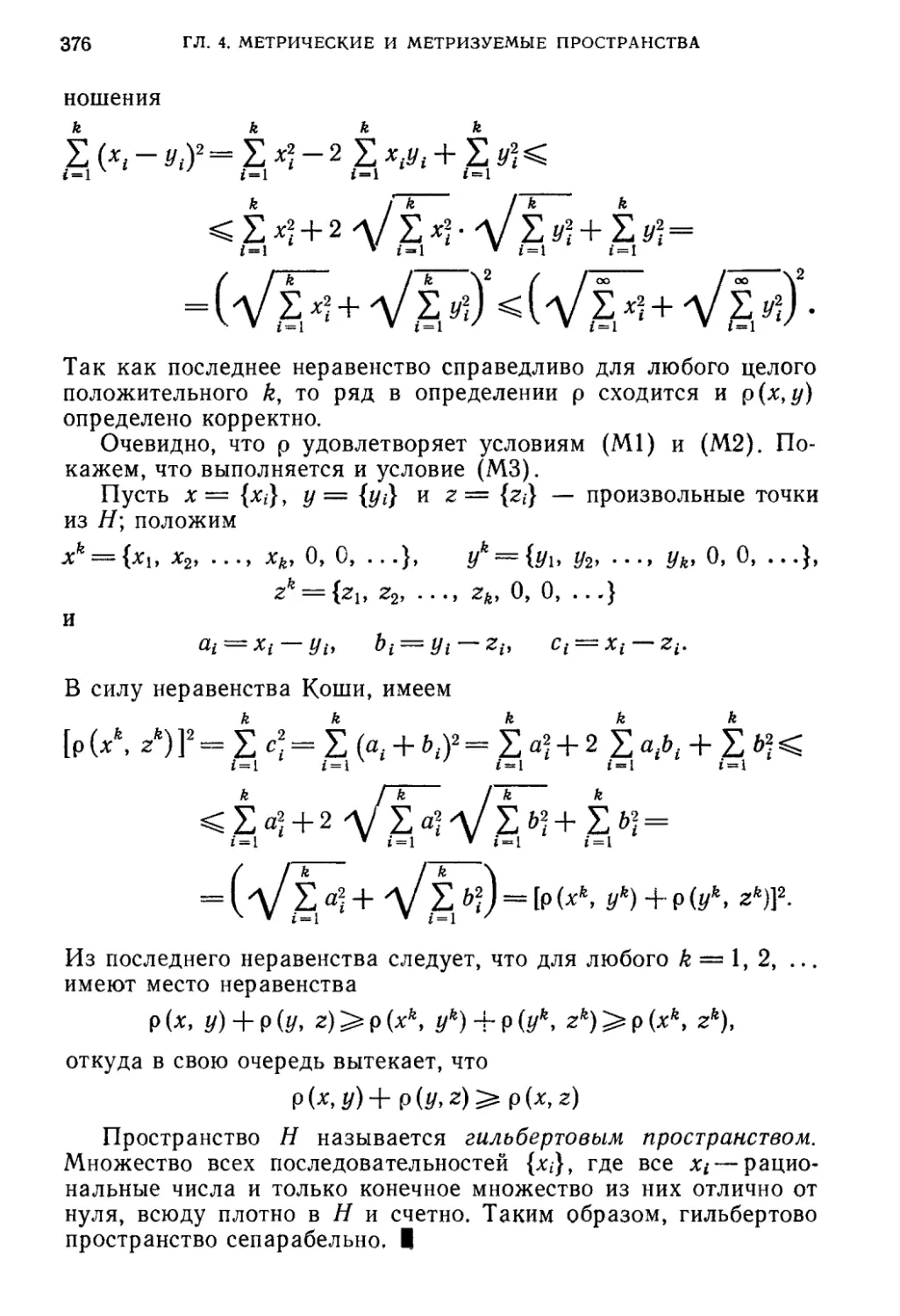Text
Р. ЭНГЕЛЬКИНГ
ОБЩАЯ
ТОПОЛОГИЯ
Перевод с английского
м. я. антоновского
и А. В. АРХАНГЕЛЬСКОГО
МОСКВА-«МИР»-1986
Monografie Matematyczne
torn 60
Ryszard Engelking
GENERAL TOPOLOGY
Panstwowe Wydawnictwo Naukowe
Warszawa 1977
Manuscript of the second
edition, 1985
ББК 22.152
Э 62
УДК 515.12
Энгелькинг Р.
Э62 Общая топология: Пер. с англ. — М.: Мир, 1986.
— 752 с.
Энциклопедически полное и сбалансированное изложение обширного круга
вопросов по общей топологии, написанное известным польским математиком.
Книга может использоваться в качестве справочника и как вводное учебное пособие
по общей топологии. Русское издание дополнено новым материалом.
Для математиков разных специальностей, для всех изучающих и использующих
методы общей топологии.
Редакция литературы по математическим наукам
1977, by Paristwowe Wydawnictwo Naukowe
(PWN — Polish Scientific Publishers)
перевод на русский язык, исправления до-
дополнения, «Мир», 1986
ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
Идеи топологии ведут начало от работ выдающихся матема-
математиков XIX века: Н. И. Лобачевского, Римана, Пуанкаре, Фреше,
Кантора, Гильберта и Брауэра.
Оформление общей топологии в самостоятельную область
математики связано с выходом в 1914 г. книги Ф. Хаусдорфа
«Теория множеств».
Важными вехами в истории общей топологии стали выход
{в 1929 г.) «Мемуара о компактных топологических простран-
пространствах» П. С. Александрова и П. С. Урысона, монографии «Торо-
logie» К. Куратовского A933 г.) и знаменитой монографии
«Topologie I» П. С. Александрова и X. Хопфа A935 г.). На этих
книгах, как и на книге Хаусдорфа, воспитывались поколения
топологов во всем мире.
Прошедшие 70 лет развития общей топологии — весьма не-
небольшой срок с точки зрения истории науки — были годами ее
молодости. Это был период активного роста общей топологии,
становления ее направлений, формирования основных принци-
принципов и методов, кристаллизации центральных понятий, создания
архитектуры общей топологии и укрепления ее взаимосвязей
с другими разделами математики, в первую очередь с анали-
анализом (в том числе функциональным), геометрией, математиче-
математической логикой и алгеброй. Довоенный период развития общей
топологии ознаменован построением П. С. Александровым и
П. С. Урысоном основ теории компактных пространств, фунда-
фундаментальной теоремой А. Н. Тихонова о компактности произве-
произведения компактных пространств, построением стоун-чеховского
расширения и теорией компактных расширений, развитой
П. С. Александровым, А. Н. Тихоновым, Э. Чехом, М. X. Стоу-
Стоуном и Г. Волманом.
В то же время были установлены основные факты теории
размерности пространств со счетной базой (П. С. Урысон, В. Гу-
ревич, К. Менгер, Л. А. Тумаркин, Н. Б. Веденисов *)).
*) Н. Б. Веденисов, доцент Московского университета, в 1941 г. вступил
добровольцем в народное ополчение и погиб в ноябре 1941 г. в боях под
Ельней.
б ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
Начало послевоенного периода развития общей топологии от-
отмечено доказательством в 1948 г. А. X. Стоуном одной из наи-
наиболее ярких и важных теорем общей топологии: теоремы о па-
паракомпактности произвольного метрического пространства. На
ее основе в 1950—1951 гг. был получен общий метризационный
критерий Бинга — Нагаты — Смирнова.
Л. В. Келдыш получила глубокие теоремы об отображениях
и размерности множеств в евклидовых пространствах, возгла-
возглавив советскую школу геометрической топологии.
Стремление распространить методы, свойственные теории
метрических пространств, за пределы этого класса привело к по-
построению А. Вейлем теории равномерных пространств, в сферу
действия которой попадают все тихоновские пространства.
В связи с понятиями паракомпактности и равномерного про-
пространства центральное значение приобрели понятие локальной
конечности и отношение звездной вписанности.
К этому моменту стало ясно, что естественная сфера дей-
действия принципов и концепций общей топологии выходит далеко
за пределы класса пространств со счетной базой или класса
метрических пространств. Первый итог развития общей тополо-
топологии, не ограниченный рамками пространств со счетной базой,
был подведен в книге Дж. Л. Келли «Общая топология», вышед-
вышедшей на английском языке в 1955 г. и изданной в русском пере-
переводе в 1968 г.
Главный объект исследования в общей топологии — понятие
непрерывности (моделируемое посредством понятий топологиче-
топологического пространства и непрерывного отображения). Вопросы,
связанные с непрерывностью, занимают центральное место во
многих разделах математики. В каждом из них они выступают
в своем облачении, на своем уровне общности, определяемом
спецификой этого раздела. Компактно-открытая топология и
топология поточечной сходимости функциональных пространств,
слабые топологии банаховых пространств, пространства мер, то-
топологические границы функциональных алгебр — появление этих
топологических объектов (заметим — не «внутри» самой общей
топологии) потребовало построения теории топологических про-
пространств за пределами пространств с первой аксиомой счет-
ности. Возникновение в связи с потребностями алгебраической
геометрии топологий Зарисского показало, что общая тополо-
топология не может априори ограничиваться рассмотрением хаусдор-
фовых пространств.
В настоящее время общая топология достигла того наиболее
естественного уровня общности, который позволяет излагать то-
пологические принципы, концепции и конструкции с наибольшей
прозрачностью и одновременно обеспечить им максимально ши-
широкую приложимость в других разделах математики.
ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ 7
С начала 50-х гг. стал наблюдаться быстрый рост активности
исследований в общей топологии буквально по всему ее фронту.
Возникло много новых, тесно связанных между собой вопросов,
направленных на более глубокое изучение паракомпактности и
близких к ней свойств; это в свою очередь вывело на передний
план метод покрытий и родственный ему метод специальных
баз. В результате в новом свете предстала метризационная про-
проблематика, совершенно по-новому зазвучала классическая тема
моровских пространств, были сделаны заметные продвижения
в теории размерности.
Весьма активно шел процесс построения новых топологиче-
топологических инвариантов; особенно большую роль стали играть карди-
кардинальные топологические инварианты, что объясняется внутрен-
внутренней идейной близостью общей топологии и теории множеств.
Последнее стимулировало глубокое проникновение в теорию то-
топологических пространств методов математической логики и
применение принципов, подобных аксиоме Мартина (см. в связи
с этим недавно вышедшую монографию X. Фремлина «Conse-
«Consequences of Martin's Axiom»). В 60-е и 70-е годы исследование
кардинальных инвариантов (а сюда попадают такие классиче-
классические вопросы, как проблема Суслина) сложилось в один из
центральных разделов общей топологии.
Новые краски обрела теория компактных пространств, в ча-
частности, в связи с исследованием пространств функций и бана-
банаховых пространств со слабой топологией (компакты Эберлейна,
компакты Корсона).
Л. С. Понтрягин еще в 30-е годы обратил внимание на кон-
конструкцию 2-произведения и применил вполне упорядоченные
(трансфинитные) спектры из компактов.
Систематически была развита теория диадических компак-
компактов— непрерывных образов обобщенных канторовых дисконти-
дисконтинуумов. Значение этой разновидности компактов связано, в ча-
частности, с тем, что к ней относятся все компактные группы.
Стержневое положение в теории диадических компактов зани-
занимают кардинальные инварианты.
Активное движение топологических концепций внутри и вне
общей топологии остро поставило задачу укрепления единства
теории топологических пространств. Именно в последние 30 лет
основную объединяющую роль в общей топологии (наряду с ме-
методом кардинальных инвариантов) стал играть метод взаимной
классификации пространств и отображений (и входящий в него
как часть метод обратных спектров).
На языке отображений удалось точно выразить соотношение
между классом метрических пространств и многими более широ-
широкими классами пространств: с первой аксиомой счетности, сек-
секвенциальных пространств, пространств Фреше — Урысона,
8 ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
пространств с равномерной базой, моровских пространств. Отме-
Отметим особо работу Г. С. Чогошвили об обобщенной сходимости.
Были доказаны фундаментальные теоремы о сохранении топо-
топологических инвариантов при отображениях (например, параком-
паракомпактности при замкнутых отображениях и метризуемости при со-
совершенных отображениях). Метод обратных спектров был раз*
вит как в аналитическом, так и в синтетическом направлении.
Это позволило получить глубокие общие теоремы (в частности»
примыкающие к теории диадических компактов), а также по-
построить тонкие примеры, относящиеся к теории кардинальных
инвариантов компактов и теории размерности компактов.
Более глубокое понимание компактности было достигнуто
посредством изучения ее важнейших граней — счетной компакт-
компактности и псевдокомпактности (ограниченности всех непрерывных
вещественных функций). Хотя различить эти понятия нелегко —
для нормальных пространств счетная компактность равносильна
псевдокомпактности, — эти понятия, как выяснилось, разделяет
пропасть: если счетная компактность наследуется замкнутыми
подпространствами, то каждое тихоновское пространство вкла-
вкладывается в качестве замкнутого подпространства в псевдоком-
псевдокомпактное пространство. Всестороннему изучению были подверг-
подвергнуты нормальность и свойство Линделёфа, в частности, был
построен пример нормального не счетно паракомпактного про-
пространства. Много тонких исследований было посвящено свой-
свойствам типа полноты: полноте по Чеху, полноте по Хьюитту, пол-
полноте по Дьедонне и др. Были введены и продемонстрировали
свое важное значение — для создания единой классификации
топологических пространств — новые классы пространств и ото-
отображений: перистые, кружевные пространства, линделефовы
S-пространства, псевдооткрытые, бифакторные отображения.
Во всех этих многообразных направлениях были получены
яркие результаты; технический уровень ведущих исследований
в общей топологии и их интенсивность значительно выросли.
Надо заметить, что это не сопровождалось ростом разобщен-
разобщенности общей топологии и потерей естественности в постановках
задач. Напротив, глубокий результат из одной области проли-
проливал, как правило, новый свет на другие разделы.
Сейчас ежегодно в мире выходит очень много книг, посвя-
посвященных той или иной области топологии. Это главным образом
учебники и монографии по отдельным вопросам алгебраической,
геометрической и дифференциальной топологии. Монографий же,
претендующих на охват всей общей топологии, совсем мало.
Такой монографией стала книга Р. Энгелькинга «Общая то*
пология», вышедшая в 1977 г. Перед ее автором стояла ело ж*
нейшая многоплановая задача. Во-первых,— такого отбора ма-
материала, который бы полно отразил основные достижения и ны-
ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ 9
нешнее состояние во всех главных разделах общей топологии.
Во-вторых, — такой организации этого материала, которая бы
продемонстрировала единство общей топологии на данном этапе
ее развития и определила бы главные дальнейшие ее задачи.
Книга должна была стать основным средством подготовки спе-
специалистов — общих топологов и одновременно быть доступной
и полезной широким кругам математиков, использующих топо-
топологические концепции. На наш взгляд, Р. Энгелькингу удалось
блестяще справиться с этими задачами.
Нет нужды говорить здесь подробно о содержании книги:
об этом хорошо сказал сам автор в своем предисловии и во
введениях к отдельным главам. Однако уместно посвятить не-
несколько слов тому, как автору удалось достичь широкого охвата
материала при сравнительно небольшом объеме и не потерять
в своем изложении единства и гармонии. Одно из средств — это
тщательный отбор материала, основанный на широком личном
опыте автора творческой работы в общей топологии и на
тесных связях автора со специалистами по общей то-
топологии из многих стран. Второе средство — это много-
многоплановая архитектура книги. Об этом следует сказать не-
несколько слов отдельно.
Во всех главах в основном тексте тщательно соблюден ба-
баланс между общими утверждениями (теоремами) и примерами.
Каждый параграф дополнен упражнениями, тесно связанными
с текстом и активно развивающими его во множестве направ-
направлений; более трудные упражнения сопровождаются указа-
указаниями; в целом они выбраны так, что самостоятельная работа
над упражнениями не должна вызывать затруднений у чита-
читателя. Это позволяет охватить множество новых понятий и при-
примеров.
Каждая глава заканчивается параграфом со скромным на-
названием «задачи». Роль этих параграфов, незаметных при чте-
чтении оглавления, чрезвычайно велика. Каждый из них на самом
деле является маленькой главой, в которой излагается множе-
множество продвинутых тем, тонких теорем и примеров в стиле, отлич-
отличном от стиля основного текста книги. Овладение материалом
этой части книги потребует от читателя творческой работы. Мно-
Многие темы задач переходят от одной главы к другой: прослежи-
прослеживается, как в различных главах освещается эта тема. Этим в
немалой степени обеспечивается единство книги: темы задач,
повторяясь, как бы «сшивают» главы воедино. В то же время,
если взять какую-нибудь из этих тем отдельно и проследить ее
движение сквозь книгу, мы увидим, что получится, в сущности,
самостоятельная глава, изложенная хотя и конспективно, но
доступно для читателя, творчески овладевшего основным тек-
текстом. Таких «скрытых» глав в книге очень много, и вес их не
10 ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
меньше веса основных глав. Назовем некоторые из них: линейно
упорядоченные пространства, борелевские множества, карди-
кардинальные функции, многозначные отображения, декартовы произ-
произведения и S-произведения, обратные спектры, пространства
замкнутых множеств, диадические компакты, пространства ото-
отображений.
Последняя важная особенность книги Р. Энгелькинга, кото-
которую хотелось бы здесь отметить, — систематический историко-
библиографический комментарий. Хотя в основном комментарий
весьма лаконичен, читатель получает представление о том, ка-
какую роль в развитии общей топологии сыграли те или иные ма-
математические школы, математические центры и отдельные вы-
выдающиеся математики.
В книге и комментариях отразилась ведущая роль, которую
играла в формировании топологии на протяжении всего 70-лет-
70-летнего периода ее развития московская топологическая школа
П. С. Александрова. Работы П. С. Александрова и П. С. Уры-
сона о компактности и метризации, теоремы А. Н. Тихонова
о компактности произведений и о погружении в тихоновские
кубы, вклад П. С. Александрова в теорию компактных расши-
расширений, труды П. С. Урысона по теории размерности, работы со-
советских математиков послевоенного периода: Ю. М. Смирнова,
A. В. Архангельского, Б. А. Пасынкова, В. И. Пономарёва,
B. В. Федорчука, В. В. Филиппова, М. М. Чобана, Е. В. Ще-
пина органически влились в книгу Энгелькинга, определив су-
существенную часть ее содержания.
По заслугам отражен выдающийся вклад в общую тополо-
топологию польской топологической школы — К. Куратовского, В. Сер-
пинского, В. Кнастера, С. Мазуркевича, 3. Янишевского и более
молодых топологов: Энгелькинга, Хабера, Пшимусинского, Поля
и др. Особенно значителен этот вклад в теорию континуумов,
теорию размерности, дескриптивную теорию множеств, теорию
многозначных отображений. Следует еще раз подчеркнуть тра-
традицию тесных связей между топологами польской и московской
школ, их огромное взаимное влияние.
В связи с изданием настоящего перевода нелишне напом-
напомнить, как высоко ценил П. С. Александров вклад польской топо-
топологической школы и конкретно монографию Р. Энгелькинга. Он
всегда подчеркивал, что для написания хорошей монографий
необходимы три ингредиента: чтобы автор был крупным ученым»
внесшим весомый вклад в развитие соответствующей области,
обладал хорошим вкусом и был исключительно добросовестен
и аккуратен. П. С. Александров с самого появления первого из-
издания монографии Энгелькинга считал необходимым перевести
ее на русский язык. По техническим причинам реализация этого
проекта задержалась на долгие годы и воспринимается сейчас
ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ Ц
как исполнение одного из пунктов завещания Павла Сергеевича
Александрова.
Продолжением традиций советско-польского содружества и
сотрудничества в области топологии явилась работа над пере-
переводом этой книги. Благодаря любезности проф. Р. Энгелькинга
переводчики имели в своем распоряжении исправленный и до-
дополненный текст второго издания книги, которое готовится к вы-
выходу в Польше в 1987 г.; с него и сделан настоящий перевод.
В книге отражен вклад в развитие общей топологии амери-
американских математиков: Э. Майкла, М. Стоуна, А. Стоуна,
Э. Хьюитта, упомянуты яркие результаты М. Э. Рудин, П. Ни-
коша, X. Викке, Дж. Уорелла, В. Флейснера, Ф. Толла, В. Ком-
Комфорта и др.
Читатель получает представление о вкладе в общую топо-
топологию японской группы: Мориты, Нагаты, Нагами, Окуя-
мы и др.
Наконец, отражены значительные достижения в общей топо-
топологии на всех этапах ее развития ученых социалистических
стран: Э. Чеха, М. Катетова, Б. Поспишила,З.Фролика, И.Юха-
са и др.
Не следует, однако, ожидать, что в учебнике по общей то-
топологии сколько-нибудь полно могут быть рассмотрены все ее
вопросы, включая применения. Например, в книге не нашло от-
отражения современное состояние дескриптивной теории множеств
в общих пространствах, ибо этот материал требует отдельной
книги. Не рассматривается метод обобщенных метрик, развитый
в конце 50-х и начале 60-х гг. М. Я. Антоновским, В. Г, Бол-
Болтянским и Т. А. Сарымсаковым. Этот метод позволил доказать
единообразным путем с помощью метризации над топологиче-
топологическими полуполями многие теоремы теории равномерных про-
пространств и пространств близости, а также получить максималь-
максимальное обобщение теорем об открытом отображении и замкнутом
графике и целый ряд результатов в теории топологических ре-
решеток и т. п. Однако книга Энгелькинга обеспечивает очень хо-
хорошую основу для приложений современной общей топологии
в различных частях математики. Она подходит вплотную к та-
таким приложениям в разделах, посвященных пространствам ото-
отображений с различными топологиями, пространствам макси-
максимальных идеалов функциональных алгебр, топологическим груп-
группам и группам гомеоморфизмов, многозначным отображениям,
равномерным пространствам.
Сам спектр приложений, к которым готовит книга Энгель-
Энгелькинга, за последние 30 лет необозримо расширился. Здесь мы
ограничимся только самым кратким обзором некоторых из этих
приложений. В математической логике топологические кон-
конструкции широко применяются при построении моделей, при
12 ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
решении вопросов о независимости и непротиворечивости. Важ-
Важную роль играет здесь счетность числа Суслина тихоновских
кубов.
Хорошо известны приложения теоремы Шаудера о неподвиж-
неподвижной точке, являющейся обобщением классической теоремы
Брауэра и в свою очередь обобщенной А. Н. Тихоновым; тео-
теоремы Банаха о сжимающих отображениях и всевозможные ее
обобщения; приложения метода Лере — Шаудера. Их даль-
дальнейшее развитие в работах Смейла, Атьи, Браудера позво-
позволило перенести упомянутые результаты на поля операторов;
в их конструкции центральное место принадлежит ком-
компактности.
Новое большое направление — теория корректных задач по
Тихонову, существенно обобщающая и развивающая понятия
корректности по Адамару.
С компактностью связано замечательное направление — тео-
теоремы вложения Соболева — Никольского — Шварца. Понятие
локальной компактности весьма плодотворно проявляет себя в
объектах, наделенных одновременно топологией и алгебраиче-
алгебраическими операциями, таких, как топологические группы, кольца,
решетки, булевы алгебры и т. п. Это понятие сыграло значи-
значительную роль в становлении большого направления в современ-
современной математике — абстрактного гармонического анализа, важ-
важного не только своей внутренней красотой, но и новыми прило-
приложениями в функциональном анализе, математической физике»
теории дифференциальных уравнений. В создании этого на-
направления большую роль сыграли работы советских матема-
математиков: Л. С. Понтрягина, А. И. Мальцева, И. М. Гельфанда,
М. Г. Крейна, М. А. Наймарка и зарубежных: А. Вейля,
Э. Хьюитта и др.
Весьма важную роль в приложениях в настоящее время на-
начали играть специальные примеры из общей топологии: канто-
рово совершенное множество, прямая Александрова, ковер Сер-
пинского, пример Кнастера, возникшие ранее из чисто внутрен-
внутренних, логических потребностей топологии. Они легли в основу
новых методов распознавания образов и теории динамических
систем.
Отметим далее, что аппарат теории метрических и псевдо-
псевдометрических пространств нашел приложение в работах по при-
прикладной статистике и распознаванию образов. Для таких прило-
приложений оказались полезными метрики Колмогорова, фон Мизеса*
Байеса и т. п. Специальные метрики в функциональных про-
пространствах позволили Ю. В. Прохорову A956 г.) по-новому по-
подойти к получению предельных теорем теории вероятностей.
Подход Ю. В. Прохорова интенсивно развивался как у нас в
стране, так и за рубежом.
ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ 13
Мы коснулись лишь небольшого числа примеров использова-
использования концепций общей топологии. В заключение еще раз хоте-
хотелось бы подчеркнуть, что данная книга будет интересна широ-
широкому кругу математиков — начиная со студентов и кончая спе-
специалистами. Переводчики благодарят автора — профессора Эн-
гелькинга за внимание к русскому изданию, а также редактора
Н. И. Плутникову за большую работу, которую ей пришлось вы-
выполнить в связи с многочисленными изменениями в процессе под-
подготовки рукописи к изданию.
М. Я. Антоновский
Л. В. Архангельский
Памяти
профессора Казимира Куратовского
ПРЕДИСЛОВИЕ
Эта книга содержит достаточно полное и современное изло-
изложение общей топологии. Она адресована в первую очередь стар-
старшекурсникам и аспирантам, но может быть полезной для ссы-
ссылок и математикам более высокого уровня.
Глава 1 содержит основные определения и результаты, отно-
относящиеся к общим топологическим пространствам и непрерывным
отображениям. Глава 2 посвящена операциям на топологических
пространствах, т. е. стандартным методам получения новых про-
пространств из старых. В следующих трех главах изучаются клас-
классы компактных, метризуемых и паракомпактных пространств, а
также некоторые отношения между классами пространств. Гла-
Глава 6 содержит обсуждение связности. Глава 7 представляет со-
собой сжатый курс теории размерности в общих топологических
пространствах. Последняя глава посвящена равномерным про-
пространствам и пространствам близости.
Первые пять параграфов гл. 1 вместе с § 2.1 и 2.3 образуют
введение в нашу книгу. Ознакомившись с этим материалом,
читатель сможет продолжить чтение в соответствии со своими
интересами или нуждами. Если же читатель мало знаком с дан-
данным предметом, мы советуем ему изучить § 4.1—4.3; сравни-
сравнительно легкие, они помогут выработать топологическую интуи-
интуицию.
Расположение материала следует предыдущей книге автора
«Outline of general topology», изданной в 1968 г. Однако дан-
данная книга написана заново и значительно более подробно. Около
40 % текста посвящено недавним достижениям общей тополо-
топологии, которые не обсуждались в предыдущей книге.
Каждый параграф оканчивается историческими и библиогра-
библиографическими замечаниями. Затем следуют упражнения, которые
прежде всего предназначены для проверки понимания и усвое-
усвоения материала читателем. Упражнения, которые начинаются
словами «проверьте», «установите», «заметьте» или «убедитесь»,
обычно достаточно легкие. Упражнения, начинающиеся словами
«покажите» или «приведите пример», несколько более трудные,
а те, которые начинаются словами «докажите», могут быть очень
трудными.
ПРЕДИСЛОВИЕ 15
Последний параграф каждой главы посвящен задачам, яв-
являющимся органической частью данной книги. Они часто снаб-
снабжены подробными указаниями, в которых фактически содер-
содержится набросок доказательства. Задачи можно и просто про-
прочитывать, не решая. Несколько серий задач обсуждается на
протяжении многих глав. Они касаются, например, линейно
упорядоченных пространств, кардинальных функций, прост-
пространств замкнутых подмножеств, полунепрерывных функций
и многозначных отображений.
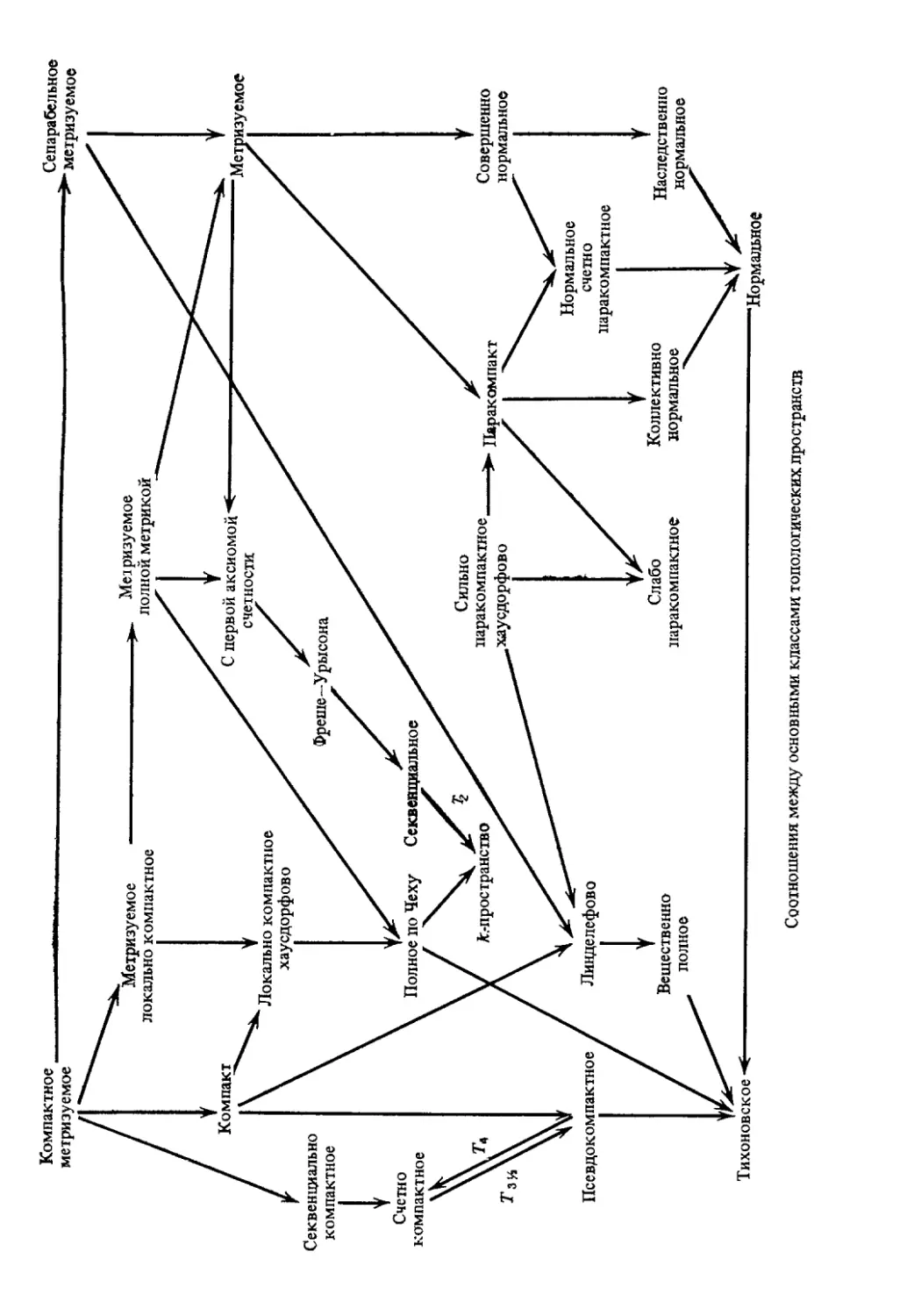
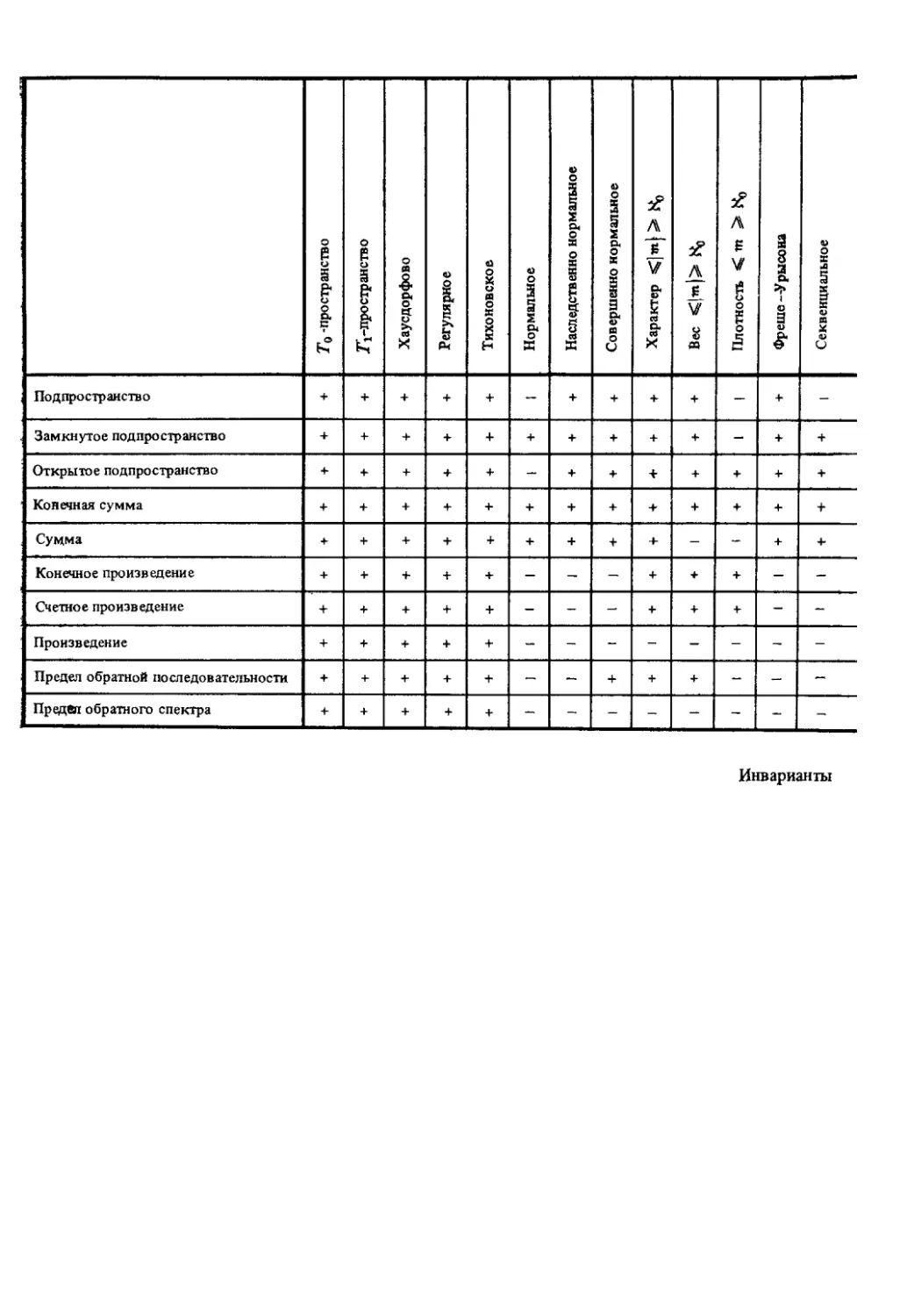
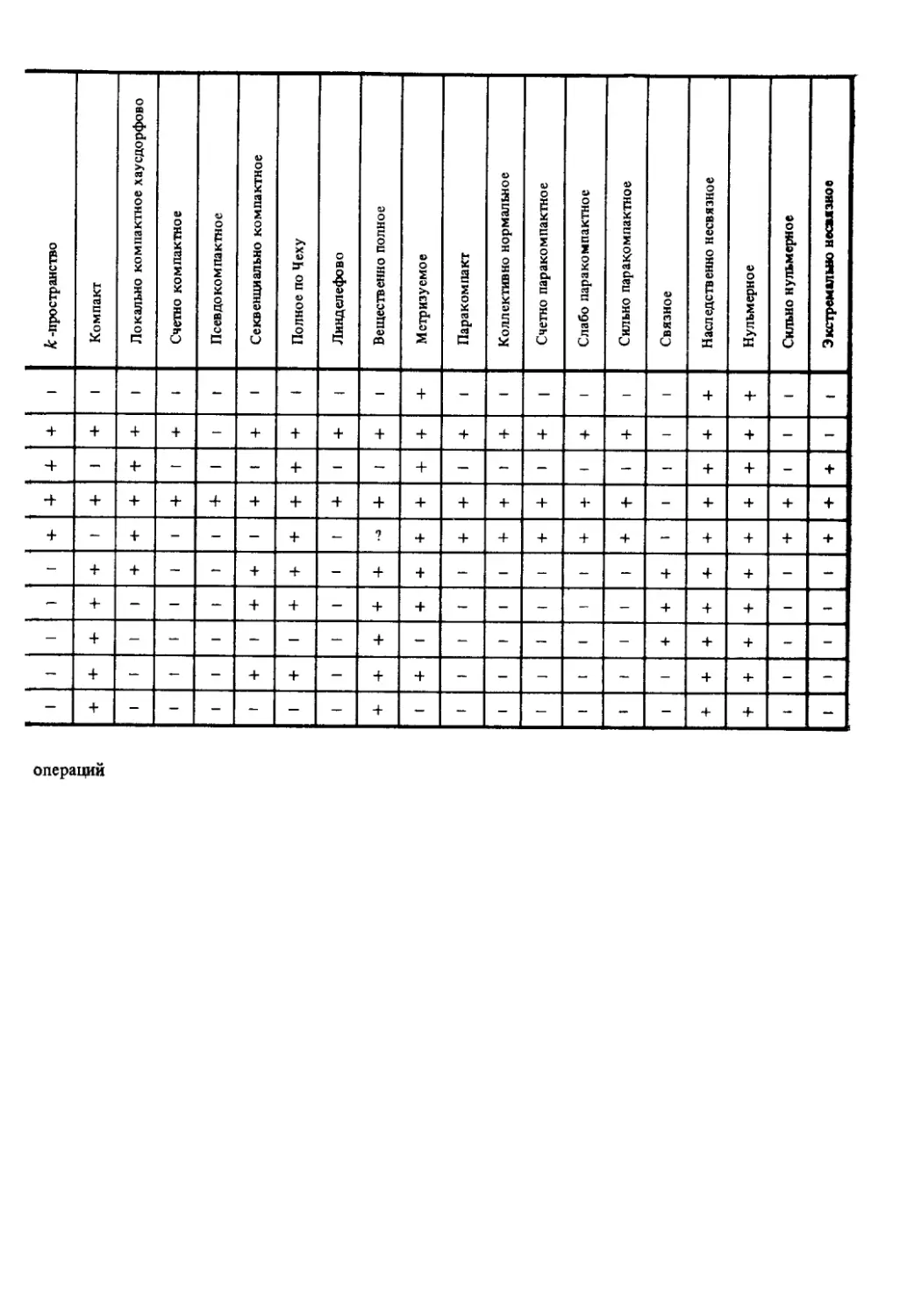
Приведенные в конце книги подробные указатели, таблица
взаимосвязей между различными классами пространств и таб-
таблицы сохранения топологических свойств при операциях и ото-
отображениях позволяют читателю лучше ориентироваться в ма-
материале.
Знаком 1 отмечен конец доказательства или примера. Если
этот знак появляется сразу после утверждения теоремы, пред-
предложения или следствия, это подразумевает, что утверждение
очевидно.
Числа в квадратных скобках после фамилий отсылают чита-
читателя к библиографии в конце книги. Работы каждого автора
пронумерованы независимо, число означает год публикации.
Мне приятно выразить свою признательность ряду коллег.
Многим я обязан за помощь при написании предыдущей книги:
помогали и вдохновляли меня профессора А. Бялыницкий-Би-
руля, Е. Бровкин, М. Карлович, А. Лелек, К. Морен, Я. Мыцель-
ский, Ч. Рылль-Нардзевский, Р. Сикорский и М. Старк. Содер-
Содержание данной книги обсуждалось в 1968—1973 гг. со студен-
студентами, посещавшими мои лекции и семинары в Варшавском уни-
университете. Их замечания позволили сделать ряд упрощений в
доказательствах и указаниях. Я благодарен К. Альстеру, Я.Ха-
беру, Я. Каневскому, П. Минцу, К. Новинскому, Я. Пшитыц-
кому, Э. Поль, 3. Слодковскому и К. Войтковской.
Особенно я обязан двум моим студентам, первым читателям
книги: Р. Полю и Т. Пшимусинскому. Их содержательные за-
замечания и предложения привели ко многим важным улучшениям
книги.
Когда готовилось английское издание книги, во время моего
пребывания в университете Питтсбурга, мне помогали профес-
профессора Д. Латцер и Э. Майкл, которые поправили мой английский
язык и внесли дальнейшие усовершенствования.
Разрешите мне также упомянуть помощь незнакомых читате-
читателей предыдущей книги, которые любезно указали на некоторые
ошибки и неточности в ней.
Варшава, июнь 1976 г.
Рышард Энгелькинг
16 ПРЕДИСЛОВИЕ
* *
*
Русское издание несколько отличается от английского ори-
оригинала: исправлен ряд ошибок, неточностей и опечаток, упро-
упрощены некоторые доказательства, добавлено несколько упраж-
упражнений и задач и включена информация о наиболее важных не-
недавних результатах, связанных с содержанием этой книги.
Я весьма обязан профессорам А. Чассару, Э. ван Дауэну,
М. А. Морису и доктору А. Мысьору, которые внимательно про-
прочитали английское издание и оказали мне большую помощь,
любезно прислав свои замечания и списки замеченных ими опе-
опечаток.
Варшава, март 1984 г.
Р. Э.
ВВЕДЕНИЕ
Все, что требуется для понимания этой книги, — знание ос-
основных фактов теории множеств и некоторых свойств веще-
вещественных чисел. Цель данного введения — перечислить эти фак-
факты и свойства и познакомить читателя с нашей терминологией
и обозначениями. Никаких доказательств в этом введении дано
не будет, за исключением доказательства эквивалентности ак-
аксиомы выбора двум принципам максимума и теореме Цермело.
Это введение ни в коей мере не заменяет курса теории множеств.
1.1. АЛГЕБРА МНОЖЕСТВ. ФУНКЦИИ
Объединение, пересечение и разность множеств А и В обо-
обозначаются соответственно А[]В, А[\В и А\В\ объединение
^l U ^2 U ... [}Ak обозначается также через (J Aiy а пересече-
ние Ах П А2 П ... [\Ak — через [\ At. Пустое множество обозна-
обозначается символом 0. На протяжении всей книги мы свободно
(т. е. не оговаривая этого) пользуемся всеми правилами вычис-
вычислений с множествами и, в частности, широко применяем за-
законы де Моргана
Мы пишем хеД, когда х является элементом множества Л,
и л;^=Л, когда х не принадлежит множеству А. Обозначения
А а В или В гэ А означают, что А содержится в В, т. е. каж-
каждый элемент множества А принадлежит множеству В. Когда
А с= В, мы говорим, что А есть подмножество множества В; если
А а В и А Ф В, то мы называем А собственным подмножеством
множества В.
Множество всех тех элементов множества X, которые удов-
удовлетворяют условию ф(х), обозначается через
{х^Х:у(х)} или {х: ф(х)};
второе обозначение используется тогда, когда из контекста ясно,
какое множество X мы рассматриваем.
Множество, состоящее из конечного числа элементов л*ьХ2, ...
..., xky обозначается через {х\, ..., хк}. Иногда мы не делаем
различия между множеством {х} и элементом х.
2 Зак. 697
18 ВВЕДЕНИЕ
Упорядоченная пара (х,у) есть множество {{х}, {х, у}}. Две
упорядоченные пары (хиу\) и (х2, г/г) равны в том и только
том случае, если xi = хг, у\ = #г-
Декартово произведение (или просто произведение) XX У
двух множеств i и У есть множество упорядоченных пар (*,#),
где хеХ, у ^ Y. Конечное произведение определяется по ин-
индукции формулой
Всякое подмножество произведения X X У есть некоторое
отношение; множество X есть область определения этого отно-
отношения, а множество У — его область значений. Отношение fez
ciXX Y называется функцией из X в У или отображением мно-
множества J в множество У, если для каждого х^Х существует
такой i/eF, что (х,у)е /, и если этот у однозначно определен
элементом х, т. е. из (х, #) <= / и (х, #') е / следует, что # = у\
Если / — функция из "множества X в множество У и хеХ,
то единственное у, удовлетворяющее условию (х,#)^/, обозна-
обозначается через /(х); оно называется значением функции / в точке
х. Образ множества А а X при отображении / есть множество
ДЛ) = {уе У: y = f(x) для некоторого х^Л};
прообраз множества ВсУ при отображении / есть множество
f-4B)=*{x(=X: f{x)<=B).
Прообразы одноточечных множеств при отображении / назы-
называются прообразами точек при отображении f.
Элементарные формулы алгебры множеств, относящиеся к
образам и прообразам множеств, часто используются в этой кни-
книге; к числу важнейших из них принадлежат следующие две
формулы:
Если / — функция из X в У, a g — функция из У в Z, то ра-
равенство (gf) (x) = g(f(x)) определяет функцию gf из X в Z,
композицию функций / и g. Легко видеть, что (gf)~l(B) =
= f~l (S~l (В)) для любого В cz Z.
Отображение / множества X в множество У называется
инъективным, если для любой пары точек хь Х2^ X
из f(x\) — f(x2) следует, что х\ = Х2.
Если отображение / множества X в множество У удовлетво-
удовлетворяет условию f(X)= У, говорят, что / отображает множество X
«а.множество У, или что / есть отображение «на». Для инъек-
тивного отображения множества X на У существует обратное
отображение /-1, являющееся инъективным отображением мно-
I. 1. АЛГЕБРА МНОЖЕСТВ. ФУНКЦИИ 19
жества У на X1); обратное отображение /-1 определяется соот-
соотношением
f~-l(y) = x в том и только том случае, когда f(x) = y.
Тождественное отображение множества X на себя обозначается
через id*; оно определяется формулой idjr(x) = # для любого
х^Х.
Произвольная функция, определенная на множестве всех
положительных целых чисел, называется последовательностью;
значение последовательности в точке п обычно обозначается
через хПу г сама последовательность — через х\, *2, ... или
(xi,X2, ...). Множество, состоящее из всех элементов последо-
последовательности xi, хь ..., обозначается {лсь Х2, .. }. Последователь-
Последовательность множеств Аи Л2, ... называется возрастающей, если Aid
сгЛ/4-1 для f=lf 2, ..., и убывающей, если Л^стЛ,- для
1 = 1,2, ... .
Множества, элементы которых суть множества, называются
семействами или классами множеств, а их элементы называются
членами или элементами семейства; семейства семейств мно-
множеств называются системами или совокупностями. В этой книге
рассматриваются как индексированные, так и неиндексирован-
ные семейства множеств. Индексированное семейство {As}s&s
есть, строго говоря, функция, приписывающая каждому sgS
множество As, а неиндексированное семейство есть просто неко-
некоторое множество множеств. Каждое неиндексированное семей-
семейство зФ можно рассматривать как индексированное: достаточно
взять каждый член семейства в качестве его собственного ин-
индекса, т. е. считать, что ^ = {A}A^t#. В этом смысле все опре-
определенные в тексте для индексированных семейств понятия (на-
(например, локальная конечность или точечная конечность) отно-
относятся и к неиндексированным семействам.
Объединение и пересечение семейства множеств {^4s}ses обо-
обозначаются соответственно (J As и П As'> B случае последова-
оо оо
тельности множеств мы употребляем символы JJ At и f| Ai9
а в случае неиндексироваиного семейства $Ф пишем \}$& и {)sf>.
Объединение и пересечение всех множеств, удовлетворяющих
условию ф(Л), обозначаются соответственно
Ф(Л)} и
Декартово произведение (или просто произведение) семей-
семейства множеств {Л5}5е5, т. е. множество всех функций / из S в
!) Инъективное отображение одного множества на другое называют так-
также взаимно однозначным отображением. — Прим, перев.
20 ВВЕДЕНИЕ
У Ast таких, что f(s)^As для любого 5 e S, обозначается
se=S
оо
И As или Ц A i в случае последовательности множеств
АиА2, ... . Для fGll4 точка f(s)^As называется 5-й коор-
S€BS
динатой /. Элемент произведения Ц Ast 5-я координата кото-
S€=S
рого есть точка xs e ASi будет обозначаться в дальнейшем сим-
символом {*$}. В частности, последовательность х\, хг, ... элемен-
элементе
тов множества Л, являющаяся элементом, ЦАь где At = A для
i = l
/=1,2, ..., будет часто обозначаться через {xt}.
Заметим, что произведение Ц Xs, где 5 ={1,2, ..., k), не
st= S
является в точности тем же самым множеством, что и произве-
произведение Xi X Х2 X ... X Xk\ тем не менее между элементами этих
двух множеств существует очевидное взаимно однозначное соот-
соответствие, и мы будем рассматривать их как одно и то же множе-
множество, элементы которого обозначаются (х\,Х2, ..., **).
Отношение Е на множестве X, т. е. подмножество произведе-
произведения XXX, называется отношением эквивалентности на X, если
оно обладает следующими свойствами (мы пишем хЕу вместо
(х,у)^Е):
(Е1) Для любого х е X имеем хЕх.
(Е2) Если хЕуу то у Ex.
(ЕЗ) Если хЕу и yEzy то xEz.
Всякое отношение эквивалентности Е на множестве X опре-
определяет разбиение X на непересекающиеся множества (классы
эквивалентности отношения Я); два элемента множества X
находятся в одном классе эквивалентности в том и только том
случае, когда они связаны отношением Е. Таким образом,
Х= (J А3 и As П ^4s'= 0, если s Ф sf\
s(=S
кроме того,
х, у ^As для некоторого sgSb том и только том случае, если
хЕу.
Класс эквивалентности, содержащий элемент xt обозначается
[х].
Обратно, всякое разбиение множества X на непересекаю-
непересекающиеся множества {>ls}56=5 задает некоторое отношение эквива-
эквивалентности Е на X, определенное условием
хЕу тогда и только тогда, когда х, y^As для некоторого $,
I. 2. КАРДИНАЛЬНЫЕ ЧИСЛА 21
1.2. КАРДИНАЛЬНЫЕ ЧИСЛА
Множества X и У называются равно мощными, если суще-
существует взаимно однозначное отображение множества X на У.
Каждому множеству X приписывается некоторое кардинальное
число (кардинал); оно называется мощностью множества X и
обозначается ]Х|; равенство |J| = |Y| имеет место в том и
только том случае, если X и У равномощны. Для конечного
множества X мощность X равна числу его элементов. Карди-
Кардинальное число, приписываемое множеству всех положительных
целых чисел, обозначается символом Ко (алеф-нуль), а карди-
кардинальное число, приписываемое множеству всех вещественных
чисел, обозначается с (континуум). Множество называется счет-
счетным, если оно либо конечно, либо имеет мощность Ко-
Для кардинальных чисел определены операции сложения и
умножения. Сумма кардиналов шип равна мощности множе-
множества X U У, где |Х\ = ш, | У| = п и X f| Y = 0. Произведение кар-
кардиналов ш и п — это мощность множества XX У, где |X| = nt и:
|У| = п. Сумма кардиналов тип обозначается т + п, произве-
произведение шип обозначается ш-п или тп. Для каждого карди-
кардинала т число 2т, обозначаемое также ехрш, определено как
мощность семейства всех подмножеств какого-нибудь множества
X, удовлетворяющего условию JX| = m. Доказано, что 28° —с.
Более общо, мы определим nm как мощность множества всех
функций из X в У, где |Аг|=ш, |У| = п. Можно доказать, что
Пусть m и п — кардиналы и |Х| = щ, |У| = п. Мы говорим*
что ш не превосходит п или что п не меньше ш, и пишем m ^ п
или n ^ m, если существует инъективное отображение X в У.
Важным фактом о неравенствах между кардиналами является
следующая теорема Кантора — Бернштейна:
если ш ^ п и п^ш, то щ = п.
Можно доказать также, что \f(X) |^|^| для любого отобра-
отображения /, заданного на X. Отсюда, в частности, следует, что се-
семейство всех подмножеств мощности ^щ произвольного множе-
множества мощности п ^ ш имеет мощность ^ищ.
Сумма двух кардинальных чисел, хотя бы одно из которых
бесконечно, равна не меньшему из них. Подобное утверждение
имеет место и для произведения любых двух кардинальных чи-
чисел, отличных от нуля. В частности,
ш + тп = тп-т = т для
22 ВВЕДЕНИЕ
Если m^tt и тфп, мы говорим, что m меньше п или что
п больше ш, и пишем m < n или п > т. Можно доказать, что
m < 2m для любого кардинального числа т;
в частности, Ко < с.
Наименьшая (точная) верхняя грань произвольного множе-
множества {ttts)s<=s каРДиналов определяется как наименьший карди-
кардинал т, такой, что m ^ ms при всех sgS,h обозначается sup ш$;
можно показать, что такое число всегда существует.
1.3. УПОРЯДОЧЕНИЯ. ПОРЯДКОВЫЕ ЧИСЛА
Пусть X — некоторое множество и < — некоторое отношение
на X. Будем говорить, что < линейно упорядочивает множество
X или что < есть линейный порядок на X, если отношение <
обладает следующими свойствами:
(LO1) Если х < у и у < г, то х < г.
(LO2) ?с./ш х < у, то отношение у <х не имеет места,
(LO3) ?о/ш хФу, то либо х<у, либо у<х.
Множество X вместе с некоторым линейным порядком на
X называется линейно упорядоченным множеством.
Будем говорить, что элемент х0 линейно упорядоченного мно-
множества X является наименьшим элементом множества Х> если
Хо < х для любого jcgA{xo}« Аналогично определяется наи-
наибольший элемент линейно упорядоченного множества. Так как
каждое подмножество линейно упорядоченного множества само
линейно упорядочено, то наибольший и наименьший элементы
подмножества линейно упорядоченного множества определены
корректно. Очевидно, что они не обязательно существуют.
Всякая пара (D,E) подмножеств множества X, линейно
упорядоченного отношением <, такая, что D[}E = X, ОФ
Ф0ФЕ и
из xeD и j/g? следует, что х<у,
называется сечением множества X. Множество D называется
нижним классом, а множество Е — верхним классом сечения;
ясно, что эти классы не пересекаются. Для каждого сечения
всякого линейно упорядоченного множества выполнено в точ-
точности одно из следующих четырех условий:
A) Существует наибольший элемент в нижнем классе и наи-
наименьший элемент в верхнем классе.
B) Существует наибольший элемент в нижнем классе, но не
существует наименьшего элемента в верхнем классе.
C) Не существует наибольшего элемента в нижнем классе,
но существует наименьший элемент в верхнем классе.
1.3. УПОРЯДОЧЕНИЯ. ПОРЯДКОВЫЕ ЧИСЛА 23
D) Не существует наибольшего элемента в нижнем классе
и не существует наименьшего элемента в верхнем классе.
Мы называем сечение скачком, если выполнено условие A),
и щелью, если выполнено условие D).
Линейно упорядоченное множество X называется плотно
упорядоченным, если никакое сечение множества X не является
скачком; если, кроме того, никакое сечение множества X не
является щелью, то X называется непрерывно упорядоченным.
Множество X плотно упорядочено в том и только том случае,
когда для любых двух элементов х, у е X, таких, что х < у,
существует элемент г, такой, что х < z < t/. Множество непре-
непрерывно упорядочено в том и только том случае, если кроме при-
приведенного условия для каждого непустого подмножества Xо с: X
множество
{х ^ X; а < х для каждого а е Хо\ {х}}
либо пусто, либо имеет наименьший элемент.
Линейный порядок < на множестве X называется вполне
упорядочением, а множество X вместе с порядком < называется
вполне упорядоченным, если порядок < обладает следующим
дополнительным свойством:
(WO) Каждое непустое подмножество множества X имеет наи-
наименьший элемент.
Можно доказать, что каждое множество кардинальных чисел
вполне упорядочено отношением <, введенным в предыдущем
параграфе.
Пусть множество X линейно упорядочено отношением <t a
множество У линейно упорядочено отношением <'. Будем гово-
говорить, что отображение f множества X в множество У сохраняет
порядок, если f(x) <'f(y) для всякой пары xjel, такой, что
х < у. Если существует сохраняющее порядок отображение ли-
линейно упорядоченного множества X на линейно упорядоченное
множество У, то X и У называются подобными.
Каждое линейно упорядоченное множество X подобно под-
подмножеству множества всех сечений множества X, удовлетворяю-
удовлетворяющему условиям A), B) или D) и линейно упорядоченному по
следующему правилу:
(D\9 Ei) < (Ds, ?2) в том и только том случае,
если ?>i с D2 и D\ Ф D%.
Указанное подмножество не имеет щелей, и если X плотно упо-
упорядочено, то оно непрерывно упорядочено.
Каждому вполне упорядоченному множеству X приписывает-
приписывается некоторое порядковое число, или ординал, а; оно называется
порядковым типом множества Х\ порядковые типы вполне
24 ВВЕДЕНИЕ
упорядоченных множеств X и Y одинаковы в том и только том
случае, когда X и Y подобны.
Каждое сохраняющее порядок отображение инъективно, по-
поэтому если X и Y подобны, то |Х| = |У|. Следовательно, каж-
каждому ординалу а соответствует некоторый кардинал — мощность
вполне упорядоченного множества типа а; этот кардинал назы-
называется мощностью ординала а и обозначается |а|. Если
| ос | ^ Ко, то ординал а называют счетным.
Пусть а и р— ординалы, являющиеся порядковыми типами
соответственно множеств X и Y. Будем говорить, что а меньше
р или что р больше а, и писать а < р или р > а, если суще-
существует такое t/0 ^ У у что множества X и {у е Y: у < у0} по-
подобны. Можно доказать, что каждое множество ординалов
вполне упорядочено этим отношением <. Всякое вполне упоря-
упорядоченное множество типа а подобно множеству всех ординалов,
меньших а, линейно упорядоченному отношением <.
Ординал X называется предельным, если не существует по-
порядкового числа, непосредственно предшествующего Х> т. е. если
для каждого g < X существует ординал а, такой, что ? < а < X.
Если ординал I непосредственно предшествует а, то говорят,
что g является предшественником а, и пишут а = | + 1; а на-
называют наследником ординала |. У каждого ординала имеется
наследник; для любого ординала а и любого целого я ^ 0 опре-
определим по индукции а + я, положив а + 0 = а и а + п =
= [а +(я— 1)]+ 1 для я ^ 1. Оказывается, любой ординал мо-
может быть единственным образом представлен в виде % -\- п, где
1 — некоторый предельный ординал, а п — неотрицательное це-
целое число. Ординал К + п четный (нечетный), если п четно (не-
(нечетно) .
Если множество всех ординалов, меньших предельного орди-
ординала X, содержит подмножество А типа а, такое, что для каж-
каждого | < к существует 5'еЛ, удовлетворяющее неравенству
I < V < X, то говорят, что ординал а конфинален X.
Бесконечный ординал X (т. е. порядковый тип некоторого
бесконечного вполне упорядоченного множества) называется
начальным (или инициальным) ординалом, если Я, —наимень-
—наименьший среди всех ординалов а, таких, что |оь| = |А,|, т. е. если
|?|<|Л| Для любого ? < X. Инициальный ординал X называет-
называется регулярным, если не существует ос < Я, конфинального X.
Для каждого кардинала щ существует начальный ординал Я,
такой, что |А,| = т, и этот X единствен (см. теорему Цермело
в следующем параграфе). Кардинал щ называется регулярным,
если отвечающий ему начальный ординал X, такой, что |Л,| = Е,
регулярен. Начальный ординал мощности &*0 обозначается че-
через <о0; это порядковый тип множества всех положительных
целых чисел с естественным порядком.
I. 3, УПОРЯДОЧЕНИЯ. ПОРЯДКОВЫЕ ЧИСЛА 25
Наименьший ординал, мощность которого больше Ко, т. е.
наименьший несчетный ординал, обозначается через соь а его
мощность — через Кь Равенство 2**° = К i называется гипотезой
континуума] гипотеза континуума независима от аксиом теории
множеств. Для каждой последовательности ai, аг, ... ордина-
ординалов, меньших соь существует такой ординал a < юь что a* < a
для i= 1, 2, ... . Наименьший ординал мощности, большей Кь
обозначается через сог, а его мощность — через &*2- Более общим
образом, каждому ординалу а соответствуют кардинал Ка и
ординал Фа, являющийся начальным ординалом мощности Ка.
Можно доказать, что каждый кардинал равен Ка для некото-
некоторого а.
Пусть а — некоторый ординал, а X — какое-нибудь множе-
множество; под трансфинитной последовательностью типа а со зна-
значениями в X понимают любое отображение / множества W(a)f
состоящего из всех ординалов, меньших а, в множество X. Эле-
Элемент множества X, поставленный в соответствие ординалу
g < а, обозначается х^ а не /(?), а сама трансфинитная после-
последовательность обозначается хо, хи ..., х^ ..., | < а. Трансфи-
Трансфинитная последовательность Ло, А\, ..., Л^, ..., | < а, множеств
называется возрастающей, если Ара Л|при g7 < | < а, и убы-
убывающей, если Л^ с= А^ при S7 < g < a.
Для определения трансфинитных последовательностей обыч-
обычно применяется
Теорема об определениях по трансфинитной индукции. Пусть
даны произвольное множество Z и некоторый ординал а. Пусть
G — множество всех трансфинитных последовательностей типов,
меньших а, со значениями в множестве Z. Для каждой функ-
функции h из G в Z существует тогда в точности одна трансфинитная
последовательность f типа а, такая, что
f{i) = h{f\W&)) привсехКа,
где f\W(\)—трансфинитная последовательность типа g, полу-
ченная сужением функции f на множество W{\) всех ординалов,
меньших g.
Теорему об определениях по трансфинитной индукции часто
применяют в случае, когда Z есть семейство всех подмножеств
множества X. Функция h определяется при этом обычно тремя
различными формулами. Первая формула дает значения h на
последовательности g типа 0 (где 0 — порядковый тип пустого
множества), являющейся пустой последовательностью, т. е. зна-
значение А@). Вторая формула дает значение h(g) на всех после-
последовательностях g типа g+ 1, и, наконец, третья формула дает
значение h(g) на всех последовательностях gy порядковый тип
26 ВВЕДЕНИЕ
которых является предельным ординалом. Например, первая
формула может быть такой:
вторая может иметь вид
а третьей может быть формула
или
где F и G — данные функции и А — некоторое множество. Тогда
последовательность Ло, Ль ...» Л^, ..., | < а, которая суще-
существует в силу теоремы об определениях по трансфинитной ин-
индукции, удовлетворяет следующим условиям:
Следовательно, для того чтобы определить трансфинитную по-
последовательность Ло, Ль ..., А^, ..., | < а, достаточно опре-
определить Ло и описать, как Л^+1 зависит от Л^ и как А\ зависит
либо от U А*9 либо от П Л|
Пусть множество X вполне упорядочено отношением <;
тогда всякое подмножество Л <^Х, при каждом х0^ X удовлет-
удовлетворяющее условию
если {xgI: х < дго}с:Л, то дг0 е Л,
совпадает с множеством X. Этот факт служит основой для ин-
индуктивных доказательств. Мы будем применять его как в слу-
случае, когда X — множество натуральных чисел (доказательства
по математической индукции), так и в случае, когда X — мно-
множество всех ординалов, меньших данного ординала а (дока-
(доказательства по трансфинитной индукции).
Пусть X — некоторое множество и <; — некоторое отношение
на нем. Мы говорим, что ^ упорядочивает X, или что ^ яв-
является упорядочением {порядком) на X, если отношение ^ об-
обладает следующими свойствами:
(OR1) Если х ^ у и у ^ 2, то х ^ г.
(OR2) Для каждого хеХ имеем х^х.
(OR3) Если х ^ у и у ^ х, то х = у.
Множество X вместе с некоторым порядком ^ на I назы-
называется упорядоченным множеством. Два элемента х и у упоря-
упорядоченного множества X могут быть несравнимыми, т. е. может
I. 3. УПОРЯДОЧЕНИЯ. ПОРЯДКОВЫЕ ЧИСЛА 27
случиться, что не имеет места ни одно из неравенств х^у9
у^х.
Всякое семейство множеств упорядочено отношением вклю-
включения с.
Если X линейно упорядочено отношением <, то, полагая для
любых х, у е X
х ^ у в том и только том случае, когда х < у или х = у9
мы получаем некоторый порядок на X. Следовательно, каждое
линейно упорядоченное множество можно рассматривать как
некоторое упорядоченное множество. Если для каждой пары
х, у элементов подмножества А упорядоченного множества X
имеет место одно из соотношений х ^ у или у ^ х, то, полагая
х < у в том и только том случае, когда х ^ у и хфу,
мы получаем некоторый линейный порядок на Л. Говорят, что
А есть линейно упорядоченное подмножество множества X, упо-
упорядоченного отношением ^.
Элемент и некоторого упорядоченного множества X назы-
называется наименьшей (точной) верхней гранью подмножества
А с= X, если х^и при всех х^А я если всякий элемент уе1,
такой, что х ^ v при всех хеД, удовлетворяет неравенству
и ^ у. Наибольшая (точная] нижняя грань подмножества
AczX определяется аналогичным образом. Зметим, что наи-
наименьшая верхняя грань множества X, если она существует, яв-
является наибольшим элементом множества X, а наибольшая
нижняя грань множества X, если она существует, является наи-
наименьшим элементом множества X.
Пусть X — произвольное множество и ^ — отношение на X.
Мы говорим, что ^ направляет множество X или что X на-
направлено отношением =^, если отношение ^ обладает следую-
следующими свойствами:
(D1) Если х^у и у ^zyro x^z.
(D2) Для всякого х^Х имеем х^х.
(D3) Для любых х, у ^ X существует такой элемент z e X, что
x^z и y^z.
Подмножество Л множества X, направленного отношением ^,
конфинально в Ху если для каждого х^Х существует такое
а^А, что х^.а. Конфинальные подмножества линейно упоря-
упорядоченных и упорядоченных множеств определяются аналогично.
Пусть множества X и У упорядочены (направлены) отноше-
отношениями ^ и </ соответственно; функция / из множества X в Y
называется неубывающей, если f(x)^ff(y) для каждой пары
xt у элементов Ху таких, что x^iy. Невозрастающие функции
определяются аналогично.
28 ВВЕДЕНИЕ
1.4. АКСИОМА ВЫБОРА
Аксиома выбора часто используется в этой книге, хотя факт
ее применения обычно не отмечается. Однако иногда удобнее
пользоваться аксиомой выбора не в ее первоначальном виде,
а в одной из альтернативных форм, которые являются важными
теоремами теории множеств. Ниже мы сформулируем теорему
Цермело о вполне упорядочиваемости и два принципа макси-
максимума, являющиеся альтернативными формами аксиомы выбора,
и докажем равносильность всех четырех утверждений. Прежде
всего дадим два необходимых определения.
Элемент х0 упорядоченного множества X называется макси-
максимальным элементом множества Ху если из х0 ^ jc e I следует,
что хо — х. Пусть дано множество X и свойство ^*, которым мо-
могут обладать подмножества множества X. Говорят, что $Р есть
свойство конечного характера, если пустое множество обладает
этим свойством, а множество А а X обладает свойством 1? в том
я только том случае, когда им обладает каждое конечное под-
подмножество А.
Аксиома выбора. Для всякого семейства {Xs}s^s непустых
множеств существует функция f из S в [] Xs, такая, что
/E) е Xs при всех seS.
Теорема Цермело о вполне упорядочиваемости. На каждом
множестве X существует отношение <, которое вполне упорядо-
упорядочивает X.
Лемма Тейхмюллера — Тьюки, Пусть задано множество X и
некоторое свойство д> его подмножеств. Если 0* есть свойство
конечного характера, то каждое множество А с= X, обладающее
свойством IP, содержится в множестве В а X, которое обладает
свойством 9* и является максимальным элементом в упорядо-
упорядоченном по включению семействе всех подмножеств множества
X, обладающих свойством 3*.
Лемма Куратовского — Цорна. Если для каждого линейно
упорядоченного подмножества А множества X, упорядоченного
отношением ^, существует такой элемент xogX, что х^.х0
при всех х^А, то в X существует максимальный элемент.
Теорема Цермело следует из аксиомы выбора.
Пусть f — функция, приписывающая каждому непустому
подмножеству А множества X некоторый элемент /(Л)еЛ.
Предположим, кроме того, что f@)=x^X. Обозначим через
Ж семейство всех вполне упорядочивающих отношений на под-
I. 4. АКСИОМА ВЫБОРА 29
множествах множества X, и пусть а — наименьший ординал,
больший всех порядковых типов подмножеств множества X, упо-
упорядоченных элементами семейства Ж.
В силу теоремы об определениях по трансфинитной индукции
существует трансфинитная последовательность xq9 x\, ..., х%, ...
..., | < а, такая, что
х$ = f(X\{xy: у < I}) для каждого | < а.
Если х^л:, то ^gI\{jcy:7<?} и a^=??a;y при у < |.
Следовательно, если бы для всех g < а было х$ Ф х, то суще-
существовала бы трансфинитная последовательность типа а, все
члены которой различны и принадлежат множеству X. Но это
невозможно в силу определения а. Поэтому существует наи-
наименьший ординал ?, такой, что л^ = х. Тогда Х = {ху: у < ?},
т. е. все элементы множества X расположены в трансфинитную
последовательность хо, х\, ..., xY, ..., у < |, и xY=^=xY, при
7 =7^ 7Л- Это и означает, что X можно вполне упорядочить. -1
Лемма Тейхмюллера — Тьюки вытекает из теоремы Цермело.
Пусть даны множество X, некоторое свойство 0* (его под-
множеств) конечного характера и множество АсХ, обладаю-
обладающее свойством 3*. В силу теоремы Цермело множество Х\А мо-
может быть вполне упорядочено. Так как каждое вполне упорядо-
упорядоченное множество подобно множеству всех ординалов, меньших
некоторого ординала а, то все элементы множества Х\А можно
расположить в трансфинитную последовательность типа а:
х0, Х\у ..., х%, ..., ! < а.
В силу теоремы об определениях по трансфинитной индук-
индукции, в доказательстве которой не используется аксиома выбора,
существует трансфинитная последовательность Ло, А\, ..., А%, ...
..., I < а + 1» такая, что
ло=л,
{U M U {ч}> если U М U {ч) обладает свойством 9>У
(J А\ в противном случае,
когда \ < а, и
Аа= U ^S-
Легко видеть, что все элементы этой последовательности об-
обладают свойством 9* и что B = Ao,zdAo = A является макси-
максимальным подмножеством множества Ху обладающим свойством
I
30 ВВЕДЕНИЕ
Лемма Куратовского— Цорна следует из леммы Тейхмюл-
лера — Тьюки.
Свойство «быть линейно упорядоченным подмножеством мно-
множества X, упорядоченного отношением О, является свойством
конечного характера. В силу леммы Тейхмюллера — Тьюки, поло-
положив А = 0, можно заключить, что существует максимальное ли-
линейно упорядоченное подмножество В множества Xt упорядо-
упорядоченного отношением ^. Выберем хо е X таким образом, чтобы
х ^ х0 для каждого х<^В. Элемент х0 является максимальным
элементом множества X. В самом деле, для каждого х^Х, та-
такого, что хо ^ х, имеем х0 = х, так как в противном случае
В[){х} было бы линейно упорядоченным подмножеством мно-
множества X, большим 5. 1
Аксиома выбора следует из леммы Куратовского — Цорна.
Пусть {J5}5eS — семейство непустых множеств. Обозначим
через Зв множество всех пар (Tff)t где Т cz S и / — функция из
Т в (J Xs, такая, что f{s)^ Xs для любого s ^ 7. Упорядочим
s eS
множество SB, полагая:
G\> /i)^(^2> /2) в том и только том случае, когда
TxczT2 и f2 (s) = fx (s) для s s= TV
Легко видеть, что для каждого линейно упорядоченного подмно-
подмножества sf* = {{Twt fw)}w <= w множества SB формулы
^O^ U Tw И /O(S) = /.(S) ДЛЯ 5€ЕГШ
ше W
определяют элемент (Г<ь/о) множества SB и (TWjfw)^(TQyfQ)
для каждого ш е IF. По лемме Куратовского — Цорна в SB су-
существует максимальный элемент (Tff)\ мы покажем, что 7 = 5,
и тем завершим доказательство. В самом деле, допустим, что
существует so^S\T; выберем х0 е XSq и положим
Г = ГиЫ, f(s) = f{s) для sgI и f(so)-=*,.
Тем самым определена пара (f,f)€3?, такая, что (Г,/)^
^(Г',/') и {Т>})Ф{Т',$')\ мы пришли к противоречию. ¦
1.5. ВЕЩЕСТВЕННЫЕ ЧИСЛА
В этой книге мы пользуемся свойствами арифметических
операций на множестве вещественных чисел, свойствами отноше-
отношения < линейного упорядочения множества вещественных чи-
чисел и свойствами функции абсолютного значения. Мы также
предполагаем у читателя знакомство с понятием предела после-
I. 5. ВЕЩЕСТВЕННЫЕ ЧИСЛА 31
довательности вещественных чисел, обозначаемого lim, и поня-
понятием непрерывной функции. Используется также тот факт, что
каждое ограниченное сверху непустое множество вещественных
чисел имеет наименьшую верхнюю грань, т. е. непрерывность
множества вещественных чисел. Наименьшая верхняя грань мно-
множества обозначается через sup, а наибольшая нижняя грань —
через inf (в том случае, когда множества конечны, используются
символы max и min соответственно). При описании некоторых
примеров топологических пространств используются тригономет-
тригонометрические функции, а также координатные системы на плоскости.
Открытые интервалы с концами а и 6, где а < Ь, обозна-
обозначаются через (а, Ь), замкнутые интервалы (отрезки) с концами
а и b — через [а, Ь]\ полуоткрытые интервалы обозначаются
через (а, Ь] и [а, Ь). Множество всех вещественных чисел обо-
обозначается через Rt а множество всех натуральных чисел — через
N. Замкнутый единичный отрезок [0, 1] обозначается через /.
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
Исчерпывающий курс теории множеств представляет собой
замечательная книга Куратовского и Мостовского [1968].
Утверждение о том, что некоторое топологическое высказывание
независимо от аксиом теории множеств, которое делается здесь в
ряде случаев, относится к системе аксиом, приведенной в этой
книге. Наше изложение общей топологии базируется на наив-
наивной теории множеств, однако легко может быть перестроено на
основе указанной системы аксиом.
Лемма Тейхмюллера — Тьюки была доказана Тейхмюллером
[1939] и Тьюки [1940], лемма Куратовского-Цорна доказана
Куратовским [1922] и Цорном [1935].
Глава 1
ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
В этой главе мы вводим основные понятия общей топологии.
В § 1.1 определяется понятие топологического пространства»
вводятся открытые множества, окрестности, базы, предбазы и
базы в точке. Мы определяем также вес и характер топологи-
топологического пространства и формулируем аксиомы счетности. Далее
мы вводим замкнутые множества и рассматриваем операторы
замыкания и взятия внутренности. В конце параграфа появляет-
появляется понятие локально конечного семейства множеств.
Параграф 1.2 посвящен различным методам построения то-
топологии в множестве.
Параграф 1.3 является прямым продолжением § 1.1. -Мы
рассматриваем операторы взятия границы и производного мно-
множества и вводим следующие важные классы множеств в топо-
топологических пространствах: всюду плотные множества, коплот-
ные множества, нигде не плотные множества и борелевские
множества (в частности, Fo~ и бб-множества).
В § 1.4 вводится понятие непрерывного отображения, кото-
которое при изучении топологических пространств оказывается не
менее важным, чем само понятие топологического пространства.
Мы рассматриваем также замкнутые отображения, открытые
отображения и гомеоморфизмы; последний класс отображений
приводит к понятию гомеоморфности пространств. Далее мы рас-
рассматриваем инварианты и обратные инварианты одного класса
отображений и в заключение приводим некоторые замечания
о предмете общей топологии.
В § 1.5 обсуждаются аксиомы отделимости, т. е. ограниче-
ограничения различного типа, касающиеся отделимости точек и замкну-
замкнутых множеств в топологических пространствах. В этом парагра-
параграфе мы доказываем лемму Урысона — одну из самых важных
теорем общей топологии.
Последний параграф посвящен направленностям и фильтрам,
которые приводят к двум различным способам описания сходи-
сходимости в общих топологических пространствах. Мы изучаем так-
также два класса топологических пространств, в которых для опи-
описания сходимости и топологии достаточно последовательностей.
I.I. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА 33
1.1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА.
ОТКРЫТЫЕ И ЗАМКНУТЫЕ МНОЖЕСТВА. БАЗЫ.
ЗАМЫКАНИЕ И ВНУТРЕННОСТЬ МНОЖЕСТВА
Топологическое пространство — это пара (X, О)у состоящая
из множества X и некоторого семейства О подмножеств множе-
множества X, удовлетворяющего следующим условиям:
@1) 0<=0 иХе±О.
@2) Если Ui^O и U2€=0, то Ui(]U2eC.
@3) Если Ж <= С, то \}& e О.
Множество X в этом случае называется пространством, его
элементы называются точками пространства; подмножества X,
принадлежащие семейству Оу называются открытыми в про-
пространстве Х\ семейство О открытых подмножеств пространства
X называется также топологией на X. Свойства @1) — @3) се-
семейства открытых множеств можно переформулировать следую-
следующим образом:
(О И) Пустое множество и все пространство суть открытые
множества.
@2') Пересечение двух открытых множеств есть открытое
множество.
@3') Объединение любого семейства открытых множеств есть
открытое множество.
Из @2) непосредственно следует, что пересечение любого
конечного семейства открытых множеств есть открытое множе-
множество.
Если для некоторого хе!и некоторого открытого множе-
множества U аХ мы имеем х^. ?/, то U называется окрестностью точ-
точки х. Множество V а X открыто в том и только том случае, если
для каждой точки х е V существует ее окрестность Ux, содер-
содержащаяся в V. Действительно, если V — открытое множество, то
положим Их = V для каждого xgV, Если выполнено это усло-
условие, то V = U Ux открыто в силу @3).
XG.V
Семейство $ с О называется базой топологического про-
пространства (X,0)t если каждое непустое открытое подмножество
пространства X можно представить в виде объединения некото-
некоторого подсемейства семейства ffi. Легко показать, что семейство
$ подмножеств X есть база топологического пространства
(Х,О) в том и только том случае, когда для любой точки
х^Х и каждой окрестности V этой точки существует такое
U е ^, что х е U с: V. Очевидно, что топологическое простран-
пространство может иметь много баз. Всякая база обладает следующими
свойствами:
(В1) Для любых U\y U2^$ и любой точки jce U\ П ^2 суще-
ствует элемент (/gJ, такой, что л:е[/с[/1ПУ2.
3 Зак. 697
34 ГЛ. 1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
(В2) Для любого х&Х существует элемент U&38, такой, что
В самом деле, первое свойство вытекает из того, что Ux П ?/г —
открытое множество, а второе есть следствие того, что X — от-
открытое множество.
Множество всех кардинальных чисел вида [#|, где 3S — база
топологического пространства (Х,0), имеет наименьший эле-
элемент (так как всякое множество кардинальных чисел вполне
упорядочено отношением <). Это наименьшее кардинальное
число называется весом топологического пространства (Х,0)
и обозначается через w{{X,0)).
Семейство 3*cz0 называется предбазой топологического про-
пространства {ХУ0)9 если семейство всех конечных пересечений
UxflUzft ... ftUk, где Ut <= 5s для i = 1, 2, ..., ky является ба-
базой пространства (Ху 0).
Семейство ${х) окрестностей точки х называется базой то-
топологического пространства (ХУ0) в точке ху если для любой
окрестности V точки х существует такой элемент U ^3!(хO что
х е U aV> Легко показать, что если $ — база пространства
(X, 0), то семейство &(х), состоящее из всех элементов &у со-
содержащих точку х, есть база пространства (ХУС) в точке х.
С другой стороны, если для каждой точки х^Х задана база
$(х) пространства (X, 0) в точке х, то объединение Ш = U & (х)
xeJf
есть база пространства (ХУ0).
Характер точки х в топологическом пространстве (Ху 0) есть
наименьшее кардинальное число вида |Я(х){, где 3S{x) — база
(Ху 0) в точке х\ это кардинальное число обозначается
%(ху (Х,<У)). Характер топологического пространства (ХУ0)
есть точная верхняя грань всех кардинальных чисел %(xf (X,0))
для х^Х; это кардинальное число обозначается %{{Х,0)).
Если %((ХУ0))^ Ко, то говорят, что пространство (ХУ0)
удовлетворяет первой аксиоме счетности; это означает, что в
каждой точке х^Х существует счетная база. Если w({X,0))^
^ Ко, то говорят, что пространство (Xt0) удовлетворяет второй
аксиоме счетности; это означает, что (Ху 0) имеет счетную базу.
Пусть (Х9 0) — топологическое пространство и для каждого
Х задана база <%(х) пространства (X,0). Семейство
}Х€Ех называется системой окрестностей топологического
пространства (Х,0). Мы покажем, что всякая система окрестно-
окрестностей {$ (х)}хех обладает следующими свойствами:
(ВР1) Для всякого хеХ имеем 3§(х)ф0 и для всякого
(/g^(jc) имеем хе(/.
(ВР2) Если хе(/е^(у), то существует такое ^еШ, что
VczU.
1.1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА 35
(ВРЗ) Для любых Uu U2&&(x) существует такое U^9S{x),
что UczUx[\ U2.
Свойство (ВР1) следует непосредственно из определения
базы в точке х. Свойства (ВР2) и (ВРЗ) также следуют из
этого определения, так как U^&(y), a U\ П &2 — открытые
множества, содержащие х*
Пусть (ХУ<У)— топологическое пространство; множество
FczX называется замкнутым в этом пространстве, если его до-
дополнение X\F— открытое множество. Используя законы де
Моргана и свойства @1) — @3) открытых множеств, мы при-
приходим к выводу, что семейство ^ замкнутых множеств обладает
следующими свойствами, двойственными к свойствам (О1) —
@3):
(Cl)
(С2) Если F1 е W и F2 е= «?, то Fx U F2 е= ^.
(СЗ) Если Л с: V, то [\s4> e V.
Эти свойства можно переформулировать следующим обра-
образом:
(С17) Все пространство и пустое множество суть замкнутые
множества.
(С2') Объединение двух замкнутых множеств есть замкнутое
множество.
(СЗГ) Пересечение любого семейства замкнутых множеств есть
замкнутое множество.
Докажем, например, (СЗ). Пусть {F8}s&s— семейство замк-
замкнутых множеств. По определению, дополнение Us === X\FS есть
открытое множество для любого s ^ S. Так как
П fs= П (x\us)=x\ U и.
S S S
и так как объединение U Us открыто в силу @3), то пересе-
чение f) F$ замкнуто.
Множества, которые являются одновременно и открытыми, и
замкнутыми, называются открыто-замкнутыми.
Пусть А а Х\ обозначим через ^А семейство всех замкну-
замкнутых множеств, содержащих А. В силу (С1) имеем *&а Ф0* а из
(СЗ) следует, что пересечение Д = ()фА замкнуто. Легко видеть,
что Л есть наименьшее замкнутое множество, содержащее А;
это множество называется замыканием А. Очевидно, что мно-
множество замкнуто в том и только том случае, если оно совпа-
совпадает со своим замыканием.
Для любых подмножеств Л, В пространства X имеем
A) если AczB, то ЛсВ.
36 ГЛ. 1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
В самом^деле, из включения AczB следует, что 9
откуда AczB.
Докажем теперь следующее предложение.
1.1.1. Предложение. Для любого AczX следующие условия
равносильны:
(i) точка х принадлежит Л;
(и) для всякой базы &(х) в точке х и любого U^3S(x)
имеем U [\АФ0\
(ш) существует база 38(х) в точке х9 такая, что 1/(]АФ0
для каждого U^t$(x).
Доказательство. Для доказательства импликации (i)=^(ii)
допустим противное, т. е. что для базы 3§(х) в точке х суще-
существует такое U е $(х), что U [}А=0. Тогда ЛсА(/ и
Х\и^фД. Следовательно, AczX\U и х^ЁА, т. е. (i) не имеет
места.
Импликация (ii)=^(iii) очевидна. Остается показать, что
(iii)=^(i). Допустим, что (i) не имеет места, т. е. хфА. Тогда
существует замкнутое множество F^Wa, такое, что хфр. Для
открытого множества V = X\F имеем
B) xebV n V(}A=0.
Далее, для любой базы ${х) в л; существует такое U^$(x),
что jc g (/ с V, и из B) следует, что Uf[A=09 т. e. (iii) не
имеет места. I
1.1.2. Следствие. Если U — открытое множество и U [)А=0, то
и ?/fU = 0.
В частности,__еслм U и V — непересекающиеся открытые мно-
множества, ToU()V = 0 = OnV.
Доказательство. Допустим, что существует xg U[\A, и, возь-
возьмем в качестве базы 9§{х) в точке х семейство всех окрестно-
окрестностей точки х. Из предложения 1.1.1 следует, что 1)[\АФ0, а
это противоречит нашему предположению. Таким образом,
U0 I
Наиболее важные свойства оператора замыкания перечис-
перечислены в следующей теореме.
1.1.3. Теорема. Оператор замыкания обладает следующими свой-
свойствами:
(СО1) 0 = 0.
(СО2) Л си Л.
(СОЗ) A U B-=A U 5.
(СО4) A) = Л.
1.1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА 37
Доказательство. Свойства (СО1) и (СО2) следуют непосред-
непосредственно из определений, а свойство (СО4) вытекает из того, что
А— замкнутое множество.
Из' A) следует, что Ас=А[)В и EczA[)B. Значит,
C) *1Г
В силу (СО2), A cz А, В а В, и потому A\jBczA]jE. По-
Последнее множество как объединение двух замкнутых множеств
замкнуто; отсюда по определению замыкания получаем
D) J{j~Bc
Формулы C) и D) устанавливают равенство (СОЗ). ¦
Внутренность множества A cz X есть объединение всех от-
открытых множеств, содержащихся в Л, или, что эквивалентно,
наибольшее открытое множество, содержащееся в А. Это множе-
множество обозначается IntA. Очевидно, что множество открыто тогда
и только тогда, когда оно совпадает со своей внутренностью.
Следующее предложение является непосредственным след-
следствием определения внутренности.
1.1.4. Предложение. Точка х принадлежит IntA тогда и только
тогда, когда существует такая ее окрестность U, что UczA. I
Как показывает следующая теорема, оператор взятия внут-
внутренности тесно связан с оператором замыкания.
1.1.5. Теорема. Для каждого А си X имеем
ЫА=Х\Х\А.
Доказательство. Из (СО2) вытекает включение Х\А с:
а Х\А\ таким образом,
Так как множество Х\Х\А открыто, то
E) X\l\AczlntA.
Для любого открытого множества U9 содержащегося в Л, имеем
используя A), получаем
X\AczX\Ut или
В частности,
lntAczX\X\A.
Последнее включение вместе с E) и устанавливает наше утвер-
утверждение. I
38 ГЛ. 1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
Свойства оператора взятия внутренности двойственны свой-
свойствам (СО1) — (СО4) и перечислены в следующей теореме, ко-
которая вытекает из утверждений 1.1.3, 1.1.5 и законов де Мор-
Моргана,
1.1.6. Теорема, Оператор Int обладает следующими свойствами:
A01) ШХ = Х.
A02) Int Лег Л.
A03) lnt(Af\B)=lntA(]lntB.
A04) Int(InM)=InM. I
1.1.7* Пример. Пусть X — произвольное множество и О —
семейство всех его подмножеств. Очевидно, что (Х,0) — топо-
топологическое пространство. Каждое множество Л cz X открыто-
замкнуто. Всякое множество, содержащее точку х, является ее
окрестностью. Семейство всех одноточечных подмножеств мно-
множества X образует базу пространства (Х,0). Эта база имеет
минимальную мощность. Поэтому вес (X, О) равен мощности
множества X. Для любой точки х^Х семейство, состоящее из
единственного множества {х}9 есть база пространства (Х9 О)
в точке х. Это показывает, что (Х9О) удовлетворяет первой ак-
аксиоме счетности. Каждое множество Л cz X совпадает со своим
замыканием и со своей внутренностью.
Такое топологическое пространство называется дискретным
пространством, а О называется дискретной топологией. I
1.1.8. Пример. Пусть X — произвольное бесконечное множество,
xq — некоторая точка в X и О — семейство, состоящее из всех
подмножеств множества Ху не содержащих хо, и всех подмно-
подмножеств множества Xt имеющих конечное дополнение. Легко уста-
установить, что (ХУС) — топологическое пространство. Все одното-
одноточечные подмножества Х9 за исключением множества {xo}f от-
открыто-замкнуты; множество {хо} замкнуто, но не открыто. Се-
Семейство, состоящее из всех одноточечных множеств {х}, хфх0,
и из всех множеств вида X\F, где F — конечное множество, об-
образуют базу пространства [XtO). Эта база имеет наименьшую
мощность. Поэтому вес пространства (X, О) равен мощности
множества X. Семейство, состоящее из всех одноточечных мно-
множеств {х}, х ф х0, и из всех множеств вида Z\ {x}, есть пред-
база пространства (Х,О). Для каждого AczX имеем
-_( А,
если Л конечно,
U {*о}» если Л бесконечно;
если Х\А конечно»
* \ {#о}> если Х\А бесконечно.
1.1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА 39
Отсюда вытекает, что любые два бесконечных замкнутых
подмножества множества X имеют непустое пересечение.!
Топологические пространства, построенные в следующих двух
примерах, имеют особенно важное значение в общей топологии.
1.1.9. Пример. Пусть R— множество вещественных чисел и 0—
семейство, состоящее из всех множеств U <zz R, обладающих тем
свойством, что для любого х е U существует такое е > О, что
(л: — е, х + s) с: U. Очевидно, что семейство 0 обладает свой-
свойствами @1) — @3). Из определения предела последовательно-
последовательности следует, что множество AczR замкнуто тогда и только
тогда, когда вместе со всякой сходящейся последовательностью
оно содержит также ее предел. Семейство всех открытых интер-
интервалов с рациональными концами образует базу пространства
(R, 0). Это база минимальной мощности; поэтому (R90) удов-
удовлетворяет второй аксиоме счетности и тем более первой.
Топология О называется естественной топологией веществен-
вещественной прямой. 1
1.1.10. Пример. Пусть / = [0,1] — замкнутый единичный интер-
интервал я 0 — семейство всех множеств вида / f) ?/, где U ci R от-
открыто относительно естественной топологии прямой R. Очевидно,
что (/, 0)— топологическое пространство. Семейство всех ин-
интервалов вида (ги г2), [0, г2) или (п, 1], где п, г2 — рациональ-
рациональные числа и 0 < г\ < т% < 1, является базой пространства
A,0). Все интервалы последних двух типов образуют предбазу.
Пространство A,0) удовлетворяет и первой, и второй аксио-
аксиомам счетности. Множество AazI замкнуто в / тогда и только
тогда, когда А замкнуто в R.
Топология С называется естественной топологией замкнутого
интервала /. 1
Из приведенных выше примеров следует, что для заданного
множества X семейство 0 можно выбрать многими различными
способами, так чтобы (X, 0) было топологическим простран-
пространством. Если 0\ и 02 — две топологии на X и 0%<zz0\, то гово-
говорят, что топология 0i сильнее (тоньше) топологии 0% или что
топология 02 слабее (грубее) 0\. Дискретная топология на X
самая сильная. Слабейшая топология на X состоит только из 0
и Х\ она называется антидискретной топологией на X. Множе-
Множество, снабженное такой топологией, называется антидискретным
пространством. Очевидно, что семейство всех топологий на мно-
множестве X упорядочено отношением включения.
Пусть X — произвольное бесконечное множество, х0 и д:^ —
две различные точки в Х> 0 — топология, определенная в 1.1.8,
и 0' — топология, определенная подобным же образом для
40 ГЛ. 1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
точки х'р Легко показать, что топологии О и О' несравнимы;
никакая из них не тоньше другой.
В дальнейшем мы будем обычно рассматривать в ходе от-
отдельного рассуждения одну фиксированную топологию О на
множестве X и для упрощения обозначений будем пользоваться
символом X вместо (Х,0). Соответственно мы будем писать
w(X), %{xyX) и %(Х). Эти обозначения не вполне точны, однако
из контекста будет всегда ясно, какая топология на X имеется
в виду. Часто мы будем говорить просто «пространство» вместо
«топологическое пространство».
Из свойства (СОЗ) оператора замыкания следует, что замы-
замыкание конечного объединения множеств совпадает с объедине-
объединением замыканий этих множеств, т. е. оператор замыкания ко-
конечно аддитивен. Как показывают простые примеры, этот опе-
оператор не является счетно аддитивным (ср. с упр. 1.1.В). Опре-
Определим теперь важный класс семейств множеств, для которых
оператор замыкания аддитивен.
Семейство D}se5 подмножеств топологического простран-
пространства X называется локально конечным, если для каждой точки
jcel существует такая окрестность ?/, что множество (seS:
U f[As?=0} конечно. Если любая точка хе! имеет окрест-
окрестность, которая пересекается не более чем с одним множеством
данного семейства, то мы называем это семейство дискретным.
Очевидно, что любое дискретное семейство, так же как и любое
конечное семейство, локально конечно.
1.1.11. Теорема. Для каждого локально конечного семейства
Ш 5 имеет место равенство (J Л5== U Л5.
s<=S s&S
S
Доказательство. Включение As a [] As для любого s e S
s&S
следует из A); значит, имеет место и включение |J Л5с |J As.
sS &S
Чтобы доказать обратное включение, заметим, что, в силу ло-
локальной конечности семейства MJsges» для л1°бой точки
x ^ U As существует такая окрестность U, что множество
So = {s g S: U(]AS ф 0} конечно. Из 1.1.1 вытекает, что хф
$ е 3T\So
так как
и л= или U
имеем
As— [] As<zz [] As. I
1.1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА 41
1.1 Л2. Следствие. Пусть &~ — локально конечное семейство и
F = \J&~. Если все элементы &~ суть замкнутые множества, то и
F — замкнутое множество. Если все элементы $Г открыто-замк-
открыто-замкнуты, то F также открыто-замкнуто. 1
1.1.13. Теорема. Пусть {As}seS— локально конечное (дискрет-
(дискретное) семейство; тогда семейство {A9}s^s также локально конечно
(дискретноI). I
В заключение этого параграфа мы приведем две теоремы
о семействах открытых множеств в пространстве веса щ. Обе эти
теоремы будут применяться в дальнейшем в этой книге.
1,1.14» Теорема. Пусть w{X)^m\ тогда для любого семей-
семейства {Us}s s s открытых подмножеств X существует такое множе-
множество S0 С S, ЧТО \Sq\ ^ Ш U U Us = U Us-
sgSo seS
Доказательство. Выберем базу $ пространства Ху удовлет-
удовлетворяющую условию \&\ ^ ш, и обозначим через $о семейство
всех U е Му таких, что существует s e S, для которого U cz Us-
Всякому и^Ло поставим в соответствие s(U)^S так, чтобы
выполнялось включение
F) U с Usm.
Таким образом определена функция 5 из 380 в S. Покажем, что
множество So = s(^7o)c=S удовлетворяет условию теоремы.
Прежде всего |So| = |s(^o) |^|Л0|^|Л|^ю. Выберем точку
хе U Us. Существуют такое seS, что хе USy и такое Uе$,
S
что x&UczUs- Ясно, что U^&q и s(U)^S0. Из включения
F) вытекает, что
x€*U<=:Us{u)Cz U U,.
Следовательно, U U8 с [} (/s. Обратное включение оче-
видно. ¦
1.1.15. Теорема. Пусть w(X)^Lm,\ тогда для любой базы $ про-
пространства X найдется такая база $о, что \ $ъ \ ^ ш и <%0с:?8.
Доказательство. Пусть сначала m ^ Ко; выберем такую базу
{1^}-г пространства X, что |Г|^ш. Пусть Я = {Us} se s;
1) Способ, которым используются скобки, позволяет нам делать одно-
одновременно два параллельных утверждения. Читая первое утверждение, не
следует принимать во внимание слова, стоящие в скобках. Читая второе
утверждение, следует опустить слова, стоящие непосредственно перед скоб-
скобками.
42 ГЛ. I. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
ПОЛОЖИМ
teT.
Так как М — база пространства X, то |J Us=Wt. В силу
se=S(t)
1.1.14, существует множество So(t)a S(t)f такое, что
G) I «о<<)!<»>
(8) Wt= U «/.= U Us.
ПОЛОЖИМ ^0 = {^}S?s0(O^er- TaK KaK 1Л^Ш> И3 G) И й3
равенства т2 =т следует, что \38о\ ^ ш. Покажем теперь, что ЗВ0
есть база. Возьмем произвольную точку х&Х и ее окрестность
V. Так как $х является базой, то существует такое /еГ, что
xeWtczV. В силу (8), найдется такое s^S0(t), что
Очевидно, что Us^{$o, а это и означает, что ^0 — база про-
пространства X.
В случае конечного щ следует показать, что если $\ — база
и |i?i| = w(X)^.m, то 3$\Ci$\ этот шаг предоставляется чита-
читателю в качестве упражнения. I
1.1.16. Замечание. Заметим, что в доказательстве теоремы
1.1.14 мы не использовали тот факт, что члены семейства $ —
открытые множества. Все, чем мы воспользовались, — это то,
что |J?|s^m и что для каждой точки jcel и ее окрестности V
существует такое U е 3$, что х е U cz V (ср. с понятием сети,
введенным в § 3.1, и теоремой 3.8.12).
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
Возникновение общей топологии есть следствие перестройки
оснований математического анализа, происходившей в течение
XIX столетия. Попытки освободить анализ от наивной геомет-
геометрической интуиции и соображений механики, к которым обра-
обращались создатели анализа И. Ньютон A642—1727) и Г. Лейб-
Лейбниц A646—1716), привели к точному определению предела
(Ж. Даламбер A717—1783) и О. Л. Коши A784—1857)), к
формулировке признаков сходимости бесконечных рядов
(К. Ф. Гаусс A777—1855)) и к прояснению понятия непрерыв-
непрерывной функции (Б. Больцано A781—1848) и Коши). Необходи-
Необходимость постановки анализа на прочный фундамент стала осоз-
осознана всеми после открытия ряда патологических явлений при
изучении сходимости тригонометрических рядов (Н. Г. Абель
A802—1829), П. Г. Лежен Дирихле A805—1859), П. Дюбуа-
1.1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА 43
Реймон A831—1889)) и построения первых примеров нигде не
дифференцируемых непрерывных функций (Больцано, Б. Риман
A826—1866) и К. Вейерштрасс A815—1897) соответственно
в 1830, 1854 и 1861 гг.). Последние примеры разрушили обще-
общепринятые представления и привели к пересмотру понятия чис-
числа и к возникновению строгих теорий вещественных чисел. Наи-
Наиболее важными из них были: теория, предложенная независимо
Ш. Мерэ A835—1911) и Г. Кантором A845—1918), в которой
вещественные числа были определены как классы эквивалент-
эквивалентности последовательностей Коши рациональных чисел, и теория,
предложенная Р. Дедекиндом A831—1916), в которой веще-
вещественные числа были определены как сечения в множестве ра-
рациональных чисел. Обе теории давали описание топологической
структуры вещественной прямой.
Общая топология обязана своим возникновением серии ра-
работ Кантора, опубликованных в 1879—1884 гг. Обсуждая про-
проблемы единственности тригонометрических рядов, Кантор сосре-
сосредоточился на изучении множеств «исключительных точек», в ко-
которых можно было опустить некоторые условия теорем, не на-
нарушая их заключений. Впоследствии он посвятил себя исклю-
исключительно исследованию множеств, создав, таким образом, одно-
одновременно теорию множеств и общую топологию. Кантор опре-
определил и изучил несколько фундаментальных понятий топологии
в рамках подмножеств евклидовых пространств. В дальнейшем
ряд важных понятий, также относящихся к подмножествам
евклидовых пространств, были введены в период 1893—1905 гг.
К. Жорданом A838—1922), А. Пуанкаре A854—1912), Э. Бо-
релем A871—1956), Р. Бэром A874—1932) и А. Лебегом
A875—1941).
Решительным шагом вперед стал переход от евклидовых про-
пространств к абстрактным пространствам. Здесь первопроходцем
был Риман. В 1854 г. он ввел и изучил понятие двумерного мно-
многообразия и указал на возможность изучения многообразий бо-
более высоких размерностей, так же как и пространств функций.
Примерно около 1900 г., когда фундаментальные топологические
понятия уже были введены, появилось несколько работ, в кото-
которых некоторые специальные множества наделялись естествен-
естественными для их структур топологиями. Среди них: множество кри-
кривых (Дж. Асколи A843—1896)), множество функций (К. Арце-
ла A847—1912), В. Вольтерра A860—1940), Д. Гильберт
A862—1943), И. Фредгольм A866—1927)) и множество прямых
и плоскостей трехмерного пространства (Борель). Таким обра-
образом была подготовлена почва для аксиоматического подхода к
понятию предела и, более общо, к понятию близости точки и
множества.
44 гл- 1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
Происхождение общей топологии, которое мы здесь подыто-
подытожили весьма кратко, исчерпывающим образом изложено в книге
Мангейма [1964]. История первых лет общей топологии тща-
тщательно описана у Розенталя и Зоретти [1924] и у Титце и Вьето-
риса [1930]. Богатую историческую информацию можно найти
также в двухтомнике К. Куратовского [1966] и [1968].
Абстрактные пространства с топологической структурой впер-
впервые были введены Фреше [1906] и Риссом [1907], [1908]. Фреше
определил свои пространства в терминах сходящихся последо-
последовательностей (см. задачу 1.7.18), а Рисе — в терминах точек на-
накопления. Серьезным недостатком подхода Фреше было огра-
ограничение счетными последовательностями, что приводило к слиш-
слишком узкому классу пространств. Тем не менее была разработана
теория, основанная на определениях Фреше (см. его книгу
[1926]). С другой стороны, определение Рисса было слишком
общим (оператор замыкания определялся присоединением к
множеству всех его точек накопления и не удовлетворял усло-
условию (СО4)) и слишком сложным. Теория, основанная на этом
определении пространства, за исключением сделанного Риссом
беглого наброска, не получила дальнейшего развития. Первое
удовлетворительное определение топологического пространства
принадлежит Хаусдорфу [1914]. Он определил топологическое
пространство как абстрактное множество, снабженное системой
окрестностей, удовлетворяющей условиям (ВР1) — (ВРЗ) и ус-
условию (ВР4) § 1.5. Хаусдорф развил идею, появившуюся в ра-
работах Гильберта [1902] и Г. Вейля [1913], которые дали аксио-
аксиоматическое описание в терминах окрестностей плоскости (Гиль-
(Гильберт) и римановой поверхности (Г. Вейль). Вклад Хаусдорфа
состоял в том, что он придал необходимую общность понятиям,
введенным предшественниками, и развил систематическую и ис-
исчерпывающую теорию. Книгу Хаусдорфа [1914] стоит просмот-
просмотреть хотя бы для того, чтобы убедиться, насколько прозрачно,
точно и изящно она написана, что позволяет с удовольствием
читать ее и через 70 лет после выхода. Другая система аксиом
была предложена Р. Мором. В своей книге [1932] (исправлен-
(исправленное издание [1962]) он приводит аксиоматическое описание
плоскости и подробно обсуждает абстрактные пространства, опи-
описываемые частичными множествами аксиом; первоначальный
вариант этого подхода можно найти в его статье [1916].
Определение топологического пространства, данное здесь и
принятое теперь повсеместно, было впервые сформулировано
Куратовским [1922] в терминах оператора замыкания, удовлет-
удовлетворяющего условиям (СО1) — (СО4). Понятия открытого и зам-
замкнутого множеств, а также замыкания и внутренности были
введены и изучены Кантором в классе подмножеств евклидовых
пространств. Хаусдорф обобщил их на абстрактные простран-
1.1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА 45
ства в своей работе [1914], где изложены также обе аксиомы
счетности. Понятие локально конечного семейства было введено
П. С. Александровым [1924].
УПРАЖНЕНИЯ
1.1.А. Проверьте, что для любых подмножеств А и В тополо-
топологического пространства имеют место включения
Заметим, что включения нельзя заменить на равенства.
1.1.В. Покажите, что для любой последовательности Аи А2, ...
подмножеств топологического пространства имеет место равен-
равенство
Покажите на примере, что это равенство перестанет быть вер-
верным, если опустить второе слагаемое в правой части.
1.1.С (Куратовский [1922а]). Подмножество U топологиче-
топологического пространства, удовлетворяющее условию U = Int ?7, на-
называется каноническим открытым множеством.
(a) Проверьте, что внутренность замкнутого множества есть
каноническое открытое множество.
(b) Покажите, что пересечение двух канонических открытых
множеств есть каноническое открытое множество. Заметим, что
объединение двух канонических открытых множеств может не
быть каноническим открытым множеством.
(c) Проверьте, что для канонических открытых множеств U
и V включение U czV имеет место в том и только том случае,
если О с= V.
(d) Докажите, что для любого семейства {Us}S€sS канониче-
канонических открытых множеств в топологическом пространстве X мно-
множество Int ( (J UА есть наименьшая верхняя грань, а множе-
ство Int ( f] (/Л есть наибольшая нижняя грань семейства
VsgS /
{Us}s^s в семействе всех канонических открытых множеств в X,
упорядоченном по включению.
(e) Подмножество А топологического пространства, удовлет-
удовлетворяющее условию А = Int Л, называется каноническим замкну-
замкнутым множеством. Покажите, что А есть замкнутое множество
в том и только том случае, если его дополнение есть канониче-
каноническое открытое множество.
46 ГЛ. 1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
Сформулируйте и докажите свойства канонических замкнутых
множеств, двойственные свойствам канонических открытых мно-
множеств, установленным в (а) — (d).
M.D. Покажите, что для любого семейства топологий
{0s}sgS на множестве X существует топология на X, являющая-
являющаяся наименьшей верхней гранью {^}5е5 (т- е- грубейшей топо-
топологией в семействе всех топологий, более тонких, чем любая
0s), а также что существует топология на X, которая является
наибольшей нижней гранью {0s}$€bS (т. е. тончайшей топологией
в семействе всех топологий, которые грубее, чем каждая 0S).
1.2. МЕТОДЫ ВВЕДЕНИЯ ТОПОЛОГИЙ
Пусть X — произвольное множество; под введением тополо-
топологии на X мы понимаем выбор семейства 0 подмножеств X,
удовлетворяющих условиям @1) — @3), т. е. такого семейства
09 что пара (Х90) есть топологическое пространство. Часто бы-
бывает удобнее давать косвенное описание семейства открытых
множеств. Мы приведем несколько методов введения топологий,
которые заключаются в том, что определяется база, или система
окрестностей, или семейство замкнутых множеств, или оператор
замыкания, или, наконец, оператор взятия внутренности.
1.2.1. Предложение. Пусть даны множество X и семейство $
его подмножеств, удовлетворяющее условиям (В1) — (В2). Пусть
0 — семейство всех подмножеств множества X, являющихся
объединениями, подсемейств семейства 3$, г. е.
U е 0 тогда и только тогда, когда U = \}SSoy где $0 — под-
подсемейство семейства $.
Семейство 0 удовлетворяет условиям @1) —@3). Семейство $
является базой топологического пространства (Х,0).
Топология 0 называется топологией, порожденной базой 3$.
Доказательство. Условие @1) выполнено, так как 0 = U^o
при &q = 0 и, в силу (В2), X = U^o при &0 = &. Пусть
Uи U2^0; тогда ^= [] Us и ?/2= [J Ui9 где Us, Ut^3S,
seSH/GT. Так как
tfi№= U
то для доказательства выполнения условия @2) достаточно
показать, что Us f| Ut есть объединение некоторого подсемей-
подсемейства из М.
1.2. МЕТОДЫ ВВЕДЕНИЯ ТОПОЛОГИЙ 47
В силу (В1), для каждого x^Us(]Ut существует такое
U(x)&$9 что xg U(x)cz Us П Uи а это влечет за собой соот-
соотношения
Usf]Ut = ЦЯ0, где 3$о =
Условие @3) выполнено по определению семейства О.
Очевидно, что 31 является базой пространства (X, О). 9
1.2.2. Пример. Пусть К — множество всех вещественных чисел, а
33 — семейство всех интервалов [х, г), где х, г&К, х<гиг —
рациональное число. Легко проверить, что семейство $ обладает
свойствами (В1) —(В2).
Элементы семейства <% суть открыто-замкнутые множества
относительно топологии, порожденной базой 3S. Ясно, что
|&| = с. Покажем, что шG() = с. Пусть 91— семейство открытых
подмножеств в К, такое, что |5?| < с. Существует точка хо е /С,
которая не является точной нижней гранью никакого элемента
семейства 91. Открытое множество [xOixo+l) нельзя предста-
представить в виде объединения подсемейства семейства 91, и, следова-
следовательно, 91 не является базой для К.
Пространство К называется прямой Зоргенфрея. I
1.2.3. Предложение. Пусть даны множество X и совокупность
{&(*)}х^х семейств его подмножеств, обладающих свойствами
(ВР1) — (ВРЗ). Пусть О — семейство всех подмножеств X, яв-
являющихся объединениями подсемейств семейства [} 38 (х). Тогда
семейство (У удовлетворяет условиям @1) — @3). Совокупность
{$(х)}х^хесть система окрестностей топологического простран-
пространства (Х,(У).
Такая топология О называется топологией, порожденной си-
системой окрестностей {&(х)}Х€вХ- И
1.2.4. Пример. Пусть L — подмножество плоскости, определен-
определенное условием у ^ 0, т. е. замкнутая верхняя полуплоскость. Обо-
Обозначим через L\ прямую у = 0 и положим L2 = L\Li. Для каж-
каждого x&Li и г>0 пусть U(xtr)— множество всех точек из L,
лежащих внутри круга радиуса г, касающегося L\ в точке дг.
Пусть далее Ui(x)= U(x, l/i)\j{x}9 t = 1, 2, ... . Для каждого
x^L% и г>0 пусть U{xtr) — множество всех точек из L, ле-
лежащих внутри круга радиуса г с центром в точке х, и пусть
Ui(x)= U(xt l/i)t /=1, 2, ... . Легко проверить, что совокуп-
совокупность {&(x)}XG.L, где #C*) = {?/i(*)}Jli, обладает свойствами
(ВР1) — (ВРЗ).
48 ГЛ. 1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
Множество L\ замкнуто относительно топологии, порожден-
порожденной системой окрестностей {$ {х)}хеХ.
Пространство L называется плоскостью Немыцкого. i
1.2.5. Предложение. Пусть даны множество X и семейство W его
подмножеств, обладающее свойствами (С1) — (СЗ). Семейство
C={X\F: F <===&}
удовлетворяет условиям @1) — @3). Семейство <& есть семей-
семейство всех замкнутых множеств топологического пространства
(Х,0).
Такая топология О называется топологией, порожденной се-
семейством замкнутых множеств %?. 1
1.2.6. Пример. Пусть X — произвольное бесконечное множество
и <g> — семейство, состоящее из всех конечных подмножеств мно-
множества X и самого X. Легко показать, что семейство *& обладает
свойствами (С1) —(СЗ).
Открытые множества в X относительно топологии, порожден-
порожденной семейством *& замкнутых множеств, суть все дополнения к
конечным множествам и пустое множество. Любые два непу-
непустых открытых множества в X имеют непустое пересечение. I
1.2.7. Предложение. Пусть даны множество X и некоторый one-
ратор, приписывающий каждому множеству AczX множество
AczX так, что выполнены условия (С01) — (С04). Семейство
О = {Х\А: А = А}
удовлетворяет условиям @1) — @3). Для каждого А а X мно-
множество А является замыканием множества А в топологическом
пространстве (Х,0).
Такая топология О называется топологией, порожденной опе-
оператором замыкания - .
Доказательство. Чтобы доказать первую часть предложения,
достаточно показать, что семейство Ф={Л: Л=А} обладает
свойствами (С1) — (СЗ). Так как AczX для любого AczX, то,
в частности, X а X, и потому, учитывая (С02), получаем Х = Х.
В силу (С01), имеем 0 = 0. Таким образом, семейство ^об-
^обладает свойством (С1). Выберем F\, F2^<&, т. е. F\ = Fi и
F2 = F2. В силу (СОЗ),
и потому F\ U F2 е %?. Таким образом, семейство ^ обладает
свойством (С2).
1.2. МЕТОДЫ ВВЕДЕНИЯ ТОПОЛОГИЙ 49
Заметим, что (СОЗ) обеспечивает монотонность оператора
замыкания:
если ЛсВ, то Acz В.
В самом деле, если Acz В, то A\JB ==~ В и А[}В = А[)В = ?.
Последнее равенство означает, что ЛсВ.
Рассмотрим теперь семейство {F8}s^s элементов W, т. е.
пусть Fs = Fst s^S. Так как f] FsczFs, то в силу A),
f] lF8cF8=F8, а отсюда следует, что fl ^^ П /> Последнее
включение вместе с (СО2) показывает, что f| Fs = f] Fs-
s&S s<=S
Таким образом, семейство *g? обладает свойством (СЗ).
Пусть символ А обозначает замыкание множества А в то-
топологическом пространстве (X,(У). Мы должны показать, что
Я = Л для каждого Лс! В силу (СО4), для каждого АсиХ
имеем Лб?5, следовательно, А с: Л. Далее, для любого замкну-
замкнутого подмножества F <=_Я, содержащего Л, т. е. такого, что
р — р и д <= F, имеем AczF—F в силу A). Следовательно,
Л с: Л = П {F: F = F и A cz F}, что и доказывает равенство
Я = Л. 1
1.2.8. Пример. Пусть X — произвольное множество, содержащее
более одной точки, и пусть х0 — некоторая точка_в X. Положим
А—А[}{хо} для каждого непустого AczX и 0 = 0. Опреде-
Определенный таким образом оператор замыкания удовлетворяет усло-
условиям (СО1)—(СО4). Множество {xq}—единственное одноточеч-
одноточечное множество в X, замкнутое относительно топологии, порож-
порожденной этим оператором замыкания. Другие одноточечные мно-
множества открыты, но не замкнуты. 1
1.2.9. Предложение. Пусть даны множество X и некоторый опе-
оператор, ставящий в соответствие каждому множеству АаХ мно-
множество intAczX таким образом, что выполнены условия
A01) —A04). Семейство
0={А\ А = ША}
удовлетворяет условиям @1) — @3). Для любого AczX мно-
множество intA является внутренностью А в топологическом про-
пространстве (Х,0).
Такая топология О называется топологией, порожденной опе-
оператором взятия внутренности Int. 1
1.2.10. Пример. Пусть X — произвольное множество, содержащее
более одной точки, и пусть Хо с= X — такое подмножество, что
4 Зак. 697
50 ГЛ. 1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
||> 1. Положим intA = ЛП^о для любого собственного
подмножества АсХ и lntX = X. Определенный таким образом
оператор взятия внутренности удовлетворяет условиям A01)—
(Ю4). Все подмножества множества Хо и все пространство —
единственные подмножества пространства X, которые открыты
относительно топологии, порожденной этим операторов. Если
Хо — пустое множество, то X является антидискретным про-
пространством.
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
Разнообразные методы порождения топологий были впервые
систематически описаны Хаусдорфом [1927]. Прямая Зоргенф-
рея фактически появилась в работе Александрова и Урысона
[1929], но только после появления работы Зоргенфрея [1947]
она стала «универсальным контрпримером» в общей топологии
(см. примеры 2.3.12, 3.8.15 и 5.1.31). Плоскость Немыцкого была
определена (со ссылкой на Немыцкого) Александровым и Хоп-
фом [1935]. Она представляет собой другой «универсальный
контрпример» (см. примеры 1.5.9 и упр. 5.2.С(Ь) и 5.3.В(а)).
Модификации прямой Зоргенфрея и плоскости Немыцкого до
сих пор поставляют важные и интересные примеры (см.
упр. 3.1. I и 5.4. В).
УПРАЖНЕНИЯ
1.2.А. Сформулируйте и докажите предложение, аналогичное
предложениям этого параграфа, о топологии, порожденной пред-
базой.
1.2.В. Пусть X — произвольное множество и ЗВи $2 — две со-
совокупности семейств его подмножеств, удовлетворяющие усло-
условиям (В1) — (В2). Покажите, что топологии, порожденные ба-
базами М\ и ^2, совпадают в том и только том случае, если для
любого х^Х и любого [/e^i, содержащего ху существует та-
такое 1/е^2, что хеУс[/, а для любого Fei2, содержащего
х, существует такое U е 31 и что х е U cz V.
Сформулируйте и докажите аналогичное утверждение для
топологий, порожденных системами окрестностей.
1.2.С. Проверьте, что для топологического пространства
(Х,0) и его базы (системы окрестностей, семейства всех замк-
замкнутых множеств, оператора замыкания, оператора взятия внут-
внутренности) топология, порожденная в X этой базой (системой
окрестностей, и т. д.), совпадает с исходной топологией про-
пространства X.
1.3. ГРАНИЦА МНОЖЕСТВА, ПРОИЗВОДНОЕ МНОЖЕСТВО 51
1.3. ГРАНИЦА МНОЖЕСТВА,
ПРОИЗВОДНОЕ МНОЖЕСТВО.
ПЛОТНЫЕ И НИГДЕ НЕ ПЛОТНЫЕ МНОЖЕСТВА.
БОРЕЛЕВСКИЕ МНОЖЕСТВА
В § 1.1 были определены два оператора на семействе всех
подмножеств топологического пространства: оператор замыка-
замыкания и оператор взятия внутренности. Были также определены и
изучены два семейства подмножеств топологического простран-
пространства: открытые множества и замкнутые множества. Этот пара-
параграф является продолжением § 1.1. Мы определим и изучим
еще два оператора и ряд новых семейств подмножеств в топо-
топологических пространствах.
Для любого подмножества Л топологического пространства
X определим границу множества Л как множество
Из предложения 1.1.1 следует
1.3.1. Предложение. Точка х принадлежит границе Ft А в том
и только том случае, если для каждого элемента некоторой
{или, что эквивалентно, любой) базы 9S{x) в точке х мы имеем
иА0иА 1
Наиболее важные свойства граничного оператора перечис-
перечислены в следующей теореме.
1.3.2. Теорема. Граничный оператор обладает следующими свой-
свойствами:
(i) 1пЫ = Л\РгЛ; (v) Fr(X\4) = Fr4;
(ii) A = A U Fr A; (vi) X=lnt A [} Fr A U Int (X \ А);
(iii) Fr(i4U?)c=Fri4UFr?; (vii) FrlcFiM;
(iv) Fr (А П В) с Fr A U Fr B\ (viii) Fr Int A cz Fr A;
(ix) А открыто тогда и только тогда, когда Fr Л =Л\Л;
(х) А замкнуто тогда и только тогда, когда Fr Л = Л\1п1;Л;
(xi) Л открыто-замкнуто тогда и только тогда, когда
FrA=0.
Доказательство. Свойства (i) — (xi) проверяются простыми
вычислениями. В качестве образца докажем соотношения (i)
и (iii):
Л \ Fr А = А \ [А П Х\А] = (А \ A) U (Л \
4*
52 ГЛ. I. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
c(AUB)f]X\A(]X\Bcz(Af]X\A)\j(B(]X\B) =
= FrA{)FrB. |
Точка х топологического пространства X называется точкой
накопления (предельной точкой) множества АаХ, если х^
gA{jc}. Множество точек накопления множества А называет-
называется производным множеством множества А и обозначается Ad.
1.3.3. Предложение. Точка х принадлежит Ad в том и только
том случае, если каждый элемент U некоторой (или, что экви-
эквивалентно, любой) базы М(х) в точке х содержит хотя бы одну
точку множества Л, отличную от х.
Доказательство. Допустим, что х — точка накопления множе-
множества Л. По определению, хеД{х}. Следовательно, для каж-
каждого U^$t(x) пересечение ?/ПЙ\М) непусто, т. е. U содер-
содержит точку множества Л, отличную от х.
Если каждый элемент U некоторой базы $(х) в точке х со-
содержит некоторую точку множества Л, отличную от х7 т. е.
U[)(А\{х})ф0 для каждого Ue&(x)9 то хеД{^} в силу
1.1.1, а это и означает, что хеДа. I
Точки множества Л\Ла называются изолированными точ-
точками множества Л. Точка х является изолированной точкой про-
пространства X в том и только том случае, если одноточечное
множество {х} открыто. В самом деле, множество {х} открыто
тогда и только тогда, когда {*} = Jf\X\{*}, т. е. когда
х<?Х\{х}.
Доказательство следующей теоремы предоставляется чита-
читателю.
1.3.4. Теорема. Производное множество обладает следующими
свойствами:
(i) A=A[)Ad;
(ii) если Л<=Я, то AdczBd\
(Hi) (AUB)d=Ad{]Bd;
(iv) IU.WU AsY.w
Введем теперь несколько новых семейств множеств в тополо-
топологических пространствах.
Множество Л cz X называется всюду плотным в А", если
Л = Х.
Множество Л сг X называется коплотным в X, если Х\А
всюду плотно.
1.3. ГРАНИЦА МНОЖЕСТВА, ПРОИЗВОДНОЕ МНОЖЕСТВО 63
Множество АаХ называется нигде не плотным в X, если А
коплотно.
Множество АаХ называется плотным в себе, если A cz Ad.
1.3.5. Предложение. Множество А всюду плотно в X тогда и
только тогда, когда любое непустое открытое подмножество в X
содержит точки множества Л.
Множество А коплотно в X тогда и только тогда, когда лю-
любое непустое открытое множество в X содержит точки дополне-
дополнения множества А.
Множество А нигде не плотно в X тогда и только тогда,
когда любое непустое открытое множество в X содержит непу-
непустое открытое подмножество, не пересекающееся с множе-
множеством Л. I
Следующие две теоремы будут часто применяться в дальней-
дальнейшем.
1.3.6. Теорема. Если А всюду плотно в X, то для любого откры-
открытого U czX
О=~Щ]А'.
Доказательство. Для любой точки х е О и любой ее окре-
окрестности W пересечение W{]U открыто и непусто. В силу 1.3.5,
W f\ U{] А Ф 0; тогда из 1.1.1 следует, что xg U(]А. Таким об-
образом, имеет место включение UczUf\A. Обратное включение
очевидно. I
Плотность пространства X определяется как наименьшее кар-
кардинальное число вида |Л|, где А—всюду плотное подмноже-
подмножество пространства X. Это кардинальное число обозначается
d(X). Если d(X)^&Ot то говорят, что пространство X сепара-
бельно.
1.3.7. Теорема. Для каждого топологического пространства X
имеет место неравенство d(X) ^ w(X).
Доказательство. Пусть $ = {?/$} ses— база пространства
X, состоящая из непустых множеств и такая, что |S| = m =
= w (X). Для каждого s ^ S выберем некоторую точку as e Us.
Покажем, что множество A={as\ s e S} всюду плотно в X.
В самом деле, каждое непустое открытое подмножество про-
пространства X содержит некоторое Us ^ $\ следовательно, оно со-
содержит точку as е Л. Так как \А \ ^|S|=m, то d{X)^. w(X). I
1.3.8. Следствие. Каждое пространство, удовлетворяющее второй
аксиоме счетности, сепарабельно. I
1.3.9. Примеры. В дискретном пространстве граница и производ-
производное множество любого множества пусты и единственным всюду
плотным множеством является само пространство. Множество
54 ГЛ. 1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
всех рациональных чисел, так же как и множество иррациональ-
иррациональных чисел, оба всюду плотны и коплотны на вещественной пря-
прямой и на прямой Зоргенфрея. Множество L% всюду плотно на
плоскости Немыцкого L, множество L\ нигде не плотно в L. Про-
Производное множество множества L\ пусто, а множество L% плотно
в себе. Точка хо — единственная точка накопления пространства
X из примера 1.1.8, другие его точки изолированы. Вещественная
прямая R, интервал /, прямая Зоргенфрея К и плоскость Не-
Немыцкого L все сепарабельны. Дискретное пространство сепара-
бельно лишь в случае, когда |Х\ ^ No. 1
Как мы знаем, пересечение счетного множества открытых мно-
множеств не обязательно открыто, так же как и объединение счет-
счетного множества замкнутых множеств не обязательно замкнуто.
Все подмножества топологического пространства X, которые мо-
могут быть получены из открытых, а также из замкнутых подмно-
подмножеств пространства X с помощью взятия счетных объединений,
пересечений и дополнения, особенно регулярны с топологической
точки зрения, и семейство таких подмножеств заслуживает изу-
изучения. Под семейством борелевских множеств в топологическом
пространстве- X мы понимаем наименьшее семейство 9 подмно-
подмножеств пространства Ху удовлетворяющее следующим условиям:
(BS1) семейство 9 содержит все открытые подмножества про-
пространства X;
(BS2) если Aez 9, то Х\А е 9\
оо
(BS3) Если At е 9 для i = 1, 2, ..., то [I ^е?.
Существование наименьшего семейства 9, удовлетворяющего
сформулированным условиям, следует из того простого сообра-
соображения, что семейство всех подмножеств пространства X удов-
удовлетворяет условиям (BS1) — (BS3) и что для любой совокуп-
совокупности семейств, удовлетворяющих (BS1) — (BS3), общая часть
всех семейств в данной совокупности есть семейство, удовлетво-
удовлетворяющее указанным условиям. Следовательно, семейство боре-
борелевских множеств в X можно было бы определить как общую
часть всех семейств 9, удовлетворяющих условиям (BS1) —
(BS3). Заметим, что в определении борелевских множеств усло-
условие (BS1) может быть заменено условием
(BS1') семейство 9 содержит все замкнутые подмножества про-
пространства X,
а условие (BS3) может быть заменено условием
оо
(BS3') если Ai<=P,i= 1,2, ..., го [\At^9.
В самом деле, объединение условий (BST) и (BS2) эквива-
эквивалентно объединению условий (BS1) и (BS2), а объединение
1.3. ГРАНИЦА МНОЖЕСТВА, ПРОИЗВОДНОЕ МНОЖЕСТВО 55
условий (BS2) и (BS37) эквивалентно объединению условий
(BS2) и (BS3).
Возникает вопрос, существуют ли подмножества простран-
пространства X, не являющиеся борелевскими множествами. Очевидно,
что ответ зависит от пространства X. Так, например, все под-
подмножества дискретного пространства суть борелевские множе-
множества. Однако, вообще говоря, в топологических пространствах
существуют множества, не являющиеся борелевскими (см.
упр. 1.3.G).
Теория борелевских множеств является хорошо разработан-
разработанной частью общей топологии, но, чтобы получить интересные
и глубокие результаты о борелевских множествах, следует огра-
ограничить класс рассматриваемых пространств (см. задачи 1.7.5,
4.5.7, 4.5.8 и 7.4.22).
Самые привычные борелевские множества кроме открытых и
замкнутых множеств суть счетные объединения замкнутых мно-
множеств и счетные пересечения открытых множеств. Первые на-
называются FVмножествами, а вторые G^-множествами. Очевидно,
что дополнение ^-множества является б6-множеством, и наобо-
наоборот. Пересечение двух ^-множеств есть опять Fo-множество.
оо оо
В самом деле, если?= 1J ?;hF== jj ^/> гДе ?* и Fj— замкну-
ОО
тые множества, то Е П F = [} (Et (]Ff)t так что Е f| F есть Fa-
i. /-I
множество. Подобным же образом объединение двух G6-mho-
жеств есть бб-множество. Очевидно, что счетное объединение
(пересечение) /^-множеств (G^-множеств) есть ^-множество
(б6-множество). Множество всех рациональных чисел является
Fo-множеством на вещественной прямой R. Тот факт, что оно
не является Ge-множеством, не столь очевиден (см. упр. 3.9.В).
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
Понятия границы множества, производного множества, всюду
плотного и нигде не плотного множества были введены Канто-
Кантором, который установил также основные свойства этих объектов.
Сепарабельные пространства были введены Фреше [1906]. Оп-
Определение борелевских множеств впервые было дано Борелем
для подмножеств вещественной прямой. Теория борелевских
множеств была заложена Лебегом [1905] (для евклидовых про-
пространств) и Хаусдорфом [1914] (для метрических пространств).
УПРАЖНЕНИЯ
1.З.А. Проверьте, что если множества А и В удовлетворяют
условию ЛЛЯ = 0=ЛПВ, то F(^(j5) F^UFB
56 ГЛ. 1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
1.3.В. Пусть{Л5}5€Е5 — локально конечное семейство подмно-
подмножеств топологического пространства X.
(a) Покажите, что Fr ( [} АЛ с: (J FvAs.
(b) Проверьте, что если все элементы семейства {>ls}ssS
нигде не плотны, то и объединение (J As нигде не плотно в X.
1.З.С. Для каждого положительного целого п множество ,
п-е производное множество подмножества А топологического
пространства X, определяется по индукции формулами
(a) Приведите пример множества вещественных чисел, имею-
имеющего три различных последовательных производных множества.
(b) Приведите пример множества вещественных чисел, кото-
которое имеет бесконечно много отличных друг от друга производ-
производных множеств.
I.3.D. (а) Обобщите 1.3.6, доказав, что для каждого откры-
открытого множества U топологического пространства X и любого
AczX
U{\A=U{\A.
Указание. Примените второе включение из упр. 1.1.А и ра-
равенство и = х\х\ и.
(Ь) Докажите, что для каждого замкнутого множества F то-
топологического пространства X и любого AczX имеет место ра-
равенство
Int(F \JlntA)=lnt(F[}A).
1.3.Е. Проверьте, что объединение коплотного множества и
нигде не плотного множества является коплотным множеством.
Заметим, что объединение двух коплотных множеств не обяза-
обязательно коплотно.
I.3.F. Покажите, что любое открытое подмножество плотного
в себе пространства плотно в себе.
1.3.G. Заметим, что открытые подмножества вещественной
прямой суть /^-множества. Покажите, что семейство всех боре-
левских множеств вещественной прямой может быть представ-
представлено как объединение U !Га, где #"о — семейство всех замк-
<
нутых множеств, ^"а состоит из всех счетных объединений мно-
множеств вида [J #"g, когда а — нечетный ординал, и из всех
1<
1<<1 I I ,7-
счетных пересечении множеств вида (J tF\, когда а — четный
1.4. НЕПРЕРЫВНЫЕ ОТОБРАЖЕНИЯ 57
ординал. Заметим, что все семейства &~а имеют мощность с; вы-
выведите отсюда, что на вещественной прямой существуют множе-
множества, не являющиеся борелевскими.
1.4. НЕПРЕРЫВНЫЕ ОТОБРАЖЕНИЯ-
ЗАМКНУТЫЕ И ОТКРЫТЫЕ ОТОБРАЖЕНИЯ.
ГОМЕОМОРФИЗМЫ
Пусть (X,О) и (У,С) — два топологических пространства;
отображение f из X в У называется непрерывным, если f~l(U)&
е<7 для любого U е О'у т. е. если прообраз любого открытого
подмножества пространства У является открытым подмноже-
подмножеством пространства X. Тот факт, что / — непрерывное отобра-
отображение пространства X в У, будет часто записываться в виде
f:X-+Y.
Наше определение непрерывного отображения опирается на
понятие открытого множества. В дальнейшем мы будем часто
пользоваться методами введения топологий, описанными в § 1.2,
поэтому удобно иметь критерии непрерывности отображений,^
сформулированные в соответствующих понятиях и терминах.
Критерии такого рода перечислены в следующем предложении.
1.4.1. Предложение. Пусть X и У — топологические пространства
и f — отображение X в У. Следующие условия эквивалентны:
(i) Отображение f непрерывно.
(и) Прообраз любого элемента предбазы 0* в У открыт в X.
(И') Прообраз любого элемента базы $ в У открыт в X.
(Hi) Существуют системы окрестностей {$(x)}XGx в X и
{8)(у)}у^у в У, такие, что для каждого xei и каждого
V &?D(f(x)) найдется U е ?8(х)t удовлетворяющее
включению f(U)c V.
(iv) Прообраз любого замкнутого подмножества простран-
пространства У замкнут в X.
(v) Для любого А с X имеем f(A)cz f(A).
(v7) Для любого BczY имеем f-l(B)a: /-1 (В).
(vi) Для любого BczY имеем /-1 (Int В) cz Int f-1 (В).
Доказательство. Импликация (i)=>(ii) очевидна.
Докажем, что (ii)=^(ii/). Пусть 9* — предбаза пространства
У, такая, что f~l{V) открыто в X для любого Уе^. Выберем
базу $ пространства У, состоящую из всех конечных пересече-
пересечений Vi П УгП ••• П Vk элементов предбазы 9>. Так как
то прообразы всех элементов семейства 08 открыты в X.
58 ГЛ. 1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
Теперь покажем, что (ii')*4-(iii). Для любого V (f())
существует такое W^&t что /(х)е W czV. Так как f~l(W) от-
открыто в X и х& f~l(W)> то существует ?/е $(х), удовлетворяю-
удовлетворяющее условию Uczf~l(W). Тогда f (U)cz ff~l (W)cz: W cz V.
Докажем импликацию (iii)=^(iv). Пусть В = В— замкнутое
подмножество в У. Так как f-l(B) = X\f~l(Y\B)f то достаточ-
достаточно показать, что прообраз множества Y\B открыт в X. Для
этого покажем, что каждая точка x^f~l(Y\B) имеет окре-
окрестность U, содержащуюся в f-l(Y\B). Для любого хе
^f~l(Y\B) имеем f(x)^ Y\B. Следовательно, существует та-
такое V&2>(f(x))9 что VczY\B. В силу (Hi), найдется U&
e$t(x), удовлетворяющее включению f(U)czV. Очевидно, что
Для доказательства (iv)=^(v) заметим, что f~l(f(A)) яв-
является замкнутым множеством, содержащим Л, и, следователь-
следовательно, A a f~l(f(A)), откуда в свою очередь получаем
Для доказательства импликации (v)=^-(v/) применим усло-
условие (v) к равенству А = f~l (В); получим включение
откуда f~l(B) cz /-1 (В).
Для доказательства того, что (v/)=^(vi), применим условие
(v') к множеству Y\B; получим включение f~l(Y\B)cz
cz f~l(Y\B), из которого следует, что
Чтобы завершить доказательство, остается показать, что
(vi)=>(i). Для каждого открытого множества UaY имеем
(/ = Int?/. Из (vi) получаем, что f-l(U)cz Int fl(U). Таким
образом, f~1(Z7)=Int/-1(Z7), т. е. f~l(U) открыто в X. I
Характеристика непрерывности, данная в (Hi), позволяет
нам определить непрерывность в точке. Будем говорить, что
отображение из X в У непрерывно в точке х^Х, если для вся-
всякой окрестности V с= У точки f(x) существует такая окрестность
U <иХ точки х, что f(U)cz V. Очевидно, что отображение / из X
в У непрерывно в том и только том случае, если оно непрерывно
в каждой точке пространства Л".
Заметим в связи с доказанным выше предложением, что если
/: Х->У, то для любого /^-множества (бб-множества) В cz У
1.4. НЕПРЕРЫВНЫЕ ОТОБРАЖЕНИЯ 59
его прообраз f~l(B) является Fa-множеством (б6-множеством)
в X.
Используя равенство (gf)~1 (U) = /-1 (g~x(U))9 легко прове-
проверить, что если / — непрерывное отображение X в У, а g— непре-
непрерывное отображение У в Z, то композиция gf — непрерывное
отображение X в Z.
1.4.2. Пример. Если X — дискретное пространство, то каждое
его отображение в любое топологическое пространство У непре-
непрерывно. Аналогично, всякое отображение любого топологического
пространства X в любое антидискретное пространство У непре-
непрерывно. I
1.4.3. Пример. Если на множестве X определены две топологии
0\ и 02, то тождественное отображение / = id* — непрерывное
отображение пространства (X, 0{) в пространство (X, 0%) в том
и только том случае, когда топология 0\ тоньше топологии 02- Ш
Пусть X — топологическое пространство, R— вещественная
прямая с естественной топологией и / — замкнутый единичный
интервал с естественной топологией. Из эквивалентности усло-
условий (i) и (iii) в 1.4.1 следует, что отображение / из X в R или /
непрерывно в том и только том случае, если для каждой точки
х е X и любого е > 0 существует такая окрестность U точки
xt что \f(x)—f{x')\< е для любой точки х;е(/. В частности,
отображение / из R в R непрерывно, если для любой точки
x^R и любого 8> 0 существует такое б > 0, что \f(x) —
— /(¦^/)|<в Для любого х'у для которого \х — л/|<6. Непре-
Непрерывное отображение в R или в / будем называть непрерывной
функцией. Эта терминология согласована с терминологией ве-
вещественного анализа.
Легко показать, что для любого f: X^~R функция |/|, где
|/| (x) = \f(x) |, непрерывна. В самом деле, |/| есть композиция
функции / и функции абсолютного значения, которые обе непре-
непрерывны. Подобным же образом легко установить, что для
/, g: X-+R непрерывны функции
= f(x)±g(x), (f
[min(f, g)](x) = min(f(x), g(x))9 [max(/, g)] (x) = max(/(x)9
Если функция /: X-+R не обращается в нуль ни в какой точке
пространства X, то функция 1/f, где A//) (х)= l/f(x), непре-
непрерывна. Подобные же утверждения имеют место для функций
f: Х-*»1 при соответствующих ограничениях.
1.4.4. Пример. Пусть К — прямая Зоргенфрея, определенная
в 1.2.2, и [х, г) — некоторый элемент базы 3§ этого пространства.
60 ГЛ. 1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
Так как множество [х, г) открыто-замкнуто в X, то формула
° при Х<У<Г>
1 в противном случае,
определяет непрерывную функцию /: /C-W. 1
1.4.5. Пример. Пусть L — плоскость Немыцкого, определенная
в 1.2.4, и Ui(x) — произвольный элемент базы Ш(х) в точке
xgL. Для каждой точки у ^ Ut(x)\{x} обозначим через у'
точку, в которой луч, выходящий из х и проходящий через у,
пересекает окружность, ограничивающую ?/,-(*). Легко пока-
показать, что формула
{0 при # = х,
1 при у e=L\ ?/,(*),
\ХУ\1\*У'\ при y^Ut(x)\{x}9
где \ab\ обозначает длину сегмента, соединяющего точки а и 6,
определяет непрерывную функцию f: L->/. I
1.4.6. Пример. Пусть X — пространство, определенное в 1.1.8.
Покажем, что для любого f: X-+R существует счетное множе-
множество Хо d X, не содержащее Xq и такое, что f {x)= f(x0) для каж-
каждой точки х е Х\Х0.
Множество Xt =X\f-l((f(x0)— i/i, f(xo)+l/t)) замкнуто и
не содержит хо. Таким образом, это конечное множество. Легко
оо
устанавливается, что множество Хо= [} Хг обладает всеми тре-
требуемыми свойствами. 1
Пусть X — топологическое пространство и {ft}—последова-
{ft}—последовательность функций из X в R или /. Говорят, что последователь-
последовательность {ft} равномерно сходится к вещественной функции /, если
для любого е > 0 существует такое &, что |/(л:)— ft(x) | < г при
каждом jcgXh любом i ^ k\ мы выразим это в символах так:
f = Hm fi.
1.4.7. Теорема. Если последовательность {ft} непрерывных функ-
функций из X в R или I равномерно сходится к вещественной функ-
функции /, то f — непрерывная функция из X в R. Если все fi —
функции в /, то f: X->L
Доказательство. Покажем, что для любой точки x0 ^ X и лю-
любого е > 0 существует такая окрестность U точки х0, что \f(xo) —
— f (x') I < е ПРИ всех х' е ?/.
Выберем целое число k так, что
(О |f(jc) — fi(x)\<e/3 при всех
1.4. НЕПРЕРЫВНЫЕ ОТОБРАЖЕНИЯ 61
Так как функция fk непрерывна, то существует такая окре-
окрестность U ТОЧКИ JCo, ЧТО
B) IM*o)—M*0l<e/3 при всех xft=U.
Покажем, что окрестность U обладает требуемыми свой-
свойствами. Пусть /g(/.B силу A) и B),
+ I fk(x') -f(x') | < 8/3 +e/3 + 8/3 = 8.
Очевидно, что если ft(X)czI, i = 1, 2, ..., то f: X-+I. 1
Опишем теперь метод введения топологий с помощью непре-
непрерывных отображений.
1.4.8. Предложение. Пусть даны множество X, семейство {Ys}seS
топологических пространств и семейство отображений {fs}s<=s,
где fs — отображение X в Ys. В классе всех топологий на X, от-
относительно которых все функции fs непрерывны, существует гру-
грубейшая топология. Это топология О, порожденная базой, со-
состоящей из всех множеств вида
п п; (V,),
где 5i, s2, ..., Sk^S и Vi — произвольное открытое подмноже-
подмножество пространства Ysr /= 1, 2, ..., k.
Такая топология О называется топологией, порожденной се-
семейством отображений {/s}seS.
Доказательство. Семейство $, состоящее из всех подмно-
подмножеств вида П frtl(Vi)f обладает свойствами (В1) — (В2), и все
fs — непрерывные отображения относительно топологии О, по-
порожденной (в силу предложения 1.2.1) базой ^. С другой сто-
стороны, легко показать, что если все fs непрерывны относительно
некоторой топологии Of на X, то М с: О'. Отсюда следует вклю-
включение О с О\ означающее, что топология О грубее сК 1
1.4.9. Предложение. Отображение f топологического простран-
пространства X в топологическое пространство У, топология которого
порождена семейством отображений {f5}seSj г^е fs — отображе-
отображение Y в Ys, непрерывно в том и только том случае, если компози-
композиция fsf непрерывна для каждого sgS.
Доказательство. Если /: X-+Y, то fsf непрерывна как компо-
композиция двух непрерывных отображений. Пусть fsf: X-+Ys для
каждого s^S\ обозначим через 0> предбазу пространства У, со-
состоящую из всех множеств вида /71 (Vs)> где Vs открыто в У5.
62 ГЛ. 1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
В силу 1.4.1, достаточно показать, что прообразы элементов 9*
при отображении f суть открытые множества в X. Но это сле-
следует из равенства
Если существует непрерывное отображение / пространства X
в пространство У, т. е. отображение /: Х-*- У,такое, что f(X)= У,
то мы говорим, что X может быть отображено на У или что У
есть непрерывный образ пространства X.
1.4.10. Теорема. Пусть У — непрерывный образ пространства X;
тогда d(Y)^d(X).
Доказательство. Пусть А — всюду плотное подмножество в
X, такое, что \А\ — d(X). В силу эквивалентности условий (i) и
(v) в 1.4.1, для отображения /: X-+Y пространства X на про-
пространство У имеем У = f{X) = f(A)a f(A). Таким образом, мно-
множество/(Л) плотно в У. Так как \f(A)\*?\A\ = d(X),?o d(Y)^
d(X) 1
1.4.11. Следствие. Непрерывный образ сепарабельного простран-
пространства сепарабелен. 1
Обратимся теперь к изучению двух важных классов непре-
непрерывных отображений: замкнутых и открытых отображений. Не-
Непрерывное отображение f: X->Y называется замкнутым (от-
(открытым) отображением, если для каждого замкнутого (откры-
(открытого) множества Ас:Х образ f(A) замкнут (открыт) в У. Ото-
Отображения, которые одновременно замкнуты и открыты, назы-
называются открыто-замкнутыми отображениями.
Очевидно, что композиция двух замкнутых (открытых) ото-
отображений является замкнутым (открытым) отображением.
1.4.12. Теорема. Непрерывное отображение f: X-+Y замкнуто
(открыто) тогда и только тогда, когда для каждого В с: У и
каждого открытого (замкнутого) множества А аХ, содержа-
щего f~l(B), существует открытое (замкнутое) множество Ccz У,
содержащее В и такое, что f~l(C)czA.
Доказательство. Мы рассмотрим случай замкнутого /; рас-
рассуждения для случая открытого отображения аналогичны.
Пусть f: X-+-Y замкнуто, Bcz У и А — открытое подмноже-
подмножество X, содержащее f~l(B). Множество С= Y\f(X\A) открыто
в У и содержит В. Кроме того,
Пусть / удовлетворяет указанным выше условиям; выберем зам-
замкнутое множество FczX. Множество А = X\F открыто, и для
1.4. НЕПРЕРЫВНЫЕ ОТОБРАЖЕНИЯ 63
В= Y\f(F) имеем
f-t(B) = X\f-4(F)cX\F =А.
Таким образом, существует открытое подмножество С с У, та-
такое, что Y\f(F)<=:C и f-l(C)czA, т. е. f~l(C)[]F = 0. Послед-
Последнее равенство означает, что Cf[f(F) = 0, т. e. Cc Y\f(F). Сле-
Следовательно, f(F)=Y\C, т. е. множество f(F) замкнуто. I
В случае замкнутых отображений условие в 1.4.12 может
быть заменено следующим более простым условием.
1.4.13. Теорема. Непрерывное отображение /: X-+Y замкнуто
в том и только том случае, если для каждой точки y^Yu каж-
каждого открытого множества U czX, содержащего f~l(у), в Y су-
существует такая окрестность V точки у, что f~l{V)czU.
Доказательство. В силу 1.4.12, достаточно показать, что если
/ удовлетворяет сформулированным выше условиям, то / зам-
замкнуто. Пусть В с= Y — некоторое множество и A czX — открытое
множество, такое, что f~l(B)aA. Для каждого у&В выберем
такую окрестность Vyc:Y точки у, что f-l(Vy)aЛ. Открытое
множество С = (J Vy удовлетворяет включению В czC и
у fi
f-l(C)czA; следовательно, / замкнуто в силу 1.4.12. 1
1.4.14. Теорема. Непрерывное отображение f: X-+Y открыто в
том и только том случае, если существует такая база & про-
пространства X, что f(U) открыто в Y для любого U&$. 1
1.4.15. Примеры. Отображение г: /?->-/, определенное формулой
замкнуто, но не открыто.
Отображение /: L~>R, сопоставляющее точке (х, у) пло-
плоскости Немыцкого ее абсциссу х е /?, открыто, но не замкнуто.
Отображение g: K-+D прямой Зоргенфрея в двухточечное
пространство D = {0, 1}, определенное формулой
0 при х < 0,
1 при #;>0,
открыто-замкнуто. 1
1.4.16. Теорема. Для любого открытого отображения f: X-+Y и
любой точки jcg! имеем y(f(x), Y) ^ y(x, X). Если, кроме того,
f(X)= У, то w(Y)^w(X) и x(Y)^x(X)-
64 ГЛ. 1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
Доказательство, Отображение f переводит базу в точке х
в базу в точке f(x) и базу пространства X в базу пространства
ПХ).Ш
В отличие от приведенного результата, при замкнутых ото-
отображениях вес и характер могут повышаться (см. теорему
3.7.19).
1.4.17. Пример. Пусть X = R — вещественная прямая и У =
= (R\N)\J{yo}t где N — множество положительных целых чисел
и yo^R. Каждой точке х^Х поставим в соответствие точку
х, если x^X\N,
у09 если x<=N.
Рассмотрим на У топологию, порожденную семейством замкну-
замкнутых множеств ?=={ЛсУ: f~l(M замкнуто в X}. Легко пока-
показать, что f: X-^Y замкнуто и окрестности точки у0 в Y имеют
вид (^\yV)U{yo}, где U открыто в X и содержит множество N.
Пусть (?/i\#)U{#o}i (?/з\#)и{|/о}| .-- — произвольная по-
последовательность окрестностей точки г/0- Для каждого i = l,
2, ... выберем такую точку хг е Ui\N, что xi > L Множество
U = X\{xi,X2, ...} открыто в А" и содержит множество N. Та-
Таким образом, 7 = (?/\Af)U{#o} является окрестностью точки уо.
Так как ни один элемент нашей последовательности не содер-
содержится в V, то пространство У не имеет счетной базы в у0- Та-
Таким образом, х(^)>^о и w(Y)>8q, тогда как w(X) =
Отображение /: X-^Y стягивает замкнутое подмножество
NaiX в точку. Подобным же образом можно получить много
других интересных примеров. Это частный случай операции пе-
перехода к факторпространству, которую мы рассмотрим в § 2.4. 1
Непрерывное отображение /: Х->-У называется гомеоморфиз-
гомеоморфизмом, если / взаимно однозначно отображает X на У и обратное
отображение f из У в X непрерывно. Два топологических про-
пространства X и У называются гомеоморфными, если существует
гомеоморфизм пространства X на пространство У.
Для любого пространства X тождественное отображение
id*: Х-^-Х является гомеоморфизмом. Легко показать, что если
/ — гомеоморфизм, то обратное отображение f~l также гомеомор-
гомеоморфизм. Композиция fg двух гомеоморфизмов / и g является го-
гомеоморфизмом. Таким образом, отношение «X и У гомео-
морфны» есть отношение эквивалентности.
1.4.18. Предложение. Пусть f—взаимно однозначное отображе-
отображение топологического пространства X на топологическое про-
пространство У. Следующие условия равносильны:
(i) / — гомеоморфизм.
1.4. НЕПРЕРЫВНЫЕ ОТОБРАЖЕНИЯ 65
(ii) / замкнуто.
(iii) / открыто,
(iv) Множество f(A) замкнуто в У тогда и только тогда,
когда А замкнуто в X,
(iv') Множество f~l(B) замкнуто в X тогда и только тогда,
когда В замкнуто в У.
(v) Множество /(Л) открыто в У тогда и только тогда,
когда А открыто в X.
(v') Множество f~l(B) открыто в X тогда и только тогда,
когда В открыто в У.
Доказательство. Равносильность (i) и (ii), а также (i) и
(iii) следует из того, что (/~1)-1(Л) = /г(Л) для любого AczX.
Равносильность (ii) и (iv), а также (iii) и (v) следует из ра-
равенства А — f~lf(A). Из равносительности (i) и (iv), а также (i)
и (v) вытекает, что как (iv'), так и (v') равносильны тому, что
/-1 — гомеоморфизм, а это равносильно (i). 1
1.4.19. Примеры. Пусть X — множество вещественных чисел, на-
наделенное одной из следующих топологий: (а) дискретной топо-
топологией; (Ь) естественной топологией; (с) топологией, определен-
определенной в 1.1.8, с хо = О; (d) топологией прямой Зоргенфрея; (е)
топологией, определенной в 1.2.6; (f) топологией, определенной
в 1.2.8, с Хо=О; (g) антидискретной топологией. Для каждого
вещественного числа а > 0 отображение fa: X-+X, определенное
формулой fa (х) s= ах, есть гомеоморфизм. При а < 0 отображе-
отображение fa не является непрерывным относительно топологии (d)f,
но является гомеоморфизмом относительно других рассмотрен-
рассмотренных здесь топологий. 1
Пусть Ж — класс непрерывных отображений, а 0* — некото-
некоторое свойство топологических пространств. Будем говорить, что
9* — инвариант класса Ж или что <Р сохраняется в сторону об-
образа при отображениях из Ж, если свойство 0* сохраняется ото-
отображениями из Ж, т. е. если для каждого f &Ж, где /: Jf-> У и
/(J)=y, пространство У обладает свойством Ф, при условии,
что им обладало пространство X. Используя эту терминологию,
можно переформулировать теорему 1.4.10, сказав, что свойство
«плотность ^т» является инвариантом непрерывных отображе-
отображений. Подобным же образом можно переформулировать тео-
теорему 1.4.16, сказав, что свойства «вес ^т» и «характер ^т»
суть инварианты открытых отображений.
Будем говорить, что свойство 9* есть обратный инвариант
класса Ж непрерывных отображений или что свойство & сохра-
сохраняется в сторону прообраза отображениями из Ж, если для
каждого fej[9 где /: X^Y и /(^)= У, пространство X обла-
обладает свойством {ру при условии, что им обладает пространство У.
Отметим, что свойство 9* есть обратный инвариант класса Ж
5 Зак. 697
66 ГЛ. 1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
тогда и только тогда, когда свойство не-^F (т. е. отрицание 9>)
есть инвариант класса Ж. Таким образом, понятие обратного
инварианта сводится к понятию инварианта. Оно введено для
упрощения ряда утверждений. Очевидно, что если Ж\ с: Ж^ то
всякий инвариант (обратный инвариант) класса Ж% является
инвариантом (обратным инвариантом) класса Ж\,
Инварианты гомеоморфизмов являются особенно важными.
Они называются топологическими свойствами. Так как обратное
отображение к гомеоморфизму также является гомеоморфизмом,
то понятия инварианта и обратного инварианта в классе гомео-
гомеоморфизмов совпадают. Таким образом, топологическое простран-
пространство X обладает свойством 9> в том и только том случае, когда
этим свойством обладает любое гомеоморфное X пространство.
Так как гомеоморфизм /: X-+Y устанавливает взаимно одно-
однозначное соответствие между точками и открытыми множествами
обоих пространств, то каждое свойство, определенное в терми-
терминах открытых множеств и в терминах теории множеств, являет-
является топологическим свойством.
Предмет топологии — изучение топологических свойств.
Когда мы рассматриваем отдельное пространство Х7 мы пытаем-
пытаемся определить, какими топологическими свойствами оно обла-
обладает. При построении какой-нибудь общей теории обычно изу-
изучается некоторое конкретное топологическое свойство 9* и его
взаимосвязи с другими топологическими свойствами; мы пы-
пытаемся определить, какие операции над топологическими про-
пространствами не изменяют 9* и каковы классы отображений, от-
относительно которых 9* инвариантно. Таким образом, с тополо-
топологической точки зрения два гомеоморфных пространства можно
рассматривать как один объект.
Мы уже определили несколько топологических свойств; наи-
наиболее важными среди них являются следующие: «вес s^Crn»,
«характер s^ta» и «плотность ^щ».
Любое свойство 9> определяет класс всех пространств, обла-
обладающих этим свойством. Если 9* — топологическое свойство, то
определенный им класс топологически инвариантен, т. е. вместе
с некоторым пространством Ху обладающим свойством 9>, он
содержит все пространства, гомеоморфные X. Топологические
свойства, перечисленные в конце предыдущего абзаца, опре-
определяют (для щ = Ко) соответственно класс пространств со вто-
второй аксиомой счетности, с первой аксиомой счетности и сепара-
бельных. Все эти классы топологически инвариантны. В даль-
дальнейшем мы определим значительное число топологических
свойств, т. е. топологически инвариантных классов топологиче-
топологических пространств. Вводя новый класс пространств, мы обычно
не останавливаемся на его топологической инвариантности. Это
следует, однако, из самого определения, в котором участвуют
1.4. НЕПРЕРЫВНЫЕ ОТОБРАЖЕНИЯ 67
лишь теоретико-множественные понятия и понятия, сводимые
к понятию открытого множества. Классы топологических про-
пространств, не являющиеся топологически инвариантными, не бу-
будут рассматриваться здесь. Подобным же образом мы будем
рассматривать лишь классы топологически инвариантных ото-
отображений, т. е. таких отображений, композиция которых с го-
гомеоморфизмами (с обеих сторон) не выводит из рассматривае-
рассматриваемого класса.
1.4.20. Примеры. Пусть X и У— два множества одной и той же
мощности. Рассмотрим в обоих дискретную топологию. Оче-
Очевидно, что каждое взаимно однозначное отображение X на У яв-
является гомеоморфизмом. С другой стороны, если дискретные про-
пространства X и У имеют различную мощность, они не могут быть
гомеоморфными. Таким образом, дискретное пространство не за-
зависит (с точностью до гомеоморфизма) от природы точек мно-
множества X, а зависит только от мощности пространства X. Ди-
Дискретное пространство мощности ш будем обозначать через
D()
()
То же самое имеет место для бесконечных множеств X и У
с топологией, определенной в 1.1.8. Однако здесь в случае, когда
оба множества имеют одну и ту же мощность, для того чтобы
получить гомеоморфизм, нужно взять такие взаимно однознач-
однозначные отображения X на У, которые переводят хо в у0 — точку на-
накопления пространства У. Пространство, полученное, как в 1.1.8,
из множества мощности m ^ &of будем обозначать через Л(т). I
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
Непрерывные отображения и гомеоморфизмы абстрактных
пространств впервые рассмотрел Фреше [1910]. В более узком
смысле понятие гомеоморфизма было введено ранее Пуанкаре.
Первое систематическое и исчерпывающее изложение этого пред-
предмета дал Хаусдорф [1914]. Топологии, порожденные семей-
семействами отображений, были рассмотрены Бурбаки [1951]. Поня-
Понятие замкнутого отображения введено Гуревичем [1926] и Алек-
Александровым [1927], понятие открытого отображения плоскости
в себя — Г. Вейлем [1913] и Стойловым [1928] (последний пред-
предполагал, что прообразы точек при этих отображениях не содер-
содержат нетривиальных континуумов). Открытые отображения топо-
топологических пространств были определены Ароншайном [1931]
(см. также Серпинский [1930]).
УПРАЖНЕНИЯ
1.4.А. Покажите, что топология прямой Зоргенфрея порож-
порождается семейством отображений в двухточечное дискретное про-
пространство.
68 ГЛ. I. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
1.4.В. Установите, что прямую Зоргенфрея можно отобразить
на Z)(&o), но нельзя отобразить на D(t).
1.4.С. Проверьте, что /: Х-> У есть замкнутое отображение
в том и только том случае, если f(A) = f(A) для каждого А сгХ,
и что / — открытое отображение в том и только том случае, если
f(lntA)<z:Intf(A) для любого АсХ. Приведите пример, по-
показывающий, что в этой характеристике открытых отображений
включение нельзя заменить на равенство.
Покажите, что f: X-+Y является открытым отображением
в том и только том случае, если f~l (В) = f~l (В), или, что экви-
эквивалентно, Intf-1(B)=f-1(IntB) для каждого ВсУ.
I.4.D. Установите следующие утверждения.
(a) Образ канонического замкнутого множества при откры-
открыто-замкнутом отображении есть каноническое замкнутое множе-
множество.
(b) Образ канонического открытого множества при открыто-
замкнутом отображении не является, вообще говоря, канони-
каноническим открытым множеством.
(c) Образ канонического замкнутого множества при замкну-
замкнутом (открытом) отображении не является, вообще говоря, кано-
каноническим замкнутым множеством.
(d) Прообраз канонического замкнутого (открытого) мно-
множества при открытом отображении есть каноническое замкну-
замкнутое (открытое) множество.
(e) Прообраз канонического замкнутого (открытого) множе-
множества при замкнутом отображении не является, вообще говоря,
каноническим замкнутым (открытым) множеством.
1.4.Е. Покажите, что прямая Зоргенфрея и плоскость Не-
мыцкого не гомеоморфны.
Указания. Примените 1.4.4.
1.4.F.(a) Докажите, что если бесконечное пространство У
является непрерывным образом пространства А (ш) при замкну-
замкнутом отображении, то существует такое кардинальное число
п ^ щ, что Y = А (п).
(Ь) Покажите, что отображение f: Л(т)-»-У пространства
А(ш) на некоторое топологическое пространство Y замкнуто
тогда и только тогда, когда для любой пары уи уч различных
точек У существуют открытые множества U\, U^a Y, такие, что
yi ^ Uи #2^ *Л и U\ П О2 = 0у т. е. У — хаусдорфово простран-
пространство (см. следующий параграф).
I.4.G. Установите, что для любого непрерывного отображе-
отображения f: X^-Y прообразы борелевских множеств из У являются
борелевскими множествами в X.
1.5. АКСИОМЫ ОТДЕЛИМОСТИ 69
1.5. АКСИОМЫ ОТДЕЛИМОСТИ
Определение топологического пространства является весьма
общим, поэтому невозможно доказать много интересных теорем
обо всех топологических пространствах сразу. В этой книге изу-
изучаются различные классы топологических пространств, от весь-
весьма общих к более и более специальным. Очевидно, что чем
уже рассматриваемый класс, тем больше теорем имеет место
об этом классе.
Ограничения, которые мы налагаем на топологические про-
пространства, имеют разнообразный характер. Мы уже обсуждали
аксиомы счетности, ограничивающие мощность баз. В этом па-
параграфе мы изучим аксиомы отделимости, касающиеся разделе-
разделения точек и замкнутых множеств в топологических простран-
пространствах.
Топологическое пространство X называется Т ^пространством,
если для каждой пары различных точек х\у Х2^Х существует
открытое множество, содержащее ровно одну из этих точек.
Примерами топологических пространств, не являющихся Го-про-
Го-пространствами, служат антидискретное пространство и простран-
пространство, описанное в 1.2.10. Все другие определенные выше про-
пространства суть Го-пространства.
1.5.1. Теорема. Пусть X есть Т^-пространство; тогда |^!^
^ exp w(X).
Доказательство, Пусть $ — такая база пространства X, что
\ = w(X)y и для любого х^Х пусть 3§(x) = {U^3t: x^U}.
з определения Г0-пространства следует, что ${х)Ф$(у) при
хФу. Так как число всех различных семейств 3§{х) не превос-
превосходит exp|Jf|, то |Х|^ехрш(Х). 1
Топологическое пространство X называется Т{-пространством,
если для каждой пары различных точек xi, Х2^Х существует
открытое множество U а X, такое, что х\ е U и X2^U. Заме-
Заметим, что существует также открытое множество VczX, такое,
что х2 ^ V и х\ ф V; достаточно рассмотреть пару х%, хи В этом
заключено отличие от Го-пространства, в котором для любой
пары несовпадающих точек х\, д:2 может существовать либо
только открытое множество U, такое, что х\ g(/, jc2 ф ?/, либо
только открытое множество V, такое, что д:2 е V, х\ ф. V.
Очевидно, что всякое ^-пространство является Го-простран-
Го-пространством. Пространство, описанное в примере 1.2.8, является Го-
пространством, но не является Ггпространством. Все другие
определенные выше пространства, за исключением описанного
в примере 1.2.10, суть ^-пространства.
Отметим, что X является ^-пространством в том и только
том случае, если каждая точка х^Х является пересечением
всех своих окрестностей. Отсюда, в частности, следует, что каж-
70 ГЛ. I. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
дое одноточечное подмножество ^-пространства с первой аксио-
аксиомой счетности является Gfi-множеством.
Оказывается, что X является ^-пространством тогда и толь-
только тогда, когда для каждого х^Х множество {х} замкнуто.
В самом деле, пусть X есть 7>пространство; тогда для любого
хеХ имеем
{x}=(\{X\U:x&UeO}9
где О — топология в множестве X. Следовательно, множество
{х} замкнуто по (СЗ). С другой стороны, пусть для каждого
х^Х множество {л;} замкнуто; тогда X есть ^-пространство.
Действительно, для каждой пары несовпадающих точек х\,х%^Х
открытое множество U = Х\{х2} содержит хи йо не содержит
х2.
Топологическое пространство X называется Т2-пространством
или хаусдорфовым пространством, если для каждой пары раз-
различных точек jti, Х2 ^ X существуют открытые множества U\, U2>
такие, что х\ е U\9 х2 e U2 и V\ П U2 = 0.
Очевидно, что каждое 72-пространство является Т^-дростран-
ством. Пространство, описанное в примере 1.2.6, является ^-про-
^-пространством, не будучи ^-пространством. Все пространства, опре-
определенные в § 1.1, а также прямая Зоргенфрея и плоскость
Немыцкого являются хаусдорфовыми пространствами.
Заметим, что X есть Г2-пространство в том и только том слу-
случае, если каждая точка х е X есть пересечение замыканий всех
своих окрестностей.
Читатель легко докажет следующее утверждение.
1.5.2. Предложение. Пусть даны множество X и совокупность
№(х)}Хевх семейств его подмножеств, обладающая свойствами
(ВР1) —(ВРЗ). Кроме того, пусть совокупность {$(х)}хеХ обла-
обладает свойством
(ВР4) Для каждой пары несовпадающих точек х, j/g! суще-
существуют открытые множества U&${x) и Уе^(у), та-
такие, что t/Л V = 0.
Тогда пространство X, наделенное топологией, порожденной со-
совокупностью {$ (х)}Х€В х, хаусдорфово.
1.5.3. Теорема. Пусть X — хаусдорфово пространство; тогда
\X\^expexpd(X) и \X\^[d{X)]*w.
Доказательство. Пусть А — всюду плотное подмножество про-
пространства X, такое, что \А\ = d(X)9 и пусть {$ (х)}х&х— неко-
некоторая система окрестностей пространства X.
Для доказательства первого неравенства сопоставим каж-
каждому xel семейство j&(x) = {U[)A: U^3t(x)} подмножеств
множества Л. Из равенства Uf]A = O следует, что пересечение
1.5. АКСИОМЫ ОТДЕЛИМОСТИ 71
замыканий всех элементов семейства зФ(х) равно {#}. Следова-
Следовательно, *$&(х)фз?{у) при хфу. Так как число всех различных
семейств $Ф (х) не превосходит ехр ехр | А \, то | X | <; exp exp d {X).
Предположим теперь, что \&(х)\^%(Х) (где %(Х)*^&о)
для каждого х е X, и обозначим через s&0 семейство всех под-
подмножеств множества Л, мощность которых не больше %(Х).Оче-
%(Х).Очевидно, что \s&o\^\d(X) |эс<*>. Для каждого U^&(x) выберем
точку а(х, U)<= Uf[A и рассмотрим множество А (х) = {а(х, U):
U^&(x)}^s&o. Для доказательства второго неравенства сопо-
сопоставим каждой точке х^Х семейство *s4q(x) = {U()А(х):
U ^M(x)}cz*s&q. Очевидно, что \$?о(х)\^%(Х). Так как хе
^ U(]A(x)cz D для каждого U^&(х), то пересечение замыка-
замыканий всех элементов <s&o(x) равно {#}. Следовательно, $?о(х)Ф
ф^о(у) при хфу. Так как число всех различных семейств
<s4-b{x) не превосходит |«5#о|х(;°> то
\X\^[[d(X)]%{X)]%iX)=[d(X)]x{X).
Когда %(Х) конечно, пространство X дискретное и второе
неравенство теоремы очевидно. 1
В дальнейшем мы будем часто пользоваться следующей тео-
теоремой.
1.5.4. Теорема. Пусть f, g — непрерывные отображения некото-
некоторого пространства X в хаусдорфово пространство У. Тогда мно-
множество
{х<=Х: f(x) = g(x)}
замкнуто в пространстве X.
Доказательство. Мы покажем, что множество А ={х^Х:
}{х)фg(x)} открыто в пространстве X. Для каждого х^А
имеем 1(х)фg(x)\ следовательно, в Y существуют открытые
множества Ui и V%,такие,что f(x)& U\f g(x)^ ?/2и f/j П U2 — 0-
Множество f~x{U\)[\g-l{U2) есть окрестность точки х, содер-
содержащаяся в Л. I
Топологическое пространство X называется Т^пространством
или регулярным пространством1), если X есть ^-пространство
и для любого х^Х и каждого замкнутого множества FaX,
такого, что x^Ft существуют открытые множества U\f ?/2, та-
такие, что
х*=ии FczU2 и Ux[\U2 = 0.
1.5.5. Предложение. Тгпространство X регулярно тогда и только
тогда, когда для каждой точки х е X и любой ее окрестности V
!) Следует предупредить читателей, что некоторые авторы не включают
в определение регулярных, вполне регулярных и нормальных пространств ус-
условие, что X есть f 1 -пространство.
72 ГЛ. 1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
из некоторой фиксированной предбазы 9> существует окрестность
U точки ху такая, что ОсК.
Доказательство. Пусть X — регулярное пространство и !? —
предбаза пространства X. Выберем некоторую точку л;е!иее
окрестность Уе^. По определению регулярного пространства
существуют открытые множества U\, U2i такие, что
Тогда U\ czX\U2cz: V, откуда в свою очередь получаем, что
О\ с: V, так как X\U2 замкнуто.
Пусть теперь выполнено условие теоремы. Выберем х е X и
замкнутое множество F так, что x^F. По определению пред-
предбазы существуют такие Vu ^2» • • -» Vk^tf*, что х s f] F/ c:X \
\ jF. Для каждого t=lf 2, ..., А выберем открестность Ш^
точки дса таким образом, что Wt cz Vt. Открытые множества
k k
Ux = П Wt и U2 = X\ji)Wiiie пересекаются, xe[/iH
ft ft
FczX\ П ^с=Х\П Г, = ?/2. I
i-l 1-1
1.5.6. Теорема, Пусть X — регулярное пространство; тогда
X)d(X)
Доказательство. Пусть {Us}seS — семейство всех непустых
открытых подмножеств пространства X. Так как X регулярно,
то семейство {Int?/s}S€5S является базой. Выберем плотное
множество AczX, такое, что \A\ = d(XI и пусть VS = A(]U$
для любого s e S. Для доказательства теоремы достаточно за-
заметить, что, в силу теоремы 1.3.6,
V8 = Vsf влечет за собой US — US' для s> s'eS,
ибо из этого вытекает, что число всех различных множеств
Int Os не превосходит ехр | А |. 1
Ясно, что всякое регулярное пространство X является хаус-
дорфовым. Именно для справедливости этого утверждения мы
предположили (кроме возможности отделять точки от замкну-
замкнутых множеств), что X является 7>пространством. Антидискрет-
Антидискретное пространство обладает требуемым свойством отделимости,
однако не является ^-пространством. Все описанные выше хаус-
дорфовы пространства регулярны. Приведем теперь пример не-
нерегулярного хаусдорфова пространства.
1.5.7. Пример. Пусть X — множество вещественных чисел и
ZczX — множество обратных для всех целых чисел, отличных
1.5. АКСИОМЫ ОТДЕЛИМОСТИ 73
от нуля. Для каждого хеX положим Ui(x) = (x— 1//, х-\- l/i) и
( {?М*))Г=1>
В (х) = \
1 {Ui(x)\Z}~_l9
если * = 0.
Легко показать, что совокупность {&{х)}х<=х обладает свой-
свойствами (ВР1) — (ВР4). Следовательно, пространство X, наделен-
наделенное топологией, порожденной системой окрестностей №(х)}хеХ>
является хаусдорфовым. Множество Z замкнуто в X и O^Z.
Кроме того, для любых открытых множеств U\, ?/2, таких, что
Oe(/i и ZczUz, имеем 1)\[\иъФ0. Следовательно, X не яв-
является регулярным. |
Еще более узкий класс пространств представляют собой ти-
хоновские пространства. Топологическое пространство X назы-
называется Г3 j_ -пространством, или тихоновским пространством, или
вполне регулярным пространством, если X есть ^-пространство
и для любого хе X и любого замкнутого множества FcX,
такого, что x^F, существует непрерывная функция /: X-+I,
такая, что
/(х) = 0 и f(y)=l для ys=F.
Так как для открытых множеств U\ = /~! ([0, 1/2)) и ?/г =
= /-1(A/2,1]) имеют место соотношения
то каждое тихоновское пространство является регулярным про-
пространством.
В определении Т \ -пространств, кроме теоретико-множе-
3Т
ственных понятий и понятий, сводимых к понятию открытого
множества, употребленных при определении ^-пространств
с f ^ 3, использовано понятие непрерывной вещественной функ-
функции. Следовательно, топологическая инвариантность класса
Г3 j_- пространств нуждается в доказательстве, тогда как для
7\-пространств с i ^ 3 она является прямым следствием способа
их определения. Однако для доказательства достаточно заме-
заметить, что композиция fh гомеоморфизма h и непрерывной функ-
функции / в / есть непрерывная функция.
1.5.8. Предложение. Т^пространство X является тихоновским
пространством в том и только том случае, если для каждой точ-
точки х^Х и любой ее окрестности V из фиксированной предбазы
& существует непрерывная функция {: X-+I, такая, что f(x) = O
и }(у)=1 дляу<=вХ\У.
74 ГЛ. 1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
Доказательство. Необходимость этого условия следует из
того, что XW замкнуто и не содержит х.
Для доказательства достаточности выберем jcel и замкну-
замкнутое множество F такими, что хф.?. По определению предбазы
существуют V\9 ..., Vk^&*t удовлетворяющие условию х е
П
П VtCzX\F. Выберем функции /*: X-+I, /=1,2, ..., А, та-
таким образом, что fi(x) = O и f{(y)= 1 при y^XWi. Легко по-
показать, что для / = max(fi,/2» ..., fk) имеют место равенства
f() 0f()\ F I
f() f(y) py
В примерах 1.4.4 и 1.4.5 мы показали, что прямая Зоргенф-
рея и плоскость Немыцкого являются тихоновскими простран-
пространствами. Очевидно, что все пространства, определенные в § \ЛТ
также являются тихоновскими пространствами.
Примеры регулярных пространств, не являющихся тихонов-
тихоновскими пространствами, сложнее рассмотренных до сих пор при-
примеров. Они не могут быть построены непосредственно; чтобы
получить их, нужно знать некоторые методы построения более
сложных пространств из более простых. Такой пример будет
приведен в следующей главе (см. пример 2.4.21 и замечания к
§ 2.4). Отметим, что существуют даже такие регулярные про-
пространства, на которых каждая непрерывная вещественная функ-
функция постоянна. Однако такие пространства весьма сложны (см.
задачу 2.7.17).
Топологическое пространство X называется Т4-пространством
или нормальным пространством, если X является ^-простран-
^-пространством и для каждой пары непересекающихся замкнутых мно-
множеств Ау BczX существуют открытые множества U, V, такие,
что
A) AczU, 5c=V и U(\V = 0.
Очевидно, что каждое ^-пространство есть ^-пространство.
Из приведенной ниже теоремы 1.5.10 следует, что каждое ^-про-
^-пространство также есть Т3х~ пространство, но этот факт отнюдь
не очевиден. Приведем теперь пример тихоновского простран-
пространства, не являющегося нормальным. Оказывается, таким про-
пространством является плоскость Немыцкого.
1.5.9, Пример. Мы должны показать, что плоскость Немыцкого
L не является нормальным пространством. Мы уже отмечали,
что производное множество L\CzL пусто. Из 1.3.4 следует, что
А& = 0 для любого A d L\ и что любое такое А замкнуто в L.
Пусть С состоит из всех точек L^ обе координаты которых ра-
рациональны. Ясно, что С — всюду плотное подмножество в L.
1.6. АКСИОМЫ ОТДЕЛИМОСТИ 75
Допустим, что L — нормальное пространство; тогда для каж-
каждого A cz L\ существуют открытые множества ?/д, Va cz L, такие,
что
AczUa, Lx\Ac:Va и Ua[\Va = 0.
Каждому Л с: Li поставим в соответствие множество СА =
= С П Uа- Мы покажем, что Сд Ф Св при А Ф В, и придем к про-
противоречию, так как L\ содержит 2е различных подмножеств, в
то время как С содержит только с различных подмножеств.
Пусть A, J3c=Li, АфВ\ без уменьшения общности можно счи-
считать, что А\В Ф 0. Так_как 0 Ф А\В cz ПА П У в и Пв П VB=0,
то, в силу 1Л.2, ЦаФИв- Из последнего соотношения и 1.3.6
следует, что С а Ф Св и потому С а Ф Св- I
Сделанное выше замечание о том, почему в определении ре-
регулярности пространства X требуется, чтобы оно было Ггпро-
странством, относится и к определению тихоновских и нормаль-
нормальных пространств. Иллюстрацией служит антидискретное про-
пространство.
Следующая теорема является одной из фундаментальных.
По историческим причинам она называется леммой Урысона.
1.5.10. Теорема (лемма Урысона). Для каждой пары А, В непе-
непересекающихся замкнутых множеств нормального пространства
X существует непрерывная функция f: X-+I, такая, что
/(х) = 0 при х<=еА и f(x)=l при х<=В.
Доказательство. Для каждого рационального числа ге
е[0,1] определим открытое множество VVcrX, удовлетворяю-
удовлетворяющее условиям
B) VrCzVr', если г<г'\
C) Лс=У0, BczXWx.
Множества W определяются индуктивно. Расположим все
рациональные числа интервала @, 1) в некоторую бесконечную
последовательность гз, Г4, ... , и пусть п = 0, /*2=1. Положим
V0 = U и Vi=X\B,
где U вместе с открытым V удовлетворяют A). Очевидно, что
А с Vo cz X\V = X\V cz Vu следовательно, Voс: Vx.
Условие C), так же как и условие
Bk) Vri cz Vrj, если г, < г, и /, / < *,
выполнено для k = 2.
Допустим, что множества Vт уже определены для i ^
^п(п^2) и выполнено B„). Обозначим через п и rm coot-
76 ГЛ. 1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
ветственно те из чисел гь г2, ..., гп, которые ближе всего к гп+г
слева и справа. Так как п < гт, то из BЛ) вытекает, что
Vr, cz УГтГ Из нормальности пространства X мы делаем вывод о
существовании открытых множеств U, V, таких, что
Отсюда следует, что U а X \ V cr VVm, а это в свою очередь
дает UczX\ V = X \V a VTm* Положив 7Гп+1 = U, мы полу-
получим множества Vfl, Fr2, ..., 7г„+1> удовлетворяющие условию
Bл+1). Полученная таким образом последовательность Fn> Vr2». •
удовлетворяет условиям B) и C).
Функцию / из X в / определим формулой
(inf{r:x^Vr} для x&Vu
f{x> = \ 1 для xz=X\Vi.
В силу C), имеем f(A)cz{0} и f(B)cz{l}. Остается доказать,
что / непрерывна. Для этого в силу 1.4.1 достаточно показать,
что прообразы интервалов [0, а) и (Ь, 1], где а ^ 1 и 6^0,—
открытые множества.
Неравенство f(x)< а имеет место в том и только том слу-
случае, если существует такое r<La, что хеУг; следовательно,
множество /-1 ([0, а)) = U { V7: г < а} открыто. Неравенство
f(x) > й имеет место в том и только том случае, если суще-
существует такое г' > й, что хфУг^ Но, в силу B), это означает,
что существует такое г > bt что х ф Vr- Следовательно, мно-
множество
r>b} = X\[\{Vr: r>b}
также открыто. 1
1.5.11. Следствие. Подмножество А нормального пространства X
является замкнутым Об-множеством в том и только том слу-
случае, если существует непрерывная функция f: X-+I, такая, что
A f40)
f4)
Доказательство, Одноточечное множество {0} cz / является
замкнутым Сб-множеством. Поэтому прообраз f~l@) при любом
непрерывном отображении /: Х~>1 является замкнутым G6-mho-
жеством.
Пусть теперь А — замкнутое бб-множество в нормальном
пространстве X. Дополнение множества А есть /^-множество,
оо
т. е. X \ А = U Fty где Ft = Fu i = 1, 2, ... . По лемме Урысона
i
1.5. АКСИОМЫ ОТДЕЛИМОСТИ 77
для каждого t=l, 2, ... существует непрерывная функция
/(•: X-+I, такая, что
fi(x) = O для х^А и /,•(#)=! для x^Ft.
оо
Из 1.4.7 вытекает, что формула f (jc)= У]т М*) определяет
непрерывную функцию f: X-+L Для х^А с очевидностью
/(jc) = O. Если хфА, то существует такое *, что x^Fi, и по-
потому /(*)>-!- ff (x) = -у > 0. Следовательно, Л = f-1 @). 1
Перейдя к дополнениям, можно переформулировать 1.5.11
следующим образом.
1.5.12. Следствие. Подмножество А нормального пространства X
есть открытое Fa-множество в том и только том случае, когда
существует непрерывная функция f: X-+I, такая, что А =
= /-4@,1]). I
Два подмножества А и В топологического пространства X
называются вполне отделимыми, если существует непрерывная
функция /: X-+I, такая, что f(x) = O при х^А и f(x)=l при
хеВ. В этом случае говорят, что / разделяет множества А и
В. Лемма Урысона утверждает, что в нормальном простран-
пространстве два непересекающихся замкнутых множества вполне отде-
отделимы. Легко показать, что если любые два непересекающихся
замкнутых множества в ^-пространстве вполне отделимы, то
пространство нормально.
Подмножество А топологического пространства X называет-
называется функционально замкнутым1), если Л=/~1@) для некото-
некоторого /: Х-*-1. Очевидно, что всякое функционально замкнутое
подмножество пространства X замкнуто в X. Пусть f, g: X^~I\
определим h\, h%: X-^-I формулами
Тогда
Ar!(O) = r!(O)Uff"l(O) и Аа-^О)- Г1 (О)П«Г!(О).
Отсюда следует, что объединение и пересечение двух (и конеч-
конечного числа) функционально замкнутых множеств — функцио-
функционально замкнутые множества. Счетное пересечение функцио-
функционально замкнутых множеств вновь является функционально
!) Принятые здесь термины «функционально замкнутое множество> и
«функционально открытое множество» кажутся нам более подходящими, чем
обычно употребляемые термины «нуль-множество» и «конуль-множество».
78 ГЛ. 1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
оо
замкнутым множеством. В самом деле, f] ffl @) = /~1@) для
оо
функции /: X-+I, определенной формулой / {х) = V —г ft (x).
t=i 2
Дополнение к функционально замкнутому подмножеству в
пространстве X называется функционально открытым. Очевидно,
что всякое функционально открытое подмножество пространства
X открыто в X. Счетное объединение и конечное пересечение
функционально открытых множеств — функционально открытые
множества. Легко показать, что ^-пространство X вполне регу-
регулярно в том и только том случае, если семейство всех функцио-
функционально открытых множеств образует базу в пространстве X. От-
Открыто-замкнутые множества одновременно функционально от-
открыты и функционально замкнуты. Прообраз при непрерывном
отображении функционально замкнутого (открытого) множества
есть функционально замкнутое (открытое) множество. Следствия
1.5.11 и 1.5.12 утверждают, что в нормальных пространствах
функционально замкнутые (открытые) множества совпадают с
замкнутыми О6-множествами (открытыми /^-множествами).
1.5.13. Теорема. Любые два непересекающихся функционально
замкнутых множества А и В в произвольном топологическом
пространстве X вполне отделимы. Более того, существует непре-
непрерывное отображение /: X-v/, такое, что Л = /-*@), Б = /-1A).
Доказательство. Пусть g, h: X^I удовлетворяют соотноше-
соотношениям
A=g-i@) и fl = /H@).
Так как Л П 5 = 0, то формула f(x) = g (х) / (g {х) + h (x)) опре-
определяет непрерывное отображение f: X-+L Легко показать, что
Л=/-1@) BB = f-l{l). 1
Очевидно, что все дискретные пространства D(m) нормальны.
Легко установить, что все пространства А(ш) также нормальны.
Приведенная ниже теорема 1.5.15 показывает, что прямая ли-
линия R и интервал / также нормальны. В примере 1.5.17 будет
показано, что прямая Зоргенфрея нормальна.
1.5.14. Лемма. Пусть X есть Ту-пространство, и пусть для лю-
любого замкнутого множества FczX и любого открытого WczX,
содержащего Ft существует последовательность Wu W%y ... от-
оо
крытых подмножеств пространства X, такая, что F с (J Wt и
Wicz W для i=l, 2, ... . Тогда пространство X нормально.
Доказательство. Пусть А и В — непересекающиеся замкну-
замкнутые подмножества пространства X. Полагая F = A и W X\B
1.5. АКСИОМЫ ОТДЕЛИМОСТИ 79
мы получим последовательность W\, W2, ... открытых подмно-
подмножеств пространства X, такую, что
оо
D) ЛсД^ и BftWt=0, /=1,2,....
Полагая F = B и № = Х\Л, мы получим последовательность
Vi, V2, ... открытых подмножеств пространства X, такую, что
оо
E) Bcz[}Vi и AflVt=0, /=1,2,
Положим
Множества G, и Я, открыты; более того, из D) и E) следует,
что
оо оо
AczU=\JGi и B<zV=\]Ht.
Для завершения доказательства остается показать, что от-
открытые множества U и V не пересекаются. Так как из F) сле-
следует, что Gi П Vf = 0 для / ^ /, то Gi Л Я/ = 0 для / ^ и По-
Подобным же образом Я/ Л ТИ^г = 0 для i ^ / и Gi Л Я/ = 0 для
i^/. Следовательно, Gi(]Hj = 0 для г, /= 1,2, ...» и потому
Легко убедиться, что условия предыдущей леммы не только
достаточны, но и необходимы для нормальности ^-простран-
^-пространства X.
1.5.15. Теорема. Любое регулярное пространство, удовлетворяю-
удовлетворяющее второй аксиоме счетности, нормально.
Доказательство. Каждое регулярное пространство X со счет-
счетной базой 3$ удовлетворяет условиям леммы 1.5.14, так как для
любого х е F существует такое Ux е ^, что х е Ux cz Ox cz W,
семейство всех Ux счетно и f с [I Ux. 1
1.5.16. Теорема. Каждое счетное регулярное пространство нор-
нормально.
Доказательство. Каждое счетное регулярное пространство
удовлетворяет условиям леммы 1.5.14, так как для всякой точ-
точки х е F существует открытое множество Ux, такое, что х е
<= Ux с: Ох cr W. Семейство всех Ux счетно hFc U Ux. |
В связи с теоремой 1.5.16 отметим, что существуют счетные
регулярные пространства, не удовлетворяющие первой и тем бо-
80 ГЛ. 1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
лее второй аксиоме счетности (см. примеры 1.6.19, 1.6.20 и
2.3.37).
1.5.17. Пример. Покажем, что прямая Зоргенфрея К является
нормальным пространством (см. пример 3.8.14). Пусть А, В —
непересекающиеся замкнутые подмножества прямой /О
Для каждого а&А возьмем интервал [atx{a))t не пересе-
"кающийся с В, а для каждого Ь&В— интервал [btx(b))f не
пересекающийся с А. Полагая U= (J [а, х (а)) и V— (J [Ь,
х(Ь)), мы получим открытые множества, такие, что Лс[/ и
В а V. Для каждого аеА и fteB имеем [a, x(a))f[[b, x(b)) =
— 0, так как иначе выполнялись бы включения Ь^[а,х{а))
или a^[b,x(b)) (в зависимости от того, какое из неравенств
имеет место: а < b или b < а). Следовательно, U(] V — 0. I
Отметим, что, применяя законы де Моргана, легко показать,
что ^-пространство X нормально в том и только том случае,
если для любой пары открытых множеств U, VczX, таких, что
Х= U[) V, существует пара замкнутых множеств Л, 5с= J, та-
таких, что AczUtBczViiX = A\JB. Для усиления этого резуль-
результата введем несколько простых понятий.
Семейство {Л5}зе_5 подмножеств множества X называется
покрытием множества X, если (J AS = X. Если X — топологи-
S
ческое пространство и все множества As открыты (замкнуты),
то мы называем покрытие {As}s^s открытым {замкнутым). Се-
Семейство {A^g-з подмножеств множества X называется точечно
конечным {точечно счетным), если для каждого xgX множе-
множество {s e S: x^As} конечно (счетно). Очевидно, что всякое
локально конечное покрытие является точечно конечным. С дру-
другой стороны, открытое покрытие интервала /, состоящее из са-
самого / и всех интервалов A/(*'+ 1), 1/0» г = 1, 2, ..., точечно
конечно, но не является локально конечным.
1.5.18. Теорема. Пусть X — нормальное пространство, и пусть
{Us}$gS—его точечно конечное открытое покрытие. Тогда су-
существует открытое покрытие {VS}SGES пространства X, такое, что
Vs с: Us для каждого seS.
Доказательство. Пусть & — семейство всех функций G:S^~C?',
(где О — топология пространства X), удовлетворяющих следую-
следующим условиям;
G) G{s)=Us или CTF)c:[/5,
(8) U
1.5. АКСИОМЫ ОТДЕЛИМОСТИ 81
Упорядочим семейство ^, положив по определению G\ ^ G2,
если G2(s)=Gi(s) для каждого seS, такого, что G\(s)=^ Us.
Мы покажем, что для всякого линейно упорядоченного подсе-
подсемейства &qCZ$ формула G0(s) = П G(s)> s^St определяет
элемент семейства $?. Условие G) выполняется очевидным обра-
образом. Проверим условие (8). Пусть х^Х; так как {Us}sgS то-
точечно конечно, существует конечное множество So={sb $2, •*•
..., sa.}c:S, такое, что x^USi, /=1, 2, ..., k и xqkUs для
s е S\50. Если Go(st) = Us. для некоторого s* e So, то
x^Gq(s()cz U GoE). Следовательно, можно считать, что для
t=l, 2, ..., /г найдется такое G*e^0, что G*(s*) Ф Usr Так
как семейство ^0 линейно упорядочено, существует такое / ^ й,
что Gi^Gj, t = l, 2, ..., й. Применяя (8) к G/, мы видим, что
jce Gf(si)= Gq(si) для некоторого s; e So.
По лемме Куратовского — Цорна в $ существует максималь-
максимальный элемент G. Для завершения доказательства достаточно по-
показать, что G(s)cz Us для каждого seS.
Допустим, что G ($0) П (X \ USo) ф 0. Множество А =
= Z \ U{C(s):5gS\ {s0}} с: G (s0) замкнуто. В силу нормаль-
нормальности пространства^ существует открытое множество V, такое,
что Л с: Ус: Fez G(so). Из G) следует, что G(so) = USQ, поэтому
формула
( V при s = s0,
Uo{S)-\G(s) при зФ so,
определяет такую функцию Go^^, что G ^ Go и G =^= Go. Это
противоречит максимальности элемента G и показывает, что
G E) cz Us для любого s eS. I
Топологическое пространство X называется совершенно нор-
нормальным, если J — нормальное пространство и каждое замкну-
замкнутое в нем множество является 6б-множеством. Очевидно, что
нормальное пространство X совершенно нормально тогда и
только тогда, когда каждое его открытое подмножество есть
/V множество.
Класс совершенно нормальных пространств существенно уже
класса нормальных пространств: для ш> Ко пространство А(ш)
не является совершенно нормальным. В самом деле, любое /V
множество в Л(ш), не содержащее единственную точку накоп-
накопления лго пространства А (т.), счетно. Отсюда следует, что от-
открытое множество Л(ш)\{хо} не является /^-множеством. От-
Отметим, что каждое нормальное пространство X со счетной базой
Ш совершенно нормально. Действительно, для любой точки х
открытого множества U czX существует такое Ux ^ 3$, что
б Зак. 697
82 ГЛ. 1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
х е Ux a Ox ci U. Таким образом, t/ = |J Ux, где объединение
x^U
счетно, ибо все множества Ux принадлежат &.
Очевидно, что все дискретные пространства и все счетные
нормальные пространства совершенно нормальны. Прямая Зор-
генфрея тоже совершенно нормальна. В самом деле, если для
каждой точки х открытого множества U а К взять объединение
U(x) всех содержащих ее открытых интервалов, лежащих в Uf
то для х,х' <= Сбудет либо U(x)= U(xf), либо U(x)[\ U(xf) = 0.
Поскольку каждое U(x) содержит рациональное число, множе-
множество различных U(x) счетно, а их объединение Uo является
/^-множеством в К. Легко проверить, что множество U\Uq
счетно, а следовательно, U есть /^-множество в /С.
Так как вещественная прямая R совершенно нормальна, то
функционально замкнутые (открытые) подмножества простран-
пространства X могут быть охарактеризованы как прообразы замкнутых
(открытых) подмножеств прямой R при непрерывных отображе-
отображениях X в R.
Отметим далее, что существуют и такие нормальные про-
пространства, в которых все одноточечные подмножества суть
G^-множества (и даже нормальные пространства с первой ак-
аксиомой счетности), но при этом пространства не являются со-
совершенно нормальными (см. пример 3.1.26).
1.5.19. Теорема Веденисова. Пусть X есть Тгпространство;
тогда следующие утверждения равносильны:
(i) Пространство X совершенно нормально.
(и) Открытые подмножества пространства X функциональ-
функционально открыты.
(iii) Замкнутые подмножества пространства X функциональ-
функционально замкнуты.
(iv) Для каждой пары непересекающихся замкнутых мно-
множеств А, ВсХ существует непрерывная функция
/: Х->/, такая, что /-!@) = Л и f~l(l) = B.
Доказательство. Импликация (i)=^(ii) вытекает из 1.5.12,
импликация (iii)=^(iv) — из 1.5.13. Импликации (ii)=^(iii) и
)^(i) очевидны. 1
Перейдем теперь к обсуждению инвариантности аксиом отде-
отделимости при различных отображениях. Начнем с простого на-
наблюдения: так как каждое пространство является непрерывным
образом некоторого дискретного пространства, то никакая из
аксиом отделимости не инвариантна при непрерывных отображе-
отображениях. Для замкнутых отображений ситуация улучшается.
1.5. АКСИОМЫ ОТДЕЛИМОСТИ 83
1.5.20. Теорема. Классы Тх- и Т'^-пространств и класс совершенно
нормальных пространств инвариантны относительно замкнутых
отображений.
Доказательство. Инвариантность ^-пространств следует из
того, что ^-пространства характеризуются как пространства, в
которых одноточечные подмножества замкнуты.
Пусть теперь /: X-^Y— замкнутое отображение нормаль-
нормального пространства X на некоторое пространство У. Как известно,
У есть ^-пространство. Для каждой пары открытых множеств
U, V czY, таких, что Y[JV=Y, множества f~l(U) и f~l(V) от-
открыты в X и покрывают пространство X. В силу нормальности
Ху существуют замкнутые множества Ло, BqczX, такие, что
Лос:/-'(?/), Boczf-l(V) и А0[}В0 = Х. Множества A = f(A0)
и В = /(В0) замкнуты в У. Более того,
Л с/f-1 (?/)=?/, Bczff~l(V)= V и A[)B = f(X)=Y.
Следовательно, У — нормальное пространство.
Если /: X-*Y — замкнутое отображение совершенно нор-
нормального пространства X на пространство У, то У нормально и
оо
для любого открытого множества U а Умы имеем /~l(C/)= (J Fif
где Fi замкнуты в X. Следовательно,
является ^-множеством в У, т. е. У совершенно нормально. I
Оказывается, аксиомы Гь Г4 и свойство совершенной нор-
нормальности— единственные аксиомы отделимости, инвариантные
при замкнутых отображениях. Чтобы получить замкнутое ото-
отображение Т3±- пространства на пространство, не удовлетворяю-
удовлетворяющее аксиоме Гг, мы должны взять любое не нормальное тихо-
тихоновское пространство Ху выделить в нем пару непересекающих
замкнутых множеств Л, ВаХ, которые не разделяются непе-
непересекающимися открытыми множествами, и отождествить мно-
множество А с некоторой точкой «а», а множество В с некоторой
точкой «&», как описано в примере 1.4.17 (ср. с примером 2.4.12).
Замкнутое отображение Г0-пространства на двухточечное анти-
антидискретное пространство построено ниже.
1.5.21. Пример. Пусть X — множество всех целых чисел с топо-
топологией, состоящей из множеств {х^Х: х^п} для ai = 0, ±1,
±2, .... Очевидно, что X есть Г0-пространство. Пусть У =
= {0,1} с антидискретной топологией, и пусть /(х) = 0, если х
четно, и f(x)= 1, если х нечетно. Легко видеть, что / — открыто-
замкнутое отображение X на У. 1
б*
84 ГЛ. 1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
Последний пример показывает, что класс Г0-пространств не
инвариантен при открытых отображениях. Оказывается, что ни-
никакая из аксиом отделимости не инвариантна при открытых
отображениях.
1.5.22. Пример. Отобразим вещественную прямую R = X на
двухточечное антидискретное пространство У = {0,1}» поставив
в соответствие 0 всем рациональным числам и 1 всем иррацио-
иррациональным числам. Легко показать, что это открытое отображение
(ср. с замечанием к упр. 4.2.D(b)). 1
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
^-пространства введены Колмогоровым (как указано у Алек-
Александрова и Хопфа [1935]), Ti-пространства — Риссом [1907], а
Т^-пространства — Хаусдорфом [1914]. Регулярные простран-
пространства определены Вьеторисом [1921]; свойство Гзу2 сформули-
сформулировано Урысоном [1925], а класс Г3у2 -пространств изучен Ти-
хоновым [1930]. Класс нормальных пространств определен Тит-
це [1923] и Александровым и Урысоном [1924]; свойство нор-
нормальности появилось ранее у Вьеториса [1921]. Свойство совер-
совершенной нормальности появилось в работе Урысона [1925] и
было изучено Александровым и Урысоном [1929] в классе ком-
компактных пространств; совершенно нормальные пространства оп-
определены Чехом [1932].
Определение Гзу2 -пространств существенно отличается от
определений других классов пространств, изученных в этом па-
параграфе. Это внешнее определение, в котором мы предполагаем
существование некоторых внешних объектов относительно рас-
сматриваемого пространства (здесь мы имеем в виду существо-
существование интервала /), в противоположность внутренним опреде-
определениям, в которых используются только внутренние объекты
относительно рассматриваемых пространств. В дальнейшем не-
несколько классов пространств будут введены посредством внеш-
внешних определений, так как иногда такие определения проще и
естественнее. Однако мы дадим, следуя установившейся в топо-
топологии традиции, и внутреннюю характеристику этих классов
(которые с очевидностью также могут служить определениями).
Так, внутренняя характеристика Гзу2 -пространств дается в
упр. 1.5.G; читатель заметит, насколько такое определение слож-
сложнее и менее естественно, чем внешнее.
Доказательство ненормальности плоскости Немыцкого, дан-
данное в 1.5.9, взято у Джоунса [1937]; доказано больше: никакое
сепарабельное пространство, содержащее множество мощности с
с пустым производным множеством, не является нормальным
1.5. АКСИОМЫ ОТДЕЛИМОСТИ 85
(другое доказательство этого факта дается в 2.1.10). Последнее
замечание широко используется при доказательствах ненормаль-
ненормальности (см. пример 2.3.12, упр. 3.1.Н(а) и задачу 2.7.20(f)).
Лемма Урысона установлена Урысоном [1925]; модификации
его рассуждений иногда используются для построения непрерыв-
непрерывных вещественных функций (см. упр. 1.5.G и задачу 2.7.2(с)).
Работа Урысона содержит также теорему 1.5.16. Теорема 1.5.15
была доказана Тихоновым [1925]; доказательство леммы 1.5.14
есть также одно из стандартных топологических рассуждений
(ср. с доказательством леммы 7.2.5). Теорема 1.5.18 принадле-
принадлежит Лефшецу [1942]. Условия совершенной нормальности в тео-
теореме 1.5.19 даны Веденисовым [1936] и [1940]. Хаусдорф [1935]
первым заметил, что нормальность есть инвариант замкнутых
отображений.
УПРАЖНЕНИЯ
1.5.А. Докажите, что X есть То-пространство в том и только
том случае, если {х}ф{у} для любой пары несовпадающих
точек х, у е X.
1.5.В. Заметим, что конечное ^-пространство дискретно. По-
Покажите, что в ^-пространствах производное множество обла-
обладает следующими свойствами:
(Лd)d сУ, (а*) = Ad = (Д)й; Ad = 0, если А конечно.
Приведите примеры, показывающие, что для Г0-простраиств эти
утверждения не имеют места.
1.5.С. Непрерывное отображение f; X-+X называется ретрак-
ретракцией пространства X, если /f = f; множество всех значений
ретракции пространства X называется ретрактом простран-
пространства X.
Покажите, что всякий ретракт хаусдорфова пространства
замкнут.
1.5.D.(a) Заметим, что в определениях регулярного и вполне
регулярного пространств мы могли бы предположить, что ис-
исходные пространства суть Го-пространства, а не ^-пространства.
Покажите, что в определении нормальных пространств такое из-
изменение невозможно.
(Ь) Покажите, что в 1.5.1 предположение, что X есть Го-про-
Го-пространство, нельзя опустить, а в 1.5.3 предположение, что X —
хаусдорфово пространство, нельзя заменить предположением,
что X есть Г!-пространство.
ГЛ. 1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
(с) Докажите, что в 1.5.6 предположение о регулярности X
нельзя заменить предположением, что X — хаусдорфово про-
пространство.
Указание. Пусть U(ztr) — множество всех точек плоскости
внутри круга радиуса г с центром в точке z. Введите топологию
на плоскости, взяв в качестве базы семейство, состоящее из всех
множеств вида ?/(г, г)\Л, где А — множество, пересекающее
каждую прямую, параллельную оси х, в конечном числе точек.
Можно также воспользоваться тем фактом, что существуют
сепарабельные хаусдорфовы пространства мощности 2е (ср.
с теоремой 2.3Л5 или следствием 3.6.11), и применить указание
к упр. 3.1.F(d).
1.5.Е.(а) Покажите, что топология ^-пространства X порож-
порождается семейством отображений в вещественную прямую тогда и
только тогда, когда X — вполне регулярное пространство.
(Ь) Докажите, что если на множестве X определены две то-
топологии Си С?2 и оба пространства (X, 0Х) и (X, О2) суть 7V/, -
пространства, то <?i=??2 в том и только том случае, когда се-
семейство всех вещественных функций на X, непрерывных отно-
относительно Ои совпадает с семейством всех вещественных функ-
функций на X, непрерывных в топологии 0%.
I.5.F. Покажите, что для любого конечного семейства {?$ых
попарно непересекающихся замкнутых множеств нормального
пространства X существует семейство {?/,}i=1 открытых подмно-
подмножеств пространства X, таких, что Fic^Ui для i=l, 2, ..., k и
Ui[\ Uj = 0 при 1ф\ (ср. с теоремой 2.1.14 и упр. 2.1.G). Уста-
Установите, что если все F, конечны, то достаточно предположить,
что X — хаусдорфово пространство.
1.5.G (Фринк О. [1964],Зайцев [1967]). Докажите,что 7\-про-
странство X вполне регулярно тогда и только тогда, когда в нем
существует база Ш, удовлетворяющая следующим условиям:
A) Для любого х е X и любого U ^<$, содержащего х, су-
существует такое 7g^, что хфУ и U\}V = X.
B) Для любой пары f/, V^38, удовлетворяющей условию
V = X, существуют такие ?/', V' еЛ, что Х\Vcz ?/', X\U a
czV и ?/'Л V" = 0.
Указание. Модифицируйте доказательство леммы Урысона.
1.5.Н.(а) Докажите, что любое замкнутое подмножество пло-
плоскости Немыцкого является Об-множеством (пространства, об-
обладающие этим свойством, называются совершенными простран-
пространствами) .
(Ь) (Смирнов [1948]). Покажите, что ^-пространство X
нормально в том и только том случае, если выполнены следую-
следующие условия:
1.5. АКСИОМЫ ОТДЕЛИМОСТИ 87
A) Любое замкнутое Оь-множество в X функционально
замкнуто.
B) Для любого замкнутого FczX и любого открытого
G cz X, содержащего F, в X существует замкнутое Оь-множество
Му такое, что FczMcz G.
(с) Установите, что никакое из условий (Ь) по отдельности
не обеспечивает нормальности пространства X.
1.5.1. Установите, что если (X, О{) есть ^-пространство
с|<2и О2 — топология в X, более тонкая, чем Ои то {Х1<У2)
также является ^-пространством. Покажите, что при / ^ 3 это
неверно.
1.5J.(а) Установите, что счетные объединения функциональ-
функционально замкнутых множеств, вообще говоря, не являются функцио-
функционально замкнутыми.
(b) Покажите, что объединения локально конечных семейств
функционально замкнутых множеств, вообще говоря, не являют-
являются функционально замкнутыми. Заметим, что в совершенно нор-
нормальных пространствах объединение любого локально конеч-
конечного семейства функционально замкнутых множеств является
функционально замкнутым.
(c) Установите, что объединение семейства функционально
открытых множеств, вообще говоря, не является функционально
открытым.
(d) Заметьте, что объединение локально конечного семейства
функционально открытых множеств функционально открыто.
1.5.К- Покажите, что ^-пространство X совершенно нор-
нормально в том и только том случае, если для каждого открытого
множества W сг X существует последовательность Wu W2, ••-
00 •
открытых подмножеств пространства X, такая, что W = [J Wt
и Wicz W для t = l, 2, ... .
1.5.L.(a) (Пономарёв [1959], Фролик [1961]). Докажите, что
если /: X-+Y — открыто-замкнутое отображение пространства
X на У, то для любого g: X^~R, ограниченного на всех прооб-
прообразах точек при /, формулы g*(у) = sup{g(x): x^f~l(y)} к
?*(#)= тНё(х): x^f~l(y)} определяют непрерывные функций
g*, g*: Y-*R (ср. с задачей 1.7.16).
(Ь) (Хабер [1972]). Покажите, что регулярность и полная:
регулярность инвариантны относительно открыто-замкнутых
отображений.
Указание. В случае вполне регулярных пространств приме-
примените (а).
Замечание. Класс хаусдорфовых пространств не инвариан-
инвариантен при открыто-замкнутых отображениях (ср. с примером Аль-
стера, который приводится у Хабера [1972], где на с. 204 в стро-
68 ГЛ. 1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
ке 7 снизу, а также на с. 205 в строках 3 и 5 сверху следует
читать R вместо Q).
1.5.М. Приведите пример открытого отображения нормаль-
нормального пространства на ^-пространство, не являющееся 7Vnpo-
странством.
1.6. СХОДИМОСТЬ
В ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ:
НАПРАВЛЕННОСТИ И ФИЛЬТРЫ.
СЕКВЕНЦИАЛЬНЫЕ ПРОСТРАНСТВА
И ПРОСТРАНСТВА ФРЕШЕ
Под направленностью в топологическом пространстве X мы
понимаем произвольную функцию, заданную на непустом на-
направленном множестве, со значениями в пространстве X. На-
Направленности обозначаются символом 5 = {ха, о е 2}, где ха—
точка в X, соответствующая элементу аеЕ. Отношение, на-
направляющее 2, обозначается через ^, и для <ть а2бЕ мы часто
пишем 01 ^ а2 вместо в2^О\.
Точка х называется пределом направленности S ={xff, ие2},
если для каждой окрестности U точки л; существует такое аое2,
что ха ^ U для любого о ^ во. В этом случае говорят, что на-
направленность S сходится к х. Направленность может сходиться,
вообще говоря, ко многим точкам. Множество всех пределов на-
направленности 5 ={ха, аеИ} обозначается Hm S или Игл х0. Когда
направленность S ={ха, сге2} имеет ровно один предел х, пи-
пишут х = lim 5 = lim xa.
Точка х называется предельной точкой направленности S =
= {x0, cr^S}, если для каждой окрестности U точки х и каж-
каждого сто е 2 существует такое о ^ а0, что ха е (/.
Говорят, что направленность S' = {хо>, о' е 2'} тоньше, чем
направленность S =={ха, сг е S}, если существует отображение
<р: 5/—>-Sf обладающее следующими свойствами:
(FN 1) Для любого ao?S найдется такое о' е 2', ^то ф(а') ^ сг
«ри (/ ^ а0.
(FN 2) хф (а') = Хо' ^ля а' <= 2".
Легко показать, что каждая неубывающая функция ф из 2'
ь 2, такая, что фB') конфинальна в 2, обладает свойством
<FN1)
1.6.1. Предложение. Если х — предельная точка направленности
«S', более тонкой, чем 5, то х — предельная точка направлен-
направленности S. Если х — предел направленности 5, то х — также пре-
предел любой направленности S', более тонкой, чем S. Если х —
1.6. СХОДИМОСТЬ В ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ 89
предельная точка направленности S, то х — предел некоторой
направленности S', более тонкой, чем S.
Доказательство. Пусть х— предельная точка направленности
S/ = {;co', а'ЕИ'}, более тонкой, чем 5 — {a;<j, a e 2}, и пусть
Ф — функция из 2' в 2, обладающая свойствами (FN1) и
(FN2). Пусть, далее, U — произвольная окрестность точки х и
(То е 2. По условию найдется такое а$е 2, что ф(а')^ а0 при
of^afo. По определению предельной точки существует такое
а"^o'Qt что ха„^ ?/. Таким образом, лгф(а,0 = ^е?/иф(а'О^схо,
т. е. х — предельная точка направленности 5.
Предположим теперь, что х — предел направленности S =
= {^,aG2}. Пусть направленность S' = {x<j', а'^2'} тоньше,
чем 5, и пусть функция ф из 2' в 2 обладает свойствами (FN1)
и (FN2). Пусть, далее, U — произвольная окрестность точки х.
Существуют такое сго^2, что х0 ^ U для каждого а ^ а0, и
такое а?е2/, что ф(а')^а0 при а'^^. Очевидно, что при
а'^а^ МЬ1 имеем xa, ^ (/, т. е. х является пределом направлен-
направленности S'.
Пусть х — предельная точка направленности S ={x0, a ^2}.
Рассмотрим множество 2', состоящее из всех упорядоченных пар
(а, ?/),где ае2,(/ — окрестность точки jch^g f/. Положим по
определению (аи ?Л)^(<*2, ^2), если О\ ^ а2 и f/2 c= IA. Легко
показать, что 2Л направлено отношением ^. Направленность
xS' = {а', ст' е 2'}, где ха> = л:а для а' = (а, ?/), тоньше, чем 2,
так как функция ф, определенная равенстйом ф((а, U))=o, яв-
является неубывающим отображением 2' в 2. Для каждой окре-
окрестности U точки х существует такое ogJ, что ха^ U. Так как
для a' ^ (a, C/)e S7 мы имеем лга'^ С/, то х— предел направлен-
направленности S'. 1
1.6.2. Пример. Пусть 2 — множество всех отрицательных рацио-
рациональных чисел, направленное отношением ^, и пусть хг = г для
любого rG2. Очевидно, что S ={xr, r e 2}—направленность
на вещественной прямой R, сходящаяся к 0. Заметим, что 0—*
единственный предел направленности S и что множество, состоя-
состоящее из всех элементов 2 и предела направленности S, не замк-
замкнуто в R. Пусть 2' — множество всех положительных целых
чисел, направленное отношением ^, и пусть ф(/г) = —1/neS
для п е 2'. Функция ф не убывает, а множество фB') конфи-
нально в 2. Направленность S' ={хп, п е 2'}, где хп = —1/л,
тоньше, чем направленность S. В силу 1.6.1, направленность S'
сходится к 0. 1
1.6.3. Предложение. Точка х принадлежит А тогда и только тогда,
когда существует направленность, состоящая из элементов А и
сходящаяся к х.
90 ГЛ. 1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
Доказательство. Из существования такой _ направленности
очевидным образом следует включение xel Пусть теперь
х еЛ, Обозначим через Щ множество всех окрестностей точки
jc, направленное по включению г>, т. е. U\ ^ U^ если U\ =э U%.
Легко показать, что х е lim хи, где хи — произвольная точка
множества A f] U. 1
1.6.4. Следствие. Множество А замкнуто тогда и только тогда,
когда вместе со всякой направленностью оно содержит все ее
пределы. I
1.6.5. Следствие. Точка х принадлежит множеству Ad в том и
только том случае, если существует направленность S = {х0, <те
е 2}, сходящаяся к х и такая, что ха^А и хафх для каждого
<JEli
Направленности обладают многими свойствами, аналогич-
аналогичными свойствам последовательностей. Именно по этой причине
направленности часто оказываются удобным средством для изу-
изучения общих топологических пространств. Читатель наверняка
заметил, что мы уже установили для направленностей аналоги
основных свойств последовательностей. В них роль подпоследо-
подпоследовательностей играют более тонкие направленности. Многие то-
топологические понятия можно охарактеризовать в терминах на-
направленностей. Кроме того, можно вводить топологию на мно-
множестве, задавая класс сходящихся направленностей (см. задачу
1.7.21). Покажем теперь, как при помощи направленностей оха-
охарактеризовать непрерывные отображения и хаусдорфовы про-
пространства.
1.6.6. Предложение. Отображение f топологического простран-
пространства X в топологическое пространство Y непрерывно в том и
только том случае, когда
/(lim xo)cz\\m f{xa)
для любой направленности {ха, ogS} б пространстве X.
Доказательство. Пусть /: Х->У и Jte lim xa. Выберем про-
извольную окрестность V точки f(x). В силу 1.4.1, суще*
ствует такая окрестность U точки х, что f((/)cl/. Так как
х е Hm xa, то найдется такое аое2, что xa^U для любых
О е 2
а ^ <то. Отсюда следует, что /(лса)е V при a ^ a0. Таким обра-
образом, f(x)^ lim /(xa), откуда вытекает включение
1.6. СХОДИМОСТЬ В ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ 91
Обратно, пусть отображение / удовлетворяет условиям на-
нашего предложения. Чтобы доказать, что / непрерывно, доста-
достаточно (опять в силу 1.4.1) показать, что f(A)czf(A) для лю-
любого AczX. Но это вытекает из предложения 1.6.3. 1
1.6.7. Предложение. Топологическое пространство X хаусдорфово
в том и только том случае, если любая направленность в X
имеет не более одного предела.
Доказательство. Пусть X — хаусдорфово пространство. Пусть,
далее, S={jco,a6S}—направленность в X и хи х2еНтха.
Выберем произвольные окрестности U\, U2 соответственно точек
хи х2. Для 1=1, 2 существуют такие Gt <= 2, что ха^ Ui для
любого а ^ а/. Так как 2 направлено, то U\ [\и2ф0. Отсюда
следует, что х\ = х2, т. е. 5 имеет не более одного предела.
Обратно, пусть X не является хаусдорфовым пространством.
Это означает, что найдутся две такие точки Х\, х2, х\ фх2, что
любая окрестность U\ точки х\ пересекается с любой окрест-
окрестностью U2 точки х2: U\[) U2?=0. Множество 2, состоящее из
всех пересечений U\ (] 02, направлено по включению гэ. Легко
показать, что хх, л:2еПтд;0, где х0 — произвольная точка эле-
мента а = U\ П t/д. 1
Сходимость в общих топологических пространствах может
быть описана также при помощи фильтров. При изложении тео-
теории фильтров мы ограничимся формулировкой основных опреде-
определений и аналогов предложений, приведенных выше для направ-
ленностей. Кроме того, мы кратко покажем, как установить эк-
эквивалентность двух этих способов описания сходимости в топо-
топологических пространствах.
Пусть $, — семейство множеств, которое вместе с любыми
множествами А и В содержит их пересечение A fl 5. Под фильт-
фильтром в 31 мы понимаем непустое подсемейство ^"с:^?, удовлет-
удовлетворяющее следующим условиям:
(F2)
(F3) Если Ае=&~ и А сАх <=&, то А{ ge#~.
Фильтр & в 31 есть максимальный фильтр, или ультрафильтр,
в 31, если для любого фильтра SFf в 31, содержащего $Г, мы
имеем #•' = 9Г.
База фильтра в 31 есть непустое семейство ^ а 31, такое, что
0ф<& и
(FB) если А\, А2^$, то существует такое А$^9, что Л3сг
АА
92 ГЛ. 1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
Легко видеть, что для любой базы фильтра ^ в 01 семейство
^ = {ДеЙ: существует такое В<^$, что BczA)
есть фильтр в 31.
Под фильтром (базой фильтра) в топологическом простран-
пространстве X мы понимаем фильтр (базу фильтра) в семействе всех
подмножеств пространства X. В этом параграфе мы будем рас-
рассматривать только фильтры и базы фильтров в топологических
пространствах; мы будем называть их просто фильтрами и ба-
базами фильтров.
Точка х называется пределом фильтра &~, если каждая ее
окрестность есть элемент #". В этом случае говорят, что фильтр
ОТ сходится к точке х, и пишут х^ lim^. Точка х называется
пределом базы фильтра *§, если x^lim^V В этом случае го-
говорят, что база фильтра 9 сходится кх,и пишут х е lim ^. Оче-
Очевидно, что xelim^ в том и только том случае, если любая
окрестность точки х содержит элемент 9.
Точка х называется предельной точкой фильтра $F {базы
фильтра W)t если она принадлежит замыканию каждого эле-
элемента из &* (из $). Очевидно, что х — предельная точка фильтра
$Г (базы фильтра *%) в том и только том случае, если любая ее
окрестность пересекает все элементы из &° (из *§). Отсюда, в
частности, следует, что каждая предельная точка некоторого
ультрафильтра есть предел этого ультрафильтра.
Говорят, что фильтр SFf тоньше, чем фильтр SF, если
1.6.8. Предложение. Пусть фильтр 9rf тоньше, чем фильтр <Г.
Тогда каждая предельная точка фильтра 2Г* является предель-
предельной точкой фильтра &~, а каждый предел фильтра SF является
пределом фильтра ^"/. Если х — предельная точка фильтра ,У\
то х есть предел некоторого фильтра ЗГ\ более тонкого, чем &~. 1
1.6.9. Предложение. Точка х принадлежит А в том и только том
случае, если существует база фильтра, состоящая из подмно-
подмножеств А и сходящаяся к точке х. 1
1.6.10. Предложение. Отображение f топологического простран-
пространства X в топологическое пространство Y непрерывно в том и
только том случае, если для каждой базы фильтра $ в про-
пространстве X и базы фильтра f(S) = {f(A): А^Щ в простран-
пространстве Умы имеем f(\im9)
1.6.11. Предложение. Топологическое пространство X хаусдор-
фово в том и только том случае, когда любой фильтр в X имеет
не более одного предела. В
Установим теперь взаимно однозначное соответствие между
направленностями и фильтрами в топологическом пространстве.
1.6. СХОДИМОСТЬ В ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ 93
1,6.12. Теорема. Пусть S ={ха, ае2}—направленность в топо-
топологическом пространстве X. Семейство #~(S), состоящее из всех
множеств A d Xy удовлетворяющих условию: существует такое
аое2, что хоеЛ при о ^ а0, является фильтром в простран-
пространстве X. При этом
Если направленность S' тоньше, чем S, то фильтр ^"E') тоньше,
4eM&~(S). I
1.6.13. Теорема. Пусть ^ — фильтр в топологическом простран-
пространстве X. Обозначим через 2 множество всех пар (х, А)у где
jCGi4eJ, и положим (xuAl)^.(x2jA2)t если А2аА\. Множе-
Множество 2 направлено отношением ^, и для направленности
S(&) { a e 2}, где ха = х для а=(х,Л)еЕ, мы имеем
#~)) и
Выше мы уже отмечали, что понятие направленности — это
модификация понятия последовательности, приспособленная для
изучения проблем сходимости в общих топологических простран-
пространствах. Необходимость модифицировать понятие последователь-
последовательности возникла потому, что существуют топологические про-
пространства, топология которых не может быть полностью описана
б терминах последовательностей, в противоположность, напри-
например, вещественной прямой, где замкнутые множества можно
охарактеризовать как множества, которые вместе со всякой схо-
сходящейся последовательностью содержат ее предел. Возникает
вопрос, в каких топологических пространствах для описания то-
топологии достаточно последовательностей. Вопрос поставлен не
совсем точно, и мы увидим, что на него можно ответить двумя
различными способами — мы определим два класса пространств,
естественных в этом контексте. Оба этих класса более широкие,
чем пространства с первой аксиомой счетности.
Для начала сделаем несколько простых наблюдений. После-
Последовательность {xi} в топологическом пространстве X очевидным
образом является направленностью, определенной на множестве
JV положительных целых чисел, направленном отношением ^.
Таким образом, для последовательностей определены понятия
предела и предельной точки, и мы знаем, когда последователь-
последовательность сходится к точке. Множество всех пределов последова-
последовательности {xi} обозначается limx*, и, когда последовательность
имеет ровно один предел х> мы пишем х = lim Xu Каждая под-
подпоследовательность {*?.} последовательности {xi} есть направ-
направленность, более тонкая, чем {xi}. Действительно, функция <р,
определенная равенством ф@ = &» не убывает, а множество
94 ГЛ. 1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
y) конфинально множеству N. Из предложения 1.6.1 следует,
что для каждой подпоследовательности {xAJ последовательности
{xi} если хе limxi, tojcg \\mxki, и что любая предельная точ-
точка для {xk^ является предельной точкой для {xi}.
Теперь определим два класса пространств, о которых мы
упомянули выше. Топологическое пространство X называется
секвенциальным пространством, если множество А а X замкнуто
тогда и только тогда, когда вместе со всякой последователь-
последовательностью оно содержит все ее пределы. Топологическое простран-
пространство X называется пространством Фреше — Урысона, если для
любого A czX я любого х^Л существует последовательность
*i, X2, ... точек множества А, сходящаяся к х.
1.6.14. Теорема. Каждое пространство с первой аксиомой счет-
ности есть пространство Фреше — Урысона, а каждое простран-
пространство Фреше — Урысона есть секвенциальное пространство.
Доказательство. Пусть пространство X имеет счетную базу
{UiO=i в точке х* и пусть х^А. Выберем для каждого /=1,
2, ... точку Xi е А П U\ П 1^2 П • • • П Ui< Мы получим последова-
последовательность {xi} точек множества Л, сходящуюся к х. Следова-
Следовательно, каждое пространство с первой аксиомой счетности яв-
является пространством Фреше — Урысона. Вторая часть теоремы
очевидна.
1.6.15. Предложение. Отображение f секвенциального простран-
пространства X в топологическое пространство Y непрерывно тогда и
только тогда, когда /(Птл:,-)с= lim f(xi) для любой последова-
последовательности {xi} в пространстве X.
Доказательство. Необходимость условия следует из предло-
предложения 1.6.6.
Мы покажем, что если / удовлетворяет условию теоремы, то
/ непрерывно. Пусть В — произвольное замкнутое подмножество
в У. Выберем некоторую последовательность х-ь точек множества
f~x(B) и точку x^limxi. Имеем f (x)e lim f(xi)czB. Следова-
Следовательно, хе /-1 (В) nf^iB) замкнуто. 1
1.6.16. Предложение. Если любая последовательность в тополо-
топологическом пространстве X имеет не более одного предела, то X
есть Т^пространство. Если, кроме того, для X выполнена пер-
первая аксиома счетности, то X — хаусдорфово пространство.
Доказательство. Если je {x}, то любая окрестность точки у
содержит точку j^hj/g lim xit где xi = х для * = 1,2, ... . Так
как и х е lim xu а каждая последовательность имеет не более
одного предела, то у = х, и потому {х} — замкнутое множество.
Доказательство второй части предложения аналогично доказа-
доказательству второй части 1.6.7. I
1.6. СХОДИМОСТЬ В ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ 95
Из 1.6.16 и 1.6.7 получаем следующее утверждение.
1.6.17. Предложение. Пространство X с первой аксиомой счет-
ности хаусдорфово тогда и только тогда, когда любая последо-
последовательность в нем имеет не более одного предела. 1
1.6.18. Пример. Пространство У, определенное в примере 1.4.17,
представляет собой пространство Фреше — Урысона, не удов-
удовлетворяющее первой аксиоме счетности. В самом деле, если
у^А для некоторого AczY я уфу0 или у = у0 и у0 е Л, то су-
существует последовательность у\, у2, ... точек множества Л,схо-
Л,сходящаяся к у. Допустим, что у е А\А и у = у$. Отметим, что
существует целое положительное k, такое, что А содержит по-
последовательность {yi}9 сходящуюся к k в R. Противное означало
бы, что любое положительное целое i имеет окрестность Ui cz R,
не пересекающуюся с Л. Отсюда следовало бы, что I \j U11 \
\ N I U {#о} — окрестность точки yQ в У, которая не пересекается
с Л, что противоречит предположению уо^А. Из определения
топологии в У вытекает, что последовательность {yi}, сходя-
сходящаяся к k e N в /?, сходится к у0 в У. В
1.6.19. Пример. Определим теперь секвенциальное простран-
пространство, не являющееся пространством Фреше — Урысона. Пусть
Х={0}[} \Jxi9 где Xi = {l/i}{} U {т + у}' Легко показать»
что Xt[\Xk=0 при [фк. Топология на X порождается сле-
следующей системой окрестностей. Все точки 1/i+l// — изолиро-
изолированные точки пространства X, т. е. <$(я) = {{х}} для любой точ-
точки х такого вида. Для точек х вида \Ц возьмем в качестве
k
семейство всех множеств Х%\ |J { — + — } для
= i2,
/2+ 1, ... . Наконец, в качестве элементов семейства ?§@) возь-
возьмем все множества, получаемые из X выбрасыванием конечного
числа членов Xi и конечного числа точек вида {1Д*+ 1//} во всех
оставшихся Xi. Легко показать, что совокупность Ф{х)}х^х
обладает свойствами (ВР1) — (ВР4), и, значит, X — хаусдорфово
пространство. Так как все элементы (J 3§(х) являются от-
*<= х
крыто-замкнутыми множествами пространства X, то X регуляр-
регулярно, а из 1.5.16 вытекает, что X совершенно нормально.
Легко заметить, что точка 0 принадлежит замыканию множе-
множества А\{0,1, 1/2, ...}, но в этом множестве нет последователь-
96 ГЛ. 1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
ности, сходящейся к нулю; таким образом, X не является про-
пространством Фреше — Урысона. Заметим еще, что X — счетное
пространство, не удовлетворяющее первой аксиоме счетности.
Покажем теперь, что X — секвенциальное пространство, т.е.
что каждое множество A czX, которое вместе со всякой сходя-
сходящейся последовательностью содержит ее предел, замкнуто в X.
Пусть х^А. Если хфО, то 3§(х) — счетная база в х и А содер-
содержит последовательность, сходящуюся к х (ср. с доказательством
1.6.14). Теперь рассмотрим случай jt = O. Пусть ОеЛ\Л. Суще-
Существует подпоследовательность х\, #2,... последовательности
1, 1/2, 1/3, ..., такая, что каждая окрестность любой точки Xi
пересекает А, так как в противном случае можно было бы дока-
доказать, что существует окрестность нуля, не пересекающаяся с Л.
Отсюда следует, что А содержит все элементы последователь-
последовательности х\, Х2, . -., и так как эта последовательность сходится к
нулю, тоОеЛ вопреки предположению. 1
1.6.20. Пример. Модифицируя пространство X предыдущего при-
примера, определим счетное совершенно нормальное пространство,
не являющееся секвенциальным. Достаточно рассмотреть У =
= Х\{1,1/2, 1/3, ...} и взять в качестве открытых множеств
все пересечения Y (] Uy где U открыто в X. Легко показать, что
сходящиеся последовательности в У суть «почти константы». Та-
Таким образом, множество У\{0} вместе с любой сходящейся по-
последовательностью содержит и ее предел. Так как У\{0} не
замкнуто, то У не является секвенциальным пространством.
Чтобы убедиться, что У совершенно нормально, можно рассуж-
рассуждать так же, как в 1.6.19. I
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
Направленности введены Мором и Смитом [1922]. Сходи-
Сходимость в общих топологических пространствах была описана в
терминах направленностей Биркгофом [1937], однако его теория
была сложной и недостаточно общей, так как он пользовался
неподходящим аналогом понятия подпоследовательности. Поня-
Понятие более тонкой направленности определено в книге Мора
[1939]. Описание сходимости в общих топологических простран-
пространствах в терминах направленностей дано Келли [1950]. Исполь-
Использование фильтров при описании сходимости встречается у Кар-
тана [1937] и [1937а]; дальнейшее развитие оно получило в ра-
работах Бурбаки [1940] (сами фильтры впервые появились у Рис-
са [1908]). На эквивалентность двух этих теорий указали Бартл
[1955], а также Брунс и Шмидт [1955]. Секвенциальные про-
пространства и пространства Фреше — Урысона были широко из-
известны почти со времени зарождения общей топологии, но впер-
1.6. СХОДИМОСТЬ В ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ 97
вые подверглись серьезному исследованию в работах Франклина
[1965] и [1967]. Пример 6.1.19 заимствован у Франклина [1965].
Пример 6.1.20 построен Аренсом [1950]. Первый пример нор-
нормального счетного пространства, не имеющего счетной базы
в одной из своих точек, дан Урысоном [1925]. Нормальное счет-
счетное пространство, не имеющее счетной базы ни в одной из своих
точек, построено Новаком [1937] (пример такого пространства
см. в 2.3.37 или упр. 2.3.Е).
УПРАЖНЕНИЯ
1.6.А. Покажите, что точка х есть предельная точка направлен-
направленности 5 ={хо, aES} в том и только том случае, если х е
П
1.6.В. Пусть S — направленное множество,?е Е,Х — тополо-
топологическое пространство и Sj = {х(%\ а е 2|} — направленность в
пространстве X, и пусть Jc^elimS^. Далее, пусть /0> fi:^->
U 2$. Покажите, что, полагая по определению (|о,/о)=^
fi) тогда и только тогда, когда g0 ^ Ei и fo(EX Mi) Для
любого |е В, мы превратим произведение Е = 2 X П %t в на-
правленное множество, и если х е lim JC|, то х е lim jco, где ха ==
-xpfc для а = F, /)еЕ.
1.6.С. Установите, что для любой направленности S =
— {х0, 0е21}, где 121 ^ **о. существует последовательность
{xt)t более тонкая, чем S.
1.6.D, Докажите, что в пространстве Фреше — Урысона X для
любой предельной точки х последовательности {я,*} в {xt} най-
найдется подпоследовательность, сходящаяся к х. Покажите, что тре-
требование, чтобы X было пространством Фреше — Урысона, нельзя
заменить предположением секвенциальности пространства X.
1.6.Е. Приведите пример нехаусдорфова пространства Фре-
Фреше— Урысона, в котором каждая последовательность имеет не
более одного предела.
Указание. Добавьте точку к пространству, описанному в
1.6.18.
I.6.F. Покажите, что секвенциальное пространство X есть
пространство Фреше — Урысона в том и только том случае, если
оператор секвенциального замыкания, который каждому мно-
множеству AczX ставит в соответствие множество всех пределов
содержащихся в нем последовательностей, обладает свойствами
(СО1) — (СО4). Покажите, что предположение о секвенциаль-
секвенциальности пространства X нельзя опустить.
7 Зак. 697
98 ГЛ. 1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
1.7. ЗАДАЧИ
Замыкание и дополнение дают только 14 различных
множеств
1.7.1 (Куратовский [1922а]). Докажите, что, чередуя опера-
операторы замыкания и взятия дополнения к множеству А в тополо-
топологическом пространстве Ху можно получить не более 14 различ-
различных множеств.
Указание. Докажите сначала, что Л-'-'-'- = Д-'-, где А~ = л
и Аг -
Левая и правая топологии на упорядоченном множестве
1.7.2. Пусть X — множество, упорядоченное отношением ^;
положим L(x) = {jeI: у ^ х) для любого элемента xg!
Левая топология, индуцированная на X упорядочением ^, есть
топология на X, порожденная системой окрестностей {{L(x)}}x^x.
(a) Покажите, что пересечение любого семейства открытых
множеств в X в этой топологии есть открытое множество.
(b) Установите, что X есть Го-пространство.
(c) Охарактеризуйте точки xeI, для которых множество
{х} замкнуто, открыто и открыто-замкнуто.
(d) Опишите замыкание {*}.
(e) Определите аналогичным образом правую топологию на
Ху индуцированную упорядочением =^.
1.7.3. Пусть X — такое Г0-пространство, что пересечение лю-
любого семейства открытых в X множеств есть открытое множе-
множество. Докажите, что в X существует такое упорядочение ^, что
исходная топология на X совпадает с левой топологией, индуци-
индуцированной отношением ^.
Линейно упорядоченные пространства I (см. задачи 2.7.5,
3.12.3, 3.12.4, 3.12.12(f), 5.5.22, 6.3.2 и 8.5.13(j))
1.7.4. Пусть X — множество, линейно упорядоченное отноше-
отношением < и содержащее хотя бы два элемента. Для a, Jel,
удовлетворяющих отношению а < 6, положим
(а, b)={x<=X: a<x<b}t
(+-,а) = {х<=Х: х< а}, (а,-ь) = {*€=*: а<х};
такие множества будем называть интервалами в X.
(а) Установите, что семейство 91 всех интервалов в ли-
линейно упорядоченном множестве X обладает свойствами (В1) —
(В2). Топология, индуцированная на X линейным упорядоче-
упорядочением <, есть топология, порожденная на X базой $. Линейно
1.7. ЗАДАЧИ 99
упорядоченное пространство — это пространство, топология ко-
которого индуцирована некоторым линейным упорядочением. По-
Покажите, что всякое линейно упорядоченное пространство есть
^-пространство.
(b) Покажите, что для всякого дискретного семейства
{{jc5}}56eS одноточечных подмножеств линейно упорядоченного
пространства X существует семейство {Us}s^s попарно непере-
непересекающихся открытых подмножеств пространства X, такое, что
xs e[/S)se S.
(c) (Мансфилд [1957а]). Докажите, что для каждого ди-
дискретного семейства {Fs}5eS замкнутых подмножеств линейно
упорядоченного пространства X существует семейство {Us}st_s
попарно непересекающихся открытых подмножеств пространства
X, такое, что Fs cz Us для s e S.
Указание (Стин [1970]). Покажите, что открытые множества
,y):x, y<=F8 и (х,у)[\ [] Fs>=0)
образуют дискретное семейство и что Fs(] U Ws*=0. Пока-
жите, что семейство всех одноточечных подмножеств объедине-
объединения U (F8\ Ws) дискретно, и примените (Ь).
(d) (Биркгоф [1940]). Докажите, что каждое линейно упо-
упорядоченное пространство нормально.
Указание, Примените (с).
(e) (Мейер [1969]). Покажите, что каждое линейно упоря-
упорядоченное секвенциальное пространство удовлетворяет первой ак-
аксиоме счетности.
Борелевские множества I (см. задачи 4.5.7, 4.5.8 и 7.4.22)
1.7.5. (а) Установите, что в совершенном пространстве X (ср.
с упр. 1.5. Н(а)) семейство борелевских множеств может быть
определено как наименьшее семейство У подмножеств простран-
пространства X, удовлетворяющее условиям (BS1), (BS3) и (BS3') или
условиям (BS1')> (BS3) и (BS3'). Выведите из этого факта,
что семейство борелевских множеств в совершенном простран-
пространстве X может быть представлено как объединение U
<
a<cui
(обьединение (J $Л где семейство fFo (семейство ^0) состоит
V а<ан / '
из всех замкнутых (открытых) множеств, семейство 9~а (семей-
(семейство $а) состоит из всех счетных объединений (пересечений)
множеств из (J &*\ (из [} ^Л для нечетных ординалов а и из
|<а V ^<а )
7*
100 ГЛ. I. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
всех счетных пересечений (объединений) множеств из |J SF\
(из U $А для четных ординалов а. Установите, что семейства
&~а и Ъа замкнуты относительно конечных объединений и пересе-
пересечений, что #~эи^э<=#~аП^а при р < а и что А ^&~а тогда и
только тогда, когда Х\А ^ ^а. Докажите, что семейство &~а (се-
(семейство &а) замкнуто относительно счетных объединений, если а
нечетно (четно) (элементы этого семейства называются множе-
множествами аддитивного класса а в X), и замкнуто относительно
счетных пересечений, если а четно (нечетно) (элементы этого
семейства называются множествами мультипликативного класса
а в X). Элементы семейства $Г\ (семейства $\) суть /^-множе-
/^-множества (<2б-множества). Элементы семейств ЗГ2у Ф*Ъу ... называют-
называются F^-множествами, F ^-множествами и т. д., а элементы се-
семейств ^2, ^з, ... называются G ^-множествами, G^^-множе-
ствами и т. д. Покажите, что если /: X-+Y — непрерывное ото-
отображение совершенного пространства X в совершенное простран-
пространство У, то прообраз любого множества аддитивного или муль-
мультипликативного класса а в У есть множество того же класса
в X.
(Ь) (Лебег [1905]). Отображение f совершенного простран-
пространства X в совершенное пространство У называется измеримым
класса а, если прообраз любого замкнутого подмножества в У
есть множество мультипликативного класса а в X.
Покажите, что отображение / измеримо класса а тогда и
только тогда, когда прообраз любого открытого множества в У
есть множество аддитивного класса а в Xt a если У удовлетво-
удовлетворяет второй аксиоме счетности, то тогда и только тогда, когда
прообразы элементов фиксированной счетной базы пространства
У суть множества аддитивного класса а в пространстве X. Уста-
Установите, что если X, У и Z — совершенные пространства, / — из-
измеримое отображение класса а из X в У и g: Y^-Z — непре-
непрерывное отображение, то композиция gf измерима класса а.
Нормально расположенные множества I (см. задачи 2.7.3
и 3.12.24)
1.7.6 (Смирнов [1951с]). Мы говорим, что множество А нор-
нормально расположено в пространстве X, если для любого откры-
открытого U d Ху содержащего Л, в X существует некоторое ^-мно-
^-множество Я, такое, что AczHczU.
(a) Покажите, что если X — нормальное пространство, то
в определении нормально расположенного множества можно
считать, что Н — открытое Ра-множество.
(b) Установите, что пространство X совершенно тогда и
только тогда, когда все его подмножества нормально располо-
расположены в нем.
1.7. ЗАДАЧИ 101
Пространства Урысона и семирегулярные пространства I (см.
задачи 2.7.6 и 6.3.17)
1.7.7 (Урысон [1925]). Топологическое пространство X назы-
называется пространством Урысона, если для любой пары точек Хи
Х2&Х, х\Фх2> существуют открытые множества Uu [/2, такие,
что х\ е Uи Х2 s ^2 и О\ П О2 = 0.
Установите, что каждое регулярное пространство есть про-
пространство Урысона и что каждое пространство Урысона есть
хаусдорфово пространство. Приведите пример хаусдорфова про-
пространства, не являющегося пространством Урысона, и пример
пространства Урысона, не являющегося регулярным.
1.7.8. (а) (Стоун М. [1937]). Топологическое пространство X
называется семирегулярным пространством, если X есть 7Vnpo-
странство, а семейство всех канонических открытых множеств
есть база пространства X.
Покажите, что каждое регулярное пространство семирегуляр-
но. Приведите пример хаусдорфова пространства, не являюще-
являющегося семирегулярным, и пример семирегулярного пространства
Урысона, не являющегося регулярным. Заметим, что существуют
Ti-пространства, в которых канонические открытые множества
образуют базу, но которые не являются ^-пространствами.
(b) (Стоун М. [1937], Катетов [1947]). Пусть (Х,0) — хаус-
хаусдорфово пространство. Постройте на X топологию 0' а 0У по-
порожденную базой, состоящей из всех канонических множеств
пространства (X, 0), и покажите, что пространство (X, 0') се-
мирегулярно и имеет те же канонические открытые множества,
что и пространство (Х,0).
(c) (Урысон [1925]). Приведите пример пространства Уры-
Урысона, не являющегося семирегулярным, и пример семирегуляр-
семирегулярного пространства, не являющегося пространством Урысона.
(d) Приведите пример счетного пространства Урысона X, та-
такого, что ни в какой его точке хе! не существует базы, со-
состоящей из канонических открытых множеств (ср. с задачей
6.3.17).
Указание. Постройте соответствующую топологию на под-
подмножестве плоскости, состоящем из всех точек, обе координаты
которых рациональны.
(e) Приведите пример счетного семирегулярного простран-
пространства Урысона X, такого, что любая его точка х е X имеет окре-
окрестность, которая не содержит замыкания никакой окрестности
точки х.
Указание. Примените указание к части (d).
1.7.9. (а) Покажите, что ни свойство быть пространством Уры-
102 ГЛ. 1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
сона, ни семирегулярность не инвариантны при замкнутых ото-
отображениях с конечными прообразами точек.
(Ь) Покажите, что семирегулярность не инвариантна при от-
открыто-замкнутых отображениях.
Замечание. Как показывает пример, упомянутый в замечании
к упр. 1.5.L (Ь), свойство быть пространством Урысона не инва-
инвариантно при открыто-замкнутых отображениях.
Теорема Кантора — Бендиксона
1.7.10. Покажите, что если каждый элемент семейства зФ под-
подмножеств пространства X плотен в себе, то и объединение [)*$Ф
плотно в себе. Покажите, что если АаХ плотно в себе, то и
замыкание А плотно в себе. Выведите отсюда, что любое топо-
топологическое пространство может быть представлено как объеди-
объединение двух непересекающихся множеств, одно из которых плот-
плотно в себе и замкнуто (такие множества называются совершен-
совершенными множествами), а второе не содержит непустого плотного
в себе подмножества (такие множества называются разрежен-
разреженными множествами).
Замечание. Не следует путать это понятие совершенного
множества с понятием совершенного пространства, определен-
определенным в упр. 1.5 Н (а).
1.7.11 (Хаусдорф [1914]; для подпространств евклидовых про-
пространств— Линделёф [1903]). Точка х топологического про-
пространства X называется точкой конденсации множества АаХу
если любая ее окрестность содержит несчетное множество то-
точек множества Л. Множество всех точек конденсации множе-
множества А обозначается Л°.
Установите, что
Л°с=Л<*, А°=1$д и (ЛиЯ)°=ЛэиЯ°.
Покажите, что если Л — подмножество некоторого пространства
со второй аксиомой счетности, то Л\Л° счетно и (Л°)°=Л0.
Выведите из предыдущего, что любое пространство со второй
аксиомой счетности может быть представлено как объединение
двух непересекающихся множеств, одно из которых совершенно,
а второе счетно (это и есть теорема Кантора — Бендиксона).
Замечание. Кантор и Бендиксон доказали этот факт незави-
независимо в 1883 г. для подмножеств вещественной прямой.
Кардинальные функции I (см. задачи 2.7.9—2.7.11, 3.12.4,
3.12.7—3.12.11, 3.12.12(j) и 8.5.17)
1.7.12. Кардинальная функция — это функция /, приписываю-
приписывающая каждому топологическому пространству X некоторое кар-
кардинальное число f(X) таким образом, что для любой пары го-
меоморфных пространств X и У имеет место равенство {(Х) =
1.7. ЗАДАЧИ
103
= /(У). Наименьшее кардинальное число m ^ Ко, такое, что
любое семейство попарно непересекающихся непустых открытых
подмножеств пространства X имеет мощность ^т, называется
числом Суслина или клеточностью пространства X и обозначает-
ся с(Х), Если с(Х)=Ко, то говорят, что пространство X обла-
обладает свойством Суслина.
Наименьшее кардинальное число m ^ Ко, такое, что каждое
подмножество пространства X, состоящее только из изолирован-
изолированных точек, имеет мощность ^ш, обозначается hc(X). Объясне-
Объяснение символа hc(X) и название этой кардинальной функции см.
в задаче 2.7.9 (Ь) (некоторые авторы пользуются символом s(X)
и называют это спредом (spread) пространства X).
Наименьшее кардинальное число m ^ Ко, такое, что каждое
замкнутое подмножество пространства X, состоящее только из
изолированных точек, имеет мощность ^т, называется экстентом
(extent) пространства X и обозначается е(Х).
В целях упрощения во всех задачах о кардинальных функ-
функциях определенные в основном тексте книги кардинальные функ-
функции (до сих пор встречались вес, характер и плотность) будут
переопределены в предположении только бесконечных значе-
значений: новое значение f(X) мы полагаем равным Ко, если старое
значение было конечным, и равным старому значению, если это
было некоторое бесконечное кардинальное число. (Иногда топо-
топологи говорят, что «в общей топологии нет конечных кардиналь-
кардинальных чисел».)
(а) Докажите, что следующая диаграмма содержит все не-
неравенства, которые имеют место между входящими в нее кар-
кардинальными функциями; стрелка из f в g означает, что g (X) ^
^ f(X) для всякого топологического пространства X:
104 ГЛ. 1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
Докажите, что если У — непрерывный образ пространства Х>
то c(Y)^ с(Х) и hc(Y)^ hc(X); если, кроме того, X есть ^-про-
^-пространство, то и е(У)^ е(Х).
Замечание. Кардинальным функциям посвящены книги Юха-
са [1971] и [1980].
1.7.13 (Архангельский и Пономарёв [1968], Архангельский
[1970]). Теснота точки х в топологическом пространстве X есть
наименьшее кардинальное число m ^ 4*0 со следующим свой-
свойством: если хеС, то существует такое Сос=С, что |С0|^ш и
л;еС0, Это кардинальное число обозначается t(x, X). Теснота
топологического пространства X есть точная верхняя грань всех
чисел t(x,X) для х^Х. Это кардинальное число обозначается
ИХ).
(a) Покажите, что для любого топологического пространства
X и любой точки х^Х имеют место неравенства t(x> X)^
^%(х,Х) и t(X)^.%(X). Приведите пример совершенно нор-
нормального пространства Ху для которого t(X)<%(X).
(b) Докажите, что для любого топологического простран-
пространства X теснота t(X) равна наименьшему кардинальному числу
ш^ Ко, такому, что для любого CczX, не явлющегося замкну-
замкнутым, существует такое Сос=С, что |С0|=^т и Со\Сф0.
Указание. Покажите, что t (X) ^ m в том и только том слу-
случае, если для каждого CczX иы имеем С = [G]m, где [С]ш =
==и{М:Л1 с=С и |Af|<m}.
(c) Покажите, что для каждого секвенциального простран-
пространства X мы имеем t(X)= Ko.
Замечание. Пространства счетной тесноты были введены
Р. К. Мором и Мрувкой [1964]; они появились также у Корсона
[1961].
Полунепрерывные функции I (см. задачи 2.7.4, 3.12.22 (g)
и 5.5.20)
1.7.14. Вещественная функция /, определенная на топологи-
топологическом пространстве ХЛ полунепрерывна снизу (сверху), если
для любого хеХи любого вещественного числа г, удовлетво-
удовлетворяющего неравенству f(x)> г (неравенству /(л;)<г), суще-
существует такая окрестность U с X точки д;,что f(x)> r (f(V) < г)
для любого х/ ^ U.
(а) Докажите, что функция f полунепрерывна снизу (сверху)
в том и только том случае, если для любого вещественного
числа г множество {х: f(x)^r} (множество {*: f(x)^r})
замкнуто. Покажите, что функция одновременно полунепре-
полунепрерывна снизу и сверху в том и только том случае, если она не-
непрерывна. Покажите, что если fug полунепрерывны снизу
1.7. ЗАДАЧИ 105
(сверху), то min(ft g)у max(ft g) и f + g полунепрерывны снизу
(сверху), а также /•#, при условии что /(лс)^О и g(x)^0 для
^е! Покажите, что функция — f полунепрерывна снизу (свер-
(сверху) в том и только том случае, если f полунепрерывна сверху
(снизу). Докажите, что для любого семейства {fs}5€55 полуне-
полунепрерывных снизу (сверху) функций, обладающего тем свой-
свойством, что (М*): sgS} ограничено сверху (снизу) для лю-
любой точки xgX, функция sup fs (функция inf fs\9 определен-
ная формулой [ sup fs] (x) = sup fs (x) (формулой [ inf fs] (x) ==
= inf fs(x))> полунепрерывна снизу (сверху). Приведите при-
мер последовательности {/,} непрерывных функций из / в себя,
такой, что inf ft не полунепрерывна снизу, a sup f,- не полунепре-
полунепрерывна сверху,
(Ь) (Форт [1955]). Докажите, что для каждой полунепре-
полунепрерывной снизу или сверху функции /, определенной на топологи-
топологическом пространстве X, существует множество G czXy которое
может быть представлено как пересечение счетного множества
всюду плотных открытых подмножеств пространства X, такое,
что / непрерывна в каждой точке G.
Указание. В случае полунепрерывной _снизу функции / поло-
положите Аг ={лг: f(x) > г} и Gr=Ar\]{X\Ar} для любого рацио-
рационального числа г. Пусть G — пересечение всех Gr.
Замечание. Для функций, определенных на вещественной
прямой, понятие полунепрерывности ввел Бэр в 1899 г., и он
же установил (а) и (Ь) в этом частном случае.
1.7.15.(а) (Бурбаки [1948]). Докажите, что Ггпространство
X вполне регулярно в том и только том случае, если для каж-
каждой полунепрерывной снизу (сверху) функции f на X, такой,
что f(x) ^ g(x) (f(x) ^ g(x)) для некоторой непрерывной функ-
функции g: X^*R и любого лсеХ, существует семейство непрерыв-
непрерывных функций {fs}s = s, такое, что / = supfs(/=: inf f3).
(b) (Тонг [1952] (заявлено в [1948]), Катетов [1951а] (ис-
(исправлено в [1953]); для паракомпактных пространств Дьёдонне
[1944]; для метрических пространств Хан [1917]). Докажите,
что ^-пространство X нормально в том и только том случае,
когда для любой пары f, g вещественных функций на Xt такой,
что / полунепрерывна сверху, g полунепрерывна снизу и f{x)^
*^g(x) для любого х^Х, существует непрерывная функция
А: Х^-R, такая, что f(x)^h{x)^g(x) для любого хе!
Указание (Тонг [1952]; ср. с задачей 2.7.2 (с)). Для начала
покажите, что если fi, gr. X-+I непрерывны для t= 1, 2, ... и
fo=inffi> go = sup?* удовлетворяют неравенству fo(x)^go(x)
106 ГЛ. 1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
при каждом х е Ху то существует непрерывная функция h:X^~I,
удовлетворяющая неравенству fo(x)^ h(x)^ go(x) для любого
хеХС этой целью предположите (без ограничения общности),
что fi+i(x)^fi(x) и gi+\(x)^ gi(x) для любого х^Ху поло-
положите ki = max [min(f/, g>)], /f = max(?t_b /,) и покажите, что
sup fo = inf U.
Возвращаясь к общему случаю, покажите, что достаточно
рассмотреть функции /, g со значениями в @, 1). Затем для каж-
каждой пары положительных целых чисел /, i9 j < / положите
Alt t = {х: g (x) < ///} и BUi = {x: f (x) > j/i + 1/2/},
выберите непрерывные функции //,,-, равные ///+ l/2j на Л/, ;, 1
на Bj, t и такие, что /7, t(x)^ j/i + l/2i для каждого jc ^ X. Уста-
Установите, что для функции fi= minbf ихеХ имеет место либо
неравенство fi(x)< g(x)y либо |//(л)— g(*)| < 3/2i и ft(x)^
^f(x). Покажите, что функция /0 ===== inf ff- удовлетворяет усло-
условиям f(x)^ fo(x)^g(x) для любого х^Х. Применяя этот ре-
результат к функциям —g и —fo, найдите go = sup gn, удовлет-
удовлетворяющую условиям fo(x) ^ go(x) ^ g(x) для любого х^Х,
и примените первую часть указания.
(с) (Тонг [1952]; для метрических пространств Хан [1917];
для вещественной прямой Бэр [1904]). Докажите, что Грпро-
странство X совершенно нормально в том и только том случае,
если для каждой полунепрерывной снизу (сверху) функции f,
определенной на X, существует последовательность {fi} непре-
непрерывных вещественных функций на Ху такая, что fi(x)^ fi^i(x)
(fi(x)> fi+\{x)) для t = l, 2, ..., x&X, и что /(*)=lim/,-(*)
при каждом х ^ X.
Указание (Тонг [1952]). Докажите, что пространство X, об-
обладающее указанными выше свойствами, удовлетворяет усло-
условию (ш) из 1.5.19. При построении последовательности {ft} для
полунепрерывной снизу функции f рассмотрите сначала случай,
когда / принимает только конечное число значений. Затем, пред-
предполагая, что 0</(х)<1, для любой пары целых чисел /, /,
0 ^ / < I, постройте
и для каждого i = l, 2, ... возьмите полунепрерывную снизу
функцию gif равную /// на С/,,-. Покажите, что gi(x)^ fix) для
xgI Выберите для любого i последовательность (glk\ непре-
непрерывных функций, такую, что g*k{x)<4+i (x), limgi(x) = gi(x)H
gik{x)'^0 для любого xg! Занумеруйте все функции g*k
в последовательность hu Л2, .-•, положите ^? = max А/ и Hx) =
1.7. ЗАДАЧИ 107
= V —r kt (л:). Покажите, что k {x) > О при ^еХи что функции
fj = max(&, kt) обладают требуемыми свойствами и принимают
только положительные значения.
1.7.16 (Исивата [1967]; ср. с упр. 1.5.L (а)). Докажите, что
если f: X-+-Y— открытое (замкнутое) отображение X на У, то
для каждого g: X-+R, ограниченного на всех прообразах точек
при отображении f, формулы g*(y)= snp{g(x): x^f~l(y)} и
g"*(у) = т^{ё(х): х^ f~l (у)} определяют соответственно полу-
полунепрерывную снизу и сверху (сверху и снизу) функцию на У.
Многозначные отображения I (см. задачи 2.7.21 и 3.12.27)
1.7.17 (Куратовский [1932] и [1963]). Отображение F, со-
сопоставляющее каждой точке у топологического пространства У
замкнутое подмножество F(y) топологического пространства Xt
полунепрерывно снизу (сверху), если для любого открытого мно-
множества U<z:X множество {у: F(y){]U ф 0} (множество {у:
F(y)a U}) открыто в У.
(a) Заметим, что F полунепрерывно снизу (сверху) в том
и только том случае, если для каждого замкнутого множества
KciX множество {у: F(y)<=K} (множество {у. Р{у)[\КФ0})
замкнуто в У. Установите, что отображение f топологического
пространства У в ^-пространство X непрерывно в том и только
том случае, если многозначное отображение F{y) = {f(y)} полу-
полунепрерывно снизу или, что эквивалентно, сверху. Докажите, что
отображение f: X-+-Y на ^-пространство У замкнуто (открыто)
в том и только том случае, когда многозначное отображение
F(y) — f-l{y) полунепрерывно сверху (снизу). Установите, что
вещественная функция f9 определенная на топологическом про-
пространстве У, полунепрерывна снизу (сверху) (см. 1.7.14) в том
и только том случае, если многозначное отображение F, при-
приписывающее точке j/eF замкнутое множество F(y) — {r^R:
г ^ f(y)}cRt полунепрерывно снизу (сверху).
(b) Покажите, что для любого семейства {Fs}ses полунепре-
полунепрерывных снизу многозначных отображений многозначное отобра-
отображение F= U Fs9 определенное формулой F(у) = [} Fs(y), по-
seS sgS
лунепрерывно снизу. Установите, что если Fu F2 — два полуне-
полунепрерывных сверху многозначных отображения, то их объедине-
объединение F = Fi U F2y определенное формулой F(у) = F\(y)[} F2(у),
полунепрерывно сверху. Покажите, что для полунепрерывных
снизу отображений аналогичное утверждение, вообще говоря, не
имеет места.
108 ГЛ. 1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
(с) Докажите, что если F\, F2— два полунепрерывных сверху
многозначных отображения пространства У в семейство замкну-
замкнутых подмножеств нормального пространства X, то их пересече-
пересечение F = Fi{\F2, определенное формулой F{y) = Fi(y)[} F2(y),
полунепрерывно сверху. Покажите, что аналогичное утвержде-
утверждение для счетных пересечений, вообще говоря, не имеет места,
так же как и соответствующее утверждение для полунепрерыв-
полунепрерывных снизу отображений.
Указание, Заметим, что {у: F(y)a U}= [)[{У- i7!(г/)cz ?/г}П
0{У- F2(y)cz U2}], где объединение берется по всем парам U\9 U2
открытых подмножеств пространства Х> таким, что U\ П U2 = t/.
Топологии, описываемые последовательностями
1.7.18 (Фреше [1906] и [1918], Урысон [1926а]). g*-noo-
странство — это пара (лД), где X — некоторое множество, а
X — некоторая функция (называемая оператором предела) при-
приписывающая некоторым последовательностям точек простран-
пространства X элемент пространства X (называемый пределом последо-
последовательности) таким образом, что выполнены следующие условия
(мы пишем kxt вместо Я ({я*}) и говорим, что xi сходится к xf
если %xt = х):
(L1) Если xi = x для /=1,2, ..., то %xt = х.
(L2) Если Kxt = х, то %Xkt = x для любой подпоследователь-
подпоследовательности {xkt} последовательности {xi}.
(L3) Если последовательность {xi} не сходится к х, то она со-
содержит подпоследовательность {хь^, никакая подпоследо-
подпоследовательность которой не сходится к х.
(a) В ^-пространстве определяют оператор замыкания, по-
полагая jcgAb том и только том случае, если А содержит после-
последовательность, сходящуюся к х. Установите, что такой оператор
замыкания обладает свойствами (СО1) — (СОЗ), но, вообще го-
говоря, не обладает свойством (СО4).
(b) Покажите, что оператор замыкания, определенный в (а),
обладает свойством (СО4) тогда и только тогда, когда выпол-
выполнено следующее условие:
(L4) Если %xi=x и Xx{p = xt для i= 1, 2, ..., то существуют
такие последовательности положительных целых чисел
]*
iu *2» - •. и /ь Ы • • •» что to]1** = х.
^-пространство X, удовлетворяющее условию (L4), назы-
называется Ф*-пространством. Топология, порожденная на X опера-
оператором замыкания, определенным в (а), называется топологией
Фреше, индуцированной оператором предела. Установите, что
любое ^-пространство с топологией Фреше является ^-про-
^-пространством.
1.7. ЗАДАЧИ 109
(с) Докажите, что для последовательности хи *2, ... точек
^-пространства с топологией Фреше х = lim х% тогда и только
тогда, когда Xxt = х, т. е. что сходимость апостериори эквива-
эквивалентна сходимости априори.
1.7.19 (Кисынский [I960]). Покажите, что в любом ^-про-
^-пространстве можно ввести топологию, взяв в качестве семейства
замкнутых множеств все множества, содержащие вместе со вся-
всякой сходящейся последовательностью ее предел. Эта топология
называется секвенциальной топологией, индуцированной опера-
оператором предела X. Установите, что любое ^-пространство с сек-
секвенциальной топологией является ^-пространством. Покажите,
что в любом ^-пространстве секвенциальная топология и топо-
топология Фреше совпадают. Докажите, что для последовательности
jci, x2, ... точек некоторого ^-пространства с секвенциальной
топологией x=limxi тогда и только тогда, когда %xi = x% т. е.
что сходимость апостериори эквивалентна сходимости априори.
1.7.20. Докажите, что в топологическом пространстве X опе-
оператор предела %, — такой, что (Х,Х) есть ^-пространство
(^-пространство) и топология Фреше (секвенциальная тополо-
топология), индуцированная Я, совпадает с исходной топологией про-
пространства X, — может быть определен тогда и только тогда, когда
X — пространство Фреше — Урысона (секвенциальное простран-
пространство), в котором любая последовательность имеет не более од-
одного предела.
1.7.21 (Келли [1950]). Сформулируйте и докажите для на-
правленностей аналоги условий (LI)—(L3) в 1.7.18. Опреде-
Определите оператор замыкания в множестве X, где классы сходя-
сходящихся направленностей и их пределы выделены таким образом,
что выполняются аналоги указанных условий, а также условие
повторных пределов из упр. 1.6.В. Докажите, что всякая тополо-
топология порождается некоторым классом сходящихся направленно-
стей, т. е. может быть получена описанным выше способом.
Глава 2
ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ
ПРОСТРАНСТВАХ
В этой главе изучаются операции на топологических про-
пространствах, т. е. методы построения новых топологических про-
пространств из заданных. Шесть параграфов главы соответствуют
шести исследуемым операциям. Из теорем об универсальности
тихоновского куба для всех 7V/a -пространств и александров-
александровского куба для всех Г0-пространств, которые будут доказаны
в § 2.3, видно, что все пространства названных классов могут
быть получены из очень простых пространств применением толь-
только двух операций. Данная глава является в некотором смысле
сердцевиной всей книги: в последующих главах, определяя раз-
различные классы пространств, мы всегда будем испытывать их по-
поведение под действием описанных здесь операций.
Параграф 2.1 посвящен подпространствам. Определив поня-
понятие подпространства, мы изучаем сужения и продолжения непре-
непрерывных отображений и функций; самым важным результатом в
этом направлении является теорема Титце — Урысона. Далее
обсуждается понятие наследственного топологического свой-
свойства. В заключение приводятся некоторые замечания о комби-
комбинациях отображений.
В § 2.2 рассмотрена операция суммы топологических про-
пространств и аддитивность топологических свойств.
Самый длинный в этой главе § 2.3 посвящен произведениям
топологических пространств. Определив на произведениях тихо-
тихоновскую топологию и доказав несколько элементарных утвер-
утверждений, мы обсуждаем мультипликативность топологических
свойств. Затем мы переходим к изучению вложений пространств
в произведения и доказываем две теоремы об упомянутых выше
универсальных пространствах. Заключительная часть параграфа
посвящена произведениям и диагональным произведениям ото-
отображений.
Факторпространства и факторные отображения обсуждаются
в § 2.4.
В § 2.5 изучаются обратные спектры пространств, их пре-
предельные пространства и отображения.
2.1. ПОДПРОСТРАНСТВА Ш
Последний параграф посвящен пространствам отображений.
Вводятся топология равномерной сходимости на множестве не-
непрерывных вещественных функций и топология поточечной схо-
сходимости на множестве непрерывных отображений. Параграф за-
завершается обсуждением приемлемых топологий на простран-
пространствах отображений. Та же тема рассматривается далее в § 3.4,
где определяется другая топология на пространствах отображе-
отображений и доказываются более глубокие результаты.
2.1. ПОДПРОСТРАНСТВА
Предположим, что заданы некоторое топологическое про-
пространство X и множество MczX. Легко видеть, что семейство О
всех множеств вида М П ?/, где U открыто в X, удовлетворяет
условиям @1) — @3). Действительно, условие (О1) выполнено,
так как 0 = М[\0иМ = М()Х,анз равенств
(Af П С/i) П (Af П С/2) == ЛГ П (C/i П С/2)»
U (М[\и8)=м[\ U и,
seS se5
следует, что выполнены также и условия @2), @3).
Взяв семейство {М[\U\ U открыто в X} в качестве семей-
семейства открытых множеств в М, мы определяем на М топологию.
Множество М с этой топологией называется подпространством
пространства X, а сама топология называется индуцированной
топологией или топологией подпространства.
2.1.1. Предложение. Пусть X—топологическое пространство
и М — его подпространство. Множество А с: М замкнуто в М
тогда и только тогда, когда A = M(]Fy где F замкнуто в X. За-_
мыкание А множества А а М в пространстве М и замыкание А
множества А в пространстве X связаны равенством А = А{]М.
Доказательство. Если А = М П F, где F = F аХу то М\А =
t=Mf\(X\F) и А замкнуто в М как дополнение к открытому
множеству. Обратно, если А — замкнутое подмножество М9 то
М\А = М П U, где U открыто в X. Значит,
и А = М П F, где F — X\U замкнуто в X.
По определению оператора замыкания А равно пересечению
всех замкнутых подмножеств пространства М, содержащих Л,
т. е. всех множеств вида Mj\F, где F — F и А с: 7\ Отсюда по-
поручаем равенство Л = !
2.1.2. Предложение. Пусть М — подпространство пространства X
и LczM\ две определенные на L топологии — топология подпро-
112 ГЛ 2. ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
странства пространства М и топология подпространства про-
странства X — совпадают. I
Подпространство М пространства X называется его замкну-
замкнутым подпространством, если множество М замкнуто в X. Если
М — замкнутое подпространство пространства X, то множество
А <=М замкнуто в М тогда_и только тогда, когда оно замкнуто
в X, и, следовательно, Я = А для каждого A <= M. Открытые под-
подпространства и всюду плотные подпространства определяются
аналогично. Ясно, что если М — открытое (всюду плотное) под-
подпространство пространства X, то множество АаМ открыто
(всюду плотно) в М тогда и только тогда, когда оно открыто
(всюду плотно) в X. В дальнейшем слова «подпространство» и
«подмножество» употребляются взаимозаменяемым образом. На-
Например, мы будем писать «сепарабельное подмножество», «ком-
«компактное подмножество» и т. д., понимая под этим подмноже-
подмножество, которое наделено топологией подпространства и является
в этой топологии сепарабельным, компактным и т. д.
Для каждого топологического пространства X и каждого его
подпространства М формула 1м(х) = х определяет отображение
М в X. Так как i^l(U) = M(]U, это отображение непрерывно.
Отображение /«: М^Х называется вложением подпространства
М в пространство X. Легко проверить, что топология подпро-
подпространства совпадает с топологией, порожденной отображением
iM множества М в топологическое пространство X. Вложение ш
замкнуто (открыто) в том и только том случае, если подпро-
подпространство М замкнуто (открыто).
Для каждого отображения /: X-+-Y и каждого подпростран-
подпространства М пространства X композиция fiM является непрерывным
отображением пространства М в пространство У. Это отображе-
отображение называется сужением отображения f на М а X и обозна-
обозначается f\M. Так как комлозиция замкнутых (открытых) отобра-
отображений является замкнутым (открытым) отображением, то су-
сужение замкнутого (открытого) отображения на замкнутое (от-
(открытое) множество МсX замкнуто (открыто).
2.1.3. Предложение. Если композиция gf непрерывных отобра-
отображений f: X^-Y и g: Y-+Z является замкнутым (открытым)
отображением, то сужение g\f(X): f(X)-+Z замкнуто (открыто).
Доказательство. Любое замкнутое (открытое) подмножество
пространства f(X) имеет вид А П f(X), где А замкнуто (открыто)
в У. Так как прообраз f~l(A) замкнут (открыт) в X и gf —
замкнутое (открытое) отображение, то множество
замкнуто (открыто) в Z. I
2.1. ПОДПРОСТРАНСТВА ЦЗ
Легко показать, что gf может быть замкнутым (открытым)
отображением и тогда, когда ни gt ни f не замкнуто (не от-
открыто) .
Сужение отображения f: X-+Y на Мс=Х и f(M)cz У опре-
определяется как отображение подпространства М в множество
f(M), которое произвольной точке х^М ставит в соответствие
точку f(x) подпространства f(M)cz У. Это сужение обозначается
через(\М; очевидно, f \M непрерывно. Отображения f\M и f\M
различаются областями значений: f\M: М-+ У и f\M: М —>-/(М);
в частности, f\X: А"->/(Х). Легко видеть, что если / и М
замкнуты (открыты), то f \ M также замкнуто (открыто).
Третьей разновидностью сужения является сужение отобра-
отображения f: X-+Y на LczY, определяемое как отображение под-
подпространства f~~l(L)czX в пространство L а У, сопоставляющее
точку f(x)^L точке x^f~l(L). Это сужение обозначается fL\
очевидно, что fL непрерывно, /i: f~l(L)-+L.
Читатель легко проверит следующие простые формулы, отно-
относящиеся к образам и прообразам при сужениях:
(f\M)(A) = f(A), AczM; (/|М)(В) = МAГ1E), BczY;
2.1.4. Предложение. Если f: X~+Y — замкнутое (открытое) ото-
отображение, то для каждого подпространства L a Y сужение
fc f-{{L)^>~L замкнуто (открыто).
Доказательство. Для А а X имеем
и наше утверждение вытекает из определения топологий на под-
подпространствах /-1 (L) и L. I
Отображение /: Х-> Y называется гомеоморфным вложе-
вложением, если оно является композицией гомеоморфизма и вложе-
вложения, т. е. если существуют подпространство L пространства Y
и гомеоморфизм f: X^>~L, такие, что f — iLff. Ясно, что тогда
L = f(X) и f' = f\ X. Если для пространства X существует го-
меоморфное вложение f: X-+Y в пространство У, то мы гово-
говорим, что X вложимо в У.
Из предложения 2.1.2 следует, что композиция гомеоморф-
яых вложений и сужения гомеоморфных вложений являются го-
меоморфными вложениями. Легко видеть, что гомеоморфное
вложение f: X^-Y замкнуто (открыто) в том и только том слу-
случае, если f(X) замкнуто (открыто) в У.
8 Зак. 697
114 ГЛ. 2. ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
2.1.5. Примеры. Интервал /, наделенный естественной тополо-
топологией, является замкнутым подпространством вещественной пря-
прямой R, взятой с естественной топологией. Естественная тополо-
топология любого интервала прямой R является индуцированной топо-
топологией. В дальнейшем под вещественной прямой или интерва-
интервалом мы всегда будем понимать эти множества, наделенные есте-
естественной топологией. Легко проверить, что любые два замкну-
замкнутых интервала, содержащих более одной точки, гомеоморфны.
То же самое имеет место для любых двух открытых и для лю-
любых двух полуоткрытых интервалов.
Дискретное пространство мощности с вложимо в плоскость
Немыцкого L: оно гомеоморфно замкнутому подпространству L\
пространства L. Дискретное пространство мощности Ко вложимо
(тоже в качестве замкнутого подпространства) в вещественную
прямую: оно гомеоморфно множеству N всех натуральных чи-
чисел с индуцированной топологией. В дальнейшем мы будем ча-
часто предполагать, что D(&0)=N. Вещественная прямая вло-
жима в отрезок /—[—1, 1]: она гомеоморфна интервалу (—1,1),
причем гомеоморфное вложение г. /?->-/ может быть определено
формулой i(x) = x/(l +\х\). I
Мы называем топологическое свойство 9* наследственным
(наследственным по отношению к замкнутым подмножествам,
открытым подмножествам и т. д.), если 9* присуще каждому
подпространству (каждому замкнутому подпространству, каж-
каждому открытому подпространству и т. д.) любого пространства
X, обладающего свойством !?. Примерами наследственных
свойств являются «вес ^щ» или «характер г^т» и, в частности,
выполнение второй или первой аксиомы счетности. Как пока-
показано в 2.1.5, сепарабельность не является наследственным свой-
свойством; однако легко проверить, что сепарабельность наследуется
открытыми подмножествами. Если само свойство 0* не является
наследственным, но каждое подпространство некоторого про-
пространства X обладает свойством д*ь то мы говорим, что X на-
наследственно обладает свойством @. В этом смысле будут упот-
употребляться в дальнейшем такие термины, как «наследственно се-
парабельное пространство» и «наследственно нормальное про-
пространство».
2.1.6. Теорема. Любое подпространство Т[-пространства яв-
является Т{-пространством, г^З—. Нормальность наследуется
замкнутыми подмножествами. Совершенная нормальность яв-
является наследственным свойством.
Доказательство. В случае Ггпространств наша теорема сле-
следует непосредственно из 2.1.1. Тот факт, что совершенная нор-
нормальность является наследственным свойством, вытекает из
2.1. ПОДПРОСТРАНСТВА Ц5
2.1.1 и равносильности условий (i) и (ш) в 1.5.19. Доказатель-
Доказательства остальных пяти случаев подобны друг другу. В качестве
примера мы докажем, что подпространство М регулярного про-
пространства X является регулярным.
Как известно, М является ^-пространством. Выберем не-
некоторую точку х s M и замкнутое множество A cz M, такое, что
хфА. В силу 2.1.1, А=М[)А, так что х^А. Тогда суще-
существуют открытые в X множества U\, V\, такие, что х^ Ь\9
AczVi и Ux{] Vi = 0. Полагая U = UX П М и V = VX [\М9 полу-
получаем открытые подмножества подпространства М, такие, что
xg[/, А<^ V я U (\V = 0. Следовательно, пространство М ре-
регулярно. 1
Как показывает приведенный ниже пример 2.3.36, нормаль-
нормальность не является наследственным свойством (ср. с упр.2.1.Е(Ь)).
Из предыдущей теоремы следует, что каждое совершенно
нормальное пространство наследственно нормально. Обратное
утверждение не имеет места: пространство Л(т) не является
совершенно нормальным для m > Мо, однако оно наследствен-
наследственно нормально, ибо все его подпространства имеют вид А (п) или
D(n) сп<ш. Заметим также, что из 2.1.4 и 1.5.20 следует, что
класс наследственно нормальных пространств инвариантен при
замкнутых отображениях.
Приведем теперь две характеристики наследственно нормаль-
нормальных пространств. Сначала введем понятие отделенных мно-
множеств. Два множества А и В топологического пространства X
отделены, если А{\В = 0 и ЛП5 = 0. Два непересекающихся
множества отделены в том и только том случае, если ни одно
из них не содержит точек накопления другого. В частности, лю-
любые два непересекающихся замкнутых множества отделены.
Всякие два непересекающихся открытых множества также отде-
отделены. Если Л, ВаХ отделены и А\ с=Л, Si czB, то множества
Ль В\ также отделены.
2.1.7. Теорема. Для любого ТгПространства X следующие усло-
условия равносильны:
(i) Пространство X наследственно нормально.
(и) Каждое открытое подпространство пространства X нор-
нормально.
(Hi) Для каждой пары отделенных множеств Л, В<^:Х су-
существуют открытые множества U, V cz Xy такие, что AczU%
BczV uU()V = 0.
Доказательство. Импликация (i)=^(ii) очевидна. Покажем
теперь, что (ii)=4-(iii)^ Пусть множества Л, Вс! отделены.По-
отделены.Положим М — Х\(Л П B)czX. Очевидно, что Л, BczM. Замыка-
Замыкания множеств Л и В в М не пересекаются. Следовательно, в
силу нормальности Af, существуют открытые в М множества ?/,
8*
116 ГЛ. 2. ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
V такие, что AczU, бсУи U f]V = 0. Так как М — открытое
подпространство пространства X, то множества U и V открыты
в X.
Для завершения доказательства осталось показать, что
(iii)=>(i). Пусть М — произвольное подпространство простран-
пространства X и A, BczM— пара непересекающихся замкнутых под-
подмножеств в М. Очевидно, что А и В отделены в Х\ следователь-
следовательно, существуют открытые множества U, V аХ, такие, что
A a U, BczV и U()V=0. Пересечения M(\U и Mf]V открыты
в М, не пересекаются и содержат соответственно А и В. |
Условие (iii) предыдущей теоремы показывает, что наслед-
наследственная нормальность может быть поставлена в ряд аксиом
отделимости; наследственно нормальные пространства иногда
называют Тъ-пространствамиу а элементы более узкого класса
совершенно нормальных пространств называют Те-прост ран-
ствами.
Пусть для отображения f: М-»-У, определенного на подпро-
подпространстве М пространства X, существует отображение F: X~+Yy
такое, что F\M = f. Тогда говорят, что f непрерывно продол-
продолжается, или, короче, продолжается на пространство X; отобра-
отображение F называется продолжением отображения / на X. Не вся-
всякое непрерывное отображение, определенное на некотором под-
подпространстве, имеет непрерывное продолжение на все простран-
пространство. Существование непрерывного продолжения скорее исклю-
исключение, чем правило. Теоремы, дающие достаточные условия про-
продолжимости непрерывных отображений или непрерывных веще-
вещественных функций, принадлежат к наиболее важным теоремам
топологии и обычно достаточно трудны. Заметим, что лемма
Урысона может быть переформулирована как теорема такого
типа. В самом деле, лемма Урысона утверждает, что если ка-
какое-либо подпространство М нормального пространства X мо-
может быть представлено как объединение двух непересекаю-
непересекающихся подмножеств Л, В, замкнутых в X, то функция /: ЛГ-^Д
определенная формулой
f ._ f 0 при xei,
rW"~tl при JceB,
непрерывно продолжается на X.
Оказывается, имеет место значительно более общее утвер-
утверждение:
2.1.8. Теорема Титце — Урысона. Каждая непрерывнаяфункция,
заданная на замкнутом подпространстве некоторого нормаль-
нормального пространства Ху со значениями в I или R непрерывно про-
продолжается на X.
2.1. ПОДПРОСТРАНСТВА Ц7
Доказательство. Прежде всего докажем нашу теорему для
функций из X в /. Для упрощения обозначений рассмотрим
случай /: M->Jt где / — интервал [—1, 1], гомеоморфный /.
Начнем с замечания, что для любого /0: Л1->-/?, удовлетво-
удовлетворяющего условию \fo{x)\^c при всех х^М, существует та-
такое g: X-+R, что
A) \g(x)\^c/3 при xs=X,
B) ! /0 (х) - g (х) | <2с/3 при х е= М.
В самом деле, множества Л=/г~1([—с, —с/3]) и В =
^f^1 ([^/3, с]) не пересекаются и замкнуты в Af; значит, они зам-
замкнуты в X, и, в силу леммы Урысона, существует такая функ-
функция k: X-+I, что k(A)cz{0} и k(B)cz{l}. Легко проверить,
9 / 1 \
что, полагая g(x) =-^clk{x)—^"J, мы получим g: X^~Ry
удовлетворяющее A) и B).
Определим теперь по индукции последовательность g\> g2,
непрерывных отображений X в /?, такую, что
C) lftWI<}(j)H при хеХ,
D)
Чтобы получить ?ь мы применим сделанное выше замечание
к функции fo = ijf и с —1, где fr — вложение / в R. Допустим,
чт0 8и ёь • • •> ^ Уже построены. Применяя то же самое заме-
чание к fо ='V/— I 2-i ?/1 ^и ?^B/3)'*, мы получим функцию
^ч-i» удовлетворяющую C) и D) с i+l вместо /.
со
Из C) и 1.4.7 следует, что формула F (х) = ]? g^M опреде-
I S5S 1
ляет непрерывную функцию F: X-+-J, и, согласно D), F (х) ~
^f(x) для всех jteAf. Таким образом, Т7 есть продолжение
/наХ
Теперь рассмотрим функцию /: X->-/?. В силу уже доказан-
доказанной части теоремы, функция ф M-+J, где /: /?-»-/ — гомео-
морфное вложение, определенное в 2.1.5, продолжается на X до
функции F\: X-**J. Очевидно, что множество L = F~X ({—1, 1})
есть замкнутое подмножество в X, не пересекающееся с множе-
множеством М. Следовательно, существует непрерывное отображение
k: X^I, такое, что k(L)a {0} и k(M)cz {1}. Легко видеть, что
отображение fV X-*Jf определенное формулой F2(x)—Fi(x)<
'k(x), также является продолжением отображения if на X и что
118 ГЛ. 2. ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
F2(X)cz i(R). Функция F: X-+-R, определенная соотношением
F(x)= i~lF2(x), является искомым продолжением f на X. I
Отметим, что свойство продолжимости, установленное теоре-
теоремой Титце — Урысона, характеризует нормальные пространства
в классе 7\-пространств. В самом деле, если некоторое ^-про-
^-пространство X не является нормальным, то оно содержит два не-
непересекающихся замкнутых подмножества Л, 5, которые не мо-
могут быть отделены открытыми множествами, и потому функцию
/: А[)В-+1, определенную соотношениями f(x) = O при х^А
и /(х)=1 при х^В, нельзя непрерывно продолжить на X.
Докажем еще одну теорему о продолжении отображений.
2.1.9. Теорема. Если непрерывное отображение f всюду плот-
плотного подмножества А некоторого топологического пространства
X в хаусдорфово пространство Y непрерывно продолжается на
X, то продолжение однозначно определено отображением f.
Доказательство. Пусть Fx: X~*Y и F%: X-*-Y — различные
продолжения отображения f. В силу 1.5.4, множество
замкнуто. Так как ЛсВ, то X = А си В, и потому В = X. 1
2.1.10. Пример. Применим теперь две последние теоремы, чтобы
получить простое доказательство того, что плоскость Немыц-
кого не является нормальной (ср. с примером 1.5.9). Как мы
уже знаем, плоскость Немыцкого L содержит замкнутое под-
подпространство Li, гомеоморфное D(c)9 и счетное всюду плотное
подмножество С. Из 2.1.9 вытекает, что каждая непрерывная
функция из L в R определяется своим сужением на множество
С. Таким образом, на L существует только ск° = с непрерывных
вещественных функций. Если же пространство L было бы нор-
нормальным, то каждая из 2е непрерывных вещественных функ-
функций, определенных на L\, могла бы быть продолжена на L, что
невозможно, ибо 2е > с. Следовательно, пространство L не яв-
является нормальным.
Приведенное только что доказательство, так же как и пред-
представленное в примере 1.5.9, показывает, что никакое простран-
пространство Ху удовлетворяющее условию d(X)=&0 и содержащее
D(t) в качестве замкнутого подмножества, не является нормаль-
нормальным. §
Иногда для определения отображения /: X-+-Y удобно стя-
стянуть пространство X в некоторое подпространство, а затем раз-
раздельно определить f (например, различными формулами) на
каждом из этих подпространств (ср. с примерами 1.4.4 и 1.4.5).
Мы приведем теперь два предложения, дающие условия непре-
непрерывности отображения, определенного таким образом.
2.1. ПОДПРОСТРАНСТВА Ц9
Пусть X — топологическое пространство, {Л5}5е$ — некото-
некоторое его покрытие и {fs}s<=s — семейство отображений fs: As —^ У.
Будем говорить, что отображения fs согласованы, если для лю-
любых 5Ь 52 S 5
1st \aSi П Л52 = fs2 \aSi П Л^2.
Полагая
f{x) = fs(x) для х<=Л5,
мы определим отображение f: X-+Y, которое назовем комбина-
комбинацией отображений {fs}s^s и обозначим символом V fs или
/iVf2V ... V/,, если 5 ={1,2, ...,?}.
2.1.11. Предложение. Если {Us}Sgs—открытое покрытие топо-
топологического пространства X и {/5}5SS, где fs: Us^- У, есть семей-
семейство согласованных непрерывных отображений, то комбинация
/= sj fs есть непрерывное отображение X в Y.
se=S
Доказательство. Для каждого открытого подмножества
U cz У имеем
Г'(?/)= U fs'iU).
Множество fsl(U) открыто в Us и, следовательно, в X. Отсюда
вытекает, что прообраз f~l(U) открыт в X. I
2.1.12. Следствие. Отображение f топологического пространства
X в топологическое пространство У непрерывно тогда и только
тогда, когда каждая точка xgX обладает такой окрестностью
Ux, что /| Ux непрерывно. 1
2.1.13. Предложение. Пусть {fe}isS- локально конечное зам-
замкнутое покрытие пространства X и {/s}seS, где fs: FS^Y, есть
семейство согласованных непрерывных отображений. Тогда ком-
комбинация f = V fs есть непрерывное отображение X в У.
se=S
Доказательство. Для каждого замкнутого подмножества
Fez У имеем
Г1(п= U
S
Множество fsl{F) замкнуто в Fs и, следовательно, в X. Так
как семейство {fsl(F)}Sf=s локально конечно, то, в силу 1.1.12,
/-1 (F) замкнуто в! I
2.1.14. Теорема. Пусть {F t}T=\ — счетное дискретное семейство
замкнутых подмножеств нормального пространства X. Тогда су-
существует семейство {Ui}fL{ открытых подмножеств пространства
120 ГЛ. 2. ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
X, такое, что Fi c= Ui для i = 1, 2, ... и Vt f| Uj = 0 для ? ^ /.
oo
Доказательство. Объединение М = И Ft есть замкнутое под-
пространство в X. Для каждого i положим fi(x)=i при любом
x^Fr, получим семейство {fi}T=*\ согласованных отображений
/*•: Fi->R. Таким образом, их комбинация / есть непрерывное
отображение. По теореме Титце — Урысона f продолжается до
отображения F:X-+R. Легко установить, что множества Ut =
= F-l((i—1/3, i+1/З)) обладают требуемыми свойствами. I
Мы завершим этот параграф предложением, в котором дают-
даются условия, при которых комбинация отображений замкнута или
открыта.
2.1.15. Предложение. Пусть X — топологическое пространство,
{AS}S€-S — его покрытие и {fs}s^s —семейство согласованных
отображений fs: As-+- У, такое, что комбинация f = V fs: X->7
непрерывна. Если все отображения fs открыты (замкнуты и се-
мейство {fs (A8}}s&s локально конечно), то комбинация f от-
открыта (замкнута).
Доказательство. Достаточно применить равенство
[)АЛ=[}Ш(]Аа).
5^S ) SES
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
Систематическое изучение подпространств было начато
в книге Хаусдорфа [1914]. Теорема 2.1.7, замечание о том, что
совершенно нормальные пространства наследственно нор-
нормальны, и теорема Титце—Урысона появились в работе Уры-
Урысона [1925]. Частные случаи указанной теоремы получены Ле-
Лебегом [1907] (для плоскости) и Титце [1915] (для метрических
пространств). Рассуждения, приведенные в 2.1.10, заимствованы
у Катетова [1950]. Теорема 2.1.14 есть частный случай одного
результата Куратовского [1935].
УПРАЖНЕНИЯ
2.1.А. Проверьте, что внутренность и граница произвольного
множества А в подпространстве М топологического простран-
пространства X равны соответственно
где черта сверху обозначает оператор замыкания в X. На ос-
основе этих соотношений выведите, что для любого множества
В a X граница в М пересечения М[)В содержится в пересече-
2.1. ПОДПРОСТРАНСТВА 121
нии М с границей В в Х\ отметим, что для внутренностей это не
имеет места.
2.1.В. (а) Проверьте, что если подпространство МаХ яв-
является /^-множеством (бб-множеством) в X, то множество
AczM есть /^-множество (<Зб-множество) в М тогда и только
тогда, когда оно является ^-множеством (бй-множеством)
в X.
(b) Докажите, что если подпространство MczX есть кано-
каноническое открытое (замкнутое) множество, то множество AczM
есть каноническое открытое (замкнутое) множество в М тогда
и только тогда, когда оно является каноническим открытым
(замкнутым) множеством в X.
(c) Докажите, что если подпространство М с= X является
функционально открытым подмножеством пространства X, то
множество А cz М функционально открыто в М тогда и только
тогда, когда оно функционально открыто в X. Приведите пример
функционально замкнутого множества М в тихоновском про-
пространстве Ху такого, что существует функционально замкнутое
множество в подпространстве М9 не являющееся функционально
замкнутым в J.
2.1.С.(а) Докажите, что если М — всюду плотное подпро-
подпространство регулярного пространства X, то %(х, Х) = %(х, М) для
любого х^М. Покажите, что предположение регулярности не
может быть ослаблено до предположения, что X — хаусдорфово
пространство.
(b) Семейство $(А) открытых подмножеств пространства X
называется базой множества АаХ в пространстве X, если все
элементы семейства ЗИ(А) содержат А и для любого открытого
множества V, содержащего А, существует множество U gJ(^),
такое, что Аа UczV. Характером множества А в топологиче-
топологическом пространстве X называется наименьшее кардинальное
число вида |^?(Л)|, где 3S(A) — база множества А ъ Х\ это
кардинальное число обозначается %(А, X).
Докажите, что если М — всюду плотное подпространство про-
пространства X и AczM обладает тем свойством, что для всякого
замкнутого множества BczX, не пересекающегося с Л, суще-
существуют открытые множества U, V с X, такие, что A cz U, В а V
и Uf]V = 0, то %(А,Х) = х(А,М) (ср. с теоремой 3.1.6).
Выведите из предыдущего, что если М — всюду плотное под-
подпространство нормального пространства X, то %{F,X) — %{F7M)
для всякого замкнутого подмножества F пространства X, содер-
содержащегося в М.
(c) Покажите, что если М — замкнутое подпространство про-
пространства X, то %(А Г) М, М)^ %(А, X) для любого ЛсХ Про-
Проверьте, что предположение о замкнутости М не может быть опу-
опушено.
122 ГЛ. 2. ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
(d) Покажите, что если /: Х->- У-^замкнутое отображение,
то %(f-l(B),X)^%(By У) для каждого В cz У; если f: Х-^У —
замкнутое отображение X на У, то %(f~l{B), Х) = %(ВУ У) для
каждого ВсУ, и если /: Х->У — открытое отображение, то
%(f(A), У) ^ %(А, X) для каждого Л сг X.
2.1.D. Проверьте, что подпространством топологического про-
пространства X является ретрактом пространства X в том и только
том случае, когда каждое непрерывное отображение, определен-
определенное на М, продолжается на все X, или, эквивалентным образом,
в том и только том случае, когда существует отображение
г: Х-+М, такое, что г\М = гдм-
2.1.Е.(а) (Урысон [1925]). Докажите, что нормальность яв-
является наследственным свойством по отношению к /^-множе-
/^-множествам.
Указание. Примените лемму 1.5.14.
(Ь) Докажите, что присоединением к плоскости Немыцкого
К одной точки можно получить нормальное пространство, для
которого К является подпространством.
2,1.F. Установите, что если х\, Х2, ••• — последовательность
точек в 72-пространстве X и Xq— предел этой последователь-
последовательности, то подпространство М ={xq, х\, *2, .. .}с: X либо дискретно
и конечно, либо гомеоморфно пространству Л (Ко)- Покажите,
что предположение о том, что X есть Г2-пространство, нельзя
заменить предположением о том, что X есть ^-пространство.
2.1.G. Покажите, что для любого счетного дискретного се-
семейства {Fi}f^x конечных подмножеств регулярного простран-
пространства X существует такое семейство {?/*}?j открытых подмно-
подмножеств пространства X, что Ft cz Ui для i = 1, 2, ... и Oi{\Uj = 0
для i Ф j.
2,1,Н. (а) Установите, что произвольное подпространство сек-
секвенциального пространства не обязано быть секвенциальным
пространством (ср. с примерами 1.6.19 и 1.6.20), однако замкну-
замкнутое подпространство или открытое подпространство являются
секвенциальными пространствами (ср. с упр. 2.4.G (Ь)).
(Ь) Проверьте, что любое подпространство пространства
Фреше — Урысона является пространством Фреше — Урысона,
2.1.1, Докажите, что прямая Зоргенфрея наследственно се-
парабельна.
2.I.J. Покажите, что предложение 2.1.13 и стоящая в скоб-
скобках часть предложения 2.1.15 не имеют места без предположе-
предположения о том, что рассматриваемые семейства множеств локально
конечны.
2.2, СУММЫ 123
2.2. СУММЫ
Пусть задано семейство {Xs}aeS попарно непересекающихся
топологических пространств, т. е. Xs П Х& = 0 Для 5 ф s'. Рас-
Рассмотрим множество Х= [} Xs и семейство О всех множеств
U сиХ, таких, что U (]XS открыто в Xs для каждого 5 <= S.
Легко видеть, что семейство С? удовлетворяет условиям @1) —
@3) и потому определяет некоторую топологию на множестве
X. Множество X с этой топологией называется суммой про-
странств{Х8}3^3 и обозначается ф Xs или Х\ © Хг © -. * © ^*,
если 5 = {1, 2, ..., k).
2.2.1. Предложение. Множество A с ф ЛГ5 замкнуто в том и
s e=S
только том случае, если пересечение A(]XS замкнуто в Xs для
каждого s e S.
Доказательство. Множество Л замкнуто в том и только том
случае, если его дополнение ф АУ\Л открыто. Следовательно,
наше утверждение вытекает из равенства
nXs, = Xs\(A
2.2.2. Следствие. Каждое множество Xs открыто-замкнуто в
Очевидно, что каждое Xs является подпространством суммы
ф Х5; вложение JTS в ф Is обозначается t5.
2.2.3. Предложение. ?сл« {^У5е55~ семейство попарно непере-
непересекающихся топологических пространств и As — подпростран-
подпространство Xs для каждого s e S, то две топологии, определенные на
множестве [} As> а именно топология суммы подпространств
{As}s^s и топология подпространства суммы ф Xs, совпадают.
s s5
2.2.4. Предложение. Если топологическое пространство X может
быть представлено как объединение семейства {Xs}s^s попарно
непересекающихся открытых подмножеству тоХ— ф Xs.
se=S
Доказательство. Множества X и ф Xs совпадают, поэтому
S
достаточно показать, что совпадают также их семейства откры-
открытых множеств. Если U открыто в X, то пересечение Uf\Xs от-
открыто в Xs для каждого sgS, следовательно, U открыто в
|24 ГЛ. 2. ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
ф Xs. Обратно, если U открыто в ф Xs> то для каждого
s&S s<= S
s^S пересечение Uf[Xs открыто в Xs, а потому и в X. Следо-
Следовательно, U = U (U П Xs) открыто в X. |
2.2.5. Следствие. Пусть {Xs}s^s — семейство попарно непересе-
непересекающихся топологических пространств. Если S = U $и г^е & Л
f\Str=0 для 1Ф1\ то фХ* = ф ( ф Xs\ г. в. q/лша про-
странств ассоциативна. I
2.2.6. Предложение. Отображение f суммы 0IS5 топологиче-
пространство Y непрерывно тогда и только тогда, когда
композиция fis непрерывна для каждого seS.
Доказательство. Если /: ф XS-^Y, то каждое fis непре-
S€ES
рывно как композиция двух непрерывных отображений. Об-
Обратно, если для отображения f суммы ф Xs в пространство Y
каждое fis непрерывно, то /= V fi8 непрерывно в силупред-
ложения 2.1.11. I
Сумму ф Xs можно также определить для семейства топо-
ssS
логических пространств {Is}se5, не являющихся попарно непе-
непересекающимися. Для этого возьмем семейство {1^е5 попарно
непересекающихся пространств, такое, что Х'5 гомеоморфно Х3
для всех seS, и положим ф Xs = ф х'8- Например, можно
s<~5 s&S
взять ^ = Х5Х{5} с топологией, порожденной отображением
ps: X^->ZS, где ps(x, s) = x. Читатель легко установит, что полу-
полученные таким путем пространства ф X* все гомеоморфны ме-
жду собой. В дальнейшем мы будем предполагать, что любое
семейство пространств имеет сумму (определенную с точностью
до гомеоморфизма), но в доказательствах будем молчаливо счи-
считать, что обсуждаемое семейство состоит из попарно непересе-
непересекающихся пространств.
Будем говорить, что топологическое свойство 9* аддитивно
(ш-аддитивно, конечно аддитивно), если для любого семейства
{J?s}seS (такого, что |5|^ш, |5|<К0) пространств, обладаю-
обладающих свойством ^, сумма ф Xs также обладает свойством ^\
2.2.7. Теорема. Любая сумма Тг-пространств есть Т(-пространство
для i < 6.
2.2. СУММЫ 125
Доказательство. В случае 7\-пространств наша теорема сле-
следует непосредственно из 2.2.1. Доказательства всех остальных
случаев подобны друг другу. В качестве примера покажем, что
нормальность аддитивна. Пусть {X8}s 8—семейство нормаль-
нормальных пространств и Л, В — два непересекающихся замкнутых
подмножества суммы ф Xs. В силу предложения 2.2.1, пересе-
чения А(]Х8 и В(]Х8 замкнуты в Xs для каждого s e S.
Из нормальности Х8 следует, что существуют такие множества
U8, VSy открытые в Х8, что
А П Х3си Us, В П Xscz Vs и С/, П Fs= 0.
Очевидно, что
^c=C/=U^ BczV=\JVs и t/n^=0;
так как U я V открыты в ф Я5, то сумма ф Z5, будучи
Ггпространством, является нормальным пространством. I
Легко видеть, что свойства «вес ^ш» и «плотность
оба т-аддитивны при ш^ Ко, однако не являются аддитивными
свойствами. Свойство «характер ^ш» аддитивно.
2.2.8. Примеры. Дискретное пространство D(m) есть сумма
одноточечных пространств.
Для любой точки х прямой Зоргенфрея К и любой окрестно-
окрестности U точки х прямая Зоргенфрея может быть представлена как
сумма Х\ ф Х2, где х е Х\ с= f/. В самом деле, в качестве Xi
можно выбрать интервал [х, г), содержащийся в [/, а в каче-
качестве Х% — его дополнение К\Х\. Так как Х\ открыто-замкнуто
в /С, то равенство /С — Х\@ Х% следует из предложения 2.2.4.
Вещественную прямую R нельзя представить как сумму
Xt @ X2 непустых множеств Х\, Хгс=/?. Допустим противное,
т. е. что R=X\ ф Х2 и Х\ф0фХ2. Выберем точки ^elj и
Jt2G Хг; не умаляя общности, можно считать, что Х\<Х2. Мно-
Множество Jfi Л1*ь*2] ограничено; пусть х0 — его наименьшая верх-
верхняя грань. Так как Х\ замкнуто, то хо^Х\, откуда xQ < x2. Так
как Х\ открыто, то существует такое г > 0, что (х0 — е, хо +
+ 8)cXi, и мы имеем Х\ fl(xo, х%)Ф 0 вопреки определению
наименьшей верхней грани. 1
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
Суммы топологических пространств впервые появились в ра-
работе Титце [1923]. Теоремы относительно этой операции обычно
весьма просты и принадлежат топологическому фольклору. Тем
не менее применение операции суммы иногда упрощает доказа-
доказательства и описание примеров.
126 ГЛ. 2. ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
УПРАЖНЕНИЯ
2.2.А. Покажите, что никакой непрерывный образ веществен-
вещественной прямой не может быть представлен как сумма Х\ © Х2
с Х\ Ф 0 ф Х2. Как усилить это утверждение?
2.2.В. Покажите, что свойство быть дискретным простран-
пространством есть аддитивное свойство.
2-2.С. Для X-0Xs выразите w(X)9 d(X)9 %{X) и %(х,Х)
S
S
через w (X,), d (Xs), х (Х8), % (х, Xs) и | S |.
2.2.D. (Куратовский [1921]). Пусть Хо, Х\9 ... — подпро-
подпространства прямой Ry определенные следующим образом:
и Xi =
Докажите, что пространства Yx = ( 0Х* J ©D (Ко) и У2 =
= Хо © ^i не гомеоморфны, однако каждое из них можно ото-
отобразить на другое непрерывно и взаимно однозначно.
Указание. При доказательстве того, что Y\ и Уг не гомео-
гомеоморфны, воспользуйтесь упр. 2.2.А.
2.2.Е. (а) Пусть заданы два семейства {X5}ssS и {ys}ees п0~
парно непересекающихся топологических пространств и семей-
семейство отображений {/x}seS, где fs: XS-*YS. Полагая f(x)=fs(x)
для х е Xs, определим отображение f суммы ф15 в сумму
ф Ys9 которое назовем суммой отображений {fs}8SS и обозначим
0f, или fie/я© ... ©/*, если 5 ={1,2, .... k).
Проверьте, что / непрерывно и что / замкнуто (открыто, яв-
является гомеоморфным вложением) в том и только том случае,
если все отображения fs замкнуты (открыты, являются гомео-
морфными вложениями).
(Ь) Пусть заданы семейство {^s}ses попаРно непересекаю-
непересекающихся топологических пространств и семейство отображений
ifs)s&s> где fs: Xs-*~Y. Сформулируйте условия, при которых
комбинация V fs: Ш L-^У является замкнутым или откры-
тым отображением (ср. с предложением 2.1.15).
2.2.F. Покажите, что пространство X гомеоморфно сумме
®JS в том и только том случае, если существует семейство
отображений {i'5}ssS, где is: X$-+X, удовлетворяющее следую-
следующим условиям:
A) для всякого пространства У и пары f, g непрерывных
отображений X в У если fis = gis при любом s е 5, то f = g;
2.3. ПРОИЗВЕДЕНИЯ 127
B) для всякого пространства Y и семейства отображений
{fs}SGSy где fs: XS^>Y, существует такое отображение /: X-+Y,
что fis = fs при любом sgS.
2.3. ПРОИЗВЕДЕНИЯ
Пусть {Zs}5eS — семейство топологических пространств. Рас-
Рассмотрим (декартово) произведение X = Ylxs множеств {^sLeo
и семейство отображений {p8}seS9 где ps соотносит точке
х = {х$} ^ YJ_XS ее 5-ю координату xs e Xs. Множество
-^= U.XS с топологией, порожденной семейством отображений
{Ps}seS> называется (декартовым) произведением пространств
{Is}sgS, а сама топология называется тихоновской топологией
на II^V» отображения ps: TJiX8->Xa называются проекциями,
s^ S s^S
Для любого семейства {^s}seS топологических пространств
символом XI Х8 мы будем далее обозначать не множество —
s&S
декартово произведение множеств {XJseS, а топологическое
пространство, снабженное тихоновской топологией. Произведе-
Произведение конечного семейства пространств №}f=1 обозначается также
через Х\ X Х2 X ... X Xk. Если Xs = X для любого s e S, то
произведение Ц Х5 обозначают также через Хш, где m=|S|.
Легко проверить, что пространство Хт не зависит (с точностью
до гомеоморфизма) от множества 5, а зависит только от его
мощности ш. Произведение Хт называется ш-й степенью про-
пространства Х\ произведение XX X называют также квадратом
пространства X.
2.3.1. Предложение. Семейство всех множеств XI И^
открытое подмножество пространства Xs и WS?*XS только для
конечного множества s e S, образует базу произведения Ц Xs.
Более того, если для каждого s e S фиксирована некоторая
база Ms пространства Xs, то подсемейство, состоящее из тех
XX В^я, в которых Ws e ^ яри Ws ?= ^s, также образует базу.
*5
5
Доказательство. В силу 1.4.8, семейство всех множеств вида
П Ps",1 fB^i)i гДе 5i, 52, ..., sk^S и W; открыто в Х8„ является
128 ГЛ. 2, ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
базой пространства Ц Xs. Следовательно, для доказательства
первой части предложения достаточно заметить, что
= П W.. где WS = XS при
S G: о
и что
Вторая часть есть непосредственное следствие первой части и
определения базы. 1
База пространства Ц Xs, описанная в первой части приве-
приведенного выше предложения, называется канонической базой
произведения.
Очевидно, что семейство всех множеств Ц Ws, где Ws —
открытое подмножество пространства Xs и WS=^XS только для
одного 5 е S, является предбазой произведения Ц Х$*
2.3.2. Предложение. Если {Xa}seS — семейство топологических
пространств и As — подпространство пространства XSy seS, to
две топологии, определенные на множестве А = П А$, а имен-
но топология произведения подпространств {As}Sf-s и топология
подпространства произведения XI Xs, совпадают.
Доказательство. Можно считать, что А5ф0 для каждого
sgS. Так как сужения ps\ A: A->AS проекций ps непрерывны,
то топология подпространства на А тоньше, чем топология про-
произведения (в силу определения последнего). Любое открытое
множество подпространства А есть пересечение А с объедине-
объединением семейства элементов канонической базы пространства
Ц Xs, т е. объединение пересечений А с элементами этого се-
se S
мейства. Так как каждое такое пересечение есть элемент кано-
канонической базы для Ц As> то топология произведения на А
тоньше, чем топология подпространства. I
2.3.3. Предложение. Для каждого семейства множеств {As}ssS>
где Ascz Xs, в произведении XX Xs имеет место соотношение
s<=S
vU 11 лв~
Доказательство. Из 1.1.1 следует, что jce ЦЛ5 в том в
2.3. ПРОИЗВЕДЕНИЯ 129
только том случае» если для каждого элемента Ц Ws канони-
ческой базы пространства Ц Xs, содержащего х, мы имеем
П Wa(\
seS seS seS
т. е. если для каждого s e S и любой окрестности Ws s-й коорди-
координаты точки х мы имеем W$ fl As Ф0. Последнее условие выпол-
выполняется тогда и только тогда, когда х € JJ
2.3.4. Следствие. Множество Ц Л„ где 0=5^i4scXs, замкнуто
ss=S
в произведении И Х3 тогда и только тогда, когда As замкнуто
s&S
в Xs для каждого s e 5.
Доказательство. Из предложения следует, что если все As
замкнуты, то П As также замкнуто. Обратно, если Ц As за-
s e S seS
мкнуто, то П Л5= XI As= T\_AS, и так как множества Л5 не
пусты, то As =AS для каждого se S. I
2.3.5. Следствие. Множество Ц Л5, где Л5 с: ^s =#= 0, всюду
плотно в произведении TL Xa в том и только том случае, если
S
S
As всюду плотно в Xs для каждого s gS. I
Отметим, что так как не каждое подмножество простран-
пространства Ц Xs допускает представление в виде Ц А$> то тихонов-
екая топология на произведении Ц Xs не может быть задана
оператором замыкания, определенным формулой A).
Из предложения 1.4.9 непосредственно вытекает
2.3.6. Предложение. Отображение f топологического про-
пространства X в произведение Ц Ys непрерывно тогда и только
тогда, когда композиция psf непрерывна для каждого seS, ¦
2.3.7. Предложение. Пусть {X3}S€BS — семейство топологических
пространств. Если S= [} Sit где S*f]S*' = 0 для гфУ, то
t €=Г
пространства Ц Х3 и П ( П Х8Л гомеоморфны, т. е. декар*
S€=S ti~T\$€SSt )
тово произведение ассоциативно.
^Доказательство. Поставим в соответствие точке x = {xs}&
точку f <*)«{*,}€= П f П Xs)f где xt = {xs}&
9 Зак. 697
130 ГЛ. 2. ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
^ II Xs. Определенное таким способом отображение f взаим-
но однозначно отображает пространство Ц Х5 на Ц ( Ц ХЛ .
Применяя 2.3.6, легко убедиться, что отображения f и /-1 не-
непрерывны. ¦
Отметим, что из последнего предложения следует, что про-
пространства (Хт) и Хт гомеоморфны для любого пространства
X и любого кардинального числа щ ^ No.
2.3.8. Предложение. Пусть {XS}SGS— семейство топологических
пространств и ф — взаимно однозначное отображение S на себя.
Тогда пространства Ц Xs и П Xq>{s) гомеоморфны, г. е. де-
s eS seS
картово произведение коммутативно. 1
2.3.9. Примеры. Пусть п — положительное целое число; про-
пространство Rn— произведение п экземпляров вещественной пря-
прямой— называется евклидовым п-мерным пространством. Про-
Пространство 1п — произведение п экземпляров замкнутого единич-
единичного отрезка — называется единичным п-мерным кубом. Если
m > л, то подпространство пространства Rm, состоящее из всех
точек, у которых последние m — п координат равны нулю, го-
меоморфно пространству Rn, т. е. Rn вложимо в Rm при m > п.
Подпространство пространства Rn+l, состоящее из всех точек
(хи Х2, ..., **и). таких, что х\ + х\ + ... + х%+1 = 1, называет-
называется единичной п-мерной сферой и обозначается Srt. Заменяя знак
равенства на ^ в определении (п—1)-мерной сферы, мы по-
получим подмножество пространства Rn, которое называется еди-
единичным п-мерным шаром и обозначается Вп. Одномерная сфера
S1 — это окружность, а произведение S1 X 51 — тор. 1
Для каждого непустого множества П^с П X* имеем
S 5
( ) = WSu, так что проекции ps: П Xs-+Xs — откры-
тые отображения. Приводимый ниже пример показывает, что,
вообще говоря, проекции не являются замкнутыми отображе-
отображениями (ср. с теоремой 3.1.16).
2.3.10. Пример. Проекция р: R2^~R плоскости R2 на ось х не
замкнута. В самом деле, множество F = {(x,y)^ R2: л#=1}
замкнуто в /?2, а его образ p(F) = R\{0} не замкнут в R. 1
Пусть заданы два семейства {Xs}seS и {Y8}se$ топологиче-
топологических пространств и семейство отображений {fe},eSt где fs:
Xs ->- У5. В силу предложения 2.3.6, отображение, переводящее
точку x = {xs}^ II Xs в точку {fs{xs)}€B П Ys, непрерывно.
2.3. ПРОИЗВЕДЕНИЯ 131
Оно называется декартовым произведением отображений
{f«h6? и обозначается П fs или /1Х/2Х ... Xfk, если
ssS
5 ={1,2, ..., k}. Отметим, что для декартова произведения
f = П fs имеют место соотношения
/ШлО-П/.М.) и г1(ПвЛ=Т[^(в3),
где fs: Xs -»¦ У5> Л8с15иВ5с У$.
Пусть заданы топологическое пространство X, семейство
{Ув}ве5 топологических пространств и семейство отображений
{fs}8&s* где fs: x^*Ys. В силу предложения 2.3.6, отображение,
переводящее точку хеХв точку {fs(x)}^ Ц У5, непрерывно.
Это отображение называется диагональю отображений {fs}SGS
(или диагональным отображением) и обозначается Д /5 или
fi A f2 А ... A /fe, если S ={1,2, ..., ?}. Отметим, что для диа-
диагонали f = A fs имеют место соотношения
/И)с=П/.(Л) и г' Г П А) = П П1 (Bs),
где fa: X^- Ys,AciXhBscz Ys.
Отметим также, что диагональ Д fs есть композиция диа-
гонали /= A idx : Х-+ TIXS, где XS = X для seS,H произ-
ведения Д /,: П^.-* П К.. Образ А = /A)сХ"=П ^,.
где nt = |S|, называется диагональю произведения Xm. Из 1.5.4
следует, что если X — хаусдорфово пространство, то диагональ
А= П {#<= Д xs: pS' (x) = ps// (jc)\ замкнута в Jfm.
s'» s^eS I seS i
Мы говорим, что некоторое топологическое свойство 0* муль-
мультипликативно {^-мультипликативно, конечно мультипликатив-
мультипликативно), если для любого семейства {^}5е5 (такого, что |5|<ш,
|5|< Ко) пространств со свойством 0* их произведение Ц Xs
также обладает свойством ^.
2.3.11. Теорема. Произведение Т(-пространств всегда есть Т{-про-
Т{-пространство при f^3—. Если произведение Ц Xs есть непустое
SGZS
Ti-пространство, то все Xs также являются 1(-пространствами
при i ^ 6.
9*
132 ГЛ. 2. ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
Доказательство, Для Грпространств теорема непосредствен-
непосредственно следует из 2.3.4. Доказательства мультипликативности Г«-про-
странств в случае i = 0, 2, 3 и 3-^- подобны друг другу, В ка-
качестве примера докажем, что произведение тихоновских про-
пространств {Xs}Sf-s есть тихоновское пространство. В силу пред-
предложения 1.5.8, достаточно показать, что для каждой точки
х= {xs} е П Xs и каждой ее окрестности V вида p~l (WSu), где
S G S
W^ — некоторое открытое подмножество пространства XSo,
существует непрерывная функция /: Ц Jfs->/, такая, что f(x) —
S
=0 и f(y)=l для у е И X8\V. Легко установить, что компо-
5
5
зиция fopSo, где f0: XS<>->I удовлетворяет условиям/о(#а) —0 и
fo (JTeto\Wrtfe) <= {1}, обладает требуемыми свойствами.
Рассмотрим теперь произведение XI Xs непустых пространств
S
Se=s* Выберем по точке x*s<^Xs для каждого sgSh поло-
положим по определению X*So= Ц A8t где -4s = {a:*} при s=?^s0 и
Л5о = Х5о. Очевидно, что сужение iSu = PsAX^->Xst есть гомео-
гомеоморфизм, и поэтому XSo вложимо в произведение Ц Xs. Более
ssS
того, если произведение Ц Xs есть ^-пространство, /^1, то
Xlu — его замкнутое подпространство и JC5o вложимо в Ц Xs
s sS
как замкнутое подпространство. В силу теоремы 2.1.6, отсюда
следует, что если П Xs — непустое ^-пространство, то все Xs
s<=S
являются ^-пространствами. I
Теперь мы приведем примеры, показывающие, что нормаль-
нормальность, наследственная нормальность и совершенная нормаль-
нормальность не являются конечно мультипликативными.
2.3.12. Пример. В примере 1.5.17 мы доказали, что прямая Зор-
генфрея К является нормальным пространством. Затем мы об-
обнаружили, что К совершенно нормально, а значит, и наслед-
наследственно нормально. Оказывается, декартов квадрат КУ^К не
является нормальным пространством. В самом деле, К^КК со-
содержит замкнутое подмножество, гомеоморфное пространству
Z)(c), а именно множество {(#,у): у = —х}, и счетное всюду
плотное подмножество — множество, состоящее из всех точек
КУ^К, обе координаты которых — рациональные числа. Рассуж-
Рассуждая так же, как в примере 1.5.9 или 2.1.10, мы заключаем, что
/СХ К не является нормальным.
2.3. ПРОИЗВЕДЕНИЯ 133
Заметим, что существуют совершенно нормальные простран-
пространства, квадрат которых — нормальное, но не наследственно нор-
нормальное пространство (см. упр. ЗЛО.С(с)). В примере 2.3.36, ко-
который мы приведем ниже, определяются два наследственно нор-
нормальных пространства с нормальным, но не наследственно нор-
нормальным произведением. Дальнейшая информация о нормаль-
нормальности произведений содержится в задачах 2.7.15 и 2.7.16. Спе-
Специального упоминания заслуживает тот факт, что iV*1 не яв-
является нормальным (см. упр. 3.1.Н(а)). I
2.3.13. Теорема. Если w(Xs)^m^ Ко для каждого smS и
|S|<m, то т(Цхж)^т.
Подобным же образом, если х№Хш^К0 для каждого
s&Su |S|<m, то П
Доказательство. Первая часть следует из предложения 2.3.1,
где в качестве $s можно взять любую базу пространства Xs, та-
такую, что |^|^т.
Доказательство второй части предоставляется читателю. 1
2.3.14. Следствие. Первая и вторая аксиомы счетности являются
^-мультипликативными свойствами. 1
2.3.15. Теорема Хьюитта — Марчевского — Пондицери. Если
^m S* Ко для каждого s^S и |5|<2т, то d П
Доказательство. Предположим, что пространства Xs непусты
и что |5| = 2т. Пусть А$ — всюду плотное подпространство про-
пространства XSy такое, что |Л5|^ш. В силу 2.3.5, достаточно дока-
доказать, что произведение Ц As содержит всюду плотное подмно-
жество мощности ^т. Так как декартово произведение f= Ц f$7
S
s<S
где fs — произвольное отображение дискретного пространства
D(m) на As> является непрерывным отображением пространства
D (ш)]21П на Ц А?> т0> в СИЛУ теоремы 1.4.10, доказательство
сводится к проверке того, что d([D (m)]2m) ^ tn.
Обозначим через Т m-ю степень двухточечного дискретного
пространства; тогда |Г|=2т и w(T)^m. Пусть $ — база про-
пространства Г, такая, что l^j^m, и пусть &~ — совокупность всех
конечных семейств {f/i, G2, ..., Uk} попарно непересекающихся
элементов базы ^. Очевидно, что |^"| ^ т.
В произведении [D (т)]2™ = Ц Yt, где Yt = D (m) для лю-
бого /еГ, выберем множество Л, состоящее из всех функций
134 ГЛ. 2. ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
f из Т в D(m), таких, что существует семейство {Uu &2> • -
..., Uk}^&~ со свойством: f постоянна на каждом множестве
Ui и на множестве T\(Ui[}U2\] ... lit/*). Так как |#"|<т,
то и |Л|^т.
Мы покажем, что множество А всюду плотно в [D(m)]2
т. е. для каждого непустого открытого множества V
пересечение A f| V непусто. Выберем точки tu t2, ...,
и ?U О()
m)]2 >
Г
иФ1} при i?*U и точки уи У2у .... ^еО(ш), такие, что
К
Л
Л Р*~1 {&*) с ^" ^ак как ^ — хаусдорфово пространство, то суще-
существует такое семейство {U\9 (/2, ...» Uk}^&~, что ti^Ut для
i = 1, 2, ..., &. Функция / из Т в Z)(m), определенная формулой
^ при *<=?/*, /= 1, 2, ... , k,
ух при <e7\(t/iU?/2U •-. Ut/*),
принадлежит обоим множествам Л и У, т. е. Л (] V Ф0. 1
2.3.16. Следствие. Сепарабельность является с-мультипликатив-
ним свойством. I
2.3.17. Теорема. Если d(Xs) ^ m ^ Ко для каждого s^S, то лю-
любое семейство попарно непересекающихся непустых открытых
подмножеств произведения Ц Xs имеет мощность =^т.
seS
Доказательство. Пусть {Ut}t(=T— семейство попарно непере-
непересекающихся непустых открытых подмножеств пространства
Ц Xs. Без ограничения общности можно считать, что {Ut}tf_T
состоит из элементов канонической базы пространства JI Xs,
smS
т. е. для каждого ieT существуют конечное множество StczS
и семейство {wt}SG.s, где Wl— открытое подмножество про-
пространства XSt причем Wfs= Xs при s ф St, такие, что Ut= Ц Wfs.
Выберем теперь произвольное подмножество Го cz T> удовлет-
удовлетворяющее соотношению |Г0К2т. Множество So= U $t так"
же имеет мощность ^2т. Поэтому, в силу теоремы Хьюитта —
Марчевского — Пондицери, произведение Ц Xs содержит всюду
плотное подмножество А мощности ^щ. Далее, семейство
| П Wl\ состоит из непустых открытых подмножеств про-
странства П Xs. Так как Ut= П ^tX П ^для каждого
S 5 5\S
2.3. ПРОИЗВЕДЕНИЯ 135
t е Го, то элементы семейства ( П Ws\ попарно не пере-
Ws\
5о )<
секаются, а так как каждый элемент этого семейства содержит
некоторый элемент множества Л, то |Г0|^|Л|^т. Таким об-
образом, мы доказали, что каждое множество Г0<=Г, такое, что
|Г0|:<2т, удовлетворяет соотношению |Г0|=^т. Отсюда в свою
очередь следует, что | Т | ^ ш. 1
2.3.18. Следствие. В произведении сепарабельных пространств
любое семейство попарно непересекающихся непустых откры-
открытых множеств счетно, I
Заметим, что (в противоположность условиям теоремы 2.3.17)
ограничение числа сомножителей в теореме Хьюитта —Марчев-
ского — Пондицери существенно (см. первую часть теоремы
1.5.3 и упр. 2.3.G).
Рассмотрим теперь вложения топологических пространств в
декартовы произведения. Начнем с двух определений и важной
технической теоремы, называемой теоремой о диагональном
отображении. Пусть X — топологическое пространство, {^J5ss —
семейство топологических пространств и #" = {fs}5eS — семей-
семейство отображений fs: X-+Ys. Говорят, что семейство (Г разде-
разделяет точки, если для каждой пары различных точек xr j/el
существует такое отображение /5е^", что fs(x)^fs(y). Если
для каждой точки х^Х и каждого замкнутого множества
F а X, не содержащего х> существует такое отображение fs ^ 9Г%
что fs (x) ф fs (F) у то говорят, что семейство ff* разделяет точки и
замкнутые множества. Заметим, что если X есть Го-простран-
Го-пространство, то каждое семейство &~, разделяющее точки и замкнутые
множества, разделяет и точки. В самом деле, если хФу, то су-
существует открытое множество U, содержащее ровно одну из этих
точек. Обозначим через z ту из двух точек ху у, которая не
принадлежит замкнутому множеству F=X\U. Тогда fs{z)$i
fs (F) для некоторого fs^!F, а это и означает, что fs (х) Ф
2.3.19. Лемма. Если отображение f: X-^Y взаимно однозначно
и одноэлементное семейство {/} разделяет точки и замкнутые
множества, то f — гомеоморфное вложение.
Доказательство. Достаточно показать, что для каждого зам-
замкнутого множества FaX имеет место соотношение
Если y = f(x)<=f(X)\f(F)t то x<?F и y = f(x)&f(F). Следо-
Следовательно, правая часть соотношения B) содержится в его левой
части. Обратное включение очевидно. 1
136 ГЛ. 2. ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
2.3.20. Теорема о диагональном отображении. Если семейство
#" = {/5}s€=s»/s: X-+Ys, разделяет точки, то диагональ /= Л fs:
S €5 5
Jf-> JX Ys есть инъективное отображение. Если, сверх того,
семейство 2F разделяет точки и замкнутые множества, то f —
гомеоморфное вложение,
В частности, если существует такое s&S, что fs — гомео-
морфное вложение, то f — гомеоморфное вложение.
Доказательство. Если семейство &* разделяет точки, то для
каждой пары различных точек xf у е X существует такое fs е ЯГ,
что fs(x)^=fs(y)> Таким образом, f(x)^f{y), a это и означает,
что f — инъективное отображение.
Если семейство $Г разделяет точки и замкнутые множества,
то семейство {f} также обладает этим свойством, ибо если
f(x)^fjF) для некоторого F = Fc:X, то fs(x) = psf{x)&
еps(f{F))с psf{F) = fs(F) для каждого seS. Для завершения
доказательства остается применить лемму 2.3.19. 1
2.3.21. Следствие. Если Xs — X для каждого s^S, то диагональ
i = Л id* : X -> П Xs есть гомеоморфное вложение.
s ^ S S s<=S
Следовательно, диагональ А произведения Хт гомеоморфна про-
пространству X. 1
Под графиком отображения f пространства X в У понимают
подмножество произведения X X Y, определенное формулой
2.3.22. Следствие. Для каждого непрерывного отображения
f: X-+Y график G(f) есть образ пространства X при гомеоморф-
ном вложении idxAf: X-+Xy(Y. Сужение p\G(f) проекции
р: Xy^Y^-X есть гомеоморфизм. Если Y — хаусдорфово про-
пространство, то G (/) — замкнутое подмножество пространства
XXY.
Доказательство. Первая часть следствия очевидна. Вторая
часть вытекает из того, что сужение p\G(f) есть обратное ото-
отображение к гомеоморфизму (id* A f)|A. Третья часть вытекает
из равенства G (f) = (/ X idr) —х (А), где А — диагональ простран-
пространства УХ^} и замкнутости А в пространстве УX Y. 1
Мы говорим, что пространство X является универсальным
для всех пространств, обладающих данным топологическим свой-
свойством 0>, если X обладает свойством 9> и каждое пространство,
обладающее этим свойством, вложимо в X.
Подчеркнем тот факт, что теоремы существования универ-
универсальных пространств весьма интересны и полезны. В самом
деле, они позволяют свести изучение класса пространств со свой-
2.3. ПРОИЗВЕДЕНИЯ 137
ством 3* к изучению подпространств некоторого фиксированного
топологического пространства (ср., однако, с упр. 2,3.1). Это есть
следствие того, что (как объяснялось в конце § 1.4) мы не раз-
различаем гомеоморфные между собой пространства.
Тихоновский куб веса ш ^ Ко есть пространство /т, т. е. про-
произведение Ц /s, где IS = I для каждого seS и |S| = m. Ти-
хоновский куб /к° называется гильбертовым кубом. Отметим,
что если n^m, то куб /п вложим в /т.
2.3.23. Теорема. Тихоновский куб 1Ш является универсальным для
всех тихоновских пространств веса ш ^ fc*0.
Доказательство. В § 1.5 мы установили, что замкнутый еди-
единичный интервал / является тихоновским пространством; следо-
следовательно, в силу теоремы 2.3*11, куб /т также является тихонов-
тихоновским пространством. Из теоремы 2.3.13 следует, что ад(/т)^т.
Теперь покажем, что каждое тихоновское пространство X
веса щ вложимо в /т. Так как дискретное пространство D(m) яв-
является тихоновским пространством веса т, то из этого следует,
в частности, что w(lm)^m, и это завершает доказательство
равенства w(lm) = nt.
Так как X — тихоновское пространство, то семейство всех
функционально открытых множеств является базой пространства
л. Из теоремы 1.1.15 вытекает, что существует такая база
{(/s}seS пространства X, состоящая из функционально открытых
множеств, что |S| = m. Для каждого seS рассмотрим непре-
непрерывное отображение /; X-+I, такое, что Us = f7l((O, 1]). Семей-
Семейство F = {/s}S6=5 разделяет точки и замкнутые множества. Так
как X есть Го-пространство, то из теоремы о диагональном ото-
отображении вытекает, что диагональ Л fs есть гомеоморфное вло-
жение пространства X в /т»
Начиная с этого места мы будем обозначать двухточечное
дискретное пространство DB) просто через D и будем отождеств-
отождествлять его с подпространством {0,1} вещественной прямой.
Канторов куб веса ш^ Ко — это пространство Z)ra, т. е. про-
произведение И Ds, где Ds = D для каждого seSn | S | = ш. Кан-
торов куб /)**° называется канторовьш множеством. Из приведен-
приведенной ниже теоремы 2.3.24 следует, что вес пространства ?>т ра-
равен т. В § 6,2 мы покажем, что канторов куб Dm также является
универсальным пространством для всех нульмерных пространств
веса m ^ Ко (см. теорему 6.2.16).
138 ГЛ. 2. ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
2.3.24. Теорема. Для каждого m ^ «0 « каждого х^Ощ имеет
место равенство %(х, Dm) = m.
Доказательство. Допустим, что%(лг, Dm)<n< m. Обозначим
через 3§{х) базу пространства Dm в точке xt такую, что
\3&(х)\^ъ. Так как Dm плотно в себе, то п^ *<0. Для каждого
U^38(x) будем рассматривать содержащуюся в нем окрест-
окрестность (точки х) вида Ц Wst где Ws ф Ds лишь для s, принад-
принадлежащих некоторому конечному подмножеству S(U)c:S. Полу-
Полученное таким путем семейство 3Sq{x) также является базой в
точке х и имеет мощность ^п. Множество 50= U S(U)
имеет мощность ^ п • Ко = ti < m, поэтому существует некото-
некоторое so^S\So. Очевидно, что окрестность р~1р^(х) точки х не
содержит элементов семейства $o(x)t а это означает, что $о(х)
не является базой в точке х. Ш
2.3.25. Следствие. Для каждого m^ fc*o и каждогоjcgT имеет
место равенство % (jc, /m) = т. |
Оказывается, существует универсальное пространство и для
всех Го-пространств веса m^ fc*0. Пусть F — топологическое про-
пространство, определенное в примере 1.2.8, где Х = {0, 1} и xq = 1,
т. е. /7 = {0,1} с топологией, состоящей из пустого множества,
множества {0} и всего пространства. Очевидно, что F является
Го-пространством.
Александровский куб веса т^^о — это пространство Fm»
т. е. произведение Ц Fs, где Fs = F для каждого $ е S и
Пусть U — произвольное открытое подмножество Го-простран-
Го-пространства Х\ определим непрерывное отображение /: X-+F, положив
, м _ ( 0 при х е Uу
Т(Х) \1 при xi=X\U.
Применяя теорему о диагональном отображении, легко доказать
следующую теорему.
2.3.26. Теорема. Александровский куб Fm универсален для всех
То-пространств веса ш ^ &0. Ш
Следующие четыре предложения описывают взаимосвязи
между замкнутостью и открытостью отображений {fs}S€BS> их
произведений Ц fs и их диагонали Д
2.3, ПРОИЗВЕДЕНИЯ 139
2.3.27. Предложение. Пусть произведение f = Ц fS9 где fs:
se=S
Xs-+Ys и Х5Ф0, s^S, замкнуто. Тогда все отображения fs
замкнуты.
Доказательство. Возьмем s0 e S и непустое замкнутое мно-
множество F с: XSo. Множество р~! (F) замкнуто в П Xs, поэтому
замкнут и его образ при отображении f в П Ys. Так как
f (Р;>ЧП)= П А,, где Л„ = /„(Л и As = fs(Xs)nw s^sQ, то
из 2.3.4 следует, что fsAF) замкнуто в У5о. |
2.3.28. Пример. Пусть f\ = idR — тождественное отображение
вещественной прямой на себя и /г — отображение той же пря-
прямой в одноточечное дискретное пространство {0}. Оба отобра-
отображения замкнуты, однако их декартово произведение f\ X h: R2^-
->i?X{0} не является замкнутым (ср. с примером 2.3.10). 1
2.3.29. Предложение. Декартово произведение f = П fs> г$е
/s: Xs~^ Ys и Xs ф 0 для s e 5, открыто в том и только том слу-
случае, если все отображения fs открыты и существует конечное
множество 5ос=5, такое, что /s(^s)== Ys для seS\So-
Доказательство. Из 1.4.14 и равенства / ( Ц Ws\ = XI fs{Ws)
VseS / sgS
следует, что если отображения fs удовлетворяют указанным в
предложении условиям, то отображение / открыто.
Обратно, пусть f — открытое отображение. Возьмем soeS и
непустое открытое множество U с= X . Множество U X П Xs
se5\{so}
непусто и открыто в Ц Xs- поэтому множество pSQf (U X
X П Xs] = fso {U) открыто в У5а, ибо проекция ps, — открытое
S\{} /
отображение. Отсюда следует, что отображение fS9 открыто. Так
как П Х,Ф0, то f ( П ХЛ = П fS {X8) — непустое открытое
подмножество пространства Ц Ys. Поэтому оно содержит
seS
множество вида Ц Wsi где Ws Ф Ys только для s, принадле-
жащих конечному множеству So c= 5. Тогда для 5 е 5\So мы
имеем fs{Xs)= Ys. I
2.3.30. Предложение. Пусть отображения fu f2, ..., fk> где
fr. X-+Yi, замкнуты, и пусть Y\ есть Т^пространство, а У2, Уз»
•.., Yk суть Tz-пространства; тогда диагональ f = f\ A /2 Л ...
•.. A fk замкнута.
140 ГЛ. 2. ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
Доказательство. Достаточно показать, что если ft: X-+Yi
замкнуто для 1=1, 2, где Y\ есть ^-пространство, а У2 есть
7Упространство, то f = /i Л f2 замкнуто. Возьмем замкнутое
множество АаХ и точку (yu y2) e Y\ X Y*\f(A). Так как Л П
1Ы1Ы0, то
В силу 1.4.13 и регулярности У2, существует окрестность
точки г/2, удовлетворяющая включению
Поэтому
f
откуда, опять в силу 1.4.13, следует существование такой окре-
окрестности V\ с: Y\ точки уи что
К1 (Vx) <= Х\А П /г G2), т. е. А Л /Г1 (Vi) П /г (F2) = 0.
Последнее равенство показывает, что окрестность V\ X V2 точки
(У\,У2) не пересекается с /(Л), откуда и следует замкнутость
отображения /. 1
2.3.31. Примеры. Для i = 1, 2 пусть /,- — проекция плоскости R2
на i-ю ось. Ни fi, ни f2 н^ являются замкнутыми отображениями
(см. пример 2.3.10), однако диагональ f\Af2 есть тождествен-
тождественное отображение плоскости R2 на себя и потому замкнута. Та-
Таким образом, замкнутость диагонали f\ A f2 не означает замкну-
замкнутости /i и f2.
Покажем теперь, что предложение 2.3.30 нельзя обобщить на
бесконечное множество отображений. Пусть Х = ЛГ и Yi = D =
= {0,1}, 1= 1, 2, ... . Отображения Д: 1->Уг определим, поло-
положив
/ ! при
при />f.
00
Эти отображения замкнуты, однако диагональ/= Д ft: N-
не замкнута. В самом деле, множество f(N) содержит все точки
вида @,0, ..., 0,1,1, ...), но не содержит точку @,0, ...), сле-
следовательно, f{N) не является замкнутым множеством простран-
пространства ?>*Ч Другие примеры, связанные с предложением 2.3.30,
приведены в упр. 2.3.J. I
2.3.32. Предложение. Если диагональ /= Д fs, fs: X->Ysf от-
крыта, то и все отображения fs открыты.
Доказательство. Утверждение следует из равенства fs = psf
и открытости проекций р5. ¦
2.3. ПРОИЗВЕДЕНИЯ 141
2.3.33. Пример. Пусть fx = f2 — id*: R-+R. Образ R при диаго-
диагональном отображении / = f\ A f% не открыт в R2. Таким образом,
диагональ двух открытых отображений, вообще говоря, не яв-
является открытым отображением. В этом примере сужение
f\\R: R-^f(R) есть гомеоморфизм и тем самым открытое ото-
отображение. Читателю предоставляется найти два открытых ото-
отображения f\ и f2 интервала / в себя, таких, что сужение /|/ диа-
диагонали f = /i Л /2 не является открытым. I
Из предложения 2.3.2 вытекает, что декартово произведение
гомеоморфных вложений есть гомеоморфное вложение. Легко
проверить, что если декартово произведение Ц f5, где f5:
Xs-+- Ys и Xs ф 0 для каждого s e 5, есть гомеоморфное вложе-
вложение, то все fs — гомеоморфные вложения. Теорема 2.3.20 дает до-
достаточное условие для того, чтобы диагональ была гомеоморф-
ным вложением. Несколько более изощренное необходимое и до-
достаточное условие содержится в упр. 2.3.D.
2.3.34. Предложение. Направленность Г={^,аЕ2} в произве-
произведении JI Xs сходится к точке х е Ц Xs в том и только том
s<=S s eS
случае, если направленность Г5={р5(ха), сгеЕ} сходится к
ps(x) для каждого s e S.
Доказательство. Если х е lim Г, то, в силу предложения
1.6.6, ps(x)G lim Ts для каждого s ^ S.
Обратно, предположим, что для х е Ц Х3 мы имеем
ps(x)^limTs при каждом s & S. Для каждой окрестности U
точки х существуют такие элементы s\, 52, ..., $k s S и откры-
открытые множества Ui ^XSii /= 1, 2, ... , k, что
* e P? (ид П P7tl (f,) П • • • П p-> (?/4) с t/.
По предположению существуют такие <п, ^2, ..., oa-^S, что
pSi{x0)czUi для любого а ^ <Ti и (=з 1, 2, ..., ft. Так как мно-
множество S направлено, то существует такое (Хо^ 2, что а(* ^ oq,
i == 1, 2, ..., А; для каждого а ^ а0 имеем
^ е р,-1 (с/,) п р-1 та п • • ¦ п рг; та с ^>
и, таким образом, х е lim Г. ¦
Следующее предложение является переложением предыду-
предыдущего на язык фильтров.
2.3.35. Предложение. Если g~ — фильтр в произведении Ц Xs$
s*bS
то для каждого seS семейство 3TS = {ps(F): Fg&~} есть
фильтр в Xs. Фильтр &* сходится к точке x^Y[Xs в том и
S
142 ГЛ. 2. ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
только том случае, если фильтр &~s сходится к ps(x) для каж-
каждого s gS, 1
Мы завершим этот параграф двумя важными примерами,
в построении которых решающую роль играют декартовы произ-
произведения.
2.3.36. Пример. Покажем, что нормальность не является наслед-
наследственным свойством (ср. с упр. 2.1 .Е(Ь)). Пусть Х = А(ш) и
Y = A(n)y где No<m<n (см. пример 1.4.20). Пусть, далее, х0
и{/0 — точки накопления соответственно пространств X и У. Про-
Произведение XX У есть нормальное пространство. Это вытекает из
того, что для любой пары непересекающихся замкнутых под-
подмножеств пространства XX У существует открыто-замкнутое
множество V X W d X X У, содержащее точку (xQi у0) и не пе-
пересекающееся по крайней мере с одним из замкнутых множеств,
и из нормальности подпространства ХХУХ^Х^7), которая
в свою очередь вытекает из 2.2.4 и 2.2.7. Заметим, что нормаль-
нормальность пространства XX У следует также из теорем 3.1.9 и 3.2.4,
приведенных ниже (ср. с примером 3.2.7).
Пусть Z = XX У\{(*о, Уо)}. Покажем, что для каждого не-
непрерывного отображения /*. Z-*R существуют такое веществен-
вещественное число r<=R и такие множества Хос=Х\{л;о}> Уо с: У\{{/о}>
что |Х0|^К0 |У[
D) /(*,*/) = г для (x,y)f=Z\Z0,
Для ^еДЦ положим по определению
E) YQ(x) = {y:f(x,y)^f(x,y0)}nY0 = Ц Y0(x)czY\{y0}.
Из свойства подмножества {х}Х У, установленного в примере
1.4.6, следует, что \Уо(х) |^ Ко, и, таким образом, |У0|^т.
Выберем теперь произвольное #е У\{Уо11{уо}} и определим
F) Хо = {х: f {ху у)Ф f (xo, 9)}czX\{x0}.
Снова в силу 1.4.6 получаем |X0|^S0. Пусть теперь
r = f(xo,y). Для любой точки (х, у) е Z\Z0, такой, что хфх0,
имеем, в силу E) и F),
f (х> У) = f (х, Уо) = f(xty)=f (хо, у) = г.
Из того, что множество (Z\Zo)\[{xo}X(y\{#o})] ВСК)ДУ плотно
в пространстве Z\Z0, следует, что если (jco,j/)g2\Zo, to
f(*o, y)=r. Таким образом, доказательство соотношения D) за-
закончено.
Фактически мы доказали, что подпространство ZcIX У не
является нормальным. В самом деле, множества А =(Х\{л:о})Х
Х{#о} и В ={хо}Х(У\{Уо}) не пересекаются и замкнуты в Z.
Так как для каждого множества Zo, определенного в D), мы
2.3. ПРОИЗВЕДЕНИЯ 143
имеем A\Zo Ф 0 ф B\Z0, то из D) же следует, что не су-
существует непрерывной вещественной функции на Z, равной нулю
на Л и единице на В. Ш
Этот пример является шагом на пути построения регуляр-
регулярного пространства, не являющегося вполне регулярным (см. при-
пример 2.4.21). Тот факт, что Z не является нормальным, можно-
установить непосредственно, показав, что множества А и В
нельзя отделить непересекающимися открытыми множествами.
Это же рассуждение можно провести при более общем предполо-
предположении &о ^ ш < и; читателю рекомендуется восполнить детали.
2.3.37. Пример. В § 1.6 мы описали два счетных пространства, не
удовлетворяющих первой аксиоме счетности. Каждое из них
имело характер =^fc*o во всех точках, кроме одной (ср.
с упр. 2.3.Е).
Из 2.3.16 следует, что канторов куб Dc = Ц Ds, где Ds = D
S€=S
для любого sgS и |S| = c, содержит всюду плотное счетное
подпространство X. Мы докажем, что %(xtX)> Ko для каждого
л;е! (отметим, что из теоремы 2.3.34 и упр. 2.1.С (а) полу-
получается даже больше, а именно что %(х,Х) = с). Для этого до-
достаточно показать, что для каждой последовательности U\9 U2, .. ¦
окрестностей точки хеХ существует такая окрестность U czX
точки х, что
G) и!\иФ0 для i = l, 2, ....
Для каждого i=l, 2, ... существуют конечное множество
StczS и семейство {tFl}S€=s непустых подмножеств пространства
Д такие, что Ws^D для s e S\S* и
(8) X П ТТ Wi cz ?/,.
seS
оо
Выберем некоторое soeS\ (J St и рассмотрим окрестность
U = Xflp;*pSt(x) точки л:. Множество (Dc\p~lpSt(x))n ~[[wi не-
пусто и открыто в Dc для 1=1, 2, ... , поэтому, в силу всюду
плотности X в ?>с, имеем (Х\?/)П ПС^Э. что вместе с (8)
дает соотношение G).
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
По сравнению с другими операциями на топологических про-
пространствах операция произведения приводит к наиболее интерес-
интересным теоремам, примерам и задачам. Декартово произведение
144 ГЛ. 2. ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
(конечного числа многообразий) появилось впервые в работе
Штейница [1908]. Фреше [1910] первым рассматривал (конеч-
(конечное) декартово произведение абстрактных пространств. Конеч-
Конечные и счетные произведения метрических пространств принад-
принадлежат к топологическому фольклору 20-х годов. Произведение
произвольного множества топологических пространств было оп-
определено Тихоновым [1930]. Теорему 2.3.15 доказали Пондицери
[1944], Хьюитт [1946], а также (для щ= No) Марчевский [1947].
Следствие 2.3.18 было установлено Марчевским [1947] (при бо-
более сильных предположениях: для пространств со второй аксио-
аксиомой счетности [1941]). Теорема 2.3.17 есть следствие более силь-
сильного результата Шанина, сформулированного здесь в задаче
2.7.11 (Ь). Теорема 2.3.23 была доказана Тихоновым [1930], а
теорема 2.3.26 — Александровым [1936]; связанные с ними ре-
результаты имеются в упр. 2.3.1 и задачах 2.7.7, 2.7.8 и 2.7.18 (Ь).
Пример 2.3.12 был построен Зоргенфреем [1947].
УПРАЖНЕНИЯ
2.З.А. Покажите, что для любых двух семейств{^5}sesH^*Ь<=г
топологических пространств пространства ( ф ХЛ X ( (В YA
и © (ISX Yt) гомеоморфны. Обобщите этот результат на
se5, t<=T
произвольную совокупность семейств топологических про-
пространств.
2.З.В. (а) Проверьте, что для любых ЛсХ и 5сУ в про-
произведении XX Y справедливы соотношения
Int(AXB)=lniAXlntB, Ft(AXB) = (AX1FtB)\j(FvAXB).
(b) Докажите, что если As есть ^-множество (бб-множе-
ство) в Xs для любоп sgSh |5|< «о A51 < Ко), то Ц As
есть Ро-множество (бб-множество) в произведении Ц Xs- За-
метим, что в обоих случаях предположение о мощности S су-
существенно.
(с) Докажите, что если At — каноническое открытое (замкну-
(замкнутое) множество в Xit /=1, 2, ..., k, то А\ХА2Х ... X^k —
каноническое открытое (замкнутое) множество в произведении
Х\ХХ2Х ..• X^ft. Заметим, что предположение о конечности
произведения существенно.
2.З.С. (а) Покажите, что X — хаусдорфово пространство в
том и только том случае, если диагональ А произведения XX X
замкнута в X X X (ср. с упр. 2.4.С (с)).
Проверьте, что диагональ А произведения XX% открыта в
2.3. ПРОИЗВЕДЕНИЯ 145
тогда и только тогда, когда пространство X дискретно
(ср. с упр. 2.4.С (Ь)).
(Ь) Приведите пример разрывной функции f прямой R в себя,
такой, что график G(f)— замкнутое подпространство плоскости
R2 (ср. со следствием 2.3.22 и упр. 3.1.D).
2.3.D. Докажите, что диагональ /= A fs, где fs: X-*YS>
S
является гомеоморфным вложением в том и только том случае,
если семейство {fs}S€=s РазДеляет точки, а семейство {/г)ге^>
где !Г — семейство всех конечных подмножеств множества 5 и
/г= Д fs> разделяет точки и замкнутые множества.
2.З.Е. Пусть X — счетное пространство, не имеющее счетной
базы в точке лс0. Покажите, что подпространство пространства
Х*°> состоящее из всех точек {х$, таких, что Xt = xo для каж-
каждого i, большего некоторого целого /, является счетным и не
имеет счетной базы ни в одной из своих точек.
2.3.F. (а) Докажите, что вес бесконечного произведения
Х= Ц Xs, где w(Xs)> 1, равен большему из двух кардиналь-
ных чисел |5| и sup{ay(Zs)}.
(b) Докажите, что для точки x={xs} бесконечного произ-
произведения Х= IXXs, где Xs есть ^-пространство и |Jfs|> 1, ха-
S
рактер %(xtX) равен большему из двух кардинальных чисел \S\
и sup{x(*s, Xs)}.
S
2.3-G. (Пондицери [1944], Марчевский [1947]). Докажите,
что произведение Х= П^> где Xs является Г2-пространством
S
S
и \Х$\ > 1, не сепарабельно, если \S\ > с.
2.3. Н. Покажите, что пространство X гомеоморфно произве-
произведению П Х$ в том и только том случае, если существует семей-
S
ство отображений {/?5}ssS, где ps: X-*~XS, удовлетворяющее сле-
следующим условиям:
A) Для любого пространства Y и пары ft g: Y-+X непре-
непрерывных отображений если psf == psg для каждого s e S, то
B) Для любого пространства У и любого семейства отобра-
отображений {fs}s&$9 где fs: Y-^XSt существует такое отображение
f: Y -> X, что psf = fs для каждого s e 5.
2.3.1. Пусть ? — топологическое пространство, определенное
в примере 1.2.10, где Х = {0, 1,2} и Хо=={0}, т. е. пусть ? =
= {0,1,2} с топологией, состоящей из пустого множества, мно-
Ю Зак. 697
146 ГЛ. 2. ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
жества 0 и всего пространства. Покажите, что пространство Еш
универсально для всех топологических пространств веса щ ^ So*
2.3J. (а) Пусть X — тихоновское пространство, не являю-
являющееся нормальным, и пусть Л, В — два непересекающихся
замкнутых подмножества пространства Ху которые нельзя отде-
отделить непересекающимися открытыми множествами. Обозначим
через Х\ и Х2 пространства, полученные из X отождествлением
соответственно Л и В в точку (см. примеры 1.4.17 и 2.4.12). Пусть
ft — естественное отображение X на Xlt i = 1, 2. Установите, что
Х\ и Х% суть Г2-пространства и что f\ и /2— замкнутые отобра-
отображения, но диагональ f\ A f2 не является замкнутой. Убедитесь,
что даже для k = 2 предположение о регулярности в предложе-
предложении 2.3.30 нельзя ослабить до предположения о том, что У2, Уз, ...
..., Yk — хаусдорфовы пространства.
(b) Пусть y1=F={0,1} с топологией, состоящей из пу-
пустого множества, множества {0} и всего пространства, и пусть
У2 = Л(К0) с единственной точкой накопления */0- Положим
Х = У!ХУ2\{@, уо)} и fi = pc\X: X-+Yh где р,— проекция
пространства Y\ X У2 на У*, i = 1, 2. Проверьте, что оба отобра-
отображения f\ и f2 замкнуты, однако диагональ fi А /2 не замкнута.
Установите, что условие в предложении 2.3.30 о том, что Y\
есть ^-пространство, нельзя ослабить до условия, что Y\ есть
Го-пространство.
(c) Видоизменяя пример из (а), определите замкнутые ото-
отображения f\ и f2 тихоновского пространства X соответственно
в хаусдорфовы пространства У! и У2 таким образом, чтобы су-
сужение f\X: X-*f(X) диагонали / = /iAf2 не было замкнутым.
Аналогично видоизмените (Ь) и вторую часть 2.3.31.
2.3.К (Франклин [1965] и [1967]). (а) Установите, что про-
произведение ХУ^Х, где X есть пространство Фреше — Урысона из
упр. 1.6.Е, не является секвенциальным пространством (ср.
с упр. 2.4.G (с) и 3.10.1 (Ь)).
Указание. Примените упражнение 2.3.С (а).
(Ь) Проверьте, что произведение X X У, где 1=/и У есть
пространство Фреше — Урысона из примера 1.6.18, не является
пространством Фреше — Урысона (из упр. 3.10.1 (Ь) следует,
что это произведение является секвенциальным пространством).
2.3.L. (а) Покажите, что если некоторое топологическое свой-
свойство & наследственно по отношению к открытым и замкнутым
множествам и счетно мультипликативно, то в классе хаусдор-
фовых пространств свойство 9* наследуется Gg-множествами.
(Ь) (Ван дер Слот [1966]). Покажите, что если некоторое
топологическое свойство 9* наследственно по отношению к замк-
замкнутым и открытым множествам и мультипликативно, то, когда
замкнутый интервал / обладает свойством #*, им обладают и все
тихоновские пространства.
2.4. ФАКТОРПРОСТРАНСТВА И ФАКТОРНЫЕ ОТОБРАЖЕНИЯ 147
2.4. ФАКТОРПРОСТРАНСТВА
И ФАКТОРНЫЕ ОТОБРАЖЕНИЯ
Пусть X — топологическое пространство и Е — некоторое от-
отношение эквивалентности на множестве X. Обозначим через
Х/Е множество всех классов эквивалентности отношения Е, а
через q— отображение множества X на Х/Еу ставящее в соот-
соответствие каждой точке х^Х ее класс эквивалентности [х]е
g!/?. В поисках хорошей топологии на Х/Е резонно потре-
потребовать, чтобы отображение q было непрерывным. В классе всех
топологий на Х/Е, относительно которых q непрерывно, суще-
существует самая тонкая: это семейство всех множеств U, таких, что
q~l(U) открыто в X. Эта топология называется фактортополо-
гией, множество Х/Е, снабженное этой топологией, называется
факторпространством, a q: X-+X/E — естественным факторным
отображением или, коротко, естественным отображением.
2.4.1. Предложение. Множество F в факторпространстве Х/Е
замкнуто тогда и только тогда, когда q~l (F) — замкнутое под-
подмножество пространства X.
Доказательство. Предложение следует из равенства
2.4.2. Предложение. Отображение f факторпространства Х/Е в
топологическое пространство Y непрерывно тогда и только тогда,
когда непрерывна композиция fq.
Доказательство. Пусть f непрерывно; тогда fq также непре-
непрерывно. Обратно, пусть fq непрерывно; тогда для каждого от-
открытого множества U с= У множество (fq)-l(U) — q~lf~l{U) от-
открыто в X, а это означает, что f-l(U) открыто в Х/Е. I
Пусть X и Y — топологические пространства и f — непрерыв-
непрерывное отображение X на Y. Рассмотрим отношение эквивалентности
E(f) на множестве Ху определенное разложением {f~x(y)}y&Y
пространства X на прообразы одноточечных подмножеств У при
отображении f. Отображение /: Х->-У можно представить как
композицию fq, где q: X-+X/E(f) — естественное отображение,
a f — отображение факторпространства X/E(f) на У, заданное
формулой f(f~l(y)) = у. Отображение f непрерывно в силу
2.4.2. Следующая диаграмма наглядно иллюстрирует сказанное:
X 1 **y
X/E(f)
10*
148 ГЛ. 2. ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
Очевидно, что f — взаимно однозначное непрерывное отображе-
отображение пространства X/EQ) на У, но, вообще говоря, не гомеомор-
гомеоморфизм. В самом деле, если / — взаимно однозначное отображение
дискретного пространства Х = ?>(с) на интервал У = /, то фак-
торпространство X/E(f) также дискретно, поэтому f не является
гомеоморфизмом. Теперь попытаемся изучить класс всех таких
отображений /, что ] — гомеоморфизм. Оказывается, эти отобра-
отображения порождают совместное обобщение замкнутых и открытых
отображений (среди отображений «на»).
Непрерывное отображение f: Х-> У пространства X на У на-
называется факторным отображением (или факторотображением),
если оно есть композиция естественного отображения и некото-
некоторого гомеоморфизма, т. е. если существуют такое отношение
эквивалентности Е на множестве X и такой гомеоморфизм
/': X/E-+Y, что f — f'q, где q: X-+X/E — естественное отобра-
отображение.
2.4.3. Предложение. Для отображения f топологического про-
пространства X на топологическое пространство У следующие усло-
условия равносильны:
(i) Отображение f есть факторотображение.
(и) Множество f~l{U) открыто в X тогда и только тогда,
когда U открыто в У.
(iii) Множество f~l(F) замкнуто в X тогда и только тогда,
когда F замкнуто в У.
(iv) Отображение f: X/E(f)-> У есть гомеоморфизм.
Доказательство. Пусть f — факторотображение, т. е. f = f'q,
где /': X/E-+Y— гомеоморфизм, a q: X-+X/E — естественное
отображение. По определению фактортопологии множество
/-1 ([)) = <pi(f')~l(U) открыто в X тогда и только тогда, когда
(^)-!({/) открыто в Х/Е\ так как f — гомеоморфизм, то послед-
последнее утверждение имеет место тогда и только тогда, когда U от-
открыто в У. Итак, мы доказали, что (i) =>* (ii).
Импликация (ii)=^(iii) следует непосредственно из равенства
fi(F) X\f*(Y\F)
f() f()
Пусть теперь f удовлетворяет условию (iii). Так как отобра-
отображение f: X/E(f)-+ У взаимно однозначно, то для доказательства
(iv) достаточно показать (см. предложение 1.4.18), что для
каждого замкнутого FczX/E(f) множество f(F) замкнуто в У.
Но f-l](F)=q~lf-lf{F)=q-l(F) замкнуто в X, поэтому множе-
множество f (F) замкнуто в У в силу (iii).
Импликация (iv)=^(i) очевидна. I
2.4.4. Следствие. Композиция двух факторотображений есть фак-
факторотображение. 1
2.4.5. Следствие. Пусть композиция gf непрерывных отображений
2.4. ФАКТОРПРОСТРАНСТВА И ФАКТОРНЫЕ ОТОБРАЖЕНИЯ 149
/: X-+Y и g: Y-+Z есть факторотображение; тогда g: Y-+-Z
есть факторотображение.
Доказательство. Очевидно, что g(Y) = Z, ибо (gf) (Х) = Z.
Если прообраз g~l(U) множества V с= Z открыт в У, то
f~l(g-l(U)) — (gf)-l(U) открыто в X, и тогда U открыто в Z,
так как gf — факторотображение. 1
Легко проверить, что если композиция gf есть факторное
отображение, то отображение / (даже если оно есть отображе-
отображение «на») не обязательно является факторным.
2.4.6. Следствие. Если для непрерывного отображения /: X-+Y
существует такое множество AczX, что f(A)=Y и сужение
f\A есть факторотображение, то и f — факторотображение.
Доказательство. Это вытекает из 2.4.5 и равенства f\A =
/4 1
2.4.7. Следствие. Любое взаимно однозначное факторотображе-
факторотображение есть гомеоморфизм. Ш
2.4.8. Следствие. Замкнутые отображения «яа» и открытые ото-
отображения «наъ суть факторотображения.
Доказательство. Если /: Х->У— отображение «на», то
//-I (В) = В для любого В cz У. 1
В связи с последним следствием встает вопрос, каким обра-
образом охарактеризовать те отношения эквивалентности, для кото-
которых естественное факторотображение замкнуто или открыто. На
этот вопрос отвечает следующее предложение.
2.4.9. Предложение. Пусть Е — некоторое отношение эквивалент-
эквивалентности на топологическом пространстве X; тогда следующие усло-
условия равносильны:
(i) Естественное отображение q: X-+X/E замкнуто (от-
(открыто) .
(ii) Для любого замкнутого (открытого) множества AczX
объединение всех пересекающихся с ним классов экви-
эквивалентности замкнуто (открыто) в X.
(Ш) Для любого открытого (замкнутого) множества AczX
объединение всех содержащихся в нем классов эквива-
эквивалентности открыто (замкнуто) в X.
Доказательство. Равносильность (i) и (ii) следует из пред-
ложения 2.4.1 и определения фактортопологии. Равносильность
(ii) и (ш) есть непосредственное следствие законов де Мор-
Моргана. Ш
2.4.10. Следствие. Факторотображение f: X-+Y замкнуто (от-
(открыто) в том и только том случае, если множество f-lf(A)czX
замкнуто (открыто) для любого замкнутого (открытого) АаХ.Ш
150 ГЛ. 2. ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
Отношение эквивалентности Е на пространстве X называется
замкнутым (открытым), если замкнуто (открыто) естественное
отображение q: Х-*Х/Е. Условия (и) и (ш) предложения
2.4.9 дают внутреннюю характеристику замкнутых и открытых
отношений эквивалентности. Из условия (И) следует, что клас-
классы эквивалентности замкнутого отношения эквивалентности на
^-пространстве суть замкнутые множества.
Как известно, существует взаимно однозначное соответствие
между отношениями эквивалентности на некотором множестве
и разбиениями этого множества на непересекающиеся подмно-
подмножества. Иногда удобнее сразу пользоваться разбиениями, а не
отношениями эквивалентности. Разбиения, соответствующие
замкнутым (открытым) отношениям эквивалентности, называют-
называются полунепрерывными сверху (снизу) (о происхождении этой
терминологии см. задачу 1.7.17 (а)). В этом контексте также
часто используется слово «отождествление» (главным образом
в связи с полунепрерывными сверху разбиениями): говорят, что
факторпространство Х/Еу где Е — отношение эквивалентности,
соответствующее разбиению <?f, получается отождествлением
каждого элемента & в некоторую точку.
2.4.11. Пример. Пусть отображение /: R^S1 определено равен-
равенством / (х) = (cos 2nx9 sin2n.x;). Очевидно, что для х, у е R мы
имеем xE(f)y в том и только том случае, когда разность
х — у есть целое число. При отображении f вещественная
прямая наматывается на единичную окружность таким обра-
образом, что каждый интервал (л:, у] длины 1 обходит всю окруж-
окружность ровно один раз (т. е. на этом интервале отображение
взаимно однозначно). Очевидно, что f переводит открытые ин-
интервалы (xt у), у — х < 1, на открытые дуги окружности S1, и,
следовательно, f есть открытое и тем более факторное отобра-
отображение. Отсюда следует, что факторпространство R/E(f) гомео-
гомеоморфно S1. Читателю предоставляется убедиться, что / не
замкнуто.
Сужение g = f\I: I-*Slt как легко проверить, есть замкну-
замкнутое (но не открытое) отображение. В частности, g— фактор-
отображение и факторпространство I/E(g) гомеоморфно S1.Раз-
S1.Разбиение замкнутого интервала /, соответствующее E(g)t состоит
из всех одноточечных множеств х, 0 < х < 1, и множества {0,1}.
Таким образом, факторпространство 51 получается отождествле-
отождествлением обоих концов / в точку. Читатель может легко проверить,
что декартово произведение gXg: I2-*SlXSl также является
факторотображением, и определить, какие отождествления в
квадрате необходимо сделать, чтобы получить тор. 1
Используя язык факторпространств, мы дадим теперь точное
описание операции отождествления замкнутых множеств в точ-
2.4. ФАКТОРПРОСТРАНСТВА И ФАКТОРНЫЕ ОТОБРАЖЕНИЯ 151
ки, которая была применена выше при построении нескольких
примеров (см. пример 1.4.17, замечание, предшествующее при-
примеру 1.5.21, и упр. 2.3.J (а)).
2.4.12. Пример. Пусть X — некоторое топологическое простран-
пространство, и пусть Аи А2, ..., Ак — последовательность попарно не-
непересекающихся замкнутых подмножеств пространства X. Обо-
Обозначим через Е отношение эквивалентности на Х9 соответствую-
соответствующее разбиению X на множества Ль А2у ..., Ak и одноточечные
множества {х}, где х е Я\ (А г [} А2 [} ... (J Ak). Для каждого
замкнутого множества АсХ объединение всех классов эквива-
эквивалентности, пересекающихся с Л, равно объединению А и тех из
Л,, для которых А{[\АФ0. Это объединение есть замкнутое
множество, и естественное отображение q: X-+X/E замкнуто
в силу 2.4.9. Факторпространство Х/Е получается из X отож-
отождествлением каждого из множеств Л,- в точку q(A{). Легко пока-
показать, что множества Jf\(Лi U ... \}Ak) и X/E\{q(Ai),
q(A2), ..., q{Ak)} гомеоморфны (см. предложение 2.1.4). Про-
Пространство, полученное отождествлением в точку только одного
замкнутого подмножества АаХ, обозначается Х/А. U
Рассмотрим теперь важный частный случай построения фак-
торпространства — так называемое присоединенное простран-
пространство. Пусть X и У— два непересекающихся топологических про-
пространства и /: M-+Y — непрерывное отображение, определен-
определенное на замкнутом подмножестве М пространства X. Обозначим
через Е отношение эквивалентности на сумме X@Y, соответ-
соответствующее разбиению пространства X Ф У на одноточечные мно-
множества {х}, х^Х\М, и множества вида {у)\})~х(у), где j/e У
(если //g Y\f(M), то последнее множество есть одноточечное
множество {у}). Факторпространство (X® Y)/E называется при-
присоединенным пространством, определенным пространствами X,
У и отображением /, и обозначается X[)f У. Легко видеть, что
если У — одноточечное пространство, то X[)fY гомеоморфно
пространству Х/М.
Пусть ix: X-+X&Y и iY: У->ХФ У— вложения X и У в
пространство X © У, и пусть q: X®Y-+X[]fY — естественное
отображение. Композиции
j = qix: X-+X[)fY и k = qiY: У-
непрерывны и множество С с= X Uf У открыто (замкнуто) в том
и только том случае, если г1 (С) и k~l(C) открыты (замкнуты)
соответственно в X и У. Легко проверить, что
A) /-1^E) = ^1E) и к-щВ) = в для BczY,
B) rlj(A) = A[)f^f(A(]M) и кгЩА)=*ПА()М) для
152 rj*. 2. ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
Из формул A) следует, что k\ У-^XUf У есть замкнутое отобра-
отображение. Так как k инъективно, оно является гомеоморфным вло-
вложением. Образ k(Y) замкнут в X[jf У. Аналогично, из формул
B) вытекает, что /JX\A1— открытое отображение. Так как
/|Х\М инъективно, оно является гомеоморфным вложением, а
образ j(X\M) есть открытое множество в X\jf Y и является до-
дополнением множества k(У). Из формул B) также следует, что
I — замкнутое отображение в том и только том случае, если
замкнуто отображение /. Поэтому факторотображение q:
X® Y -*• X[)fY замкнуто тогда и только тогда, когда замкнуто
отображение /.
Если, кроме того, /(Л1)=У, то j(X) = X\]fY, а так как
замкнутость / влечет за собой замкнутость /, то имеет место сле-
следующая теорема.
2.4.13. Теорема. Пусть М — замкнутое подпространство про-
пространства X и JS — полунепрерывное сверху разбиение множе-
множества М\ тогда разбиение пространства X на элементы с? и од-
одноточечные множества {х}, хеАМ, полунепрерывно сверху. I
Операция образования факторпространства сохраняет мало
топологических свойств по сравнению с операциями, изученными
в § 2.1—2.3. Очевидно, что сохраняются в точности те топологи-
топологические свойства, которые инвариантны при факторотображе-
ниях. Так как и замкнутые, и открытые отображения «на» фак-
факторные, то инварианты факторотображений являются инвариан-
инвариантами замкнутых и открытых отображений. Следовательно, среди
топологических свойств, инвариантность которых обсуждалась
в § 1.4 и 1.5, только свойство «плотность =^т» могло бы со-
сохраняться факторными отображениями. Как мы знаем (теорема
1.4.10), это свойство сохраняется даже всеми непрерывными
отображениями. Чтобы получить факторпространство Х/Е с хо-
хорошими топологическими свойствами, обычно налагают дополни-
дополнительные условия на классы эквивалентности отношения Е или
на их взаимосвязи. Такие условия могут быть выражены в виде
дополнительных свойств естественного отображения, соответ-
соответствующего ?. Например, как легко видеть, факторпространство
Х/Е является ^-пространством в том н только том случае, когда
классы эквивалентности замкнуты в X, а из теоремы 1.5.20 сле-
следует, что если X нормально и отношение эквивалентности Е на
X замкнуто, то и факторпространство Х/Е нормально.
2.4Л4. Предложение. Факторпространство некоторого фактор-
пространства пространства X является факторпространством
пространства X.
Точнее, если Е — отношение эквивалентности на простран-
пространстве Х9 а Ег — отношение эквивалентности на факторпростран-
2.4. ФАКТОРПРОСТРАНСТВА И ФАКТОРНЫЕ ОТОБРАЖЕНИЯ 153
стае Х/Еу то отображение q'q\ X/E(q'q)->(X/E)/E', где
q: Х-+Х/Е и qr\ Х/Е-+(Х/Е)/Е'— естественные факторотобра-
женил, является гомеоморфизмом.
Доказательство. В силу 2.4.4, композиция qfq есть фактор-
отображение. Следовательно, q'q— гомеоморфизм в силу равно-
равносильности условий (i) и (iv) в предложении 2.4.3. Ш
Пусть X — некоторое топологическое пространство и Е — от-
отношение эквивалентности на X. Тогда на любом подпростран-
подпространстве Л пространства X определено отношение эквивалентности
Е\А=(АУ,А){\Е — сужение Е на Л, причем E\A=E(q\A),
где q: X-+X/E — естественное отображение. Возникает вопрос,
будет ли отображение q\A: A{(E\A)-+q(A)c:XlE гомеоморфиз-
гомеоморфизмом. Очевидно, что этот вопрос равносилен такому: будет ли
сужение/| Л: Л->/(Л) факторного отображения / факторным
отображением. Как показано в примерах 2.4.16 и 2.4.17 ниже,
ответ, вообще говоря, отрицателен. Заметим, однако, что из
предложения 2.4.3 немедленно получается следующий положи-
положительный результат (ср. с упр. 2.4.F).
2.4.15. Предложение. Если f: X-*Y — факторотображение, то
для любого открытого или замкнутого множества В с= У сужение
[я: f-l(B)-> В есть факторотображение.
Другими словами, если Е — некоторое отношение эквивалент-
эквивалентности на пространстве X, то для любого открытого или замкну-
замкнутого множества ЛсХ, удовлетворяющего условию qrxq(A) = A,
где q\ X^-X/E — естественное отображение, отображение q\A:
А/(?|Л)-ьq(A)с= Х/Е есть гомеоморфизм. I
2.4.16. Пример. Пусть g: I-+S1— факторотображение, опреде-
определенное в 2.4.11. Сужение g\A: A-+g(A) = Sl на открытое под-
подмножество Л=@, 1]с:/ взаимно однозначно, но не является
гомеоморфизмом, следовательно, g\A не является факторото-
бражением. Более того, комбинацияh = \&s*4{g\A): Sl®A-*Sl
есть факторотображение в силу следствия 2.4.6, ибо A|5I = ids«,
однако сужение h\A = g\A на открыто-замкнутое подмноже-
подмножество Аа S1 (В А факторотображением не является. I
2.4.17. Пример. Пусть Х=(о, у] U { Ь 1 + », 1 +у, ••¦}
с топологией, индуцированной из R, и пусть Е — отношение
эквивалентности на X, определенное следующим образом: хЕу
в том и только том случае, когда \х — z/j= 1 или х = у. Легко
заметить, что множество Л = {1} u[(o, у] xly, j, ...jlc^f
имеет вид qrl(B) для B = q(A)czX/E, a сужение qB: A-*q(A)
взаимно однозначно. Так как 1 — изолированная точка в Л, а
154 ГЛ. 2. ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
?вA) не изолирована в q(A), то сужение qB не является гомео-
гомеоморфизмом, а потому не является и факторотображением.
Читатель легко установит, что если ограничиться соответ-
соответствующим счетным подпространством пространства X, то можно
получить в качестве факторпространства пространство примера
1.6.19 (ср. с упр. 2.4.G(a)). 1
2.4Л8. Предложение. Пусть X— топологическое пространство,
{А3}3€в3— некоторое его покрытие и {f^s^s —семейство со-
согласованных отображений fs: AS^>~Y, такое, что комбинация
f= у fs:X^>~Y непрерывна. Если существует такое множество
So с: S, что сужения fs\As: As->fs(As) суть факторотображения
для s^So и {fs(As)}SGSa является либо открытым покрытием
пространства У, либо его локально конечным замкнутым по-
покрытием, то комбинация f есть факторотображение.
Доказательство* Пусть {fs(As)}Sf=Sa — открытое покрытие про-
пространства У, и пусть прообраз fl (U) множества U czY от-
открыт в X. Так как множество As[\f~x(U) = {fs\As)~x(U[\fs(As))
открыто в ASi то для каждого 5eS0 множество U{]fs(As)
открыто в fs(As), а потому и в У. Следовательно, объединение
[} U(]fs (As) = U П U /, (As) = U(]Y = U открыто в У. Подоб-
seSo seSfl
ным же образом доказывается, что если {/5(Л5)}5е5о—локаль-
{/5(Л5)}5е5о—локально конечное замкнутое покрытие пространства У, то из замкну-
замкнутости f~l(F) в X следует замкнутость F в У. В обоих случаях
утверждение о том, что / — факторотображение, следует из пред-
предложения 2.4.3. I
Пусть теперь {Xs}5eS — семейство топологических про-
пространств и Es — отношение эквивалентности на Xs для каждого
s e S. Определим отношение эквивалентности Е на произведе-
произведении Ц Xs, полагая {xs}E{ys} в том и только том случае, когда
s<=S
xsEsys для каждого sgS. Отношение Е называется (декарто-
(декартовым) произведением отношений {ES}S€.S и обозначается XI Es
S €= S
или Z^X^X ... X?fc, если S={1,2, ..., k}. Легко видеть,
что XI ?$ = ?A1 <7sV гДе <7*: Xs^>~Xs/Es — естественное ото-
s e S \ssS /
бражение. Возникает вопрос, является ли отображение Ц qs:
ss=S
П Xs/Yi Es-+ П (Xs/Es) гомеоморфизмом. Очевидно, что
этот вопрос равносилен такому: является ли декартово произве-
произведение факторотображений факторотображением. Как показано
в примере 2.4.20 ниже, ответ, вообще говоря, отрицателен даже
2.4. ФАКТОРПРОСТРАНСТВА И ФАКТОРНЫЕ ОТОБРАЖЕНИЯ 155
в случае двух факторотображений, одно из которых тожде-
тождественно, а другое замкнуто (ср. с теоремой 3.3.17 и задачей
3.12.14 (Ь)). Отметим, что для открытых отношений эквивалент-
эквивалентности имеет место следующий положительный результат, выте-
вытекающий из предложения 2.3.29.
2.4.19. Предложение. Для каждого s^S пусть Es— открытое
отношение эквивалентности на пространстве XSt a qs: Xs ->¦ Xs/E9—
естественное отображение; тогда отображение Ц qs:
П Xs/TlEs-> П (Xs/Es)ecTb гомеоморфизм. ¦
seS sgeS sgS
2.4.20. Пример. Пусть Хх = YX = R \ {у, у, ...} наделены
топологией как подпространства R, и пусть /i = id*,: Xx-*- Y\.
Пусть Y2— факторпространство, полученное из X2=1R отож-
отождествлением множества положительных целых чисел в точку
(ср. с примерами 1.4.17 и 2.4.12), и пусть f2: Х2-+ Y2— етествен-
ное отображение; как известно, отображение/г замкнуто. Мы по-
покажем, что декартово произведение f = f\ X fz- Xi X X2-* У1ХУ2
не является факторотображением.
Множество F^jxel!: || - ^|<у} Х {' ™ 7 } ^^Х^
замкнуто для /, ]' = 2, 3, ... и семейство {/r^}^/es2 локально ко-
нечно. Поэтому объединение F= [} F^ замкнуто в
ut=%
Так как @, f2(l))<zif{F)\f(F), то множество f(F) не замкнуто
в У1ХУ2. Из очевидного равенства F = f-lf(F) следует, что /
не является факторотображением. 1
Опишем теперь регулярное пространство, не являющееся
вполне регулярным, используя операцию образования фактор-
пространств.
2.4.21. Пример. Пусть Z — пространство, определенное в примере
2.3.36; положим Z,*=ZX{i} Для каждого положительного це-
лого i, и пусть Z* = @Zt. Выберем некоторую точку гфЪ* и
введем топологию на множестве Г* = Z* (J {z} при помощи си-
системы окрестностей {^(^)}леГ*, где $(х) для любого jcgZ*
есть семейство всех открытых подмножеств множества Z*, со-
содержащих х, и 3$(z) = {Ul(z)}^l, где ?/,(г) = Г\ [}Zf. Чита-
Читатель легко проверит, что Г* — вполне регулярное пространство,
a Z* — его подпространство.
156 ГЛ. 2. ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
Определим отношение эквивалентности Е на Г*, полагая t\Et2
в том и только том случае, когда t\ = t2 или выполнено одно из
следующих условий:
C) {tu t2} = {(*, уо> i)9 (х, у0, i + 1)} Для xs=X\ {х0}
и нечетного if
4) {tu 4} = {(xq> У> '). (*о. У> i + 0} Для у €= Г \
и четного /.
Следовательно, факторпространство Т=Т*/Е получается
отождествлением соответствующих точек в А X{*} и Л Х{^ + 1}
для каждого нечетного t и отождествлением соответствующих
точек в ВХ{0 и BX{i+O Для каждого четного г. Заметим,
что полные прообразы точек при естественном отображении
q: Г*->Г суть одноточечные и двухточечные множества.
Пространство Т и служит искомым примером. Так как клас-
классы эквивалентности отношения Е замкнуты, Т есть Ггпростран-
ство. Проверка регулярности Т предоставляется читателю (до-
(достаточно заметить, что q замкнуто, и применить теорему 3.7.20).
Мы докажем, что Т не является вполне регулярным простран-
пространством. Для этого достаточно показать, что для точки t = q(z)9
не содержащего ее замкнутого множества F —#(ЛХ{1}) и
каждого непрерывного отображения f: 7->/, такого, 4Tof(F)={l},
мы имеем f(t)=l. Рассмотрим функцию fi = f(q\Zi): Zi-+I,
i = 1, 2, .... В силу свойства Z, установленного в 2.3.36, суще-
существуют такое вещественное число п и такие множества Xq t a
Х\{} У0|i с= Y\{y0}, что \Х0> t\ < «0, | Ум| < m и
ft (х. У, 0 = П для (л, ^) <= Z\Z0> /,
Полагая Го = Д ^ г Го = Д ^ f и ZJ- (^ XУ) U (XXTQ,
получаем
E) ^\z;^0^5\z;
F) ft(xf у, i) = rt для (х, y)<==Z\Z*0 и /= 1, 2, ....
В результате выполненных отождествлений имеем
ft (*> Уо> i) = /i+i (*» %»*+ 1) Для #е=Х \ {х0} и любого нечетного i9
fi(*о> У> 0 = fi+i (xo> bU i + 1) Для y^Y\ {y0} и любого четного i%
а это вместе с соотношениями E) и F) означает, что r,-+i ^=Гг
для i = l, 2, ... . Так какД(Л X{l})==f(^) = {!}» ™ ^ = 1 для
2.4. ФАКТОРПРОСТРАНСТВА И ФАКТОРНЫЕ ОТОБРАЖЕНИЯ 157
/ = 1, 2, ... . Замыкание множества M={q(x,y,i): (x, у)&
е Z \ Z*o> i = 1, 2, ...} содержит точку t, и так как f(M)= {1},
то /@=1. ¦
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
Факторпространства впервые появились в работе Р. Л. Мора
[1925] и Александрова [1927] (объявлено в [1925]). Оба автора
изучали частный случай, когда факторпространство порождает-
порождается полунепрерывным сверху разбиением (Мор изучал только
разбиения плоскости на континуумы). Понятие факторпростран-
факторпространства в полной общности, так же как и понятие факторотобра-
жения введены Бэром и Леви [1932] и впервые систематически
изучены в книгах Бурбаки [1940] и [1951]. Присоединенное про-
пространство введено Борсуком [1935] (для компактных метриче-
метрических пространств). Пример 2.4.21 (и вспомогательный пример
2.3.36) получен как комбинация примеров Тихонова [1930] иНо-
вака [1948]. Простой пример регулярного пространства, не яв-
являющегося вполне регулярным, построен недавно Мысьором
[1981а].
УПРАЖНЕНИЯ
2.4.А. (М. Стоун [1936]). Пусть X — произвольное топологи-
ческоемяространство; положим хЕоу в том и только том случае,
если {*}=={#}. Покажите, что Ео — отношение эквивалентности
на X и что Х/Ео есть Г0-пространство. Покажите, кроме того,
что если для некоторого отношения эквивалентности Е на X
факторпространство Х/Е есть 70-пространство, то Ео cz Я.
Указание. Множество {х} есть объединение классов эквива-
эквивалентности отношения ?0.
2.4.В. Пусть Е — отношение эквивалентности на пространстве
Х> Ег — отношение эквивалентности на пространстве Y и отобра-
отображение /: X-+-Y таково, что хЕу влечет за собой f(x)E'f(y). Оп-
Определим отображение /*: X/E^-Y/E' равенством f*q = q'f, где
q: X-+-X/E и qf\ Y^>~Y/Ef — естественные отображения. Дока-
Докажите, что если f — факторотображение, то f* тоже фактор-
отображение, а если оба отображения / и q' замкнуты (откры-
(открыты), то /* тоже замкнуто (открыто).
Заметим, что если заданы замкнутые подмножества А с X и
ВсУи такое отображение /: Х-> У, что f(A)c В, то /*: Х/Л->
-*• Y/B замкнуто, когда / замкнуто.
2.4.С. (а) Приведите пример замкнутого (открытого) отно-
отношения эквивалентности Е на каком-либо пространстве X, та-
такого, что множество Е не является замкнутым (открытым) в
158 ГЛ. 2. ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
произведении Х^Х. Приведите пример отношения эквивалент-
эквивалентности Е на пространстве Х> такого, что Е не является замкну-
замкнутым отношением эквивалентности, однако множество Е замкнуто
в произведении X X X.
(b) Покажите, что если Е — некоторое отношение эквива-
эквивалентности на пространстве X и множество Е открыто в произ-
произведении ^Х^> то факторпространство Х/Е дискретно и ? —
открытое отношение.
(c) Пусть Е — отношение эквивалентности на топологическом
пространстве X. Покажите, что если факторпространство Х/Е
хаусдорфово, то Е — замкнутое подмножество произведения
ХУ^Х. Пусть Е — замкнутое подмножество произведения X X Х>
а отношение Е открыто; проверьте, что тогда Х/Е — хаусдор-
хаусдорфово пространство.
2.4.D. (а) Пусть {XJseS и {У«}ве5~ Два семейства тополо-
топологических пространств, таких, что Xs {] Ys — 0 для sgS,h пусть
{/s}seS— семейство отображений fs\ Ms-*YSy где Ms — некото-
некоторое замкнутое подпространство пространства Xs. Установите, что
присоединенное пространство ( ф ХЛ U/ ф f \ f ф Y$\ гомео-
морфно сумме ф 0X*sUf-!%)•
(b) Для /~1 и 2 определите такие непересекающиеся топо-
топологические пространства X/, Yi и такое отображение ff. Afj-> Yu
где Mi — замкнутое подпространство пространства Хи что при-
присоединенное пространство {Хх X Х2) [}{fl х fa) (Yx X ^2) не гомео-
морфно произведению (Х\ Ufl ^1) X (-^2 Uf,^)-
Указание. См. пример 2.4.20.
2.4.Е. (а) Установите, что сумма ф fs является фактор-
S
отображением в том и только том случае, когда отображения
fs факторные.
(b) Приведите пример двух открытых отображений f\\X-+Yi
й fa Х-^-Уа» таких, что сужение f\X: X-+f(X) диагонали f =
= f 1 Л f2 не является факторным.
Указание. Возьмите X = [0,1).
(c) Покажите, что для каждой ретракции /: Х-^Х сужение
f \X: X-*-f(X) есть факторотображение.
2.4.F (Макдугл [1958] и [1959], Архангельский [1963], Динь
Ньё Тонг [1963], Филиппов [1969а]). Непрерывное отображение
f: X-**Y называется наследственно факторным, если для каж-
каждого бег У сужение /V. f-l{B)^>~B есть факторотображение.
(а) Докажите, что отображение f: X-+Y наследственно фак-
факторное в том и только том случае, если множество f(f~l(B))cz У
замкнуто для каждого В czY> или, что равносильно, в том и
2.4. ФАКТОРПРОСТРАНСТВА И ФАКТОРНЫЕ ОТОБРАЖЕНИЯ 159
только том случае, если для каждого j/еУи каждого открытого
UczXy содержащего f~l(y), мы имеем y^Intf(U).
(b) Проверьте, что композиция двух наследственно фактор-
факторных отображений является наследственно факторным отображе-
отображением, что сумма наследственно факторных отображений есть на-
наследственно факторное отображение и что предложение 2.4.18
имеет место также для наследственно факторных отображений.
(c) Покажите, что любое факторотображение /: X-+-Y на
пространство Фреше — Урысона, в котором каждая последова-
последовательность имеет не более одного предела (в частности, на Г2-
пространство Фреше — Урысона), является наследственно фак-
факторным.
(d) Применяя (с) к соответствующим примерам фактор-
отображений, покажите, что сужения наследственно факторных
отображений на открыто-замкнутые подмножества области опре-
определения, декартовы произведения двух наследственно фактор-
факторных отображений и сужения диагоналей (см. упр. 2.4.Е (Ь))
двух наследственно факторных отображений, вообще говоря, не
являются факторотображениями.
2.4.G (Архангельский [1963а],Франклин [1965] и [1967]). (а)
Покажите, что образ секвенциального пространства при фактор-
отображении есть секвенциальное пространство и что образ про-
пространства Фреше — Урысона при наследственно факторном
отображении есть пространство Фреше — Урысона.
Покажите, что образ секвенциального пространства при не-
непрерывном отображении не обязан быть секвенциальным про-
пространством, а образ пространства Фреше — Урысона при фак-
торотображении, вообще говоря, не является пространством
Фреше — Урысона.
(Ь) Пусть X — секвенциальное пространство и % — семей-
семейство всех таких последовательностей х0, хи хь ... точек про-
пространства X, что Хо^ liraxi. Для каждого c = {xt}^<S' положим
#с={с}Х@, 1, 1/2, 1/3, ...}, где {с}—одноточечное дискретное
пространство и {0,1, 1/2, 1/3, ...} наделено топологией подпро-
подпространства из /?. Определим fc: XC-*X формулами
fc((c,O)) = xo и М(
Покажите, что комбинация fx— V fe: © ХС->Х есть фак-
факсе^ се?
торотображение и что секвенциальные пространства можно оха-
охарактеризовать как образы пространств, удовлетворяющих пер-
первой аксиоме счетности, при факторотображениях (ср. с упр.
4.2.D (с)). Установите, что подпространство М секвенциального
пространства X является секвенциальным в том и только том
случае, если сужение (!х)м: f^{ Ш)-> М есть факторотображе-
факторотображение. Выведите отсюда, что пространство X наследственно сек-
160 ГЛ. 2. ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
вендиально тогда и только тогда, когда оно является простран-
пространством Фреше — Урысона (ср. с задачей 3.12.15). Покажите, что
пространства Фреше — Урысона можно охарактеризовать как
образы пространств, удовлетворяющих первой аксиоме счет-
ности, при наследственно факторных отображениях (ср.
с упр. 4.2.D (с)).
(с) Покажите, используя пример 2.4.20, что произведение
нормального пространства со второй аксиомой счетности и нор-
нормального пространства Фреше — Урысона не обязано быть сек-
секвенциальным пространством (ср. с упр. 2.3.К (а) и примером
3.3.29).
2.5. ПРЕДЕЛЫ ОБРАТНЫХ СПЕКТРОВ
Пусть 2 — направленное множество, и пусть каждому deS
поставлено в соответствие топологическое пространство Хо*
Пусть, далее, для любых а, реЕ, таких, что р ^ а, определено
непрерывное отображение л?: Ха^Х9. Пусть, кроме того,
Jignjj = n;* для любых а, р, teS, таких, что т ^ р ^ а, и
n%=idx для каждого а ^2. В этом случае говорят, что се-
семейство S = |Х0, п^ 2} есть обратный спектр пространств Ха\
отображения п°0 называются связующими отображениями об-
обратного спектра S.
Обратный спектр Я = {Х^ я*, Щу где N — множество всех
положительных целых чисел с естественным порядком, назы-
называется обратной последовательностью и обозначается через
{Xt, я)}.
Пусть S = {Хау л;?, 2} •— обратный спектр; элемент {ха} про-
произведения И Ха называется нитью обратного спектра S, если
^р {ха) = хр для Л1°6ых а, р е 2, удовлетворяющих неравенсгву
р ^ а. Подпространство пространства XI Ха, состоящее из всех
нитей спектра S, называется пределом обратного спектра
S = {Ха, я?, Щ и обозначается через lim S или Нт |Ха> я?, 2}.
2.5.1. Предложение. Предел обратного спектра S —{Ха, jt?, 2}
хаусдорфовых пространств Х0 есть замкнутое подпространство
произведения XI Ха.
Доказательство. Для любых р, те 2, таких, что х ^ р, по-
положим
Так как, в силу теоремы 1.5.4, множества Мрх замкнуты в про-
2.5. ПРЕДЕЛЫ ОБРАТНЫХ СПЕКТРОВ 161
изведении Ц Хо, то множество lim S = [") ^рт также зам-
замкнуто в произведении Д Jf0. |
Из теорем 2.1.6 и 2.3.11 следует
2.5.2. Теорема. Предел обратного спектра Т^пространств есть
Тг пространство, если I ^ 3 -г-. |
Из примера 2.5.3 и упр. 3.1.Н(а) (или задачи 2.7.16(а)) выте-
вытекает, что предел обратного спектра совершенно нормальных
пространств не обязан быть нормальным. Однако предел обрат-
обратной последовательности совершенно нормальных пространств
является совершенно нормальным (см. задачу 2.7.15 (Ь)). Это
последнее заключение неверно для нормальных или наслед-
наследственно нормальных пространств (см. замечание к задаче 2.7.15).
2.5.3. Пример. Пусть {Xs}s e s —- семейство топологических про-
пространств, причем |S|^=No. Заметим, что семейство 2 всех ко-
конечных подмножеств множества S направлено по включению,
т. е. направлено отношением ^, определенным так: р^ав том
и только том случае, когда рсо. Пусть Ха= П Xs для каж-
каждого 0gS. Для любы* <г, ре2, таких, что р ^ а, определено
непрерывное отображение яа: Х0-^Х —сужение элементов
пространства Ха на подмножество рса. Легко установить, что
S = pf0, я?, Щ — обратный спектр топологических пространств.
Для любого seS положим <rs={s}e2. Легко проверить,
что, поставив в соответствие каждой точке {ха} е lim S точку
{xOs} e П X8f мы определим гомеоморфизм пространства limS
на произведение Ц Xs. Следовательно, применяя операцию пре-
предела обратного спектра, можно выразить бесконечные произве-
произведения в терминах конечных произведений. 1
2.5.4. Пример. Пусть 2 — семейство подпространств топологи-
топологического пространства X, направленное по включению =э, т. е.
обладает тем свойством, что для любых Lu ?2 ^2 существует
такое М е 2, что М a L\ П L2. Для любых М, L е 2, таких, что
MaLt пусть ot^: M-*L — вложение М в L. Легко установить,
что S — {M, n?, 2}— обратный спектр (где пространство, соот-
соответствующее MgS, есть само М) и что limS гомеоморфен
подпространству f]2 пространства X. В частности, каждое под-
подпространство А ^-пространства X можно представить как пре-
предел обратного спектра открытых подпространств пространства X.
В самом деле, А = П2, где 2 —направленное семейство всех от-
П Зак. 697
162 ГЛ. 2. ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
крытых подмножеств пространства X, которые содержат множе-
множество А и имеют дополнение, состоящее из конечного числа то
чек. 1
Пусть S = {XG, я?, 2} — обратный спектр топологических
пространств, и пусть X = limS. Для каждого а^2 определим
отображение яа = ра|Х: Х-+ХСу где ро: Г1 Хо->Ха— проек-
ция. Отображение яа называется проекцией предела обратного
спектра S на Хо. Очевидно, что для любых а, ре2, таких, что
р ^ а, проекции я0 и яр удовлетворяют равенству яр = я?яа.
2.5.5. Предложение. Семейство всех множеств я'1 Шо\ где UG —
открытое подмножество пространства Хо и а пробегает подмно-
подмножество 2', конфинальное множеству 2, есть база предела об-
обратного спектра S = 1Ха, яа, Е}.
Более того, если для каждого а е 2 база SSa пространства
Ха фиксирована, то подсемейство, состоящее из тех я™1 (U а)
для которых Uо е 3$а> также образует базу.
Доказательство. Обозначим через М семейство, описанное
в первой части предложения, и пусть Z = HmS.TaK как проек-
проекции я0 непрерывны, то все элементы семейства 3§ открыты в про-
пространстве X. Поэтому остается показать, что каждое непустое
открытое множество U а X может быть представлено как объ-
объединение подсемейства семейства $. Очевидно, достаточно по-
показать, что для каждого х —{ха}е U существуют такое ogS;
и такое открытое подмножество UG cz XGy что х е я^1 ШЛ cz [/.
По определению индуцированной топологии, существует от-
открытое множество VczYl Ха, такое, что f/ = Xfl V, и, в силу
предложения 2.3.1, найдутся сть а2, ..., ak e 2 и открытые в
Ха^у %о2> •••> Xak соответственно множества U\, ^2> ..-, Uk,
для которых
A) хер-' (U,)ПР-1 (f/2)П • • • ПРо-; (f/ft) c= F.
Так как множество 2 направлено, а 2' конфинально 2, то
существует такое абЕ', что Oi ^. а для i= 1, 2, ..., /г. Все
k
множества (п° \~l (U.) и их пересечение f/a= П (na)~l(Ui) от"
крыты в Za- Далее, так как я? (ха) = х0 , то
B) х[е(/,
Очевидно, что имеет место соотношение
C) я. 1
2.5. ПРЕДЕЛЫ ОБРАТНЫХ СПЕКТРОВ 153
используя B), C) и A), мы получаем включение
«*.-CJ - «.-(Д(»«" СО)-Д %-№)"
которое завершает доказательство того факта, что $ — база про-
пространства X.
Вторая часть данного предложения есть непосредственное
следствие первой части и определения базы. 1
2.5.6. Предложение. Для каждого подпространства А предела X
обратного спектра S = {Хо, я?, Щ семейство SA={A0, я?, Щ, где
Ла —яа(Л) и п°(х) = я?(х) для xg1o, является обратным спек
тром и Пт5л = Л czX.
Доказательство. Так как яр (х) = я?яа(х)для х^А и р^о,
имеют место соотношения
которые доказывают, что SA есть обратный спектр.
Очевидно, что HmSAc=JC. Из предложений 2.3.2 и 2.1.2
следует, что lim SA есть подпространство пространства Х\ более
того, оно является замкнутым подпространством пространства X.
В самом деле, для каждого х = {х0} е X \ lim SA существует
такое а(л)е1, что л;0(х)^^а(х) \ Ла(х). Таким образом,
n~fx)(Xoix)\AG{x)) является окрестностью точки х, не пересе-
пересекающейся с lim SA. Из очевидного включения Л cz lim SA сле-
следует, что A cz lim SA.
Выберем теперь любую точку х == {jca} e lim SA. В силу пред-
предложения 2.5.5, семейство всех множеств я~1(?/А где Ua — ок-
окрестность точки ха в пространстве Ха, есть база пространства X
в точке х. Для каждого элемента я^1 (Ua) этой базы имеем
ха^ Л0П ^а и, таким образом, ЛаП ^а=т^ 0, или, что равносиль-
равносильно, Л []п~1 (?/о) =т^= 0. Отсюда следует, что #^ Л, т. е. HmS^ ^
с=Л. | *~
2.5.7. Следствие. Всякое замкнутое подпространство А предела
X обратного спектра S = {Ха, я?, 2} есть предел обратного
11*
164 ГЛ. 2. ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
спектра SA = {Aa, n°, 2} замкнутых подпространств Аа про-
пространств ХФ 1
Из 2.5.1, 2.5.3 и 2.5.7 получается
2.5.8. Теорема. Пусть 9* — топологическое свойство, наследуемое
замкнутыми подмножествами и конечно мультипликативное.
Топологическое пространство X гомеоморфно пределу обратного
спектра Т2-пространств, обладающих свойством {р, в том и толь-
только том случае, если X гомеоморфно замкнутому подпространству
произведения Т2-пространете, обладающих свойством <р. 1
Пусть даны два обратных спектра S = {Ja, л?, SJ и S' =
= {YO,, я?', 2'}. Отображение обратного спектра S в обратный
спектр S' есть семейство |ср, fG,\, состоящее из неубывающей
функции ф: 2'-^ 2, такой, что множество tpB') конфинально 2,
и непрерывных отображений /0,: Хф(а,}-^Ка/, определенных для
всех а' е 2' и таких, что
т. е. таких, что диаграмма
Ху (а') * IV
ф(р>1 f, \ р
^ф (р') ^ ^р'
коммутативна для любых а\ р' е S', удовлетворяющих неравен-
неравенству рл ^ а'.
Любое отображение обратного спектра S в обратный спектр
S' индуцирует непрерывное отображение предела lim S в lim S .
Чтобы убедиться в этом, рассмотрим отображение (ф, /0Л об-
обратного спектра S = {Ja, я?, 2} в S/ = {Kp,, я^, 2'}. Для нити
# = {xaj s J = limS и каждого а'е? положим
полученная таким образом точка |#a,} e П Ка, есть нить, т. е.
^а,} eF = lim S'. Действительно, для любых ef,p' e S',р' ^ а\
имеем, в силу D) и E),
К (Ус) = </а'
Поставим в соответствие точке х = {xa}e X точку у = |ya,} e К.
Тем самым мы определим отображение /: X->Y. Покажем, что
2.5. ПРЕДЕЛЫ ОБРАТНЫХ СПЕКТРОВ 165
/ непрерывно. В силу предложения 2.5.5, достаточно показать,
что прообразы при отображении / всех множеств я~{ (U0X где
Uа, — открытое подмножество пространства Ка„ открыты в про-
пространстве X. Из E) следует, что для х = Ме1 имеют место
равенства
значит, прообраз fln~l (?/о,) = %/^f ~/(?/а,) открыт, ибо /а, и
я @,j непрерывны. Отображение f: Jf-*- У называется предель-
предельным отображением, индуцированным семейством |<р, ДА и обо-
обозначается через lim {ф, ДЛ,
2.5.9. Лемма. Пусть {ф, /у} — отображение обратного спектра
S = {Za, я?, 2} в обратный спектр S' = {Y0,, я?, 2'}. ?сл« все
отображения /а' инъективны, то предельное отображение f =
= lim{qp, /а'} также инъективно. Если, более того, все for —
отображения «на», то f также есть отображение «на».
Доказательство. Пусть х = {ха} и 2=={га}—две различные
точки пространства lim S. Выберем элемент сго^2, такой, что
Хац Ф zGq, и элемент а'еИ', удовлетворяющий неравенству
а0 ^ф(а'). Ясно, что лгф(а') Ф 2ф(а')- Так как отображение fa,
инъективно, то /а,(л:ф(а0) Ф /a'K(a'))- Таким образом, f(x)^f(z).
Предположим теперь, что fo> для каждого a'ej' является
взаимно однозначным отображением пространства Хф(а') на про-
пространство IV. Выберем точку у = {yG>} <= limS^. Из соотношения
D) следует, что равенство ф(а')=ф(р') влечет за собой равен-
равенство f~,x (#a,) = f~,1 (yQ*). Таким образом, для каждого элемента
(') B') точка
г) = 'а'
вполне определена. Для каждого a e 2 выберем такой элемент
a' G 2', что a ^ ф(а'), и положим
Легко показать, что л:а не зависит от выбора а', что лг = {х0} —
нить спектра S и f(x) = у. 1
2*5.10. Предложение. Пусть {ф, fa'} — отображение обратного
спектра S = {Ja, я^, S} в обратный спектр S' = (К^, я^, S'}.
?сла все отображения fa< — гомеоморфизмы^ то предельное ото-
отображение / = Нт{ф, jFa'} также является гомеоморфизмом.
166 ГЛ. 2. ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
Доказательство, В силу леммы и предложения 2.5.5, доста-
достаточно показать, что для каждого a' e 2' и любого откры-
открытого ?/с=Хф(а/) образ при отображении f множества ^^(С/)
открыт в Hm S'. Из соотношения F) вытекает, что для А с: YG'
мы имеем \x{a,)f~}{A) = f~[n0',{ (Л). Положим Л = /а,(?/); так как
/а' — взаимно однозначное отображение пространства Х
на Уа', то мы получаем
Поэтому множество
f \ in GO = f Г Vk «О = *Л («О
открыто в пространстве lim S/. I
2.5.11. Следствие. Пусть S = {Xa, л?, 2} — обратный спектр и
2'— подмножество, конфинальное 2. Отображение, состоящее
в сужении всех нитей из X = \\mS на 2', есть гомеоморфизм
пространства X на пространство Xr = lim S', где S7 — |Ха„ л^
V). I
2.5.12. Следствие. Яусгб S = {Ха, я?, 2] — обратный спектр.
Пусть, далее, в направленном множестве 2 имеется такой эле-
элемент 0о, что а ^ 0о для каждого cgI Тогда предел обратного
спектра S гомеоморфен пространству Jao. |
Из следствия 2.5.11 вытекает, что, рассматривая отображе-
отображение^, fff,} обратного спектра S = {Xa, л^, 2J в обратный спектр
S' — {YG,, л^', 27}, можно всегда считать, что фB')=2. В са-
самом деле, когда мы отождествляем предел обратного спектра S
и предел обратного спектра S" = {XGy njj, <pB7)}, как описано
в 2.5.11, то предельные отображения пространства limS в про-
пространство lim S' и пространства lim S" в пространство lim S'
совпадают.
Легко установить, что каждое счетное направленное множе-
множество содержит конфинальное подмножество, линейно упорядо-
упорядоченное отношением ^ и подобное множеству Af всех положи-
положительных целых чисел. Поэтому из 2.5.11 вытекает, что вместо
обратного спектра {Ха, п°, 2} с |2|=К0 можно рассматривать
обратную последовательность. Рассматривая отображение {ср, /*}
обратной последовательности в обратную последовательность,
можно считать, что ср = id#.
Приступим теперь к доказательству двух теорем, показы-
показывающих, что предельные отображения можно выразить в терми-
2.5. ПРЕДЕЛЫ ОБРАТНЫХ СПЕКТРОВ 167
нах декартовых произведений, а проекции обратных спектров —
в терминах предельных отображений. Эти теоремы найдут при-
применение в дальнейшем при доказательстве принадлежности пре-
предельных отображений и проекций некоторым классам отобра-
отображений (см. следствие 3.2.15, теоремы 3.7.11, 3.7.12 и задачу
6.3.16 (а)).
2.5.13* Теорема. Для любого отображения {ф, /у} обратного
спектра S = {Ха, я?, 2} в обратный спектр S' = \Уа„ я?', 2'} су-
существует гомеоморфное вложение h: lim S -^ XI ^а'> где
Za, = Xy{a,y такое, что Ит{<р, /„/}=( Ti Jj\h. Если все про-
пространства Ху(о') хаусдорфовы, то A(limS) является замкнутым
подпространством произведения П Zy.
Доказательство. Для каждого аеф(У) диагональное ото-
отображение ia= A id;r : XG -> Ц Z</ является гомео-
морфным вложением, и если пространство Хо хаусдорфово, то
iG(Xa) замкнуто. Композиция h описанного в 2.5.11 гомеомор-
гомеоморфизма HmS на HmS", где S" = {XO, n^, фB')}, и сужения
( П ^^IlimS^: limS"-> П Za/ также является гомеомор-
фным вложением, и если все Х^^) хаусдорфовы, то Л (HmS) —
замкнутое подпространство пространства Ц Za^. Равенство
lim {ф, f0'} = ( П М Л очевидно
2.5.14. Теорема, Дугл каждого обратного спектра S = {Jp, я^, S}
и любого сг0 е 2 существуют обратный спектр S' = $Y&y я^, S'j
(в котором Fa' = ^ao «рм любом а'Е?), гомеоморфизм
h: HmS'-^X^ а отображение {ф, /а,} спектра S в S', где for —
связующие отображения спектра S, такие, что яао = /гПт{ф, f Л.
Доказательство. Определим обратный спектр 5/={К0„ п^„ S'J,
полагая 2/ = {а/еЕ: ап<а'), У„, = Хп для a'eS' и Jt? = idr
для любых a', p'eS', таких, что р'^с/. Предел спектра S'
совпадает с диагональю А произведения Ц Ytf = X™u, где
m = |2^|. Обозначим через h гомеоморфизм А на Хв<>, обратный
гомеоморфизму ( A idX\\XOa: Jao->A. Семейство {ф, f^}, где
ф(а') = о' и /:0/ = я^ при а'еУ, есть отображение обратного
168 ГЛ. 2. ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
спектра S в обратный спектр S'. Соотношение яао —ЛПт{ф, fa,}
очевидно. | ° "*""
Мы закончим этот параграф рассмотрением двух важных
частных случаев отображений обратных спектров.
Пусть X — топологическое пространство и 2— непустое на-
направленное множество. Обратный спектр S(X, 2) = {Ja, я?, 2},
в котором Ха = Х для cell и ^p — id^ для любых a, pel
удовлетворяющих неравенству р ^ а, называется постоянным
обратным спектром пространства X над множеством индексов 2.
Ясно, что отображение h: X -> lim S (Ху 2), относящее точке х^Х
нить {ха} с ха = х для аеЕ, является гомеоморфизмом про-
пространства X на пространство Hm S (X, 2), совпадающее с диа-
диагональю произведения Ц Хо = Хщ, где 12 | = т.
Если заданы обратный спектр S = {Ха, я?> 2} с 2 ф 0, топо-
топологическое пространство X и семейство {/о}ое2 отображений
/0: Х~+Ха, такие, что я?/о = /р, когда а, р е 2 и р ^ а, то се-
се? р
мейство {ids, fa} является отображением постоянного обратного
спектра S(X, 2) в обратный спектр S. Тем самым определено
предельное отображение / = lim(id2, fo} из Hm S(X, 2) в Hm S
Композиция fh: X -> lim S, где Л — определенный выше гоме-
гомеоморфизм пространства X на Hm S (X, 2), называется предель-
предельным отображением, индуцированным семейством {/a}ae=2, и обо
значается через lim/a.
Аналогично, если заданы обратный спектр S = {Xa>n^,2J
с2^0, топологическое пространство X и семейство {/0}аеа
таких отображений /ff: Ха~+Х, что /ая?= /о Для любых a, p e 2,
удовлетворяющих неравенству р ^ а, то семейство {ids, fa) яв-
является отображением обратного спектра S в постоянный обрат-
обратный спектр S(X, 2), так что определено предельное отображение
f — lim {ids, fo} пространства lim S в ton S {X, 2). Композиция
h~lf: limS->X, где h — определенный выше гомеоморфизм X
на HmS(Jf, 2), называется предельным отображением, индуци-
индуцированным семейством отображений {fa}0€=2> и обозначается че-
через lim/0.
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
Понятие предела обратной последовательности появилось в
несколько другой форме в работе П. С. Александрова [1929];
2.5. ПРЕДЕЛЫ ОБРАТНЫХ СПЕКТРОВ 169
настоящее определение впервые появилось у Лефшеца [1931].
Отображения обратных последовательностей и индуцированные
ими предельные отображения впервые изучались Фрейденталем
в работе [1937]. Стинрод [1936] рассматривал частный случай
обратных спектров, у которых 2 — множество ординалов, на-
направленное по своему естественному порядку; в полной общно-
общности обратные спектры введены Лефшецом в [1942]. Всесторон-
Всестороннее обсуждение обратных спектров было дано Эйленбергом и
Стинродом в их книге [1952]; после выхода этой книги обрат-
обратные спектры начали широко изучаться и применяться. Отме-
Отметим, что понятия обратного спектра и его предела можно ввести
без учета топологии пространств Хо. Эти понятия изучаются
также в алгебре и анализе.
УПРАЖНЕНИЯ
2.5.А.(а) Покажите, что если все связующие отображения
в обратной последовательности S = {X., nj| непустых про-
пространств являются отображениями «на», то Hm S Ф 0.
(b) (Уотерхаус [1972]). Пусть 5 — произвольное несчетное
множество и 2 — семейство всех конечных подмножеств множе-
множества 5, направленное по включению. Рассмотрите обратный
спектр S = {Х0, я?, 2}, где Ха — дискретное пространство, со-
состоящее из всех вложений множества а с= S в N, и я? (/) = f | p
для [gI0 и а, реХ, таких, что р ^ а. Заметьте, что все свя-
связующие отображения обратного спектра S являются отображе-
отображениями «на» и тем не менее HmS = 0 (ср. с упр. 3.1.К (Ь) и
теоремой 3.2.13). *~~
Замечание. Первый пример обратного спектра, обладающего
аналогичными свойствами, появился у Хенкина [1950].
(c) Приведите пример обратной последовательности
S = {^, я*} непустых пространств, в которой все связующие
отображения инъективны и lim S — 0.
2.5,В.(а) Покажите, что если в обратной последовательности
5 = |if., я*} все связующие отображения являются отображе-
отображениями «на», то и все проекции — отображения «на». Заметим,
что для произвольных обратных спектров этот факт, вообще
говоря, не имеет места (см. упр. 2.5.А (Ь)).
(Ь) Покажите, что если в обратном спектре S = {Z0, я?, IX
все связующие отображения инъективны, то и все проекции
также инъективны. Проверьте, что если, кроме того, все свя-
связующие отображения являются отображениями «на», то все
проекции также являются отображениями «на».
170 ГЛ. 2. ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
2.5.С. Приведите пример таких обратных последовательно-
последовательностей S = {Xp я'} и S' = {F?, Щ и отображения {id*, //} из S
в S', что все отображения я], «* и /,- являются отображениями
«на», а предельное отображение lim {id#, / J не является.
2.5.D. (а) Проверьте, что если для каждого seS задан
обратный спектр S(s) = {X(s)a, я($)°, 2} и X(s)a(\X(s\ = 0
при 5=7^=5' и сг^2, то семейство © S(s) = ( © ^(s)o,
0 я EH, 2) является обратным спектром и lim f 0 S(s)\ =
= 0 HmS(s).
5 *
(b) Проверьте, что если для каждого seS задан обратный
спектр S(s) = (X(s) у n(s)°, 2}, то семейство Ц S(s) —
= ( П ^E)flf И дE)п» ^) является обратным спектром и про-
странство lim (YL S(s)\ гомеоморфно пространству Ц li
2.5.E. (а) Заметьте, что предел обратной последовательности
пространств с первой (второй) аксиомой счетности есть про-
пространство с первой (второй) аксиомой счетности, но предел
обратного спектра пространств со второй аксиомой счетности не
обязательно является пространством с первой аксиомой счет-
счетности.
(Ь) Покажите, что предел обратной последовательности се-
парабельных пространств не обязательно является сепарабель-
ным пространством.
Указание. Примените пример 2.5.4 к плоскости Немыцкого.
Замечание. Предел обратной последовательности пространств
Фреше — Урысона не обязан быть секвенциальным простран-
пространством (см. упр. З.З.Е(Ь)).
2.5.F. Покажите, что пространство X гомеоморфно пределу
обратного спектра (Ха, я?, Щ тогда и только тогда, когда су-
существует семейство {я>о}в<=ъ отображений яа: Х-+Ха со следую-
следующими свойствами:
A) Для любых а, р ^ 2, таких, что р ^ а, имеем яаяа=я
B) Для произвольного пространства Y и любых двух не-
непрерывных отображений /, g пространства Y в X из того, что
яа/ = n<jg для каждого а е 2, следует равенство f=g.
C) Для каждого Y и семейства {/а}ае=2 отображений /0:
У-+XGy таких, что я^/ст = / где o.pEll мр^а, найдется та-
такое отображение f: Y-+X, что яа/ = fa при каждом ogX.
2.6. ПРОСТРАНСТВА ОТОБРАЖЕНИЙ I 171
2.6. ПРОСТРАНСТВА ОТОБРАЖЕНИЙ I:
ТОПОЛОГИЯ РАВНОМЕРНОЙ СХОДИМОСТИ
НА Rx И ТОПОЛОГИЯ ПОТОЧЕЧНОЙ
СХОДИМОСТИ
Последняя из операций, обсуждаемых в настоящей главе,—
операция образования пространств отображений. Каждой паре
А", У топологических пространств отвечает множество Yx всех
непрерывных отображений из X в У; мы постараемся ввести на
нем естественную топологию. Оказывается, в отличие от рас-
рассмотренных выше операций, множество Yx имеет несколько до-
довольно естественных топологий. Мы начнем с определения то-
топологии на множестве Rx всех вещественных функций на про-
пространстве X. После этого мы введем топологию на Vх для про-
произвольных X и У. Параграф завершается обсуждением условий,
которым должна удовлетворять «приемлемая топология» на Ух.
Еще одна топология на пространстве отображений, удовлетво-
удовлетворяющая этим условиям для достаточно широкого класса про-
пространств, будет введена и изучена в § 3.4, после того как в на-
нашем распоряжении будет понятие компактности.
Для A czRx и / <= Rx определим Л следующим образом:
A) / ^ Л тогда и только тогда, когда / = lim //,
где/ieA, 1 = 1,2, ... .
Равенство f = lim Д- означает, как определено в § 1.4, что по-
последовательность {//} равномерно сходится к /.
2.6.1. Предложение. Оператор замыкания, определенный в Rx
формулой A), удовлетворяет условиям (СО1) — (СО4).
Доказательство. Условие (СО1) с очевидностью выполнено.
Поскольку lim ft = f для /,• = f при /=1,2, ..., условие (СО2)
также выполняется.
Из A) немедленно следует, что
B) если А а 5, то Л<=Я;
следовательно, для установления (СОЗ) достаточно показать, что
C) ЛЦВ
Возьмем f <= A (J В и такую последовательность {/,•} функ-
функций, принадлежащих А [} В, что / = lim ft. В одном из множеств
А или В, скажем в Л, имеется подпоследовательность \fk^ по-
последовательности {/,-}; по определению равномерной сходимости
/ = lim fkp т. е. / е Л, так что C) выполнено.
172 ГЛ. 2. ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
Поскольку из B) следует включение Лс (Л), для доказа-
доказательства (СО4) достаточно показать, что
D) (Х)с=Л.
Возьмем / е (Л) и такую последовательность {Д} функций
из Л, что / = lim ft. Для каждого положительного целого k су-
существует такое i(k)> что
E) |/(*) — //<*)(*) К 1/2* для xgI
Поскольку /?{А)^Л, имеем /i(ft) = limg*, где g^ei для
/= 1, 2, ..., и существует положительное целое /(*), такое, что
(в) | W*)-*/(*)<*) |< 1/2* для *е*-
Функция gk = g){k) принадлежит А при * = 1, 2, ... ; по-
поскольку из E) и F) следует равенство / = limgftl имеем
/бЛ, что завершает доказательство соотношения D). I
Топология, порожденная (в соответствии с предложением
1.2.7) на Rx с помощью оператора замыкания, определенного
формулой A), называется топологией равномерной сходимости
на Rx. Читатель может легко проверить, что для любого / е Rx
семейство {Ut(f)}^v где
U;(f) — {g e Rx: существует такое а < 1/t,
что |/(х)—?(*) |< а при jcg!},
является базой в точке / пространства Rx с топологией равно-
равномерной сходимости.
Мы не намерены изучать сейчас топологию равномерной схо-
сходимости; ее природа будет прояснена в § 4.2 и 8.2. Отметим,
однако, что топология равномерной сходимости на Rx индуци-
индуцирует на Iх топологию подпространства и из теоремы 1.4.7 выте-
вытекает
2.6.2. Предложение. Для каждого топологического пространства
X множество Iх замкнуто в пространстве Rx с топологией рав-
равномерной сходимости. 1
Пусть X и У — произвольные топологические пространства.
Для AczX n В с Y положим
G) Af(i4,B) = {/€=y*: f(A)czB).
Обозначим чер^з V семейство всех конечных подмножеств мно-
множества Ху и пусть О — топология на У. Семейство $ всех мно-
к
жеств вида f| M (Au Ut), где At е Т и Ut е О при i = 1, 2, ...
,.., ky порождает (согласно предложению 1.2.1) топологию на
2.6. ПРОСТРАНСТВА ОТОБРАЖЕНИЙ I 173
Yx, называемую топологией поточечной сходимости. Семейство
38 является базой пространства Yx с топологией поточечной схо-
сходимости.
2.6.3. Предложение. Топология поточечной сходимости на Yx
совпадает с топологией подпространства произведения IX Ух
где Yx — Y для каждого xg!
Доказательство. Каждое открытое подмножество простран-
пространства Yx с топологией подпространства произведения Ц Ух
является объединением множеств вида
(8) Y* П Р-' (С/,) Л Р-1 (U2) Л • • • П p;l (Uk),
где Xi е X и Ut е О для / = 1,2, ..., k. Но
9) Yx{\P'xx{U)
Таким образом, все множества вида (8) и все множества, от-
открытые относительно топологии подпространства декартова про-
произведения, суть открытые множества в топологии поточечной
сходимости.
Обратно, из (9) вытекает, что для Л={хь^2» . •¦> хк}^&~
и U g(? имеем
М(Л, U) = Y*{] />-¦ (U) П р (?/) П • • • ПР^1 (U).
Таким образом, все множества, открытые в топологии поточеч-
поточечной сходимости, открыты в топологии подпространства декар-
декартова произведения. I
Из последнего предложения и теорем 2Л.6, 2.3.11 следует
(см. пример 2.6.7)
2.6.4. Теорема. Если Y есть 7^-пространство, то пространство Yx
с топологией поточечной сходимости также есть Т(-пространство
для /<3~. |
Из предложений 2.6.3 и 2.3.34 получаем
2.6.5. Предложение. Направленность {/0, ogS} б пространстве
Yx с топологией поточечной сходимости сходится к элементу
f^Yx в том и только том случае, если направленность {/0(*Ь
ogX} сходится к f(x) для каждой точки jcg! I
Топология поточечной сходимости на Yx может быть также
определена как топология подпространства произведения или
так топология, порожденная семейством отображений. Приня-
Принятое нами определение — хотя оно и выглядит неоправданно
сложным — выбрано потому, что оно аналогично определению
174 ГЛ. 2. ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
компактно-открытой топологии на Yx> где вместо семейства $F
конечных подмножеств множества X взято семейство %?{Х)
всех компактов пространства X (ср. § 3.4).
2.6.6. Предложение. Для каждого топологического пространства
X топология равномерной сходимости на Rx сильнее топологии
поточечной сходимости.
Доказательство. Эквивалентность условий (i) и (v) пред-
предложения 1.4.1 показывает, что достаточно доказать следующее:
если f е Rx принадлежит замыканию множества А с= Rx в топо-
топологии равномерной сходимости, то f принадлежит замыканию
множества А в топологии поточечной сходимости. Пусть U =
k
= /?хП П PJ.1 (Ui)~~ окрестность элемента/ в топологии поточеч-
поточечной сходимости. Так как множества Ut открыты в /?, найдется
такое е >0, что (/(*/)— е, /(*/) + e)cz U{ для г = 1, 2, ..., k.
Далее, так как f = lim/7, где f/GA для / = 1, 2, ..., то суще-
существует такое /, что \f(x)—//(^)|<е для каждого xg! В ча-
частности fj(Xi)^Ui, /=1, 2, ..., &, а это означает, что
и(А0 I
Отметим, что определенные выше топологии на Rx и Vх не
зависят от топологии пространства X, хотя множества Rx и Yx
зависят от топологии пространства X.
2.6.7. Пример. Выберем У=/С, X = D. Из предложения 2.6.3
и примера 2.3.12 следует, что пространство Vх с топологией
поточечной сходимости, вообще говоря, не является нормальным
пространством даже для совершенно нормального простран-
пространства У. 1
2.6.8. Пример. На множестве RN топология равномерной сходи-
сходимости отличается от топологии поточечной сходимости. В самом
деле, легко проверить, что функция f0 ^ Я^, определенная усло-
условием fo(x) = O для хе№, принадлежит замыканию множества
А={/е=/?": f(tf)c:{0, 1} и |f-l@) |< КО}<= Я* в топологии по-
поточечной сходимости, однако /0 не принадлежит замыканию мно-
множества А в топологии равномерной сходимости. 1
Пусть Y — топологическое пространство и {р} — одноточечное
пространство. Каждой точке у е У поставим в соответствие эле-
элемент iY(y)^Y{p\ где [iV(#)] (Р) = У- Тем самым определено
взаимно однозначное отображение пространства Y на простран-
пространство У^. Отображение iY: Y-*Y^ является гомеоморфизмом
относительно топологии поточечной сходимости на Y&\ а при
У = R также относительно топологии равномерной сходимости
на RM.
Из предложений 2.1.11 н 2.2.6 следует, что если Х$Ф0 для
5 g S, то комбинация V есть взаимно однозначное отображение
2.6. ПРОСТРАНСТВА ОТОБРАЖЕНИЙ I 175
произведения Ц {Yx$) на пространство y\seS v. Подобным
же образом из предложения 2.3.6 вытекает, что диагональ А
взаимно однозначно отображает произведение Ц (У*) на про-
пространство ГЦ УЛХ. Читатель может легко доказать следую-
VsgeS /
щие два предложения.
2.6.9. Предложение. Пусть {Xs}s^s — семейство непустых топо-
топологических пространств и У — топологическое пространство. Ком-
р
бинация V: ii\Y s)-^yV5eS /
S
ii\ ) есть гомеоморфизм относи-
seS
тельно топологии поточечной сходимости в пространствах ото-
отображений. 1
2.6.10. Предложение. Пусть X — топологическое пространство и
{K5}seS— семейство топологических пространств. Диагональ
А : П (У?)-*Г П УЛХ есть гомеоморфизм относительно то-
пологий поточечной сходимости в пространствах отображений. 1
Легко установить, что для У == R аналог предложения 2.6.9
в случае топологии равномерной сходимости имеет место в том
и только том случае, если семейство {^5}se5 конечно (ср. с при-
примером 2.6.8).
Заметим, что любые отображения g: Y^Z и h: T-+X по-
порождают отображения Ф^: Yx^-Zx и Ч^: YX-*YT, определен-
определенные формулами
(Ю) <S>g(f) = gf для f^Yx и
Wk(f) = fh для ?eF.
Так как
A1) Ф?(М(А, В)) = М(А, g
1 )y В),
то оба отображения (Dg и Wh непрерывны относительно топо-
топологии поточечной сходимости в функциональных пространствах.
Легко установить, что для каждого h: T-*X отображение
^п: RX^RT также непрерывно относительно топологии равно-
равномерной сходимости на Rx и RT. С другой стороны, отображение
<Dg пространства Rx в себя необязательно непрерывно даже для
гомеоморфизма g: R^-R (см. пример 4.2.14). Это показывает,
что соотношение между естественной топологией на R и тополо-
топологией равномерной сходимости на Rx не вполне удовлетвори-
удовлетворительно. Мы покажем в дальнейшем, что топология равномер-
равномерной сходимости на Rx ассоциирована с конкретной метрикой на
176 ГЛ. 2. ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
R или, точнее, с конкретной равномерной структурой на /?, а не
с топологией на R (см.теорему 4.2.19и упр.4.2.А (с) и 8.1.А (а)).
Если i: Y-+-Z— гомеоморфное вложение, то Ф*: YX-*ZX
также есть гомеоморфное вложение относительно топологии по-
поточечной сходимости на пространствах отображений. Если
i: Т-^Х — вложение, то Ч?г. YX-*YT есть сужение. Вообще го-
говоря, отображение Ч^ не является ни инъективным, ни отобра-
отображением «на», так как некоторые элементы пространства YT мо-
могут не допускать продолжения на все пространство X. С другой
стороны, если h: Т-*Х есть отображение «на», то, как легко
понять, Ч*/,: Yx -> YT есть гомеоморфное вложение относительно
топологии поточечной сходимости, а когда Y = R — относительно
топологии равномерной сходимости.
Отображения Ф^ и Wh связаны с операцией 2 композиции
отображений. В действительности из формул A0) непосред-
непосредственно вытекает, что
Возникает вопрос, можно ли определить топологию на про-
пространствах отображений ZY, Yx и Zx таким образом, чтобы Б
было непрерывным отображением произведения Zy X У* в Zx.
Оказывается, при естественных дополнительных предположениях
(исключающих, например, дискретную топологию) для того,
чтобы определить такую топологию, нужно сузить класс рас-
рассматриваемых пространств (см. теорему 3.4.2 и упр. 3.4А).
Отображение Q пространства Yx X X в пространство У, оп-
определенное формулой fi(f, x) = f(x)> называется отображением
вычисления для пространства Yx. Оно также связано с опера-
операцией 2. А именно, Q есть композиция отображений
A2) Yx X X 1уХ > Yx X XV* -^ YM — У, т. е.
Легко видеть, что формула
A3)
где / — отображение пространства ZXX в У, определяет
взаимно однозначное соответствие Л между множеством всех
(необязательно непрерывных) отображений пространства ZXX
в У и множеством всех отображений пространства Z в множе-
множество всех отображений пространства X в У. Это соответствие
называется экспоненциальным отображением. Естественно изу-
изучать поведение Л и Л~1 на множествах непрерывных отображе-
отображений Y^zxX) и (Yx)z; последнее множество определенно корректно,
если на Yx задана топология.
2.6. ПРОСТРАНСТВА ОТОБРАЖЕНИЙ I 177
Прежде всего встает вопрос, принадлежит ли A(f) множе-
множеству (Yx)zy если f ^y(zx^); это так, если топология на Vх не
слишком сильная. Другой естественный вопрос: принадлежит
ли h~x(g) пространству FxJf>, если ge(Y*)z; это так, если
топология на Yx не слишком слабая. Наконец, можно спросить,
когда экспоненциальное отображение непрерывно и при каких
условиях оно является гомеоморфизмом.
Топологию на Yx называют собственной, если для каждого
пространства Z и любого f gFzxjc отображение A(f) принад-
принадлежит пространству (Yx)z. Аналогично топологию на Yx назы-
называют допустимой, если для каждого пространства Z и любого
f gGxJ отображение A~l(g) принадлежит пространству
y(zxx) Топология на Yx9 которая одновременно собственная и
допустимая, называется приемлемой.
2.6.11. Предложение. Топология на Yx допустима в том и только
том случае, если отображение вычисления для пространства Yx
непрерывно, т. е. если непрерывно отображение Q: YXY^X-*Y.
Доказательство. Если топология на Yx допустима, то для
Z — Yx и g = idy;c отображение A~l(g): YXX%^~Y непре-
непрерывно. Так как
A4) {[Л (О)] (/)}(*) = Q(/, x) = f{x), т. е. A(Q) = idyx,
отсюда следует, что Я = Л*1 (g), поэтому Q непрерывно.
Обратно, если отображение вычисления для пространства Yx
непрерывно, то для каждого пространства Z и любого элемента
gG(F)z отображение Л-1^) непрерывно, так как A~l(g) =
= Q(g X idx): Zy^X-+Y. В самом деле, для любых (г, х)е
gZX^ мы имеем
{ [Л (Я (g X id*))] (г)} (х) = [Q (g X idx)] (г, х) =
так 4ToA(Q(gXidx)) = g и A~l(g) =
2.6.12. Предложение. Для каждой пары топологических про-
пространств Ху Y и любых двух топологий О, Of на пространстве
Yx имеют место следующие утверждения.
(I) Если топология О собственная и Of <z:0t то топология
Of также собственная.
(и) Если топология 0 допустимая и Са0*\ то топология
0f также допустима.
(Hi) Если топология 0 собственная, а топология 0' допусти-
допустимая, то 0 a 0f.
(iv) На Yx существует не более одной приемлемой тополо-
топологии.
12 Зак. 697
178 ГЛ. 2, ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
Доказательство. Оба утверждения (i) и (и) следуют не-
непосредственно из определений собственной и допустимой топо-
топологий, a (iv) вытекает из (ш). Для доказательства (ш) выбе-
выберем собственную топологию О и допустимую топологию С на
Yx и обозначим пространство (Yx\O) через У*, а простран-
пространство (YX1O/) через У*.
Определения допустимой и собственной топологий приводят
к следующим включениям:
) и *[№*)] с: (
из которых вытекает, что idYx = AA~l(idYx)^(YfpaK т. е,
О a Of. I
Из предложения 2.3.6 следует, что топология поточечной
сходимости является собственной. В самом деле, A(f) непре-
непрерывно в том и только том случае, если pxJS. (/) непрерывно
для любой точки xogI Из соотношения A3) вытекает, что
[PxA(f)](z) = f(z, х0). Поэтому если /е У<гх*>, тоЛ(/)<=(У*J.
С другой стороны, топология поточечной сходимости, вообще
говоря, не является допустимой. В самом деле, для этой тополо-
топологии факт принадлежности g множеству (Yx)z означает, что для
всех zoeZ и Хо^Х отображения [gBo)](*) и [g(z)]{x0) не-
непрерывны, в то время как факт принадлежности Л (g) множе-
множеству У<2 х *> означает, что отображение g непрерывно по обеим
координатам.
Из предложения 2.6.11 непосредственно вытекает, что то-
топология равномерной сходимости допустима. С другой стороны,
топология равномерной сходимости, вообще говоря, не является
собственной. Читателю предоставляется определить функцию
/: RXR-+-R, такую, что A(f) не принадлежит пространству
(RR)R, где RR наделено топологией равномерной сходимости.
Отметим, что предложение 2.6.6 есть непосредственное след-
следствие части (iii) предложения 2.6.12 и фактов, установленных
в последних двух абзацах.
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
Топология равномерной сходимости берет свое начало из
классического понятия равномерно сходящейся последователь-
последовательности функций, а топология поточечной сходимости — из понятия
сходящейся последовательности функций. Допустимые тополо-
топологии впервые рассматривал Арене в [1946]; они были опреде-
определены через непрерывность отображения вычисления. Арене и
Дугунджи [1951] определили собственные топологии и доказали
предложения 2.6.11 и 2.6.12.
2.6. ПРОСТРАНСТВА ОТОБРАЖЕНИЙ I 179
УПРАЖНЕНИЯ
2.6.А. Покажите, что множества M({x},U), где х^Х и U
принадлежит фиксированной предбазе {Р пространства У, обра-
образуют предбазу пространства Yx с топологией поточечной схо-
сходимости.
2.6.В. Проверьте, что для любых двух семейств {^}5e=s и
{Ys} eSтопологических пространств произведениеЦ: XI
есть гомеоморфное вложение относи-
тельно топологии поточечной сходимости в пространствах ото-
отображений.
2.6.С (Арене и Дугунджи [1951]). Говорят, что направлен-
направленность {/<т, 0GH) в пространстве Yx непрерывно сходится к ото-
отображению fm Yx, если для каждой направленности {xj, o'g?}
в пространстве X и любого хе lim ха' направленность {fa(xa')f
(сг, а')еЕХ2'} в пространстве Y сходится к точке /(х);
здесь множество 2X2' направлено по следующему правилу:
(аг <O^(tf2» а^) тогда и только тогда, когда al^a2 и о'{^.в'г
(a) Покажите, что топология на пространстве Yx собствен-
собственная в том и только том случае, если для каждой направлен-
направленности {/0, сг е 2} в Yx из непрерывной сходимости направлен-
направленности {/a, a g Е} к отображению / е Yx следует, что/е lim fa
относительно этой топологии.
(b) Покажите, что топология на пространстве Yx допустима
в том и только том случае, если для каждой направленности
{fay о е 2} в Yx и любого/е lim fa относительно этой тополо-
гии направленность {fa, ueS} непрерывно сходится к f.
2.6.D. (а) Покажите, что операция композиции 2, вообще
говоря, не является непрерывной относительно топологии по-
поточечной сходимости.
(b) Проверьте, что операция композиции 2, вообще говоря,
не является непрерывной относительно топологии равномерной
сходимости.
(c) Докажите, что если топологии на ZY и Yx допустимы,
а топология на Zx собственная, то операция композиции 2 есть
непрерывное отображение пространства ZYY^YX в пространство
Zx.
Указание. Выразите 2 в терминах отображений Q и А.
2.6.Е (Фокс [1945]). Докажите, что не существует приемле-
приемлемой топологии на пространстве RQ, где Q — пространство ра-
рациональных чисел (ср. с теоремой 3.4.3 и упр. 3.4.А).
12*
180 ГЛ. 2. ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
Указание. Покажите, что если топология на RQ собственная,
то IntM(f7, @, 1)) = 0 для каждого открытого подмножества
U a Q. Для этого покажите, что О содержит D(K0) как замкну-
замкнутое подпространство, и при помощи теоремы Титце — Урысона
определите для любого f^M (О, @, 1)) функцию F: [0, 1]Х
XQ~>-/?, такую, что F(Q,x) = f(x) для xeQ и [A(F)](z)&
<?М(О, @, 1)) дляг>0.
2.6.F. Докажите, что для любых топологических пространств
X, У, Z экспоненциальное отображение Л: Y^zxX^^(Yx)z есть
гомеоморфное вложение относительно топологии поточечной
сходимости на пространствах отображений.
Указание. Используйте упр. 2.6.А.
2.6.G. Покажите, что сложение и вычитание функций есть
непрерывное отображение произведения Rx X Я* в Rx как от-
относительно топологии равномерной сходимости, так и относи-
относительно топологии поточечной сходимости на Rx. Проверьте, что
умножение функций есть непрерывное отображение произведе-
произведения Rx X Rx в Rx относительно топологии поточечной сходи-
сходимости. Покажите, что умножение функций на вещественные
числа не является непрерывным отображением Rx X R в Rx от-
относительно топологии равномерной сходимости.
2.7. ЗАДАЧИ
Локально замкнутые множества
2.7.1 (Куратовский и Серпинский [1921а]). Подмножество Л
топологического пространства X называется локально замкну-
замкнутым, если каждая точка х^А имеет такую окрестность U в
пространстве X, что пересечение Af\U замкнуто в подпростран-
подпространстве U с: X.
Покажите, что для подмножества А топологического про-
пространства X следующие условия равносильны:
A) Множество А локально замкнуто.
B) Разность Л\А замкнута.
C) Множество А есть разность двух замкнутых множеств.
Отделенные Fa-множества в нормальных пространствах
2.7.2. (а) (Урысон [1925]). Докажите, что для каждой пары
Л, В отделенных /v-множеств в нормальном пространстве X су-
существуют открытые множества U, V с X, такие, что A a U>
BczV nU(]V = 0.
оо оо
Указание. Пусть Л == М At и В= \J Biy где Лг и Bt — зам*
2.7. ЗАДАЧИ 181
кнутые множества. Определите по индукции две последователь-
последовательности Uu U2, •-• и V\t V2, ... открытых подмножеств простран-
пространства Ху такие, что
Vi-X U At с Ut и Vt П (В U Fz-i) = 0,
а также
Pi-! U Я* с= V, и Vt П (Л U ?7/) = 0,
где f/0 = Vo = 0.
(b) (Урысон [1925]). Выведите из (а), что нормальность на-
наследуется /^-множествами (ср. с упр. 2.1.Е).
(c) (Бонан [1970]). Примените (а) для решения задачи
1.7.15 (Ь).
Указание (Катетов [1951а]). Модифицируя доказательство
леммы Урысона, определите для каждого рационального числа
г открытое множество Vr cr X, такое, что
и Кгс V/, где г < гг.
Нормально расположенные множества II (см. задачи 1.7.6
и 3.12.24)
2.7.3. (Смирнов [1951с]). Докажите следующие свойства нор-
нормально расположенных множеств.
(a) Если At — нормально расположенное множество в про-
оо
странстве Xt i = 1, 2, ..., то объединение (J At нормально рас-
«=1
положено в пространстве X.
(b) Если А — нормально расположенное множество в про-
пространстве X и В — множество типа Fo в подпространстве Л, то
В нормально расположено в X.
(c) Если А — нормально расположенное множество в про-
пространстве X, а В — нормально расположенное множество в под-
подпространстве А, то В нормально расположено в X.
(d) Если X — нормальное пространство, то каждое его нор-
нормально расположенное подмножество с топологией подпростран-
подпространства является нормальным пространством.
Полунепрерывные функции II (см. задачи 1.7.14—1.7Л6,
3.12.22 (g) и 5.5.20)
2.7.4. (а) (Хаусдорф [1919]). Покажите, что теорема Тит-
це — Урысона легко следует из характеристики нормальности,
данной в задаче 1.7.15(Ь).
182 ГЛ. 2. ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
(b) (Тонг [1952]; для метрических пространств — Титце
[1915]). Докажите, что ^-пространство X нормально тогда и
только тогда, когда для каждого замкнутого подмножества
А сг X и каждой вещественной функции k, определенной и огра-
ограниченной снизу на X и непрерывной во всех точках множества
Л, существует непрерывная функция h: X^~Ry такая, что
h | А = k | А и h (x) ^ k (х) для каждого х е X.
Указание. Покажите, что функция g, определенная форму-
формулой g(x) = sup( inf k{z))y где sup берется по всем окрестностям
U ze=U
U точки ху полунепрерывна снизу. Далее примените характе-
характеристику нормальности, данную в задаче 1.7.15(Ь).
(c) (Тонг [1952]; для метрических пространств — Титце
[1915]). Докажите, что ^-пространство X является совершенно
нормальным в том и только том случае, если для каждого
замкнутого множества АаХ п любой полунепрерывной снизу
(сверху) функции /, определенной на X и такой, что f\A непре-
непрерывна, существует последовательность {/;} непрерывных функ-
функций на Ху такая, что f(x)=limfi(x) для каждого х^.Х, ft\A =
= /|Л, t = l,2, .... и fi(x)^fi+x(x) (и fi(x)^fi+x(x)) для
1 = 1, 2, ...hxg!
Указание. Примените части (с) и (Ь) задачи 1.7.15.
Линейно упорядоченные множества II (см. задачи 1.7.4,
3.12.3, 3.12.4, 3.12.12@, 5.5.22, 6.3.2 и 8.5.13(j))
2.7.5. (а) Пусть X — пространство с топологией, индуцирован-
индуцированной линейным порядком <С. Установите, что для любого под-
подмножества МаХ, содержащего не менее двух элементов, топо-
топология на М как на подпространстве пространства X сильнее, чем
топология, индуцированная на М сужением линейного порядка
< на М. Приведите пример открыто-замкнутого подмножества
М линейно упорядоченного пространства X, такой, что две ука-
указанные топологии на М различны. Проверьте, что если М всюду
плотно в X в смысле порядка (т. е. для каждых х, j/gX, таких,
что х < yt существует 2GM, такое, что х < z < у), то две то-
топологии на М совпадают. Покажите, что это заключение, вообще
говоря, не имеет места, если предполагать только, что М топо-
топологически всюду плотно в X, т. е. что М = X.
(Ь) Подмножество С линейно упорядоченного множества X
выпукло, если (х, у) а С для любых х, у^С.
Установите, что если семейство ^ состоит из выпуклых под-
подмножеств пространства X и [)$Ф0У то \J& — выпуклое множе-
множество. Покажите, что каждое подмножество М cz X может быть
представлено как объединение попарно непересекающихся мак-
максимальных выпуклых множеств, т. е. выпуклых множеств, кото-
которые не могут быть расширены до выпуклых подмножеств про-
2.7. ЗАДАЧИ 183
странства X, содержащихся в М. Эти множества называются
выпуклыми компонентами подмножества М. Проверьте, что в
каждом выпуклом подмножестве С пространства X, содержа-
содержащем хотя бы два элемента, топология подпространства про-
пространства X и топология, индуцированная сужением линейного
порядка из пространства X на С, совпадают. Покажите, что вы-
выпуклые компоненты открытого подмножества М а X открыты
в пространстве X.
(с) (Бурбаки [1948]). Докажите, что каждое линейно упо-
упорядоченное пространство наследственно нормально.
Указание. Примените (Ь) и задачу 1.7.4(d).
Пространства Урысона и семирегулярные пространства II
(см. задачи 1.7.7—1.7.9 и 6.3.17)
2.7.6. (а) Установите, что свойство быть пространством Уры-
Урысона наследственное и мультипликативное.
(Ь) Покажите, что семирегулярность мультипликативна и
наследуется открытыми подмножествами и всюду плотными под-
подмножествами.
Вложение в произведения
2.7.7 (Шанин [1944], Мрувка [1956]). Покажите, что для
Го-пространства X и топологического пространства У следующие
условия равносильны:
A) Пространство X вложимо в некоторую степень простран-
пространства У.
B) Семейство всех множеств вида f-l(U), где f: X-^Y не-
прерывно и U —открытое подмножество пространства Y, обра-
образует предбазу пространства X.
C) Топологию пространства X можно задать с помощью се-
семейства отображений в пространство У.
D) Для любого xgX и любого замкнутого подмножества
F а X, такого, что x^F, существует непрерывное отображение
f пространства X в конечную степень пространства У, такое,
что fW
2.7.8 (Мрувка [1956]). (а) Докажите, что не существует та-
такого ^-пространства У, что каждое ^-пространство вложимо
в некоторую степень пространства У (ср. с задачей 2.7.18(Ь)).
Указание. Примените задачу 2.7.7.
(Ь) Для каждого ш ^ Ко обозначим через L(m) простран-
пространство, определенное в примере 1.2.6, где |Х| = ш. Покажите, что
каждое /^-пространство X, такое, что ] Х\ ^ m ^ fc*0 и w{X) ^ ш;
вложимо в ш-ю степень L(m).
184 ГЛ. 2. ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
Кардинальные функции II (см. задачи 1.7.12, 1.7.13, 3.12.4,
3.12.7—3.12.11, 3.12.12(j) и 8.5.17)
2.7,9. Для кардинальной функции / мы обозначим через hf
кардинальную функцию, значение которой на пространстве X
равно sup f{M)t где sup берется по всем подпространствам М
пространства X. Функция hf называется наследственной f—
в этом смысле употребляются такие термины, как наследствен-
наследственная всюду плотность, наследственное число Суслина и т. п.
(a) Проверьте, что
hw(X)=w(X), Ax(*) = X<*) и ht(X) = t(X).
(b) Проверьте, что функция he, определенная в задаче 1.7.12,
есть наследственное число Суслина и что hc(X) = he(X) для
каждого топологического пространства X.
(c) Покажите, что hd(X)^ t(X) для каждого топологиче-
топологического пространства X, и приведите пример пространства X, для
которого hd(X)> d(X) и hd(X)>t(X).
(d) Установите, что если А — всюду плотное подпространство
пространства X, то с(Л) —с(Х), но, вообще говоря, неравенство
d(A)^ d(X) не имеет места.
(e) (Смирнов [1951 d]; для &*0 — Серпинский [1921а]). До-
Докажите, что топологическое пространство X удовлетворяет усло-
условию hd(X)^: Ка в том и только том случае, если для каждой
возрастающей трансфинитной последовательности FqCZ F\Ci
с= F2 cz ... с: Ft c= ..., | < (оа+1, замкнутых подмножеств про-
пространства X существует такое ?о < <*>а-н, что Fi = Fi0 для каж-
каждого ? ^ |о (СР- с задачей 3.12.7(Ь)).
(f) (Серпинский [1921а]). Приведите пример хаусдорфова
пространства X, такого, что hd(X) > hc(X)= Ko.
Указание. Возьмите прямую R с топологией, порожденной
базой, состоящей из всех множеств вида (а,Ь)\А, где
|Д|К
Замечание. Тодорчевич [1984] описал вполне регулярное
пространство X, удовлетворяющее неравенствам hd(X)>
> hc(X)> &o. В рамках наивной теории множеств неизвестно
ни одного примера регулярного пространства X, такого, что
hd(X) > hc(X)= Ko. Существование такого пространства свя-
связано с проблемой Суслина — вопросом, поставленным М. Сусли-
ным в 1920 г.: существует ли линейно упорядоченное простран-
пространство X, такое, что с(Х)=&0 и d(X)>&0 (пространство Сус-
Суслина). В самом деле, можно доказать, что для любого про-
пространства Суслина X выполняется неравенство hd(X)>hc(X) =
= So (см. задачу 3.12.4(е)). Как показано йехом в [1967] и
Тенненбаумом в [1968], существование пространства Суслина
не противоречит аксиомам теории множеств и не зависит от них
2.7. ЗАДАЧИ 185
(история проблемы Суслина и ее связи подробно изучены Ку-
репой в [1968] и М. Рудин в [1969]).
Наследственно нормальное пространство X, такое, что
hd(X)> /ic(X)=K0, было построено Хайналом и Юхасом
[1974] в предположении континуум-гипотезы. Намного более
простая конструкция была описана Ван Дауэном, Толлом и
Вейсом в [1977] (ср. с замечанием к задаче 3.12.7(с)).
(g) (Зенор [1980]). Покажите, что если семейство {^}
топологических пространств удовлетворяет условию hd( Ц
^ шдля каждого конечного So <= S и |5| ^ m, Tohdf Ц
VseS
2.7.10.(а) Приведите пример совершенно нормального про-
пространства Ху такого, что hd(X) = hc(X) = e(X)= So и
hd(XXX)h(XXX)(XXX)
Указание. См. упр. 2.1.1.
(Ь) (Курепа [1950]). Пусть X — пространство Суслина. До-
Докажите, что сAХХ)> Ко.
Указание. Для каждого а < ом определите по трансфинит-
трансфинитной индукции, как показано ниже, замкнутое сепарабельное
подпространство facl и обозначьте через °U^ семейство всех
выпуклых компонент подпространства X\Fa- Пусть Fo = 0;
для предельного числа а положим Fa = М Ffl и для а = р+ 1
Э<а р
положим Fa = F$[)A$> где Лр состоит из тех U ^.°U§, для ко-
которых существует такая точка x(U), что U\{x(U)}=U'\JU"f
где ?/', U" — непустые непересекающиеся открытые в простран-
пространстве X множества. Затем покажите, что для каждого а суще-
существует такое Ua^fyl, что x(Ua) определено, и рассмотрите се-
мейство KU:}
Замечание. Как вытекает из (Ь) и замечания к предыдущей
задаче, нельзя доказать, что свойство Суслина конечно муль-
мультипликативно. Оказывается, конечная мультипликативность
свойства Суслина не зависит от аксиом теории множеств (см.
Архангельский [1971] или Юхас [1971]).
(с) (Шанин [1948] (объявлено в [1946])). Покажите, что
для каждого семейства {St}t<=r конечных множеств, где |Г| =
= m>N0 — регулярный кардинал, существуют такое множе-
множество Го cz Т мощности m и такое множество Z, что St Л S? = Z
для любой пары tt V различных элементов множества Го.
Указание (Юхас [1971]). Можно считать, что |S*| = /i< No.
Примените индукцию относительно п. Рассмотрите максималь-
максимальное подмножество Тх cz Г, такое, что S* Л S*'= 0 для любых пар
/, f различных элементов множества Т\.
186 ГЛ. 2. ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
(d) Докажите, что произведение Ц Xs обладает свойством
sgS
Суслина в том и только том случае, если для каждого конечного
So cz S произведение JI Xs обладает свойством Суслина.
Указание. Примените (с) для m = Ni.
Замечание, Курепа доказал в [1962], что если c(Xs)^nt для
каждого seS, то с ( Ц ХЛ <; 2т; доказательство этого факта
можно также найти у Юхаса [1971].
2.7.11 (Шанин [1948] (объявлено в [1946а]). Говорят, что
кардинал m > Мо есть калибр пространства X, если каждое се-
семейство мощности т, состоящее из непустых открытых подмно-
подмножеств пространства X, содержит подсемейство мощности m с не-
непустым пересечением. Наименьший кардинал ш ^ Ко, такой, что
каждое семейство мощности >щ, состоящее из непустых откры-
открытых подмножеств пространства X, содержит подсемейство мощ-
мощности >ш с непустым пересечением, называется числом Шанина
пространства X и обозначается через s(X). Очевидно, что
s(X)—наименьший кардинал ш ^ Ко с тем свойством, что сле-
следующий за ним кардинал есть калибр пространства X.
(a) Покажите, что c(X)^.s(X)^. d(X), и приведите примеры
хаусдорфовых пространств X и У, таких, что s{X)> hc{X) и
d(Y)>S(Y).
(b) Докажите, что если регулярный кардинал является ка-
калибром пространства Xs для любого s e S, то этот кардинал
также является калибром произведения Ц Xs- Выведите от-
сюда, что если s (Xs) = ш для каждого seS, to s ( Ц ХЛ == tit.
Указание. Сначала рассмотрите конечные произведения, а
затем используйте задачу 2.7.10(с).
(c) Приведите примеры вполне регулярных пространств X
и У, таких, что s(X) > с(Х) и d(Y) > s(У).
Замечание. Существование нормальных пространств, удов-
удовлетворяющих указанным выше неравенствам, следует из задачи
2.7.14 и теорем 2.3.17 и 3.1.9.
Функции на произведениях
2.7.12. (а) (Росс и Стоун [1964]). Пусть {X9}8eS — семей-
семейство сепарабельных пространств. Покажите, что замыкание от-
открытого множества U cz Ц Xs (являющееся каноническим
замкнутым множеством; ср. с упр. 1.1.С(е)) зависит лишь от
счетного множества координат, т. е. существует счетное мно-
2.7. ЗАДАЧИ 187
жество So ^ S, такое, что если
{xs}<=U, {ys}s== П Х$ и ys = xs Для seS0, то
Указание. Рассмотрите максимальное семейство непересе-
непересекающихся элементов канонической базы пространства И Xs9
содержащихся в [/, и примените 2.3.18.
(Ь) (Бокштейн [1948], Росс и Стоун [1964]). Используя (а),
покажите, что для каждой пары непустых непересекающихся
открытых множеств U, V cz д Is, где Xs — сепарабельное
se5
пространство, существует счетное множество So cz S, такое, что
проекции U и V на П Xs не пересекаются. Проверьте, что
se5o
если все Xs удовлетворяют второй аксиоме счетности, то су-
существуют открытые множества U\t V\ с: Ц Xs, являющиеся
счетными объединениями элементов канонической базы про-
пространства П^ и такие, что
^UcUu VcVt и ?/iflVi=0.
(с) (Мазур [1952], Корсон [1959], Корсон и Исбелл [1960],
Росс и Стоун [1964]). Пусть {X?}5?=s ~~ семейство топологиче-
топологических пространств. Говорят, что непрерывное отображение
/: Л->У подпространства А произведения Ц Xs в пространство
s e S
Y зависит от счетного множества координат, если существует
счетное множество SqCzS, такое, что f(x) — f(y) для каждой
пары х= {xs}, у = {ys}> удовлетворяющей условию xs = ys для
Пусть {JJ5^S— семейство сепарабельных пространств и У —
хаусдорфово пространство со второй аксиомой счетности. До-
Докажите, что каждое непрерывное отображение /: П XS^>Y
S€=S
зависит от счетного множества координат и существуют счет-
счетное множество So с: 5 и непрерывное отображение fo: ±[ XS->Y9
такие,что /совпадаете композицией fopSo проекции ps: U_XS-^
s s 5
П Xs и отображения f0 (ср. с упр. 3.2.Н и 4.1.G и зада-
чей 2.7.13)
Замечание. Дальнейшие сведения о функциях на произве-
произведениях можно найти в работах: Энгелькинг [1966] и Нобл и
Ульмер [1972].
188 ГЛ. 2. ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
2-произведения I (см. упр. 3.10. D и задачи 3.12.23 и 4.5.12)
2.7.13 (Корсон [1959]; ссылка на Э. М. Глисона в книге
Исбелла [1964]). Пусть {I5}5eS — семейство топологических
пространств, и пусть а = {as}—точка произведения П Xs,
Через 2(а) обозначим подпространство произведения Ц Xs,
s&S
состоящее из всех таких точек {xs}t что х5фа5 только для
счетного множества s e S. Все подпространства пространства
П Xs вида 2(а) для аеД^ называются ^-произведениями
пространств {Xs}5€e5.
(а) Пусть {Xs}se s — семейство сепарабельных топологиче-
топологических пространств и Y — хаусдорфово пространство, одноточеч-
одноточечные подмножества которого суть G^-множества. Докажите, что
для каждого а^\П Xs и каждого непрерывного отображения
/: 2(а)->У существуют счетное множество 50cS и непрерыв-
непрерывное отображение/о: П XS^Y, такие, что f совпадает с компо-
зицией fnipq |2(а)) сужения проекции р~: П Xs-> П Xs на
2 (а) и отображения fo. Покажите, что, в частности, f зависит от
счетного множества координат.
Указание. Прежде всего покажите, что для каждого х =
= {xs}^2(a) существует счетное множество S(x)cnSy такое,
что если х' = \х[) е 2(а) и x's = xs для 5 eS(x), то f(x') = f(x).
Затем определите по индукции счетные подмножества 2ь 2г, ...
множества 2(а), где 2j = {а}, и счетные подмножества Si,
S2, ... множества S, такие, что Si = (J U S (x) и проекции
мнол^еств 2(+i на пространства П Xs всюду плотны в про-
°°
странствах П Xs. Затем рассмотрите множество So = M Si-
(b) Выведите из сказанного выше, что при предположениях
задачи (а) каждое непрерывное отображение/: 2(а)-^У не-
непрерывно продолжается на все пространство П Xs.
(c) Покажите, что (а) остается верным, если 2(а) заменить
любым открытым подмножеством пространства П Xs, т. е.
что в предположениях задачи (а) для каждого открытого мно-
множества U cz Ц Xs и каждого непрерывного отображения
2.7. ЗАДАЧИ 189
/: U' ->- У существуют счетное множество SqCiS я непрерывное
отображение/0: pSq(U)-+Y, такие, что / —/0(psJ?/). Покажите,
что этот результат дает решение задачи 2.7.12 (Ь).
2.7.14 (Комбаров и Малыхин [1973]). Пусть {Xs}sgS — се-
семейство топологических пространств со следующим свойством:
для каждого счетного множества SoczS произведение П Xs
нормально и наследственно сепарабельно. Докажите, что тогда
любое 2-произведение пространств {^s}5t=s нормально (ср. с
задачей 2.7.9(g)).
Указание. Рассмотрите 2-произведение 2(а), где a = {as}^
е П Xs- Для любого x={xs}^2(a) положите 5(х) =
= {s€eS: ХзФпз) и S(AT)= U S (х) для любого МаЪ(а).
Для пары Л, В непересекающихся замкнутых подмножеств про-
пространства 2 (а) выберите soeS и определите по индукции воз-
возрастающую последовательность 5i с: S2 сг ..., где Si = {$о},
А\ cz A<i с: ... и Si cz В2 с: ..., счетных подмножеств множеств
5, Л и В соответственно, таких, что для /=1,2, ...
Pst(A)<=Plffi)' РзАВ)<=^ГЩ и S(Ai)US(Bi)czSi+l.
оо оо оо
Установите, что для 50== U Sh Ло= U At и Во= U #/ имеют
i=l f=I i=\
место включения
: PsQ (Bo)
и что pSq (Ло) П Psq {Bo) = 0 -
Декартовы произведения и нормальность
2.7.15.(а) (Катетов [1948]). Пусть произведение ХХУ на-
наследственно нормально. Покажите, что либо все счетные под-
подмножества пространства X замкнуты, либо пространство У со-
совершенно нормально.
Указание. Допустим, что существуют счетное подмножество
М czX, такое, что М\М ф 0, и замкнутое подмножество г cz: У,
не являющееся Gg-множеством. Выберите х^М\М и рас-
рассмотрите подмножества A=MXFnB = {x} X(Y\F) си XX У.
(Ь) (Кук и Фицпатрик [1968]). Докажите, что предел об-
обратной последовательности совершенно нормальных пространств
совершенно нормален.
Указание. Примените условие (ш) теоремы 1.5.19.
190 ГЛ. 2. ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
(c) (Катетов [1948] ). Покажите, что счетное произведение
IiXj совершенно нормально в том и только том случае, когда
все конечные произведения Х\ X Х2 X • • • X Xi совершенно нор-
нормальны.
(d) (Катетов [1948]). Докажите, что счетное произведение
оо
И Xiy где |Х/|^2 для i= 1, 2, ..., совершенно нормально в
том и только том случае, если оно наследственно нормально.
Замечание. Как отметил Майкл [1971], существует не нор-
оо
мальное произведение Ц Xi9 такое, что все конечные произве-
произведения XiX^X ... Х-& наследственно нормальны (в действи-
действительности наследственно паракомпактны). В самом деле, доста-
достаточно взять пространство X из примера 5.1.32 в качестве Х\ и
счетное дискретное пространство Лг в качестве пространства
Xt, i> 1 (см. пример 5.1.32 и упр. 4.3.G).
2.7.16.(а) (А. Стоун [1948]). Докажите, что декартово про-
произведение N*x не является нормальным (ср. с упр. 3.1. Н(а)).
Указание. Пусть N*1 = П Xs, гце Xs = N и \S\ = «ь Для
I = 1 и 2 рассмотрите множество At cz П Xs> состоящее из
всех таких {xs}t что для каждого / Ф i равенство xs = j имеет
место не более чем для одного seS. Проверьте, что А\ и Л2
замкнуты и не пересекаются, и покажите (применяя задачу
2.7.12(Ь) или 2.7.13(с)), что А\ и А2 не могут быть отделены
непересекающимися открытыми множествами.
(Ь) (Поспишил [1937а]). Покажите, что никакое декартово
произведение несчетного множества пространств, каждое из
которых имеет мощность > 1, не является наследственно нор-
нормальным.
Указание. Примените либо (а), либо 2.7.15(а).
Регулярное пространство X, на котором каждая непрерыв-
непрерывная вещественная функция постоянна
2.7.17 (Херрлих [1965а]). (а) Определите регулярное про-
пространство Я, содержащее точки t и f, удовлетворяющее усло-
условию f(t) — f(t') для каждой непрерывной функции f: Я->/?.
Указание. Измените конструкцию примера 2.4.21, взяв сум-
ОО 00
му ф Zf ф ф Z_f и добавив две точки.
2.7. ЗАДАЧИ 191
(b) Для каждого регулярного пространства S определите
регулярное пространство #E), содержащее S как замкнутое
подпространство и обладающее тем свойством, что каждая не-
непрерывная функция f: H(S)-*R постоянна на S.
Указание. Рассмотрите произведение K = SX# с тополо-
топологией, порожденной окрестностями следующего вида: для точки
(s, h), кф(, в качестве окрестностей взяты все множества
{s} X Vt где V пробегает множество окрестностей точки h в про-
пространстве Я, таких, что / Щ V, а для точки (s, t)— все множества
вида U ({s'} X VV)> где U — окрестность точки 5 в простран-
стве Sf a Vs' — окрестность точки / в пространстве Н. Отожде-
Отождествите замкнутое подмножество 5 X {f} пространства Y в
точку.
(c) Определите регулярное пространство X, такое, что \Х\ >
> 1 и каждая непрерывная функция /: X-+-R постоянна.
Указание. Возьмите Хо = {0} и Xt+\ = H(Xi) для i = 1, 2, ...
оо
и рассмотрите объединение X — JJ Хг.
Замечание. Пространства с подобными свойствами были ра-
ранее определены Хьюиттом [1946] и Новаком [1948], однако их
конструкции более сложны.
2.7.18 (Херрлих [1965а]). (а) Для каждого ^-пространства
Y определите регулярное пространство X, такое, что |АГ|> 1 и
каждая непрерывная функция /: X-*~Y постоянна.
Указание. Поступайте так, как предложено в указаниях к
предшествующей задаче; начните с соответствующего изменения
пространства Z из примера 2.3.36.
(Ь) Выведите из (а), что не существует ^-пространства Y
с тем свойством, что каждое регулярное пространство вложимо
в некоторую степень пространства Y.
Замечание. Часть (Ь) была получена независимо Рамером
в [1965].
Обратные спектры I (см. задачи 3.12.13 и 6.3.16)
2.7.19. (а) (Джентри [1969], Э. Поль [1973]). Приведите
пример обратных последовательностей5 = {-Х"г я?| и S'={K,, sxj}
подпространств вещественной прямой и отображения {icU, ft] из
S в о', где я', й/ и /, — открыто-замкнутые отображения «на»,
такие, что Hm{id^, /J есть отображение «на», не являющееся
факторным.
(Ь) (Локуциевский [1954]). Докажите, что если все свя-
связующие отображения nj обратной последовательности {Xt, я]}
192 ГЛ. 2. ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
открыты и являются отображениями «на», то проекции я, от-
открыты.
Замечание. Последнее заключение не имеет места для про-
произвольных обратных спектров (см. Э. Поль [1973] ).
(c) Приведите пример обратной последовательности {Xt> л'}»
где все связующие отображения я| открыты, в то время как
проекции Hi не являются открытыми.
(d) (Зенрр [1969] ). Докажите, что если все связующие ото-
отображения я} обратной последовательности {Xiy nj} замкнуты,
то проекции я» также замкнуты.
Замечание. Последнее заключение, вообще говоря, не имеет
места для произвольных обратных спектров (см. Э. Поль
[1973]).
(e) (Э. Поль [1973] ). Докажите, что если все связующие
отображения я* обратной последовательности iXp ftj} наслед-
наследственно факторны, то проекции я,- также наследственно фак-
факторны.
Замечание. Это утверждение несправедливо для произволь-
произвольных обратных спектров даже в случае, когда проекции Па —
отображения «на». Если же только предположить, что все свя-
связующие отображения обратной последовательности {Xi9 я|} фак-
факторные, то проекции я,-, вообще говоря, не являются фактор-
факторными (см. Э. Поль [1973]).
Пространства замкнутых подмножеств I (см. задачи 3.12.26,
4.5.22, 6.3.22 и 8.5.16)
2.7.20. (а) (Вьеторис [1922]). Для любого топологического
пространства X обозначим через 2х семейство всех его непустых
замкнутых подмножеств. Проверьте, что семейство 3§ всех мно-
множеств вида
U2, ..., Uh) =
e=2*: Be [}ut и В[\1)гФ 0, /=1, 2, ...,
где Uи U2f ..., Uk — последовательность открытых подмножеств
пространства X, удовлетворяет условиям (В1) и (В2). Таким
образом, это семейство $ порождает топологию на множестве
2х; эта топология называется топологией Вьеториса. Множество
2х с топологией Вьеториса называется экспоненциальным про-
пространством пространства X.
(Ь) (Майкл [1951]). Пусть Ji{X)% f = l, 2, ..., есть подпро-
подпространство пространства 2х, состоящее из всех множеств мощ-
оо
ности ^ *, и пусть /(Х)= U Ji(X). Пусть X есть Грпростран-
2.7. ЗАДАЧИ 193
ство; поставим в соответствие элементу (х\, х2, ..., JC/jeX'
точку {хих2, ..., Xi} ^ Ji (X). Проверьте, что тем самым опре-
определено непрерывное отображение /,-: Xl-^Ji(X)cz2K.
Заметьте, что для ^-пространства X пространство J\(X) го-
меоморфно пространству X. Покажите, что если X есть 7>про-
странство, то все множества h(X) замкнуты в пространстве 2х,
а если X есть ^-пространство и J\(X) замкнуто в пространстве
2х, то X есть Г2-пространство.
Установите, что если X есть 7\-пространство, то J(X) всюду
плотно в 2х, и покажите, что dBx)= d{X) для каждого беско-
бесконечного 7>пространства X. Заметьте, что если X есть ^-про-
^-пространство, то 2х плотно в себе тогда и только тогда, когда про-
пространство X плотно в себе.
(c) Покажите, что если X есть Гг-пространство, то отобра-
отображение /г: Xl-^Ji(X) замкнуто для t = l, 2, ... . Отметьте, что,
вообще говоря, отображения \i не являются открытыми.
(d) (Майкл [1951] ). Проверьте, что отображение F, ставя-
ставящее в соответствие каждой точке у топологического простран-
пространства У непустое замкнутое подмножество F(y) топологического
пространства Ху есть непрерывное отображение пространства Y
в экспоненциальное пространство 2х в том и только том случае,
если F полунепрерывно и сверху, и снизу (см. задачу 1.7.17).
(e) (Майкл [1951] ). Покажите, что 2х всегда является
Го-пространством и если X есть 7Упространство, то и 2х есть
Ti-пространство, но не наоборот. Докажите, что для Ti-npo-
странстваХ экспоненциальное пространство 2х хаусдорфово (ре-
(регулярно, или, что равносильно, вполне регулярно) в том и
только том случае, если X— регулярное (нормальное) про-
пространство (ср. с замечанием к задаче 3.12.26(а)).
(f) (Иванова [1955] ). Докажите, что экспоненциальное про-
пространство 2N не является нормальным.
Указание (Кислинг [1970] ). Разложите ./V в объединение
Nil]N2\ где Ni(]N2 = 0 и |tfi| = |tf2| = K0. Для /==1> 2 ВЫ'
берите взаимно однозначное отображение fi множества N на Nt
и проверьте, что {fi (A )[}f2(N\A); AczN} — замкнутое подпро-
подпространство пространства 2N, гомеоморфное пространству D(t).
Многозначные отображения II (см. задачи 1.7.17 и 3.12.27)
2.7.21 (Куратовский [1963] ). Докажите, что Тгпространство
X нормально в том и только том случае, если, сопоставляя каж-
каждой паре (Л, В)е2^Х 2х пересечение А П В е: X, мы определяем
полунепрерывное сверху многозначное отображение (на 2х рас-
рассматривается топология Вьеториса).
13 Зак. 697
Глава 3
КОМПАКТНЫЕ ПРОСТРАНСТВА
Компактные пространства, изучение которых является глав-
главной целью этой главы, составляют один из наиболее важных
классов топологических пространств. Они определяются как
пространства, каждое покрытие которых открытыми множе-
множествами содержит конечное подпокрытие. Класс компактных про-
пространств содержит все ограниченные замкнутые подмножества
евклидовых пространств, и оказывается, что многие хорошо из-
известные свойства таких подмножеств в действительности явля-
являются свойствами всех компактных пространств. В § 3.10 изу-
изучаются три класса пространств, тесно связанные с классом
компактных пространств. Эти классы совпадают с классом ком-
компактных пространств, когда мы ограничиваемся подпростран-
подпространствами евклидовых пространств, однако в общем случае они
ведут себя не так хорошо, как класс компактных пространств.
Исследование этих классов, а также класса линделёфовых
пространств и класса вещественно полных пространств позво-
позволяет глубже понять роль и место компактности в общей то-
топологии.
В § 3.1 дается определение компактных пространств, дока-
доказывается несколько простых теорем о компактности и приво-
приводятся некоторые примеры. В этом же параграфе вводится
понятие сети; оно оказывается хорошим средством для доказа-
доказательства теорем о весе компактных пространств.
Параграф 3.2 посвящен изучению поведения компактных
пространств при различных операциях, определенных в преды-
предыдущей главе. В этом параграфе доказываются теорема Тихо-
Тихонова, утверждающая, что произведение компактных пространств
является компактным пространством (один из самых полезных
результатов общей топологии), и теорема Стоуна — Вейер-
штрасса.
В § 3.3 обсуждаются локально компактные хаусдорфовы
пространства и их факторпространства — так называемые k-upo-
странства.
Компактно-открытая топология на пространствах функций,
которой мы уже коснулись в § 2.6, обсуждается в § 3.4. В по-
последней части этого параграфа рассматриваются теоремы типа
3.1. КОМПАКТНЫЕ ПРОСТРАНСТВА 195
теоремы Асколи, дающие необходимые и достаточные условия
компактности множеств в пространствах функций.
Параграф 3.5 посвящен компактификациям. В семействе
Х) всех компактификаций тихоновского пространства X
определяется порядок; доказывается, что относительно этого
порядка в ^(Х) есть все точные верхние грани. Оказывается,
существование точных нижних граней в %?(Х) равносильно ло-
локальной компактности пространства X.
В § 3.6 изучается расширение Стоуна — Чеха $Х простран-
пространства X — наибольший элемент семейства ^(Х), а также расши-
расширение Волмэна (йХ — аналог расширения рХ определенный для
всех 7>пространств.
Совершенные отображения определяются и изучаются в §3.7.
Мы показываем, что этот важный класс отображений хорошо
ведет себя относительно операций над отображениями и что
многие топологические свойства сохраняются такими отображе-
отображениями в сторону образа и в сторону прообраза.
Последние четыре параграфа имеют несколько более спе-
специальный характер. Параграф 3.8 посвящен линделёфовым
пространствам. В § 3.9 изучаются пространства, полные по
Чеху. Среди прочих вещей мы показываем, что для таких про-
пространств и, в частности, для локально компактных хаусдорфо-
вых пространств имеет место теорема Бэра о категории. В § 3.10
рассматриваются три класса пространств, связанные с классом
компактных пространств, а именно: счетно компактные, псевдо-
псевдокомпактные и секвенциально компактные пространства. Мы при-
приводим несколько примеров (в которых участвует расширение
Стоуна — Чеха), чтобы продемонстрировать, что ни один из
этих трех классов не ведет себя по отношению к операциям так
же хорошо, как класс компактных пространств. В частности,
произведение двух счетно компактных (псевдокомпактных) про-
пространств не обязательно счетно компактно (псевдокомпактно).
Вещественно полные пространства, которые имеют некоторые
применения в функциональном анализе, изучаются в § 3.11.
3.1. КОМПАКТНЫЕ ПРОСТРАНСТВА
Напомним, что покрытием множества X называется такое
семейство {4}seS его подмножеств, что U AS = X. В случае
s&S
когда X — топологическое пространство, это покрытие назы-
называется открытым (замкнутым) покрытием пространства X, если
все множества As открыты (замкнуты). Мы говорим, что покры-
покрытие $ = {Bt}t<=,r является измельчением другого покрытия
*s? —{Л$}5е5 того же множества Ху если для каждого t^T су-
существует такое s(t)^St что BtCzAS(t). В этом случае мы гово-
13*
196 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
рим также, что Я вписано в S&. Покрытие $&' = {A's} f мно-
множества X является подпокрытием покрытия s& = {As}s^s мно-
множества X, если S' cr S и Afs = As для всех s <= S'. В частности,
каждое подпокрытие является измельчением.
Топологическое пространство X называется компактным, если
каждое его открытое покрытие содержит конечное подпокрытие,
т. е. если для каждого открытого покрытия {^s}seS простран-
пространства X существует конечное множество {s\, s2, *¦•» s^}c:5, та-
такое, 4ToX = USl{) ... [}U8k.
Семейство 5F = {Fs}s e s множеств называется центрирован-
центрированным, если &~Ф0 и /7s1 П ••• П/7^^ 0 для каждой конечной
системы si, ..., $k^ S.
3.1.1. Теорема. Пространство X компактно в том и только том
случае, если каждое центрированное семейство замкнутых мно-
множеств в X имеет непустое пересечение.
Доказательство. Пусть X — компактное пространство и
{Fs}5eS — семейство замкнутых в X множеств, такое, что П F
s'f=S
пусто. Рассмотрим открытые множества Us = X\FS. Так как
U U8= U (X\F8)=X\ П Fa = X,
s<=S s&S se=S
семейство {Us}s^s является открытым покрытием пространства
X. Но пространство X компактно. Значит, покрытие Ws}s^s со-
содержит конечное подпокрытие {USl, ..., f/5fe}. Следовательно,
= U U8i= U (X\FSi) = X\ П
k
откуда вытекает, что П Fs. = 0- Таким образом, если семей-
ство {F8}seS замкнутых в X множеств центрировано, то
П рвф0.
S€=S
Доказательство компактности пространства, в котором все
центрированные семейства замкнутых множеств имеют непустое
пересечение, предоставляется читателю. I
Следующая теорема является следствием теоремы 3.1.1.
3.1.2. Теорема. Каждое замкнутое подпространство компактного
пространства компактно. I
Мы докажем теперь несколько теорем о компактных подпро-
подпространствах произвольных топологических пространств.
3.1. КОМПАКТНЫЕ ПРОСТРАНСТВА 197
Из определения топологии подпространства немедленно сле-
следует
3.1.3. Теорема. Если подпространство А топологического про-
пространства X компактно, то для любого семейства {US}SGS
открытых в X множеств, такого, что А си \j Us, найдется ко-
конечное множество {su s2, ..., sk} cr S, для которого A cz
<= U uSi. i
i=i i
3.1.4. Следствие. Пусть {F\t F%, ..., Fk) — семейство замкнутых
k
подмножеств пространства X. Подпространство F = \J Ft про-
пространства X компактно в том и только том случае, если все
подпространства Fi компактны. I
3.1.5. Следствие. Пусть U — открытое множество в топологиче-
топологическом пространстве X. Если семейство {Fs}seS замкнутых под-
подмножеств пространства X содержит по крайней мере одно ком-
компактное множество (в частности, если X компактно) и если
Р) FsczU, то существует конечное множество {su 52, ..., Sk} cr
: 5, такое, что [\ Fs. cr U.
Доказательство. Пусть множество FSo компактно. Заменив
пространство X его подпространством FSo, множество U множе-
множеством U(]Fson семейство {Fs}s^5 семейством {/%П^}ses* мы
сведем нашу задачу к случаю компактного пространства. Зна-
Значит, можно предположить, что пространство X компактно. При-
Применив теорему 3.1.3 к множествам A=X\U и Us — X\FS, мы
получим конечное множество {si, ..., sJcS с нужным свой-
свойством. I
3.1.6. Теорема. Если А —компактное подпространство регуляр-
регулярного пространства X, то для каждого замкнутого множества
В е: Х\А найдутся открытые множества U, V с Ху такие, что
Лс[/, BczV и U(]V = 0.
Если, кроме того, В является компактным подпространством
пространства X, то достаточно предполагать X хаусдорфовым
пространством.
Доказательство. Так как пространство X регулярно, то для
каждого х^Х найдутся открытые множества Ux, Vx cr X, та-
такие, что
A) xt=UXf BczVx
x
198 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
Ясно, что Л с: (J Ux; поэтому, в силу 3.1.3, существует конеч-
х<=А
к
ное множество {хи х2у ... у xk} czA, такое, что Лс [} Ux..
k l~k
Легко проверяется, что множества U= [} Ux. и V= Г) VXf
обладают нужными свойствами.
Заметим, что, когда множество В одноточечно, в доказатель-
доказательстве первой части теоремы используется только хаусдорфовость
пространства X. Если В является компактным подпространством
пространства X, то для каждого х^А мы получаем открытые
множества UXy Vx cz X, удовлетворяющие условию A), приме-
применив предшествующее замечание к компактному подпространству
В и одноточечному множеству {х}. I
3.1.7. Теорема. Если А — компактное подпространство тихонов-
тихоновского пространства Ху то для каждого замкнутого множества
ВаХ\А найдется непрерывная функция f: X-+I, такая, что
f(x) = 0 при всех х^А и f(x) ===== 1 при всех ^еВ.
Доказательство. Для каждого хеЛ существует функция
fx:X^Iy такая, чтоМ*) = 0 и fx(B)cz {1}. Так как A cz
U f~l{[0, 1/2)), то, в силу 3.13, найдется конечное множество
€= А
U
Х€= А
{хи х2, ... , xk) cz Л, такое, что А с= JJ f~* ([0, 1/2)). Функция
g: Х->1, определенная следующим образом:
удовлетворяет включениям
Acg-ЩО, 1/2)) и g(B)cz{l}.
Легко проверяется, что функция f: X-*I, определенная форму-
формулой f(x) = 2 max (g(x) —у, OJ f обладает нужными свой-
свойствами. I
3.1.8. Теорема. Каждое компактное подпространство хаусдор-
фова пространства X является замкнутым в X множеством.
Доказательство. Пусть А — компактное подпространство про-
пространства X. В силу второй части утверждения 3.1.6, для каж-
каждого хеХ\А найдется открытое множество V<z:Xy такое, что
х ^V n Af\V = 0. Значит, множество Х\А открыто в X. I
Из второй части утверждения 3.1.6, взятой вместе с 3.1.2,
следует
3.1. КОМПАКТНЫЕ ПРОСТРАНСТВА 199
3.1.9. Теорема. Каждое компактное хаусдорфово пространство
нормально. 1
В следующих трех теоремах рассматриваются свойства не-
непрерывных отображений компактных пространств.
3.1.10. Теорема. Если компактное пространство X непрерывно
отображается на пространство У, то У — компактное простран-
пространство.
Иными словами, непрерывный образ компактного простран-
пространства компактен.
Доказательство. Пусть {Us}s<=$ — открытое покрытие про-
пространства У. Семейство {f~l {Us)}se=s является открытым по-
покрытием пространства X. Значит, существует конечное множе-
множество {su s2y ..., Sk) cr 5, такое, что
а отсюда следует, что U3l[) ¦•• \}Usk = Y. |
3.1.11. Следствие. Если f: А'->У — непрерывное отображение
компактного пространства X в хаусдорфово пространство У, то
f (Л) = f (Л) для каждого А а X.
Доказательство. Так как / непрерывно, f(A)czf(A) в силу
предложения 1.4.1. Обратное включение вытекает из определе-
определения замыкания и из теорем 3.1.2, 3.1.10 и 3.1.8. I
Из последнего утверждения сразу следует
3.1.12. Теорема. Каждое непрерывное отображение компактного
пространства в хаусдорфово пространство замкнуто. 1
Из 3.1.12 и 1.4.18 мы получаем следующую важную теорему
(см. задачу 3.12.5(е)):
3.1.13. Теорема. Каждое непрерывное взаимно однозначное ото-
отображение компактного пространства на хаусдорфово простран-
пространство является гомеоморфизмом. 1
3.1.14. Следствие. Пусть 0\ и 02— две топологии на множестве
X, и пусть О\ тоньше, чем Оъ. Тогда если пространство (X, 0{)
компактно, а (X, 02) является хаусдорфовым пространством, то
01=02.
Иными словами, среди всех хаусдорфовых топологий ком-
компактные топологии являются минимальными.
Доказательство. Тождественное отображение множества X
на себя является взаимно однозначным непрерывным отображе-
отображением пространства (X, 0\) на пространство (X, <72). По тео-
теореме 3.1.13, это отображение является гомеоморфизмом. I
Теперь мы дадим интересную характеристику компактных
пространств в терминах декартовых произведений.
k
d
200 ГЛ. З. КОМПАКТНЫЕ ПРОСТРАНСТВА
3.1.15. Лемма. Если А — компактное подпространство простран-
пространства X и у — точка пространства У, то для каждого открытого
множества W а X X Y, содержащего А X {у}, существуют от-
открытые множества U сг X и V сг У, такие, что А X {у} cz
с= U X V с= W.
Доказательство. Для каждого х^А точка (х, у) имеет
окрестность вида Ux X VXy содержащуюся в W. Очевидно,
Л X {{/} с U Ux X Vx, так что по теореме 3.1.3 существует
яе A
конечное множество {хь х2)..., х&} сг Л, для которого Л X {#}<=
U ?^ X VXi* Легко проверяется, что множества U = (J ^**
и т/ = (| Vjcf. обладают нужными свойствами. 1
3.1.16. Теорема Куратовского. Для произвольного пространства
X следующие условия равносильны:
(i) Пространство X компактно.
(ii) Для каждого топологического пространства У проекти-
проектирование р: Xy^Y^-Y является замкнутым отображением.
(iii) Для каждого нормального пространства У отображе-
отображение р: XXY^Y замкнуто.
Доказательство. Пусть X — компактное пространство я F =
= FczXy^Y. Возьмем точку y^p(F). Так как ХУС{у}с2
cz(JX Y)\F, из леммы 3.1.15 вытекает, что у точки у есть та-
такая окрестность V, что (ХУ( V)f\F = 0. Имеем тогда p(F)(] 7=
= 0, значит, p(F) является замкнутым в У множеством. Импли-
Импликация (i)=^(ii) доказана.
Импликация (ii)=^(iii) очевидна; докажем, что (iii)=^(i).
Пусть пространство X обладает свойством (iii). Предположим,
что нашлось центрированное семейство {Fs}S€=s замкнутых мно-
множеств в X, такое, что П Fs=0. Возьмем точку уо^Х и на
множестве Y = X{J{yo} рассмотрим топологию, состоящую из
всех подмножеств множества X и всех множеств вида
{yo}\i(Fai{]Fs2{]"-uFsk)UK9 где su s2, ..., sk e 5 и KczX.
Из (| Fs= 0 следует, что У является Грпространством*
Так как каждое подмножество пространства У, не содержащее
уо, открыто, пространство У нормально.
Так как X обладает свойством (iii), проекция p(F) мно-
множества /7={(х, х): хе!}с1ХУ является замкнутым в У
множеством. Из включения Xczp(F) следует, что yo^p(F)f
так как уо^Х =Y. Значит, существует точка дго^X, для ко-
которой (х0, yo)^F. Для каждой окрестности UczX точки х0 и
3.1. КОМПАКТНЫЕ ПРОСТРАНСТВА 201
каждого s e S имеем тогда [U X ({уо} UFs)]{]{(xt х): х е X} Ф
Ф0, т. е. U П ^s Ф 0. Значит, х0 е Fs при всех л; е 5, и, следо-
следовательно, П Fs Ф 0 ~~ противоречие. |
3.1.17. Замечание. Небольшое изменение в проведенном рас-
рассуждении (см. задачу 3.12.14(а)) дает компактное простран-
пространство У, такое, что w(Y)^ w(X). Следовательно, чтобы доказать,
что пространство X компактно, достаточно показать, что проек-
проектирование/?: XX Y —> Y замкнуто для каждого компактного про-
пространства У, для которого w(Y)^w(X).
Определим теперь понятие сети и связанное с ним понятие
сетевого веса. Оба понятия определяются для любых топологи-
топологических пространств, но особенно полезными они оказываются
при изучении классов пространств, более или менее тесно свя-
связанных с классом компактных пространств.
Семейство Л — {Ms}s^s подмножеств топологического про-
пространства X называется сетью пространства X (или сетью в X),
если для каждой точки х<= X ц каждой окрестности U точки х
найдется такое s e S, что x^Mscz U. Ясно, что каждая база
пространства X является сетью этого пространства, причем
сетью особого сорта: ее элементы — открытые множества. Се-
Семейство всех одноточечных подмножеств пространства является
другим примером сети. Сетевой вес пространства X определяется
как наименьший кардинал вида |«^|, где Jf — сеть простран-
пространства X. Этот кардинал обозначается через nw(X). Ясно, что для
каждого топологического пространства X выполняются соотно-
соотношения nw(X)^ w{X) nnw(X)^\X\.
Заметим, что если в X есть сеть мощности ^ nt, то в X есть
и всюду плотное множество мощности ^ ш (см. доказательство
теоремы 1.3.7), так что для каждого топологического простран-
пространства X имеем: d(X)^. nw{X).
Противоположное неравенство, вообще говоря, не верно: рас-
рассуждая так же, как в примере 1.2.2, легко показать, что птю(К) =
= с для прямой Зоргенфрея К. Таким образом, nw(K)> d(K) =
= Ко. Если X является Г0-пространством, то |Х\ ^ exp nw(X).
Это можно доказать точно так же, как более слабое неравен-
неравенство из 1.5.1.
3.1.18. Лемма. Для каждого хаусдорфова пространства X суще-
существует непрерывное взаимно однозначное отображение этого
пространства на хаусдорфово пространство У, такое, что w(Y)^
^nw(X).
Доказательство. Пусть nw(X)^=m, и пусть Jf — сеть прост-
пространства X, для которой | ИГ | ===== т. Легко проверить, что если
m <; Ко, то X является дискретным пространством мощности ш,
w(X)—mt и можно взять Y == X,
202 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
Предположим, что ш ^ Ко. Обозначим через О\ топологию
пространства X. Рассмотрим те пары (Мь М2) элементов се-
семейства JF, для которых существуют непересекающиеся откры-
открытые множества U\9 ?/2е(?ь содержащие М\ и М2 соответствен-
соответственно. Для каждой такой пары (М\, М2) фиксируем некоторые
f/i, f/2, обладающие названными свойствами. Семейство всех
отобранных таким образом элементов топологии О\ обозначим
через З&о. Семейство ЗВ всех конечных пересечений элементов се-
семейства ЗВо обладает свойствами (В1)—(В2).
Из определения сети и того факта, что (X, Ох) является
хаусдорфовым пространством, вытекает, что множество X, на-
наделенное топологией О% порожденной базой ЗВ, является хаус-
хаусдорфовым пространством — мы обозначаем это пространство че-
через Y. Так как |#|^т, имеем w(Y)^nw(X). Из включения
02а0\ следует, что тождественное отображение множества X
на себя является взаимно однозначным непрерывным отображе-
отображением пространства X на пространство Y. I
Предыдущая лемма и теорема 3.1.13 дают такой результат:
3.1.19. Теорема. Для каждого компактного хаусдорфова про-
странетва X имеем nw(X)=w(X). I
3.1.20. Следствие. Если компактное хаусдорфово пространство
X обладает таким покрытием {As}se_Sf что w(As)^ ш ^ Ко при
всех s^S и |5|^га, то w(X)^m.
Доказательство. Семейство U &s> где 3SS есть база мощ-
ности ^ ш подпространства As, является сетью пространства Ху
и мощность этого семейства не превосходит m. I
Заметим, что в приведенном выше следствии достаточно
предполагать, что nw(As)^ ш.
Из теоремы 3.1.19 вытекают две другие важные теоремы.
3.1.21. Теорема. Для каждого компактного хаусдорфова прост-
ранства X имеем w(X)^.\X\. I
3.1.22. Теорема. Если компактное хаусдорфово пространство Y
является непрерывным образом пространства X, то w(Y)^.
()
Доказательство. Из условия (Hi) теоремы 1.4.1 следует, что
если f отображает X на К, то семейство {f(U): U е^?}, где & —
база пространства X, является сетью пространства У. 1
Ясно, что в условиях приведенной выше теоремы выполня-
выполняется более сильное неравенство w(Y)^nw(X).
Так как существуют счетные пространства без счетной базы
(см. примеры 1.6.19, 1.6.20 или 2.3.37), предположение о ком-
компактности в теоремах 3.1.19 и 3.1.21 опустить нельзя. Рас-
3.1. КОМПАКТНЫЕ ПРОСТРАНСТВА 203
сматривая любое отображение пространства N на счетное про-
пространство без счетной базы, мы видим, что предположение о
компактности нельзя опустить и в теореме 3.1.22. Оказывается,
однако, что во всех этих трех теоремах компактность можно
заменить более слабыми предположениями (см. теоремы 3.3.5,
37.19 и упр. 3.9.Е).
Следующая теорема характеризует компактность в терминах
направленностей.
3.1.23. Теорема. Пространство X компактно в том и только том
случае, если каждая направленность в X имеет предельную
точки.
Доказательство. Пусть X — компактное пространство и S =
= {ха, аеИ} — направленность в X. Семейство {Fa}ae52;, где
состоит из замкнутых множеств и центрировано, так как
FOlczFa2 при (Т2 ^ <*!• По теореме 3.1.1 существует х^ \\ Fa.
Точка х является предельной точкой направленности S. Дей-
Действительно, если бы х не было предельной точкой для S, то
нашлись бы окрестность U точки х и оое2, такие, что
И было бы X ф FaB.
Пусть теперь X — любое пространство, в котором каждая
направленность имеет предельную точку. Рассмотрим любое
центрированное семейство $Г замкнутых в X множеств. Обо-
Обозначим через 2 множество, состоящее из всех конечных подсе-
подсемейств {Fu F2, ..., Fk) семейства У, и для а = {Fi, F2,..., F^},
о' = {F[, F'2, ..., F[) €= S положим а < а', если Fx f] F2 П ... П
П Fk zd F[ П Ff2 П ... П F'r Множество 2 направлено отношением
<;. Выбрав для каждого a={Fu F2, ..., Fk} e 2 точку ха в
пересечении F\ П F2 П ... П Fk9 получаем направленность S =
= {хо, аб2) в X. Для завершения доказательства достаточно
показать, что если х является предельной точкой для S, то х
принадлежит всем членам семейства #".
Пусть Fo — любой член семейства У. Для каждой окрест-
окрестности U точки х найдется а = {Fi, F2, ..., Fk) ^ а0 = Fo, та-
такое, что ха е С/. Так как х0 е F\ П F2 П • • • П Fk <= Fo, имеем
Fo П ^ =7^ 0, откуда следует, что х е Fo, так как множество Fo
замкнуто. I
Относящийся к фильтрам аналог доказанной выше теоремы
звучит так:
204 гл- 3- КОМПАКТНЫЕ ПРОСТРАНСТВА
3.1.24. Теорема. Пространство X компактно в том и только том
случае, если каждый фильтр в X имеет предельную точку, I
3.1.25. Примеры. Дискретное пространство D(m) компактно в
том и только том случае, если ш конечно.
Вещественная прямая и прямая Зоргенфрея не компактны:
открытое покрытие {(— /, 0}Г=* не содержит конечного подпо-
подпокрытия.
Покажем теперь, что пространство Л(т), определенное в
1.4.20, компактно для каждого ш ^ Ко. Пусть {Us}s<=s ~~ откры-
тое покрытие пространства А(ш). Найдется такое so^S, что
единственная точка накопления х0 множества Л(т) принадле-
принадлежит USo- По определению топологии пространства А(ш) мно-
множество A(m)\USo конечно. Пусть A(m)\USo = {xu х2, ..., xk}
и Xi^Us. при i=l, 2, ..., k. Ясно, что {^}* — конечное
подпокрытие покрытия {Us}s s s.
Докажем, что каждый замкнутый интервал /=[а, 6] с/?
является компактным пространством. Возьмем любое открытое
покрытие Ws}S(=s пространства /. Пусть Л — множество всех
хе/, таких, что отрезок [а, х] содержится в объединении ко-
конечного числа членов семейства {^s}5e=5- Достаточно показать,
что множество /\Л пусто.
Предположим, что /\Л Ф 0, и обозначим через дго точную
нижнюю грань множества /\Л. Ясно, что xQ e /\Л. Суще-
Существует So e S, для которого Хо е ?/5о. Легко видеть, что а < х0;
поэтому для некоторого уе[с, лг0) выполняется включение
(у, хц] a USo- По определению хо имеем у^А. Значит, [a, y]cz
k
cz U Ust для некоторых s\, S2, .-., 5ft e S. Следовательно,
k
[a, xo]cz \j Us.~- мы получили противоречие. I
3.1.26. Пример. Рассмотрим на плоскости R2 две концентричные
окружности Ci={(x, y)^R2: x2-\-y2 = i}, где i—1, 2, и их
объединение X =Ci\JC2. Отображение проектирования окруж-
окружности Сх на окружность С2 из точки @, 0) будет обозначаться
через р. На множестве X будет определена топология с помощью
системы окрестностей {$(z)}z<=x' А именно, положим ,SB(z)==
= {^/И}Г=1 при 2ECi и %{z)={{z}} при z^C2, где Uj =
= Vj[}p(V?\{z}) и V/ является дугой длины 1// окружности
Cj с серединой в точке г. Легко проверяется, что семейство
{$(z)}Z€=x обладает свойствами (ВР1)—(ВР4). Значит, по
предложению 1.5.2, множество X вместе с топологией, порожден-
3.1. КОМПАКТНЫЕ ПРОСТРАНСТВА 205
ной семейством {$(%)}г^х> является хаусдорфовым простран-
пространством.
Пространство X называется двойной окружностью Алексан-
Александрова.
Подпространство С2 с X является дискретным простран-
пространством мощности с; оно открыто и всюду, плотно в X. Подпро-
Подпространство С\ сг X является окружностью S1 единичного радиуса
с обычной топологией. Оно компактно, так как S1 является не-
непрерывным образом компактного пространства /.
Покажем теперь, что пространство X компактно. Пусть
UMs€=s—какое-нибудь открытое покрытие пространства X. Не
теряя общности, можно предполагать, что множества Us явля-
являются членами определенной выше системы окрестностей. Так
как подпространство С\ компактно, найдется конечное множе-
множество {si, s2, -• •, Sk} с S, для которого
B) QczUSlUUs2[j ... [}Usk.
Если мы отбросим те из стоящих справа в этом соотношении
множеств, которые одноточечны, включение будет по-прежнему
выполняться. Значит, можно считать, что USi = U\ь (г*), где
Zi е С\ при i=l,2, ..., k. Таким образом,
X\{p(z{), Р(г2\ ..., P(zk)}czUSl\JUs2U ... UUak.
При i=l,2, ..., k выберем s|eS так, чтобы было р(г.) е Us\.
Ясно, что семейство Ш Xk [} W Лк является конечным подпо-
крытием, выбранным из семейства {Us}s<=s> и это доказывает,
что X компактно.
Легко проверяется, что Сг не является /^-множеством в Х\
следовательно, пространство X не совершенно нормально. С дру-
другой стороны, нетрудно установить, что X—наследственно нор-
нормальное пространство. Пространство X удовлетворяет первой
аксиоме счетности, но не удовлетворяет второй аксиоме счет-
ности — оно даже не сепарабельно.
Легко строится непрерывное отображение пространства X на
пространство А (с): достаточно как-нибудь взаимно однозначно
отобразить множество С2 на множество всех изолированных то-
точек пространства А (с), а всю окружность С\ отобразить в точку
накопления пространства Л (с). Это показывает, что аналогичное
теореме 3.1.22 утверждение, относящееся к характеру, не
верно. I
3.1.27. Пример. Пусть W — множество всех ординалов, меньших
(или равных) первого несчетного ординала а>ь Множество W
вполне упорядочено естественным упорядочением <. Рассмот-
206 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
рим топологию на W, порожденную базой 3$, состоящей из всех
интервалов вида (ytx]= {zef: у < г ^ х), где у < х ^ coi, и
одноточечного множества {0}, где 0 — порядковый тип пустого
множества. Легко видеть, что W является хаусдорфовым про-
пространством.
Докажем, что пространство W компактно. Пусть {Us}s€=s —
открытое покрытие пространства W и А — множество всех
х е W, таких, что отрезок [0, л:] содержится в объединении ко-
конечного числа членов семейства {^Л56Е5- Достаточно показать,
что множество W\A пусто.
Предположим, что 1^\Л Ф 0, и обозначим через хо наимень-
наименьший элемент множества W\A. Существует soeS, такое, что
Xq е Us9- Как легко видеть, 0 < х0. Значит, найдется у е [0, дс0),
для которого (уу xq] е USq* По определению х0 имеем у^А.
Следовательно, [0, у] cz (J US( для некоторых $i, s2, ..., s^^S.
Заключаем отсюда, что 10, х0] cz (J USi — получили противо-
противоречие.
Рассмотрим теперь подпространство Wq = ti7\{o>i} простран-
пространства W. Пространство Wo нормально. Более того, каковы бы ни
были непересекающиеся замкнутые подмножества Л, В про-
пространства Wo, их замыкания А и В в пространстве W не пересе-
пересекаются. Это следует из того, что самое большее одно из мно-
множеств А и В может быть конфинально Wq. Действительно, если
бы Л и В оба были конфинальны Wq, мы могли бы определить
по индукции две последовательности аи а% ... и bu b2y ... счет-
счетных ординалов, удовлетворяющих условиям
ai<bi<ai+i и а,-еЛ, bt e В при i'=I, 2, ....
Так как никакое счетное множество не конфинально W70, мно-
множество С всех элементов множества Wo, больших чем каждое щ
и каждое bt, было бы не пусто, — а это невозможно, так как
наименьший элемент множества С тогда принадлежал бы А П В,
что легко проверяется.
Из сказанного выше можно вывести (см. теорему 3.2.1 или
следствие 3.6.4), что каждая непрерывная функция f: Wq->I
продолжается на W. Оказывается, можно утверждать нечто боль-
большее: для каждой непрерывной функции /: Wo-+I найдется орди-
ординал Xq < @!, ТаКОЙ, ЧТО f {х) = f (Xq) ПрИ ВСвХ X ^ Л'о, — Т. е. /,
начиная с некоторого члена, является константой.
Достаточно показать, что для каждого целого положитель-
положительного числа / найдется х-ь е Wo, такое, что \f(x) — f(Xi)\<il/i
при всех х ^ Xi. Действительно, легко проверить, что любое а-0,
большее чем все xt, будет обладать требуемым свойством.
3.1. КОМПАКТНЫЕ ПРОСТРАНСТВА 207
Предположим, что для некоторого i и каждого x^W0 можно
найти х; G fo, такое, что \f(x)—f(x')\^ \/i и х/ ^ х. Это по-
позволяет нам определить по индукции две последовательности
аи 0-2, • • • и Ь\, Ь2у ... счетных ординалов, удовлетворяющих
условиям
aj<bj<aM и \f(aj)-f(bj)\^\/i при /=1,2, ....
Оказывается, однако, что существование таких последователь-
последовательностей входит в противоречие с непрерывностью f. В самом деле,
пусть с — наименьший ординал, больший, чем все щ и все ft*.
Имеем с е WOy и, как легко проверяется, каждая окрестность
элемента с содержит почти все члены обеих последователь-
последовательностей. Так как множество f~{((f(c)—l/2?, f(c)+l/2/)) содер-
содержит самое большее одну из точек аь Ь,- при каждом /=1,2,
это множество не является окрестностью точки с.
Множество F всех счетных предельных ординалов замкнуто
в Wo. Так как не существует непрерывной функции f: Wo-+I,
такой, что F = f~l(O), из теоремы Веденисова следует, что про-
пространство Wo не совершенно нормально. Значит, и пространство
W не совершенно нормально. С другой стороны, можно пока-
показать (см. задачи 3.12.3(с) и 2.7.5(с)), что W является наслед-
наследственно нормальным пространством. Пространство Wo удовле-
удовлетворяет первой аксиоме счетности; пространство W не имеет
счетной базы в точке @| — в действительности W даже не яв-
является секвенциальным пространством.
Как читатель несомненно заметил, топологии, рассмотрен-
рассмотренные на W и на Wq9 так же как и естественные топологии на R
и /, тесно связаны с естественными линейными упорядочениями,
определенными на этих множествах. Подобным образом можно
определить некоторую топологию на каждом линейно упорядо-
упорядоченном множестве. Топологические пространства, так получен-
полученные, образуют интересный класс линейно упорядоченных про-
пространств (см. задачи 1.7.4, 2.7.5, 3.12.3, 3.12.4, 3.12.12(f), 5.5.22,
6.3.2 и 8.5.130)). 1
3.1.28. Пример. Мы покажем сейчас, что канторово множество
DK° гомеоморфно некоторому подпространству вещественной
прямой. Рассмотрим множество С всех вещественных чисел сег-
сегмента /, в троичном разложении которых не встречается 1, т. е.
множество всех чисел вида
оо
C) X = Y;~T> где ^е{0, 1} при 1=1,2,....
Любой элемент х множества С представим в виде C) един-
единственным образом. Значит, полагая f(x)={xi}9 мы получаем
взаимно однозначное отображение f множества С на простран-
208 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
ство D*°. Из 2.3.6 следует, что / непрерывно относительно топо-
топологии подпространства пространства R на С. По теореме 3.1.13,
чтобы установить, что / является гомеоморфизмом, достаточно
показать, что пространство С компактно. Последнее следует, од-
со
нако, из равенства С= |) Fit где Ft— подмножество отрезка /,
1=1
состоящее из всех чисел, в троичном разложении которых в /-м
разряде (при всех / ^ i) стоит не единица. Действительно, все
множества Ft замкнуты. Легко видеть, что множество F\ полу-
получается из / удалением «среднего» интервала A/3, 2/3), мно-
множество F^ получается из F\ удалением «средних» интервалов
A/9, 2/9) и G/9, 8/9) из двух сегментов, составляющих F\,
и т. д.
Из сказанного выше следует, что канторово множество D**0
компактно. В следующем параграфе мы покажем, что канторов
куб Dm компактен при каждом т ^ Ко (см. теорему 3.2.4). I
В заключение параграфа приведем важную теорему, из ко-
которой следует, в частности, что мощность каждого компакта1)
с первой аксиомой счетности не превосходит с (см. задачи
3.12.11 (d) и 3.12.10(а)).
3.1.29. Теорема. Для каждого бесконечного компакта X имеем
||
|р
Доказательство. Пусть X — бесконечный компакт и %(Х)=щ.
Ясно, что т^ Ко. Для каждого хеХ возьмем базу $(х) про-
пространства X в точке х, такую, что \$(х) | ^ т.
Пусть т—наименьший начальный ординал мощности, боль-
большей чем ш; этот ординал т регулярен. По трансфинитной индук-
индукции будет определена трансфинитная последовательность Fo,
Fu . -., Fa, ..., а < т, замкнутых подмножеств пространства
Ху такая, что для каждого а < т
D) IFaKf, FfitzFa при р<а
и
E) для каждого конечного подсемейства Ш семейства
\j\${x): xs= U FA, если
X\[)<U^0, то Fa\\)<U=?0.
Предположим, что осо = 0 или что а0 > 0 и множества Fa,
удовлетворяющие условиям D) и E), определены для всех
1) Компактами мы именуем компактные хаусдорфовы пространства. —
Прим. перев.
3.1. КОМПАКТНЫЕ ПРОСТРАНСТВА 209
а < а0. Положим
<*): х^ U ?а)>
a<a0 J
z%: \<U\ конечно и Х\\}<иф0}.
Ясно, что |^|<2т и |В|<2т. Обозначим через В множе-
множество, которое получается, если для каждого Ш^В выбрать
точку из дополнения kU^. Очевидно, | В | <] 2т. В силу второго
неравенства теоремы 1.5.3, мощность множества FaQ = B{] \j Fa
а<а0
не превосходит 2Ш, так что условия D) и E) при а = а0 вы-
выполняются.
Для завершения доказательства достаточно показать, что
объединение F = [j Fa совпадает с X. Так как ординал т ре-
а<т
гулярен, из второй части условия D) следует, что для каждого
множества Acz F мощности,_не большей чем т, найдется а < т,
такое, что Л с: Fa. Значит, AczFa<^F, а отсюда и из %(Х)=ш
следует, что множество F замкнуто в X. В частности, простран-
пространство F компактно.
Предположим теперь, что существует точка у ^ X\Ft и для
каждого xEf выберем Ux^$(x)y для которого y^Ux. Най-
Найдется конечное подсемейство °U семейства {Ux}X(=F, такое, что
F cz U Ш, и найдется ординал а < т, для которого °U a
[}{3& (х): х €= (J FA. Значит, Х\1Ш Ф 0, а FaXU^ = 0, что
противоречит E). i
3.1.30. Следствие. Если компакт удовлетворяет первой аксиоме
счетности, то его мощность не превосходит с. 1
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
Зарождение понятия компактности связано с теоремой Бо-
реля (доказанной в 1894 г.), утверждающей, что каждое счетное
открытое покрытие замкнутого интервала содержит бесконечное
подпокрытие этого интервала, и с наблюдением Лебега, что это
остается верным и для любого открытого покрытия замкнутого
интервала (в [1903] Борель распространил этот результат
(в формулировке Лебега) на все замкнутые ограниченные под-
подмножества конечномерных евклидовых пространств). Когда об-
общая топология была еще в пеленках, за основу при определении
новых классов пространств часто принимали различные свой-
свойства отрезка / или вещественной прямой R: брали класс всех
пространств, обладающих таким свойством. По этой схеме были
14 Зак. 697
210 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
определены классы сепарабельных, компактных, полных и связ-
связных пространств. Сначала этим методом выделяли классы ме-
метрических пространств, затем определения были распространены
на топологические пространства. Иногда свойства, равносильные
в классе метрических пространств, после распространения на
топологические пространства приводили к разным классам про-
пространств (см., например, теорему 4.1.15), и не сразу было ясно,
какой из этих классов являлся правильным обобщением. Так
произошло с компактностью: некоторое время были сомнения,
является ли правильным расширением класса компактных ме-
метрических пространств класс компактных пространств, класс
счетно компактных пространств или класс секвенциально ком-
компактных пространств (см. § ЗЛО). Сейчас совершенно ясно, что
таким классом является класс компактных хаусдорфовых про-
пространств (компактов). Этот класс хорошо себя ведет по отноше-
отношению к операциям над топологическими пространствами, наибо-
наиболее часто встречается в приложениях и приводит к самым инте-
интересным задачам.
Понятие (регулярного) компактного пространства было вве-
введено Вьеторисом в [1921]. Данное им определение сходно с усло-
условием, которое фигурирует в теореме 3.1.23. В той работе Вьето-
рис доказал теоремы 3.1.1, 3.1.8 и 3.1.9. Понятие компактного
хаусдорфова пространства (аналогично определенное) появи-
появилось ранее в работе Янишевского [1912]; в этой работе, однако,
нет результатов об этом классе пространств. (Рисе утверждает
в [1908], что каждое центрированное семейство ограниченных
замкнутых подмножеств евклидова пространства имеет непустое
пересечение.) Эквивалентность некоторых топологических
свойств условию Бореля — Лебега, определяющему компактные
пространства, была доказана Куратовским и Серпинским в
[1921] и Саксом в [1921], но они не рассматривали класс ком-
пактных пространств. Данное здесь определение компактности
было сформулировано П. С. Александровым и П. С. Урысоном
в [1923]. Они определили класс компактных хаусдорфовых
пространств совершенно независимо от Вьеториса и осуществили
глубокий анализ понятия компактности в важной работе [1929]
(основные определения и результаты были объявлены в [1923]
и [1924]). В частности, их работа содержит теоремы 3.1.1, 3.1.2,
3.1.3, 3.1.8 и 3.1.9. Теоремы 3.1.10, 3.1.12 и 3.1.13 были доказаны
П. С. Александровым в [1927] (объявлены в [1925] ).
Теоремы 3.1.6 и 3.1.7 свидетельствуют о достаточно общей, но
несколько туманной закономерности, обычно выражаемой фра-
фразой: «компактные множества ведут себя как точки» (см. тео-
теоремы 3.2.10 и 3.3.2). Куратовский доказал в [1931], что в классе
метрических пространств проекции параллельно компактному
пространству являются замкнутыми отображениями. Это
3.1. КОМПАКТНЫЕ ПРОСТРАНСТВА 211
утверждение было распространено на топологические простран-
пространства Бурбаки [1940], а Мрувка заметил в [1959], что данное
свойство характеризует компактные пространства.
Сети были введены Архангельским в [1959], где теорема
3.1.9 была установлена; наше доказательство этой теоремы осно-
основано на работе Голштынского [1966а]. Теорема 3.1.21 легко
следует из ранних результатов П. С. Александрова (см.
упр. 3.1.F(a)). Теорема 3.1.22 была доказана П. С. Алексан-
Александровым в [1939]. Двойная окружность Александрова была опре-
определена в работе Александрова и Урысона [1929]. Теорема 3.1.29
была доказана Архангельским в [1969а]; она решает известную
проблему общей топологии, которой занимались около 50 лет.
Наше доказательство взято из работы Р. Поля [1974] (оно тесно
связано с доказательством, данным Пономаревым в [1971] );
аналогичное доказательство содержится в работе Шапировского
[1974]; оглядываясь сейчас назад, мы видим, что идея доказа-
доказательств Поля и Шапировского содержалась в оригинальном рас-
рассуждении Архангельского.
Кроме многих важных теорем глава 3 содержит ряд при-
примеров, имеющих основополагающее значение для общей тополо-
топологии. Не все они рассматриваются в основном тексте книги. При-
Примеры, намеченные в упр. 3.1.1, 3.2.Е, 3.6.1 (а) и 3.10.С, а также
примеры в задачах 3.12.18 и 3.12.19 заслуживают особого вни-
внимания читателя.
УПРАЖНЕНИЯ
З.1.А. Покажите на примерах, что теоремы 3.1.8, 3.1.9, 3.1.12,
3.1.13, 3.1.19, 3.1.21 и 3.1.22 перестают быть верными, если в
них вместо компактных хаусдорфовых пространств говорить о
компактных ^-пространствах.
3.1.В. Докажите, что каждое компактное подпространство
прямой Зоргенфрея счетно.
Указание. Примените теорему 3.1.13,
3.1.С. Непрерывное отображение f: X-> Y пространства X на
пространство Y называется неприводимым, если \(А)ФУ для
каждого собственного замкнутого подмножества А простран-
пространства X.
(a) Покажите, что для каждого непрерывного отображения
/: X-*~Y пространства X на пространство Y с компактными про-
прообразами точек существует замкнутое подпространство ХосиХ,
такое, что f(X0)=Y и отображение f\X0: Xo^-Y неприводимо
(см. задачу 5.5.12).
Указание. Примените лемму Куратовского — Цорна.
(b) Проверьте, что каждое неприводимое открытое отобра-
отображение хаусдорфова пространства является гомеоморфизмом, и
заметьте, что это не верно для отображений 7>пространств.
14*
212 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
(с) Заметьте, что если множество всех одноточечных прооб-
прообразов при непрерывном отображении f: X —>• У пространства X
на пространство У всюду плотно в X, то / неприводимо. Приве-
Приведите пример неприводимого отображения f: X-+Y компакта X
на компакт У, при котором нет одноточечных прообразов
точек.
3.I.D. Покажите с помощью теоремы Куратовского, что ото-
отображение / пространства X на компакт У непрерывно в том и
только том случае, если график отображения / является замкну-
замкнутым в XX У множеством (см. упр. 2.3.С(Ь)).
3.1.Е (Архангельский [1965], Чобан [1967]). (а) Докажите,
что если подмножества А\ и А2 пространства X таковы, что
А\ а А2 и для каждого замкнутого в А2 множества F czA2\A\
существуют непересекающиеся открытые множества в X, содер-
содержащие соответственно А\ и F, то %(А\, Х)^.%(А\, А2)%(А2, X)
(см. теорему 3.1.6 и упр. 3.8.В).
Выведите отсюда, что для компактных подмножеств F\ и F2
хаусдорфова пространства Х% таких, что F\ cz F2, всегда
(FX)(FF)(FX) '
Указание. Пусть ш = %(Аи А2)%{А2, X) и i^bes»
eT— базы множества А2 в X и множества А\ в Л2 соответ-
соответственно, причем |S|^m и |7|^га. Для каждого t^T возь-
возьмите непересекающиеся открытые множества Gt, Ht cz X, такие,
что А\ a Gt и A2\Vt cz Я/, и проверьте, что множества Ut,s =
= Gt П Ws составляют базу множества А\ в X.
(Ь) Хаусдорфово пространство X называется пространством
точечно счетного типа, если для каждой точки хеХ найдется
компактное множество F(x)aXt такое, что x<=F(x) и
Заметьте, что компакты и хаусдорфовы пространства с пер-
первой аксиомой счетности являются пространствами точечно счет-
счетного типа. Докажите, что замкнутые подпространства и бб-под-
пространства пространства точечно счетного типа являются про-
пространствами точечно счетного типа. Приведите пример нормаль-
нормального пространства, не являющегося пространством точечно счет-
счетного типа; обратите внимание на то, что свойство быть простран-
пространством точечно счетного типа не является наследственным (мож-
(можно применить теорему 3.2.4).
3.1.F. (а) (П. С. Александров [1924а]). Псевдохарактер
^-пространства X в точке х определяется как наименьший кар-
кардинал вида |^|, где °U—семейство открытых в X множеств,
такое, что {\Ш= {х}\ этот кардинал обозначается через ty(xyX).
Псевдохарактер Т^пространства X определяется как супремум
всех кардиналов г^(х, X), где хеХ; обозначается этот кардинал
через (X)
3.1. КОМПАКТНЫЕ ПРОСТРАНСТВА 213
Заметьте, что ty(xt X)^%(x, X) и ^(Х)^.%(Х) для каждого
^-пространства X и любого х е X. Докажите, что если X — ком-
компакт, то ty(xt Х)=%(ху X) для всех х^Х и •$(Х)=%{Х).
Убедитесь, что отсюда следует теорема 3.1.21. Покажите, что
^(Х) expd(X) для каждого хаусдорфова пространства X (см.
теорему 1.5.6).
(b) Для любого хаусдорфова пространства X обозначим че-
через h(X) наименьший кардинал ш, такой, что, какова бы ни была
точка хеХ, найдется компакт F(x)cz X со свойствами: х е F(x)
и %(F(x)t Х)^ш. Таким образом, хаусдорфово пространство X
является пространством точечно счетного типа (см. упр. 3.1.Е(Ь))
в том и только том случае, если h(X)^. Ko.
Докажите, что ixt(X)=ty(X)h(X) для каждого хаусдорфова
пространства X
(c) Заметьте, что если хаусдорфово пространство X допу-
допускает открытое отображение на хаусдорфово пространство Y, то
h{Y)^h(X)y и что для замкнутых отображений это не обяза-
обязательно так (см. упр. 3.7.F(b)).
(d) Покажите, что \Х\ ^ exp[d(X)ty (X)], если пространство
X регулярно. Проверьте, что здесь не достаточно требовать хаус-
хаусдорфовости вместо регулярности.
Указание. Имея в виду, что d (/с) = Ко» определите хаусдор-
хаусдорфово пространство X мощности 2е, со счетным всюду плотным
множеством А изолированных в X точек, такое, что подпростран-
подпространство Х\А дискретно.
3.1.G. Пусть X — компакт, Ij = IX W, где f=l, 2, и
А(Х) = Х\ [}Х2. В обобщение примера 3.1.26 определите на
А(Х) топологию компактного хаусдорфова пространства таким
образом, чтобы Хх было гомеоморфно Xt а Х2 было дискретным
подпространством. Проверьте, что для каждого множества
Мс^Х подпространство XiU^2 пространства А(Х), где М2 =
= А1Х {2}с:Х2, компактно и что при дополнительном предпо-
предположении, что М всюду плотно в Ху а X плотно в себе, множество
М2 всюду плотно в Х\ [}М2.
3.1.Н. (а) (Энгелькинг [1968]). Докажите, что дискретное
пространство D(t) вложимо в качестве замкнутого подпростран-
подпространства в [D(i$0)]c. Выведите отсюда, что декартово произведение
[D(^0)]c не нормально (см. задачу 2.7.16(а)).
Указание. Пусть Х\ — отрезок / с естественной топологией, и
пусть Х2 — тот же отрезок с дискретной топологией. Для каж-
каждого t е / определим отображение ft множества / в дискрет-
дискретное пространство Z)(S0) = N ® {0}, положив ft(t) = 0 и //(х) =
при < | х — /К —. Проверьте, что f- Д f( является
гомеоморфным вложением пространства Х2 в пространство
214 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
У = [О(К0)]с>и заметьте, что если у = {yt} <? f(I) n yt = 0 для
некоторого t е /, то у точки у в пространстве Y есть окрестность,
не пересекающаяся с f(/). Покажите, что если у= {yt}^f(I),
то yt = 0 для некоторого t е /; для этого рассмотрите семейство
{f~l (U)}Ug$ замкнутых подмножеств пространства Хи где 38 —
некоторая база в точке 1/еУ.
(Ь) (Юхас [1969] ). Пользуясь тем, что существует компакт
X, для которого \Х\ = 2т и %(х, Х)—т при всех х^Х (см.
теоремы 2.3.24 и 3.2.4), покажите, что, каково бы ни было
nt ^ Ко, дискретное пространство О Bт) можно вложить в ка-
качестве замкнутого подпространства в [D(m)]2TU.
Указание. Для каждого t^X возьмем базу {Us(t)}s^s в
точке t, где S — некоторое вполне упорядоченное множество
мощности иг, такое, что 0 ф. 5, и определим отображение ft мно-
множества X в дискретное пространство Z)(nt)= S © {0}, положив
/г@ = 0 и (при хф1) ft(x) — sy где s — наименьший элемент в
5, такой, что хф. Us(t). Следуйте теперь указанию из (а).
3.1.1 (Александров и Немыцкий [1938], Маколей [1956]).
Зададим топологию на плоскости, оставив неизменными окрест-
окрестности всех точек (х, у), для которых уфО, и приняв за базу
в точке (х, 0) семейство {{(х> 0)} U Ut {x)}^v где Ut(x)—мно-
Ut(x)—множество всех точек, лежащих внутри круга радиуса \/i с центром
в (ху 0), но вне двух кругов радиуса ?, касающихся оси х в
точке (х, 0).
Покажите, что полученное таким образом пространство X со-
совершенно нормально и что на множествах Х\ = {(х, 0): x^R}
и Х2 = Х\Х\ топология, порожденная топологией пространства
X, совпадает с топологией, порожденной обычной топологией
плоскости R2. Проверьте, что d(X)= %(X)— nw(X)= Ko и что
(Х
)
3.1.J. (а) Заметьте, что если М — подпространство простран-
пространства X, то nw(M)^ nw(X).
(b) Докажите, что сетевой вес бесконечного декартова про-
произведения X=sll XS9 где nw(Xs)> 1, равняется наибольшему
из кардиналов |5| и sup {nw(Xs)}.
3.1.К. (а) Применив теорему о диагональном отображении
и пример 3.1.28, докажите, что для каждого счетного ординала
а подпространство Ya= {у: у ^ «} пространства W, определен-
определенного в 3.1.27, вложимо в вещественную прямую.
Заметьте, что подпространство Wo пространства W не вло-
вложимо в вещественную прямую.
(Ь) (Хигман и Стоун [1954], Исбелл [1964]). Пусть Уа,
ае Wq, — пространства, определенные в (а); рассмотрим обрат-
3.2. ОПЕРАЦИИ НАД КОМПАКТАМИ 215
ный спектр S = {Xa, я<*, WQ}, где Ха — дискретное пространство,
состоящее из всех гомеоморфных вложений пространства Уа в
вещественную прямую, и я<*(/) = /|Ур при fela и а, ре Wo,
где Р ^ а. Все отображения я<* являются отображениями «на»,
и тем не менее Hni S = 0 (см. упр. 2.5.А(Ь) и теорему 3.2.13).
3.2. ОПЕРАЦИИ НАД КОМПАКТАМИ
Обсудим сначала задачи, связанные с переходом к подпро-
подпространству. Отметим прежде всего, что компактность в классе
хаусдорфовых пространств наследуется при переходе к замкну-
замкнутым и только таким подпространствам (см. теоремы 3.1.2 и 3.1.8).
Следующая теорема дает критерий того, что отображение в
компакт можно продолжить.
3.2.1. Теорема. Пусть А — всюду плотное подпространство топо-
топологического пространства X и f—непрерывное отображение
пространства А в компакт У. Отображение f можно непрерывно
продолжить на X в том и только том случае, если для каждой
пары Ви В2 непересекающихся замкнутых в У множеств замы-
кания их прообразов f~l(B\) и f~1(B2) в пространстве X не пе-
пересекаются.
Доказательство^ Пусть F: X^-Y—продолжение отображе-
отображения /. Если Bi = Bi<^Y при ?=1,2 и В\ П В2 = 0, то
) ()v i=l,2 и
так что
Значит, условие теоремы необходимо для того, чтобы / можно
было продолжить.
Покажем теперь, что это условие также и достаточно. Для
каждого х^Х обозначим через $(х) семейство всех окрестно-
стей точки х в пространстве X и рассмотрим семейство &~(х) =
= {f (А П ^)}уе^(Я) замкнутых множеств в У.
Так как при Uu ..., Uk^$(x)
A) f{AnU{(]U2{] ... nUk)df(A{]Ux)(] ... {\f(A(]Uk)9
семейство !F{x) центрировано. По теореме 3.1.1, пересечение
F(x) = 0@~(х) не пусто для каждой точки х е X.
Докажем, что множество F(x) состоит ровно из одной точки;
отсюда будет следовать, в частности, что F(x)= {f(x)} для всех
xgA Пусть у и y2^F(x) и У\?=У2- Найдутся ^окрестности V\
и V2 точек у\ и у2 соответственно, такие, что У\ П ^2 = 0- По
216 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
условию теоремы тогда f"l(V\)(]f~l(V2) = 09 так что
X=Wl[)W2, где Wi = X\rl(Vi) при /=1,2.
Тогда x^Wio для /0= 1 или для /0 = 2. Так как
(\f{A\f~x(ViQ))==0 и множество К*о открыто, имеем
откуда следует, что
и мы получили противоречие.
Поставив в соответствие точке хеХ точку F(x), мы опре-
определим отображение F пространства X в пространство У, являю-
являющееся продолжением отображения f. Остается показать, что F
непрерывно. Покажем, что F удовлетворяет условию (ш) пред-
предложения 1.4.1.
Пусть V — окрестность точки F(x) в пространстве У. Так как
{F(x)}= fl f(Af\U)czV, из 3.1.5 следует, что существует
конечное семейство {Uu U2 U!t} cz&(x), такое, что
B) '
Ясно, что t/i П ^2П ... n^* = t/e^(jc)> и, в силу A) и B),
имеем f^'Je f(A (] f/)cz У для каждого x'^Ut т. е. F(U)cz
Следующая теорема является следствием теоремы 3.2.1.
3.2.2. Теорема. Каждый компакт веса ш ^ Ко является непре-
непрерывным образом замкнутого подпространства канторова куба
Доказательство. Пусть У—компакт веса nt. Из теоремы 2.3.26
следует, что У гомеоморфно подпространству александровского
куба Fm.J\nn простоты предположим, что У cz F™. Пространства
Fm и Dm состоят из одного и того же множества точек, и каж-
каждый элемент канонической базы $ пространства Fm является
открыто-замкнутым множеством в Dm, так что тождественное
отображение h пространства ?т на пространство Fm непре-
непрерывно.
Покажем, что предположения теоремы 3.2.1 будут выполне-
выполнены, если положить A = h~l(Y)9 X = Ac=Dm и f = h\A: A -> У.
Пусть Ви В2 — любая пара непересекающихся замкнутых
множеств в У. Существуют замкнутые множества К\ я Къ в Fm,
такие, что 5,- = У П Ki при i = 1, 2. Так как В\ П ^2 = 0, имеем
3.2. ОПЕРАЦИИ НАД КОМПАКТАМИ 217
YczFm \(K\ ПК2)- Так как последнее множество открыто, для
каждого хеУ найдется Ux е 38, такое, что х <= Ux cz Fm \ (К\ Л
Г)*2).
По теореме 3.1.3, найдется конечное множество {х\,... ,Xk}cz
cz У, такое, что
YcUXl[)UX2\) ... UUXhczFn\(KiUK2).
Объединение U = UXl\i U*2 (J ... U U x% является открыто-
замкнутым множеством в Dm, содержащим А. Значит,
Так как /-1 (В?) = А П Kt a A ft Ki при /= 1, 2, имеем
и, по теореме 3.2.1, существует продолжение F: X-+Y отобра^
жения /. Так как /(Л)=У, пространство У является непрерыв-
непрерывным образом замкнутого подпространства X пространства Dm. I
Единственная наша теорема, относящаяся к операции сум-
суммы, такова:
3.2.3. Теорема. Сумма ф Xs, где Х3ф 0 при s e= S, является
компактом (компактным пространством) в том и только том
случае, если все пространства Xs являются компактами (соот-
(соответственно компактны) и множество S конечно.
Доказательство. Если сумма X = ф Xs является компакт-
ным пространством, то все пространства Xs компактны как
замкнутые подпространства пространства X, и множество S
конечно, так как иначе открытое покрытие {Is}5eS не содер-
содержало бы конечного подпокрытия.
Обратно, если {Х(}^х — конечное семейство компактов
(компактных пространств), то сумма X = X\® Х2® >.. @ Х&
является компактом (компактным пространством) в силу тео-
теоремы 2.2.7 и следствия 3.1.4. I
Рассмотрим теперь операцию (декартова) произведения. Сле-
Следующая теорема является основной в этом отношении и одной
из главных теорем общей топологии.
3.2.4. Теорема Тихонова. Произведение Ц Xs, где Xs ф 0 при
S€=S
5^5, является компактом (компактным пространством) в том
и только том случае, если компактами (соответственно компакт-
компактными пространствами) являются все пространства Xs.
218 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
Доказательство. Пусть произведение Х=П ^ является
непустым компактом. Тогда все Xs — хаусдорфовы пространства
(по теореме 2.3.11) и все Xs являются компактными простран-
пространствами в силу теоремы 3.1.10, так как проекция р5: X-*-Xs яв-
является непрерывным отображением пространства X на про-
пространство Xs.
Рассмотрим теперь произвольное семейство {^s}se=s компак-
компактов. По теореме 2.3.11, произведение Х= Ц Xs является хаус-
дорфовым пространством. Возьмем любое центрированное се-
семейство ^о замкнутых множеств в X. Так как центрированность
является свойством конечного типа, из леммы Тейхмюллера —
Тьюки (см. введение) вытекает, что семейство &~о содержится
в некотором максимальном центрированном семействе @~ мно-
множеств в X.
Чтобы доказать, что П^о Ф 0, достаточно найти точку
х е Ху для которой
C) xel при всех А ^ У.
Из максимальности ЯГ получаем
D) если Ль Л2, ..., i4*<=y, то Ах П . -. {\Ak еУ,
и
E) если А о с: X и Ао[)АФ0 для каждого Ле?*,
ТО -fiQ ^^ *5^ •
Так как ЯГ центрировано, семейство #"s = {ps(A)}A ^^ также
обладает этим свойством при всех s e S. Значит, для каждого
5GS существует точка
xs^ П р8{А)аХа.
AeSr
Пусть Ws — любая окрестность точки xs в Xs. Из выписанной
выше формулы следует, что Ws П ps(A )Ф 0 для всех Лее ^, т. е.
р;х (Ws) (}Аф 0 для каждого Ле^.
На основании E) заключаем, что P~l (Ws) ^ У9 а из D) сле-
следует, что все члены канонической базы пространства Ху которые
содержат точку л:= {xs}, принадлежат семейству У. Так как У
центрировано, каждое А^.@~ пересекает все члены канониче-
канонической базы пространства X, содержащие точку ху а это дает
нам C). I
Заметим, что компактность конечного произведения ком-
компактов можно доказать непосредственно и проще; она выте-
3,2. ОПЕРАЦИИ НАД КОМПАКТАМИ 219
кает также из теоремы Куратовского, так как для каждого
пространства У проекция р: Х\ X Х2 X ... X%kX У-* Y яв-
является замкнутым отображением как композиция замкнутых
отображений
Pi: XxXXsX ... XXkXY^X2XX3X ••- XXhXY,
ft: X2XX3X .-• XXkXY^X3XX4X ... X^X^
Теорема Тихонова вместе с теоремой 2.3.23 дает следующие
две теоремы.
3.2.5. Теорема. Тихоновский куб 1т является универсальным
(по вложению) пространством для всех компактов веса ш ^
^ Ко ¦
3.2.6. Теорема. Пространство X является тихоновским в том и
только том случае, если его можно вложить в некоторый ком-
компакт. 1
3.2.7. Пример. Из теоремы Тихонова и теоремы 3.1.9 следует,
что рассмотренное в примере 2.3.36 произведение XX Y яв-
является нормальным пространством. Однако с помощью теоремы
Тихонова легко получить другой пример не нормального под-
подпространства нормального пространства: по теореме 2.3.23, ти-
тихоновский куб Iе содержит подпространство, гомеоморфное
плоскости Немыцкого. ¦
Подмножество А я-мерного евклидова пространства Rn на-
называется ограниченным, если существует такой отрезок / =
= [а, b]czRy что A cz Jncz Rn. Вещественная функция /, опре-
определенная на топологическом пространстве X, называется огра-
ограниченной, если образ f(X) является ограниченным множеством
Теорема Тихонова позволяет охарактеризовать компактные
подмножества евклидова пространства.
3.2.8. Теорема. Подпространство А п-мерного евклидова про-
пространства Rn является компактом в том и только том случае,
если множество А замкнуто и ограничено.
Доказательство. Пусть А — компактное подпространство про-
пространства Rn. Из теоремы 3.1.8 следует, что множество А замк-
оо
нуто. Так как Л с: JJ /С?, где Ki = (—/, /), и /С? cz Kf при i ^ /,
найдется такое iQ, что A cz /f",» а это означает, что А ограничено.
Обратно, так как для каждого J = [a, b] пространство Jn
является, по теореме Тихонова, компактом, каждое замкнутое
220 ГЛ, 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
ограниченное подпространство пространства Rn есть компакт
в силу теоремы 3.1.2. 1
3.2.9. Следствие. Каждая непрерывная вещественная функция
на компактном пространстве ограничена и достигает своих наш
большего и наименьшего значений. 1
Докажем еще одну теорему, относящуюся к произведениям.
3.2.10. Теорема Уоллеса. Пусть As — компактное подпростран-
подпространство топологического пространства Xs при s <= S и W — открытое
множество в произведении П Xs> содержащее множество
П As. Найдутся открытые множества Us a Xs, такие, что
Us Ф Xs лишь для конечного числа sgS и Ц Ascz YLusczW.
Доказательство. Рассмотрим сначала случай произведения
двух пространств, т. е. предположим, что 5 = {1, 2}. Из леммы
3.1.15 следует, что для каждого у^А2 найдутся открытые мно-
множества Ui(y)czXi и U2(y)<=X2y такие, что ~А{ X {у} a U\(y)X
XU2(y)cz W. Так как пространство Л2 компактно, существует
конечное множество {уи #2, ..., Ук}^А2, для которого A2cz
k k
cz U U2{yd-Легко проверяется, что множества?Л = f] Ux(yt) и
k
U2= U U2(yt) обладают всеми нужными свойствами.
i = \
Предположим теперь, что теорема выполняется для произ-
произведения k— 1 пространств для некоторого k ^ 3, и рассмотрим
открытое подмножество W произведения XiX^X ... Х^,
содержащее множество Л^^гХ ... Х^й. Так как произве-
произведение Л2ХЛ3Х ... Y,Ak компактно, то, в силу частного слу-
случая теоремы, доказанного выше, существуют открытые множе-
множества UlczX{ и f/^cIgX^X • • - X Xk, такие, что
А{Х{А2ХАгХ ... XA^czU.XU^cWcz
с^ХЙХ^зХ ... XXk).
По индуктивному предположению, найдутся открытые множе-
множества U2 cz X2, UaCzXz, ..., ?/* с: Xk, для которых
Легко видеть, что множества U\, U2y ... у Uk обладают всеми
нужными свойствами; таким образом, теорема установлена для
конечных произведений.
Рассмотрим, наконец, произвольное произведение и множе-
множество А = XI Ascz WczYl Xs. Для каждого а^А возьмем ка-
3.2. ОПЕРАЦИИ НАД КОМПАКТАМИ 221
кой-нибудь элемент канонической базы произведения Ц Xs,
s<=S
содержащий а и содержащийся в W. По теореме Тихонова, А
содержится в объединении конечного семейства таких множеств:
A cz П Wl U П ulU ¦ • • U UWsCzW.
Найдется конечное множество So = {su s2» ..., si}, такое,
что Wt8 = Xs при s е 5\5о и / = 1, ..., k. Положим
Wi= U П Wi, Wt= П Xs и Л2= П А,.
г = 1 5 е 50 5 е S \ SQ se5\S0
Имеем
и, так как наша теорема для конечных произведений доказана,
существуют открытые множестваUS{ cz XS[, Us2 c= Х$2у ..., t/5/ с
cl5/, такие, что
ASlXAs2X ... X^c^X^X .-• X^cIFl
Положим Us — Xs при всех s e S\S'o; открытые множества
Us cz Xs определены теперь для всех s e 5. Легко проверить,
что эти множества искомые. 1
В связи с операцией перехода к факторпространству имеет
место следующая простая теорема.
3.2.11. Теорема П. С. Александрова. Для каждого замкнутого
отношения эквивалентности Е на компакте X существуют ровно
одно (с точностью до гомеоморфизма) хаусдорфово простран-
пространство Y и непрерывное отображение f: X^Y пространства X на
У, такие, что E — E(f)t а именно: факторпрост ранет во Х/Е и
естественное факторное отображение qp: X-+X/E; более того, Y
при этом является компактом.
Обратно, для каждого непрерывного отображения компакта
X на хаусдорфово пространство Y отношение эквивалентности
E(f) замкнуто.
Доказательство. Если Е — замкнутое отношение эквивалент-
эквивалентности на компакте Х\ то естественное отображение q: Х^-Х/Е
замкнуто; поэтому, в силу теорем 3.1.9 и 1.5.20, факторпростран-
ство Х/Е нормально. Более того, по теореме 3.1.10, простран-
пространство Х/Е является компактом.
Если У — хаусдорфово пространство и существует отображе-
отображение f: X^-Y пространства X на пространство У, такое, что Е —
= ?"(/), то отображение / замкнуто и f: X/E^-Y является го-
гомеоморфизмом в силу 2.4.3 и 2.4.8. Ясно, что если отождествить
222 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
Х/Е с У посредством гомеоморфизма f, то отображение f совпа-
совпадает с естественным отображением q\ Х^Х/Е.
Вторая часть теоремы является переформулировкой теоремы
3.1.12. I
3.2Л2. Примеры. Покажем, что предположение о компактности
существенно в первой части приведенной выше теоремы. Пусть
X = D(t) и fi: X-*It f2: X-+I®{2}—произвольные взаимно
однозначные отображения «на». Ясно, что E(fi) = E(f2) — отно-
отношение тождества на Х\ таким образом, одно и то же замкнутое
отношение эквивалентности на X определяется отображениями
пространства X на различные компакты.
Нельзя опустить и предположение, что пространство У хаус-
дорфово. Действительно, пусть 1 = / и У— отрезок / с тополо-
топологией, описанной в примере 1.2.6. Непрерывное отображение
f: X-+Y, определенное правилом f(x) = x< порождает то же
замкнутое отношение эквивалентности, что и тождественное
отображение id*: X->X, а именно отношение тождества, хотя
X я Y при этом не гомеоморфны. ¦
Перейдем теперь к обсуждению обратных спектров из ком-
компактов.
3.2.13. Теорема. Предел обратного спектра S = {Xa, я?, ?} не-
непустых компактов является непустым компактом.
Доказательство. Для каждого р е 2 положим
2р = {{*„НоГиа: «?(*„) = *, при т<р}.
Возьмем точку гр<=ХрФ0, положим z% = я?(гр) при т^р
и выберем произвольно га е Хо для всех остальных о ^ Е.
Ясно, что z= {га} GZp, так что 1$ф0. Из теоремы 1.5.4
следует, что множество Zp замкнуто в Ц Ха- Так как Z9{ с: Z92
при Р2 ^ Pi и множество 2 направлено, семейство {^P}pes
замкнутых подмножеств произведения П Ха центрировано.
По теореме Тихонова (| ^0Ф 0t что вместе с очевидным со-
отношением lim S = f] ZD завершает доказательство. 1
3.2.14. Теорема. Пусть {q>, fa,} — отображение обратного спектра
S = {A0, я^, Е} компактов в обратный спектр S' = {yCT,, я^', 2'}
Т\-пространств. Если все отображения /а, являются отображе-
отображениями «на», то предельное отображение / = lim ^ф, /а.} тоже
является отображением «на».
3.2. ОПЕРАЦИИ НАД КОМПАКТАМИ 223
Доказательство. В силу следствия 2.5.11, можно предполо-
предположить, что фB')=2. Рассмотрим вспомогательный обратный
спектр S" = {Xv(ar nl%y 2'}, где каждое пространство Ха
встречается ^-1(a)l Раз и гДе связующие отображения те же,
что и в S. Далее, рассмотрим отображение {id2,, /a,} обратного
спектра S" в обратный спектр S'h обозначим через \* предельное
отображение Hm {ids,, f0,}.
Пусть у = \уЛ — любая точка из lim S'. Для каждого о' е 2'
множество Za' = fo>1 (уа') замкнуто в X^{af) и, следовательно,
является компактом. Для произвольных о'у р' е 2', таких, что
р'^с/, имеем
Таким образом, S"' = {Z0,, «•{«?,, 2'}, где й${$ (*) = *$;>
при jf e Za', есть обратный спектр из непустых компактов. По
теореме 3.2.13, существует точка х' = {х0'} е lim S'"; очевидно,
Рассмотрим теперь отображение {<р, ^хф(а/)} обратного спек-
спектра S в обратный спектр S'\ Из предложения 2.5.10 следует, чго
предельное отображение f" = lim {ф, idx(p({J/)} является гомеомор-
гомеоморфизмом, так что существует точка х е lim S, для которой
f"(x) = х'. Так как f = ff (что легко проверить), то f(x) = y. I
Из теорем 3.2.14 и 2.5.14 вытекает
3.2.15. Следствие. Если в обратном спектре S = {X0, я?, 2} ком-
компактов все связующие отображения я? являются отображениями
«на», то и проекции л0: limS—*Ха также являются отображе-
отображениями «на». I
Вот еще два следствия, относящиеся к двум частным случаям
отображений обратных спектров, обсуждавшимся в конце § 2.5.
3.2.16. Следствие. Если S = {Xa, я°, 2} где 2 Ф0У есть обрат-
обратный спектр Т\-пространству X—компакт и {Мае2> г&е f<*: ^"^
XOj — семейство отображений «на», такое, что ii°fg = f для
д
всех а, ре2, удовлетворяющих условию р^о, то предельное
отображение Пт/а также является отображением «на». I
3.2.17. Следствие. Если S = {X0, я?, 2}, где 2 ф 0, — обратный
спектр компактов, X есть Тгпространство w{fa}asS» где f0'- ^a~*
»> X, — семейство отображений «на», такое, что /рл^ = /а для
224 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
всех сг, ре 2, удовлетворяющих условию р ^ а, то предельное
отображение Игл /а гсмег является отображением «на». 1
Завершает этот параграф важная теорема о пространстве
всех непрерывных вещественных функций на компакте. Общие
функциональные пространства будут обсуждены в § 3.4.
Семейство Р czRx непрерывных вещественных функций на
топологическом пространстве X является кольцом функций, если
для всех /, g^P функции f + g, f — g и f-g тоже принадле-
принадлежат P.
Как показано в § 1.4, пространство Rx является кольцом
функций, содержащим все константы и замкнутым относительно
равномерной сходимости. Более того, если X — тихоновское про-
пространство, то семейство Rx разделяет точки, т. е. для любой
пары различных точек х,г/е! существует функция /еRx, та-
такая, что f(x)=?f(y). Для компактов верно и обратное: каждое
кольцо непрерывных вещественных функций на компакте Ху
удовлетворяющее указанным выше условиям, совпадает со всем
Rx. Доказательству этой теоремы будут предпосланы три лем-
леммы. Вторая из них является частным случаем хорошо известной
теоремы из курса анализа; она включена для полноты. Первая
лемма нужна только для доказательства второй.
3.2.18. Лемма (теорема Дини). Пусть X — компакт и {ft} — по-
последовательность непрерывных вещественных функций на X, та-
кая, что fi{x)^fi+\(x) для всех хе! и i=l, 2, ... . Если
существует функция f^Rxt для которой f(x) = limfi(x) при
каждом xel, to f = lim/,-, т. е. последовательность {ft} схо-
сходится к f равномерно.
Доказательство. Пусть е — произвольное положительное
число. Множества Ft = {х: {(х) — Д(х)^е} замкнуты и обра-
образуют убывающую последовательность F\^>F2^> ... . Так как
[}Fi = 0, семейство {^J^i не может быть центрированным.
Значит, найдется to, для которого Ло— 0, а это доказывает
лемму. 1
3.2.19. Лемма. Существует последовательность {wi} полиномов,
равномерно сходящаяся к функции л/t на отрезке I.
Доказательство. Последовательность {wi} определяется ре-
рекуррентными формулами
F) ш,(/) = 0 и wi+x(t) = w.(t) + j(t-wz(t)) при*'=1,2,... .
Докажем по индукции, что
G) WiitXt^T при t<=I и /=1,2,
3.2. ОПЕРАЦИИ НАД КОМПАКТАМИ 225
Последнее^ неравенство верно при /=1. Предположим, что
Щ (t) ^ л/t . Так как
V?" - Щ+1 @ = V'~ - ™i @ ™ у (' - «* @) =
из индуктивного предположения и неравенства t ^ 1 следует,
что
л/Г - a»,+i @> (л/Г ~ »i@) (i - 4 2 л/Г) > о,
чем доказательство G) завершено.
Из F) и G) вытекает, что Wi(t)^wi+\(t) при t^I и i =
== 1, 2, ... . Вместе с G) это показывает, что при каждом t^I
существует предел f{t) последовательности {о>*(')}•_
Переход к пределу в F) дает равенство / (t) = л/t при всех
L Из предшествующей леммы следует, что f = lim Wi. I
3.2.20. Лемма. Пусть Р — некоторое кольцо непрерывных огра-
ограниченных вещественных функций на топологическом простран-
пространстве X. Если кольцо Р содержит все постоянные функции и
замкнуто относительно равномерной сходимости, то для всех
f,g^P функции max(f,g) и min(f9g) тоже принадлежат Р.
Доказательство. Так как
tnn(ftg) = ±(f + g-\f-g\) и
достаточно показать, что если /еР, то |/|еР. Возьмем любое
feP и положительное число с, такое, что \f{x)\^c при всех
х е X. Достаточно доказать, что — I /1 e P; поэтому можно пред-
предположить, что \f(x) | ^ 1 при всех j^gIIIo предыдущей лемме,
функция I f I = V~F является пределом равномерно сходящейся
последовательности функций, принадлежащих Р, а именно по-
последовательности {//}, где fi(х) = Wi[(f(x)J]. I
3.2.21. Теорема Стоуна — Вейерштрасса. Если кольцо Р непре-
непрерывных вещественных функций на компакте X содержит все по-
постоянные функции, разделяет точки и замкнуто относительно
равномерной сходимости (т. е. замкнуто в пространстве Rx, на-
наделенном топологией равномерной сходимости, то Р совпадает
с кольцом всех непрерывных вещественных функций на X.
Доказательство. Достаточно доказать, что для каждого
f^Rx и любого е>0 найдется /е ^ Р, такое, что \f(x) —
— fвМ | < е при всех jcg!
15 Зак. 697
226 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
Для каждой пары различных точек а, &б! существует
функция fteP, такая, что к(а)фк(Ь). Функция g9 определен-
определенная формулой g(x) = (h(x) — h(a) )(h{b)— h(a))~\ принадле-
принадлежит P и обладает тем свойством, что g(a) = 0 и #(&)= 1. Для
функции fa,b^P, определенной формулой fa, ь(х )=(/(& )—
— f(a))g(x)+f(a)> имеем
fa,b(a)=f(a) и fa,b(b)
Множества
Ua.b = {x: fa.bW<f(*) + *} и Va,b = {x: fa,b(x)>f(x)-B]
являются соответственно окрестностями точек а и Ь. Зафикси-
Зафиксируем точку 6 и возьмем конечное подпокрытие {Ua.t ь}&= откры-
того покрытия {Uatb}a(_x пространства J. В силу леммы 3.2.20,
функция fb = min {/ai, 6, ffl2, &> ... ,fak, ь) принадлежит Р\ оче-
очевидно, fb{x)<f(x)+ г при хеХи Ы<*0>/(л;) — е при хе
Множество Vb является окрестностью точки Ь. Возьмем ко-
конечное подпокрытие {Vbt}l_ открытого покрытия {Уь}ь^х ПР°'
странства X. В силу леммы 3.2.20 функция /8 = max {/&1, ..., fb^
принадлежит Р, и ясно, что \f&(x) — f(x)\<.e для каждого
Важность теоремы Стоуна — Вейерштрасса в том, что она
дает метод равномерной аппроксимации всех непрерывных ве-
вещественных функций, определенных на каком-либо компакте X,
специальными классами функций. Действительно, каждая не-
непрерывная вещественная функция на X может быть сколь
угодно хорошо аппроксимирована полиномами (от нескольких
переменных) от элементов произвольного фиксированного се-
семейства непрерывных функций, разделяющего точки. Так как
для каждого отрезка J a R семейство {/}, состоящее из функ-
функции f: J^~R, заданной правилом 1(х) — х, разделяет точки, тео-
теорема 3.2.21 влечет за собой классическую теорему Вейерштрасса,
которая утверждает, что каждая непрерывная вещественная
функция на / является пределом равномерно сходящейся после-
последовательности полиномов.
3.2.22. Пример. Покажем, что предположение о компактности
в теореме 3.2.21 существенно. Действительно, кольцо Р, являю-
являющееся замыканием по отношению к топологии равномерной схо-
сходимости в пространстве RR множества всех непрерывных ото-
отображений пространства R в себя, постоянных вне какого-нибудь
интервала, удовлетворяет всем предположениям теоремы Стоу-
3.2. ОПЕРАЦИИ НАД КОМПАКТАМИ 227
на — Вейерштрасса, но не совпадает со всем RR9 так как оно не
содержит функцию sin jc — это легко проверить. Можно доказать,
что если вполне регулярное пространство X удовлетворяет тео-
теореме Стоуна — Вейерштрасса, то X является компактом (см.
упр. 3.2.К). ¦
Читатель легко проверит, что для не хаусдорфовых ком-
компактных пространств аналоги теорем 3.2.1, 3.2.2, 3.2.11, 3.2.13,
3.2.14 и 3.2.21 не верны.
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
Теорема 3.2.1 была доказана Таймановым в [1952] и, в виде
двойственного утверждения (см. упр. 3.2.А(а)), Эйленбергом и
Стинродом в [1952]. Теорема 3.2.2 доказана П. С. Алексан-
Александровым в [1936]. Тихонов доказал теоремы 3.2.5 и 3.2.6 в [1930].
В частности, он показал, что все кубы /ш компактны, откуда
легко следует, что теорема 3.2.4 верна, но сама эта теорема была
впервые сформулирована в работе Тихонова [1935а]. Данное
нами доказательство теоремы Тихонова следует Шевалле и
и О. Фринку [1941]. Конечный случай теоремы Уоллеса по-
появился в работах Готшелка и Хедлунда [1955] и Келли [1955],
где отмечается, что результат принадлежит Уоллесу; теорема
в полной общности была доказана Фроликом в [I960] и Лином
в [1960]. Теорема П. С. Александрова была объявлена в [1925]
и доказана в [1927]. Теорема 3.2.13 по существу доказана Стин-
Стинродом в [1936]. Следствие 3.2.15 можно найти в работе Эйлен-
берга и Стинрода [1952]. Лемма 3.2.18 установлена У. Дини
в 1878 г. для функций, определенных на отрезке. Теорема Стоу-
Стоуна— Вейерштрасса, обобщающая классический результат
Вейерштрасса, полученный в 1885 г. (он сформулирован перед
примером 3.2.22), доказана М. Стоуном в [1937]. Простое ее
доказательство, приведенное нами, и интересное обсуждение
предмета можно найти в статье М. Стоуна [1947].
УПРАЖНЕНИЯ
З.2.А. (а) (Эйленберг и Стинрод [1952]). Пусть А — всюду
плотное подпространство топологического пространства X и f —
непрерывное отображение пространства А в компакт У. Дока-
Докажите, что отображение / можно продолжить до непрерывного
отображения всего X в том и только том случае, если для каж-
каждого открытого покрытия {Vt}^={ пространства Y существует от-
открытое покрытие {^t}(=1 пространства Ху такое, что открытое
покрытие {Ui{\A}\=x подпространства А вписано в покрытие
15*
228 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
(Ь) (Бурбаки и Дьедонне [1939]). Пусть А — всюду плот-
плотное подпространство топологического пространства X и f — не-
непрерывное отображение пространства Л в регулярное простран-
пространство У. Докажите, что f можно продолжить до непрерывного
отображения всего X в том и только том случае, если / непре-
непрерывно продолжается на Л11М для каждого х^Х\А. За-
Заметьте, что предположение о регулярности Y нельзя ослабить до
предположения, что пространство Y хаусдорфово.
З.2.В. Покажите, что формула
где x={Xi}, определяет непрерывное отображение канторова
множестваОйо на отрезок /. Докажите с помощью этого факта
теорему 3.2.2. Проверьте, что существует счетное множество
Лс/, такое, что |f (у) \ = 2 для каждого г/еЛ и |f~l(у) | = 1
для г/<=/\Л.
З.2.С. Сегмент в Rn с концами х, y^Rn есть множество всех
точек вида A—f)x + ty, где O^fsgll, а сложение точек и
умножение точки на число определяются так же, как в начале
приложения к § 7.3. Луч в Rn с началом в точке х е Rn, проходя-
проходящий через точку у е Rn, отличную от х, есть множество всех
точек вида A — t)x~\- ty, где / > 0. Подмножество А множества
Rn называется выпуклым, если для каждой пары х, у точек
множества А сегмент с концами в х, у содержится в Л.
Покажите, что каждый выпуклый компакт А сг Rn, такой, что
1п1Аф0, гомеоморфен единичному гс-шару Вп, а его граница
Fr А гомеоморфна (п—1 )-сфере Sn~l. В частности, гомео-
морфны пространства 1п и Вп, так же как и пространства
Fr ln c= Rn и Sn'\ при п = 1, 2, ... .
Указание. Зафиксируйте точку x^lntA и докажите, что
каждый луч с началом в точке х пересекает РгЛ в точности
в одной точке.
3.2.D. Заметьте, что теорема Тихонова вытекает из теоремы
Куратовского и теоремы Уоллеса.
3.2.Е. (Келли [1955]). Докажите, что подпространство X ти-
тихоновского куба Iе = П It> где It = I для каждого t e /, кото-
рое состоит из всех неубывающих отображений отрезка / в /,
обладает следующими свойствами:
(a) X — компакт.
(b) Пространство X содержит подпространство, гомеоморф-
ное дискретному пространству D(с), и подпространство, гомео-
морфное прямой Зоргенфрея К.
(c) Пространство X не наследственно нормально.
3.2. ОПЕРАЦИИ НАД КОМПАКТАМИ 229
Указание, Проверьте, что X2 можно вложить в X.
(d) Пространство X удовлетворяет первой аксиоме счет-
ности.
Указание. Множество точек разрыва произвольной функции,
входящей в X, счетно.
(e) Пространство -X" сепарабельно.
Указание. См. доказательство теоремы Хьюитта — Марчев-
ского — Пондицери.
Пространство X называется пространством Хелли.
3.2.F (Архангельский [1965]). Покажите, что произведение
XI ХЗУ где Х3ф0 при seS, является пространством точечно
S
S
счетного типа в том и только том случае, если все Xs являются
пространствами точечно счетного типа и существует счетное
множество So cz S, такое, что Xs является компактом для всех
s€~S\S0 (см. упр. ЗЛ.Е(Ь)).
3.2.G. Покажите, что если X — компакт, то отношение экви-
эквивалентности Е на X замкнуто в том и только том случае, если
множество Е замкнуто в произведении ХУ(Х.
З.2.Н. (а) (Мибу [1944]). Докажите с помощью теоремы
Стоуна — Вейерштрасса, что каждая непрерывная вещественная
функция/: II XS->R, определенная на произведении компак-
тов, зависит лишь от счетного числа координат (см. определение
в задаче 2.7.12(с)).
(b) Покажите, что существует непрерывная вещественная
функция (в действительности непрерывная функция, принимаю-
щая лишь значения 0 и 1) на произведении 1 — ГХ Ц ?>/, где
T = D(t) и Dt = D при всех t^T, которая зависит от несчет-
несчетного множества координат.
Указание. Рассмотрите разбиение пространства X на непере-
непересекающиеся открыто-замкнутые множества Atti={x^X:
р(л:) = ^ и pt(x) — i}, где t^T, i^D, p — проекция простран-
пространства X на Т и pt — проекция пространства X на D*.
(c) (Келлерер [1968]). Докажите, что если Xs для каждого
«eS — хаусдорфово пространство, в котором есть всюду плот-
плотное подпространство, являющееся объединением счетного се-
семейства компактов (в частности, если каждое Xs сепарабельно),
то любая непрерывная вещественная функция /: П^"*^
зависит лишь от счетного числа координат (см. задачу 2.7.12(с)
и упр. 4.1.G).
Указание. Пусть XStu Xs,2, ... — возрастающая последова-
оо
тельность компактов в Xs, такая, что объединение и %s, г всюду
230 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
плотно в Xs. Рассмотрите произведения Xi= Ц XSt t\\ заметьте,
оо
что объединение и Хг всюду плотно в Ц Xs.
i = l s<=S
(d) Докажите аналоги утверждений (а) и (с) для непрерыв-
непрерывных отображений декартовых произведений в тихоновские про-
пространства веса ш.
3.2.1. (а) Покажите, что для любого тихоновского простран-
пространства X и произвольного кардинала m Г5= Ко каждое из следую-
следующих условий вытекает из предыдущего и что если X — компакт,
то все эти условия равносильны:
A) Пространство Rx с топологией равномерной сходимости
содержит всюду плотное подмножество мощности ^ ш.
B) Пространство X имеет базу мощности ^ т.
C) В множестве Rx есть подмножество мощности ^ т, раз-
разделяющее точки.
Примените этот результат для доказательства теоремы 3.1.21
и — при дополнительном предположении, что X компактно, —
для доказательства теоремы 3.1.22.
Проверьте, что ни условия A) и B), ни условия B) и C)
не равносильны.
Указание. Доказывая теорему 3.1.22, заметьте, что если су-
существует непрерывное отображение пространства X на про-
пространство У, то RY можно (гомеоморфно) вложить в Rx> и про-
проверьте, что если d(Rx) < щ, то и w (Rx)^ m.
(b) Докажите, что условие C) в (а) равносильно такому:
D) Пространство Rx с топологией поточечной сходимости
содержит всюду плотное множество мощности <; щ.
Выведите отсюда, что d{R2j^vx (сравните этот результат
с теоремой Хьюитта — Марчевского — Пондицери).
3.2.J (М. Стоун [1947]). (а) Покажите, что каждая непре-
непрерывная вещественная функция, определенная на компактном
подпространстве М тихоновского пространства Xt непрерывно
продолжается на X.
Указание. Вложите X в тихоновский куб и примените тео-
теорему Титце — Урысона.
(Ь) Заметьте, что утверждение (а) вытекает из теоремы
Стоуна — Вейерштрасса без помощи теоремы Титце — Урысона
(см. упр. 3.6.С).
3.2.К (Хьюитт [1947]). Заметьте, что если вполне регулярное
пространство X удовлетворяет теореме Стоуна — Вейерштрасса,
то X — компакт.
Указание. Вложите X в тихоновский куб.
3.3. ЛОКАЛЬНО КОМПАКТНЫЕ ПРОСТРАНСТВА 231
3.3. ЛОКАЛЬНО КОМПАКТНЫЕ ПРОСТРАНСТВА
И ^-ПРОСТРАНСТВА
Топологическое пространство X называется локально ком-
компактным, если для каждого х^Х существует окрестность U
точки х, такая, что О является компактным подпространством
пространства X.
3*3.1. Теорема. Каждое локально компактное хаусдорфово про-
пространство является тихоновским пространством.
Доказательство. Пусть х — точка локально компактного хаус-
дорфова пространства X и F— замкнутое в X множество, такое,
что хф?. Возьмем окрестность U точки х, для которой U яв-
является компактом. Множество Fo = (U\U)\j^O f\F)— замкну-
замкнутое подмножество пространства П. Так как x^U\FOi существует
непрерывная функция ft: B-+J, такая, что f\(x) — O и f\(F0)cz
с {1}. Так как U(](X\U)= U\UczFo, комбинация / функции
fx и постоянной функции /г: Х\ [/->-/, определенной правилом
Ы#)—1 Для всех y^X\U, является непрерывной функцией
в силу 2.1.13. Легко видеть, что f(x) = O и f(F)cz {1}. I
3.3.2. Теорема. Для каждого компактного подпространства А
локально компактного хаусдорфова пространства X и каоюдого
открытого множества V а X, содержащего Л, найдется откры-
открытое множество U а X, такое, что AczUczfJczVuU — компакт.
Доказательство. Для каждого хеЛ возьмем окрестность Vx
точки ху такую, что Vx cz У, и окрестность Wx точки ху для ко-
которой Wx является компактом. Множество UXt где Ux = Vxf\ Wx,
компактно, так как оно замкнуто в компактном пространстве
Wx. В силу теоремы 3.1.3, найдется конечное множество
{*ь *2, ..., xk) а Л, такое, что A cz U = UXl U Ux% U •.. U Uxk.
Множество U=^UXi [} UXz U ... (J UXk — компакт в силу теоремы
3.1.4, и очевидно, что U c= VXi U VXiU . ¦. UVXk^V. I
Из теорем 3.3.1, 3.1.7 и 3.1.2 получаем
3»3.3. Следствие. Для каждого компактного подпространства А
локально компактного хаусдорфова пространства X и каждого
открытого множества V, содержащего Л, существует непрерыв-
непрерывная функция f: Х->-/, такая, что f(x) = O при х^А, f(х) = 1
при a;g!\F и множество f~l([0, a]) является компактом для
каждого а < 1. 1
Следующая теорема дает оценку характерам точек в локаль-
локально компактном хаусдорфовом пространстве (см. упр. 3.1.F(a)).
3.3.4. Теорема. Характер произвольной точки х в локально ком-
компактном хаусдорфовом пространстве X равен наименьшему кар-
232 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
диналу вида \°U\> где Ш — семейство открытых множеств в Ху
такое, что [Щ = {х}.
Доказательство. Пусть {х}= fj V8, где Vs открыто в X и
s eS
|5|^щ. Достаточно показать, что %(х, Х)^.ш. Можно предпо-
предположить, что m ^ Ко> так как если m конечно, то х — изолирован-
изолированная точка _в X и %(х, X)— 1 ^ ш. Из теоремы 3.3.2 следует, что
[х\ = fj Us, где Us — окрестность точки х, такая, что Os ком-
пактно. В силу 3.1.5, для каждой окрестности U точки х най-
найдется конечное множество {su s2, ..-, sk}<z:S, такое, что
USl(]Us2n ... n^crt/^n^n ••• [\U8k^U. Значит, все ко-
конечные пересечения элементов семейства {Us}seS образуют
базу в точке х. Так как мощность семейства всех таких пересе-
пересечений не превосходит т, имеем %(х,Х)^ш. ¦
Оказывается, теорему 3.1.19, как и ее следствия, можно
распространить на локально компактные хаусдорфовы простран-
пространства (см. упр. 3.9.Е).
3.3.5. Теорема. Для каждого локально компактного хаусдорфова
пространства X имеем nw(X)=w(X).
Доказательство. Достаточно показать, что w(X)^ nw(X).
Очевидно, можно предположить, что /ш(Х)=т :js Ко. Пусть
Jf — сеть в X, для которой |^Г| = т. Из определения локальной
компактности следует, что семейство {M5)seS, состоящее из всех
членов семейства Jf, замыкание которых компактно, покрывает
X. В силу 3.3.2, для каждого s e= S найдется открытое множество
UsCzX, такое, что MsczUs я U$ — компакт. Так как nw(Us)^
^nw(X) = m, из теоремы 3.1.19 следует, что te>([/s)^m, т. е.
подпространство Us пространства X обладает базой $s мощ-
мощности =^т. Легко видеть, что объединение U $s является ба-
зой мощности ^т пространства X Значит, w(X)^.m. I
Заметим, что последняя теорема немедленно следует из тео-
теоремы 3.1.19 и теоремы 3.5.11, которая будет доказана далее.
3.3.6. Следствие. Для каждого локально компактного хаусдор-
хаусдорфова пространства X имеем w(X)^\X\. 1
3.3.7. Следствие. Если локально компактное хаусдорфово про-
пространство Y является непрерывным образом пространства X, то
Y(X) 1
3.3.8. Теорема. Если X — локально компактное хаусдорфово про-
пространство, то каждое подпространство пространства X, пред-
ставимое в виде F П V, где F замкнуто в X, а V открыто в X,
тоже локально компактно.
3.3. ЛОКАЛЬНО КОМПАКТНЫЕ ПРОСТРАНСТВА 233
Доказательство. Достаточно показать, что локальная ком-
компактность хаусдорфова пространства наследуется как замкну-
замкнутыми подпространствами, так и открытыми подпространствами,
поскольку F(]V является открытым подпространством замкну-
замкнутого подпространства F пространства X.
Пусть F— замкнутое подпространство локально компактного
пространства X. Для каждого х^ F найдется окрестность U
точки х в пространстве X, такая, что V компактно. Пересечение
FQ U—окрестность точки х в пространстве F, и замыкание
F(]U(]F = Ff\U этой окрестности в F компактно как замкну-
замкнутое подпространство компактного пространства О1).
Тот факт, что локальная компактность хаусдорфова про-
пространства наследуется открытыми подпространствами, следует
сразу из теоремы 3.3.2, примененной к одноточечному множе-
множеству А. I
3.3.9. Теорема. Локально компактное подпространство М хаус-
хаусдорфова пространства X является открытым множеством в за-
замыкании М множества М в пространстве X; следовательно, М
можно представить в виде F П V, где F замкнуто в Ху а V от-
открыто в X.
Доказательство. Достаточно показать, что всюду плотное
локально компактное подпространство М хаусдорфова простран-
пространства X открыто в X.
Каждая точка х^М обладает окрестностью U в подпро-
подпространстве М, такой, что множество О[\М компактно и, значит,
замкнуто в X. Так как U cr V П М, имеем О с: О f| M с: М. Пусть
W — открытое множество в Ху для которого U — MflW. В силу
теоремы 1.3.6,
откуда следует, что каждая точка х^М обладает окрестностью
W в пространстве Ху содержащейся в подпространстве М. Зна-
Значит, М открыто в X. I
Последние две теоремы дают
3.3.10. Следствие. Подпространство М локально компактного
хаусдорфова пространства X локально компактно в том и только
том случае, если его можно представить в виде FflV, где F
замкнуто в X, а V открыто в X. 1
Из 3.3.10, 3.3.1 и 3.2.6 получаем
1) Предположение, что X — хаусдорфово пространство, в этой части рас-
рассуждения не использовалось. — Прим. перев,
234 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
3.3.11. Следствие. Хаусдорфово пространство локально ком-
компактно в том и только том случае, если оно гомеоморфно откры-
открытому подпространству некоторого компакта. I
3.3.12. Теорема. Сумма © Х3 является локально компактным
se=S
(хаусдорфовым) пространством в том и только том случае, если
все пространства Xs локально компактны (и хаусдорфовы).
Доказательство. Если сумма (В Xs локально компактна, то
S€=S
и все Xs локально компактны (см. следствие 2.2.2 и доказатель-
доказательство теоремы 3.3.8).
Обратно, пусть все Xs локально компактны. Тогда для каж-
каждого х е= X = © Xs найдется $0 ^ 5, такое, что х е XSo, и най-
Sf=S
дется окрестность V точки х в XSq, замыкание которой в Xs*
компактно. Ясно, что U является окрестностью точки х в X и
что замыкание множества (/ в I, совпадающее с замыканием
множества U в XSa, компактно. |
3.3.13. Теорема. Декартово произведение Ц Xst где Х3ф0
s<=S
при 5^5, локально компактно в том и только том случае, если
все пространства Xs локально компактны и существует конеч-
конечное множество So сг 5, такое, что Xs компактны при всех s e
€= S\So-
Доказательство. В силу теоремы Тихонова и предложения
2.3.7, достаточность этого условия будет установлена, если мы
покажем, что произведение любого конечного числа локально
компактных пространств локально компактно. Возьмем точку
х—(хи %2> ..., ^)g!iX^X ... XAV В силу локальной
компактности X/, при i = h 2, ..., k найдется окрестность Vi
точки Xt в Xtt такая, что Vi компактно. Множество V = V\ X
X У г X ••• X Vk является окрестностью точки х в Хг X Х2 X ...
... X Хи и V компактно в силу 2.3.3 и теоремы Тихонова.
Обратно, предположим, что П Xs — непустое локально ком-
пактное пространство. Возьмем sogSh точку х ^ XSo и пока-
покажем, что у точки х есть окрестность WczXSQt для которой W
является компактным подпространством пространства Xs^ Пусть
xs — любая точка пространства Xs при 5^=50 и xSo = x. Точка
{xs} g]I^ обладает окрестностью U, замыкание которой О
$ eS
компактно. Ясно, что существует член П Ws канонической
s<=S
базы пространства П Xs, такой, что {xs} e П WsczU n Ws =
= XS при sgS\S0, где |50|< Ko. В силу теоремы 3.1.2, произ-
3.3. ЛОКАЛЬНО КОМПАКТНЫЕ ПРОСТРАНСТВА 235
ведение JJ Ws = Ц Ws с: 0 компактно. Следовательно, W =
s eS S(=S
= 1^5о с Х5о — окрестность точки х, замыкание которой ком-
компактно, и Xs компактно при s e S\So- I
Из последней теоремы и примера 2.5.3 следует, что предел
счетного обратного спектра локально компактных хаусдорфовых
пространств может не быть локально компактным простран-
пространством.
3.3.14. Примеры. Каждое дискретное пространство локально
компактно. Вещественная прямая локально компактна так как
она гомеоморфна открытому подпространству (—1, 1) компакта
[—1, 1]. Из последней теоремы следует, что я-мерное евклидово
пространство Rn тоже локально компактно. Локально компактно
и пространство В^о всех счетных ординалов.
Пространство Z, определенное в примере 2.3.36, локально
компактно как открытое подпространство компакта XX У; оно
является примером не нормального локально компактного хаус-
дорфова пространства. 1
3.3.15. Теорема. Если f: X-+ У — открытое отображение локально
компактного пространства X на хаусдорфово пространство У, то
У — локально компактное пространство.
Доказательство. Пусть у — любая точка из У. Возьмем про-
произвольную точку x^f-l(y) и окрестность U точки х в X, для
которой О — компактное подпространство пространства X.
Образ /(?/) является окрестностью точки у в Y. Множество f(O)
компактно и, значит, замкнуто в У; следовательно, f(U)czf(O)
и f(U)—компакт. 1
С другой стороны, локальная компактность не сохраняется
замкнутыми отображениями:
3.3.16. Пример. В примере 1.4.17 мы определили замкнутое ото-
отображение f: X-+Y вещественной прямой R — X на факторпро-
странство R/N = У, полученное отождествлением множества N
положительных целых чисел в точку г/о ^ У. Было отмечено, что
пространство У не имеет счетной базы в точке уо; в силу след-
следствия 3.3.7, это означает, что пространство У не локально ком-
компактно.
Другой пример можно получить, отождествив в точку зам-
замкнутое подмножество А локально компактного пространства Z,
описанного в примере 2.3.36; факторпространство Z/A не регу-
регулярно— значит, оно и не локально компактно. 1
Как показано в примере 2.4.20, декартово произведение фак-
факторного отображения и тождественного отображения не обязано
быть факторным отображением. Однако для тождественных
236 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
отображений локально компактных пространств имеет место
следующее утверждение (см. задачу 3.12.14 (Ь)):
3.3.17. Теорема Уайтхеда. Для каждого локально компактного
хаусдорфова пространства X и произвольного факторного ото-
отображения g: Y-+Z декартово произведение f = \йх X g: XX У-*
->-1Х2 является факторным отображением.
Доказательство. Предположим, что прообраз /-1 (W) cz X X У
множества W<=XXZ открыт, и возьмем произвольную точку
(#о, 2о)е W. Выберем точку уо eg-!Bo) и возьмем окрестность
U точки х0, для которой О компактно и ОХ {уо} ci f~ (W). Для
каждого у ^ У имеем
A) OXg-lg(y)ctl(W> если OX{y}<=f~l(W)l
поэтому выполняется включение BXg~l(zo)c^f~'l(W). Множе-
Множество V={z^Z: 0Xg~lB)<=f~l(W)} удовлетворяет условию
(хо, 2о) s U X V с= W; значит, достаточно показать, что V откры-
открыто в Z. Так как отображение g факторно, это сводится к дока-
доказательству открытости в Y множества
Из A) следует, что g-l(V)={yeY: PX^c^ff)}, a
по теореме Куратовского последнее множество открыто, так как
оно является дополнением проекции замкнутого множества
(OX Y)\f~l(W) при проектировании р: UX Y-+Y параллельно
компактному сомножителю U. 1
Вторая половина этого параграфа посвящена изучению
^-пространств; класс этих пространств тесно связан с классом
локально компактных хаусдорфовых пространств. Топологиче-
Топологическое пространство X называется k-пространством, если оно хаус-
дорфово и представимо в виде образа некоторого локально ком-
компактного хаусдорфова пространства при факторном отображе-
отображении. Иными словами, ^-пространства — это хаусдорфовы про-
пространства, являющиеся факторпространствами локально ком-
компактных хаусдорфовых пространств. Ясно, что каждое локально
компактное хаусдорфово пространство есть ^-пространство.
3.3.18. Теорема. Хаусдорфово пространство X является k-npo-
странством в том и только том случае, если в X замкнуто каж-
каждое множество AczX, пересекающееся со всяким компактным
подпространством Z пространства X по замкнутому в Z мно-
множеству.
Доказательство, Пусть X есть ^-пространство и f: Y-+X —
факторное отображение локально компактного хаусдорфова
пространства У на X. Предположим, что пересечение множества
А сг X с каждым компактным подпространством Z пространства
3.3. ЛОКАЛЬНО КОМПАКТНЫЕ ПРОСТРАНСТВА 237
X замкнуто в Z. Возьмем любую точку yef~l(A) и произволь-
произвольную окрестность U <= Y точки у, такую, что О компактно. Мно-
Множество f~l(A (\f(O))c: f-1 (А) замкнуто в У и содержит множе-
ство f~l (А )П О; значит, у е f-1 (A). Отсюда следует, что f~l(A)—
/*(Л), и так как отображение f факторно, мы заключаем, что
Рассмотрим теперь произвольное хаусдорфово пространство
X и обозначим через Э?(Х) семейство всех непустых компакт-
компактных подпространств пространства X. Пространство Х= © Z
локально компактно и хаусдорфово, а отображение/= V iz
Ze2 (X)
Х-+Х, где iz — тождественное вложение подпространства
Z в пространство X, непрерывно в силу 2.1.11. Легко видеть, что
если в X замкнуто каждое множество Лс1, пересечение А Л Z
которого с Z замкнуто в Z для всех Z^3C(X), то отображение
/ факторно. I
Заметим, что в приведенной выше теореме можно с тем же
успехом предполагать, что все пересечения А (] Z компактны или
что все они замкнуты в X.
3.3.19. Следствие. Хаусдорфово пространство X является k-npo-
странством в том и только том случае, если в X открыто каждое
множество АсХ9 пересечение которого со всяким компактным
подпространством Z пространства X открыто в Z. I
3.3.20. Теорема. Каждое секвенциальное хаусдорфово простран-
пространство— «, в частности, каждое хаусдорфово пространство с пер-
первой аксиомой счетности — является k-пространством.
Доказательство. Предположим, что подмножество А секвен-
секвенциального пространства X не замкнуто. Существуют последова-
последовательность хи Х2, ... точек множества А и точка jcoelimjc/, та-
такие, что Хо^А. Если X является к тому же хаусдорфовым про-
пространством, то, как легко проверить, подпространство Z =
— {#о, хи Х2, ...} пространства X гомеоморфно пространству
А(Ко); при этом хо — единственная предельная точка для Z.
Отсюда следует, что пересечение множества А с компактным
подпространством Z пространства X не замкнуто. I
3*3.21. Теорема. Отображение f k-пространства Х в топологиче-
топологическое пространство Y непрерывно в том и только том случае,
если для каждого компактного подпространства ZczX сужение
f\Z: Z-*-Y является непрерывным отображением.
Доказательство. Достаточно показать, что из непрерывности
всех таких сужений f\Z следует непрерывность f. Возьмем лю-
любое замкнутое множество А а У. Для каждого компактного
238 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
ZczX множество f~l(A)()Z = (f\Z)~l(A) замкнуто, откуда сле-
следует, что f~x(A) замкнуто. Следовательно, / непрерывно. I
3.3.22. Теорема. Непрерывное отображение f: X-+Y топологи-
топологического пространства X в k-пространство У замкнуто (открыто,
факторно) в том и только том случае, если для каждого ком-
компактного подпространства ZaY сужение fz: f~l(Z)-+Z является
замкнутым (открытым, факторным) отображением.
Доказательство. В силу предложений 2.1.4 и 2.4.15, доста-
достаточно показать, что если все такие сужения fz замкнуты, от-
открыты или факторны, то таким же будет и отображение /.
Предположим сначала, что сужение fz: f~l(Z)-+Z замкнуто
(открыто) для каждого компактного подпространства Z<=y, и
рассмотрим произвольное замкнутое (открытое) множество
A cz X. Равенства
и тот факт, что fz замкнуто (открыто), показывают, что мно-
множество f(A)(]Z замкнуто (открыто) в Z для каждого компакт-
компактного подпространства Zc:Y. Так как У есть ^-пространство,
заключаем, что f(A) замкнуто (открыто), а это означает, что
отображение / замкнуто (открыто).
Предположим теперь, что сужение fz: f~l(Z)-+Z является
факторным отображением для каждого компактного подпро-
подпространства Z с У, и рассмотрим любое множество В cz У, такое,
что f~l(B) замкнуто в X. Множество /"' (B(]Z) = rl(B) Л Г1 (Z)
замкнуто в f~l(Z); значит, пересечение B(]Z замкнуто в Z для
каждого компактного подпространства Z <nY. Так как У явля-
является ^-пространством, множество В замкнуто в У, а это показы-
показывает, что отображение f факторно. 1
Из определения ^-пространства получаем сразу следующий
результат:
3.3.23. Теорема. Если f: X^-Y— факторное отображение k-npo-
странства X на хаусдорфово пространство У, то Y является
k-пространством. 1
3.3.24. Примеры. Отметим, что существуют не регулярные &-про-
странства; одно из таких пространств определено во втором
примере из 3.3.16.
Существуют также совершенно нормальные пространства, не
являющиеся ^-пространствами: таково пространство У, опреде-
определенное в примере 1.6.20. Чтобы доказать, что У не является
^-пространством, достаточно показать, что все компактные под-
подпространства пространства У конечны, так как множество
У\{0} не замкнуто в У, но пересекается по замкнутому мно-
множеству с каждым конечным подмножеством пространства У.
3.3. ЛОКАЛЬНО КОМПАКТНЫЕ ПРОСТРАНСТВА 239
Предположим, что Z — бесконечное компактное подпространство
пространства У. Так как каждое из пересечений^ Л у— > — + -^г|
конечно, найдется последовательность хи *2, ... точек мно-
множества Z, сходящаяся к 0 относительно естественной топологии
вещественной прямой. Множество {х\9 х2, ...} cz Z, наделенное
топологией подпространства пространства У, гомеоморфно ди-
дискретному пространству /)(Ко) и замкнуто в У, а это противоре-
противоречит предположению, что Z компактно.
Данное пространство У — непрерывный образ пространства
D(i&o), являющегося ^-пространством. Значит, непрерывный
образ ^-пространства не обязан быть ^-пространством, даже
если он совершенно нормален.
Заметим, что пространство У является подпространством сек-
секвенциального пространства (а именно пространства X, описан-
описанного в примере 1.6.19). Таким образом, как показывает теорема
3.3.20, свойство быть ^-пространством не наследственно (см.
задачу 3.12.15). I
Из 3.3.8 и 2.4.15, однако, следует
3.3.25. Теорема. Свойство быть k-пространством наследуется как
замкнутыми, так и открытыми подпространствами. 1
Из теоремы 3.3.18 вытекает
3.3.26. Теорема. Сумма ф Xs является k-пространством в том
и только том случае, если все Xs суть k-пространства. I
Теорема Уайтхеда влечет за собой такой результат:
3.3.27. Теорема. Декартово произведение XX У локально ком-
компактного хаусдорфова пространства X и k-пространства У яв-
является ^пространством. 1
Из теоремы 3.3.23 следует, что если непустое произведение
11 Х3 является ^-пространством, то ^-пространствами явля-
s<= S
ются и все Xs.
Докажем теперь теорему о декартовых произведениях, из
которой будет вытекать важный факт: свойство быть /г-простран-
ством не мультипликативно.
3.3.28. Теорема. Если /г. Jfj-^У/ — факторные отображения при
i = 1, 2 и как Хи так и Y\ X Y2 являются k-пространствами, то
декартово произведение f = f\X h"- X\ X Х2 ->¦ Y\ X Y2 является
факторным отображением.
Доказательство. Покажем сначала, что если XX Т есть
^-пространство, то, каково бы ни было факторное отображение
g: У^-71, декартово произведение h = id* X g'- ХХУ-^ХХ^
является факторным отображением. Для этого рассмотрим ком-
240 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
пактные подпространства Z\ cz X и Z2 cz Г, их произведение
Z = ZiX22 и сужение hz: h-l(Z)-+Z. Из равенства hrx(Z) =
==Z1Xg-1(Z2) следует, что ^z = idZi Xg2- Значит, /iz — фак-
факторное отображение по теореме Уайтхеда. Так как каждое ком-
компактное подпространство произведения ХХТ содержится в
произведении его проекций в X и Т, т. е. в компактном множе-
множестве вида Z\XZ%% из теоремы 3.3.22 следует, что отображение h
факторно.
Рассмотрим теперь частный случай этой теоремы, а именно
случай локально компактного хаусдорфова пространства Х\.
Так как, в силу 3.3.27, произведение Х\ X Y2 является ^-про-
^-пространством, из установленного в предшествующем абзаце факта
следует, что отображения
являются факторными. Следовательно, и отображение / как
композиция этих отображений тоже является факторным.
Наконец, рассмотрим случай произвольного ^-пространства
Х\. Существуют локально компактное хаусдорфово пространство
Х/ и факторное отображение f: Xf-*~X\ пространства X' на про-
пространство Х\. Согласно частному случаю доказываемой теоремы,
уже установленному выше, декартово произведение (jiff)Xf2'
XfXX2^~Y\XY2 является факторным отображением. Так как
(UP) X /2 = (fx X f2) (/' X idXi), то декартово произведение f =
= /i X /2 является факторным отображением в силу 2.4.5. I
3.3.29. Пример. В 2.4.20 мы рассмотрели подпространство Х\ =
= Yi — R\{l/2, 1/3, ...} вещественной прямой и факторпро-
странство У2, полученное из Х% = R отождествлением множе-
множества всех положительных целых чисел в точку. Оба пространства
Fi и Y2 являются ^-пространствами, и тем не менее их произве-
произведение Y\ X Y2 ^-пространством не является. Действительно, как
показано в 2.4.5, декартово произведение f == f 1 X /2, где f{ = idXi
и f2 — естественное факторное отображение, не является фактор-
факторным отображением. Значит, из последней теоремы следует, что
Y\ X Y2 не может быть ^-пространством. 1
Мы завершаем этот параграф конструкцией, которая ведет
от произвольного хаусдорфова пространства к некоторому ^-про-
^-пространству, состоящему из того же множества точек. Пусть X —
любое хаусдорфово пространство. Легко проверяется, что се-
семейство & всех подмножеств пространства X, пересекающихся
с каждым компактным подпространством пространства X по
замкнутому подпространству, обладает свойствами (С1)—(СЗ).
Множество X вместе с топологией, порожденной семейством Ф
замкнутых подмножеств, будет обозначаться через kX. Ясно,
3.3. ЛОКАЛЬНО КОМПАКТНЫЕ ПРОСТРАНСТВА 241
что подмножество пространства kX открыто в том и только том
случае, если его пересечение с каждым компактным подпро-
подпространством Z пространства X открыто в Z. Топология простран-
пространства kX сильнее топологии пространства Х\ значит, простран-
пространство kX хаусдорфово и формула х»х(х) = х определяет непрерыв-
непрерывное отображение кх: kX-*X. Из теоремы 3.1.10 вытекает, что
если Z— компактное подпространство пространства kX, то Z
является также компактным подпространством пространства X.
С другой стороны, если Z—компактное подпространство про-
пространства X, то обе топологии на Z — а именно индуцированная
топологией пространства X и индуцированная топологией про-
пространства kX — совпадают; значит, Z в этом случае является
компактным подпространством и пространства kX. Таким обра-
образом, пространства kX и X обладают одними и теми же компакт-
компактными подпространствами, причем эти подпространства несут
одну и ту же топологию. Следовательно, kX является &-про-
странством и, в силу теоремы 3.3.21, имеет место такой факт.
По произвольному непрерывному отображению /: X-+Y хаус-
дорфовых пространств X и У определим отображение kf: kX-+
~->kY9 поставив в соответствие точке x^kX точку f(x)^kY.
Отображение kf непрерывно; ясно, что для kf выполняется ра-
равенство fax = Kykf.
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
Понятие локально компактного хаусдорфова пространства
было введено П. С. Александровым в [1923]; в этой работе
были объявлены теорема 3.3.4 и следствие 3.3.11 (доказатель-
(доказательства были даны в [1924b] ). Теорема 3.3.17 была доказана Уайт-
хедом в [1948]. Класс ^-пространств был введен в статье Гэйла
[1950] (где это понятие приписывается Гуревичу). Характери-
Характеристика ^-пространств, установленная в теореме 3.3.18, в статье
Гэйла принята за определение, и затем доказано, что локально
компактные хаусдорфовы пространства и пространства с первой
аксиомой счетности являются ^-пространствами. Статья Д. Коэ-
на [1954] содержит теорему 3.3.27, построение kX и вторую по-
половину доказательства теоремы 3.3.18. Келли доказал в [1955]
теоремы 3.3.21 и 3.3.23. Теорема 3.3.25 была доказана в статье
Архангельского [1965] (объявлена в [1963]), а теорема 3.3.28
получена Майклом в [1968а]. Первый пример двух &-про-
странств, произведение которых не является ^-пространством,
был приведен Даукером в [1952].
УПРАЖНЕНИЯ
З.З.А. Докажите, что каждое пространство X, представимое
в виде объединения локально конечного семейства локально
16 Зак. 697
242 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
компактных замкнутых хаусдорфовых подпространств, само ло-
локально компактно (и хаусдорфово) (см. теорему 3.7.22).
З.З.В. (а) Проверьте, что каждое хаусдорфово пространство,
которое можно представить в виде объединения некоторого се-
семейства локально компактных открытых подпространств, само
локально компактно,
(Ь) Приведите пример ^-пространства, представимого в
виде объединения двух открытых компактных хаусдорфовых
подпространств, но не являющегося 72-пространством.
З.З.С. Определите подпространство вещественной прямой, яв-
являющееся объединением двух локально компактных подпро-
подпространств, которое тем не менее не локально компактно.
3.3.D (Пархоменко [1941] ). Покажите, что каждое локально
компактное хаусдорфово пространство можно взаимно одно-
однозначно и непрерывно отобразить на некоторое компактное хаус-
хаусдорфово пространство.
Указание. Примените следствие 3.3.11 и теорему 3.2.11.
З.З.Е. (а) (Келли [1955]). Проверьте, что декартово произ-
произведение N^1 не является ^-пространством.
Указание. Рассмотрите в N**1 подмножество, состоящее из
всех точек х, таких, что для некоторого / > 1 самое большее i
координат точки х равны 1, а остальные координаты равны и
(Ь) Покажите, что предел обратного спектра пространств
Фреше — Урысона не обязан быть /^-пространством.
Указание. Представьте пространство Yx из примера 3.3.29 в
виде предела обратного спектра локально компактных хаусдор-
хаусдорфовых пространств и примените теорему 3.3.17 и упр. 2.5.D(b).
3.3.F. Докажите теорему 3.3.27, применив характеристику
^-пространств, данную в теореме 3.3.18.
3.3.G (Архангельский [1965] ). Приведите пример &-про-
странства X, подмножества АаХ и точки хеЛ, таких, что
x^A(]Z, каково бы ни было компактное подпространство
ZczX.
Указание. Существует даже секвенциальное пространство с
этим свойством.
3.3. Н (Архангельский [1965] ). Покажите, что для каждого
хаусдорфова пространства существует ровно одно й-простран-
ство, обладающее тем же множеством точек и теми же самыми
компактными подпространствами.
3.3.1 (Архангельский [1965]). (а) Заметьте, что каждое ло-
локально компактное хаусдорфово пространство является про-
пространством точечно счетного типа.
(Ь) Докажите, что каждое пространство точечно счетного
типа является ^-пространством.
Указание. Видоизмените доказательство теоремы 3.9.5.
3.4. ПРОСТРАНСТВА ОТОБРАЖЕНИЙ II 243
(с) Приведите пример ^-пространства, не являющегося про-
пространством точечно счетного типа.
3.4. ПРОСТРАНСТВА ОТОБРАЖЕНИЙ II:
компактно-открытая топология
В § 2.6 мы определили топологию поточечной сходимости на
множестве Yx всех непрерывных отображений пространства X
в пространство У как топологию, порожденную базой, состоящей
из всех множеств вида П M(Ait Ut), где At— конечное множе-
множество в X и Ui — открытое в У множество при i= 1, 2, ..., k и
где при любых А аХ н В <zz Y
Компактно-открытая топология на Yx — это топология, по-
порожденная базой, состоящей из всех множеств вида
П M(Ct, Ut), где Ct — компактное множество в X и Ui— от-
открытое множество в У при t=l, 2, ..., k.
Как и в случае обеих топологий, о которых шла речь в § 2.6,
каково бы ни было топологическое пространство У и одноточеч-
одноточечное пространство {р}, поставив в соответствие точке у ^ Y эле-
элемент ir(y) пространства Y{p}, где [ir(y)] {р)=У, мы получаем
гомеоморфизм пространства У на пространство Y{p] с компакт-
компактно-открытой топологией.
Формулы A1) из § 2.6 позволяют заключить, что
A) Ф^: YX->ZX непрерывно для каждого непрерывного ото-
отображения g: Y ^*Zy
и
B) 4V- YX->YT непрерывно, каково бы ни было непрерывное
отображение А: Г^1в топологическое пространство Х>
где G)g(f) — gf при f^Yx, Wh(f) = fh при f e У*, и рассматри-
рассматриваемые пространства отображений несут компактно-открытую
топологию.
Читатель легко проверит, что для каждого гомеоморфного
вложения /: Y^-Z и отображения h: T-+X в топологическое
пространство X, такого, что для каждого компактного C<z:X
найдется компактное С'с: Г, удовлетворяющее равенству
h(C')=C (см. задачу 5.5.11 и теорему 3.7.2), — в частности, для
каждого непрерывного отображения h; Т^Х компактного про-
16*
244 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
странства Т на топологическое пространство X, — отображения
Ф*: YX^~ZX и Ч^: Yx-±-YJ являются гомеоморфными вложе-
вложениями.
Заметим, что на Rx компактно-открытая топология обычно
отличается от топологии равномерной сходимости (см. теоремы
4.2.17 и 4.2.19); действительно, это следует из примера 2.6.8, так
как на RN компактно-открытая топология совпадает с топо-
топологией поточечной сходимости. Компактно-открытая топология
обычно отличается и от топологии поточечной сходимости. Чи-
Читатель легко проверит, что множество Р служит тому примером.
3.4.1. Теорема. Для каоюдой пары X, Y топологических про-
пространств компактно-открытая топология на Yx является соб-
собственной.
Доказательство. Пусть Z — произвольное топологическое про-
пространство и f — отображение из У(гхх). Возьмем множество
М(С, U)aYxy где С—компактное подмножество в X и U —
открытое множество в У. В силу равенства A3) § 2.6,
=U при
: f(z,x)<==U при х€=С
= {z€eZ: {z}XCczf-l(U)}.
Из леммы 3.1.15 вытекает, что последнее множество открыто.
Так как множества M(Ct U) составляют предбазу топологии
пространства Yx, это означает, что A(f)^(Yx)z. 1
Из последней теоремы, части (Hi) предложения 2.6.12 и пред-
предпоследнего абзаца § 2.6 следует, что на Rx компактно-открытая
топология слабее топологии равномерной сходимости. Так как
одноточечные множества компактны и для каждого конечного
А = {хи Х2, ..., Xk) имеет место соотношение M(A,U) =
k
= П М({хЛ, U), компактно-открытая топология сильнее, чем
топология поточечной сходимости.
3.4.2. Теорема. Для каждой пары Xt Z топологических про-
пространств и произвольного локально компактного хаусдорфова
пространства У композиция 2: ZYXYX-+ZX является непрерыв-
непрерывным отображением по отношению к компактно-открытой тополо-
топологии на пространствах отображений.
Доказательство. Мы покажем, что если множество С а X
компактно, а множество U a Z открыто, то прообраз
2-1(Л1(С, ?/)) открыт. Для каждой пары (g, f)^2-I(M(C, U))
имеем gf(C)czU, т. е. f(C)czg-l(U). Так как пространство У
локально компактно и хаусдорфово, из теоремы 3.3.2 следует,
3.4. ПРОСТРАНСТВА ОТОБРАЖЕНИЙ II 245
что существует открытое множество W а У, для которого f(
aWczWci g~l(U) и W компактно. Легко проверяется, что
(*, f)^M(W, U)XM(C, W)aX-4M(C, ?/));
значит, множество Ъ~1(М(С9 U)) открыто. 1
3.4.3. Теорема. Если X — локально компактное хаусдорфово про-
пространство, то для каждого топологического пространства Y
компактно-открытая топология на Yx является приемлемой.
Доказательство. Из теоремы 3.4.2, формулы A2) § 2.6 и
предложения 2.6.11 следует, что компактно-открытая топология
на Yx является допустимой. Значит, достаточно применить тео-
теорему 3.4.1. I
Оказывается, предположение о локальной компактности про-
пространства X нельзя заменить. Действительно, можно доказать
(см. упр. 3.4.А), что если для вполне регулярного пространства
X на множестве Rx существует приемлемая топология, то про-
пространство X локально компактно.
Читатель легко докажет следующие аналоги предложений
2.6.9 и 2.6.10:
3.4.4. Предложение. Для каждого семейства {Xs}s^s непустых
топологических пространств и любого топологического простран-
пространства У комбинация отображений V: И (У s)->yvseS / явля-
s&S
ется гомеоморфизмом по отношению к компактно-открытой то-
топологии на пространствах отображений. 1
3.4.5* Предложение. Для любого топологического пространства
X и произвольного семейства {Ys}s^s топологических про-
пространств диагональное отображение А : Ц (У*) -> ( П УЛ
является гомеоморфизмом относительно компактно-открытой то-
топологии на пространствах отображений. 1
Рассмотрим теперь сужение экспоненциального отображения
Л на множество Y{Z x х\ Для простоты это сужение тоже будет
обозначаться через Л и называться экспоненциальным отобра-
отображением.
3.4.6. Лемма. Пусть X — хаусдорфово пространство. Тогда для
любого топологического пространства У и любой предбазы &
пространства У множества М(С, J7), где С — компактное мно-
множество в X и U ^<Р, составляют предбазу пространства Yx в
компактно-открытой топологии.
Доказательство. Достаточно доказать, что для каждого ком-
компактного множества С аХу каждого открытого множества
Uа У и произвольного f^M(C, U) найдутся компактные мно-
246 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
жества Си С2, ,.., Ck в X и элементы ?/}, U\, ..., f/^, ?/?, i/L •••
..., [/*ft семейства ^, такие, что
a ni
C) /еВ7=П П Af(C,, UficzMiC, U).
По определению предбазы, для каждого х е С найдутся мно-
множества ?/f, f/f, ..., ?/„х e ^, удовлетворяющие условиям
|
D) жеПГ'М и f|u?cl/.
Из теоремы 3.1.3 следует, что найдется конечное множество
{xu *2, .. •, хк) с С,такое, что С с= |J Ц Г1 (^/)> где U)^U^
i = \ / —1
и п. = пх,- По теореме 1.5.18, существует замкнутое покры-
покрытие {C;)t=i пространства С, для которого
E) Qcflr1^/) при i= 1, 2 &
(это можно доказать и непосредственно, воспользовавшись ре-
регулярностью и компактностью С). Ясно, что множества С» ком-
компактны, а из E) следует, что отображение / принадлежит мно-
множеству W, определенному в C). Остается доказать, что W а
аМ(С, U). Возьмем любое ge W и любую точку х^С. Най-
nt
дется i^k, для которого хеС*; тогда ff(x)e П ^/- Отсюда
и из второй части соотношения D) следует, что g(x)^U; зна-
значит, geM(C, t/). 1
3.4.7. Теорема. Для каждой пары X, Z хаусдорфовых про-
пространств и произвольного топологического пространства Y экспо-
ненциальное отображение Л: Y }^{Y ) является гомео-
морфным вложением по отношению к компактно-открытой топо-
топологии на пространствах отображений.
Доказательство. Если С с: X, U a Y и С aZ, то очевидно,
что
F) А~ЧМ(С М(С, С/))]=М(С'ХС, U).
Следовательно, последняя лемма влечет за собой непрерывность
Л. Так как отображение Л взаимно однозначно, остается до-
доказать, что для каждого открытого множества WaYzx его
3.4. ПРОСТРАНСТВА ОТОБРАЖЕНИЙ II 247
образ A{W) открыт в подпространстве Л(УBхХ)) пространства
(Yx)z. Из равенства F) вытекает, что
Л (М (С X С, U)) = Л (Yiz ХХ))ПМ (С, М (С, ?/)).
Следовательно, в силу взаимной однозначности отображения Л,
достаточно показать, что множества
G) М (С X С, U), где CczX и C'czZ компактны
и U a У открыто,
составляют предбазу пространства У(гхД).
Возьмем компактное подмножество С" пространства Z X Ху
открытое множество U в У и отображение f^M(C", U). Так
как С" компактно, найдутся открытые множества V\, F2, ...
..., Vk с= ^ и !/[, V^, ..., V'k с: Z, для которых
(8) С" с: UCWX^Oc:/^).
Найдем, как в доказательстве леммы 3.4.6, покрытие {CJ^
пространства СЛ/, состоящее из компактных множеств, таких,
что
(9) CiczVfiXVi при /=1, 2, ..., А.
Из формул (8) и (9) следует, что f е {] М (р' (С,) X р (Ct), U) cz
аМ(С", С/), где р': ZXX->Z n p: Z ХХ^Х— проекции. Так
как Z и X — хаусдорфовы пространства, мтюжества pf{Ci) и
p(Ci) компактны; тем самым доказано, что множества G) обра-
образуют предбазу пространства Y{ZxX). |
Из теорем 3.4.3 и 3.4.7 вытекает
3.4.8. Теорема. Каковы бы ни были топологическое пространство
У, хаусдорфово пространство Z и локально компактное хаусдор-
фово пространство X, экспоненциальное отображение A: Y ->
—>(У У является гомеоморфизмом относительно компактно-
открытой топологии на пространствах отображений. 1
3.4.9. Теорема. Если ZXX есть k-пространство, то для любого
топологического пространства У экспоненциальное отображение
Л: Y{ZxX)->{Yx)z является гомеоморфизмом относительно ком-
компактно-открытой топологии на пространствах отображений.
Доказательство. В силу теоремы 3.4.7, достаточно показать,
что если ZXX является ^-пространством, то для каждого ^е
^(Yx)z отображение A~l(g) пространства ZXX в простран-
пространство У непрерывно. Как следует из теоремы 3.3.21, достаточно
248 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
доказать, что сужение A~l(g)\C: C-+-Y непрерывно, каково бы
ни было компактное подмножество С пространства ZX^. Верно
даже большее: сужение отображения A~!(g) на более широкое
множество ZX^o, где Хо— проекция множества С в простран-
пространство X, непрерывно. Действительно, так как Хо компактно, из
теоремы 3.4.3 мы заключаем, что экспоненциальное отображение
Ло: У ° —> (У °) является отображением «на»; очевидно, что
где gQ <= (Yx°)z определено формулой [go(z)] (x)= [g(z)] (x)
при xelo. I
3.4.10. Следствие. Если X и Z— хаусдорфовы пространства с
первой аксиомой счетности, то для каждого топологического про-
пространства У экспоненциальное отображение Л: YiZxX)->(Yx)z
является гомеоморфизмом по отношению к компактно-открытой
топологии на пространствах отображений. I
Покажем теперь, как представить пространство отображений
произвольного ^-пространства X в топологическое пространство
У в виде предела обратного спектра пространств отображений
Ус, где С — компактное подпространство пространства X.
Пусть 9?(Х)—семейство всех непустых компактных подмно-
подмножеств хаусдорфова пространства X. Семейство 3?(Х) упорядо-
упорядочено отношением ^, определенным так:
Сч ^ С\ в том и только том случае, если Сг с: С\.
Более того, семейство Z(X) направлено отношением ^, так
как объединение двух компактных множеств снова является
компактным множеством. Для любых Си Сг^^(Х), таких, что
Сг ^ Си и для произвольного топологического пространства У
определено непрерывное отображение^: УС]-^УС2, а именно
яс1 = 1^> г^е 1: ^2 -> С\ — тождественное вложение. Ясно, что
ng(/) = /IC2 при всех /еУс«.
3.4.11. Теорема. Если X есть k-npotr ранет во, то для всех топо-
топологических пространств У пространство Yx с компактно-открытой
топологией (с топологией поточечной сходимости) гомеоморфно
пределу обратного спектра S (X) = {Ус, я?«, % (Хц пространств
Ус с компактно-открытой топологией (с топологией поточечной
сходимости).
Доказательство. Для всех f = {fc}^\imS(X) отображения
{Wcezm согласованы, и из теоремы 3.1.21 следует, что ото-
отображение F(f)— V fc' X^-Y непрерывно, т. е. F(f)^Yx.
С<=%{Х)
Ясно, что F взаимно однозначно отображает limS(A') на Yx.
3.4. ПРОСТРАНСТВА ОТОБРАЖЕНИЙ II 249
Так как для всех /= {/с}, всех С ^ ЗС(Х) и любого А а С
F(f)^M(A, U) в том и только том случае, если fc^M(At U),
то, по предложению 2.5.5, F — гомеоморфизм. I
Теперь мы обсудим, как топологические свойства простран-
пространства Yx с компактно-открытой топологией зависят от свойств
X и У. Начнем с аксиом отделимости. Так как компактно-откры-
компактно-открытая топология сильнее, чем топология поточечной сходимости,
из теоремы 2.6.4 немедленно следует, что если У является
^^пространством, то Yx с компактно-открытой топологией тоже
является ^-пространством при i ^ 2. Покажем, что то же самое
имеет место при i = 3 и Зу.
3.4Л2. Лемма. Каковы бы ни были топологические пространства
X, У, подмножество А пространства X и замкнутое подмножество
В пространства У, множество М(А, В) замкнуто в пространстве
Yx с топологией поточечной сходимости и тем более в простран-
пространстве Yx с компактно-открытой топологией.
Доказательство. Ясно, что
М(А, В) = П Af ({jc}, В),
А
и так как множество М({х}, B)=Yx\M({x}9 Y\B) замкнуто
при всех х^Л, множество M(At В) замкнуто. I
3.4.13. Теорема. Если У — регулярное пространство, то простран-
пространство Yx с компактно-открытой топологией тоже регулярно.
Доказательство. В силу предложения 1.5.5, достаточно по-
показать, что для каждого /еУ^и каждой окрестности М(С, U)
точки /, где С — компактное множество в X и U — открытое
множество в У, найдется открытое множество V cz У, такое, что
A0) /e=Af(C, V)aM(Ct V)czM(C, U).
Из теорем 3.1.10 и 3.1.6 следует, что существует открытое
множество V czY, удовлетворяющее условию
A1) f(C)cFcFc U.
В силу последней леммы, множество М(С, V) замкнуто; по-
этому М(С, V)czM(C, F), и A0) следует из A1). I
3.4.14. Лемма. Пусть X—топологическое пространство и С —
компактное подпространство в X. Приписывая каждому f^Ix
число S(/)=sup f(x)9 мы получаем функцию В: 1х->19 непре-
С
рывную относительно компактно-открытой топологии на Iх,
250 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
Доказательство. Покажем, что, каков бы ни был открытый
интервал (a, b)aR, прообраз S^1 (/П(^» Ь)) открыт в Iх. След-
Следствие 3.2.9 показывает, что sup f(x)<b в том и только том
х е С
случае, если f(x)<b при всех х^С. Значит, для Д = {хе/:
х ^ a} hB={jcg/:x<6} имеем
) = (F\M(C, Л))ПМ(С, В).
Отсюда и из леммы 3.4.12 следует, что множество Е-{A(](а7 Ь))
открыто в Iх. 9
3.4.15. Теорема. Если У'->- тихоновское пространство, то простран-
пространство Yx с компактно-открытой топологией тоже является тихо-
тихоновским пространством.
Доказательство. В силу предложения 1.5.8, достаточно пока-
показать, что для каждого / ^ Yx и произвольной окрестности
М(С, U) функции /, где С — компактное множество в X и U —
открытое множество в У, найдется непрерывная функция
G: У*->/, такая, что G(/) = 0 и G(h)= 1 при Ле= У*\Л*(С, U).
В силу теорем 3.1.10 и 3.1.7, существует функция g: У-*/,
для которой g(f(C))cz {0} и g(y)=l при г/е У\?/. Положим
G(A) = sup g7*(x) при всех Л е У*. Так как G = S<Dg, последняя
лемма показывает, что G является непрерывным отображением
пространства Yx в /. Ясно, что G(f) = O; если кфМ(С, U), то
найдется точка хеС, для которой h(x)^ Y\U. Тогда gh(x) =
= 1, откуда следует, что G(h)= 1. 1
Как легко видеть, если пространство X дискретно, то про-
пространство Yx с компактно-открытой топологией гомеоморфно
декартову произведению XI Yx> гДе Yx — У при всех х ^ X
Так как существует совершенно нормальное пространство, ква-
квадрат которого не нормален (см. упр. 2.3.12), то пространство
Yx с компактно-открытой топологией не обязано быть нормаль-
нормальным, даже если У — совершенно нормальное пространство, а
X — дискретное двухточечное пространство.
3.4.16. Теорема. Если вес пространств X и У не превосходит
m ^ i<o и X локально компактно и хаусдорфово, то вес про-
пространства Yx с компактно-открытой топологией не превосхо-
превосходит т.
Доказательство. Пусть $ — база пространства X, такая, что
\$\ ^ ш, конечные объединения элементов семейства $ при-
принадлежат $ и V компактно для каждого Уе1 Пусть 2) — база
пространства У, содержащая все конечные объединения своих
элементов и такая, что |й)|^ю. Мощность семейства & всех
множеств М(Р, W), где Ке^и f е2), не превосходит ш. Зна-
Значит, для завершения доказательства достаточно показать, что
3.4. ПРОСТРАНСТВА ОТОБРАЖЕНИЙ II 251
S — предбаза пространства Yx. Действительно, если /^Ух,
С — компактное множество в X и О — открытое множество в У,
для которых f^M(Ct U)t то найдется V^$, удовлетворяющее
условию С dV ciV cz f~l(U)y и найдется W^3), такое, что
f(V)aW^U. Следовательно, /е=Л1G, W)cM(C, U) и
Можно доказать (см. упр. 3.4.Е), что если пространство Rx
с компактно-открытой топологией удовлетворяет первой аксиоме
счетности и X — тихоновское пространство с первой аксиомой
счетности, то X локально компактно. Аналогично можно дока-
доказать (см. упр. 5.1.Н), что если пространство Rx с компактно-
открытой топологией удовлетворяет первой аксиоме счетности
и -X"—метризуемое пространство, то пространство X локально
компактно и обладает счетной базой.
В заключение этого параграфа приведем две характеристики
компактных подпространств пространств отображений с ком-
компактно-открытой топологией. В этих характеристиках приме-
применяется понятие однообразной непрерывности семейства отобра-
отображений. Как читатель увидит в гл. 8, это понятие является топо-
топологическим аналогом понятия равностепенной непрерывности
семейства отображений. Мы говорим, что семейство F отобра-
отображений пространства X в пространство У однообразно непре-
непрерывно, если, каковы бы ни были ^еХ, у е У и окрестность V
точки у, найдутся окрестность U точки х и окрестность W точки
у, такие, что Q[(F{]m({х}, №))ХФ] с: V, т. е. условия f^F и
f(x)e W влекут за собой включение f(U)a V. Из этого опреде-
определения прямо следует, что если семейство F отображений про-
пространства X в пространство У однообразно непрерывно, то все
отображения из F непрерывны, т. е. F cz Yx.
3.4.17. Лемма. Если У—регулярное пространство, то для каэю-
дого однообразно непрерывного семейства отображений F с: У*
замыкание F множества F в произведении П Yx, где Yx = Y
х<=Х
при всех л;еХ, является однообразно непрерывным семейством
отображений и, в частности, F cz Yx.
Доказательство. Возьмем произвольно точку jcqgX и точку
Уо е= У. Каждой окрестности_У точки уо сопоставим окрестность
V этой точки, такую, что V а V. Так как семейство F однооб-
однообразно непрерывно, для каждого V найдутся окрестность Uv
точки х0 и окрестность Wv точки г/о, удовлетворяющие условию
&1(РМ{} Wv))XUv]czV'. Отсюда следует, что
<= IT Yx:e^Hf(xQ)^WVi то f(Uv)ciV7) =
252 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
Последнее множество замкнуто; следовательно, f cF(xo, Уо> V).
Значит, множество F содержится в пересечении всех множеств
F(x, у, V), где хеХ9 y^Y и V—произвольная окрестность
точки у> а отсюда вытекает, что семейство отображений F одно-
однообразно непрерывно. 1
3.4.18. Лемма. Если Fez Yx — однообразно непрерывное семей-
семейство отображений^ то сужение Q \ F X X отображения вычисления
является непрерывным отображением по отношению к топологии
поточечной сходимости на F.
Доказательство, Для f^F, х^Х, y=f(x) и произвольной
окрестности V точки у найдутся окрестность U точки х и окрест-
окрестность W точки у, такие, что Q[(F(]M({x}, W))X iJ]cz V\ Доста-
Достаточно теперь заметить, что множество (F(]M({x}f W))X& яв-
является окрестностью точки (/, х) в пространстве FXX. I
3.4.19. Лемма. Пусть Y — регулярное пространство^ X — произ-
произвольное топологическое пространство и Yx — пространство всех
непрерывных отображений пространства X в пространство Y
с топологией поточечной сходимости. Если множество F cz Yx
компактно и сужение Q | F X X отображения вычисления непре-
непрерывно, то F — однообразно непрерывное семейство отображений.
Доказательство. Пусть igX, у е У и V—произвольная
окрестность точки у. Так как пространство Y регулярно, найдется
окрестность W точки уу для которой W''cz V. Из леммы 3.4.12
следует, что множество F0 = Ff)M({x}, W) компактно. Так как
Q(FoX{x})czV9 то FoX {x} cz{Q\FXX)-l(V) и, по лемме
3.1.15, найдется окрестность О точки х, такая, что Q(F0XU)cz
czV. Очевидно, Q[(Ff\M({x}f W))XU]aQ(F0XUyy значит,
семейство F однообразно непрерывно. 1
3.4.20. Теорема Асколи. Пусть X есть k-пространство, a Y — ре-
регулярное пространство. Тогда замкнутое подмножество F про-
пространства Yx с компактно-открытой топологией является ком-
компактом в том и только том случае, если F — однообразно непре-
непрерывное семейство отображений и замыкание множества
Q(FX ix)) " {f(x):f^F}czY компактно при всех xg!
Доказательство. Предположим, что F <^YX — однообразно
непрерывное семейство отображений и что множество Fx=
= Q(FX {x})cz Y компактно при всех xgI Декартово произ-
произведение П Fх компактно; значит, замыкание F множества F
в произведении Ц Yx, где YX=Y при всех xel, является
компактом. По лемме 3.4.17, FczYx — однообразно непрерыв-
непрерывное семейство отображений, и из леммы 3.4.18 следует, что су-
сужение Qq = Q\FXX непрерывно, т. е. что Q0^YF хх. В силу
3.4. ПРОСТРАНСТВА ОТОБРАЖЕНИЙ II 253
теоремы 3.4.1, A{QQ)&(Yxy, где Yx взято с компактно-открытой
топологией. Так как [Л(й0)] Ш=/ при всех /eF, из теоремы
3.1.13 вытекает, что на г компактно-открытая топология совпа-
совпадает с топологией поточечной сходимости. Значит, F = Fh мно-
множество F— компакт.
Обратно, предположим, что F— компактное подмножество
в Yx. В силу леммы 3.4.19, достаточно показать, что сужение
Q\FX>X отображения вычисления непрерывно, так как ком-
компактность множеств Q(FXW) следует немедленно из ком-
компактности F и непрерывности отображения Q\FXX. Так как,
в силу теоремы 3.3.27, пространство FXX является &-простран-
ством, достаточно для каждого компактного пространства CczX
проверить непрерывность сужения Qo^Ql^XC. По теореме
3.4.3, отображение вычисления Qc: YCXC~*Y непрерывно, а
это влечет за собой непрерывность отображения Qo, так как
Qo=BS5fic[Dri|i?)Xidc]t где /: С-+Х — тождественное вложение
подпространства С в X I
Следующая теорема — разновидность теоремы Асколи. В ее
формулировке через F\Z при Fez Yx и Zcz X обозначено семей-
семейство сужений {f\Z: f^F} cz Yz.
3.4.21. Теорема. Пусть X есть k-пространство, a Y — регулярное
пространство. Тогда замкнутое подмножество F пространства
Yx с компактно-открытой топологией является компактом в том
и только том случае, если F\Z — однообразно непрерывное се-
семейство отображений для всякого компактного подпростран-
подпространства Z а: X и замыкание множества Q(F X {х}) = {/(х): /е F)cz
с: У компактно при всех хеХ
Доказательство. В силу теоремы Асколи, достаточно пока-
показать, что из условий теоремы вытекает компактность множества
F. Последнее, однако, является следствием утверждений 2.5.7,
3.4.17, 3.4.20,3.4.11 и 3.2.13. 1
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
Компактно-открытая топология была определена Фоксом в
f 1945]. Фокс доказал теоремы 3.4.1 и 3.4.3 и показал, что экспо-
экспоненциальное отображение Л в следствии 3.4.10 является взаим-
взаимно однозначным отображением «на». Тот факт, что Л — гомео-
гомеоморфизм, был доказан Джексоном в [1952а]. Работа Джексона
содержит также лемму 3.4.6 и теоремы 3.4.7 и 3.4.8. Теорема
3.4.9 доказана Моритой в [1956а]. Теоремы 3.4.13, 3.4.15 и 3.4.16
доказаны Аренсом в [1946]. Понятие однообразно непрерыв-
непрерывного семейства отображений было введено Келли и Морсом
(см. Келли [1955]). Они доказали также теоремы 3.4.21 и
3.4.20, причем последнюю при более ограничительном предполо-
254 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
жении, что пространство X локально компактно и хаусдорфово;
обобщение на случай ^-пространств было получено Бэгли и
Янгом в [1966]. Различные варианты теоремы Асколи (обоб-
(обобщающие классический результат Асколи, полученный в 1883 г.)
часто применяются в анализе — главным образом в доказатель-
доказательствах теорем существования (например, в доказательстве су-
существования решения дифференциального уравнения у'=и(х,у)
при единственном предположении, что функция и(х, у) непре-
непрерывна).
УПРАЖНЕНИЯ
3.4.А (Фокс [1945], Арене [1946]). Докажите, что если X —
вполне регулярное пространство и на Rx существует приемлемая
топология, то пространство X локально компактно (см.
упр. 2.6.Е).
Указание, Определим f: X^~R, положив /(х) = 0 при всех
хе! Для произвольной точки хо^Х возьмите любую ее
окрестность V и окрестность ^функции /, такие, что Q(Wy^V)cz
с:(—1, 1), и покажите, что V компактно. С этой целью для
произвольного семейства {Vrs}se5 открытых множеств в X, по-
покрывающего F, рассмотрите топологию на Rx, порожденную ба-
k
зой, состоящей из всех множеств вида (l iW (Лг-, ?Д), где А{
замкнуто и содержится либо в некотором Vs, либо в X\V, a
Ui — открытое множество в R при i ===== 1,2, ..., k.
3.4.В. Проверьте, что для произвольного семейства {#Л5е5
хаусдорфовых пространств и произвольного семейства {Fs}seS
топологических пространств декартово произведение Ц:
S6EtS '
y^Ues s) является гомеоморфным вложе-
нием по отношению к компактно-открытой топологии на про-
пространствах отображений.
З.4.С. (а) Покажите, чго если X — компакт, а У — хаусдор-
хаусдорфово пространство, то множество всех непрерывных отображе-
отображений пространства X на пространство У замкнуто в пространстве
Yx с компактно-открытой топологией. Проверьте, что предполо-
предположение о компактности пространства X нельзя опустить.
(Ь) Пусть X — компакт и Я— подпространство пространства
Xх, состоящее из всех гомеоморфизмов пространства А" на себя.
Покажите, что, поставив в соответствие всякому Л е Я обрат-
обратный к нему гомеоморфизм hrl е Я, мы получим гомеоморфизм
пространства Я на себя (см. теорему 3.4.2 и пример 8.1.17).
Проверьте, что предположение о компактности X существенно.
3.4. ПРОСТРАНСТВА ОТОБРАЖЕНИЙ II 255
3.4.D (А. Стоун [1963]). Проверьте, что пространство всех
непрерывных отображений отрезка / в тихоновский куб Iе с
компактно-открытой топологией не нормально (см. упр. 3.8.D).
Указание. Заметьте, что пространство V содержит D(H0) в
качестве замкнутого подпространства, затем примените предло-
предложение 3.4.5 и упр. 3.1.Н(а).
3.4.Е (Арене [1946]). Хаусдорфово пространство X называ-
называется хемикомпактным, если в семействе всех компактных под-
подпространств пространства X, упорядоченном отношением <=, су-
существует счетное конфинальное подсемейство.
(a) Докажите, что каждое хемикомпактное пространство с
первой аксиомой счетности локально компактно.
(b) Приведите пример счетного хемикомпактного простран-
пространства, не являющегося ^-пространством.
(c) Покажите, что в классе пространств со счетной базой
хемикомпактность равносильна локальной компактности.
(d) Докажите, что если пространство Rx с компактно-откры-
компактно-открытой топологией удовлетворяет первой аксиоме счетности, а X
является тихоновским пространством, то пространство X хеми-
компактно.
3.4.F. Заметьте, что если X — тихоновское пространство, а
У содержит подпространство, гомеоморфное R, то пространство
Yx с компактно-открытой топологией компактно тогда и только
тогда, когда Y компактно, а X дискретно.
3.4.G. (а) (Майкл [1961]). Покажите, что nw(Yx)^
^,w(X)w(Y) по отношению к компактно-открытой топологии и
по отношению к топологии поточечной сходимости на Yx. Вы-
Выведите отсюда, что если X и Y—пространства со счетной базой,
то пространство Yx наследственно сепарабельио как по отноше-
отношению к компактно-открытой топологии, так и по отношению к то-
топологии поточечной сходимости1).
Указание. Пусть $ и 3) — базы мощности ^ w(X)w(Y) про-
пространств X и Y соответственно. Рассмотрите топологию на Yx,
порожденную базой, состоящей из множеств f] Ai(Ut9 Vi)t где
Ui^$ и Vi^S) при i=l, 2, ..., k\ примените теорему 3.4.1
и предложение 2.6.11.
(Ь) (Уорнер [1958]). Докажите, что если X—тихоновское
пространство, то пространство Rx с компактно-открытой тополо-
топологией содержит всюду плотное подпространство мощности
^ щ ^ Ко в том и только том случае, если существует взаимно
однозначное непрерывное отображение пространства X на тихо-
тихоновское пространство веса ^ ш.
1) В работе Майкла [1961] нет понятия сети и сетевого веса. В ней до-
доказывается именно последнее утверждение. — Прим. перев.
256 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
Указание. Выведите из упр. 3.2.J(a), что если h: X-^Z —
взаимно однозначное непрерывное отображение пространства X
на пространство Z, то ^?h отображает Rz на всюду плотное в
Rx множество, и примените (а).
(с) Покажите, что, каковы бы ни были тихоновское про-
пространство X и кардинал ш ^ Ко, следующие условия равно-
равносильны:
AM пространстве Rx с компактно-открытой топологией
есть всюду плотное множество мощности ^ ю.
B) В пространстве Rx с топологией поточечной сходимости
есть всюду плотное множество мощности ^ ш.
Указание. См. упр. 3.2.1.
3.4.Н (Кол [1969]). Назовем семейство F отображений про-
пространства X в пространство У равномерно регулярным, если,
каково бы ни было открытое покрытие Т пространства У, най-
найдется открытое покрытие Ш пространства X, которое вписано в
каждое покрытие вида {f~l(V): Vef}, где f^F.
Докажите, что если X есть ^-пространство, а У — регулярное
пространство, то замкнутое в пространстве Yx с компактно-от-
компактно-открытой топологией множество F компактно в том и только том
случае, если F — равномерно регулярное семейство отображений
и замыкание множества Q(F X {х} )= {/(*): f^F}aY ком-
компактно для каждого хе!
Указание. Покажите, что если замыкание множества {f(x):
f eF} компактно при всех xel, то семейство F равномерно
регулярно в том и только том случае, если оно однообразно не-
непрерывно.
3.4.1. Покажите, что сложение, вычитание и умножение функ-
функций являются непрерывными отображениями произведения
Rx X Rx в Rx и что умножение на вещественные числа является
непрерывным отображением пространства Rx X R в Rx по отно-
отношению к компактно-открытой топологии на Rx.
3.5. КОМПАКТИФИКАЦИИ
Пара (У, с), где У—компакт, а с: Х-* У—гомеоморфное
вложение пространства X в У, такое, что c(X)=Y, называется
компактификацией пространства X (или компактным хаусдор-
фовым расширением пространства X). Если некоторое простран-
пространство X вложимо в компакт У, т. е. существует гомеоморфизм
f: Х-*М на подпространство M = f(X) пространства У, то
ясно, что пара (/(X), if), где / — тождественное вложение про-
пространства М в М, является компактификацией пространства X.
Следовательно, каждое пространство, вложимое в компакт, об-
обладает компактификацией. Этот факт вместе с теоремами 3.2.6,
3.2.5 и 2.3.23 влечет за собой следующие две теоремы:
3.5. КОМПАКТИФИКАЦИИ 257
3.5.1* Теорема. Пространство X обладает компактификацией в
том и только том случае, если оно тихоновское. 1
3.5.2« Теорема. Каждое тихоновское пространство X имеет та-
такую компактификацию (У, с), что w(X) = w{Y). I
В дальнейшем под компактификацией пространства X мы
понимаем не только пару (У, с), но и любой компакт У, в кото-
который X можно вложить в качестве всюду плотного подпростран-
подпространства. Компактификации пространства X обычно обозначаются
через сХу аХ, уХ и т. д., где с, ci и у символизируют гомеоморф-
ные вложения пространства X в соответствующие компактифи-
компактификации. Таким образом, когда компактификация будет рассма-
рассматриваться как пространство, будет каждый раз известно, какое
гомеоморфное вложение используется: для компактификации
сХ пространства X имеем
с: Х-^сХу с\Х: X —> с (X) — гомеоморфизм и с(Х) = сХ.
Назовем компактификации С\Х и С2Х пространства X экви-
эквивалентными, если существует гомеоморфизм /: С\Х—*С2Х, такой,
что диаграмма
с2Х
коммутативна, т. е. fc\(x) — C2(x) при всех л;е! Таким обра-
образом, две компактификации пространства X эквивалентны, если
они гомеоморфны и пространство X вложено в них одинаковым
образом. Легко проверяется, что эквивалентность компактифи-
компактификации является отношением эквивалентности.
В дальнейшем мы будем часто отождествлять эквивалентные
компактификации; любой класс эквивалентности компактифика-
компактификации будет рассматриваться как одна компактификация и будет
обозначаться символом сХ, где сХ — произвольная компактифи-
компактификация этого класса.
Если сХ—компактификация компакта X, то с(Х)=сХ и
с — гомеоморфизм. Значит, для любых двух компактификации
С\Х и счХ компакта X отображение / —с2сГ1: С\Х->С2% явля-
является гомеоморфизмом и fc\(х) = с2(х) при всех л;е1, т. е.
любые две компактификации произвольного компакта эквива-
эквивалентны. В частности, каждая компактификация компакта X
эквивалентна компактификации (Xt id*), которую мы отожде-
отождествляем с самим пространством X.
Теоремы 1.5.3 и 1.5.6 приводят к следующему результату:
3.5.3. Теорема. Для каждой компактификации Y пространства X
имеем: [У!^ехрехр^(Х) и w{Y)^expd(X). I
17 Зак. 697
258 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
Из последней теоремы и теоремы 3.2.5 вытекает, что все ком-
пактификации пространства X (с точностью до эквивалентности)
являются подпространствами тихоновского куба /ехР <*<*). Это
позволяет для любого пространства X рассмотреть семейство
^(Х) всех его компактификаций. Строго говоря, &(Х) является
семейством классов эквивалентных компактификаций простран-
пространства X, являющихся подпространствами тихоновского куба
Определим теперь упорядочение на семействе ^(Х). Поло-
Положим czX ^ с\Х, если существует непрерывное отображение
/: С1Х-+С2Х, такое, что /ci = С2. Таким образом, неравенство
с2Х ^ С\Х означает, что с\Х можно отобразить на с2Х таким об-
образом, что каждая точка пространства X, рассматриваемого как
подпространство каждого из пространств с\Х, с2Х, перейдет в
себя. Как легко видеть, если С\Х ^ с2Х и с2Х ^ СзХ, то С\Х ^
^ с3Х Значит, чтобы показать, что ^ является упорядочением
на семействе ^{Х), достаточно доказать следующую теорему.
3.5.4. Теорема. Компактификаций С\Х и с2Х пространства X
эквивалентны в том и только том случае, если с\Х ^ с2Х и
с2Х ^ с\Х.
Доказательство, Ясно, что если С\Х и с2Х эквивалентны, то
сгХ ^ с2Х и с2Х ^ аХ.
Предположим теперь, что с\Х ^ с%Х и с%Х ^ с\Хш Пусть
fu С\Х-+с2Х и jf2: c2X-*CiX удовлетворяют условиям: f\C\ = с2
и /2^2 = ^1. В силу теоремы 3.1.13, чтобы доказать, что f\ явля-
является гомеоморфизмом, откуда будет следовать, что С\Х и с2Х
эквивалентны, достаточно показать, что
A) /2/1 (х) =х при всех х е с{Х,
Композиция f2f\: С\Х-^-С\Х удовлетворяет равенству f2fxCi = C\;
поэтому /гЫ*) —* ПРИ всех х^С\(Х)ас\Х. Это означает, что
сужение отображения fefi на всюду плотное подпространство
С\(Х) пространства С\Х совпадает с сужением тождественного
отображения \АСхх на сх (Х\ соотношение A) вытекает теперь из
теоремы 2.1.9. 1
Другое необходимое и достаточное условие эквивалентности
двух компактификаций содержит следующая теорема.
3.5.5. Теорема. Компактификаций С\Х и с9шХ пространства X
эквивалентны в том и только том случае, если для любых замк-
замкнутых в X множеств А и В выполняется условие:
B) С\(А)Г\С\(В)=0 тогда и только тогда, когда
3.5. КОМПАКТИФИКАЦИИ 259
Доказательство. Ясно, что если С\Х и с2Х эквивалентны, то
условие B) выполняется для каждой пары Л, В замкнутых в X
множеств.
Пусть теперь компактификации С\Х и С2Х таковы, что усло-
условие B) выполняется для каждой пары замкнутых множеств в X.
В силу теоремы 3.2.1, отображения
и c2h\\
где ht\ Ci(X)->X — обратные отображения к гомеоморфизмам
d\X при i = 1, 2, продолжаются до отображений
С2: С2Х-*~С\Х и С\\
Так как, очевидно, С2с2 = С\ и С\С\ = с2, из теоремы 3.5.4 выте-
вытекает эквивалентность С\Х и с2Х. 1
Пусть сХ — произвольная компактификация пространства X.
Множество сХ\с(Х), т. е. множество всех точек, которыми сХ
отличается от с(Х), называется наростом компактификации сХ.
Главное свойство наростов устанавливается ниже в теореме
3.5.7. В доказательстве этой теоремы применяется следующая
лемма.
3.5.6. Лемма. Пусть А — всюду плотное подпространство хаус-
дорфова пространства X и f: X-+Y — отображение пространства
X в произвольное пространство Y. Если f\A: Л-*/(Л)с=К —
гомеоморфизм, то f(X\A)(]f(A) = 0.
Доказательство. Пусть существует точка х^Х\А, для ко-
которой f(x)^ f(A). He теряя общности, можно предположить, что
Х = А[}{х} и Y = f(A). Пусть f(x) = f(y)9 где y<=At и пусть
?/, Vc^X — непересекающиеся окрестности точек х, у соответ-
соответственно. Множество f(A \ У) = (/|Л)(Л \ V) замкнуто в У =
= /(Л), поэтому множество /~1/И\^)==^>44^ замкнуто в X.
Так как х ^ F, это доказывает замкнутость множества А в Ху
и мы получили противоречие. 1
3.5.7. Теорема. Если С\Х и с2Х — компактификации пространства
X и отображение f: C1X-+C2X удовлетворяет условию fc\ = c2, то
f(Cl(X))=c2(X) и f(clX\cl(X))=c2X\c2(X).
Доказательство. Первое из равенств следует из условия
fc\ = C2. Второе равенство вытекает из первого равенства, по-
последней леммы и того, что f(ciX)= c2X. I
Оказывается, некоторые классы тихоновских пространств
можно охарактеризовать свойствами наростов компактифика-
компактификации. Мы покажем, как охарактеризовать таким образом локаль-
локально компактные хаусдорфовы пространства. Другой важный
класс пространств, допускающих такую характеристику, класс
17*
260 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
полных по Чеху пространств, будет рассмотрен в § 3.9 (см. так-
также упр. 3.5.G, теорему 3.11.10, задачи 3.12.24, 3.12.25 и 8.5.13(Ь)).
3.5.8. Теорема. Для каждого тихоновского пространства X сле-
следующие условия равносильны:
(i) Пространство X локально компактно.
(И) Для каждой компактификации сХ пространства X на-
нарост сХ\с(Х) замкнут в сХ.
(ш) Существует компактификация сХ пространства X, для
которой нарост сХ\с(Х) замкнут в сХ.
Доказательство. Импликации (ii)=>(iii) и (iii)=^(i) оче-
очевидны; импликация (i)=^(ii) вытекает из теоремы 3.3.9. 1
В следующей теореме устанавливается важное свойство се-
семейства *&{Х) всех компактификации произвольного простран-
пространства X.
3.5.9. Теорема. Каждое непустое подсемейство ^ос:^(Х) обла-
обладает точной верхней гранью в W(X) по отношению к упорядо-
упорядочению ^.
Доказательство. Пусть ^o™W}ses' Рассмотрим декарто-
декартово произведение П csX и отображение cs— Д cs: J-> Ц csX>
которое по теореме о диагональном отображении является го-
меоморфным вложением. Покажем, что csX = csX с: Д csX яв-
S€=S
ляется наименьшей верхней гранью семейства Wo.
Так как проекция /V- П csX -> csX удовлетворяет условию
pscs = cs, имеем csX ^ csX при всех s^S. Пусть сХ — некото-
некоторая компактификация пространства X, для которой с3Х ^ сХ
при всех s^S, т. е. существуют отображения fs: cX-*-c$Xy та-
такие, что f$c == с$ при всех s e S. Легко видеть, что диагональное
отображение F= Л fs удовлетворяет условию Fc = cs; значит,
csX < сХ. I
3.5.10. Следствие. Для каждого тихоновского пространства X су-
существует наибольший элемент относительно упорядочения ^ на
Х) ¦
Наибольший элемент семейства W(X) называется стоун-че-
стоун-чеховской компактификацией (или стоун-чеховским расширением)
пространства X или максимальной компактификацией простран-
пространства X и обозначается через рХ Эта компактификация будет
подробно изучена в следующем параграфе.
В связи с последней теоремой возникает вопрос, для каких
пространств X каждое подсемейство семейства W обладает наи-
наибольшей нижней гранью. Если для подсемейства &о семейства
3.5. КОМПАКТИФИКАЦИИ 261
Я? (X) множество Vo = {с'Х: с'Х ^ сХ при всех сХ е= Wq} не-
непусто, то его наименьшая верхняя грань будет наибольшей ниж-
нижней гранью семейства Фо. Следовательно, наибольшие нижние
грани в ^(Х) существуют в том и только том случае, если в
Ф(Х) есть наименьший элемент. Оказывается, это условие экви-
эквивалентно локальной компактности пространства X.
3.5.11. Теорема об александровской компактификацин. Каждое
некомпактное локально компактное хаусдорфово пространство X
обладает компактификацией аХ с одноточечным наростом. Эта
компактификация является наименьшим элементом семейства
*&(Х) по отношению к упорядочению ^, а ее вес равен весу
пространства X.
Доказательство, Возьмем любую точку Q <ф. X и положим
aX = XU {Q}. Назовем открытыми множествами в аХ множе-
множества вида {^}U(^\/7), где F — любое компактное множество
в Ху а также все открытые в X множества. Легко видеть, что
аХ с этой топологией является хаусдорфовым пространством и
что отображение а: Х-+аХ, определенное правилом a(x)=xt
является гомеоморфным вложением, образ при котором а(Х) =
==Х всюду плотен в аХ. Покажем, что пространство аХ ком-
компактно. Пусть {Us}Ses ~~ произвольное открытое покрытие про-
пространства аХ. Существует s0 ^ $, такое, что ?2 е USo, и из
определения топологии на аХ следует, что множество F=X \ U$
компактно. По теореме 3.1.3, найдется конечное множество
{$ь 52, ..., Sk} а 5, для которого F с: \] Us\ значит, покрытие
{?/Л5е5с°ДеРжит конечное подпокрытие {Us^ -
Соотношение сХ^аХ, где сХ — любая компактификадия
пространства Ху будет доказано, если мы покажем, что отобра-
отображение f пространства сХ в пространство aXt определенное пра-
правилом
а(с-1(х)) при хшс(Х),
при х<=сХ\с(Х),
удовлетворяет условию fc — а и непрерывно. Равенство fc = a
следует прямо из определения, а по теореме 3.5.8 прообраз каж-
каждого открытого в аХ множества открыт в сХ — либо как откры-
открытое подмножество открытого подпространства с(Х), либо как
дополнение компактного множества в сХ.
Последняя часть теоремы вытекает из 3.1.20. I
Компактификация аХ локально компактного хаусдорфова
некомпактного пространства X называется александровской
компактификацией, одноточечной компактификацией или мини-
262 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
малъной компактификацией этого пространства. Можно сказать,
что она получается присоединением к пространству X «беско-
«бесконечно удаленной точки».
3.5.12. Теорема. Если в семействе ^(Х) всех компактификации
некомпактного тихоновского пространства X есть наименьший
элемент сХ по отношению к упорядочению ^, то X локально
компактно и сХ эквивалентно александровской компактифика-
компактификации аХ пространства X.
Доказательство. Для доказательства теоремы достаточно
показать, что нарост сХ\с(Х) является одноточечным множе-
множеством, так как это влечет за собой локальную компактность X
и, в силу теорем 3.5.11 и 3.5.4, эквивалентность сХ и аХ.
Предположим, что нарост сХ\с(Х) содержит две различные
точки х\ и х2. Пространство Х\ =сХ\{хи х2} локально ком-
компактно, и александровская компактификация пространства Х\
является компактификацией также и пространства X, т, е.
аХ\ = с\Х. Так как сХ ^ схХу существует отображение f: C\X—>
-+сХ, такое, что f\c(X) = idC(X). В силу теоремы 2.1.9, f\Xi =
= icUt; применив теорему 3.5.7 к компактификациям С\Х и сХ
пространства Хи заключаем, что /({&})= {хи х2}, а это не-
невозможно* I
3.5.13. Теорема. Если компакт У является непрерывным обра-
образом нароста сХ\с(Х) компактификации сХ локально компакт-
компактного хаусдорфова пространства X, то у пространства X есть
компактификация стХ ^ сХу нарост которой гомеолюрфен У.
Доказательство. Пусть / — непрерывное отображение про-
пространства сХ\с(Х) на У. Из теорем 3.5.8 и 2.4.13 следует, что
разбиение пространства сХ на прообразы точек при f и одното-
одноточечные подмножества множества с(Х) полунепрерывно сверху.
Отношение эквивалентности ?*, отвечающее этому разбиению
пространства сХ, замкнуто, а факторпространство сХ/Е яв-
является компактом. Подпространство с(Х) открыто в сХ. По-
Поэтому из предложения 2.4.15 следует, что пространство сХ/Е =
— сХ, где c' = qc и q\ сХ^-сХ/Е — естественное факторное
отображение, является компактификацией пространства X с на-
наростом, гомеоморфным У. I
3.5.14. Примеры. Окружность S1 и отрезок / являются компак-
тификациями вещественной прямой /?; при этом окружность S1
является александровской компактификацией прямой R.
Вообще, n-мерная сфера Sn и n-мерный куб 1п являются
компактификациями евклидова n-мерного пространства Rn\ при
этом сфера Sn является александровской компактификацией Rn.
Пространство W, описанное в примере 3.1.27, является алек-
александровской компактификацией своего подпространства №0.
3.5. КОМПАКТИФИКАЦИИ 263
Пространство Л(т), определенное в 1.4.20, является алек-
александровской компактификацией дискретного пространства D(m).
Каждая конечная сумма Л(т)ФЛ(т)Ф ... ®А(ш) также яв-
является компактификацией пространства D(m). Двойная окруж-
окружность Александрова, определенная в 3.1.26, является компакти-
компактификацией дискретного пространства D(t)\ эта компактифика-
ция не сравнима (по отношению к упорядочению ^) с компак-
компактификацией Л (с)® Л (с) пространства Ь(с). I
3.5.15. Пример. Рассмотрим подпространство X = X\{JX2\J Х$
плоскости/?2, где Xi = {0}X[—l, l],*2 = {(*> sin»):0<x<
^-^л;> и Х$— какая-нибудь дуга с концамив точках @, —1) и
Г у я, — 1J , которая не имеет других общих точек с Х\ U Х2. Так
как X — замкнутое и ограниченное множество в R2, пространство
X является компактом. Подпространство Х\Х\ пространства X
гомеоморфно R и всюду плотно в X, так что X является компак-
тификацней пространства R. Нарост этой компактификации го-
меоморфен /. Заменив Х\ХХ подходящим дискретным подпро-
подпространством Y мощности Ко, мы получим компактификацию
У U^i пространства D(No), нарост которой гомеоморфен /.
Из теоремы 3.5.13 следует, что каждый компакт, являющийся
непрерывным образом отрезка / (см. задачу 6.3.14), служит на-
наростом некоторой компактификации пространства R, а также
наростом некоторой компактификации пространства Ь(К0). Из
примера 3.1.26 мы заключаем, что каждое такое пространство
является также наростом некоторой компактификации простран-
пространства D(t) (см. упр. 3.5.Н). I
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
Компактификации (открытых подмножеств плоскости) впер-
впервые изучал Каратеодори в [1913] в связи с некоторыми пробле-
проблемами, касающимися аналитических функций. Ранее похожие
конструкции использовались в различных теориях веществен-
вещественных чисел. Теоремы 3.5.1 и 3.5.2 можно найти в работе Тихо-
Тихонова [1930]. Упорядочение ^ в семействе всех компактифика-
компактификации произвольного пространства было определено Люббеном в
[1941], где были доказаны теоремы 3.5.9 и 3.5.12. Существование
наибольшей компактификации было установлено ранее Чехом
в [1937] и М. Стоуном в [1937]. Теорема 3.5.5 доказана Смир-
Смирновым в [1952] (приведенное нами доказательство принадлежит
Мрувке [1956а]). Теорема 3.5.11 была доказана П. С. Алек-
Александровым в [1924b]. Теорема 3.5.13 являлась частью топологи-
топологического фольклора в тридцатые годы (по крайней мере в классе
264 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
метризуемых пространств); см. заключительные замечания в
книгах Хаусдорфа [1938] и Куратовского [1938]. Видимо, впер-
впервые она была сформулирована в явном виде в работе Ма-
гилла [1966].
УПРАЖНЕНИЯ
3.5.А, Покажите, что если csXs — компактификация про-
пространства Xs при 5 е S, то произведение П csXs является ком-
пактификацией произведения Ц Xs.
З.5.В. Пусть сХ — компактификация пространства X и Е —
замкнутое отношение эквивалентности на сХ. Покажите, что
если все одноточечные подмножества множества с(Х) явля-
являются классами эквивалентности отношения ?, то сХ/Е— тоже
компактификация пространства X.
З.5.С. Покажите, что предел обратного спектра {соХ, я?, Щ
компактификаций пространства X, где cp = n^cG при любых
а, ре 2, таких, что р ^ а, является компактификацией про-
пространства X.
3.5.D. Обратите внимание на то, что любые две компакти-
компактификаций C\N и c2N пространства Af = D(K0), обладающие ко-
конечными наростами одной мощности, гомеоморфны, и что тем
не менее они могут быть не сравнимы по отношению к упоря-
упорядочению ^. Приведите пример двух негомеоморфных компак-
компактификаций пространства ?(с), наросты которых двухточечны.
3.5.Е. Покажите, что максимальную компактификацию тихо-
тихоновского пространства X можно получить, взяв в II If замы-
кание образа пространства X при отображении А /, где $Г—
семейство всех непрерывных отображений пространства X в
отрезок / и If — / при \^SF.
3.5.F. Докажите, что для каждой компактификаций сХ про-
пространства X существует компактификация cfX ^ сХ, такая, что
w(c'X)=w(X).
3.5.G. (а) (Архангельский [1965]). Докажите, что для про-
произвольного тихоновского пространства X следующие условия
равносильны:
A) Пространство X точечно счетного типа.
B) Какова бы ни была компактификация сХ пространства
X, подпространство с(Х) можно представить в виде объединения
некоторого семейства G^-множеств в сХ.
C) Существует компактификация сХ пространства Ху для
которой с(Х) представимо в виде объединения некоторого се-
семейства д6~множеств в сХ.
3.6. СТОУН-ЧЕХОВСКАЯ КОМПАКТИФИКАЦИЯ И РАСШИРЕНИЕ ВОЛМЭНА 265
(Ь) Покажите, что для любого тихоновского пространства
X следующие условия равносильны:
A) Пространство л хемикомпактно.
B) Для каждой компактификации сХ пространства X имеет
место неравенство %(сХ\с(Х)у сХ)^ Ко-
C) Существует компактификация сХ пространства X, для
которой %(сХ\с(Х), сХ)^к0.
3.5.Н. Покажите, что для каждого компакта X, такого, что
^(Х)^ш^К0> найдется компактификация дискретного про-
пространства D(m), нарост которой гомеоморфен X.
Указание. Примените упр. 3.1.G и теорему 3.5.13.
Замечание. Как доказано Паровиченко в [1963], каждый
компакт X веса ^ Xi является непрерывным образом нароста
$N\N (см. доказательство в работе Уокера [1974]), так что
(в силу теоремы 3.5.13) найдется компактификация простран-
пространства Ny нарост которой гомеоморфен X,
3.5.К Докажите, что окружность и отрезок являются един-
единственными компактификациями вещественной прямой, наросты
которых конечны.
Указание. Примените заключительную часть примера 2.2.8.
3.5.J (Леви и Макдауэлл [1975], Ван Дауэн [1977]).
(а) Покажите, что для любого тихоновского пространства X все
его компактификации имеют одну и ту же плотность.
Указание. Примените упр. 3.1.С (с) и заметьте, что неприво-
неприводимое замкнутое отображение не может понизить плотность.
(Ь) Приведите пример тихоновского пространства X и его
компактификации сХу таких, что d(cX)<d(X).
Указание. Воспользуйтесь следствием 2.3.16.
3.6. СТОУН-ЧЕХОВСКАЯ КОМПАКТИФИКАЦИЯ
И РАСШИРЕНИЕ ВОЛМЭНА
Напомним, что наибольший элемент в семействе всех ком-
компактификации тихоновского пространства X называется ком-
пактификацией Стоуна — Чеха пространства X и обозначается
через pX
Для простоты в этом параграфе мы будем отождествлять
пространство X с подпространством с(Х) любой его компакти-
компактификации сХ, т. е. будем предполагать, что X является подпро-
подпространством любой своей компактификации сХ (это предпола-
предполагается и в некоторых других местах книги уже без специаль-
специальных оговорок). Тождественное вложение подпространства X в
сХ будет обозначаться через с. Отождествление X и с(Х) позво-
позволяет ставить и обсуждать вопрос о возможности продолжения
отображений пространства X на его компактификации.
266 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
3.6.1. Теорема. Каждое непрерывное отображение f: X-+Z про-
произвольного тихоновского пространства X в любой компакт Z
можно продолжить до непрерывного отображения F: pX->Z.
Если каждое непрерывное отображение тихоновского про-
пространства X в компакт можно непрерывно продолжить на не-
некоторую компактификацию уХ пространства X, то уХ эквива-
эквивалентна стоун-чеховской компактификации пространства X.
Доказательство. Теорема о диагональном отображении по-
показывает, что с = р A/: X-+$Xy{Z является гомеоморфным
вложением, так что сХ = c(X)cz РХХ Z — компактификация
пространства X. В силу максимальности компактификации $ХУ
существует непрерывное отображение g: §Х~+сХ, такое, что
g$ = c. Пусть р: cX^-Z — сужение на сХ проекции простран-
пространства $XyiZ на Z; положим F — pg: pZ->-Z. Так как F$ =
= pg$ = pc — /, отображение F является продолжением ото-
отображения /.
Если какая-нибудь компактификация уХ тихоновского про-
пространства X обладает свойством, сформулированным во второй
части теоремы, то найдется продолжение В: уХ-*$Х тожде-
тождественного вложения Р: Х->- (ЗХ Имеем тогда By = C, т. е. рХ ^
^ уХ, откуда следует, что компактификации уХ и рХ эквива-
эквивалентны. I
Из теоремы 3.6.1 вытекает ряд важных следствий.
3.6.2. Следствие. Замыкания в $Х любых двух вполне отделен-
отделенных подмножеств тихоновского пространства X не пересекаются.
Если в компактификации уХ тихоновского пространства X
замыкания любых двух вполне отделенных подмножеств про-
пространства X не пересекаются, то уХ эквивалентна стоун-чехов-
стоун-чеховской компактификации пространства X.
Доказательство. Пусть А, В — любые два вполне отделен-
отделенных подмножества тихонопского пространства X и /: Х-**1 —
непрерывная функция, отделяющая А и 5. В силу последней
теоремы, f можно_ продолжить до_непрерывной_функции F: рХ->
-*/. Значит, А П В = 0, так как Ас^(О) и B<=F-l(l).
Если компактификация 7-^ тихоновского пространства X
обладает свойством, сформулированным во второй части след-
следствия, то вполне отделенные подмножества пространства X и
(в силу леммы Урысона и теоремы 3.1.9) только такие подмно-
подмножества имеют непересекающиеся замыкания в уХ. То же самое
выполняется и для рХ, так что компактификации уХ и рХ экви-
эквивалентны по теореме 3.5.5. 1
3.6.3. Следствие. Каждое непрерывное отображение f: Х->1 ти-
тихоновского пространства X в отрезок I продолжается до непре-
непрерывной функции F: $Х->1.
3.6. СТОУН-ЧЕХОВСКАЯ КОМПАКТИФИКАЦИЯ И РАСШИРЕНИЕ ВОЛМЭНА 267
Если каждая непрерывная функция на тихоновском про-
пространстве X со значениями в отрезке I непрерывно продолжается
на компактификацию уХ пространства X, то уХ эквивалентна
стоун-чеховской компактификации пространства X. I
3»6.4. Следствие. Для любых двух непересекающихся замкнутых
подмножеств нормального пространства X их замыкания в рХ
не пересекаются.
Если компактификация уХ тихоновского пространства X
обладает тем свойством, что, какова бы ни была пара непересе-
непересекающихся замкнутых подмножеств пространства X, их замыка-
замыкания в уХ не пересекаются, то X нормально и уХ эквивалентна
стоун-чеховской компактификации пространства X. I
3.6.5. Следствие. Для каждого открыто-замкнутого подмноже-
подмножества А тихоновского пространства X замыкание А множества А
в рХ открыто и замкнуто. 1
Пусть X и У— тихоновские пространства, сХ и с'У — ком-
компактификации пространств X и У соответственно, и пусть
f: X-+Y— любое непрерывное отображение. Если существует
непрерывное отображение F: cX->c'Y9 такое, что F(x) = f(x)
при х е X, то мы говорим, что отображение f продолжается на
компактификации сХ и crY, и называем F продолжением ото-
отображения f на сХ и crY. Эта модификация понятия продолжае-
продолжаемости позволяет просто сформулировать следующее важное
свойство стоун-чеховского расширения,
3.6.6. Следствие. Для каждой компактификации yY тихонов-
тихоновского пространства У и любого непрерывного отображения
f: X-+Y тихоновского пространства X в пространство У суще-
существует продолжение F: рХ-^уУ на рХ и yY. 1
3.6.7. Следствие. Если М — подпространство тихоновского про-
пространства X и каждая непрерывная функция f: М->1 непре-
непрерывно продолжается на X, то замыкание М множества М в РХ
является компактификацией пространства М, эквивалентной $М.
Если, сверх того, М всюду плотно в X, то рХ = рМ. 1
Последнее следствие и теорема Титце — Урысона приводят
к таким утверждениям.
3.6.8. Следствие. Для каждого замкнутого^ подпространства М
нормального пространства X замыкание М множества М в рХ
является компактификацией пространства М, эквивалентной
pAf. I
3.6.9. Следствие. Для каждого тихоновского пространства X и
любого пространства Т, такого, что X cr T с: рХ, имеет место
равенство рГ = рХ. I
268 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
3.6.10. Пример. Как показано в примере 3.1.27, всякая непре-
непрерывная функция /: U70-Wt определенная на пространстве 1Г0
всех счетных ординалов, продолжается на пространство W всех
ординалов ^ coi; имеем, следовательно, W = $Wq.
Пространство Wo имеет только одну компактификацию. Дей-
Действительно, александровская компактификация <xWq получается
отождествлением нароста $Wo\Wo в точку. Значит, для нашего
пространства aWo = $Wo. Вообще, равенство аХ — $Х выпол-
выполняется для любого пространства X вида рУ\{л}, где хе РУ\У,
так как для такого пространства аХ = рУ и, в силу следствия
3.6.9, рХ = рУ. 1
Изучим теперь подробно стоун-чеховские компактификации
дискретных пространств и, в частности, компактификацию piV,
где N—пространство положительных целых чисел с дискретной
топологией.
3.6.11. Теорема. Для каждого ш ^ Ко стоун-чеховская компак-
компактификация дискретного пространства D(m) имеет мощность
22т и вес 2т.
Доказательство. Тихоновский куб Рт является компактом
мощности 22tn и веса 2т. В силу теоремы Хьюитта — Марчев-
ского — Пондицери, /2П содержит всюду плотное множество А
мощности га. Пусть /: Z)(m)-^/— произвольное отображение
пространства D(m) в /2"\ для которого /ф(ш)) = Л. Из тео-
теоремы 3.6.1 следует, что / продолжается до непрерывного отобра-
отображения F: p/)(tn)-^/2m. Очевидно, F(^D(m)) = I^f так как мно-
множество F($D(m)) замкнуто в /2tn и содержит всюду плотное в
Рт множество Л. Имеем теперь I $D (in) | ^ | Рт \ = 22Ш и, в силу
теоремы 3.1.22, ш(р/)(т))>ау (/2tn) = 2m. Чтобы завершить до-
доказательство, достаточно применить теорему 3.5.3 и теорему
Кантора — Бернштейна. I
3.6.12. Следствие. Мощность пространства $N равна 2е, а вес
его равен с. I
3.6.13. Теорема. Для каждой точки x^$D(m) и любой окрест-
окрестности V точки х существует открыто-замкнутое множество U
в р?)(га), такое, что л:^ U cz V.
Доказательство. Пусть W — произвольная окрестность точки
х, удовлетворяющая условию х е У с f с У; положим А =
= Wf\D(ut). В силу следствия 3.6.5, множество U — А открыто-
замкнуто в PD(m), а из теоремы 1.3.6 следует, что U =
Теорему 3.6.11 можно значительно усилить в случае ш=
А именно, имееа место следующий результат.
3.6. СТОУН-ЧЕХОВСКАЯ КОМПАКТИФИКАЦИЯ И РАСШИРЕНИЕ ВОЛМЭНА 269
3.6.14. Теорема. Каждое бесконечное замкнутое множество
F с р# содержит подмножество, гомеоморфное piV. В част-
частности, мощность F равна 2е, а вес F равен с.
Доказательство. По индукции без труда определяются по-
последовательность точек аи а2, ... и последовательность откры-
открытых множеств Vu V2y ..., такие, что а(- е К», Vi(]Vj = 0 при
1Ф1 и А = {аи a2f ...} <=/\
Пусть g: Л-*/— произвольная непрерывная функция. Функ-
Функция go: Л/'-*-/, определенная формулой
{g (а*), если л е ЛГ П Vh
О, если neJV\U^.
имеет продолжение Go: $N->I. Так как N всюду плотно в |W,
для всех x^Vi = Nf] Vi имеем Go(x) = g(ai)t так Что О0|Л =#.
Значит, для каждой непрерывной функции g: A-+I существует
продолжение G = Go| Л: Л->-7 на компактификацию Л простран-
пространства А9 и, в силу следствия 3.6.3, Л = рЛ. Так как пространство
А гомеоморфно N, заключаем, что пространство рЛ=Лс=/7 го-
меоморфно рЛ/". I
3.6.15. Следствие. Пространство pAf не содержит никакого под-
подпространства, гомеоморфного Л(Ко), г. е. в p,/V нет нетривиаль-
нетривиальных сходящихся последовательностей. 1
3.6.16. Следствие. Никакое недискретное подпространство про-
пространства р# не является секвенциальным пространством. 1
3.6.17. Следствие. Никакое пространство N[) {x} cz$Nf где х^
е $N\N, не удовлетворяет первой аксиоме счетности. I
3.6.18. Пример. В пространстве $N\N, наросте стоун-чеховской
компактификации дискретного пространства мощности Ко, су-
существует семейство мощности с попарно непересекающихся не-
непустых открытых множеств.
Отметим сначала, что в множестве # есть семейство {Nt} tG
бесконечных подмножеств, такое, что пересечение Nt П Nr ко-
конечно для каждой пары t, t' различных чисел из отрезка /.
Действительно, достаточно организовать все рациональные чис-
числа отрезка / в последовательность q\t ?2, ... и положить Nt =
= {пи П2, ...}, где^л,> Чп2, ... —какая-нибудь подпоследова-
подпоследовательность последовательности <7ь Ц% •.., сходящаяся к ty все
элементы которой различны. _ _
Семейство {Ut}t€El, где Ut=($N\N')()Nt, имеет мощность с
и состоит из непустых открытых в &N\N множеств. Для каж-
каждой пары t, f различных чисел из отрезка / имеем Nt' = F[)M9
270 I1 Л. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
где |F| < К0_и MJ]Nt = 0. Так как F = FczN и, согласно след-
следствию 3.6.4, M(]Nt=0t то
3.6.19. Пример. С помощью семейства {Ut}t^n построенного в
предыдущем примере, мы определим теперь интересное ненор-
ненормальное тихоновское пространство, которое пригодится нам
в § 6.2.
Выберем точку Xt^Ut для каждого ^е/ и положим Х =
= N\J U {jcJ.TaK как N локально компактно и всюду плотно в
t e/
X, из теоремы 3.3.9 следует, что множество X\N замкнуто в X.
Так как все точки пространства X\N изолированы, оно гомео-
морфно D(t). Рассуждая так же, как в примере 2.1.10 или в
примере 1.5.9, заключаем, что пространство X не нормально. 1
Пространство piV участвует в построении многих интересных
примеров; некоторые из них будут рассмотрены в последующих
параграфах этой главы.
Из теорем 3.6.11 и 2.3.23 следует, что пространство &D(m)
можно вложить в тихоновский куб /2Ш. Опишем теперь подпро-
подпространство канторова куба D2™ а Рш> гомеоморфное pZ)(m).
3.6.20. Пример. Пусть ^~—семейство всех отображений про-
пространства D(m), где m ^ Ь$о, в двухточечное дискретное про-
пространство D = {0, 1}. Ясно, что |#"| = 2Ш. По теореме о диаго-
диагональном отображении, отображение/7 = А /:?>(тп)->/JШ= Ц Df
где Df = Z) при всех f ^ ff", является гомеоморфным вложением.
Значит, замыкание F (D (ш)) cz D2™ является компактификацией
пространства D(m). Для каждой пары Л, В непересекающихся
замкнутых множеств в D(m) замыкания множеств ^(-4) и F(B)
в этой компактификации не пересекаются. В самом деле, для
функции f: D(m)—>Dy определенной формулами
f(x) = Q, если хеД и ?(x)=lt если x^D(m)\A,
имеем
F(A)czpf40) и F(B)<=:pfl(i)f
причем множества pjx @) и р^A)не пересекаются и замкнуты в D2m.
Следствие 3.6.4 показывает, что F(D(m))—компактификация
пространства D(m), эквивалентная pD(m). I
Определим теперь для каждого ^-пространства X компакт-
компактное Грпространство соХ, содержащее X в качестве всюду плот-
плотного подпространства и обладающее тем свойством, что каждое
непрерывное отображение /: X—*-Z пространства X в любой
3.6. СТОУН-ЧЕХОВСКАЯ КОМПАКТИФИКАЦИЯ И РАСШИРЕНИЕ ВОЛМЭНА 271
компакт Z продолжается до непрерывного отображения F:
->Z. Таким образом, соХ играет роль стоун-чеховской компакти-
фикации в случае произвольного ^-пространства X. Оказы-
Оказывается, пространство соХ является хаусдорфовым в том и только
том случае, если пространство X — нормально. Очевидно, в этом
случае соХ является компактификацией пространства А", эквива-
эквивалентной рх
Пусть X есть ^-пространство и 2)(Х)—семейство всех замк-
замкнутых в X множеств. Из леммы Тейхмюллера — Тьюки следует,
что каждое центрированное семейство замкнутых в X множеств
содержится в некотором ультрафильтре на 3)(Х)\ обычно такой
ультрафильтр не единствен. Семейство всех ультрафильтров на
Ф(Х) будет обозначаться через F(X). Каждый ультрафильтр
F(X) обладает следующими свойствами:
A) 0<^<Г.
B) Если Аи А2^&~, то АХ(]А2^^.
C) Если А0<=2)(Х) и АоПАф0 при всех А<==&~, то А0ев$~.
D) Если А^ЗГ и А^АХ^3){Х), то АХ^Т.
E) Если Аи А2^2)(Х) и Ai[}A2e~y9 то либо АХ^Т, либо
А2^ЗГ.
F) Если ЗГф$Г\ то существуют А^@~ и Л'е^, такие, что
А(]А/ = 0.
Свойства A), B) и D) вытекают из определения фильтра,
свойство C) следует из того, что семейство ^UHo}c2)(X)
центрировано и, значит, содержится в некотором ультрафильтре
&' на 3)(Х), который должен совпадать с #". Для доказательства
E) заметим, что если Ахф&~ и А2ф3гу то, в силу C), най-
найдутся Л[, Ле^, такие, что Л1 ПА\ = 0 = А% ПА'г
Значит, '2(Al[)A2)flA'{ftA'2=0, откуда, в силу (I) и B),
следует, что А\\)А2ф&г. Наконец, свойство F) вытекает из то-
того факта, что если ЗГ Ф&~\ то, в силу максимальности^", суще-
существует ief, для которого А ф&~\ и, согласно C), найдется
Л' е &", такое, чтоЛГ|Л/ = 0.
Легко видеть, что свойства A)—C) характеризуют ультра-
ультрафильтры в классе всех подсемейств семейства 3)(Х).
Каждому х е X отвечает ультрафильтр &* (х) = {Л е 3) (X):
х<=А}\ ясно, что {\У{х) = {х}. Если $~se:F{x) и х<^[\&~> то
&*cz@~(x)t так что <У = <Г(х). Значит, для каждого ультра-
ультрафильтра ^"ef(I) пересечение (}@~ либо является одноточеч-
одноточечным множеством, либо пусто. Ультрафильтры с пустым пере-
пересечением называются свободными ультрафильтрами; они со-
составляют подсемейство Fq(X) семейства F(X).
272 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
Положим (йХ = X\JFo(X); для каждого открытого множе-
множества U а X пусть
U* = UU {#"е^о(X): AczU для некоторого ЛеУ}с<*ХУ
и для каждого замкнутого множества А а X пусть
A# = A\J{&-seF0(X): Л 6=0-} с ©X.
В силу C), если ^ef(X) и множество UczX открыто, то
Х\иф&~ тогда и только тогда,
когда Л с= U для некоторого Л ^ #".
Поэтому
G) У == ©Z \ (Я\С/). и Л# = ®Х\(Х \ Л)\
Из B), E) и D) следует, что если множества Ль Л2с=Х замк-
замкнуты, то
(8) (Л! Л Л2)# = Аи П Л2# и (Л! U Л2)# = Аи [} Л2#,
откуда, в силу G) и формул де Моргана, следует, что если мно-
множества Uи U2czX открыты, то
(9) (UxUU$y = U\liUl и (Ux[\V%)* =
Второе соотношение в (9) вместе с равенством Х* = ®Х по-
показывает, что семейство $ всех множеств С/*, где U открыто в
Ху обладает свойствами (В1)—(В2) из § 1.1. Множество соХ
с топологией, порожденной базой $, называется волмэновским
расширением (расширением Волмэна) пространства X.
3.6.21. Теорема. Для каждого Т\-пространетва X его волмэнов-
ское расширение соХ является компактным Тупрост ранет во м, со-
содержащим X в качестве всюду плотного подпространства, при-
причем каждое непрерывное отображение f: X-+-Z пространства X
в произвольный компакт Z можно продолжить до непрерывного
отображения F: (dX-*Z.
Доказательство. То, что на X топология подпространства
пространства &Х совпадает с исходной топологией пространства
Ху и то, что X всюду плотно в (дХ, вытекает прямо из определе-
определения множеств U*.
Покажем, что toJ является ^-пространством.
Прежде всего из второй части G) следует, что множество
Л* замкнуто в юХ для всех Л ^3)(Х). Так как ясно, что {х} =
= Ш* для каждого хеХ, и, в силу F), {#"}= П ^* при
любых У е Fo(X), все одноточечные подмножества простран-
пространства (дХ замкнуты.
3.6. СТОУН-ЧЕХОВСКАЯ КОМПАКТИФИКАЦИЯ И РАСШИРЕНИЕ ВОЛМЭНА 273
Для доказательства компактности а>Х рассмотрим произволь-
произвольное центрированное семейство {Fs}sgS замкнутых в ыХ мно-
множеств. По определению топологии на (oXf при всех s e 5 имеем
Fs— П Аи> где At — замкнутое множество в X. Семейство
{At}tezT> г#е ^= U ^s> центрировано. Первая формула из (8)
показывает, что семейство {At}t<=T замкнутых множеств в X
также центрировано; значит, семейство {At}t^T содержится в
некотором ультрафильтре ЗГ на 2)(Х). Если (K?~Ф0, то су-
существует точка xel, такая, что ЗГ = &~(х); тогда хе f| At cr
с П Л*,= П />Если П^ = 0, то Fe=F0(X) и^е П 4,,=
= П ^s* Значит, в обоих случаях пересечение семейства
S He ПУСТО.
Рассмотрим теперь произвольное непрерывное отображение
f: X-+-Z пространства X в компакт Z. Для любых непересекаю-
непересекающихся замкнутых множеств В\ и В2 в Z их прообразы /~!(^1)
и f~1(B2) замкнуты в X и не пересекаются. Значит, в силу пер-
первого равенства в (8), множества [f^i)]» и If (Яг)]» не пе-
пересекаются. Так как последние два множества замкнуты в соА
и содержат соответственно f-l(B\) и f~l(B2), то замыкания мно-
множеств f~l(Bi) и f-l(B2) в (оХ не пересекаются. Существование
продолжения F: &X^Z отображения f следует теперь из тео-
теоремы 3.2.1. 1
3.6.22. Теорема. Волмэновское расширение соХ Т^пространства
X является хаусдорфовьш пространством в том и только том
случае, если X нормально.
Доказательство. Если пространство (оХ хаусдорфово, то <х)Х
является компактификацией пространства X. Так как замыка-
замыкания в (оХ произвольной пары непересекающихся замкнутых в X
множеств не пересекаются, пространство X нормально.
Предположим теперь, что X — нормальное пространство.
В силу F), для любых двух различных элементов #", &"
семейства F(X) найдутся замкнутые множества ^ef и
Л'еЗ*"', такие, что А(]А' = 0. Далее, в силу нормаль-
нормальности X, найдутся открытые множества U(&~, &"), V(&~, &~')а
сX, для которых AcU(9*, &% A'czV{Т> 9") и U(Г, Я")П
(\V{Tf <F')=0m Легко видеть, что для каждой пары различ-
различных точек Ту $Ff <^l F0(X) <=ooj (для каждой пары различных
точек х, х' е X cz ©J, для каждой пары точек ^efo(I), д:е
€=Х) множества U(&*, $"\ и F(#", Т\ (множества U {Т {х),
& {х% и VW (х), Т (*')Ь множества U (Tt T {х)\ и
18 Зак. 697
274 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
)\) являются непересекающимися окрестностями этих
точек в пространстве соХ Значит, пространство а>Х хаусдор-
фово. I
3.6.23. Следствие. Если пространство X нормально, то его вол-
мэновское расширение ыХ является компактификацией простран-
пространства Ху эквивалентной стоун-чеховской компактификации этого
пространства. I
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
Стоун-чеховская компактификация была введена Чехом в
[1937] и М. Стоуном в [1937]. Эти работы, вместе со статьей
М. Стоуна [1948], содержат все фундаментальные результаты о
рХ, а именно теорему 3.6.1 и следствия 3.6.2—3.6.9. Первый из
этих двух авторов определил максимальную компактификацию
с помощью метода, указанного в упр. 3.5.Е, развив таким обра-
образом идею, появившуюся в работе Тихонова [1930]. Второй автор
применил конструкцию, описанную в задаче 3.12.21 (с) ниже.
Заметим, что Тихонов определил пространство, гомеоморфное
PjV, в [1935] (см, упр. 3.6.Н). Пример 3.6.10 приведен Чехом
в [1937]. Теорема 3.6.11 доказана Поспишилом [1937]; ее до-
доказательство, приведенное нами, принадлежит Мрувке [1959а]
(эту теорему можно вывести также из более раннего результата
теории множеств (см. упр. 3.6.F)). Теорема 3.6.14 была доказана
Новаком в [1953а]. Существование в наросте $N\N семейства
мощности с попарно непересекающихся непустых открытых мно-
множеств было замечено Накамурой и Какутани в [1943]. Построе-
Построение такого семейства, приведенное в примере 3.6.18, так же как
и пример 3.6.19, взяты из работы Катетова [1950] (семейство
{Nt}t^T в принципе было определено Серпинским [1928а] ).
Вол мэновское расширение было построено Волмэном в [1938];
там же доказаны теоремы 3.6.21 и 3.6.22. Большое число ре-
результатов, относящихся к стоун-чеховской компактификации,
собрано в книге Уокера [1974].
Проблемы, связанные со стоун-чеховской компактификацией,
относятся к числу наиболее интересных проблем общей тополо-
топологии. Некоторые из них, в частности проблемы, относящиеся к
стоун-чеховским компактификациям дискретных пространств,
очень близки к теории множеств. Компактификация $Х может
быть построена многими способами (см. упр. 3.5.Е, 3.6.К, за-
задачи 3.12.21 (с), 8.5.8(а), примеры 8.3.18 и 8.4.14). Она обла-
обладает множеством интересных свойств (см., например, теоремы
7.1.15 и 7.1.17), применяется при построении большого числа ин-
интересных примеров (см. примеры 3.10.19, 3.10.29, 5.1.23, задачи
3.12.17 и 4.5.19(с)), а также при доказательстве ряда теорем
(см. указания к задачам 5.5.8(а), 7.4.15 и 7.4.16).
3.6. СТОУН-ЧЕХОВСКАЯ КОМПАКТИФИКАЦИЯ И РАСШИРЕНИЕ ВОЛМЭНА 275
УПРАЖНЕНИЯ
3.6.А (Новак [1953], У. Рудин [1956]). Проверьте, что все
открыто-замкнутые подмножества нароста $N\N имеют вид
W(M)=M()($N\N), где McJV,h что W(Mx)cz W(M2) в том
и только том случае, если разность М\\М2 конечна. Покажите,
что внутренность каждого непустого Gg-множества в $N\N не
пуста.
З.6.В. Определите функцию f: D (с)->-/, которую нельзя не-
непрерывно продолжить на компактификации пространства ?>(с),
описанные в 3.5.14.
3.6.С (М. Стоун [1948]). Выведите следствие 3.6.8 из след-
следствия 3.6.4 и, применив упр. 3.2J(b), получите теорему Титце —
Урысона.
3.6.D. (а) Выведите из упр. 3.2.Н, что произведение РХХРУ
не обязательно является стоун-чеховской компактификацией
пространства XX У (даже если У—компакт).
Замечание. Необходимое и достаточное условие равенства
П РХ*= рП Xs дано в задаче 3.12.20.
S S
П s
(b) Покажите, что функцию f: ЛГХЛГ-^Л определенную
формулой
f (т, n) = п^т при (т, n)e=NX N,
нельзя непрерывно продолжить на pAf X PiV. Выведите отсюда,
что произведение $N X Р^ не является стоун-чеховской компак-
компактификацией пространства NXN (см. задачу 6.3.21 (Ь)).
(c) Докажите, что, каков бы ни был сепарабельный компакт
X, произведение Й^Х^ является стоун-чеховской компактифи-
компактификацией пространства Wo X X.
Замечание. Предположение о сепарабельности не сущест-
существенно (см. задачи 3.12.19(с) или 3.12.20(с)).
(d) Докажите, что для каждого вполне регулярного про-
пространства У существует вполне регулярное пространство Z, та-
такое, что PZ\Z = У.
Указание. Если ш(У)^К0, то существование такого Z сле-
следует из (с); если зд(У) = с, то искомое заключение вытекает из
(с) и следствия 2.3.16. Чтобы получить общее утверждение,
видоизмените (с), рассмотрев подходящее пространство ордина-
ординалов вместо Wo.
Замечание. Этот результат прямо следует из задачи
3.12.19(с) и задачи 3.12.23(с).
(e) Заметьте, что стоун-чеховская компактификация предела
обратного спектра {Ха, я?, 2} тихоновских пространств может
отличаться от предела обратного спектра {&ХоУ й?, 2}, где п° —
продолжение отображения я? на рХа и $ХР.
18*
276 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
3.6.Е. Докажите, что для любого непрерывного отображения
/: X-*Y тихоновского пространства X на тихоновское простран-
пространство У существуют компактификации сХ и c'Y, такие, что
ш(сХ) = w(X)w(Y), w(c'Y)= w(Y) и / продолжается до непре-
непрерывного отображения F: cX-^c'Y.
3.6.F. Будем говорить, что семейство {^5}5е5 подмножеств
множества X состоит из независимых множеств, если для каж-
каждой конечной последовательности su s2, ..., Sk различных эле-
элементов множества S и каждой последовательности i\, 12, • • •, ik
из нулей и единиц всегда A*sl Л А8* Л • • • Л Ask Ф 0, где А0 — А
(a) (Хаусдорф [1936а]; при т = К0 и т = 2*° — Фихтен-
гольц и Канторович [1934] ). Покажите, что семейство всех под-
подмножеств множества X мощности ш^80 содержит подсемей-
подсемейство мощности 2т, состоящее из независимых множеств.
Указание. Примените теорему Хьюитта — Марчевского —
Пондицери и возьмите в качестве X всюду плотное множество в
канторовом кубе D2™.
(b) Выведите из (а), что канторов куб?JШ содержит всюду
плотное множество мощности т.
Указание. Воспользуйтесь семейством независимых подмно-
подмножеств на множестве мощности m для нумерации 2т сомножите-
сомножителей канторова куба D2™.
(c) Заметьте, что теорема 3.6.11 следует из (а).
3.6.G. (а) (Чех [1959], Гиллман и Джерисон [I960]). До-
Докажите, что для любого тихоновского пространства X мощность
всякого непустого замкнутого О6-множества в рХ, содержаще-
содержащегося в наросте рХ\Х, не меньше, чем 2е.
Указание. Пусть f: $Х^>-1 — непрерывная функция, обращаю-
обращающаяся в нуль только в точках рассматриваемого множества.
Определите последовательность аи #2, .-. точек пространства
X, такую, что f (fli)> f(a2) > ... и f(ai)^ \/i при / = 1,2, ... .
Воспользовавшись нормальностью отрезка [0, 1], заметьте, что
каждая пара непересекающихся замкнутых множеств подпро-
подпространства А = {fli, a2i ...} вполне отделена в Ху и выведите
отсюда, что замыкание множества А в рХ гомеоморфно Р#.
(Ь) (Чех [1937]). Покажите, что тихоновские пространства
X и У, удовлетворяющие первой аксиоме счетности, гомеоморф-
ны в том и только том случае, если компактификации РХ и рУ
гомеоморфны.
З.6.Н. Для всякого /е/ и i = l}2, ... обозначим через dtit)
i-я разряд двоичного разложения числа ty причем если у t есть
два таких разложения, то рассмотрим то из них, в котором
число нулей бесконечно. Этим при каждом i определена точка
ъ.7. СОВЕРШЕННЫЕ ОТОБРАЖЕНИЯ 277
тихоновского куба /с = П /*, где h = / при /е/. Покажите,
что подпространство {</ь <й>, ...} пространства /с гомеоморфно
N и что его замыкание в Iе гомеоморфно (W.
3.6.1. (а) (Мрувка [1954], Франклин [1967]). Пусть {NS}S^ST
где «Sf|W = 0,— бесконечное семейство бесконечных подмно-
подмножеств множества N, такое, что пересечение Ns П М* конечно для
каждой пары 5, s/ различных элементов семейства S, причем
{NS}S(=S максимально относительно последнего свойства (см.
пример 3.6.18 и лемму Тейхмюллера — Тьюки). Зададим топо-
топологию на множестве X = N (J 5 системой окрестностей Ш (х)}х<=х*
где #(*)= {{п}} при x = ti€EN и #(*) = {{s)\}{Ns \ {1, 2, ...
• • • >*})}ILi пРи x = s ^S. Проверьте, что X — не нормальное ло-
локально компактное хаусдорфово пространство, и докажите, что
ссХ является секвенциальным пространством, но не простран-
пространством Фреше — Урысона.
(Ь) Из существования локально компактного хаусдорфовз
пространства X со счетным всюду плотным множеством А изо-
изолированных в X точек, такого, что подпространство Х\А содер-
содержит с изолированных точек, легко следует наличие в наросте
$N\N семейства мощности с попарно непересекающихся непу-
непустых открытых множеств.
3.6.J (Гиллман и Джерисон [I960] ). Заметьте, что теорема
Тихонова вытекает как из теоремы 3.6.1, так и из теоремы
3.6.21.
Указание. Рассмотрите стоун-чеховскую компактификацию и
волмэновское расширение декартова произведения.
3.6.К (Гиллман и Джерисон [1960] ). (а) Проверьте, что если
X — тихоновское пространство, то, видоизменив построение вол-
мэновского расширения, а именно взяв ультрафильтры на се-
семействе S)q(X) всех функционально замкнутых подмножеств
пространства X вместо ультрафильтров на 2)(X), мы получим
стоун-чеховскую компактификацию пространства X.
В этом случае семейство всех множеств вида ?/*, где U — лю-
любое функционально открытое множество в X, образует базу про-
пространства X[)F0(X).
(b) Тихоновское пространство X компактно в том и только
том случае, если каждое центрированное семейство функцио-
функционально замкнутых множеств в X имеет непустое пересечение.
3.7. СОВЕРШЕННЫЕ ОТОБРАЖЕНИЯ
Непрерывное отображение f: X^-Y называется совершен-
совершенным, если X — хаусдорфово пространство, / — замкнутое отобра-
отображение и все прообразы f~*(y) являются компактными подмно-
278 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
жествами в X. Инъективное отображение /: X-*Y хаусдорфова
пространства X совершенно в том и только том случае, если оно
является замкнутым отображением, т. е. если f — гомеоморф-
ное вложение и множество f (X) замкнуто в У. В частности, вло-
вложение iM: M-+X является совершенным отображением в том и
только том случае, если пространство М хаусдорфово и М=М.
Теоремы 3.1.2 и 3.1.12 показывают, что каждое непрерывное
отображение компакта в хаусдорфово пространство совершенно.
Из теоремы Куратовского следует
3.7.1. Теорема. Если X — компакт, a Y — хаусдорфово простран-
пространство, то проекция р: ХУ( Y-+Y является совершенным отобра-
отображением. I
3.7.2. Теорема. Если f: X^Y — совершенное отображение, то
для каждого компактного подпространства Z<nY его прообраз
f~l(Z) является компактом.
Доказательство. Очевидно, f~l (Z) — хаусдорфово простран-
пространство. Остается показать, что для каждого центрированного се-
семейства ^~ = {^s}5<=s замкнутых множеств в f~l(Z) пересече-
пересечение П Fs непусто. При этом можно предполагать, что все
конечные пересечения элементов семейства У входят в (F, так
как, добавив к $Г эти пересечения, мы снова получим центриро-
центрированное семейство. В силу предложения 2.1.4, сужение fz\ f~l(Z)-*
~>Z является замкнутым отображением. Значит, {f(Fs)}SGS—
центрированное семейство замкнутых множеств в Z, и суще-
существует точка уе П /(Fs)' Таким образом, для всех sgS
55
5е5
имеем f~l (у) (] Fs Ф 0, и так как f~l(y) компактно, а У замк-
замкнуто относительно конечных пересечений, найдется точка
х<= П (f-[(y)OFs)^ П F8. 1
s^S s^5
Последняя теорема влечет за собой
3.7.3. Следствие. Композиция совершенных отображений явля-
является совершенным отображением. 1
Из предложения 2.1.4 получаем
3.7.4. Предложение. Если f: X-+Y—совершенное отображение,
то для каждого замкнутого А с: X и любого В czY сужения
f\A: A-*Y и fe: f~l(B)^B являются совершенными отображе-
отображениями. I
Из предложений 2.1.15, 2.1.11 и 2.1.13 вытекают следующие
два предложения.
3.7.5. Предложение. Пусть X — хаусдорфово пространство,
{At}i=\—конечное покрытие пространства X u{fi}i=l — семей-
3.7. СОВЕРШЕННЫЕ ОТОБРАЖЕНИЯ 279
ство согласованных отображений /,•: Ai^Y, комбинация f =
= /iV/2V ... Vfft которых является непрерывным отображе-
отображением. Тогда если все отображения ft совершенны^ то и их ком-
комбинация f — совершенное отобраоюение. Ш
3.7.6. Предложение. Если {Ai}i=[ — конечное замкнутое покры-
покрытие или конечное открытое покрытие хаусдорфова пространства
X и {fi}i=s{ — семейство согласованных совершенных отображе-
отображений fr, Л-~>У, то их комбинация / = /iVf2V ... V/ft является
совершенным отображением пространства X в У. I
3.7.7. Теорема. Декартово произведение /==11 fs, где fs: Xs-*-
s&S
-» Ys и Xs Ф 0 при s e S, является совершенным отображением
в том и только том случае, если совершенны все отображения fs.
Доказательство. Из предложения 3.7.4 следует, что если де-
декартово произведение f совершенно, то и все отображения fs
совершенны.
Предположим теперь, что все отображения /s совершенны.
По теореме 2.3.11, произведение П Xs является хаусдорфовым
пространством и, по теореме Тихонова, прообраз f~l(y) =
= П /Г1 (У8) является компактом при всех у= {у$}^ П Ys.
Значит, остается показать, что отображение f замкнуто.
Возьмем любую точку у = {ys} e Ц Ys и произвольное от-
крытое множество U <= Ц Xs9 содержащее f~l{y)~ П /Г1 (ys)*
ssS seS
По теореме Уоллеса, существуют открытые множества UsaXs>
такие, что Us Ф Xs лишь для s e {sp s2, ..., sAJ cz S и
11 fs^1 (ys) с: П ?/$ c: ?/. Так как /5. — замкнутое отображение,
$€=S S(=S l
в силу теоремы 1.4.13 при /=1, 2, ..., k найдется окрестность
Vsi(^Ysi точки yst, для которой f~{ (Vs\ cz USt. Окрестность
V = П Vs точки у, где Ks = У5 при s ф {su s2, ..., sk}> удовлет*
seS
воряет условию
Г1 (V) = П /Г1 (К,) cllf/.cd;
значит, отображение f замкнуто по теореме 1.4.13. 1
Из теоремы о декартовом произведении совершенных отобра-
отображений мы выведем серию важных свойств таких отображений.
Чтобы сразу дать читателю представление о том, как сильна эта
теорема, отметим, что и теорема Тихонова и теорема Уоллеса
Для хаусдорфовых пространств Xs являются ее непосредствен-
280 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
ными следствиями. Действительно, если {A"s}se5 — произволь-
произвольное семейство компактов, то отображение fs: Xs-+Ys простран-
пространства Xs в одноточечное пространство Ys совершенно при всех
5^5; значит, отображение f = П fs тоже совершенно и про-
изведение TL Xs = f~l(y), где {у} — Ц Ys, является компак-
том. Чтобы вывести теорему Уоллеса из 3.7.7, рассматривают
естественные факторные отображения fs: Xs~-* Xs/As.
Из теоремы 3.7.7 легко вытекает
3.7.8. Теорема. Диагональное произведение любого семейства
совершенных отображений является совершенным отобра-
отображением.
Доказательство. Диагональное отображение можно предста-
представить как сужение декартова произведения отображений на замк-
замкнутое множество. 1
Заметим, что если диагональное произведение f\ А /г является
совершенным отображением, то это еще не означает, что отобра-
отображения fi и $2 совершенны (см. 2.3.31).
Последнюю теорему можно значительно усилить.
3.7.9. Теорема. Пусть дано семейство {fs}s<=s непрерывных ото-
бражений fs: X-*-Ys. Если существует so^S, такое, что fS9 со-
совершенно и Ys — хаусдорфово пространство при всех seS\{s0},
то диагональное произведение A fs является совершенным ото-
se=S
бражением.
Доказательство. Достаточно рассмотреть диагональное про-
произведение h — fAg любого совершенного отображения /: Х-*-
->У и произвольного непрерывного отображения g: X-+Z на
хаусдорфово пространство Z. Это диагональное произведение h
можно представить в виде композиции
id* Ag f X idz
X > XXZ ^ YXZ.
Отображение id* Ag совершенно в силу следствия 2.3.22, а ото-
отображение / X idz совершенно по теореме 3.7.7. Таким образом,
из следствия 3.7.3 вытекает, что отображение h совершенно. 1
Последняя теорема фактически является усилением теоремы
3.7.8. Действительно, если f: X-+Y — совершенное отображение,
то, как показано ниже в теореме 3.7.20, f(X) — хаусдорфово
пространство и замкнутое подпространство в У.
3.7.10. Предложение. Если композиция gf непрерывных отобра-
отображений f: X-+Y и g: Y-+Z является совершенным отображением
и Y — хаусдорфово пространство, то отображения g\f(X) и f
тоже совершенны.
3.7. СОВЕРШЕННЫЕ ОТОБРАЖЕНИЯ 281
Доказательство. Для каждой точки z e Z прообраз
(g\f(X))-l(z) = f(X)ftg-l(z) = f[(gf)~l(z)} компактен, так как
компактен прообраз (gf)~l(z). Замкнутость отображения g\f(X)
следует из предложения 2.1.3.
Отображение f можно представить в виде композиции
X J^IL, YXZ -^ Y,
где р — проекция. Диагональное произведение Л = /Л(^/) яв-
является совершенным отображением в силу последней теоремы.
Легко видеть, что множество h(X)cz YY^Z совпадает с графи-
графиком отображения g\f(X) и потому содержится в графике G{g)
отображения g. Значит, / = (р | G (^) )Ло(^>, откуда следует, что
отображение f совершенно, так как р\ G(g) — гомеоморфизм:
(см. следствие 2.3.22) и отображение ho(g) совершенно в силу
предложения 3.7.4. I
Теорема 3.7.7 вместе с теоремами 2.5.13 и 2.5.14 приводит к
следующим двум теоремам.
3.7.11. Теорема. Если {<р, /0'} — отображение обратного спектра
S в обратный спектр S' и все отображения fof совершенны, то
предельное отображение Нт {ф, /v} тоже является совершенным
отображением. I
3.7.12. Теорема. Если все связующие отображения я° обратного
спектра S = \Х0> :гс?, 2} совершенны, то и все проекции являются
совершенными отображениями. I
Следующая интересная характеристика совершенных ото-
бражений тоже связана с теоремой 3.7.7.
3.7.13. Теорема. Для произвольного непрерывного отображения
f: X-*Z хаусдорфова пространства X следующие условия равно-
равносильны:
(i) Отображение f совершенно.
(и) Для каждого хаусдорфова пространства Y декартово
произведение /Xidy является совершенным отображением.
(in) Для каждого хаусдорфова пространства Y декартово
произведение f X id/ является замкнутым отображением.
Доказательство. Импликации (i)=^(ii) и (ii)=^(iii) оче-
очевидны. В силу предложения 2.3.27, для доказательства импли-
импликации (iii)=^(i) достаточно показать, что из (iii) вытекает ком-
компактность всех прообразов точек при f. Возьмем любое zoeZ
и произвольное хаусдорфово пространство У. Сужение go =
eg({zo)xy)' f~l (z0) X Y ->{z0} X Y замкнутого отображения g =
p=/Xidy замкнуто. Значит, композиция pogo, где pom. {20} X^
-*Y — проекция, тоже является замкнутым отображением. Эта
композиция совпадает с проекцией р: f^(zo)X У->У. Таким об-
282 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
разом, поскольку f~1(zo)<z:X— хаусдорфово пространство, ком-
компактность f~l{zo) следует из теоремы Куратовского. I
Из замечания 3.1.17 вытекает также следующее: если для
отображения f; X->Z декартово произведение /Xidy является
замкнутым отображением при любом выборе компакта У, та-
такого, что w(Y)^ w(X), то отображение / совершенно. Ясно, что
декартово произведение /Xg совершенного отображения f и
произвольного замкнутого отображения g не обязательно явля-
является замкнутым отображением (см. пример 2.3.28).
Среди тихоновских пространств класс совершенных отобра-
отображений можно охарактеризовать в терминах расширений. Мы
дадим сейчас две характеристики такого рода, основанные на
общей лемме. В первой из этих характеристик предполагается,
что пространства X и Y являются подпространствами рассматри-
рассматриваемых в теореме компактификаций.
3.7.14. Лемма. Совершенное отображение f: X->Y нельзя непре-
непрерывно продолжить ни на какое хаусдорфово пространство Z,
содержащее X в качестве всюду плотного подпространства.
Доказательство. Если F: Z-+Y—продолжение отображения
/ на хаусдорфово пространство Z, содержащее X, то, так как
композиция Fix = f является совершенным отображением, из
предложения 3.7.10 следует, что отображение ix совершенно.
Значит, X — замкнутое подпространство пространства Z. 1
3.7.15. Теорема. Для произвольного непрерывного отображения
f: X^-Y, где X и Y — тихоновские пространства, следующие
условия равносильны:
(i) Отображение f совершенно.
(и) Какова бы ни была компактификация yYy продолжение
Fy: $X-+yY отображения f удовлетворяет условию Fy($X\X)cz
Y\Y
y
(iii) Продолжение F: ($Х->|ЗУ отображения f удовлетворяет
условию F(ftf\X)cz$Y\Y.
(iv) Существует компактификация yY, такая, что для про-
продолжения Fy: $X-*yY отображения f выполняется условие
F(X\X)Y\Y
($)y
Доказательство. Предположим, что отображение f: X-+Y
совершенно, и рассмотрим его продолжение Fy\ $X-*yY. Так
как / можно продолжить на Z = F~x{Y)t не изменив области
значений, из леммы вытекает, что Z = X, т. е. 4toF~{(Y) cz X
и Fy($X\X)cz yY\Y. Этим импликация (i)=^(ii) доказана.
Импликации (ii)=^(iii) и (iii)=^(iv) очевидны; импликация
(iv)=^(i) вытекает из предложения 3.7.4. 1
3.7.16. Теорема. Непрерывное отображение f: X-+Yt где X и
У — тихоновские пространства, совершенно в том и только том
3.7. СОВЕРШЕННЫЕ ОТОБРАЖЕНИЯ 283
случае, если его нельзя непрерывно продолжить ни на какое
хаусдорфово пространство Z, содержащее X в качестве всюду
плотного собственного подпространства.
Доказательство. Достаточно заметить, что если f: X-+Y не
совершенно, то, по последней теореме, для продолжения F: |ЗХ->
->РУ отображения f имеет место соотношение ^((ЗХХЛ^Л Уф0;
значит, / продолжается на пространство Z = F~l(Y), содержа-
содержащее X в качестве всюду плотного подпространства, hZ=^I. I
Применяя теорему 3.3.22, получаем следующую характери-
характеристику совершенных отображений со значениями в ^-простран-
^-пространствах.
3.7.17. Теорема. Непрерывное отображение /: X->Y хаусдор-
фова пространства X в k-пространство Y совершенно в том и
только том случае, если для каждого компактного подпростран-
подпространства Za У сужение fz: f-1(Z)->Z совершенно. 1
Из последней теоремы и теоремы 3.7.2 получаем следующий
результат.
3.7.18. Теорема. Непрерывное отображение f: X^>Y хаусдор-
фова пространства X в k-пространство У совершенно в том и
только том случае, если прообраз f~l(Z) каждого компактного
множества ZczY компактен. I
Рассмотрим теперь вопрос о сохранении топологических
свойств совершенными отображениями в сторону образа и в
сторону прообраза.
3.7.19. Теорема. Если пространство X совершенно отображается
на пространство У, то w(Y)^w(X).
Доказательство. Пусть /: X-+Y—совершенное отображение
на У и n = w(X). Очевидно, теорема верна при ш< Ко, поэтому
можно предположить, что ш ^ Ко. Пусть {f/s}5e5—база про-
странства X, для которой |5| = ш, и пусть ЗГ — семейство всех
конечных подмножеств множества S. Так как |^J = m, доста-
достаточно показать, что семейство {^т)т^€г^ гДе WT — Y\f(X\ \J [/s)f
T
seT
является базой пространства У. Из определения вытекает,
что множества WT открыты. Возьмем точку у е У и произ-
произвольную ее окрестность Wc^Y. Прообраз f~l{y)—компактное
подмножество множества f~l{W); значит, найдется Ге^", та-
такое, что f~l(y)cz U Usa f~l(W). Ясно, что y&Wr, и так как
Y \ W = f (X \. /-' (W)) <= f (*\UTU.) ,
имеем frcf.l
Как отмечено в последнем абзаце примера 3.1.26, совершен-
совершенные отображения могут увеличивать характер пространств. Из
284 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
последней теоремы следует, что при отождествлении конечного
числа компактных попарно непересекающихся подмножеств
хаусдорфова пространства в точки (см. пример 2.4.12) вес не
возрастает. Пример 1.4.17 показывает, что предположение о
компактности существенно.
3.7.20. Теорема. Класс Ti-пространств инвариантен относительно
совершенных отображений при i = 2, 3, 4, 5 и 6.
Доказательство. В силу теоремы 1.5.20 и отмеченной в § 2.1
инвариантности класса наследственно нормальных пространств
относительно замкнутых отображений, достаточно эту теорему
доказать для / = 2 и 3. Эти случаи аналогичны друг другу, по-
поэтому мы рассмотрим только случай / = 2.
Пусть f: X-+Y — совершенное отображение хаусдорфова
пространства X на пространство У и у и #2 — любые две различ-
различные точки пространства У. Прообразы f~l(y\) и /"ЧУг) ком-
компактны и не пересекаются. Следовательно, по теореме 3.1.6, су-
существуют открытые множества U, Ус X, такие, что f~l(t/\)cz U,
f-l(y2)czV и U(]V = 0. Множества Y\f(X\U) и y\f(*W)
открыты в У, причем первое из них содержит уи а второе со-
содержит #2- Далее,
Y\f(X\U)]n[Y\f(X\V)]=Y\[f(X\U)[}f(X\V)] =
Отображение q: 7*->Г, описанное в примере 2.4.21, совер-
совершенно. Следовательно, вполне регулярность не сохраняется со-
совершенными отображениями.
Теоремы 3.7.20 и 3.1.10 влекут за собой инвариантность
класса компактов относительно совершенных отображений. Ана-
Аналогично из теорем 3.7.20 и 3.3.23 следует, что и свойство быть
^-пространством инвариантно относительно совершенных ото-
отображений.
То же имеет место и для локально компактных хаусдорфо-
вых пространств.
3.7.21. Теорема. Локальная компактность сохраняется совершен-
совершенными отображениями.
Доказательство. Пусть f: X ->- У — совершенное отображение
локально компактного (хаусдорфова) пространства X на про-
пространство У. По теореме 3.3.2, для каждого у е У_найдется от-
открытое множество VczX, такое, что f~l(y)a V и V компактно.
Множество W=Y\f{X\V) является окрестностью точки у, и
так как
W = Y\f(X\V)cz Y\f(X\V)cz f{V)9
замыкание W является компактным подпространством про-
пространства У. 1
3.7. СОВЕРШЕННЫЕ ОТОБРАЖЕНИЯ 285
3.7.22. Теорема. Пусть & — (конечно) аддитивное топологиче-
топологическое свойство, инвариантное относительно совершенных отобра-
отображений. Если пространство X можно представить в виде объеди-
объединения локально конечного (конечного) семейства {XS}S€BS замк-
замкнутых подпространств, обладающих свойством &*, то X тоже
имеет свойство $Р.
Доказательство. Отображение V ixJ ф Х8-+Х совер-
шенно. 1
Обсудим теперь, какие свойства сохраняются совершенными
отображениями в сторону прообраза.
3.7.23. Теорема. Регулярность сохраняется в сторону прообраза
совершенными отображениями.
Доказательство, Пусть /: Х->У— совершенное отображение
на регулярное пространство У. Возьмем точку ^еХи замкнутое
множество F cz X, такие, что x^F. Множество F(]f~{f(x) ком-
компактно и не содержит х; следовательно, по теореме 3.1.6, су-
существуют непересекающиеся открытые множества Uu V\ с: л,
для которых х е Ux и F П f~lf(x) ^ У\- Множество f(F\V{) замк-
замкнуто в У и не содержит Да:); значит, в силу регулярности У,
найдутся непересекающиеся открытые множества f/g, У 2 с: У,
такие, что f(x)f=U2 и f(F\V{)a:V2, Множества U=Uifif-l(U2)
и V=V\[}f~l(V2) открыты в Х9 не пересекаются и содержат
точку х и множество F соответственно. I
Остальные аксиомы отделимости не сохраняются в сторону
прообраза совершенными отображениями. Чтобы убедиться в
этом в случае наследственной нормальности и совершенной нор-
нормальности, достаточно отобразить /с на одноточечное простран-
пространство (см. упр. З.Ю.С(с)). По поводу нормальности см. за-
задачу 3.12.19(е) или пример 5.1.40, а по поводу вполне регуляр-
регулярности см. замечания к этому параграфу.
3.7.24. Теорема. Компактность и локальная компактность со-
сохраняются в сторону прообраза совершенными отображениями.
Доказательство, Сохранение компактности прямо следует из
теоремы 3.7.2. Если f: X -* У — совершенное отображение, а
У — локально компактное пространство, то для каждой точки
х^Х найдется окрестность U с X, такая, что f(U) содержится
в некотором компактном подпространстве Z пространства У.
Так как f@)a f(U)aZ, множество Dczf-l(Z) компактно. 1
3.7.25. Теорема. Если f: Х-^У—совершенное отображение про-
странства X на k-прост ранет во У, то X—тоже k-пространство.
Доказательство. Рассмотрим пространства kX и kY и отобра-
отображение kf: kX^-kY, определенное в конце § 3.3. Так как У есть
^-пространство, то Y = kY и kf = fax. В силу теоремы 3.7.17,
286 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
отображение kf совершенно, а отсюда и из теоремы 37.10 сле-
следует, что %х совершенно. Будучи взаимно однозначным, отобра-
отображение кх является гомеоморфизмом. Значит, X есть ^-простран-
^-пространство. I
Из теоремы 3.7.1 вытекает, что если топологическое свой-
свойство !Р сохраняется в сторону прообраза совершенными отобра-
отображениями, то произведение компакта X на ^пространство У со
свойством & тоже имеет свойство Л Следовательно, теоремы
о сохранении в сторону прообраза совершенными отображе-
отображениями топологических свойств являются обобщениями соответ-
соответствующих теорем о произведениях. Как показано в следующей
теореме, в классе тихоновских пространств для всех топологи-
топологических свойств, наследуемых замкнутыми подпространствами,
сохранение в сторону прообраза совершенными отображениями
равносильно сохранению этих свойств при умножении на любые
компакты.
3.7.26. Теорема. Пусть 3*— топологическое свойство, наследуе-
наследуемое замкнутыми подпространствами и сохраняющееся при умно-
умножении на любой компакт. Тогда если тихоновское пространство
X совершенно отображается на пространство У со свойством д>7
то и само X обладает свойством 0*.
Доказательство. По теореме 3.2.6, существует гомеоморфное
вложение g: X-+Z пространства X в компакт Z. Диагональное
отображение fAg: Х->УХ2 является одновременно гомео-
морфным вложением (см. теорему 2.3.20) и совершенным ото-
отображением (см. теорему 3.7.9). Значит, X гомеоморфно замкну-
замкнутому подпространству пространства У X Z и, следовательно,
обладает свойством 9*. 1
Вполне регулярность наследуется замкнутыми подпростран-
подпространствами и сохраняется при умножении на компакт; тем не менее
она не сохраняется в сторону прообраза совершенными отобра-
отображениями. Значит, в последней теореме существенно предположе-
предположение, что X является тихоновским пространством.
3.7.27. Теорема. Пусть 3* — топологическое свойство, наследуе-
наследуемое замкнутыми подпространствами и конечно мультипликатив-
мультипликативное. Предположим, что пространство X допускает инъективное
непрерывное отображение f: X->Y в хаусдорфово пространство
Y со свойством 3* и совершенное отображение g: X-+Z в про-
пространство Z со свойством 3*. Тогда и пространство X обладает
свойством д>.
Доказательство. Диагональное отображение f Ag\ X^-Y\Z
совершенно и инъективно и, значит, является гомеоморфным
вложением. Следовательно, X гомеоморфно замкнутому подпро-
подпространству пространства УХ2 и, значит, обладает свойством 9*. ¦
Простые примеры показывают, что ни первая, ни вторая
3.7. СОВЕРШЕННЫЕ ОТОБРАЖЕНИЯ 287
аксиомы счетности не сохраняются в сторону прообраза совер-
совершенными отображениями (см. упр. 3.7.Е). Однако из последней
теоремы вытекает
3.7.28. Следствие. Если nw(X)^m и пространство X можно со-
совершенно отобразить в пространство Y веса ^ ш (характера
s^m), то w(X)^m {то %(Х)^ш).
Доказательство. Утверждение очевидно при ш < &о; поэтому
можно предположить, что ш ^ Мо. Свойства «вес ^ ш» и «ха-
«характер =^т» наследственны и конечно мультипликативны. Да-
Далее, пространство X хаусдорфово, так как на нем определено
совершенное отображение. Значит, следствие вытекает из леммы
3.1.18 и теоремы 3.7.27. 1
3.7.29. Теорема. Если топологическое свойство 9* сохраняется в
сторону прообраза совершенными отображениями и наследуется
открыто-замкнутыми подпространствами, то в хаусдорфовых
пространствах свойство & наследуется и замкнутыми подпро-
подпространствами.
Доказательство. Пусть F— замкнутое подпространство хаус-
дорфова пространства Ху обладающего свойством 9*. Комбина-
Комбинация ifVidx является совершенным отображением суммы F®X
на X. Так как F — открыто-замкнутое подпространство простран-
пространства F(BX, пространство F обладает свойством IP. 1
Топологические свойства хаусдорфовых пространств, сохра-
сохраняемые совершенными отображениями как в сторону образа,
так и в сторону прообраза, называются совершенными свой-
свойствами. Класс всех хаусдорфовых пространств с фиксированным
совершенным свойством называется совершенным классом про-
пространств. Из теорем этого параграфа вытекает, что классы ре-
регулярных пространств, компактов, локально компактных хаус-
хаусдорфовых пространств и ^-пространств являются совершенными
классами.
Помимо совершенных отображений рассматривается и более
Широкий класс почти совершенных отображений. Непрерывное
отображение f: Х->У называется почти совершенным, если f
замкнуто и все прообразы точек f~l(y) — компактные подпро-
подпространства пространства X. Следовательно, совершенные отобра-
отображения— это в точности почти совершенные отображения, опре-
определенные на хаусдорфовых пространствах. Читателю не соста-
составит труда проверить, что теоремы и предложения 3.7.1—3.7.7 и
теорема 3.7.13 остаются верными (вместе с их доказательства-
доказательствами), если заменить «совершенное» на «почти совершенное»,
«компакт» на «компактное пространство» и «хаусдорфово про-
пространство» на «топологическое пространство». Легко проверяется
также, что теорема 3.7.9 и предложение 3.7.10 верны и для
288 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
почти совершенных отображений; однако предположение, что
эти отображения принимают значения в хаусдорфовых простран-
пространствах, существенно в обоих утверждениях (см. упр. 3.7.А).
Рассмотрев отображения в одноточечные пространства, легко
убедиться, что в теоремах о сохранении топологических свойств
в сторону прообраза необходимо налагать некоторые ограниче-
ограничения на прообразы точек. В этом параграфе было показано, что
предположение о компактности прообразов точек вместе с пред-
предположением о замкнутости отображения ведет к серии теорем
о сохранении свойств в сторону прообраза. Оказывается, топо-
топологические свойства, как правило, не сохраняются в сторону
прообраза открытыми отображениями с компактными прооб-
прообразами точек (см. упр. 3.7.Н). Поэтому в дальнейшем, обсуж-
обсуждая вопросы сохранения свойств в сторону прообраза, мы огра-
ограничиваемся замкнутыми отображениями, прообразы точек при
которых удовлетворяют различным требованиям «типа ком-
компактности».
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
Класс совершенных отображений (для метрических про-
пространств) был введен Вайнштейном в [1947]. Независимо со-
совершенные отображения были введены и исследованы (в классе
локально компактных хаусдорфовых пространств) Л ере в [1950]
и Бурбаки в [1951]. Два последних автора определили этот
класс отображений посредством характеристики, содержащейся
в теореме 3.7.18. Теорема 3.7.2 была доказана Люббеном в
[1941]. Важная теорема 3.7.7, которая показывает, что совер-
совершенные отображения играют среди всех непрерывных отобра-
отображений роль, сходную с ролью компактов среди всех топологи-
топологических пространств, была доказана Фроликом в [1960] и Бур-
баки в [1961]. Теорема 3.7.9 доказана Архангельским в [1967а]
(В. И. Пономарев показал в [1966], что эта теорема имеет место
в классе тихоновских пространств). Теорема 3.7.10 доказана
Бурбаки в [1961], а теорема 3.7.16 была сформулирована Исбел-
лом в [1962]. Приведенные нами доказательства этих трех тео-
теорем взяты из работы Майкла [1971b]. Бурбаки в [1961] опре-
определил совершенные отображения как отображения, удовлетво-
удовлетворяющие условию (ш) теоремы 3.7.13, и доказал эквивалентность
всех условий этой теоремы. Работа Хенриксена и Исбелла
[1958] содержит теорему 3.7.15 (импликация (i)=>-(ii) была за-
замечена Таймановым в [1955]), с помощью которой эти авторы
доказали сохранение совершенными отображениями многих
свойств в сторону образа и в сторону прообраза. Книга Келли
[1955] содержит теоремы 3.7.19, 3.7.20 и 3.7.21 (теорема 3.7.19
при ш = No была доказана Уайберном в [1942]). Теорема 3.7.23
3.7. СОВЕРШЕННЫЕ ОТОБРАЖЕНИЯ 289
получена Хенриксеном и Исбеллом в [1958], теорема 3.7.24
была в принципе доказана Вайнштейном в [1952] (объявлена
в [1947]), а теорема 3.7.25 доказана Архангельским в [1965]
(объявлена в [1963]). Работа ван дер Слота [1966] содержит
теорему 3.7.26, статья Архангельского [1967а] содержит тео-
теорему 3.7.27, а работа Хенриксена и Исбелла [1958] содержит
теорему 3.7.29. Пример, показывающий, что вполне регулярность
не сохраняется в сторону прообраза совершенными отображе-
отображениями, был приведен Хенриксеном и Исбеллом в [1958]. Хабер
в [1972] упростил и усилил этот их результат.
УПРАЖНЕНИЯ
З.7.А. (а) Диагональное произведение двух почти совершен-
совершенных отображений может не быть замкнутым отображением.
(b) Докажите существенность в теоремах 3.7.9 и 3.7.10 пред-
предположения о том, что рассматриваемые отображения принимают
значения в хаусдорфовых пространствах.
(c) Укажите пример совершенного отображения /: Х->19 ко-
которое можно непрерывно продолжить на некоторое Грпростран-
ство У, содержащее X в качестве собственного всюду плотного
подпространства.
З.7.В. Проверьте, что сумма © fs является совершенным
отображением в том и только том случае, если все отображения
fs совершенны.
З.7.С. Докажите, что отображение /*: XjE^YjE', определен-
определенное в упр. 2.4.В, является совершенным отображением, когда
оба отображения /: X->Y и qf\ Y^Y/Е' совершенны и про-
пространство Х/Е хаусдорфово.
3.7.D (Динь Ньё Тонг [1963]). Пусть /: Х^- Y— наслед-
наследственно факторное отображение с компактными прообразами
точек, определенное на хаусдорфовом пространстве X. Дока-
Докажите, что w(Y)^w(X) и что если пространство X локально
компактно и хаусдорфово, а пространство У хаусдорфово, то У
локально компактно.
З.7.Е. (а) Докажите, что если /: Х-> У — замкнутое отобра-
отображение регулярного пространства X в топологическое простран-
пространство У и для каждого х^Х выполняются неравенства
(f() n(HWK (Х)<
(b) Заметьте, что если отображение / совершенно, то в
утверждении (а) можно опустить предположение о регуляр-
регулярности X.
3.7.F (Чобан [1967]). (а) Если пространство X можно со-
совершенно отобразить на пространство У, то h(X)^h(Y).
19 Зак. 697
290 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
(Ь) Приведите пример совершенного отображения простран-
пространства с первой аксиомой счетности X на пространство У, такое,
что А (У) = 24
Указание. Воспользуйтесь упр. 3.1.1.
3.7.G (Годел [1969а]). Пусть 9>— топологическое свойство,
наследственное по замкнутым множествам и такое, что каж-
каждое пространство X, представимое в виде объединения локально
конечного семейства №}Ses замкнутых подпространств со свой-
свойством 9*у само обладает свойством 9> (см. теорему 3.7.22).
(а) Покажите, что если существует открытое покрытие 41 =
со
= U Qli пространства X, такое, что все семейства 411 локально
конечны и П обладает свойством 9* для каждого U e °U, то и
все пространство X обладает свойством 9*.
оо
(b) Пусть Ш — U 41 i — открытое покрытие пространства X,
где все °Ub — локально конечные семейства множеств. Если
каждое U^°U обладает свойством 9* и может быть представ-
представлено в виде объединения счетного семейства открытых мно-
множеств, содержащихся в U вместе с замыканием (в частности,
оо
если покрытие 41 = JJ 411 состоит из функционально откры-
открытых множеств, обладающих свойством ^), то и само простран-
пространство X имеет свойство 9*.
оо
(c) Пусть <U= U cUi — открытое покрытие хаусдорфова про-
пространства X, где все семейства °Ui локально конечны, каждое
U e °U обладает свойством 9* и Fr U компактна для всех U е °11.
Тогда пространство X тоже обладает свойством ^\
(d) Приведите пример нерегулярного хаусдорфова простран-
пространства, представимого в виде объединения двух нормальных под-
подпространств со счетной базой, граница одного из которых ком-
компактна.
З.7.Н. Приведите пример открытого отображения не нормаль-
нормального вполне регулярного пространства на отрезок /, при кото-
котором все прообразы точек гомеоморфны /.
Указание. Возьмите сужение определенного в 1.4.15 отобра-
отображения плоскости Немыцкого на вещественную прямую.
3.8. ЛИНДЕЛЕФОВЫ ПРОСТРАНСТВА
Мы называем топологическое пространство X линделёфовым
пространством, или пространством со свойством Линделёфа,
если X регулярно и из каждого открытого покрытия этого про-
3.8. ЛИНДЕЛЁФОВЫ ПРОСТРАНСТВА 291
странства можно выбрать счетное подпокрытие1). Ясно, что
регулярное пространство X является линделёфовым простран-
пространством в том и только том случае, если в каждое открытое по-
покрытие пространства X можно вписать счетное покрытие. Из
этих определений следует, что каждый компакт является лин-
линделёфовым пространством.
Из теоремы 1.1.14 следует
3*8-1. Теорема. Каждое регулярное пространство со счетной ба-
базой является линделёфовым пространством. 1
Из леммы 1.5.14 вытекает
3.8.2, Теорема. Каждое линделёфово пространство нормально. I
Будем говорить, что семейство ^" = {^?в}$€=$ подмножеств
множества X счетно центрировано, если f ^0и П ^ ^ 0
S
для каждого счетного множества So cz S.
Доказательства следующих четырех теорем параллельны до-
доказательствам теорем 3.1.1, 3.1.2, ЗЛ.З и 3.1.10; мы оставляем их
читателю.
3.8.3. Теорема. Регулярное пространство X обладает свойством
Линделёфа в том и только том случае, если каждое счетно
центрированное семейство замкнутых в X множеств имеет не-
непустое пересечение. 1
3.8.4. Теорема. Каждое замкнутое подпространство линделёфова
пространства является линделёфовым пространством. ¦
3.8.5. Теорема. Если подпространство А топологического про-
пространства X обладает свойством Линделёфа, то для любого се-
семейства {Us}s<=$ открытых в X множеств, такого, что A cz
cz (J Us, найдется счетное множество {si, 5г, ...} с: S, такое, что
5
3*8.6. Теорема. Если f: X->Y — непрерывное отображение лин-
линделёфова пространства X на регулярное пространство У, то Y —
линделёфово пространство. I
Доказать следующую теорему предоставляется читателю.
8.8.7. Теорема. Сумма ф Xs, где Xs ф 0 при s^S, обладает
S
свойством Линделёфа в том и только том случае, если все про-
пространства Xs обладают свойством Линделёфа и множество S
счетно. Ш
г) Если X — произвольное топологическое пространство и из каждого его
открытого покрытия можно выделить счетное подпокрытие, то пространство
X называется финально компактным. — Прим. перев.
19*
292 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
Из теоремы 3.8.5 следует, что если регулярное пространство
является объединением счетного семейства подпространств со
свойством Линделёфа, то оно само является линделёфовым про-
пространством. В частности, каждое регулярное пространство, яв-
являющееся объединением счетного семейства компактных под-
подпространств (пространства с этим свойством называются о-ком-
пактными), обладает свойством Линделёфа и, следовательно,
нормально. Применив теорему 3.8.4, мы заключаем, что каждое
^-множество в линделёфовом пространстве является линделё-
линделёфовым пространством.
Тривиальным видоизменением доказательства теоремы 3.7.2
получается
3.8.8. Теорема. Если f: X-> Y — замкнутое отображение регуляр-
регулярного пространства X и все прообразы точек f~l(y) обладают
свойством Линделёфа, то для каждого линделёфова подпро-
подпространства ZczY его прообраз f~l (Z) тоже является линделёфо-
линделёфовым пространством. I
3.8.9. Теорема. Класс всех линделёфовых пространств является
совершенным классом.
Доказательство. Сохранение свойства Линделёфа (в сторону
образа) при совершенных отображениях вытекает из теорем
3.7.20 и 3.8.6; сохранение его в сторону прообраза следует из
теорем 3.7.23 и 3.8.8. 1
3.8.10. Следствие. Декартово произведение линделёфова про-
пространства и компакта является линделёфовым пространством. 1
В следующей теореме устанавливается важное свойство лин-
линделёфовых пространств.
3.8.11. Теорема. В каждое открытое покрытие линделёфова про-
пространства можно вписать локально конечное открытое покрытие.
Доказательство. Пусть °U — открытое покрытие линделёфова
пространства X. Так как X регулярно, для каждой точки х^Х
найдутся открытые множества Ux, Vx cz X, такие, что х^ Ux cr
<= Ох с Vx и Vx содержится в некотором элементе покрытия CU.
Пусть {UXi}T=\ ~ счетное подпокрытие покрытия {Ux}x<=x ПР°"
странства X. Множества
№) где i=l, 2, ...,
открыты и покрывают X. Действительно, для любого хеХ
имеем x^Wi(x), где i(x) — наименьшее натуральное число i,
такое, что х^ V*.. Покрытие{Wi}™=x вписано в Ш и локально
конечно, так как UXj П W% = 0 при i > /. |
Понятие линделёфова пространства приводит к понятию
числа Линделёфа: наименьший кардинал т, такой, что из каж-
3.8. ЛИНДЕЛЁФОВЫ ПРОСТРАНСТВА 293
дого открытого покрытия пространства X можно выбрать подпо-
подпокрытие мощности ^ ш, называется числом Линделёфа про-
пространства X и обозначается через 1(Х). Таким образом, регу-
регулярное пространство X обладает свойством Линделёфа в том и
только том случае, если l(X)^. Ko.
Из замечания 1.1.16 сразу вытекает
3.8.12. Теорема. Для каждого топологического пространства X
имеет место неравенство l(X)^nw(X). ¦
3.8.13. Примеры. Плоскость Немыцкого — сепарабельное не лин-
делёфово пространство (пример нормального пространства с
теми же свойствами приведен в упр. 3.8.Е).
Пространство Л(т) при ш > *<о является линделёфовым не
сепарабельным пространством.
Так как каждое счетное регулярное пространство обладает
свойством Линделёфа, из 3.3.24 вытекает, что существуют лин-
делёфовы пространства, не являющиеся ^-пространствами. I
3.8.14. Пример. Покажем теперь, что прямая Зоргенфрея А' яв-
является линделёфовым пространством. Пусть {Us)s^s — произ-
произвольное открытое покрытие пространства К и Vs — внутренность
множества Us по отношению к обычной топологии вещественной
прямой. Покажем, что множество L = /C\ \j Vs счетно. Дей-
ствительно, для каждого x^L найдутся s(x)eS и веществен-
вещественное число г{х)> х, такие, что [х, r(x) )cr US(x). Далее, из опре-
определения множества L следует, что если хфх\ то [х, г(х))(]
Г\[х\ г(х'))=0. Так как мощность каждого семейства попарно
не пересекающихся полуоткрытых интервалов не превосходит
*%о, имеем |L| ^ Ко.
Множество K\L с топологией, индуцированной обычной то-
топологией вещественной прямой, обладает счетной базой. Зна-
Значит, покрытие {Fj5eS множества K\L содержит счетное под-
подпокрытие {^-}П=1 этого множества. Ясно, что семейство
{Us(x)}Xf=i U{^(}Ili является счетным подпокрытием покрытия
{(/JseS; следовательно, К — линделёфово пространство. Про-
Пространство К является примером сепарабельного линделёфова
пространства с первой аксиомой счетности, но без счетной
базы1).
3.8.15. Пример. В примере 2.3.12 было показано, что произве-
произведение /СХ/( не нормально. Применив теорему 3.8.2, мы заклю-
!) Прямая Зоргенфрея К является также наследственно линделёфовым
пространством без счетной сети. — Прим. перев.
294 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
чаем, что произведение двух линделёфовых пространств может
не быть линделёфовым пространством (см. упр. 3.8.G и 3.9.F). I
Существует пространство X, все конечные степени которого
являются линделёфовыми пространствами и все же Х*° не нор-
нормально. В частности, отсюда следует, что предел обратной по-
последовательности линделёфовых пространств может не быть лин-
линделёфовым пространством (этот факт можно установить проще;
см. задачу 5.5.4(с)).
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
Понятие линделёфова пространства было введено П. С. Алек-
Александровым и П. С. Урысоном в [1929] (Линделёф доказал в
[1903], что произвольное семейство открытых в Rn множеств
содержит счетное подсемейство с тем же объединением). Тео-
Теорема 3.8.9 доказана Хенриксеном и Исбеллом в [1958]. Теорема
3.8.11 была доказана Моритой в [1948] (а при дополнительном
предположении локальной компактности или метризуемости —
Дьедонне в [1944] ). Примеры 3.8.14 и 3.8Л5 приведены Зорген-
фреем в [1947]. Пространство X, упомянутое в конце парагра-
параграфа, было определено Пшимусинским в [1980]. Ранее такое про-
пространство было определено Майклом в [1971] при дополни-
дополнительном предположении континуум-гипотезы.
УПРАЖНЕНИЯ
З.8.А. (а) Пространство X является наследственно линделё-
линделёфовым пространством в том и только том случае, если все от-
открытые подпространства пространства X обладают свойством
Линделёфа.
(Ь) Покажите, что линделёфово пространство X является на-
наследственно линделёфовым пространством в том и только том
случае, если X совершенно нормально.
3.8.В (Ю. М. Смирнов [1950]). Пусть А и В — непересекаю-
непересекающиеся замкнутые множества в регулярном пространстве X, при-
причем А я В обладают свойством Линделёфа. Покажите, что най-
найдутся открытые множества U, V с Ху такие, что AczUy В а V
и Uf] V = 0.
З.8.С. (а) Каждое хемикомпактное пространство а-компакт-
но, но обратное (в классе хаусдорфовых пространств) может не
иметь места (см. упр. 3.4.Е).
(Ь) Докажите, что для локально компактного хаусдорфова
пространства X следующие условия равносильны:
A) Пространство X линделёфово.
B) Пространство X хемикомпактно.
C) Пространство X о-компактно.
3.8. ЛИНДЕЛЁФОВЫ ПРОСТРАНСТВА 295
D) Существует последовательность Аи А% ... компактных
подпространств пространства X, такая, что Ai <=lntAi+i и
E) Пространство X компактно или %(Q, aX)= Ко-
3.8.D (М. Рудин и Кли [1956], Майкл [1961]). Докажите,
что если X и Y — пространства со счетной базой и У регулярно,
то пространство Yx наследственно линделёфово как в компактно-
открытой топологии, так и в топологии поточечной сходимости
(см. задачу 5.5.13).
Указание. Примените упр. 3.4.G(a).
3.8.Е (Энгелькинг [1968]). Пусть Y—подпространство тихо-
тихоновского куба Т — /с, гомеоморфное пространству Wo всех счет-
счетных ординалов, и пусть С — счетное всюду плотное множество
в Г. Рассмотрим пространство АG), определенное в упр. 3.1.G,
и его подпространство Х= Y\\}C2. Докажите, что X — нормаль-
нормальное сепарабельное не линделёфово пространство (см. задачу
Указание. Если А и В — непересекающиеся замкнутые мно-
множества в Wo, то хотя бы одно из них компактно.
Замечание. Первые примеры пространств с подобными свой-
свойствами были построены М. Рудин в [1956] и Маколеем в
[1956а].
3.8.F (Хенриксен, Исбелл и Джонсон [1961]). (а) Пусть X —
подпространство компакта Z и {^*}П=1 — счетное семейство
замкнутых в Z множеств, причем для любых хеХ hj/gZ\X
найдется такое г, что x^Fi и у ф Fu Докажите, что тогда про-
пространство X линделёфово *).
Указание. Пусть {Us}Sgs ~~ открытое покрытие пространства
X. Множества Vs = Z\X\US открыты в Z и XczV= [] Vs.
s<=S
Покажите, что X содержится в объединении всех конечных пере-
пересечений Fi{ ПFt2П ••• ПFift, не имеющих общих точек с ZW.
(Ь) Пусть X — компакт и 9? — наименьшее семейство под-
подпространств пространства X, содержащее все замкнутые мно-
множества и замкнутое относительно счетных объединений и пере-
пересечений. Докажите, что все элементы семейства S обладают
свойством Линделёфа.
3.8.G (Хейджер [1969]). Докажите, что произведение счет-
счетного семейства регулярных а-компактных пространств является
линделёфовым пространством.
Указание. Примените упр. 3.8.F(a).
*) Класс всех пространств X, таких, как в этом примере, совпадает с клас-
классом линделёфовых ^-пространств, введенным Нагами в [1969*].
296 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
З.8.Н. Пусть 9* — топологическое свойство, наследуемое замк-
замкнутыми подпространствами и такое, что если какое-либо про-
пространство X является объединением локально конечного семей-
семейства {Is}5eS замкнутых подпространств, обладающих свойством
9>, то и само X имеет свойство 9> (см. теорему 3.7.22 и упр.
3.7.G).
(a) Пусть пространство X регулярно и существует локально
конечное открытое покрытие Ш этого пространства, такое, что
каждое U е Ш обладает свойством 9> и Fr U является линделё-
фовым пространством для всех U^°U. Покажите, что тогда и
само X имеет свойство 9*.
Указание. Примените упр. 3.8.В.
(b) Приведите пример не нормального тихоновского про-
пространства, представимого в виде объединения счетного семей-
семейства открытых нормальных подпространств, граница каждого
из которых линделёфова.
(c) Покажите, что если нормальное пространство X допу-
оо
екает открытое покрытие <Ы= JJ °Uu где каждое семейство °Ui
локально конечно, все U ^°U обладают свойством 9> и Fr U —
линделёфово пространство для каждого U<^°и, то и все про-
пространство X имеет свойство 9*.
3.9. ПОЛНЫЕ ПО ЧЕХУ ПРОСТРАНСТВА
Следующая теорема, аналогичная теореме 3.5.8, ляжет в
основу последующего определения.
3.9.1. Теорема. Для каждого тихоновского пространства X сле-
следующие условия равносильны:
(i) Нарост сХ\с(Х) каждой компактификации сХ простран-
пространства X является Fa-множеством в сХ.
(И) Нарост рХ\Р(Х) является Fa-множеством в $Х.
(iii) Существует компактификация сХ пространства X, та-
такая, что нарост сХ\с(Х) является Fa-множеством в сХ.
Доказательство. Импликации (i)=^(ii) и (ii)=^(iii) оче-
очевидны; остается доказать, что (iii)=>-(i).
Покажем сначала, что (ш)=^(П). В силу максимальности
рЯ, существует непрерывное отображение f: $X^cX, такое, что
/Р = с. По теореме 3.5.7, f-l(cX\c(X) )= рГ\р(Х). Значит, так
как нарост сХ\с(Х) является /^-множеством в сХ, нарост
является ^-множеством в рХ.
Покажем теперь, что (ii)=^(i). Пусть pZ\P(X)= U Fu где
Fi — замкнутые в рХ множества. Рассмотрим произвольную
компактификацию сХ пространства X и непрерывное отображе-
3.9. ПОЛНЫЕ ПО ЧЕХУ ПРОСТРАНСТВА 297
ние /: $Х-+сХ, для которого /Р = с. По теореме 3.5.7, имеем
со
сХ \с{Х) — U / (Ft). Так как множества/(Т7/) замкнуты в сХ,
U
нарост сХ\с(Х) является /^-множеством в сХ. I
Топологическое пространство X называется полным по Чеху,
если X — тихоновское пространство, удовлетворяющее условию
(i), а следовательно, и всем остальным условиям теоремы 3.9.1.
Заметьте, что каждый компакт полон по Чеху. Локально
компактные хаусдорфовы пространства тоже полны по Чеху, так
как каждое не компактное локально компактное хаусдорфово
пространство обладает компактификацией с одноточечным на-
наростом. Пространство всех иррациональных чисел с топологией
подпространства вещественной прямой служит примером не ло-
локально компактного пространства, полного по Чеху.
Данное нами определение полных по Чеху пространств яв-
является внешним определением: оно характеризует полные по
Чеху пространства через их отношение к другим топологиче-
топологическим пространствам, а именно их компактификациям. Установим
теперь внутреннюю характеристику полных по Чеху пространств.
Сначала введем вспомогательное понятие. Будем говорить,
что диаметр подмножества А топологического пространства X
меньше, чем покрытие зФ = ?4s}S€eS этого пространства, и пи-
писать Ь(А)<зФ, если существует s^S, такое, что AczAs.
3.9.2. Теорема. Тихоновское пространство X полно по Чеху
тогда и только тогда, когда существует счетное семейство
i^i}T=\ открытых покрытий пространства X со свойством: если
#" — центрированное семейство замкнутых в X множеств, такое,
что для каждого / = 1, 2, ... в $Г есть множество диаметра,
меньшего чем *s&i, то пересечение семейства ЗГ не пусто.
Доказательство. Предположим, что тихоновское пространство
XczfiX обладает семейством {^*}Г=1 открытых покрытий с тре-
требуемым свойством. Пусть ^i== {USti}s^s. при i=l, 2, ... и
Vs, t — открытое множество в рХ, такое, что Us, ,- = X fl Vs, t при
s e Si и i = 1, 2, ... . Ясно, что
U у,.,;
будет доказано, что X полно по Чеху, если мы установим обрат-
обратное включение.
оо
Возьмем любую точку хе f| [I KS)/ и пусть $(х)—се-
t = l se=St
мейство всех окрестностей точки х в рХ Семейство #" =
298 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
= {X()V: Vel(x)}, где V — замыкание множества V в рХ,
центрировано и состоит из замкнутых в X множеств. Так как
для каждого i существует s е S/, такое, что х е Vs, и из регуляр-
регулярности рХ следует, что семейство У содержит множества диа-
диаметра, меньшего чем sti, при /= 1, 2, .... По предположению,
ХП(}{?: Уе=$(х)}Ф0. Так как []{?: V е Я(х)} = {х}, за-
заключаем, что л; ^ X
Рассмотрим теперь произвольное полное по Чеху простран-
пространство XczpX Множество X— типа Gb в рХ, т. е. существует се-
оо
мейство {Gt}™=l открытых в рХ множеств, такое, что X = (] Ог.
Для каждого jjeXh f = l, 2, ... выберем открытое множество
Vx, t сг рХ, такое, что х ^ Vx, t a Vx> i cz G/, и положим j^i =
= {^П Vjt. Jjcejc- Покажем, что семейство {^J^! открытых по-
покрытий пространства X обладает нужным свойством.
Рассмотрим произвольное центрированное семейство {Fs}s^s
замкнутых в X множеств, содержащее множества диаметра,
меньшего чем $f>i, при I = 1, 2, ... . Так как {/^bes ~ центри-
центрированное^ семейство замкнутых в рА' множеств, найдется точка
х е П Fs- Будет доказано, что х <= f] Fs, если мы установим,
S S
что jueI
Для каждого целого положительного / выберем Si ^ S, та-
такое, что б (F8i) < &i, и XfEl, такое, что Fs. cz X f] Кх?, /. Так
как
при /=1, 2, ..., то д:е П G? = J. I
Следующая теорема важна разнообразными приложениями.
Ее название объясняется тем, что счетные объединения нигде
не плотных множеств иногда называют множествами первой
категории.
3.9.3. Теорема Бэра о категории. В полном по Чеху простран-
сю
стве X объединение А = (J At любой последовательности нигде
i = \
не плотных множеств является коплотным множеством, т. е.
его дополнение Х\А всюду плотно в X.
Доказательство, Покажем, что множество G\A не пусто,
каково бы ни было непустое открытое множество G а X.
Пусть {«$#/}^lj —семейство открытых покрытий пространства
X, такое, как в теореме 3.9.2. Так как множество А\ нигде не
3.9. ПОЛНЫЕ ПО ЧЕХУ ПРОСТРАНСТВА 299
плотно, найдутся точка хе G\A\ и ее окрестность G\, такие, что
GxczG\Ai и 6(G1)<^1.
Аналогично, пользуясь тем, что Gi\A2— непустое открытое
множество, получаем непустое открытое множество G2, для ко-
которого
G2czGx\A2 и
По индукции определяется последовательность Gb G2, ...
непустых открытых множеств в X, удовлетворяющая условиям
G^dGx-z>G2zd ..., Gi[]Ai=0 и 6(Gi)<^ при i=l9 2,
Легко проверяется, что 0==П
Следующее утверждение является двойственным вариантом
теоремы Бэра о категории.
3.9.4. Следствие. В полном по Чеху пространстве X пересечение
оо
G= П G,- любой последовательности G\, G2, ... всюду плотных
открытых множеств всюду плотно. I
3.9.5. Теорема. Каждое полное по Чеху пространство является
k-пространством.
Доказательство. Пусть X — полное по Чеху пространство и
{GJ~=i ~ семейство открытых множеств в рХ, такое, что
оо
Х= Р G*.Рассмотрим произвольное множество AczX, пересече-
пересечение которого с каждым компактным подпространством простран-
пространства X замкнуто, и предположим, что само А не замкнуто в X,
т. е. что существует точка л;^ХП(А\Л), где черта обозначает
замыкание в рХ. Пусть Uo = рХ, Uu U2y... — последовательность
окрестностей точки х в рХ, такая, что Di с: Ui-\ П Gi при / ==
оо
= 1, 2, ... . Пересечение Z= f] C/f czz X компактно; значит, ком-
компактно и множество Af\Z. Так kukjc^A{]Z, найдется окрест-
окрестность V с рХ точки х, для которой Vf\Af\Z = 0.
Окрестность V'fl^ точки л: пересекает множество Л. Выбе-
Выберем точку xi^Af\Vf\Ui при t = l, 2, ... и положим В =
= {хь х2, ...}. Из 3.1.5 следует, что
A) если U открыто в рХ и Z с: U, то для некоторого ? имеем
С/* с ?/,
а отсюда вытекает, что множество ZU5 компактно. Значит, пе-
300 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
ресечение ЛП[^П(^и5)] тоже компактно. Так как BczA(]V9
то
откуда следует, что U = $X\B открыто в $Х и Z c= U. В силу
A), найдется такое /, что Ui[)B — 0, — что невозможно, так
как Xi ^ Ui П В. Полученное противоречие показывает, что А
замкнуто, т. е. что X есть ^-пространство1). 1
3.9.6. Теорема. Полнота по Чеху наследуется замкнутыми мно-
множествами и G^-множествами.
Доказательство. Первая часть теоремы вытекает сразу из
теоремы 3.9.2. Вторая часть следует из того, что если X есть
б6-множество в рХ и А есть бб-множество в X, то А есть GЛ-мно-
жество в $Х и тем более в замыкании Л cz pX, которое является
компактификацией пространства Л. I
3.9.7. Теорема. Сумма ф Xs полна по Чеху в том и только том
случае, если все пространства Xs полны по Чеху.
Доказательство. Если сумма © Xs полна по Чеху, то все
S€=S
пространства Xs полны по Чеху в силу 2.2.2 и 3.9.6
Предположим теперь, что все пространства Xs полны по
Чеху, и для каждого s ^ S возьмем некоторую компактифика-
цию csXs пространства Xs; имеем csXs \ Xs== jj Fs,,-, где FSi i —
замкнутые множества в csXs при seS и / = 1, 2, ... . В силу
3.3.12, сумма Х= © csXs — локально компактное хаусдорфово
пространство; тем более X полно по Чеху. Так какХ \ф Xs =
оо
= U Г и Ps*t\ и множества U FSti замкнуты в А" при i =
= 1,2, ..., сумма ф Xs полна по Чеху в силу 3.9.6. 1
3.9.8. Теорема. Произведение счетного семейства полных по
Чеху пространств является полным по Чеху пространством.
Доказательство. Пусть {^Jjli — семейство полных по Чеху
пространств. Для каждого /=1, 2, ... возьмем произвольную
компактификацию dXi пространства Х(. Тогда dXi\Xi есть
^-множество в dXi при t = 1, 2, .... В силу 2.3.5 и 3.2.4, про-
[) Не всегда G$- множество в ^-пространстве является ^-пространством,
как можно было бы предположить после теоремы 3.9.5 (см. пример 1.6.19).—
Прим. перев.
3.9. ПОЛНЫЕ ПО ЧЕХУ ПРОСТРАНСТВА 301
оо
странство П ctXi является компактификацией произведения
оо оо
ЛXt. Множество ^/ = 11^4^/, где Л/,/ = CjXj\X}- и Ai,j = ctXi
оо
при i ф }У является множеством типа Fa вЦсА при /=1, 2,... .
оо оо оо оо
Так как П с*Х* \ IIХ* = LI ^у» произведение П^ является
полным по Чеху пространством. 1
3.9.9. Следствие. Предел обратной последовательности полных
по Чеху пространств является полным по Чеху пространством. 1
Из упр. 3.9.С(Ь) следует, что предположение о счетности
существенно в последней теореме и что следствие 3.9.9 не рас-
распространяется на произвольные обратные спектры.
Из определения полноты по Чеху и теоремы 3.7.15 получаем
следующий результат:
3.9.10. Теорема. Пусть X и У — тихоновские пространства и
/: Х->У—совершенное отображение пространства X на про-
пространство У. Тогда пространство X полно по Чеху в том и только
том случае, если пространство У полно по Чеху. ¦
С другой стороны, полнота по Чеху не сохраняется ни замк-
замкнутыми, ни открытыми отображениями (см. упр. 3.9.1 и задачи
3.12.18(d) и 5.5.8(Ь)).
Предположение, что X и У — тихоновские пространства, су-
существенно в последней теореме. Действительно, совершенное
отображение в примере 2.4.21 преобразует полное по Чеху про-
пространство в пространство, не являющееся тихоновским. Суще-
Существуют также примеры открытых совершенных отображений не
тихоновских пространств на пространства, полные по Чеху. Та-
Таким образом, класс полных по Чеху пространств совершенен
лишь «по модулю аксиом отделимости».
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
Полные по Чеху пространства были определены в работе
Чеха [1937]; эта работа содержит также доказательство тео-
теоремы Бэра о категории, известной до этого для более узкого
класса пространств, метризуемых полной метрикой (см. заме-
замечания к § 4.3). Внутренняя характеристика полных по Чеху
пространств, данная в теореме 3.9.2, была независимо установ-
установлена Фроликом в [1960b] и Архангельским в [1961]. Аналогич-
Аналогичная характеристика была дана Шаниным в [1943а]. Теорема
3.9.5 была доказана Архангельским в [1965], а теорема 3.9.10 —
Хенриксеном и Исбеллом в [1958]. Пример открытого совер-
302 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
шенного отображения не тихоновского пространства на нор-
нормальное полное по Чеху пространство приведен Хабером в
[1972].
УПРАЖНЕНИЯ
З.9.А. Покажите, что если полное по Чеху пространство X
является подпространством хаусдорфова пространства У, то най-
найдется Gб-множество Zcz У, такое, что X = Xf\Z.
Выведите отсюда, что подпространство М полного по Чеху
пространства X полно по Чеху в том и только том случае, если
М можно представить в виде F[)Z> где F замкнуто в X, a Z
есть бб-множество в X.
З.9.В. Покажите, что пространство всех рациональных чисел,
наделенное топологией подпространства вещественной прямой,
не полно по Чеху. Выведите отсюда, что множество всех ирра-
иррациональных чисел не является /^-множеством на вещественной
прямой.
З.9.С. (а) (Окстоби [1961]). Докажите, что теорема Бэра о
категории выполняется для произведения любого множества
полных по Чеху пространств.
(b) Заметьте, что произведение ЛГ*1 не полно по Чеху.
Указание. См. упр. 3.3.Е(а).
(c) Выведите теорему Бэра о категории прямо из определе-
определения полноты по Чеху.
3.9.D. Покажите с помощью теоремы 3.9.2, что плоскость
Немыцкого полна по Чеху.
Указание. Заметьте сначала, что подпространство L<i<^L
полно по Чеху.
3.9.Е (Архангельский [1960а], Архангельский и Голштын-
ский [1963]). Пусть X—тихоновское пространство. Обозначим
через g(X) наименьший кардинал m ^ Ко, для которого суще-
существует компакт У, содержащий X, и семейство Ш открытых в У
множеств, такие, что \Ш\ = т, и если jcgXh^g У\Х, то най-
найдется U e °U со свойствами: х е U и у ф U.
(a) Заметьте, что g(X)=i&o для каждого полного по Чеху
пространства X. Покажите, что h(X)^ g(X), каково бы ни было
тихоновское пространство X (см. упр. 3.1.F), и приведите при-
пример совершенно нормального пространства Ху для которого
h(X)<g(X).
(b) Внешней базой подпространства X в пространстве У на-
называется семейство Я открытых в У множеств, такое, что если
х^Х и U — любая окрестность точки х в пространстве У, то
найдется V^SS, для которого x^VczU. Докажите, что для
любого подпространства X компакта У и любого кардинала
ш ^ Ко следующие условия равносильны:
3.9. ПОЛНЫЕ ПО ЧЕХУ ПРОСТРАНСТВА 303
A) Сетевой вес пространства X не превосходит т, и суще-
существует семейство °U открытых в У множеств, такое, что
\°U\ ^ т, и для любых хе! и j/g Y\X найдется U^<Ut удов-
летворяющее условиям x^U и у фи.
B) Существует семейство #~ замкнутых множеств в У, такое,
что \&~\ =?1 т, и для любой пары различных точек х\^Х, х2е У
найдутся непересекающиеся множества F\, F2^fF, такие, что
X\^F\ U X2 ^ F2.
C) Существует семейство У открытых множеств в У, для
которого \У°\ ^ т, и, каковы бы ни были различные точки Х\^Х,
ХгеУ, можно найти непересекающиеся множества Vi, V2^T$
такие, что хх е V\ и х2 е V2.
D) Существует внешняя база % пространства X в простран-
пространстве У, для которой | J?| ^ т.
(c) Выведите из (Ь), что ау(Х)=пау(Х)^(Х) для каждого
бесконечного тихоновского пространства X и что w(X) = nw(X),
если пространство X полно по Чеху.
(d) Покажите, что если пространство X можно вложить в
совершенно нормальный компакт, то w (X) = nw (X).
3.9.F (Фролик [1960], Энгелькинг [1966]). Докажите, что
произведение счетного семейства полных по Чеху линделёфовых
пространств является полным по Чеху линделёфовым простран-
пространством (см. задачу 5.5.9 (Ь)).
Указание (Хейджер [1969]). Примените упр. 3.8.F (а).
3.9.G (Зенор [1970]). Заметьте, что пространство полно по
Чеху в том и только том случае, если оно является пределом
обратной последовательности локально компактных хаусдорфо-
вых пространств.
3.9.Н (Майкл [1963а]; для метрических пространств Арене
[1958]). Пусть S = {Xit я|}—- обратная последовательность не-
непустых полных по Чеху пространств, такая, что ^(Х() всюду
плотно в Xj при всех i, j> таких, что / ^ и Покажите, что для
каждого i проекция nt(X) предела X — lim S всюду плотна в Xi
и что, в частности, предел X не пуст.
Указание. Рассмотрим обратную последовательность
*S = {Z(, nj}, где Xi = $Xi и п) — продолжение отображения я'
на РХ; и рХ/. Положим G.==iir1 (J.), где nt — проекция пре-
предела X=limS в Xi. Покажите, что все Gt являются всюду
плотными О6-множествами в Х> и примените следствие 3.9.4.
3.9.L Заметьте, что каждое полное по Чеху пространство
является пространством точечно счетного типа, и выведите от-
отсюда, что полнота по Чеху не сохраняется замкнутыми отобра-
отображениями.
304 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
ЗЛО. СЧЕТНО КОМПАКТНЫЕ,
ПСЕВДОКОМПАКТНЫЕ И СЕКВЕНЦИАЛЬНО
КОМПАКТНЫЕ ПРОСТРАНСТВА
Топологическое пространство X называется счетно компакт-
компактным, если из каждого счетного открытого покрытия простран-
пространства X можно выбрать конечное подпокрытие. Значит, каждое
компактное пространство счетно компактно. Точнее, имеет место
3.10.1. Теорема. Топологическое пространство является компак-
компактом в том и только том случае, если оно счетно компактно и
обладает свойством Линделёфа. I
Примеры счетно компактных, но не компактных хаусдорфо-
вых пространств приводятся ниже (см. примеры 3.10.16—3.10.19).
Следующие две теоремы содержат характеристики счетно
компактных пространств в терминах центрированных семейств
множеств и в терминах локально конечных семейств множеств.
Доказательство первой теоремы можно получить, слегка видо-
видоизменив доказательство теоремы 3.1.1.
3.10.2. Теорема. Для произвольного пространства X следующие
условия равносильны:
(i) Пространство X счетно компактно.
(ii) Пересечение каждого счетного центрированного семей-
ства замкнутых в X множеств не пусто.
(ш) Для любой убывающей последовательности F\ zd F21Э ...
оо
непустых замкнутых в X множеств пересечение П Fi He пУ~
сто. I
3.10.3. Теорема. Для любого пространства X следующие уело*
вия равносильны:
(i) Пространство X счетно компактно.
(ii) Любое локально конечное семейство непустых множеств
в X конечно.
(Hi) Каждое локально конечное семейство одноточечных
подмножеств пространства X конечно.
(iv) Каждое бесконечное подмножество пространства X
имеет в X строгую предельную точку.
(v) Любое счетное бесконечное подмножество пространства
X имеет в X строгую предельную точку1).
1) Точка х называется строгой предельной точкой для множества Л, если
в любой ее окрестности лежит бесконечно много точек из А. Множество всех
таких точек обозначается через Ah. Если X — хаусдорфово пространство,
можно слово «строгую» в (iv) и (v) опустить. — Прим. перев.
ЗЛО. СЧЕТНО КОМПАКТНЫЕ ПРОСТРАНСТВА 305
Доказательство. Покажем сначала, что (i)=^(ii). Предполо-
Предположим, что (ii) не выполняется. Существует, таким образом, ло-
локально конечное семейство {Л*}!°=1 непустых подмножеств в X.
Легко проверяется, что непустые замкнутые множества F\,
оо
F%, ..., где Fi = U A-v составляют убывающую последователь-
оо
ность и что ["] /7/ = 0. Значит, по последней теореме, простран-
пространство X не счетно компактно.
Импликации (и)=^(ш), (iii)=^(iv) и (iv)=^(v) очевидны.
Для завершения доказательства достаточно показать, что (v)=>-
=^(i). Пусть (i) не выполняется. Тогда, по последней теореме,
найдется убывающая последовательность F\ zd F2 ^> ... непу-
оо
стых замкнутых в X множеств, такая, что f] Ft— 0. Выберем
по точке xi^Fi при i = l, 2, ... и положим Л—{xi, x2j ...}.
Множество А бесконечно, так как в противном случае некото-
некоторая его точка принадлежала бы бесконечному числу множеств
оо
Fi и было бы f| ргфф. Покажем, что Ан = 0, т. е. что (v)
не выполняется. Действительно, для каждого хеХ найдется
такое /, что x^Fr, тогда множество U = Х\ Fi является
окрестностью точки х и UftA cz {хи х2, ..., Xi-i} — конечное
множество. I
Следующая теорема является следствием теоремы 3.10.2.
3.10.4. Теорема. Каждое замкнутое подпространство счетно ком-
компактного пространства счетно компактно. 1
Заметим, что счетно компактное хаусдорфово пространство
может не быть нормальным; существуют даже не регулярные
счетно компактные хаусдорфовы пространства (см. упр. 3.10.В
или пример 5.1.40).
Доказательство следующей теоремы аналогично доказатель-
доказательству теоремы 3.1.10; провести его предоставляем читателю.
3.10.5. Теорема. Если f: X-+Y— непрерывное отображение
счетно компактного пространства X на топологическое простран-
пространство У, то пространство Y счетно компактно. В
Каждое подпространство вещественной прямой обладает
счетной базой; значит, в силу 3.8.1 и 3.10.1, каждое счетно ком-
компактное подпространство вещественной прямой компактно. При-
Применив 3.10.5 и 3.2.8, приходим к следующему утверждению.
20 Зак. 697
306 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
3.10.6. Теорема. Каждая непрерывная вещественная функция на
счетно компактном пространстве ограничена и принимает наи-
наименьшее и наибольшее значения. I
3.10.7. Теорема. Пусть X—счетно компактное пространство и
У— секвенциальное пространство (в частности, пространство с
первой аксиомой счетности). Тогда проекция р: Xy^Y-^-Y яв-
является замкнутым отображением.
Доказательство. Пусть F — замкнутое множество в 1ХУ-
Рассмотрим последовательность г/ь Уъ ••• точек множества
p(F) и любую точку y^limyt. Выберем точку Xi^X так, что-
чтобы было (xiyyi)^F при t = l, 2, ... . Если множество Л =
= {*i, X2, .-.} конечно, то найдется xgI, такое, что xki = x
для бесконечной последовательности k\ < k2 < ... натураль-
натуральных чисел. Тогда {ху у)^ lim(xfe., yki), откуда следует, что
(х, у)<= F = F и, значит, j/ep(F). С другой стороны, если А
бесконечно, то найдется х е Ah. Легко проверяется, что тогда
(х,у)^ F = F, откуда получаем j/Ep(F)% Так как простран-
пространство Y секвенциально, множество p(F) замкнуто в У. I
Характеристика счетно компактных пространств в терминах
проекций, аналогичная характеристике компактных пространств,
содержащейся в теореме 3.1.16, сформулирована в упр. 3.10.А
(Ь).
В последней теореме предположение, что Y — секвенциаль-
секвенциальное пространство, нельзя заменить предположением, что У есть
^-пространство. Действительно, можно определить счетно ком-
компактное хаусдорфово пространство X и компакт У, для которых
проекция р: XXY-+Y не является замкнутым отображением
(см. пример 3.10.16).
Читатель легко докажет следующую теорему.
3.10.8. Теорема. Сумма ф Xs, где Х3ф0 при всех s^S, яв-
ляется счетно компактным (хаусдорфовым) пространством в том
и только том случае, если все пространства Xs счетно компакт-
компактны (и хаусдорфовы), а множество S конечно. I
Тривиально видоизменяя доказательство теоремы 3.7.2, по-
получаем следующий результат:
3.10.9. Теорема. Если f: X-+Y — замкнутое отображение топо-
топологического пространства X и все прообразы точек f_i (у), счетно
компактны, то для каждого счетно компактного подпространства
Z czY прообраз f-1 (Z) счетно компактен. I
Из последней теоремы и теорем 3.10.5 и 3.7.20 вытекает
3.10.10. Теорема. Класс всех счетно компактных хаусдорфовых
пространств совершенен. 1
ЗЛО. СЧЕТНО КОМПАКТНЫЕ ПРОСТРАНСТВА 307
Счетная компактность не сохраняется, вообще говоря, ко-
конечными произведениями: в примере 3.10.19 ниже будут опреде-
определены два счетно компактных хаусдорфовых пространства, произ-
произведение которых не счетно компактно. Однако если один из со-
сомножителей является ^-пространством, то произведение двух
счетно компактных пространств счетно компактно.
3.10.11. Лемма. Если f: X-+Y — совершенное отображение, то
для каждого локально конечного семейства М- множеств в X
семейство {/(Л): Ле^} их образов локально конечно в У.
Доказательство. Из компактности прообразов точек при /
вытекает, что для каждого у е У найдется открытое множество
U(y)aX, содержащее f~l(y) и пересекающееся лишь с конеч-
конечным числом членов семейства зФ. Так как / замкнуто, из тео-
теоремы 1.4.13 следует, что у точки у есть окрестность V(y), для
которой f~l(V(y))cz U(y). Очевидно, окрестность V(y) пересе-
пересекается лишь с конечным числом членов семейства {/(Л): Ле
^} I
3.10.12. Лемма. Пусть {As XBS}S(=S, где |S|> К 0, — произволь-
произвольное локально конечное семейство непустых множеств в произ-
произведении XX Yy где X — любое топологическое пространство, а
У есть k-пространство. Тогда найдется бесконечное подмноже-
подмножество Sqcz S, такое, что либо семейство {Л5}5(_5о, либо семейство
{Bs}s€BSo локально конечно.
Доказательство. Если семейство {Ss}se=s локально конечно,
то годится So = S. Значит, можно предположить, что семейство
}s не локально конечно.
Покажем, что существуют компакт Z с У и бесконечное
множество So с S, для которых Z П Bs Ф0 при всех 5 е So.
Пусть у — любая точка пространства У, каждая окрестность ко-
которой пересекается с Bs для бесконечного числа s ^ S. Если
множество S(j/) = {5eS: y^Bs} бесконечно, можно положить
Z={y} и So = S(y)m Если, напротив, множество S(y) конечно,
то объединение B = [){BS: s^S\S(y)} не замкнуто, так как
у^В\В. В этом случае возьмем в качестве Z произвольное
компактное подмножество пространства У, для которого пере-
пересечение Zf]B = \j{Zf]Bs: s^S\S(y)} не замкнуто, и поло-
положим So ={s^S\S(y): гГ\В3Ф0}. Очевидно, что последнее
множество бесконечно.
Семейство {Л^Х (Z Л Bs)}s&s непустых подмножеств про-
пространства Xy^Z локально конечно. Применив теорему 3.7.1 и
лемму 3.10.11, заключаем, что семейство {Л5}5е5о тоже локально
конечно. ¦
20*
308 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
Из эквивалентности условий (i) и (ш) в 3.10.3 и последней
леммы получается
3.10.13. Теорема. Произведение счетно компактного простран-
пространства X и счетно компактного k-пространства Y счетно компакт-
компактно. I
Первое из двух приведенных ниже следствий вытекает из
теоремы 3.10.9, а второе следует из теорем 3.10.7 и 3.10.9.
3.10.14. Следствие. Произведение X\Y счетно компактного
пространства X и компактного пространства Y счетно компакт-
компактно. I
3.10.15. Следствие. Произведение XX Y счетно компактного
пространства X и счетно компактного секвенциального простран-
пространства Y счетно компактно. I
Счетно компактные пространства были определены и изу-
изучались раньше компактных пространств. Сначала казалось, что
они составляют класс, более отвечающий сути вещей. До неко-
некоторой степени, это объяснялось тем, что для широкого и важ-
важного класса метризуемых пространств оба определения равно-
равносильны (см. теорему 4.1.17). В те времена счетно компактные
пространства именовались компактными пространствами, а наши
компактные пространства назывались бикомпактными простран-
пространствами. Сейчас в ходу терминология, принятая нами в этой кни-
книге1). Главная причина превосходства компактных пространств
над счетно компактными пространствами — в том, что компакт-
компактность мультипликативна, в то время как счетная компактность
даже не конечно мультипликативна (см. пример 3.10.19).
3.10.16. Пример. Пространство Wo всех счетных ординалов (см.
пример 3.1.27) служит примером счетно компактного неком-
некомпактного пространства.
Ясно, что пространство Wo не компактно, — ведь оно вло-
вложено в пространство W = WoU{o>i} в качестве не замкнутого
подпространства. С другой стороны, для каждого счетного бес-
бесконечного множества A a WQ найдется xQ < (оь такое, что Лс
с1^1= [0, Хо] cz Wo. Но W\ компактно как замкнутое подпро-
подпространство в W. Значит, Ah = 0, а это показывает, что простран-
пространство Wo счетно компактно.
Легко проверяется, что проекция р: U7oX W->> W не являет-
является замкнутым отображением (см. теорему 3.10.7). I
3.10.17. Пример. Мы определим теперь всюду плотное подпро-
подпространство в /с, которое счетно компактно, но не компактно.
]) См. примечание переводчика на стр. 208. — Прим. перев.
ЗЛО. СЧЕТНО КОМПАКТНЫЕ ПРОСТРАНСТВА 309
Пусть Iе = И 1и где U = I при /gJ?, и X — подпространство
пространства /с, состоящее из всех тех точек {xt}> не более чем
счетное число координат которых отлично от нуля. Так как X —
всюду плотное в Iе подпространство, отличное от всего /с, про-
пространство X не компактно. Пусть А — произвольное счетное бес-
бесконечное подмножество в I, В силу определения пространства
X, найдется счетное множество Ro<^R, такое, что pt(x) = O при
всех хе^и всех / е /?\ /?о, где pt — проекция пространства
Iе на It. Значит, А является подмножеством произведения
П Xit где Xt = It при t е= Ro к Xt = {0} при t e R\R0. Так
tR
R
как последнее произведение компактно, у множества А есть пре-
предельная точка в Ц Xt. Так как Ц Xt cz X, множество А имеет
t<=R teR
предельную точку и в X; значит, X счетно компактно. 1
3.10.18. Пример. Еще одним примером счетно компактного не
компактного пространства может служить пространство Х =
= pyv\{x}, где х е $N\ N. Так как X всюду плотно в $N
и не совпадает с piV, пространство X не компактно. С другой сто-
стороны, для каждого счетного бесконечного подмножества А про-
пространства Xa$Nt в силу теоремы 3.6.14, |Л| = 2С, откуда сле-
следует, что Ан(]Хф0. Таким образом, в X есть предельная для
множества А точка. Значит, пространство X счетно компактно. I
3.10.19. Пример. Определим теперь счетно компактные тихонов-
тихоновские пространства X и К, такие, что произведение XX Y не
счетно компактно. Они будут подпространствами пространства
PJV, подчиненными условиям: X[}Y = $N и XflY = N.
Для каждого М cz $N обозначим через &(М) семейство всех
счетных бесконечных подмножеств множества Му и пусть / —
отображение, которое каждому члену А семейства 3*($N) сопо-
сопоставляет некоторую предельную точку множества А в простран-
пространстве рлл
Полагая Хо = N и
ДЦ 0<а<ш„
мы определяем по трансфинитной индукции трансфинитную по-
последовательность Хо, Хи ••-, Ха, ..-, а < ©ь подмножеств про-
пространства pAf. Пространство Х= [} Ха счетно компактно, так
a<wi
как каждое А^0>{Х) содержится в некотором Ха и имеет, сле-
следовательно, предельную точку в Ха+\ и тем более в X. Легко
показывается по трансфинитной индукции, что | Ха \ ^ с • с +
+(с.с)*о = с. Значит, \Х\^с. Положим Y = N[)($N\X). По
310 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
теореме 3.6.14, \А | = 2С для каждого Ле^(У). Значит, каждое
бесконечное подмножество пространства У имеет предельную
точку в У и пространство У счетно компактно.
Рассмотрим теперь произведение XX У и обозначим через
До пересечение множества XX У и диагонали А произведения
$NX$N. Так как X()Y = N, имеем До ={A, 1), B, 2), ...}.
Множество {i} открыто в $N при i = l, 2, ..., поэтому До —
открытое дискретное подпространство пространства XX У.
С другой стороны, так как Д — замкнутое множество в РЛ^Х PN,
множество До замкнуто в XX У, а это показывает, что про-
пространство XX У не счетно компактно.
По теореме 3.10.13, ни X, ни У не являются ^-пространства-
^-пространствами. В частности, X и У не полны по Чеху (см. теорему 3.9.5). I
Отметим в связи с последним примером, что можно по-
построить хаусдорфово пространство X, все конечные степени ко-
которого счетно компактны, а Х*° не счетно компактно. Отсюда
следует, в частности, что предел обратной последовательности
счетно компактных пространств может не быть счетно компакт-
компактным пространством (последнее можно установить непосред-
непосредственно, видоизменив конструкцию в примере 3.10.19 таким об-
образом, чтобы получилась убывающая последовательность Х\ =>
zd Х2 и> ... счетно компактных подпространств пространства рЛ/\
для которой fl Xi = N).
Изучим теперь еще один класс пространств, имеющих пря-
прямое отношение к компактным пространствам.
Топологическое пространство X называется псевдокомпакт-
псевдокомпактным, если X — тихоновское пространство и каждая непрерывная
вещественная функция на X ограничена. Как легко проверить,
последнее условие равносильно тому, что каждая непрерывная
вещественная функция на X принимает наибольшее и наимень-
наименьшее значения. Из теоремы 3.10.6 следует
3.10.20. Теорема. Каждое счетно компактное тихоновское про-
пространство псевдокомпактно. I
Для нормальных пространств справедлива и обратная импли-
импликация.
3.10.21. Теорема. Каждое псевдокомпактное нормальное про-
странство счетно компактно.
Доказательство. Пусть X — нормальное не счетно компакт-
компактное пространство. Существует множество А={х\9 х2, ...}с:Х,
такое, что х{ ф х\ при i ф j и Ай = 0. Ясно, что А — замкнутое
дискретное подпространство пространства X. По теореме Тит-
це — Урысона, существует непрерывная функция /: X->-/?, для
ЗЛО. СЧЕТНО КОМПАКТНЫЕ ПРОСТРАНСТВА 311
которой f(Xi) — i при / = 1, 2, ... . Так как функция / не огра-
ограничена, пространство X не псевдокомпактно. I
Следующие две теоремы характеризуют псевдокомпактные
пространства в терминах локально конечных и центрированных
семейств множеств.
3.10.22. Теорема. Для любого тихоновского пространства X сле-
следующие условия равносильны:
(i) Пространство X псевдокомпактно.
(и) Каждое локально конечное семейство непустых откры-
открытых множеств в X конечно.
(ш) Каждое локально конечное покрытие пространства X
непустыми открытыми множествами конечно.
(iv) Каждое локально конечное открытое покрытие простран-
пространства X содержит конечное подпокрытие.
Доказательство. Покажем сначала, что (i)=^(ii). Предпо-
Предположим, что условие (ii) не выполняется. Тогда существует ло-
локально конечное семейство {и^=1 непустых открытых множеств
в X. Выберем по точке xi е [// при i = 1, 2, ... . Так как X —
тихоновское пространство, при / = 1, 2, ... найдутся функции
/(•: X-+R, такие, что fi(xt) = i и fi(X\ ?/;)<= {0}. В силу локаль-
ной конечности семейства {?/j}°li> формула f(x)=^i\fi(x)\
i = \
определяет некоторую непрерывную функцию /: X-+R. Так как
функция / не ограничена, пространство X не псевдокомпактно.
Импликации (ii)=^(iii) и (iii)=^(iv) очевидны. Для завер-
завершения доказательства остается показать, что (iv)=^(i). Пусть
/ — произвольная непрерывная вещественная функция на про-
пространстве X, удовлетворяющем условию (iv). Ясно, что
{f^((i —I, i+l)): i=0, ±1, ±2,...}—локально конечное
открытое покрытие пространства X. Из существования в этом
покрытии конечного подпокрытия следует, что функция f огра-
ограничена. I
3.10.23. Теорема. Для произвольного тихоновского простран-
пространства X следующие условия равносильны:
(i) Пространство X псевдокомпактно.
(ii) Для каждой убывающей последовательности W\ =>
оо
zd W2 =з ... непустых открытых множеств в X пересечение f| Wt
не пусто.
(Hi) Для каждого счетного центрированного семейства
оо
{Vi}T=\ открытых множеств в X пересечение f| Vt не пусто.
312 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
Доказательство. Покажем сначала, что (i)=^(ii). Пусть X —
псевдокомпактное пространство и W\ zd W2 => ... — убывающая
последовательность непустых открытых множеств в X. Из тео-
теоремы 3.10.22 следует, что семейство {Wi}™==x не локально ко-
конечно. Значит, существует точка х^Х, каждая окрестность ко-
которой пересекает бесконечно много множеств Wi. Ясно, что
Для доказательства импликации (ii)=^(iii) достаточно рас-
рассмотреть последовательность V\t V\ f] У2, •.. . Наконец, (ш)=ф-
=>(i), так как если существует не ограниченная непрерывная
функция /: X^R, то семейство {FJJlp где Vi ={x: \f(x) |> i}f
00
центрировано, и тем не менее f] F/—0. I
Из определения псевдокомпактности следует
3.10.24. Теорема. Если f\ X-+Y — непрерывное отображение
псевдокомпактного пространства X на тихоновское простран-
пространство У, то Y псевдокомпактно, 1
Читатель легко докажет следующую теорему.
3.10.25. Теорема. Сумма ф Xst где Х3ф0 при s<=S, являет-
ся псевдокомпактным пространством в том и только том случае,
если все пространства Xs псевдокомпактны и множество S ко-
конечно. I
Как показано ниже в примере 3.10.29, псевдокомпактность не
наследуется, вообще говоря, замкнутыми подпространствами.
Так как, очевидно, псевдокомпактность наследуется открыто-
замкнутыми подпространствами, из теоремы 3.7.29 следует, что
псевдокомпактность не сохраняется (вообще говоря) в сторону
прообраза совершенными отображениями даже в классе тихо-
тихоновских пространств (см. упр. 3.10.G).
Псевдокомпактность не конечно мультипликативна. Действи-
Действительно, пространства X и У, определенные в примере 3.10.19,
псевдокомпактны, а произведение XX У содержит D(Ko) = Ao
в качестве открыто-замкнутого подпространства. Значит, произ-
произведение XX У не псевдокомпактно. Оказывается, однако, что
если хотя бы один из сомножителей является ^-пространством,
то произведение двух псевдокомпактных пространств псевдо-
псевдокомпактно.
3.10.26. Теорема. Произведение Xy(Y псевдокомпактного про-
пространства X и псевдокомпактного k-пространства У псевдоком-
псевдокомпактно.
ЗЛО. СЧЕТНО КОМПАКТНЫЕ ПРОСТРАНСТВА 313
Доказательство. Достаточно заметить, что каждое непустое
открытое в декартовом произведении Xyjt множество содержит
непустое открытое множество вида UX,V, применить лем-
лемму 3.10.12 и воспользоваться эквивалентностью условий (i) и
(и) в теореме 3.10.22. I
3.10.27. Следствие. Произведение псевдокомпактного простран-
пространства X и компакта Y псевдокомпактно. ¦
3.10.28. Следствие. Произведение Xyjf псевдокомпактного про-
пространства X и псевдокомпактного секвенциального пространства
У псевдокомпактно. I
Можно построить пространство X, все конечные степени ко-
которого псевдокомпактны, но Х*° не псевдокомпактно1). Отсюда
следует, в частности, что предел обратной последовательности
псевдокомпактных пространств может не быть псевдокомпакт-
псевдокомпактным пространством (последнее можно установить непосред-
непосредственно, применив задачу 3.12.23(с): см. указание к задаче
6.3.25).
Приведем теперь пример псевдокомпактного пространства Ху
содержащего дискретное пространство D(Ko) в качестве зам-
замкнутого подпространства. Этот пример показывает, что псевдо-
псевдокомпактное пространство не обязано быть счетно компактным
и что псевдокомпактность не всегда наследуется замкнутыми
подпространствами.
3.10.29. Пример. R силу следствия 3.6.8, стоун-чеховская ком-
пактификация $N является подпространством стоун-чеховской
компактификации $R. Рассмотрим пространство X=$R\
\($N \ N). Ясно, что X содержит дискретное пространство
N = D(&o) в качестве замкнутого подпространства. Покажем,
что X псевдокомпактно. Предположим, что нашлась не ограни-
ограниченная непрерывная функция f: X-^R. Так как множество
R\ N всюду плотно в X, найдется последовательность х\у х2, ...
различных точек множества R\N, такая, что \f(xi)\> i при
t = l, 2, ... . Так как функция / непрерывна, множество Л =
= {хи х2, .-.} не имеет предельных точек в X. Значит, А —
замкнутое в R дискретное^ подпространство пространства X.
В силу следствия 3.6.4, А (] N = А П Р# = 0, т. е. А сг X. Следо-
Следовательно, Л = Л — бесконечный дискретный компакт. Получен-
Полученное противоречие показывает, что X псевдокомпактно2). 1
1) Отметим, что если пространство G топологической группы псевдоком-
псевдокомпактно, то и любая степень пространства G псевдокомпактна (см. Комфорт,
Росс [1966*]). — Прим. перев.
2) Можно построить псевдокомпактное пространство X, каждое счетное
подпространство которого замкнуто и дискретно. Примеры таких пространств,
обладающих дополнительными интересными свойствами, построены Д. Б. Шах-
Шахматовым и Е. А. Резниченко. — Прим. перев.
314 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
Секвенциальная компактность — еще одно свойство, связан-
связанное с компактностью. Топологическое пространство X называет-
называется секвенциально компактным, если каждая последовательность
точек вХ содержит сходящуюся подпоследовательность. Из экви-
эквивалентности условий (i) и (v) в теореме 3.10.3 следует
3Л0.30. Теорема. Каждое секвенциально компактное простран-
пространство счетно компактно. I
Обратная импликация не верна. Существуют даже не сек-
секвенциально компактные компакты: в силу следствия 3.6.15,
стоун-чеховская компактификация $N является таким простран-
пространством (см. пример 3.10.38). Однако имеет место
3.10.31. Теорема. Секвенциальная компактность и счетная ком-
компактность равносильны в классе секвенциальных Т ^пространств
и, в частности^ Т^пространств с первой аксиомой счетности.
Доказательство. Достаточно показать, что в любой последо-
последовательности хи *2, ... точек счетно компактного секвенциаль-
секвенциального пространства X есть сходящаяся подпоследовательность.
Конечно, можно предположить, что х-г Ф х\ при i ф /. Пусть х —
какая-нибудь предельная точка для бесконечного множества
А = {хи х2у ...}. Множество Л\{л:} не замкнуто, так как х е
gA{x}. Но пространство X секвенциально. Значит, в множе-
множестве Л\{лс} есть последовательность, сходящаяся к некоторой
точке дополнения к Л\{л:}. Расположив подходящим образом
члены этой последовательности, мы получим сходящуюся под-
подпоследовательность последовательности х\, х2, ... . ¦
Из последней теоремы следует, что пространство Wo всех
счетных ординалов секвенциально компактно как счетно ком-
компактное пространство с первой аксиомой счетности. Это пример
секвенциально компактного некомпактного пространства. Заме-
Заметим в связи с последней теоремой, что существуют секвенциаль-
секвенциально компактные пространства, не являющиеся секвенциальными
пространствами. К числу таких пространств относится, очевид-
очевидно, пространство всех ординалов ^соь Существуют также не
регулярные секвенциально компактные хаусдорфовы простран-
пространства (см. упр. 3.10.В и пример 5.1.40).
Следующие три теоремы вытекают непосредственно из опре-
определения секвенциальной компактности.
3.10.32. Теорема. Если f: X—>¦ У—непрерывное отображение
секвенциально компактного пространства X на топологическое
пространство У, то У секвенциально компактно. Щ
На примере отображения компактного, но не секвенциально
компактного пространства на одноточечное пространство видно,
что секвенциальная компактность не сохраняется в сторону про-
прообраза совершенными отображениями.
3.10. СЧЕТНО КОМПАКТНЫЕ ПРОСТРАНСТВА 315
3.10.33. Теорема. Каждое замкнутое подпространство секвен-
секвенциально компактного пространства секвенциально компактно. I
3.10.34. Теорема. Сумма ф XS9 где Xs?=0 при seS, секвен-
s<=S
циально компактна в том и только том случае, если все простран-
пространства Xs секвенциально компактны и множество S конечно. 1
В заключение этого параграфа приведем три теоремы о про-
произведениях секвенциально компактных пространств.
3.10.35. Теорема. Произведение любого счетного семейства сек-
секвенциально компактных пространств является секвенциально
компактным пространством.
Доказательство. Пусть {Х*}^ — счетное семейство секвен-
секвенциально компактных пространств и ги г2, Zs, ..., где ?/
последовательность точек произведения П^. Последователь-
ностьл;}, х\у х\> .. .точек пространства Х\ содержит сходящуюся
подпоследовательность x*htf д^**-1, x^lt ...; пусть х\ — предел
этой подпоследовательности. Аналогично последовательность
X2ltl> X22tl> X2*'l> • • • точек пространства Х2 содержит сходящую-
сходящуюся подпоследовательность jc*1»2, лф*2> лф'2 ...; пусть Х2 — предел
этой подпоследовательности. По индукции определяем для / —
= 3, 4, ... подпоследовательность я*1.', хк.2>1, хк^>1, ...последо-
...последовательности xk.ui~l, x^(~lt я*3*', ..., сходящуюся к точке
Xi^Xi, Заметим, что если опустить первые / — 1 членов после-
последовательности &i, ь &2,2, &з, з, ..., то она станет подпоследова-
подпоследовательностью последовательности &i,/, &2, *, &з,;, .... Теперь не
составляет труда показать, применив предложение 2.3.34, что
точка {Xi} ^JJ.X( является пределом подпоследовательности
zk%v ... последовательности zu z2, г3, ... . ¦
3.10.36. Теорема. Произведение ХУ^У счетно компактного про-
пространства X и секвенциально компактного пространства Y счетно
компактно.
Доказательство. Рассмотрим счетное бесконечное множество
A = {zu z2, Z3, ...}czXXY, где Zi = (Xi,yi) при t'=l, 2, ... и
Zi Ф Zjt если 1ф\. Пусть #*„ г/^2, ... — некоторая подпоследова-
подпоследовательность последовательности y\f г/2, ..., сходящаяся к точке
у е У. Если множество {Xkv Xk2, ...} конечно, то найдутся точка
х^Х и подпоследовательность kmi, km2, ... последовательности
ku k2y ,.., такие, что xkfn = х при i = 1,2, ... . Если множество
{Xkt> Xk2> •..} бесконечно, то у него есть строгая предельная
316 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
точка Jtel Легко видеть, что и в том, и в другом случае
является строгой предельной точкой для Л. I
3.10.37. Теорема. Произведение XX Y псевдокомпактного про-
пространства X и секвенциально компактного тихоновского про-
пространства Y псевдокомпактно.
Доказательство. Предположим, что нашлась не ограничен-
ограниченная непрерывная функция f: XX Y->R, и выберем точки zt =
= (Xitj//)eXX Y так, чтобы было \f(zi) \ ^ i при / = 1,2,....
Пусть tjhxy #ь>. • • *— подпоследовательность последовательности
Ни Уъ • •., сходящаяся к точке i/gK Подпространство Уо=
= {#> Укху yk2> ...} cz У является компактом; поэтому простран-
пространство XX^о псевдокомпактно в силу следствия 3.10.27. Тем не
менее непрерывная функция /|ХХУо: Xy^Y0~^R не ограни-
ограничена. Это противоречие показывает, что каждая непрерывная
вещественная функция на XX Y ограничена. 1
Так как существуют секвенциально компактные хаусдорфовы
пространства, не являющиеся ^-пространствами (см.упр. 3.10.Н),
теоремы 3.10.36 и 3.10.37 не зависят от теорем 3.10.13 и 3.10.26.
3.10.38. Пример. Мы заметили выше, применив следствие 3.6.15
что пространство $N не секвенциально компактно. Это можно
доказать и непосредственно. Последовательность 1, 2, ... точек
пространства р# не содержит никакой сходящейся подпоследо-
подпоследовательности, так как для любой возрастающей последователь-
последовательности k\ < k2 <Z ... положительных целых чисел замыкания
множеств A={kx,kz9kb, ...} и В={&2, А4, &е, ...} в piV не пе-
пересекаются, а отсюда вытекает, что последовательность k\, k%,
из, ... не сходится. 1
Как показано в примере 3.6.20, пространство $N можно вло-
вложить в канторов куб Dc. Значит, по теореме 3.10.33, канторов
куб Dz не секвенциально компактен, и мы видим, что предполо-
предположение о счетности в теореме 3.10.35 существенно.
Из того, что Z)c не секвенциально компактно, и примера 2.5.3
вытекает, что предел обратного спектра секвенциально компакт-
компактных пространств может не быть секвенциально компактным про-
пространством. С другой стороны, из теорем 3.10.33 и 3.10.35 сразу
следует, что предел обратной последовательности секвенциально
компактных пространств является секвенциально компактным
пространством.
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
Счетно компактные пространства были введены Фреше в
[1906]. Характеристика счетной компактности условием (iv)
теоремы 3.10.3 была установлена Хаусдорфом в [1914]. Теоре-
ЗЛО. СЧЕТНО КОМПАКТНЫЕ ПРОСТРАНСТВА 317
ма 3.10.7 доказана Флейшером и Франклином в [1967] (Ханаи
[1961] и Исивата [1963] доказали эту теорему при более силь-
сильных предположениях, что Y — пространство с первой аксиомой
счетности и что У — пространство Фреше — Урысона соответ-
соответственно). Теорема 3.10.10 была установлена Хенриксеном и Ис-
беллом в [1958]. Теорема 3.10.13 доказана Ноблом в [1969]
(следствие 3.10.14 получено Ю. М. Смирновым в [1951d], а след-
следствие 3.10.15 — Франклином в [1965]). В примере 3.10.17, при-
приведенном Понтрягиным в [1954], применено важное понятие
2-произведения; оно обсуждается также в упр. 3.10.D и зада-
задачах 2.7.13, 2.7.14, 3.12.23 и 4.5.12. Пример 3.10.19 был построен
Новаком в [1953а] (данное нами описание следует статье Фро-
лика [1959]). Сходный пример был приведен Терасакой в [1952]
Существование тихоновского пространства X, все конечные сте-
степени которого счетно компактны, тогда как Х^° не счетно ком-
компактно, было установлено Фроликом в [1967]. В примере Фро-
лика пространство Х*° даже не псевдокомпактно. Однако в
случае псевдокомпактности аналогичные примеры можно опре-
определить проще (см. Комфорт [1967] и Фролик [1967а]).
Псевдокомпактные пространства были определены Хьюит-
том в [1948]; в этой его статье были доказаны теоремы 3.10.20
и 3.10.21. Эквивалентность псевдокомпактности условиям (ii),
(iii) и (iv) теоремы 3.10.22 была замечена Гликсбергом в [1952],
Керстаном в [1957] и Ю. М. Смирновым в [1954] соответствен-
соответственно. Теорема 3.10.23 приведена Колмесом в [1951]. Теорема
3.10.26 установлена Тамано в [I960] (следствие 3.10.27 было
независимо доказано Гликсбергом в [1959] и Мрувкой в [1959];
следствие 3.10.28 было доказано Бэгли, Коннеллом и Макнайтом
в [1958] при более сильном предположении, что пространство Y
удовлетворяет первой аксиоме счетности). Пример 3.10.29 при-
приведен Катетовым в [1951а].
Понятие секвенциально компактного пространства, как и
теоремы 3.10.30 и 3.10.32—3.10.35, долгое время принадлежало
топологическому фольклору. Возникновение этого понятия свя-
связано с характеристикой компактности в классе метрических про-
пространств. Теорема 3.10.31 была доказана Франклином в [1965]
(эквивалентность секвенциальной компактности и счетной ком-
компактности в метрических пространствах была установлена Хаус-
дорфом в [1914]). Теорема 3.10.36 доказана Мрувкой в [1959]
(Рыль-Нардзевский в [1954] доказал эту теорему при более
сильном предположении, что Y счетно компактно и удовлетво-
удовлетворяет первой аксиоме счетности). Теорема 3.10.37 появилась в
статье Скарборо и А. Стоуна [1966].
В связи с тем что Dc не секвенциально компактно (см. при-
пример 3.10.38), а каждый компакт мощности < 2**1 секвенциально
318 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
компактен (см. задачу 3.12.11 (е)), возникает вопрос, является
ли секвенциально компактным пространство ?>Kl. Как показано
Бутом в [1974], ответ на этот вопрос не зависит от обычных
аксиом теории множеств. Иными словами, существуют модели
теории множеств, в которых D*1 является секвенциально ком-
компактным пространством, и есть модели, в которых D**1 не сек-
секвенциально компактно.
Дальнейшие результаты о произведениях счетно компактных,
псевдокомпактных и секвенциально компактных пространств
можно найти в работах Гликсберга [1959], Скарборо и А. Стоу-
Стоуна [1966], Кендерова [1968], Стефенсона [1968] и Нобла [1969].
УПРАЖНЕНИЯ
3.10.А. (а) Заметьте, что топологическое пространство X
счетно компактно в том и только том случае, если каждое его
счетное замкнутое подпространство компактно.
(Ь) (Ханаи [1961]). Проверьте, что пространство X счетно
компактно в том и только том случае, если проекция р: XX
X Л(Ко)->-Л(Ко) является замкнутым отображением (см. тео-
теоремы 3.1.16 и 3.10.7 и задачу 3.12.14(а)).
3.10.В (Бурбаки [1948]). Покажите, что пространство, кото-
которое получается из пространства W всех ординалов =^а>ь если
дополнительно объявить множество Z всех счетных предельных
ординалов замкнутым (см. пример 1.5.7), является нерегуляр-
нерегулярным счетно компактным (и даже секвенциально компактным)
хаусдорфовым пространством (см. пример 5.1.40).
3.10.С (П. С. Александров и Урысон [1929]). Положим Х =
= CoUC1czi?2, где Со= {(*,0): 0 < х ^ 1} и Ci={(*, 1):
0 ^ jc < 1}, и возьмем на X топологию, порожденную базой, со-
состоящей из множеств вида
{{xfi)^X: *о— 1/А < х <х0 и t = 0, 1}|Д(*о,О)},
где 0<jc0^1 и Л = 1, 2, ..., а также из множеств вида
{(xJ)<=X; хо<х<Хо + 1/Ь t = 0, l}U{(*o, 1)},
где 0 ^ хо < 1 и k= 1, 2, .... Так полученное пространство X
называется две стрелки.
(a) Заметьте, что подпространства Со и С\ пространства X
гомеоморфны прямой Зоргенфрея. Выведите отсюда, что про-
пространство X наследственно сепарабельно, наследственно линде-
лёфово и, значит, совершенно нормально.
Указание. См. упр. 2.1.1, 3.8.А(Ь) и пример 3.8.14.
(b) Докажите, что пространство X компактно, и выведите
отсюда, что прямая Зоргенфрея не полна по Чеху.
ЗЛО. СЧЕТНО КОМПАКТНЫЕ ПРОСТРАНСТВА 319
Указание. Примените теорему 3.10.1.
(с) Заметьте, что пространство X2 не наследственно нор-
нормально, и выведите отсюда, что ни наследственная нормаль-
нормальность, ни совершенная нормальность не сохраняются в сторону
прообраза при открытых совершенных отображениях, при ко-
которых прообразы точек совершенно нормальны.
3.10.D (Нобл [1970]). Пусть {Xs}ssS — семейство топологи-
топологических пространств и a ={as} —точка произведения Ц Xs. Че-
рез 2 (а) обозначим подпространство пространства Ц Xs, co-
coses
стоящее из всех точек x={xs}, для которых множество 5(х) =
= {5 gS: xs ?= as} счетно. Докажите, что если все пространства
Xs удовлетворяют первой аксиоме счетности, то 2 (а)—про-
(а)—пространство Фреше — Урысона. Отсюда следует, в частности, что
пространство, рассмотренное в примере 3.10,17, является про-
пространством Фреше — Урысона (и, значит, ^-пространством); про-
проверьте, что оно не полно по Чеху.
Указание. Пусть х = {хя} еЛс2(а) и {UStt}^x — база
пространства Xs в точке xs. Определите по индукции последо-
последовательность х\, Х2, -•- точек множества А так, чтобы было
H USt iX И Xs\ где Si = {sft k: 0 ^ /, k < /} и
индексы
5/,^ определяются равенствами S(xi) = {sito9 Sifu •••} и x0 = x.
Покажите, что х = limxt.
3.10.E. (а) (Хьюитт [1948]). Покажите, что тихоновское
пространство X псевдокомпактно в том и только том случае,
если нарост $Х\Х не содержит никакого непустого множества
типа G6 в рХ
(b) (Колмес [1951], Гликсберг [1952]). Докажите, что ти-
тихоновское пространство X псевдокомпактно в том и только том
случае, если X удовлетворяет теореме Дини, т. е. если для
каждой последовательности {ft} непрерывных вещественных
функций на X, такой, что fi(x)^.fi+\(x) при всех х е X и i =
= 1,2, ..., для которой существует функция / е Rx> такая, что
f(x) = limfi(x) при всех xel, имеет место соотношение / =
= lim/,-, т. е. последовательность {ft} равномерно сходится к /
(см. лемму 3.2.18).
(c) Заметьте, что если каждое замкнутое подпространство
пространства X псевдокомпактно, то пространство X счетно
компактно.
(d) (Колмес [1951]). Покажите, что псевдокомпактность на-
наследуется каноническими замкнутыми множествами.
(e) (Колмес [1952]). Заметьте, что теорема Бэра о катего-
320 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
рии выполняется в регулярных счетно компактных простран-
пространствах и в псевдокомпактных пространствах.
3.10.F (Мрувка [1954]). Покажите, что пространство X,
определенное в упр. 3.6.1 (а), псевдокомпактно, но не счетно
компактно.
3.10.G (Ханаи и Окуяма [1962]; для открытых совершенных
отображений — Пономарев [1960а]). Если f: X~*Y— открытое
отображение тихоновского пространства X на псевдокомпактное
пространство У, при котором образ каждого функционально
замкнутого подмножества пространства X замкнут в У и все
прообразы точек псевдокомпактны, то пространство X псевдо-
псевдокомпактно.
Указание. Примените упр. 1.5.L (а).
3.10.Н. Действуя по той же схеме, что и в примере 3.1.27,
определите на множестве всех ординалов ^оJ некоторую топо-
топологию (см. задачу 1.7.4) и проверьте, что подпространство, ко-
которое получается, если удалить все ординалы, конфинальные соь
секвенциально компактно, но не является ^-пространством.
3.10.1. Топологическое пространство X называется локально
секвенциально компактным, если для каждой точки х е X и
каждой ее окрестности U найдется окрестность V точки х, такая,
что V секвенциально компактно и Fez U.
(a) Проверьте, что теорема 3.3.17 остается справедливой и
в том случае, когда У — секвенциальное, а X — локально сек-
секвенциально компактное пространство.
(b) (Бёме [1965]). Докажите, что произведение XX У сек-
секвенциальных пространств секвенциально, если пространство X
локально секвенциально компактно (см. упр. 2.3.К(а)).
Указание. Примените (а) и упр. 2.4.G(b).
3.11. ВЕЩЕСТВЕННО ПОЛНЫЕ ПРОСТРАНСТВА
Топологическое пространство X называется вещественно пол-
полным (или R-полным, или полным по Хьюитту), если оно яв-
является тихоновским пространством и не существует тихонов-
тихоновского пространства X, которое удовлетворяло бы следующим
двум условиям:
(RC1) Существует гомеоморфное вложение г: Х-^R, такое, что
7
(RC2) Для каждой непрерывной вещественной функции /: Х-*
->•/? найдется непрерывная функция f: X-+R, такая, что
1) Вещественно полные пространства именуются также Q-пространствами,
вещественно компактными пространствами, функционально замкнутыми про-
пространствами, Я-компактными пространствами, пространствами Хьюитта —
Нахбина и полными по Хьюитту пространствами.— Прим. перев.
3.11. ВЕЩЕСТВЕННО ПОЛНЫЕ ПРОСТРАНСТВА 321
Из этого определения сразу следует, что каждый компакт
является вещественно полным пространством. Точнее, имеет ме-
место.
ЗЛЫ. Теорема. Топологическое пространство является компак-
компактом в том и только том случае, если оно псевдокомпактно и
вещественно полно.
Доказательство. Каждый компакт псевдокомпактен и веще-
вещественно полон. Если не компактное пространство X вещественно
полно, то, так как X ф рХ, найдется непрерывная функция f:
X->•/?, которую нельзя непрерывно продолжить на $Х. Ясно,
что функция / не ограничена; следовательно, X не псевдоком-
псевдокомпактно. I
3.11.2. Примеры. Из последней теоремы следует, что простран-
пространства, рассмотренные в примерах 3.10.16—3.10.19 и 3.10.29, не
вещественно полны. В частности, заключаем, что существует не
вещественно полное локально компактное хаусдорфово про-
пространство. I
Теперь мы установим важную характеристику вещественно
полных пространств и выведем из нее несколько следствий. Две
дальнейшие характеристики полных пространств будут даны в
теоремах 3.11.10 и 3.11.11.
3.11.3. Теорема. Топологическое пространство вещественно пол-
полно в том и только том случае, если оно гомеоморфно замкнутому
подпространству произведения некоторого множества копий ве-
вещественной прямой.
Доказательство. Пусть X—вещественно полное простран-
пространство. Через &~ обозначим семейство всех непрерывных ве-
вещественных функций на X и рассмотрим отображение
F= A f: X-+ П Rf> где Rf = R при fe#". Так как про-
f?" f?~
f f
странство X тихоновское, из теоремы о диагональном отображе-
отображении следует, что F— гомеоморфное вложение. Положим
X = F(X)cz Ц Rf- Для каждой непрерывной вещественной
функции f: X—*R найдется непрерывная функция f: X—»R> та-
такая, что JF = f, а именно такой функцией является сужение
pf\X проекции pfi Ц Rf-+Rf. Значит, по определению веще-
ственной полноты, ^=/7(Х), т. е. пространство X гомеоморфно
замкнутому подпространству F(X) произведения Ц Rfl
Рассмотрим теперь произвольное замкнутое подпростран-
подпространство X произведения Ц R3, где Rs^ R при sgS, и пусть
S
21 Зак. 697
322 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
даны тихоновское пространство X и гомеоморфное вложение г:
Х-*Х, удовлетворяющие условию (RC2). Очевидно, можно пред-
предположить, что г(Х)=Х. Для каждого seS найдется непре-
непрерывная функция ps: X^~RS = R, такая, что psr=ps. Положим
F— A р8: X->II/?S. TaK Ka^ Fr(x) = x при всех xel, то
5 S
F(X)=F(r(X)) cFr(X)=X=X; таким образом, сужение Fx
отображает X на X При всех х&Х имеем rFx(r(x))= r(x).
Значит, отображение rFx: X-+X при сужении на г(Х) совпа-
совпадает с idr(*). Из теоремы 1.5.4 теперь следует, что rFx = id^.
Так как rFx(X)czr(X), заключаем, что г(Х) — Х. Следователь-
Следовательно, не существует тихоновского пространства X, которое удов-
удовлетворяло бы условиям (RC1) и (RC2), т. е. пространство X
вещественно полно. I
Следующая теорема вытекает из теоремы 3.11.3.
3.11.4. Теорема. Каждое замкнутое подпространство веществен-
вещественно полного пространства вещественно полно. I
Из теоремы 3.11.3 и утверждений 3.11.4, 2.3.7 и 2.3.4 полу-
получается
3.11.5. Теорема. Произведение П Xs, где Xs?=0 при sgS,
вещественно полно в том и только том случае, если все про-
пространства Xs вещественно полны. I
Из теорем 3.11.4 и 3.11.5 вытекает
3.11.6. Следствие. Предел обратного спектра вещественно пол-
полных пространств является вещественно полным пространством. I
3.11.7. Следствие. Пусть X — топологическое пространство и
{As}s^s — некоторое семейство его подпространств. Тогда если
все As вещественно полны, то и пересечение {] As вещественно
полно.
Доказательство. Пространство f| As гомеоморфно замкну-
тому подпространству произведения Ц Л5» а именно пересече-
нию множества Ц As с диагональю произведения Ц Xst где
XS=X при sgS. Остается заметить, что пространство Ц As
вещественно полно (см. также пример 2.5.4). I
3.11.8. Следствие. Если /: X-*Y — непрерывное отображение
вещественно полного пространства X в хаусдорфово простран-
пространство Y, то для каждого вещественно полного подпространства В
3.11. ВЕЩЕСТВЕННО ПОЛНЫЕ ПРОСТРАНСТВА 323
пространства У его полный прообраз f~x{B)aX вещественно
полон.
В частности, вещественная полнота наследуется функцио-
функционально открытыми подмножествами.
Доказательство. График G(fB) сужения fB: f~1(B)^-B совпа-
совпадает с пересечением (Х*Х B){)G(f) и, следовательно, замкнут
в вещественно полном пространстве ХУ^В. Так как прообраз
f~l(B) гомеоморфен G(fB), пространство f~l(B) вещественно
полно. I
3.11.9. Лемма. Пусть X — топологическое пространство и А —
его подпространство. Если каждая непрерывная функция g:
Л -»-/?, для которой g{x)^l при всех х<=А, продолжается на
X, то и любая непрерывная функция f: A^-R продолжается
на X.
Доказательство. Пусть /: A-*R— любая непрерывная функ-
функция. Положим
gi(x)= I + max(/(*), 0) и g2(x)= 1 - min(/(*),0).
Ясно, что функция gc Л-)-/? непрерывна и gi{x)^ 1 при всех
х е А и i = 1, 2. Так как f(x) = gi(x) — g2(x) при х^ А, функ-
функция F: X^~R, где F(x)= G\(x)— G2(x) и Gt — непрерывное
продолжение функции gt на X при ?= 1, 2, является продолже-
продолжением функции f на X. I
3.11.10. Теорема. Тихоновское пространство X вещественно пол-
полно в том и только том случае, если для каждой точки хо ^
epjf\X найдется непрерывная функция h: $Х^>-1, такая, что
h(xo) = 0 и h(x)> 0 при всех х^Х.
Доказательство. Пусть X — вещественно полное простран-
пространство и хо ^ рХ\Х. Так как для X = ZU{*o}<= $X выполняется
условие (RC1), существует непрерывная функция /: X ->-/?, ко-
которую нельзя продолжить на X. Последняя лемма позволяет
предположить, что f(x)^ 1 при всех xg! Функция 1/f: X^I
продолжается до непрерывной функции h: рХ-^7, причем оче-
очевидно, что h(x)>0 при всех х^Х. Если бы было к(хо)фО,
можно было бы определить продолжение f: X-+R функции f,
положив j(x)= l/h(x). Значит, h(xo) = O.
Предположим теперь, что для каждой точки г е $Х\Х най-
найдется непрерывная функция hz: $Х^>~1, такая, что Аг(г) = 0 и
hz(x)>0 при всех х<=Х. Тогда Х= П ^4@, 1]) и X ве-
щественно полно в силу следствия 3.11.7 и второй части след-
следствия 3.11.8. I
Характеристики вещественно полных пространств, данные в
теоремах 3.11.3 и 3.11.10, так же как и определение этого класса
пространств, носят внешний характер. Внутренняя характери-
21*
324 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
стика вещественной полноты содержится в следующей теореме
Через 2)q(X) в формулировке этой теоремы обозначено семей-
семейство всех функционально замкнутых подмножеств тихоновского
пространства X.
3.11.11. Теорема. Тихоновское пространство X вещественно пол-
полно в том и только том случае, если каждый счетно центриро-
центрированный ультрафильтр на 3)q{X) имеет непустое пересечение.
Доказательство. Рассмотрим произвольное не вещественно
полное тихоновское пространство X и возьмем точку х0 е рХ\Х,
такую, что для всякой функции / из семейства ?Г={/е/Р*:
f(#o) = O} имеет место соотношение Zf =Х(I~1@)ф 0. Семей-
Семейство $& = {Zf}f sg. cziZH(X) замкнуто относительно счетных пе-
пересечений, и, значит, пересечение любого счетного множества
его элементов не пусто.
Покажем, что ^ — ультрафильтр на 2>о{Х). Рассмотрим лю-
любое центрированное семейство <2/с= 3H(Х), содержащее «2J.
Возьмем ZeS>', непрерывную функцию g: X-*Iy удовлетво-
удовлетворяющую условию g~]@)=Z, и продолжение G: $Х-+1 отобра-
отображения g. Если jto^G-I(O)> то найдется f^&~, для которой
Г1<О)П<Н(О) = 0 и
что невозможно. Значит, xo^G~l(Q)y т.е. Gef и, следова-
следовательно, Z = ZG ^ Ж. Таким образом, Ж— счетно центрирован-
центрированный ультрафильтр на Ю0(Х). Так как {\Ж = 0, условие теоре-
теоремы не выполняется для пространства X.
Рассмотрим теперь произвольное вещественно полное про-
пространство X и любой счетно центрированный ультрафильтр
2Е> = {Zs}seS на З)о(Х). Из максимальности Ж сразу следует,
что семейство Ж замкнуто относительно счетных пересечений.
Семейство {Es}s^s замыканий элементов семейства Ж в |ЗХ
имеет непустое пересечение. Для завершения доказательства до-
достаточно показать, что любое х0 е [] Z$ принадлежит X, так
как тогда Jtoe (J ^*-
Предположим, что хо^$Х\Х, и рассмотрим непрерывную
функцию f: рХ^-7, для которой f(xo) = O и f(x)>0 при всех
хеХ. Положим Zi = X()f-l([0yl/i]). Ясно, что Zfe2)o(I)
при t=l, 2, .., . Так как f~l([0, l/i))—окрестность точки х0,
имеем 1^13ф0 при всех seS и f=l, 2, ... , Из макси-
максимальности семейства ЗС следует, что Z,-e<2J при t = 1,2, ...;
оо оо
таким образом, |J Zt^3Z. Так как U Z(= 0, мы пришли к
противоречию; значит, хоеХ. I
3.11. ВЕЩЕСТВЕННО ПОЛНЫЕ ПРОСТРАНСТВА 325
Из теоремы 3.11.11 вытекает
ЗЛ1.12. Теорема. Каждое линделёфово пространство веществен-
вещественно полно. I
Последняя теорема вместе с 3.8.13 показывает, что не все
вещественно полные пространства являются ^-пространствами
(см. упр. З.З.Е(а)).
3.11.13. Пример. Так как прямая Зоргенфрея К является лин-
делёфовым пространством (см. пример 3.8.14), она вещественно
полна. Значит, произведение КУС К вещественно полно. Это при-
пример не нормального вещественно полного пространства (см. при-
пример 2.3.12). Пространство КУ\К содержит дискретное простран-
пространство D{t) в качестве замкнутого подпространства; значит,
пространство D(t) вещественно полно. I
В связи с последним примером естественно задать вопрос:
каждое ли дискретное пространство вещественно полно?
Это вопрос теоретико-множественного характера; он равно-
равносилен вопросу о том, каждый ли кардинал неизмерим (см.
упр. 3.11.D(а)). Чтобы определить, какие кардиналы называют-
называются неизмеримыми, нам нужно одно вспомогательное понятие.
Пусть s& — семейство множеств, замкнутое относительно
счетных объединений. Под счетно аддитивной двузначной мерой
на s& мы понимаем любое отображение семейства $& в множе-
множество {0, 1}, такое, что
1=1
если Ai е зФ и At (] А}- = 0 при / ф ]. Кардинал m называется
неизмеримым, если каждая двузначная мера на семействе всех
подмножеств множества X мощности т, обращающаяся в нуль
на всех одноточечных подмножествах, тривиальна — равна то-
тождественно нулю.
Очевидно, что класс Jf всех неизмеримых кардиналов содер-
содержит кардинал Ко. Можно доказать, что если m e Jf> то в Jf
входят все кардиналы, меньшие ш, сумма любого семейства
K}seS кардиналов из Jfy где |5|^т (т. е. мощность множе-
множества (J As, где |Л,| = тв и As()As'= 0 при s=^s'), а также
кардинал 2т. Можно также доказать, что первый сильно не-
недостижимый кардинал принадлежит Jf (кардинал Ка называет-
называется сильно недостижимым, если а > 0, ординал <оа регулярен
и из неравенства ш < Ка следует, что2т< Ка). Известно, что
предположение о неизмеримости всех кардиналов (и даже пред-
предположение о том, что не существует сильно недостижимого кар-
кардинала) совместимо с обычными аксиомами теории множеств.
326 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
Известно также, что предположение о существовании измери-
измеримого кардинала сильнее предположения о непротиворечивости
теории множеств.
Сделаем несколько замечаний о сохранении вещественной
полноты в сторону образа и в сторону прообраза при отобра-
отображениях. Так как пространство всех счетных ординалов является
непрерывным образом пространства D(t), мы заключаем, что
вещественная полнота не сохраняется непрерывными отобра-
отображениями. Оказывается, вещественная полнота не сохраняется в
сторону образа ни открытыми отображениями (см. упр. 3.11-Е),
ни совершенными отображениями (см. упр. 3.11.G). Последнее
следует из существования не вещественно полного тихоновского
пространства, представимого в виде объединения двух замкну-
замкнутых вещественно полных подпространств (см. теорему 3.7.22).
Однако такое пространство довольно сложно устроено, и описы-
описывать его в этой книге мы не будем.
Из теорем 3.11.4, 3.11.5 и 3.7.26 вытекает
3.11.14. Теорема. Если /: X-+Y— совершенное отображение ти-
тихоновского пространства X на вещественно полное пространство
У, то пространство X вещественно полно. I
В заключение параграфа мы построим для каждого тихо-
тихоновского пространства X вещественно полное пространство оХ,
свойства которого параллельны свойствам |5Х.
3.11.15. Лемма. Пусть X—топологическое пространство и А —
его подпространство. Если каждая непрерывная вещественная
функция f: A^-R непрерывно продолжается на X, то каждое
непрерывное отображение f: А -> И Rs в произведение копий
вещественной прямой тоже непрерывно продолжается на X. Ес-
Если, кроме того, А всюду плотно в X, то каждое непрерывное
отображение f: Л->В = Вс Пй5 в замкнутое подпростран-
ство В такого произведения продолжается до непрерывного ото-
отображения всего X в В.
Доказательство. Пусть дано непрерывное отображение /:
А-> Ц Rs, где Rs = R при sgS. Для каждого seS опреде-
лено продолжение fs: X^~RS композиции psf: A-+Rs. Как легко
видеть, диагональное отображение F = A fs: X -> И Ws яв-
ляется продолжением отображения f. Если А = X и f: A^>B =
= Bcz Ц Rsy то для продолжения F: Х-> П Rs композиции
iBf: A -> Ц Rs имеют место соотношения F(X)=F{A)cz
5
3.11. ВЕЩЕСТВЕННО ПОЛНЫЕ ПРОСТРАНСТВА 327
czF(A)cz Б= В, так что сужение Fb: Х~+В является продол-
продолжением отображения /. I
ЗЛЫ6, Теорема. Для каждого тихоновского пространства X су-
существует ровно одно (с точностью до гомеоморфизма) веще-
вещественно полное пространство т>Х, обладающее следующими дву-
двумя свойствами:
(i) Существует гомеоморфное вложение и: Х->оХ, для ко-
которого и(Х) = оХ.
(п) Какова бы ни была непрерывная вещественная функция
f: Х-)-/?, найдется непрерывная функция f: оХ->-/?, такая, что
h-f-
Пространство оХ удовлетворяет также условию
(iii) Для каждого непрерывного отображения /: Х->- У про-
пространства X в произвольное вещественно полное пространство Y
найдется непрерывное отображение J: оХ-^У, такое, что fu=f.
Доказательство, Для каждого непрерывного f: X^-R возь-
возьмем продолжение F: $X^aR, где aR— одноточечная компак-
тификация вещественной прямой, и положим Wf = F~l(R).
Очевидно, Xcz Wf. Пусть fF — семейство всех непрерывных ве-
вещественных функций на I и ul= f] Wf. Отображение и:
Х-)-иХ, определенное правилом u(jc) = |3(я) при х е X, является
гомеоморфным вложением и и(Х) = т>Х, т. е. условие (i) выпол-
выполнено. Из построения следует, что иХ удовлетворяет и условию (п).
Вещественная полнота пространства иХ вытекает из следствий
3.11.7 и 3.11.8.
Из теоремы 3.11.3, свойств (i) и (п) и леммы 3.11.15 сле-
следует, что иХ удовлетворяет также условию (iii).
Пусть uiX — какое-нибудь вещественно полное пространство,
для которого выполняются условия (i) и (п). Тогда uiX удов-
удовлетворяет также условию (iii), откуда следует, как в доказа-
доказательстве теоремы 3.5.4, что uiX гомеоморфно иХ. I
Пространство т>Х называется хьюиттовым пополнением {по-
{пополнением по Хьюитту) пространства X.
Отметим, что другое построение хьюиттова пополнения про-
пространства X указано в доказательстве теоремы 3.11.3: простран-
пространство иХ можно получить, взяв в Ц Rft где &~ — семейство всех
непрерывных вещественных функций на X и Rf = R при / е #",
замыкание образа пространства X при отображении F == Д f
(см. упр. 3.11.F(b)).
328 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
Вещественно полные пространства были введены Хьюиттом
в [1948]. Он определил их посредством условия, близкого к ха-
характеристике, приведенной ниже в задаче 3.12.21 (g). Эквива-
Эквивалентность принятого нами определения и первоначального опре-
определения Хьюитта была установлена Катетовым в [1951]. Нах-
бин в [1950] независимо определил тот же класс пространств
в терминах равномерностей — а именно условием, что слабей-
слабейшая равномерность, относительно которой все непрерывные ве-
вещественные функции равномерно непрерывны, полна (см. при-
примеры 8.1.19, 8.3.19 и упр. 8.1.D). Статья Хьюитта [1948] содер-
содержит теоремы 3.11.1, 3.11.11, 3.11.12 и 3.11.16. Теоремы 3.11.3,
3.11.4 и 3.11.5 были доказаны Широтой в [1952] (теорема 3.11.4
получена также Катетовым в [1951]). Теорема 3.11.10 установ-
установлена Мрувкой в [1957]. Результаты о замкнутости класса Jf
всех неизмеримых кардиналов относительно указанных в тексте
арифметических операций были получены Уламом в [1930]. Не-
Неизмеримость первого сильно недостижимого алефа (и даже не-
некоторых больших кардиналов) доказана Кейслером и Тарским
в [1963]. Доказательства этих результатов и дальнейшую ин-
информацию можно найти в книге Куратовского и Мостовского
[1968]. Некоторые теоремы о сохранении вещественной полноты
при отображениях установлены Исиватой в [1967] и Кендеро-
вым в [1967]. Не вещественно полное тихоновское пространство,
которое можно представить в виде объединения двух веще-
вещественно полных замкнутых подпространств, описано в работе
Мрувки [1958] (исправление —в [1970]). Более простой при-
пример был приведен Мысьором в [1981]; как заметид Р. Л. Блэр
(на него ссылается Исбелл в [1962а]), примеры такого рода
показывают, что вещественная полнота может не сохраняться
совершенными отображениями. В нашем изложении вопросов
вещественной полноты мы следуем Энгелькингу и Мрувке [1958]
и Ван дер Слоту [1972]. Книга Гиллмана и Джерисона [1960]
содержит важное развитие теории вещественно полных про-
пространств. Обзор последующих результатов можно найти в книге
Вейра [1975].
УПРАЖНЕНИЯ
3.11.А (Гиллман и Джерисон [I960]). Пусть А — веществен-
вещественно полное подпространство, а В — компактное подпространство
тихоновского пространства X. Докажите, что пространство Ли
U В вещественно полно.
3.11.В. (а) (Широта [1952], Гиллман и Джерисон [I960]).
Докажите, что для произвольного тихоновского пространства X
следующие условия равносильны:
3.U. ВЕЩЕСТВЕННО ПОЛНЫЕ ПРОСТРАНСТВА 329
A) Пространство X наследственно вещественно полно.
B) Для каждого х^Х пространство Х\{х} вещественно
полно.
C) Любое тихоновское пространство, которое можно непре-
непрерывно отобразить на пространство X так, что прообразы всех
точек компактны, вещественно полно.
D) Каждое тихоновское пространство, уплотняющееся1) на
пространство X, вещественно полно.
Указание. Примените упр. 3.11.А и следствие 3.11.8.
(b) Выведите из (а), что плоскость Немыцкого вещественно
полна.
(c) Выведите из (Ь), доказательства теоремы 3.11.3 и тео-
теоремы о диагональном отображении, что пространство Rc не нор-
нормально (см. упр. 3,1.Н (а) и задачу 2.7.16 (а)).
3.11.С. Заметьте, что тихоновское пространство X псевдоком-
пактно в том и только том случае, если vX = pX.
3.11.D. (а) (Макки [1944], Хьюитт [1950]). Докажите, что
пространство D(m) вещественно полно в том и только том слу-
случае, если ш — неизмеримый кардинал.
Указание. Примените теорему 3.11.11.
(Ь) (Гиллман и Джерисон [I960]). Покажите, что сумма
ф Xs, где Xs ф 0 при s ^ Sy вещественно полна в том и
только том случае, если все пространства Xs и пространство
D(|S|) вещественно полны.
Указание. Сумма ф Xs гомеоморфна замкнутому подпро-
странству произведения D(\ S |) X И Xs.
3.11-Е (Фролик [1961]). Нормальное пространство, являю-
являющееся непрерывным образом вещественно полного пространства
при открытом отображении, может не быть вещественно полным.
Указание. Возьмите в качестве области значений простран-
пространство Wq всех счетных ординалов, а в качестве области опреде-
определения сумму ф Ха, где Ха = {х^ Wo: x ^ а}.
а<а>|
3.II.F. (а) (Вулих [1952], Энгелькинг [1964]). Докажите,
что непрерывное отображение f: A-+Y всюду плотного под-
подпространства топологического пространства X в вещественно
полное пространство Y непрерывно продолжается на X в том
и только том случае, если для каждой последовательности
Z7!, F2, ... функционально замкнутых в Y множеств, такой, что
!) Напомним, что уплотнением называется взаимно однозначное непре-
непрерывное отображение одного пространства на другое. — Прим. перев.
330 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
со оо
Р| Fi—Q), имеет место соотношение [\ /~1(^*)=0> где черта
обозначает замыкание в X.
Указание. Рассмотрите сначала случай Y = R: примените
теорему 3.2.1.
(Ь) (Гиллман и Джерисон [I960]). Покажите, что если
взять в конструкции рХ, описанной в упр. 3.6.К (а), только те
ультрафильтры на 3)${Х)У которые счетно центрированы, то по-
получится хьюиттово пополнение ьХ.
3.11.G (Пономарев [1959], Фролик [1961]). Докажите, что
если /: X->Y — совершенное открытое отображение веществен-
вещественно полного пространства X на тихоновское пространство У, то У
вещественно полно.
Указание. Примените упр. 1.5.L (а) и теоремы 3.7.15 и 3.11.10.
3.11.Н (Пасынков [1965]). Топологическое пространство X
вещественно полно в том и только том случае, если оно гомео-
морфно пределу обратного спектра линделёфовых пространств
(или — что эквивалентно — гомеоморфно пределу обратного
спектра из подпространств гильбертова куба I*0).
3.12. ЗАДАЧИ
Дальнейшие характеристики компактности: точки полного
накопления и теорема Александера о предбазе
3.12.1 (Куратовский и Серпинский [1921], Вьеторис [1921],
П. С. Александров и Урысон [1929] (объявлено в [1923])).
Точка х топологического пространства X называется точкой
полного накопления для множества А<=ХУ если |ЛП^| = И1
для каждой окрестности U точки х.
Докажите, что для произвольного топологического простран-
пространства X следующие условия равносильны:
A) Пространство X компактно.
B) Для каждого бесконечного подмножества пространства
X в X есть точка полного накопления.
C) Для каждой убывающей трансфинитной последователь-
последовательности FqZd Т7! => ... => Ft zd ..., I < а, непустых замкнутых
в X множеств пересечение П Fg не пусто.
Указание. Для каждого бесконечного ординала К существует
начальный ординал, конфинальный % (см. Куратовский и Мо-
стовский [1968]).
Замечание. Легко показать, что если для каждого несчетного
множества Лс!вХ есть точка полного накопления, то 1(Х)^
^ Ко. С другой стороны, пространство всех ординалов <(йт с
3.12. ЗАДАЧИ 331
топологией, порожденной естественным линейным упорядоче-
упорядочением <, является линделёфовым пространством, в котором нет
точки полного накопления (для всего пространства). П. С. Алек-
Александров и Урысон доказали в [1929], что если 1(Х)^80, то
каждое несчетное множесто АаХ регулярной мощности имеет
в X точку полного накопления. А. С. Мищенко в [1962а] опре-
определил тихоновское не линделёфово пространство X, в котором
каждое несчетное множество АаХ регулярной мощности имеет
точку полного накопления, и доказал, что каждое счетно пара-
компактное нормальное пространство, обладающее последним
свойством, является линделёфовым пространством (см. зада-
задачу 3.12.7 (d)).
3.12.2 (Александер [1939]). (а) Пусть X — топологическое
пространство и & — некоторая его предбаза. Покажите, что X
компактно в том и только том случае, если из каждого покры-
покрытия пространства X элементами семейства 9* можно выделить
конечное подпокрытие (это и есть теорема Александера о пред-
базе).
Указание. В классе всех семейств открытых подмножеств
пространства X свойство не содержать никакого конечного под-
подсемейства, покрывающего X, является свойством конечного ха-
характера. Если X не компактно, то найдется максимальное се-
семейство 91, которое обладает указанным свойством и покры-
покрывает X. Покажите, что если G\, G2, ..., Gk— открытые множе-
множества и 0ьф91 при i = 1, 2, ..., k, то Gi П G2 П • • • [\Gk^9t,
и что если G\ ф. 91 и G\ c= G2, то Очф. 91. Выведите отсюда, что
пересечение Ш[\9> покрывает X.
(Ь) Докажите теорему Тихонова с помощью характеристики
компактности, установленной в (а).
Линейно упорядоченные пространства III (см. задачи 1.7.4,
2.7.5, 3.12.12(f), 5.5.22, 6.3.2 и 8.5.13(j)).
3.12.3. (а) (Хаар и Кёниг [1910]). Покажите, что простран-
пространство X с топологией, порожденной линейным упорядочением <>
компактно в том и только том случае, если каждое подмноже-
подмножество AczX обладает в X наименьшей верхней гранью.
Указание. Наименьшей верхней гранью пустого множества
служит наименьший элемент множества X.
(Ь) Докажите, что каждое пространство X с топологией, по-
порожденной линейным упорядочением <, обладает компактифи-
кацией сХ, топология которой порождается некоторым линей-
линейным упорядочением </, таким, что x<.fy равносильно х < у
для всех ^,jgX.
Указание. Рассмотрите множество сечений множества Х\
примените задачу 2.7.5 (а).
332 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
Замечание. Линейно упорядоченные компактификации ли-
линейно упорядоченных пространств были исследованы Федорчу-
ком в [1969] (объявлено в [1966а]) и Кауфманом в [1967].
(c) Проверьте, что топология на множестве всех ординалов
г^юь определенная в примере 3.1.27, совпадает с топологией,
порожденной естественным линейным упорядочением <.
(d) Рассмотрите линейное упорядочение < на квадрате /2,
определенное правилом: (х\, У\) <(*2, */г), если х\ < х2 или если
xi = х% и у\ < У2 (это упорядочение называется лексикографи-
лексикографическим упорядочением). Докажите, что квадрат с топологией,
порожденной указанным линейным упорядочением, компактен и
удовлетворяет первой аксиоме счетности, но не сепарабелен и
не совершенно нормален. Проверьте, что наделенный такой то-
топологией квадрат содержит пространство «две стрелки», опре-
определенное в упр. 3.10.С.
3.12.4. (а) (Мардешич и Папич [1962]). Покажите, что для
каждого линейно упорядоченного пространства X имеют место
неравенство %(Х)^ с(Х).
(b) (Латцер и Беннет [1969]; для компактного X — Марде-
Мардешич и Папич [1962]). Покажите, что для каждого линейно упо-
упорядоченного пространства X имеет место неравенство hl(X)^
^с(Х), где hi — наследственное число Линделёфа (см. зада-
задачу 2.7.9 и §3.8).
Указание. Применив 3.12.3 (Ь), сведите задачу к случаю
компактного пространства X. Заметьте, что каждое открытое
множество может быть представлено как объединение некото-
некоторого семейства попарно не пересекающихся интервалов, приме-
примените (а) и подходящее обобщение упр. 3.8.А (а).
(c) (Скула [1965]). Покажите, что для каждого линейно
упорядоченного пространства X имеет место равенство d(X) =
= hd(X).
Указание (Латцер и Беннет [1969]). Пусть D — всюду плот-
плотное множество в X, такое, что \D\ = d(X). Для произвольного
AczX выберем по одной точке из каждого непустого пересече-
пересечения Af\(a9b)f где a, b e D и а < 6. Проверьте, что объедине-
объединение Е так полученного множества и множества всех изолиро-
изолированных точек множества А всюду плотно в Л; с помощью (Ь)
покажите, что \Е\^ d(X).
(d) Покажите, что для каждого линейно упорядоченного
пространства X имеют место равенства lxt{X)=t$(X)=t(X) и
w(X)=nw(X).
(e) Проверьте, что следующая диаграмма (см. зада-
задачу 1.7.12 (а)) содержит все равенства и неравенства, которые
выполняются в классе всех линейно упорядоченных пространств
для вошедших в нее кардинальных функций (символ | | обо-
3.12. ЗАДАЧИ
333
значает мощность; по поводу соотношений между d{X) и с(Х)
см. замечание к задаче 2.7.9(f)):
/
x-t-
„-*-«
/
I
' )
\
Замечание. Хайнал и Юхас доказали в [1969], что если про-
пространство X линейно упорядочено, то либо d(X)=c(X), либо
d(X) —наименьший кардинал, больший, чем с(Х).
Я-замкнутые и Я-минимальные пространства
3.12.5 (а) (П. С. Александров и Урысон [1929] (объявлено
в [1923]), П. С. Александров [1939]). Хаусдорфово простран-
пространство X называется Н-замкнутым, если X замкнуто в каждом
хаусдорфовом пространстве, содержащем его в качестве под-
подпространства.
Докажите, что для хаусдорфова пространства X следующие
условия равносильны:
A) Пространство X Н-замкнуто.
334 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
B) Если {V8}seS — центрированное семейство открытых в X
множеств, то f] Vs ф 0.
C) Каждый ультрафильтр в семействе всех открытых в X
множеств сходится в X.
D) Каждое открытое покрытие {U$}$^s пространства X со-
содержит конечное подсемейство {Us, Us , ..., ?/5jJ, такое, что
uuuv[iux
{2k
Выведите отсюда, что регулярное пространство Я-замкнуто
в том и только том случае, если оно компактно, и приведите
пример нерегулярного Я-замкнутого пространства.
Заметьте, что Я-замкнутость не наследуется, вообще говоря,
замкнутыми подмножествами.
(b) (Катетов [1940]). Заметьте, что Я-замкнутость насле-
наследуется каноническими замкнутыми множествами и сохраняется
(в сторону образа) непрерывными отображениями на хаусдор-
фовы пространства.
(c) (М. Стоун [1937], Катетов [1940]). Докажите, что хаус-
хаусдорфово пространство X компактно в том и только том случае,
если все его замкнутые подпространства Я-замкнуты.
Указание (Катетов [1940]). Покажите, что каждое семей-
семейство SF непустых Я-замкнутых подпространств хаусдорфова про-
пространства X, линейно упорядоченное по включению, имеет непу-
непустое пересечение. С этой целью убедитесь, что семейство всех
открытых множеств UczX, для которых существует f еУ, та-
такое, что F czF(\U, центрировано.
(d) (Шевалле и О. Фринк [1941]). Докажите, что произве-
произведение П Xs, где Xs ф 0 при s e S, Я-замкнуто в том и толь-
ко том случае, если все пространства Xs Я-замкнуты.
(e) (Пархоменко [1939], Катетов [1940]). Хаусдорфово про-
пространство X называется Н-минимальным, если каждое уплотне-
уплотнение пространства X на хаусдорфово пространство является го-
гомеоморфизмом.
Докажите, что хаусдорфово пространство X является Я-ми-
нимальным в том и только том случае, если X семирегулярно
и Я-замкнуто. Приведите пример не компактного Я-минималь-
ного пространства.
Указание. Примените задачу 1.7.8 (Ь).
Замечание. Помимо Я-замкнутых и Я-минимальных про-
пространств рассматривают аналогично определяемые ^-замкнутые
и ^-минимальные пространства для различных топологических
свойств 9. Этой теме посвящена обширная литература, обсу-
обсуждаемая в статье Берри, Портера и Стефенсона [1968].
3.12. ЗАДАЧИ 3 35
3.12.6 (Катетов [1940]). Обозначим через 0{Х) семейство
всех открытых подмножеств хаусдорфова пространства X. Рас-
Рассмотрим семейство Т(Х) всех ультрафильтров на (У(Х), не схо-
сходящихся ни к какой точке пространства X, и определим топо-
топологию на множестве %Х = Х[}Т(Х), взяв в качестве окрестно-
окрестностей точки х^Х семейство всех ее окрестностей в простран-
пространстве X, а в качестве окрестностей произвольной точки УеГ(X)
семейство всех множеств вида {ЗГ}\} U, где ?/е#~. Простран-
Пространство хХ, полученное таким образом, называется катетовским
расширением пространства X.
(a) Заметьте, что X является открытым всюду плотным под-
подпространством пространства хХ и что подпространство хХ\Х
пространства хХ дискретно.
(b) Докажите, что хХ есть Я-замкнутое пространство и что
для каждого непрерывного отображения /: J~> У пространства
X в хаусдорфово пространство У, такого, что f(J?)— У, найдется
подпространство Z пространства хХ, содержащее X, и продол-
продолжение F: Z-+Y отображения /, удовлетворяющее условию
F(Z)=Y.
Заметьте, что указанное свойство характеризует хХ (с точ-
точностью до гомеоморфизма) в семействе всех хаусдорфовых про-
пространств, содержащих X в качестве всюду плотного подпро-
подпространства.
(c) Покажите, что если в ситуации, описанной в (Ь), про-
пространство У компактно или является Я-замкнутым простран-
пространством, содержащим X в качестве всюду плотного подпростран-
подпространства, причем / = id*, то Z = хХ.
Кардинальные функции III (см. задачи 1.7.12, 1.7.13, 2.7.9—
2.7.11, 3.12.4, 3.12.12(j) и 8.5.17)
3.12.7. (а) Заметьте, что hnw(X) = nw{X) и /гяр (X) = -ф {X)
для каждого топологического пространства X и что ф(Х)^
^hl(X) для произвольного хаусдорфова пространства X.
(b) (Ю. М. Смирнов [1950]; для Ко — Серпинский [1921а]).
Докажите, что топологическое пространство X удовлетворяет
условию hl(X)^.i^a в том и только том случае, если для ка-
каждой возрастающей трансфинитной последовательности Uo cz
с Ui a ... с Ui cz ..., I < ©а+ь открытых в X множеств най-
найдется go < Оси-ь такое, что ?/| = ?/ge при всех g ^ |0 (см. зада-
задачу 2.7.9 (е)).
(c) (Серпинский [1921а]). Приведите пример хаусдорфова
пространства X, такого, что М(Х) > Ы(Х)= Ко.
Указание. Рассмотрите некоторое вполне упорядочение <
вещественной прямой R и возьмите топологию на /?, в которой
336 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
окрестностями произвольной точки х е R служат множества
Ut(x)={x}[){yeR: \х — у\<1/1шу<х] при i = 1, 2, ... .
Замечание. Тодорчевич описал в [1984] вполне регулярное
пространство X, для которого hl(X)> hd(X)> Ко. Регулярное
пространство X, такое, что hl(X) > hd(X)= Ко, называется
5-пространством. Первый пример 5-пространства был приведен
М. Э. Рудин в [1972]: в предположении, что существует про-
пространство Суслина (см. замечание к задаче 2.7.9 (f)), она опре-
определила нормальное наследственно сепарабельное пространство
X, которое не обладает свойством Линделёфа (и удовлетворяет
условию if(X)> Ко). Пример наследственно нормального и на-
наследственно сепарабельного счетно компактного пространства X,
не являющегося линделёфовым пространством, был построен в
11974] Хайналом и Юхасом в предположении континуум-гипо-
континуум-гипотезы. Осташевский в [1976] вывел из одного теоретико-множе-
теоретико-множественного утверждения, совместимого с аксиомами теории мно-
множеств, что существует наследственно сепарабельное счетно ком-
компактное локально компактное хаусдорфово пространство с пер-
первой аксиомой счетности, не являющееся линделёфовым про-
пространством. Слив воедино последние две конструкции, Юхас,
Кунен и М. Э. Рудин привели в [1976] (в предположении кон-
континуум-гипотезы) намного более простой пример наследственно
сепарабельного локально компактного хаусдорфова простран-
пространства с первой аксиомой счетности, не являющегося линделёфо-
линделёфовым пространством. Из примера Осташевского и одного резуль-
результата Сентмиклоси [1978] следует, что существование компакт-
компактных S-пространств совместимо с обычными аксиомами теории
множеств и не зависит от них. Как показал Тодорчевич в [1981],
существование S-пространства также не зависит от аксиом тео-
теории множеств (доказательство этого и дальнейшие сведения
см. в работе Ройтман [1984]).
Тодорчевич также описал в [1984] вполне регулярное про-
пространство Ху для которого hd(X)> hl(X)> Ко. Регулярное про-
пространство X, для которого hd(X)> hl(X)=80, называется
L-пространством. Пример L-пространства в рамках классической
теории множеств не известен (хаусдорфово пространство X,
определенное в указании к задаче 2.7.9 (f), удовлетворяет усло-
условиям hd(X)> hl(X)= Ко). Любое пространство Суслина яв-
является наследственно линделёфовым несепарабельным про-
пространством (см. задачу 3.12.4(е)); таковы же пространства,
построенные в предположении континуум-гипотезы и упомя-
упомянутые в последнем абзаце замечания к задаче 2.7.9 (f) (про-
(пространство, построенное Хайналом и Юхасом, удовлетворяет не-
неравенству hl(X)<Zt(X)). Существование компактного L-про-
L-пространства совместимо с обычными аксиомами (достаточно ука-
указать на континуум Суслина), Юхас [1970] показал, что суще-
3.12. ЗАДАЧИ
337
ствование компактного L-пространства не зависит от аксиом
теории множеств 1).
(d) (Куратовский и Серпинский [1921]). Покажите, что ре-
регулярное пространство X наследственно линделёфово в том и
только том случае, если каждое несчетное множество А а X об-
обладает точкой конденсации, лежащей в А, т. е. если А П А0 Ф 0
(см. задачу 1.7.11).
(e) Воспользовавшись приведенным выше замечанием к ча-
части (с), проверьте, что следующая диаграмма (см. зада-
задачу 1.7.12(а)) содержит все неравенства, которые выполняются
для кардинальных функций, входящих в эту диаграмму (через
| | обозначена мощность):
*) Сентмиклоси в [1978] показал, что в предположении аксиомы Марти-
Мартина и отрицания континуум-гипотезы (совместимом с обычными аксиомами тео-
теории множеств) каждый наследственно сепарабельный компакт совершенно
нормален, а Юхас в [1970] вывел из того же предположения, что каждый
совершенно нормальный компакт наследственно сепарабелен. Федорчук в
[1976] установил, что с аксиомами теории множеств совместимо существо-
существование наследственно сепарабельного компакта X мощности 2**i, в котором
нет ни одной нетривиальной сходящейся последовательности, а А. В. Иванов
в [1980*] показал, что можно дополнительно потребовать, чтобы простран-
22 Зак. 697
338 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
(f) С помощью сделанного выше замечания к части (с) про-
проверьте, что следующая диаграмма содержит все неравенства,
выполняющиеся для входящих в эту диаграмму кардинальных
функций (символ Ti рядом со стрелкой означает, что соответ-
соответствующее неравенство выполняется для 7\-пространств):
(g) Для кардинальной функции / обозначим через hel (че-
(через hopf) кардинальную функцию, значение которой на про-
пространстве X равно sup/(Af), где супремум берется по всем зам-
замкнутым (по всем открытым) подпространствам М простран-
пространства X. Покажите, что для каждого топологического простран-
пространства X имеют место соотношения:
held (X) < hd (X), hopd (X) = d (X),
hele (X) = he (X), hope (X) = с (X),
hell (X) = I (X), hopl (X) = hi (X),
hole (X) = e (Z), hope (X) < he (X).
Покажите, что hope(X) = hc(X) для каждого Ti-простран-
ства X, и приведите пример Го-пространства X, такого, что
hope(X)=?hc{X).
Приведите пример хаусдорфова пространства X, для кото-
которого held(X)= «о < hd(X).
Указание. Измените топологию «двух стрелок» (см.
упр. ЗЛО.С), объявив открытыми все множества вида U\A,
ство Хп было наследственно сепарабельным при всех целых положительных
п. Как заметил Толл в [1969], с аксиомами теории множеств совместимо
существование L-простраиства, вес которого больше 2**° Нельзя в рамках
классической теории множеств доказать, что если пространство наследствен-
наследственно линделёфово, то его плотность не превосходит »i (или »2» **з и т. д.) —
см. Юхас [1971]. В той же работе показано, что если регулярное простран-
пространство наследственно сепарабельно, то это еще не означает, что его число
Линделёфа не превосходит »i (или К2, »з и т. д.). К. Кунен в [1977*] до-
доказал, что в предположении аксиомы Мартина и стрицания континуум-гипо-
континуум-гипотезы следующие утверждения о регулярном пространстве X равносильны:
(а) пространство Хп наследственно линделёфово при всех целых положи-
положительных п и (Ь) Хп наследственно сепарабельно при всех целых положи-
положительных л. — Прим. перев.
3.12. ЗАДАЧИ 339
где U открыто в исходной топологии, а А — счетное подмноже-
подмножество множества Со; примените упр. 3.1.В.
Замечание. Пространство, определенное выше в указании,
является модификацией первого примера пространства с ана-
аналогичными свойствами, приведенного Оллом в [1975]. Пример
регулярного пространства X, такого, что ксЫ(Х)фкй(Х), не
известен (см. задачи 3.12.9(d) и (е)) *).
(h) (Зенор [1980]). Покажите, что если семейство {Xs}S€s5
топологических пространств таково, что hit Ц хЛ<Сю для
каждого конечного So c= S и | S | ^ m, то hi ( TL ХЛ ^ тп.
Vse=S /
(i) (Зенор [1980]). Докажите, что если Нс(ХХ У)<^ ш 5*
^ Ко, то либо hl(X) ^ m, либо hd(Y) ^ m.
Указание. Воспользуйтесь пунктом (Ь) и задачей 2.7.9 (е).
3.12.8. (а) (Архангельский и В. И. Пономарев [1968]). По-
Покажите, что если /: X-+Y— факторное отображение «на», то
(Y)(X)
)()
Указание. Примените задачу 1.7.13 (Ь).
(b) Если X есть ^-пространство, то t(X) является точной
верхней гранью всех кардиналов вида t(F), где F— компактное
подпространство пространства X.
(c) Теснотой множества А в топологическом пространстве X
называется наименьший кардинал m ^ Ко, такой, что если_ЛП
П С Ф 0, то найдется Со с= С, для которого | Со| ^ ш и А П Со Ф
Ф 0. Этот кардинал обозначается через t(AtX).
Заметьте, что для произвольного топологического простран-
пространства X и любого множества А с: X имеет место неравенство
(AX)(AX)
)x()
Докажите, что если А\ и А2 — подмножества пространства X,
такие, что А\ с Л2, и для каждого замкнутого в А2 множества
^с=Л2\^1 найдутся непересекающиеся открытые в X множе-
множества, содержащие А\ и F соответственно, то t(AX)
(AA)(AX)
Выведите отсюда, что если F\, F2 — компактные подмноже-
подмножества хаусдорфова пространства X и Fi<zzF2, то t(Fi,X)^
^ t(Fu F2)t(F2j X), и что для любого замкнутого в регулярном
пространстве X множества F и каждой точки x^F имеет место
неравенство t (х, X) ^ t (x9 F) t (F, X).
Указание. Положим m = t(Ai, A2)t{A2, X). Предположим
что нашлось CczX, такое, что А\{]С Ф 0, и тем не менее
]) В. И. Малыхин построил (в предположении континуум-гипотезы) не
наследственно сепарабельное тихоновское пространство, все замкнутые под-
подпространства которого сепарабельны. — Прим. перев.
22*
340 гл- 3- КОМПАКТНЫЕ ПРОСТРАНСТВА
Ах[)[С]т=0, где [C]m= U {М: М с=С и |М|<т}. Проверьте,
что Ах П Л2 П [С]т = 0 > возьмите открытое множество U czX,
для которого Л i с: ?/ и ?/ Л Л2 П[С]т = 0, и заметьте, что
A2[\U[\С Ф 0.Примените неравенство t(A2> X) ^m.
(d) Заметьте, что если отображение /: X-+Y замкнуто, то
t(f~l(B),X)^t(B9 Y) для всех В с У.
Выведите отсюда, что если /: X-+Y— замкнутое отображе-
отображение регулярного пространства X в топологическое пространство
У и для каждого х е X выполняются неравенства t(f(x), У) ^ ш
и t(x,f-lf(x))^m, то t(x9X)^m.
Если отображение / совершенно, то предположение о регу-
регулярности пространства X можно опустить.
(e) (Архангельский [1972]). Определите нормальные про-
пространства X и У, такие, что t{X)=t(Y)=K0 и t(XX У) > «о-
Указание, В качестве X возьмите сумму счетного множества
копий пространства Л(&*0), в которой все предельные точки
отождествлены, а в качестве У возьмите пространство, получен-
полученное таким же образом из суммы континуума копий простран-
пространства Л («о) J)-
({) (Малыхин [1972]). Покажите, что если X — локально
компактное хаусдорфово пространство, то для каждого хаус-
дорфова пространства У имеет место неравенство t(Xy^Y)
((*)))
)())
Докажите, что если семейство {^5}56=s топологических
пространств таково, что t ( Ц ХЛ ^ ш для каждого конечного
Soc:S и |S|<tn, то /(П*5)<™.
Указание. Примените (d) в доказательстве первой части.
(g) Пусть {X5}s€=5~ семейство хаусдорфовых пространств,
такое, что t (Xs) ^юий (Xs) ^ m при sgSh | S \ ^ m. Покажи-
Покажите, что тогда / ( Ц ХЛ ^ т.
3.12.9. (а) (Шапировский [1972]). Докажите, что для ка-
каждого открытого покрытия {Us}s^s топологического простран-
пространства X существует So с: S, обладающее следующими свойства-
свойствами: при всех sgS0 можно выбрать точку xs e Us таким об-
образом, чтобы было xs Ф xS' при s Ф s\ подпространство
А = U {xs} было дискретным и имело место равенство Х =
S(=Sq
= U U.VA.
5
1) Пространство, которое получается отождествлением всех неизолирован-
неизолированных точек в сумме m экземпляров пространства Л(«о), называется веером
Фреше — Урысона мощности m и обозначается через V(m). — Прим. перев.
3.12. ЗАДАЧИ 341
Выведите отсюда, что Х= \] US\JA, где |50|<Лс(Х) и
Указание. Применив трансфинитную индукцию, определите
точки jc0, х\, ..., xi, ..., ? < а, пространства X и элементы
?/о, f/ь • > #ь ••> I < a» данного покрытия, такие, что
f U c/v
где
= U W и х= U
(b) (Шапировский [1972]; для компактов —Архангельский
[1971]). Покажите, что для каждого хаусдорфова пространства
X выполняется неравенство t(X)^. hc(X)h(X).
Выведите отсюда, что t(X)^. hc(X) для каждого &-простран-
ства X.
Указание. Применив 3.12.8 (с), сведите задачу к^случаю
компакта X. Пусть m — hc(X); докажите, что если СФ[С]Ш
для некоторого С а X, то [С]ш ф С. С этой целью для произ-
произвольной точки х0 е С \ [С]т возьмите семейство {Us}Se=$ откры-
открытых в X множеств, такое, что хо^[/5 и Сс [} Us, и, приме-
нив (а), выберите So с: 5 и AczC> для которых |S0K|m,
|Л|<шиСс: U US\}A. Определите семейство {Vt}ts.T от-
крытых в X множеств так, чтобы было |Г|^тп, {xo} = (C\J
иЫ)ПП^и П Vt= П Vt. Заметьте, что x(Z, Z)<m
для Z= (] F^, и рассмотрите базу $ пространства X в Z, для
которой |J?|^m. Составьте множество 5, взяв по точке из
каждого пересечения С f| ?/, где U е ^, и покажите, что произ-
произвольное Zq^ B[)Z удовлетворяет условию z0 е [С]т \С
(c) Воспользовавшись замечанием к задаче 3.12.7(с), про-
проверьте, что диаграмма на с. 342 (см. задачу 1.7.12(а)) содержит
все равенства и неравенства между входящими в нее кардиналь-
кардинальными функциями, которые выполняются в классе всех компактов
(ясно, что для каждого компакта X имеют место равенства
1(Х)=е(Х)=Яо).
Замечание. Шапировский доказал в [1974], что если X —
компакт, то либо hd(X)=hc(X), либо hd(X) равно наимень-
наименьшему кардиналу, большему чем hc{X).
(d) Для каждого пространства X имеет место неравенство
hd{X)^hcld(X)t{X). Заметьте, что hcld(X) = hd(X)y если X —
пространство счетной тесноты.
(e) Покажите, что для каждого хаусдорфова пространства X
имеет место неравенство hd(X)^hcld{X)h(X). Заметьте, что
342 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
hcld{X) = hd{X)y если X — пространство точечно счетного типа.
Указание. Примените (Ь).
(f) Приведите примеры нормальных пространств X и У, для
которых h(X)<t(X) и t(Y)<h(Y).
3.12.10. (а) (Архангельский [1969]). Докажите, что для ка-
каждого хаусдорфова пространства X выполняется неравенство
|X|[/(X)(X)]
|X|<exp[/(X)x()].
Указание (Р. Поль [1974]). Видоизмените доказательство
теоремы 3.1.29 1).
(Ь) (Хайнал и Юхас [1967]). Докажите, что для каждого
хаусдорфова пространства X выполняется неравенство \Х\^.
^[(Х)(Х)]
р()%()]
Указание (Р. Поль [1974]). Видоизмените доказательство
каждого xg! возьмем базу 38(х) в точке х, такую, что
\${х) |^т. Определим возрастающую трансфинитную последо-
последовательность Ао cz А\ с: ... с: Аа с= ..., а < т, подмножеств
пространства X, где т — наименьший начальный ординал мощ-
мощности, большей чем ш, такую, что | Аа | ^ 2т и выполняется усло-
условие: для каждого семейства {?/5}5eS подсемейств семейства
]) См. также упрощенные варианты доказательства теоремы 3.1.29 и ее
обобщений в работах Архангельского 1974, 1976 и 1978 гг. — Прим. перев.
3.12. ЗАДАЧИ 343
(J АЛ, где |S|<m и |%|<тпри seS, если
«* р)
, to Ла\1Ни%: 5eS}=^0. Покажи-
ПокажиU{U }, 1Ни }
те, что объединение А = U Ла равно X. Для этого предполо-
а<х
жите, что нашлась точка у^Х\А, положите &(y) = {Vs}s&Sf
где |S|^nt, и для каждого se5 рассмотрите максималь-
максимальное семейство <2/5 попарно непересекающихся открытых мно-
множеств, содержащееся в семействе {U е $(х): л; е Л и U П V$ =
==0}.
(с) (Хайнал и Юхас [1967]). Докажите, что для ка-
каждого ^-пространства X имеет место неравенство |^|^S
^exp[hc(X)ty{X)] (см. (h) ниже).
Указание (Годел [1976]). Положим ш = hc(X)^(X). Для
каждого х^Х возьмем семейство °U{x) открытых множеств,
такое, что f\cU(x) = {x} и \Щ(х)\^ш. Определим возрастаю-
возрастающую трансфинитную последовательность Лосихе: ... с=Лас=
с: ..., а < т, подмножеств пространства X, где т — наимень-
наименьший начальный ординал мощности, большей чем ш, для которой
|Ла|<[2ш и выполняется условие: для каждого подсемейства
{Us}s^s семейства [}Ш(х): jcg U АЛ, где |S|<m, и каждо-
го семейства {Вг}шт подмножеств множества (J А§> гДе 1^1^
если Х\\{] Us[) [] ВЛф 0, то
UsU U ВЛ ф 0. Покажите, что объединение А —
= U Аа равно X. С этой целью предположите, что нашлась
точка у^Х\А, положите Х\{у}= [] ?и гДе 1^1 ^ю и
t <=т
Ft = Ft при /g7, ис помощью задачи 3.12.9(а) получите при
каждом /gT подсемейство Ti семейства \]^U(x): x^AflFt)
и подмножество Bt с: Л П Л, мощность каждого из которых не
превосходит т, такие, что Af\Ft cz([}Tt)[} Bt с Х\{у}. В ка-
качестве {t/s}S€E$ возьмите объединение (J У%.
(d) (Шапировский [1972]). Покажите, что для каждого
хаусдорфова пространства X имеет место неравенство ф(Х)^
^ exp he (X).
Указание. Возьмите точку xq^X и, применив задачу 3.12.9(а),
найдите семейство {Us}s<=s °ткРытых подмножеств простран-
пространства X и подмножество AczХо — Х\{х0], такие, что xo^USi
и XQ= \j USU(A{]XO). Воспользо-
S
344 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
вавшись упр. 3.1.F(a), заметьте, что для Х\ =(АП
имеет место неравенство tf(Xi) ^ exp hc{X).
(е) (Шапировский [1972]). Докажите, что для каждого
^-пространства X найдется множество S cz X мощности
*? № (X) ] Лс<*>, такое, что
Х=\){М: MczS и \M\^hc(X)}.
Указание. Пусть т — наименьший начальный ординал мощ-
мощности, большей чем hc(X). Определите трансфинитную последо-
последовательность So, Si, ..., Sa, ..., a < т, подмножеств простран-
пространства X и трансфинитную последовательность °U^ °U\, ...
..., °Ua, • •., а<т, семейств открытых подмножеств простран-
пространства X так, чтобы при всех a < т выполнялись следующие
условия:
A) I Se| <[¦(*)]*<* И |««|<M>W)]te(X).
B) Если a > 0 и Sa с= (U <U) U Л, где <U a \J <UV А с |J SB,
\<U\^hc{X) и | Л К /гс (X), то Х=~{\]Ш)\}А.
C) Каждая точка множества Sa является пересечением не-
некоторого подсемейства семейства °Ua-
Примените затем задачу 3.12.9(а).
(О (Шапировский [1972]). Покажите, что для каждого хаус-
дорфова пространства X найдется множество ScX мощности
^ exp he {X), такое, что
Х = [){М: MczS и \M\^hc{X)}.
(g) (Хайнал и Юхас [1967]; для регулярного X — де Гроот
[1965]). Докажите, что для каждого хаусдорфова простран-
пространства X имеет место неравенство |Х|^ехрехрЛс(Х).
Указание (Шапировский [1972]). Примените (f) и теоре-
теорему 1.5.3.
Замечание. Более слабое неравенство [Х\ ^ exp exp exp hc(X)
было доказано для вполне регулярных пространств Исбеллом
в [1964а], а для хаусдорфовых пространств де Гроотом в [1965]
и Б. А. Ефимовым в [1965].
(h) (Шапировский [1972]). Заметьте, что для регулярных
пространств неравенство в (с) следует из (f) и упр. 3.1.F(d).
(i) (Ю. М. Смирнов [1950]; для hl(X)=&0 — П. С. Алек-
Александров и Урысон [1929]). Докажите, что для произвольного
хаусдорфова пространства X имеет место неравенство |^|^
^expht(X).
Указание. Докажите сначала, что \X\*?L exp [d{X)hl(X)]9 и
выведите^ отсюда, что множества М из (f) удовлетворяют усло-
условию | М | ^ exp hi(X). Видоизменив доказательство теоре-
теоремы 3.1.29, можно показать также, что если хаусдорфово про-
3.12. ЗАДАЧИ 345
,m
странство X удовлетворяет неравенствам ty(X)^m и |Х|>2
то у него есть подпространство М, для которого 1(М)> ш.
(j) (Хайнал и Юхас [1967]). Покажите, что для каждого
хаусдорфова пространства X имеет место неравенство hd(X)^L
^exphc(X).
Указание. Примените (f).
(к) (Шапировский [1972]). Покажите, что если простран-
пространство X регулярно, то nw (X) ^ exp he (X).
Выведите отсюда, что hl(X)^ exp hc(X) для каждого регу-
регулярного пространства X. __
Указание. Заметьте, что множества М из (f) образуют сеть
пространства X.
A) (Шапировский [1972]). Докажите, что если пространство
X регулярно, то w{X)^exp(hc(X)h(X)].
Указание. Пусть m = exp[hc(X)h(X)]. Заметьте, что d(X)^
^шй %(Х)^т (воспользуйтесь для этого упр. 3.1.Е(а)). Возь-
Возьмите базу мощности ^щ в каждой точке некоторого всюду
плотного множества мощности ^ш, рассмотрите объединение 41
этих баз и докажите, что семейство {Int((J^o): aUo<^°U и
\°U\(X)} является базой пространства X.
3.12.11. (а) (Чех и Поспишил [1938]). Докажите, что если
для каждой точки х компакта X имеет место неравенство
%(х, Х)^ ш ^ Ко, то [Xl^expm (здесь имеется в виду опре-
определение характера, принятое в основном тексте этой книги, т. е.
мы отходим от соглашения, введенного в задаче 1.7.12, по ко-
которому значениями кардинальных функций могут служить лишь
бесконечные кардиналы).
Указание. Пусть % — начальный ординал мощности ш. Для
каждого а^т обозначим через D(a) множество всех транс-
трансфинитных последовательностей типа а, принимающих только
значения 0 и 1. Для каждого f^D(a) и любого р<а обо-
обозначим через /з элемент множества Z)(P), определенный так:
fo(v)=f(v) ПРИ У < Р- Для каждого /<=?>(«), где а < т, и
i=0, 1 обозначим через /* элемент множества Z)(a-j- 1), опре-
определенный следующим образом: f'(P) = /(P) при р<аи р(а) =
Применив трансфинитную индукцию, определите для каждо-
каждого а < т и каждого f^D(a) открытое множество Va(f)c^X
таким образом, чтобы выполнялись следующие условия:
A) Va+l(fJ)^Va(f) при / = 0, 1 и /gD(o).
B) ^а+1(Г)П^а+1(/1)=0 при /eD(a).
D) Ка(/)==Агдля каждого предельного ординала а и ка-
каждого f e Ь(а).
346 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
Каждому f^D(x) поставьте в соответствие какую-нибудь
точку из пересечения f) Va(fa) и покажите, что если f и f от-
0<Т
личаются на некотором непредельном ординале, то соответ-
соответствующие f и ? точки различны.
(b) (Чех и Поспишил [1938]). В обобщение (а) покажите,
что предположение о компактности X можно заменить предпо-
предположением, что X является пересечением Ко открытых множеств
в некотором компакте (т. е. что пространство X полно по Чеху).
(c) Заметьте, что Ко в (Ь) нельзя заменить на ш.
Указание. Примените конструкцию, описанную в упр. 2.3.Е,
кХ = Л(с).
(d) (Архангельский [1969]). Покажите, что каждый ком-
компакт, удовлетворяющий первой аксиоме счетности, либо счетен,
либо имеет мощность ровно с.
Указание. Покажите, что множество точек конденсации про-
пространства X плотно в себе, и примените (а).
(e) (Франклин [1969]). Выведите из (Ь), что каждый ком-
компакт мощности < 2^1 секвенциально компактен.
Указание. Из (Ь) следует, что каждый несчетный компакт
мощности < 2*1 содержит несчетное множество точек, характер
в которых
Диадические пространства I (см. задачи 4.5.9—4.5.11)
3.12.12. Компакт X называется диадическим (П. С. Алек-
Александров [1936]), если он является непрерывным образом канто-
рова куба Dm при некотором щ ^ Ко.
(a) (Марчевский [1941], Тьюки [1941]). Заметьте, что
с(Х)=&о для каждого диадического компакта X, и выведите
отсюда, что компакт А{т) не диадический, если m > Ко.
Указание. См. теорему 2.3.17.
(b) (Шанин [1948] (объявлено в [1946b])). Покажите, что
каждый диадический компакт веса ш ^ Ко является непрерыв-
непрерывным образом канторова куба Dm.
Указание (Энгелькинг и Пелчинский [1963]). Примените
упр. 3.2.H(d).
(c) (Энгелькинг и Пелчинский [1963]). Докажите, что для
каждой непрерывной вещественной функции f: X-^R на диади-
ческом компакте X найдется компакт Хо <= X веса Ко, такой, что
) f()
Заметьте, что R здесь можно заменить на любое тихонов-
тихоновское пространство веса Ко.
(d) (Энгелькинг и Пелчинский [1963]). Выведите из (с),
что компакт «две стрелки» не диадичен и что если стоун-чехов-
3.12. ЗАДАЧИ 347
ское расширение пространства X диадично, то X псевдоком-
пактно.
Указание, Покажите, что $R не является диадическим ком-
компактом, и заметьте, что любое не псевдокомпактное тихонов-
тихоновское пространство можно непрерывно отобразить на всюду
плотное подпространство пространства R.
(e) (Есенин-Вольпин [1949]). Покажите, что если компакт
X диадичен, то w{X)—%{X) (см. (g) и (h) ниже).
Указание. Докажите аналог задачи 2.7.13 (а) для простран-
пространства У, одноточечные подмножества которого являются пересе-
пересечениями m ^ Ко открытых множеств.
(f) (Шанин [1948] (объявлено в [1946а])). Докажите, что
каждый линейно упорядоченный диадический компакт обладает
счетной базой.
Указание, Примените (е) и задачу 3.12.4(а).
(g) (Б. А. Ефимов [1963а]). Докажите, что если %(х, Х)^.
^ m ^ Ко для каждого х из некоторого всюду плотного под-
подмножества диадического компакта X, то w(X)^ ш.
Указание (Э. Поль и Р. Поль [1976]). Пусть %(х,Х)^ш
для каждого х из множества В, всюду плотного в X. Рассмот-
Рассмотрите отображение f: Dn^>X канторова куба ?)п= Ц Ds кг X
и при каждом аеЛ = /-1(В) выберите S(a)c:S, такое, что
Psla)Ps(a)(a) = f~lf(a) и IS (а) |< т. Определите по индукции
возрастающие последовательности S\ а S2 с: ... и А\ с: Л2 ci
d ... подмножеств множеств S и А соответственно, такие, что
|S,|<m, |ЛКш»
Ps. W <= PSi (Ад и S*+i = Si U U {S (а): а е А,}.
оо оо
Заметьте, что для 50= (J St и Ло= М At имеют место соот-
ношения pSu(A)czps (Ло) и f(PslPs (a))~/(a) ПРИ всех а^ А-
Рассмотрите множество Af = /?„ (А) X П {«Л » где as = О
при 5gS\5Ojh покажите, что f(A') — X.
(h) (Архангельский и В. И. Пономарев [1968]). Докажите,
что w(X)=t(X) для каждого диадического компакта X.
Указание (Архангельский [1969]). Рассмотрите отображение
/: От->Хна X и множество 2n c:Z)m, где n = t(X), состоящее из
тех точек пространства Dm, не более чем п координат которых
отличны от нуля. Покажите, что / BП) = X, и заметьте, что те-
теперь достаточно доказать неравенство d(X)^n. С помощью
теоремы 2.3.15 убедитесь, что для каждого f ^ n и произволь-
произвольного множества Acz X мощности ^lexp f найдется множество
Bel, такое, что А а В я |В|^1. Трижды воспользовавшись
348
ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
этим наблюдением и применив теорему 1.5.3, покажите, что
jXJ^expn (с этой целью рассмотрите произвольное множе-
множество ЛсХ, для которого | А | ^ ехр ехр ехр п). Еще дважды вос-
воспользовавшись тем же соображением, докажите, что d(X)^n.
(i) (Энгелькинг 11965]; для кардиналов m вида «a+i —
Б. А. Ефимов [1965а]). Докажите, что если X — диадический
компакт и х(дго, X) = ш ^ «о, то X содержит подпространство М,
гомеоморфное ?>(т), такое, что М U {*о} гомеоморфно Д(т).
Указание. Рассмотрите непрерывное отображение f: П Ds~+
-+Х на X, прообраз А = f-l(x0) и множество 50 с S, состоящее
из тех sgS, для которых можно найти точки a(s)^ A n b(s)^
фА, такие, что ps,(a($)) = pff(b{s)) при sr Ф s. Для каждого
sgS0 выберем точки a{s) и b(s) с этими свойствами. Дока-
Докажите, что Л = р5(Л)Х П Ар и выведите отсюда, что
|So|^m. Прообразы точек при отображении Ь множества So
на множество B = b{S0) конечны; выведите отсюда, что |В|^
^ш. Проверьте, что все предельные точки множества В при-
принадлежат Л, и положите М = f(B).
(}) Проверьте, что следующая диаграмма (см. задачу
1.7.12(а)) содержит все равенства и неравенства, выполняю-
выполняющиеся для входящих в нее кардинальных функций в классе всех
диадических компактов (символ \Х\ обозначает здесь мощность
множества Х\ в силу (а), с(Х)=К0 для каждого диадического
компакта Х\ ясно, что 1(Х) =е(Х)= «о для такого компакта X):
3.12. ЗАДАЧИ 349
(к) (Б. А. Ефимов [1963а]). Докажите, что каждый наслед-
наследственно нормальный диадический компакт обладает счетной
базой.
Указание. Рассмотрите любое непрерывное отображение /:
?>m->Z на X и 2-произведение 2(a)c=Z)m. Покажите, что если
f(L(a)) = X, то а>(*)<К0 (см. задачу 3.12.23(f)). С этой
целью заметьте, что каждое сепарабельное подпространство
пространства X обладает счетной базой и что это же относится
и к каждому подпространству мощности ^с. Примените затем
(i) и (е). Если 1A,(а))ФХ, возьмите любую точку jcgX\
\/B(а)) и покажите с помощью (i) и теоремы 3.10.21, что
пространство X\{x} не нормально.
Обратные спектры II (см. задачи 2.7.19 и 6.3.16)
3.12.13 (Мардешич [1971]). Пусть S = {Za, л?, 2} —обратный
спектр хаусдорфовых пространств и Аа для каждого a ^ 2 —
компактное подпространство пространства Ха, такое, что
я?(Ла)с:Лр при любых a, pGS, удовлетворяющих условию
р^а, т. е. S' = {Aa, яЦ, 2}, где п°(х) = п°(х) при лге=Ла, яв-
является обратным спектром. Докажите, 4toS" — {Xg/Ao, (я?)\ 2},
где (я?)\* Х0/А0^>Хр1А9 определено в упр. 2.4.В, является
обратным спектром и что предельное пространство lim S" го-
меоморфно факторпространству (lim S)/(lim S').
Проверьте, что предположение о компактности пространств
Ао нельзя опустить.
Вокруг теоремы Куратовского и теоремы Уайтхеда
3.12.14. (а) (Мрувка [1959]). Пусть X — такое топологиче-
топологическое пространство, что проекция р: XX У ~*¦ Y является замкну-
замкнутым отображением для каждого компакта У, удовлетворяющего
неравенству w(Y)^ w(X). Докажите, что тогда X компактно.
Указание. Воспользуйтесь условием C) задачи 3.12.1, за-
заметьте, что можно предполагать, что \a\^w(X)t и возьмите
в качестве Y пространство всех ординалов ^а с топологией, по-
порожденной естественным линейным упорядочением <.
(b) (Майкл [1968]). Докажите, что если декартово произ-
произведение id*X?> где X — регулярное пространство, является
факторным отображением для каждого факторного отображе-
отображения g, то пространство X локально компактно (см. теоре-
теорему 3.3.17).
Указание. Воспользуйтесь конструкцией, приведенной в ука-
указании к пункту (а), и примените пример 2.4.20.
(c) (Майкл [1968]). Докажите, что если произведение
350 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
XX У. где X — регулярное пространство, является /г-простран-
ством для каждого /^-пространства У, то пространство X ло-
локально компактно (см. теорему 3.3.27).
Указание. Примените (Ь) и пример 3.3.29.
(d) (Майкл [1968]). Докажите, что если произведение
XX У у где X — регулярное пространство, является секвенциаль-
секвенциальным пространством для каждого секвенциального пространства
У, то пространство X локально секвенциально компактно (см.
упр. 3.10.1 (Ь)).
Указание. Примените теорему 3.10.33 и видоизмените кон-
конструкцию, приведенную в указании к пункту (а).
Наследственно ^-пространства совпадают с пространствами
Фреше — Урысона
3.12.15 (Архангельский [1968]). Докажите, что хаусдорфово
пространство является наследственно /^-пространством в том и
только том случае, если оно пространство Фреше — Урысона.
Указание. Заметьте прежде всего, что если X — наследствен-
наследственно ^-пространство, то для каждого подмножества Лс! и лю-
любой точки jcg1\4 найдется компакт Zcz^UM, такой, что
. Возьмите затем такой компакт Z наименьшей мощ-
мощ{}
ности щ, покажите, что %(xt Z) = т, и рассмотрите базу Vu V2, . • .
..., У ay .-., а < т, пространства Z в точке х, где т— началь-
начальный ординал мощности ш. Применив трансфинитную индукцию,
определите трансфинитную последовательность U\t U2, •••
..., Uа, • • •, а < т, окрестностей точки х в Z и трансфинитную
последовательность хи х2, ..., ха, ..., а < т, точек множе-
множества Z, такие, что
( U {*эГ)П?/а=0> Uaa:Va и ха^( П ?V)\{*} при а<т.
Покажите, что {х} (J [} {ха} содержит А(ж).
<%
Компактификации
3.12.16. (а) (Хьюитт [1947]). Докажите, что для каждого
тихоновского пространства X следующие условия равносильны
(см. задачу 8.5.11):
A) Пространство X обладает единственной (с точностью до
эквивалентности) компактификацией.
B) Пространство X компактно или \$Х\Х\=1.
C) Из любых двух замкнутых вполне отделенных подмно-
подмножеств пространства X по крайней мере одно компактно.
(Ь) Покажите, что каждое тихоновское пространство, удов-
удовлетворяющее условиям в (а), псевдокомпактно и локально ком-
компактно (см. задачу 3.12.19(а)).
3.12. ЗАДАЧИ 351
(c) Приведите пример счетно компактного локально ком-
компактного пространства, у которого есть бесконечно много не-
неэквивалентных компактификаций.
(d) Заметьте, что если f: X-*Y — непрерывное отображение
тихоновского пространства X, обладающего единственной ком-
пактификацией, на некомпактное тихоновское пространство Y>
то У обладает единственной компактификадией, а отображение /
совершенно.
(e) (Вислисени и Флаксмайер [1965]). Докажите, что если
для любых двух компактификаций тихоновского пространства X
с первой аксиомой счетности существует наибольшая нижняя
грань (т. е. семейство ^(Х) является решеткой), то простран-
пространство X локально компактно. Покажите, что предположение о
первой аксиоме счетности существенно.
Указание. Покажите, что если некоторая последователь-
последовательность точек множества $Х\Х сходится к точке из X, то у про-
пространства X есть компактификаций схХ и с2Х, для которых не
существует компактификаций сХ, удовлетворяющей неравен-
неравенствам сХ ^ аХ при i = 1 и 2.
3.12.17 (Франклин и Раджагопалан [1971]). (а) Определите
по трансфинитной индукции трансфинитную последовательность
U\ с: U2 cz ... a Uacz ..., а < a>i, открыто-замкнутых под-
подмножеств пространства $N\ N, такую, что Ua Ф U$ при Р < а,
и проверьте, что формула
при xs=($N\N)\ U Uat
] inf{a: x^Ua} при хе [) ?/a
<
задает непрерывное отображение f: $N \ N ->- W на простран-
пространство W всех ординалов sgcoi.
Указание. Примените упр. З.б.А.
(b) Определите трансфинитную последовательность U\ с:
с: U% с: ... a Uacz ..., a < б, открыто-замкнутых собствен-
собственных подмножеств пространства fiN \N, такую, что Up Ф Ua при
Р < а и объединение \J Ua всюду плотно в $N\ N. Заметьте,
а<б
что i^i^|6|^c и что в предположении континуум-гипотезы
можно взять б=соь Определите непрерывное отображение /:
р#\ 1^F + 1) на пространство W(8+l) всех ординалов
<б +1 с топологией, порожденной естественным линейным
упорядочением <.
(c) Покажите, что существует компактификация yN про-
пространства N, нарост которой совпадает с W. Отметьте, что yN —
сепарабельный компакт мощности Кь не являющийся секвен-
352 гл- 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
циальным пространством. Проверьте, что yN\{<di}—сепара-
бельное локально компактное нормальное пространство с пер-
первой аксиомой счетности, не являющееся линделёфовым про-
пространством.
Указание, Примените (а) и теорему 3.5.13.
(d) Покажите, что существует компактификация yfN про-
пространства N, нарост которой совпадает с 1^F+ 1), такая, что
никакая последовательность точек из N не сходится к точке б.
Заметьте, что y'N\ {6} — сепарабельное, локально компактное,
секвенциально компактное нормальное пространство, которое не
компактно.
Замечание. Первый пример секвенциально компактного не
компактного нормального пространства, содержащего в каче-
качестве всюду плотного подпространства локально компактное се-
сепарабельное метрическое пространство, был определен (в пред-
предположении континуум-гипотезы) М. Рудин в [1965].
(e) Заметьтье, что в предположении континуум-гипотезы
пространство y'N\{6} в (d) удовлетворяет первой аксиоме
счетности.
Длинная прямая и длинный отрезок
3.12.18. Пусть Wo — множество всех счетных ординалов. Рас-
Рассмотрим линейное упорядочение < на множестве Vo = Wo X
Х[0, 1J, определенное так: (аь ^i) < (а2, t2), если ai < а2 или
аг = а2 и U < t2. Множество Уо с топологией, порожденной ли-
линейным упорядочением <, называется длинной прямой. При-
Присоединив к множеству Vo точку o)i и приняв, что х < coi при
всех jcg Vo, мы получим некоторое линейно упорядоченное
множество V. Это множество V с топологией, порожденной ли-
линейным упорядочением <, называется длинным отрезком.
(a) Покажите, что длинный отрезок является стоун-чехов-
стоун-чеховской компактификацией длинной прямой.
(b) Докажите, что для любого х0 е Vo подпространство
М=={хеУ0: х ^ хо} пространства Vo гомеоморфно отрезку
[0,1].
Указание. Пусть Q — множество всех рациональных чисел
интервала @,1). Покажите, что элементы множеств Q и М П
fl(WoXQ) можно так расположить в последовательности
ги ?2> -•• и Si, s2, .-., что неравенство п < г/ будет выпол-
выполняться в том и только том случае, если s,- < s/. Проверьте, что
формула f{ri)=Si определяет непрерывное отображение /: Q->
-*Mt и примените теорему 3.2.1.
(c) (Архангельский [1961], Фролик [1961]). Тихоновское
пространство X называется локально полным по Чеху, если у
каждой точки xgX есть полная по Чеху окрестность.
3.12. ЗАДАЧИ 353
Покажите, что пространство, получающееся при удалении из
длинной прямой всех точек (а, 0), где а — любой непредельный
ординал, локально полно по Чеху, но не полно по Чеху (см.
задачу 5.5.8(с)).
(d) Заметьте, что каждое локально полное по Чеху про-
пространство является образом некоторого полного по Чеху про-
пространства при открытом отображении, и выведите отсюда, что
полнота по Чеху не является инвариантом открытых отобра-
отображений (см. задачу 5.5.8 (Ь)).
Плоскость Тихонова и близкие к ней пространства
3.12Л9. (а) (Тихонов [1930], Хьюитт [1948], Тонг [1949]).
Пусть W — пространство всех ординалов ^©i и W— его под-
подпространство, состоящее из всех ординалов ^©о. Пространство
Г= В7Х^'\ {(о)Ь coo)} называется плоскостью Тихонова.
Заметьте, что §T=Wy(,Wy и выведите отсюда, что про-
пространство Т не нормально. Плоскость Тихонова обладает един-
единственной компактификацией и не счетно компактна (см. зада-
задачу 3.12.16(Ь)).
(b) (П. С, Александров и Урысон [1929]). Докажите, что
если каждому счетному ординалу а > 0 поставить в соответ-
соответствие ординал ф(сс) таким образом, что ср(а)< а при всех а <
< соь то найдется ординал «о < ©ь Для которого |ф-1(ао)| =
= «ь
(c) Докажите, что для каждого компакта X произведение
Wy^X является стоун-чеховской компактификацией простран-
пространства Wo XX где Wo — пространство всех счетных ординалов
(см. задачу 3.12.20(с)).
Указание (Ван Дауэн [1978]). Пусть/: Wo X ^-^/ — произ-
произвольное непрерывное отображение. Возьмите любое положитель-
положительное целое число i и покажите, что для каждого счетного орди-
ординала а>0 найдется ординал ф(а)<а, такой, что \f(a',x) —
— f(a, x)\<.l/i при всех х е X и всех а', удовлетворяющих
условию ф(а) <С о! ^ а. Примените затем (Ь).
(d) (Дьедонне [1939b], Хьюитт [1948]). Покажите, что про-
произведение W X W является стоун-чеховской компактификацией
пространства Т^оХ W» и выведите отсюда, что пространство
foX^ не нормально. Отметьте, что пространство 1^0Х^
счетно компактно.
(e) Выведите из (d), что нормальность не сохраняется в
сторону прообраза совершенными отображениями.
Стоун-чеховская компактификация произведений
3.12.20. (а) (Исивата [1969], Нобл [1969а] и [1969b], Ком-
Комфорт и Хейджер — ссылка в работе Нобла [1969а]). Докажите,
23 Зак. 697
354 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
что для произвольных тихоновских пространств X и У следую-
следующие условия равносильны:
A) Проекция р: XX Y-*X отображает функционально
замкнутые подмножества пространства XX У на замкнутые
подмножества пространства X.
B) Каждую ограниченную непрерывную функцию f: XX ^-^
—* R можно непрерывно продолжить на XX рУ.
C) Для каждой непрерывной ограниченной вещественной
функции f: XXY-+R формула F (х) = sup / (x, у) определяет
непрерывную функцию F: X-+R.
Указание (Комфорт и Хейджер — цитировано в работе Ноб-
ла [1969а]). Доказывая, что C)=>A), рассмотрите для произ-
произвольного функционально замкнутого множества Z = g~l@)cz
cIX ^ и любой точки xo^X\p(Z) функцию /: ХХУ^/?,
определенную правилом: f(x,y)=—min(\g(x,y)/g(xQ,y)\fl).
(b) (Тамано [I960]). Докажите, что произведение XX У ти-
тихоновских пространств X и У псевдокомпактно в том и только
том случае, если пространства X и У псевдокомпактны и при
проекции р: ХХ^-^Х образами функционально замкнутых
подмножеств пространства XX У служат замкнутые подмноже-
подмножества пространства X.
Указание (Комфорт и Хейджер [1971]). Доказывая, что если
XX У псевдокомпактно, то p(Z) замкнуто в X для каждого
функционально замкнутого множества ZcIX ^ рассмотрите
произвольную точку хо е p(Z)\ p(Z) и непрерывную функцию
/: 1Х^^Д такую, что Z = f~l @) и f (х0, у)= 1 при всех г/sF
(см. указание в пункте (а)). Определите затем по индукции по-
последовательность (xuyi), (x2, #2), ... точек множества Z, а так-
также последовательности Wu W2, ... и W[, W'v ... открытых
подмножеств пространства XX У, где Wi = UiXVi — окрест-
окрестность точки (л;*, #/), удовлетворяющая условию f(Wi)cz [0, 1/3],
и W\ = U'. X Уi — окрестность точки (лго, уд, такая, что / (Wty cz
cz [2/3, 1], и где иш [} U'i+l czU'. при i = 1, 2, .... С помощью
теоремы 3.10.22 получите противоречие. При доказательстве об-
обратной импликации воспользуйтесь эквивалентностью условий
A) и C) в (а).
(c) (Гликсберг [1959]). Докажите, что если произведение
XX У пространств X и У псевдокомпактно, то рХХ Р^ является
стоун-чеховской компактификацией пространства XX У, т. е.
каждая непрерывная функция f: XX У-*/ непрерывно продол-
продолжается на рХХРУ. Покажите, что если рХХрУ—стоун-чехов-
рХХрУ—стоун-чеховская компактификация пространства XX У и оба пространства
X, У бесконечны, то произведение XX У псевдокомпактно.
Указание (Комфорт и Хейджер [1971]). Заметьте, что если
3.12. ЗАДАЧИ 355
при проекции р: ZXT-+Z, где Z — произвольный бесконечный
компакт, образы функционально замкнутых подмножеств про-
пространства Z X Т являются замкнутыми подмножествами про-
пространства Z, то пространство Т псевдокомпактно. Для этого
определите непрерывную функцию f: Z->I, такую, что при не-
некотором г0 е Z выполняются условия: /(го) = О и гоф Int f~l@).
Предположив, что пространство Т не псевдокомпактно, опреде-
определите непрерывную функцию g: 7-^@,1], для которой
infg(/) = 0. Рассмотрите функцию h: ZXT-+R, заданную
* <=г
формулой Л (г, 0=~?@Д2)> и воспользуйтесь эквивалентностью
условий A) и C) в (а). При доказательстве псевдокомпактно-
псевдокомпактности XX У примените сделанное выше наблюдение к произведе-
произведениям $XXY иХХРУ-
(d) (Гликсберг [1959]). Докажите, что если произведение
Ц Xs тихоновских пространств Xs псевдокомпактно, то
S
Р П Xs = П $XS, и что если р П Xs = Ц рХ5 и произведение
Sf=S s^S ssS seS
Ц Xs бесконечно при всех s0 e 5, то произведение JJ Х3
5\ {s0} sgS
псевдокомпактно.
Указание. Сначала убедитесь, что если произведение JI Xs
псевдокомпактно, то для каждой непрерывной функций
/•' II XS->I и каждого е > 0 найдется конечное множество
So c= S, такое, что выполняется условие: если x,jg]]^h
Ps(x) = ps(y) при всех seS0) то \f(x) — /(f/)|<e. Для этого
предположите, что такого So не существует, и определите по-
последовательность Si, S2, ... попарно не пересекающихся конеч-
конечных подмножеств множества S и последовательности х\, Х2> ...
и у и г/2, ... точек множества Ц Xsf такие, что \f(xi)— f{yi) [^
^ е/2 и ps(xi)= ps(yi) при s^Si. Найдите окрестности
U% = П Us, i и Vt = П Vs, i точек xi и уи для которых Us, t =
= Vs,i при ss?Si и |/(л:) — f(j/)|^e/4, когда ^et/(- и уеУ(,
и выведите отсюда противоречие.
Рассмотрите затем произвольную пару Л, В вполне отде-
отделенных подмножеств пространства Ц Xs и для произволь-
S€=S
ной непрерывной функции /, отделяющей А и В, и числа е = 1/3
возьмите конечное множество So с: S с указанным выше свой-
свойством. Применив (с), продолжите f до непрерывной функции
23»
356 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
Г- П P^s X П Xs->/и заметьте, что проекции множеств
5 5\S
0 ^\0
А и В на пространство Ц Xs имеют непересекающиеся замы-
кания в И $XS.
(е) (Гликсберг [1959]). Докажите, что если X — любое
псевдокомпактное пространство и {^}ses произвольное се-
семейство локально компактных псевдокомпактных пространств, то
произведение ХХП^ псевдокомпактно.
Указание. Заметьте сначала, что достаточно рассмотреть
случай счетного семейства {Xi}™^ некомпактных пространств.
Покажите затем, что никакая бесконечная последовательность
U\, U2i ... элементов канонической базы произведения
оо
X X П Xt не локально конечна. С этой целью рассмотрите про-
i = \
оо
изведение XXП a%i и последовательность Vu У2, ••• его от-
крытых подмножеств, где Vk получается из Uk заменой каждого
сомножителя Xt на aXi.
Кольца непрерывных функций и компактификации
3.12.21 (М. Стоун [1937], Гельфанд и Колмогоров [1939],
Хьюитт [1948] и [1950]). Для произвольного тихоновского про-
пространства X через С(Х) (через С*(Х)) обозначается кольцо
всех непрерывных вещественных (всех ограниченных непрерыв-
непрерывных вещественных) функций на пространстве X. Идеалом в С(Х)
(в С*(Х)) называется произвольное собственное подмножество Д
кольца С(Х) (кольца С*(Х)), такое, что если /, ^еД, то
f + geA, и если feAHge C(X) (если g^ C*(X)), то fg e Д.
Идеал Д называется максимальным идеалом, если для каждого
идеала Д', содержащего Д, имеет место равенство К = Д.
(a) Покажите, что каждый идеал содержится в некотором
максимальном идеале.
(b) Докажите, что тихоновское пространство X компактно
в том и только том случае, если для каждого максимального
идеала Д в кольце С(Х), или, что равносильно, для каждого
максимального идеала Д в кольце С*(Х), найдется точка jcgI,
такая, что условия Дх) = 0 и[еД эквивалентны.
Указание. Предположите, что для компакта X нашелся идеал
Д, содержащий при каждом xg! неотрицательную функцию
fx, такую, что fx(x)=ly и рассмотрите покрытие
{/^(U/2, 3/2))}Х€еЛ пространствах
3.12. ЗАДАЧИ 357
Пусть X — некомпактное тихоновское пространство. Возьмите
открытое покрытие {Us}s<-S, в котором нет конечного подпокры-
подпокрытия. Для каждого хеХ выберите s(x)e S, такое, что хе Us(x)>
и функцию /*е С*(Х), для которой Ы*)= 1 и fx(xWS(x)) =
= {0}; рассмотрите любой идеал, содержащий все отобранные
функции.
(c) На множестве Ж всех максимальных идеалов кольца
С(Х) (кольца С*(Х)) введите топологию, взяв в качестве базы
семейство всех множеств вида Uf = {А: \ф А}, и покажите, что
Ж— компакт. Проверьте, что если поставить в соответствие ка-
каждой точке х е X максимальный идеал А(х) всех функций, об-
обращающихся в точке х в нуль, то получится гомеоморфное вло-
вложение пространства X в пространство Ж. Докажите, что Ж яв-
является стоун-чеховской компактификацией пространства X.
Выведите отсюда, что компакты X и Y гомеоморфны в том
и только том случае, если кольца С(Х) и С (У) изоморфны,
т. е. если существует взаимно однозначное отображение
Ф множества С{Х) на множество C(Y)t такое, что <t>(f + g") =
= Ф(/) + Ф(?) и Ф(/-я) = Ф(П-Ф(г) при всех f, g<=C(X).
Покажите, что тихоновские пространства X и У, удовлетворяю-
удовлетворяющие первой аксиоме счетности, гомеоморфны в том и только том
случае, если кольца С(Х) и C(Y), или, что равносильно, кольца
С*(Х) и С*(У), изоморфны.
Указание, Чтобы доказать, что Ж является стоун-чеховской
компактификацией пространства Ху примените теорему 3.2.1.
(d) Проверьте, что если А — максимальный идеал в С(Х),
то ЗГ (А) = {f~l @): f e А}—ультрафильтр на семействе З)о(Х)
всех функционально замкнутых подмножеств пространства X,
и что если У — произвольный ультрафильтр на 2H(Х), то
Д (#") = {/<= С(Х): f-l(Q)e:&~}— максимальный идеал в С(Х).
Покажите, что Д(#~(Д)) = А и #~(A(^"))==iF, т. е. имеет место
взаимно однозначное соответствие между ультрафильтрами на
З)о(Х) и максимальными идеалами в С(Х). Заметьте, что кон-
конструкция пространства (ЗХ, указанная в (с), по существу иден-
идентична конструкции, описанной в упр. З.б.К(а).
Приведите пример максимального идеала А в C*(N), такого,
что семейство {f~l @): / е А} не центрировано, и приведите при-
пример ультрафильтра У на Й5О(ЛО» для которого множество {/ е
^C*(N): /-1@)e^"} не является максимальным идеалом.
(e) Будем называть кольцо Ра С*(X) полным кольцом
функций на тихоновском пространстве X, если Р содержит все
постоянные функции, разделяет точки и замкнутые множества
и замкнуто относительно топологии равномерной сходимости.
Докажите, что конструкция из (с), примененная к множеству Ж
всех максимальных идеалов в полном кольце функций Р на ти-
358 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
хоновском пространстве X, дает некоторую компактификацию
пространства X и что семейство всех функций на X, допускаю-
допускающих непрерывное продолжение на эту компактификацию, сов-
совпадает с Р. Проверьте, что таким образом установлено взаимно
однозначное соответствие между всеми полными кольцами функ-
функций на тихоновском пространстве X и всеми компактификация-
ми пространства X.
Указание. Доказывая, что пространство всех максимальных
идеалов в Р хаусдорфово, заметьте, что если /еР и 1/2 ^Г
/(K/2 при всех xgI, то / не принадлежит никакому
идеалу (примените равенство 1// = 1 + ? fl0> где /0 = 1 — /)«
Рассмотрите компактификацию сХ пространства X, для которой
семейство всех функций на X, непрерывно продолжаемых на сХ>
совпадает с Р.
(f) Линейно-мультипликативный функционал на С(Х) (на
С*(Х))—это функционал ср, сопоставляющий каждому /е
^С(Х) (каждому f ^ С*(X)) вещественное число cp(f) таким
образом, что для всех fu f2 и всех вещественных чисел tu h
выполняются условия:
Функционал ф называется нетривиальным, если существует
функция /, для которой ф(/)=7^0. Функционал ф определяется
точкой х ^ Ху если ф(/) = f(x) при всех /.
Покажите, что тихоновское пространство X компактно в том
и только том случае, если каждый нетривиальный линейно-муль-
линейно-мультипликативный функционал на С* (X) определяется некоторой
точкой.
Заметьте, что имеется взаимно однозначное соответствие ме-
между нетривиальными линейно-мультипликативными функциона-
функционалами на С*(Х) и максимальными идеалами в С*(Х), т. е. точ-
точками стоун-чеховской компактификации пространства X.
Указание. Если ф — нетривиальный линейно-мультиплика-
линейно-мультипликативный функционал, то множество A={f: ф(/) = 0} является
максимальным идеалом.
(g) Покажите, что тихоновское пространство X вещественно
полно в том и только том случае, если каждый нетривиальный
линейно-мультипликативный функционал на С(Х) определяется
некоторой точкой.
Заметьте, что имеет место взаимно однозначное соответствие
между нетривиальными линейно-мультипликативными функцио-
функционалами на С(Х) и точками пополнения по Хьюитту (т. е. веще-
вещественного пополнения) пространства X.
3.12. ЗАДАЧИ 359
Выведите отсюда, что вещественно полные пространства X
и Y гомеоморфны в том и только том случае, если кольца С(Х)
и C(Y) изоморфны.
Указание. Примените (f) и теорему 3.11.10.
Замечание. Так как uJdpX, возникает вопрос, чем харак-
характеризуются те максимальные идеалы в С(Х) (в С*(Х)), которые
отвечают точкам пространства иХ Как мы знаем, в конструкции
пространства $Х в терминах ультрафильтров на SDo(X) счетно
центрированные ультрафильтры отвечают точкам пространства
ьХ (см. упр. 3.11 .F(b)). Оказывается, этим ультрафильтрам со-
соответствуют те идеалы А (идеалы А П С*{Х))9 для которых фак-
торкольцо С(Х)/А изоморфно полю вещественных чисел; см.
книгу Гиллмана и Джерисона [1960].
Счетная компактность
3.12.22. (а) (Акуаро [1965]). Докажите, что если каждое
дискретное семейство непустых подмножеств пространства X
конечно (имеет мощность ^ш^^о), то каждое открытое то-
точечно конечное покрытие %L (каждое открытое покрытие °U
с тем свойством, что никакая точка пространства X не принад-
принадлежит более чем m ^ Ко элементам семейства °U) простран-
пространства X содержит конечное подпокрытие (подпокрытие мощности
Заметьте, что если пространство X счетно компактно, то ка-
каждое открытое точечно счетное покрытие °U пространства X
(каждое открытое покрытие °U со свойством, что никакая точка
пространства X не принадлежит более чем at ^ Ко элементам
семейства °U) содержит конечное подпокрытие (подпокрытие
мощности ^ш).
Указание. Рассмотрите максимальное множество Лс:Х, та-
такое, что |ЛП^|^1 Для всех U e °Uy и покажите, что Х =
{ А}
{ }
(b) (Исэки и Касахара [1957], Левшенко [1957]). Докажи-
Докажите, что регулярное пространство X счетно компактно в том и
только том случае, если каждое точечно конечное открытое по-
покрытие пространства X содержит конечное подпокрытие.
Указание. Примените упр. 2.I.G.
(c) (Фролик [1960а]). Покажите, что предположение о ре-
регулярности существенно в (Ь).
Указание. При i = l, 2, ... пусть At обозначает множество
всех чисел вида k/2\ где & = 1, 3, ..., 2* — 1. На множестве
2, ...}, где Хо=(/\ U АЛ и
&I при i = l9
2 ..., введем топологию следующим образом. Множество Jo
наделим топологией, порожденной /, и объявим открытым под-
360 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
пространством пространства X; в качестве базы топологии в
точке Xi возьмем семейство всех множеств вида {xi}(](U П Хо),
где U — любое открытое множество в /, для которого AtczU.
С помощью теоремы Бэра о категории покажите, что для ка-
каждой возрастающей последовательности k\ < &2 < • • • нату-
натуральных чисел и произвольного семейства {Ui}{^m{ открытых в /
множеств, такого, что Akt cz Ut при /=1,2, ..., найдется точка
хо е Xq, принадлежащая бесконечно многим Ui.
(d) (Р. С. Хьюстон — цитировано в работе Флейшмана
[1970]; для регулярных пространств —Флейшман [1970]). До-
Докажите, что хаусдорфово пространство X счетно компактно в
том и только том случае, если для каждого открытого покры-
покрытия Щ пространства X найдется конечное множество F czX>
такое, что X =* [} {U e= °U\ F П U ф 0}.
Указание. Пусть X — хаусдорфово пространство, в котором
есть счетное бесконечное множество Л, для которого никакая
точка пространства X не является предельной. Представьте А
сю
в виде объединения [j Ai9 где \At | = i и Аг (]А}==0 при i ф /.
Для каждого х ^ А возьмите окрестность Ux, такую, что А П
П Ux = {х} и UxOUy = 0, когда х и у различны и принадле-
принадлежат одному и тому же множеству Л*. Рассмотрите покрытие
{Ux)xmAVlX\A}.
(e) (Хабер [1976]). Докажите, что если пространство X
счетно компактно и диагональ Д является б6-множеством в про-
произведении Х\Х, то X компактно.
Указание. Определите сначала счетное семейство {Уi}°°=x от-
открытых покрытий пространства X, такое, что для каждой пары
лс, у различных точек множества X найдется натуральное чис-
число i, при котором никакой член семейства У°1 не содержит од-
одновременно х я у. Предположите, что X обладает открытым по-
покрытием Ш, у которого нет счетного подпокрытия. Заметьте, что
если множество F cz X нельзя покрыть счетным подсемейством
семейства °U, то для каждого х е X найдется такое /, что и
множество F\ \){V ^Tr. xgF} не покрывается никаким счет-
счетным подсемейством семейства °U. Определите последователь-
последовательность Х\у х%, ... точек пространства X и последовательность
iu i2, ... натуральных чисел таким образом, чтобы выполнялись
следующие условия:
A) **е/\=Х\ Ц [){V<=r4i xf^V}.
B) Множество Fk \U{Kg Tik: xk^V) не покрывается ни-
никаким счетным подсемейством семейства °U.
3.12. ЗАДАЧИ 361
C) Для каждого х ^ Fk и любого i < ik множество
Fk\\]{V ^Ti: xe V) может быть покрыто счетным подсемей-
подсемейством семейства °U.
Покажите, что некоторое натуральное число / встречается
в последовательности i!f i2t ... бесконечно много раз, и полу-
получите противоречие.
(f) (А. С. Мищенко [1962], Корсон и Майкл [1964]). Дока-
Докажите, что если некоторая база $ счетно компактного (компакт-
(компактного) ^-пространства X точечно-счетна (обладает тем свой-
свойством, что никакая точка пространства X не принадлежит более
чем ш ^ No элементам базы Ш), то 0$ счетна (имеет мощность
)
Указание. Докажите, что d(X)^m. Для этого определите
последовательность С\ с: С2 с: ... подмножеств пространства Х>
оо
такую, что |Ci\ ^ ш при i = 1, 2, ... и U С,- всюду плотно в X:
примите за С\ произвольное одноточечное подмножество про-
пространства X и определите C,-+i как множество, полученное из d
присоединением по одной точке из каждого непустого множества
вида X\\JT, где Y — произвольное конечное подсемейство се-
семейства {В <= Я: В П Ct ф 0}.
В случае компактного пространства можно воспользоваться
также следующим фактом, известным под названием леммы Ми-
Мищенко: если семейство si подмножеств множества X обладает
тем свойством, что никакая точка множества X не принадлежит
более чем ш ^ Ко элементам семейства *s#, то существует самое
большее ш неприводимых (т. е. не содержащих собственных под-
подпокрытий) конечных покрытий множества X элементами семей-
семейства si. Чтобы установить лемму Мищенко, поступите следую-
следующим образом. Предположите, что для некоторого целого k се-
семейство А всех неприводимых покрытий множества X, состоящих
ровно из k элементов семейства si, имеет мощность >ш, и опре-
определите по индукции различные члены Аи А2> ..., Ak семейства
М- таким образом, чтобы при каждом / ^ k семейство
А(А\У А2, ..., Л) всех покрытий из А, содержащих множества
А\9 Л2, ..., Ai, имело мощность >ш.
(g) (Фролик [1959]). Покажите, что хаусдорфово простран-
пространство X счетно компактно в том и только том случае, если ка-
каждая полунепрерывная снизу (сверху) вещественная функция,
определенная на Ху ограничена снизу (сверху).
2-произведения II (см. задачи 2.7.13, 2.7.14, 4.5.12 и
упр. 3.10.D)
3.12.23. (а) (Энгелькинг [1966]). Пусть {Js}5e5—некоторое
семейство топологических пространств и a={as)—точка про-
362 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
изведения JJ Xs. Через 2/(а) обозначим подпространство про-
S
s
s S
странства Д Xs, состоящее из всех точек {xs}> таких, что xs?=
S ?5
ф as лишь для конечного числа seS. Докажите, что если все
конечные произведения XS{ X Xs2 X • • • X Xsk, где su 52, ...
..., s^eS, обладают свойством Линделёфа, то для каждого
семейства точек {xt}t^T в 2'(а), где \Т\> Хо, найдется точка
jcoeS'fa), каждая окрестность которой содержит точки xt для
бесконечного числа t e Т.
Указание. Примените задачу 2.7.10(с).
(Ь) (Энгелькинг [1966]). Пусть {Xjse5 — семейство топо-
топологических пространств, причем все конечные произведения
Х$1 Х^2Х"- XXsk, где 5i, s2, ..., ^eS, обладают свой-
свойством Линделёфа (см. упр. 3.8.G и 3.9.F) и У — такое хаусдор-
фово пространство, что диагональ Дет УХ У является G6-mho-
жеством. Докажите, что тогда для каждой точки а е Ц Xs и
любого непрерывного отображения /: 2 (а)-»- У найдутся счетное
множество So си S и непрерывное отображение /0: Ц Xs-+Y,
такие, что / совпадает с композицией /0(/?sJ2(a)) сужения про-
проекции р • П Xs-+ П Х5на 2(а) и отображения /0.
Указание. Сначала покажите, применив (а), что множество
So всех тех seS, для которых существуют точки xf xfe 2х(а),
отличающиеся только на 5-й координате и удовлетворяющие
условию 1(х)Ф1(х/), счетно. Проверьте затем, что если для
точек x={xs}, x' = {x's} из S7(a) множество (seS: х$Фх'^
конечно и не пересекается с So, то f(x)—f(x'). Чтобы завер-
завершить доказательство, воспользуйтесь непрерывностью f и тем,
что 27(а) всюду плотно в 2(а).
(c) (Гликсберг [1959]). Докажите, что для каждого семей-
семейства {JTs}seS компактов и любой точки ае Д ^произведение
JJ Xs является стоун-чеховской компактификацией Е-произве-
дения 2(а).
(d) (Корсон [1959], Энгелькинг [1966]). Пусть {Xs}se5 —
семейство тихоновских пространств, для которого все конечные
произведения Х$1 ХХ$2 X ... X XSft, где su s2, ..., sk e S, об-
обладают свойством Линделёфа (см. упр. 3.8.G и 3.9.F). Дока-
Докажите, что для любой точки а е JJ Xs произведение JJ JTS яв-
ляется пополнением по Хьюитту 2-произведения 2 (а).
ЗЛ2. ЗАДАЧИ 363
(e) (Корсон [1959]). Приведите пример нормального про-
пространства, для которого пополнение по Хьюитту не нормально.
Указание. Примените (d) и задачи 2.7.14 и 2.7.16(а).
(f) (Б А Е [1963а]). П {} й
р () ()
(f) (Б. А. Ефимов [1963а]). Пусть {X5}seS — семейство ком-
компактов, таких, что w(Xs)^m^ &q при всех s e 5, и пусть
а ={а5} — какая-нибудь точка произведения Ц Xs. Обозначим
через 2т (а) подпространство пространства Ц XSJ состоящее из
всех точек {xs}> для которых мощность множества {s e S: xs Ф
Ф as} не превосходит ш. Докажите, что если компакт X является
непрерывным образом пространства Sm(a), то ш(Х)^т.
Указание. Примените (с) и указание к задаче 3.12.12 (h).
Нормально расположенные множества III (см. задачи 1.7.6
и 2.7.3)
3.12.24. (а) (Ю. М. Смирнов [1951с]). Покажите, что если
пространство X линделёфово, то каждое нормально расположен-
расположенное подмножество пространства X, наделенное топологией под-
подпространства, является линделёфовым пространством. Докажи-
Докажите, что для каждого тихоновского пространства X следующие
условия равносильны:
A) Пространство X обладает свойством Линделёфа.
B) Пространство X нормально расположено в каждой своей
компактификации.
C) Пространство X нормально расположено в рХ.
D) Пространство X нормально расположено в некоторой
своей компактификации.
Выведите отсюда, что никакая точка х ^$N\ N не являет-
является б6-множеством в $N (см. упр. 3.6.G(a)).
(b) Проверьте, что тихоновское пространство X обладает
свойством Линделёфа в том и только том случае, если для
каждого компакта ZcrpX\X найдется непрерывная функция
h: pX-v/, такая, что ft(Z)cr{0} и Л(л:)>0 при всех x e X. За-
Заметьте, что в приведенной выше характеристике компактифика-
цию рХ можно заменить любой компактификацией простран-
пространства X.
Регулярно расположенные множества
3.12.25 (Мрувка [1957]). Будем говорить, что множество А
регулярно расположено в пространстве X, если для каждой точ-
точки хеХ\/1 в X существует множество Н типа Fo, такое, что
АсН<=:Х\{х}.
(а) Заметьте, что каждое множество, нормально располо-
расположенное в 7\-пространстве X, регулярно расположено в X.
364 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
(b) Покажите, что тихоновское пространство X вещественно
полно в том и только том случае, если X регулярно располо-
расположено в рХ. Приведите пример вещественно полного простран-
пространства X и его компактификации, в которой X не регулярно рас-
расположено.
(c) Докажите, что если X — вещественно полное простран-
пространство, то каждое регулярно расположенное в нем подмножество
в топологии подпространства вещественно полно.
(d) Выведите из (Ь) и (с), что произведение любого мно-
множества вещественно полных пространств вещественно полно.
Пространства замкнутых подмножеств II (см. задачи 2.7.20,
4.5.22, 6.3.22 и 8.5.16)
3.12.26. (а) (Вьеторис [1922]). Докажите, что если X — ком-
компактное пространство, то экспоненциальное пространство 2х
тоже компактно и wBx) = w(X). Заметьте, что если X есть
7\-пространство и пространство 2х компактно, то и простран-
пространство X тоже компактно.
Указание (Майкл [1951]). Проверьте, что семейство всех
множеств вида {В^2Х: В а Щ и {В^2Х: В(]иФ0}, где
U — произвольное открытое множество в X, является предбазой
пространства 2х, и примените задачу 3.12.2.
Замечание. Кислинг доказал в [1970], что нормальность про-
пространства 22* эквивалентна тому, что X—компакт. В [1970а]
он доказал, что в предположении континуум-гипотезы простран-
пространство 2х нормально в том и только том случае, если X — ком-
компакт. Как показано Величко в [1975], равносильность послед-
последних условий можно доказать без помощи континуум-гипотезы.
Заметим также, что, как доказал Л. Б. Шапиро в [1976], про-
пространство 2х может не быть диадическим компактом, если X —
диадический компакт.
(b) (Майкл [1951]). Для произвольного 7\-пространства X
обозначим через Ж(Х) подпространство пространства 2х, обра-
образованное всеми непустыми компактными замкнутыми подмноже-
подмножествами пространства X. Покажите, что 3?(Х) является 7Vnpo-
странством в том и только том случае, если X является
^-пространством при i =2, 3 и 3 j. Приведите пример совер-
совершенно нормального линделёфова пространства X, для которого
ЗС(Х) не нормально. Проверьте, что wCZ(X))= w(X) для ка-
каждого Т\-пространства X.
(c) (М.М. Чобан [1971]). Проверьте, что если X — подпро-
подпространство компакта Z, то, ставя в соответствие произвольному
Де? (X) то же А ^ 2Z, мы определяем гомеоморфное вложе-
вложение пространства Z(X) в пространство 2Z. Выведите отсюда,
что пространство ??{Х) локально компактно и хаусдорфово в
3.12. ЗАДАЧИ 365
том и только том случае, если пространство X локально ком-
компактно и хаусдорфово. Заметьте, что пространство 2* не локаль-
локально компактно.
Покажите для произвольного ^-пространства X, что, сопо-
сопоставляя каждому А^2Х замыкание А в волмэновском расши-
расширении (дХ, мы получаем гомеоморфное вложение пространства
2х в пространство 2соХ. Докажите, что wBx)— w(<uX) для ка-
каждого Трпространства X.
(d) (М. М. Чобан [1971] (объявлено в [1969]); для ш =
= fci0 — Вулберт [1968]). Докажите, что для произвольного
хаусдорфова пространства X неравенство х(^(^))^т^^о
выполняется в том и только том случае, если d(A)^Lm и
(ЛХ)^шпри всех Ле?(Х).
Выведите отсюда, что для компакта X неравенство %BХ)<^.
m ^ &о выполняется в том и только том случае, если
(X)m, и %(А,Х)^ш для каждого замкнутого АаХ.
Указание. Заметьте, что T{UU U2, ..., Uk)czT(Vu V2, ...
k m
..., Vm) в том и только том случае, если |J Ut a \] V> и в
i=i /=i
каждом Vj содержится некоторое [/,-. Воспользуйтесь тем, что
если %(Х)^ш и d(A)^m для каждого замкнутого A<z:Xy то
hd(X)^.m (это следует из задачи 3.12.9(d), но может быть до-
доказано и прямо).
(e) (М. М. Чобан [1971]). Проверьте, что если X и У —
хаусдорфовы пространства и f: X-+Y — непрерывное отобра-
отображение, то, положив f(A) = f(A) для каждого Ле?A), мы
получим непрерывное отображение f: Z?{X)-> 2?(Y). Покажите,
что если X и У — тихоновские пространства, то / совершенно
в том и только том случае, если f совершенно.
Указание. Привлеките стоун-чеховскую компактификацию.
(f) (Зенор [1970]; для компактов С. Сирота [1968]). Дока-
Докажите, что если 5 = [Хо, я?, 2} — обратный спектр хаусдорфовых
пространств, то S = {Ж (Ха), й«, 2}, где й? Z (Хо) -> X (Х9)
определено как в (е), тоже обратный спектр и что предел lim S
гомеоморфен пространству 3Z (lim S).
Выведите отсюда, что если S = {Xa, я^, S} — обратный
спектр компактов, то S = {2*a, ftp, E} тоже является обратным
спектром и что предел lim S гомеоморфен пространству 2<- .
(g) (М. М. Чобан ^11971] (объявлено в Ц969]), Зенор
[1970]). Докажите, что пространство 3Z(X) полно по Чеху в том
и только том случае, если X полно по Чеху.
Указание. Примените (с) или воспользуйтесь (f) и упр. 3.9.G.
366 ГЛ. 3. КОМПАКТНЫЕ ПРОСТРАНСТВА
(h) (Зенор [1970]). Докажите, что пространство 3Z(X) ве-
вещественно полно в том и только том случае, если X веществен-
вещественно полно.
Указание. Либо воспользуйтесь (с) и задачей 3.12.25(с),
либо примените (f) и упр. 3.11.Н.
(i) (Марьянович [1966]). Докажите, что произведение
П Xs, где все пространства Xs являются компактами, можно
вложить в экспоненциальное пространство одноточечной ком-
пактификации суммы © Xs, и заметьте, что отсюда следует
теорема Тихонова для хаусдорфовых пространств.
(j) Покажите, что если X — компакт и У — хаусдорфово про-
пространство, то, сопоставляя каждому f ^ Yx график G(f)cz
сзХХУ, мы получаем гомеоморфное вложение функциональ-
функционального пространства Yx с компактно-открытой топологией в экс-
экспоненциальное пространство 2х ХУ.
(к) Проверьте, что если X — компакт и У — хаусдорфово
пространство, то, поставив в соответствие каждой паре (/, Л)е
е Ух X 2х образ f(A)^2Y, мы получаем отображение из
У*Х2* в 2У, непрерывное по отношению к компактно-открытой
топологии на Yx.
Многозначные отображения III (см. задачи 1.7.17 и 2.7.21)
3.12.27. (а) (Энгелькинг [1963]; для метрических про-
пространств— Куратовский [1932]). Докажите, что для любого
семейства {Fs}5gS полунепрерывных сверху многозначных ото-
отображений топологического пространства У в хаусдорфово про-
пространство X с компактными образами точек пересечение
F= Г\ Ft, определенное формулой F(y)= f] Ft(y)y является
полунепрерывным сверху отображением.
Указание. Заметьте, что {у: F(у) с:U} = (J П {У- Ft(y)cz
с=С/^},где объединение берется по всем семействам{Ut}t(sT от-
открытых множеств в X, для которых f| Ut = U и множество
{t еГ: Ut?= X} конечно.
(Ь) (Энгелькинг [1963]). Для каждого /еГ пусть Ft — не-
некоторое многозначное отображение, сопоставляющее точкам то-
топологического пространства У замкнутые подмножества про-
пространства Xt. Проверьте, что если все отображения Ft полуне-
полунепрерывны снизу, то декартово произведение F= Ц Ft, onpe-
t e= T
деленное формулой F(y)= Ц Ft(yO является полунепрерывным
ts=T
3.12. ЗАДАЧИ 367
снизу многозначным отображением, при котором точкам про-
пространства У соответствуют замкнутые подмножества произведе-
произведения IX AY
t<=T
Покажите, что если при всех отображениях Ft образы точек
компактны и все Ft полунепрерывны сверху, то декартово про-
произведение F = IX Ft т°же является полунепрерывным сверху
отображением.
Выведите отсюда, что для произвольного семейства {Xt}t^T
хаусдорфовых пространств, приписывая каждой точке {At}^
е Ц 3C(Xt) произведение П^^^ГП^Л» мы получаем
непрерывное отображение.
(с) (Энгелькинг [1963]). Докажите, что хаусдорфово про-
пространство X компактно в том и только том случае, если, каково
бы ни было индексное множество Г, поставив в соответствие
произвольной точке {A t} e XI 2х', где Xt=X при (еТ и 2^
взято с топологией Вьеториса, пересечение ("] Л* е 2х (или, что
П xt
полунепрерывное сверху многозначное отображение.
тт ( t)\
равносильно, произведение _и_Л^е2^еГ ^1, мы получаем
t е=г /
Глава 4
МЕТРИЧЕСКИЕ
И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА
Понятие топологического пространства можно рассматривать
как аксиоматизацию понятия близости точки к множеству: точка
близка к множеству, если она принадлежит его замыканию.
В этой главе мы будем изучать теорию метрических пространств,
которая является аксиоматизацией понятия близости точек: в
метрическом пространстве каждой паре точек соответствует ве-
вещественное число — расстояние между ними, основные свойства
которого описывает система аксиом. Расстояние между точками
можно использовать для определения расстояния между точкой
и множеством; считая все точки, расстояние которых до мно-
множества А равно нулю, близкими к множеству А и определяя
замыкание множества А как множество всех таких точек, мы
получаем топологическое пространство. Топологические про-
пространства, которые могут быть получены таким образом, назы-
называются метризуемыми пространствами.
В гл. 8 мы обсудим две другие системы аксиом, описываю-
описывающие родственные понятия равномерных пространств и про-
пространств близости. В равномерных пространствах тоже рас-
рассматривается расстояние между парами точек, но оно изме-
измеряется не так, как в метрических пространствах. Теория про-
пространств близости есть аксиоматизация понятия близости между
парами множеств.
Итак, эти три понятия — метрическое пространство, равно-
равномерное пространство и пространство близости — существенно
отличаются от понятия топологического пространства. Причина,
по которой они изучаются в данной книге, заключается в мно-
многочисленных и интересных взаимосвязях этих пространств с то-
топологическими пространствами, что и делает их частью общей
топологии.
Из чисто логических соображений мы должны были бы от-
отложить изучение метрических пространств до гл. 8, как мы по-
поступили с равномерными пространствами и пространствами бли-
близости, и завершить прежде всего ту часть этой книги, которая
целиком посвящена топологическим пространствам. Однако
класс метрических пространств внутренним образом связан с
представляющим большой интерес классом метризуемых про-
пространств (которые образуют особый класс топологических про-
пространств). Метризуемые пространства играют важную роль в
4.!. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА 369
приложениях общей топологии, и, кроме того, работа с этим
классом способствует развитию правильной топологической ин-
интуиции, а наш запас топологических понятий и фактов уже до-
достаточен для того, чтобы установить наиболее важные резуль-
результаты о метрических и метризуемых пространствах.
Параграф 4.1 открывается определениями метрического и
метризуемого пространства; мы показываем, как метрика ин-
индуцирует топологию, и называем две метрики эквивалентными,
если они индуцируют одну и ту же топологию. Затем мы пока-
показываем, что всякое метризуемое пространство является совер-
совершенно нормальным и удовлетворяет первой аксиоме счетности
и что для метризуемого пространства наличие счетной базы
(т. е. выполнение второй аксиомы счетности) равносильно сепа-
сепарабельности и свойству Линделёфа. Параграф завершается дву-
двумя важными теоремами, утверждающими, что для метризуемых
пространств понятия компактности, счетной компактности и сек-
секвенциальной компактности эквивалентны и что эти свойства
влекут за собой сепарабельность.
В § 4.2 определяются и изучаются операции на метрических
пространствах. Мы доказываем, что подпространства, суммы и
счетные декартовы произведения метризуемых пространств мет-
ризуемы. Более того, показано, что для топологического про-
пространства X пространство отображений Rx, наделенное тополо-
топологией равномерной сходимости, метризуемо. Приводятся также
несколько условий, достаточных для метризуемости факторпро-
странств, пределов обратных спектров и пространств отображе-
отображений, наделенных компактно-открытой топологией. Параграф за-
завершается определением метрики на множестве всех ограничен-
ограниченных отображений топологического пространства в метрическое
пространство, что в свою очередь приводит к определению то-
топологии равномерной сходимости в этой более общей ситуации.
Параграф 4.3 посвящен изучению двух важных классов мет-
метрических пространств: вполне ограниченных пространств и пол-
полных пространств. Далее мы даем топологические характеристики
этих классов пространств. Кроме того, для каждого метриче-
метрического пространства X мы определяем его пополнение X — наи-
наименьшее полное пространство, содержащее X. В конце этого
параграфа обсуждаются метрические свойства метризуемых
компактов.
По сравнению с классическими результатами первых трех
параграфов результаты § 4.4 относительно новы. Они связаны
с теоремой А, Стоуна о возможности вписать локально конечное
подпокрытие в любое открытое покрытие метризуемого про-
пространства и дают топологические условия, характеризующие
метризуемость, и условия сохранения метризуемости при ото-
отображениях.
24 Зак. 697
370 ГЛ. 4. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА
4.1. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ
ПРОСТРАНСТВА
Метрическое пространство есть пара (X, р), состоящая из
множества X и функции р, определенной на множестве ХУ^Х,
принимающей неотрицательные вещественные значения и удов-
удовлетворяющей следующим условиям:
(Ml) p(xt у) = 0 тогда и только тогда, когда х = у.
(М2) р(х,у) = р(у,х) для всех jcje!
(МЗ) p(x,y)-{-p(y,z)^p(x,z) для всех x9y,z<=X.
Множество X в таком случае называется пространством, его
элементы — точками, функция р — метрикой на множестве Ху
а число р(х, у) — расстоянием между х и у. Условие (Ml) озна-
означает, что расстояние между двумя разными точками положи-
положительно и что каждая точка находится на нулевом расстоянии
от самой себя. Условие (М2) утверждает, что функция расстоя-
расстояния симметрична, т. е. не зависит от порядка точек х и у.
Условие (МЗ), называемое неравенством треугольника, утвер-
утверждает, образно говоря, что сумма двух сторон треугольника не
меньше третьей стороны.
Неотрицательная вещественная функция р, определенная на
множестве XX X и удовлетворяющая условиям (М2), (МЗ) и
условию
(МГ) р(х9 х) = 0 для каждого xel,
называется псевдометрикой на множестве X.
Пусть (Xt р) — метрическое пространство, х0 — точка про-
пространства X и г — положительное число; множество В(хо, г) =
= {xel: р(*о, х)<г} называется открытым шаром с центром
Хо радиуса г или просто r-шаром с центром xq. Для множества
A cz X и положительного числа г под r-шаром вокруг А мы по-
понимаем множество В (Л, г)= U В(х> г)- Заметим, что так как
х е В(х, г), то ЛсгВ(Л, г) и что если х\^В[хОу г), то В(jci, r\)cz
d В {xq, г) для п = г — р (хо, х\) > 0. В самом деле, если х s
е В (х\, г\), то, в силу (МЗ),
р(д:0, л;)<р(xOt хх) + р(хи х)<р(*0> х^ + г -р(д:0, хх) = г.
Из последнего неравенства следует, что, положив 38(х) =
= {В(х, г): г > 0} для каждого хеХ, мы получим совокуп-
совокупность семейств подмножеств пространства X, обладающую свой-
свойствами (ВР1) — (ВР2) и, следовательно, в силу предложения
1.2.3, порождающую некоторую топологию О на множестве X.
Поэтому каждое метрическое пространство (X, р) определяет
топологическое пространство (X, О). При этом элементами то-
топологии О, т. е. открытыми подмножествами пространства
(X, О), являются объединения открытых шаров. Очевидно, что
4.1. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА 371
семейство всех открытых шаров есть база пространства (X, О),
Семейство всех A/0-шаров с центром х0, где / = 1, 2, 3, ...,
есть база пространства (Ху О) в точке х0. Отсюда следует, что
пространство (Ху О) удовлетворяет первой аксиоме счетности.
Топология О на множестве X называется топологией, индуци-
индуцированной метрикой р.
Так как p(xi,x2)>0 для любой пары Х\> х2 различных точек
пространства X, из неравенства треугольника следует, что мно-
множества В(х\,г/2) и В(х2,г/2)—непересекающиеся окрестности
точек Xi и Х2. Таким образом, всякое пространство с топологией,
индуцированной метрикой, является хаусдорфовым простран-
пространством.
Как и в случае топологического пространства, мы будем
обозначать метрическое пространство просто через X Из кон-
контекста всегда будет ясно, какая метрика на множестве X рас-
рассматривается.
Аналогичную конструкцию можно осуществить в предполо-
предположении, что функция р является псевдометрикой. При этом по-
получается весьма широкий класс топологических пространств, ко-
который мы здесь рассматривать не будем. Заметим только, что
пространство X с топологией, индуцированной псевдометрикой р,
является Го-пространством тогда и только тогда, когда р — мет-
метрика. В самом деле, если p(xi,x2) = 0 для xi ф Хг, то каждая
окрестность точки xi содержит точку Х2, и наоборот, так что X
не является Го-пространством. Легко также установить следую-
следующее: если X — множество, состоящее более чем из одной точки,
то, полагая р(х, у)=0 для любых x,j/eX, мы получим псев-
псевдометрику на множестве X, которая индуцирует на нем анти-
антидискретную топологию. Хотя мы и не изучаем здесь псевдомет-
псевдометрики ради них самих, мы пользуемся ими в дальнейшем как
удобным техническим средством.
Понятие метрического пространства приводит к важному то-
топологическому понятию, а именно к понятию метризуемого про-
пространства. Топологическое пространство X метризуемо, если су-
существует такая метрика р на множестве X, что индуцированная
этой метрикой топология совпадает с исходной топологией про-
пространства X. Те метрики, которые индуцируют исходную топо-
топологию пространства X, называются метриками на простран-
пространстве X.
Мы уделяем такое внимание метрическим и метризуемым
пространствам потому, что многие важные топологические про-
пространства, используемые в разных областях математики, мет-
ризуемы и, более того, их топология часто индуцирована есте-
естественной метрикой.
Заметим, что метризуемость есть топологическое свойство,
однако приведенное здесь определение класса метризуемых про-
24*
372 ГЛ. 4. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА
странств не является внутренним определением. Возникает во-
вопрос, существует ли внутренняя характеристика метризуемых
пространств. Как мы увидим в дальнейшем, ответ на этот во-
вопрос положителен. Теоремы , дающие необходимые и достаточ-
достаточные внутренние условия метризуемости топологических про-
пространств, сформулированные в терминах топологических инва-
инвариантов, называются метризационными теоремами. Две из них
будут доказаны в § 4.4, другие — в § 5.4.
Две метрики pi и р2 на множестве X называются эквивалент-
эквивалентными, если они индуцируют на нем одну и ту же топологию.
Очевидно, что определенное таким образом отношение является
отношением эквивалентности. Мы рассматриваем две метрики,
индуцирующие одну и ту же топологию как эквивалентные объ-
объекты по той причине, что в этой книге нас интересуют в первую
очередь топологии, а метрики играют только вспомогательную
роль, подобную той, которую играют системы координат при
изучении евклидовых пространств.
Ниже, в теореме 4.1.2, мы приведем удобный критерий экви-
эквивалентности метрик. Сначала покажем, как описать в терминах
метрики замыкание множества.
Последовательность х\, х2у ... точек метрического простран-
пространства (X, р) сходится к точке х е X, если последовательность ве-
вещественных чисел р(х, х\), р(х,х2), ... сходится к нулю. Точка х
в этом случае называется пределом последовательности хих2, ...
и обозначается limjt,-. Из условий (Ml) и (МЗ) вытекает, что
всякая последовательность точек метрического пространства
имеет не более одного предела.
4.1.1. Предложение. Точка х принадлежит замыканию А множе-
множества AczX в топологии, индуцированной на X метрикой р, в том
и только том случае, если существует последовательность точек
множества А, сходящаяся к х.
Доказательство. Пусть х^Л. Для каждого натурального
числа i выберем точку Х{ е Af\ В(х, \/i). Очевидно, что
р(х, Xi)<i \/i и х = limxi. С другой стороны, если хф А, то су-
существует такое г > О, что А П В (х, г) = 0. Следовательно,
р(х,х')^г для любого xr ^ Л, и потому не существует после-
последовательности точек множества Л, сходящейся к х. 1
Из предложения 4.1.1 вытекает
4.1.2. Теорема. Две метрики pi и рг на множестве X эквивалент-
эквивалентны тогда и только тогда, когда они индуцируют одну и ту же
сходимость, т. е. для каждой точки х е X и каждой последова-
последовательности х\, Х2, ... точек множества X условия Y\mpl(xyXi) = O
и lim p2(x, Xi) = 0 эквивалентны. ¦
В связи с понятиями, изученными в § 1.6, заметим, что по-
последовательность х\, JC2, ... в метрическом пространстве (X, р)
4.1. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА 373
сходится в точке хе! в том и только том случае, если х =
= limx; в пространстве X с топологией, индуцированной мет-
метрикой р. Тем самым оправдано использование одних и тех же
символов и терминов в обоих случаях. Очевидно, что предло-
предложение 4.1.1 есть непосредственное следствие сделанного выше
замечания и теоремы 1.6.14. Заметим также, что из предложе-
предложения 1.6.15 (или предложений 4.1.1 и 1.4.1) вытекает, что ото-
отображение f метризуемого пространства X в метризуемое про-
пространство Y непрерывно в том и только том случае, если для
любой последовательности ху х\, х2, ... в пространстве X ра-
равенство x=limxi влечет за собой равенство f(x) = Hm f(xi).
Диаметр непустого множества А в метрическом простран-
пространстве (X, р) определяется как точная верхняя грань всех рас-
расстояний между точками множества А и обозначается через
б (Л). Диаметр может быть конечным или равным оо. Таким
образом,
A) 8(A)=snp{p(xux2): xu хг<=А}\
положим также б@) = О. Легко проверить, что 6(Л) = б(Л).
Множество А называется ограниченным, если б(Л)<оо.
Метрика р на множестве X ограничена вещественным числом г
(ограничена), если 8(Х)^ г (если Ь(Х)< оо). Аналогично опре-
определяются те же понятия относительно псевдометрики.
4.1.3. Теорема. Для каждого метрического пространства (Х,р)
существует метрика р{ на множестве Ху эквивалентная метри-
метрике р и ограниченная числом 1.
Доказательство. Положим
р\(х,у)=тЩ\,р{х, у)) для всех х, уеХ
Покажем, что pi — метрика. Тот факт, что pi удовлетворяет
условиям (Ml) и (М2), вытекает непосредственно из того, что
р удовлетворяет этим условиям. Пусть х, у и z — три произ-
произвольные точки множества X, и пусть а = р(х,у), b = p(yyz) и
с = р(х, г). Так как каждое из чисел 2, 1 + а, I-\-b и а + 6
больше или равно 1, либо с, то
minB, 1 + а, 1 + 6, а + b) ^ min(l,c),
поэтому
Pi(*> У) + Piiy, z) = minA, a)+min(l, b) =
= min B, 1 + a, 1 + b, a + b) > min A, c) = px (x, z).
Следовательно, pi удовлетворяет и условию (МЗ). Очевидно,
что р\ ограничена числом 1 и ее эквивалентность метрике р
следует из теоремы 4.1.2. I
374 гл- 4- МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА
4.1.4. Примеры. Пусть X — произвольное множество; для лю-
любых х, у е X положим
1, если хфу,
О, если х = у.
Легко видеть, что р — метрика на X. Так как В(х, 1) = {л;} для
каждого jtel, метрика р индуцирует дискретную топологию
на множестве X. Следовательно, каждое дискретное простран-
пространство метризуемо. Термин дискретное пространство будет при-
применяться также к описанному выше метрическому пространству
Вещественная прямая R и единичный отрезок / также мет-
ризуемы: расстояние между двумя точками на них можно опре-
определить как абсолютное значение разности соответствующих чи-
чисел. Легко показать, что в § 1.1 мы определили открытые мно-
множества в R и / как объединения открытых шаров относительно
указанных метрик.
Так как каждое метризуемое пространство удовлетворяет
первой аксиоме счетности, то пространство Л(т) с в > Ко яв-
является примером неметризуемого пространства. ¦
4.1.5. Пример. Пусть m—бесконечный кардинал, S — множе-
множество мощности щ и Is = / X{s} для каждого s^S. Полагая
(х, Si)E(yy s2) тогда и только тогда, когда х = 0 = у
или х — у и s\ = S2,
мы определим отношение эквивалентности Е на множестве
Читатель может легко установить, что формула
1 х — у |, если Si = $2,
^ + г/, если Sj ф s2,
определяет метрику на множестве классов эквивалентности от-
отношения Е. Полученное таким образом метризуемое простран-
пространство для фиксированного кардинала m не зависит (с точностью
до гомеоморфизма) от выбора множества S. Это пространство
назовем ежом колючести щ и обозначим через /(т). Легко ви-
видеть, что для каждого sgS отображение js отрезка / в /(т),
определенное формулой js(x)= [(*, s)], является гомеоморфным
вложением. Семейство всех шаров с рациональными радиусами
и центрами в точках вида [(г, s)], где г — рациональное число,
образует базу в /(т). Таким образом, ш(/(т))^ш. Так как
подпространство пространства /(ш), состоящее из всех точек
4.1. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА 375
вида 1A,5)], является дискретным пространством мощности т,
то ш(/(т)) = т. I
4.1.6. Пример. Пусть Х = R X /?; положим
% I + I*! — x2\, если ххфх2,
для каждой пары точек 2i=(xi,#i), 22 =(#2, У2) плоскости X.
Читатель может легко проверить, что р — метрика на X, не
эквивалентная метрике, определенной в примере 4.1.4. (Такой
метрикой могли бы пользоваться обитатели джунглей, по кото-
которым протекает река у = 0: чтобы иметь доступ к воде, они про-
прорубили тропы, ведущие к реке, и путь от точки (х\,у\) к (х2уу2)
проходит сначала по такой тропе к реке, затем по реке до
точки, ближайшей к (х2,у2), и снова по тропе.) I
4.1.7. Пример. Пусть Я— множество всех бесконечных после-
последовательностей {xi} вещественных чисел, удовлетворяющих
оо
условию X х\ < оо. Покажем, что, полагая
для х = {хt}9 у = {(/;} €= Я,
мы определяем метрику на Н.
Прежде всего покажем, что р определена корректно, т. е. что
ряд в определении р сходится. Для доказательства применим
неравенство Коши
справедливое для всех конечных последовательностей аь а2, ...
..., ak и &ь Ь2, ..., bk вещественных чисел !).
Заметим, что для каждой пары точек х = {л;;}, у = {yi} из Н
и любого положительного целого числа k имеют место соот-
к k к
1) Пусть a = J] а% 6==S&? и с ^Х aib0 чтобы Доказать неравен-
i = \ t = l i = \
ство Коши, т. е. неравенство с2 ^ aby достаточно заметить, что многочлен
ах2 + 2сх + b = ^ (а^л: + &(-J не имеет различных вещественных корней,
и потому 4с2 ^ 4а6.
376 ГЛ. 4. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА
ношения
к k k k
Z/ v \2 V <и2 О V v // _L V //2 <**
I л. Уi) — /La •** ^j $i ~T" ^j i/* ^^
i = l v l l/ t = l i = l t-1
k
i = \
й*?" Vй^ + /§^=
Так как последнее неравенство справедливо для любого целого
положительного &, то ряд в определении р сходится и р(х,у)
определено корректно.
Очевидно, что р удовлетворяет условиям (Ml) и (М2). По-
Покажем, что выполняется и условие (МЗ).
Пусть х = {xi}, у = {(/(} и г= {гг} — произвольные точки
из Н\ положим
xk = {xu х2У ..., xk, 0, 0, ...}, ук = {Уъ У2> •••> У к* °» °» •••}»
z* = {zb г2, ..., zft, 0, 0, ...}
В силу неравенства Коши, имеем
[р (/, **) ]2
Из последнего неравенства следует, что для любого & = 1, 2, ...
имеют место неравенства
Р(*. У)+ 9 (У,
откуда в свою очередь вытекает, что
Р(х,у)+ р{у,г)^ р(х,г)
Пространство Н называется гильбертовым пространством.
Множество всех последовательностей {х$, где все Xt — рацио-
рациональные числа и только конечное множество из них отлично от
нуля, всюду плотно в Я и счетно. Таким образом, гильбертово
пространство сепарабельно, I
4.1. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА 377
Эквивалентность условий (i) и (Hi) в предложении 1.4.1 не-
непосредственно влечет за собой следующие характеристики не-
непрерывности отображений метризуемых пространств.
4.1.8. Предложение. Отображение f пространства X с тополо-
топологией, индуцированной метрикой р, в пространство У с тополо-
топологией, индуцированной метрикой а, непрерывно в том и только
том случае, если для каждого х е X и любого г > О существует
такое б>0, что o(f(x),f(x'))<i е, как только р(х, х')< б. I
Метрические пространства позволяют также ввести понятие
равномерно непрерывных отображений. Отображение / про-
пространства X с метрикой р в пространство У с метрикой а на-
называется равномерно непрерывным относительно метрик р и а,
если для каждого е > 0 существует такое б > 0, что
<*(/(*)»/(*'))< 8 Для каждой пары х, /gI, удовлетворяющей
условию р(х,х/)<б. Очевидно, что каждое равномерно непре-
непрерывное отображение непрерывно, однако обратное не имеет
места. Понятие равномерной непрерывности не является топо-
топологическим; оно относится к конкретным метрикам на простран-
пространствах X и У. Отображение f: X-+Y может быть равномерно
непрерывным относительно одних метрик и не быть таковым
относительно других метрик (см. теорему 4.3.32), Понятие рав-
равномерной непрерывности относится к теории равномерных про-
пространств, развитой в гл. 8 (см. упр. 8.1.А (а) и задачу 8.5.19 (а)).
Отображение / пространства X с метрикой р в простран-
пространство У с метрикой а называется изометрией, если р(ху у) =
= o(f(x),f(y)) для каждой пары точек х,у^Х. Если суще-
существует изометрия пространства X на пространство У, то гово-
говорят, что X и У изометричны. Легко видеть, что изометрия —
равномерно непрерывное инъективное отображение. Так как об-
обратное отображение к некоторой изометрии «на» также является
изометрией, то изометрии «на» — это гомеоморфизмы и изомет-
ричные пространства гомеоморфны.
Расстояние р(х, А) от точки х до множества А в метрическом
пространстве (X, р) определяется выражением
р(х, А)= inf p(x> а), если А Ф 0, и р(х, 0)=1.
Подобным же образом для двух множеств Л, В в метрическом
пространстве (X, р) мы полагаем
р (Л, 5) = inf {p (flj):ae^je В}, если А ф 0 Ф В,
и р(Л, 0)=1=р@, В).
4.1.9. Предложение. Пусть {Х9р)—метрическое пространство,
х, у gI и АаХ; тогда
378 гл- 4- МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА
Доказательство. Можем считать, что А = 0. Для каждого
flG^ имеем
откуда, поскольку точка а е Л произвольна, следует, что
р(*, Л)< pU, у)+ р((/, Л), т. е.
р(х,А)—р(у,А)^р{х,у).
Из соображений симметрии имеем также
р(у9 А)— р(х, А)^ р(х9у). I
Из предложений 4.1.8 и 4.1.9 следует
4.1.10. Теорема. Пусть множество ЛсХ фиксировано; тогда
функция р, сопоставляющая каждой точке х е X расстояние
р(х, А) у непрерывна на пространстве X. I
Из 4.1.1 и 4.1.10 мы получаем
4.1.11. Следствие. Для каждого множества AczX имеем
А={х: р{х,А) = 0}.Ш
Сформулируем еще три следствия теоремы 4.1.10.
4.1.12. Следствие. Каждое замкнутое подмножество метризуе-
мого пространства функционально замкнуто и, в частности, яв-
является G^-множеством.
Доказательство. Если А = Л, то, полагая f(х) = р(х,Л),
имеем A = f~l(O). I
Предыдущее следствие и теорема 1.5.19 позволяют получить
4.1.13. Следствие. Каждое метризуемое пространство совершен-
совершенно нормально. I
Заметим, что нормальность метризуемого пространства X
непосредственно следует из того, что для любой пары Л, В не-
непересекающихся замкнутых подмножеств пространства X и лю-
любой метрики р на пространстве X формула
1 w р (х, Л) + р {х, В)
определяет непрерывную вещественную функцию на простран-
пространстве X, такую, что f(A)cz{0}t f{B)cz{l}.
4.1.14. Следствие. Пусть (Х,р)—метрическое пространство.
Для каждого компактного множества AczX и любого открытого
множества U, содержащего Л, существует такое г > 0, что
В(Дг)с U.
Доказательство. Положим f(x)=p(x, X\U); тем самым
определена функция /: X—>R, положительная на множестве Л.
4.1. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА 379
Поэтому, в силу следствия 3.2.9, существует такое г > О, что
f(x)^r для каждого х е А\ следовательно, В (Af r)czU. I
Как уже известно, все метризуемые пространства удовлетво-
удовлетворяют первой аксиоме счетности, но не все — второй аксиоме
счетности. Следующая теорема дает необходимые и достаточные
условия того, что метризуемое пространство удовлетворяет вто-
второй аксиоме счетности.
4.1.15. Теорема. Пусть т — произвольный кардинал и X — про-
произвольное метризуемое пространство; тогда следующие условия
равносильны:
(i) Пространство X имеет базу мощности
(и) Пространство X имеет сеть мощности
(iii) Каждое открытое покрытие пространства X имеет под-
подпокрытие мощности ^ т.
(iv) Каждое замкнутое дискретное подпространство про-
пространства X имеет мощность ^щ.
(v) Каждое дискретное подпространство пространства X
имеет мощность ^щ.
(vi) Каждое семейство попарно непересекающихся непустых
открытых подмножеств пространства X имеет мощность ^.ш.
(vii) Пространство X имеет всюду плотное подмножество
мощности ^щ.
Доказательство. Легко установить, что если ш — конечное
число, то все сформулированные утверждения равносильны не-
неравенству |Х|^щ. Поэтому будем считать, что &^К0.
Импликация (i)=^(ii) очевидна; (ii)=^(iii) следует из тео-
теоремы 3.8.12 или замечания 1.1.16.
Пусть А — замкнутое дискретное подпространство простран-
пространства X. Для любого х е А существует открытое множество
UxczXy такое, что A{\Ux=^{x}. Так как открытое покрытие
{Ux}xgA[]{X \А} пространства X не содержит подпокрытия
мощности <|Л|,то (iii)=^(iv).
Перейдем теперь к доказательству импликации (iv)=^(v).
Пусть А — дискретное подпространство пространства X. Легко
установить, что А — открытое подмножество замыкания Лс!
В силу совершенной нормальности пространства X, существует
последовательность Ль Л2, ... замкнутых подмножеств множе-
ства Л, такая, что А = U Аг. Так как множества Д- также зам-
кнуты в X, то из условия (iv) следует, что |Д-|^т для ** =
= 1, 2, ..., а из этих неравенств в свою очередь вытекает, что
Для доказательства импликации (v)=>(vi) достаточно заме-
заметить, что, выбирая по точке из каждого элемента некоторого се-
380 ГЛ. 4. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА
мейства попарно непересекающихся непустых открытых подмно-
подмножеств пространства Ху мы получим дискретное подпространство
пространства X, имеющее ту же мощность, что и рассматривае-
рассматриваемое семейство.
Для доказательства импликации (vi) =>- (vii) выберем какую-
нибудь метрику р на пространстве X и, применяя лемму Тейх-
мюллера — Тькжи, возьмем для каждого t = l, 2, ... макси-
максимальное подмножество Aid X с тем свойством, что р(х, у) ^ \/i
для любых х, г/ G Л. Так как A/2?) -пары с центрами в точках
множества Д попарно не пересекаются, то |Д-|^т. Поэтому
оо
достаточно доказать, что объединение А = U At всюду плотно
i = \
в X. Тем не менее если бы существовала точка х е Х\А, то
для некоторого целого положительного /о выполнялось бы нера-
неравенство р(лг, Aio)^p{x, А) > 1Д*0 что невозможно в силу мак-
максимальности множества Л/о.
Остается показать, что (vii)=^(i). Пусть р — некоторая мет-
метрика на пространстве X, и пусть А — всюду плотное подмноже-
подмножество пространства X, имеющее мощность =^щ. Обозначим через
$ семейство всех шаров Б(х, г), где х <~ Л, а г — рациональное
число. Очевидно, что |^|=^т. Докажем, что $ — база про-
пространства X. Выберем произвольную точку х е X и некоторую
ее окрестность U. Можно считать, что t/ = S(jc, г). Так как
множество А всюду плотно в X, существует точка х0^
^ А{] В{х, г/3). Для любого рационального числа г0, удовле-
удовлетворяющего условию г/3 < го < г/2, имеем
х <ее В (хо, го) а В (х, г) = U и В{х0, ro)ez$. I
4.1.16. Следствие. Для любого метризуемого пространства X
следующие условия равносильны:
(i) Пространство X удовлетворяет второй аксиоме счетности.
(п) Пространство X обладает свойством Линделёфа.
(iii) Пространство X сепарабельно.
(iv) Каждое семейство попарно непересекающихся непустых
открытых подмножеств пространства X счетно. I
Из равносильности условий (iii) и (iv) теоремы 4.1.15 и
утверждения теоремы 3.10.3 следует, что любое счетно компакт-
компактное метризуемое пространство обладает свойством Линделёфа.
Поэтому, в силу теорем 3.10.1 и 3.10.31, имеет место
4.1.17. Теорема. Для любого метризуемого пространства X сле-
следующие условия равносильны:
(i) Пространство X — компакт.
(ii) Пространство X счетно компактно.
(ш) Пространство X секвенциально компактно. 1
4.1. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА 381
Заметим, что, в силу теорем 3.10.20 и 3.10.21, к сформулиро-
сформулированным выше условиям можно присоединить псевдокомпакт-
псевдокомпактность пространства X.
Из равносильности условий (iv) и (vii) теоремы 4.1.15 сле-
следует
4.1.18. Теорема. Каждое компактное метризуемое пространство
сепарабельно. I
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
Класс метрических пространств стал первым классом аб-
абстрактных пространств, на который был успешно обобщен ряд
понятий и результатов, открытых на заре общей топологии при
изучении подмножеств вещественной прямой и евклидовых про-
пространств. Класс метрических пространств достаточно обширен
и включает в себя много объектов, изучаемых в различных об-
областях математики. Это позволяет описывать эти объекты на
геометрическом языке. В то же время пространства этого класса
кажутся достаточно простыми, к ним применима геометрическая
интуиция. Понятие метрического пространства было введено
Фреше в его диссертации [1906]. В течение многих лет внима-
внимание топологов было приковано к метрическим пространствам и,
в частности, к сепарабельным метрическим пространствам. Не-
Несомненно, это наиболее изученный класс топологических про-
пространств. Двухтомная монография Куратовского [1966] и [1968]
представляет собой настоящую энциклопедию по этому пред-
предмету.
Равносильность условий (и) и (ш) следствия 4.1.16 и усло-
условий (i) и (ii) теоремы 4.1.17 установлена Гроссом в [1914].
Хаусдорф [1914] доказал равносильность условий (i) и (Hi)
следствия 4.1.16 и условий (и) и (Hi) теоремы 4.1Л7, а также
теорему 4.1.18. Пространство J(m) было открыто Урысоном в
[1927]. Гильбертово пространство, описанное в примере 4.1.7,
как показал Андерсон [1966], гомеоморфно произведению Ко
копий вещественной прямой; это трудный и глубокий результат.
УПРАЖНЕНИЯ
4.1.А. Покажите, что в метрическом пространстве (X, р) за-
замыкание шара В(хо, г), вообще говоря, не совпадает с множе-
множеством {х: р(х0, х) ^ /-}.
4.1.В. (а) Покажите, что для каждого метрического про-
пространства (X, р) формула
9{(х, у)- 1 + 9{х у)
определяет метрику на множестве X, эквивалентную метрике р
и ограниченную числом 1.
382 ГЛ. 4. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА
(b) Назовем две метрики pi и р2 на множестве X равномерно
эквивалентными, если для каждого е > 0 существуют такие
6i > 0 и б2 > 0, что при всех х, /е! мы имеем p2(jt, xf) < г,
как только pi(x, xf) < 6i, и pi(x, x/)<e, как только р2(х, x')<Z
<б2.
Покажите, что любые равномерно эквивалентные метрики
эквивалентны, и приведите пример двух метрик на вещественной
прямой, которые эквивалентны, но не равномерно эквивалентны.
Покажите, что метрики pi и р2 на пространстве X равномерно
эквивалентны тогда и только тогда, когда тождественное ото-
отображение id*: X->Y равномерно непрерывно относительно pi
и р2, а также относительно р2 и рь или, что равносильно, когда
для каждого метрического пространства (У, о) класс всех ото-
отображений 1в У, равномерно непрерывных относительно pi и аг
совпадает с классом всех отображений I в У, равномерно не-
непрерывных относительно р2 и а (ср. с упр. 8.1.А(Ь) и зада-
задачей 8.5.19 (Ь)).
(c) Покажите, что метрика pi из теоремы 4.1.3 и метрика pi
из пункта (а) равномерно эквивалентны метрике р.
(d) Покажите, что метрика, равномерно эквивалентная огра-
ограниченной метрике, вообще говоря, не является ограниченной.
4.1.С. Покажите, что гильбертов куб /я° гомеоморфен под-
подмножеству гильбертова пространства, состоящему из всех точек
{xi}, где 0 ^ xt ^ 1/7 для i = 1,2, ... .
4.1.D. Приведите пример метризуемого пространства, кото-
которое нельзя вложить в локально компактное метризуемое про-
пространство.
4.1.Е. (а) Покажите, что для замкнутого подмножества Л
метризуемого пространства X неравенство %(A,X)^L fc$0 выпол-
выполняется в том и только том случае, если множество Ft А есть
компакт. Докажите, что плотное в себе метризуемое простран-
пространство X есть компакт в том и только том случае, если %(А, Х)^
^ Ко для любого замкнутого Лс!
(Ь) (Хенриксен и Исбелл [1958]). Докажите, что если сХ —
компактификация метризуемого пространства X, то нарост
сХ\Х обладает свойством Линделёфа.
Указание. Примените (а) и упр. 2.1.С(Ь).
4.1.F (Хаусдорф [1919]). Покажите, что если Л —замкнутое
подпространство метризуемого пространства X, то для любой
функции f: Л-»-/ и любой метрики р на пространстве X фор-
формула
inf {f(а)+ р/ al — Ц, если хеХ\Л,
j (x)t если хеД
4.2. ОПЕРАЦИИ НА МЕТРИЗУЕМЫХ ПРОСТРАНСТВАХ 383
определяет непрерывное продолжение F функции f яг X (ср. с
теоремой 2.L8).
4.I.G. Покажите, что в упр. 3.2.Н(а) и (с) можно считать,
что отображение / принимает значения в произвольном метри-
зуемом пространстве.
Указание. Воспользуйтесь теоремой 4.1.18.
4.1.Н (Эрдеш и Тарский [1943]; неявно — Харатоми [1931]).
(а) Покажите, что в любом метризуемом пространстве веса ш
существует семейство попарно непересекающихся непустых от-
открытых множеств, имеющее мощность т.
Указание, Трудности возникают, когда w (X) = щ есть точ-
точная верхняя грань кардиналов пц, Щ, • • • > где >*0 ^ Ш < ш для
* = 1, 2, ... . Сначала рассмотрите случай, когда существует
непустое открытое множество UczXt такое, что w(V) = m для
каждого непустого открытого множества VczU. Затем, пред-
предполагая, что такого множества не существует, рассмотрите мак-
максимальное семейство {U$}Sf=s попарно непересекающихся не-
непустых открытых подмножеств пространства X, таких, что
w (Us) < ш для каждого sgS.h покажите, что sup w (Us) = m.
Замечание. Проблема существования регулярного простран-
пространства X, в котором точная верхняя грань мощностей всех се-
семейств попарно непересекающихся непустых открытых множеств
не достигается ни для какого из таких семейств, имеет теоре-
теоретико-множественный характер. Ее обсуждение см. в работе
Комфорта [1971].
(Ь) Выведите из (а), что всякое метризуемое пространство
веса ш содержит дискретное подпространство мощности т. При-
Приведите пример метрического пространства веса ш > Ко, не со-
содержащего замкнутого дискретного подпространства мощно-
мощности т.
Указание. Рассмотрите подходящее подпространство про-
пространства /()
4.2. ОПЕРАЦИИ НА МЕТРИЗУЕМЫХ ПРОСТРАНСТВАХ
Начнем с простого замечания о том, что любое подпростран-
подпространство метризуемого пространства метризуемо. В самом деле,
пусть X — метризуемое пространство и р — метрика на нем.
Пусть расстояние между двумя точками некоторого подмноже-
подмножества М с: X равно расстоянию между этими точками в метрике р.
Тем самым мы определяем метрику из М. Легко показать, что
индуцированная этой метрикой топология совпадает с тополо-
топологией на М как подпространстве пространства X. Сужение
р\МХМ метрики р, заданной на X, на подпространство М сХ
384 ГЛ. 4. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА
будет обозначаться рм, а метрическое пространство (М,рм) —
просто (М, р).
4.2.1. Теорема. Сумма ф Xs метризуема в том и только том
случае, если метризуемы все пространства Xs.
Доказательство, В силу сделанных выше замечаний, доста-
достаточно доказать, что сумма попарно непересекающихся метри-
зуемых пространств {Xs}5e=s метризуема. Согласно теореме 4.1.3,
можно считать, что для каждого sgS топология на Xs инду-
индуцирована метрикой ps, ограниченной числом 1, т. е. что ps(x,y)^
^ 1 для jc, j/ EI5, s e S. Для каждой пары точек ху уеХ =
= Ф %s ПОЛОЖИМ
Ps(*> У)у ecjm существует такое seS, что х, у ^ Xs*
1 в противном случае.
Покажем, что р — метрика на множестве X. Условия (Ml)
и (М2) с очевидностью выполнены, и остается проверить усло-
условие (МЗ). Пусть х, у и z — любые точки пространства X. По-
Покажем, что
A) р (х, z) ^ р (х, у) + р (у, z).
Если х, 2 ^ Xs для некоторого sgS, to левая часть неравен-
неравенства A) равна ps(x, г), а правая часть равна ps(xyy)-{- ps(y,z)y
если j/eXs, или равна 2, если y^Xs. Таким образом, неравен-
неравенство A) выполнено. С другой стороны, если x^XSl и z^XS2
для s\ Ф s2, то левая часть неравенства A) равна 1, а правая
часть не меньше 1, так как либо уФХ8о либо y^XS2- Следо-
Следовательно, неравенство A) выполнено и в этом случае.
Далее, для каждого se5 множество Xs открыто в простран-
пространстве X с топологией, индуцированной метрикой р. Так как
рх = ps индуцирует исходную топологию на Xs, то, в силу пред-
предложения 2.2.4, р индуцирует на X топологию суммы топологи-
топологических пространств {Xs}5e5. 1
Пусть Х\9 Хг, ... — последовательность метризуемых про-
пространств и pi — метрика на пространстве Xiy ограниченная чис-
оо
лом 1, / = 1, 2, ... . Рассмотрим множество X=JIa^h для
каждой пары х ={#*}, у ={#*} его точек положим
B) Р(х,у) =
Читатель может легко установить, что р удовлетворяет усло-
условиям (Ml) —(МЗ). Возникает вопрос, совпадает ли топология,
4.2. ОПЕРАЦИИ НА МЕТРИЗУЕМЫХ ПРОСТРАНСТВАХ 385
индуцированная метрикой р, с тихоновской топологией на про-
оо
язведении Ц Х^ Положительный ответ на него содержится в
следующей теореме.
4.2.2. Теорема. Пусть Хи Х2, ... — последовательность метри-
зуемых пространств и р/ — метрика на пространстве Xi, ограни-
ограниченная числом 1, /=1, 2, ... . Топология, индуцированная на
оо
множестве X = Ц Х{ метрикой р, определенной в B), совпадает
с топологией произведения пространств {Xjjlr
Доказательство. Для точек х = {xi}, y= {yi} elc очевид-
очевидностью р(х, у)< е, как только р* (#*,#/)< г/21. Поэтому, в силу
предложения 4.1.8, проекция pi пространства X в Xi непрерывна
в топологии, индуцированной метрикой р. Далее, по определе-
определению тихоновской топологии топология, индуцированная метри-
метрикой р, сильнее топологии произведения на X.
Покажем теперь, что каждое множество U с: Х> открытое в
топологии, индуцированной метрикой р, открыто и в топологии
произведения. Возьмем произвольную точку x = {xi}& U\ суще-
существует такое г > 0, что B(xtr)<z: U. Для завершения доказа-
доказательства достаточно найти положительное число k и открытые
множества Bt ci Xu i = 1, 2, ..., k> такие, что
k
C) х^[\^
Пусть k — положительное целое число, удовлетворяющее
условию
для / = 1,2, ..., k положим
Вг - В (xit r/2) = {2G Xt: Pi (xu z) < г/2}.
к
Для каждой точки y = {yt}<= f] PJl{Bi) имеем pt(xp y.)<r/2,
где i^k, так что (в силу соотношений B) и D))
k оо
~9i (xit уг)+ ?
р (.г, у) = ^ ~-9i (xit уг)+ ? ± р (xh yt) < г/2 + г/2 - г,
что и доказывает включение C). I
25 Зак. 697
386 ГЛ. 4. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА
Предположение последней теоремы о том, что метрики р*
ограничены числом 1, необходимо только для сходимости ряда
в формуле B). Для конечной последовательности Х\, Х2, ...
..., Хк метризуемых пространств расстояние между двумя точ-
точками х = {xi} и у = {tji} множества X = Х\ X Х2 X ¦ • • X %k
можно определить, полагая
Р (*. У) = Pi (хи Ух) + Р2 (*2> У2)+ • • • + Р* (Ч> Ук)>
где pi — некоторая метрика на пространстве Xi. Легко прове-
проверить, что р — метрика на Х> индуцирующая топологию произ-
произведения.
Из теоремы 4.2.2 вытекает несколько следствий.
4.2.3. Следствие. Гильбертов куб 1*° метризуем. |
4.2.4. Следствие. Произведение JI ХЗУ где Xs ф 0 для s e S,
8 eS
метризуемо в том и только том случае, если все пространства
Xs метризуемы и существует счетное множество 5о ci S, такое,
что Xs есть одноточечное пространство для seS\S0.
Доказательство, Из теоремы 2.3.24 следует, что произведе-
произведение несчетной совокупности метризуемых пространств, каждое
из которых содержит не менее двух точек, не удовлетворяет пер-
первой аксиоме счетности. I
4.2.5. Следствие. Предел обратной последовательности метри-
метризуемых пространств метризуем. I
4.2.6. Следствие. Пусть (Х,р)—метрическое пространство. По-
Поставив в соответствие каждой точке (x,j/)gIX^ расстояние
р(х,у), мы получим непрерывную функцию р: ХУ^Х-^R.
Доказательство. Легко проверить, что
\р(х,у)-р(х?,у')\<р(х9х')+р(у,у'). I
Из теоремы 4.2.2 несложным подсчетом получается такое
следствие (его можно также вывести непосредственно из пред-
предложения 2.3.34).
4.2.7. Следствие. Последовательность точек {atI}» (jc?|, . •. произ-
оо
ведения Па*^ метризуемых пространств сходится к точке
П
LXi тогда и только тогда, когда последовательность
х\у х% ... сходится к Xi, i = 1, 2, ... . I
4.2.8. Теорема. Компактное пространство метризуемо в том и
только том случае, если оно удовлетворяет второй аксиоме счет-
счетности.
4.2. ОПЕРАЦИИ НА МЕТРИЗУЕМЫХ ПРОСТРАНСТВАХ 387
Доказательство. Из 4.1.18 и 4.1.16 следует, что каждый мет-
ризуемый компакт удовлетворяет второй аксиоме счетности. Так
как каждый компакт является тихоновским пространством, из
2.3.23 и 4.2.3 следует, что каждый компакт со второй аксиомой
счетности метризуем. I
4.2.9. Теорема. Пространство, удовлетворяющее второй аксиоме
счетности, метризуемо в том и только том случае, если оно ре-
регулярно.
Доказательство. Из 4.1.13 следует, что каждое метризуемое
пространство регулярно. Так как каждое регулярное простран-
пространство со второй аксиомой счетности в силу 1.5.15 является тихо-
тихоновским пространством, то из предложений 2.3.23 и 4.2.3 выте-
вытекает, что каждое регулярное пространство со второй аксиомой
счетности метризуемо. I
4.2.10. Теорема. Гильбертов куб /*° является универсальным
пространством для всех метризуемых компактов и всех сепара-
бельных метризуемых пространств, I
Теоремы 4.2.8 и 4.2.9 — это метризационные теоремы: они
устанавливают в терминах топологических инвариантов (вто-
(вторая аксиома счетности и регулярность соответственно) необхо-
необходимые и достаточные условия метризуемости для двух специ-
специальных классов топологических пространств: компактов и про-
пространств со второй аксиомой счетности.
4.2.11. Пример. Пусть Xi — метризуемое пространство, i =
= 1,2, ..., ky и пусть pi — метрика на пространстве Хи Опре-
Определим расстояние между двумя точками х = {xi} и у {i}
множества X = Xi X Х2 X • • • X %&> полагая
E)
Как в примере 4.1.7, легко проверить, что р удовлетворяет не-
неравенству треугольника. Условия (Ml) и (М2) выполняются
очевидным образом, так что р — метрика на X. Легко устано-
установить, что р индуцирует на X топологию произведения. Отсюда,
в частности, следует, что топология произведения на евклидо-
евклидовом я-мерном пространстве Rn, определенном в 2.3.9, совпадает
с топологией, индуцированной естественной метрикой на этом
пространстве, т. е. метрикой р, определенной формулой E), где
Pi(xt, #*) = !** -" yt\- Читатель легко проверит, что понятие огра-
ограниченного подмножества пространства Rn, определенное в § 3.2,
совпадает с понятием ограниченного множества в метрическом
пространстве (Rnt p). I
25*
388 ГЛ. 4. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА
4.2.12. Пример. Пусть Xi, i= 1,2, ..., —дискретное простран-
пространство D(m) мощности ш^К0 с метрикой р,, определенной сле-
следующим образом:
pi(x,y)=l, если хфу, и р,(х, х) = 0.
Из теоремы 4.2.2 следует, что пространство B(m)= [Z)(m)]*° =
оо
= П^0 метризуемо и формула
оо
определяет метрику на пространстве \\ Xt.
Легко можно проверить, что формула
1/&, если Хь Ф yk и xt — У( при / < k,
( ) . ^--.,. w.,, ^ ^ если Х/_^ при всех *,
определяет метрику на множестве JJ Xf*. Последовательность
{*}}» {^1}» ••• в пространстве S(m) сходится к точке x={xi}
в том и только том случае, если для каждого i существует та-
такое k(i), что а:{~х., как только j^k(i). To же условие не-
необходимо и достаточно для сходимости последовательности
{Х1}» {Х1}> • • * к точке ^={^} в пространстве E(ш),р), где
метрика р определена формулой F). Таким образом, в силу
теоремы 4.1.2, F) определяет метрику на пространстве В(т).
Пространство В(ш) называется пространством Бэра веса т.
Говоря о метрике на пространстве Бэра, мы всегда будем иметь
в виду метрику, определенную формулой F). I
Факторпространства метризуемых пространств, вообще го-
говоря, не метризуемы. Примеры 1.4,17 и 2.4.12 показывают, что
для сепарабельного метризуемого пространства X и замкнутого
отношения эквивалентности Е на X факторпространство Х/Е,
вообще говоря, не удовлетворяет первой аксиоме счетности.
В § 4.4 мы покажем, что если Е — замкнутое отношение экви-
эквивалентности на метризуемом пространстве X и факторпростран-
факторпространство Х/Е удовлетворяет первой аксиоме счетности или классы
эквивалентности отношения Е компактны, то Х/Е — метризуе-
мое пространство. Заметим, что уже сейчас, основываясь на
теоремах 3.7.19, 3.7.20 и 4.2.9, мы можем сформулировать не-
несколько более слабый результат.
4.2.13. Теорема. Если Е — замкнутое отношение эквивалентно-
эквивалентности на сепарабельном метризуемом пространстве X с компакт-
4.2. ОПЕРАЦИИ НА МЕТРИЗУЕМЫХ ПРОСТРАНСТВАХ 389
ныли классами эквивалентности, то факторпространство Х/Е
метризуемо. I
Заключительная часть этого параграфа посвящена простран-
пространствам отображений.
Пусть X — топологическое пространство и (У,р) — метриче-
метрическое пространство. Говорят, что отображение f: X-+Y ограниче-
ограничено, если ограничено множество f(X)czY. На множестве всех
ограниченных непрерывных отображений X в У опредлим метри-
метрику р, положив
G) р(/, g)= sup p (/(*), g(x)).
xz=X
Так как множества f(X) и g(X) ограничены, то р (/, g) — кор-
корректно определенное число. Легко проверить, чтор удовлетво-
удовлетворяет условиям (Ml) — (МЗ).
Понятие ограниченного отображения не является топологи-
топологическим понятием: оно зависит от выбора конкретной метрики
на У. Из теоремы 4.1.3 вытекает, что на У существует метрика,
относительно которой все непрерывные отображения X в У огра-
ограничены. Таким образом, существует метрика на множестве Yx
всех непрерывных отображений X в У, и эта метрика индуцирует
топологию на Vх. К сожалению, эта топология на Yx зависит
от выбора ограниченной метрики на У.
4.2.14. Пример. Пусть pi —метрика на множестве R веществен-
вещественных чисел, определенная формулой р\(х,г/) = min(l, \х — у\),
а р2 —другая метрика на множестве R, определенная равен-
равенством p*(xty)=p(h(x)fh(y))9 где А: Я-^Ч {@, 1)} с/?* —
некоторый гомеоморфизм и р — естественная метрика на /?2.
Очевидно, что метрики pi и р2 эквивалентны, хотя pi(—i,i)= I,
i = 1, 2, ..., тогда как lim p2(—t, i) = 0.
Для X = Af и У = R множество Yx состоит из всех отобра-
отображений X в У. Метрики pi и р2 на /? порождают соответственно
метрики pi и р2 на У*. Покажем, что метрики р{ и рг не экви-
эквивалентны.
Рассмотрим отображение fr. X-+Y, / = 1, 2, ..., определен-
определенное формулами
U (i) =—i и fi(k)=k при НФ L
Определим отображение /: Х->-У, положим /(/) = «. Очевидно,
что p\(f,fi)=l, i=}, 2» •••, тогда как Hmp2(/, fi) = 0. Следо-
Следовательно, метрики pi и р2 не эквивалентны в силу теоре-
теоремы 4.1.2. I
Итак, с топологической точки зрения нет оснований рассмат-
рассматривать топологию на Yx> индуцированную метрикой р, опреде-
определенной формулой G). Тем не менее пространство всех ограни-
390 ГЛ. 4. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА
ченных непрерывных отображений из X в У с топологией, инду-
индуцированной метрикой р, обладает интересными свойствами и
весьма полезно, причем главным образом потому, что (как мы
увидим в следующем параграфе) в нем справедлива теорема
Бэра о категории, когда (У, р) —полное пространство. Отметим
также, что (как показано ниже в теореме 4.2.17) для компак-
компакта X топология, индуцированная метрикой р, совпадает с ком-
компактно-открытой топологией и, следовательно, не зависит от
выбора конкретной метрики р на пространстве У.
Докажем теперь следующую теорему.
4.2.15. Теорема. Для каждого топологического пространства X
и любого метрического пространства (У, р), где р ограничена,
топология на Yx, индуцированная метрикой р, допустима.
Доказательство. В силу предложения 2.6.11, достаточно по-
показать, что отображение вычисления Q: Yx X Х-+ X непрерыв-
непрерывно. Пусть (/о, хо)е У* XX и fo(xo) = yo. Так как /0 непрерывно,
для любого е > 0 найдется такая окрестность V а X точки хо,
что fo(V)cz В (у о, в/2). Легко установить, что Q(B(/o> е/2)Х V)cz
czB(yo,s). Отсюда вытекает непрерывность отображения Q. 1
Последняя теорема вместе с 3.4.1 и 2.6.12 дает
4.2.16. Следствие. Для любого топологического пространства X
и любого метрического пространства (У, р), где р ограничена,
топология, индуцированная метрикой р из Yx, сильнее, чем ком-
компактно-открытая топология. I
Пусть X — компакт; тогда, в силу 4.2.6 и 3.2.9, каждое не-
непрерывное отображение X в метризуемое пространство У огра-
ограничено относительно любой метрики р на пространстве У. Та-
Таким образом, в случае, когда X — компакт, р — метрика на всем
множестве У*.
4.2.17. Теорема. Пусть X —компакт, У — метризуемое простран-
пространство и р — метрика на У. Тогда топология на Yx, индуцирован-
индуцированная метрикой р, совпадает с компактно-открытой топологией и
не зависит от выбора метрики р.
Доказательство. В силу 4.2.16, достаточно показать, что для
каждого f e Yx и любого г > 0 существует такое множество
V a Yx, открытое относительно компактно-открытой топологии,
что
(8) fc=VczB(f,r).
Семейство {Ux}xeX множеств Ux = f~l(B(f(x),r/4)) является
открытым покрытием компакта X, поэтому существует конечное
множество {хи Х2, .. -, Xk}czXt такое, что
(9) X=UXlUUx9\) ... \}UXk.
4.2. ОПЕРАЦИИ НА МЕТРИЗУЕМЫХ ПРОСТРАНСТВАХ 391
Для t = l,2, ..., k положим
A0) С, = UH = Г (В (f (*,), г/4)) и Vt = В (f (xt)t г/3).
Так как подмножества Сь С2, ..., Ck пространства X компакт-
компактны, а подмножества V\, V2, • •, У к пространства У открыты, то
множество
открыто в компактно-открытой топологии на У*. Покажем, что
V удовлетворяет включению (8).
Из равенств A0) вытекает, что f(Ci)cz Vt, /=1, 2, ..., ky
поэтому |еУ. Рассмотрим теперь произвольное jgV. В силу
(9) и A0), для любой точки х ^ X существует такое / ^ k, что
x<=d. Очевидно, g(x)<=Vt и f(x)e=Vi. Так как б(^)<2г/3,
то p(f(x),g(x))^i 2г/3 и, в силу произвольности выбора точки х,
P(f,g)<- r* Тем самым включение (8) доказано. I
Теоремы 4.2.17 и 3.4.16 дают
4.2.18. Следствие. Для всякого метризуемого компакта X и лю-
любого сепарабельного метрического пространства (У, р) про-
странство (Yx,p) сепарабельно. I
Читатель легко может установить, что в последнем след-
следствии требование компактности пространства X нельзя ослабить
до локальной компактности и сепарабельности.
В заключение этого параграфа приведем теорему, проясняю-
проясняющую природу топологии равномерной сходимости на Rxt вве-
введенной в § 2.6. Для этого сначала обобщим понятие равномерно
сходящейся последовательности функций.
Пусть X — топологическое пространство, (У, р) —метриче-
—метрическое пространство и {//}—последовательность отображений X
в У. Будем говорить, что последовательность {/*} равномерно
сходится к отображению f пространства X в У, если для каждого
е > 0 найдется такое k, что p(f (x), fi(x)) < г для любого xgZ
и i ^ k. Доказательство следующей теоремы, аналогичное до-
доказательству теоремы 1.4.7, предоставляется читателю.
4.2.19. Теорема. Пусть X — топологическое пространство,
(У, р)—метрическое пространство и {ft}—последовательность
непрерывных отображений fr. X-+Y. Если последовательность
{fi} равномерно сходится к отображению f, то f: X-+Y непре-
непрерывно. Если все отображения fi ограничены, то f также ограни-
ограничено. ¦
Легко видеть, что последовательность {/*} непрерывных ото-
отображений из X в (У, р) равномерно сходится к отображению f:
JC-> У в том и только том случае, если Iim i (/,//)== 0, где
392 ГЛ. 4. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА
Pi(*>!/)= min(l, p(x, у))у т. е. в том и только том случае, если
f = limfi в метрическом пространстве (У*,pi). Следовательно,
из предложения 4.1.1 и формулы A) § 2.6 вытекает
4.2.20. Теорема. Для каждого топологического пространства X
пространство отображений Rx с топологией равномерной схо-
сходимости метризуемо.
Точнее, топология равномерной сходимости на Rx индуци-
индуцируется метрикой р, где р — метрика на вещественной прямой,
заданная формулой р(х, у) = min(l, \x~-y\). I
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
Информация о происхождении операций на метрических и
метризуемых пространствах содержится в замечаниях к гл. 2.
Теоремы 4.2.8 и 4.2.9 были доказаны Урысоном в [1924] (объяв-
(объявлено в [1928]) и в [1925а] соответственно. В первоначальной
формулировке последней теоремы вместо регулярности была
нормальность. Тихонов в [1925] установил, что теорема верна
в приведенной здесь более сильной форме (ср. с теоремой 1.5.15).
Топологическая характеристика метризуемых компактов была
дана также Читтенденом и Питчером в [1919]. Бэровские про-
пространства В(ш) были определены Бэром в [1909] для т=К0.
Теорему 4.2.13 доказал Уайберн в [1942]. Пространство огра-
ограниченных отображений с метрикой р, задаваемой формулой G),
было изучено Фреше в [1906] (идея приписывается там Вейер-
штрассу). Следствие 4.2Л6 было отмечено впервые в работе
Джексона [1952].
УПРАЖНЕНИЯ
4.2.А. (а) Покажите, что если две метрики р и а на множе-
множестве X равномерно эквивалентны, то для каждого M<z:X мет-
метрики рм и ом на подпространстве М также равномерно эквива-
эквивалентны.
(b) Установите, что если для /= 1,2, ... метрики р,- и а* на
множестве Xi равномерно эквивалентны и ограничены 1, то мет-
оо
рики р и а на JJ хь определенные формулой B), также рав-
номерно эквивалентны.
(c) Докажите, что если две метрики р и а на множестве Y
равномерно эквивалентны и ограничены, то для каждого про-
пространства X метрики р и d на Yx, определенные формулой G),
также равномерно эквивалентны и, следовательно, индуцируют
одну и ту же топологию на Yx (ср. с упр. 4.3.1 (Ь)).
4.2.В (Шнейдер [1945]). Покажите, что компактное про-
пространство X метризуемо тогда и только тогда, когда диагональ
4.2. ОПЕРАЦИИ НА МЕТРИЗУЕМЫХ ПРОСТРАНСТВАХ 393
А есть бб-множество в произведении ХУ^Х (см. задачу 3.12.22 (е);
ср. с задачей 4.5.15 и упр. 5.1.1).
Указание, Определите счетное семейство {Тг}^х конечных
открытых покрытий пространства X, такое, что для любой пары
х, у различных точек пространства X найдется номер /, при ко-
котором точки х и у не принадлежат одновременно замыканию
никакого элемента покрытия У и Покажите, что семейство всех
конечных пересечений V\ П Vi П • • • П Vk, где Vt e Т-ь для
/ = 1,2, ..., k, является базой пространства X.
Можно также выбрать функцию f: X\X-+I таким образом,
что А = /-1 @), и положить р (х, у) = sup \f{x, z) — f (у, г) |.
4.2.С (Вон [1937]). Докажите, что для метризуемого про-
пространства X сепарабельность и локальная компактность являют-
являются необходимым и достаточным условием существования на X
такой метрики, что подпространство ЛсгХ компактно в том и
только том случае, когда множество А замкнуто и ограничено.
4.2.D. (а) (Пономарев [I960]). Докажите, что Го-простран-
Го-пространство X удовлетворяет первой аксиоме счетности в том и только
том случае, когда X есть непрерывный образ метризуемого про-
пространства при открытом отображении.
Указание. Пусть пространство X удовлетворяет первой
аксиоме счетности, и пусть {[/s}seS — его база. Рассмотрите бэ-
оо
ровское пространство В(ш) = ЦXi, где Xi = S, снабженное
дискретной топологией, и подмножество Т cz В (т), состоящее из
всех точек {$;}, таких, что {USi}T является базой в точке х ^ X.
Точке {St}e T поставьте в соответствие точку х е X.
(Ъ) (Майкл [1971а]). Покажите, что каждое пространство X
с первой аксиомой счетности есть непрерывный образ хаусдор-
фова пространства с первой аксиомой счетности при открытом
отображении, и выведите отсюда, что в (а) предположение о
том, что X является ^-пространством, можно опустить.
Указание (Шимрат [1956]). Определите в S(m), где т =
= \Х\У семейство {Ах}Х(=х попарно непересекающихся всюду
плотных подмножеств и возьмите подмножество U ({х}У^Ах)
произведения X()
Замечание, Конструкция, приведенная в указании, говорит
о том, что каждое топологическое пространство есть непрерыв-
непрерывный образ хаусдорфова пространства при некотором открытом
отображении. Исбелл [1969] доказал более сильное утвержде-
утверждение: каждое топологическое пространство есть непрерывный об-
образ наследственно паракомпактно*о и наследственно сильно
нульмерного пространства при открытом отображении. Допол-
394 ГЛ. 4. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА
нительную информацию, относящуюся к пунктам (а) и (Ь),
можно найти в работах Юннилы [1978] и Р. Поля [1981].
(с) (Архангельский [1963], Франклин [1965]). Покажите, что
конструкция, описанная в упр. 2.4.G(b), показывает, что секвен-
секвенциальные пространства можно охарактеризовать как образы
метризуемых пространств при факторных отображениях, а про-
пространства Фреше — Урысона — как образы метризуемых про-
пространств при наследственно факторных отображениях.
4.2.Е (Куратовский [1947]; для вещественных функций —
Хан [1921]). Докажите, что если X—метризуемый компакт и
(У, р)—метрическое пространство, то последовательность {ft}
непрерывных отображений из X в У равномерно сходится к ото-
отображению f ^ Yx тогда и только тогда, когда для каждой по-
последовательности Х\, х%, ... точек пространства X, сходящейся
к точке х^Х, последовательность fi(xt) сходится к f(x)
(ср. с упр. 2.6.С).
4.2.F (Куратовский [1931]). Покажите, что если X — мет-
метризуемый компакт, а У — хаусдорфово пространство, то все то-
топологические вложения пространства X в У образуют G6-mho-
жество в пространстве Yx с компактно-открытой топологией.
4.2.G (Джексон [1952]). Пусть X — тихоновское простран-
пространство, У—метризуемое пространство, содержащее подпростран-
подпространство, гомеоморфное прямой R, и р — ограниченная метрика на
пространстве У. Покажите, что если метрика р индуцирует ком-
компактно-открытую топологию на У*, то X — компакт.
Указание. Видоизмените рассуждение, предложенное в ука-
указании к упр. 3.4.А.
4.2.Н (Арене [1946]). Докажите, если X — хемикомпактное
пространство, то для любого метризуемого пространства У про-
пространство Yx с компактно-открытой топологией метризуемо
(ср. с упр. 3.4.Е, 3.5.G(b), 3.8.C(b) и 4.3.F).
4.2.1. Пусть р — псевдометрика на множестве Х\ положим
хЕ(р)у в том и только том случае, если р(х, у) = 0. Покажите,
что тем самым определено отношение эквивалентности Е(р)
на X. Проверьте, что формула р([х]у [#])=р(х,у) определяет
метрику на множестве всех классов эквивалентности отношения
?(р). Полученное так метрическое пространство обозначается
через Х/р.
Пусть X — топологическое пространство и р — псевдометрика
на множестве X, такая, что р: XX X->R — непрерывная функ-
функция. Покажите, что, относя точке ^е! класс [х]еХ/р, мы
определяем непрерывное отображение /: Х^-Х/р. Установите,
что, вообще говоря, топология на Х/р, индуцированная метри-
метрикой р, слабее топологии факторпространства Х/Е(р) и что две
эти топологии совпадают, если топология на X индуцирована
псевдометрикой р.
4.3. ВПОЛНЕ ОГРАНИЧЕННЫЕ И ПОЛНЫЕ МЕТРИЧЕСКИЕ ПРОСТРАНСТВА 395
Пусть X— топологическое пространство и р — псевдометрика
на множестве X, такая, что р: XX.X-+R — непрерывная функ-
функция. Покажите, что в этом случае топология на X, индуцирован-
индуцированная псевдометрикой р, слабее исходной топологии.
4.3. ВПОЛНЕ ОГРАНИЧЕННЫЕ
И ПОЛНЫЕ МЕТРИЧЕСКИЕ ПРОСТРАНСТВА.
КОМПАКТНОСТЬ В МЕТРИЧЕСКИХ ПРОСТРАНСТВАХ
Пусть (X, р)—метрическое пространство и А — подмноже-
подмножество пространства X. Говорят, что А г-плотно в (X, р), если для
каждого xgI существует такое xf ^ Л, что р(лс, х') < е.
Метрическое пространство (Х> р) называется вполне ограни-
ограниченным, если для каждого е > 0 существует конечное множе-
множество Лс1, е-плотное в (X, р). Метрика р на множестве X на-
называется вполне ограниченной, если пространство (X, р) вполне
ограничено. Топологическое пространство X метризуемо вполне
ограниченной метрикой, если на нем существует вполне ограни-
ограниченная метрика.
Первое из приведенных выше определений задает некоторый
класс метрических пространств. Третье определение задает
класс топологических пространств, который вместе с некоторым
пространством X содержит и все гомеоморфные ему простран-
пространства. Однако определение последнего класса не является внут-
внутренним, так как в нем использовано понятие метрики.
Теперь мы коротко обсудим класс всех вполне ограниченных
метрических пространств и покажем, что класс всех пространств,
метризуемых вполне ограниченной метрикой, совпадает с клас-
классом всех сепарабельных метризуемых пространств. Как мы уви-
увидим, последний факт приводит к внутренней характеристике
класса всех пространств, метризуемых вполне ограниченной мет-
метрикой.
Сначала рассмотрим несколько примеров.
4.3.1. Примеры. Дискретное пространство (^,р), определенное
в 4.1.4, не является вполне ограниченным, если множество X
не является конечным. В самом деле, если X бесконечно, то ни-
никакое конечное множество не может быть е-плотным в (X, р)
при е = 1.
Читатель легко установит, что вещественная прямая R, про-
пространство /(т), плоскость с метрикой р из примера 4.1.6, гиль-
гильбертово пространство Я и бэровское пространство В(ш) не яв-
являются вполне ограниченными.
С другой стороны, каждый отрезок / = [а, b]c=R вполне
ограничен. В самом деле, для любого е > 0 множество / П
396 ГЛ. 4. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА
f\{i/k: f=0, + 1» ±2, ...}, где k — целое положительное число,
удовлетворяющее неравенству l/k < е, конечно и е-плотно в 7.
Более общо, каждый метрический компакт вполне ограничен
(см. теорему 4.3.27). Каждый открытый интервал также вполне
ограничен. Так как вещественная прямая гомеоморфна интер-
интервалу (—1,1), то ясно, что пространство, гомеоморфное вполне
ограниченному пространству, может не быть вполне ограничен-
ограниченным. Однако оно метризуемо вполне ограниченной метрикой.
Читатель легко установит, что пространство, изометричное впол-
вполне ограниченному пространству, является вполне ограничен-
ограниченным. I
4.3.2. Теорема. Пусть (X, р) — вполне ограниченное простран-
пространство] тогда для любого подмножества М а X пространство
(М, р) вполне ограничено.
Если (X, р) —произвольное метрическое пространство и под-
подмножество Мс! таково, что (Му р) вполне ограничено, то про-
пространство (М, р) также вполне ограничено.
Доказательство. Выберем некоторое е>0 и конечное мно-
множество A — {xi, х2, ..., Xk}, е/2-плотное в (Ху р). Пусть
{хщ^ Хт2> •--» Хт\ — подмножество множества Д состоящее из
всех точек, расстояние которых от М меньше е/2, и пусть
х[, х'%, ..., ^ — произвольные точки множества М, такие, что
A) рD*;.)<е/2, /=1, 2, ...,/.
Мы покажем, что множество Af = {x'v x'v ..., х^ 8-плотно в М.
Пусть х^М\ по определению множества А существует такое
i ^ k, что
B) р(*,*,)< е/2.
Следовательно, хг — хт для некоторого j^t и, в силу A) и B),
р (х, х]) < 8.
Вторая часть теоремы вытекает из следующего простого фак-
факта: любое множество, е/2-плотное в (М, р), е-плотно в (М, р). I
Читатель может легко установить, что если {(XSi P5)}5e=s—
семейство непустых метрических пространств, причем метрика
р5 при каждом sgS ограничена числом 1, то сумма ф Xs
с метрикой р, определенной в доказательстве теоремы 4.2.1,
вполне ограничена тогда и только тогда, когда все пространства
(Xs, p5) вполне ограничены и |5|< Ко.
4.3.3. Теорема. Пусть {(Xi, Pi)}°°=l — семейство непустых метри-
метрических пространств, таких, что метрики pi ограничены числом 1,
4.3. ВПОЛНЕ ОГРАНИЧЕННЫЕ И ПОЛНЫЕ МЕТРИЧЕСКИЕ ПРОСТРАНСТВА 397
t = 1, 2, ... . Произведение Д^ с метрикой р, определенной
формулой B) в § 4.2, вполне ограничено тогда и только тогда,
когда все пространства (Xi, р,-) вполне ограничены.
Доказательство, Предположим, что пространство
(й*<- О
вполне ограничено. Подпространство Х^ = ЦЛ* с IIX*, гДе
А} = Х] и At = {x*^ — одноточечное подмножество пространства
Xi при всех i ф /, вполне ограничено в силу теоремы 4.3.2. Легко
установить, что если множество А и е/2^-плотно в(Х!, р), то мно-
множество Р)(А) является е-плотным в (Х/,ру). Таким образом,
пространство (Xj, p;) вполне ограничено.
Допустим теперь, что все пространства (Xi, pi) вполне огра-
ограничены. Выберем е > 0 и натуральное число k, такое, что
1/2* < е/2. Для каждого / ^ k выберем конечное множество
[х\у х*2, ..., х1т{()}, е/2-плотное в Xi, а для каждого i > k выбе-
выберем произвольную точку х^^Х^
оо
Множество А с= Ц Xit состоящее из всех точек вида
C) у=*{х)х, хJ, ..., х*к, х^К х*+\ ...}, где 1</,<т(/)
для i ^ к,
конечно. Для завершения доказательства достаточно показать,
что А е-плотно в пространстве I Ц Xt, р 1.
оо
Пусть х={хЛ—произвольная точка пространства Ц Х(.
(=1
Для каждого i ^ k существует такое // ^ m(i), что 9t(xv х1Л<
<е/2. Для точки г/, определенной в C), имеем
f- I
Таким образом, множество А е-плотно в ( П^, Р ) • I
4.3.4. Следствие. Гильбертов куб /*° с метрикой р, определен-
определенной формулой
оо
Р(х> У) = X! ~^Г I xi — Vi I» г(?е х = {^J « У {
является вполне ограниченным пространством. I
398 ГЛ. 4. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА
4.3.5. Теорема. Метризуемое пространство метризуемо вполне
ограниченной метрикой в том и только том случае, если оно
сепарабельно.
Доказательство. Достаточность условия сепарабельности
следует из 4.2.10, 4.3.4 и 4.3.2. Для доказательства его необхо-
необходимости заметим, что если р — вполне ограниченная метрика
на пространстве X и At с: X — конечное множество, 1/7-плотное
оо
в (X, р), то объединение А = [} At — счетное всюду плотное
подмножество пространства X. I
Последняя теорема вместе с 4.1.16 и 4.2.9 дает
4.3.6. Следствие. Топологическое пространство метризуемо впол-
вполне ограниченной метрикой в том и только том случае, когда оно
регулярно и удовлетворяет второй аксиоме счетности. I
Перейдем теперь к классу полных метрических пространств.
Пусть (Ху р) — метрическое пространство и {xi} — последо-
последовательность точек X. Будем называть {xi} последовательностью
Коши в (X, р), если для любого е>0 существует натуральное
число k, такое, что p(xt, Xk)^ е, как только i ^ k. Легко видеть,
что каждая сходящаяся последовательность в метрическом про-
пространстве есть последовательность Коши.
Метрическое пространство (X, р) называется полным, если
любая последовательность Коши в (X, р) сходится к некоторой
точке пространства X. Метрика р на множестве X называется
полной, если пространство (X, р) полное. Будем говорить, что
топологическое пространство X метризуемо полной метрикой,
если существует полная метрика на пространстве X.
Замечание, сделанное в начале этого параграфа в связи с
вполне ограниченными пространствами и пространствами, мет-
ризуемыми вполне ограниченными метриками, применимо к пол-
полным метрическим и метризуемым полной метрикой простран-
пространствам.
Вначале рассмотрим класс полных метрических пространств,
затем класс пространств, метризуемых полной метрикой, и в
заключение дадим внутреннюю характеристику пространств,
метризуемых полной метрикой.
Рассмотрим сначала несколько примеров.
4.3.7. Примеры. Дискретное пространство (X, р), определенное
в 4.1.4, полное. В самом деле, каждая последовательность Коши
в (X, р) постоянна, начиная с некоторого члена.
Мы покажем, что вещественная прямая R с естественной
метрикой есть полное пространство. Пусть {xt} —последователь-
—последовательность Коши в R. Существует натуральное число 6, такое, что
\xi — Xk\^, 1, как только i^k. Таким образом, все члены по-
4.3. ВПОЛНЕ ОГРАНИЧЕННЫЕ И ПОЛНЫЕ МЕТРИЧЕСКИЕ ПРОСТРАНСТВА 399
следовательности {х,}, начиная с 6-го, содержатся в замкнутом
интервале / = [xk — 1, Xk + 1]. Из компактности / и теоре-
теоремы 4.1.17 следует, что найдется подпоследовательность {хк(} по-
последовательности {Xi}t сходящаяся к точке хе/. Прямое вы-
вычисление показывает, что последовательность {xi} также схо-
сходится к точке х.
Каждый замкнутый интервал — тоже полное пространство
(см. теорему 4.3.28). С другой стороны, открытый интервал
(—1, 1) и любой другой открытый интервал не являются пол-
полными. В самом деле, 11 } — последовательность Коши в
интервале (—1,1), которая не сходится ни к какой его точке.
Так как интервал (—1, 1) гомеоморфен вещественной прямой,
мы видим, что пространство, гомеоморфное полному простран-
пространству, не обязательно полно, хотя и метризуемо полной метри-
метрикой. Читатель легко проверит, что пространство, изометричное
полному пространству, само является полным пространством.
Стоит также отметить, что открытое подмножество полного
пространства необязательно полно, как видно на примере под-
подпространства (—1,1)^/?. I
Заметим, что для каждого полного метрического простран-
пространства (X, р) существует полная метрика pi на множестве Ху
эквивалентная метрике р и ограниченная числом 1. В самом
деле, метрика pi из теоремы 4.1.3 полна, так как последователь-
последовательность {х(} точек пространства X есть последовательность Коши
в (X, р) тогда и только тогда, когда она есть последовательность
Коши в (Xtpi).
Следующие две теоремы содержат две характеристики пол-
полноты. Первая аналогична характеристике счетной компактности,
данной в теореме 3.10.2(ш), вторая — характеристике компакт-
компактности, данной в теореме 3.1.1.
4.3.8. Теорема Кантора. Метрическое пространство (X, р) полно
тогда и только тогда, когда каждая убывающая последователь-
последовательность F\ zd F2 => ... непустых замкнутых подмножеств простран-
пространства X, таких, что lim 6 (Fi) = 0, имеет непустое пересечение:
Д Р(ф0'
Доказательство. Пусть (X, р)—полное пространство и
F\, F%, ... — последовательность непустых замкнутых подмно-
подмножеств пространства X, таких, что
D) Hm6(Fi) = 0 и Fi+.czFi, i = l, 2, ... .
Выберем точку Xi^Fu / = 1, 2, ... . Легко видеть, что все
члены последовательности {л;,-}, начиная с j-ro, содержатся в
множестве Fu Таким образом, в силу первого соотношения из
400 ГЛ. 4. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА
D), {xt} — последовательность Коши и потому сходится к не-
некоторой точке xg! Так как множества Ft замкнуты, то х е
оо
?^,/ = 1,2, ..., и, следовательно, f] F( Ф 0.
Пусть теперь (X, р) — метрическое пространство, удовлетво-
удовлетворяющее условиям нашей теоремы, и пусть {xt} — последователь-
последовательность Коши в (X, р). Множества Ft = {xu xi+u -..}, i= 1,2, ...,
замкнуты и удовлетворяют соотношениям D). Следовательно,
оо
существует точка л: s f] Ft. Легко показать, что х = limxi. По-
Поэтому пространство (X, р) полное. ¦
4.3.9. Следствие. Пусть (X, р)—метрическое пространство и
М cz X — такое подмножество, что (М, р) — полное простран-
пространство; тогда М замкнуто в X.
Доказательство. Для каждой точки х ^ М последователь-
последовательность Fu F2t ... подмножеств Mt где Ft =M[}B(x, l/i)t удов-
удовлетворяет условиям теоремы Кантора. Следовательно, в силу
оо
полноты пространства (М, р), мы имеем f] Ft Ф 0. Так как
оо
f] F{ cr {х}, то jc g М и потому М — М. I
4.3.10. Теорема. Метрическое пространство (X, р) полно в том
и только том случае, когда каждое центрированное семейство
замкнутых подмножеств пространства X, в котором для любого
е > 0 содержится множество диаметра <е, имеет непустое пе-
пересечение.
Доказательство. Достаточность этого условия вытекает из
теоремы Кантора.
Докажем теперь его необходимость. Пусть (X, р) — полное
пространство. Пусть {Fs}Sf=s— центрированное семейство замк-
замкнутых подмножеств ^сгХ. Пусть для любого натурального
числа /это семейство содержит такое множество Fs.t что 6Gv)<
< 1//. Легко видеть, что последовательность F\9 F2, ..., где
Ft = П Fs» удовлетворяет условиям теоремы Кантора. По-
ОО ОО
этому существует точка х^ f] Ft. Очевидно, что f| /rt- = {x}.
Выберем теперь произвольное So ^ 5 и положим
pf _ с и рг — F П F / = 93
4.3. ВПОЛНЕ ОГРАНИЧЕННЫЕ И ПОЛНЫЕ МЕТРИЧЕСКИЕ ПРОСТРАНСТВА 401
Мы получим последовательность F[, Fr2, ... , удовлетворяющую
условиям теоремы Кантора. Так как
то х е Fs0- Следовательно, х е [) /v |
Изучим теперь операции над полными пространствами.
4.3.11. Теорема. Пусть (Х,р)—полное пространство. Для того
чтобы пространство (М, р), МаХ, было полным, необходимо и
достаточно, чтобы М было замкнутым в X.
Доказательство. В силу следствия 4.3.9, достаточно пока-
показать, что если М — М, то пространство (М, р) полное. Каждая
последовательность Коши в (М, р) является последователь-
последовательностью Коши в (X, р) и, следовательно, сходится к точке х е X.
Так как М = Я, то очевидно, что х^М. Ш
Пусть {(Xs, P$)}s^s~" семейство непустых метрических про-
пространств, таких, что метрика ps ограничена числом 1 для ка-
каждого s^S. Легко установить, что сумма © %s> снабженная
sgS
метрикой р, определенной в доказательстве теоремы 4.2.1, яв-
является полным пространством тогда и только тогда, когда все
пространства (Xs, ps) полны. Следовательно, сумма © Xs
se S
пространств Xs, метризуемых полной метрикой, тоже метризуе-
ма полной метрикой.
4.3.12. Теорема. Пусть {(Xit Р*)}^°=1 — семейство непустых мет-
метрических пространств, таких, что метрика pi ограничена чис-
лом 1, i = 1, 2, ... . Произведение TLx? с метрикой р, опре-
деленной формулой B) в § 4.2, полно тогда и только тогда, когда
все пространства (Xif p(-) полны.
Доказательство. Допустим, что пространство (Д^, pi
оо оо
полное. Подпространство X) = Ц At cz Ц Хи где А\ = X/ и
А. = {х*| — одноточечное подмножество пространства X. при
1ф], замкнуто и, в силу теоремы 4.3.11, полно. Легко уста-
установить, что Р;* —Р/|^/: Xj-*-^ —гомеоморфизм и что для
каждой последовательности Коши {л;*} в (Xjt р/) последователь-
последовательность {р* (л: t)} есть последовательность Коши в X*. Образ
предела последовательности {р)~{ (xt)} есть предел последова-
последовательности {xi}. Таким образом, пространство (Xj, p/) полно.
26 Зак. 697
402 ГЛ. 4. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА
Допустим теперь, что все пространства (Хц р;) полны. Если
{*!}> {xi}j * * • —последовательность Коши в (IT Xt, p I, то для
i = l, 2, ... последовательность х\, х\> ... является последова-
последовательностью Коши в пространстве (Xi, р;) и, таким образом, схо-
сходится к точке xt e Xi. Из следствия 4.2.7 вытекает, что после-
довательность {х\}, \х2^, ... сходится к точке х = {х(}
Значит, пространство III Xi9 p 1
Jl
полно.
4.3.13. Теорема. Для каждого топологического пространства X
и любого полного метрического пространства (У, р) простран-
пространство всех ограниченных непрерывных отображений из X в У
с метрикой р, определенной формулой G) § 4.2, является пол-
полным пространством.
Доказательство. Пусть {/;} — последовательность Коши в
рассматриваемом пространстве. Очевидно, что {/;(#)} — после-
последовательность Коши в пространстве (У, р) для любой точки
х е X. Поставим в соответствие каждой точке х ^ X предел по-
последовательности {fi(x)}. Тем самым определено некоторое ото-
отображение f из X в У. Легко видеть, что последовательность
{/;} равномерно сходится к /. Поэтому, в силу теоремы 4.2.19,
отображение f ограничено и непрерывно. Следовательно,
limp(f, fi) = 09 т. е. последовательность {f/} сходится к /. I
4.3.14. Теорема. Каждое метрическое пространство изометрично
подпространству полного метрического пространства.
Доказательство. Пусть {Ху р)—произвольное метрическое
пространство. В силу последней теоремы, пространство (Y,a)
всех ограниченных непрерывных вещественных функций на X,
где a (f, g) = sup [ / (л:) — g (x) |, полно. Зафиксируем некоторую
точку flGl Поставим в соответствие каждой точке xg! функ-
функцию fx e Rx, определенную следующей формулой:
Mz) = p(z,*)—р(г, а), ге!
Так как \fx(z)\^p{ayx) в силу неравенства треугольника, то
fx ^ У для каждого xgI Мы покажем, что
E) a (fx, fy)=p (х, у) для всех х, у е X.
Заметим сначала, что для любого геХ имеет место неравен-
неравенство
fx(z) — fg(z) = p(z, x) — p(z, a) — p(z9 y) + p(z, a)<p(x, у).
4.3. ВПОЛНЕ ОГРАНИЧЕННЫЕ И ПОЛНЫЕ МЕТРИЧЕСКИЕ ПРОСТРАНСТВА 403
Из симметрии предположений вытекает, что \fx{z)~ fy{z) | ^
<р (*,#), т. е.
С другой стороны, так как fx(y)—fy(y)= р(у,х)—р(у,а) +
+ ) = р(У,х)9 то
Таким образом, равенство E) доказано, а с ним и утверждение
теоремы. I
4.3.15. Следствие. Каждое метризуемое пространство можно
вложить в пространство, метризуемое полной метрикой. I
Заметим в связи с последним доказательством, что если
(X, р) ограничено, то изометрию между (X, р) и (У, а) можно
получить более простым способом: достаточно поставить в со-
соответствие каждой точке х ^ X функцию fx s У, определенную
равенством fx(z)= p(x, z).
Очевидно, что для данного метрического пространства (X, р)
есть много полных метрических пространств (У, а), содержащих
изометричное (X, р) подпространство. Однако если добавить тре-
требование, что подпространство, изометричное (X, р), должно быть
всюду плотно в (У, а), то пространство (У, а) определяется од-
однозначно (с точностью до изометрии). Для доказательства этого
факта нам потребуется теорема о продолжаемости отображе-
отображений в полные метрические пространства.
Пусть X — топологическое пространство, (Y,o) —метриче-
—метрическое пространство и f: A^-Y— непрерывное отображение всю-
всюду плотного подмножества А пространства X. Будем говорить,
что колебание отображения f в точке х <= X равно нулю, если
для любого е > 0 найдется такая окрестность U точки х, что
6{f(A(]U))<B. Для любого целого i множество всех точек
xgJ, имеющих такую окрестность ?/, что 8(f(A(] ?/))< 1//,
открыто и содержит Л. Поэтому множество всех точек, в кото-
которых колебание отображения / равно нулю, есть бб-множество,
содержащее А.
4.3Л6. Лемма. Пусть X — топологическое пространство, (Y.g) —
полное метрическое пространство и /: Л->- У — непрерывное ото-
отображение, определенное на плотном подмножестве А простран-
пространства X. Тогда отображение f продолжимо до непрерывного ото-
отображения F: B^Y, определенного на множестве В, состоящем
из всех точек пространства X, в которых колебание f равно
нулю.
Доказательство. Для каждого jcgB обозначим через $(х)
семейство всех окрестностей точки х. Рассмотрим семейство
26*
404 ГЛ. 4. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА
{/(Л Л U)}uez$(x) замкнутых подмножеств пространства У. Ука-
Указанное семейство центрировано и для любого е > 0 содержит
множество, диаметр которого меньше е. Таким образом, в силу
теоремы 4.3.10, пересечение f) f(A[)U) не пусто. Так как
диаметр этого пересечения равен нулю, оно состоит из един-
единственной точки ^(х). Очевидно, что F(x) — f(x) для х <= Л. По-
Поставим в соответствие каждой точке хеБ точку F(x). Тем са-
самым мы определим отображение F: B^-Y, являющееся продол-
продолжением отображения /. Остается доказать непрерывность ото-
отображения F. Возьмем произвольную точку xgB и е > 0. Из
определения множества В следует, что существует t/e^(x),
удовлетворяющее соотношению б(/(ЛЛ^О)<е. Для любого
/eBfl^ имеем U е $(х') и, следовательно, ^(х')^ /(Л Л U).
Так как F(x)e /(Л Л ^0, то имеет место соотношение
((),()): 8(f (А Л ?/))< е, из которого следует непрерыв-
непрерывность отображения А I
4.3.17. Теорема. Пусть (Х,р) —метрическое пространство и
(Y,o)—полное метрическое пространство] тогда каждое ото-
отображение f: Л->- Y всюду плотного подмножества А простран-
пространства X в пространство У, равномерно непрерывное относительно
р и а, продолжается до отображения F: X-^Y, равномерно не-
непрерывного относительно р и о.
Доказательство, Из равномерной непрерывности отображе-
отображения f вытекает, что колебание отображения / в каждой точке х
равно нулю. Следовательно, в силу леммы, существует продол-
продолжение F: X-*Y отображения /. Остается доказать равномер-
равномерную непрерывность отображения F.
Выберем произвольные е > 0 и б > 0, такие, что для любых
х, х'е Л мы имеем а(/(х), f (х')) < е/2, как только р(х, х') < б.
Для любой пары х0, х?е X, такой, что р(г0, х?) < б, множество
U = В (х0, г) U 5 (Xq, г), где г = — (б — р (х0, *?)), открыто и его
диаметр меньше б. Следовательно, б (/ (Л Л U)) <е/2и6 (/ (Л Л Щ)
^ е/2 < е. Так как F (х0) и F (х^) принадлежат множеству
НАЩ, то a(F(x0), FD))<s. I
Изометрии равномерно непрерывны, поэтому последняя тео-
теорема вместе с 1.5.4 и 4.2.6 дает
4.3.18. Следствие. Пусть (Х,р) и (К, а)—полные метрические
пространства; тогда каждая изометрия между (Л, рл) и (BtGB)}
где А и В — всюду плотные подмножества в пространствах X
и У соответственно, продолжается до изометрии между (Х} р)
(Y)*
4.3. ВПОЛНЕ ОГРАНИЧЕННЫЕ И ПОЛНЫЕ МЕТРИЧЕСКИЕ ПРОСТРАНСТВА 405
4.3.19. Теорема. Для любого метрического пространства (X, р)
существует ровно одно (с точностью до изометрии) полное мет-
метрическое пространство (X, р), такое, что X содержит всюду
плотное подпространство, изометричное пространству (X, р). Бо-
Более того, w(X)= w(X), и если пространство (X, р) вполне огра-
ограничено, то (Х,р) также вполне ограничено.
Доказательство. Пусть (X, р) — метрическое пространство.
В силу теоремы 4.3.14, существуют полное метрическое про-
пространство (К, а) и изометрия f: X-+Y. Положим X = f(X)aY
и р = а^; мы получим метрическое пространство (Х> р) с тре-
требуемыми свойствами. Единственность (Х,р) следует из 4.3.18.
Равенство w(X) = w(X) следует из теоремы 4.1.15. Если про-
пространство (X, р) вполне ограничено, то в силу второй части тео-
теоремы 4.3.2 пространство (Х,р) также вполне ограничено. I
Пространство (Хр), удовлетворяющее условиям теоремы
4.3.19. называется пополнением метрического пространства
№р).
Теперь перейдем к рассмотрению класса пространств, мет-
ризуемых полной метрикой. Начнем с одной простой теоремы
о продолжении отображений.
4.3.20. Теорема. Пусть Y — пространство, метризуемое полной
метрикой. Тогда каждое непрерывное отображение f: A —>¦ Y, где
А — всюду плотное подмножество топологического простран-
пространства X, продолжается до непрерывного отображения F: B^-Y,
определенного на G у множестве Вс^Х, содержащем множе-
множество А.
Доказательство. Достаточно рассмотреть любую полную мет-
метрику на пространстве У, взяв в качестве В множество всех тех
точек, в которых колебание отображения / равно нулю, и при-
применить 4.3.16. 1
Наша следующая теорема — важный результат о продолже-
продолжении гомеоморфизмов.
4.3.21. Теорема Лаврентьева. Пусть X и Y — пространства, мет-
ризуемые полной метрикой, и пусть А а X и С cz Y—произволь-
Y—произвольные подпространства. Любой гомеоморфизм /: А —> С продол-
продолжается до гомеоморфизма F: B-*Dy где A cz В cz X, С a D a Y
и В, D суть О6-множества в X и Y соответственно.
Доказательство. Без ограничения общности можно считать,
что Л=1иС=У. Пусть g: С->Л — обратное отображение к f.
Из 4.3.20 вытекает существование продолжений
^о: BQ-*Y и Go: Dq-+X
отображений f и g на Об-множества ВоаХ и DQczY. Пере-
Пересечения J6 = i?on/7o(^o) и D~Dof\Gol (Во) суть О6-множества
406 ГЛ. 4. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА
в X и Y соответственно. Очевидно, что ЛсВ, CczD, Покажем,
что
F) G0F0(x) = x для каждого хеВ и F0(B)c=D.
Согласно теореме 1.5.4, из того, что сужение отображения
GqFo\B на А совпадает с вложением 1а\ А-*-Х, вытекает первая
часть F), откуда в свою очередь следует, что Fo(B)cz GoX (В) cz
cz Go1 (Во). Так как F0(B)cz Do, то справедлива и вторая
часть F). В силу симметричности наших предположений,
G) FQG0(y) = y для каждого y^D и G0(D)czB.
Из соотношений F) и второй части G) следует, что GQ(D)==B.
Подобным же образом имеем F0(B)=D. Отсюда следует, что
отображения F — F0\B: B^D и G — G0\D: D-+ В взаимно об-
ратны, а это означает, что F — гомеоморфизм. Щ
В следующих двух теоремах мы обсуждаем операцию пере-
перехода к подпространству.
4.3.22. Лемма. Каждое G^-множество в метризуемом простран-
пространстве X гомеоморфно замкнутому подпространству произведения
XXR*0-
Доказательство. Пусть А есть б6-множество в X и р — про-
произвольная метрика на пространстве X. Представим дополнение
оо
Х\Л как объединение (J Ft замкнутых множеств Ft и рас-
смотрим отображение /= Л ft: A->{J_Xi,rjief0: A^-XQ = X —
t=0 t=0
вложение и fr. A^>~Xi = R определено формулой
Ы*) = [р(*>Л*)]Л i -1, 2, ... .
По теореме о диагонали, f — гомеоморфное вложение. Следова-
тельно, остается показать, что образ f{A) замкнут в
оо
Мы покажем, что каждая точка х = {хЛ еП^Х/ (А) обла-
облако
дает окрестностью С/, содержащейся в дополнении к множеству
ПА).
Рассмотрим сначала случай, когда х0 ^ Л. Так как х ф f(A),
найдется такое / > 0, что хьф fi{xo). Пусть U\ и V^ — непересе-
непересекающиеся окрестности точек хь и fi{xo) соответственно. Так как
функция /(• непрерывна, существует такая окрестность Uo<^ X
точки дсо, что fi{A(] Uq)cz U2. Легко проверить, что
(8) x = {xi}^U = pol(Uo)[\p7X(Ul)^U
4.3. ВПОЛНЕ ОГРАНИЧЕННЫЕ И ПОЛНЫЕ МЕТРИЧЕСКИЕ ПРОСТРАНСТВА 407
Пусть теперь х0 ф. А. Очевидно, что Хо ^ Fi для некоторого
i > 0. Пусть г > 0 таково, что xi + 1 < 1/г, и пусть ?/0 =
= fi(xo, г), ?Л = {я е /?: jc < jc^ + 1}. Легко видеть, что форму-
формула (8) верна также и в этом случае. I
Эта лемма вместе с теоремами 4.3.11 и 4.3.12 приводит
(ср. с упр. 2.3.L(а)) к следующей теореме.
4.3.23. Теорема. Метризуемость полной метрикой наследуется
G6-множествами. 1
4.3.24. Теорема. Если подпространство М метризуемого про-
пространства X метризуемо полной метрикой, то М есть G^-множе-
ство в X.
Доказательство. По теореме 4.3.20, отображение icU: M->M
всюду плотного подмножества М пространства М czX продол-
продолжается до непрерывного отображения F: В-*МУ определенного
на бб-множестве ВаМ9 содержащем М. Предположение о су-
существовании точки х е В\М противоречит непрерывности ото-
отображения F. Таким образом, В = А1 и М есть Об-множество
в Mt а потому и в X. I
Так как всякое сепарабельное метризуемое пространство
вкладывается в i?K°, из 4.3.22—4.3.24 получаем
4.3.25. Следствие. Сепарабельное метризуемое пространство
метризуемо полной метрикой в том и только том случае, когда
оно вкладывается в /?к° как замкнутое подпространство. 1
Из теорем 4.3.14, 4.3.23 и 4.3.24 следует, что среди метризуе-
мых пространств пространства, метризуемые полной метрикой,
можно охарактеризовать как абсолютные Оь~множества, т. е.
пространства, являющиеся Gg-множествами в любом метризуе-
мом пространстве, в которое они вложены.
4.3.26. Теорема. Топологическое пространство метризуемо пол-
полной метрикой в том и только том случае, если оно есть полное
по Чеху метризуемое пространство.
Доказательство. Пусть X метризуемо полной метрикой и
р — полная метрика на нем. Из теоремы 4.3.10 следует, что лю-
любое центрированное семейство замкнутых подмножеств про-
пространства Ху содержащее множества, диаметр которых меньше
чем диаметр множеств покрытия s?i = {B(x, l/t)}Xs=x> * —
= 1, 2, ..., имеет непустое пересечение. Следовательно, про-
пространство X полно по Чеху в силу теоремы 3.9.2.
Пусть теперь X— метризуемое пространство, полное по Чеху.
Возьмем его пополнение X и компактификацию сХ простран-
пространства X. Очевидно, что сХ — компактификация пространства X,
Из теоремы 3.9.1 следует, что X есть 6б-множество в сХ% а по-
408 ГЛ. 4. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА
тому ив1. Теорема 4.3.23 показывает тогда, что X метризуемо
полной метрикой. I
Отметим, что, поскольку классы метризуемых пространств и
полных по Чеху пространств допускают внутреннюю характери-
характеристику (см. § 4.4, 5.4 и теорему 3.9.2), последняя теорема дает
внутреннее описание пространств, метризуемых полной мет-
метрикой.
Теоремы 4.3.26 и 3.9.10 показывают, что метризуемость пол-
полной метрикой сохраняется в сторону прообраза совершенными
отображениями, определенными на метрических пространствах.
Отметим также, что метризуемость полной метрикой сохраняется
при замкнутых и открытых отображениях на метризуемые про-
пространства (см. задачи 4.5.13 (е) и 5.5.8 (d)).
Мы закончим этот параграф исследованием метрик на ком-
компактах.
4.3.27. Теорема. Каждая метрика на компакте вполне ограни-
ограничена.
Доказательство. Пусть р —метрика на компакте X. Возьмем
некоторое е > 0. Открытое покрытие {В(х, s)}Xf=x компакта X
имеет конечное подпокрытие, т. е. существует конечное множе-
множество Л={хь Х2, ..., Xjfe}c: X, такое, что
Х = В(хив)[}В(х2,г)\) ... [}В(хь,г)я
Легко видеть, что множество А е-плотно в X. I
Из теоремы Кантора следует
4.3.28. Теорема. Каждая метрика на компакте полна. I
Наша следующая теорема характеризует компактность мет-
метризуемых пространств в терминах метрики.
4.3.29. Теорема. Метризуемое пространство X есть компакт в
том и только том случае, когда на нем существует полная и
вполне ограниченная метрика р.
Доказательство. Необходимость условия теоремы следует
из 4.3.27 и 4.3.28.
Пусть теперь (X, р)—метрическое пространство, вполне
ограниченное и полное. Для любого натурального числа i вы-
выберем конечное множество {хь х\, ..., х1кц)}> A/2/)-плотное в {Х>
р). Полагая B) = B{xlh 1/2/) для /= 1, 2, ..., &(/), получаем
ft (о
(9) х = U В) и б (В)) < 1Д" для / < k (i).
/-1
Мы покажем, что каждое бесконечное подмножество А про-
пространства X имеет предельную точку. Согласно теоремам 3.10.3
и 4.1.17, этого достаточно для завершения доказательства тео-
теоремы.
4.3. ВПОЛНЕ ОГРАНИЧЕННЫЕ И ПОЛНЫЕ МЕТРИЧЕСКИЕ ПРОСТРАНСТВА 409
Так как множество Л бесконечно, то, в силу первого равен-
равенства (9), найдется такое j^k{\), что пересечение ЛП#) бес-
бесконечно. Обозначим это пересечение Ль Тогда
Aid Аи б(Л0< 1 и \АХ\^ Ко.
Аналогичным образом мы получим множество Лг, равное од-
одному из пересечений A{(]Bj и удовлетворяющее условиям
А=>А^А2, б(Л2)<1/2 и \А2\>Н0-
Определим по индукции последовательность Ль Л2, ... мно-
множеств, удовлетворяющих условиям
A0) Л=ЭЛ!=ЭЛ2=Э ..., 6(Лг-)<1Д И |Л;|>К0'
ОО
По теореме Кантора, существует точка х е f| At. Из соотноше-
ний A0) следует, что каждая окрестность точки х содержит бес-
бесконечно много точек множества Л. Следовательно, х — предель-
предельная точка множества Л. 1
4.3.30. Следствие. Пополнение метрического пространства (Х> р)
есть компакт в том и только том случае, если (X, р) — вполне
ограниченное пространство, I
Мы завершим этот параграф простой, но полезной теоремой
об открытых покрытиях компактных метрических пространств.
4.3.31. Теорема Лебега о покрытиях. Для любого открытого по-
покрытия зФ метрического компакта X существует такое е > 0,
что покрытие {В(х> g)}xgX вписано в s&.
Доказательство. Для каждой точки х е X выберем такое
гх > 0, что шар B(xf 2гх) содержится в элементе покрытия з$>.
Открытое покрытие {В(х, вх}х^х пространства X имеет конеч-
конечное подпокрытие, т. е. существует конечное множество точек
{хи %%•> . - -, Xk}cn X, такое, что
Х = В(хи e^UB^ e,2)U ... [}B(xh9 sXk).
Легко видеть, что число е = гшп(е*1> е*2, - • -, sXk) обладает тре-
требуемым свойством. |
Всякое число е, удовлетворяющее требованиям последней
теоремы, называется числом Лебега покрытия «s#.
Из теоремы Лебега о покрытиях следует
4.3.32. Теорема. Всякое непрерывное отображение f: X->Y мет-
ризуемого компакта X в метризуемое пространство Y равномер-
равномерно непрерывно относительно любых метрик р и о соответственно
на пространствах X и Y.
410 ГЛ. 4. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА
Доказательство. Для произвольного е > 0 пусть б = б(е) —
число Лебега открытого покрытия {(-1(В(у,е/2))}у^у простран-
пространства X. Если р(х, х')<б, то найдется такая точка у е У, что
)/еВ(х,в)сН(в(у,е/2)), и потому о(/(*), f (*'))< е. ¦
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
Вполне ограниченные пространства были введены Хаусдор-
Хаусдорфом в [1914], а полные и метризуемые полной метрикой про-
пространства— Фреше в [1906]. Куратовский в [1933] доказал тео-
теоремы 4.3.3, 4.3.10 и 4.3.13; в [1930] он обнаружил, что условие
теоремы Кантора достаточно для полноты. Необходимость этого
условия была установлена Хаусдорфом в [1914] (Кантор до-
доказал эту теорему для вещественной прямой в [1880]). Замеча-
Замечание о том, что каждое вполне ограниченное метрическое про-
пространство сепарабельно, можно найти в книге Хаусдорфа [1927].
Теорема 4.3.14 была доказана Хаусдорфом в [1914]; наше до-
доказательство заимствовано из работы Куратовского 11935а]
(аналогичной конструкцией пользовался Фреше в [1910]). По-
Пополнение метрического пространства было описано Хаусдорфом
в [1914] (единственность была отмечена в [1927]); конструк-
конструкция Хаусдорфа (см. задачу 4.5.6) связана с теорией веществен-
вещественных чисел Кантора — Мерэ. Теоремы 4.3.20 и 4.3.21 доказал Лав-
Лаврентьев в [1924]. Теорема 4.3.23 была доказана Александровым
в [1924] для сепарабельных пространств и обобщена на произ-
произвольные метризуемые пространства Хаусдорфом в [1924]. Лем-
Лемма 4.3.22 была установлена в книге Куратовского [1933]. Тео-
Теорема 4.3.24 легко следует из факта, установленного Лаврен-
Лаврентьевым в [1924] (для подмножеств евклидовых пространств —
Мазуркевичем в [1916]), что свойство быть (/^-множеством в
полном пространстве топологически инвариантно. Теорема 4.3.26
была доказана Чехом в [1937]; из нее следует, что теорема Бэра
о категории имеет место для всех пространств, метризуемых
полной метрикой (ср. с упр. 4.3.С), — это впервые было доказа-
доказано Хаусдорфом в [1914] (Бэр доказал эту теорему для веще-
вещественной прямой в 1889 г.). Теорема Бэра о категории в при-
применении к пространствам отображений (см. теорему 4.3.13) или
к пространствам замкнутых подмножеств (см. задачи 4.5.21 (с)
и (d)) дает эффективный и широко применяемый метод для
установления существования некоторых математических объек-
объектов (так называемый категорный метод). Читатель может по-
попытаться доказать, используя категорный метод, что существует
непрерывная функция f: /?->-/?, не дифференцируемая ни в ка-
какой точке прямой R (это классическая теорема Вейерштрасса;
доказательство категорным методом дано Банахом в [1931]).
Теоремы 4.3.27—4.3.29 доказаны Фреше в [1910а], однако он не
4.3. ВПОЛНЕ ОГРАНИЧЕННЫЕ И ПОЛНЫЕ МЕТРИЧЕСКИЕ ПРОСТРАНСТВА 411
рассматривал класс вполне ограниченных пространств. Теоре-
Теорему 4.3.31 доказал Лебег в работе [1921] (там эта теорема при-
приводится в двойственной формулировке); наше доказательство
основано на идее Мазуркевича [1920а]. Теорему 4.3.32 можно
найти в книге Хаусдорфа [1914].
УПРАЖНЕНИЯ
4.З.А. (а) Покажите, что метрическое пространство (X, р)
вполне ограничено тогда и только тогда, когда для любого е >
> 0 существует конечное покрытие X множествами, диаметр
которых меньше е.
(b) Установите, что если отображение /: J?->Y метризуе-
мого пространства X на метризуемое пространство У равномерно
непрерывно относительно метрик р и а соответственно на про-
пространствах X и У и пространство (X, р) вполне ограничено, то
и пространство {Y,o) вполне ограничено.
(c) Пусть пространство (X, р) вполне ограничено и метрика
р равномерно эквивалентна метрике а на пространстве X: тогда
пространство (X, а) также вполне ограничено.
4.3.В. (а) Приведите пример полного метрического простран-
пространства (X, р), которое допускает равномерно непрерывное относи-
относительно метрик р и а отображение на неполное пространство
(Y,o).
(b) Пусть (X, р)—полное пространство и метрика р равно-
равномерно эквивалентна некоторой метрике а на пространстве X;
покажите, что тогда пространство (X, о) также полное.
(c) Покажите, что еж /(ш), плоскость с метрикой из при-
примера 4.1.6, гильбертово пространство Я и пространство Бэра
В(ш) —полные пространства.
4.З.С. (а) Приведите прямое доказательство теоремы Бэра
о категории для пространств, метризуемых полной метрикой
(ср. с упр. 4.4.F(d) и (е)).
Указание, Для непустого открытого множества G определите,
как при доказательстве теоремы 3.9.3, последовательность
Gu G2, ... непустых открытых множеств, таких, что
G =э Gx zd Gj => G2 => ..., Ъг Г) At = 0 и b(Gt)< I//, /=1,2,... .
(b) Приведите пример подпространства X на плоскости, для
которого справедлива теорема Бэра о категории, несмотря на
то что X не метризуемо полной метрикой.
Указание. Используйте такой факт: если теорема Бэра о ка-
категории имеет место для всюду плотного подпространства про-
пространства X, то она имеет место и для X
412 ГЛ. 4. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА
4.3.D (Линденбаум [1926]). (а) Покажите, что если {Х7 р) —
вполне ограниченное пространство, то для каждой изометрии f:
Х-+Х образ f{X) всюду плотен в X (ср. с задачей 4.5.4).
Указание. Воспользуйтесь тем, что для каждой точки xgX
последовательность f (x), f(f(x)), ... содержит подпоследователь-
подпоследовательность, сходящуюся к х.
(Ь) Выведите из (а), что если (X, р)—компакт, то каждая
изометрия /: Х-*-Х есть отображение «на». Покажите, что пред-
предположение о компактности нельзя ослабить до условия, что (X, р)
вполне ограничено.
4.3.Е, (а) Пусть (X, р) и (У, а)—метрические пространства
и /: X-^Y — непрерывное отображение. Покажите, что формула
p{xfy)=p(x9y)+a(f{x)9f(y))
определяет метрику р на пространстве X, эквивалентную мет-
метрике р, и что отображение f равномерно непрерывно относи-
относительно метрик р и ст. Проверьте, что если метрики р и су вполне
ограничены, то р вполне ограничена.
(b) Пусть (X, р)—метрическое пространство и /: Х-**Х~
непрерывное отображение; покажите, что формула
р(х, y) = p(x,y) + YJ-^rP(f (*), f (у)),
где fl(x) = f(fl~l{x)) при i^l и /°(х) = х, определяет метрику
р на пространстве X, эквивалентную метрике р, и что отобра-
отображение f равномерно непрерывно относительно р и р. Покажите
также, что если р вполне ограничена, то и р вполне ограничена.
(c) Покажите, что метризуемое пространство X — компакт
в том и только том случае, когда каждая метрика на нем вполне
ограничена, или, что равносильно, каждая метрика на нем огра-
ограничена (ср. с задачей 4.5.20 (d)).
(d) (Немыцкий и Тихонов [1928]). Докажите, что метри-
метризуемое пространство X является компактом в том и только том
случае, когда каждая метрика на нем полна (ср. с упр. 4.4.Е(Ь)
и задачей 4.5.20(d)).
Указание. Пусть X — некомпактное метризуемое простран-
пространство и F\ZdF2^> ... — убывающая последовательность непу-
непустых замкнутых подмножеств пространства X, такая, что пере-
оо
сечение П Ft пусто. Выберите некоторую метрику а на про-
i = 1
странстве X, ограниченную числом 1, и проверьте, что для / =
= 1,2, ... формула
Pi (х, У) = \<у (*, Ft) - <* (У, /V I + Ып (о (х, Ft)9 а (у, Ft))] а {х9 у)
определяет псевдометрику на множестве X. Используя построен-
4.3. ВПОЛНЕ ОГРАНИЧЕННЫЕ И ПОЛНЫЕ МЕТРИЧЕСКИЕ ПРОСТРАНСТВА 413
ные так псевдометрики, определите метрику р на пространстве
X, такую, чтобы б(/г/)^ 1/2', /=1, 2, ... (ср. с леммой 4.4.6).
4.3.F. (а) Пусть X — локально компактное пространство
Линделёфа, a Y — пространство, метризуемое полной метрикой.
Докажите, что пространство Vх с компактно-открытой тополо-
топологией метризуемо полной метрикой (см. упр. 4.2.Н и 3.8.С(Ь)).
(Ь) Приведите пример хемикомпактного пространства X, та-
такого, что пространство Iх с компактно-открытой топологией не
метризуемо полной метрикой (ср. упр. 4.2.Н).
Указание, Возьмите в качестве X пространство Y из при-
примера 1.6.20 и рассмотрите множество, состоящее из всех функ-
функций / е Iх, принимающих только значения 0 и 1 и постоянных
на каждом подпространстве вида Yf\(l/i, 1/7+ 1Д2].
4.3.G (Бэр [1909]). Докажите, что пространство Р всех ир-
иррациональных чисел (с топологией подпространства веществен-
вещественной прямой) гомеоморфно пространству Бэра B(&0) = N*° (ср.
с упр. 6.2.А).
Указание. Прежде всего покажите, что для каждой метрики
р на пространстве Р, всякого е > 0 и любого непустого откры-
открытого множества U cz P существует последовательность F\, F2, ...
попарно непересекающихся непустых открыто-замкнутых под-
подмножеств пространства Р% такая, что б(/7/)<е, г'=1,2, ..., и
оо
?/ = U Ft. Затем выберите полную метрику р на пространстве Р
и для каждой последовательности iu 12, ..., 4 натуральных чи-
чисел определите по индукции непустое открыто-замкнутое
множество Fixi2...ik <^P диаметра, меньшего l/k, такое, что
оо оо
Р = JJ Fu Ftli2... h = JJ Fili2... iki и Fitt2... ik[\Filh ... ih= 0,
если последовательности индексов различны.
4.З.Н. (а) (Брауэр [1913]; неявно —Фреше [1910]). Дока-
Докажите, что для любых двух счетных всюду плотных подмножеств
Л, В вещественной прямой R существует гомеоморфизм f: /?->-
->/?, такой, что f(A) = B (ср. с задачей 4.5.2).
Указание. Пусть А={аи а2, ...} и В={Ьи Ь2, ...}. Опреде-
Определите по индукции функцию /: Л->7?, полагая f(ai)=b\ и вы-
выбирая в качестве /(#;) элемент В с наименьшим возможным ин-
индексом, такой, что условия а}- < ak и f(afXf(ak) равносильны
при /, k ^ и Рассмотрите продолжение функции f на R и дока-
докажите, что это — гомеоморфизм.
(Ь) (Фреше [1910]). Покажите, что пространство Q всех
рациональных чисел (с топологией подпространства веществен-
вещественной прямой) есть универсальное пространство для всех счетных
метризуемых пространств.
414 ГЛ. 4. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА
Указание. Заметьте, что счетные метризуемые пространства
вкладываются в R. Для счетного X a R рассмотрите множе-
множества X U Q и Q и примените (а).
(c) Пусть А\, Л2, В\ и Z?2 — счетные всюду плотные подмно-
подмножества прямой R, удовлетворяющие условию А\ Л Аг = 0 =
= Bif[B2\ покажите, что существует гомеоморфизм /: R-+Ry
такой, что f(Ai)= Bt при i = 1, 2.
(d) Покажите, что для любых двух счетных всюду плотных
подмножеств Л, В пространства Р иррациональных чисел суще-
существует гомеоморфизм /: Р-+Р9 такой, что f(A) — B.
(e) Покажите, что для любых двух счетных всюду плотных
подмножеств Л, В канторовского подмножества С существует
гомеоморфизм f: C-+C, такой, что/(Л) = В.
Указание, Заметьте, что для каждого счетного множества
А<=С существует гомеоморфизм g: C-+C, такой, что множе-
множество g(A) не пересекается с множеством концов всех интерва-
интервалов, выброшенных из / при построении канторовского множе-
множества, и примените упр. 3.2.В.
4.3.1. (а) Покажите, что любые две метрики на метризуемом
компакте равномерно эквивалентны.
(Ь) Пусть У — метризуемый компакт. Покажите, что для ка-
каждого топологического пространства X топология на У*, инду-
индуцированная метрикой р, определенной по формуле G) в § 4.2,
не зависит от выбора конкретной метрики р на пространстве У.
Покажите, что так определенная топология на Yx, вообще го-
говоря, не совпадает с компактно-открытой топологией.
Указание. См. упр. 4.2.А(с) и 4.2.G.
4.3.J (Банах [1922]). Пусть (X, р)—метрическое простран-
пространство. Отображение f: Х-^Х называется сжимающим, если су-
существует такое число се@, 1], что p(f(x)yf(y))^ cp(x,y) для
всех х, у е X, Покажите, что для каждого сжимающего отобра-
отображения полного метрического пространства X в себя существует
в точности одна точка Хо^Х, такая, что /(хо)=хо (это и есть
теорема Банаха о неподвижной точке).
Указание. Возьмите любую точку х^Х и покажите, что
/ (х) у f (f (x)) у - • • — последовательность Коши.
4.4. МЕТРИЗАЦИОННЫЕ ТЕОРЕМЫ I
Семейство множеств называется о-локально конечным
(о-дискретным), если оно может быть представлено как счетное
объединение локально конечных (дискретных) семейств.
Следующая теорема устанавливает одно из самых важных
свойств метризуемых пространств.
4.4.1. Теорема Стоуна. В каждое открытое покрытие метризуе-
4.4. МЕТРИЗАЦИОННЫЕ ТЕОРЕМЫ I 415
мого пространства можно вписать открытое подпокрытие, яв-
являющееся одновременно локально конечным и о-дискретным.
Доказательство. Пусть {Us}sgS — открытое покрытие метри-
зуемого пространства X. Выберем метрику р на пространстве X
и отношение вполне упорядочения < на множестве 5. Опреде-
Определим индуктивно семейства F/ = {Vs> t}s^s подмножеств про-
пространства X, полагая
Va,i = [}B (с, 1/2*),
где объединение берется по всем точкам cgI, удовлетворяю-
удовлетворяющим следующим условиям:
A) 5 — наименьший элемент множества S, такой, что с^ Us;
B) c&Vut при j < I и /eS;
C) В (с, 3/2*) си Us.
Из определения непосредственно вытекает, что множества
Vs, i открыты. Включение C) показывает, что Vs, i сз Us. Пусть
xgI; выберем наименьшее s е S, такое, что хе Us, и нату-
натуральное число I, такое, что В(х, 3/2г')с: Us. Очевидно, что либо
х е Vt, i для некоторых / < * и <eS, либо х е У5> *. С ледова-
оо
тельно, объединение Ж = (J ^°,- является открытым покрытием,
/-I
вписанным в покрытие {C/5}seS.
Мы докажем, что для каждого i
D) если Xi е VSu и *2е ^2, t и Si=?s2, то р (jc^ jc2) > l/2?.
Эти соотношения в свою очередь означают, что семейства Ti
дискретны, ибо каждый A/2'+1)-шар пересекается не более чем
с одним элементом семейства Ti.
Допустим, что S\ < 52. По определению множеств VSl, t и
Vs2, i найдутся такие точки сг и с2, удовлетворяющие соотно-
соотношениям A) —C), чтохк&В(ск9 1/2')с: VSk, h k=l, 2. Из вклю-
включения C) следует, что В(си 3/21) czUSl, а из A) видно, что
c2&Uslf так что p(cj, с2)^3/2*. Значит,
р(хи х2)^р(сх, с2) — р{си хх) — р(с2, х2) > 1/2*,
что и доказывает неравенство D).
Для завершения доказательства теоремы достаточно пока-
показать, что для каждого /gS и любой пары /г, / натуральных
чисел
если В (х, 1/2*) с У,.,, то 5 (х. 1/2/+*) П Vs, t = 0
' при i^j+k и 5^5.
416 ГЛ. 4. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА
В самом деле, для каждого хе! существуют такие k, j и ty
что В(х, l/2k)cz Vt,jt и, таким образом, шар В (xt \/2i+k) пере-
пересекается не более чем с / + k — 1 элементами семейства Т.
Из B) вытекает, что точки с в определении множеств Vs, г
не принадлежат Vt,jt если i^j + k. Так как В(ху \/2k)a Vt,jy
то p(xt c)> \/2k для каждого такого с. Из неравенств / + &^=
^ k + 1 и i ^ k + 1 вытекает, что 5(jc, 1/2>+*)П В {с, 1/20 = 0,
откуда следует E). ¦
4.4.2. Замечание. Отметим, что доказательство теоремы Стоуна
дает больше, чем утверждается теоремой: во всякое открытое
покрытие пространства X, топология которого индуцирована не-
некоторой псевдометрикой, можно вписать покрытие, одновремен-
одновременно локально конечное и а-дискретное.
4.4.3. Теорема. Каждое метризуемое пространство имеет о-дис-
кретную базу.
Доказательство, Пусть р — метрика на метризуемом про-
пространстве X и 98 i— открытое а-дискретное покрытие, вписанное
в открытое покрытие пространства X, состоящее из всех
A//)-шаров. Легко показать, что а-дискретное семейство
оо
5lf= U $г есть база пространства X I
4.4.4. Следствие. Каждое метризуемое пространство имеет а-ло-
кально конечную базу. I
Мы докажем, что существование а-локально конечной базы
также и достаточно для метризуемости регулярного простран-
пространства. Начнем с леммы, обобщающей теорему 1.5.15.
4.4.5. Лемма. Каждое регулярное пространство, имеющее сг-
локально конечную базу, совершенно нормально.
оо
Доказательство. Пусть $ = М Яи где семейства 98г локально
(=i
конечны, есть база регулярного пространства X. Рассмотрим от-
открытое множество W а X. Для каждого х ^ W существуют на-
натуральное число i(x) и открытое множество и(х)а$цХ), такие,
что;се [/(х)сЩГ)с W. Положим Wi=*[}{U(x): /(х) = /}.Мы
получим последовательность W\, W2, .. • открытых подмножеств
оо
пространства X, такую, что W— U Wt и, в силу теоремы 1.1.11,
i = i
WtczW, i=l> 2, .... Нормальность пространства X теперь
оо
следует из леммы 1.5.14. Так как 1^=11 Wit пространство X
совершенно нормально (ср. с упр. 1.5.К). I
4.4. МЕТРИЗАЦИОННЫЕ ТЕОРЕМЫ I 417
4.4.6. Лемма. Пусть X есть Т^пространство, {${\™=х счетное се-
мейство псевдометрик на множестве X, которые все ограничены
числом 1 и удовлетворяют следующим условиям:
(i) р*: Xy^X-^R — непрерывная функция, / = 1, 2, ... .
(и) Для каждой точки хе! « каждого непустого замкну-
замкнутого множества А а X, такого, что хф А, найдется i, при кото-
котором р? (х, А) = inf Qi (х, а) > 0.
Тогда пространство X метризуемо и функция р, определенная
формулой
есть метрика на пространстве X.
Доказательство. Легко видеть, что р(х, х) = 0 для каждого
^еХ и р удовлетворяет условиям (М2) и (МЗ). Так как X
есть Го-пространство, то для любой пары различных точек х,
!/е! либо хф{у), либо уф{х). Следовательно, р(хуу)>0
в силу (И), т. е. р — метрика на множестве X Для того чтобы
доказать, что р — метрика на пространстве .X", достаточно по-
показать, в силу следствия 4.1.11, что
р(х, А) = 0 в том и только том случае, когда хе!
_^Л, то, в силу (п), существует такое число t, что
Р<(хД)=г>0, и р(*,А)^р(х,Л)^г/2''>0. С другой сто-
стороны, из (i) вытекает (в силу теоремы 1.4.7), что р: ХУ^Х-^R —
непрерывная функция, а тогда предложение 4.1.9 показывает,
что функция /: X-+R, определенная формулой f (x)= р(х, Л),
также^непрерывна. Следовательно, если xei, то f(x)^f(A)cz
= {0},т. е. р(х,А) = 0. 1
4.4.7. Метризационная теорема Нагаты — Смирнова. Топологи-
Топологическое пространство метризуемо в том и только том случае, ко-
когда оно регулярно и имеет а-локально конечную базу.
Доказательство. Необходимость условий теоремы следует
из 4.1.13 и 4.4.4. Мы покажем, что эти условия также и доста-
достаточны.
00
Пусть X — регулярное пространство с базой 38= {] $„ где
38i = {Us}s^s локально конечное семейство. Для фиксирован-
фиксированной пары натуральных чисел t, k и любого 5 е S,-, в силу лем-
леммы 4.4.5 и следствия 1.5.12, существует непрерывная функция
fs: X-+I, такая, что Ua = f Iх ((О, 1]). Так как семейство {Ws}seS ,
где Ws =(US X Х)Щ^Х Us), есть локально конечное открытое
27 Зак. 697
418 ГЛ. 4. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА
покрытие пространства XXX и \fs(x)— fs{y) | = 0 для {х,у)ф
^ WSy то, полагая
8t(x, y)= I I /,(х) - fa(у)| для (х, у)^ХХ X,
мы определяем (в силу следствия 2.1.12) непрерывную функцию
gn XXX-+R. Очевидно, что формула pi{x,y) = min(l7gi(x%y))
задает псевдометрику на множестве X, ограниченную числом 1.
Семейство (pj°°=i удовлетворяет условию 4.4.6(i). Выполнено и
условие (и). В' самом деле, для каждого jcgXh каждого не-
непустого замкнутого множества AczX, такого, что хфА, суще-
существует такое Ue3$, что х <= U и A cz X \ U. Далее, U = Us e
е 38 i при некоторых / и s gS(-, и так как fs(x) >0и /5(Л) = {0},
получаем inf Pi{x, a)^fs(x)>0. Метризуемость пространства
а ^ Л
X вытекает теперь из леммы 4.4.6 (ср. с упр. 4.4.A(d)). I
Отметим также, что из последней теоремы непосредственно
вытекает, что условия теорем 4.2.8 и 4.2.9 достаточны для мет-
метризуемости.
Из теорем 4.4.3 и 4.4.7 следует
4.4.8. Метризационная теорема Бинга. Топологическое простран~
ство метризуемо в том и только том случае, когда оно регулярно
и имеет о-дискретную базу. I
Покажем теперь, что существует универсальное пространство
для всех метризуемых пространств веса их^&о (ср. с упр. 4.4.К).
4.4.9. Теорема. Произведение [7(tn)]*°, составленное из Ко копий
ежа J (ш), универсально для всех метризуемых пространств веса
ш ^ Ко.
Доказательство. Очевидно, что [/(nt)]*° — метризуемое про-
пространство веса т.
Пусть X — метризуемое пространство веса ш ^ Мо. По тео-
теореме 4.4.3, существует база 3S = {Us}sgS пространства X, такая»
оо
что S= U SJf где 3i = {Us}s<=s ~~ дискретное семейство.
i = l l
В силу теоремы 1.1.15, можно считать, что |S| = m. Без ограни-
ограничения общности можно предполагать, что множество S совпа-
совпадает с множеством, использованным в примере 4.1.5 при по-
построении ежа 7(т).
Для каждого натурального числа i и любого s ^Si суще-
существует (в силу следствия 4.1.12) непрерывная функция fs: X-W,
такая, что J7e = /i~4@» 1]). Так как семейство U/s}ssS дискрет-
4.4. МЕТРИЗАЦИОННЫЕ ТЕОРЕМЫ I 419
но, то, полагая
fi(x) = jsfs(x) при хе=?/5 и Ы*) = /в0@)
при х&Х\ U USf
где 5о — фиксированный элемент множества 5, мы определяем
(согласно предложению 2.1.13) непрерывную функцию /,-: Х->
->/(ш). Легко показать, что семейство (МП-i разделяет точки
и замкнутые множества. И потому, в силу теоремы о диагональ-
диагональном отображении пространство X вложимо в [7(m)]s°. |
Заключительная часть этого параграфа посвящена изучению
сохранения метризуемости при отображениях. Для начала на-
напомним, что в примере 1.4.17 мы определили замкнутое отобра-
отображение вещественной прямой на пространство, не удовлетворяю-
удовлетворяющее первой аксиоме счетности. Таким образом, метризуемость не
сохраняется при замкнутых отображениях (ср. с теоремой 4.4.17).
Теперь мы приведем два примера, показывающих, что метри-
метризуемость не сохраняется и при открытых отображениях (ср. с
упр. 4.2.D и задачей 4.5.17).
4.4.10. Пример. Рассмотрим подпространство плоскости:
* = {@, 0)}U U HU 1/0}U«О, 1}XU О
i=l i=l /-1
и определим на X отношение эквивалентности Е\ {у)(У)
в том и только том случае, когда у\ = г/2. Естественное фактор-
отображение q: Х^>~ Х/Е — Y открыто. В самом деле, пусть
множество AczX открыто; тогда множество q~lq(A) также от-
открыто, ибо оно получается присоединением к А нескольких изо-
изолированных точек пространства Ху и, следовательно, множество
q(A)cz У также открыто. Легко видеть, что У— хаусдорфово
пространство. Покажем, что У не является регулярным про-
оо
странством. Множество q{F), где F= U {(U 1//)}, замкнуто в Y
и не содержит точки p = q((Oi 0)); тем не менее для каждой
пары U, V открытых подмножеств пространства У, таких, что
р<= U и q(F)a Vt мы имеем []{\Уф0. В самом деле, суще-
существует такое (о, что (о, — + ут^) е q~l {U)> как только / ^ i ^
>to, и такое /о ^ to, что Г1, 4-+ r-^-A s= q~l (V), как только
/ > /о- Таким образом, для # = -!- + j^ имеем @, у) е q~l (U)
и (l,y)<= q~l(V), откуда следует, что q{O,y)= q(l,y)eUf[V.
27*
420 ГЛ. 4. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА
Заметим, что прообразы точек при отображении q — одноточеч-
одноточечные или двухточечные множества. I
4.4.11. Пример. Пусть У= Wo — пространство всех ординалов,
меньших (Oi (см. пример 3.1.27). Положим Х= © Ха> где Ха =
= {jfG Wq: x ^ а} с топологией подпространства. Так как все
Ха открыты, комбинация /= v *a.' X-+Y, где ia: Xa-*Y —
<
вложение, является открытым отображением в силу предложе-
предложений 2.1.11 и 2.1.15. Каждое пространство Ха удовлетворяет вто-
второй аксиоме счетности, поэтому они метризуемы согласно тео-
теореме 4.2.9. Тогда, в силу теоремы 4.2.1, пространство X также
метризуемо. С другой стороны, пространство Y = f(X) не мет-
ризуемо, так как это счетно компактное, но не компактное про-
пространство (см. пример 3.10.16 и теорему 4.1.17). Отметим, что
прообразы точек при отображении / все гомеоморфны дискрет-
дискретному пространству Z)(Ki). I
Докажем теперь, что метризуемость —инвариант совершен-
совершенных отображений. При доказательстве будут использованы сле-
следующие две леммы (вторая является важным частным случаем
теоремы 5.1.33).
4.4.12. Лемма. Пусть в каждое открытое покрытие топологиче-
топологического пространства X можно вписать локально конечное замкну-
замкнутое покрытие. Тогда в каждое открытое покрытие пространства
X можно вписать локально конечное открытое покрытие.
Доказательство, Пусть °U — открытое покрытие простран-
пространства X. Выберем локально конечное покрытие M = {As}s^sf
вписанное в °U. Для каждой точки хеХ выберем ее окрест-
окрестность Vx, которая пересекается лишь с конечным числом эле-
элементов покрытия $Ф* Пусть, далее, У — локально конечное зам-
замкнутое покрытие, вписанное в открытое покрытие {Vx}XfsXf
пусть для любого $ е S
Очевидно, что множество Ws открыто и содержит As. Более
того, для каждого sgSh любого F е & имеем
F) Ws[\F Ф0 тогда и только тогда, когда As Л F Ф 0.
Для каждого sgS возьмем такое U{s)^(Uy что As c= Us. По-
Положим Vs= Ws[}U(s). Семейство {Vs}Ses является открытым
покрытием, вписанным в покрытие 41. Каждая точка xgX
имеет окрестность, пересекающуюся не более чем с конечным
числом элементов покрытия ЗГ, и каждый элемент покрытия $Г
пересекается не более чем с конечным числом элементов по-
4.4. МЕТРИЗАЦИОННЫЕ ТЕОРЕМЫ I 421
крытия Ж. Поэтому, в силу F), покрытие (Ks}seS локально ко-
конечно. I
4.4.13. Лемма. Пусть f: Х-> У— совершенное отображение мет-
ризуемого пространства X на пространство У. Тогда в каждое
открытое покрытие пространства У можно вписать открытое ло-
локально конечное покрытие.
Доказательство. Пусть Т — открытое покрытие пространства
У. По теореме Стоуна, в открытое покрытие {f~x (V)}Ve.r про-
пространства X можно вписать локально конечное покрытие
Wsis^s- Применяя теорему 1.5.18, выберем замкнутое покрытие
&* — {FS}SGS пространства X, такое, что FS<=US для каждого
seS. Так как &" локально конечно, из 3.10.11 следует, что се-
семейство (f(Fs)}seS есть локально конечное измельчение покры-
покрытия Т пространства У. Теперь утверждение леммы вытекает
из 4.4.12. I
4.4.14. Замечание. Заметим, что в доказательстве леммы 4.4.13
использовались только нормальность пространства X и тот факт,
что в каждое его открытое покрытие можно вписать локально
конечное открытое покрытие.
4.4.15. Теорема. Метризуемость сохраняется при совершенных
отображениях.
Доказательство. Пусть f: X^-Y—совершенное отображение
метризуемого пространства X на некоторое пространство У. Вы-
Выберем метрику р на X и для i = 1, 2, ... и каждого у е У рас-
рассмотрим открытые множества
Ut (у) = В (Г1 (У), 1//), W, (у) = Y \ f (X \ Ut (у)),
Vi(y) = rl(Wl(y))czUi(y).
Отсюда следует, что для y^Y имеем
G) Ul(y)cUi(y), j^i.
Семейство ^°i:={Wi(y)} Y является открытым покрытием
пространства У. Заметим, что для каждого у еУ
(8) {^(#)}°li-6a3a Y в точке У-
В самом деле, для любой окрестности V точки у имеем f~l(y)cz
czf-x(V). В силу 4.1.14, существует такое /, что Ut(у)cr f~l(V),
откуда следует включение Wi(y)cz V.
Теперь покажем, что
(9) для каждого уеУи каждого i найдется такое /,
что W7(z)cz Wi(y), где ys=Wf(z).
422 гл- 4- МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА
В силу 4.1.14 и G), существует такое j^2i, что U}(y)cz
<= ^2i(y). Рассмотрим такое 2еУ,чтог/е W}(z). Тогда f~1\y)cz
cz Vj (z) cz Ui (z), т. e. существуют такие x e /-1 (z) и xf e /-1 (y),
что p(x,x/)< 1//. Отсюда следует, что Uj(y)(}f-l{z)?=0 и
/-1 (z)cz V2t(y), ибо последнее множество вместе с любой точ-
точкой х содержит также f~~l(f(x)).
Выберем теперь некоторую точку tfe Wj(z). Тогда f~l(t)a
cz Uj{z) и для любой точки хе/-*(/) существует такая точка
x'^f-l(z)t что р(х,xf) < 1// ^ l/2i. Как показано выше,
/-1(г)с: l/2i(y)c= U2i{y), следовательно, найдется такая точка
х" е/-1 (*/), что р(х', х//)< 1/2/. Поэтому р(х, х")< 1Д откуда
следует, что /-1(/)cz: Ui{y), т. е. что t e ^(г/), и доказательство
утверждения (9) завершено.
В силу леммы 4.4.13, в покрытие Wi пространства Y можно
вписать локально конечное покрытие 3Si. Из утверждений (8)
оо
и (9) вытекает, что объединение 3$ = (J ^« ~~ база простран-
пространства У. Следовательно, будучи нормальным по теореме 1.5.20»
пространство Y метризуемо по теореме Нагаты — Смирнова. I
Следующая теорема дает необходимые и достаточные усло-
условия метризуемости замкнутых образов метризуемых пространств.
4.4.16. Лемма Вайнштейна. Пусть /: X^-Y — замкнутое отобра-
отображение метризуемого пространства X на пространство У. Тогда
для каждого y^Y, такого, что %(y,Y)^^oy множество
Ff f (у) — компакт.
Доказательство. Пусть Л={*1, Хг, ...}— подмножество мно-
множества F = Fr/-1 (у), такое, что |Л| = К0, и пусть {Vt}™=x —
база пространства У в точке у. Рассмотрим метрику р на про-
пространстве X и для i = l, 2, ... выберем такую точку х\^
s f~l(Vi) \f~] (y)> чтор(х; ,Xi) < 1//. Такая точка обязательно су-
существует, ибо отображение f замкнуто, множества {у}, f~l(y)
замкнуты и потому jt(- e F cz f~l (у) cz f-1 (Vi). Следовательно,
множество B{xi,l/i)f[f~l(Vi) является окрестностью точки хи
Для множества В = {х[, х'2, ...} имеем у е f(B)\f (В); так как
/ — замкнутое отображение, ВфВ и В6Ф0. Поскольку
р (х., х\) < 1//, i = l, 2, ..., имеем А6 = 5d ф 0. Следователь-
Следовательно, каждое счетное бесконечное подмножество множества F
имеет предельную точку. Этот факт, в силу теорем 3.10.3 и 4.1.17,
означает, что F — компакт. I
4.4.17. Теорема Ханаи — Мориты — Стоуна. Для любого замкну-
того отображения f: X-+Y метризуемого пространства X на про-
пространство У следующие условия равносильны:
4.4. МЕТРИЗАЦИОННЫЕ ТЕОРЕМЫ I 423
(i) Пространство Y метризуемо.
(и) Пространство Y удовлетворяет первой аксиоме счетно-
сти.
(ш) Для каждой точки y^Y множество Frf~l(y)—ком-
Frf~l(y)—компакт.
Доказательство. Импликация (i)=^(ii) очевидна, a (ii)=>-
=»-(iii) вытекает из предыдущей леммы. Покажем, что
Пусть для любого y^Y множество A{y)<z:X равно
если последнее множество непусто, и является некоторым одно-
одноточечным подмножеством множества \~~1(у), если Fr /-1 (у) = 0,
т. е. если \~х{у)—открыто-замкнутое подмножество простран-
пространства X. Множество А = (J А (у) замкнуто в X, так как Х\А —
объединение открытых множеств lntf~l(y) не более чем с одной
выброшенной точкой каждое. Сужение f\A: A-+Y есть замкну-
замкнутое отображение множества А на У. Так как прообразы точек
при отображении f\A либо имеют вид FTf~l(y), либо суть од-
одноточечные множества, то отображение f\A совершенно. Мет-
Метризуемость пространства Y следует теперь непосредственно из
теоремы 4.4.15. I
Теоремы 1.4.16 и 4.4.17 приводят к следующей теореме.
4.4.18 Теорема. Метризуемость сохраняется открыто-замкнуты-
открыто-замкнутыми отображениями. I
Заметим, что метризуемость не сохраняется в сторону про-
прообраза при совершенных открытых отображениях, как показы-
показывает отождествление в точку любого неметризуемого компакта.
Следующая теорема, последняя в этом параграфе, является
следствием теорем 3.7.22, 4.2.1 и 4.4.15.
4.4.19. Теорема. Пусть топологическое пространство X имеет ло-
локально конечное замкнутое покрытие, состоящее из метризуемых
подпространств', тогда и само пространство X метризуемо. I
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
Теорема 4.4.1 была доказана в работе А. Стоуна [1948]. Это
одна из самых важных теорем общей топологии. Приведенное
нами доказательство заимствовано из работы М. Рудин [1969а].
Нагата и Смирнов доказали теорему 4.4.7 соответственно в
[1950] и [1951а]. Теорема 4.4.8 доказана Бингом в [1951]. Даль-
Дальнейшие метризационные теоремы будут приведены в § 5.4. Тео-
Теорема 4.4.9 принадлежит Ковальскому и доказана в [1957]: дан-
данное здесь доказательство принадлежит Свордсону [1979]. При-
Пример 4.4.10 взят из книги Александрова и Хопфа [1935], а при-
пример 4.4.11 —из работы А. Стоуна [1956]. Теоремы 4.4.15 и 4.4.17
независимо доказаны Моритой и Ханаи в [1956] и А. Стоуном
424 ГЛ. 4. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА
в [1956] (для сепарабельных пространств Уайберн доказал пер-
первую из них в [1942], а равносильность условий (i) и (и) второй
теоремы — в [1950]). Лемма 4.4.12 доказана Майклом в [1953],
лемма 4.4.13 — Моритой и Ханаи в [1956], а лемма 4.4.16 —
Вайнштейном в [1947]. Теорема 4.4.18 доказана Балачандраном
в [1955], а теорема 4.4.19 —Нагатой в [1950].
УПРАЖНЕНИЯ
4.4.А. (а) Покажите, что локально конечное открытое по-
покрытие метрического пространства не обязательно а-дискретно.
Указание. Рассмотрите дискретное пространство D(c).
(b) Покажите, что пространство X в примере 1.5.7 удовле-
удовлетворяет второй аксиоме счетности и потому имеет а-дискретную
базу.
(c) Покажите, что 7\-пространство X обладает локально ко-
конечной базой, или, что эквивалентно, базой, представимой в
виде конечного объединения локально конечных семейств, в том
и только том случае, когда X — дискретное пространство.
(d) Рассмотрите псевдометрики р*, ь> определенные в дока-
доказательстве метризационной теоремы Нагаты—Смирнова, и за-
заметьте, что семейство {fit ^}°%=1 отображений /,-,*: Х-*X/pi,k,
определенных в упр. 4.2.1, разделяет точки и замкнутые множе-
множества. Применяя теорему о диагональном отображении, выведите
отсюда, что пространство X метризуемо.
4.4.В. Докажите, что каждое метризуемое полной метрикой
пространство веса ^ ш ^ Ко гомеоморфно замкнутому подпро-
подпространству произведения [7(т)]х°.
Указание. Заметьте, что вещественная прямая гомеоморфна
замкнутому подпространству пространства [/(Ко)]2, и приме-
примените лемму 4.3.22.
4.4.С. (а) Докажите, что для каждого метризуемого про-
пространства X веса ^с существует взаимно однозначное отобра-
отображение f: X-*Y на сепарабельное метризуемое пространство У.
Указание, Сначала рассмотрите пространство X = /(с), а за-
затем примените теорему 4.4.9.
(Ь) (Видосич [1972]). Пусть X — тихоновское пространство
и существует его взаимно однозначное отображение на метри-
метризуемое пространство. Докажите, что тогда каждое семейство
попарно непересекающихся непустых открытых подмножеств
пространства Rx с компактно-открытой топологией счетно.
Покажите, что в пространстве Rm каждое семейство попарно
непересекающихся непустых открытых множеств счетно (ср. со
следствием 2.3.18).
4.4. МЕТРИЗАЦИОННЫЕ ТЕОРЕМЫ I 425
Указание. Рассмотрите сначала случай метризуемого про-
пространства X и модифицируйте доказательство теоремы 2.3Л 7,
используя (а) и упр. 3.4.G(b), а затем примените указание к
упр. 3.4.G(b).
4.4.D. (а) Непрерывное отображение /: X-+Y называется
локальным гомеоморфизмом, если для каждой точки х^Х су-
существует такая ее окрестность U(x)y что f\U(x)— гомеомор-
гомеоморфизм окрестности U(x) на открытое подпространство простран-
пространства У.
Установите, что каждое открытое отображение f: X->Y9
определенное на хаусдорфовом пространстве Ху при котором
прообразы всех точек — конечные множества одинаковой мощ-
мощности, является локальным гомеоморфизмом.
(b) (Архангельский [1966]). Покажите, что каждый локаль-
локальный гомеоморфизм f: X~^Y, определенный на хаусдорфовом
пространстве X, при котором прообразы всех точек конечны и
состоят из одного и того же числа точек, есть замкнутое ото-
отображение.
(c) Покажите, что если существует открытое отображение
f: X-^Y метризуемого пространства X на пространство У, при
котором прообразы всех точек конечны и состоят из одного и
того же числа точек, то пространство У метризуемо.
4-4.Е. (а) Примените метризационную теорему Нагаты —
Смирнова для решения упр. 4.4.D(c).
(b) Примените метризационную теорему Нагаты —Смирно-
—Смирнова для выполнения упр. 4.3.E(d).
Указание. Для некомпактного метризуемого пространства X
определим такую последовательность х\, #2» •-• его точек, что
для некоторой метрики р на пространстве X имеем р(х*, х/)^ 1
при i ф ]. Присоедините к пространству А' точку х0 таким обра-
образом, чтобы пространство XU{*o} было метризуемым и х0 =
= \imxt.
4.4.F. Топологическое пространство X называется локально
сепарабельным в точке хеХ, если х имеет сепарабельную
окрестность. Топологическое пространство X называется локаль-
локально сепарабельным, если оно локально сепарабельно в каждой
своей точке хе!
(a) Проверьте, что еж /(с) не является локально сепара-
сепарабельным.
(b) (Урысон [1927а]). Приведите пример метризуемого про-
пространства веса с, не являющегося локально сепарабельным ни
в какой точке.
(c) (Александров [1924b]). Покажите, что если X — локаль-
локально сепарабельное метризуемое пространство, то Х= ф Xs, где
все пространства Xs сепарабельны (ср. с упр. 5.3.А(Ь)).
426 ГЛ. 4. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА
Указание. Возьмите локально конечное открытое покрытие
°Ы, вписанное в некоторое открытое покрытие пространства X
сепарабельными подмножествами. Определите отношение экви-
эквивалентности Е на °U, полагая UEU', если существует последова-
последовательность Uo, U\t ..., Uk элементов покрытия Ш, такая, что
Uo =U, Uk = U' h Ut П ?/,-+! Ф 0 для i = 1, 2, ..., k - 1. Для
каждого класса эквивалентности aU%(Zioil отношения Е рассмот-
рассмотрите объединение Xs = U °US-
(d) (Степанек и Вопенка [1967]). Покажите, что каждое
метризуемое пространство X, не являющееся локально сепара-
бельным ни в какой своей точке, может быть представлено как
объединение возрастающей трансфинитной последовательности
А\ cz А2 а ... cz Аа с= ..., а < щ, состоящей из нигде не плот-
плотных множеств.
Указание, Пусть {t/,}s es есть а-локально конечная база про-
пространства X, и пусть Us, и Us,2> . • •, Us, a, ..., seS,ct<©i, —
семейство попарно непересекающихся непустых открытых мно-
множеств, содержащихся в Us. Рассмотрите множества Аа = Х\
\ U U
(е) (Степанек и Вопенка [1967]). Покажите, что каждое
метризуемое пространство без изолированных точек может быть
представлено как объединение семейства нигде не плотных мно-
множеств мощности ^с.
Указание. Примените (с) и (d).
4.4.G. Покажите, что лемма Вайнштейна легко следует из
упр. 2.1.C(d) и4.1.Е(а).
4.4.Н. (а) (Архангельский [1960]; для локально компактных
пространств — Смирнов [1956а]). Покажите, что если полное
в смысле Чеха пространство X имеет счетное покрытие, состоя-
состоящее из сепарабельных метризуемых пространств, то простран-
пространство X метризуемо.
Указание. См. упр. 3.9.Е(с).
(Ь) Покажите, что условие сепарабельности в (а) суще-
существенно даже в случае двухэлементного покрытия.
4.4.1. Покажите, что если существует замкнутое отображе-
отображение f: X—>Y метризуемого пространства X на пространство Y
точечно счетного типа (в частности, на полное по Чеху про-
пространство У), то У метризуемо.
Указание. Примените упр. 3.1.F(b).
4.4.J (Морита [1955]). Докажите, что каждое метризуемое
пространство X веса m ^ Хо есть непрерывный образ некоторого
подпространства бэровского пространства В(ш) при совершен-
совершенном отображении (ср. с указанием к упр. 4.2.D(a)).
Указание. Применяя теорему Стоуна, определите последова-
последовательность @~\УЗГ2, ... локально конечных замкнутых покрытий
4.4. МЕТРИЗАЦИОННЫЕ ТЕОРЕМЫ I 427
пространства Ху таких, что <?", = {Fe( t}S€BS, |S| = m и 8(FS, i)^
^ \/1 для каждого s^S. Рассмотрите подмножество Тег
оо
с: B(m) = S°, состоящее из всех точек {s,}, таких, что р Fs., гФ
Ф0,н поставьте в соответствие точке {si}eT единственную
оо оо
точку пересечения Р Fs. i с X. Покажите, что f~{ (х) = П (sg
eS:xeFSif} для каждого jcg!
4.4.К (Даукер [1947а]). Пусть m — бесконечный кардинал и
S — множество мощности т. Рассмотрим множество всех веще-
вещественных функций х, определенных на S и таких, что
| {s е S: xs ф 0} | ^ Ко и ? х\ < оо, где xs — значение функ-
f eS
ции х на s; формула р(jc, t/) = a/sZs U*~&Jопределяет мет-
метрику на этом множестве. Полученное так метрическое простран-
пространство не зависит (с точностью до изометрии) от выбора множе-
множества S. Оно называется гильбертовым пространством веса ш
и обозначается через #(т). Очевидно, что гильбертово простран-
пространство Я, определенное в примере 4.1.7, совпадает с Я(К0).
Докажите, что гильбертово пространство Н{ш) универсально
для всех метризуемых пространств веса m ^ Ко.
Замечание. Даукер в [1947а] получил этот результат при
дополнительном предположении паракомпактности; тот факт,
что все метризуемые пространства паракомпактны, не был еще
известен.
4.5. ЗАДАЧИ
Расширение открытых и замкнутых множеств
4.5.1 (Куратовский [1948а]). (а) Покажите, что для каждо-
каждого семейства {^5}5е5 открытых подмножеств подпространства
М метризуемого пространства X существует семейство {f/J5sS
открытых подмножеств пространства X, такое, что Vs—M[\ Us
при всех s e S и для каждого конечного множества So с: S,
удовлетворяющего условию f| Fs=0, мы имеем f| U8=0.
ss50 5 ^ So
Указание. Положите [/s={xg X: р(х, Vs) < р(х, М \ Vs)},
где р — метрика на пространстве X.
(Ь) Покажите, что для каждого семейства {Л5}5е5 замкну-
замкнутых подмножеств подпространства М метризуемого простран-
пространства X существует семейство {Fs}s<=s замкнутых подмножеств
пространства X, такое, что А$ = Mf\ Fs при всех sgS и для
428 ГЛ. 4. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА
каждого конечного множества 5о сг S, удовлетворяющего соот-
соотношению U AS = M, мы имеем (J FS = X.
sg5o seSa
Пространство Rn однородно относительно счетных всюду
плотных подмножеств
4.5.2 (Брауэр [1913а]; неявно —Фреше [1910]). Докажите,
что для любых двух счетных всюду плотных подмножеств А, В
евклидова n-мерного пространства Rn существует такой гомео-
гомеоморфизм /: Rn^Rn, что f(A) = B (ср. с упр. 4,3.Н(а)).
Указание. Говорят, что множество A a Rn находится в об-
общем положении относительно координатных осей, если для лю-
любой пары различных точек х={хг}, у ={yi}^ А разность
Xi — yi не обращается в нуль при t = l, 2, ..., п. Докажите
сначала, что для каждого счетного множества Ac^Rn суще-
существует гомеоморфизм Rn на себя, при котором А переходит в
некоторое множество в общем положении относительно коорди-
координатных осей. Затем покажите, что элементы двух счетных бес-
бесконечных множеств в общем положении относительно коорди-
координатных осей можно упорядочить в две последовательности
хи Х2, ... и г/ь уъ .. • , где xi = {х{} и у} = {*/>}, / = 1, 2,
таким образом, чтобы разности х\ — х\ и у\ — у\ имели одина-
одинаковый знак для /, k = 1, 2, ... и I = 1, 2, ..., п.
Топология поточечной сходимости и метрики
4.5.3. (а) Установите, что пространство V с топологией по-
поточечной сходимости не метризуемо.
Указание. Примените упр. 2.1.С (а).
(b) Определите две топологии О\ и <У2 на счетном множе-
множестве X таким образом, чтобы пространство (X, <У\) было метри-
зуемым, а пространство (Xt <У2)—нет и чтобы х = lim xi отно-
относительно топологии О\ в том и только том случае, когда х =
== lim Xi относительно топологии 02.
(c) (Форт [1951]). Докажите, что не существует метрики р
на множестве /7, обладающей тем свойством, что limp(/, //) = 0
тогда и только тогда, когда f = lim // относительно топологии
поточечной сходимости.
Указание (Дугунджи [1966]). Допустим, что существует
метрика р на /7, обладающая указанным выше свойством. Для
каждого лее/ и t = 1,2, ... положим di(x)= sup{/(#): f^F
и P(f»/o)< 1/0» г^е /о е I* тождественно равна нулю. Покажи-
Покажите, что lim di(x) = 0 для каждого х^Х и что для некоторого
числа 10 существуют последовательность х\у х2, ... точек отрез-
отрезка/и последовательность U\9 U2, ... открытых подмножеств
отрезка /, такие, что ^@(а:.)< 1, xi^Ui, i' = l, 2, ..., и Ui{\
(]U} = 0 при i ф j.
4.5. ЗАДАЧИ 429
Рассмотрите последовательность fu /2, ..., где /,• (/ =
= 1, 2, ...)—непрерывное отображение отрезка / в себя, та-
такое, что fi(I\Ui) = {0] и U(xi)= 1.
Расширяющие и сжимающие отображения метрических про-
пространств
4.5.4 (Фрейденталь и Гуревич [1936]). (а) Покажите, что
если (Xt р)—вполне ограниченное пространство, то любое ото-
отображение / пространства X в себя, удовлетворяющее условию
р(х,у)^ p(f(x)>f(y)) при всех xf i/6l, является изометрией
(ср. с упр. 4.3.D).
Указание, Установите, что f обладает свойством, упомяну-
упомянутым в указании к упр. 4.3.D(a), и примените этот факт к ото-
отображению /X /•
(Ь) Покажите, что если (X, р)—вполне ограниченное про-
пространство, то каждое отображение / пространства X в себя,
удовлетворяющее условию р(х, у)^ р(/(х)9f(y)) для всех х,
!и такое, что f{X) всюду плотно в X, является изометрией.
Указание. Рассмотрите продолжение / до отображения /:
Х-*Х, где X — пополнение X, и примените (а).
Всякое плотное в себе метризуемое полной метрикой про-
пространство содержит канторово множество
4.5.5 (Хаусдорф [1914]). (а) Покажите, что каждое непу-
непустое плотное в себе метризуемое полной метрикой пространство
содержит подпространство, гомеоморфное канторову множеству.
Указание. Пусть р — полная метрика на плотном в себе про-
пространстве X. Для каждой последовательности /ь i2f ..., ik, со-
состоящей из нулей и единиц, определите по индукции непустое
открытое множество Vti2... %h с: X, диаметр которого меньше
l/kt такое, что
Vilt2...ikot)Vllt2...iki = 0 и V\,2...vcrF,V2...tV / = 0,1.
(b) Покажите, что каждое сепарабельное метризуемое пол-
полной метрикой пространство либо счетно, либо имеет мощность с.
Указание. Примените задачу 1.7.11 и пункт (а) или устано-
установите, что этот результат непосредственно следует из задачи
ЗЛ2.11(Ь).
Прямая конструкция пополнения
4.5.6 (Хаусдорф [1914]). Пусть (X, р)—метрическое про-
пространство. Определим отношение эквивалентности Е на множе-
множестве всех последовательностей Коши в пространстве (X, р), по-
полагая {xi}E{tfi} в том и только том случае, если lim р(х/, у{) = 0.
430 ГЛ. 4. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА
Покажите, что формула р ([{*,-}], [{у*}] )= limp(^f у{) опреде-
определяет метрику на множестве X всех классов эквивалентности от-
отношения Е. Каждой точке х е X поставьте в соответствие точку
[{х(}]^Х, где Xi = x, i=l, 2, ..., и покажите, что (X,р) —
пополнение пространства (X, р).
Борелевские множества II (см. задачи 1.7.5 и 7.4.22)
4.5.7. Будем говорить, что метризуемое пространство X —
абсолютно мультипликативного (аддитивного) класса а, где
а < ©I, если для каждого гомеоморфного вложения ft: X-*Y
пространства X в метризуемое пространство У образ h(X) яв-
является множеством мультипликативного (аддитивного) клас-
класса а в У.
(a) (Лаврентьев [1924]). Докажите, что для каждого а > 0
(каждого а > 1) метризуемое пространство X — абсолютно
мультипликативного (аддитивного) класса а в том и только том
случае, если существует гомеоморфное вложение Л: Х-+- У про-
пространства X в метризуемое полной метрикой пространство У, та-
такое, что образ h(X) есть множество мультипликативного (ад-
(аддитивного) класса а в У.
Указание. Примените теорему Лаврентьева.
(b) Покажите, что (а) не имеет места ни для мультиплика-
мультипликативного класса 0, ни для аддитивных классов 0 и 1. Покажите,
что метризуемое пространство X — абсолютно мультипликатив-
мультипликативного (аддитивного) класса 0 в том. и только том случае, если
X — компакт (пусто).
(c) Покажите, что метризуемое сепарабельное пространство
X—абсолютно аддитивного класса 1 в том и только том случае,
когда X сг-компактно.
Замечание. А. Стоун доказал в [1962], что метризуемое про-
пространство X—абсолютно аддитивного класса 1 в том и только
том случае, когда X может быть представлено как счетное объ-
объединение локально компактных, или, что равносильно, замкну-
замкнутых локально компактных подпространств.
4.5.8- (а) (Майкл [1954]). Докажите, что в метризуемом
пространстве X объединение локально конечного семейства, со-
состоящего из множеств мультипликативного (аддитивного) клас-
класса а, есть множество того же класса.
Указание. Примените теорему Стоуна и трансфинитную ин-
индукцию.
Замечание. Тот же результат (и доказательство) имеет ме-
место, если X — совершенно нормальное паракомпактное простран-
пространство.
(Ь) (Монтгомери [1935]). Покажите, что если каждая точка
подмножества А метризуемого пространства X обладает такой
4.5. ЗАДАЧИ 431
окрестностью U в X, что Af\U — множество мультипликативно-
мультипликативного класса а > О (аддитивного класса а) в подпространстве U
пространства Ху то А — множество того же класса (ср. с зада-
задачей 2.7.1).
Указание (Майкл [1954]). Примените (а) и тот факт, что X
обладает а-локально конечной базой.
(с) (Монтгомери [1935]). Докажите, что если X и У— мет-
ризуемые пространства и /: X->Y— измеримое отображение
класса а, то график G(f) есть множество мультипликативного
класса а в произведении XX У-
Указание (Энгелькинг [1967]). Покажите, что для любой
базы {Bs}seS пространства У существует семейство {y45}s<=sOT"
крытых подмножеств пространства У, такое, что {X X У) \ G(/)—
U С/ (As) X Bs). Примените (а) и тот факт, что про-
S
ssS
странство У имеет а-локально конечную базу.
Диадические пространства II (см. задачу 3.12.12)
4.5.9. (а) (Серпинский [1928]). Покажите, что каждое не-
непустое замкнутое подмножество А канторовского множества С
есть ретракт пространства С.
Указание (Халмош [1963]). Покажите, что метрика а на
множестве Z)N°t определенная формулой
v (*> У) = ? -^г I xt - yt |, где х = {xt}y у = {yt}t
индуцирует топологию на декартовом произведении. Отметьте,
что если сг(х, у)= о(х, г), то у = г, и выведите отсюда, что для
каждого х е ?)к° существует ровно одна точка а е Л, такая, что
о(х, а)=о(х,А).
(Ъ) (Александров [1927] (объявлено в [1925]), Хаусдорф
[1927]). Покажите, что из (а) и теоремы 3.2.2 вытекает, что
каждый непустой метризуемый компакт есть непрерывный образ
канторова множества, т. е. является диадическим пространством
(ср. с теоремой 3.2.2 и задачей 3.12.12(а)).
4.5.10 (Ефимов [1963]). Покажите, что каждое непустое
замкнутое бб-множество FcDm есть ретракт пространства Dm'
Покажите, что диадичность наследуется непустыми замкнутыми
Сб-множествами.
Указание (Энгелькинг и Пелчинский [1963]). Выберите
функцию /: Dm^Rt такую, что f = /-1@), примените
упр. 3.2.Н(а) и задачу 4.5.9(а).
432 ГЛ. 4- МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА
4.5.11 (Ефимов [1963а]). Покажите, что каждая диадическая
компактификация сХ метризуемого пространства X удовлетво-
удовлетворяет второй аксиоме счетности, т. е. метризуема.
Указание (Энгелькинг и Пелчинский [1963]). Заметьте сна-
сначала, что пространство X сепарабельно, затем примените
упр. 3.5.F и задачу 3.12.12(с).
Можно также использовать задачу 3.12.12(g) и упр. 2.1.С (а).
2-произведения III (см. задачи 2.7.13, 2.7.14, 3.12.23 и
упр. 3.10.D)
4.5.12. (а) (Гулько [1977], М. Рудин [1977]). Пусть 2 (а)
есть 2-произведение метризуемых пространств {Js}56_s, где а =
={а5}е Ц Js. Докажите, что для каждого дискретного семей-
сгва &~ замкнутых подмножеств пространства 2 (а) существует
открытое а-локально конечное покрытие Ш пространства 2(а),
такое, что замыкание каждого элемента °U пересекается не бо-
более чем с одним элементом семейства SF.
Указание. Для каждого пересечения ?/ = 2(а)П XI f/5 npo-
seS
странства 2 (а) с элементом XI Us канонической базы $ произ-
ведения XI ^положим S((/) = {sgS: Us ф Х^}. Для каждого
х = {xs} = 2 (а) пусть {s <= S: xs ф as) = {sx, и sx, 2, ...}, и для
каждого открытого подмножества t/cz2(a), пересекающегося
более чем с одним элементом семейства У, пусть A(U)cz U со-
состоит из двух точек, выбранных в двух различных элементах
семейства У. Для любого seS определим последовательность
^5?ь %, 2, ••• локально конечных открытых покрытий про-
пространства Xs, такую, что каждый элемент покрытия °US, t имеет
диаметр меньше 1// и может быть представлен как объедине-
объединение элементов покрытия °US, м-ь и положим ^ f
пИ зЦ5 Us^^ls,i для sgS([/)}. Допу-
s^S s^S
стим, что |^"|^2, и рассмотрим семейство 9* всех конечных
последовательностей Uo, U\, ..., Un открытых подмножеств про-
пространства 2 (а), где 2(а)= Uo => U\ =э ... zd Un, Ui^Mi для
i = l, 2, ..., п. Каждое Ui при /^n —1 пересекается более
чем с одним элементом семейства^" и S(Ui) = {sx /: х ^ A(Uq)\J
[)A(Ui)[} ... [}A(Ui-i)9 / = lf 2, ..., i] для i = l, 2, ..., п.
Рассмотрите семейство <Ыо, состоящее из всех последних эле-
элементов Un последовательностей из У, которые пересекают не
более одного элемента семейства У, и покажите, что <2/0 есть
ст-локально конечное открытое покрытие пространства 2 (а).
4.5. ЗАДАЧИ 433
Для доказательства того, что °U§ — покрытие, допустим про-
противное, т. е. что существует точка х ={xs}^ 2(a)\ U °И^ Рас-
Рассмотрим бесконечную последовательность ?/о, 13и &2, . - -, такую,
что x<=Ut для «' = 0, 1, 2, ... и (/о, Uu • •-, Un принадлежат
множеству 9? для п = 0, 1, 2, ... . Определите / = {^}еЕ(а),
оо
положив x's^=xs для se U S(Ui) и x's = as в противном
случае, и получите противоречие, установив, что хг е{ао, аь
а2, ...}, где а;<= A(Ui)[}[){F ^&~: x'$?F}. Затем покажите по
индукции, что семейство последних элементов последовательно-
последовательностей из & длины п + 1 является локально конечным для п =
= 0, 1, 2, .... Чтобы получить °U, заметьте, что элементы по-
покрытия °Uq функционально открыты. Замените каждый из них
счетным множеством подходящих открытых множеств.
(Ь) (Гулько [1977], М. Рудин [1977]; для пространств, мет-
ризуемых полной метрикой, — Корсон [1959]). Докажите, что
любое 2-произведение метризуемых пространств нормально.
Указание. Пусть fF ={Fu ^2}, где F\, F2 — замкнутые и не-
непересекающиеся множества. Примените (а), определите локаль-
локально конечное подпокрытие Му вписанное в покрытие Щ (см. лем-
лемму 5.1.10), и рассмотрите множества Ui= X\\J{A* А^^Ф и
A[\Fi = 0} для / = 1, 2.
Замечание. Те же рассуждения показывают, что любое
2-произведение метризуемых пространств коллективно нор-
нормально.
Продолжение замкнутых и открытых отображений
4.5.13. (а) (Вайнштейн [1952]). Непрерывное отображение
f: X^Y замкнуто в точке y^Y, если для каждого открытого
множества (/gI, содержащего f~l(y)> B Y существует окрест-
окрестность V точки у, такая, что f~l(V)cz 13. Множество всех точек
пространства У, в которых отображение /: Х-+- У замкнуто, обо-
обозначается через C(f).
Покажите, что C(f){](f(X)\f(X)) = 0 и B(]C(f)czC(fB)
для каждого ВсУ. Заметьте, что C(f\A)aC(f) для каждого
непрерывного отображения f: X-+Y нормального пространства
X в 7Упространство У, где А — всюду плотное множество в X.
(Ъ) (Энгелькинг [1971]). Докажите, что для каждого непре-
непрерывного отображения f: Х-> У, где X — пространство, метризуе-
мое полной метрикой, а У — хаусдорфово пространство, удовле-
удовлетворяющее первой аксиоме счетности, множество C(f) есть
С6-множество в У.
Указание. Заметьте, что для каждого y^C(f) множество
Frf~l(y)—компакт. Возьмите полную метрику р на простран-
пространстве X и для /=1,2,... рассмотрите множество Wu состоящее
28 Зак. 697
434 ГЛ. 4. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА
из всех точек у е У, имеющих окрестность W с тем свойством,
что каждое множество K<=f~l(W), такое, что p(x,x')^z \/i и
/ для любой пары различных точек множества К,
оо
конечно. Покажите, что С(/)= f] Wt,
(c) (Вайнштейн [1952] (объявлено в [1947])). Докажите,
что если /: X-+Y — непрерывное отображение пространства Ху
метризуемого полной метрикой, в хаусдорфово пространство У,
удовлетворяющее первой аксиоме счетности, то для всякого мно-
множества A cz Ху такого, что сужение /1А: А -> / (А) замкнуто, най-
найдется такое бб-множество В cz X, что Л с: В и сужение f\B:
B-+f(B) замкнуто. Заметьте, что если сужение f\A совершен-
совершенно, то существует такое <36-множество В azX, что А а В и
сужение f\B совершенно.
Указание. Примените (а) и (Ь).
(d) Пусть X и У — пространства, метризуемые полной мет-
метрикой, и пусть АаХ и С а У— произвольные подпространства.
Выведите из (с), что любое замкнутое отображение /: Л->С
подпространства Л на С продолжается до замкнутого отображе-
отображения F: B-+D подпространства В на подпространство Z), где
AdBazX, CczDczY и В есть <Зб-множество в X. Заметьте,
что если / — совершенное отображение, то существуют такие В
и D, что F: B-+D — также совершенное отображение.
Замечание. Из теорем 4.3.23, 4.3.24 и задачи (е) ниже вы-
вытекает, что D есть <Зб-множество в У.
(e) (Вайнштейн [1952] (объявлено в [1947])). Докажите,
что если метризуемое пространство У является непрерывным
образом пространства X, метризуемого полной метрикой, при
замкнутом отображении /, то У также метризуемо полной мет-
метрикой.
Указание. Примените (а) и (Ь); можно также воспользо-
воспользоваться теоремами 4.3.26 и 3.9.10 и сузить замкнутое отображе-
отображение до совершенного отображения, как при доказательстве тео-
теоремы 4.4.17.
4.5.14. (а) (Мазуркевич [1932]). Докажите, что если /: Х-*-
-> У — непрерывное отображение сепарабелыгого пространства
X, метризуемого полной метрикой, в метризуемое пространство
У, то для каждого множества 4с1, такого, что сужение
f\A: A->f(A) открыто, существует О6-множество BazX, такое,
что AazB и сужение f\B: B~>f(B) открыто.
Указание (Хаусдорф [1934]). Без ограничения общности
можно считать, что Л —X и С= У, где C = f(A). Возьмем пол-
полную метрику р на пространстве X и любую метрику а на про-
пространстве У. Для фиксированной счетной базы к пространства
X положим Л*={(/еЯ: 8(U)<l/k и 6(/(?/))< 1/Л}. Для
4.5. ЗАДАЧИ
каждой последовательности м, /2, .
определите по индукции множество U
ti ...
435
ik натуральных чисел
3&& такое, что
Выберите открытые множества Vii2... iS^Y диаметра
удовлетворяющие соотношениям
ili2...ik и V,ltt...th,czVilia...ik,
Пусть далее
Установите, что
U
'.',¦•¦'*)
есть /^-множество, не пересекающееся с С. Рассмотрите мно-
множество
(b) Пусть X — сепарабельное пространство, метризуемое
полной метрикой, У — пространство, метризуемое полной метри-
метрикой, я Аа X, Ccz Y — произвольные подпространства. Выведите
из (а), что каждое открытое отображение f: A-+C подпростран-
подпространства Л на С продолжается до открытого отображения F: B-+D
подпространства В на Z), где ЛсВсХ, CcDcF и В есть
(/^-множество в X.
Замечание. Из задачи 5.5.8 (d) и теорем 4.3.23, 4.3.24 выте-
вытекает, что D есть О6-множество в У.
(c) (Р. Поль [1981]). Докажите, что предположение о се-
сепарабельности пространства X в (а) и (Ь) существенно.
Указание. Пусть Q — множество всех рациональных чисел,
P = R\Q и S = Z)(c). Пусть далее {Cs}3&$ — семейство всех
счетных всюду плотных подмножеств пространства Р. Рассмот-
Рассмотрите подпространство X = {(s, *)e S X R: te=R\Cs}aSXR
и отображение f: X-+R, определенное формулой /(s, t)= t. По-
Покажите, что сужение f |Л, где A = SXQ, открыто. Рассмотрите
б 5 В X А В П
у
любое Eб-множество
Q р р
X, такое, что А а В. Покажите, что
28*
436 ГЛ. 4. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА
существует бб-множество Сс=/?, такое, что QaCczf(B), и
рассмотрите множество f(B (}[{s}X(R\ Cs)])> где CsaC.
(d) Докажите, что если X-+Y — непрерывное отображение
метризуемого пространства X в метризуемое пространство У,
то для каждого множества АаХу такого, что сужение f\A:
A-+f(A) открыто и f(A) есть бб-множество в У, найдется та-
такое E6-множество BczX, что А а В и сужение /1 В: В -> f (В) от-
открыто.
Указание. Можно считать, что f(A) = У.
Метризуемость компактов и счетно компактных пространств
4.5.15. (а) (Катетов [1948]). Покажите, что компакт X мет-
ризуем в том и только том случае, когда произведение ХУ^ХУ^Х
наследственно нормально (ср. с упр. 4,2,В).
Указание. Используйте задачу 2.7.15(а) и упр. 4.2.В.
Замечание. Как показал Никош в [1977], существование не-
метризуемых компактов X, таких, что произведение XX X на-
наследственно нормально, совместимо с аксиомами теории мно-
множеств.
(Ь) (Хабер [1976]). Покажите, что предположение о ком-
компактности в (а) можно ослабить до счетной компактности.
Указание. См. задачу 3.12.12 (е).
Произведения с метризуемым сомножителем
4.5.16. (а) (Майкл [1953]). Докажите, что произведение
XX У совершенного пространства X и метризуемого простран-
пространства У есть совершенное пространство.
Указание. Воспользуйтесь тем фактом, что пространство У
имеет сг-локально конечную базу.
(b) (Морита [1963]). Докажите, что произведение XX У
совершенно нормального пространства X и метризуемого про-
пространства У совершенно нормально.
Указание. Примените упр. 1.5.К.
Замечание. В примере 5.1.32 будет показано, что нормаль-
нормальность и наследственная нормальность не сохраняются при умно-
умножении на метризуемое пространство.
(c) (Бурбаки [1958], Дьедонне [1958]; объявлено А. Стоу-
Стоуном [1948]). Докажите, что произведение IX ^ счетно ком-
компактного нормального пространства X и метризуемого про-
пространства У нормально.
Указание. Модифицируйте доказательство леммы 5.2.7; при-
примените теорему 3.10.7.
Замечание. Тот же результат (и доказательство) имеет ме-
место, если У — паракомпактное пространство, удовлетворяющее
первой аксиоме счетности (ср. с примером 5.1.40).
4.5. ЗАДАЧИ 437
(d) Уиллард [1971]). Докажите, что произведение XX Y
наследственно линделёфова пространства X и сепарабельного
метризуемого пространства У является наследственно линделё-
фовым пространством.
Указание. Примените (а) и следствие 3.8.10.
Замечание. В работе [1964] Морита описал топологические
пространства, произведения которых с любым метрическим про-
пространством нормальны.
Сохранение метризуемости при открытых и факторных ото-
отображениях
4.5.17 (А. Стоун [1956]). Докажите, что если /: X-+Y —
открытое отображение локально сепарабельного метризуемого
пространства X на регулярное пространство У и все прообразы
точек при отображении f сепарабельны, то пространство У мет-
ризуемо (ср. с задачей 5.5.8 (d)).
Указание. Пусть Х= ф Xs, где все пространства Xs cena-
рабельны (ср. с упр. 4.4.F(b)). Определите отношение эквива-
эквивалентности Е на множестве S, полагая sEs', если существует та-
такая последовательность s0, su ..., sk, что s0 = s, sk = s' и
!(Х$()П!{Х$1+1)ф 0, i = 0, 1, ..., k—\. Установите, что объ-
объединение Xs, принадлежащих одному и тому же классу эквива-
эквивалентности отношения ?, образуют сепарабельные подпростран-
подпространства пространства X. Образы этих подпространств при отобра-
отображении / открыты и попарно не пересекаются.
4.5.18 (Чобан [1966]; для сепарабельных X — А. Стоун
[1956]). Докажите, что если /: Х->-У — факторное отображение
метризуемого пространства X на сепарабельное регулярное про-
пространство У, удовлетворяющее первой аксиоме счетности, и все
прообразы точек при отображении / — сепарабельные подпро-
подпространства, то пространство У метризуемо.
Указание. Покажите, что для любого счетного всюду плот-
плотного множества ВсУ подпространство A = f~l(B)czX сепара-
бельно. Выберите для пространства А счетную базу $, замкну-
замкнутую относительно конечных объединений, и докажите, что се-
семейство {Int f(U): U ^M) — база пространства У.
Продолжение функций и метрик
4.5.19. (а) (Дугунджи [1951]; для сепарабельных X — Бор-
сук [1933]). Пусть X — метризуемое пространство и М — его
замкнутое подпространство. Докажите, что для каждого непре-
непрерывного отображения /: M^-R можно задать его непрерывное
438 ГЛ. 4. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА
продолжение e(f)= F: Х-+- R таким образом, что
sup|[e(/)](jc)|=sup|/(;c)|
X Af
при всех f:
где [tf] (jc)== t-f(x), при всех fi, f2: M-*R и вещественных tu *2.
Указание (Дугунджи [1951], Арене [1952]). Выберем метрику
р на пространстве X и локально конечное открытое подпокры-
подпокрытие {Fs}seS, вписанное в покрытие \в fjc, —р(лг, M)j\ под-
подпространства Х\М. Для любого seS выберем такую точку
xs е X \ М, что Vs с В (xs, -j- p (xs, Мп , и такую точку as e M,
что р(а5, *5)<-^p(jcs, M). Используя теорему 1.5.18, определим
функции gs: Х\М->1, такие, что & (-У Ws) с: {0} для любого
5eS и X gs(x)=l Для любого хеХ\Л1; положим
г / (jc) при х^ Mt
[е(/)] (х) = ] ^ /(ae)gs(x) при хеХ\Л1.
Для доказательства непрерывности ^(/) заметьте, что для ка-
каждого а ^ М и любого х ^ Vs имеет место неравенство
p(,)p()
(b) (Дугунджи [1951]). Пусть X — метризуемое простран-
пространство и М — его замкнутое подпространство. Докажите, что для
каждого непрерывного отображения /: M-+C*{Y), где C*{Y) —
кольцо всех ограниченных непрерывных вещественных функций,
определенных на пространстве У, с топологией, индуцированной
метрикой д, определенной формулой G) § 4.2, где а — есте-
естественная метрика вещественной прямой, существует продолже-
продолжение F: X-+C*(Y) отображения f на все пространство X.
Указание. Следуйте конструкции, предложенной в предыду-
предыдущем указании, и определите F по формуле, задающей e{f).
Замечание, Подобная же конструкция проходит для линей-
линейного продолжения функций со значениями в любом локально
выпуклом топологическом векторном пространстве.
(c) (Гемба и Семадени [I960]). Покажите, что не суще-
существует оператора продолжения е, задающего для каждой непре-
непрерывной функции /: $N\N-^R некоторое продолжение e(f):
fW ->/? таким образом, что
sup |И/)](х)|= sup \f(x)
4.5. ЗАДАЧИ 439
при всех /: $N\N-+R и
для всех /i,/2: $N\N-+R.
Указание. Рассмотрите семейство {Ut}t^I открытых подмно-
подмножеств пространства $N\Ny определенных в примере 3.6.18, и
семейство {ft}t^I функций ft: $N\ N->-R, определенных фор-
формулой
1, если x^Uu
U (Х) \0, если х е ($N\N)\Ut.
4.5.20. (а) (Хаусдорф [1938]). Пусть М — замкнутое подпро-
подпространство метризуемого пространства X и /: M-+L — непрерыв-
непрерывное отображение М на метрическое пространство L. Докажите,
что пространство L может быть изометрично вложено как зам-
замкнутое подмножество в некоторое метрическое пространство Y
таким образом, что отображение / продолжается до непрерыв-
непрерывного отображения F: Х->У, сужение которого F\X\M есть
гомеоморфизм Х\М на Y\L.
Указание (Куратовский [1938], Арене [1952]). Рассмотрите
продолжение композиции /': Af->C*(L) отображения f и изо-
метричного вложения L в C*(L), определенного в доказатель-
доказательстве теоремы 4.3.14, до непрерывного отображения f: X-> C*(L)
(ср. с задачей 4.5.19(Ь)). Рассмотрите произведение Z =
= C*(L)X R X С*(Х) и отображение F: X-+Zy определенное
формулой F{x) = (f'(x),p(x,M),p(xtM)-fx), где р — ограничен-
ограниченная метрика на пространстве X и fx(y)= р{х,у). Установите,
что в качестве Y можно взять подпространство F{X)c^Z.
(b) Установите, что если отображение f в (а)—гомеомор-
(а)—гомеоморфизм, то продолжение F, определенное выше в указании, также
является гомеоморфизмом.
Указание. Покажите, что если {Vs} 5es — открытое покрытие
подпространства Х\М и {as: s sS} — подмножество в М9 опи-
описанное в указании к задаче 4.5.19(а), то для каждого а еМ и
любого x^Vs имеет место неравенство р(а, х) < р(а, а5) +
+ 2(Af)
p()
(c) (Хаусдорф [1930]). Докажите, что если М — замкнутое
Подпространство метризуемого пространства X, то каждая мет-
метрика на М продолжается до метрики на пространстве X.
(d) Убедитесь в том, что с) немедленно решает 4.3.Е(с)
и (d).
(e) Покажите, что если М — замкнутое подпространство про-
пространства X, метризуемого вполне ограниченной метрикой, тогда
каждая вполне ограниченная метрика на М продолжается до
вполне ограниченной метрики на всем пространстве X.
440 ГЛ. 4. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА
(f) (Бэкон [1968]). Покажите, что если М — замкнутое под-
подпространство пространства X, метризуемого полной метрикой,
то каждая полная метрика на М продолжается до полной мет-
метрики на пространстве X.
Указание. Пусть р — полная метрика на подпространстве М.
Продолжите метрику р до метрики р на пространстве X и
возьмите пополнение (X, р) пространства (X,р). Представьте
оо
разность Х\Х как счетное объединение \J Ft замкнутых под-
подмножеств пространства X и рассмотрите метрику а на X, опре-
определенную формулой
оо
М) I \
Пространство R1 метрически универсально для всех сепара-
бельных метрических пространств
4.5.21. (а) Покажите, что для каждого счетного семейства
{/^^Ij ограниченных непрерывных вещественных функций, опре-
определенных на сепарабельном метризуемом пространстве X, су-
существует метризуемая компактификация сХ пространства X,
такая, что все функции ft непрерывно продолжаются на сХ.
Указание. См. упр. 4.3Е(а).
(b) Отметьте, что для каждого метрического компакта (X, р)
пространство (Rx7a), где а — естественная метрика веществен-
вещественной прямой, изометрично подпространству пространства (Rc, a),
где С — канторово множество.
Указание. Используйте задачу 4.5.9 (Ь).
(c) (Банах и Мазур, как указано Банахом в [1932]). До-
Докажите, что каждое сепарабельное метрическое пространство
(X, р) изометрично подпространству пространства (R!,d), где
а — естественная метрика вещественной прямой.
Указание. Заметьте сначала, что пространство (/?с, д) изо-
изометрично подпространству (/?7,а). Затем выберите счетное всю-
всюду плотное подмножество А={аи а2, ...} пространства X и
рассмотрите семейство {/j}°°=1 вещественных функций на Ху
определенных формулой fi(x) = p(x, а()— р(х, а), где аеХ-
фиксированная точка. Далее примените (а), (Ь) и теорему 4.3.17.
Замечание. Урысон в работе [1927] первым описал метри-
метрическое пространство, метрически универсальное для всех сепа-
рабельных метрических пространств.
4.5. ЗАДАЧИ 441
Пространства замкнутых подмножеств III см. задачи 2.7.20,
3.12.26,6.3.22 и 8,5.16)
4.5.22. Хаусдорфова метрика на семействе всех ограниченных
непустых замкнутых подмножеств метрического пространства
(X, р) определяется формулой
Ря(Л, Я) = max {sup p (а, В), sup p(b, Л)}.
А bB
(a) (Хаусдорф [1914], Майкл [1951]). Установите, что ря —
метрика на семействе всех ограниченных непустых замкнутых
подмножеств метрического пространства (X, р). Проверьте, что
(X, р) изометрично некоторому замкнутому подпространству по-
полученного таким образом метрического пространства. Приве-
Приведите пример двух эквивалентных вполне ограниченных метрик р
и а на пространстве X, таких, что топологии на 2х, индуциро-
индуцированные метриками ря и ан> различны. Приведите пример огра-
ограниченного сепарабельного метрического пространства (X, р), та-
такого, что топология Вьеториса на 2х и топология, индуцирован-
индуцированная метрикой ря, несравнимы. Покажите, что топология, инду-
индуцированная хаусдорфовой метрикой ря на семействе 2?(Х) всех
непустых компактных подпространств метрического простран-
пространства (X, р), совпадает с топологией Вьеториса на 3j{X).
Замечание. Помпейю в [1905] исследовал сходимость, ин-
индуцированную метрикойРр (Л, В) = sup p(a, ?)+ supp(&, Л) на
семействе всех ограниченных непустых замкнутых подмножеств
плоскости.
(b) Проверьте, что если пространство (X, р) вполне огра-
ограничено, то пространство Bх, ря) также вполне ограничено. При-
Приведите пример сепарабельного ограниченного метрического про-
пространства (X, р), такого, что пространство Bх, ря) не сепара-
бельно.
(c) (Хан [1932]). Покажите, что если пространство (X, р)
полно, то пространство всех ограниченных непустых замкнутых
подмножеств пространства (X, р) с хаусдорфовой метрикой ря
также полно.
(d) (Куратовский [1956]). Покажите, что если пространство
{X, р) полно, то и пространство (<2^(Х),ря) полно.
(e) Установите, что если X есть ^-пространство, то экспо-
экспоненциальное пространство 2х метризуемо в том и только том
случае, если X — метризуемый компакт. Убедитесь в том, что
пространство ЗС(Х) метризуемо в том и только том случае, если
пространство X метризуемо.
Указание. Используйте задачу 2.7.20 (f).
(f) (Куратовский [1948]). Пусть (X, р)—метрическое про-
442 ГЛ. 4. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА
странство исеХ Каждому ограниченному непустому замкну-
замкнутому подмножеству Аа X поставим в соответствие функцию
fA^Rx, определенную формулой fA(x)= p(x, А) — р(х, а). По-
Покажите, что это соответствие определяет изометрию между про-
пространством всех ограниченных непустых замкнутых подмно-
подмножеств пространства (X, р) с хаусдорфовой метрикой ря и про-
пространством всех ограниченных непрерывных вещественных функ-
функций на X с метрикой &, определенной формулой G) § 4.2, где
а — естественная метрика на вещественной прямой.
Выведите отсюда, что для каждого метризуемого компакта
X пространство 2х с топологией Вьеториса вложимо в простран-
пространство отображений Rx с компактно-открытой топологией. Устано-
Установите, что оба условия — метризуемость и компактность простран-
пространства X—являются существенными (ср. с задачей 3.12.26(j)).
Глава 5
ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА
Паракомпактные пространства одновременно обобщают ком-
компактные пространства и метризуемые пространства. Хотя они
были определены намного позже, чем два предыдущих класса,
паракомпактные пространства быстро завоевали популярность
у топологов и аналитиков и считаются теперь одним из важ-
важнейших классов топологических пространств. Благодаря введе-
введению паракомпактности многие теоремы топологии и анализа
получили обобщения, а многие доказательства упростились.
Кроме того, понятие локально конечного семейства и понятия,
связанные с ним, оказались весьма эффективными и естествен*
ными средствами изучения топологических пространств.
Параграф 5.1 посвящен паракомпактным пространствам. Мы
начинаем с трех теорем, содержащих различные характеристики
паракомпактности хаусдорфовых пространств (описания ее в
терминах разбиений единицы особенно важны для анализа).
Далее доказываем, что паракомпактные хаусдорфовы простран-
пространства обладают свойством коллективной нормальности, намного
более сильным, чем простая нормальность, и приводим несколь-
несколько примеров. Во второй части этого параграфа изучаются опе-
операции над паракомпактными пространствами и поведение этого
класса пространств при отображениях. Параграф завершается
теоремой Тамано, в которой устанавливается интересная внеш-
внешняя характеристика паракомпактных хаусдорфовых пространств.
В § 5.2 мы изучаем класс счетно паракомпактных про-
пространств. Теоремы этого параграфа содержат различные харак-
характеристики счетной паракомпактности.
Параграф 5.3 посвящен слабо паракомпактным и сильно па-
паракомпактным пространствам. Как и класс счетно паракомпакт-
паракомпактных пространств, эти два класса имеют гораздо меньшее зна-
значение, чем класс паракомпактных пространств. Однако они
играют определенную роль в теории размерности и алгебраиче-
алгебраической топологии. Среди теорем этого параграфа самыми важ-
важными являются теорема Нагами — Майкла о том, что каждое
коллективно нормальное слабо паракомпактное пространство
паракомпактно, и теорема Уоррелла о сохранении слабой пара-
паракомпактности замкнутыми отображениями.
444 ГЛ. 5. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА
Последний параграф является продолжением § 4.4; в нем
приводятся еще пять метризационных теорем.
5.1. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА
Понятие локально конечного семейства множеств, введенное
в гл. 1, приводит к определению важного класса топологических
пространств — паракомпактных пространств. Топологическое
пространство X называется паракомпактным, если в каждое его
открытое покрытие можно вписать локально конечное открытое
покрытие *).
Заметим, что, в противоположность определению компактно-
компактности, в определении паракомпактности нельзя заменить «вписан-
«вписанное покрытие» на «подпокрытие». Действительно, легко видеть,
что каждое дискретное пространство паракомпактно: покрытие,
состоящее из всех его одноточечных подмножеств, открыто, ло-
локально конечно и вписано в любое покрытие этого простран-
пространства,— и тем не менее открытое покрытие {N [\ П> *]}JLi ПР°"
странства натуральных чисел N не содержит никакого локально
конечного подпокрытия (ср. с упр. 5.1.A(d)).
Из определения паракомпактного пространства вытекает
5.1.1- Теорема. Каждое компактное пространство паракомпакт-
паракомпактно. 1
С помощью понятия паракомпактности теоремы 3.8.11 и 4.4.1
можно сформулировать следующим образом:
5Л.2. Теорема. Каждое линделёфово пространство параком-
паракомпактно. I
5.1.3. Теорема. Каждое метризуемое пространство параком-
паракомпактно. I
Читатель легко выведет из теоремы 5.1.12 и замечания 5.1.7,
что возможность вписывать открытые покрытия, которые одно-
одновременно локально конечны и а-дискретны, установленная для
метризуемых пространств в теореме 4.4.1, лишь формально силь-
сильнее паракомпактности в классе хаусдорфовых пространств.
5.1.4. Лемма. Пусть X — паракомпактное пространство и А, В —
два непересекающихся замкнутых множества в X. Если для
каждой точки х е В существуют открытые множества Ux, Vx,
такие, что A a Ux, xg Vx и ихГ\Ух — 0, то найдутся открытые
множества 1)у V, для которых AczU, В а V и U f\V — 0.
Доказательство. Семейство {VX}X^B U {X \В} является от-
1) Паракомпактные хаусдорфовы пространства называются также пара-
компактами. — Прим. перев.
5.1. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА 445
крытым покрытием паракомпактного пространства X, Значит,
существует вписанное в него локально конечное открытое по-
покрытие {W$}S€BS. Для S0 = {se=S: №8[\Вф 0} имеем
А П Ws = 0 при всех sgS0 и В cz \] Ws.
В силу теоремы 1.1.11, множество U = X \ [} Ws открыто.
se=So
Как легко видеть, множества U и V = [} Ws обладают всеми
нужными свойствами. I
5.1.5. Теорема. Каждое паракомпактное хаусдорфово простран-
пространство нормально.
Доказательство. Подставляя одноточечные множества вме-
вместо А в последней лемме, мы видим, что каждое паракомпакт-
паракомпактное хаусдорфово пространство регулярно. Пользуясь этим фак-
фактом и применяя лемму снова, мы получаем теорему. 1
Отметим, что последняя теорема обобщает одновременно
теоремы 1.5.15, 3.1.9 и 3.8.2. Так как каждое регулярное про-
пространство с а-локально конечной базой паракомпактно (это вы-
вытекает из следующей далее теоремы 5.1.11), она обобщает так-
также лемму 4.4.5.
Семейство {/5}seSнепрерывных отображений пространства X
в единичный отрезок / называется разбиением единицы на про-
пространстве X, если Yi М*)=1ПРИ всех х^Х- Последнее ра-
венство имеет тот смысл, что при произвольном фиксированном
Хо ^ X лишь счетное множество функций fs не обращается в нуль
в точке х0 и ряд X fs,(xQ)9 где {su s2, ...} = {s^S:
t=i *
сходится к I. Так как этот ряд абсолютно сходится, порядок
членов не имеет значения, и сходимость к 1 означает, что 1 яв-
является наименьшей верхней гранью множества всех чисел вида
fsii(xo) + fSl2(Xo)+ ... +fsik(*o), где su s2J ..., s&e=S.
Мы говорим, что разбиение единицы {fs}SG$ на простран-
пространстве X локально конечно, если покрытие {/7l(@, l])}seS про-
пространства X локально конечно. Это означает, что для каждой
точки хо е X найдутся ее окрестность ?/0 и конечное множество
So—{si, S2t •¦•• s*}c:S, такие, что fs(x) = O при всех xg[/0
и всех s e S \ So и X fst (х) = 1 •
Разбиение единицы {/s}se=s на пространстве X подчинено
покрытию зФ пространства X, если покрытие {/J1 (@, 1])} впи-
вписано в si-.
446 ГЛ. 5. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА
Наша следующая теорема содержит две характеристики па-
ракомпактов в терминах разбиений единицы. Эти характеристи-
характеристики очень полезны не только в топологии, но и в анализе, и в
дифференциальной геометрии. Теореме будут предпосланы две
леммы. Первая из них будет применяться еще и потом, поэтому
мы устанавливаем ее в несколько более общей форме, чем тре-
требуется сейчас. В доказательстве нашей теоремы можно приме-
применить вместо этой леммы — менее элементарно — теорему 1.5.18.
5.1.8. Лемма. Если в каждое открытое покрытие регулярного
пространства X можно вписать локально конечное покрытие
{произвольными множествами), то для каждого открытого по-
покрытия {Us}s eS пространства X найдется замкнутое локально
конечное покрытие (F5}seS этого пространства, такое, что Fscz
с Us при всех s e S1).
Доказательство, В силу регулярности Х> существует откры-
открытое покрытие Ж пространства X, такое, что {W: W ^Ж} впи-
вписано в {US}S(^S. Возьмем локально конечное покрытие {At}t^Ty
вписанное в покрытие Ж, для каждого / ^Г выберем s(t)^S>
такое, что At а 1/я<о> и положим Fa = U Л*. Из теорем 1.1.11
и 1.1.13 легко следует, что {Fs}st=s — замкнутое локально ко-
конечное покрытие пространства X, а определение множеств Fs
показывает, что Fs cz Us при всех sgS. I
5.1.7. Замечание. Отметим, что если покрытие {At}t^T в послед-
последнем доказательстве открыто, то множества Vs= M At откры-
ты и Fy= Vs. Значит, для каждого открытого покрытия {Us}s^
паракомпакта существует локально конечное открытое покрытие
iVis* такое> что ^ cr f/s при всех sgS.
5.1.8. Лемма. Если для открытого покрытия °U пространства X
существует подчиненное ему разбиение единицы {fs}seS, то в <Ы
можно вписать открытое локально конечное покрытие.
Доказательство. Для начала заметим, что если g: X-+I —
непрерывная функция, хое1 и g(*o)>O, то найдутся окрест-
окрестность Uq точки а'о и конечное множество So cz 5, такие, что
A) fs(x)<g(x) при хе[/0 и 5g5\50.
Действительно, легко проверяется, что условию A) удовле-
удовлетворяют любое множество 50 = {si, s2,..., s^} cz S, для которого
]) Говорят при этом, что покрытие {F5}5eS комбинаторно вписано в по-
покрытие {Us}s€bS*~ Прим. перев.
5.1. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА 447
к
Y*Ut (*о) < g (*о)> и открытое множество [/0 = {xg А\* 1 —
Для каждого xg! выберем s(x)eS так, чтобы было
/*<*)(*)> 0- Взяв g = fs(x) в предыдущем замечании, мы заклю-
заключаем из 2.1.12, что формула / (лг)== sup fs(x) определяет некото-
рую непрерывную функцию /: Х-*-(О, 1]. При каждом ^gS
множество
открыто, и семейство Т = {Vs}8eS вписано в °U. Положив
gs=yf(jc) в нашем первоначальном замечании, мы приходим
к выводу, что семейство Т локально конечно.
5.1.9. Теорема. Для каждого Т\-пространства X следующие
условия равносильны:
(i) Пространство X — паракомпакт.
(и) Для каждого открытого покрытия пространства X най-
найдется подчиненное ему локально конечное разбиение единицы.
(iii) Для каждого открытого покрытия пространства X най-
найдется подчиненное ему разбиение единицы.
Доказательство. Предположим, что X — паракомпакт, и рас-
рассмотрим произвольное открытое покрытие $Ф пространства X.
Пусть <M = {US}S&sлокально конечное открытое покрытие, впи-
вписанное в з?. По лемме 5.1.6, найдется замкнутое покрытие
{Fs}5eS пространства X, такое, что Fs с Us при всех 5 е S. Из
леммы Урысона следует, что для каждого sgS можно найти
непрерывную функцию gs: Х->19 такую, что gs(x) = Q при хе
eX\Us и gs(x)=l при х е Fs. Так как семейство °U ло-
локально конечно, то полагая #(#)=? gs(x)> мы получаем не-
прерывную функцию g". Z->/?. Легко видеть, что семейство
ifs}ses* где U^Ss/gj является локально конечным разбиением
единицы, подчиненным зФ. Тем самым импликация (i)=^(ii)
установлена.
Так как импликация (ii) => (iii) очевидна, для завершения
доказательства достаточно показать, что (iii)=^(i), а это, в силу
леммы 5.1.8, сводится к доказательству того, что каждое 7Vnpo-
странство J, удовлетворяющее условию (iii), является хаусдор-
фовым пространством. Мы покажем, что X — тихоновское про-
пространство. Рассмотрим любую точку хо е X и произвольное
448 ГЛ. 5. ПАРАКОМПАКТИЫЕ ПРОСТРАНСТВА
замкнутое множество F cz Xt такое, что х0 ф F. Открытому по-
покрытию °и ={X\Fy X\{xo}} пространства X подчинено не-
некоторое разбиение единицы if ) . Возьмем s0 e S, для которого
/S9(jc0) = а > 0, и заметим, что множество f~l (@, 1]) содержи-
содержится в X\F> т. е. fSji{F)cz {0}. Непрерывная функция f: Jf->/,
определенная формулой f (х) = 1 — min(l, /w(x)/a), удовлетворяет
условиям /(jco)=O и /(F)c:{l}. |
Три дальнейшие характеристики паракомпактов устанавли-
устанавливаются в следующей теореме.
5.1.10. Лемма. В каждое открытое Q-локально конечное покры-
покрытие Т произвольного топологического пространства X можно
вписать локально конечное покрытие (произвольными множе-
множествами).
оо
Доказательство. Пусть Т = (J Tt, где Тг— {Vs}s&s ™ ло~
кально конечное семейство открытых множеств и Sif\Sf = 0
при i ф \. Для каждого 50 е Si положим
U U Vs.
Семейство ^ = {Л5}5е5> где S= IJ Sit покрывает Х и вписано
в Т. Покажем, что $Ф локально конечно. Для произвольной точ-
точки х ^ X обозначим через k наименьшее натуральное число, та-
такое, что х е U Vs, и возьмем s0 ^ Sk> для которого х е VSa.
Ясно, что VSo — окрестность точки х, не пересекающаяся с теми
ASy для которых 5 e U Sj. Так как семейства Ti локально ко-
>
нечны, для каждого i ^ k найдется окрестность Ui точки х, пе-
пересекающаяся лишь с конечным числом членов семейства У°*.
Окрестность f/i П U2 П • • • П ^ft П Vs, точки х пересекается толь-
только с конечным числом элементов семейства зФ. I
5.1.11. Теорема. Для каждого регулярного пространства X сле-
следующие условия равносильны:
(i) Пространство X паракомпактно.
(и) В каждое открытое покрытие пространства X можно
вписать открытое о-локально конечное покрытие.
(iii) В каждое открытое покрытие пространства X можно
вписать локально конечное покрытие (произвольными множе-
множествами).
(iv) В каждое открытое покрытие пространства X можно
вписать замкнутое локально конечное покрытие.
5.1. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА 449
Доказательство. Эта теорема вытекает из 5.1.10, 5.1.6 и
4.4.12. I
Из последней теоремы немедленно следует, что каждое лин-
делёфово пространство паракомпактно. Следует отметить также,
что в (ii) нельзя заменить второе слово «открытое» на слово
«замкнутое» (см. задачу 5.5.3(а)).
Мы введем теперь несколько понятий, связанных с понятием
покрытия, с помощью которых будут установлены дальнейшие
характеристики паракомпактности. Пустьзф = {i4e}eeS — произ-
произвольное покрытие множества X. Звезда множества М czX отно-
относительно $!> есть множество St {М, si-) = U {As: М Л As Ф 0}.
Звезда одноточечного множества {х} относительно покрытия ^Ф
называется звездой точки х относительно $Ф и обозначается че-
через St(x, «$?). Мы говорим, что покрытие $ = {Bt}t^T множества
X сильно звездно вписано в покрытие s4> = {^s}s^s того же мно-
множества X, если для каждого /еГ найдется s(t)^ S, такое, что
St {Bu 3$) с: AS(t). Если для каждого х^Х существует s(x)^S,
такое, что St(jc, 38) cz AS{X)9 то мы говорим, что 3S звездно впи-
вписано в j#. Ясно, что из сильной звездной вписанности следует
звездная вписанность, а из звездной вписанности вытекает впи-
вписанность.
Следующая теорема содержит еще три характеристики па-
ракомпактов. Она будет выведена прямо из лемм 5.1.13, 5.1.15
и 5.1.16, формулируемых и доказываемых ниже.
5.1.12. Теорема. Для каждого Тгпространства X следующие
условия равносильны:
(i) Пространство X — паракомпакт.
(ii) В каждое открытое покрытие пространства X можно
звездно вписать открытое покрытие.
(iii) В каждое открытое покрытие пространства X можно
сильно звездно вписать открытое покрытие.
(iv) Пространство X регулярно, и в каждое открытое покры-
покрытие пространства X можно вписать открытое ^-дискретное по-
покрытие.
5.1.13. Лемма. Если в открытое покрытие °U топологического
пространства X можно вписать замкнутое локально конечное по-
покрытие, то в °U можно звездно вписать открытое покрытие.
Доказательство* Пусть &* = {Ft}t е т — замкнутое локально
конечное покрытие, вписанное в (U = {Us}seS. Для каждого
/еГ выберем s(/)e S, такое, что Ft cz US(t)- Из локальной ко-
конечности семейства 8Г следует, что множество T(x) = {t ^Т:
х е Ft) конечно при каждом х ^ X, а отсюда вытекает, что мно-
29 Зак. 697
450 ГЛ. 5. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА
жество
B) V*sss
открыто при всех xgX. Так как х е Vx, семейство Т = {Vx}Xf=x
является открытым покрытием пространства X. Пусть х0— лю-
любая точка пространства X и to — некоторый элемент множества
Т(х0). Из B) следует, что если х0 е Vx, то to^T(x) и, значит,
VxaUS{u). Таким образом, St(x0, У°)<^и3(П) и Т звездно впи-
вписано в <U. §
5Л.14. Замечание. Если °U — локально конечное открытое по-
покрытие, то семейство всех множеств вида B) является локально
конечным покрытием, звездно вписанным в Щ.
5.1.15. Лемма. Если покрытие $$> — {As}$^s множества X звезд-
но вписано в покрытие $ = {Bt}t s т множества Ху a SS звездно
вписано в покрытие ^? = {Cz}zgbZ того же множества, то s? силь-
сильно звездно вписано в Ф.
Доказательство. Возьмем SoeS и для каждого хs A^ вы-
выберем /(х)еГ так, что
C) St(xtst)cBtW.
Имеем, таким образом,
D) stou, .*)= U st(x, а) с U
Пусть хо — произвольный элемент множества Лв0. Из C) сле-
следует, что хо е Вцх) при всех х е ASo, так что
U Bt(X)
A
Вместе с D) последнее включение показывает, что
St (As,,, si) с: St (jc0» Я) cr Сг при некотором 2eZ. I
5.1.16. Лемма. Если в каждое открытое покрытие пространства
X можно сильно звездно вписать открытое покрытие, то в ка-
каждое открытое покрытие этого пространства можно вписать
о-дискретное открытое покрытие.
Доказательство. Рассмотрим произвольное открытое покры-
покрытие <U = {Us}seBS пространства X. Положим <U0 = <U9 и пусть
Ши °U2, ... — какая-нибудь последовательность открытых по-
покрытий пространства X, такая, что
E) °Ui+\ сильно звездно вписано в Щ% при 4 = 0, 1, ... .
5.1. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА 451
Для каждого s e S и i = 1, 2, ... возьмем открытое множество
Us,i=z{x^X: х обладает окрестностью V, такой, что
St(V,<Ui)<=:Us}.
Семейство {?/s, J5eS вписано в Щ при i = 1, 2, ... и состоит из
открытых множеств. Заметим, что
если x^Us%i и y&USt м, то не существует ?/е^/+1,
' для которого jc, y^U.
Действительно, в силу E), для каждого U^°Ui+\ найдется
W е%, такое, что St(l/, %+i)cz W. Следовательно, если хе
е С/ПС/,,1, то IFcSt (*,<%)<= С/, и, значит, St<C/,<Wi+1)ci С/,
и С/en ?/5, ад.
Зафиксируем какое-нибудь вполне упорядочение < на мно-
множестве S и положим
G) V*.t = Usbt\ U С/а. Ж-
<
Для произвольной пары Si, 52 различных элементов множества
S либо si < 52 либо 5г < Si; в зависимости от того, какое из
этих двух соотношений выполняется, имеем в силу G):
либо VsbiczX\Uaiti+i, либо V8l,iCzX\Uabt+\'
Значит, из F) вытекает, что если х е VSlt i иуЕ VS2, i* где
si ф S2, то нет такого C/e<W/+i, чтобы было х, j/e(/. Следо-
Следовательно, семейство {Ve, JaeS открытых множеств дискретно
при i* = lf 2, ... .
Для завершения доказательства осталось показать, что се-
семейство {VSt j?,i ses покрывает X. Пусть х — любая точка из X.
Обозначим через s(x) наименьший элемент множества {s e S:
xeUs,i при каком-нибудь положительном целом i}\ существо-
существование s(x) следует из того, что при i = l, 2, ... семейство
{и* i}s<=s покрывает X. Так как х ф Us> г+2 яри 5 < s(x), из F)
вытекает, что
StU%+2)f] U С/,. ,+1 = 0,
<U)
а это показывает, что х (),
Доказательство теоремы 5.1.12. В силу последних трех лемм
и теоремы 5.1.11, достаточно показать, что каждое ^-простран-
^-пространство X, которое удовлетворяет условию (ш), регулярно. Рас-
Рассмотрим любые точку xgIh замкнутое множество F а X, для
которых х ф Ft и возьмем открытое покрытие 41, сильно звездно
вписанное в открытое покрытие {X\F, X\{x}} пространства
29*
452 ГЛ. 5. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА
X. Пусть U — любой элемент семейства °U, содержащий х. Так
как St([/, Ш)а X\Ft то О П F = 0, так что пространство X
регулярно. I
Понятие сильной звездной вписанности ведет к понятию нор-
нормального покрытия (см. упр. 5.4.Н(с) и (d)). Открытое покры-
покрытие Ж пространства X называется нормальным, если существует
такая последовательность Ж и *№% ... открытых покрытий про-
пространства X, что Ж\ =Ж и Wi+\ сильно звездно вписано в Wi
при i = l, 2, .... Из теоремы 5.1.12 следует, что среди ^-про-
^-пространств требование нормальности каждого открытого покрытия
характеризует паракомпакты. Теорема 1.5.18, леммы 5.1.13,
5.1.15 и замечание 5.1.14 показывают, что каждое локально ко-
конечное открытое покрытие нормального пространства нормально.
Оказывается, нормальные пространства характеризуются этим
свойством в классе ^-пространств (см. упр. 5Л.А(а)). Таким об-
образом, хотя в названии подчеркнута аналогия между параком-
паракомпактностью и компактностью, паракомпактность в соединении с
хаусдорфовостью может также рассматриваться как значитель-
значительное усиление нормальности.
Коллективная нормальность — другое усиление нормально-
нормальности, более слабое для хаусдорфовых пространств, чем параком-
паракомпактность. Топологическое пространство X называется коллек-
коллективно нормальным, если X есть ^-пространство и для каждого
дискретного семейства {/?5}5sS замкнутых множеств в X суще-
существует дискретное семейство {V5}5€sS открытых множеств в X,
такое, что Fs cz Vs при всех sgS. Ясно, что каждое коллектив-
коллективно нормальное пространство нормально.
5.1.17. Теорема. Ti-пространство Х коллективно нормально в
том и только том случае, если для каждого дискретного семей-
семейства {Fs}S€aS замкнутых множеств в X найдется семейство
{Us}seS открытых множеств в X, такое, что FsczUs при всех
s <=S и US()US'= 0 при s Ф s'.
Доказательство. Достаточно доказать, что каждое Трпро-
странство X, которое удовлетворяет условию теоремы, коллек-
коллективно нормально. Ясно, что X нормально. Поэтому для произ-
произвольного дискретного семейства |/7s}5eS замкнутых множеств
в X непересекающиеся замкнутые множества А = (J Fs и В =
= X \ U Us содержатся соответственно в непересекающихся
открытых множествах U и V. Легко проверяется, что семейство
0M5eS> r*e Va = VaflU, дискретно. |
Так как каждое локально конечное семейство непустых под-
подмножеств счетно компактного пространства конечно (см. тео-
5.1. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА 453
рему 3.10.3), из теоремы 2.1.14 вытекает, что каждое счетно
компактное нормальное пространство коллективно нормально.
5.1.18. Теорема. Каждый паракомпакт коллективно нормален.
Доказательство. Пусть {Fs}ssS —дискретное семейство зам-
замкнутых множеств в паракомпакте X. Для каждого х^Х возь-
возьмем окрестность Нх точки х, пересекающую самое большее одно
множество Fs, и, применив теорему 5.1.12, возьмем открытое по-
покрытие W = {Wt}t^T, сильно звездно вписанное в покрытие
{Hx}xgX. Осталось показать, что каждый член семейства Ж
пересекается самое большее с одним элементом семейства
{Vs}se5, где Vs = St(Fs,W). Однако для любого /еГ най-
найдется хеХ, такое, что St(Wt, Ж) а Нх; тогда если Wtf\Vs^ 0,
го Нх(\РвФ0. ¦
5.1.19. Замечание. Как легко проверить, для любого локально
конечного семейства (Fs}seS замкнутых множеств в параком-
паракомпакте конструкция из последнего доказательства дает локально
конечное семейство {V5}seS открытых множеств, такое, что
Fs с: Vs при всех seS (см. задачи 5.5.17 и 5.5.18).
Как показано в теореме 4.1.17, компактность и счетная ком-
компактность в классе метризуемых пространств равносильны. По-
Покажем теперь, что то же самое верно и в более широком классе
паракомпактных пространств (см. теорему 5.3.2).
5.1.20. Теорема. Каждое счетно компактное паракомпактное
пространство компактно.
Доказательство. Пусть $Ф — произвольное открытое покры-
покрытие счетно компактного паракомпактного пространства X. Из
теоремы 3.10.3 следует, что каждое локально конечное открытое
покрытие $, вписанное в «5#, конечно. Значит, пространство X
компактно. I.
Обсудим теперь некоторые примеры.
5Л.21. Пример. Из последней теоремы и примера 3.10.16 сле-
следует, что пространство Wo всех счетных ординалов не параком-
пактно. Так как WQ счетно компактно и нормально, оно кол-
коллективно нормально. I
Конструкция нормального не коллективно нормального про-
пространства намного труднее. Мы предпошлем ей вспомогатель-
вспомогательный пример, в котором обсуждается одна простая операция над
топологическими пространствами, оказавшаяся полезной при
построении контрпримеров.
5.1.22. Пример. Пусть М — любое подпространство топологиче-
топологического пространства X. Легко проверить, что семейство всех мно-
454 ГЛ. 5. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА
жеств вида U\j К, где U — открытое множество в X и К
составляет некоторую топологию на X. Множество X с этой но-
новой топологией будет обозначаться через Хм. Таким образом,
пространства X и Хм имеют одно и то же множество точек, но
различные, вообще говоря, топологии: топология пространства
Хм тоньше (т. е. сильнее) топологии пространства X Множество
Х\М и все его подмножества открыты в Хм, так что Х\М
является открытым дискретным подпространством пространства
Хм- Подпространство МаХм замкнуто, и его топология совпа-
совпадает с топологией, порожденной на М топологией простран-
пространства X
Некоторые свойства пространства X разделяет с ним и про-
пространство Хм: например, как легко видеть, если X есть ^-про-
^-пространство, где i—0, 1 или 2, то Хм тоже ^-пространство. Чи-
Читатель может легко проверить, что то же самое верно при i = 3
и 37г. С другой стороны, пространство Хм не обязано быть нор-
нормальным, если X — нормальное пространство или даже компакт
(см. упр. 5.1.D).
Покажем теперь, что Хм нормально, если X есть ^-простран-
^-пространство и для каждой пары непересекающихся замкнутых мно-
множеств Ль Si подпространства MczX существуют открытые в
пространстве X множества U и V, такие, что
(8) AiczU, BiczV и U(\V = 0.
В частности, Хм нормально, если X нормально и М замкнуто
в X. Как нам уже известно, Хм является ^-пространством.
Пусть Д В — два любых непересекающихся замкнутых множе-
множества в Хм- Множества Ах = Af\M n Bi — Bf\M замкнуты в под-
подпространстве MczX я не пересекаются. Значит, найдутся от-
открытые множества С/, V а X, удовлетворяющие условию (8).
Легко видеть, что множества
(U\B)(J(A\M) и (V\i4)U(B\Af)
открыты в Хм, не пересекаются и содержат множества А и В
соответственно. Значит, пространство Хм нормально.
Покажем также, имея в виду применить это в дальнейшем,
что если пространство X наследственно паракомпактно (т. е.
каждое подпространство пространства X паракомпактно — что
выполняется, например, для любого метризуемого пространства
X), то пространство Хм тоже наследственно паракомпактно. Так
как каждое подпространство пространства Хм имеет вид Хгт
где X' czX и M' — Mf\X'9 достаточно проверить, что Хм пара-
компактно. Каждое открытое покрытие пространства Хм имеет
вид {Us U Ks}s е s, где Us открыто в X и Ks cz X \ М.
5.1. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА 455
В открытое покрытие {Us}s^s пространства U — [} Uscz
X можно вписать локально конечное открытое покрытие
JT- Как легко проверить, присоединив к этому последнему
семейству множеств все одноточечные подмножества множества
X\U, мы получаем локально конечное открытое покрытие про-
пространства Хм, вписанное в покрытие {US\JKS}S€B$-
Дальнейшие свойства операции Хм, определенной в этом
примере, можно найти в задаче 5.5.2. I
Опишем теперь нормальное пространство, которое не коллек-
коллективно нормально.
5Л.23. Пример (Бинг). Обозначим через У семейство всех ото-
отображений дискретного пространства Ь(с) мощности с в двухто-
двухточечное дискретное пространство D == {0,1}. Ясно, что |#"| = 2С.
По теореме 2.3.20, диагональное отображение F = Д /:Z)(c)->
D?c = Ц Df, где Df = D при всех f e #", является гомео-
морфным вложением. Для каждой пары непересекающихся зам-
замкнутых подмножеств Аи Вг подпространства М — F(D(t)) czZJ
множества
?/ = />?(!) и V = pft@),
где А = F~l (A\) и fA^&~ определено правилом:
fA(x)= 1, если хеЛ, и /л(^) = 0, если x&D(t)\A, удовлетво-
удовлетворяют соотношениям (8). Значит, в силу примера 5.1.22, простран-
пространство X = Dj^ нормально.
Остается показать, что пространство X не коллективно нор-
нально. Предположим, что X коллективно нормально. Так как
М cz X дискретно и Х\А1 открыто, семейство {{х}}хеМ одно-
одноточечных подмножеств пространства X дискретно. Значит, су-
существует семейство {^jJjcesM попаРно непересекающихся откры-
открытых подмножеств пространства X, таких, что x&Vx при всех
х f= 7W. Так как Vx = Ux U Кх, где Ux открыто в D2C иКх^ D2C\
\Mf имеем x^Ux- Следовательно, Wx}x^M — семейство
мощности с попарно непересекающихся непустых открытых мно-
множеств bZJ0, а это противоречит теореме 2.3.18.
Как показано в примере 3.6.20, замыкание множества М в
D2' является стоун-чеховской компактификацией пространства
D(c). Как легко проверить, нормальное не коллективно нормаль-
нормальное пространство можно точно так же получить, взяв произволь-
произвольное гомеоморфное вложение h пространства D(t) в D2C или в 12\
для которого A(D(c)= pD(c), вместо специального вложения F,
456 ГЛ. 5. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА
использованного выше (см. теоремы 3.6.11, 3.6.13 и 6.2.16 или
3.6.11 и 2.3.23). I
В следующих двух теоремах описываются соотношения ме-
между паракомпактностью и свойством Линделёфа.
5.1.24. Лемма. Каждое локально конечное семейство непустых
подмножеств линделёфова пространства счетно.
Доказательство. Пусть s4> — любое локально конечное семей-
семейство непустых подмножеств линделёфова пространства X Для
каждого х е X выберем окрестность Ux точки х, пересекающую-
пересекающуюся лишь с конечным числом элементов семейства j#, и возьмем
счетное подпокрытие °U покрытия {Ux}xeX пространства X. Так
как каждый элемент семейства зФ пересекает некоторое U^.°Uy
заключаем, что |*я?|^ Ко. ¦
5.1.2.5. Теорема. Если паракомпакт X содержит всюду плотное
подпространство Л, обладающее свойством Линделёфа, то X —
линделёфово пространство.
Доказательство. Пусть °U = {[/s}seS — произвольное открытое
покрытие пространства X. В силу замечания 5.1.7, найдется ло-
локально конечное открытое покрытие {^Jse=s пространства X,
такое, что V$ cz Us при всех s e S. По предшествующей лемме,
существует счетное множество So с: S, такое, что А = (J А Л Vs>
а отсюда следует, что
= А= U A{]V8= U AnV$a [} Vscz [} Us.
s e So seSo $e5o S
Значит, в °U есть счетное подпокрытие. I
5.1.26. Следствие. Каждый сепарабельный паракомпакт являет-
является линделёфовым пространством1). I
х) Следующий результат заметно сильнее утверждения 5.1.26:
Теорема А. Если число Суслика паракомпакта X счетно, то X является
линделёфовым пространством.
Пусть Rx — пространство непрерывных вещественных функций на X в
топологии поточечной сходимости. Число Суслина пространства Rx счетно,
так как оно всюду плотно в топологической степени прямой. Значит, из тео-
теоремы А вытекает
Следствие. Для пространства Rx в топологии поточечной сходимости
паракомпактность и свойство Линделёфа равносильны.
Пространство X называется слабо финально компактным, если из каж-
каждого его открытого покрытия можно выделить счетное семейство множеств,
объединение которого всюду плотно в X. К числу слабо финально компакт-
компактных пространств относятся все пространства со счетным числом Суслина
все пространства, обладающие всюду плотным линделёфовым подпростран-
подпространством. Имеет место более общая, чем теорема А,
Теорема Б. Паракомпактное слабо финально компактное пространство
5.1. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА 457
5.1.27. Теорема. Каждый локально компактный паракомпакт X
можно представить в виде объединения некоторого семейства
попарно не пересекающихся открыто-замкнутых подпространств
пространства X, каждое из которых обладает свойством Линде-
лёфа.
Доказательство. Для каждого х^Х выберем окрестность Ux
точки х, такую, что Пх компактно, и возьмем какое-нибудь ло-
локально конечное открытое покрытие Т, вписанное в покрытие
{их}х^х пространства X. Для каждого V^Т я любого хе V
существует окрестность Wx точки ху пересекающаяся лишь с ко-
конечным числом членов покрытия Т. Так как V сг V с: (J Wx
и V компактно, множество V содержится в объединении конеч-
конечного числа множеств Wx. Значит, каждое VgF пересекает
лишь конечное число членов семейства Т. Для произвольного
Vo^T пусть 9*k(Vo)czT состоит из всех тех FeF, для ко-
которых существует конечная последовательность Vu • • • > V& эле-
элементов семейства Т, такая, что Vk = V и У* fl V^+i ф 0 при
оо
? = 0, 1, ..., k— 1. Положим далее ^(Vo)= U &k(Vo) и
fei
S(V0)= U^(Vo). Как легко видеть, все семейства &k{Vo) ко-
конечны, откуда вытекает, что |^(Vo)|^^o. При VQ, V'0^T
множества S(V0) и S(y'Q) либо совпадают, либо не пересе-
пересекаются, поэтому все множества S(Vo) открыто-замкнуты. Из
равенства S(Vo)= S(Vo) следует, что S(V0)= [}{V: 7g^(V0)}.
Значит, все подпространства S(Vo) обладают свойством Линде-
лёфа как счетные объединения компактов. I
Обсудим теперь операции над паракомпактами. Начнем с
двух теорем.
5.1.2.8. Теорема. Подпространство типа Fo паракомпакта яв-
является паракомпактом.
Доказательство. Пусть М — подпространство паракомпакта X
оо
и М= [} Fiy где все Ft замкнуты в X. Рассмотрим произвольное
открытое покрытие {Us}se.s пространства М и возьмем семей-
семейство {7s}seS открытых множеств в X, такое, что Us=M[)Vs
при всех s<~S. При каждом / = 1, 2, ... семейство {P%}Se$U
(J {X \ Fi} является открытым покрытием пространства X; сле-
финально компактно. В частности, слабо финально компактный паракомпакт
является линделёфовым пространством.
Теорема Б вытекает из следующей очевидной леммы:
Лемма. В слабо финально компактном пространстве каждое локально
конечное семейство открытых множеств счетно. — Прим. перев.
458 ГЛ. 5. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА
довательно, в него вписано некоторое локально конечное откры-
открытое покрытие sti. Положим
оо
Ясно, что^= U ^ — открытое а-локально конечное покрытие
пространства М, вписанное в {Us}sgS. Следовательно, простран-
пространство М паракомпактно в силу теоремы 5.1.11. I
Из последней теоремы вытекает следующий результат, кото-
который можно вывести и прямо из определения паракомпактности.
5.1.29. Следствие. Каждое замкнутое подпространство параком-
пакта является паракомпактом. I
5.1.30. Теорема. Сумма ф Х$ является паракомпактом в том
и только том случае, если все Xs — паракомпакты.
Доказательство. Если сумма ф Jfs— паракомпакт, то и все
seS
Xs — паракомпакты в силу последнего следствия.
Обратно, если все Xs являются паракомпактами и Т =
= {У*Ьег произвольное открытое покрытие суммы ф XSJ то се-
мейство [J s?s, где s?s — локально конечное открытое по-
крытие, вписанное в открытое покрытие {Xs Л Vt}t e г подпро-
подпространства Xs, является открытым локально конечным покрытием
суммы ф Х8, вписанным в Т. I
stsS
Как показано в следующем ниже примере, паракомпактность
не мультипликативна.
5.1.31. Пример. Из примера 3.8.14 и теоремы 5.1.2 следует, что
прямая Зоргенфрея К является паракомпактом. Так как произ-
произведение /СХ^С не нормально (см. пример 2.3.12), на основании
теоремы 5.1.5 мы заключаем, что произведение двух параком-
пактов не обязательно является паракомпактом (см. задачи
5.5.5 и 5.5.6). I
Покажем теперь, что паракомпактом может не быть даже
произведение паракомпакта и сепарабельного метризуемого про-
пространства. С другой стороны, произведение паракомпакта и
компакта всегда является паракомпактом (см. теорему 5* 1.36)*
5.1.32. Пример (Майкл). Через Q и Р обозначим подпростран-
подпространства пространства R, состоящие из рациональных и иррацио-
иррациональных чисел соответственно. В силу примера 5.1.22, простран-
пространство X = Rq наследственно паракомпактно. Покажем, что про-
произведение XX У, где У = Р, не нормально.
5.1. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА 459
Рассмотрим непересекающиеся замкнутые множества Л, В
в XX Y, определенные следующим образом:
):уеР) и B =
Достаточно показать, что, каково бы ни было открытое множе-
множество t/cIXl", содержащее Л, всегда В(]Пф0. Пусть
{piy Р2, ..•}—какое-нибудь счетное множество, всюду плотное
в Р. Так как A cz Ut то для каждого у е Р найдутся окрест-
окрестность Uy czP точки у у такая, что
(9) {y}XUya:U,
и натуральное число i{y)9 удовлетворяющие условию
(Ю) Pt(v)<=Uy.
Положим Pi—{y^P: i(y)=i) при f=l, 2, ... . Из теоремы
Бэра о категории сразу следует, что Р не является Ра-множе-
Ра-множеством в R (см. упр. 3.9.В). Значит, найдутся натуральное число
lo и qo e Q, для которых q0 e Р*о, где черта обозначает замы-
замыкание в /?; очевидно, (#0> Ph)^B. Пусть FX ^ — произвольная
окрестность точки (<7о> PiQ) в произведении XX Y = /?q X Р- Так
как <7о е Pt-0, то У Л РьФ0> т. е. существует #е V П Ри- Но / (у)=
=/0. Поэтому, в силу A0), piQ^Uff, а отсюда и из (9) следует, что
(у, pio)^U. Очевидно, {у> pt0)^ FX W. Значит, каждая окрест-
окрестность точки (доу рь) е В пересекает множество С/, т. е. В Л 1?Ф0.
Заметим, что в проведенном выше доказательстве мы вос-
воспользовались только тремя свойствами множеств Р и Q, а имен-
именно тем, что Р и Q — взаимно дополнительные подмножества то-
топологического пространства, Р — не типа Fa и сепарабельно. I
Приступим теперь к обсуждению вопроса об инвариантности
паракомпактности при отображениях. Для начала заметим, что
паракомпактность не является инвариантом непрерывных ото-
отображений; действительно, каждое топологическое пространство
является непрерывным образом дискретного — следовательно,
паракомпактного — пространства. Пример 4.1.10 или примеры
4.4.11 и 5.1.21 показывают, что паракомпактность не является
инвариантом и открытых отображений. С другой стороны, имеет
место
5Л.33. Теорема Майкла. Образ паракомпакта при замкнутом
отображении является паракомпактом.
Доказательство. Пусть /: Х-> Y — замкнутое отображение
паракомпакта X на топологическое пространство У. Из теорем
1.5.20 и 5.1.5 следует, что пространство Y нормально. Значит,
в силу теоремы 5.1.11, достаточно доказать, что в каждое от-
открытое покрытие {US}SGS пространства У можно вписать от-
открытое а-дискретное покрытие.
460 ГЛ. 5. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА
Пусть < —какое-нибудь вполне упорядочение на множестве
S. Определим по индукции при i = 1, 2, ... замкнутое локально
конечное покрытие &~i = {Fs, *}5eS пространства X, удовлетво-
удовлетворяющее условиям
A1) Fsti<=f-l(Us) при sgS и * = 1, 2, ...,
A2) f(Fs,i){)f(Es,i-l)=0, где Es. t-x= U Pt.t-i при />1.
t <s
Существование $Г\ следует из леммы 5.1.6. Предположим,
что покрытия &~и &~2, .. •, &~k-\ уже определены и удовлетво-
удовлетворяют условиям A1) и A2) при i < k. Так как покрытие ^-i
локально конечно, а отображение / замкнуто, множества
A3) Ws, к = f-HUs)\f-4(Es, ft-Ocz f-HUs)
открыты. Для каждого jcg! обозначим через s(x) наимень-
наименьший элемент множества S, для которого xg f~l (US(X))- Так
как ?,uu-ic U Г1(и8) в силу A1), то rlf(ES(x)t*-i)c:
S<()
<= U / l(^s)- Значит, хе= 1Г5(*),й, т. е. {lFs>u}se5—открытое
s<s(x)
покрытие пространства X. Применив лемму 5.1.6, получаем ло-
локально конечное замкнутое покрытие ^ = {^5, k}s^s простран-
пространства X, такое, что Fs, н с: Ws, % при всех s e 5. Из A3) следует,
что покрытие Ук удовлетворяет условиям A1) и A2) при i = k.
Таким образом, построение покрытий &*% завершено.
Рассмотрим открытые множества VSt t = Y\f ( \] Ftii\. Так
как семейство {/ (FSt d}SGS покрывает У, имеем Vs, i cz f{Fs, i),
откуда следует, что
A4) Vsti[\Vt,i = 0 при s*?L
Покажем, что семейство У = {К5, t}T=u se~s покрывает про-
пространство У. Для каждого у е Y обозначим через s{y) наимень-
наименьший элемент множества S, такой, что у е f(FS(y), /) при некото-
некотором целом положительном i, и возьмем какое-нибудь целое i{y)>
для которого y^f(FS(y),i(y)-i). Значит, у е f(Es,i(y)-\) при всех
s>s(y) и, в силу A2), y&f(F8,ny)) при s>s(y). С другой
стороны, y&f(Fs,i(y))t когда s<s(y), так что yG^j,^.
Следовательно, Т покрывает У. Из Vs,i c= f (Fs, i) и A1) выте-
вытекает, что Т вписано в {?/s}Se=s-
Применив еще раз лемму 5.1.6, возьмем замкнутое покры-
покрытие {Ki}T=i пространства X, такое, что KiCzf~l(Vt)9 где Vi =
=: U V8, t при i = l, 2, ... . Пространство У нормально, no-
noses
5.1. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА 461
этому существуют открытые множества Wt c= У, для которых
A5) f(Ki)cWiczWiczVi при i = l, 2, ....
Применив A4) и последнее включение в A5), мы сразу обна-
обнаруживаем, что при фиксированном i семейство {VSt t(] Wi}SGS
дискретно. Из первого включения в A5) вытекает, что семей-
семейство {Vs, *f|W*}JLi. ess покрывает У. Ясно, что это открытое
а-дискретное покрытие, вписанное в {US}S(-S. "
В связи с теоремой Майкла отметим, что есть характеристи-
характеристики паракомпактов, из которых сразу следует сохранение пара-
паракомпактности при замкнутых отображениях хаусдорфовых про-
пространств; некоторая такая характеристика неявно используется
в приведенном выше доказательстве (см. упр. 5.1 .G). Заметим,
что важный частный случай теоремы Майкла: образ параком-
паракомпакта при совершенном отображении является паракомпак-
том, — можно установить гораздо проще (см. лемму 4.4.13 и
замечание 4.4.14).
Из последнего утверждения и теорем 5.1.30 и 3.7.22 получаем
следующий результат:
5.1.34. Теорема. Если топологическое пространство X обладает
локально конечным замкнутым покрытием из паракомпактов,
то X само паракомпакт. I
Последнюю теорему можно вывести также из эквивалентно-
эквивалентности условий (i) и (iv) в теореме 5.1.11.
5.1.35. Теорема. Прообраз паракомпакта при совершенном ото-
отображении является паракомпактом.
Доказательство. Пусть f: X-+Y — совершенное отображение
на паракомпакт У. Рассмотрим открытое покрытие {t/5}seS про-
пространства X и для каждого у е У выберем конечное множество
S(y)cS, такое, что f~~l(y)cz M Us. Воспользовавшись тео-
ремой 1.4.13, возьмем окрестность Vy точки у, такую, что
Г1(у)сГ1(У9)с U U
S()
,.
В открытое покрытие {V9} Y пространства У вписано некото-
некоторое локально конечное открытое покрытие {Wt}t&T. Семейство
{f~l(Wf)}t&Tявляется открытым покрытием пространства X, и
для каждого (бГ найдется yte У, такое, что
rl(Wt)czrl(Vyt)cz U U
462 гл* 5- ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА
Легко проверяется, что семейство {f~l(Wt)[}Us: t eT и sg
ES(//f)} является открытым локально конечным покрытием,
вписанным в {Us}seS. I
Из теорем 3.7.1 и 5.1.35 следует
5.1.36. Теорема. Произведение XX Y паракомпакта X и ком-
компакта Y является паракомпактом. I
Из теоремы 5.1.35 и теоремы Майкла вытекает
5.1.37. Теорема. Класс паракомпактов совершенен. I
В заключение этого параграфа приведем интересную внеш-
внешнюю характеристику паракомпактов:
5.1.38. Теорема Тамано. Для каждого тихоновского пространства
X следующие условия равносильны:
(i) Пространство X паракомпактно.
(ii) Для каждой компактификации сХ пространства X про-
произведение XX сХ нормально,
(iii) Произведение X X $Х нормально.
(iv) Существует компактификация сХ пространства X, та-
такая, что произведение XX сХ нормально.
Доказательство. Импликация (i)=^(ii) следует из теоремы
5.1.36. Очевидно, (ii)=^(iii) и (iii)=>-(iv); остается показать, что
(i)(i)
)()
Пусть {f/5}S6S- произвольное открытое покрытие простран-
пространства X. Для каждого sgS возьмем открытое множество Vs <= сХ,
такое, что Us = X f| W Так как дополнение Z = сХ\ \J Vs яв-
ляется компактным подмножеством нароста сХ\Х, диагональ
АсХу^Х и произведение XX Z — непересекающиеся замкну-
замкнутые подмножества пространства Ху^сХ. Следовательно, в силу
(iv), найдется непрерывная функция /: ХУ(сХ-+1, для которой
/(Д)с={0} и f(XXZ)cz{l}.
Положив
р(х, У)= SUp\f(x, z) — f(y, 2I,
X
cX
получаем некоторую псевдометрику р на множестве X. Тополо-
Топология О и порожденная псевдометрикой р, содержится в исходной
топологии 02. Действительно, для каждого х0 е X и любого
е >0 найдутся открытые множества G\ X #ь 62X^2, ...
..., GkXHkdXXcX, такие, что xQe=Gi и 6(/(G/X#/))<e
k
при /= 1, 2, ..., k, и {х0} X сХ a U (Gt X Ht). Значит, хв<=
k
е П GiCiB(xQt 8) = {ш1: р(х0, х) < г), откуда следует, что
5.1. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА 463
все открытые шары по отношению к р принадлежат О%, т. е. О\ с=
cz<72.
Из замечания 4.4.2 следует, что в покрытие {В (х, 1/Щх<=х мно~
жества X вписано некоторое покрытие {Wt}t(-Tj открытое и ло-
локально конечное по отношению к топологии Си а значит, и по
отношению к топологии 0г- При всех хе! и (/ей(х,1/2)
имеем f(x,у) = \f{x,y)—f(y,y)\^p(xf у) < 1/2; следовательно,
f(x9y)^l/2t если //gB(jc,1/2), где черта обозначает замыка-
замыкание в сХ. Так как f(x, z) = 1 при 2 е Z, то Wt{\Z = 0 для всех
/бГ. Множество Wt компактно, значит, существует конечное
множество S(t)aS, такое, что W*cz U Us. Как легко npO-
верить, семейство {Wtf[Us: (еГ, s^S(t)} является локально
конечным открытым покрытием пространства Ху вписанным в
Из теоремы 5.1.36 и 5.1.38 вытекает
5.1.39. Теорема. Топологическое пространство X в том и только
том случае является паракомпактом, если произведение IX ^
нормально для каждого компакта Y. Ш
5.1.40. Пример. Из теоремы Тамано следует, что произведение
Wo X W пространства Wo всех счетных ординалов и простран-
пространства W всех ординалов ^.щ не нормально (это можно доказать
и прямо — см. задачу 3.12.19 (Ь)). В самом деле, W — компакти-
фикация пространства Wo, и в примере 5.1.21 было показано,
что пространство Wo не паракомпактно. Значит, в пространстве
Wo X W существуют замкнутые непересекающиеся множества А
и 5, которые нельзя отделить непересекающимися открытыми
множествами. Легко проверить, имея в виду, что пространство
FoX li^ счетно компактно (см. 3.10.14), что полученное отож-
отождествлением в точку множества А факторпространство (IFOX
y^W)/A (см. пример 2.4.12) является счетно компактным (даже
секвенциально компактным) не регулярным хаусдорфовым про-
пространством (см. упр. 3.10.В).
На примере проекции пространства WQ X W на Wo видно, что
нормальность может не сохраняться в сторону прообраза от-
открытыми совершенными отображениями. 1
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
Понятие паракомпактности было введено Дьедонне в [1944];
в этой же работе содержатся теоремы 5.1.5 и 5Л .36, а также
следствие 5.1.29. Как отмечено выше, теорема 5.1.2 была уста-
установлена Моритой в [1948], а теорема5.1.3 — А. Стоуном в [1948]
(паракомпактность метризуемых пространств со счетной базой
и локально компактных метризуемых пространств была установ-
464 гл- 5- ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА
лена Дьедонне в [1944]). Теоремы 5.1.9 и 5.1.11, как и равно-
равносильность условий (i) и (iv) в теореме 5Л.12, были доказаны
Майклом в [1953]. Приведенное простое доказательство леммы
5.1.8 принадлежит Мазеру [1964]. Равносильность условий (i)
и (ш) в теореме 5.1.12 была установлена А. Стоуном в [1948].
Тьюки ввел в [1940] класс звездно нормальных пространств как
пространств, удовлетворяющих условию (ш) теоремы 5.1.12. Он
доказал, что каждое метризуемое пространство звездно нор-
нормально (см. упр. 5.1.А(с)), установил эквивалентность условий
(и) и (ш) в теореме 5.1.12 и ввел понятие нормального покры-
покрытия. Класс коллективно нормальных пространств был определен
Бингом в [1951] (посредством условия, фигурирующего у нас
в теореме 5.1.17; то, что это условие эквивалентно данному нами
определению, было доказано Даукером в [1952а]). Работа
Бинга содержит также теорему 5.1.18 и пример 5.1.23; сейчас не
известны примеры нормальных не коллективно нормальных про-
пространств, отличные от этого примера Бинга и его модификаций
(см. задачу 5.5.3). Модификация топологий, описанная в при-
примере 5.1.22, была предложена Бингом в [1951] и Ханнером в
[1951]. Она была вновь применена Майклом в [1963], где при-
приведен пример 5.1.32 (дальнейшие сведения можно найти в зада-
задачах 5.5.2 и 5.5.4). Примеры 5.1.31 (принадлежащий Зоргенфрею
[1947]) и 5.1.32 наводят на вопрос, следует ли из нормальности
произведения двух паракомпактных пространств, что это произ-
произведение паракомпактно. Как показано Пшимусинским в [1980],
ответ отрицателен. С другой стороны, М. Рудин и Страбёрд до-
доказали в [1975], что если произведение метрического простран-
пространства и паракомпакта нормально, то оно паракомпактно (см. за-
задачу 5.5,19(d)). Теорема 5.1.25 была замечена Уиллардом в
[1971]. Как легко показать, каждый паракомпакт со свойством
Суслина (см. задачу 1.7.12) тоже является линделёфовым про-
пространством. Цитированная выше работа Мориты [1948] содер-
содержит также теорему 5.1.27. Теоремы 5.1.28 и 5.1.34 были дока-
доказаны Майклом в [1953], а теорема 5.1.33 доказана им же в
[1957] (для совершенных отображений ее доказали Морита и
Ханаи в [1956]). Теорема 5.1.35 была в принципе доказана Ха-
наи в [1956]. Равносильность условий (i) и (ш) в теореме 5.1.38
и теорема 5.1.39 доказаны Тамано в [1960а]. Равносильность
условий (i) и (iv) в теореме 5.1.38 была получена независимо
Корсоном в [1962], Моритой в [1962] и Тамано в [1962].
УПРАЖНЕНИЯ
5.1.А. (а) Заметьте, что если в каждое двухэлементное от-
открытое покрытие ^-пространства X можно сильно звездно впи-
вписать открытое покрытие, то пространство X нормально.
5.1. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА 465
(b) Покажите непосредственно, что в каждое конечное от-
открытое покрытие нормального пространства можно сильно звезд-
звездно вписать конечное открытое покрытие.
Указание. Рассмотрите сначала случай двухэлементного по-
покрытия.
(c) (Тьюки [1940]). Покажите непосредственно, что в каж-
каждое открытое покрытие метризуемого пространства можно силь-
сильно звездно вписать открытое покрытие.
Указание. Пусть Щ — произвольное открытое покрытие мет-
метризуемого пространства X. Рассмотрите метрику на простран-
пространстве X и для каждого х^Х возьмите гх > 0, такое, что шар
B(xf Агх) содержится в некотором элементе семейства °U. Про-
Проверьте, что покрытие {В (х, gx)}xgX звездно вписано в °U.
(d) Заметьте, что пространство X компактно в том и только
том случае, если каждое открытое покрытие пространства X со-
содержит локально конечное подпокрытие.
(e) Заметьте, что регулярное пространство X обладает свой-
свойством Линделёфа в том и только том случае, если каждое от-
открытое покрытие пространства X содержит а-локально конечное
(или, что равносильно, о-дискретное) подпокрытие.
5.1.В (Архангельский [1965]). (а) Покажите, что регулярное
^-пространство X паракомпактно в том и только том случае, если
в каждое открытое покрытие °U пространства X можно вписать
замкнутое покрытие дГ, такое, что каждый компакт, лежащий
в Ху пересекается лишь с конечным числом членов семейства #~.
(Ь) Покажите, что нормальное ^-пространство X параком-
паракомпактно в том и только том случае, если в каждое открытое по-
покрытие Ш пространства X можно вписать открытое покрытие Y,
такое, что каждый компакт, лежащий в X, пересекается лишь
с конечным числом членов семейства Т.
5.1.С. (а) Проверьте, что коллективная нормальность насле-
наследуется замкнутыми подмножествами (см. задачу 5.5.1 (Ь)) и яв-
является аддитивным свойством.
(b) Покажите, что коллективная нормальность сохраняется
замкнутыми отображениями, но не сохраняется открытыми ото-
отображениями (см. упр. 4.2.D).
(c) Заметьте, что коллективная нормальность не сохраняется
в сторону прообраза совершенными отображениями.
(d) Приведите пример обратной последовательности пара-
компактов, предел которой не нормален (см. задачу 5.5.4(с)).
Указание. Воспользуйтесь примером 5.1.32.
5.1.D. Приведите пример компакта X и его подпространства
М cz X, таких, что пространство Хм, определенное в примере
5.1.22, не нормально.
Указание. Рассмотрите пространство ^Х^ из примера
2.3.36 или любой другой не наследственно нормальный компакт.
30 Зак. 697
466 ГЛ. 5. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА
5.1.Е. Заметьте, что у каждой точки пространства X из при-
примера 5.1.23 есть паракомпактная открыто-замкнутая окрест-
окрестность.
5.1.F. (а) (Дьедонне [1944]). Заметьте, что X наследственно
паракомпактно в том и только том случае, если все открытые
подпространства пространства X паракомпактны.
(b) (Даукер [1947а]). Каждое совершенно нормальное па-
ракомпактное пространство наследственно паракомпактно.
(c) Покажите, что каждое сепарабельное наследственно па-
ракомпактное хаусдорфово пространство является наследственно
линделёфовым пространством и, значит, совершенно нормально
(см. упр. 3.8.А (Ь)). Приведите пример наследственно параком-
пактного хаусдорфова пространства, которое не совершенно нор-
нормально.
5.1.G (Майкл [1957]). Семейство {^s}5e=s подмножеств топо-
топологического пространства называется консервативным, если
U ^5= U ^5 Для каждого S0<^S.
5SSo 5 €= So
Докажите, что для произвольного регулярного пространства
X следующие условия равносильны:
A) Пространство X паракомпактно.
B) В каждое открытое покрытие пространства X можно впи-
вписать открытое консервативное покрытие.
C) В каждое открытое покрытие пространства X можно впи-
вписать консервативное покрытие (состоящее из произвольных мно-
множеств).
D) В каждое открытое покрытие пространства X можно впи-
вписать замкнутое консервативное покрытие.
Указание. При доказательстве импликации D)=^A) за-
заметьте сначала, что для каждого открытого покрытия {#s}5€=s
пространства X существует замкнутое консервативное покрытие
{F8}8es* такое, что Fs с: Us при всех s e S. Заметьте затем, что
X нормально, и рассуждайте далее по аналогии с доказатель-
доказательством теоремы 5.1.33, где У = X и / = id*.
5.1. Н. Докажите, что если пространство X метризуемо, а про-
пространство Rx с компактно-открытой топологией удовлетворяет
первой аксиоме счетности, то X локально компактно и обладает
счетной базой; заметьте, что и Rx при этом имеет счетную базу
(см. теорему 3.4.16).
Указание. Сначала с помощью упр. 3.4.Е покажите, что X ло-
локально компактно. Затем воспользуйтесь 5.1.27, 3.4.4 и 2.3.F(b).
5.1.1. (Нагата [1950]). Покажите, что полное по Чеху пара-
компактное пространство X метризуемо в том и только том слу-
случае, если диагональ А является б6-множеством в произведении
XXX (см. упр. 4.2.В и задачу 5.5.9 (с)).
5.1. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА 467
Указание. Определите счетное семейство {Ti}^=[ локально
конечных открытых покрытий пространства Xt такое, что:
A) Если семейство s& подмножеств пространства X центри-
центрировано и содержит множества диаметра, меньшего чем Ти для
каждого 1 = 1,2, ..., то пересечение (]{А: Л е $?} не пусто.
B) Для каждых двух различных точек х, у пространства X
найдется натуральное число /, при котором замыкание никакого
элемента семейства Ti не содержит одновременно х и у.
Проверьте, что семейство всех конечных пересечений
V\ П V2 П • • • Л Vky где Vi e Tt при / = 1, 2, ..., ky является ба-
базой пространства X.
Можно взять также непрерывную функцию f: ХХ$Х-+1, для
которой А = f-! @), и положить р (д:, у) = sup | / (х, z) — f (y> г) |.
5.1.J (Тьюки [1940], А. Стоун [1948], Майкл [1953], Морита
[1964]).
(a) Покажите, что для каждого а-локально конечного по-
покрытия {Us}S€eS пространства X функционально открытыми мно-
множествами существуют псевдометрика р на X, такая, что отобра-
отображение р: ХХ^-^/? непрерывно, и покрытие {Fs}se5 множества
X, открытое относительно топологии на X, порожденной псевдо-
псевдометрикой р, для которого Vs с: Us при всех seS.
Указание. Рассмотрите непрерывные функции fs: Х->1, для
которых Us = f-l((O, 1]).
(b) Выведите из (а), что для каждого а-локально конечного
покрытия {?/*}$€= s пространства X функционально открытыми
множествами существуют непрерывное отображение f: X~>- Y на
метризуемое пространство Y и открытое покрытие {Ws}s^$ про-
пространства У, такие, что f-l(Ws)cz Us при всех s &S.
Указание. Примените упр. 4.2.1.
(c) Заметьте, что (а) и (Ь) выполняются для любого откры-
открытого покрытия {Us}sgS пространства X, обладающего подчинен-
подчиненным ему разбиением единицы (см. упр. 5.4.Н (с)).
(d) Заметьте, что (а) и (Ь) выполняются, если пространство
X нормально и открытое покрытие {Us}s^s либо локально ко-
конечно, либо точечно конечно и счетно (см. упр. 5.2.F (Ь)).
(e) Докажите, что ^-пространство X паракомпактно в том
и только том случае, если для каждого открытого покрытия
{Us}s^s пространства X найдутся непрерывное отображение
f: X—>-У на метризуемое пространство У и открытое покрытие
{fJseS пространства У, такие, что f-l(Ws)<= Us при всех
seS.
30*
468 ГЛ. 5. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА
(f) Выведите из (е), что каждый паракомпакт гомеоморфен
замкнутому подпространству произведения некоторого множе-
множества метризуемых пространств (см. задачу 8.5.13).
5.2. СЧЕТНО ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА
Топологическое пространство X называется счетно параком-
пактным, если в каждое его счетное открытое покрытие мож-
можно вписать локально конечное открытое покрытие. Ясно, что
каждое паракомпактное пространство счетно паракомпактно и
что таковы все счетно компактные пространства. Из последнего
замечания следует, что существуют коллективно нормальные
счетно паракомпактные пространства, не являющиеся параком-
пактами (см. пример 5.1.21), и что существуют счетно параком*
пактные хаусдорфовы не регулярные пространства (см. пример
5.1.40). Из теоремы 3.10.22 вытекает, что каждое псевдокомпакт-
псевдокомпактное счетно паракомпактное пространство счетно компактно. Зна-
Значит, пространство X из примера 3.10.29 является тихоновским не
счетно паракомпактным пространством (см. также упр. 5.2.С).
С другой стороны, найти нормальное пространство, которое не
счетно паракомпактно, было известной задачей общей тополо-
топологии на протяжении примерно двадцати лет. Сейчас такие про-
пространства известны, но они слишком сложны для того, чтобы их
можно было здесь описать.
В этом параграфе содержится несколько характеристик счет-
счетно паракомпактных пространств и нормальных счетно параком-
пактных пространств. Дальнейшую информацию можно найти в
упражнениях (см. также задачу 5.5.15),
5.2.1. Теорема. Следующие условия равносильны для произволь-
произвольного топологического пространства X:
(i) Пространство X счетно паракомпактно.
(и) Для каждого счетного открытого покрытия {Ui}T=\ про-
странства X существует локально конечное открытое покрытие
{Vt}T=\ пространства X, такое, что Vi с: I/,- при 1 = 1,2, ... .
(iii) Какова бы ни была возрастающая последовательность
ОО
W\ cz W2 a ... открытых в X множеств, для которой [} Wt = J,
найдется последовательность F\, F2, ... замкнутых в X множеству
ОО
такая, что Fi a Wt при i = 1, 2, ... и М Int Ft = X.
ы\
(iv) Для каждой убывающей последовательности F\ n>
ОО
zd F2^ ... замкнутых в X множеств, такой, что f| Fi= 0»
5.2. СЧЕТНО ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА 469
дется последовательность W\, W2, ... открытых в X множеств,
оо
такая, что Fi cz Wi при i = 1, 2, ... и f| Wt= 0 .
Доказательство. Для доказательства импликации (i)=^(ii)
достаточно взять любое локально конечное открытое покрытие
Т, вписанное в покрытие {Ui)T-u выбрать для каждого V ^ Т
номер i(V), такой, что V с: Uim, и положить Vt = М К.
nv)=t
Покажем, что (и)=^(ш). Так как {W(}Т=\ — счетное откры-
открытое покрытие пространства X, существует локально конечное от-
открытое покрытие {Vi}^ пространства X, такое, что Vt с: Wi при
f=l, 2 ... . Множества Ft = X\ U F/ с: jj Vt замкнуты и
Fi<=Wi при /=1,2, ... , так как [J V} a \] Wi=Wt>
Семейство {Vi}7=\ локально конечно, поэтому у каждой точ-
точки xg! есть окрестность, которая содержится в некотором Ft,
00
т. е. U lntFt = X.
Из формул де Моргана легко следует, что условия (ш) и
(iv) равносильны. Значит, для завершения доказательства до-
достаточно показать, что (iii)=^(i). Пусть {иг}Г=\ — счетное откры-
открытое покрытие пространства X. Рассмотрим возрастающую после-
последовательность W\ a И?2 с: ... открытых множеств в X, где
оо
Wi= U С//. Так как И Wt = X, найдется последовательность
Fu F2, ... замкнутых в X множеств, для которой Ft a Wi и
оо
U Int Fi = X. Множество Ff = ?/f\ И FtCiUi открыто при
г=1,2, ...;таккак U Fjcz [j W}^ [j Ut% то U\ [j Ut с Vi9
i<i i<i i<i !<i
откуда следует, что семейство {VjH-i покрывает X. У каждой
точки х^Х есть окрестность вида Int/7/. Эта окрестность не пе-
пересекается с теми множествами Vu Для которых i > /; значит,
покрытие {Vt}^L\ локально конечно. I
5.2.2. Следствие. Нормальное пространство X счетно параком-
пактно в том и только том случае*, если для каждой убывающей
последовательности Л => F2=> ... замкнутых в X множеств, удов-
оо
летворяющей условию [\Ft=0, найдется последовательность
470 ГЛ. 5. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА
W\, №2, ... открытых в X множеств, такая, что Ft<^Wi при
/=1,2, ...и П И^=0. I
5.2.3. Теорема. Для каждого Т\-пространства X следующие усло-
условия равносильны:
(г) Пространство X нормально и счетно паракомпактно.
(п) Каково бы ни было счетное открытое покрытие {?/*}?! i
пространства X, найдется локально конечное открытое покрытие
{ViiT=\ пространства Ху для которого Vi c= Ut при /=1,2, ... .
(Hi) Для каждого счетного открытого покрытия {U^f^x про-
пространства X существует замкнутое покрытие {Ff}^,1 простран-
пространства X, такое, что Ft cz ?/,• при /=1,2, ... .
Доказательство. Для доказательства импликации (i)=^(ii)
достаточно заметить, что, в силу теоремы 5.2.1, существует ло-
локально конечное открытое покрытие {IFJ^Lj пространства X, для
которого WiczUi при /=1,2 ... , и применить затем тео-
теорему 1.5.18.
Импликация (ii)=^(iii) очевидна. Покажем, что (iii)=>(i).
Заметим сначала, что каждое ^-пространство X, которое удов-
удовлетворяет условию (Hi), нормально. Действительно, для произ-
произвольных открытых подмножеств ?/, V пространства Ху таких, что
U U V = X, положим Ux = U, U2 = V, ?/3 = ?/4 ==... = 0; усло-
условие (iii) дает нам тогда замкнутые множества F\, F2CZX, такие,
что F\cz U, F2 cz V и F\ [} F2 = X. Из формул де Моргана сле-
следует, что, какова бы ни была последовательность Fu F2, ...
замкнутых в пространстве X множеств, удовлетворяющая усло-
вию (iii) и такая, что f) /7i=0, найдется последовательность
W\, W2* ... открытых множеств в X, такая, что FiCiWi при
оо
? == 1, 2, ... и П TF^=0. Следовательно, X счетно параком-
пактно по следствию 5.2.2. I
Помимо локально конечных и точечно конечных семейств
множеств рассматривают также звездно конечные и звездно
счетные семейства: семейство {Aj}5(E_s подмножеств множества
X звездно конечно (звездно счетно), если при каждом soeS
множество {s eS: As П As* Ф 0} конечно (счетно). Ясно, что
каждое звездно конечное семейство точечно конечно. Отметим,
что произвольное звездно конечное семейство подмножеств то-
топологического пространства не обязано быть локально конеч-
конечным; однако любое звездно конечное открытое покрытие топо-
топологического пространства локально конечно.
5.2. СЧЕТНО ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА 471
Нашей следующей теореме, содержащей еще два условия,
равносильных счетной паракомпактности в классе нормальных
пространств, предшествует лемма.
5.2.4. Лемма. В каждое счетное покрытие {?/J?Li топологиче-
топологического пространства X функционально открытыми множествами
Ui можно вписать счетное звездно конечное покрытие, состоя-
состоящее из функционально открытых множеств.
Доказательство. Пусть t/? == /Г1 (@> 1])» где ft: Х->1 —
оо
непрерывное отображение. Полагая /(*) = ]!? —М*), мы оп"
оо
ределяем непрерывную функцию /: Х->1. Так как U Ut = Xy
то /(л;)>0 при всех х^Х. Семейства {Vk}?=i и {Fk}T^u где
покрывают X и состоят из функционально открытых и функ-
функционально замкнутых множеств соответственно.
Докажем, что функционально открытые множества Uk / =
= Uj()(Vk+i\Fk-l)t где 1 *^j^kt k = l9 2, ... и Fo = 0, об-
образуют звездно конечное покрытие пространства X. Пусть х —
произвольная точка из X. Обозначим через k наименьшее целое
число k, такое, что х е Fk- Как легко проверить, Fk с: (J Uf, по-
этому найдется j^k, для которого х е С//, откуда следует, что
x&Uj П (Fk\Fk~\) с= Uk, /. Для каждого /<fe имеем Ukt / с: Vk+\ cz
czFk+\, так что
A) Uk,ittUm,i = 0 при m^k + 2 и i<m.
Из A) следует,что покрытие {Uk, /}Г=о, /<^ звездно конечно. I
Заметим, что приведенная выше лемма и теорема 1.5.19 дают
5.2.5. Следствие. Каждое совершенно нормальное пространство
счетно паракомпактно. 1
5.2.6. Теорема. Для любого нормального пространства X следую-
следующие условия равносильны:
(i) Пространство X счетно паракомпактно.
(п) В каждое счетное открытое покрытие пространства X
можно вписать звездно конечное открытое покрытие.
(Hi) В любое счетное открытое покрытие пространства X
можно вписать точечно конечное открытое покрытие.
Доказательство, Импликация (i)=^(ii) вытекает из теоремы
5.2.3, леммы Урысона и леммы 5.2.4. Импликация (i)()
очевидна, a (iii)=^(i) следует из теорем 1.5.18 и 5.2.1.
472 ГЛ. 5. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА
Мы завершаем этот параграф интересной характеристикой
счетно паракомпактных нормальных пространств в терминах
произведений.
5.2.7. Лемма. Произведение X X Y счетно паракомпактного нор-
нормального пространства X и компакта со счетной базой У нор-
нормально.
Доказательство. Пусть {Wi}T=\ — база пространства У. Обо-
Обозначим через 9* семейство всех конечных множеств натураль-
натуральных чисел и для каждого Sg^ положим TF5= (J WV В силу
теоремы 3.1.16, проекция р\ XX Y-+X является замкнутым ото-
отображением. Пусть q: XX Y-+ У —другая проекция, и для каж-
каждого МсXX Y пусть Мх = q[({x}X Y)(\М].
Рассмотрим произвольные непересекающиеся замкнутые мно-
множества Л, В в X X Y и при всех 5 е У положим
B) Us = {х е= X: Ах с Ws cz Ws
Так как
X\US = {xs= X: Ах П (Y\WS) Ф 0}{){х<
= Р U П
множества Us открыты. Приняв во внимание компактность У,
легко проверить, что семейство {(/5}Sg^ покрывает Х\ очевидно,
оно является счетным открытым покрытием. Следовательно, по
теореме 5.2.3, существует локально конечное открытое покрытие
{e^ пространства X, такое, что Vs <= Vs cz Us при всех
Множество U= [) (Vs X Ws) открыто. Для завершения
5^
доказательства достаточно показать, что
C) Лс[/ и Bd V = (XX
Для каждого (х, у)^А существует Se^, такое, что x^VsCZ
cz (/s. Из B) вытекает, что (л:, j/)gVsX^sC U; значит, пер-
первое из соотношений C) выполняется. Предположим теперь, что
нашлась точка (х9у)^В[]О. В силу локальной конечности се-
семейства {V$}$<=;&> существует окрестность WcX точки Jfel,
пересекающая лишь конечное число множеств Vs. Значит, ок-
окрестность W X У точки (х, у) пересекает лишь конечное число
произведений VsXWs — например, Vsx X WSl Vs2 X Ws2, ...
VSk X WSk. Так как (*, у) e U, то (х, у) е Ц (Vst X WS()
5.2. СЧЕТНО ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА 473
и существует i^k, для которого
D) (х, */) е В Л (VSiXWSi) = ВП (VSi X WSi) с= ВП(USi X WSi).
Из D) следует, что xe?/Sj и #<= BxftWsi9 что противоречит
B). Таким образом, доказательство второго соотношения в C)
завершено. I
5.2.8. Теорема, Топологическое пространство X нормально и счет-
счетно паракомпактно в том и только том случае, если произведение
ХУA пространства X на отрезок I нормально.
Доказательство. В силу предшествующей леммы, для любого
счетно паракомпактного нормального пространства X произведе-
произведение XXI нормально.
Рассмотрим теперь произвольное топологическое простран-
пространство X, такое, что XXI нормально. Так как X гомеоморфно
замкнутому подпространству ХХ{0} пространства XXЛ про-
пространство X нормально. Покажем, что X удовлетворяет условию
(iv) теоремы 5.2.1. Пусть F\ => F2 => ... — убывающая последо-
оо
вательность замкнутых множеств в X, такая, что f\ Fi~—0. Мно-
Множества
не пересекаются и замкнуты в X X Y. Следовательно, суще-
существуют открытые множества U, V с: X X У» Для которых А с U,
Bel/ и U{]V = 0. Множества Wi={x&X: {xtl/i)<=U} от-
оо
крыты при t= 1, 2, ... и Г] Ц7,= 0, так как 0(\5 = 0. Для
завершения доказательства достаточно заметить, что Ft cz Wi
при i = 1, 2, ... . I
5.2.9. Замечание. В последнем доказательстве использовалось
только то, что в пространстве / есть нетривиальная сходящаяся
последовательность; значит, мы доказали несколько больше — а
именно, что если произведение ZX^(^o) нормально, то про-
пространство X нормально и счетно паракомпактно.
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
Класс счетно паракомпактных пространств был независимо
введен Даукером в [1951] и Катетовым в [1951]. Внимание то-
топологов фокусировалось на счетно паракомпактных простран-
пространствах в течение двадцати лет после 1951 г. в связи с поиском
474 ГЛ. 5. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА
нормального не счетно паракомпактного пространства. Такое
пространство было, наконец, описано М. Рудин в [1971]; это
пространство даже коллективно нормально. Класс счетно пара-
компактных хаусдорфовых пространств интересен главным обра-
образом из-за того, что им указывается граница той области, в ко-
которой выполняются некоторые важные теоремы (см. задачи
5.5.18 и 5.5.20). В цитированных выше работах Даукер и Кате-
Катетов независимо доказали следствие 5.2.2, теорему 5.2.3, след-
следствие 5.2.5 и эквивалентность условий (i) и (ш) в теореме 5.2.6.
Теорема 5.2.1 доказана Исикавой в [1955]. Лемма 5.2.4 была
в принципе доказана в работе Мориты [1948]. Равносильность
условий (i) и (п) в теореме 5.2.6 доказана Исэки [1954]. Тео-
Теорема 5.2.8 н лемма 5.2.7 доказаны Даукером в [1951].
УПРАЖНЕНИЯ
5.2.А. Покажите, что ^-пространство X счетно паракомпактно
и нормально в том и только том случае, если каждому счетному
открытому покрытию пространства X подчинено разбиение еди-
единицы или, что равносильно, локально конечное разбиение еди-
единицы.
Указание. Покажите, видоизменив доказательство леммы
5.1.8, что если каждому двухэлементному открытому покрытию
^-пространства X подчинено некоторое разбиение единицы, то
пространство X нормально.
5.2.В. Проверьте, что счетная паракомпактность наследуется
замкнутыми подмножествами и является аддитивным свойством
(см. задачу 5.5.16).
5.2.С. (а) Проверьте, что пространство А (&о)ХА (**i)\{(#o, Уо)}
где хо и у о — единственные предельные точки пространств Л (Ко)
и Л(К1) соответственно, не счетно паракомпактно (см. пример
2.3.36).
(b) Покажите, что плоскость Немыцкого и квадрат прямой
Зоргенфрея не счетно паракомпактны.
Указание. Пусть Q={xu х2, ...} — множество всех точек пло-
плоскости Немыцкого L вида (qy 0), где q рационально. Применив
теорему Бэра о категории, покажите сначала, что Q и L\\Q
нельзя отделить непересекающимися открытыми множествами.
Рассмотрите затем открытое покрытие {L\Q} [} {U\ (х*)}П=1 и по-
получите противоречие.
(c) Приведите пример не нормального тихоновского про-
пространства, которое счетно паракомпактно.
(d) Проверьте, что пространство X в примере 5.1.23 счетно
паракомпактно.
(e) Покажите, что произведение XX Y в примере 5.1.32 не
счетно паракомпактно, и выведите отсюда, что предел обратной
5.2. СЧЕТНО ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА 475
последовательности счетно паракомпактных хаусдорфовых про-
пространств может не быть счетно паракомпактным пространством
(см. задачу 5.5.19 (d)).
5.2.D (Олл [1965]; для счетно компактных хаусдорфовых
пространств — П. С. Александров и Урысон [1929]). Покажите,
что каждое счетно паракомпактное хаусдорфово пространство
с первой аксиомой счетности регулярно.
5.2.Е. Докажите, что для каждого счетного покрытия {иг}Т=\
топологического пространства X функционально открытыми мно-
множествами Ui существует покрытие {Ft}T=\ функционально замк-
замкнутыми множествами, такое, что FiczUi при i = l, 2, ... .
Указание. Возьмите какую-нибудь непрерывную функцию
/,-: Jf-*/, такую, что ?/г = /Г1(@> 1]) при / = 1, 2, ..., и рассмот-
оо
рите функции fi/l где / (х) = ? -+г /, (х).
Можно применить также упр. 5.1.J (Ь).
5.2.F (Морита [1964]). (а) Покажите, что в каждое а-ло-
кально конечное открытое покрытие счетно паракомпактного
нормального пространства можно вписать локально конечное от-
открытое покрытие.
(Ь) Заметьте, что утверждения (а) и (Ь) из упр. 5.1.J вы-
выполняются, если X — произвольное счетно паракомпактное нор-
нормальное пространство, а открытое покрытие {Us}s^s а-локально
конечно.
5.2.G. (а) (Ханаи [1956], Хенриксен и Исбелл [1958]). По-
Покажите, что счетная паракомпактность сохраняется в обе сто-
стороны замкнутыми отображениями со счетно компактными про-
прообразами точек. Заметьте, что класс счетно паракомпактных
пространств совершенен.
Указание. При доказательстве сохранения счетной параком-
паракомпактности в сторону образа воспользуйтесь условием (iii) тео-
теоремы 5.2.1; доказывая ее сохранение в сторону прообраза, мо-
модифицируйте доказательство теоремы 5.1.35, заменив множества
Vy на множества Y\f(X\ []
\ $*вЗ(у)
(b) (Даукер [1951]). Выведите из (а), что произведение
XX Y счетно паракомпактного пространства X и компактного
пространства У счетно паракомпактно. Заметьте, что этот ре-
результат следует также из теоремы 3.1.16 и условия (iv) теоремы
5.2.1.
(c) (Зенор [1969]). Докажите, что счетная паракомпакт-
паракомпактность не сохраняется замкнутыми отображениями в классе хаус-
хаусдорфовых пространств.
476 ГЛ. 5. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА
Указание. Пусть Z — не нормальное тихоновское простран-
пространство, которое счетно паракомпактно. Возьмем любые непере-
непересекающиеся замкнутые множества Л, В в Z, не отделимые не-
непересекающимися открытыми множествами (см. упр. 5.2.С (с)).
Рассмотрите естественное факторное отображение суммы
оо
Х= фХр где Xz* = ZX{i}> на пространство У, получающееся
00
из X при отождествлении множества (J (В X 0'}) в точку.
(d) (Ханаи [1956]). Покажите, что класс счетно параком-
паракомпактных нормальных пространств инвариантен относительно
замкнутых отображений.
Указание. Примените следствие 5.2.2.
(e) Покажите, что счетная паракомпактность сохраняется
открыто-замкнутыми отображениями на хаусдорфовы простран-
пространства.
5.3. СЛАБО И СИЛЬНО ПАРАКОМПАКТНЫЕ
ПРОСТРАНСТВА
Топологическое пространство X называется слабо параком-
пактным1), если в каждое открытое покрытие пространства X
можно вписать точечно конечное открытое покрытие. Каждое
паракомпактное пространство слабо паракомпактно, но обратное
неверно (см. пример 5.3.4 и задачу 5.5.3 (с)). Из теоремы 5.2.6
вытекает, что каждое слабо паракомпактное нормальное про-
пространство счетно паракомпактно; предположение о нормальности
здесь существенно (см. упр. 5.2.С (а) и 5.3.В (Ь)).
Обсуждению слабо паракомпактных пространств мы предпо-
предпосылаем простую теорему о точечно конечных покрытиях. По-
Покрытие {Л5}5е5 пространства X называется неприводимым, если
U As ф X для каждого собственного подмножества So множе-
sgSo
ства S.
5.3.1. Теорема. Каждое точечно конечное покрытие {AS}SGS про-
пространства X содержит неприводимое подпокрытие.
Доказательство. Рассмотрим семейство 9 всех отображений
G множества S в семейство всех подмножеств множества X,
подчиненных следующим условиям:
A) G(s) = As или G(s) = 0
*) Употребляются также названия: метакомпактное пространство и го-
чечно паоакомпактное пространство.
5.3. СЛАБО И СИЛЬНО ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА 477
И
B) U
s
Упорядочим семейство ^, положив G\ ^ G2 в том и только
том случае, если Gz(s) = 0 при всех s е 5, таких, что G\ (s) == 0.
Как в доказательстве теоремы 1.5.18, легко проверяется, что
если подсемейство tfocrW линейно упорядочено, то формула
Go($)= [~] G(s) для каждого sgS определяет некоторый эле-
мент семейства ? и G < Go при всех G <= Sq.
Из леммы Куратовского — Цорна следует, что в % существует
максимальный элемент G.
Покрытие {^U}5«=St>rAe 5i={seS: G(s)=^0}> является не-
неприводимым подпокрытием покрытия {^5}seS. I
Покажем, обобщая теоремы 4.1.17 и 5.1.20, что в классе слабо
паракомпактных пространств компактность равносильна счетной
компактности (см. задачу 5.5.23).
5.3.2. Теорема. Каждое счетно компактное слабо паракомпакт-
нов пространство компактно.
Доказательство. Пусть Ш — произвольное открытое покрытие
счетно компактного слабо паракомпактного пространства X.
В силу теоремы 5.3.1, существует неприводимое точечно конеч-
конечное открытое покрытие У — {Vt}t еГ, вписанное в °U. Так как по-
покрытие Т неприводимо, при каждом /еГ найдется точка
U Vv- Множества Vt покрывают пространство X; зиа-
чит, у каждой точки х^Х есть окрестность, которая содержит
ровно одну точку множества А = [} {xt}. Следовательно,
tT
v4d = 0, и из счетной компактности пространства X вытекает,
что множество А конечно; значит, множество Т тоже конечно и
У—конечное открытое покрытие, вписанное в Щ. 1
5.3.3. Теорема Майкла — Нагами. Каждое слабо паракомпактное
коллективно нормальное пространство паракомпактно.
Доказательство. В силу теоремы 5.1.11, достаточно доказать,
что в каждое точечно конечное открытое покрытие ^=={(/s}seS
коллективно нормального пространства X можно вписать а-ло-
кально конечное открытое покрытие.
Мы определим по индукции относительно г = 0, 1, ... ди-
дискретные семейства Tt = {VV}re^- открытых в X множеств, та-
такие, что каждый элемент семейства У",- будет содержаться в не-
478 ГЛ. 5. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА
котором Us и множества Ц7$ = и^ будут удовлетворять усло-
условию
i
C) если |{seS: jte=?/s}|</, то x^{jwr
Положим Уо={0} и предположим, что семейства Ти удов-
удовлетворяющие условию C), уже определены при i^k. Обозна-
Обозначим через iT"ft+i семейство всех подмножеств множества S, со-
состоящих ровно из k + 1 элементов, и для каждого Т е ёГк+х по-
положим
Отметим, что
E) Лгс j] Us при всех
Действительно, если бы при некоторых х^Ат и sogT было
х ф t/So> то, в силу D), точка х принадлежала бы самое большее
k элементам семейства Щ — а это противоречило бы C).
Покажем теперь, что у каждой точки х е X есть окрестность
V(x), пересекающаяся не более чем с одним элементом семей-
семейства {Ат}т^р . Если в 41 есть k + 2 элементов Us^ U$2> ..¦
fc+2
... , Usk+2, которым х принадлежит, то для V {х) = [} USi, в силу
D), имеем V(x)[)At = 0 при всех Tef^i. Если х принадле-
принадлежит только i ^ k элементам семейства ^, то, в силу C), мно-
множество V(x)— U Wi — окрестность точки х, не пересекаю-
/«о
щаяся ни с одним Л г. Наконец, если точка х принадлежит ровно
k + 1 членам семейства °U, например USl, f/s2, ... , USk+l, то ок-
ft+i
рестность У(х)= П Ust точки пересекается самое большее с
одним членом семейства {Ат}т<=&к ~а именно с множеством
Атоу где Tq = {s{9 s2> ... , 5a+i}.
Следовательно, Wj-}^^^^ — дискретное семейство замкну-
замкнутых в X множеств. Пусть {Ог}Ге_^ — дискретное семейство
открытых множеств в X, такое, что ATcz От при всех
Покажем, что семейство Yk+\ — {Ут}т е &к , где
F) VT = GT П
обладает всеми нужными свойствами.
5.3. СЛАБО И СИЛЬНО ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА 479
Ясно, что семейство Tk+\ дискретно, состоит из открытых в X
множеств и что каждый элемент семейства У%+1 содержится
в некотором Us. Рассмотрим любую точку xel; пусть она при-
принадлежит не более чем k + 1 элементам семейства °U. Тогда
найдется Ге^ц, для которого х е Х\ U Us. Имеем
U с/.=Г(*\U w,) и U w{] л (x\U и.)<=Ати U wr
^t L\ /-о / /~о J V s&t ) /-о
s&T
Г/ k \ k 1
I I .. I I „V II I . . I I I _ •
же
Последняя формула вместе с E), F), и включением Ат<=: Gt
показывает, что х е (J W».
/-о '
Так как покрытие °U точечно конечно, из C) следует, что
со
[J Tt есть а-локально конечное открытое покрытие, вписанное
b"W. 1
5.3.4. Пример. Нерегулярное хаусдорфово пространство X, опи-
описанное в примере 1.5.7, слабо паракомпактно.
Пусть ?/ = {(/s}se5 — произвольное открытое покрытие
пространства X. Открытое подпространство X\Z пространства
X, где Z — множество обратных всем целым числам, отличным от
нуля, наделено топологией подпространства вещественной пря-
прямой. Значит, пространство X\Z паракомпактно, и в открытое по-
покрытие {^$\Z}S^S пространства X\Z можно вписать локально
конечное открытое покрытие Т. Для каждого z e Z выберем
s (г) е S, такое, что z e VS(zb и положим
(О, 2г)П ?/*<*). если г>0,
у =,
2 l Bz, 0)Пи8ю, если z < 0.
Как легко видеть, семейство ^°[}{VZ}Z^Z является точечно
конечным открытым покрытием, вписанным ъШ.Ш
Существуют коллективно нормальные пространства, которые
не слабо паракомпактны; в силу теоремы 5.3.2 и примера 5.1.21,
пространство Wo всех счетных ординалов является таким про-
пространством. Существуют также слабо паракомпактные нормаль-
нормальные пространства, которые не коллективно нормальны (см. за-
задачу 5.5.3 (с)).
Мы завершаем первую часть этого параграфа теоремой о со-
сохранении слабой паракомпактности замкнутыми отображениями
на хаусдорфовы пространства. Заметим, что этот результат
вместе с теоремой 5.3.3 и инвариантностью коллективной нор-
нормальности при замкнутых отображениях (см. упр. 5.1.С (Ь)) дает
другое доказательство теоремы 5.1.33. Еще одно доказатель-
480 ГЛ. 5. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА
ство теоремы 5.1.33 можно получить, сделав небольшие измене-
изменения, предлагаемые ниже в упр. 5.3.Е, в доказательстве теоремы
об инвариантности слабой паракомпактности. Однако оба эти
доказательства труднее, чем исходное доказательство, приведен-
приведенное в § 5.1.
5.3.5. Лемма. Для каждого открытого покрытия {[/,}5е5 слабо
паракомпактного пространства X существует точечно конечное
открытое покрытие {Vs}s^s пространства X, такое, что Vscz Vs
при всех seS. I
5.3.6. Лемма. Если f: X-*Y — замкнутое отображение слабо па-
паракомпактного пространства X на пространство У, то в каждое
открытое покрытие пространства У, представимое в виде объеди-
объединения счетного семейства точечно конечных семейств, можно
вписать точечно конечное открытое покрытие.
оо
Доказательство. Пусть ^= I) %t ™ открытое покрытие про-
странства У, причем каждое <2^— {Us}s<=s —точечно конечное
семейство. По лемме 5.3.5, найдется точечно конечное открытое
покрытие {Gi)T=\ пространства X, такое, что Gi<z:f-l(Ui) при
i=l,2, ..., где Ui = U °U>u Множество Ek = X\ [} Gt замкнуто
при й = 1,2, ... ; как легко видеть, ?jc?2C ... и {Ек}^[ по-
покрывает X. Далее,
/(?*)<=/( U Gt)c U f(Gt)<= U Ut при fe=l, 2
Положим S== M St) очевидно, можно предполагать, что
Si fl 5/ = 0 при i ф /. Для завершения доказательства достаточ-
достаточно показать, что семейство Ж = {fJseS, где
Ws = Us\f(Ei) При SGSi,
является точечно конечным открытым покрытием пространства У.
Так как отображение f замкнуто, множества Ws открыты; мы
покажем, что они образуют точечно конечное семейство. Из
оо
Y — U / (Ek) следует, что каждая точка у е У принадлежит не-
й в* 1
которому множеству f(Ek)', значит, у не входит ни в одно из
множеств Ws, для которых seSfHi^ k. Семейства °Uu <%2> . -.
..., <Uk-\ точечно конечны, поэтому у принадлежит лишь конеч-
конечному числу членов семейства Ж. Остается показать, что Ж по-
покрывает У. Для произвольного //еУ обозначим через i(y) наи-
наименьшее натуральное число, для которого y^U%y). Так как
5.3. СЛАБО И СИЛЬНО ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА 481
f(EHy))cz U Uit то найдется s(y)€=Siiyh такое, что i/g
i < i (У)
Ш
5.3.7. Теорема Уоррела. Если f: X^Y— замкнутое отображение
слабо паракомпактно го пространства X на хаусдорфово про-
пространство У, то пространство У слабо паракомпактно.
Доказательство. По лемме 5.3.6, достаточно доказать, что в
каждое открытое покрытие {Us}s^s пространства У можно впи-
вписать открытое покрытие, являющееся объединением счетного се-
семейства точечно конечных семейств.
Пусть < — произвольное вполне упорядочение на множе-
множестве S. Определим по индукции относительно / = 1,2, ... откры-
открытые точечно конечные покрытия ^ = {GS, *}se5 пространства Ху
удовлетворяющие условиям
G) GSticzr{(Us) при *e=S и /=1, 2, ... ,
(8) 1{Оы)П?(Е8.1-х) = 0,тАе Ea.t-i = X\U Gt.t-i при*>1.
t >
Существование *&\ следует из леммы 5.3.5. Предположим, что
покрытия 9и $2, . - •, 8k-\ уже определены и удовлетворяют G)
и (8) при i < k. Из замкнутости отображения / следует, что
множества
(9) WSt и = /-1 (Us)\rlf (Es, *-0 c= r\Us)
открыты. Для каждого х через $(х) обозначим наименьший
элемент множества 5, такой, что х е f~~l (Us{x))- Так как
Es{x),k~icz U G,. *-! и, в силу G), U G8,k-i<=z [} f~{(Us\
s<s{x) s<s(x) s<s(x)
имеем rlf(Esix)tk^)cz [} f'l(Ua). Значит, x<=W8{x)ik9
T- e* {Ws k}s&s ~~ открытое покрытие пространства X.
Воспользовавшись леммой 5.3.5, получаем точечно конечное
покрытие Эй = {GSt k}s^s пространства X, такое, что Gs, и с= Ws, к
при всех 5 е S. Из (9) следует, что покрытие 9k удовлетворяет
условиям G) и (8) при i = k\ таким образом, построение покры-
покрытий *§1 завершено.
Заметьте, что при всех soeSH всех i = 1, 2, ...
A0) E,bt = X\ U Gs,,c= U (X\U Ом).
s>s0 s <So t>s
Действительно, если х ф U GS| it то найдется 5 < s0, такое,
что х ф U Gt iy а именно наибольшее seS, для которого
t >s
Gs, j. Подобным же образом получаем
31 Зак. 697
482 гл- 5* ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА
A1) х = U (X\ U Gt,t) при i=l, 2
seS \ t> s /
Рассмотрим открытые множества Vs, i• = Y\f(X\Gs, *)• Так
как
A2) f-l(Vs,i)^Gs,i при sgS и /=1, 2, ...,
семейство У% = {Vs, t}s<=s точечно конечно при / = 1,2, ... . По-
оо
кажем, что семейство У° = [} У% покрывает пространство Y. Для
произвольного y^Y обозначим через s(y) наименьший элемент
множества 5, для которого y^f(X\ [j Gt Л при некото-
ром целом положительном г, — такой элемент существует в силу
A1). Возьмем какое-нибудь целое число i(y), такое, что у е
^f(X\ U Gt,i(y)-A. Тогда j/ef(?,,^H) при всех
V t>s(y) J
s> s(y) и, в силу (8),
U f(Gs^(tf)) = /f U G*,,^, т. е.
УФ U f(^(tf) /f U
s>s(y) \s>s(y)
Г1(У)\] U Ge.Mtf)=0-
С другой стороны, в силу A0),
f(x\ U о..«„>)<=/( U (A U
= U f(X\{] Gt.t{yA.
s<s{y) \ t> s J
Так как у не принадлежит последнему объединению,
то ГХ(У)<= U Gs,i(y). Значит, f-'ft/lcG^^, т. е.
^(y)
у^: Vs(y), i(y). Следовательно, У покрывает Y. Для завершения
доказательства достаточно заметить, что Т вписано b{?/s}ssS —
последнее вытекает из соотношений G) и A2). I
Перейдем теперь к классу сильно паракомпактных про-
пространств. Топологическое пространство X называется сильно па-
ракомпактным1), если в каждое открытое покрытие простран-
пространства X можно вписать звездно конечное открытое покрытие.
Каждое сильно паракомпактное пространство паракомпактно;
следовательно, хаусдорфово сильно паракомпактное простран-
пространство нормально. Однако не всякий паракомпакт сильно пара-
компактен (см. упр. 5.3.F(a) и 6.1.D).
Пусть ^ = {4}seS—некоторое семейство подмножеств
множества X. Под цепочкой от As до Asf условимся понимать
]) Иногда используется термин гипокомпактное пространство.
5.3. СЛАБО И СИЛЬНО ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА 483
любую конечную последовательность ASl, As2, • •. » A$k элемен-
элементов семейства зФ, такую, что S\ = 5, Sk = s' и As. [}ASi+l Ф 0
при f= 1, 2, ..., k — 1. Скажем, что семейство s& связно, если
для любых двух членов As, Asf семейства М- найдется цепочка
от As до AS'. Компоненты семейства s& определяются как макси-
максимальные связные подсемейства семейства $Ф, т. е. связные под-
подсемейства семейства «5$, не являющиеся собственными подмно-
подмножествами никакого связного подсемейства семейства st>.
Отметим два простых факта (см. доказательство теоремы
5.1.27):
5.3.8. Лемма. Каждое семейство подмножеств произвольного
множества X распадается в объединение своих компонент. Если
зФ\ и $&2 — различные компоненты семейства sf>, то (U^OR
2) = 0. ¦
5.3.9. Лемма. Каждое связное звездно счетное семейство мно-
множеств счетно. I
5.3.10. Теорема. Для каждого регулярного пространства X сле-
следующие условия равносильны:
(i) Пространство X сильно паракомпактно.
(и) В каждое открытое покрытие пространства X можно
вписать замкнутое покрытие, которое одновременно локально
конечно и звездно конечно.
(iii) В каждое открытое покрытие пространства X можно
вписать замкнутое покрытие, которое одновременно локально
конечно и звездно счетно.
(iv) В каждое открытое покрытие пространства X можно
вписать звездно счетное открытое покрытие.
Доказательство. Покажем, что (i)=^(ii). Пусть °U — любое
открытое покрытие пространства X и Т = {Vs}sgS — звездно ко-
конечное открытое покрытие, вписанное в °U. Так как простран-
пространство X нормально, а покрытие У локально конечно, то, по тео-
теореме 1.5.18, найдется замкнутое покрытие #" = {/7a}JSs ПР°"
странства X, такое, что Fs cr Vs при всех s ^ S. Ясно, что У
вписано в °11 и что У одновременно локально конечно и звездно
конечно.
Импликация (и) =4-(Hi) очевидна; покажем, что (iii)=^(iv).
Рассмотрим любое открытое покрытие cM = {lJs}s€=s простран-
пространства X и вписанное в него замкнутое покрытие ЗГ, локально ко-
конечное и звездно счетное одновременно. Пусть $F = |J &*t9 где
t gt
!Ft — компоненты семейства SF.
Из леммы 5.3.9 следует, что все семейства &~t счетны; пусть
&~t — {Ft, i}7=\- Множества Ct = \J3Tt попарно не пересекаются
31*
484 ГЛ. 5. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА
и, в силу локальной конечности семейства 2Г> открыто-замкнуты.
При каждом ^еГи любом натуральном i выберем s(t7i)^S
так, чтобы было Ftj ,• <= US{t, /). Семейство {Cf f] Us(t 0}°°=МеГяв-
ляется звездно счетным открытым покрытием, вписанным в °U.
Докажем теперь, что (iv)=^(i). Пусть °Ы — произвольное от-
открытое покрытие пространства X и Т — звездно счетное откры-
открытое покрытие, вписанное в Ш. Рассмотрим семейство {Tt}t^T
всех компонент покрытия Т. В силу леммы 5.3,9, Tt — {Vt, {}Г=\
при каждом t^T. Семейство {Vt,i}t^T Дискретно при / =
= 1, 2, ... ; следовательно, Т является а-локально конечным
открытым покрытием, вписанным в °U. Значит, пространство X
паракомпактно по теореме 5.1.11. Положим Ct = [)Tt при всех
t e Т. Множества Ct открыты и попарно не пересекаются, следо-
следовательно, они открыто-замкнуты. Значит, пространство Ct пара-
компактно при каждом t е Г, и, в силу теоремы 5.2.6, в откры-
открытое покрытие Tt пространства Ct можно вписать некоторое
звездно конечное открытое покрытие °Ut> Объединение (J <?/*
является звездно конечным открытым покрытием, вписанным
в покрытие Ш. 1
Заметим, что предположение о локальной конечности в (И)
и (Hi) выше нельзя опустить. Действительно, для произвольного
Ti-пространства Х семейство всех одноточечных подмножеств
множества X является звездно конечным замкнутым покрытием,
вписанным в произвольное покрытие пространства X.
Последняя теорема дает
5.3.11. Следствие. Каждое линделёфово пространство сильно па-
паракомпактно. 1
5.3.12. Пример. Из следствия выше и примера 3.8.15 вытекает,
что произведение двух сильно паракомпактных хаусдорфовых
пространств не обязательно сильно паракомпактно. I
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
Слабо паракомпактные пространства были введены Аренсом
и Дугунджи в [1950]. Их работа содержит теоремы 5.3.1 и 5.3.2
(другое доказательство последней намечено в указании к за-
задаче 3.12.22(а)). Теорема 5.3.3 была доказана независимо Майк-
Майклом в [1955] и Нагами в [1955]. Теорема 5.3.6 доказана Уорре-
лом в [1966].
Сильно паракомпактные пространства определены Даукером
в [1947]. Теорема 5.3.10 доказана Ю. М. Смирновым в [1956];
следствие 5.3.11 появилось ранее в работе Мориты [1948] (Кап-
лан доказал в [1947], что каждое сепарабельное метризуемое
пространство сильно паракомпактно).
5.3. СЛАБО И СИЛЬНО ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА 485
УПРАЖНЕНИЯ
5.З.А. (а) (Трэйлор [1964], Годел [1969]). Докажите, что
если пространство X локально сепарабельно и в каждое откры-
открытое покрытие пространства X можно вписать точечно счетное
открытое покрытие, то в каждое открытое покрытие простран-
пространства X можно вписать звездно счетное открытое покрытие. Вы-
Выведите отсюда, что каждое локально сепарабельное слабо пара-
компактное пространство сильно паракомпактно.
(Ь) (А. Стоун [1962]). Если в каждое открытое покрытие
пространства X можно вписать точечно счетное открытое покры-
покрытие и у каждой точки хе! есть окрестность 1)у такая, что
m^z &о, то Х== 0XS, где w(Xs)^m при всех s^S
s<=S
(см. упр. 4.4.F(c)).
(с) (Чарльзуорт [1976]). Если топологическое пространство
X обладает базой $, такой, что у каждой точки jcg! есть
окрестность U> для которой мощность семейства {KgJ: U[)
П V Ф0} не превосходит т, то Х= ф xs, где w(Xs)^m. при
всех s <= S.
Указание. Рассмотрите подсемейство семейства $у состоя-
состоящее из тех множеств, которые пересекают самое большее m эле-
элементов семейства Ш.
5.З.В. (а) Проверьте, что плоскость Немыцкого, квадрат
прямой Зоргенфрея и пространство всех счетных ординалов не
слабо паракомпактны.
Указание. Примените упр. 5.3.А(а).
(b) Покажите, что произведение Л (Ко)X ^4(^i) наследствен-
наследственно слабо паракомпактно.
(c) Проверьте, что пространство X из примера 5.3.4 совер-
совершенно, но не счетно паракомпактно.
5.3.С. (а) Отметьте, что слабая паракомпактность является
аддитивным, но не конечно мультипликативным свойством.
Замечание. Предел обратной последовательности слабо па-
ракомпактных пространств может не быть слабо паракомпакт-
ным пространством (см. задачу 5.5.4(с)).
(b) (Чобан [1970]). Покажите, что слабая паракомпакт-
паракомпактность наследуется /^-множествами.
(c) Заметьте, что сильная паракомпактность является адди-
аддитивным свойством и наследуется замкнутыми множествами
(см. упр. 5.3.F(c)).
5.3.D (Майкл [1955], Нагами [1955]). (а) Покажите, что для
каждого счетного точечно конечного открытого покрытия {Wt}T=\
нормального пространства X найдется локально конечное от-
486 ГЛ. 5. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА
крытое покрытие {Vi}7-\ этого пространства, такое, что Vi a W-t
при i = 1, 2, ... .
Указание. Примените либо теорему 1.5.18 и лемму 5.2.4, либо
упр. 5.U(d).
(b) Покажите, что в каждое точечно конечное открытое по-
покрытие коллективно нормального пространства можно вписать
локально конечное открытое покрытие.
Указание. Заметьте, что покрытие {Wt}T=b определенное в
доказательстве теоремы 5.3.3, точечно конечно; примените за-
затем (а).
5.3.Е (Уоррел [1966]). Докажите теорему 5.1.33, видоизме-
видоизменив доказательство теоремы 5.3.7.
Указание. Пусть покрытия $\, $2, • ••> фигурирующие в до-
доказательстве теоремы 5.3.7, локально конечны; возьмем замкну-
замкнутое покрытие {Ki}7=\ пространства X, такое, что /С(С/-1(У,-),
где Vi = [)Ti. Рассмотрим при / = 1, 2, ... открытое покрытие
Ti\j{Y\f(Ki)} пространства У и применим теорему 1.5.18. За-
Заметьте, что каждое точечно конечное консервативное (см.
упр. 5.1.G) семейство замкнутых множеств локально конечно.
5.3.F. (а) (Нагата [1957]). Докажите, что произведение от-
открытого единичного интервала @,1) и пространства Бэра
B(&i) не сильно паракомпактно. Выведите отсюда, что предел
обратной последовательности сильно паракомпактных хаусдор-
фовых пространств не обязан быть сильно паракомпактным про-
пространством (см. задачу 5.5.4(с)).
(b) Покажите, что пространство Бэра В(т) сильно пара-
компактно при всех m ^ Ко (см, упр. 7.2.Е и пример 7.3.14).
Указание. Объединение произвольного семейства A//)-шаров
открыто-замкнуто.
(c) Заметьте, что из (а), (Ь) и упр. 5.3.Н(Ь) ниже следует,
что даже в классе метризуемых пространств сильная параком-
паракомпактность не наследуется /^-множествами и не конечно муль-
мультипликативна.
(d) Приведите пример метризуемого пространства, которое
можно представить в виде объединения двух замкнутых сильно
паракомпактных подпространств, но которое само не сильно па-
паракомпактно.
Замечание. Ясуи доказал в [1967], что если регулярное про-
пространство X покрывается локально конечным семейством зам-
замкнутых сильно паракомпактных подпространств, границы кото-
которых в X обладают локально свойством Линделёфа (т. е. у ка-
каждой точки есть окрестность, замыкание которой является лин-
делёфовым пространством), то пространство X сильно параком-
паракомпактно.
5.4. МЕТРИЗАЦИОННЫЕ ТЕОРЕМЫ II 487
(е) (Морита [1954]). Покажите, что каждое сильно пара-
компактное метризуемое пространство веса щ ^ Ко можно вло-
вложить в произведение /*° X В(ш).
5.3.G. (а) Покажите, что сильная паракомпактность равно-
равносильна паракомпактности в классе локально компактных хаус-
дорфовых пространств.
(Ь) Приведите пример не нормального слабо паракомпакт-
ного локально компактного хаусдорфова пространства.
Указание, Посмотрите упр. 5.3.В(Ь).
5.3.Н. (а) (Ханаи [1956]). Покажите, что слабая параком-
паракомпактность и сильная паракомпактность сохраняются в сторону
прообраза совершенными отображениями.
(b) (Бегль [1949] для сильной паракомпактности). Убеди-
Убедитесь, что произведение XX У слабо (сильно) паракомпактного
пространства X и компактного пространства У слабо (сильно)
паракомпактно.
(c) (В. И. Пономарев [1962]). Заметьте, что сильная пара-
паракомпактность не является инвариантом совершенных отображе-
отображений.
Указание. Примените упр. 5.3.F(d) и теорему 3.7.22.
(d) (В. И. Пономарев [1962а]). Докажите, что сильная па-
паракомпактность сохраняется открытыми совершенными отобра-
отображениями.
Указание. Пусть /: X-^Y— открытое совершенное отобра-
отображение пространства X на пространство У. Проверьте, что если
{Us}s^s — звездно конечное открытое покрытие пространства X,
то множества
U(su s2> ... , sk) =
где si, s2, ..., sk e 5, образуют звездно конечное открытое по-
покрытие пространства У.
(e) Покажите, что если f: X^Y — открытое отображение
паракомпактного пространства X на топологическое простран-
пространство У и все прообразы f~~l(y) точек компактны, то пространство
У слабо паракомпактно.
5.4. МЕТРИЗАЦИОННЫЕ ТЕОРЕМЫ II
В этом параграфе с помощью понятий паракомпактности,
коллективной нормальности и слабой паракомпактности уста-
устанавливаются дальнейшие топологические характеристики клас-
класса метризуемых пространств.
Последовательность Ж\у Жч, ... покрытий топологического
пространства X называется измельчающейся, или измельчением
488 ГЛ. 5. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА
пространства Ху если все покрытия Wt открыты и для каждой
точки х <= X и произвольной ее окрестности U найдется нату-
натуральное число i, такое, что $t(xyWi)a ?/. Как легко заметить,
последовательность открытых покрытий пространства X яв-
является его измельчением в том и только том случае, если для
каждой точки jcg! любое семейство {И^}П=1> такое, что х е
^Wi^Wi при 1=1,2, ...., является базой пространства X
в точке х,
5,4.1. Метризационный критерий Бинга. Топологическое про-
пространство метризуемо в том и только том случае, если оно кол-
коллективно нормально и обладает измельчением.
Доказательство. Пусть X—метризуемое пространство и р —
метрика на X. Для каждого дискретного семейства {Fs}se.s
замкнутых в X множеств семейство {Us}s^s,, где Us= ix e X:
р(х, Fs) < р (х, И Fs*\\> удовлетворяет условию теоремы 5.1.7;
V э'Фз Л
следовательно, X коллективно нормально. Легко проверяется,
что последовательность Ж\, Жч> . •-, гдеЯ^ = {?(*, 1А)}л;ех»яв"
ляется измельчением пространства X.
Рассмотрим теперь коллективно нормальное пространство Ху
обладающее измельчением Ж\, Ж%% .... Покажем сначала, что
в каждое открытое покрытие {US}SG.S пространства X можно
вписать 0-локально конечное открытое покрытие (в силу тео-
теоремы 5.1.11, это означает, что X паракомпактно).
Возьмем произвольное вполне упорядочение < на 5 и по-
положим
Замкнутые множества Fs,,-, где sgS и t=l,2, ..., покры-
покрывают пространство X. Действительно, взяв для каждого xgX
наименьший элемент s(x) в 5, такой, что хе US(x), и выбрав
натуральное число 1{х), для которого St (jc, Жцх))*^. Us(x), мы по-
получаем х е FS(x), цх). Так как при фиксированном i окрестность
US(x) П St(jc,5fi) точки х пересекается только с одним членом се-
семейства STг = {FSt i}S(=s> а именно с множеством FS(X), и семейство
{Ft дискретно. В силу коллективной нормальности X, найдутся
открытые множества USt и Для которых Fs> ,• с: Us, i c= Us при
seS и i= 1,2, ... и семейство {U8ti}seS дискретно при каж-
каждом L Следовательно, {us j^j se5 есть 0-локально конечное от-
открытое покрытие, вписанное в {?/5}5G=s.
Пусть (при i = 1, 2, ...) 3Si есть о-локально конечное откры-
открытое покрытие, вписанное в покрытие Жи Легко проверяется, что
5.4. МЕТРИЗАЦИОННЫЕ ТЕОРЕМЫ II 489
оо
$= (J $ь — база пространства Х\ значит, X метризуемо по мет-
метризационной теореме Нагаты — Смирнова. I
Заметим, что при доказательстве сохранения метризуемости
совершенными отображениями (см. теорему 4.4.15) мы сначала
определили некоторое измельчение пространства У, а затем,
пользуясь паракомпактностью У (установленной ранее в лем-
лемме 4.4.13), определили сг-локально конечную базу пространства
У— в точности так, как и при доказательстве метризационной
теоремы Бинга.
Покажем теперь, как получить, усилив понятие измельче-
измельчения, необходимое и достаточное условие метризуемости Го-про-
Го-пространств.
Последовательность Wu У2, ••• покрытий топологического
пространства X называется сильным измельчением простран-
пространства X, если все покрытия Wi открыты и для каждой точки
xgIh произвольной ее окрестности U найдутся окрестность V
точки х и натуральное число /, такие, что St(V, W*i)cz U. Ясно,
что каждое сильное измельчение является измельчением.
5.4.2. Метризационная теорема Мора. Топологическое простран-
пространство метризуемо в том и только том случае, если оно является
Т^пространством и обладает сильным измельчением.
Доказательство. Легко проверяется, что для произвольной
метрики р на X последовательность Ж\, F^, . • •, где
Жг = {В{ху l/i)}xeX> является сильным измельчением простран-
пространства X.
Рассмотрим теперь произвольное ^-пространство Ху обла-
обладающее сильным измельчением Ж\, Ж2, .... В силу метриза-
метризационного критерия Бинга, достаточно показать, что X коллек-
коллективно нормально.
Покажем сначала, что X есть ^-пространство. Возьмем лю-
любые две различные точки х, у пространства X. Так как X есть
Го-пространство, найдется открытое множество [/, которое со-
содержит ровно одну из точек х, у\ можно предположить, что
х^ U и у ф. U. Выберем натуральное число /, такое, что
St(x, Wi)cz U, и возьмем какое-нибудь множество W^Wi, со-
содержащее у. Так как х ф. W, мы видим, что X есть ^-простран-
^-пространство.
Заменив, если нужно, покрытия У,- покрытиями, состоящими
из всевозможных пересечений W\ Л W2 П • • • П Wi, где Wk e Wk
лри k ^С /, можно считать, что Ж\ вписано в Wi при / ^ и Для
сильного измельчения, удовлетворяющего этому дополнительно-
дополнительному условию, имеем _
A) если х^Л = Лс1, то St(x, Жг)[\Ъ\{А> Wt)=0 при не-
некотором натуральном /.
490 гл- 5- ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА
Действительно, по определению сильного измельчения, суще-
существуют окрестность V точки х и натуральное число /, такие, что
St(l/, Ж}) а Х\ А] применив снова определение сильного из-
измельчения, мы находим k, для которого St(x, Wk)cz V. Для но-
номера / = max(/, k) условие A) выполняется, так как St(x, Wi)cz
St(jcf3rfc)c= V и St(V,Wi)czSt{Vjri)czX\A1 т. е.
(AW>)X\V
(9)
Для произвольного дискретного семейства {Fs}s^s замкнУ*
тых множеств в X определим теперь семейство {Us}s^s откры-
открытых множеств, такое, что Fs cz Us при всех s e 5 и Us{] US'= 0,
когда 5 ^s'; по теореме 5.1.17, это завершит доказательство.
При каждом s^S множество А$= [} FS' замкнуто, тогда
s' ф s
как множества
U8. i = U Ув> ь где ЗГЛ ^{ГбГ,: Г П St (A8, Wt) =
оо
и множество ?/s= U ^s * открыты. Так как FsczX\As> из A)
следует, что Fs cz Us при всех s e S. Будет установлено, что
US[\US'= 0 при s^sf> если мы покажем, что f/s, i f| f/S', / = 0
при s^s' и />/. Но если W^Ws,i и И^'еЗГ^,/, то
W[\$i(As> Wi)=0 и It7/n/7S'^0- Из последнего неравен-
неравенства следует, что W <=$i(As, F)/)c:St(Лs, ЗГ,); значит,
W[)W = 0, откуда получаем, что t/s, i (]Usr, /= 0- I
Следующие две метризационные теоремы формулируются в
терминах специальных баз.
Назовем базу <М топологического пространства X точечно
регулярной1), если для каждой точки jcgIh произвольной ее
окрестности О множество всех элементов базы $, содержащих х
и пересекающихся с Х\ U, конечно. Легко заметить, что база
$ пространства X точечно регулярна в том и только том случае,
если, какова бы ни была точка xel, любое бесконечное се-
семейство элементов базы J?, содержащих точку х, является ба-
базой пространства X в точке х.
Назовем базу <М топологического пространства X регулярной,
если для каждой точки хе!и произвольной ее окрестности U
найдется окрестность V cz U точки х, такая, что множество всех
элементов базы Ш, пересекающихся с У и с Д(/, конечно.
Ясно, что каждая регулярная база точечно регулярна.
Доказательства теорем 5.4.6 и 5.4.8 основаны на нескольких
леммах, которые мы сейчас докажем. Чтобы упростить форму-
формулировки этих лемм, условимся для произвольного семейства $$>
:) Точечно регулярные базы называют также равномерными базами.
5.4. МЕТРИЗАЦИОННЫЕ ТЕОРЕМЫ II 491
множеств обозначать через sfim подсемейство семейства бФ> со-
состоящее из всех максимальных его элементов (т. е. множеств
Ле^, таких, что если ЛсгЛ'е^, то А = А'); через У(Х)
будем обозначать семейство всех открытых одноточечных под-
подмножеств произвольного топологического пространства X.
5.4.3. Лемма. Если $ — точечно регулярная (регулярная) база
пространства X, то семейство 3§m a $ является точечно конеч-
конечным (локально конечным) покрытием пространства X.
Доказательство. Покажем сначала, что [}$т = Х. Для про-
произвольного х е X найдется Uo^$, содержащее х. Предполо-
Предположив, что х не содержится ни в каком элементе семейства $т,
можно определить бесконечную последовательность Uo cz U\ a
с= U2 с= ... элементов базы ^?, такую, что Ui ф ?A+i при i =
= 1, 2, ... . Получаем бесконечное подсемейство {и?}Т=\базы $у
все элементы которого содержат х и пересекают X\Uo, что
невозможно. Следовательно, х е (J ^ш и U $т = X.
Покажем теперь, что если база $ точечно регулярна (регу-
(регулярна), то покрытие $т точечно конечно (локально конечно).
Возьмем любую точку хеХи какое-нибудь множество U e ^m,
содержащее х.
Множество всех элементов базы J7, пересекающих X\U и
{х} (и произвольную фиксированную окрестность V точки х),
конечно. Но каждое f//e^m\{[/}, содержащее х (пересекаю-
(пересекающее V) пересекает также и!\(/, так что лишь конечное число
членов семейства $т содержит х (пересекает V). Это показы-
показывает, что J?m — точечно конечное (локально конечное) покрытие
пространства X. I
5.4.4. Лемма. Если $ — база Т{-пространства X, то для произ-
произвольного точечно конечного покрытия Ж а $ семейство Ы" =
= CS \ $') U У (X) является базой пространства X. Далее, если
база $ точечно регулярна (регулярна), то и база Ш" тоже то-
точечно регулярна (регулярна).
Доказательство. Пусть х — любая точка пространства X и
U — произвольная ее окрестность. Если точка х изолирована, то
jfG{i}eJ(I) ихе{х}с(/; если точка х не изолирована, то
пересечение (]{W^$': хеУ} содержит некоторую точку
у ф х, и любая окрестность Уе^ точки х, удовлетворяющая
условию Vcz U\{y}, принадлежит <Я\ЗВ/. Вторая часть лем-
леммы очевидна. I
5.4.5. Лемма. Пусть $ — точечно регулярная (регулярная) база
7'{-пространства X; положим
B) &1 = ЗГ и &t = \\3t\\] 9&Л\)ЗГ(Х)\ при i = 2, 3, ... .
492 гл- 5- ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА
Этим определена последовательность З&и $ъ ¦ • • точечно конеч-
конечных (локально конечных) открытых покрытий пространства X,
оо
такая, что $ =[}$;.
Доказательство. Из лемм 5.4.3 и 5.4.4 следует, что $и
$2, ••¦ — последовательность точечно конечных (локально ко-
конечных) открытых покрытий пространства X. База $ точечно
регулярна, поэтому для каждого U е J? лишь конечное число
множеств W е $ удовлетворяет включению U a Uf. Следова-
оо
тельно, 9i= U &г в силу B). |
i = \
5.4.6. Метризационная теорема Архангельского. Топологическое
пространство метризуемо в том и только том случае, если оно
является Т ^пространством и обладает регулярной базой.
Доказательство. Проверим сначала, что каждое метризуемое
пространство X имеет регулярную базу. Пусть р — некоторая
метрика на X и SSi — локально конечное открытое покрытие, впи-
вписанное в покрытие {В (х, 1/4г)}хеХ (см. теорему 4.4.1). Ясно, что
00
,$= у <gt является базой пространства X. Для каждой точки
хеХи произвольной ее окрестности U найдется натуральное
число г, такое, что B(x,l/i)cz U. Положим VQ = B(x,l/2i), и
пусть Vj при / = 1, 2, ... — окрестность точки х> пересекающая-
пересекающаяся лишь с конечным числом членов семейства 9&\. Легко прове-
проверяется, что множество всех элементов семейства ^?, пересекаю-
i
щихся и с F= П Viy и с X\U, конечно.
Рассмотрим теперь любое ^-пространство X с регулярной
базой ^?. Легко проверить, что множества U и V, фигурирую-
фигурирующие в определении регулярной базы, удовлетворяют включению
V a U, Следовательно, пространство X регулярно. Для заверше-
завершения доказательства достаточно применить лемму 5.4.5 и метри-
метризационную теорему Нагаты — Смирнова. I
Чтобы выяснить соотношение между измельчениями и точеч-
точечно регулярными базами, мы формулируем следующую лемму в
несколько более общем виде, нежели это требуется для дока-
доказательства теоремы 5.4.8.
5.4.7. Лемма. Для произвольного хаусдорфова пространства X
следующие условия равносильны:
(i) Пространство X обладает точечно регулярной базой.
(и) Пространство X слабо паракомпактно и имеет измель-
измельчение.
5.4. МЕТРИЗАЦИОННЫЕ ТЕОРЕМЫ II 493
(Hi) Пространство X имеет измельчение, состоящее из то-
точечно конечных покрытий.
Доказательство. Покажем сначала, что (i)=>-(ii). Пусть °Ы —
любое открытое покрытие хаусдорфова пространства X, обла-
обладающего точечно регулярной базой Я. Семейство 3$0 всех эле-
элементов семейства Ш, содержащихся хотя бы в одном элементе
покрытия °U, очевидно, образует точечно регулярную базу про-
пространства X. Значит, по лемме 5.4.3, семейство &™ является
точечно конечным открытым покрытием, вписанным в °U. Сле-
Следовательно, пространство X слабо паракомпактно.
Остается доказать, что пространство X обладает измельче-
измельчением. Рассмотрим последовательность SSu $% •-• открытых по-
покрытий пространства Ху определенную в B). В силу леммы 5.4.5,
оо
,$= М ^.. Для произвольной точки хе!и любой ее окрест-
t=\
ности U лишь конечное число членов семейства J? — пусть это
Uи U2, ••-, Uk — содержат х и пересекаются с X\U. Так как
dii П &\ a3f(X) при i ф j и множества Uu V%, ..., Uk содержат
более одной точки, найдется натуральное число /, такое, что
Uj^$i при / = 1, 2, ..., k. Следовательно, St (x, Щ a U\ это
показывает, что ^?ь ^?2, ••• — измельчение пространства X.
Импликация (ii)=>-(iii) очевидна. Покажем, что (iii)=^(i).
Пусть Жи ТР%* ••• — измельчение пространства X, состоящее из
точечно конечных покрытий. Без ограничения общности можно
предположить, что W\ вписано в Wi при / ^ I. Ясно, что семей-
оо
ство J?= у ffli является базой пространства X. Эта база то-
точечно регулярна, так как для каждого х е X и любой окрест-
окрестности U точки х существует натуральное число i, такое, что
St(x,Wj)cz U при /^ i, и в каждом из покрытий Ж\, W%, ...
..., 39^1—1 лишь конечное число членов содержит точку х. I
5.4.8. Метризационный критерий Александрова. Топологическое
пространство метризуемо в том и только том случае, если оно
коллективно нормально и обладает точечно регулярной базой.
Доказательство. Каждое метризуемое пространство коллек-
коллективно нормально и, в силу 5.4.6, имеет точечно регулярную базу.
Произвольное коллективно нормальное пространство с то-
точечно регулярной базой метризуемо в силу леммы 5.4.7 и мет-
метризационного критерия Бинга. I
Заметим, что в последнем доказательстве вместо метриза-
метризационного критерия Бинга можно было бы применить лемму 5.4.7,
теорему Майкла — Нагами и метризационную теорему Нага-
ты — Смирнова.
494 ГЛ. 5. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА
Мы заключаем этот параграф наиболее ранней в хроноло-
хронологическом отношении метризационной теоремой.
5.4.9. Метризационная теорема Александрова — Урысона. Топо-
Топологическое пространство метризуемо в том и только том слу-
случае, если оно является 7^-пространством и обладает измельче-
измельчением Ж и Ж2, ..., таким, что для каждого натурального числа i
и любых двух пересекающихся множеств W\, W2^Wt+\ най-
найдется множество W <= Ж и такое, что W\ U №'2 с= W.
Доказательство. Легко проверяется, что для любой метрики
р на X последовательность^!, ЗРг» . • • > где Ж(=^{В(х, Щ1)}х<=х*
является измельчением пространства X и обладает нужным
свойством.
Рассмотрим теперь Г0-пространство Аг и его измельчение
Жи Ж^ •*., обладающее указанным в теореме свойством. По-
Покажем, что Ж и Жь ... — сильное измельчение пространства Х>
чем, в силу метризационной теоремы Мора, доказательство бу-
будет завершено. Пусть х — произвольная точка пространства X
и U—любая ее окрестность. Возьмем натуральное число /, для
которого St(x, Wi)cz U, и выберем УеУ,-+ь для которого
хе 1/. Для каждого W^Жь+\, пересекающегося с V, найдется
W'<=W*it такое, что V[}WczW'. Так как jceV, то V[)Wa
'ti^dcz U, т. е. St(V,3fm)c= U. I
5.4.10. Следствие. Топологическое пространство X метризуемо в
том и только том случае, если оно является Т^-пространством и
обладает измельчением Ж\, Ж%, ..-, таким, что Жь+\ сильно
звездно вписано в Ж{ при /=1,2, ... . I
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
Бинг установил свой метризационный критерий в [1951]. По-
Понятие измельчения было введено Читтенденом и Питчером в
[1919]; существование измельчения является одной из аксиом
Р. Л. Мора для абстрактных пространств (см. замечания
к § 1.1). Измельчения появляются также в работе П. С. Алек-
Александрова и П. С. Урысона [1923].
Регулярные пространства с измельчением называются мо-
ровскими пространствами. Со времени работы Джоунса [1937],
где было показано, что в предположении неравенства 2**° < 2**1
каждое сепарабельное нормальное моровское пространство мет-
метризуемо, много усилий было посвящено проблеме: метризуемо
ли каждое нормальное моровское пространство? Предположе-
Предположение о нормальности существенно: плоскость Немыцкого яв-
является моровским пространством. Дж. X. Силвер, в сотрудниче-
сотрудничестве с Толлом, доказал совместимость с обычными аксиомами
5.4. МЕТРИЗАЦИОННЫЕ ТЕОРЕМЫ II 495
теории множеств существования неметризуемого сепарабельного
нормального моровского пространства (см, диссертацию Толла
[1969]), Из этих результатов Джоунса и Силвера и Толла сле-
следует, что существование неметризуемого сепарабельного нор-
нормального моровского пространства не зависит от обычных
аксиом теории множеств. Этот факт и результаты Хита в [1964]
показывают, что существование неметризуемого сепарабельного
нормального пространства с точечно регулярной базой тоже не
зависит от обычных аксиом теории множеств (см. упр. 5.4.В).
Флейснер доказал в [1982], что существование неметризуемого
нормального моровского пространства вытекает из континуум-
гипотезы. Как вытекает из результатов Никоша [1980] и Флейс-
нера [1982], несуществование такого пространства связано с
аксиомами о больших кардиналах (подробности см. у Флейс-
нера [1984]).
Метризационная теорема Мора имеет длинную историю.
В настоящем виде она была доказана независимо А. Стоуном в
[1960] и Архангельским в [1961а], где было введено понятие
сильного измельчения. В несколько иной форме (предполага-
(предполагалось, что последовательность Ж\, Ж2> ... удовлетворяет усло-
условию A) этого параграфа) эта теорема была приведена
Р. Л. Мором в [1935] (см. также Джоунс [1966]) и переоткрыта
Моритой в [1951]. Метризационная теорема А. X. Фринка, уста-
установленная в [1937] (см. упр. 5.4.С), может рассматриваться как
еще одна разновидность той же теоремы. Отметим также, что
Куратовский в [1933] объявил принадлежащую Ароншайну мет-
метризационную теорему, весьма близкую к теореме 5.4.2.
Понятие точечно регулярной базы и теорема 5.4.8 появились
в работе П. С. Александрова [I960]; эта работа содержит до-
доказательство равносильности условий (i) и (iii) леммы 5.4.7
(то, что условия (i) и (и) равносильны, было установлено Хи-
Хитом в [1964]), Теорема 5.4.6 была доказана Архангельским
в [I960]; в его работе было введено понятие регулярной базы
и дано доказательство теоремы 5.4.8, приведенное выше.
Грубо говоря, понятия сильного измельчения и регулярной
базы получаются из понятий измельчения и точечно регулярной
базы путем замены точек открытыми множествами; модифика-
модификации этого рода приводят к условиям, равносильным метризуе-
метризуемости. Другое усиление измельчений и точечно регулярных баз,
тоже дающее условия, равносильные метризуемости, обсуждает-
обсуждается в упр. 5.4.Е.
Теорема 5.4.9 была доказана Александровым и Урысоном
в [1923а]. Следствие 5.4.10 (называемое некоторыми теоремой
Александрова — Урысона) появилось в книге Тьюки [1940] —
это слабая форма теоремы о порождении равномерностей мет-
метриками (см. теорему 8.1.21): она устанавливает только, что
496 ГЛ. 5. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА
если топология пространства X порождена некоторой равномер-
равномерностью Ш, обладающей счетной базой, то пространство X мет-
ризуемо, в то время как теорема 8.1.21 устанавливает боль-
большее— а именно что на X существует метрика, которая поро-
порождает равномерность °U.
Известно много других метризационных теорем. Некоторые
из них формулируются ниже в упражнениях. Есть также много
способов выводить их одну из другой. Ясно, что доказательство
теоремы, устанавливаемой первой, должно содержать построе-
построение метрики. В этой книге мы начали с теоремы Нагаты —
Смирнова. Можно было бы начать со следствия 5.4.10 (эскиз
построения метрики для этого случая дан в упр. 5.4.Н(а)) —
упорядочение метризационных теорем по этому принципу пред-
представлено в книге Нагаты [1968] (см. упр. 5.4.1). До открытия
метризационной теоремы Нагаты — Смирнова и теоремы 8.1.21
в качестве первого звена обычно бралась теорема Читтендена
(формулируемая ниже в упр. 5.4.G), которая сводит существо-
существование метрики к существованию функции р с более слабыми
свойствами. Хотя характеристика метризуемости, данная Чит-
тенденом, не является чисто топологической, она была важным
достижением в изучении метризуемости.
УПРАЖНЕНИЯ
5.4.А (Ю. М. Смирнов [1951а]). Убедитесь, что каждый ло-
локально метризуемый паракомпакт (т. е. паракомпакт, каждая
точка которого обладает метризуемой окрестностью) метризуем.
Указание. См. теорему 4.4.19.
5.4.В (Хит [1964]). Пусть X — подмножество плоскости,
определенное условием у ^ 0, т. е. замкнутая верхняя полу-
полуплоскость. Введем топологию на X, объявив все точки, лежащие
выше оси х, изолированными и объявив базой в точке (х, 0)
семейство всех отрезков, начинающихся в (х, 0) и образующих
с осью х угол 90°, если х рационально, и угол 45°, если х ирра-
иррационально. Докажите, что X — вполне регулярное не нормаль-
нормальное пространство с точечно регулярной базой. Покажите, что X
слабо паракомпактно и полно по Чеху, но не счетно параком-
пактно. Заметьте, что X можно представить в виде объединения
двух открытых метризуемых подпространств.
Указание. Примените теорему Бэра о категории для дока-
доказательства не нормальности X и не счетной паракомпактно-
паракомпактности X.
5.4.С (А. X. Фринк [1937]). Покажите, что Г0-пространство
X метризуемо в том и только том случае, если оно обладает си-
системой окрестностей {й(х)}хеХ, где J7(x) — {Bt(x)} Jt-ь такой,
что для каждого х е X и каждого натурального числа i най-
5.4. МЕТРИЗАЦИОННЫЕ ТЕОРЕМЫ II 497
дется /, для которого из В}(х)[]В1(у)Ф0 следует, что Bj(y)d
czBi(x).
Указание. См. замечания к этому параграфу.
5.4.D. (а) (Морита [1955]). Докажите, что Г0-пространство
X метризуемо в том и только том случае, если оно обладает
последовательностью #~ь ^2, ... локально конечных замкнутых
покрытий, такой, что для каждой точки х <= X и произвольной
ее окрестности U найдется натуральное число /, такое, что
St(^-/)ci U.
Указание. Можно предположить, что #~h-i вписано в &*i при
* = 1, 2, ... . Проверьте, что последовательность Ж и *№ъ •.-,
где Уг= {Int St(x, @~д}х^х> является сильным измельчением
пространства X.
(Ь) Докажите теорему Ханаи — Мориты — Стоуна с по-
помощью характеристики метризуемости, установленной в (а).
5.4.Е. (а) (Джоунс [1958]). Покажите, что Г2-пространство
X метризуемо в том и только том случае, если оно обладает
последовательностью Ж\, Ж%, ... открытых покрытий, такой, что
для каждого компакта ZcX и произвольного открытого мно-
множества U, содержащего Z, найдется натуральное число /, для
которого St(Z,W?)с U.
Указание. Примените теорему 5.4.2.
(Ь) (Архангельский [1965] (объявлено в [1963])). Пока-
Покажите, что ^-пространство X метризуемо в том и только том
случае, если у него есть база ^, такая, что для каждого ком-
компакта Z а X и произвольного открытого множества ?/, содержа-
содержащего Z, множество всех элементов базы $, пересекающих и Z,
и Х\0, конечно.
Указание. Примените теорему 5.4.6.
5.4.F (Нагата [1957а]). Докажите, что Г0-пространство X
метризуемо в том и только том случае, если для каждой точки
х^Х найдутся последовательность U\(x)y ?/г(-лО> .•• окрестно-
окрестностей точки х и последовательность А\(х)у А2{х), ... подмно-
подмножеств множества X, удовлетворяющие условиям:
(i) Для каждой точки х^Х и произвольной ее окрестности
U существует i, такое, что Ai(x)cz V.
(ii) Если Ui(x){]Ui(y)=?0,Toy<=Ai(x).
(iii) Если y^L Ui(x)t то (Ji(y)czAi(x).
Указание. Можно предположить, что Uj(x)a Ut(x) при
j^i и х^Х. Проверьте, что последовательность Ж\, Ж\, ...
где ffli = {Ut {x)}xeXJ является сильным измельчением про-
пространства X.
5.4.G (Читтенден [1917]). Докажите, что Г0-пространство X
метризуемо в том и только том случае, если существует неотри-
неотрицательная вещественная функция р на множестве ХУ^Х, такая,
32 Зак. 697
498 ГЛ. 5. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА
что для каждого А а X выполняется условие
infp(x, а) = 0 тогда и только тогда, когда Jtei,
а также условия (Ml) и (М2) из определения метрики и условие
(МЗ') Существует отображение f множества всех неотрицатель-
неотрицательных вещественных чисел в себя, для которого из
Hm tn = 0 следует, что lim/(^) = 0 « при всех х, у, г^Х
неравенства р(х, у)^ е и p(y,z)^ e влекут за собой не-
неравенство р (х, z) ^ f (e).
5.4.Н. (а) (Тьюки [1940]). Докажите, что для каждой по-
последовательности Жо> Ж\, ••• покрытий множества X, где Жо =
= {X} и Wi+\ сильно звездно вписано в Wt при i= 1, 2, ...,
найдется псевдометрика р на множестве X, такая, что при всех
/ ^ 1 покрытие Жг вписано в покрытие {В(ху 1/21Ч)}хеХ и по-
покрытие {В (х, 1/2')}^^ вписано в yfVi.
Заметьте, что если X — топологическое пространство, а по-
покрытия Wi открыты, то р — непрерывное отображение простран-
пространства X X X в R.
Воспользовавшись замечанием 4.4.2, выведите из этого ре-
результата лемму 5.1.16.
Указание. Определите отображение /множества XXX в R
правилом
{оо
0, если у^ П St(x, ЖЬ)У а иначе
1/2', где у ее St(x, Г,) \St(x,
Определите р(я, у) как наибольшую нижнюю грань множества
всех чисел вида ? f{%i-u xt), где х0, хь ..., х^ — любая после-
i = \
довательность точек множества X, такая, что х0 = х и х& = у,
и покажите, что A/2)/(х, у) ^ р(х, у) ^ /(х, у) (см. доказатель-
доказательство теоремы 8.1.10).
(b) (Тьюки [1940]). Проверьте, что если Жо, Жи ..., где
W\ = {X} и У,-+1 сильно звездно вписано в Жг при i = 1, 2, ...,
является измельчением 70-пространства X, то псевдометрика
р, фигурирующая в (а), является метрикой на X (см. след-
следствие 5.4.10).
(c) (Тьюки [1940], Морита [1962] и [1964]). Покажите, что
для каждого открытого покрытия {[/s}seS произвольного то-
топологического пространства X следующие условия равносильны:
A) Покрытие {Us}s^s нормально.
B) Существуют псевдометрика р на множестве X, для ко-
которой отображение р: Xy^X^R непрерывно, и покрытие
5.5. ЗАДАЧИ 499
множества Xt открытое по отношению к топологии, по-
порожденной псевдометрикой р, такие, что Vs c= Us при всех s е S.
C) Существуют непрерывное отображение f: X^Y на мет-
ризуемое пространство Y и открытое покрытие {Ws}SfBS про-
пространства У, такие, что /-1(Ws)cz Us при всех seS.
D) В покрытие {U8}S€sS можно вписать локально конечное
покрытие, состоящее из функционально открытых множеств.
E) В покрытие {Us}s<=s можно вписать а-локально конеч-
конечное покрытие, состоящее из функционально открытых мно-
множеств.
Указание. Примените упр. 5.I.J.
(d) (A. X. Стоун [1948]). Проверьте, что открытое покрытие
нормального пространства нормально в том и только том слу-
случае, если в него можно вписать локально конечное открытое
покрытие.
5.4.1 (Нагата [1950]). Выведите из следствия 5.4.10, что
каждое регулярное пространство, обладающее а-локально ко-
конечной базой, метризуемо.
оо
Указание. Пусть X — регулярное пространство и ^= U Шг—
база пространства X, где $i = {Us}S(^s —локально конечное
покрытие пространства X. При каждом i обозначим через Wi
семейство всех конечных подмножеств множества St. С помощью
леммы 4.4.5 при каждом seS; получите замкнутые множества
оо
Fs,u Fs,2> ..., такие, что Us= [} Fs,j. Затем при ГеУ,- и
/=1, 2, ... положите WT,= fl ?/*flf*\U Л.Л- Пока-
жите, что при /, /= 1, 2, ... семейство F'j,/ = \Wt,\\t^& . яв"
ляется локально конечным открытым покрытием пространства X
и что если расположить покрытия JTit у как-нибудь в виде после-
последовательности, то они составят измельчение пространства X
С помощью теоремы 1.5.18, лемм 5.1.13 и 5.1.15 и замеча-
замечания 5.1.14 получите измельчение W\, ^2, ..., такое, что Jf\-+i
сильно звездно вписано в Wi при i= 1, 2, ... (можно восполь-
воспользоваться также теоремами 5.1.11 и 5.1.12).
5.5. ЗАДАЧИ
Коллективная нормальность
5.5.1. (а) (Маколей [1958]). Докажите, что для любого
7гпространства X следующие условия равносильны:
A) Пространство X наследственно коллективно нормально.
32*
500 ГЛ. 5. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА
B) Каждое открытое подпространство пространства X кол-
коллективно нормально.
C) Для любого семейства {Fs}8eS подмножеств простран-
пространства Ху дискретного в объединении F = у Fs, найдется семей-
ство {US}S€3S попарно не пересекающихся открытых в X мно-
множеств, такое, что Fs cr Us при всех s^S.
(b) (Шедива [1959]). Покажите, что коллективная нормаль-
нормальность наследуется /^-множествами. Заметьте, что совершенно
нормальное коллективно нормальное пространство наследствен-
наследственно коллективно нормально.
Указание. См. задачу 2.7.2(а).
(c) Докажите, что ^-пространство X коллективно нормально
в том и только том случае, если для каждого кардинала m ^ Но
произвольное непрерывное отображение /: Л-^/(т) любого
замкнутого подпространства А пространства X в пространство
/(ш) можно непрерывно продолжить на всё X.
Указание. Пусть непрерывное отображение /: Л-^/(ш) опре-
определено на замкнутом подпространстве А коллективно нормаль-
нормального пространства X. Рассмотрите отображение g: J(m)-*If
определенное так: g( [(x, s)]) = х при всех хе/ и s^St где
[(х, s)] и 5 —такие, как в примере 4.1.5. Возьмите какое-ни-
какое-нибудь непрерывное продолжение G: X-+I композиции gf: A-+L
Заметьте, что множества Fs = f~l{{[{xts)]: 0<x^l}) со-
составляют дискретное семейство замкнутых подмножеств в
G'~!(@, 1]). Воспользовавшись (Ь), возьмите семейство {Us}s^s
попарно не пересекающихся открытых множеств в Ху таких, что
Fs cz Us при всех seS. Продолжите функцию h: A U (X \ (J Us] ->
V se=S )
->/, определенную условиями h\A = gf и h (X \ U иЛ cz
cr {0}, до некоторой непрерывной функции Я: Х->1. По-
Положите F(x) = [(H(x),s)] при x<=Us и F(x) = [@, s)] при
Х€=Х\ U Us-
Операция Хм
5.5.2. (а) Проверьте, что для каждого подпространства М
наследственно нормального пространства X пространство Хм
наследственно нормально.
(b) Проверьте, что для каждого подпространства М наслед-
наследственно коллективно нормального пространства X пространство
Хм наследственно коллективно нормально.
(c) (Фурдзик [1968]). Покажите, что если М — подпростран-
подпространство совершенно нормального пространства Ху то пространство
5.5. ЗАДАЧИ 501
Хм совершенно нормально в том и только том случае, если
М — множество типа G6 в X.
(d) Покажите, что если М — подпространство метризуемого
пространства Xt то пространство Хм метризуемо в том и только
том случае, если М — множество типа G6 в X.
Вокруг примеров Бинга и Майкла
5.5.3. (а) (Бинг [1951]). Заметьте, что пространство X в при-
примере 5.1.23 наследственно нормально, но не совершенно нор-
нормально.
оо
Рассмотрите множество Z = (MU{0})U U (^ХО/0) и вве"
дите топологию на Z, приняв за базу в каждой точке (х, 0) со-
оо
вокупность всех множеств вида{(х, 0)} (J [] (t/XO/О)» где U —
i=k
произвольная окрестность точки х в пространстве X и k= 1,
2, ..., а все остальные точки объявив изолированными. Про-
Проверьте, что пространство Z совершенно нормально, но не кол-
коллективно нормально. Убедитесь, что Z обладает а-дискретной
сетью, и выведите отсюда, что в каждое открытое покрытие
пространства Z можно вписать замкнутое а-локально конечное
покрытие.
Замечание. Топологическое пространство Xt в любое откры-
открытое покрытие которого можно вписать замкнутое а-локально ко-
конечное покрытие, называется субпаракомпактным. Класс суб-
паракомпактных пространств широко изучался. Он был введен
Маколеем в [1958] под названием Fa-просеянных пространств.
Позднее Архангельский определил в [1966b] класс а-параком-
пактных пространств. Пространство X называется о-параком-
пактным, если для каждого открытого покрытия °U простран-
пространства X найдется последовательность Ж\у Жч, ... открытых по-
покрытий пространства X, обладающая тем свойством, что для
каждой точки хе! существуют натуральное число i и множе-
множество U^l°U, такие, что St(x,Wi)cz 0 (таким образом, каждое
топологическое пространство с измельчением а-паракомпактно).
Бурке доказал в [1969] совпадение /^-просеянности и а-пара-
комиактности; он ввел также термин «субпаракомпактность»
и дал другие характеристики субпаракомпактности.
(b) Покажите, что пространство X в примере 5.1.23 и про-
пространство Z в (а) не слабо паракомпактны.
Указание, С помощью задачи 2.7.11 (Ь) покажите, что только
счетное число членов произвольного точечно конечного откры-
открытого покрытия пространства X может пересекать множество М.
(c) (Майкл [1955]). Пусть 5 — подпространство простран-
пространства X из примера 5.1.23, состоящее из всех точек множества
502 ГЛ. 5. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА
D2\ лишь конечное число координат которых отлично от нуля.
Проверьте, что пространство Хо = S [} М cz X нормально и слабо
паракомпактно, но не коллективно нормально. Приведите при-
пример совершенно нормального пространства с этими свойствами.
5.5.4. (а) (Майкл [1963]). Видоизменив пример 5.1.32, опре-
определите наследственно паракомпактное пространство X со свой-
свойством Линделёфа и сепарабельное метризуемое пространство У,
такие, что произведение XX У не нормально (см. задачу 5.5.5
и упр. 5.1.F(c)).
Указание (Куратовский и Серпинский [1926]). Применив
трансфинитную индукцию, докажите, что для каждого множе-
множества X мощности с и произвольного семейства *& мощности с, со-
состоящего из подмножеств мощности с множества X, найдется
множество AczX, такое, что |Л| = с и А{\Сф 0 Ф(Х\А)[\С
при всех Се?. Выведите отсюда, воспользовавшись зада-
задачей 4.5.5, что существует подмножество А мощности с веществен-
вещественной прямой, для которого каждый компакт, лежащий либо в Л,
либо в R\A, счетен (произвольное множество AczR, обладаю-
обладающее последним свойством, называется множеством Бернштейна;
такие множества были впервые определены Бернштейном в
[1908]).
(b) (Майкл [1963]). Видоизменив пример 5.1.32, определите
сепарабельное линделёфово пространство X и сепарабельное
метризуемое пространство У, такие, что произведение XX У не
нормально.
Указание. Определите сепарабельное линделёфово простран-
пространство, содержащее пространство X из (а) в качестве замкнутого
подпространства.
(c) Определите обратную последовательность линделёфовых
пространств, предел которой не нормален и не слабо параком-
пактен.
Указание. Разложите R на непересекающиеся множества
Аи А2> ... мощности с, такие, что при i= 1, 2, ... каждый ком-
компакт, лежащий в R\At, счетен.
Паракомпактность произведений
5.5.5. (а) (Майкл [1953]). Докажите, что произведение
XX У совершенно нормального паракомпактного пространства
X и метризуемого пространства У паракомпактно.
Указание. Покажите, что произведение XX У удовлетворяет
условию (п) теоремы 5.1.11. Воспользуйтесь задачей 4.5.16(а)
и тем, что определенное в доказательстве теоремы 5.1.28 семей-
семейство 9И су-локально конечно в X.
(Ь) (Майкл [1953]). Докажите, что произведение XX У па-
5.5. ЗАДАЧИ 503
ракомпакта X и регулярного а-компактного пространства У па-
ракомпактно.
(c) (Морита [1953]). Докажите, что произведение XX У
паракомпакта X и локально компактного паракомпакта У па-
ракомпактно.
(d) (Уиллард [1971]). Заметьте, что произведение XX У
линделёфова пространства X и пространства У, обладающего
всюду плотным су-компактным множеством (в частности, произ-
произведение линделёфова пространства X и сепарабельного про-
пространства У), паракомпактно в том и только том случае, если
оно обладает свойством Линделёфа.
Указание. См. теорему 5.1.25.
(e) (Тамано [1962]). Выведите из теоремы Тамано, что для
каждого топологического пространства X следующие условия
равносильны:
A) Для каждого паракомпакта У произведение X X Y яв-
является паракомпактом.
B) Для каждого паракомпакта Y произведение Xy^Y нор-
нормально.
Замечание. Не существует внутренней характеристики класса
пространств, для которых произведение на каждый параком-
пакт является паракомпактом (см., однако, Катута [1971]).
Работа Тельгарского [1971] содержит новые результаты в этом
направлении и обсуждение более ранних результатов (см. за-
задачу 5.5.9 (Ь)).
5.5.6 (А. X. Стоун [1948]). Докажите, что следующие усло-
условия равносильны для произвольного семейства {^s}se5 метри-
зуемых пространств:
A) Произведение JJ Xs нормально.
B) Произведение Ц Xs коллективно нормально.
C) Произведение Ц Xs паракомпактно.
D) Множество некомпактных подпространств семейства
{Xs}S€eS не более нем счетно.
Указание. Примените задачу 2.7.16(а).
Замечание. Как отмечено в замечании к задаче 2.7.15 (d),
оо
существует не нормальное произведение Г1^> Для которого
все конечные произведения Х\ X ^2 X • • • X %t наследственно
паракомпактны и хаусдорфовы. С другой стороны, Нагами до-
доказал в [1972], что предел произвольной обратной последова-
последовательности совершенно нормальных паракомпактных пространств
является совершенно нормальным паракомпактом.
504 ГЛ. 5, ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА
Паракомпакты с диагональю типа G6
5.5.7 (Окуяма [1964], Борджес [1966]). (а) Покажите, что если
X — паракомпакт и диагональ А является множеством типа G6
в Ху^Х, то существует взаимно однозначное непрерывное ото-
отображение1) пространства X на некоторое метризуемое про-
пространство.
Указание. Определите счетное семейство {Уь}°°=1 локально
конечных открытых покрытий пространства X так, чтобы для
каждой пары х, у различных точек пространства X существо-
существовал номер /, при котором никакой элемент семейства Ti не
содержит одновременно х и у. Каждому покрытию Yi поставьте
в соответствие подходящую псевдометрику рх-: ХУ^Х^-R, а за-
затем определите метрику на множестве X.
Можно взять также замкнутое (?6-множество FсХХР^.
для которого F(](Xy^ X) = А, определить непрерывную функ-
функцию f: X X pj-> /, такую, что F = f~l @), и положить р (х, у) =
= SUp \f(x9 Z)~f(yy 2I
(b) Докажите, что паракомпакт X с диагональю А типа G6
в!Х^ метризуем в том и только том случае, если X допускает
совершенное отображение на метризуемое пространство.
Указание. Примените теорему 3.7.27.
(c) Заметьте, что утверждением (Ь) решается упр. 4.2.В,
(d) Приведите пример паракомпакта, который не допускает
совершенного отображения на метризуемое пространство.
(e) (Нагата [1969]). Заметьте, что топологическое простран-
пространство X допускает совершенное отображение на метризуемое про-
пространство в том и только том случае, если X гомеоморфно
замкнутому подпространству произведения YXZ метризуемого
пространства У на компакт Z.
Замечание. Класс всех пространств, допускающих совершен-
совершенное отображение на метризуемое пространство, был недавно
подробно изучен. Обсуждение результатов, полученных в этом
направлении, можно найти в работах Архангельского [1966b]
и Мориты [1971] (см. задачу 5.5.9(а) и (d)).
Паракомпактность и полные по Чеху пространства
5.5.8. (а) (Пасынков [1967]; для метризуемого X — Майкл
[1959]). Докажите, что для произвольного открытого отобра-
отображения /: X-+Y полного по Чеху пространства X на параком-
паракомпакт Y найдется замкнутое C6-множество А^.ХУ такое, что су-
сужение f\A: A-^Y является совершенным отображением про-
пространства А на У.
]) Такие отображения называются уплотнениями. — Прим. перев.
5,5. ЗАДАЧИ 505
Указание. Рассмотрите непрерывное продолжение F: $Х-+-
->рУ отображения / и совершенное отображение g = FY: Z-*Yf
где Z = F~l(Y). Покажите сначала, что для каждого открытого
множества G пространства Z, такого, что f(Xf}G)=Y, най-
найдется открытое множество HczZ, для которого f(X[)H)=Y
и flcG, где черта обозначает замыкание в Z. С этой целью
выберите для каждого y^Y открытое множество V(y)czZ, та-
такое, что f~l(y)() У{у)Ф 0 и V(y)czG. Возьмите затем какое-
нибудь локально конечное открытое покрытие {Us}sgeS про-
пространства У, вписанное в покрытие {f(X[}V(y))}yeY этого про-
пространства. При каждом s^S выберите j/(s)ey, такое, что
Us^f[X(]V(y(s))]t и положите Н= (j [V(y(s))(]g'l(Us)l
sgS
оо
Представьте X в виде {] Gt, где каждое Gt открыто в Z.
i = \
Определите по индукции последовательность #о = Z, Ни #2, . •.
открытых подмножеств в Z, такую, что Я,-с G,-f| #i-i и f(X[)
оо оо
fl Hi) = Y при i = 1, 2, ... . Положите А = П Ht = П #;•
(b) (Пасынков [1967]). Покажите, что если /: X-*-Y — от-
открытое отображение локально полного по Чеху пространства X
на паракомпакт У, то У полно по Чеху.
Указание. Каждое локально полное по Чеху пространство
является образом некоторого полного по Чеху пространства при
открытом отображении.
(c) (Архангельский [1961], Фролик [1961]). Выведите из
(Ь), что каждый локально полный по Чеху паракомпакт полон
по Чеху.
(d) (Майкл [1959]; для метризуемого У — Хаусдорф [1934];
для сепарабельных метризуемых X и Y — Серпинский [1930]).
Докажите, что если паракомпакт У является образом полного
метризуемого пространства X при открытом отображении, то У
метризуемо полной метрикой.
Замечание. Майклом было доказано в [1959], что если
f: X^-Y — открытое отображение метризуемого пространства X
на паракомпакт У, такое, что прообразы f~l(y) всех точек полны
относительно некоторой метрики на пространстве X, то про-
пространство Y метризуемо.
5.5.9. (а) (Фролик [I960]). Докажите, что топологическое
пространство X паракомпактно и полно по Чеху в том и только
том случае, если оно допускает совершенное отображение на
некоторое метризуемое полной метрикой пространство.
Указание. Если X — полный по Чеху паракомпакт, то най-
найдется непрерывная функция /: ХХ,$Х-*1У для которой Дс
506 ГЛ. 5. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА
f^ Рассмотрите псевдометрику р на множествеX,
определенную формулой р(лг, у)= sup \f(x, z) — f{y, z)\, и
пространство У = Х/р (см. упр. 4.2.1).
(b) (Фролик [I960]). Выведите из (а) и теоремы 3.7.7, что
произведение счетного семейства полных по Чеху паракомпак-
тов является полным по Чеху паракомпактом (см. упр. 3.9.F).
(c) Заметьте,что (а) и задача 5.5.7 (Ь) дают решение упр. 5.1.1.
(d) (Шостак [1974]). Покажите, что топологическое про-
пространство X веса =^m ^ So является полным по Чеху параком-
паракомпактом в том и только том случае, если X гомеоморфно замк-
замкнутому подпространству произведения [/(m)]s°X/m-
Указание. Воспользуйтесь задачей 5.5.7(е) и упр. 4.4.В.
Паракомпактность и вещественно полные пространства
5.5.10 (Катетов [1951]). (а) Докажите, что паракомпакт X
вещественно полон в том и только том случае, если каждое
замкнутое дискретное подпространство пространства X веще-
вещественно полно (см. задачу 8.5.13(h)).
Указание (Мрувка [1964]). Возьмем какую-нибудь точку
А'о е РХ\Х и а-дискретное замкнутое покрытие У простран-
пространства X, такие, что х^фР при всех F ^&~, где черта обозначает
оо
замыкание в рХ Положим Fi = [} ЗГ^ где $Г — [} 3Tt и семей-
ства !Fi дискретны. Если Xq^Fi при i=l, 2, ..., то легко
определяется непрерывная функция h: Х->19 такая, что /i(xo) =
= 0 и А(лс)>0 при всех л;бХ. Значит, можно предположить,
что x0effo. Рассмотрите отношение эквивалентности Е на про-
пространстве y = f\oU{#o}, отвечающее разбиению «? = ^"^11 {#0}»
возьмите факторпространство Z = Y/E и естественное фактор-
факторное отображение q: Y^~Z. Заметьте, что Z — тихоновское про-
пространство и что выполняется условие pZ = рГ, где T = q(F.y,
воспользуйтесь теперь вещественной полнотой пространства Т.
(b) Заметьте, что если мощность каждого замкнутого дис-
дискретного подпространства паракомпакта X является неизмери-
неизмеримым кардиналом, то X вещественно полно (см. задачу 8.5.13(h)).
Указание. Примените упр. 3.11.D(a).
(c) Убедитесь, что если f: X-^-Y — непрерывное отображе-
отображение вещественно полного пространства X на паракомпакт У,
то У вещественно полно.
Компактно накрывающие отображения
5.5.11. Непрерывное отображение f: Х->У называется ком-
компактно накрывающим, если для каждого компакта В а У най-
найдется компакт A a Xt такой, что f(A)— 5.
5.5. ЗАДАЧИ 507
(a) (Архангельский [1964]). Покажите, что каждое ком-
компактно накрывающее отображение со значениями в ^-простран-
^-пространстве является факторным.
(b) (Майкл [1964а]). Покажите, что если f: X-+Y— замк-
замкнутое отображение пространства X на пространство Y точечно
счетного типа, то для каждой непрерывной функции g: X->R
и любого г/EF множество g(Fvf~~l(y)) ограничено1). Выве-
Выведите отсюда, что если пространство X нормально, то множества
Frf~l(y) счетно компактны (см. лемму 4.4.16 и упр. 4.4Л).
Указание. Каждая точка i/еУ имеет такую систему окрест-
окрестностей {Vi}7=\, что для любой последовательности уи #2, ..•>
где yt^Vi при i= 1, 2, ... и уьфу] при / ф /, у множества
{уи #2, . • •} есть предельная точка.
(c) (Майкл [1964а]; объявлено для метризуемого X — Ар-
Архангельский [1964]). Докажите, что каждое замкнутое отобра-
отображение f: X^Y паракомпакта X на произвольное2) простран-
пространство Y является компактно накрывающим.
Указание. См. доказательство теоремы 4.4.17.
(d) Покажите, что в (с) нельзя заменить предположение
о паракомпактности X предположением о коллективной нор-
нормальности X.
(e) (Архангельский [1966а] (объявлено в [1964]); для мет-
метризуемого X — Бурбаки [1958]). Докажите, что каждое откры-
открытое отображение f: X^-Y полного по Чеху пространства X на
произвольное пространство Y является компактно накры-
накрывающим.
Указание. См. задачу 5.5.8(а).
(f) (Майкл [1959]). Приведите пример открытого отобра-
отображения сепарабельного метризуемого пространства на (замкну-
(замкнутый) единичный отрезок /, не являющегося компактно накры-
накрывающим.
Указание. В квадрате /2 уберите подходящим образом по
точке с каждого вертикального отрезка.
Непроводимые отображения
5.5.12 (Лашнев [1965]). Докажите, что если /: X->Y—
замкнутое отображение паракомпакта X на пространство Фре-
ше — Урысона У, то найдется замкнутое подпространство Xocz
*) Сейчас принято называть подмножество А топологического простран-
пространства X R-ограниченным в X (или просто ограниченным), если каждая непре-
непрерывная вещественная функция на X ограничена на А снизу и сверху. —
Прим. перев.
2) Обратим внимание читателя на то, что в определении компактно на-
накрывающего отображения фингурируют не произвольные компактные подпро-
подпространства, а компакты. — Прим. перев.
508 r. 5. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА
cr X, для которого f(X0)=Y и отображение f\X0: XQ-*Y не-
приводимо (см. упр. 3.1.С).
Указание. Рассмотрите замкнутое множество В = А [}
{}f-l(Yd)czX, где А получено путем выбора по точке из про-
прообраза f~l(y) каждой изолированной точки //eF, и возьмите
семейство 2Г всех замкнутых подмножеств Fa: В, таких, что
f(F)= У, упорядоченное отношением zd. Предположите, что для
некоторого линейно упорядоченного подсемейства {Fs}5eS се-
семейства $~ нашлась точка yo^Y, такая, что/~!(#0)П П ^s —
S
s
= 0. Возьмите произвольную нетривиальную последователь-
последовательность у\, У2, •-., сходящуюся к #о, и, воспользовавшись зада-
оо
чей 5.5.11(Ь), заметьте, что множество f~{(yo){] U f~l(tfi) ком-
компактно. Выведите отсюда противоречие. Примените затем лемму
Куратовского — Цорна.
Паракомпактность пространств отображений
5.5.13. (а) (О'Мира [1971]). Докажите, что если X — сепа-
рабельное метризуемое пространство и У-—метризуемое про-
пространство, то пространство Yx с компактно открытой тополо-
топологией совершенно нормально и наследственно паракомпактно
(см. упр. 3.8.D).
Указание. Пусть {xi, х2, ...}—счетное всюду плотное в X
множество и $ есть а-дискретная база пространства У. Зафик-
Зафиксируем метрику р на пространстве X и для каждой (конечной)
последовательности м, h, •••> ik натуральных чисел, произволь-
произвольной последовательности Ви В2, ..., В/г элементов базы $ и лю-
любого натурального числа т положим
A) U(h, l%, ... , ik\ В{, В2> ••• » Bk)= \ I ^({xi/}> ^/)
и
k
B) Mm(iv iv ... , V, Bv B2, ... , Bk) = ^M(B(xijt l//n),B.).
Проверьте, что множества в A) составляют а-дискретное от-
открытое покрытие пространства У*, а множества в B) образуют
сеть в Yx.
(b) Докажите, что если X — сепарабельное метризуемое про-
пространство и У — метризуемое пространство, то пространство Yx
с топологией поточечной сходимости совершенно нормально
и наследственно паракомпактно (см. упр. 3.8.D).
Указание. Проанализируйте доказательство утверждения (а).
5.5. ЗАДАЧИ 509
Пространство N*1 не является ни счетно паракомпактным, ни
слабо паракомпактным
5.5.14. (а) (Нагами [1972]). Покажите, что пространство
#Kl не счетно паракомпактно (см. задачу 5.5.6).
Указание. Положим 7VKl = Yl Xs, гДе XS = N и |5|=Кь
Для каждого натурального числа k рассмотрите множество
Ak^ П Xs, состоящее из всех {xs}, таких, что при всяком
У Ф k равенство xs = / выполняется самое большее для одного
оо
s^S. Положите Ft= (J Ak и примените теорему 5.2.1 и за-
задачу 2.7.12(а).
(Ь) Убедитесь, что пространство N**1 не слабо параком-
паракомпактно.
Счетная паракомпактность в нормальных пространствах
5.5.15 (Мансфилд [1957]). Докажите, что для каждого нор-
нормального пространства X следующие условия равносильны:
A) Пространство X счетно паракомпактно.
B) В каждое счетное открытое покрытие пространства X
можно вписать локально конечное замкнутое покрытие.
C) В каждое счетное открытое покрытие пространства X
можно вписать о-локально конечное замкнутое покрытие.
D) В каждое счетное открытое покрытие пространства X
можно вписать о-дискретное замкнутое покрытие.
E) В каждое счетное открытое покрытие пространства X
можно сильно звездно вписать счетное открытое покрытие.
F) В каждое счетное открытое покрытие пространства X
можно сильно звездно вписать открытое покрытие.
Fa-множества в счетно паракомпактных пространствах
5.5.16 (Зенор [1976]). (а) Покажите, что свойство быть
счетно паракомпактным нормальным пространством насле-
наследуется /^-множествами.
(Ь) Докажите, что если все /^-подмножества произведения
(Y — счетно паракомпактные хаусдорфовы пространства, то
либо X нормально, либо все счетные дискретные подпростран-
подпространства пространства Y замкнуты.
Указание. Предположим, что {уи 1/2, . • }—счетное дискрет-
дискретное подпространство пространства У, у которого есть в Y пре-
предельная точка г/о- Возьмем замкнутое множество F cz X, от-
открытое множество WczX, содержащее F, и рассмотрим под-
510 ГЛ. 5. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА
со
пространство А = (J Ft пространства XX У, где /ч) —
j0
и Ft = ZX {yi} при t^l. В открытое покрытие {?Л}I0 под-
подпространства Л, где ?/о = (И?Х У)П^ и Ui — Ft при i ^ 1>
можно вписать локально конечное открытое покрытие {Vi}^=Qy
такое, что ViCzUi при / = 0, 1, ... . Проверьте, что последова-
последовательность Wu W2, ..., где Wi = X\'p(VT) и р: XXY-+X —
проекция, удовлетворяет условиям леммы 1.5.14.
(с) Выведите из (Ь), что счетная паракомпактность не на-
наследуется /^-множествами.
Продолжение локально конечных семейств множеств
5.5,17 (Мансфилд [1957]). Покажите, что хаусдорфово про-
пространство X счетно паракомпактно в том и только том случае,
если для каждого счетного локально конечного семейства
(Л)П=1 замкнутых множеств в X найдется локально конечное
семейство {V^}°°=1 открытых множеств, такое, что Ft a Vi при
1=1,2, ... .
Указание. Пусть 9> — семейство всех конечных множеств на-
натуральных чисел. Для каждого х^Х возьмем окрестность
U(x) точки х и множество 5(лг)е^, такие, что Fif]U(x)= 0
при i^S(х). Пусть U$ = [}{U(x): S(х) = S}; возьмем локально
конечное открытое покрытие {lfs}5G^ пространства X, такое,
чю Ws a Us при всех 5еУ,и положим Vt = U Ws.
5.5.18. (а) (Даукер [1956]). Докажите, что нормальное про-
пространство X коллективно нормально и счетно паракомпактно
в том и только том случае, если для каждого локально конеч-
конечного семейства (FS}J6S замкнутых в X множеств найдется
локально конечное семейство {VS}S(_5 открытых множеств, та-
такое, что Fs cz Vs при всех sgS.
Указание (Катетов [1958]). Заметьте сначала, что при до-
дополнительном предположении, что никакая точка пространства
X не принадлежит более чем i множествам Fs, существование
такого семейства {Vs}se5 следует из коллективной нормально-
нормальности X (примените индукцию по /). Затем, обратившись к об-
общему случаю, положите F = U Fs и обозначьте через Wt под-
множество множества Fy состоящее из всех точек, которые при-
принадлежат самое большее к i множествам Fs. Рассмотрите
локально конечное замкнутое покрытие {Е^^х пространства Т7,
вписанное в открытое покрытие {Wi}°°=x этого пространства.
5.5. ЗАДАЧИ 511
Воспользовавшись задачей 5.5.17, возьмите локально конечное
семейство {Vi}^L{ открытых множеств в X, такое, что EiczVi
при /= 1, 2, ... . Для каждого i рассмотрите локально конеч-
конечное семейство {Vs, i}S(=s открытых множеств в X, такое, что
с»
Fs ftEt a V8t t и положите Vs= [} (V8m tu\Vi).
i = l
(b) (Смит и Краевский [1971]). Докажите, что для каждого
локально конечного семейства {FJjeS замкнутых множеств
в слабо паракомпактном пространстве X существует точечно
конечное семейство {VS}5€5S открытых множеств, такое, что
Fs a Vs при всех s e S.
Указание. См. указание к задаче 5.5.17.
Коллективная нормальность и произведения
5.5.19. (а) (Алас [1971]). Докажите, что если пространство
X коллективно нормально и счетно паракомпактно, то при каж-
каждом m ^ Ко произведение IX^W нормально.
(b) (Алас [1971]). Покажите, что если произведение XX
УСА(т)у где т = |Х|, нормально, то пространство X коллек-
коллективно нормально и счетно паракомпактно.
(c) (Алас [1971]). Докажите, что если произведение XX
А()$ где т^|Х|, нормально, то оно также и коллективно
нормально.
(d) (Морита, цитировано в Исии [1966]). Докажите, что
если произведение X X У нормального пространства X и метри-
зуемого пространства У счетно паракомпактно, то Xy^Y нор-
нормально.
Указание (М. Э. Рудин и Старбёрд [1975]). Возьмите ка-
какую-нибудь метрику на пространстве У и рассмотрите последо-
последовательность <U\, °11ч, ... локально конечных открытых покрытий
пространства У, где 6(U) < l/i при ?/е °Ui: и 4li+\ вписано в Щ{.
Рассмотрите произвольное замкнутое множество FczXXY и
любое открытое множество WczXy^Y, содержащее F. Для каж-
каждого U e °Ui возьмите множество
где р обозначает проекцию пространства XX Y на X. Убедитесь,
что множества Л< = [){A(U)X О: ?/е%} замкнуты, образуют
убывающую последовательность и удовлетворяют условию
оо
П At= 0. Воспользовавшись теоремой 5.2.1, возьмите убываю-
убывающую последовательность V\9 ^2> ... открытых множеств в ХХ^>
512 ГЛ. 5. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА
такую, что At c= Vi при i = 1, 2, ... и f] Vt = 0. Проверьте, что
для каждого Ut=°Ui множества ?(?/) = р[(*Х #)ПЛ\рI(*Х
Xf/jnVi] и C{U)=p[(XXU)\W] замкнуты и не пересе-
пересекаются. Возьмите открытое множество W(U)czX, для которого
C(U)f]W(U)=0 и B(U)czW(U). Убедитесь, что множества
Wi— U{^(t/)X U~ U^°Ui) удовлетворяют условиям лем-
леммы 1.5.14.
Замечание. В [1975] Рудин и Старбёрд доказали также, что
если произведение -XX У счетно паракомпактного пространства
X и метризуемого пространства У нормально, то XX У счетно
паракомпактно.
(е) Докажите, что произведение JX Y совершенно нормаль-
нормального коллективно нормального пространства X и метризуемого
пространства У коллективно нормально (см. задачи 4.5.16(Ь)
и 5.5.5(а)).
Указание. Пусть т = |ХХУ|^^о- Воспользовавшись зада-
задачей 4.5.16(Ь), следствием 5.2.5 и упр. 5.2.G(b), заметьте, что
(Xy(Y)y^A(m) счетно паракомпактно. Выведите затем из (а),
что пространство ZX^W нормально, и примените (d) и (Ь).
Полунепрерывные функции III (см. задачи 1.7.14—1.7.16, 2.7.4
H3.12.22(g)).
5.5.20 (Даукер [1951], Катетов [1951а]; для паракомпакт-
ных пространств — Дьедонне [1944]). Докажите, что ^-про-
^-пространство X нормально и счетно паракомпактно в том и только
том случае, если для любых вещественных функций f и g на Х>
таких, что f полунепрерывна сверху, g полунепрерывна снизу
и f(x)<g(x) при всех xgI, найдется непрерывная функция
h: X->¦/?, для которой f(x) < h(x) < g{x) при всех х^Х.
Указание. Определяя А, рассмотрите счетное открытое по-
покрытие пространства X, образованное всеми множествами Ur =
= {х^Х: f(x)<Z г < g(x)}, где г — любое рациональное число.
Теорема Борсука о продолжении гомотопии
5.5.21 (Даукер [1951]; для метризуемого X — Борсук [1937]).
Пусть X и У — топологические пространства и /0. h — непре-
непрерывные отображения пространства X в У. Если существует
такое непрерывное отображение F: ХУA-+УУ что F(xy i)= fi(x)
при i = 0 и i = 1, то мы говорим, что отображения fQ и f\ гомо-
гомотопны; отображение F при этом называется гомотопией между
fo и fu
Докажите, что если X — счетно паракомпактное нормальное
пространство, М — замкнутое подпространство пространства X
5.5. ЗАДАЧИ 513
и /о, fx— гомотопные непрерывные отображения пространствам
в n-сферу Sny причем /0 непрерывно продолжается на все X, то
fi тоже непрерывно продолжается на X и, более того, для каж-
каждого непрерывного продолжения отображения /0 найдется гомо-
гомотопное ему продолжение отображения f\ (это и есть теорема
Борсука о продолжении гомотопии).
Указание (Даукер; цитировано в книге Гуревича и Волмэна
[1941]). Пусть F: М XI-+Sn — гомотопия между /0 и /ь и пусть
/*: X->Sn — непрерывное продолжение отображения /0. Комби-
Комбинация отображения F и отображения /* (рассматриваемого как
отображение множества XX {0} в Sn) продолжается, в силу
теоремы 2.1.8 и упр. 3.2.С, до непрерывного отображения
G: U-+Sn, где UaXyil — некоторое открытое множество, со-
содержащее (XX {0})ЩМX/). По теореме 3.1.16, существует
открытое множество УсХ, для которого МУ^1 с VX/с ?/.
Рассмотрите отображение F: XXI—*Sn, определенное так:
F(x,t)=G(x,tg(x)), где g: X-+I — произвольная непрерывная
функция, удовлетворяющая условиям g(X\V)cz {0} и g(M)cz
с{1}.
Замечание. Морита в [1975] и Старбёрд в [1975] незави-
независимо доказали, что теорема Борсука о продолжении гомотопии
выполняется и для любого нормального пространства X, но
доказывается это существенно более сложным рассуждением.
Линейно упорядоченные пространства IV (см. задачи 1.7.4,
2.7.5, 3.12.3, 3.12.4, 3.12.12(f), 6.3.2 и 8.5.13(j)).
5.5.22. (а) (Беннет [1971]). Пусть $$> — произвольное связ-
связное семейство выпуклых подмножеств множества X, линейно
упорядоченного отношением <. Покажите, что в \}s4> суще-
существуют последовательности jci, x^ ... и уи у2, ..., конечные
или бесконечные, для которых выполняются условия
A) х{ = уи **<**+! и ум<уг при i=l, 2, ...;
B) xM<?St(xi9 s4>) и yi+l^St(yh s4>) при i= 1, 2, ...;
C) St {xit бФ) П St (хм, Ж)Ф®Ф$1 (y0 Ж) П St (yi+l, st)
при *=1, 2, ...;
D) 0 stu,, sf)\} U st(^, a)=va.
(b) Выведите из (а), что для каждого открытого покрытия
Щ произвольного линейно упорядоченного пространства следую-
следующие условия равносильны:
A) В покрытие °U можно вписать звездно конечное откры-
открытое покрытие.
B) В покрытие <U можно вписать точечно счетное открытое
покрытие.
33 Зак. 697
514 ГЛ. 5. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА
(c) (Болл [1954], Гиллман и Хенриксен [1954]). Покажите,
что каждое линейно упорядоченное пространство счетно пара-
компактно.
(d) (Гиллман и Хенриксен [1954], Федорчук [1966]). Пока-
Покажите, что для каждого линейно упорядоченного пространства X
следующие условия равносильны:
A) Пространство X сильно паракомпактно.
B) Пространство X паракомпактно,
C) Пространство X слабо паракомпактно.
D) В каждое открытое покрытие пространства X можно впи-
вписать точечно счетное открытое покрытие *).
(e) (Гиллман и Хенриксен [1954]). В произвольном линейно
упорядоченном множестве X кроме щелей, определенных во вве-
введении (которые иногда называют внутренними щелями), мы бу-
будем рассматривать концевые щели: если в X нет наибольшего
элемента, то пара (X, 0) будет именоваться правой концевой
щелью множества J, а если в X нет наименьшего элемента, то
пара @, X) будет называться левой концевой щелью множества
X. Щель (Л, В) в X называется левой Q-щелью, если либо
Л=0, либо найдется возрастающая трансфинитная последова-
последовательность Хо, Х\у ..., х%, ..., | < а, элементов множества А,
конфинальная всему А и такая, что, каков бы ни был предель-
предельный ординал Я < а, у множества {х^: g < %} нет наименьшей
верхней грани в Х\ правая Q-щель в X определяется аналогично.
Под Q-щелью в линейно упорядоченном множестве X мы будем
понимать такую щель в X, которая является одновременно и ле-
левой, и правой Q-щелью.
Докажите, что линейно упорядоченное пространство X пара-
компактно в том и только том случае, если каждая щель в X
является Q-щелью.
Указание. С помощью (а) покажите, что в связное покрытие
Щ линейно упорядоченного пространства X, состоящее из интер-
интервалов, можно вписать точечно счетное открытое покрытие в том
и только том случае, если концевые щели множества X (если
таковые существуют) являются Q-щелями.
(f) (Энгелькинг и Латцер [1977]). Для произвольного орди-
ординала а пусть W(a) — множество всех ординалов, меньших а,
с топологией, порожденной естественным упорядочением <. Ста-
Стационарным подмножеством множества W(a) называется такое
множество SczW(a), что Б{\СФ0 для каждого замкнутого
множества С, конфинального W(a).
Докажите, что линейно упорядоченное пространство X не па-
паракомпактно в том и только том случае, если найдется предель-
предельный ординал а, не конфинальный соо, такой, что в X есть замк-
*) Топологические пространства, которые удовлетворяют условию D),
называются металинделёфовыми. — Прим. перев.
5.5. ЗАДАЧИ 515
нутое подпространство, гомеоморфное некоторому стационар-
стационарному множеству в W(a).
Указание. Если X не паракомпактно, то в X есть щель (Л, В),
которая не является Q-щелью. Можно предположить, что эта
щель не является левой Q-щелью. Рассмотрите произвольную
возрастающую трансфинитную последовательность хо, хи ...
..., *б> ..., | < а, элементов множества Л, конфинальную А,
и покажите, что X содержит замкнутое подпространство, гомео-
гомеоморфное подпространству 5 пространства W(a), состоящему из
всех тех предельных ординалов Ху для которых множество
{х%° ? < М обладает наименьшей верхней гранью в X.
Показать, что произвольное стационарное подмножество S
пространства W(a) не паракомпактно, можно следующим обра-
образом. Предположим, что нашлось локально конечное открытое
покрытие Ш пространства 5, такое, что никакой элемент покры-
покрытия °U не конфинален 5. Рассмотрите множество Сс W(a)\St
состоящее из всех точек пространства W(a)> каждая окрестность
которых пересекает бесконечно много элементов семейства Щ.
(g) (Латцер [1971]). Покажите, что каждое совершенно нор-
нормальное линейно упорядоченное пространство паракомпактно.
Заметьте, что лексикографически упорядоченный квадрат (см.
задачу 3.12.3(d)) является наследственно паракомпактным ли-
линейно упорядоченным пространством, которое не совершенно
нормально.
Указание (Энгелькинг и Латцер [1977]). Примените (f).
(h) Заметьте с помощью подходящей модификации (Ь), что
каждое линейно упорядоченное пространство наследственно
счетно паракомпактно. Убедитесь, что если линейно упорядочен-
упорядоченное пространство наследственно удовлетворяет одному из усло-
условий в (d), то оно наследственно удовлетворяет и всем остальным
условиям в (d).
(i) (Мансфилд [1957а]). Покажите, что каждое линейно упо-
упорядоченное пространство коллективно нормально, и выведите
отсюда, что условия B) и C) в (d) равносильны.
Указание. См. задачу 1.7.4(с).
(j) (Стин [1970]). Покажите, что каждое линейно упорядо-
упорядоченное пространство наследственно коллективно нормально.
Указание. См. указание к задаче 2.7.5(с).
(к) (Латцер [1969]). Докажите, что линейно упорядоченное
пространство X метризуемо в том и только том случае, если диа-
диагональ А является множеством типа G6 в произведении JXX.
Указание (Латцер [1970]). Определите измельчение в Х\
примените затем 5.4.1 и (i).
A) (Латцер [1969]). Выведите из (к), что на прямой Зор-
генфрея не существует линейного упорядочения, порождающего
ее топологию.
33*
Глава 6
СВЯЗНЫЕ ПРОСТРАНСТВА
Свойство, называемое «связностью», которое мы собираемся
изучить в этой главе, имеет совершенно другую природу, чем
топологические свойства, исследованные в предыдущих главах.
В частности, из связности ни одно из этих свойств не вытекает
и сама она не является следствием никакого из них. Говоря не
строго, связные пространства состоят из одного куска в отличие
от пространств, состоящих из многих удаленных друг от друга
кусков, — таких, как дискретные пространства.
В § 6.1 мы определяем связность и изучаем поведение связ-
связных пространств при различных операциях. Оказывается, класс
связных пространств замкнут относительно произведений, а в
случае компактов — относительно перехода к пределу обрат-
обратного спектра. Затем вводятся понятия компоненты и квазиком-
квазикомпоненты и показывается, что для компактов эти понятия совпа-
совпадают. Параграф завершается теоремой Серпинского, утверждаю-
утверждающей, что никакой связный компакт нельзя представить в виде
объединения счетного семейства попарно не пересекающихся
замкнутых множеств, отличных от всего компакта, и кратким ис-
исследованием монотонных отображений — отображений со связ-
связными прообразами точек.
Параграф 6.2 посвящен изучению четырех классов топологи-
топологических пространств, обладающих высокой степенью несвязности,
а именно: наследственно несвязных пространств, нульмерных
пространств, сильно нульмерных пространств и экстремально не-
несвязных пространств. Эти четыре класса идут в убывающей по-
последовательности. Понятия нульмерного и сильно нульмерного
пространства имеют отношение к концепции размерности про-
пространства. В теории размерности для каждого непустого топо-
топологического пространства X определяют его размерность, яв-
являющуюся либо неотрицательным целым числом, либо «беско-
«бесконечным числом» оо. Сделать это можно несколькими способами,
однако во всех случаях размерность пространства выступает как
некоторая мера его связности. Названия «нульмерное» и «сильно
нульмерное» пространства связаны с тем, что такие простран-
пространства имеют размерность нуль по отношению к двум различным
определениям размерности. Эти два класса пространств иссле-
6.1. СВЯЗНЫЕ ПРОСТРАНСТВА 517
дуются в § 6.2 без ссылок на теорию размерности. Однако изуче-
изучение этих классов служит введением в теорию размерности, разви-
развиваемую в гл. 7. Обсудив взаимоотношения между первыми тремя
классами и исследовав их поведение относительно операций, мы
определяем два класса отображений — легкие отображения и
нульмерные отображения — и доказываем, что каждое совершен-
совершенное отображение имеет единственное представление в виде ком-
композиции монотонного отображения и нульмерного отображения.
Заключительная часть этого параграфа посвящена экстремально
несвязным пространствам. Это весьма специальный класс про-
пространств; на первый взгляд он может показаться несколько
искусственным. Однако этот класс играет важную роль в теории
булевых алгебр и в некоторых задачах функционального анализа.
6.1. СВЯЗНЫЕ ПРОСТРАНСТВА
Топологическое пространство X называется связным, если X
нельзя представить в виде Х{ФХ2у где Х\ и Х2— непустые под-
подпространства пространства X. Начнем с ряда характеристик
связности.
6.1.1. Теорема. Для произвольного топологического простран-
пространства X следующие условия равносильны:
(i) Пространство X связно.
(и) Пустое множество и все пространство — единственные
открыто-замкнутые в пространстве X множества.
(Ш) Если Х = Х\\}Х2 и множества Х\ и Х2 отделены, то
одно из них пусто.
(iv) Каждое непрерывное отображение f: X^-D простран-
пространства X в двухточечное дискретное пространство ?>={0, 1} по-
постоянно, т. е. либо /(Х)с={0}, либо f(X)cz{l}.
Доказательство. Для доказательства импликации (i)=^(ii)
достаточно заметить, что если множество Х\ cz X открыто-замк-
открыто-замкнуто в X, 0 Ф Xi Ф X и Х2 — дополнение к Ii в I, то X =
= Xi © Х2 в силу предложения 2.2.4 и Хх Ф 0 Ф Х%. _
Покажем, что (ii)=^(iii). Пусть X = ZiU^2» где Х\(]Х2 =
= 0 =Х\ П Х2. Тогда X\CzX\X2a:Xi и Х\=Хи Аналогично
Х2 = Х2. Так как множества Х\ и Х2 замкнуты и не пересе-
пересекаются, они также открыты и, в силу (ii), одно из них пусто.
Установим импликацию (iii)=^(iv). Достаточно заметить, что
если /: X^>~D — непрерывное отображение, для которого Хх =
= /-1 (О)Ф0 и Х2 = 1-Х{\)Ф0, то, в силу очевидных равенств
X = Х{ U Х2 и Xi П %2 = 0 = %\ П ^2, пространство X не удовлет-
удовлетворяет условию (III).
Импликация (iv)=^(i) следует из того, что если не выпол-
выполняется (i), т. е. X = Х\ ФХ2, где Х\Ф0ФХ2, то, полагая
518 ГЛ. 6. СВЯЗНЫЕ ПРОСТРАНСТВА
Дх) = 0 при х^Хх и /(х)= 1 при х^Х2, мы получаем непре-
непрерывную функцию /: X->D, такую, что f(X) = D. I
6.1.2. Следствие. Пространство X связно в том и только том
случае, если его нельзя представить в виде объединения
Х\ U Х2 двух непустых замкнутых непересекающихся множеств. ¦
Легко видеть, что последнее следствие остается верным, если
слово «замкнутое» всюду заменить в нем на слово «открытое».
6.L3. Следствие. Каждое связное тихоновское пространство, в ко-
котором есть по крайней мере две различные точки, имеет мощ-
мощность, не меньшую с.
Доказательство. Пусть X — связное тихоновское пространство
и х\, х% — две различные точки пространства X По определению
тихоновских пространств, существует непрерывная функция
/: Х-*1, для которой /(xi)=0 и f(x2)=l. Если бы нашлось
r^I\f(X), то мы бы имели Х = {х: f(x)<r}®{x: f(x)>r} —
противоречие. Значит, f(X) = I и, следовательно, |Х|^с. I
Из равносильности условий (i) и (iv) в теореме 6.1.1 выте-
вытекает
6.1.4. Теорема. Связность сохраняется непрерывными отображе-
отображениями (в сторону образа). I
6.1.5. Примеры. Из 2.2.8 следует, что любое дискретное простран-
пространство, содержащее не менее двух точек, равно как и прямая Зор-
генфрея, не связны. Кроме того, из 2.2.8 вытекает, что веще-
вещественная прямая связна. Значит, в силу теоремы 6.1.4, связны
и все интервалы вещественной прямой. Пустое пространство и
одноточечное пространство, очевидно, связны. Как легко видеть,
двухточечное пространство i7 ^{0, 1} с топологией, состоящей
из пустого множества, множества {0} и всего пространства,
тоже связно1). I
6.1.6. Пример. Опишем бесконечное счетное связное хаусдор-
фово пространство. Из 6.1.3 следует, что счетного связного ти-
тихоновского пространства, содержащего более одной точки, не
существует. По теореме 1.5.16, нет и регулярного пространства
с указанными свойствами.
Обозначим через X множество всех точек (г\,г2) плоскости
R2y таких, что п и г2 рациональны и г2 ^ 0; ясно, что \Х\ — Ко.
Для каждого х = (п, /*г) ^ X и i = 1, 2, ... положим
Ut (х) = {х} U {(г, 0): | г - (г, - Га/УЗ ) | < l/i} [}
U {(г, 0): | г - (п + /Уд/З") | < 1/«}.
1)) Пространство F = {0, 1} с указанной топологией называется связ-
связным двоеточием. Связные двоеточия полезны при изучении Г0-пространств
Прим. перев.
6.1. СВЯЗНЫЕ ПРОСТРАНСТВА 519
Для произвольной точки х, лежащей выше первой оси (т. е. оси
первой координаты), множество Ui(x) состоит из х и всех ра-
рациональных точек первой оси, удаленных менее чем на \/i от
одной из вершин равностороннего треугольника с вершиной в
точке х, основание которого лежит на первой оси. Если точка л:
расположена на первой оси, то множество Ui(x) состоит из всех
рациональных точек этой оси, лежащих от х на расстоянии,
меньшем 1/L Легко проверяется, что семейство {^W}xep где
#(*) = UM*)}fli» обладает свойствами (ВР 1) — (ВР 4); следо-
следовательно, оно порождает на множестве X некоторую топологию
хаусдорфова пространства.
Замыкание множества Ui(x) по отношению к этой тополо-
топологии состоит из всех точек пространства X, расстояние от которых
до какой-нибудь из прямых, проходящих через точку х под
углом 60° и 120° к первой оси, не превосходит д/3/2/. Значит,
для любых точек х\, хгЕ! и любых натуральных чисел i\, i2
имеем Uil(xx)(]Ui3(x2)?s 09 а это показывает, что простран-
пространство X нельзя представить в виде объединения двух непустых
непересекающихся открыто-замкнутых множеств. Таким обра-
образом, пространство X связно. I
Рассмотрим теперь, как действуют операции на связные про-
пространства.
Очевидно, подпространство связного пространства может не
быть связным. Обсудим вкратце вопрос о том, когда подпро-
подпространство произвольного топологического пространства связно.
Начнем с простой характеристики.
6.1.7. Теорема. Подпространство С топологического пространства
X связно в том и только том случае, если, каковы бы ни были
отделенные подмножества Хи Х2 пространства Ху такие, что
С = Х\ U Х2, всегда либо Хх = 0, либо Х2 = 0.
Доказательство. ^Предположим, что С связно и С = Х\ U Х2,
где Х\ П Х2 = 0 = Х\ П Х2. Ясно, что множества Х\ и Х2 отде-
отделены в пространстве С Значит, по теореме 6.1.1, одно из этих
множеств пусто.
С другой стороны, если С не связно, то найдутся непересе-
непересекающиеся замкнутые в С множества Х\ и Х2, для которых
С = Х\ U Х2. Ясно, что множества Хг и Х2 отделены в простран-
пространстве X; таким образом, условие теоремы не выполняется. I
6Л.8. Следствие. Если подпространство С топологического про-
пространства X связно, то для любых двух отделенных подмно-
подмножеств Хи Х2 пространства X, таких, что CczXi []Х2, всегда либо
С d Xu либо С а Х2.
Доказательство. Множества С(]Х\ и С[\Х2 отделены ь X, я
их объединение равно С. В силу последней теоремы, одно из
520 ГЛ. 6. СВЯЗНЫЕ ПРОСТРАНСТВА
этих множеств пусто и, значит, множество С содержится в дру-
другом из них. 1
6.1.9. Теорема. Пусть {Cs}s<=s— некоторое семейство связных
подпространств топологического пространства X. Тогда если най-
найдется такое so e S, что множество CSu не отделено ни от одного
из множеств Cs, то объединение (J Cs связно.
Доказательство. Предположим, что С= [] Cs = Xx[}X2, где
Хх и Х2 — отделенные подмножества пространства X. В силу
следствия 6.1,8, либо CSoc=Jb либо CSoc=J2. Пусть C^dXi.
Так как каждое из множеств Cs содержится либо в Хи либо в
Х2 и ни одно из них не отделено от С5о, имеем Cs с: Хх при всех
sezS. Значит, CczXlnX2 = 0. I
6.1.10. Следствие. Если семейство {Cs}s^s связных подпро-
подпространств топологического пространства имеет непустое пересе-
пересечение, то его объединение |J Cs связно. |
6.1.11. Следствие. Если подпространство С пространства X
связно, то и каждое подпространство А пространства X, для ко-
которого СсЛс?, тоже связно.
Доказательство. Семейство {C}U {{*}}*<= л удовлетворяет ус-
условию теоремы 6.1.9, где CSo = C |
6.1.12. Следствие. Если топологическое пространство X содержит
всюду плотное связное подпространство, то X само связно. I
6.1.13. Следствие. Если каждые две точки топологического про-
пространства X можно соединить связным подпространством этого
пространства, то пространство X связно.
Доказательство. Зафиксируем произвольно точку xq простран-
пространства X и для каждого х^Х через Сх обозначим какое-нибудь
связное подпространство пространства Ху соединяющее л:о и х.
Семейство {Сх}х^х удовлетворяет посылкам утверждения
6.Ы0 и U СХ = Х. |
лее X
Отметим, что из 6.1.12 и 3.6.5 вытекает
6.1.14. Теорема. Стоун-чеховская компактификация $Х тихонов-
тихоновского пространства X связна в том и только том случае, если
пространство X связно. I
Из определения связности немедленно следует, что никакая
нетривиальная сумма топологических пространств не является
связным пространством.
6.1. СВЯЗНЫЕ ПРОСТРАНСТВА 521
6.1.15. Теорема. Произведение Ц Xs, где Х5ф0 при всех
sgS, связно в том и только том случае, если все пространства
Xs связны.
Доказательство. Если произведение 1=П ^s связно и не
пусто, то все пространства Xs связны по теореме 6.1.4, так как
проекция ps: X-+Xs является непрерывным отображением про-
пространства X на пространство Xs.
Докажем теперь, что произведение связных пространств связ-
связно. Для начала рассмотрим произведение JX Y двух связных
пространств. Любые две точки (х\,у\) и (*2, #г) пространства
XX Y можно соединить множеством (^Xfei})U(WX^)- Это
множество связно как объединение двух пересекающихся связ-
связных множеств. Значит, пространство XX Y связно в силу след-
следствия 6.1.13.
Легко показать прямым рассуждением по индукции, что про-
произведение любого конечного множества связных пространств
связно.
Рассмотрим теперь произвольное семейство {^}5eS непустых
связных пространств и зафиксируем при каждом sgS точку
as e Xs. Обозначим через 2Г семейство всех конечных подмно-
подмножеств множества 5 и для каждого Ге^ положим
Сг= П А8, где As={a8), если s<?7\ и AS = XS при seT,
Согласно конечному случаю нашей теоремы, {Сг}Ге5г —се-
—семейство связных пространств. Так как a = {as}^ П СТФ 0,
из следствия 6.1.10 вытекает, что объединение С= (J Ст
связно. Но С — всюду плотное подпространство пространства
JI Xs. Значит, можно завершить доказательство, применив
ss
следствие 6.1.12. 1
6.1.16. Следствие. Евклидово п-пространство Rn, тихоновский
куб /т и александровский куб Fm — связные пространства. I
Очевидно, факторпространства связных пространств всегда
связны.
Приведем теперь пример, который показывает, что предел
обратной последовательности связных пространств может не
быть связным пространством.
6.1.17. Пример. Пусть X — плоскость R2, из которой выкинут от-
открытый интервал с концами в точках Х\=(—1,0) и #2 =A,0).
При i = l, 2, ... обозначим через Хг пересечение множества X
522 гл. 6. связные пространства
с областью, заключенной внутри прямоугольника с вершинами
в точках (-1-1Д 1/0, (-1-1Д -1/0, A + 1Д -1/0 и
A + 1/t, 1/0- Пространства Xt связны и Xi<^Xj при j^i. Че-
Через п* обозначим вложение пространства Xt в X/. В соответствии
с примером 2.5.4 семейство |А\, я*} составляет обратную после-
последовательность связных пространств, причем предел этой после-
последовательности состоит из точек х\ и х2> т. е. не связен. |
Пространства в примере 6.1.17 не компактны. Из теоремы
6.1.20 следует, что предел обратного спектра связных компактов
связен.
Топологическое пространство X называется континуумом,
если X одновременно связно и является компактом. В силу тео-
теорем 3.2.4 и 6.1.15, произведение континуумов является континуу-
континуумом. Аналогично, из теорем 3.1.10 и 6.1.4 вытекает, что непре-
непрерывный образ континуума есть континуум — в предположении,
что этот образ является хаусдорфовым пространством.
6.1.18. Теорема. Пусть {С s}s^s — некоторое семейство подпро-
подпространств топологического пространства Х% каждое из которых яв-
является континуумом. Если для любых s\, s2^S существует
s3eS, такое, что CS3czCSl[}CS2<> т. е. если семейство {CJS€_S
континуумов направлено отношением иэ, то пересечение [} C
S
s
является континуумом.
Доказательство. Можно предположить, что X — компакт. Дей-
Действительно, зафиксируем некоторое /gSh для каждого «jgS
выберем s'eS, такое, что CS'<^Ct[}Cs- Заменяя пространство
X на пространство С* и континуум Cs на континуум CV, мы сво-
сводим задачу к случаю, когда X — континуум.
Предположим, что С= П С3 = Ху[]Х2> где Х\ и Х2 —непе-
ресекающиеся замкнутые в С множества. Так как множества Х\
и Х2 замкнуты в X, можно найти непересекающиеся открытые
множества ?/ь U2czX, для которых X\czU\ и Х2с U2. В силу
следствия 3.1.5, существует конечное множество {sb 52,-.
k
..., sk}czSt такое, что f] CSi с= С/х U ?/2. Семейство {CS}S(EE s на-
h
правлено отношением zd, значит, CSo c= f] Cs. для некоторого
sq g S. Таким образом, С с: CSo t= U\ U U2 и, в силу следствия
6.1.8, либо С с: CSu cz Ux, либо С a CSo c= f/2, откуда вытекает, что
Х2 = 0 или Х\ =0. Следовательно, пространство С связно; оно
также является компактом, как замкнутое подпространство ком-
компакта X. 1
6.1. СВЯЗНЫЕ ПРОСТРАНСТВА 523
оо
6.1Л9. Следствие. Пересечение f] Xt убывающей последователь-
последовательности X\ZdX2^> ... континуумов является континуумом. I
6.1.20. Теорема. Предел обратного спектра S = {X0, я?, 2} кон-
континуумов является континуумом.
Доказательство. Для каждого pGS положим
*р = {{*«,} е* *8(*р)-*а"Ри °<Р] и 2р = 2\{ае2:
где J= XI Ха- Пространство Zp— континуум. Действительно,
оно является образом континуума Ц Ха при непрерывном
отображении, сопоставляющем точке {ха} <= Г1 Ха точку {2а}е
^ZpczX, где 20 = д:а при а^ 2р и za = nf{x9) при а<р.
Так как ZPlc=Zp2, когда p2^Pi» и множество 2 направлено,
пересечение П ^р является континуумом по теореме 6.1.18.
Так как это пересечение совпадает с lim S, доказательство
завершено. |
Пространство отображений Yx, как правило, не является
связным для связных пространств X и У. Исследование условий
связности пространств отображений приводит к важым резуль-
результатам. Оно требует, однако, специальных методов, не развивае-
развиваемых в этой книге. Например, доказывается, что если X — под-
подпространство пространства Rn, то пространство (Sn-l)x с ком-
компактно-открытой топологией связно в том и только том случае,
если связно пространство Sn\X (n-сфера Sn здесь рассматри-
рассматривается как компактификация евклидова n-пространства Rn9 по-
полученная присоединением к Rn «точки в бесконечности»; для
компактного подпространства X пространства Rn пространство
Sn\X связно в том и только том случае, если связно простран-
пространство Rn\X), Так как для гомеоморфных подпространств Хи Х2
пространства Rn пространства отображений (Sn~l)Xl и (Sn-l)x
гомеоморфны, получается, что Sn\X\ связно в том и только том
случае, если связно Sn\X2. Это важный и глубокий результат,
обобщающий классическую теорему Жордана, которая говорит,2
что если подпространство X плоскости R2 гомеоморфно окруж-
окружности S\ то дополнение R2\X не связно.
Компонентой точки х в топологическом пространстве X на-
называется объединение всех связных подпространств простран-
пространства X, содержащих точку х. Из 6.1.10 и 6.1.11 вытекает, что
компоненты являются связными замкнутыми в X множествами.
524 ГЛ. б. СВЯЗНЫЕ ПРОСТРАНСТВА
Компоненты двух различных точек топологического простран-
пространства X или совпадают, или не пересекаются, так что в совокуп-
совокупности компоненты составляют разбиение пространства X на по-
попарно непересекающиеся связные замкнутые множества, назы-
называемые компонентами пространства X.
Следующий простой результат будет применен в § 6.2.
6.1.21. Теорема. Компонента точки x={xs} в произведении Ц Xs
совпадает с произведением Ц Csy где Cs — компонента точки
xs в пространстве Xs.
Доказательство. Обозначим компоненту точки х в простран-
пространстве П Xs через С. Так как при каждом 5GS проекция ps(C)
связна, то ps(C)czCs при всех s е S. Значит, С cz Ц Cs; ра-
венство C = ПС5 вытекает из теоремы 6.1.15. |
S
Квазикомпонентой точки х в топологическом пространстве X
называется пересечение всех открыто-замкнутых множеств в X,
содержащих точку х.
Квазикомпоненты являются замкнутыми в X множествами.
Квазикомпоненты различных точек пространства X либо совпа-
совпадают, либо не пересекаются. Таким образом, в совокупности
квазикомпоненты составляют разбиение пространства X на по-
попарно непересекающиеся замкнутые множества, называемые
квазикомпонентами пространства X.
6.1.22. Теорема. Компонента С точки х в топологическом про-
пространстве X содержится в квазикомпоненте Q точки х.
Доказательство. Пусть F — любое открыто-замкнутое в X
множество, содержащее х. Множества F и X\F, и тем более
множества Cf\F и C\F, отделены. Так как C[\F?=0, из тео-
теоремы 6.1.7 следует, что C\F — 0, т. е. что CczF. Значит,
CczQ. I
6Л.23. Теорема. В произвольном компакте X компонента любой
точки х^Х совпадает с квазикомпонентой точки х.
Доказательство. В силу последней теоремы, достаточно пока-
показать, что квазикомпонента Q точки х связна.
Предположим, что непересекающиеся замкнутые подмноже-
подмножества Х\9 Х2 пространства Q удовлетворяют условиям Q=^Xi{jX2
и х^Х\. Так как Х\ и Х2 замкнуты в X, то, в силу нормаль-
нормальности компактов, найдутся открытые в X множества U и V, та-
такие, что
A) Xx^Uy X2czV a U(]V = 0.
6.1. СВЯЗНЫЕ ПРОСТРАНСТВА 525
Значит, Qc^U\JV и, в силу следствия 3.1.5, существует конеч-
конечное семейство открыто-замкнутых множеств Fu Р2, ..., Fk, для
k
которого Q<zz F= П Fi<^U\JV. Ясно, что множество F открыто-
замкнуто. Так как
то пересечение U f] F тоже окрыто-замкнуто. Но х е U П F, по-
поэтому Q cz U П F и
B) X2c=Qc=(/n^c= t/.
Из A) и B) вытекает, что Х2 = 0. Следовательно, множе-
множество Q связно. I
6.1.24. Пример. Опишем теперь пространство, в котором компо-
компоненты и квазикомпоненты отличаются друг от друга.
Пусть X — подпространство плоскости, состоящее из отрез-
отрезков /;=[0, 1]Х{1/0> где / = 1, 2, ..., и точек ро=(О,О) и
Р\ =A,0). Отрезки /j и точки р0, р\ являются компонентами
пространства X. Покажем, что квазикомпонента Q точки р0 со-
совпадает с множеством {ро, pi}.
Каждое открыто-замкнутое множество F, содержащее р0, со-
содержит и почти все члены последовательности {@, 1/0}* Так как
отрезки /,• связны, почти все они содержатся в Р. Значит, мно-
множество F содержит почти все члены последовательности {A, 1/0}»
и предел р\ этой последовательности тоже принадлежит F. Та-
Таким образом, {pOtpi}cz Q, и так как никакая другая точка про-
пространства X не может принадлежать Q, то Q—{p0, pj.
Заменив точки р0 и рх полуинтервалами [0, 1/2)Х{0} и
A/2, 1]Х{0}, мы получаем локально компактное хаусдорфово
пространство с теми же свойствами. 1
Оказывается, никакой континуум нельзя разложить на счет-
счетное число отличных от него попарно не пересекающихся непу-
непустых замкнутых множеств (см. упр. 6.1.F). Доказательству этого
факта мы предпошлем две леммы.
6.1.25. Лемма. Пусть А—произвольное замкнутое подпростран-
подпространство континуума X, такое, что 0ФАФХ. Тогда для каждой
компоненты С пространства А выполняется соотношение
СА0
Доказательство. Из теоремы 6.1.23 вытекает, что С = {\Ж,
где Ж — семейство всех открыто-замкнутых подмножеств про-
пространства Л, содержащих некоторую точку х0 е С. Предполо-
Предположим, что Cf)Fr^=0. Так как семейство Ж замкнуто относи-
относительно конечных пересечений и множество Fr А компактно, най-
найдется К^ЖУ для которого /СПРгЛ = 0. Возьмем открытое
526 ГЛ. 6. СВЯЗНЫЕ ПРОСТРАНСТВА
множество UczXt такое, что U(]A = K. Из равенства
%()FrA=0 вытекает, что K==Uf\lntA; таким образом, мно-
множество К открыто в X. Но множество К также замкнуто в X и
содержит xq. Значит, К — Х. Следовательно, FrA = 0, и мы по-
получили противоречие. I
6.1.26. Лемма. Если континуум X покрыт попарно непересе-
непересекающимися замкнутыми множествами Хх, Х2, ..., хотя бы два
из которых не пусты, то для каждого i найдется континуум
СczX, такой, что C{\Xi = 0 и по крайней мере два множества
в последовательности С[\Х\, С{\Х2, ...не пусты.
Доказательство. Если Xt = 0, положим С = Х. Значит, мож-
можно предположить, что Xi ф 0. Возьмем / Ф i, для которого
Xf Ф 0, и выберем непересекающиеся открытые множества U,
V cz X, такие, что Xi cz U и Xt cz V. Пусть х — произвольная точ-
точка множества Xj и С — компонента точки х в подпространстве V.
Ясно, что С —континуум, C[\Xi = 0 и С(]Х}Ф0. Так как, по
предыдущей лемме, С[\?т7Ф0 и так как Xt cz Int F, то най-
найдется k ф j, для которого С П Xk ф 0. I
6.1.27. Теорема Серпинского. Если континуум X можно покрыть
счетным семейством {Xi}°°=l попарно не пересекающихся замкну-
замкнутых множеств, то самое большее одно из множеств Xi не пусто.
оо
Доказательство. Пусть Х= (J xit гДе множества Xi замк-
замкнуты и Xi(\Xj = 0 при 1ф\. Предположим, что по крайней
мере два из множеств Xi не пусты, Из леммы 6.1.26 следует, что
найдется убывающая последовательность Сх =э С2 zd^ ... конти-
континуумов, содержащихся в Ху для которой
C) Ci(]Xt=0 и Сьф0 при /=1,2
Первое из соотношений C) показывает, что ( f| СЛ П I U ^)=Я0»
оо
т. е. что р| с^=0, а из второго условия в C) и компакт-
оо
ности X вытекает, что (| СгФ 0. |
Понятие связности приводит к новому классу отображений.
Мы называем непрерывное отображение f: X-^Y монотонным,
если все прообразы f~l(y) точек связны. Название «монотонное
отображение» происходит от того, что при непрерывном отобра-
отображении / вещественной прямой в себя все прообразы точек связ-
связны в том и только том случае, если f — не возрастающая или не
убывающая функция (см. упр. 6.1.G).
6.1. СВЯЗНЫЕ ПРОСТРАНСТВА 527
6.1.28. Теорема. Если /: X^Y— монотонное факторное отобра-
отображение, то для каждого связного подмножества С пространства
У, открытого или замкнутого в У, прообраз f~~l(C) связен.
Доказательство. В силу предложения 2.4.15, достаточно до-
доказать, что если У связно, то и X связно. Рассмотрим произ-
произвольное разбиение Z = XiU^2 пространства X на два непере-
непересекающихся открыто-замкнутых множества. Так как прообразы
точек при f связны, то Xi = /-1 (У,) при i = l9 2, где У = Y\ U У2
и Y\ П Уг = 0. Отображение / факторно, поэтому множества УЬ
У2 открыто-замкнуты. Значит, в силу связности У, одно из мно-
множеств Yi пусто. Отсюда с очевидностью следует пустота одного
из множеств Xi. Таким образом, пространство X связно. 1
6.1.29. Теорема. Если f: X-+Y — монотонное отображение про-
пространства X на пространство У, причем f открыто или замкнуто,
то прообраз f~l(C) произвольного связного подмножества С
пространства У связен.
Доказательство. По предложению 2.1.4, достаточно показать,
что если У связно, то и X связно. Но последнее немедленно сле-
следует из предшествующей теоремы. 1
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
Приведенное определение связности было дано Жорданом в
1893 г. для компактных подмножеств плоскости. Обобщение на
абстрактные пространства было осуществлено Риссом [1907],
Леннесом [1911] и Хаусдорфом [1914]. Условие в упр. 6.1.С,
равносильное связности в классе компактных метрических про-
пространств, было введено Кантором в 1883 г. Систематическое изу-
изучение связности было начато Хаусдорфом в [1914] и Кнастером
и Куратовским в [1921]. Книга Хаусдорфа [1914] содержит след-
следствия 6.1.10 — 6.1.13, определения компоненты и квазикомпо-
квазикомпоненты, теорему 6.1.22 и теорему 6.1.23 для случая компактных
метрических пространств (обобщение последней на произволь-
произвольные компакты было сделано Шурой-Бурой в [1941]). Работа
Кнастера и Куратовского [1921] содержит теоремы 6.1.7 и 6.1.9.
Первый пример счетного связного хаусдорфова пространства
был приведен Урысоном в [1925]; наш пример 6.1.6 взят из
статьи Бинга [1953]; он намного проще первоначального при-
примера. Теорема 6.1.15 для конечных произведений была доказана
Ван Данцигом в [1930], теорема 6.1.20 фигурирует в качестве
задачи в книге Эйленберга и Стинрода [1952]. Как утверждает-
утверждается в статье Зоретти [1905], следствие 6.1.19 (в несколько иной
форме) было доказано П. Пэнлеве для континуумов на пло-
плоскости. Тот факт, что для подпространства X пространства Rn
пространство (Sn-l)x связно в том и только том случае, если
528 ГЛ. 6. СВЯЗНЫЕ ПРОСТРАНСТВА
связно пространство Sn\X, был независимо доказан П. С. Алек-
Александровым в [1932] и Борсуком в [1932] в предположении ком-
компактности пространства X (для топологии на (Sn~})xt порож-
порожденной метрикой, определенной формулой G) в § 4.2). В полной
общности этот факт был доказан Куратовским в [1959]. Теорема
6.1.27 доказана Серпинским в [1918]. Монотонные отображения
континуумов первым изучал Р. Л. Мор в [1925] (в терминах
полунепрерывных сверху разбиений). Класс монотонных отобра-
отображений был введен Уайберном в [1934].
УПРАЖНЕНИЯ
6.1.А. Опишите все связные подпространства вещественной
прямой.
Указание. Заметьте, что каждое связное подпространство ве-
вещественной прямой выпукло.
6.1.В. Проверьте, что для каждой последовательности
С\, С2, ...связных подпространств топологического пространства,
оо
такой, что Сг f] С(+1 Ф 0 при i = 1, 2, ..., объединение [] С(
?-1
связно.
6.1.С. (а) Проверьте, что если пространство X с топологией,
порожденной метрикой р, связно, то для каждой пары х, у
точек из X и любого 8 >0 найдется последовательность
xi, х2, ..., Xk точек пространства X, такая, что х\ = х, хц = у
и p(xi, *,-+i) < 8 при i = 1, 2, ..., k — 1.
(b) Покажите, что каждый компакт (X, р), удовлетворяю-
удовлетворяющий условию в (а), связен, и что предположение о компактно-
компактности существенно.
6.1.D. Докажите, что в классе связных пространств сильная
паракомпактность равносильна свойству Линделёфа. Выведите
отсюда, что ёж /(ш) не сильно паракомпактен при щ> Ко.
6.1.Е. (а) Приведите пример континуума, который непред-
непредставим в виде непрерывного образа никакого связного метри-
зуемого пространства.
Указание. С помощью следствия 3.6.15 покажите, что р/? не
является непрерывным образом никакого связного секвенциаль-
секвенциального пространства.
(Ь) Покажите, что при каждом m ^ Ко тихоновский куб I™
можно представить как непрерывный образ некоторого связного
метризуемого пространства.
6.1.F. Приведите пример связного подпространства плоско-
плоскости, которое можно разложить на счетное семейство попарно
непересекающихся непустых замкнутых подмножеств.
6.2. РАЗЛИЧНЫЕ ВИДЫ НЕСВЯЗНОСТИ 529
6.1.G. Докажите, что непрерывное отображение f: R^-R мо-
монотонно в том и только том случае, если f{x)^f(y) при х^у
или f(x)^f{y) при х^у.
6.1.Н. Заметьте, что теорема 6.1.29 выполняется для моно-
монотонных наследственно факторных отображений, и заметьте, что
она не имеет места для монотонных факторных отображений.
Указание. Видоизмените пример 2.4.17.
6.2. РАЗЛИЧНЫЕ ВИДЫ НЕСВЯЗНОСТИ
Топологическое пространство X называется наследственно
несвязным, если X не содержит никакого связного подпростран-
подпространства, содержащего более одной точки. Следовательно, простран-
пространство X наследственно несвязно в том и только том случае, если
компонента каждой точки хе! состоит только из этой точки х.
Так как компоненты пространства замкнуты, каждое наслед-
наследственно несвязное пространство является ^-пространством. От-
Отметим, что в контексте несвязности термин «наследственно»
имеет значение, несколько отличающееся от принятого на про-
протяжении этой книги: стандартное понимание этого термина при-
привело бы к пустому классу пространств.
Топологическое пространство X называется нульмерным,
если X — непустое ^-пространство, обладающее базой из от-
открыто-замкнутых множеств. Ясно, что каждое нульмерное про-
пространство является тихоновским пространством.
6.2.1. Теорема. Каждое нульмерное пространство наследственно
несвязно.
Доказательство. Пусть А — подмножество нульмерного про-
пространства I и |Л|> 1. Возьмем любые две различные точки
хь Х2 множества А и такое открыто-замкнутое подмножество U
пространства X, что х\ е UаХ\{х2}. Так как множества A\U
и А П U отделены и непусты, множество А не связно. I
Покрытие пространства функционально открытыми (функ-
(функционально замкнутыми) множествами в дальнейшем будет на-
называться функционально открытым (функционально замкну-
замкнутым) покрытием.
Топологическое пространство X называется сильно нульмер-
ным, если X — непустое тихоновское пространство и в каждое
конечное функционально открытое покрытие {Ui}.=l простран-
пространства X можно вписать конечное открытое покрытие {У(}^и
такое, что Vt{\ V/ = 0 при i ф /. Ясно, что покрытие {^Jjlj со-
состоит из открыто-замкнутых множеств и, таким образом, яв-
является функционально открытым покрытием пространства X.
34 Зак. 697
530 ГЛ. 6. СВЯЗНЫЕ ПРОСТРАНСТВА
6.2.2. Лемма. Для любых вполне отделенных подмножеств А
и В сильно нульмерного пространства X найдется открыто-замк-
открыто-замкнутое множество U cz X, такое, что A <= U а Х\В.
Доказательство. Пусть /: X-+I — непрерывная функция, для
которой
/(Л)с={0} и
Множества /—! (@, 1]) и /—1 ([0, 1)) составляют функционально
открытое покрытие пространства X. Возьмем какое-нибудь по-
покрытие Т, состоящее из попарно непересекающихся открытых
множеств, вписанное в это покрытие. Множество (/= \j{V^T:
А П V Ф 0} открыто-замкнуто и, очевидно, Лс(/с Х\В. Ш
6.2.3. Лемма. Пусть для любых двух вполне отделенных под-
множеств А, В топологического (нормального) пространства X
существует открыто-замкнутое множество ?/с=Х, такое, что
А с: U <^Х\В. Тогда в каждое конечное функционально откры-
открытое (открытое) покрытие {?/;}f=1 пространства X можно вписать
конечное открытое покрытие {Vi}ki=v такое, что ViczUt при
i = 1, 2, ..., k и Vi П Vj = 0, когда i Ф /.
Доказательство. Применим индукцию по k. При k = 1 лемма
верна. Предположим, что она верна при всех k < /n, и рассмот-
рассмотрим произвольное функционально открытое (открытое) покры-
покрытие {Ui}™^ пространства X. По индуктивному предположению,
найдется покрытие {Wi, W%, ..., Wm-i} пространства X, состоя-
состоящее из попарно непересекающихся открыто-замкнутых мно-
множеств, удовлетворяющих условиям
Wi^Ut при i<m-\ и Wm^^Um_xUUm.
Множества Wm-\\Um-\ и Wm-i\Um не пересекаются и функ-
функционально замкнуты (замкнуты). Значит, по теореме 1.5.13 (по
теореме 1.5.10) они вполне отделены. Следовательно, суще-
существует открыто-замкнутое множество U czX, такое, что
Wm-x \ Um-\ d U и U с X\{Wm_x \ Um) = (X \ Wm_x)\}Um.
Ясно, что
Легко проверяется, что семейство {Vt}™=v где
Vi = Wt при i<m-U Vm-i=Wm_x\U и Vm = Wm.xUU9
является открытым покрытием пространства Ху для которого
VidUi при 1=1, 2, ..., m и Vif[Vj = 0, когда 1ф]\ I
Из лемм 6.2.2 и 6.2.3 вытекает
6.2. РАЗЛИЧНЫЕ ВИДЫ НЕСВЯЗНОСТИ 531
6.2.4. Теорема. Непустое тихоновское пространство X сильно
нульмерно в том и только том случае, если для любых двух
вполне отделенных подмножеств А и В пространства X суще-
существует открыто-замкнутое множество U а X, такое, что А а
cUczX\B. ¦
Из последней теоремы и леммы 6.2.3 следует
6.2.5. Теорема. Непустое нормальное пространство X сильно
нульмерно в том и только том случае, если в каждое открытое
покрытие {Ut}i=sl пространства X можно вписать конечное от-
крытое покрытие {V^=v такое, что Vt{\ Vj = 0 при I ф /. I
Заметим, что из леммы 6.2.2 немедленно получается
6.2.6. Теорема. Каждое сильно нульмерное пространство нуль-
нульмерно. I
6.2.7. Теорема. Каждое нульмерное линделёфово пространство
сильно нульмерно.
Доказательство. Достаточно показать, что, каковы бы ни
были замкнутые непересекающиеся подмножества А и В нуль-
нульмерного линделёфова пространства X, найдется открыто-замкну-
открыто-замкнутое множество U <и X, такое, что A a U а Х\В.
Для каждого хе! выберем открыто-замкнутое множество
Wxc^X, содержащее х и удовлетворяющее одному из условий:
A[\Wx = 0 или Bf]Wx = 0.
Пусть {WXi}™_ —счетное подпокрытие покрытия {Wx}x^x про-
пространства X. Множества
Ut = Wx\ U WXft где *=1, 2, ....
открыто-замкнуты, попарно не пересекаются и покрывают про-
пространство X. Множество U = \}{Ui\ Af\Ui=^0} обладает нуж-
нужными свойствами. I
6.2.8. Следствие. Каждое непустое регулярное пространство X,
для которого \Х\^ Ко» сильно нульмерно.
Доказательство. Так как X — линделёфово пространство, до-
достаточно показать, что совокупность всех открыто-замкнутых
множеств пространства X является его базой. Для этого возь-
возьмем любую точку х^ X п произвольную ее окрестность У. Рас-
Рассмотрим любую непрерывную функцию /: Х—>19 для которой
f(x)= 0 и f(X\V)cz {1}. Так как пространство X счетно, суще-
существует г е I\f(X). Очевидно, прообраз U = f~l ([0, г)) =
= f~1([0, r]) является открыто-замкнутым множеством, содер-
содержащим х и содержащимся в V. I
34*
532 ГЛ. 6. СВЯЗНЫЕ ПРОСТРАНСТВА
6.2.9. Теорема. Наследственная несвязность, нульмерность и
сильная нульмерность равносильны в классе непустых локально
компактных паракомпактов.
Доказательство. В силу теорем 6.2.1 и 6.2.6, достаточно до-
доказать, что каждое непустое наследственно несвязное локально
компактное паракомпактное хаусдорфово пространство X силь-
сильно нульмерно. Из теорем 5.1.27 и 6.2.7 следует, что достаточно
для каждой точки хеХи каждой ее окрестности VczX найти
открыто-замкнутое множество U, такое, что хе Uа V (см. тео-
теорему 6.2.13 ниже).
Возьмем какую-нибудь окрестность W точки х, для которой
W cz V и замыкание W является компактом. Теорема 6.1.23 по-
показывает, что множество {х} cz W совпадает с пересечением
семейства Ж всех открыто-замкнутых в пространстве W мно-
множеств, содержащих точку х. Значит, по следствию 3.1.5, най-
найдется конечное число множеств F\, F2, ..., ?к^Ж, таких, что
х е U = Fi П F2 П ... П Fk сг W cz V. Множество V замкнуто в X,
так как оно замкнуто в W. Оно открыто в X, так как оно от-
открыто в W. I
6.2.10. Следствие. Наследственная несвязность, нульмерность и
сильная нульмерность равносильны в классе непустых ком-
компактов. I
6.2.11. Теорема. Наследственная несвязность является наслед-
наследственным свойством, а нульмерность наследуется непустыми
подмножествами.
Если X — сильно нульмерное пространство и М — непустое
подпространство пространства X, обладающее тем свойством,
что каждая непрерывная функция /: M-+I продолжается до
непрерывной функции на X, то и пространство М сильно нуль-
нульмерно.
В частности, в нормальных пространствах сильная нульмер-
нульмерность наследуется непустыми замкнутыми подмножествами.
Доказательство. Первая часть теоремы очевидна. Вторая ее
часть вытекает из теоремы 6.2.4, так как при сделанном об М
предположении любые вполне отделенные подмножества про-
пространства М вполне отделены в X. I
Как замечено в последнем абзаце примера 6.2.20, сильная
нульмерность не является наследственным свойством (см. за-
задачу 7.4.6).
6.2.12. Теорема. Стоун-чеховская компактификация $Х тихонов-
тихоновского пространства X сильно нульмерна в том и только том
случае, если пространство X сильно нульмерно.
Доказательство. В силу последней теоремы, достаточно по-
показать, что если X сильно нульмерно, то и $Х сильно нульмерно.
6.2. РАЗЛИЧНЫЕ ВИДЫ НЕСВЯЗНОСТИ 533
Пусть А и В — произвольные вполне отделенные подмножества
пространства $Х и /: Х->1— непрерывная функция, для кото-
которой /(Л)с={0} и f{B)cz{l]. Множества АХ = X(\f-l([Q,l/3))
и В\ = Xf\f-1 (B/3, 1]) вполне отделены в Х\ значит, по тео-
теореме 6.2.4, найдется открыто-замкнутое множество U czX, та-
такое, что A\c=U и B\czX\U. Следствие 3.6.5 показывает, что
U — открыто-замкнутое множество в_рХ,_а из теоремы 1.3.6 ^ле-
дуе2, что А с: А\ и В а Бь Так как В\ П О = 0, имеем A cz A\ cz
czU а $Х\Б\ cz $Х\В. Следовательно, $Х сильно нульмерно
по теореме 6.2.4. I
В заключительной части примера 6.2.20 мы покажем, что
аналоги теоремы 6.2.12 для наследственно несвязных про-
пространств и для нульмерных пространств не имеют места.
Из теоремы 6.2.11, предложения 2.2.1 и определения тополо-
топологии суммы пространств вытекает
6.2.13. Теорема. Сумма ф Xs, где S ф 0 u Xs Ф 0 при s e 5,
наследственно несвязна (нульмерна, сильно нульмерна) в том
и только том случае, если все пространства Xs наследственно
несвязны (нульмерны, сильно нульмерны). I
6.2.14. Теорема. Произведение XI Xs, где S ф 0 и Х3ф 0 при
s^S, наследственно несвязно (нульмерно) в том и только том
случае, если все пространства Xs наследственно несвязны (нуль-
(нульмерны) .
Доказательство. Каждое из пространств Xs гомеоморфно
подпространству пространства Ц Xs; значит, по теореме 6.2.11,
достаточно показать, что произведение Д Xs наследственно
несвязных (нульмерных) пространств наследственно несвязно
(нульмерно). В случае наследственной несвязности это сле-
следует из теоремы 6.1.21. В случае нульмерности это следует из
того факта, что множества вида XI ^> где Ws открыто-замк-
s<=S
нуто в Xs и множество {s eS: Ws ф Xs} конечно, составляют
базу пространства Ц Xs и открыто-замкнуты. I
6.2.15. Следствие. Предел обратного спектра наследственно не-
связных (нульмерных) пространств является наследственно не-
несвязным (нульмерным или пустым) пространством. I
Произведение двух сильно нульмерных пространств не обя-
обязано быть сильно нульмерным пространством; соответствующий
пример слишком сложен, чтобы его здесь обсуждать. Подобным
же образом предел обратной последовательности сильно нуль-
534 гл. 6. связные пространства
мерных пространств может не быть сильно нульмерным про-
пространством (см. задачу 6.3.25).
6.2.16. Теорема. Канторов куб Dm универсален для всех нуль-
нульмерных пространств веса ш ^ Ко.
Доказательство. В силу последней теоремы, достаточно до-
доказать, что каждое нульмерное пространство X веса га. можно
вложить в D.
Из теоремы 1.1.15 вытекает, что у пространства X есть база
}s состоящая из открыто-замкнутых множеств и такая,
что |S| = ra. При каждом s^S определим отображение /s: X->
-*DS = D, положив
Г 1 при xg[/5(
0 при xe=X\U3.
f Г 1
ГЛХ) \0
По теореме о диагональном отображении, отображение /= Д f
S
s
является гомеоморфным вложением пространства X в канторов
куб Dm= UDS. I
6.2Л7. Следствие. Каждое нульмерное пространство X веса ш об-
обладает нульмерной компактификацией веса ш.
Доказательство. Можно предположить, что m ^ Ко; тогда
замыкание подпространства пространства Dm, гомеоморфного X,
является требуемой компактификацией. I
По теореме 3.2.2 (см. также упр. 3.2.В), существует непре-
непрерывное отображение f некоторого замкнутого подпространства
X канторова множества /)8° на отрезок /. Из теоремы 3.2.11
вытекает, что факторпространство X/E(f) гомеоморфно от-
отрезку /. Следовательно, факторпространство наследственно не-
несвязного (нульмерного, сильно нульмерного) пространства
может не быть наследственно несвязным (нульмерным, сильно
нульмерным) пространством.
6.2.18. Примеры. Каждое непустое дискретное пространство
сильно нульмерно.
Пространство W всех ординалов ^coi (см. пример 3.1.27)
нульмерно; так как это пространство — компакт, оно сильно
нульмерно. В силу теоремы 6.2.11 и примера 3.1.27, простран-
пространство Wo всех счетных ординалов тоже сильно нульмерно.
Прямая Зоргенфрея К нульмерна (см. пример 2.2.8); так
как это пространство линделёфово (см. пример 3.8.14), оно
сильно нульмерно.
Из 6.1.5 вытекает, что любое нульмерное подпространство
вещественной прямой не содержит никакого интервала. Как
6.2. РАЗЛИЧНЫЕ ВИДЫ НЕСВЯЗНОСТИ 535
легко проверить, каждое непустое подпространство веществен-
вещественной прямой, которое не содержит никакого интервала, нуль-
нульмерно. Значит,- непустое подпространство вещественной прямой
нульмерно, или, что равносильно (по теоремам 6.2.7 и 3.8.1),
сильно нульмерно в том и только том случае, если оно не со-
содержит никакого интервала. В частности, множества рацио-
рациональных чисел и иррациональных чисел нульмерны. Теоре-
Теоремы 6.2.7 и 6.2.14 показывают, что подпространство евклидова
л-пространства Rn (я-куба /я, гильбертова куба /к°), состоящее
из всех точек с рациональными координатами, сильно нуль-
нульмерно. Аналогично подпространство евклидова п-пространства
Rn (n-куба /л, гильбертова куба /**°), образованное всеми точ-
точками с иррациональными координатами, сильно нульмерно.
Из теоремы 6.2.14 следует, что пространство Бэра В(ш)
нульмерно при всех m ^ Ко. В примере 7.3.14 мы покажем, что
пространство В (ш) сильно нульмерно. ¦
Опишем теперь наследственно несвязное сепарабельное мет-
метрическое пространство, которое не нульмерно.
6.2.19. Пример (Эрдёш). Пусть J? —подпространство гильбер-
гильбертова пространства Я, определенное в примере 4.1.7, которое со-
состоит из всех бесконечных последовательностей {г,} рациональ-
рациональных чисел.
Пространство X наследственно несвязно. Действительно, для
любых двух различных точек я = {/^} и У = {/"/'} пространства
X найдется натуральное число /0, такое, что r'io Ф r"Q; очевидно,
можно предположить, что г'и < г". Возьмем любое иррацио-
иррациональное число /, для которого rfu < t < r?. Множество
открыто-замкнуто, содержит л: и не содержит у. Следовательно,
каждое связное подпространство пространства X содержит не
более одной точки.
Пусть хо = @, 0, ...) — точка пространства X, все коорди-
координаты которой равны нулю; положим V = В (лг0, 1) = |{г Jel:
? f? < 1 Г " Мы покажем, что для каждой окрестности U
t=i l )
точки Хо, содержащейся в окрестности V этой точки, всегда
Ггиф0, т. е. что никакое такое множество не является от-
открыто-замкнутым. Последнее означает, что пространство X не
нульмерно.
536 ГЛ. 6. СВЯЗНЫЕ ПРОСТРАНСТВА
Определим по индукции последовательность аи а2, ... ра-
рациональных чисел, удовлетворяющую условиям
A) xk = (au а2, ..., ак> О, 0,...)е[/ и p(xk,X\U)^ l/k.
Очевидно, если мы положим й\ = 0, то A) будет выполнено
при k=l. Предположим, что рациональные числа п\у п27 ...
..., flm-i уже определены и условия A) выполняются при всех
k^m — 1. Последовательность
xf = (av a2, ..., ат.р Цт, О, 0, ...)
является точкой множества X при / = 0, 1, ..., т. Так как
x™^U и x™&U, найдется i < m, для которого xf^U и
*Д-1 ^ ^ • Легко видеть, что, положив ат = i/m, мы обеспечи-
обеспечиваем выполнение условий A) при k = т. Таким образом, по-
последовательность аи «2, ... определена. Из A) вытекает, что
к
^ а2. < 1 при k = 1, 2, ...; значит, точка а = {at} является эле-
ментом множества X. Из A) также следует, что а^О{\
IT7T
Построим теперь нульмерное нормальное пространство, ко-
которое не сильно нульмерно.
6.2.20. Пример (Даукер). Пусть Q — множество всех рациональ-
рациональных чисел отрезка /. Положив
хЕу в том и только том случае, если \х — y\^Qt
мы определяем отношение эквивалентности на множестве /.
Ясно, что каждый класс эквивалентности Е счетен и всюду пло-
плотен в /. Значит, мощность семейства всех классов эквивалент-
эквивалентности равна с. Выберем из этого семейства подсемейство мощ-
мощности 4*ь не содержащее класса эквивалентности Q, и распо-
расположим члены этого подсемейства в трансфинитную последова-
последовательность Qo, Qu -.. > Qa> .. •, a < (Оь
В силу 6,2.18, для каждого a < an множество 5a=/\ U QY
нульмерно. Пусть W — пространство всех ординалов ^coi
и Wo=W\{coi}. при каждом a < coi множество Ха={у^
^W: у ^ а} открыто-замкнуто в W. Рассмотрим произведение
Wyil и его подпространства
^a= U ((y}X5y), y= U Uy}xsy) и r = yu(WX/).
У<а Y<g>i
Пространство Ya= Y0(Xay(I) открыто-замкнуто в У; так
как Уа е: Ха XSa, T0 пространство Уа нульмерно в силу теорем
6.2. РАЗЛИЧНЫЕ ВИДЫ НЕСВЯЗНОСТИ 537
6.2.11 и 6.2.14. Значит, пространство У тоже нульмерно. Так как
произведение ХаУ^1 является компактом со счетной базой,
оно метризуемо по теореме 4.2.8. Подпространство yacXaXi
тоже метризуемо и тем более нормально.
Покажем, что пространства У и У* тоже нормальны. Пусть
А и В— непересекающиеся замкнутые множества в У*. Множе-
Множества Л! = ЛП(У*\У) и B{ = B[](Y*\Y) являются компак-
компактами; поэтому, по теореме 3.1.6, существуют открытые множе-
множества U, V cz У*, такие, что
B) AicU, BxczV и U{]V=0.
Применив следствие 3.1.5 к воспользовавшись компакт-
компактностью Wy^I, мы легко убеждаемся, что при некотором a < <о\
выполняются включения
C) Al)(Y*\Ya)cU и ВП(У*\Уа)сК.
Из формул B) и C) и нормальности пространства Уа следует,
что множества А и В можно отделить в У* открытыми множе-
множествами, т. е. что пространство У* нормально.
Пусть теперь А и В — любые два непересекающихся замк-
замкнутых множества в У. Мы покажем, что замыкания множеств Л
и В в У* не пересекаются; очевидно, отсюда будет следовать,
что У нормально и что, в силу следствия 3.6.4, имеет место ра-
равенство р У* = р У.
Предположим, что нашлась точка ((д\,х)еА(\В, и возьмем
a<©i, для которого xgSy при всех у ^ а. Без труда опре-
определяются по индукции две последовательности оы, аг, ... и
Pi, P2, ... счетных ординалов, больших а, и две последователь-
последовательности хи *2, ... и уи У2у ... точек множества /, такие, что
<*i < Pi < a*+i> | х — хг | < 1//, \x — yt\< 1//,
(a,-, Xi)e±A и (р?, yt)^B
при t=lf 2, ... . Рассуждая так же, как в примере 3.1.27, мы
заключаем, что А[\В ф 0 — противоречие.
Предположим, что пространство У сильно нульмерно. По
теореме 6.2.4, найдется открыто-замкнутое множество f/сгУ,
такое, что W0X{0}czU и У0Х{1}сЛ[/. Как доказано
выше, Of\(Y\U)=0, Так как Y*=O\)(Y\U)t (юьО)е=0
и (coi, l)e Y\U9 наше предположение противоречит связности
пространства {coi} X /. Следовательно, пространство У не сильно
нульмерно.
Из нульмерности пространства У и следствий 6.2.10 и 6.2.17
вытекает, что сильно нульмерное пространство может содер-
содержать непустое нормальное подпространство, которое не сильно
538 ГЛ. 6. СВЯЗНЫЕ ПРОСТРАНСТВА
нульмерно. На примере пространства У мы видим также, что
из нульмерности пространства не следует, вообще говоря, нуль-
нульмерность его стоун-чеховской компактификации (см. теорему
6.2.12). Действительно, в силу теорем 6.2.12 и 6.2.7, простран-
пространство рУ не может быть нульмерным, так как пространство У
не сильно нульмерно. I
Введенные в этом параграфе понятия приводят к двум новым
классам отображений.
Непрерывное отображение /: Х->У называется легким
(нульмерным), если все прообразы f~{(y) точек наследственно
несвязны (нульмерны или пусты). Ясно, что каждое нульмер-
нульмерное отображение является легким и что среди отображений,
при которых все прообразы точек являются компактами, эти
два класса совпадают. В отношении строения прообразов точек
легкие отображения и нульмерные отображения являются пол-
полной противоположностью монотонных отображений. Как пока-
показано в теореме 6.2.22 ниже, каждое совершенное отображение
можно представить в виде композиции монотонного отображе-
отображения и нульмерного отображения.
6.2.21. Лемма. Для каждого совершенного отображения f: X-+
-*¦ У отношение эквивалентности Е на пространстве X, опреде-
определенное разбиением всех прообразов f~l(y) точек на компоненты,
замкнуто.
Доказательство. Достаточно показать, что естественное фак-
факторное отображение g: Х^Х/Е = Z замкнуто. Пусть C^Z —
произвольная компонента прообраза f~l(y) и U — любое откры-
открытое в X множество, содержащее g~l{C) — С. По теореме 6.1.23,
найдется открыто-замкнутое множество F в пространстве f~l(y),
для которого С a F cz U. Множества F и f~l(y)\F являются
компактами и не пересекаются; значит, в силу теоремы 3.1.6,
существуют открытые непересекающиеся множества W\y W2czX,
такие, что F <zz W\ cz U и f~l(y)\F cz W2. Из замкнутости / вы-
вытекает, что найдется открытое множество W cz У, для которого
С cz /-1 (у) cz f-1 (W)czWi\J W2. Множество V = Wi П f~l (W)
удовлетворяет равенству g~l(g(V))— V\ значит, g(V) является
окрестностью точки СeZ, Так как g~l(g{V))cz U, отображение
g замкнуто. I
6.2.22. Теорема. Каждое совершенное отображение f: X-^Y
можно представить в виде композиции f = hg, где g: X^-Z —
монотонное совершенное отображение и h: Z^Y — нульмерное
совершенное отображение.
Доказательство. Пусть Е — отношение эквивалентности, оп-
определенное в приведенной выше лемме, и g: X/E^-Z — есте-
естественное факторное отображение. Для каждого класса эквива-
эквивалентности [x]^Z обозначим через h([x]) точку f(x)^Y. Так
6.2, РАЗЛИЧНЫЕ ВИДЫ НЕСВЯЗНОСТИ
539
как hg = /, отображение h: Z-+Y непрерывно в силу предло-
предложения 2.4.2.
Из леммы, приведенной выше, следует, что отображение g
совершенно; значит, по теореме 3.7.20, Z— хаусдорфово про-
пространство. В силу предложения 2.1.3, h — совершенное отобра-
отображение.
Отображение g монотонно по определению. Остается дока-
доказать, что h нульмерно. Прообразы точек при h являются ком-
компактами, поэтому достаточно проверить, что для каждой точки
j/g7 ее прообраз hrx{y) наследственно несвязен. Пусть С —
произвольное связное подмножество пространства hrl(y). По
теореме 6.1.29, множество g~l (С) cz f~l (у) связно и, значит, со-
содержится в некоторой компоненте пространства f~](y). Следо-
Следовательно, множество gg~l(C)= С содержит самое большее одну
точку. I
Заметьте, что в последней теореме пространство Z является
непрерывным образом пространства X при совершенном ото-
отображении, равно как и прообразом пространства У при совер-
совершенном отображении. Поэтому многие топологические свой-
свойства пространств X и У являются также свойствами простран-
пространства Z. Например, если X или У являются компактами, локально
компактными хаусдорфовыми пространствами или паракомпак-
тами, то и пространство Z таково же (см. теоремы 3.7.21, 3.7.24,
5.1.33 и 5.1.35), и если X метризуемо, то и Z метризуемо (см. тео-
теорему 4.4.15).
Следуя схеме доказательства теоремы 6.2.22, для произволь-
произвольного непрерывного отображения f: X^-Y в ^-пространство У
можно определить пространство Z, монотонное факторное ото-
отображение g: J-^Z и легкое отображение h: Z^-Y, такие, что
f s= hg. Однако если / не совершенно, то даже для «хороших»
пространств X и У пространство Z обычно не будет хаусдорфо-
вым (см. упр. 6.2.Е). Следующая теорема показывает, что опре-
определенная нами факторизация отображения f единственна.
6.2.23. Теорема. Если непрерывное отображение f: J-^У пред-
представлено (при i = 1 и i — 2) в виде композиции higiy где
gi\ X-^Zi — монотонное факторное отображение и he Zt^^Y—
легкое отображение, то существует гомеоморфизм h: Z\-^Z2>
такой, что коммутативна следующая диаграмма:
540 ГЛ. 6. СВЯЗНЫЕ ПРОСТРАНСТВА
Доказательство, Для каждого z^ Z{ положим h(z)=g2g~l(z).
Так как g~{ (z) — связное подмножество пространства f~lhx (г)=
= g2lh2lhi(z)> множество h{z) состоит ровно из одной точки:
действительно, оно является связным подмножеством в Л^~1/г1 (аг).
Из равенства hgx = g2 следует, что h является непрерывным
отображением пространства Z\ в пространство Z2. Аналогично,
положив hf {z) — gxg~l (z) для каждого z^Zv мы определяем
непрерывное отображение h! пространства Z2 в Zj. Так как
hh' = idz2 и h'h = idzl, отображение h является гомеоморфиз-
гомеоморфизмом. Читатель легко проверит, что h2h = hu I
Так как каждое отображение компакта в точку совершенно,
лемма 6.2.21, теорема 6.1.29 и следствие 6.2.10 влекут за собой
следующую теорему.
6.2.24. Теорема. Для каждого компакта X разбиение простран-
пространства X на компоненты — или, что равносильно, на квазикомпо-
квазикомпоненты — определяет замкнутое отношение эквивалентности Е на
пространстве X. Факторпрост ранет во Х/Е является при этом
нульмерным компактом. I
Заключительная часть этого параграфа посвящена классу
еще более несвязных пространств.
Топологическое пространство X называется экстремально не-
несвязным, если для каждого открытого множества U<^X замы-
замыкание U открыто в X. Каждое дискретное пространство экстре-
экстремально несвязно. Пространство всех рациональных чисел может
служить примером сильно нульмерного не экстремально несвяз-
несвязного пространства. Ясно, что каждое экстремально несвязное
хаусдорфово пространство наследственно несвязно. Любое непу-
непустое экстремально несвязное регулярное пространство нульмер-
нульмерно. Действительно, в силу регулярности, для каждой точки
jteIh каждой ее окрестности V найдется окрестность W точ-
точки х, такая, что xg W czWczV. В силу экстремальной несвяз-
несвязности X множество U = W открыто и замкнуто. Значит, семей-
семейство всех открыто-замкнутых множеств составляет базу про-
пространства X. Подобным же образом доказывается и следующая
теорема.
6.2.25. Теорема. Каждое непустое экстремально несвязное тихо-
тихоновское пространство сильно нульмерно. I
6.2.26. Теорема. Топологическое пространство X экстремально не-
несвязно в том и только том случае, если для каждой napu_JJ, V
неперескающихся открытых в X множеств всегда U {]V=0.
Доказательство. Пусть U и V — непересекающиеся открытые
множества в экстремально несвязном пространстве X. Так как
6.2. РАЗЛИЧНЫЕ ВИДЫ НЕСВЯЗНОСТИ 541
LJ П V = 0± то 0[) V = 0; учитывая, что множество V открыто,
получаем uf\V = 0.
Предположим теперь, что для каждой пары ?/, V непересе-
непересекающихся открытых подмножеств топологического пространства
X выполняется условие U f\V = 0. Пусть U — произвольное от-
открытое в X множество. Открытые множества U и Х\О не пере-
секаются, значит, V П Х\ #_= 0- Следовательно, О czX \X\ О =
= Int U, т. е. множество О открыто и пространство X экстре-
экстремально несвязно. I
6.2.27, Теорема. Стоун-чеховская компактификация рХ тихонов-
тихоновского пространства X экстремально несвязна в том и только том
случае, если пространство X экстремально несвязно.
Доказательство. Пусть X — экстремально несвязное тихонов-
тихоновское пространство и U — открытое множество в рХ. Замыкание
Xf\Uf\X множества U(]X в пространстве X является открытым
и замкнутым множеством. По теореме 1.3.6 имеем
Поэтому, в силу следствия 3.6.5, множество U = Xf\Uf\X от-
открыто и замкнуто в EХ.
Рассмотрим теперь произвольное тихоновское пространство X,
стоун-чеховская компактификация рХ которого экстремально не-
несвязна, и пусть UczX — любое открытое в X множество. Возь-
Возьмем какое-нибудь открытое множество WczfiX, для которого
W()X_=U. По теореме 1.3.6, Е/ = 1Г[]1=|, Значит, замыка-
замыкание U[)Х— Wf\X множества U в пространстве X замкнуто и
открыто. I
6.2.28. Следствие. При каждом m 2^ Ко стоун-чеховская компак-
компактификация р?)(т) дискретного пространства D(m) является
экстремально несвязным пространством. I
6.2.29. Следствие. Пространство pW экстремально несвязно. I
6.2.30. Теорема. Сумма © Xs экстремально несвязна в том и
только том случае, если все пространства Xs экстремально не-
несвязны. I
Как свидетельствует пример канторова множества ?)к°, про-
произведение экстремально несвязных пространств, как правило, не
экстремально несвязно (см. упр. 6.2.G(a) и задачу 6.3.21 (а)).
6.2.31. Пример. Покажем, что пространство $N\N не экстре-
экстремально несвязно. Отсюда будет следовать, что экстремальная
несвязность не наследуется, вообще говоря, замкнутыми подпро-
подпространствами.
542 ГЛ. 6. СВЯЗНЫЕ ПРОСТРАНСТВА
Пусть X не нормальное тихоновское пространство, опреде-
определенное в примере 3.6.19. В пространстве X есть непересекаю-
непересекающиеся замкнутые множества А и В, которые нельзя отделить не-
непересекающимися открытыми множествами. Конечно, можно
предположить, что Л,Вс X\N. Положим
xte=A} и WB =
где {Ut}te/ — семейство открытых множеств в $N\N, рассмот-
рассмотренное в примере 3.6.19.
Предположим, что пространство $N\N экстремально не-
несвязно. Так как WahWb — непересекающиеся открытые подмно-
подмножества пространства $N\N, их замыкания в $N\N не пересе-
пересекаются. Но пространство $N\N замкнуто в $N; поэтому
Wa П ^в = 0, где черта обозначает замыкание в piV. В силу нор-
нормальности пространства (W, найдутся открытые множества
У, Ус Р#, такие, что
Множества Xf\ U и Xf\ V открыты в X, не пересекаются и содер-
содержат множества А и В соответственно. Полученное противоречие
показывает, что пространство $N\N не экстремально несвязно. I
Из примеров 2.5.4 и 6.2.31 следует, что предел обратной по-
последовательности экстремально несвязных пространств может
не быть экстремально несвязным пространством.
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
Наследственно несвязные пространства были введены Хаус-
дорфом в [1914]. Иногда такие пространства называют вполне
несвязными; однако теперь вполне несвязным называют обычно
пространство, в котором квазикомпонента каждой точки х со-
состоит только из этой точки х (этот класс пространств был вве-
введен Серпинским в [1921]). Легко проверяется, что каждое нуль-
нульмерное пространство вполне несвязно и что каждое вполне не-
несвязное пространство наследственно несвязно. Имеет отношение
к названным классам пространств класс пунктформных, или
разрывных, пространств. Это такие пространства, которые не
содержат никакого континуума, состоящего более чем из
одной точки (данный класс пространств был введен Янишевским
в [1912]). Ясно, что каждое наследственно несвязное простран-
пространство пунктиформно. Пространство в примере 6.2.19 вполне не-
несвязно. Примеры наследственно несвязных, но не вполне не*
связных пространств, равно как и примеры связных пункта-
формных пространств, можно найти в задачах 6.3.23 и 6.3.24.
6.2. РАЗЛИЧНЫЕ ВИДЫ НЕСВЯЗНОСТИ 543
Нульмерные пространства были введены Серпинским в
[1921] — до того, как возникла теория размерности. С другой
стороны, сильно нульмерные пространства изучались только в
контексте теории размерности, и наши теоремы об этом классе
пространств являются специальными случаями теорем теории
размерности (см. замечания к § 7.1). Теоремы 6.2.5, 6.2.7 и
6.2.16, а также следствие 6.2.10 были доказаны Веденисовым в
[1939]. Пример сильно нульмерного нормального пространства
X, такого, что произведение ХУ^Х нормально, но не сильно
нульмерно, был построен Ваге в [1977] (см. также Ваге [1978]).
В своем оригинальном построении Ваге применил континуум-
гипотезу; Пшимусинский (цитировано Ваге в [1977]) показал,
как модифицировать конструкцию Ваге таким образом, что
ссылка на континуум-гипотезу будет не нужна (детали можно
найти в работе Пшимусинского [1979]). Пример 6.2.19 описан
в статье Эрдёша [1940] (первый пример сепарабельного метри-
метрического пространства с аналогичными свойствами был определен
Серпинским в [1921]; пространство Серпинского еще и метри-
зуемо полной метрикой). Пример 6.2.20 описан в статье Дау-
кера [1955].
Легкие отображения и нульмерные отображения введены
Стойловым в [1928]. Теорема 6.2.22 доказана Эйленбергом в
[1934] и Уайберном в [1934] для компактных метрических про-
пространств X и F. Для любых метрических пространств она была
доказана Вайнштейном в [1947а]; в нынешней форме эта тео-
теорема была установлена Пономаревым в [1959а]. Теорема 6.2.23
отмечена Уайберном в [1942].
Экстремально несвязные пространства были определены
М. X. Стоуном в [1937а]. Доказательство того, что $N\N не
экстремально несвязно, приведенное в примере 6.2.31, взято из
книги Гиллмана и Джерисона [I960]; сам этот факт был дока-
доказан (на другом языке; см. Энгелькинг [1972]) Хаусдорфом
в [1936].
УПРАЖНЕНИЯ
6.2.А. (а) (Мазуркевич [1917]). Пусть множество А и его
дополнение Х\А всюду плотны в сепарабельном нульмерном
пространстве X, метризуемом полной метрикой, причем А яв-
является множеством типа G6 в X. Докажите, что А тогда гомео-
морфно пространству иррациональных чисел.
Указание. Воспользовавшись указанием к упр. 4.3.G, пока-
покажите, что каждое пространство А с перечисленными выше свой-
свойствами гомеоморфно пространству В(&0)-
(Ь) (Александров и Урысон [1928]). Покажите, что каждое
сепарабельное нульмерное метризуемое полной метрикой про-
544 ГЛ. 6. СВЯЗНЫЕ ПРОСТРАНСТВА
странство, которое не содержит никакого непустого открытого
компактного подмножества, гомеоморфно пространству иррацио-
иррациональных чисел.
(c) (Брауэр [1910]). Докажите, что каждый плотный в себе
нульмерный метризуемый компакт гомеоморфен канторову со-
совершенному множеству.
Указание. Видоизмените конструкцию, описанную в указании
к упр. 4.3.G, таким образом, чтобы множества Ftlt2... tk были
определены при i\ ^ ти t2 ^ п%2, •.., ik^ rrik, где m\t тг, ... —
некоторая последовательность степеней числа 2.
(d) (Серпинский [1920а] (объявлено в [1915])). Докажите,
что каждое плотное в себе счетное метризуемое пространство го-
гомеоморфно пространству рациональных чисел.
Указание. В силу упр. 4.3.H(d), достаточно показать, что
каждое плотное в себе счетное метризуемое пространство X го-
гомеоморфно некоторому всюду плотному подпространству про-
пространства Р иррациональных чисел. Вложите X в Р, уберите
подходящим образом &0 точек из Х\Х и примените (а).
Можно воспользоваться также упр. 4.3.Н(е) и применить (с).
6.2.В. (а) Покажите, что непустой компакт нульмерен в том
и только том случае, если он гомеоморфен пределу обратного
спектра конечных дискретных пространств.
(Ь) (Терасава [1972]). Покажите, что непустое тихоновское
пространство X сильно нульмерно в том и только том случае,
если каждое функционально замкнутое подмножество простран-
пространства X можно представить в виде пересечения счетного семей-
семейства открыто-замкнутых множеств.
6.2.С (Даукер [1955]). Покажите, что к пространству У в
примере 6.2.20 можно таким образом присоединить одну точку,
что получится, по нашему усмотрению, либо нормальное не нуль-
нульмерное пространство, либо нормальное и сильно нульмерное про-
пространство (см. упр. 6.2.D).
Указание. Присоедините точку (соьО); отождествите множе-
множество У*\У с: У* в точку.
6.2.D. (а) Докажите, что если пространство, полученное при-
присоединением нульмерного компакта к сильно нульмерному про-
пространству, является тихоновским, то оно также и сильно нуль-
нульмерно.
Указание. Примените упр. 3.2.J.
(Ь) Докажите, что если пространство, полученное присоеди-
присоединением к сильно нульмерному пространству другого сильно нуль-
нульмерного пространства в качестве замкнутого подпространства,
нормально, то оно также и сильно нульмерно.
6.2.Е. (а) Приведите пример непрерывного отображения
/: X~-*Y, такого, что X и У — сепарабельные метризуемые про-
пространства, все прообразы f~l{y) точек компактны, но в разло-
6.2. РАЗЛИЧНЫЕ ВИДЫ НЕСВЯЗНОСТИ 545
жении f = hg, где g: X-+Z— монотонное факторное отображе-
отображение и h: Z-+Y — легкое отображение, пространство Z не яв-
является хаусдорфовым.
Указание. Возьмите в качестве X пространство, определенное
в примере 6.1.24.
(b) Приведите пример замкнутого отображения /: Х->-У,
где X и У — сепарабельные метризуемые пространства, такого,
что в разложении / = hg, где g: X^*Z— монотонное фактор-
факторное отображение и h: Z^~Y — легкое отображение, простран-
пространство Z не является хаусдорфовым.
(c) (Майкл [1964]). Покажите, что если пространства X п Y
в теореме 6.2.22 вполне регулярны, то и пространство Z вполне
регулярно.
6.2.F (Куратовский [1928]). Покажите, что любое разбиение
компакта на счетное семейство континуумов задает замкнутое
отношение эквивалентности.
Указание. Примените теоремы 6.1.27 и 6.2.24.
6.2.G. (а) Убедитесь, что никакое подпространство экстре-
экстремально несвязного хаусдорфова пространства X не гомеоморфно
^(^о), т. е. что в X нет нетривиальных сходящихся последова-
последовательностей.
Выведите отсюда, что каждое экстремально несвязное сек-
секвенциальное пространство дискретно.
(b) Покажите, что экстремальная несвязность наследуется
каноническими замкнутыми множествами, открытыми множе-
множествами и всюду плотными множествами.
(c) Заметьте, что каждое экстремально несвязное наслед-
наследственно нормальное пространство наследственно экстремально
несвязно. Приведите пример недискретного пространства с та-
такими свойствами.
(d) Покажите, что волмэновское расширение (оХ ^-простран-
^-пространства X экстремально несвязно в том и только том случае, если
пространство X экстремально несвязно.
6.2.Н. (а) Покажите, что нульмерность и сильная нульмер-
нульмерность не сохраняются ни совершенными отображениями, ни от-
открытыми отображениями (даже в классе сепарабельных метри-
зуемых пространств), но они сохраняются открыто-замкнутыми
отображениями.
Указание. См. упр. 3.2.В, 4.2.D(a) и 1.5.L(b).
(b) Покажите, что экстремальная несвязность не сохраняет-
сохраняется совершенными отображениями, но сохраняется открытыми
отображениями (в сторону образа).
(c) Заметьте, что наследственная несвязность не является
инвариантом ни совершенных отображений, ни открытых отобра-
отображений.
35 Зак. 697
546 ГЛ. 6. СВЯЗНЫЕ ПРОСТРАНСТВА
Замечание. Э. Поль и Р. Поль привели в [1974] пример со-
совершенно открытого отображения наследственно несвязного се-
парабельного пространства на нетривиальное связное простран-
пространство. Некоторые результаты о сохранении наследственной не-
несвязности открыто-замкнутыми отображениями при дополни-
дополнительных ограничениях можно найти в статье Комбарова [1971].
6.3. ЗАДАЧИ
Одна характеристика связности
6.3.1. Покажите, что пространство X связно в том и только
том случае, если для каждого открытого покрытия {Us}sgS про-
пространства X и любых двух точек х\, х2 из X найдется последо-
последовательность s\y s2, ..., sk элементов множества 5, такая, что
xxgUSi, x2^USk и USi{\USj ф 0 в том и только том случае,
если \i — /1^ 1.
Линейно упорядоченные пространства V (см. задачи 1.7.4,
2.7.5, 3.12.3, 3.12.4, 3.12.12(f), 5.5.22 и 8.5.13(j))
6.3.2. (а) Покажите, что пространство X с топологией по-
порожденной линейным упорядочением <, связно в том и только
том случае, если X непрерывно упорядочено отношением <.
(b) Покажите, что каждый сепарабельный линейно упорядо-
упорядоченный континуум X гомеоморфен отрезку /.
Указание. Возьмите счетное множество S ={s\t s2, .. ¦}, всюду
плотное вХ, в которое не входят ни наименьший, ни наиболь-
наибольший элементы множества X. Упорядочите множество рациональ-
рациональных чисел, заключенных (строго) между 0 и 1, в последователь-
последовательность п, г2у ... таким образом, чтобы п < г/ было в том и толь-
только том случае, если st < s/. Проверьте, что равенством f(si) = ri
определено непрерывное отображение /: S-*I, и примените тео-
теорему 3.2.1.
(c) Докажите, что каждое сепарабельное линейно упорядо-
упорядоченное метризуемое пространство X можно вложить в веще-
вещественную прямую.
Указание. Заметьте сначала, что можно предположить, что
X — компакт (см. указание к задаче 3.12.3 (Ь)). Отметьте, что
множество скачков в X счетно, замените каждый скачок отрез-
отрезком / и примените (Ь).
(d) Приведите пример неметризуемого сепарабельного ли-
линейно упорядоченного пространства.
(e) (Херрлих [1965]). Докажите, что каждое наследственно
несвязное линейно упорядоченное пространство сильно нуль-
нульмерно.
6.3. задачи 547
(f) (Херрлих [1965]; для сепарабельных пространств — Линн
[1962]). Докажите, что топология каждого сильно нульмерного
метризуемого пространства X порождается некоторым линейным
упорядочением < на X.
Указание. Покажите сначала, что для каждого е > 0 найдет-
найдется покрытие °U пространства X, состоящее из попарно непересе-
непересекающихся открыто-замкнутых множеств диаметра, меньшего е
(можно или воспользоваться теоремой 7.3.15, или применить
теорему 4.4.1 к покрытию пространства X шарами радиуса е/4
и воспользоваться свойством D) семейств Ти определенных в
доказательстве этой теоремы). Такое покрытие Щ, так линейно
упорядоченное некоторым отношением <, что в Щ есть наимень-
наименьший и наибольший элементы и индуцированная отношением <
топология на °U дискретна, будет называться е-цепью в X.
Но индукции определите при i = l, 2, ... 1/2'-цепь <Ui в X
и два отображения //, gt множества °Ui в X так, чтобы выполня-
выполнялись следующим условия:
A) При всех U <~<Ui имеем ft(U)& U и gi{U)^ [/.
B) Если fi(U)=gi(U) = x, то U={x}.
C) Семейство °Ui+\ является объединением \j{%i+i(U):
U^tUi} с естественным упорядочением, где Щ^\{и) — некото-
некоторая 1/2'+1-цепь в U, такая, что }u{U) принадлежит наименьшему
элементу семейства °Ui+\{lJ) и gi(U) принадлежит наибольшему
элементу семейства <2/h-i(?/).
D) Если fi(U)*BV<=<UH.u то f/+i(V)=fi(?/).
E) Если #(?/)€= V €=<&,+,, то gw(V) = gi(U).
Для xt у е X положим х < у, если существует /, такое, что
Локальная связность
6.3.3. Топологическое пространство X называется локально
связным, если для каждой точки ^gIh любой ее окрестности
U существует связное множество С а ?/, такое, что х е Int С.
(a) Покажите, что пространство X локально связно в том
и только том случае, если компоненты всех открытых подпро-
подпространств пространства X открыты.
Замечание. Не лишне отметить здесь, что необязательно в
любое открытое покрытие локально связного паракомпакта
можно вписать локально конечное открытое покрытие, состоящее
из связных множеств (даже в классе сепарабельных метризуе-
мых пространств); см. Филиппов [1974]. С другой стороны, в
любое открытое покрытие произвольного локально связного па-
паракомпакта можно вписать ог-дискретное открытое покрытие, со-
состоящее из связных множеств; см. Пшимусинский [1973].
(b) Убедитесь, что в локально связном пространстве компо-
компоненты совпадают с квазикомпонентами.
35*
548 ГЛ. 6. СВЯЗНЫЕ ПРОСТРАНСТВА
(c) Заметьте, что локальная связность не сохраняется не-
непрерывными отображениями даже в классе сепарабельных мет-
ризуемых пространств.
(d) (Уайберн [1952]). Покажите, что локальная связность
сохраняется факторными отображениями.
6.3.4. (а) Заметьте, что локальная связность наследуется от-
открытыми множествами, и приведите пример замкнутого множе-
множества на плоскости, которое не локально связно.
(Ь) Убедитесь, что сумма ф Xs локально связна в том и
только том случае, если все пространства Xs локально связны,
(с) Покажите, что произведение Ц Xs, где Х3ф0 при
se=S
sgS, локально связно в том и только том случае, если все про-
пространства Xs локально связны и существует конечное множество
So c= 5, такое, что Xs связно при всех s e S\So-
6.3.5. (а) (Уоллес [1951] для нормальных пространств). До-
Докажите, что для тихоновского (нормального) пространствах функ-
функционально открытое (открытое) множество U а рХ связно в том
и только том случае, если пересечение Xf\ U связно.
Указание. Примените лемму 7.1.13 и упр. 2.1.В (с).
(b) (Банашевский [1956]). Покажите, что если стоун-чехов-
стоун-чеховская компактификация рХ тихоновского пространства X локаль-
локально связна, то X псевдокомпактно.
Указание (де Гроот и Макдауэлл [1967]). Заметьте, что
компактификация вещественной прямой, описанная в примере
3.5.15, не локально связна, и примените задачу 6.3.3 (d).
(c) (Хенриксен и Исбелл [1957]). Покажите, что если псев-
псевдокомпактное пространство X локально связно, то каждое регу-
регулярное пространство, содержащее X в качестве всюду плотного
подпространства, тоже локально связно.
Указание (де Гроот и Макдауэлл [1967]). Воспользовавшись
равносильностью условий (i) и (и) в теореме 3.10.22, покажите,
что если открытые множества U, V с: X удовлетворяют вклю-
включению VczU, то лишь конечное число компонент множества U
пересекает множество К.
(d) (Банашевский [1956], Хенриксен и Исбелл [1957]). До-
Докажите, что стоун-чеховская компактификация рХ тихоновского
пространства X локально связна в том и только том случае, если
пространство X локально связно и псевдокомпактно.
6.3.6. (а) (Хенриксен и Исбелл [1957]). Покажите, что сле-
следующие условия равносильны для произвольного регулярного
пространства X:
A) В каждое конечное открытое покрытие пространства X
можно вписать конечное покрытие, состоящее из связных мно-
множеств.
6.3. ЗАДАЧИ 549
B) В каждое конечное открытое покрытие пространства X
можно вписать конечное открытое покрытие, состоящее из связ-
связных множеств.
C) Пространство X локально связно и счетно компактно.
(b) Заметьте, что если X — нормальное пространство, то ус-
условия A) — C) в (а) равносильны следующему условию:
D) В каждое конечное открытое покрытие пространства $Х
можно вписать конечное покрытие, состоящее из континуумов.
(c) Покажите, что компакт X локально связен в том и толь-
только том случае, если в каждое открытое покрытие пространства X
можно вписать конечное покрытие, состоящее из континуумов.
6.3.7. Покажите, что ^-пространство X связно и локально
связно (одновременно) в том и только том случае, если, каковы
бы ни были открытое покрытие {Us}s^s пространства X и точки
jti, x2 из X, найдутся последовательность (конечная) s\, 52, ...,$&
элементов множества S и последовательность Vu V2> ..., Vk
связных открытых подмножеств пространства X, такие, что
хх е= Vx, х2 е= Vht Vt с Us. при / = 1, 2, ..., k и Vi [\VS?*0 в
точности тогда, когда \i — /| ^ 1.
Топологическая характеристика отрезка
6.3.8. Назовем точку х связного пространства X разбиваю-
разбивающей точкой пространства X, если Х\ {*}=?/U У> где множе-
множества U, V открыты, не пересекаются и не пусты, т. е. если про-
пространство Х\{х} не связно. Если х не является разбивающей
точкой пространства X, назовем ее не разбивающей точкой.
(a) Проверьте, что если х — разбивающая точка континуума
X и Х\{х}= U {) V, где U и V — непустые непересекающиеся
открытые множества, то множества U\){x] и KUW являются
континуумами.
(b) (Уоллес [1942]; для метризуемых континуумов —
Р. Л. Мор [1920]). Покажите, что в каждом континууме X мощ-
мощности >1 есть по крайней мере две неразбивающие точки.
Указание. Докажите, что для каждого х^Х найдется нераз-
бивающая точка уе Х\{х}. Для этого упорядочите семейство 9
всех собственных подконтинуумов континуума X, содержащих
точку х, положив С\^С2 в том и только том случае, если
С\ cz Int C2. Возьмите затем любое максимальное линейно упоря-
упорядоченное подсемейство Wocz^, содержащее {х}, и рассмотрите
объединение (J *&0.
(c) (Серпинский [1916], Страшевич [1918], Р. Л. Мор [1920];
для континуумов на плоскости — Леннес [1911]). Докажите, что
произвольный сепарабельный континуум, ровно две точки кото-
которого являются неразбивающими, гомеоморфен отрезку /.
Указание. Пусть а, Ъ — две неразбивающие точки такого кон-
550 ГЛ. 6. СВЯЗНЫЕ ПРОСТРАНСТВА
тинуума X, Воспользовавшись (Ь), покажите, что для каждого
xei\{fl,l>} имеет место равенство X\{x} = A(x)\J B(x)t где
А(х) и Б(jc) — открытые множества, А(х)ПВ(х) = 0 и а^А(х),
Ь^В(х). Для различных х, y^X\{ayb} положим х<у, если
Л (jc) с= А (у), и пусть а<Х<Ь для всех ^Gl\{a,J}, Убеди-
Убедитесь, что <—линейное упорядочение на X, порождающее ис-
исходную топологию пространства X, Примените задачу 6.3.2(Ь).
Линейная связность и локальная линейная связность
6.3.9. Пространство X линейно связно, если для любых двух
точек х\, х2 пространства X существует непрерывное отображе-
отображение f: I-+-X отрезка / в пространство X, такое, что f{O) = x\ и
/0)
)
(a) Проверьте, что каждое линейно связное пространство
связно, и приведите пример континуума на плоскости, не яв-
являющегося линейно связным.
(b) Заметьте, что линейная связность сохраняется (в сто-
сторону образа) непрерывными отображениями.
(c) Покажите, что произведение Ц Xs> гДе Х8ф 0 при
sgS, линейно связно в том и только том случае, если все про-
пространства Xs линейно связны.
6.3.10. Пространство X локально линейно связно, если для
каждой точки хеХи произвольной ее окрестности U найдется
окрестность V точки х, такая, что, каково бы ни было у е V,
существует непрерывное отображение /: /->-?/, удовлетворяющее
условиям f(O) = x и f(l)= г/.
(a) Проверьте, что каждое локально линейно связное про-
пространство локально связно, и приведите пример локально связ-
связного подпространства плоскости, которое не является локально
линейно связным. Покажите, что каждое связное локально ли-
линейно связное пространство линейно связно.
(b) Заметьте, что локальная линейная связность сохраняет-
сохраняется факторными отображениями, но не сохраняется непрерыв-
непрерывными отображениями — даже если ограничиться сепарабель-
ными метризуемыми пространствами.
(c) Убедитесь, что локальная линейная связность наследует-
наследуется открытыми множествами.
(d) Покажите, что произведение Ц Xs, где Xs Ф 0 при
s e S, локально линейно связно в том и только том случае, если
все пространства Xs локально линейно связны и существует ко-
конечное множество So с: 5, такое, что Xs линейно связно при всех
s e S\S0.
6.3.11 (Менгер [1929],Р. Л.Мор [1932] (объявлено в [1927]);
для компактов —Мазуркевич [1913], [1913а] и [1920], Р. Л. Мор
6.3. ЗАДАЧИ 551
[1916]). Докажите, что для любых двух различных точек Х\, хг
произвольного связного открытого подпространства V локально
связного пространства Х7 метризуемого полной метрикой, в V
существует подпространство, гомеоморфное отрезку /, которое
содержит jci и х2.
Выведите отсюда, что каждый локально связный метризуе-
мый континуум линейно связен и локально линейно связен.
Указание, Определите при т = 1, 2, ... конечную последо-
последовательность V?> Vf, ...» Vrkm связных открытых подмножеств
пространства V, такую, что
A) xxeV?\(V?[) ... иЯЦ, x2^Vfm\(vTU^-UVfm^)
и 6(УГ)<1М при /=1, 2, ..., kn.
B) V?(}VT?=0 в точности тогда, когда \i — /|<l.
C)_При всех /<&„,, где т> 1, найдется /(')^&jn-i> такое»
что V?cV?w> и если /i</2> то j(hXj(i2).
С помощью задачи 6.3.8 (с) покажите, что пересечение
LI
П LI VT гомеоморфно /.
m=l i = \
Можно также определить непосредственно гомеоморфное вло-
вложение h: /-> У, такое, что хи jc2e/i(/). Для этого разбейте от-
отрезок / на km следующих друг за другом замкнутых отрезков
^Г> /Г» • • • > I*km с попарно непересекающимися внутренностями
таким образом, что iT^lfd) ПРИ ё = 1.2 fcm, где /п > 1,
и 6(/f ) = 6 ('"), как только /@ = /(tr) - Определите затем Л,
оо
взяв в качестве ft(tf) единственную точку пересечения Р U
6.3.12. (а) Покажите, что хаусдорфово пространство X ли-
линейно связно в том и только том случае, если для каждой пары
jci, X2 различных точек пространства X существует гомеоморф-
гомеоморфное вложение h: 1->Х замкнутого отрезка / в пространство X,
удовлетворяющее условиям /t(O) = jti и AA) = jc2 (т. е. если X
дугообразно связно).
Указание. Примените задачу 6.3.11.
(Ь) Покажите, что хаусдорфово пространство X локально
линейно связно в том и только том случае, если для каждой
точки xgX я произвольной ее окрестности U найдется окре-
окрестность V точки х, такая, что, какова бы ни была точка
ye V\{*}, существует гомеоморфное вложение А: /->•{/, удов-
удовлетворяющее условиям Л(О) = л; и ft(l) = # (т. е. если X локаль-
локально дугообразно связно).
552 ГЛ. 6. СВЯЗНЫЕ ПРОСТРАНСТВА
6.3.13. Пусть (X, р) — локально связное компактное метриче-
метрическое пространство. Докажите, что для каждого е > 0 найдется
б > 0, такое, что, каковы бы ни были точки ху у пространства
X, удовлетворяющие условию 0 < р(х, у) < б, существует гомео-
морфное вложение h: I-*X, такое, что h@) = x, h(\) = y и
в(А()
())
Указание. Примените задачу 6.3.11.
6.3.14 (Хан [1914], Мазуркевич [1913], [1913а] и [1920а],
Серпинский [1920b]). Докажите, что для каждого метризуемого
континуума X следующие условия равносильны:
A) Пространство X является непрерывным образом отрезка I.
B) Для каждой метрики р на пространстве1) X и любого
е > 0 существуют связные замкнутые множества F\, F2, ..*, Fkj
такие, что X = Fi{]F2U ... [}Fk и 6(Fi) ^ е при I = 1, 2, ..., k.
C) Пространство X локально связно.
Указание. При доказательстве импликации C)=^A) восполь-
воспользуйтесь теоремой 3.2.2 и задачами 6.3.11 и 6.3.13.
Квазикомпоненты произведений
6.3.15 (Куратовский [1961]). Докажите, что квазикомпонента
точки x={xs} в произведении Ц Xs совпадает с прозведением
Ц Qs, где Qs — квазикомпонента точки xs в пространстве^.
Обратные спектры III (см. задачи 2.7.19 и 3.12.13)
6.3.16. (а) (Джентри [1969], Э. Поль [1973]). Пусть
{ф, /^ — отображение обратного спектра 5==|Ха, я?, 2} ком-
компактов в обратный спектр S' = {Ya,, л?,2'} ^-пространств. Дока-
Докажите, что если все отображения fa, монотонны, то предельное
отображение f = Пт|ф, fa,} тоже монотонно.
Выведите отсюда, что если в обратном спектре S={Ja, я^, 2}
компактов все связующие отображения я? монотонны, то проек-
проекции яо: HmS-> Хатоже являются монотонными отображениями.
(Ь) (Э. Поль [1973]). Приведите пример обратных последо-
последовательностей 3 = {Х{1 я|} и S' = {Yr Щ подпространств пло-
плоскости и отображения {id*, /,-} из S в S7, где я|, зх| и ft — моно-
монотонные замкнутые отображения «на», таких, что lim {id^, ft) яв-
является замкнутым, но не монотонным отображением «на».
*) Напомним, что выражение «метрика на пространстве X» следует по-
понимать как «метрика на множестве X, порождающая топологию простран-
пространства Хъ. — Прим. перев.
6.3. ЗАДАЧИ 553
Приведите пример обратной последовательности S = {XP я?}
связных подпространств плоскости, в которой все связующие
отображения я| являются монотонными отображениями «на»,
такой, что предел Iim S не связен. Выведите отсюда, что суще-
существует обратная последовательность S = {Xr ли связных про-
пространств, в которой все связующие отображения nj монотонны
и «на», такая, что некоторые проекции я^: WxnS^Xi не моно-
монотонны.
(с) (Э. Поль [1973]). Докажите, что если все связующие
отображения я* обратной последовательности S = {Jt., njj связ-
связных пространств являются наследственно факторными монотон-
монотонными отображениями, то Iim S — связное пространство.
Выведите отсюда, что если все связующие отображения тс1.
обратной последовательности S = {X.> nfy являются наследствен-
наследственно факторными монотонными отображениями, то проекции
щ: limS->J(- тоже монотонны.
Пространства Урысона и семирегулярные пространства III
(см. задачи 1.7.7— 1.7.9 и 2.7.6)
6.3.17. Покажите, что если применить операцию, описанную
в задаче 1.7.8 (Ь), к пространству X в примере 6.1.6, то получится
счетное семирегулярное пространство, ни у каких двух различ-
различных точек которого нет окрестностей с непересекающимися за-
замыканиями (см. задачу 1.7.8(d)).
Экстремально несвязные пространства и аксиомы отделимости
6.3.18. Убедитесь, что каждое экстремально несвязное хаус-
дорфово пространство является урысоновым пространством и
что каждое экстремально несвязное семирегулярное простран-
пространство является тихоновским пространством. Приведите пример
экстремально несвязного хаусдорфова пространства, которое не
семирегулярно, и пример экстремально несвязного тихоновского
пространства, которое не нормально.
Проективные пространства и проективные резольвенты (абсо-
(абсолюты)
6.3.19 (Глисон [1958],Рейнуотер [1959]). Мы называем ком-
компакт Р проективным в классе компактов, если для любых ком-
компактов X и У, каждого непрерывного отображения g компакта
X на компакт У и любого непрерывного отображения h: P-+Y
существует непрерывное отображение /: Р->-Х, такое, что
*/ = *-
554 ГЛ. 6. СВЯЗНЫЕ ПРОСТРАНСТВА
(a) Покажите, что пространство проективно в классе ком-
компактов в том и только том случае, если оно является ретрактом
стоун-чеховской компактификации дискретного пространства.
Указание. Каждый компакт является непрерывным образом
стоун-чеховской компактификации дискретного пространства.
(b) Докажите, что каждый компакт X является непрерывным
образом некоторого проективного в классе компактов простран-
пространства А (X) при неприводимом отображении пх-
Проверьте, что если некоторое пространство Р и отображе-
отображение / обладают указанными выше свойствами пространства А(Х)
и отображения лх, то найдется гомеоморфизм h: A(X)^P, та-
такой, что fh = nx. Пара (А(Х),пх) называется проективной ре-
резольвентой или абсолютом пространства X.
Указание. Проверьте, что если непрерывное отображение /
хаусдорфова пространства У о в себя не является тождественным
отображением, то найдется собственное замкнутое подмножество
Y\ с= Уо, такое, что Y\ \] j~l(Yi)= Уо. Рассмотрите затем непре-
непрерывное отображение какого-нибудь проективного пространства
У на X и примените упр. 3.1.С (а).
(c) Покажите, что каждое неприводимое замкнутое отобра-
отображение хаусдорфова пространства на экстремально несвязное
пространство является гомеоморфизмом.
(d) Докажите, что компакт проективен в классе компактов
в том и только том случае, если он экстремально несвязен.
Указание. Убедитесь, что экстремальная несвязность сохра-
сохраняется ретракциями.
6.3.20 (Флаксмайер [1963], Илиадис [1963], Пономарёв
[1963]; для паракомпактов — Пономарёв [1962]). Скажем, что
регулярное пространство Р проективно в классе регулярных про-
пространств, если для любых двух регулярных пространств X и У,
каждого совершенного отображения g пространства X на про-
пространство У и произвольного совершенного отображения h:
Р->У найдется непрерывное отображение f: Р-^Х, такое, что
uf = h.
(a) Покажите, что каждое экстремально несвязное регуляр-
регулярное пространство X проективно в классе регулярных про-
пространств.
Указание. Рассмотрите множество S={(^p)gXX^-
g(x) = h(p)}czXy<KP и заметьте, применив теорему 3.7.7 и пред-
предложение 3.7.10, что сужения на 5 проекций произведения ХУ^Р
на X и Р являются совершенными отображениями. Примените
затем упр. 3.1.С (а) и задачу 6.3.19 (с).
(b) Пусть О (X) — семейство всех открытых множеств регу-
регулярного пространства X. Рассмотрите семейство А (X) всех
ультрафильтров в 0{Х)У сходящихся к точкам пространства Х>
6.3. ЗАДАЧИ 555
и введите на А(Х) топологию, взяв в качестве базы семейство
всех множеств (/#={^еЛ(Х): U €= #"}, где U *=0 (X).
Заметьте, что A(X)\U* = {X\U)*, и покажите, что А{Х) —
экстремально несвязное регулярное пространство и что отобра-
отображение пх: А(Х)->Х> сопоставляющее произвольному ультра-
ультрафильтру Уе/1 (X) его предел в X, является неприводимым со-
совершенным отображением.
Убедитесь, что если некоторое пространство Р и отображе-
отображение f обладают свойствами А(Х) и ях, то найдется гомеомор-
гомеоморфизм h: A(X)^P, такой, что fh = nx. Пара (А(Х),пх) назы-
называется проективной резольвентой или абсолютом простран-
пространства X.
(c) Заметьте, что для каждого тихоновского пространства X
пара ($А(Х),И)Х где П: рЛ(Х)->-рХ обозначает продолжение
отображения пх: А(Х)-*Х, является проективной резольвентой
пространства рХ.
(d) Покажите, что каждое пространство Р, проективное в
классе регулярных пространств, экстремально несвязно.
Указание, Рассмотрите А(Р).
Замечание. Дальнейшую информацию об абсолютах можно
найти в обзоре Вудса [1978].
Произведение piVXPiV не является экстремально несвязным
6.3.21 (Гиллман и Джерисон [I960]), (а) Покажите, что
произведение р# X Р# не экстремально несвязно.
Указание, Рассмотрите открытое множество {(i,i): i=l,
2, ...}c(WVXptf.
(b) Выведите из (а), что стоун-чеховская компактификация
пространства Ny^N не гомеоморфна произведению piVXpN
(см. упр. 3.6.D(b) и задачу 3.12.20(с)).
Пространства замкнутых множеств IV (см. задачи 2.7.20,
3.12.26, 4.5.22 и 8.5.16)
6.3.22. (а) (Вьеторис [1923], Майкл [1951]). Докажите, что
если X есть Ггпространство, то экспоненциальное пространство
2х и пространство 2?{Х) всех непустых замкнутых компактных
подмножеств пространства X связны в том и только том случае,
если X связно. Приведите пример связного сепарабельного огра-
ограниченного метрического пространства (X, р), для которого про-
пространство Bх,р#) не связно.
Указание. Примените задачу 2.7.20 (Ь).
(Ь) (Майкл [1951]). Покажите, что если пространство X
нормально, то подпространство пространства 2х, состоящее из
всех непустых замкнутых связных подмножеств пространства
X, замкнуто. Отметьте, что предположение о нормальности су-
существенно.
556 ГЛ. 6. СВЯЗНЫЕ ПРОСТРАНСТВА
Указание. Воспользуйтесь длинным отрезком.
(c) (Майкл [1951]). Покажите, что если X есть ^-простран-
^-пространство, то пространство 3?(Х) локально связно в том и только
том случае, если X локально связно. Убедитесь, что 2R не ло-
локально связно.
(d) (Майкл [1951]). Проверьте, что если X есть Грпро-
странство, то пространство ЗС(Х) нульмерно в том и только том
случае, если X нульмерно.
(e) Покажите, что если X — нормальное пространство, то
пространство 2х нульмерно в том и только том случае, если
пространство X сильно нульмерно.
(f) (Сигал [1959] для метризуемых континуумов). Пусть
&~{Х)—подпространство пространства 2х, состоящее из всех
непустых континуумов, содержащихся в X. Покажите, что
если S = {Ха, я?, 2} — обратный спектр хаусдорфовых прост-
пространств, то S = {^"(ZCT), я?, 2}, где я«: Т(Ха)^Т{Х9) опреде-
определено правилом Яр(С) = Яр(С), является обратным спектром, и
что предел lim S гомеоморфен пространству <T(limS).
Указание. См. задачу 3.12.26 (f).
Веер Кнастера — Куратовского
6.3.23 (Кнастер и Куратовский [1921]). Пусть С —канторово
множество на отрезке [О, 1]Х {0} czR2. Обозначим через Q мно-
множество всех концевых точек интервалов, удаленных из отрезка
[0, 1]Х{0} в процессе построения канторова множества, опи-
описанном в примере 3.1.28, и положим Р= C\Q. Соединим каж-
каждую точку се С с точкой q = A/2, 1/2)^R2 отрезком Lc и обо-
обозначим через Fc множество всех точек (х, y)^Lc, таких, что у
рационально, если cgQ, и j/ иррационально, если с^ Р. Под-
Подпространство F = U Fc плоскости называется веером Кнасте-
С<Е=С
ра — Куратовского.
(а) Докажите, что пространство F связно и пунктиформно.
Указание. Пусть п, Ъ, ... — последовательность всех рацио-
рациональных чисел отрезка [0, 1/2] и PiCiR2 — горизонтальная пря-
прямая у = г и Предположим, что F = (F[\A)\J(Ff\B), где множе-
множества А и В замкнуты в/?2, F[]A{]B = 0 и ?еЛ. Рассмотрите
множества ^={cgC: A{\B[\Lc{\ Pi Ф 0}. Проверьте, что
оо
Я/ == Kt при i — 1, 2, ... и U Ki с: Р. Покажите, что Fc П В = 0
оо
для каждой точки cgP\ N Ki, и, воспользовавшись теоремой
Бзра о категории, выведите, что F[\B = 0.
6.3. ЗАДАЧИ 557
(b) Докажите, что пространство F\{q} наследственно не-
несвязно, но не вполне несвязно.
Вокруг примера Эрдёша
6.3.24. (а) Пусть X — пространство, рассмотренное в при-
примере 6.2.19. Заметьте, что, поставив в соответствие произвольной
точке х = {xi} gI ту же точку х = {л:,-} е Q*4 мы получаем
непрерывное отображение; выведите отсюда, что существует
непрерывное инъективное отображение /: Х-+С пространства X
в канторово множество С, такое, что f{xo)= 0. Определим ото-
отображение g: Х->12, положив
при x = {Xi).
Покажите, что пространство Х\ = g(X)\] {@, 1/2)} с=/2 наслед-
наследственно несвязно, но не вполне несвязно и что пространство
Х2 = g(X)\J {@, 1)} с: Я связно и пунктиформно.
Указание. Заметьте, что существует непрерывное взаимно
однозначное отображение пространства g{X) на пространство
f(X)a С и что если для какого-нибудь открыто-замкнутого мно-
множества AczX множество {||jc||: х^А} ограничено, то А — 0.
(b) (Роберте [1956]). Докажите, что отображение g в (а)
является гомеоморфным вложением.
Указание. Докажите, что последовательность д;1, л:2, ... в про-
пространстве X, где xk — {xi}, сходится к точке x={xi} в том
и только том случае, если последовательность \\xk\\ сходится
к ||я|| и последовательность х\9 х\, ... сходится к xi при i=l,
2, ....
(c) Приведите примеры метризуемых полной метрикой про-
пространств Y, Yu Yz<^I2 со следующими свойствами: У вполне
несвязно, но не нульмерно, Y\ наследственно несвязно, но не
является вполне несвязным, и Y% связно и пунктиформно.
Указание. Рассмотрите подпространство гильбертова про-
пространства Я, состоящее из всех последовательностей иррацио-
иррациональных чисел; рассуждайте так же, как в (а) и (Ь).
Замечание. Первый пример связного и пунктиформного се-
парабельного метрического пространства был построен Серпин-
ским в [1920]. Пространство с этими свойствами, которое, сверх
того, метризуемо полной метрикой, было описано Мазуркевичем
в [1920]. Первый пример сепарабельного метрического про-
пространства, которое наследственно несвязно, но не вполне не-
несвязно, был приведен Серпинским в [1921]; построенное им
пространство, кроме того, метризуемо полной метрикой.
558 гл. 6. связные пространства
Обратная последовательность сильно нульмерных про-
пространств, предел которой не сильно нульмерен
6.3.25. Покажите, что предел обратной последовательности
сильно нульмерных пространств может не быть сильно нуль-
нульмерным пространством.
Указание. Применив задачу 3.12.23(с), определите в DKl
последовательность подпространств Х\ id Х2 =э ..., такую, что
оо
рХг = ?)Kl при f=l, 2, ... и П %i гомеоморфно пространству
Y из примера 6.2.20.
Глава 7
РАЗМЕРНОСТЬ ТОПОЛОГИЧЕСКИХ
ПРОСТРАНСТВ
В этой главе, обобщая понятие размерности евклидовых про-
пространств, мы припишем определенным топологическим про-
пространствам неотрицательное целое число — размерность этого
пространства. Кроме того, пустому пространству будет припи-
приписано число —1, а «бесконечномерным» пространствам будет
сопоставлен символ оо. Такое соответствие будет установлено
тремя различными способами; топологическому пространству X
будет сопоставлено три числа: indX, IndX и dimX, каждое из
которых обладает свойствами размерности. Областями, в кото-
которых естественно изучать ind, Ind и dim, служат соответственно
классы регулярных пространств, нормальных пространств и
тихоновских пространств. При рассмотрении в более широких
классах пространств у названных размерностных функций раз-
развиваются патологические свойства.
Теория размерности не является частью классического курса
общей топологии. Главная причина этого в том, что развитая
первоначально для метризуемых компактов и распространен-
распространенная затем на сепарабельные метризуемые пространства теория
размерности только частично обобщается на топологические
пространства. Более того, фундаментальная теорема теории раз-
размерности для сепарабельных метризуемых пространств, которая
утверждает, что ind, Ind и dim совпадают, не выполняется ни
в классе всех метризуемых пространств, ни в классе всех ком-
компактов. Таким образом, для общих пространств мы имеем три
теории размерности вместо одной, каждая из которых несколько
беднее1) и менее гармонична, чем теория размерности сепара-
сепарабельных метризуемых пространств. Однако все эти теории сей-
сейчас развиты достаточно для того, чтобы быть включенными
в книгу по общей топологии. Читатель увидит, что они содержат
много интересных теорем и проливают свет на классическую
теорию размерности.
*) Не совсем ясно, следует ли согласиться с этой оценкой: теории раз-
размерности общих пространств беднее едиными общими теоремами, но богаче
контрпримерами и специальными теоремами, представляющими немалый
интерес. — Прим. перев.
560 ГЛ. 7. РАЗМЕРНОСТЬ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ
Эта глава тесно связана с § 6.2, в котором, как читатель
теперь увидит, мы развили часть теории размерности: теорию
размерности нуль. Связи с другими главами слабее. Хотя мы
используем многие предшествующие результаты, рассмотренные
здесь задачи и развитые методы имеют свой особый характер.
Следующая глава не зависит от этой. Данная глава предназна-
предназначается главным образом тем читателям, которые знакомы с
классической теорией размерности сепарабельных метризуемых
пространств. Читатели, которые интересуются только основными
понятиями и результатами общей топологии, могут ее про-
пропустить.
Параграф 7.1 открывается определениями ind, Ind и dim
и некоторыми немедленными следствиями этих определений.
Затем мы доказываем две вспомогательные теоремы о разду-
раздутиях и ужатиях покрытий, которые играют ключевую роль в тео-
теории размерности в смысле покрытий (dim). В частности, из
этих теорем мы выводим, что в классе нормальных пространств
определение размерности в смысле покрытий можно сформули-
сформулировать проще. Параграф завершают доказательства того, что
IndpX=IndX и dimCX = dimX, но, вообще говоря, т&$Х Ф
Ф'т&Х.
В § 7.2 изучается размерность в смысле покрытий (dim).
Мы начинаем с двух «теорем о сумме», утверждающих, что если
нормальное пространство можно представить в виде объедине-
объединения счетного или локально конечного семейства замкнутых
подпространств размерности ^п, то размерность этого про-
пространства тоже ^п. Лемма, которая нужна для теоремы
о локально конечной сумме, влечет за собой важную характе-
характеристику размерности в смысле покрытий в классе нормальных
пространств. Эта характеристика применяется в следующем
параграфе. В § 7.2 мы доказываем также, что dim X ^. ind X
для каждого линделёфова пространства X и dim X ^ Ind X для
каждого нормального пространства X. В заключительной части
параграфа размерность dim характеризуется в терминах пере-
перегородок.
Последний параграф посвящен теории размерности метри-
метризуемых пространств. Сначала размерность в смысле покрытий
метрических пространств характеризуется в терминах специаль-
специальных последовательностей покрытий, а затем доказывается фун-
фундаментальная теорема Катетова — Мориты, утверждающая, что
Ind X = dim X для любого метризуемого пространства X. По-
Последняя теорема вместе с результатами § 7.2 показывает, что
ind X = IndX = dim X для каждого сепарабельного метризуе-
метризуемого пространства X. Затем мы устанавливаем две характери-
характеристики размерности Ind метризуемых пространств, одна из ко-
которых формулируется в терминах специальных баз, а другая —
7.1. ОПРЕДЕЛЕНИЕ И ОСНОВНЫЕ СВОЙСТВА РАЗМЕРНОСТЕЙ Ind, Ind И dim 561
в терминах разбиений на подпространства размерности нуль.
Эти характеристики приводят к теореме о сумме и теореме
о размерности произведений. В доказательствах всех упомяну-
упомянутых выше теорем применяется теорема Катетова— Мориты; в
упр. 7.3.С(а) намечено, как можно обойтись без этого довольно
трудного результата. Параграф завершается теоремой о раз-
размерности евклидовых пространств, которая говорит, что
indRn = lndRn = dim/?" = п. Эта теорема, доказательство ко-
которой требует более глубокого проникновения в строение евкли-
евклидовых пространств, выводится здесь из теоремы Брауэра о не-
неподвижной точке.
Чтобы достичь замкнутости изложения, доказательство тео-
теоремы Брауэра о неподвижной точке приведено в приложении
к § 7.3.
7.1. ОПРЕДЕЛЕНИЕ И ОСНОВНЫЕ СВОЙСТВА
РАЗМЕРНОСТЕЙ ind, Ind и dim
Пусть X — регулярное пространство и п — неотрицательное
целое число; положим тогда
(MU1) indJ —— 1 в том и только том случае, если Х—0.
(MU2) ind Х^п, если для каждой точки х е X и каждой ее
окрестности V существует открытое множество U cz X,
такое, что
x<=UczV и indFr?/</i—1.
(MU3) indX = n> если т&Х^п и неравенство indZ^n— 1 не
выполняется.
(MU4) indX=oo, если неравенство хп&Х^п не выполняется
ни для какого п.
Условия (MU1) — (MU4) сопоставляют каждому регуляр-
регулярному пространству X число indZ, являющееся либо целым чис-
числом ^ — 1, либо «бесконечным числом» оо. Число ind X назы-
называется размерностью Менгера — Урысона или малой индуктив-
индуктивной размерностью пространства X. Легко проверяется, что если
пространства X п Y гомеоморфны, то ind X = ind У.
В силу регулярности Х> можно предполагать, что множество
U в (MU2) удовлетворяет более сильному условию U cz V. Та-
Таким образом, неравенство ind X ^ п ^ 0 означает, что каждую
точку xgI можно отделить от произвольного не содержащего
ее замкнутого множества F посредством некоторого множества
размерности ^.п—1.
Из определения размерности Менгера—Урысона сразу сле-
следует, что indX ^л^Ов том и только том случае, если суще-
существует база $ пространства X, такая, что indFrt/^n—1 для
36 Зак. 697
562 ГЛ. 7. РАЗМЕРНОСТЬ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ
всех U ^ $. В частности, ind X = 0 в том и только том случае,
если пространство X нульмерно в смысле § 6.2.
Чтобы упростить формулировки некоторых доказываемых
дальше результатов, будем предполагать, что соотношения
п^оо и п-\-оо = оо-\-п = оо выполняются при каждом це-
целом п.
Так как регулярность — наследственное свойство, то если
размерность ind определена для некоторого пространства X, то
она определена и для каждого подпространства М а X.
7.1.1. Теорема. Для каждого подпространства М регулярного
пространства X выполняется неравенство ind M ^ ind X.
Доказательство. Ясно, что это неравенство выполняется, если
indZ = —1 и если indX=oo. Предположим, что наше нера-
неравенство доказано для всех пространств X, таких, что indX^
^п—1. Рассмотрим регулярное пространство Ху для которого
indA'==AZ, любое подпространство Mel, точку х^М и про-
произвольную окрестность V точки х в М. Пусть V\ — любое от-
открытое в X множество, такое, что V = M(]V\. Так как indX^
^ п, найдется открытое множество U\ a X, для которого
A) xeUiczVi и indFrf/i</i —1.
Множество U = М (] U\ является окрестностью точки х в М,
а его граница Fr U = Л1ПЛ1П Ui (\M\U\ в М является под-
подпространством границы множества U\ в X. Следовательно, в
силу A) и индуктивного предположения, ind М^п, и доказа-
доказательство завершено. I
Пусть X — нормальное пространство и п—неотрицательное
целое число; положим
(ВС1) IndJf = —1 в том и только том случае, если Х= 0.
(ВС2) Ind X*^n, если для каждого замкнутого множества
А а X и произвольного открытого множества V с X, со-
содержащего А, найдется открытое множество (/сХ, такое,
НТО
Ac^UcV и IndFrf/<n—1.
(ВСЗ) IndX = n, если indX^n и неравенство indX^n — 1
не выполняется,
(ВС4) IndJ = oo, если неравенство lndX^.n не выполняется
ни для какого п.
Условия (ВС1) — (ВС4) сопоставляют каждому нормальному
пространству X число indX, являющееся либо целым числом
^—1, либо «бесконечным числом» оо. Число IndX называется
размерностью Брауэра — Чеха или большой индуктивной раз*
мерностью пространства X. Легко проверяется, что если про-
пространства X и У гомеоморфны, то Ind X = Ind У.
7.1. ОПРЕДЕЛЕНИЕ И ОСНОВНЫЕ СВОЙСТВА РАЗМЕРНОСТЕЙ ind, Ind И dim 563
В силу нормальности X, можно предполагать, что множество
U в (ВС2) удовлетворяет более сильному условию UaV. Та-
Таким образом, неравенство lndX^Zn^O означает, что любые
два непересекающихся замкнутых в X множества А и В могут
быть отделены множеством размерности ^.п— 1.
Теорема 6.2.4 показывает, что если пространство X нор-
нормально, то IndX = 0 в том и только том случае, если простран-
пространство X сильно нульмерно в смысле § 6.2.
Читатель легко докажет по индукции следующую теорему,
которой оправдываются названия малая и большая индуктив-
индуктивная размерность.
7.1.2. Теорема. Если пространство X нормально, то
*=? Ind X. I
Так как нормальность не является наследственным свой-
свойством (см. пример 2.3.36), может случиться, что размерность
Ind определена для пространства X, но не определена для не-
некоторого подпространства MczX. Однако теорема 2.1.6 пока-
показывает, что если IndX определена, то IndM определена для
каждого замкнутого подпространства М а X. Доказательство
следующей теоремы, аналогичное доказательству теоремы 7.1.1,
предоставляется читателю.
7.1.3» Теорема. Для каждого замкнутого подпространства М
нормального пространства X выполняется неравенство IndM^
<IndX. I
Из заключительной части примера 6.2.20 следует, что по-
последняя теорема перестает быть верной, если предположение
о замкнутости подпространства М в X заменить более слабым
предположением, что пространство М нормально, т. е. что раз-
размерность Ind M определена.
В определение размерности в смысле покрытий входит по-
понятие порядка покрытия. Под порядком семейства $& подмно-
подмножеств множества X мы понимаем наибольшее целое число п>
такое, что семейство <$& содержит п + 1 множеств с непустым
пересечением, или «бесконечное число» оо, если такого целого
числа не существует. Таким образом, если порядок семейства
,s& — {As}$^s равен п, то для любых п + 2 различных индексов
s\9 $2, • ••» %2^S имеет место соотношение A8lflAs2(] ••• П
f\ASn, = 0.B частности, непустое семейство порядка —1 со-
состоит лишь из пустого множества, а семейство порядка 0
состоит из попарно непересекающихся множеств, не все из ко-
которых пусты. Порядок семейства $& обозначается через ord^.
Пусть X — тихоновское пространство и п — целое число
^ — 1. Положим
36*
564 ГЛ. 7. РАЗМЕРНОСТЬ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ
(CL1) dimX^in, если в каждое конечное функционально откры-
открытое покрытие пространства X можно вписать конечное
функционально открытое покрытие порядка ^.п.
(CL2) dim Х — п, если dim Х^п и неравенство dim X ^ п — 1
не выполняется.
(CL3) dimX=oo, ecm неравенство АхтХ^п не выполняется
ни при каком п.
Условия (CL1) — (CL3) приписывают каждому тихоновскому
пространству X число dimX, являющееся либо целым числом
^—1, либо «бесконечным числом» оо. Число dimjf называется
размерностью Чеха — Лебега или размерностью в смысле по-
покрытий пространства X. Ясно, что если пространства X и Y
гомеоморфны, то dim X = dim У.
Из определения размерности в смысле покрытий сразу сле-
следует, что dimZ^—1 в том и только том случае, если Х=0,
и dimX=0 в том и только том случае, если пространство X
сильно нульмерно.
Свойство быть тихоновским пространством наследственно,
поэтому если размерность dim для некоторого пространства X
определена, то она определена и для каждого подпространства
МсХ. Чтобы доказать аналоги теорем 7.1.1 и 7.1.3 для раз-
размерности в смысле покрытий, потребуются некоторые свойства
функционально замкнутых и функционально открытых мно-
множеств. Две теоремы о функционально замкнутых и функцио-
функционально открытых множествах, которые мы сейчас докажем, бу-
будут часто применяться в дальнейшем. Аналогичные теоремы
для нормальных пространств (формулируемые в скобках)
имеют место для всех замкнутых и всех открытых множеств.
Раздутием семейства {i4s}seS подмножеств пространства X
называется любое такое семейство {Bs}s^s подмножеств этого
пространства, что AsczBs при всех sgSh, каково бы ни было
конечное множество индексов si, s2, ..., sm e S, выполняется
следующее условие:
(]ASfn=0 в том и только том случае,
если BSl(]BS2[] ..
Sfn
7.1.4. Теорема. Для каждого конечного семейства {Fi}*^ функ-
функционально замкнутых (замкнутых) множеств топологического
(нормального) пространства X существует раздутие {?/*}^=1
этого семейства, состоящее из функционально открытых мно-
множеств. Если, кроме того, дано некоторое семейство {V^^функ-
{V^^функционально открытых (открытых) множеств в X и Ft cz Vi при
7.1. ОПРЕДЕЛЕНИЕ И ОСНОВНЫЕ СВОЙСТВА РАЗМЕРНОСТЕЙ ind, Ind И dim 565
t=l, 2, ..., А, то раздутие можно выбрать так, чтобы было
Ui<=Vitipui= 1,2, .... ft.
Доказательство. Объединение Si всех пересечений /^ Л Fi% Л ...
• • • Г) Лт> удовлетворяющих условию Fx Л Л: Л Fit П • • • П Fim= 0,
является функционально замкнутым (замкнутым) множеством,
не пересекающимся с F\. Следовательно, по теореме 1.5.13 (по
лемме Урысона) существует непрерывная функция f\\ X-+I,
такая, что
ЫЛ)<={0} и
Как легко видеть, семейство {К\, F2, F3, ..., F^}, где К\ =
= /f *([(), 1/2]), является раздутием семейства {Ft}ki=sV
Предположим теперь, что при каждом /= 1, 2, ..., / опре-
определена непрерывная функция fr, X-+I таким образом, что
/,(Л)с:{0} и семейство {К\, К2, ..., /С/, ^/+ь ..., Fk}, где
Л'^ = /Г1([0, 1/2]), является раздутием семейства {FJ*=1. Объ-
Объединение S/+1 всех тех пересечений элементов семейства {/Сь
/С2, ..., К{, Fy+j ..., Fjfe}, которые не пересекаются с F/+i,
является функционально замкнутым (замкнутым) множеством,
не пересекающимся с F}-+\. Следовательно, существует непре-
непрерывная функция //+ь X-+I, такая, что
//+i(f/+1)c{0} и //
Как легко видеть, семейство {К\, /С2> - • •» ^С/+ь ^/+2» • • •, ^а},
где /C/+i = //+i(fO» 1/2]), является раздутием семейства {Fi}i=v
Таким образом, можно предположить, что для каж-
каждого i^k определена непрерывная функция fr. X-+I та-
таким образом, что fi (Ft) cz {0} и семейство {/С,}^=1> где /(; =
/Г!([0, 1/2]), является раздутием семейства {/\-}^=г Легко
видеть, что семейство {f/J/=1, где t/t = /t~I([^' V2))> удовлетво-
удовлетворяет требованиям первой части теоремы.
Для доказательства второй части надо заменить множества
Ui множествами g^l([0, 1/2)), где gr. X-*I — какая-нибудь не-
непрерывная функция, удовлетворяющая условиям
Ужатием покрытия {^5}seS пространства X называется лю-
любое покрытие {Bs}s^s этого пространства, такое, что Bsc=As
при всех sg5. Ясно, что порядок произвольного ужатия по-
покрытия зФ не превосходит ord $?.
566 ГЛ. 7. РАЗМЕРНОСТЬ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ
7*1.5. Теорема. Каждое конечное функционально открытое (от-
(открытое) покрытие {Ut}ki = l топологического (нормального) про-
пространства X обладает ужатиями {Fi}ki={ и {Wt}ki=v функцио-
функционально замкнутым и функционально открытым соответственно
и такими, что Ft a Wi czWtczUi при ? = 1,2 Л.
Доказательство, Семейство {X \t/J^==l состоит из функцио-
функционально замкнутых (замкнутых) множеств, и пересечение всех
элементов этого семейства пусто. По теореме 7.1.4, данное се-
семейство обладает раздутием {VJ^j, состоящим из функцио-
функционально открытых множеств. Семейство {Fi}i={, где Fi = X\Vi>
является функционально замкнутым ужатием семейства {f/jf^.
Существование множеств Wi следует из теоремы 1.5.13 (из
леммы Урысона). I
Заметим, что вариант последней теоремы, относящийся
к нормальным пространствам, следует также из теоремы 1.5.18
и леммы Урысона.
Из теорем о раздутиях и ужатиях мы выведем некоторые
полезные характеристики размерности в смысле покрытий.
7.1.6. Теорема. Для каждого тихоновского пространства X сле-
следующие условия равносильны:
(i) dixnX^n.
(ii) Каждое конечное функционально открытое покрытие
пространства X обладает функционально открытым ужатием
порядка ^.п,
(ш) Каждое конечное функционально открытое покрытие
пространства X обладает функционально замкнутым ужатием
порядка ^.п.
(iv) В каждое конечное функционально открытое покрытие
пространства X можно вписать конечное функционально замк-
замкнутое покрытие порядка ^п.
Доказательство. Пусть tf/J*el — произвольное функциональ-
функционально открытое покрытие тихоновского пространства X, удовлетво-
удовлетворяющего условию dimX^Crt. Возьмем вписанное в него конеч-
конечное функционально открытое покрытие {V/}^ порядка ^.п и
для каждого / ^.ш выберем i(j) ^ k так, чтобы было V/ с: ?/,-(/).
Семейство {W^v где Wi = [){V}: i(j)=i}y является функцио-
функционально открытым ужатием покрытия {?/*}(-=1 и его порядок ^п.
Значит, (i)=^(ii). Импликация (ii)=^(iii) вытекает из тео-
теоремы 7.1.5, импликация (iii)=^(iv) очевидна, а импликация
(iv)=^(i) является следствием теоремы 7.1.4. I
7.1. ОПРЕДЕЛЕНИЕ И ОСНОВНЫЕ СВОЙСТВА РАЗМЕРНОСТЕЙ ind. Ind И dim 567
В классе нормальных пространств все условия последней
теоремы можно сформулировать проще; из теорем 7.1.4—7.1.6
вытекает
7.1.7. Теорема. Для каждого нормального пространства X сле-
следующие условия равносильны:
(i) dimX^n.
(ii) В каждое конечное открытое покрытие пространства X
можно вписать конечное открытое покрытие порядка ^.п.
(iii) Каждое конечное открытое покрытие пространства X
обладает открытым ужатием порядка ^.п.
(iv) Каждое конечное открытое покрытие пространства X
обладает замкнутым ужатием порядка ^.п,
(v) В каждое конечное открытое покрытие пространства X
можно вписать конечное замкнутое покрытие порядка
7.1.8. Теорема. Если подпространство М тихоновского простран-
пространства X обладает тем свойством, что каждая непрерывная функ-
функция f\ М->1 продолжается непрерывно на X, то dimM ^ dim X.
В частности, для каждого замкнутого подпространства М
нормального пространства X имеет место неравенство dim M ^
dX
Доказательство. Пусть X — тихоновское пространство, для
которого dimX^n, и М — подпространство пространства X,
удовлетворяющее условию теоремы. Рассмотрим произвольное
функционально открытое покрытие {C/J*el пространства М.
Применив теорему 7.1.5, возьмем функционально замкнутое
ужатие {Ft}kis=l рассматриваемого покрытия. По теореме 1.5.13,
при i=lf 2, ..., k найдутся непрерывные функции /(-: М->19
такие, что
B) fi(M\Ut)c:{0} и
Пусть ft: X-*-1 — продолжение функции fi на X. Мно-
Множества ff1 (A/2, 1]), fa (A/2, 1]) /V((l/2, 1]), .nfr'([O, 1))
составляют конечное функционально открытое покрытие s& про-
пространства X. Из B) следует, что
C) Af Л/Г1 (A/2, 1]) с: Ut при/ = 1,2, ..., к и Af П Ц/Г1 ([0,1))=0.
Так как dimZ^n, в покрытие ^ можно вписать конечное
функционально открытое покрытие ^, такое, что oxd$^n.
Из C) вытекает, что пересечения элементов семейства 9И с М
образуют конечное функционально открытое покрытие про-
568 ГЛ. 7. РАЗМЕРНОСТЬ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ
странства М9 вписанное в покрытие {?/J*=1. Ясно, что порядок
этого вписанного покрытия ^п и, таким образом, dimM ^ /г. I
Из заключительной части примера 6.2.20 следует, что по-
последняя теорема не распространяется на произвольные подпро-
подпространства МаХ.
Читатель, несомненно, заметил, что некоторые теоремы этого
параграфа обобщают на более высокие размерности ряд тео-
теорем, доказанных в § 6.2 для размерности нуль: теоремы 7.1.1,
7.1.3 и 7.1.8 обобщают теорему 6.2.11, теорема 7.1.2 является
обобщением теоремы 6.2.6, а теорема 7.1.7 обобщает тео-
теорему 6.2.5. Наша следующая теорема является обобщением тео-
теоремы 6.2.13; доказательство ее предоставляется читателю.
7.1.9. Теорема. Сумма X = ф Xs удовлетворяет условию
SZES
indX^n (IndX^ln, dlmX^Zn) в том и только том случае,
если mdXs^n (lndXs^.ny d\mXs^n) при всех sgS. I
Воспользовавшись определениями размерностных функций
ind, Ind и dim, можно переформулировать теоремы 6.2.5, 6.2.7
и 6.2.9 следующим образом:
7.1.10. Теорема. Для каждого нормального пространства X ус-
условия Ind X = 0 и dim X = 0 равносильны, I
7.1.11. Теорема, Для каждого линделёфова пространства X
условия indX = 0, IndX = 0 и dimX = 0 равносильны. I
7.1.12. Теорема, Для каждого непустого локально компактного
паракомпакта X условия ind X = 0, Ind X = 0 и dim X = 0 рав-
равносильны наследственной несвязности X. I
Заметим, что теоремы 7.1.10 и 7.1.11 на более высокие раз-
размерности не обобщаются. Действительно, существует компакт X,
для которого ind X = Ind X = 2, но dim X = 1 (см. задачу 7.4.5).
Существует также компакт Х> для которого indX = dimX = 2,
но IndX=3. Однако последнее пространство устроено очень
сложно, и в этой книге оно описано не будет (см. тео-
теорему 7.2.8).
Мы завершаем этот параграф двумя теоремами, утверждаю-
утверждающими, что IndpX = IndJ и dimpX=dimX, и обобщающими,
таким образом, теорему 6.2.12. В доказательствах обеих теорем
применяется некоторый оператор продолжения открытых в X
множеств до открытых множеств в рХ. Основные свойства этого
оператора, обозначаемого через Ех, устанавливаются в двух
леммах. До конца доказательства теоремы 7.2.17 чертой будет
обозначаться замыкание в рХ Замыкание множества А в X
записывается как Х[\А,
7.1. ОПРЕДЕЛЕНИЕ И ОСНОВНЫЕ СВОЙСТВА РАЗМЕРНОСТЕЙ ind, Ind И dim 569
Для каждого открытого множества U тихоновского про-
пространства X множество
открыто в рХ Так как
X\(X\U) = X\[X(](X\U)] = U
и так как для каждого открытого множества VczfiX, такого,
что X П V = Uy имеют место соотношения
т. е.
множество Ex U является наибольшим открытым множеством
пространства pZ, пересечение которого с X равно U. Ясно, что
ExUczU.
7.1.13. Лемма. Для любых двух открытых множеств U, V тихо-
тихоновского пространства X выполняются условия
Ex(Uf\V) = ExU{]ExV и Ех (С/ U V) => Ex U U Ех V.
Если, кроме того, множества U, V функционально открыты или
пространство X нормально, то
Доказательство. Первые две формулы теоремы непосред-
непосредственно вытекают из определения оператора Ex. Следовательно,
достаточно доказать, что если множества U, V функционально
открыты или пространство X нормально, то
D)
Полагая А = X\U иВ- X\Vf заменяем формулу D) рав-
равносильным включением
E) Af]BczA(]B.
Возьмем любую точку х^А(]В и произвольную ее окрест-
окрестность GczfiX. Пусть F — какое-нибудь функционально замкну-
замкнутое в рХ множество, для которого х е Int F cz F cz G. Имеем
х е А{\ Int F cz AflF и х е В Л Int F с B{]F.
Значит, в силу следствия 3.6.2, множества A(]F и B{\F не
вполне отделены в X. Так как A[\F и B[)F — либо функцио-
функционально замкнутые множества, либо замкнутые подмножества
570 ГЛ. 7. РАЗМЕРНОСТЬ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ
нормального пространства, то
Множество G является произвольной окрестностью точки х;
поэтому х^А(]В. Следовательно, включение E) установ-
установлено. I
7.1.14. Лемма. Для каждого открытого множества U нормаль-
нормального пространства X выполняется равенство
FrExU^FrU,
где Ft U — граница множества U в пространстве X, a FvExU —
граница множества Ex U в пространстве $Х.
Доказательство. Отметим сначала, что
F) РХ \Ех{Х \U) =X\(X\U) = U = U.
Применяя F) и последнюю формулу леммы 7.1.13, получаем
FrExU= ExUЛ Ext/ = U\ExU= pJ\[Ex (X \U)[]ExU] =
7.1.15. Теорема. Если пространство X нормально, то IndpX =
= Ind X.
Доказательство. Докажем сначала, что IndZ^ Ind pX Ясно,
что это неравенство выполняется, если IndpZ = —1 и если
IndpX=oo. Предположим, что рассматриваемое неравенство
уже доказано для всех нормальных пространств, большая ин-
индуктивная размерность стоун-чеховских компактификаций ко-
которых ^.п—1. Рассмотрим произвольное нормальное простран-
пространство X, такое, что Ind $Х ^ п, замкнутое множество А с= X и от-
открытое множество VaX, содержащее Л. В силу следствия 3.6.4,
замыкания множеств А и X\V в $Х не пересекаются, поэтому
существует открытое множество W cz $Xy для которого
G) Аа W<=$X\X\V и lndFvW^n—1.
Пересечение U = X (] W открыто в X и
Граница Fr U множества U в пространстве X содержится в Х(]
П Fr U7; значит, Fr Ua Fr W и IndFrt/^n—1 в силу тео-
теоремы 7.1.3 и второй из формул G). Применяя следствие 3.6.8
и индуктивное предположение, мы заключаем, что Ind Fr U ^
^Zn — 1. Следовательно, Ind X ^ п, и неравенство Ind X ^
^ Ind рХ установлено.
Докажем теперь, что Ind $X ^ Ind X. Ясно, что это неравен-
неравенство выполняется, если lndX = —1 и если IndX=oo. Пред-
7.1. ОПРЕДЕЛЕНИЕ И ОСНОВНЫЕ СВОЙСТВА РАЗМЕРНОСТЕЙ ind, Ind И dim 571
положим, что рассматриваемое неравенство доказано для всех
нормальных пространств, большая индуктивная размерность
которых ^п—1, и рассмотрим произвольное нормальное про-
пространство X, для которого Ind X ^ п. Пусть А —любое замкну-
замкнутое множество в $Х и Vczpj— любое открытое множество, со-
содержащее А, Возьмем открытые множества G, Яс=рХ, для ко-
которых
(8) А с G c= G с Я с Н с= у.
Так как Ind X ^ /г, существует открытое множество ?/ cz X, та-
такое, что
(9) ХA<?с:(/с:ХЛ// и IndFr?/</i—1,
где Fr U — граница множества U в пространстве X.
Из формул (8) и (9) вместе с леммой 7.1.13 получаем
A a G cz Ех (X П G) с Ex U с: Ех (X Л Я) с= Я с: 1/.
Воспользовавшись последней формулой, второй из формул (9),
леммой 7.1.14, следствием 3.6.8 и индуктивным предположением,
мы заключаем, что
ЛсЕхУсК и IndFrEx(/<n—1.
Следовательно, IndfiX ^L nt и неравенство IndpA'^IndZ уста-
установлено. ¦
Последняя теорема вместе со следствием 3.6.7 дает
7.1.16. Следствие. Для каждого нормального пространства X и
любого всюду плотного в нем нормального подпространства
М сг Ху обладающего тем свойством, что каждая непрерывная
функция /: M-+-I непрерывно продолжается на X, имеет место
равенство Ind М = Ind X.
Иными словами, для каждого нормального пространства Y
и любого нормального подпространства ТсгрУ, содержащего Y>
имеем Ind У = Ind Т. I
7.1.17. Теорема. Для каждого тихоновского пространства имеет
место равенство dim $Х = dimX.
Доказательство. Из теорем 3.6.1 и 7.1.8 следует, что dimZ^
^ dim р^; таким образом, достаточно доказать, что если
dim X ^ п, то dim $Х ^ п.
Пусть X — произвольное тихоновское пространство, для ко-
которого dimXt^n. Рассмотрим любое конечное открытое покры-
покрытие {Ui}ki=i пространства $Х. По теореме 7.1.5, найдется функ-
функционально открытое ужатие{1Г(-}г.^1 покрытия {U^i=sV такое, что
A0) WiCzUt при i=l, 2, ..., k.
572 гл. 7. размерность топологических пространств
Для покрытия {X{\Wi}i=x пространства X существует функ-
функционально открытое ужатие {Kjf^ порядка ^.п. Формула A0)
показывает, что _ __
ExVidVtCzWiCzUi.
Следовательно, по лемме 7.1.13, семейство {Ex Vi}ki=sV является
открытым ужатием покрытия {U(}i={ пространства $Х. Так как
порядок этого ужатия ^.п, имеем dimpX^ п. I
Последняя теорема вместе со следствием 3.6.7 дает
7.1.18. Следствие. Если X — тихоновское пространство и подпро-
подпространство Мс! всюду плотно в X и обладает тем свойством,
что каждая непрерывная функция f: M-+I непрерывно продол-
продолжается на X, то dimM = dimX
Иными словами, для каждого тихоновского пространства У
и любого подпространства Г с: (ЗУ, содержащего У, имеем
dim У = dim Г. 1
Напомним читателю в связи с теоремами 7.1.15 и 7.1.17, что
для пространства У в примере 6.2.20 выполняются соотношения
ind У = 0 и indpy>0.
7.1.19. Примеры. Для каждой точки х вещественной прямой R
или окружности S1 и произвольной окрестности V точки х най-
найдется окрестность U этой точки, такая, что [/сК и граница
Fr U состоит из двух точек. Значит, indR ^ 1 и indS1 ^ 1. Так
как Ind/>0 по теореме 6.2.18, из теоремы 7.1.1 следует, что
indR = indS1 = ind/= 1.
Для каждой точки х евклидова /г-пространства Rn или /г-сфе-
ры Sn и любой окрестности V точки х найдется окрестность U
этой точки, такая, что U cz V и граница Fr U гомеоморфна Sn~l.
Следовательно, как легко доказывается по индукции,
ind Rn^n, ind Sn ^ п и ind In^n
для всех натуральных чисел п.
Малая индуктивная размерность пространств Rn, Sn и 7rt, так
же как большая индуктивная размерность и размерность в
смысле покрытий этих пространств, в действительности равна п.
Доказательство этого факта гораздо труднее осуществленных
выше оценок; оно будет приведено в § 7.3. I
7.1.20. Пример. Пусть У и У* — пространства, определенные в
примере 6.2.20. Мы уже знаем, что indy = 0, Ind У > 0 и
dim У > 0. Из следствий 7.1.16 и 7.1.18 вытекают равенства
Ind У = Ind У* и dim У = dim У*. Покажем теперь, что Ind У* ^ 1.
Пусть AcnY* — произвольное замкнутое множество и V cz
cz У* — открытое множество, содержащее А. Возьмем на отрезке
/ какое-нибудь открытое множество G, которое является конеч-
1Л. ОПРЕДЕЛЕНИЕ И ОСНОВНЫЕ СВОЙСТВА РАЗМЕРНОСТЕЙ ind, Ind И dim 573
ным объединением непересекающихся открытых интервалов и
удовлетворяет условию
А П (Ы X /) с: {со,} X G с V Л (W X /).
Воспользовавшись тем, что пространства I\G и G обладают
счетной базой, мы легко убеждаемся, что при некотором а < coi
выполняются включения
A1)
Так как Ya — сепарабельное метризуемое пространство и
ind Ya = 0, то, по теоремам 3.8.1 и 7.1.11, существует открыто-
замкнутое в Уа и тем более в У* множество Я, такое, что
A2) Af]YaczHczV.
В силу A1) и A2), множество ?/ = H{J{Y* f][(W\Xa)X G]}
удовлетворяет включениям AczU cz V. Так как Fr U cz (Ц7\Ха) Х
X Fr G и Fr G— конечное множество, то, по теореме 7.1.9, мы
имеем Ind Fr U ^ 0. Следовательно, Ind У* ^ 1.
Подобным же образом можно доказать, что dimF*s<Cl, но
это неравенство будет также следствием теоремы 7,2.8» приве-
приведенной ниже.
Отметим, что из неравенства Ind 7*^ 1 и теорем 7.1.1 и 7.1.2
вытекает, что ind У* = 1. Таким образом, имеем окончательно
ind У = 0, ind У* = 1, Ind У = Ind У* = 1,
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
Индуктивное определение размерности наметил Пуанкаре в
[1912]. Первое точное определение размерностной функции было
сформулировано Брауэром в [1913]. Функция Брауэра совпа-
совпадает с размерностью Ind в классе локально связных пространств,
метризуемых полной метрикой. Однако в работе Брауэра раз-
мерностная функция выступает лишь как вспомогательное сред-
средство при доказательстве того, что пространства Rm и Rn не го-
меоморфны, если тфп (первое корректное доказательство этого
важного факта было дано Брауэром в [1911]).
Теория размерности была основана Менгером и Урысоном.
Определение размерности ind было сформулировано Урысоном
в [1922] и Менгером в [1923]. Определение размерности Ind
было сформулировано Чехом в [1931]. Размерность в смысле
покрытий dim была определена (условием (п) теоремы 7.1.7)
в работе Чеха [1933]. Статья Лебега [1911] содержит теорему
о том, что dim In — n (в качестве следствия Лебег получает тот
факт, что пространства Rm и Rn не гомеоморфны при тфп),
574 ГЛ. 7. РАЗМЕРНОСТЬ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ
однако данный там набросок доказательства содержит пробел,
который был заполнен лишь в работе Лебега [1921]. Определе-
Определение размерности в смысле покрытий, данное Чехом, оказалось
удачным только в классе нормальных пространств. Модифика-
Модификация этого определения, получающаяся, если рассматривать функ-
функционально открытые покрытия, принадлежит Катетову [1950а].
Другой класс покрытий, который приводит к той же размерно-
стной функции, был рассмотрен Ю. М. Смирновым в [1956b].
Первое систематическое изложение теории размерности тихонов-
тихоновских пространств было дано в книге Гиллмана и Джерисона
[1960].
Теорема 7.1.8 доказана Катетовым в [1950а] (для нормаль-
нормальных пространств — Чехом в [1933]). Первый пример компакта Y,
для которого ind X Ф Ind X, был приведен В. В. Филипповым
в [1969] (нормальное пространство с тем же свойством было
описано Ю. М. Смирновым в [1951b]). Дальнейшие примеры
таких компактов, упрощенные, но все еще очень сложные, были
построены В. В. Филипповым в [1970], Пасынковым и Лифано-
вым в [1970] и Пасынковым в [1970]. Оператор Ех был введен
Шаниным в [1943]. То включение в лемме 7,1.13, которое нетри-
нетривиально, было установлено (для нормальных пространств)
Ю. М. Смирновым в [1952] и Уоллесом в [1951]. Теорема 7.1.15
была доказана Веденисовым в [1941], а теорема 7.1.17 — Волмэ-
ном в [1938] для нормальных пространств (в [1950а] Катетов
заметил, что эту теорему можно распространить на тихоновские
пространства). В связи с теоремами 7.1.3, 7.1.8 и заключитель-
заключительной частью примера 6.2.20 (см. также задачу 7.4.12) следует от-
отметить, что Э. Поль и Р. Поль определили в [1977] наследствен-
наследственно нормальное пространство X, такое, что dimX = 0, но в X есть
подпространство Л, для которого dim Л > 0. Те же авторы опре-
определили в [1979] наследственно нормальное пространство Х>
такое, что dimX = 0, но при каждом натуральном п в X есть
подпространство Л„, для которого dimAn = 1пйАп = п. В пред-
предположении, что существует пространство Суслина (см. замеча-
замечание к задаче 2.7.9(f)), такое пространство было определено
В. В. Филипповым в [1973].
Читателю, желающему лучше понять происхождение и гео-
геометрическое значение теорем этой главы, мы советуем обра-
обратиться к книге Гуревича и Волмэна [1941] или к книге Энгель-
кинга [1978]. Каждая из этих книг содержит полный курс тео-
теории размерности сепарабельных метризуемых пространств.
УПРАЖНЕНИЯ
7.1.А (Эрдёш [1940]). Убедитесь, что малая индуктивная раз-
мерность пространства X в примере 6.2.19 равна единице.
7.1. ОПРЕДЕЛЕНИЕ И ОСНОВНЫЕ СВОЙСТВА РАЗМЕРНОСТЕЙ ind, Ind И dim 575
Указание. Достаточно показать, что для каждого натураль-
натурального числа / у точки xq есть окрестность VtczX, такая, что
6(Vi)^ \/i и IndFr V/ = 0. С этой целью заметьте, что при всех
г множество {хеХ; р (х0, х) — г) гомеоморфно подпространству
гильбертова куба, образованному всеми точками с рациональ-
рациональными координатами.
7.1. В. Докажите, что каждое локально конечное функцио-
функционально открытое покрытие {0s}se.s произвольного топологиче-
топологического пространства X допускает ужатия{/^}5€_5 и {W8}8eS, функ-
функционально замкнутое и функционально открытое соответственно,
такие, что Fs с: Ws с: Ws <= Us при всех s <s S.
Указание. Возьмите непрерывные функции /5: Х->19 для
которых Us = fsl((Oy 1]), и рассмотрите функцию /: X-+I,
определенную так: f (x) = sup fs(x). Можно применить также
упр. 5.1.J(b).
7.1,С. Пусть X — нормальное пространство, для которого
Ind X ^Г/г $= 0, и нормальное пространство У получено присое-
присоединением к X некоторого замкнутого в Y сильно нульмерного
пространства. Докажите, что тогда Ind Y ^ п.
7.1.D. Докажите, что если X — нормальное пространство, для
которого dixnX^.n^Ot и нормальное пространство Y полу-
получается присоединением замкнутого в Y сильно нульмерного про-
пространства, то dim Y ^ п (см. теорему 7.2.1).
7Л.Е. Покажите, что если пространства X и Y являются ком-
компактами и dim Y =0, то dim (XX 30 = dimA' (см. задачу 7.4.10).
7.1.F (В неявном виде — Фрейденталь [1973]). Докажите,
что если S —(Ха, я;?, 2} — обратный спектр из компактов и
dimXa^Ln при всех ае2, то предел X==lim S удовлетворяет
неравенству бхтХ ^ п.
7.1.G. (а) (Морита [1950а]). Докажите, что если для семей-
семейства {Fs}s^s замкнутых подмножеств нормального пространства
X существует локально конечное семейство {Vs}s&s открытых в X
множеств, такое, что Fs с: Vs при всех seS, то у семейства
{Fs}$^s есть состоящее из открытых множеств раздутие {Us}sgS>
такое, что Ds cz Vs при всех seS.
Указание. Примените трансфинитную индукцию.
(b) Покажите прямо, видоизменив доказательство теоремы
5.1.18, что у каждого локально конечного семейства замкнутых
множеств в паракомпакте существует раздутие, состоящее из от-
открытых множеств.
(c) Для произвольного локально конечного семейства замк-
замкнутых множеств в метризуемом пространстве определите (с по-
576 ГЛ. 7. РАЗМЕРНОСТЬ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ
мощью некоторой метрики на этом пространстве) раздутие, со-
состоящее из открытых множеств.
Указание. Пусть {Fs}seS—локально конечное семейство
замкнутых подмножеств метризуемого пространства X. Для каж-
каждого х^Х возьмите е* > 0, такое, что если Fs (] В(х, 2гх)Ф0,
тохе Fs, и положите Us = [} В(х, вх).
X€=FS
7.2. ДАЛЬНЕЙШИЕ СВОЙСТВА РАЗМЕРНОСТИ dim
Начнем с двух теорем, которые часто будут применяться в
этом и следующем параграфах. Эти теоремы называются теоре-
теоремами о сумме,
7.2.1. Теорема о счетной сумме. Если нормальное пространство X
допускает счетное замкнутое покрытие {Fj}°°={, такое, что
dim Fj ^ п при /=1,2, ..., то dim X ^ п.
Доказательство. Пусть {f/J*=1 — произвольное конечное от-
открытое покрытие пространства X. Определим по индукции по-
последовательность <U^ °U\, ... открытых покрытий пространства
X, где <Mi = {?//, i}ki=,p удовлетворяющую условиям:
A) U^tcU^ui при/>1 и UmcUi;
B) ord ({[/,, t П Ff}ki=l) < n9 где Fo = 0.
Положим Uoti = Ui при / = 1, 2, ..., k. Условия A) и B)
при / = 0 оказываются выполненными. Предположим, что удов-
удовлетворяющие условиям A) и B) покрытия °Uj определены при
всех / < m ^ 1. По теореме 7.1.7, открытое покрытие
{Fm П^/щ-ь »*}*=! подпространства Fm<^X обладает открытым
ужатием {FJ^=1 порядка ^.п. Как легко заметить, семейство
{Wifi=v где Wi = (Um_Ui\Fm)[)ViczUm_Ui1 является откры-
открытым покрытием пространства Хн ord ({Wi(]Fm}k(^^^n. По
теореме 7.1.5, найдется открытое ужатие aUm = {Um, t}ki=l послед-
последнего покрытия, такое, что Um, i с: Wi при i = lt 2, ..., k. Ясно,
что покрытие Щш удовлетворяет условиям A) и B) при / = тп\
таким образом, построение последовательности Ш^ 4lu ¦•• за-
завершено.
Для каждого х^Х существует l(x) ^ k, такое, что х принад-
принадлежит бесконечному числу множеств ?//, ,•(*>; следовательно, в
оо
силу A), имеем xg f| Ujti(X). Применяя A) и B), мы заклю-
7.2. ДАЛЬНЕЙШИЕ СВОЙСТВА РАЗМЕРНОСТИ dim 577
пи,, Л
чаем, что семейство \ \ \ UIt t г является замкнутым ужатием
покрытия {С/*}1==1 и имеет порядок ^.п. Следовательно, dimX ^ п
в силу теоремы 7.1.7. I
Теорема о локально конечной сумме будет выведена из лем-
леммы. Лемма эта формулируется более общим образом, что позво-
позволяет получить из нее другую теорему, играющую основную роль
в теории размерности метризуемых пространств.
7.2.2. Лемма. Пусть <U = {Us}aeS — произвольное открытое
покрытие нормального пространства X и существует локально
конечное замкнутое покрытие SF пространства X со следующими
свойствами: размерность в смысле покрытий каждого элемента
покрытия ОТ не превосходит пУ и каждый элемент семейства 8Г
пересекается лишь с конечным множеством элементов семейства
<U. Тогда покрытие Ш обладает открытым ужатием порядка ^п.
Доказательство. Присоединим к покрытию У множество
Fo = 0 и расположим элементы этого покрытия в трансфинит-
трансфинитную последовательность Fo, Fu . ••» ^а, ..., а ^ ?, типа ?+1.
Мы определим по трансфинитной индукции трансфинитную по-
последовательность <2/о, ^ь • • > *%<*> ...» а ^ |, открытых покры-
покрытий пространства X, где (Ma = Rs}ses, удовлетворяющую ус-
условиям
C) Uа. s cz ?/р. 89 если р < а и UOt s с: U8;
D)
E) U*a\Ua.acz U *V если
Полагая L/o, 5 = Us для всех s б S, мы добьемся выполнения
условий C) — E) при <х=0. Предположим, что покрытия Ф/а,
удовлетворяющие условиям C) — E), определены для всех
а < а0 ^ 1.
Покажем сначала, что семейство всех множеств
где s ^ S, является открытым покрытием пространства X. Это
ясно, если ao = ai + l, так как тогда и^8 = иаиа9 следова-
следовательно, можно предположить, что ао — предельный ординал.
У каждой точки хе! есть окрестность ?/, пересекающая
лишь конечное число элементов семейства ^"; очевидно, най-
найдется р < ао, такое, что U [)Fy = 0 при любом у, удовлетво-
удовлетворяющем условию fj <; 7 < a0. Так как <U§ — покрытие простран-
пространства X, то существует s е S, для которого х е U&, s. Из E) сле-
37 Зак. 697
578 ГЛ. 7. РАЗМЕРНОСТЬ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ
дует, что U П Uл s с: Uat «, когда р ^ а < а0; таким образом,
x^Uf\U&scz U^ s. Следовательно, множества U^ s открыты
и покрывают пространство X.
Открытое покрытие {Т7^ Л U'aQt s} подпространства F^czX
обладает открытым ужатием {^Л5е5 п0РяДка ^п, так как—
в силу C) и посылок леммы—число непустых элементов этого
покрытия конечно. Семейство Щп = Ш_ Л , где Un e =
=== (^аа, s \ ^а0) U ^*i является открытым покрытием пространства
X, удовлетворяющим условиям C) — E) при а = а0. Построение
последовательности %, Щ\, ••-, ^а, ..., а ^ |, таким обра-
образом, завершено. Из D) теперь следует, что ord^^ n. Так как
покрытие <Ui, в силу C), является ужатием покрытия <U, лемма
доказана. ¦
Из леммы 7.2.2 и теоремы 7.1.7 вытекает
7.2.3. Теорема о локально конечной сумме. Если пространство X
нормально и существует локально конечное замкнутое покрытие
{Fs}sg5 этого пространства, такое, что dim Fs ^ n при всех
s^S, то dim X ^ п. I
Заметим, что из теорем 7.2.1 и 7.2.3 вытекает теорема о а-ло-
кально конечной сумме: каждое нормальное пространство X, до-
допускающее 0-локально конечное замкнутое покрытие {FJ^^
такое, что dim F$ ^ п при всех s ^ S, удовлетворяет неравенству
dimX ^ п.
7.2.4. Теорема Даукера. Для каждого нормального пространства
X следующие условия равносильны:
(i) dimJ^/z.
(ii) Каждое локально конечное открытое покрытие простран-
пространства X обладает открытым ужатием порядка =^/г.
(iii) В каждое локально конечное открытое покрытие про-
странства X можно вписать открытое покрытие порядка ^п.
Доказательство. Покажем, что (i):=^(ii). Пусть X — нормаль-
нормальное пространство, удовлетворяющее условию dim X ^ /г, и
(U = {Us}sgS— произвольное локально конечное открытое по-
покрытие пространства X. Через У обозначим семейство всех не-
непустых конечных подмножеств множества S и для каждого
IgJ' рассмотрим замкнутое множество
Рт= П U,[\ П (X\US).
T &T
По теореме 7.1.8, имеем dim Ft ^ n. Семейство
&* — {Рт}т<=&— замкнутое покрытие пространства X, причем
каждый элемент этого покрытия пересекает лишь конечное число
7.2. ДАЛЬНЕЙШИЕ СВОЙСТВА РАЗМЕРНОСТИ dim 579
множеств ?/s. Покрытие ЗГ локально конечно. Действительно,
для каждой точки хе! найдутся окрестность U(x) этой точки
и конечное множество S(x)czS, такие, что U{x){\ Us — 0, если
s^S(x). Очевидно, U(x){]Us = 0 при s^S{x)\ значит, если
U (х) П Ft Ф 0, то TczzS(x). Это показывает, что семейство ST
локально конечно. Из леммы 7.2.2 вытекает, что у покрытия Щ
есть открытое ужатие порядка ^п.
Импликация (ii)=^(iii) очевидна. Доказательство имплика-
импликации (iii)=^(i) предоставляется читателю (см. доказательство
теоремы 7.1.6). I
Легко проверяется, что если пространство X — паракомпакт,
то в последней теореме можно заменить слова «локально конеч-
конечное открытое покрытие» словами «открытое покрытие». В случае
паракомпактов можно также брать вместо открытых ужатий
(вписанных открытых покрытий) замкнутые ужатия (локально
конечные замкнутые вписанные покрытия) порядка ^/г; это
легко следует из замечания 5.1.19 и упр. 7.I.G.
Изучим теперь соотношения между размерностью dim и ин-
индуктивными размерностями ind и Ind. Будут доказаны две тео-
теоремы, устанавливающие неравенства между различными размер-
размерностями пространства (см. теорему 7.1.2). Начнем с леммы,
обобщающей теорему 6.2.7.
7.2.5. Лемма. Пусть X — линделёфово пространство и Ш — база
пространства X. Для любых непересекающихся замкнутых мно-
множеств А и В пространства X найдутся тогда открытое множество
W аХ и счетное семейство {Wt}^x элементов базы Шу такие, что
AczWczWczX\B и Fr Wcz [} Fr Wt.
Доказательство, Для каждого xeJ возьмем окрестность
Wx e $ точки х, такую, что либо AftWx = 0, либо B{\Wx = 0,
и рассмотрим счетное подпокрытие ^ = {^г}^в1 открытого по-
покрытия {Wx}xs_x пространства X. Обозначим через {и(}^{ семей-
семейство всех элементов покрытия Ж, замыкания которых пересе-
пересекают множество Л, а через {KJ^j обозначим семейство всех
остальных элементов покрытия 3f\ Тогда
оо оо
F) Ac: [}ui9 Bc[]Vi и Ui(]B=0^Vif]A
i = \ i = l
при i = 1, 2, ... .
Положим
G) Oi^Vt^JJ/t и Hi = Vi\UUf
37*
580 гл. 7. размерность топологических пространств
при i= 1, 2, .... Из формул F) и G) следует, что для откры-
оо оо
тых множеств W= М Gt и V = М Ht выполняются условия
?1 ii
Поэтому W[\V = 0 и ^c=X\Vc=X\S. Так как FvWcz
c=X\(U^U V), для завершения доказательства достаточно про-
проверить, что
X\(WVV)c= U FrС/,U U FrVt= \JFrWi.
i=\ i-\ i->\
Возьмем любую точку x^X\(W\}V) и обозначим через F
первый элемент последовательности Пи V\, &2, %, . ., который
содержит х. Если F = Пи то х е Fr ?// = Hi\Uu так как я ^= G(-
и х ф Vj при / < L Если, с другой стороны, F = 7», то х е
е Fr Vj = Pi\Vu так как хфН( и хф\3\ при / ^ /. Значит,
оо оо
в обоих случаях хе [J Frf/^U |J FrK^. I
?=1 *-I
7.2.6. Лемма. Если для каждой пары А, В замкнутых непересе-
непересекающихся подмножеств нормального пространства X найдется
открытое множество W сг X, такое, что
AaW<=WaX\B и dimFr W^n— I,
то dim Xa^n.
Доказательство. Пусть {Ui}ki=x — произвольное конечное от-
открытое покрытие пространства X и {Л,}(.=1—некоторое замкнутое
ужатие покрытия {Ui}ki=v При i= 1, 2, ..., k возьмем какое-ни-
какое-нибудь открытое множество Wi cz X, такое, что At cz Wt cz Wi a Ui
и dimFr Wt^n— 1. Так как пространство F — (J Fr Wt нор-
мально, то dimf^n—1 по теореме 7.2.1. Из теорем 7.1.7 и
7.1.4 следует, что существует семейство {V^}^ открытых мно-
множеств пространства X, такое, что ViCzUi при /=1, 2, ..., ky
составляют замкнутое покрытие, вписанное в {t/J*el- Значит, в
силу теоремы 7.1.7, для завершения доказательства достаточно
(8) FczV=UVt и
Множества Vu V2, -•-, Vk9 Fu F2i ..., Fk, где
7.2. ДАЛЬНЕЙШИЕ СВОЙСТВА РАЗМЕРНОСТИ dim 581
показать, что порядок этого вписанного покрытия ^.п. Послед-
Последнее неравенство сразу следует из второй формулы в (8) и того
факта, что при / < i ^ k выполняются соотношения
Из 7.2.5, 7.2.6 и 7.2.1, рассуждая по индукции относительно
X, получаем следующий результат (см. упр. 7.2.F):
7.2.7. Теорема. Для каждого линделёфова пространства X имеет
место неравенство dimX ^ indX I
Применяя индукцию относительно IndX, получаем из леммы
7.2.6 следующий вывод:
7.2.8. Теорема. Для каждого нормального пространства X имеет
место неравенство dinxX ^ IndX. I
Из леммы 7.2.5 и теорем 7.1.11, 7.2.1 и 7.1.2 вытекает также
7.2.9. Теорема. Для каждого линделёфова пространства X усло-
условия indX= 1 и IndX= 1 равносильны. I
7.2.10. Пример. Из 7.1.19, 7.2.7, 7.2.8 и 7.1.11 вытекает, что
Ind/? = Ind51 = Ind/= 1 и dim/? = dimS1 = dim/= 1. Ана-
Аналогично, из 7.1.19 и 7.2.7 следует, что dim Rn^n, dim Sn^.n и
dim/" ^ n для каждого натурального числа /г. 1
7.2.11. Пример. Для каждой пары n, m целых чисел, такой, что
0 ^ m ^ /г, обозначим через Qm подпространство пространства
Rn, состоящее из всех точек, ровно m координат которых рацио-
рациональны. Пусть п^ 1.
Как бы ни были выбраны m различных натуральных чисел
*ь к, ..., i'm, не превосходящих п> и m рациональных чисел
п
г\, г2, ..., rmt пространство П#*> где Ru = {rk} при & = 1,
2, ..., т и Ri — R при 1ф1%У является замкнутым подпростран-
п
ством пространства /?п. Следовательно, пространство Q2* П П Rt
замкнуто в Q^. Так как пространство Qm П П Rt гомеоморф-
но подпространству пространства Rn~my образованному всеми
точками, все координаты которых иррациональны, из 6.2.18 и
7.1.11 следует, что dim I Qmfin#* 1 = 0. Из теоремы о счетной
сумме теперь вытекает, что dimQm —0, так как семейство всех
п
множеств вида QmflII#* является счетным замкнутым покры-
тием пространства Qtn- |
582 ГЛ. 7, РАЗМЕРНОСТЬ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ
Мы завершаем этот параграф характеристикой размерности
в смысле покрытий в терминах перегородок. Начнем с определе-
определения и двух лемм.
Пусть X—-произвольное топологическое пространство и А,
В — любая пара непересекающихся множеств в X. Замкнутое
множество LczX называется перегородкой между А и В> если
существуют открытые множества U, V с: Ху такие, что
(9) Лс(/, ВсК, U(]V=0 и X\L = U[}V.
7.2.12. Лемма. Если перегородка L между подмножествами А и
В топологического пространства X функционально замкнута, то
множества U и V в (9) функционально открыты.
Доказательство. Пусть f: X-*~R — непрерывная функция, для
которой f-l(O) = L, По теореме 2.1.13, формула
f (х)у если х е U U L,
О, если xe=VUL,
(
определяет непрерывную функцию g: X-+R. Так как
g~l(R\{0}) = U, множество U функционально открыто. В силу
симметрии наших посылок, множество V тоже функционально
открыто. I
7.2.13. Лемма. Если каждое (п + 2) -элементное функционально
открытое {открытое) покрытие {Ut}"** тихоновского (нормаль-
(нормального) пространства X обладает функционально открытым (от-
крытым) ужатием {Wi}*1^, таким, что f) Wt=09 то dimX<
Доказательство. Покажем, что каждое тихоновское (нор-
(нормальное) пространство X, для которого dimX>n, обладает
(п +2)-элементным функционально открытым (открытым) по-
покрытием {?/J*^fi каждое функционально открытое (открытое)
ужатие {Н^}*^2 которого удовлетворяет неравенству f) Wt=?0.
Так как dim X > щ найдется конечное функционально открытое
(открытое) покрытие Т пространства X, которое не допускает
функционально открытого (открытого) ужатия порядка ^л.
Кроме того, можно предположить — заменив, если нужно, по-
покрытие У подходящим его ужатием, — что У* является разду-
раздутием любого функционально открытого (открытого) своего ужа-
ужатия. Действительно, если элементы Vu Уг» ••-, Vk покрытия У*
имеют непустое пересечение и у У есть функционально откры-
открытое (открытое) ужатие, пересечение соответствующих элементов
которого пусто, то мы заменим У этим ужатием. Ясно, что
7.2. ДАЛЬНЕЙШИЕ СВОЙСТВА РАЗМЕРНОСТИ dim 583
после конечного числа шагов будет получено покрытие с нуж-
нужным свойством. Так как ordF>n, можно предположить, что
п+2
Рассмотрим теперь (л+ 2)-элементное функционально от-
открытое (открытое) покрытие {Ui}"** пространства X, где Ut =
= Vi при 1=1,2,..., л + 1 nUn+2= U Vt. Пусть ^
t ~п+2
любое функционально открытое (открытое) ужатие покрытия
{Ui)tl Покрытие {Wu .... Wn+b Wn+%()Va+29 .... Wn+2 Л Vm]
является функционально открытым (открытым) ужатием по-
покрытия У°. Значит, У0 является раздутием этого покрытия и
п+2 и+1
П Wt=>[) К^
Из теорем 7.1.6 и 7.1.7 следует, что условие приведенной
выше леммы является и необходимым для неравенства dimZ^
^ п. Следовательно, мы, между прочим, получаем некоторую
характеристику размерности. Эта характеристика и характери-
характеристика, двойственная к ней, которая легко получается примене-
применением законов де Моргана, формулируется в следующем утверж-
утверждении.
7.2Л4. Следствие. Тихоновское (нормальное) пространство X
удовлетворяет условию dim X ^ п в том и только том слу-
случае, если каждое (п-\- 2) -элементное функционально откры-
открытое (открытое) покрытие {?/*}^2 пространства X обладает функ-
функционально открытым (открытым) ужатием {Wi}"*** таким, что
л+2
П Wt=- 0, или —что эквивалентно — в том и только том слу-
чае, если для каждого (п + 2)-элементного семейства {ЯJ"l^
функционально замкнутых (замкнутых) подмножеств простран-
rt+2
ства X, удовлетворяющего условию fj В(=0, найдется функ-
ционально замкнутое (замкнутое) покрытие {Fi}^ пространства X,
п+2
такое, что f) Ft= 0 и Bt<^Fi при i = 1, 2, ..., п + 2. |
7.2.15. Теорема о перегородках. Тихоновское (нормальное) про-
пространство X удовлетворяет условию dim X ^ п ^ 0 в том и
только том случае, если для каждой последовательности
(АиВ^, (А2уВ2), ..., (An+uBn+i)
584 ГЛ. 7. РАЗМЕРНОСТЬ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ
п +1 пар непересекающихся функционально замкнутых
{замкнутых) подмножеств пространства X существуют функ-
функционально замкнутые (замкнутые) множества Lu L2, ..., Ln+u
такие, что Li является перегородкой между At и Bi и L\ (] L2 П • • •
... Л Ln+i = 0.
Доказательство. Докажем сначала, что условие теоремы не-
необходимо для неравенства dimX^/г. Пусть X — тихоновское
(нормальное) пространство, такое, что dimX^n^O, и
(АиВ{), (Л2, В2), ..., (Ап+и Вп+х) — последовательность п+1
пар непересекающихся функционально замкнутых (замкнутых)
подмножеств пространства X. Семейство {SJ^f, где ?п+2 =
/Н-1
= U Аи состоит из функционально замкнутых (замкнутых) в
X множеств, и выполняется условие f] В^ = 0. Значит, по
следствию 7.2.14 и теореме 7.1.4, найдется функционально от-
открытое (открытое) покрытие {иг}п.^ пространства X, такое, что
п+2
П Ut=0 и BtCzUi при /=1, 2, ..., п + 2.
Семейство {KJ^f, где Vi = Ut\Ai при /=1, 2, ..., п + 1
и ^гл+2:=г^л+2» является функционально открытым (открытым)
покрытием пространства X. Пусть {Fty}** — какое-нибудь функ-
функционально замкнутое (замкнутое) ужатие последнего покры-
покрытия. Положим при i = 1, 2, ..., п + 1
A0) Ei = Fn+2\Ut, Ct^AtUEt и Х>, =
Так как
U (Л, Л /w) U № П Bt) U (?, Л Ft) = 0.
найдется, по теореме 1.5.13, непрерывная функция Д-: Х^*1 для
i= 1, 2, .... п+ 1, такая, что /i(G)c= {0} и Д(Д)сг {1}. Мно-
Множество
(П) ^ = /-41/2)^X4^^^)
является функционально замкнутой (замкнутой) перегородкой
между множествами At и Я,- при i = l, 2, ..., п+1. Из A0),
п+2
равенства П {/;= 0 и включения Fn+2C= {/л+2 получаем
7.2. ДАЛЬНЕЙШИЕ СВОЙСТВА РАЗМЕРНОСТИ dim 585
Следовательно, в силу A0) и A1),
n+1 n+1 /п+1 п+1
П Lt<=X\ U (C,U0f)ci*\( U Ег\} U
а это показывает, что условие теоремы необходимо для нера-
неравенства dim X ^ п.
Рассмотрим теперь произвольное тихоновское (нормальное)
пространство X, удовлетворяющее условию теоремы. Пусть
WiYltl —любое (п +2)-элементное функционально открытое
(открытое) покрытие пространства X. Возьмем какое-нибудь
функционально замкнутое (замкнутое) ужатие {5J"^f покрытия
{?/*}"= f н положим
At = X\Ut при i = 1, 2, ..., п + 1.
Последовательность (Ль В\), (Л2, В2), ..., (Лл+ь Вп+\) состоит
из п +1 пар непересекающихся функционально замкнутых
(замкнутых) подмножеств пространства X. Значит, при t=lf
2, ..., п+1 существуют множества У,-, 1^,-, функционально от-
открытые по лемме 7.2.12 (открытые), удовлетворяющие условиям
A2) AtczVb BtczWh Vi(]Wi=0 при i = 1, 2, ..., n + 1
+ +i
и такие, что f] U\(^U^)] = ^\ U (Vi[]Wi)=0, т. е.
л+l n+1
A3) U Vti) U f,=jt.
i=i i=i
Из A3), A2) и включения 5л+2сг [/л+2 вытекает, что
[п-Ы п+1 Г п + 1 т
ип+2(] U vf и U Wi = \ ?/««U U ^ П
t=i J t-i L i=i J
[n+l ft+1 T n+2
U ^u U у«Ь0 Bi=x-
t=i t=i j «-1
Следовательно, семейство {WiI^9 где
n+l
wn+2=un+2f] U к„
i=l
является функционально открытым (открытым) ужатием по-
покрытия {?/(}^2. Кроме того, из A2) следует, что
п+2 п+1 г п+1 -| п+1 п+1
Д Wi=Д Гг п гп+2 п »У,к'Jс Д Wt П ,У,Vi=0;
таким образом, dimX ^ /г в силу леммы 7.2.13. I
586 ГЛ. 7. РАЗМЕРНОСТЬ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
Теорема 7.2.1 доказана Чехом в [1933]; приведенное выше
доказательство принадлежит Хаберу (цитировано Энгелькин-
гсм в [1973]). Теорема о счетной сумме для размерности ind
была доказана Менгером в [1924] и Урысоном в [1926] (объ-
(объявлено в [1922]) для метризуемых компактов; она была обоб-
обобщена на случай сепарабельных метризуемых пространств Ту-
маркиным в [1926] (объявлено в [1925]) и Гуревичем в [1927].
Лемма 7.2.2 доказана Катетовым в [1952]; теорема 7.2.3 полу-
получена независимо Моритой в [1950а] и Катетовым в [1952]. Тео-
Теорема 7.2.4 была доказана Даукером в [1947]. Теорема 7.2.7 до-
доказана Менгером в [1924] и Урысоном в [1926] (объявлено
в [1922]) для метризуемых компактов; она была распростра-
распространена на сепарабельные метризуемые пространства Гуревичем
в [1927b]. Для компактов неравенство dimX ^ ind X было уста-
установлено П. С. Александровым в [1941], а его обобщение на
линделёфовы пространства принадлежит Морите [1950] и
Ю. М. Смирнову [1951b]. Теоремы 7.2.8 и 7.2.9 обе принадле-
принадлежат Веденисову; первая из них была доказана в [1939], вто-
вторая— в [1941]. Теорема 7.2.15 была установлена Эйленбергом
и Отто в [1938] для сепарабельных метризуемых пространств;
обобщение ее на нормальные пространства появилось в работе
Хеммингсена [1946] (которая содержит также следствие 7.2.14).
Приведенное нами доказательство этой теоремы взято из рабо-
работы Голштынского [1966]. Важность теоремы 7.2.15 — в том, что
через теорему о продолжении отображений в Sn (см. задачу
7.4.13) она ведет к гомологической характеристике размерности.
Теорема о счетной сумме для размерности Ind выполняется
в совершенно нормальных пространствах (Чех [1932] (объяв-
(объявлено в [1931])) и в наследственно паракомпактных хаусдорфо-
вых пространствах (Даукер [1955]). Теорема о локально конеч-
конечной сумме для Ind тоже выполняется в названных двух классах
пространств (Кимура [1963]). Доказательства этих утверждений
можно найти в книге Энгелькинга [1978]. В классе всех ком-
компактов не выполняется даже теорема о конечной сумме для
размерности Ind (см. задачу 7.4.5).
Размерность ind не удовлетворяет теореме о конечной сумме
ни в классе компактов (см. задачу 7.4.5; более простой пример
нормального пространства, не удовлетворяющего этой теореме,
приведен в упр. 7.2.С), ни в классе метризуемых пространств.
Последнее — как замечено Ван Дауэном в [1973] и Пшимусин-
ским в [1974] — является простым следствием того, что суще-
существует метризуемое пространство X, для которого йХф
Ф Ind X (см. замечания к § 7.3).
7.2. ДАЛЬНЕЙШИЕ СВОЙСТВА РАЗМЕРНОСТИ dim 587
Малая индуктивная размерность ind — с которой теория раз-
размерности началась — оказалась впоследствии не столь важ-
важной, как размерности dim и Ind.
УПРАЖНЕНИЯ
7.2.А. Пусть X — тихоновское пространство и М — его под-
подпространство, удовлетворяющее условиям: йшМ^п и каждая
непрерывная функция /: Af —>-/ непрерывно продолжается на X.
Покажите, что для каждого функционально открытого покры-
покрытия {иг}к^{ пространства X существуют семейство {Vj}$=1 функ-
функционально открытых множеств и функционально замкнутое мно-
множество F, такие, что
к
Vt^Ui при /=1,2,..., Л, MczF<=[}Vi и
7.2.В (Катетов [1950а]). Покажите, что если тихоновское
пространство X обладает счетным замкнутым покрытием
{M/Jjlj, таким, что dimM/^n и каждая непрерывная функция
/: Mj^I непрерывно продолжается на X при /= 1, 2, ..., то
dimX ^ п.
Указание. Видоизмените доказательство теоремы 7.2.1 и при-
примените упр. 7.2.А.
Можно также применить теорему 7.1.17 и воспользоваться
тем фактом, что каждое <у-компактное регулярное пространство
нормально.
7.2.С (Пшимусинский [1974]). Пусть Y и F* — простран
ства, определенные в примере 6.2.20. Обозначим через X про-
пространство, которое получается при отождествлении в точки
замкнутых подмножеств ^Х{0} и WX{1} подпространства
У U ({toi} X {0,1}) пространства У*. Покажите, что простран-
пространство X нормально, indX= 1, но тем не менее X можно пред-
представить в виде объединения Х—Х\ U^2> где Х\ и Х2 замкнуты
в X и ind Х\ = 0 = ind Хг (см. задачу 7.4.5).
7.2.D. (а) (Даукер [1947]). Заметьте, что нормальное про-
пространство X удовлетворяет неравенству dimZ^/z в том
и только том случае, если в каждое звездно конечное открытое
покрытие пространства X можно вписать звездно конечное от-
открытое покрытие порядка ^п.
(Ь) (Пасынков [1965]). Покажите, что тихоновское про-
пространство X удовлетворяет неравенству dimX^Zn в том и
только том случае, если в каждое локально конечное функцио-
функционально открытое покрытие пространства X можно вписать
588 ГЛ. 7. РАЗМЕРНОСТЬ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ
локально конечное функционально открытое покрытие по-
порядка г^Я.
Указание (Р. Поль — цитировано Энгелькингом в [1973]).
Возьмите произвольное локально конечное функционально от-
открытое покрытие {Us}S(=s пространства X; рассмотрите функ-
функционально замкнутое ужатие {Fs}seS покрытия {US}S€ES (cm.
упр. 7.1.В) и непрерывные функции fs: Х->1, такие, что fs(Fs)cz
с: {1} и fs(X\Us)cz {0}. Определите псевдометрику р на мно-
множестве X правилом р (л;, у) = ? | fs (х) — fs (у) I и рассмотрите
ssS
отображение /: X-+Y = Х/р (см. упр. 4.2.1). Возьмите непре-
непрерывное продолжение F: р^->рУ отображения / и примените
теоремы 5.1Д 5.1.35, 7Л.17 и 7.2.4.
Для определения / можно воспользоваться также
упр. 5.1.J(b).
7.2.Е. Заметьте, что каждый сильно нульмерный параком-
пакт сильно паракомпактен.
7.2.F (Морита [1950а]). Усильте теорему 7.2.7, показав, что
неравенство dimX^indX выполняется для каждого сильно
паракомпактного хаусдорфова пространства X.
Указание. Видоизмените лемму 7.2.5, примените леммы 5.3.8,
5.3.9 и теорему 7.1.9.
7.2.G (А. X. Стоун [1962а]). Докажите, что каждое сильно
нульмерное пространство X веса m > Ко, метризуемое полной
метрикой и обладающее тем свойством, что w(U)= ш для каж-
каждого непустого открытого множества U а X, гомеоморфно про-
пространству Бэра В(т) (см. упр. 6.2.А(Ь) и 4.3.G).
Указание. Видоизмените конструкцию из указания к
упр. 4.3.G; примените упр. 4.1.Н и теорему 7.2.4.
7.3. РАЗМЕРНОСТЬ МЕТРИЗУЕМЫХ
ПРОСТРАНСТВ
Начнем с теоремы, характеризующей размерность dim мет-
ризуемых пространств в терминах специальных последователь-
последовательностей покрытий. Приведенные в этой теореме характеристики
будут применены при доказательстве теоремы Катетова — Мо-
риты, утверждающей, что IndX = dimX для каждого метризуе-
мого пространства Х\ эта теорема является одной из важнейших
теорем теории размерности. Отметим, что условия (и) и (iii)
в теореме 7.3.1 сформулированы в терминах метрик; чисто то-
топологические характеристики этого типа формулируются ниже
в упр. 7.З.А.
7.3.1. Теорема. Для каждого метризуемого пространства X сле-
следующие условия равносильны:
7.3. РАЗМЕРНОСТЬ МЕТРИЗУЕМЫХ ПРОСТРАНСТВ 589
(i) dimX^/z.
(ii) Для каждой метрики р на пространстве X существует
последовательность °U\, <2/2, ... локально конечных открытых
покрытий пространства Ху такая, что ord °Ui ^ п, б (U) < l/i
для всех U^L°Ui и для каждого Uе<W,-+i найдется Vе4iif со-
содержащее О.
(iii) Существуют метрика р на пространстве X и последо-
последовательность Ж\, >^2, ... открытых покрытий пространства X, та-
такие, что ordWi^n, 8{W)< l/i для всех W<=Wi и FVh впи-
вписано в Ж и
Доказательство. Покажем прежде всего, что (i)=>(ii). По-
Последовательность <UU %, . ¦ • будет определена по индукции.
Предположим, что k = 1 или что k > 1 и покрытия °Ui уже
определены при i < k. Для каждой точки х^Х возьмем ее
окрестность UXt такую, что 8(UX)< l/k и Ох содержится в не-
некотором члене семейства Шн-и если й>1. Из теорем 5.1.3
и 7.2.4 вытекает, что в покрытие {Ux}xeiX пространства X можно
вписать локально конечное открытое покрытие %Lk порядка ^.п.
Полученная таким образом последовательность °U\y %, • • •
удовлетворяет условию (ii).
Так как импликация (ii)=^(iii) очевидна, остается показать,
что (iii)=^(i).
При каждом / возьмем отображение /j+1 множества Жь+\
в множество Жи такое, что W с: f*+1 (W) при всех W е Ж1+{9
Положим /? = /{+1/Ц? ••• fk-i ПРИ i<k и /|(Юв^ ПРИ w^
^ Wv Очевидно,
A) Wczfk.(W) для всех Ws=Wk и /<?.
Пусть {Я/}|=1—произвольное открытое покрытие простран-
пространства X. Множества Х\, ^2, ..., где
B) Xk = U {W e ^ft: существует /</, такое, что St (Г, Ж*Л) сгЯу},
составляют открытое покрытие пространства X. Рассмотрим
подсемейства
где /г = 1,2 Для каждого U(=<Uk имеем f* (f/) П ( U
обозначим через /(?/) наибольшее целое число i^k, такое,
что /J(?/)fl(.U|^/)saa0- Оказывается, Н{и){и)[\Хци)Ф 0.
Действительно, если i{U)<k, то равенство f*{U)(U){]Xl{U)= 0
590 ГЛ. 7. РАЗМЕРНОСТЬ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ
противоречит максимальности i(U), и если i(U) — k, то
fki{U)W)ПXtm = fkk{U)[\Xk = U[\Xk^0. Таким образом,
C) W
Для каждого Ve.Tt возьмем открытое множество
D) Т = U. [U {f/ П Хк: U е <М4, /* (?/) = К и / (С/) = /}].
Й {
U.
Й — {
Так как V Л */ # 0, то, в силу B), найдутся Г е= Wt и / (К) ^ /,
для которых V{\W^0 и V<=.St(W,7Pi)czHm. В силу A),
имеем V* cz V\ значит, V*czHf{V). Так как Ti[\Yf = 0 при
1ф]\ то множество К* и целое число j(V) корректно опреде-
лены для каждого V е Т = М F^.
Для завершения доказательства достаточно показать, что
семейство {Vtfl=v где Vf = [}{V: V<=T и /(У) = /}с=Я/, по-
покрывает X и имеет порядок ^я, или —равносильное условие —
что F*= {V*: V е F} — покрытие пространства J, порядок ко-
которого ^.п.
Для произвольного хе! возьмем целое число ky такое, что
E) ^1А\ U X»
и множество U e Wk, содержащее точку х. Так как 11Г\Хкф 0,
то ?/€=%. Из C) и D) следует, что x^U(]Xk cz (/fw(t/))'e
е F*; таким образом, F* покрывает пространство X.
Рассмотрим любое непустое пересечение К* П ^ П • • • П V*k,
где Kf e Fmf и Kj =7^= F/ при / =т^= /, и возьмем точку х в этом
пересечении. Из определения семейства Tmi следует, что целое
число k в формуле E) удовлетворяет неравенствам mt ^ k при
/ = 1, 2 А. В силу D), существуют множества t/fG?/ft ,
такие, что Ц(?/.) = У\, i(Ui) = rni и *€=?^П*А.. Так как
xelfef, из E) вытекает, что k^kt. Все множества Wx, W2, ...» W/t,
где Wi = fki{U^^:Wky содержат точку х\ значит, учитывая,
что ord Wk ^ п> достаточно показать, что Wi Ф W\ при
1ф /. Заметим, что множества Wi принадлежат семейству
°Uk и что i(Wi)= i(Ui) — rrii по определению t(?//). Следова-
Следовательно, Wt ф Wj9 если mi ф ntj. При mt- = /и/ мы тоже имеем
Wi Ф Wj, так как тогда
7.3. РАЗМЕРНОСТЬ МЕТРИЗУЕМЫХ ПРОСТРАНСТВ 591
7.3.2. Теорема Катетова — Мориты. Для каждого метризуемого
пространства X имеет место равенство IndX = dimX.
Доказательство. По теореме 7.2.8, достаточно показать, что
IndX^ dimX. Очевидно, можно предположить, что dimZ<; оо.
Применим индукцию по отношению к dimZ. Если dimZ = —1,
то X = 0 и IndX ^ dimX Предположим, что наше неравенство
выполняется для всех метризуемых пространств, для которых
размерность в смысле покрытий ^/г—1. Рассмотрим произ-
произвольное метризуемое пространство X, такое, что dimZ = n,
замкнутое множество Л с X и открытое множество V с X, со-
содержащее Л.
Пусть а — произвольная метрика на пространстве X и
/: X-+I — непрерывная функция, удовлетворяющая условиям
/(Л)сз{0} и /E)с{1}, где В = XW. Формула р(х,у) =
= в(х, y) + \f(x) — f(y)\ определяет метрику на пространстве X,
и, по теореме 7.3.1, существует последовательность Ши %, •••
локально конечных открытых покрытий пространства Х> такая,
что ord^//^n, б(?/)< \/i при всех U ^°Ui> где б обозначает
диаметр по отношению к метрике р, и для каждого f/e%+i
найдется V е °Ui, содержащее ?7.
Положим /Со = Л, Мо = В и при / ^ 1 положим Кг = X\Hi
M X\G где
7f-i= 0} и
Таким образом, определены две последовательности /Со,
/Сь ... и Л10, -Mi, .... Заметим, что
F) если U<=<Ui и 0 0^-1=^0, то
Утверждение F) при i == 1 вытекает из определения мет-
метрики р, так как никакое множество диаметра, меньшего 1, не
пересекает множества Л и Б одновременно. Если U^Ши при-
причем i>\ и Uf\Mi~\ ф 0, то для любого Уе^ч, содержа-
содержащего О, имеем У(]М(~\ф 0, так что V не содержится в G,_i.
Отсюда следует, что Ус: Ям, а это дает равенство U[)Ki-i=0.
Из локальной конечности семейств °Uu определений мно-
множеств Gt и Hi и утверждения F) вытекает, что Gif\Mi-i == 0 =
= Я(П^"-1 при_^= 1, 2, ..., а это влечет за собой соотноше-
соотношения /С;_1 с: X\Hi = Int /С/ и Alf-i с: X\G/ = Int Af,-. Кроме того,
так как G; (J Я(- = X, то /G П A^t = 0- Следовательно, множества
оо с»
/С= У /Сг иМ= UiWj открыты, не пересекаются и содержат
множества Л и В соответственно. Имеем, таким образом, Л с:
czKczV и FrKaL = Х\(К{)Щ- Для завершения доказа-
доказательства достаточно показать, что dimL^n—1, так как, по
592 ГЛ. 7, РАЗМЕРНОСТЬ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ
теореме 7.1.3 и индуктивному предположению, отсюда будет
следовать, что Ind Fr /С ^ Ind L ^ dim L ^ п — 1.
оо оо
Так как K\JM=\] (KtUMi), имеем L= П Lu где Lr- =
i = l i = l
При i=l, 2, ... семейство
7!# 0}
является открытым покрытием пространства LczHi ^
^ n— 1, так как любая точка jcgLcLjC G; принадлежит по
крайней мере к одному Uе^/г, такому, что U(]Mi-i = 0. Если
U e %+i и О[\М(Ф 0, то для каждого У е <UU содержащего
U, имеем У^М^ф 0; значит, V не содержится в G,, откуда
следует, что VftMi-хФ 0, т. е. что V[\L^Wi. Значит, покры-
покрытие 3Pj+i вписано в Ж и и, так как, очевидно, 6{W)< \/i при
W €Е ЗГ/, то dim L ^ /г — 1 по теореме 7.3.1. I
Из теорем 7.1.2, 7.2.7, 7.3.2 и следствия 4.1.16 вытекает
7.3.3. Теорема. Для каждого сепарабельного метризуемого про-
пространства X имеют место равенства indA"= IndX—dimX. I
В связи с теоремами 7.3.2, и 7.3.3 возникает вопрос, может
ли малая индуктивная размерность метризуемого пространства
отличаться от большой индуктивной размерности и размерности
в смысле покрытий этого пространства. Оказывается, суще-
существует метризуемое полной метрикой пространство Ху такое, что
ind X = 0, но Ind X = dim X = 1. Однако определение этого
пространства и вычисление его размерностей ind и Ind связаны
с большими трудностями и в этой книге обсуждаться не будут.
Так как каждое подпространство пространства X, удовле-
удовлетворяющего условию (Hi) теоремы 7.3.1, тоже удовлетворяет
этому условию, из теорем 7.3.1 и 7.3.2 вытекает
7.3.4. Теорема. Для каждого подпространства М произвольного
метризуемого пространства X выполняется неравенство If
Заметим также, что из теорем 7.2.1, 7.2.3 и 7.3.2 получается
7.3.5. Теорема о 0-локалыю конечной сумме. Если метризуемое
пространство X допускает о-локально конечное замкнутое по-
покрытие {Fs}Ss=s> такое, что IndFs^n при всех seS, то
indX^n. I
Докажем теперь теорему, характеризующую размерность Ind
метризуемых пространств в терминах специальных баз и в тер-
терминах разбиений на множества меньшей размерности.
7.3.6. Лемма. Если метризуемое пространство X обладает а-ло-
кально конечной базой 38, состоящей из открыто-замкнутых мно-
множеств, то Ind X ^ 0.
7.3. РАЗМЕРНОСТЬ МЕТРИЗУЕМЫХ ПРОСТРАНСТВ 593
Доказательство. Пусть $ — М $it где семейства 911 локаль-
но конечны. Рассмотрим любое замкнутое множество АсиХ
и открытое множество УсиХу содержащее А. При i= 1, 2, ...
положим
G) K« = U{?/e^: ?/сУ} и
Множества V2f и У2гч-1 открыто-замкнуты и удовлетворяют ус-
условиям
со со
U V2I = V и U V2i+l = X\A9
так что {1^}°^ является покрытием пространства X. Семейство
{t/jjlp где 6^ = V^\ U ^/» образует покрытие пространстваX
попарно непересекающимися открыто-замкнутыми множествами.
Из G) следует, что множество U=[}{Ui: U-t с: V} открыто-
замкнуто и удовлетворяет включениям А <^ U czV. I
7.3.7. Лемма. Пусть X — метризуемое пространство и Z — под-
подпространство пространства X. Если Ind Z ^ 0, то для каоюдого
замкнутого множества АсиХ и произвольного открытого множе-
множества V cz X, содержащего Л, найдется открытое множество
U сX, такое, что Аа Uа О аУ и ZflFr U = 0.
Доказательство. Возьмем открытые множества W\y W2^Xy
удовлетворяющие включениям
Так как Ind Z = 0, найдется открыто-замкнутое в Z множество
Uо, такое, что Z [)ШХ a UoczZ(] W* Очевидно,
Легко проверяется, что множества A[}Uqh [(X\V)\J(Z\Uq)]
отделены. В силу следствия 4.1.13 и теоремы 2.1.7, найдется
открытое множество U а X, такое, что A[)Uq<=.U и О()[ (Х\ V) [}
[)(Z\Uo)] = 0. Ясно, что множество U обладает требуемыми
свойствами, I
7.3.8. Теорема. Для каждого метризуемого пространства X и
произвольного целого числа п^О следующие условия равно-
равносильны:
A) IndJ^n.
(и) Пространство X обладает а-локально конечной базой
$, такой, что Ind Fr U ^ n — 1 при всех U е $.
38 Зак. 697
594 ГЛ. 7. РАЗМЕРНОСТЬ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ
(iii) X = У U Zt где Ind У ^ п — 1 и Ind Z ^ 0.
Доказательство. Покажем, что (i)=^(ii). Пусть X — метри-
зуемое пространство, для которого indX^n, и р — произволь-
произвольная метрика на пространстве1) X. Из теоремы 5.1.3 следует, что
при каждом / = 1, 2, ... пространство X обладает локально ко-
конечным открытым покрытием Ti = {Vs}seS,9 состоящим из мно-
множеств диаметра, меньшего 1/L По теореме 1.5.18, при каждом /
найдется замкнутое ужатие {F$}S€Es. покрытия Ти Так как
IndX ^ я, то при каждом 5 e Si существует открытое множество
Us cz X, такое, что
FsdUsCzVs и lndFrUs^n—1.
Семейство ^ = {t/5}S6S —локально конечное открытое покры-
покрытие пространства X, состоящее из множеств диаметра, меньшего
оо
1/7. Значит, ,$— М $г есть а-локально конечная база простран-
ства X.
Для доказательства импликации (ii)=^(iii) заметим, что по
теореме 7.3.5 подпространство y = U{Fr(Z: U^$}czX удовлет-
удовлетворяет неравенству Ind У ^ я — 1 и что подпространство Z =
= X\Y обладает а-локально конечной базой {Z fl U: U ^$}, со-
состоящей из открыто-замкнутых множеств. Значит, IndZ^O по
лемме 7.3.6.
Импликация (iii)=^(i) прямо следует из леммы 7.3.7 и тео-
теоремы 7.1.3. I
Последняя теорема влечет за собой такой результат:
7.3.9. Теорема о разложении. Метризуемое пространство X удо-
удовлетворяет неравенству Ind X ^ п ^ 0 в том и только том слу-
случае, если X = Zi\jZ2\J ... U Z/M-i, где Ind Zt ^ 0 при i = 1, 2, ...
.... /i+l. I
Из теоремы о разложении вытекает в свою очередь
7.3.10. Теорема о сложении. Для каждой пары X, Y подпро-
подпространств метризуемого пространства имеет место неравенство
Ind(*U10<IndJr+Indy+l. I
Следующая наша теорема обобщает лемму 7.3.7.
7.3.11. Теорема об отделении. Пусть X — метризуемое простран-
пространство и М — подпространство пространства X. Тогда если
Ind М ^ п ^ 0, то для каждого замкнутого множества AczX и
произвольного открытого множества V аХ, содержащего А,най-
1) Предполагается, что р порождает топологию пространства X. — Прим.
перев.
7.3. РАЗМЕРНОСТЬ МЕТРИЗУЕМЫХ ПРОСТРАНСТВ 595
дется открытое множество U а X, такое, что A cz U a U czV и
(MFU)l
()
Доказательство. По теореме 7.3.8, имеем М = Y [} Z, где
Ind У ^ л — 1 и Ind Z ^ 0. Открытое множество U, такое, как
в лемме 7.3.7, удовлетворяет также и требованиям нашей тео-
теоремы, так как М П Fr U cz M\Z сУи Ind (M f] Fr U) ^ n — 1 no
теореме 7.1.З. I
Из теоремы об отделении мы получаем следующий вывод,
являющийся, по теореме Катетова — Мориты, частным случаем
теоремы 7.2.15.
7.3.12. Следствие. Для каждого набора
(Ль 50, (Л2,52), ..., (Ап+иВп+{)
п + 1 пар непересекающихся замкнутых подмножеств метризуе-
мого пространства X, где Ind X ^ п ^ 0, найдутся открытые мно-
множества Uи U2, >•>, ^л+ь такие, что
Ai<z.UiCiUiCzX\Bi при i=l, 2, ..., я+ 1
« Fr t/i П Fr ?/2 П ... nFrt/«+I=0. I
7.3.13. Пример. Из 7.3.3 и 7.1.19 или из 7.3.3 и 7.2.10 следует,
что Indi?" ^ n, IndS" ^ n и Ind/" ^ n для каждого натураль-
натурального числа п.
Разложение пространства Rn на п+ 1 нульмерных множеств
(см. теорему 7.3.9) дается, согласно примеру 7.2.11, формулой
Последняя формула дает также другое доказательство нера-
неравенства \uR I
7.3.14. Пример. Покажем, что пространство Бэра 5(ш), опреде-
определенное в примере 4.2.12, удовлетворяет равенству Indfi(m) = 0
при всех m ^ ?t0.
Рассмотрим произвольные две точки x — {xi} и y = {yi} про-
пространства 5(ш) и вещественное число г, для которого 0 < г ^ 1.
Если пересечение B(xt r)[)B(yyr) непусто, то найдется точка
2 = йеВ(ю), такая, что xi = z{=yu х2 = г2 = у% .... xft =
= г& = уй, где ft —целое число, для которого * t <г<-^-;
тогда 5(х, r) = B(yt r). Следовательно, в В(ш) любые два г-шара
либо не пересекаются, либо совпадают. В частности, при каж-
каждом натуральном / семейство всех l/i-шаров является покрытием
пространства В(ш) попарно непересекающимися открыто-замк-
открыто-замкнутыми множествами. Следовательно, по лемме 7.3.6,
Indfi(m) = 0. I
38*
596 ГЛ. 7. РАЗМЕРНОСТЬ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ
7.3.15. Теорема. Пространство Бэра В(ш) универсально для всех
метризуемых пространств X, таких, что Ind^ = 0 и w(X) =
= ш ^ Ко.
Доказательство. Ввиду последнего примера достаточно пока-
показать, что каждое метризуемое пространство X, для которого
Ind X = 0 и w (X) = т, вкладывается в В (ш).
Пусть р — произвольная метрика на пространстве X. Из тео-
теоремы 7.1.10 и импликации (i)=^(ii) в теореме 7.3.1 следует, что
при 1 = 1, 2, ... существуют покрытия Yi пространства X по-
попарно непересекающимися открыто-замкнутыми множествами
диаметра, меньшего 1//. Такие покрытия можно также опреде-
определить прямо: в соответствии с теоремой 7.3.8 существует сг-ло-
кально конечная база <$ пространства X, состоящая из открыто-
замкнутых множеств. Семейство Ж={[/е1: 8(U)l/t} можно
представить как объединение локально конечных семейств 3Sit и
$i,2> •.. . Расположим члены семейства 9St в трансфинитную по-
последовательность Uu 11ъ - • •, ?/сы ... у ^ < |, взяв сначала все
члены семейства 3&i,u затем все члены семейства ^j2 и т. д.
Ясно, что при каждом а<? семейство {иЛа<а локально ко-
конечно; поэтому семейство ^i = {V^a<v где Va = Ua\ U ^e»
есть покрытие пространства X попарно непересекающимися от-
открыто-замкнутыми множествами диаметра, меньшего 1/7. По
теореме 1.1.14, покрытие Ti содержит такое подпокрытие
ihss чт0 I5l<
Не теряя общности, можно предположить, что множество Si
является подмножеством дискретного пространства Xt мощности
ш, фигурирующего в определении пространства В(ш) как произ-
ведения И Xt. Ставя в соответствие каждой точке х е X индекс
s g S^ такой, что x^Vs, мы получаем непрерывное отображе-
отображение fr. X->Xi. Легко видеть, что семейство {/J7=i отделяет точки
от замкнутых множеств; значит, по теореме 2.3.20, диагональное
оо
отображение /7==А ft: X->B(m) является гомеоморфным вло-
t=i
жением. 1
Так как произведение Ко копий пространства В(ш) гомео-
морфно 5(ш), из теорем 7.3.4 и 7.3.15 вытекает
с»
7.3.16. Теорема. Произведение X=TLxt метризуемых про-
странств удовлетворяет условию IndX = 0 в том и только том
случае, если Ind Xt = 0 при /=1,2, ... . 1
7.3. РАЗМЕРНОСТЬ МЕТРИЗУЕМЫХ ПРОСТРАНСТВ 597
Докажем еще одну теорему о размерности произведения мет-
ризуемых пространств.
7.3Л7. Теорема. Для любых двух метризуемых пространств Ху У,
хотя бы одно из которых непусто, имеем
Доказательство. Это неравенство очевидно, если IndJ = oo
или IndF = oo; поэтому можно предположить, что indX и
Ind У конечны. Применим индукцию по числу Ind X+Ind у. Если
IndX+Indy =—1, то либо Х = 0, либо У = 0 и наше нера-
неравенство выполняется.
Предположим, что неравенство доказано для каждой пары
метризуемых пространств, сумма больших индуктивных размер-
размерностей которых не больше k—1 ^—1, и рассмотрим метризуе-
мые пространства X и Y, такие, что Ind X = m ^ 0, Ind У = п ^ О
и т + ^ = &. По теореме 7.3.8, у пространства X есть база
со
Я? = [] Wi, где семейства Vi локально конечны и Ind Fr U ^
=^/n—1 для каждого t/e®7. Аналогично, у пространства Y
оо
есть база 3) = U З)*, где все семейства 3)j локально конечны и
Ind Fr V ^ п — 1 для каждого V е 2). Семейство
состоит из открытых в XXY множеств и локально конечно. Так
как
Ft(UXV)cz(XXFtV)U(FtUXY)9
то для каждого (UX У)е^-,/, по теореме 7.3.5 и индуктивному
предположению, имеем Ind Ft (U XV) ^ k—1. Семейство
оо
J?= 1J $ы является базой пространства XXY\ значит,
Ind (XX Y) ^ k = m + п по теореме 7.3.8. I
Отметим, что неравенство в последней теореме нельзя заме-
заменить на равенство: существуют сепарабельные метризуемые про-
пространства X и У, такие, что Ind(XX Y) < IndX + Ind У (см.
упр. 7.3.G). Существуют даже метризуемые компакты с этим
свойством, но они устроены гораздо сложнее.
Заметим также, что, по теореме Катетова — Мориты, все тео-
теоремы этого параграфа, начиная с теоремы 7.3.4, выполняются
также и для размерности в смысле покрытий dim.
В завершение этого параграфа мы показываем, что размер-
размерности ind, Ind и dim евклидова n-пространства Rn (а также
л-сферы Sn и л-куба 1п) все равны /г. Этот факт оправдывает
598 гл. 7. размерность топологических пространств
определения наших трех размерностных функций —действитель-
—действительно, размерностная функция, приписывающая Rn число, отличное
от п9 противоречила бы интуитивному представлению о размер-
размерности и была бы, следовательно, неприемлема. Пространства Rnt
Sn и In — первые наши примеры пространств размерности, боль-
большей единицы; до сих пор мы не показали, что такие простран-
пространства существуют.
Доказательство того, что топологическая размерность про-
пространства Rn равна п, требует более глубокого проникновения
в строение этого пространства; при этом непременно потре-
потребуются некоторые комбинаторные рассуждения. Чтобы сохра-
сохранить единообразие рассуждений, проводимых в этой книге,—
а все они имеют теоретико-множественный характер, — мы вы-
выведем равенство indRn = lndRn = dimRn = n (довольно легко)
из теоремы Брауэра о неподвижной точке. Доказательство тео-
теоремы Брауэра о неподвижной точке тоже требует некоторых
комбинаторных или алгебраических рассуждений, но сам резуль-
результат, вероятно, известен большинству читателей. Для полноты
книги мы приводим элементарное комбинаторное доказательство
теоремы Брауэра о неподвижной точке в приложении к этому
параграфу.
7.3.18. Теорема Брауэра о неподвижной точке. Для каждого на-
натурального числа п и каждого непрерывного отображения
f: In-+In найдется точка xg In, такая, что /(х) = х.
7.3.19. Теорема. При каждом натуральном п имеют место равен-
равенства ind Rn = Ind Rn = dim Rn = n.
Доказательство. В силу теорем 7.3.3 и 7.1.3 и примера 7.3.13,
достаточно показать, что Ind/">n—1. Предположим, что
Ind In ^п — 1. При /=1,2, ..., п положим
Аг = {{xf} €= Г: Xi = 0} и Bt = {{х}} е Iя: xt = 1}.
По следствию 7.3.12, существуют открытые множества U\, f/2, >>.
..., Un, такие, что
Ai^UiczUi^In\Bi при i=l, 2, .... л
и
(8) Fr?/,nFrt/2n ..• f]Frt/ft = 0.
Из предложения 2.1.13 следует, что при / = 1,2, ..., п формулы
, Т к«. Pro,)+ P(«.-t.L"? пр"
7.3. РАЗМЕРНОСТЬ МЕТРИЗУЕМЫХ ПРОСТРАНСТВ 599
где р — естественная (обычная) метрика на /я, определяют не-
непрерывные функции ft: In^-I. Ясно, что
(9) fl
Из формул (8) и (9) следует, что диагональное отображение
/ = /1Л/гЛ ... Л fn: In^-In не принимает значения а =
= A/2, 1/2, ..., 1/2)е/п. Композиция g: In^In отображения f
и проекции множества 1п\{а} из точки а на границу множества
п
1п — т. е. на множество В= \j (AiUBi)— удовлетворяет усло-
вию g(In)czB> В силу второй и третьей формул в (9), имеем
g(Ai)czBi и g(Bt)czAi. Последние три включения показывают,
что g(x):?=x при всех х^1п, что противоречит теореме Брауэра
о неподвижной точке. Следовательно, lndln = n. I
7.3.20. Следствие. При каждом натуральном п выполняются ра-
равенства indSrt = IndS" = dim5rt = n и ind In = Ind Г =
= dim/rt= n. I
7.3.21. Следствие, Для гильбертова куба /й° имеем ind/Ko=r-
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
Равносильность условий (i) и (ii) теоремы 7.3.1 была уста-
установлена Даукером и Гуревичем в [1956], равносильность усло-
условий (i) и (Hi) — Вопенкой в [1959]; приведенное нами доказа-
доказательство получено путем небольшой адаптации рассуждения из
работы Нагами и Робертса [1967]. Заметим, что предположение
в (ii) и (ш) о том, что каждое покрытие вписано в предыдущее,
существенно: Ситников в [1953] определил сепарабельное метри-
метрическое пространство размерности 2, которое при каждом нату-
натуральном i имеет открытое покрытие порядка 1, состоящее из мно-
множеств диаметра, меньшего \/i (см. упр. 7.3.А(с)).
Теорема 7.3.2 доказана Катетовым в [1952] и Моритой в
[1954]; наше доказательство, полученное комбинацией теоремы
7.3.1 я упрощенного рассуждения из статьи Даукера и Гуревича
[1956], было опубликовано Энгелькингом в [1973] (эскиз другого
доказательства, в котором удается обойтись без ссылки на тео-
теорему 7.3.1, дан в упр. 7.3.С(Ь)). Равенство размерностей ind и
Ind для метризуемых компактов было объявлено Брауэром в
[1924] (с указанием, что этот факт известен также Урысону).
Приведенное здесь доказательство было дано Менгером в [1924]
(неявно) и Урысоном в [1926]. Для сепарабельных метризуемых
пространств равенство ind и Ind было установлено Тумаркиным
600 ГЛ. 7. РАЗМЕРНОСТЬ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ
в [1926] (объявлено в [1925]) и Гуревичем в [1927]. Равенство
ind и dim для метризуемых компактов было доказано Урысоном
в [1926] (в [1922] он объявил неравенство dimX^indX); оно
было обобщено на сепарабельные метризуемые пространства
Гуревичем в [1927b]. Пример пространства X, метризуемого пол-
полной метрикой, для которого indX = 0 и IndX=l, кратко опи-
описан Роем в [1962]; подробно он обсуждается в статье Роя [1968].
Теорема 7.3.4 установлена Чехом в [1932] (объявлено в
1931]). История теорем о сумме обсуждается в замечаниях к
предыдущему параграфу. Для метризуемых компактов и размер-
размерности ind равносильность условий (i) и (Hi) теоремы 7.3.8, а
также теоремы 7.3.9 и 7.3.10, были установлены Урысоном в
[1926] (объявлено в [1922]). Обобщение на сепарабельные мет-
метризуемые пространства принадлежит Тумаркину [1926] (объяв-
(объявлено в [1925]) и Гуревичу [1927]. Теорема 7.3.11 для метризуе-
метризуемых компактов и размерности ind была доказана Менгером в
[1924] и обобщена на сепарабельные метризуемые простран-
пространства Гуревичем в [1927]. Для произвольных метризуемых про-
пространств теоремы 7.3.9—7.3.11 и 7.3.15—7.3.17 установлены Кате-
товым в [1952] и Моритой в [1954]; теорема 7.3.8 доказана Мо-
ритой в [1954]. Для сепарабельных метризуемых пространств и
размерности ind теорема 7.3.15 была доказана Серпинским в
[1921], теорема 7.3.16 — Куратовским в [1933] и теорема
7.3.17 — Менгером в [1928]. Пример двумерных метризуемых
компактов X и У, таких, что произведение X X У трехмерно, был
приведен Понтрягиным в [1930]. Работа Брауэра [1913] содер-
содержит доказательство равенства lndRn — dim/?" = п (см. замеча-
замечания к § 7.1). Равенство ind Rn — n было доказано (без помощи
результата Брауэра, из которого оно легко следует) Менгером
в [1924] и Урысоном в [1925b] (объявлено в [1922]).
Теорема Брауэра о неподвижной точке установлена Брауэ-
ром в [1912]. Ее доказательство, данное в приложении, а также
теорема 4 приложения принадлежат Кнастеру, Куратовскому и
Мазуркевичу [1929]; лемма Шпернера была доказана Шперне-
ром в [1928].
УПРАЖНЕНИЯ
7.З.А. (а) (Нагами и Роберте [1967]). Докажите, что метри-
зуемое пространство X удовлетворяет неравенству dimX^n
в том и только том случае, если X обладает сильным измельче-
измельчением Ж\, Ж% ..., таким, что oxAWi^n и Jf\-+i вписано в Wi
при /==1,2, ... .
Указание. Видоизмените доказательство теоремы 7.3.1.
(Ь) (Нагата [1956]). Докажите, что метризуемое простран-
пространство X удовлетворяет неравенству dim X ^Ln в том и только том
7.3. РАЗМЕРНОСТЬ МЕТРИЗУЕМЫХ ПРОСТРАНСТВ 601
случае, если X обладает измельчением Ж\у Жь ..-, таким, что
ordWi ^п и Wi+\ звездно вписано (сильно звездно вписано)
вЗГ*при 1 = 1, 2, ... .
Указание. См. доказательство теоремы 5.4.9.
(c) Заметьте, что метризуемый компакт X удовлетворяет не-
неравенству dimZ^n в том и только том случае, если для каж-
каждой метрики р на пространстве X и произвольного е > 0 най-
найдется открытое покрытие пространства X, порядок которого ^Zn
и все члены имеют диаметр, меньший е, или, что равносильно,
в том и только том случае, если существует метрика р на про-
пространстве X, обладающая указанным свойством.
(d) Убедитесь, что в (а) нельзя опустить предположение,
что Ж%1 вписано в Ж%.
7.3.В (Морита [1950а]). Докажите, что для каждого метри-
зуемого пространства Ху представимого в виде объединения
а-локально конечного семейства сильно паракомпактных замк-
замкнутых подпространств, имеют место равенства indX = IndX =
= dim JT.
Указание. Примените упр. 7.2.F.
7.З.С. (а) Докажите теоремы 7.3.4, 7.3.5, 7.3.8—7.3.11, 7.3.15—
7.3.17 и 7.3.19, не используя теорему Катетова — Мориты, а при-
применяя только теорему 7.1.10 и теорему 7.2.1 при п = 0.
Указание (Морита [1954]; для сепарабельных метризуемых
пространств — Гуревич [1927]). Заметьте прежде всего, восполь-
воспользовавшись теоремой 4.4.1, что в метризуемых пространствах из
теоремы о счетной сумме следует теорема о а-локально конеч-
конечной сумме. Затем, обозначив через 2(п) теорему о счетной сум-
сумме для размерности п и через А (п) теорему 7.3.8 для размер-
размерности п, убедитесь, что в приведенном доказательстве теоремы
А(п) применяется только 2(п—1), и покажите, что из 2@) и
А(п) следует 2(л). Доказывая последнюю импликацию, за-
заметьте, что множества Xf = Fi\ M Fit где {FAT,— замкну-
тое покрытие пространства X, являются /^-множествами и по-
покрывают пространство X.
(Ь) Докажите теорему Катетова — Мориты, не пользуясь тео-
теоремой 7.3.1.
Указание (Пшимусинский [1974]). Пусть запись ds(X,p)^n
обозначает, что пространство X обладает последовательностью
покрытий Щи Щ2у —, удовлетворяющей условию (ii) теоремы
7.3.1. Заметим сначала, видоизменив доказательство теоремы
7.3.2, что если ds(X, р) ^ п ^ 0, то для каждого замкнутого мно-
множества АсиХ и любого открытого множества VczX, удовлетво-
удовлетворяющего условию р(Л, X\V)> 0, найдется открытое множество
U czX, такое, что ЛсУсУи ds (Fr t/, p^r и) ^ п — 1. Покажите
602 ГЛ. 7. РАЗМЕРНОСТЬ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ
затем с помощью сделанного выше наблюдения, что из неравен-
неравенства ds(X, р) ^ п ^ 0 следует условие (И) теоремы 7.3.8.
7.3.D (Нагами [1957]). Покажите, что если метризуемое про-
пространство X можно представить в виде объединения трансфинит-
трансфинитной последовательности /Сь ^2> • •. > Ка, ..., а < ?, подпро-
подпространств пространства X, таких, что Ind/Ca^n и множество
F = У /Св замкнуто при каждом a < ?, то IndJ ^ п.
0< p
Указание. Возьмите метрику на пространстве X и проверьте,
что при г = 1, 2, ... семейство {Fi,a}a<$> Г^е ^/, a = tfa \-В (^а»
оо
1/0» дискретно и что Х= U [J FUa.
7.З.Е. Убедитесь, что в теореме 7.3.8 можно заменить а-ло-
кальную конечность базы 9? на <х-дискретность.
7.3.F (Хаусдорф [1934], де Гроот [1956]). Метрика р на
множестве X называется неархимедовой (или ультраметрикой),
если
р (х, z) < max [р (х, у), р (у, г) ]
при всех ху у, 2Е X.
Покажите, что непустое метризуемое пространство X удов-
удовлетворяет условию IndX = 0 в том и только том случае, если
существует неархимедова метрика на пространстве X,
Указание, Метрика пространства В(ш) является неархиме-
неархимедовой.
7.3.G. Покажите, что неравенство в теореме 7.3.17 нельзя за-
заменить на равенство.
Указание. Примените упр. 7.1.А.
7.3.Н. Докажите, что каждое метризуемое полной метрикой
пространство X, для которого IndX = 0 и ш(Х) = т, гомео-
морфно некоторому замкнутому подпространству пространства
Бэра В(ш). Выведите отсюда, что каждое Gg-подпространство
пространства В(ш) гомеоморфно некоторому замкнутому под-
подпространству пространства S(m).
7.3Л (Нагами [1959]). Докажите, что если S = {Х., я|} —
обратная последовательность метризуемых пространств, для ко-
которых dimXi^Zn при /=1, 2, ..., то предел Jl == lim S тоже
удовлетворяет неравенству dimX ^ /г.
Указание. Примените условие A11) теоремы 7.3.1.
ПРИЛОЖЕНИЕ. ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ БРАУЭРА
О НЕПОДВИЖНОЙ ТОЧКЕ
Пусть x = {xi) и y={yi} — точки евклидова /г-пространства
/?п. Сумма х-\-у точек х и у и произведение %х точки х на ве-
7.3. РАЗМЕРНОСТЬ МЕТРИЗУЕМЫХ ПРОСТРАНСТВ 603
щественное число % определяются формулами
x + y = z={zi}> где zi = Xi + yif и
где tt = %Xi.
Точка пространства Rn> все координаты которой равны 0, бу-
будет обозначаться символом 0; расстояние р@, х) будет обозна-
обозначаться через \х\. Легко проверяется, что
последнее неравенство является переформулировкой неравенства
треугольника для Rn.
Точки хо, хи • • • > Xk^Rn называются линейно независимыми,
если для каждой системы Яо, *ь ••*> Xk вещественных чисел ус-
условия %0Х0 + X\Xi + • - • + hkXk = 0 И к0 + к\ + . . . + %k — 0
вместе влекут за собой Я/ = 0 при всех / = 0, 1, ..., k (заметьте,
что это не то же самое, что понятие линейной независимости
векторов в линейном пространствеI).
Пусть ао, аь ,.., ат — произвольная система из т + 1 ли-
линейно независимых точек пространства Rn. Подмножество про-
пространства Rny состоящее из всех точек вида
A) л;
где
B) Хо + h + ... + Ят = 1 и Л/ > 0 при / = 0, 1, ..., т,
называется т-мерным симплексом, натянутым на точки а0,
аь ..., ат, и обозначается через поп\ ... аот. Ясно, что сим-
симплекс аоа\ ... amczRn не зависит от упорядочения точек
по, а\у ..., ат, а зависит только от множества {а0, пи ..., dm}-
Рассмотрим произвольный симплекс aod\ ... amaRn\ для
любых k + 1 различных неотрицательных целых чисел /о, /ь . • -
..., Ik, не больших т, точки а, 9 а,, ..., а, линейно незави-
симы и, значит, определен ^-мерный симплекс а, а. ... а, .
Каждый симплекс такого вида называется k-мерной гранью
симплекса aoai ... ат\ 0-мерные грани ао, аи .-., ат назы-
называются также вершинами симплекса аоп\ ... am. Сам симплекс
cl<ju\ ... ат тоже считается своей гранью. Легко проверяется,
что ^-мерная грань а. а, ... а, состоит из всех точек вида A),
удовлетворяющих условиям B) и, кроме того, условию
%1 = 0, если / Ф ji при i = 0, 1, ..., k.
х) Однако имеется тривиальный канонический переход от одного понятия
к другому — Прим. перев.
604 ГЛ. 7. РАЗМЕРНОСТЬ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ
Из линейной независимости вершин следует, что каждая
точка xeaoai ... amczRn представляется в виде A) при со-
соблюдении условий B) единственным образом. Коэффициенты
Ко, Ки •.-, Кт> входящие в A), называются барицентрическими
координатами точки х; барицентрические координаты точки х
будут обозначаться также через Ко(х), ^iW. • ••> Km(x).
Теорема 1. Для любых m-j-l линейно независимых точек
ао, аи • • •, flm & Rn симплекс S = поп\ ... ат является компакт-
компактным подпространством пространства Rn, и барицентрические ко-
координаты Ко, Ки ..., Km являются непрерывными отображе-
отображениями пространства S в I.
Доказательство. Положим 6' = 0 при i-Ф] и б|==1. Точки
d0, d[t ..., dm в /?m+1, где d/=={6{+1}, линейно независимы, так
что симплекс T=dodi ... dmcz Rm+l определен корректно. Ба-
Барицентрические координаты точек симплекса Т совпадают с их
координатами в Rm+lt и, следовательно, в силу B), Т является
замкнутым и ограниченным подмножеством пространства Rm+l.
Теорема 3.2.8 показывает, что Т — компакт.
Из предложения 2.3.6 вытекает, что формула
f (х) = X&Q + х2а{ + ... +xm+lamt где ^
определяет некоторое непрерывное отображение f: T^Rn.
В силу линейной независимости точек ао, #ь •••> #т, отобра-
отображение f инъективно. Так как f{dj)=aj при / = 0, 1, ..., /п,
имеем f(T) = S9 и, по теореме 3.1.13, f\T является гомеомор-
гомеоморфизмом пространства Т на S. Значит, S — компактное подпро-
подпространство пространства Rn, и барицентрические координаты А,/
непрерывны при / = 0, 1, ..., т, потому что Х^(х) =
P/+i(/|r)~l(#)i где pi обозначает проекцию произведения Rm+X
на г-ю ось. I
Тот факт, что f\T является гомеоморфизмом, можно также
вывести из элементарных теорем линейной алгебры. Эти тео-
теоремы показывают, кроме того, что у / есть обратное отображе-
отображение, определенное формулами, аналогичными тем, которыми
было определено f\ разница заключается лишь в том, что вме-
вместо точек ao> ai, ..., ат в формуле для обратного отображения
к / участвуют некоторые точки а'о, а[, ...» а!п_х е Rm+l в каче-
качестве коэффициентов.
Из непрерывности барицентрических координат немедленно
вытекает
Следствие. Любые два m-мерных симплекса гомеоморфны. I
Симплициальным подразделением симплекса S a Rn назы-
называется любое семейство ^> = {S/}*_1 симплексов в Rn, удовле-
7.3. РАЗМЕРНОСТЬ МЕТРИЗУЕМЫХ ПРОСТРАНСТВ 605
творяющее следующим трем условиям:
C) 5= US,.
D) При любых /, / ^ k пересечение Si Л S/ либо пусто,
либо является общей гранью симплексов Si и 5/.
E) При i = 1, 2, , k все грани симплекса S,- принадлежат ^\
Мелкость симплициального подразделения {S/}^ симплекса
5 определяется как наибольшее из чисел 6(Si), бEг), ...
6(S)
()
Для каждого симплекса 5 = aoai ... amc^Rn точка
называется барицентром (или центром тяжести) симплекса S;
ясно, что ft(S)eS и b(S) не принадлежит никакой (т—1)-
мерной грани симплекса S.
Теорема 2. Пусть S = a§a\ ... am — произвольный симплекс.
Тогда для каждой убывающей последовательности So => Si гэ...
. ..r^Sft различных граней симплекса S точки 6 (So), &(Si), •••
..., 6Eа) линейно независимы. Семейство 0* всех симплексов
вида b(So) b(S\) ... b(Sk) является симплициальным подраз-
подразделением симплекса 5; каждый (т—I)-мерный симплекс
Ге^1 является гранью одного или двух m-мерных симплексов
семейства $Р — в зависимости от того, содержится или нет сим-
симплекс Т в какой-нибудь (т—1) -мерной грани симплекса S.
Доказательство. Каждая убывающая последовательность
различных граней симплекса 5 может быть дополнена до по-
последовательности Sqzd S\zd ... zd Sm, состоящей из m + 1 гра-
граней симплекса S и такой, что
F) So = aioait ... a,m, S, = atai2 ... Ntm, ..., Sm = a,m>
где /о, i\9 ..., im — некоторая перестановка элементов 0, 1, ...
..., m. Для доказательства первой части теоремы достаточно
показать, что точки b(So)9 ft (Si), ..., ft(Sm) линейно неза-
независимы.
Рассмотрим произвольную линейную комбинацию
G) |*oft(So) + »iiftEi)+ ... +M>(S,«).
Воспользовавшись определением барицентра, мы можем пред-
представить G) как линейную комбинацию точек а, , а. , ..., а, ; а
именно, она равна
606 ГЛ. 7. РАЗМЕРНОСТЬ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ
где
i
(9) Ч^Е (TO + n-fe»** ПРИ / = 0,1,..., т.
fe=0
Кроме того, имеем
mm} mm
do) Еч=ЕЕ (т+о-^^ЕЕ^Л-^
Если линейная комбинация G) равна 0 и \xq + щ + ... + Цт=0,
то, так как точки а. , а{, ..., at. линейно независимы, из A0)
следует, что Af/—0 при / = 0, 1, ..., т. Применив (9), мы
видим, что ^0 = 0, щ = 0, ..., \х,т = 0. Следовательно, точки
6(So), b(S\)y ..., 6(Sm) линейно независимы и симплекс
6(So) 6(Si) ... b{Sm) корректно определен.
Каждый симплекс из 9* является гранью некоторого т-мер-
ного симплекса вида b(So)b(S\) ... b(Sm). Из формул G) —
A0) следует, что симплекс b(So)b{S\) ... b(Sm) является под-
подмножеством симплекса S; покажем, что это подмножество сов-
совпадает с множеством
A1) {jcgS: A^UX^^xX-..^*, (jc)}.
В силу (9), достаточно показать, что каждая точка х мно-
множества A1) может быть представлена в виде G) таким обра-
образом, что [10 + ^1+ ... + \im = 1 и fi/^О при / = 0, 1, ..., /п.
Читатель легко проверит, что получается такое представление,
если определить коэффициенты Ц,/ формулами
A2) ib = (m+l)Kh(x) и |i/ = [(iit+I)
при/= 1, 2, ..., т.
Из A2) следует, что грани симплекса b(So)b(Si) ... b(Sm)
описываются путем присоединения к условиям, определяющим
множество A1), некоторого числа условий вида Я^ (х)==Л,*._1(д:)»
где 1 ^ / ^ /п, а также, возможно, условия Л*о(;с) = 0.
Так как пересечение грани, определенной таким множеством
условий, с гранью другого симплекса b (Sj) b (S[) . •. b (Sm)r
отвечающего другой перестановке i'0> iv ..., irm элементов 0,
1, ..., m, само определяется множеством условий подобного
типа или пусто, семейство 9* удовлетворяет условию D). Усло-
Условие C) также выполнено, так как каждая точка множества S
принадлежит некоторому множеству вида A1). Условие E)
вытекает из определения семейства 9*. Следовательно, семей-
семейство 9* является симплициальным подразделением симплекса S.
7.3. РАЗМЕРНОСТЬ МЕТРИЗУЕМЫХ ПРОСТРАНСТВ
607
Рассмотрим теперь произвольный (т—1)-мерный симплекс
Т — b(So)b(S\) ... b(Sm-i)^&** Если симплекс Т содержится
в некоторой (т—1)-мерной грани симплекса 5, т. е. если
50 ?=¦ 5, то Т является гранью в точности одного m-мерного сим-
симплекса семейства &>, а именно симплекса b(S)b(So) ... 6EOT_i).
С другой стороны, если Т не лежит ни в какой (т— 1)-мерной
грани симплекса 5, т. е. если 5о = S, то либо найдется / ^
^ m—1, такое, что симплекс 5/ получается из симплекса S/_i
опусканием двух вершин, либо Sm-\ — одномерный симплекс.
Легко проверяется, что и в том и в другом случае Т является
гранью в точности двух m-мерных симплексов семейства 9*. I
Симплициальное подразделение симплекса 5, определенное
в теореме 2, называется барицентрическим подразделением
симплекса 5. Для каждого натурального числа / мы определим
теперь 1-е барицентрическое подразделение симплекса 5. Ба-
Барицентрическое подразделение симплекса S является первым
барицентрическим подразделением этого симплекса; если /-е
барицентрическое подразделение {5*}/=1 симплекса S уже из-
известно, то его (/+1)-е барицентрическое подразделение опре-
определяется как объединение |J 8*t, где {?г — барицентрическое
подразделение симплекса Si. Для каждой грани 5' симплекса
51 и каждого члена S" семейства &i пересечение Sf[\S" либо
пусто, либо является гранью симплекса S" и членом барицент-
барицентрического подразделения симплекса S'. Пользуясь этим фак-
к
том, читатель легко проверит, что объединение \j {Pt является
t=i
симплициальным подразделением симплекса S.
Рассмотрим произвольный симплекс S = аоа[ ... amczRn,
точку х = Хоао + hcti + ... +Xmami где %о + %\ + ... + Яш = 1
и Л/ ^ 0 при / = 0, 1, ..., пг, т. е. любую точку xgS,h произ-
произвольную точку у е Rn. Покажем, что
A3)
р(х, r/)<maxp(a7 у).
Действительно, имеем
Р(*> У) = \х — у\ =
т т
— у К max | а} — у |
== max p (а;, г/).
Лемма 1. Диаметр любого симплекса а$а\ ... amczRn равен
диаметру множества {ао, ai, ..., ат} вс^л: его вершин.
608
ГЛ. 7. РАЗМЕРНОСТЬ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ
Доказательство. Пусть х, у<=аоа{ ... ат. В силу A3),
р{х, #)<maxp(a/f у). Применив A3) снова, заключаем, что
p(a/> yXmax(a/, аг); таким образом, р(х, #)< max р(а*, аг),
т. е. 6@^ ... ат) = 6({а0, olf ..., ат}). |
Лемма 2. Мелкость барицентрического подразделения
m-мерного симплекса S = a0Oi ... am «е превосходит——-у- 5(S)
Доказательство. По лемме 1, достаточно показать, что рас-
расстояние между любыми двумя точками вида
где k< i *?Lm и toi M, • • ¦ > ^*m — перестановка из 0, 1, ..., ту не
превосходит J7] 1 6(S). Из A3) следует, что p(b{Sk),
( )
при
). Следовательно,
/
Z(a~ — a
¦
Из последней леммы вытекает
Теорема 3. Для каждого симплекса S и произвольного е>0
найдется натуральное число I, такое, что мелкость 1-го бари-
барицентрического подразделения симплекса S меньше е. I
Лемма Шпернера. Пусть 3* есть 1-е барицентрическое под-
подразделение т-мерного симплекса а^а\ ... аш и V — множество
всех вершин всех симплексов из ЗЙ. Тогда если функция h,
определенная на V и принимающая значения в множестве {О,
1, ..., т), удовлетворяет условию
h (v) е {/0, i{9 ..., ik}> как только v ^a
. ¦. at
то число симплексов семейства &у на вершинах которых функ-
функция h принимает все значения от 0 до т, нечетно.
Доказательство. Применим индукцию относительно пг. Если
m = 0, то лемма выполняется, так как #*= {ао} и ft(oo) = 0.
7.3. РАЗМЕРНОСТЬ МЕТРИЗУЕМЫХ ПРОСТРАНСТВ 609
Предположим, что лемма установлена при т< п. Рассмотрим
произвольный я-мерный симплекс S = aQai ... ап, /-е барицент-
барицентрическое подразделение ?Р симплекса S и любую функцию Л,
удовлетворяющую посылкам леммы. Обозначим через &г се-
семейство всех (п—1)-мерных симплексов семейства ^, на вер-
вершинах которых h принимает все значения от 0 до п—1. Ясно,
что единственной (п—1)-мерной гранью симплекса S, содер-
содержащей симплексы семейства &\ является грань аоа\ ... ап-ь
По индуктивному предположению, число симплексов семейства
9>\ лежащих в а§а\ ... ап-и нечетно; обозначим это число че-
через а.
Расположим все я-мерные симплексы семейства 9* в после-
последовательность Si, S2, -.., St. Для каждого j^t обозначим
через Ь\ число граней симплекса S/, принадлежащих 9*ry и через
Nj обозначим множество значений функции h на вершинах
симплекса S/.
Читатель легко проверит, что:
A4) Если Nj={0, 1, ..., n}, то 6/=1.
A5) Если Nf= {0, 1, ..., п— 1}, то 6/= 2.
A6) Если включение {0, 1, ..., п— 1} с: Nj не выполняется,
то bj = 0.
Через с обозначим число симплексов в ^, на вершинах ко-
которых h принимает все значения от 0 до п. В силу A4) — A6),
существует целое число d\y такое, что
A7) c-{bx + b2+ ... +bt)=2du
Если мы сопоставим каждому симплексу S/ его bj граней,
принадлежащих &*у то каждый симплекс Т из i?f будет постав-
поставлен в соответствие, как это легко следует из последней части
теоремы 2, одному или двум симплексам S/ — в зависимости от
того, содержится или нет симплекс Т в какой-нибудь {п—1)-
мерной грани симплекса S. Следовательно, существует целое
число d2, такое, что
A8) а-(Ьг + Ь2+ ... +bt) = 2d2.
Формулы A7) и A8) показывают, что с — a = 2{dx — d2)\ та-
таким образом, с — нечетное число. 1
Теорема 4. Пусть {Ft}fLQ — семейство замкнутых подмно-
подмножеств симплекса S = а$а\ ... ат. Тогда если для каждой грани
а. а{ ... а. симплекса S выполняется соотношение
39 Зак. 697
610 ГЛ. 7. РАЗМЕРНОСТЬ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ
Доказательство. Предположим, что F\ f] F2 Л • • • П Fm = 0.
Семейство {?/^}^0, где ?Д- = SNF,-, является открытым покры-
покрытием симплекса 5; значит, в силу компактности 5 и тео-
теоремы 4.3.31, существует е > 0, такое, что каждое подмножество
симплекса S, диаметр которого меньше е, содержится в неко-
некотором Uи т. е. не пересекается с Ft.
По теореме 3, найдется натуральное число /, такое, что
мелкость /-го барицентрического подразделения & симплекса S
меньше е. Обозначим через V множество всех вершин всех сим-
симплексов из 9*. Для каждого yeF пересечение всех граней сим-
симплекса 5, содержащих v, является некоторой гранью симплекса
S, т. е. имеет вид а. а ... а. . Так как v^a.a, ... а. , то по
предположению теоремы найдется / ^ k, такое, что v e Ft*
Полагая h(v) = ijy мы определяем на V функцию h, кото-
которая удовлетворяет посылкам леммы Шпернера; значит, най-
найдется хотя бы один симплекс Т = vov\ ... vm^fF, такой, что
h(vi) = i при / = 0, 1, ..., /п. Значит, vi^Ft и тем более Г Л
f]Ft?=0 при i = 0, 1, ..., /п. Получили противоречие, так как
б(Г)<е. ¦
Доказательство теоремы Брауэра о неподвижной точке. Куб
/* (я-мерный) содержится в n-мерном симплексе Т = аоаг ...
... an<=Rn, где aQ = 0, а} = {пЩ при /=1,2, ..., л, б{=0, когда
1ф'и и *'=!. Если бы существовало непрерывное
отображение f: In^In, такое, что \(х)Фх при всех хе/п, то
для непрерывного продолжения f: T->In отображения /, суще-
существующего в силу 2.1.8 и 2.3.6, было бы Цх)Фх при всех
х'еГ Значит, достаточно доказать, что для каждого непре-
непрерывного отображения f: T-**T найдется точка ^еГ, такая, что
J(x) = x. Заметим, что возможность замены n-куба 1п симплек-
симплексом Т также вытекает из того, что Iя и Т гомеоморфны
(см. упр. 3.2.С).
Для каждой точки х^Т имеем
A9) * = Л0(х)а0 + Мх)а1+ ••• +К(х)ап,
где
B0) Я0(х) + Я1(х)+ ... +М*)=1
и Kf(x) ^ 0 при / = 0, 1, ..., п.
Образ каждой точки хеГ при отображении f можно запи-
записать так:
B1) f(x) = K0(f
где
B2) h(f(x))
7.4. ЗАДАЧИ 611
При i = О, 1, ..., п множество
B3) Fi={x<=T: MfOOXM*)}
замкнуто, так как Л,- и f непрерывны. Покажем, что семейство
удовлетворяет посылкам теоремы 4. Пусть a?at
а. —
произвольная грань симплекса Т. Рассмотрим любую точку
х^ а. а, ... а, . Имеем
1 ь\ 1к
так что, в силу B2),
Значит, hi}(f(x))^Xif(x) по крайней мере для одного / < ky
и тогда х е Fir Мы установили, таким образом, что
В силу теоремы 4, существует точка х ^ Fo П ^i П • • • П Fn\ из
B3) следует, что
Однако, в силу B0) и B2), строгое неравенство Mf(*))<
не может выполняться ни для какого /; значит,
и, в силу A9) и B1), имеем f(x) = x. I
7.4. ЗАДАЧИ
Теоремы сложения
7.4.1 (Урысон [1925b]). Пусть X — наследственно нормаль-
нормальное пространство и М — любое его подпространство. Покажите,
что ind М ^ п ^ 0 в том и только том случае, если для каждой
точки х е М и произвольной окрестности V точки л: в простран-
пространстве X найдется открытое множество U czX, такое, что х е
е= t/cz V и ind(Af ПFr t/)< n — 1.
Выведите отсюда, что для любых двух подпространств X, У
произвольного наследственно нормального пространства вы-
выполняется неравенство
ind(XU У)< ind X + ind У + 1.
Указание. Примените индукцию относительно ind X + ind У.
7.4.2 (Ю. М. Смирнов [1951b]). Пусть X — наследственно
39*
612 ГЛ. 7. РАЗМЕРНОСТЬ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ
нормальное пространство и М — подпространство пространства
X, Покажите, что IndiW^n^O в том и только том случае,
если для каждого замкнутого множества AczX и произволь-
произвольного открытого множества VczX, содержащего Л, найдется
открытое множество UczX, такое, что ^czf/czV и Ind (Mfl
nFr?/)</i—1.
Выведите отсюда, что для каждой пары X, Y подпространств
любого наследственно нормального пространства имеет место
неравенство
Ind (X U Y) ^ Ind X + Ind Y + 1.
7.4.3 (Чех [1932а]). Пусть X — наследственно нормальное
пространство и М — подпространство пространства X. Пока-
Покажите, что у каждого открытого покрытия пространства М есть
раздутие, состоящее из открытых в X множеств.
Указание. Применяя индукцию относительно k, покажите,
что для каждого конечного семейства {K/}f=1 открытых мно-
k
жеств в Му удовлетворяющего условию f| Vt= 0, найдется
i = \
семейство {Ut}i=<i открытых множеств в X, такое, что ViCzUt
k
при «= 1,2, ...,k и [\иь=0.
1АА (Ю. М. Смирнов [1951b]). Пусть X — наследственно
нормальное пространство и М — подпространство пространства
X. Покажите, что dimM^n в том и только том случае, если
для каждого конечного семейства {Ut}i=l открытых множеств
k
в Ху удовлетворяющего условию М cz (J Ut, найдется семей-
ство {Vi}ki=x открытых множеств в X, такое, что ViCzUt при
k
/=1,2 ft,Alc[J^
Выведите отсюда, что для любых двух подпространств X, У
произвольного наследственно нормального пространства имеет
место неравенство
Указание. При доказательстве первой части утверждения
примените задачу 7.4.3.
Компакт X, для которого indX Ф dimX
7.4.5 (Локуциевский [1949]). Пусть V — длинный отрезок
(см. задачу 3.12.18) и f: DK°->/— функция, определенная в
7.4. ЗАДАЧИ 613
упр. З.2.В. На произведении V^D**0 рассмотрим отношение
эквивалентности ?, определенное правилом: (х\, C\)E(x2t с2) в
том и только том случае, если (x\t С\) = {х2у с2) или х\ = х2 = o>i
и /(ci) = /(c2). Докажите, что для факторпространства
Х\ = (V X D**Q)/E выполняются равенства ind X\ = Ind X\ =
diX I
Пусть А\ — подпространство пространства Х\, состоящее из
всех точек, прообразы которых при естественном факторном
отображении q: KXOKo-^^i двухточечны. Пусть Х2 — копия
пространства Х\у не пересекающаяся с Х\, и А2 — подмножество
множества Х2> соответствующее множеству А\сХ\. Применив
упр. 4.3.Н(а), соедините Х\ с Х2 вдоль отрезка я({щ} X^Ro)
таким образом, чтобы никакая точка множества А\ не соеди-
соединилась ни с какой точкой множества А2. Проверьте, что для
полученного таким образом компакта X выполняются равен-
равенства IndX = тйХ = 2 и dimX= 1.
Заметьте, что теорема о счетной сумме и даже теорема о ко-
конечной сумме не выполняются для размерностей ind и Ind
в классе всех компактов.
Замечание, Первый пример компакта Ху такого, что тйХФ
Ф dim X, был построен Лунцем в [1949].
Тихоновское престранство Z и замкнутое подпространство М
пространства Z, для которых dimZ < dimAl
7.4.6 (Ю. М. Смирнов [1956b]). С помощью пространства У
из примера 6.2.20 определите тихоновское пространство Z, та-
такое, что dimZ = 0, но dimM>0 для некоторого замкнутого
подпространства М aZ.
Указание. Пусть cY — какая-нибудь нульмерная компакти-
фикация пространства У, и пусть W обозначает пространство
всех ординалов ^соь Покажите, применив задачу 3.12.19(с),
что для пространства Z = (WX cY)\ [{coi} Х(сУ\с(У))] имеет
место равенство CZ = WX cY.
Нормальное пространство Z, для которого indZ — Ои
dimZ = оо
7.4.7 (Ю. М. Смирнов [1958])* Видоизменив построение про-
пространства У в примере 6.2.20, определите нормальное простран-
пространство Z, такое, что ind Z = 0 и dim Z = оо.
Указание. Замените отрезок гильбертовым кубом и множе-
множества Sa произведениями So0. Примените следствие 7.1.18.
Полиэдры
7.4.8. Пространство Р называется полиэдром, если суще-
существуют симплекс S и семейство & граней симплекса S, такие,
614 ГЛ. 7. РАЗМЕРНОСТЬ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ
что Р = (J !?. Вершины симплекса 5, принадлежащие Р, назы-
называются вершинами полиэдра Р. Размерность полиэдра Р есть
максимум размерностей симплексов из ^.
Заметьте, что определения вершины и размерности поли-
полиэдра не зависят от выбора симплекса S и семейства !Р. Убеди-
Убедитесь, что каждый полиэдр является компактом.
Пусть Р — полиэдр и по, а\у •••> йт — все его вершины. По-
Покажите, что каждая точка хеР единственным образом пред-
представляется в виде
х=
т
где 2 %i (х) = 1 и Kj(x) ^ О при / = О, 1, ..., т. Проверьте, что
Яо, Ки ..-, Ят — непрерывные функции на Р со значениями в /.
Подмножество
G/= (xeP: Я;(х)>0}
полиэдра Р называется звездой вершины а}-. Покажите, что для
последовательности а, > а. , ..., а, вершин полиэдра Р пере-
передо м }k
сечение G/o f| G}l П • • • П G;& непусто в том и только том случае,
если а, а, ... а, с: Р.
Докажите, что для каждого полиэдра Р размерности ind/\
IndP и dimP совпадают с размерностью полиэдра Р.
Характеристика размерности dim в терминах ^-отображений
7.4.9 (неявно — Куратовский [1933а]; для метризуемых ком-
компактов— П. С. Александров [1928]). Пусть X и У — топологиче-
топологические пространства и s& — произвольное покрытие пространства
X. Непрерывное отображение /: X-+Y называется ^-отображе-
^-отображением, если существует открытое покрытие {(/JseS пространства
У, такое, что {f~l (Us)}seS вписано в *я?.
(а) Докажите, что тихоновское (нормальное) пространство X
удовлетворяет неравенству dimX^n в том и только том слу-
случае, если для каждого конечного функционально открытого
(открытого) покрытия зФ пространства X существует ^-отобра-
^-отображение пространства X в полиэдр размерности ^п.
Указание. Пусть Т = {Vt}^ — какое-нибудь функционально
открытое покрытие, вписанное в s?, для которого ord T ^ п, и
{/^}JLo— функционально замкнутое ужатие покрытия Т. Возь-
Возьмите любой m-мерный симплекс S = аоа\ ... аш и семейство
ш},-=о непрерывных функций /г\ X-+-I, удовлетворяющих уело-
7.4. ЗАДАЧИ 615
виям fi(X\Vi)cz{0} и fi{Fi)cz{l}, и положите
Рассмотрите отображение /: X-*S, определенное формулой
() Я()
f() () ) ()
(Ь) Покажите, что в данной в пункте (а) характеристике
размерности dim слова «в полиэдр» можно заменить словами
«на полиэдр».
Указание. Покажите, что для каждого подмножества А по-
полиэдра Р= U^найдутся подсемейство ^0 семейства 9 и непре-
непрерывное отображение g: Л->Р, такие, что g(A) = Pq— U^o и
^)с=Г при всех
Размерность в смысле покрытий произведений
7.4.10 (Хеммингсен [1946]). Докажите, что для любых двух
компактов X, У, хотя бы один из которых не пуст, имеет место
неравенство
dim {X X Y) ^ dim X + dim Y
(см. задачу 7.4.12 (b)).
Указание. Покажите, что для каждого конечного открытого
покрытия пространства XX Y найдется вписанное в него покры-
покрытие вида {{/XV: U е <я?, V е .$}, где j# и J? — конечные откры-
открытые покрытия пространств X и У соответственно. Примените
задачу 7.4.9(а).
Размерность подпространств
7.4.11 (Даукер [1955]). Пусть X — нормальное пространство
и М — замкнутое подпространство пространства Ху такое, что
dimAf^n. Покажите, что dimX^n в том и только том слу-
случае, если каждое замкнутое подпространство F<^X, не пересе-
пересекающееся с М9 удовлетворяет условию dim F ^п.
7.4.12 (Чех [1933], Ю. М. Смирнов [1951с]). (а) Пусть X —
нормальное пространство, удовлетворяющее неравенству
ЛшХ^п. Докажите, что для каждого подпространства МаХ,
являющегося /^-множеством или (более слабое требование)
нормально расположенного в X, выполняется неравенство
dimM ^ п.
Выведите отсюда, что для каждого подпространства М про-
произвольного совершенно нормального пространства X имеем
dimAf < dimX.
Замечание. Чех доказал в [1932] (объявлено в [1931]), что
IndAf ^ IndX для каждого подпространства М совершенно нор-
нормального пространства X; доказательство см. в работе Нагами
[1970] или Энгелькинга [1978].
616 ГЛ. 7. РАЗМЕРНОСТЬ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ
(Ь) Покажите, что неравенство в задаче 7.4.10 остается вер-
верным для любых тихоновских пространств X, У, таких, что про-
произведение XX У является линделёфовым пространством.
Характеристика размерности dim в терминах отображений в
сферы
7.4.13. (а) (Хеммингсен [1946], Александров [1947], Даукер
[1947]; для компактов — Александров [1940], Морита [1940];
для метризуемых компактов—Александров [1932] и Гуре-
вич [1935]). Докажите, что нормальное пространство X удовлет-
удовлетворяет неравенству dimX^nl^O в том и только том случае,
если каждое непрерывное отображение /: A-^Sn, определенное
на каком-нибудь замкнутом подпространстве А пространства X,
можно непрерывно продолжить на все X.
Указание. Рассмотрите сначала случай компакта X. Восполь-
Воспользуйтесь характеристикой размерности dim, установленной в тео-
теореме 7.2.15. Вместо Sn возьмите границу S? (п+ 1)-куба /"+1 в
/?"+*; примените задачу 5,5.21 и тот факт, что для каждой точки
лсое/л+1\5/ граница 5/ является ретрактом пространства
1п+1\{хо}. Чтобы распространить эту характеристику на нор-
нормальные пространства, примените теорему 7.1.17.
(b) (Ю. М. Смирнов [1955b]) Докажите, что тихоновское
пространство X удовлетворяет неравенству dimX ^n^fl в том
и только том случае, если каждое непрерывное отображение
/: Л->5Л, определенное на замкнутом подпространстве А про-
пространства X, для которого существует непрерывное отображение
F: Х~>Вп+\ такое, что F(x) = f(x) при всех хеЛ, непрерывно
продолжается на X.
(c) Покажите, что если А — замкнутое подпространство нор-
нормального пространства X и каждое замкнутое подпространство
F пространства X, не пересекающееся с Л, удовлетворяет нера-
неравенству dim^F^n^O, то каждое непрерывное отображение
/: Л—>Sn непрерывно продолжается на X.
(d) Пусть X! и Х2—-замкнутые подпространства метризуе-
мого пространства X, такие, что Х11)Х2 = Х1 и ft: Xi-+Sn и
f2: X2->S" — некоторые непрерывные отображения. Покажите,
что если множество D={x^Xx[\X2: fi(x)^/2W} удовлетво-
удовлетворяет неравенству dimD^n—1, то оба отображения f\ и /2 не-
непрерывно продолжаются на X.
Указание. Примените задачу 5.5.21.
Факторизационная теорема Мардешича
7.4.14 (Мардешич [I960]). Докажите, что для каждого не-
непрерывного отображения /: X->Y любого компакта X, удовлет-
удовлетворяющего условию dimX^n, в произвольный компакт У, та-
7.4. ЗАДАЧИ 617
кой, что тю(У)^шу найдутся компакт Z и непрерывные отобра-
отображения g: I^Z и ft: Z^-У, для которых выполняются условия
dimZ^tt, w(Z)^m, g(X) = Z и f — hg (это и есть фактора-
зационная теорема Мардешича).
Указание (Архангельский [1967]). Возьмите любую базу $
пространства У, для которой |^|^т, и рассмотрите семейство
^/s}seS всех конечных покрытий пространства У, состоящих из
элементов семейства $. Положим VO = {TS}S^S, где Т$ —
= {/-1(f/): ?/е%}, и определим последовательность V\f V% •,.
семейств открытых покрытий пространства X, где V/+i получает-
получается путем выбора для каждой пары У, Т''е Vi некоторого конеч-
конечного открытого покрытия порядка ^л, сильно звездно вписан-
вписанного и в У9, и в У*\ Убедитесь, что, полагая хЕу в том и только
том случае, если У ^ [\ П Stfa, Дмы определяем замкнутое
отношение эквивалентности Е на пространстве X. Проверьте,
что факторпространство Z = X/E, естественное факторное ото-
отображение g и отображение А, определенное равенством А([лг] ) =
= f(x), удовлетворяют требуемым условиям.
Компактификации, сохраняющие размерность и вес
7.4.15 (Скляренко [1958]; для сепарабельных метризуемых
пространств — Гуревич [1927b] и [1930]). Докажите, что для
каждого тихоновского пространства Ху удовлетворяющего усло-
условиям dimX^n и w(X)^mt найдется компактификация сХ, та-
такая, что dim сХ ^ л и w (сХ) ^ т.
Указание (Мардешич [I960]). Продолжите гомеоморфное
вложение i: Х-+Г на рХ и примените задачу 7.4.14.
Универсальные пространства размерности п и веса m
7.4.16 (Зарелуа [1964], Пасынков [1964]). Докажите, что для
каждого натурального числа л и любого кардинала щ^ Ко най-
найдется компакт, являющийся универсальным пространством для
всех тихоновских пространств X, таких, что dimX^.n и
(X)
Указание (Пасынков [1964]). Пусть ^ — семейство всех под-
подпространств X пространства /ш, для которых dimX^n. Поло-
Положим Y= ф X и /= v ix- У^Г, где ix: X->/m— тожде-
ственное вложение пространства X в /т. Рассмотрите непрерыв-
непрерывное продолжение /: рУ-^/т отображения / и примените за-
задачу 7.4.14.
618 ГЛ. 7. РАЗМЕРНОСТЬ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ
Замечание. Нёбелинг показал в [1931], что при каждом п^ О
п
пространство Л/!**1 = (J Qm + \ т. е. подпространство простран-
пространства /?2"+!, состоящее из всех точек, не более чем п координат
которых рациональны, является универсальным пространством
для всех сепарабельных метризуемых пространств размерности
^п. Отсюда следует, в частности, что любое сепарабельное
метризуемое пространство размерности ^п можно вложить в
/?2л+1. Последний факт был доказан также Лефшецем в [1931],
равно как Понтрягиным и Толстовой в [1931]. Доказательства
можно найти в книге Гуревича и Волмэна [1941] и в книге Эн-
гелькинга [1978].
Расширение я-мерных множеств до n-мерных С6-множеств
7.4.17 (Катетов [1952], Морита [1954]; для сепарабельных
метризуемых пространств — Тумаркин [1926] (объявлено в
[1925])). Покажите, что для каждого подпространства М про-
произвольного метризуемого пространства X найдется б6-множество
М* а X, такое, что М а М* и Ind М* = Ind M.
Выведите отсюда, что каждое метризуемое пространство X
гомеоморфно всюду плотному подпространству некоторого мет-
метризуемого полной метрикой пространства X*, такого, что Ind X* =
() ()
Указание. Рассмотрите сначала случай, когда подпростран-
подпространство М удовлетворяет условию IndM = 0. Видоизмените первую
часть доказательства теоремы 7.3.8 и примените лемму 7.3.7;
можно также воспользоваться теоремами 7.3.15 и 4.3.21.
Для доказательства в общем случае примените теорему 7.3.9.
При доказательстве второго утверждения примените теоремы
4.3.19 и 4.3.23.
п- мерные подпространства пространства Rn
7.4.18 (Менгер [1924], Урысон [1925b] (объявлено в [1922])).
Докажите, что подпространство М евклидова n-пространства Rn
имеет размерность п в том и только том случае, если \п\Мф0.
Выведите отсюда, что для каждого непустого открытого мно-
множества UaRn, такого, что \ЗфКп, размерность границы Fr U
равна /г— 1.
Указание. Примените задачу 4.5.2.
Отображения, повышающие размерность, и отображения, по-
понижающие размерность
7.4.19. (а) (Энгелькинг [1973]). Заметьте, что метризуемое
пространство X удовлетворяет неравенству IndX^n^O в том
7.4. ЗАДАЧИ 619
и только том случае, если X обладает 0-локально конечной
сетью JF, такой, что Ind Fr М <! п — 1 при всех М е Jf\
(b) (Морита [1955]; для сепарабельных метризуемых про-
пространств— Гуревич [1927а]). Докажите, что если /: X-+Y—
замкнутое отображение метризуемого пространства X на метри-
зуемое пространство К и [/-1 (у) | ^ k + 1 ^ 1 при всех у е У, то
Idy^IdJ + Л
Указание (Энгелькинг [1973]). Примените индукцию относи-
относительно Ind У + k. Возьмите а-локально конечную базу $ про-
пространства X, для которой IndFr U ^ IndX— 1 при всех 11^38,
рассмотрите семейство {f(U): U ^Щу воспользуйтесь леммой
3.10.11 и утверждением (а).
7.4.20. (а) (Гуревич и Волмэн [1941] для сепарабельных мет-
метризуемых пространств). Пусть метризуемое пространство X об-
обладает замкнутым покрытием Ж, таким, что Ind/C^n^O при
всех /С <=«#*, и открытым а-локально конечным покрытием Щ,
таким, что для каждого К^Ж и произвольного открытого
V cz X, содержащего К, найдется U е Ш, удовлетворяющее усло-
условиям К cz U cz V и IndFr ?/^| я—-1. Докажите, что тогда
Указание. Докажите, что каждое непрерывное отображение
f: Л»>5Л, определенное на каком-нибудь замкнутом подпро-
подпространстве А пространства X, имеет непрерывное продолжение
F: X->-Sn (см. задачу 7.4.13(а)). Сначала, применив задачу
7.4.13(с), для каждого К^Ж определите f/j^e^, такое, что
Kcz Uк, IndFr Uк ^ п— 1 и / допускает непрерывное продол-
продолжение на Л U Ок. Расположите все члены семейства {?/*: К^Ж)
в трансфинитную последовательность U0,Uu ..., Ua* .-•, а<?
таким образом, чтобы семейство {^в}й<а было локально конечно
при каждом а < |. Положите Ло = A U по и Аа = Оа при а > 0.
Применяя задачу 7.4.13(d), определите по трансфинитной индук-
индукции трансфинитную последовательность отображений Fq, F\y ...
..., F^ .... а < |, где Fa: ( (J ^el^5"' такую, что
^a — IГ U ^r^^^v ПРИ Y^a и /70|Л = /. Положите F =
|V3<Y P/
(b) (Морита [1956], Нагами [1957]; для сепарабельных мет-
метризуемых пространств — Гуревич и Волмэн [1941]; для метри-
метризуемых компактов — Гуревич [1927а]). Докажите, что если
/: X-*~Y — замкнутое отображение метризуемого пространства X
в метризуемое пространство Y и Indf~l(y)^ k ^ 0 при всех
уе Г, то IndX^Indy + A.
Указание, Зафиксируйте k и примените индукцию относитель-
относительно Ind У. Возьмите a-локально конечную базу $ пространства У,
620 ГЛ. 7. РАЗМЕРНОСТЬ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ
такую, что IndFr ?/^ Ind У—1 для всех U^$, рассмотрите
семейство {f~l(U): U е Щ и воспользуйтесь (а).
Замечание. Обзор результатов об отображениях, повышаю-
повышающих размерность, и об отображениях, понижающих размер-
размерность, можно найти в работе Лелека [1971] (см. также статьи
Нагами [1970] и Энгелькинга [1978]). В работе В. В. Филип-
Филиппова [1972] описан общий метод, который упрощает многие до-
доказательства в этой области.
Вокруг теоремы Брауэра о неподвижной точке
7.4.21. (а) Покажите, что теорема Брауэра о неподвижной
точке влечет за собой лемму Шпернера и следующие два факта:
A) Сфера Sn не является ретрактом шара Вп+К
B) Тождественное отображение ids«: Sn^»Sn не гомотопно
постоянному отображению сферы Sn в точку х е S".
Покажите, что каждый из приведенных выше двух фактов,
равно как и теорема о том, что dim/" = я, влечет за собой тео-
теорему Брауэра о неподвижной точке.
(Ь) Докажите, что для каждого непрерывного отображения
/: /к° ¦-> /к° существует точка х е /*°, такая, что f(x) = x.
Борелевские множества III (см. задачи 1.7.5, 4.5.7 и 4.5.8)
7.4.22 (Лебег [1905]). Докажите, что для каждого счетного
ординала а найдется в гильбертовом кубе /**° множество Ма
мультипликативного класса а, которое не входит в аддитивный
класс а, а также найдется множество Аа аддитивного класса а,
которое не принадлежит мультипликативному классу а.
Указание (Энгелькинг, Голштынский и Сикорский [1966]).
Определите по индукции множества Ма и Аа = /к° \ Ма, взяв
в качестве Мо произвольное одноточечное подмножество про-
пространства /**° и при а > 0 положив
{Л^с=(/ко)«о = /«о, если сс=р+Ь
IX Аа cz (/*о)*о = /\ если а — предельный ординал.
Р< р
Покажите, что для каждого метризуемого пространства X и лю-
любого множества В<^Х мультипликативного (аддитивного) клас-
класса а существует непрерывное отображение f: X-+I**0, такое,
что f~l(Ma) = B (такое, что f~l(Aa) = В). Примените задачу
7.4.21 (Ь).
Глава 8
РАВНОМЕРНЫЕ ПРОСТРАНСТВА
И ПРОСТРАНСТВА БЛИЗОСТИ
Понятия равномерного пространства и пространства бли-
близости можно рассматривать с двух позиций — либо как аксиома-
аксиоматизации некоторых геометрических объектов, близкие к понятию
топологического пространства, хотя и совершенно независимые
от него, либо как удобные средства изучения топологических про-
пространств. Когда А. Вейль впервые ввел равномерности, они рас-
рассматривались именно как такое средство, пригодное в отличие
от метрик для изучения топологических пространств без каких-
либо предположений о счетности. Близости также могут быть
использованы для изучения топологий; они особенно эффективны
при исследовании компактификаций. Бурбаки, весьма подробно
излагающий в своей книге теорию равномерных пространств,
подчеркивает ее независимый характер, хотя она и очень тесно
связана с теорией топологических пространств. Связь между
этими двумя теориями основана на том, что равномерным про-
пространствам и равномерно непрерывным функциям ставятся в со-
соответствие (неким стандартным образом) топологические про-
пространства и непрерывные отображения. Этот переход от равно-
равномерных пространств к топологическим разбивается на два этапа;
промежуточное положение занимают пространства близости.
Теория равномерных пространств обладает разительным
сходством с теорией метрических пространств, но область ее
применения значительно шире. В частности, каждая топологи-
топологическая группа обладает тремя естественными равномерностями,
которые применяются в теории топологических групп.
В § 8.1 мы вводим понятия равномерности и равномерного
пространства и показываем, как равномерность порождает топо-
топологию. Затем определяются два понятия, широко используемые
в теории равномерных пространств: равномерные покрытия и
равномерные псевдометрики. Из важного результата о том, что
для каждой равномерности Ш существует много псевдометрик,
равномерных относительно Ш, мы выводим, что всякое про-
пространство с топологией, индуцированной некоторой равномер-
равномерностью, есть тихоновское пространство. Затем мы показываем,
что топология любого тихоновского пространства порождена не-
некоторой равномерностью. Далее мы рассматриваем три упомя-
622 ГЛ. 8. РАВНОМЕРНЫЕ ПРОСТРАНСТВА И ПРОСТРАНСТВА БЛИЗОСТИ
нутые равномерности на топологических группах и устанавли-
устанавливаем необходимое и достаточное условие, чтобы равномерность
порождалась метрикой. Параграф заканчивается обсуждением
равномерно непрерывных отображений и равномерных изомор-
изоморфизмов.
В § 8.2 изучаются три операции на равномерных простран-
пространствах: рассматриваются подпространства, декартовы произведе-
произведения и пространства отображений. В отличие от метрических про-
пространств произведение любого семейства равномерных про-
пространств является равномерным пространством, поэтому нет
нужды вводить ограничения на мощность семейства. Равномер-
Равномерности в пространствах отображений позволяют определить поня-
понятие равностепенно непрерывного семейства отображений и до-
доказать аналоги классической теоремы Асколи.
Параграф 8.3 посвящен вполне ограниченным и полным рав-
равномерным пространствам. Здесь отчетливо видна аналогия
между равномерными и метрическими пространствами. Многие
теоремы этого параграфа являются обобщениями теорем § 4.3,
причем их формулировки и доказательства почти дословно сов-
совладают с исходными. В заключительной части этого параграфа
мы определяем пополнение равномерного пространства и об-
обсуждаем свойства компактных равномерных пространств.
В § 8.4 изучаются близости и пространства близости. Мы по-
показываем, что каждая близость порождает некоторую тополо-
топологию, и изучаем взаимосвязи между равномерностями и близо-
близостями. Наиболее важным результатом этого параграфа являет-
является теорема Смирнова, устанавливающая взаимно однозначное
соответствие между близостями на тихоновском пространстве X
и его компактификациями.
8.1. РАВНОМЕРНОСТИ И РАВНОМЕРНЫЕ
ПРОСТРАНСТВА
Сначала введем некоторые обозначения. Пусть X—некото-
X—некоторое множество и Л, В — подмножества произведения Х\Х,
т. е. отношения на множестве X. Обратное к А отношение будет
обозначаться через —Л, а композиция отношений А и В — че-
через А + В\ так,
—А={(х,у): (у,х)<=А}
и
А + В = {(х, г): существует такой yel,
что (х, у)^А и (у, г)еВ).
Легко видеть, что композиция отношений ассоциативна, т. е.
(Л + В)-\- С = А -\-(В + С). С другой стороны, как показывают
8.1. РАВНОМЕРНОСТИ И РАВНОМЕРНЫЕ ПРОСТРАНСТВА 623
простые примеры, композиция отношений не коммутативна, т. е.,
вообще говоря, А + В Ф В + Л. Для произвольного отношения
AczXyiX и натурального числа п отношение пА<^Ху^Х опре-
определяется индуктивно формулами
\А=А и пА =(п— \)А + Л.
Из ассоциативности композиции следует, что тА -f- пА = пА +
-}- тА =(/п + я)Л.
В § 2.3 мы определили диагональ произведения Ху^Х как
множество
А={(х,л:): jkge X}.
Каждое множество VczX^X, которое содержит А и удовлет-
удовлетворяет условию У =—У, называется окружением диагонали;
множество всех окружений диагонали AczXX^ будет обозна-
обозначаться 2>*. Если для пары х, у точек X и некоторого У <= Ж>х
мы имеем (хуу)^. У, то будем говорить, что расстояние меоюду
х и у меньше У, и писать \х — у\< У; в противном случае бу-
будем писать \х — у\^ У. Если для любой пары х, у точек мно-
множества А а X и некоторых V е Ж)х мы имеем \х — у\ < V, т. е.
если А X A d V, то будем говорить, что диаметр А меньше У,
и писать б(Л) < V. Легко проверить, что для любых х, у, г е!
и любых V, Vi, Уг ^ ®х выполнены следующие условия:
A) \x-x\<V;
B) |jc — у\ < У тогда и только тогда, когда | у — л:| < У;
C) если \х — у\< Vi и |у — г|< У2, то |jc — z|< Vi + V2.
Пусть х0 — точка Х9 и пусть V^S)x\ множество B(xQyV) =
= {х^ X:\xo — х | < У} называется шаром с центром х0 радиуса
V или просто V-шаром с центром х0. Из C) сразу следует, что
диаметр У-шара меньше 2У. Для множества Л с: X и некото-
некоторого У е 2>х под V-шаром вокруг А мы подразумеваем мно-
множество В (А, У)= U В(ху У).
Равномерность на множестве X есть подсемейство ^ с: Юк,
которое удовлетворяет следующим условиям:
(Ul) EcauV <=<U uV aW €=3>x>toW <=<U.
(U2) ?сла Vu V2 e ^, то Vi fl V2 e ^/.
(U3) Для любого V ^Ш существует такое W е ^/, что 21F с У.
(U4) П ^ = А.
Семейство $<^Щ называется базой равномерности 41, если
для любого V ^°U существует такое W <= ^, что Wcz К. Оче-
Очевидно, что равномерность °Ц может иметь много баз; наимень-
624 ГЛ. 8. РАВНОМЕРНЫЕ ПРОСТРАНСТВА И ПРОСТРАНСТВА БЛИЗОСТИ
ший кардинал вида |Л|, где 38 — база для Щ, называется весом
равномерности Щ и обозначается wDl).
Любая база 3& равномерности на множестве X обладает сле-
следующими свойствами:
(BU1) Для всех Vi, V2^& существует такое Ve^J, что
(BU2) Для всякого V <= 3$ существует такое W ^38, что 2W а V.
(BU3) П^ = Д.
Отметим, что каждое окружение диагонали 1/е2)х порож-
порождает покрытие <ff(V) = {B(x, V)}x^x множества X. Пусть °U —
какая-нибудь равномерность на множестве Х\ всякое покрытие
множества Ху в которое можно вписать покрытие вида ff(V),
где Уе%, называется равномерным относительно °U. Совокуп-
Совокупность С всех покрытий множества X, равномерных относи-
относительно некоторой равномерности °U на Ху обладает следую-
следующими свойствами:
(UC1) Если зФ^С и зФ вписано в некоторое покрытие <М мно-
множества Ху то 3$^ С.
(UC2) Для любых зФь зФ2^ С существует зФ^С, которое впи-
вписано и в зФ\у и в <$Ф2-
(UC3) Для любого зФ^С существует ^еС, сильно звездно
вписанное в зФ.
(UC4) Для любой пары ху у различных точек X существует та-
кое ^gC, что ни один член зФ не содержит одновре-
одновременно х и у.
Свойство (UC1) очевидно, свойство (UC2) есть следствие
(U2) и равенства В(ху Vx П V2) = B(x, V\)(\B(x9 72), а свойство
(UC4) следует из (U4) и (U3). Остается установить (UC3);
для этого достаточно показать, что для любого зФ = <&'(У)^С
покрытие ЗИ = ff (W), где W e °U удовлетворяет включению
4W a Vy сильно звездно вписано в зФ. Рассмотрим элемент
В(х, W) покрытия 3S и такую точку yel, что В(х, W)f\
Л В (у, W) Ф0. Из последнего неравенства получаем х — у\<С
<2Wy так что для любого z^B(yy W) имеем \х — z <31Fc
c=4lFc=K, т. е. zeB(x9V). Следовательно, St(B(x9W)93S)c
czB(x, У)^зФ9 откуда видно, что $ сильно звездно впи-
вписано в зФ.
Равномерное пространство — это пара (X, °U), состоящая из
некоторого множества X и равномерности °U на нем. Вес рав-
равномерного пространства (Ху °U) определяется как вес равномер-
равномерности °U.
Каждая равномерность Щ на множестве X порождает неко-
некоторую топологию О на X; значит, каждое равномерное простран-
пространство (J, °U) определяет топологическое пространство (Ху О).
Точнее, имеет место
8.1. РАВНОМЕРНОСТИ И РАВНОМЕРНЫЕ ПРОСТРАНСТВА 625
8.1.1. Теорема. Для любой равномерности Щ на множестве X
семейство
0 = {G а X: для каждого х ^ G существует
такое V d°U> что В(х, V) a G)
есть топология на множестве X, и топологическое пространство
(X, О) есть 7'{-пространство.
Топология О называется топологией, порожденной (или ин-
индуцированной) равномерностью °U.
Доказательство. Из определения семейства О следует, что
оно удовлетворяет условиям @1) и @3). Покажем, что вы-
выполнено и условие @2). Рассмотрим два множества G\9 G2^0
и точку хе Gi П ^2. По определению О существуют такие
Vu Уг^Ш, что B(xf Ki)cz Gi и В(х, V2)<=G2. Из (U2) следует,
что V= Vif] V2^°Uy и так как В(х, V) = B(xt Vi)(\B(x9 V2)a
czGif] G2, то Gi П G2 e 0.
Остается проверить, что (X, О) есть ^-пространство. Для
этого достаточно показать, что при каждом х^Х множество
G = X\{x} открыто. Для любого y^G имеем хфу, так что,
согласно (U4), существует Уе^, удовлетворяющее неравен-
неравенству \х — y\^V. Так как В (у, V)aG, то множество G от-
открыто. I
Мы покажем в следствии 8.1.13, что топологическое про-
пространство (Х,(У)У полученное из равномерного пространства
(Х,<М)9 всегда является тихоновским пространством. Так же
как в случае метрик, можно спросить, когда для топологиче-
топологического пространства (X, О) существует такая равномерность Щ
на множестве X, что порожденная ею топология совпадает с ис-
исходной топологией О. В теореме 8.1.20 мы докажем, что такая
равномерность существует тогда и только тогда, когда (X, О) —
тихоновское пространство. Поэтому некоторые авторы называют
тихоновские пространства униформизуемыми пространствами.
Если X — топологическое пространство и равномерность °U
на множестве X индуцирует исходную топологию X, то мы бу-
будем говорить, что Щ есть равномерность на пространстве Х\
вообще говоря, существует много равномерностей на данном
тихоновском пространстве (см. пример 8.1.7 и упр. 8.1.В
и 8.1.С).
8.1.2. Предложение. Внутренность множества Лс! относитель-
относительно топологии, индуцированной равномерностью °U на множестве
X, совпадает с множеством
В={хе1: существует такое Уе^, что В{х, V)czA}.
Доказательство. Так как каждое открытое множество Сс=Л
содержится в 5, достаточно показать, что В —¦ открытое множе-
40 Зак. 697
626 ГЛ. 8. РАВНОМЕРНЫЕ ПРОСТРАНСТВА И ПРОСТРАНСТВА БЛИЗОСТИ
ство. Для любой точки хеВ существует такое Уе?/, что
В(х7 V)czА\ возьмем W<^°U, удовлетворяющее условию 2W<ziV.
Из C) следует, что для каждого j/eB(x, W) имеем В (у, W)cz
с~ В(х, V)a A\ следовательно, В(х, W)czB, откуда видно, что
В — открытое множество. I
8.1.3. Следствие. Если топология пространства X индуцирована
равномерностью Шу то для каждой точки х^Х и каждого
Fg% множество IntВ(ху V) — окрестность точки х.
Доказательство. Так как В(х, V)czB(xy У), точка х принад-
принадлежит внутренности шара В{х, V). I
8.1.4. Следствие. Если топология пространства X индуцирована
равномерностью 41, то для каждого хеХ « каждого Лс!
имеем
х^А тогда и только тогда, когда А П В (х, V) ф 0
для каждого Уе% I
8.1.5. Следствие. Если топология пространства X индуцирована
равномерностью °U, то для каждого А а X и каждого V е °Ы
имеем
б(Л)<ЗУ, как только 6{A)<V.
Доказательство. Согласно последнему следствию, для лю-
любых х, у^А существуют такие х7, /g/1, что х'^B(x,V)
ку'<=В(у,У). Поэтому |* — y\<V+V+V = 3V. I
Заметим, что, как вытекает из приведенных выше следствий,
пространство X с топологией, индуцированной равномерностью
°U на множестве X, есть регулярное пространство (ср. со след-
следствием 8.1.13). В самом деле, в силу теоремы 8.1.1, X есть
^-пространство. Поэтому для любой точки хе! и любого
замкнутого множества FczX, такого, что x<?F, окрестность
IntJ5(x, W) точки х9 где W^Ш удовлетворяет условию 6Wcz V
с некоторым У^УХ, таким, что F[\B{xy V)= 0, обладает свой-
свойством hdB(x9W) П F = 0.
8.1.6. Пример. Для любого множества X семейство °U = 3)x
есть равномерность на Х\ она называется дискретной равномер-
равномерностью на X, а пространство (X, °U) называется дискретным
равномерным пространством. Одноэлементное семейство .59 —
= {А} есть база для °U, так что w{cU)^= 1. Так как В(х, А) =
= {л:}, то всякое покрытие множества X равномерно относи-
относительно °U. Ясно, что каждое подмножество Аа X открыто отно-
относительно топологии, индуцированной °Uy т. е. дискретная рав-
равномерность порождает дискретную топологию. 1
Этот пример показывает, что вес топологического простран-
пространства (X,О), где топология 0 индуцирована равномерностью Ш*
8.1. РАВНОМЕРНОСТИ И РАВНОМЕРНЫЕ ПРОСТРАНСТВА 627
может оказаться больше веса °U. С другой стороны, легко про-
проверить, что характер (X, О) не больше веса °11,
8.1.7. Пример. Пусть X — произвольное множество; для каждой
конечной последовательности х\, ..., Xk элементов множестваX
положим по определению
Множества V(xu x2, ..., Xk) являются окружениями диагонали.
Рассмотрим семейство °Ucz2Dx, состоящее из всех окружений
диагонали, которые содержат множество V(x\, x2, ..., Xk). Се-
Семейство °U составлено теми элементами ?>х, которые полу-
получаются из ХХ^ удалением некоторого множества, покрывае-
покрываемого конечным объединением множеств (IXW)(W^)
Мы покажем, что Щ — равномерность на X.
Тот факт, что Щ удовлетворяет условиям (U1) и (U2), сле-
следует из определения. Легко проверить, что 2V{x\, х2> ..., xk) =
= V(x{7 х2, ..., Xk), поэтому условие (U3) также выполнено.
Наконец, условие (U4) выполнено потому, что (х, у)ф V(x),
когда хфу.
Так как В {ху V(x)) = {х}, равномерность °U индуцирует дис-
дискретную топологию на X, Если множество X бесконечно, то
Щф$Ьх, поэтому, согласно примеру 8.1.6, разные равномер-
равномерности могут индуцировать одну и ту же топологию. Легко про-
проверить, что если \Х\ ^ No, то w{(U) = \X\. I
8.1.8. Пример. Пусть / = [0,1] — единичный отрезок. Читатель
легко проверит, что семейство °Ы всех окружений диагонали
Дсг/ХД которые содержат какое-нибудь открытое подмноже-
подмножество в /ХЛ содержащее А, есть равномерность на /; очевидно,
Щ индуцирует естественную топологию отрезка / и w (<%() =
= No. ¦
Пусть Щ — равномерность на множестве Х\ тихоновская то-
топология на произведении XX X, где X взято с топологией, инду-
индуцированной равномерностью °U, называется топологией, инду-
индуцированной равномерностью °М на множестве Ху^Х. Простран-
Пространство ХУ^Х с этой топологией играет важную роль в теории рав-
равномерных пространств.
Рассмотрим равномерное пространство (X, 41) и некоторую
псевдометрику р на множестве Х\ будем говорить, что псевдо-
псевдометрика р равномерна относительно Щ, если для каждого е > О
найдется такое Kg?/, что p(xt y)<e, как только \х — у\<. У.
8.1.9. Предложение. Если псевдометрика р на множестве X рав-
равномерна относительно равномерности °U на X, то р — непрерыв-
40*
628 ГЛ. 8. РАВНОМЕРНЫЕ ПРОСТРАНСТВА И ПРОСТРАНСТВА БЛИЗОСТИ
ное отображение множества XXX с топологией, индуцирован-
индуцированной равномерностью °11, в вещественную прямую.
Доказательство. Пусть (х0, уо) — точка ХХХ\ выберем 8 > О
hI/g?/ так, что
р(х,у)<г/2, когда \х — y\<V.
Согласно следствию 8.1.3, множество Int В(хо, V)X Int5(t/o, V)
есть окрестность точки (хо, уо)у поэтому достаточно показать,
что | р (хо, уо) — р(х,у)\<г при всех (х, у) е В (хОу V)XB (yQy V).
Если (x,y)€=B(xotV)XB(yo,V),To \xo~x\<Vn \yo—y\<V,
и, согласно неравенству треугольника, получаем
o. Уо) -P(^J/)I<P {хо, х) + Р (У Й< {
Наша следующая теорема представляет собой один из наи-
наиболее важных результатов теории равномерных пространств;
она утверждает, грубо говоря, что для всякой равномерности °И
существует много псевдометрик, равномерных относительно Щ.
Этот факт будет широко применяться в последующем. В част-
частности, мы выведем из него, что всякое пространство с тополо-
топологией, индуцированной равномерностью, есть тихоновское про-
пространство.
8,1.10, Теорема, Для каждой последовательности Vo, Vu ••• эле-
элементов равномерности °U на множестве X, где
D) V0 = ^X^ и 3Vi+l<=Vi при /=1, 2, ...,
существует такая псевдометрика р на множестве X, что при
всяком i ^ 1
ViC{(x,y): p(x,j/)<l/2'}cVw.
Доказательство. Определим отображение / из XXX в R,
положив
• °°
О, если (х, j)e p Vi9
i-Q
оо
1/2', где (*, ^) е= К, \ Vi+1, если (дс, у) ф {] Vt.
Из определения / следует, что для любых х, у е X имеем
E) /(*,*)= 0 и f{xfy) = f(y,x).
Далее, для любой пары х, у точек X определим р(х, у) как
наибольшую нижнюю грань всех чисел ? f(xi-i> xt)> гДе хо,
хи ..., xk — последовательность точек Xt такая, что хо = х
и xk = у. Из E) следует что р (х, х) = 0 и р (х, у) = р (у, х) для
8.1. РАВНОМЕРНОСТИ И РАВНОМЕРНЫЕ ПРОСТРАНСТВА 629
всех х, у е Х\ так как, по определению, р удовлетворяет нера-
неравенству треугольника, р есть псевдометрика на X.
Доказательство остальной части теоремы будет выведено из
двойного неравенства
F) у/(*,*/)<Р(*,*/)</(*, У).
Для доказательства F) достаточно показать, что при любых
х, j/eX и каждой последовательности хо, хь ..., xk, такой, что
хо—х и Xk=y, имеет место неравенство
k
G) у/<*. *)
Мы докажем G) индукцией по /г. При /г = 1 неравенство G)
очевидно. Предположим, что /п>1 и что G) верно для всех
k<Lm. Рассмотрим последовательность х0, хь ..., хт, такую,
ЧТО Хо = X Н Хт = у, Я ПуСТЬ а= Y* f (xi-\> xi)- ^СЛИ п ^ 1/2,
t = l
тс G) справедливо для k = m, так как f{x,y)^Z. 1; поэтому мы
можем считать, что а < 1/2.
Рассмотрим сначала случай, когда а > 0. Очевидно, что вы-
выполнено одно из неравенств /(хо, х\) ^ а/2 или /(xm_i,xm)^
^ а/2. В силу симметрии наших предположений, можно счи-
считать, что f(xOiXi)^a/2. Пусть / — наибольший индекс, такой,
что
/+1 m
Тогда 2 /Ui-ь xt) >а/2, откуда X /(**-ь
1=1 /=/+2
По индуктивному предположению, /(хо, ху)^ а и f(Xj+u xm) ^ а.
Из определения а следует, что и /(х/, лгу+i) ^ а. Обозначим че-
через / наименьшее целое число, удовлетворяющее неравенству
1/2* ^ а; так как а < 1/2, то / ^ 2. Очевидно, что (х0, д:/)е У/,
(х/, x/+i)e^ и (x/+i,xm)e Уг; из D) следует, что (xOfxm) =
= (x,y)€=Vi-i. Итак, f(x,y)^l/2l-l^2a, т. е. у/(х,
и G) выполнено для k = m, если а > 0.
Далее, в случае, когда а = 0, для / = 1, 2, ..., т мы имеем
/(хг~1, Хг) = 0 и, по определению f, (jcj, Jti-i)e V/ при / = 0,
1, .... Отсюда видно, что (х, у) е тУ;- при / = 0, 1, ...; по-
оо
этому, согласно D), (х, у) е f] К(-, т. е. /(х,#)=0. Итак, G)
0
630 ГЛ. 8. РАВНОМЕРНЫЕ ПРОСТРАНСТВА И ПРОСТРАНСТВА БЛИЗОСТИ
выполнено для k = т в случае а = 0. Поэтому G) имеет место
для всех k и F) доказано. Из F) и определения / следует, что
Vtc{(xty): p(x,y)^l/2i}<=Vi-l при /=1, 2, ...;
тем самым доказательство закончено. I
8.1.11. Следствие. Для каждой равномерности °U на множестве
X и любого Уе^ существует псевдометрика р на множестве Xt
которая равномерна относительно Щ и удовлетворяет условию
{(х,у): p(x,y)<l}<=V.
Доказательство. Из (U3) вытекает, что существует последо-
последовательность Т/о, Vu ... членов Щ, для которой V\ = V и D) вы-
выполнено. Легко проверить, что псевдометрика р = 4р0, где ро —
псевдометрика, удовлетворяющая теореме 8.1.10, обладает тре-
требуемым свойством. I
8.1.12. Следствие. Для каждой равномерности °U на множестве
X семейство всех элементов °U, открытых относительно тополо-
топологии, индуцированной °U на ХУ(Х, а также семейство всех эле-
элементов Ш, замкнутых относительно этой топологии, являются
базами для °U.
Доказательство. Пусть V — элемент Щ и р — псевдометрика,
определенная в доказательстве следствия 8.1.11. Согласно (U1),
множества
W = {[x, у): р(х, г/)<1}с=1/ и U = {(x,y):p(x,y)^l№czV
являются элементами °U. Из предложения 8.1.9 следует, что
лервое множество открыто, а второе замкнуто. I
8Л.13. Следствие. Для каждой равномерности °U на множествеX
множество X с топологией, индуцированной °И, есть тихоновское
пространство.
Доказательство. Для любой точки хе!и замкнутого мно-
множества FaX, таких, что хфР, существует Уе% удовлетво-
удовлетворяющее условию F[\B{x, V)= 0. Функция /: X^It определен-
определенная равенством f(y)— min(l, р(х, у)), где р — псевдометрика
из следствия 8.1.11, непрерывна, равна 0 в х и равна 1 на F. 1
Пусть (X, °Ы)—-равномерное пространство; мы покажем, что
семейство Р всех псевдометрик на множестве X, равномерных
относительно CU, обладает следующими свойствами:
(UP1) Если рь р2е Р, то тах(рь рг)^ Р-
(LJP2) Для каждой пары xt у различных точек X существует
такая реР, что р(х, у) > 0.
Для проверки свойства (UP1) рассмотрим pi, р2 ^ Р, р =
= max(pi, P2), и произвольное г > 0. По определению псевдо-
псевдометрики, равномерной относительно °Uy найдутся такие Vu У2 ^
8.1. РАВНОМЕРНОСТИ И РАВНОМЕРНЫЕ ПРОСТРАНСТВА 631
е<2/, что pi(x, */)<е, как только \x — y\<V\, и р2(х, #)<е,
как только |х — у|< У2. Так как У = Vi П V2e^/ и р(х, у)<е,
когда | д; — у | < У, мы имеем рЕР.
Свойство (UP2) следует из (U4) и следствия 8.1.11.
При определении равномерности на множестве часто более
удобно не описывать непосредственно семейство °U окружений
диагонали. Мы приведем три способа задания равномерностей:
определение базы, семейства равномерных покрытий или семей-
семейства равномерных псевдометрик.
8.1.14. Предложение. Пусть даны множество X и семейство
ШаЖ)х окружений диагонали, обладающее свойствами (BU1) —
(BU3). Семейство Ш, состоящее из всех элементов 2)х, содер-
содержащих некоторый элемент семейства 3§, есть равномерность на
множестве X и $ — ее база.
Если при этом X — топологическое пространство и семейство
$ состоит из открытых подмножеств произведения ХУХ и если
для каждой точки х е X и любой ее окрестности G существует
такое Уе^, что В(х, V)a G, то °U — равномерность на про-
пространстве X.
Такая равномерность Щ называется равномерностью, порож-
порожденной базой $. ¦
8.1.15. Пример. Читатель может легко проверить, что способ
задания равномерности определением базы был применен в при-
примерах 8.1.7 и 8.1.8. I
8.1.16. Предложение. Пусть заданы множество X и совокупность
С его покрытий, обладающая свойствами (UC1) — (UC4). Се-
Семейство $а2)х всех окружений диагонали вида U{^X#*
H^s4), где s?e=C, есть база равномерности °U на множестве
X. При этом С есть совокупность всех покрытий X, равномерных
относительно Щ.
Если к тому же X — топологическое пространство и С со-
состоит из открытых покрытий X и если для каждой точки х!
и каждой ее окрестности G найдется такое s?^C что St(x,
<= G, тоШ — равномерность на пространстве X.
Такая равномерность Щ называется равномерностью, по-
порожденной совокупностью С равномерных покрытий.
Доказательство. Для каждого покрытия М- множества X по-
положим
Так как V(s&)^ 2Е)х, достаточно проверить, что семейство $ =
= {У(^): ^еС} обладает свойствами (BUI) —(BU3). Но эти
свойства следуют непосредственно из свойств (UC2) — (UC4),
если заметить, что У(^)<=У(^) для покрытия s&, вписанного
632 ГЛ. 8. РАВНОМЕРНЫЕ ПРОСТРАНСТВА И ПРОСТРАНСТВА БЛИЗОСТИ
в покрытие 3Sy и что 2V'{<s4-) cz V'{$), если s& сильно звездно
вписано в ^. Тот факт, что С — совокупность всех покрытий X,
равномерных относительно Ш, следует из (UC1) и легко уста-
устанавливаемого равенства В(х, К(^))= St(x, зФ).
Из последнего равенства мы получаем также вторую часть
теоремы. I
8.1.17. Пример. Группа — это такое множество G, что для лю-
любой пары х, у его элементов определен элемент ху е G — про-
произведение х и у и выполнены следующие три условия:
(G1) (ху)г = x(yz) для всех х, у, ге G.
(G2) Существует такой элемент eeG, что хе=ех = х для
каждого xgG.
(G3) Для каждого x^G существует такой элемент x~l e G,
что хх~1 = е.
Элемент е называется единицей в С, а г1 называется обрат-
обратным элементом для х. Легко проверить, что существует только
одна единица в G и что для каждого xgC существует ровно
один обратный элемент. Если в группе G кроме условий (G1) —
(G3) выполнено условие
(G4) ху = ух для всех х, y^Gy
то G называется абелевой или коммутативной группой.
Топологическая группа — это группа G, которая одновре-
одновременно является ^-пространством, причем выполнены следую-
следующие два условия:
(TG1) Формула f(x,y) = xy определяет непрерывное отобра-
отображение f: GXG-+G.
(TG2) Формула f(x) = x~l определяет непрерывное отображе-
отображение /: G->G.
Пусть G — группа и Л, В —ее подмножества; положим
А~1 =={х~1: х<ебА} и АВ = {ху: х<=А и у^В}.
Для подмножества A cz G и элемента x^G вместо {х}А и
А {х} мы пишем просто хА и Ах. Легко проверить, что если А —
открытое подмножество топологической группы G, то множество
Л также открыто. Аналогично множество АВ открыто, если
хотя бы одно из множеств Л и В открыто. В частности, для
каждого открытого множества HczG множества хН и Нх от-
открыты.
Пусть G — топологическая группа и $ = $(е) — ее база в
точке е. Каждый элемент Я семейства Ш определяет три по-
покрытия G:
Обозначим через С/, Сг и С соответственно совокупности всех
покрытий G, в которые вписаны покрытия вида в7/(Я), *^(Я)
8.1. РАВНОМЕРНОСТИ PI РАВНОМЕРНЫЕ ПРОСТРАНСТВА 633
или W(H), где #^Jf. Каждая из совокупностей Cit Cr и С
обладает свойствами (UC1) — (UC4) и поэтому порождает рав-
равномерность на множестве G. Более того, топология, индуциро-
индуцированная каждой из этих равномерностей, совпадает с исходной
топологией G. Во всех трех случаях доказательства одинаковы,
поэтому мы обсудим только случай Си Отметим, что если G —
абелева группа, то С/, Сг и С совпадают и поэтому порождают
одну и ту же равномерность на множестве G.
Рассмотрим топологическую группу G и определенную выше
совокупность Ct ее покрытий. Из определения С/ немедленно
вытекает, что С% обладает свойством (UC1). Так как для лю-
любых #i, Н2^$ существует такое Яе^, что HczH\f\H2, то
Ct обладает свойством (UC2).
Для доказательства того, что Ci обладает свойством (CU3),
достаточно показать, что
(8) Для каждого Я <= $ существует такое Н\ е $7,
что St(xHit Wi(Hi))(^xH при всех x^G.
Так как формула f(x{, хг х3) = х{х~1х3 определяет непрерыв-
непрерывное отображение /: GXGXG^G и f(e, e, е) = е, для каждого
Яе ^найдется такое#1<ЕЕ.$, что/(#, X #i X#i) = #i#r'#ici
сг Я; мы покажем, что Н\ удовлетворяет (8). Ясно, что если
хНх {\Х\НХФ 0 при некотором фиксированном х е G, то xho =
= x\huT. е. jci == хЛо/гГ1 Для некоторых Ао, h\ e Н\\ поэтому для
каждого элемента x\h из х\Н\ имеем
X[h = xhohr[h<= xH\H\{Hi axH,
что доказывает утверждение (8).
Для каждой пары х, у различных точек G имеем х"ху Ф е.
Так как G есть ^-пространство, существует такое Яе^, что
х~1уфН. Мы покажем, что ни один элемент покрытия Wi{HiO
где Н\^3& удовлетворяет включению НГ1Н\ cz Я, не содержит
одновременно х и у. В самом деле, из равенств х = xohi и у =
= х0к2у где h\, Л2еЯь следует, что х~{у = h\Xh2 e H\{H\ cz H>
что противоречит выбору окрестности Н\. Поэтому Сг обладает
и свойством (CU4).
Проверим, что топология, индуцированная равномерностью,
порожденной С/, совпадает с исходной топологией G. Так как
Ci состоит из открытых покрытий С, достаточно заметить, что
для каждой точки х е G и любой ее окрестности V найдется
такое Яе^, что xHczU, и применить (8). В частности, мы
получим важное следствие о том, что каждая топологическая
группа есть тихоновское пространство. I
634 ГЛ. 8. РАВНОМЕРНЫЕ ПРОСТРАНСТВА И ПРОСТРАНСТВА БЛИЗОСТИ
8.1.18. Предложение. Пусть дано множество X и семейство Р
псевдометрик на нем, обладающее свойствами (UP1) — (UP2).
Семейство $cz?Dx всех окружений диагонали вида {(х, у):
р(х,у)<1 1/2*}, где реР и i= 1, 2, ..., образует базу равно-
равномерности Ш на множестве X Каждая псевдометрика р ^ Р рав-
равномерна относительно Щ.
Если к тому же X — топологическое пространство и все псев-
псевдометрики семейства Р — непрерывные функции из Ху(Х в ве-
вещественную прямую и если для каждого х ^ X и каждого не-
непустого замкнутого множества А с= X, такого, что хфА, най-
найдется такое р^Р, что inf р (х, а) > 0, то °U — равномерность
а е А
на пространстве X.
Равномерность Щ называется равномерностью, порожден-
порожденной семейством Р равномерных псевдометрик. I
8.1.19. Пример. Пусть X — тихоновское пространство; обозна-
обозначим через С(Х) семейство всех непрерывных вещественных
функций, определенных на Ху и через С*(Х) — подсемейство
в С{Х), состоящее из всех ограниченных функций. Для каждой
конечной последовательности f\, f2, ..., fk элементов С(Х)
формула
(9) Pf» fr.... fk(x, у) = тах{\Ш-Ш\, \Ш~ Ш\, ...
.¦•. \fk(x)-fk(y)\)
определяет псевдометрику на множестве X. Пусть Р — семей-
семейство всех псевдометрик pfl, f2 ffe, где fu f2, ..., fftSC(X),
и пусть Р* — подсемейство в Р, состоящее из всех псевдометрик
PfP f2 fh> где fu f2, ..., fh<=C*(X).
Оба семейства Р и Р* обладают свойствами (UP1) — (UP2),
так что они порождают равномерности W и ^* на множестве X.
Мы покажем, что топологии, индуцированные ^ и #*, совпа-
совпадают с исходной топологией X.
Из (9) следует, что все псевдометрики в семействе Р — не-
непрерывные функции из Ху^Х в вещественную прямую. Рас-
Рассмотрим х е X и непустое замкнутое множество A cz X, такое,
что хфА. Так как X — тихоновское пространство, существует
функция f ^ С*(Х)а С(Х), удовлетворяющая условиям f(jc) = О
и f(A)cz{l}. Псевдометрика pf^P*czP с очевидностью удов-
удовлетворяет равенству inf Pf{x, a)=l , так что, согласно второй
аЕД
части предложения 8.1.18, ^ и ^* — равномерности на простран-
пространстве X. I
В связи с описанными выше способами задания равномер-
ностей мы обращаем внимание читателя на следующий простой
факт: если °U§ — равномерность на множестве X, то для базы $
8.1. РАВНОМЕРНОСТИ И РАВНОМЕРНЫЕ ПРОСТРАНСТВА 635
равномерности Шо (совокупности С всех покрытий X, равно-
равномерных относительно <%>; семейства Р всех псевдометрик на X,
равномерных относительно °U§) равномерность %L, порожден-
порожденная на X базой $ (совокупностью С, семейством Р) в соответ-
соответствии с предложением 8.1.14 (предложением 8.1.16, предложе-
предложением 8Л.18), совпадает с исходной равномерностью %.
Пример 8.1 Л 9 и следствие 8.1.13 приводят к следующему
утверждению:
8.1.20. Теорема. Топология пространства X индуцирована неко-
некоторой равномерностью на множестве X тогда и только тогда,
когда X — тихоновское пространство. 1
Пусть X — некоторое множество и р — метрика на нем. Так
как семейство {р}, состоящее из единственной псевдометрики р,
обладает свойствами (UP1) — (UP2), оно порождает равномер-
равномерность Щ на множестве X. Более того, согласно следствиям 4.2.6
и 4.1.11, топологии, индуцированные на X метрикой р и равно-
равномерностью <U, совпадают. Равномерность °U называется равно-
мерностью, индуцированной (или порожденной) метрикой р.
Равномерное пространство (X, °Ц) метризуемо, если на множе-
множестве X существует такая метрика р, что индуцированная ею рав-
равномерность совпадает с исходной равномерностью °U. Возникает
естественный вопрос: существуют ли внутренние характеристики
метризуемых равномерных пространств. Наша следующая тео-
теорема содержит такую характеристику.
8.1.21. Теорема. Равномерность Щ на множестве X порождена
некоторой метрикой на X тогда и только тогда, когда w {%L) ^ Ко.
Доказательство. Очевидно, что каждая равномерность, инду-
индуцированная метрикой, имеет вес =^К0.
Рассмотрим равномерность °U на множестве X, которая
имеет счетную базу {t/J^L^ Существует такая последователь-
последовательность Vo, V\, ... элементов Щ, что
V0 = XXX, 3Vi+lczVi и ViCUi для /=1,2,....
оо
Последнее включение влечет за собой равенство Г) V(=A,
так что псевдометрика р из теоремы 8.1.10, соответствующая
нашей последовательности Vo, Vu • • • элементов Ш, есть мет-
метрика. Из второго включения в теореме 8.1.10 немедленно полу-
получаем, что р индуцирует исходную равномерность Щ. I
Заметим в связи с последней теоремой, что, как показывает
пример 8.1.7, может случиться, что метризуемая топология на
множестве X индуцируется такой равномерностью <U на X, кото-
которая не порождается никакой метрикой на X.
636 ГЛ. 8. РАВНОМЕРНЫЕ ПРОСТРАНСТВА И ПРОСТРАНСТВА БЛИЗОСТИ
Отметим также, что из 8.1.21 и 8.1.18 вытекает лемма 4.4.6,
а из 8.1.21 и 8.1.16 —следствие 5.4.10.
Мы закончим этот параграф кратким обсуждением равно-
равномерно непрерывных отображений. Пусть {Х,Щ) и (У, Т) — два
равномерных пространства; отображение f множества X в мно-
множество У называется равномерно непрерывным относительно
равномерностей Ш иТ, если для каждого V е Т существует та-
такое U ^l<U, что при всех х, xf e X мы имеем \f(x)— f(x') | < V,
когда \х — jc'|< U. Из этого определения сразу вытекает, что
/ — непрерывное отображение пространства X с топологией, ин-
индуцированной Щ, в пространство У с топологией, индуцирован-
индуцированной Y. Тот факт, что / — равномерно непрерывное отображение
относительно равномерностей °U и У на X и У соответственно,
будет записываться в виде /: (X,41)^G,Т).
Читатель может легко проверить, что если f: (X,<U)^(Y,Y)
и?: (Y,r)-+(Z,W)9 то gf: (X,<U)^{Z,W) т. е., композиция рав-
равномерно непрерывных отображений равномерно непрерывна.
Так же как и в случае топологических пространств, можно
сформулировать признаки равномерной непрерывности отобра-
отображения в соответствии с разными способами задания равномер-
равномерностей.
8.1.22. Предложение. Пусть (X,<U) и (У\Т) — равномерные про-
пространства и f — отображение X в У. Следующие условия равно-
равносильны:
(i) Отображение f равномерно непрерывно относительно ЙЛ
и Т.
(П) Существуют базы Ш и W для Щ и У соответственно, та-
такие, что для каждого V ^Ч? найдется U ^ $, удовлетворяющее
условию U<={fXf)~l(V).
(Hi) Для каждого покрытия $Ф множества У, равномерного
относительно Y, покрытие {f~x(A): Aei} множества X равно-
равномерно относительно Ш.
(iv) Для каждой псевдометрики р на множестве У, равно-
равномерной относительно Y, псевдометрика а на множестве Ху опре-
определенная равенством a(xt y) = p{f(x),f(y))> равномерна относи-
относительно <U. 1
Взаимно однозначное отображение / множества X на множе-
множество У есть равномерный изоморфизм относительно равномер-
равномерностей Ш иТ на множествах X и У соответственно, если f рав-
равномерно непрерывно относительно Щ и У3 и обратное отображе-
отображение f~l равномерно непрерывно относительно Y и Щ. Равномер-
Равномерный изоморфизм есть гомеоморфизм индуцированных топологи-
топологических пространств.
Два равномерных пространства (Xt<U) и (YtT) называются
равномерно изоморфными, если существует равномерный изо-
8.1. РАВНОМЕРНОСТИ И РАВНОМЕРНЫЕ ПРОСТРАНСТВА 637
морфизм {X,°U) на (Y,T). Изучение равномерных свойств или
равномерных инвариантов, т. е. инвариантов равномерных изо-
изоморфизмов, и есть предмет теории равномерных пространств.
Очевидно, что каждый топологический инвариант есть равномер-
равномерный инвариант.
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
Понятие равномерного пространства введено Вейлем в [1938].
Первое систематическое изложение теории равномерных про-
пространств дано в книге Бурбаки [1940]. Наше определение рав-
равномерности слегка отличается от первоначального определения
Вейля: под окружением диагонали Вейль понимал любое множе-
множество V а ХУ^Х, содержащее А (т. е. не предполагалось выпол-
выполнение условия симметрии V = —F), а под равномерностью —
семейство 41 окружений диагонали, удовлетворяющее условиям
(Ul) — (U4) и содержащее вместе с каждым V также и множе-
множество — V. То, что мы рассматриваем лишь симметричные окру-
окружения, немного упрощает наше изложение.
Работа Вейля содержит теоремы 8.1.1, 8.1.20, 8.1.21, пример
8.1.17 и определения равномерно непрерывного отображения и
равномерного изоморфизма. В своем доказательстве теоремы
8.1.20 Вейль обобщил одно неопубликованное рассуждение
Л. С. Понтрягина, доказавшего, что каждая топологическая
группа является тихоновским пространством. Аналог теоремы
8.1.21 для топологических групп (см. упр. 8.1.G) также был из-
известен ранее: он был получен Биркгофом в [1936] и Какутани
в [1936]. Теорему 8.1.21 можно рассматривать как аналог метри-
метризационной теоремы Александрова — Урысона для равномерных
пространств, доказанную этими авторами в [1923] (ср. с заме-
замечаниями по поводу теоремы 5.4.9).
Другое, но эквивалентное предыдущему понятие равномер-
равномерного пространства, определенное в терминах совокупности по-
покрытий (ср. с теоремой 8.1.16), было введено и изучено Тьюки
в [1940], где он доказал теорему 8.1.10, сформулированную в
терминах покрытий (см. упр. 5.4.Н(а)). В настоящее время язык
покрытий получил более широкое распространение, чем язык
окружений диагонали. Книга Исбелла [1964], в которой теория
равномерных пространств получила важное развитие, написана
в терминах покрытий.
Из теоремы 8.1.10 вытекает, что равномерные пространства
могут быть также описаны в терминах псевдометрик (см. за-
задачу 8.5.5); такое описание дано Бурбаки в [1948]. Язык псев-
псевдометрик использовали Гиллман и Джерисон в книге [1960].
Мы следовали этой книге, когда описывали равномерности Й7
и W* в примерах 8.1Л9, 8.3.4, 8.3.18 и 8.3.19.
638 ГЛ. 8. РАВНОМЕРНЫЕ ПРОСТРАНСТВА И ПРОСТРАНСТВА БЛИЗОСТИ
УПРАЖНЕНИЯ
8.1.А. (а) Пусть (X, р) и (У, о)—метрические пространства,
и пусть °U и Т — равномерности, индуцированные метриками р
и а на X и У соответственно. Покажите, что отображение
{: X-^Y равномерно непрерывно относительно Ш и Т в том и
только том случае, если / равномерно непрерывно относительно
р и а (ср. с задачей 8.5.19(а)).
(Ь) Заметьте, что две метрики pi и р2 на множестве X рав-
равномерно эквивалентны (см. упр. 4.1.В(Ь)) тогда и только тогда,
когда они индуцируют одну и ту же равномерность.
8.1.В. Пусть Щ\ и % — Две равномерности на множестве X
и % cz Щ\\ мы говорим, что равномерность^! сильнее (тоньше)
равномерности % или что Шъ слабее (грубее), чем °U\.
(a) Проверьте, что если равномерность Щ\ на множестве X
сильнее равномерности %, то топология, индуцированная рав-
равномерностью °U\y сильнее топологии, индуцированной равномер-
равномерностью <2/2.
(b) Покажите, что каждое семейство {^е5 равномер-
равномерностей на множестве X имеет наименьшую верхнюю грань, т. е.
существует равномерность °U на X, которая слабее любой равно-
равномерности на X, более сильной, чем все равномерности 4ls. Про-
Проверьте, что если равномерность °US индуцирует топологию OSy
то топология, индуцированная наименьшей верхней гранью се-
семейства {%}5е5, есть наименьшая верхняя грань семейства
{(?s}5eS топологий на множестве X. Заметьте, что если каждая
из равномерностей °US индуцирует одну и ту же топологию О
на Ху то наименьшая верхняя грань семейства {°HS}S^S также
индуцирует топологию <?.
(c) Приведите пример двух равномерностей °Ц\ и Щ% на счет-
счетном множестве X, таких, что не существует равномерности на Х>
которая была бы слабее их обеих одновременно.
8.1.С. Наименьшая верхняя грань всех равномерностей на ти-
тихоновском пространстве X, т. е. сильнейшая из всех равномер-
равномерностей на пространстве Ху называется универсальной равномер-
равномерностью на пространстве X (см. упр. 8.1.В(Ь); ср. с задачей 8.5.8).
Мы называем равномерное пространство (X, Щ) сильным (тон-
(тонким), если Ш — универсальная равномерность на пространстве
X с топологией, индуцированной равномерностью Ш.
(а) Покажите, что каждое непрерывное отображение тихо-
тихоновского пространства X в тихоновское пространство У равно-
равномерно непрерывно относительно универсальной равномерности
на пространстве X и любой равномерности на пространстве У.
Заметьте, что сформулированное выше свойство характеризует
универсальную равномерность на X.
8.1. РАВНОМЕРНОСТИ И РАВНОМЕРНЫЕ ПРОСТРАНСТВА 639
(b) Покажите, что для каждого тихоновского пространства
X совокупность всех нормальных покрытий пространства X об-
обладает свойствами (UC1) — (UC4); убедитесь, что равномер-
равномерность, порожденная этой совокупностью, является универсаль-
универсальной равномерностью на X.
(c) Покажите, что для каждого тихоновского пространства X
семейство всех псевдометрик на множестве X, которые являются
непрерывными вещественными функциями на произведении
ХУ(Х, обладает свойствами (UP1) — (UP2). Заметьте, что рав-
равномерность, порожденная этим семейством, есть универсальная
равномерность на X.
8.1.D. Проверьте, что для любого тихоновского пространства
X равномерность V (равномерность <&*) есть слабейшая равно-
равномерность в семействе всех равномерностей °U на пространстве X,
таких, что каждая непрерывная функция f: X^-R (каждая не-
непрерывная функция /: X-+-I) равномерно непрерывна относи-
относительно °U и равномерности, индуцированной на вещественной
прямой (замкнутом единичном интервале) естественной метри-
метрикой.
8.I.E. Пусть X — топологическое пространство, х — точка про-
пространства X и F — замкнутое подмножество X, такое, что хф?.
Покажите, что для каждой равномерности Щ на пространстве X
существует отображение f: X-*I> равномерно непрерывное отно-
относительно °Ы и равномерности на /, индуцированной естественной
метрикой, и такое, что f(x) = O и f(F)c{\}.
8.I.F. Пусть X — некоторое множество, {(Ys, Bls)}S€sS—се-
Bls)}S€sS—семейство равномерных пространств и {/$}Se=s—семейство отобра-
отображений fs: Х->У5. Покажите, что в классе всех равномерностей
на множестве X, относительно которых все fs равномерно непре-
непрерывны, существует слабейшая равномерность Щ. Определите
базу равномерности °U и докажите, что топология, индуцирован-
индуцированная °U, совпадает с топологией, порожденной семейством отобра-
отображений {fs}Si=s> где Ys имеет топологию, индуцированную %. Та-
Такая равномерность.^ называется равномерностью,порожденной
семейством отображений {/Л5е5*
8.1.G. (а) (Биркгоф [1936], Какутани [1936]). Покажите, что
топологическая группа метризуема тогда и только тогда, когда
она удовлетворяет первой аксиоме счетности.
(Ь) Выведите (а) из метризационного критерия Бинга.
8.1.Н (Тьюки [1940]). Покажите, что для тихоновского про-
пространства X совокупность всех его покрытий, в которые можно
вписать конечные нормальные покрытия, обладает свойствами
(UC1) — (UC4); убедитесь, что равномерность, порожденная этой
совокупностью, есть равномерность W*.
640 ГЛ. 8. РАВНОМЕРНЫЕ ПРОСТРАНСТВА И ПРОСТРАНСТВА БЛИЗОСТИ
Указание (Исбелл [1964]). Устанавливая свойство (UC3),
проверьте, что если покрытие $ сильно звездно вписано в ко-
конечное покрытие s& и для любой пары j^0, «s#i подсемейств се-
семейства s& определено 3t(*s&o,J&\) как семейство всех BgJ,
таких, что ^Фо—{А <=^: BczA} и зФх ={^Gi: St(Вf SB)cz A),
то множества U i?(^o> <s4-\) образуют сильно звездно вписанное в
М> конечное покрытие. В доказательстве заключительной части
воспользуйтесь следствием 8.1.11.
8.1.1. (а) (Широта [1952]). Покажите, что для каждого тихо-
тихоновского пространства X семейство всех его покрытий, имеющих
счетное нормальное вписанное покрытие, обладает свойствами
(UC1) —(UC4).
Указание (Куцья [1973]). Устанавливая свойство (UC3),
проверьте, что если покрытие J? сильно звездно вписано в сче
ное покрытие ^Ф^^{Аг}^=1 и для любого натурального числа k
и каждого подсемейства *я?0 семейства {А$=\ определяется
^й(^о) как семейство всех BeJf, таких, что зФо={Аг. BczAi,
i ^ k) и St(B, J?)c: Ak, то множества SBki^o) образуют счетное
покрытие, звездно вписанное в «я?.
(Ь) Покажите, что равномерность, порожденная совокуп-
совокупностью всех покрытий тихоновского пространства X, имеющих
счетные нормальные вписанные покрытия, сильнее равномер-
равномерности W и, вообще говоря, отличается от >(& (ср. с примером
8.3.19 и упр. 8.3.F).
Указание. Каждое покрытие, равномерное относительно W,
имеет вписанное покрытие конечного порядка.
8.2. ОПЕРАЦИИ НА РАВНОМЕРНЫХ
ПРОСТРАНСТВАХ
Пусть даны равномерное пространство (X, °U) и множество
МаХ. Легко видеть, что семейство °Ым ={(МУ(М)(} V: Ve
е^}с:^>м удовлетворяет условиям (Ul) — (U4),t. e. (М.Шм) —
равномерное пространство. Равномерное пространство (М.^м)
называется подпространством равномерного пространства (Х,°и).
Легко проверить, что топология, индуцированная на М равно-
равномерностью °Um, совпадает с топологией на М как подпростран-
подпространстве пространства X, где X имеет топологию, индуцированную Щ.
Если равномерность °U индуцирована метрикой р на множе-
множестве X, то равномерность °Um совпадает с равномерностью, инду-
индуцированной рм на множестве М.
Для каждого равномерного пространства (X, °U) и любого
множества М аХ формула iM(x) = x определяет равномерно не-
непрерывное отображение и*: (М,сИм)~^(Х,Щ); отображение ш
8.2. ОПЕРАЦИИ НА РАВНОМЕРНЫХ ПРОСТРАНСТВАХ 641
называется вложением подпространства Ш, Щы) в пространство
(X9<U).
Перейдем к (декартовым) произведениям равномерных про-
пространств. Пусть {(X$J ^)}5gS — семейство равномерных про-
пространств. Семейство 9S всех окружений диагонали Дсг ( Ц ^ЛХ
вида
У31 Для * = 1, 2, ..., k}9
где 5Ь 52, ..., sk e S и Ks. е <2/5. при t = 1, 2, ..., А, обла-
обладает свойствами (BUI) — (BU3), так что, согласно предложе-
предложению 8.1.14, семейство $ порождает равномерность на множестве
IX Xs\ эта равномерность называется (декартовым) произведе-
нием равномерностей {^4}5eS и обозначается Ц <2/5.Произве-
S €5 о
дение конечного семейства равномерностей {Ф/*}^ обозначается
^iX%X ••• Х%. Если все равномерности <US равны друг
другу, т. е. если Xs = X и Ш5 = °U при всех s e S, то произве-
произведение XI Щк обозначается также <Um, где m = |S|. Равномер-
ное пространство (Ц Xs, Д °иЛ называется (декартовым)
произведением равномерных пространств {(Xs, ^5)}ses- Чита-
Читатель может легко проверить, что топология, индуцированная на
Ц Xs равномерностью Ц Ш^ совпадает с тихоновской топо-
ssS sgS
логией на произведении Ц Xs, где Xs имеют топологию, инду-
цированную Щ^
Если для ?=1, 2, ... равномерность % на множестве Х\
индуцирована метрикой р(* на пространстве Хи ограниченной чис-
оо оо
лом 1, то равномерность Ц Шг на множестве Ц Хг совпадает
i=i f-i
с равномерностью, индуцированной метрикой р, определенной
формулой B) в § 4.2.
Легко видеть, что если ( Ц Xs, Ц ^/s^i — произведение
равномерных пространств {(Xs> (Us)}s^st то для любого seS
проекция ps произведения Ц Xs на s-ю ось Xs, определенная
формулой p5({.x:s}) = *s, равномерно непрерывна относительно
П % и «,.
41 Зак. 697
642 ГЛ. 8. РАВНОМЕРНЫЕ ПРОСТРАНСТВА И ПРОСТРАНСТВА БЛИЗОСТИ
Имеет место следующий равномерный аналог предложе-
предложения 2.3.6.
8.2.1. Предложение. Пусть (Ху <Щ — равномерное простран-
пространство, {(Ys, Ts)}s^s — семейство равномерных пространств и f —
отображение множества X в произведение XI Ys. Отображение f
равномерно непрерывно относительно 41 и Ц Fs тогда и только
S
тогда, когда композиция psf равномерно непрерывна относи-
относительно 41 uTs при всех sgS, I
8.2.2. Пример. Возьмем интервал / с равномерностью °U, инду-
индуцированной естественной метрикой на /. На произведении /т,
где т ^ Ко, рассмотрим равномерность °U™ — произведение ш
копий равномерности °U. Очевидно, что <Um индуцирует на/т то-
топологию тихоновского куба веса т. Легко видеть, что w (^m)^ nt
и из следствия 2.3.25 следует, что w (<2/m) = m.
Каждое тихоновское пространство X веса s^m можно рас-
рассматривать как подпространство /т. Так как равномерность
Ш™ индуцирует на /т топологию тихоновского куба, равномер-
равномерность {°Um)x индуцирует исходную топологию на X. Поэтому
опология всякого тихоновского пространства веса ^т индуци-
индуцирована некоторой равномерностью веса ^ш. 1
8.2.3. Теорема. Каждое равномерное пространство равномерно
изоморфно подпространству произведения некоторого семейства
метризуемых равномерных пространств.
Доказательство. Рассмотрим равномерное пространство
{ХУЧ1). Согласно (U3), для каждого УеЩ существует после-
последовательность Vo, Vu ... элементов °U, такая, что
A) KO = IXI, Vi = V и 3VMczVi для /=1,2,....
Воспользуемся теоремой 8.1.10. Для этого возьмем такую псев-
псевдометрику pv на множестве X, что для любого / ^ 1
B) Vi<z{{x,y): pv(x,y)^ 1/2'} с Vw.
Полагая xEvy тогда и только тогда, если pv{x,y) = 0, мы опре-
определим отношение эквивалентности Ev на множестве X (ср. с
упр. 4.2.1); пусть Ху — множество всех классов эквивалентности
для Ev- Из неравенства треугольника следует, что для всех
х* х'> У у У' s Xt таких, что xEvxf и yEvy\ мы имеем
Таким образом, полагая fiv{[x], [y])= pv(x,y) для всех
[х], [j/] e Ii/, мы определим метрику р у на множестве Xv. Пусть
8.2. ОПЕРАЦИИ НА РАВНОМЕРНЫХ ПРОСТРАНСТВАХ 643
%Ly — равномерность на множестве Xv, индуцированная метри-
метрикой jiv. Из B) следует, что, полагая fv(x) = [x], мы определим
равномерно непрерывное отображение }v пространства {X,°U)
в пространство (Xv, Щу).
Из предложения 8.2.1 следует, что диагональ Л fv есть
равномерно непрерывное отображение (Xt °U) в произведение
( П Xv> Ц «глЛ.Мы покажем, что сужение / = f Л fy\\X
есть равномерный изоморфизм.
Из (U4), A) и B) следует, что для каждой пары х, у раз-
различных точек пространства X существует такое V^°U> что
pv{x,y)> 0; поэтому f(x)=?f(y)t откуда видно, что / — взаимно
однозначное отображение.
Осталось доказать, что f равномерно непрерывно относи-
относительно ( П ШуЛ и °Uy т. е. показать, что для любого
\V^n Jf(X)
f(X)
существует такое W& П ^v, что \х — и|< Vo, когда
\f(x) — f(y)\<W. Но из A) и B) следует, что
обладает требуемыми свойствами. ¦
8.2.4. Замечание. Отметим, что если в доказательстве предыду-
предыдущей теоремы мы рассмотрим только такие V, которые принад-
принадлежат некоторой базе равномерности Ш, то отображение / —
также равномерный изоморфизм. Поэтому каждое равномерное
пространство веса щ равномерно изоморфно подпространству
произведения щ метризуемых равномерных пространств.
Отметим также, что не существует универсального простран-
пространства для всех равномерных пространств веса =^т, т. е. не су-
существует равномерного пространства (Xt Щ) веса ^ш, такого,
что для любого равномерного пространства {Y,T) веса <jm оно
содержит равномерное подпространство, равномерно изоморф-
изоморфное (Y,T). В самом деле, из примера 8.1.6 следует, что вес дис-
дискретного равномерного пространства равен 1, и так как мощ-
мощность множества X может быть произвольно большой, не суще-
существует равномерного пространства, содержащего подпростран-
подпространства, равномерно изоморфные — или даже подмножества, рав-
номощные — всем дискретным равномерным пространствам.
В оставшейся части этого параграфа мы обсудим простран-
пространства отображений.
Пусть X — топологическое, а (У, °U) — равномерное простран-
пространства. Через Yx обозначается множество всех непрерывных ото-
отображений пространства X в пространство У, где У снабжено
топологией, индуцированной °U. Для каждого V ^ Ш обозначим
41*
644 ГЛ. 8. РАВНОМЕРНЫЕ ПРОСТРАНСТВА И ПРОСТРАНСТВА БЛИЗОСТИ
через V окружение диагонали А с: Yx X Yx> определенное фор-
мулой
9={{ftg): \f(x) — g{x)\<V для любого х<=Х}.
Из легко устанавливаемых формул
GnV=UT{V и U + Vczlf+V
следует, что семейство {V: V^Ш)обладает свойствами (BU1) —
(BU3). Равномерность на множестве Ух, порожденная этим се-
семейством, будет называться равномерностью равномерной схо-
сходимости, индуцированной Щ, и обозначаться °й.
Если равномерность Щ индуцирована ограниченной метри-
метрикой р на У, то хю{Ш)^ Ко, так что (по теореме 8.1.21) равно-
равномерность °й индуцирована некоторой метрикой на У*. Легко
проверить, что метрика р, определенная формулой G) в § 4.2,
индуцирует равномерность Щ. Поэтому из примера 4.2.14 сле-
следует, что для двух равномерностей Щ\ и Щ% на У, которые
индуцируют одну и ту же топологию, топологии на Ух, индуци-
индуцированные °п\ и <г/г> могут различаться. Оказывается, для ком-
компакта X — как и в случае метрических пространств — топология
на Yx не зависит от выбора равномерности °U на пространстве
У, поскольку топология, индуцированная °йу совпадает с ком-
компактно-открытой топологией на У*. Этот факт есть следствие
доказываемой ниже теоремы 8.2.6. Чтобы сформулировать ее,
нужно ввести другую равномерность на У*.
Для хаусдорфова пространства X и равномерного простран-
пространства (У, (Щ обозначим через °U\S?{X) равномерность на Yx,
порожденную базой, состоящей из всех конечных пересечений
множеств вида
={(/,*): |f(*)-*(*)|<V Д^ всех xe=Z},
где Fg^, Zg2(I) и 2?(Х) — семейство всех компактных
подмножеств пространства X (читатель легко может проверить,
что семейство всех конечных пересечений множеств в C) обла-
обладает свойствами (BUI) — (BU3)). Равномерность <М\%(Х) бу-
будет называться равномерностью равномерной сходимости на
компактах, индуцированной равномерностью Щ.
8.2.5. Лемма. Если топология пространства X индуцирована не-
некоторой равномерностью Ш, то для каждого компактного мно-
множества Z czX и всякого открытого множества G, содержащего
Z, найдется такое V^°Uy что B(Z, V)a G.
Доказательство. Для каждого x^Z выберем УХ^.°И так,
чтобы В(х, 2Vx)cz G. Из следствия 8.1.3 вытекает, что семей-
8.2. ОПЕРАЦИИ НА РАВНОМЕРНЫХ ПРОСТРАНСТВАХ 645
ство {Z f)lntB(x, Ух)}хе.2естъ открытое покрытие множества Z;
поэтому существует конечное множество {х\, х2, ..., xk}aZ,
для которого
D) ZczIntS^, VX]){)IntB(x2, VXt)U-^[}lntB(xk9 VXk)\
положим V = VXl Л Vx2 П ¦ ¦ • П VXk e ^/. Из D) следует, что для
любого x<=Z существует такое i^.kf что |х — хt\ < VXi- Для
любой точки х'^В (х, V)<zzB (x, VXi) мы имеем /ей (#„ 2VX.)<^G,
так что 5(Z, V)czG. 1
8.2.6. Теорема. Для всякого хаусдорфова пространства X и каж-
каждого равномерного пространства (Y.^U) топология на Yx, ин-
индуцированная равномерностью (U\Z(X) равномерной сходимо-
сходимости на компактах, совпадает с компактно-открытой топологией
на Yx, где Y снабжено топологией, индуцированной (U.
Доказательство. Обозначим через О\ топологию на Yx, ин-
индуцированную равномерностью Ш\3?(Х), а через О2 компактно-
открытую топологию. Вначале мы докажем, что Ог сг G\* Оче-
Очевидно, достаточно показать, что все множества M(Z,G), где
Zg?(I) и G — открытое подмножество в У, принадлежат 0\.
Рассмотрим Ze?(i), открытое множество бсУ и некоторое
f^M(Z, G). Так как Y — тихоновское пространство, f(Z)—ком-
f(Z)—компакт в G. Применяя лемму 8.2.5, возьмем такое Ке?/, что
B(f(Z),V)czG. Очевидно, B(f,V\Z)<=:M(Z9G)f и так как f —
произвольный элемент M(Z, G), то M(Z, G)e^i.
Докажем теперь, что О\ с: О2. Очевидно, достаточно пока-
показать, что для любых Z^lSL(X), Vg^ и f^Yx существуют
компактные подмножества Z\, Z2i ..., Zk пространства X и от-
открытые подмножества G\, G2> ..., Gk пространства У, такие, что
k
/еДм(г„ Gt)czB(f, V\Z).
В силу следствия 8.1.12, найдется окружение W^.Ш диагонали
А с: УХ У, которое замкнуто относительно топологии, индуци-
индуцированной %L на УХУ» и удовлетворяет включению 3WCZV.
Так как f(Z) — компакт, то существует конечное множество
{*,, х2, ..., xk) cZ, такое, что / (Z) с: (J B(f(xt)t W). Мы по-
кажем, что множества
Zi=Zf\rl(B(f(xi)iW)) и G, = IntB(ffo), 2Г)
обладают необходимыми свойствами.
Заметим, что из замкнутости W в УХ У следует замкнутость
шаров B(f(Xi), IF) в У и компактность множеств Zt. Более того,
646 ГЛ. 8. РАВНОМЕРНЫЕ ПРОСТРАНСТВА И ПРОСТРАНСТВА БЛИЗОСТИ
k k
/е[1 M(Zit Gt). Рассмотрим отображение gsf] M(Ziy G^).
Для каждого xeZ существует такое i ^ ky что хеZt\ оче-
очевидно,
g(x)ezB{f(xi),2W) и /W
Поэтому \f(x) — g(x)\<3WczV для каждого xeZ, а это по-
показывает, что g^ B(f, V\Z). I
8.2.7. Следствие. Пусть Х —компакт и (Y,<U) —равномерное
пространство. Топология на Yxt индуцированная равномер-
равномерностью Щ равномерной сходимости, совпадает с компактно-от-
компактно-открытой топологией на Yx и зависит только от топологии, инду-
индуцированной на Y равномерностью Ш. ¦
Отметим, что из теоремы 8.2.6 следует теорема 3.4.15 в слу-
случае хаусдорфова пространства X. На самом деле для каждого
тихоновского пространства У существует равномерность Щ на
У, которая индуцирует первоначальную топологию пространства
У. По теореме 8.2.6, компактно-открытая топология на Yx ин-
индуцирована равномерностью на У*, так что пространство Yx
с компактно-открытой топологией есть тихоновское про-
пространство.
Для отображений топологического пространства X в тихо-
тихоновское пространство У можно определить понятие равносте-
равностепенной непрерывности относительно равномерности °11 на про-
пространстве У: семейство F отображений X в Y называется рав-
равностепенно непрерывным относительно равномерности °Ы на
пространстве У, если для каждой точки xgIh всякого Vg%
существует такая окрестность G точки лс, что \f(x) — f (xf) | < Vf
когда /ef и x'^G. Для такой равностепенной непрерывно-
непрерывности справедливы аналоги классической теоремы Асколи. Прежде
чем сформулировать аналоги, докажем две леммы, которые
показывают, как равностепенная непрерывность связана с по-
понятием однообразной непрерывности, введенной в § 3.4.
Напомним читателю, что семейство отображений FczYx
однообразно непрерывно, если для каждой точки xgI, каждой
точки уеУ и всякой окрестности Н точки у существуют окре-
окрестность G точки х и окрестность Н' точки г/, такие, что из усло-
условий / е F и f (х) ^ #' следует включение f(G) cz H.
8.2.8. Лемма. Пусть X — топологическое пространство, У — ти-
тихоновское пространство и Ш — равномерность на пространстве
У. Если семейство FczYx отображений X в У равностепенно
непрерывно относительно °U, то семейство F однообразно не-
непрерывно.
Доказательство. Предположим, что F^YX равностепенно
непрерывно относительно °U\ рассмотрим х^Х, y^Y и окре-
8.2. ОПЕРАЦИИ НА РАВНОМЕРНЫХ ПРОСТРАНСТВАХ 647
стность Я точки у. Выберем УеЧ/, удовлетворяющее включе-
включению В {у, 2 V) с: Я, и такую окрестность G точки х, что |/(х) —
— f(*') I < ^» как только fef и/eG. Положим Я' = В(у, V)
и рассмотрим такое /ef, что f(x)^H'. Тогда |z/ — f(x) | < V,
так что для каждой точки /gG мы имеем |# — /(х/)|<2У,
т. е. f(x')^B(y,2V)<^H. Отсюда /(<5)с=Я, и тем самым одно-
однообразная непрерывность семейства F доказана. I
8.2.9. «Лемма. Пусть X — топологическое пространство, У—ти-
У—тихоновское пространство и Щ — равномерность на пространстве
У. Если семейство F aYx отображений X в Y однообразно не-
непрерывно и для каждой точки х^Х множество {f(x): f^F}
имеет компактное замыкание, то семейство F равностепенно не-
непрерывно относительно °LL*
Доказательство. Предположим, что F cz Yx однообразно не-
непрерывно и множества Л(х)= {f(x): f^F}—компакты; рас-
рассмотрим точку хеХй Уе?/. Выберем элемент Уе?/, такой,
что 2W<^V, и для каждой точки у^А(х) и ее окрестности
Я (у) = IntE(#, W)) выберем окрестность G(y) точки х и окрест-
окрестность Н'{у) точки у таким образом, чтобы из условий feF
и f(x)^H/(y) следовало включение f(G(y))cz H(y). Так как
множество А (х) компактно, существует конечное множество
{уи У2, ..., Ук} cz А {х), такое, что А (х) с= [] Н' (yt).
Пусть / — функция в F и х' — точка в окрестности G =
— П О(Уд точки х. Найдется такое i^ky что f{x)^H/(yi)i
так что f(G(yi))cz Н(у{). Так как х и хг принадлежат G(yi),
имеем f{x)Jf{x/)^H(yi)t т. е. \f(x)~~ f(x') \ < У; это показы-
показывает, что семейство F равностепенно непрерывно относи-
относительно CU. I
Эти леммы и теоремы 3.4.20 приводят к следующей теореме.
8.2.10. Теорема Асколи. Пусть X есть k-пространство, Y — тихо-
тихоновское пространство и Щ — равномерность на пространстве У.
Замкнутое подмножество F пространства Yx с компактно-откры-
компактно-открытой топологией компактно тогда и только тогда, когда F рав-
равностепенно непрерывно относительно °tt и множество {f{x):
f^F} cz Y имеет компактное замыкание для каждого х^Х. Ш
Следующий вариант теоремы Асколи представляет собой
аналог теоремы 3.4.21; он вытекает из лемм 8.2.8, 8.2.9 и тео-
теоремы 3.4.21. В формулировке теоремы мы используем символ
F\Z, где Fc=Yx и ZczJ, для обозначения семейства сужений
{f\ZfF}Yz
8.2.11. Теорема. Пусть X есть k-пространство, Y — тихоновское
пространство и °U — равномерность на пространстве У. Замкну-
648 ГЛ. 8. РАВНОМЕРНЫЕ ПРОСТРАНСТВА И ПРОСТРАНСТВА БЛИЗОСТИ
тое подмножество F пространства Vх с компактно-открытой то-
пологией компактно тогда и только тогда, когда для каждого
компакта Z<=X семейство F\Z равностепенно непрерывно отно-
относительно °U и множество {f(x): f^F}a:Y имеет компактное
замыкание для каждого jcel I
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
Понятия подпространства и декартова произведения равно-
равномерных пространств введены А. Вейлем в [1938]; там же дока-
доказана теорема 8.2.3. Равномерность равномерной сходимости на
компактах введена в работе Аренса [1946], и там же доказана
теорема 8.2.6. Равномерность равномерной сходимости для ло-
локально компактных X была введена в книге Бурбаки [1949]
и там же доказана теорема 8.2.10. Обобщение теоремы 8.2.10
на ^-пространства получено Бэгли и Янгом в [1966]. Теорема
8.2.11 доказана Келли в [1955]; неявно она сформулирована
как задача в книге Бурбаки [1949].
УПРАЖНЕНИЯ
8.2.А. (а) Пусть {(Xs, <2/s)}5(_5 — семейство равномерных про-
пространств. Покажите, что равномерность Ц °US на множестве
JJ Xs совпадает с равномерностью, порожденной семейством
отображений {ps}s&s* где Ps — проекция множества Ц Xs на
Xs (см. упр. 8.1.F).
(Ь) Покажите, что равномерное пространство {ХУЩ) равно-
равномерно изоморфно произведению ( Ц Xs, Ц ШЛ в том и
только том случае, если существует семейство {ps}s^s Равн0"
мерно непрерывных отображений ps: (Xy iU)-^(XS9cMs)t удовле-
удовлетворяющее равномерным аналогам условий A) и B) упр.2.3.Н.
8.2.В. (а) Пусть {{Xs, *WJ}aeS — семейство равномерных про-
пространств, такое, что XS[}XS'= 0 при 5 Ф $'. Покажите, что се-
семейство °U = [ U Vs: Vs e <иЛ есть равномерность на множе-
м lse5 i
стве Х= [j Xs и что для каждого sgS формула is{x) = x-
S
определяет равномерный изоморфизм (Xs, *%) на подпро
странство (Xs, ^xs) пространства {X, °U). Покажите, что топо-
топология, индуцированная равномерностью Ш на X, совпадает
8.2. ОПЕРАЦИИ НА РАВНОМЕРНЫХ ПРОСТРАНСТВАХ 649
с топологией, индуцированной равномерностью °US. Равномер-
Равномерное пространство ( \] Xs, ЩЛ называется суммой равномерных
пространств {{XSi ^5)}5e5. Определите сумму произвольного
семейства {{Xs, ^5)}se=5 равномерных пространств таким обра-
образом, чтобы выполнялся равномерный аналог упр. 2.2.F.
(b) Пусть (X, CU) — равномерное пространство и Е — отно-
отношение эквивалентности на множестве X. Заметьте, что сильней-
сильнейшая равномерность Т на множестве Х/Е, при которой есте-
естественное отображение X в Х/Е равномерно непрерывно отно-
относительно Щ и Ту индуцирует на множестве Х/Е топологию,
отличную, вообще говоря, от фактортопологии на Х/Е, где на А'
рассматривается топология, индуцированная равномерностью Ф/.
Покажите, что для равномерности Т справедлив равномерный
аналог предложения 2.4.2.
(c) Обратный спектр равномерных пространств есть се-
мейство S = {(Xa, <2/а), я?, 2}, где S' — {Хо, п°0, 2} — обратный
спектр топологических пространств и для любых a, peS,
р ^ а, отображение эт? равномерно непрерывно относительно
Шо и °и$. Подпространство {Х> °U) произведения ( XI Ха9
И °U0\ , где X = limS' и °U = ( Ц ШЛ > называется преде-
oeS ) < VoeS Jx
лом обратного спектра S. Проверьте, что для (X, °U) и отобра-
отображений яа: (X, Ш)^{Х0, Шо) имеет место равномерный аналог
упр. 2.5.F.
8.2.С. Пусть (X, Щ) — равномерное пространство. Проверьте,
что топология, индуцированная равномерностью °U на множе-
множестве X X X, совпадает с топологией, индуцированной произведе-
произведением ШУШ. Покажите, что псевдометрика р на множестве X
равномерна относительно равномерности °LL на множестве X
в том и только том случае, если р — равномерно непрерывное
отображение пространства (ХХХ^Х^) в вещественную
прямую с равномерностью, порожденной естественной метри-
метрикой.
8.2.D. Пусть X — топологическое пространство и {Y,T) —
равномерное пространство. Применяя предложения 2.6.11, 3.4.1
и 2.6.12, покажите, что топология на пространстве Ух, индуци-
индуцированная равномерностью равномерной сходимости, сильнее,
чем компактно-открытая топология.
8.2.Е. Заметьте, что из леммы 8.2.5 вытекает теорема 3.2.10,
если сделать дополнительные предположения о том, что все
пространства Xs являются тихоновскими пространствами.
650 ГЛ. 8. РАВНОМЕРНЫЕ ПРОСТРАНСТВА И ПРОСТРАНСТВА БЛИЗОСТИ
8.3. ВПОЛНЕ ОГРАНИЧЕННЫЕ
И ПОЛНЫЕ РАВНОМЕРНЫЕ ПРОСТРАНСТВА.
КОМПАКТНОСТЬ В РАВНОМЕРНЫХ ПРОСТРАНСТВАХ
Пусть (X, °U) — равномерное пространство, V — произволь-
произвольный элемент равномерности °U и A cz X. Будем говорить, что
множество А V-плотно в (X,°U)y если для каждого хе! най-
найдется такое /еД что |х — х'| < V.
Равномерное пространство (X, Щ) вполне ограничено, если
для каждого V^Ш существует конечное множество А с= X,
V-плотное в пространстве (X, Ш). Равномерность °U на множе-
множестве X вполне ограничена, если пространство (X, °U) вполне
ограничено.
Легко установить, что если существует равномерно непре-
непрерывное отображение / вполне ограниченного равномерного про-
пространства (X, °U) в равномерное пространство (У, Т), такое, что
f(X)=Y, то пространство {У>У) также вполне ограничено.
В частности, вполне ограниченность есть равномерный инва-
инвариант.
8.3.1. Предложение. Пусть равномерность %L на множестве X
индуцируется метрикой р; тогда равномерное пространство
(X, °U) вполне ограничено в том и только том случае, если мет-
метрическое пространство (X, р) вполне ограничено. I
Приведенное выше определение описывает некоторый класс
равномерных пространств. Возникает вопрос, существует ли
внутренняя характеристика топологических пространств, топо-
топология которых индуцирована вполне ограниченной равномер-
равномерностью. Подобная характеристика существует, но не представ-
представляет интереса: мы покажем в примере 8.3.4, что топология лю-
любого тихоновского пространства индуцирована вполне ограни-
ограниченной равномерностью.
Теперь сформулируем две теоремы относительно операций
на классе вполне ограниченных равномерных пространств. До-
Доказательство первой из них можно получить из доказательства
теоремы 4.3.2, если взять V^°U вместо е>0 и заменить е/2
таким f е^, что 2Wc V. Для доказательства второй теоремы
следует рассмотреть базу равномерности JJ <2/s> описанную
в предыдущем параграфе, и заметить, что каждое пространство
(Х5, <%) равномерно изоморфно некоторому подпространству
произведения ( XI Xs, Ц ШЛ, а затем следовать рассужде-
ниям доказательства теоремы 4.3.3.
8.3. ВПОЛНЕ ОГРАНИЧЕННЫЕ И ПОЛНЫЕ РАВНОМЕРНЫЕ ПРОСТРАНСТВА 651
8.3.2. Теорема. Пусть (Xy°U)— вполне ограниченное равномер-
равномерное пространство; тогда для каждого подмножества М cz X про-
пространство {M,°Um) вполне ограничено.
Пусть (Ху°и)—произвольное равномерное пространство, и
пусть для М си X пространство (Mt °Um) вполне ограничено',
тогда пространство {M,°U^) также вполне ограничено. I
8.3.3. Теорема. Пусть {(Xs, <Us)}s^s— семейство непустых рав-
равномерных пространств. Произведение ( Ц Xs, Ц ^^] вполне
ограничено в том и только том случае, когда все пространства
(XSy °US) вполне ограничены. I
8.3.4. Пример. Пусть X — тихоновское пространство и 9* — рав-
равномерность на пространстве X, определенная в примере 8.1.19.
Мы покажем, что равномерное пространство (X,ff*) вполне
ограничено.
Достаточно доказать, что для любой конечной последова-
последовательности /ь /^2, ..-> fk элементов С*(Х) и любого е>0 можно
определить конечное множество А cz X, такое, что для каж-
каждого х^Х существует /еЛ, удовлетворяющее условию
9fv f2 fk (x, x') = max {| fx (x) - h (x') I, I h (x) - f2 (xf) I, ...
Выберем ограниченный замкнутый интервал / cz R, который
содержит все множества fi(X), f2(X), ..., fk(X), и рассмотрим
некоторое покрытие {А^™=х интервала / множествами, диаметр
которых меньше е. Множества вида
где 1 ^ if ^ m при / ^ ky образуют покрытие пространства X,
и диаметр каждого из них относительно псевдометрики
р^ f f меньше е. Выбирая по точке из каждого непустого
множества вида A), мы получим конечное множество А, обла-
обладающее требуемым свойством.
Читатель может легко установить, что вещественная пря-
прямая R с равномерностью V, определенной в примере 8.1.19, не
является вполне ограниченной. I
Пусть (X, °U) — равномерное пространство и SF — некоторое
семейство подмножеств множества X. Говорят, что ST содержит
произвольно малые множества, если для каждого V^°U най-
найдется такое FeJ, что б(/7)< V. Из (U4) вытекает, что если
семейство @~ содержит произвольно малые множества, то пере-
пересечение П У состоит не более чем из одной точки.
652 ГЛ. 8. РАВНОМЕРНЫЕ ПРОСТРАНСТВА И ПРОСТРАНСТВА БЛИЗОСТИ
Равномерное пространство (X,°U) называется полным, если
каждое семейство iF подмножеств множества X, замкнутых
в топологии, индуцированной равномерностью °U, центрирован-
центрированное и содержащее произвольно малые множества, имеет непус-
непустое пересечение. Равномерность °U на множестве X называется
полной, если пространство (X, °U) полное.
Легко установить, что полнота есть равномерный инвариант,
но не является инвариантом равномерно непрерывных отобра-
отображений (ср. с упр. 4.3.В(а) и 8.1.А(а)).
Из теоремы 4.3.10 вытекает
8.3.5. Предложение. Пусть равномерность °Ы на множестве X
индуцирована метрикой р; тогда равномерное пространство
(X, Щ) полно в том и только том случае, когда полно метриче-
метрическое пространство (X, р). I
8.3.6. Теорема. Пусть {X,°U)— полное равномерное простран-
пространство-, тогда для подмножества М cr X равномерное пространство
(М^Чбм) полно в том и только том случае, когда М замкнуто
в X относительно топологии, индуцированной равномерно-
равномерностью °U.
Доказательство. Предположим^ что пространство (М, °Um)
полное, и рассмотрим точку х?М. Пусть iF— семейство всех
множеств вида В(х, V)f\M, где V — элемент из °U, замкнутый
в топологии, индуцированной равномерностью °U на ХУ^Х. Из
следствий 8.1.4 и 8.1.12 вытекает, что семейство ЗГ центриро-
центрировано. Легко видеть, что 5Г состоит из подмножеств простран-
пространства М9 замкнутых в топологии, индуцированной равномер-
равномерностью °Um, и что #"* содержит произвольно малые множества.
Так как [}@~ cz {x}9 то из полноты пространства {M,°Um) выте-
вытекает, что xg М.
Из определения полноты непосредственно вытекает полнота
пространства (М, Шм), при условии что пространство (X, °U)
полное, а М замкнуто в топологии, индуцированной равномер-
равномерностью Щ. I
Теорема 4.3.14, предложение 8.3.5 и очевидный факт, что
«изометрия на» есть равномерный изоморфизм индуцированных
равномерных пространств, приводят к следующему предло-
предложению.
8.3.7. Лемма. Для любого метризуемого равномерного простран-
пространства {Х,Ш) существует полное метризуемое равномерное про-
пространство {Y,T)> такое, что для некоторого MczY пространство
{X,°U) равномерно изоморфно пространству (М,Тм)- I
Из теорем 8.2.3, 8.3.6 и предыдущей леммы легко получается
8.3.8. Теорема. Каждое полное равномерное пространство рае*
номерно изоморфно замкнутому подпространству произведения
семейства полных метризуемых равномерных пространств. I
8.3. ВПОЛНЕ ОГРАНИЧЕННЫЕ И ПОЛНЫЕ РАВНОМЕРНЫЕ ПРОСТРАНСТВА 653
8.3.9. Теорема. Пусть {(Xs. <US)}S(_S —семейство непустых рав-
равномерных пространств. Произведение ( Ц Xs, Ц ЩЛ полно
в том и только том случае, если полно каждое пространство
(XSy<Us).
Доказательство. Если произведение ( Ц XSJ Ц <US\ полно,
то каждое пространство (Xs, °US) полно, ибо оно равномерно
изоморфно замкнутому подпространству произведения.
Доказательство полноты произведения полных равномерных
пространств аналогично доказательству теоремы Тихонова.
Нужно только заметить, что если семейство ^"о> рассмотренное
в этом доказательстве, содержит произвольно малые множества,
то определенные там семейства 3TS также содержат произ-
произвольно малые множества. I
Из теорем 8.3.9, 8.3.6 и 3.11.3 следует, что топология любого
вещественно полного пространства X порождается некоторой
полной равномерностью на X. Можно показать (см. задачу
8.5.13(h)), что если топология пространства X порождается не-
некоторой полной равномерностью и кардинал \Х\ неизмерим,
то X — вещественно полное пространство. Можно также дока-
доказать (см. задачу 8.5.13(а)), что класс топологических про-
пространств, топология которых порождается полной равномер-
равномерностью, совпадает с классом замкнутых подпространств произ-
произведений метризуемых пространств. Заметим, что из последнего
утверждения следует, что топология любого метризуемого про-
пространства порождается некоторой полной равномерностью. Ока-
Оказывается, все паракомпакты обладают тем же свойством (см.
задачи 8.5.13 (Ь) и (d)). Следовательно, каждый паракомпакт
(и, в частности, каждое метризуемое пространство) неизмери-
неизмеримой мощности является вещественно полным (ср. с задачей
5,5.10 (Ь)).
8.3.10. Теорема. Если {X,°U) — равномерное пространство и
(У, У)—полное равномерное пространствоу то каждое равно-
равномерно непрерывное отображение f: (А,с16а)'^{УуТ)у где А —
всюду плотное подмножество в X относительно топологии, ин-
индуцированной равномерностью °U, продолжается до равномерно
непрерывного отображения F: {X,cU)-^(YiЖ).
Доказательство. Для каждого х е X семейство
{f{B{x,Щ\]А)}и^ш центрировано и содержит произвольно ма-
малые множества. Следовательно, в силу полноты пространства
(У, Т)> формула
B) F(x)= П T(B(x,U)ftA)
654 ГЛ. 8. РАВНОМЕРНЫЕ ПРОСТРАНСТВА И ПРОСТРАНСТВА БЛИЗОСТИ
определяет отображение X-+-Y. Легко видеть, что для каждого
х <= А мы имеем F(x) = f(x).
Мы покажем, что отображение F равномерно непрерывно.
Для любого W^T выберем такое 7е7, что QVczW, и такое
U е °Ы, открытое в топологии, индуцированной равномерностью
Ш на ХУ^Х, что для любых а, а'^А если |а — a'\<2Uf то
|/(а) — /(a')|<V. Из следствия 8.1.5 вытекает, что для лю-
любого М cz X
C) 6(/(Affli4))<3K, когда 6(М)<2?/.
Рассмотрим теперь такую пару точек х, j/eX, что |х — #|<
< ?/, и положим 51 = 5 (х, i7) и В2 — В (у, [/). Пересечение
5i f] 52 непусто и открыто в X, следовательно, существует точка
аеЛпадг. Тогда f(a)s=f(Bl[)A)nf(B2[)A) и, согласно
C), 8(f(Bi(]A)UnB2nA))<6V. Поэтому, в силу B), \F(x)-
—F(y)\<6VczW. I
Последняя теорема вместе с теоремой 1.5.4 дает
8.3.11. Следствие. Если {X,°U) и (Y,T) — полные равномерные
пространства, то каждый равномерный изоморфизм {А.Ша) на
(В, Тв), где А и В — всюду плотные подмножества X и Y соот-
соответственно, продолжается до равномерного изоморфизма (X, °U)
на {У,Г). I
8.3.12. Теорема. Для каждого равномерного пространства (X, °п)
существует ровно одно (с точностью до равномерного изомор-
изоморфизма) полное равномерное пространство (X, Щ), такое, что
для некоторого плотного подмножества AczX пространство
{Х,Щ) равномерно изоморфно пространству (А,°йА). Более
того, имеет место равенство w((U) = w(<:U), и если {Х,Ш)
вполне ограничено, то (Х,Ш) также вполне ограничено.
Доказательство. Существование пространства (X, Ш) вы-
вытекает из 8.2.3, 8.3.7, 8.3.9 и 8.3.6, а его единственность — из
следствия 8.3.11.
Равенство w(cU)= w{°U) вытекает из замечания 8.2.4 и сле-
следующего факта: если ш(<2/)<&о> то 41 — дискретная равно-
равномерность. Наконец, в силу второй части теоремы 8.3.2, если
(X, °tt) вполне ограничено, то {X, Ш) также вполне ограни-
ограничено. I
Пространство (Х,Ш), удовлетворяющее условиям теоремы
8.3.12, называется пополнением равномерного пространства
{Х
{,)
Мы закончим этот параграф исследованием равномерностей
на компактах.
8.3. ВПОЛНЕ ОГРАНИЧЕННЫЕ И ПОЛНЫЕ РАВНОМЕРНЫЕ ПРОСТРАНСТВА 655
8.3.13. Теорема. Для каждого компакта X существует точно
одна равномерность °U на множестве X, индуцирующая исход-
исходную топологию пространства X. Все окружения диагонали Дс
czXy^X, открытые в произведении Ху^Х, образуют базу рае-
номерности °п.
Доказательство. Существование равномерности °U на про-
пространстве X вытекает из теоремы 8.1.20. Мы покажем, что все
окружения диагонали ДсХХ^, открытые в XXX, образуют
базу °U. Очевидно, что из этого факта вытекает единствен-
единственность °U.
Согласно следствию 8.1.12, каждое V<^°U содержит некото-
некоторое окружение диагонали, открытое ь ХХХ. Рассмотрим ка-
какое-нибудь открытое окружение _Й7 диагонали Hs.cz ХУ^Х. В силу
(U4) и следствия 8.1.12, А = Л{^: Fe^}c W. Пользуясь ком-
компактностью пространства ХУХ я следствием 3.1.5, мы заклю-
заключаем, что существует конечное семейство {Vi, F2, -.., У^аШ,
для которого AczVifl^n ... П^с^Л^Л ••• [\Vk<z:W.
Следовательно, в силу (U1) и (U2), W^Ш. I
Доказательство следующей теоремы, аналогичное доказа-
доказательству теоремы 4.3.27, предоставляется читателю.
8.3.14. Теорема. Каждая равномерность на компакте вполне
ограничена. I
Из определения полноты непосредственно следует (ср. с за-
задачей 8.5.12)
8.3.15. Теорема. Каждая равномерность на компакте полна, I
Равномерное пространство (X, °U) называется компактом,
если множество X с топологией, индуцированной равномер-
равномерностью °U, есть компакт.
8.3.16. Теорема. Равномерное пространство {Х,%1) есть компакт
в том и только том случае, когда оно одновременно вполне огра-
ограниченное и полное.
Доказательство. В силу теорем 8.3.14 и 8.3.15, достаточно
доказать, что каждое равномерное пространство, которое одно-
одновременно вполне ограничено и полно, есть компакт. Из тео-
теоремы 8.3.8 следует, что {Х,Ш) равномерно изоморфно замк-
замкнутому подпространству произведения ( Ц Xs, Ц ШЛ, где
пространства (XSt °Us) полны и метризуемы. Без ограничения
общности можно считать, что Х = Хcz Ц Xs, <2/=(П 41Л
se=S \se=S Jx
и ps(X) = Xs для каждого s^S. Так как вполне ограниченность
сохраняется при равномерно непрерывных отображениях, про-
пространства (ps{X), ((Us)ps(X)) вполне ограничены, и из второй
части теоремы 8.3.2 вытекает, что пространства (Xs, °US) также
656 ГЛ. 8. РАВНОМЕРНЫЕ ПРОСТРАНСТВА И ПРОСТРАНСТВА БЛИЗОСТИ
вполне ограничены. Следовательно, в силу 8.3.1, 8.3.5, 4.3.29,
пространства (Xs, Щ5) — компакты. Применяя теорему Тихо-
Тихонова, мы заключаем, что и пространство {X, °U) — компакт. I
8.3.17. Следствие. Пополнение равномерного пространства
(A', °U) является компактом в том и только том случае, когда
(Xt °U) вполне ограничено. I
8.3.18. Пример. Пусть X — тихоновское пространство. Как пока-
показано в примере 8.3.4, равномерность W* на пространстве X
вполне ограничена. Следовательно, пополнение (X, W*) — ком-
компакт, а пространство X есть компактификация пространства X.
Мы докажем, что X — стоун-чеховская компактификация про-
пространства X.
Для этого достаточно показать, что каждая непрерывная
функция f: Х->1 непрерывно продолжается на X. Так как един-
единственная равномерность У на отрезке /, индуцирующая его
естественную топологию, полна, то по теореме 8.3.10 достаточно
показать, что f — равномерно непрерывное отображение про-
пространства (Х,Ф*) в A,Т) (ср. с упр. 8.1.D).
Семейство всех окружений диагонали А с= / X Л которые
имеют вид Ух= {(f,z)e/X/: p(f,z)< 1/2'}, где /=1, 2, ...
и p(t,z) = \t — z\9 образует базу равномерности Т на /. Так
как f ^ С*(Х), множество
Wi=*{(x,y)eXXX: pf(x,y)<l/2*}
принадлежит^* при /=1, 2, .... Далее, \f(x)—f(y)\<Vu
как только \х— у\< Wt и, значит, отображение / равномерно
непрерывно. I
8.3.19. Пример. Пусть X — тихоновское пространство и W — рав-
равномерность на нем, определенная в примере 8.1.19. Мы дока-
докажем, что пространство X, где {Х,Ф) — пополнение пространства
(X, Ф), является вещественной компактификацией по Хьюитту
пространства X.
Пусть для любого f^C=C(X) пространство (Rf.^Uf) —
вещественная прямая с равномерностью, индуцированной есте-
естественной метрикой на R. В силу 8.3.5 и 8.3.9, произведение
ШЯь П <иЛ полно. Легко проверить, что сужение
, с f<=c )
F~( Д f\\ X есть равномерный изоморфизм пространства
\f^c )\
{Х^) на подпространство произведения ( XI Rf> П ^/fV Из
KfezC f<=C )
единственности пополнения и из теоремы 8.3.6 следует, что
X = F(X) cz И Rf. Таким образом, X — вещественно полное
fs=C
пространство по теореме 3.11.3. Далее, каждая функция /е
8.3. ВПОЛНЕ ОГРАНИЧЕННЫЕ И ПОЛНЫЕ РАВНОМЕРНЫЕ ПРОСТРАНСТВА 657
geC(X) непрерывно продолжается на Ц Rf и тем более на К,
поэтому пространство л есть вещественная компактификация
по Хьюитту пространства X. I
Полноту равномерных пространств можно охарактеризовать
в терминах направленностей и фильтров. Пусть (Х,°11)— равно-
равномерное пространство и {%ае2}—направленность в X. Бу-
Будем называть {ха,(те2} направленностью Коши в (X, °U)%
если для каждого Уе% найдется такое аое2, что \х0 —
—Xao|<V, как только а ^ ао. Подобным же образом фильтр @*
в семействе всех подмножеств пространства X называется
фильтром Коши в (X,Щ), если для каждого Уе<?/ существует
такое F^tF, что 8(Р)< V. Читатель может легко установить,
что направленности и фильтры Коши отвечают друг другу при
взаимно однозначном соответствии, установленном между на-
правленностями и фильтрами в § 1.6.
8.3.20. Теорема. Равномерное пространство (X, °U) полно в том
и только том случае, если каждая направленность Коши в
(X, 41) сходится к точке пространства X.
Доказательство. Ход рассуждений тот же, что в доказатель-
доказательстве теоремы 3.1.23; следует только заметить, что установлен-
установленное там соответствие между направленностями и центрирован-
центрированными семействами замкнутых множеств переводит направлен-
направленности Коши в семейства, содержащие произвольно малые мно-
множества, и наоборот. I
Доказательство аналога теоремы 8.3.20 для фильтров предо-
предоставляется читателю.
8.3*21, Теорема. Равномерное пространство (X,°U) полно в том
и только том случае, если каждый фильтр Коши в {X,°U) схо-
сходится к точке пространства X. I
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
Понятие вполне ограниченного равномерного пространства
введено Бурбаки в [1940]; там же доказаны теоремы 8.3.3
и 8.3.9. Понятие полного равномерного пространства введено
А. Вейлем в [1938], где доказаны теоремы 8.3.6, 8.3.8, 8.3.10,
8,3.12, 8.3.13 и 8.3.16 (в последней неявно использовано поня-
понятие вполне ограниченности).
УПРАЖНЕНИЯ
8.З.А. (а) Заметьте, что каждая равномерность °U\ на мно-
множестве X, которая слабее какой-нибудь вполне ограниченной
равномерности % на X, сама вполне ограничена.
42 Зак. 697
658 ГЛ. 8. РАВНОМЕРНЫЕ ПРОСТРАНСТВА И ПРОСТРАНСТВА БЛИЗОСТИ
(Ь) Убедитесь, что каждая равномерность °U\ на простран-
пространстве Xt которая сильнее какой-нибудь полной равномерности,
сама полна. Заметьте, что, вообще говоря, это неверно для рав-
номерностей на множестве.
8.3. В. Пусть °U — равномерность на множестве X и А — под-
подмножество в X, всюду плотное в топологии, индуцированной
равномерностью %1. Покажите, что если для каждого центриро-
центрированного семейства $Г подмножеств множества Л, содержащего
произвольно малые множества, пересечение [){F: F^ST) не-
непусто (здесь F — замыкание множества F в пространстве X),
то пространство (X, %L) полное.
8.З.С. (а) Покажите, что для каждого топологического про-
пространства X и любого равномерного пространства (У,°U) рав-
равномерность равномерной сходимости, индуцированная равно-
равномерностью °U на У*, полна.
(Ь) Покажите, что для каждого ^-пространства X и любого
полного равномерного пространства (У, °U) равномерность рав-
равномерной сходимости на компактах, индуцированная равномер-
равномерностью °U на Yx, полна. Заметьте, что предположение о том,
что X является ^-пространством, существенно.
Указание. См. упр. 4.3.F(b).
8.3.D. (а) Проверьте, что равномерность °U, порожденная
совокупностью С равномерных покрытий множества X, вполне
ограничена тогда и только тогда, когда для каждого покрытия
s? ^С существует вписанное в него конечное покрытие М^С*
(b) Проверьте, что равномерность °U, порожденная совокуп-
совокупностью С равномерных покрытий множества X, полна в том
и только том случае, если каждое центрированное семейство ЗГ
подмножеств X, замкнутых в топологии, порожденной равно-
равномерностью °Uy которое для любого покрытия М^С включает
в себя множество F, содержащееся в некотором элементе зФ,
имеет непустое пересечение.
(c) Установите, что равномерность Щ, порожденная семей-
семейством Р равномерных псевдометрик на множестве X, вполне
ограничена в том и только том случае, если для каждого
реР и каждого е > 0 найдется конечное множество A cz X,
такое, что для каждой точки хе! существует х*'^Л, удовле-
удовлетворяющее неравенству р(х, х') <С е,
(d) Установите, что равномерность Ш, порожденная семей-
семейством Р равномерных псевдометрик на множестве X, является
полной в том и только том случае, если всякое центрированное
семейство ЗГ подмножеств пространства X, замкнутых в топо-
топологии, индуцированной равномерностью %L, которое для каж
дой псевдометрики реР и каждого е > 0 содержит множест-
множество F, диаметр которого относительно р меньше е, имеет непустое
пересечение.
8.3. ВПОЛНЕ ОГРАНИЧЕННЫЕ И ПОЛНЫЕ РАВНОМЕРНЫЕ ПРОСТРАНСТВА 659
8.З.Е. (а) Докажите, что полное равномерное пространство
(YtT) является пополнением равномерного пространства (J,°U)
в том и только том случае, если существует равномерно непре-
непрерывное отображение /: {Xy°U)^{Y,T)y такое, что f(X)=Y,
и для каждой псевдометрики р на множестве Ху равномерно
непрерывной относительно °Uy существует псевдометрика р на
множестве У, равномерно непрерывная относительно Т и такая,
что р [f(x), \(у)) = р (х, у) при х,уеХ.
(Ь) Пусть {(Х$, (Ms)}s<=s — семейство равномерных про-
пространств и (XSy 41s) — пополнение пространства (Xs, Qls). По-
Покажите, что произведение ( П Xs, JJ <иЛ есть пополнение про-
изведения ( П X8f П <иЛ-
8.3.F (Широта [1952]). Пусть X — тихоновское пространство
и °Ы — равномерность, порожденная семейством всех покрытий
пространства Ху в которые можно вписать счетное нормальное
покрытие (см. упр. 8Л.1(а)). Докажите, что пространство Ху
где (Я, Щ) — пополнение пространства (X, cU)t является веще-
вещественной компактификацией по Хьюитту пространства X (ср. с
примером 8.3.19 и упр. 8.1.1 (Ь)).
Указание. Заметьте, что семейство Р всех псевдометрик р
на множестве X, таких, что отображение р: ХУ^Х-^R непре-
непрерывно и пространство Х/р, определенное в упр. 4.2.1, сепара-
бельно, обладает свойствами (UP1) — (UP2). Покажите, что
равномерность, порожденная семейством Р равномерных псев-
псевдометрик, совпадает с °Uy и воспользуйтесь упр. 8.3.Е(Ь),
8.1.1 (Ь) и теоремой 8.2.3.
8.3.G. Покажите, что если (X,°U) — равномерный компакт,
тс каждое открытое покрытие пространства X с топологией,
индуцированной равномерностью Ш, равномерно относи-
относительно °U.
Указание. Примените упр. 5.1.А(Ь), предложение 8.1.16
и теорему 8.3.13. Прямое доказательство можно получить мо-
модификацией доказательства леммы 8.2.5.
8.3.Н. Заметьте, что упр. 4.2.В можно решить с использова-
использованием теорем 8.1.21 и 8.3.13.
8.3.1. (а) Проверьте, что если пространство X с топологией,
индуцированной равномерностью °U, связно, то для всякой пары
а:, у^Х и всякого V^l°U существует такая последовательность
хи #2, •. • у %k точек пространства X, что х\ = х, хц = у и \xi —
— *,+1|< Т/при i= 1, 2, ..., k— 1.
(b) Покажите, что каждый равномерный компакт (X, Ш),
удовлетворяющий условию (а), связен и что предположение
о компактности существенно.
42*
660 гл- 8. РАВНОМЕРНЫЕ ПРОСТРАНСТВА И ПРОСТРАНСТВА БЛИЗОСТИ
8.4. БЛИЗОСТИ И ПРОСТРАНСТВА БЛИЗОСТИ
Пусть X — произвольное множество и б —• некоторое отноше-
отношение на семействе всех подмножеств X, Мы будем писать АбВ,
если множества А, В czX находятся в б-отношении; в противном
случае мы будем писать АдВ. Отношение б на семействе всех
подмножеств множества X называется близостью на множе-
множестве X, если оно удовлетворяет следующим условиям:
(PI) A8B тогда и только тогда, когда В8А.
(Р2) А8(В[]С) тогда и только тогда, когда либо А8В, либо
А8С.
(РЗ) {х}8{у} тогда и только тогда, когда х = у.
(Р4) 08Х.
(Р5) Если Л63, то существуют такие С, DczXy что А8С, B8D
и C[}D = X.
Пара {X, б), состоящая из множества X и близости б на нем,
называется пространством близости. Два подмножества А и В
множества X близки относительно б, если А8В\ в противном
случае они далеки относительно б.
Из условий (Р1) — (Р5) вытекают следующие свойства бли-
близостей:
A) Если А8В и В d С, то А8С.
B) Если А Л В Ф 0, то А8В.
C) 06А для каждого А а X.
Чтобы установить соотношение A), достаточно заметить,
что если В cz С, то В [} С = С, т. е. из А8В следует, что А8С
в силу (Р2). Свойство B) вытекает из (РЗ), (Р1) и A). В са-
самом деле, если х^А[\В, то {х}б{х}, {х}8Ау А8(х) и А8В. На-
Наконец C) следует из (Р4) и A).
Каждая близость б на множестве X индуцирует топологию О
на X. Следовательно, каждое пространство близости (X, 8)
определяет топологическое пространство (X, 0). Точнее, как
мы увидим, формула
D) 1={^1: {х}8А}
определяет оператор замыкания на множестве X. Начнем с
леммы.
8.4.1. Лемма. Для каждой близости 8 на множестве X и любых
множеств Л, В аХ
E) если ВЬАУ то Б64.
8.4. БЛИЗОСТИ И ПРОСТРАНСТВА БЛИЗОСТИ 661
Доказательство. Если ВЬА, то в силу (Р5), существуют та-
такие С, D си X, что
F) ВЪС, A6D
и
G) C[)D = X, т. е. X\D с= С.
Из A) и второй части F) вытекает, что AczX\D) поэтому
ЛсСв силу G) и ВЬК в силу первой части F). I
8.4.2. Теорема. Для каждой близости б на множестве X фор-
формула D) определяет оператор замыкания, удовлетворяющий
условиям (СО1) — (СО4). Пространство X с топологией Оу по-
порожденной этим оператором замыкания, является Т{-простран-
Т{-пространством.
Такая топология О называется топологией, индуцированной
(или порожденной) близостью б.
Доказательство. Условия (СО1), (СО2) и (СОЗ) вытекают
непосредственно из C), B) и (Р2) соответственно. Для дока-
доказательства условия (СО4) достаточно показать, что для каж-
каждого АаХ выполнено включение (Л)с=Л, или, что эквива-
эквивалентно,
(8) если хфА, то хф (Л).
Но (8) следует из леммы, примененной к одноточечному множе-
множеству В = {%}.
То, что (X, О) есть ^-пространство, вытекает непосред-
непосредственно из (РЗ). I
Ниже мы покажем (см. теорему 8.4.9), что, как и в случае
равномерностей, топология пространства X индуцируется неко-
некоторой близостью на множестве X в том и только том случае,
когда X — тихоновское пространство.
Отметим, что из леммы 8.4.1, свойства A) и условия (Р1)
вытекает, что для каждой близости б на множестве X оператор
замыкания, определенный соотношением D), обладает следую-
следующим свойством:
(9) АгВ тогда и только тогда, когда ЛбЛ.
8.4.3. Пример. Пусть X — произвольное множество. Проверим,
что, полагая А8В тогда и только тогда, когда А(]В ф 0, мы
определим близость на множестве X. В самом деле, легко ви-
видеть, что б удовлетворяет условиям (Р1) — (Р4). Для того чтобы
доказать условие (Р5), достаточно заметить, что для каждой
пары Л, В далеких, т. е. непересекающихся подмножеств мно-
множества X множества С = Х\А и D = Х\В обладают требуе-
требуемыми свойствами. Очевидно, что топология, индуцированная
662 ГЛ. 8. РАВНОМЕРНЫЕ ПРОСТРАНСТВА И ПРОСТРАНСТВА БЛИЗОСТИ
отношением б, — это дискретная топология на X. Близость б
называется дискретной близостью на X, а пространство (X, б) —
дискретным пространством близости. Ш
8.4.4. Пример. Пусть X — тихоновское пространство. Для любых
двух множеств Л, BczX положим АЬВ тогда и только тогда,
когда А Ф 0 ф В и не существует непрерывной функции
f: Х^1У такой, что f(x)=0 для х^А и f(x)= 1 для хеВ,
т. е. множества Л и В не вполне отделены. Покажем, что б —
близость на множестве X.
Непосредственно из определения следует, что б удовлетво-
удовлетворяет условиям (Р1), (РЗ) и (Р4).
Чтобы проверить условие (Р2), достаточно показать, что,
если Л6В и ЛбС, то А8(В\]С). Выберем непрерывные функции
f, g'- X-+I, такие, что
f(x) = g(x) = 0 для хеД f(x)=l для хеВ,
g(x)= 1 для хеС.
Функция A = max(/,g) примет значение 0 на множестве Л
и значение 1 на множестве В[)С, так что А6{В[}С).
Наконец, б удовлетворяет условию (Р5), ибо если АдВ
т. е. если существует непрерывная функция f: X-+-I, такая, что
f(x) = О для хеАи f(x) = 1 для х е 5, то
множества С = /-411/2,1]) и D = f-'([0, 1/2])
обладают требуемыми свойствами.
Из определения тихоновского пространства вытекает, что
близость 6 на I индуцирует исходную топологию простран-
пространства X. 1
Теперь мы вкратце обсудим отображения пространств бли-
близости. Пусть (X, б) и (К, б') — два пространства близости. Ото-
Отображение f множества X в множество У называется близостно
непрерывным относительно близостей б и б', если для любых
множеств Л, BczX, близких относительно б, образы f(A)9
f(B)cz Y близки относительно б'. Из формулы D) и равносиль-
равносильности условий (i) и (v) предложения 1.4.1 следует, что f —
непрерывное отображение пространства X с топологией, инду-
индуцированной отношением б, в пространство Y с топологией, инду-
индуцированной отношением 8'. Очевидно, что композиция близо-
близостно непрерывных отображений близостно непрерывна.
Взаимно однозначное отображение f множества X на мно-
множество Y называется близостным изоморфизмом относительно
близостей б и б' на множествах X и Y соответственно, если f
близостно непрерывно относительно б и бг и обратное отобра-
отображение f~{ близостно непрерывно относительно б' и б. Близостный
8.4. БЛИЗОСТИ И ПРОСТРАНСТВА БЛИЗОСТИ 663
изоморфизм есть гомеоморфизм индуцированных топологиче-
топологических пространств.
Говорят, что два пространства близости (X, б) и (У, б') бли-
зостно изоморфны, если существует близостный изоморфизм
(X, б) на (У, б'). Изучение близостных инвариантов, т. е. инва-
инвариантов близостных изоморфизмов, является содержанием тео-
теории пространства близости. Очевидно, что каждый топологиче-
топологический инвариант является близостным инвариантом.
Теперь мы перейдем к изучению связей между близостями
и равномерностями на множестве.
8.4.5. Теорема. Пусть °U — равномерность на множестве X. По-
Положив для А, В czX
А8В тогда и только тогда, когда V[](Ау^В)Ф 0
для каждого Fg?/,
мы определим близость на множестве X. Топология, индуциро-
индуцированная отношением б, совпадает с топологией, индуцирован-
индуцированной %1.
Такая близость б называется близостью, индуцированной
равномерностью °U.
Доказательство. Сначала заметим, что АЬВ тогда и только
тогда, когда для каждого V ^°U найдутся такие xgAhi/eB,
что | jc — y\<ZV. Очевидно, отношение б удовлетворяет усло-
условиям (Р1) и (Р4), а из (U4) вытекает, что б удовлетворяет
также (РЗ).
Для проверки условия (Р2) достаточно показать, что если
АЬВ и АЬС, то Ад[В[]С). Выберем такие Vu V2^aU, что
\х — у\^ V\ и \х — z\z^ V2 для всех хеЛ, у е В и zgC.
Ясно, что \х—1\^ V = V\ П Кг» как только xg/I и t^B{]C;
так как Fe^, то, в силу (U2),А6(В[}С).
Наконец, б удовлетворяет условию (Р5), так как если АдВ,
т. е. если существует такое V^Ql, что \х— у\^ V при xgA,
у е В, то множества
C = X\B{A,W) и D = X\B{B,W),
где W^°U удовлетворяет включению 2WcnV, обладают тре-
требуемыми свойствами.
Из следствия 8.1.4 вытекает, что топология на X, индуциро-
индуцированная близостью б, которая в свою очередь индуцирована рав-
равномерностью °U на множестве X, совпадает с топологией, инду-
индуцированной равномерностью °U. I
Легко проверить, что если отображение f множества X в
множество Y равномерно непрерывно относительно равномер-
ностей °U и У3 на множествах X и Y соответственно, то f бли-
664 ГЛ. 8. РАВНОМЕРНЫЕ ПРОСТРАНСТВА И ПРОСТРАНСТВА БЛИЗОСТИ
зостно непрерывно относительно близостей б и б', индуцирован-
индуцированных равномерностями °U и У0.
8.4.6. Пример. В § 8.1 мы установили, что каждая метрика р
порождает некоторую равномерность °U на множестве X. В силу
последней теоремы, равномерность Щ в свою очередь порождает
близость б на множестве X. Легко установить, что два множе-
множества А, В с: X близки относительно б в том и только том слу-
случае, если р (Л, В) = 0. Следовательно, если р — произвольная
метрика на множестве X и мы положим
А8В тогда и только тогда, когда р(Л,В) = 0,
то тем самым мы определим близость б на множестве X. Бли-
Близость б называется близостью, индуцированной метрикой р. I
Для обсуждения перехода от близости к равномерностям
удобно рассмотреть отношения строгого включения. Пусть б —
некоторое отношение на множестве X. Будем говорить, что
множество Л строго содержится в множестве В относительно б,
и писать А шВ, если А8(Х\В). Заметим, что, используя отно-
отношение строгого включения, мы можем переписать (Р5) в сле-
следующем виде:
(Р5') Если А6В, то существуют Аи B\czX, такие, что Л<^Ль
ВтВх и А\{\В\ = 0.
Покажем теперь, что отношение ш обладает следующими
свойствами (в (SI5) и (SI7) рассматривается топология, инду-
индуцированная отношением б):
E11) Если АшВ,то Х\В ш Х\А.
E12) Если АшВ,то Лей.
E13) Если Л1 с: А Ш В с: Ви то Аг Ш 5Ь
E14) Если AimBxuA2m B2, то Аг (J Л2 <^ Вг U В2.
{SI5) Если AmВу то существует открытое множество С, та-
кое, что АшСаСШВ.
E16) 0Ш0.
E17) Для каждой точки xeZ и каждой ее окрестности А
имеем {х} ш Л.
Свойство (SI1) вытекает из определения строгого включе-
включения и из тождества А = Х\(Х\А). Свойства (SI2) и (SI3)
следуют из B) и A) соответственно.
Чтобы установить (SI4), достаточно заметить, что если
А\шВ\ и А2шВ2, то, в силу A), при *'=1, 2 имеем
M(*\Bi)n(*\Sa)], так что (АхUА2)~д[Х\(Вх[}В2)], т. е.
Al[}A2mBi\jB2B силу (Р1) и (Р2).
Несколько сложнее доказать (SI5). Если АшВ, то, в силу
(Р5'), существуют такие Ль В\ с: X, что
АшАи
8.4. БЛИЗОСТИ И ПРОСТРАНСТВА БЛИЗОСТИ 665
В силу_(811), имеем AidX\B\mB9 так что А\д{Х\В). Так
как Лб(Х\Л1), то из E) вытекает, что Лб(Х\Л1), т. е.
Л6(^\_IntЛ1). Полагая С=1гйЛь получаем АтСаА\. Так
как А\6(Х\В), то C6{X\B)t откуда в свою очередь следует,
что С6(Х\В)9т. е.СшВ.
Свойства (SI6) и (SI7) следуют из (Р4) и D) соответ-
соответственно. Заметим, что из (SI1) и законов де Моргана следует»
что свойство (SI4) можно переписать в следующем виде:
(SI40 Если AlmBl и А2шВ2, то Ах{\А2шВх(\В2.
Более общо, если при /=1, 2, ..., k мы имеем Ai<^Bit то
k k
(как читатель легко может установить) М At m (J Bt и
Пл,еПд,.
i = \ i = l
Заметим также, что из (SI5) следует, что пространство X
с топологией, индуцированной близостью на множестве Ху яв-
является регулярным пространством (ср. с теоремой 8.4.9).
Пусть б — близость на множестве X. Конечное покрытие
^/}f=1 множества X называется б- рае номерным, если суще-
существует такое покрытие {В^=1 множества J, что
A0) BtmAi при /=1, 2, ..., k.
8.4.7. Лемма. Пусть б — близость на множестве X. Для Л, ВаХ
мы имеем А8В в том и только том случае, если каждое 5-рав-
номерное покрытие {Л*}^ множества X содержит такое мно-
множество Л/, что А[\А\Ф0 фВ[\ А\.
Доказательство. Рассмотрим такие Л, BczX, что Л65.
Пусть st- = {Ai}ki=x есть б-равномерное покрытие множества X,
и пусть $== {В(}^=1 —покрытие пространства X, удовлетворяю-
удовлетворяющее A0). Из упомянутого выше обобщения (SI4) следует, что
множества
A1) C = St(At?) и D = St(Atst)
удовлетворяют включению СШО. Так как Л с С, то АЬ(X\D)t
откуда следует, что
A2) В(\ВФ0.
В самом деле, в противном случае было бы BczX\D и А6В>
что невозможно. Из второй части A1) и A2) вытекает суще-
существование такого / ^ k, что Л П Л/ Ф 0 ф В (] Л/.
Рассмотрим теперь такие Л, ВаХ, что А6В. В силу (Р5')
существуют B\t B^cnX, удовлетворяющие соотношениям АШ
666 ГЛ. 8. РАВНОМЕРНЫЕ ПРОСТРАНСТВА И ПРОСТРАНСТВА БЛИЗОСТИ
<тХ\Ви В<тХ\В2 и (Х\ВХ)П(Х\В2)= 0. Множества Аг =
= Х\А и А2 = Х\Б образуют покрытие $Ф множества X. По-
Поэтому, в силу (SI1), ВхШАх и В2<^А2. Так как ВХ[]В2 = Х,
то *я? есть б-равномерное покрытие пространства X, никакой
элемент которого не пересекает одновременно А и В. I
8.4.8. Теорема. Для каждой близости б яа множестве X со-
совокупность С всех покрытий пространства X, в которые можно
вписать Ь-равномерные покрытия, обладает свойствами
(UC1) — (UC4). Равномерность Ш на множестве X, порожден-
порожденная совокупностью С, вполне ограничена и индуцирует близость
б. Топология, порожденная равномерностью °U, совпадает с то-
топологией, порожденной близостью б.
Такая равномерность Щ называется равномерностью, по-
порожденной (или индуцированной) близостью б.
Доказательство. Пусть Со — совокупность всех б-равномер-
ных покрытий множества X. Так как совокупность С обладает
свойством (UC1), то для доказательства первой части теоремы
достаточно показать, что Со обладает свойствами (UC2)—
(UC4).
Сначала покажем, что Со обладает свойством (UC2). Рас-
Рассмотрим st-u s$2^C0n положим st>x = {Аи i}\=i> ^Ф2 = {А% /J/Lj.
Возьмем такие покрытия ^\=^{В\^кых и ^2 = {52, /}^L, множе-
множества X, что
BXyimAhi при i= 1, 2, ..., k
и В2,}ША2,! при /=1, 2, ..., т.
Из свойства (SI4') вместе с A3) следует, что семейство $Ф
всех пересечений AXti[\A2t/, где i^k и j^m, есть б-равно-
б-равномерное покрытие множества X. Так как М> вписано и в *s^i,
и в s&2, то семейство Со обладает свойством (UC2).
Доказательство того, что Со обладает свойством (UC3),
несколько длиннее. Прежде всего заметим, что, в силу лем-
леммы 5.1.15, достаточно показать, что для каждого «^еС0 суще-
существует покрытие 3$ е Со, звездно вписанное в s&.
Рассмотрим сначала двухэлементное покрытие s& =
= {Л1,Л2}еС0, и пусть В\, B2czX удовлетворяют условиям
A4) ВгШАи В2ША2 и ВХ\}В2 = Х.
Из A4) следует, что семейство i^= ^i\52, A2\BU Ai(]A2}
есть покрытие множества X. Так как (A\\B2)(](A2\Bi)=^ 0,
то покрытие $ звездно вписано в покрытие s&. В силу (SI5),
найдутся такие Сь С2 с= X, что
A5) ВхШСхШАх и 52<^С2<^Л2.
8.4. БЛИЗОСТИ И ПРОСТРАНСТВА БЛИЗОСТИ 667
Из свойств (SI1) и (SI4') с помощью формул A4) и A5) по-
получаем, что
d \С2ШАХ\В2У С2\С{шА2\Ви С1[\С2ШАХ[\А2
т. е. что J? е Со. Следовательно, в каждое двухэлементное по-
покрытие ^gC0 можно звездно вписать покрытие J?eC0.
Рассмотрим теперь произвольное покрытие $Ф = {Л/}^=1 ^ Со>
и пусть ВьВ2,.,.,ВАсХ удовлетворяют условиям
A6) Я,^Л, при /=1,2,..., /г и fiiLJS2U ..
Из свойств (SI5) и (SI1) вытекает, что М-г = {Л,-, )
при i = 1, 2, ..., &. В силу уже доказанной части теоремы, при
i= 1, 2, ..., k для каждого ^ существует звездно вписанное
в него покрытие SBt е Со и, кроме того, существует покрытие
Ш^Со, вписанное во все 3St. Для каждого х^Х и любого
t ^ ? имеем St (x, $) с: St (x, ^г), так что
St (jc, Л) с= Л/ или
Так как, в силу A6), вторая часть альтернативы не может
иметь место для всех /, то существует такое i ^ kt что
St(x, &)czAi, т. е. $ звездно вписано в *s#. Таким образом, до-
доказательство свойства (UC3) завершено.
Тот факт, что семейство Со обладает свойством (UC4), так
же как и то, что равномерность °U, порожденная совокупностью
С, индуцирует близость б, следует непосредственно из лем-
леммы 8.4.7. Так как равномерность Ш индуцирует близость б, то
по теореме 8.4.5 топология, индуцированная равномерностью Ш,
совпадает с топологией, индуцированной близостью б.
В силу предложения 8.1.16, множества
где ^ = {Л/}ыеС0, образуют базу равномерности °U. Выби-
Выбирая по точке в каждом непустом элементе *я?, мы получаем ко-
конечное множество, которое У(^)-плотно в (X, °U). Следова-
Следовательно, равномерность Щ вполне ограничена. ¦
Оказывается, если близость б индуцирована вполне огра-
ограниченной равномерностью Ш, то равномерность, индуцирован-
индуцированная близостью б, совпадает с Щ (см. упр. 8.4.D). Следова-
Следовательно, существует взаимно однозначное соответствие между
близостями и вполне ограниченными равномерностями на мно-
множестве.
Из теорем 8.4.8, 8.1.20 и примера 8.4.4 следует
668 ГЛ. 8. РАВНОМЕРНЫЕ ПРОСТРАНСТВА И ПРОСТРАНСТВА БЛИЗОСТИ
8.4.9. Теорема. Топология пространства X индуцирована неко-
некоторой близостью на множестве X в том и только том случае,
если X — тихоновское пространство. I
Если X — топологическое пространство и близость б на мно-
множестве X индуцирует исходную топологию на X, то будем гово-
говорить, что б — близость на пространстве X. Вообще говоря, су-
существует много близостей на данном тихоновском пространстве.
Этот параграф мы закончим теоремой, устанавливающей вза-
взаимно однозначное соответствие между близостями на тихонов-
тихоновском пространстве X и компактификациями пространства X.
Сначала мы покажем, что на компакте существует только одна
близость.
8.4.10. Теорема. Для каждого компакта X существует в точно-
точности одна близость б на множестве X, которая индуцирует исход-
исходную топологию пространства X, а именно близость б, определен-
определенная следующим образом:
A7) А8В в том и только том случае, если А(]Б^ 0.
Доказательство. Из примера 8.4.4 вытекает, что A7) опре-
определяет близость на пространстве X.
Пусть б' — некоторая близость на пространстве X. Из B)
и (9) следует, что если А8В, то АЬ'В. Следовательно, для за-
завершения доказательства достаточно показать, что если А и
Б — непересекающиеся замкнутые подмножества пространства
Ху то АЬ'В. Для каждого х^.А имеем {х}д'В, так что, в силу
(SI5), существует открытое множество Vx, удовлетворяющее
условию
A8) x^Vx и VA'B.
По теореме 3.1.3, существует конечное множество {х\, х% ...
..., xk] cz Л, такое, что
A9) AcVXlUVXtU ... UV4
Теперь из (Р2),A), A8) и A9) следует, что Ад'В. I
8.4.11. Лемма. Пусть X — тихоновское пространство и сХ — его
компактификация. Для А, В czX положим
А8(с)В в том и только том случае, когда с{А)(\с(В)ф 0,
где замыкание взято в сХ. Тем самым мы определили близость
б (с) на пространстве X.
Для компактификаций с\Х и с2Х пространства X имеем
) 6(c2) в том и только том случае, если кочпактификации
С\Х и с2Х эквивалентны.
8.4. БЛИЗОСТИ И ПРОСТРАНСТВА БЛИЗОСТИ 669
Доказательство. Проверка того, что б (с) —близость на про-
пространстве X, предоставляется читателю. Вторая часть леммы
следует непосредственно из теоремы 3.5.5. I
8.4.12. Лемма. Для каждой близости б на тихоновском про-
пространстве X существует компактификация сХ пространства X,
такая, что б = б (с).
Доказательство. Пусть °U — равномерность, индуцированная
близостью б, и {%,Ш) — пополнение равномерного простран-
пространства (Ху °U). Так как равномерность Щ вполне ограничена, то
пространство Ху в силу следствия 8.3.17, есть компакт. Рассмот-
Рассмотрим отображение с: Х-^Я, равномерно непрерывное относи-
относительно %L и Щ и такое, что с \Х — равномерный изоморфизм
(X,°U) на {АуЧ1а), где А = с(Х) — некоторое всюду плотное
подпространство пространства К. Очевидно, что X = сХ — ком-
компактификация пространства X.
Пусть б' — близость, индуцированная на множестве X рав-
равномерностью CU. По теореме 8.4.8 равномерность °U индуцирует
близость б, и так какс\Х — равномерный изоморфизм, то для
Л, В^Х
B0) А8В тогда и только тогда, когда с(А)8'с(В).
С другой стороны, из компактности К и теоремы 8.4.10 получаем
B1) с(А)8'с(В) тогда и только тогда, когда с(А)(]с(В)Ф 0;
таким образом, б = б (с). I
Леммы 8.4.11 и 8.4.12 приводят к следующей теореме.
8.4.13. Теорема Смирнова. Сопоставив каждой компактифика-
ции сХ тихоновского пространства X близость б (с) на простран-
пространстве X, мы установим взаимно однозначное соответствие между
всеми компактификациями пространства X и всеми близостя-
близостями на X. I
8.4.14. Пример. Читатель может легко проверить, что близость,
определенная в примере 8.4.4 на тихоновском пространстве X,
соответствует стоун-чеховской компактификации простран-
пространства X. I
ИСТОРИЧЕСКИЕ И БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
Рисе в [1908] сформулировал аксиомы, описывающие поня-
понятие близости пары множеств; хотя введенное им понятие не эк-
эквивалентно рассмотренному здесь отношению близости, оно ему
аналогично. Однако ни сам Рисе, ни кто-либо из математиков —
его современников не проявил интереса к подробной разработке
этой идеи. Понятие близости (в нашем смысле) введено Ефре-
670 ГЛ. 8. РАВНОМЕРНЫЕ ПРОСТРАНСТВА И ПРОСТРАНСТВА БЛИЗОСТИ
мовичем в [1951]. Там же доказана теорема 8.4.2. Теорема
8.4.10 доказана в работе Ефремовича [1952]. Анализ про-
пространств близости проведен Смирновым в [1952]. В этой же
работе доказаны теоремы 8.4.5, 8.4.8, 8.4.9 и 8.4.13. Наиболее
полное изложение теории пространств близости приводится
в книге Наимпалли и Воррэка [1970].
УПРАЖНЕНИЯ
8.4.А. (а) Покажите, что каждое непрерывное отображение
компакта X в тихоновское пространство Y близостно непре-
непрерывно относительно любых близостей б, б' на пространствах X
и Y соответственно.
(Ь) (Ефремович [1952]). Пусть (X,б) — пространство бли-
близости, и пусть Л, В — два далеких относительно б подмноже-
подмножества X. Покажите, что существует близостно непрерывное ото-
отображение /: X-+I (где близость на отрезке / индуцирована
естественной метрикой на нем), такое, что f(A)cz {0} и /E)с:
8.4.В. (а) Пусть б и б' — близости на X и Y соответственно,
и пусть 41 и Щг — равномерности, индуцированные б и б'. По-
Покажите, что каждое отображение X в Y, близостно непрерывное
относительно б и б', равномерно непрерывно относительно
<U и Щ1.
Указание. Покажите, что / близостно непрерывно относи-
относительно б и б' в том и только том случае, если для каждого
б'-равномерного покрытия {^}*в1 множества У покрытие
I/ (Л*)}^=1 множества X б-равномерно.
(Ь) Выведите из (а), что каждое отображение /: X-+Yr
близостно непрерывное относительно близостей б и б' на про-
пространствах X и Y соответственно, продолжается до непрерыв-
непрерывных отображений F: cX^c'Y, где сХ и cfY—компактификации
пространств X и У, удовлетворяющие условиям 6 (с) = 6 и
6(с') = 6'.
8.4.С. Если 6i и бг — две близости на множестве X и для
всех Л, В d X из А8\В следует Л6г5, то говорят, что близость
6j сильнее (тоньше) близости б2, а бг слабее [грубее) бь и пи-
пишут б2 ^ бь
(a) Проверьте, что отношение ^ задает некоторое упорядо-
упорядочение семейства всех близостей на X.
(b) Убедитесь, что для компактификации С\Х и с%Х тихо-
тихоновского пространства X неравенство С\Х ^ с2Х имеет место
в том и только том случае, если 6(ci) ^ б(с2).
8.4.D (Смирнов [1952]). (а) Покажите, что в семействе всех
равномерностей на множестве X, которые индуцируют фиксиро-
фиксированную близость б, существует слабейшая равномерность.
8.5. ЗАДАЧИ 671
Указание. Это равномерность, индуцированная близостью б.
(Ь) Проверьте, что в семействе всех равномерностей на мно-
множестве X, индуцирующих некоторую фиксированную близость
б, существует ровно одна вполне ограниченная равномерность —
слабейшая. Установите, что для любого тихоновского простран-
пространства X существует взаимно однозначное соответствие между
близостями и вполне ограниченными равномерностями на про-
пространстве X.
8.4.Е. Дайте прямое описание близости на локально ком-
компактном пространстве X, соответствующей компактификации
Александрова пространства X.
8.5. ЗАДАЧИ
Характеристика паракомпактности в терминах окружений
диагонали
8.5.1. (Келли [1955]). Покажите, что если в открытое по-
покрытие {Us}s^s топологического пространства X можно вписать
замкнутое локальное конечное покрытие {Ft}t€-T, то существует
окружение V диагонали AczJX^, открытое в произведении
XX X и такое, что покрытие {В(х, V)}xeX вписано в {Us}s&s.
Указание. Для любого (g?1 выберите такое s(t)^S, что
FtczUs{th и положите Vt = (Usit)XUsit))[j[(X\Ft)X(X\Ft)).
Проверьте, что V = П V t обладает требуемыми свойствами.
8.5.2 (Келли [1955]). Докажите, что регулярное простран-
пространство X есть паракомпакт тогда и только тогда, когда в каждое
открытое покрытие пространства X можно вписать покрытие
вида {В(х, V)}xeX, где V — некоторое окружение диагонали
Д с X X X, открытое в произведении X X X.
Указание. При доказательстве паракомпактности простран-
пространства X воспользуйтесь условием (п) теоремы 5.1.12. Выберите
вписанное покрытие вида {В{х, V)}xeiX, для каждой точки
х е X возьмите окрестность WXy такую, что WxXWxc:Vt и рас-
рассмотрите покрытие {W}
р-адические равномерности
8.5.3. (а) Пусть Z — множество всех целых чисел и р — про-
простое число. Покажите, что семейство ^ = {^Л7=1 окружений
диагонали AczZXZ, где ^^{(^j/JeZX^ % — у делится
на р1}, обладает свойствами (BUI) — (BU3). Равномерность,
порожденная такой базой ^, называется р-адаческой равномер-
равномерностью на Z и обозначается Жр.
672 ГЛ. 8. РАВНОМЕРНЫЕ ПРОСТРАНСТВА И ПРОСТРАНСТВА БЛИЗОСТИ
Покажите, что если /?i и р2— различные простые числа, то
равномерности WPl и ЖРг, а также топологии на Z, индуциро-
индуцированные этими равномерностями, несравнимы, т. е. ни одна из
них не сильнее другой.
(b) Пусть р— простое число; рассмотрим произведение
со
Хр = 1[Хй, где *,= {-р+1, -р + 2, ..., -1, 0, 1, ...
?=0
..., р — 1}—дискретное пространство, и единственную равно-
равномерность °UP на пространстве Хр. Обозначим через Y подмноже-
подмножество пространства XPt состоящее из всех последовательностей
{лгг}, в которых не более чем конечное число Х{ отлично от нуля,
со
и положим /({xj)— X xiP*> ГДе {xi}^Y. Проверьте, что / —
равномерный изоморфизм (У,(^)у) на (Z, Жр), а убедитесь,
что (Хр, °UP) — пополнение равномерного пространства (Z, Жр).
Используя упр. 6.2.А(с), заметьте, что Хр гомеоморфно канто-
рову совершенному множеству.
(c) Пусть Q — множество всех рациональных чисел и р —
простое число. Покажите, что семейство ^ — {VJ^lj окруже-
окружений диагонали AczQXQ, где Vi= {(x,y)^Qy(tQ: существуют
такие ky m^Z, что х—у=—р1> и т не делится на р}, обла-
обладает свойствами (BUI) — (BU3). Равномерность, порожденная
такой базой Ш, называется р-адической равномерностью на Q
и обозначается Тр. Проверьте, что (Тр)г = Жр, где WP есть
р-адическая равномерность на Z. Пространство Qp с тополо-
топологией, индуцированной равномерностью TPi где (QP,TP) — по-
пополнение равномерного пространства (Q,TP), называется про-
пространством р-адических чисел. Докажите, что Qp гомеоморфно
сумме Ко экземпляров канторова множества.
(d) Пусть р — простое число; положим 1^@) = 0 и для каж-
каждого рационального числа х ф 0 обозначим через vp(x) нату-
натуральное i, такое, что Х——Р1* гДе k и m пе делятся на р.
Покажите, что формула рр(х, y) = p~vP{x~y) определяет неко-
некоторую метрику на множестве Q рациональных чисел и что эта
метрика индуцирует р-адическую равномерность на Q.
Топологические группы
8.5.4. (а) Пусть {Gs}5e5 — семейство групп. Проверьте, что про-
произведение Ц Gs — группа относительно покоординатного умно-
жения. Эта группа называется декартовым произведением
групп {}
8.5. ЗАДАЧИ 673
Покажите, что декартово произведение топологических групп
}5_5 есть топологическая группа относительно тихоновской
топологии и что равномерность на Ц G$> порожденная одним
из трех семейств равномерных покрытий, определенных в при-
примере 8.1.17, есть декартово произведение соответствующих рав-
номерностей на группах Gs.
(b) Подмножество Go группы G называется подгруппой,
если х-1 gG0 и ху е Go для х, у е Go. Покажите, что под-
подгруппа Go топологической группы G есть топологическая группа
относительно топологии подпространства и что если °U — рав-
равномерность на G, порожденная одной из трех совокупностей
равномерных покрытий, определенных в примере 8.1.17, то Шв^
совпадает с соответствующей равномерностью на группе Go-
(c) (А. Стоун [1948]). Заметьте, что Z**1, где Z — множество
всех целых чисел, не является нормальной топологической
группой.
Указание. См. задачу 2.7.16(а).
(d) (Тьюки [1940]). Докажите, что Z)KlX2, где Sc=Z)Kl
состоит из всех точек с не более чем счетным множеством от-
отличных от нуля координат, является счетно компактной не нор-
нормальной топологической группой.
Указание. См. пример 3.10.17, задачу 3.12.23 (с) и теоре-
теорему 5.1.38.
Равномерности в терминах псевдометрик
8.5.5. Пусть даны множество X и семейство Р псевдометрик
на нем, обладающее свойствами (UP1) — (UP2) и следующим
свойством:
(UP3) Если а — псевдометрика на множестве X и для любого
е > 0 существуют такие реР и б > 0, что а(х}у)< 8,
как только р(х, г/) < 6, то аЕ Р.
Проверьте, что Р — семейство всех псевдометрик на X, рав-
равномерных относительно равномерности Щу порожденной семей-
семейством Р.
Заметьте, что существует взаимно однозначное соответствие
между равномерностями на X и семействами псевдометрик на Х>
обладающими свойствами (UP1) —(UP3).
Продолжения равномерных псевдометрик и равномерно не*
прерывных функций
8.5.6. (а) (Исбелл [1959]). Пусть (ХУШ) — равномерное про-
пространство и Mel. Докажите, что каждая ограниченная псев-
псевдометрика р на множестве X, равномерная относительно %
43 Зак. 697
674 ГЛ. 8. РАВНОМЕРНЫЕ ПРОСТРАНСТВА И ПРОСТРАНСТВА БЛИЗОСТИ
продолжается до ограниченной псевдометрики а на множестве
X, равномерной относительно %1.
Указание. Можно считать, что р ограничена числом 1/2.
Для i=l, 2, ... выберем Vi^°U, удовлетворяющее условию
Vi()(MXM)cz{(xiy)€zMXM: р(х,у)< 1/2*}, и псевдомет-
псевдометрику Gi на множестве X, ограниченную числом 1 и такую, что
{(x,j/)gXX^: <т;(х,у)< 1/4} cz V*. Установите, что формула
оо
о'(х, у) = 8 2^ —<*i(x> У) определяет псевдометрику а' на Х9
2
равномерную относительно °11 и удовлетворяющую неравенству
Р (х, у) ^ Qf (х> У) Для всех пар ху у^М. Пусть а(х, у) =
= min (а'(*,#), о"(х,у)), где о"(х,у)= inf ('( (
+ ( ^))
(b) (Катетов [1951а]). Пусть {X,%L) — равномерное про-
пространство иМс! Докажите, что каждая ограниченная веще-
вещественная функция f на Му равномерно непрерывная относи-
относительно °11м и равномерности Т на /?, индуцированной естествен-
естественной метрикой, продолжается до ограниченной вещественной
функции F на Ху равномерно непрерывной относительно °U и Т.
Указание (Гантнер [1969]). Рассмотрите функцию f, прини-
принимающую только неотрицательные значения и удовлетворяющую
условию f~1(O)=7lt0. Примените (а), продолжите псевдометрику
р на М, определенную формулой p{xty) = \f(x) — f{y)\f до
псевдометрики а на X и положите F{x) = о(х, f~l @)).
(c) Убедитесь, что предположение об ограниченности р в
(а) и предположение об ограниченности f в (Ь) оба суще-
существенны.
Слабейшие вполне ограниченные равномерности и компак-
тификации Самюэля
8.5.7. (а) (Самюэль [1948]). Покажите, что для каждой
равномерности °U на тихоновском пространстве X равномер-
равномерность %, порожденная семейством всех отображений X в I,
равномерно непрерывных относительно °U и единственной рав-
равномерности на /, есть вполне ограниченная равномерность на
пространстве X, которая слабее равномерности Щ. Проверьте,
что °U<s — сильнейшая равномерность на пространстве X, вполне
ограниченная и более слабая, чем °U. Пространство sX9 где
(sX^o) — пополнение равномерного пространства (Х,^о), на-
называется компактификацией Самюэля пространства X относи-
относительно равномерности °U.
Докажите, что компактификация Самюэля пространства X
относительно °Ы содержит X, где (Я, %?) — пополнение равно-
равномерного пространства (X, Щ) (ср. с задачей 8.5.20).
8.5. ЗАДАЧИ 675
(b) Докажите, что для каждой равномерности Ш на тихо-
тихоновском пространстве X совокупность С всех покрытий про-
пространства X, в которые можно вписать конечные покрытия,
равномерные относительно Шу обладает свойствами (UC1) —
(UC4). Покажите, что равномерность, порожденная совокуп-
совокупностью С равномерных покрытий, совпадает с равномерностью
%ь определенной в (а).
Указание. См. указание к упр. 8.1 .Н.
Замечание. Естественный вопрос — для каждого ли карди-
кардинала m ^ Ко совокупность Ст всех покрытий пространства Х>
имеющих вписанные покрытия мощности <т, равномерные
относительно °U, обладает свойством (UC3). Исбелл в [1964]
заметил, что ответ положителен для m=i*i; Куцья в [1973]
обнаружил, что в предположении обобщенной гипотезы конти-
континуума (т. е. в предположении, что для каждых кардиналов
tt, ш, таких, что п < ш, выполняется неравенство 2n^ш) ответ
всегда положителен. Пелант в [1975] доказал, что этот вопрос
независим от аксиом теории множеств.
Универсальные равномерности
8.5.8. (а) Пусть Щ — универсальная равномерность на тихо-
тихоновском пространстве X. Покажите, что сильнейшая (тончай-
(тончайшая) равномерность °U§ на пространстве X, вполне ограничен-
ограниченная и более слабая, чем °U (см. задачу 8.5.7), совпадает с рав-
равномерностью в7*, определенной в примере 8.1.19. Установите,
что компактификация Самюэля тихоновского пространства X
относительно универсальной равномерности на X совпадает со
стоун-чеховской компактификацией пространства X.
(b) Пусть °U — универсальная равномерность на тихонов-
тихоновском пространстве X и (\лХ9<Ы) — пополнение равномерного про-
пространства {ХуЩ). Докажите, что \iX — подпространство веще-
вещественной компактификации по Хьюитту vX пространства X, так
что Xcz\iXczvXcz рЛГ.
(c) Пусть Ш — универсальная равномерность на тихонов-
тихоновском пространстве X и {^Х.Щ) — пополнение равномерного про-
пространства {Xy°U). Заметьте, что каждая псевдометрика р на
множестве Ху являющаяся непрерывным отображением ХУ^Х
в R, может быть продолжена до псевдометрики р на множестве
цХ, являющейся непрерывным отображением \iXX\*>X^R.
Указание. Примените упр. 8.3.Е(а).
Пространства со слабейшей равномерностью
8.5.9 (Самюэль [1948]). Покажите, что слабейшая равно-
равномерность на тихоновском пространстве X существует в том
и только том случае, если пространство X локально компактно.
43»
676 ГЛ. 8. РАВНОМЕРНЫЕ ПРОСТРАНСТВА И ПРОСТРАНСТВА БЛИЗОСТИ
Указание. Примените задачу 8.5.7 и теоремы 3.5.12, 8.3.10
и 8.3.16.
Характеристика псевдокомпактности в терминах равномер-
ностей
8.5.10 (Досс [1947]). Докажите, что для каждого тихонов-
тихоновского пространства X следующие условия равносильны:
A) Пространство X псевдокомпакт но.
B) Каждая равномерность на пространстве X вполне огра-
ограничена.
C) Равномерности ?? и <&* на пространстве X совпадают.
Указание. Чтобы доказать, что из A) вытекает B), пока-
покажите, что если B) не выполнено, то существует бесконечное
дискретное семейство непустых открытых подмножеств про-
пространства X. Импликация C)=^A) следует из упр. 3.11.С.
Пространства с единственной равномерностью
8.5.11 (Досс [1949]). Докажите, что для каждого тихонов-
тихоновского пространства X следующие условия равносильны (ср. с
задачей 3.12.1б(а)):
A) Пространство X обладает единственной (с точностью
до эквивалентности) компактификацией.
B) Существует только одна равномерность на простран-
пространстве X.
C) Существует только одна вполне ограниченная равно-
равномерность на пространстве X.
Указание. При доказательстве импликации A)=>-B) вос-
воспользуйтесь задачами 3.12.1б(а) и 8.5.10.
Пространства без полных равномерностей
8.5.12 (Дьедонне [1939а]). Заметьте, что если некомпактное
тихоновское пространство X имеет единственную компактифи-
кацию, то не существует полной равномерности на X (ср. с за-
задачей 3.12.16(а)).
Полные по Дьедонне пространства
8.5.13. Топологическое пространство X называется полным
по Дьедонне, если на нем существует полная равномерность.
Легко видеть, что топологическое пространство X полно по
Дьедонне в том и только том случае, если X — тихоновское про-
пространство и универсальная равномерность на X полна.
(а) (Дьедонне [1939]). Проверьте, что полнота по Дьедонне
наследуется замкнутыми множествами и мультипликативна.
Докажите, что для каждого топологического пространства X
следующие условия равносильны:
8.5. ЗАДАЧИ 677
A) Пространство X полно по Дьедонне.
B) Пространство X гомеоморфно замкнутому подпростран-
подпространству произведения пространств, метризуемых полной метри-
метрикой.
C) Пространство X гомеоморфно замкнутому подпростран-
подпространству произведения метризуемых пространств.
D) Пространство X гомеоморфно пределу обратного спектра
пространств, метризуемых полной метрикой.
E) Пространство X гомеоморфно пределу обратного спек-
спектра метризуемых пространств.
Установите, что вещественно полные пространства полны
по Дьедонне (это можно также вывести из примера 8.3.19 или
задачи 8.5.8 (Ь)). Заметьте, что из упр. 5.1.J(f) следует, что
каждый паракомпакт является полным по Дьедонне простран-
пространством (ср. с (Ь) и (d) ниже).
Указание. Для доказательства импликации C)=^B) до-
достаточно показать, что каждое метризуемое пространство X
гомеоморфно замкнутому подпространству произведения про-
пространств, метризуемых полной метрикой. Для этого рассмотрите
метризуемое полной метрикой пространство У, содержащее X,
и произведение JJ (У \ {#}).
Y\X
(b) (Кац [1954], Фролик [1961b], Тамано [1962]). Дока-
Докажите, что для каждого тихоновского пространства X следую-
следующие условия равносильны:
A) Пространство X полно по Дьедонне.
B) Для каждой точки хо^$Х\Х существует такой пара-
компакт Та:$Х,что XczTcz рХ\ {хо}.
C) Для каждой точки х0 е РА\Х существует локально ко-
конечное функционально открытое покрытие s4> пространства X,
такое, что точка хо не принадлежит замыканию в $Х никакого
элемента покрытия $&.
D) Для каждой точки хо е РХ\Х существует локально ко-
конечное разбиение единицы {fs}S(=s на пространстве Ху такое,
что точка хо не принадлежит замыканию в $Х никакого мно-
множества /74@, 1]).
Установите, что каждый паракомпакт является полным по
Дьедонне пространством.
Указание. При доказательстве того, что A)=>B), заметьте,
что существует псевдометрика р: Xy^X-^R, которую нельзя
непрерывно продолжить на пространство (X\j {xo})X(^U {*o}).
Рассмотрите отображение /: X—> У = Х/р (см. упр. 4.2.1), его
продолжение F: pA'-^pf, где f — пополнение пространства У,
и сужение F?: F~l (?)-*?. Покажите, что пространство Г =
= F~l(Y) обладает требуемыми свойствами (примените тео-
678 ГЛ. 8. РАВНОМЕРНЫЕ ПРОСТРАНСТВА И ПРОСТРАНСТВА БЛИЗОСТИ
рему 5.1.35). При доказательстве импликации C)=>D) вос-
воспользуйтесь упр. 7.1.В. При доказательстве того, что D) =^A),
рассмотрите пополнение \iX cr рх пространства X относительно
универсальной равномерности на X. Допуская, что существует
точка хо е iiX\X с: $Х\ХУ используйте разбиение единицы
в D) для определения псевдометрики р: Xy(X-+Rt которую
нельзя непрерывно продолжить на pJf X М-Х
(c) Заметьте, что на множестве полных по Дьедонне про-
пространств компактность, счетная компактность и псевдокомпакт-
псевдокомпактность эквивалентны.
(d) (Нагата [1950а]). Приведите прямое доказательство
того факта, что на каждом паракомпакте существует полная
равномерность (ср. с (а) и (Ь) выше).
Указание. Проверьте, что семейство всех открытых покрытий
пространства X обладает свойствами (UC1) — (UC4). Предпо-
Предположите, что существует центрированное семейство & замкну-
замкнутых подмножеств пространства X, которое содержит произ-
произвольно малые множества и удовлетворяет условию П^" = 0-
Для каждой точки хе! выберите ее окрестность Ux, не пере-
пересекающуюся с каким-нибудь элементом семейства ^", и рас-
рассмотрите покрытие {Ux}xgX пространства X
(e) (Кац [1954]). Докажите, что если X — подпространство
полного по Дьедонне пространства У и для каждой точки хое
е Y\X существует локально конечное функционально открытое
покрытие $?> пространства X, такое, что точка х0 не принадле-
принадлежит замыканию в У никакого элемента покрытия s4>y то про-
пространство X полно по Дьедонне.
Указание. Предположите, что X всюду плотно в У, рассмот-
рассмотрите продолжение /: рХ-^рУ вложения пространства X в про-
пространство У и заметьте, что pX\Z = [fLl(y)\^]U[/py)\
f4Y)h
4Y)h
(f) (Дьедонне [1939]). Докажите, что если X — подпро-
подпространство полного по Дьедонне пространства У и для каждой
точки хоеУ\Х существует счетное семейство {HFJ^ откры-
тых подмножеств пространства У, такое, что хое П WtczY \Х,
то пространство X полно по Дьедонне.
Установите, что полнота по Дьедонне наследуется TVmho-
жествами.
(g) (Дьедонне [1939b], Кац [1954]). Пусть А" —полное по
Дьедонне пространство, удовлетворяющее первой аксиоме счет-
ности. Пусть топология 02 на множестве X сильнее исходной
топологии О и и пусть (X, О2) — тихоновское пространство. До-
Докажите, что (X, 02) полно по Дьедонне.
8.5. ЗАДАЧИ 679
Указание. Рассмотрите продолжение тождественного ото-
отображения (Ху С2) в (X, О\) на стоун-чеховскую компактифи-
кацию.
(h) (Широта [1952]). Докажите, что полное по Дьедонне
пространство X является вещественно полным тогда и только
тогда, когда каждое дискретное замкнутое подпространство
пространства X вещественно полно. Пусть мощность каждого
замкнутого дискретного подпространства полного по Дьедонне
пространства X — неизмеримый кардинал. Докажите, что тогда
X вещественно полно. Пусть, наконец, мощность каждого се-
семейства попарно непересекающихся непустых открытых под-
подмножеств полного по Дьедонне пространства — неизмеримый
кардинал. Докажите, что тогда X вещественно полно.
Указание. Примените (а) и задачу 5.5.10(а).
(i) (Зенор [1970]). Докажите, что пространство 2Z(X) всех
непустых компактов в X полно по Дьедонне в том и только том
случае, когда X полно по Дьедонне.
Указание. Примените задачу 3.12.26(f).
(j) (Исии [1959]). Докажите, что линейно упорядоченное
пространство X полно по Дьедонне в том и только том случае,
когда X — паракомпакт.
Указание (Энгелькинг и Латцер [1977]). В силу 5.5.22(f),
достаточно доказать, что не существует полного по Дьедонне
стационарного подмножества S пространства W(a)t где а —
предельный ординал, такой, что о>о не конфинально а. Так как
семейство @" = {S(}{x, ~^)}x<=s Центрировано и П^= 0, то
достаточно показать, что для любой открытой окрестности U
диагонали AciSXS существует такой элемент x(U)^S, что
(x,y)^U, как только х, j/eSn(x(f/),->). Допуская против-
противное, определите две трансфинитные последовательности хо,
хи ..., x%i ..., I < у, и уо, уи ... у Уь • • •» I < Tt конфинальные
в S и такие, что (л^, у^фи и xl<yl< хг> для всех |< ?' < \>-
Рассмотрите множество {х^: | <; у}.
Прямое построение пополнения
8.5.14 (Самюэль [1948]). (а) Пусть {Х.Щ) — равномерное
пространство. Мы называем фильтр Коши У в (X, Щ) мини-
минимальным, если для каждого фильтра Коши &*' в \ХУ%1), со-
содержащегося в ir> имеем #"' = У. Покажите, что любой фильтр
Коши в {X, °U) содержит ровно один минимальный фильтр
Коши. Установите, что для любой точки х е X семейство всех
подмножеств пространства Х> содержащих какую-нибудь окре-
окрестность точки х, если минимальный фильтр Коши в (X, Щ).
680 ГЛ. 8. РАВНОМЕРНЫЕ ПРОСТРАНСТВА И ПРОСТРАНСТВА БЛИЗОСТИ
(Ь) Пусть (Х> Щ) — равномерное пространство. Обозначим
через X семейство всех минимальных фильтров Коши в (X, %L)
и для каждого Уе% положим
(?={(Г1,ЗГ2)е1Х X: 8(F)<V для некоторого fG^ifl^}.
Установите, что семейство {V: Уе^} окружений диагонали
Aci^X^ обладает свойствами (BUI) — (BU3) и потому по-
порождает равномерность °п на множестве X. Покажите, что рав-
равномерное пространство (Х>Ш) есть пополнение пространства
()
Указание. Воспользуйтесь упр. 8.З.В.
Пополнение абелевой группы есть абелева группа.
8.5.15. Пусть G — абелева топологическая группа. Рассмот-
Рассмотрите равномерное пространство (О,Ш), где °Ы — равномерность
на G, определенная в примере 8.1.17, и его пополнение (<?,<?/)*
Покажите, что на О можно определить операцию умножения,
относительно которой G — абелева топологическая группа, та-
таким образом, что G станет подгруппой группы G.
Пространства замкнутых подмножеств V (см. задачи 2.7.20,
3.12.26, 4.5.22 и 6.3.22)
8.5.16. Пусть (X, Щ) — равномерное пространство и 2х— се-
семейство всех непустых подмножеств пространства X, замкну-
замкнутых в топологии, индуцированной равномерностью °U.
(a) Покажите, что семейство Ш всех множеств
2V = {(Л, Л') с 2х X 2х: А с В (А\ V) и Аг сг В (Л, К)},
где Fe?/, обладает свойствами (BUI) —(BU3). Равномер-
Равномерность на множестве 2х, порожденная базой Л?, обозначается
24 Проверьте, что (X, °U) равномерно изоморфно подпростран-
подпространству полученного таким образом равномерного пространства,
которое замкнуто в топологии, индуцированной на 2х равно-
равномерностью 2Ч.
(b) Проверьте, что если равномерность °U на множестве X
индуцирована метрикой р на множестве X, то равномерность
2% на семействе Ж всех ограниченных непустых замкнутых
подмножеств пространства (X, р) совпадает с равномерностью,
индуцированной метрикой Хаусдорфа.
(c) (Майкл [1951]). Покажите, что для любой равномер-
равномерности °Ы на топологическом пространстве X топология на SZ(X),
индуцированная равномерностью 2^), совпадает с топологией
Вьеториса.
(d) Пусть {Х> °U) — вполне ограниченное равномерное про-
пространство. Проверьте, что в этом случае пространство Bх, 2ой)
также вполне ограничено.
8.5. ЗАДАЧИ 681
(e) Приведите пример полного равномерного пространства
{Х> °U)> такого, что пространство Bх, 2й) не полно.
Указание. Рассмотрите равномерность на вещественной пря-
прямой, порожденную базой, состоящей из всех множеств вида
и{ЛХ>1: A^sf-}, где s4- — счетное покрытие вещественной пря-
прямой попарно непересекающимися множествами.
(f) Покажите, что если равномерное пространство (X, °U) —
компакт, то пространство Bх, 2ой) также компакт.
Кардинальные функции IV (см. задачи 1.7.12, 1.7.13, 2.7.9—
2.7.11, 3.12.4, 3.12.7—3.12.11 и 3.12.12(j))
8.5Л7. Наименьший кардинал m ^ Ко, такой, что на тихо-
тихоновском пространстве X существует равномерность веса ^ш,
называется равномерным весом пространства X и обозна-
обозначается и(Х).
(a) (Шерф [1968]). Покажите, что для каждого тихонов-
тихоновского пространства X мы имеем w(X) = с(Х)и(Х).
Указание (Юхас [1971а]). Примените замечание 8.2.4.
(b) Установите, что для каждого тихоновского простран-
пространства X имеет место равенство w(X) — e(X)u(X)t и выведите из
него, что w(X) = f(X)u(X) для каждой кардинальной функ-
функции / из диаграммы задачи 3.12.7(е), кроме f = \ |.
(c) Приведите пример топологического пространства X
веса ш и равномерностей Щ\ и %L% на пространстве X, таких, что
(<U){U)
Строгие включения
8.5.18 (Александров и Пономарев [1959]). Пусть X есть
^-пространство, и пусть О и W — семейства всех открытых
и всех замкнутых подмножеств пространства X соответственно.
Отношение Ш между элементами семейств W и О называется
строгим включением на пространстве X, если оно обладает свой-
свойствами (SI1) — (SI7), сформулированными в § 8.4.
Покажите, что для каждого ^-пространства X существует
взаимно однозначное соответствие между близостями и стро-
строгими включениями на пространстве X.
Близостно непрерывные отображения метрических про-
пространств
8.5.19 (Ефремович [1952]) (а) Пусть (X, р) и (У,а) —
метрические пространства и б, б' — близости, индуцированные
метриками р, а на X и У соответственно. Покажите, что отобра-
отображение f: X-+Y близостно непрерывно относительно б и б' в том
и только том случае, если / равномерно непрерывно относи-
относительно р и а (ср. с упр. 8.1.А(Ь)).
682 ГЛ. 8. РАВНОМЕРНЫЕ ПРОСТРАНСТВА И ПРОСТРАНСТВА БЛИЗОСТИ
Указание. (Исбелл [1964]). Если отображение / не является
равномерно непрерывным, то найдутся такое е > 0 и такие
последовательности х[У х2> ... и х[, х'2> ... точек пространства
[ 2 [ 2
Ху что limp(v., *J) = 0 и or (/(*.), f(*'i))>& при i= I, 2, ... .
Определите конечное множество Л1 натуральных чисел, такое,
что а (/ (xt)y f (*,)) > е/4 при всех it j e M.
(Ь) Заметьте, что две метрики pi и р2 на множестве X рав-
равномерно эквивалентны (см. упр. 4.1.В(Ь)) в том и только том
случае, если они индуцируют одну и ту же близость.
Равномерности и близости
8.5.20 (Смирнов [1952]). Покажите, что если равномерность
Щ на пространстве X индуцирует близость б на J, то опреде-
определенная в задаче 8.5.7 равномерность % — сильнейшая равно-
меность на пространстве X, вполне ограниченная и более сла-
слабая, чем °U, также индуцирует близость б, т. е. равномерность
Шъ совпадает с равномерностью, индуцированной близостью б,
которая индуцирована равномерностью °U. Проверьте, что ком-
пактификация Самюэля тихоновского пространства X относи-
относительно равномерности °U — это та компактификация, которая
соответствует близости б, индуцированной равномерностью °lt
(ср. с теоремой 8.4.13).
8.5.21 (Смирнов [1952]). Пусть б — близость на множестве
X. Покрытие si> множества X называется слабо ^-равномерным,
если существует последовательность sf>\ = s4<y s?2> ... покрытий
пространства X, удовлетворяющая следующим двум условиям:
A) Mi+\ сильно звездно вписано в Mi при i= 1, 2, ... .
B) Для каждой пары А, В подмножеств пространства Ху
удовлетворяющих условию АЬВУ и для каждого i существует
множество Ai e s?iy такое, что А П Д/ ф 0 Ф В П Аи
(a) Покажите, что каждое б-равномерное покрытие про-
пространства X является слабо б-равномерным.
(b) Докажите, что для каждого слабо б-равномерного по-
покрытия зФ пространства X существует равномерность °U на
множестве Ху которая индуцирует близость б и содержит мно-
множество [){А У, А: А е«я?}.
8.5.22 (Катетов [1959], Даукер [1961]). Проверьте, что со-
совокупность С всех покрытий множества X = Ny^N, где N —
множество натуральных чисел, в которые можно вписать по-
покрытие вида {{х}Х.А: x^N, i4E^}, где зФ — конечное по-
покрытие множества N попарно непересекающимися множествами,
обладает свойствами (UC1) — (UC4). Пусть °U — равномер-
равномерность, порожденная С, и б — близость на X, индуцированная
равномерностью CU. Установите, что Дб[(#Х #)\A]. Пока-
Покажите, что покрытия {{*} XN}xgN и {NX{y}}yfE:N оба слабо
8.5. ЗАДАЧИ 683
6-равномерны и что единственное покрытие, вписанное одно-
одновременно в эти оба покрытия, состоит из всех одноточечных
подмножеств пространства X. Установите, что в семействе всех
равномерностей на множестве X, индуцирующих близость б, не
существует сильнейшей равномерности.
8.5.23 (Смирнов [1952]). Пусть б — близость на множестве
X, индуцированная метрикой на X. Докажите, что в семействе
всех равномерностей на множестве X, которые индуцируют
данную близость б, существует сильнейшая равномерность.
Указание. Покажите, что если для окружения V диагонали
ДсгХХ^ существуют две последовательности х[9 х2, ... илу,
х2, ... точек пространства X, такие, что | хь — х\ I ^ V при
i = 1, 2, ..., то для любого окружения W диагонали А с: X X Х>
удовлетворяющего включению 4W с У, существует бесконечное
множество М натуральных чисел, такое, что Iл:^ — J^i^W для
всех /, / е М.
ЛИТЕРАТУРА
Акуаро (Aquaro G.)
[1965] Ricovrimenti puntualmente numerabili di uno spazio numerabilmente
compatto.—Atti Acad. Naz. Lincei 39 A965), 19—21.
Алас (Alas О. Т.)
[1971] On a characterization of collectionwise normality. — Canad. Math.
Bull. 14 A971), 13—15.
Александер (Alexander J. W.)
[1939] Ordered sets, complexes and the problem of compactifications. — Proc.
Nat. Acad. Sci. USA 25 A939), 296—298.
Александров П. С.
[1923] Sur les proprietes locales des ensembles et la notion de compacitee. —
Bull. Intern. Acad. Pol. Sci. Ser. A A923), 9—12.
[1924] Sur les ensembles de la premiere classe et les ensembles abstraits.—
С R. Acad. Paris 178 A924), 185—187.
[1924a] Uber die Struktur der bikompakten topologischen Raume.— Math.
Ann. 92 A924), 267—274.
[1924b] Uber die Metrisation der in kleinen kompakten topologischen Rau-
Raume.—Math. Ann. 92 A924), 294—301.
[1925] Uber stetige Abbildungen kompakter Raume. — Proc. Akad. Amster-
Amsterdam 28 A925), 997—999.
[1927] Uber stetige Abbildungen kompakter Raume. — Math. Ann. 96 A927),
555—571.
[1928] Uber den allgemeinen Dimensionsbegriff und seine Beziehungen zur
elmentaren geometrischen Anschauung. — Math. Ann. 98 A928), 617—
636.
[1929] Untersuchugen uber Gestalt und Lage abgeschlossener Mengen belie-
biger Dimension. —Ann. of Math. 30 A929), 101—187.
[1932] Dimensionstheorie. Ein Beitrag zur Geometrie der abgeschlossenen
Mengen. —Math. Ann. 106 A932), 161—238.
[1936] К теории топологических пространств. — ДАН СССР 2 A936), 51—
54.
[1939] О бикомпактных расширениях топологических пространств. — Ма-
тем. сб. 5 A939), 403—423.
[1940] О размерности бикомпактных пространств. — ДАН СССР 26 A940),
619—622.
[1941] Теорема сложения в теории размерности бикомпактных про-
пространств. — Сообщ. АН Груз. ССР 2 A941), 1—6.
[1947] On the dimension of normal spaces.— Proc. Roy. Soc. London 189
A947), 11—39.
[1960] О метризации топологических пространств. — Bull. Acad. Pol. Sci.
Ser. Math. 8 A960), 135—140.
!) Звездочкой отмечены работы, добавленные при переводе. — Прим. пе-
рев.
ЛИТЕРАТУРА 685
Александров П. С, Немыцкий В. В.
[1938] Условие метризуемости топологических пространств и аксиома сим-
симметрии. — Матем. сб. 3 A938), 663—672.
Александров П. С, Пасынков Б. А.
[1975*] Введение в теорию размерности. — М.: Наука, 1975.
Александров П. С, Пономарев В. И.
[1959] О бикомпактных расширениях топологических пространств. — Вест.
Моск. унив., сер. матем. A959), № 5, 93—108.
Александров П. С., Урысон П. С.
[1923] Sur les espaces topologiques compacts. — Bull. Intern, Acad. Pol. Sci.
Ser. A A923), 5—8.
[1923a] Une condition necessaire et suffisante pour qu'une classe (L) soit
une classe (/>). — С R. Acad. Sci. Paris 177 A923), 1274—1276.
[1924] Zur Theorie der topologischen Raume. —Math. Ann. 92 A924), 258—
266.
[1928] Uber nulldimensionale Punktmengen. — Math. Ann. 98 A928), 89—
106.
[1929] Memoire sur les espaces topologiques compacts. — Verh. Akad. We-
tensch. Amsterdam 14 A929).
Александров П. С, Федорчук В. В.
[1978] Основные моменты в развитии теоретико-множественной тополо-
топологии. — УМН, т. 33, вып. 3 A978), с. 3—48.
Александров П. С, Хопф X. (Alexandroff P., Hopf H.)
[1935] Topologie I. —Berlin, 1935.
Альстер, Поль (Alster К., Pol R.)
[1980*] On function spaces on compact subspaces of 2-products of the real
line.— Fund. Math. 107 A980), 135—143.
Амирджанов Г. П.
[1977*] О всюду плотных подпространствах счетного псевдохарактера и
других обобщениях сепарабельности.—ДАН СССР 234 A977), 993—
996,
Амирджанов Г. П., Шапировский Б. Э.
[1974*] О всюду плотных подмножествах топологических пространств. —
ДАН СССР 214 A974), 249-252.
Андерсон (Anderson R. D.)
[1966] Hilbert space is homeomorphic to the countable infinite product of
lines. —Bull. Amer. Math. Soc. 72 A966), 515—519.
Антоновский М. Я.
[1961*] К аксиоматике топологических полуполей. — ДАН УзССР 10 A961),
3—6.
[1961*] Метрические пространства над полуполями. — Proceedings of the
Symposium on General Topology, Prague, 1961, pp. 64—68.
[1970*] Гомоморфизмы тихоновских полуполей и обобщенные полуметри-
полуметрики.—Fund. Math. 69 A970), 109—123.
[1972*] Some algebraic and topological characteristics of Ulam's measurable
cardinals. In: Topology and its applications (Budva, 1972). — Beo-
grad, 1973, pp. 25—30.
[1982*] Обобщенные метрики и меры и некоторые их приложения. — Math.
Vesnik 6 A9) C4) A982), 9—21.
Антоновский М. Я., Болтянский В. Г., Сарымсаков Т. А.
{1961*] Метрические пространства над полуполями. — Тр. Таш. ун-та, 191
П961).
[1962*] Конечномерные модули над полуполями. — Тр. Таш. ун-та, 208
A962), 3-29.
[1963*] Топологические алгебры Буля. — Ташкент: Издат. АН УзССР, 1963,
с. 1—124.
686 ЛИТЕРАТУРА
[1966*] Очерки теории топологических полуполей. — УМН 21 A966), 185—
218.
[1970*] Тихоновские полуполя и некоторые проблемы общей топологии.—
УМН 25 A970), 3—48.
[1977*] Topological Semifields and Their Application to General Topology.—
Amer. Math. Soc. Trans. Ser. 2, 106 A977), vi — 142.
Антоновский М. Я., Кошевникова И. Г.
[1970*] К вопросу о полуметризации полуравномерных структур. — Тр. Tain.
ПИ (матем.) 56, A970), 12-28.
[1972*] Пространства сходимости типа Фреше — Урысона и обобщенная ме-
метризация. — Матем. вестник 9 B4) A972), 373—378.
Антоновский М. Я., Миронов А. В.
[1967*] К теории топологических /-групп. — ДАН УзССР 6 A967), 6—8.
Антоновский М. Я., Поляков В. 3.
[1971*] О некоторых решетках топологического типа и их гомоморфизмах.—
ДАН СССР 198 A971), № 3.
[1972*] Несимметричные близости и метрики. —ДАН СССР 206 A972),
13—16.
Антоновский М. Я-, Хьюитт Э.
[1977*] Структура гипервещественных полей. Proc. of the 3d Int. Symp. on
Topology and its Appl. — Beograd, 1977, pp. 25—30.
Антоновский М. Я., Чобаи М. M.
[1981*1 Инвариантные обобщенные метрики на топологических алгебрах.—
Math. Vesnik 5 A8), A981), 1—18.
[1981а*]Радиальные метрики и их применение к топологическим группам.—
Math. Vesnik, 5 A8) A981), 129—138.
Антоновский М. Я-, Чудновский Д. В.
[1976*] Некоторые вопросы общей топологии и тихоновские полуполя, II. —
УМН 31 A976), 71—128.
Арене (Arens R.)
[1946] A topology for spaces of transformations. — Ann. of Math. 47 A946),
480—495.
[1950] Note on convergence in topology. — Math. Mag. 23 A950), 229—
234.
[1952] Extension of functions on fully normal spaces. — Pacific J. of Math.
2 A952), 11—22.
[1958] Dense inverse limit rings. — Michigan Math. J. 5 A958), 169—182.
Арене, Дугунджи (Arens R., Dugundji J.)
[1950] Remark on the concept of compactness.— Portugaliae Math. 9 A950),
141_H3.
[1951] Topologies for function spaces. — Pacific J. of Math. 1 A951), 5—31.
Арнаутов В. И.
[1970*] Недискретная топологизуемость бесконечных коммутативных ко-
колец.—ДАН СССР 194 A970), 991—994.
[1970а*] Недискретиая топологизуемость счетных колец. — ДАН СССР 191
A970), 747—750.
Арнаутов В. И., Марин Е. И., Михалев А. В.
[1984*] Необходимые условия продолжения топологий группы и поля на их
групповую алгебру. — Вестиик МГУ, сер. матем. A984), № 6,
58—61.
Ароишайн (Aronszajn N.)
[1931] Uber ein Urbildproblem. — Fund. Math. 17 A931), 92—121.
Архангельский А. В.
[1959] Аддиционная теорема для веса множеств, лежащих в бикомпак-
бикомпактах.—ДАН СССР 126 A959), 239—241.
[1960] О метризации топологических пространств, — Bull. Acad. Pol. Sci.
Ser. Math. 8 A960), 589—595.
ЛИТЕРАТУРА 687
[1960а] О внешних базах множеств, лежащих в бикомпактах. — ДАН СССР
132 A960), 495—496.
[1961] О топологических пространствах, полных в смысле Чеха.— Вест.
Моск. унив., сер. матем. A961), № 2, 37—40.
[1961а] Новые критерии паракомпактности и метризуемости произвольного
^-пространства. — ДАН СССР 141 A961), 13—15.
[1963] Бикомпактные множества и топология пространств. — ДАН СССР
150 A963), 9-12.
[1963а] Некоторые типы факторных отображений и связи между классами
топологических пространств. — ДАН СССР 53 A963), 743—746.
[1964] О факторотображениях метрических пространств. — ДАН СССР 155
A964), 247—250.
[1965] Бикомпактные множества и топология пространств. — Тр. Моск. ма-
матем. об-ва 13 A965), 3—55.
[1965*] Об одном классе пространств, содержащем все метрические и все
локально бикомпактные пространства. — Матем. сб. 67 A09), A965),
№ 1, с. 55—85.
[1966] Признак существования бикомпактного элемента в непрерывном
разбиении. Теорема об инвариантности веса при открыто-замкнутых
конечнократных отображениях. — ДАН СССР 196 A966), 1263—
1266.
[1966а] Отображения открытые и близкие к открытым. Связи между про-
пространствами.— Тр. Моск. матем. об-ва 15 A966), 181—223.
[1966b] Отображения и пространства. — УМН 21 A966), вып. 4, 133—
184.
[1966с*] О замкнутых отображениях, бикомпактных множествах и одной
задаче П. С. Александрова. — Матем. сб. 69 A11), A966), № i,
с. 13—34.
[1967] О факторизации отображений по весу и размерности. — ДАН СССР
174 A967), 1243—1246.
[1967а] О совершенных отображениях и уплотнениях. — ДАН СССР 176
A967), 983—986.
[1968] A characterization of very fc-spaces. — Czech. Math. J. 18 A968),
392—395.
[1968a*] Об отображениях, связанных с топологическими группами. — ДАН
СССР 181 A968), 1303—1306.
[1969] Аппроксимация теории диадических бикомпактов. — ДАН СССР 184
A969), 767—770.
[1969а] О мощности бикомпактов с первой аксиомой счетности. — ДАН
СССР 187 A969), 967—970.
[1970] Число Суслина и мощность, характеры точек в секвенциальных би-
бикомпактах. — ДАН СССР 192 A970), 255-258.
[1971] О бикомпактах, которые удовлетворяют условию Суслина наслед-
наследственно. Теснота и свободные последовательности. — ДАН СССР
199 A971), 1227—1230.
[1971а*] Об отображениях всюду плотных подпространств топологических
произведений. — ДАН СССР 197 A971), 750—753.
[1972] Спектр частот топологического пространства и классификация про-
пространств. — ДАН СССР 206 A972), 265—268.
[1976*] О некоторых топологических пространствах, встречающихся в функ-
функциональном анализе. — УМН, 31 A976) № 5, с. 17—32.
[1976а*] Теоремы о мощности семейств множеств в бикомпактах. — ДАН
СССР 226 A976), №5.
[1976b*] Аксиома Мартина и строение однородных бикомпактов счетной тес-
тесноты.—ДАН СССР 226 A976), 1249—1252.
[1977*] О пространствах, растянутых влево. — Вестник МГУ, сер. матем.,
5 A977), 30-36.
588 ЛИТЕРАТУРА
[1978*1 О топологиях, допускающих слабую связь с упорядочениями.—
ДАН СССР, 238 A978), 773—776.
[1978а*] О пространствах непрерывных функций в топологии поточечной
сходимости. — ДАН СССР, 240 A978), 505—508.
[1978b*] Строение и классификация топологических пространств и карди-
кардинальные инварианты. — УМН 35 A978) № 6, с. 29—84.
[1979*] Об инвариантах типа характера и веса. — Тр. Моск. матем. об-ва,
38 A979), 3—23.
[1979а*] Спектр частот топологического пространства и операция произведе-
произведения. — Тр. Моск. матем. об-ва 39 A979), 171—206.
[1980*] О некоторых свойствах радиальных пространств. — Матем. заметки
27 A980), № 1, с. 95—104.
[1980а*] Метод звезд, новые классы пространств и счетная компактность.—
ДАН СССР 251 A980), 1033—1037.
[1980b*] О соотношениях между инвариантами топологических групп и их
пространств. — УМН 35 A980), № 3, с. 3—22.
[1981*] Классы топологических групп.— УМН 36 A981), № 3, с. 127—
146
[1982*] Факторизационные теоремы о пространствах функций: устойчивость
и монолитность. — ДАН СССР 265 A982), 1039—1043.
[1982а*] О линейных гомеоморфизмах пространств функций. — ДАН СССР
264 A982), 1289—1292.
[1982b*] Теорема о т-аппроксимации и функциональная двойственность.—
Матем. заметки 31 A982), № 3, с. 421—432.
[1983*] Топологические свойства пространств функций: теоремы двойствен-
двойственности. — ДАН СССР 269 A983), № 6, с. 1289—1292.
[1983а*] Пространства функций и условия типа полноты. — Вестн. МГУ,
сер. матем., № 6 A983), 3—9.
[1983b] Functional tightness, Q-spaces and т-embeddings.— Comment. Math.
Univ. Carol. 24 A983), 105—120.
[1984*] Непрерывные отображения, факторизационные теоремы и про-
пространства функций. — Тр. Моск. матем. об-ва 47 A984), 3—21.
[1984а*] Пространства функций в топологии поточечной сходимости и ком-
компакты.—УМН 39 A984), № 5, с. 11—50,
[1985*] Клеточные структуры и однородность. — Матем. заметки, 37 A985),
№ 4, с. 580—586.
Архангельский А. В., Голштынский В.
[1963] Sur les reseaux dans les espaces topologiques.— Bull. Acad. Pol. Sci.
Ser. Math. 11 A963), 493—497.
Архангельский А. В., Пономарев В. И.
[1968] О диадических бикомпактах. — ДАН СССР 182 A968), 993—996.
996.
[1974*] Основы общей топологии в задачах и упражнениях. — М.: Наука,
1974.
Архангельский А. В., Ранчин Д. В.
[1982*] О всюду плотных подпространствах топологических произведений и
о свойствах, связанных с финальной компактностью. — Вести. МГУ,
сер. матем., A982), № 6, с. 21—28.
Архангельский А. В., Чинчура Ю.
[1984*] On continuous images of almost Tychonoff cubes,—Comment. Math.
Univ. Carol. 25 A984), 287—295.
Асанов М. Ом Величко Н. B.
[1981*] Компактные множества в Ср(Х).—Comment. Math. Univ. Carol.
22 A981), 255—266.
Балачандран (Balachandran V. K.)
[1955] A mapping theorem for metric spaces.— Duke Math. J. 22 A955),
461-464.
ЛИТЕРАТУРА 689
Балог 3.
[1979*1 Об относительной счетной компактности. — УМН, 34 A979), № 6,
с. 139—143.
Банах (Banach S,)
[1922] Sur Ies operations dans Ies ensembles abstraits et leurs applications
aux equations integrates--Fund. Math. 3 A922), 133—181.
[1931] Ober die Bairesche Kategorie gewisser Funktionenmengen. Studia
Math. 3 A931), 174—179.
[1932] Theorie des operations lineaires — Warszawa 1932, [Украинский пере-
перевод: Банах С. Курс функционального анализу. — Ки;в, 1948.]
Банашевский (Banaschewski В.)
[1956] Local connectedness of extension spaces. — Canad. J. of Math. 8
A956). 395—398.
Бандлов И.
[1978*] Гиперабсолют отображения. — ДАН СССР 240 A978), 760—763.
Бандлов И., Пономарев В. И.
[1980*] Кардинальнозначные инварианты типа тесноты. Абсолюты про-
пространств и непрерывных отображений. — УМН 35 A980), № 3,
с. 23—30.
Бартл (Bartle R. G.)
[1955] Nets and filters in topology. — Amer. Math. Monthly 62 A955), 551—
Бегль (Begle E. G.)
[1949] Anote on S-spaces. — Bull. Amer. Math. Soc. 55 A949), 557—579.
Бельнов В. К.
[1976*] О нульмерных топологических группах.— ДАН СССР 226 A976),
749—753.
Беннет (Bennett H. R.)
[1971] A note on point-countability in linearly ordered spaces. — Proc. Amer.
Math. Soc. 28 A971), 598—606.
Бернштейн (Bernstein F.)
[1908] Zur Theorie dcr trigonometrischen Reihe. — Berichte Konigl. Sachs.
Gesellschaft der Wiss. Leipzig Math. — Phys. Klasse 60 A908), 325—
338.
Берри, Портер, Стефенсон (Berri M. P., Porter J. R., Stephenson R. M.
jr.)
[1968] A survey of minimal topological spaces. In: General Topology and
its Relations to Modern Analysis and Algebra (Proceedings of the
Kanpur Topological Conference 1968).— Prague 1971, 93—114.
Бёме (Boehme Т. К.)
[1965] Linear s-spaces. — Preprint of a talk presented at the Symposium on
Convergence Structures, Univ. of Oklahoma, 1965.
Бинг (Bing- R. H.)
[1951] Metrization of topological spaces. — Canad. J. of Math. 3 A951),
175—186.
[1953] A connected countable Hausdorff space. — Proc. Amer. Math. Soc. 4
A953), 474.
Биркгоф (Birkhoff G.)
[1936] A note on topological groups. — Сотр. Math. 3 A936), 427—430.
[1937] Moore-Smith convergence in general topology.— Ann. of Math. 38
A937), 39—56.
[1940] Lattice cheory. — New York, 1940. [Русский перевод: Биркгоф Г.
22 A974), 821-825.
Теория структур. — М.: ИЛ, 1952.]
Богатый С. А.
[1974*] Об «-подвижности в смысле К. Борсука. — Bull. Acad. Polon. Sci.,
44 За к. 697
690 ЛИТЕРАТУРА
Богатый С. А., Смирнов КХ М.
[1974а*] Аппроксимация полиэдрами и факторизационные теоремы для
Л##-бикомпактов. — Fund. Math. 87 A974), 195—205.
Бокштейн М. Ф.
[1948] Un theoreme de separabitite pour les produits topologiques,— Fund.
Math. 35 A948), 242—246.
Болл (Ball B. J.)
[1954] Countable paracompactness in linearly ordered spaces. — Proc. Amer.
Math. Soc. 5 A954), 190—192.
Болтянский В. Г.
[1961*] Аксиомы отделимости и метрика. — ДАН СССР 197 A971), 1239™
1242.
Бонан (Bonan E.)
[1970] Sur un lemme adapte au theoreme de Tietsze-Urysohn. — C. R. Acad.
Sci. Paris 270 A970), Ser. A, 1226—1228.
Борджес (Borges C. J.)
[1966] On stratifiable spaces. — Pacific J. Math. 17 A966), 1—16.
Борель (Borel E.)
[1903] Sur Tapproximation des nombres par es nombres rationnels. — C. R.
Acad. Sci. Paris 136 A903), 1054—1055.
Борсук (Borsuk K.)
[1932] Uber Schnitte der n-dimensionalen Euklidischen Raume.—Math. Ann.
106 A932), 239—248.
[1933] Uber Isomorphie der Funktionalraume. — Bull. Intern. Acad. Pol. Sci.
Ser. A A933), 1—10.
[1935] Quelques retracts singuliers. —Fund. Math. 24 A935), 249—258.
[1937] Sur les prolongements des transformations continues. — Fund. Math.
28 A937), 99—110.
Брауэр (Brouwer L. E. J.)
[1910] On the structure of perfect sets of points. — Proc. Akad. Amsterdam
12 A910), 785—794.
[1911] Beweis des Invarianz der Dimensionenzahl. — Math. Ann. 70 A911),
16J —165.
[1912] Ober Abbildung von Mannigfaltigkeiten. — Math. Ann. 71 A912),
91—115.
[1913] Uber den naturlichen Dimensionsbegriff.—J. fur die relne
und angew. Math. 142 A913), 146—152.
[1913a] Some remarks on the coherence type t\. — Proc. Akad. Amsterdam 15
A913), 1256—1263.
[1924] Bemerkungen zum naturlichen D!mensionsbegriff. — Proc. Akad, Ams-
Amsterdam 27 A924), 635—638.
Брунс, Шмидт (Bruns G., Schmidt J.)
[1955] Zur Aquivalenz von Moore — Smith-Folgen und Filtern. — Math.
Nachr. 13 A955), 169—186.
Бурбаки (Bourbaki N.)
[1940] Topologie generate ch. I et II. —Paris, 1940.
[1948] Topologie generale ch. IX. —Paris, 1948.
[1949] Topologie generale ch. X. — Paris, 1949. [Русский перевод 3-го франц.
изд. в книге: Бурбаки Н. Общая топология. Основные структуры.—
М.: Наука, 1975, с. 173—261.]
[1951] Topologie generale ch. I et II. B-me ed.).— Paris, 1951. [Русский
перевод: Бурбаки Н. Общая топология. Основные структуры. — М.:
Физматгиз, 1958.]
[1958] Topologie generale ch. IX B-me ed.). —Paris, 1958. [Русский пере-
перевод 3-го франц. изд. в книге: Бурбаки Н. Общая топология. Основ-
Основные структуры. — М.: Наука, 1975, с. 11—172.]
[1961] Topologle generale ch. I et II C-me ed.). —Paris, 1961. [Русский пе-
ЛИТЕРАТУРА 691
ревод: Бурбаки Н. Общая топология. Основные структуры. — М.:
Наука, 1968.]
Бурбаки, Дьедонне (Bourbaki N., Dieudonne J.)
[1939] Note de teratopologie IL —Revue Scientifique 77 A939), 180—181.
Бурке (Burke D. K.)
[1969] On subparacompact spaces. — Proc. Amer. Math. Soc. 23 A969),
655—663.
Бут (Booth D.)
[1974] A Boolean view of sequential compactness.—Fund. Math. 85 A974),
99-102.
Бэгли, Коннелл, Макнайт (Bagley R. W., Connell E. H., McKnight J. D.)
[1958] On properties characterizing pseudo-compact spaces. — Proc. Amer.
Math. Soc. 9 A958), 500—506.
Бэгли, Янг (Bagley R. W., Yang J. S.)
{1966] On й-spaces and function spaces. — Proc. Amer. Math. Soc. 17 A966),
703—705.
Бэкон (Bacon P.)
[1968] Extending a complete metric. — Amer. Math. Monthly 75 A968), 642—
643.
Бэр (Baire R.)
[1904] Sur les series a termes continus et tous de meme signe. — Bull. Soc.
Math. France 32 A904), 125—128.
[1909] Sur la representation des fonctions discontinus (deuxieme partie), Ac-
ta Math. 32 A909), 97—176.
Бэр, Леви (Baer R. W., Levi F.)
[1932] Stetige Funktionen in topologischen Raumen. — Math. Zeitschr. 34,
A932), 110—130.
Bare (Wage M. L.)
[1977] The dimension of product spaces. — Preprint 1977.
[1978] The dimension of product spaces. — Proc. Mat. Acad. Sci. USA 75
A978), 4671—4672.
Вайнштейн И. А.
[1947] О замкнутых отображениях метрических пространств. — ДАН СССР
57 A947), 319—321.
[1947а] Об одной проблеме П. С. Александрова. — ДАН СССР 57 A947),
431—434.
[1952] О замкнутых отображениях. — Учен. зап. Моск. унив. 155 A952),
3—53.
Ван Данциг (Van Dantzig D.)
[1930] Uber topologisch homogene Kontinua. — Fund. Math. 15 A930), 102—
125.
Ван Дауэн (van Douwen E. K.)
[1973] The small inductive dimension can be raised by the adjunction of a
single point. — Indag. Math. 35 A973), 434—442.
[1977] Density of compactifications. In: Set-theoretic Topology (G. M. Reed,
ed.). — New York, 1977, pp. 97—110.
[1978] If К is a compact space then P(coj X K) = ((Oi + 1) X K. — Preprint
1978.
Ван Дауэн, Толл, Вейс (van Douwen E. K-, Tall F. D., Weiss W. A. R.)
[1977] Non-metrizable hereditarily Lindelof spaces with point-countable ba-
bases from CH. —Proc. Amer. Math. Soc. 64 A977), 139—145.
Ван дер Слот (van der Slot J.)
[1966] Universal topological properties. — Afd. Zuiv. Wisk. Z. W. 1966—011,
Amsterdam, 1966.
[1972] A survey of realcompactness. — Theory of sets and topology (in ho-
honour of Felix Hausdorff). —Berlin, 1972, 473—494.
44*
692 ЛИТЕРАТУРА
Веденисов Н Б.
[1936] Sur les fonctions continues dans les espaces topologiques. — Fund.
Math. 27 A936), 234—238.
[1939] Замечания о размерности топологических пространств. — Учен. зап.
Моск. унив. 30 A939), 131—140.
[1940] Generalisation de quelques theoremes sur la dimension. — Сотр.
Math. 7 A940), 194—200.
[1941] О размерности в смысле Е. Cech'a. — Изв. АН СССР, Сер. матгм.
5 A941), 211—216.
Вейль A. (Weil A.)
[1938] Sur les espaces a stiuciure uniforme et sur la topologie generate.—
Paris, 1938.
Вейль Г. (Weyl H.)
[1913] Die Idee der Riemannschen Flache.— Leipzig, 1913.
Вейр (Weir M. D.)
[1975] Hewitt — Nachbin spaces. — Amsterdam. 1975.
Величко Н. B.
[1967*] Пример открытого компактного монотонного отображения неметри-
зуемого бикомпакта на компакт. — ДАН СССР 177 A967), 995—
996.
[1972*] О непрерывных отображениях топологических пространств. — Сиб.
матем. ж. 13 A972), № 3, с. 541—557.
[1973*] О перистых пространствах и их непрерывных отображениях. — Ма-
Матем. сб. 90 A973), № 1, с. 34—47.
[1975] О пространстве замкнутых множеств. — Сиб. матем. ж. 16 A975),
627—629.
[1975а*]Заметка о перистых пространствах. — Cechoslov. Math. J. 25 A975),
8—19.
[1976*] К теории разложимых пространств. — Матем. заметки 19 A976),
109—114.
[1976а*]Упорядоченные р-пространства. — Изв. ВУЗов, матем., 9 A976),
25—36.
[1981*] О слабой топологии пространств непрерывных функций. — Матем.
заметки 30 A981), № 5. с. 703—712.
[1982*] К теории пространств непрерывных функций. — УМН 37 A982),
№ 4, 149—150.
Видосич (Vidossich G.)
[1972] Function spaces which are pseudo-K-compact spaces. — Preprint 1972.
Вислисени Ю., Флаксмайер Ю.
]1965[ Мощность и строение структуры бикомпактных расширений вполне
регулярного пространства. — ДАН СССР 165 A965), 258—260.
Волмэн (Wallman H.)
[1938] Lattices and topologocal spaces.— Ann. of Math. 39 A938). 112—
126.
Boh (Vaughan H.)
[1937] On locally compact metrisabie spaces. — Bull. Amer. Math. Soc. 43
A937), 532—535.
Вопенка (Vopenka P.)
[1959] Замечание о размерности метрических пространств. — Czech. Math.
J. 9 A959), 519—522.
Вудс (Woods R. G.)
[1978] A survey of absolutes of topological spaces. In: Topological Struc-
Structures II. Math. Centre Tracts 116 (Proceedings of the Symposium in
Amsterdam 1978).— Amsterdam, 1979, pp. 323—362.
Вулберт (Wulbert D. E.)
[1968] Subsets of first countable spaces. — Proc. Amer. Math. Soc. 19 A968),
1273-1277.
ЛИТЕРАТУРА 693
Вулих Б. 3.
[1952] О распространении непрерывных функций в топологических про-
пространствах. — Магем. сб. 30 A952), 167—170.
Вьеторис (Vietoris L.)
[1921] Stetige Mengen. — Monatsh. fur Math, und Phys. 31 A921), 173—
204.
[1922] Bereiche zweiter Ordnung — Monatsh, fur Math, und Phys. 32 A922),
258—280.
[1923] Kontinua zweiter Ordnung.— Monatsh, fur Math, und Phys. 33
A923), 49—62.
Гантнер (Gantner Т. Е.)
[1969] Some corollaries to the metrization lemma. — Amer. Math. Monthly
76 A969), 45—47.
Гельфанд И. М., Колмогоров А. Н.
[1939] О кольцах непрерывных функций на топологических простран-
пространствах.™ ДАН СССР 22 A939), 11—15.
Гемба, Семадени (Ggba К., Semadeni Z.)
[1960] Spaces of continuous functions V. — Studia Math. 19 A960), 303—
320.
Герлич (Gerlits J.)
[1983*] Some properties of C(X), II, —Topology and Appl. 15 A983), 255—
262.
Герлич, Надь Ж. (Gerlits J., Nagy Zs.)
[1980*] Об а-левых и а-растянутых пространствах. — УМН 35 A980) № 3,
с. 162—168.
Гиллман, Джерисон (Gillman L., Jerison M.)
[1960] Rings of continuous functions. —New York, 1960.
Гиллман, Хенриксен (Gillman L., Henriksen M.)
[1954] Concerning rings of continuous functions. — Trans. Amer. Math. Soc.
77 A954), 340—362.
Гильберт (Hilbert D.)
[1902] Ober die Grundlagen der Geometrie. — Math. Ann. 56 A902), 381—
422. [Русский перевод: Гильберт Д. Основания геометрии. — М.—
Л.: ОГИЗ, 1948.]
Гинзбург, Вудс (Ginsburg J., Woods R. G.)
[1977*] A cardinal inequality for topological spaces, involving closed discrete
sets. — Proc. Amer. Math. Soc. 64 A977), 357—360.
Гликсберг (Glicksberg I.)
[1952] The representation of functionals by integrals. — Duke Math., J. 19
A952), 253—261.
[1959] Stone-Cech compactifications of products. — Trans. Amer. Math. Soc.
90 A959), 369—382.
Глисон (Gleason A. M.)
[1958] Projective topological spaces, —III, J. of Math. 2 A958), 482—439.
Годел (Hodel R. E.)
[1969] Separability and the point countable property. — Notices Amer. Math.
Soc. 16 A969), 96.
[1969a] Sum theorems for topological spaces. — Pacific. J. of Math. 30 A969),
59—65.
[1976] New proof of a theorem of Hajnal and Juhasz on the cardinality of
topological spaces. — Bull. Acad. Pol. Sci., Ser, Math. 24 A976),
999-1000.
Голштынский (Holsztynski W.)
[1966] Topological dimension of lattices. — Bull. Acad. Pol. Sci. Ser. Math.
14 A966), 63—69.
[1966a] Хаусдорфовы пространства минимального веса.— ДАН СССР 168
A966), 508—509.
694 ЛИТЕРАТУРА
Готшелк, Хедлуид (Gottshalk W. H., Hedlund G. А.)
[1955] Topological dynamics. — Providence, 1955.
Граев М. И.
[1948*1 Свободные топологические группы. — Изв. АН СССР, сер. матем.,
12 A948), 279—324.
[1950*] Теория топологических групп. —УМН 5 A950), № 2, с. 3—56.
де Гроот (de Groot J.)
[1956] Non-archimedean metrics in topology. — Proc. Amer. Soc. 7 A956),
948—953.
[1965] Discrete subspaces of Hausdorff spaces. — Bull. Acad. Pol. Sci, Ser.
Math. 13 A965), 537—544.
де Гроот, Макдауэлл (de Groot J., McDowell R. H.)
[1967] Locally connected spaces and their compactifications. — 111. J. of Math.
11 A967), 353—364.
Гросс (Gross W.)
[1914] Zur Theorie der Mengen, in denen em Distanzbegriff definiert ist. —
Sitzungsberichte Akad. Wiss. Wien Abt. Ila 123 A914), 801—819.
[19771 О свойствах множеств, лежащих в 2-произведениях. — ДАН СССР
237 A977), 505—508.
Гротендик (Grothendieck A.)
[1952*] Criteres de compacite dans les espaces fonctionnels generaux. — Amer.
J. Math. 74 A952), 168—186.
Грызлов A. A.
[1979*] О фильтрующихся покрытиях и определяемых ими точках рЛГ. В кн.:
Современная топология и теория множеств, вып. 2. — Ижевск, 1979,
с. 25—36.
[1980*] Две теоремы о мощности топологических пространств. — ДАН
СССР 251 A980), 708—713.
Грюнхаге Г.
[1980*] Паракомпактность и субпаракомпактность в совершенно нормальных
пространствах. — УМН, 35 A980), № 3, с. 44—50.
Грюнхаге, Майкл и Танака (Gruenhage G., Michael E. and Tanaka Y.)
[1984*] Spaces determined by point-countable covers. — Pacif. J. Math. 113
A984), 303—332.
Гулько С. П.
[1977] О свойствах множеств, лежащих в 2-произведениях. — ДАН СССР
237 A977), 505—508.
[1978*] О свойствах функциональных пространств. — ДАН СССР 243 A978),
339—342.
[1979*] О структуре пространств непрерывных функций и их наследствен-
наследственной паракомпактности. — УМН 34 A979), № 6, с. 33—40.
[1981*] О свойствах функциональных пространств. — В кн.: Семинар по об-
общей топологии. — М.: Изд. МГУ, 1981.
Гуран И. И.
[1981*] О топологических группах, близких к финально компактным. — ДАН
СССР, 256, A981), №6.
Гуревич (Hurewicz W.)
[1926] Uber stetige Bilder von Punktmengen. — Proc. Akad. Amsterdam 29
A926), 1014—1017.
[1927] Normalbereiche und Dimensionstheorie. — Math. Ann. 96 A927), 736—
764.
[1927a] Uber stetige Bilder von Punktmengen (Zweite Mitteilung). — Proc.
Akad. Amsterdam 30 A927), 159—165.
[1927b] Uber des Verhaltnis separabler Raume zu kompakten Raumen. —
Proc. Akad. Amsterdam 30 A927), 425—430.
[1930] Einbettung separabler Raume in gleich dimensional kompakte Rau-
Raume.—Monatsh, fur Math, und Phys. 37 A930), 199—208.
ЛИТЕРАТУРА 695
[1935] Cber Abbildungen topologischer Raume auf die n-dimensionale Spha-
re. —Fund. Math. 24 A935), 144—150.
Гуревич, Волмэн (Hurewicz W., Wallman H.)
[1941] Dimension theory.— Princeton, 1941. [Русский перевод: Гуревич В.,
Волмэн Г. Теория размерности. — М.: ИЛ, 1948.]
Гэйл (Gale D.)
[1950] Compact sets of functions and function rings. — Proc. Amer. Math.
Soc. 1 A950), 303—308.
Даукер (Dowker С. Н.)
[1947] Mapping theorems for non-compact spaces.—Amer. J. of Math. 69
A947), 200—242.
[1947a] An imbedding theorem for paracompact metric spaces. — Duke Math.
J. 14 A947), 639—645.
[1911] On countably paracompact spaces. — Canad. J. of Math. 3 A951),
219—224.
[1952] Topology of metric complexes. — Amer. J. of Math. 74 A952), 555—
577.
[1952a] On a theorem of Hanner. — Ark. for Math. 2 A952), 307—313.
[1955] Local dimension of normal spaces. — Quart. J. of Math. Oxford 6
A955), 101—120.
[1956] Homotopy extensions theorems. — Proc. London Math. Soc. 6 A956),
100—116.
[1961] Mappings of proximity structures. In: General Topology and its Rela-
Relations to Modern Analysis and Algebra (Proceedings of the Sympo-
Symposium held in Prague in September 1961). —Prague 1962, pp. 139—
141.
Даукер, Гуревич (Dowker С. H., Hurewicz W.)
[1956] Dimension of metric spaces. — Fund. Math. 43 A956), 83—88.
Дектярев И. М.
[1964*] О (р-полных пространствах, метризуемых над полуполями. — ДАН
СССР 154 A964), с. 23—25.
Джексон (Jackson J. R,)
[1952] Comparison of topologies on function spaces. — Proc. Amer. Math.
Soc. 3 A952), 156—158.
[1952a] Spaces of mappings on topological products with applications to ho-
homotopy theory. — Proc. Amer. Math. Soc. 3 A952), 327—333.
Джентри (Gentry K. R.)
[1969] Some properties of the induced maps, Fund Math. 66 A969), 55—59.
Джоунс (Jones F. B.)
[1937] Concerning normal and completely normal spaces. — Bull. Arner.
Math. Soc. 43 A937), 671—677.
[1958] R. L. Moore's axiom Г and metrization. — Proc. Amer. Math. Soc. 9
A958), 487.
[1966] Metrization. — Amer. Math. Month. 73 A966), 571—576.
Динь Ньё Тонг
[1963] Предзамкнутые отображения и теорема А. Д. Тайманова. — ДАН
СССР 152 A963), 525—528.
Досс (Doss R.)
[1947] On continuous functions in uniform spaces. —Ann. of Math. 48 A947),
843-844.
[1949] On uniform spaces with a unique structure. — Amer. J. of Math. 71
A949), 19—23.
Дранишников А. Н.
[1981*] О счетнозначных ретрактах тихоновского куба. — УМН 36 A981),
№3.
[1984*] Абсолютные экстензоры в размерности п и /i-мягкие отображения,
повышающие размерность. — УМН 39 A984), № 5, с. 55—95.
596 ЛИТЕРАТУРА
Дугунджи (Dugundji J.)
[1951] An extension of Tietze's theorem. — Pacific J. of Math. 1 A951),
353—367.
[1966] Topology. — Boston, 1966.
Дьедонне (Dieudonne J.)
[1939] Sur les espaces uniformes complets. — Ann. Sci. Ecole Normale Sup.
56 A939), 277—291.
[1939a] Un exemple d'espace normal поп susceptible d'une structure d'espace
complet. —C. R. Acad. Sci. Paris, 209 A939), 145—147.
[1939b] Sur les espaces topologiques susceptibles d'etre munis d'une struc-
structure uniforme d'espace complet. — C. R. Acad. Paris 209 A939), 666—
668.
[1944] line generalisation des espaces compacts. — J. de Math. Pures et
Appi. 23 A944), 65—76.
[1958] Un critere de normalite pour les espaces produits. — Coll. Math. 6
A958), 29—32.
Дэвис, Рид, Bare (Davis S. W., Reed G. M. and Wage M. L.)
[1976*] Further results on weakly uniform bases. — Houston J. of Math., 2
A980), 57—63.
Елькин А. Г.
[1969*] О разложимости пространств. — ДАН СССР 186 A969), 9—12.
[1980*] О регулярных максимальных пространствах. — Мат. заметки, 27
A980), № 2, с. 301—305.
Есенин-Вольпин А. С.
[1949] О зависимости между локальным и интегральным весом в диади-
ческих бикомпактах. — ДАН СССР 68 A949), 441—444.
Ефимов Б. А.
[1963] О диадических бикомпактах. — ДАН СССР 149 A963), 1011—1014.
[1963а] О диадических пространствах. — ДАН СССР 51 A963), 1021—1024.
[1963b] Метризуемость и 2-произведение бикомпактов. — ДАН СССР 152
A963), 794—797.
[1965] О мощности хаусдорфовых пространств. — ДАН СССР 164 A965),
967—970.
[1965а] Диадические бикомпакты. — Тр. Моск. матем. об-ва 14 A965), 211—
247.
[1975*] О мощности расширений диадических пространств. — Матем. сб. 96
A975), № 4, с. 614—632.
[1977*] Отображения и вложения диадических пространств. — Матем. сб.
103 A977), № 1.
Ефремович В. А.
[1951] Инфинитезимальные пространства. — ДАН СССР 76 A951), 341—
343.
[1952] Геометрия близости I. Матем. сб. 31 A952), 189—200.
Зайцев В. И.
[1967] К теории тихоновских пространств. — Вестн. Моск. унив., сер, ма-
матем. A967), №3, с. 48—57.
Замбахидзе Л. Г.
[1977*] О функциях размерностного типа. — Тр. Тбил. матем. ин-та 56
A977), 52—98.
[1979*] О взаимоотношениях между периферическими свойствами тихонов-
тихоновских пространств, их степеней, экспонент, свободных групп и под-
подгрупп. — УМН 33 A979) № 6, с. 154—157.
[1980*] О соотношениях между размерностями свободных базисов свобод-
свободных топологических групп. — Сообщ. АН ГССР 97 A980), № 3,
с. 569—572.
Зарелуа А. В.
[1963*] О равенстве размерностей. — Матем. сб. 62 A963), № 3, с. 295—319.
ЛИТЕРАТУРА 697
[1964] Универсальный бикомпакт данного веса и данной размерное! и. ДАН
СССР 154 A964), 1015—1018.
[1964а*] О продолжении отображений на расширения, обладающие некото-
некоторыми специальными свойствами. — Сиб. матем. ж. 5 A964), № 3,
с. 532—548.
[1974*] Построение сильно бесконечномерных компактов с помощью колец
непрерывных функций. —ДАН СССР 214 A974), № 2, с. 264—267.
Зенор (Zenor P.)
[1969] On countable paracompactness and normality. — Prace Mat. 13 A969),
23—32.
[1970] On the completeness of the space of compact subsets. — Proc. Amer.
Math. Soc. 26 A970), 190—192.
[1976] Countable paracompactness of Fa-sets.— Proc. Amer. Math. Soc. 55
A976), 201—202.
[1980] Hereditary m-teparability and the hereditary m-Lindelof property in
product spaces and function spaces. — Fund. Math. 106 A980) ,i 175—
ISO.
Золотарев В. П.
[1975*] О размерности подпространств. — Вестник МГУ, матем. A975),
№ 5, с. 10—12.
Зоргенфрей (Sorgenfrey R. Н.)
[1947] On the topological product of paracompact spaces. — Bull. Amer.
Math. Soc. 53 A947), 631—632.
Зоретти (Zoretti L.)
[1905] Sur les fonctions analytiques unformes qui possedent un ensemble
parfait discontinu de points singuliers. — J. de Math. Pures et AppL
1 A905), 1—51.
Иванов А. В.
[1978*] О наследственной сепарабельности и размерности произведений би-
бикомпактов. — ДАН СССР 239 A978), 1037—1040.
[1978*] О бикомпактах, все конечные степени которых наследственно сепара-
бельны.—ДАН СССР 243 A978), 1109—1112.
[1980*] О нульмерных прообразах бикомпактов с 1-й аксиомой счетностн.—
УМН 35 A980), № б, с. 161—162.
[1981*] Суперрасширения открыто-порожденных бикомпактов. — ДАН СССР
259 A981), 275—278.
Иванова В. М.
[1955] К теории пространства подмножеств. — ДАН СССР 101 A955),
601—603.
Илиадис С. Д.
[1963] Абсолюты хаусдорфовых пространств. — ДАН СССР 149 A963),
22—25.
Исаридзе X. Н.
[1966*] О расширениях и наростах конечного порядка вполне регулярного
пространства. — ДАН СССР 166 A966), 1043—1045.
[1966а*] Об одном обобщении совершенных отображений. — ДАН СССР 168
A966), 266—268.
Исбелл (Isbell J. R.)
[1959] On finite-dimensional uniform spaces. — Pacific J. of Math. 9 A959),
107—121.
1962] Review A 3547. —Math. Rev. 23 A962), 675.
;i962a] Review A 4122. —Math. Rev. 23 A962), 787.
1964] Uniform spaces. — Providence, 1964.
1964a] Remarks on spaces of large cardinal number. — Czech. Math. J. 14
A964), 383—385.
[1969] A note on complete closure algebras. — Math. Systems. Theory 3
A969), 310—312.
698 ЛИТЕРАТУРА
Исивата (Isiwata T.)
[1963] Normality and perfect mappings. — Proc. Japan Acad. 39 A963), 95—
97.
[19671 Mappings and spaces. — Pacific J. of Math. 20 A967), 455—480.
[1969] Z-mappings and C*-embeddings. — Proc. Japan Acad. 45 A969), 889—
893.
Ксии (Ishii T.)
[1959] A new characterization of paracompactness. — Proc. Japan Acad. 35
A959), 435—436.
[1966] On product spaces and product mappings. — J. Math. Soc. Japan 18
A966), 166—181.
Исикава (Ishikawa F,)
[1955] On countably paracompact spaces. — Proc. Japan Acad. 31 A955),
686—687.
Исэки (Iseki K.)
[1954] A note on countably paracompact spaces. — Proc. Japan. Acad 30
A954), 360—351.
Исэки, Kacaxapa (Iseki K., Kasahara S.)
[1957] On pseudo-compact and countably compact spaces. — Proc. Japan
Acad. 33 A957), 100—102.
Какутани (Kakutani S.)
[1936] Uber die Metrisation der topologischen Gruppen. — Proc. Imp. Acad.
Tokyo 12 A936), 82—84.
Каплан (Kaplan S.)
[1947] Homology properties of arbitrary subsets of Euclidean spaces.—
Trans. Amer. Math. Soc. 62 A947), 248—271.
Каратеодори (Caratheodory C.)
[1913] Uber die Begrenzung einfach zusammehangender Gebiete. — Math.
Ann. 73 A913), 323—370.
Картан (Cartan H.)
[1937] Theorie des flitres. — С A. Acad. Sd. Paris 205 A937), 595—598.
[1937a] Filtres et ultrafiltres. — С R. Acad. Sci. Paris 205 A937), 777—779.
Катетов (Katetov M.)
[1940] Uber Я-abgeschIossene und bikompakte Raume. — Casopis Pest. Mat.
Fys. 69 A940), 36—49.
[1947] On tf-closed extensions of topological spaces. — Casopis Pest. Mat.
Fys. 72 A947), 17—32.
[1948] Complete normality of Cartesian products. — Fund. Math. 36 A948),
271—274.
[1950] On nearly discrete spaces. — Casopis Pest. Mat. Fys. 75 A950), 69—
78.
[1950a] A theorem on the Lebesgue dimension. — Casopis Pest. Mat. Fys. 75
A950), 79—87.
[1951] Measures in fully normal spaces. — Fund. Math. 38 A951), 73—84.
[1951a] On real-valued functions in topological spaces. — Fund. Math. 38
A951), 85—91.
[1952] О размерности несепарабельных пространств. I. — Czech. Math. J. 2
A952), 333—368. (On the dimension of non-separable spaces. I.).
[1953] Correction to «On real-valued functions in topological spaces». —
Fund. Math. 40 A953), 203—205.
[1958] О продолжении локально конечных покрытий. — Coll. Math. 6
A958), 145—151.
[1959] Pine normalni prostory (Fully normal spaces). Appendix to: Cech E.
Topologicke prostory (Topological spaces).—Praha, 1959.
Катута (Katuta Y.)
[1971] On the normality of the product of a normal space with a paracom-
paracompact space. —General Topology and Appl. 1 A971), 295—319.
ЛИТЕРАТУРА 699
Кауфман (Kaufman R.)
[1967] Ordered sets and compact spaces. —Coll. Math. 17 A967), 35—39.
Кац Г. И.
[1954] Топологические пространства, в которых можно ввести полную рав-
равномерную структуру. — ДАН СССР 99 A954), 897—900.
Кашуба Р. П.
[1980*] К теории пространств очановского типа. — УМН 35 A080), № 3,
с. 192—193.
Кейслер, Тарский (Keisler H. J., Tarski A.)
[1964] From accessible to inaccessible cardinals. —Fund. Math. 53 A964),
225—308.
Келдыш Л. В.
[1959*] Нульмерные открытые отображения. — Изв. АН СССР, сер. матем.
23 A959), №2, с. 165—184.
Келлерер (Kellerer H. G.)
[1968] Stetige Funktionen auf Produktraumen. — Arch, der Math. 19 A968),
79—82.
Келли (Kelley J. L.)
[1950] Convergence in topology. — Duke Math. J. 17 A950), 277—283.
[1955] General topology. — New York, 1955. [Русский перевод: Келли Дж,
Общая топология. 2-е изд.—М.: Наука, 1980.]
Кендеров П.
[1967] О Q-пространствах. — ДАН СССР 175 A967), 288—291.
[1968] Об одном вопросе А. Стоуна. — Вест. Моск. унив., сер. матем. A968),
№ 2, с. 5—7.
[1980*] Многозначные отображения и их свойства подобные непрерывно-
непрерывности.—УМН 35 A980), № 3, с. 194—196.
Керстан (Kerstan J.)
[1957] Zur Charakterisierung der pseudokompakten Raume.— Math. Nachr
16 A957), 289—293.
Кимура (Kimura N.)
[1963] On the inductive dimension of product spaces. — Proc. Japan Acad. 39
A963), 641—646.
Кислинг (Keesling J.)
[1970] Normality and properties related to compactness in hyperspaces.—
Proc. Amer. Math. Soc. 24 A970), 760—766.
[1970a] On the equivalence of normality and compactness in hyperspaces. —
Pacific J. of Math. 33 A970), 657—667.
Кисынский (Kisynski J.)
[1960] Convergence du type L — Coil. Math. 7 A960), 205—221.
Клебанов Б. С.
[1978*] О замкнутых образах произведений метрических пространств.—
ДАН СССР 240 A978), 1285—1288.
[1982*] О факторизации отображений произведений топологических про-
пространств. — ДАН СССР 262 A982), 1059—1064.
Клюшин В. Л.
[1964*] О совершенных отображениях паракомпактных пространств. — ДАН
СССР 109 A964), 734—737.
Кнастер, Куратовский (Knaster В., Kuratowski К.)
[1921] Sur les ensembles connexes. — Fund. Math. 2 A921), 206—255.
Кнастер, Куратовский, Мазуркевич (Knaster В., Kuratowski К., Mazurkie*
wicz S.)
[1929] Ein Beweis des Fixpunktsatzes fur n-dimensionale Simplexe. — Fund.
Math. 14 A929), 132-137.
Ковальский (Kowalsky H. J.)
[1957] Einbettung metrischer Raume. — Arch, der Math, 8 A957), 336—
339.
700 ЛИТЕРАТУРА
Кол (Kaul S. К,)
[1969] Compact subsets in function spaces. — Canad. Math. Bull. 12 A969),
461—466.
Колмес (Colmex J.)
[1951] Sur ies espaces precompacts. — C. R. Acad. Sci. Paris 233 A951),
1552—1553.
[1952] Sur ies espaces precompacts. — C. R. Acad. Sci. Paris 234 A952),
1019—1021.
Колмогоров А. Н.
[1941*] Точки локальной топологичности счетнократных открытых отобра-
отображений компактов. — ДАН СССР 30 A941), 477—478.
Комбаров А. П.
[1971] О наследственно несвязных пространствах. — Вест. Моск. унив.,
сер. матем. A971), № 4, с. 21—25.
[1971а] О 2-произведениях топологических пространств. — ДАН СССР 199
A971), 526—528.
[1978*] О тесноте и нормальности 2-произведений. — ДАН СССР, 239
A978), 775—778.
[1981*] О пространствах с точечно-счетной полубазой. — Вестник МГУ, сер.
матем. A981), № 3, с. 28—31.
[1983*] Об одной теореме А. X. Стоуна. —ДАН СССР 270 A983), 37—40.
Комбаров А. П., Малыхин В. И.
[1973] О 2-произведениях. — ДАН СССР 213 A973), 774—776.
Комфорт (Comfort W. W.)
[1967] A nonpseudocompact porduct space whose finite subproducts arepseu-
docompact — Math. Ann. 170 A967), 41—44.
[1971] A Survey of cardinal invariants. — General Topology and Appl. 1
A971), 163—199.
Комфорт, Росс (Comfort W. W., Ross K. A.)
[1966*] Pseudocompactness and uniform continuity in topological groups. —
Pacif. J. Math. 16 A966), 483—496.
Комфорт, Сакс (Comfort W. W., Saks V.)
[1973*] Countably compact groups and finest totally bounded topologies.—
Pacif. J. Math. 49 A973), 33—44.
Комфорт, Хейджер (Comfort W. W., Hager A. W.)
[1971] The projection mapping and other continuous functions on a product
space. —Math. Scand. 28 A971), 77—90.
Корсон (Corson H. H.)
[1959] Normality in subsets of product spaces.—Amer. J. of Math. 81 A959),
785—796.
[1961] The weak topology of a Banach space.— Trans. Amer. Math. Soc. 101
A961), 1—15.
[1962] Review A 2186. —Math. Rev. 23 A962), 407.
Корсон, Исбелл (Corson H. H., Isbell J. R.)
[1960] Some properties of strong uniformities. — Quart. J. of Math, Oxford
11 A960), 17—33.
Корсон, Майкл (Corson N. H., Michael E.)
[1964] Metrizability of certain countable unions. — Illinois Journ. of Math. 8
A964), 351—360.
Коэн (Cohen D. E.)
[1954] Spaces with weak topology. — Quart. J. of Math. Oxford 5 A954),
77—80.
Кристенсен (Christensen J. P. R.)
[1981*] Joint continuity of separately continuous functions. — Proc. Amer.
Math. Soc. 82 A981), 455—461.
ЛИТЕРАТУРА 701
Кузьминов В. И.
[1959*] О гипотезе П. С. Александрова в теории топологических групп.—
ДАН СССР, 125 A959), 727—729.
[1961*] Пример размерно неполноценного компакта. — ДАН СССР 141
A961), 312—315.
Кук, Фицпатрик Б. (Cook H., Fitzpatrick В. jr.)
[1968] Inverse limits of perfectly normal spaces. — Proc. Amer. Math. Soc.
19 A968), 189—192.
Кунен (Kunen K.)
[1977*] Strong S and L spaces under MA. In: Set-theoretic Topology. — New
York: Academic Press, 1977.
Куратовский (Kuratowski K.)
[1921] Solution d'un probleme concernant Ies images continues d'ensembles
de points. — Fund. Math. 2 A921), 158—160.
[1922] Une methode d'elimination des nombres transfinis des raisonnements
mathernatiques. — Fund. Math. 3 A922), 76—108.
[1922a] Sur l'operation A de l'Analysis Situs.—Fund. Math.3 A922), 182—199.
[1928] Sur Ies decompositions semi-continues d'espaces metriques compacts.—
Fund. Math. 11 A928), 169—185.
[1930] Sur Ies espaces complets. — Fund, Math. 15 A930), 301—309.
[1931] Evaluation de la classe borelienne d'un ensemble de points a Taide
des symboles logiques. — Fund. Math. 17 A931), 249—272.
[1932] Les fonctions semi-continues dans Tespace des ensembles fermes. —
Fund. Math. 18 A932), 148—159.
[1933] Topologie I. — Warszawa, 1933.
[1933a] Sur un theoreme fondamental concernant le nerf d'un systeme d'en-
d'ensembles. — Fund. Math. 20 A933), 191—196.
[1935] Sur le prolongement des fonctions continues et les transformations en
poly topes, Fund. Math. 24 A935), 259—268.
[1935] Quelques problemes concernant Ies espaces metriques non-separables.—
Fund. Math. 25 A935), 534—545.
[1938] Remarques sur les transformations continues des espaces metriques.—
Fund. Math. 30 A938), 48—49.
[1947] Sur la topologie des espaces fonctionnels. — Ann. Soc. Pol. Math. 20
A947), 314—322.
[1948] Topologie I (second ed.). —Warszawa, 1948.
[1948a] Une methode de prolongement des ensemf
ouverts. — Coll. Math. 1 A948), 273-278.
[1956] Sur une methode de metrisation complete de certains espaces d'en-
d'ensembles compacts. — Fund. Math. 42 A956), 114—138.
[1959] Un critere de coupure de I'espace euclidien par un sous-ensemble ar-
bitraire.— Math. Zeitschr. 72 A959), 88—94.
[1961] Topologie II (third ed.).—Warszawa, 1961.
[1963] Operations on semi-continuous set-valued mappings. 1st. di Alta Mat.
Roma, Seminar! 1962—1963, vol. II. Roma, 1965, pp. 449—461.
[1966] Topology, vol. I. —New York, 1966. [Русский перевод: Куратов-
Куратовский К. Топология. Т. 1. —М.: Мнр, 1966.]
[1968] Topology, vol. П.—New York, 1968. [Русский перевод: Куратов-
Куратовский К. Топология. Т. 2. — М,: Мир, 1969.]
Куратовский, Мостовскнй (Kuratowski K-, Mostowski A.)
[1968] Set theory. — Amstredam, 1968. [Русский перевод: Куратовский К.,
Мостовский А. Теория множеств. — М.: Мир, 1970.]
Куратовский, Серпинский (Kuratowski К-, Sierpinski W.)
[1921] Le theoreme de Borel—Lebesgue dans la theorie des ensembles ab-
straits. — Fund. Math. 2 A921), 172—178.
[1921a] Sur les differences de deux ensembles fermes. — Tohoku Math. J. 20
A921), 22—25.
ensembles relativement fermes ou
702 ЛИТЕРАТУРА
[1926] Sur un probleme de M. Frechet concernant les dimensions des ensem-
ensembles lineaires. — Fund. Math. 8 A926), 193—200.
Kypena (Kurepa D.)
[195Q] La condition de Souslin et une propiete caracteristique des nombres
reels. —С R. Acad. Sci. Paris 231 A950), 1113—1114.
[1962] The cartesian multiplication and the cellularity number. — Publ. Inst.
Math. Beograd 2 A962), 121—139.
[1966*] On numerical and non-numerical ecart. — Proceedings of the Second
Prague Topological Symposium, 1966, pp. 236—237.
[1968] Around the general Suslin porblem. In: Proceedings of the Internatio-
International Symposium on Topology Herceg-Novi 1968. — Beograd, 1969,
239—245.
Кунья (Kucia A.)
[1973] On coverings of a uniformity. — Coll. Math. 27 A973), 73—74.
Лаврентьев М. A.
[1924] Contribution a la theorie des ensembles homeomorphes.— Fund. Math.
6 A924), 149—160.
Латцер (Lutzer D. J.)
[1969] A metrization theorem for linearly ordered spaces. — Proc. Amer.
Math. Soc. 22 A969), 557—558.
[1970] Autorreferat — Zentralblatt fur Math. 177 A970), 507.
[1971] On generalized ordered spaces. — Dissertationes Math. 89 A971).
Латцер, Беннет (Lutzer D. J., Bennett H. R.)
[1969] Separability, the countable chain condition and the Lindelof property
in linearly orderabie spaces. — Proc. Amer. Math. Soc. 23 A969),
664—667.
Лашнев H. C.
[1965] О непрерывных разбиениях и замкнутых отображениях метрических
пространств. —ДАН СССР 165 A965), 756—758.
Лебег (Lebesgue H.)
[1905] Sur les fonctions representables analytiquement. — J. de Math. Pures
et Appl. 1 A905), 139—216.
[1907] Sur le probleme de Dirichlet. — Rend, del Circ. Mat. di Palermo 24
A907), 371—402.
[1911] Sur la non applicabilite de deux domaines appartenant respectivement
a des espaces, de n et n-\-p dimensions. — Math. Ann. 70 A911),
166—168.
[1921] Sur les correspondences entre les points de deux espaces. — Fund.
Math. 2 A921), 256—285.
Леви, Макдауэлл (Levy R., McDowell R. H.)
[1975] Dense subsets of pX. —Proc. Amer. Math. Soc. 50 A975), 426—
430.
Левшенко Б. Т.
[1917] О понятии компактности и точечно-конечных покрытиях. — Матем.
сб. 42 A957), 479—484.
[1961*] О бесконечномерных пространствах. — ДАН СССР 139 A961), 286—
289.
[1965*] Пространства трансфииитной размерности.—Матем. сб. 67 A965),
№ % с. 255—266.
Лейбо И. М.
[1975*] О замкнутых образах метрических пространств. — ДАН СССР 224
A975), 756-759.
[1976*] О факторизации равномерных отображений. — Bull. Acad. Pol. Sci.,
Ser. Math., 24 A976), 75—79.
Лелек (Lelek A.)
[1971] Dimension inequalities for unions and mappings of separable metric
spaces. —Coll. Math. 23 A971), 66—91.
ЛИТЕРАТУРА 703
Леннес (Lennes N. J.)
[1911] Curves in non-metrical analysis situs with an application in the cal-
calculus of variations. — Amer. J. of Math. 33 A911), 287—326.
Лере (Leray J.)
[1950] L'anneau spectral el l'anneau filtre d'homologie d'un espace locale-
ment compact et d'une application continue. — J. de Math. Pures et
Appl. 29 A950), 1—80.
Лефшец (Lefschetz S.)
[1931] On compact spaces. —Ann. of Math. 32 A931), 521—538.
[1942] Algebraic topology. — New York, 1942. [Русский перевод: Лефшец С.
Алгебраическая топология. — М.: ИЛ, 1949.]
Лин (Lin Y. F.)
[1960] A note on the Wallace theorem. — Portugaliae Math. 19 A960), 199—
201.
Лннделёф (Lindelof E.)
[1903] Sur quelques points de la theorie des ensembles.—C. R. Acad. Sci.
Paris 137 A903), 697—700.
Линденбаум (Lindenbaum A.)
[1926] Contributions a i'etude de l'espace metrique I, —Fund. Math. 8 A926),
209—222.
Линн (Lynn I. L.)
[1962] Linearly orderable spaces. — Proc. Amer. Math. Soc. 13 A962), 454—
456.
Лисица Ю. Т.
[1973*] Продолжение непрерывных отображений и факторизационная тео-
теорема.—Сиб. матем. ж., 14 A973), Кя 1, с. 128—139.
Лифанов И. К.
[1968*] О размерности произведений бикомпактов. — ДАН СССР 182
A968), 1274—1277.
[1969*] О большой индуктивной размерности. — ДАН СССР 184 A969),
1288—1291.
[1973*] О размерности нормальных пространств. — ДАН СССР 209 A973),
291—294.
Локуциевский О. В.
[1949] О размерности бикомпактов. — ДАН СССР 67 A949), 217—219.
[1954] Пример открытого отображения одномерного компакта на гильбер-
гильбертов параллелепипед. — Уч. записки Моск. унив. 165 A954), 118—
130.
[1973*] Аксиоматическое определение размерности бикомпактов. — ДАН
СССР 212 A973), 813—815.
Лунц А. Л.
[1949] Бикомпакт, индуктивная размерность которого больше, чем размер-
размерность, определенная при помощи покрытий. — ДАН СССР 66 A949),
801—803.
Люббен (Lubben R. G.)
[1941] Concerning the decomposition and amalgamation of points, upper se-
micontinuous collections, and topological extensions. — Trans. Amer.
Math. Soc. 49 A941), 410—466.
Магилл (Magill K. D. jr.)
[1966] A note on compactifications. — Math. Zeitschr. 94 A966), 322—325.
Мазер (Mather M. R.)
[1964] Paracompactness and partitions of unity. — Preprint, 1964.
Мазур (Mazur S.)
[1952] On continuous mappings on Cartesian products. — Fund. Math. 39
A952), 229—238.
Мазуркевич (Mazurkiewicz S.)
[1913] О arythmetyzacji continuow. — C. R. Varsovie 6 A913), 305—311.
704 ЛИТЕРАТУРА
[1913а] О arytmetyzacji continuow II. —С. R. Varsovie б A913), 941—945.
[1916] Ober Borel'sche Mengen. — Bull. Intern. Acad. Pol. Sci. Ser. A. A916),
490—494.
[1917] Teoria zbiorow Ga. - Wektor 6 A917—18), 129—185.
[1920] Sur un ensemble G& punctiforms qui n'est homeomorphe a aucun en-
ensemble lineaire. — Fund. Math. 1 A920), 61—81.
[1920a] Sur les lignes de Jordan. — Fund. Math. 1 A920), 166—209.
[1932] Sur les transformations interieurs. — Fund. Math. 19 A932), 189—
204.
Майкл (Michael E.)
[1951] Topologies on spaces of subsets. — Trans. Amer. Math. Soc. 71
A951), 152—182.
[1953] A note on paracompact spaces. — Proc. Amer. Math. Soc. 4 A953),
831—838.
[1954] Local properties of topological spaces. — Duke Math. J. 21 A954),
163—172.
[1955] Point-finite and locally finite coverings. — Canad. J. of Math. 7
A955), 275—279.
[1957] Another note on paracompact spaces. — Proc. Amer. Math. Soc. 8
A957), 822—828.
[1959] A theorem on semi-continuous set-valued functions. — Duke Math. J.
26 A959), 647—651.
[1961] On a theorem of Rudin and Klee. — Proc. Amer. Math. Soc. 12 A961),
921.
[1963] The product of a normal space and a metric space need not be nor-
normal. — Bull. Amer. Math. Soc. 69 A963), 375—376.
1963a] Review 4480. —Math. Rev. 25 A963), 873—874.
1964] Cuts. — Acta Math. Ill A964), 1—36.
1964a] A note on closed maps and compact sets.— Israel J. of Math. 2
A964), 173—176.
[1968] Local compactness and Cartesian products of quotient maps and k-
spaces. — Ann. Inst. Fourier 18 A968), 281—286.
[1968a] Bi-quotient maps and Cartesian products of quotient maps. — Ann.
Inst. Fourier 18 A968), 187—302.
[1971] Paracompactness and the Lindelof property in finite and countable
Cartesian products. — Сотр. Math. 23 A971), 199—214.
[1971a] On representing spaces as images of metrizable and related spaces.—
General Topology and Appl. 1 A971), 329—343.
[1971b] A theorem on perfect maps.— Proc. Amer. Math. Soc. 28 A971),
633—634.
[1972*] A quintuple quotient quest. — General Topology and Appl. 2 A972),
91—138.
[1973*] On ^-spaces, ^-spaces and k(X).~Pacif. J. Math. 47 A973), 487—
498.
[1976*] Quotients of countable complete and metric spaces. — Proc. Amer.
Math. Soc. 57 A976), 371—372.
[1981*] Inductively perfect maps and tri-quotient maps. — Proc. Amer. Math.
Soc. 82 A981), 115—119.
Макдугл (McDougle P.)
[1958] A theorem on quasi-compact mappings. — Proc. Amer. Math. Soc. 9
A958), 474—477.
[1959] Mappings and spaces relations. — Proc. Amer. Math. Soc. 10 A959),
320—323.
Макки (Mackey G. W.)
[1944] Equivalence of a problem in measure theory to a problem in the theo-
theory of vector lattices.— Bull. Amer. Math. Soc. 50 A944), 719—
722.
ЛИТЕРАТУРА 705
Маколей (McAuley L. F.)
[1956J A relation between perfect separability, completeness and normality
in semi-metric spaces. — Pacific J. of Math. 6 A956), 315—326.
[1956a] Paracompactness and an example due to F. B. Jones. — Proc. Amer.
Math. Soc. 7 A956), 1155—1156.
[1958] A note of complete collectionwise normality and paracompactness.—
Proc. Amer. Math. Soc. 9 A958), 796—799.
Малыхин В. И.
[1972] О тесноте и числе Суслина в ехр Л" и в произведении пространств. —
ДАН СССР 203 A972), 1001—1003.
[1975*] Экстремально несвязные и близкие к иим группы. — ДАН СССР 220
A975), 27—30.
[1978*] О разреженных пространствах, не имеющих разреженных биком-
бикомпактных расширений. — Матем. заметки 23 A978), с. 127—136.
[1979*] Об экстремально несвязных топологических группах. — УМН 34
A979), №6, с. 59—66.
[1980*] О лузинских пространствах. — Матем. сб. 111 A980), № 3, с. 453—
464.
[1982*] О мощности бикомпактов со слабой первой аксиомой счетности.—
Матем. заметки, 32 A982), № 2, с. 261—268.
[1983*] Топология и форсинг. —УМН 38 A983), № I, с. 69—118.
Малыхин В. И., Пономарев В. И.
[1975*] Общая топология. — В кн.: Итоги науки и техники, т. 13 A975),
с. 149—231.
Малыхин В. И., Шапировский Б. Э.
[1973*] Аксиома Мартина и свойства топологических пространств. — ДАН
СССР 213 A973), 532—535.
Мангейм (Manheim J. H.)
[1964] The genesis of point set topology. — Oxford, 1964.
Мансфилд (Mansfield M. J.)
[1957] On countably paracompact normal spaces. — Canad. J. of Math. 9
A957), 443—449.
[1957a] Some generalizations of full normality. — Trans. Amer. Math. Soc.
86 A957), 489—505.
Мардешнч (Mardesic S.)
[I960] On covering dimension and inverse limits of compact spaces. — 111.
J. of Math. 4 (I960), 278—291.
[1971] On the shape of the quotient space Sn/A, — Bull. Acad. Pol. Sci. Ser.
Math. 19 A971), 623—629.
Мардешич, Папич (Mardesic S., Papic P.)
[1962] Continuous images of ordered compacta, the Suslin property and dia-
dic compacta. — Glasnik Mat 17 A962). 3—25.
Мардешич С, Шостак А.
[1980*] О совершенных прообразах кружевных пространств. — УМН 35
A980), №3, 84-93.
Марчевский (Шпильрайн) (Marczewski E. (Szpilrajn E.))
[1941] Remarque sur les produits cartesiens d'espaces topologiques. — ДАН
СССР 31 A941), 525—527.
[1947] Separabilite et multiplication cartesienne des espaces topologiques. —
Fund Math. 34 A947), 127—143.
Марьянович (Marjanovic M.)
[1966] Topologies on collections of closed subsets. — Publ. Inst. Math. Beo-
grad 6 A966), 125—130.
Матвеев М. B.
[1984*] Замкнутые вложения в псевдокомпактные пространства. — В сб. Кар-
Кардинальные инварианты и отображения топологических про-
пространств.— Ижевск, 1984.
45 Зак. 697
706 ЛИТЕРАТУРА
Медников Л. Э.
[1984*1 Гомеоморфизмы Z-множеств в тихоновском кубе. — УМН 39 A984).
№ 3, с. 239—240.
Мейер (Meyer P. R.)
[1969] Sequential properties of ordered topological spaces. — Сотр. Math.
21 A969), 102—106.
Менгер (Menger K-)
[1923] Ober die Dimensionalitat von Punktmengen I. — Monatsh. fur Math.
und Phys. 33 A923), 148—160.
[1924] Ober die Dimension von Punktmengen II. — Monatsh. fur Math, und
Phys. 34 A926), 137—161.
[1928] Dimensionstheorie. — Leipzig — Berlin, 1928.
[1929] Uber die Dimension von Punktmengen III. Zur Bergrundung einer
axiomatischen Theorie der Dimension.—Monatsh. fur Math, und Phys.
36 A929), 193—218.
Мибу (Mibu Y.)
[1944] On Baire functions on infinite product spaces.— Proc. Imp. Acad.
Tokyo 20 A944), 661—663.
Мищенко А. С
[1962] О пространствах с точечно счетной базой. — ДАН СССР 144 A962),
985—988.
[1962а] О финально компактных пространствах. — ДАН СССР 145 A962),
1224—1227.
Монтгомери (Montgomery D.)
[1935] Nonseparable metric spaces. —Fund Math. 25 A935), 527—533.
Mop P. К., Мрувка (Moore R. C, Mrowka S.)
[1964] Topologies determined by countable objects.— Notices Amer. Math.
Soc. 11 A964), 554.
Mop P. Л. (Moore R. L.)
[1916] On the foundations of plane analysis situs. — Trans. Amer. Math. Soc.
17 A916), 131—164.
[1920] Concerning simple continuous curves. — Trans. Amer. Math. Soc. 21
A920), 333—347.
[1925] Concerning upper semi-continuous collections of continua. — Trans.
Amer. Math. Soc. 27 A925), 416—428.
[1927] Abstract sets and the foundation of analysis situs. — Bull. Amer.
Math. Soc. 33 A927), 141.
[1932] Foundations of point set theory. —New York, 1932.
[1935] A set of axioms for plane analysis situs. — Fund. Math. 25 A935),
13—28.
[1962] Foundations of point set theory (second ed.). — Providence, 1962.
Mop Э. (Moore E. H.)
[1939] General analysis I. Pt. П. —Philadelphia, 1939.
Mop Э., Смит (Moore E. H., Smith H. L.)
[1922] A general theory of limits. — Amer. J. of Math. 44 A922), 102—
121.
Морита (Morita K.)
[1940] On uniform spaces and the dimension of compact spaces. — Proc.
Phys.-Math. Soc. Japan 22 A940), 969—977.
[1948] Star-finite coverings and star-finite property. — Math. Japonicae 1
A948), 60—68.
[1950] On the dimension of normal spaces. I. —Jap. J. of Math. 20 A950),
5—36.
[1950a] On the dimension of normal spaces II. — J. of Math. Soc. Japan 2
A950), 16—33.
[1951] On the simple extension of a space with respect to a uniformity. IV.—
Proc. Japan. Acad. 27 A951), 632—636.
ЛИТЕРАТУРА 707
[1953] On the dimension of product spaces. — Amer. J. of Math. 75 A953),
205—223.
[1954] Normal families and dimension theory for metric spaces. — Math. Ann.
128 A954), 350—362.
[1955] A condition for the metrizability of topological spaces and for n-di-
mensionality.— Sci. Rep. Tokyo Kyoiku Daigaku Sec. A 5 A955),
33-36.
[1956] On closed mappings and dimension. — Proc. Japan Acad. 32 A956),
161—165.
[1956a] Note on mapping spaces. — Proc. Japan Acad. 32 A956), 671—675.
[1962] Paracompactness and product spaces. — Fund. Math. 50 A962), 223—
236.
[1963] On the product of a normal space with a metric space.— Proc. Japan
Acad. 39 A963), 148—150.
[1964] Products of normal spaces with metric spaces. — Math. Ann. 154
A964), 365—382.
[1971] A survey of the theory of M-spaces.— General Topology and Appl. 1
A971), 49—55.
[1975] On generalizations of Borsuk's homotopy extension theorem. — Fund.
Math. 88 A975), 1—6.
Морита, Ханаи (Morita К., Hanai S.)
[1956] Closed mappings and metric space.— Proc. Japan Acad. 32 A956),
10—14.
Моторов Д. Б.
[1984*] Бикомпакты счетного характера являются (в СН) непрерывными
образами однородных бикомпактов. — В сб. Кардинальные инвариан-
инварианты и отображения топологических пространств. — Ижевск, 1984.
Мрувка. (Mrowka S.)
[1954] On completely regular spaces. — Fund. Math. 41 A954), 105—106.
[1956] On universal spaces. — Bull. Acad. Pol. Sci. Cl. Ill 4 A956), 479—
481.
[1956a] Замечание к работе П. Александрова «О двух теоремах Ю. Смир-
Смирнова».—Fund. Math. 43 A956), 399—400.
[1957] Some properties of Q-spaces. — Bull. Acad. Pol. Sci. Cl. Ill 5 A957),
947—950.
[1958] On the unions of Q-spaces. — Bull. Acad. Pol. Sci. Ser. Math. 6
A958), 365—368.
[1959] Compactness and product spaces. — Coll. Math. 7 A959—60), 19—22.
[1959a] On the potency of $N, — Coll. Math. 7 A959—60), 23—25.
[1964] An elementary proof of Katetov's theorem concerning Q-spaces. — Mi-
Michigan Math. J. И A964), 61—63.
[1970] Some comments on the author's example of a non-$-compact space.—
Bull. Acad. Pol. Sci. Ser. Math. 18 A970), 443—448.
Мысьор (Mysior A.)
[1981] A union of real compact spaces.— Bull. Acad. Pol. Sci. Ser. Math. 29
A981), 169—172.
[1981a] A regular space which is not completely regular. — Proc. Amer. Math.
Soc. 81 A981), 852—853.
Нагами (Nagami K.)
[1955] Paracompactness and screenability. — Nagoya Math. J. 8 A955),
83—88.
[1957] Some theorems in dimension theory for non-separable spaces. — J.
Math. Soc. Japan 9 A957), 80—92.
[1959] Finite-to-one closed mappings and dimension. TI. — Proc. Japan Acad.
35 A959), 437—439.
[1969*] 2-spaces. — Fund. Math. 61 A969), 169—192.
[1970] Dimension theory. —New York, 1970.
45*
708 ЛИТЕРАТУРА
[1972] Countable paracompactness of inverse limits and products. — Fund.
Math. 73 A972), 261— 270.
Нагами, Роберте (Nagami К., Roberts J. H.)
[1967] A study of metric-dependent dimension functions.—Trans. Amer.
Math. Soc. 129 A967), 414—435.
Нагата (Nagata J.)
[1950] On a necessary and sufficient condition of metrizabilfty. — J. Inst.
Polyt. Osaka City Univ. 1 A950), 93—100.
[1950a] On topological completeness.—J. of Math. Soc. Japan2 A950), 44—47.
[1956] Note on dimension theory.—Proc. Japan Acad. 32 A956), 568—569.
[1957] On imbedding theorem for non-separable metric spaces.— J. Inst. Po-
Polyt. Osaka City Univ. 8 A957), 9—14
[1957a] A theorem for metrizability of a topological space.— Proc. Japan
Acad. 33 A957), 128—130.
[1968] Modern general topology.—Amsterdam, 1968.
[1969] A note on M-space and topologically complete space.— Proc. Japan
Acad. 45 A969), 541—543.
[1983*] Обзор теории размерности III.— Тр. матем. инст. АН СССР, 1983,
т. 154, с. 186—199.
Наимпалли, Воррэк (Naimpally S. A., Warrack В. D.)
[1970] Proximity spaces. — Cambridge, 1970.
Накамура, Какутани (Nakamura M., Kakutani S.)
[1943] Banach limits and the Cech compactification of a countable discrete
set— Proa Imp. Acad. Tokyo 19 A943), 224—229.
Намиока (Namioka I.)
[1974*] Separate continuity and joint continuity. — Pacif. J. Math. 51 A974),
515—531.
Нахбин (Nachbin L.)
[1950] On the continuity of positive linear transformations. In: Proceedings
of the Internation Congress of Mathematicians, Cambridge, Mass.
1950, vol. I. — Providence, 1952, pp. 464—465.
Недев С. И.
[1971*] О-метризуемые пространства, — Тр. Моек матем. об-ва 24A971),
201—236.
Недев С. И., Чобан М. М.
[1970*] О Д-метризуемых р-пространствах. — Вестник МГУ A970), Кя 6,
с. 3—9.
[1974*] Факторизационные теоремы для многозначных отображений, много-
многозначные сечения и топологическая размерность. — Math. Balcanica 4
A974), 457—460.
Немыцкий В. В., Тихонов А. Н.
[1928] Beweis des Satzes dass ein metrisierbarer Raum dann und nur dann
kompakt ist, wenn er in jeder Metrik vollstandig ist.— Fund. Math.
12 A928), 118—120.
Непомнящий Г. М.
f 1981*] О спектральном разложении многозначных абсолютных ретрактов. —
УМН 36 A981), № 3, с. 221—222.
Нёбелинг (Nobeling G.)
[1931] Uber eine /z-dimensionale Universalmenge im R2n+l. —Math. Ann. 104
A931), 71—80.
Никош (Nyikos P.)
[1977] A compact nonmetiisable space P such that P2 is completely normal.—
Topology Proc. 2A977), 359—363.
[1980] A provisional solution to the normal Moore space problem. — Proc.
Amer. Math. Soc. 78 A980), 429—453.
[1983*] Топологическое пробное пространство для многих аксиом теории
множеств. — УМН 38 A983), № 6, с. 97—103.
ЛИТЕРАТУРА 709
Нобл (Noble N.)
[1969] Countably compact and pseudocompact products.— Czech. Math, J. 19
A969), 390—397.
[1969a] A note on z-closed projections.—Proc. Amer. Math. Soc. 23 A969),
73—76.
[1969b] Products with closed projections. — Trans. Amer. Math. Soc. 140
A969), 381—391.
[1970] The continuity of functions on Cartesian products. — Trans. Amer.
Math. Soc. 149 A970), 187—198.
Нобл, Ульмер (Noble N.. Uimer M.)
[1972] Factoring functions on Cartesian products. — Trans. Amer. Math. Soc.
163 A972), 329—339.
Новак (Novak J.)
[1937] Spocetny ARU-prostor, jenz neobsahuje Шпу bod spocetnosti. — Ca-
sopis Pest. Mat. Fys. 67 A937—38), 97—99.
[1948] Regulanri prostor, na nemz je kazda spojita funkce konstantni. — Ca-
sopis Pest. Mat. Fys. 73 A948), 58—68.
[1953] О некоторых проблемах Лузина, касающихся частей натурального
ряда. —Czech. Math. J. 3 A953), 385—395.
[1953а] On the Cartesian product of two compact spaces. — Fund. Math. 40
A953), 106—112.
Окромешко Н. Г.
[1983*] О ретракциях однородных пространств. — ДАН СССР 268 A983),
548—551.
[1984*] Ретракции бикомпактов, близких к однородным. — Вестник МГУ,
сер. матем. A984), № 6, с. 7—10.
[1984а*] Факторные отображения и вложения топологических пространств.—
В кн.: Отображения и функторы. — М.: Изд. МГУ, 1984.
Окстоби (Oxtoby J. С.)
[1961] Cartesian products of Baire spaces. —Fund. Math. 49 A961), 157—
166.
Окунев О. Г.
[1984*] Хьюиттовские расширения и пространства функций. — В сб.: Кар-
Кардинальные инварианты и отображения топологических пространств.—
Ижевск, 1984.
Окуяма (Okuyama A.)
[1964] On metrizability of Af-spaces.—Proc. Japan Acad. 40 A964), 176—179.
Олл (Aull С. Е.)
[1964] A note on countably paracompact spaces and metrization. — Proc.
Amer. Math. Soc. 16 A965), 1316—1317.
[1975] Quasi-developments and 69-bases. — J. London Math. Soc. 9 A975),
197—204.
О'Мира (O'Meara P.)
[1971] On paracompactness in function spaces with the compact-open topo-
topology.—Proc. Amer. Math. Soc. 29 A971), 183—189.
Осташевский (Ostaszewski A. J.)
[1976] On countably compact, perfectly normal spaces. — J. London Math.
Soc. 14 A976), 501—516.
Островский А. В.
[1976*] Об открытых отображениях нульмерных пространств. — ДАН СССР
228 A976), 34-37.
Очан Ю. С.
[1943*] Пространство подмножеств топологического пространства. — Матем.
сб. 12 A943), № 3, с. 340—352.
Павловский Д. С.
[1980*] О пространствах непрерывных функций.—ДАН СССР 253 A980),
38—41.
710 ЛИТЕРАТУРА
Паровиченко И. И.
[1963] Об одном универсальном бикомпакте веса «—ДАН СССР 150
A963), 36—39.
Пархоменко А. С.
[1939] О взаимно однозначных и непрерывных отображениях. — Матем.
сб. 5 A939), 197—210.
[1941] Об уплотнениях в компактные пространства. — Изв. АН СССР, сер.
матем. 5 A941), 225—232.
Пасынков Б. А.
[1964] Об универсальных бикомпактах данного веса и данной размерно-
размерности. — ДАН СССР 154 A964), 1042—1043.
[1965] О спектральной разложимости топологических пространств. — Ма-
Матем. сб. 66 A965), 35—79.
[1965а*]Частичные произведения. — Тр. Моск. матем. об-ва 13 A965), 136—
245.
[1965b*] О почти метризуемых группах, —ДАН СССР 161 A965), 281—284.
[1967] Об открытых отображениях.— ДАН СССР 175 A967), 292—295.
[1970] О бикомпактах с несовпадающими размерностями. — ДАН СССР
192 A970), 503—506.
[1975*] О размерности прямоугольных произведений. — ДАН СССР 221
A975), 291—294.
[1976*] Размерность пространств с бикомпактной группой преобразований. —
УМН 31 A976), № 5, с. 112—120.
[1976а*] О пространствах с бикомпактной группой преобразований. — ДАН
СССР 231 A976), 39—42.
[1981*] Факторизационные теоремы в теории размерности. — УМН 36 A981),
№ 3, с. 147—176.
[1981а*] Об открытых счетнократных отображениях. — В кн.: Семинар по
общей топологии. — М.: Изд. МГУ, 1981.
[1984*] О распространении на отображения некоторых понятий и утвержде-
утверждений, касающихся пространств. — В кн.: Отображения и функто-
функторы.—М.: Изд. МГУ, 1984.
Пасынков Б. А., Лифанов И. К.
[1970] Примеры бикомпактов с несовпадающими индуктивными размерно-
размерностями.—ДАН СССР 192 A970), 276—278.
Пасынков Б. А., Федорчук В. В., Филиппов В. В.
[1979*] Теория размерности. — В кн.: Итоги науки. Алгебра. Топология. Гео-
Геометрия. Т. 17. —М.: ВИНИТИ, 1979.
Пелант (Pelant J.)
[1975] Cardinal reflections and point-character of uniformities — countere-
counterexamples.— Seminar Uniform Spaces 1973—1974 dicrected by Z. Frolik,
Matematicky ustav CSAV v Praze, Prague, 1975, pp. 149—158.
Перегудов С. А.
[1975*] О некоторых свойствах топологических пространств, лежащих ме-
между паракомпактностью и слабой паракомпактностью. — Вестник
МГУ, сер. матем., A975), № 1, с. 71—77.
[1976*] О я-равномерных базах и я-базах. — ДАН СССР 229 A976), 542—
545.
Пестов В. Г.
[1982*] Совпадение размерностей dim /-эквивалентных топологических про-
пространств. — ДАН СССР 266 A982), 553—556.
[1982а*] О вложениях и уплотнениях топологических групп. — Матем. за-
заметки, 31 A982), № 3, с. 443—446.
[1982b*] Некоторые свойства свободных топологических групп. — Вестн.
МГУ, сер. матем. A982), № 1, с. 35—37.
Плыкин Р. В.
[1963*] Хаусдорфова метрика над полуполями. — ДАН УзССР 9 A963).
ЛИТЕРАТУРА 711
Поль P. (Pol R.)
[1974] Short proofs of two theorems on cardinality of topological spaces,—
Bull Acad. Eol. Sci. Ser. Math. 22 A974), 1245—1249.
[1979*] A function space C(X) which is weakly Lindelof but not weakly com-
compactly generated. — Studia Math. 64 A979), 279—285.
[1981] On category-raising and dimension-raising open mappings with dis-
discrete fibers, —Coii. Math. 44 A981), 65—76.
Поль Э. (Пузё) (Pol E. (Puzio E.))
[1973] Limit mappings and projections of inverse systems. — Fund. Math. 80
A973), 81—97.
Поль Э. (Пузё, Пузё-Поль), Поль Р. (Pol E., Pol R.)
[1974] An open-perfect mapping of a hereditarily disconnected space onto
a connected space. — Fund. Math. 86 A974), 271—278.
[19761 Remarks on Cartesian products. — Fund. Math. 93 A976),
57—69.
[1977] A hereditarily normal strongly zero-dimensional space with a sub-
space of positive dimension and an Af-compact space of positive di-
dimension. — Fund. Math. 97 A977), 45—52.
[1979] A hereditarily normal strongly zero-dimensional space containing sub-
spaces of arbitrarily large dimension.—Fund. Math. 102 A979),
137—142.
Помпейю (Pompeiu D.)
[1905] Sur la continuite des functions de variatables complexes.— Ann. Fac.
Sci. Toulouse 7 A905), 265—315.
Пондицери (Pondiczery E. S.)
[1944] Power problems in abstract spaces. — Duke Math. J. 11 A944), 835—
837.
Пономарев В. И.
[1959] Об открытых отображениях нормальных пространств. — ДАН СССР
126 A959), 716—718.
[1959а] О замкнутых отображениях. — УМН 14 A959), № 4, с. 203—206.
[I960] Аксиомы счетности и непрерывные отображения. — Bull. Acad. Pol.
Sci. Ser. Math. 8 A960), 127—133.
[1960a] О свойствах топологических пространств, сохраняющихся при много-
многозначных непрерывных отображениях. — Матем. сб. 51 A960), 515—
536.
[1962] О паракомпактных пространствах и их непрерывных отображе-
отображениях.—ДАН СССР 143 A962), 46—49.
[1962а] О сохранении сильной паракомпактности при открытых совершен-
совершенных отображениях. — Bull. Acad. Pol. Sci. Ser. Math. 10 A962),
425—428.
[1963] Об абсолюте топологического пространства. — ДАН СССР 149
A963), 26—29.
[1966] О пространствах, соабсолютных с метрическими. — УМН 21 A966),
№ 4, с. 101—132.
[1971] О мощности бикомпактов с первой аксиомой счетности. — ДАН
СССР 196 A971), 296—298.
Пономарев В. И,, Шапиро Л. Б.
[1976*] Абсолюты топологических пространств и их непрерывных отображе-
отображении.—УМН 31 A976), № 5, с. 120—136.
Понтрягин Л. С.
[1930] Sur une hypothese fondamentale de la theorie de la dimension. —
С R. Acad. Paris 190 A930), 1105—1107.
[1954] Непрерывные группы. — M.: Физматгиз, 1954.
Понтрягин Л. С., Толстова Г. В.
[1931] Beweis des Mengerschen Einbettungssatzes.— Math. Ann. 105 1931,
734-747.
712 ЛИТЕРАТУРА
Попов В. В.
[1980*] Метризуемость и пространство замкнутых множеств. — УМН 35
A980), №3, с. 209—213.
Поспишил (Pospisil В.)
[1937] Remark on bicompact spaces. —Ann. of Math. 38 A937), 845—
846.
[1937a] Trois notes sur les espaces abstraits.— Publ. Fac. Sci. Univ. Masa-
rykBrno 249 A937), 3—9.
Прохоров Ю. В.
[1956*] Сходимость случайных процессов и предельные теоремы теории ве-
вероятности.— Теор. вер. и прилож. 1 A956), № 2, с. 177—228.
Паункаре (Poincare Н.)
[1912] Pourquoi Tespace a trois dimensions. — Revue de Mataph. et de Mo-
Morale 20 A912), 483—504.
Пшимусинский (Przymusiriski T.)
[1973] On a-discrete coverings consisting of connected sets.— Coll. Math.
27 A973), 237—239.
[1974] A note on dimension theory of metric spaces. — Fund. Math. 85 A974),
277—284.
[1979] On the dimension of product spaces and an example of M. Wage.—
Proc. Amer. Math. Soc. 76 A979), 315—321.
[1980] Normality and paracompactness in finite and countable Cartesian
products. — Fund. Math. 105 A980), 87—104.
Пьпкеев Е. Г.
[1977*] К теории уплотнений на компакты.— ДАН СССР 223 A977),
1046—1048.
[1977а*] К теории взаимно однозначных непрерывных отображений. — Ма-
тем. зап. Уральск, ун-та 10 A977), № 2, с. 121—132.
[1980*] О наследственно перистых пространствах. — Матем. заметки 28
A980), 603—618.
[1982*] О тесноте пространств непрерывных функций. — УМН 37 A982),
№ 1, с. 157—158.
[1982а*] О секвенциальности пространств непрерывных функций. — УМН 37
A982), № 5, с. 197—198.
[1983*] О максимально разложимых пространствах. — Тр. Матем. ин-та АН
СССР, т. CLIV. —М., 1983.
Пыткеев Е. Г., Яковлев Н. Н.
[1980*] On bicompacta which are unions of spaces defined by means of co-
coverings. — Comment. Math. Univ. Carol. 21 A980), 247—261.
Рамер (Ramer A.)
[1965] Some problems on universal spaces. — Bull. Acad. Pol. Sci. Ser.
Math. 13 A965), 291—294.
Ранчин Д. В.
[1977*] Теснота, секвенциальность и замкнутые покрытия. — ДАН СССР
232 A977), 1015—1018.
[1980*] О наследственно бесконечномерных пространствах. — УМН 35
A980), №3, с. 213—217.
Рейнуотер (Rainwater J.)
[1959] A note on projective resolutions.—Proc. Amer. Math. Soc. 10 A959).
734—735.
Рисе (Riesz F.)
[1907] Die Genesis des Raumbegriffes.— Math, und Naturwiss. Berichte aus
Ungarn 24 A907), 309—353.
[1908] Stetigkeitsbegriff und abstrakte Mengenlehre. In: Atti del IV Congres-
so Internazionale dei Matematici, Roma 1908, vol. II. — Roma, 1909,
pp. 18—24.
ЛИТЕРАТУРА 713
Роберте (Roberts J. Н.)
[1956] The rational points in Hilbert space.—Duke Math. J. 23 A956).
489—492.
Розенталь, Зоретти (Rosenthal A., Zoretti L.)
[1924] Die Punktmengen. — Encyklopadie der Mathematischen Wissenschaf-
ten, II С 9а, Leipzig, 1924.
Рой (Roy P.)
[1962] Failure of equivalence of dimension concepts for metric spaces. —
Trans. Amer. Math. Soc. 68 A962), 609-613.
[1968] Nonequality of dimensions for metric spaces.— Trans. Amer. Math
Soc. 134 A968), 117—132.
Ройтман (Roitman J.)
[1984] Basic S and L. In: Handbook of set-theoretic topology (K. Kunen
and J. E Vaughan, eds.).— Amsterdam, 1984, pp. 295—326.
Росс, Стоун (Ross К. A., Stone A. H.)
[1964] Products of separable spaces. — Amer. Math. Monthly 71 A964), 398—
403.
Рудин (Rudin M. E.)
[1956] A separable normal nonparacompact space.— Proc. Amer. Math. Soc.
7 A956), 940—941.
[1965] A technique for constructing examples.— Proc. Amer. Math. Soc 16
A965), 1320-1323.
[1969] Souslin's conjecture.—Amer. Math. Monthly 76 A969). 1113—1119.
[1969a] A new proof that-metric spaces are paracompact,— Proc. Amer. Math.
Soc. 20 A969), 603.
[1971] A normal space X for which Xxl is not normal.—Fund. Math. 73
A971), 179—186.
[1972] A normal hereditarily separable non-Lindelof space. — 111. J. of Math.
16 A972), 621—626.
[1977] 2-products of metric spaces are normal—Preprint, 1977.
Рудин М., Кли (Rudin M. E., Klee V. L. jr.)
[1956] A note on certain function spaces.—Arch, der Math. 7 A956), 469—470.
Рудин М., Старбёрд (Rudin M. E., Starbird M.)
[1975] Products with a metric factor. — General Topology and Appl. 5 A975),
235—248.
Рудин У. (Rudin W.)
[1956] Homogeneity problems in the theory of Cech compactifications.—
Duke Math. J. 23 A956), 409—419.
Рыль-Нардзевский (Ryll-Nardzewski C.)
[1954] A remark on the Cartesian product of two compact spaces, Bull. Acad.
Pol. Sci. CI. Ill 2 A954), 265—266.
Савинов Н. B.
[1976*] Пример совершенно нормального бикомпакта без промежуточных
размерностей. — Вестник МГУ, сер. матем. A976), № 3, с. 52—56.
[1977*[ Два примера к теории размерности бикомпактов. — ДАН СССР 233
A977), 41—44.
Сакс (Saks S.)
[1921] Sur l'equivalence de deux theoremes de la theorie des ensembles.—
Fund. Math. 2 A921), 1—3.
Самюэль (Samuel P.)
[1948] Ultrafilters and compactifications of uniform spaces. — Trans. Amer.
Math. Soc. 64 A948), 100—132.
Свордсон (Swardson M. A.)
[1979] A short proof of Kowalsky's hedgehog theorem. — Proc. Amer. Math.
Soc. 75 A979), 188.
Сентмиклоси (Szentmikloszy Z.)
[1978] S-spaces and L-spaces under Martin's axiom. In: Colloquia Math. Soc.
714 ЛИТЕРАТУРА
J. Bolyai 23 (Proceedings of Colloquium on Topology, Budapest
1978). —Amsterdam, 1980, pp. 1139—1145.
Серпинский (Sierpinski W.)
[1915] Homeomorfizm przestrzeni wymiernych.— Wektor 4 A914—15).215—
221.
[1916] Kontynuum Hniowe jako wnogosc abstrakcyjna. — Prace Mat. — Fix.
27 A916), 203—227.
[1918] Un theoreme sur Ies continus,— Tohoku Math. J. 13 A918), 300—303.
[1920] Sur un ensemble ponctiforme connexe. — Fund. Math. 1 A920), 7—
10.
[1920a] Sur une propriete topologique des ensembles denombrables denses en
soi. — Fund. Math. 1 A920), 11 — 16.
[1920b] Sur une condition pour qu'un continu so:t une courbe jordanienne. —
Fund. Math. 1 A920), 44—60.
[1921] Sur Ies ensembles connexes et non connexes. — Fund. Math. 2 A921),
81—95.
[1921a] Sur l'equivalence de trois proprietes des ensembles abstraits —Fund.
Math. 2 A921), 179—188.
[1928] Sur Ies projections des ensembles complementaires aux ensembles
(A). —Fund. Math. 11 A928), 117—122.
[1928a] Sur une decomposition d'ensembles. — Monatsh. fur Math, und Phys.
35 A928), 239-242.
[1930] Sur une propriete des ensembles G6. — Fund. Math. 16 A930), 173—
180.
Сигал (Segal J.)
[1959] Hyperspaces of the inverse limit spaces. — Proc. Amer. Math. Soc. 10
A959), 706—709.
Симон П.
[1978*[ Расходящиеся последовательности в бикомпактах. — ДАН СССР
243 A978), 1398—1401.
[1980*] О двух теоремах М. Г. Ткаченко. — УМН 35 A980), 220—221.
Сирота С.
[1968] О спектральном представлении пространства замкнутых подмно-
подмножеств бикомпактов. — ДАН СССР 181 A968), 1069—1072.
[1969*] Произведение топологических групп и экстремальная несвязность.—
Матем. сб. 79 A969), № 2, с. 179—192.
Ситников К. А.
[1953] Пример двумерного множества в трехмерном евклидовом простран-
пространстве, допускающего сколь угодно малые деформации в одномерный
полиэдр, и некоторая новая характеристика размерности множеств
в евклидовых пространствах. — ДАН СССР 88 A953), 21—24.
Скарборо, Стоун (Scarborough С. Т., Stone A. H.)
[1966] Products of nearly compact spaces. — Trans. Amer. Math. Soc. 124
A966), 131—147.
Скляренко Е. Г.
[1958] О вложении нормальных пространств в бикомпакты того же веса
и той же размерности. — ДАН СССР 123 A958), 36—39.
Скула (Skula L.)
[1965] Dedicna m-separabilita uspofadaneho prstoru. — Casopis Pest. Mat.
Fys. 90 A965), 451-454.
Смирнов Ю. M.
[1948] К теории вполне регулярных пространств. — ДАН СССР 62 A948),
749—752.
[1950] О топологических пространствах, компактных з данном отрезке
мощностей. - Изв. АН СССР, сер. матем. 14 A950), 155—178.
[1951] О покрытиях топологических пространств. — Уч. записки Моск. унив.
148 A951), 204-215.
ЛИТЕРАТУРА 715
[1951а] О метризации топологических пространств. — УМН 6 A951), № 6,
с. 100—111.
[1951b] Некоторые соотношения в теории размерности. — Матем. сб. 29
A951), 151—172.
[1951с] О нормально расположенных множествах нормальных пространств.—
Матем. сб. 29 A951), 173-176.
[1951а] К теории финально компактных пространств. — Укр. матем. ж. 3
A951), 52—60.
[1952] О пространствах близости. — Матем. сб. 31 A952), 543—574.
[1954] О полноте пространств близости. — Тр. Моск. матем. общ-ва 3
A954), 271—306.
[1956] О сильно-паракомпактных пространствах. — Изв. АН СССР, сер. ма-
матем. 20 A956), 253—274.
[1956а] О метризуемости бикомпактов, разлагаемых в сумму множеств со
счетной базой. — Fund. Math. 43 A956), 387—393.
[1956b] О размерности пространств близости. — Матем. сб. 38 A956), 283—
302.
[1958] Пример нульмерного пространства, имеющего бесконечную размер-
размерность в смысле покрытий. — ДАН СССР 123 A958), 40—42.
Смит, Краевский (Smith J. С., Krajewski L. L.)
[1971] Expandability and collectionwise normality. — Trans. Amer. Math.
Soc. 160 A971), 437—451.
Старбёрд (Starbird M.)
[1975] The Borsuk homotopy extension theorem without the binormality con-
condition.—Fund. Math. 87 A975), 207—211.
Степанек, Вопенка (Stepanek P., Vopenka P.)
[1967] Decomposition of metric spaces into nowhere dense sets. — Comm.
Math. Univ. Caroiinae 8 A967), 387—404.
Стефенсон (Stephenson R. M. jr.)
[1968] Pseudocompact spaces. —Trans. Amer. Math. Soc. 134 A968), 437—
448.
[1971*] Minimal topological groups. — Math. Ann. 192 A971), 198.
Стин {Steen L. A.)
[1970] A direct proof that a linearly ordered space is hereditarily collection-
wise normal. —Proc. Amer. Math. Soc. 24 A970), 727—728.
Стинрод (Steenrod N.)
[1936] Universal homology groups. — Amer. J. of Math. 58 A936), 661—
701.
Стоилов (Sfollow S.)
[1928] Sur les transformations continues et la topologie des fonctions ana-
lytiques. — Ann. Sci. Ecole Normale Sup. 45 A928), 347—382.
Стоун A. (Stone A. H.)
[1948] Paracompactness and product spaces. — Bull. Amer. Math. Soc. 54
A948), 977—982.
[1956] Metrizability of decomposition spaces. — Proc. Amer. Math. Soc. 7
A956), 690—700.
[1960] Sequences of coverings. — Pacific. J. of Math. 10 A960), 689—
691.
[1962] Absolute Fa-spaces. — Proc. Amer. Math. Soc. 13 A962), 495—499
[1962a] Non-separable Borel sets. — Rozprawy Mat. 28 A962).
[1963] A note on paracompactness and normality of mapping spaces. — Proc.
Amer. Math. Soc. 14 A963), 81—83.
Стоун M. (Stone M. H.)
[1936] Applications of Boolean algebras to topology. — Матем. сб. 1 A936),
765—772.
[1937] Applications of the theory of Boolean rings to general topology.—
Trans. Amer. Math. Soc. 41 A937), 375—481.
716 ЛИТЕРАТУРА
[1937а] Algebraic characterizations of special Boolean rings. — Fund. Math.
29 A937), 223-302.
[1947] The generalized Weierstrass approximation theorem. — Math. Mag. 21
A947—48), 167—183 and 237—254.
[1948] On the compactification fo topological spaces. — Ann. Soc. Pol. Math.
21 A948), 153—160.
Страшевич (Straszewics S.)
[1918] Ober den Begriff des einfachen Kurvenbogens. — Math. Ann. 78
A918), 369—377.
Тайманов А. Д.
[1952] О распространении непрерывных отображений топологических про-
пространств. — Матем. сб. 31 A952), 459—463.
[1955] О замкнутых отображениях. L — Матем. сб. 36 A955), 349—352,
Тамано (Tamano H.)
[1960] A note on the pseudo-compactness of the product of two spaces. —
Mem. Coll Sci. Univ. Kyoto Ser. A 33 (I960), 225—230.
[1960a] On paracompactness. —Pacific J. of Math. 10 A960), 1043—1047.
[1962] On compactifications. — J. Math. Kyoto Univ. 1 A962), 161—193.
Тейхмюллер (Teichmuller O.)
[1939] Braucht der Algebraiker das Auswahlaxiom? — Deutsche Math. 4
A939), 567—577.
Тельгарский (Telgarsky R.)
[1971] C-scattered and paracompact spaces. — Fund. Math. 73 A971), 59—74.
Тенненбаум (Tennenbaum S.)
[1968] Souslin's problem. — Proc. Nat. Acad. Sci. USA 59 A968),
Терасава (Terasawa J.)
[1972] On the zero-dimensionality of some non-normal product spaces.—
Sci. Rep. Tokyo Kyoiku Daigaku Sec. A 11 A972), 95—102.
Терасака (Terasaka H.)
[1952] On Cartesian product of compact spaces. — Osaka Math. J. 4 A952),
11-15.
Терпе Ф., Флаксмайер Ю.
[1977*] О некоторых приложениях теории расширений топологических про-
пространств и теории меры. — УМН 32 A977), № 5, с. 125—162.
Тише (Tietze H.)
[1915] Cber Funktionen, die auf einer abgeschlossenen Menge stetig sind.
J. fur die reine und angew. Math. 145 A915), 9—14.
[1923] Beitrage sur allgemeinen Topologie I.™Math. Ann. 88 A923), 290—
312.
Титце, Вьеторис (Tietze H., Vietoris L.)
[1930] Beziehungen zwischen den yerschiedenen Zweigen der Topologie.—
Encyklopadie der Mathematischen Wissenschaften. Ill AB 13, Leip-
Leipzig,'1930.
Тихонов А. Н.
[1925] Uber einen Metrisationssatz von P. Urysohn. — Math. Ann 95 A925),
139-142.
[1930] Uber die topologische Erweiterung von Raumen.— Math. Ann. 102
A930), 544-561.
[1935] Uber einen Funktionenraum.— Math. Ann. Ill A935), 762—766.
[1935a] Ein Fixpunktsatz. — Math. Ann. Ill A936), 767—776.
Ткаченко М. Г.
[1979*] О непрерывных образах всюду плотных подпространств топологиче-
топологических произведений. — УМН 34 A979), № 6, с. 199—202.
[1983*] О бикомпактности счетно-компактных пространств, обладающих до-
дополнительной структурой.™Тр. Моск. матем. об-ва 46 A983), 145—
163.
ЛИТЕРАТУРА 717
[1983а*]О полноте свободных абелевых топологических групп. — ДАН
СССР 269 A983), 299—303.
[1984*] О топологии свободных групп над бикомпактами. — В кн.: Отобра-
Отображения и функторы. — М.: Изд. МГУ, 1984.
Ткачук В. В.
[1983*] О кардинальных инвариантах типа числа Суслина. — ДАН СССР
270 A983), 795—798.
[1984*] О мультипликативности некоторых свойств пространств отображе-
отображений в топологии поточечной сходимости. — Вестник МГУ, сер. ма-
тем. A984), №6, с. 36—39.
Тодорчевич (Todorcevic S.)
[1981] A model for no S-spaces. — Preprint, 1981.
[1984] Generalized S and L. — Preprint, 1984.
Толл (Tail F. D.)
[1969] Set-theoretic consistency results and topological theorems concerning
the normal Moore space conjecture and related problems. Thesis, Univ.
of Wisconsin 1969. — Dissertationes Math. 148 A977).
Тонг (Tong H.)
[1948] Some characterizations of normal and perfectly normal spaces.—
Bull. Amer. Math. Soc. 54 A948), 65.
[1949] On some problems of Cech.— Ann. of Math. 50 A949), 154—157.
[1952] Some characterizations of normal and perfectly normal spaces.—
Duke Math. J. 19 A952), 289-292.
Трейлор (Traylor D. R.)
[1964] Concerning metrizability of pointwise paracompact Moore spaces.—
Canad. J. of Math. 16 A964), 407—411.
Трнкова В. (Шедива В.)
[1979*] Гомеоморфизмы произведений пространств. — УМН 34 A979), № 6,
с. 124—139.
Тумаркин Л. А.
[1925] Zur allgemeinen Dimensionstheorie. — Proc. Akad. Amsterdam 28
A925), 994—996.
[1926] Beitrag zur allgemeinen Dimensionstheorie. — Матем. сб. 33 A926),
57—86:
Тьюки (Tukey J. W.)
[1940] Convergence and uniformity in topology. — Ann. of Math. Studies 2,
Princeton, 1940.
[1941] Review. — Math. Rev. 2 A941), 178.
Уайберн (Whyburn G. T.)
[1934] Non-alternating transformations. — Amer. J. of Math. 56 A934), 294—
302.
[1942] Analytic topology. — New York, 1942.
[19501 Open and closed mappings.—Duke Math. J. 17 A950), 69—74.
[1952] On quasi-compact mappings. — Duke Math. J. 19 A952), 445—446.
Уайтхед (Whitehead J. H. C.)
[1948] A note on a theorem due to Borsuk. — Bull. Amer. Math. Soc. 54
A948), 1125—1132.
Уиллард (Willard S.)
[1971] Paracompactness in small products. — Canad. Math. Bull. 14 A971),
127.
Улам (Ulam S.)
[1930] Zur Masstheorie in der allgemeinen Mengenlehre. — Fund. Math. 16
A930), 140—150.
Ульянов В. М.
Г1975*] О бикомпактных расширениях счетного характера и абсолютах. —
Матем. сб. 98 A975), № 2, с. 223—254.
718 ЛИТЕРАТУРА
[1975а*] О вполне замкнутых и близких к ним отображениях. — УМН 30
A975), №3, с. 177—178.
[1977*] Решение основной задачи о бикомпактных расширениях волмэнов-
ского типа. —ДАН СССР 233 A977), № 6, с. 1056—1059.
Уокер (Walker R. С.)
[1974] The Stone — Cech compactification.—Berlin, 1974.
Уоллес (Wallace A. D.)
[1942] Monotone transformations. — Duke Math. J. 9 A942), 487—506.
[1951] Extensional invariance. — Trans. Amer. Math. Soc. 70 A951), 97—
102.
Уорнер (Warner S.)
[1958] The topology of compact convergence on continuous function spa-
spaces. —Duke Math. J. 25 A958), 265—282.
Уоррел (Worrell J. M. jr.)
[1966] The closed continuous images of metacompact topological spaces.—
Portugaliae Math. 25 A966), 175—179.
Уотерхаус (Waterhouse W. C.)
fl972] An empty inverse limit. — Proc. Amer. Math. Soc. 36 A972), 618.
Успенский В. В.
[1978*] О вложениях в функциональные пространства. — ДАН СССР 242
A978), 544—546.
[1982*] О спектре частот функциональных пространств. — Вестник МГУ,
сер. 1, матем. A982), № 1, с. 35—37.
[1982а*] Топологическая группа, порожденная линделефовым 2-просгран-
ством, обладает свойством Суслина. —ДАИ СССР 265 A982),
823—826.
[1983*] К теореме Бальцара — Франека об отображении экстремальных не-
несвязных бикомпактов на канторов дисконтиуум. — Comment. Math.
Univ. Carol. 24 A983), 155—165.
[1983a*] A characterization of realcompactness in terms of the topology of po-
intwise convergence on the function space. — Comment. Math. Univ.
Carol. 24 A983), 121—126.
Урысон П. С.
[1922] Les multiplicites Cantoriennes. — С. R. Acad. Paris, 175 A922), 440—
442.
[1923] Sur la metrisation des espaces topologiques.— Bull. Intern. Acad. PoL
Sci. Sen A A923), 13—16.
[1924] Uber die Metrisation der kompakten topologischen Raume.—Math.
Ann. 92 A924), 275—293.
[1925] Uber die Machtigkeit der zusammenhangenden Mengen. — Math. Ann,
94 A925), 262—295.
[1925a] Zum Metrisationsproblem. — Math. Ann. 94 A925), 309—315.
[1925b] Memoire sur les Multiplicates Cantoriennes. — Fund. Math. 7 A925).
30-137.
[1926] Memoire sur les multiclicites Cantoriennes (suite), — Fund. Math. 8
A926), 225—359.
[1926a] Sur les classes (L) de M. Frechei—Enseign. Math. 25 A926), 77—
83.
[1927] Sur un espace metrique universel. — Bull Sci. Math. 51 A927), 43—
64, 74—90.
[1927a] Beispiel eines nirgends separablen metrischen Raumes.—Fund. Math.
9 A927), 119—121.
Федорчук В. В.
[1966] Упорядоченные множества и произведение топологических про-
пространств. — В естн. Моск. уни-та, сер. матем. A966), № 4, 66—71.
[1966а] Об упорядоченных пространствах. — ДАН СССР 169 A966), 777—
780.
ЛИТЕРАТУРА 719
[1968*] О бикомпактах с несовпадающими размерностями. — ДАН СССР
182 A968), 275—277.
[1969] Некоторые вопросы теории упорядоченных пространств. — Сибир-
Сибирский матем. ж. 10 A969), 172—187.
[1971*] Пример однородного бикомпакта с несовпадающими размерностя-
размерностями.—ДАН СССР 198 A971), 1283—1286.
[1975*] Бикомпакт, все конечные замкнутые подмножества которого л-мер-
ны. — Матем. сб., 96 A975), № 1, с. 41—62.
[1975а*] О мощности наследственно сепарабельных бикомпактов. — ДАН
СССР 222 A975), 302—305.
[1976*] Вполне замкнутые отображения и совместимость некоторых теорем
общей топологии с аксиомами теории множеств. — Матем. сб. 99
A976), № 1, с. 3—33.
[1977*] A compact space having the cardinality of the continuum with no
convergent sequences. — Math. Proc, Cambridge Phil. Soc. 81 A977),
177—181.
[1978*] Бесконечномерные бикомпакты. — Изв. АН СССР, сер. матем. 42
A978), 1162—1178.
[1972а*] Об упорядоченных множествах. — ДАН СССР 240 A978), 280—282.
[1980*] Метод развертываемых спектров и вполне замкнутых отображений в
общей топологии. — УМН 35 A980), № 3, с. 112—121.
[1981*] Козариантные функторы в категории компактов, абсолютные ретрак-
ты и Q-многообразия. —УМН 36 A981), № 3, с. 177—198.
[1984*] О некоторых геометрических свойствах ксвариантных функторов.—
УМН 39 A984), № 5, с. 169—208.
Филиппов В. В.
[1967*] О совершенном образе паракомпактного перистого пространства.—
ДАН СССР 176 A967), 533—536.
[1968*] О перистых паракомпактах. — ДАН СССР 178 A968), 553—558.
[1969] Бикомпакт с несовпадающими индуктивными размерностями. —
ДАН СССР 184 A969), 1050—1053.
[1969а] Факторпространства и кратность базы. — Матем. сб. 80 A969),
521—532.
[1969b*]О совершенно нормальных бикомпактах. — ДАН СССР 189 A969),
36—39.
[1969с*] Бикомпакт с первой аксиомой счетности с несовпадающими размер-
размерностями ind и Ind. — ДАН СССР 186 A969), 1020—1022.
[1970] О бикомпактах с несовпадающими индуктивными размерностями.—
ДАН СССР 192 A970), 289—292.
[1970а*] Решение одной задачи П. С. Александрова (Бикомпакт с несовпа-
несовпадающими индуктивными размерностями). — Матем. сб. 83 A970),
№ I, с. 42—60.
[1972] О размерности замкнутых отображений. — ДАН СССР 205 A972),
40—43.
[1973] О размерности нормальных пространств. — ДАН СССР 209 A973),
805-807.
[1974] О локально-связных пространствах. — ДАН СССР 215 A974),
1061—1062.
[1978*] О поведении размерности при замкнутых отображениях. — Тр. семи-
семинара имени И. Г. Петровского, МГУ A978), № 3, с. 177—196.
[1979*] О весовых характеристиках пространства с действием бикомпактной
группы. — Матем. заметки 25 A979), № 6, с. 939—947.
[1980*] On the existence of solutions of differential equations. — Colloq.
Math. Soc. Janos Bolyai, 23, North-Holland, Topology, v. I. pp. 397—
412.
[1983*] О нормально расположенных пространствах. — Тр. Матем. ин-та АН
СССР 154 A983), 239—251.
720 ЛИТЕРАТУРА
Фихтенгольц Г. М., Канторович Л. В.
[1934J Sur les operations lineaires dans l'espace des fonctions bornees. —
Studia. Math. 5 A934), 69—98.
Флаксмайер (Flachsmeyer J.)
[1963] Topologische Projektivraume. — Math. Nachr. 26 A963). 57—66.
[1983*] Топологические полуполя и соответствующие им булевы алгебры. —
Тр. Матем. ин-та АН СССР, 154 A983), 252—263.
Флейснер (Fleissner W. G.)
[1982] If all normal Moore spaces are metrisable, then there is an inner mo-
model with a measurable cardinal. — Trans. Amer. Math. Soc. 273 A982),
365—373.
[1984] The normal Moore space conjecture and large cardinals. In: Hand-
Handbook of set-theoretic topology (X. Kunen and J. E. Vaughan, eds.).—
Amsterdam, 1984, pp. 733—760.
Флейшер, Франклин (Fleischer I., Franklin S. P.)
[1967] On compactness and projections. In: Contributions to Extension Theo-
Theory of Topological Structures (Proceedings of the Symposium held in
Berlin August 14—19, 1967).™ Berlin, 1969, pp, 77—79.
Флейшман (Fleischman W. M.)
[1970] A new extension of countable compactness. — Fund. Math. 67 A970),
1—9.
Фокс (Fox R. H.)
[1945] On topologies for function spaces. — Bull. Amer. Math. Soc. 51
A945), 429—432.
Форт (Fort M. K. jr.)
[1951] A note on pointwise convergence. — Proc. Amer. Math. Soc. 2 A951),
34-35.
[1955] Category theorems. — Fund. Math. 42 A955), 276—288.
Франклин (Franklin S. P.)
[1965] Spaces in which sequences suffice.— Fund. Math. 57 A965), 107—
115.
[1967] Spaces in which sequences suffice II. —Fund. Math. 61 A967), 51—
56.
[1969] On two guestions of Moore and Mrowka. — Proc. Amer. Math. Soc.
21 A969), 597—599.
Франклин, Раджагопалан (Franklin S. P., Rajagopalan M.)
[1971] Some examples in topology. — Trans. Amer. Math. Soc. 155 A971),
305—314.
Фрейденталь (Freudenthal H.)
[1937] Entwicklungen von Raumen und ihren Gruppen. — Сотр. Math. 4
A937), 145—234.
Фрейденталь, Гуревич (Freundenthal H., Hurewicz W.)
[1936] Dehnungen, Verkurzungen, Isometrien. — Fund. Math. 26 A936),
120—122.
Фреше (Frechet M.)
[1906] Sur quelques points du calcul fonctionnel. — Rend, del Circ. Mat. di
Palermo 22 A906) 1—74.
[1910] Les dimensions d'un ensemble abstrait. — Math. Ann. 68 A910), 145—
168.
[1910a] Les ensembles abstraits et le calcul fonctionnel. — Ren. del Circ.
Math, di Palermo 30 A910), 1—26.
[1918] Sur la notion de voisinage dans les ensembles abstraits. — Bull. Sci.
Math. 42 A918), 138—156.
[1926] Les espaces abstraits. — Paris, 1926.
Фринк A. (Frink A. H.)
[1937] Distance functions and the metrization problem. — Bull. Amer. Math.
Soc. 43 A937), 133—142.
ЛИТЕРАТУРА 721
Фринк О. (Frink О.)
[1964] Compactifications and semi-normal spaces. — Amer. J. of Math. 86
A964), 602—607.
Фролик (Frolik Z.)
[1959] Обобщения компактности и свойства Линделёфа. — Czech. Math.
J. 9 A959), 172—217.
[1960] On the topological product of paracompact spaces. — Bull. Acad. Pol.
Sci. Ser. Math. 8 A960), 747—750.
[1960a] An example concerning countably compact spaces. — Czech. Math. J.
10 A960), 255—257.
[1960b] Generalization of the Ga-property of complete metric spaces.—
Czech. Math. J. 10 (I960), 359—379.
[1961] Applications of complete families of continuous functions to the
theory of Q-spaces. — Czech. Math. J. 11 A961), 115—133.
[1961a] Локально топологически полные пространства. — ДАН СССР 137
A961), 790—792.
[1961b] On approximation and uniform approximation of spaces. — Proc. Ja-
Japan Acad. 37 A961), 530—532.
[1967] Sums of ultrafillers. — Bull. Amer, Math. Soc. 73 A967), 87—91.
[1967a] On two problems of W. W. Comfort. — Comm. Math. Univ. Carolinae
8 A967), 139—144.
Фурдзик (Furdzik Z.)
[1968] On absolute Gg in perfectly normal topological spaces. — Zeszyty
Nauk. U. J. 167, Prace Mat. 12 A968), 17—18.
Хаар, Кёниг (Haar A., Konig D.)
[1910] Uber einfach geordnete Mengen. — J. fur die reine und engew. Math.
139 A910), 16—28.
Хабер (Chaber J.)
[1972] Remarks on open-closed mappings. — Fund. Math. 74 A972), 197—208.
[1976] Conditions which imply compactness in countably compact spaces.—
Bull. Acad. Pol, Sci. Ser. Math. 24 A976), 993—998.
Хайнал, Юхас (Hajnal A., Juhasz I.)
[1967] Discrete subspaces of topological spacel. — Indag. Math. 29 A967),
343—356.
[1969] Some remarks on a property of topological cardinal functions.—Acta
Math. Acad. Sci. Hung. 20 A969), 25—37.
[1974] On hereditarity a-Lindelof and a-separable spaces, II. — Fund. Math.
81 A974), 147—158.
Халмош (Halmos P. R.)
[1963] Lectures on Boolean algebras. — Princeton, 1963.
Хан (Hahn H.)
[1914] Mengentheoretische Charakterisierung der stetigen Kurve. — Sitzung-
sberichte Akad. Wiss. Wien Abt. Ha 123 A914), 2433—2489.
[1917] t)ber halbstetige und unstetige Funktionen. — Sitzungsberichte Akad.
Wiss. Wien Abt. Ha 126 A917), 91 — 110.
[1921] Theorie der reeilen Funktionen. — Berlin, 1921.
[1932] Reelle Funktionen I. — Leipzig, 1932.
Ханаи (Hanai S.)
[1956] On closed mappings. II. —Proc. Japan Acad. 32 A956), 388—391.
[1961] Inverse images of closed mappings. I. — Proc. Japan Acad. A961),
298—301.
Ханаи, Окуяма (Hanai S., Okuyama A.)
[1962] On pseudocompactness and continuous mappings.— Proc. Japan
Acad. 38 A962), 444—447.
Ханнер (Hanner O.)
[1951] Solid spaces and absolute retracts. — Ark. for Mat. 1 A951), 375—
382.
46 Зак. 697
722 ЛИТЕРАТУРА
Харатоми (Haratomi К.)
[1931] Uber hoherstufige Separabilitat und Kompaktheit I. —Jap. J of Math
8 A931), 113—141.
Хаусдорф (Hausdorff F.)
[1914] Grundzuge der Mengenlehre,— Leipzig, 1914.
[1919] Uber halbstetige Funktionen und deren Verallgemeinerung. — Math
Zeitschr. 5 A919), 292—309.
[1924] Die Mengen Gq in vollstandigen Raumen. — Fund. Math. 6 A924),
146—148.
[1927] Mengenlehre. — Berlin, 1927. [Русский перевод: Хаусдорф Ф. Теория
множеств. —М. —Л.: ГТТИ, 1937.]
[1930] Erweiterung einer Homoomorphie. — Fund. Math. 16 A930), 353—360.
1934
1935
1936
Uber innere Abbildungen. — Fund. Math. 23 A934), 279—291.
Gestufte Raume. —Fund. Math. 25 A935), 486—502.
Summen von «i Mengen. — Fund. Math. 26 A936), 241—255.
1936a] Uber zwei Satze von G. Fichtenholz und L. Kantorovitch. — Studia
Math. 6 A936), 18—19.
[1938] Erweiterung einer stetigen Abbildung. — Fund. Math. 30 A938), 40—
47.
Хейджер (Hager A. W.)
[1969] Approximation of real continuous functions on Lindelof spaces.—
Proc. Amer. Math. Soc. 22 A969), 156—163.
Хеммингсен (Hemmingsen E.)
[1946] Some theorems in dimension theory for normal Hausdorff spaces. —
Duke Math. J. 13 A946), 495—504.
Хенкин (Henkin L.)
[1950] A problem on inverse mapping systems. — Proc. Amer. Math. Soc.
1 A950), 224—225.
Хенриксен, Исбелл {Henriksen M., Jsbell J. R.)
[1957] Local connectedness in the Stone-Ceeh compactification. — 111. J. of
Math. 4 A957), 574—582.
[1958] Some properties of compactificatins. — Duke Math. Ж 25 A958),
83—106.
Хенриксен, Исбелл, Джонсон (Henriksen M., Isbell J. R., Johnson D. G.)
[1961] Residue class fields of lattice-ordered algebras. — Fund. Math. 50
A961), 107-1117.
Херрлих (Herrlich H.)
[1965] Ordhugsfahigkeit total-diskontinuierlicher Raume.— Math. Ann. 159
A965), 77—80.
[1965a] Wenn sind alle stetigen Abbildungen in Y konstant. — Math. Zeitschr.
90 A965), 152—154.
Хигман, Стоун (Higman G., Stone A. H.)
[1954] On inverse systems with trivial limits. — J. London Math. Soc. 29
A954), 233—236.
Хит (Heath R. W.)
[1964] Screenability, pointwise paracompactness and metrization of Moore
spaces. —Canad. J. of Math. 16 A964), 763—770.
Хьюитт (Hewitt E.)
[1946] On two problems of Urysohn. — Ann. of Math. 47 A946), 503—509.
[1946a] A remark on density characters. — Bull. Amer. Math. Soc. 52 A946),
641—643.
[1947] Certain generalizations of the V/eierstrass approximation theorem. —
Duke Math. J. 14 A947), 419—427.
[1948] Rings of real-valued continuous functions, I. — Trans. Amer. Math.
Soc. 64 A948), 45—99.
[1950] Linear functionals on spaces of continuous functions.— Fund. Math.
37 A950), 161—189
ЛИТЕРАТУРА 723
Цорн (Zorn М.)
[1935] A remark on method in transfinite algebra. — Bull. Amer Math Soc
41 A935), 667—670.
Чарльзуорт (Charlesworth A.)
[1976] A note on Urysohn metrisation theorem. — Amer. Math. Monthly 83
A976), 718—720.
Чертанов Г. И.
[1975*] Произведение линейно упорядоченных пространств и непрерывные
отображения. — ДАН СССР 223 A975), 1322—1325.
[1984*] Псевдорадиальность произведения конечного числа линейно упоря-
упорядоченных бикомпактов. — В сб.: Управление, надежность, навига-
навигация.— Саранск, 1984.
Чех (Cech E.)
[1931] Sur la theorie de la dimension. — С. R. Acad. Paris. 193 A931),
976—977.
[1932] Sur la dimension des espaces parfaitement normaux.—Bull. Intern.
Acad. Tcheque Sci. 33 A932), 38—55.
[1932a] Theorie generate de l'homologie dans un espace quelconque. — Fund.
Math. 19 A932), 149—183.
[1933] Pnspevek k theorii dimense. — Casopis Pest. Mat. Fys. 62 A933),
277—291.
[1937] On bxompact spaces. —Ann. of Math. 38 A937), 823—844.
[1959] Topologicke prostory. — Praha. 1959.
Чех, Поспишил (Cech E., Pospisil B.)
[1938] Sur les espaces compacts. — Publ. Fac. Sci. Univ. Masaryk Brno 258
A938), 3—7.
Чигогидзе А. Ч.
[1977*] О неравенстве Урысона—Менгера. — Труды Тбил. гос. ун-та, 185
A977), 51—57.
[1980*] On some questions in dimension theory. — Colloq. Math. Soc. Janos
Bolyai, 23, Topology, v. I, North-Holland, 1980, pp. 273—286.
[1980a*] О совершенно х-нормальных пространствах. — ДАН СССР 250
A980), 308—311.
[1982*] О бесконечных бикомпактах. — Сиб. матем. ж. 23 A982), № 2,
с. 157—164.
Читтенден (Chittenden E. W.)
[1917] On the equivalence of ecart and voisinage. — Trans. Amer. Math. Soc.
18 A917), 161-166.
Читтенден, Питчер (Chittenden E. W., Pitcher A. D.)
[1919] On a theory of developments of an abstract class in relation to the
calcul fonctionel.— Trans. Amer. Math. Soc. 20 A919), 213—233.
Чобан М. M.
[1966] О поведении метризуемости при факторных s-отображениях.— ДАН
СССР, 166 A966), 562—565.
[1967] Совершенные отображения пространств счетного типа. — Вестник
МГУ, сер. матем. A967), № 6, с. 87—93.
[1967а*] Некоторые метризационные теоремы для перистых пространств. —
ДАН СССР 173 A967), 1270—1272.
[1969] Об экспоненциальной топологии, — ДАН СССР 186 A969), 272—
274.
[1969а*] О <г-паракомпактных пространствах. — Вестник МГУ, сер. матем.
A969), № 1, с. 20-27.
[1970] К теории р-пространств. — ДАН СССР 194 A970), 528—531.
[1971] Note sur la topologie exponentielle. — Fund. Math. 71 A971),27—41.
[1971a*] Многозначные отображения и борелевские множества, L —Тр.
Моск. матем. об-ва, 22 A971), 229—250.
[1972*] Многозначные отображения и борелевские множества, II. — Тр.
Моск. матем. об-ва, 23 A972), 277—301.
46*
724 ЛИТЕРАТУРА
[1973*] Редукционные теоремы о существовании непрерывных сечений. —
Матем. исслед. 8 A973), № 4, с. 111—156.
[1974*] Непрерывные образы полных пространств. — Тр. Моск. матем. об-
ва, 30 A974), 23-59.
[1975*] Об операциях над множествами. — Сиб. матем. ж. 16 A975), № 6,
с. 1322—1351.
[1975а*] Модификации топологий и непустота классов. — Сердика, Българ-
ско матем. списание, 1 A975), 133—143.
[1976*] Топологическое строение подмножеств топологических групп и их
факторпространств. — ДАН СССР 228 A976), 52—55.
[1977*] Топологическое строение подмножеств топологических групп и их
факторпространств. — В сб.: Матем. исслед. — Кишинев: Штиинца,
1977, вып. 44, с. 117—163.
[1978*] Общие теоремы о сечениях и приложения — Българска матем. спи-
списание, 4 A978), с. 74—90.
[1979*] Открытые отображения и классы пространств. В кн.: Топологиче-
Топологические пространства и алгебраические системы. — Кишинев: Штиинца,
1979, с. 148—173.
[1983*] Отображение и размерностные свойства пространств. — Тр. Матем.
ин-та АН СССР, 154 A983), 296—305.
Чобан М. М., Додон М. К.
[1979*] Теория ^-разреженных пространств. — Кишинев: Штиинца, 1979.
Чогошвили Г. С.
[1941*] О пространствах сходимости. — Матем. сб. 9 E1), A941), № 2,
с. 377—381.
[1966*] Обобщенные произведения, пределы и их применения. — УМН 21
A966), № 4.
Шанин Н. А.
[1943] О специалньых расширениях топологических пространств. — ДАН
СССР 38 A943), 7—11.
[1943а] К теории бикомпактных расширений топологических пространств. —
ДАН СССР 38 A943), 166—169.
[1944] О погружениях в степень топологического пространства. — Изв.
АН СССР, сер. матем. 8 A944), 233—242.
[1946] Одна теорема из общей теории множеств. — ДАН СССР 53 A946),
403—404.
[1946а] О взаимном пересечении открытых подмножеств произведения то-
топологических пространств. — ДАН 53 A946), 503—506.
[1946b] О диадических бикомпактах. — ДАН СССР 53 A946), 785—788.
[1948] О произведении топологических пространств.—¦ Тр. матем. ин-та АН
СССР 24 A948), 1—112.
Шапнро Л. Б. к
[1976] Пространство замкнутых подмножеств D 2 не является диадиче*
ским бикомпактом. — ДАН СССР 228 A976), 1302—1305.
[1976*] Об абсолютах топологических пространств и непрерывных отобра-
отображений.—ДАН СССР 226 A976), 523—526.
[1976а*] О пространствах замкнутых подмножеств бикомпактов. — ДАН
СССР, 231 A976), 295—2Э8.
Шапировский Б. Э.
[1972] О дискретных подпространствах топологических пространств. Вес,
теснота и число Суслина. — ДАН СССР 202 A972), 779—782.
[1974] Канонические множества и характер. Плотность и вес в биком-
бикомпактах. — ДАН СССР 218 A974), 58—61.
[1975*] О я-характере и я-весе в бикомпактах,—ДАН СССР 223 A975),
799—802.
[1975а*] О мощности наследственно нормальных пространств. — ДАН СССР,
225 A975), 767—770.
ЛИТЕРАТУРА 725
[1976*] О тесноте, я-весе и близких к ним понятиях. — Уч. зап. Рижск.
ун-та 3 A976), 88—99.
[1980*] Об отображениях на тихоновские кубы. — УМН 35 A980), № 3,
с. 122—130.
[1981*] Кардинальные инварианты в бикомпактах. — В кн.: Семинар по об-
общей топологии. — М.: Изд. МГУ, 1981.
Шахматов Д. Б.
[1983*] Кардинальные инварианты топологических полей.— ДАН СССР 271
A983), 1332-1336.
[1984*] О псевдокомпактных пространствах с точечно счетной базой.—
ДАН СССР 279 A984), 825—829.
Шевалле, Фринк (Chevalley С, Frink О. jr.)
[1941] Bicompactness of Cartesian products. — Bull. Amer. Math. Soc. 47
A941), 612—614.
Шедива (Трнкова) (Sediva V.)
[1959] О коллективно нормальных и сильно паракомпактных пространст-
пространствах.—Czech. Math. J. 9 A959), 50—62.
Шерф (Schaerf H. M.)
[1968] Topological cardinality theorems. In: Proceedings of the Internatio-
International Symposium on Topology, Herceg Novi 1968. — Beograd, 1969,
pp. 292.
Шимрат (Shimrat M.)
[1956] Decomposition spaces and separation properties.—Quart. J. of Math.
Oxford 7 A956), 128—129.
Широков Л. В.
[1982*] Внешняя характеристика пространств Дугунджи и каппа-метризуе-
мых бикомпактов. — ДАН СССР 263 A982), 1073—1077.
Широта (Shirota Т.)
[1952] A class of topological spaces. — Osaka Math. J. 4 A952), 23—40.
Шнейдер В. Е.
[1945] Непрерывные образы суслинских и борелевских множеств. Метри-
Метризационные теоремы.— ДАН СССР 50 A945), 77—79,
Шостак А. П.
[1974] Характеристика класса полных по Чеху паракомпактов как класса
^-компактности. — Bull. Acad. Pol. Sci. Ser. Math. 22 A974), 839—
844.
Шпернер (Sperner E.)
[1928] Neuer Bewies fur die Invarianz der Dimensionszahl und des Gebie-
tes. — Abh. Math. Semin. Hamburg. Univ. 6 A928), 365—272.
Штейниц (Steinitz E.)
[1908] Beitrage zur Analysis situs. —Arch, der Math, und Phys. 13 A908),
Sitzungsberichte Berl. Math. Ges. 7 A908), 29—49.
Шура-Бура М. P.
[1941] К теории бикомпактных пространств. — Матем. сб. 9 A941), 385—
388.
Щепин Е. В.
[1973*] Аксиоматика размерности метрических пространств.— Матем. сб. 92
0973), № 1, с. 135—141.
[1976*] Топология предельных пространств нечетных обратных спектров.- —
УМН 31 A976), Но 5, с. 191-226.
[1976а*] Вещественные функции и канонические множества в тихоновских
произведениях и топологических группах. — УМН 31 A.976), № 6,
с. 17—27.
[1977*] Конечномерный бикомпактный абсолютный окрестностный ретракт
метризуем. — ДАН СССР 233 A977), 304—307.
[1979*] О тихоновских многообразиях. — ДАН СССР 246 A979), № 3.
[1979а*] О х-метризуемых пространствах. — Изв. АН СССР 43 A979),
№ 2.
726 ЛИТЕРАТУРА
[1981*] Функторы и несчетные степени компактов. — УМН 36 A981), № 3,
с. 3—62.
[1984*] Мягкие отображения многообразий. — УМН 39 A984), № 5, с. 209—
224.
Эйленберг (Eilenberg S.)
[1934] Sur les transformations continues d'espaces metriques compacts.—
Fund. Math. 22 A934), 292—296.
Эйленберг, Otto (Eilenberg S., Otto E.)
[1938] Quelques proprietes caracteristiques de la theorie de dimension. —
Fund. Math. 31 A938), 149—153.
Эйленберг, Стинрод (Eilenberg SM Steenrod N.)
[1952] Foundations of algebraic topology. — Princeton. 1952. [Русский пере-
перевод: Стинрод Ы., Эйленберг С. Основания алгебраической тополо-
топологии. М.: Физматгиз, 1958.]
Энгелькинг (Engelking R.)
[1963] Quelques remargues concernant les operations sur les fonctions se-
semi-continues dans les espaces topologiqes. — Bull. Acad. Pol. Sci.
Sen Math. 11 A963), 719—726.
[1964] Remarks on real-compact spaces. — Fund. Math. 55 A964), 303—308.
[1965] Cartesian products and dyadic spaces. — Fund. Math. 57 A965), 287—
304.
[1966] On functions defined on Cartesian products. — Fund. Math. 59 A966),
221—231.
[1967] On Bore! sets and ^-measurable functions in metric spaces.— Prace
Mai 10 A967), 145—149.
[1968] On the double circumference of Alexandroff. — Bull. Acad. Pol. Sci.
Ser. Math. 16 A968), 629—634,
[1971] Closed mappings on complete metric spaces. — Fund. Math. 70 A971),
103—107.
[1972] Hausdorff's gaps and limits and compactifications. In: Theory of
sets and topology (in honour of Felix Hausdorff). — Berlin, 1972,
pp. 89—94.
[1973] Some new proofs in dimension theory. In: Proceedings of the Sym-
Symposium on General Topology, Rome 1973.— 1st. di Alta Mat. Sympo-
Symposia Math. 16 A975), 83—91.
[1978] Dimenison theory.—Amsterdam, 1978.
Энгелькинг, Голштынский, Сикорский (Engelking R., Holsztynski W., Sikor-
ski R.)
[1966] Some examples of Borei sets. —Coll. Math. 15 A966), 271—274.
Энгелькинг, Латцер (Engelking R., Lutzer D. J.)
[1977] Paracompactness in ordered spaces. — Fund. Math. 94 A977), 49—58.
Энгелькинг, Мрувка (Engelking R,, Mrowka S.)
[1958] On ^-compact spaces. — Bull. Acad. Pol. Sci. Ser. Math. 6 A958),
429—436.
Энгелькинг, Пелчинский (Engelking R., Pekzyriski A.)
[1963] Remarks on dyadic spaces. — Coll. Math. 11 A963), 55—63.
Эрдёш (Erdos P.)
[1940] The dimension of tiie rational points in Hilbert space.—Ann. of
Math. 41 A940), 734—736.
Эрдёш, Тарский (Erdos P., Tarski A.)
[1943] On families of mutually exclusive sets. — Ann. of Math. 44 A943),
315—329.
Юннила (Junnila H. J. K.)
[1978] Stratifiable pre-images of topological spaces. In: Colloquia Math.
Soc. J. Bolyai 23 (Proceedings of Colloquium on Topology, Buda-
Budapest 1978).—Amsterdam, 1980, pp. 689—703.
ЛИТЕРАТУРА 727
Юхас (Juhasz I.)
[1969] On closed discrete subspaces of product spaces. — Bull. Acad. Pol.
Sci. Ser. Math. 17 A969), 219—223.
[1970] Martin's axiom solves Ponomarev's problem. — Bull. Acad. Pol. Sci.
Ser. Math. 18 A970), 71-74.
[1971] Cardinal functions in topology. — Math. Centre Tracts 34, Amster-
Amsterdam, 1971.
[1971a] Proof of a theorem of H. M. Schaerf. — Math. Balk. 1 A971), 129—
133.
[1980] Cardinal functions in topology—ten years later. — Math. Centre
Tracts 123, Amsterdam, 1980.
Юхас, Кунен, Рудиы (Juhasz I., Kunen K., Rudin M. E.)
[1976] Two more hereditarily separable non-Lindelof spaces. — Canad. J.
of Math. 28 A976), 998—1005.
Яковлев Н. H.
[1976*] К теории о-метризуемых пространств. — ДАН СССР 229 A976),
1330—1332.
[1980*] On bicompacta in 2-products and related spaces. — Comment. Math.
Univ Carol. 21 A980), 263—283.
Янишевский (Janiszewski Z.)
[1912] Sur les continus irreductibles entre deux points. — J. Ecole polyt. 16
A912), 79—170.
Ясуи (Yasui Y.)
[1967] Unions of strongly paracompact spaces, — Proc. Japan Acad. 43
A967), 263—267.
УКАЗАТЕЛЬ ОБОЗНАЧЕНИЙ
А[}В,А1[)Ааи...\)Аъ \JA, 17 l<piP>a 24
* ' 6+1 24
ЛПВ. i4,ni4,fl ¦•• l)А*. П Л, 17 »a 25
«=1 No 25
A\B, Ac=B, В=зА 17 *0, *j x5 |<a 25
0 17 (a> b), [a, b], (a, ft], [a, 6) 31
xeAxfid U R.N.I 31
{ж е ЛГ: ф (х)}, {х: Ф (*)} 17 w ({Х> в)), w (X) 34, 40
{*»' *2 xft} 17 x (jc, (X, <?)), x (ж. А-) 34, 40
XXY,XlXX2X-..XXk 18 x ({Xi a)), x (X) 34,40
f(A) 18 J 35
/"'(S) 18 InM 37
gf 18 Ft A
Г1 18 ^d
51
52
19 rf(X) 53
Jti, *2. • • ¦ 19 л*-' 56
.} 19 /:JT->K 57
19 |/| 59
.У/^У/"^ 19 ш1а(/.Лш«(/.в) 59
oo Нт/г 60
f| As, f\ At. ГЦ* 19 Z)(m) 67
sss ':' A(m) 67
П4П^ 20 {*a.ors?> 88
{*.}¦{*«} 20 mn<FaeS 92
|51 21 Hm xt 93, 372
f° Г (a, b), (*-. a), (a, ->) 98
2m,expnt 21 eW ,03
n™ ^ 21 /(x.JT), /(JT) 104
m<n, n> m 21 f 112
TJsms 22 Л./1^/л ИЗ
УКАЗАТЕЛЬ ОБОЗНАЧЕНИИ 729
V fs, /jVf2V ...V/fc 119 У(ЛГ) 258
?i^ ^ ^2-^ 258
Х|Л*) 121 p* 260
123 aX 261
<o* 271
126 l(X) 293
6 (Л) < ^ 297
127 g(*) 302
s^S ' ~ " vx 327
Xm 127 tJ 335
p5 127 t(AfX) 339
Ял, /я, 5я, Вп 130 С (Я), С* (X) 356
П/в./,х/2х-..хъ i31 *(Х) ш
s*=s B(x,r), В (А, г) 370
A fs, fj Af2 Д ... Д/л 131 б (Л) 373
Г5 131 /(m) 374
cm зб 9{Х>Л) 377
^^ 136 р(Л,В) 377
/m, /Ro 137 р„ 384
137 В (т) 388
F- 138 Р 389
Х/Е 147 Z/P 394
E(f) 147 №р) 405
f 147 Я(т) 427
JT/Л 151 рЯ 441
ХМ.Г 151 St(AI, st), St(jc,j#) 449
HmS, lim{^a, nj, 2} 160 м
Т~ *" 1АО ^ 491
я<у lb2 indX 561
lim {ф, /Д 165 jn(j х 562
limfff 168 ord^ 563
*7 dim ^ 564
Ex U 568, 569
-Л 622
А + В 622
пЛ 623
\x-yl<V, |JC-y|>V 623
5 (л:, V), В (Л, F) 623
w (Ш) 624
Q? B?* СО Л
f: (Xt<U)->(Y, T) 636
^Л, 640
У
М (Л, 5)
2, Й, Л
hd (X)t he (X), he (X)
*(Х)
2 (a)
2х
nw(X)
$ {x, X), ф (X)
h(X)
kX,kf
cX
171
172
175
176
184
186
188
192
201
212
213
240, 241
257
730 УКАЗАТЕЛЬ ОБОЗНАЧЕНИЙ
Щ
Л 6S, А 6В
и (X)
@1) —(ОЗ)
(В1)-(В2)
644
644
654
660
664
675
680
681
33
33—34
(BPI)-(BP4)
(C1)-(C3)
(CO1)-(CO4)
ПОП — A04)
(RC1)-(RC2)
(M1)-(M3)
(U1)-(U4)
(BUI) —(BU3)
(UC1) —(UC4)
(UP1)-(UP3)
(P1)-(P5)
(SI1) —(SI7)
34—35, 70
35
36
38
320
370
623
624
624
630, 673
660
664
ИМЕННОЙ УКАЗАТЕЛЬ
Абель (Abel N. Н.) 42
Акуаро (Aquaro G.) 359
Алас (Alas О. Т.) 511
Александер (Alexander J. W.) 331
Александров П. С. 45, 50, 67, 84, 144,
157, 168, 210—212, 214, 227, 241,
263, 294, 318, 330, 331, 333, 344,
346, 353, 410, 423, 425, 431, 475,
494, 495, 528, 543, 586, 614, 616,
637, 681
Альстер (Alster К.) 87
Андерсон (Anderson R. D.) 381
Арене ((Arens R.) 97, 178, 179, 253—
255, 303, 394, 438, 439, 484, 648
Ароншайн (Aronszajn N.) 67, 495
Архангельский А. В. 104, 158, 159,
185, 211, 212, 229, 241, 242, 264,
288, 289, 301, 302, 339—342, 346,
347, 350, 352, 394, 425, 426, 465,
495, 497, 501, 504, 505, 507, 516
Ариела (Arzela С.) 43
Асколи (Ascoli G.) 43, 254
Балачандран (Balachandran V. К.)
424
Банах (Banach S.) 410, 414, 440
Банашевский (Banaschewski В.) 548
Бартл (Bartle R. G.) 96
Бегль (Begle Е. G.) 487
Бендиксон (Bendixson I.) 102
Беннет (Bennett H. R.) 332, 513
Бернштейн (Bernstein F.) 502
Берри (Berri M. Р.) 334
Бёме (Boehme Т. К.) 320
Бинг (Bing Я Н.) 423, 455, 464,
494, 501, 527
Биркгоф (Birkhoff G.) 96, 99, 637,
639
Блэр (Blair R. L.) 328
Бокштейн М. Ф. 187
Болл (Ball В. J.) 514
Больцано (Bolzano В.) 42, 43
Бонан (Bonan E.) 181
Борджес (Borges С. J.) 504
Борель (Borel E.) 43, 55, 209
Борсук (Borsuk К.) 157, 437, 512,
528
Брауэр (Brouwer L. E. J.) 413, 428,
544, 573, 599, 600
Брунс (Bruns G.) 96
Бурбаки (Bourbaki N.) 67, 96, 105,
157, 183, 211, 228, 288, 318, 436,
507, 621, 637, 648, 657
Бурке (Burke D. К.) 501
Бут (Booth D.) 318
Бэгли (Bagley R. W.) 254, 317, 348
Бэкон (Bacon P.) 440
Бэр (Baire R.) 43, 106, 157, 392, 410
413
Ваге (Wage M. L.) 543
Вайнштейн И. А. 288, 289, 424, 433,
434, 543
Ван Данциг (Van Dantzig D.) 527
Ван Дауэн (Van Douwen E. К.) 185,
265, 353, 586
Ван дер Слот (Van der Slot J.) 146,
289, 328
Веденисов Н, Б. 5, 85, 543, 574, 586
Вейерштрасс (Weierstrass К.) 43,227,
392
Вейль A. (Weil A.) 621, 637, 648, 657
Вейль Г. (Weyl H.) 44, 67
Вейр (Weir M. D.) 328
Вейс (Weiss W. A. R.) 185
Величко Н. В. 364
Видосич (Vidossich G.) 424
Вислисени Ю. 351
Волмэн (Wallman H.) 274, 513, 574,
618, 619
Вольтерра (Volterra V.) 43
Вон (Vaughan H.) 393
Вопенка (Vopenka P.) 426, 599
Воррэк (Warrack В. D.) 670
Вудс (Woods R. G.) 555
Вулберт (Wulbert D. Е.) 365
Вулих Б. 3. 329
Вьеторис (Vietoris L.) 44, 84, 192,
210, 330, 364, 555
Гантнер (Gantner Т. Е.) 674
Гаусс (Gauss К. F.) 42
Гельфанд К М. 356
Гемба (Geba К.) 438
Гиллман (Gillman L.) 276, 277, 328—
330, 359, 514, 543, 555, 574, 637
Гильберт (Hilbert D.) 43, 44
Гликсберг (Glicksberg I.) 317—319,
354—356, 362
732
ИМЕННОЙ УКАЗАТЕЛЬ
Глисон (Gleason A. M.) 188, 553
Годел (Hodel R. Е.) 290, 343, 485
Голштынский (Holsztynski W.) 211,
302, 586, 620
Готшелк (Gottshalk W. Н.) 227
Гроот де (de Groot J.) 344, 548, 602
Гросс (Gross W.) 381
Гулько С. П. 432, 433
Гуревич (Hurewicz W.) 67, 241, 429,
513, 574, 586, 599—601, 616—619
Гэйл (Gale D.) 241
Даламбер (D'AIembert J. L.) 42
Даукер (Dowker С. Н.) 241, 427, 464,
466, 473—475, 484, 510, 512, 513,
536, 543, 544, 586, 587, 599, 615,
616, 682
Дедекинд (Dedekind R.) 43
Джексон (Jackson J. R.) 253, 392,
394
Джентри (Gentry К. R.) 191, 552
Джерисон (Jerison M.) 276, 277,
328—330, 359, 543, 555, 574, 637
Джонсон (Johnson D. G.) 295
Джоунс (Jones F. В.) 84, 494, 495,
497
Дини (Dini U.) 227
Динь Ньё Тонг 158, 289
Дирихле (Dirichlet L.) 42
Досс (Doss R.) 676
Дугунджи (Dugundji J.) 178, 179,
428, 437, 438, 484
Дьедонне (Dieudonne J.) 105,228 294,
353, 436, 463, 464, 466, 512, 676,
678
Дюбуа-Реймон (Du Bois-Reymond P.)
42—43
Есенин-Вольпин А. С. 347
Ефимов Б. А. 347, 348, 363, 431,
432
Ефремович В. А. 669, 670, 681
Жордан (Jordan С.) 43, 527
Зайцев В. И. 86
Зарелуа А. В. 617
Зенор (Zenor P.) 185, 192, 303, 339,
365, 366, 475, 509, 679
Зоргенфрей (Sorgenfrey R. Н.) 50,
144, 294, 464
Зоретти (Zoretti L.) 44, 527
Иванов А. В. 337
Илиадис С. Д. 554
Исбелл (Isbell J. R.) 187, 188, 214,
288, 289, 294, 295, 301, 317, 328,
382, 393, 475, 548, 637, 640, 673,
675, 682
Исивата (Isiwata T.) 107, 317, 328,
353
Исии (Ishii T.) 511, 679
Исикава (Ishikawa F.) 474
Исэки (Iseki К.) 359, 474
йех (Jech Т.) 184
Какутани (Kakutani S.) 274, 637,
639
Кантор (Cantor G.) 43, 44, 55, 102,
410, 527
Канторович Л. В. 276
Каплан (Kaplan S.) 484
Каратеодори (Caratheodory С.) 263
Картан (Cartan H.) 96
Касахара (Kasahara S.) 359
Катетов (Katetov M.) 101, 105 120,
181, 189, 190, 274, 317, 328, 334,
335, 436, 473, 474, 506, 510, 512,
574, 586, 587, 599, 600, 618, 674,
682
Катута (Katuta Y.) 503
Кауфман (Kaufman R.) 332
Кац Г. И. 677, 678
Кейслер (Keisler H. J.) 328
Келлерер (Kellerer H. G.) 229
Келли (Kelley J. L.) 96, 109, 227, 228,
241, 242, 253, 288, 648, 671
Кендеров П. 318, 328
Керстан (Kerstan J.) 317
Кёниг (Konig D.) 317
Кимура (Kimura N.) 586
Кислинг (Keesling J.) 193, 364
Кисынский (Kisynski J.) 109
Кли (Klee V. R.) 295
Кнастер (Knaster B.) 527, 556, 600
Ковальский (Kowalsky H. J.) 423
Кол (Raul S. K.) 256
Колмес (Colmez J.) 317, 319
Колмогоров А. Н. 84, 356
Комбаров А. П. 546
Комфорт (Comfort W. W.) 313, 317,
353—355, 383
Коннелл (Connell E. H.) 317
Корсон (Corson H. H.) 104, 187, 188,
361—363, 433, 464
Коши (Cauchy A. L.) 42
Коэн (Cohen D. E.) 241
Краевский (Krajewski L. L.) 511
Кук (Cook H.) 18Э
Кунен (Kunen K.) 336, 338
Куратовский Kuratowski K.) 31, 44,
45, 98, 107, 120, 126, 180, 193, 210,
ИМЕННОЙ УКАЗАТЕЛЬ
733
264, 328, 330, 337, 366, 381, 394,
410, 427, 439, 441, 495, 502, 527,
528, 545, 552, 556, 600, 614
Курепа (Kurepa D.) 184—186
Куцья (Kucia A.) 640, 675
Лаврентьев М. А. 410, 430
Латцер (Lutzer D. J.) 332, 515, 515,
679
Лашнев Н. С. 507
Лебег (Lebesgue H.) 43, 55, 100, 120,
209, 411, 573, 574, 620
Леви P. (Levy R.) 265
Леви Ф. (Levi F.) 157
Левшенко Б. Т. 359
Лейбниц (Leibniz G.) 42
Лелек (Lelek A.) 620
Леннес (Lennes N. J.) 527, 549
Лере (Leray J.) 288
Лефшец (Lefschetz S.) 85, 169, 618
Лин (Lin Y. F.) 227
Линделёф (Lindelof E.) 102, 294
Линденбаум (Lindenbaum A.) 412
Линн (Lynn I. L.) 547
Лифанов И. К. 574
Локуциевский О. В. 191, 612
Лунц А. Л. 613
Люббен (Lubben R. G.) 263, 288
Магилл (Magill К. D.) 264
Мазер (Mather M. R.) 464
Мазур (Mazur S.) 187, 440, 464
Мазуркевич (Mazurkiewicz S.) 410,
411, 434, 543, 550, 552, 557, 600
Майкл (Michael E.) 190, 192, 193,
241, 255, 288, 294, 295, 303, 349,
350, 361, 364, 393, 424, 430, 431,
436, 441, 458, 464, 467, 484, 485,
501, 502, 504, 505, 507, 545, 555,
556, 680
Макдауэлл (McDowell R. Н.) 265,
548
Макдугл (McDougle P.) 158
Макки (Mackey G. W.) 329
Макнайт (McKnight J. D.) 317
Маколей (McAuley L. F.) 214, 295,
499, 501
Малыхин В. И. 189, 339, 340
Мангейм (Manheim J. H.) 44
Мансфилд (Mansfield M. J.) 99, 509,
510, 515
Мардешич (Mardesic S.) 312, 348,
616, 617
Марчевский (Marczewski Е.) 144,
145, 346
Марьянович (Marjanovic M.) 366
Мейер (Meyer P. R.) 99
Менгер (Menger К.) 550, 573, 586,
599, 600, 618
Мерэ (Мёгау С.) 43
Мибу (Mibu Y.) 229
Мищенко А. С. 331, 361
Монтгомери (Montgomery D.) 430,
431
Мор Р. К. (Moore R. С.) 104
Мор Р. Л. (Moore R. L.) 44, 157,
494, 495, 528, 549, 550
Мор Э. (Moore E. Н.) 96
Морита (Morita К.) 253, 294, 423,
424, 426, 436, 437, 463, 464, 467,
474, 475, 484, 487, 495, 497, 498,
503, 504, 511, 513, 575, 586, 588,
599—601, 616, 618, 619
Морс (Morse А. Р.) 253
Мостовский (Mostowski A.) 31, 328,
330
Мрувка (Mrowka S.) 104, 183, 211,
263, 274, 277, 317, 320, 328, 349,
363, 506
Мысьор (Mysior A.) 157, 328
Нагами (Nagami К.) 295, 484, 485,
503, 509, 599, 600, 602, 615, 619,
620
Нагата (Nagata J.) 423, 424, 466,
486, 496, 497, 499, 504, 600, 678
Наимпалли (Naimpally S. A.) 670
Накамура (Nakamura M.) 274
Нахбин (Nachbin L.) 328
Немыцкий В. В. 50, 214, 412
Нёбелинг (Nobeling G.) 618
Никош ((Nyikos P.) 436, 495
Нобл (Noble N.) 187, 317—319, 353,
354
Новак (Novak J.) 157, 191, 274, 275,
317
Ньютон (Newton I.) 42
Окстоби (Oxtoby J. С.) 302
Окуяма (Okuyama A.) 320, 504
Олл (Aull С. Е.) 339, 475
О'Мира (О'Меага Р.) 508
Осташевский (Ostaszewski A. J.) 336
Отто (Otto E.) 586
Папич (Papic P.) 332
Паровиченко И. И. 265
Пархоменко А. С. 242, 334
Пасынков Б. А. 330, 504, 505, 574,
587, 617
Пелант (Pelant J.) 675
Пелчинский (Pelczynski A.) 346, 431,
432
Питчер (Pitcher A. D.) 392, 494
734
ИМЕННОЙ УКАЗАТЕЛЬ
Поль P. (Pol R.) 211, 342, 347, 394
435, 546, 574, 588
Поль Э. (Poi E.) 191, 192, 347, 546,
552, 553, 574
Помпейю (Pompeiu D.) 441
Пондицери (Pondiczery E. S.) 144,
145
Пономарев В. И. 87, 104, 211, 288
320, 330, 339, 347, 393, 487, 554,
681
Понтрягин Л. С. 317, 600, 618
Портер (Porter J. R.) 334
Поспишил (Pospisil В.) 190,274,345,
346
Пуанкаре (Poincare H.) 43, 67, 573
Пшимусинский (Przymusinski Т.) 294,
464, 543, 547, 586, 587, 601
Пэнлеве (Painleve P.) 527
Раджагопалан (Rajagopalan M.) 351
Рамер (Ramer A.) 191
Резниченко Е. А. 313
Рейнуотер (Rainwater J.) 553
Риман (Riemann В.) 43
Рисе (Riesz F.) 44, 84, 96, 210, 527,
669
Роберте (Roberts J. H.) 557, 599,600
Розенталь (Rosenthal A.) 44
Рой (Roy P.) 600
Ройтман (Roitman J.) 336
Росс (Ross К. А.) 186, 187, 313
Рудин М. (Rudin M.) 184, 295, 336,
352, 423, 432, 433, 464, 474, 511,
512
Рудин У. (Rudin W.) 275
Рыль-Нардзевский (Ryll-Nardzew-
ski С.) 317
Сакс (Saks S.) 210
Самюэль (Samuel P.) 674, 675, 679
Свордсон (Swardson M. А.) 423
Семадени (Semadeni Z.) 438
Сентмиклоси (Szentmikloszy Z.) 336,
337
Серпинский (Sierpinski W.) 67, 180,
184, 210, 274, 330, 335, 337, 431,
502, 505, 528, 542, 543, 544, 549,
552, 557, 600
Сигал (Segal J.) 556
Сикорский (Sikorski R.) 620
Силвер (Silver J. H.) 494, 495
Сирота С. 365
Ситников К- А. 599
Скарборо (Scarborough С. Т.) 318
Скляренко Е. Г. 617
Скула (Skula L.) 332
Смирнов Ю. М. 86, 100, 181, 184,
263, 294, 317, 335, 344, 363, 423,
426, 484, 496, 574, 586, 611—613
615, 616, 670, 682, 683
Смит Г. (Smith H. L.) 96
Смит Дж. (Smith J. С.) 511
Старбёрд (Starbird M.) 464, 511,
512
Степанек (Stepanek P.) 426
Стефенсон (Stephenson R. М.) 318
334
Стин (Steen L. А.) 99, 517
Стинрод (Steenrod N.) 169, 227, 527
Стоилов (Stoiiow S.) 67, 543
Стоун A. (Stone A. H.) 186, 187,
190, 214, 255, 318, 423, 430, 436,
437, 463, 464, 467, 485, 495, 499,
503, 588, 673
Стоун М. (Stone M. Н.) 101, 157,
227, 230, 263, 274, 275, 334, 356,
543
Страшевич (Straszewicz S.) 549
Суслин М. Я. 184
Тайманов А. Д. 227, 288
Тамано (Tamano H.) 317, 354, 464,
503, 677
Тарский (Tarski A.) 328, 383
Тейхмюллер (Teichmuller О.) 31
Тельгарский (Telgarsky R.) 503
Тенненбаум (Tennenbaum S.) 184
Терасава (Terasawa J.) 543
Терасака (Terasaka H.) 317
Титце (Tietze H.) 44, 84, 120, 125,
181, 182
Тихонов А. Н. 84, 85, 144, 157, 227,
263, 274, 353, 392, 412
Тодорчевич (Todorcevic S.) 184, 336
Толл (Tall F. D.) 185, 338, 494, 495
Толстова Г. В. 618
Тонг (Tong H.) 105, 106, 181, 182,
353
Трейлор (Traylor D. R.) 485
Тумаркин Л. А.
Тьюки (Tukey J. W.) 31, 346, 465,
467, 495, 498, 637, 639, 673
Уайберн (Whyburn G. Т.) 288, 392,
424, 528, 543, 548
Уайтхед (Whitehead J. H. С.) 241
Уиллард (Willard S.) 437, 464, 503
Улам (Ulam S.) 328
Ульмер (Ulmer M.) 187
Уокер (Walker R. С.) 265, 274
Уоллес (Wallace A. D.) 227, 548,549,
574
Уорнер (Warner S.) 255
Уоррел (Worrell J. M.) 484, 486
Уотерхаус (Waterhouse W. C.) 169
ИМЕННОЙ УКАЗАТЕЛЬ
735
Урысон П. С. 50, 84, 85, 101, 108,
120, 122, 180, 181, 210, 211, 294,
318, 330, 331, 333, 344, 353, 381,
392, 425, 440, 475, 494, 495, 527,
543, 573, 586, 599, 600, 611, 618,
637
Федорчук В. В. 332, 337, 514
Филиппов В. В. 158, 547, 574, 620
Фихтенгольц Г. М. 276
Фицпатрик (Fitzpatrick В.) 189
Флаксмайер (Flachsmeyer J.) 351,
554
Флейснер (Fleissner W. G.) 495
Флейшер (Fleischer I.) 317
Флейшман (Fleischman W. М.) 360
Фокс (Fox R. Н.) 179, 253, 254
Форт (Fort M. К.) 105, 428
Франклин (Franklin S. Р.) 146, 159,
277, 317 346, 351, 394
Фредгольм (Fredholm I.) 43
Фрейденталь (Freudenthal H.) 169,
429
Фреше (Frechet M.) 44, 55, 67, 108,
143, 317, 381, 392, 410, 413, 428
Фринк A. (Frink A. H.) 495, 496
Фринк О. (Frink О.) 86, 227, 334
Фролик (Frolik Z.) 87, 227, 288, 301,
303, 317, 329, 330, 352, 359, 361,
505, 506, 677
Фурдзик (Furdzik Z.) 500
Хаар (Нааг А.) 331
Хабер (Chaber X) 87, 289, 302, 360,
436, 586
Хайнал (Hajnal A.) 185, 333, 336,
342-345
Халмош (Halmos P. R.) 431
Хан (Hahn H.) 105, 106, 441, 552
Ханаи (Hanai S.) 317, 318, 320, 423,
424, 464, 475, 476, 487
Ханнер (Hanner О.) 464
Харатоми (Haratomi К.) 383
Хаусдорф (Hausdorff F.) 44, 50, 55,
67, 84, 85, 102, 120, 181, 264, 276,
317, 381, 382, 410, 411, 429, 431,
434, 439, 441, 505, 527, 542, 543,
602
Хедлунд (Hedlund G. А.) 227
Хейджер (Hager A. W.) 295, 303,
353-355
Хеммингсен (Hemmingsen E.) 586,
615, 616
Хенкин (Henkin L.) 169
Хенриксен (Henriksen M.) 288, 289,
294, 295, 301, 317, 382, 475, 514,
548
Херрлих (Herrlich H.) 190, 191, 546,
547
Хигман (Higman G.) 214
Хит (Heath R. W.) 495, 496
Хопф (Hopf Н.) 50, 423
Хьюитт (Hewitt E.) 144, 191, 230,
319, 328, 329, 350, 353, 356
Хьюстон (Houston R. S.) 360
Цорн (Zorn M.) 31
Чарльзуорт (Charlesworth A.) 485
Чех (Cech E.) 84, 263, 274, 276, 301,
345, 346, 410, 573, 574, 586, 600,
612, 615
Читтенден (Chittenden E. W.) 392,
494, 496, 497
Чобан М. М 212, 289, 364, 365, 437,
485
Шанин Н. А. 144, 183, 185, 186, 301,
346, 347, 574
Шапиро Л. Б. 364
Шапировский Б. Э. 211, 340, 341,
343—345
Шахматов Д. Б. 313
Шевалле (Chevalley С) 227, 334
Шедива (Sediva V.) 500
Шерф (Schaerf H. М.) 681
Шимрат (Shimrat M.) 393
Широта (Shirota Т.) 328, 640, 659,
679
Шмидт (Schmidt J.) 96
Шнейдер В. Е. 392
Шостак А. П. 506
Шпернер (Sperner E.) 600
Штейниц (Steinitz E.) 143
Шура-Бура М. Р. 527
Эйленберг (Eilenberg S.) 169, 227,
527, 586
Энгелькинг (Engelking R.) 187, 213,
295, 303, 328, 329, 346, 348, 361,
362, 366, 367, 431—433, 514, 515,
543, 574, 586, 588, 599, 615, 618—
620, 679
Эрдёш (Erdos P.) 383, 535, 543, 574
Юннила (Junnila H. J. К.) 394
Юхас (Juhas I.) 104, 185, 186, 214,
333, 336—338Г 342—345, 681
Янг (Yang J. S.) 254, 648
Янишевский (Janiszewski Z.) 210,
542
Ясуи (Yasui Y.) 486
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абсолют 554, 555
Абсолютно мультипликативный, аб-
абсолютно аддитивный класс а 430
Аддитивное свойство 124
Аддитивный класс а 100
Аксиома выбора 28
Аксиомы отделимости 69—70
Александера теорема о предбазеЗЗ!
Александрова двойная окружность
205, 263
— метризационный критерий 493
— теорема 221
— Урысона метризационная теорема
494
Александровская (одноточечная) ком-
пактификация 261
Александровский куб 138
Антидискретная топология 39
Антидискретное пространство 39, 59,
75, 78, 81, 374
Архангельского метризационная тео-
теорема 492
Асколи теорема 253, 647
База множества в топологическом
пространстве 121
— равномерности 623
— топологического пространства 33
-в точке 34
— фильтра 91, 92
Банаха теорема о неподвижной точ-
точке 414
Барицентр 605
Барицентрические координаты 604
Барицентрическое подразделение 607
Бернштейна множество 502
Бикомпактные пространства 308
Бита метризационная теорема 418
— метризационный критерий 488
— пример 455, 501
Близкие подмножества 660
Близостно изолированные простран-
сгва 663
— непрерывное отображение 662
Близостный изоморфизм 662
Близость 660
— индуцированная метрикой 664
равномерностью 663
— на топологическом пространстве
668
Большая индуктивная размерность
562, 568, 570, 573, 575, 618, 619
Борелевские множества 54, 57, 68,
99, 430, 620
Борсука теорема о продолжении го-
мотопии 513
Брауэра теорема о неподвижной точ-
точке 598, 610, 620
— Чеха размерность 562, см. Боль-
Большая индуктивная размерность
Бэра пространство 388, 395, 535,
595, 596, 602
— теорема о категории 298, 302,
319—320, 411
Вайнштейна лемма 422
Веденисова теорема 82
Верхняя грань (точная) кардиналов
22
подмножества 27
Вершины полиэдра 614
— симплекса 603
Вес равномерного пространства 624
— равномерности 624
— топологического пространства 34,
41, 64, 72, 138, 145, 201—202, 230,
232, 250, 257, 283, 287, 289, 303,
332—333, 347, 363, 617
Вещественно полное (^-полное, пол-
полное по Хьюитту) пространство
320—330, 358—359, 364, 366, 506
Взаимно однозначное отображение
19
Вложение подпространства в равно-
равномерное пространство 640—641
топологическое простран-
пространство 112
Вложимое пространство 113
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
737
Внешнее определение 84
Внешняя база подпространств 302
Внутреннее определение 84
Внутренность множества 37
Волмэновское расширение 272, 273,
365, 545
Вписанное покрытие 196
Вполне несвязное пространство 542
557
— ограниченная метрика 395
равномерность 650, 655, 657,
674—676
— ограниченное метрическое про-
пространство 395—399, 408, 411
равномерное пространство 650,
651, 655
— отделимые подмножества 77
— регулярное пространство 73, см.
Тихоновское пространство
— упорядоченное множество 23
Всюду плотное множество 52
подпространство 112
Вторая аксиома счетности 34
Выпуклая компонента 182
Выпуклое подмножество (в линейно
упорядоченном пространстве) 182
(в л-мерном евклидовом про-
пространстве) 228
Вьеториса топология 192
Гильбертов куб 137, 382, 386, 387,
620
Гильбертово пространство 376, 382,
427
Гипокомпактное пространство 482,
см. Сильно паракомпактное про-
пространство
Гипотеза континуума 25
Гомеоморфизм 64
Гомеоморфное вложение 113
Гомеоморфные пространства 64
Гомотопия 512
Граница множества 51
Грань симплекса 603
График отображения 136
Группа 632
Даукера пример 536
— теорема 578
«Две стрелки» 318, 332, 338, 346
Де Моргана законы 17
Декартово произведение групп 672
множеств 19
отношений 154
отображений 131, 138, 139, 154,
155, 239—240, 254, 279, 281, 349
равномерностей 641
равномерных пространств 641—
643, 648—651, 653
топологических пространств
127—146, 160—162, 170, 185—191,
193, 200, 201, 217, 218, 220—222,
228—230, 234, 239, 240, 264, 275,
279—281, 301, 308, 309, 313, 315,
316, 319, 321, 322, 326, 334, 340,
348, 353—356, 385—388, 436, 459,
462, 463, 472—474, 487, 502—504,
511, 512, 521, 533, 548, 550, 552,
596, 615, 677
Диагональ отображений 130, 139—
141, 145, 175, 245, 280
— произведения 131, 623
Диагональное отображение 131, см.
Диагональ отображений
Диадические пространства 431
Диадический компакт 346
Диаметр множества 373
Дини теорема 224, 319
Дискретная близость 662
— равномерность 626
— топология 38
Дискретное пространство 38, 59, 67,
78, 82, 137, 204, 235, 270, 325, 330,
374, 388, 395, 455, 534
близости 662
метрическое 374
равномерное 626
— семейство множеств 40
Длинная прямая 352
Длинный отрезок 352
Допустимая топология 177, 390
Дугообразно связное пространство
551
Евклидово пространство 130
Единичная сфера 130
Единичный куб 130
— шар 130
Еж 374, 395, 528
Естественная топология вещественной
прямой 39
замкнутого интервала / 39
интервала 114
Естественное факторное отображение
147
Замкнутое в точке отображение 433
— множество 35
— отношение эквивалентности 150,
157—158, 221, 229
— отображение 62, 68, 83, 112, 113,
120, 121, 138—140, 146, 149, 158,
47
к. 697
738
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
199, 200, 210, 235, 238, 292; 306,
340, 422, 426, 434, 459, 475, 476,
479, 481, 507, 527, 619
— подпространство 112
— покрытие 80
Замыкание 35
Звезда вершины 614
— множества, точки 449
Звездно вписанное покрытие 449
— конечное, звездно счетное семей-
семейство 470
Зоргенфрея прямая 47, 50, 54, 59,
63, 67, 68, 78, 80, 82, 122, 125,
204, 211, 293, 319, 325, 458, 474,
485, 534
Идеал 356
Измельчение покрытия 195
— пространства (измельчающаяся
последовательность покрытий)
487—488
Измеримое отображение класса а 100
Изолированные точки 52
Изометрия 377
Инвариант класса отображений 65
Индексированное семейство 19
Индуцированная топология 111
Инъективное отображение 18
Калибр пространства 186
Каноническая база произведения 128
Каноническое замкнутое множество
45, 68, 121, 144, 186
— открытое множество 45, 68, 121,
144
Кантора — Бендиксона теорема 102
— Бернштейна теорема 21
— теорема 399
Канторов куб 137, 143, 216, 316, 347,
534
Канторово множество 137, 207, 228,
414, 544
Кардинал (кардинальное число) 21
— регулярный 24
Кардинальные функции 102, 183, 335
Категорный метод 410
Катетова — Мориты теорем а 591,601
Катетовское расширение 335, 336
Квазикомпонента 524
Кнастера — Куратовского веер 556
Коллективно нормальное простран-
пространство 452, 455, 465, 477, 486, 499—
500, 511—512, 515
Кольцо функций 224—226
непрерывных 356
Комбинация отображений 119, 154,
174, 245, 279
Компакт 208
Компактификация 256—274, 282 283
296, 332, ЗоО—352, 358, 363, 432*
462, 534, 617, 668—671, 676
Компактно накрывающее отображе-
отображение 506, 507
Компактное топологическое простран-
пространство 196—230, 252, 253, 274, 285,
304, 308—310, 313, 320, 321, 330—
332, 334, 345, 348, 349, 358, 360,
362, 364, 366, 367, 380, 386, 390—
392, 412, 436, 444, 453, 462, 465,
475, 477, 532, 540, 647, 648, 654,
655, 668, 678
Компактно-открытая топология 243—
256, 295, 366, 390, 394, 413, 466,
508, 646—649
Композиция функций 18
Компонента пространства 524
— семейства множеств 483
— точки 523
Консервативное семейство 466
Континуум (мощность) 21
— (пространство) 522, 523, 526, 546,
549-551
Конфинальное подмножество 27
Конфинальный ординал 24
Коплотное множество 52
Коши направленность 657
— последовательность 398
— фильтр 657
Куратовского теорема 200, 349
— Цорна лемма 28
Лаврентьева теорема 405
Лебега теорема о покрытиях 409
~ число
Левая топология 98
Легкое отображение 538
Лексикографическое упорядочение 332
Линделёфа свойство 290
— число 293, 342
Линделёфово пространство (про-
(пространство со свойством Линделё-
Линделёфа) 290—294, 303, 304, 325, 330,
331, 362, 363, 380, 444, 456, 484,
502, 528, 531
Линейно независимые точки 603
— связное пространство 550—552
— упорядоченное множество 22, 182
подмножество упорядоченного
множества 27
пространство 98—99, 182, 331—
333, 346, 513—515, 546-547
Линейное упорядочение 22
Линейно-мультипликативный функ-
функционал 358
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
739
Локально дугообразно связное про-
пространство 551
— замкнутое подмножество 180
— компактное пространство 231—
237, 241, 242, 244, 245, 247, 250,
254, 260, 261, 284, 285, 290, 297,
303, 340, 351, 364—365, 457, 487,
503, 675
— конечное разбиение единицы 445
семейство множеств 40
— линейно связное пространство
550—552
— полное по Чеху пространство 352,
505
— связное пространство 547, 548,
550, 551, 556
— секвенциально компактное про-
пространство 320, 350
— сепарабельное пространство 425,
485
Локальный гомеоморфизм 425
Луч в я-мерном евклидовом про-
пространстве 228
Майкла—Нагами теорема 477
— пример 458—459, 501—502
— теорема 459
Максимальная компактификация 260,
см. Стоун-чеховская компактифи-
компактификация
Максимальный идеал 356
— фильтр 91, 92
— элемент 28
Малая индуктивная размерность 561,
562, 569, 570, 573, 574, 581
Мардеишча факторизационная теоре-
теорема 617
Мелкость симплициального подразде-
подразделения 605
Менгера — Урысона размерность 561,
см. Малая индуктивная размер-
размерность
Метакомпактное пространство 476,
см. Слабо паракомпактное про-
пространство
Метризационные теоремы 372, 386—
392, 417, 418, 436, 466, 488, 489,
492—494, 496—499
Метризуемое пространство 371, 378—
384, 398, 403, 405, 407—409, 411 —
423, 433—442, 504, 511, 512, 515,
588—597, 677
.— — вполне ограниченной метрикой
395, 398, 439
полной метрикой 398
— равномерное пространство 635
Метрика на множестве 370
топологическом пространстве
371
Метрическое пространство 370
Минимальная компактификация 261,
см. Александровская компактифи-
компактификация
Минимальный фильтр Коши 679
Мищенко лемма 361
Многозначные отображения 107, 193,
366
Множества первой категории 298
— типа F6 55, 58—59, 77, 121, 122,
144, 180—181, 302, 457, 486, 500,
509-510, 678
Об 55, 58-59, 76, 121, 144, 146,
276, 300, 378, 393, 405—407, 466,
504, 515, 618
Монотонное отображение 526, 538,
552, 553
Мора метризационная теорема 489,
495
Моровские пространства 494
Мощность множества 21
— ординала 24
Мультипликативное свойство 131
Мультипликативный класс а 100
Нагаты — Смирнова метризационная
теорема 417
Направленное множество 27
Направленность 88—92, 109, 141,173,
203
Нарост компактификации 259, 261,
263, 269, 276, 277, 296, 319, 382
Наследственно линделёфово про-
пространство 294, 437
— несвязное пространство 529, 532,
533, 535, 546, 557
— нормальное пространство 114—
116, 183, 189, 190, 284, 348
— сепарабельное пространство 114,
255
— факторное отображение 158—159,
192, 289, 394, 553
Наследственное свойство 114
Неархимедова метрика 602
Независимые множества 276
Неизмеримый кардинал 325
Немыцкого плоскость 48, 50, 54, 60,
63, 68, 86, 118, 122, 293, 329, 474,
485
Непрерывная функция 59
Непрерывно сходящаяся направлен-
направленность 179
— упорядоченное множество 23
Непрерывное отображение 57
Непрерывный образ 62
47*
740
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Неприводимое отображение 211,507—
508
— покрытие 476
Неравенство треугольника 370
Нетривиальный функционал 358
Нигде не плотное множество 53
Нижняя грань (точная) подмноже-
подмножества 27
Нить обратного спектра 160
Нормально расположенное множе-
множество 100, 181, 363
Нормальное покрытие 452
Нормальное пространство 74—82,
85—88, 105, 115, 116, 119, 142, 174,
181—182, 189, 190, 199, 270, 284,
291, 310, 353, 416, 436, 445, 454,
462, 464, 465, 471—473, 511
Нульмерное отображение 538, 539,
545
— пространство 529—538, 543—545,
556
Образ 18
Обратная последовательность 160,
167, 168, 189, 190, 192, 301, 303,
386, 474—475, 485, 502, 558, 602
Обратный инвариант класса отобра-
отображений 65
— спектр 160—168, 191, 192, 214—
215, 222, 223, 242, 248, 264, 275,
322, 348—349, 365, 533, 552—553,
575, 677
равномерных пространств 649
Ограниченная метрика 373
— функция 219
Ограниченное множество в п-мерном
евклидовом пространстве 219
метрическом пространстве
373
— отображение 389
Однообразно непрерывное семейство
отображений 251
Окрестность 33
Окружение диагонали 623
Ординал 23
— инициальный (начальный) 24
— наследник 24
— нечетный 24
— предельный 24
— предшественник 24
— регулярный 24
— счетный 24
— четный 24
Отделенные множества 115
Отделимость 69
Открытое множество 33
— отношение эквивалентности 150,
157
— отображение 62, 68, 83, 112, 113,
120, 121, 138—140, 149, 158, 235,
238, 290, 320, 330, 353, 393, 420,
435, 487, 507, 527, 545
— подпространство 112
—¦ покрытие 80
Открыто-замкнутое множество 35
— отображение 62
Открытый шар 370
Отношение 18
— эквивалентности 20
Отображение 18
— вычисления 176
— обратного спектра в обратный
спектр 164
Отождествление 150
Паракомпакт 444
Паракомпактное пространство 444—
468, 477, 502—506, 514, 515, 588,
671, 677, 678
Первая аксиома счетности 34
Перегородка 582
Плотное в себе множество 53
Плотность 53, 62, 70—72, 134, 184,
213, 230, 255, 257, 265, 332—333,
379
Подгруппа 673
Подмножество 17
Подобные множества 23
Подпокрытие 196
Подпространство равномерного про-
пространства 640
— топологического пространства
111—120, 128, 142, 163, 164, 196—
200, 230, 231, 239, 291, 299, 305,
312, 313, 322, 383, 457, 486, 519,
520, 532, 541, 550, 562, 563, 567,
615, 616, 677, 678
Покрытие 80, 195
Полиэдр 613
Полная метрика 398
Полное кольцо функций 357
— метрическое пространство 398—
403, 406, 410
— по Дьедонне пространство 676—
678
Чеху пространство 297—301,
346, 365, 408, 426, 466, 504, 505
Полунепрерывная функция 104, 181,
512
Полунепрерывное отображение 107
— разбиение 150
Пополнение метрического простран-
пространства 405, 429—430
— равномерного пространства 654,
655, 658, 678
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
741
Порядковый тип 23
Порядок семейства множеств 563
Последовательность 19
Постоянный обратный спектр 168
Почти совершенное отображение 287
Предбаза 34
Предел направленности 88
— обратного спектра равномерных
пространств 649
— топологических пространств
160
— последовательности в метрическом
пространстве 372
— фильтра 92
Предельная точка множества 52
направленности 88
фильтра 92
Предельное отображение 165—168,
222, 281, 552
Приемлемая топология 177—179, 245,
254
Присоединенное пространство 151,
158
Продолжение отображения 116, 267
Проективная резольвента 553—555
Проективное пространство 553, 554
Проекции 127
Произведение см. Декартово произве-
произведение
Производное множество 52, 56
Прообраз 18
Пространство близости 660
— р-адических чисел 672
— точечно счетного типа 212, 213,
229, 242, 264, 303, 342
Псевдокомпактное пространство 310—
312, 314, 318—320, 329, 347, 351,
354, 355, 548, 676, 677
Псевдометрика 370
Псевдохарактер 212
Пунктиформное (разрывное) про-
пространство 542
Равномерная псевдометрика 627
Равномерно изоморфные простран-
пространства 636
— непрерывное отображение метри-
метрического пространства 377
— равномерного пространства
636
— сходящаяся последовательность 60,
391
— эквивалентные метрики 382
Равномерное покрытие 624
— пространство 624
Равномерность на множестве 623
индуцированная близостью
666
— — топологическом пространстве
625
— равномерной сходимости 644, 645
Равномерные инварианты 637
Равномерный вес 681
— изоморфизм 636
Равномощные множества 21
Равностепенно непрерывное семейство
646
Разбивающая точка 549
Разбиение единицы 445
Разделение точек 135
и замкнутых множеств 135
Раздутие семейства 564
Размерность в смысле покрытий 564,
566, 570, 575—592, 600, 613—616
— полиэдра 614
Разреженные множества 102
Расстояние в метрическом простран-
пространстве 370, 377
Регулярная база 490
Регулярно расположенные множества
363
Регулярное пространство 71, 79, 85>
87, 115, 121, 122, 124—125, 131,
155, 161, 173, 190, 191, 197, 249,
284, 285, 343, 344, 416, 448
Ретракт 85, 122, 431, 620
Ретракция 85, 160
Самюэля компактификация 674
Свободные ультрафильтры 271
Свойство конечного характера 28
Связное пространство 517—529, 546,
555-557, 659
— семейство множеств 483
Связующие отображения 160
Сегмент 228
Секвенциальная топология 109
Секвенциально компактное простран-
пространство 314—316, 318, 320, 346, 352,
380
Секвенциальное пространство 94—96,
99, 104, 122, 146, 159, 160, 170, 237,
269, 277, 306, 313, 314, 320, 350,
394
Семейство 19
Семирегулярное пространство 101,
183, 553
Сепарабельное пространство 53, 62,
134, 135, 145, 170, 187, 381, 387,
391, 398, 456
Серпинского теорема 526
Сетевой вес топологического про-
пространства 201, 202, 214, 232, 255,
287, 293, 303, 333
Сеть 201
742
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Сечение множества 22
Сжимающее отображение 414
Сильно звездно вписанное покрытие
449
— недостижимый кардинал 325
— нульмерное пространство 529—
533, 537, 539—545, 555, 557, 588
— паракомпактное пространство
482—484, 514, 528, 588
Сильное (тонкое) равномерное про-
пространство 638
Симплекс 603
Симплициальное подразделение 604
Система окрестностей 34
Скачок 23
Слабо паракомпактное пространство
476—482, 485—487, 501, 502, 506,
514
— б-равномерное покрытие 682
Смирнова теорема 669
Собственная топология 177—179, 244
Собственное подмножество 17
Совершенно нормальное простран-
пространство 8—83, 87, 106, 174, 189, 190,
284, 378, 436, 466, 471, 512
Совершенное множество 102
— отображение 277—290, 301, 307,
319, 326, 340, 353, 365, 421, 461,
486, 487, 537, 538, 545
— пространство 86, 102, 435
— свойство 287
Совершенный класс 287, 306
Согласованные отображения 119
Спред 103
Сравнение топологий 39
Стационарное подмножество 514
Стоуна — Вейерштрасса теорема 225
— теорема 414
Стоун-чеховская компактификация
260, 265—274, 283, 296, 353—356,
362, 363, 462, 520, 532, 541, 548,
670, 676, 677
Строгая предельная точка 304
Строгое включение 664, 681
Субпаракомпактное пространство 501
Сужение 112, 113
Сумма отображений 126
— пространств 123—126, 143, 170,
217, 234, 239, 291, 300, 306, 312,
329, 384, 458, 485, 533, 541, 548,
568
— равномерных пространств 649
Суслина проблема 184
— пространство 184, 185
— свойство 103, 185
— число (клеточность) 103, 184—186,
337—346
Сходимость в метрическом простран-
пространстве 372
Счетно аддитивная двузначная мера
325
— компактное пространство 304—
310, 314, 315, 318-320, 353, 359-
361, 380, 436, 453, 477, 678
— паракомпактное пространство
468—476, 509—513
— центрированное семейство 291
Счетное множество 21
Тамано теорема 462
Тейхмюллера •— Тьюки лемма 28
Теорема о диагональном отображе-
отображении 136
локально конечной сумме 578
перегородках 583
разложении 594
— — сложении 594
счетной сумме 576
а-локально конечной сумме 592
— об отделении 594
Теоремы о сумме 576, 578
Теснота множества 339—341
— пространства 104, 333, 339—341,
347
Титце — Урысона теорема 116
Тихонова плоскость 353
— теорема 217
Тихоновская топология 127
Тихоновский куб 137—139, 219
Тихоновское пространство 73, 85—87,
115, 124, 131, 138, 155, 161, 173,
198, 219, 250, 270, 284, 310, 319,
635, 668
Тождественное отображение 19
Топологическая группа 632, 639, 673,
680
Топологические свойства 66
Топологическое пространство 33
Топология 33, 46
— индуцированная близостью 661
— — метрикой 371
упорядочением 98
— порожденная базой 46
классом сходящихся направлен-
ностей 109
оператором взятия внутрен-
внутренности 49
замыкания 48
равномерностью 625
семейством отображений 61
системой окрестностей 47
— поточечной сходимости 173
— равномерной сходимости 172—174
Тор 130
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
743
Точечно конечное, точечно счетное
семейство множеств 80
— паракомпактное пространство 476,
см. Слабо паракомпактное про-
пространство
— регулярная база 490
Точка конденсации 102
— накопления 52
— полного накопления 330
Трансфинитная индукция 25
— последовательность типа а 25
Уайтхеда теорема 236, 349
Ужатие покрытия 565
Ультрафильтр 91, 92
Универсальная равномерность 638,
675
Универсальное пространство 136—
138, 145, 219, 387, 413, 418, 440,
534, 596, 617
Униформизуемое пространство 625,
см. Тихоновское пространство
Уоллеса теорема 220
Уоррела теорема 481
Уплотнение 329
Упорядочение 26
Упорядоченная пара 18
Упорядоченное множество 26
Урысона лемма 75
— пространство 101, 183, 553
Факторотображение (факторное ото-
отображение) 148—155, 157—158, 235,
238, 349, 437
Факторпространство 147, 152, 157,
221, 289, 349, 389
Фактортопология 147
Фильтр 91, 92, 141, 203—204
Финально компактное пространство
291
Фреше топология 108
— Урысона веер 340
пространство 94, 95, 97, 109,
159, 350, 394
Функционально замкнутое множество
77, 78, 85, 91, 121, 378
— — покрытие 529
— открытое множество 78, 85, 91,
121, 323
— — покрытие 259
Функция (отображение) 18
Ханаи — Мориты — Стоуна теорема
422
Характер множества 121, 212
—- пространства 34, 63, 71, 143, 208,
287, 332, 333, 342, 346, 365
— точки 34, 63, 120, 212, 231, 345—
348
Хаусдорфова метрика 441
Хаусдорфово пространство 70, 71,
85—87, 115, 121, 124, 131, 133, 161,
173, 193, 198, 199, 284, 341—344
Хелли пространство 229
Хемикомпактное пространство 255,
256, 294, 394, 413
Хьюитта — Марчевского — Лондице-
ри теорема 133
Хьюиттово пополнение (пополнение
по Хьюитту) 327, 329, 358, 675
Центрированное семейство 196
Цепочка 482
Цермело теорема о вполне упорядо-
чиваемости 28
Чеха — Лебега размерность 564, см.
Размерность в смысле покрытий
Шанина число 186
Шар в метрическом пространстве 370
равномерном пространстве 623
Шпернера лемма 608
Щели 514
Щель (сечение) 23
Эквивалентные компактификации
257—259
— метрики 372
Экспоненциальное отображение 176,
245
— пространство 192, 364—366, 441—
442, 555—556, 680—681
Экстент 103
Экстремально несвязное пространства
540, 541, 553
Эрдёша пример 543, 574
^-отображение 614
^-просеянные пространства 501
Я-замкнутое пространство 333
Я-минимальное пространство 334
^-пространство 236—240, 247, 248,
299, 312, 350, 647
744
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
«^-пространство, ^-пространство
108
р-адическая равномерность 671, 672
Го-пространство 69, 85, 87, 115, 124,
131, 156, 161, 173, 193
Гшространство 69, 78, 85, 87, 105,
106, 115, 124, 131, 161, 173, 193,
342—344, 447, 449
Т2-пространство 70, см. Хаусдорфово
пространство
Гз-пространство 71, см. Регулярное
пространство
^/¦¦пространство см. Тихоновское
пространство
Т4-пространство 74, см. Нормальное
пространство
Гб-пространство 116, см. Наследствен-
Наследственно нормальное пространство
Гб-пространство 116, см. Совершенно
нормальное пространство
6-равномерное покрытие 665
2-произведение 188, 189, 361—363,
432
а-дискретное семейство множеств
414
а-компактное пространство 292, 294,
295, 430
а-локально конечное семейство мно-
множеств 414
0-паракомпактное пространство 501
Компактное т
метризуемое
Секвенциально
компактное
Счетно
компактное
Сепарабельное
"^" метризуемое
Метризуемое
^ Ме1ризуемое
Метризуемое
локально компактное
полной метрикой
С первой аксиомой*^
счетности
Локально компактное
хаусдорфово
Фреще-Урысона
Сильно
паракомпактное
хаусдорфово
Нормальное
счетно
паракомпактное
Псевдокомпактное
Коллективно
нормальное
Слабо
наракомпактное
Вещественно
полное
Совершенно
нормальное
Наследственно
нормальное
Тихоновское -<-
"Нормальное
Соотношения между основными классами топологических пространств
Подпространство
Замкнутое подпространство
Открытое подпространство
Конечная сумма
Сумма
Конечное произведение
Счетное произведение
Произведение
Предел обратной последовательности
Предел обратного спектра
v
A
Ч
i
Инварианты
1
+
1
1
1
1
1
1
4-
I
1
1
1
!
1
1
+
+
t
I
1
+
1
t
1
+
+
1
4-
+
1
1
1
1
1
1
+
+
1
1
1
4-
I
1
1
1
1
1
4-
I
1
1
1
1
1
+
+
4-
1
1
1
+
1
1
1
4-
4-
1
+
+
1
1
t
1
1
+
+
+
I
1
I
+
+
1
1
4-
+
1
+
1
1
I
I
1
+
4-
4-
'
I
+
I
1
1
+
1
+
+
+
+
+
1
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
1
+
+
+
+
+
+
1
1
t
+
1
I
+
1
1
1
)
t
!
+
+
1
+
+
+
4-
+
+
+
+
+
+
+
+
+
+
+
1
+
+
1
1
1
'
1
t
1
1
1
1
1
+
1
1
1
1
1
+
+
1
t
к -пространство
Компакт
Локально компактное хаусдорфово
Счетно компактное
Псев до компактное
Секвенциально компактное
Полное по Чеху
Линделефово
Вещественно полное
Метризуемое
Паракомпакт
Коллективно нормальное
Счетно паракомпактное
Слабо паракомпактное
Сильно паракомпактное
Связное
Наследственно несвязное
Нульмерное
Сильно нульмерное
Экстремально несвязное
Сохраняются
в сторону
образа
Непрерывные
Факторные
Открытые
Замкнутые
Открыто-замкнутые
Совершенные
Открытые совершенные
\7
Сохраняются в сторону
прообраза
Совершенные
Открытые совершенные
/\
Свойства, сохраняемые отображениями
8.
+
+
(
+
+
1
1
+
+
1
1
1
1
1
¦
1 +
1
1
+
1
1
1
1
1
+
+
+
+
+
+
+
+
+
+
+
1
+
1
1
1
1
1
+
¦ о
+
+
к»
1
+
+
+
+
1
+
1
1
]
+
+
1
1
1
1
1
1
+
V»
+
1
!
i
1
1
1
1
!
1
1
I
+
+
1
СП
I
1
I
1
1
I
1
i
1
i
i
1
J
+
I
+
«*
1
!
1
1
1
1
I
I
1
1
1
fc-пространсгво
Компакт
Локально компактное хаусдорфово
Счетно компактное хаусдорфово
Псевдокомпактно&
Секвенциально компактное
хаусдорфово
Полное по Чеху
Лннделефово
Вещесавенно полное
Метризуемое
Ларакомпактное
Коллективно нормальное
Счетно паракомпактное хаусдорфово
Хаусдорфово слабо паракомпактное
Хаусдорфово сильно паракомпактное
Связное
Наследественно несвязное
Нульмерное
Сильно нульмерное
Экстремально несвязное
ОГЛАВЛЕНИЕ
ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ 5
ПРЕДИСЛОВИЕ 14
ВВЕДЕНИЕ 17
I. 1. Алгебра множеств. Функции 17
~. 2. Кардинальные числа 21
. 3. Упорядочения. Порядковые числа 22
. 4. Аксиома выбора 28
. 5. Вещественные числа 30
ГЛАВА 1. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА 32
1.1. Топологические пространства. Открытые и замкнутые множества.
Базы. Замыкание и внутренность множества , 33
1.2. Методы введения топологий 46
1.3. Граница множества, производное множество. Плотные и нигде не
плотные множества. Борелевские множества 51
1.4. Непрерывные отображения. Замкнутые и открытые отображения.
Гомеоморфизмы 57
1.5. Аксиомы отделимости 69
1.6. Сходимость в топологических пространствах: направленности и
фильтры. Секвенциальные пространства и пространства Фреше . . 8&
1.7. Задачи 98
ГЛАВА 2. ОПЕРАЦИИ НА ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ. ПО
2.1. Подпространства 111
2.2. Суммы 123
2.3. Произведения 127
2.4. Факторпространства и факторные отображения 147
2.5. Пределы обратных спектров 160
2.6. Пространства отображений /: топология равномерной сходимости
на Rx и топология поточечной сходимости 171
2.7. Задачи 180
ГЛАВА 3. КОМПАКТНЫЕ ПРОСТРАНСТВА 194
3.1. Компактные пространства 195
3.2. Операции над компактами 215
3.3. Локально компактные пространства и ^-пространства .... 231
3.4. Пространства отображений II: компактно-открытая топология 243
3.5. Компактификации 256
ОГЛАВЛЕНИЕ 751
3.6. Стоун-чеховская компактификация и расширение Волмэна . . 265
3.7. Совершенные отображения 277
3.8. Линделёфовы пространства 290
3.9. Полные по Чеху пространства 296
ЗЛО. Счетно компактные, псевдокомпактные и секвенциально компакт-
компактные пространства 304
3.11. Вещественно полные пространства 320
3.12. Задачи € 330
ГЛАВА 4. МЕТРИЧЕСКИЕ И МЕТРИЗУЕМЫЕ ПРОСТРАНСТВА . . 368
4.1. Метрические и метризуемые пространства 370
4.2. Операции на метризуемых пространствах 383
4.3. Вполне ограниченные и полные метрические пространства. Ком-
Компактность в метрических пространствах 395
4.4. Метризационные теоремы I 414
4.5. Задачи 427
ГЛАВА 5. ПАРАКОМПАКТНЫЕ ПРОСТРАНСТВА 443
5.1. Парокомпактные пространства 444
5.2. Счетно паракомпактные пространства 468
5.3. Слабо и сильно паракомпактные пространства 476
5.4. Метризационные теоремы II 487
5.5. Задачи 499
ГЛАВА 6. СВЯЗНЫЕ ПРОСТРАНСТВА 516
6.1. Связные пространства 517
6.2. Различные виды несвязности 529
6 3. Задачи 546
ГЛАВА 7. РАЗМЕРНОСТЬ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ . . 559
7.1. Определение и основные свойства размерностей ind, Ind и dim . 561
7.2. Дальнейшие свойства размерности dim 576
7.3. Размерность метризуемых пространств 588
Приложение. Доказательство теоремы Брауэра о неподвижной точке 602
7.4. Задачи 611
ГЛАВА 8. РАВНОМЕРНЫЕ ПРОСТРАНСТВА И ПРОСТРАНСТВА
БЛИЗОСТИ 621
8.1. Равномерности и равномерные пространства 622
8.2. Операции на равномерных пространствах 640
8.3. Вполне ограниченные и полные равномерные пространства. Ком-
Компактность в равномерных пространствах 650
8.4. Близости и пространства близости 660
8.5. Задачи 671
УКАЗАТЕЛЬ ОБОЗНАЧЕНИИ 728
ИМЕННОЙ УКАЗАТЕЛЬ 730
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ 736
ПРИЛОЖЕНИЕ 745