Алгебра и геометрия интегрируемых гамильтоновых дифференциальных уравнений

Author: Фоменко А.Т. Трофимов В.В.
Tags: математика геометрия алгебра дифференциальные уравнения
Similar
Лекции по дифференциальной геометрии
Дифференциальные уравнения
Обыкновенные дифференциальные уравнения
Краткий курс дифференциальной геометрии и топологии
Text
                    В.В. Трофимов, А. Т. Фоменко
АЛГЕБРА И ГЕОМЕТРИЯ ИНТЕГРИРУЕМЫХ ГАМИЛЬТОНОВЫХ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Посвящена интересному и актуальному направлению, бурно развивающемуся
в последние годы, в рамках которого открыты важные методы интегрирования
гамильтоновых уравнений и получены новые результаты о геометрической
структуре интегрируемых уравнений. Большинство вопросов впервые изложены в
виде, доступном для широкого круга специалистов.
Для научных работников — математиков, физиков, механиков, аспирантов и
студентов соответствующих специальностей. Может быть использована как
пособие по специальным курсам: симплектическая геометрия, интегрируемые
системы и др.
Содержание
Введение 3
ЧАСТЫ
ЭЛЕМЕНТАРНЫЕ АЛГЕБРО-ГЕОМЕТРИЧЕСКИЕ СВОЙСТВА 11
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Глава 1. Краткий экскурс в классическую механику 11
§ 1. Принцип Даламбера — Лагранжа 11
§ 2. Уравнения Лагранжа второго рода 16
§ 3. Уравнения Гамильтона 20
§ 4. Первые интегралы дифференциальных уравнений 23
§ 5. Динамика твердого тела 29
§ 6. Вариационные принципы в механике 38
§ 7. Интегральные инварианты 42
§ 8. Канонические преобразования 48
§ 9. Скобки Пуассона 51
Глава 2. Интегрирование канонических систем 55
§ 10. Алгебра Ли векторных полей 55
§11. Теорема Якоби 62
§ 12. Теорема Лиувилля 67
§ 13. Теорема Ли 70
§ 14. Дополнительные сведения из теории групп Ли и алгебр Ли 75
Глава 3. Симплектическая геометрия в линейном пространстве 84
§ 15. Симплектические пространства 84
§ 16. Группы симплектических преобразований линейного пространства 86
§ 17. Лагранжев грассманиан 95
Глава 4. Симплектическая геометрия 102
§ 18. Симплектические многообразия 102
§ 19. Гамильтоновы векторные поля 111
§ 20. Геодезические потоки 118
§21. Алгебра Ли функций Гамильтона 126
§ 22. Симплектическая структура на орбитах коприсоединенного 134
представления группы Ли

§ 23. Уравнения Эйлера 139
§ 24. Канонические преобразования 145
§ 25. Теорема Дарбу 150
§ 26. Вложения симплектических многообразий 153
§ 27. Пуассоновы многообразия 157
ЧАСТЬ 2
АЛГЕБРАИЧЕСКИЕ СВОЙСТВА ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Глава 5. Гамильтоповы системы с симмстриямп. Симплсктичсскис 163
действия групп Ли на симплектических многообразиях
§ 28. Вполне интегрируемые гамильтоновы системы 163
§ 29. Структура вполне интегрируемых гамильтоновых систем 166
§ 30. Некоммутативное интегрирование гамильтоновых систем 171
§31. Интегрируемые алгебры Ли 179
§ 32. Симплектические действия групп Ли 184
§ 33. Редукция гамильтоновых систем с симметриями и псевдогруппы Ли 190
Глава 6. Методы построения функций в инволюции на орбитах 197
коприсоединенного представления групп Ли
§ 34. Метод сдвига аргумента 197
§ 35. Метод построения коммутативных наборов функций по цепочкам 203
подалгебр
§ 36. Семейства функций в инволюции, связанные с согласованными 206
скобками Пуассона
§ 37. Сжатия алгебр Ли 208
§ 38. Метод тензорных расширений алгебр Ли 212
§ 39. Метод сходных функций 221
§ 40. Метод Я-матрицы 222
Глава 7. Полнота инволютивных наборов функций 223
§ 41. Критерий полноты 223
§ 42. Полнота семейств функций, построенных методом сдвига аргумента 229
§ 43. Функции в инволюции на симметрических алгебрах Ли 232
§ 44. Скобки Пуассона, связанные с лиевыми пучками 237
§ 45. Инволютивные семейства функций на полупрямых суммах 249
Глава 8. Секционные операторы 261
§ 46. Динамические системы и Симплектические структуры, порождаемые 261
секционными операторами
§ 47. Секционные операторы для коприсоединенного представления и вполне 267
интегрируемые системы
§ 48. Основные примеры секционных операторов 274
§ 49. Бигамильтоновость уравнений Эйлера 278
Глава 9. Полная интегрируемость по Лиувиллю некоторых 281
гамильтоновых систем на алгебрах Ли
§ 50. Уравнения Эйлера на алгебрах Ли, возникающие в задачах 281
математической физики
§51. Уравнения Эйлера на полу простых алгебрах Ли 288

§ 52. Уравнения Эйлера на разрешимых алгебрах Ли 294
§ 53. Уравнения Эйлера на неразрешимых алгебрах Ли с нетривиальным 299
радикалом
§ 54. Интегрируемые системы и симметрические пространства 304
§ 55. Коммутативные подалгебры универсальной обертывающей алгебры 316
ЧАСТЬ 3
ГЕОМЕТРИЧЕСКИЕ И ТОПОЛОГИЧЕСКИЕ СВОЙСТВА
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Глава 10. Качественная топологическая теория интегрируемых систем 325
на симплсктичсских многообразиях
§ 56. Элементы теории Морса 325
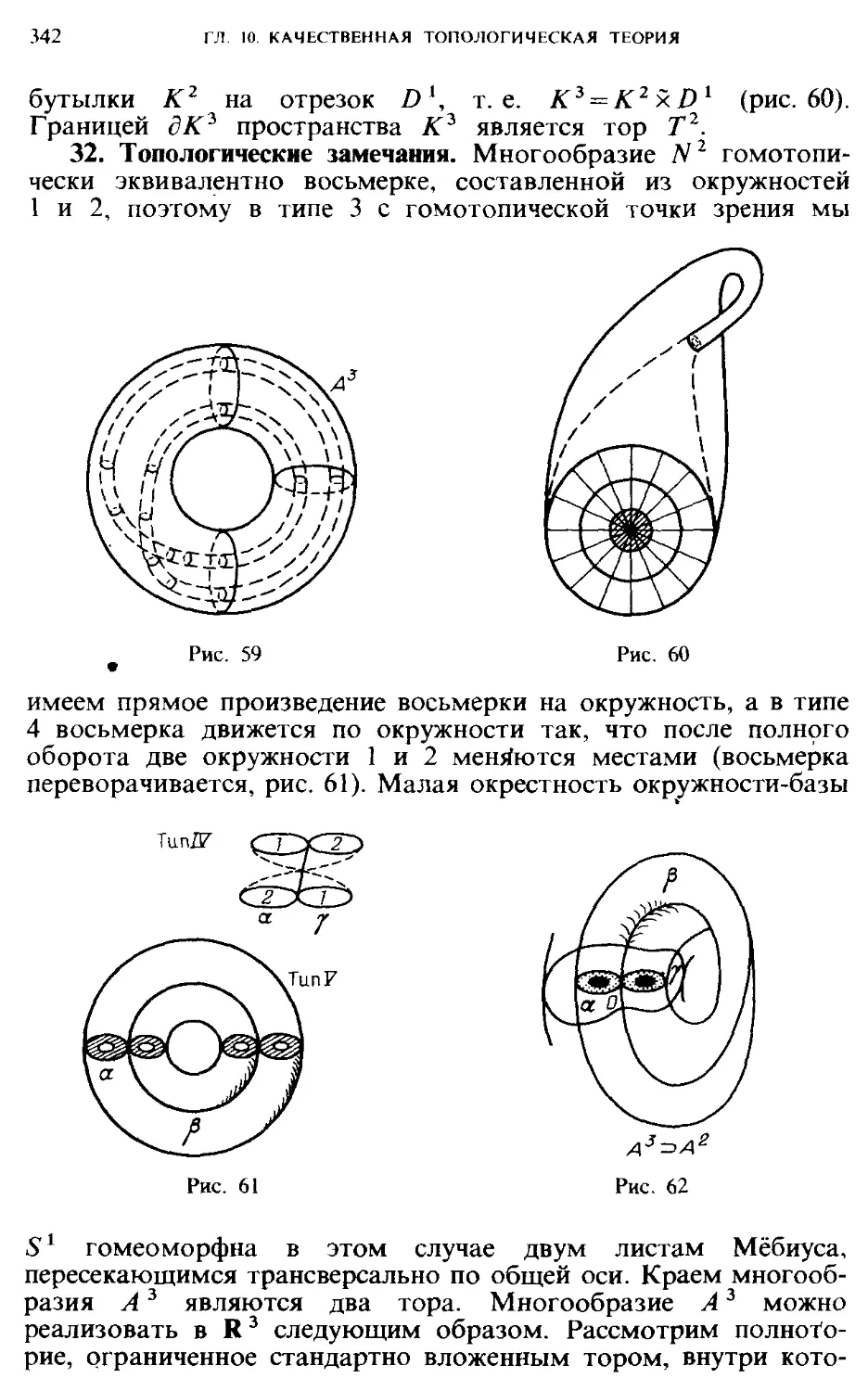
§ 57. Классификация трехмерных поверхностей постоянной энергии 333
интегрируемых систем
§ 58. Граф, естественно связанный с интегрируемой гамильтоновой системой 346
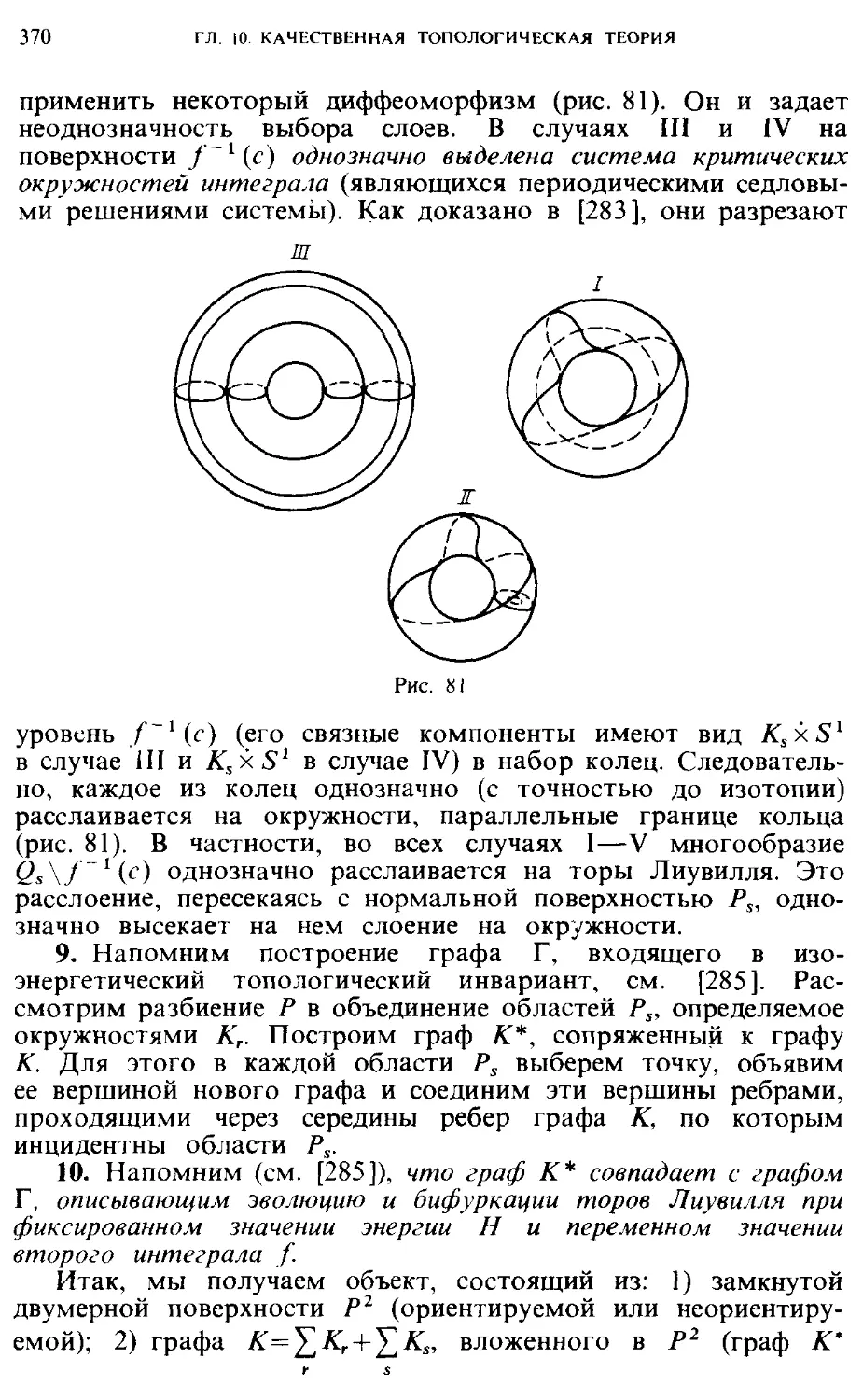
§ 59. Новый топологический инвариант гамильтоновых систем 349
дифференциальных уравнений, интегрируемых по Лиувиллю
§ 60. Построение меченого инварианта интегрируемых систем 366
§ 61. Классификация перестроек торов Лиувилля на многомерных симп- 378
лектических многообразиях в окрестности бифуркационной диаграммы
отображения моментов
Глава 11. Характеристические классы 396
§ 62. Характеристические классы лагранжевых слоений 396
§ 63. Обобщенные классы Маслова лагранжевых подмногообразий и 399
симплектические связности
§ 64. Вполне интегрируемая гамильтонова система, торы Лиувилля которой 406
имеют нетривиальные индексы Арнольда — Маслова.
Приложение. Нерешенные задачи 411
Список литературы 416
Предметный указатель 439
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Алгебра кватернионов 93, п. 23 сохраняющая скалярное
— Ли 55, п. 1 произведение 56, п. 13
абелева 56, п. 4 — самосопряженная 220, п. 30
72-градуированная 208, п. 2 — с двойственностью Пуанкаре 214,
группы Ли 75, п. 4 п- 6
двойная 222, п. 1 — Фробениуса 220, п. 28
интегрируемая 179, п. 2 алгоритм (t) 212, п. 3
коммутативная 56, п. 4 (Ь) 215, п. 9
полупростая 56, п. 12 аналог уравнения движения твердого
разрешимая 56, п. 9 тела 275, п. 2
редуктивная 56, п. 12 аннулятор ковектора 84, п. 34
симметрическая 232, п. 1 Базис Вейля 84, п. 33
совершенная 281, п. 7 — Гельфанда—Цетлина 323, п. 23
— симплектический 86, п. 6

Вложение динамической системы в
алгебру Ли 160, п. 19
волчок Лагранжа 303, п. 14
— полностью симметричный 303,
п. 14 время в уравнении
Гамильтона—Якоби 147, п. 6
вставка 391, п. 24
вырождение предельное 385, п. 9
Гамильтониан 112, п. 7
— неориентируемый 386, п. 12
— нерезонансный 349, п. 2; 363, п. 38
— ориентируемый 386, п. 12
геодезическая 119, п. 7 гессиан
325, п. 2
гомоморфизм алгебр Ли 56, п. 6
— касательный 76, п. 11
— накрывающий 185, п. 3
градиент косой 112, п. 9
грассманиан лагранжев
вещественный 96, п. 3
приведенный 403, п. 17
граф редуцированный 371, п. 11
группа голономии 403, п. 17
— диффеоморфизмов
однопараметрическая 58, п. 21
локальная 58, п. 23
порожденная векторным
полем 59, п. 25
— Ли 75, п. 1
— Гамильтона—Ли 195, п. 27
— пуассонова 195, п. 27
— симметрии гамильтоновой
системы 185, п. 5
— симплектическая вещественная 86,
п. 1
компактная 94, п. 25
комплексная 88, п. 8
группоид симплектический 191, п. 2
группы пуассоновы сопряженные
196, п. 32
Движение условно периодическое
169, п. 10
действие 147, п. 6
— гамильтоново 184, п. 3
— группоида 193, п. 14
— группы Ли 76, п. 7
— коприсоединенное псевдогруппы
Ли 195, п. 21
— по Гамильтону 38, п. 1
— присоединенное 76, п. 12
— пуассоново псевдогруппы Ли 194,
п. 15
— свободное от кратностей 308, п. 9
— строго симплектическое 184, п. 3
диаграмма бифуркационная 378, п. 2
— сепаратрисная 336, п. 9; 354, п. 15
диаграмма сепаратрисная входящая
336, п. 9
диаграмма сепаратрисная исходящая
336, п. 9
дифференциал абсолютный 119, п. 4
дополнение косоортогональное 85, п.
2
Задача вариационная с подвижными
концами 40, п. 3
— Гамильтона—Якоби 149, п. 14
— Неймана 124, п. 25
Значение критическое 378, п. 2
Идеал 56, п. 3
изотония гамильтонова 406, п. 32
импульс 21, п. 2; 147, п. 6
инвариант 78, п. 19; 81, п. 26
— интегральный 43, п. 1
абсолютный 43, п. 1
относительный 43, п. 1
полного порядка 43, п. 1
Пуанкаре—Картана 45, п. 5
— коприсоединенного представления
78, п. 19
— меченый 372, п. 11
— топологический интегрируемого
гамильтониана 351, п. 9
изоэнергетический 355, п.
19
меченый 372, п. 11; 377,
п. 23
полный 355, п. 19
/f-инвариант канонический 221, п. 4

инварианты сходные 222, п. 5
инволюция антикомплексная 100, п.
13
— Картана 233, п. 7
индекс алгебры Ли 84, п. 34; 251, п.
12
— критической точки 325, п. 5
вырожденной 326, п. 17
— представления 251, п. 12
— регулярной точки проекции 406, п.
28
— ручки 327, п. 13
интеграл 24, п. 1
— боттовский 334, п. 4
ориентируемый 336, п. 10
неориентируемый 336, п. 10
— момента количества движения 35,
п. 14
— первый 24, п. 1
— полный 62, п. 1
— тривиальный геометрический 35,
п. 14
— циклический 19, п. 7
— энергии 35, п. 14
— Якоби19, п. 8
Кватернион 93, п. 23
— сопряженный 93, п. 23
— чисто мнимый 93, п. 23
кернфункция Бергмана 109, п. 28
класс Арнольда—Маслова 400, п. 5;
401, п. 6
— Годбийона—Вея 398, п. 14
— когомологический диагональный
215, п. 11
— Маслова 400, п. 3
— многообразий (Я) 345, п. 41
@ 345, п. 41
(S) 345, п. 41
(W) 345, п. 41
— характеристический типа Маслова
403, п. 18
лагранжева
подрасслоения 405, п. 26
полного инволютивного
семейства 404, п. 23
количество движения 12, п. 4
коммутатор векторных полей 60, п.
29
компонента седловая 353, п. 14
координаты в уравнении
Гамильтона—Якоби 147, п. 6
— лагранжевы 16, п. 1
корень алгебры Ли 82, п. 30
положительный 83, п. 32
простой 83, п. 32
кривая интегральная 57, п. 20
Линия толстая 374, п. 16
— тонкая 274, п. 16
— узлов 33, п. 9
Матрица Гесса 325, п. 2
метрика отображения моментов 305,
п. 2
— Фубини—Штуди 108, п. 23
многообразие кэлерово 107, п. 20
— лагранжево грассманово
вещественное 96, п. 3
комплексное 96, п. 3
— пуассоново 157, п. 1
— редуцированное 372, п. 11
— симплектическое 102, IL 1
— точек /f-значных 111, п. 36
— Тёрстона 109, п. 29
многообразия пуассоновы взаимно
полярные 193, п. 12
множество бифуркационное 378, п. 2
множитель Якоби последний 29, п.
10
модуль кватерниона 93, п. 23
момент внешних сил главный 15, п.
12
— инерции 30, п. 1
осевой 30, п. 1
относительно оси 31, п. 4
полярный 30, п. 1
центральный 31, п. 3
центробежный 30, п. 1
— количества движения 14, п. 9
Набор коммутативный 319, п. 8

— разделяющий 319, п. 8
Область ограниченная 108, п. 26
овал 356, п. 22; 368, п. 4
ограничение 113, п. 17
окружность толстая 374, п. 16
— тонкая 374, п. 16
оператор Ли 126, п. 1
— отвечающий базисному вектору
79, п. 20
— секционный 261, п. 2
канонический 262, п. 2
операция приклейки ручки 327, п. 13
— сдвига аргумента 197, п. 2
орбита точки 58, п. 21; 77, п. 14
ось инерции главная 31, п. 6
отображение изотропное 147, п. 7
— моментов 185, п. 4; 194, п. 19
— симплектическое 154, п. 2
— экспоненциальное 76, п. 9
Пара гамильтонова 207, п. 1
— пуассонова 207, п. 1
— сферическая 309, п. 15
переменные действие—угол 171, п.
17
перемещение возможное 11, п. 1
— действительное 11, п. 1
перестройка симплектического
многообразия ПО, п. 31
перестройки торов Лиувилля
канонические 344, п. 37
плоскость вещественная лагранжева
100, п. 15
поверхность интегральная 385, п. 10
подалгебра 55, п. 3
— Картана 82, п. 29
— конечного типа 317, п. 3
— сферическая 309, п. 15
подгруппа изотропии 77, п. 14
— однопараметрическая 75, п. 5
— стационарная 77, п. 14
— сферическая 309, п. 15
подмногообразие лагранжево 147, п.
7
подмножество алгебраическое в СРп
108, п. 24
поднятие 185, п. 3
подпространство изотропное 85, п. 3
— коизотропное 85, п. 3
— коммутативное 317, п. 1
главное 321, п. 14
— лагранжево 85, п. 3
— симплектическое 85, п. 3
подъем функции 203, п. 1
поле векторное левоинвариантное 75,
п. 2
правоинвариантное 75, п. 2
— гамильтоново 112, п. 7
поле гамильтоново локально 112, п. 6
— параллельное 119, п. 7
— полное 59, п. 25
полноторие 340, п. 31
— диссипативное 380, п. 6
— расслоенное типа (а, Ь) 351, п. 9
положение общее для перестроек
385, п. 10
полуинвариант 79, п. 19
поток геодезический 118, п. 2
представление алгебры Ли
коприсоединенное 76, п. 12
присоединенное 76, п. 12
— группы Ли 76, п. 10
коприсоединенное 76, п. 12
присоединенное 76, п. 12
— изотропии 189, п. 21
представления эквивалентные 77, п.
15
^-представление группы Ли 201, п. 10
преобразование каноническое 48, п.
1; 145, п. 1
унивалентное 49, п. 4
— Лежандра 23, п. 7
— симплектическое вещественное
86, п. 1
комплексное 88, п. 8
приклейка ручки 327, п. 13
торической 387, п. 20
принцип Гамильтона 38, п. 1
— поглощения 149, п. 14

— Якоби41, п. 3
произведение внутреннее 111, п. 1
— тензорное 212, и. 1
производная ковариантная 119, п. 4
пространство кэлерово 93, п. 19
положительное 93, п. 21
— линзовое 338, п. 17
— симметрическое 263, п. 3
максимального ранга 267, п. 14
— симплектическое 84, п. 1
— фазовое над пуассоновым
многообразием 191, п. 5
Р-пространство симплектическое
184, п. 1
однородное 184, п. 1
псевдогруппа Ли 191, п. 2
соответствующая пуассонову
многообразию 191, п. 2
пучок лиев 237, п. 1
замкнутый 241, п. 12
неприводимый 241, п. 12
Радикал 56, п. 11
разложение гамильтоново 344, п. 36
— корневое 82, п. 30
— топологическое 344, п. 36
размерость лиева пучка 237, п. 1
размерность ручки 327, п. 13
ранг алгебры Ли 83, п. 31
— компактной группы Ли 267, п. 14
— симметрического пространства
266, п. 14
— скобки Пуассона 158, п. 4
— фундаментальной группы 339, п.
22
расслоение пуассоново 191, п. 5
расширение алгебры Ли 249, п. 3
— несущественное 251, п. 9
— существенное 251, п. 9
— универсальное 251, п. 11
расширения эквивалентные 250, п. 7
реализация, гамильтонова векторного
поля 160, п. 17
— пуассонова многообразия 159, п.
15
— системы 160, п. 18
редукция 176, п. 15
решение уравнения Гамильтона —
Якоби 148, п. 14
род системы 358, п. 26
ручка 327, п. 13
— торическая 387, п. 19
ряд канонический 321, п. 19
— подчиненный 321, п. 16
— регулярный 321, п. 15
ряды канонически эквивалентные
322, п. 20
Связность аффинная 118, п. 3
согласованная с метрикой 119,
п. 5
— почти симплектическая 401, п. 7
— симплектическая 402, п. 10
— согласованная с формой 401, п. 7
связь 113, п. 17
— голономная 11, п. 1
— идеальная 12, п. 2
сдвиг аргумента 197, п. 2
— левый 75, п. 1
— правый 75, п. 1
седло неориентированное 341, п. 31
торическое 381, п. 6
— ориентированное 340, п. 31
торическое 381, п. 6
семейство полное 159, п. 9
инволютивное 163, п. 1
— производящее для лагранжевой
иммерсии 406, п. 29
— — — — — квадратичное на
бесконечности 406, п. 29
— решений невырожденное п-
параметрическое 164, п. 4
сепаратриса 354, п. 15
серия секционных операторов
компактная 276, п. 4; 278, п. 12
— — — комплексная полупростая
275, п. 2; 278, п. 11
серия секционных операторов
нормальная 276, п. 6; 278, п. 13
сжатие алгебры Ли 209, п. 3

сила 21, п. 2
— потенциальная 16, п. 16
симплектоморфизм 145, п. 1
система координат каноническая 117,
п. 25
— типа Калоджеро—Сазерленда 310,
п. 20
— уравнений боттовская 334, п. 4
вполне интегрируемая 163, п. 1
алгебраическая 292, п. 12
в коммутативном смысле
172, п. 4
— — — — в некоммутативном
смысле 172, п. 4
полная 71, п. 7
— функций канонически
сопряженная 170, п. 14
полная инволютивная 163, п. 1
системы гамильтоновые
эквивалентные геометрически
364, п. 38
топологически 364, п. 38
скобка Березина 138, п. 13
— инвариантная 196, п. 30
— Пуассона 51, п. 1; 113, п. 11; 157,
п. 1
фундаментальная 51, п. 3
а-скобка Березина 208, п. 6
Я-скобка 222, п. 1
скобки Пуассона согласованные 206,
п. 1
скорость лагранжева 16, п. 1
слоение колежандрово 396, п. 5
— лагранжево 396, п. 1
слой симпдектический 158, п. 7
случай Ковалевской 35, п. 14
— Лагранжа обобщенный 302, п. 12
— Лагранжа—Пуассона 35, п. 14
— Эйлера—Пуансо 35, п. 14
сокращение разложения
многообразия 391, п. 24
степень вырождения критической
точки 325, п. 2
структура комплексная 92, п. 18
— пуассонова 157, п. 1
— симплектическая 102, п. 1
каноническая на орбитах 135,
п. 2
связности 107, п. 18
сумма полупрямая 251, п. 9
Тензор структурный 55, п. 2
— кривизны симплектический 402, п.
12
— Риччи 402, п. 14
тор максимальный 267, п. 14
точка>4-значная 111, п. 36
— критическая 325, п. 1; 378, п. 2
вырожденная 325, п. 2
невырожденная 325, п. 2
— регулярная 378, п. 2
траектория устойчивая 335, п. 7
Угол нутации 33, п. 9
— прецессии 33, п. 9
— собственного вращения 33, п. 9
— Эйлера 33, п. 9
уравнение Гамильтона каноническое
40, п. 2
— Гамильтона—Якоби 49, п. 5; 148,
п. 14
стационарное 147, п. 6
— движения триплета 144, п. 13
— Лагранжа второго рода 18, п. 3; 21,
п. 2
— Эйлера 140, п. 1
— Якоби 42, п. 4
уравнения Лагранжа 21, п. 2
— Пуассона кинематические 34, п. 11
— Эйлера динамические 34, п. 12
кинематические 33, п. 10
уровень критический
невырожденный 328, п. 16
М-условие 222, п. 6
Форма Киллинга 82, п. 27
— Кириллова 135, п. 2
— связности универсальная 106, п.
17
— симплектическая 84, п. 1; 102, п. 1
— целочисленная 155, п. 7

функции в инволюции 113, п. 13; 159.
п. 9
функции функционально зависимые
24, п. 2
функция боттовская 334, п. 5
— Гамильтона 147, п. 6
— Казимира 158, п. 4
—: коллективная 309, п. 10
— Лагранжа 18, п. 5
— Морса 325, п. 3
— производящая 112, п. 7
— Рауса 41, п. 3
— центральная 158, п. 4
функции сходные 222, п. 5
Центр алгебры Ли 56, п. 7
— масс 13, п. 7
цилиндр 340, п. 31; 381, п. 6
Частота условно периодического
движения 169, п. 10
часть кватерниона вещественная 93,
п. 23
мнимая 93, п. 23
число степеней свободы 16, п. 1
Штаны 341, п. 31
Элемент Казимира 319, п. 6
— регулярный 82, п. 29
— слабо регулярный 253, п. 16
элементы коммутирующие 317, п. 1
эллипсоид инерции 31, п. 6
энергия системы 21, п. 4
кинетическая 15, п. 14
Ядро гомоморфизма 56, п. 6
— кососимметрической билинейной
формы 85, п. 3
якобиан 24, п. 2

ВВЕДЕНИЕ
Цель данной книги — доступно рассказать о некоторых новых
методах интегрирования гамильтоновых дифференциальных
уравнений на симплектических многообразиях. Проблема интег-
рирования дифференциальных уравнений как обыкновенных, так
и в частных производных является классической. К настоящему
времени в математике имеется достаточно мощный арсенал
различных средств, используемых при интегрировании уравне-
ний. Выбор средств и методов, которые используются при
решении конкретных задач, возникающих, например, в геомет-
рии, механике или математической физике, сильно зависит от
того, какой смысл мы вкладываем в выражение «решить
уравнение». Например, если искать решение в каком-нибудь
функциональном пространстве, то естественно привлекать мето-
ды функционального анализа. Выделим три аспекта в изучении
дифференциальных уравнений: а) явное интегрирование; б)
качественные методы; в) интегрируемость по Лиувиллю.
Традиционный подход к изучению свойств решений диф-
ференциальных уравнений состоит в том, что сначала явно
определяют полное множество решений и лишь потом анализи-
руют их свойства. Именно так поступали Лежандр, Лагерр,
Бессель, Эрмит при изучении дифференциальных уравнений
второго порядка. Однако, помимо уравнений данного типа,
в различных приложениях возникают линейные или нелинейные
уравнения выше второго порядка. Возникает вопрос о возмож-
ности отыскания полного набора решений для качественного
описания поведения общих решений уравнений, моделирующих
интересующую нас систему.
Главная трудность при интегрировании дифференциальных
уравнений, как отмечал еще Якоби, «состоит во введении
удобных переменных, для разыскания которых нет никакого
общего правила. Поэтому мы должны идти обратным путем:
найдя какую-нибудь замечательную подстановку, разыскивать
задачи, в которых она может быть с успехом применена» [299].
Систематическое изложение метода разделения переменных
и его связь с теорией алгебр Ли можно найти в книге [179].

4 ВВЕДННИК
Активно развивавшаяся в прошлом веке теория эллиптичес-
ких и абелевых функций нашла применение в классической задаче
о движении тяжелого твердого тела, имеющего неподвижную
точку. Усилия крупнейших математиков были направлены на
установление аналитических свойств решений, поиски случаев
сведения задачи к квадратурам, доказательствам теорем сущест-
вования (или несуществования) интегралов в том или ином
классе функций. Сильные результаты были получены, например,
С. В. Ковалевской и С. А. Чаплыгиным. Работу С. В. Ковалев-
ской отличает эффектная математическая постановка задачи —
она ищет условия, при которых зависимость основных перемен-
ных от времени (которое полагается комплексной переменной)
представляется мероморфными функциями. Получив эти усло-
вия, Ковалевская указывает и четвертый интеграл задачи
(оказавшийся алгебраическим) и искусными заменами сводит
задачу к квадратурам. Такое же высокое аналитическое мастер-
ство присуще и известной работе С. А. Чаплыгина.
В настоящее время происходит возвращение (на новом
уровне) к классическим ценностям: мы имеем в виду новые
современные методы явного интегрирования уравнений, с кото-
рыми можно познакомиться по книге В. Е. Захарова,
С. В. Манакова, С. П. Новикова, Л. П. Питаевского [104] или
по обзору Б. А. Дубровина, В. Б. Матвеева, С. П. Новикова
[100], а также по обзору С. П. Новикова [199].
Выдающийся французский ученый А. Пуанкаре убедительно
показал, что во многих случаях необходим лишь ограниченный
объем информации качественного характера, которая, собствен-
но, и представляет интерес при изучении конкретных систем
уравнений. Основы современного подхода к определению
качественных изменений в поведении решений обыкновенных
дифференциальных уравнений были заложены почти сто лет
назад А. Пуанкаре.
При изучении неинтегрируемых многомерных динамических
систем методы качественного исследования являются, по
существу, единственной альтернативой численных методов. При
этом ряд важных вопросов, в частности, исследование общих
свойств поведения решений для всех значений параметров или
существование счетного множества решений, обладающих ка-
ким-либо исключительным свойством, во многих задачах
успешно решаются качественными методами и принципиально
не могут быть решены с помощью одних только численных
методов.
В середине семидесятых годов были обнаружены глубокие
связи между эффектом интегрируемости систем и их скрытыми
алгебраическими свойствами. Особо отметим важные идеи
В. И. Арнольда (представление геодезических потоков в тер-
минах уравнений Эйлера), Марсдена, Вейнстейна (идея редук-

ВВЕДЕНИЕ 5
ции) и С. В. Манакова (сдвиги орбитальных инвариантов на
ковектор общего положения). На первое место следует поста-
вить «симметрии систем», понимаемые не просто как группы их
инвариантности, а, более общо, как совокупность алгебраичес-
ких свойств системы дифференциальных уравнений, позволя-
ющих естественно связать с системой некоторую алгебру
(группу) Ли, орбиты которой инвариантны относительно
данной системы. Оказалось, что такого рода механизмы
управляют интегралами многих интересных гамильтоновых
систем в геометрии, механике и физике. Этим вопросам
посвящены многие работы. Отметим здесь школы
С. П. Новикова, В. И. Арнольда, В. П. Маслова, И. М. Гель-
фанда, Мозера, Марсдена, Вейнстейна, ван Мербеке, Адлера,
Костанта.
Структура книги следующая. Она состоит из трех частей,
разделенных на главы и параграфы. Все формулы, рисунки
и таблицы в тексте пронумерованы, причем используется
сквозная нумерация.
Первая часть книги вводная. Отметим, что классическое
механическое и физическое происхождение многих важных
понятий геометрии часто игнорируется и не сообщается
студенту. Мы хотим вернуться к исходному пониманию этих
объектов и в связи с этим намеренно ведем изложение на
элементарном уровне, достаточном для понимания современ;
ных дифференциально-геометрических построений. В частности,
именно поэтому все теоремы в первой части книги приведены
с полными доказательствами.
В первой главе дано введение в классическую механику
в том виде, в котором она нам потребуется в основном тексте.
При этом мы специально отказались от современного абстракт-
ного языка, часто используемого во многих книгах по
гамильтоновой геометрии, намеренно постарались максимально
упростить изложение, ведя его на классическом уровне. От
читателя не требуется ничего, кроме знания элементарных
понятий классической механики (элементы кинематики, законы
Ньютона). Читателя, желающего Продолжить знакомство с за-
тронутыми вопросами, мы отсылаем, например, к [8], [12],
[76], [79], [80], [129], [145], [243], [299].
Во второй главе собраны классические методы интегрирова-
ния систем гамильтоновых дифференциальных уравнений.
В этой же главе мы приводим необходимые сведения из теории
групп Ли и алгебр Ли; подробности см., например, в [65], [81 ],
[88], [112], [124], [263], [279], [293].
. . В третьей и четвертой главах приведены основные понятия
симплектической геометрии, а! также зафиксированы обозначе-
ния, используемые в дальнейшем; рм. такжЬ [8], [10], [102],
[279], [2861.

6 ВВЕДЕНИЕ
Вторая часть посвящена некоторым современным методам
интегрирования систем гамильтоновых уравнений. Мы не
претендуем на полный обзор. Этот раздел математики в насто-
ящее время бурно развивается, количество публикаций по
данной тематике исчисляется сотнями работ, и имеется масса
обзоров по этой актуальной области. Читатель, желающий
познакомиться с другими методами, может обратиться, напри-
мер, к обзорам С. П. Новикова, В. И. Арнольда, Д. В. Аносова,
Я. Г. Синая, В. В. Козлова в замечательной серии: Фундамен-
тальные направления. Современные проблемы математики.
Итоги науки и техники. ВИНИТИ, т. 1—6, 17. Мы остановимся
лишь на некоторых методах, связанных с коммутативной
и некоммутативной интегрируемостью по Лиувиллю.
В пятой главе излагаются вопросы, связанные с полной
интегрируемостью по Лиувиллю, в частности, рассмотрена
схема редукции гамильтоновых систем с симметриями по
Марсдену и Вейнстейну.
В шестой главе мы даем обзор различных методов
построения функций в инволюции, т. е. строятся большие серии
примеров гамильтоновых систем с богатым набором первых
интегралов.
Известно, что поиск интегралов конкретной системы уравне-
ний— трудная задача. Более того, дифференциальные уравнения
«общего положения» обычно вообще не имеют достаточного
числа интегралов (позволяющих проинтегрировать систему).
Поэтому задача отыскания редких интегрируемых случаев
в безбрежном океане всех гамильтоновых систем («большинст-
во» из которых неинтегрируемы) требует эффективных методов
поиска интегралов. Некоторые из общих методов обсуждаются
в шестой главе. Здесь, в частности, описаны результаты
B. И. Арнольда, А. А. Архангельского, А. В. Беляева, О. И. Бо-
гоявленского, А. В. Болсинова, А. В. Браилова, А. П. Веселова,
Дао Чонг Тхи, Б. А. Дубровина, М. В. Карасева, С. В. Манако-
ва, В. П. Маслова, М. В. Мещерякова, А. С. Мищенко,
C. П. Новикова, М. А. Олыианецкого, А. А. Ошемкова,
Т. А. Певцовой, А. М. Переломова, А. Г. Реймана, М. А. Семе-
нова-Тян-Шанского, В. В. Трофимова, А. Т. Фоменко, М. Ад-
лера, П. ван Мёрбеке, В. Гийемина, Дж. Мозера, Б. Куперш-
мидта, С. Стернберга, Ф. Магри, Дж. Марсдена, А. Вейнстейна,
Т. Ратью, Маккина.
В седьмой главе рассмотрены вопросы полноты инволютив-
ных семейств функций. После того как построена гамильтонова
система с большим запасом коммутирующих первых интег-
ралов, возникает естественный вопрос о функциональной незави-
симости этого семейства интегралов. Этот вопрос является
центральным при исследовании полной интегрируемости и, как
правило, очень трудоемким. В частности, в настоящее время

ВВЕДЕНИЕ 7
обнаружен красивый эффективный критерий полноты интег-
ралов, полученных методом сдвига аргумента (А. В. Болсинов).
Он излагается в этой главе.
Восьмая глава посвящена некоторому специальному, важ-
ному для приложений в геометрии классу уравнений Эйлера,
связанных с так называемыми секционными операторами,
введенными А. Т. Фоменко,— это уравнения Гамильтона со
специальной квадратичной функцией Гамильтона.
В девятой главе результаты, полученные в шестой и седьмой
главах, применяются к конкретным дифференциальным уравне-
ниям. В частности, дан список физически интересных уравнений,
полная интегрируемость которых получается изложенными
в шестой главе методами теории групп Ли. Здесь же
обсуждается связь, обнаруженная Э. Б. Винбергом, между мето-
дом построения коммутативных наборов функций по цепочкам
подалгебр и методом сдвига аргумента.
Третья часть посвящена топологии гамильтоновых систем.
Она представляет интерес не только для математиков, но и для
механиков и физиков. Изложены современные топологические
аспекты теории гамильтоновых интегрируемых уравнений.
В этой части предполагается знакомство читателя с простей-
шими элементами трехмерной топологии (см. [172], [201]).
В десятой главе излагаются элементы симплектической
топологии интегрируемых систем. Традиционно считается, что
полная интегрируемость по Лиувиллю гамильтоновои системы
дает более или менее полное качественное описание поведения
интегральных траекторий системы. Безусловно, в принципе это
так. Однако при этом часто игнорируется то обстоятельство,
что для такого описания требуется эффективно найти перемен-
ные действие — угол (относительно которых траектории систе-
мы превращаются в прямолинейные обмотки торов) в окре-
стности торов Лиувилля. Вложения торов Лиувилля в объем-
лющее пространство могут быть весьма сложными. Ясно, что
сложность вложения торов растет по мере усложнения интег-
ралов системы. Обычно интегралы являются полиномами (с
растущими степенями) или рациональными функциями, поэто-
му конкретное исследование торов и переменных действие —
угол часто затруднено, так как связано с решением нетривиаль-
ных алгебраических и аналитических проблем. (На этом пути
фундаментальные результаты получены С. П. Новиковым и его
школой.)
Поэтому уместно поставить следующий вопрос. Как распола-
гаются торы Лиувилля в фазовом пространстве? Как они
примыкают друг к другу? Как они заполняют открытые области?
Как они перестраиваются в окрестности критических поверхно-
стей интегралов? Другими словами, как построить качественную
теорию топологического расположения и взаимодействия торов

g ВВЕДЕНИЕ
Лиувилля (и тем самым расположения интегральных траекторий
системы), например, на поверхности постоянной энергии систе-
мы? Как классифицировать интегрируемые системы по их
топологическому типу?
В десятой главе на основе теории, построенной
А. Т. Фоменко, даются ответы на некоторые из этих вопросов.
При этом развивается новая специфическая теория типа Морса
для интегрируемых гамильтоновых систем, отличающаяся от
обычной теории Морса и от теории Ботта функций с вырожден-
ными особенностями. В частности, находят свое развитие
некоторые важные идеи, высказанные в свое время
Д. В. Аносовым [5], С. П. Новиковым [196], [198], В. В. Коз-
ловым [131], С. Смейлом [235].
Теория А. Т. Фоменко включает в себя, например, описание
изоэнергетических поверхностей боттовских интегрируемых га-
мильтоновых систем, классификацию бифуркаций торов Ли-
увилля в таких системах, новые топологические препятствия
к интегрируемости и т.д. [281]—[286]. Дальнейшее развитие
теории выполнено А. Т. Фоменко совместно с X. Цишангом,
С. В. Матвеевым, В. В. Шарко, А. В. Браиловым, А. В. Болси-
новым, А. А. Ошемковым [54], [171]—[173], [207]—[209],
[287], [288]. В [509] можно найти нужную информацию.
В одиннадцатой главе излагаются различные конструкции
топологических инвариантов гамильтоновых систем и, более
общо, лагранжевых слоений. В связи с этим отметим в первую
очередь работы В. П. Маслова, В. И. Арнольда, М. В. Карасе-
ва. Эти работы были затем развиты В. В. Трофимовым,
который обнаружил новые характеристические классы лагран-
жевых слоений, см. [257], [260]—[262], [510], [511].
В книгу включены не только классические результаты
и обзор по современным направлениям интегрирования гамиль-
тоновых систем дифференциальных уравнений, но и результаты,
полученные авторами книги и участниками научно-исследова-
тельского семинара «Современные геометрические методы»,
действующего на механико-математическом факультете МГУ
(под руководством А. Т. Фоменко, В. В. Трофимова), в частно-
сти А. В. Беляевым, А. В. Болсиновым, А. В. Браиловым, Дао
Чонг Тхи, Ле Нгок Тьеуеном, Ле Хонг Ван, М. В. Мещеряко-
вым, А. А. Ошемковым, Ю. А. Тюриной, К. Шваей. Многие
результаты, включенные в книгу, обсуждались на семинаре
«Геометрия и механика», работающем на механико-математи-
ческом факультете МГУ под руководством В. В. Козлова
и А. Т. Фоменко.
Книга рассчитана на широкий круг читателей, интересу-
ющихся приложениями современной геометрии к гамильтоно-
вой механике, теории интегрирования уравнений на многооб-
разиях. Первая треть книги доступна читателю с минимальной

ВВЕДЕНИЕ 9
подготовкой. По поводу простейших понятий геометрии,
которые не поясняются в основном тексте книги (а это
относится в основном к третьей части), см. книги [26], [76],
[102], [103], [126], [190], [201], [239], [263], [279], [293].
Различные разделы книги обсуждались авторами с разными
специалистами. Авторы выражают благодарность за плодо-
творные научные дискуссии С. П. Новикову, В. И. Арнольду,
В. П. Маслову, В. В. Козлову, Д. В. Аносову, В. В. Румянцеву,
О. И. Богоявленскому, Я. В. Татаринову, Б. Костанту, Дж. Ма-
рсдену, Т. Ратью.

СПИСОК ОСНОВНЫХ ОБОЗНАЧЕНИЙ
R — множество всех вещественных чисел;
С — множество всех комплексных чисел;
Z — множество всех целых чисел;
Q — множество всех рациональных чисел;
Н — множество всех кватернионов;
К"—п-мерное линейное пространство над К=9., Q, С, Н;
@^@2 — внешнее произведение дифференциальных форм шь ш2;
А"', X—матрица, транспонированная к А";
ad * — коприсоединенное представление алгебры Ли;
Ad * — коприсоединенное представление группы Ли;
ехр — экспоненциальное отображение алгебры Ли в группу Ли;
vx = npxv—проекция вектора v на ось х\
D = D(M) — алгебра Ли векторных полей на многообразии М;
еь ..., еп — стандартный базис в R";
Х\, ..., х„—стандартные координаты в R";
е(п) — алгебра Ли группы движений пространства R";
Е(п)—группа движений пространства R";
С (М) — пространство гладких функций на многообразии М;
(а, Ь) — скалярное произведение;
а х Ь = [а, Ь ] — векторное произведение;
с[и] — альтернирование;
V1 — ортогональное дополнение;
— xtt)—касательный вектор в точке x(t0) к кривой x(t);
at t=t0
id — тождественное отображение;
R"(/>) обозначает пространство с координатами /> = (/>ь ...,/»„);
Hom(G)—пространство линейных отображений векторного пространства
G;
GL(F) — множество невырожденных линейных преобразований векторного
пространства V;
М„{К)—матрицы размера пхп с коэффициентами из поля К;
{иь ...,и„} — подпространство, порожденное векторами иь ..., и„;
il'JM)—пространство р-форм на многообразии М;
S,—группа перестановок на п символах;
II v ||—длина вектора v: || и ||2 = (i>,- и);
lloiyll—матрица с элементами ац;
л*(F)—k-я внешняя степень пространства V;
d—внешняя производная;
g^X'dt , = 0(ехР{8)х—векторное поле на многообразии М, отвечающее
элементу g алгебры Ли G при действии группы Ли Р (соответствующей алгебре
Ли G) на многообразии М.
Группы Ли, как правило, обозначаются буквами Р, Q, R, S, Т,
а соответствующие алгебры Ли—буквами G, H, J, К, L.

ЧАСТЬ 1
ЭЛЕМЕНТАРНЫЕ АЛГЕБРО-ГЕОМЕТРИЧЕСКИЕ
СВОЙСТВА ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Глава 1
КРАТКИЙ ЭКСКУРС В КЛАССИЧЕСКУЮ МЕХАНИКУ
t+dt
Действительное
перемещение
t
§ 1. Принцип Даламбера — Лагранжа
1. Напомним, что в основу построения классической меха-
ники можно положить принцип Даламбера—Лагранжа. Для
того чтобы его сформулировать, приведем нужные нам опреде-
ления понятий, связанных с различными типами связей.
Рассмотрим систему к ма-
териальных точек с массами
ти ..., тк. Выберем инерци-
альную систему координат.
Положения материальных то-
чек определим радиус-вектора-
ми гь ..., гк. На точки действу-
ют силы Ft, ..., Fk. Пред-
положим, что наложены а)
удерживающие связи, которые
задаются уравнениями
fj(ri,r2,...,rt,t) = 0{j=l, 2, ...
..., /, 1<к); б) неголономные
связи /.(г,, ..., гк, ги ..., гк, ?) = 0
(»=1, 2, ..., s, s<k). Связи
первого типа называются так-
же голономными. Перемещения
делятся на два типа: а) действительные, происходящие под
действием заданных систем сил; б) возможные, происходящие
при «замораживании» связей (см. рис. 1).
В окрестности изучаемой точки рассмотрим семейство
траекторий r = r(t, а), зависящих от параметра а, причем
считаем, что при <х = 0 получаем действительную траекторию
r(t, 0) = г(/). Кроме того, предполагаем, что r(t, а) удовлетворя-
Возможные
'перемещения
_
ет уравнениям связей. Определим вариацию 5г = ( —
\с<х
5а.

12 ГЛ. 1. КРАТКИЙ ЭКСКУРС В МЕХАНИКУ
Если имеем голономные связи fj{rl3 ..., rk, t) = 0, то дейст-
вительные перемещения должны удовлетворять уравнению
^-Г^г^Л-О, A)
* Bf
а возможные — уравнению 5/,-= У -^5г; = 0, т.е. действитель-
, = 1 or,
ные перемещения не обязательно находятся среди возможных
(см. рис. 1). Если связь стационарная, то, как следует из
предыдущих выкладок, действительные перемещения лежат
среди возможных.
2. Определение. Пусть Ru R2, ..., Rk — силы реакций,
т. е. равнодействующие сил реакций, приложенных к точкам,
в которых находятся массы ти т2, ..., тк. Связь, наложенная
на систему, называется идеальной, если
? (*«, 5rf) = 0 B)
i=i
для любого возможного перемещения.
3. Принцип Даламбера—Лагранжа. Для того чтобы переме-
щение механической системы, подчиненной удерживающим
идеальным связям, было действительным, необходимо и до-
статочно, чтобы выполнялось равенство
*-F,, &-,) = <). C)
Этот принцип верен также и для неудерживающих связей,
в этом случае он постулируется. В случае удерживающих
идеальных связей его можно доказать, исходя из второго закона
Ньютона. Мы примем принцип Даламбера—Лагранжа как
постулат, подтвержденный экспериментом.
4. Определение. Величина <7= ? /и,-г( называется количе-
i=i
ством движения рассматриваемой механической системы. Сим-
волом G, будем обозначать проекцию пр/<7 вектора G на ось /.
Символом е° обозначим единичный вектор оси /. Тогда
5. Теорема (об изменении количества движения). Если
связи, наложенные на систему, идеальны и допускают в качестве
возможных^ перемещений группу поступательных движений вдоль
некоторого направления, то производная количества движения
системы по времени вдоль <этого направления равна сумме'
проекций на это. направление сил, приложенных к системе.

§ 1. ПРИНЦИП ДАЛАМБЕРА—ЛАГРАНЖА 13
к
Доказательство. Пусть G( = np/<7= ? т&ц, где Vu = nplri.
dG k
Надо проверить равенство —'-= ? Fu, где Fu = nplFi. Группа
i=i
поступательных перемещений имеет вид 8г = 6ге°. Из принципа
Даламбера—Лагранжа следует равенство
0. D)
i it
Поскольку дгфО, то с0 ? щг\= ? /^е0, т. е.
d к
и, следовательно,
f-I*, F)
6. Замечание. Если ^ ^« = 0, то имеем закон сохранения
к i=i
Gt = const. Условие ? Fu = 0 всегда выполняется для замкнутых
систем, т. е. для систем, на которые не действуют
внешние силы.
7. Определение. Точка С, радиус-вектор гс которой
равен гс= ? т{гг/ ? w(, называется центром масс.
i=i i=i
8. Следствие (теорема о движении центра масс).
Предположим, что выполнены условия теоремы 5; и пусть связи
допускают поступательное движение вдоль оси xt. Тогда
dG, •• ..
~ = тх1С, где
«=!«,, G)
;=i
к
*ic= ? ntiXu/m, (8)

14 ГЛ. I. КРАТКИЙ ЭКСКУРС В МЕХАНИКУ
к
Если система изолирована (Х^и=0)> ТО xlc=0, т.е.
Си С2=const.
9. Определение. Вектор Ко= ? (rsxmjfj) называется мо-
ментом количества движения относительно центра О. Момен-
том количества движения относительно оси а называется
проекция Ка = щ)аКо момента количества движения Ко относи-
тельно произвольной точки Оеа на ось а.
Момент M0(F) силы F относительно центра О равен rxF.
Момент силы / относительно оси а—это проекция npaMo(F)
момента силы F относительно центра Оеа.
10. Лемма. Момент количества движения твердого тела,
вращающегося вокруг оси Ох3 с постоянной угловой скоростью
(о, равен K3 = wJ3, где J3= X "^(х?,•.+*!>) — момент инерции
тела относительно оси Ох3.
Доказательство. Если радиус-вектор гг имеет коор-
динаты (хи, x2i, x3l), то vi = (oxri = (-(i>X2i, сохц, 0). Поэтому
к к
a> X щ(хги+х1^га1г. A0)
11. Теорема (о моменте количества движения системы).
Если связи, наложенные на систему, идеальны и среди возмож-
ных перемещений есть бесконечно малый поворот системы как
целого вокруг неподвижной оси, то производная момента
количества движения системы по времени относительно этой
оси равна сумме моментов относительно той же оси всех
внешних сил, приложенных к системе.
Доказательство. Поскольку система допускает поворот
как целое, то
dф dф / \ dri
v. = a> хrt = e3m хп=е3-?--х.г( = -?(е3 хг() = ~,
где w = d((>/dt, ф — угол поворота. Следовательно, 5г,=
= 5<р(г3хг(). Поэтому из принципа Даламбера—Лагранжа
следует равенство
-F,), 6ф(«3хг,)) = 6ф Е ((тД-F,), (*зХг,)) = 0. A2)
к
Отсюда J ((т{гг — F,), е3хг{) = 0, и, следовательно,
i=i
/ к \ / * к
[е3, Х»-;Х(/и,г;-^)) = [е3, X Е F

§ 1. ПРИНЦИП ДАЛАМБЕРА—ЛАГРАНЖА
15
ПОСКОЛЬКУ — (г,ХГ,) = Г,Х Г, + Г, X Г,-= Г
ТО
{ х г,- = -
A4)
Г ,„ к "I
Итак, е3 —^ — V Л/о (i^i) = 0. Из этого следует равенство
d '" '=1 ^
— (е3, К0) = е3 X M0(Ft)= X Л/*3(Т)> ^ea — внешние силы. Внут-
ренние силы дают равные по величине, но противоположные по
направлению моменты. Действительно, по третьему закону
Ньютона Ft = — Fj (рис. 2). То-
гда
г,х,
А,т.
rj X Fj = ri x Fi — rj x Ff =
i-;) x Fj = ^i x F, = 0,A5)
т. е. сумма моментов всех вну-
тренних сил равна нулю.
12. Определение. Вели-
чина М3= X МХг(??) называ-
B,wi
Рис. 2
ется главным моментом внеш-
них сил.
13. Следствие. В предположениях теоремы 11 имеют место
следующие утверждения, а) Если М3 = 0 {тождественно по
времени), то К3 = const, б) Если среди возможных перемещений
системы есть бесконечно малые повороты вокруг осей хх, х2, х3, то
ЧГ
dK2
It
=м2,
A6)
и, следовательно, —- = М0. в) Если М0 = 0, то Ко = const.
dt
k
14. Определение. Величина T=2~l X mirf называется
кинетической энергией системы.
15. Теорема (о кинетической энергии системы). Если на
систему наложены идеальные связи, причем действительные
перемещения входят в число возможных, то дифференциал
кинетической энергии равен сумме элементарных работ всех
внешних сил на действительных перемещениях.
Доказательство. Из принципа Лагранжа — Даламбера
следует равенство I X (mfi — Fi)> <4",-1 = 0, и X tnfidfi= X ^'fol Из

16 ГЛ. 1. КРАТКИЙ ЭКСКУРС В МЕХАНИКУ
соотношения Г;drt = —-drt = dri-~ = rtdrt = V;<fv,- = 2~1d(viJ = d(vf/2)
следует равенство
* vf k
к к
т. е. d(
U=l
16. Определение. Силы, действующие на систему, назы-
ваются потенциальными, если существует силовая функция
U{xn, x2i, x3i) такая, что F,=
17. Следствие. Предположим, что: а) связи идеальные; б)
связи не зависят от времени; в) существует силовая функция U,
не зависящая от времени. Тогда имеется интеграл энергии
Т- U = const.
Доказательство вытекает из равенства
§ 2. Уравнения Лагранжа второго рода
1. Пусть О, хи х2, х3—инерциальная система координат.
Предположим, что движение системы описывается соотно-
шениями
rt = ri(q1,q2,...,qn;t), /=1, 2, ..., к, A9)
где qu q2, ..., qn—независимые параметры. Параметры qu ...
..., qn называются лагранжевыми координатами, производные
qu ..., qn—лагранжевыми скоростями, п — число степеней
свободы. Для возможных перемещений имеем
2. Теорема. В лагранжевых координатах уравнения движе-
ния механической системы имеют вид
к к
где Г=2~1 ^ mtvf — кинетическая энергия, Qj= У Ft — , j—
i=l i=l 8<lJ
= 1, 2, ..., и — обобщенные силы.

§ 2. УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА 17
Доказательство. Из принципа Даламбера—Лагранжа
следует равенство
?>,*-F,)?!^ = 0, B2)
т. е.
Отсюда
где 7=1, 2, ..., и, так как q, — независимые параметры. Введем
обозначения
',-?,"*?. *-,?,'¦?•;" "¦ <25)
Тогда имеем равенство Pj — Qj, 7=1, 2, ..., и.
Из равенства
следует соотношение dri/dqj = dri/dqj.
Продифференцируем B6) по переменной
f!^= У s*r' д ' 82т'
Из того, что
rf 3fi 3 dr,
получим —т1 = - .
dtdqf dqs dt
Преобразуем теперь выражение
Имеем

18 ГЛ. 1 КРАТКИЙ ЭКСКУРС В МЕХАНИКУ
Подставим C0) в формулу для Ру.
где r=2-1?miuf, *, = *„ tf = v? = vf. Итак, pJ
Подставляя это выражение в P( = Qi, получим требуемое
соотношение.
3. Определение. Уравнение
d дТ дТ _ ... ,.»,
—= &> 7=1, 2> •••' и' C2)
полученное в теореме 2, называется уравнением Лагранжа
второго рода.
4. Предложение. Если силы, действующие на систему,
потенциальны (т. е. существует потенциальная функция
U(r1, ..., rk, /)), то уравнения Лагранжа второго рода имеют
вид
ddL_dL
где L=T+U.
к .
Доказательство. Поскольку Qj= ^ Ft^ и
„ ... \ди ди ди\
Fi = grad U =< — ,—,-—>, C4)
[Вхи dx2i dXii\
то обобщенные силы равны
_ v вг,_ v /ди дхи dU dx2i dU 8x3\_8U ,.,.\
,•=1 ^9; i=i V^ii c?j o^2i oqj дхЪ; oqj I dqj
Итак, уравнения Лагранжа имеют вид
d дТ дТ dU • , т ,1^
7,7Г-^Г = 7Г> ¦/=1' 2' ••' и- C6)
5. Определение. Функция L = Т+ U из предложения 4 на-
зывается функцией Лагранжа. Она полностью описывает пове-
дение механической системы.

§ 2. УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА 19
6. Замечание. Кинетическая энергия системы допускает
представление в виде Т=Т2 + Т1 + Т0, где Tt — форма степени /.
Действительно,
у тХдп Д 8r<aY-
здесь qu ..., qn — лагранжевы координаты.
7. Предложение. Если \-Qt = 0, mo уравнения Лагранжа
допускают первый интеграл dL/dqj=fij = const, который называ-
ется циклическим интегралом.
л
8. Предложение. Предположим, что: а) ? Qiqt~O, т. е.
силы гироскопические; б) dL/dt = O. Тогда уравнения Лагранжа
допускают первый интеграл T2—T0=U+h, h = const, который
называется интегралом Якоби. Если дополнительно Т= Т2, то
интеграл Якоби имеет вид T—U=h = const.
Доказательство. Имеет место равенство
dT зт Д дт.. Д ёт.
**)^0*' C8)
<//аг\ ёт ёи „ „
так как ?Iq = i!l*q+?Ilq = 2T2 + T1. Итак,
0<7 0^ 0^
|(r2-r0).-^+IfiA, D0)
откуда следует наше утверждение.
9. Теорема. Если движение механической системы описыва-
ется уравнениями Лагранжа второго рода — ( —) = \-Q(
dt \dqil Sqt eqt

20 ГЛ. 1. КРАТКИЙ ЭКСКУРС В МЕХАНИКУ
и кинетическая энергия Т инвариантна относительно группы
преобразований ?, = 4,(/, ос), причем ?f(f, 0) = qt(t), то
D1)
о
Доказательство. Из соотношения T(q, q, /)=Г(^, ?,, t)
вытекает • равенство
Следовательно,
?[г(г) +?(й 1=°- D3)
Из уравнений Лагранжа получим
поэтому
' ( }
10. Замечания, а) Если У (—+ g ,)(^ ) =0, то
т(д?\ ,ЛСЛ
- г = const, D6)
т. е. получили циклические интегралы.
б) Если (?¦ = 0, то вместо Г можно взять L и получим первый
интеграл
= const. D7)
Это утверждение носит название теоремы Э. Нётер.
§ 3. Уравнения Гамильтона
1. Напомним, что механическая система полностью харак-
теризуется функцией Лагранжа L=T—U(qi,...,qX В общем
случае на функцию L = L(qu ..., qn, qu ..., qn, t) мы будем
накладывать условие невырожденности, состоящее в том, что ее

§ 3. УРАВНЕНИЯ ГАМИЛЬТОНА 21
гессиан относительно обобщенных скоростей qt не равен
тождественно нулю, т. е.
feW D8)
2. Определение. Импульсомрг, канонически сопряженным
с координатой qr, называется производная pr = dL/dqr функции
Лагранжа L по соответствующей скорости qr.
Сила Fr находится дифференцированием функции L по
соответствующей координате qr, т. е. Fr = dLj3qr.
Уравнения движения системы (уравнения Лагранжа) имеют вид
dteqr dq/
3. Замечание. Уравнения движения в развернутом виде
можно переписать так:
" Я2 Л
J O, E0)
где Ft—сумма членов, не содержащих обобщенных ускорений
qk (k= 1, ..., и). В силу предположения о невырожденности гессиана
эту систему можно разрешить относительно обобщенных ускоре-
ний и записать ее в виде '4i = Qi(t, qk, Як\> ' = 1, •••> п. Отсюда можно
сделать вывод об однозначном определении движения системы
путем задания начальных данных qf, qf (/'=1, .., и).
4. Определение. Величина H=—L+Y,PrQr называется
энергией системы.
5. Предложение. Если — = 0, т. е. если функция Лагран-
ot
жа не зависит от времени явно, то dH/dt = 0, т. е< энергия
системы сохраняется.
Доказательство вытекает из следующей выкладки:
It
6. Теорема. Пусть дана некоторая функция f[xi, .... х„\,
гессиан которой отличен от нуля, т.е. det(d2//cJxId.x/)#O.
Предположим, что имеется преобразование переменных, «поро-
ждаемое» функцией f(xi, ..., дгя),. которое имеет вид v ,,
* , _df(xly ...,x.) •_ *
У: -~? , t—l,..., п.
?

22 ГЛ. 1. КРАТКИЙ ЭКСКУРС В МЕХАНИКУ
Тогда существует преобразование, обратное к преобразованию
E2), также порождаемое некоторой функцией g(ji, ..., у„), т. е.
Xi = Bg{y^...,y.)^ /=!,...,„. E3)
Порождающая функция g обратного преобразования связана
с порождающей функцией f прямого преобразования формулой
g =-/+?*; Ji E4)
(здесь предполагается, что все переменные jc, выражены через у().
Если функция f содержит параметры аь ..., <хт, то функция
g также зависит от этих параметров и выполняется равенство
— = — — /=1 E5)
Доказательство. Якобиан системы у{ = '"' со-
впадает с гессианом det(d2f/dXjdx^ функции /, и по теореме
о неявных функциях переменные xt можно выразить через у-р
т.е. хг=Ъ\ух, ..., уп), /=1, ..., и. Определим функцию
g= — f(xu ..., х„)+ 51 Х1У>> переменные xt заменены их выражени-
¦ =1
ями xi=fi(yl, ..., уя), i=l, ..., п. Тогда
- L ^гтг- E6)
Справедливо равенство
8у~^
так как уг = /1г
Пусть теперь функция / зависит дополнительно от парамет-
ров <хь ...., ос,,. Тогда эти параметры фигурируют как в прямом
преобразовании, так и в обратном. Имеем по правилу
дифференцирования сложной функции
u ..., ^ а1; ...,аД ..., хт{уи ..., >>„; аь ...,txm),ab
Итак, dg/daLj= —df/doLj.

I 4. ПЕРВЫЕ ИНТЕГРАЛЫ 23
7. Определение. Переход от переменных хх к переменным
Ур i, у=1, ¦••, и, описанный в предыдущей теореме 6, называется
преобразованием Лежандра.
8. Теорема. Преобразование Лежандра с порождающей
функцией f=L[qu ..., qn, qu ..., qn, t) переводит уравнения Лаг-
ddL dL n
ронжа —-—— = v в уравнения
r dtdqi Oq,
dPl _ _дН
dt dq,'
dp,__dH
Tt~ B~q~.' E9)
dqi дН
dq,_ дН
~dt~ ~др~п'
которые называются уравнениями Гамильтона или канониче-
скими уравнениями.
Доказательство. Применим предыдущую теорему
6 к функции f=L(q1,...,qql,...,qn,t), считая (qu...,qn) =
= (хи ..., хп) и (qt, ..., qn, t) = (<xi, ..., а», ая + 1). По теореме 6 надо
п
составить функцию H=Y.4iPt-L(qu...,qn,qu...,qn,t), т.е.
=l,..., л, F0)
взять энергию системы. Тогда
. дН 0L дН .
op, oqi cq,
и — =-—. Уравнения Лагранжа с учетом замены
pi = dL(q1, ..., qn, qu ..., qm t)jdqt имеют вид -^=——-. Эти
at OC[i
уравнения совместно с равенствами F0) приводят к канониче-
ским уравнениям Гамильтона —= , — = , i, /=1, •••, л.
dt Bq, dt dpj
§ 4. Первые интегралы дифференциальных уравнений
1. Пусть дана система обыкновенных дифференциальных
уравнений
F1)

24
ГЛ 1. КРАТКИЙ ЭКСКУРС В МЕХАНИКУ
Первым интегралом (или просто интегралом) этой системы
называют такую функцию <p(xlt —,xH, t) аргументов хи ..., хп, t,
полный дифференциал которой
F2)
обращается тождественно в нуль в силу уравнений, т. е.
dt
дх
TJ
дх.
F3)
По-другому можно сказать так: функция ф(хь ...,хп t) посто-
янная вдоль решений уравнений F1), т.е. <p(xi(t), ..., xn(t),
/) = const.
2. Определение. Пусть дана система т функций
м1=ф1(хь х2, ...,
ит = Ц>т(хи х2, ...,
F4)"
аргументов xlt х2, ..., хп, причем ф1; ..., фтеС°°(П), где ilcR" —
некоторое открытое подмножество. Функции (фЛ называются
функционально зависимыми на подмножестве Sczil, если суще-
ствует открытое множество ?2'z>/(S) (здесь /=(фь ..., фт):
fi-»RM) и функция geC°°(ii') такая, что g~l@) нигде не плотно
в И' и g(/(jt)) = O для всех xeS.
Якобианом системы функций hl(xl, ..., хп), ..., hn{xu ..., хп)
называется определитель вида
D(hu h2, ..., I
D(xu x2, ...,.
dh^ dhi
дхх дх2
dh2 dh2
dxl Sx2
дх, ёх.
дх,
dh,
дх.
F5)
3. Теорема. Если f: i2-»Rm есть С™-отображение
/=(/i, •-,/«)> "w набор {fjj функционально зависим на каждом

§ 4. ПЕРВЫЕ ИНТЕГРАЛЫ
25
компактном подмножестве ATcflcR" в том и только том
случае, когда на il выполняется неравенство
гк
д/г
dXl
а/_
дх.
дх2
дх2
'а/я
дх.
дх
е/
дх,
г/
дх
F6)
4. Теорема. Если между функциями йь ...,hn существует
зависимость ^(Ль Л2, ..., hn) = 0, то их якобиан F5) тождествен-
но равен нулю. Если по крайней мере один из миноров 1-го поряд-
, D(hu H2, ..., К) Л
ка определителя -^ не равен нулю, а сам определитель
?>(*!, х2, ..., х„)
D(huh2, ...,,
u x2, ..., х„)
F7)
тождественно равен нулю, то между функциями hv, ..., hn
существует зависимость вида F(hi, h2, ..., Лп) = 0.
5. Лемма. Число функционально независимых интегралов
системы F1) не превышает п.
Доказательство. Пусть срь ..., ф„ — функционально неза-
висимые интегралы системы F1); тогда у*1''"' '-ф§ в силу
D(Xi, ..., Хн)
п. 4. Предположим, что имеется еще один интеграл ср„+1.
Покажем, что cpn + i есть функция интегралов ср1; ..., ф„. По
определению интегралов имеем тождества
ЙЧ>1 ЙЧ>1
dt dxi
дх2
дх„
III— «5
F8)
dt
ёх,
ёх2
дх„
Рассматривая полученную систему тождеств как систему одно-
родных линейных уравнений, видим, что она имеет нетривиаль-
ное решение 1, /ь ...,/„. Поэтому ее определитель
ф2,
D(t,xly ...,*„)
тождественно равен нулю. Следовательно,
Фл + i является функцией остальных интегралов.
F9)
функция

26
ГЛ. 1. КРАТКИЙ ЭКСКУРС В МЕХАНИКУ
6. Замечание. Пусть <рь ..., ср„ — функционально независи-
мые интегралы системы F1). Поскольку
ь ф2, ....
#0,
то систему
D(xu хг, -,хп)
i, ..., х„, t) =
<р„(хи ...,х„, t) =
G0)
G1)
можно решить относительно хи ..., х„, здесь
сь ..., с„ — произвольные константы. Итак, получим выражение
для неизвестных функций хи ..., х„:
1' С2,
1' С2,
и с г,
Сп, t),
С„, t),
с„, t),
G2)
т. е., зная полный набор первых интегралов системы F1),
можем найти общее решение G2) системы F1).
7. Знание первого интеграла / системы F1) позволяет
понизить порядок системы. Рассмотрим фиксированную гипер-
поверхность {/=с}. Из определения интеграла следует, что если
траектория xl = x1(t), ..., xn = xJt) имеет общую точку с {/=с},
то вся траектория лежит в {/=с}. Поэтому вся поверхность
{f=c} расслоена на траектории. Это позволяет понизить
порядок исходной системы уравнений на единицу, ограничив ее
на поверхность S={/=c} (рис. 3). Если нам даны два функци-
онально независимых интеграла/ь/2, то порядок системы уже
понижается на две единицы (рис. 4) и т. д.
8. Предложение. Пусть дана система дифференциальных
уравнений —'- = Xi(xl, ..., х„, t), i=l,...,n. Рассмотрим преоб-
разование -Xf = (p(ji, ..-, у„, t) к новым переменным уи...,у„.
S= \f = const}
Рис. 3

§ 4. ПЕРВЫЕ ИНТЕГРАЛЫ
27
Рис. 4
Предположим, что в новых переменных система запишется
в виде —=Yj(yi...,yn,t), 7=1,..., п. Введем обозначение
D = det(dxi/dyJ). Тогда
А 8Х,_1 Д д^) ,_,
? —— 2-t —а ' ^ '
Доказательство. Имеют место следующие равенства:
^ eXi v-> v eXidyk ^ ^ дУк ^х'
В силу того, что
дУ
к_ Д йуцйл^ГО,
* t=i d*i ду. \ 1,
О, если
если k = s,
^i^fl G4)
byb»\- G4)
G5)
и j- = Aki/D (правило вычисления обратной матрицы), где
Аы—алгебраическое дополнение к элементу aki в якобиане D,
" ёХ-
? ~ можно продолжить:
1 т-< *шт ии г-^ ёх,
= \ у 1_ \ ?
предыдущее равенство для суммы
л к
У ^fj_
Ati ё2х,

28
ГЛ. 1. КРАТКИЙ ЭКСКУРС В МЕХАНИКУ
(здесь использовали правило дифференцирования определителя
D). Далее
Из полученных соотношений вытекает утверждение теоремы.
9. Теорема. Пусть система дифференциальных уравнений
^ = ...=? = 1, G8)
где Xi = Xi(xl, ..., х„, х), X=X(xt, ..., х„, х), имеет первые интег-
ралы fi(xi, ..., хп, x) = ct, /=1, ..., п— 1. Потребуем, чтобы
A = D(flt ...,fn-l)ID{xy, ..., хя-х)^<Ь, т. е. интегралы независимы.
Ограничим нашу систему на поверхность S=<fi(xu ..., хп, x) = ct,
i=l, 2, ..., и—1} и предположим, что на S система имеет вид
dx._dx
Если известно какое-либо решение М уравнения
G9)
А а* °' (80)
то последнее уравнение G9) интегрируется «в квадратурах»;
точнее, для уравнения G9) в явном виде можно указать
интегрирующий множитель ц.
Доказательство. Из (80) следует равенство
дх
дх
Поскольку —'¦=—, то (81) эквивалентно
dx х
(81)
(82)
Сделаем замену переменных yt=fu /= 1, ..., и— 1, ^и=д::,, y,+i=x.
При такой замене Г1 = ... = Уя_1=0 {в обозначениях п.8) и
,'! О
Го
(83)

§ 5 ДИНАМИКА ТВЕРДОГО ТЕЛА 29
Сделаем в уравнении (82) указанную замену переменных,
используя предложение 8, получим
ИеE)к(г)>? (84)
или
TA/^AWYL *JL^ *JL = 0. (85)
д г* А* дхп
Напомним, что ц—интегрирующий множитель уравнения
X dxn-Xndx = O, если -*^^ =— -цА„ , т.е.
дх дхп
Н—- = 0. Если положить и = М'/А', то в силу (85) мы имеем
dx
интегрирующий множитель для —" = —, что доказывает нашу
теорему.
10. Определение. Решение М уравнения (80) из теоремы
9 называется последним множителем Якоби.
11. Теорема. Каноническая система уравнений Гамильтона
всегда имеет последний множитель Якоби М=\.
Доказательство. Канонические уравнения Гамильтона
= =
Л дрС Л dq,
можно переписать в виде =——— = —. Уравнение (80) для
dH/op oHjoq I
(87)
q
последнего множителя Якоби имеет вид
и, следовательно, М=\ является его решением, что и утверж-
далось.
§ 5. Динамика твердого тела
1. Определения. Пусть ?1—твердое тело, (О, х, у, z)
— инерциальная система координат (рис. 5). Интеграл
, i+y+k=n, (88)

30 ГЛ. I. КРАТКИЙ ЭКСКУРС В МЕХАНИКУ
называется моментом инерции п-го порядка. Величины
am
(89)
(90)
(91)
называются осевыми моментами, а /0 = Щг2<Ля — полярным
п
моментом. Центробежные моменты инерции D, E, F определя-
ются равенствами
(92)
(93)
(94)
2. Предложение. Рассмотрим систему координат, начало
которой находится в центре масс С, а оси параллельны осям
X
Рис. 5
Рис. 6
исходной инерциалъной системы координат. Обозначим коор-
динаты в исходной системе буквами х, у, z, а в новой —
буквами ?,, г), С,. Тогда
(95)

§ 5. ДИНАМИКА ТВЕРДОГО ТЕЛА 31
(96)
где ОС={хс, ус, zc}, а т— масса тела (рис. 6).
3. Определение. Моменты инерции, вычисленные относи-
тельно системы координат, начало которой находится в центре
масс, называются центральными.
4. Определение. Пусть /—некоторая прямая в простран-
стве. Интеграл
dm (97)
п
называется моментом инерции тела il относительно оси /, где
Р(х, у, z)— расстояние от точки (х, у, z) до оси /.
5. Предложение. Пусть е° = {а, Р, у}—направляющий
вектор оси /, а2 + р2 + у2 = 1. Тогда момент инерции Jt относи-
тельно оси I равен
J, = Jxxol2 + Jyy p2 + Jzzy2 - 2Л,оф - 2jxzay - 2Jy?y. (98)
Доказательство вытекает из следующей цепочки равенств:
2-(', e°J)dm =
— 2yz$y — 2jczay] dm =
n
- 2xya.fi - 2yz$y - 2xzay] dm = Jxxa2 +
+JfyP2 + J*rf - 2аРЛ, - 2<tyJxz - 2$yjyz. (99)
6. Определение. На каждой оси /, проходящей через
фиксированную точку О, отложим отрезок ОА, равный 1/^/TJ.
Тогда точка А опишет поверхность, являющуюся эллипсоидом.
Существуют такие оси X, Y, Z, что уравнение эллипсоида име-
ет вид JXXX2 + JYYY2 + JZZZ2=\, т.е. для этих осей JXY =
=JYZ = jxz = 0, Построенный эллипсоид называется эллипсо-
идом инерции, оси X, Y, Z называются главными осями инер-

32 ГЛ. 1. КРАТКИЙ ЭКСКУРС В МЕХАНИКУ
ции. Если эллипсоид инерции построен для центра масс, то
главные оси инерции называются главными центральными
осями. Аналогичные названия используются для моментов
инерции.
7. Теорема. Пусть тело закреплено в начале координат О,
оси х, у, z направлены по главным осям. Тогда кинетическая
энергия Т твердого тела il, вращающегося с угловой скоростью
<o = fp, q, г), равна T=2~1(Ap2 + Bq2 + Cr2).
Доказательство. По определению кинетическая энергия
Т твердого тела ?2 равна интегралу
2T=\\\v2dm, A00)
а
где v = {uxp = {qz — ry, rx—pz, py — qx).
Имеем
2T=M[(qz-ryJ+(rx-pzJ+(py-qx)Ydm =
а
— 2pq Щ ху dm — 2pr j jj xz dm — 2qr JJJ yzdm= •
a a a
= Jxxp2 + Jnq2 + Jzzr2-2Jxypq-2Jxzpr-2Jyzqr. A01)
Поскольку оси х, у, z главные, то Jxy = Jv = JyZ = 0 и,
тельно, 2T=Jxxp2+Jyyq2+Jzzr2=Ap2 + Bqr+Cr2.
8 Т П д П
следова-
8. Теорема. Пусть твердое тело ?2 закреплено в начале
координат О. Тогда момент количества движения К={КХ, Ку,
Kz} относительно точки О (кинетический момент) твердого
тела ?2, вращающегося с угловой скоростью <я={р, q, r},
равен
кх=Jxxp—Jxyq—Jxzr,
Ky=- J^p + Jy,q- Jyzr, A02)
Если х, у, z—главные оси инерции, то К={Ар, Bq, Cr)
и A:=gradeJ.
Доказательство. По определению кинетический момент
К твердого тела ?2 равен интегралу

§ 5. ДИНАМИКА ТВЕРДОГО ТЕЛА
33
где р = {х, у, z} — радиус-вектор текущей точки. Поскольку
pxv = px[o>, p] = wp -р(р, to), то
A04)
Далее, если К={КХ, Ку, Kz} и ча = {р, q, r}, то
a n n
A05)
Аналогично проверяются остальные равенства.
9. Определение. Пусть ?,, г\, ? — неподвижная система
координат, х, у, z — система координат, жестко связанная
с телом (подвижная). Линия ON
пересечения плоскости О^г) с плос-
костью Оху называется линией уз-
лов. Угол ф между осью 0?, и лини-
ей узлов называется углом прецес- i>
сии, угол ф между линией узлов 0Л
и осью Ох называется углом соб-
ственного вращения, угол 9 между
осями 0^ и Qz называется углом
нутации. Углы vj/, ф, 9 дают коор-
динаты в группе вращений, которые
называются углами Эйлера (рис. 7).
10. Углам Эйлера ф, vj/,.9 отвеча-
ют три скорости ф, vj/, 9. В силу рис. i
правила сложения скоростей, если
угловая скорость в подвижной системе координат равна ш = {р,
q, r}, то
р = v|/ sin 9 sin ф + 9 cos ф,
q = ij/ sin 9 cos ф — 9 sin ф,
A06)
Эти соотношения называются кинематическими уравнениями
Эйлера.
11. Пусть ^0 = Yiei+Y2e2+y3^3 — единичный вектор,
У^зтЭэтф, у2 = 51п9созф, y3=cos9. Тогда d%°/dt = O. Напом-
ним следующее правило дифференцирования: для любого
вектора а = {аи а2, а3} имеет место равенство — = —hox|°, где

34
ГЛ. 1. КРАТКИЙ ЭКСКУРС В МЕХАНИКУ
da . . „
— = a1el+a2e2+a3e3. Применим это правило к вектору
dt
Получим следующую систему равенств:
d2l = ry ay
dt
dt
A07)
dt т'1 "z
Эти соотношения называются кинематическими уравнениями
Пуассона.
12. Динамические уравнения Эйлера. Направим координатные
оси по главным направлениям. По теореме о моменте
dK . g.
количества движения имеет место равенство — = М, здесь оба
момента К и М вычислены относительно точки О. Пусть <я = {р,
q, r}—вектор угловой скорости в подвижной системе коор-
динат; поскольку рассматриваются главные направления, то
в силу теоремы 8, используя правило дифференцирования
dK dK жг ш .
— = ЬгахА = М, получим уравнения
dt dt
Afr(B-C)qr=Mx,
A08)
которые называются динамическими уравнениями Эйлера. Если
к этим уравнениям добавить кинематические уравнения Эйлера,
то получим замкнутую систему дифференциальных уравнений.
Интегрируя полученную
систему из шести диф-
ференциальных уравнений,
найдем закон движения
твердого тела.
13. Случай тяжелого
твердого тела. Пусть с —
центр масс твердого те-
ла, а рс = {хс, ус, zc} — его
радиус-вектор в подви-
жной системе коорди-
Рис. 8 нат. Тогда M=pcxmg,
С
с0'
А
{
И
v\
Vi
^^
тд
У
1

§ 5. ДИНАМИКА ТВЕРДОГО ТЕЛА 35
g= —gC,0 (рис. 8). В этом случае имеем следующую полную
систему дифференциальных уравнений:
d = mg(zcy2 -усУз),
Cj-(A~B)pq = mg (усу 1 - хсу2),
A09)
14. Интегралы уравнений Эйлера. Время t явно в уравнения
A09) не входит, поэтому порядок можно понизить на единицу,
приняв за новую переменную одну из неизвестных величин.
Считаем, что в точке крепления нет трения, силы, при-
ложенные к телу, описываются силовой функцией
U=—mg(xcyl+ycy2 + zcy3). Следовательно, можно ввести функ-
цию Гамильтона, и поэтому имеется последний множитель
Якоби, см. п. 11 § 4.
Уравнения A09) имеют интеграл энергии Т— ?/=const или
{A2 + B2 + C2)-U = h, см. п. 7.
Уравнения A09) имеют интеграл момента количества
движения Apyt +Bqy2 + Cry3= const, так как сила mg параллель-
на оси 0?.
Наконец, система A09) имеет тривиальный геометрический
интеграл у\ + у2\ + у\=\-
Для того чтобы проинтегрировать систему A09), надо найти
дополнительный интеграл. Он существует, например, в следу-
ющих трех случаях:
а) случай Эйлера — Пуансо, когда xc = yc = zc = 0;
б) случай Лагранжа — Пуассона, когда А = В, хс = ус = 0\
в) случай Ковалевской, когда А = В = 2С, zc = 0.
15. Интегрирование уравнений в случае Эйлера — Пуансо.
Умножая первое из уравнений
Ap = {B-C)qr,
Bq = (C-A)pr, (ПО)
Cr = {A-B)pq

36 ГЛ. 1. КРАТКИЙ ЭКСКУРС В МЕХАНИКУ
на р, второе на q и третье на г, получим
Ар dp Bq dq _ Cr dr
В-С С-А A-B^dt- AП)
Перейдем от времени / к времени х: dx=pqr dt. Тогда
р2 = b\(x + bl), q2=b'2(x + b2), r2 = b'3{x + b3), где bh
b)—константы. Величину т находим, обращая интеграл
* , (П2)
где X — (b\b'2b'3) 1/2, что приводит к эллиптическим функциям.
Приведем окончательный ответ. Пусть для определенности
А<В<С и К2>2ЕВ (Е—константа энергии) (в случае К2<2ЕВ
надо поменять местами р и г). Начало отсчета времени можно
выбрать так, что <7 = 0 при ? = 0. Выполняя интегрирование,
получим p=pocn(s, x), q = qosn(s, x), r = rodn(s, к), где
A13)
(С-В)(К2-2ЕА) (В-А)BЕС-Кг)
~4 ~АЖ '' %~{С-В)(К2-2ЕАУ
a sn(s, x), cn(s, x), dn(s, x) — стандартные эллиптические
функции, см., например,' [83].
Направим ось аппликат неподвижной системы координат
вдоль вектора К={КХ, Ку, Kz). Тогда К=Ку1е1+Ку2е2 + КУзез,
и поскольку K=Ape1 + Bqe2 + Cre3, то
A15)
A16)
A17)
Из третьего уравнения следует cos 9 = — = const, т. е. 9 = 90=const.
К t
Из второго уравнения и го соотношения <7 = \j/sin9sin<p (п. 10) вы-
К ' 'К
текает равенство - sin 9 sin (p = \j/ sin 9 sin (p, т. е. \\i = K/A и \j/ = -?+\j/0.
А Л
К К
Далее, ф = г0—-cos90 и> следовательно, ф-=(/-0 —- cos90)/+/H.
16. Интегрирование уравнений.в случае Лагранжа—Пуассона.
Уравнения движения в этом случае имеют вид
Ap-(A-C)qr = mgzcy2,
Aq + (A-C)pr=-mgzcyu A18)

§ 5. ДИНАМИКА ТВЕРДОГО ТЕЛА 37
В качестве недостающего последнего интеграла можно взять
/• = i|/cos9 + (p. Интеграл энергии имеет вид A(p2+q2)+Cr2 +
+ 2mgzcy3 = const, т. е. v4(\j/2 sin2 S + &2) + 2mgzccos& = h. Интеграл
момента количества движения имеет вид ^(^Yi+472) +
+ Сгу3 = к, т.е. A\\i sin2 9 +О cos 9 = к. Из интеграла момента
,' к — OcosS
количества движения следует равенство Ц1= —2—, подстав-
ляя которое в интеграл энергии, получим
A19)
Положим и = cos 9. Тогда для нахождения и имеем дифференци-
альное уравнение
^X = ±2[A{l-u2){h-2mgzeu)-(k-CruJl A20)
т. е. ( —I =Р3(и), где Р3(и)— кубический многочлен, следова-
du , Т1
тельно, / — /о = —эллиптическая функция. Из интеграла
из
jJA)
v4»|/sin2 9+Crcos9 = fc найдем \)/ — v|/0= ^—-~-dt, а
I j4 sin У11\
Ф = г —\)/cosS найдем (р — (р0 = J(г —1|/cos9)rff.
17. Интегрирование уравнений в случае Ковалевской. Если
А = В = 2С, zc = 0, yc —0, то уравнения имеют вид
2Cp-Cqr = 0,
2Cq + Cpr = mgxcy2, A21)
Cf=-mgxcyl.
Положим mgxcIC = n. Тогда имеем следующую систему:
A22)
Отсюда
{ + i) i( + i) + i A23)
{
( ) ()( A24)

38
ГЛ. 1. КРАТКИЙ ЭКСКУРС В МЕХАНИКУ
Если первое равенство умножить на p + iq, а второе на
и сложить, то получим
Аналогично получается равенство
jt[(p-^J-n(yi-iy2)-] = ir[(p
Отсюда
( — я)
A25)
A26)
A27)
A28)
A29)
A30)
§ 6. Вариационные принципы в механике
1. Принцип Гамильтона. Рассматривается голономная меха-
ническая система, на которую действуют потенциальные силы;
таким образом, система характеризуется функцией Лагранжа
L = L(t, qly ..., qn, qly ..., qn). Дви-
жение системы описывается ура-
внениями Лагранжа второго ро-
Складывая и интегрируя, получим соотношение
[(p2-q2-ny1) + iBpq-ny2)][{p2-q2-nyl)-
-iBpq-ny2)~\ = const,
из которого следует последний недостающий интеграл
Действительная
траектория
Рис. 9
d (dl\ dL ,. ..
да - — - —= 0. Интеграл
dt \SqJ dq
W=\L{t,ql,...,qn,ql,...,qK)dt
A31)
называется действием по Гамиль-
тону, здесь t0, /x фиксированы.
В пространстве с координатами (q, t) рассматриваются возмож-
ные движения q — q{t, а) (а—параметр), причем q{i) — q{t, 0) —
действительная траектория (рис. 9). Здесь не варьируются А,
В и ?0, h-

§ 6. ВАРИАЦИОННЫЕ ПРИНЦИПЫ в МЕХАНИКЕ 39
Принцип Гамильтона утверждает, что на действительных
траекториях 5PF=0. Действительно, вычислим вариацию
dfV. Имеем
to
= 0, A32)
так как 5q\l=^ =8q\l=h=0.
Равенство 8W=0 означает, что действие W минимально, если
точки А, В близки. Действительно, вторая вариация 5 21^ имеет вид
. A33)
'о
так как форма ? ——г5</E<77- положительно определена.
2. Предложение. Если выполняется принцип Гамильтона,
то траектории описываются уравнениями Гамильтона.
Доказательство. На действительной траектории выпол-
няется равенство 5 J L dt = 0 и, следовательно,
'о
«1 I,
8 IT I Pi9i~ I Pi4i + L)dt = b [( ? ptqt-H)dt = 0, A34)
to U
n
так как Н= ^ p^ — L. Отсюда
i= 1
A35)

40 ГЛ. I. КРАТКИЙ ЭКСКУРС В МЕХАНИКУ
так как
'i '1
5 I ? л&*= | I (Pi&4t+4fiPi)dt=
J i=l J i=l
t,
j i=i
f ? ?,8Л* = Г ? (q^-p^dt, A36)
J i=l J i=l
to 'o
fii 4 dt +
i = 1 i = 1
'o
и 8^i(/o) = 8^i(?i) = 0- Итак,
дН . дН
следовательно, л = —, pt= ——, т.е. получили канонические
уравнения Гамильтона.
3. Принцип Якоби. Рассматривается механическая система, на
которую наложены идеальные связи, предполагается, что
активные силы потенциальны и Т=Т2 (см. п. 6 §2), T—U—h.
В пространстве лагранжевых координат (ql) рассматриваются
траектории, проходящие через фиксированные точки А, В, но
момент времени прохождения А и В может быть различным,
5/г = 0 на всех траекториях. Получили так называемую вариаци-
онную задачу с подвижными концами.
Рассмотрим такую вариацию времени x = x(t, а), что при
а = 0 получим время на действительной траектории, т. е. x(t,
0) = f; если то = тAо, a), Ti=t('i, °0> то т0 и Tt будут общими для
всех траекторий, т.е. 5то = 6т!=0. Тогда
и т,
\Ldt=\L1t'dx, A38)
где L = L(q1, ..., qn, qt, ..., qn) и L1 =
так как qi = — — = q'i/t'. Итак, переходим к и+1 переменной
di at
Я\, ••¦> Я», t.

§ б. ВАРИАЦИОННЫЕ ПРИНЦИПЫ В МЕХАНИКЕ 41
Поскольку лагранжиан Lx от / явно не зависит, • то
t—циклическая переменная и имеется первый интеграл
_-i = const, который имеет вид
it'
-2T=U-T=-h, A39)
так как L = Т+ U, т. е. циклический интеграл совпадает
с интегралом энергии. Рассмотрим функцию Рауса
j () ()t' = 2Tt'. Тогда
принцип Гамильтона можно записать в виде
Ti Т,
8jiJrfr = 0, или 8|27УЛ = 0, A40)
То То
1 "
где Т=- Yj aij4i4j- Введем метрику
ds2= ? a^dqidq^lTdt2. A41)
Тогда вариационный принцип можно переписать в виде
равенства
То
Поскольку T=U+h, то -I —) =U+h и, следовательно, -I —) =
= (t'J(U+h), т. е. /'= , . Итак, вариационный принцип
имеет вид
5 ||%/2(С/+Л)Л = 0. A43)
То
Окончательно получаем принцип Якоби, который утверждает,
что на действительных траекториях имеет место равенство
5 | ч/2(С/+Л)Л = 0. A44)
лв

42 ГЛ. 1 КРАТКИЙ ЭКСКУРС В МЕХАНИКУ
4. Уравнение Якоби. Примем переменную qx за независи-
мую. Тогда вариационный принцип Якоби перепишется
в виде
A45)
/ и и
Обозначим квадратный корень 2(U+h) У ау —— буквой
ОТ ГТ d ?S\ dS П
Л. Тогда соответствующее-уравнение Лагранжа — —г — — = 0,
dqi \SqiJ eqt
i = 2, ..., п, называется уравнением Якоби. Отметим, что
для понижения порядка уравнения использовали интеграл
энергии.
5. Пример. Рассмотрим движение материальной точки
в однородном поле тяжести. Пусть ось Ох направлена по
горизонтали, а ось Оу— вертикально вниз. Кинетическая энер-
гия Т имеет вид Т=-(х2+у2) и U+h = h — mg. Поэтому
S= / {h — mgy)m\ 1 -Н — I ). Уравнение Якоби имеет вид
(V . \ \ / /
dS\ dS „ , dy
— - — = 0, где у =~, т. е.
dy I dy dx
A46)
следовательно, 2(h — mgy)y" + mg{\ +(y'J) = 0. Продифференци-
руем это равенство по х, получим у =0.
6. Замечание. Вывод уравнений Лагранжа из вариацион-
ного принципа 5 И^= 0 можно найти в [275].
§ 7. Интегральные инварианты
1. Определение. Рассмотрим систему дифференциальных
уравнений -^ = Xi(t, xx, ..., х„) (i=\, 2, ..., п) с начальными
условиями Xi(to) = xf. Решение этой задачи обозначим хг = хг{1,
х\, ..., х®). Для заданной области fioc:Rp рассмотрим ее
отображение xf = xf (Хх, ..., Хр), (X.l5 ..., Xp)eQ0, в пространство
R", т. е. в R" дана /7-мерная поверхность, заданная парамет-
рически. Определим однопараметрическое семейство поверх-

7. ИНТЕГРАЛЬНЫЕ ИНВАРИАНТЫ
43
ностей ?2,, которое задается в виде x^t, Xi(X.1;
..., -Xn(^-i> ••-, \))- Выражение
Хр),
J J it ip- 1
называется интегральным инвариантом р-ro порядка, если
/(?) = const; если р = п, то J называется интегральным инвариан-
том полного порядка. Если равенство J(t) = const выполняется
для любой поверхности, то J называется абсолютным интег-
ральным инвариантом. Если же это верно для компактных
ориентируемых подмногообразий без края, то J—относитель-
ный интегральный инвариант. В формуле A47) 8jCf,... 5лг,-
обозначает дифференциальную форму, индуцированную из
формы dxt, л ... л dxi,.
Теория относительных интегральных инвариантов сводится
к теории абсолютных интегральных инвариантов. Пусть,
например,
A48)
— относительный интегральный инвариант. Тогда в силу
теоремы Стокса его можно записать в виде
т. е. получили абсолютный интегральный инвариант второго
порядка. Аналогично, каждому относительному интегральному
инварианту р-ro порядка отвечает абсолютный интегральный
инвариант (р+1)-го порядка.
Отметим связь интегральных инвариантов с первыми интег-
ралами.
2. Теорема. Пусть система дифференциальных уравнений
xi = Xi(xl, ..., лг„), (=1, ..., и, имеет интегральный инвариант
A48). Тогда величина
) , ..., хп)уп A50)
ной систем
8^Уп, i, k=\, ..., «.A51)
является первым интегралом расширенной системы
!, ..., х„), Ук =

44
ГЛ. I КРАТКИЙ ЭКСКУРС В МЕХАНИКУ
3. Пример. Рассмотрим систему х= —xf(r)/r, у = —yf(r)lr,
где г = ^/х2+у2. Пусть х = и, y = v. Тогда величина
J=| (v6x - иЪу—уЪи + x6v)
A52)
является интегральным инвариантом. Действительно, поскольку
ху—ух = XV—уи = const = с — интеграл площадей, то
J = J (v6x — иЪу —ybu + at5d) = J 8 (ид; — г/j) = 18с = const A53)
для любой области.
4. Теорема Лиувилля. Величина
J '" J 4l"
A54)
является интегральным инвариантом для канонической системы
„ dp, дН dqt дН .
Гамильтона от п переменных: J—= , — = —, г=1, ..., п.
dt dq{ dt dp.
Доказательство. Пусть AJ=J(t + dt) — J(t) и q[ = qi +
+ q\dt, p'^Pi+Pidt. Тогда
A55)
b.J=\...\lbq\...bq'nbp\...bp'n-\...\bqi...bqnbpl...bpn =
a' a
где
i+dAdt+... dA
cq\ dq2
dq2
dp»
dp»
d^dt+ i+fdt+...
cqi dq2 др„
= 1+ Y, I — + -p-1Л+члены высшего порядка. A56)

§ 7. ИНТЕГРАЛЬНЫЕ ИНВАРИАНТЫ
45
Итак, d/=0, так как D=l + ... в силу того, что %=дН/дрг, р\=
= —dHjdqi. Следовательно, /=const и J—интегральный инвариант.
5. Определение. Величина
У=Ф -
A57)
называется интегральным инвариантом Пуанкаре—Картана.
6. Теорема. Величина У является интегральным ин-
вариантом.
Доказательство. Рассмотрим функционал W=\Ldt;
_ 'о
вычислим его вариацию, причем t0, rt также будем варьиро-
вать, т.е. to = to(oi), ti = t1((x), qi = qAt, a), 4i = qdt, а) (при а = 0
получим значения лагранжевых координат и скоростей соответ-
ствующей действительной траектории). Полная вариация 8</
имеет вид bq = — 8a + q5t. Символом [5</] обозначим изохрон-
на
ную вариацию, т. е. [8^,-]|,=,. = —8ос|,=,., г = 0, 1. Положим также
' да '
bqf = 8<7,-(f0) и 8^=5<7('i). Тогда имеет место равенство
dL
, A58)
так как на действительной траектории — — г = 0. Поскольку
dqi at dqi
п
dL/dqt=pt и H=-L+YJPi4i, то
5W=L18t1—Lo8to+ У (dql — q'lbt!) —
- ? p?5^P = l -H8t+ X j
i=l \ i=l
A59)

46
ГЛ. 1. КРАТКИЙ ЭКСКУРС В МЕХАНИКУ
Рассмотрим теперь в пространстве (qlt ..., qn, plt ..., р„, t) две
замкнутые кривые: кривая Со задается уравнениями q( = qf(a),
?( () 0/ °(O) f(l) ?@)?(/)
у р
р,=р?(а), ' =
С
ур
, и q°(O) = qf(l),
й
); кривая
С, являющаяся образом кривой Со при действии гамильтонова
потока qt = dH/dph pt= —dH/dqt, задается уравнениями
Pt=Pi(t, a),( qi = qi(t, а) и Pi(t, 0)=Pi(/,/), qt{t, 0) = ^(f, /). Из
равенства J 5 И^= W(l)— W@) = 0 вытекает соотношение
о
и поэтому ф( — Hbt+
J
С
У=(Ь1 —Я8?+
J V
? ;5д( =Ф I— H8t+ ? р;
i=i / J \ ( = i
Со
— интегральный инвариант.
т.е.
7. Теорема Ли Хуачжуна. Любой относительный
интегральный инвариант вида
A61)
для гамильтоновой системы пропорционален инварианту Кар-
тана— Пуанкаре.
Доказательство этой теоремы приведем только для случая си-
стемы с одной степенью свободы. Вычислим производную dJ'jdt:
dJ' Г [(дА дА . дА
J L V q p
с
^г
. A62)

§ 7. ИНТЕГРАЛЬНЫЕ ИНВАРИАНТЫ 47
Поскольку §b(Aq) = Q, jb(Bp') = 0, то для любого контура
с с
С выполняется равенство
dJ' _
It'
дВ дВ . , дВ Д к . /зд s , ЗВ - \1
о/ dq dp J \dg dp /J
ъ~2тч
тг2тР\^^ A63)
где Z= . Интеграл от дифференциальной формы вдоль
dp dq
замкнутого пути (любого) обращается в нуль тогда и только
тогда, когда подынтегральное выражение является полным
дифференциалом, а это, в свою очередь, эквивалентно тому, что
д [дА
выполняется соотношение —
d\d
д [дА r,dHl д [дВ ~дн]
— Z— =— ——Z— , т.е.
dp\_dt dq J dq\_dt dp J
A64)
(для любой функции Н). Поэтому — = 0, — = 0, — = 0, т. е.
dt dq dp
dt dp dq dpdq dq dp dpdq
— 0,
dq dp
дА dB
Z = const и = const или d(A — cp)/dp = dB/dq, а это озна-
dp dq
чает, что (A— cpMq+ B8p = 5V. Следовательно, A5q + B8p —
и поэтому
Г Г Г
A65)
так как |5F=0 (рис. 10).
с
Отметим без доказательства следующий интересный ре-
зультат.

48
ГЛ. 1. КРАТКИЙ ЭКСКУРС В МЕХАНИКУ
i
Рис. 10
8. Теорема. Если система дифференциальных уравнений
допускает интегральный инвариант вида У=ф ? />;8<7; — Hbt, то
J;=i
с
она может быть приведена к гамильтонову виду.
§ 8. Канонические преобразования
1. Определение. Преобразование /:R2n(qt, ..., qn, Pi, ...
..., /7n)->R (?i, ..., Ь,п, t)i> •••> Лп) называется каноническим, если
оно сохраняет каноническую форму уравнений для любой
функции Гамильтона, см. также п. 1 § 24.
Если ?( = ?,•(?, р) и П^Пг(?./>), то предполагаем, что /)(^,
r\)/D(p, q)^0. При этом отображении система .уравнений
4i = dH/dpi, p'i= — dH/dqi переходит в систему ?,i = dK/d
д/дЬ
2. Теорема. Пусть задана функция V=V(t, д1г ...
¦¦-, Чп> ?,i, •••, %п)> называемая производящей, и константа c = const,
называемая валентностью преобразования. Тогда преобразование
dv
dV
является каноническим. Будем предполагать, что
82V
det
#о,
т. е. преобразование обратимо.
Доказательство. Используя равенства
огУ
с [ Sq.dt ,i
A66)
A67)
A68)

§ 8. КАНОНИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 49
получим следующие соотношения:
- ¦ +
+~ z z?s—~~^~-z zhj—^-—• (i7°)
Поскольку
ft 2 n / \ n
_ 1 dijfsd^j dx\i _ 1 dqs \ 5^j / 3t\i ^?\ ^Яа ^Л|
5Я 1 A 5 /eA 5e. 1 t/E, db д ( TT dv\ .
то —=— > — —) H и —I сЯН . Аналогично
5T)i с _, dqs \ dt I dr\i с dt dt dr\t \ dt I
rfTi, d I „ , dV\
получается, что —-= \cH-\—).
dt dt,,y dt)
3. Следствие. Преобразование cpt = —, r\t=—— переводит
. dH . dH
каноническую систему qt = —, pt= с гамильтонианом
dpi dqi
H в каноническую систему с гамильтонианом К^сН + -—.
4. Определение. Если с = 1, то соответствующее преоб-
разование называется унивалентным.
5. Уравнение Гамильтона — Якоби. С помощью канониче-
ского преобразования из п. 2 можно попытаться привести
каноническую систему к простейшему виду 4, = 0, ть = О. Этого
можно добиться, если выбрать такую производящую функцию
V, что К=сН-\ = 0. Для этого надо решить уравнение
dt
dV
dt
которое называется уравнением Гамильтона—Якоби. С этим
Уравнением подробнее ознакомимся в следующей главе.

50
ГЛ. 1 КРАТКИЙ ЭКСКУРС В МЕХАНИКУ
6. Структура канонических преобразоваиий. Пусть Со — такой
контур в пространстве (q, р, t), который лежит в гиперплоскости
t = t0, а С*о — его образ при каноническом преобразовании
^; = ^j(^, p), r\i = r\i(q, p). Обозначим через С и С* образы
контуров Со и С*о относительно соответствующих гамиль-
тоновых потоков (т. е. сдвиг на время t в силу соответствующей
динамической системы для некоторого фиксированного значе-
ния /) qt = dH/dpi, р,= -дН/д<], и ^ = дК/д^, г\{=-дК/д^
(рис. 11). Интегральный инвариант Картана — Пуанкаре дает
равенства
Со
Г "
И ф > Г\гОС,1 =
Ji=l
Со С*
Ли Хуачжуна
тельно,
с
так как 5/|Со = 0
так как 5г|Сп- = 0. В силу теоремы
-НЫ и, следова-
A73)
X Л,-8?,--*8<-с X Pibqi-НЫ ) =0
для любого контура С, а следовательно,
F^)+r&- (l74)

§ 9. СКОБКИ ПУАССОНА 51
Рассмотрим четыре случая.
а) Пусть />(^, ..., Z»)/D(pi, ..., />„)#0. Тогда />;=/>,(?, q) и
V=V(t, q,Q. Из равенства f гь^.-^-с(? PtSqt-H8t) =
и К=сН+д*
ot
= — > I —oqt+—ос. — — 6t вытекает, что гъ= ,
^-^ \ Я/7. № . I Pit ЛГ.
б) Аналогично, если Di^, ..., ?>n)/D(ql, ..., дп)ф0, то
V=V(t,p,ty и ц — dV/dpi, cq,= -dVldpt, K=cH+dV/dt.
в) Аналогично, если D(r\1, ..., i]n)jDip1, ..., р„)?=0, то
V=V(t,q,i]) и 4,- = 5К/дп,, ОД= -dV/dq,, K=cH+dV/dt.
г) Аналогично, если ^(т)!, ..., r|J/Z)(^j, ..., ^„)#0, то
К=К(?, ?, л) и ^,. = гк/гль сд(=-дУ/др(, K=cH+dV/dt.
§ 9. Скобки Пуассона
1. Определение. Пусть на пространстве R2" с коор-
динатами q^,...,qn, pi, ..., р„ заданы две функции f(t,q,p)
и g(^q,P)- Функция {/,#•}, определенная равенством
(,75)
называется скобкой Пуассона функций fug.
2. Лемма. Пусть q(t) и p(t)—решение канонической
системы qt = dH/dpi, р\= — dH/dqj. Тогда полная производная —
dFtt, а, р) dF(t, о, р) г_ гг1 _ „
равна —' '=—v '+{F, H\. В частности, уравнения Гами-
льтона имеют вид 4i = {qi, H}, р\ = {рг,Н).
Доказательство вытекает из равенства
ui+ ? (?ljl-?:jl)=?+{f, h}.
dt St' .f'l \dqi Spi dp, dq;J dt l *
3. Определение. Скобки Пуассона {qt, Pj} = &ij,
{?b?j}=0, {л,Р;}=0 называются фундаментальными.
4. Теорема. Скобки Пуассона не меняются при каноничес-
ких преобразованиях.
Для доказательства теоремы потребуется следующая
5. Лемма. Фундаментальные скобки Пуассона не меняются
при канонических преобразованиях.

52 ГЛ. 1 КРАТКИЙ ЭКСКУРС В МЕХАНИКУ
Доказательство. Пусть x = x(q,p) и y=y(q,p) — кано-
ническое преобразование. Если xi = dH/dyi, ух = — dH/dXi, то
• _ у (дх<ди_дх'дн\_
ех; у (дНдх, дНду\_дх, у (dHdxj дНду\]_
дНfdxidxj_dxidx\ у у дн/дх,¦dyj_dxi?y\_
^^Л+-{^,^ = ^, 077)
здесь Н—произвольная функция. Отсюда, если H=Xj, то
{jCj, at,-} = 0, если H=yt, то (л:;, Jj}=l, и, наконец, если H=yj, то
U} 0 (#)
U,^} G)
Равенство {/,-, Jj) = O проверяем аналогично, вычислив про-
изводную yt.
Доказательство теоремы 4. Для каждого j=\, ...
..., п имеет место равенство
у
, Л) ,. ^ ! \D{x,, xk)D{qj, Pj)
Просуммировав эти равенства и воспользовавшись леммой 5,
получим
6. Теорема. Скобка Пуассона обладает следующими
свойствами: а) Для произвольной константы с имеет место
равенство {<р, с} = {с, <р} = 0. б) Для произвольной константы
с имеет место равенство {(р, с\(/} = с{(р, i|/}. в) Если обе функции
<р и v|/ не зависят от аргументов одного какого-нибудь класса
q1, ..., qn или Pi, ..., р„, то {(р, х)/}=0. г) Выполняется соотноше-
ние {<р, \|/}= — {v|/, (р}. д) Имеем {ц>, — \j/}= — {(р, \)/}. е) Если
<р=/((р!, ..., (р),), где <р!, <р2. ••¦. Ф* — функции аргументов обоих

9. СКОБКИ ПУАССОНА 53
классов qx, ..., qn и ри ..., рп, то {ф, \|/}= ? {(pj, ^}у~- ж)
ф и \j/ зависят от какого угодно параметра t (в частности,
t может быть одним из аргументов qt, ..., qn или р%, ..., р„), то
^5J^=J-2 \|/> + <ш, — >. з) Выполняется тождество Якоби
Доказательство. Докажем тождество Якоби, остальные
свойства легко вытекают из определения 1. Пусть ф1; ф2,
фз — функции аргументов (qt) и (о,) каждая. Введем обозначе-
ния {ф1, Ф2}=4'з; {фг, Фз} = ^1, {фз. Ф1} = ^2- Тогда тождест-
во Якоби принимает вид {tyi, Ф1} + { v|/2, Фг} + { ^з, Фз}=0.
Заметим, что —- = —(ф2, ф3} = < —, Фз ? + \Ч>2, -г^г и ^ =
opt dpi | dpi I dpi 1 oq{
= < -—, Фз > + \ Ф2»-~ \. Вычислим первое слагаемое в тождестве
Якоби:
5ф, Mф2 ( <3ф! ) Gфз I /1СПЛ
-^i^-, Фз>-^-^Ф2,7~Г • <18°)
Далее,
' .,^11, 081)
-^Ui.^H- 082)
Вычислим скобку {xj/j, ф!} при помощи свойства е), рас-
сматривая

54 ГЛ. I. КРАТКИЙ ЭКСКУРС В МЕХАНИКУ
как сложную функцию qt и pt, зависящую от них посредством
переменных dip2/8pi, <Э(р2/д<7;, d<f>3/dpiy d(p3/d<7(, где i=l, ..., п.
Тогда по формуле в утверждении е) теоремы имеем
Ф1 >= Z <^,
dp,) \S4l
Из равенства A83) находим
5*1*1 йфз 5(|/i йфз ,.„.,
— , — ^-=— , (loJj
cqi ,/5ф2\ dp-,
i.T1 Сфг сН|/, да>2 /ю^ч
= . ~~7^Ч"= ' A°«)
и поэтому
Г | ) V ^Ф3 )^Ф2 ( сф3 ] ^Ф2
Аналогично,
5<Pi ) ^фз ]^ф1 / I
—~~' Ф 2 Y ~1 Л ~ ' Ф 2 Г 11
A88)
A89)
Сложив равенства A80), A81), A87) — A89), получим после
приведения подобных членов равенство
, Фз}=0. A90)

§ 10. АЛГЕБРА ЛИ ВЕКТОРНЫХ ПОЛЕЙ 55
Действительно, рассмотрев, например, сумму членов, содер-
жащих множитель 5<р2/#/>,•, видим, что
*!i{^, ф1}-^{^, фЛ = 0 A91)
вр, I a», v J вр, I s4i V3J v '
в силу свойства г) из теоремы.
7. Теорема Пуассона. Пусть /(/, а, р) и g (t, q, p) —
первые интегралы системы канонических уравнений qx = bH\dpb
Р;= —dHldqt. Тогда {/, g] также первый интеграл этих же
уравнений.
Доказательство. Из теоремы 6 вытекает равенство
|+{g, Я},/}=0, A92)
так как f=f+{f, Я}=0 и g = |+{g, Я} = 0.
Глава 2
ИНТЕГРИРОВАНИЕ КАНОНИЧЕСКИХ СИСТЕМ
§ 10. Алгебра Ли векторных полей
1. Определение. Векторное пространство G называется
алгеброй Ли, если в G задана операция [х, у ], х, у е G, которая
удовлетворяет следующим свойствам: а) [х, у] — билинейная
функция; б) [х, у]= — [у, х]; в) выполнено тождество Якоби
[[x,y],z]+[[y,z],x]+[[z,x],y] = 0.
2. Определение. Пусть G — конечномерная алгебра Ли,
a d, ..., еп — ее базис. Тогда [е{, е}] = Ск^ек. Набор С*у является
тензором, который называется структурным.
На языке структурного тензора свойство б) из п. 1 перепи-
шется в виде Ck,j=—C)i, а в) — в виде
\ O. A93)
Пусть G — алгебра Ли. Не все подпространства в G равно-
ценны, выделяются специальные подпространства.
3. Определение. Подпространство Н в алгебре Ли
G называется подалгеброй, если [х, у]еН для любых х, yeH.

56 ГЛ 2. ИНТЕГРИРОВАНИЕ КАНОНИЧЕСКИХ СИСТЕМ
Подалгебра К в алгебре Ли G называется идеалом, если
[х,у]еК для любых хеК, yeG.
4. Определение. Алгебра Ли G называется коммутатив-
ной (или абелевой), если [х, у] = 0 для любых ее элементов
х, yeG. Если G — коммутативная алгебра Ли, то любое ее
подпространство является подалгеброй и идеалом. В любой
алгебре Ли произвольная прямая является подалгеброй.
5. Конструкция. Если К—идеал в алгебре Ли G, то
в факторпространстве G/K определена структура алгебры Ли:
<x(x + K)+P(y + K) = <xx+Py + K и [х + К, у + К]=[х,у] + К.
6. Определение. Гомоморфизм алгебры Ли Gx в алгебру
Ли G2 — это такое линейное отображение /: G^^G2, что
f[x,y]= [f(x), f(y)]. Подпространство Кег/= {хеGy \f{x) = 0}
называется ядром гомоморфизма /. Ядро любого гомоморфиз-
ма является идеалом, и так получается любой идеал.
7. Определение. Пусть G—произвольная алгебра Ли.
Определим линейное отображение adx: G -»G формулой
ad* (у) = [х, у ]. Пространство Z(G) = {хе G | ad* = 0} называется
центром алгебры Ли G; Z(G) — идеал в G.
8. Пусть G — произвольная алгебра Ли. Определим цепочку
идеалов G => Ga) => ... з G(i) => ... формулой G^ = {G{i~i))w, где
Ga) — производная подалгебра, которая является линейной
оболочкой коммутаторов [х, у], х, yeG. Для конечномерной
алгебры Ли G эта цепочка стабилизируется, т. е. найдется такой
номер I, что G(i) = G(i+1) = ...
9. Определение. Если цепочка производных алгебр Ли
G => G(i) з ... => G(i) з... стабилизируется на нуле, то G называет-
ся разрешимой алгеброй Ли.
10. Замечание. Если G — разрешимая алгебра Ли и Н—
подалгебра в G, то Н—разрешимая алгебра Ли, так как G{1) => Hil\
11. Рассмотрим максимальный по размерности разрешимый
идеал в G — он называется радикалом алгебры Ли G. Возможно,
что радикал J равен нулю. Радикал определен единственным
образом, так как если бы существовал разрешимый идеал К, не
содержащийся в радикале J, то K+J было бы разрешимым
идеалом, строго содержащим J.
12. Определение. Если радикал J алгебры Ли G равен
нулю, то G называется полупростой алгеброй Ли. Алгебра Ли
G называется редуктивной, если С7 = ЯфС71, где Я—абелева
алгебра Ли, a Gx — полупростая алгебра Ли и [х, у ] = 0 для
хеН, yeGt.
13. Определение. Пусть в алгебре Ли G задано скалярное
произведение <х, у}, х, yeG. Говорят, что алгебра Ли G со-
храняет скалярное произведение, если <adzx, уУ + (х, adzjy> = 0
для всех х, у, zeG.
14. Теорема. Пусть конечномерная алгебра Ли G сохраня-
ет скалярное произведение. Тогда G редуктивная.

§ 10. АЛГЕБРА ЛИ ВЕКТОРНЫХ ПОЛЕЙ 57
Доказательство вытекает из следующих четырех лемм.
15. Лемма. Пусть алгебра Ли G сохраняет скалярное
произведение. Тогда если Я—идеал в G, то его центр Z(H)
содержится в центре Z{G) алгебры Ли G. В частности, всякий
абелев идеал содержится в Z(G).
Доказательство. Пусть х, yeG, zeZ(H). Тогда
<[z, х\, [z, *]> + <*, [z, [z, х]]> = 0, A94)
но [z, x] = аеЯ, так как zeZ(Я) с Я и xeG, следовательно,
[z, а] = 0, поскольку zeZ(H), aeH. Итак, <[z, x], [z, x]} = 0.
Отсюда [z, х] = 0 для любого xeG, т.е. zeZ(G).
16. Лемма. Алгебра, сохраняющая скалярное произведение,
полупроста тогда и только тогда, когда ее центр Z(G) нулевой.
Доказательство. Алгебра G полупроста тогда и только
тогда, когда G не содержит разрешимых идеалов, что эк-
вивалентно тому, что G не содержит коммутативных идеалов.
Поэтому необходимость условия Z(G) = 0 очевидна.
Достаточность. Если Z(G) = 0 и Я с G—разрешимый
идеал, то существует коммутативный идеал К ci G, Кф 0. В силу
леммы 15 имеем включение К a Z(G) = 0, поэтому К=0,
полученное противоречие доказывает лемму.
17. Лемма. Если G — конечномерная алгебра Ли, сохраня-
ющая скалярное произведение, то производная алгебра Ли GA)
полупроста.
Доказательство. Алгебра GA> сохраняет скалярное
произведение, поэтому достаточно доказать, что Z(GA)) — 0.
Пусть heZ(GA)). Тогда heZ(G) в силу леммы 15. Для любых
х, yeG имеем ([х, у], hy + (y, [x, А]>=0, следовательно,
([х, у], /г> = 0, так как xeG, heZ(G) и [х, /г] = 0. Итак, h±GA)
и heG{l), следовательно, </г, /г> = 0, поэтому /г = 0.
18. Лемма. Пусть конечномерная алгебра Ли G сохраняет
скалярное произведение. Тогда справедливо утверждение
теоремы 14.
Доказательство. Пусть Н—ортогональное дополнение
к Сг'1) в G. Тогда Н—идеал в G. Действительно, для heH
имеем <[и, /г], [х, y]} + (h, [v, [x, y]]} = 0, так как
</г, [v, [x,y]]} = 0, x,yeG. Итак, [v, h]eH=(Ga))L. Поскольку
Я—идеал, то [Я,Я]сЯПСA) = 0, т.е. Я—абелев идеал.
Пусть veH, yeGw. Тогда ([v, у], [v,y]) + (y, [v, [v,y]]> = 0,
следовательно, [v, y] = 0. По предыдущей лемме A7) Gw —
полупростая алгебра Ли и, следовательно, G—редуктивная
алгебра Ли.
19. Замечание. Теперь после напоминания нужных нам
понятий из теории алгебр Ли приведем основные понятия,
связанные с геометрией векторных полей на многообразиях.
20. Определение. Пусть X— векторное поле на многооб-
разии М. Кривая x{t) называется интегральной кривой поля X,

58
ГЛ. 2. ИНТЕГРИРОВАНИЕ КАНОНИЧЕСКИХ СИСТЕМ
если для любого t0 вектор Хх(,о) касается кривой x(t) в точке
d
x(t0), т.е.
Л
x(t).
Из основных теорем для систем обыкновенных дифференци-
альных уравнений вытекает, что для любой точки роеМ
найдется такое е>0, что для |/|<е определена единственная
интегральная кривая x(t) поля X такая, что х@)=ро.
21. Определение. Однопараметрическая группа диффе-
оморфизмов многообразия М—это такое гладкое отображение
F: RxM-»M, что: а) (ро(х) = х, хеМ; б) ф, +, = ф, »ф, , где
Ф, (*) = *"(*,*). . « . «
Из определения вытекает, что ф, — диффеоморфизм много-
образия М.
Отображение ф, определяет гладкое векторное поле X на
М по формуле Хр=ц>,—
dt
q>t(p):— это касательный
о
вектор к кривой x(t) = (pt(p), называемой орбитой точки р
(рис. 12).
ft(P)
О t
Рис. 12
22. Лемма. Орбита ф,(р) есть интегральная кривая поля X.
23. Определение. Гладкое отображение F:
( — е, е) х U-* М, где U—открытое множество в многообразии
М, называется локальной однопараметрической группой преоб-
разований, если отображение F удовлетворяет следующим
условиям: а) для любого U|<e отображение <pt(p) = F(t, p)
является диффеоморфизмом множества U на открытое множе-
ство фг(С/), причем фо = 1с1; б) для любых t, s, p таких, что t, s,
t + se( — e,e), p, <f>s(p)eU, выполняется следующее равенство:
Ф<+Лр) = Фг(ф« (/>))•
Так же, как в п. 21, локальная однопараметрическая группа
преобразований (диффеоморфизмов) индуцирует векторное поле
X, определенное на U.
Справедливо обратное утверждение.

§ 10. АЛГЕБРА ЛИ ВЕКТОРНЫХ ПОЛЕЙ 59
24. Предложение. Пусть X— векторное поле на многооб-
разии М. Для произвольной точки реМ существуют окре-
стность U точки р, положительное число г и локальная
однопараметрическая группа преобразований ф,: V-*M, te
б ( — 6, е), которая индуцирует заданное поле X.
Доказательство. Пусть х1, ... х" — локальная система
координат в окрестности W точки р. Пусть
X— X V(xl> ¦¦¦> х")—• в W. Рассмотрим систему обыкновенных
дифференциальных уравнений — =^'(/1@> -./"(О), i=U •••, и,
at
с неизвестными функциями fl, ..., /". Пусть f'(t, и) — такое
решение этой системы, определенное для \xJ(q) — xJ(p)\<8
и И<е, что /'@, х) = х'. Положим <p,(u) = (f1 (t, и), ...,f"(t,u))
для И<е в U={q\\xi(q) — х'(р)\<г]. Это искомая локальная
однопараметрическая группа.
25. Определение. В условиях предложения 24 будем
говорить, что поле X порождает локальную однопараметричес-
кую группу преобразований ф, в окрестности точки р. Если
существует глобальная однопараметрическая группа преоб-
разований многообразия М, которая порождает X, то поле
X называется полным.
26. Предложение. На компактном многообразии каждое
векторное поле полное.
27. Предложение. Пусть ф: М-*М—диффеоморфизм
многообразия М. Если векторное поле X порождает локальную
однопараметрическую группу преобразований <р,, то векторное
поле ц>,Х порождает группу ф о ф, о ф ~1.
Доказательство. Ясно, что ф°ф(оф~х—локальная од-
нопараметрическая группа преобразований. Покажем, что она
индуцирует векторное поле <р,Х. Поскольку ф, порождает X,
Ф((ф~1(/')Х поэтому в силу определения
Ф(ф<(ф(/')))' A95)
ТО "Ф УР) df
<$>,Х имеем
л d
dt
т.е. ф(ф,(ф^1 (р))) порождает ф,*.
28. Следствие. Векторное поле X инвариантно относи-
тельно диффеоморфизма ф (т. е. <р,Х=Х) тогда и только
тогда, когда диффеоморфизм ф перестановочен с группой ф(,
т. е. фф, = ф,ф.
d
Доказательство. В силу п. 27 имеем (<р,Х)р = —
dt
1 = 0
фо
°Фг°Ф * (р)- Поэтому если поле инвариантно, то

60
ГЛ. 2 ИНТЕГРИРОВАНИЕ КАНОНИЧЕСКИХ СИСТЕМ
{«>,Х)Р = ХР = — Ф,(р), так как ф, порождает X, т. е. векторное
at ,=0
поле (р,Х=Х порождается двумя однопараметрическими груп-
пами фоф, оф~1иф,ив силу теоремы единственности решений
дифференциальных уравнений они совпадают, т. е. ф°ф,»ф~' =
= Ф,. Обратно, пусть это равенство имеет место. Тогда
ф°ф,°ф
A96)
так как X порождает ф,.
29. Определение. Напомним определение коммутатора
векторных полей. Пусть х1, ..., х"—локальная система коор-
динат на многообразии М, а Х=Х'—:
дх'
У=У'/7—два
дх
векторных поля. Тогда формула Z=\X, Y] = XY— YX,
[X,
дх1
Их1
A97)
определяет некоторое векторное поле на М, которое называется
коммутатором полей X, Y.
30. Лемма. Пусть ф: М -»N—диффеоморфизм. Тогда
Ф,[^, У]=[ф.^,Ф.У].
31. Теорема. Пусть X, Y—векторные поля на М. Если
X порождает локальную однопараметрическую группу преоб-
разований ф,, то
[X, y] = limi[y-
0 '
A98)
Доказательство. Пусть/— произвольная гладкая функ-
ция на М. Очевидно, что
A99)
Вычисляя производную под знаком интеграла, получим равен-
ство /(ф,(д))=/(а)-Иа((а), где
ds.
B00)

10 АЛГЕБРА ЛИ ВЕКТОРНЫХ ПОЛЕЙ
61
Ясно, что
1
'тИ
dx
'дх'
dx
Имеем равенство
1 at'
= Х„/. B01)
.7 4.) B02)
и, следовательно,
.0 '
= Xa{Yf)- Ya(a0) = Ха(Г/)- Ya(Xf) = [X, Г] J, B03)
так как ao = Xf и
B04)
32. Следствие, в обозначениях предыдущей теоремы
имеем
f --» 0 '
B05)
любого s.
Доказательсдво. В силу леммы 30 имеем (ф5), [Z, Y] =
= [(Ф,).АГ, (ф,).У]. Далее [(ф5).ДГ, (Ф,).У ]= [X (ф,).У], так как
(ф5),Х=Х в силу Следствия 28. Теперь, применив предыдущую
теорему 31 к векторному полю (ф5), Y, получим
= Нт![(ф,).У-(ф, + |).Г]. B06)
/-•о ^
33. Замечание. Предыдущее следствие 32 можно записать
в виде равенства
так как
B07)

62 ГЛ. 2. ИНТЕГРИРОВАНИЕ КАНОНИЧЕСКИХ СИСТЕМ
34. Предложение. Пусть векторные поля X и Y порожда-
ют локальные однопараметрические группы ср, и \)rs
соответственно. Тогда cpi<K = <K(p( для всех, t, s тогда и толь-
ко тогда, когда [X, Y] = 0.
Доказательство. Если (р^^^Фо то ^=(ф|)»^ B силу
п. 28. Тогда по теореме 31 имеем
[X, r] = lim![y-(<p,).r] = 0. B08)
Пусть теперь [Л', Y ] = 0. Тогда в силу п. 33 имеем
— (ф,), У=0 для всех t. Поэтому (ф,), Y есть постоянный вектор
dt
в каждой точке а, и, следовательно, он совпадает
с (ф,),У|, = о = (фо).У= Y. Итак, поле Y инвариантно относитель-
но каждого диффеоморфизма ф,. Поэтому \jrs коммутирует
с каждым отображением <р,, см. п. 28.
35. Предложение. Коммутатор векторных полей превра-
щает линейное пространство всех гладких векторных полей на
многообразии М в алгебру Ли, которую будем обозначать D(M).
Каждый диффеоморфизм /: М -» jV индуцирует гомоморфизм
/,: D(M)->D(N) алгебры Ли D{M) в алгебру Ли D{N).
Доказательство. Единственное, что надо проверить,—
это тождество Якоби, которое получается прямым вычислением.
§ 11. Теорема Якобн
1. Определение. Пусть дано нелинейное уравнение
первого порядка в частных производных
) 0. B09)
Функция z = <p(xl, ..., хп, Сь ..., С'„), зависящая от постоянных
Ci, ..., С„, называется полным интегралом уравнения B09), если
эта функция является решением уравнения B09) и
D(CuC2,...,Cn) ^ V '
2. Замечание. Общее решение уравнения в частных
производных зависит от нескольких произвольных функций.
Поэтому полный интеграл уравнения B09) отнюдь не является
общим решением. Полный интеграл по сравнению с общим
решением охватывает только небольшую «горстку» решений
уравнения B09).

§11. ТЕОРЕМА ЯКОБИ 63
3. Теорема Якоби. Пусть z = (p(x1, ..., х„, h, Cx, ...
..., Ca-i) + Cn—полный интеграл уравнения в частных произ-
водных
Тогда уравнения движения канонической системы обыкновенных
дифференциальных уравнений
i,...,p.,Xi,...,Xn)
dt dpi
B12)
dpi cF^pi, ..., pn, хг, ..., xn)
dt ox-,
(=1, 2, ..., л, можно записать в виде
= <5q> ^Ф__> dJ?_ = t , т B13)
/=1, 2, ..., и, 5=1, 2, ..., и—1, м ?s, т — произвольные константы.
Доказательство. Покажем сначала, что уравнения B13)
разрешимы как относительно xi, ..., х„, р±, ..., р„, так и относи-
тельно 2л постоянных d, d. •••, d-i, ^i> ^2. ¦•¦> i.-i, Л, т.
Действительно, уравнения d<p/dCs = bs, s=l, 2, ..., п—\, раз-
решимы относительно xit ..., xn-i, так как определитель
U\Xi, x2, ..., Jrn-i) WIC,, С2, ..., Cn_i)
отличен от нуля в силу определения полного интеграла, см. п. 1.
Итак, xs = <ps(xn, Cs, bs, h), 5=1, ..., n—\. Подставив найденные
значения в уравнение d<p/dh = t + z, получим соотношение
П(х„, Cs, bs, h) = t + z, s=\, ..., л—1. Разрешив это уравнение
относительно х„, подставив полученное значение в выражение
¦xs = (ps(xn, Cl, ..., Cn-i, Ь1,...,Ь„~1, И), а затем подставив эти
соотношения в уравнения pi = dq>ldxi, получим решение системы
B13) относительно х, и р{:
B15)
Уравнения B13) разрешимы относительно 2л постоянных.
Для этого достаточно показать, что уравнения р( = д<р/дх/,

64 ГЛ. 2. ИНТЕГРИРОВАНИЕ КАНОНИЧЕСКИХ СИСТЕМ
/=1, 2, ..., п, разрешимы относительно С\, С2, •¦¦¦, Cn_l5 h. Это
имеет место в силу того, что определитель
DfaP !>) B16)
Й(С,,С2,..., С..,, A)
отличен от нуля. Таким образом, решив систему B13)
относительно 2« постоянных, получим следующие выражения:
Cs = As(xi, х2, ..., хп, pi,p2, ..., Рп),
bs = Bs(Xl, х2, ..., хп, рир2, ..., рп),
h = F(Xl, x2, ...,xn,pi,p2, ...,ря),
т = Т(х1, х2, ..., х„, pi, р2, ..., pn)~t.
Покажем, что B15) дает общий интеграл, а уравнение
B17) — совокупность 2п различных интегралов канонической систе-
мы B12). Подставив выражения B15) в уравнение B13), получим
тождества, дифференцируя которые, найдем новые соотношения
Tr^j^^^ B18)
" J\_d±
?х дсЕдхк dt х
i^-^=h B20)
kf j ohPxk dt
i=\, ..., n, 5=1, ..., n— 1. Функция 2 = ф является полным интег-
ралом уравнения B11) с частными производными, следователь-
но, заменив в нем /?f на pi = 3q>/dxi, получим тождество
F\ —-¦, —Li ••¦, —!-, -fi, .^2, •••, хп =«• Дифференцируя это тождест-
\схх <\х2 гх„ }
во по X;, Cs, /г, получим новые тождества
B22)
?iS=1> B23)
(=1, ..., n, 5=1, ..., и-1. Вычитая B19) и B20) из B22) и B23),
получим

S 11. ТЕОРЕМА ЯКОБИ
65
Получили систему п линейных однородных уравнений, ее
определитель
02ф
гх2дс2
8х„дС2
дх, dh
dx.dh
дх2
D(Ct, С2. ..., С„_„ Л)
B25)
отличен от нуля, и, следовательно, — = 0, к—\, ..., и. Склады-
дрь dt
вая B18) и B21) и принимая во внимание последние тождества,
получим, что —(-— тождественно обращается в нуль (;= 1, ..., л).
0Xi dt
4. Замечание. В п. 5 §8 мы получили уравнение Гамиль-
тона— Якоби. Теперь мы видим, что, найдя полный интеграл
этого уравнения, мы можем проинтегрировать систему канони-
ческих уравнений.
Отметим, что если S(t, qh a,) — полный интеграл уравнения
Гамильтона — Якоби, то уравнения
— (t, qu a,)=A.
B26)
в пространстве V=R" (p) x R" (q) x R" (t) задают одномерное
подмногообразие, поскольку матрица Якоби этой системы
имеет вид
1
0
0
0
1
a4i dqs
dq, daj
B27)
и detJ=det(d2Sldqjda.j)^O и rkJ—2n, и по теореме о неявных
функциях М—гладкое одномерное подмногообразие
в V (рис. 13).

66
ГЛ. 2. ИНТЕГРИРОВАНИЕ КАНОНИЧЕСКИХ СИСТЕМ
М
Имеются три важных слу-
чая, когда можно найти пол-
ный интеграл уравнения Гами-
льтона— Якоби, см. пп. 5—7.
5. Пусть функция Н не
зависит явно от t, т. е.
dH/dt = 0. Тогда задача оты-
скания полного интеграла ура-
внения — +H\t, с—, ос =0 эк-
ct \ cq )
вивалентна задаче отыскания
(p)^R"(q)mR\t) полного интеграла уравнения
Ну ~, q\ = h, если искать
5 в виде S~-ht+W(q\
Рис. 13
>. Пусть дН/дд„ = О. Тогда
полный интеграл 5 уравнения
Гамильтона — Якоби ищем в виде S = anqn+ W(t, q-i, ..., qn).
7. Разделение переменных. Пусть
H = G(fi(ql,pl),...,fn(qn,pn)),
B28)
с/,
и предположим, что —-#0, т. е. в этом случае в выражении для
функции Н переменные разделились, в каждую.функцию входит
только одна пара сопряженных переменных qh p{. Уравнение
Гамильтона — Якоби перепишется в следующем виде:
B29)
dV
Положим/; qh — =a,, /= 1, ..., и, где а, — произвольные посто-
янные. Тогда постоянную h можно выразить через постоянные
а,, ..., а„, т.е. h = G(al, ..., а„). Из предположения д/(/др(ф0
( \
следует, что соотношение
dv\
^ — ) = а1- можно разрешить
Sq,J
и получить ~ = Fi(qj, a,), j=l, ..., п. Тогда V= ^ jFi(q» ^i)dqi,
и поэтому для действия 5 получим
5= -G(o,, ..., *n)t+ X SF,(qt, at)dq, B30)

§ 12. ТЕОРЕМА ЛИУВИЛЛЯ
67
Покажем, что формула B30) определяет полный интеграл.
Имеем
dq;da.k
B31)
при
тл det
d2s
oqt
цирования обратной
ЛЯ*
ЛЯ
= YI —i:^0, так как по правилу дифферен-
._ j 00.1
функции имеем dFi/dcti — (cfi/dpi)
§ 12. Теорема Лиувнлля
1. Теорема Лиувилля. Предположим, что канонические
уравнения
dq, _ cH
dt
B32)
обладают п независимыми первыми интегралами Fj(qu .... qn,
рь ..., р„), j~ 1, ..., п, которые находятся в инволюции и которые
можно разрешить относительно переменных ри ..., р„. Тогда
уравнения B32) интегрируются в квадратурах.
Для доказательства этой теоремы нам потребуется сле-
дующая
2. Лемма. Пусть задана каноническая система уравнений
B32), которая обладает п функционально независимыми первыми
интегралами FAqu ..., qn, /?ь ..., р„), находящимися попарно в ин-
волюции, т.е. {Fj,Fj}=0, i,j=\,...,n. Предположим, что
B33)
Тогда система уравнений Fj(q1, ..., qn, pi, ..., pn) = a.j может быть
разрешена относительно pj=fj(ql, ..., qm ось ..., а„). Утвержда-
ется, что {pk-fk, Pi-f,)=0.
Доказательство. Имеем тождество
Fhiflu-, Чп, Pi{4i,-, Ч«, «ь ..., а„), ...
..., pn(qu ..., qn, au ..., an)) = ctk.
Вычислив производную по а, получим
или —-= У —*°^т т% так как dpy/dqs =
B34)
—-+ У — — гО
Принимая во

68 ГЛ. 2. ИНТЕГРИРОВАНИЕ КАНОНИЧЕСКИХ СИСТЕМ
внимание, что dfy/dps = 0, тождество dFk/dps = dFk/dps можно
переписать в виде
^*= у 8Ftdb>y-A) B35)
8Р* у = 1 8Ру 8Р*
В результате имеем равенство
dJ±dJl=Y у dFk8Flгfa~Л)д(р«-fb) B36)
8Ч> 8Р* у=! g=i 8Ру дРь 84s 8Р,
Аналогично,
Отсюда
fdFtdF, dF,dFk
" PF
Введем обозначение z^= У —-{л—//, л^/в}- Тогда
Ф8
B39)
к, /= 1, ..., п. Соотношения B39) представляют собой п2 тож-
деств, которые можно разбить на п систем однородных
линейных уравнений порядка п относительно переменных z<,° (с
фиксированным значением /) и с отличным от нуля определи-
телем B33). Следовательно, каждая такая система имеет только
тривиальное решение
*У=1?{Ру-U Рь-Л} = 0, B40)
5=1 °Р*
у, 1=1, ..., п. Эти п2 тождеств снова распадаются на п систем
однородных линейных уравнений порядка п относительно
переменных {py—fy, Ps—fs} (с фиксированным индексом 8)
с отличным от нуля определителем B33). Поэтому {py—fy,
Рь~/s} = 0. Лемма доказана.
3. Доказательство теоремы. Пусть pj—fj(q,a1,...
..., а„), у'=1, ..., п,— решения системы
Fi(qi, ..., qn, Pi, ...,/»„) = аь
B41)
Fn(qi, ...,qn, Pi, ...,pn) = an.

§ 12 ТЕОРЕМА ЛИУВИЛЛЯ 69
Тогда по лемме {рк — fk, Pi~fi} = 0 и, следовательно, 8fk/dqi =
= df,/dqk, к=1,...,п, так как {/ь/;}=°> {рк, р,} = 0 и {рк, /} =
= df/8qk. Поэтому дифференциальная форма <o=fidqi + ...
...+fndqn является точной, т. е. ? fjdqj = dW. Поэтому
pj=fj=dW/8qj. Подставляя это выражение в первый интеграл
F1=H=ct1, получим уравнение
) B42)
Итак, W удовлетворяет уравнению B42) первого порядка
в частных производных. Покажем теперь, что W будет полным
интегралом уравнения B42), т. е. выполняется неравенство
det \\d2Wjdqkdctl \\ фО, которое в силу равенства fk = dW/dqk
можно переписать в виде
7=det
К .... а.)
B43)
Для доказательства неравенства B43) рассмотрим тождество
Fj{qu ..., qn, к, ..., /.) = <Х; B44)
и очевидное соотношение , ""а"; = 1. Подставляя в это
О(аь ..., а„)
соотношение вместо аь ..., а„ левые части тождеств B44),
получим
l, .., F,)D(fu .... /„)
1
й(а„ ..., а„) D(px, ...,Л)й(а„ ..., а,)'
Отсюда 1фО. Таким образом, функция
= J hdqx + ...+fndqn, B46)
где у — любой путь, соединяющий начальную точку
х0 с текущей точкой р, является полным интегралом уравнения
B42). Поэтому по теореме Якоби остальные п первых интег-
ралов системы B32) можно найти из соотношений
-+%->•• ?-*•¦•¦•?-*• <™>
заменяя в их левых частях все постоянные а,- на соответст-
вующие выражения a.J = Fj(q1, ..., qn, pu ..., рн), здесь-р7—произ-
вольные постоянные.

70 ГЛ. 2. ИНТЕГРИРОВАНИЕ КАНОНИЧЕСКИХ СИСТЕМ
4. Замечание. Теорема Лиувилля в настоящее время
является одной из общих теорем, постоянно используемых
в гамильтоновой геометрии, математической физике. Она лежит
в основе исследования интегрируемых систем.
§ 13. Теорема Ли
1. Замечание. Пусть в фазовом пространстве R2" канони-
ческой системы р= —дН/dq, q = dH/dp заданы п независимых
функций: H=F1(p,q),...,Fn(p,q) таких, что {F,, Fi] = CkiiFk,
С \j = const. Тогда линейное пространство С, натянутое на
функции Fu ..., Fn, будет конечномерной алгеброй Ли, а числа
Cij будут ее структурным тензором в базисе Fx, ..., Fn.
2. Теорема. Предположим, что: а) на множестве
Ма={(р, q)\F1=ai, ..., Fn = an} функции Fu ..., Fn функционально
независимы; б) ? Ckjak = 0 для всех i,j=\, ..., п; в) алгебра Ли
G разрешима, причем {Fu Fj} = C\iFl. Тогда решения системы
дН . дН
лежащие на Ма, можно найти в квадратурах.
3. Замечание. Множество П наборов a = (at, ..., а„), удов-
летворяющих условию б) теоремы 2, является линейным
подпространством FIczR" в R", размерность которого не
меньше dimG — dimGA), где GA) — производная алгебры Ли G.
Поскольку G разрешима, то dim П ^ 1.
4. Теорема Ли. Пусть в области ficR"(^', ..., х") задана
система дифференциальных уравнений
х'=Дх), х = {х\ ..., xn)e?l<=R" B49)
и п линейно независимых векторных полей Xl7 ..., Х„ таких,
что: а) Аг1=^/(д;) —; б) [Хь A'i] = XiA'1, X, = const; в) про-
i = I <*Xi
странство линейных комбинаций полей Xt, ..., Хп является
разрешимой алгеброй Ли относительно коммутатора \Х, У]
векторных полей. Тогда уравнение B49) интегрируется в квад-
ратурах.
5. Теорема. В условиях теоремы 4 уравнение XlF= 0
интегрируется в квадратурах.
6. Замечание. Доказательство теоремы 2 базируется на
теореме 4, а теорема 4 будет получена из теоремы 5. При
доказательстве последней будем пользоваться некоторыми
фактами из теории систем дифференциальных уравнений в част-
ных производных первого порядка (линейных).

§ 13. ТЕОРЕМА ЛИ 71
7. Определение. Пусть дана система линейных диф-
ференциальных уравнений первого порядка в частных про-
изводных
B50)
Она называется полной, если [Л,> Л;]= ? b\jAk, где
? fj-—некоторые константы.
8. Теорема. Полная система дифференциальных уравнений
B50), где Аи ..., А, — линейно независимые векторные поля,
имеет n — s функционально независимых решений.
9. Лемма. Полная система дифференциальных уравнений
B50), где Ау, ..., As — линейно независимые векторные поля,
эквивалентна такой полной системе дифференциальных уравне-
ний Xvf=Q, ..., XJ~=0, что векторные поля Хи ..., XS линейно
независимы, линейно выражаются через Аи ..., As и \Х„ А^]=0.
Доказательство. Пусть хи ..., х„ — произвольная систе-
ма координат в области ?2. Тогда
Мх)=
'й
B51)
7 = 1
Тогда поле X, имеет вид Х{ = -—h X Qjj-> гДе Cj6C
В силу линейной независимости полей At, ..., As матрица
А(х)= || atj{x) ||, 1<г<5, 1</<и, имеет ранг s. He теряя
общности, предположим, что det || а{)(х) \\ фО, l^i^s, l^j^s.
Пусть В(х)= || bij(x) || =А(х)~1 в некоторой меньшей окрестно-
сти и b4eCx{U), t/czQ, 1</, j^s. Положим Z,= ? ЬиА^
-—
Поскольку —, — =0, то отсюда следует, что поля Х1, .... Xs
VXi VXj I
искомые. Лемма доказана.
10. Лемма. Пусть Хи ..., Xs — векторные поля на V, линей-
но независимые в каждой точке хе V и такие, что [Xt, Zj = 0.
Тогда для любой точки aeV в окрестности Uс: V найдется
локальная система координат х1, ..., х", определенная в меньшей
окрестности V и такая, что Xi = d/8x', i=l,...,s.
Доказательство. Пусть z , ..., z" — такая система коор-
д
динат, что векторы Хг{а), ..., Xs(a),
' ¦"' 8z"
линейно

72 ГЛ. 2. ИНТЕГРИРОВАНИЕ КАНОНИЧЕСКИХ СИСТЕМ
независимы. Такая система координат существует: для ее
построения достаточно подвергнуть пространство R" линейному
преобразованию. Обозначим cpA) локальные однопараметрические
группы преобразований, порожденные полями Xt, см. п. 23 § 10.
Пусть tu ..., ts, zs+1, ..., z"—достаточно малые числа. Опре-
делим отображение h: Cl->V, Q = {xeR"\\x\<8}, равенством
h(tu ..., ts, zs+1, ..., z") =
= ф,A1)°...оф<*>оХ|/-1@, ..., 0, zs+1, ..., z"), B52)
где \j/ — координатный гомеоморфизм, отвечающий координа-
там z1, ..., z" (v|/(a) = 0). По определению имеем равенство — (/°
°h)@) = X1(a)f, так как фA) индуцирует поле ХХ. Поскольку
[Хг, Ау] = 0, то в силу утверждения п. 37 § 10 отображения
ф|'' коммутируют и, следовательно, zr(f°h)@) = Xi(a)f,
(=1, ..., s, т. е. ht,a((d/dti)a) = Xi(a). Далее, h,A—. ) = — при
s<j^n. Поэтому отображение /г,0 имеет ранг п, и, значит, по
теореме об обратной функции отображение h является диффе-
оморфизмом Q на открытое множество U с V, если 5 достаточ-
но мало. Система координат (С/, /г) искомая. Лемма доказана.
11. Доказательство теоремы 8 вытекает из леммы 10, так
как исходная система после подходящей замены переменных
превращается в простейшую -4 = 0, ...,-4 = 0, для которой
утверждение теоремы очевидно.
12. Доказательство теоремы 5. С помощью ли-
нейных преобразований заменим систему Хи ..., Х„ на
систему Yt, ..., Yn так, чтобы Xl = Y1
{Yl, ..., У;} — подалгебра, порожденная Уь ..., У,-, причем- эта
последовательность подалгебр удовлетворяет требованию, что
{Уь ..., Yk} — идеал коразмерности один в {Уь ..., Yk+l}. Это
всегда можно сделать. Действительно, из разрешимости алгеб-
ры G вытекает, что существует ряд 0 с Gx с G2 <= •¦¦ <= Gn с G,
обладающий вышеуказанным свойством. Пусть теперь J—
идеал алгебры Ли G. Образуем ряд подалгебр
Для соседних членов Kh Ki+l этого ряда выполнено одно из
двух утверждений: а) либо Kt = Ki+1; б) либо Kt — идеал кораз-
мерности один в К1+1. Теперь, убирая лишние члены из ряда
B53), получим ряд OcLt <= ... cLnc G, где каждый член имеет
либо вид Li = Gi[)J, либо вид 1,, = С7>ф/. Заметим, что если

§ 13. ТЕОРЕМА ЛИ 73
dim/=l, то Ll=J. Поле Хх порождает идеал алгебры Ли G,
применяя к нему приведенную выше конструкцию, получим
требуемый ряд.
В этом случае система дифференциальных уравнений
Yxf=Q, ..., Yn-lf=0 является полной и, следовательно, имеется
нетривиальное решение M^const. Пусть <p(u)=Yn(u). Докажем,
что ф(м) — решение системы Yif=0, ..., Yn-1f=0. Пусть
i=l,..., п — 1. Имеем равенства
Y, (Yn (и)) = [ Yt, Yn] и + Yn (Y, (и)) = "^ С ?„ Yk (и) = 0. B54)
* = i
В силу линейной независимости векторных полей Yt, ..., Yn
функция Yn(u) = q>(u) отлична от нуля. Положим и1 =jdu/(p(u).
Легко проверяется, что и1—решение системы Y1f=0, ...
..., Yn_1f=0, Ynf=l. Но решение этой системы находится
в квадратурах, так как из нее можно найти выражения для
производных df/dx', что позволяет найти / по полному
дифференциалу df=-^1dx1+-^dx2 + ...+-~dx". С другой сто-
роны, решения этой системы действительно существуют.
Сделаем замену переменных (в случае необходимости коор-
динаты х1, ..., х" можно перенумеровать): (х1, ¦¦¦, х")->(и1,
-> _> _ lilt д ди1 д д ди1 д „
х2, ..., хп). Тогда д дх1=-—--1, т- = ]П-Т7 + -7, где i = 2, ..., п.
ди1 дх дх ди' дх дх
В переменных и1, х2, ..., х" имеем Yk(f)= ? —-^[(и1, х2, ...
..., х"), к=\, ..., и—1. Поэтому и1 можно считать параметром.
Решая систему Yxf=0, ..., Yn-2(f) = O, Yn-1(f)=\ и продолжая
процесс, мы получим все решения уравнения Х1/=0 в квад-
ратурах. Теорема доказана.
13. Доказательство теоремы 4. Пусть uu...,uH-i
представляют собой п — 1 независимое решение уравнения
X1F=Q, полученное методом, описанным при доказательстве
теоремы 5. В координатах мь ..., и„_1, хп уравнение XtF=0
имеет простой вид X^F=—-b\(uu ...,un-u x"). Соответству-
ющее обыкновенное дифференциальное уравнение имеет вид
«!=0, п2 = 0, ..., п„_! = 0, хп = Ь\(и1, ..., и„_ь хп). Найдем реше-
ние, проходящее через точку (xq, ..., х). Тогда
B55)

74 ГЛ. 2. ИНТЕГРИРОВАНИЕ КАНОНИЧЕСКИХ СИСТЕМ
Подбирая соответствующую константу, получим требуемое
решение. С другой стороны, имеем отображение
ul=u1(x1, ..., х"),
иа'.1=ия.1(х\.'.,х%
t = un(x\ ..., хя)
такое, что «„(xj, ..., х?) = 0. Отображение B56) является локаль-
ным диффеоморфизмом v: R"->R". Обратное отображение
задается функциями х1 =vf' [uu ..., ип-и /),..., х" = \~1(и1, ...
..., и„-и t). Решение, проходящее через точку (х?, ..., Хо), имеет
вид xf = vf 1(u°, ..., и°~и t), ..., xn = v~1(u\, ..., Un-U t). Теорема
доказана.
14. Доказательство теоремы 2. Рассмотрим п линей-
но независимых векторных полей Х1г ..., Х„, определяемых
канонической системой уравнений B48). Естественное отображе-
ние алгебры Ли G функций {Fly .... Fn} на алгебру Ли D полей
{Xi, ..., Х„} является изоморфизмом, так как линейная ком-
бинация ? XjFi является константой только при Xt = 0 в силу
функциональной независимости функций {Ft}.
Векторные поля Xt касаются многообразия Ма, так как
F,, Fj}sO на Ма по условию. В локальных координатах
х , ..., х") на Ма уравнения B48) будут иметь вид xk=fk{x),
п л
к=\, ..., п. При этом, очевидно, поле Хк= ? /*—; удовлетворя-
ет теореме 4. Теорема доказана.
15. Пример. Рассмотрим движение на одной прямой трех
точек, взаимодействующих между собой с силой, обратно
пропорциональной кубу расстояния между ними. Эту задачу
рассматривали Якоби и Пуанкаре. Пусть дяь т2, тъ — массы
точек, а х, у, z — их координаты. Потенциальная энергия этой
системы имеет вид
Рассмотрим три функции
Н=р1=й+ё;+й+и{х>у>^ B58)
F2 = xpx+ypy+zpz, F^=px+py+pz. B59)
Здесь рх, РУ, Pz — координаты, канонически сопряженные с х, у,
z. Ясно, что /\ — полная энергия системы, F2 = 2~1 — [т1х1 +

§ 14. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ 75
+ т2у2 +m3z2), a F3— импульс всей системы. Функции Ft, F2,
F3 функционально независимы, и {Ft, F3}=0, {F2, F3}= — F3,
{Flt F2}=2F1. Соответствующая алгебра Ли G разрешима, так
как G ~=> HsL э {0}, где одномерная подалгебра L порождается
функцией Fu а двумерная подалгебра Я порождается функци-
ями Ft, F3. Подалгебры Я и L являются идеалами в G и Я со-
ответственно.
Применяя теорему 2, заключаем, что решения этой
задачи, лежащие на нулевой поверхности уровня энергии
и импульса, можно найти с помощью квадратур. Полученный
результат справедлив и для более общего случая, когда
потенциальная энергия U зависит только от разностей
х — у, x — z, y — z и является однородной функцией переменных
х, у, z степени — 2.
§ 14. Дополнительные сведения
из теории групп Ли и алгебр Ли
1. Определение. Гладкое многообразие Р, на котором
введена структура группы, называется группой Ли, если отоб-
ражение /: Ру.Р-*Р, задаваемое формулой f{g,h) = g'lh,
является гладким.
Для каждого элемента geP группы Ли Р определены два
диффеоморфизма Rg: P-*P\ L0: P^P, называемые соответст-
венно правым и левым сдвигом и определяемые равенствами
Rg(x) = xg и Lg(x) = gx соответственно, где хеР.
2. Определение. Векторное поле X на группе Ли
Р называется левоинвариантным (соответственно правоинвари-
антным), если (LaVX=X для любого аеР (соответственно
(Яа),Х=Х).
Каждое левоинвариантное векторное поле однозначно опре-
деляется своим значением в единице ееР группы Ли Р.
3. Лемма. Пространство левоинвариантных векторных по-
лей на группе Ли является конечномерным линейным подпрост-
ранством в пространстве всех векторных полей. Его размер-
ность равна размерности группы Ли. Если X, Y—левоинвари-
антные векторные поля, то их коммутатор [X, У] — левоинва-
риантное векторное поле.
4. Определение. Алгебра Ли G левоинвариантных ве-
кторных полей на группе Ли Р называется алгеброй Ли
группы Ли Р.
5. Определение. Гладкое отображение/: R1^/5 называ-
ется однопараметрической подгруппой в группе Ли Р, если:
a) f(a + b)=f (a) f(b) для всех a, beR1; б)/@) = е, где е — еди-
ница группы Ли Р.
6. Лемма. Каждое левоинвариантное векторное поле на
группе Ли Р является полным. Если ф, — однопараметрическая

76 ГЛ 2 ИНТЕГРИРОВАНИЕ КАНОНИЧЕСКИХ СИСТЕМ
группа диффеоморфизмов, порожденная левоинвариантным по-
лем X, то ф, (е) — однопараметрическая подгруппа. Из этой
конструкции получаются все однопараметрические подгруппы.
7. Определение. Говорят, что группа Ли Р действует на
многообразии М, если задано такое гладкое отображение h:
РхМ-уМ, что: a) gig2=gig2, gugi^P; б) е =id, где g (x) =
= h{g, х) и id(x) = x — тождественное отображение.
8. Замечание. Имеются естественные биекции между
следующими объектами: а) однопараметрические подгруппы
в группе Ли Р; б) касательные векторы Хе ТеР в единице
е группы Ли Р; в) левоинвариантные векторные поля на группе
Ли Р; г) левоинвариантные действия группы R1 на Р.
9. Определение. Все однопараметрические подгруппы
группы Ли Р можно собрать в одно универсальное отображение
exp: G-+P, при котором exptX: R1-^-»/1 задает однопарамет-
рическую подгруппу с вектором скорости X в единице ее Р.
Отображение ехр называется экспоненциальным отображением
группы Ли Р (G—алгебра Ли группы Ли Р).
10. Определение. Действие группы Ли Р на многооб-
разии R" называется и-мерным линейным представлением
группы Ли Р, если все диффеоморфизмы g, определенные в п. 7,
являются линейными отображениями g: R"->R". В этом опреде-
лении вместо R" можно взять любое линейное пространство V.
11. Конструкция. Пусть группа Ли Р действует на мно-
гообразии М. Тогда определен касательный гомоморфизм
ф: G-*D(M) алгебры Ли G группы Ли Р в алгебру Ли
D(M) векторных полей на многообразии М. Он определяется
равенством
exptX(a). B60)
¦ 12. Конструкция. Группа Ли Р действует на Р посредством
сопряжения g (x)=gxg~l, хеР. Этоддействие называется присо-
единенным и обозначается ig(x) = g (x). Оно индуцирует уже
линейное действие группы Ли Р на алгебре Ли G, обозначаемое
Ad, т. е. Adg(X) = (deig)(X). Это представление называется
присоединенным представлением группы Ли Р. Дифференциал
ad = ^e(Ad): G->Hom(G) называется присоединенным представле-
нием алгебры Ли G.
Пусть G* — пространство, дуальное к G, т. е. пространство
всех линейных отображений a: G->R. Определим коприсоединен-
ное представление Ad* группы Ли /"равенством (Ad*/)(x) =
=/(Adg-iJc), где geP, xeG, feG*. Коприсоединенное представ-
ление задает отображение Ad*: />->GL(G*), дифференциал кото-
рого в единице еЕР называется коприсоединенным представлени-
ем алгебры Ли G, т. е. имеем отображение ad*: G->Hom(G*).

§ 14. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ 77
13. Пред л ожени-е. Для X, YeG и feG" имеют место
следующие равенства: a) adxY=\X, Y~\; б) (ad"x f)(Y) —
= -/([*, Г]).
14. Определение. Пусть группа дЛи Р действует на
многообразии М. Множество O[x0) = {gxo\ geP} называется
орбитой точки хоеМ, a PXo = {geP\gxo = xo}—ее стационар-
ной подгруппой или подгруппой изотропии.
15. Определение. Каждое линейное «-мерное представле-
ние (т. е. представление в и-мерном линейном пространстве V)
группы Ли Р можно рассматривать как отображение р:
P^GL(V), p{g) = g ¦ Пусть имеются два представления
pl: />^GL(K1) и р2: P->GL(K2) группы Ли Р. Они называются
эквивалентными, если существует такое невырожденное линей-
ное отображение /: Vi^>V2, что диаграмма
^ У B61)
коммутативна для всех geP, т.е. /°pi(g)=p2(g)°/
16. Предложение. Если на алгебре Ли G существует
такое невырожденное скалярное произведение (х, v), x, yeG, что
(Adgx, Adgy) = (x, у), gtP, т.е. все операторы Ad9 являются
ортогональными преобразованиями, то присоединенное и коприсо-
единенное представления группы Ли Р эквивалентны, в частно-
сти они имеют одинаковые орбиты.
Доказательство. Скалярное произведение задает изо-
морфизм/: G^-G*, каждому элементу xeG отвечает линейный
функционал fx(y) = (x, у). Поскольку
Ad A-W = (Ad9x,j) = (Ad9x, Ad9Ad9 ,,) =
= {х, Adg ,y)=fx(Ade ,y) = (Ad*9fx)(y), B62)
то fAd x = Ad*gfx, т.е. диаграмма
G' >G*
Ad;
коммутативна, что и требовалось доказать.
17. Замечание. Для любой алгебры Ли компактной
группы Ли выполнены условия предыдущего предложения 16.
Следовательно, для компактных групп Ли представления Ad
и Ad* эквивалентны, и поэтому орбиты этих представлений
совпадают.

78
ГЛ. 2. ИНТЕГРИРОВАНИЕ КАНОНИЧЕСКИХ СИСТЕМ
18. Пример. Простейший пример группы Ли, для которой
орбиты присоединенного и коприсоединенного представлений
различны, дает группа Р={х-*ах + Ь\афО, a, b, хеЩ аффинных
преобразований прямой R . Эта группа допускает матричную
реализацию
Р =
а Ь
О 1
B64)
Легко проверить, что алгебра Ли G группы Ли Р изоморфна
следующему пространству матриц
Si S2
О О
B65)
с обычным матричным коммутатором \_А, В]=АВ—
В G выберем базис ej =
базис, fu /2, т. е. ft
1 О
О О
В
О 1
0 0
, а в G —сопряженный
базисе /,, /2 координаты
обозначим хь х2. Тогда простые вычисления показывают, что
B66)
B67)
где а= "' ~" и ?= "' "" . Из этих вычислений легко
0 1 0 0
получить, что орбиты присоединенного представления имеют
Рис. 14. Орбиты:
1. прямые {х = const # 0},
2. j* = 0, j#0|.
al
0
«2
1
И %=¦
0
0
\;
вид, приведенный на рис. 14, а орбиты коприсоединенного
представления -—вид, указанный на рис. 15.
19. Определение. Пусть /"—группа Ли, отвечающая
алгебре Ли G. Функция /eCc0(G*) называется инвариантом

§ 14. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
79
(коприсоединенного представления группы Ли Р), если для
любых geP, xeG' выполняется равенство f(Ad'ex)=f(x),
и полуинвариантом, если f (Adgx) = %(g)f (х), где х—некоторое
одномерное представление группы Ли Р.
Рис. 15. Орбиты:
2. отдельные точки на
прямой {у=0}
20. Конструкция. Коприсоединенное представление Ad* группы
Ли Р индуцирует гомоморфизм алгебры Ли G в алгебру Ли D(G')
векторных полей на G', см. п. 11. Опишем его подробнее. Итак,
пусть U—открытое подмножество в G', a D(U)—пространство
векторных полей на U, D{U)—алгебра Ли относительно
коммутатора векторных полей, см. п. 35 § 10. Представление
<р: G-*D(U) на базисных векторах еи ..., е„ алгебры Ли G опреде-
ляется равенством i$(el) = Xi = X(ei) = Cikxj —, i=l, ..., и, здесь
C'ik — структурный тензор алгебры Ли (г в базисе (et), (xj)
— координаты в G', соответствующие базису eJ, сопряженному еь
т. е. eJ(ei) = 8Jr Поскольку используемые здесь операции имеют
тензорный характер, то полученное представление не зависит от
выбора базиса в G. Векторные поля Хи как следует из тождества
Якоби в G, удовлетворяют соотношению \Xh Х/\=Сцек. Отсюда
вытекает, что ф — гомоморфизм алгебр Ли. Будем говорить, что
оператор Х( отвечает базисному вектору eteG.
21. Лемма. Для любой функции F на пространстве G *
выполняется равенство
d"
It"
Доказательство. Имеем соотношения
B68)
B69)
так как x>(Ad;xp,1,/)=(Ad;ip№/)(^)=/(Adeip(_<l,) et). В силу того,

80
ГЛ. 2. ИНТЕГРИРОВАНИЕ КАНОНИЧЕСКИХ СИСТЕМ
что/—линейная функция, а дифференциал от Ad есть ad, имеем
f{Adt,pl-№)el)=f{-[v,et-])=-f{C)lv>ek)=-CkJtv>fk.
dt
Итак,
dF
. B7°)
т. е. при п=\ лемма доказана. В предположении, что лемма при
п < т справедлива, получим
d"
dx"
П
-1
t-1
d
dt
F
•i
( = 0
(Ac
dm
dx"
lexp
-1
- 1
, + <
-ф(и))Ш- 1
F(Ad
f) d"
)VJ ' dsm
=? + x. B71)
22. Лемма. Для любой аналитической функции F на С
выполняется равенство
B72)
"¦
Доказательство вытекает из разложения F{Ad*nplvf) в ряд
Тейлора с использованием леммы'21.
23. Теорема. Пусть F—аналитическая функция на G*.
Тогда: a) F—инвариант коприсоединенного представления связ-
ной группы Ли Р (отвечающей алгебре Ли G) в том и только
том случае, когда XjF=0, /=1, ..., « = dimG; б) F—полуинвари-
ант коприсоединенного представления группы Ли Р, отвечающей
характеру х, в том и только том случае, когда XtF= — X(F,
i=\, ..., n — dimG, Xi = d%{ei), dx — производная % в единице
группы Ли Р.
Доказательство, а) Поскольку F(Ad\xptvf) = F(f), то
— F{Ad\xptvf) = 0, и поэтому в силу леммы 21 при и=1
получаем XjF=O, i=l, ..., п. Обратно, если X{F=0, то (p(v)F=O,
поэтому Г —ф(г)]"/"= 0, и тогда по лемме 22 F(Ad*txptvf) —
= F(f). Поскольку Р—связная группа Ли, то F(Ad'gf) = F(f)
для любого g e Р.
б) Из равенства F(Adlxptvf) = %(exptv)F(f) вытекает
и I —ф
at
at

§ 14. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ 81
= X,(v)F(f). Обратно, [( — <p(u))ll].F=[x.(i>)]'t.F, следовательно,
в силу леммы 22
F(Ad-tIpll,f)Jl + ? btlEfl! ,-]/•(/), B73)
и так как x(exPtv) = exP(tX*(v% то мы получаем наше
утверждение.
24. Итог. Окончательно, для того чтобы найти инварианты,
надо решить систему дифференциальных уравнений
CkijXkd? = d, i=l л, B74)
а для нахождения полуинвариантов — систему
^ = hF, i= 1 л. B75)
Методы решения этих систем см., например, в [227], [338].
25. Предложение. Пусть W— конечномерное подпрост-
ранство в пространстве аналитических функций на простран-
стве G*, дуальном к алгебре Ли G связной группы Ли Р. Если
feW, то Ad^/eH/((Ad*,/)(x)=/(Ad^,x)) для любого geP
тогда и только тогда, когда XifeW, /=1, ..., и.
Доказательство. Если/еРК, то из того, что f(Adgx)e
е W для любого geP, следует, что — f(AdlIfl,vx)e W, так как
любое конечномерное подпространство замкнуто и тогда по
лемме 21 XifeW. Обратно, достаточно проверить, 4To/(Ad*,x)e
? W для g = exptv, veG, так как связная группа Ли порождается
любой своей окрестностью единицы, а достаточно малая
окрестность единицы порождается однопараметрическими под-
группами. Имеем равенство
/(Ad;xp№x)=/(x)+f Ь*Ш/{х)г, B76)
и так как W замкнуто, то f(Ad*lvx)eW.
26. Замечание. Пусть р: />->GL(F) — произвольное коне-
чномерное представление группы Ли Р в линейном простран-
стве V. Функция /'называется инвариантом, если F(p(g)x) = F(x)
для всех geP, xeV. Пусть dp(ei)f = akjfk, где/ — базис V,
a et — базис алгебры Ли G группы Ли Р. Функция F является
инвариантом тогда и только тогда, когда
аЧухк^ = 0, B77)
что доказывается так же, как это было сделано в случае p = Ad*.

82 ГЛ. 2. ИНТЕГРИРОВАНИЕ КАНОНИЧЕСКИХ СИСТЕМ
Отметим более общее утверждение. Если ф,—локальная
однопараметрическая группа на многообразии М, а X—соот-
ветствующее векторное поле, то функция Fe С °° (М) инвариан-
тна относительно ф, тогда и только тогда, когда XF=0 (см.,
например, [263 ]).
27. Определение. Пусть G — алгебра Ли. Билинейная
форма В(х, y) = tradxady называется формой Киллинга алгебры
Ли G.
28. Теорема. Алгебра Ли G полупроста тогда и только
тогда, когда ее форма Киллинга не вырождена.
В следующих пунктах мы дадим обзор теории полупростых
алгебр Ли над полем комплексных чисел С, доказательства
и более подробное изложение можно найти в книгах [65], [81],
[263], [279], [293].
29. Подалгебры Картана. Максимальная абелева подалгебра
Н с G в полупростой алгебре Ли G называется подалгеброй
Картана, если операторы ad,, полупросты для всех heH, т. е.
существует такой базис, в котором adh записывается диагональ-
ной матрицей. Если xeG — произвольный элемент, то обозна-
чим G(x, 0) подпространство коммутирующих с х элементов
в G. Элемент х называется регулярным, если размерность
dimGbc, 0) минимальная. Если xeG — регулярный элемент, то
G(x, 0)—подалгебра Картана в G; эту подалгебру обозначим
Н\х). Регулярные элементы образуют в G открытое всюду
плотное подмножество. Любая подалгебра Картана по опреде-
лению коммутативна.
30. Корни. Пусть G—полупростая алгебра Ли над полем
комплексных чисел С. Фиксируем некоторую подалгебру Кар-
тана Н. Линейная форма а (А) на Н называется корнем, если
существует такой элемент E^eG, Ехф0, что [А, ?а] = а(/г)?о для
любого heH. Пусть G" — собственное подпространство, от-
вечающее а. Тогда
G = H® X G\ B78)
знак © означает прямую сумму линейных пространств.
В полупростой алгебре Ли G все подпространства G" одномер-
ны при а^О (над полем С). Разложение B78) называется
корневым разложением полупростой алгебры Ли G относитель-
но подалгебры Картана Н.
31. Свойства корней. Имеет место включение
[G",GP]cG"+p, т.е. [?а, Ef]=Naf>Ea+fi. Если а+МО, то
Е„ и Е$ ортогональны относительно формы Киллинга В(х, у).
Векторы Еа и Е-а, напротив, неортогональны. Ограничение
формы В(х, у) на Н не вырождено. Если r = dimc7/, то
существует г линейно независимых корней алгебры Ли G от-

§ 14. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ 83
носительно Я. Число г называется рангом G. Полное семейство
корней, вообще говоря, линейно зависимо. Если а, Р, а+Р—
корни, не равные нулю, то [G", GP] = GO+P; единственные
корни, пропорциональные корню ос,—это 0, + ос. Корень
а можно представить вектором h'aeH; поскольку В(х, у) не
вырождена на Я, то для каждого осе Я* существует единствен-
ный элемент h'aeH такой, что cc(h) = B(h, п'„) для всех heH.
Тогда если ос/0, то [х, ЕЛ] = В(Е„ х)Еа для хеН и В(а, ос)/О.
Обозначим Яо подпространство в Я, порожденное всеми
векторами h'x с рациональными коэффициентами, Яо явля-
ется «вещественной» частью Я. Оказывается, что
сИт0Я0 = сИтсЯ=-с11ткЯ (здесь Q — поле рациональных чи-
сел). Далее, ограничение на Яо формы B(h, h') положительно
определено и принимает рациональные значения, h,h'eH0.
Далее, a(A')eQ при любом ос/0. В частности, а (Л') — вещест-
венное число, если /г'еЯ0. В дальнейшем обозначаем Д множе-
ство ненулевых корней алгебры Ли G.
32. Простые корни. Пусть ht, ..., hr—какой-нибудь фиксиро-
ванный базис в Яо. Если X, \i — две линейные формы на Яо, то
говорят, что X>\i, если Х,(/гг) = ц(/г,) при /=1, ..., к и X{hk + 1)>
>(i(Ak + 1). Напомним, что если X,, (х—корни, то X(h'\ \i(h')
— вещественные числа. Таким образом, в множестве А возника-
ет линейное упорядочение. Корень осеД называется положи-
тельным, если а>0, т.е. ос(А,) = О при i=l,...,k и a(hk + 1)>0.
Линейная упорядоченность вводится неоднозначно: для даль-
нейшего предполагаем, что базис hu ..., hr (r = rgG—ранг G)
фиксирован. Обозначим множество положительных корней Д+.
Тогда Д = Д+ (J Д ~, где Д+ f] Д~ =0, причем существует взаимно
однозначное соответствие между А и А~, устанавливаемое
инволюцией ос-> — а. Ясно, что если аеД+, то ( —а)еА~.
Положительный корень а называется простым, если его нельзя
представить в виде суммы двух положительных корней. Если
r = rgG = dimcH—ранг алгебры Ли G, то существует ровно
г простых корней ось ..., осг, которые образуют базис в Я над
С и базис в #0 над Q. Кроме того, каждый корень РД
г
представляется в виде Р= X т№и гДе w,eZ — целые числа
одного знака; если /и,-^0, то РеД + , а если wf^0, то РеД^.
Система простых корней ось ..., осг обычно обозначается буквой
П. Система Д+ однозначно восстанавливается по системе П.
Положим К+ = ? G", V~ = ? G". Тогда корневое разложение
а>0 а<0
B78) принимает вид G=V~@H@V + .
33. Базис Вейля. Для дальнейшего в полупростой алгебре Ли
G фиксируем базис специального вида. Произвольный базис

84 ГЛ. 3. СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ ПРОСТРАНСТВА
hu ..., hr в Я (над С) порождает базис {h'a} в Яо (над Q)
и в Я (над Q). Этот базис дополним векторами ЕлеС. <х^0,
аеА. Векторы Ел можно выбрать так, что В(Еа, Е-х) = — 1.
Тогда операция коммутирования в G задается следующим
образом: [h, Е<Л = a(h)Ea, heH (a(A)eQ, если АеЯ0);
[?„ ?_J=-A;: (X, ^p] = ArIp?a+p, если a + Р^О—корень,
и [?¦„, ?р] = 0, если а + Р^О не корень; B(h, А;) = а(А), /геЯ.
Векторы ЕаеС" можно выбрать так, что Лг„р = Лг„11_р. Констан-
ты jV^p можно считать вещественными (после соответствующей
нормировки векторов Ел). Имеется алгоритм для определения
Л^р по системе корней (см. [504]). В дальнейшем все обозначе-
ния, связанные с полупростыми алгебрами и их системами
корней, мы будем использовать из [55]. Построенный базис
называется базисом Вейля.
34. Определение. Для данного ковектора /eG*, где
G* — пространство, дуальное к алгебре Ли G, определим
подпространство Ann(/) = {xeG |ad* /=0}. Это подпространст-
во называется аннулятором элемента /. Число
г = min dim Ann (/) B79)
feC
называется индексом алгебры Ли G и обозначается r = ind(G).
35. Предложение. Если G — полупростая алгебра Ли, то
ее индекс совпадает с ее рангом, равным размерности подалгебры
Картана.
Глава 3
СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ
В ЛИНЕЙНОМ ПРОСТРАНСТВЕ
§ 15. Симплектические пространства
1. Определение. Пусть V—конечномерное векторное
пространство. Билинейная форма со на Ух V называется
симплектической, если она не вырождена, т. е. если w{x, у) = 0
для всех уеУ при некотором хе V, то х = 0; co(jc, у) кососиммет-
рична, т.е. w(x, у)=—т(у, х) для всех х, yeV или, что
эквивалентно, со(х, х) = 0, хеУ.
Пара (V, со) называется в этом случае симплектическим
пространством.
Если е1; ..., еп — базис пространства, то со определяется своей
матрицей Грама Г= ||со(е(, е,.)|| = ||со,7 ||, которая кососимметрич-
на и не вырождена. Поскольку невырожденная кососимметрич-
ная матрица имеет четный порядок, то размерность симплек-
тического пространства четна.

§ 15 СИМПЛЕКТИЧЕСКИЕ ПРОСТРАНСТВА 85
Пусть Ь(х, у)—ненулевая кососимметрическая билинейная
форма в п-мерном линейном пространстве V.
2. Определение. Если W—подпространство простран-
ства V, то ортогональное дополнение к W относительно
Ь обозначается WL и называется косоортогопальным дополнени-
ем, по определению W1 = {xeV\b(x, у) = 0 для всех yeW}.
Заметим, что WП W1 может содержать ненулевые векторы.
3. Определение. Векторное подпространство W<= V на-
зывается: а) изотропным, если W с W1; б) коизотропным, если
WL(=-W; в) лагранжевым, если W=WL; г) симплектическим,
если Wf]W1 = {0}. Пространство V1 называется ядром формы
Ъ. Для любого подпространства W а V имеем
1)- B80)
4. Лемма. Для изотропного подпространства W<^V эк-
вивалентны следующие условия: a) W является максимальным
изотропным подпространством; б) dim W =-(dim K+dim VL); в)
W^> WL; г) W—WL. Если эти условия выполнены, то W^> V1.
5. Теорема. Найдется такой базис пространства V, в ко-
тором форма Ь(х, у) запишется в следующем каноническом виде:
Ь(х, y) =
1^<?. B81)
Доказательство. Пусть в некотором базисе имеем
л
Ь(х, у)— ? aijxiyj. Изменив нумерацию неизвестных, можно
считать а12^0. Запишем форму в виде
Ь(х, у) = х1(а12у2+...+а1„уп)-у1(а12х2+...+а1лхп) + Ь1(х, у),
B82)
и произведем невырожденное преобразование неизвестных
х\=х1, х'2 = а12х2+...+а1пхп, х'3 = х3, ..., х'„ = х„ B83)
и такое же преобразование для yt. Получим
Ь(х, у) = х\у'2 — х'2у\+Ь2{х, у). Если форма Ь2(х, у) не содер-
жит х'2, у 2, то поступаем с ней аналогично. Иначе
п
Ьг(х, у)= ? a'ijx'ty'j, где а'2кФ0 для некоторого к, 2^к^п.
Произведя невырожденное преобразование
х=х\-а'гзх'3- ...-а'2пх'„, х=х'2, ..., xl = x'n B84)
и такое же преобразование над у\, получим
Ъ{х,у) = х\у\ — х"гу\+Ъъ(х,у\ где Ь3{х, у) не содержит х\,
Х2> у"\, У "г- Если Ь3(х, у)^0, то поступаем с ней .аналогично.

86 ГЛ. 3. СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ ПРОСТРАНСТВА
6. Определение. Симплектическим базисом в (V, со)
называется такой базис et, ..., еп, ft, ..., fn, что
и(е,, ek) = a>{f}, /k) = 0, <о(е,, fk) = 8jk. B85)
7. Следствие. Каждое симплектическое пространство
имеет симплектический базис.
8. Теорема. Каждое изотропное подпространство содер-
жится в лагранжевом подпространстве. В частности, нулевое
подпространство содержится в лагранжевом подпространстве,
т. е. лагранжевы подпространства существуют для формы Ь.
Доказательство. Пусть W— изотропное подпростран-
ство, которое не является лагранжевым, т. е. W <=¦ W и \?ф
^W1. Выберем вектор ueWL\W. Тогда кем1. С другой
стороны, ueW1, так что Wczu1. Пространство W+uR
изотропно. Продолжая этот процесс, получим искомое лагран-
жево подпространство.
§ 16. Группы снмплектическнх преобразований
линейного пространства
1. Определение. Линейное преобразование g: V-+V
симплектического пространства (К, со) в себя называется
симплектическим, если оно сохраняет симплектическую струк-
туру, т. е. сохраняет кососимметрическое скалярное произведе-
ние: w(ga, gb) = (u(a, b) для любых a, beV. Совокупность всех
симплектических преобразований пространства V образует
группу, которая называется вещественной симплектической
(некомпактной) группой и обозначается Sp(«, R), если
dimF=2n.
2. Лемма. Симплектическое преобразование переводит лю-
бое изотропное подпространство в изотропное. В частности,
образ лагранжева подпространства при симплектическом преоб-
разовании снова является лагранжевым подпространством.
Доказательство. Согласно определению симплектиче-
ского преобразования оно сохраняет кососкалярное произведе-
ние любой пары векторов. Следовательно, подпространство,
в котором произведение любой пары векторов равно нулю,
переходит в подпространство с тем же свойством. Лемма
доказана.
3. Замечание. Рассмотрим группу Р всех диффеоморфиз-
мов /: V -> V симплектического пространства (V, со), сохраня-
ющих со. Тогда группа Р не исчерпывается линейными
преобразованиями, сохраняющими со (см. п. 2 § 24). Этим
свойством группа Р отличается от группы изометрий евклидова
пространства.
4. Лемма. Группа Sp(l, R) изоморфна группе вещественных
матриц порядка два с определителем 1, т. е. группе SLB, R).

§ 16. ГРУППЫ СИМПЛЕКТИЧЕСКИХ ПРЕОБРАЗОВАНИЙ
87
С топологической точки зрения эта группа матриц некомпак-
тна, имеет размерность 3 и гомеоморфна прямому произведению
окружности на двумерную плоскость (рис. 16). В частности,
группа Sp(l, R) неодносвязна и ее фундаментальная группа
изоморфна группе целых чисел 7t1(Sp(l, R))^Z.
Рис. 16
Доказательство. Ясно, что кососкалярное произведение
пары векторов a, b равно площади параллелограмма, натянуто-
го на а, Ъ. С другой стороны, если Я= —произвольное
линейное преобразование плоскости, то площадь параллело-
грамма, натянутого на векторы g(a) и g(b), получается из
первоначальной площади умножением на определитель преоб-
разования g. Следовательно, преобразование g сохраняет
кососкалярное произведение векторов тогда и только тогда,
когда оно унимодулярно, т.е. detg=ps — rq=\. Группа SLB,
\а b , , ,\ _
ad—bc=\y является поверхностью S в простран-
i-bc=\\
стве К4, задаваемой уравнением ad—bc=\. Перейдем к новым
координатам «t, i»j, u2, v2: a = u.+v1, d=u1 — vl, b = u
2 — v2 Тогда группа SLB R) будет з
i
= u
t j 2 2 1 1 l 2 2
— v2. Тогда группа SLB, R) будет задаваться уравнением
ui + vi — vi — ui = l, т.е. это квадрика в четырехмерном про-
странстве. Рассмотрим цилиндр W с уравнением и \ + v 1 = 1. Он,
очевидно, гомеоморфен произведению S1 xR2^S1xD2. Отоб-
разим" поверхность S на цилиндр W: через точку aeS проведем
прямую /, перпендикулярную к плоскости (vt, u2) и параллель-
ную плоскости (м15 v2), получим
f(a) = lf]W, являющееся
/ в координатах имеет
отображение /: S -» W,
Действительно,
гомеоморфизмом.
вид /(и1э
u2, vl I, и оно имеет обратное, которое в координатах
записывается в виде
V2\/1 +^l + U2, U2,
f— гомеоморфизм.
u2,
v1)=(u1>/T+v
1
(рис. 17). Итак,/и/ непрерывны, т. е.

ГЛ. 3. СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ ПРОСТРАНСТВА
5. Определение. В пространстве С2
митову форму |zj|2 — \z2\2. Преобразования А = \
рассмотрим эр-
•\а All
, со-
,1е А\
храняющие эту форму и имеющие определитель, равный
единице, образуют группу, ко-
торая обозначается SUA, 1).
Преобразования из этой груп-
4 \\" Ь
пы имеют вид А = _
а,
ЬеС,
6. Лемма. Если матрица
оператора в вещественном ба-
зисе пространства С2 вещест-
венная унимодулярная, то ма-
трица этого оператора в ком-
плексно сопряженном базисе
ft —ev + ie2, fz = ei~ге2 принад-
Рис. 17. Сечение плоскостью лежит группе SUA, 1). Итак,
{u2=const, u1=const} три группы Sp(l, R), SLB, R),
S U A, 1) изоморфны.
7. Замечание. Укажем еще на связь групп SLB, R),
SUA, 1) с геометрией Лобачевского. Рассмотрим две модели
плоскости Лобачевского: модель на верхней полуплоскости Н2
имеет метрику ds2 = R2 y~2(dx2 + dy2), R = const; модель
в единичном круге D2 имеет метрику
ds2—AR2{\ — (х2 +у2))~ {dx2 + dy2). Группа изометрий плос-
кости Лобачевского в модели Н2 состоит из преобразований
а Ъ\
таких, что
w = (az + b)/(cz
eSLB, R), а в модели
D2 — из преобразований w = (pz + q)j(rz + t) таких, что
eSU(l, 1), см. [190].
8. Определение. Невырожденное комплексное линейное
преобразование g: C2"->C2" называется симплектическим, если
оно сохраняет симплектическую структуру в С2", т. е. сохраняет
внешнюю 2-форму dzl л dzn+1 + ... +dzn л dz2n (zt, ..., z2n —
координаты в С2"). Совокупность всех симплектических преоб-
разований пространства С образует группу, которая называет-
ся комплексной симплектической группой и обозначается
Sp(B, С).
9. Предложение. Группа Sp(и, С) является некомпактной
группой Ли вещественной размерности 2лBи + 1). Алгебра Ли
sp(n, С) этой группы Ли состоит из комплексных матриц вида
-z\
B86)

§ 16. ГРУППЫ СИМПЛЕКТИЧЕСКИХ ПРЕОБРАЗОВАНИЙ
89
ХеМ2п(С), где Zt—произвольная комплексная матрица порядка
п, а комплексные матрицы Z2 и Z3 симметричны.
Группа Sp («, R) является некомпактной группой Ли размер-
ности п Bи+1). Алгебра Ли sp(/2, R) этой группы состоит из
вещественных матриц вида B86), где Zt—произвольная вещест-
венная матрица порядка п, а матрицы Z2 и .Z3 имеют порядок
п и симметричны.
Доказательство. Рассмотрим случай группы Sp(n, R).
Для Sp(«, С) все аналогично. Матрица g является симплектиче-
ской тогда и только тогда, когда glg' = l, где /—симплектичес-
кая единица, равная
/=
|0 -E
U 0
B87)
Итак, группа Sp(/2, R) в пространстве матриц M2n(R) размера
2их2и выделяется системой полиномиальных уравнений. При-
меним к этой системе теорему о неявных функциях.
10. Теорема (геометрическая формулировка теоремы о не-
явных функциях). Рассмотрим в пространстве R" с коор-
динатами х1, ..., х" множество ZcR", состоящее из точек
Р(хг, ..., х"), координаты {х1, ..., х") которых удовлетворяют
системе уравнений
B88)
fs(x\ ..., х") = 0.
Если ранг rkJx матрицы Якоби
V =
г/,
дх1
з/,
ах,
х - ах«
а/.
X
X
B89)
всюду на X равен s, то множество X является гладким
многообразием размерности n — s. Точнее, в некоторой окрестно-
сти точки х0 6 X в качестве локальных координат можно взять
координаты, дополнительные к (х-'1, ..., х'ш) в (х1, ..., х"), где
det
дх''
дх1-
дх'-
B90)
— минор в JXo, отличный от нуля.

90
ГЛ. 3. СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ ПРОСТРАНСТВА
11. Замечание. С системой уравнений B88) связано
отображение F: R"(x\ ..., x")->Rs(x\ ..., х"), F(x\ ..., х") =
= {у\ ...,у"), где yl=Mxl, .... х") и ^=^"'@). Ясно, что
k dil^
Продолжим доказательство, теоремы 9. Группа Sp(«, R)
вложена в пространство R4"\ поскольку любую матрицу
можно записать в строку
длины An2. Соотношение
glg' = l дает 4и2 ура-
внений, причем среди них
2п2 — п попарно различ-
ных. Определим отобра-
жение Ф: R4"'->R4 фор-
мулой Ф(Г)=Г/Г'-/.
Ясно, что Sp(«, R) =
= Ф  @). Вычислим диф-
ференциал с1ФХо. Для это-
го рассмотрим такую
кривую F(t)eR4"', что
Рис. 18
и - F(t) =
( = 0
= X— данная матрица
(рис. 18). Имеем
l, B91)
t = 0
т. е. S=XIX'0 + X0IX'. Очевидно, что S—кососимметрическая
матрица, так как /—кососимметрическая матрица. Любая
кососимметрическая матрица S представима в виде
S=XIX'0 + X0IX', где AroeSp(n, R) для некоторой матрицы X.
Достаточно положить Х= — SIX0I. Итак, образ Гт^Ф^
отображения <1ФХо совпадает с пространством кососимметричес-
ких матриц, следовательно, ранг матрицы Якоби системы,
описывающей группу Sp(«, R), постоянен, т. е. Sp(«, R) —
гладкое многообразие. Вычислим размерность этого многооб-
разия. Имеем гкУх = dimlm^>x = dim {кососимметрические мат-
рицы} = пBи—1). Поэтому dimSp(/2, R) = 4« — пBп— 1) =
= 2иу+и = иBи+1)
()
Ясно, что матричные элементы произведения и обратной
матрицы гладко зависят от координат на группе Sp(«, R)
в силу теоремы о неявных функциях.
Вычислим теперь алгебру Ли sp(n, R) группы Ли Sp(«, R).
Для этого продифференцируем тождество #(т)/?(т)' = / по
т при т = 0 в предположении, что g@) = E, получим gI+Ig' = 0.

§ 16. ГРУППЫ СИМПЛЕКТИЧЕСКИХ ПРЕОБРАЗОВАНИЙ
91
Записывая матрицу g в виде
' 2
найдем, что
Zi+Z4 = 0, Z1=Z'1, Zi = Z\, и предложение 9 доказано.
12. Замечание. Для доказательства связности симплек-
тических групп воспользуемся следующим утверждением: если
подгруппа Q а р и факторпространство Р /Q связны, то группа
Р также связна.
13. Замечание. Группа Sp(n, R) может быть отождеств-
лена с множеством симплектических базисов в пространстве
R2", так как любое преобразование geSp(«, R) переводит
симплектический базис в симплектический.
14. Теорема. Для любого и ^ 1 группа Sp(«, R) связна.
Доказательство. Пусть ех, ..., еп, ft, ...,/„ — симплек-
тический базис пространства (R2", со). Определим в R2"
скалярное произведение, относительно которого выбранный
базис ортонормированный, обозначим это скалярное произведе-
ние символом (х, у). Множество L={(u, v)eR2"x R2"|(«,
v)=l} связно. Любую пару (и, v)eL можно соединить с такой
парой («0, vo)eL, что \vo\=\,
с помощью кривой ф(/) = (/ы,
Г1!)), Гб[1, \v\~i]. ЕСЛИ \v\=l,
то с помощью вращения перей-
дем к северному полюсу v0 еди-
ничной сферы S2". Далее, мно-
жество таких векторов и, что
(и, vo)=\ связно,, представляет
собой «горизонтальную» гипер-
плоскость, проходящую через v0
(рис. 19).
Пусть J: R2"->R2n — стан-
дартная комплексная структура
в R2", определенная равенствами
Jek=fk, Jfk=-ek, k=l, ..., п.
Тогда (я(и, v) = (Ju, v) и, следовательно, множество таких пар
(«, u)eR xR2", что со(м, v)=l, связно. Обозначим это множе-
ство Мп.
Группа Sp(n, R) транзитивно действует на Мп по правилу
g(u, v) = (gu, gv), так как если (м, v)—l, то R2"= V@VX, V={u,
v}, и, следовательно, стационарная подгруппа пары (и, v)eMn
изоморфна Sp(« —I, R). Отсюда Mn^Sp(n, R)/Sp(«— I, R).
Теперь по индукции, учитывая связность гиперповерхности М„
и замечание 12, получим связность группы Sp(«, R), так как
Sp(l, R) связна в силу п. 4.
15. Следствие. Если ^4e-Sp(n, R), то det^4= + l.
Доказательство. Из равенства glg' = l для geSp(n, R)
вытекает (detgJ=l, поэтому detg=+l, так как группа
Sp(/i, R) связна и det?=l, EeSp(n, R).
Рис. 19

92 ГЛ. 3 СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ ПРОСТРАНСТВА
16. Замечание. В пространстве R2" (при доказательстве
теоремы 14) введены скалярное произведение (х, у) и комплекс-
ная структура, которые полезны при изучении симплектических
пространств. Ортогональная группа ОBп)— это группа всех
вещественных линейных преобразований пространства R2",
сохраняющих (х, у). Унитарная группа U(n) — это группа всех
комплексных линейных преобразований пространства C" = R2",
сохраняющих эрмитово скалярное произведение <дг, y} = (i)(Jx,
y) + iu>{x, у). Имеет место равенство U{n) = OBn)f]Sp(n, R).
Топологию группы Sp(n, R) описывает следующая
17. Теорема. Для каждого элемента ^eSp(«, R) суще-
ствует единственная такая пара (U, S), где U—унитарное,
a S—ком/ijieKCHoe линейное симметрическое преобразование
пространства C" = R2", что A = UexpS. В частности, группа
S(rc, R) диффеоморфна произведению С"(л+1)/2 х (/(«)¦ Отсюда
S(R)) (U())Z
p) l(())
Доказательство. Изложим схему доказательства этой
теоремы. Преобразование А'А симметрично и положительно
определено, поэтому определен корень квадратный R = (A'AI12.
Пусть С/=Л-1С/. Тогда UeOBn). Далее, R2kIR2k=I, k = 0, 1, 2, ...
Выберем такую матрицу ТеОBп), что TRT'1=R0 диагональна,
и положим G=TIT~1. Тогда R2)kGR2)k = G для всех неотрицатель-
ных целых к, что можно переписать в виде равенства
(fl,)*=grf, . B92)
uj
где С'г{ — соответствующие матричные элементы,
а а)—диагональные элементы матрицы Rok (r, s—l, ..., 2п).
Соотношение B92) выполняется при всех значениях keZ.
Отсюда следует, что B92) справедливо при всех значениях к ^ 0.
Итак, Лт/7?т = /для любого т>0. Матрицу R, которая является
положительно определенной симметричной, единственным об-
разом можно записать в виде R = expS, S—симметрическая
матрица. Подставляя это выражение в кх1Яг = 1 и дифферен-
цируя по т при т = 0, получим SI+IS=0. Отсюда легко
получить утверждение теоремы 17.
18. Определение. Пусть V—вещественное векторное
пространство. Вещественно линейное преобразование /: V -* V
такое, что J2 = — id, называется комплексной структурой на V.
Ясно, что в этом случае размерность dim V четная. Если
в пространстве V задана комплексная структура J, то V—
комплексное векторное пространство, для этого достаточно
положить (x + iy)v = xv+yJv для х, yeR и veV. Обратно, если
V—комплексное векторное пространство, то его можно считать
вещественным пространством, в котором определена комплекс-
ная структура, задаваемая умножением на i=yf~--~\.

§ 16. ГРУППЫ СИМПЛЕКТИЧЕСКИХ ПРЕОБРАЗОВАНИЙ 93
При доказательстве теоремы 14 определили комплексную
структуру в симплектическом пространстве. Обобщая эту
конструкцию, дадим
19. Определение. Симплектическое пространство (V, а>)
с комплексной структурой J называется кэлеровым, если
JeSp(V).
20. Лемма. Каждое кэлерово векторное пространство имеет
псевдоевклидово скалярное произведение b(v, w) = co(f, Jw), инвари-
антное относительно комплексной структуры J.
Доказательство. Произведение b(v, w) = <u(v, Jw) сим-
метрично, поскольку
b(w, v) = w(w, Jv) = (o(Jw, J2v)= — w(Jw, v) =
= io(v,Jw) = b(v,w), B93)
так как JeSp(V), J2=—E и co(x, y)= — v)(y, x).
Произведение b(v, w) не вырождено. Действительно, если
(о(х, Jy) = 0 для всех xeV, to Jy = 0, так как форма со не
вырождена. Следовательно, w= — J2w = 0.
Произведение b(x, у) является /-инвариантным, т.е.
b(Jv, Jw) = b(v, w). Действительно, b(Jv, Jw) = (o(Jv, J2w) =
= (o(v, Jw) = b(v, w).
Заметим также, что симплектическая структура ю восстанав-
ливается с помощью произведения Ь(х, у) по формуле
ю(х, y) = b(Jx, у).
21. Определение. Кэлерова структура на пространстве
V называется положительной, если соответствующая форма
Ь{х, у) положительно определена.
22. Замечание. Наряду с «вещественной формой» Sp(n, R)
группа Sp(«, С) содержит важную подгруппу Sp(«), называе-
мую компактной симплектической. Напомним ее определение.
23. Кватернионы. Алгебра кватернионов Н—это веществен-
ное четырехмерное пространство с базисом 1, /, у, к и законом
умножения i2=j2 = k — — 1, ij=k, ji=—k, jk = i, kj=—i, ki=j,
ik=-j.
Модулем кватерниона q = a + bi+cj+dk называется число
\q\ = y/a2 +b2 + c2-\-d2, сопряженным кватернионом — кватерни-
он q = a — bi—cj—dk. Имеют место соотношения qq = qq = \q\2
и <71<72 = <72<71- Далее q~l =q/\q\2 — обратный кватернион к q.
Е bdk R
7172 7271 Д q q/\q\ р р q
Если q = a + bi+cj+dk, то a = Re<? называется вещественной
частью кватерниона q, a bi+cj+dk = lmq—мнимой частью.
При а = 0 кватернион называется чисто мнимым.
24. Кватериионное пространство. Рассмотрим и-мерное ли-
нейное кватернионное пространство Н" с базисом elt ..., еп.
п
Каждый вектор аеН" допускает однозначную запись а= ? а,е,,
где а,еН. Рассмотрим в Н" кватернионнозначную форму

94 ГЛ. 3. СИМШ1ЕКТИЧЕСКАЯ ГЕОМЕТРИЯ ПРОСТРАНСТВА
<д, by'— ? 0{Ьг, где ah ?,еН, и вещественнозначное невырож-
п
денное скалярное произведение <а, A> = Re ? а,Лг
25. Определение. Симплектической компактной группой
Sp(«) называется множество всех линейных кватернионных
преобразований g пространства Н", оставляющих на месте
точку ОеН" и сохраняющих вещественнозначное скалярное
произведение <я, 6> в Н", т. е. (ga, gbs) = (a, b~). Группа Sp(«)
совпадает с группой преобразований, сохраняющих кватернион-
нозначную форму (а, by.
26. Замечание. Кватернионное пространство Н" можно
канонически отождествлять с комплексным пространством С2".
При п = 1 это отождествление устроено следующим образом.
Очевидно, что кватернион q = ro\+r1i+r2j+r3k можно перепи-
сать в виде q = (ro + r1i)+j(r2 — r3i) = zl+jz2, где zl=r0 + rli,
z2 = r2 + r2i—комплексные числа. Выполняя эту операцию вдоль
каждой кватернионной координаты в Н", получим отождествле-
ние Н" с Cin.
27. Лемма. Множество Sp(«) является связной компакт-
ной группой Ли вещественной размерности иBя+1). При
отождествлении Н" с С2" группа Sp(«) вкладывается как
подгруппа в группу UB«). При этом вложении алгебра Ли sp(«)
группы Sp(«) состоит из комплексных матриц порядка 2«
следующего вида:
А В
-В А
B94)
где А—комплексная косоэрмитова матрица порядка п, а В—
комплексная симметрическая матрица порядка п. Если матрицы
\\р r\\
из группы UB«) представить в виде , где Р, R, S,
Т—комплексные матрицы, то подгруппа Sp(«) в UB«)
состоит из унитарных матриц вида B94). При этом матрица
\\ А В\\ , ¦ ,
_ _ является унитарной в том и только том случае, когда
\\~в А\\
комплексные матрицы А и В удовлетворяют уравнениям
АА' + ВВ' = Е, ВА' = АВ'.
Доказательство. То, что Sp(«) — гладкое многооб-
разие, доказывается аналогично утверждению п. 9. Доказатель-
ство связности группы Sp(«) следует схеме п. 14, только вместо
равенства Mn^Sp(n, R)/Sp(«— I, R) используется равенство
5'4''-1S()/S(l)
Легко проверить, что при отождествлении Н" с С2"
кватернионнозначная форма <а, by переходит в сумму

17 ЛАГРАНЖЕВ ГРАССМАНИАН 95
, fe>2, где а,=/
), <«, ?>'2 = ? {qkck-Pkdk). B95)
Поэтому кватернионный оператор g: H"-»H" является уни-
тарным.
28. Предложение. Группа Ли SpA) изоморфна в алгебра-
ическом смысле группе SU B) = {geUB)|det,?j=l} м обе они
гомеоморфны сфере S3.
Доказательство. Группа SpA) действует в простран-
стве Н'=Н как умножение на «скаляр» — кватернион, т.е.
каждое преобразование g: H-*H, где geSp(l), имеет вид
gq = qa, где qeH, яеН. Здесь элемент а фиксирован и полно-
стью задает преобразование g. Поскольку кватернионная форма
(<7i> ЧгУ~Ч\Чг сохраняется при действии преобразования g, то
q1q2 = qlaaq2 = \a\2qiq1, т.е. |а|2 = 1 и |о|=1. Поскольку для
любых кватернионов а, Ь выполнено равенство |а?| = |а||?|, то
группа Sp A) изоморфна группе всех кватернионов а таких, что
|о| = 1. Все такие кватернионы образуют сферу S3 в R4.
Рассмотрим описанное в п. 27 вложение Sp(«)-»UB«). При
п=\ это вложение имеет вид
р 1
где |/>|2 + |<?|2 = 1, Р, Ч —
_
комплексные числа. Итак, группа Sp A) изоморфна группе
матриц
р ч
-ч р
где \р\2 + \q\2 =\, а эта группа есть в точности
Ч И
SUB).
29. Замечание. Группа SpB) изоморфна группе SpinE),
являющейся универсальным накрытием над группой SO E).
Напомним, что при л^З односвязная группа Spin (и), дважды
накрывающая группу SO (и), называется спинорной группой. Ее
построение см., например, в [102]. Все остальные группы Sp(«),
п>2, уже не сводятся к унитарным и ортогональным группам.
30. Предложение. Группа Sp(«) односвязна, т.е.
Jii(Sp(«))=l. Группа Sp(«) является максимальной компактной
подгруппой в группе Sp(«, С),
Доказательство односвязности получается из точной гомото-
пической последовательности расслоения Sp(«— l)-»Sp(«)-*
-*S*H~1, см. [102].
§ 17. Лагранжев грассманиан
1. Замечание. Будем заниматься изучением лагранжевых
подпространств V симплектического пространства (R , со), см.
определение 3 § 15. Оказывается, множество всех лагранжевых

96 ГЛ. 3 СИМШ1ЕКТИЧЕСКАЯ ГЕОМЕТРИЯ ПРОСТРАНСТВА
подпространств можно организовать в некоторое гладкое
многообразие, играющее большую роль в симплектической
топологии. Это так называемый лагранжев грассманиан LG*.
Его роль в симплектической топологии обусловлена тем, что
любое лагранжево многообразие (см. п. 7 § 24) в R2" естествен-
но отображается в LGjf. В самом деле, если L — гладкое
лагранжево подмногообразие в R2", то, сопоставляя каждой
точке xeL касательную плоскость TXL в точке х и перенося ее
в начало координат, получим гладкое отображение/: L->LGJJ,
которое позволяет построить характеристические классы Ар-
нольда— Маслова. Кроме того, если рассмотреть тавтологичес-
кое расслоение р: E-+LG* (векторное) над LG", то простран-
ства Тома этого расслоения играют большую роль в теории
лагранжевых и лежандровых кобордизмов в смысле Арнольда,
см. [10].
Следующее утверждение дает важный алгоритм для постро-
ения лагранжевых подпространств.
2. Предложение. Пусть (V, ©) — симплектическое про-
странство, a V0<^Vi<^...czVn — такая возрастающая цепочка
подпространств, что dim V{ = i, Vn=V. Пусть со( = ©/К;
и U, = Ni + N2 +... + Nt, где Nt—ядро формы ш(. Тогда Un явля-
ется максимальным изотропным подпространством относи-
тельно (о и Unf)Vj— U{ для всех L
Доказательство. Проведем индукцию по п. Пред-
положим, что Nn<=Vn-x. Тогда NncNn-1. Отсюда Un=Un-1. По
предположению индукции Un[\Vi=Un-l[\Vi=Ui для всех i<n
и Un=Un-l изотропно относительно con-i, а следовательно,
относительно со.
Предположим теперь, что Nn<?Vn-i. Тогда Лг„_1 =
= Nn(\Vn-l—гиперплоскость в Nn. Поэтому UnC\Vn-i = Un-i +
+(^лПК„_1)=С/я-1 и, значит, Unf]Vi=Ui для всех i<n по
предположению индукции. С другой стороны, подпространство
Un=Un-l+Nn изотропно и dim Gn=l+dim (/„_!, так что
и„—максимальное изотропное подпространство.
3. Определение. По аналогии с обычным грассмановым
многообразием определим вещественное лагранжево грассмано-
во многообразие LGj| (или, короче, вещественный лагранжев
грассманиан) как множество всех лагранжевых подпространств
в симплектическом пространстве (R , со).
Аналогично определяется комплексное лагранжево грассма-
ново многообразие LGJ как совокупность всех лагранжевых
подпространств в комплексном симплектическом пространстве
С2", см. определение 8 § 16.
Изучим сначала комплексный случай.
4. Предложение. Любые две комплексные лагранжевы
плоскости могут быть совмещены друг с другом при помощи
подходящего симплектического преобразования.

§ 17. ЛАГРАНЖЕВ ГРАССМАНИАН 97
Доказательство. В качестве примера лагранжевого
подпространства (плоскости) возьмем координатную и-мерную
изотропную плоскость С", порожденную первыми п коор-
динатами z,,..., zn. Докажем, что для любой лагранжевой
плоскости ПсС2" существует симплектическое преобразование
g такое, что оно переводит С" в П, т. е. П=#С\ Фиксируем
в С2" стандартный базис еt, ..., е2п- Тогда получим, что
плоскость С" натянута на первые п векторов этого базиса.
Поскольку П является комплексным и-мерным подпростран-
ством в С 2", то в П всегда можно выбрать ортонормированный
комплексный базис из векторов а1г...,ая. Разложим эти
векторы по базису elt ..., е2п, т. е.
л л
я*= I акрер+ X Ькрея+Р. B96)
Выписывая координаты векторов п\, ..., а„ относительно базиса
ei> ¦¦¦, е2п, мы получаем прямоугольную комплексную матрицу
I из л строк и 2и столбцов вида \\ А В\\, где А = \\ акр \\,
В= II Ькр ||—матрицы порядка п. Построим теперь матрицу
А В
g порядка 2и, положив по определению g =
-в л
. Оказывает-
ся матрицы А и В не могут быть произвольными. Они связаны
следующим соотношением.
5. Лемма. Матрицы А_и В+ образующие матрицу g,
удовлетворяют уравнению АА' + ВВ' = Е.
Доказательство. Векторы ау,...,ая образуют ортонор-
мированный базис в комплексной плоскости П, поэтому
скалярный квадрат каждого из них равен единице, а попарные
их произведения (относительно эрмитовой формы) равны нулю.
Очевидно, эти условия в точности эквивалентны уравнению
А1 ВВ' Е
6. Лемма. Матрицы А и В, образующие матрицу g,
удовлетворяют уравнению АВ' = ВА'.
Доказательство. Плоскость П является лагранжевой,
что накладывает дополнительные ограничения на матрицы
А и В. Лагранжевость плоскости П означает, что попарные
кососкалярные произведения всех векторов базиса at, ..., а„
тождественно равны нулю. Следовательно, мы должны запи-
сать равенство нулю попарных произведений векторов относи-
тельно кососимметрической формы, задаваемой матрицей
/=
О -Е\
Е О
. Ясно, что это условие принимает вид XIX'= 0, где
Х=\\А, В\\. Отсюда
\А В\
10 -Е\
\Е 0
=о,
что эквивалентно уравнению АВ' = ВА*. Лемма доказана.

98
ГЛ. 3 СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ ПРОСТРАНСТВА
7. Доказательство предложения 4. Из условия
ортогональности базиса а1; ..., ап в плоскости П мы получили
соотношение АА' + ВВ' = Е, а из условия лагранжевости плоско-
сти П — соотношение АВ' = ВА'. Оказывается, отсюда уже
А В\\
-В А\\
симплектической. В самом деле, мы должны проверить выпол-
нение тождества glg' = l. Подставляя сюда явную формулу для
g и используя леммы 5, 6, получаем равенство
вытекает, что матрица g =
является комплексной
ВА'-АВ' -ВВ'-АА'
АА' + ВВ' ВА'-АВ1
О -Е
Е О
B97)
где AeGL(n, С)
что и требовалось доказать.
В частности, любая лагранжева плоскость может быть
представлена в виде gC", где geSp(n, С) и С" — координатная
лагранжева плоскость, натянутая на первую половину базиса.
8. Определение. Из предложения 4 вытекает, что можно
определить действие группы Sp(/j, С) на грассманиане LG^,
полагая, что подпространство V переходит в ^К, это действие
транзитивно. Обозначим буквой Н стационарную подгруппу
симплектической группы Sp(«, С) в точке С" = С(е1, ..., е„).
9. Предложение. Лагранжево комплексное грассманово
многообразие LG^ допускает представление в виде однородного
пространства Sp(«, С)/Н, здесь стационарная подгруппа Н со-
ч А В
стоит из матриц вида g =
и АВ' = ВА'.
Доказательство. Достаточно найти стационарную под-
группу Н, т. е. подгруппу симплектических преобразований,
переводящих в себя плоскость С(е1, ..., е„). Симплектическое
преобразование можно представить в виде g= _ , где
glg' = l. Следовательно, матрицы А, В, С, D удовлетворяют
соотношениям ВА' = АВ', BC'-AD'=-E и DC' = CD'. Накла-
дывая на g условие инвариантности плоскости C{ei, ..., еп),
получаем С = 0. Отсюда ВА' = АВ' и AD' = E. В качестве
матрицы А можно брать произвольную невырожденную ком-
плексную матрицу. Предложение доказано.
10. Предложение. Лагранжево комплексное грассманово
многообразие LG? диффеоморфно однородному пространству
Sp(«)/U(«), где группа U(«) вложена в компактную группу Sp(«)
как подгруппа матриц вида
[А
П
-м, L AeU(n).
) ||
II [ ) ||
Доказательство. Пусть П—произвольная комплексная
лагранжева плоскость. Выше доказали, что П можно пред-
ставить в виде n=gC", где g—комплексное симплектическое
преобразование, geSp(n, С), см. доказательство предложения 4.

17 ЛАГРАНЖЕВ ГРАССМАНИАН
99
В действительности мы доказали более сильное утверждение,
а именно: можно считать, что преобразование g не только
симплектическое, но и унитарное, т. е. geUBn). В самом деле,
из лемм 5, 6 следует, что преобразование g допускает
представление в виде
А_ В
-В А
, где АВ' = ВА', АА' + ВВ'^Е. Эти
А
-В
В
А
А1
В1
-В'
А'
Е
0
0
Е
Н имеют вид g=
два условия эквивалентны унитарности матрицы g, так как
унитарность матрицы записывается в виде соотношения
B98)
Очевидно, что эти две системы уравнений совпадают. Посколь-
ку Sp(«, C)f]\JBn) = Sp(n), то мы тем самым получили ком-
пактную симплектическую группу Sp(«). Таким образом, ком-
пактная симплектическая группа транзитивно действует на
множестве всех лагранжевых комплексных плоскостей.
Осталось найти стационарную подгруппу, т. е. подгруппу тех
преобразований, которые переводят в себя плоскость
С"(е!,..., е„). В силу предложения 9 достаточно вычислить
пересечение Hf]UBn). Поскольку матрицы из подгруппы
Л Й
,,-iy и условие унитарности означает
U \А )
gg' = E, то отсюда получаем В = 0. Предложение доказано.
П. Замечание. Предыдущие рассуждения можно было бы
повторить для случая вещественного лагранжева грассманова
многообразия. Однако мы будем использовать информацию
о структуре многообразия LGJ, полученную выше.
12. Предложение. Лагранжево вещественное грассманово
многообразие LG* диффеоморфно однородному пространству
U(«)/O(«), где группа О (и) естественно вложена в группу U(«)
как подгруппа вещественных матриц.
13. Замечание. Для доказательства п. 12 нам потребуется
установить естественную связь между комплексными и вещест-
венными лагранжевыми плоскостями. Рассмотрим в С2" веще-
ственное «-мерное подпространство R2", порожденное линей-
ными комбинациями базисных векторов ех, ..., е2п с веществен-
ными коэффициентами. Ясно, что R является «вещественной
частью» С2". Ограничение формы (х, у) с С2л на подпростран-
ство R2" задает на нем кососимметрическую вещественнознач-
ную форму, которую обозначим для простоты тем же
символом. Ясно, что R2" является симплектическим простран-
ством с формой (х, у). Рассмотрим в С2" операцию а комплекс-
2л
ного сопряжения, т. е. переводящую вектор а=
^ в вектор
а=
«.-?;• Ясно, что это отображение а(д) = « является

100 ГЛ. 3 СИМШ1ЕКТИЧЕСКАЯ ГЕОМЕТРИЯ ПРОСТРАНСТВА
антикомплексной инволюцией, т. е. a2 = id и о(Ха) = Ха(а). При
этом подпространство R2" состоит в точности из всех непод-
вижных точек этой инволюции, т. е. a (R2") = R2".
14. Лемма. Операция комплексного сопряжения а:
С2"-»С2" переводит любую лагранжеву комплексную плоскость
снова в лагранжеву плоскость.
Доказательство. Пусть П — произвольная лагранжева
плоскость. Тогда для любых двух векторов а, ЬеП имеем
(а, Ь) = 0. В то же время (оа, ob) = (a, b) = (a, b) = 0. Таким
образом, плоскость аП также лагранжева.
15. Определение. Лагранжева плоскость П в комплекс-
ном пространстве С2" называется вещественной лагранжевой
плоскостью, если она инвариантна относительно операции
комплексного сопряжения.
16. Лемма. Пусть П — произвольная вещественная лагран-
жева плоскость в С2". Тогда: 1) n|")R2" = n°, где П" —
подпространство неподвижных векторов преобразования а;
2) плоскость П f) R 2" является
лагранжевой (вещественной)
плоскостью в вещественном сим-
плектическом пространстве
= (Uf)R2n)®i(nf]R2n), т. е.
n = Ren©Imn (рис.20).
Доказательство. Первое
утверждение следует из того, что
подпространство R2" в С2" со-
стоит в точности из неподвиж-
ных векторов преобразования а.
Далее, так как плоскость П изо-
тропна в С2", то любое его
подпространство также изотроп-
но, поэтому для доказательства утверждения 2 (достаточно
проверить, что dim (Yl(~}R2") = n. Для этого нам потребуется
сначала доказать утверждение п. 3).
Рассмотрим более подробно действие антикомплексной
инволюции а: С2"-»С2". Если аеПа = П[]Я2п, то 1афП", так
как ia = ia= —ia. Следовательно, П"П'П" = 0. В то же время
для любого вектора аеП можно однозначно определить
векторы х = 2~1(а + а\еП" и у = 2~1(а-а)еП". Ясно, что
a = x + iy, где х, yen". Таким образом, мы представили
плоскость П в виде прямой суммы П"©Ша, что и доказывает
п. 3). Поскольку умножение на число i определяет обратимое
линейное преобразование пространства С2", то
dimR na = dimR г'Па, откуда dimRn = 2dimR nc = 2dimc П = 2«.
Таким образом, dimcn = «. Лемма доказана.

§ 17. ЛАГРАНЖЕВ ГРАССМАНИАН 101
17. Обсуждение. Итак, существует взаимно однозначное
соответствие между вещественными лагранжевыми плоскостя-
ми {комплексной размерности п) в пространстве С2" и лагран-
жевыми {вещественными) плоскостями вещественной размер-
ности п в пространстве R2".
Следует обратить внимание на несколько различное упот-
ребление здесь термина «вещественный». Особенно наглядно
это различие видно на рис. 20, где «настоящая вещественная»
плоскость Па в R2" определяет плоскость П"+Ща, инвариант-
ную относительно сопряжения а: С2"->С2". Ясно, что вещест-
венная плоскость П°@/П° в С2л отнюдь не содержится
в множестве неподвижных точек отображения а. Другими
словами, мы доказали, что каждая вещественная лагранжева
плоскость П в С2" получается комплексификацией вещественной
лагранжевой плоскости П°, лежащей в R2"cC2".
Лемма 16 важна для установления соответствия между
вещественными и комплексными лагранжевыми грассмановыми
многообразиями.
18. Доказательство предложения 12. В лемме 16
мы фактически доказали, что вещественное лагранжево грас-
сманово многообразие LGJJ диффеоморфно множеству Р\„ всех
вещественных лагранжевых плоскостей (комплексной размер-
ности п) в С2". Ясно, что PjfcLG^. Рассмотрим в С
стандартное действие ортогональной группы ОB«). Напомним,
что эта группа вложена в группу UB«) как подгруппа
вещественных матриц. Рассмотрим в С2" стандартную лагран-
жеву вещественную плоскость (С2")" = R2". Пусть/: Sp(«)-»LG^
естественное отображение, построенное при доказательстве
предложения 10 и сопоставляющее каждому симплектическому
преобразованию geSp(n) плоскость gC", являющуюся образом
стандартной лагранжевой плоскости С(ех, ..., е„) в С2". По-
скольку /—отображение «на», то Р*„ содержится в образе
отображения/ Рассмотрим в Sp(n) подгруппу ортогональных
преобразований в С2", т. е. пересечение Q = Sp(n)f]OBn). Здесь
ОB«) — группа ортогональных преобразований в базисе
<?!, ..., е2п- Утверждается, что f(Q) = P*n. Это следует из того,
что группа ОB«) транзитивна на множестве всех 2«-мерных
(над R) вещественных плоскостей в С2". Значит, P\n = QjR, где
R—стационарная подгруппа, т. е. подгруппа преобразований,
переводящих в себя какую-то фиксированную вещественную
лагранжеву плоскость. Утверждается, что Q=U(n). Пусть
g—вещественное симплектическое преобразование из Q, т. е.
geSp(n) и geOln). Симплектичность g означает, что glg' = l.
Поскольку geO(/?), то g'=g~1. Отсюда следует, что gl=lg.
Поэтому каждое преобразование g e Q задает ортогональное
преобразование вещественного пространства R2", коммутиру-
ющее с преобразованием /. Как мы знаем, преобразование

102
ГЛ. 4. СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ
/ позволяет определить в R2" комплексную структуру; при этом
операторы, коммутирующие с /, оказываются комплексными.
Следовательно, каждое преобразование geQ оказывается уни-
тарным преобразованием из и(и). Таким образом, Qc\J(n).
Верно и обратное утверждение. Пусть ge\J(n)— произволь-
ное унитарное преобразование пространства R2", т. е. оператор,
коммутирующий с /. Тогда получаем, что geOBn) и gl=lg-
Отсюда glg' = l, что и означает симплектичность преобразова-
ния. Тем самым Q = U(n). Осталось найти преобразования из
U (и), переводящие в себя какую-то фиксированную веществен-
ную лагранжеву плоскость. Ясно, что вещественные унитарные
преобразования из группы U(«) образуют группу О(я). Пред-
ложение доказано.
Глава 4
СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ
§ 18. Симплектические многообразия-
1. Определение. Пусть М—гладкое многообразие. Сим-
плектической структурой на М называется замкнутая невырож-
денная дифференциальная 2-форма coeQ2(Af). Пара (М, со)
называется симплектическим многообразием, а сама форма
со симплектической.
Если х1, ..., х"—локальная система координат на многообра-
зии М, то a) = (uijdx' л dx'. Условие невырожденности формы
со эквивалентно тому, что матрица || со,7 || не вырождена в каждой
точке хеМ. Форма со замкнута тогда и только тогда, когда Ло = 0,
где d—операция внешнего дифференцирования, а это, в свою
очередь, эквивалентно тому, что дсо^/дх' — д(ош/дх] — dwji/dxk = 0.
2. Форма со определяет в каждом касательном пространстве
ТХМ невырожденное кососимметрическое скалярное произведение
со(а, Ь) = ща Ь}, где а= \\ а' ||, b=\\bJ ||, а, ЬеТхМ. Как показано
в части I, в пространстве ТХМ существует симплектический базис,
в котором со,7 (х) приводится к каноническому виду (см. п. 5 § 15)
B99)
0
-1
t
0
0
0
о
-1
1
0

§ 18. СИМПЛЕКТИЧЕСКИЕ МНОГООБРАЗИЯ 103
3. Кососимметрическое скалярное произведение в ТХМ,
индуцированное симплектическои структурой, позволяет опреде-
лить каноническое отождествление касательного пространства
ТХМ и кокасательного Т'ХМ. Это отождествление задается
классической операцией опускания индексов !;'->м, = со;;!;1, здесь
\еТхМ, а иеТхМ.
4. На произвольном многообразии, вообще говоря, не
существует симплектическои структуры. Например, любое сим-
плектическое многообразие четномерно, поскольку кососиммет-
рическая матрица нечетного порядка вырождена, т. е. она имеет
определитель, равный нулю.
Более содержательное ограничение на топологию таких
многообразий дает следующая
5. Теорема. Симплектическое многообразие ориентируемо.
Доказательство. Пусть форма соеП2(М) задает сим-
плектическую структуру на многообразии М. Если dim M=2k,
то определим форму П, как /с-кратное внешнее произведение
формы ©, т. е. П= © л ... л со . Покажем, что Q^O. Действитель-
Y
к
но, как отмечено в п. 2, в каждом касательном пространстве
ТХМ найдутся такие координаты д;1, ..., хк, у1, ..., ук, что
(о = х1 а у1 +...+хк а ук. Тогда очевидно, что
Q = (-l) 2 klx1 A ... АХк Ay1 A ... Аукф0. C00)
6. Не на любом четномерном ориентируемом многообразии
существует симплектическая структура. Отметим одно из
простейших топологических препятствий к существованию
симплектических структур на многообразии.
7. Теорема. Если на компактном многообразии М2к
существует симплектическая структура, то все четномерные
группы когомологии H2s(M2k, R) многообразия М2к отличны от
нуля, s = 0, 1, ..., к.
Доказательство. Пусть H2s(M2k) = 0 и на М2к суще-
ствует симплектическая структура со, придем к противоречию.
Положим ф= сол... л со. Ясно, что dq> = 0 и <p = dy?, так как
Y
Н2ЧМ2к) = 0.
Поэтому
Н=^сол...лсо=фл©л...лсо==д|\|;лсол...лсо;|. C01)
к k-s k-s
В п. 5 было показано, что форма ?2 = ©л...лсо не обращается
в нуль ни в одной точке многообразия М, поэтому П =/¦ vol, где

104 ГЛ. 4. СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ
/—некоторая гладкая функция, отличная от нуля на М2к,
a vol — форма объема на М2к. Поэтому по формуле Стокса
J п= J </(Ч'лсол...лсо) = 0, C02)
но, с другой стороны,
f/vol
J vo1 = wd(M2'')^0, C03)
где v(M2k)—объем многообразия М2к, а"т — некоторая кон-
станта, т>0. Полученное противоречие доказывает теорему.
8. В качестве примера многообразий, на которых нет
симплектических структур в силу теоремы 7, отметим сферы
S" Ъ
В силу предыдущих замечаний ясно, что большую роль
играют примеры симплектических многообразий. Остаток этого
параграфа посвящен построению трех важных классов симплек-
тических многообразий: а) двумерные многообразия; б) кокаса-
тельные расслоения; в) кэлеровы многообразия.
9. Первый источник симплектических многообразий — глад-
кие двумерные ориентируемые замкнутые римановы многооб-
разия, т. е. сферы с ручками. В качестве симплектической
структуры на них можно взять стандартную форму двумерного
риманова объема, являющуюся замкнутой невырожденной
внешней 2-формой. Если поверхность задана параметрически:
r = r(u, v), то форма объема имеет вид
(дг дг\/дг дг\ (Ьг Ьг\г , ,
ди duj\dv dvJ \du dvj
Любая сфера с ручками допускает явное параметрическое
задание, например, уравнение
3 3
C05)
(x-at) ft {x + a,Jx2j = в2,
i=i J
uj^cij, i-ф}, при достаточно малом е описывает сферу с 8 руч-
ками. Аналогичное уравнение можно написать и для сферы
с п ручками.
10. Второй источник получения симплектических многооб-
разий— это кокасательные расслоения. Как правило, простран-
ство положений механической системы является гладким много-
образием М. Это так называемое конфигурационное простран-
ство механической системы. Гамильтонову механику строят
в пространстве импульсов — в фазовом пространстве. Фазовое
пространство с математической точки зрения совпадает с кока-
сательным расслоением Т'М к многообразию. М. Точкой

§ 18. СИМПЛЕКТИЧЕСКИЕ МНОГООБРАЗИЯ 105
пространства Т'М является пара (х, t,), где хеМ, ^еТ'хм, т. е.
Ъ, — ковектор в точке х. Легко проверяется, что Т'М—гладкое
2и-мерное многообразие, n = dimM. Естественная проекция р:
Т'М-*М определяется с помощью равенства р(х, ?,) = х. Ясно,
что Т'М является расслоенным пространством с базой М,
а слоем р ~1 (х) этого расслоения над точкой х будет кокасатель-
ное пространство Т'ХМ.
11. Теорема. Для любого гладкого многообразия М на
кокасагпельном расслоении Т'М существует естественная сим-
плектическая структура.
Доказательство. Пусть U—координатная окрестность
на многообразии М, a ql, ..., q"—координаты в U. Пусть
U^T'M—множество ковекторов, точка приложения которых
находится в U, а —г,..., базисные векторные поля в U.
dq dq"
Если Pi, ..., р„ — значения ковектора на этих полях, то (q1, ..., q",
Pi, ¦¦¦, Рп) можно взять за координаты в U. В этих координатах
определим форму a> = dpl Adql-\-... + dpn /\dq". Проверим, что
это определение корректно. Предположим, что Uf]V^0. Тогда
в Uf] V справедливы следующие формулы перехода:
ql = ql(q\...,qn), C06)
Pi=Pi{p,,...,Pn, q\ ...,q") = ^;Pj, ^ C07)
и поэтому dq' = —.dqj, dpi = ~dpA——dq'. Следовательно,
dq1 dpj ' dq1
n n n
™= Z dPi A d4j= Z dPi A dcl'+ Z asid(lS A d(i'' CO8)
j=l j=l j,s=l
Д dq' b dq1
где a-=^wwPt
,tl dq' dq' d? Pt ~ Д dq- dq1 dq'dq" P''
n
то ajs = asj и, следовательно, ? asjdqs a dqJ = O. Итак, в пересе-
чении карт J^ dp,/\dql= ? dpjAdq1, и поэтому это выражение
i=1 i= 1
корректно определяет дифференциальную форму на Т'М. Из
координатной записи очевидно, что со—замкнутая невырожден-
ная форма.
12. Следствие. Для любого гладкого многообразия М про-
странство Т'М ориентируемо.

106 ГЛ. 4. СИМШ1ЕКТИЧЕСКАЯ ГЕОМЕТРИЯ
Изложенная конструкция дает не все симплектические
многообразия, как показывает следующее утверждение.
13. Лемма. Симплектическое многообразие Т'М некомпак-
тно. Каноническая симплектическая структура на Т'М являет-
ся точной, т. е. найдется такая форма аеП1 (Т'М), что со = doc.
Доказательство. В системе координат, описанной
п
в п. 11, положим ос= ? Pidq1. Надо доказать, что эта форма не
зависит от выбора системы координат. Для этой цели дадим
геометрически инвариантное .определение формы aeQ1 (Т'М).
Каноническая проекция я: ТМ-+М индуцирует отображение я,:
~ ~" " ~,М, где (х, г\)еТ'М, хеМ, цеТ'хМ. Положим
C10)
Если \ = V.±
Поэтому а(^) = г1(я,(^)) = т1;^'(^), что и требовалось проверить.
14. Можно дать другое доказательство теоремы 11. Опреде-
лим симплектическую структуру со на Т'М равенством co = da.
Очевидно, что d(o = d2(o = 0. Невырожденность формы со вытека-
ет из ее координатной записи.
15. Любая форма (реО.1(М) определяет сечение S9: M-*T'M
кокасательного расслоения, где S9(x) = <pxeT'xM. Форма ае
О.1 (Т'М), построенная в п. 13, однозначно характеризуется
следующим свойством универсальности: 5'*(а) = феП (М).
16. На практике иногда встречаются ситуации, когда сим-
плектическая структура фазового пространства Т'М отличается
от канонической. Оказывается, что возможен единый подход,
когда та или иная геометрия фазового пространства объясняет-
ся наличием связности в одномерном тривиальном расслоении
над пространством конфигураций.
17. Определение. Пусть в одномерном тривиальном
расслоении р: М х R->M над многообразием М имеется связность,
которая задается формой aeQ.l(M). Дифференциальная форма
аеП (Т'М) называется универсальной формой связности, если для
любой формы фбПх(М) выполняется равенство 5'5,(а) = ф —а.
Универсальная форма связности всегда существует. Поло-
жим a = a — я* (а), где a — каноническая универсальная форма на
Т'М. Тогда
Единственность формы, а вытекает из единственности формы а.
Итак, a—универсальная форма связности тогда и только тогда,
когда a = a —л*(а).

§ 18 СИМПЛЕКТИЧЕСКИЕ МНОГООБРАЗИЯ 107
18. Определение. Пусть в одномерном тривиальном
расслоении р: AfxR->M над многообразием М имеется
связность, которая задается формой аеП'^М). В этой ситуации
определим на Т'М симплектическую структуру со формулой
(a = ddL = da — dn'(a) = da. — n'(d<j). Назовем эту структуру сим-
плекгпической структурой связности.
Проверим невырожденность формы со. Пусть р1,...,рп,
q1, ..., q"— каноническая система координат на Т*М. Тогда
о^о^Ц', C12)
i = 1 i=l i = 1
со = й?а= ? dpi л dg' — ? Jjkdq'л Jg*, C14)
где y,i = —- —^, 1 <л /с<«. Из этой записи следует невырож-
ex-s дхк
денность формы со = й?а.
Заметим, что универсальная форма локально интегрируемой
связности задает ту же симплектическую структуру, что
и форма а.
19. Третий источник симплектических многообразий — кэле-
ровы многообразия. Пусть М2п — комплексное многообразие
с эрмитовой метрикой (?,, г|). Рассмотрим со(^, г|) = 1т(^, г\).
Очевидно, что со — кососимметрическая невырожденная 2-
форма. Для того чтобы получить симплектическую структуру
на М2", необходимо равенство й?со = 0. В произвольном ком-
плексном многообразии с эрмитовой метрикой это свойство не
выполняется.
20. Определение. Комплексное многообразие, снабжен-
ное эрмитовой метрикой, называется кэлеровым, если мнимая
часть со скалярного произведения D, л) ^ть замкнутая диф-
ференциальная форма, т. е. da> = 0.
21. Классический пример кэлерова многообразия дает ком-
плексное проективное пространство СР". Для построения
канонической симплектической структуры на СР" рассмотрим
на пространстве С" + 1\0 ковариантный тензор
Ы lzkzk) X ад I dzk®dzk\-
? zk®dzk)\, C15)
t=0 / \k=0 /J
где z0, ..., zn — стандартные координаты в C"+1.

108 ГЛ. 4 СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ
22. Предложение. На СР" существует кэлерова метрика
F такая, что n*F=F, где F—определенная выше форма, к:
Сп+1 \0->СР"—естественная проекция.
Это утверждение вытекает из следующих четырех очевидных
свойств тензора /: а) сужение тензора^/1 на слой отображения я:
С"+1\0-»СР" равно нулю; б) тензор Fинвариантен относитель-
но естественного действия группы С* = С\0 на _С"+1\0:
z(z0, ..., zn) = (zz0, ..., zzn), zeC; в) сужение тензора F на ор-
тогональное дополнение к слою относительно плоской метрики
в С"+1 положительно определено; г) дифференциальная форма
d(lmF) степени три на СР" инвариантна относительно отоб-
ражений, индуцированных унитарными преобразованиями
А пространства C"+1, Ae\J(n+l).
23. Определение. Построенная метрика F на проектив-
ном пространстве СР" называется метрикой Фубини—Штуди,
см. подробности в [293].
24. Определение. Алгебраическим подмножеством в СР"
называется всякое подмножество вида
V(A, ...,fN) = {P = (a0:...:an)eCP"\fl (ао:...ап) =
...=/„ Ц:...:«„) = 0}, C16)
где {fi, ...,fx}—любое множество однородных многочленов
в кольце С [Хо, ..., Хп~\.
25. Если градиенты grad/j 0=1, ..., N) линейно независимы,
то алгебраическое множество V(ft, ...,/#) является комплекс-
ным многообразием, лежащим в СР", что непосредственно вы-
текает из теоремы о неявных функциях. Пусть у: V{f\, •••,/#)->
->СР" — вложение комплексного многообразия V(/x, ...,/jv)
в комплексное проективное пространство СР" и П=ут F, где
F—метрика Фубини — Штуди. Дифференциальная форма П за-
дает на многообразии V(fi, ...,У]у) симплектическую струк-
туру. Это утверждение вытекает из того, что
^(/i> ¦¦¦у/n) — комплексное подмногообразие в СР". Изложен-
ная конструкция дает примеры компактных кэлеровых многооб-
разий и, в частности, компактных симплектических многооб-
разий.
26. Определение. Ограниченной областью D назовем
ограниченное открытое связное подмножество в пространстве
С*
27. Теорема. Любая ограниченная область является кэле-
ровым многообразием и, в частности, симплектическим многооб-
разием.
Приведем схему доказательства этой классической теоремы,
см. подробности в [293]. Обозначим H{D) гильбертово
пространство голоморфных комплексных функций на D, для

§ 18. СИМПЛЕКТИЧЕСКИЕ МНОГООБРАЗИЯ 109
которых J \f\2dn<oo, где d\i — мера Лебега в R2N^CN.
Скалярное произведение в H(D) имеет вид
и II / II = >/(/>/)• Функции, совпадающие всюду вне некоторого
множества меры 0, рассматриваются как одинаковые элементы
пространства L2(D), H(D)<=L2(D)— множество функций, голо-
морфных в D. Множество H(D) является замкнутым линейным
подпространством в L2(D) и, следовательно, гильбертовым
пространством относительно скалярного произведения (/, g).
Выберем произвольный ортонормированный базис ф0,
00
<Pi, ..., ф„, ... пространства H(D). Тогда ряд ? cpn(z)cpn(?)
л = 0
равномерно сходится на каждом компактном подмножестве
в D х D. Его сумма обозначается K(z, Q и не зависит от выбора
ортонормированного базиса. Для области D определим ком-
плексное тензорное поле F на D равенством
F== I ^-^ln K(z,z)dzt®dzj, C18)
где zt, ..., zN — стандартные координаты в С*'.
Тензорное поле F задает на D структуру кэлерова многооб-
разия и, следовательно, симплектическую структуру.
28. Определение. Функция K(z, Q называется кернфункцией
Бергмана области D, а метрика Re F, индуцированная построенной
кэлеровой структурой, называется метрикой Бергмана в области D.
29. Имеются компактные симплектические многообразия, не об-
ладающие кэлеровой структурой. Для этой цели рассмотрим много-
образие Тёрстона, являющееся факторпространством M4 = R4/F,
где Г—дискретная группа преобразований, порожденная единич-
ными сдвигами вдоль осей xt, x2, х3 вместе с преобразованием
(х,, х2, х3, х4)->-(х1+Х2, х2, х3, х4+1). C19)
Симплектическая форма а многообразия М* поднимается
в форму dxl л dx2 + dx3 л dx^ на пространстве R4. Итак, М4
является расслоением над двумерным тором Т2 со слоем Т2.
Если Р1(И/) обозначает k-е число Бетти пространства W, то для
многообразия Тёрстона имеют место равенства р\(М) =
= Рз(Л^) = 3. С другой стороны, известно, что для кэлерова
многообразия эти числа четные, см., например, [82].
30. Классическая конструкция раздутия из алгебраической
геометрии (см. [82]) переносится в теорию симплектических
многообразий. Будем называть ее в этом случае перестройкой

1 10 ГЛ. 4. СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ
симплектического многообразия. Если симплектическое многооб-
разие (М, со) вложено в симплектическое многообразие (X, а), то
можно определить операцию перестройки многообразия X вдоль
М и получить новое симплектическое многообразие (X, со). Итак,
пусть М—компактное подмногообразие в X коразмерности 2к
такое, что структурная группа его нормального расслоения ?-»М
редуцирована к унитарной группе U(k). Предположим, что к^2,
так как в противном случае будем считать, что при перестройке
многообразие X не изменяется. Пусть U—трубчатая окрестность
подмногообразия М в X, V—подрасслоение в Е на диски,
гомеоморфное U, РЕ—проективизация расслоения Е, РЕ—
комплексное линейное расслоение над проективизациеи РЕ. Имеем
отображение ср: РЕ->Е, так как слой L над точкой хеМ можно
рассматривать как подпространство в Ск.
31. Определение. Перестройкой X многообразия X вдоль
подмногообразия М называется многообразие
X=X\U U
где 5ф~'(К) отождествляется с BV очевидным образом.
Подробности этой конструкции см. в работе [434]. Там же
можно найти построение симплектической структуры на пере-
стройках X, описанных выше.
32. Общий метод построения так называемых однородных
симплектических многообразий связан с теорией групп Ли
и будет подробно обсуждаться ниже. Соответствующие сим-
плектические многообразия играют важную роль не только
в теории гамильтоновых систем, но и в теории групп Ли и их
представлений, см., например, [124].
33. Теорема. Каждая орбита коприсоединенного представ-
ления группы Ли обладает симплектической структурой.
Доказательство этой теоремы см. в § 22.
34. Пусть (М 2", со) — симплектическое многообразие. Форма
со определяет следующие топологические данные: класс когомо-
логий а = [оз~\еН2(М, R), гомотопический класс редукции струк-
турной группы касательного расслоения многообразия
М к группе SpB/j, R) и, следовательно, гомотопический класс
[/ ] почти комплексной структуры на М. Громов показал, что
если М—открытое многообразие, то любая пара (а, [/]) может
быть реализована некоторой симплектической формой на
многообразии М, см. [376].
35. Замечание. Пусть X, Y—симплектические многооб-
разия с формами сох, coy. Тогда произведение XxY превращается
в симплектическое многообразие, если снабдить его 2-формой
С321)

§ 19 ГАМИЛЬТОНОВЫ ВЕКТОРНЫЕ ПОЛЯ ||1
где рх: Хх Y-+X—проекция на X, а ру — проекция на Y.
Используя примеры симплектических многообразий, описанных
выше, мы тем самым получим много новых примеров.
36. Конструкция. Пусть А—локальная алгебра (коммутатив-
ная, с единицей), dim^<oo, максимальный идеал которой имеет
коразмерность 1. Тогда определено гладкое многообразие А-
значных точек, которое будем обозначать МА, см. [518]. Точка
Ъ,еМА есть гомоморфизм ^: Сх(А/)->Л алгебры СХ(Л/) в А.
Имеется каноническое расслоение я: МА^М: /(rt(?)) = aug^( Л,
для любой функции/еС^(М) и любой точки ?,еМ , aug: Л->К.
Касательное пространство Т^МЛ описывается следующим
образом [463], [464].
37. Лемма. Для каждой точки ?,еМЛ отображение
W^{\dA® W)°у задает изоморфизм пространства Т^МЛ на
Der(Cx(M), А), у: С* (М)-М®С°° (МА), /Ч/* (?) = ?(/).
38. Лемма. Отображение X^>{\dA®X)°y задает изоморфизм
СхША)-модуля D(MAJ на модуль Der(Cx (М), А®СХ(МА)).
39. Замечание. Если А—фробениусова алгебра, то кон-
струкция расширения МА многообразий переводит симплек-
тические многообразия в симплектические, т. е. если на М име-
ется симплектическая структура, то и на МА также имеется
естественная симплектическая структура. Это замечание принад-
лежит А. В. Браилову, и оно получается в рамках тензорных
расширений алгебр Ли, см. § 38.
40. Четвертый источник симплектических многообразий воз-
никает из топологии. Имеет место следующая
41. Теорема (С. В. Матвеев, А. Т. Фоменко). Пусть Мъ —
любое гладкое компактное замкнутое ориентируемое трехмер-
ное многообразие. Тогда прямое произведение Мг х D1 {где
D1—отрезок) является симплектическим многообразием.
42. Замечание. В качестве следствия отметим, что любое
замкнутое ориентируемое 3-многообразие М3 является поверх-
ностью постоянной энергии некоторой гладкой гамильтоновой
системы дифференциальных уравнений (определение гамиль-
тоновых полей см. в п. 7 § 19).
§ 19. Гамильтоновы векторные поля
1. Определение. Пусть X—векторное поле, со — диффе-
ренциальная форма степени к на многообразии М. Определим
операцию внутреннего произведения \{Х)(а = XL- со формулой
= I (-О'ЦГь -. Yi, X, yi + 1, ..., yt_,) C22)
i = 0
и i(A')/=0 для любой гладкой функции /бС°°(М).

112 ГЛ. 4. СИМШ1ЕКТИЧЕСКАЯ ГЕОМЕТРИЯ
2. Если /еС°°(М)—гладкая функция, то i(X)df=df(X)
= Xf—производная функция / вдоль векторного поля X.
3. Если соеП2(М)—форма степени два, то
\y{X)<u\(Y) = (a(X, Y)-w(Y, Х) = 2а>(Х, Y). C23)
4. Лемма. Операция внутреннего произведения обладает
следующими свойствами: a) i(X+ Y) = i(X) + i(Y); б) i(aX) =
= ai(X) для любой гладкой функции аеС (М); в) i(X)i(Y) =
= -i(Y)x(X); г) i(X)x(X) = 0.
5. В п. 3 § 18 было определено каноническое отождествление
/: ТМ-*Т'М в случае, когда М—симплектическое мно-
гообразие с симплектической структурой со. На языке вну-
треннего произведения этот изоморфизм задается равенством
f\) ()
) ()
. Определение. Векторное поле X на симплектическом
многообразии (М, со) называется локально гамильтоновым, если
d((X)) 0
))
. Определение. Поле X на симплектическом многооб-
разии (М, со) называется гамильтоновым, если -i(X)(o = df.
Функция (—/) называется производящей функцией, или гамиль-
тонианом векторного поля X.
8. Введем обозначения: Н(М) — гамильтоновы вектор-
ные поля на М, а Н0(М) — локально гамильтоновы вектор-
ные поля. Имеет место включение Н(М)а Н0(М), так
как d2 = 0.
9. Для данной функции F можно построить гамильтоново
векторное поле X с гамильтонианом F. Оно однозначно
определяется из равенства dF=—i(A')o), т.е. для любо-
го векторного поля Y должно выполняться равенство dF(Y) =
= —со^, У). Векторное поле X будет называться косым
градиентом функции F и обозначаться символом Х=
= sgrad F.
10. Предложение. Пусть х1, ..., х" — локальная система
координат на симплектическом многообразии (М, со), со^ —
координаты формы со и co'J определены из равенства co'scosj = 8j-.
Тогда (sgrad F)' = со1}—-., т. е. векторное поле X'= sgrad F получа-
ется стандартной операцией поднятия индексов у ковекторного
поля dF/dx'.
Доказательство. Равенство dF{Y)= — а>{Х, Y) в коор-
динатах перепишется в виде —-j Y'= — (HjiX'Y1. Поскольку
Y—произвольное векторное поле, то dF/dx'= — со^А'-' = со,7А'-/,
и отсюда вытекает наше утверждение.

§ 19. ГАМИЛЬТОНОВЫ ВЕКТОРНЫЕ ПОЛЯ 113
11. Определение. Скобкой Пуассона {/, g) функций /
geCm[M) на симплектическом многообразии (М, со) называется
функция, определенная равенством
{/ g} = ~со (sgrad/ sgrad g) = co1J ~ -?,. C24)
Второе равенство имеет место в силу соотношения
co(sgrad f. sgrad e) = co.;co'-'1 —4- со- —?- =
v ' '¦> дх'1 дх'2
дх'1 ' дх'2 дх'1 дх'2 дх'1 дх'1
12. Из определения скобки Пуассона вытекает цепочка
равенств
{/,*}=-<»(sgrad/ sgradg)=-dg(sgrad/) = df (sgmdg). C26)
13. Определение. Если скобка Пуассона {/ g] двух
функций / и g на симплектическом многообразии (М, со)
обращается в нуль, то говорят, что функции / g находятся
в инволюции.
14. Предложение. Функция F является первым интегра-
лом системы дифференциальных уравнений х = sgrad H тогда
и только тогда, когда {F,H}=0.
Доказательство. Напомним, что функция F является
первым интегралом систе?лы дифференциальных уравнений
x = v(x), если v(x)F=0. В нашем случае имеет место равенство
(sgrad Я)F=dF(sgrad H) = {F, H}=0. C27)
15. Следствие. Гамильтонова система x = sgrad#(;t) все-
гда имеет первый интеграл—гамильтониан Я.
Доказательство. Действительно, {Я, Н) = со (sgrad H,
sgrad Я) = 0 в силу кососимметричности скалярного произведе-
ния, ассоциированного с симплектической структурой со.
16. В терминах скобки Пуассона очень просто описывается
геометрия гамильтоновых систем на подмногообразиях сим-
плектических многообразий. Следующие пункты посвящены
этому вопросу.
17. Определение. Пусть на гладком многообразии iV за-
даны функции/!, ...,/т, которые функционально независимы на
подмногообразии Nf = {xeN\fj(x) = 0, 7=1, 2, ..., т}, гладко
вложенном в N. Набор функции /i, ...,/„ называется ограничени-
ями, или связями.
18. Лемма (см. [90], [91], [337]). Предположим, что на
симплектическом многообразии М2п заданы связи flt ...,/гт,

114 ГЛ. 4. СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ
т<п. Ограничение ©у симплектической формы со на подмногооб-
разие Mf является невырожденной 2-формой тогда и только
тогда, когда матрица || {/-,/}}«, ||, составленная из скобок
Пуассона {fi,fj} связей fi, ...,f2m, не вырождена в каждой точке
хе Mf подмногообразия Mr.
Доказательство. Если матрица || {/i,/)•}„, || в точке
хеМг вырождена, то найдутся такие числа с1? ..., с2т, что
2т
X ck {fj'fk }=0 приу'=1, 2, ..., 2т, причем все с,- одновременно
k-l
не равны нулю. В силу равенства C26) имеет место
соотношение
dfj ( f ck sgrad/,) =f ck {fj,fk} =0, C28)
а это равенство означает, что вектор v= ? C/Sgrad/j принад-
лежит касательному пространству TxMf. Поскольку функции
/i, -ч/гт по определению связей функционально независимы, то
градиенты grad/j линейно независимы. Операция поднятия
индексов с помощью симплектической структуры является
изоморфизмом, который переводит grad/] в sgrad/, следова-
тельно, вектор v отличен от нуля. Итак,
2m
k=l
/ 2m
\J=1
r,- sgrad fj
j
И
C29)
? cisgrad/t,
для любого касательного к Mr вектора ueTxMf, т.е. форма
©у вырождена на Mf, здесь (!;, г\) — скалярное произведение,
ассоциированное с симплектической структурой со.
Обратно, пусть для некоторого ненулевого вектора veTxMf
выполняется равенство (м, v) = 0 для всех ueTxMf. Тогда
2/п
v= ^] uj sgrad fj, причем не все ah j~ I, 2, ..., 2т, равны нулю, и,
следовательно,
\fj, 2fajk\ =dfj(sgmd2faJk) = dfj(v) = O, C30)
(. k=l )ш \ *=1 /
так как veTxMf. Итак, если со вырождена на Mf, то матрица
II {/(,/}} II сингулярна.
19. Если матрица ||{/j,/}}|| не вырождена, то 2-форма
K>feQ.2{Mf) определяет на Mf симплектическую структуру, так

§ 19. ГАМИЛЬТОНОВЫ ВЕКТОРНЫЕ ПОЛЯ 115
как d(Hf = (d(u)f = 0. Пусть Н—гладкая функция на М (гамиль-
тониан). Обозначим символом sgrad (Я IA/,-) гамильтоново
векторное поле на Ms относительно симплектическои структуры
Ю/, а символом sgradЯ—гамильтоново векторное поле на
М относительно данной симплектическои структуры со на М.
Вообще говоря, sgrad(#| A/^^sgrad^lA/f. Однако имеет
место следующее утверждение.
20. Лемма (см. [192], [337]). Равенство sgrad(Я|Mf) =
= (sgrad H)\Mf имеет место тогда и только тогда, когда
на Mf выполняется соотношение {H,fj}=0, j=l, 2, ..., 2m.
Введем обозначение || {/-,/}}•> И ~1 = И/гё1 II- Тогда для любой
функции FeCx(M) имеет место равенство sgrad (F | Mf) =
^dtfJIM, где
H=F+ I fj Е /д1 {*¦>/»}.• C31)
Доказательство. Если {^/^„^^(sgrad/^^O на
Мг для j=\, 2, ..., 2m, то sgrad #=?1 (sgrad)#e TxMf для всех
xeMf, и поэтому sgrad (Я| Mf ) = (sgrad H) | Mf, где ?2—невыро-
жденная кососимметрическая матрица. Обратно, если
sgradftflMj-Hsgradtf^M^T^M,), xeMf, то {H,fj}a =
= dH(sgrad/j) = O, j=l, 2, ..., 2m, для всех xeMf. Последнее
утверждение следует из равенства
sgrad (F\ Mf ) = sgrad (H\ Mf ) = (sgrad H) \ Mf. C32)
Рассмотрим вопрос о вычислении скобок Пуассона на Mf.
Имеет место следующая лемма Дирака (см. [90], [91]).
21. Лемма. Пусть {h,g}mf — скобка Пуассона функций h,
g е С °° (Mf) относительно симплектическои структуры coy на
Mf. Тогда
{*,*}., = {*>*}.- I {h,f3}»nl{fb,g}., C33)
где || fjkl || = || {fj,fk} W'1- Правая часть вычисляется для произ-
вольного гладкого продолжения функций h, geCX3(Mf) до
функций h, geC'iy) на открытой окрестности V подмногооб-
разия Mf в М.
Доказательство. Предположим, что {/г, /,}т =
= {g,fj}e, = 0, j=\, 2, ...,2т. Тогда по предыдущей лемме
{h, g } Ш/ = - со/ (sgrad (h \ Mf), sgrad (g \Mf)) =
= -co(sgrad/i, sgrad^) = {A, g}M. C34)

116
ГЛ. 4. СИМПЛЕКТИЧЕСКЛЯ ГЕОМЕТРИЯ
В общем случае имеем равенства
? f?{h,fk}mfj,g+
j,k=l i.
+ I f?{hAUfj,g+
j,k=l i,
+ I
« C35)
из которых следует наше утверждение.
22. В заключение этого параграфа рассмотрим несколько
примеров вычисления гамильтоновых векторных полей и скобок
Пуассона.
23. Лемма. Пусть T'R" — кокасательное расслоение над
пространством R" с декартовыми координатами х^,...,х". На
7"R" имеется каноническая симплектическая структура
w = dpl Adx1+ ... +dpnAdx", см. п. 11 § 18. Гамильтоново век-
торное поле sgrad.// на T'R" относительно формы ю имеет вид
,. . .! .„, / дн дн ЪН дн\
^ р"х х >-Va?"- "a?* *:••-*;;
Доказательство. Матрица ||с»у|| формы ю равна
C36)
-1
0
0
0
-1
1
0
и
0
1
, II ы
if
II
1
0
0
0
и
0
Поэтому если (sgradН)' = а}'] —.=а\ то
.
а1
а
1
0
1
-1
0
-1
— II
дИ
дЯ
дх"
C37)

§ 19 ГАМИЛЬТОНОВЫ ВЕКТОРНЫЕ ПОЛЯ 117
24. Лемма. В условиях леммы 23 скобка Пуассона {F, Н}
функций F, Н на кокасательном расслоении VR" вычисляется по
формуле
V1' 0/7, BpiBx'J'
Доказательство вытекает из определения скобки Пуассона
и леммы 23.
25. Определение. Систем.: координат (х1, ..., х", р1, ...
...,рп) на симплектическом мнгч оооразии (М2", со) называется
канонической, если {х1, х'} = {р\ р') = 0 и {х1, р'} = Ъ'К
26. Лемма. На кокасательном расслоении Т*М" рассмот-
рим симплектическую структуру со связности, задаваемой
формой оеО.1 (Мп). Каноническая система координат на Т*М"
для формы со связана со стандартными координатами (х1, ...
...,х", pi, ...,р„) на Т*М" функциями перехода х' = х\
Pj—Pj — aj(x),i,j=l,2,...,n, где Oj—координаты формы а.
Доказательство. Система функций д:ь...,д:„, ру,...,рп
образует систему координат, так как обратной заменой будет
Pi=Pi + ai(x)- Эти координаты являются каноническими, так
л л
как Р = X (Pi ~ а' (х)) dxi= X Pi dx' и> следовательно, dp =
i = 1 i = 1
л
= ? dptAdx', см. п. 18 § 18.
27. Лемма. На кокасательном расслоении Т'М" к многооб-
разию М" рассмотрим симплектическую структуру со связ-
ности, задаваемой формой ае?11{М"). Если Н,Н1,Н2е
ёСх {Т*М") — гладкие функции на Т'М", то
дН с ? ( дн дн
dpi дх
л
и \Н1, Н2) = {ль Н2)Л-\- 2_, То ~ ;—' г"е \"i> jci — клас-
сическая скобка Пуассона на Т*М", описанная в п. 24,
1
Доказательство вытекает из равенства

118 ГЛ. 4 СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ
28. Замечание. На кокасательном расслоении r*R" урав-
нения Гамильтона
dpt дН dx> дН .
'1
переписываются в терминах скобки Пуассона в следующем
виде:
%={Р„Н}, d-^ = {xj,H}, i,j=\,...,n. C42)
Действительно, в силу уравнений Гамильтона имеем
dF_BF у 8F dx' у dF dp, _
.....
C43)
§ 20. Геодезические потоки
1. Пусть М—компактное гладкое риманово многообразие,
т. е. на М задано такое тензорное поле gtJ, что: a) gij = gju
б).#ц^;>0 Для ^ = (V> •••> ^.")#0. Определим gij из условия
g'igj]i = 8'k. Тензорное поле g1' определяет скалярное произведе-
ние в каждом кокасательном пространстве Т*х М, в частности,
для реТ'М имеем \\p\\2=g1'PiPj- На пространстве Т*М имеется
каноническая симплектическая структура со, см. п. 11 §18.
Рассмотрим на Т'М функцию Гамильтона
и отвечающий ей гамильтонов поток i = sgrad# относительно
симплектической структуры со на Т*М. Поскольку Н—первый
интеграл этого потока, то единичный кокасательный пучок
Т\М={хе Т*М\ \\р\\ = 1} инвариантен относительно потока
sgrad H.
2. Определение. Ограничение потока х = sgradH, где
H=2~1g'Jpjpj, на Т\М называется геодезическим потоком на
многообразии М.
Напомним некоторые понятия, связанные с аффинной
геометрией, подробности см., например, в [102].
3. Определение. Говорят, что на многообразии М зада-
на аффинная связность, если в каждой системе координат на
М задан набор функций Т)к, который при переходе от одной
системы координат к другой меняется по закону
г =дх^д?8х^ . г2х' дх<'
ук' дх1 дх''дхк ^дх'дх"' в*'' 1 '

§ 20. ГЕОДЕЗИЧЕСКИЕ ПОТОКИ Ц9
4. Определение. Если на многообразии М задана аффин-
ная связность Т)к и тензорное поле V1} -'», то определен
абсолютной дифференциал DV'.1'1.' поля F'.1"!' формулой
DV'} - \- = с1У1.' - 1- + П1 Vril ¦:i>dxs+ ... +V/S V1} - y^
Jl ¦•¦ Jq ]\ •••Jq Jt ••• Jq J\ ••• Jq
а также ковариантная производная DVly'y = ^7kVl>"\pdxk. Если
тензорное поле У)\-у задано вдоль кривой {xs(t)}, то
определена ковариантная производная DV'r-yjdt формулой
5. Определение. Аффинная связность Гд называется
согласованной с римановой метрикой gtJ, если Гд = Г^- и Dgij = 0.
6. Теорема (см. [102]). Для любой метрики gtJ на
многообразии М существует единственная согласованная с ней
аффинная связность, причем она вычисляется по формуле
+&-ё)- C47)
7. Определение. Тензорное поле V)\"'j' называется па-
раллельным вдоль кривой x(t), если DV'jY"у']а!=0. Кривая x(t)
называется геодезической, если ее касательный вектор dx(t)/dt
параллелен вдоль кривой x(t).
8. Лемма. Пусть х1, ...,х" — локальная система координат
на многообразии М". Кривая x(t) = (x1 (/),..., x"(t)) на многооб-
разии М" с аффинной связностью Т)к является геодезической
тогда и только тогда, когда
^ ^ = О. C48)
Эта система имеет однозначно определенное решение, если
задать начальные данные xl@) = x'o, xl@) = v'o.
9. Лемма. Кривая x(t) на поверхности M"cR"+1 является
геодезической относительно аффинной связности, согласованной
с метрикой, индуцированной из R"+1, тогда и только тогда,
когда вектор ускорения d2x(t)/dt2 перпендикулярен касательной
плоскости Tx(t)M".
Доказательство. Из п. 6 следует, что для метрики
gij = (dr/du', drjdu3) согласованная аффинная связность Гд равна
T)k = g's I —^—, — ), где r = r(ul,..., и") — параметрическое
уди'ди ди* J

120
ГЛ. 4. СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ
задание поверхности М", см. [102]. Условие перпенди-
d2x(t) . ._„ (d2x(t) дг \ п
кулярности —^ ±М имеет вид —=—, —г =0. Поскольку
dt2 \ dr дик)
d2x{t)
dt2
дг
дгг
ди'ди'
TO
d2x(t)
C49)
C5O)
т. е. ?цй'+?ьГу«'и; = 0 или мк + Гуи'м7 = 0, что совпадает
с уравнениями геодезических.
10. Метрика gtj устанавливает естественный диффеоморфизм
/: ТМ -> Т*М, который линеен на каждом слое. Если i; e TM, то
f(v)(x)=gijvixi. Обратное отображение/ задается поднятием
индексов f~l (p)'=g'iPj- Следующая теорема проясняет смысл
термина «геодезический поток».
11. Теорема. При естественном изоморфизме Т'М-> ТМ
траектории геодезического потока переходят в кривые, состав-
ленные из касательных векторов к геодезическим линиям в М.
Отдельное преобразование Т' переводит пару (х0, Ро) в пару
(•**> Pt)= Т'{х0, р0), где для получения х, следует провести
геодезическую через точку хоеМ в направлении р0 и тогда
х, отстоит от х0 на расстояние t вдоль этой геодезической,
а вектор рг касается этой геодезической в х, и направлен так
же, как и р0.
Доказательство. Запишем уравнения Гамильтона для
функции H = 2~1giJpipJ:
i
(з51)
Перейдем к контравариантным переменным vl=gl'pf. dqljdt = v' и
Из равенства gk'g,m = bkm следует j--gim= -gk'8glm/dqj, и по-
этому
gii~gkmg,nvmv"=-giigklgkm Вф vmv"= -g« |t vlv\ C53)

§ 20 ГЕОДЕЗИЧЕСКИЕ ПОТОКИ 121
Следовательно,
= -Ti,vkvl, C54)
так как g'J % i,V = gijЩ vlvk.
dq dq
12. Замечание. Пусть поверхность M2cR3 представлена
в виде графика z=f(x, у). Тогда простые вычисления показыва-
ют, что гамильтониан геодезического потока на М2 имеет вид
н_0 +/?(¦*¦ y))pl-2fxfyPxPy + 0 +/*(*, у))р]
2A+/?+/?)
где х, у, рх, pv—координаты в Т*М2, fx = — и /v = —.
ох ду
13. Рассмотрим геодезический поток на сфере S"<=R"+1.
В этом частном случае продемонстрируем конструкцию рас-
ширения геодезических потоков, принадлежащую Мозеру. Она
превращает геодезический поток на нелинейном многообразии
S" в гамильтонов поток на линейном пространстве. Уравнения
геодезического потока на S" имеют вид х = Хх, см. п. 9.
Множитель Лагранжа А. найдем из условия |х| = 1. Из равенства
(х, х) = \ следует (х, х) + (х, х) = 0, следовательно,
\(х, х) + (х, х) = 0, т.е. Х= — \х\2. Итак, уравнения, описыва-
ющие геодезические на S", примут вид х=— \х\2х.
14. Предложение. Геодезический поток на сфере S"
получается ограничением на T*S" гамильтонова потока sgrad H
на T'Rn+1=R" + 1(xu...,xn + l)®R»+i(yl,...,yn + 1), где
Н=]-\х\2\у2\=]-(х2+ ... +х2+1)(у2+ ... +у2+1). C56)
Доказательство. Возможность ограничения потока
sgrad// на T'S" вытекает из п. 20 § 19, так как T*S" выделяется
в T*R" + l связями (х, х) = х\ + ... +x2+i = 1 и (х, у) = х1у1+ ...
... +хп + 1у„+1=0. Уравнения Гамильтона с функцией Гамиль-
тона Н = 21 \х\2\у\ имеют вид
... +х2+1)уп + и
+- +у2+1)хи
2 л C57)
2)х

122 ГЛ. 4. СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ
которые при ограничении на сферу xj+ ... +х%+1 = \, очевидно,
дают уравнения геодезических х = — |jc|2jc.
15. Рассмотрим теперь случай произвольной поверхности М"
в R" + 1. Для гладкой строго выпуклой функции/(х) в R"+1 такой,
что/(а)-> оо при |jc|->oo, определим функцию F(x, >>), х,уе
eR" + 1, равенством F(x, y) = mmf(x+ty). Гамильтонова система
x = 8F/8y, y= —dFjdx имеет два первых интеграла h=\y\2
и I2 = F(x, у), поэтому можно рассмотреть решения, удовлетво-
ряющие дополнительному условию |j>| = 1, F(x, y) = 0. Каждой
точке (х, y)eRn+1 xR"+1 поставим в соответствие прямую
1(х, у), проходящую через точку jceR"+1 в направлении >>eR"+1.
16. Теорема (см. [192]). Предположим, что градиент
функции f{x) не обращается в нуль при /(д:) = 0, т. е. f(x) — O
задает гладкое многообразие. Если x = x(t), y = y(t)—решение
cF cF
уравнения х = — , у'= —— при \у\ = \, F(x, y)~0, то прямая
l(x{t), y(t)) касается поверхности f{x) = О, а точка касания Ь, (t)
прямой l(x(t),y(t)) с поверхностью {/=0} движется по
геодезической этой поверхности.
Доказательство. Пусть F(x, y)=f(x + a.{x, у) у), т.е.
функция f(x + ty) имеет минимум при / = а(л:, у). Тогда
dF) = dxf(L,)(y), где ?, = х + а(х, у)у. Отсюда получим
C58)
i(x, у). C59)
„ . dF . OF
Следовательно, гамильтонова система х = —, у= принимает
ду ох
вид x = a.-f-(?,), $=——(?,)¦ Для точки l, = x+cty получим \ = х+
+ щ> + &у = &у, у= — df/dx. Если использовать <х = а(х(?), y(t))
в качестве независимой переменной, то уравнения принимают вид
dA=y, d-f=-(«rld/ C60)
da. da. дх
d2\ . .._. df ,,
или —\= — (a) —, а эти уравнения являются дифференциаль-
ными уравнениям^ для геодезических на поверхности /= const,
так как вектор \ перпендикулярен поверхности.
Если ограничиться рассмотрением случая F=0, то
/(?)/(* + «(*> У)у) = О, где Ь,—точка касания прямой x+ty
с поверхностью /=0.
17. В п. 16 показано, что гамильтонова система х = —,
By
у'= связана с геодезическими на поверхности/= 0. Докажем

§ 20. ГЕОДЕЗИЧЕСКИЕ ПОТОКИ 123
утверждение, аналогичное п. 14. Рассмотрим в пространстве
R2a + 2(x,, ..., хл+1, уи ..., уп+1) подмногообразие М={(х, у)е
eR2n+2 | M2=l, dxf(x)(y) = 0}. В силу п. 18 § 19 это подмного-
образие является симплектическим, так как {\у\2, dxf(x)(y)} =
(d2f(x) \
——— у, у I < 0, так как в п. 15 мы предположили, что
дхдх I
функция/(jc) строго выпуклая. Ограничим Я на М. Из п. 20 § 19
следует, что поток sgrad (Я| М) получается ограничением некото-
рого потока sgrad Яо из М. Применим эту конструкцию
к связям F1 = 2~l (\у\2—1) = 0, F2=dxf{x)(y) = 0 и гамильтони-
ану H=F(x, y) = minf(x + ty). Тогда Н0 = Н— XiFl — ~k2F2. Из
равенств
{Яо, Fj} = {H, Fj}-^ {Fu Fj}-X2{F2, F}}=0 C61)
находим Xt и Х2. Поскольку {Я, F1}=0, то Х2=0. Далее,
Xt = {Я, F2] j {Fx, F2}. Поток х = дН0/ду, у=—дН0/дх, ограни-
ченный на поверхность Яо = 0, после введения нового параметра
х такого, что —dx/dt = Xi, принимает более простой вид
*=_k-i3Ho * = 3L-i^.. C62)
dx 1 ду dx 1 дх v '
На М справедливо равенство minf(x + ty)=f{x), поскольку
dxf(x)(y) = 0, так что на М: dyH(x,y) = 0 и dxH(x, y) = dxf(x).
Итак, на М выполняется равенство dyK(x, y) — dFl/dy=y,
а дифференциальные уравнения приводятся к виду dx/dx=y,
dy)dx— — Xi 1dxH= — Xi ldxf или d2x/dx2= — \i idxf, которые
совпадают с дифференциальными уравнениями для геодезичес-
ких. Итак, доказано следующее утверждение.
18. Предложение. Геодезический поток на поверхности
/=0 получается ограничением гамильтоновой системы х = —-,
ду
дН0 -
у= на многообразие
M={(x,y)eR2" + 2 \\y\2 = \, dxf(x)(y) = 0}. C63)
19. В заключение этого параграфа рассмотрим геометричес-
кие свойства гамильтонова потока на R6(xb x2, х3, уи у2, Уъ) —
= r*R3 = R3(jcb x2, x3) ® R3(_vb у2, Уз) с гамильтонианом
Н=\ I aiXf+l- (x2y2-(x, уJ), C64)
где (!;, г\) обозначает обычное скалярное произведение
^1 ^ пространстве R3.

124 ГЛ. 4. СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ
На пространстве Г*Ы3 определим три функции
РЛх,У) = х1-1(ХкУ'-Х1УкJ. C65)
20. Лемма. Гамильтониан Я представим в виде
Н=\ X atF,. C66)
Доказательство получается непосредственным вычислением.
21. Лемма. Функции Fu F2, F3 находятся в инволюции
относительно стандартной симплектической структуры на T*R3.
Доказательство вытекает из явного вида скобки Пуассона на
кокасательном расслоении T*R3, см. п. 24 § 19.
22. Лемма. Функции Fu F2, F3 являются первыми интег-
ралами гамильтонова потока sgrad Я.
Доказательство. Воспользуемся предложением 14 § 19:
функция Fk — первый интеграл потока sgrad Я тогда и только
тогда, когда {Fk, H) = 0. Имеем
{Н, Fk} = I { ? atFh Fk} = i X a, {Fh Fk}=0. C67)
Z i=l l i = l
23. Лемма. Функции Fu F2, F3 функционально независимы
почти всюду.
тт г, г d(FiyF2,F3)
Доказательство. Якобиан /= — — является рацио-
д(х1,х2,х3)
нальной функцией х{ и yt, и поэтому достаточно показать, что
/#0 в некоторой точке. Положим У1=у2=Уз=®1 тогда
l23^
24. Лемма. Поверхность xl+x2 + xl=l инвариантна от-
j ^
носительно потока sgrad//, Н=- ? flj/v
Доказательство вытекает из леммы 20 § 19, так как
{Я, xl + x22 + x23}=2((xl + x22 + xl)(x, y)-
\\ l) = Q. C68)
25. Определение. Задача интегрирования гамильтонова
потока sgrad Я с гамильтонианом Я из п. 19 на сфере
х\ + х\ + х~3 = \ называется задачей Неймана.
Оказывается, эта задача связана с геодезическими потоками.
26. Предложение. Гамильтонов поток sgrad Я на T*R3 =
= R3 (—у) © R3 (jc) является геодезическим потоком метрики
\\gll\\ =
-У\Уг ~У\Уъ
-У\Уг +yl+yl -У2У3
-У1У3 -УгУъ
C69)

§ 20. ГЕОДЕЗИЧЕСКИЕ ПОТОКИ
125
т. е. указанный поток переходит в геодезический при
замене у -> —у.
Доказательство вытекает из непосредственного сравнения
системы jc = sgrad// с уравнениями, описывающими геодезичес-
кий поток указанной метрики ||gy||.
27. Обозначения. Рассмотрим динамическую систему
с п степенями свободы, т. е. систему, описывающуюся обобщен-
ными координатами ql,...,q". Пусть Т=- a^q' q>—кинетичес-
кая энергия этой системы, ац—гладкие функции координат q',
i= I, ..., п. Вдоль траектории ql = q'(t), i= I,..., и, нашей системы
сохраняется энергия E=T+V, где К—функция, зависящая
только от координат q\ i=\,...,n (консервативная система).
Движение системы определяется из уравнения Лагранжа
i=\,...,n, где L = T—V—функция Лагранжа.
28. Теорема. Траектории динамической системы (с полной
энергией Е), конфигурационное пространство которой отнесено
к координатам ql,...,q", можно отождествить с геодезиче-
скими линиями метрики ds2=gijdq'dqJ = 2(E—V)aijdq'dqi, опре-
деленной на конфигурационном пространстве, после подходящей
замены параметра вдоль геодезической линии.
Доказательство. Уравнения Лагранжа
L=T-V=2~1ahkqhqk-V(q1,...,q"), имеют вид
: : = 0,
dt oq' dq'
C7,)
Из равенства T+V=E= const вытекает / =1, и, следова-
тельно, уравнение Лагранжа можно переписать в виде
C72)
или
d(
\dB(E-V)a№)
~2
dq'
2(E-V)a№qkq
jj^ = O. C73)

126 ГЛ. 4. СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ
Введем метрику ds2 — 2(E—V)aijdqidqi=gijdqidqi. Тогда пре-
дыдущее соотношение перепишется в виде
)¦??? = (>, C74)
ds J 2 dq ds ds
так как gij=2(E—V)aij. Полученное выражение эквивалентно
равенству
giJ ds2 *~2\8qk~rdqh' dq1 J ds ds
После поднятия индекса i получим равенство —-r + Г?.- — — = 0,
ds ds ds
где Гд — связность, согласованная с метрикой gy. Итак,
уравнения Лагранжа эквивалентны уравнениям геодезических
линий для римановой метрики #;,.
§ 21. Алгебра Ли функций Гамильтона
1. Определение. Пусть К—любое тензорное поле на
многообразии М, Y—векторное поле на М, ф,—локальная
однопараметрическая группа преобразований, отвечающая по-
лю Y, ф, — индуцированное отображение в тензорах. Определим
оператор Ли Lr соотношением
(LYK)X= lim - [*,-(№,)*),]• C76)
г —о •
2. Предложение. Оператор Ли LY обладает следующими
свойствами: a) LY—линейное отображение; б) LY(K1(g)K2) =
= (LYK1)®K2 + Ki® (LYK2); в) отображение LY сохраняет тип
тензора; г) для любой функции f имеет место равенство
LYf= Y(f); д) отображение LY перестановочно с операцией
свертки.
Доказательство. Пусть ф, — локальная однопарамет-
рическая группа преобразований, порожденная полем Y. Тогда
Lr(K1®K2)=Hm -[а:1®а:2-ф,(/:1®а:2)] =
1
+ lim - [&,К,(Е)К->— ф.Л^^ф.ЛГ-Л = lim -
C77)

i 21. АЛГЕБРА ЛИ ФУНКЦИЙ ГАМИЛЬТОНА
Поскольку ф, сохраняет тип тензора и перестановочно со
сверткой, то и отображение LY обладает этими же свойствами.
Далее,
1
t~-О t
= -lim 1[/(фГ1(^))-/(х)]=Пт/(ф-(дг))~/(х)=7(Л- C78)
t —о ' t — о —'
3. На пространстве ?lk (M) дифференциальных форм степени
к на многообразии М имеем три операции d: Qk (M)-+Qk + 1 (M),
i(У): ?2*(М)-*а*-1 (М) и LY: Пк (M)-*Clk (M). Они обладают
следующими двумя важными свойствами:
C79)
(?усо2). C80)
Второе равенство вытекает из обычного правила дифферен-
цирования произведения.
4. Предложение. Для любых дифференциальных форм
<хеПк (М) и Ре?2"(М) имеет место равенство
1(У)(алр) = A(У)а)Ар + (-1)»алг(Г)р. C81)
Доказательство. В локальной системе координат
х1, ..., Xs на многообразии М имеет место равенство
(ЛУ)^1...1к.1=кщ1...,к_1Г1, C82)
так как (г(У)со)(У1, ..., Yk_l) = kw(Y, Yu ..., Yk^l). Далее,
'> C83)
C84)
C85)
где | i | означает, что индекс i не участвует в альтернации. Итак,
мы должны доказать равенство
1)Чл...и.Р|'1;2...у.]У- C86)
С этой целью рассмотрим подгруппу Н в группе Sn+k всех
перестановок на п+к символах /, i2, ..., *'*, j\, ..., jn, которая
состоит из преобразований, оставляющих первый индекс / на

128 ГЛ. 4 СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ
месте. Обозначим V-u1...i$j1...j, символом Xu2...ikjt...j,- Тогда по
определению альтернации
!
где первая сумма ?A) берется по всем смежным классам, для
которых а(/)е[г2, ..., jt]. а вторая сумма УB) — по всем смеж-
ным классам, для которых ос(/)ё[/1, ...,у„] (каждый смежный
класс <хН элемента а однозначно определяется значением а (г)).
Заметим, что все слагаемые как в первой, так и во второй
сумме равны между собой. Поэтому альтернация А равна
C88)
где <т0 — одна из перестановок, для которой o0(i)e[jlt ...,jn\
В качестве а0 можно взять, например,
Л «2 -к Л л-уД C89)
\h h-ji i ji-uj
Действительно, рассмотрим слагаемое, содержащее
и транспозицию t, которая переставляет р и /, оставляя
остальные символы на месте. Тогда
<xP...i..At ...*,= -<*t(P...i...$st...,.)= -<Xi-4i2...it$jl...j.y C91)
Проконтролируем теперь знаки: ao(H2...itPj1...jB) входит в рас-
сматриваемое слагаемое со знаком (—1)". Поскольку a = tx, то
(-!)« = (-1)'(-1)'=-(-1)\ Поэтому (-1)ааа(»2..лкРЛ...;„) =
= -(-l)t(-l)ai,(i2...i,Py1...i.) = (-l)tai,(i2...i4Py1..j1I), т.е. для каж-
дого слагаемого в сумме ? (— 1)°-^о(«2—/,) мы найдем равное

§ 21. АЛГЕБРА ЛИ ФУНКЦИЙ ГАМИЛЬТОНА
129
и поэтому эти суммы
ему слагаемое в сумме ? (— l)"^,,^
пеЯ
равны. Сумма, отвечающая смежному классу ао#, очевидно,
равна (— I)*ati2j3...fl_1ji$\i\j2..../„]• Аналогично рассматривается
первая сумма.
5. Лемма. Имеем равенство LY°d=d°LY.
Доказательство. Имеет место равенство
так как d—
dt
f
Г = 0
1 = 0
d
Jt
1 = 0
d
dt
d
C92)
= — d в силу того, что d—это дифферен-
цирование по аргументам х, а по аргументу /.
6. Теорема. Имеет место тождество
C93)
Доказательство. Из предложения 4 и формул для
d((?>lAG32), i(Y)((ol лсо2) вытекает, что если равенство C93)
имеет место для coj и со2, то оно справедливо и для
сох лсо2. Поскольку любая форма имеет вид cof ...itdx^ л ... Adx'k,
то равенство C93) достаточно доказать для функций / и форм
вида df.
Если со=/, то LYf=Yf, i(Y)f=O и i(Y)df=Yf; тем самым
все доказано.
Если со = <//, то di(Y)df+i(Y)ddf=d(YJ), так как
i(Y)df=Yf, ddf=O. Далее, LYdf=dLYf=d(YJ), и, следователь-
но, LYdf=[di(Y)+i(Y)d)df.
7. Следствие. Векторное поле Y является локально
гамильтоновым тогда и только тогда, когда ?усо = 0, где со—
симплектическая структура. В частности, Z,sgrad yco = 0, так как
любое гамильтоново поле является локально гамильтоновым.
Доказательство. Напомним, что поле Y называется
локально гамильтоновым, если df— — 2 ~ii(Y)to. Утверждение
вытекает из равенства LYa> = di(Y)a> + i(Y)d<u и d(o = 0.
8. В качестве еще одного следствия теоремы 6 получим
бескоординатное выражение внешней производной. Для этой
цели вспомним, что
[X, 7]=limi[7-
1—0 •
C94)
и, следовательно, Lx Y= — LYX= [X, У], где ср,—локальная
однопараметрическая группа преобразований, порожденная век-
торным полем X.

130 ГЛ. 4. СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ
9. Теорема. Пусть сое?У(А/). Тогда
da(X0, Хи ..., Xr) = — ? (-\)%<а(Х0, .... Х„ .... Х,) +
r+1 i=o
+ Л X ЫГМГА^О]' Xo, ..., X» ..., Хр ..., Xr). C95)
Докажем это утверждение индукцией по г. Пусть г=1, т.е.
coeil1 (M). Из равенства C93) вытекает соотношение da>(X, Y) =
= 2~4i(X)da){Y) = 2-4Lxw]{Y)-2-1{dh(X)w]}(Y), так как
[i(X)(o)\y) = 2(o(X, Y). Из равенства (?А-ю)(У) = X(o(Y)-(o(LxY)
и предыдущего соотношения следует
da(X, Y) = 2-1(X(o(Y)-Y(a{X)-(a(LxY)) =
= 2 '1 (Ха (Y) - Усо (X) - со ([X 7])), C96)
т.е. Ло(Х, 7) = 2-1(ХсоG)-Усот-со([А', У])), так как 41МХ
х со](Y) — dUa(Xj](Y)=Y(u(X). Итак, при г = 1 утверждение
доказано. Пусть теперь г>1. Имеем равенство
(r+\)dw(X, Хи ..., Xr) = (i(X)d(a)(X1, ..., Хг) =
= (Lxv)(Xu ..., Х)-^!^©)^. -, ХТ). C97)
Далее,
- X со(Хь ..., [X, X,-], ..., JTr) C98)
в силу того, что (й(Х1: ..., А"г) получается из тензорного
произведения сверткой. Поскольку 1(А')сое?2г~1(М), то в силу
индуктивного предположения имеем равенства
{di{X)<o)(Xu ..., Х,) =
= - ? (-^-^(гДОш^, ..., Х„ ..., Хг)) +
Г i=l
+~ X (-1)'+уAA)ш)([1„ Xj], Хи ..., Х„ ..., Xj, ..., Хг) =
Г 1 « I < j s; r
- I (-\)i+Jw{[XhXj], X, Xu...,Xh...,Xj,...,Xr), C99)
из которых немедленно следует наше утверждение.

§ 21. АЛГЕБРА ЛИ ФУНКЦИЙ ГАМИЛЬТОНА 131
10. Пусть (М2и, со)—симплектическое многообразие
С00(А/2")—пространство гладких функций на М2', на этом
пространстве определена скобка Пуассона {F, G}, F, GeCcc(M),
см. я. 11 § 19. Ясно, что скобка Пуассона линейна по каждому
аргументу.
11. Предложение. Для любых функций /, g на сим-
плектическом многообразии выполняется равенство
sgrad{g,f}-[sgrad/, sgradg~\.
Доказательство. Векторное поле X является гамиль-
тоновым с гамильтонианом g тогда и только тогда, когда
— 2~1i(X)(a = dg. Применив к этому равенству оператор LY, где
Y= sgrad/, получим — 2~1 Ьг{х(Х)щ = LYdg. Имеют место равен-
ства .LYdg = dLyg = d(Yg) = d[\sgradf)g] = d{g,f}. Далее
со, D00)
так как (i(A')co), = 2col7A'i. Поскольку dio=0 (со—симплектическая
структура) и д(гG)со) = 0. то LY(u = i(Y)d(u + di(Y)m = 0. Следо-
вательно, Ly[i(l)co]=i([V, Г))со и -2-h([Y, X])(a = d{g,f}.
Поэтому в силу определения косого градиента имеем равенства
sgrad {^/} = [7, X] = [sgrad/, sgradg]. D01)
12. Теорема. Скобка Пуассона {f,g} задает в простран-
стве гладких функций С" (М) на симплектическом многообразии
структуру алгебры Ли.
Доказательство. Равенство {/, g} = — {g,/} вытекает из
соотношения
{/,?}=-<»(sgrad/, sgradg) =
= -(-co(sgrad?, sgrad/)) =-{g,f}. D02)
Проверим далее тождество Якоби. Имеем {/, {g, h}} =
=-(sgmd f){g,h}=-Lstr>d/{g,h} и {g,/,} = (o^^. Введем
обозначение Y= sgrad/ Тогда
D03)
OX CX*
так как
D04)
Докажем, что (Lyco)'v = 0. Применив оператор LY к равенству
coi-'(Oj.t = 5i, получим (LyCo)'-'co,]k-|-co'-'(LyCo)jk = 0, так как LY5'k = 0.

132 ГЛ. 4. СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ
Поскольку LYw = i(Y)d<u + di(Y)(u = 0-2d2f=0, то (Lyco)'JcojVk = 0,
следовательно, (Z,yra)'-' = 0. Итак,
Ly{g,h} = {Yg,h} + {g, Yh} =
= {(sgrad/)g, h} + {g,{sgnidf)h} = {{g,f},h} + {g,{h,f}}, D05)
что и требовалось доказать.
13. Теорема Пуассона. Пусть Fl, F2— первые интег-
ралы потока X=sgrad Я(Х). Тогда {Flt F2)—тоже первый
интеграл потока X=sgraaH(X).
Доказательство. Функция F является первым интегра-
лом потока Х= sgrad Я тогда и только тогда, когда {F, Я}=0.
Из тождества Якоби {Я, {Fu F2}} + [Fu {F2, H}} +
+ {F2, {Я, F1}}=0 следует равенство {H,{FU F2})=0, так как
{F2,H} = {H,Fl}=0.
14. Следствие. Пусть F{M) — алгебра Ли функций Гами-
льтона относительно скобки {F, G}'= — {F, G], a D[M) —
алгебра Ли векторных полей относительно коммутатора век-
торных полей. Отображение sgrad: F(M)-+D(M) является
гомоморфизмом алгебр Ли, т.е. sgrad {F, G}' = [sgrad F,
sgrad GJ. Его ядро состоит из локально постоянных функций;
если М связно, то Ker sgrad =R.
15. Следствие. Гамильтоновы векторные поля образуют
подалгебру в алгебре Ли векторных полей D(M).
16. Следствие. Для того чтобы гамильтоновы потоки
sgrad F и sgrad G коммутировали, необходимо и достаточно,
чтобы функция {F, G} была локально постоянной.
17. Лемма. Пусть X—гамильтоново векторное поле, ф,—
отвечающая ему локальная однопараметрическая группа, со—
симплектическая структура. Тогда (ф,)»со = со для любого t.
Доказательство. Мы уже знаем, что ?А-ю = 0, т.е.
Шп![а>-(ф,)„ю] = 0. D06)
1—0 '
Применим к этому равенству отображение (ф5).:
I
Пт-((ф5).со-(ф,+5).ю) = 0, D07)
I—.0 '
d
т. е. —
(фТ).со = 0 и, следовательно, (ф,),со = const, (ф,).со =
о).со = со.
1». Лемма. Имеет место формула {/, uv} = v{/, м} +
+ м{/, v} для любых трех функций /, и, v.
Доказательство. Очевидно, что
{/, uv}= -(sgrad/)(uv) =
= {/, u}v + u{f, v}. D08)

§21. АЛГЕБРА ЛИ ФУНКЦИЙ ГАМИЛЬТОНА 133
19. Теорема. Пусть L — конечномерная алгебра Ли функ-
ций на компактном симплектическом многообразии (М2п, со).
Тогда алгебра Ли L редуктивна.
Доказательство. В пространстве ССО(М) гладких функ-
ций на многообразии М определим скалярное произведение
D09)
м
где со" = сол... лсо — форма объема на М2п. Проверим, что
алгебра Ли СХ'(М) сохраняет скалярное произведение </, g},
т. е. для /, и, vеС °°(М) выполнено равенство
<м, {/, !?}> + <{/, и}, г> = 0. Докажем, что если/, gsCco{M), то
J {/, g}co" = 0. Тогда требуемое утверждение следует из фор-
мулы {/, uv} =u{f, v} + v {/, и} после ее интегрирования:
J{/ uv}(an = |м{/ v}wn+\v{f, м}со", D10)
МММ
так как
|м{/г}со" = <м, {/г}>, D11)
м
J «{/, и} ш« = <»,{/,«}>, D12)
м
J{/мг;}со" = 0. D13)
м
Заметим сначала, что имеет место равенство
{/ g}co"= — d[nfdgл<й"~1]. Справа и слева здесь стоят тензоры,
поэтому достаточно проверить это равенство в какой-нибудь
специальной системе координат. Выберем такую систему
координат, что в точке х форма со имеет канонический вид
п
юх= ]Г dx' Adx"+1. Тогда, как мы уже знаем,
x" + i), . D14)
так как сол...лсо = и! /\dxlAdx" + i. Далее,
i=i
л л
сол ... л со = (и—1)! ^ Д dx' Adx" + I. D15)

134
ГЛ. 4. СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ
Поэтому
= л^^Л*лЛ'л (л-1)!
-• (z ?
Рис. 21
Тогда
= -Г J d
\_M\D
= -Г J
L«(m\d)
= -[ J
л <*¦ -*
так как при
dxkAdxlna. Л(<
умножении
лучим, очевидно, не нуль
только в одном-единственном
случае, когда k=j и l=n+j
или k = n+j, a /=/.
Теперь применим теорему
Стокса. Для этой цели вы-
режем из многообразия Л/2"
маленький 2и-мерный диск
D с границей S2" (рис. 21).
J
1 =0,
J
D17)
так как ориентации на 8(M\D) и на <3D противоположны, см.
рис. 21. Тем самым теорема полностью доказана, если вспом-
нить утверждение теоремы 14 § 10.
§ 22. Симплектическая структура на орбитах
копрнсоединенного представления группы Ли
1. Предложение. Пусть Р—группа Ли, G — ее алгебра
Ли и О (f)—орбита коприсоединенного представления Ad*
группы Ли Р, проходящая через точку /е G *. Тогда касательное

§ 22. СИМПЛЕКТИЧЕСКАЯ СТРУКТУРА НА ОРБИТАХ
135
пространство TrOif) допускает следующее описание: TrO(f) =
{ad[/|^6G}CG*
Доказательство. Для любого касательного вектора
() найдется такой элемент geG, что
d
v = —
dt
d'aptg feTfO(f).
D18)
Пусть еь ..., е„ — базис алгебры Ли G, а е1, ..., е" — базис
в пространстве G*, сопряженный к {е,}, т. е. e'(e/) = 8j. Тогда для
любого xeG имеем х = х'е{, а для любого/eG* имеем/=/;е',
причем fi=f{ei). Координаты х1 и ft — линейные функции'на
соответствующем пространстве. Пусть vl — это г-я координата
вектора v. Из цепочки равенств
dt
dt
( = 0
d
~ dt
=/(-[?, е,])=-Н*/)(е,) D19)
следует соотношение v=— ad*/, которое доказывает наше
утверждение.
2. Определение. На каждой орбите O(f) коприсоединен-
ного представления Ad* группы Ли Р определим симплектичес-
кую структуру со, которую будем называть канонической
симплектической структурой (форма со также называется
формой Кириллова). Пусть ?, r\eTfO(f). Тогда в силу п. 1
найдутся такие элементы ?ь r\ieG, что % = ad*^/H ri = ad*i/
Положим по определению со (^, ri)=/([Sb T|i])-
Ближайшие пункты будут посвящены доказательству того
факта, что со задает симплектическую структуру на орбите
/)
3. Лемма. Определение 2 корректно.
Доказательство. Если ^ = ad^/=adj2/, то %у— %ге
eAnn(/), Ann(/) — аннулятор ковектора /. Поэтому для про-
верки корректности определения надо показать, чт/([^ ^
Л1 + Ло])=/(|Ль Л1'])> гДе So. ПоеАпп(/). Имеем
D20)
так как adjo/=ad*o/=0.
4. Лемма. Форма a>eA2(TfO(f)) не вырождена.

136
ГЛ. 4. СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ
Доказательство. Проверим, что если со(%, г|) = 0 для
всех ^eTrO(f), то ц=0. Пусть ?, = ай\ /, r\ = ad' f
и а>($, л)=ЛЙ1. 4i]) = 0 для любого ^eG. Итак,'(ad*, JHU) = O
для любого 4i?G. Следовательно ad_/=0 и r| = adni/=0.
5. Следствие. Размерность каждой орбиты коприсоеди-
ненного представления четна.
6. Предложение. Форма ю инвариантна относительно
коприсоединенного представления Ad*, т. е. (Ad*,)(»,, = (»<•, где
* = Ad;/ (рис. 22); а)9бЛ2(Г9О(/)), ю/бЛ2(Г/О(/)).
Рис. 22
Доказательство. Операция увлечения форм определяет-
ся равенством [(AdJ)*ca?1(^, ri) = cae(rf(AdH)^, rf(Ad;)ri). Вычис-
лим дифференциал d(Aa\), где Adfr: G'-+G . Поскольку AdJ—
линейное отображение, то его дифференциал совпадает с ним
самим, т. е. rf(Ad*,) = Ad;. Если отображение ограничить на
подмногообразие, то его дифференциал также ограничивается,
поэтому rf(Ad*,)^ = Ad^.
Для завершения вычислений нам потребуется равенство
Adgad^/=adAd 5iAd*/. Докажем его. Для любого элемента
xeG имеем
D21)
что и требовалось проверить.
Пусть ? = ad^/, ^=ad*1/. Тогда
D22)

§ 22. СИМПЛЕКТИЧЕСКАЯ СТРУКТУРА НА ОРБИТАХ 137
так как Ad*hf=g и, следовательно, f=Ad*h-ig. Кроме того,
использовалось следующее свойство присоединенного представ-
ления Ad: Ada[^, riJ^Ad.,2;, Adar|].
7. Следствие. Каноническая форма соеО2(О(/)) является
гладкой формой на орбите O(f).
Доказательство. Для того чтобы задать форму со
на всей орбите, достаточно задать со в одной точке и раз-
нести ее по всей орбите с помощью преобразований Ad*,,
heP.
8. Замечание. Для проверки равенства <&о=0 воспользу-
емся следующим утверждением.
9. Предложение. Пусть на многообразии М2п задана
невырожденная дифференциальная 2-форма сое02(М211). Тогда
с помощью со можно определить скобку Пуассона
{/ g} = mi'—.—., здесь х1, ..., х"— локальные координаты на
Mln, co,-j-—координаты формы са в этих координатах
и II <вц || ~' = || cou'||. Равенство rfco = 0 имеет место тогда
и только тогда, когда скобка {/ g} удовлетворяет тождеству
Якоби {/ {g,h}} + {g, {h,f}} + {h, {/,*}} =0.
Доказательство. Необходимость доказана в теореме
12 § 21.
Для доказательства обратной импликации достаточно про-
делать все выкладки этой теоремы в обратном порядке.
10. Замечание. Для того чтобы применить это ут-
верждение, вычислим скобку Пуассона относительно кано-
нической формы ш. С этой целью сначала вычислим sgrad/
относительно ш.
Скобку Пуассона на орбитах можно «склеить» в единую
скобку Пуассона на всем пространстве G*. Если/, geC°°(G*), то
положим по определению {/, g}(x)={f\O(x), g\O(x)}(x). По-
скольку пространство G* расслаивается на орбиты представле-
ния Ad*, то это определение корректно.
11. Лемма. Пусть f—гладкая функция на пространстве
G", дуальном к алгебре Ли G. Тогда (sgrad/)x = ad*,y(x)(x). Здесь
df(x)e(G-y^G.
Доказательство. По определению векторного поля
sgrad/ имеем равенство са(У, sgrad/) = df(Y) для любого по-
ля Y. Покажем, что это равенство выполнено, если поло-
жить (sgrad/)x = ad*(/(x)(jc). Пусть Y=ad*yx для некоторого
вектора yeG. Тогда со(У, ad*,/(x)jc)=a>(ad*;c, ad*,/(JC)x) =
= х([у, df\x)\). С другой стороны, dfx(Y) = dfx(ad'yx) = (adyx)
Шх) = х([у, dfx]), здесь использовали определение изоморфизма
(Gj'^G. Поскольку форма со не вырождена, то поле sgrad/
определено однозначно и, следовательно, sgradx(/|O(x)) =
ad*x

138 ГЛ. 4. СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ
12. Лемма. Пусть /, g—гладкие функции на простран-
стве G*, дуальном к алгебре Ли G. Тогда имеет место ра-
венство
^Ь-CUgg. D23)
Здесь е1у ..., е„ — базис алгебры Ли G, е1, ..., е" — сопряженный
базис пространства С, а х1, ..., х" и хь ..., х„ — соответст-
вующие координаты в G и в G', Ckj—структурный тензор
алгебры Ли G в базисе ех, ..., е„, т. е. [е{, e^\ = CkVlek.
Доказательство. Из определения изоморфизма G" = G
ясно, что йях = -~е{ и dfx = ~e:. Тогда
dxi dxj
{/. gb=-fi>(sgrad/c, sgradgj = ro(sgradgx, sgrad/x) =
= dfx (sgrad gx) = dfx (ad\{x) x) = (ad*dg{x) x) (dfx) = x (\dgx, dfx]) =
oxt
-СЪ*??-, D24)
0Xj dXj
здесь мы использовали естественный изоморфизм G"^G.
13. Замечание. Итак, на пространстве G* определена
скобка Пуассона {/, g}= — С^хк — -^-. Эту скобку впервые
рассмотрел Березин [21 ], будем называть ее скобкой Березина.
Для доказательства того, что {/, g} на орбитах удовлетворяет
тождеству Якоби (а именно это и надо проверить для
доказательства замкнутости канонической формы со), мы
покажем, что скобка Березина на G* удовлетворяет тождеству
Якоби. Тогда ее ограничение на каждую орбиту также
удовлетворяет тождеству Якоби, а это ограничение совпадает со
скобкой Пуассона относительно канонической симплектической
структуры на орбитах коприсоединенного представления Ad*.
14. Теорема. Скобка Пуассона —{f,g} = CkijXk — — на
пространстве G", дуальном к алгебре Ли G, удовлетворяет
тождеству Якоби.
дх
Доказательство. Учитывая равенство —^ = §1!, получим
дхг
k
С» Сг х ^LEl^-4-C Ck x x — df 5?
v iJ "dxq дх, dxj qr h " "dxq dxrdx, dx/
D25)

§ 23. УРАВНЕНИЯ ЭЙЛЕРА 139
Поэтому
{А. {/,*}} + {/, {*,*}} + {*, {И, /}} =
*r iJ дх, Зхс 3xj+ 'r J« ад:, 5^ ад:,+ jr * ид:, ах, Вх,
Cx x 8f
^ + ytjrtqlxpxk^ ^
D2б)
Во втором слагаемом заменили <? на г, г на у, _/ на q, а в третьем,
седьмом, восьмом и девятом слагаемых заменили q на _/, i на q,
j на г. Первая квадратная скобка равна
(C^Cy+C^C^+C^C,,)—— —-0, D2/)
так как равенство [е„, [е„ еу]] + [е„ [еу, е,]] + [еу, [е„ <?,•]] = О
эквивалентно соотношению CijCJr+CjeCfr+C^Cj'r = O. Вторая
и третья квадратные скобки перепишутся так:
Гк ГР Г М
Г С,,- С,г С „)
С1,)х,хк1 +
&-C;CWx,,^gg. D28)
Заметим, что тензор- /4erij = (CJrC*j —Cj^Cf,)^^ кососиммет-
ричен по г, г, а вторые частные производные 81FI8xr8xi
симметричны по г, i, поэтому при суммировании мы получим
нуль. Теорема полностью доказана.
15. Теорема. На орбитах коприсоединенного представле-
ния любой группы Ли имеется естественная инвариантная
симплектическая структура.
Доказательство вытекает из утверждений п. 3, 4, 6, 14.
§ 23. Уравнения Эйлера
1. Определение. Пусть /— гладкая функция ,на орбите
O(t), teG*, коприсоединенного представления Ad* группы Ли Р,
отвечающей алгебре Ли G. Тогда в силу п. 11 § 22 гамиль-

140 ГЛ. 4 СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ
тоновы уравнения jc = sgrad/x на орбите О (t) относительно
канонической формы со имеют вид x = ad'dfix)(x), xeG*.
Если /?С°С(С), где G' — пространство, дуальное к алгеб-
ре Ли G, то на каждой орбите возникают гамильтоновы урав-
нения
x = addfM(x), xeG', feC»(G'). D29)
Эту систему на G' будем называть уравнениями Эйлера.
Важность изучения уравнений Эйлера определяется прежде
всего тем фактом, что многие физически интересные системы
имеют указанный вид. В качестве примера укажем, что такое
представление допускают: а) уравнения движения твердого тела
с закрепленной точкой; б) уравнения, описывающие динамику
твердого тела с распределенным электрическим зарядом в иде-
альной жидкости при наличии постоянного гравитационного
и электрического полей и при условии равенства вытал-
кивающей силы и силы тяжести и нулевом суммарном заряде
тела; в) уравнения, описывающие вращение намагниченного
твердого тела вокруг неподвижной точки в однородном
гравитационном и магнитном поле, см. § 50.
2. Конструкция. Большой интерес представляют уравнения
Эйлера, когда гамильтониан /—квадратичная функция. Рас-
смотрим этот случай более подробно. Квадратичные функции
на G* находятся во взаимно однозначном соответствии с линей-
ными операторами С: G*-*G: если f{x) — квадратичная функ-
ция, то ее можно представить в виде f{x) = 2~ x(C(x)), xeG*.
Билинейная форма/(х, у) = х(С(у)) симметрична тогда и только
тогда, когда оператор С самосопряжен, <С(х), у} = (х, С(у)},
где <;с, у} — обозначает значение х на у. Будем предполагать,
что С самосопряжен. В этом случае, если f(x) = 2~1x(C(x)), то
dfx = C(x). Поэтому уравнения Эйлера примут вид x = ad'C(x)(x).
Эта система уравнений на G* гамильтонова на каждой ор-
бите представления Ad' — гамильтонианом является ограни-
чение функции f(x) = 2lx(C(x)) на рассматриваемую ор-
биту.
3. Координаты. Перепишем уравнения Эйлера в координатах.
Пусть еь ..., еп — базис алгебры Ли G, е1, ..., е"— сопряженный
базис в пространстве G*, т. е. е'(е,) = 8} и С(е') = а'-'е,-. Тогда,
очевидно, f(x) = 2~1a'}XiXj. Условие самосопряженности опера-
тора С имеет вид aiJ = aJl. Здесь хи ..., х„ — координаты в G*,
отвечающие базису е'.
4. Лемма, а) Пусть f—гладкая функция на G*. Тогда
уравнения Эйлера, отвечающие /, имеют вид
xs = C%^xk, s=l, ..., n = dimG. D30)
8xj

S 23 УРАВНЕНИЯ ЭЙЛЕРА ]4|
б) Пусть С: G*->G — самосопряженный линейный оператор
с матрицей а''. Тогда ему отвечают уравнения Эйлера
х, = а{'С%х{хк, s=l,...,n, n = dimG. D31)
Эта система имеет первый интеграл T=21a'sxixs— интеграл
энергии.
Доказательство. Легко видеть, что ad'e.ek = C)ses. По-
этому &&'ух = &&'у1е.хкек = хку]ad'e.ek-xkyiCkses. Отсюда следует
утверждение о виде уравнений Эйлера. Утверждения о том, что
Т—интеграл, следует из того, что ограничение уравнений
Эйлера на орбиты представления Ad* есть гамильтонова
система с функцией Гамильтона, равной ограничению Т на
рассматриваемую орбиту. Это утверждение можно проверить
и непосредственной выкладкой. Имеем равенства
J = Vs *!Х,+ 1-а"х,х, = aisxiXs = aisa4bCpbixqapxs =
= a"bC^aisxsxqxp = -a"bCfbaisxsxqxp = -aisCfba"bxsxqxp =
= -asiC4babqxsxqxp, D32)
здесь второе и седьмое равенства написаны в силу симметрич-
ности a's = as', а пятое равенство вытекает из кососимметрич-
ности Сы=-С?ь.
Поскольку aqbCgialsxsxqxp = as'Cfbabqxsxpxq, то из получен-
ного выше соотношения
~ = a«bC?iaisxsxqxp= -asiCfbabllxsxqxp D33)
dT „
следует — = 0.
at
5. Замечание. Уравнения Эйлера \s = aljCksxixk можно
написать в более широкой ситуации, чем это указано в лемме 4,
а именно, предположим, что в пространстве V заданы два
тензора aij и С*,. Тогда имеют смысл уравнения Эйлера
и функция T=2~l aksxkxs — первый интеграл, если только
aiJ = aji и Ckj=-Ckji.
6. Предложение. Любая функция F, удовлетворяющая
системе уравнений в частных производных
CkjXk~ = 0, i=l, ...,И, D34)
CXj
является первым интегралом нелинейной системы обыкновенных
дифференциальных уравнений D30).
Доказательство. Функция F, удовлетворяющая ука-
занной системе уравнений в частных производных, является
инвариантом коприсоединенного представления Ad*, т. е.

142
ГЛ. 4. СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ
постоянна на орбитах представления Ad*. Следовательно,
ограничение F\O{t) функции F на любую орбиту О(п
постоянно, т. е. F\OQj находится в инволюции с любой
функцией на орбите. Это же утверждение можно проверить
непосредственными вычислениями:
7. Замечание. Предложение 6 дает некоторый аналог
метода Якоби, при использовании которого мы переходим от
обыкновенных дифференциальных уравнений к уравнению
dS ..( ds\ - , т,
в частных производных —\-Н \ t, q, — =0 (уравнению Гамиль-
dt \ dqj
тона — Якоби), вообще говоря, нелинейному. В п. 6 также
предлагается перейти от обыкновенных уравнений D30) к урав-
нениям в частных производных D34), но в отличие от метода
Гамильтона—Якоби к линейным. В п. 3 § 34 опишем регуляр-
ный алгебраический процесс, который позволяет строить боль-
шой запас интегралов системы D30). Этот метод позволяет
проинтегрировать многие интересные системы.
8. Пример. Рассмотрим алгебру Ли soC) = {eb е2, е3} с ком-
мутаторами [еь ег~\=еъ, [еи еъ\— —е2> \_е2, еъ\ = е1- Соответст-
вующие уравнения Эйлера имеют вид
а интегралы, описанные в п. 4 и 6, принимают форму
+ ai3x1x3 + a23x2x3,
9. Теорема. Пусть
С =
a
0
0
0
P -
0
0
0
у ~
D37)
D38)
D39)
— диагональный оператор, С: soC)*->soC). Уравнения Эйлера на
soC)* эквивалентны уравнениям движения трехмерного твердого
тела, закрепленного в одной точке и имеющего моменты инерции
а, Р, у. Эквивалентность задается оператором С: soC)*->soC).

§ 23. УРАВНЕНИЯ ЭЙЛЕРА
143
Доказательство. Уравнения Эйлера, отвечающие ал-
гебре Ли soC) и оператору С, имеют вид
D40)
Перепишем эти уравнения с помощью оператора С на soC),
1 1 1
т.е. сделаем замену переменных у1=-х1, у2 = -х2, у3 = -х3.
а р у
Тогда, очевидно, получим уравнения ау\ =(Р~ у)угУъ,
$У2={у — у)у1Уъ, ЧУъ = (у- — $)У\У21 которые описывают движение
твердого тела, см. п. 12 § 5.
10. Лемма. Алгебра Ли soC) изоморфна алгебре Ли косо-
симметрических матриц, точнее, если
0 -ш,
0 -ш,
D41)
то /([«, 6]) =[/(«)> /(*)]=/(«)/(*) ~/(*)/(fl).
Доказательство получается непосредственным вычислением.
11. Предложение. Уравнения, описывающие движение
твердого тела
Ap = (B-C)qr,
Bq = (C-A)pr, D42)
Cf = (A-B)pq,
эквивалентны следующей системе на soC): фХ=[фЛ', Х\ Хе
esoC), где ф(X) = IX+ XI, /=diag(A.1, Л.2, Х.3) и
, -Л + й+С . А-В+С . Л + й-С ,..лч
А.!= —, ^2=~у-, А.з = ^—. D43)
Эквивалентность задается изоморфизмом, описанным в п. 10.
Доказательство. Если
Х=
0
D44)
то непосредственное вычисление дает
-^13-^32»
) здесь предполагается, что

144 ГЛ. 4. СИМПЛККТИЧССКАЯ ГЕОМЕТРИЯ
Хц^—х^. После подстановки выражений для Х,- и замены
xi2=—r, xl3 = q, х23=—р получим уравнения, описывающие
движение твердого тела.
12. Определение. Система уравнений ц>Х=[ц>Х, X], Хе
eso(w), на алгебре Ли so(w) кососимметрических матриц порядка
ихя, где ф(X) = XI+IX и /=diag(A.,, ... Х„), А., + ^#0, называется
системой уравнений, описывающих движение w-мерного твердо-
го тела с закрепленной точкой.
13. Замечание. Общие уравнения Эйлера из п. 8 совпада-
ют с так называемыми уравнениями движения триплета, см.
[75]. В этой же работе показано, как с помощью линейной
замены переменных уравнения D36) привести к уравнениям,
описывающим движение твердого тела.
14. Уравнения Эйлера естественным образом возникают при
изучении геодезических потоков левоинвариантных метрик на
группах Ли. Рассмотрим это более подробно. Касательный ТР
и кокасательный Т Р пучки группы Ли Р допускают триви-
ализацию с помощью левых Lg(H) = gh и правых Rg(h) = hg
сдвигов на элементы g из группы Ли Р. Определим отображе-
ния X: TR-+PxG, X: T"P-+PxG' формулами lk(xg) = (g, dLg_lxg),
~ ~ " СЦ) = (*. dL'?.% Ъ е Т\Р, где G - алгебра Л]
1и Р. Здесь dLg, dL * — индуцированные отображения касатель-
ных и кокасательных пространств, a G* — пространство, со-
пряженное к алгебре Ли G. Каноническая 1-форма 0 на Т*Р
в терминах левой тривиализации Т. запишется следующим
образом: 0(9 5I(jc, P)=<E,, х) для geP, t,, PeG* и xeG. Симплек-
тическая структура d% на касательных векторах (g, E; xt, B{), (g,
?; х2, р2) задается формулой d%Uxu р,), (х2, Р2)) = <|,
[х,,^2]> + <Р2, *1>-<Рь х2}, в которой Xl\g) = dLe\xl), X2(g) =
= dLg(x2) — левоинвариантные поля на Р и р1? р2—левоинвари-
антные ковекторные поля на группе Ли Р.
15. Лемма. Если функция Гамильтона H(t) на Т'Р левоин-
вариантна (т. е. H(Lgt) = H(t), teT'P, geP), то векторное поле
sgrad H тоже ¦ левоинвариантно.
16. Таким образом, если функция Гамильтона левоинвари-
антна, то соответствующее ей гамильтоново векторное поле
sgrad// тоже левоинвариантно и, значит, проекция /: Т*Р-+Т*еР,
задаваемая с помощью левых сдвигов формулой l(t) = Ln.,^-i(t),
согласована с векторным полем sgrad H. Следовательно, на
кокасательном пространстве Т*еР существует векторное поле
Е(Н), согласованное с полем sgrad H. Покажем, что соответст-
вующие полю Е(Н) уравнения совпадают с уравнениями
Эйлера.
17. Предложение. Уравнения Гамильтона на Т'Р, опре-
деляемые левоинвариантной функцией Гамильтона HeC™(G')
в терминах левой тривиализации Т., имеют вид % = d!
dL(dH(ty)

<j 24. КАНОНИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 145
§ 24. Канонические преобразования
1. Определение. Пусть (М\п, raj и (М\п, со2) — симплек-
тические многообразия. Диффеоморфизм/: М1->М2 называется
симплектоморфизмом или каноническим преобразованием, если
/*С02 = (й1.
2. Теорема. Пусть S(<xk, qk)— такая гладкая функция, что
det || d2Sjdak8qi \\ #0. Тогда преобразование пространства T*R",
задаваемое формулами
является каноническим относительно стандартной симплек-
тической структуры на кокасательном расслоении T*R".
Доказательство. Напомним, что симплектическая стру-
ктура на расслоении Т'М определена в п. 11 § 18. Из равенств
D45) получим соотношения
, d2S , d2S , ,..,,
dPi = T-r-daJ+-^rdqJ, D46)
dp^-^jLdoLj-^daj. D47)
Из D47) найдем dqj. Пусть apl находится из условия
• B2S
apl = 8?, что всегда можно сделать в силу невырожденности
матрицы \\d2S/da.idqj\\. Тогда
dqs=-asid^i-a'l-^-da.j, D48)
и из D46) следует
dp'-l^-^a'J^lda^a-d*.. D49)
\_dtjidaj dqtdqs Bafia.^ BqtBqm
Поэтому
. D50)

146 ГЛ. 4. СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ
Вычислим коэффициент при */<хлл*/ал. Пусть Л = ||ар'||,
C=\\d2S/daidqj\\. Тогда АС=Е и А = С~1, следовательно,
СА=Е, т.е. -^-ajs = bl Поэтому
д a idqj
д2$ ^^^. D51)
т. е. получили симметричное по индексам jlf j2 выражение.
п d2S h B2S . .
Далее, а также симметрично по индексам j 1; j2, т. е.
dqfiqi 8a,doiA
коэффициент Fjj2 при daJAda.]i симметричен по индексам у,, j2,
поэтому сумма ? FhHdah л daji равна нулю, так как
JlJl 62s ¦
da: Ada: = —da: Ada, . Аналогично, выражение a'salk сим-
oqidqi
метрично по индексам s, к, поэтому слагаемое с d$s л d$k
в D50) равно нулю. Коэффициент при ( — dv.h Ad$k) равен
d2S d2S ,. a2S 1a | aim d2S d2S a,k_
lslk + lslk 6jt. D52)
a 6
oa.,oa.h
n
Итак, /*ю= Y, d$iAda.t.
3. Предложение. При канонических преобразованиях
гамильтоновы векторные поля переходят в гамильтоновы
векторные поля.
Доказательство. Применим к соотношению df(X) =
= X(f) = m(X, sgrad/), определяющему гамильтоново векторное
поле sgrad /, каноническое отображение g: (M, Q)->(jV, ю).
Получим
g.X, g,sgmd /), D53)
, g.sgrad /). D54)
Здесь g,X= Y—любое поле. Итак, для произвольного поля
Y имеет место соотношение ?2(У, sgrad (g*f)) = d(g*f)(Y) = Cl(Y,
g,sgrad /). Отсюда g,sgrad/= sgrad (gf), т.е. g^,sgrad/—
гамильтоново векторное поле с гамильтонианом g"f=f°g-
4. Замечание. Утверждение, обратное к п. 3, неверно:
преобразования, сохраняющие форму со, и преобразования,
переводящие гамильтоновы векторные поля в гамильтоновы,—
это разные преобразования. Действительно, преобразование
txi = aqi, p;=P/>,- переводит гамильтоново векторное поле sgrad Я

§ 24. КАНОНИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 147
на T'R" в гамильтоново векторное поле sgrad/7, где
^, ^). Однако /*со= ? <*а,л<*Р,- = аР ? dPiAdqt =
\ / ii f i
= арю, т.е. преобразование ai = aqi, Р,= р/>; не является
каноническим при ар#1, см. также п. 1 §8.
5. Замечание. Закон преобразования гамильтониана при
преобразованиях D45) получен в теореме 2 § 8. В частности,
если взять в качестве функции S такую функцию, что
— + H\t, —, ..., —, ql7 ..., qn) = 0, D55)
то преобразования pt = — (t, a, q), pt=— — (t, a, q) переводят
vqi с (X i
dp: ёН da. дН „ д
систему -^-= , ^- = ^— в простейшую систему a, = 0, 6f = 0.
Л Of/,- a( op,
6. Обозначения. Для уравнения вида D55) обычно использу-
ются следующие обозначения: решение S(ql, ..., qn, t) уравнения
D55) называется действием, функция n(t, pY, ..., рп, qt, ...
..., qn) — функцией Гамильтона или гамильтонианом, переменные
qt, ..., qn — координаты, а рх, ..., р„ — импульсы, t — время.
Рассмотрим стационарный случай, когда гамильтониан Н не
зависит от времени /. Тогда действие S ищем в виде
S— — ht+ W[q) и для нахождения функции W получим стаци-
онарное уравнение Гамильтона — Якоби H{8Wjdq, q) = h.
Рассмотрим инвариантную теорию уравнения Гамильтона —
Якоби. Для этого нам потребуется новое понятие.
7. Определение. Пусть N—произвольное многообразие,
а (Л/2", са) — симплектическое многообразие. Отображение
/: 7v->M2" называется изотропным, если/*са = 0. Предположим
дополнительно, что/—иммерсия, т. е. дифференциал с?/инъек-
тивен во всех точках. В этом случае N (вместе с /) называется
погруженным лагранжевым подмногообразием в А/2", если
di21diMi"
8. Лемма. Пусть aefi1 (Г*Мп)—\-форма на^ Т*М", опреде-
ленная в и. 13 § 18, a s—сечение расслоения п: Т*М"^М", т. е.
n°s = id. Тогда s'a = s.
оказательство. Напомним, что если С,теТт(Т'М), то
>wK.rc(Q], dmn: Tm(T'M)->Tnim)M. Поэтому для
Г М) имеем
°s%m)\=s{m%m), D56)
так как n°s = i&. Итак, (s*v.)m = s(m).
9. Следствие. Нулевое сечение кокасательного расслоения
является лагранжевым подмногообразием.

148 ГЛ. 4. СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ
Доказательство. Из соотношения s*ol = s = 0 вытекает
равенство s*(da) = d(s'ah=0.
10. Следствие. Пусть ц>еСх(М). Тогда A = dip(M) —
лагранжево подмногообразие в Т*М, т. е. график любого
дифференциала является лагранжевым подмногообразием.
Доказательство. Имеет место равенство
d2q> = 0. D57)
11. Следствие. Пусть есть такое сечение s: R"->r*R",
что s(R") — лагранжево подмногообразие. Тогда найдется такая
функция 9?C°°(R"), что s = dq>.
Доказательство. Пусть са—симгиектическая структура
на r*R". Тогда ю = й?а, аепЦТ'Я"), см. п. 13 § 18. Лагран-
жевость означает, в частности, что ^*ю = 0, т. е.
0 = s'(o = s*da. = ds*a.. Поскольку любая замкнутая форма на R"
является точной (лемма Пуанкаре), то s*a = d(p, где cpeC^R").
Мы уже доказали, что s'ol = s, поэтому s = dq>.
12. Замечание. Итак, лагранжевы подмногообразия
в T*R", однозначно проектирующиеся на R", исчерпываются
графиками дифференциалов.
13. Обсуждение. Рассмотрим стационарное уравнение Гами-
льтона— Якоби #|tfi, ..., а., —, ..., — ) = c = const, см. п. 6.
\ 81 dqj
Вместе с функцией u(q^, ..., qn), являющейся решением
уравнения Гамильтона — Якоби, все функции w^ + const также
являются решениями этого уравнения. Ввиду того, что такая
совокупность функций однозначно характеризуется дифференци-
алом каждой из них, можно сказать, что уравнение Гамильто-
на— Якоби есть уравнение относительно дифференциала du
неизвестной функции u(q). Рассмотрим поверхность уровня
Г функции Н на T*R". Если и является решением уравне-
ния Гамильтона — Якоби, то график ее дифференциала L =
= <(<?, p)\p = — (q)> лежит на Г. Но графики дифференциалов
функций на R" суть лагранжевы подмногообразия в r*R",
однозначно проектирующиеся на R". Следовательно, решения-
ми уравнения Гамильтона—Якоби являются лагранжевы мно-
гообразия, лежащие на Г и однозначно проектирующиеся на R".
Обобщим нашу задачу, отказавшись от требования одно-
значной проектируемости.
14. Определение. Пусть (М, ш) — симплектическое много-
образие. Уравнение Гамильтона — Якоби на М—это произволь-
ная гиперповерхность V в многообразии М. Произвольное
лагранжево подмногообразие, лежащее на V, называется реше-

§ 24. КАНОНИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
149
нием уравнения Гамильтона — Якоби. Задачей Гамильтона —
Якоби на симплектическом многообразии М называется задача
нахождения лагранжевых подмногообразий, лежащих на по-
верхности V.
Для исследования решений уравнения Гамильтона — Якоби
нам потребуется следующее утверждение, известное как принцип
поглощения.
15. Предложение. Функция Н постоянна на лагранжевом
подмногообразии M"<^N2n тогда и только тогда, когда гамиль-
тоново векторное поле sgrad H касается подмногообразия
M"^N2".
Доказательство достаточности. Поскольку поля
sgrad Я и X касаются лагранжева подмногообразия, то а(Х,
sgrad Я) = 0. Следовательно, dH(X) = X(H) = a>(X, sgrad Я) = 0,
т. е. dH(X) = 0 для всех ХеТаМ, аеМ. Поэтому #|M" = const.
Необходимость. Допустим, что многообразие М"
лежит на поверхности уровня функции Я, т.е. Н\Мп = 0.
Отсюда юm(sgradHm, Xm) = 0 для всех XmeTmM". Если бы
вектор sgrad Hm не принадлежал пространству ТтМ", то
в подходящей системе координат билинейная форма сат имела
бы матрицу, у которой квадрат размера (w+l)x(n+l) состоял
бы из нулей:
0
0 0 • • • 0
А
0
0
0
0
*
в
ж-
D58)
так как форма сат на ТтМ тождественно обращается в нуль
в силу лагранжевости подмногообразия М. Теперь определи-
тель detcam обращается в нуль, так как он равен произведению
определителей выделенных матриц А, В, а в них есть либо
нулевая строка, либо нулевой столбец. Поэтому форма са была
бы вырожденной, что на самом деле не так.
16. Предложение. Пусть задано п-параметрическое се-
мейство лагранжевых подмногообразий Lv<^M2n, расположен-
ных на поверхности уровня как функции ft, так и функции /2
(/i,/2eC00(M2''))- Тогда {A,f2} = 0 (каждое ^расположено на
своей поверхности уровня).
Доказательство. Векторное поле sgrad/i касается лаг-
ранжева подмногообразия Lv в силу принципа поглощения, так

150 ГЛ. 4. СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ
как Lv<={/,= const}. Поскольку подмногообразия Lv лежат на
поверхностях уровня /2=const (v), то поле sgrad/i касается
поверхности уровня /2= const (v) и, следовательно, производная
(sgrad/! )/2 обращается в нуль. Поэтому {/j, /2} =
= -(sgrad/1)(/2)=0.
§ 25. Теорема Дарбу
1. Замечание. Как известно, любая метрика может быть
приведена в одной точке к каноническому (диагональному) виду
путем выбора подходящих локальных координат. В этом
смысле обе структуры — риманова и симплектическая — похожи,
см. п. 5 § 15. Однако между ними имеется и серьезное различие,
проявляющееся в тот момент, когда мы переходим к рассмотре-
нию целой окрестности точки. Как известно, риманова метрика,
вообще говоря, не может быть приведена (путем замены
координат) к диагональному виду в целой окрестности,
поскольку этому может препятствовать ненулевой тензор
римановой кривизны. Симплектическая структура, напротив,
всегда может быть приведена к каноническому виду путем
замены координат сразу в целой достаточно малой окрестности.
Это утверждение составляет содержание классической теоремы
Дарбу. Итак, в этом смысле симплектического тензора кривиз-
ны нет.
2. Теорема Дарбу. Пусть ш—невырожденная замкну-
тая 2-форма в окрестности точки х0 е R 2". Тогда в некоторой
окрестности точки х0 можно выбрать такую систему локаль-
ных координат (plt ..., ря, qi, ..., qn), что форма ш принимает
стандартный вид са= ? dpjAdqt.
3. Лемма. Пусть в окрестности точки х0 е R2" имеются
п независимых функций ф1; ..., ф„ в инволюции. Тогда в некото-
рой окрестности точки х0 существуют такие функции ^fi, ...
..., \|/„, что набор (ф1; ..., ф„, \\flt ..., \|/„) является канонической
системой координат.
Доказательство. Поскольку [sgrad ф(, sgrad ф,] =
= sgrad !фь ф;}=0, то в силу свойства коммутирующих полей
из п. 10 § 13 существуют такие координаты щ, ..., и„, vt, ..., vn,
что sgrad ф, = й/йм,-. Отсюда
{щ, фЛ=^^ <р,•)(«,•) = — = 8.(. D59)
OUj
В силу того, что {ф;, ф;}=0, и в силу равенства D59) имеем
{ф„ф,.} {„„„,} 110 -Е ( 60)
Ц, ф;} {и,, и,} \\е Л У '

§ 25. ТЕОРЕМА ДАРБУ 151
и (<pt, ..., ю„, ul, ..., ип) можно принять за координаты. Пусть
А = || {щ, и-} || = || a(J ||. В силу D59) и тождества Пуассона имеем
равенства
= {6W, и,}-{8ы, и,.} = 0. D61)
Следовательно, {м,-, и,} = аи(ф,, ..., ф„). Тогда
л
Ю=- X й?ф,Лй?М;-Хя;,(ф1> -' ф»)^ф(Л^ф_,. D62)
? = 1 ( <7
Форма Y, а{]с1<$>i/\ d<$> j как разность двух замкнутых форм
замкнута, и, следовательно, в достаточно малой окрестности
/ " \
точки jc0 она точна, т.е. ^ aijd(piAd(pj =
о Д. '<J
В этом случае форма со приводится к виду
\i=i ' 7 \i=i ' 7 \i=i ' ' 7
Полагая tyi = ui—fi(q>l, ..., ф„), мы получим канонические коор-
динаты.
4. Лемма. В пространстве (R2", со) локально всегда
существует п функций в инволюции.
Доказательство. Докажем более сильное индуктивное
утверждение: если имеется к<п независимых функций ф1( ...
..., фк в инволюции, то существует не зависящая от них функция
Фи+i такая, что {фь фц + 1} = 0 (ясно, что одну функцию
в инволюции мы всегда предъявить можем, так как {ф, ф} = 0).
В силу свойства п. 10 § 13 найдутся такие координаты щ, ..., ик;
vu ..., v2n~k, что sgrad Ui = d/8ui. При этом ф; = ф;(г1, ..., v2n-k\
так как — = (sgrad ф>)ф, = {ф1, ф;}=0. Поскольку к<2п — к, то
существует функция <pk+i(v), не зависящая от ф1( ..., ц>к. Тогда
{фк+i, ф,}= ф"'=0. Лемма доказана.
5. Доказательство теоремы 2. Оно сразу следует из
лемм 3 и 4.
6. Замечание. Теорема Дарбу допускает обобщение,
принадлежащее А. Б. Гивенталю, см. п. 8. Теорема Гивенталя
утверждает, что не существует внешней геометрии подмногооб-
разий симплектических многообразий: подмногообразия с оди-
наковой внутренней геометрией локально переводятся друг

152
ГЛ. 4 СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ
в друга сохраняющим симплектическую структуру диффеомор-
физмом объемлющего пространства.
7. Замечание. Нам потребуется следующая формула.
Пусть X—векторное поле на многообразии М,
а ф, — соответствующая однопараметрическая группа диффе-
оморфизмов. Тогда
dtK
D64)
для любой формы а. Равенство D64) сразу вытекает из
определения 1 § 21.
8. Теорема. Пусть М—гладкое многообразие, Y—замкну-
тое подмногообразие в М, а са0, «>i—такие симплектические
структуры на М, что их ограничения на TY совпадают.
Предположим, что а>0, а>1 можно соединить кусочно гладкой
кривой со,, 0<г^1, в пространстве симплектических форм
на М, совпадающих с са0 {или с (oj на Y. Тогда существуют
такие две окрестности U, V подмногообразия Y в М и такой
диффеоморфизм Ф: U-+ V, что ограничение Ф на Y является
тождественным отобра-
жением и Ф*сй1=са0, ины-
ми словами, Ф — симпле-
ктоморфизм (?/, са0) на
У {V, a>i).
Доказательство.
Обозначим линейное от-
ображение из ТХМ
в Т'ХМ, определенное
формой (о, символом /ш.
Пусть U—достаточно
малая трубчатая окре-
стность подмногообразия
Y, X—«радиальное» век-
торное поле на U, каса-
тельное к слоям нор-
мального расслоения
л: U-* Y и обращающееся
в нуль на Y (рис. 23), а <р,—локальная однопараметрическая
группа, порожденная полем X. Предположим, что гомотопия
(а, гладкая. Пусть v, = I^ia,, где
D65)
Ясно, что vt\Y=0. Обозначим Ф(г) локальную однопарамет-
рическую группу, порожденную векторным полем и„ т. е.
-ы
Рис. 23. Расслоение л: U-+Y

§ 26 ВЛОЖЕНИЯ СИМПЛЕКТИЧЕСКИХ МНОГООБРАЗИЙ 153
положим x(t) = <b(t)x0, где x(t) = v,(x(t)), jc@) = jco. Покажем, что
в качестве Ф из формулировки теоремы можно взять отображе-
ние ФA). Проверим, что Ф(;)*ю, = са0, te[O, 1]. В самом деле,
D66)
в силу формулы Лейбница и формулы D64). Из соотношения
D65) следует равенство
L, ю, = d(v, 1ю,) = d(Iov,) = d%. D67)
Из определения D65) легко проверить, что da, = —'-. Из всего
сказанного следует равенство Ф(/)*ю, = ю0, ?е[0, 1], поэтому,
в частности, ФA)*ю1=ю0. Теорема доказана.
9. Замечание. Локальный вариант теоремы 8 не требует
гомотопности форм соо, а>1 в классе симплектических структур,
так как в этом случае можно положить ro, = cao + ?((»i—соо)-
10. Замечание. Теорема 8 в предположении, что симплек-
тические структуры ю0, <»! совпадают на ограничении ТМ\ Y
расслоения ТМ на подмногообразие Y, известна как теорема
Вейнстейна. Ее доказательство можно найти, например, в [74].
Другие доказательства теоремы Дарбу см. например, в [8],
[74], [102], [194], [227], [243], [301], [374].
11. Замечание. Из теоремы Вейнстейна можно получить
следующее важное утверждение о строении лагранжевых под-
многообразий, которое принадлежит Костанту, см. его до-
казательство, например, в [74].
12. Теорема. Пусть L — вложенное лагранжево подмного-
образие в симплектическом многообразии М с симплектической
структурой са. Рассмотрим L как нулевое сечение в T'L, и пусть
о/ — каноническая симплектическая структура на T'L. Тогда
у L существует такая окрестность U в М и такой
диффеоморфизм h: U-+VdT*L, что h\L — '\u и /г*со' = са.
§ 26. Вложения снмплектических многообразий
1. Замечание. Теорему Дарбу можно рассматривать как
теорему о существовании локального вложения окрестности
любой точки симплектического многообразия А/2" в симплек-
тическое пространство R2N с канонической структурой
N
О. = Yj dpi л dqj. Мы естественным образом приходим к следу-
ющему вопросу. Можно ли вложить симплектическое многооб-
разие М2п в некоторое пространство R2N таким образом, чтобы
симплектическая структура са на А/2" индуцировалась стандарт-

154 ГЛ. 4. СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ
ной симплектической структурой Q на R2N, т. е. чтобы со=/*?2,
где /: M2"->R2N — вложение?
2. Определение. Отображение/: M->N симплектического
многообразия (М, rox) в симплектическое многообразие (N, со2)
называется симплектическим, если /*со2=со1.
3. Лемма. Необходимым условием существования симплек-
тического отображения из многообразия (А/, со) в многообразие
(R2N, ? dpiAdq^ является точность формы со, т. е. возмож-
ность ее записи в виде со = й?а, где а — некоторая 1 -форма.
Доказательство. Отображение /: M->R2)V порождает
гомоморфизм /*: H2(R2N; R)-+H2(M; R) групп когомологий,
и поскольку H2(R2N; R) = 0, то [со] =/* [Ь] = О, что и утверж-
далось.
4. Следствие. Компактное замкнутое симплектическое
многообразие нельзя симплектически вложить ни в какое
симплектическое пространство (R2N, ?1).
Доказательство. Точная 2-форма coi на компактном
замкнутом ориентируемом многообразии не может быть
невырожденной. В самом деле, если допустить существование
точной невырожденной формы, то, с одной стороны, ее и-я
внешняя степень дает 2«-мерную форму со" объема на
многообразии М2п. Следовательно, J со" =volM^0. С другой
стороны, форма со" точна, так как а1 =da и со" =d(a Ada л... л da).
По формуле Стокса интеграл по замкнутому компактному
многообразию М от точной формы со" равен нулю. Полученное
противоречие доказывает утверждение.
5. Теорема. Пусть (М2п, со)—произвольное вещественно
аналитическое некомпактное симплектическое многообразие,
причем симплектическая структура со является точной: со = й?ст.
Тогда существует симплектическое вложение многообразия
(М2п, со) в (R , ?2) для некоторого N<co. Более того,
в действительности можно считать, что N=nBn+\).
Доказательство получается из результатов Громова [369],
[376].
6. Замечание. Напомним, что для построения конкретных
примеров симплектических многообразий важно уметь вклады-
вать одно симплектическое многообразие в другое, в этом
случае определены перестройки X, см. п. 30 § 18.
7. Определение. Рассмотрим канонический гомоморфизм
E.Hk(M, Z)->Hk(M, R), отображающий группы целочисленных
когомологий многообразия М в группы его вещественных
когомологий. Этот гомоморфизм возникает, когда мы вклады-
ваем Z в R и рассматриваем каждую целочисленную коцепь как
вещественную. Замкнутая внешняя &-форма на многообразии

§26. ВЛОЖЕНИЯ СИМПЛЕКТИЧЕСКИХ МНОГООБРАЗИЙ 155
М называется целочисленной, если ее класс когомологий
является образом некоторого целочисленного класса когомоло-
гий при гомоморфизме е.
8. Теорема. Комплексное проективное пространство CPN
со стандартной кэлеровой формой Q (см. п. 21 § 18) является
универсальным целочисленным симплектическим многообразием.
Другими словами, любое многообразие М с целочисленной
симплектической формой а может быть вложено в CPN для
подходящего достаточно большого N с помощью такого
отображения /, что /*?2 = а. Если dimA/ = m, то можно
положить N=2m+\.
Доказательство этой теоремы было получено Тишлером в
[503], Нарасимхамом, Рамананом в [460] и Громовым в [369].
9. Пример. Если М*—-многообразие Тёрстона (см. п. 29 § 18),
то его можно вложить в СР5 со стандартной симплектической
структурой, так как симплектическая структура многообразия А/4
является целочисленной. Пусть X—многообразие, полученное из
СР5 перестройкой вдоль МА. Тогда_ имеет место следующая
10. Теорема. Многообразие X является односвязным
симплектическим многообразием с рх (Л/4)=р3(Л) = 3. Следова-
тельно, X не кэлерово.
Доказательство см. в работе [434].
11. Для доказательства обобщения теоремы о вложении
в пространство CPN потребуется следующая важная теорема 12,
известная как теорема Мозера о стабильности, см. [452].
12. Теорема. Пусть М" — замкнутое многообразие
и со,@</<1) — гладкое семейство невырожденных 2-форм из
одного класса когомологий. Тогда существует семейство диффе-
оморфизмов Ft: М-+М, 0<?<1, такое, что F*(coo) = co,.
13. Теорема Тишлера. Пусть М—замкнутое компакт-
ное многообразие и со— целочисленная замкнутая 2-форма на
многообразии М (не обязательно невырожденная). Тогда для
достаточно большого N существует симплектическое отоб-
ражение /: M-*CPN такое, что f ?2 = со, где С1 — стандартная
симплектическая форма на CPN.
Доказательство. Приведем идею доказательства те-
оремы Тишлера, см. [503]. Искомое отображение / строится
в несколько этапов; у-й этап обозначается /,-, O^j^p (p—
некоторое число, зависящее от числа элементов некоторого
открытого покрытия компактного многообразия М). Выберем
/о: M-+CPN таким, что f'0Q и со лежат в одном классе
когомологий. Это можно сделать, так как СР" является
2л-остовом комплекса Маклейна — Эйленберга типа K^L, 2).
Обозначим da точную форму d<x = (o—f'0Cl. Для каждой точки
хеМ найдем такую ее окрестность Wx, что множество
fo(Wx)<^CP" покрывается симплектической картой на СР"
достаточно малых размеров. Существование симплектического

156 ГЛ. 4 СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ
атласа следует из теоремы Дарбу (см. п. 2 § 25) и явно строится
на С/ Тишлером. Выберем конечное подпокрытие Wx, ..., Wp
этого покрытия. Тогда существует набор вещественных функций
р
hk, tk, l^k^p, таких, что л ? dhiAdti = da и их носители
содержатся в одном из элементов покрытия {Wt}.
Для каждого j, I ^j^p, предположим выполненным индук-
тивное предположение: существует отображение fj-\-
M-+CPn+i~^ такое, что
/•_1а"+^1=/оал + -'х dhkAdtk. D68)
71 *=i
Заметим, что отображение fp было бы искомым. Остается
проверить шаг индукции, т. е. построить отображение/,, исходя
из отображения /}_!. На M\Wj положим fj=ifj_l, где
i: CP"+i~i->CP"+J—естественное включение. Существует сим-
плектическая карта на CPn+J со значениями в шаре радиуса 1,
Bn+ii\)<zR2{n+i>. Обозначим символом л^ проекцию шара
B"+J(l) на шар fi"+-'~1(lJcR2("+-'), а символом я2, проекцию
шара Bn+i{\) на шар В1(\)сЪ2.
Пусть фх: Dx-fBN(l)—карта. Определим отображение
() J^
g/. Wj->Bn+i(l), положив я^=фх^_ь K2g] = hj + J^\tj, и от-
ображение /, = Фх gj- Обозначим фх симплектическое коор-
динатное отображение фх: DX-*BN(\), DxczCPN (для любого N).
Теорема М озера о стабильности симплектических форм позво-
ляет аппроксимировать построенное симплектическое погруже-
ние /: M-*CPN симплектическим вложением g: M-*CPN. Чтобы
получить симплектическое вложение g замкнутого симплектиче-
ского многообразия М с целочисленной симплектической
формой со в CPN, исходя из имеющегося симплектического
погружения /: M-*CPN, аппроксимируем / вложением
go'- M-*CPN таким, что все формы A — ?)oj + tg*oQN = oj/, 0</<l,
не вырождены. Тогда по теореме Мозера существует диффе-
оморфизм F: М-*М такой, что /г*со1=юо, т.е. F'g0ClN = a.
Вложение gF: M->CPN будет искомым. Теорема доказана.
14. Замечание. Модифицируя доказательство теоремы
Тишлера, В. А. Попов доказал следующие две теоремы 15, 16.
15. Теорема. Пусть (А/, со)—произвольное симплектическое
многообразие размерности т = 2п с точной симплектической
формой a = dcc. Тогда существует собственное симплектиче-
ское отображение (погружение) /: M-*R2N такое, что
? dpi^dqi J = co, где N=(m+l)(m + 2).
16. Теорема. Пусть (Л/, со)—произвольное симплектическое
многообразие с целочисленной симплектической формой со. Тогда

§ 27. ПУАССОНОВЫ МНОГООБРАЗИЯ 157
существует симплектическое погружение /: M-fCPN, N~m3,
dimM=m = 2n. Существует симплектическое погружение
g: M-*CP2N+1, образ которого g(M) содержится в v2N+l =
= {(z0: ... : zN: zN+u ... : z2N + ij\ существует k^N, гкф0}, и отоб-
ражение g: M-*V собственное. Тогда g гомотопно вложению.
§ 27. Пуассоновы многообразия
1. Определение. Пуассоновой структурой на многооб-
разии М называется билинейная операция {/, g} в пространстве
С°°(Л/) гладких функций на М, удовлетворяющая требованиям:
а) {/, g} = — {g, f) — антикоммутативность; б) выполняется
тождество Якоби {/, {g, h)} + {g, {h, f}} + {h-, {/, g})=0; в)
справедливо тождество Лейбница {h, /1/2} = {Л, fijfi+fi {h, /2}-
Многообразие с пуассоновой структурой называется пуас-
соновым многообразием, а операция {/", g} — скобкой Пуассона.
2. Предложение. Скобка Пуассона однозначно определяет
тензорное поле А1' такое, что А1'=—А'х, причем
Доказательство. Пусть {/, g} — произвольная пуас-
сонова структура на М, a U—открытый шар с центром в OeR".
Если (реС0(U) и ср(О) = О, то существуют такие функции
срь ..., ф„еС°°((У), что ф(м)= X И'*МИ)- Их можно построить по
1
формуле v|/j (и) = J —-t (tu) dt. Тогда очевидно, что —.
= v|/,@). Если
/, geCco{M), то, выбирая на Л/ такие локальные координаты,
что х1{р) = 0 в точке реМ, получим
f[x\ ..., *")= I х;а,; ^(х1, ..., *")= X х'р„ D70)
и по определению пуассоновой структуры
Bul
= {*', xJ}
dg_
3. Лемма. Гладкое кососимметрическое тензорное поле А1'
задает скобку Пуассона тогда и только тогда, когда
?yo. D72)
Вх J

158 ГЛ 4. СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ
4. Определение. Рангом скобки Пуассона в фиксирован-
ной точке хоеМ называется ранг тензора А1'(х0). Рангом
скобки Пуассона на всем многообразии М называется число
* = maxrg^D D73)
Функция feCx{M) называется центральной функцией или
функцией Казимира скобки Пуассона, если она принадлежит центру
алгебры Ли гладких функций, т. е. {/, g}=0 для любой гладкой
функции g. Если скобка Пуассона не вырождена, т. е. ее ранг равен
dim M, то центральными функциями являются только константы.
5. Предложение. Пусть ранг тензорного поля A'j
локально постоянен в точке хеМ и равен R. Тогда в некоторой
окрестности У(х) определены независимые функции /ь ...,/9, где
g = dim M— R, которые являются центральными для ограничения
скобки Пуассона на окрестность У(х).
6. Определение. Каждой гладкой функции Н на пуас-
соновом многообразии М ставится в соответствие векторное
поле v = sgraAH, задаваемое соотношением v(g) = {H, g] для
любой гладкой функции g или в локальных координатах
u' = (sgrad H)' = AJ'~-.. Векторные поля вида i> = sgrad# называ-
ются гамильтоновыми.
7. Конструкция. Пуассоново многообразие М разбивается на
симплектические слои, каждый из которых является локально
симплектическим подмногообразием, размерность которого
равна рангу скобки Пуассона в любой его точке. Касательное
пространство к слою в точке хеМ образовано векторами вида
sgrad/(x), ортогональное дополнение в Т'х М к касательному
пространству слоя совпадает с ядром 2-формы А1'(х), от-
вечающей скобке ¦{/, g). Более точно см. [10], [228]. Назовем
две точки х, уеМ эквивалентными, если их можно соединить
кусочно гладкой кривой, каждый сегмент которой является
интегральной траекторией гамильтонова векторного поля.
Тогда симплектический слой Ох, проходящей через точку х, есть
класс эквивалентности этой точки.
8. Пример. Пусть G—вещественная алгебра Ли, G* —
дуальное к G пространство. Для/, geC"(G*) определена скобка
Березина, см. п. 13 § 22:
{/,#}(ф)=<Ф,[</ф, *,]>. ФеС*> D74)
здесь считаем, что G" = G. В этом примере симплектические
слои совпадают с орбитами коприсоединенного представления
группы Ли Р, отвечающей алгебре Ли G. Векторное поле
sgrad/x имеет вид ad j/ (X) (x). Центральные функции — это
инварианты коприсоединенного представления.

§ 27. ПУАССОНОВЫ МНОГООБРАЗИЯ 159
9. Определение. Функции/, g на многообразии Пуассона
находятся в инволюции, если {/, g}=0. Семейство функций
В в инволюции называется полным в точке хеМ, если
размерность подпространства в Т*ХОХ, порожденного дифферен-
циалами df функций /еВ, ограниченных на слой 0х, равна
2" * dim О,.
10. Предложение. Пусть К<=Т'ХМ—подпространство,
порожденное дифференциалами функций из инволютивного семей-
ства F, а К={^еТ'хМ\А(^, К) = 0}—ортогональное дополнение
к К относительно 2-формы А = \\А li(x)\\ на Т'ХМ, отвечающей
скобке Пуассона. Инволютивное семейство Fполно в точке хеМ
тогда и только тогда, когда К=К+КетА.
11. Замечание. Пусть F: М^М2— гладкое отображение
пуассоновских многообразий Mt, /=1, 2. Определено отображе-
ние F': С™ (U)^>CCO (F'1 (U)), U с М2 — открытое подмноже-
ство в М2. Возникает естественный вопрос: когда это отображе-
ние является гомоморфизмом алгебр Ли.
12. Предложение. Отображение F' индуцирует гомомор-
физм пуассоновых структур тогда и только тогда, когда имеет
место одно из следующих трех эквивалентных требований:
a) F.A1=A2, где At — соответствующее тензорное поле на Mt,
i=\, 2; 6) диаграмма
C°{UX)^CX{U2)
Isgrad Isgrad D75)
коммутативна, где U2 — открытое множество в М2,
U1=F~1 (U2), D(U) — алгебра Ли гладких векторных полей на
U; в) если <о1, со2 — симплектические структуры на симплек-
тических слоях в Mir M2, то F'a>2 \ F=C0j | V, где
V(u) = (KetF,\DuI и Du ={sgrad/J/eC°°(f/)}.
13. Рассмотрим случай скобки Березина (п. 8). Итак, пусть
F: M-+G"—гладкое отображение, М—многообразие с пуас-
соновой структурой {/, g}. Обозначим Ф: G->CCC(M) линейное
отображение Фх(и) = <7г(м), X}, т. е. ФХ = /Г*Х.Х, где \% —
линейный функционал на G', определенный равенством О*-х->
Ф> = <Ф, X}, XeG, cpeG*.
14. Предложение. Отображение F': C°°(G')->С"(М)
является гомоморфизмом пуассоновых структур тогда и толь-
ко тогда, когда Ф: (G, [X, Г])->(С°° (М), {/, g}) — гомомор-
физм алгебр Ли.
15. Определение. Пуассоново многообразие М допуска-
ет реализацию в пуассоновом многообразии N, если существует
такое отображение/: M^N, что F*: С00(N)->С<°{М) — гомо-
морфизм пуассоновых структур. Если N—инвариантное от-
носительно коприсоединенного представления подмногообразие

160 ГЛ. 4. СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ
в пространстве С, на котором в качестве пуассоновой
структуры взята скобка Березина, то в этом случае говорят, что
пуассоново многообразие допускает реализацию в алгебре Ли G.
16. Следствие. Пусть пуассоново многообразие М до-
пускает реализацию с помощью f в алгебре Ли G. Если F,
Н находятся в инволюции на всех орбитах коприсоединенного
представления, то F°f, H°f находятся в инволюции на М.
17. Определение. Пусть симплектическое многообразие
М допускает реализацию / в алгебре Ли G и на М задано
гамильтоново векторное поле sgrad F. Говорят, что оно
реализуется в G с помощью /, если на подмногообразии N, на
котором реализуется М, существует такая функция F,, что
F=Ft°f.
18. Очень часто динамические системы не являются гамиль-
тоновыми. Например, векторное поле v, определяющее динами-
ческую систему, может быть задано на нечетномерном много-
образии М. В этом случае под реализацией системы v будем
понимать задание такой пуассоновой структуры на М, которая
допускает реализацию в некоторой алгебре Ли G, при этой
реализации система x = v(x) должна перейти в гамильтонову
систему. Более подробно, это означает следующее.
19. Определение. Говорят, что векторное поле v на М"
допускает вложение в алгебру Ли, если М" можно отождествить
с инвариантным относительно коприсоединенного представле-
ния подмногообразием V с G' в пространстве G *, дуальном
к некоторой алгебре Ли G, причем: а) векторное поле v касается
орбит коприсоединенного представления группы Ли Р на G'\
б) векторное поле v на V оказывается гамильтоновым на
орбитах относительно стандартной симплектической структуры
{Р—группа Ли, отвечающая алгебре Ли G).
20. Пусть G — алгебра Ли, а р: G->End(F) — ее представле-
ние. Символом G®V обозначим полупрямую сумму G и V.
Коммутатор в G®V определяется формулой [(l1, vt), (/2,
]Vi 2}(p(l)v2-P(l2)v1), /,-eG, v(eV, ;=1, 2.
21. Предложение. В обозначениях предыдущего пункта
пространство T'V с канонической симплектической структурой
со допускает реализацию в алгебре Ли G®V.
р
Доказательство. Для алгебры Ли G отображение R:
T*V=V@V'-^{G®V)', определенное формулой 7?(а®а*)
Р
(/, 1>) = <а*, V — р(/)а>, где а, veV, ot*e V, leG, задает нужную
реализацию.

! 27 ПУАССОНОВЫ МНОГООБРАЗИЯ
161
22. Предложение. Каноническое симплектическое про-
странство R2"(<7j, pt) допускает реализацию в алгебре Ли
верхних треугольных матриц.
Доказательство. Пусть
0N
О
к_ =
D76)
т.е. К+—верхние треугольные матрицы, а К_—нижние
треугольные. Имеется естественное невырожденное спаривание
/: К+ х К_ -* R, f(X, Y) = tiXY, которое позволяет отождест-
вить К\=К_ и К'-=К+. Положим
N=
О .
О
о
-1 р. I
D77)
легко видеть, что N—инвариантное относительно Ad* подпро-
странство. Нужная реализация задается формулами
х„, ух, ..., уя) = U л. , D78)
.-^+i)- D79)
23. Алгебраизация системы Неймана. Рассмотрим материаль-
ную точку на сфере S" = {x||x| = l}, находящуюся в поле
квадратичного потенциала U(x) = 2~l (х, Ах), где А — вещест-
венная симметричная матрица, которую без ограничения
общности можно считать диагональной. Такая система была
проинтегрирована для и = 2 в 1859 г. К. Нейманом, он использо-
вал метод разделения переменных в уравнении Гамильтона —
Якоби (см. § 11). Уравнения движения этой системы имеют вид
Xj= —djXj + vxj, где v = (x, Ах) — \х\2— множитель Лагранжа.
Эти уравнения можно переписать в виде
х(=У(, yj=-ajxj+(Ax@x-\y\2E)xj. D80)
Введем матрицы Х=х®х, Р=х®у—у®х. Тогда уравнения
D80) можно переписать в виде
Х=[Х, Р], Р=[А, X], \х\ = 1, (х, у) = 0. D81)
Если в этих уравнениях сделать замену переменных Х-*Х~п~*Е
и А -> А—п~1 (trA)E, то можно считать, что X, Pes\(n, R).

162 ГЛ. 4. СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ
Для реализации системы Неймана на орбите коприсоединен-
ного представления рассмотрим алгебру Ли Q(sl(«, R)) =
= sl(«, R)®R [x]/(x2), ей отвечает группа Ли Q(SL(n, R)) =
= SL(«, R)xsl(«, R) с умножением (gt, ^)(g2, ^2) = (gi?2,
^j + Ad,, ^2). Рассмотрим в ?2(si(и, R)) подалгебру L = so(n) + S,
где S—векторное пространство всех симметрических матриц,
и подпространство V=S+so(n). Пространство L* отождествим
с V, используя прямую сумму форм Киллинга (А, В} —
= — 2~1trAB. Система Неймана реализуется на специальной
орбите коприсоединенного представления группы Ли Г, от-
вечающей алгебре Ли L.
24. Теорема. Рассмотрим орбиту группы T=SO(n)x S,
проходящую через точку z(g)z — n~1E в пространстве
L* = so(n)@S, z = (\, ..., 1)/ч/й. Она состоит из пар (X, Р),
Х=х®х — п~1 Е, Р = х®у—у®х, |х| = 1, (х, у) = 0. Эта
2(и— \)-мерная орбита с симплектической структурой Кирил-
лова диффеоморфна касательному расслоению TS"~ при отоб-
ражении (X, Р)—*{х, у) с симплектической структурой,
п
индуцированной на TS"'1 структурой ? dXj л dy} в простран-
стве R2"(x;, yj). Гамильтониан
Н(х,р)=-2-1(Р,Р) + <А,Х) D82)
определяет на этой орбите уравнения движения для системы
Неймана {см. D81)).
Доказательство см. в [482]. Гамильтоновость уравнений
D81) была также установлена в [305].

ЧАСТЬ 2
АЛГЕБРАИЧЕСКИЕ СВОЙСТВА
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Глава 5
ГАМИЛЬТОНОВЫ СИСТЕМЫ С СИММЕТРИЯМИ.
СИМПЛЕКТИЧЕСКИЕ ДЕЙСТВИЯ ГРУПП ЛИ
НА СИМПЛЕКТИЧЕСКИХ МНОГООБРАЗИЯХ
§ 28. Вполне интегрируемые гамильтоновы системы
1. Определение. Система гамильтоновых уравнений
x = sgrad// на симплектическом многообразии (М2п, со) называ-
ется вполне интегрируемой, если существуют такие гладкие
функции /i, ..., /„ на многообразии М2п, что: а)/] — первые
интегралы потока х, т. е. {Н,/<}=0, /=1, ..., «; б) функции/!, ...
...,/„ находятся попарно в инволюции, {/;, /}}=0; в) функции
fi, ...,/„ функционально независимы почти всюду на М , т. е.
их дифференциалы линейно независимы на открытом всюду
плотном подмножестве в М2п.
Семейство функций /\, ...,/„, удовлетворяющее свойствам
а) — в), будем называть полным инволютивным.
2. Пример. Система х = sgrad Н, где Н определена в
п. 19 § 20, является вполне интегрируемой: функции F1? F2,
F3, определенные в п. 19 § 20, дают полный инволютив-
ный набор первых интегралов, что вытекает из лемм
21—23 в § 20.
3. Предложение. Геодезический поток на поверхности
вращения является вполне интегрируемым.
Доказательство. Пусть М2 — поверхность вращения.
Геодезический поток определен на Т*М . Поскольку dim
Т* М2 = 4, то для полной интегрируемости надо указать полное
инволютивное семейство функций, состоящее из двух функций,
т. е. достаточно указать один первый интеграл геодезического
потока, см. п. 1 § 20.
Для геодезических на поверхности вращения выполнено
соотношение х sin ю = const, где со — угол, который геодезическая
линия образует с меридианом в точке пересечения с ним,
а х — радиус параллели, на которой лежит рассматриваемая
точка, или, что то же самое, расстояние до оси вращения

164
ГЛ. 5. ГАМИЛЬТОНОВЫ СИСТЕМЫ С СИММЕТРИЯМИ
(рис. 24). Это утверждение в элементарной дифференциальной
геометрии известно как теорема Клеро.
4. Определение. Пусть К2"— симплектическое многооб-
разие, Н—гладкая функция на К2". Рассмотрим однопарамет-
рическое семейство
Vc = {H=c), ceR, по-
верхностей уровня га-
мильтониана Н и соот-
ветствующее семейство
задач Гамильтона —
Якоби в симплектиче-
ском многообразии
К2". Говорят, что за-
дача Гамильтона —
Якоби имеет невырож-
денное п-параметричес-
кое семейство решений
в области Uс К2", ес-
ли существует отобра-
жение ф: U-* V на об-
ласть K<=R" такое,
что: а) ф регулярно,
т. е. ранг й?ф максима-
лен; б) для любого ve V прообраз (p1(v) = Lv является лагран-
жевым подмногообразием, лежащим на некоторой поверхности
уровня функции Н, т. е. Lv — решение соответствующей задачи
Гамильтона — Якоби, см. п. 14 § 24. Пусть Qt: K->R (/=1, ...
..., п) — координатные функции на V. 'Если Vbv = (c1, ..., с„),
п
Геодезаческая
Рис. 24
то Lv =
где Qi = (
> — параметры лагран-
жевых многообразий Lv, понимаемые как функции на U.
5. Теорема. Пусть задача Гамильтона—Якоби имеет
невырожденное п-параметрическое семейство решений в некоторой
области U симплектического многообразия М2п. Тогда соответ-
ствующая гамильтонова система х — sgrad H вполне интегрируема
в U, причем за набор коммутирующих первых интегралов можно
принять параметры, рассматриваемые как функции на U.
Доказательство. Дифференциалы функций Qt линейно
независимы в силу регулярности отображения ф (Lv —
подмногообразие в силу теоремы о неявных функциях, так как
Ф — регулярное отображение).
Лагранжевы многообразия Lv лежат на поверхностях уровня
Н = с по определению решения уравнения Гамильтона^—Якоби.
Далее, Lv лежат на поверхности уровня функции Qj = Qj°q>,
поэтому по предложению 16 ^24 имеем {Н, Qj} = 0, т.е.
Qi — первые интегралы потока х = sgrad//, и по тому же

§ 28. ВПОЛНЕ ИНТЕГРИРУЕМЫЕ СИСТЕМЫ
165
предложению {Qt, Qj}=Q, т. е. функции Qt в инволюции и их
число по определению равно половине размерности многооб-
разия Л/2".
6. Предложение (А. В. Браилов). На любом симплектиче-
ском многообразии существует полное инволютивное семейство
гладких функций, функционально независимых почти всюду на
многообразии.
Доказательство. Согласно теореме Дарбу п. 2 § 25
в некоторой шаровой окрестности любой точки существуют
симплектические координаты, т. е. симплектическая структура
имеет каноническое представление dp i л dq t +... + dpn Adqn. Ha
этом шаре рассмотрим функции fi=Pi+ql¦ Ясно, что {/f, f]}=0,
т. е. эти функции находятся в инволюции. Пусть
л л
/= ? /;= ? (p? + qf)- Построим теперь на шаре гладкую
функцию h=g°f, зависящую только от «радиуса» / шара, равную
единице в центре шара, равную тождественно нулю на границе
шара и монотонно убывающую с ростом / от единицы в центре
шара до нуля на границе (рис. 25).
Эту функцию продолжим нулем на
все многообразие. Ясно, что {А,
ft} = 0, следовательно, {hfi, hfJ}=0.
Утверждается, что функции
hfi, ..., hfn независимы внутри
шара. В самом деле, если допустить
функциональную зависимость, то
существует такая функция F^Q,
ЧТО Fihfi, ..., hfn) = O, Т.е.
Y "
z-g(t)
Рис. 25. е—радиус координат-
ного шара
Z/i)/i> •••' ? E-/i)/»)-°- Ясно, что функции /1;
..., jn независимы, поэтому можно заменить их формальными
переменными /t, ..., tn. Если мы докажем, что функция
(л \ / л \
^ tt \ti, ..., gl ^ tj \tn) не равна тождественно нулю, то тем
самым докажем независимость функций hfi, ..., hfn.
Допустим противное, пусть указанная функция тождественно
обращается в нуль, т.е. функции g(? '¦ )h, ¦•-, g
функционально зависимы. Якобиан
очевидно, равен
vi / v=i /
J этой системы функций,
1 о
О'i
D83)
dt

166 ГЛ. 5. ГАМИЛЬТОНОВЫ СИСТЕМЫ С СИММЕТРИЯМИ
где t = ti + ... + tn. Если J=0, то g+t — = 0, т. е. g(t)—линейная
функция, что не так.
Покрывая теперь многообразие счетным числом дисков
и выполняя на каждом из них только что описанную конструк-
цию, получим искомый на-
бор функций кх, ..., к„, кото-
рые попарно находятся в ин-
волюции и каждая kt от-
лична от нуля на открытом
всюду плотном подмножест-
ве (рис. 26).
7. Замечание. Кон-
струкция, изложенная в п. 6,
носит формальный харак-
тер: она показывает, что
в гладком случае на любом
Рис 26 симплектическом многооб-
разии существует хотя бы одна вполне интегрируемая гамиль-
тонова система. Однако ясно, что построенный в п. 6 набор
функций не представляет интереса с точки зрения содержатель-
ных физических приложений. Поэтому следует сузить класс
функций, среди которых нужно искать вполне интегрируемые
гамильтоновы системы и полные инволютивные семейства
функций. Часто рассматривается класс аналитических функ-
ций. Другой естественный класс таких функций указан в § 57 —
это так называемые боттовские функции на гладких многооб-
разиях.
§ 29. Структура вполне интегрируемых
гамнльтоновых систем
1. Теорема Лиувилля. Пусть на симплектическом 2п-
мерном многообразии Мг" задана система п функций /,, ...,/„,
находящихся попарно в инволюции, т. е. {/;,./}} =0, i, 7=1, ..., п.
Рассмотрим множество уровня этой системы функций, т. е.
М^ = {хе М |/; [х) = ?;, г=1, ..., п). Предположим, что на М% функ-
ции fj, j=l,...,n, независимы, т.е. l-формы df,, j=\,...,n,
линейно независимы в каждой точке хеМ^. Тогда: а) М^ —
гладкое многообразие, инвариантное относительно потока sgrad//
с функцией Гамильтона H=ft; б) если многообразие М^ компак-
тно и связно, то оно диффеоморфно п-мерному тору Т"; в)
фазовый поток sgrad Н с функцией Гамильтона Н определяет на
М^ условно периодическое движение.
Доказательство. По теореме о неявных функциях
М^ — гладкое многообразие размерности dimM,.=n.

§ 29. СТРУКТУРА ВПОЛНЕ ИНТЕГРИРУЕМЫХ СИСТЕМ 167
2. Лемма. На п-мерном многообразии М^ существуют
п касательных векторных полей, попарно коммутирующих
и линейно независимых в каждой точке.
Доказательство. Поля i;, = sgrad/;, /=1, ..., п, искомые.
Действительно, по условию dfi линейно независимы, а операция
поднятия индексов с помощью со является изоморфизмом,
поэтому поля vt также линейно независимы. Далее,
[sgrad/b sgrad/,] = sgrad{/,, /t}=sgrad0 = 0 D84)
в силу предложения 11 § 21. Итак, поля vt коммутируют. Поля
vt касаются поверхности М^. Действительно, вектор X касается
поверхности Н=const тогда и только тогда, когда dH(X) = 0,
так как уравнение dH=0 задает касательную плоскость к по-
верхности Н—const. В нашем случае
fi?fi(sgrad/t) = {/;, fk} = 0. D85)
3. Следствие. Многообразие М^ инвариантно относитель-
но каждого из п коммутирующих фазовых потоков i = sgrad/f
с функцией Гамильтона ft.
4. Следствие. Многообразие М^ является лагранжевым.
Доказательство. Векторы sgrad/f образуют базис
в ТХМ, и со (sgrad/,, sgrad/,) = {/b /}}=0.
5. Предложение. Пусть Р" — компактное связное п-мер-
ное многообразие, на котором задано п попарно коммутирующих
векторных полей, линейно независимых в каждой точке. Тогда
Р" диффеоморфно п-мерному тору.
Доказательство. Построим действие группы Ли R" на
Р". Пусть ф|, i=l,..., «,— однопараметрическая группа, от-
вечающая векторному полю vh которое задано на Р" по
условию. Поскольку \vu Vj]=O, то потоки <р\, ф; коммутируют,
см. п. 34 § 10. Поскольку многообразие компактно, то вектор-
ные поля vt порождают не локальные однопараметрические
группы, а глобальные, т. е. vt — полные поля. Определим
действие ф': М-*М, teR", группы R" на Р" формулой
ф'(х) = ф'1...ф'"(х), где t = (ti, ..., ?n)eR". Очевидно, что <p'<ps = <pt+s
для всех t, seR".
6. Лемма. Построенное действие группы R" на Р" тран-
зитивно, т. е. любую точку хоеР" можно с помощью
некоторого отображения ф' перевести в любую наперед
заданную точку хеР".
Доказательство. Рассмотрим отображение ф: R"->P,
ф(г) = ф'(;с0). Вычислим его дифференциал d<p: ToR"-*TXoP.
Имеем'
D86)

168
ГЛ. 5. ГАМИЛЬТОНОВЫ СИСТЕМЫ С СИММЕТРИЯМИ
Поэтому матрица отображения d<p имеет вид || v-,j ||, где v{j—это
j-я координата вектора v(. Следовательно, detdcp^O, так как
vx, ..., vn линейно независимы. Итак, существует такая окре-
стность U точки х0 и окрестность V точки OeR", что
Ф отображает V на U диффеоморфно.
Рис. 27
Рис. 28
Соединим точку х с х0 кривой y(t), покроем эту кривую
конечным числом окрестностей Uu ..., UN, построенных выше
(рис.27). Пусть хге Uip\U2, ¦¦¦, xN-xe UN-iC)UN. Тогда имеем
xl = q>tlx0, ..., x=(ptrixN-i, и окончательно x = (pttl+'"+tlx0
(рис. 28).
7. Лемма. Стационарная подгруппа любой точки хоеР
относительно построенного действия группы R" на Р дискретна.
Доказательство. Поскольку R" — абелева группа, то
стационарная подгруппа Z={teR"\(p'(xo) = xo} не зависит от
выбора точки хоеР. Проверим, что в достаточно малой
окрестности V точки 0 в Z нет других точек стационарной
подгруппы Z кроме точки t — О. Это вытекает из того, что
ф: V-*U—диффеоморфизм, см. п. 6.
8. Предложение. Пусть Г с R" — дискретная подгруппа.
Тогда существует линейно независимая система векторов
еи ..., e*eR" такая, что r = <xeR"|x = ? ntet, «;eZ>.
Доказательство. Проведем индукцию по п. Пусть п = 1.
Если Г#{0}, то выберем наименьший по абсолютной величине
элемент ^еГ, ехф0 (такой элемент существует в силу
предположения о дискретности Г). Если уеГ, то найдется такое
целое число meZ, что \y-mei\<\e1\, но у — теуеТ, следова-
тельно, у — me^=Q, т.е. у = тех и et порождает группу Г.
Предположим, что для размерности п—\ утверждение
доказано, докажем его для размерности п. Пусть Г—ди-
скретная подгруппа в R". Считаем, что Г#{0}; ехеГ—такой
элемент, что ехФ0 и ехфту, уеГ, т>\, т.е. et не
является кратным некоторого элемента уеГ. Рассмотрим

§ 29. СТРУКТУРА ВПОЛНЕ ИНТЕГРИРУЕМЫХ СИСТЕМ 169
(«— 1)-мерное пространство R^R^ и естественную проекцию
л: R -+R"/Re!. Докажем, что л(Г) — дискретная подгруппа
в R"/Re1. Пусть я (Г) не дискретна, это означает, что существует
такая последовательность у„еГ, что я (у„)->() при и-юо, но
я (у „) фО. Пусть R" = Re1® V. Можно считать, что я есть проекция
на V. Тогда уп = с„е1 + у'л, я(уп) = у^->0 при «->оо. Будем считать,
что с„е,—ограниченное множество. Действительно,
Уп = Уп-[сп]е1еГ и ?„ = {сп}е1 + у; = с|,е1+у;. Множество {с„}
ограничено. Следовательно, из него можно выбрать сходящуюся
подпоследовательность ся-*с, и->оо. Тогда уп-*сеи и-»со, так как
yJ,->0, «-+00, причем у„^сеь так как у'„т*О. Если {св}е1+у1, = се1,
то ({с„} —с)е!+у^ = О, поэтому {с„} —с = 0 и у„ = 0. Итак, у„еГ,
у„->сеь и-^оо, упфсеи а это противоречит дискретности группы Г.
По предположению индукции существует система линейно
независимых векторов fi,---,fk такая, что
n(r) = <xeR"|x= ? Wj/j, w,eZ>. Выберем такие векторы
е2, ..., et, что л(е()=/;(/ = 2, ..., к), и рассмотрим систему еи
е2, ¦¦¦, ек. Очевидно, что эти векторы линейно независимы. Это
искомая система: если уеГ, то
* (Г) =?#*,./; = л (?»!,*,), D87)
к к
следовательно, у— ? »»;?,• eRej, т. е. у— ^ miei = m1e1.
9. Доказательство предложения 5. Многообразие
Р диффеоморфно факторпространству R"/Z, где Z—стационар-
f " 1
ная подгруппа. Поскольку Z=< ? Wjgj, WjeZ> в силу предложе-
ti=i J
ния 8, то P = R"/Z=T", что и утверждалось.
10. Определение. Пусть Т" — и-мерный тор, ср =
= (фь ..., ср„) — угловые координаты. Однопараметрическая
группа диффеоморфизмов тора Т" называется условно пери-
одическим движением, если она описывается дифференциальным
уравнением ф = со, со = (соь ..., con) = const.
Эти уравнения немедленно интегрируются: cp(?) = cp(O) + co?.
Таким образом, в карте {ср;} траектории являются прямыми
линиями. Величина со называется частотой условно периодиче-
ского движения.
11. Доказательство теоремы 1. В силу леммы
2 многообразие М^ удовлетворяет условиям предложения 5.
На М^ построена карта ср: V->U, <p(tu ..., tn) = <p'1.x.q>'nx0.
Очевидно, что координатная линия {?j = const, 7=1, ... i, ..., п\
переходит в интегральную траекторию векторного поля sgrad/f.
Теорема 1 доказана.

170 ГЛ. 5. ГАМИЛЬТОНОВЫ СИСТЕМЫ С СИММЕТРИЯМИ
12. Замечание. Если поверхность уровня М^ некомпакт-
на, то векторные поля sgrad/j, вообще говоря, не полные
и действие группы Ли R" на М^ мы не получим. Если такое
действие существует, то поверхность уровня М^ диффеоморфна
цилиндру T"~kxRk.
13. Замечание. Если выполняются условия теоремы 1,
то соответствующая гамильтонова система локально может
быть явно решена при условии, что симплектическая струк-
тура со точна, т. е. <a = da. Это утверждение вытекает из
теоремы 1 § 12.
14. Определение. Инволютивная система функциональ-
но независимых функций/ь ..., /„ на симплектическом многооб-
разии М" называется канонически сопряженной с инволютивной
ункционально независимой системой функций gb ..., gn, если
/} 8 l
. Теорема. Пусть (М2п, со) — симплектическое многооб-
разие с точной симплектической структурой со = й?а. Тогда для
любой инволютивной -функционально независимой системы
fi, ..., /„ канонически сопряженная система gi,..., gn функций
строится с помощью квадратур.
Доказательство. По предположению функции /ь ...,/„
функционально независимы, дополним их произвольным об-
разом до некоторой локальной системы координат /ь ..., /„,
hi, ..., hn. Имеем равенство
«= t ajdfj+ | bjdkj, D88)
где ah bj, i, j=\,...,n,— некоторые гладкие функции. На
подмногообразии Л/^ = {/; = ^, /= 1, ..., п} 2-форма со обращается
в нуль, см. п. 4, т.е. со|Л/^ = 0. Тогда ограничение а\М^
локально является полным дифференциалрм некоторой функции
QeCco(M) (т.е. a.\M^ = dQ), так как d(a\M^ = (da)\M!.=
= со | М^ = 0. Имеем
dQ= ^ —dfj+ ? —dhj. D89)
Ограничим соотношения D88), D89) на М%, получим
I d?dfj+ t bjdhj = dQ, D90)
4= ? — А= Z bidhj- Отсюда
и, следовательно,
^ (a.-W\dfj. D91)

§ 30. НЕКОММУТАТИВНОЕ ИНТЕГРИРОВАНИЕ 171
Положим gi = ~ — ai, i=l, ..., л. Тогда из D91) следует, что
п
форма а имеет вид cc = dQ — ? gidft. Таким образом,
i=i
<в = </«=?<//, л rfg,. D92)
i=l
Из невырожденности формы со следует, что функции /ь ..., /„,
glt ..., gn функционально независимы в совокупности, причем
{/;> gj}=&ij и {gu gj} = 0, i, 7=1, ..., п.
16. Замечание. Конструкции п. 15 выполняются только
локально. Построение аналогичных координат в некоторой
окрестности тора представляет собой отдельную сложную
задачу.
17. Определение. Координаты срь ..., ср„, sx, ..., sn,
действующие в окрестности тора М^, называются переменными
действие—угол для данной гамильтоновой системы, если: а)
фь ..., ф„—угловые координаты на торах, близких к М^; б)
со= '? d<pi/\dsi; в) исходная гамильтонова система имеет вид
i; = 0, ф^шДхь ..., sn), 1, 7=1, ..., п.
Заметим, что в целом на всем многообразии координаты (ф(,
Sj) определить нельзя. Соответствующее препятствие указано
в работе [341 ], там же рассмотрен пример, когда оно отлично
от нуля.
18. Конструкция. Укажем алгоритм построения перемен-
ных действие — угол. Пусть уи ..., у„ — базисные циклы тора
М^, Ри ..., рп, <7ь ..., <7„ — координаты. Положим
^§t D93)
Y, * = 1
Переменные sl7 ..., sn канонически сопряжены с угловыми
переменными фь ..., ф„, см. [8], [102], [374].
§ 30. Некоммутативное интегрирование гамильтоновых систем
1. В теореме Лиувилля 1 § 29 основную роль играет
коммутативность набора функций fu ..., /„. Другими словами,
линейное пространство G функций, натянутое на /ь ..., /„,
является коммутативной алгеброй Ли размерности п. При этом
гамильтониан интегрируемой системы включен в эту алгебру
как один из ее элементов: F=fl. Во многих конкретных
ситуациях гамильтоновы системы обладают набором интег-
ралов /ь ..., /„, которые не образуют коммутативной алгебры
Ли, т. е. не находятся в инволюции. Поэтому было бы весьма

172 ГЛ. 5. ГАМИЛЬТОНОВЫ СИСТЕМЫ С СИММЕТРИЯМИ
полезно располагать методом, позволяющим интегрировать
некоторые такие системы. Следующая теорема 2 естественно
обобщает теорему Лиувилля, см. работы А. С. Мищенко,
А.Т.Фоменко [187], [191].
2. Теорема. Пусть на симплектическом многообразии М1п
задан набор из к гладких функций /ь ...,/*, линейная оболочка
G которых является алгеброй Ли относительно скобки Пуас-
k
сона, т.е. {/,, /,•}= Y, C1jfq, где Cfj = const. Пусть М% — со-
4=1
вместная поверхность уровня общего положения функций fh
т.е. M^ = {xeM[fi(x) = t,i, 1</<л). Предположим, что на
этой поверхности уровня все к функций /ь ..., fk функцио-
нально независимы, алгебра Ли G удовлетворяет условию
dimG + indG = dimA/. Тогда поверхность М^ является гладким
r-мерным подмногообразием (где r = indG), инвариантным от-
носительно каждого векторного поля i> = sgradA, ЛеАпп(^) = {хе
eG|adx?, = 0}. Пусть далее v—одно из следующих гамилътоно-
вых полей на М: а) либо i> = sgradA, где гамильтониан h является
элементом алгебры интегралов G и лежит в аннуляторе Ann(i;)
ковектора Ь,, определяющего поверхность уровня М^; б) либо
f = sgradf—гамильтоново поле на М, для которого все функции
алгебры G являются интегралами, т. е. {F, /} = 0 для всех /е G.
Тогда, как и в случае «коммутативной теоремы» Лиувилля, если
многообразие М^ связно и компактно, то оно диффеоморфно
r-мерному тору Тг, и на этом торе можно ввести такие
криволинейные координаты «Pi, ..., срг, что векторное поле и,
будучи записано в этих координатах, на торе приобретает вид
<Pi = 9i(^i, ..., ?*), т. е. компоненты этого поля v постоянны на
торе, и интегральные траектории поля определяют условно
периодическое движение системы v, m. e. задают «прямолиней-
ную обмотку» тора Тг.
3. Замечание. Если алгебра Ли G интегралов коммутатив-
на, то условие dimG + indG = dimA/ превращается в условие
k + k = 2n, так как indG = dimG = &. Итак, к = п, и мы получаем
классическую «коммутативную теорему» Лиувилля, доказанную
в предыдущем параграфе.
4. Определение. Гамильтонова система i> = sgradA на
симплектическом многообразии М2п называется вполне интег-
рируемой в некоммутативном смысле, если она обладает такой
алгеброй Ли G интегралов, что dimG + indG = dimA/. Вполне
интегрируемую систему в смысле определения 1 § 28 будем
также называть интегрируемой в коммутативном смысле.
5. Опишем простую и красивую конструкцию, позволяющую
превращать гамильтонову систему, обладающую группой сим-
метрии, в гамильтонову систему на симплектическом многооб-
разии меньшей размерности (Марсден и Вейнстейн [431]).

§ 30. НЕКОММУТАТИВНОЕ ИНТЕГРИРОВАНИЕ
173
Соответствующая процедура называется редукцией гамиль-
тоновой системы. Эта конструкция используется, в частности,
при доказательстве теоремы 2.
Пусть на симплектическом многообразии (А/2", со) задана
гамильтонова система i; = sgradF с алгеброй Ли G интегралов,
аддитивными образующими которой являются к независимых
(почти всюду) гладких функций /1; ..., fk. Пусть Р—соответст-
вующая группа Ли, действующая на М симплектическими
диффеоморфизмами (т. е. сохраняющими со). Каждой точке
хеМ сопоставим линейный функционал ф(х) на алгебре Ли G.
Положим ф(х)/=/(х), где feG. Итак, cp(x)eG*.
Следовательно, имеем отображение ср: M-*G*.
6. Лемма. Пусть ?eG* — произвольный ковектор. Тогда его
полный прообраз ср'1^) при отображении ср является совмест-
ной поверхностью уровня М^ интегралов /ь ..., fk — образующих
алгебры Ли G.
Доказательство. По определению ф~1(У = {х?
еА/|/(;с) = !;(/)}, где feG. Поскольку (/,) — аддитивный базис
d- Если
в G, то /=?>/, т.е. f( l
l^i^k, то */<(*) = Ф(*)/| = 5(Л) = ^ ' Для хеМ^. Итак,
Л/4 = ср i(?,) = {xeM\fi(x) = ?)i}, ^ = (^i, ..., Ъ). Лемма доказана.
7. Предложение. Пусть элемент /еG лежит в ан
нуляторе Ann (?) и хеМ^, где М^ — неособая поверхность. Тогд
d/()rM
элемент /еG лежит в ан-
^ — неособая поверхность. Тогда
A /r°
/E
Доказательство. Рассмотрим аддитивные образующие
/ь ..., fk в G и градиенты grad/b ..., grad/*. Поскольку
Мк—неособая поверхность, то
все эти градиенты независимы во
всех точках поверхности, поэто-
му они трансверсальны А/5, т. е.
А:-мерная плоскость V, натянутая
на grad/j, пересекается только по
нулю с ТХМ^, V@TxMii=TxM
(рис. 29). Удобно считать, что на
М задана риманова метрика.
Тогда векторы grad/,- орто-
гональны поверхности М^. Что-
бы доказать соотношение
sgrad/(x)e TXM%, достаточно
проверить, что (sgrady)g = O для любой функции geG, т. е. что
производная вдоль sgrad/ любой функции geG, постоянной на
А/5, равна нулю. В самом деле, (sgradf)g = (sgrad/, sgrad g), где
(x, у) — риманова метрика на М. Из равенства нулю скалярных
произведений вектора sgrad/ на все векторы grad/ вытекает
ортогональность sgrad/к плоскости V, т. е. sgrad/e TXMK. Итак,
Рис. 29

174 ГЛ. 5. ГАМИЛЬТОНОВЫ СИСТЕМЫ С СИММЕТРИЯМИ
(sgrad/)*={/; g}. Далее, {f, g}{.x) = <& {/ g}> = <ad}^ ?>=0, так
как ad}% = 0, /eAnn(^), что и требовалось доказать.
8. Предложение. Имеет место равенство (рис.30)
(Тх ЩП{sgrad Д/е G} = Кх = {sgrad Л|h е Ann ft)}. D94)
Доказательство. В п. 7 доказано, что {sgradA|Ae
е Ann (?;)}<= rxM^n{sgrad/|/eG}. Докажем обратное включение.
Пусть ХеТхМ^ и Х= sgrad/ где /еС Надо доказать, что
Рис. 30 Рис. 31
/eAnn(?,). Рассмотрим <at/}^, g> = <^, {/ ?}>=0 для любого
geG, так как \j\ g}(x) = 0. Последнее равенство вытекает из
того, что [/; g}(.x) = (sgrad/)g|;c = A'(g) = O, так как A"e ГХМ^, а все
geG постоянны на поверхности уровня А/с. Итак, <а
при любом geG. Это означает, что лс1}\ = 0, т.е.
Предложение доказано (рис. 31).
9. Следствие. Поверхность уровня М^ инвариантна от-
носительно действия группы S^ отвечающей алгебре Ли Ann (^),
на многообразии М.
10. Рассмотрим форму со на М, и пусть
E = co|Mf—ограничение ее на поверхность М^. Действие под-
группы 5^ на М^ порождает в каждой точке х е М? подпростран-
ство КХ<^ТХМ^, образованное векторами sgrad/, /еАпп(^).
11. Предложение. Ядро формы со совпадает с подпрост-
ранством КХ^ТХМ^.
Доказательство. Покажем, что КегсопА^. Пусть
A'=sgrad/7, /;eAnn(Q, ХеКХ<=ТХМ^. Требуется доказать, что
X лежит в ядре формы со, т. е. что со(Х, У) = 0 для любого
вектора Y из подпространства ТХМ^. В самом деле, co(A", Y)~
= со (sgrad h, У)— У(Л) = 0, так как вектор Y касается поверхности
уровня, а функция h, являясь элементом алгебры интегралов G,
постоянна на поверхности уровня. Докажем обратное, т. е. что
Кег со с: Л"*. Пусть (?>(Х, У) = 0 для любого вектора YeTxM^.
Требуется представить вектор X в виде X=sgrddh для
некоторой функции ЛеАпп(^). Рассмотрим форму со как
кососимметрическое скалярное произведение на касательном

S 30 НЕКОММУТАТИВНОЕ ИНТЕГРИРОВАНИЕ
175
пространстве ТХМ и обозначим (TXM^)L ортогональное допол-
нение относительно формы со к подпространству ТХМ^ в ТХМ.
Поскольку форма со не вырождена, то имеет место равенство
d\m{TxM()t=d\mM-d\mTxM!.=d\mV=k. Ясно, что
Кета=ТхМ^О(ТхМ01- Докажем, что {sgrad/|/eG} = (ТхМ01.
В самом деле, пусть YtTxMK. Тогда co(sgrad/; Y)=Y(f) = 0, так
как y^const на М%. Итак, {sgrad/|/eG} с {ТХМ1I. Далее,
dim {sgrad/|/eG}=? = dimG. Это равенство вытекает из того,
что линейная оболочка градиентов (grad/|/e G) имеет размер-
ность к, а кососимметрическое скалярное произведение не
вырождено и линейная оболочка косых градиентов также имеет
размерность к. Наконец, было доказано, что dimG'xM^)± = ^,
поэтому {sgradf\feG} = (TxMiI. Предложение доказано.
12. Соберем вместе все факты и изучим геометрическую
картину взаимодействия описанных подмногообразий. Основ-
ными объектами являются: а)
поверхность уровня М^,
dimM^ = 2n — k; б) орбита Р(х)
точки х, dimP(x) = k; в) орбита
S^(x) точки х при действии под-
группы Sf, отвечающей алгебре
Ли Ann (у. Ясно, что TxG(x) =
= isgrad/|/eG}, TxS^(x) = Kx =
= {sgrad/!|/!eAnn(^)}. Отсюда
следует, что Р(х) П М^ = S^ (x)
(рис. 32). Отметим, что размерность орбиты S^(x) равна
размерности S^ и равна г.
13. Конструкция. Рассмотрим действие группы Р на
М и предположим, что в малой окрестности поверхности М^ это
действие имеет один тип стационарных подгрупп, т. е. что все
орбиты группы Р, близкие к орбите Р(х), ей диффеоморфны.
Рассмотрим проекцию п: М-*М/Р многообразия М на про-
странство орбит N=M/P. Это пространство может не быть
гладким многообразием и иметь особенности. Для нас важно
то, что в малой окрестности точки пР(х)вМ / Р пространство
М/Р—гладкое многообразие размерности 2п — к. В действите-
льности, если, например, Р—компактная группа и она гладко
действует на М, то объединение множества орбит общего
положения, диффеоморфных друг другу, является открытым
всюду плотным подмножеством в М, поэтому пространство
./V является Bи —/с)-мерным многообразием всюду, за исключе-
нием подмножества меры нуль. Отметим, что пространство
(многообразие) ./V не обязано быть симплектическим, так как,
например, оно может быть нечетномерным. Проекция п, будучи
ограничена на поверхность М^, проектирует ее на пространство
Q^ = M^ I Sf. Поэтому пространство ./V расслоено на поверхности
(?5 (рис. 33). Здесь мы опираемся на предложение 8.
Рис. 32

176
ГЛ. 5. ГАМИЛЬТОНОВЫ СИСТЕМЫ С СИММЕТРИЯМИ
14. Предложение. Многообразия Q$, т. е. фактормного-
образия поверхностей уровня М^ по действию подгруппы S^,
являются симплектическими многообразиями с невырожденной
замкнутой формой р, являющейся проекцией формы й> на Mf при
отображении п: А
с~~у^ ~)м*' /°* При этом п* р = й> = <
^У5/ / Доказательство.
/ / / Поскольку ядро формы
со на ТХМ^ совпадает
с подпространством
KxczTxM^, то наше ут-
верждение вытекает из
предложения 11.
15. Редукция. Вернем-
ся теперь к изучению га-
мильтоновых систем на
М. Пусть v = sgrad F—си-
стема с алгеброй интег-
ралов G, т. е. {F, h} = 0,
heG. Поскольку F ком-
мутирует (в смысле скоб-
ки Пуассона) со всеми
элементами из G, то
F инвариантна относительно группы Ли Р. В самом деле,
(sgrad/) F={f, F} = Q, fsG. В частности, подгруппа 55, действуя
на М, переводит функцию F в себя. Итак, определена
естественная проекция векторного поля sgrad F на пространство
N=MjP. При этом векторное поле sgrad F касается поверхности
М^ и также проектируется в некоторое поле E(F) на фактор-
многообразии б5, так как поле
sgrad F инвариантно относитель-
но 54. Итак, пространство N рас-
слоено на симплектические мно-
гообразия б4 и на JV определено
векторное поле E(F), касающееся
всех поверхностей Q^ (рис. 34).
Окончательно мы сопоставили
тройке (М2п, sgrad F, со) новую
тройку {Q%, E(F), p). Этот про-
цесс называется редукцией.
16. Предложение. Век-
торное поле E(F) является гами-
льтоновым относительно симплектической формы р на многооб-
разии Qk для функции Гамильтона F, равной проекции функции
F\M^ на многообразие Q^, т.е. E(F) = sgradp (k*F\M^).
Доказательство вытекает из предложения 14 и инвариант-
ности гамильтониана при действии группы.
ш
щ
V/ /
//
N
Рис. 34

! 30. НЕКОММУТАТИВНОЕ ИНТЕГРИРОВАНИЕ
177
17. Предложение. Пусть G — конечномерная алгебра ин-
тегралов потока sgrad F на М, удовлетворяющая всем перечис-
ленным условиям, и пусть E[F)—редуцированная система на
многообразии N={}Q^, являющаяся гамильтоновой на каждом
подмногообразии Qt. Пусть G'— линейное пространство функций
на многообразии N таких, что их ограничения на подмногооб-
разия Q^ образуют конечномерную алгебру Ли интегралов
потока E{F). Тогда пространство функций G@G", где G" = n*G',
т.е. G" = {gn\geG'}, к: M-+N, является алгеброй Ли интег-
ралов системы sgrad F, причем \G, G"'] = 0.
Доказательство. Пусть g—некоторая функция на про-
странстве N. Тогда ее прообраз gn при отображении п: M-*N
является функцией на М, очевидно инвариантной относительно
действия Р на М. Это означает, что функция gn находится
в инволюции со всей исходной алгеброй функций (интегралов)
G. Итак, всякая новая функция g, являющаяся интегралом для
редуцированного потока E(F) на N, дает дополнительный
интеграл gn исходного гамильтонова потока sgrad F на М. То,
что эти дополнительные интегралы независимы от функций
алгебры G, следует из того, что их градиенты отличны от нуля
по направлению подмногообразий Q$, лежащих (локально)
в поверхности уровня Mt, в то время как градиенты функций из
G ортогональны М^. Предложение доказано.
18. Доказательство теоремы 2. Пусть v—одна из
систем, указанных в формулировке теоремы, т. е. либо
v = sgrad F, {F, G} — 0, либо v = sgrad h, где h e Ann (?). Рассмот-
рим описанную выше редукцию. Поскольку теперь выполне-
но дополнительное условие
dim G + ind G = dim M, т.е.
k + r = 2n, то размерность по-
верхности М5 равна г. Размер-
ность орбиты 5^(х), содержа-
щейся в М^, также равна г.
Отсюда сразу следует, что
M^ = S^(x), т. е. в условиях
теоремы 2 поверхность уровня
М^ является орбитой точки
х при действии группы Ли 5^,
алгебра Ли которой является
аннулятором ковектора !;,
определяющего данную поверхность уровня. В
dim Q^ = 2n—k — r = Q. Поэтому в данном случае
редуцированной системы особенно проста.
Q^ является точкой, то поток Е (F) нулевой (рис. 35). Здесь
пространство N имеет размерность и. Поскольку
М^ — поверхность уровня интегралов G, то поток v касается
Рис. 35
частности,
структура
Поскольку

178 ГЛ. 5 ГАМИЛЬТОНОВЫ СИСТЕМЫ С СИММЕТРИЯМИ
М^ в обоих случаях а) и б), т. е. М^ — r-мерное подмногооб-
разие, инвариантное относительно всех полей вида sgrad/i,
ЛеАпп (?), и sgradi% {F, G}=0. Осталось доказать, что поверх-
ность уровня является r-мерным тором в том случае, когда
М^ компактна и связна. Для этого нам потребуется важная
теорема, см. [513].
19. Теорема Вернь. Пусть ?,еG' — ковектор общего
положения. Тогда его аннулятор Ann (^) = {xeG|ad^ = 0} ком-
мутативен, в частности, подгруппа S^ коммутативна.
Доказательство. Рассмотрим коприсоединенное пред-
ставление группы Ли Р на пространстве G*, сопряженном
к алгебре Ли G группы Ли Р. Обозначим О" (!;} орбиту,
проходящую через точку ?еС*. Посколь-
ку dim Ann (?) = /• и dimG' = k, то
dim О* (!;) = & — г. Tajc как ковектор ? об-
щего положения, то орбиты, близкие
к <?*(?), диффеоморфны ей и можно
считать, что достаточно малая окре-
стность U точки ?, расслоена на гомео-
U морфные слои (рис. 36). Обозначим
. Хо локальное сечение расслоения U на
°\& орбиты представления Adj.. Пользуемся
тем, что U представимо в виде прямого
с' произведения базы Хо на слой — часть
орбиты. Пусть h (т|) — гладкая функция на U, постоянная на
орбитах. Утверждается, что adSj,(^ = O, где dh (дифференциал)
интерпретируется как элемент дуального пространства G" = G,
т.е. dh(?)eG. Другими словами, -утверждается, что dh(Qe
eAnn(?). Мы должны убедиться в том, что (ad^^,^) (g) = 0 для
любого geG. Имеем
\, g} = <S, [dh (%). g]> = - <ad* %, dh(ф =0;
D95)
так как ковектор ad*? лежит в касательной плоскости Т^О*
к орбите О* в точке %, а функция h постоянна на орбитах,
в частности, постоянна и на орбите О'. На сечении Хо,
являющемся гладкой поверхностью размерности г, трансвер-
сально пересекающей орбиты, близкие к орбите О' (?,), рассмот-
рим набор из г независимых функций hu ..., hr и продолжим их
до гладких функций на всей окрестности U, продолжив их
с сечения Хо значениями, постоянными вдоль орбит О*.
Получим adj^(?)!; = 0, 1</<г. Таким образом, dht(?)еAnn(?),
1 </</¦. Так как функции hx были выбраны независимыми, то
все дифференциалы dht (?) независимы в Ann (?) и число их равно
г, т. е. в точности совпадает с размерностью аннулятора
Ann (?). Итак, дифференциалы образуют базис в Ann (?) и для
доказательства коммутативности аннулятора достаточно до-

§ 31. ИНТЕГРИРУЕМЫЕ АЛГЕБРЫ ЛИ 179
казать, что попарные коммутаторы этих дифференциалов dht(?,)
равны нулю, т.е. [dhAty, dft,-(?)]=0. Поскольку ad'dh (O?, = Q, то
biQidbQidhfc^O. Отсюда
i dhi(%)y = i\, [dh^), dhj($]} = 0. D96)
Рассмотрим произвольное направление т\ в окрестности U и про-
дифференцируем вдоль этого направления функцию b(Q O
(j] = 0,D97)
<ad;M^, <
так как ad5hj(y^ = ad5»i(y^ = O. Поскольку net/ciG* произвольно,
то из равенства <л, [<#!;(?), dhj(ty]}=0 вытекает, что [dht(Q,
dhj(?,J\ = O. Теорема доказана.
20. Продолжим доказательство теоремы 2. Мы доказали,
что Mi — орбита группы 5^, и так как dim М$ = dim S& то
М^ есть факторгруппа S$ по дискретной решетке Г. Так как
группа S^ = exp Ann (^) коммутативная, то М^ в случае компакт-
ности и связности является r-мерным тором, см. п. 8 § 29.
§ 31. Интегрируемые алгебры Ли
1. Обсуждение. Если гамильтонова система на симплектиче-
ском многообразии М вполне интегрируема по Лиувиллю
в некоммутативном смысле, т. е. допускает конечномерную
алгебру Ли G функционально независимых интегралов, причем
dim G + ind G = dim M и алгебра Ли G некоммутативна, то
возникает естественный вопрос: является ли эта же гамиль-
тонова система вполне интегрируемой в обычном коммутатив-
ном смысле, т. е. существует ли коммутативная алгебра Ли Go
функционально независимых функций такая, что 2 dim Go =
= dim M.
Хотя в случае существования такой алгебры Go инвариант-
ные поверхности имеют размерность, большую, чем dimM^,
тем не менее ответ полезно знать, так как в этом случае торы
маленькой размерности можно организовать в торы большей
размерности. Оказывается, что для широкого класса алгебр Ли
G ответ является положительным.
2. Определение. Алгебра Ли G называется интегриру-
емой (или удовлетворяет условию FJ), если на G* существует

180 ГЛ. 5. ГАМИЛЬТОНОВЫ СИСТЕМЫ С СИММЕТРИЯМИ
линейное подпространство ЯсС°°((/'), в котором можно
выделить аддитивный базис функционально независимых функ-
ций/^, ...,fq, q = dimH, таких, что они находятся в инволюции
на G относительно скобки Пуассона, причем q = dm\H=
21(idG diG)
( )
3. Замечание. Если G—интегрируемая алгебра Ли, то
ограничения /, \O = hi, ...,fq\O = hq функций /i, ...,/, алгебры
Ли Я на орбиту О коприсоединенного представления Ad* дают
набор функций, который обладает следующим свойством.
Рассмотрим всевозможные функциональные комбинации
F(h!, ..., hq) функций И1г ..., hq. Тогда в пространстве всех таких
функций найдется * линейно независимых, где s = 2~l dimO =
= 2~1 (dimG* — indG), т.е. на каждой орбите OczG* общего
положения имеем вполне интегрируемую гамильтонову си-
стему.
В работах [187], [191] были высказаны следующие две
гипотезы.
4. Гипотеза эквивалентности. Пусть гамильтонова система
х = sgrad/ на симплектическом многообразии М вполне интегри-
руема в некоммутативном смысле, т. е. коммутативная алгебра
Ли ее интегралов Н (feH) включается в некоторую объемлю-
щую, вообще говоря, некоммутативную алгебру Ли функций
G такую, что dimG + indG = dimM. Тогда эта же система вполне
интегрируема и в обычном коммутативном смысле, т. е.
существует другая Коммутативная алгебра Ли Go независимых
интегралов такая, что 2 dim Go = dim М и /е Go. При этом
интегралы алгебры Go принадлежат к тому же функционально-
му классу, что и функции, составляющие алгебру Ли G (если,
например, функции из G аналитические, то и функции из Go
также аналитические). При этом функции алгебры Go функцио-
нально выражаются через функции алгебры G.
5. Гипотеза о слоении орбит на торы Лиувилля. Любая
алгебра Ли интегрируема.
Между гипотезами 4, 5 имеется тесная связь. Имеет место
следующая теорема, принадлежащая А. С. Мищенко
и А. Т. Фоменко [187], [191].
6. Теорема. Пусть М—симплектическое многообразие,
L—алгебра Ли функционально независимых интегралов гамиль-
тоновой динамической системы, dimZ, + indZ, = dim M. Если
алгебра Ли Lo интегрируема, то найдется другая, коммутатив-
ная алгебра Ли Lo функционально независимых интегралов,
причем 2 dim Lo = dim M.
Доказательство. Алгебру Ли Lo будем искать среди
таких функций, которые функционально выражаются через
интегралы из алгебры L. Пусть х1, ..., x"eL — линейный базис
алгебры Ли L. Тогда функции из алгебры Ли Lo будут иметь
вид fix1, ..., х"), где /—гладкая функция п независимых

§ 31. ИНТЕГРИРУЕМЫЕ АЛГЕБРЫ ЛИ 181
переменных. Заметим, что скобка Пуассона двух функций
/(х1, ..., х") и g(x\ ..., х") задается формулой
I ^(х\...,х»)^(х\...,х"){х\х*}. D98)
i,j=l0X Ox
С другой стороны, всякая функция /и независимых переменных
определяет функцию /* на дуальном пространстве V, а именно,
/*(?)=/«? х1) <? х">) ?е?* Тогда скобка Пуассона пары
у рр
/(?)/«?, ), , <?, >), ?,е?*. Тогда скобка Пуассона пары
функций f (?), g* (?) на орбите коприсоединенного представле-
ния задается формулой
|« [jc', хф. D99)
Формулы D98), D99) показывают, что соответствие f-*f
является изоморфизмом бесконечномерных алгебр Ли. Учиты-
вая свойство FI, получаем доказательство нашей теоремы.
7. Замечание. Имеются достаточно богатые серии приме-
ров интегрируемых алгебр Ли. Например, все полупростые
алгебры Ли G таковы, в качестве коммутативной алгебры Ли
Я следует взять функции f(E, + \a), Z,eG\ где /—функции,
постоянные на орбитах коприсоединенного представления.
Интегрируемыми алгебрами Ли являются также широкие
классы разрешимых алгебр Ли и некоторые полупрямые суммы
алгебр Ли. По этому поводу см. работы [11], [18], [33], [39],
[40], [45], [47], [50], [150], [151], [198], [205], [206], [212],
[213], [215], [228], [229], [231], [246]—[249], [253], [254],
[256], [258], [265]—[270], [278], [296].
Класс всех интегрируемых алгебр Ли обозначим FILA.
8. Лемма, а) Если G — абелева алгебра Ли, то GeFILA.
б) Если G, tfeFILA, то G@HeFlLA.
Доказательство очевидно.
9. Приведем список интегрируемых алгебр Ли, см. п. 10—
35. Полный инволютивный набор функций на алгебре Ли
G обозначим F(G) = {fl, ...,/,}, f{eCx(G'). Итак: а)/;,...,/,
функционально независимы; б) {/;,/,}=0, i,j=l,...,q;
в) q = 2~l(dimG + indG).
10. Произвольная полупростая комплексная или веществен-
ная полупростая алгебра Ли G интегрируема, причем F(G)
построено А.С.Мищенко и А.Т.Фоменко [186], [188], [189],
F(G) состоит из полиномов, см. также теорему 7 § 42.
11. Компактная вещественная форма Gc полупростой алгеб-
ры Ли G интегрируема. Семейство F{GC) построено

182 ГЛ. 5. ГАМИЛЬТОНОВЫ СИСТЕМЫ С СИММЕТРИЯМИ
А.С.Мищенко и А.Т.Фоменко [186], [188], [189], F(GC)
состоит из полиномов.
12. Нормальная компактная подалгебра Gn в компактной
вещественной форме Gc комплексной полупростой алгебры Ли
G интегрируема. Семейство F(Gn) построено А. С. Мищенко
и А. Т. Фоменко [186], [188], [189], F(Gn) состоит из поли-
номов.
13. Полупрямая сумма E(n) = so(n)@R", где р — представле-
р
ние минимальной размерности, интегрируема. Семейство F(E(n))
построено В. В. Трофимовым и А. Т. Фоменко [264], [266],
[267], оно состоит из полиномов. Другое семейство построено
А. В. Браиловым в работе [52], оно также состоит из полиномов.
14. Полупрямая сумма G = su(«)©C, где р — представление
р
минимальной размерности, интегрируема. Семейство F(G)
построено А. В. Браиловым и А. В. Болсиновым, оно состоит
из полиномов.
15. Полупрямая сумма G = u(«)©C", где р — представление
р
минимальной размерности, интегрируема. Семейство F(G)
построено А. В. Браиловым, оно состоит из полиномов.
16. Полупрямая сумма G = K@V, где p = adK:F-*F (V—
р
идеал, К—компактная алгебра Ли), интегрируема. Семейство
F(G) построено В. В. Трофимовым (в некоторых частных
случаях) и А. В. Браиловым (в общем случае), оно состоит из
полиномов.
17. Полупрямая сумма G = glBи)©RN, где ц=Л2р, р —
р
представление минимальной размерности, Л2р — вторая внеш-
няя степень представления р, интегрируема. Семейство F(G)
построено Т. А. Певцовой, см. [212]. Оно состоит из рацио-
нальных функций.
18. Полупрямая сумма G = si Bи) © RN, где ц = 52р, р — пред-
р
ставление минимальной размерности, S2p — вторая симмет-
рическая степень представления р, интегрируема. Семейство
F(G) построено Т. А. Певцовой, см. [212]. Оно состоит из
рациональных функций.
19. Полупрямая сумма sp Bи) © RN = G, где ц = р + т, р —
и
представление минимальной размерности, т — одномерное триви-
альное представление, интегрируема. Семейство F(G) построено
Т. А. Певцовой, см. [212]. Оно состоит из рациональных функций.
20. Полупрямая сумма G = K@V, где К—произвольная
р
простая алгебра Ли, а р — произвольное неприводимое линей-

§ 31 ИНТЕГРИРУЕМЫЕ АЛГЕБРЫ ЛИ 183
ное представление, V—абелев идеал (V—пространство предста-
вления), интегрируема. Семейство F(G) построено А. В. Болси-
новым. Этот результат обобщает многие из перечисленных
выше. Семейство F(G) состоит из полиномов, см. теорему 2 § 45.
21. Полупростые алгебры Ли, как уже отмечалось, интег-
рируемые. Новое семейство F(G) построено О. И. Богоявлен-
ским [30], [31]. Оно состоит из полиномов.
22. Вещественные формы В G борелевских подалгебр простых
комплексных алгебр Ли G интегрируемы. Семейство F(BG)
построено В. В. Трофимовым [246]—[249], А. А. Архангельским
[11] и для В?8 — С. Сяровым. Оно состоит из полиномов.
23. Разрешимая алгебра Ли G = Z,© ? RiT^- интегрируема,
где L — подалгебра алгебры диагональных матриц. Семейство
F{G) построено Ле Нгок Тьеуеном, см. [150], [151]. Оно
состоит из полиномов.
24. Операция тензорного произведения G®A на фробениу-
сову алгебру А не выводит за пределы класса FILA интегриру-
емых алгебр Ли, т. е. если GeFILA, то G®^4eFILA. Впервые
алгоритм для размножения полных инволютивных семейств
был найден в работах В.В.Трофимова [250], [251], [253],
[254], затем он был развит А. В. Браиловым и Ле Нгок
Тьеуеном [47], [151].
25. Полупростые алгебры Ли являются интегрируемыми, см.
п. 10, 21. Новое семейство F{G) построено О. И. Богоявленским
в работе [36]. Оно состоит из полиномов.
26. Алгебры Ли малых размерностей интегрируемы, см. [253 ].
27. Полупрямая сумма K@V=G, где К—полупростая ал-
р
гебра Ли, р — представление, у которого стационарная под-
алгебра регулярного элемента относительно представления р
тривиальна, является интегрируемой. Семейство F(G) постро-
ено А. В. Браиловым, Т. А. Певцовой [53], [212]. Все функции
этих полных инволютивных наборов являются линейными.
28. Алгебра Ли G@G — H интегрируема, см. п. 24. Новое
семейство F(H) построено А. В. Болсиновым, см. [39].
29. Алгебра Ли G = so(«)©R" является интегрируемой, как
р
уже отмечено в п. 13. Новое семейство построено
А. М. Переломовым, А. Г. Рейманом, функции этого семейства
являются интегралами «и-мерного случая Клебша», см. [213],
[228].
30. Алгебра Ли G = so(«)©R" является интегрируемой. Но-
р
вое семейство F(G) построено А. М. Переломовым [215]

184 ГЛ. 5 $*МИЛЬТОНОВЫ СИСТЕМЫ С СИММЕТРИЯМИ
и А. Г. Рейманом [228], функции этого семейства являются
интегралами аналога случая Ковалевской в и-мерном случае.
31. Новое семейство F(G) для алгебры Ли G = so(n)©R", где
р
р — представление минимальной размерности, построено
A. В. Беляевым [18]. Оно состоит из полиномов, которые являются
интегралами аналога случая Лагранжа в и-мерном случае.
32. Алгебры Ли so D) и soC)©R3 интегрируемы, как
р
отмечено выше. Они играют важную роль в современных
исследованиях и им посвящены работы [415], [208], [165],
[188], [189], [30], [60], [63], [183], [193], [61], [8], [202], [134],
[87], [391], [309], [307], [379], [59], [32], [237].
33. Любая нильпотентная вещественная алгебра Ли является
интегрируемой. Семейство F(G) построено М. Вернь [513]. Оно
состоит из полиномов.
34. Любая вполне разрешимая вещественная алгебраическая
алгебра Ли интегрируема. Семейство F(G) построено
B. А. Гинзбургом. Оно состоит из полиномов.
35. Любая разрешимая вещественная алгебраическая алгебра
Ли, для которой существует флаг из алгебраических подалгебр
G = Gn=>Gn-l=>...z>G1=>Go = 0, dim Gt = i, является интегрируе-
мой. Семейство F{G) построено А. В. Болсиновым.
§ 32. Симплектические действия групп Ли
1. Определение. Пусть Р—группа Ли, действующая на
симплектическом многообразии (М, со) симплектоморфизмами,
т. е. для любого gsP соответствующее отображение g: M->M
является каноническим преобразованием, см. п. 1 § 24. В этом
случае М называется симплектическим Р-пространством. Если
группа Р действует на многообразии М транзитивно, то
М называется однородным симплектическим Р-пространством.
2. В том случае, когда группа Р действует на многообразии
М, определен гомоморфизм ср: G-*D(M) алгебры Ли G группы
Ли Р в алгебру Ли D(M) векторных полей на М:
(р(Х)т = Х(т)=- expTxim), XeG, msM, E00)
at i = o
см., например, [102], [263]. Пространство векторных полей на
симплектическом многообразии (М2п, со) вида sgrad/ является
алгеброй Ли относительно коммутатора. Эту алгебру Ли будем
обозначать символом Нат(М) (см. § 10 и § 19).
3. Определение. Симплектическое действие группы Ли
Р на симплектическом многообразии М называется строго
симплектическим, если cp(G)<=Ham(M), и гамильтоновым, если
существует такой гомоморфизм X: G -* С°° {М) алгебр Ли

§ 32 СИМПЛЕКТИЧЕСКИЕ ДЕЙСТВИЯ ГРУПП ЛИ 185
(который назовем поднятием или гомоморфизмом, накрыва-
ющим ф), что диаграмма
О >R—~С™(М) —?-^ Нат(М) —> О
E01)
коммутативна, где отображение р: Сж (М) -> Нат(М) определе-
но равенством p(f) = sgradf.
4. Определение. Пусть {М, со)— строго симплектическое
f-многообразие с поднятием X: G -* С°° (М). Отображение
Ф: M-»G*, определенное формулой Ф(т)(Х) = Х(Х)т, называ-
ется отображением моментов.
5. Определение. Если Р—группа, действующая симплек-
тически на многообразии (М, со), сохраняет функцию Н (т. е. Н
постоянна на орбитах группы Р), то группа Р является по опреде-
лению группой симметрии гамильтоновой системы i = sgradH.
6. Теорема ограничения. Пусть Р—компактная
группа симметрии гамильтоновой системы х = sgradffl H,
a FcC" (М) — Р-инвариантная алгебра интегралов, Fp — Р-непод-
вижная подалгебра, N—многообразие неподвижных точек, F—
множество ограничений интегралов F на ./V. Тогда: a) (N, со) —
симплектическое многообразие, где со = ю | ./V; б) множество
F замкнуто относительно скобки Пуассона {/, g) N и отображе-
ние ограничения является _ эпиморфизмом алгебр Ли
{FP, {/, g)N) -> (F, {k, 1}нУ, _в) F—алгебра интегралов гамиль-
тоновой системы х = sgradM// на N, где Н—ограничение Н на N.
7. Лемма. Пусть (W, со) — симплектическое векторное про-
странство, р: Р —* End (W) — вполне приводимое симплектичес-
кое представление группы Р, WQ — неподвижное подпространст-
во. Тогда со| WQ—невырожденная форма.
Доказательство. Пусть ?,е\У0, а ^х — ортогональное
дополнение. Поскольку ^elV0, то Ъ,1 инвариантное относитель-
но Р. Следовательно, существует инвариантное одномерное
подпространство Rr| такое, что W/=?,1©Rri. Из определения
вектора г\ вытекает, что со(^, г|)^0. Вместе с /"-инвариант-
ностью Rr| это означает, что ц е WQ.
8. Лемма. Если feFP, то sgradM/= sgrad№/.
Доказательство. Пусть qeN. Из инвариантности / по-
лучаем, что sgradM/( q)e TqN. Поэтому для доказательства
леммы достаточно для любого векторного поля X на М прове-
рить равенство
w(sgradM/, X)=(u(sgr<idNf,X). E02)
Обе части E02) равны X(F). Лемма доказана.

186 ГЛ. 5 ГАМИЛЬТОНОВЫ СИСТЕМЫ С СИММЕТРИЯМИ
Доказательство теоремы 6. Пусть qeN— неподвиж-
ная точка. Тогда соответствие а -> dqo: TqN -* TqN является
симплектическим представлением группы Р в пространстве TqN.
Так как по условию группа Р компактна, то это представление
вполне приводимо. Применяя лемму 7, получаем утверждение
а). Гомоморфность ограничения и замкнутость образа
FP в F относительно скобки Пуассона следуют из ее определе-
ния и равенства E02). Эпиморфность получается из того, что
ограничение функции / на N совпадает с композицией ограниче-
ния и операции S{f) усреднения по группе:
E03)
Таким образом, доказано утверждение б) теоремы ограничения.
Докажем утверждение в). Действительно, пусть feF—интеграл
системы i = sgradJ//_Ha (М, со). Тогда {Я,/}м = 0; применяя б),
получим, что {H,f}N — 0. Утверждение в), а вместе с ним
и теорема ограничения полностью доказаны.
Приведем простейший пример, когда возникают симплек-
тические действия групп.
9. Теорема. Пусть Р—компактная группа, действующая
автоморфизмами на алгебре Ли G, Gn — неподвижная подалгеб-
ра, xeG*nczG', ОР(х) — орбита представления Ad* группы Ли Р,
отвечающей G, проходящая через х, ОР (х) — орбита группы Р„,
отвечающей алгебре Ли Gn. Тогда: &) Р действует симплек-
тически на ОР(х); б) ОР^(х) открыто в многообразии Р-
неподвижных точек орбиты ОР(х); в) если со, со„—формы
Кириллова алгебр Ли G, Gn соответственно, то mn = co|G*.
10. Лемма. Пусть Р, ОР(х) те же, что и в теореме 9. Если
аеР, то a": G*->G' обозначает сопряженное к о линейное
отображение. Тогда a'(OP(x))czOP(x).
Доказательство. Пусть хеG*. Определим окрестность
Vx. в О, (*'):
K,. = {exp(ad;)(x'), geG}. E04)
Применяя а* к E04), получим
a'(Fx.)={exp(ad;-49l)(a*x'), geG}, E05)
откуда следует включение
a'{Vx.)<zOP(x'). E06)
Таким образом, локально лемма доказана. Для перехода
к глобальному утверждению достаточно заметить, что орбита
ОР(х) — связное множество, а OP(x)C\a'~i(OP(a*(x))) — откры-
тое множество в силу E06).

§ 32 СИМПЛЕКТИЧЕСКИЕ ДЕЙСТВИЯ ГРУПП ЛИ 187
11. Лемма. Пусть хеС, ?, г\еТхОР(х), со—форма Кирил-
лова. Тогда ых(?„ г)) = соа.х (а'Ё,, о'ц).
Доказательство. По определению векторов ?, г\ найдут-
ся векторы ?,', r\'sG такие, что
Z, = ad\.(x), ri = ad;.(jc). E07)
Тогда по определению формы Кириллова
сох(^, т)) = <;с, [?', г|']>. Применяя к E07) преобразование а*,
получим
a^ = ad;.,6.(o'jc), a-r, = ad*a-,n.(a-.v). E08)
Используя E08), легко вычислить форму Кириллова в точке
а*х:
= <а'х,а-1[?>',ц']> = (йх(%,ч). E09)
12. Доказательство теоремы 9. Утверждение а) вы-
текает из лемм 10, 11. Докажем утверждение б). Пусть
N—многообразие неподвижных точек. Из E05) вытекает, что
в окрестности точки х множество N задается уравнениями
exp(adn-,(9))(x) = exp(ad*)(x), aeP. E10)
Из E10) получаем, что ad* (x)e TXN тогда и только
тогда, когда
Пусть Ann(x) = {usG\'dd*u(x) = 0}, geG, g=g'+g", где g' e
eGn + Ann (x), a g" e W, где W— Р-инвариантное дополнение
к Gn + Ann(x) в G. Тогда ad*»(jc) = ad*,g..(.x), откуда g" = 0.
Действительно, если g"ф0, то найдется такое преобразование
аеР, что g"^ag", значит, 0=?g" — ag" <г\?, а это противоречит
тому, что g" — ag"e Ann (х). Поэтому можно усилить E11):
¦ddg(x)eTxN тогда и только тогда, когда g" = 0. Это, в свою
очередь, означает, что
TxN=TxOPn{x). E12)
Очевидно, что ОР (x)aN, поэтому из E12) вытекает утвержде-
ние б). Утверждение в) теоремы 9 тривиально следует из
определения формы Кириллова. Теорема 9 доказана.
13. Пример отображения моментов. Группа P=Sp(n, R)
действует на многообразии (R2", со). Пространство G* = sp(«, R)
отождествляется с алгеброй Ли G, которая состоит из матриц
X порядка 2и вида
С -А' ' В=В> С=С E13)

188 ГЛ. 5. ГАМИЛЬТОНОВЫ СИСТЕМЫ С СИММЕТРИЯМИ
(см. § 16). Отображение моментов ц: R2"->RJV, N—2n2 + n,
переводит вектор х = (р, q) в матрицу
E14)
14. Пример. Пусть имеются два действия группы Ли Р на
симплектических многообразиях М, N с отображениями момен-
тов Фм и Ф#. Тогда группа Р действует на М х N с отображени-
ем момента Ф/цхц(т, п) = Фм(т) + Фц(п).
15. Пример. Если р: Р\-*Р%— гомоморфизм групп Ли
и Р2 действует на М с отображением моментов Фг: M-^G\, то
Р^ действует на М (с помощью гомоморфизма р) с отображени-
ем момента Ф1 = (а"р)* °Ф2.
16. Теорема. Пусть Р— связная группа Ли, G — ее алгебра Ли.
Предположим, что Н1 (G) = Н2(G) = 0. Если группа Ли Р действует
симплектически на симплектическом многообразии (М, со), то
существует такой однозначно определенный гомоморфизм X:
G->-C00(Af), где ССС(М) — алгебра Ли всех гладких функций на
М относительно скобки Пуассона, что со(|, Х) = а"к(?,)(Х), где
\—векторное поле на М, отвечающее элементу ?е С В этом случае
определено отображение моментов Ф: M-*G* формулой (Ф(т),
?> = X(Q(m). Отображение моментов эквивариантно относительно
заданного действия группы Ли Р на многообразии М и коприсоединен-
ного представления группы Ли Р на пространстве G*.
17. Замечание. Теорема 16 дает критерий гамильтоново-
сти данного симплектического действия группы Ли в терминах
когомологий алгебр Ли. Доказательство теоремы 16 можно
найти в [374]. С теорией когомологий алгебр Ли можно
познакомиться по работам [81], [291]. Отметим только, что
если G — полупростая алгебра Ли, то H1(G) = H2(G) = 0, см.,
например, [65], [81]. Критерий существования отображения
моментов в терминах топологии многообразия дает теорема 18,
доказательство ее см. в [374].
18. Теорема. Пусть группа Р действует симплектически
на компактном симплектическом многообразии М. Если Н1 (М,
R) = 0, то Ц!;) однозначно можно найти из условия \ Ц^)со" = 0.
19. Замечание. В п. 20—26 будет дан обзор результатов,
связанных со свойством выпуклости отображения момента. Мы
будем следовать работам Атьи, Гийемина, Стернберга [313],
[314], [372], [375], подробное изложение затронутых здесь
вопросов можно найти в книге [374].
20. Обозначения. Пусть V—векторное пространство и аь ...
..., ansV. Тогда >?(аь ¦¦¦, ап) обозначает выпуклое множество

§ К СИМПЛЕКТИЧЕСКИЕ ДЕЙСТВИЯ ГРУПП ЛИ 189
21. Определение. Если группа Ли Р действует на
многообразии М, хоеМ—неподвижная точка этого действия,
то гомоморфизм из Р в группу линейных преобразований
пространства ТХаМ, который сопоставляет каждому элементу
geP дифференциал dg в точке х0, называется представлением
изотропии.
22. Теорема о локальной выпуклости. Пусть
М — симплектическое многообразие, V — r-мерный тор,
Тг х М-»А/—гамильтоново действие тора Тг на М с отображе-
нием моментов Ф: М—>//, x—-неподвижная точка действия
тора Tr, L—алгебра Ли тора Т', а р = Ф(х). Тогда найдется
такая окрестность U точки хвМ и окрестность U' точки
реЬ*, что Ф(Ц)= U'(~){p + S((Xi, ..., ос„)}, где аь ..., а„ — веса
линейного представления изотропии тора ТТ в касательном
пространстве ТХМ.
23. Теорема. Предположим, что r-мерный тор Тг гамиль-
тоново действует на симплектическом многообразии М с отоб-
ражением моментов Ф: M-*L*. Тогда образ отображения
моментов является выпуклым многогранником.
Эти теоремы можно применить к изучению структуры орбит
коприсоединенного представления связных компактных групп Ли.
24. Теорема. Орбиты коприсоединенного представления
связной компактной группы Ли Р односвязны.
Доказательство. Приведем схему доказательства.
Пусть Ф — отображение моментов. Тогда <Ф(х), ^> = <^, х> для
любого элемента Ь, алгебры Ли G группы Ли Р, где <(^,
х} — инвариантное скалярное произведение на G. Для почти
всех ^eG функция <?,, х>, ограниченная на данную орбиту О,
является такой функцией Морса на О, что индексы всех
критических точек четны. В этом случае соответствующее
многообразие О односвязно.
25. Теорема. В коприсоединенном представлении связной
компактной группы Ли Р стационарная подгруппа Р„ любого
элемента r\eG* связна (G — алгебра Ли группы Ли Р).
Доказательство. Отображение п: Р->О, g->Ad*gr\, явля-
ется расслоением над орбитой О группы Р со слоем
Рц (стационарная подгруппа). Поскольку группы я^О) и п0(О)
тривиальны, то из точной гомотопической последовательности
....-ии^-и^Тд-Яо^)-... E15)
вытекает, что Рл связна.
26. Пример. Пусть P=SOD), M—орбита коприсоединенного
представления в soE)*. На рис. 37 изображено множество
Ф(М)(~)Ь*. Положительный квадрант есть L*+. Итак, Ф(М)(~)Ь',
вообще говоря, не выпуклое множество.
27. Теорема (А. В. Браилов). Пусть i: = sgrad//—гамиль-
тонова система на симплектическом многообразии (М, со),

190
ГЛ. 5 ГАМИЛЬТОНОВЫ СИСТЕМЫ С СИММЕТРИЯМИ
Рис. 37
а Н—ее алгебра Ли интегралов. Предположим, что для любого
hеR изоэнергетическая поверхность Мн = {хёМ\Н{х) = И} ком-
пактна. Тогда Н—компактная алгебра Ли.
Доказательство. Пусть geH, Х9 — соответствующее
гамильтоново поле на М. Векторное поле Хд касается Mh для
любого h и поэтому полно на
М (т. е. интегральные траектории
можно продолжать неограниченно
долго). Поэтому определено дейст-
вие связной односвязной группы Ли
Q, отвечающей алгебре Ли Н, на
многообразии М. Это действие га-
мильтоново, так как по определе-
нию векторного поля Хд оно явля-
ется гамильтоновым векторным по-
лем с гамильтонианом g. Пусть Р:
М->Н* — соответствующее отобра-
жение момента, P(x)(g) = g(x). По-
скольку Н—алгебра Ли интегралов
гамильтоновой системы x=sgrad.F, то изоэнергетические по-
верхности Mh инвариантны относительно действия Q и их
образы P(Mh) инвариантны относительно Ad* для любого h.
Так как по предположению Mh компактно, то P(Mh) также
компактны. Пусть gsH—нильпотентный элемент в алгебре Ли
Н. Тогда ad* — нильпотентный эндоморфизм Н* и отображение
t—>exp(ad*9)x полиномиально для каждого хеЯ*. В силу
инвариантности Р(Мр) для xsP(Mh) это отображение является
отображением из R в P(Mh). Поскольку P(Mh) компактно,
а отображение t-*exp(ad*tg)x полиномиально, то это постоянное
отображение, exp(ad*9)x = x для всех t. Поэтому для любого
хеР(М) имеем ad*x = 0. Следовательно, всякий нильпотентный
элемент g лежит в центре Z алгебры Ли Н. Пусть R —
разрешимый радикал Н. Тогда [R, R] состоит из нильпотент-
ных элементов и, следовательно, [R, R]<=Z. Поэтому весь
радикал R состоит из нильпотентных элементов и, следователь-
но, R = Z. Итак, Н—редуктивная алгебра Ли. Пусть S=[H,
Н] — ее полупростой идеал. Поскольку Sf)Z = O, то в 5 нет
ненулевых нильпотентных элементов. Следовательно, S—ком-
пактная полупростая алгебра Ли. Поэтому Н—компактная
алгебра Ли. Теорема доказана.
§ 33. Редукция гамильтоновых систем с симметриями
и псевдогруппы Ли
1. Определение. Пусть Е—некоторое множество, О —
точка, не принадлежащая Е. Множество Е называется группо-
идом, если на Е{]О задана бинарная ассоциативная операция

§ 33. РЕДУКЦИЯ ГАМИЛЬТОНОВЫХ СИСТЕМ 191
* такая, что: а) О*О = О\ б) выделено непустое подмножество
tfcE такое, что для произвольного элемента а^О существует
элемент а'1^®, обладающий свойством a*a'1, a~1*asN; в)
если eeN и а*ефО, то а*е = а и е*е = е. По поводу свойств
группоидов см. [377], [485]. Множество N называется подмно-
жеством единиц. Обозначим Е* с ЕхЕ область определения
частичной операции: (а. Ь)еЕ* тогда и только тогда, когда
существует а*ЬеЕ, т. е. а*Ь=?0. Обозначим буквами г и / отоб-
ражения сокращения E->N, заданные формулами
г(а) = а~1*а, 1(а) = а*а~\ E16)
Отметим, что элементы а и Ъ перемножаемы (т. е. (а, Ь)еЕ*)
тогда и только тогда, когда r(a) = l(b). При этом l(a*b) = l{a)
и r(a*b) = r(b).
2. Определение. Группоид Е называется симплектиче-
ским или конечномерной псевдогруппой Ли, если: а) Е—симплек-
тическое многообразие, его подмножество единиц N—лагран-
жево подмногообразие; б) отображения сокращения /, г.
E-*N—субмерсии, трансверсальные N; в) отображение а-^я
и умножение (а, Ь)-щ*Ь являются антиканоническим и канони-
ческим отображением соответственно из Е в Е и из Е* в Е.
Каноничность означает, что прообраз формы со? совпадает
с сужением формы со?©ю? на Е*. Конечномерная псевдогруппа
Ли Е соответствует пуассонову многообразию N, если N вложе-
но в Е как подмногообразие единиц и отображение сокращения
антиканоническое.
3. Теорема (М. В. Карасев [118], [119]). Любому пуас-
сонову многообразию соответствует локальная конечномерная
псевдогруппа Ли. Каждая конечномерная псевдогруппа Ли соот-
ветствует единственному пуассонову многообразию.
4. Замечание. Теорема 3 представляет собой аналог
третьей классической теоремы Ли о связи между группами Ли
и алгебрами Ли. Реальному вычислению структуры псевдогруп-
пы из теоремы 3 посвящена следующая теорема 8. С этой
целью введем
5. Определение. Симплектическое многообразие Е назы-
вается фазовым пространством над пуассоновым многообразием
N, если: a) JV вложено в Е как лагранжево подмногообразие; б)
задано антиканоническое расслоение г: E-*N и каноническое
расслоение /: E^N; в) / и г косоортогональны (полярны) друг
другу; г) / и г трансверсальны N и на ./V тождественны. Будем
называть /иг пуассоновыми расслоениями над N.
6. Теорема (М. В. Карасев [118]). Над любым пуассоновым
многообразием N существует фазовое пространство.
7. Обозначения. Символом sgrad H, как обычно, обозначим
гамильтоново поле на Е, отвечающее функции Гамильтона Н,
возможно зависящей явно от времени, а символом

192 ГЛ. 5 ГАМИЛЬТОНОВЫ СИСТЕМЫ С СИММЕТРИЯМИ
7 я обозначим сдвиг вдоль траекторий этого поля за единичное
время. Нижние индексы (sgrad//)а будут указывать переменную
(в данном случае а), по которой действует оператор.
8. Теорема (М. В. Карасев [118], [119]). Если Е—псевдо-
группа Ли, отвечающая пуассонову многообразию N, и ф —
гладкая функция на Е, то функция Ф(а, b) = q>(a*b) на Е*
удовлетворяет системе уравнений
(sgrad rj). - (sgrad /,)„ Ф {а, Ь) = О, E17)
Ф(а, b)\beN = 4>(a), j= I, ..., dimJV. E18)
Наоборот, если Е—фазовое пространство над данным пуас-
соновым многообразием N, а г и I—его пуассоновы расслоения,
то для любой функции ц> на Е система E18) на многообразии
Е* ={(а, b)\r(a) = l(b)} имеет единственное решение
Ф(а, Ь) = ц>(а*Ь); получающаяся таким образом операция а*Ъ
задает на Е структуру конечномерной псевдогруппы Ли,
отвечающей пуассонову многообразию N. Эта же псевдогруппа
может быть вычислена так: точки а и b перемножаемы, если
a = Y[.f(l(b)) для некоторой функции f на N; при этом
a*b = Yt.f(b). Такое определение корректно, т. е. не зависит от
выбора функции /.
9. Замечание. Доказательства и обсуждения теорем 3, 6,
8 содержатся в работах [118], [119], [120].
10. Обсуждение. Один из главных механизмов возникновения
пуассоновых многообразий — это процедура редукции гамиль-
тоновых систем с симметриями.
Пусть X—симплектическое многообразие, Я—функция Га-
мильтона на нем, А=(А1, ..., Ап) — набор независимых первых
интегралов гамильтонова векторного поля sgradH. Возникает
естественный вопрос: каким условиям должен удовлетворять
набор А для того, чтобы поле sgrad Я допускало редукцию, т. е.
понижение числа степеней свободы на поверхностях
M!i = {Ai = ^i = const, 1<г<и} с сохранением гамильтоновой
структуры.
Понизить число степеней свободы можно, избавившись от
координат вдоль траекторий полей sgrad Ay Обозначим
аг линейную оболочку этих полей в точке zsX. Условием
существования редукции является интегрируемость распределе-
ния плоскостей {<xz}. В силу критерия Фробениуса данное
распределение интегрируемо тогда и только тогда, когда набор
А замкнут относительно скобок Пуассона {/, g}x на многооб-
разии X, т. е.
{Aj,Ak} = tykJ(A), j,k=\, ..., п. E19)
Соотношения E19) и представляют собой искомые условия
существования редукции поля sgrad H.

§ 33 РЕДУКЦИЯ ГАМИЛЬТОНОВЫХ СИСТЕМ 193
11. Обозначения. Набор независимых функций, постоянных
на слоях распределения {<хг}, обозначим В = (Ви ..., Вт)
(/и + и = dim А"). Поскольку Н также постоянна на слоях, то
H = h(B), т. е. гамильтоново поле sgradH является линейной
комбинацией полей sgrad-Bj. Линейная оболочка pz этих полей
совпадает с касательной плоскостью к поверхности {At = const}
в точке z. Таким образом, распределение {Рг} заведомо
интегрируемо и поэтому набор В замкнут относительно скобки
Пуассона:
{Bj, Bk}x = <&kj(B), j,k=\, ..., т. E20)
Обозначим буквой М базу отображения В. Тензор || Ф,* ||
задает на базе новую скобку Пуассона, а исходное поле sgrad//
после проектирования вдоль В (т. е. вдоль слоев распределения
{az}) превращается в гамильтоново поле sgrad/г на пуассоновом
многообразии М: dB (sgradH) = sgradh, H=h(B). Редуцирован-
ное поле sgradA направлено вдоль симплектических листов на
М (на которых скобка не вырождена). Коразмерность этих
листов равна cork Ф = cork Ч*. Итак, размерность фазового
пространства в результате редукции уменьшилась на
(гкЧ' + гсогк4?) единиц.
12. Определение. Важно, что на базах отображений А,
В возникают новые скобки Пуассона, порожденные тензорами
Ч*, Ф. Будем предполагать, что оба отображения являются
глобальными расслоениями
М
E21)
В каноническое, А каноническое, А и В косоортогональны.
Пуассоновы многообразия М и N в диаграмме E21) называют-
ся взаимно полярными.
13. Оказывается, слои канонических расслоений А и В в диа-
грамме E21) являются орбитами пуассоновых действий на двух
конечномерных псевдогруппах, отвечающих пуассоновым мно-
гообразиям М и N.
14. Определение. Действие абстрактного группоида Е на
множестве X—это такая операция
{a,z)^aoz, E22)
заданная на некотором подмножестве Х*сЕхХ, что выпол-
нены условия: а) если a°z определено, то b°(a°z) определено
тогда и только тогда, когда в Е определено произведение Ь*а,

194 ГЛ. 5. ГАМИЛЬТОНОВЫ СИСТЕМЫ С СИММЕТРИЯМИ
и в этом случае b°(a°z)-{b*a)°z; б) для любого zeX
существует «единица» е в Е такая, что e°z = z.
15. Определение. Конечномерная псевдогруппа Ли Е пу-
ассоново действует на симплектическом многообразии X, если
это действие E22) — каноническое отображение.
16. Замечание. При выполнении условий а), б) из п. 14
пуассоновость действия эквивалентна лагранжевости подмного-
образия aiX, E)—{{a°z, z, a)}czXxXxE относительно симплек-
тической формы а>х®а>х®а)Е. Это «сплетающее» лагранжево
подмногообразие было введено в работе [21 ]. Точно так же
лагранжевость подмногообразия Н(Е, Е) = {(a*b, b, а)}<^ЕхЕхЕ
эквивалентна каноничности операции умножения * в псевдо-
группе Е. А. Вейнстейн [525] именно с его помощью определяет
симплектический группоид.
Буквами г и / обозначим отображения сокращения псевдо-
группы Е.
17. Теорема. Пусть задана диаграмма E21) и Е—псевдо-
группа, отвечающая пуассонову многообразию N. Тогда для лю-
бой гладкой функции <р на X система уравнений
(sgrad r})a -(sgrad Aj)z<b {a, z) = 0,
E23)
на подмногообразии X* = {(a, z) | г (а) = A (z)} czExX имеет един-
ственное решение Ф(а, г) = ц>(а° z). Определенная таким способом
операция a°z — это пуассоново действие псевдогруппы Е на X. То
же самое пуассоново действие можно задать так: если
a = 4t*f(A(z)) для некоторой функции f на N, то по опреде-
лению а° z = yA.f(z). Орбиты этого действия совпадают со
слоями В.
В некотором смысле это утверждение можно обратить.
18. Теорема. Пуассоново действие любой конечномерной
псевдогруппы Е на X порождает (по крайней мере локально)
диаграмму E21), в которой N—подмногообразие единиц из Е,
а В—расслоение на Е-орбиты. Это действие псевдогруппы
Е удовлетворяет формулам теоремы 17.
19. Замечание. В случае обычного пуассонова действия
группы Ли [430], [496], [8] многообразие N оказывается
л
линейным и скобка на нем линейна, т. е. \)/;t(^)= ? ?Ajy,
Xski = const (или отличается от нее на' постоянный коцикл).
Отображение А — это обычное отображение моментов. Мы
сохраним этот термин в общей ситуации теоремы 18.
20. Замечание. Действие a°z определено тогда и только
тогда, когда r(a) = A(z). При этом B(a°z) = B(z) и A{a°z) = l(a).
Последнее свойство моментов А показывает, что действие

§ 33. РЕДУКЦИЯ ГАМИЛЬТОНОВЫХ СИСТЕМ 195
псевдогруппы Е на X проектируется вдоль А и задает некоторое
действие Е на N.
21. Определение. Естественное действие псевдогруппы
на своем многообразии единиц назовем коприсоединенным.
Вычисляется это действие по формулам теоремы 17, в которой
вместо X нужно взять многообразие N, а вместо А —
тождественное отображение id: N-*N.
22. Замечание. Если 1(а) = С, и r{a) = t>, то а°^ = С,. Таким
образом, орбитами коприсоединенного действия являются сим-
плектические листы многообразия N. На каждом листе это
действие пуассоново.
23. Следствие. Пуассоново действие псевдогруппы Е на
симплектическом многообразии X переводится отображением
моментов A: X—>N в коприсоединенное действие Е на своем
многообразии единиц N.
24. Рассмотрим теперь псевдогруппу, отвечающую пуас-
сонову многообразию М, полярному N. Следующая теорема
служит источником примеров глобальных псевдогрупп.
25. Теорема. Пусть псевдогруппа Е, отвечающая пуас-
сонову многообразию N, действует на X пуассоново и свободно,
ее орбиты задают глобальное расслоение В: Х—>М, а расслоение
моментов A: X-+N также глобально. Тогда глобальная псевдог-
руппа, отвечающая пуассонову многообразию М, полярному N,
существует и пуассоново действует на X вдоль слоев А. Ее
действие коммутирует с действием Е.
26. В заключение рассмотрим интересный класс скобок
Пуассона, тесно связанный с квадратичными коммутационными
соотношениями [234], [240].
27. Определение. Группа Ли К, наделенная скобкой
Пуассона так, что умножение ц: КхК-*К канонично, а обраще-
ние v: K^>K (v(x) = x~l) антиканонично, называется пуассоно-
вой группой или группой Гамильтона — Ли [93].
Пуассоново действие такой группы на симплектическом
многообразии X задается каноническим отображением
КхХ->Х. Подробности см. в [93], [233].
28. Замечание. Множество АГ-инвариантных функций на
X будет замкнуто относительно скобки Пуассона, и поэтому,
если /if-орбиты порождают расслоение В: Х^М, то на базе
М возникает единственная пуассонова структура, относительно
которой В—каноническое отображение. Буквой А обозначим
косоортогональное В отображение в диаграмме E21). Пред-
положим, что A: X->N является глобальным расслоением.
29. Обозначения. Обозначим Dt базисные левоинвариантные
векторные поля на группе Ли. Скобку на К запишем в виде
(К—группа Ли, отвечающая алгебре Ли G)
{и, v}K = (RDu, Dv), u,veCK (К), E24)

196 ГЛ. 5. ГАМИЛЬТОНОВЫ СИСТЕМЫ С СИММЕТРИЯМИ
где R: G*-*G, R = R(<x)— гладкая функция точки <хеК. Оказыва-
ется [93 ], тензор R полностью характеризуется своими первыми
производными в единице ее К. Точнее, числа
*1НА4и)И E25)
задают на С структуру алгебры Ли, и две структуры Ли на
G и С согласованы друг с другом в следующем смысле [7]:
л -X(Jf)sgrad(F)'-sgrad Y-ЦХ), E26)
где X, YeG, Цх)=\\ ? хД^Ц.
i — 1 ~.
30. Если вещественные числа k)k удовлетворяют всем перечи-
сленным условиям, то на односвязной группе Ли К, отвечающей
алгебре Ли G, существует единственная скобка E24), которая
превращает К в пуассонову группу и для которой выполнены
равенства E25). Эту скобку на К будем называть инвариантной.
31. Лемма. Пусть тензор R = R(oi) задает по формуле E24)
инвариантную скобку на группе К, и пусть <хоеК. Тогда тензор
R(a) — R(ac0) задает скобку Пуассона на К, причем левый сдвиг
8: ol-kxq1!* переводит эту скобку в ^инвариантную,
32. Определение. Обозначим К односвязную группу Ли
со структурными константами Цк. В силу сказанного выше на
К существует единственная инвариантная скобка
{/, g}~ = <RDf, Dg), f, ge С00 (К), E27)
такая, что Vjk = (DjRki) (е)—структурные константы алгебры Ли
G. Группы К и К называются сопряженными, см. [93], [233].
33. Теорема. Пусть пуассонова группа К пуассоново
действует на односвязном симплектическом многообразии
X и задает расслоение В: Х->М. Пусть A: X—>N—каноническое
расслоение, косоортогональное В. Тогда выполнено следующее.
1) База N диффеоморфна области в сопряженной пуассоновой
группе К, причем скобка Пуассона на N отличается^ от
инвариантной скобки E27) на «константу» {/, g}N = ({R+C)
Df,Dg}, Cjk = const.
2) Числа Cjk подчинены условию «коцикличности»
,Clm-CjsUm) = 0, E28)
здесь суммирование идет по повторяющимся индексам и по
циклической перестановке произвольной тройки индексов (/, к, т),
a Xsi и %skm—структурные константы групп К и К соответст-
венно.
3) «Коцикл» {Сд} тривиален, если Cjk = RkJ(?,0) для некоторое
го Z,oeK; в этом случае после левого сдвига о скобка на NxK
становится инвариантной.

§ 34. МЕТОД СДВИГА АРГУМЕНТА 197
4) При выполнении условия C) конечномерная псевдогруппа Ли
Е, отвечающая пуассонову многообразию'N'«К, диффеоморфна
К у-К и пуассоново действует на X по формуле (a, ^)°z = a-z,
если t, = A(z) (здесь z->ol-z—действие К на X). Расслоение
А является отображением моментов.
5) Коприсоединенное действие Е на К имеет вид (а, ?)°
°2; = а-?, если ? = ? (здесь ?-юг?— некоторое пуассоново дейст-
вие группы К на сопряженной группе К, орбитами которого
являются симплектические листы в К). Умножение в псевдог-
руппе Е=КхК задается формулой (Р, С)*(а> ^) = (Ра> ?)> если
6) Пусть К действует на X свободно. Тогда база М рас-
слоения В обладает структурой глобальной конечномерной
псевдогруппы Ли.
34. Замечание. Подробные формулы см. в работе [120].
Глава 6
МЕТОДЫ ПОСТРОЕНИЯ ФУНКЦИЙ В ИНВОЛЮЦИИ
НА ОРБИТАХ КОПРИСОЕДИНЕННОГО ПРЕДСТАВЛЕНИЯ ГРУПП ЛИ
§ 34. Метод сдвига аргумента
1. Замечания. Весьма эффективным методом построения
функций в инволюции на орбитах коприсоединенного представ-
ления группы Ли является метод сдвига аргумента.
2. Определение. Пусть f(x) — функция, заданная на
линейном пространстве V, а aeV—фиксированный вектор. На
пространстве К построим семейство функций/x,a(jc)=/(x+ )tа),
где X — произвольное число (>»eR, если V—вещественное
линейное пространство). Будем говорить, что функции f^a(x)
получаются из f(x) операцией сдвига аргумента. Если f\,a(x)
можно разложить в ряд по X, то
А.а(х)= ? Х"Л.в,.(дс) E29)
п = 0
и операция сдвига порождает из функции /(х) целое семейство
функций УКа,п{х)}.
Эта идея для случая алгебры Ли so (я) впервые появилась
в работе СВ. Манакова [165]. Затем для случая общих алгебр
Ли метод был разработан А. С. Мищенко и А. Т. Фоменко
[186]—[189]. В теории гамильтоновых систем сдвиг аргумента
используется в силу следующей важной теоремы.
3. Теорема (см. [186]—[189]). Пусть F(x) и G(x) — dee
функции на пространстве L', дуальном к алгебре Ли L,

198 ГЛ. 6. МЕТОДЫ ПОСТРОЕНИЯ ФУНКЦИЙ
постоянные на орбитах 0(t) коприсоединенного представления
группы Ли Т, отвечающей алгебре Ли L, aeL* — фиксированный
ковектор,_Х, \xeR — фиксированные числа. Утверждается, что
функции Fx a{t) = F(t + \a) и G~a{i) = G(t + \\.a) находятся в ин-
волюции на всех орбитах 0(t) относительно стандартной
симплектической структуры (для любых X, цеЯ).
^Доказательство. Нужно доказать равенство <7,
[dFXa(t), й?СМ11@]> = 0, где <А", Y) — значение линейного функ-
ционала X на векторе Y, так как sgrad,/r=adjF(I)(r). Действи-
тельно,
{F, G}= -co(sgradF, sgrad G)= -a>(ad;F(|)@, ad;-(t)(/)) =
= -t([dF,,dG,]). E30)
Пусть Х.#ц и t = a(t + \a) + $(t + \ia), где $ = \/(k-\i), ое =
l(p.-'k). Тогда
(t,[dFk(t), rf
) ^,a(')>=0' E31)
так как функции F a G постоянны на орбитах представления
Ad*.
Равенство нулю при ^ = |i получается из соображений
непрерывности.
4. Замечание. Теорему 3 можно обобщить на случай
функций из конечномерного пространства представления груп-
пы Ли в пространстве функций на орбитах представления Ad*,
см. [249].
5. Обозначения. Пусть W— такое подпространство
в пространстве аналитических функций A(L') на пространстве
L', дуальном к алгебре Ли L, что: a) dimfi/<oo; б) для любых
элементов geT, fsW имеет место включение /(Ad*jc)s W, т. е.
W инвариантно относительно представления, индуцированного
коприсоединенным представлением в пространстве функций на
L*, Т—группа Ли, отвечающая L.
Фиксируем в W базис/ь ..., fs. Тогда каждая функция feW
определяет на группе Т, отвечающей алгебре Ли L, набор
функций Су, по правилу
E32)
и набор линейных функционалов C[(J)sL*:
rfCVfa E33)

§ 34. МЕТОД СДВИГА АРГУМЕНТА 199
т. е. C',(f) — дифференциал отображения С/ в единице
группы Ли Т.
6. Предложение. При сделанных выше предположениях
выполняется равенство (sgrad/) (х) = С,1 {f)/^ (дг) +... + CJ (f)fs (x).
Доказательство. Дифференцируя равенство
d;pUx) = C1(expt^)/1(x) + ... + Cs(exp!^)/s(x) no t при 1 = 0,
получим
M>, E34)
здесь ftxeL", но имеется канонический изоморфизм L" = L,
поэтому /.tJCeL. Итак, ad}-ж(д) = -С.1/, (*)-...-CJ/, (*)• Про-
верим, что определение векторного поля sgrad/ будет вы-
полнено, если положить sgrad/=C»1/1 + ... + C*/s. В силу не-
вырожденности симплектической структуры со тем самым
все будет доказано. Имеем
<o{ClJ,{x), ad\x) = <o(-adyjx), ad\x) = (x, -[/sx, ф =
adjx>. E35)
7. Теорема (см. [249]). Пусть в A(L*) выделено конечномер-
ное подпространство W, инвариантное относительно коприсо-
единенного представления группы Ли Т, отвечающей алгебре Ли
L (см. п. 5), а /ь ..., fs — базис в W. Если в W заданы такие
функции hx, ..., hpeW, что
Ckj.{dhUx) = O, Ui, j^p, l^k^s, E36)
где С*. = Cj (Л,-) относительно базиса /ь ..., fs, то: а)
на всех орбитах коприсоединенного представления Ad* группы
Ли Т функции hh l^i^p, находятся в инволюции, т.е.
{hi, hj}=0, К/, j^p; б) сдвиги функций ht находятся
в инволюции на всех орбитах коприсоединенного представления
Ad* группы Ли Т, т. е.
{hi(x + ka), hj(x + \ia)}=0, l^i, j^p, X, цеЫ, aeU. E37)
Для доказательства этого утверждения потребуются следу-
ющие две леммы.
8. Лемма. В пространстве гладких функций С°° (If) на If
о
рассмотрим дифференциальные операторы Ari = C*7-xt—, где
ОХ;

200 ГЛ. 6 МЕТОДЫ ПОСТРОЕНИЯ ФУНКЦИЙ
jc; — координаты относительно базиса е1, ..., е", сопряженного
к базису еь ..., eneL, a C\j—структурный тензор алгебры Ли
L в базисе еи ..., еп. Тогда: а) если W—инвариантное
подпространство в С °° (L*), то XJs W для любой функции /е W;
б) если feW и fu ...,fs —базис в W, Xif=C{fj, то С{(/)=-С\е1.
Доказательство. Из равенства /(Ad*xp(^x) =
= C'(txptQf(x) следует, что ~
dt
но
поэтому (Х,/)е'=-Мх)С1..
Утверждение а) вытекает из конечномерности W, так как
в этом случае W—замкнутое подпространство и, следователь-
но, —
dt
f(Adlxptkx)eW.
0
Утверждение б) получается из равенства — f С, =
X(f)](t) C\ft
[lf)]() \fj
9. Лемма. Пусть f geC°°(L*) — гладкие функции на L'.
Тогда функции fug находятся в инволюции на всех орбитах
представления Ad* тогда и только тогда, когда
здесь Скц — структурный тензор алгебры Ли L в базисе еи ..., е„,
а Хх, ..., х„ — координаты в пространстве L" в базисе,
сопряженном с еи ..., е„.
Доказательство. Для скобки Пуассона имеем вы-
ражение
"'>--«'*?& E40)
см. п. 12 § 22. Используя его,получим, что функции/и g в ин-
волюции на всех орбитах тогда и только тогда, когда С^хк х
х ——- = 0, что и утверждалось.
дх, dxj
Доказательство теоремы 7. Проверим, что
СЪхкд?(х+Ха)г?{х+ца) = 0. E41)
Обозначим х + Ха буквой у. Тогда левая часть E41), которую

§ 34. МЕТОД СДВИГА АРГУМЕНТА 201
обозначим буквой А, равна
A = Cby^(y)d^(y + va)-XCba^(y)^(y + va), E42)
где у = ц — X. Из равенства
C}j (Л + VflJ ^ (у + vfl) = CYp,;/r (>• + ve) E43)
(C\,i — /-я координата ковектора С\„
следует, что
ff() l[lA )b^ j E44)
поэтому
= - (\ + ^i(z(y))b(y)
-±С1,(с1К(у))/у(у + уа)^0. E45)
Наконец, предельный переход в E41) доказывает равенство при
10. Определение. Конечномерное подпространство
W в A(L*) (где L—алгебра Ли) с выделенным набором функций
Аь ..., нре ^называется S-представлением группы Ли Т, ассоци-
ированной с L, если выполнены следующие два условия: а)
W—инвариантно относительно коприсоединенного представле-
ния Ad*G); б) <.Ck.(hj), dhp(x)) = 0 на U.

202 ГЛ 6. МЕТОДЫ ПОСТРОЕНИЯ ФУНКЦИЙ
11. Замечание. Условие <С? (//,•), dhp(x))=0, очевидно, не
зависит от выбора базиса /,, ...,/s в пространстве W.
12. Замечание. В теореме 7 утверждается, что если
(И,, ..., h' W) — S-представление группы Ли Г, то сдвиги
hi(x+Xa), hj(x + \xa) находятся в инволюции на всех орбитах
представления Ad*(Т) относительно стандартной симплектиче-
ской структуры.
13. Частным случаем теоремы 7 является методика сдвига
полуинвариантов (см. [11]). Отметим, что в этом случае
условие C),(dhix) = Q можно опустить, что является глубоким
фактом из теории представлений, который вытекает из резуль-
татов работ [188], [324], [486]. [339], [246].
14. Операцию сдвига аргумента можно скомбинировать
с операцией ограничения функций на подпространства в L*.
Приведем соответствующие формулировки для инвариантов.
Эти результаты принадлежат А. В. Браилову. На произвольные
представления они обобщаются очевидным образом.
15. Обозначения. Пусть V—векторное пространство, а —
инволютивный автоморфизм V, т. е. a^ = id, а Уо — собственное
подпространство для а, отвечающее собственному значению
+ 1, Vi—собственное подпространство для а, отвечающее
собственному значению —1. Тогда V= V0©Vi—разложение
для V относительно инволютивного автоморфизма а. Пусть
а'-у*_>у* — дуальный к а автоморфизм сопряженного про-
странства V. Ясно, что а* — инволютивный автоморфизм.
Символом У = {уH®(у"\ обозначим соответствующее раз-
ложение пространства К\ Отображение ограничения функци-
оналов хе V на подпространство V0<^V устанавливает естест-
венный изоморфизм (V*H->V*0, где V'o — пространство, дуальное
к Vo. Аналогично, отображение ограничения функционалов
yeV на К, с: К позволяет отождествить (V*I с пространством
V\, дуальным к Vl.
Пусть теперь V=L — алгебра Ли, a — инволютивный авто-
морфизм L, L = L0©Ll—разложение L относительно а,
L' = L*0©L\—разложение L* относительно а. Поскольку а —
автоморфизм L, то [L,-, Lj]czLi+j, где i,j = 0, 1—вычеты по
модулю два. Для произвольной гладкой функции / на L*
обозначим / ее ограничение на L*o.
16. Лемма. Пусть а — инволютивный автоморфизм алгеб-
ры Ли L, L = L0®L1 и L* = L*0®L\—соответствующие разложе-
ния L и L*, aeL\, X, |ieR и /, g—два инварианта коприсоединен-
ного представления Ad*. Тогда ограничения fka и gM а сдвигов
инвариантов f, g находятся в инволюции на всех орбитах
коприсоединенного представления в Ad*(r0), То — группа Ли,
отвечающая Lo.
Доказательство. Заметим, что для сдвига любой
гладкой функции / на элемент aeL\ имеет место равенство

! 35 МЕТОД ПОСТРОЕНИЯ КОММУТАТИВНЫХ НАБОРОВ 203
dfa(x)=\(dfa(x) + df.a(x)), xeL'o, где Дх)=Да*(х)). Отметим
также, что если fel(L)—инвариант коприсоединенного пред-
ставления Ad*(Г), то и /e/(L). Поэтому
{Л.„ ?ц,Л (х) = \ <Х, [dfKa (x) + df-XM (х), dg^ (x) +
+ \<х, {dh,a{x\ </?-„.„(*)]> + \ <х, [df-Ka (x),
dg,,a (x)]> + l- <x, [df-Ua{x), dg-^ (х)]У =
= \{А,а g»,a) (x)+ \{fKa, g-ц,а} (*) +
+ J{/-X.e, g,...} (X)+ '{/-X,«,g-M,a}(A-) = 0 E46)
в силу теоремы 3, так как /, g, f и g—инварианты копри-
соединенного представления АсГ(Г) группы Ли Т, отвечаю-
щей L.
§ 35. Метод построения коммутативных
наборов функций по цепочкам подалгебр
1. Определение. Предположим, что Н—подалгебра Ли
в алгебре Ли G. Имеет место естественная проекция л: G*-*H*.
которая определяется ограничением линейных функционалов,
n(h) = h\H. В этом случае функции, заданные на Н", можно
поднимать на G', точнее, если FeCco(H*), то определена
функция n'F^FoneC"(G*), которую будем называть подъемом
функции F на G*.
2. Лемма (см. [246]). Если функции/, geCcc(//*) находятся
в инволюции на всех орбитах представления Ad*, то их подъемы
iff, n*g на G* находятся в инволюции на всех орбитах
коприсоединенного представления Ad* группы Ли Р, отвечающей
алгебре Ли G.
Доказательство. Пусть е\, ..., es—базис в Н. Дополним
его до базиса е\, ..., es, es+i, ..., е„ в G. Введем следующие
обозначения для индексов: i, ... = 1, ..., s; a, ... = s+\, ..., и;
а, ...= 1, ..., п. Эти обозначения сохраним до конца параграфа.
В этих обозначениях подъем функции с Н* на G* не зависит от

204 ГЛ. 6. МЕТОДЫ ПОСТРОЕНИЯ ФУНКЦИЙ
координат л:а. Инволютивность будем доказывать с помощью
леммы 9 § 34. Имеем
Г'иГ df dg -Гс v Sf dg -i-Г' v df dg j-
^ аЬЛс -— - ^ o,R Лс -— 1- (_ ;„ Лс — h
дха дхь дх, дх$ дх{ дх„
+ dxt f f- + СЬхс f ^=CbXc f f = СЪх™ =0. E47)
дхл Ox-, dxt dxj J dxt dxj dxidxj
Мы воспользовались тем, что — =0, и равенством Су = 0,
охр
которое выполняется в силу того, что [et, e^\ e H. Окончательно
получаем 0, так как на всех орбитах представления Ad* B)
функции / и g находятся в инволюции (Q отвечает Н), т. е.
&й = СЬ*??=°- E48)
3. Лемма (см. [246 ]). Предположим, что G^H, f—
инвариант коприсоединенного представления Ad*(/>), a g—подъем
функции с Н*. Тогда fug находятся в инволюции на всех
орбитах коприсоединенного представления группы Ли Р, от-
вечающей алгебре Ли G.
Доказательство вытекает из равенства
Cbxkf f Jc'jXbf)^ =0. E49)
dxi dxj у dxi J dxj
4. Лемма (см. [246]). Пусть Н и G — такие алгебры Ли,
что HczG', где G' — производная алгебра Ли uf—полуинвариант
представления Ad*(.P). Если dg/dxx = 0, то {/, g} = 0 на всех
орбитах коприсоединенного представления Ad'(P), P отвечает G.
Доказательство. Функция / является полуинвариантом
тогда и только тогда, когда Ckuxk—=XJ, поэтому
dXj
- г &\* -
аХ ¦I <- Ьс ха ~ I "Г
дхь дхс у дхь J дхс
^^ёУ-0- <55О)
но ^j = 0, так как характер на производной алгебре—тождест-
венный нуль.
5. Итак, по каждой цепочке подалгебр G^>Hx^>H2zi...z>Hs
в алгебре Ли G можно строить функции в инволюции на G',
используя достаточно большой запас функций в инволюции на
Н*, например полученных с помощью сдвигов инвариантов,
и на каждом шаге добавляя инварианты коприсоединенного
представления группы Ли Qh отвечающей алгебре Ли Ht. Если

§ 35. МЕТОД ПОСТРОЕНИЯ КОММУТАТИВНЫХ НАБОРОВ 205
выполняется условие 1122^15,
то на каждом шаге можно добавлять полуинварианты. Оказы-
вается, эту конструкцию можно обобщить: на каждом шаге
можно добавлять не только полуинварианты, но и функции из
некоторых представлений. Точнее, справедлива следующая
6. Лемма. Пусть К—подалгебра в алгебре Ли G и Va A (С)
— инвариантное относительно Ad*(P) конечномерное подпрост-
ранство в пространстве аналитических функций на G". Функция
fe V, как описано в п. 5 § 34, при выборе базиса в пространстве
V определяет ковекторы C\sG". Если подъем функции geA(K*)
на G* постоянен вдоль этих ковекторов, то он находится
в инволюции с функцией f на всех орбитах коприсоединенного
представления группы Ли Р, отвечающей алгебре Ли G.
Доказательство аналогично доказательству предыдущей
леммы 2.6.
7. Простейший вариант изложенной конструкции мы полу-
чим в том случае, когда HscG — максимальная абелева
подалгебра в G'czG. В качестве инвариантов абелевой подалгеб-
ры Hs можно взять любой ее элемент, рассматриваемый как
функция на дуальном пространстве //*. Вообще говоря,
инвариантов максимальной абелевой подалгебры не хватает для
построения вполне интегрируемых систем, и приходится ис-
пользовать несколько подалгебр.
8. Лемма. Предположим, что в алгебре Ли G есть такая
цепочка подалгебр GzdH\^>Hx, что G=>G' =>НХ=>Н\^>Нг, Н'2 = 0,
\_Н1у Я2] = 0. Тогда любая функция feА(Н\) и элементы хеН2,
которые рассматриваются как функции на Н'2, находятся
в инволюции на всех орбитах представления Ad*(F), здесь группа
Ли Р отвечает алгебре Ли G.
Доказательство получается применением леммы 9 § 34
с учетом того, что [//ь//2]=0.
Итог исследования подводит следующая
9. Т е о р е м а (В. В. Трофимов [246]). Пусть дана пара алгебр
Ли (К, L), K^>L. Тогда если функции /, g на L* находятся
в инволюции на всех орбитах представления Ad* (Т^ где Т— группа
Ли, отвечающая алгебре Ли L, то подъемы /, g функций f,
g находятся в инволюции на всех орбитах представления Ad* E),
где S—группа Ли, отвечающая алгебре Ли К, м/=/ол, g = gon,
п: 1С-*U — отображение ограничения; если f—инвариант копри-
соединенного представления группы Ли S и g — подъем функции
geCx(Lx), то {/, g} = 0 на всех орбитах представления Ad*^);
если цепочка KzdL такова, что K-^K'zdL, f—полуинвариант
представления Ad*E) и g—подъем функции geCco(L*), то
{f,g}=0Ha всех орбитах коприсоединенного представления Ad*E)
группы Ли S.
10. Замечание. Методика этого параграфа является обо-
бщением конструкции М. Вернь (см. [513]). В работе [513] для

206 ГЛ. 6. МЕТОДЫ ПОСТРОЕНИЯ,ФУНКЦИЙ
построения глобальных симплектических координат на орбитах
максимальной размерности представления Ad* в нильпотентной
алгебре Ли использовались цепочки идеалов G1cG1^ — ^G
такие, что dim GiIGi-l = \ и инварианты представления Ad*(/",-)
(Pt — группа Ли, отвечающая алгебре Ли G(), г=1, ..., dimG,
поднимались с помощью естественной проекции щ: G*-*G' на
G*, что давало требуемые координаты.
В заключение приведем два утверждения 11 и 12, в которых
операции сдвига аргумента и подъема функций работают
одновременно.
11. Лемма. Пусть aeG* — элемент дуального пространства
к алгебре Ли G, G" — аннулятор a, f—инвариант коприсоединен-
ного представления группы Ли, отвечающий алгебре Ли G,
a g—гладкая функция на {G")'. Тогда функция fa(x)=f(x + a)
и функция g, рассматриваемая как функция на G', находятся
в инволюции на всех орбитах коприсоединенного представления
группы Ли Р, отвечающей алгебре Ли G.
Доказательство. Имеем равенства
{fa,g}(x)=<X,[dfa(x),dg(x)]) =
= -<в, [dfa(x), </?(*)]>=-<ad;9(x)(a), <//.(*)> = 0, E51)
так как dg(x)eG". Лемма доказана.
12. Лемма. Пусть о — инволютивный автоморфизм алгеб-
ры Ли G и G — G0 + Gu G* = Gq + G\ — соответствующие раз-
ложения пространств G и G* на собственные подпространства,
отвечающие собственным значениям +1 и —1. Для _asG\
и инварианта f представления Ad*(/") положим fa(x) =
=/(jc + a)|Go — ограничение на G"o сдвига инварианта f на
элемент а. Если g—подъем функции geCx(Ga)* на G", то
fa и g находятся в инволюции на G', группа Р отвечает G.
Доказательство. Имеем равенства
{fa,g} (X) = <Х, [dfa(X), dg(x)]} =
\ (x), dg(x)]) =
= -i (a, [df.{x)-d7-a{x), dg(x)]> =
= i<(ad;,(Jt)(e), dfa(x)-df-a(x)) = 0, E52)
так как dg(x)eGo- Лемма доказана.
§ 36. Семейства функций в инволюции,
связанные с согласованными скобками Пуассона
1. Определение. Две скобки Пуассона на многообразии
М называются согласованными, если любая их линейная
комбинация снова является скобкой Пуассона на М.

§ 36. СЕМЕЙСТВА ФУНКЦИЙ В ИНВОЛЮЦИИ 207
В другой терминологии согласованные скобки Пуассона
называются пуассоновыми или гамильтоновыми парами. Со-
гласованные скобки изучались в работах Магри [424], [425].
2. Предложение. Скобки Пуассона {/, g}0, {f, g]i со-
гласованы тогда и только тогда, когда выполнено тождество
{g, *}o,/h +
}o, g}i + {{h,f}u g}0 = 0. E53)
3. Обозначения. Пусть на многообразии М заданы две
согласованные скобки Пуассона {/, g}0 и {f,g}y. Обозначим
буквой J двумерное линейное семейство скобок вида
{/> ?}х,ц = М/> #}о + д{/> g}i- Отождествим семейство J с соот-
ветствующим подпространством в пространстве кососиммет-
рических тензорных полей типа B, 0). Положим R =
= max rkC(x), см. п. 2 § 27.
хеМ. CeJ
4. Теорема, а) Пусть f и g—центральные функции
пуассоновых структур A,BeJ соответственно, причем А и В ли-
нейно независимы (т. е. непропорциональны). Тогда f и g находят-
ся в инволюции относительно всех скобок из семейства J.
б) Пусть f и g—центральные функции пуассоновой струк-
туры AeJ, причем ранг тензорного поля А равен R почти всюду
на М. Тогда fug находятся в инволюции относительно всех
скобок семейства J.
Доказательство. Первое утверждение очевидно. Дейст-
вительно, в силу линейной независимости А и В пространство
J порождается этими пуассоновыми структурами. Функции
/ и g находятся в инволюции относительно А и В и,
следовательно, относительно их произвольной линейной ком-
бинации.
Пусть хеКегЛ, уеКетВ, С—произвольная форма из J.
Если А и В линейно независимы, то С = <хА + р>В. Следовательно,
С(х,у) = а.А(х,у) + $В(х,у) = О. Если В = ХА и rkA = R, то
утверждение следует из соображений непрерывности. Действи-
тельно, существует последовательность форм At такая, что
A(eJ, Aj->A, At и В линейно независимы, rk^4, = 7? и последова-
тельность векторов {*,-} такая, что х(-*х, д^еКегЛ,-. Тогда
С{х, y)=\im С{х„ у) = 0. E54)
п-> ос
5. Замечание. Таким образом, взяв объединение цент-
ральных функций всех скобок из семейства J, имеющих почти
всюду на М ранг R, мы получим инволютивное семейство
относительно всех скобок Пуассона {/, g}eJ одновременно.
Недостаток этой конструкции состоит в том, что центральные
функции могут быть глобально не определены. Поэтому будем
рассматривать локальную ситуацию.

208 ГЛ. 6 МЕТОДЫ ПОСТРОЕНИЯ ФУНКЦИЙ
Фиксируем точку хеМ такую, что ранг почти всех скобок из
семейства J в точке х максимален, т. е. равен R. Рассмотрим
семейство функций Fj, состоящее из локальных центральных
функций тех скобок Пуассона из J, которые в точке х имеют
ранг R. Отметим, что функции из семейства Fj могут иметь
разные области определения, при этом пересечение этих
областей может состоять из одной точки х. Чтобы избежать
такой ситуации, семейство F} уменьшим, оставив лишь конеч-
ное число независимых в точке х функций. Обозначим это
семейство по-прежнему Fj. В силу конечности F} существует
окрестность U{x), в которой все функции feFj определены
и пуассоновы структуры, отвечающие этим функциям, имеют
постоянный ранг R. Из теоремы 4 следует, что построенный
набор Fj инволютивен в окрестности U(x).
6. Замечание. Метод сдвига аргумента является частным
случаем общей методики построения инволютивных семейств
по произвольной паре согласованных скобок Пуассона. В дан-
ном случае кроме скобки Березина на пространстве G",
дуальном к алгебре Ли G, надо рассмотреть еще одну скобку
Пуассона {/, g}a(x) = (a, [df(x), dg(xJV), где aeG*— фиксиро-
ванный ковектор. Назовем эту скобку а-скобкой Березина.
Тензорное поле, определяющее скобку {/, g}a, постоянно и име-
ет вид Фа(Х, Y) = (a, [X,Y]>.
7. Лемма. Скобка Березина и а-скобка Березина образуют
гамильтонову пару для любого aeG*. Функции вида f\<a\x) =
=f(x + Xa), где f—инвариант коприсоединенного представления
Ad* группы Ли Р, отвечающей алгебре Ли G, являются
центральными для линейной комбинации {f,g} + X{f,g}a.
§ 37. Сжатия алгебр Ли
1. Операцию сжатия в теории гамильтоновых систем ввел
С. П. Новиков в работах, посвященных интегрированию уравне-
ний Эйлера на алгебре Ли ?C) = soC)©R3 группы движений
евклидова пространства R3. Результаты, изложенные в этом
параграфе, принадлежат А. В. Браилову [51].
2. Определение. Алгебра Ли G называется Ъ2-граду-
ированной, если G = Н® V, причем \Н, Н]сН, \Н, V\ci V.
[V, V]^H. L J
Пусть H*(V) — подпространство в G* всех ковекторов,
аннулирующих V (соответственно Н). Тогда G* = H*®V*. Для
любых xeG* и geG везде ниже хн и xv обозначает //*-
компоненту и К'-компоненту вектора х, gH и gv — //-компоненту
и К-компоненту вектора geG. Определим на G новый ком-
мутатор [jc, y\ формулой
[g, g'\ = [gH, gH] + [gv, g'v] + [gH, gv] + k[gv, g'v]. E55)

§ 37 СЖАТИЯ АЛГЕБР ЛИ 209
Коммутатор [х, у]к удовлетворяет тождеству Якоби. Получен-
ную алгебру Ли обозначим G^.
3. Определение. Пусть G— Z2-rpaflyHpoBaHHaH алгебра.
G». — построенная выше серия алгебр Ли, соответствующая
коммутаторам [.г, у\. Сжатием Z2-rpaflyHpoBaHHOH алгебры
Ли G называется алгебра Ли Go.
4. Обозначения. Пусть G — Z2-гpaдyиpoвaннaя алгебра Ли.
Обозначим скобку Пуассона для сжатия Go символом {х, у}0,
а аннулятор элемента х символом Anno(x).
5. Теорема (А. В. Браилов). Пусть G — полупростая Z2-
градуированная алгебра Ли, Go — соответствующее сжатие.
Тогда индекс mdG0 алгебры Ли Go равен индексу алгебры Ли
G (рангу G).
6. Лемма. Пусть G — Ъ2-градуированная алгебра Ли, xeG*,
geG, G = H®V. Тогда
(g) ;f gv gHXy. E56)
Доказательство. Если g'eG, то
= <Х, [gH, g'H]+[gv, g'H] + [gH, g'v]+^[gv, g'v]} =
= <xH, [gH, g'H]) + (xv, [gv, g'H] + [gH, g'v]) + k(xH, [gy, g'v]} =
xH, g'>. E57)
Полагая здесь ^ = 0, мы получим E56).
7. Обозначения. Пусть G — полупростая алгебра Ли, В(Х, Y)
— форма Киллинга G, geG. Двойственный ковектор g*
к вектору g относительно В определяется равенством g'(X) =
= B(X,g), XeG.
8. Определение. Если geG^, то g'eG{ определяется
формулой g*[u\ = B{g, и), ueGx, где форма В(Х, Y) на Gx та же,
что и на G (напомним, что G и Gx, рассматриваемые как
векторные пространства, совпадают). Если W<^G — подпрост-
ранство, то W* = {g' | g е W}.
9. Теорема. В G можно выбрать подалгебру Картана
J так, что будут выполнены следующие условия: a) J=Jh@Jv,
где JH = Jf]H, Jv = Jf]V; б) если geV и [g, Jv]=0, то geJv\ в)
JH — подалгебра Картана в К, где К—централизатор Jv в Н; г)
Jv—редуктивная подалгебра в G.
Доказательство см. в [88].
10. Лемма. Пусть G — полупростая алгебра Ли, J—под-
алгебра Картана в G такая, что выполнены условия а) — г),
J'czG*—двойственное к J в смысле определения 8 подпростран-
ство в G*o. Тогда для xeJ* общего положения имеет место
равенство Anno(jc) = /.

210 ГЛ. 6. МЕТОДЫ ПОСТРОЕНИЯ ФУНКЦИЙ
Доказательство. Пусть х = хн + xv, хнеН*, xveV* и ие
eAnno(jc), u = uH + uv, инеН, uveV. Из E56) вытекает, что
ad:Hxv 0.
По определению x — g' для некоторого geJ, g = gH+gv,
gHeH, gve V. Поскольку Н ортогональна V, то g*H = xH, g*v = xv.
По) i ому равенства E58) запишутся так:
|> ] + |> ] 0
|>я, «я] + |>к, Ик] 0,
кк,«я] = 0. E59)
Для элемента gK общего положения из второго равенства E59)
вытекает, что инеК, так как gHeJH<=.K, то и [gH, uH\eK.
Поэтому если коммутировать первое равенство E59) с gv, то
получим
[*к,[*к,«к]] = 0; E60)
так как Jv редуктивна в G, то из E60) вытекает, что [gK> uv~\=0.
Из этого равенства и первого равенства E59) получаем
"" = 0. Отсюда для gH и gv общего положения (используя
= 0) получим, что uveJv, uHeJH. Окончательно ueJ.
мы доказали, что Anno(x)aJ. Обратное включение легко
получить из формул E59).
11. Лемма. Если G — произвольная Ъ2-градуированная алгеб-
ра Ли, Go — ее сжатие, то indG^indG0.
Доказательство. Пусть Gx — семейство алгебр Ли,
введенное при определении сжатия, см. п. 2. Соответствие
4>(gH+gv) = gH+ -rr gv является изоморфизмом ср: Gr->GX при
Из этого
[gH, «я] = '
[gr, Uy] = (
Итак, мы
X', А."#0. Поэтому indGx = const(A.) при 'КфО. Докажем, что при
^#0 индекс может только увеличиться. Действительно, индекс
равен корангу матрицы || С^(Х)хк ||, где Су(Х) — структурный
тензор алгебры Ли Gx, а хк — координаты ковектора общего
положения. При малом изменении X ранг матрицы || Су(\)хк \\
может только увеличиться, поэтому индекс алгебры Ли
Gk может только уменьшиться, значит, при ХфО имеет место
неравенство ind Go S= ind Gx-
12. Доказательство теоремы 5. Из леммы 10 полу-
чаем
ind Go < dim Ann (t') = dim J = rk G = ind G, E61)
где teJ—элемент общего положения в картановской подалгеб-
ре J. С другой стороны, из леммы 11 следует, что
ind Go ^ ind Gi = ind G, значит, ind Go = ind G. Теорема 5 полно-
стью доказана.

§ 37. СЖАТИЯ АЛГЕБР ЛИ 211
13. Замечание. Пусть G = H®V—г2-градуированная ал-
гебра Ли. Подобно тому как мы выше определили сжатие
коммутатора [х, у\-*\х, у\0, для некоторых функций F на G*
можно определить нечто вроде сжатия.
14. Определение. Предположим, что разложение по
степеням V для функции F обрывается на некотором члене, т. е.
оно имеет вид Fb(xH) + F1 (хн, xv) + ... + F"(xH, xv) и Fk(xH, xv)
при фиксированном хн является к -формой от xv. Положим
в этом случае Fx(x) = "K^ F(xH, X~ll~ xv). Заметим, что Fx(x)
определено и при ^ = 0: F0(x) = Fn(xH, xv).
15. Предложение. Пусть G = H©V—Z 2-градуированная
алгебра Ли, F, F'—функции на G" такие, что: a) {F, F'}=0;
б) определены Fx и F'x (см. п. 14, например, F и F'—полиномы).
Тогда {Fx, F'x}=0, в частности, {F", F'"}0 = 0, где Fn, F'~—
максимальные компоненты при разложении на однородные
составляющие по V.
Доказательство. Соответствие gH+gv->gH + X~112 gv яв-
ляется гомоморфизмом алгебр Ли G->GX при Х.#0. При этом
гомоморфизме функция F переходит в Х~2 Fx, поэтому
{Fx, F'k}^ = 0 при^.#0. Это равенство верно и при Х = 0, так как
коммутатор и функции непрерывно зависят от X.
16. Замечание. Предложение 15 можно использовать для
построения инволю^ивных наборов функций на G#o. Покажем,
как это утверждение^южно применить к нахождению инвариан-
тов сжатой алгебры Ли Go.
17. Предложение. Пусть G = H©V—Ъ2-градуированная
алгебра Ли, F—полином на G*, инвариантный относительно
коприсоединенного представления, Fo — сжатие F (см. определе-
ние 14), a Go—-сжатие G. Тогда F—инвариант коприсоединен-
ного представления G.
Доказательство. Пусть usGg. Тогда и можно рассмат-
ривать как линейную функцию на Go. Очевидно, что при этом
сжатие и — и0 будет равно uv, если wK#0, и ин в противном
случае. Тот факт, что F—G-инвариант, может быть записан
в виде равенств
{F, и„} = 0, {F,uv} = 0, E62)
инеН, uveV. Из сделанного выше замечания вытекает, что
{Fo, ин}=0, {Fo, uv}0 = 0. Оба этих тождества в совокупности
и означают, что сжатие Fo является G0-инвариантом.
18. Пример. Алгебра Ли so D) задается соотношениями
\.еч-> ejk\ — eik, индексы i,j,k пробегают значения от 1 до 4,
еи=-еИ. Подалгебра #=soC) натянута на векторы
е12, е13, е2з. V—линейная оболочка векторов е14, е24, ^34-
Нетрудно проверить, что разложение so D) = Н © V является
Z2-гpaдyиpoвкoй на so D), а соответствующее сжатие soDH —

212 ГЛ. 6 МЕТОДЫ ПОСТРОЕНИЯ ФУНКЦИЙ
это полупрямая сумма soC)©R3, или, другими словами,
алгебра Ли группы движений евклидова пространства R3.
Инвариантами коприсоедингнного представления для so D), как
4
известно, являются функции F= ? xf. и F' = xl2x34,— х13х2д +
+ Х25Х1л- Сжимая Fh F', получаем инварианты коприсоединен-
ного представления для алгебры Ли soC)®R3: F0 = x\A + x\^ +
+ х§4 и F'0 = F'.
§ 38. Метод тензорных расширений алгебр Ли
1. Замечание. Этот метод был впервые предложен
В.В.Трофимовым в [250], [251], [253], а затем развит
А. В. Браиловым в [47] и Ле Нгок Тьеуеном в [151]. Пусть
А — коммутативная ассоциативная (конечномерная) алгебра
с единицей. Тензорное произведение G®A алгебры Ли G и А яв-
ляется алгеброй Ли относительно коммутатора
\g®a, A®6] = [g, /i]® ab, g, heG, a, be А. Вопрос, который
здесь возникает, состоит в том, чтобы, зная полное инволютив-
ное семейство функций на пространстве G", построить полное
инволютивное семейство функций на пространстве (G ® А )*.
Впервые эта задача изучалась в работах В. В. Трофимова [250],
[251], [253] для алгебр A =R[jc1, ..., *„]/(*?¦+ f, ..., jc™-+1), где
R[xj, ..., xnj — кольцо полиномиальных функций переменных
х1,...,хп, a (х™1 + 1, ..., x™"+1)— идеал, натянутый на
x™i + 1, ...,x™"+1. Затем эта задача рассматривалась А. В. Бра-
иловым для алгебр с двойственностью Пуанкаре.
2. Конструкция. Рассмотрим случай кольца A =R [jc1; ..., хп~\/
/(x"' + 1, ..., x™" + 1). Пусть s. обозначает образ элемента х{
в кольце А при естественном отображении п; R[^i, ¦••, х„]->А,
т. е. 8; = п(л:(), а е1, ..., ег—базис алгебры Ли G. Тогда векторы
?j'...?^-ej, O^y'^r, О^ос.^ш,, 1 </<и, образуют базис алгебры
Ли G®A. Дуальный базис в G* обозначим е\ он определяется
из соотношения <V, е>/ = Ъ), где </, jc> — значение feG" на
векторе xeG*. Координаты в пространстве G®A в базисе,
дуальном к е ¦... ¦e""eJ., Ky^r, 0<а,^т,, l</^w, обозначим
х{а1, ..., а„)., а координаты в G* в базисе, дуальном к et.
Обозначим Jxt, I </<r. Введем в пространстве G®A новые
переменные
z,= Y. e«-...e--Jr(p1 рД. E63)
3. Алгоритм (t) В. В. Трофимова. Пусть F(xt, ..., хп) — ана-
литическая функция на пространстве G* (или на открытом

§ 38. МЕТОД ТЕНЗОРНЫХ РАСШИРЕНИЙ АЛГЕБР ЛИ 213
подмножестве в G*) со значениями в R. Раскладывая
F(xl, ..., хя) ъ ряд Тейлора и подставляя вместо xi выражения
для Zj из E63), мы получим конечную сумму, так как
достаточно высокие степени элементов et равны нулю. Итак,
F(z1, ..., zr)— корректно определенная функция на пространстве
(G<S>A)* со значениями в кольце А; ее можно представить в виде
F(Zl,...,zr)= X e"'...e;-F.i...B>(x(p1, ....ft,),), E64)
поскольку г"'..г"—базис алгебры A = R[_xl, ..., хя~\/
1{х^ + \х™-+\ здесь Fai...a.(x(pi)...,Pn).)eR. Алгоритм (?)
б ф F срансве
...,
1{^ \\ ai...a.((pi,Pn)) р ()
по определению будет переводить функцию F на пространстве
G' в набор функций F.,....,, т.е. (t)(F) = {Fa^}.
4. Теорема (В. В. Трофимов, [251], [253]). Пусть функции
F1 (x), ..., FN(x), определенные на пространстве G*, находятся
в инволюции относительно формы Кириллова на всех орбитах
коприсоединенного представления группы Ли Р, ассоциированной
с алгеброй Ли G. Тогда все функции (/)(/r1)U---U(O(^r\) Ha
выходе алгоритма (t) находятся в инволюции относительно
формы Кириллова на всех орбитах коприсоединенного представ-
ления группы Ли Р®А, ассоциированной с алгеброй Ли G®A.
При этом, если /"j,...,^ функционально независимы на про-
странстве G', то все функции семейства (O(^i)U--lj(O(^jv)
функционально независимы на пространстве {G®A)'. Если
Fl, ..., FN — полный набор, то (?)(Fj) U"-U(')(^jv)—также пол-
ный набор функций.
Доказательство этой теоремы будет дано в несколько более
общей ситуации, см. п. 27.
5. Примеры. В работе Такифа [501 ] построены инварианты
алгебры Ql(G) = G®R[x]/(x2). Рассмотрим следующее кольцо
Л = Я [х]/(х3). В пространстве O.2(G) = G®A имеем координаты
х@)г, хA){, xB)i и переменные zi = .x@I-e2 + x(l)iE +
+ xB)i (здесь е3 = 0). Воспользовавшись формулой Тейлора,
получим F(zl, ..., zr) = F0(z) + F1(z)e + F1(z)e2, где
E65)
E66)
'^ E67)
(рис. 38).
Рассмотрим алгебру Ли, отвечающую кольцу A=R[xt,
1{х\,х22). Тогда ull(G) G®A GG G G

214
ГЛ. 6. МЕТОДЫ ПОСТРОЕНИЯ ФУНКЦИЙ
= Ё2 = 0. Координаты в Q1A(G)' мы обозначили х@,0),,
хA, 0),-, х@, l)j, x(l, 1), в соответствии с написанным разложе-
нием Cliд (G) в прямую сумму линейных пространств. Имеем
Рис. 38
переменные zi = z1z2x (О, O)i + z1x(O,
и снова по формуле Тейлора F(z1,
| с fn 1 -4- ? ? /* • 1 ГЛС
р /7\ = pixn j\ у
Рис. 39
z2x(\,Q\+x(\, 1),.,
E68)
E69)
E70)
градуированная коммутатив-
AA П
(рис. 39).
6. Определение. Пусть рур у
ная алгебра, т.е. А = А0@...@Ап и A;AjCiAi+j, i+j^n. Пред-
положим, что дш\Аа=\. Пусть Q — линейный функционал на А,
равный тождественно нулю на Ai при i^n—l и не равный нулю
на Ап. Пусть р(а, b) = Q,{ab) — симметричная билинейная форма
на А. Если р — невырожденная форма, то алгебра А называется
алгеброй с двойственностью Пуанкаре.
7. Конструкция. Легко видеть, что для алгебр с двойствен-
ностью Пуанкаре имеем Ao-R. Пусть zt — \. Выберем произ-
вольный базис е2,...,е^ в At, затем выберем произвольный
базис e А\ /2
Ji +!,
...,е^ в At, затем выберем произвольный
в А\ и так далее до градуировки и/2.

i) 38. МЕТОД ТЕНЗОРНЫХ РАСШИРЕНИЙ \.irt-sp ЛИ 215
В Апп выберем базис, в котором матрица формы \\ диагональ-
на. В пространствах At, i>n/2, выберем базисы, сопряженные
относительно Р к уже выбранным в Anl2-i- В итоге получим
e1,...,eJV — однородный самосопряженный относительно Р ба-
зис алгебры А, Р(е„, ?,) = б,7, где * — перестановка.
8. Обозначения. Пусть е,,...,<?„ — базис в G\ xl,...,xm—
соответствующие координаты. Линейные функции на G" естест-
венно рассматривать как элементы алгебры Ли G. Напротив,
элементы .г,-®е7- алгебры Ли GA = G® А, рассматриваемой как
алгебра Ли над R, можно рассматривать как линейные
координатные функции на G*A. Пусть лг / = .г,-® е^—координаты
на GA.
9. Алгоритм (J>) А. В. Браилова. Для полиномиальной функ-
ции Р(х) на G , имеющей вид
P{xu...,xm)=t I Pil...ltxli...xl=PIxl, E72)
k = 0 (», i,)
определим функции Ри)(х), l^j^N, на пространстве
G \ формулой
Pfl)(x\, ...,xNm) =
QC
= ZZ Pli...it(Ej,Eji...Ejt)x'lK.x'>- = Pl(zJ,Zj)xy, E73)
«1 = 0 (i, ij)
(J,-A)
здесь (zj, zJt...Zjk) — проекция элемента ?;,•••?;, на базисный вектор
е-. Пусть F—набор полиномиальных функций на G*. Алгоритм
(о) переводит семейство F в семейство (b)(F) = FA = {PU)\ PeF,
j}
10. Теорема (А. В. Браилов, [47]). 1) Если F—инволютив-
ный набор на G*, то FA — инволютивный набор на G'A = (G ® А)'.
2) Если F—полный инволютивный набор и число независимых
полиномиальных инвариантов алгебры Ли G равно ее индексу, то
FA — полный инволютивный набор на G'A = (G ® А)*. 3) Если
набор F содержит невырожденную квадратичную форму, то
набор FA также содержит невырожденную квадратичную
форму.
11. Обозначение. Звездочкой обозначим также линейный
оператор *е, = е,г, *2 = id. Пусть (X, Y) — скалярное произведение
в алгебре А, соответствующее базису ex,...,eN. Легко прове-
рить, что для любых элементов a, be А выполнено равенство
(*а, b) = (zN, ab).
N
Пусть АеА ® А, где А = ]Г (*Е() ® е;. Элемент А есть точный
аналог диагонального когомологического класса, см. [181].

216 ГЛ. 6 МЕТОДЫ ПОСТРОЕНИЯ ФУНКЦИЙ
12. Лемма. Имеет место равенство (*а, bc) = (*b, ас) для
любых элементов а, Ь, се А.
Доказательство очевидно.
13. Лемма. Имеет место равенство АA ® а) = А(а® 1)
для любого элемента as А.
Доказательство вытекает из равенств
А A ® а) = *е,: ® е, а = (*е;-, е, а) *е, ® *е,- =
= (*е,-, Zja)*z, <S> *е; = е,я® *е; = А(а® 1). E74)
14. Определение. Для многочлена Ре9.[х1, ...,х„] опре-
делим PeA[xi, ...,xm] равенством P(x) = P,Zjx'{J, где мульти-
индексные обозначения понятны из формул E72), E73). Роль
полиномов, обозначенных буквой с тильдой, объясняет
15. Лемма. Имеет место равенство
>, Qli)}={Si<g>Ej, А{р7Ь}® 1), Лбе С" (С). E75)
Доказательство. Поскольку
j, ^® %>{*;, Л{}\ E76)
то достаточно показать, что
^^Ъ®1- E77)
Левую часть E77) обозначим {Р, Q}®. Введенная таким
образом операция {Р, Q}® билинейна и при фиксации одного из
аргументов становится дифференцированием второго. Это
означает следующее:
{р,р2,е}®=л® 1 -{р2,q}®+p2®\{р„е}®, E78)
{Р, 6162}®=! ®& "{Л 22}® + 1 ® &-{Л Ci}®- E79)
Левая часть E77) также обладает аналогичными свойствами:
= Р1 ® 1 (А• {/Сб} ® 1) + Р2 ® 1 -(А• {P~Q} ® 1), E80)
® йг '(А • {Л1М ® 1)- E81)
Свойство E80) вытекает из мультипликативности операции
Р-*Р и свойств стандартной скобки {/, g}: Свойство E81)

§ 38. МЕТОД ТЕНЗОРНЫХ РАСШИРЕНИЙ АЛГЕБР ЛИ 217
получается из леммы 13. Сопоставляя равенства E78), E79)
и E80), E81), видим, что равенство E77) достаточно доказать
для линейных Р и Q. Имеем равенства
t-v, xq] — *ь5 ^х; *ьр\лг, \aj
= (zk, zs-zp)*zs®*zpC'rqxk = (*zk, zs-zp)*zs®*zpC'rqx"k =
= (*es, zk-zp)*zs® *zpC'rqx'k =
= zkzp®*zpC'rqx*k = A-zk® 1 -С^х*1 = Л-{д:г, xj® 1. E82)
16. Лемма. Пусть P,, ..., PreR [xl, ..., xm]—полиномы,
независимые в точке уеС, где у = {)\, ...,ут). Тогда полиномы
Pj1', ..., P(rN) независимы в любой точке xeG*A, у которой
старшие координаты xf=}'i, I ^i^m.
Доказательство. Предположим для определенности,
что полиномы />!, ..., Рг независимы по первым г координатам,
т.е. det || dPj(y)ldx;\\ Ф0. Рассмотрим матрицы Msq(x):
E83)
где 1 ^i, q^N, 1^/, j^r. Если s>q, то (zq, azs) = 0. Поэтому,
если (zq, е7)/0, то 8х//дхТ = 0- Значит, при s>q матрица Мщ(х)
состоит из нулей. При s = q имеем
"itf—(%'b)P,j^-L^.'xi,-xi, 'j^Xi^-Xi-—^~- р84)
Рассмотрим матрицу Msqij(x), составленную из матриц Msq(x),
эта матрица является блочно треугольной, причем на диагонали
стоят невырожденные матрицы SPjiy^/By^ поэтому она не
вырождена и, значит, полиномы Р[1), ..., Р™ независимы
в точке х.
17. Теорема (А. В. Браилов). Пусть Р1,...,РГ—набор
независимых инвариантов коприсоединенного представления груп-
пы Ли Р, ассоциированной с алгеброй Ли G, и ее индекс равен г.
Тогда: a) indG/4 = dimy4indG; б) Р^\ ..., P(rN)—полный набор
независимых инвариантов коприсоединенного представления груп-
пы Ли Р, ассоциированной с алгеброй Ли G.
Доказательство. Пусть Р(х) — инвариант. Это эквива-
лентно тому, что {Р, xs} = 0, \^s^m. Из леммы 15 получаем
{P(l), Jt*j} = {P(", x1sJ)}=(e,® Zj, A-{P, xs} ® l) = 0, E85)
значит, Р<0 — инварианты алгебры Ли GA = G®A. Если
Pj, ..., Рг независимы, то из леммы 16 следует независимость

218
ГЛ 6. МЕТОДЫ ПОСТРОЕНИЯ ФУНКЦИЙ
rN штук инвариантов Р{*\ ..., P(rN) алгебры Ли GA = G®A,
значит, indGA^rN. Обратное неравенство получается следу-
ющим образом. Пусть Ьщ (х) — квадратная матрица
(Lsq(х))^ = {.Х{, х'/} (х). Если s>q, то Lsq(x) = 0. Если s = q, то
(Lsq(x)).j = XbC'{j. Если yeG' (r, = .\-:v, t=l, ..., т) — регулярная
точка, то ранг матрицы bij = x!tCij равен т — indG. Отсюда
ind GA sjmN— rk Lsq (x) = mN—(m — ind G)N = rN.
18. Доказательство теоремы 10. 1) Инволютивность
семейства FA вытекает из леммы 15.
2) Пусть Р}. ..., PkeF независимы и образуют полный
коммутативный набор. В этом случае к = 2~1 (m + r), r = indG.
Из леммы 16 вытекает независимость kN штук находящихся
в инволюции полиномов Р'1', ..., Р^. Для полноты этрго
набора достаточно, чтобы kN = 2~1 (dimG^ + indG^), что выте-
кает из теоремы 17: 2 (dimG^ + ind GA) = 2~l (mN+rN) = kN.
3) Пусть QeF—невырожденная квадратичная форма, мож-
но считать, ^ что Q{x) = qi{xiI, gf#0, l^i^m. Тогда
Q* (x) = qjXJx*J—также невырожденная квадратичная форма.
Нетрудно видеть, что в вещественном случае эта форма всегда
индефинитна. Теорема доказана.
19. Замечание. Алгоритмы (/) (см. п. 3) и (Ь) (см. п. 9)
имеют разные области определения (рис. 40), где условно
изображены области действия этих алгоритмов.
Класс
алгебр
Рис. 40. X={R[xi, ...
Пуанкаре}, U—мноп
многочлены на G*
Класс
функций на (>
*7' + 1)}, К={алгебры с двойственностью
V—аналитические функции на областях
в G*
20. Теорема (В.В.Трофимов, см. [256]). Пусть (hlt ...
..., hp; W) является S-представлением группы Ли Р. Тогда
утверждается, что {(t)(ht),..., {t){hp); (t){W)) является S-
представленчем группы Ли Р, ассоциированной с алгеброй Ли G.
21. Предложение. Пусть FeC™(G'). Тогда имеем
E86)

§ 38 МЕТОД ТЕНЗОРНЫХ РАСШИРЕНИЙ АЛГЕБР ЛИ 219
где Fti
ti Р.
Доказательство. Непосредственно из определения ком-
мутатора в G ® А следует, что
, E87)
где С*.— структурный тензор алгебры Ли G в базисе et. Из
этого соотношения легко получить, что X(z\l...z'1n-ei)F{zi, ...
..., zr) = e'1'...t'AX(el)F)(zu ..., zr), где Zfe) — оператор в C°°(G*),
отвечающий базисному вектору eteG, и вместо z,- подставлено
его выражение E63). Применяя к функции F(z1; ..., zr) =
= ?>'¦...е^...„XPi, ..., Р„)Л оператор *(ej-... ??¦<?,•) и восполь-
зовавшись соотношением X(z*1'...z*"ei)F=z11...Er'n-(X(ei)F), мы
очевидно, получим наше утверждение.
22. Следствие. ?сли И^— инвариантное подпространство
в С°°(С*) относительно Ad>, wo @(И^) = {(/<)(^)|*е ^} —мн-
вариантное подпространство относительно А.д.Р(&Л, здесь Р®А
отвечает алгебре Ли G ® А.
23. Предложение. Если W— конечномерное инвариантное
подпространство в С* {G'), то (t)(W) — конечномерное инвари-
антное подпространство в С°° ((G ® А)').
Доказательство. Докажем, что если /i,.--,/s — базис
пространства W, то (O(/i)U-U(O(/s) —базис в (t)(W). Это
утверждение вытекает из явного вида функций fe(t){F),
который легко получается из разложения f(zA, ..., zr) в ряд
Тейлора.
24. Обозначения. Пусть (hy,...,hp, W) — 5-представление
группы Ли Р и X(ei)hk = Ci(hk)fj. Тогда
X{z\'...zl-et)hk,, ,T. = C?-"'-(At.Ti....,T.)ta ,a./jPl,...,P,, E88)
так как (^(И7)—инвариантное конечномерное пространство,
здесь At>Ti,...^ne{t){hk).
25. Предложение. Имеет место равенство
С^-ЦИ^ Jiai..^ = Ci(hk)^l.Xi...6^. E89)
Доказательство. Из предложения 21 следует, что
Сравнивая полученное выражение с E88), получим наше
утверждение.
26. Доказательство теоремы 20. Инвариантность
пространства {t)(W) вытекает из п. 22. Проверим условие б)

220 ГЛ. 6. МЕТОДЫ ПОСТРОЕНИЯ ФУНКЦИЙ
определения 10 § 34. Распишем это условие в коо
<Ckt(hj),dhp(x)y = Ct.t{hJ)dhpjdxt, где Ctt{hj) = c({j){
координаты ковектора C*(h}) в базисе eteG. Умножим
на jj
равенство нулю выражения С^р^'.'.'.Ур (й^ ,.,^ )dh(z)/dxipl...рл,
что, очевидно, равно С *1,Гр1||'.'.'.]'|11| (/»(,& i5J e™i~pi...e™»~p"——, что
в силу п. 25 равно
^.^^ЦИ^ E92)
и получим нуль, так как по условию C*(hj)t—— = 0, теорема
доказана.
27. Доказательство теоремы 4 вытекает из теоремы 7 § 34,
если применить теорему 20.
28. Определение. Ассоциативная коммутативная алгебра
А с единицей называется алгеброй Фробениуса, если на
А существует невырожденное скалярное произведение (х, у),
которое удовлетворяет условию «инвариантности» (ab, с)=
= (а, be), a, b, се А.
29. Конструкция. Рассмотрим конечномерную ассоциатив-
ную коммутативную алгебру А с единицей, dim A= N. Фи-
ксируем в А некоторый базис ех, ..., zN и линейный оператор
П: А-*А такой, что Пе( = еш, 1^/^TV, где со — некоторая
перестановка индексов. Определим на А скалярное произведение
<*, у}, относительно которого базис ei,...,eN будет ор-
тонормированным.
30. Определение. Ассоциативная коммутативная алгебра
с единицей называется самосопряженной относительно тройки
(A, Cl, E;), если скалярное произведение <х, у} удовлетворяет
условию <еШ1-, Ejek> = <emj, E,-et>, l^i, j, k^N.
31. Теорема. Ассоциативная коммутативная алгебра А яв-
ляется самосопряженной тогда и только тогда, когда А явля-
ется алгеброй Фробениуса.
32. Алгоритм. Пусть е; — базис алгебры A, xs — координаты
на G* (пространстве, дуальном к алгебре Ли G); тогда
обозначим xf функцию х,®еа. Для многочлена Р вида E72)
определим функцию Р формулой
P=I I I Pll...lk*hzh...4x?...x?. E93)
fe = 0 i1,....it=l jy jk=l

§ 39. МЕТОД СХОДНЫХ ФУНКЦИЙ 221
Для любого элемента аеА построим функцию Р" = (О.а, Р), т. е.
P" = (Cla, P,?jX?J).
Рассмотрим только такие расширения, для которых скобка
Пуассона обладает следующим свойством. Для всех многочле-
нов Р, Q на пространстве G* имеет место равенство
{P",Qb}(G®A)- = {P,Q}f'b\ где a, be А, а я: АхА^А —
некоторое отображение.
33. Теорема (Ле Нгок Тьеуен). Пусть А — ассоциативная
коммутативная алгебра с единицей и [А, П, е,) — ее тройка, я:
АхА^А—некоторое отображение и для каждой полиномиаль-
ной функции Р на дуальном пространстве G* к алгебре Ли
G и элемента аеА определено продолжение Р" функции
Р относительно тройки (А, €1, еД Тогда если справедливо
тождество {Ра, Q }<о®лг = {Л Q}"a,b) для всех полиномиаль-
ных функций Р, Q на G*, то к (a, b) = ab.
34. Теорема (Ле Нгок Тьеун [151]). Пусть А—ассоци-
ативная коммутативная алгебра с единицей. Для существования
некоторой тройки (A, Q, е,-) для алгебры А, относительно
которой расширенные функции Ра и Qb удовлетворяют равенст-
ву {Ра, Q"}g'a = {P, Q}% для всех многочленов Р, Q, где
G — произвольная алгебра Ли, необходимо и достаточно, чтобы
алгебра А была алгеброй Фробениуса, G"A = {G®A)'.
§ 39. Метод сходных функций
1. Обозначения. Пусть Н—полупростая подалгебра Ли G.
Рассмотрим присоединенное действие алгебры Ли Н в G.
Алгебра Ли G превращается в //-модуль. Пусть V—Н-
подмодуль в G, не содержащий Н. Если в V фиксировать базис
Xi, ..., х„, то на Н определена (ихи)-матрица W 1-форм.
Значение этой матрицы на векторе heH будем обозначать WH.
Таким образом, Wh — матрица преобразования ad,,: K->K
в базисе хг, ..., х„. Матричные элементы юG- матрицы W явля-
ются 1-формами на Н. Поскольку алгебра Н полу проста, то
со,-; можно считать принадлежащим Н.
2. Предложение. Пусть В—инвариантная r-форма от-
носительно действия алгебры Н на строках (Х\, ..., Х„), XteV.
Функции на G* вида B(XW'», ..., XW1') находятся в инволюции со
всеми линейными функциями соу (l^i, j^n).
3. Замечание. Может оказаться, что Я-модуль G 'имеет
несколько подмодулей Vt, ..., Vm, изоморфных V. В этом
случае имеет смысл говорить о функциях вида B(XWl1,
X' W1*, ..., X{m)W1^*"). По-прежнему функции такого вида
находятся в инволюции со всеми линейными функциями
co,v, Is;г, _/<и.
4. Определение. Будем называть каноническими Н-ин-
вариантами функции вида B(XWil, ..., X(m)Wlf+").

222 ГЛ. 6. МЕТОДЫ ПОСТРОЕНИЯ ФУНКЦИЙ
5. Определение. Согласно теореме Гамильтона — Кэли
и- 1
W= ? ai{W)Wl. В записи канонического //-инварианта явно
i = 0
присутствуют степени матрицы W. Назовем два канонических
//-инварианта сходными, если один получается из другого
заменой матрицы W на W, причем степень i такова, что
функция at(W) тождественно не равна нулю.
6. Определение. Пусть G — алгебра Ли, а Н—ее под-
алгебра. Скажем, что пара (G, Н) удовлетворяет М-условию,
если выполнены следующие условия. Предположим, что
G = H® V1@...@Vk—разложение Я-модуля G на неприводимые
подмодули. Требуется, чтобы: а) Н была простой подалгеброй
Ли в G классического типа А„, В„, С„, /)„; б) все Vt являлись
либо тривиальными //-модулями, либо отвечающее подмодулю
К,- (i=l, ..., к) представление алгебры Ли было эквивалентно
минимальному.
7. Теорема (А. В. Беляев [20]). Пусть G — алгебра Ли,
а Н—ее подалгебра. Предположим, что пара {G, Н) удовлет-
воряет М-условию, Fi = X'WlBX' — канонический Н-инвариант.
Тогда скобка Пуассона {Ft, Fn} сходных функций Ft, Fn (X
может совпасть с X') равна нулю.
§ 40. Метод /У-матрицы
1. Определение. Алгебра Ли G называется двойной
алгеброй Ли, если задан такой линейный оператор R: G->G, что
скобка
[X, Y]R = l-([RX, У] + [ЛГ, RYJI E94)
задает в G структуру алгебры Ли, т. е. для нее выполнено
тождество Якоби. Алгебру Ли со скобкой E94) будем обозна-
чать символом GR. Скобку Березина алгебры Ли GR будем
называть R-скобкой.
2. Пример. Пусть алгебра Ли G как векторное пространство
представлено в виде прямой суммы двух своих подалгебр
G = G+@G-. Обозначим Р± проектор на G± параллельно
дополнительной подалгебре и положим R — P+—P^. Тогда
R задает на G структуру двойной алгебры Ли.
3. Замечание. Общая теория Л-скобок изложена, напри-
мер, в [206]. Через I(G) обозначим кольцо инвариантов
коприсоединенного представления группы Ли Р, отвечающей
алгебре Ли G.
4. Теорема (см. [206]). Функции из I(G) находятся
в инволюции относительно R-скобки на G*. Уравнения движения,

§ 41. КРИТЕРИЙ ПОЛНОТЫ 223
задаваемые функцией <р е I(G), относительно R-скобки имеют вид
?=-ad'G,M($), M = 2 '/?(Лр(!;)). E95)
Доказательство. Пусть <р, vJ/eC^G*). Тогда их R-
скобка имеет вид
{Ф, Ф}«И = 2<[^ф(-4 <Л|/(*)], х) +
+ 2<[^ФD Rd^{.x)l х). E96)
Поскольку ф — инвариантная функция, то <[^ф(х), Х~\, х) = 0
для всех XeG. Отсюда вытекает первое утверждение. Очевидно,
что для всех <peI(G) уравнение Эйлера \|/={ф, \\>}ц имеет вид
^(x) = 2-\[Rd<p(x), di,(x)l х) =
= -2-1(d^(x),ad'Rd9Mx), E97)
т. е. х=-2~1 ad'Rd9(x)x.
5. Замечание. Обзор систем, интегрируемых с помощью
метода /{-матрицы, можно найти в работе [206].
Глава 7
ПОЛНОТА ИНВОЛЮТИВНЫХ НАБОРОВ ФУНКЦИЙ
§ 41. Критерий полноты
1. Обозначения. В этом параграфе будем изучать вопрос
о полноте семейства функций Fj, построенного в п. 5
§ 36. Определение полноты дано в п. 9 § 27. Напомним,
что Fj — это объединение центральных функций всех скобок
из линейного семейства J, порожденного парой согласованных
скобок Пуассона.
Вместе с пространством J рассмотрим его комплексифика-
цию Ус, т. е. семейство комплексных тензорных полей вида
"КА + \х.В (к, цеС), где А и В—произвольные линейно незави-
симые пуассоновы структуры из J. Для почти всех Се J имеем
vkC{x) = R, поэтому с точностью до пропорциональности
существует лишь конечное число ненулевых элементов
С], ..., CNeJc таких, что rkCi(x)<R, /=1, ..., N. Для каждого из
них определим подпространство К,¦ с Кег С,(х) с Т*ХМС:
/Г,- = {?еКегС( (*)[?(?, Кег С,(.*)) = 0 для всех BeJ}. E98)
Обозначим буквой L подпространство в Т_*ХМ, порожденное
дифференциалами функций feFj. Пусть LcTxM—косоор-
тогональное дополнение к L относительно некоторой 2-формы
С(х), CeL. Полнота семейства Fj в точке х означает, что
? = L + Ker C(x), поэтому выясним строение L.

224 ГЛ. 7. ПОЛНОТА ИНВОЛЮТИВНЫХ НАБОРОВ ФУНКЦИЙ
2. Теорема, а) Косоортогональное дополнение L к подпро-
странству L не зависит от выбора пуассоновой структуры CeJ.
б) Подпространство Lc содержит ядра всех 2-форм С(х) на
(Т'ХМ)С, где CeJc\{0}. 1 '
N
в) Равенство LC = LC+ ^ kerC,(x) имеет место тогда
и только тогда, когда dim АГ( = dim M — /?, i=l, ..., TV.
Из этой теоремы легко получить необходимое и достаточное
условие полноты семейства Fj в точке хеМ.
3. Теорема (критерий полноты А. В. Болсинова, см. [43],
[46]). Инволютивное семейство Fj полно в точке хеМ
относительно фиксированной пуассоновой структуры CeJ тогда
и только тогда, когда: a) rkA(x) = R для всех AeJc, Аф\С\
б) dim Кс = dim M-R, где
Кс= ,.екетС{х)\В(?„ KerC(x)) = 0 для всех BeJ). E99)
Доказательство. Условие полноты имеет вид
L = L +Кег С(х), поэтому достаточность сразу следует из
утверждения в) предыдущей теоремы 2. Оттуда же следует
необходимость условия dim Kc = dim M — R. Покажем необходи-
мость первого условия. Предположим, что существует элемент
C'eJc, С' ф\С, такой, что rkC'(x)<R. Условие
L = L + KerC(x) тогда не выполняется, поскольку каждая «осо-
бая» форма с" дает независимый вклад в размерность L,
равный R — rkC'(x), см. п. 15.
4. Замечание. При rk C(x) — R, т. е. в случае симплектиче-
ского слоя 0х максимальной размерности, условие
dim Kc = dim M — R выполняется автоматически. Для этого слу-
чая утверждение теоремы впервые было доказано А. В. Бра-
иловым при дополнительном требовании аналитичности рас-
сматриваемых скобок Пуассона.
Оставшаяся часть параграфа посвящена доказательству
теоремы 2.
5. Пусть Т—конечномерное линейное вещественное про-
странство размерности п. Рассмотрим двумерное линейное
семейство J кососимметрических билинейных форм на Т,
порожденное фиксированными формами Ао и А^. Пусть
/? = maxrkC Обозначим буквой L подпространство в Т,
CeJ
порожденное ядрами форм А е J ранга R.
6. Предложение. Подпространство L^T изотропно от-
носительно всех форм CeJ.
7. Кососимметрические формы на Т будем рассматривать
как кососимметрические операторы из Г в Т". Фиксируем две
произвольные линейно независимые формы А и В из семейства
J, пусть при этом rk A = R.

§ 41. КРИТЕРИЙ ПОЛНОТЫ 225
8. Предложение. В пространстве L<zT можно выбрать
базис х{, (=1, ..., n — R, j=0, I, ¦-., kj, для которого справедливы
соотношения
Axf=Bxf,
F00)
для любого /=1, ..., n — R.
Доказательство. Рассмотрим уравнение (А — ХВ)х = 0
относительно хеТ с параметром X. Ясно, что подпространство
L с Т порождается решениями этого уравнения при малых А,.
Пусть у\, ..., yl~R — базисные решения, аналитические по А, (А,
мало). Разлагая векторы у} в ряд по А и подставляя
в уравнение, получим соотношения Ayf = 0, Ay} =Byf,
ос
Ayf = By}, ..., где у}= Yj у№- Система векторов у\ порождает
L, но базисом не является. Обозначим Uk подпространство в L,
порожденное векторами у{, j^k, i=l, ..., n — R. Имеем
Uo с Ui с U2 с ..., причем, начиная с некоторого N, имеем
Un=Un + i=... = L. Кроме того, справедливы соотношения
A(Uo) = 0, A(UN) = B(UN), ^(t/t) = fi(C/t_1), k=l,...,N.
9. Лемма. Существуют подпространства Ко,
V1,...,VN<=L такие, что: a) Uk=Uk-1@Vk, k=\, ..., N;
5) A(Vk) = B(Vk_1), k=\,...,N; в) ?/„= K0 = Ker A, VNcKerB.
Доказательство. Подпространства Vk строятся по ин-
дукции, начиная с VN.
Шаг 1. Имеем B(UN) = B(UN-l), следовательно, существует
подпространство VNcUN такое, что VNcKerB, C/N=C/N_1©KN.
Шаг N-k. Пусть Uk + 1 = Uk@Vk + l. Тогда B(Uk) = A(Uk+l) =
= A(Uk®Vk+1). Учитывая, что KerAcUk, имеем B(Uk) =
= A(Uk)®A(Vk + 1) = B(Uk-1)@A(Vk+l). Ясно, что существует
подпространство VkcUk такое, что Uk=Uk-l®Vk, A(Vk+l) =
= B(Vk). Лемма доказана.
Продолжим доказательство предложения. В силу леммы
9 корректно определен оператор А'1 В: Kt->Kt+1, поскольку
VkP\KerA = {0}, кфО. Определим цепочку подпространств
V\cz ... cV»=v0, полагая V'0 = {^e УоЦА'1 В)% = 0}. Выберем
произвольный базис в Ко, дополним его до базиса в Ко и т. д.,
получим базис x°,...,x°-R в пространстве Ко. Остальные
векторы базиса xJ. в L определяются по формуле xJ. = (A ~1 B)Jx?
(нулевые векторы отбрасываются).
10. Следствие. Косоортогональное дополнение ? = {^е
еТ\ВA„ L) = 0} к подпространству L в Т не зависит от выбора
нетривиальной формы BeJ.

226 ГЛ. 7. ПОЛНОТА ИНВОЛЮТИВНЫХ НАБОРОВ ФУНКЦИЙ
Доказательство. Косоортогональное дополнение
LB к подпространству Lс Т относительно формы BeJ совпада-
ет с ортогональным дополнением в Т к подпространству
B(L)<zT*. Из соотношений F00) следует, что A(L) = B(L) для
любых двух нетривиальных форм A, BeJ, поэтому LB = LA = L.
11. Предложение. Пусть, как и раньше, А и В—две
линейно независимые формы из семейства J, причем rk A = R.
Тогда L является максимальным среди всех подпространств
К<^Т, удовлетворяющих условию В (К) с А (К).
Доказательство. Покажем сначала, что любое подпро-
странство КсТ такое, что В(К)сА(К), содержится в L.
Воспользуемся соотношением A(Vk) = B(Vk-1), k=\,...,N. До-
кажем по индукции, что А (К, Vk) = 0 для любого к. При А:=0
имеем А {К, У0) = А{К, КегЛ) = 0. Пусть А (К. Kt) = 0. Тогда
А(К, Ук + 1)=-(К, A(Vk + l))=-(K, B(Vk)) = (B(K), Vk) с
с(А(К), Vk) = A(K,Vk) = 0. __
Покажем теперь, что_ B(L)<^A(L). Действительно, B(L)c
<^L^czT*, но L1 = A(L), так как Кег А с L. Предложение
доказано.
12. Для более подробного описания пространства L необ-
ходимо перейти к полю комплексных чисел. Обозначим Тс, Lc,
Lc, Jc комплексификацию пространств Т, L, L, J.
В семействе Ус содержится с точностью до пропорциональ-
ности лишь конечное число форм немаксимального ранга.
Рассмотрим все такие формы Сь..., CN, С,еУс, rkC,</?,
QjtXCj. Положим Л:; = {?,еКегС(|5(?„ КегС;) = 0}, где
В и С,- линейно независимы uBeJ. Проверим, что подпростран-
ство Ki не зависит от выбора формы BeJ. Действительно, если
B' = ^B+yCh то B'fe, KerC,) = p\e(^, КегС,). Следовательно,
/^={^еКегС,-|5(^ КегС;) = 0 для всех BeJ}.
13. Предложение, а) Подпространство LC^TC содер-
жит ядра всех нетривиальных форм из семейства Jc.
N
б) Имеет место равенство LC = LC+ ^ КегС,, т. е. Lc
;=i
поромсдается ядрами всех нетривиальных форм из семейства Jc
тогда и только тогда, когда dimKj = n — R, i=l,...,N.
Доказательство. Чтобы не усложнять обозначений, все
пространства предполагаются комплексифицированными, ин-
декс С не пишется.
Первое утверждение вытекает из предложения 11. В самом
деле, 0 = В(КегВ)а А(КегВ), т.е. KerficL^ Форма BeJ была
выбрана произвольно, поэтому Кег С с: L для всех Се J,
отличных от нуля.
Отметим отсюда одно следствие: сптА^и — R. Действитель-
но, для любой формы С,- имеем 5(КегС,П^, КегС;) = 0, т.е.
KCO Kh но Ct{L) = A{L) для любой формы A eJ ранга R.

§ 41. КРИТЕРИЙ ПОЛНОТЫ 227
поэтому dim Кег С(П? = dim Кег Л Р)? = dim Кег Л =n — R, следо-
вательно, dim Kj ^ п — R.
Для доказательства второго утверждения выберем произ-
вольное алгебраическое дополнение К к L в_ L. __ Тогда
L=V0®Vi® ¦¦¦ ®VN®K. Рассмотрим оператор Ф: L->?, опре-
деляемый соотношением А(ФЬ) = В^, ?eL, Ф?,еУ1®У2® ¦¦¦
...®VN®K. Из F00) следует, что подпространство L инвариан-
тно относительно Ф и ограничение Ф\Ь нильпотентно. Раз-
ложим пространство L на обобщенные собственные подпрост-
ранства оператора Ф. Имеем L=U0+ ? Ux, причем LcU0. Без
ограничения общности можно считать, что rkB=R. Покажем,
что в этом случае L=U0. Предположим противное. Тогда
существует элемент Ь,е Uo такой, что ?,$L, Ф^еЬ. По определе-
нию оператора Ф имеем А(Ф(Ъ)) = В{^), но A(L) = B(LI
поэтому существует такой элемент r\eL, что Вг\=В^. Отсюда
г) —^eKer5<=L, следовательно, Z,eL. Получили противоречие.
Итак, L = L+ X U-,.
Введем обозначение: подпространство в С/ь состоящее из
собственных векторов, обозначим С/°.
14. Лемма. Подпространство L0 = L+ ^ ?/? порождено
ядрами форм Се7\{0}. Другими словами,
Y Y KerQ. F01)
j. # о i=i
Доказательство. Покажем, что Lo содержит все ядра
КегС(, i=l,...,N. Пусть Ci = aiiA + $iB. Тогда KerCf =
= KeT(B-liA), где А,;=-а,/р;. Покажем, что КегE-Х.,-^)с:
cL+[/°. Из определения оператора Ф следует, что
С/?, = КегE-А,,Л)П1тФ. Отсюда dim Ul^R-rk(B-'kiA), по-
скольку dimKerE->L,^) = « —rkE —A,jfi), codim 1тФ = n — R. Да-
лее, dimLf)KerE — "К{А)=п — R, следовательно, KerE —
-A,i^) = (?nKerE-A,,vl))©C/l),ciL©C/$'jc:Lo. С другой стороны,
U°.<^KeT(B—XiA). Лемма доказана.
Из утверждения леммы следует, что L = L+Y, KerQ тогда
и только тогда, когда ?/?,.= ?/).,, т. е. отсутствуют присоединен-
ные векторы оператора Ф веса А,,/0, где А,,= —', Ci = a.iA + $iB.
Pi
Пусть присоединенный вектор веса А,, существует. Это эк-
вивалентно тому, что система уравнений
(Ф-Х,Е)х = у, (Ф-Х1Е)у = 0 F02)

228 ГЛ. 7. ПОЛНОТА ИНВОЛЮТИВНЫХ НАБОРОВ ФУНКЦИЙ
имеет решения при уфО. Учитывая определение оператора Ф,
перепишем эту систему следующим образом:
(B~XiA)x = Ay, (B-XiA)y = 0,
F03)
хекпФ, уе1тФ.
Легко видеть, что первые два уравнения разрешимы тогда
и только тогда, когда yeKi<^KeT(B — 'kiA). Если dimК, = n — R,
то Ki=KerCif)L, т.е. yeL. На пространстве L оператор
Ф нильпотентен, поэтому у не может быть собственным
вектором ненулевого веса. Следовательно, система F02) не
имеет решений при уфО. Если dimK{>« — /?, то существует
уоеК(С\1тФ, уоФО. Уравнение (B — 'kiA)x = Ay0 разрешимо,
и множество его решений имеет вид xo + KeT(B — XtA), где
х0 — частное решение. Поэтому (хо + Кет(В-Х1А))(]1тФф0,
так как dim Ker (В -А,,-,А )>n — R. Следовательно, система F02)
имеет нетривиальное решение и присоединенный вектор суще-
ствует. Предложение доказано.
15. Следствие. Имеют место следующие оценки:
N
dim?>dim?+ ? (Я-гкС,), F04)
dimL^n-~— ? (Л-rkCj), F05)
причем равенства имеют место тогда и только тогда, когда
dim Ki = n-R. i=l,...,N.
16. Следствие. Подпространство L является максималь-
ным изотропным (лагранжевым) относительно произвольной
нетривиальной формы из семейства J тогда и только тогда,
когда все нетривиальные формы из семейства Jc имеют
одинаковый ранг.
Доказательства следствий. Все обозначения^ из
доказательства предложения 13 сохраняются. Разложим L на
обобщенные собственные подпространства UXl оператора
Ф. Имеем
N N
dimL = dimL+ ? dim Uu^dimL+ ? dim [/?, F06)
;=i i=i
где U°i<^Ux,— подпространство, состоящее из собственных
векторов. Из доказательства последней леммы 14 следует, что
dim ?/?( = /? — rk С,-. Это доказывает справедливость первой оцен-
ки. Условие dim Ki = n — R, как это было показано, в точности
означает совпадение подпространств С/Х| и U°,, поэтому первая
оценка переходит в точное равенство. Отметим, что каждая
форма С; дает независимый вклад в размерность пространства

i 42. ПОЛНОТА СЕМЕЙСТВ ФУНКЦИЙ 229
L, поэтому Кег С;ф1+^ Кег С(. Вторая оценка следует из
первой и равенства dim L + dim L = n + (n — R). Докажем следст-
вие 16. Лагранжевость подпространства L означает, что L = L,
поэтому из первой оценки необходимо следует равенство
rkCi = R, т.е. все формы из Jc имеют одинаковый ранг.
Условие dim Ki = n — R в этом случае выполняется автоматичес-
ки, и первая оценка переходит в равенство.
17. Доказательство теоремы 2. Утверждение а) яв-
ляется точным аналогом следствия 10. В самом деле, до-
казательство теоремы легко сводится к задаче из линейной
алгебры. Действительно, подпространство L<^T*XM порождает-
ся ядрами 2-форм С(х) (CeJ) такими, что rkC(x) = R.
Поэтому при доказательстве мы можем забыть о скобках
Пуассона и рассматривать двумерное семейство кососиммет-
рических билинейных форм на Т*ХМ. Утверждения б) и в)
теоремы в точности соответствуют утверждениям а) и б)
предложения 13.
§ 42. Полнота семейств функций, построенных
методом сдвига аргумента
1. Применим общий критерий А. В. Болсинова из п. 3 § 41
к скобке Березина на G* и а-скобке Березина на G*. Получим
критерий полноты семейства функций, построенных в [188]
методом сдвига аргумента, см. п. 2 § 34.
Обозначим Fa семейство функций Р1 (х), Р2(х),..., получен-
ных следующим образом. Пусть f(x) — произвольный локаль-
ный инвариант коприсоединенного представления Ad* группы
Ли, отвечающей алгебре Ли G. Положим f(a + Xx) = P0(x) +
1Р) 12Р()
х{
2. Теорема (критерий А. В. Болсинова, случай орбит
общего положения, см. [46]). Пусть G — произвольная конеч-
номерная комплексная (вещественная) алгебра Ли, S= {уеС*\
|dimAnn(^)>indG}—множество сингулярных элементов в G*
(соответственно в (GC)*J, aeG*—регулярный элемент. Ин-
волютивное семейство Fa полно на G* тогда и только тогда,
когда codim 5^2.
Доказательство. Пусть элемент хеG* регулярен. Будем
проверять полноту семейства Fa в точке х, пользуясь теоремой
3 § 41. Второе условие этой теоремы выполнено автоматически
в силу регулярности элемента xeG*. Первое условие пе-
реписывается следующим образом: rk(aOx+pOa) = dimG — indG
для а, ре С, не обращающихся одновременно в нуль. Гео-
метрически это означает, что двумерная плоскость, натянутая
на векторы х и а в пространстве G* (или в пространстве

230 ГЛ. 7. ПОЛНОТА ИНВОЛЮТИВНЫХ НАБОРОВ ФУНКЦИЙ
(Gе)* в вещественном случае), пересекается с множеством
S только в нуле. Ясно, что элементы xeG*, удовлетворяющие
этому условию, существуют тогда и только тогда, когда
codimS>2 (рис.41). Теорема доказана.
3. Замечание. Множество сингулярных элементов в G*
и в (Gc)* в случае вещественной алгебры Ли G могут иметь
различные размерности. Поэто-
му в условиях теоремы 2 множе-
ство S нельзя заменить в вещест-
венном случае на множество син-
гулярных элементов в G*.
4. "Рассмотрим теперь случай
сингулярных орбит. Пусть хе
eG* — сингулярный элемент, т. е.
Рис 41 dimAnn(x)>indG, а О(х) — ор-
бита точки х при действии груп-
пы Ли Р на G* коприсоединенным образом (Р отвечает алгебре
Ли G), Когда семейство Fa сдвигов инвариантов при ограниче-
нии на сингулярную орбиту О(х) образует полный инволютив-
ный набор на этой орбите? Известно, что так бывает не всегда,
даже если семейство Fa полно на всем пространстве G*, т. е.
если из него можно выбрать 2 ~l (dim G + ind G) функционально
независимых на G* функций.
5. Теорема (критерий А. В. Болсинова, случай сингуляр-
ных орбит, см. [46]). Пусть G—произвольная конечномерная
комплексная (вещественная) алгебра Ли, S—множество син-
гулярных элементов в G* (соответственно в (GC)*J. Пусть
aeG*—произвольный регулярный элемент, xeG' — произвольный
сингулярный элемент, к: G*->Ann(x)*— естественная проекция.
Инволютивное семейство Fa полно в сингулярной точке xeG*
тогда и только тогда, когда: а) комплексная прямая х+Ха
(ХеС) пересекает множество сингулярных элементов S только
в точке х; б) имеет место равенство dim Ann rc(a) = indG, где
Ann n(a) — аннулятор элемента 7t(a)eAnn(x)* в алгебре Ли
Ann (х).
Доказательство. Это утверждение является точной
переформулировкой теоремы 3 § 41. Действительно, первое
условие означает, что все линейные комбинации аФх+рФа
при Р#0, а, Ре С, имеют максимальный ранг R = dim G — ind G.
Далее, следуя обозначениям теоремы 3 S 41, положим
А:х = {^еКегФ,|Ф„(^КегФх) = 0}. Учитывая, "что КегФх =
= Апп(х), получаем Ax = {^eAnn(x)|(ad^a, Ann(x)) = 0}, или
А^ = Апп7г(а). Таким образом, условие б) доказываемой тео-
ремы в точности соответствует второму условию теоремы 3
§ 41.
6. Следствие. Пусть семейство сдвигов инвариантов
Fa полно на всем пространстве G*, xeG*—сингулярный эле-

§ 42. ПОЛНОТА СЕМЕЙСТВ ФУНКЦИЙ 231
мент, причем ind Ann (х) = ind G. Тогда найдется регулярный
элемент beG* такой, что инволютивное семейство Fb полно на
сингулярной орбите О (х).
Доказательство. Полнота семейства Fa на G* гаран-
тирует выполнение условия codimS^2, где S—множество
сингулярных элементов. Это, в свою очередь, гарантирует
выполнение условия а) теоремы 5 почти для всех beG'.
Равенство ind Ann (x) = ind G означает, что dim Ann к (b) = ind a
для регулярных проекций n(b), т. е. почти для всех beG'. Ясно,
что beG* можно выбрать удовлетворяющим двум условиям
одновременно. Тогда семейство Fb будет полно в точке xeG' и,
следовательно, на всей орбите О(х).
Рассмотрим теперь случай полупростых алгебр Ли.
7. Теорема. Пусть G — полупростая алгебра Ли (ком-
плексная или вещественная). Тогда семейство сдвигов ин-
вариантов коприсоединенного представления Ad* группы Ли
Р, отвечающей алгебре Ли G, является полным инволютивным
семейством на G'.
Доказательство. Если G — полупростая алгебра Ли, то
коразмерность множества сингулярных точек равна трем
и теорема вытекает из критерия п. 2.
8. Замечание. Эта теорема ранее была доказана другими
методами А. С. Мищенко и А. Т. Фоменко, см. [186], [188],
[189].
9. Пример. Пусть G — фробениусова алгебра Ли ([298]), т. е.
алгебра Ли с нулевым индексом. В этом случае орбиты об-
щего положения представления Ad* открыты в G* и, следова-
тельно, инвариантами являются только константы. Поэтому
семейство сдвигов тривиально. С другой стороны, множество
сингулярных элементов задается одним уравнением
det(C'jk_xi) = 0, где С)к — структурный тензор алгебры Ли, т. е.
codimS= 1.
10. Теорема. Пусть G — полупростая алгебра Ли. Тогда
семейство сдвигов инвариантов коприсоединенного представления
Ad* группы Ли Р, отвечающей алгебре Ли G, является полным
инволютивным семейством на полупростых сингулярных ор-
битах.
Доказательство. Если алгебра Ли G полупроста, то
условие ind Ann (x) = ind G выполнено для всех полупростых
сингулярных элементов и утверждение следует из критерия
п. 5.
11. Замечание. Эта теорема была доказана в [85], [185],
[53]. В некоторых случаях условие полупростоты сингулярного
элемента xeG' существенным не является.
12. Предложение. Для всех элементов xesl(n) выполнено
равенство ind Ann (x) = ind si (и). Таким образом, методом сдвига
аргумента можно построить полные инволютивные семейства

232 ГЛ. 7 ПОЛНОТА ИНВОЛЮТИВНЫХ НАБОРОВ ФУНКЦИЙ
функций на всех сингулярных орбитах коприсоединенного дейст-
вия группы Ли Sh(n).
Доказательство получаем явным вычислением централизато-
ра произвольного элемента xes\(ri) и его индекса, используя
стандартную жорданову нормальную форму.
§ 43. Функции в инволюции
на симметрических алгебрах Ли
1. Определение. Симметрической алгеброй Ли называет-
ся пара (G, 9), где G—алгебра Ли, а 0 — ее автоморфизм
такой, что 0 = id. Обозначим буквой Н множество таких
элементов xeG, для которых д(х) — х, а буквой V—множе-
ство таких xeG, что 0(jc)=-jc. Ясно, что G = HQV, [Н, Н]с
<=#, [H,V]cV, [V, V]czH. В частности, Я—подалгебра в
G. Если В—форма Киллинга алгебры Ли G, т.е. В(х, у) =
= tradxady, то подпространства Н и V ортогональны относи-
тельно В.
2. Конструкция. Обозначим Ge полупрямую сумму подалгеб-
ры Н и коммутативного пространства V по представлению ad:
#->End(F), т. е. зададим на линейном пространстве G = H+V
еще один коммутатор [х, у]в по формуле [h1^-v1,h2 + v2\ =
= [hl,h2]+[hi,v2]+[v1,h2], ht + VieH+V, hteH, v.eV,
(=1, 2.
На пространстве G* = H*+V* рассмотрим три различные
скобки Пуассона: а) скобку Пуассона Ли {х, у}, отвечающую
алгебре Ли G; б) скобку Пуассона — Ли {х, у}в, отвечающую
алгебре Ли Ge; в) скобку \х, у}а, ае V, см. п. 6 § 36.
3. Лемма. Три скобки {х, у}, {х, у}в, {х, у}а на G*
согласованы, т. е. любая линейная комбинация этих трех скобок
является скобкой Пуассона на G*.
4. Предложение. Центральными функциями скобки
а{х, у} + ${х, у}в + у {х, у}а при а + р/0, а/0 являются
функции вида
(J^ ^) F07)
где f пробегает кольцо инвариантов алгебры Ли G.
Доказательство см. в [228].
5. Замечание. Класс полупрямых сумм, возникающих из
рассмотрения симметрических алгебр Ли, содержит серию
алгебр Ли, кольца инвариантов коприсоединенного представле-
ния которых совпадают с кольцами инвариантов представлений
изотропии неприводимых симметрических пространств. Список
симметрических алгебр Ли этого вида приведен в табл. 1, см.
[293], гл. 9.

§ 43. ФУНКЦИИ В ИНВОЛЮЦИИ
233
I .i i ¦. i и ц а 1
Тип по
Картану
А\
BDI
а
El
?(V)
?VIII
Л
G2
Симметрическое
пространство М
SU(n)/SO(n)
SOBp+ l)ISO(p) x SO(/>+ 1)
Sp(n)/U{n)
E6/SpD)
E7/SU(8)
E8/SOA6)
E4/Sp'3)xSUB)
G2/SUB)xSUB)
n2 + n-2
2
/>(/>+0
n(n+\)
42
70
128
28
8
rkM
n-1
P
n
6
7
8
4
2
Индекс
алгебры G,
n 1
P
n
6
7
8
4
2
Имеется связь между операцией сдвига инвариантов из
кольца I{G%) и операцией подъема функций, см. п. 9 § 35.
6. Предложение. Операция сдвига инвариантов из кольца
I(G%) эквивалентна взятию абелевой подалгебры L в V в качест-
ве алгебры первых интегралов.
Доказательство. Пусть /х, ..., /г — набор однородных
полиномиальных образующих в кольце J(G%) и «г = deg/,-, / =
= 1, ..., г. Тогда согласно теории инвариантов групп, порож-
г
денных отражениями, имеем ? щ = 2 ~1 (dim Ge + rk Ge) =
= dim V. Следовательно, сдвиг образующих /,- на регулярный
элемент приводит к семейству функций в инволюции, зависящих
только от координат в пространстве V.
7. Инволютивное семейство. Для построения функций в ин-
волюции на G* = H*+V" применим общую конструкцию § 36,
рассмотрев любое двумерное подпространство в простран-
стве, порожденном скобками {/, g}, {/, g}e и {/, #}„. Тогда
из п. 4 следует, что функции вида f(kh + v + X а) находятся
в инволюции относительно всех скобок вида ot({/, g} + {/, #}„) +
+ Р{/, #}е- Проанализируем полноту этого семейства, ис-
пользуя критерий Болсинова.
Рассмотрим следующий важный случай. Пусть G — полу-
простая вещественная алгебра Ли, а 6 — инволюция Картана,
т.е. форма (X, Y)= —B(X, 6 У) положительно определена,
где В—форма Киллинга. Будем отождествлять Не Н*
и К с К* с помощью формы Киллинга. В общем
случае семейство функций в инволюции FaB = {f(Xh+v + }.2a)\fe
eI(G), A,eR} полным не является. Однако функции feFa e
коммутируют с элементами подалгебры St(a), где St(a) —
стационарная подалгебра элемента а е V при действии
Н на V, ср. п. 11 § 35. Рассмотрим произвольный полный

234 ГЛ. 7. ПОЛНОТА ИНВОЛЮТИВНЫХ НАБОРОВ ФУНКЦИЙ
инволютивный набор Fsm на двойственном пространстве St(a)*.
Функции geFSHa) естественным образом продолжаются на все
пространство G* с помощью проекции к; G*-->St(a)*, см. п. 1 § 35.
Объединяя семейства Fa в и FSl,a), получим инволютивное семейст-
во на G* в смысле скобки {/, g}e.
8. Теорема. Пусть G—полупростая вещественная алгебра
Ли, 0 — инволюция Картана, G = Н® V— соответствующее раз-
ложение алгебры Ли G, ае V—произвольный элемент. Тогда
инволютивное семейство Fa^[jFSi(a) полно на G = H©Vomnocu-
тельно скобки Пуассона {/, g}e.
Доказательство. Фиксируем точку h + veH+V. Обозна-
чим М подпространство в G, порожденное дифференциалами
функций вида fQJi + v + Х2а). Обозначим М косоортогональное
дополнение к М относительно. 2-формы на G, задаваемой
скобкой {/, #}в в точке h + v. Утверждение теоремы эквивален-
тно существованию точки h + v такой, что M = M+St(a).
Перейдем к комплексным алгебрам Ли. Чтобы не услож-
нять обозначений, будем сразу считать алгебры Ли
G и Ge комплексными. Отметим, что после перехода к ком-
плексным алгебрам Ли элемент aeV произвольным уже считать
нельзя, поскольку вещественное подпространство V состоит из
полупростых элементов. Поэтому и в комплексном случае
мы будем считать aeV полупростым. Обозначим
А. р кососимметрическую форму на G, задаваемую скобкой
щ{/, g} + {f> g}a)+f>{f, g}b B точке h + v. Покажем, что точка
h + v может быть выбрана так, что: a) rkAa p = /? = dimG — indG,
а+Р^О, афО; б) ткА0 1=.fi = dimG-indG;'B) dim/^ -^indG,
где *1,_1 = {?еКегЛ1/_1Мо.1&КегЛ1._1) = 0}.
В силу утверждения в) теоремы 2 § 41 эти условия
эквивалентны тому, что М=М+КетА1 _t.
9. Лемма Условие а) эквивалентно регулярности элемента
вида Xh + v + X2a (keC, ХфО) в алгебре Ли G.
Доказательство. Форма А^р задается кососимметриче-
ским оператором к: G -»G вида
, аА]), F08)
+ aa]+[r\, ah]eV. Сделаем замену %' = \1'К, Х= /—^-. Тогда
ядро формы Ля_ р совпадает с пространством решений системы
уравнений
[V,

§ 4J ФУНКЦИИ В ИНВОЛЮЦИИ 235
т. е. ?,' + ц принадлежит централизатору элемента Xh + v + X2a
в алгебре Ли G. Поэтому условие гкЛа p = /? = dim G — ind G
эквивалентно регулярности элемента Xh + v + X2a в алгебре
Ли G.
Поскольку indG = indGe (см. [52]), то второе условие
эквивалентно регулярности элемента h + v как вектора двойст-
венного пространства GI.
Рассмотрим теперь третье условие. Ядро формы
Ах _! совпадает с пространством решений системы уравнений
[л,а] = 0, [л, *] + [?, а] = 0. F10)
Введем следующие обозначения: С (а) — централизатор эле-
мента а в алгебре Ли G, V(a)= Vf]C(a), St(aI— ортогональное
дополнение к St(a) в Н относительно формы Киллинга,
V{a)L — ортогональное дополнение к V{a) в V. Имеют место
разложения в прямые суммы G=H+ V=St(a) + St(a)L + V(a) +
+ V(a)x, C(a)= V(a) + St(a). Здесь мы учли то, что элемент ае V
полупрост.
В системе уравнений F10) положим h = hl+h2, ?, = ^l+{,2, гДе
/гь ?>1eSt(a), /г2, E,2eSt(a)±. Тогда второе уравнение системы
запишется в виде
[Л, /rJ = O, [л, А2] + К2, «] = 0- F11)
Второе из уравнений F11) однозначно разрешимо относи-
тельно ^s'StfoI- при любых r\eV(a), A2eSt(a)x. Элемент
^!eSt(a) в уравнения не входит, т. е. St(a)cKer^, _t. Из этого
следует, что размерность ядра формы Alt-i равна сумме
dimSt(a) + dim W, где W—пространство решений следующей
системы уравнений относительно л:
[Л, д]=0, [л, Ai] = 0. F12)
10. Лемма. Почти для всех ht e St(a) имеет место равенст-
во dim W=indG — indSt(a).
Доказательство. Пусть К— подалгебра Картана в St (а).
Утверждается, что централизатор подалгебры К в С (а) есть
подалгебра Картана в С (а) (и, следовательно, в G, поскольку
ind G — ind С (а)). Достаточно проверить, что централизатор
подалгебры К в С(а) коммутативен. Предположим противное,
т.е. существуют такие элементы h' + v', h" + v"еС(а), что [ЛГ,
h' + v'J = [K, А" + и"]=О, но [h' + v1, h" + v"~\^0. Легко видеть, что
/г', he К, поэтому \К, v'] = [К, v"] = 0, но [i/, d"]#0. Имеем
[К, [у', v"]]=0; с другой стороны, [у', у"] eSt(a). Подалгебра
KczSt(a) является максимальной коммутативной в St(a). Следо-
вательно, [v',v"~\eK. Ограничение формы Киллинга на К не

236 ГЛ. 7 ПОЛНОТА ИНВОЛЮТИВНЫХ НАБОРОВ ФУНКЦИЙ
вырождено, поэтому найдется хеАтакой, что (х,[V, i)"])^0, но
это невозможно, так как [лс, >;'] = [*, i>"] = О. Далее, существует
такой элемент hteK, что его централизатор в С [а) совпадает
с централизатором подалгебры К в С(а), причем такие
элементы образуют в К множество, являющееся дополнением
к некоторому конечному семейству гиперплоскостей. Цент-
рализатор такого элемента hl в алгебре Ли С (а) совпадает
с прямой суммой К+ W, где W— пространство решений
системы F12). Следовательно, dim W=indC(a) — dimK=
= ind G — ind St (а). Лемма доказана.
Пусть h = h1+h2eH, причем ^eSt^a) удовлетворяет услови-
ям леммы 10, в частности, h1 регулярен в St(a). Пусть
К—подалгебра Картана в St(a), содержащая ht. Рассмотрим
разложение St(a) = K+B + +В ~, где В+ и В~—нильпотент-
ные подалгебры в St(a), отвечающие соответственно множест-
вам положительных и отрицательных корней. Утверждается,
что ограничение формы Аол на подпространство В + +В~
не вырождено. В самом деле, на этом пространстве форма
Аол имеет вид ^0,i(^i> b2) = (hl, \b1, 62])- Поэтому невырож-
денность следует из регулярности элемента hy в St(a). Следо-
вательно, размерность подпространства Кх _1; т.е. ядра фор-
мы Ао !, ограниченной на ядро формы Alt-t, не превос-
ходит
dim Ker^!,-! -dim(B +
= dim St(a) + indG-ind St(a)-(dim St(a)-ind St(a)) = indG. F13)
Итак, мы показали, что третье условие выполнено почти для
всех элементов h + veH+V. Аналогичное утверждение справед-
ливо, очевидно, и для второго условия. Наконец, первое условие
означает, что комплексная кривая Xh + v + X2a (XeC\{0}) не
пересекает множество сингулярных элементов S в алгебре Ли G.
Ясно, что это условие также выполняется почти для всех h + v,
так как codim5'=3>l. Итак, можно выбрать точку h + v,
в которой условия а), б), в) выполняются одновременно. В этой
точке М=М+КетА1 __!.
Покажем, что М+КегЛь_, =M+St(a). Все предыдущие
обозначения сохраняются. Рассмотрим цепочку вложений
М+(В + +B-)aM+St(a)<=M+KerAu-1. Сумма М+(В + +В~)
прямая. В противном случае существует ?,еМ(\В + + В "), ?/().
Тогда Аол(%, В + +В~) = 0, так как В + +ВсМ. Это проти-
воречит невырожденности формы А01 на В + +В~. Теперь
остается сравнить размерности:
dim(M+KerA1 _1) = dimM+dim
St(a) + ind G-ind St(a)-

§ 44. СКОБКИ ПУАССОНА 237
-indG = dimM+dim St(a)-ind St(a) =
), F14)
здесь использовано то, что dimMf]KerAj^^i^indG.
§ 44. Скобки Пуассона, связанные с лиевыми пучками
1. Определение. Пусть L — конечномерное линейное
пространство. Линейное семейство структур алгебры Ли на
L называется лиевым пучком. Пусть ([х, y\^sj—соответст-
вующее семейство коммутаторов на L. Линейность означает,
что множество параметров J является линейным простран-
ством, при этом а[х, у~\а + Ь[х, у]р = [х, у]ая+ьр> aa + bfieJ.
Размерность пространства J называется размерностью лиева
пучка.
2. Согласованные скобки. Если на пространстве L задан лиев
пучок (Гх, y\)aeJ, то на двойственном пространстве естествен-
ным образом возникает линейное семейство согласованных
скобок Пуассона {{f, g}a)aeJ, где {/, g}a(x) = lx, [df, dg~]a). Для
того чтобы применить общую конструкцию § 36, мы должны
рассмотреть произвольное двумерное семейство скобок Пуас-
сона ({/ g}y)yzj0, где J0<=J—двумерное подпространство, содер-
жащее а. Итак, пусть на конечномерном комплексном простран-
стве L задан пучок ([х, y~\<l}aej размерности два, J^C . На L*
рассмотрим соответствующее семейство скобок Пуассона
({/> g}a)aej- Пусть максимум рангов скобок из этого семейства
равен R, т.е. R = dimL — min indLx. Следуя общему методу,
огеУ
рассмотрим семейство функций Fj, состоящее из центральных
функций скобок ({/, g}a)bej, ранга R, т.е.
аеУ, indZ. = dim Z. — R
где l(L^) — кольцо инвариантов коприсоединенного представле-
ния группы Ли Na, отвечающей алгебре Ли La, задаваемой
коммутатором [х, у]а. Будем предполагать, что алгебры Ли из
пучка обладают полными полиномиальными наборами инвари-
антов (или рациональными инвариантами), например, все
алгебры Ли La алгебраические.
3. Обозначения, а) Множество сингулярных элементов в L*
в смысле коприсоединенного представления алгебры Ли La,
осе/, обозначим 5„. б) Стационарную подалгебру вектора xeL'
относительно коприсоединенного действия алгебры Ли La на L*
прис
,(х).
обозначим АппЛх). в) Центр алгебры Ли ЬЛ обозначим Za.

238 ГЛ. 7. ПОЛНОТА ИНВОЛЮТИВНЫХ НАБОРОВ ФУНКЦИЙ
4. Предложение. Пространство Za является подалгеброй
в любой алгебре Ли Lp, fieJ.
Доказательство. Легко видеть, что для любых двух
алгебр La и Lp из пучка выполняется тождество
У» л]р+[К, УР, л].=о. F16)
Пусть 4, Ле^а- Тогда из тождества F16) немедленно следует,
что [[?, л]р, Q* = o Для любого ^eL, т.е. [?,, л]р?^о,-
Следовательно, z,,— подалгебра в Lp.
5. Замечание. Условие F16) означает в точности, что
операция \х, у] р является коциклом в смысле когомологий
алгебры Ли La относительно присоединенного представления,
см. [291].
Пучки, которые будут рассматриваться ниже, обладают
одним весьма удобным свойством; все алгебры Ли пучка за
исключением конечного числа (с точностью до пропорциональ-
ности параметра) изоморфны между собой. Будем предполагать,
что это условие выполнено, и фиксируем какой-нибудь предста-
витель Lm из этих алгебр «общего положения». Пусть
Lai, ..., L4 — все с точностью до пропорциональности алгебры
Ли из пучка, которые не являются алгебрами общего положения.
6. Элементы центра Za мы будем рассматривать как
линейные функции на L*. Любая функция peZ,. принадлежит
кольцу инвариантов I(La.) и поэтому коммутирует со всеми
функциями из Fj относительно произвольной скобки {/, g}a,
аФХа(. Обозначим Ft полный инволютивный набор функций на
Z\. относительно скобки {f,g}a «общего положения». Скобка
{/>'?}m естественным образом ограничивается на Z;, так как
Za—подалгебра в Ью. Функция feFj продолжается на все
пространство L* с помощью естественной проекции тс;:L*~*Z\.,
см. § 35. В силу выбора семейств Ft и теоремы 4 § 36 семейство
Fj\JF\\J — \JFk является инволютивным относительно любой
скобки {/, g} а, a e J.
7. Предложение (А. В. Болсинов). Пусть для любой
алгебры Ли Ьл выполняется равенство \п<1Ьа. = '\п6Ьы +
+ dimZcl. — indZ,,.'(здесь Zx. рассматривается как подалгебра
в Ьш, т. е. алгебра Ли с коммутатором [х, у~\ш). Пусть для
алгебры Ли La «общего положения» выполнено условие
codim5'm^2. Тогда инволютивное семейство Fj\JFi\J...\JFk явля-
ется полным на L* относительно скобки {/, g}m.
Доказательство. Условие codim5'm>2 гарантирует, что
существуют точки xeL*, которые являются регулярными
в смысле коприсоединенного представления всех алгебр Ли
Lj, из пучка одновременно. Действительно, достаточно пока-

S 44 СКОБКИ ПУАССОНА 239
зать, что дополнение к множеству Sj = (J S^ в L' содержит
всюду плотное открытое множество. Множество Sj является
объединением множеств коразмерности два за исключением,
быть может, конечного числа S1^, ..., Sat. При этом объединение
происходит фактически не по двум, а по одному параметру,
поскольку Sa = SXa (удобно считать, что параметр а пробегает
не множество J^C2, а соответствующее проективное простран-
ство />(J) = C/>1). Поэтому размерность Sj может увеличиться
только на единицу по сравнению с размерностью типичного
множества S^, т.е. codimS/^1.
Потребуем далее, чтобы точка xeL* удовлетворяла одновре-
менно трем условиям: а) точка х регулярна как ковектор
в смысле всех алгебр Ли La из пучка, т. е. xeL"\Sj\ б) ковектор
я,(х) регулярен в Z*., /=1, ..., к, где я,-: L*->Z*.—естественная
проекция, Za. рассматривается как подалгебра в LM; в) все
инволютивные семейства F, полны в точке х, или, более строго,
инволютивные семейства Ft на Z*. полны в точках я,(дг).
Обозначим буквой М подпространство в L, порожденное
дифференциалами функций feFj в точке х. Пусть М —
косоортогональное дополнение к М в L относительно 2-формы,
задаваемой произвольной скобкой {/, ,§¦}„• Напомним, что М не
зависит от выборка скобки {/, е}„, ос^О, в силу теоремы 2 § 41.
Покажем, что М = Л/+АппA1(х) + ... + Аппа|,(д:). Из теоремы 2
§ 41 следует, что для этого необходимо и достаточно, чтобы
выполнялось условие dim AT,- = ind Lw, i=\, ..., к, где Kj = {?,e
е АпПаДхШх, к, Ann. (лг)]ш) = О}. Рассмотрим подпространство
A^J = {?,'eza.)(x, [^, ZCI.]a) = O}. Другими словами, К[ — это ан-
нулятор ковектора я,(дг) в подалгебре Z^.czL^,. Точка я,(х)
регулярна в Z* , поэтому dim A^J = ind Z>.'
8. Лемма. Йусть на конечномерном пространстве К задана
кососимметрическая форма В, К' — подпространство в К,
В\К' — ограничение формы В на К'. Тогда имеет место оценка
dim AT-dim Кег fi^dim К'-dim Кег В\К'.
Доказательство. Разность dim К— dim Кег В равна ран-
гу формы В на К; аналогично, ранг ограничения В\К' равен
dim К' — dim Ker В\К', но ранг ограничения не превосходит
ранга формы на объемлющем пространстве.
Из утверждения леммы следует, что dim Аппп(д:) —
— dim A^dim Za—dim K\. По условию dim Anna (x) = ir
= ind Lm + dim Za! — ind Za. Поэтому dim Arj = indZ.A), так как
всегда dim A^irid Lm.
Отметим еще одну оценку, которая пригодится в даль-
нейшем:
ind X@^dim AT.sSdim Ann^.^J-dim Z^-l-ind Zx. F17)

240 ГЛ. 7. ПОЛНОТА ИНВОЛЮТИВНЫХ НАБОРОВ ФУНКЦИЙ
или
ind La.^ind ?M + dim Za — ind Za.. F18)
Итак, Й=М+Аппх.(х) + ... + Аппа,к(х). Покажем, что на
самом деле M = M+Zai + ... + Za. Ясно, что M+Z^.a
^М+АпПаДх). Подпространство Za содержится в косоор-
тогональном дополнении М к м, поэтому M{\ZK\
следовательно,
dim (M + Za.) = dim M+dim Zx-
>dim M + dim Z^.-ind Z,, F19)
С другой стороны,
dim(M + Ann<,.(x)) = dim M+dim Anna.(x) — dim(Mf) Ann,.(*)) =
= dim M+ind La— dim Кг = <Ит M+ind La— ind La. F20)
Поэтому dim(M+Z0I.)^dim(M+Anna.(jc)). Следовательно,
М+гл1 = М+Апп..(х) и M=M+Zai + ...+Zak. Пусть Mi-
подпространство в Zx., порожденное дифференциалами функций
feFi в точке х. По построению семейства F, полны в точке х,
поэтому подпространства М, являются максимальными изо-
тропными подпространствами в Za. в смысле скобки {х, у}т.
Учитывая, что все подпространства М,- косоортогональны
между собой, заключаем, что подпространство М+М1+М2 +
+ ... + Мк является максимальным изотропным в L. Это
означает полноту семейства />U-^i U ¦•• ^ Fk в точке xeL' и,
следовательно, на всем пространстве L .
9. Замечание. Если условие об изоморфизме почти всех
алгебр Ли из пучка не выполняется, то нужно ввести несколько
иное определение алгебры Ли «общего положения», накладывая
на такие алгебры Ли два условия: a) ind La = min ind Lp = r;
ре J
6) codim Sx = max codim Sp. Все алгебры Ли любого двумерного
PeJ.ind Lf = r
лиева пучка за исключением конечного числа являются алгеб-
рами «общего положения» в этом смысле.
10. Замечание. Утверждение предложения 7 допускает
следующую эквивалентную переформулировку. Рассмотрим се-
мейство функций F=Fj{JZnt 0... U-Z<v И3 предложения 4 сле-
дует, что F—^алгебра Ли относительно любой из скобок {х, у}л,
aeJ. Предложение 7 фактически утверждает, что алгебра Ли
F является полной в некоммутативном смысле относительно
скобки {х, у}т.
11. Конец этого параграфа будет посвящен изучению неко-
торых важных конкретных примеров лиевых пучков: неприводи-
мых замкнутых лиевых пучков.

§ 44. СКОБКИ. ПУАССОНА 241
12. Определение. Лиев пучок называется неприводимым,
если не существует нетривиального подпространства K<pL,
которое является идеалом для всех элементов пучка одновре-
менно.
Пусть А—линейная операция на L, а В—билинейная
операция. Определим действие операции А на множестве всех
билинейных операций, полагая
A(B)(X,Y) = A(B(X,Y))-B(AX,Y)-B(X,AY), X,YeL. F21)
Если ([х, >>]«), ае/,— лиев пучок на L, то для xeL, осе/
определим оператор Ах ,а{у) = [х, у~\а. Будем говорить что лиев
пучок замкнут, если множество коммутаторов ([х, y^^^j
инвариантно относительно действия всех операторов АХ_Т
Имеется полная классификация замкнутых неприводимых ли-
евых пучков.
13. Теорема (И. Л. Кантор, Д. Б. Персиц [117]). Неприво-
димые замкнутые лиевы пучки над С исчерпываются следующим
списком:
1) L — множество кососимметрических матриц размера
п х п; J—множество симметрических матриц размера п х п;
коммутатор \Х, Y~\A, AeJ, задается формулой fx, Y]A =
= XAY-YAX;
2) L—множество симметрических матриц размера пхп\
J—множество кососимметрических матриц размера пхп;
коммутатор [X, YlA, AeJ, задается формулой \Х, YlA =
= XAY-YAX;
3) L—множество матриц размера пхт; J—множество
матриц размера тхп; коммутатор [X, Y~\A, AeJ, задается
формулой [X, Y]A = XAY-YAX;
4) L — четномерное линейное пространство, J=L; коммута-
тор \_Х, YlA, AeJ, задается формулой [X, Y]A = (A, X} Y—
— (A, Y}X— (X, Y}A, где <Х, Y} — невырожденная кососим-
метрическая форма на L;
5) одномерный пучок, порожденный простой алгеброй Ли.
14. Программа изучения. Установим, какие неизоморфные
алгебры Ли содержатся в данном пучке. Укажем индексы этих
алгебр Ли, их центры и явный вид инвариантов коприсоединен-
ного представления типичных алгебр Ли из пучка (множество
параметров J содержит открытое по Зарисскому множество U,
такое, что алгебры Ли LA и LB изоморфны для любых A, BeU,
такие алгебры Ли называются типичными или алгебрами
«общего положения» в пучке {Lc}CsJ). Наконец, проверим
полноту инволютивных семейств, построенных по некоторому
двумерному подпучку.
Случай 1.
15. Замечание. Пусть A, BeJ—симметрические матрицы.
Если С—некоторая невырожденная матрица, то алгебры Ли

242
ГЛ. 7. ПОЛНОТА ИКВОЛЮТИВНЫХ НАБОРОВ ФУНКЦИЙ
LA и LCTAr изоморфны. Изоморфизм устанавливается отображе-
нием / (X) = СХС . Отсюда следует, что класс алгебры Ли LA,
т. е. множество алгебр LB, изоморфных LA, определяется
рангом матрицы А, так как в комплексном случае любая
симметрическая матрица А ранга к может быть приведена
к стандартному виду
у. =
О
F22)
16. Предложение. Имеет место равенство
indZ,?t = indso(«) + dim so (я — к) — ind so (я — к). F23)
Доказательство. Алгебра Ли LE является полупрямой
суммой алгебры Ли so (А:) и радикала V, который естественным
образом разлагается в прямую сумму Vх + К2. На V^ действие
алгебры Ли so (А:) является суммой п — к экземпляров простей-
шего представления so (к) на С*, на V2 действие so (к)
тривиально, Г Vu V{\ cz V2, Vi — центр алгебры Ли LE. Центр
Zk алгебры Ли LEt является подалгеброй в алгебре L?"=so(n),
изоморфной so (и — к). Поэтому формулу F23). которую надо
доказать, можно переписать в виде
ind LE = ind LE + dim Zk — ind
F24)
где Zk рассматривается как подалгебра в so (и) (ср. с предложе-
нием 7). Рассмотрим два случая. Пусть сначала п — к четно.
Отождествим пространства L и L* при помощи невырожден-
ного скалярного произведения (X, Y) = trXY. Тогда коприсо-
единенное действие алгебры Ли LA на L" = L имеет вид
(ad*A)xZ = AXZ — ZXA. Положим
F25)
где detZ2#:0, элемент Z) полупрост и регулярен в so (А). Тогда
аннулятор ковектора Z в алгебре Ли LE имеет вид
AnnF (z) =
Я
НеК
F26)

i 44 СКОБКИ ПУАССОНА
243
где К—подалгебра Картана в so (А:), содержащая Zj. Таким
образом, dim Ann* (Z) = ind so (к) + dim so (n — к) = ind so Ы) +
+ dim so (я — к) — ind so (я — к). Следовательно, indLE^
<dim AnnEi(z), при доказательстве леммы 8 была получе'на
обратная оценка F18). Поэтому indL? =indL? +dimZ!t — indZt.
Пусть п — к нечетно. Положим
Z=
z,
0
0
0
0
0
-1
0
0
1
0
0
0
0
0
z2
F27)
Тогда
Ann (Z ) = ¦
H
0
0
0
0
0
-I
0
0
I
У/
V,
0
0
///////
Mm
He К
F28)
Подсчитывая размерность, получим оценку indL? <
^dimAnnEtZ=indL?+dimZ,i —indZt. Из F18) получим обрат-
ную оценку.
17. Инварианты. Если det^/O, то кольцо полиномиальных
инвариантов алгебры Ли LA при отождествлении L с L * состоит
из функций вида f(CXCT), где feI{LE), Е„ = САСТ. Кольцо
I(LE) порождается функциями вида try2' B/<я), когда
п нечетно, и txY11 B1<п), Pf(y) = v/det Y, когда п четно.
Поэтому в качестве образующих кольца I(LA) можно взять
функции tr(CXCTJl = tr(XA~1J1 B/<и), когда п нечетно,
и triXA^1J' B/<n), РЦХ), когда п четно.
18. Инволютивное семейство. Рассмотрим двумерный пучок,
порожденный алгебрами LE и LB(>, где ?'=diag(l, ..., 1),
B0 = diag(bu ¦-., hi , b2, ..., b2 , ..., bs,°...,bs). Следуя общей
конструкции, выделим из пучка
все алгебры Ли,
б
конструкции, выделим из пучка (?х? + "В0)х,Цес все алгебры Ли,
которые не изоморфны LE^so(n). Ясно, что такими будут

244
ГЛ. 7. ПОЛНОIА ИНВОЛЮТИВНЫХ НАБОРОВ ФУНКЦИЙ
только алгебры Lc, где Ci = B0 — biE. Центр Z, алгебры Ли
Lc имеет вид
z, =4
0
0
0
щ
0
0
¦-.
0
F29)
и как подалгебра в LE = so(n) изоморфен so(&;). Пусть
Ft — произвольное полное инволютивное семейство функций на
Z*{k)'
{)
19. Теорема (А. В. Болсинов). Семейство функций
FBo = Fl(J...[JFs{J( U I(LBt>+XE)) на пространстве L* инволютив-
't-Ф -Ь,
но и полно относительно скобки Пуассона, отвечающей алгебре
Ли LE = so(n), или, более общим образом, относительно скобок
{х, у}хе+1хв0 таких, что indLi?+MBo = indLE.
Доказательство вытекает из предложения 7. В самом деле,
indLc =indLE + dimZi — indZ; (см. п. 16) и codim SE = 3 > 2, где
SE — множество сингулярных элементов в L* = so(n)*.
20. Следствие. Пусть Ci = BQl--biE. Для того чтобы
получить полное инволютивное семейство на L* относительно
скобки {х, у}с, достаточно добавить к семейству FB функции из
центра Zt.
Доказательство. Нужно проверить, сколько новых
функций добавится к семейству FBo. Набор Ft выражается через
линейные функции veZ,. Набор Ft состоит из 2(dimZ, + indZ,)
функционально независимых функций, поэтому добавится не
более dimZ, — 2~'(dimZ,- + indZ,) функций (на самом деле ровно
столько, иначе набор FBo можно было бы расширить с сохране-
нием инволютивности относительно скобки {х, у}Е, что невоз-
можно). Итак, в наборе FBo было 2~1(dimLE + indZ,?) независи-
мых функций. Добавив 2~* (dimZj — indZj) новых функций,
получим семейство, состоящее из 2~l (dim LE + ind LE +
+ dimZ, — indZj) = 2 l (dimLc +ind?c) функций, т.е. полное
относительно скобки {х, у}с..
21. Следствие. Семейство функций (J (l(LiAo+jJiB))
где
инволютивно и полно на L относительно скобки {х,у\А,
^40 = diag(l, ..., 1, 0), отвечающей алгебре Ли Е(п—\).
Доказательство. Пусть ^0 = diag(l, ..., 1, 0). Алгебра Ли
ф этом случае алгебре Ли Е{п—\) группы
LA() изоморфна в

i 44. СКОБКИ ПУАССОНА
245
движений (п — 1)-мерного евклидова пространства. Пусть
2f = diag(Z>i, ..., ЬЛ, Ь„фО. Тогда тахгк(Х.Л0 б)
>ц
= я, и можно
ц
применить к пучку, натянутому на алгебры Ли LAq и Lb,
теорему 19, поскольку такой пучок изоморфен стандартному
(bb)
j
Случай 2.
22. Замечание. Алгебры Ли из пучка (LA)AeJ разбиваются
на [я/2] + 1 классов, каждый из которых содержит изоморфные
между собой алгебры. Алгебры Ли LA и LB принадлежат
одному и тому же классу тогда и только тогда, когда
гкЛ = гк.б. Канонические представители классов имеют вид LF,
FkeJ, где
0 1
-1 0
0
-1
0
0
1
0
0
-1
1
0
о
о
F30)
Алгебра Ли LF^ является полупрямой суммой симплектической
алгебры Ли spBA:, С) и радикала V, который разлагается
в прямую сумму Vi + V2. На V1 действие алгебры Ли spB?, С)
является суммой п — 2к экземпляров простейшего представления
р0 размерности 2к. На V2 действие тривиально, [Vb Vi~\=V2,
V2 — центр алгебры Ли LF. Если п четно, то алгебра Ли
LF изоморфна симплектической алгебре Ли sp (и, С).
23. Предложение. Имеет место равенство
mALFt = -{n-2k)(n-lk+\) + k.
F31)
Доказательство. Продемонстрируем метод вычисления
индекса, который удобно применять в случае, когда стационар-
ные подалгебры общего положения представления Ad* со-
пряжены. Этот метод предложен А. Г. Элашвили [297] и ос-
нован на следующем утверждении.
24. Лемма. Пусть G—комплексная конечномерная алгебра
Ли, xeG* — некоторый элемент, а Апп(х)—стационарная под-

246
ГЛ. 7. ПОЛНОТА ИНВОЛЮТИВНЫХ НАБОРОВ ФУНКЦИЙ
алгебра Этого ковектора х относительно коприсоединенно-
го представления группы Ли Р, отвечающей алгебре Ли G.
Пусть Ann(x)f)[G, Апп(д:)]=0. Тогда элемент х регулярен
и ind G = dim Ann\x).
Доказательство. Обозначим Кх подпространство вС,
состоящее из ковекторов yeG* таких, что Ann(y)<= Ann(jc), т. е.
Kx={yeG*\ad\y = 0, ?eAnn(x)}. Легко видеть, что
KX=[G, Апп(дг)]1. Кроме того, Апп(хI = ТхО(х). Поэтому
условие Ann(*)n[G, Апп(д:)]=0 в точности означает, что
G' = KX+ TxO(x). Выпуская орбиты из точек уеКх, близких
к xeG*, мы заполним этими орбитами некоторую окрестность
точки х. Ясно, что стационарные подалгебры точек этих орбит
сопряжены аннулятору Апп(дг). Итак, имеется открытое под-
множество в G', состоящее из точек veG*, стационарные
подалгебры которых имеют одинаковую размерность. Ясно,
что это возможно лишь в том случае, когда все эти точки
регулярны. Лемма доказана.
Докажем теперь предложение 23, подобрав подходящим
образом ковектор xeL'. Как и в предыдущем случае, коприсо-
единенное действие алгебры Ли Lfj имеет вид
(adf )*YX=Fk YX— XYFk, если отождествить L с L' с помощью
скалярного произведения XxXY. Положим
Х=
лг, О
О х2
F32)
Xi — регулярный ковектор в смысле алгебры Ли spB&, С),
detJ!f2#0. Тогда
AnnFt(X) =
heH},
F33)
где Y3 — произвольная матрица, Y\=Y$, H—стационарная
подалгебра элемента Xt в смысле алгебры Ли spB&, С), т. е.
подалгебра Картана в spBk, С). Очевидно, что Annf (X)f)
n[AnnFk(X), LjFt = O. Поэтому *
dim?F =dimAnnF (Ar) = dim//+dim V2 —
= k+X-{n-2k)(n-2k+\). F34)
Отметим, что при доказательстве предложения 16 этот
метод применить нельзя, так как стационарные подалгебры
минимальной размерности не сопряжены.

: 44 СКОБКИ ПУАССОНА
247
25. Обозначения. Положим
0
Л
0
0
A
-ь
0
0
0
0
0
0
0
0
0
F35)
Обозначим Zk подпространство в L вида
0
0
0
ФЩ
гк
Пусть
А, =
0
0
0
0
0
0
0
0
0
2|
2
я,
0
0
0
0
2/
F36)
F37)
26. Теорема (А. В. Болсинов). а) Пусть п — четное число.
Тогда семейство функций I (J I(LB-kFk) )U^i U ••• UA \J Zk яв-
\ФЬ, )
ляется инволютивным и полным на пространстве L* относи-
тельно скобки {х, у}вк- б) Пусть п — нечетное число. Тогда
семейство функций \J /(Z.fj+lB,) является инволютивным и пол-
ным на пространстве L* относительно скобки {х, y}Fk-
Доказательство. Теорема доказывается аналогично
теореме 19 и является непосредственным следствием пред-
ложений 7 и 23.
Случай 3.
27. Замечание. Как и в предыдущих двух случаях,
алгебры Ли LA и LB изоморфны между собой тогда и только

248
ГЛ. 7 ПОЛНОТА ИНВОЛЮТИВНЫХ НАБОРОВ ФУНКЦИЙ
тогда, когда rk А = rk В. Рассмотрим только случай алгебр Ли
LA «общего положения», т.е. rkA=min(n,m). Пусть для
определенности п^т. Тогда алгебра Ли LA является полупря-
мой суммой алгебры Ли gl (т) и коммутативного идеала V,
действие gl(w) на V является прямой суммой п — т экземпляров
простейшего представления.
28. Теорема (А. В. Болсинов). Пусть пфО mod(n — m),
либо п = т. Тогда для любой матрицы А ранга т найдется
матрица В ранга т такая, что семейство функций IJ I(LA + lB)
инволютивно и полно на L* относительно скобки {х,у}А.
Доказательство. Если т = п, то без ограничения об-
щности можно считать, что ^4 = diag A, ..., 1). Пусть
B=d\ag(bl, ..., Ь„), bi^bj при /#_/. Тогда все алгебры Ли пучка,
порожденного алгебрами Ли LA и LB, за исключением абелевой
алгебры Lo имеют индекс п. Поэтому семейство {]
i
инволютивно. Полнота следует из того, что почти все алгебры
из этого пучка изоморфны LA = gl (т) и codim SA = 3 > 2, где
SAciL* — множество сингулярных элементов в смысле коприсо-
единенного действия алгебры Ли LA. Если п>т, то положим
А =
1 О
1 О
о
1 О
о
1 О
, в -
О 1
О 1
о
О 1
о
О 1
F38)
Тогда rk (\А + \\.В) = т при всех А., цеС, не обращающихся
одновременно в нуль. Поэтому все нетривиальные алгебры Ли
из пучка (^хх + цвКиес изоморфны между собой. Кроме того,
codim SA 5=2 в случае пфО mod (я — т). Оценка коразмерности
множества SA легко проводится по индукции с использованием
общей методики оценки коразмерности множества сингулярных
элементов в случае полупрямых сумм, см. п. 19 § 45. Теперь
инволютивность и полнота семейства (J I(LA + tB) непосредствен-
но следуют из предложения 7.
29. Замечание. Если я = 0 mod («— т), то алгебра Ли
LA является фробениусовой (см. [298], [478]), поэтому
codimSA=\, кольца инвариантов I(La+Xb) тривиальны.
Случай 4.
30. Замечание. Все алгебры Ли LA изоморфны между
собой (исключение — абелева алгебра Ли Lo). Покажем, что

§ 45. ИНВОЛЮТИВНЫЕ СЕМЕЙСТВА ФУНКЦИЙ 249
все эти алгебры Ли являются фробениусовыми, т. е. ind LA = 0
при АфО. Отождествим L и L* с помощью формы <Х, Y}.
Тогда коприсоединенное действие алгебры Ли ЬА на L*
запишется в виде {adA)\Y=(A, X) Y+(A, Y)X+<X, Y}A.
Пусть (A, F>/0. Решим уравнение (ad*A)xY=0 относитель-
но X. Ясно, что X линейно выражается через Y и А. Поло-
жим X=<xY+fiA и подставим в выражение для (ad^^y,
получим
(A, v.Y+$A)Y+(A, У>(аУ+рл) + <аУ+рл, Y)A =
) = 0. F39)
Итак, осУ+рл=О, т.е. Х=0 и ind?j4=0. Следовательно,
пользуясь методом построения инволютивного семейства по
двумерному лиеву пучку, мы не сможем получить полного
семейства на L*. Полное семейство функций в инволюции на L*
можно построить другим способом, взяв произвольное лагран-
жево подпространство в L, содержащее А. Легко видеть, что это
подпространство является абелевой подалгеброй размерности
2~1d\mL и поэтому полно и инволютивно на V.
§ 45. Инволютивные семейства функций
на полупрямых суммах
1. Замечание. Пусть К—полупростая алгебра Ли,
р: K-+End(V)—линейное представление, G = K+V—полупря-
мая сумма. Задача построения полных инволютивных наборов
на двойственном пространстве G* решалась в работах
А. Г. Реймана [228], В.В.Трофимова и А.Т.Фоменко [266],
А. В. Браилова [48], [49], Т. А. Певцовой [212]. Здесь мы
докажем общую теорему о существовании полного инволютив-
ного семейства функций.
Докажем следующую теорему, принадлежащую А. В. Бол-
синову.
2. Теорема. Пусть К—классическая комплексная простая
алгебра Ли, р: К-* End(V) — неприводимое представление,
G = K+V—полупрямая сумма. Тогда сдвиги инвариантов ко-
присоединенного представления Ad* на произвольный регуляр-
ный ковектор aeG* образуют полный инволютивный набор
на G*.
Прежде чем доказывать эту теорему, напомним основные
моменты, связанные с коприсоединенным представлением полу-
прямых сумм алгебр Ли. Начнем с общего понятия расширения
алгебры Ли.
3. Определение. Алгебра Ли (Е, [х, у]) называется
расширением алгебры Ли L с помощью абелевой алгебры Ли А,

250 ГЛ. 7 ПОЛНОТА ИНВОЛЮТИВНЫХ НАБОРОВ ФУНКЦИЙ
если эдана точная последовательность алгебр Ли:
F40)
Выберем в Е такое подпространство S, что E=i(A)@S.
4. Лемма. Каждое расширение Е алгебры Ли L с помощью
А определяет представление р алгебры Ли L в пространстве А
Доказательство. Пусть met, aeА. Определим действие
р(т) алгебры Ли L в А формулой ip(m)a= [д\ ад], где х— такой
элемент в Е, что п(х) = т. Из тождества Якоби
[[.v, у], ib ]= [.y, [у, ib~\]—[)', [х, ib]] получим равенство
р( [т. п]) = р(т) р(«) — р(п)р(т), где п(х) = т, п(у) = п.
5. Лемма. Произвольное расширение (Е, [х, у]) алгебры Ли
L с помощью А определяет некоторый класс когомологий
fieH2(L;A) алгебры Ли L со значениями в А.
Доказательство. Фиксируем подпространство S такое,
что Е= i(A) © S. Ограничение я = я | S задает изоморфизм между
S и L. Обозначим р1 (соответственно р2) каноническую
проекцию пространства Е на (А (соответственно на S). Для
m,neL выберем такие элементы x,yeS, что к(х) = т, к(у) = п.
Положим iC(m, п)=р1 [х, у]. С: LxL->A — кососимметри-
ческое полилинейное отображение, т. е. 2-коцепь алгебры Ли L со
значениями в А. Более того, ЬС{х1, .г2. х3) = 0, т. е. С—коцикл.
Пусть теперь 5"—другое дополнительное подпространство к i(A),
т.е. ?= i(A)@ S'. Тогда С — С = дТ, где Т: L—>A—линейное
отображение, т. е. 1-коцепь алгебры Ли L со значениями в А.
6. Лемма. Пусть задано представление р: L -* End (A)
алгебры Ли L в векторном пространстве А, рассматриваемом
как абелева алгебра Ли, и класс когомологий Pe//2(L; А). Тогда
существует расширение Е алгебры Ли L с помощью А,
ассоциированное с представлением р и классом р.
Доказательство. Положим E=A@L. Определим на
Е коммутатор: [а, х ] = р (х) а, если xeL, aeA, и
[xi+ai, x2 + a2] = [xu х2~\ + С(хи х2) + р(х1)а2-р(х2)а1, F41)
если xfeL, ateA и [а, />] = 0, a, be А. Ясно, что Е—искомое
расширение.
7. Определение. Пусть есть два расширения ?\ и Е2 ал-
гебры Ли L с помощью А. Они называются эквивалентными,
если существует такой изоморфизм /: Ех -> Е2 алгебр Ли, что
диаграмма
II и lf«2W F42)
А - Е2 -+L
коммутативна.

I» 45. ИНВОЛЮТИВНЫЕ СЕМЕЙСТВА ФУНКЦИЙ 251
8. Предложение. Два расширения Ех, Е2 алгебры Ли
L с помощью А эквивалентны тогда и только тогда, когда они
определяют одно и то же представление р алгебры Ли L на
А и один и тот же элемент когомологий $eH2(L;A).
9. Определение. Расширение, отвечающее нулевому
классу когомологий $еН2(ЦА) называется несущественным
расширением или полупрямой суммой E=Lp + A. Если C/0, то
расширение существенное.
10. Замечание. Поскольку для каждого конечномерно-
го модуля V над полупростой алгеброй Ли G выполняет-
ся равенство Н2 (G; V) = 0, то любое расширение полупро-
стой алгебры Ли несущественно, т. е. является полупрямой
суммой.
11. Пример. Построим существенное расширение. Пусть D,
как обычно, алгебра Ли векторных полей на многообразии М",
а С1р — пространство /?-форм на М. Алгебра Ли D представлена
в пространстве Qp с помощью операции производной Ли (см.
п. 1 § 21), поэтому можно рассмотреть пространство когомоло-
гий Н2 (D; Qp), см. [291 ]. Выберем на М" связность Гд без
кручения, ее производная Ли определяется формулой
() 1.rf1-arjrirr1.+5ljr'r;i+ajjrrrfr, F43)
где XeD. Равенство
СГ(Х,?)и = {ЬхГ)ЦЬгГук]-(ЬуГ)^(Ьхгук] F44)
задает 2-коцепь алгебры Ли D со значением Q2- Легко видеть,
что 5 Сг (х, у, z) — 0, т.е. это коцикл и, следовательно, он
определяет некоторый класс когомологий. Оказывается, что
этот класс когомологий ненулевой для любого многообразия
М", причем он не зависит от выбора связности, т. е. получили
выделенный класс когомологий. Итак, имеем существенное
расширение Е алгебры Ли D с помощью Q2, которое
называется универсальным расширением алгебры Ли D.
12. Определение. Для произвольного представления
р алгебры Ли G в вещественном пространстве V индексом этого
представления называется число ind p = {коразмерность орбиты
общего положения представления группы Ли, отвечающей
алгебре Ли G). Напомним, что индекс коприсоединенного
представления по определению — это индекс алгебры Ли, indG =
= ind ad* [88].
Пусть G — некоторая алгебра Ли, W<^G — векторное под-
пространство, xeG* — элемент двойственного к G простран-
ства. Определим подпространство
(H/, x) = {ge W\ad*x = 0}a V. F45)
Если W—подалгебра, то и IVх также подалгебра.

252 ГЛ. 7. ПОЛНОТА ИКВОЛЮТИВКЫХ НАБОРОВ ФУНКЦИЙ
13. Теорема (М.Раис, [478], [479]). Пусть G—полупря-
мая сумма алгебры Ли Н по представлению р алгебры Ли Н в V.
Тогда для элемента xeG* общего положения выполнено
равенство
indG^ndtf' + indp*, F46)
где р* — представление Я в V*, двойственное к р.
Доказательство. Пусть xeG*, x = xH + xv, хнеН*, xve
V,— такой элемент, что выполнены следующие условия:
a)dimp*=dimtf-dimtfx; б) ind HXy = inf{ind H\ yeV*};
в) dim Ann (НХу, x\ HXy) = indHXy. Все такие элементы х образу-
ют непустое открытое по Зарисскому множество в G*. Таким
образом, элементы общего положения в G* удовлетворяют
условиям а) — в). Поэтому для доказательства теоремы до-
статочно проверить, что из а) — в) следует равенство dimGJr =
= ind #* + indp*. Пусть g=gH+gveGx. Тогда
ad*H{xH)+ad*v{xv) = 0, F47)
аA*„Ы = 0. F48)
Из F48) следует, что gHeHXy. Рассмотрим ограничение
равенства F47) на НХу:
<ad*r(xv), HXy)=-(ad*H,y(xv), gv) = 0; F49)
<ad*H(xH), HXy) = (xH, ad*H(HXy)) =
= (х„\НХу, ad9H(HXy)) = (ad*H(xH\Hxy), H*y). F50)
Таким образом, ограничивая F47) на НХу, получим
(ad*н) (л:| НХу) = 0. Пусть кн—проекция из G в Я вдоль V. Мы
доказали, что ян (Gx)cz Ann (НХу, х\ НХу). Пусть, напротив,
gHe Ann {HXy, x\HXy). Тогда уравнение F48) выполняется авто-
матически. Покажем, что можно так подобрать gve V, что
будет выполнено и уравнение F47).
14. Лемма. Если уеН* и у\НХу = 0, то найдется такой
элемент gveV, что y = ad* (xv).
Доказательство. Выше было показано, что
(ad*y) xv\HXy = 0, поэтому достаточно проверить, что
dim (adK)* xK = dim {уеН*\ у\НХу = 0]. Очевидно, что dim {ye
eH*\y\HXy = 0}=dimH/HXy. С другой стороны, dim (adK)* хк =
= dimF/F^. Пусть L (X, Y)=(xv, [X, Y]> — билинейная косо-
симметричная форма на G. Легко проверяется, что Я и V—
изотропные относительно формы L подпространства
и НХу@ VXy = KerL, откуда следует, что dim V/VХу — dimH/HХу.
Лемма доказана.
Поскольку ((adgH)* хн)\НХу = 0, то в силу леммы можно
подобрать gv так, что
(adj* xH+(ad9y)* xv = 0. F51)

§ 45. ИНВОЛЮТИВНЫЕ СЕМЕЙСТВА ФУНКЦИЙ 253
Отсюда следует, что gHenH(Gx) и л„ (G*) = Ann (НХу, х\ Нху).
Теперь подсчитаем размерность слоя проекции л»: Gx:-*nH(Gx).
Из уравнения F47) следует, что dim(nH)~ {gn) = dimVXv,
откуда dimG* = dim Ann (#*", x\Hxr) + dim VXv. Теперь заме-
тим, что dim VXv = d\v& V— dim V/V**. Выше было доказано, что
I, поэтому dim Fx^ = dim V-dimH+
Теперь из условия в) получаем dimG* =
p Теорема доказана.
15. Формулы. Пусть Q — конечномерная группа Ли (с
алгеброй Ли Я), действующая в линейном пространстве V, Р =
= QxV—соответствующее полупрямое произведение. Алгебра
ф
Ли G группы Ли Р является полупрямой суммой G=H+V
ф
алгебры Ли Я и пространства V по индуцированному представ-
лению ф = ^Ф: Я->Еп<з(К). Пространство G* будем отождеств-
лять с прямой суммой H*+V*, полагая H*=V1, V* = HL.
Тогда коприсоединенное представление группы Ли Р и алгебры
Ли G на V запишутся так:
Ad(* a) (x+v) = {{Ad?)gx + A (а, Ф* (g) v^ + Ф* (g) v, F52)
D)i;, F53)
здесь первая скобка в F52) и F53) принадлежит Я*, а вторая —
пространству V*, где Ad? — коприсоединенное действие группы
Ли Q на Н*, ad% — коприсоединенное действие алгебры
Ли Я на Я*, Ф* — действие группы Ли Q на V*,
сопряженное с Ф, ср* — действие алгебры Ли Я на V*,
сопряженное с ср, A: VxV* -+ Н* — линейное преобразование,
определенное равенством (A (a, v), ?) = (q> (?)a, v), geQ, ^еЯ,
aeV, xeH*, veV*.
16. Определение. Элемент veV* называется слабо регу-
лярным, если для стационарной подалгебры St (v) cz Я выполня-
ется условие dim St (v) + ind St (v) = min (dim St (и) + ind St (и)).
ueV*
Элементы общего положения являются слабо регулярными;
обратное, вообще говоря, неверно. Пусть S={x + veH* +
+ V* | dim Ann (x + v) > ind G} — множество сингулярных элемен-
тов в G*:
17. Предложение. Элемент veV* слабо регулярен тогда
и только тогда, когда существует такой элемент хеН*, что
x + veS.
Доказательство. Пусть x + veG*, к: Я* -»St(t>)* —
естественная проекция. Вычислим размерность dim Ann (x + v).
Имеем
dim Ann (x + v) = dim Ann n (x) + codim О (v) =
= dim Ann л (x) + dim V— dirr^+dim St (t>)^
2* (ind St (v) + dim St (v)) + dim V- dim H, F54)

254 ГЛ 7 ПОЛНОТА ИНВОЛЮТИВНЫХ НАБОРОВ ФУНКЦИЙ
причем если ковектор я (jc) регулярен в St (f)*, то в точности
dim Ann (x + v) = (ind St (v) + dim St (v)) + dim V— dim H. Таким об-
разом,
veH'
mindimAnn(jc + t;) = indSt(t;) + dim St (u) + dim K-dim#; F55)
indG= min dim Ann (x + v) =
x + veH' + V
= min (ind St (u) + dim St (u)) + dim V- dim H. F56)
ueV*
Утверждение сразу следует из этих равенств.
18. Обозначения. Символом Sv обозначим дополнение
к множеству слабо регулярных точек в пространстве V*,
символом 5s,o — множество сингулярных элементов в St*
в смысле представления ad*, где Stoc://—стационарная под-
алгебра общего положения.
19. Предложение. Условие codim 5^2 выполняется
тогда и только тогда, когда codim Sv > 2 и codim 5s,o > 2.
Доказательство. Рассмотрим сечение множества
5с: Н*+ V* аффинными плоскостями вида v + H*, veV*. Легко
видеть, что условие codim 5=1 эквивалентно выполнению
одного из следующих двух условий: 1) множество точек ve V*,
для которых коразмерность пересечения (v + H*)f]S в плоско-
сти v + H* равна единице, открыто' по Зарисскому в V*
и непусто; 2) множество точек veV* таких, что v + H*cS,
имеет коразмерность один в V*.
В силу предложения 17 условие 2) в точности означает, что
codim Sr=l. Рассмотрим пересечение (v + H*)f]S. Пусть
v + H*<?S, т.е. точка veV% слабо регулярна. Элемент x+v
содержится в пересечении (v + H*)f]S тогда и только тогда,
когда л (x)eSSl(v)cz St (v)*, где 5St(l)i — множество сингулярных
элементов в St (t>)*. Поэтому codim (v + //*) f] 5=-codim5St(l;).
Следовательно, первое условие означает, что существует непус-
тое открытое по Зарисскому множество V а V*, состоящее из
элементов v таких, что codim 5St ,„, = 1. Поскольку множество
точек общего положения тоже открыто по Зарисскому, то
условие 1) эквивалентно тому, что codim 5s,o=l. Предложение
доказано.
20. Доказательство теоремы п. 2. Пусть сначала
dimA">dimK, что эквивалентно нетривиальности стационар-
ной подалгебры общего положения [3]. В работе
А. Г. Элашвили [297] получен список представлений простых
алгебр Ли, удовлетворяющих этому условию, и найдены
стационарные подалгебры общего положения. В данном слу-
чае существует открытое по Зарисскому непустое подмножест-

§ 45 ИНВОЛЮТИВНЫЕ СЕМЕЙСТВА ФУНКЦИЙ 255
во в V, все точки которого имеют сопряженные стационар-
ные подалгебры. Именно эти точки естественно назвать
точками общего положения, и при доказательстве теоремы
мы будем придерживаться такой терминологии. В силу кри-
терия полноты семейства сдвигов и предложения п. 19 до-
статочно проверить выполнение двух условий: 1) codim Sv^2;
2) codim5s,o>2.
Известно, что представления ф и ф*, вообще говоря, не
эквивалентны даже для полупростых алгебр Ли, однако
полупрямые суммы К+ V и К+ V* изоморфны как алгебры Ли.
Ф Ч>*
Поэтому будем рассматривать только одно из этих представле-
ний. Разберем два случая: 1) стационарная подалгебра общего
положения редуктивна; 2) стационарная подалгебра общего
положения не редуктивна.
21. Случай 1. В этом случае автоматически codim Ss,o > 2, где
St0 — стационарная подалгебра общего положения, которая
предполагается редуктивной. Остается проверить первое усло-
вие. Элемент vneV* назовем нильпотентным, если замыкание
его орбиты O(vn)aV* при действии группы Т, отвечающей
алгебре Ли К, на V* содержит нуль. Пусть, как и выше,
Sv — дополнение в К* к подмножеству слабо регулярных
элементов.
22. Лемма. Если существует слабо регулярный нилыготент-
ный элемент vn е V, то codim Sv > 2.
Доказательство. Предположим, что условие codimSv 5=2
не выполняется, т. е. Sv является алгебраической гиперповерх-
ностью и задается уравнением P(v) = 0, где Р—некоторый
однородный полином. Кроме того, множество Sv инвариантно
относительно действия группы Т, отвечающей алгебре Ли К,
поэтому полином Р является полуинвариантом представления
ф*, но у полупростых алгебр Ли не существует нетривиальных
характеров, поэтому на самом деле Р—инвариант. Пусть
vn — слабо регулярный нильпотентный элемент. Тогда
Р|О(vn) = const, но замыкание орбиты O(vn) содержит нуль,
следовательно, P\O(vn) = 0 и P(vn) — 0, т. е. vneSv. Проти-
воречие доказывает лемму.
23. Замечание. Если алгебра Ли К простая классическая,
представление ф* неприводимо и dimK^dimA", то слабо
регулярные нильпотентные элементы всегда существуют. Для
того чтобы их найти, достаточно иметь классификацию типов
орбит представления ф*. Если представление ф* не слишком
сложно, то изучение типов орбит не представляет больших
трудностей. Наиболее нетривиальными являются случаи пред-
ставлений в пространстве тривекторов, спинорных и полуспи-
норных представлений. Однако и в этих случаях необходимые
для нас сведения получены в работах [493], [84], [222], [361],

с;
ю
тз ел
¦ч
О а"
с ел
е
~°
СЛ
9-
S
я
9-
*
я:
с
я:
(N
О.
с
и
^ ъ.
!N +
, О
ей О.
Х II
1
С
(sp
С
<!
-
| |
я:
я:
СЛ
и
+ а°
С
О
Q.
ел
(Ч
1
я:
1
«
i
с
и
и
тз
я
СЛ
i2
X
*
п-i
<
(9)
"?,
oo
и
+ .о
^—- Q.
rs X
*""*" о
«л с
X «
-—'
ел
а.
"ел
00
,
и

Q.
1
гч
с
1
&:
_ ** ^
1
1
с
so(
и
(^
s:
о
СЛ
а.
g
Г-
"^
(N
с
и
и
S
ч*
и
СЛ
а
s

10
11
12
13
14
15
16
17
so (9)
so A1)
so A3)
spBn)
sp Bи)
spF)
so A2)
so A4)
spin
spin
spin
Л2р0 = ф + х
ad
Л3ро = ф+Ро
л —spin
s— spin
62 + C7
spD)+l/14
slB)+(/13
*
slB)+t/3A,_1)
¦
C"
si B)+ C5
s4Po
spF) + C14, Л2р0 = х|/ + т
ad
so G)
si E)
slC)xslC)
slB)x...xslB)
n
C"
slC)
si F)
g2xg2
21
24
16
3n
n
8
35
28
3
4
4
n
n
2
5
4

258
ГЛ 7 ПОЛНОТА ИНВОЛЮТИВНЫХ НАБОРОВ ФУНКЦИЙ
[386]. Классификация орбит действия группы Ли SL(«)
в пространстве тривекторов получена при и=6, 7 Рейхелем
и Схоутеном [493], при п = % — Г. Б. Гуревичем [84]. Клас-
сификация орбит действия группы SpF, С) в пространстве
тривекторов размерности 6 получена В. Л. Поповым в [222],
в этой же работе дана классификация спиноров размерности 14.
Классификация спиноров до размерности двенадцать включи-
тельно проведена Игузой [386], размерности 13 — Э. Б. Винбер-
гом и В. Г. Кацем [361]. Список стационарных подалгебр слабо
регулярных нильпотентных элементов vne V* приведен в табл. 2.
В таблице указаны также для сравнения стационарные под-
алгебры общего положения, индексы и размерности. Слабая
регулярность элементов следует из равенств dimSt(i;n) = dimSt0,
indSt(un) = indSt0.
24. Пояснения к табл. 2. Использованы следующие обозначе-
ния: U, — унипотентный некоммутативный радикал размерности
/; С ' — коммутативная алгебра размерности /; р0 — простейшее
представление; т — одномерное тривиальное представление;
в графе 11 1|/=ро + ро + Л2р и UlA=Vl+V2+V3, [V2, V3]=Vt;
в графе 12 v|/ = po + x + po + ad + po + x+po и U13= K, +... + V7,
[Vh Vj]czVij при i+j^l, исключения: [V2, V2]=[V2, И4] = 0;
3A1_1)= V, + ... + К„_1; [V,, V}] =
в графе 13 i|/ = ad+...+ad и t/
= Vi
n—\, другими словами, siB) +
где А=С[х]/С[х"].
Разберем один случай подробно.
25. Пусть K=sp(n, С), ф = Л2р0. Элементы алгебры Ли
sp(n, С) представим в стандартном виде
D С
В -D1
F57)
где С=С, В = В'. Представление ф = Л2р0 реализуется в про-
странстве кососимметрических матриц ц>(Х)А=ХА+АХ\
А'= —А. Положим
F58)
0
-1
0
0
-1
0
0
0
-1 0
0
1
0
0
1
0
0
. 1
. 0

i 45 ИНВОЛЮТИВНЫЕ СЕМЕЙСТВА ФУНКЦИЙ
259
0
0 .¦
с„ с, ¦ •
ап-\
«0
¦г-
¦ С ПА
Ьп-\
ь1 ¦ '
-ап , ¦
0
0
Решая уравнение ХАо + АоХ' = 0, находим стационарную
подалгебру
F59)
Легко проверяется, что St(/Io) = slB)®/1, где Л = С[х]/
/С[х"]. Поэтому indSt(/lo) = indslB)dim/f =« = indSt0, см.
[253], dimSt(/40) = dimSt0. Остается проверить, что элемент Ао
нильпотентен. Имеется следующее простое достаточное условие
нильпотентности.
26. Лемма. Если элемент vneV является собственным
вектором ненулевого веса для некоторого оператора ty{X), XeK,
то vn нильпотентен.
Доказательство. Рассмотрим кривую y(t) = tvn, te [0, 1 ].
Утверждается, что y(t)^O(vn). Достаточно проверить, что
j(t)€Tn,)O(y(i)), т.е. vneT,LnO(tvn) для всех te [0, 1 ]. Это
условие выполнено, так как в" силу линейности представления
Т„. O(tvn)=Tv O(vn), и по предложению существует такой
элемент XеК," что (p(X)vn = OLVne TvО(vn), ^
Элемент Ао ур фу
ному условию леммы 26, так как является собственным
вектором единичного веса оператора Ц>(Х) при A'=diag A, 2, ...
..., п, -1, -2, ..., -п).
Остальные случаи рассматриваются аналогично.
27. Случай 2. Стационарная подалгебра общего положения
нередуктивна. Имеются 4 представления с таким свойством:
a)A"=sl(n), ф = р0; б) A"=sp(n, С), ф = р0; в) A"=s1Bm + 1),
Ф = Л2р0; r)A"=soA0), 9 = .s-spin.
Представление ф* во всех случаях локально транзитивно,
поэтому выполнено условие codim Sv > 2. Действительно, лю-
бой элемент общего положения является нильпотентным. Итак,
остается проверить условие codim 5Sto > 2 для стационарной
подалгебры общего положения. Стационарные подалгебры
pn n vn
о удовлетворяет сформулированному достаточ-
26 б
в этих четырех случаях имеют вид: 1) St0 1 =sl (и — 1) + С";
р
2) St0 2 = spB« — 2, С)+ U2n-i, радикал U2n-i некоммутативен,
U2n^=V1+V2, \VX,V,\=V2, V2 = Z(St02), dimK2=l;
3)St0 3=spBn, C) + C2"; 4) St04 = soG) + С8. Случай 4) уже

260 ГЛ. 7. ПОЛНОТА ИНВОЛЮТИВНЫХ НАБОРОВ ФУНКЦИЙ
разобран выше. Случай 1) легко рассматривается по индукции.
Действительно, мы только что доказали, что codim 5 2s 2 тогда
и только тогда, когда codim5012;2, где 5—множество
сингулярных элементов в (sl(n) + C")*, S0l—множество син-
Ро
гулярных элементов в (sl(«— 1 ) + С~1)'. Снижая размерность,
Ро
доходим до алгебры Ли sl^J + C1, а она абелева, поэтому
Ро
множество сингулярных элементов пусто. Случаи 2) и 3) тесно
связаны друг с другом и тоже рассматриваются по индукции
с использованием следующей леммы.
28. Лемма. Пусть L0 = L/M—фактор-алгебра Ли L по
идеалу М, SL и S^—1-множества сингулярных элементов в U
и L'o соответственно, и indL0 = indL — dim А/. Тогда если
codim SLa 2* 2, то codim SL > 2.
Доказательство. Пусть тс: L-*L0—естественная проек-
ция. Тогда определено естественное вложение л': L*0^L'. Ko-
присоединенные представления алгебр Ли L и L обозначим ad
и ad0 соответственно. Легко проверить, что 7t*(adl(,)x)=ad*Tc(jc).
Проверим равенство n'(SLJ = SL f]n'(L*0). Из тождества
7t*(ado^(g)x) = ad*7t*(x) следует, что Апптс'(х) = 7с~1 (Аппх) для
любого xeL'o. Сингулярность элемента xeL'o означает, что
dim Ann* > indL0, следовательно, dim Ann л* (х) = dim Ann* +
+ dim M > ind L, т.е. элемент п'(х) сингулярен в U. Таким
образом, 7t*Eto) c SL f)i'(to). Обратное включение доказыва-
ется аналогично. Поскольку отображение п* является вложени-
ем, то коразмерность SLo в L'o равна коразмерности множе-
ства n'(SLJ = SL f]n'(Lr0)\ n'(L'o). Множество SL выделяется
в U некоторым набором однородных полиномов, поэтому
при переходе к сечению SLC]n'(L'o) коразмерность может
только возрасти (коразмерность в 7t*(Z,o)), поэтому
codim SLo 2= codim SL. Лемма доказана.
29. В нашем случае L = spBn — 2, С) + U2n_l, M=
= Z(L)=V2, LO = L/M=spBn-2,C) + C2"-2. Известно, что
indStOi2 = ind(Sto 2/Z(StO2))+l, см. [479]. Поэтому если
codim SLa 2=2, то codim SSl<i2 2=2. Это позволяет в случаях 2) и 3)
п. 27 применить индукцию, переходя на каждом шаге к стаци-
онарной подалгебре общего положения St0 2, затем от нее,
пользуясь леммой 28, к алгебре Ли L0 = St0 2/Z(St0 2) и т.д.
В результате мы придем к алгебре Ли spB, С) + С2. Стаци-
р
онарная подалгебра в этом случае одномерна, следовательно,
удовлетворяет условию codim 5sto 2=2.

S 46 ДИНАМИЧЕСКИЕ СИСТЕМЫ 261
Осталось рассмотреть случаи, когда dim F^dimA", стаци-
онарная подалгебра общего положения в этом случае тривиаль-
на, поэтому следует проверить условие codim5K > 2. В [395]
получен полный список представлений простых алгебр Ли, для
которых выполнены условия dim V > dim К и codim Sv = 1.
Оказывается, все такие представления приводимы. Теорема
доказана.
30. Предложение. Пусть G = K + V—полупрямая сумма
ф
простой алгебры Ли К и линейного пространства V по
представлению ф, aeG*—регулярный элемент. Если:
1) K=s\(n), ф= ро+ ... + р0, пфО modp, либо р=\; 2) K=so(n),
Ф=Ро+•••+Ро> Р произвольно; 3) K=sp(n, С), ф = ро+...+р0 ,
р раз р раз
р нечетно или р > п, то семейство сдвигов инвариантов
коприсоединенного представления алгебры Ли G на ковектор
а полное. Если ограничения на число слагаемых не выполнены, то
семейство сдвигов неполное.
Доказательство аналогично доказательству теоремы 2.
Глава 8
СЕКЦИОННЫЕ ОПЕРАТОРЫ
§ 46. Динамические системы и симплектические
структуры, порождаемые секционными операторами
1. Замечание. В работах [274], [278] А. Т. Фоменко
предложил конструкцию построения операторов, названных
секционными и позволяющих получать достаточно богатые
серии как вполне интегрируемых гамильтоновых систем на
орбитах представлений групп Ли, так и примеры разнообразных
симплектических структур, обладающих интересными свойст-
вами. Частными случаями таких гамильтоновых систем оказы-
ваются, например, уравнения движения многомерного твердого
тела с закрепленной точкой в отсутствие силы тяжести,
уравнения движения многомерного твердого тела по инерции
в идеальной жидкости и т. п., см. [266], [267].
2. Конструкция. Пусть Н—алгебра Ли, Q — соответству-
ющая группа Ли, р: Н->End(K) — представление Н на линей-
ном пространстве V и О(Х) — орбита действия Q на V. Пусть
XeV. Если задать линейный оператор q: V-* Н (который
назовем секционным), то на орбитах возникает векторное поле
X=p{q{X))(X). Предъявим специальный класс секционных

262
ГЛ. 8. СЕКЦИОННЫЬ ОПЕРАТОРЫ
операторов, образующих многопараметрическое семейство, ос-
новными параметрами которого являются два элемента а е V,
ЬеК=КетФа, где Фя: H->V, Фв(А) = р(Л)а.
Пусть а—элемент общего положения в Я. Предположим, что
в алгебре К есть полупростые элементы. Пусть b e К— произволь-
ный полупростой элемент. Рассмотрим П = КегрF) <= V; пусть
Н = К+К', где К' — произвольное алгебраическое дополнение к К.
Имеем К=П + 1трF) (в силу полупростоты b), T\(*\\mp(b) = Q.
Плоскость ФаК' = ФаН cz V определена однозначно (при заданном
а). Положим В = И(]ФаК', А' = ФаК' C)lmp(b). В силу выбора
b оператор р(Ь) изоморфно отображает ImpF) на себя. Пусть
р(Ь) —обратный оператор
= p(bIR'. Тогда
lmp(b) = R + Z, где Z—произвольное алгебраическое дополнение.
Пусть Т—алгебраическое дополнение к В в П.
Окончательно получаем разложение пространства V в пря-
мую сумму четырех подпространств: V= T+B + R + Z. Если на
V задано скалярное произведение, то Z и Т однозначно
определяются как ^ортогональные дополнения. Положим
В = Ф~1В, Фа^' = Л, получаем разложение алгебры^ Ли
Н в прямую сумму четырех noflnpocTpaHCTB:_// = A'+.e + .fi+Z,
где Z — алгебраическое дополнение к B + R в К' (рис. 42).
Рис. 42
Определим ^секционный оператор
-+K+B+R + Z, положив
T+B+R+Z
4 =
ф;'рF)
О D'
F60)
где D: Т->К и D': Z^>Z—произвольные линейные операторы,
Фа: В -> В, Ф~1р(Ь): R-*R. Такие операторы назовем
каноническими секционными. Итак, получили многопарамет-
рическое семейство операторов q = q(a, b, D, D').
3. Определение. Пусть M = P/Q — компактное однород-
ное пространство. Тогда алгебра Ли G группы движений

<j 46. ДИНАМИЧЕСКИЕ СИСТЕМЫ 263
Р разлагается в прямую сумму G = H+V двух подпространств
Я и К где H=TeQ — стационарная подалгебра, касательная
плоскость к стационарной подгруппе Q, а V можно отождест-
вить естественным образом с касательным пространством
к многообразию М. Ясно, что Н присоединенным образом
действует на V, т. е. p = ad.
Пространство М называется симметрическим, если суще-
ствует такой инволютивный автоморфизм 6: Р^Р группы Р,
что (Рв H el Q с />е, где Рв = {х е Р \ 0 (.v) = х } — множество непод-
вижных точек автоморфизма 0, а {РвH— компонента связности
единицы е е Рв.
4. Теорема (А.Т.Фоменко). Пусть M=P/Q — компакт-
ное симметрическое пространство, где Р, Q — полупростые
компактные группы Ли. Пусть ае V—точка общего положения.
Тогда разложение пространства V=T+B+R + Z, определяющее
канонический секционный оператор С: V—>H, имеет следующий
вид: Т—максимальное коммутативное подпространство в про-
странстве V, aeT, R = R', Z = 0, ФаН+Т= V= T+B+R,
ФаН=В + R, R=\mp(b). Плоскости Т, В, R попарно ор-
тогональны. Если q. С: V -> Н—два канонических секционных
оператора, то наряду с динамической системой X=p(q(X))(X)
на орбитах O(X)cV возникает внешняя 2-форма F(X,
?,, л) = <?*, [?, л]>. где ?,, цеТхО(Х). Здесь <Х, Г> —
невырожденное скалярное произведение Киллинга на полупростой
алгебре Ли Н.
Доказательство. Пусть aeV—произвольный элемент
общего положения. Из теории симметрических пространств
(см., например, [160]) следует, что в плоскости V всегда
существует максимальное коммутативное подпространство Т,
содержащее а. Фиксируем такое подпространство, и пусть
Т — ортогональное дополнение к Т относительно формы
Киллинга. Напомним, что на алгебре G=H+V задана
форма Киллинга (X, F> = tradA-ady, ограничение которой
на V также задает невырожденное положительно определенное
скалярное произведение на V.
Следуя общей схеме построения секционного оператора, мы
должны теперь рассмотреть в подалгебре Н аннулятор К=К{а)
элемента а, т. е. совокупность всех таких кеН, что [к, а] = 0.
Это означает равенство К=КетФа. Из тождества Якоби
следует, что аннулятор является подалгеброй в Н (не обязатель-
но коммутативной). Можно считать, что К (а) является
аннулятором любого элемента t общего положения из Т, т. е.
K(a) = K(t), где a, t — элементы общего положения в Т. Теперь
мы должны рассмотреть в К произвольный элемент b общего
положения. Отметим, что при этом элемент b не обязан быть
элементом общего положения с точки зрения всей алгебры Ли
Н. Согласно нашей общей схеме мы должны рассмотреть

264 ГЛ. 8 СЕКЦИОННЫЕ ОПЕРАТОРЫ
подпространство П = КегрF) в V. Ясно, что оно совпадает
с аннулятором К, т.е. Kerp(b) = {ve K|[f, ?1 = 0}. Подпрост-
ранство П не зависит от выбора элемента b общего положения
в К. Очевидно, TczYl. Пусть В—ортогональное дополнение
к плоскости Г в П.
5. Лемма. Плоскость В совпадает с ФаН(~]П, где Фа:
H-+V, Фа(й) = р(й)(а)=[й, а]. Кроме того, Ф„#IT.
Доказательство. Согласно определению оператора Фа
пересечение ФаН с П состоит из всех элементов вида [И, а],
коммутирующих с а, где ИеН. Докажем, что плоскость ФаН
ортогональна к Т. Рассмотрим скалярное произведение <ФаЛ,
О, где ИеН, teT. Тогда <Ф„/г, t) = ([h, a], ?> = <Я [a, t]} = 0,
так как teT, т.е. [а, Т] = 0. Кроме того, мы использовали
свойство операции ad: (ad^ Y, Z>= — < Y, adxZ). Другими
словами, операторы ad^ кососимметричны относительно формы
Киллинга. Таким образом, Т±ФаН и Т±(ФаНf]TL), следова-
тельно, В = ФаН П П. Лемма доказана.
6. Замечание. Использованное нами обозначение В для
плоскости, ортогональной к Т в П, полностью согласуется
с обозначениями п. 2, где дана общая схема построения
секционного оператора.
Пусть Т — ортогональное дополнение к Т в V, а К' —
ортогональное дополнение к К в Н.
7. Лемма. Для элемента аеТ общего положения отоб-
ражение Фа: Н -> V, где Фа(И)= [h, а], устанавливает линейный
изоморфизм между плоскостями К' и Т'. При этом А^=КегФа,
Т' = ФаК'.
Доказательство. Отметим, что плоскости Н и V ор-
тогональны в G. Имеем ФаН=Фа(К+К') = ФаК', так как
А^=КегФа. В силу леммы 5 плоскость ФаК' ортогональна Г в К,
следовательно, ФаК' с Т'. При этом отображение Ф„ явля-
ется мономорфизмом на плоскости К', так как КегФа(~)К' =
= К[)К' = 0. Исследуем действие стационарной подгруппы Н
на плоскости V. Ясно, что из каждой точки t ? Т вы-
растает орбита этого действия. Рассмотрим орбиты общего
положения O(t), вырастающие из точек / общего положения,
лежащих в Т. Имеем dim V= dim0@ + dim T. Ясно, что
dim0(O = dim T'. В то же время касательная плоскость к ор-
бите 0@ в точке t естественно отождествляется с фактор-
пространством Н /кегФа = Н i К= К'. Отсюда следует, что
dim A^' = dim0@ = dim Т'. Поскольку отображение Фа мономор-
фно вкладывает К' в Г', то ФаК'=Т\ что и требовалось
доказать.
8. Лемма. В пространстве V выполнены следующие соотно-
шения: a) V=\m p(?)+Ker р(Ь), причем Im p(b)f) Ker pF) = 0;
б) Л = 1т р(Ь) с 1тФа = ФаК' = А + В, в частности, в обозначени-
ях п. 2 R = R' и R+B=T'.

§ 46. ДИНАМИЧЕСКИЕ СИСТЕМЫ 265
Доказательство. Оператор р(Ь), будучи ограничен на
плоскость V, кососимметричен относительно формы Киллинга,
поэтому может быть записан кососимметрической матрицей.
При подходящем выборе базиса она принимает канонический
блочно диагональный вид, и соответствующее разложение
пространства V в сумму плоскостей, на одной из которых
оператор р(Ь) тривиален, а на другой сводится к поворотам
в двумерных плоскостях, совпадает с разложением в сумму
образа и ядра оператора р(Ь).
Далее, образ р{Ь) ортогонален ядру оператора р(Ь), а так
как КегрF) = П и Г<=П, то 1трF)±П и lmp{b)±T.
Поэтому \тр{Ь)аТ' = ФаК', т.е. \тр(Ь)с ФаК' = ФаН. По-
скольку Я' = ФаК' (~) Im p(b), то R' = \mp(b). Отсюда ФаК' =
= 1тр(Ь) + Кегр(Ь)С)ФаК' = ]тр(Ь) + В. Итак, ФаК' = Я' + В.
Поскольку R' = \mp(b), то R = R', т.е. ФаК' = R+B. Лемма
доказана.
9. Таким образом, канонический секционный оператор С:
V'-*Н приобретает в нашем случае вид С: T+B+R -^K+B+R,
где аеТ, К=К(а) = Апп?а), ЬеК, П = В+ Т=Кетр(Ь),
R = lmp(b), ФaH = B+R, В = Фа1В, К = ФйГ1 (Ь)Я Ф~1 R'
Значит,
С=
D
0
Ф;1
ф;
0
'Р(А)
F61)
Первые утверждения теоремы 4 доказаны. Осталось опреде-
лить внешнюю 2-форму F. Пусть С—секционный оператор.
Рассмотрим произвольную точку Хе V, и пусть ?, ц—произ-
вольные векторы из V, приложенные в точке X. Тогда [?, ц ]еН
и СХеН, следовательно, определено скалярное произведение
<СХ, [<;, г|])> которое мы примем за значение формы Fc
в точке X на паре векторов <;, г\. Корректность определения
основана на свойстве симметрического пространства: если
G = H+V—разложение из п. 3, то [V, К]сЯ (включения [Н,
Н]аН и [Н, К]<=К выполняются для любого однородного
пространства). Теорема доказана.
10. Лемма. Пусть/—гладкая функция на пространстве V.
Обозначим sgradc/e V векторное поле на V такое, что для
произвольного векторного поля YeV выполнено равенство
Fc(sgradcf, Y)—Y{f). Здесь Y(f) — производная функции
f вдоль поля Y. Тогда grad f= [CX, sgradc/]. Поле sgradc/
определено, вообще говоря, неоднозначно.
Доказательство. Из равенства F(/) = < Y, grad/> следу-
ет < Y, grad/> = <Cr, [sgradc/, Г]> = < [CX, sgradc/ ], Y). Отсюда
< Y, grad/— [CX, sgradc/ ]> = 0. В силу произвольности поля
Y получаем grad/— [CX, sgradc/ ] = 0, что и требовалось доказать.

266 ГЛ. 8. СЕКЦИОННЫЕ ОПЕРАТОРЫ
11. Замечание. Существуют такие важные симметрические
пространства, что форма Fc при подходящем выборе канониче-
ского секционного оператора определяет на орбитах (или почти
всюду на орбитах) симплектическую структуру. Возьмем,
например, в качестве симметрического пространства полупрос-
тую группу Ли Q = M. Тогда M=P/Q, где Р = Q x Q и инволюция
9: Р-+Р задается формулой в(х, у) = (у, х). Соответствующее
разложение в алгебре Ли Н@Н имеет вид V={(X, — Х)\ХеН},
Н={(Х, Х)\ХеН}. Здесь одной буквой обозначена Я и ее
реализация в G = H@H. Далее, dQV=-V, dQH=H.
12. Лемма. Имеют место равенства В = В = 0, H=K+R,
и V=T+R—картановское разложение алгебры Ли Я.
Доказательство. Здесь T={(t, — t)\teTr}, T — карта-
новская подалгебра в Я. Ясно, что K={(t, t)\teTr}. Поэтому
Т и К изоморфны Т'. Поскольку К и Я соответствуют одной
и той же группе, то присоединенное действие adH на V имеет
вид ad{h k)(X, — X) = ([h,X], — [h, X])e V, т. е. совпадает с дей-
ствием adhX. Следовательно, для нахождения В достаточно
найти централизатор Тг в Я. Отсюда (ввиду полупростоты)
получаем, что й = 0и централизатор совпадает с Т''. Вследствие
полупростоты ортогональное дополнение R к Т (и R к К)
натянуто на корневые подпространства алгебры ^Ли Я, а это
означает, что разложения V=T+R и H=K+R изоморфны
картановскому разложению. Отметим, что хотя М и диффе-
оморфно Q, но вложено в P=QxQ не как подгруппа. Можно
считать, что плоскости Н={(Х, Х)\ХеН} и V={(X, -X)\Xe
еЯ} отождествлены с помощью естественной операции а:
(X, Х)-*(Х, —X). В частности, орбиты О <=-V совпадают
с орбитами стандартного присоединенного действия.
13. Предложение. Форма FC(X; ?, r\), где С=С(а,
а, О, Е), совпадает с формой Кириллова на алгебре Ли
Я (линейно изоморфной V); в частности, не вырождена
и замкнута (и инвариантна) на орбитах О присоединенного
действия группы Q на V.
Доказательство. Поскольку V=T+R, то Х=пХ+ Y, где
пХеТ, YeR и CX=DnX+ad^ adb Y=nX+ Y=XeH. Следова-
тельно, FC = (X, [?, г)]>. В полупростом случае эта форма
фактически совпадает с формой Кириллова, отличаясь от нее на
линейное преобразование в одной точке. Формы (X, [%, т) ]> и <А",
[?'> Л' ]) инвариантны на К относительно Ad, поэтому достаточно
сравнить их только в одной точке X общего положения на V;
^ = ad^', Ti=adxri'; (X, [%', П'1> и <Х, [ad^', adxT|']> отлича-
ются на невырожденное линейное преобразование adx, переводя-
щее касательное пространство ТХО в себя.
14. Определение. Рангом симметричного пространства
(компактного) M=P/Q называется размерность максимального
коммутативного подпространства Т в плоскости V, где

§ 47 СЕКЦИОННЫЕ ОПЕРАТОРЫ 267
G = H@V, G, H—алгебры Ли групп Ли Р и Q соответственно,
здесь симметрическое пространство М определяется инволюци-
ей а: Р-*Р такой, что (РаH с: Q а Ра, Ра — множество непод-
вижных точек автоморфизма а, (РаH — связная компонента
единицы (см. [160]) и da\H=id, da\V=— id. Рангом компакт-
ной группы Ли Р называется размерность максимальной
компактной связной коммутативной подгруппы в Р. Такая
подгруппа называется максимальным тором. Пространство
М=РIQ называется пространством максимального ранга, если
ранг М равен рангу группы Ли Р.
В качестве примера симметрического пространства мак-
симального ранга рассмотрим пространство SU(n)/SO(n).
Группа SO (и) вложена в SU(«) как подгруппа вещественных
матриц. Можно проверить, что ранг этого пространства
максимален и равен п — 1.
15. Лемма. В случае пространства максимального ранга
разложение пространства V и Н, соответствующее каноничес-
кому секционному оператору, имеет вид Z = Z = 0, R = R = 0,
К=0, аеТ, Ь = 0, С = @, Фо1) и С: Т+В-+В.
Доказательство. Поскольку ранг М максимален, тоГс Г
является одновременно и картановской подалгеброй в G.
Следовательно, аннулятор плоскости Т в G равен Т, и, значит, его
пересечение с Н <= G нулевое, т. е. К=0иЬ — 0. Поскольку р (Ь) = 0,
то П = КегрF) = С lmp(b) = 0, т.е. R = R = 0, <t>aH=B + R = B.
Поэтому V= Т+ФаН и группа Q действует на плоскости К таким
образом, что всё орбиты общего положения в V диффеоморфны
группе Q. Итак, из всех компонент оператора остается только
отображение Ф,,, что доказывает лемму.
16. Предложение. Если симметрическое пространство
M=P/Q имеет максимальный ранг, то внешняя форма Fc на
пространстве V (и, в частности, на орбитах группы Ли Q в V,
гомеоморфных Q), определяемая каноническим секционным опе-
ратором С=С(а, 0, 0, 0) = @, Ф.Г1), порождается тензором
римановой кривизны симметрического пространства. А именно,
имеет место равенство FC(X; %, т|) = 4<а, R{X, ^)r)>, где
R — тензор римановой кривизны, а ае Т—фиксированный вектор.
§ 47. Секционные операторы
для коприсоединенного представления
и вполне интегрируемые системы
1. Замечание. Общую конструкцию Фоменко в предыду-
щем параграфе применим к задаче построения вполне интег-
рируемых гамильтоновых систем на орбитах коприсоединен-
ного представления. Итак, пусть G — конечномерная алгебра
Ли, G' — пространство, дуальное к G, aeG"—регулярный
элемент, Fa — семейство полиномов, полученных при разложе-

268 ГЛ. 8 СЕКЦИОННЫЕ ОПЕРАТОРЫ
нии в ряд локальных инвариантов алгебры Ли G в точке aeG'.
Общее определение секционного оператора в случае коприсо-
единенного представления можно конкретизировать.
2. Определение. Самосопряженный оператор С: G'—>G
называется секционным, если для некоторого элемента be
eAnn(a) выполняется равенство
a^Cfx^adjjc. F62)
3. Предложение. Пусть С—секционный оператор, h(x) =
= 2~1(Сх, х) — соответствующий квадратичный гамильтониан.
Тогда {/;,/}= О для всех feFa, т.е. семейство Fa состоит из
первых интегралов в инволюции уравнения Эйлера x = adjhx.
Доказательство. Пусть fb — локальный инвариант пред-
ставления Ad* в окрестности точки aeG* такой, что df(a)= —b.
Рассмотрим разложение в ряд /i(a + jc) = />0 + P1(jc) + />2(jc) + ...,
где Р((х) — однородные полиномы степени /. Легко видеть, что
дифференциалы полиномов Р{ удовлетворяют цепочке рекур-
рентных соотношений
F63)
Напомним, что Ф„^ = аё*.а. В силу • выбора fbeI[G) имеем
dPl=-b. Поэтому ФаС(х)-Ф^Р2(х) = а6'ьх-ФхЬ = 0, т.е.
sgrada(// — P2) = 0. Функция И — Р2 является, таким образом,
центральной для скобки {/; g}a и, следовательно, коммутирует
с семейством Fa. Функция РгМ принадлежит инволютивному
семейству Fa по определению. Поэтому {/г, /} = 0 для BcexfsFa.
4. Замечание. Рассмотрим подпространство К(а) = {уе
бС*|Фа(Апп(а)) = 0}. Из равенства (G, ФуАпп(а)) =
= ({G, Ann (a)], у) следует, что K(a) = \G, Апп(аН±. В силу само-
сопряженности оператора С из условия С (К (а)) с Ann (а) следу-
ет включение С(Апп(а)х)с=Л:(а)\ т. е. C(TaO(a))<=[G, Ann (а)].
5. Предложение. Имеет место включение С(К(а))а
с: Ann (о).
Доказательство. Пусть уеК(а). Тогда ad*,j = 0, так как
ЬеАпп(а). Таким образом, ФаС(у) = 0, т. е. C(j)eAnn(a).
6. Предложение. Если Ann (а) не является максимальной
коммутативной подалгеброй в G, то секционный оператор
С вырожден.
Доказательство. Пусть Z(Ann(a)) — централизатор под-
алгебры Ann (а) в G. Имеем dimAnn(a)<dimZ(Ann(a))<

§ 47. СЕКЦИОННЫЕ ОПЕРАТОРЫ 269
b. Поскольку C(Keradt)cAnn(a), то
H^{}
7. Предложение. Если [G,Ann(af\ +Ann(a)^G, то опера-
тор С не может быть положительно определен.
Доказательство. Если [G, Ann(aj] + Ann(a)^G, то
ТаО(а)Г\К(а)ф{0}. Пусть Офуе ТаО(а)(\К\а). Тогда С{у)е
eAnn(a)=TaO{af и (С(у), у) = 0.
8. Предложение. Пусть h(x) = 2 1 (Сх, х) — квадратич-
ный гамильтониан, отвечающий секционному оператору
С: G*-*G. Тогда уравнения Эйлера x = ad'dh(x)x на G* являются
гамильтоновыми относительно скобки Пуассона
X{f, g} + n{f, g}a при всех X, и и aeG*.
Доказательство. Гамильтоновость уравнений относи-
тельно скобки {/, g}+X{f, g}a при XфО проверяется тривиаль-
но. В качестве гамильтониана следует рассмотреть функцию
g(x) = h(x)-X(b, x). Тогда
-ХЬ) = Фх+,а<1ё(х). F64)
Гамильтоновость относительно скобки {/, g}a можно прове-
рить, например, следующим образом. Для локальной гамиль-
тоновости необходимым и достаточным является выполнение
следующих двух условий: а) производная Ли постоянного
тензорного поля Ф„ вдоль векторного поля v = ad*dhx равна
нулю; б) векторное поле u = adJAx касается симплектических
слоев формы Ф„, или (adjhx, Ann(a)) = 0. Первое условие
выполнено из соображений непрерывности, так как производная
Ли любого тензорного поля Ф„ + >.ФХ при ХфО вдоль v = ad*dhx
равна нулю. Второе условие также выполнено, так как любой
элемент Ь'еАпп(а) можно рассматривать как линейную функ-
цию на G*, поэтому (ad'dhx, b)={h, b'}=0, поскольку b'eFa.
Глобальная гамильтоновость следует из того, что скобка {/, g}a
постоянна на всем пространстве G*.
9.. Конструкция. Дадим теперь явное описание секционных
операторов Фоменко для произвольной алгебры Ли G. Выберем
произвольное алгебраическое дополнение L к Ann (а) в G. Пусть
LL — ортогональное дополнение к L в G*. Тогда G'=TaO(a)@
®Z/. Имеет место изоморфизм Ф„: L-»ТаО(а), поэтому коррек-
тно определен оператор Фа1'- TaO(d)-*L. Положим С0(х) =
= Ф„~^);л:. Определение корректно, так как ad*b(G*)c: ТаО(а).
Оператор Со: С*->С не является, вообще говоря, секционным
в смысле определения 2, так как может быть несамосопряжен-
ным. Поэтому его следует подправить. Обозначим
я: G*-*TqO(a) проекцию, соответствующую разложению
G'=TaO\a)®LL, Положим С=С0 + С*0 — Соп. Утверждается, что
С—секционный оператор. Для доказательства следует прове-

270 ГЛ. 8 СЕКЦИОННЫЕ ОПЕРАТОРЫ
рить справедливость соотношения F62) и самосопряженность
оператора Соп. Оператор Со удовлетворяет соотношению F62),
поэтому необходимо показать, что Фа(С"ох — Со(п(х))) = 0. Для
любого вектора Z,eG имеем
{Фв(СГох-Со(п{х))), Ъ,) = {-х, С0ФД)-(ФаФа-1ас^я(х), ^) =
= (-*, ф-1ай1Ф^)-{ай1п(х), ?,)=-{*, Ф.^Ф-С*. У) +
+ {п(х), [Ь, У)= -(*(*), (Ф.-'Ф.-^) [*, У). F65)
Мы использовали в последнем равенстве тот факт, что
1тФ~1 = Ь, поэтому (х, ц) = (п(х), х\) для любого г^тФ.
Далее, (Фа1Фа — Е)[Ь,^]-^еАпп(а), поэтому [п(х),?] = 0.
Докажем самосопряженность оператора Соп: G*-*G. Для
произвольных x,yeG* имеем (Соп(х), у) = (Ф^1аА'ьп(х), п(у)).
Положим п(х) = Фа^, п(у) = Фач\. Тогда
(С0(я(*)), у) = (Ф:1гА\ФпУ, Фац)= -(Ф.Ф-^с!^^, ц) =
Ь, л])= -(^, Ф«[А, П]) =
= (х, Со (я (>-))). F66)
Мы использовали тождество асЦФ^Ф^ас^, которое следует из
того, что ЬеАпп(а). Итак, показано, что оператор
С=Со+Со — Соп, где п: G*-*TaO(a), является секционным. Из
определения секционного оператора следует, что этот оператор
при фиксированных элементах аеС, ЬеАпп(а) определен не
однозначно, а с точностью до произвольного самосопряженного
оператора D: G*-*G, образ которого содержится в Апп(а).
Поэтому общий вид секционного оператора С при фиксированных
aeG', beAnn(a) такой: С=Со + С*о-Соя + Д где С0 = Ф~1ас11,
Фа1: TaO(a)->L,n: G'^TaO{a), D самосопряжен и ImZ)<=Ann(a).
10. Применим предыдущую конструкцию секционного опера-
тора к симметрической алгебре Ли. Итак, пусть G — вещественная
полупростая алгебра Ли, 9 — инволюция Картана, a G = H+ V—
соответствующее разложение. Рассмотрим гамильтоновы систе-
мы, связанные с семейством скобок <х({/, g} + {f, g}o)+P{/, g}9,
см. § 43. Введем следующие обозначения: С(а)—централизатор
элемента ае V в алгебре Ли G; St(a)—стационарная подалгебра
элемента aeV при действии Н на V, или St(a) = Hf)C(a);
V(a)=Vf]C(a), St(aI — ортогональное дополнение к St(a) в Н,
v\a.y — ортогональное дополнение к V{a) в V. Выберем элемент
beV, удовлетворяющий условиям \р, aJ = O, \b, Stfa)] = O. Легко
проверить, что в данном случае adb(St(aI)<= V(a) , кроме того,
ada: St(a)x->V(aY — изоморфизм. Поэтому корректно определен
оператор Leib>D(/i) = ad~1adfc/z2-|-Z)/z1, где h = h1+h2, AieSt(a),
h2eSt{aI, a D: St(a)->St(a)—произвольный самосопряженный
оператор.

§ 47 СЕКЦИОННЫЕ ОПЕРАТОРЫ 271
11. Предложение. Оператор LuybyD: H-*H самосопряжен
относительно ограничения формы Киллинга на Н.
Доказательство. Достаточно показать самосопряжен-
ность оператора ad ad,,: St(a)±-»St(aI, т. е. выполнение тож-
дества (ad^adj,*, >) = (*, aA~ladby) для любых х, yeSi(a)L.
Представим х, jeSt(a) в виде jc = adajc', у = айау', где х',у'е
е V(aI. Это возможно, так как St(a)±c=Imada. Имеем
= (adbx', aday') =
= -(*', ad6ada/) = -(x1, adaadfc>-') = (adox', adby') =
= (adox', ad~1adbaday') = (x, ad^'ad^j). F67)
12. Предложение. Функции вида g(h + v) = 2~1 (LabyD(h),
h) — (b, v) являются центральными функциями скобки Пуассона
{f,g} + {f,g}a-{f,g}e-
Доказательство. Необходимо проверить, что дифферен-
циал dg функции g(h + v) является решением системы уравнений
F47), F48). Дифференциал dg в силу предыдущего утверждения
имеет вид dg(h + v) = LaybiD(h) — b. Имеем \р, а] = 0 по условию.
Далее,
]
-[*. /?i+/i2] = [ad-ladb/i2, a]-[b, /г2]=0. F68)
13. Следствие. Функции из семейства Fae являются
первыми интегралами гамильтоновых относительно скобки
{/> g}e систем на G с гамильтонианами g(h + v).
14 З Сй F{f(kn + v + \2a)\f
g}e g(
14. Замечание. Семейство Fa^={f(kn
R} может оказаться неполным, поэтому при произвольном
выборе оператора D: St(a)->St(a) гамильтонова система
h = [La,btD(h),h]~[b,v], F69)
v = [La,b,D(h), v]
относительно скобки {/, g}e может оказаться неинтегрируемой.
Для получения вполне интегрируемой системы оператор D следует
выбрать так, чтобы уравнения Эйлера /ij = \_Dhu /гх] на St(a) бы-
ли вполне интегрируемы. Тогда, добавив к семейству Fa e полное
семейство интегралов Fsi{a) уравнения h1 = [_Dhi, h^], в силу тео-
ремы 8 § 43 получим полное семейство первых интегралов
в инволюции уравнений Эйлера F69). Если положить D = XE, то
мы получим систему, вполне интегрируемую в некоммутативном
смысле (см. [187], [191]), некоммутативная алгебра первых
интегралов — это i7aeUSt(a). Итак, имеет место следующее
15. Предложение. Пусть гамильтонова система А. =
= \^Dhl, hi] интегрируема по Лиувиллю на алгебре Ли St(a),
^si(a) — полное семейство первых интегралов в инволюции. Тогда
уравнения Эйлера F69), отвечающие скобке {/, g}8, вполне

272 ГЛ 8. СЕКЦИОННЫЕ ОПЕРАТОРЫ
интегрируемы по Лиувиллю на G, и первыми интегралами
в инволюции являются функции из семейства Fae[JFStM.
16. Замечание. В рамках изложенной конструкции получа-
ются интересные примеры гамильтоновых систем: л-мерное
обобщение случая Лагранжа (см. [18], [39], [228]) и движение
«-мерного твердого тела в квадратичном потенциале [228], [33],
некоторые другие примеры см. в [228].
17. Пусть L — пространство кососимметрических матриц,
для любой симметрической матрицы А на L определен
коммутатор [X, Y]A = XAY— YAX. Рассмотрим двумерный под-
пучок, порожденный алгебрами LE и LB, где ? = diag(l, ..., 1),
i?=diag(Z>1, ..., bn). Семейство функций F= (J I(LB + lE) ин-
волютивно на L* относительно скобки {X, Y}E, отвечающей
алгебре Ли so (и), см. § 44.
18. Предложение. Семейство F эквивалентно стандарт-
ному семейству сдвигов в случае нормальной серии на so (и), т. е.
семейству первых интегралов уравнений движения п-мерного
твердого тела, обнаруженных С. В. Манаковым [165].
Доказательство. Для того чтобы в этом убедиться,
можно рассмотреть коэффициенты разложения функций
tr(X+KBf и tr(X(E+KB)~1I в ряд по А, и проверить их
совпадение. Такая проверка, однако, громоздка, мы поступим
другим способом. Пусть матрица В регулярна в gl(«), т. е.
b{^bj при 1ф). Тогда оба семейства (J f(LB + XE) и tr(X+\B)k,
KeR, k=\, 2, ..., инволютивны и полны относительно скобки
{X, Y}E, поэтому для доказательства их эквивалентности до-
статочно проверить, что они коммутируют между собой. Итак,
пусть f(X) = (X+XB)\ geI(LE + vl?). Дифференциал dg(X)sL
удовлетворяет тождеству (E+\iB)dg(X)X-Xdg(X){E+\iB) = O,
а дифференциал df(X)eL имеет вид df(X) = n\k(X+XB) ),
где п: gl(n)->so(«) — ортогональная проекция относительно ска-
лярного произведения (X, Y) = trXY. Имеем {/, g}E(X) =
= lr(dfdg-dgdf)X=irdf{dg-X-X-dg), но dgX-XdgeL.
Поэтому
{f,g}E{X) = kiT(X+XBf~1(dg X-Xdg) =
= ktT(X+XBf'2((X+XB)dgX-X dg-(X+\B)) =
= Xktr(X+XBf-z{B dg ¦ X-X dg ¦ B) =
= --ktr(X+XBf'2(dg-X~X dg) =
= --ktr{X+XBf-3((X+\B)dgX-Xdg-(X+\B)) = ...
... = k(--\ tr{X+XB)(dg-X-X-dg) = O. F70)

§ 47. СЕКЦИОННЫЕ ОПЕРАТОРЫ 273
19. Лемма. Стандартные уравнения движения твердого
тела на so (и): Х=[Х, п]Е, Х=Вп + пВ, X, QeL (см. п. 12 § 23),
гамильтоновы не только относительно обычной скобки Пуассона
{X, Y}E, но и относительно любой нетривиальной линейной
комбинации Х{Х, Y}E + y.{X, Y}B.
Доказательство. Рассмотрим функции fk(X), которые
являются коэффициентами при Хк в разложении tr(X+XB)k + по
степеням X:
... + X2Bk)+..., F71)
() { k), F72)
где fo(X) = tvX2, f1(X) = tr3BX2, f2(X) = trDB2X2 + 2BXBX).
Обозначим sgrad? и sgradB косые градиенты относительно
скобки {X, Y}E и {X, Y}B соответственно. Непосредственной
выкладкой легко убедиться в справедливости соотношений
sgrad ? /о = 0, sgrad ? ft = sgrad в /0,
sgradE/2 = sgradB/!, ..., sgrad?/t = sgradB/t-1, ... F73)
Гамильтониан, соответствующий уравнениям
Х=[Х, О]?, Х=ВП + пВ, X, ПеЦ F74)
является конечной линейной комбинацией функций /0, fy, f2, ...,
т. е. g(X)= X Cifi(X) и sgradEg(X)= ? с,-sgradE/;(x), поэтому
i = 1 i = О
Х=[Х, П] = sgradEg(X) =
= ? с,sgradB/,_1(Jr) = sgrad,,( t Ci/i-i(Jr)). F75)
Таким образом, показана гамильтоновость уравнений F74)
относительно скобки {X, Y}B. Аналогично,
JT=sgrad? + ,B ? d,ft(X), F76)
i = 0
где коэффициенты dt находятся из системы линейных уравнений
Xds-t=cs,
Xds-2 = cs-i—ds-i, F77)
20. Пусть ^0 = diag A, 1, ..., 1, 0). Тогда LAo = E(n) =
= so(n) + R". Положим B0 = diag(b1, ... Ь„+1), Ь{фЬ„ *„+1^0.
Семейство функций (J 1\^\а„+^в^ инволютивно на L*
(X, ц)/@, 0)

274 ГЛ- 8. СЕКЦИОННЫЕ ОПЕРАТОРЫ
относительно скобки {X, Y} Aii, отвечающей алгебре Ли Е{п), см.
§ 44. Посмотрим, какие квадратичные гамильтонианы содер-
жатся в этом семействе. В кольце инвариантов I(LAa+iiBt>)
содержится квадратичная функция вида
/„(X) = trX(A0 + vB0)-iX(A0 + \iB0)-1. F78)
Чтобы получить удобное описание линейных комбинаций
функций /ц(А'), сделаем замену Y=BqII2XBq112¦ Тогда
fjYj^trY^E+AoBo^-'Y^E+AoBo1)-1. F79)
Общий вид линейных комбинаций таких функций следующий:
g(Y) = 2~1 (ad 7,,s(/adc Y, Y), С диагональна. Итак, с помощью
инволютивного семейства (J l(LkAn+ilBii) можно проинтег-
(>., |1)^@. 0)
рировать по Лиувиллю уравнения Эйлера для алгебры Ли Е(п),
т. е. уравнения Эйлера на Е(п)* с гамильтонианом
() (oii1/2, Boll2XBoli2) F80)
или, используя стандартные координаты х^, у\ на Е(п)*,
Z у'Ч^- {681)
Рассмотрим на Е(п)' квадратичные гамильтонианы общего
вида
h(X)= X xfja(J+ I aiyf. F82)
Тогда гамильтонианы g(X) вида F81) выделяются условиями
^ + «i^ + ^ = o, UA-, /,/$«, F83)
"i, <ijk aki
что в точности соответствует «-мерному обобщению случая
Клебша, обнаруженному А. М. Переломовым [213].
§ 48. Основные примеры секционных операторов
1. Определим аналоги уравнений движения твердого тела на
произвольной полупростой алгебре Ли, см. [186], [188], [189].
Пусть G — комплексная полу простая алгебра Ли,
a G=T+ V+ + V~—ее корневое разложение, т. е. Т—подалгеб-
ра Картана и V+= ]Г СЕа, V~ = ]Г С?„. Предположим, что а,
а>0 оКО
ЬеТ—два произвольных регулярных элемента картановской
подалгебры Т. Рассмотрим оператор ada: G—>G, айаЬ = [а, b\

: 48 основные примьры сккционных опьраторов
275
Ясно, что оператор ado сохраняет корневое разложение.
Поскольку а — элемент общего положения, то оператор ada
обратим на V=V + ®V~. Согласно общей методике определим
секционный оператор <pa,b,D- G->G формулой Ч>а.ь.о{Х) =
= <pa.h(X') + D(t) = ada^adhX' + D(tl где X^X' + t— однозначное
разложение вектора X по V и Т, a D: Т-> Т— произвольный
линейный оператор, симметричный на Т относительно формы
Киллинга. Оператор фа-(, D параметризован с помощью а, b, D.
В базисе Вейля (?а, ?_„, Я„) полупростой алгебры Ли
G оператор <ра.ь. о задается матрицей
<?„„,
Ч 0
о Ч
1)
1)
0
к о
°'ч
0
0
0
D
F84)
где Xa = tx(b)/а.\а), q = d\mV±—число положительных корней.
Построенные операторы фо,ь.с играют роль операторов инер-
ции для комплексных полупростых алгебр Ли.
2. Определение. Уравнение Эйлера на комплексной
полупростой алгебре Ли G, которое отвечает построенному
оператору ф„,(,,о, называется аналогом уравнения движения
твердого тела на полупростой алгебре Ли G. Операторы
<Pa.b,D называются комплексной полупростой серией секционных
операторов.
3. Построим семейство гамильтоновых систем на про-
извольной компактной вещественной алгебре Ли, использовав
для этого вещественные формы комплексных простых алгебр
Ли, см. [186], [188]. Каждая комплексная полупростая
алгебра Ли G обладает компактной вещественной формой
Gc. Напомним, что Gc={Ea + E-a, /(?„ — ?_„), «'//„}. Пусть
a, beiT0 (То — вещественное подпространство в картановской
подалгебре Т, натянутое на все корни НаеТ) — элементы
общего положения. Ясно, что ada(?a + ?-a) = a(a')(((?'a — ?-„)),
ас1в(/(?я-?_я))=-а(а')(?'«+?'-01), где a = ia', a'eT0. Итак,
оператор ada переводит вектор Ех + Е-а в вектор, про-
порциональный /(?„ — ?_„), и наоборот. Поэтому все векторы
?7 + ?-а и /(?„—?_„) являются собственными векторами
с собственными числами а(й)а(а)~'=а(й')а(а')~', a = ia', b = ib',
а', Ь'еТ0. Оператор q> = (pabD: GC->GC определим так: <р(Х) =
= <p(X' + t) = (pa,b(X') + D(t) = ad;1 adbX'+ D(t), где X=X' + t —
однозначное разложение X на такие составляющие, что
'е;Т0, Х'ИТ0. В базисе {?а + ?_а, /(?„ — ?_„), /#„} оператор
IX*

276
ГЛ. К СЕКЦИОННЫЙ ОПЬРАТОРЫ
Ф задается матрицей
V 0
() "ч
0
0
0
°\
0
0
0
I)
' (К
F85)
где числа Я.я = а(й)/а(а) вещественны.
4. Определение, Серия операторов ф„,(,,с: GC^>GC называ-
ется компактной серией секционных операторов.
5. Аналогичные операторы можно построить на некоторых
простых компактных вещественных алгебрах Ли, отвечающих
классическим нормальным компактным подалгебрам в ком-
плексных полупростых алгебрах Ли. В каждой компактной
форме Gc рассмотрим подалгебру Gn, называемую нормальной
компактной подалгеброй, которая натянута на векторы
Еа + Е-а, а пробегает множество всех корней алгебры Ли
G относительно подалгебры Картана Т. Поскольку все эти
векторы собственные для операторов ф компактной серии, то
при ограничении их на подалгебру Gn получим некоторую
серию операторов на Gn. Эти операторы совпадают
с ф = фа,„: GC^GC1 ср (Jf) = ad .Г1 ad ,,(*), XeGn, a, beiT0, a(a)^0,
(й) В базисе {?, + ?-„} оператор ф задается матрицей
о
F86)
Отметим, что здесь a, beGn, т. е. операторы нормальной серии
фа,ь; Gn-fGn требуют для своего определения элементов некото-
рой большей алгебры Ли.
6. Определение. Серия операторов ц>а,ь'- Сл->G„, по-
строенная в п. 5, называется нормальной серией секционных
операторов.
7. Лемма. Среди гамильтоновых систем нормальной серии
содержатся классические уравнения движения многомерного
твердого тела с неподвижной точкой.
Доказательство. Рассмотрим алгебру Ли so (я) и пред-
ставим ее в виде нормальной подалгебры в алгебре Ли su(«).
Вложим su(«) стандартным образом в и (и) и рассмотрим два
регулярных элемента а, Ъ из картановской подалгебры ;Т0

§ 48 ОСНОВНЫЕ ПРИМЕРЫ СЕКЦИОННЫХ ОПЕРАТОРОВ 277
в и(и) (а не в su(n)). Пусть a = diag(ia1, ..., /аД b = diag(ibl, ...
..., ibH), at, bteR, а,ф ±а}, Ь,ФЬ, при /#/'. Тогда оператор
Фа,ь: Gn^Gn действует так: Ф.,ь(?. + ?_.) = ^(?. + ?_A). По-
этому гамильтонова система Х=\_Х, ф„ ЬХ] имеет вид
Пусть теперь a=—ib2, т.е. ар = Ъ\. Отсюда
Итак, при a=—ib2 получаем известную систему п. 12 § 23.
8. Построим секционные операторы для алгебры Ли группы
движений евклидова пространства. Алгебра Ли Е(п) группы
движений R" является полупрямой суммой so(n) + R", где
ф: so(n)->End(R") — дифференциал стандартного представления
группы SO (и) в пространстве R", причем R" рассматривается
как коммутативная алгебра Ли. Пространство Е(п)', дуальное
к Е(п), отождествим с Е(п); для этого определим невырожден-
ное скалярное произведение в Е(п). Пусть В(Х, Y)—форма
Киллинга алгебры Ли so (и), а (X, Y)e — евклидово скалярное
произведение на R". Тогда положим ((xb yt), (x2, y2)) = B(x1,
X2l + (yu yi)e, где хи x2eso(n), yu ^->?R". С помощью этого
произведения отождествим Е(п)' с Е(п) и все подпространство
в Е(п)' будем изображать как подпространства в Е(п),
используя это отождествление. Ортогональное дополнение
к подпространству W в Е(п) или в Е(п)' относительно
скалярного произведения В(Х, Y) + (Z, R)e обозначим W1. Пусть
а — элемент общего положения, а л = КегФа. Тогда Ф„ отобра-
жает К1 в К'1, где К=К' при отождествлении Е(п)'
с Е(п). Отображение Ф„: K^-fK'1—изоморфизм. По общей
методике пусть E(n) = KL + K, E(n)' = K'1 + K' и аеК', ЬеК,
причем а—элемент общего положения. Тогда если z = x+ye
еЕ(п)', xeK'L, уеК', то С (а, Ь, D)(z) = ^;lad^(x) + D(y),
где D: К'^>К—произвольный самосопряженный линейный опе-
ратор.
9. Пусть A = R[x~]/(x2). Положим Cl(G) = G®A. Построим для
алгебр Ли ii(G), где G — полупростая алгебра Ли, секционные
операторы.
10. Лемма. Пусть G — комплексная полупростая алгебра
Ли, aeil(G)' — элемент общего положения. Тогда КегФ„ =
= Н+еН, где е = ж[х), п: И[х\-*А — естественная проекция,
Н—подалгебра Картана в G. Пусть Ь = Ь1+еЬ2еКетФа = Н+ЕН,
причем Ьх—элемент общего положения. Тогда Kerp(b) =
= H+eH=?i(G)'^G + ?G Утверждается, что Фв(КегФ^)с

278 ГЛ. 8 СЕКЦИОННЫЕ; ОПЕРАТОРЫ
,; и pF)(Kerp(ftI)ciKerp(ft)i для любого 6еКегФ„, где
W1 означает ортогональное дополнение относительно прямой
суммы форм Киллинга на G, p = ad*.
Доказательство получается прямым вычислением.
11. Определение. Комплексная серия секционных операто-
ров С: ?1 ((?)*->?2 (G) задается матрицей [253]
С=С(а, Ь, Л)=||Ф'7а:д|| F89)
(G — полупростая комплексная алгебра Ли) в соответствии
с разложениями ?2(С) = КегФ„©КегФ,;, Q(G)* = Kerp(/>)©
©Кегр(бI, здесь D: Ker р(Ь)->КегФа— произвольный самосоп-
ряженный оператор.
12. Определение. Пусть Gc — компактная вещественная
форма в комплексной полупростой алгебре Ли G. Компактная
серия секционных операторов С: fi(Gc)*->f2(Gt.) также задается
формулой F89), только J): Н0 + еН0->Н0 + еН0, где Но —
вещественная часть подалгебры Картана Н в G [253].
13. Определение. Пусть G„ — нормальная подалгебра в G.
Нормальная серия секционных операторов С: D(Gn)*->f2(Gn)
является ограничением операторов компактной серии на ?2 (<?„)•
§ 49. Бигамильтоновость уравнений Эйлера
1. Теорема (М. В. Мещеряков [176]). Пусть ср/ G^>G —
самосопряженный относительно формы Киллинга по.лупростой
алгебры Ли G линейный оператор. Уравнение Эйлера Х=\_Х, <рХ]
гамильтоново относительно скобки Пуассона {Y, Z}a тогда
и только тогда, когда ф = ф„,ь,в для некоторых ЬеН и D: Н^Н.
2. Замечание. Таким образом, гамильтоновость потока
Эйлера с квадратичным гамильтонианом F{X) = 2~1 B(X, ц>(Х)\
одновременно относительно пары скобок: скобки Пуассона {/
g} и скобки {/, g}a = <a, [dfa, dga]y характеризуют тензоры
инерции ср„ 6 д многомерных «твердых тел» среди всех тензоров
инерции на алгебре G.
3. Лемма. Пусть FeI(G)—полиномиальный инвариант коприсо-
единенного представления и Fx(?,) = F(Е, + Ха) = ]Г Fk(E,, a) Xk. Тог-
да дифференциалы Uk (?,) = dFk (^) функций Fk удовлетворяют
цепочке рекуррентных соотношений
F90)

§ 49. БИГАМИЛЬТОНОВОСТЬ УРАВНЕНИЙ ЭЙЛЕРА 279
Доказательство. Поскольку I(G) лежит в ядре скобки
Пуассона {/, *}(?,) = <Е, Ш\), dg($]>, то {/, F}(|) = 0 для
любой функции /е С00 IG ). Это означает, что ad df(yq = 0 для
любого вектора ?;eG*. Замена ?;->?; +Ал, если учесть разложение
dFi (?;) = ? dFk (Е,, а) А.1, приводит к цепочке соотношений F90) на
векторы*^ (&)=[/*(?).
4. Лемма. Пусть G — такая алгебра Ли, что стационарные
подалгебры общего положения в коприсоединенном представлении
линейно порождаются дифференциалами инвариантов представ-
ления Ad*. Тогда уравнения Эйлера E, = ad*<tI)<yE, гамильтоновы
относительно скобки Пуассона {/, g}a.
Доказательство. Оператор cp = cpa.ь,в удовлетворяет со-
отношениям ad*(^a = adjE,, ad^a = 0. Пусть алгебра Ли G тако-
ва, что любое beGa={xeG\ad'xa = 0} реализуется как дифферен-
циал некоторого полиномиального инварианта h, т. е. dh(a) = b.
я
Положим hx{Q= Yj hjXJ. Из леммы 3 получаем соотношения
adj^_^ + ad«f га = 6, ad'dh^ + ad'dKia=0, причем dhq-y{\) = b
в силу линейности hq-1 по \. Рассмотрим функцию ?(?,) =
= F{Q + hq-2(?). Тогда add*f(a) = 0 и, следовательно, F принад-
лежит ядру скобки Пуассона {/, g}a. Ясно, что F—квадратичная
функция, и поскольку ядро скобки {/, g}a порождается
линейными функциями /;(?;)=<?;, ?>, где bi=dFi(a)
и Ft — однородные полиномиальные образующие кольца ин-
вариантов /(G), то F=X Vijfifj + c, v,j = Vj,eR, с = const. Значит,
F= — hq-2 + YjVijfifj + C- Теперь находим, что скобка {F, /}
функций F и / eC'lG') равна
{f,b,-2}-I,ViA{f,f,}fj+{fJj}fi). F91)
i.j
Учитывая соотношения {/, А,_2}= -{/, Л,-з}«, {/../}} =
= -{/, Я,-},, где
/•Л^+М=^(у+...+яА"-2+/Ав' + ^^D F92)
<7у = deg Fj, перепишем скобку {F, /} в виде
{F, Л = {Л.-э, /}«-Е^Д{Яь f}afj+{Hj, f}Jt). F93)
Далее, [Нф, f}a = {Ht, f}afj+{fj, f}aHi для любых i,
j=\, ...,&imGa. Поскольку _/} лежат в ядре скобки {/, g}a, то
{Я,/у, /}а = {Яь /}0/j и соотношение F93) примет вид {F,
f} = {hq-3-Y,vij(Hifj+fiHj), /} для любой функции /е С00(G').

280 ГЛ. 8. СЕКЦИОННЫЕ ОПЕРАТОРЫ
Поэтому функцию Fi=hq-3 — 2_,Vij{Hifj + Hjfi) можно считать
гамильтонианом уравнения Эйлера ?,'=ad*(^ относительно
скобки {/, g]a. Лемма доказана.
5. Лемма. Пусть G—полупростая алгебра Ли, а уравнение
Эйлера х = [х, ф (х)] гамильтоново относительно скобки {/, g}a.
Тогда <р = Ц>ауь,э для некоторых beGa = H и D: Н-*Н.
Доказательство. Обозначим векторное поле, задающее
уравнение Эйлера, через У. Если поле У гамильтоново отно-
сительно скобки {/, g}, то производная Ли LY вдоль У—
дифференцирование алгебры Ли (C°°(G), {/, g}), см. § 21. Пусть
и, veG — произвольные элементы алгебры G и fu(x) = B(x, и),
fv(x) = B(x, v) — отвечающие им линейные функции на G. Тогда
Ly{fu, fv}a = {LYfu, fv}a + {fu, LYfv}a, так как {/„, fv)a(x) =
= В(а,[и, i;]) = const. Кроме того, LYfu = {F, /„}, LYfv = {F, /„}
в силу гамильтоновости поля У относительно скобки {/, g}.
Здесь Fjx) = 2~lB(x, ф(х)). Отсюда следует, что {{F, /„},/„L +
+ {L,{F, /»}}« = 0 для любых и, veG. Далее, {F, /„}(х) =
= В(х, [ф(х), и\)= —В(х, adu°ф(x)) и (ad„oф)* = ф*oad*= —фoadu.
Положим Фu(x) = 2~1fi(x,(фoad„—ad„oф)A1. Ясно, что {•/%/„}=<!>„,
— ad„oф(x), «]). Следовательно, оператор ф удовлетворяет
соотношению
B(a,[(p°adu(x)-adu°(p(x),v]) = B(a,[(p°adv(x)-advoq>(x),u]).
F94)
В силу самосопряженности линейного оператора ф получим
еще одно соотношение B(<p([v, а]), [и, х]) — B([v, а\ [и, ф(х)]) =
= В(и, adаoфcad„(x)) — В(и, aaa°adv°(p(x)f для любого элемента
ueG. Учитывая невырожденность формы В, получим из преды-
дущего равенства функциональное уравнение на оператор ф
[х, y([v, а])]-[Ф(х), [v, aj] = [a,4>([v, x])]-[a,[«, Ф(х)]]. F95)
Отсюда [ф (х)Аа, vj\ - [х, ф ([a, v])] = [а, [ф (х), vj] - [а, ц>([х, d])] для лю-
бого veG. Поэтому
ad, (х) о ada — ad* о ф о ada = ada ° ad, (x) — ado ° ф о adx. F96)
Окончательно
[ad, м, ada] = adx с ф о ada- ada ° ф о ad,. F97)
В силу тождества Якоби в алгебре Ли G, имеем [ad,,,x), ado] =
= ad[Q/ix>,a] и, следовательно, adt,(x) „^ас^офс^,, —adao<poadx
для люоого xeG. Обозначим оператор ad<1oф буквой \|/ и подей-
ствуем операторами из соотношения F97) на произвольный
вектор у еG Получим Г[ср(х),а],у]=[х, Ф([а,у])~] - [а, ф([х,у])]
или \|/([х,у\) — [\|i(x), >'J + [x, фoadа(^')^. Докажем теперь, что

§ 50. УРАВНЕНИЯ ЭЙЛЕРА НА АЛГЕБРАХ ЛИ 281
Ф о ada = acL ° ср. Из соотношения F97) вытекает равенство
ГГф(Д а],а]= — [а,ф([лг,а])]. Таким образом, аё„ оф = абаофоас1а.
При пеН имеем ada (ф(Л)) = 0. Поэтому в силу невырожденности
оператора ф вектор ф(Л) лежит в ядре оператора ad^.
Последний оператор самосопряжен относительно формы Кил-
линга и на ортогональном дополнении V к подалгебре Н не
вырожден, так как элемент а регулярен. Значит, Kerade=#
и ц>(И)еН для любых heH. Заметим далее, что оператор
Ф сохраняет разложение G = Н© V. Отсюда ясно, что для любых
veV имеет место равенство ad(,°ф(l>) = ф°ad1I(l^), причем на
подалгебре Картана Н операторы ada и ф также коммутируют.
Итак, доказано, что линейный оператор \|/ = ado°9 — дифферен-
цирование полупростой алгебры Ли G. Все дифференцирования
алгебры G внутренние, и, следовательно, найдется такой
элемент beG, что *P = ad6. Таким образом, оператор ф удовлет-
воряет соотношению [ф(лс), а] = [6, лс], т.е. Ф = Ф„,ь,d-
6. Доказательство теоремы 1. Утверждения лемм
4 и 5 дают доказательства необходимости и достаточности
условий теоремы.
7. Замечание. В доказательстве леммы 5 существенным
образом используются два обстоятельства. Первое — наличие
симметрической невырожденной инвариантной билинейной
формы, ограничение которой на централизатор регулярного
элемента не вырождено. Второе — отсутствие у алгебры Ли
G внешних дифференцирований. Алгебры Ли такого типа
называются совершенными. Лемма 4 для них верна в силу их
алгебраичности. Поэтому теорема 1 имеет место для класса
совершенных алгебр Ли, обладающих инвариантной симмет-
рической билинейной формой, ограничение которой на цент-
рализатор регулярного элемента не вырождено.
8. Замечание. Имеется классификация алгебр Ли G,
которые допускают невырожденное инвариантное скалярное
произведение (X, Y), (A.dgX, AdgY) = (X, Y). По этому поводу см.
[439].
Глава 9
ПОЛНАЯ ИНТЕГРИРУЕМОСТЬ ПО ЛИУВИЛЛЮ НЕКОТОРЫХ
ГАМИЛЬТОНОВЫХ СИСТЕМ НА АЛГЕБРАХ ЛИ
§ 50. Уравнения Эйлера на алгебрах Ли,
возникающие в задачах математической физики
1. Приведем список уравнений Эйлера, которые возникают
в различных вопросах механики и математической физики.
В этих примерах гамильтониан Н не обязательно является
квадратичной формой на пространстве G*. Для того чтобы,

282 ГЛ. 9. ПОЛНАЯ ИНТЕГРИРУЕМОСТЬ ПО ЛИУВИЛЛЮ
например, учесть потенциал, рассматриваются гамильтонианы,
являющиеся суммой квадратичного и некоторого линейного
функционала.
2. Уравнения движения трехмерного твердого тела, закреп-
ленного в одной точке, являются уравнениями Эйлера для
алгебры Ли soC) кососимметрических вещественных матриц
размера 3x3, см. п. 12 § 5, п. 9 § 23. Напомним, что они
имеют вид a>X*=[tpX, ХЛ, JTesoC), q>X=IX+XI, 1=
= diagjA..,X.2,A.3), где Х.1=2-*(-Л + Л+С), Х2 = 2~1(А-В+С),
Х3=2 1(А + В — С), А, В, С—моменты инерции тела относи-
тельно осей Ox, Оу, Oz.
Инвариантное описание оператора ср см. в п. 7 § 48.
3. Уравнения движения свободного твердого тела. Движение
твердого тела, в трехмерном пространстве R3 описывается
уравнениями К=[К, со] + [е, и], ё=\е, со], где К—кинетичес-
кий момент тела, со—угловая скорость тела, а векторы
е и и определяются физическим содержанием задачи, описыва-
ют взаимодействие внешних сил. Указанные общие уравнения
имеют три классических интеграла; /х = Н, где полная энергия
Я имеет вид Н=2~1(К, h~f(K)) + m(r, e), затем /2=(К, е)
и /з = (е, е). Рассмотрим, например, задачу о движении тяже-
лого твердого тела вокруг неподвижной точки. Тогда
е—единичный вектор, направленный по вертикальной оси Oz,
и, следовательно, третий интеграл/3 имеет вид/3=(е, е)=\.
Общее уравнение движения твердого тела задает векторное
поле на шестимерном евклидовом пространстве R 6 = R3 (К) х
х R3 (е). Оказывается, это векторное поле гамильтоново на
совместной поверхности уровня двух интегралов /2 = с2= const
и /з = с3 = const относительно некоторой естественной скобки
Пуассона. Пусть M1-i = \f2 — c2, /3 = с3>0}. Эта поверхность
является четырехмерным подмногообразием в R6. Поверх-
ность М2з диффеоморфна кокасательному расслоению двумер-
ной сферы. Определим на пространстве R6(K, e) пуассонову
структуру {/, g). Если К=(К1г К2, К3) и е = {ех, е2, е3), то на
образующих Kt, et операция задается табл. 3. Эта операция
продолжается на C°°(R ) и там задает структуру алгебры Ли.
Проверяется, что эта пуассонова структура изоморфна скобке
Березина для алгебры Ли soC) + R3 (алгебры Ли группы
р
движений евклидова пространства). Эту скобку Пуассона
можно ограничить на поверхность М23, и там она задает
невырожденную скобку.
4. Теорема (СП. Новиков, И. Шмельцер). Уравнения
движения твердого тела К=\_К, со] + [е, и], ё = \е, со] можно
представить на совместной поверхности уровня М23 двух
интегралов /2 и /3 в гамильтоновом виде /={/, h], где
h — сужение функции Н на М23.

8 50. УРАВНЕНИЯ ЭЙЛЕРА НА АЛГЕБРАХ ЛИ
Таблица 3
283
к,
к2
к3
е\
е2
к,
0
к,
-К2
0
е3
— е2
К2
-к3
0
к,
0
е,
к,
К2
-к,
0
е2
0
е\
0
еъ
-е2
0
0
0
е2
0
ei
0
0
0
^3
е2
-е,
0
0
0
0
5. Вращение твердого тела вокруг неподвижной точки в нью-
тоновском поле с потенциалом фС*^, х2, х3). Пусть а, C, у — три
орта неподвижной системы координат, отнесенные к системе
отсчета 5, жестко связанной с твердым телом. Уравнения
вращения твердого тела в системе S имеют вид
8U.
~да'
ги
ги
F98)
а = ахш, Р = Cхсо, у = Ухт>
где U(а., C, у)—потенциальная функция:
U(а, C, у) = |р(г)Ф((г, ос), (г, C), (г, y))dridr2dr3, F99)
т
здесь Т—твердое тело, a rt, r2, г3 — координаты в системе
отсчета S.
Определим алгебру Ли L. По определению она является
полупрямой суммой soC) + R3 + R3 + R3 с базисом Xt, Y", i,
У= 1, 2, 3, в котором коммутационные соотношения имеют вид
k, [Xh
?, YJ]=O. G00)
6. Теорема (О. И. Богоявленский [33]). Уравнения F98) яв-
ляются уравнениями Эйлера вида x = ad*df{x)(x) в пространстве
L и имеют гамильтониан
)-?/(a, C, у), М,=
G01)

284 ГЛ. 9 ПОЛНАЯ ИНТЕГРИРУЕМОСТЬ ПО ЛИУВИЛЛЮ
7. Динамика твердого тела с распределенным электрическим
зарядом в идеальной несжимаемой жидкости. При наличии
постоянного гравитационного и электрического полей и при
условии равенства выталкивающей силы и силы тяжести
и нулевом суммарном заряде тела уравнения движения в свя-
занной с твердым телом системе отсчета S, центр которой
совпадает с центром масс твердого тела при условии безвих-
ревого обтекания, имеют вид
М=Мх (д+р х u + mgr х y + Edx 5,
s- х G02)
р=рх&, Y = Yxt0> o = oxg),
где ю — угловая скорость, и—скорость твердого тела в жид-
кости, р — полный импульс, М—полный момент импульса (в
системе отсчета S), т — масса тела, g—ускорение силы
тяжести, у—направление силы тяжести, вектор г определяет
положение центра масс вытесненного объема жидкости, Е—
напряженность электрического поля, d—вектор дипольного
момента, 5—направление электрического поля.
8. Теорема (О. И. Богоявленский, см. [33]). Уравнения
G02) являются уравнениями Эйлера в пространстве L* и имеют
гамильтониан
-mg(r, y)-E(d, 5), G03)
где (Oi — dH/dMi, ut = dH/dpt, здесь atJ, b{j, ctj—произвольные
постоянные коэффициенты, обеспечивающие положительную
определенность указанной квадратичной формы.
9. Вращение яамагниченного твердого тела вокруг неподвиж-
ной точки в однородном гравитационном и магнитном полях.
В этом случае уравнения, описывающие движение твердого
тела, имеют вид
M=Mx(u + mgrxy + hzx 5,
*• * G04)
где z — вектор магнитного момента твердого тела, 5 — направ-
ление магнитного поля, h—его напряженность.
10. Теорема (О. И. Богоявленский [33]). Уравнения G04)
являются уравнениями Эйлера в пространстве М' с гамильтони-
аном H=2~l(M, (u) — mg(r, y) — h(z, 5), Мt= ? Iiku>k, где
k= 1
алгебра Ли М имеет коммутационные соотношения, описанные
в п. 5 при а, C=1, 2. При z = 0 это уравнение переходит
в классические уравнения Эйлера—Пуассона.

§ 50. УРАВНЕНИЯ ЭЙЛЕРА НА АЛГЕБРАХ ЛИ 285
11. Динамика твердого тела с эллипсоидальной полостью,
заполненной магнитной жидкостью, совершающей однородное
вихревое движение. Уравнения движения в системе отсчета
S имеют вид
М=МхА, K=KxB+uxw, й = ихВ, G05)
где М — суммарный момент количества движения твердого тела
и жидкости относительно общего центра масс, А — угловая
скорость вращения твердого тела, В—угловая скорость внут-
реннего вращения жидкости, К—вектор вихря скорости жид-
кости, векторы и и w связаны с магнитным полем, вморожен-
ным в жидкость. Координаты векторов А, В линейно выража-
ются через координаты векторов М и К, координаты векторов
и, w также связаны линейными соотношениями.
12. Теорема (О. И. Богоявленский [33]). Уравнения G05)
являются уравнениями Эйлера в сопряженном пространстве
к алгебре Ли soC)©?'C) и имеют гамильтониан Н=2~1((М,
А) + (К, В) + [и, и>)), где Е(Ъ) — алгебра Ли группы движений
евклидова пространства R3.
13. Динамика твердого тела с л эллипсоидальными полостями,
заполненными магнитной жидкостью, совершающей однородное
вихревое движение. В этом случае динамика описывается
уравнениями
М = МхА, Ка = Ках Ba + uaxwa,
„ G06)
иа = иахВа,
где а=1, .., п, М—суммарный момент количества движения
(относительно общего центра масс) твердого тела и жидкости
во всех эллипсоидальных полостях, А — угловая скорость
вращения твердого тела, векторы Ка, Ва, иа, wa характеризуют
движение жидкости и вмороженное магнитное поле в а-полости.
Координаты векторов А, Blt ..., В„ линейно выражаются через
координаты векторов М, Кг, ..., К„, координаты векторов
иа и wa связаны линейными соотношениями; коэффициенты этих
линейных связей зависят от компонент тензора инерции
твердого тела и параметров эллипсоидальных полостей. Обо-
значим LKm прямую сумму soC)©...©soC)©?'C)©...©?'C),
состоящую из к экземпляров алгебры Ли so C) и т экземпляров
алгебры Ли ?C).
14. Теорема ([33]). Уравнения G06) являются уравнениями
Эйлера в сопряженном пространстве к алгебре Ли L = L1<n
и имеют гамильтониан
? ((ЛГ„ Ва) + (и„, w.))). G07)

286 • ГЛ. 9 ПОЛНАЯ ИНТЕГРИРУЕМОСТЬ ПО ЛИУВИЛЛЮ
При отсутствии магнитного поля в к полостях (ма = но = 0,
ос=1, ..., к) алгебра Ли L редуцируется к алгебре Ли Lk+ln-k.
15. Вращение твердого тела с л эллипсоидальными полостями,
заполненными магнитной жидкостью, вокруг неподвижной точки
в ньютоновском поле с потенциалом <p(.Ci, х2, х3). В этом случае
динамика описывается уравнениями
ди си п си
—xty> + ~xp+—xy,
foe cE <;y
0 = РхЛ, у = ухА, G08)
которые являются нераспадающейся комбинацией уравнений из
п. 5 и 11.
16. Теорема (О.И.Богоявленский [33]). Уравнения G08)
являются уравнениями Эйлера в сопряженном пространстве
к алгебре Ли L@L0 „ и имеют гамильтониан
Н=2~1{М, А) + 2-1 ?((*., Вв) + (и9, we))-U(a, C, у)- G09)
в= 1
При отсутствии магнитного поля в к полостях алгебра Ли
L@LOn редуцируется к алгебре Ли L@Lkn-k.
17. Уравнения Кирхгофа движения твердого тела в жидкости.
Свяжем систему координат с движущимся телом. Пусть
и{ — компоненты скорости поступательного движения начала
координат, а ш( — компоненты угловой скорости вращения
твердого тела. Тогда кинетическая энергия системы жидкость —
твердое тело имеет вид Г=2~1(у11ут1(в7 + Л,уМ1Му)+С^т(м;-, где
Aij, B;j, Cij—постоянные, зависящие от формы тела и от
плотностей тела и жидкости; по дважды повторяющемуся
индексу производится суммирование от 1 до 3. Пусть N=(yx,
У2, Уз), где yi = dT/d(Oi, и К=(х^ х2, х3), где х, = 5Г/5м,. Тогда
уравнение движения тела по инерции в идеальной жидкости
описывается уравнениями
— = N
L г G10)
dt
где м = («!, и2, и3), й) = (со1, (?>2, тз)-
18. Т е о р е м а (см. [266], [267]). Система уравнений Эйлера
для алгебры Ли ЕC) группы Ли движений евклидова простран-
ства R3 совпадает с уравнениями движения твердого тела по
инерции в идеальной жидкости G10).
19. Уравнения движения твердого тела по инерции в несжима-
емой идеально проводящей жидкости. Рассмотрим классические

§ 50. УРАВНЕНИЯ ЭЙЛЕРА НА АЛГЕБРАХ ЛИ 287
уравнения магнитной гидродинамики несжимаемой идеально
проводящей жидкости
^ x v= p~l(rot Я) х Я-gradП,
G11)
Как показано в работе [67], эти уравнения имеют в качестве
простейшего конечномерного аналога уравнения
M=[?l, M]+[J, Я],
• г п
я=[а я],
где М, Я, J, iiesoC). Физический смысл величин М, Я, J, ?2 см.
в [67].
20. Теорема (В. В. Трофимов [253]). Уравнения Эйлера для
алгебры Ли so C)®R [x]/(jc ) совпадают с уравнениями G12),
являющимися конечномерными аппроксимациями уравнений маг-
нитной гидродинамики G11).
21. Квазиннстантон и уравнения Эйлера. Пусть
A\j—связность в главном SU B)-расслоении над R4,
Rllv = dllAv — 8y/Au + lAt,, А Л — ее тензор кривизны, где
Лм= II Apj |[ eSUB), см. [263]. На пространстве связностей
рассмотрим функционал
5[^,,]=1Л"Ч^. *.,>, G13)
где ?MV — метрика на R4, (X, Y} — форма Киллинга алгебры Ли
suB). Экстремали этого функционала описываются уравнениями
Эйлера—-Лагранжа Z>mjRAV = O, А^ — поле Янга—Миллса.
Пусть •i?0I<J = -E,<I(lvi?(lv. Любая автодуальная конфигурация
ЛМУ = »/?AУ автоматически удовлетворяет уравнению Эйлера —
Лагранжа и приводит к экстремуму функционала действия G13).
Положим Ац = А"оа/И, где аа — матрицы Паули, см. [226].
Рассмотрим обобщенный анзац т'Хоофта
А2ц(х)=-рт]1д^2{х), G14)
Al{x)=-yT\lvdvy3(x),
здесь автодуальные тензоры т'Хоофта т|° определены ра-
венствами т1цУ=-Л?м = Ем" если ц, v=l, 2, 3, и ца^= -rjVM = 5J,
если v = 4.

288 ГЛ. 9. ПОЛНАЯ ИНТЕГРИРУЕМОСТЬ ПО ЛИУВИЛЛЮ
Следующее утверждение показывает, как возникают уравне-
ния Эйлера на алгебре Ли si B, R) при решении уравнений
автодуальности для зависящих от г = хцхц (ц=1, 2, 3, 4)
конфигураций полей Янга — Миллса А„, см. [113], а также
[300], [517].
22. Теорема (Т. А. Иванова). Для обобщенного анзаца
т'Хоофта G14) уравнения автодуальности для полей А^и)
приводятся к уравнениям Эйлера на алгебре Ли si B, jft)
с гамильтонианом 7/=a11(z1J — а22(г2J — a33(z3J, где z —ф1,
z2 = i\r2, z3 = v)J3 и ап =+ 1 /у^2 + а33, а22 = + ^/2 + аъъ, аъъе
eR — произвольное число.
a
§ 51. Уравнения Эйлера на полупростых алгебрах Ли
1. Замечание. Вложение гамильтоновой системы в алгебру
Ли гарантирует тривиальное семейство первых интегралов —
функции, постоянные на орбитах коприсоединенного представ-
ления. Этих интегралов, как правило, не хватает для полной
интегрируемости. Если алгебра Ли двумерна, то функции,
постоянные на орбите, полностью решают задачу. Для постро-
ения полного набора интегралов на полупростых алгебрах Ли
используется метод сдвига инвариантов, см. § 34. Эта общая
схема является развитием идеи, предложенной в [165] для
случая алгебры Ли so (и).
2. Теорема (А. С. Мищенко и А. Т. Фоменко [186], [188]).
Пусть G — комплексная полупростая (или редуктивная) алгебра
Ли, Х=\_Х, фА']—уравнения Эйлера с оператором ф комплекс-
ной серии. Тогда эта система вполне интегрируема по Лиувиллю
на орбитах алгебры Ли G, находящихся в общем положении.
Более точно, пусть /— любая гладкая инвариантная функция на
G. Тогда все функции hx(X, a)=f(X-\-Xd) являются интегралами
векторного поля X при любых комплексных числах X. Любые два
интеграла hx и d^, построенные по функциям /, geI(G),
находятся в инволюции на любой орбите (регулярной или
сингулярной). Гамильтониан F(X)=(X, фА"> векторного поля
X также находится в инволюции со всеми интегралами вида h-^.
Из множества указанных интегралов можно выбрать функци-
онально независимые на орбитах общего положения интегралы
в количестве, равном половине размерности орбиты. Интеграл
F функционально выражается через интегралы вида hk.
Доказательство вытекает из п. 7 § 42 и результатов § 47.
3. Теорема (А. С. Мищенко и А. Т. Фоменко [186], [188]).
Пусть Gc — вещественная компактная форма полупростой ком-
плексной алгебры Ли G и Х—\Х, фХ~\— уравнения Эйлера
с оператором ф компактной серии. Тогда эта система
дифференциальных уравнений вполне интегрируема по Лиувиллю

§ 51 УРАВНЕНИЯ ЭЙЛЕРА НА ПОЛУПРОСТЫХ АЛГЕБРАХ ЛИ 289
на орбитах общего положения. Более точно, пусть feI(Gc) —
любая гладкая инвариантная функция. Тогда все функции вида
h±(X, a)=f[X+Xa) являются интегралами векторного поля
X для любого вещественного X. Любые два интеграла пх и dv,
построенные по функциям /, geI(Gc), находятся в инволюции на
любой орбите (регулярной или сингулярной). Гамильтониан
F(X) = (X, (pX) векторного поля X также находится в ин-
волюции со всеми интегралами вида hx. Из множества
указанных интегралов (оно, вообще говоря, избыточно) можно
выбрать функционально независимые в количестве, равном
половине размерности орбиты общего положения. Интеграл
F функционально выражается через интегралы вида hx.
Доказательство вытекает из п. 7 § 42 и результатов § 47.
4. Теорема (А. С. Мищенко и А. Т. Фоменко [186], [188]).
Пусть Gn — нормальная компактная подалгебра в полупростой
комплексной алгебре Ли G и Х=[Х, срА']—уравнения Эйлера
с оператором ф нормальной серии. Тогда эти уравнения вполне
интегрируемы по Лиувиллю на орбитах алгебры Ли Gn,
находящихся в общем положении. Более точно, пусть /е
eI(Gc) — любая гладкая инвариантная функция. Тогда все функ-
ции hx{X, a)=f(X+Xa)\ Gn являются интегралами потока X для
вещественных X. Любые два таких интеграла находятся
в инволюции на любой орбите (регулярной или сингулярной).
Гамильтониан F(X)=(X, q>X) потока X также находится
в инволюции со всеми этими интегралами. Из множества
указанных интегралов можно выбрать функционально независи-
мые на орбитах общего положения в количестве, равном
половине размерности орбиты. Интеграл F функционально
выражается через интегралы вида hx. В частности, мы
получаем полную интегрируемость уравнений движения классиче-
ского т-мерного твердого тела.
Доказательство вытекает из результатов гл. 8.
5. Замечание. Итак, уравнения Эйлера на всех орбитах
общего положения в полупростых алгебрах Ли вполне интег-
рируемы по Лиувиллю. Однако в действительности верно более
сильное утверждение. Оказывается, полный инволютивный
набор алгебраических функций существует на любой полупрос-
той орбите в алгебре Ли; в частности, эта орбита не обязана
быть орбитой общего положения. Впервые этот результат был
объявлен Дао Чонг Тхи в [85], однако в доказательстве этой
теоремы в [85] были допущены пробелы. Эти пробелы
окончательно устранены А. В. Браиловым. Точную формули-
ровку теоремы см. в п. 10 § 42.
6. В табл. 4 приведен список компактных вещественных
форм GС, нормальных вещественных форм Go и компактных
нормальных подалгебр Gn в классических простых комплексных
алгебрах Ли G.

290
ГЛ. 9. ПОЛНАЯ ИНТЕГРИРУЕМОСТЬ ПО ЛИУВИЛЛЮ
Таблица 4
Тип
алгебры
в„
с„
о„
G2
Ft
?6
Е-,
Е»
С
si (я. С)
soBn+l, С)
sp(n. С)
soBn. С)
82 (С)
f4(C)
е6(С)
67 (С)
е8(С)
С,
su(n)
soBn+l)
sp(n)
so Bл)
g2
f4
e6
e7
e8
Co
sl(n, R)
soBn+l, R)
sp(n, R)
so(n, n)
82 (R)
f,(R)
MR)
e,(R)
ee(R)
С„
so(n)
so(n+ l)x so(n)
u(n)
so(n)x so(n)
suB)xsuB)
spC)xsuB)
spD)
su(8)
so A6)
7. Уравнения Эйлера на алгебре Ли so D). В этом случае
состояние системы описывается шестью переменными /у = — lJh
г, у=1,..., 4. Перейдем к новым переменным /j =2~1 (/гз + ЛД
/2 = 2-1(/3i+V), /з=2(/12 + /з4), «1=2-1(/23-/14), т2 =
= 2 (/л—/24)> W3 = 2 (/12—^34). которые соответствуют раз-
ложению so D) = so C)©so C) алгебры Ли so D) на простые
слагаемые. Имеем {/,-, 4}=Едт/от, {ту-, тк} = ?jksms, {lj,mk}=0.
Рассмотрим гамильтониан Я общего вида, являющийся одно-
родным квадратичным:
Такой гамильтониан характеризуется тремя 3 х 3-матрицами
А= |f ai} ||, Д= || by || и С= || Су ||, две из которых (Л и С)
симметричны и зависят, следовательно, от 21 параметра. За-
метим, что, пользуясь преобразованиями из группы G = SOC)x
х SO C), мы можем привести матрицы А и С к диагональному
виду, так что без ограничения общности можем считать, что
Н имеет вид
ЦГя,/,2 + 2 I V.-'M-I <V?1 G16)
1 . i.J=l 1=1 J
и зависит от 15 параметров.
Гамильтонова система с гамильтонианом Н общего вида
всегда обладает тремя интегралами движения 11 = 12, 12=т2
и /3 = Н. Орбита коприсоединенного представления имеет
размерность 4 и выделяется уравнениями /1=const, /2=const.
С топологической точки зрения орбиты являются произведени-
ем двумерных сфер O = S2 x S2.
Имеет место следующая теорема 8, решающая вопрос
о существовании дополнительного квадратичного интеграла

!; Ч УРАВНЕНИЯ ЭЙЛГРА НА ПОЛУПРОСТЫХ АЛГЕБРАХ ЛИ 291
движения. Ответ на этот вопрос был дан в различной, хотя
и эквивалентной форме в работах [30], [60].
8. Теорема (А. П. Веселое, см. [60]). Пусть Н имеет вид
G16), причем собственные значения как матрицы А, так
и матрицы С различны, а матрица В не вырождена (det.8#0).
Тогда для существования четвертого независимого квадратич-
ного интеграла движения необходимо выполнение следующих
условий.
а) Матрица В одновременно с А и С приводится к диагональ-
ному виду, так что матрицы А, В и С молено считать
диагональными с элементами я,-, bj, Cj соответственно.
б) Должны выполняться условия
ах -а2)(а2-«з)х
x(a3-fl4) = 0, G17)
x(c3-f,) = 0. G18)
Дополнительный квадратичный интеграл движе>шя существует
лишь в случае Манакова [165] и для гамильтонианов вида
aj = a + Uj\ Bj = bj + Xb](blb2b3)-1,
cj = (b1b2b3)-lbj{bi + b22+b23~bj) + \c. }
Приведем иную форму интегралов движения, взятую из
работы [30].
9. Теорема (О. И. Богоявленский [30]). Следующие три
функции на so D) находятся в инволюции:
а,-а2
'"-й21 12+
1/2 / _л \ 1/2 ~J
' а2-аъ
G20)
- <721)
19"
1\а2-а,)
1/2 /, , \ 1/2 -12
(^ А G22)

292 гл. ч полная интегрируемость по лиувиллю
10. Замечание. Функции /,, /2 и /4, /5, А, связаны одним
линейным соотношением, так что среди них имеются четыре
независимые функции. Поэтому общий вид гамильтониана,
допускающего дополнительный интеграл движения, таков:
4 ss b
11. Замечание. Во многих случаях торы Лиувилля явля-
ются вещественной частью комплексного тора, причем этот тор
является абелевым многообразием. Выделим эту ситуацию
в виде следующего определения.
12. Определение. Пусть на R" задана пуассонова структура
,, ч / .eh 0е\ ch ( ch ch\ , ,, •.
\h, g} = I У—, — \, где — = —,..., — , a J = J(x)— кососиммет-
\ ex ex Ox \Pxt ixn)
рическая матрица. Если Яь ..., Нк — функционально независимый
к
набор функций Казимира, то f] {Hi{x) = c[\xeR"}—четномерное
подмногообразие, п — к = 2т. Гамильтонова система x = J—,
сх
xeR", при сделанных предположениях называется алгебраически
вполне интегрируемой, если выполняются следующие два свойства.
а) Система имеет т полиномиальных интегралов
Hk+i, ..., Hk + m в инволюции (т. е. {#,-, Hj}=0, {Я, //,} = 0) таких,
к + т
что Тт= П {.*eR"| Hl(x) = c\} — инвариантное компактное связ-
i= 1
ное подмногообразие (являющееся m-мерным тором) для
c = (ci, ..., ст) общего положения. Движение системы на Тт —
прямолинейная обмотка тора Тт = Rm/Г, где Г — решетка в Rm.
б) Многообразие Тт можно считать некомпактным аффин-
ным алгебраическим многообразием в С". Требуется, чтобы это
к + т
подмногообразие имело вид [\ {хеС" \ Я,(х) = г,} = T"\S, где
S—объединение нескольких подмногообразий коразмерности
один, а Т™ — комплексный алгебраический тор: Г™ = Ст/Л,
Л — решетка периодов. Алгебраичность означает, что
м
Т"с= П {Fi(xo, •••,-*п) = 0}> гДе ^; — однородные многочлены.
Требуется, чтобы координаты z,-(?) были мероморфными функ-
циями на Т™.
13. Рассмотрим подробнее геодезический поток левоинвари-
антной метрики на группе Ли SO D). Имеет место следующее
утверждение, фактически подводящее итог исследованиям
М. Адлера, П. Мёрбеке, С. В. Манакова, О. И. Богоявленского,
А. П. Веселова, М. Ланглуа, А. С. Мищенко, А. Т. Фоменко.
14. Теорема. Геодезический поток левоинвариантной мет-
рики на группе Ли SO D) алгебраически вполне интегрируем

§ 51 УРАВНЕНИЯ ЭЙЛЕРА НА ПОЛУПРОСТЫХ АЛГЕБРАХ ЛИ 293
тогда и только тогда, когда метрика имеет один из трех
указанных низке видов.
а) Метрика Манакова. В этом случае H = 2l ? hjxfj
и числа Xtj подчинены соотношению
б) Алгебру Ли soD) представим в виде soD) = soC)©soC).
В этом случае метрика имеет вид
з
Н= _
где
= -42i А54А32А65А 13А46\
\ Л65/132
причем знак произведения А,14Х25^зб выбирается из условия
= A2lAS4A32A6SAl3AA6(A5A~A2i)(A6S-A32)(A4f,~Ai3), G25)
здесь AiJ = Xi — 'kj.
в) В этом случае метрика имеет вид
H = Y> ? (i0ci + di)xf+(ci + 3di)xf+3 + 6(di-cl)xixi + 3l G26)
i- 1
причем Ci = bi/ai и </, = -^—-, где (/, j, k) — перестановка A, 2, 3),
Cj — ak
параметризованы такими числами (аь а2, а3) и [Ь^. Ь2, Ь3\ что
a1+a2 + ai = 0 и й1+й2 + ^з=0.
15. Пример. В качестве примера системы, являющейся алгеб-
раически вполне интегрируемой, отметим динамическую систе-
му Неймана, полная интегрируемость которой доказана в п. 2
§ 28. Подробное исследование этой системы с точки зрения
алгебраической полной интегрируемости см. в книге [164].
16. Конструкция. Приведем метод построения интегрируемых
уравнений Эйлера, который связан с рассмотрением фильтраций
в алгебрах Ли. Рассмотрим уравнение Эйлера Х=[Х, С(Х\\, где
G—полупростая алгебра Ли, XeG, а С: G-*G—секционный

294 ГЛ. 9 ПОЛНАЯ ИНТЕГРИРУЕМОСТЬ ПО ЛИУВИЛЛЮ
оператор. Пусть задано разложение G в прямую сумму
линейных подпространств: G = L0 + Ll + ... + Ln, где все Ц ор-
тогональны относительно формы Киллинга и их коммутаторы
удовлетворяют условию [Ьк_ь Z.Jc:Lk при />0. Ясно, что
Gk = Lt + ... + Lk— подалгебра. Поэтому мы получаем фильтра-
цию алгебры Ли G = Gn=>...z>G1 =>G0 = L0. Обратно, по каждой
фильтрации, такой, что ограничение формы Киллинга на
подалгебру G, является невырожденным, восстанавливается
нужное разложение G в прямую сумму подпространств
J-k — Gk П GI - 1 • Обозначим Рк ортогональный проектор на
подпространство Lk. Произвольный элемент leG имеет пред-
ставление /=/0 + ...+/„, /; = /"((/) 6 L;. Рассмотрим операторы С:
G^>G вида
C(t) = aQ(t) + \lll + ... + \Hln, G27)
где а0 — любой симметрический оператор в подалгебре Lo.
Пусть /, gel(G) — функции, постоянные на орбитах присо-
единенного представления в алгебре Ли G.
17. Теорема (О. И. Богоявленский [33]). Уравнение Эйлера
Х=[Х, С(Х)\ с оператором С. G^G вида G27) эквивалентно
уравнению /0 = [/0, а0 (/0)] в подалгебре Ли Lo и цепочке линейных
дифференциальных уравнений в пространствах Lk. Уравнение
Эйлера Х=[Х, С(Х)\ имеет набор первых интегралов f(<xmk + $lk),
где mk — l0 + ... + lk, т„ = Х, ЛГ=/0+ ... + /„, зависящих от спектраль-
ных параметров а, р\ О^к^п. Скобки Пуассона этих интегралов
{/(awt + p/t), g{ymj-\-blj)} обращаются в нуль в следующих
случаях: a) k=j; б) k>j, a=l, р = 0 или а = 0, Р=1.
§ 52. Уравнения Эйлера на разрешимых алгебрах Ли
1. Обозначения. Пусть G—комплексная простая алгебра Ли,
Н—ее подалгебра Картана, G = H® ? G" — корневое разложе-
ние, {hh е^ — базис Шевалле. Рассмотрим в G борёлевскую
подалгебру bG, определяемую равенством
6G = ©R/r,©X Rea. G28)
Ей отвечает группа Ли BG. Выберем в группе Вейля W(G, H)
алгебры Ли G элемент w0 наибольшей длины, см. [55].
2. Теорема (А. А. Архангельский [11]). Пусть d{ — полуин-
варианты представления Ad* группы Ли ВА„. Существует
открытое всюду плотное подмножество Uc(bAn)' такое, что
если функция f на (ЬА„)' функционально зависит от функций
d^x + Xa), i=\,...,n, XeR, aeU, то система уравнений
x = ad*dfM(x) вполне интегрируема по Лиувиллю на орбитах
общего положения представления Ad* группы Ли ВАп.

§ 52. УРАВНЕНИЯ ЭЙЛЕРА НА РАЗРЕШИМЫХ АЛГЕБРАХ ЛИ 295
3. Теорема (В.В.Трофимов [246]). Пусть dt — полуин-
варианты представления Ad* группы Ли BSp(n). Существует
открытое всюду плотное подмножество ?/c(dsp(m))* такое,
что если функция f на (bsp(/i))* функционально зависит от
функций di(x + Xa), 1=1, ..., п, Хек, aeU, то система уравнений
x = ad'dfW(x) вполне интегрируема по Лиувиллю на орбитах
общего положения представления Ad* группы BSp(n).
4. Замечание. Явное описание полуинвариантов для ВА„
можно найти в работе А. А. Архангельского [11], а для
BSp(n)—в работе В. В. Трофимова [246]. В работе [249] дано
описание полуинвариантов и, в частности, инвариантов для всех
борелевских подалгебр bG в простых алгебрах Ли G.
Пусть Aj(A')—нижний левый угловой минор порядка i мат-
рицы X, Oij(s)—окаймление минора AS(X), соответствующее
элементу xtj.
5. Теорема (В. В. Трофимов [246]). Пусть функция f на
(bso(n))* функционально зависит от полуинвариантов представле-
ния Ad* группы Ли BSO(n) и, кроме того, в случае п = 2к — от
координат максимальной абелевой подалгебры bso(n), т. е. от
yiJ+n(i+j<n), в случае BSODA:+1) — от сдвигов Ak+l и коор-
динат ytj+k (i+j<k) абелевой подалгебры, в случае BSODs + 3) —
от сдвигов Ok + l k+2{k— 1) и координат ytj+k {i+j<k) абелевой
подалгебры (алгебра Ли so(Ar) реализована матрицами, кососим-
метричными относительно побочной диагонали). Тогда система
уравнений x = a.d'df(x)(x) вполне интегрируема по Лиувиллю на
орбитах общего положения представления Ad* группы Ли
BSO(n).
6. Теорема (см. [246]). Если функция f на (bG2)* функци-
онально зависит от полуинвариантов коприсоединенного пред-
ставления Ad* группы Ли BG2 и координат максимальной
абелевой подалгебры в bG2, то система уравнений jc = adjy(x)(x)
вполне интегрируема по Лиувиллю на орбитах общего положения
представления Ad*,G2.
7. Теорема (см. [249]). В пространстве многочленов на
(bF^Y и \ЬЕЬ)* в явном виде предъявляется конечномерное
подпространство W, инвариантное относительно представления
Ad* группы Ли BF4. или ВЕ6, такое, что если функция
f функционально зависит от сдвигов базисных функций простран-
ства W, то система уравнений jc = ad*)y(I)(x) вполне интегриру-
ема по Лиувиллю на орбитах общего положения представления
Ad* группы Ли BF^ или ВЕ6 соответственно.
Доказательство теоремы 6 основано на использовании мето-
да цепочки подалгебр (см. § 35), а доказательство теоремы 7
проводится на основе обобщенной методики сдвига, см. § 34.
Подробности см. в работах В.В.Трофимова [246]—[249].
8. Замечание. Для построения полного инволютивного
семейства функций на (bG)' надо знать индекс алгебры Ли bG.

296
ГЛ 9. ПОЛНАЯ ИНТЕГРИРУЕМОСТЬ ПО ЛИУВИЛЛЮ
Эту задачу решает следующая теорема, принадлежащая
В. В. Трофимову. . _ _
9. Теорема (см. [249]). Пусть G—простая алгебра Ли,
bG—описанная выше вещественная форма борелевской подалгеб-
ры в G, woeW{G, H) — элемент группы Вейля максимальной
длины. Тогда если О — орбита максимальной размерности
представления Ad *BG, то ind bG = codim О = - card A, где
A = {(XjeA|( — wo)ai#a(}, A — система простых корней алгебры
Ли G, сага А — мощность множества А.
Таблица 5
тип
алгебры
Система простых корней
Инволюция . -ш0
д.
а. а3 ос- а5 а6 а, а
id
id
если п четно, то id
если п нечетно,то
a.i~^a.i , i-г re-2
id
id
id
Id

§ 52. УРАВНЕНИЯ ЭЙЛЕРА НА РАЗРЕШИМЫХ АЛГЕБРАХ ЛИ 297
10. Действие инволюции ( — и>0) на схеме простых корней
простой алгебры Ли G приведено в табл. 5, см. [55].
11. Теорема (Ле Нгок Тьеуен, см. [150]). Пусть L —
любая подалгебра в алгебре Ли Кп всех верхних треугольных
матриц вида L=V+ ? R-?y> г&е Ец—элементарная мапгри-
ца порядка пхп, а V— произвольное подпространство п-мерногд
пространства диагональных матриц. Тогда на пространстве L*
существует полный инволютивный набор, который состоит из
полиномов и который можно предъявить в явном виде.
12. Замечание. Общая теорема существования полного
инволютивного семейства функций для нильпотентных алгебр
Ли доказана в работе Вернь [513]. Однако представляет интерес
явное построение такого набора функций. В качестве примера
приведем результат, принадлежащий Т. А. Певцовой.
13. Теорема. Пусть ft — полуинварианты представления
Ad* группы Ли Рп верхних треугольных матриц п-го порядка
с единицами на диагонали. Существует открытое всюду плотное
подмножество U cG*n такое, что если функция f на G'n функци-
онально зависит от функций вида fj(x + \a), XeR, aeU, то
система уравнений х = adjy(ж) (х) вполне интегрируема по Лиувил-
лю на орбитах общего положения представления Ad*^ (Gn —
алгебра Ли верхних треугольных матриц п-го порядка с"нулями
на диагонали).
14. Цепочки Тоды. Описанные ниже системы были найдены
в работе О.И.Богоявленского [321]. Пусть q = (qt, ..., qn)
и /» = (/»i, ..., р„) — векторы координат и импульса в и-мерном
евклидовом пространстве. Пусть <х1? ..., <хг—линейно независи-
мые векторы в этом пространстве, a (jv = (a,, q) — линейные
функции (г^п).
Цепочки Тоды описываются гамильтонианом вида
\ ?2,-,*.)• G29)
г
где U(q!, ..., qn)= X si expB^aJ—потенциал системы.
* = i
Если система векторов at, ..., ar произвольна, то относитель-
но соответствующей гамильтоновой системы сейчас почти
ничего сказать нельзя. Однако если {<х;} образуют систему
корней простой алгебры Ли, то можно полностью исследовать
соответствующую гамильтонову систему. Приведем описание
соответствующих интегрируемых потенциалов.
15. Тип Am_t. Система простых корней <xl=e1— ег, ..., an_t =
= е„ _! — еп. Потенциал U имеет вид
U=e1l~tl + ...+e*'-1~\ G30)

298 ГЛ. 9. ПОЛНАЯ ИНТЕГРИРУЕМОСТЬ ЦО ЛИУВИЛЛЮ
16. Тип Д,. Система простых корней a.i=ei— е2, —, an-i =
= еп-1— е„, а.„ = е„. Потенциал U имеет вид
U=e*1~t* + ... + e1'-1~t-+e\ G31)
17. Тип С„. Система простых корней al=ei—e2, ..., а„_! =
-е„-!— еп, ап = 2е„. Потенциал U имеет вид
U=eqi~qi + ...+eq-l~q- + e2q: G32)
18. Тип О„. Система простых корней а.1=е1—е2, <х2 =
= е2-е3, ..., а.„-1=е„-1-е„, а„ = еп-1+еп. Потенциал (/имеет
вид
U=e9l~q2 + ...+eq-l~q- + e^-l+q: G33)
19. Тип G2. Система простых корней а1=е1—е2, <х2=— 2et +
+ е2 + е3. Потенциал U имеет вид
20. Тип F4. Система простых корней а1=е1— е2, а.2=е2 — е3,
п.3 = е3, а.4. = 2~1(е4. — е1—е2—е3). Потенциал U имеет вид
21. Тип Е6. Система простых корней а.1 = 2~1 (~е1+е2 +
+ ... + е7-е8), а.2 = е1-е2, а.3 = е2-е3, а.4 = е3-еА, а5=е4-е5,
а6 = — (et + е2). Потенциал U имеет вид
22. Тип Е7. Система простых корней a1 = 2~1(e1— es+e2 +
+ ... + еп), а2 = е!-е2, ..., n.6 = e5-OL6, a7=-(e1+e2). Потенциал
U имеет вид
23. Тип ?8. Система простых корней a1 = 2~1( — ex— es+e2 +
+ ... + е7), ci2 = e1-e2, ..., а-, = еь-е-,, а8=-(е1+е2). Потенциал
U имеет вид
U=eq^4> + ...+eq*-4T + e^+4i) + e^-q>+9i + -+qi~''*). G38)
24. Предложение. Цепочки Тоды (п. 15—2Ъ) допускают
реализацию в соответствующей борелевской подалгебре.
Доказательство. Приведем конструкцию для цепочки
Тоды типа А„. Обозначения возьмем из п. 15, 22 § 27.

i 53. УРАВНЕНИЯ ЭЙЛЕРА НА НЕРАЗРЕШИМЫХ АЛГЕБРАХ ЛИ
299
В качестве функции Ft (см. п. 15 § 27) возьмем функцию
F1(X)=l-tr{X+aJ, XeN и
О а,
о
О
О
G39)
Прямое вычисление показывает, что H=Fl°f.
Аналогичное построение можно выполнить для остальных
типов цепочек.
25. Теорема. Цепочки Тоды типов А„, ..., Е8, описанные
выше, являются вполне интегрируемыми гамильтоновыми си-
стемами.
Доказательство см. в работе [231].
§ 53. Уравнения Эйлера на неразрешимых алгебрах Ли
с нетривиальным радикалом
1. Первый (после важной работы В. И. Арнольда [8])
пример интерпретации уравнений Эйлера на алгебре Ли еC)
группы движений трехмерного пространства R3 был обнаружен
С. П. Новиковым в [198], где указано, что соответствующие
уравнения есть уравнения Кирхгофа, описывающие свободную
динамику твердого тела в жидкости, см. п. 17 § 50. Эти
уравнения были исследованы на интегрируемость В. В. Коз-
ловым и Д. А. Онищенко [134]. Как указал С. П. Новиков
в [198], при стягивании алгебры Ли soD) на алгебру еC)
семейство метрик уа,ъ,о переходит в случай Клебша. Затем
аналогичное наблюдение было сделано в [59], предельным
переходом получено известное семейство Стеклова — Ляпуно-
ва— Колосова.
2. Замечание. Уравнения движения многомерного твердо-
го тела вкладываются в алгебру Ли е(п) группы движений
пространства R". Оказывается, что в этом случае метод сдвига
аргумента позволяет построить полный коммутативный набор
интегралов на орбитах общего положения.
Отметим, что полнота сдвигов инвариантов есть следствие
общей теоремы А. В. Болсинова (п. 2 § 45).
3. Теорема (В.В.Трофимов и А.Т.Фоменко [2661,
[267]). а) Система дифференциальных уравнений Х—аЛ*^Х){Х),
где q = C(a,b,D)—секционный оператор, построенный в п. 8
§ 48 для е(п), вполне интегрируема на орбитах общего положе-
ния, б) Пусть/—инвариантная функция на е(п)*. Тогда функции

300 ГЛ. 9. ПОЛНАЯ ИНТЕГРИРУЕМОСТЬ ПО ЛИУВИЛЛЮ
hx(X)=f{X+'ka) являются интегралами движения при любых
числах X. Любые два интеграла hx и gv находятся в инволюции на
всех орбитах представления Ad* группы Ли Е(п), причем число
независимых интегралов указанного вида равно половине размер-
ности орбиты общего положения. При этом если О — орбита
максимальной размерности коприсоединенного представления, то
,. _ Г"+'1 ГП
codimO = ,
т.е.
, т.е. тае[п) = \ .
4. Замечание. В явном виде интегралы описаны в работе
[266], или см., например, обзор [268] или [269], [270]. В [255]
доказана интегрируемость соответствующего геодезического
потока на группе Ли Е(п).
5. Обозначения. Построенный в теореме 3 полный ком-
мутативный набор функций на пространстве е(п)* играет роль
«компактной» серии интегралов для полупростых алгебр Ли,
см. п. 3 § 51. Аналог «нормальной» серии построен
А. В. Браиловым. Пусть е(п) — алгебра Ли группы Ли Е(п)
движений евклидова пространства R" Стандартный базис
алгебры Ли е(п) состоит из элементов Jci;- и ук, где
Xjj—инфинитезимальное вращение в (i,j)-u плоскости,
ук— инфинитезимальный сдвиг по к-й координате, /, j=\, ..., п,
i<j, k=\,...,n. Линейные координатные функции на е(п)*,
соответствующие элементам хи, ук, обозначим ху и ук. Пусть
at, ..., а„ — произвольные числа. Определим матрицы размера
(и+1)х(и+1): Eks= || 5it5SJ-1|, здесь 5№ — символ Кронекера,
G40)
^ i, Xl = \\xij\\,
где Xij=-Xji, xkin + l = xn+Uk = Q при к=1, ..., n+1;
И
X_! = Yj Ji-^iTn+i' X=X1+X-l. Таким образом, X, Xt,
i = O
X-i—матричные функции на пространстве е{п)*.
6. Теорема (А. В. Браилов). Пусть at>...>an-1, апф0, ЬХ,
Ь2, ..., Ьп — некоторые числа. Тогда дифференциальные уравне-
ния x = adJH(x)(jc), хее(п)', с квадратичной функцией
п — 2 п—I , , п—1 ,
л~1

§ 53 УРАВНЕНИЯ ЭЙЛЕРА НА НЕРАЗРЕШИМЫХ АЛГЕБРАХ ЛИ 301
вполне интегрируемы по Лиувиллю на орбите О представления
Ad* группы Е(п) в е(п)* для орбиты О общего положения в е(п)'.
Полным набором коммутирующих интегралов являются функци-
ональные коэффициенты his (k = 2, ..., п + 2; 5 = 0, ..., к) при Xs\i~2
в многочлене hk(X, ц~1)=Д*(Л'1+Ы1+ц2(Л'_1+Ы-1)), где
Ак — сумма всех симметричных миноров к-го порядка.
7. Замечание. Метод тензорных расширений позволяет
строить полные коммутативные наборы первых интегралов для
конечномерных аналогов уравнений магнитной гидродинамики,
описанных в п. 19 § 50. Пусть G—комплексная полупростая
алгебра Ли, If(G)—множество функций на С, которые
являются сдвигами инвариантов F коприсоединенного представ-
ления ad* алгебры Ли G, т. е. If[G) состоит из функций вида
hx(X) = F(X+Xf), где ХеС, feG—фиксированный ковектор.
Используя процедуру тензорного расширения (см. п. 3 § 38), мы
построим семейство функций (t)(jf(G)) на пространстве Cl(G)*.
Следующая теорема была доказана В. В. Трофимовым.
8. Теорема (см. [253], [258]). а) Пусть функция h функци-
онально зависит от семейства (t)(la(G)). Тогда уравнения Эйлера
X=a.d*di,ix)(X) являются вполне интегрируемой гамильтоновой
системой на всех орбитах общего положения коприсоединенного
представления Ad* группы Ли fi(-P), ассоциированной с алгеброй
Ли Q(G). б) Пусть G—комплексная полупростая алгебра Ли,
X=adc(abD)(X)—уравнения Эйлера на fl(G)*, A'efl(G)*, с опера-
тором «комплексной» серии, см. п. 11 § 48. Тогда эта система
вполне интегрируема по Лиувиллю на всех орбитах коприсо-
единенного представления группы Ли С1(Р), ассоциированной
с Cl(G). Более точно, пусть F[x)— любая главная, инвариантная
относительно коприсоединенного представления группы Ли &(Р)
функция на Q(G)'. Тогда все функции F(X+Xf), ХеС, являются
первыми интегралами уравнений Эйлера для всех ХеС. Любые
два таких интеграла F(X+Xf), H(X+\if), X, цеС, находятся
в инволюции на всех орбитах относительно формы Кириллова.
Из указанного множества интегралов можно выбрать функци-
онально независимые интегралы в количестве, равном половине
размерности орбиты общего положения коприсоединенного пред-
ставления группы Ли fi(/>), ассоциированной с алгеброй Ли Q{G).
9. Замечание. Аналогичная теорема справедлива для
компактной вещественной формы полупростой алгебры Ли,
а также для нормальной компактной подалгебры в простой
комплексной алгебре Ли G. Список таких подалгебр приведен
в табл. 4, определение соответствующих серий операторов см.
в п. 12, 13 § 48. Подробности см. в работах [253], [258].
10. Многомерный случай Лагранжа. Впервые вполне интегриру-
емый случай уравнений движения и-мерного твердого тела
с закрепленной точкой в поле силы тяжести был найден А. В. Бе-
ляевым [18]. Найденный случай является обобщением классиче-

302 ГЛ 9 ПОЛНАЯ ИНТЕГРИРУЕМОСТЬ ПО ЛИУВИЛЛЮ
ского случая Лагранжа, см. п. 14 § 5. Несколько другое обобщение
случая Лагранжа на произвольную размерность было найдено
Ратью [483]. Далее, как заметил А. В. Болсинов, случай Лагранжа
можно включить в серию вполне интегрируемых гамильтоновых
систем на алгебрах Ли вида Q(G) = G®(R[x]/(jc2)).
11. Обозначения. Свяжем с и-мерным твердым телом ор-
торепер О, е(, ..., е„ (О — точка закрепления). Тогда движение
тела в неподвижной системе координат О, е\, ..., е'„ можно
представить как путь в группе P=SO(n). Фазовое пространство
этой системы есть T'SOin), а движение задается векторным
полем sgrad//, где Не С (Т* SO (л)) — функция полной энергии,
которая имеет вид H=T+n*(U\, где Т—левоинвариантная
часть гамильтониана, п: Т'Р^Р— проекция кокасательного
расслоения, U&CCO{P)— потенциал. Потенциал U обладает тем
свойством, что при действии группы Р сдвигами U порождает
конечномерное пространство V. Определена полупрямая сумма
G:1 = G:+F, G = so(n), где V рассматривается как абелева алгебра
Ли. Как заметил А. В. Бочаров (см. дополнение к [66]),
исходная система эквивалентна гамильтоновой системе
sgrad//^ где Hl = Tl + U1 и 7\—функция компоненты G*,
равная ограничению Г на G *, a f/t — функция компоненты V,
равная значению функционала среК* на ие V. Итак, движение
твердого тела с закрепленной точкой в поле силы тяжести
описывается гамильтоновым уравнением на пространстве (so(и)
+ R")*. В качестве координат на (so(«) + R")* возьмем линейные
формы v,7, yk на (so(«) + R")*, являющиеся базисами so(«) и R"
соответственно. Их выбираем так, чтобы {v,j, vjk } = vy,
{Vij, Jj} = Ji- Гамильтониан Я в переменных v^, yk имеет вид
здесь а,—диагональные элементы матрицы /моментов инерции
(все остальные элементы равны нулю), /¦, — координаты центра
масс в базисе О, е±, ..., е„.
12. Определение. Обобщенным случаем Лагранжа в смы-
сле [18] называется случай, когда
О
о с
к с
о. G43)
13. Теорема (см. [18]). Динамическая система, отвеча-
ющая случаю Лагранжа (п. 12), является вполне интегрируемой
гамильтоновой системой.
14. Определение. Гамильтонова система на (so(«) + R")*
с гамильтонианом Я=2<М, Q> + <A', Г>, где М = || w,-; )| e

§ S3. УРАВНЕНИЯ ЭЙЛЕРА НА НЕРАЗРЕШИМЫХ АЛГЕБРАХ ЛИ ч 303
eso(n)—вещественная кососимметрическая ихи-матрица, М=
= QJ+JCl = C-1il, J^diagih, ..., /„), А>0, ЛГ=||Х« II—Фик-
сированная матрица в so (и), М, Peso (и), называется волчком
Лагранжа в смысле [48 3], если /1=/2 = а, 13 = /Л = ... = 1„ = Ь
и Xi2= "~X2i =Х> все остальные Ху = 0- Полностью симметрич-
ный волчок определяется как система, у которой 1\=1г —
...=1„ = а и X—произвольный элемент алгебры Ли so(n).
15. Теорема (см. [483], [484]). Предположим, что Xi2^0-
Тогда уравнения Эйлера движения п-мерного твердого тела
Г = [Г,П], М=[М,С1] + [Г, X] G44)
можно переписать в виде — (Г + Х.М +Х2С) = \Т + ХМ+Х2С,
AJf] в том и только том случае, когда G44) описывает
п-мерный волчок Лагранжа или полностью симметричный
волчок. Величины К = и(Г + Ш+\2С) и р{(Г + ХМ+Х2С) =
= [det(r + X.M+X.2C)]1/2 (для четного п) дают полный ком-
мутативный набор интегралов.
16. Замечание. Пусть G— полупростая алгебра Ли,
Cl(G) = G®(R[x']/(x2))—тензорное расширение алгебры Ли
G с помощью R[jc]/(x2) = R + eR, e2 = 0. Рассмотрим на
u(G)^Q(G)* гамильтониан F(x + ?y) = 2~1(q>abD(x), x>— (b, у).
При отождествлении il(G) = Q(G)' уравнения Эйлера Х=
= ad;fm(A') примут следующий вид:
*=[фа,ь,в(х)> х]-[*^1
G45)
У=[ч>а,ь,о{х), у],
где х, у, Ь, фа ь D (дг) е G. В случае (j = soC) система G45)
принимает вид классического случая Лагранжа движения
твердого тела в поле силы тяжести. Это замечание принадлежит
А. В. Болсинову. Итак, случай Лагранжа оказался включенным
в семейство гамильтоновых систем на двойственных простран-
ствах к алгебрам Ли типа u(G).
17. Теорема (А. В. Болсинов [39]). Система уравнений
G45) вполне интегрируема по Лиувиллю на всех орбитах
общего положения представления Ad* группы Ли &(Р),
отвечающей Q (G).
18. Замечание. Заметим, что у нас еще остался не
обобщенным на и-мерное пространство случай Ковалевской, см.
п. 14 § 5. Это будет сделано в следующем параграфе.
19. Замечание. Хотя теорема А. В. Болсинова (п. 2 § 45)
и решабт принципиально вопрос о существовании полного
инволютивного семейства функций на пространстве, дуальном
к полупрямой сумме G+V, большой интерес представляют

304 ГЛ. 9. ПОЛНАЯ ИНТЕГРИРУЕМОСТЬ ПО ЛИУВИЛЛЮ
явные конструкции таких семейств. В качестве примера приве-
дем две теоремы такого сорта, см. п. 20, 21.
20. Теорема (Т. А. Певцова [212]). Пусть G—полупрямая
сумма простой алгебры Ли Н и абелевой алгебры по представле-
нию и. Тогда если: а) алгебра Ли H = g\{ln), а представление
ц = Л р; б) алгебра Ли //=slBn), а представление (i = S2p;
в) алгебра Ли # = spBn), а представление ц = р + т, где р —
минимальное представление, а т — одномерное тривиальное пред-
ставление, то метод цепочек подалгебр в явном виде позволяет
построить полное инволютивное семейство рациональных функ-
ций на пространстве G*. Здесь Л*р и S р обозначают к-ю
внешнюю и к-ю симметрическую степени представления р.
21. Теорема (Е. Г. Шувалова; К. Швая [296]). Пусть
G—полупрямая сумма простой алгебры Ли si B) и абелевой V по
неприводимому представлению ц>к: si B)-» End (к), которое зада-
k
ется своими числовыми отметками о на схеме простых корней.
Тогда при к=\, ..., 6 метод сдвига инвариантов в явном виде
позволяет построить полное инволютивное семейство функций
на пространстве G*.
22. Теорема (см. [33]). Пусть V—пространство, со-
пряженное к одной из алгебр Ли L, М, soC)©R3, Lkm, L@LOn
(соответствующие обозначения были введены в § 50j. Тогда на
V существует полное инволютивное семейство функций, явля-
ющихся первыми интегралами уравнений Эйлера F98), G02),
G04) — G06), G08), т. е. эти уравнения вполне интегрируемы по
Лиувиллю.
§ 54. Интегрируемые системы
и симметрические пространства
1. Конструкция. Пусть группа Ли R с алгеброй Ли J действу-
ет на многообразии М. Действие группы R индуцирует
симплектическое действие R на кокасательном расслоении Т*М.
Этому действию соответствует отображение момента Р:
T'M-*J", которое в данном случае определяется следующим
образом: (Р(х), g> = <x, g(m)), где xeT*mM, <X, Y) в левой
части обозначает спаривание У* с У, а в правой части —
спаривание Т*тМ и ТтМ. Пусть на J имеется невырожденная
билинейная симметричная инвариантная форма Q. Отождеств-
ляя /'с/с помощью Q, мы будем рассматривать отображение
момента P = PQ: T'M-*J, Q(P(x), j) = <x, g(m)), где geJ,
xeT*mM. При фиксированной точке теМ отображение момента
Р линейно по хеТ*тМ. Поэтому если на J определен оператор
4>a,b,D (элементы а и Ъ могут быть элементами алгебры Ли,
содержащей J), то Ha,biD(x) = 2~lQ(P(x), сра,г,,в(-Р(*)))—квад-
ратичная функция на Т*М.

§ 54 ИНТЕГРИРУЕМЫЕ СИСТЕМЫ 305
2. Определение. Если квадратичная функция HabD(x)
является положительно определенной невырожденной квад-
ратичной формой, то ей соответствует риманова метрика dsl ь D
на М. Это соответствие определено в общей ситуации
и называется преобразованием Лежандра, см., например, [8],
[102]. Метрики dsibD называются метриками отображения
моментов Р.
3. Теорема (А. В. Браилов). Пусть М—риманово глобаль-
но симметричное пространство, rk М—его ранг, R — связная
компонента группы изометрий М, J—ее алгебра Ли, Q —
Aut (^)-инвариантная симметричная невырожденная билинейная
форма на J. Предположим, что R — компактная полупростая
группа Ли. г) Если rkA/ = rk/, срв,(,,в—произвольный положи-
тельный оператор на J (а и b могут быть элементами большей
алгебры Ли) и /^ (X), ...,fk{X)— полный инволютивный набор
независимых интегралов уравнения Х=\_Х, <р„ ¦, n(A')], XeJ,
A; = 2(rkJ+dimJ), то k = dimM и функции fy (Р(х)), ...,fk(P(x))
являются независимыми интегралами в инволюции геодезиче-
ского потока на Т'М римановой метрики ds^b D отображения
моментов Р: T'M-+J. б) Если tkM<tkJ, a, beG, cpe>ft,D —
положительный оператор, то геодезический поток на Т*М
римановой метрики dsjbD отображения моментов Рп'. T*M-*J
имеет инволютивный набор интегралов движения F(P(x) + Xa),
Fel(j), X.eR, и для элемента aeJ общего положения в J из
этого набора можно выбрать независимые на Т*М функции
в количестве, равном размерности М.
Доказательство, а) Фиксируем какую-либо точку теМ.
Изометрия многообразия М, оставляющая точку т неподвиж-
ной и переворачивающая геодезические, проходящие через т,
определяет инволютивный автоморфизм /: R-+R. Этот авто-
морфизм R определяет инволютивный автоморфизм алгебры
Ли J, который мы обозначим буквой а. Пусть J=H+ V—такое
разложение J, что a\H=id и a\V=— id. Для точки т имеем
Р(Т^,[М))= V. Поскольку гкМ=гкУ, то мы можем выбрать
подалгебру Картана К в J так, что К а V. Ввиду компактности
алгебры Ли J отсюда следует, что всякая орбита R в J пересека-
ет V. Как известно, действие R на Т'М при отображении
моментов переходит в (ко)присоединенное действие на J.
Поэтому J=P(T'M). Следовательно, функции f1(P(X)), ...
•~>fk(P(x)) независимы на Т'М. Их инволютивность вытекает
из формулы {f°P, g°P} = {f, s}°P- Поэтому осталось доказать,
что dimM=2~1(dimy+rk7). Пусть а — прризвольный элемент
из V, У—централизатор а в J, Ha = Hf]J", V=vf]Ja.
Поскольку. [Н,Н~\сН, [y,V\czH, [H,V~\czV и aeV, то
Ja = Ha+Va. Определим на J кососимметрическую форму
La(X, Y)=Q(a, [X, У]), Поскольку Q инвариантна относитель-
но Aut (У), то она инвариантна, в частности, относительно ст.

306 ГЛ. 9. ПОЛНАЯ ИНТЕГРИРУЕМОСТЬ ПО ЛИУВИЛЛЮ
Поэтому Я и V являются g-ортогональными дополнениями
друг друга в J. Отсюда следует, что HX = V+H", V1=H+V,
где Я и V1—косоортогональные дополнения к Я и V в J от-
носительно La. Следовательно, факторформа La на У/У = Я/
Ha©V/V не вырождена и осуществляет спаривание простран-
ства Н/Н" с VIV. Поэтому dim Н/Н" = dim V/ V. Пусть
К—подалгебра Картана в J такая, что К а V, аеК—регуляр-
ный в J элемент. Тогда J"=V = K, Я" = 0. Имеем
= -(dim#-dim#e + dim K-dim K") + dim V =
= dim V/ V + dim F" = dim K=dimM. G46)
б) Пусть К—такая подалгебра Картана в J, что
Kv = Kf]V—максимальное коммутативное подпространство
в V. В этом случае dim Kv = rk М. Для элемента а е Kv общего
положения в Ку имеем V = KV, поэтому для орбиты О группы
R в J, проходящей через точку а, имеем -dimO = -dimy/y =
= - (dim Я/Я" + dim V/ Fa) = dim V/ V. Воспользуемся теперь
тем, что сдвиги инвариантов образуют полный инволютивный
набор на каждой полупростой орбите, см. п. 10 § 42. Получим,
что набор функций F(x + Xa), Fel(j), XeR, содержит -dimО
независимых на О функций.
4. Лемма. Пусть J—вещественная или комплексная полу-
простая алгебра Ли, aeJ—полупростой элемент, J" — цент-
рализатор a, Cent У" — его центр, <X, Г) — инвариантная сим-
метрическая билинейная невырожденная форма, с помощью
которой мы отождествляем J и J', f1, ...,fk — образующие
алгебры инвариантов I(J). Тогда дифференциалы dfx (a), ..., dfk{a)
порождают Cent J".
Доказательство, а) Случай поля комплексных чисел.
Пусть Я—подалгебра Картана в J. Тогда, как известно,
отображение ограничения j: I{J)-*S(H), где S(H) — алгебра
полиномиальных функций на Я, является вложением на
jI{J) = S(H)w, где S(H)W — подалгебра в S(H) инвариантных
многочленов относительно группы Вейля W, соответствующей
подалгебре Картана Я. Пусть b e Cent J", W — стабилизатор
а в W, Wb—стабилизатор Ъ в W. Тогда имеем W с Wh. Пусть
{в!, ..., ап} — орбита а относительно группы Вейля. Подберем
положительную функцию g на Я так, чтобы dg(a) = b и ^g(a,) = 0

§ 54 ИНТЕГРИРУЕМЫЕ СИСТЕМЫ 307
при агфа. Пусть g = n ? g<o. Тогда dg(a) = b и geS(H)w.
Следовательно, f=j~i(g)—инвариант J такой, что df{a) = b.
Итак, показано, что если fx, ...,fk — образующие алгебры
инвариантов I(J), то f=P(ft, ...,fk) для подходящего полинома
* дР
Р. Следовательно, Ь= ? — dft(a), что и требовалось доказать.
i = 1 ¦*'
б) Пусть J—вещественная алгебра Ли. Рассмотрим ее
комплексификацию Jc. Тогда J—вещественная форма J , пусть
а — сопряжение относительно J. Пусть /- k
и /i, ...,/г — образующие алгебры I(J). Положим
i =/i +/1 ° о, -. grrfr+fro о; G47)
G48)
черта обозначает комплексное сопряжение. Тогда glt ..., g2re
I(JC) и все они принимают вещественные значения на J,
следовательно, их ограничения на J, которые мы также
обозначим gi, ..., g2r, являются инвариантами J. Пусть g —
инвариант J, gc—его комплексное продолжение на Jc. Тогда
gc — инвариант Jc и gc = P(fi, ¦¦¦¦,/,) для подходящего полино-
ма Р. ПОСКОЛЬКУ fi=gi+yf^\gr + i, -,fr=g, + yf--lg2r, ТО gC
и g полиномиально выражаются через #ь ..., g2r. Пусть (JCY —
централизатор а в Jc и Cent(yc)° — его центр. Тогда Cent(y )" =
= Cent J' + yJ — 1 Cent J" и всякий элемент бе Cent J" является
линейной комбинацией дифференциалов dfl(a), ..., dfr(a) с ком-
плексными коэффициентами в силу а), следовательно, Ъ являет-
ся линейной комбинацией дифференциалов dgl(a), ..., dg2r(a)
с вещественными коэффициентами, что и требовалось доказать.
5. Поскольку инварианты J постоянны на О, но не
постоянны на Кг, то, используя лемму 4, на образе отображе-
ния Р, т.е. на Р(Т*М), получим - dim О + dim Kv независимых
функций из набора FKa, Fel(j), keR. Следовательно, среди
функций F(P(x) + Xa) имеется по меньшей мере - dimO+ dimKv
независимых на Т*М функций. Далее, - dim О + dim Kv =
= dim V/V+ dim V= dim V= dim M.
Функции F^a(X) являются интегралами движения в ин-
волюции уравнения Эйлера Х=[Х, фв,ь,в(^)], которое гамиль-
тоново на орбитах R в J с гамильтонианом hebyD (X) = - Q (X,

308 ГЛ. 9. ПОЛНАЯ ИНТЕГРИРУЕМОСТЬ ПО ЛИУВИЛЛЮ
ФаьвРО) В силу соотношения {/оР, goP} = {f, g}oP получаем,
что функции F(P(x) + Xa) являются интегралами движения
в инволюции гамильтоновой системы на Т'М с гамильтониа-
ном HabD(X) = habJ)(P(X)). Поскольку гамильтониан
Ha,b,D является гамильтонианом геодезического потока на Т'М
метрики dSa,b,D и набор интегралов движения F(P(X) + Xa)
содержит независимые функции на Т'М в количестве, равном
размерности М, то теорема доказана.
6. Обозначения. Пусть S" — стандартная единичная сфе-
ра в R"+1. Группа SO(«+1) стандартным образом действует на
сфере S".
7. Теорема (А. В. Браилов). Пусть a, beg\(n+\, R
a = diag(au ..., an+l), b = diag(bu ..., bn + l), аг >...>ап+1
bi>...>bn+l; Q(X, Y)= — -trXY— инвариантная билинейная сим-
метрическая невырожденная форма на gl (и + 1, R), положитель-
но определенная на so(n+ l)c gl(«+1, R); фаЬ = ас1~1аA(,—
Q-симметричный оператор; группа SO(n+l) стандартным об-
разом действует на сфере S" = { у\ +...+у%+1 = 1}, P = PQ:
T'S"-*so(n+\) — соответствующее отображение моментов;
dSa.b—риманова метрика на S", соответствующая (при преоб-
разовании Лежандра) квадратичному гамильтониану НаЬ, где
Ha,b(q)=-Q{P(q), Ч>а,ь(Р{я))) для qeT'S". Тогда: а) геодезический
поток на T*S" римановой метрики ds\b имеет п независимых
квадратичных интегралов в инволюции Н1, ..., Н„, где Hk(q) =
= \Q{P(q)^ak(P{q)% ak = dmg(ak1,...,akn + 1) и qeT'S"; б) если
', ..., а„+\), то при замене yi = xilsjai, /=1, ..., и+1,
Гх2 х2 ~\
метрика dslj, переходит в метрику —^+ ...-{—^ х
х {dx\ + ... + dx%+1), конформно эквивалентную стандартной
метрике
%+1), фр у
dx\ + ...+dx^+l эллипсоида <—+...-I—— = 1 >.
(«1 а„+1 J
( J
Доказательство получается непосредственным вычислением,
см., например, [353].
8. Замечание. Мы обобщим предыдущую конструкцию.
Для этого нам потребуется новое понятие. Алгебра операторов,
коммутирующих с представлением группы Ли, коммутативна
тогда и только тогда, когда каждое неприводимое представле-
ние группы Ли R входит в данное представление с кратностью
не выше один. По аналогии с этим «квантовым» свойством
дадим следующее
9. Определение. Гамильтоново действие группы Ли R на
симплектическом многообразии М называется свободным от

§ 54 ИНТЕГРИРУЕМЫЕ СИСТЕМЫ 309
кратностей, если кольцо Л-инвариантных функций на М ком-
мутативно относительно скобки Пуассона.
10. Определение. Рассмотрим отображение моментов
Р: M2n-+J', отвечающее гамильтонову действию группы Ли
R с алгеброй Ли J на симплектическом многообразии М. Функции
вида /о Р на М2п, где /еСж(У'), назовем, следуя терминологии
Гийемина и Стернберга, коллективным, см. [370]. Вполне интегри-
руемую систему, гамильтониан которой является коллективным
и все первые интегралы таковы же, назовем вполне интегрируемой
системой коллективного типа, см. [187], [370], [441].
11. Теорема (см. [374]). Пусть на симплектическом
многообразии М гамильтоново действует группа Ли R. Тогда
если М допускает вполне интегрируемую гамильтонову систему
коллективного типа, то действие группы Ли R на М свободно от
кратностей.
12. Замечание. В случае групп U(n) и О (и) действие
свободно от кратностей тогда и только тогда, когда на
М имеется вполне интегрируемая гамильтонова система коллек-
тивного типа, см. [371], [374].
В следующей теореме устанавливается связь между пред-
ставлениями групп Ли, свободными от кратностей, и сущест-
вованием вполне интегрируемых гамильтоновых систем коллек-
тивного типа, см. [373].
13. Теорема. Действие группы Ли R на симплектическом
многообразии М свободно от кратностей тогда и только тогда,
когда представление Тд группы Ли R в пространстве L2(M)
свободно от кратностей, где Tgf(m)=f((g ){т)\, feL2(M).
14. Замечание. Для компактных групп (Р, Q) следующие
три условия эквивалентны: а) все /"-инвариантные гамиль-
тоновы системы на T*(PlQ) являются вполне интегрируемыми
системами коллективного типа; б) спектр представления Тд,
geP, в пространстве L2(P/Q) прост; в) алгебра /"-инвариантных
функций на T*(P/Q) коммутативна. Выделим эту ситуацию
в виде отдельного определения, см. [185].
15. Определение. Пусть G — редуктивная вещественная
(или комплексная) алгебра Ли, ф — невырожденная билинейная
инвариантная форма на G, Н—редуктивная в G подалгебра,
Gx — централизатор элемента х, Hx = Hf]Gx. Пусть М={хе
G\cp(x, Н) = 0). Подалгебра Н алгебры G называется сферической,
а пара (G, Н) — сферической парой, если для всех точек из
некоторого открытого множества UcM выполнены эквивалент-
ные условия:
1) dim (GХ/Нх) + idim (G /G х) = dim (G/#);
2) dim(GX/Hx)+ dim(H/H*)= dimM;
3) (rkG—ткНх)+ dim{HjHx)= dim(G/ff).

310 ГЛ 9. ПОЛНАЯ ИНТЕГРИРУЕМОСТЬ ПО ЛИУВИЛЛЮ
Пара групп (Р, Q) называется сферической, если соответст-
вующая пара алгебр (G, Н) сферическая. В этом случае
Q называется сферической подгруппой в Р.
16. Замечание. В [402 ] получена классификация сферичес-
ких подгрупп простых компактных групп Ли.
17. Замечание. Все симметрические пары (G, Я), т. е. такие
пары, что //—алгебра неподвижных точек инволютивного авто-
морфизма редуктивной алгебры G, сферические, см. [184], [185].
18. Обозначения. Пусть G — полупростая комплексная
алгебра Ли, К—ее подалгебра Картана. Символом /?(Л) будем
обозначать неприводимое представление алгебры Ли G со
старшим весом Л (см. [65], [81]), символом Я'(А) — контра-
градиентное представление, буквой г\ — одномерное тривиаль-
ное представление. Если {а,-} — простые корни G относительно
К, {ф(}—соответствующие фундаментальные веса, то Л = ?Л,ф,,
Л.-eN. Простые корни нумеруем в том же порядке, как в [55].
19. В табл. 6 приведен список несимметрических сферических
пар (G, //), где G—простая классическая комплексная алгебра
Ли, Н—редуктивная в G подалгебра, указано также представле-
ние у, определяющее вложение Н в G.
20. Определение. Система типа Калоджеро — Сазерлен-
да—это система, определяемая гамильтонианом
H=\ipj+g2iv(qj-qk), G49)
где потенциал имеет специальный вид. В [328] изучался
потенциал, для которого v(Q = b,~2+^J,2, а в [498] — потенци-
ал, для которого v(?,) = sin~2?,.
Эти классические системы допускают обобщение, использу-
ющее симметрические пространства. При этом варьируется как
набор функций и(^), так и область изменения индексов
суммирования.
21. Класс функций. Будем предполагать, что функция v(L,)
является одной из следующих пяти: I) v{l,) = ^ ; II) и(^) =
= sh; Ш) »($) = sin-2S; IV) !>($)= Т®; V) v(Q = ?,-2+?.?,
где Т —функция Вейерштрасса.
Таблица 6
1
2
3
G
Ar, r ^2
Ar, r^2
A2r,r>2
H
Ак®Аг^к-,,г-к-\^к^\
А,-,
с.
j
Л(ф1)(Х)Г) + Г)(Х)/?(ф1)
/?(ф! )+ Г)
Л(Ф.) + Л

54. ИНТЕГРИРУЕМЫЕ СИСТЕМЫ
311
Продолжение табл. 6
4
5
6
7
8
9
10
11
12
13
14
15
G
Л2„ г>2
В„ г>2
C,,r»3
D2r+i
й5
Д4
Д4
Д4
ВА
в,
Е6
Н
СгфС
Сг-,фС
Л2г
ВзФС
Л,©В2
в,
G2
Въ
G2
D5
Л2
j
Л(ф!) + Г1
Л(ф,) + Л'(ф1) + П
Л(ф1) + 2г|
Л(ф,) + Л'(ф1)
«(Фэ) + 2Т1
Л(ф1)®Л(ф2)
Л(Фз)
R(<?i) + r\
Л(фз) + Л
Л(Ф1)
Л(ф1) + Л(ф5) + т1
Л(ф1) + Л(ф2) + т1
22. Индексы. С каждым римановым симметрическим про-
странством M=P/Q, где Q — максимальная компактная под-
группа, связана неприводимая ограниченная система корней,
которая имеет тип А„, Вп, С„, Dn, Еь, Е-,, Е8, F4, G2 или ВС„
[160]. Пусть А+—подсистема положительных корней.
23. Потенциалы. Определим потенциал U(q) формулой
G50)
е Д+
где !;(?) имеет вид, описанный в п. 21.
В случае системы корней А„ мы имеем потенциал Калод-
жеро — Сазерленда G49).
24. Пример. Системы, отвечающие ВС„, имеют потенциал
+gl I vBqk). G51)
it = i
25. Теорема (см. [206 ]). Гамильтоновы системы с потен-
циалами Калоджеро — Сазерленда (см. п. 23) являются вполне
интегрируемыми системами для неособых систем корней.
26. Замечание. Системы, описанные выше, допускают
явное интегрирование. С этими вопросами можно познакомить-
ся по обзору [206].
Теперь мы изложим еще одну конструкцию гамильтоновых
систем, связанных с эрмитовыми симметрическими простран-
ствами и принадлежащую Форда, Войцеховскому и Маршаллу
[354]. По этой схеме получаются гамильтоновы системы

312 ГЛ. 9. ПОЛНАЯ ИНТЕГРИРУЕМОСТЬ ПО ЛИУВИЛЛЮ
1 "
с гамильтонианом Н=- ? pl+ V(qi, ...,qn), У которого потен-
2 t=i
циал V имеет степень 4. Важность рассмотрения таких систем
связана с линейными аппроксимациями четных потенциалов в
окрестности особой точки. В настоящее время известно ограни-
ченное число вполне интегрируемых потенциалов степени 4.
В качестве примеров отметим
к к к
27. Обозначения. Пусть симметрическое пространство связа-
но с симметрической алгеброй Ли (G^ а) и G = H+V—
соответствующее разложение симметрической полупростой ал-
гебры Ли G. Имеют место включения [Н, Н]аЩ [Н, V]cV,
[V, V]czH. В случае эрмитова симметрического пространства
существует такой элемент АеН, что H—CG(A)={be
eG\ [А, Ь] = 0}. Пусть К—подалгебра Картана в G. Элемент
А можно выбрать из подалгебры К. Имеем F= V+® V~, [А, Н] = 0,
[А, Х±]=±аХ± (число а одно и то же для всех X±eV±).
28. Спектральная задача. Рассмотрим следующую задачу,
которая приводит к интегрируемым потенциалам. Для Q(x, t)e
е V рассмотрим спектральную задачу
Ч', = (М + е)Ч', G52)
где ц — спектральный параметр, /—время и временная зависи-
мость ищется из условия
Ч, = Р(х, t, ц)Т. G53)
Условие совместности G52) и G53) вместе с изоспектральным
условием ц, = 0 имеет вид Qt = Px—\^A-\-Q,P\.
Пусть е±а—базис пространства К*, Л — постоянная диаго-
нальная матрица,
^^ G54)
Уравнения совместности имеют вид
, G55)
Р. Г, 8
-«Т" = г«"+ Z R-i-1.-Sr-'r-'qt + <oar-; G56)
Р.Т.*
где /?p,Y,-g—тензор кривизны данного симметрического про-
странства, числа сэа—линейные комбинации собственных значе-
ний матрицы Л.

§ 54 ИНТЕГРИРУЕМЫЕ СИСТЕМЫ 313
29. Потенциалы. Интегрируемые потенциалы соответствуют
стационарным потокам уравнений совместности G55), G56).
Стационарные потоки являются гамильтоновыми системами,
и если положить r~"=—q" (^_a= —/>„), то соответствующий
гамильтониан имеет вид
+^IX-aM<?°J- G57)
30. Явный вид. Имеются четыре бесконечные серии эр-
митовых симметрических пространств М. Им отвечают по-
тенциалы
qff,
G58)
, G59)
I CO, E,2
3
I (8,2+ l)??J-(«i«3-dJ' G60)
, G61)
J- G62)
Первые два потенциала отвечают симметрическому про-
странству SU(w + «)/S(U(w)xU(«)) класса АШ. Третий потен-
циал отвечает симметрическому пространству Sp(«)/U(«) клас-
са CI в случае и = 2. Четвертый потенциал отвечает симмет-
рическому пространству SOBn)/U(«) класса Dili для и = 4.
Пятый потенциал отвечает симметрическому пространству
SO(n + 2)/SOB)xSO(«) класса BDI для и = 4.
31. Теорема (см. [354]). Гамилътоновы системы, от-
вечающие перечисленным выше потенциалам G58) — G62), явля-
ются вполне интегрируемыми.
32. Замечание. В рамках теории симметрических про-
странств можно дать многомерное обобщение случая Ковалев-
ской. С этой целью рассмотрим компактную простую группу
Ли Р и ее замкнутую подгруппу Q такую, что факторпростран-
ство P/Q является симметрическим, см. [293]. Тогда G-H+V,

314 ГЛ. 9 ПОЛНАЯ ИНТЕГРИРУЕМОСТЬ ПО ЛИУВИЛЛЮ
где Н—алгебра Ли группы Ли Q, а V—ортогональное
дополнение к Н в G относительно формы Киллинга.
33. Конструкция. Изложим схему построения интегрируемых
гамильтонианов, предложенную А. М. Переломовым. Сохра-
ним обозначения предыдущего пункта. Имеем неприводимое
представление ц: Q -» GL (V) стационарной подгруппы Q в про-
странстве V. Рассмотрим такое неприводимое представление р:
Р -> GL (W) группы Ли Р, что неприводимое представление
ц группы Q в V входит в ограничение p\Q с единичной
кратностью. Пространство W, в котором действует представле-
ние р, разложим в прямую сумму W=Wo@Wu где
Wo — подпространство, в котором действует представление,
изоморфное ц, a Wx — ортогональное дополнение
к Wo (пространство Wo изоморфно V).
Пусть G = G + W—полупрямая сумма G и W по представле-
р
нию р, P = P-W—соответствующее полупрямое произведение.
В итоге мы имеем разложение алгебры Ли G в прямую
сумму четырехподпространств: G = H+V+W0+Wl. Тогда для
пространства G* имеем представление G* = H'+V*+W*0+W\,
где dim V* = dim Wo = п и К* и W'o изоморфны относительно
действия группы Q.
34. Обозначения. Обозначим la, rtj, pk и q» базисные линейные
функции в пространствах Н", V, W*o и W\. В пространствах
гладких функций на Н' и V* существуют инвариантные
относительно действия коприсоединенного представления груп-
пы Q квадратичные функции, которые обозначим /2(/а) и I (rtj)
соответственно.
35. Гамильтонианы. Интересующая нас динамическая систе-
ма задается гамильтонианом
G63)
где ур = улР], у = (у1, —, у")—постоянный вектор пространства
36. Случай симметрического пространства SO(n+l)/SO(n).
Итак, пусть P = SO(n+l), Q = SO(n), P = PW=E(n+\)—груп-
па движений (и+1)-мерного евклидова пространства, W=Rn+l,
W0 = R~, Wt=Rl. Пусть ljk=-tkj и рт (j,k,m^\,...,n+\)-
стандартный базис в пространстве линейных функций на
G' = H'@V* и W"=W'0@W\ соответственно со скобками
Пуассона
{1ц, и=Ь»1ш + Ь1тГ»-Ь1кГ]т-Ьм1л, G64)
{1ц, ,Рь} = 8д/>,-bapj, {pj, pk}=0. G65)

§ 54 ИНТЕГРИРУЕМЫЕ СИСТЕМЫ 315
В соответствии с п. 36 в качестве гамильтониана возьмем
h=\U i iib+vini+iwX G66)
где nj = ljn+l, q=pn+1.
Уравнения движения имеют вид
37. Замечание. Гамильтонианы, определенные в п. 35,
зависят от параметров а, Р, yJ, /=1,..., п. В силу инвариант-
ности скобок Пуассона при замене pj -> Xpj свойства системы
существенно зависят лишь от параметра а/р.
38. Теорема (А. М. Переломов). Динамическая, система
G67) при а = 2р обладает представлением Лакса L= [L, М],
M = cl, где /=||/у||,
L=-^/2 + P«®« + (Y®/7+p®Y). G68)
При и = 2 эта система совпадает с системой, описывающей
движение твердого тела в случае Ковалевской.
39. Замечание. Конструкция, изложенная в предыдущих
пунктах, допускает обобщение, найденное А. Г. Рейманом
и М. А. Семеновым-Тян-Шанским, см. [490]. Это обобщение
я
связано с алгеброй Ли е(р, q) = so(p)+®Rp, p^q, являющейся
полупрямой суммой q копий пространства Rp и so(p) (здесь
ч
©Rp — абелев идеал в e{p,q)).
40. Определение. На пространстве e(p,q)\ дуальном
к алгебре Ли е(р, q), определим гамильтониан
I 'Ь+с I lb+ I 'у)" I (Л. е,), G69)
где еи...,вр—фиксированный ортонормированный репер,
/= ||/0,||еso (р), /ь ...,/, — векторы Пуассона, c = const.
Обозначим / матрицу размера pxq, составленную из
столбцов /ь ...,/,, и пусть а — матрица размера pxq с элемен-
тами atj = 8ij. Введем ортогональный проектор Р на подпрост-
ранство R", натянутое на векторы еи ..., е^.
41. Теорема (см. [490]). Уравнения Эйлера на e(p,q)*
с гамильтонианом G69) обладают представлением Лакса

316 ГЛ. 9. ПОЛНАЯ ИНТЕГРИРУЕМОСТЬ ПО ЛИУВИЛЛЮ
— = [L, М], где L, Meso(p, q) [X, X'1 ]. В естественных блоч-
dt
ных обозначениях имеем
и . и н _ и
G70)
а
||o о ||1| *.- о Iя" G71)
здесь (oeso(p)—матрица угловой скорости, а)^ = 2/у для i,j^q,
(?>ij = clij для i,j>q и соу = /у для i^q,j>q. Инварианты матрицы
L (к) являются интегралами уравнений Эйлера с гамильтонианом
G69).
42. Замечание. Эквивалентное представление Лакса в слу-
чае q=p— 1 было найдено А. М. Переломовым [472], см. выше.
43. Замечание. Конструкцию п. 39 можно обобщить на
симметрические пары (Р, Q), когда Q не является простой.
Например, с римановой симметрической парой (SOC, 3),
SO C) х SO C)) связана система с гамильтонианом
h = \ (Ij + l22+2l23 + v2)+ X (К%, х)(х, <?,)- X (К%, е,), G72)
являющимся обобщением случая Ковалевской и задачи Нейма-
на (см. [490]).
§ 55. Коммутативные подалгебры универсальной
обертывающей алгебры
1. Определения. Универсальная обертывающая алгебра
U(L) алгебры Ли L имеет возрастающую фильтрацию
U(L)= U Uk(L), G73)
* = о
в которой U (L) есть подпространство элементов, представля-
емых в виде (некоммутативных) многочленов степени не выше
к от элементов алгебры L, см. [88]. Из определяющих
соотношений алгебры U(L) следует, что
[Uk(L), U\L)\cUk+l-\L). G74)
Ассоциированная градуированная алгебра
grU(L) = P(L)=® Pk(L), Pk(L)=Uk(L)/Uk-1(L) G75)
Jt = O
согласно теореме Пуанкаре—Биркгофа —Витта канонически
изоморфна симметрической алгебре пространства L. Однако
помимо коммутативно-ассоциативной операции умножения

§ 55. КОММУТАТИВНЫЕ ПОДАЛГЕБРЫ 317
в ней благодаря G74) естественным образом вводится лиевская
операция {х, у} — скобка Пуассона — Ли — Березина (мы будем
называть ее просто скобка Пуассона), для которой {Pk(L),
P,(L)}cPk+l-l(L). А именно, при ueUk(L), veUl(L) принима-
ется, что
{и+ик~1{Ь), t)+t/'-1(L)} = [M, v] + Uk+l~2(L). G76)
Это определение корректно ввиду G74). Другие эквивалентные
определения см. в [270].
Скобка Пуассона связана с умножением тождеством
Лейбница
{x,yz} = {x,y}z+y{x, z). G77)
Она однозначно определяется этим свойством и «начальными
условиями» {х, у} = [х, у ] при х, yeL.
Элементы х, yeP(L) будем называть коммутирующими,
если {х, у}=0. В соответствии с этим будем понимать и такие
термины, как «коммутативное подпространство» (в частности,
коммутативная подалгебра) и «централизатор» (какого-нибудь
подмножства) в алгебре P(L). Из G77) следует, что если
какие-либо элементы алгебры P(L) попарно коммутируют, то
порожденная ими подалгебра коммутативна.
2. Замечание. Пусть Т—связная группа Ли, имеющая
L своей алгеброй Ли. Если понимать элементы алгебры P(L)
как многочлены на пространстве L*, сопряженном к L, то
скобка Пуассона в P{L) будет совпадать с обычной скобкой
Пуассона функций на орбитах коприсоединенного представле-
ния группы Ли Т относительно канонической симплектической
структуры на этих орбитах. Отсюда следует, что степень
трансцендентности любой коммутативной подалгебры алгебры
P(L) не превосходит d(L) = - (dimL-bindL), где indL (индекс
алгебры Ли L) — коразмерность орбиты общего положения
коприсоединенного представления группы Ли Т. В работе [188]
для любой полупростой алгебры Ли L методом сдвига
инвариантов были построены коммутативные подалгебры ал-
гебры P(L), степень трансцендентности которых равна d(L).
3. Определение. Если А — коммутативная подалгебра
алгебры U(L), то grA = B—коммутативная подалгебра алгебры
P(L). Будем говорить, что А—подалгебра конечного типа, если
алгебра В конечно порождена. Нетрудно показать, что в этом
случае степени трансцендентности алгебр А и В совпадают.
Таким образом, степень трансцендентности любой коммутатив-
ной подалгебры конечного типа алгебры U(L) не превосходит
d(L). Существуют ли в U(L) коммутативные подалгебры
конечного типа, степень трансцендентности которых равна

318 ГЛ 9 ПОЛНАЯ ИНТЕГРИРУЕМОСТЬ ПО ЛИУВИЛЛЮ
d(Ly. Примеры таких подалгебр, во всяком случае, имеются.
Так, конструкция «базиса Гельфанда — Цетлина» в простран-
ствах неприводимых представлений алгебр Ли si (и) и so (и)
связана именно с такими подалгебрами алгебр U(s\(n))
и U(so(n)) соответственно.
4. Замечания. В настоящем параграфе, следуя работе
Э. Б. Винберга [64 J, для произвольной полупростой алгебры Ли
L делается попытка «квантования», т. е. поднятия в U(L),
коммутативных подалгебр алгебры P{L), получаемых методом
сдвига инвариантов.
Проведенные исследования дают также новый подход
к определению самих подалгебр Мищенко — Фоменко, показы-
вающих большую естественность, чем это можно было пред-
положить, исходя из первоначального определения.
5. Обозначения. Пусть L — произвольная алгебра Ли.
Алгебры U(L) и P(L) можно рассматривать как алгебры Ли
относительно операции коммутирования и скобки Пуассона
соответственно. Алгебра L канонически вкладывается в эти
алгебры Ли. Образ элемента xeL в P(L) будем отождествлять
с х (и обозначать той же буквой), а образ х в U(L) будем
обозначать х. Вложение L^>U(L) продолжим до изоморфизма
векторных пространств P(L) -> U(L), при котором
xl...xk^x1 ...xk = - ^ xar..xOk (xu...,xkeL). G78)
' aeSk
Вложения алгебры L в U(L) и P(L) определяют на этих
пространствах структуры L-модулей. Отображение G78) являет-
ся изоморфизмом /.-модулей. Положим Uk(L) = Pk(L). Тогда
U(L)= © Uk(L) G79)
* = о
— разложение в прямую сумму L-подмодулей (но, вообще
говоря, не градуировка алгебры).
6. Конструкция. Пусть теперь L — полупростая комплексная
алгебра Ли, Я—ее картановская подалгебра, А — система
корней алгебры Ли L относительно Н. Пусть (X, Y) —
какое-нибудь инвариантное скалярное произведение в L. В каж-
дом корневом подпространстве La выберем элемент ел так,
чтобы (еа, е~а)=\.
Будем рассматривать коммутативные подалгебры алгебры
P(L) (соответственно U(L)), содержащие Н (соответственно Я).
Централизатор Я в P1(L) = L совпадает с Я; централизатор
Я в P2(L) есть прямая сумма Рг{Н) и линейной оболочки
произведений вида еяе_„ (аеА), которую обозначим буквой Q.
Соответственно этому централизатор Я в U2(L) есть

S 55. КОММУТАТИВНЫЕ ПОДАЛГЕБРЫ 319
Всякий элемент qeQ однозначно представляется в симмет-
ризованной форме
9= !?.<?«<?-. (?.=*?-.еС). G80)
ore Д
При этом
q= Z qaeae-.. G81)
ае Д
В частности, если {Л,,..., Л,} — ортонормированный базис
подалгебры Я, то элемент
c(L)=Zhf+?e*e^eP2(H)®Q G82)
1=1 3 ? Д
лежит в центре всей алгебры P(L). В алгебре U(L) ему
соответствует элемент Казимира
<?(?)= ?й,2+?е.е_,,е1/2(Я) + <2, G83)
i=l аеД
лежащий в центре алгебры V{L). Элемент c(L) также будем
называть элементом Казимира.
Рассмотрим произвольный набор (^i. •••> 9*)сB> гДе
?i= I *..<?«*-. (?,.„ = ?,.-«еС). G84)
аеД
Каждому корню аеА сопоставим точку paL = (qy,^,¦¦¦,pkiX)eCk
(так что />„=/>_„).
7. Теорема. Следующие условия эквивалентны:
[7 ?Л Р /
2) W.-> ^J=° пРи всех 'J'
3) Зля любых корней а, р, уеА таких, что а + Р + у = 0, точки
Р*> Р& Ру лежат на одной прямой.
8. Определение. Набор (?i, .•.,?*)> удовлетворяющий
эквивалентным условиям из теоремы 7, назовем kotktkj-
тативным. Набор (qu ..., qk) назовем разделяющим, если
Ря=?р$ при a?t±p.
9. Теорема. Для любого регулярного элемента hoeH
и любых элементов /гь ..., hke H набор (qt, ..., qk)eQ, определя-
емый формулами
9<=1^7П ««*-.. '=1'-'/?' G85)
коммутативен. Обратно, если алгебра L проста, то любой
разделяющий коммутативный набор (^ь •••> 0*)CQ ранга не
меньше 3 получается этим способом.

320 ГЛ 9 ПОЛНАЯ ИНТЕГРИРУЕМОСТЬ ПО ЛИУВИЛЛЮ
10. Замечание. Очевидно, что ранг набора (qi,...,qk),
определяемого формулами G85), ^>авен рангу набора (ht,..., hk)
и, значит, не превосходит / = rkL.
11. Следствие. Для любой полупростой алгебры Ли
L в пространстве Q не существует разделяющего коммутатив-
ного набора ранга, большего /=rkL.
12. Пример. Условие разделяемости в формулировке те-
оремы существенно, как показывает следующий пример. Пусть
алгебра L содержит собственную полупростую регулярную
подалгебру Ly того же ранга /. Пусть AtcA — система корней
алгебры Lx. Обозначим Qt линейную оболочку произведений
вида еае^а, где гхеА1. Тогда по формулам G85), примененным
к алгебре Lt, мы можем построить линейно независимый
коммутативный набор из / элементов пространства Qx. Присо-
единяя к нему элемент ? еае-а (проекцию на Q элемента
ае Д
Казимира алгебры L), мы получим линейно независимый
коммутативный набор из /+1 элементов пространства Q.
Условие на ранг также существенно, так как проекция на
Q элемента Казимира вместе с любым элементом q e Q
образует коммутативный набор, но в общем случае далеко не
всякий элемент qeQ может быть представлен в виде
V aW с е
13. Замечания. Согласно первой части теоремы с каждым
регулярным элементом ИоеН можно связать /-мерное ком-
мутативное подпространство
Q. G86)
-д«(Ао) "
С другой стороны, методом сдвига инвариантов по каждому
регулярному элементу hoeH строится однородная коммутатив-
ная подалгебра L(h0) алгебры P{L), имеющая степень транс-
цендентности d{L). При этом известно, что [274]
Т IU \Г\Т t/ Т (U \Г\ Т> 11 \ Т> t U\(?s ГЛ (U \ /C74!
Lj\TIq)\ |х^ — П, х^^/7о^[ \12\*-'/ — * 2 \^ / ^f ^ Vo/- V' '/
В силу теоремы 7 подпространство Q(ho\cQ поднимается до
коммутативного подпространства Q(ho)<^Q, элементы которого
к тому же коммутируют с элементами из Н. Таким образом,
образующие первой и второй степени алгебры L(h0) поднима-
ются до попарно коммутирующих элементов алгебры U(L).
14. Определение. Путем предельного перехода из под-
пространств вида Q(h0) можно получить другие /-мерные
коммутативные подпространства пространства Q. Все получен-
ные таким образом подпространства (включая сами подпрост-

§ 55. КОММУТАТИВНЫЕ ПОДАЛГЕБРЫ 321
ранства Q{h0)) будем называть главными коммутативными
подпространствами. Для их явного описания введем некоторые
понятия.
15. Определение. Будем рассматривать сходящиеся сте-
пенные ряды с коэффициентами из Н от переменной /,
принимающей значения в С. Будем называть ряд А0 = /г@0> +
+ h{o)t-\-hio)t2+ ... (h^eH) регулярным, если он удовлетворяет
следующим эквивалентным условиям:
1) /г0 — регулярный (полупростой) элемент алгебры L®C((/))
над полем С((/)) рядов Лорана;
2) элемент ho{t)eH регулярен при всех достаточно
малых ?#0;
3) никакой корень осеЛ не обращается в нуль на всех
элементах h^\ /г</>, И<2), ...
16. Обозначения. Для всякого ряда h = hm + hn)t + h{2)t2 + ...
(hik)eH) обозначим Ak(h) подсистему корней, обращающихся
в нуль на /г@), /гA), ...,/г^». Ясно, что А = А0(Л)=эД1(Л)=>
Д(Л) ... Ряд /г0 регулярен тогда и только тогда, когда
o) = 0 для некоторого т. Будем называть ряд h подчинен-
ным ряду /г0, если Лк (Л)=>Лк (Ло) при всех к. В этом случае при
<xeAk(h0)\Ak + 1(h0) существует предел
,_оа(йо(О) <*С«")' '
и, следовательно, если ряд h0 регулярен, существует предел
При фиксированном h0 элементы вида G89) образуют подпро-
странство, которое обозначим Q(h0).
17. Теорема. Для всякого регулярного ряда Ио имеем
e(Ao)=lime(Ao(O), G90)
г —о
и, следовательно, Q(h0) есть главное коммутативное подпрост-
ранство пространства Q. Обратно, всякое главное коммутатив-
ное подпространство получается таким способом.
18. Замечание. Различным регулярным рядам может,
конечно, отвечать одно и то же коммутативное подпространст-
во. Пользуясь этим, можно сделать описание главных ком-
мутативных подпространств более эффективным.
19. Определение. С помощью инвариантного скалярного
произведения отождествим Н* с Я и, таким образом, будем
рассматривать корни как элементы Я. Регулярный ряд
h0 называется каноническим, если для любого к выполнены
условия:

322 ГЛ 9. ПОЛНАЯ ИНТЕГРИРУЕМОСТЬ ПО ЛИУВИЛЛЮ
) о<*(о)>;
С2) проекция ho на линейную оболочку каждой нераз-
ложимой компоненты системы Ак(И0) отлична от нуля.
Из С2) следует, что если Ak(ho)=?0, то Ак + 1 (по)фАк(по).
Поэтому канонический ряд автоматически конечен.
20. Определение. Канонические ряды /г0 и Ио называются
эквивалентными, если для любого к выполнены условия:
El) Ak(h0) = Ak(h0);
Е2) проекции элементов /ij,' и Л&° на линейную оболочку
каждой неразложимой компоненты системы Ак(И0) пропорци-
ональны.
Заметим, что если условия Е1) и Е2) выполнены для
какого-то к, то автоматически Ак + 1 (И0) = Ак+1 (/Го).
21. Теорема. Всякое главное коммутативное подпростран-
ство пространства Q имеет вид Q(h0), где h0 — канонический
регулярный ряд, причем ряд п0 определен однозначно с точ-
ностью до эквивалентности.
22. Замечания. К этому можно добавить, что если
/г0 — канонический регулярный ряд, то в приведенном выше
определении пространства Q(h0) можно ограничиться (ав-
томатически конечными) рядами /г, в которых h(k)е (Ак(/г0))
при всех к.
23. Пример. Пусть L — s\(n), H—подалгебра диагональ-
ных матриц и ho = hioO) + h^)t+ ... + Л(ОП~2)/В , где /j{j° =
= diag(l,..., 1, — (и — к— 1), 0,..., 0). Если обозначить е,- линей-
ную функцию на Н, равную г'-му диагональному элементу, то
At(^o) — подсистема корней вида б, — Ej, где i,j^n — k, т. е.
система корней алгебры si (и —/с), естественным образом (в виде
«левого верхнего угла») вложенной в si (я). В частности,
Аи _! (Ло) = 0, так что ряд Ио является регулярным (и канониче-
ским). Ряд hk = h(°) + h@1)t+ ... +h^~l)tk^1 (k=\,...,n-\), очевид-
но, подчинен ряду h0 и
^к^'--Л:-'- G91)
Следовательно, подпространство Q(h0) совпадает с линейной
оболочкой элементов
X е„е-„, к = 0, 1,...,п-2, G92)
представляющих собой проекции на Q элементов Казимира
подалгебр si (и — Л:).
Подпространство Q(h0) в этом примере является частью
коммутативной подалгебры М алгебры P(s\(n)), порожденной
подалгеброй Н и центрами подалгебр P(s\(n — k)), /c = 0, 1,...
..., и — 2. Подалгебра М поднимается до коммутативной под-

§ 55. КОММУТАТИВНЫЕ ПОДАЛГЕБРЫ 323
алгебры А алгебры U(sl(n)), порожденной подалгеброй Н и цен-
трами подалгебр U(s\(n — k)). Весовые подпространства алгебры
А в пространстве V любого неприводимого линейного представ-
ления алгебры sl(n) одномерны; их базисные векторы и состав-
ляют базис Гельфанда—Цетлина пространства V.
24. Замечания. Докажем, что коммутативная подалгебра
алгебры P(sl(n)), порожденная подалгеброй Н и центрами
подалгебр P(s\(n — k)), к = 0, 1,..., п — 2 (см. пример выше),
является пределом коммутативных подалгебр, получаемых
методом сдвига инвариантов.
Нам будет технически удобнее иметь дело не с алгеброй
si (и), а с алгеброй gl(«), хотя она и не полупроста. Имеется
гомоморфизм проектирования п: gl(n) ->sl(w), X-+X-- (lrX)E.
Он индуцирует гомоморфизм проектирования f(gl («))->
->P(s\(n)), который обозначим той же буквой п. С помощью
этого гомоморфизма из любого результата, который мы
получим для алгебры gl(«), можно будет вывести соответст-
вующий результат для алгебры si (и).
25. Определение. Центр Zn алгебры P(g\(n)), как извес-
тно, состоит из инвариантов естественного действия алгебры
gl(«) в P(g\(n)). Опишем его образующие.
Обозначим etj{\ ^i,j^n) матричные единицы, составляющие
базис алгебры gi(«), и определим «главные миноры порядка г»
алгебры gl (n) как элементы
М„...,= XCsgna)^...^, G93)
где умножение понимается не как умножение матриц, а как
операция в алгебре P(gl(n)). Тогда суммы
Fr= I M,,...ir, r=\,...,«, G94)
i, <...<ir
алгебраически независимы и порождают Zn.
Пусть dijeDeTP(g\(n)) обозначает дифференцирование по etJ.
Для любой матрицы Jf=||ay|| положим дхи = ^а^8ии (ие
eP(gl(n))). В частности, пусть X=di&g(al, ...,ап), причем
аь...,а„ различны. Тогда согласно общему результату [188]
элементы
F,ik(au ..., аК)=±дкхРг, г=\, ...,«, к = 0, 1, ..., г- 1, G95)
алгебры P(g\(n}) попарно коммутируют и алгебраически незави-
симы. Порожденную ими коммутативную подалгебру обозна-
чим L(a,, ..., ап). Она имеет максимальную возможную степень
трансцендентности, равную d(gl(n)) = 2ln(n+l).

324 ГЛ. 9 ПОЛНАЯ ИНТЕГРИРУЕМОСТЬ ПО ЛИУВИЛЛЮ
Заметим, что элемент Frk(ai, ..., а„) есть сумма всевозмож-
ных членов, получаемых из членов выражения элемента Fr через
матричные единицы заменой каких-либо к диагональных мат-
ричных единиц соответствующими диагональными элементами
матрицы X.
26. Утверждение. Докажем, что подалгебра
-1, ..., t, \)cP(g\(n)) G96)
t—о
порождается центрами Zn-k подалгебр P(g\(n — k)), k = 0, 1, ...
..., и—1.
В выражении элемента Frk(t", ..., t, 1) члены наименьшей
степени по t, равной 2~1k(k—l), получаются при замене
в подходящих членах выражения Fr множителей en-k + ln-k+l, ...
..., е„„ соответствующими степенями /. При этом в качестве
коэффициента при tk{k~1)l2 получается сумма главных миноров
порядка г —к алгебры g\(n — k) (вложенной в gl(«) в виде левого
верхнего угла). Следовательно, эта сумма принадлежит С.
Отсюда и вытекает доказываемое утверждение.
27. Конструкция. Переходя к алгебре si (и), заметим, что
подалгебра P(s\(n))cPfg\(n)) аннулируется оператором дЕ и,
значит, dxu = drtXueP{s\\n)) при ueP(sl(n)), Xeg\(n). Поэтому,
применяя метод сдвига инвариантов к алгебре si (и), в качестве
исходной диагональной матрицы X можно без увеличения
общности рассматривать матрицу с произвольным следом.
Центр алгебры P(s\(n)) равен nZn и порождается элементами
7iFr, r = 2, ..., п. Поскольку эти же элементы вместе с элементом
Ft=E могут быть взяты в качестве образующих Zn, ком-
мутативная подалгебра алгебры P(sl(n)), получаемая методом
сдвига инвариантов исходя из матрицы X =diag(ab ..., an)eg\(n),
совпадает с подалгеброй nL{al, ..., а„).
Подалгебра nL = \\mnL(tn~l, ..., t, 1) порождается проекци-
ями на f(sl(«)) центров Zn~k подалгебр P(gl(n — k)),
к = 0, 1, ..., п— 1. Выберем в качестве образующих Zn-k проекции
на P(s\(n — к)) сумм главных миноров порядков не меньше
2 алгебры si (и —А:) и единичную матрицу En-keg\(n — к) (проек-
ция которой на P(sl(n — к)) равна нулю). Тогда мы получим, что
подалгебра nL порождается центрами подалгебр P(s\(n — к))
и проекциями на P(sl(n)) матриц Е„-к (к= 1, ..., п— 1), состав-
ляющими, как легко видеть, базис пространства всех диагональ-
ных матриц с нулевым следом.
Таким образом, коммутативная подалгебра алгебры P(sl(n)),
порожденная подалгеброй диагональных матриц (с нулевым
следом) и центрами подалгебр P(s\(n — к)), является пределом
подалгебр, получаемых методом сдвига инвариантов.

ЧАСТЬ 3
ГЕОМЕТРИЧЕСКИЕ И ТОПОЛОГИЧЕСКИЕ
СВОЙСТВА ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Глава 10
КАЧЕСТВЕННАЯ ТОПОЛОГИЧЕСКАЯ ТЕОРИЯ ИНТЕГРИРУЕМЫХ
СИСТЕМ НА СИМПЛЕКТИЧЕСКИХ МНОГООБРАЗИЯХ
§ 56. Элементы теории Морса
1. Определение. Пусть /: A/->R—гладкая функция на
многообразии М. Точка реМ называется критической точкой
функции/, если отображение df: ГРА/->Г/(Р)К = К касательных
пространств обращается в нуль. Если в окрестности U точки
р выбрана некоторая локальная система координат х1, ..., х", то
это условие примет вид —.(р) = 0, i—\,...,n.
2. Определение. Критическая точка реМ функции / на-
зывается вырожденной, если матрица вторых частных про-
изводных
н=Мр)=
дх'дх'
(Р)
G97)
вырождена, т. е. det #=0. Матрица Н называется матрицей
Гесса, а ее определитель — гессианом функции / в точке ре М.
Коранг матрицы /*,( р) называется степенью вырождения крити-
ческой точки реМ функции /: A/-»R. Критическая точка
р с нулевым индексом вырождения называется невырожден-
ной.
3. Определение. Гладкая функция / на многообразии
М называется функцией Морса, если все ее критические точки не
вырождены.
4. Лемма. Пусть/—гладкая функция на многообразии М,
а реМ—невырожденная критическая точка функции /. Тогда
в некоторой открытой окрестности точки р существуют такие
локальные координаты у1, ..., у", что в этих координатах
функция f запишется в виде f=f(p) — (V1J —... — (Vх) 2 +
+(ук+1)Ч...+(упУ-
Доказательство леммы 4 см., например, в [180], [103], [279].

326
ГЛ. 10 КАЧЕСТВЕННАЯ ТОПОЛОГИЧЕСКАЯ ТЕОРИЯ
5. Определение. Число X из леммы 4 называется индек-
сом критической точки реМ функции/: M-»R. Квадратичную
форму с матрицей /••(/>) на пространстве TjM) можно
привести к каноническому виду—(м J —...— (и1^ +(ик+1J +
+ ...+(и"J. Тогда число отрицательных коэффициентов равно
индексу X критической точки реМ. На рис. 43 схематично
указано строение окрестностей различных критических точек.
ЛЛ7
7 О
\О О
Рис. 43
6. Следствие. Невырожденные критические точки явля-
ются изолированными.
7. Лемма. Пусть /: U—>R — гладкая функция на области
t/czR". Тогда почти для всех линейных отображений L: R"->R
функция /+ L имеет только невырожденные критические точки.
Доказательство леммы 7 см. например, в [180], [103], [279].
8. Теорема. На всяком компактном гладком многообразии
существует функция Морса.
Доказательство см., например, в [180], [103], [279].
9. Замечание. Существует тесная связь между критиче-
скими точками гладких функций на многообразии и топологи-
ческими инвариантами многообразия. Точные формулировки
и доказательства соответствующих утверждений можно найти,
например, в [180], [103], [279].
10. Обозначения. Пусть/— функция Морса на многооб-
разии М. Введем обозначение /„ =/ ~ * (а) — поверхность уровня
функции/, отвечающая значению aeR. Пусть Qa={xeQ\)'(x)^
<а}, т. е. Qa состоит из всех точек, в которых значения функции
/ не превосходят а. Ясно, что dQa=fa (рис. 44).
11. Лемма (см. [180]). Пусть отрезок [а, Ь\ {где а<Ь) не
содержит критических значений функции /, т. е. в множестве
f~i[<a,b~\, лежащем в многообразии Q, на котором задана

§ 56. ЭЛЕМЕНТЫ ТЕОРИИ МОРСА
327
функция f, нет критических точек функции /. Тогда многооб-
разия fa и /j, диффеоморфны, кроме того, многообразия
Qa и Qb также диффеоморфны. При этом Qa является
деформационным ретрактом Qb (рис. 45).
12. Лемма (см. [180]). Пусть в слое f ~i [а, Ь1 = Qb\ Qa
имеется ровно одна критическая точка индекса А. Тогда
многообразие Qb гомотопически эквивалентно конечному клеточ-
ному комплексу, получающемуся из многообразия Qa приклейкой
к краю fa = 5Qa одной клетки <зк размерности X (рис. 46).
Рис. 45
13. Определение. Ручкой Н" размерности п и индекса
X называется прямое произведение DxxD"~x двух дисков Dx
и D"~x размерностей п и п — Х соответственно. Край ручки
имеет вид dHl = (Sk~l xDn'k)[j(Dxx S").
Определим операцию приклейки ручки Н к многообразию
Q" с краем V~1=8Q". Пусть S^'c V"'1— такая гладко
вложенная в многообразие V сфера, что ее достаточно
малая трубчатая окрестность NtS*~1=N"~1' радиуса ? представ-
ляется в виде прямого произведения Sx~1xZ)"~x', где D"~x —

328
ГЛ. 10. КАЧЕСТВЕННАЯ ТОПОЛОГИЧЕСКАЯ ТЕОРИЯ
нормальный диск размерности я —А. и радиуса е. Тогда можно
построить новое гладкое многообразие О" с краем, рассмотрев
склейку HI с Q" по отображению %: S xD"~x->iV?(Sx~1) =
Sl~ D"~x ффф
у
% ?
хD"~x, являющемуся диффеоморфизмом части
Sx~* xD"~x границы ЗЯ" на трубчатую окрестность NtSx'1.
На рис. 47 показана операция приклейки ручки Н\, а на
рис. 48 — операция приклейки ручки Н\.
¦v\ -. J¦. - ¦. Л.ъ. .-.¦.'.'.-
V1
и
и?
Рис. 47
14. Лемма (см. [180]). Пусть f: A/->R — функция Морса
на многообразии М. Тогда многообразие Qb получается из
многообразия Qa описанной выше операцией приклейки к краю
многообразия Qa ручки индекса
X в обозначениях п. 12.
Доказательство см., напри-
мер, в [180], [103], [279].
15. Обобщением обыкно-
венной теории Морса на слу-
чай функций, вырожденных
особым образом, служит так
называемая эквивариантная
теория Морса. Аналогом по-
нятия критической точки в эк-
вивариантной теории является
понятие критического уровня.
16. Определение. Зам-
кнутое подмногообразие
N многообразия М называется
невырожденным критическим
уровнем функции /: M-»R, если: а) N связно; б) для любой
точки xeN выполняется равенство df(x) = 0; в) в некоторой
окрестности U^N кроме N нет других критических точек
функции /; г) коранг матрицы Гесса функции / совпадает
с размерностью многообразия N во всех точках из N.
Рис 4g

i 5<v ЭЛЕМКНТЫ ТЕОРИИ МОРСА 329
17. Замечание. Из соображений непрерывности следует,
что все точки связной компоненты критического уровня имеют
одинаковый индекс. Квадратичную форму/..(х) на пространстве
ТХМ, xeN, приведем к каноническому виду — (и1J —...— (и*J +
+ (г/+1J + ...+(мгJ. Число Я. отрицательных коэффициентов
в этом разложении по определению называется индексом
вырожденной критической точки xeN.
18. Замечание. Функции, критические точки которых
образуют целые подмногообразия, естественным образом воз-
никают в случае, когда на многообразии действует группа Ли
и функция инвариантна относительно преобразований группы.
Другой пример дают функции f, полученные из многообразий
меньших размерностей при отображении \|г. M"->M"~* как
функции вида /(x)=g(\|/(x)).
19. Теорема Ботта. Если критическое значение с функции
/ изолировано, поверхность уровня f~l(c) компактна, /"'(с) —
невырожденный критический уровень, то найдется такое г>0, что
множество К+ ={х\/{х)^с + е} содержит подмножество К вида
{x\f{x)^.e — z}\JQ, где Q — топологическая сумма конечного числа
замкнутых шаров, являющаяся деформационным ретрактом для
К+. Размерность шаров, составляющих О, не меньше наименьшего
из индексов критических точек pef~l(c) (рис. 49).
Рис. 49
20. Замечание. Аналог утверждения 7 для эквивариант-
ных функций, вообще говоря, неизвестен. Рассмотрим два
примера, когда существует сколь угодно близкая к данной
функции эквивариантная функция Морса.
21. Пример. Рассмотрим в пространстве R3 стандартное
действие группы Ли SO[3), при котором отображение /?eSOC)
переводит вектор xeR /?(ЛТ)Н5
22 Т
р ()
22. Теорема. Для любой функции /е С х (R\ инвариантной
носительно действия группы Ли SOC) на R3 (см. п. 21),

330
ГЛ. 10 КАЧЕСТВЕННАЯ ТОПОЛОГИЧЕСКАЯ ТЕОРИЯ
найдется функция И е Сх (R3), сколь угодно близкая к /,
инвариантная относительно того же действия группы Ли SOC)
и имеющая только невырожденные критические орбиты.
Доказательство. Функция/постоянна на сферах с цент-
ром в нуле, так как / инвариантна относительно действия
группы Ли SOC). Поэтому она
порождает функцию на луче
[0, оо), которую продолжим
гладким образом до функции
geC^R) (рис.50). Произволь-
ную гладкую функцию на R мо-
жно сделать функцией Морса,
изменив ее не более чем на
С^'1'. Если мы подвергнем
такому преобразованию функ-
цию g, то значения индуцирован-
ной функции /на R3 и ее производных в нуле не изменятся.
Полученная функция / может иметь вырождение только в i очке
О. Это вырождение можно устранить сколь _угодно малым
шевелением. Выберем точку х0, в которой grad/не равен нулю.
Пусть grad/#O в некотором сферическом слое W=Bl\B2, где
BY — шар радиуса ?ь В2 — шар радиуса е2, ?2<е1, с центром
в нуле, B={xeR3} \\\х\\ =е}. Рас-
смотрим две гладкие функции
Фь 92eCcc(R3) и 0<фь ф2<1:
функция ф! равна нулю на
В 2 и единице на R3\Z?b
а ф2 = 1— Ф1 (рис. 51). Функция
Рис. 50
Рис. 51
искомая.
23. Замечание. В п. 22 мы
рассмотрели пример такой функ-
ции f(x), что g(x) = const — ор-
бита заданного действия группы
Ли. Рассмотрим более сложный
пример аналогичной ситуации.
Группа Ли SOC) x SOC) действу-
ет на GLC, R) по следующему правилу: A-tR^1 AR2, где /?],
/?2eSOC) и ^eGLC, R).
На GLC, R) рассмотрим функцию Fc(A) = cl \x{AA') +
+ C2[tr(^^')]2 + c3tr(^^'J, c = (ct, c2, c3). Поверхности уровня
функции Fc (X) являются орбитами действия группы Ли SO C) х
хБО(зГна GlC, R).
24. Теорема. Функция вида FC(X), c = (ct, c2, c3), не вырож-
дена на GLC, R) в смысле определения 16, т. е. все ее
критические подмногообразия не вырождены для почти всех

§ 56. ЭЛЕМЕНТЫ ТЕОРИИ МОРСА 331
наборов c = {ci, с2, с3). Кроме того, если для набора с = (сь с2, сЛ
функция FC(X) вырождена, то найдется набор с' — (с\, с'2, с'3\
сколь угодно близкий к с = {с1, с2, с3), такой, что соответст-
вующая функция FC(X) уже не вырождена на GLC, R).
Доказательство. Заметим сначала, что каждая орбита
содержит диагональную матрицу. Кроме того, диагональные
матрицы, лежащие в одной орбите, имеют общий спектр.
Действительно, рассмотрим образ A [S2) единичной сферы S2
при линейном отображении А е GL C, R). Ясно, что A [S2)
— эллипсоид. Пусть Я.ь Х2, Х3 — его полуоси. Заметим, что
полуоси эллипсоида гладко зависят от коэффициентов матрицы
линейного преобразования А. Умножением А слева на Rte
eSOC) повернем эллипсоид так, чтобы его полуоси совпали
с базисными векторами. Теперь применим преобразование
с матрицей D —
Хг1 О О
о ).;' о
о о и1
. Получим снова сферу. Следова-
тельно, композиция DRlA является ортогональным преоб-
разованием, т. е. прообразы осей эллипсоида ортогональны.
Найдется такая матрица /?2eSOC), что R2~1(DR1a) = E. Отсюда
A = RiiD~1Rz, т.е. орбита О(А), содержащая произвольную
матрицу А из GLC, R), содержит также и диагональную
матрицу. Нетрудно видеть, что другие диагональные матрицы
получаются из нее перестановкой базисных векторов и поэтому
имеют тот же спектр.
Итак, достаточно исследовать степень вырождения функции
на диагональной матрице, представляющей данную орбиту.
Имеем
а..
0
0
0
^2
0
0
0
^3
(+b42 + li). G98)
Рассмотрим ограничение функции FC[X) на множество диаго-
нальных матриц. Таким образом, мы свели задачу к исследова-
нию функции на пространстве R3 с координатами (A,i, A,2, Х3).
Первое и второе слагаемые в G98) постоянны на сферах
с центром в начале координат. Поэтому для выявления
критических точек надо рассмотреть поведение третьего слага-
емого на этих сферах. Очевидно, что эта функция имеет
максимум в точках Л = гA,0, 0), В = г(-1, 0, 0), С = г@, 1, 0).
D = r@, -1,0), ?=/-@,0, 1), F=r@, 0, -I) (рис. 52). Минимум
эта функция имеет в точках Р = — A, 1, 1), Q = — (— 1, 1, 1),
v/з -Л

332
ГЛ. 10. КАЧЕСТВЕННАЯ ТОПОЛОГИЧЕСКАЯ ТЕОРИЯ
t/=-^(-l, 1, -1), V=-!-(-l, -1, -1), W=-j={\, -1, -1), где
r—радиус сферы, на которой изучается поведение функции, см.
рис. 52. Функция FC(X) допускает группу симметрии такую же,
как октаэдр, поэтому можно рас-
смотреть ее поведение в одной
точке максимума и в одной точке
минимума, точнее, на лучах, про-
ходящих через нуль и выбранную
точку. Один из «максимальных»
лучей задается уравнением %-i — t,
А. 2 = А. 3 = О, а «минимальный»
луч — уравнением X1 = 'k2 = 'k3 = t.
На «максимальном» луче функ-
ция имеет вид Fi(f) =
= clt2 + c2tA + c3tA, а на «мини-
мальном» имеет вид F2(t) =
= 3c1t2 + 9c2t4' + 3c3t4. Критичес-
кие точки находятся дифферен-
цированием указанных выраже-
ний по t, т. е. из условий
G99)
(800)
Точка @, 0, 0) является невырожденной (при с^О). Остальные
критические точки находятся из квадратных уравнений
(801)
(802)
+ 36c2t2+l2c3t2 = 0,
решая которые, найдем ?х= /—2——-, t2= —2——-.
Исследуем эти решения, а) Оба подкоренных выражения
отрицательны. Тогда кроме нуля критических точек нет,
а в нуле при ct>0 максимум, при с^ <0 минимум, б) Если t\>0,
t\<Q, то имеется критическая точка на «максимальном» луче,
причем матрица Гесса в каноническом виде имеет на диагонали
один минус и два плюса, в) Если tj<0, t\>0, то критическая
точка есть на «минимальном» луче, причем в этой точке
матрица Гесса в каноническом виде на диагонали имеет один
минус и два плюса, г) Если ff >0, t\>0, то на «максимальном»
луче имеется точка перегиба, матрица Гесса в каноническом
виде на диагонали имеет один минус и два плюса. На

§ 57. КЛАССИФИКАЦИЯ ТРЕХМЕРНЫХ ПОВЕРХНОСТЕЙ 333
«минимальном» луче находятся абсолютные минимумы, мат-
рица Гесса в каноническом виде на диагонали имеет три
минуса.
Доказательство утверждения о существовании невырожден-
ной функции, достаточно близкой к данной, проводится так же,
как и в теореме 22.
25. Замечание. Ниже будет показано, как построить
аналог теории Морса, если заменить функцию /еС"" (М) на
отображение моментов симплектического многообразия, порож-
денное полным набором коммутирующих интегралов.
§ 57. Классификация трехмерных поверхностей
постоянной энергии интегрируемых систем
1. Традиционно считается, что полная интегрируемость по
Лиувиллю гамильтоновой системы дает более или менее полное
качественное описание поведения интегральных траекторий
системы. Безусловно, в принципе это так. Однако при этом
часто игнорируется то обстоятельство, что для такого описания
требуется эффективно найти переменные действие —угол (от-
носительно которых траектории системы превращаются в пря-
молинейные обмотки торов) в окрестности торов Лиувилля.
Новый подход состоит в построении качественной гео-
метрической теории, позволяющей описывать симплектичес-
кую топологию слоения фазового многообразия на торы
Лиувилля.
В настоящем параграфе мы начнем изложение теории
А. Т. Фоменко интегрируемых боттовских систем, развитой
затем X. Цишангом, С. В. Матвеевым, А: В. Болсиновым,
А. А. Ошемковым и др. Уместно поставить следующие во-
просы. Как располагаются торы Лиувилля в фазовом про-
странстве? Как они примыкают друг к другу, как заполняют
открытые области и как перестраиваются в окрестности
критических поверхностей интегралов и т. п.? Другими словами,
как построить качественную теорию топологического рас-
положения и взаимодействия торов Лиувилля (и тем самым
взаимного расположения интегральных траекторий системы),
например, на поверхности постоянной энергии системы?
2. Пусть Л/4— четырехмерное симплектическое многооб-
разие, на котором задана гамильтонова система x = sgrad H,
которую мы будем отождествлять с векторным полем
f = sgrad Н, здесь Н—гладкий гамильтониан. Положения равно-
весия х0 системы v — это критические точки функции Н. Поле
v можно ограничить на инвариантную трехмерную поверхность
Q = {xeM\H(x) = const}, так как Н—интеграл системы v.
Являясь симплектическим многообразием, М4 ориентируемо,
а поэтому многообразие Q также ориентируемо.

334 ГЛ. 10. КАЧЕСТВЕННАЯ ТОПОЛОГИЧЕСКАЯ ТЕОРИЯ
Рассмотрим некритические поверхности уровня Q, т. е.
такие, на которых grad НФО. Для полной интегрируемости по
Лиувиллю системы v на многообразии М достаточно найти еще
один (второй) интеграл /, независимый с Н (почти всюду)
и находящийся с ним в инволюции на поверхности уровня.
Пусть такой интеграл существует. Ограничим его на поверх-
ность Q и получим гладкую функцию. Мы будем изучать
интегрируемость системы лишь на какой-то одной поверхности
постоянной энергии.
3. Не исключено, что у многих гамильтоновых систем,
в целом неинтегрируемых, существует «одинокая» поверхность,
на которой имеет место интегрируемость. Интеграл /, который
интегрирует систему x = sgrad Я лишь на одной поверхности
уровня гамильтониана, удовлетворяет более слабому уравне-
нию, чем обычное уравнение инволютивности {Я, /} = 0.
А именно, он должен коммутировать с гамильтонианом
Я лишь на самой поверхности уровня Q, а вне ее он уже не
обязан коммутировать с Я. В простейшем случае это условие
можно записать так: {//,/} = >.(Я), где функция Х{Н) такова,
что А,@) = 0 и <^{Я,/}=0 на Q, см. [131 ]. Мы предполагаем, что
интересующая нас изолированная поверхность уровня гамиль-
тониана задается уравнением Я = 0.
4. Определение. Гладкий интеграл / будем называть
боттовским на поверхности Q, если критические точки функции
/ на Q образуют невырожденные критические гладкие подмно-
гообразия, см. определение 16 § 56. В этом случае гамильтонову
систему на Q назовем боттовской.
5. Замечание. Общие свойства таких гладких функций
(не интегралов) изучены в работах Р. Ботта, см., например,
[325]. На этом основании такие функции уместно назвать
боттовскими.
Из накопленного опыта исследования конкретных систем
(см., например, работы Т. И. Погосяна, М. П. Харламова,
Я. R. Татаринова, А. Т. Фоменко, А. А. Ошемкова, А. В. Бол-
синова, К. Шваи, Л. С. Поляковой, 3. Тевдорадзе [218—220],
[221], [241], [281—288], [207—209], [296]) можно извлечь, что
подавляющее большинство уже обнаруженных интегралов явля-
ются боттовскими в указанном смысле. Поэтому введенный
класс боттовских интегралов представляется естественным.
В качестве простейшего примера приведем следующий резуль-
тат, принадлежащий К. Швае.
6. Теорема (К. Швая, см. [296]). а) Пусть G = slB, К)ф
©R2 — полупрямая сумма алгебры Ли siB, R) и R2 по неприводи-
мому двумерному представлению, /I x° Xl , (fo>.Fi)) =
~xiy\ — инвариант коприсоединенного представ-

§ 57. КЛАССИФИКАЦИЯ ТРЕХМЕРНЫХ ПОВЕРХНОСТЕЙ 335
ления, f{x + Xa)=f(x)+fl(x, a)X + f2(x, a)X2+f{a)X3. Система
x = sgradfl вполне интегрируема на орбитах общего положения.
Все орбиты коприсоединенного представления расслоены на
изоэнергетические поверхности Q3 = {fi (х) = const}, обладающие
тем свойством, что для всех этих поверхностей Q3 функция
fi\Qb является боттовским интегралом потока х. Точнее,
функция f2\Q3 на некомпактном многообразии Q3 не имеет
критических точек. Многообразие Q3 в общем положении
диффеоморфно тривиальному одномерному векторному рас-
слоению над R2 \ {0}.
б) Пусть G = slB, R)©R3— полупрямая сумма алгебры Ли
si B, R) и R3 по неприводимому трехмерному представлению,
f(x) = xoyi+2xly2-2xlyo, g(x) = 4y0y2-yzu где х = [ *° ** \\,
(Уо, У\.1 з^г) Ie G,— инварианты коприсоединенного представления
(полный набор), f(x + l.a)=f(x)+f1(x,a)X+f(a)X2 и g(x + Xa) =
= g(x)+gl (x, a)X+g(a)X2. Система x = sgradfl(x) вполне интег-
рируема на орбитах общего положения. Все орбиты коприсо-
единенного представления расслоены на изоэнергетические по-
верхности Q ={/i (x) = const}, обладающие тем свойством, что
для всех поверхностей Q 3 функция f2\Q3 является боттовским
интегралом потока х для вектора сдвига а общего положения.
Точнее, функция f2 на некомпактном многообразии не имеет
критических точек. Многообразие Q 3 можно представить в виде
Q3 = М2 х@, 1), где М2 — одна из двумерных поверхностей:
а) цилиндр Л/2^^1 х@, 1); б) плоскость М =R2; в) два экземп-
ляра плоскости M2 = S°xR2.
7. Определение. Пусть у — замкнутая траектория систе-
мы y = sgrad H на поверхности Q (т. е. периодическое решение).
Траектория у называется устойчивой, если некоторая ее
трубчатая окрестность целиком расслоена (без щелей) на
концентрические двумерные торы, инвариантные относительно
системы v. Это означает, что все интегральные траектории,
близкие к у, «укладываются» на инвариантные двумерные торы,
общей осью которых является траектория у.
8. Замечание. Система может быть интегрируемой, но не
иметь при этом ни одной замкнутой устойчивой траектории
(хотя замкнутых траекторий может быть очень много). Про-
стейший пример: геодезический поток двумерного плоского
тора Г2 с локально евклидовой метрикой. Легко видеть, что
этот геодезический поток имеет дополнительный интеграл,
однако все замкнутые траектории системы являются неустой-
чивыми.
9. Обозначения. Пусть Q—поверхность постоянной энергии,
на которой задан второй интеграл. Если он определен не только

336
ГЛ. 10 КАЧЕСТВЕННАЯ ТОПОЛОГИЧЕСКАЯ ТЕОРИЯ
Рис. 53
на поверхности Q = {H=0}, но и в некоторой ее окрестности, то
/удовлетворяет уравнению {#,/} = А,(Я), А,@) = 0, d{H,/} = 0.
Буквой Т обозначим критические невырожденные подмного-
образия интеграла / на Q. Каждое из них обладает сепаратрис-
ной диаграммой — это объединение интегральных траекторий
пояя grad /, входящих в Г и исходящих из Т. В соответствии
с этим будем говорить о входя-
щей сепаратрисной диаграмме
Р(Т) и исходящей сепаратрис-
ной диаграмме Р+(Т). В малой
окрестности подмногообразия
Т обе диаграммы (входящая
и исходящая) являются двумер-
ными гладкими многообразиями
с общим краем Т (край понима-
ется здесь не в общетопологиче-
ском смысле, а в смысле теории многообразий). Они могут
быть как ориентируемыми, так и неориентируемыми. Итак,
определены три объекта Q3, Т и P+(T)\JP-(T) (рис.53).
Заметим, что последний объект зависит от выбора метрики на
Q, и если это важно, то эта зависимость будет специально
отмечаться.
10. Определение. Боттовский интеграл / на поверхности
Q называется ориентируемым, если все его критические подмно-
гообразия ориентируемы. Если хотя бы одно критическое
подмногообразие неориентируемо, то будем
говорить, что интеграл неориентируем.
11. Замечание. Без существенного огра-
ничения общности можно изучать лишь ори-
ентируемые интегралы / на Q. Дело в том,
что рассматривая изоэнергетические поверх-
ности Q с точностью до двулистного накры-
тия (над ними), всегда можно считать, что
интеграл / ориентируем.
12. Предложение (см. [283]). Пусть
Q3 — неособая компактная поверхность по-
стоянной энергии в МА и f—боттовский
неориентируемый интеграл на Q. Тогда все его
неориентируемые критические подмногообра-
зия гомеоморфны бутылке Клейна (рис. 54),
причем интеграл f достигает на них либо минимума, либо
максимума (локального). Пусть U(Q) — достаточно малая
трубчатая окрестность цоверхности Ь в М. Тогда существует
двулистное накрытие п: (U(Q), H,j)-*(U{Q), H,f) (со слоем
Z2), где U(Q) — симплектическое многообразие с гамцлътоновой
системой v = sgrad /У (где гамильтониан Н имеет вид Н=п*Н),
интегрируемой на E = л ~' (Q) при помощи боттовского ориен-
Рис. 54

§ 57. КЛАССИФИКАЦИЯ ТРЕХМЕРНЫХ ПОВЕРХНОСТЕЙ 337
тируемого интеграла f=n' f. При этом все критические бутыл-
ки Клейна «разворачиваются» в критические торы Т2 в Q (мак-
симумы или минимумы интеграла J). Многообразие 0{Q)
является трубчатой окрестностью Q.
13. Следствие. Если f—не ориентируемый интеграл на Q,
то Л! @)ф® и в группе п^ (Q) содержится подгруппа индекса два.
Если, например, Q гомеоморфно сфере S3 (частный случай из
механики),. то любой боттовский интеграл f на S3 всегда
ориентируем.
14. Обозначения. В дальнейшем будем обозначать m = m(Q)
число устойчивых периодических решений системы x = sgrad H
на Q = {H=const}. Пусть далее r = r(Q) — число критических
подмногообразий интеграла / на Q, гомеоморфных бутылке
Клейна. Если интеграл ориентируем, то г = 0.
15. Теорема (А.Т.Фоменко, см. [283]). Пусть Не-
гладкое симплектическое четырехмерное многообразие (ком-
пактное или некомпактное) и y = sgrad H—гамильтоново век-
торное поле на МА, где Н—гладкий гамильтониан. Пред-
положим, что система интегрируема по Лиувиллю на какой-то
неособой компактной трехмерной поверхности уровня Q гамиль-
тониана Н, причем второй гладкий интеграл f коммутирует
с Н на Q и является боттовским на Q. Тогда число m = m(Q)
устойчивых периодических решений системы x = sgrad H на
поверхности Q следующим образом оценивается снизу через
топологические инварианты поверхности Q.
1) В том случае, когда интеграл f ориентируем на Q, мы
имеем:
а) если группа гомологии Hl(Q;Z) конечна, то
б) если фундаментальная группа nl(Q) = Z, то
2) В том случае, когда интеграл f неориентируем на Q, мы
имеем:
а) если группа гомологии H1(Q;Z) конечна, то т + г^2;
б) если Hl(Q;Z) = 0 (при этом группа 7tiF) может быть
бесконечной), то т^2;
в) если группа Ht(Q; Z) конечная циклическая, то w^l;
г) если Kl(Q) = Z или если л, (Q) — конечная группа, то w^l;
д) если группа Hl {Q; Z) конечная циклическая и поверхность
Q не принадлежит к небольшой серии многообразий Q0 — {Sl x D 2)
+ sA3 + гКъ, которые описаны в явном виде ниже, то т^-2.
В обоих случаях 1) и 2) интеграл f достигает локального
минимума или максимума на каждом из этих устойчивых
периодических решений системы v (или на бутылках Клейна).
Если группа гомологии H^^Q;!^ бесконечна, т.е. ранг Ht(Q;
Z) ^ 1, то система x = v может вообще не иметь на поверхности
Q устойчивых периодических решений.
16. Замечание. У многих интегрируемых систем поверх-
ности постоянной энергии часто диффеоморфны либо сфере S3,

338 ГЛ. 10 КАЧЕСТВЕННАЯ ТОПОЛОГИЧЕСКАЯ ТЕОРИЯ
либо проективному пространству RP 3, либо S1 х S2. Например,
для уравнений движения тяжелого твердого тела в зоне
больших скоростей после подходящей факторизации можно
считать, что поверхности Q гомеоморфны RP3. Кроме того,
если гамильтониан Н имеет изолированный минимум или
максимум (т. е. изолированное положение равновесия системы)
на М , то все достаточно близкие поверхности уровня
2={H = const} являются трехмерными сферами S3.
17. Определение. Обозначим Lpq так называемое лин-
зовое пространство, которое определяется следующим образом.
Циклическую группу q-ro порядка Zq представим как мульти-
пликативную группу корней q-й степени из единицы
— l[- Пусть р, q — взаимно простые натура-
ехр —
ч
льные числа. Группа Zq свободно действует на трехмерной
сфере S3 по правилу
/ \ ( 2jtlV 2nivp\ /orv->\
(z1,z2)-*[z1exp , z2exp , (803)
V ч ч !
где 5'3<=R4^C2 описывается уравнением z1z1+z2z2 = l. Лин-
зовое пространство Lp q есть факторпространство S 3/Zg относи-
тельно описанного действия группы Z, на сфере S3.
Выделим случаи, представляющие интерес для гамиль-
тоновой механики, в виде отдельного утверждения.
18. Предложение. Пусть гамильтонова система
х = sgrad H интегрируема при помощи боттовского интеграла
f на какой-то отдельной поверхности Q постоянной энергии,
гомеоморфной одному из многообразий S3, RP3, SlxS2, Lpq.
1) В том случае, когда интеграл f ориентируем, мы всегда
имеем т^2, т.е. система х обязательно имеет по меньшей
мере два устойчивых периодических решения на каждой из этих
поверхностей.
2) В том случае, когда интеграл / неориентируем, мы имеем
для сферы S3 неравенство т^2, а для многообразий RP3,
SlxS2, Lpq — неравенство т^\. В частности, на сфере S3
интегрируемая система всегда имеет по меньшей мере два
устойчивых периодических решения для любого боттовского
интеграла.
19. Замечание. Два устойчивых периодических решения
у интегрируемой системы существует не только на трехмерных
малых сферах, близких к изолированному положению равнове-
сия (минимуму или максимуму энергии Н), но и на всех
расширяющихся поверхностях уровня функции Н до тех пор,
пока они остаются гомеоморфными сфере S3.
20. Замечание. Критерий теоремы 15 является точным
в следующем смысле. Известны случаи, когда интегрируемая

& 57. КЛАССИФИКАЦИЯ ТРЕХМЕРНЫХ ПОВЕРХНОСТЕЙ 339
система v имеет на поверхности Q — RP3 или на Q = S3 ровно
два (и не больше) устойчивых периодических решения.
21. Следствие. Пусть двумерная гладкая поверхность
гомеоморфна сфере и снабжена гладкой римановой метрикой
общего положения, т. е. на поверхности нет ни одной устой-
чивой замкнутой геодезической. Тогда соответствующий этой
метрике геодезический поток неинтегрируем (на каждой неосо-
бой поверхности постоянной энергии) в классе боттовских
интегралов,
22. Определение. Рангом R фундаментальной группы
я, (Q) называется наименьшее возможное число образующих (в
копредставлении этой группы).
23. Примеры. Если ранг пх (Q) равен единице, то система
г, интегрируемая на Q при помощи боттовского интеграла j\
обязательно имеет на Q хотя бы одно устойчивое периодическое
решение. Например, в некоторых интегрируемых случаях задачи
движения четырехмерного твердого тела по инерции с закреп-
ленной точкой (см. [279]) некоторые трехмерные неособые
поверхности постоянной энергии диффеоморфны S' х S 2 (заме-
чание А. В. Браилова; до конца ситуация проанализирована
А. А. Ошемковым). Это означает, что n1(SlxS2) = Z и R=\.
Аналогично, как хорошо известно, в интегрируемом случае
Ковалевской (для трехмерного тяжелого тела) некоторые
поверхности постоянной энергии (после подходящей факториза-
ции) также гомеоморфны S1xS2.
24. Предложение. Пусть гамильтонова система
х = sgrad H интегрируема на какой-то одной неособой компакт-
ной трехмерной поверхности Q постоянной энергии с помощью
боттовского интеграла /. Тогда, если система х не имеет на
Q устойчивых периодических решений, то: 1) группа Hi(Q; Z) не
является конечной циклической, 2) ранг iti(Q)^2, причем хотя
бы одна из образующих в группе п^ (Q) имеет бесконечный
порядок.
25. Пример. Рассмотрим геодезический поток плоского
двумерного тора Т2, т. е. тора, снабженного локально евк-
лидовой метрикой. Этот поток интегрируем в классе боттовс-
ких интегралов и, очевидно, не имеет замкнутых устойчивых
траекторий. В силу предыдущего предложения 24 должно
выполняться неравенство R ^2 (R — ранг группы nt@). В са-
мом деле, неособые поверхности Q диффеоморфны здесь
трехмерному тору Г3, у которого Нх (Г3; Z) = Z©Z©Z.
26. Следствие. Пусть х — sgradH—гамильтонова система
на МА ,и Q — некоторая неособая компактная трехмерная
поверхность постоянной энергии. Предположим, что выполнены
следующие два условия: 1) система х имеет на Q не более одного
устойчивого периодического решения; 2) группа гомологии
H1(Q;Z) конечная циклическая, либо ранг группы 74@ Ие

340 ГЛ 10. КАЧЕСТВЕННАЯ ТОПОЛОГИЧГ.СКАЯ ТНОРИЯ
больше 1. Тогда система х — sgrad H неинтегрируема в классе
гладких боттовских интегралов на данной поверхности Q.
27. Следствие. Пусть гамильтонова система х = sgradH
интегрируема на М2" в некоммутативном смысле и G — алгебра
Ли функций на М2" (относительно скобки Пуассона) с функци-
онально независимыми (вообще говоря, некоммутативными)
образующими /i, ...,fk, где f\ = H, A=dim(j
и dim G + ind G = dim M. Пусть indG = 2. Предположим, что
среди функций есть хотя бы одна функция /„ такая, что ее
ограничение на какую-то одну совместную трехмерную ком-
пактную поверхность уровня Q остальных функций j), j^1*,
является боттовской функцией. Тогда для системы х на
Q выполнены все утверждения из теоремы 15.
28. Утверждение. «Далеко не каждое» трехмерное
гладкое компактное замкнутое ориентируемое многообразие
может быть поверхностью постоянной энергии гамильтоновой
системы, интегрируемой при помощи боттовского гладкого
интеграла, см. [41 ].
29. Замечание. Таким образом, препятствием к итегриру-
емости гамильтоновой системы может быть топология поверх-
ности постоянной энергии. Детали см. в [283], [286].
Мы предъявим в явном виде топологическое препятствие,
мешающее «подавляющему большинству» трехмерных много-
образий реализовываться в виде поверхностей постоянной
энергии интегрируемых систем.
30. Перечисленные выше результаты в действительности
являются следствиями общей теоремы А. Т. Фоменко о тополо-
гическом описании поверхностей постоянной энергии интегриру-
емых боттовских систем. Прежде чем сформулировать ее,
опишем в следующем пункте пять типов простейших трехмер-
ных многообразий, оказывающихся теми «элементарными кир-
пичиками», из которых склеена произвольная поверхность
постоянной энергии интегрируемой системы.
31. Пять типов многообразий. Дадим описание элементарных
трехмерных многообразий Р3 (или I), Z3 (или II), С3 (или III),
А3 (или IV), К3 (или V), из которых склеивается произвольная
интегрируемая изоэнергетическая поверхность.
Тип 1. Прямое произведение S1' х?Н окружности 51 на диск
D2 называется полноторием Р3. Его край дР3 — один тор Т2
(рис. 55).
Тип 2. Прямое произведение Т2 х D1 тора Г2 на отрезок D 1
называется цилиндром Z3. Его край 8Z3 — два тора Т\{]Т\
(рис. 56).
Тип 3. Прямое произведение N2 х S' двумерной сферы
с тремя выброшенными дисками D \, D2,, D\ (или диска
с двумя дырками, рис. 57) N2 = S2\(D\ (J D\ (J d\) и окружно-
сти Sl называется ориентированным седлом С (или, более

57. КЛАССИФИКАЦИЯ ТРЕХМЕРНЫХ ПОВЕРХНОСТЕЙ
341
образно, «штанами»). Многообразие ./V2 гомотопически эк-
вивалентно восьмерке, т. е. букету двух окружностей (рис. 58).
Край d(N2xS1) — три тора Т\{]Т22[]Т1.
Рис. 55
Рис. 56
\<:
- s
/s'
Рис
^?$^
. 57
)
СО
Рис. 58
Тип 4. Реализуем многообразие N2 как диск с двумя
дырками, которые зафиксируем и обозначим цифрами 1 и 2.
Рассмотрим нетривиальное расслоение N2 -> А3 -> S1 с базой —
окружностью S1 и слоем ./V2. Над окружностью существуют
лишь два неэквивалентных расслоения со слоем N2. Это —
прямое произведение N2 x S1 (см. выше тип 3) и расслоение А 3
(рис. 59). Оно характеризуется тем, что после переноса слоя N2
вдоль базы S1 он возвращается на прежнее место с переменой
местами дырок 1 и 2. Многообразие А3 называется неориен-
тируемым седлом.
Тип 5. Символом К2 обозначим бутылку Клейна, а симво-
лом К3 — пространство ориентированного косого произведения

342
ГЛ. 10 КАЧЕСТВЕННАЯ ТОПОЛОГИЧЕСКАЯ ТЕОРИЯ
бутылки К2 на отрезок D1, т.е. K3 = K2xDl (рис.60).
Границей дКъ пространства Къ является тор Т2.
32. Топологические замечания. Многообразие N2 гомотопи-
чески эквивалентно восьмерке, составленной из окружностей
1 и 2, поэтому в типе 3 с гомотопической точки зрения мы
Рис. 59
Рис. 60
имеем прямое произведение восьмерки на окружность, а в типе
4 восьмерка движется по окружности так, что после полного
оборота две окружности 1 и 2 меняются местами (восьмерка
переворачивается, рис. 61). Малая окрестность окружности-базы
TunZZ
Рис. 61
S1 гомеоморфна в этом случае двум листам Мёбиуса,
пересекающимся трансверсально по общей оси. Краем многооб-
разия А3 являются два тора. Многообразие А3 можно
реализовать в R3 следующим образом. Рассмотрим полнот'о-
рие, ограниченное стандартно вложенным тором, внутри кото-

§ 57 КЛАССИФИКАЦИЯ ТРЕХМЕРНЫХ ПОВЕРХНОСТЕЙ 343
рого высверлим тонкое полноторие, два раза наматывающееся
на образующую большого полнотория (рис. 62). Ясно, что А 3
является пространством ориентированного косого произведения
N2 х S'. С топологической точки зрения многообразие А 3 не
является новым. Оно получается склейкой полнотория и штанов
по некоторому диффеоморфизму тора. Условно это можно
записать так: A 3 = l + lll = (S1 x D2) + (N2 x S1).
С топологической точки зрения многообразие К3 типа
5 также не является принципиально новым, так как оно
представляется в виде следующей склейки вида:
AT3 = I + IV = E'1 xD2) + A 3 = 21 + lll = 2(S1 x D 2)+.(N2 x S 1).
Наконец, многообразие типа 2 также получается склейкой
многообразий типов 1 и 3, а именно: Z3 = P3 + C3.
Таким образом, из указанных пяти типов многообразий
лишь два (I и III) являются топологически независимыми,
остальные разлагаются в комбинации многообразий типов
1 и 3. Однако при изучении траекторий системы x = sgrad//
(динамики системы) многообразия Z3, А3 и К3 представляют
большой самостоятельный интерес, так как соответствуют
интересным движениям механических систем.
Пусть М4 — гладкое симплектическое многообразие (ком-
пактное или некомпактное) и x = sgradH—гамильтонова систе-
ма, интегрируемая по Лиувиллю на какой-то одной неособой
компактной трехмерной поверхности постоянной энергии Q при
помощи боттовского интеграла/. Пусть т — число периодичес-
ких решений системы х на поверхности Q, на которых интеграл
/ достигает строгого локального минимума или максимума
(тогда они устойчивы). Пусть р — число двумерных критических
торов интеграла / (минимумов или максимумов интеграла);
q— число критических окружностей интеграла / (неустойчивых
траекторий системы) с ориентируемой сепаратрисной диаграм-
мой; 5—число критических окружностей интеграла / (неустой-
чивых траекторий системы) с неориентируемой сепаратрисной
диаграммой; г—число критических бутылок Клейна (миниму-
мы или максимумы интеграла). Это полный список всех
возможных критических подмногообразий интеграла / на Q.
33. Теорема (А.Т.Фоменко; см. [283]). Многообразие
Q представляется в виде склейки (по некоторым диффеоморфиз-
мам граничных торов) следующих «элементарных кирпичей»:
Q = ml +pll + q\\\ + Л V + rV =
1) 21) 3 3 (804)
Если интеграл f ориентируемый, то последнего слагаемого нет, т. е.
г=0. Указанное разложение поверхности Q назовем гамильтоновым.
34. Замечание. Таким образом, в полученном нами
каноническом гамильтоновом представлении многоообразия

344 ГЛ. 10. КАЧЕСТВЕННАЯ ТОПОЛОГИЧЕСКАЯ ТЕОРИЯ
Q все неотрицательные целые числа т, р, q, r, s имеют четкую
интерпретацию—они сообщают нам, сколько критических
подмногообразий каждого типа имеет данный интеграл / на
данном многообразии Q. Если же мы будем игнорировать эту
интерпретацию чисел т, р, q, s, r и поставим вопрос о наиболее
простом топологическом представлении изоэнергетической по-
верхности Q, то на этот вопрос отвечает следующая
35. Теорема (А.Т.Фоменко). Пусть Q—компактная
неособая поверхность постоянной энергии гамильтоновой систе-
мы х = sgrad H, интегрируемой при помощи боттовского интег-
рала /. Тогда Q допускает следующее топологическое представ-
ление:
Q = m'l + q'Ul = m'(SlxD2) + q'(N2xS1), (805)
где т', q' — некоторые неотрицательные целые числа. Эти числа
связаны с числами т, р, q, s, r из теоремы 33 равенствами
m' = m + s + 2r+p, q' = q+s+r+p.
36. Определения. Для изоэнергетической поверхности Q3
возникает два разложения: Q3 = mI+pll+qlII + sYV + rV
и Q3 = m'\ + q'\\l. Первое из них называется гамильтоновым
разложением, а второе — топологическим разложением.
37. Канонические перестройки торов Лиувилля. Рассмотрим
следующие пять типов перестроек торов Лиувилля, отвечающие
указанным в п. 31 многообразиям Р3, Z3, С3, А3, К3.
Реализуем тор Т2 как одну из компонент края соответст-
вующего многообразия. Тогда тор Т2, увлекаемый изменением
интеграла /, преобразуется в объединение торов Лиувилля,
являющихся остальными компонентами края. Эти перестройки
имеют следующий вид.
Тип 1: перестройка Г2->5'1-»0. Тор Т2 стягивается на
осевую окружность полнотория и «исчезает» затем с поверх-
ности уровня интеграла /.
Тип 2: перестройка 2Т2 -> Т2 -> 0. Два тора Т2 движутся
навстречу друг другу по цилиндру, сливаются в один тор
и «исчезают».
Тип 3: перестройка Т2-*2Т2. Тор Т2 распадается на два
тора, проходя через центр штанов (ориентированного седла),
которые затем «остаются» на поверхности уровня интеграла /.
Тип 4: перестройка Т2 -> Т2. Тор Т2 два раза наматывается
на тор Т2 (следуя при этом топологии неориентированного
седла А3) и «остается» затем на поверхности уровня
интеграла /.
Тип 5: перестройка Г2->А^2->0. Тор Т2 превращается
в бутылку Клейна (два раза накрывая ее) и затем «исчезает»
с поверхности уровня интеграла /.
Пять перестроек, получающихся из указанных выше заменой
стрелок на обратные, мы не будем считать новыми.

§ 57. КЛАССИФИКАЦИЯ ТРЕХМЕРНЫХ ПОВЕРХНОСТЕЙ 345
38. Замечание. Теперь мы можем дать полную клас-
сификацию всех перестроек торов Лиувилля, возникающих при
изменении значения интеграла /. Меняя Ни/ местами, можно
было бы говорить о бифуркации торов Лиувилля, когда они
проходят через критический уровень энергии при фиксирован-
ном втором интеграле /. Ответ на этот вопрос дает следующая,
принадлежащая А. Т. Фоменко теорема о классификации бифур-
каций двумерных торов Лиувилля.
39. Теорема. Пусть f— боттовскип интеграл на неособой
поверхности постоянной энергии Q3. Тогда любая перестройка
общего положения тора Лиувилля, возникающая при его проходе
через критическую поверхность уровня интеграла /, является
композицией перечисленных выше элементарных перестроек
типов 1—5. Более того, из этих пяти перестроек независимы (с
топологической точки зрения) лишь первая и третья. Пере-
стройки типов 4 и 5 распадаются в композиции перестроек
типов 1 и 3.
40. Обсуждение. В качестве важного следствия этих резуль-
татов мы получаем возможность представить каждую изоэнер-
гетическую поверхность Q с интегралом / на ней в виде
одномерного графа Г (Q, /), все типы вершин которого E
типов), оказывается, допускают точное и полное описание.
Такое представление, вообще говоря, неоднозначно и будет
подробно описано ниже. В рамках изложенной конструкции
доказывается теорема 41 § 18, принадлежащая С. В. Матвееву
и А. Т. Фоменко.
41. Определение. Рассмотрим четыре класса (Н), (Q),
(W), (S) трехмерных компактных ориентируемых замкнутых
многообразий.
Класс (Н). Многообразие М3 принадлежит классу (Н), если
М3 является поверхностью постоянной энергии (изоэнергетиче-
ской поверхностью) интегрируемой гамильтоновой системы
(при помощи боттовского интеграла).
Класс (Q). Многообразие М3 принадлежит классу ((?), если
оно разлагается в сумму «элементарных кирпичей» типов
1 и 3 из п. 31, т.е. M3 = m'l + q'lU, или M3 = m'{Si xD 2) +
'^^S11)
^)
Класс (W). Многообразие М3 принадлежит классу (И7), если
в М3 существует набор непересекающихся двумерных торов,
выбросив которые получим многообразие, каждая компонента
связности которого расслаивается со слоем — окружностью над
двумерным многообразием (возможно, с краем).
Класс E). Многообразие М3 принадлежит классу E), если
на М3 существует гладкая функция g, все критические точки
которой организованы в невырожденные окружности, а все
неособые поверхности уровня функции g являются несвязным
объединением двумерных торов.

346 ГЛ 10 КАЧЕСТВЕННАЯ ТОПОЛОГИЧЕСКАЯ ТЕОРИЯ
42. Замечания. Из теоремы 33 вытекает, что класс (Н)
содержится в классе @. Класс (И7), возникший в задачах
трехмерной топологии, подробно изучался Вальдхаузеном
в [516] и был назван им Graphenmannigfaltigkeiten. Класс (S)
ввел С. В. Матвеев, развивая идеи А. Т. Фоменко.
43. Теорема. Все четыре класса трехмерных многообразий,
описанных в л. 41, совпадают, т.е. (H) = (Q) = (IV) = (S).
44. Замечание. Равенство (H) = (Q) доказано А. В. Бра-
иловым и А. Т. Фоменко, равенство (W) = {Q)— А. Т. Фоменко
и X. Цишангом, равенство (S) = (Q) — С. В. Матвеевым.
45. Обозначения. Ранг группы гомологии Hl (Q; Z) обозна-
чим буквой Р (т. е. р — одномерное число Бетти), е — число
элементарных множителей в конечной части Tor Ht (Q; Z)
группы #i (Q; Z). Если Tor //t (Q; Z) разложена в упорядочен-
ную сумму подгрупп, где порядок каждой подгруппы делит
порядок предыдущей, то е — число таких слагаемых.
46. Пусть Q е(Н) и Q = m'\ + q'l\l — топологическое раз-
ложение изоэнергетической поверхности Q = ml+pll + qlU +
+ rl\ + s\ интегрируемой боттовской системы. Здесь т — число
устойчивых периодических решений системы, 5—число неустой-
чивых периодических решений с неориентируемой сепаратрис-
ной диаграммой, г—число критических бутылок Клейна.
47. Теорема (А. Т. Фоменко, X. Цишанг). Всегда выпол-
нены неравенства m + s + 2r^e — 2fi+\, q'^m'—2 при
m + r+s + q>0. Если же m = r = s = q = O, то
? —2Р^0, причем равенство е = 2р действи-
тельно достигается для некоторых пар (Q, /).
48. Случай m = r = s = q = 0 реализуется тог-
да и только тогда, когда многообразие
Q является расслоением с базой S1 и слоем
гор (рис. 63). Если интеграл / «полностью
ориентируем», т. е. s = r = 0, то мы получим
>_/ неравенство т^е~2р+1, т. е. получаем оцен-
ку снизу на число устойчивых периодических
ijhc 63 решений системы. Детали см. в [288].
49. Замечание. Выше мы разобрали
случай, когда совместная поверхность уровня обоих интегралов
Н и / компактна. Однако не составляет труда сформулировать
и доказать аналогичные утверждения и для некомпактного
случая.
§ 58. Граф, естественно связанный
с интегрируемой гамильтоновой системой
1. Конструкция. Многообразие Q удобно задавать в виде
некоторого графа Г = Г(G,/). Пусть 0</<1 на поверхности Q.
Все минимумы и максимумы можно считать абсолютными.

§ 58. ГРАФ. СВЯЗАННЫЙ С ГАМИЛЬТОНОВОЙ СИСТЕМОЙ 347
Граф Г строится следующим образом. Начнем с частного
случая.
а) Сначала предположим, что каждая связная компонента
каждого критического слоя/ (с) содержит ровно одно связное
критическое подмногообразие. В этом случае граф Г = Г(?>,/)
строится однозначно следующим образом. Поскольку /—
боттовская функция на Q, то картина распада и уничтожения
неособых торов Лиувилля вблизи критических седловых окру-
жностей строго определенная, см. выше.
Изобразим неособые двумерные торы Лиувилля обычными
точками (на каждый тор отведем по одной точке). Меняя
значение функции/, мы заставля-
ем эти точки перемещаться, так
как каждый неособый слой функ-
ции (интеграла) изображается те-
перь набором точек (по числу
торов Лиувилля). В результате
получится некоторый одномер-
ный граф, начинающийся на
плоскости (/=0) и заканчивающийся на плоскости (/=1). При
этом введем следующие обозначения (рис. 64).
1) Большой черной точкой (черным кружочком) с ис-
ходящим (соответственно входящим) ребром графа мы обозна-
чим минимальную (соответственно максимальную) окружность
для интеграла.
2) Белым кружочком с двумя исходящими (соответствен-
но входящими) ребрами графа мы обозначим минимальный
(соответственно максимальный) двумерный тор для инте-
грала.
3) Трилистником («треножником»), т. е. точкой с тремя
ребрами графа, встречающимися в этой точке, мы обозначим
связную трубчатую окрестность критической седловой окружно-
сти с ориентированной сепаратрисной диаграммой sdS11.
4) Звездочкой (с входящими и исходящими ребрами) обозна-
чим трубчатую окрестность критической седловой окружности
с неориентированной сепаратрисной диаграммой sd S .
5) Кружочком с точкой внутри и с исходящим (соответст-
венно входящим) ребром графа мы обозначим минимальную
(соответственно максимальную) критическую бутылку Клейна.
Каждый трилистник (треножник) описывает либо распад
одного тора на два тора, либо, наоборот, слияние двух торов
в один. Это зависит от того, как ориентирован трилистник:
либо двумя ребрами вверх, либо одним ребром вверх.
Получающийся таким образом граф Г = Г(?>,/) можно
реализовать в R3. Очевидно, существует непрерывное отображе-
ние h поверхности Q на граф Г (Q, /). Меняя интеграл / (но
сохраняя поверхность Q), мы будем, вообще говоря, менять

348 ГЛ 10. КАЧЕСТВЕННАЯ ТОПОЛОГИЧЕСКАЯ ТЕОРИЯ
граф Г. Поэтому в обозначении графа Г учтено как многооб-
разие Q, так и интеграл /.
б) Теперь рассмотрим общий случай, когда на некоторых
связных компонентах критических поверхностей /~1{с) лежат
несколько критических подмногообразий интеграла /. В этом
случае конструкция, описанная выше (случай а)), не проходит.
Но тем не менее оказывается и здесь естественным путем
возникает граф Г, точное описание которого дается ниже в § 59
в теореме 3 и п. 10—17. Для случая а) этот общий граф,
конечно, превращается в граф Г, описанный выше.
Отметим также следующее полезное обстоятельство. В о.б-
щем случае б) можно построить некоторый граф Г {Q, /),
«возмутив» интеграл /. В самом деле, в работе Фоменко [283 ]
было построено возмущение /-*/ интеграла / в некоторую
близкую функцию /, которая, вообще говоря, не является
интегралом, но зато имеет на каждой связной компоненте
критического слоя /~l (с) ровно одно критическое подмногооб-
разие. Следовательно, по схеме случая а) мы можем построить
граф Г (Q,f). При этом возмущении/-+/многообразие Q не
меняется. Таким образом, мы можем сопоставить паре (Q, /) (в
общем случае) некоторый граф Г (Q, /). Конечно, такое
сопоставление, неоднозначно, так как существует много воз-
мущений /-»¦_/. Однако из сказанного выше ясно, что все такие
графы Г (Q, /) задают одно и то же (исходное) многообразие Q.
Таким образом, от тройки (Q, Н, /)_ можно путем гладкой
деформации перейти к тройке (Q, H,f). Далее, из теоремы
Браилова и Фоменко следует, что можно всегда подобрать
такую пару (Н, g), что (Н, g)— «боттовская пара», интегралы
Hug коммутируют и определяемое ими слоение Q на
двумерные ^поверхности совпадает со слоением, определяемым
парой Ни/ Другими словами, по заданному симплектическому
действию абелевой группы R2, порожденной коммутирующими
функциями Ни/ всегда можно построить новое симплектичес-
кое действие группы R2, отвечающее интегралам Н и g. При
этом каждая связная компонента каждого критического слоя
g~* (с) содержит ровно одно связное критическое подмногооб-
разие интеграла g.
2. Замечание. Вершины графа Г (в случае а)) занумерова-
ны цифрами 1, 2, 3, 4, 5 не случайно. Дело в том, что имеется
взаимно однозначное соответствие между этими пятью видами
вершин графа Г и пятью типами простейших трехмерных
многообразий, перечисленных в п. 31 § 57. Оказывается, до-
статочно малая «окрестность» вершины графа типа i, /=1, 2, 3,
4, 5, гомеоморфна (с точки зрения поверхности /) элементар-
ному многообразию типа /.
Рассмотрим связное критическое подмногообразие L и близ-
кие к нему неособые поверхности уровня Ва + е и Ва-С. Пусть

I) 54 НОВЫЙ ТОПОЛОГИЧЕСКИЙ ИНВАРИАНТ 349
U(L) — связная компонента слоя между Ва + С и Ва-С, содер-
жащая L.
3. Следующие факты доказаны в [283]. 1) Пусть S1 —
критическая седловая окружность и ее сепаратрисная диаграмма
/"_ ориентируема. Тогда трехмерное многообразие (/E11)
с краем TiiC\JT2.e\JT-c гомеоморфно прямому произведению
N2xS\ где N —двумерная сфера с тремя дырками (диск
с двумя дырками).
2) Пусть теперь сепаратрисная диаграмма Р неориен-
тируема. Тогда U(S') гомеоморфно многообразию А3, т. е.
нетривиальному расслоению Аъ —> S1 со слоем Л'2: U(S1) =
= N2xS1 (косое произведение).
3) Пусть L = 5"' — максимальная (или минимальная) окру-
жность для интеграла. Тогда t/E1) = 51 x D2 (полноторие).
4) Пусть L=T —максимальный (или минимальный) тор.
Тогда U(L)=T2xD1 (цилиндр).
5) Пусть L = K2 — максимальная (или минимальная) бутыл-
ка Клейна. Тогда U(K2) = K3 = K2 xSl (косое произведение).
§ 59. Новый топологический инвариант '
гамильтоновых систем дифференциальных
уравнений, интегрируемых по Лиувиллю
1. Классическая бифуркационная диаграмма Z, при помощи
которой обычно описывают топологию интегрируемых случаев,
при всех несомненных достоинствах обладает существенным
недостатком — она зависит от выбора второго интеграла, т. е.
не является топологическим инвариантом системы. Две кон-
струкции построения инвариантов вполне интегрируемых си-
стем мы опишем в гл. 11. Эти конструкции копируют
в некотором смысле конструкцию классических характеристи-
ческих классов векторных расслоений, см. [103], [181]. Мы
приведем здесь другую конструкцию топологических инвариан-
тов, предложенную А. Т. Фоменко на основе построенной им
топологической теории интегрируемых систем.
2. Определение. Назовем гамильтониан Н нерезонанс-
ным на данной изоэнергетической поверхности g3, если в Q3
всюду плотны торы Лиувилля, на которых интегральные
траектории системы v образуют плотную иррациональную
обмотку.
3. Теорема (А. Т. Фоменко [285]). Пусть v — гамилыпоно-
ва система с нерезонансным гамильтонианом Н, интегрируемая
при помощи некоторого боттовского интеграла f на компактной
неособой трехмерной изоэнергетической поверхности Q. Тогда
можно однозначно построить некоторый граф Г (Q, /) со
следующим свойством: по графу T{Q,f) однозначно (с точ-
ностью до гомеоморфизма) восстанавливается вся топологичес-

350 ГЛ. 10 КАЧЕСТВЕННАЯ ТОПОЛОГИЧЕСКАЯ ТЕОРИЯ
кая картина эволюции и перестроек (бифуркаций) торов
Лиувилля внутри поверхности Q при изменении значения
интеграла /
4. Обозначения. Пусть/: Q-+R — боттовский интеграл, <xeR
и /,с/"' (а) — связная компонента поверхности уровня интег-
рала (особая или неособая). Если а = а—регулярное (некрити-
ческое) значение/, то/ (а) — это объединение конечного числа
торов Лиувилля. Критические значения / обозначим буквой с,
связную компоненту критической поверхности уровня интег-
рала— символом /, а множество критических точек интеграла
/ на /— символом Nc. Как доказано в [285], связные
компоненты множества Nc могут быть только следующих
типов: 1) минимаксная окружность S1 (локальный минимум
или максимум /), тогда Nc=fc = Sl; 2) минимаксный тор Г2,
тогда Nc=fc=Ti; 3) седловая критическая окружность S1
с ориентируемой сепаратрисной диаграммой, тогда Nc = S1=^fc;
4) седловая критическая окружность S1 с неориентируемой
сепаратрисной диаграммой, тогда NC = S1 ф/с; 5) минимаксная
бутылка Клейна К , тогда Nc=fc = K2.
Символом ?/(/), где с—критическое значение интеграла,
обозначим регулярную связную замкнутую трубчатую окре-
стность компоненты/ в многообразии Q3. Можно считать, что
?/(/) — связное трехмерное многообразие, край которого состо-
ит из несвязного объединения торов. В качестве U(fc) можно
взять связную компоненту многообразия/'1 [с — г, с + е]. Мож-
но считать, что Q = ^U{fc), т.е. Q получается из всех
многообразий U(fc) склейкой их границ по некоторым диффе-
оморфизмов граничных торов.
5. Теорема (А.Т.Фоменко). Пусть Q—компактная не-
особая изоэнергетическая поверхность системы v с гамиль-
тонианом Н (не обязательно нерезонансным), интегрируемая
при помощи некоторого боттовского интеграла / Тогда
многообразие U(fc), входящее в разложение Q = Y,U(fc), до-
с
пускает следующее представление (в зависимости от типа
множества Nc):
тип 1: [7(/) = Р^х5'1, где P}=D2 (диск);
тип 2: U(fc) = P\ x S1, где P^S'xD1 (цилиндр);
тип 3: U(fc) = P} x 51, где Р2 — некоторая двумерная по-
верхность с краем;
тип 4: U(fc) = P2 xS1, где Р2 — некоторая двумерная поверх-
ность с краем, а Р2 х S1—пространство расслоения Зейферта
с базой Р2 и слоем S1 (описание см. ниже);
тип 5: U(fc) = P2 x S1, где P2 = \l (лист Мёбиуса), a (xxS11
обозначает косое произведение (с краем — тором Т2).

S 59. НОВЫЙ ТОПОЛОГИЧЕСКИЙ ИНВАРИАНТ 351
6. Следствие. С каждой изоэнергетической поверхностью
Q (в условиях теоремы 5) можно однозначно (с точностью до
гомеоморфизма) связать некоторую замкнутую двумерную
поверхность Р((?,/) = ? Р2, получающуюся склейкой поверх-
ностей Р2, индуцируемой склейкой 2 = Х U(fc)-
7. Теорема (основная; А.Т.Фоменко [285]). Пусть v —
гамильтонова система, интегрируемая на Q при помощи
боттовского интеграла. Тогда существует однозначное (с
точностью до гомеоморфизма) каноническое вложение h[Q,/')
графа T(Q,f) в поверхность P2(Q,f). Если гамильтониан
Н нерезонансный на Q, то тройка (Г, Р, h) не зависит от выбора
второго интеграла f. А именно: если f и f — любые боттовские
интегралы системы v, то соответствующие графы Г(Q,f)
и T{Q,f), как и поверхности P(Q,f) и P{Q',f), гомеоморфны,
а диаграмма
(806)
коммутативна.
8. Следствие. В нерезонансном случае тройка (Г, Р, h)
является топологическим инвариантом самого интегрируемого
случая (гамильтониана) и позволяет классифицировать интег-
рируемые гамильтонианы по их топологическому типу и слож-
ности.
9. Определение. Тройку (Г, Р, h) назовем топологиче-
ским инвариантом интегрируемого гамильтониана. Разбиение
поверхности P(Q) на области (определяемое графом Г(?))
также является топологическим инвариантом. Поверхность
P(Q) не обязана вкладываться в Q. Теперь определим
многообразие PfxS1. Расслоенным полноторием типа (а. Ь)
называется полноторие, полученное склейкой двух оснований
полного цилиндра D2 x D1 при помощи отображения
(z, 0)-fехр ^, \\ где zeC, |z|<l, a, beZ, (a, b)=l. Слоем
является
2Kib \ ( 4nib
... ехр2тп (fl-')fe, O^Kli. (807)
а )
Тогда на полнотории D2 x S1 определяется расслоение со
слоем S1 над D2, локально тривиальное для всех ненулевых

352 ГЛ. 10 КАЧЕСТВЕННАЯ ТОПОЛОГИЧЕСКАЯ ТЕОРИЯ
точек диска D2. Слой — окружность {@, /)|0<Г< 1} является
особым, если а > 1.
Теперь рассмотрим многообразие Р2 с отмеченными на нем
точками х1у ..., хт и окружим их малыми дисками D2, ..., D2,.
Затем возьмем прямое произведение Р2 х Sx и выбросим из
него т полноторий D?xS\ l^i^m. Вклеим вместо них
расслоенные полнотория типа B, 1). Полученное многообразие
обозначим P^xS1. Оно является расслоением Зейферта, а Р2—
его базой, см. [172].
10. Дадим явное построение инвариантов. Предположим
сначала, что на каждой компоненте fc критического уровня
расположено ровно одно критическое связное многообразие Nc.
В этом случае построение графа Г(Q,f) было фактически
описано в § 58 (а также в [283]). Построим граф Г в общем
случае. Теперь на одной компоненте критического уровня может
лежать несколько критических многообразий. В отличие от
обычных функций Морса критические многообразия боттов-
ского интеграла, лежащие на одном уровне, вообще говоря,
нельзя «развести» на разные уровни путем малого возмущения
интеграла (оставаясь в классе интегралов). Возмущение / интег-
рала / может не быть интегралом. Пусть/ (а) — поверхность
уровня интеграла. Если а—регулярное значение, то /"'(а)
— объединение конечного числа торов. Изобразим их точками
в R3 на уровне а, где ось R направлена вверх. Меняя
а в области регулярных значений, мы заставляем эти точки
заметать некоторые дуги — часть ребер будущего графа Г.
Пусть Nc — множество критических точек / на fc. Выделим два
случая: a) Nc=fc; б) Nccfc, причем Nc^fc. В работе [285]
найдены все возможные варианты для Nc. Рассмотрим случай
а). Здесь возможны лишь три типа критических множеств.
11. Тип «минимаксная окружность». Здесь Nc=fc гомеоморфно
окружности, на которой / достигает локального минимума или
максимума. Ее трубчатая окре-
стность S1 х D2 гомеоморфна пол-
. ноторию (в ()ъ). При а-*с неособые
торы стягиваются на ось полното-
I рия и при а = с вырождаются в 51.
t • Условно изобразим эту ситуацию
черной жирной точкой (вершина
I графа), в которую входит (или из
которой выходит) одно ребро графа
(рис. 65).
Рис 65 12. Тип «тор». Здесь Nc=fc и го-
меоморфно тору Т2, на котором
/ достигает локального минимума или максимума. Его трубча-
тая окрестность гомеоморфна цилиндру Т2 х D1. Граница
цилиндра — два тора. При а->с они движутся навстречу друг

§ 59 НОВЫЙ ТОПОЛОГИЧЕСКИЙ ИНВАРИАНТ
353
другу и при а = с сливаются в один тор. Изобразим эту
ситуацию белым кружком (вершина графа), в который входят
(или выходят) два ребра графа (рис. 66).
13. Тип «бутылка Клейна». Здесь Nc=fc и гомеоморфно
бутылке Клейна А/2, на которой / достигает локального
минимума или максимума. Ее трубчатая окрестность К2 х D1
гомеоморфна косому произведению К2 на отрезок. Граница
Рис. 66
Рис. 67
с(К2 х D1) — один тор. Когда а->с, он сремится к К2 и двули-
стно накрывает ее при а = с. Изобразим эту ситуацию белым
кружочком с точкой внутри (вершина графа), в который входит
(или выходит) одно ребро графа (рис. 67).
Рис. 68
14. Случай б). Здесь Nccfc, причем dim7Vc=l, a dimfc = 2.
Тогда (см. § 58 и [285]) Nc есть несвязное объединение
непересекающихся окружностей. Каждая из них будет седловой
для /. Компоненту /с также назовем седловой. Условно ее можно
изобразить плоским горизонтальным квадратом, лежащим на
уровне с в R3 (рис. 68). Снизу в него втыкаются некоторые
ребра графа (при а->с и а<с), вверх уходят другие ребра графа
(когда а>с). В результате мы определили некоторый граф А,

354
ГЛ. 10. КАЧЕСТВЕННАЯ ТОПОЛОГИЧЕСКАЯ ТЕОРИЯ
состоящий из регулярных дуг (ребер), часть из которых
втыкается в квадраты, а часть заканчивается вершинами трех
описанных типов.
15. Фиксируем седловое значение с и построим граф Тс,
показывающий, как именно соединяются ребра графа А,
взаимодействующие с fc. Рассмот-
рим на Q векторное поле w = grad /
Его траектории, входящие в крити-
ческие точки интеграла или ис-
ходящие из них, называются сепа-
ратрисами. Их объединение — это
сепаратрисная диаграмма критиче-
ского подмногообразия. Из каждой
седловой критической окружности
S1 на уровне fc выпустим ее сепара-
трисную диаграмму. Если она ори-
ентируема, то она получается
склейкой двух плоских колец (цили-
ндров) по осевой окружности,
см. § 58. Если она неориентируема,
то она получается склейкой двух
листов Мёбиуса по их осевой окру-
жности. Рассмотрим некритические
значения с — г и с-1-е, близкие к с.
Поверхности fc_t и fc+c состоят из
торов (рис. 69). Сепаратрисные диаграммы критических окру-
жностей, лежащих в /с, пересекают эти торы трансверсально по
некоторым окружностям и разбивают торы в объединение
областей, которые мы назовем регулярными. Выберем на
уровне/С_Е в каждой из них по точке и выпустим из этих точек
интегральные траектории поля w. Они пройдут мимо критичес-
ких окружностей на уровне /с и попадут в некоторые другие
регулярные области торов, составляющих /с+?. Очевидно, что
тем самым мы получаем гомеоморфизм между открытыми
регулярными областями из /с_с и открытыми регулярными
областями из /С+Е.
16. Ориентируемый случай. Итак, предположим, что все
сепаратрисные диаграммы ориентируемы (т. е. нет листов
Мёбиуса). Поскольку каждый неособый тор — это точка на
графе А, то можно соединить точки на уровне/с_е и на уровне
fc+e дугами (отрезками), изображающими пучки интегральных
траекторий поля w. Получим некоторый граф Тс. Его ребра
показывают нам движение открытых регулярных областей
торов. Торы разваливаются на куски, которые затем поднима-
ются (спускаются) и перегруппировываются в новые торы.
Каждый верхний тор составлен из кусков нижних торов (и
наоборот).
Рис. 69

§ 59. НОВЫЙ ТОПОЛОГИ 4F.CKHfl ИНВАРИАНТ 355
17. Неориентируемый случай. Итак, на /с имеется хотя бы
одна критическая окружность с неориентируемой диаграммой.
На каждом торе, подходящем к /с, отметим звездочкой
регулярные области, инцидентные с неориентируемыми сепарат-
рисными диаграммами (т. е. листами Мёбиуса). Следовательно,
можно пометить звездочками и со-
ответствующие ребра конструиру-
емого графа. Итак, строим граф по
схеме ориентируемого случая, после \/
чего отмечаем звездочками те его 1. nVe©
ребра, которые изображают движе- 1 А I
ние регулярных областей со звездо- I / \ I
чками. Полученный граф обозна-
чим Тс (рис. 70). Ясно, что концы рис 70
ребер графа Тс отождествляются
с концами некоторых ребер графа А. Окончательно определим
граф Г как объединение (склейку) Г = Л+?Г„ где {с} —
с
критические седловые значения интеграла.
18. Предложение. Пусть f, f — два любых боттовских
интеграла. Тогда при гомеоморфизме q{Q,f,f)'- T{Q, f)-*T(Q, f )
(см. теорему 7) седловые подграфы Тс для интеграла f гомеомо-
рфно переходят в седловые подграфы Т'с для интеграла f.
Звездочки графа Г переходят в звездочки графа Г'. Вершины
типов «минимаксная окружность» и «бутылка Клейна» графа
Г переходят в вершины того же типа (соответственно) на
графе Г'. Вершины типа «тор» графа Г могут отобразиться
в обычные внутренние точки ребер графа Г'. Наоборот, обычные
внутренние точки ребер графа Г могут отобразиться в вершины
типа «тор» на графе Г".
19. Определение. Тройку (ГB), P{Q), h{Q)) назовем
изоэнергетическим топологическим инвариантом l(H, Q) интег-
рируемого гамильтониана Н на данной изоэнергетической
поверхности Q. Полным топологическим инвариантом 1(Н)
назовем набор всех троек {ГB), P{Q\ M2)} по всем Q.
Гомеоморфные тройки считаем, конечно, эквивалентными.
Полный инвариант /(//) зависит уже только от гамильтониана
Н. Итак, если две интегрируемые системы имеют негомеоморф-
ные топологические портреты, то системы не эквивалентны,
между ними нельзя установить инварианты, траекторный
изоморфизм. В то же время существуют заведомо не эк-
вивалентные интегрируемые системы с одинаковыми топологи-
ческими инвариантами /(//).
20. Конструкция. Построим поверхность P(Q,f). Мы опре-
делим ее как объединение (склейку) вида Р(А) + ^Р(ТС), где
Р(А) и Р(ТС) — двумерные поверхности с краем. Определим

356 ГЛ. 10 КАЧЕСТВЕННАЯ ТОПОЛОГИЧЕСКАЯ ТЕОРИЯ
P(A) = (Si х lntA)' + l,D2 + I,\i + l.S1 xD1. Здесь intA — объеди-
нение всех открытых ребер графа А. Следовательно,
S1 х IntA — это объединение открытых цилиндров. Многооб-
разие (Sl х Int A)' получается из него добавлением граничных
окружностей. Пусть ребро графа А заканчивается в черной
вершине. Тогда заклеим диском D2 соответствующую ей
граничную окружность на крае многообразия E1 х IntA)'.
Приклейку таких дисков мы обозначаем 1.D 2. Пусть два ребра
графа А встретились в белой вершине. Она определяет две
граничные окружности на (S'xlnt^), которые мы заклеим
(соединим) цилиндром Sl x D1. Эту операцию мы обозначаем
Z51 xD1. Пусть ребро графа А заканчивается белой вершиной
с точкой внутри. Заклеим соответствующую ей граничную
окружность на (Sl x Int A) листом Мёбиуса ц. Эта операция
обозначается ?ц. Итак, 2.D2, l,S1xD1, Ец соответствуют
минимаксным окружностям, торам и бутылкам Клейна. Теперь
построим Р(ТС) = РС. Рассмотрим сначала ориентируемый слу-
чай, когда все критические седловые окружности на /с имеют
ориентированные сепаратрисные диаграммы. Как показал
А. Т. Фоменко в [283 ], /с гомеоморфно прямому произведению
Кс х S1, где Кс — некоторый граф, получающийся из нескольких
окружностей путем отождествления на них некоторых пар
точек. Локально из каждой вершины графа Кс выходит ровно
4 ребра.
21. Предложение. Комплекс fc получается склейкой не-
скольких двумерных торов по окружностям, реализующим
ненулевые циклы у на торах. Если на одном торе расположено
несколько таких окружностей, то они не пересекаются. Окру-
жности, по которым касаются торы, входящие в состав fc,
являются критическими для /. Они гомологичны и разрезают
fc в объединение нескольких плоских колец.
21. Итак, на fc однозначно определен цикл у. Выберем на
каждом торе в fc некоторую окружность — образующую а,
дополнительную к у (пересекающуюся с у ровно в одной точке).
Назовем ее овалом. Можно считать, что овалы касаются друг
друга в точках, лежащих на критических окружностях интег-
рала. В ориентируемом случае объединение овалов дает граф
Кс. Он не обязан быть плоским. Пусть х — точка касания двух
овалов, т. е. критическая для /. Тогда отрезки интегральных
траекторий поля w и линии уровня функции / определяют (на
двумерном диске с центром в точке х, лежащем в Q и ор-
тогональном критической окружности, на которой лежит точка
х) около точки х «координатный крест», на каждом конце
которого стоит стрелка, указывающая направление w. Постро-
им такие нормальные двумерные кресты в каждой вершине
графа Кс. Разные кресты соединены отрезками, являющимися
частями овалов. Соединим теперь концы крестов узкими

<j 59. НОВЫЙ ТОПОЛОГИЧЕСКИЙ ИНВАРИАНТ 357
лентами, идущими вдоль дуг овалов-. Эти ленты состоят из
отрезков интегральных траекторий поля w, ортогонально
пересекающих овалы (вне критических точек). Дуги овалов идут
по оси этих лент. В результате получаем гладкую двумерную
поверхность с краем. Знаком « —» отметим граничные окружно-
сти, соответствующие торам, подошедшим к/с снизу. Знаком « + »
отметим граничные окружности, соответствующие торам, подхо-
дящим к/с сверху. Полученную поверхность обозначим Р(ТС) = РС.
Ее граничные окружности разбиты на два класса: нижние
(отрицательные) и верхние (положительные). Граф Кс однозначно
(с точностью до гомеоморфизма поверхности) вложен в Р*.
Построим теперь Р? в неориентируемом случае. Схема
рассуждения в основном сохраняется. Пусть сначала для
простоты на fc лежит ровно одна критическая окружность
с неориентируемой диаграммой. Тогда fc имеет вид, показанный
на рис. 71. Следовательно, каждый овал а, лежащий на таком/с,
должен быть удвоен. Любая другая критическая
окружность с ориентируемой диаграммой, лежа-
щая на этом /с, встречает два экземпляра цикла
а в двух точках. Это заставляет нас удваивать
циклы а и на тех торах, которые касаются друг
друга вдоль окружностей с ориентируемыми
диаграммами, но входят в состав связного /с,
содержащего окружность с неориентируемой
диаграммой. Количество окружностей с неори- _
ентируемыми диаграммами на связном /с не
влияет на процесс удвоения, т. е. удвоить циклы нужно лишь
один раз. Дальнейшие построения повторяют ориентируемый
случай. В результате получаем поверхность Рс. Отличие лишь
в, том, что теперь каждая граничная окружность поверхности
Рс (т. е. соответствующая одному тору) встречается ровно
в двух экземплярах (удвоена).
Теперь построим поверхность Р(ТС). Из построения
Рс видно, что на ней корректно определено гладкое действие
группы Z2 (инволюция а). При этом а(х) = х в том и только
том случае, когда точка х принадлежит критической окружно-
сти с неориентируемой сепаратрисной диаграммой. Обозначим
такие точки хи ..., хт, а соответствующие им ^окружности
Si, ..., Sm. Рассмотрим факторпространства PC = A/Z2. Ясно,
что РС = Р(ТС) является двумерным многообразием с краем.
Теперь каждая его граничная окружность отвечает ровно
одному тору Лиувилля (верхнему или нижнему). Легко видеть,
что xi, ..., xm являются внутренними точками на поверхности Рс.
Отметим их звездочками. В частном случае, когда /с имеет вид,
показанный на рис.71 (т.е. m=l), поверхность Рс является
двумерным цилиндром с одной звездочкой. Теперь мы можем
построить всю поверхность P(Q, /).

3?S ГЛ 10 КАЧЕСТВЕННАЯ ТОПОЛОГИЧЕСКАЯ ТЕОРИЯ
Ясно, что существует взаимно однозначное соответствие между
граничными окружностями поверхности Р(А) и граничными
окружностями объединения поверхностей Рс. Это соответствие
задается ребрами графа А. Отождествив соответствующие
окружности при помощи некоторых гомеоморфизмов, однозначно
получаем двумерную поверхность P(Q, /) (ориентируемую или
неориентируемую). Очевидно, что замена склеивающих гомеомор-
физмов другими индуцирует лишь iомеоморфизм поверхности на
себя. На P(Q, /) однозначно (с точностью до гомеоморфизма
поверхности) расположен некоторый, вообще говоря, несвязный
граф, который мы обозначим K(Q, /). Рассмотрим окружности,
рассекающие пополам цилиндры, входящие в состав поверхности
S1 х inlA. Можно считать, что каждая из них имеет вид S1 х р, где
р — середина соответствующего ребра графа А. Теперь определим
граф К как несвязное объединение всех графов Кс и окружностей
вида 5 ' х р. Граф К имеет лишь вершины кратности 4. Построение
поверхности P(Q, /) полностью завершено.
23. Предложение [285]. Если f, f — любые боттовские
интегралы на Q, то P(Q, /) гомеоморфно P(Q, /') (в нерезо-
нансном случае).
24. Обозначение. Обозначим К* граф, сопряженный графу
К в поверхности P(Q. /). Его вершины — это центры q облас-
тей, на которые граф К разбивает Р, а ребра — это дуги,
соединяющие вершины через середины ребер графа К.
25. Предложение (см. [285]). Граф T{Q, f) совпадает
с графом K*(Q, /). Следовательно, граф Г (Q, /) допускает
вложение h(Q, /): V(Q, f)->P{Q, /), однозначно (с точностью
до гомеоморфизма поверхности) определяемое исходной интег-
рируемой нерезонансной системой. Граф К разбивает поверх-
ность Р на области, гомеоморфные либо диску, либо плоскому
кольцу, либо листу Мёбиуса.
26. Определение. С каждой интегрируемой гамильтоно-
вой системой естественно связано целое число, которое называ-
ется родом системы,— это род поверхности P{Q)-
27. Доказательство предложения 18. Пусть /и
/' — два боттовских интеграла на Q. В силу нерезонансности
гамильтониана Н каждый неособый тор с иррациональной
обмоткой одновременно является компонентой поверхности
уровня для каждого из интегралов, поскольку интегралы
постоянны на траекториях системы i> и, следовательно, постоян-
ны на замыкании каждой траектории. Каждый неособый тор
с рациональной обмоткой аппроксимируется сколь угодно
близко неособыми торами с иррациональной обмоткой. Следо-
вательно, он тоже является компонентой поверхности уровня
для каждого из интегралов.
Рассмотрим поля w = grad/ и ii'' = grad/'. Они определяют
одно и то же одномерное слоение поверхности Q на интеграль-

§ 59. НОВЫЙ ТОПОЛОГИЧЕСКИЙ ИНВАРИАНТ 359
ные траектории, ортогональные (в какой-либо метрике) всем
неособым поверхностям уровня, т. е. торам. Скорость движения
по траекториям (определяемым полями w и w') может быть
различной и может обращаться в нуль сразу на всем торе для
одного из полей (в то время как другое поле ненулевое).
Поскольку особые компоненты уровня аппроксимируются не-
особыми торами (при их движении вдоль w и w'), то особые
компоненты связности поверхности уровня для /, отличные от
тора, совпадают с аналогичными компонентами для/'. Если же
поверхность уровня была критическим тором для /, то она
может стать некритической для /' (и наоборот). Однако каждая
особая компонента для/является особой компонентой и для/'
(и наоборот). Торы образуют одномерное семейство в окрестно-
сти каждого неособого тора. Локально, рассматривая операции
/-»/2=/' или/ -»>//"=/', мы можем превратить некритический
тор в критический и наоборот. Все другие функциональные
операции, локально сохраняющие боттовость, сводятся к этим
двум, так как гладкая морсовская функция на одномерном
многообразии может иметь лишь квадратичные особенности.
С геометрической точки зрения операция / -»/2 отвечает
перегибанию ребра графа и появлению на нем локального
минимума или максимума. Операция / -+>//' отвечает распрям-
лению ребра графа и уничтожению локального минимакса.
Построим гомеоморфизм графа Г на граф Г'. Чтобы
определить его на подграфе А, достаточно рассматривать
каждый неособый тор для интеграла /как тор для интеграла/'
(особый или неособый). Это отображение продолжается и на
подграфы вида Тс, так как одномерные слоения поверхности Q,
порожденные w и w', совпадают всюду, кроме, быть может,
некоторых критических или некритических торов (где скорость
движения вдоль w или w' обращается в нуль). Как следствие,
отметим, что полные поверхности уровня интегралов / и /'
(содержащие одну и ту же компоненту связности) могут
состоять из разного числа связных компонент. При этом
значения / и /' могут быть различны на одной и той же
компоненте связности. Предложение доказано.
28. Доказательство предложения 21 можно найти в [283],
[286].
29. Доказательство предложения 23. Рассмотрим
подробнее процесс построения поверхности Р. Ограничимся
пока ориентируемым случаем. Комплекс/ получается склейкой
нескольких экземпляров торов Ти ..., TN по циклам, гомологич-
ным циклу у на / (см. выше). Пусть Sb ..., Sp—критические
окружности на/. Выберем на каждой из них по точке дь ..., qp.
Рассмотрим какое-нибудь из плоских колец у, на которые
/ разрезается окружностями St. Тогда на каждой из его

360 ГЛ. 10. КАЧЕСТВЕННАЯ ТОПОЛОГИЧЕСКАЯ ТЕОРИЯ
граничных окружностей лежит ровно по одной точке вида qa.
Пусть это точки цл и q$. Соединим их гладкой дугой т„р,
целиком лежащей внутри кольца. Эта дуга строится, конечно,
неоднозначно, но на окончательный результат это не влияет.
Самонепересекающуюся дугу т^р можно было бы связать
с интегралом /. Для этого нужно рассмотреть поле sgrad / на
кольце у. Это поле может обращаться в нуль только на границе
кольца. Можно было бы выпустить из точки qa короткий
отрезок, идущий внутрь кольца, затем из его конца выпустить
интегральную траекторию поля sgrad/и двигаться по ней, пока
не приблизимся достаточно близко к противоположной границе
кольца, на которой расположена точка q§. Затем свернем
с интегральной траектории и проведем короткий отрезок
в точку ^р.
Повторим процесс построения гладкой дуги в следующем
кольце, начиная с точки q^, и т. д., пока не исчерпаем все
кольца, входящие в состав /с. В результате получим систему
окружностей — овалов. Каждая из них составлена из дуг вида
т„,р. Рассмотрим во всех внутренних точках дуги т^ нормальный
отрезок вдоль интегральных траекторий поля grad/. Концы
полученной ленты определяются координатными крестами
точек <7„ и q$. Заменяя дугу т„р дугой т^р, лежащей в у исоединя-
ющей qa и ^р, получаем поверхность, гомеоморфную пре-
дыдущей. Замена / на /' приводит к гомеоморфизму Р и может
существенно повлиять на вид вложения Рс в Q.
30. Доказательство предложения 25 следует из конструкции,
изложенной выше. Граф Кс состоит из дуг вида таЭ. Каждая из
них определяет свое кольцо вида у на fc.
31. Доказательство теоремы 5 следует из [283], а также из
явной конструкции Рс, описанной выше. Остановимся подробнее
на случае PcxSl. Пусть U(fc)={xeQ | с — ?</(х)<с + е} — регу-
лярная окрестность fc, причем /с содержит критические окружно-
сти Su ..., Sm с неориентируемыми диаграммами. Пусть
U(S^ — малая трубчатая окрестность 5( (полноторие) в U(fc).
Тогда U(fc)\(U(S1)\J...{JU(Sn.)) гомеоморфно прямому произ-
ведению (/>c\(.x1\j...U-*m)) x S > при этом каждое полноторие
U(Si) является расслоенным полноторием типа B, 1).
В серии важных работ М. П. Харламова была детально
исследована топология отображения моментов некоторых слу-
чаев интегрируемости классических механических систем. Этой
информации оказалось достаточно для того, чтобы сразу
выписать значения топологического изоэнергетического инвари-
анта I(H, Q) для этих случаев интегрируемости. Однако
следующий шаг — вычисление окончательного, меченого ин-
варианта I(H, Q)' — потребовал привлечения новых идей друго-
го характера, что и было сделано А. В. Болсиновым,
А. А. Ошемковым и А. Т. Фоменко [208], [209]. Дело в том,

« 54 НОВЫЙ ТОПОЛОГИЧЕСКИЙ ИНВАРИЛН1
361
что вычисление рациональных и целочисленных параметров,
окончательно классифицирующих интегрируемые системы, тре-
бует специального (и нетривиального) исследования «функций
склейки» элементарных «блоков», определяющих слоение изо-
энергетического многообразия на торы Лиувилля.
;с. 72
Рис. 73
32. Пример. Рассмотрим случай Ковалевской, см. п. 14 § 5.
На рис. 72 приведена бифуркационная диаграмма IcR2 (вычи-
сленная М. П. Харламовым), а на рис. 73 — полный список всех
графов ГB), встречающихся в случае Ковалевской.
Рис. 74
Рис. 75
33. Пример. Случай Горячева — Чаплыгина. Бифуркационная
диаграмма показана на рис. 74, а полный список графов
Г (g) — на рис. 75.
Рис. 76
34. Пример. Гиростат. Полный список графов Г (Q) приве-
ден на рис. 76.

362
ГЛ 10 КАЧЕСТВЕННАЯ ТОПОЛОГИЧЕСКАЯ ТЕОРИЯ
35. Пример. Четырехмерное твердое тело. Полный список
графов ГШ) приведен на рис. 77, а бифуркационная диаграмма
на рис. 78.
36. Дальнейшие примерения инварианта I(H, Q) были выпо-
лнены А. Т. Фоменко и X. Цишангом. В частности, они
X
Y v
Рис. 77.
(A)
Рис. 78. Цифрами обозначено число торов Лиувилля в F ' О')
получили полную классификацию всех стабильно эквивалент-
ных интегрируемых боттовских гамильтоновых систем (на
достаточно сложных и неприводимых изоэнергетических 3-
многообразиях).
37. Резюме. Подведем промежуточные итоги. Интегриру-
емая система называется боттовской, если она имеет боттов-
ский интеграл. В работах А. Т. Фоменко построена теория типа
Морса для боттовских интегралов на изоэнергетических
3-поверхностях. В частности, получена структурная теорема,
дающая топологическое описание изоэнергетических многооб-
разий Q интегрируемых боттовских систем. Оказалось, что
Q допускает представление вида ml+pU + qlU + sW + rV, т.е.
представляется как склейка некоторого числа экземпляров
элементарных 3-многообразий типов I, II, III, IV, V. Наряду
с этим (гамильтоновым) разложением есть более «грубое»
(топологическое) разложение ?> = т'1 + <7'Ш, где числа т' и q'
являются линейными комбинациями чисел т, р, q, s, r.
Как доказали затем С. В. Матвеев и А. Т. Фоменко, условие
боттовости интеграла / можно существенно ослабить, заменив
его условием, чтобы / был всего лишь «ручным» интегралом.

§ 59. НОВЫЙ ТОПОЛОГИЧЕСКИЙ ИНВАРИАНТ 363
Однако, поскольку подавляющее большинство исследованных
классических интегралов, известных в механике и математиче-
ской физике, являются боттовскими (это выяснено в работах
А. А. Ошемкова, А. Т. Фоменко, А. В. Болсинова, Л. С. Поля-
ковой, К. Шваи, см. [207]—[209], [283]—[286], [296]), мы
будем считать, что все рассматриваемые в настоящей книге
интегралы боттовские, см. также [509].
Интеграл / задает отображение /: Q->R. Символом aeR
обозначим регулярное значение отображения /, а символом
ceR — сингулярные (критические) значения. Тогда полный про-
образ f ~1 (а) каждого регулярного значения а состоит из
несвязного объединения торов Лиувилля. Обозначим /"'(с)
критический уровень интеграла /. Пусть fs обозначает связную
компоненту критического уровня / ~1 (с). Индексом s будем
пользоваться также для разных уровней с, т. е. индекс
s перечисляет все связные компоненты всех критических уровней
функции /.
Класс замкнутых трехмерных ориентируемых многообразий,
допускающих представление вида m'1 + q'lll, обозначим (Q).
Пусть (//) — класс всех трехмерных изоэнергетических замк-
нутых поверхностей гамильтоновых систем, интегрируемых
при помощи боттовских интегралов. Согласно [283] имеем
(Н) с= (Q). Затем в работах А. В. Браилова, С.В.Матвеева,
А.Т.Фоменко и X. Цишанга [283], [54], [287], [288] было
доказано, что класс (H) = (Q) совпадает также с классом (S)
3-многообразий и с классом (W) граф-многообразий. Далее,
А. Т. Фоменко и X. Цишанг [287], [288] изучили топологичес-
кие свойства многообразий класса (Я) = (И/), в частности,
получили оценки числа устойчивых периодических решений
интегрируемых боттовских гамильтоновых систем. Связь класса
(H) = \W) с классом [R) 3-многообразий, допускающих круглую
функцию Морса, изучена А. Т. Фоменко и В. В. Шарко [289].
Затем неожиданные и глубокие связи класса (H) = (W) с теорией
трехмерных замкнутых гиперболических многообразий обнару-
жены С. В. Матвеевым и А. Т. Фоменко в [171].
38. Напомним, что гамильтониан Н называется нерезонанс-
ным на изоэнергетической поверхности Q, если в Q всюду
плотны торы Лиувилля, на которых интегральные траектории
системы у образуют плотную иррациональную обмотку, см.
[352], [285]. Опыт изучения конкретных интегрируемых систем
математической физики [285], [207], [131], [208] показывает,
что на МА гамильтонианы в большинстве случаев нерезонансны
на почти всех поверхностях Q3. Важные геометрические
свойства интегрируемых систем см. в работах О. И. Богоявлен-
ского [37], В. В. Козлова [131]. О резонансности и нерезонанс-
ности многомерных систем в связи с некоммутативной интегри-
руемостью см. работу В. В. Трофимова и А. Т. Фоменко [270].

364 ГЛ. 10. КАЧЕСТВЕННАЯ ТОПОЛОГИЧЕСКАЯ ТЕОРИЯ
Следуя [352], [285], назовем две интегрируемые гамиль-
тоновы системы Vy и v2, заданные на многообразиях
Qi и 0.2 соответственно, топологически (или геометрически)
эквивалентными, если существует диффеоморфизм d: Qi~>Q2,
переводящий торы Лиувилля системы vt в торы Лиувилля
системы v2- В частности, в нерезонансном случае, этот
диффеоморфизм переводит друг в друга критические поверх-
ности уровня интеграла /t и критические поверхности уровня
интеграла /2, см. [285] (не путать с траекторной эквивалент-
ностью!).
39. В [352], [285] А. Т. Фоменко обнаружил новый тополо-
гический инвариант I(H, Q) интегрируемых нерезонансных
боттовских гамильтоновых систем (названный изоэнергетиче-
ским топологическим инвариантом). Он представляет собой
граф Г, вложенный в замкнутую двумерную поверхность Р2.
Инвариант не зависит от выбора боттовского интеграла
/ и полностью определяется самим гамильтонианом Н. Как
доказано в [285], если две нерезонансные системы vl и v2 имеют
различные {т. е. не гомеоморфные) инварианты, то системы
топологически не эквивалентны. В [285] введен также полный
инвариант 1{Н), не зависящий от конкретного выбора поверхно-
сти Q. Наряду с графом Г на поверхности Р определен другой
граф К такой, что К* = Г. Здесь К* — это граф, сопряженный
к графу К (см. [285], а также ниже). Удобно иногда вместо
пары (р2, Г) рассматривать пару (Р2, К). Она также однозначно
определяет изоэнергетический инвариант /(//, Q).
В [285] отмечено, что, снабдив инвариант 1{Н, Q) некоторы-
ми числовыми метками, т. е. рассмотрев «меченый» инвариант
1{Н, Q )*, можно получить критерий топологической эквивалент-
ности интегрируемых гамильтоновых систем. Эта программа,
намеченная в работе [285], полностью реализована Фоменко
и Цишангом. Сейчас мы дадим точное определение «меченого»
инварианта 1{Н, QY, укажем оптимальные числовые метки,
превращающие /(//, Q) в /(#, Q)*. Мы будем говорить, что
меченые изоэнергетические топологические инварианты
1{Ни 2i)* и I(H2, Q2)* гомеоморфны (или равны), если суще-
ствует гомеоморфизм, переводящий поверхность Р\ ъ поверх-
ность Р\, граф Tj в граф Г2 и сохраняющий все числовые
метки.
40. Теорема (Фоменко, Цишанг). Критерий эквива-
лентности интегрируемых систем. Пусть даны два
трехмерных замкнутых ориентируемых изоэнергетических мно-
гообразия Q\ и Qx, и пусть иь v2 — интегрируемые (при помощи
боттовских интегралов) нерезонансные гамильтоновы системы
на них. а) Если соответствующие им меченые инварианты
I(HU gt)* и 1{Нг, Q2)' не гомеоморфны (различны), то системы
D! и v3 топологически не эквивалентны. При этом многообразия

§ 59 НОВЫЙ ТОПОЛОГИЧЕСКИЙ ИНВАРИАНТ 365
Q \ и Q 2 могут быть гомеоморфны. б) Обратно, пусть меченые
инварианты двух интегрируемых систем vt и v2 гомеоморфны
(равны). Тогда: 1) многообразия Q\ и Q\ гомеоморфны;
2) системы и, и v2 топологически эквивалентны.
Эта теорема позволяет приступить к топологической класси-
фикации всех интегрируемых боттовских гамильтоновых систем.
41. Следствие. Пусть на одном и том же изоэнергетиче-
ском многообразии Q 3 заданы две интегрируемые нерезонансные
боттовские гамильтоновы системы v, и v2 с одинаковыми
мечеными инвариантами I(H1, Q)" и I\H2, Q). Тогда системы
vl и v2 топологически эквивалентны. •
В действительности можно описать множес i во всех значе-
ний, которые принимает меченый инвариант /(//, Q)* для
всевозможных интегрируемых боттовских систем. Тогда из
теоремы 40 мы получим, что инвариант /(//, Q) классифицирует
интегрируемые системы и можно предъявить «список» всех
возможных интегрируемых боттовских систем.
42. В работе [41] А. В. Болсинова, С. В. Матвеева
и А. Т. Фоменко была полностью завершена топологическая
классификация интегрируемых (боттовских) гамильтоновых си-
стем (с двумя степенями свободы). Эффективно и алгоритмичес-
ки описано все множество допустимых значений, которые
может принимать инвариант /(//, Q)*, доказано, что каждое из
этих допустимых значений реализуется на некоторой интегриру-
емой системе. Это позволило построить дискретную таблицу
всех интегрируемых систем (указанного типа), рассматриваемых
с точностью до топологической эквивалентности. Обнаружен
простой способ кодирования интегрируемых систем, при кото-
ром каждая такая система записывается в виде некой
«химической молекулы», составленной из атомов, список
которых также алгоритмически предъявлен. Оказалось далее,
что можно ввести естественное понятие сложности интегриру-
емой системы и, следовательно, упорядочить все системы
в порядке возрастания их сложности. Затем при помощи
компьютера были перечислены все интегрируемые системы
«малой сложности», т. е. системы, сложность которых не
превосходит некоторого фиксированного (не очень большого)
числа. Наконец, были вычислены значения инварианта для
многих классических интегрируемых систем, т. е. найдены
соответствующие им «химические формулы». В результате на
таблице всех возможных интегрируемых систем обозначилась
«физическая зона», заполненная системами, уже обнаруженными
в физике и механике. Это позволяет представить то место,
которое занимают «физические интегрируемые системы» среди
множества всех мыслимых (формально существующих и полно-
стью перечисленных в указанной таблице) интегрируемых
систем.

366 ГЛ. 10. КАЧЕСТВЕННАЯ ТОПОЛОГИЧЕСКАЯ ТЕОРИЯ
§ 60. Построение меченого инварианта интегрируемых систем
1. Пусть Q3—замкнутое изоэнергетическое многообразие
(оно автоматически ориентируемо) и /—боттовский интеграл.
Следуя [285], рассмотрим регулярную связную е-окрестность
связной компоненты /s критического уровня. Обозначим эту
окрестность U(fs). Она является гладким 3-многообразием,
компактным, связным, край которого состоит из некоторого
числа неособых торов Лиувилля. Будем считать, что U(fs)
заключено между уровнями / ~1 (с — е) и/ '(с + е). Напомним,
что индекс с нумерует критические значения интеграла /,
а индекс s—связные компоненты всех критических уровней
f~l{c). В дальнейшем мы предполагаем (не повторяя этого
каждый раз), что система f нерезонансна на Q. Многообразие
Q разлагается в объединение конечного числа 3-многообразий
с торическими краями. Обозначая для краткости U(fs) симво-
лом Qs, получим Q = ? Qs. Здесь сумма (объединение) берется
5
фактически по всем критическим значениям с (индекс .у пробега-
ет все компоненты всех критических уровней). Это разложение
Q в сумму «кусков» Qs однозначно определено (в нерезонансном
случае) гамильтоновой системой v, т. е. не зависит от выбора
боттовского интеграла / на Q, см. [285]. (Не путать это
разложение с гамильтоновым!)
2. Однозначно определено расслоение ns: Qs -* Ps, базой
которого является двумерная связная поверхность Ps с краем.
Край состоит из конечного числа гладких окружностей, которые
обозначим Ss\;. Слоем расслоения ns является окружность.
Подробнее об определении слоев (и об их однозначности) см.
ниже. Над каждой граничной окружностью 5i?j однозначно
определен тор Лиувилля Т1л = к^ (S\,i), являющийся одной из
компонент края многообразия Qs. Поскольку Q склеено из
кусков Qs, то для каждого граничного тора Tjj определен
некоторый диффеоморфизм на другой граничный тор, определя-
емый разложением Q = Y^Qs- Следовательно (см. [285]), одно-
значно определяется взаимно однозначное соответствие между
граничными окружностями кусков Ps. Склеивая соответст-
вующие окружности, получаем замкнутую поверхность Р2. На
ней однозначно (с точностью до изотопии) определяется
конечная система окружностей Кг, являющихся результатом
склейки граничных окружностей 5*, и Sl.v кусков Ps и Ps.
Окружности типа Кг не пересекаются. Они образуют граф,
который мы обозначим {Кг}.
3. Замечание. Мы будем употреблять термин «разрезать
поверхность». Он означает следующее. Поверхность Р склеена
из кусков Ps. Граничные окружности кусков отождествляются
диффеоморфизмами, которые мы считаем фиксированными.

i 60 ПОСТРОЕНИЕ МЕЧЕНОГО ИНВАРИАНТА
367
Операция разреза обратна склейке. Мы не используем труб-
чатые окрестности окружностей для определения разреза (как
это обычно делается).
Упростим обозначения. Склеивая окружности 5'; и
Ss',1- (при склейке кусков Ps и Ps), мы получаем окружность
типа Кг в графе К. Заменим пару индексов (s, i) в обозначении
Slj на один индекс. Для этого будем считать, что, разрезав
Р по окружности Кг, мы получаем две окружности (два берега
разреза): Кг на куске Ps и Кг на куске Ps. Вместо Slsi будем
писать Кг, а вместо S'-?г напишем Кг..
4. Нам потребуется подробное описание поверхности Р,
построенной в [285]. Напомним о связи Ps с многообразиями
Qs— U(fs). Многообразия Qs разбиваются на пять типов
в соответствии с разбиением поверхностей Ps на пять типов.
Многообразия Qs типов I, И, III имеют вид прямого
произведения PJxS1, где Р2 — связная двумерная поверхность
с краем. Поверхность Р2 типа I — это диск D2, поверхность
Р2 типа II — это кольцо S1xD1, поверхность Р2 типа III
является поверхностью с краем такой, что ее одномерная
группа гомологии не имеет кручения и ранг не менее двух.
Многообразие Qs типа IV имеет вид Р2 х S1 (расслоение
Зейферта с базой Р2 и слоем S1), причем Pf является
поверхностью (типа IV) с краем, и одномерная группа гомоло-
гии Р2 не имеет кручения, и ее ранг не менее двух.
Многообразие Qs типа
V имеет вид P2xSl (ко-
сое произведение). Здесь
Р2 типа V — это лист Мё-
биуса ц.
Поверхности Ps типов
I, И, V отвечают мини-
мальным и максималь-
ным (локально) значени-
ям интеграла. Тип I от-
вечает критической
окружности, тип II — кри-
тическому тору, тип V —
критической бутылке
Клейна. Поверхности
Ps типов III и IV отвеча-
ют седловым значениям интеграла. Каждая из поверхностей
Ps содержит связный граф, который мы обозначим Ks. Его
можно понимать как «пересечение» Рг (нормальной к поверх-
ности f~l(c)) с поверхностью f~l(c). Граф Ks изображен на
рис. 79.
Тип I: Ks является точкой в центре диска P2 = D2. Тип II:
Ks является осевой окружностью кольца Pj=S1xZI. Тип III:
Рис. 79

368 ¦ ГЛ 10 КАЧЕСТВЕННАЯ ТОПОЛОГИЧЕСКАЯ ТЕОРИЯ
Ks является графом, получающимся попарным касанием гладких
окружностей в числе, не меньшем двух. Каждая пара таких
окружностей либо не пересекается, либо касается в одной или
нескольких точках. В каждой точке касания могут касаться лишь
две окружности. На рис. 79 точки касания отмечены черными
точками. Граф Ks (как и поверхность Ps) связен и отвечает
критическим седловым окружностям интеграла /, имеющим
лишь ориентируемые сепаратрисные диаграммы. Точки касания
окружностей графа Ks (эти окружности мы называем овалами)
соответствуют критическим седловым окружностям на поверхно-
сти уровня/ (с). Итак, граф Ks составлен из овалов, и каждая
его вершина имеет кратность 4 (локально из нее выходят ровно
4 ребра графа). Овалы, составляющие граф Ks, выделим
и зафиксируем в каком-либо порядке. Условие касания в одной
точке лишь двух овалов следует из боттовости интеграла / см.
[285]. Тип IV; граф Ks аналогичен графу типа III, однако среди
критических седловых окружностей есть по крайней мере одна
с неориентируемой сепаратрисной диаграммой. Как доказано
в [285 ], это влечет за собой появление группы Z2, действующей
на нормальном сечении к уровню/ г (с). Факторизуя по этому
действию, мы получим поверхность Ps, в которой лежит граф Ks,
составляющий «половину» первоначального набора овалов на
уровне/~'(с). В случае IV на графе Ks выделены звездочки,
отвечающие неподвижным точкам действия группы Z2. Они
соответствуют критическим седловым окружностям с неориенти-
руемыми сепаратрисными диаграммами. Тип V: Ks является
осевой окружностью листа Мёбиуса Ps = n, см. рис. 79.
5. Предложение (см. [285]). Связная поверхность Ps (ти-
пов I—V) является трубчатой окрестностью вложенного в нее
графа Ks. Более того, определена (с точностью до изотопии)
ретракция Ps на граф Ks. Многообразие PS\KS гомеоморфно
прямому произведению полуинтервала на некоторое множество
непересекающихся окружностей. Это множество гомеоморфно
границе поверхности Ps и состоит из окружностей вида Кг.
В случаях I—IV поверхность Ps ориентируема, в случае
V неориентируема.
Ретракция Ps на Ks осуществляется вдоль интегральных
траекторий поля grad/ (для этого на Q задается риманова
метрика). Поверхность Ps не обязана быть плоской. В случаях
III и IV каждая вершина графа Ks окружена на
Ps «координатным крестом», задающим структуру морсовской
особенности интеграла/по нормали к критической окружности.
Эти кресты соединены тонкими лентами, образованными
отрезками интегральных траекторий поля grad/ ортогональных
овалам, составляющим Ks, см. [285].
6. Итак, если на Q задана интегрируемая система, то она
однозначно (с точностью до изотопии) определяет слоение (с

§ 60 ПОСТРОЕНИЕ МЕЧЕНОГО ИНВАРИАНТА
369
особенностями) поверхности Р на окружности. На графах
Ks типов III и IV однозначно определена система образу-
ющих— овалов. Их объединение дает граф Ks. Овалы могут
лишь касаться друг друга. Рассматривая «нижние» торы
Лиувилля, лежащие на близком уровне с — е, и пронумеровав их,
переносим чту нумерацию на образующие — овалы графа Ks.
Если же фиксировать «верхние» торы Лиувилля, лежащие на
близком уровне с+е, можно получить другие образующие
графа Ks. «Нижняя»
система образующих
превращается в «верх-
нюю», если мы перене-
сем критический уро-
вень с, двигаясь от
уровня с —? к уровню
с + е. Договоримся рас-
сматривать «нижнюю»
систему образующих.
Граф К, введенный
в [285], представля-
ется как объединение
Нис. 80
K={Kr} + {Ks} или К=
Каждая компонента вида
Кг или Ks связна. Компоненты Кг являются окружностями, по
которым склеены поверхности Р„ (рис. 80). Разрезав поверх-
ность Р по всем окружностям Кг, получаем набор связных
поверхностей Ps. Каждая из них содержит ровно одну связную
компоненту графа вида Ks.
7. Предложение (см. [283], [285]). В случаях I, II, III
имеем Qs = PsxS\ При этом Qs[)f~l(c) = KsxSl. В случае IV
имеем Qs = PsxSl. При этом QsC\f~l(c) = KsxS1. В случае
V имеем Qs = PsxS\ причем 6S П / ~' (с) = Ц х S * (бутылка
Клейна).
8. Представление многообразий типов I (полноторие), II
(цилиндр T2xD1) и V (косое произведение бутылки Клейна на
отрезок) в виде расслоения (со слоем окружность) неоднозначно.
Неоднозначность не устраняется с привлечением данных об
интегральных траекториях системы. Напротив, многообразия
Qs типов III и IV однозначно (с точностью до изотопии)
представляются соответственно как прямое произведение
PsxSl и как расслоение Зейферта PsxSK Согласно [283]
критические подмногообразия интеграла / в случаях I, II,
V таковы: окружность, тор, бутылка Клейна (соответственно).
Поэтому слой окружность может наматываться вокруг «оси»
много раз, что влияет на представление Qs в виде произведения.
А именно, чтобы совместить два таких представления, нужно

370
ГЛ. 10 КАЧЕСТВЕННАЯ ТОПОЛОГИЧЕСКАЯ ТЕОРИЯ
применить некоторый диффеоморфизм (рис. 81). Он и задает
неоднозначность выбора слоев. В случаях III и IV на
поверхности f~l (с) однозначно выделена система критических
окружностей интеграла (являющихся периодическими седловы-
ми решениями системы). Как доказано в [283], они разрезают
Рис. 81
уровень f~l(c) (его связные компоненты имеют вид A^xS1
в случае III и ^xS1 в случае IV) в набор колец. Следователь-
но, каждое из колец однозначно (с точностью до изотопии)
расслаивается на окружности, параллельные границе кольца
(рис. 81). В частности, во всех случаях I—V многообразие
QsXf1 (с) однозначно расслаивается на торы Лиувилля. Это
расслоение, пересекаясь с нормальной поверхностью Ps, одно-
значно высекает на нем слоение на окружности.
9. Напомним построение графа Г, входящего в изо-
энергетический топологический инвариант, см. [285]. Рас-
смотрим разбиение Р в объединение областей Р„ определяемое
окружностями Кг. Построим граф К*, сопряженный к графу
К. Для этого в каждой области Ps выберем точку, объявим
ее вершиной нового графа и соединим эти вершины ребрами,
проходящими через середины ребер графа К, по которым
инцидентны области Ps.
10. Напомним (см. [285]), что граф К* совпадает с графом
Г, описывающим эволюцию и бифуркации торов Лиувилля при
фиксированном значении энергии Н и переменном значении
второго интеграла /.
Итак, мы получаем объект, состоящий из: 1) замкнутой
двумерной поверхности Р2 (ориентируемой или неориентиру-
емой); 2) графа К=^КГ + ^К„ вложенного в Р2 (граф К'

i) 60 nOCTPOF.HHI- МКЧКНОГО ИНВАРИАНТА
371
совпадает с Г). Этот объект и является изоэнергетическим
топологическим инвариантом /(//, Q), обнаруженным
А. Т. Фоменко.
11. Модифицируем граф К. Рассмотрим все Qs типа II, т. е.
цилиндры T2xD1. Им отвечают на Р2 двумерные цилиндры
Ps = Sl х D1. Внутри Qs лежит критический тор Т2 (отвечающий
белой вершине графа Г, см. [283], [285]). «Внизу», на Р, этому
тору отвечает окружность A^s (осевая окружность цилиндра Ps).
Редуцируем граф К следующим образом. Стянем в Q каждое
многообразие Qs типа II на его критический тор. Затем «внизу»,
на Р, стянем соответствующее кольцо на его осевую окруж-
ность Ks (типа II). Итак, мы убираем из разложения Q (в сумму
элементарных кирпичей) все цилиндры T2xDl (тип II) и убира-
ем из разложения Р (в сумму кусков Ps) все кольца типа II. На
языке графа Г происходит следующее: белая вершина на нем
исчезает и заменяется обычной точкой ребра (рис. 82). Напри-
Рис. 82
мер, иногда можно считать, что мы распрямляем ребро графа,
в результате чего критический гор становится некритическим.
Эта процедура может изменить интеграл, но не меняет слоения
Q на торы (в нерезонансном случае). Поскольку нас интересует
топологическая эквивалентность систем, то описанная операция
приводит нас к системе, топологически эквивалентной исходной.
Итак, на графе Г мы можем «вытереть» все белые вершины,
заменив их обычными точками ребер графа. При стягивании
кольца по поверхности Р мы получаем окружность. Естественно
обозначить ее символом Кг, так как теперь она является
границей двух соседних областей типа Ps. Пояснение: две пары
прежних окружностей типа Кг и одна окружность типа
Ks слились в одну окружность, которую мы обозначим Кг.
Выполним эту операцию со всеми двумерными цилиндрами на
Р. Получаем новое разбиение поверхности и новый граф. Граф
мы по-прежнему обозначим буквой К, чтобы не вводить новые
обозначения, но будем говорить о нем как о редуцированном

372 ГЛ. 10. КАЧЕСТВЕННАЯ ТОПОЛОГИЧЕСКАЯ ТЕОРИЯ
графе К. Точно так же мы сохраним прежние обозначения
и для многообразий Qs, но будем говорить о редуцированных
многообразиях. В дальнейшем считаем, что все наши объекты
редуцированы.
Описанная редукция нужна для корректного решения про-
блемы классификации интегрируемых систем. Дело в том, что
соответствующим образом изменяя интеграл / (например,
извлекая из него квадратный корень, как описано в [285]), мы,
с одной стороны, получаем систему, топологически эквивалент-
ную исходной, а с другой стороны, уничтожаем на графе
Г белую вершину. Соответственно на графе К нужно отождест-
вить две окружности типа КТ с одной окружностью типа Ks. Как
доказано в [285], единственными допустимыми (локальными)
операциями над боттовским интегралом являются возведение
его в квадрат или извлечение из него квадратного корня. Как
мы покажем ниже, редуцированный граф К и редуцированная
поверхность Р уже позволяют (после нанесения числовых меток)
различать неэквивалентные системы.
Перейдем к построению меченого изоэнергетического топо-
логического инварианта, который обозначим I(H, Q)* и для
краткости назовем меченым инвариантом (Фоменко, Цишанг).
12. Начнем с рассмотрения ориентируемого случая. Пусть:
1) редуцированная поверхность Р ориентируема (фиксируем эту
ориентацию); 2) боттовский интеграл / также ориентируем.
Напомним, что ориентируемость интеграла означает ориентиру-
емость всех его критических многообразий. При этом сепарат-
рисные диаграммы некоторых критических многообразий могут
быть неориентируемы. Интеграл ориентируем в том и только
том случае, когда в разложении Q на кирпичи нет многообразий
типа V. Общий случай (т. е. когда Р и интеграл / могут быть
неориентируемыми) лишь технически сложнее. Общая схема
рассуждений останется той же, как и в ориентируемом
случае. Более того, в [283 ] доказано, что если на Q задан
ориентируемый интеграл /, TOj переходя к двулистному
накрытию Q, мы получаем на Q ориентированный интеграл
/. Следовательно, рассматривая изоэнергетические поверхности
с точностью до двулистного накрытия, можно считать
интеграл ориентируемым.
После редукции ориентированной поверхности Р она скле-
ивается лишь из кусков следующих трех типов: тип I—диск D2
с границей Кг и центральной точкой Ks; тип III — более сложная
поверхность Ps (отвечающая окружностям с ориентированными
диаграммами); тип IV — также более сложная поверхность
Р„ (отвечающая окружностям, среди которых есть по крайней
мере одна с неориентируемой диаграммой).
13. Поскольку Р предположена ориентируемой, то фиксиру-
ем индуцированную ориентацию на каждом куске Ps. Фиксиру-

60. ПОСТРОЕНИЕ МЕЧЕНОГО ИНВАРИАНТА
373
ем ориентацию на каждой граничной окружности S,',- так, чтобы
она была согласована с ориентацией Ps. Пусть склеены два
куска Ps и Ps.. Выделим какую-нибудь пару склеиваемых
окружностей Kr = Sl4 и Kr=Slr. Рассмотрим многообразие 2s-
расслоенное над базой Ps со слоем S . Пусть каким-либо
образом заданы и фиксированы эти расслоения. Для типов III
и IV эта процедура однозначна, для типа I — нет. Поскольку на
Qs задана ориентация и на базе Ps также фиксирована
ориентация, то однозначно определяется ориентация на слое —
окружности. Фиксируем ориентацию слоя на каждом Qs.
Рассмотрим над каждой окружностью Кг граничный тор
Лиувилля Т2 = тт5Г1 (К), расслоенный над Кг со слоем S1. Из
предыдущего следует, что можно однозначно задать ориен-
тацию на торе. Более того, можно считать, что на торе
фиксирован базис из двух циклов — меридиана и параллели.
Параллель отвечает слою проекции tts, а меридиан отвечает,
например, окружности Кг.
14. Замечание. Рассмотрим Qs типов I, III, IV. Они
содержат критические окружности интеграла / (периодические
решения системы и). Поскольку система задана на всем Q, то
она однозначно определяет ориентацию на всех своих решениях.
В случаях I, III, IV эти решения (окружности) являются слоями
расслоений ns. Но в общем случае мы не будем пользоваться
этой ориентацией, так как для Qs типов II
и V нет выделенных критических окружно-
стей. Здесь критические многообразия —
тор и бутылка Клейна. Рассмотрим рас-
слоения иs: QS-*PS и 7ts.: Qs-+Ps- Пусть
Ps и Ps. — поверхности типов III или IV
(независимо друг от друга). В частности.
Р5 и Ps, отличны от диска. Прообразы
окружностей Кг и Кг, т.е. торы к~ (Кг)
и npl(Kr-), обозначим Т2 и Т2. В каждом
из них однозначно (с точностью до изо-
топии) определены слои расслоения, т. е.
окружности Si = it (хг) и Si' = 7i 5Тl (,xr). p
где xr и -v — некоторые точки на '
Кг и Кг соответственно (рис. 83).
15. Введем удобную систему координат
на торах Т2 и Т2.. Окружности S'r и Si—
образующие на торах Т? и Т^ соответст-
венно. Дополним образующую S'r на торе трансверсальной
окружностью D}, а образующую 5ГХ—трансверсальной окру-
жностью D1,-. Пары окружностей (Si, Dl) и [Si-, ?)',) дают,
Tts
Рис. 83
очевидно, системы
координат на Т2 и Tf. Отображения
тс5 и 7ts. определяют расслоение торов Т* и ТЬ на окружности
(однозначно для типов III и IV). Ясно, что D; и D\. являются

374 ГЛ 10 КАЧЕСТВЕННАЯ ТОПОЛОГИЧЕСКАЯ ТЕОРИЯ
сечениями этих расслоений на торах Т? и Т*,. Выбор сечений
D) и D\' неоднозначен, однако этот произвол не повлияет на
наши окончательные конструкции.
Поскольку Р склеена из кусков Ps, следовательно, торы
Г, и Т}- склеиваются «наверху» (т. е. внутри Q) некоторым
диффеоморфизмом X. Он задается структурой Q и системой v.
Учитывая введенную систему координат на торах, мы однозна-
чно получаем две целочисленные матрицы
М„.=
а(г.г') р(г.г')
у (г, г') 6 (г, г')
а (г', г) Р(г\ г)
у (г', г) 5 (с', г)
(808)
Матрица М„, записывает диффеоморфизм Tj->T}-, а матрица
МГ'Г — диффеоморфизм Т?—>Т?. Можно считать, что обе
матрицы имеют определитель, равный — 1. Этого можно
добиться выбором ориентации на базисных окружностях торов.
Эти матрицы связаны соотношением A/rr-A/r.r=id, т.е. они
взаимно обратны. Для дальнейшего особую роль играет первая
строка матрицы М„- (или Мг>), т. е. пара целых чисел а (г, г'),
Р(г, г'). Будем обозначать эту пару (а, Р), если нет опасений
перепутать матрицы М„. и Мгг. Числа а и C можно считать
взаимно простыми, причем 0<а<|Р|, если Р/0.
16. Выделим среди окружностей Кг те, для которых пара
чисел (а, Р) имеет вид (±1,0). Эти окружности однозначно
выделяются из множества всех окружностей Кг. Для нагляд-
ности будем говорить (и изображать на рисунках), что такие
окружности Кг нарисованы тонкими линиями. Остальные
окружности К, (т. е. те, для которых (а, Р)#(±1, 0), изобразим
толстыми линиями. Итак, граф {А"г} разбивается в объединение
тонких и толстых окружностей.
На каждой толстой окружности поставим рациональное
число ое/Р (здесь мы считаем, что О^ое<|Р|). Мы пользуемся
тем, что Р/0.
17. Пусть теперь хотя бы одна из двух граничащих по
К, областей Ps и Ps. гомеоморфна диску. Возможны два случая:
1) обе области Ps и Ps, гомеоморфны диску; 2) лишь одна из них
гомеоморфна диску, а другая имеет тип III или IV. Пусть
в случае 2) область Ps гомеоморфна диску.
Компонента графа Ks состоит в данном случае из одной
вершины — центра диски (граница диска — окружность Кг).
Наша цель — построить здесь для Кг аналог рациональной
дроби ое/р. Построение усложняется тем, что над диском PS = DZ
не определено однозначно расслоение на окружности ks: Qs-yPs.
Предположим сначала, что область Ps = Di граничит (по Кг)
с областью Ps. типа III или IV. На языке графа Г это означает,
что единственное ребро, выходящее из черной вершины,
приходит в седловую вершину (компоненту графа Г). Как мы

1 Ы) ПОСТРОЕНИЕ МЕЧЕНОГО ИНВАРИАНТА
375
покажем ниже, эта ситуация является типичной. В этом случае
выбор системы координат на торе T^ = n^i(Kr) осуществляется
так. Поскольку тор Т* одновременно является одним из
граничных торов Т^ многообразия <2s=Jts~1 С«')> то на тоРе
Тг:, отождествленном с тором Т? при помощи некоторого
фиксированного диффеоморфизма, уже ранее нами построено
слоение на окружности — слои — и выбрано сечение. Эти сло-
ение и сечение можно перенести на тор Т?. Итак, мы вводим на
торе Т? координаты, которые берем «от соседа», т. е. многооб-
разия Qs.. Эта операция определена однозначно. Рассмотрим на
полнотории Qs меридиан, однозначно задаваемый следующим
условием. Он определяется (с точностью до изотопии и ориен-
тации) как простая кривая, лежащая на граничном торе
полнотория и стягиваемая внутри полнотория, но не стягива-
емая на торе. Разложим этот меридиан по базису, только что
введенному нами на торе Т? (слой и сечение от соседа).
В результате получаем два числа р и q—коэффициенты
разложения меридиана по базису. Их отношение p/q мы
и сопоставим окружности Кг. Эта дробь — аналог дроби ое/р.
18. Когда применима конструкция п. 17, т. е. когда можно
считать, что область Р, типа I граничит с областью Р,- типа III
или IV?
19. Лемма. Рассмотрим ориентированный редуцированный
случай. Тогда на связной поверхности Р каждая область Ps типа
I всегда граничит с областью типа III или типа IV, за
исключением того единственного слу-
чая, когда граф Г имеет вид, показан-
ный на рис. 84, а, т. е. когда Q получа-
ется склейкой двух полнотории по
некоторому диффеоморфизму гранич-
ных торов.
Доказательство. В силу усло-
вий леммы в составе Р нет областей
типов II и V. Рассмотрим два случая:
1) граф Г содержит ровно две вер-
шины; 2) граф Г содержит более двух
вершин. В случае 1) вид графа Г см.
на рис. 84,а (две черные вершины,
соединенные ребром). В случае 2) граф
Г показан на рис. 84,6—все его вер-
шины черные, и каждое ребро, ис-
ходящее из черной вершины, втыкает-
ся в какое-то седлб (ориентированное
или неориентированное). Конкретный пример такого графа см.
на рис. 84, в. Лемма доказана.
20. Итак, конструкция п. 17 применима во всех случаях,
кроме одного, а именно, когда Q есть склейка двух полнотории
Рис. 84

376 ГЛ 10 КАЧЕСТВЕННАЯ ТОПОЛОГИЧЕСКАЯ ТЕОРИЯ
(рис. 84,а). Легко видеть, что инвариант I(H, Q) в случае
1) имеет вид, показанный на рис. 84,а, т.е. является сферой,
разрезанной пополам экватором. Здесь Q = Qi + Qz, P = P\ + Pi,
имеется ровно одна окружность Кг (экватор), ровно две
компоненты графа Ks, а именно — два центра дисков. Этот
случай прост, и его можно рассмотреть отдельно. Для
классификации всех систем с таким простым значением инвари-
анта /(Я, Q) можно ввести системы координат на каждом
полнотории, повторить описанные конструкции, построить (а,
Р) и т. д. Теперь мы основное внимание уделим случаю 2).
21. Поскольку мы предположили ориентируемость редуци-
рованной поверхности Р и ориентируемость интеграла /, то
каждая область Ps гомеоморфна либо диску (тип I), либо
кольцу S1 х D1 (тип II), либо ориентируемой поверхности типа
III или типа IV. Рассмотрим все толстые окружности Кг и раз-
режем по ним поверхность Р. Получим набор областей, часть
из них совпадают с прежними Ps, а часть являются объединени-
ем нескольких прежних областей Ps. Назовем новые области
«большими» и обозначим их Rb, где индекс b пробегает
некоторое конечное множество целых чисел. Граница каждой
области Rb состоит из окружностей Кг (толстых). Все прежние
тонкие окружности Кг лежат строго внутри областей Rb. Над
каждой областью Rb мы получаем расслоение со слоем
окружность. Пространство расслоения Qb либо совпадает
с некоторым Qs, либо является объединением нескольких таких
многообразий Qs. Граница Qh состоит из торов Лиувилля. На
каждом из них определено сечение расслоения, задаваемое
окружностью D\ (рис. 83). Следовательно, на границе Qb задано
сечение расслоения Qb ->Rb. Поэтому однозначно определен
целочисленный инвариант — препятствие к продолжению этого
сечения внутрь Qb. Обозначим этот числовой инвариант еь.
Итак, мы имеем следующий объект, состоящий из: 1) замкну-
той ориентируемой поверхности Р2; 2) графа K={Kr} + {Ks},
причем некоторые окружности Кг нарисованы тонкими линиями,
а некоторые толстыми; 3) на каждой толстой окружности
Кг поставлена числовая метка—пара взаимно простых чисел (а,
Р), Ка<|Р| (эта пара отлична от (+1,0)); 4) поверхность
Р представлена как объединение областей Rb, получающихся
разрезанием Р по всем толстым окружностям К„ при этом
каждой области Rb, отличной от диска, приписано некоторое
целое число еь; 5) элемент ае//х(Г; Z2).
Тонким окружностям Кг мы числовые метки не приписываем
(лишь из методических соображений им можно было бы
приписать (+1, 0)).
Далее, каждой области Rb сопоставим новое рациональное
число Ц(, = е,,— ?а/р. Сумма берется по всем толстым окружно-

§ 60. ПОСТРОЕНИЕ МЕЧЕНОГО ИНВАРИАНТА 377
стям К„ составляющим границу Rb. Индекс г в обозначении
чисел а/р опущен, так как мы помним, что числа <х/Р зависят от
окружности К,.
22. Подведем итоги. Мы получили следующий объект.
1) Замкнутая ориентируемая поверхность Р2, разбитая в объе-
динение областей Rb, границами которых являются толстые
окружности Кг. 2) Редуцированный граф K={Kr} + {Ks} на
поверхности Р, причем некоторые окружности А, нарисованы
тонкими линиями, а некоторые толстыми. Все тонкие окру-
жности Кг лежат внутри областей Rb. 3) Каждая толстая
окружность Кг снабжена рациональным числом <х/Р, где
1 < а < | В |. Вместо предыдущего можно просто писать - mod 1.
р
При этом предполагается, что области Rb, граничащие
по Кг, не являются дисками. Если же хотя бы одна
из областей Rb, граничащих по Кг, является диском, то
сопоставляем окружности Кт число p/q (см. выше). 4) Каждой
области Rb, отличной от диска, сопоставлено рациональное
число ць = е6— ?<х/р. 5) Задан аеЯ^Г, Z2).
23. Объект l(H, QY = (P2=ZRb; {К,};{ф, p/q}; {цр}) назовем
меченым изоэнергетическим топологическим инвариантом интег-
рируемой боттовской системы v на многообразии Q. Скажем,
что значения инвариантов /(Я, Q)' и /(Я', Q')' для двух систем
и и и' равны, если существует гомеоморфизм <р: Р->Р',
переводящий граф Г в граф Г', граф К в граф К', области
Rb в области Ry, числовые метки <х/Р в числовые метки а'/Р'
и числа \ib в числа ц^.. (Здесь мы имеем в виду, что а/Р = а'/Р'
и ць = и.'ь..) В противном случае скажем, что значения инвариан-
тов /(Я, Q)' и 1(Н', Q')' для систем v и и' различны.
24. Дополнительные комментарии. С точки зрения меченого
инварианта становятся нагляднее результаты работы [285].
Рассмотрим два случая: а) боттовский интеграл / на Q3 таков,
что каждая связная компонента каждого критического уровня
/содержит ровно одно критическое подмногообразие; б) общий
случай, когда таких подмногообразий может быть несколько.
В случае а) все бифуркации торов Лиувилля являются элемен-
тарными и, следовательно, совпадают с какой-либо из перестро-
ек 1—5, указанных в [282], [283]. В случае б) любая
бифуркация торов является композицией этих элементарных
перестроек. Такое разложение перестроек в композицию элемен-
тарных неоднозначно. Нужно возмутить интеграл / получить
близкую функцию / (вообще говоря, не являющуюся интегра-
лом), описывающую (согласно алгоритму работы [283]) ис-
комое разложение. При возмущении функции / многообразие
б3 не меняется. Другой подход состоит в рассмотрении (в

378 ГЛ. 10. КАЧЕСТВЕННАЯ ТОПОЛОГИЧЕСКАЯ ТЕОРИЯ
окрестности компоненты критического уровня) графа Ks. Семей-
ство «нижних» торов, пересекая критический уровень, трансфор-
мируется в семейство «верхних» торов в-точном соответствии
с геометрией графа Ks. В этом смысле все возможные
боттовские перестройки торов Лиувилля классифицируются
графами Ks, структура которых описана в [285] и получила
дополнительное объяснение в рамках изложенной конструкции.
Отметим очень интересные и важные компьютерные экс-
перименты по численному интегрированию гамильтоновых
систем, описанные в работе Ченела и Сковела [329]. Многие из
результатов работы [329] получают новое объяснение на языке
графа К.
§ 61. Классификация перестроек торов Лиувилля
на многомерных симплектических многообразиях
в окрестности бифуркационной диаграммы отображения
моментов
1. В настоящем параграфе мы даем классификацию элемен-
тарных перестроек общего положения торов Лиувилля, возника-
ющих в тот момент, когда тор пересекает критический уровень
интеграла энергии. Оказывается, все перестройки общего
положения распадаются в композицию некоторых канонических
(элементарных) перестроек пяти типов и эти последние явно
описываются и имеют простую геометрическую природу. При
этом мы, в частности, развиваем некоторые идеи, высказанные
С. Смейлом в работе [235].
2. Определения. Пусть v = sgradH— гамильтонова систе-
ма на симплектическом многообразии М2п. Пусть система
v интегрируема, т. е. существуют п независимых (почти всюду)
гладких интегралов/j, ...,/„, находящихся в инволюции. Будем
считать, что fx—H. Пусть F: M2n->R" — соответствующее этим
интегралам отображение моментов, т.е. F(x) = (fl(x), ...,/„{х))е
eR". Напомним, что точка хеМ называется регулярной для
отображения F, если ранг дифференциала dF(x) равен п, т. е.
отображение dF(x): ГХМ->К"=7^(Х)К" является эпиморфизмом.
В противном случае точка х называется критической, а ее образ
F(xj—критическим значением.
Пусть NczM—множество всех критических точек отображе-
ния моментов. Ясно, что оно замкнуто. Пусть T. = F(N)
— множество всех критических значений. Оно называется
бифуркационной диаграммой (бифуркационным множеством).
Поскольку отображение F гладко, то dim ? < п — 1. Если точка
jceR" не является критическим значением, т. е. xeR"\Z, то ее
полный прообраз Ba = F~1{a)czM (т.е. неособый слой) не
содержит критических точек отображения F. В силу теоремы
Лиувилля каждая его компактная связная компонента диффе-

§ М КЛАССИФИКАЦИЯ nEPECTPOF,K ТОРОВ
379
Рис. 8з
оморфна тору Лиувилля Т". Предположим пока для простоты,
что весь слой Ва компактен (рис. 85). Из полученных ниже
результатов легко будут следовать соответствующие утвержде-
ния и для некомпактных слоев, т. е. для «цилиндров». Если
деЕ, то совместная поверх-
ность уровня (т. е. слой)
Ва является особой (критиче-
ской) и dim Ва^п.
3. Постановка задачи. При
деформации точки д в R" ее
прообраз, т. е. слой Ва, как-то
деформируется. До тех пор,
пока точка д, двигаясь по R",
не встречается с бифуркацион-
ной диаграммой Е, слой Ва преобразуется посредством диффе-
оморфизмов, т. е. не претерпевает качественных топологических
перестроек. В частности, любые два слоя Ва и Вь, где точки
д и b могут быть соединены гладкой кривой yczR" /Y, (т. е. не
содержащей ни одного критического значения отображения
моментов), диффеоморфны, состоят
из одного и того же числа торов
Лиувилля.
Если же непрерывная кривая
у встречает в какой-то точке би-
фуркационную диаграмму Е, то
слои Ва и Вь могут быть то-
пологически различными. Если точ-
ка д при своем движении протыкает
Е, то слой За подвергается, вообще
говоря, качественному топологичес-
кому преобразованию, перестройке
(рис. 86).
Сформулируем общую задачу:
описать топологические перестрой-
ки торов Лиувилля, возникающие
в тот момент, когда точка а пересе-
кает бифуркационную диаграмму Е.
4. Замечание. При классифи-
кации перестроек естественно выде-
лить два случая: 1) dimE <и—1;
2) dimE = H—1. В случае 1) диаграм-
ма Е не разделяет R", т. е. любые две точки д, ЬеЛ."
соединяются гладкой кривой ycR"\S. Следовательно, ком-
пактные неособые слои диффеоморфны между собой, в частно-
сти, состоят из одного и того же числа торов Лиувилля.
Существенно более сложным является случай 2). Здесь диаграм-
ма Е, вообще говоря, разбивает R" на несколько открытых
Рис. 86

380 ГЛ 10 КАЧЕСТВЕННАЯ ТОПОЛОГИЧЕСКАЯ ТЕОРИЯ
непересекающихся областей. В каждой из них топология
неособого слоя (например, количество торов Лиувилля), вообще
говоря, своя. Она может меняться от области к области.
Итак, пусть dimS = n—1. Рассмотрим точку сеЕ и изучим
перестройки торов Лиувилля, когда гладкая кривая у (след
движения точки а) протыкает диаграмму ? в точке с. При этом
достаточно рассматривать лишь малую окрестность U=U(c)
точки с в R".
5. Общее положение. Мы изучим случай общего положения,
т. е. когда путь у трансверсально протыкает Е с ненулевой
скоростью в точке с, лежащей на (л — 1)-мерном страте (листе)
диаграммы ?. Другими словами, будем предполагать, что
U[)Т является гладким (л — 1 )-мерным подмногообразием в R".
В случае общего положения можно считать, что множество
Nf]F~l(U) критических точек является объединением конеч-
ного числа гладких подмногообразий в М, стратифицированных
рангом dF. Это означает, что N можно представить в виде
объединения непересекающихся подмногообразий Nt, на каж-
дом из которых ранг dF в точности равен i (некоторые из этих
подмногообразий могут быть пустыми).
Понятие общего положения можно уточнить еще и так.
Поскольку мы предположили, что в окрестности точки с множе-
ство X является (л — 1 )-мерным подмногообразием, то можно
считать, что в окрестности какой-то одной связной компоненты
В° особого слоя Вс последние л—1 интегралов /2, ..., /„
независимы, а первый интеграл j\ = Н (энергия) становится
зависимым с ними на подмножестве критических точек
T=N [)В°. В самом деле, ограничим отображение F на
подмножество Nf]F~1(U), являющееся согласно требованию
общего положения объединением конечного числа гладких
подмногообразий. Поскольку ограничение F на каждый, в том
числе и на максимальный, страт N'f]F~l(U) является гладким
отображением гладкого подмногообразия, то dF(.x):
TxN'—>TF{y)Y является эпиморфизмом и ранг dF(x)^ п— 1, так
как dim Uf]Y, = n— 1. В то же время, так как xeN—критическая
точка, то ранг dF(x) ^n — 1. Следовательно, ранг dF(x) = n— 1.
Поэтому можно считать (в случае необходимости, заменяя
базис в множестве интегралов), что/2, ...,/„ независимы на fi,°.
Следовательно, интеграл /t становится зависимым с ними на
множестве T=Nf)B°.
6. Пять типов многообразий. Теперь мы рассмотрим
пять типов (п+ 1)-мерных многообразий, краями которых
являются торы.
Тип 1. Рассмотрим стандартное вложение в R"+1 «пол-
нотория» D2xTnl с «осью», являющейся тором Т" 1.
Его граница — тор Т". Назовем D2xT"~1 диссипатшнъш
полноторием.

§ 61 КЛАССИФИКАЦИЯ ПЕРЕСТРОЕК ТОРОВ 381
Тип 2. Прямое произведение T"xD1 называется цилиндром.
Его край—два тора Т".
Тип 3. Пусть N —диск с двумя дырками, Прямое произ-
ведение N2xT"~1 называется торическим ориентированным
седлом. Его край—три тора Т".
Тип 4. Над тором тп~ рассмотрим все неэквивалентные
друг другу расслоения со слоем отрезок D1=[—l, +1]. Они
классифицируются элементами ос группы гомологии Н1(Т"~1;
Z2) = Z2@...@Z2 (n— 1 раз). Обозначим F" пространство рас-
слоения, отвечающего элементу ос. Ясно, что У" является
и-мерным гладким многообразием, край которого состоит из
двух торов Т"'1, если <х = 0, и из одного тора, если <х#0.
Поскольку нас интересуют интегрируемые системы, то мы
будем рассматривать далее только такие расслоения, краями
которых являются торы.
Рассмотрим теперь новое расслоение N2->AZ+1->T"~1 с ба-
зой тор 7 и со слоем N2, которое ассоциировано
с расслоением D1-* Y" ->Т"~1, рассмотренным выше. Оно
определяется следующим образом. Диск с двумя дырками
гомотопически эквивалентен восьмерке. На N рассмотрим
отрезок D1 = [— 1, +1 ], проходящий через центр диска и соеди-
няющий (после его продолжения) центры двух выброшенных
дисков (дырок). С каждым расслоением D1-*Yl-*T"~l можно,
заменив слой D1 на слой N2, ассоциировать расслоение
N2-*A"+l-+T"~l, причем такое, что его границей являются
торы. Частным его случаем является прямое произведение
N хГ, т.е. многообразие типа 3. Оно получается в том
случае, когда а = 0. Если же а/О, то соответствующее
расслоение Al+1 нетривиально. Многообразия А%+1, имеющие
размерность п +1, называются неориентированными ториче-
скими седлами, если ое/0. Краем многообразия А^+1 являются
два тора, если ое/0.
Тип 5. Пусть р: Т"->К" — двулистное накрытие над неори-
ентируемым многообразием К". Все такие накрытия можно
классифицировать. Для каждого р = 0, 1 обозначим Gp груп-
пу преобразований тора 7"" = R"/Z", порожденную инво-
люцией
а1У а2 + -, а3, ..., а,
а2, ах, а3+1-, аА, ..., аЛ Р=1,
где а=(ах, ..., an)eR"/Zn. Здесь предполагается, что л^О при
Р = 0 и и ^ 3 при р = 1. Группа Gp действует на торе Т" без

382 ГЛ 10 КАЧЕСТВЕННАЯ ТОПОЛОГИЧЕСКАЯ ТЕОРИЯ
неподвижных точек, следовательно, фактормножество К$ =
= rn/Gp является гладким многообразием. Преобразование /?р
меняет ориентацию, поэтому А"р — неориентируемое многооб-
разие. Многообразия Ко, К" не гомеоморфны. Обозначим
Кр+1 цилиндр отображения р: Т"-+Кр. Ясно, что
%1=n+\ и дК;+1 = Т", |3 = 0, 1.
7. Топологические замечания. Все многообразия Л"+1 при
диффеоморфны друг другу. Это следует из того, что
любая несамопересекающаяся траектория на торе может быть
взята в качестве одной из образующих на нем. Таким образом,
как и в четырехмерном случае, получаем лишь два топологичес-
ки различных многообразия.
Многообразия Л"+1 и K^+s представляются в виде склейки
многообразий первых трех типов, т. е. с топологической точки
зрения независимыми «элементарными кирпичами» являются
лишь многообразия T"xD\ N2xT"~\ D2xT"~l. Доказа-
тельство этого утверждения аналогично четырехмерному
случаю.
Отметим, что К0 = К21хТ"-2 и К\=К\хТп'г.
8. Теорема (А. В. Браилов, А. Т. Фоменко [54]). Пусть fx,
...,/„— полный инволютивный набор гладких функций на симплек-
тическом многообразии М2" и F: M2n—>R — соответствующее
отображение моментов. Пусть А'"+1 = {хбМ2"|/-(х) = ^, /=1,
..., л—1}. Предположим, что ограничение fn\Xn+1 является
боттовской функцией и X0 = {fi(x) = ?)i, 1</<и}—неориен-
тируемое многообразие минимума функции fn\Xn+1. Тогда
X диффеоморфно либо Kq (при п ^ 2), либо К\ {при п ^ 3).
Доказательство. На многообразии Хо глобально опреде-
лены векторные поля I'^sgrad/j, /=1, ..., и—1, и локально
определено векторное поле vn = sgrad d ^J /„ — %n. Эти поля ком-
мутируют друг с другом и в каждой точке хеХ0 линейно
независимы. Пусть W—трубчатая окрестность Хо в Хп+1 вида
И/={./,(х) = ^,,/=1, ...,и+1;/„(х)<5. + е}. Пусть я: dW-^Xo —
соответствующее двулистное накрытие. Нетрудно видеть, что
на 8 W имеется глобально определенное векторное поле
v'n такое, что n,v'a = vn. Векторные поля vt, /=1, ..., п—\, также
поднимаются в 8 W, nmv\ = vt. Все векторные поля v\, /=1, ..., п,
по-прежнему коммутируют и независимы в каждой точке
xedW. Преобразование 8W, состоящее в сдвиге вдоль интег-
ральной кривой поля v] за время t, обозначим g\. Для а= (а,,
..., aJeR" композицию g"i---ug'n обозначим g".
Итак, группа R" действует на dW по формуле x—>ga(x). Из
неориентируемости Хо вытекает, что многообразие д W связно.
Следовательно, для любой точки хоеХо ее R"-op6nTa совпадает
с д W. Пусть L = LXi—стационарная подгруппа точки xoeR".
Тогда отображение а -*g"(x0), aeR"/L, является диффеомор-

<j 6! КЛАССИФИКАЦИЯ ПЕРЕСТРОЕК ТОРОВ 383
физмом R"/L на dW. Для любой точки xedW компоненты
вектора aeR" такого, что g"{xo) — xo, назовем (неоднознач-
ными) координатами точки х. Пусть а — инволюция д W,
переставляющая листы. Тогда a,v'n= —v'n. Следовательно,
a(g"{x)) = g"°la)(o(x)), где (-«,, а2, ..., ан) = а0(а).
Фиксируем точку .v0 e д W и соответствующие ей (многознач-
ные) координаты а.. В этих координатах преобразование
а задается формулой a(a) = (q1—a1, q2+a2 qn + an), где
qi — координаты точки а(х0). Заменяя при необходимости
точку х0 на точку с координатами (qt/2, О, ..., 0), мы будем
считать, что ^!=0. Пусть Tq(a) = a + q — преобразование сдвига
на вектор q no модулю L. Ясно, что о = о0Г5 и <т07"ч=Г9о0.
Поскольку ao = aT^q — корректно определенное преобразование
многообразия dW и ао(хо) = хо, то ao(L) = L. Поскольку
T2q = olT2q = a2 = id\ew, то 2qeL.
Определим решетки L± = {/eL|o0 (/)=+/}, L' = L++L~.
Тогда либо L = L', либо Lj^L. Рассмотрим сначала первый
случай. Выберем базис (/,) в L~ и базис (/,-), /=2, ..., и,
в L+. Тогда (/,) = (/;), /=1, ..., п,— базис в L = L. Следо-
вательно, в базисе (/,) линейный оператор <т0 задается матри-
цей diag (—1, 1, ..., 1). Выше мы видели, что qt=0,
2qeL. Следовательно, 2qeL+ и можно считать, что ба-
зис (/;) выбран таким образом, что I2 = 2q. В координатах,
связанных с базисом (/,), имеем <т(а,, ..., ап) = ( — а,,
а2 + -, а3, ..., а„), следовательно, Хо диффеоморфно К"о.
Пусть L'=?L. Для любого aeR" j L определим
а± =(а + ао(а))/2. Возьмем /[6L\L'. Предположим, что l^eL~.
Поскольку li=ll — l^, то в этом случае и lfeL+. Сле-
довательно, l1=li+l^eL'; получили противоречие. Поэто-
му /f^L~, тогда, очевидно, 2/f eL. Покажем, что 11
порождает L по модулю L'. Действительно, пусть lsL\L.
Тогда 2l~eL~ и 1~фЬ~. Следовательно, /f—/~eL~
и (/,— l)+eL+. Поэтому /,-leL', что и требовалось доказать.
Пусть /* — образующий элемент в L . Тогда для 11<eL\L'
и подходящего целого числа т имеем 2l\=ml*. Число
т нечетно, так как 1^фЬ~. Заменим /, на l\=ll—nl*, где
т = 2п+\. Тогда 2/f =тГ — 2п1=Г. Таким образом, lleL\L'
можно выбрать так, что 2/f—образующий элемент в L .
Пусть /r, i = 2, ..., п,— базис в L+. Докажем, что /, = /,, /=1, ••., л,
— базис в L. Пусти leL—произвольный элемент. Необходимо
найти целые числа т{, i=\, ..., п, такие, что l=Y,mih-
Поскольку /j порождает L по модулю L', то можно считать, что
leL'. Тогда /=/++/~, где /±eL±, а поскольку /~=2w/j~, то

384
ГЛ 10 КАЧПСТВ1.ННАЯ ТОПОЛОГИЧГС КАЯ Т1ОРИЯ
отсюда следует, что /= ? /и,/, для подходящих целых чисел т{.
\= 1
В базисе /, линейный оператор ст0 задается матрицей
•V-Is, Л -
-vl.
¦VJ1
0
1
1
0
0
0
1
(810)
-1
р
0
0
1
1
0
0
0
1
Имеем ,?и=-1. так как det i"= — 1. Путем элементарных
преобразований базиса /;, / = 2, ..., п, в L + можно добиться того,
чтобы выполнялась цепочка равенств s3l =s4t =.,, = snl = 0.
В итоге получаем, что ап задается матрицей
(811)
Заменим теперь в базисе /,, i=\, 2 я, первый вектор 1Х на
l\=ll+kl2. В новом базисе ст0 задается той же матрицей, но
с заменой Р на Р'=Р — 2к. Поэтому можно считать, что C = 0
или 3=1. Первый случай соответствует L = L' и был разобран
ранее. Рассмотрим случай Р=1. Вектор qeL+f)l-\L\ коор-
динат точки ст(х0) определен по модулю L. Поэтому можно
п
считать, что q= ^ </,¦/;, где qt = 0, 1/2. Если qz=\:2, то заменим
i = 2
точку отсчета дг0 на точку с координатами A/2. 0, ...
..., 0). Поскольку ао(/!)= —1{ +/2, то сдвиг q в новых
координатах даст тождество q + ~l2 = 0 (mod L). Следовательно,
можно считать, что q2 = 0- Далее, совершая элементарные
преобразования над векторами /,-, / = 3, ..., п, можно добиться
того, чтобы g = (/3/2)mod L. Наконец, заменяя /2 на 1'2—— h+li-
получаем, что о задается в координатах, связанных с базисом (/,),
формулой o(ai, ..., а„) = (а2, alt a3+-, а4, ..., «„). Следовательно,
многообразие Хо диффеоморфно К\. Теорема доказана.
9. Перестройка торов Лиувилля. Опишем пять типов канони-
ческих перестроек.

§ 61. КЛАССИФИКАЦИЯ ПЕРЕСТРОЕК ТОРОВ 385
Тип 1. Тор задается как граница диссипативного полнотория
D2xTnl и затем стягивается на его ось, т.е. на тор Т.
Назовем эту операцию предельным вырождением. Обозначим
эту перестройку символом Т" -> Т"~1 -» 0.
Тип 2. Два тора Т\ и Т, являющиеся границей цилиндра
T"xDl, движутся по нему навстречу друг другу и в середине
цилиндра сливаются в один тор Т". Условное обозначение
27 ^ Г"-> 0.
Тип 3. Тор Г", являющийся нижним краем ориентирован-
ного торического седла N2 х Т"~1, поднимается вверх и в соот-
ветствии с топологией многообразия N2xT"~1 распадается на
два тора Т" и Т. Обозначение: Т"^>2Т".
Тип 4. Тор Т", являющийся одним из краев многообразия
А"+1, где а#0, поднимается по A"+l «вверх» и в его середине
перестраивается, превращаясь в один тор — в верхний край
многообразия А^. Обозначение: Тп-+Тп. Все такие перестройки
параметризуются ненулевыми элементами,
Тип 5. Реализуем тор Т" как край многообразия Кр+1.
Деформируя тор внутрь К^+1 вдоль проекции р, мы, наконец,
двулистно накрываем тором Т" многообразие К1, После этого
тор «исчезает». Условное обозначение: Т" -»Kf-tO.
10. Определение. Фиксируем значения последних и—1
интегралов/2, ...,/„ и рассмотрим получившуюся (л+1)-мерную
поверхность уровня X"+l. Ограничивая на нее первый интеграл
(энергию) Л = Н, мы получим гладкую функцию / на многооб-
разии X" , которую будем называть интегральной поверх-
ностью. Будем говорить, что перестройка торов Лиувилля,
образующих неособый слой Ва, является перестройкой общего
положения, если в окрестности перестраивающегося тора Т"
поверхность Xn+l является компактным и неособым подмного-
образием, а ограничение энергии/! = Я на X"+l является (в этой
окрестности) боттовской функцией.
11. Теорема (А.Т.Фоменко [283]). 1) Если dimZ<n—1,
mo все неособые слои Ва диффеоморфны между собой.
2) Пусть dimZ = n—1 и невырожденный тор Лиувилля Т"
движется вдоль совместной неособой поверхности X"+l уровня
последних интегралов /2, ...,/„, увлекаемый изменением значения
интеграла энергии fx = Н. Это эквивалентно тому, что точка
a = F(T")eR" движется по гладкому отрезку у по направлению
к бифуркационной диаграмме S. Пусть в некоторый момент
времени тор Т" подвергся топологической перестройке, т. е.
вышел на критический уровень энергии. Это происходит в том
и только в том случае, когда тор Т" встречает на своем пути
критические точки N отображения моментов F: M2"->R" (т. е.
путь у в точке с трансверсально и с ненулевой скоростью
протыкает (п — \)-мерный лист диаграммы Т.). Предположим,
что эта перестройка является перестройкой общего положения.

386 ГЛ. 10. КАЧЕСТВЕННАЯ ТОПОЛОГИЧЕСКАЯ ТЕОРИЯ
Тогда все возможные типы перестроек тора Лиувилля исчер-
пываются композициями указанных выше (и обратных к ним)
канонических перестроек типов 1, 2, 3, 4, 5. В действительности,
с топологической точки зрения независимыми из них являются
лишь первая и третья, а перестройки 2, 4 и 5 являются их
композицией.
12. Определение. Гамильтониан называется ориенти-
руемым, если все его критические подмногообразия (на
Х"+1) ориентируемы, т.е. нет ни одного критического
многообразия А"?. В противном случае гамильтониан на-
зывается неориентируемым.
13. Предложение. Если (U(X"+1y sgradtf, /2, ...,./„) —
интегрируемая гамильтонова система с боттовским неориен-
тируемым гамильтонианом Н на поверхности Хп+1, то ее
всегда можно двулистно^ накрыть гамильтоновой системой
(U(Xn+l); sgrad H,^J2, •••,/л) c ориентируемым гамильтонианом
Н на накрытии Х"+1. Здесь U(X"+1) — двулистное накрытие
окрестности U(X" + 1) многообразия Хп+1.
14. Теорема (А. Т. Фоменко [283]). Пусть М2"— гладкое
симплектическое многообразие и система v = sgrad H интегриру-
ема с помощью гладких независимых коммутирующих интег-
ралов H=fi, f2, ..., /„. Пусть X"+1—любая фиксированная
компактная неособая совместная поверхность уровня последних
п—\ интегралов /2, ..., /„. Пусть ограничение Н на Xn+l
является боттовской функцией. Тогда поверхность Xn+l имеет
вид m{D2xT"~1)+p(T"xD1) + q(N2xT"-') + sAl + 1+rKy1,
т. е получается в результате склейки граничных торов (при
помощи некоторых диффеоморфизмов) следующих «элементар-
ных кирпичей»: т диссипативных полноторий, р цилиндров,
q торических неориентированных седел, s торических неориен-
тированных седел и г многообразий K$+l. Число т в точности
равно числу предельных вырождений системы v на поверхности
Х"+1, на которых энергия Н достигает локального минимума
или максимума.
15. Обозначения. Пусть eel. и малая окрестность 1/(с)[)Т.
точки с на ? является гладким (п— 1)-мерным подмногообрази-
ем. Пусть у — гладкий путь, трансверсально протыкающий
S в точке с и соединяющий два некритических значения а и Ь,
расположенных по разные стороны от гиперповерхности Z.
Рассмотрим связную компоненту В° особого слоя BC = F~1 (с).
Пусть Т=В° f]N, a Xq+1 — связная компонента слоя F~iU(c),
заключенная между двумя близкими неособыми слоями Ва и Вь.
Поскольку а и b — некритические значения, то Ва и Вь являются
объединениями торов Лиувилля. Пусть B^ = Xq+1 f]Ba
и B2 = X+1f)Bb, т.е. дХЪХх=В°а(\В1. Обозначим буквой
f ограничение первого интеграла j\ на интегральную поверх-
ность Х+1=Х0.

§ 61. КЛАССИФИКАЦИЯ ПЕРЕСТРОЕК ТОРОВ 387
16. Лемма. Точка хеХ0 является критической для функции
/ тогда и только тогда, когда в ней первый интеграл fi зависим
(на М) от последних п—\ интегралов /2, ...,/„•
Доказательство. Поскольку Хо— совместная поверх-
ность уровня последних интегралов, то их градиенты образуют
базис в плоскости, нормальной к Хо в М. Зависимость функции
1\ с функциями/2, ..., /„ эквивалентна тому, что в этой точке
вектор grad/j является линейной комбинацией градиентов
grad/j, 2г$г^л. Ясно, что grad/на Хо получается ортогональ-
ным проектированием grad/j на Хо. Лемма доказана.
17. Лемма. Множество Т критических точек функции / на
Хо является несвязным объединением некоторого числа п-мерных
торов Т". (п—\)-мерных торов Т"'~1, п-мерных неориентируемых
многообразий К\.
Доказательство. Если Т=В°, то Т является совместной
(особой) поверхностью уровня всех п интегралов /l5 ..., /„.
Близкие к ней поверхности уровня R являются неособыми
компактными торами Лиувилля. Ясно, что R — граница трубча-
той окрестности Уп+1 подмногообразия Т в Хо. Если dim T=k,
то R=T0 расслаивается над Т со слоем S"~k. Это может быть
только в том случае, когда п — к = 0 или п — к=1, т. е. когда
либо dim Т—п, либо dim Т= п— 1. Если Го — связная компо-
нента Г, то 7^=7"" или Т = К"р. Если В°ФТ, то рассуждение
усложняется. Ясно, что в этом случае dim T<dim B° = n, т.е.
dim T^п— 1. Из условий, наложенных, на интегралы системы,
следует, что на Т интегралы /2, ..., /„ независимы (они
независимы на всем В"). Следовательно, на Tq-1 имеется л—1
независимых коммутирующих векторных полей sgrad/;, i = 2, ...
..., п. Как известно, отсюда сразу следует, что Т~1 = Тп~1.
Лемма доказана.
18. Если критический тор имеет размерность л, то
он является множеством либо локального минимума, либо
локального максимума энергии Н. В этом случае либо
два близких неособых тора Лиувилля пиваются в один
тор Т", либо тор Т" распадается на два тора Т". Пусть
Р" =р"_(Тп~1) и Р"+ =Р\ (Г") — соответственно входящая
и исходящая сепаратрисные диаграммы критического под-
многообразия Т" ~ .
19. Определение. Назовем торической ручкой индекса
X и степени вырождения к прямое произведение
TkxDxxDn+lkx, подошвой ручки — следующую часть ее
границы: (Tk xSl~1)xDn+1~k~x, осью подошвы — пространство
20. Определение. Определим операцию приклейки ториче-
ской ручки к краю V (п+ 1)-мерного многообразия W+i. Пусть
край содержит вложенное подмногообразие TkxSx~l. Пред-
положим, что его трубчатая окрестность гомеоморфна прямому

388 ГЛ 10. КАЧЕСТВЕННАЯ ТОПОЛОГИЧЕСКАЯ ТЕОРИЯ
произведению (Тк xSx~l)xDn+l'k"x. Можно выбросить эту
трубчатую окрестность, край которой гомеоморфен
Тк х Sx~i x S"~k~x. С другой стороны, край подошвы ториче-
ской ручки также гомеоморфен произведению
Ткх S*-'1 х Sn~k~k. Отождествляя этот край с краем выброшен-
ной окрестности, получаем новое (л + 1 )-мерное многообразие.
Его край будем называть торической перестройкой края V".
Для дальнейшего можно считать, что гладкий путь y = y(t) с R"
моделируется отрезком вещественной оси R1, на которой лежат
три точки а<с<Ь, где с — критическое значение, а и b близки
к с. Положим Ca = F~1 (t^a), Cb = F1 (ЩЬ). Тогда Са с Сь.
Другими словами, можно считать, что /': ArS+1->R1
и Са = (/<«), Cb = (f^b), B°c=f-'(c).
21. Лемма. Предположим, что на особом слое В° лежит
роено один критический (седловой) тор Т"'1.
1) Пусть Р"- (Г" ') — ориентируема. Тогда Сь получается из
Са приклейкой к краю Ва торической ручки индекса 1 и степени
вырождения п—\. При этом Сь гомотопически эквивалентно Са,
к которому приклеено многообразие T"~ly.Dl no двум непересе-
кающимся торам Т\~а и Т~а ¦
2) Пусть Р"_(Т"~1) неориентиру ема. Тогда множество
Сь гомотопически эквивалентно Са, к краю В° которого по тору
Тпа~1 приклеено п-мерное многообразие Ya, имеющее край Т
и являющееся расслоением Dl -> YZ-* Т"~1, отвечающим ненуле-
вому элементу oeeZ^ = НХ (Т"~ ; Z2).
22. Лемма. Пусть тор Т"~1, вложенный в какой-то
неособый тор Лиувилля Т"аа В®, является либо одной из подошв
торической ручки (индекса 1 и степени вырождения п—\), либо
краем многообразия F" (в случае, когда /"„(Г") неориентиру-
ема). Тогда этот тор 7JJ всегда реализует одну из
образующих в группе гомологии Н1(Т1^; Z) = Z"~1. Если обе
подошвы торической ручки приклеены к одному и тому же тору
Лиувилля Т"а, то соответствующие оси этих подошв, т. е. торы
Т\~а и Т~а , не пересекаются, реализуют одну и ту же
образующую группы гомологии Н„-1(Т"; Z) и, следовательно,
изотопны внутри тора Тпа.
Доказательство. Рассмотрим критический седловой тор
Т. Из леммы 17 следует, что он является орбитой действия
абелевой подгруппы R"^1, вложенной в группу R", порожден-
ную полями sgrad/;, l^i^n. При этом базис в подгруппе R"
образуют поля sgrad/b 2^i^n. Фиксируем эту подгруппу.
Поскольку действие R" (и R") определено на всем М2", то мы
всегда можем рассмотреть орбиты группы R" ', близкие
к орбите Тп~1. Рассмотрим достаточно близкий к слою
В° неособый тор Лиувилля Тпа, на котором сепаратрисная
диаграмма Рп- высекает некоторый тор Т"'1. Этот тор,
конечно, не является орбитой действия группы R" на торе Т"а.

I) 61 КЛАССИФИКАЦИЯ ПЕРЕСТРОЕК ТОРОВ 389
Однако, как мы сейчас покажем, тор 7"" ! можно аппрок-
симировать некоторой орбитой действия группы R" '. Для
этого рассмотрим элемент а.еНп^1{Тп1; Z2). Из леммы 21 мы
знаем, что тор Г" является одной из компонент края
многообразия F?, приклеенного к тору Г". Если ое^О, то
dYl=Tna-1; если а = 0, то BY^diT"-1 x Dl)= Т\~а1(]ТТ},
Г л - 1 *гп— 1
1, а — 1
Задание элемента а определяет некоторое число к образу-
ющих в критическом торе Т, обходя вокруг которых
нормальный отрезок сепаратриснои диаграммы Р меняет свою
ориентацию. Выделим эти образующие. В ориентируемом
случае & = 0, так как а = 0. Поскольку тор fn~l является
орбитой действия группы R", то, заменяя образующие
в группе R" ' (если это необходимо), всегда можно считать, что
в неориентируемом случае (Аг^О) среди полей sgrad/f, 2^г<л,
есть ровно к полей sgrad/2, ..., sgrad/t + 1 таких, что однократ-
ный обход вдоль орбит точки хеГ", порожденных соответст-
вующими им одномерными подгруппами R2, ..., R* + i, меняет
ориентацию нормального отрезка сепаратриснои диаграммы.
Рассмотрим сначала ориентируемый случай, когда А: = 0. Тогда
в подгруппе R"+1 можно выделить (л—1)-мерный парал-
лелепипед П — фундаментальную область действия группы
R" ' на торе Г". При естественном отображении группы
R" на тор Т"'1 этот параллелепипед П накрывает весь тор,
т. е. тор 7"" получается отождествлением противоположных
граней этого параллелепипеда. Поскольку параллелепипед П со-
стоит из преобразований на М, то можно рассмотреть орбиту
этого параллелепипеда при действии его на некоторую точку
heT"rJ с Та- Конечно, эта орбита уже не будет замкнутым
(п— 1)-мерным тором в Т"а.
Однако так как точка h e T\ ~J близка к точке х е Т", то
можно считать, что орбита П (И) является «почти тором», т. е.
каждая из образующих параллелепипеда П переходит в отрезок,
концы которого близки на торе Т"а (т. е. получается «почти
окружность»). Выберем на торе Г" координаты фь ..., ф„
в соответствии с теоремой Лиувилля. Мы используем здесь то
обстоятельство, что точки параллелепипеда П представлены
симплектическими преобразованиями.
Тогда в этих координатах «почти тор» П(Д) является
линейным вполне геодезическим подмногообразием, быть мо-
жет, с непустым краем. Изображая тор Т" (в этих координатах)
в виде стандартного куба, противоположные грани которого
отождествлены, мы получим в нем плоскость П'. Ее пересече-
ния с противоположными гранями являются (я — 2)-мерными
подпространствами, которые оказываются близкими после
отождествления граней. Ясно, что плоскость П' можно слегка
повернуть так, что она превратится (после факторизации куба

390 ГЛ. 10. КАЧЕСТВЕННАЯ ТОПОЛОГИЧЕСкАЯ ТЕОРИЯ
на тор) в некоторый (и— 1)-мерный линейный вполне геодезичес-
кий тор Г" в торе Т". Ясно, что тор Г" близок к «почти
тору» П(й) и в то же время близок к тору Т\~}. Отсюда
следует, что эти торы изотопны.
Итак, мы доказали существование малой изотопии тора
Т"х~а в торе Т"а, переводящей его в линейный тор. Но в таком
случае тор Т\~? реализует образующую в группе Я„_!(Г2; Z),
что и требовалось доказать. Итак, в ориентируемом случае
лемма доказана. Отметим, что при малом шевелении плоскости
П мы получили новую плоскость П„ образующие которой уже
могут включать в себя образующую sgrad/b которая была
исключена на исходной плоскости П. Ясно, что Г"~1=П,(Л).
Рассмотрим теперь неориентируемый случай. Здесь рассуж-
дения более деликатные. Дело в том, что здесь нельзя обойтись
самим параллелепипедом П. В самом деле, из определения
неориентируемой сепаратрисной диаграммы следует, что ор-
биты (ТЩЯ^/г, ...,(UPiRl+1Jh образующих R^, ..., Rj+i (соот-
d/ 2^i^k\)
(Щ^ (Pil+1J ру ^, j
ветствующих полям sgrad/, 2^i^k+\) не являются «почти
замкнутыми» траекториями на торе Т"а. Обозначим П, соответ-
ствующие ребра параллелепипеда П, т. е. П^ППН?,
2^i^k+]. При действии П; на точку h она успевает пробежать
лишь половину полного оборота на торе Т". Для того чтобы
она сделала почти полный оборот, следует еще раз подей-
ствовать на нее ребром параллелепипеда П;. Другими словами,
чтобы заставить точку h сделать полный оборот на торе Т"а,
к ней следует применить преобразования из 2П(, т. е. удвоить
соответствующую сторону параллелепипеда П. Итак, мы
подходим к следующей схеме.
Нужно удвоить все стороны параллелепипеда П2, ..., nt+J.
В результате получится новый (вытянутый) параллелепипед П,
растянутый в к направлениях в два j»a3a. Теперь подействуем
этим растянутым параллелепипедом П на точку h. В результате
мы получим некоторую орбиту П(Д). Ясно, что теперь эта
орбита изображается (в переменных действие — угол на торе
Лиувилля) линейной плоскостью, которая «почти замкнута»
после факторизации куба на тор. Дальнейшие рассуждения
повторяют рассуждения ориентируемого случая. Лемма до-
казана.
23. Доказательство теорем 11, 14. После доказатель-
ства основных лемм дальнейшая схема повторяет соответст-
вующие рассуждения для четырехмерного случая, см. [283].
24. Теорема (А. В. Браилов, А. Т. Фоменко [54]). Пусть
Хп+1—компактное замкнутое ориентируемое многообразие,
получающееся склейкой произвольного числа элементарных мно-
гообразий типов 1, 2 и 3 (т. е. диссипативных полноторий,
цилиндров и штанов) по любым диффеоморфизмам их граничных
торов Т". Тогда всегда существует гладкое компактное

§ 61. КЛАССИФИКАЦИЯ nEPFXTPOEK ТОРОВ 391
симплектическое многообразие М1п с краем, диффеоморфным
несвязному объединению некоторого числа многообразий вида
S"'1xT", и полный инволютивный набор гладких функций
Л, ..., /„ на М2п такой, что Xn+1 = {xeM2"\f2(*) = ... =/„(*) = 0}.
Доказательство. Искомое многообразие М2п констру-
ируется из симплектических многообразий, соответствующих
тем «элементарным кирпичам», из которых склеено многооб-
разие Xn+l. Поэтому на первом шаге доказательства мы
построим примеры интегрируемых систем, в которых реализу-
ются перестройки типов 1, 2, 3.
Пусть <в„ — симплектическая структура на торе
л
Г2" = {(фь ..., ф2„)тоA2л}, со„= Y, d<p2i-idq>2i- На торе Т2 мож-
но, очевидно, построить гладкие функции фм, где 5=1,2,3
и подмногообразия MsczT2 так, что Nt — точка невырожден-
ного максимума для /[1], N2— невырожденная седловая точка
для /[2] и jV3—невырожденная критическая окружность для
/[3]. Можно, например, взять /'1I=/t2I = cos((p1+2(p2), Ni =
= {@,0)}, N2 = {(n, 0)}, /[3] = со8ф1, N3 = {@, ф2)тос12л}. Если
cs=fls](Ns) — критическое значение, то Cj=c3 = l, c2= —1.
Построим примеры s, s=l, 2, 3. Многообразие М2п = Т2п,
со„ — симплектическая структура на нем. Для г = 2, ..., п имеем
/•(ф, ..., ф2п| = 8Шф2, + 1. Для /=1 имеем /i(cpi, ..., ф2„) =
=/ (фь Фг)- Тогда гамильтонова система u = sgrad fx вполне
интегрируема на М2" с полным инволютивным набором
интегралов ft, a N=NsxT2n~2 — невырожденное критическое
подмногообразие функции fy \Xn + l, где А'"+1 = {/2 = ...=/п = 0}.
Критическое значение fi(N) = cs.
Пусть многообразие Х" + 1= (J Xj склеено из «кирпичей»
Xj и s(j) — тип Xj. Если многообразие Xj типа 2 склеивается
с различными многообразиями X, и XJ2 по диффеоморфизмам
u?i и d2, то из разбиения Х"+^ можно удалить Xj, склеив
XJi и XJ2 по диффеоморфизму d2dil. Описанный процесс
назовем сокращением разложения многообразия Х"+1 на эле-
ментарные кирпичи. Обратный процесс, при котором в разложе-
нии Х"+1 добавляется новый кирпич типа 2, назовем вставкой.
Оба процесса не меняют многообразия Xn + 1 с точностью до
диффеоморфизма. Далее очевидно, что путем подходящей
последовательности сокращений и вставок из исходного раз-
ложения многообразия Xn+1 можно получить такое разложение,
для которого буДут выполнены следующие условия: 1) для
любого кирпича Xj типа 2 номера склеенных с Xj кирпичей либо
оба больше j, либо оба меньше j; 2) для любого кирпича
Xj типа 3 номера всех трех склеенных с Xj кирпичей не могут
быть одновременно больше или меньше j.

392 ГЛ 10 КАЧЕСТВЕННАЯ ТОПОЛОГИЧЕСКАЯ ТЕОРИЯ
Итак, пусть Х"+1= \J Xj—разлэжение, удовлетворяющее
этим двум условиям. Для каждого7= 1, •••, т копии объектов ft,
N, М2п из примера s = s[j) обозначим соответственно /у, N,,
М]". Путем подходящей линейной замены/1J->/',j = aJ/1 ^ +о,
можно добиться того, чтобы отображение моментов Fj(x)
= (fij(x), ...,fnj(x)) удовлетворяло следующим условиям: 1) для
каждого j=\,...,m при движении точки yeR" вдоль первой
координатной оси от 0 до т+1 точка у пересекает бифуркаци-
онное множество Е,- отображения Fj только один раз — в точке
?,j = (j, 0, ..., 0); 2) если ,$(_/)= 1 и кирпич Xj склеен с кирпичом
Xjt, то при указанном движении в точке y = \j происходит
рождение тора FJi (у) в случае j\ >j и уничтожение в случае
jx <j; 3) если s(j) — 2 и кирпич Xj склеен с Xj и XJ2, то в точке
y = t,j происходит рождение двух торов F]'l(y) в случае ju j2>j
и уничтожение двух торов в случае jt, J2<f, 4) если .sG') = 3
и кирпич Xj склеен с XJt, XJ2, Х1ъ, то при ji<j<j2, j3 B точке
y = %j происходит перестройка одного тора в два тора, а при/ь
72<7<7з — перестройка двух торов в один.
Для любых r>0, a<b определим цилиндр
п
С\а, Ь)=\уе^\ X yf<r2, а<у!<Ь}. (812)
i=2
Нетрудно видеть, что Y.jf)C1/2@, т+ 1) = ПУП Сц2@, т+ I), где
Ylj={yeR"\ }'i=j} — гиперплоскость. Многообразие М2п полу-
чается из многообразий
/ ,\\ / , \
--, «1+1 (813)
приклеиванием соединяющих их трубок. Возможность прикле-
ивания трубок вытекает из следующей леммы.
25. Лемма. Пусть заданы числа ax<bx <Cx<a2<b2<c2,
г>0. Предположим, что для каждого 7=1, 2 имеется симплек-
тическое многообразие Mj" и на нем полный инволютивный
набор гладких функций /у, где j=\, ..., п такой, что отображе-
ние моментов Fj является расслоением со слоем — тором Т" над
цилиндром Cr(ah ct). Тогда для достаточно малого е>0 суще-
ствует симплектическое многообразие Z, содержащее в качест-
ве открытых подмногообразий прообразы Vx =FГ1 (СЕ(аь ^i))
и V2 = F21 (Cc(b2, c2)) и полный инволютивный набор гладких
функций fi на V такой, что соответствующее отображение
моментов F является расслоением со слоем Т" над Ce(tfi, с2)
и F\ Vj = Ej\ Vj для у'=1, 2.
Доказательство. Пусть й1<й?1<с1 и a2<d2<c2,
Dj = (dj, 0, ..., 0), 7=1> 2. Выберем в окрестности Oj тора

§ 61. КЛАССИФИКАЦИЯ ПЕРЕСТРОЕК ТОРОВ
393
l(Dj) переменные /у, фу типа действие—угол. Уменьшая
необходимости Oj, мы будем считать, что переменные
0 B {
T-j=FJ
при не „ ...
/у задают расслоение If. Oj-*Bb над малым шаром Bs =
eK"||j|<5}. Таким обр_азом, переменные /у, фу задают
диффеоморфизм 1,х<ру. О,—>i>8x Г". _ _
Положим f=(/2x(p2)(/1 хф^. Очевидно, что Р: Oi~>O2 —
симплектический диффеоморфизм. Поскольку переменные
/0 выражаются через ftJ и независимы, то существует диффе-
оморфизм Jj-. Bb->Oj = Fj(Oj) такой, что Fj=JjIt. Пусть,
наконец, P = J2Jl . В итоге имеем коммутативную диаграмму
(814)
Ее построение неоднозначно, поскольку введение переменных
типа действие — угол зависит от выбора базиса циклов на торе,
в окрестности которого эти переменные вводятся, см. п. 18 § 29.
Обсудим характер этой неоднозначности. Пусть (Л,) и (Л;)
= A(Aj)—два различных базиса в группе Hl(Fj 1(b) )
Тогда h\=
для подходящей матрицы Л=||Л№||е
eGL(n, Z). Поскольку переменные It типа действие определяют-
ся путем интегрирования фиксированной 1-формы по циклам ht,
п
то замена к{-^к\ приводит к линейной замене /, = /;= ? Л,*Д.
Замена угловых переменных производится при помощи обрат-
п
ной матрицы Ф;->Ф;= ? (А~1)()(ФI. Заменяя при необходимости
h1 на A'i= — hi, мы можем считать, что якобиан диффеоморфиз-
ма Р больше нуля.
Пусть Ct(a, e)—такой цилиндр, что правый его- торец
находится внутри Оь а точка Dt — внутри Ct(a, e) (рис. 87).
Соединим цилиндр Се(Ь2, с2) трубкой Т с образом цилиндра
Сг(аи г) при диффеоморфизме Р так, чтобы трубка Т была
гладким продолжением обоих цилиндров и имела открытые
непустые пересечения с ними. Пусть
= T[jCc(b2,c2),
y= 1,2.(815)

394
ГЛ. 10. КАЧЕСТВЕННАЯ ТОПОЛОГИЧЕСКАЯ ТЕОРИЯ
Диффеоморфизм Р. симплектический, следовательно, склеивая
Z, и Z2 при помощи Р, мы получим симплектическое
многообразие Z=ZX\)Z2. Для A=Al\JA2, учитывая положи-
? р
тельность якобиана диффеоморфизма Р, имеем, что существует
о,
1
1 '
1 1
\
/
1
1
Рис. 87
диффеоморфизм L: A-*Cc(ait с2), тождественный на Се(аи bi)
и Cz(b2, с2). Отображение F(x) = L(Fj(x)), xeZj, является ис-
комым расслоением.
26. Вернемся к доказательству теоремы 24. Для каждого
7=1, ..., т ограничение отображения моментов Fj на М) будем
обозначать F). Для любых а<Ь пусть [а, Ь\х—отрезок первой
координатной оси в R" от а до Ь. Нетрудно видеть, что
прообраз (F'j)~l([0, m+\]l) = (F'j)'1( \j—-, j+- ) диффеомор-
фен кирпичу Xj. Далее эти многообразия отождествляются. При
этом каждый тор Тк , ограничивающий Xj, является, очевидно,
связной компонентой множества
-\, 0, ...,
))'l(j+\, 0, ..., о\
(816)
Для кирпичей
d
р
dXJ
положим
Xj
Tk2<zdXJ2
четверки2 а, используя
тическое многообразие
пересечения Vki и Vkj
отображение моментов
, ji<j2, склеенных по торам Тк cBXj ,
= {Xjr Tk , XJ2, Ткг). Для любой такой
лемму 2?5, можно2 построить симплек-
Za, имеющее непустые (размерности 2«)
с Mji и MJ2 соответственно, а также
Fa: Z,a->R", продолжающее отображения
Более подробно: пусть Vki—связная компонента прообраза
содержащая тор Tki
1-, О,

§ 61 КЛАССИФИКАЦИЯ ПЕРЕСТРОЕК ТОРОВ 395
О,..., 01; Укг—связная компонента прообраза Fjsl[cAj2—,
)\ / \
), содержащая тор Tk2cz Fj~2l lj2 —, 0, ..., 0 1. Здесь черта
сверху обозначает топологическое замыкание в R". Из леммы
25 вытекает, что существует симплектическое многообразие
Z, и отображение моментов Fa: Z0,-»CE(y1+-, J2~-j такие,
что для каждого /=1,2 пересечение M'jf]Za совпадает
с Ук, Fa\yk=F'j\yk и отображение F, является расслоением
со слоем Т".
Пусть Fl: M'j [jZzlJM'j -»R" — отображение, совпадающее
с F'j^ на M'Jr с 'F, на Za2n с F'J2 на МJ. Тогда прообраз
(F;')Jl ([0, от+l]i) диффеоморфен склейке 1XJi[JXJ2 кирпичей
е
Xjx и Xj по диффеоморфизму граничных торов 0: Tki-*Tkl.
Возможно, однако, что диффеоморфизм 0 неизотопен диффе-
оморфизму 0а, при помощи которого торы Tki и Ткг отождеств-
ляются в многообразии X"+l. В этом случае при построении
многообразия Za необходимо изменить выбор базисных циклов
п
hi в Hi(Tki; Z), Л,—»А;= ? Л,-Д, Л= || Л,-, || eSL(n, Z) так, чтобы
диффеоморфизм 0' = Л~Х0 стал изотопен 0„,.
Таким образом, мы можем считать, что каждое многооб-
разие (F^') ([0, т+ 1]х) диффеоморфно объединению
Xj и Xs в А'"+1. Следовательно, для многообразия
М1" = ((J M'j)\j((J Za) и отображения F, совпадающего по опреде-
лению с F'j на M'j и с F, на Za, имеем F~l([0, m+ 1]1) = A'"+1.
К сожалению, многообразие М' является многообразием
с кусочно-гладким краем и поэтому не удовлетворяет требова-
ниям теоремы. Однако можно гладким образом обрезать углы
многообразия М' и получить многообразие МсМ', сколь
угодно мало отличающееся от М' и уже с гладким краем dW.
Вырезаемое множество W необходимо взять в виде
W= M'\M = F~l (У), К с F(M'). Тогда край дМ тривиально
расслаивается над F(dM) со слоем Т". Образ F((dM)a) каждой
компоненты связности [дМ\ края дМ является связной суммой
двух (л—1)-мерных сфер и, следовательно, диффеоморфен 5".
Следовательно, край дМ диффеоморфен несвязной сумме
г копий многообразия S"~i х Г", где г — число пар склеиваемых
торов в данном разложении многообразия А'" + 1. Теорема
доказана.
27. В заключение этого параграфа приведем работы, по
которым читатель может познакомиться с темами, близкими
к затронутым в этой главе: [2], [4], [9], [29], [34], [37], [38],

396 ГЛ. 11. ХАРАКТЕРИСТИЧЕСКИ!: КЛАССЫ
[41], [44], [69], [77], [108]—[111], [127]—[129], [131], [132],
[134], [136], [137], [142], [153]—[156], [197], [210], [218] —
[221 ], [241], [242], [244], [315], [330], [331], [342], [345], [367],
[414], [421], [458], [468], [469], [509], [526].
Глава 11
ХАРАКТЕРИСТИЧЕСКИЕ КЛАССЫ
§ 62. Характеристические классы
лагранжевых слоений
1. Определение. Пусть М2п + Г — многообразие, со — за-
мкнутая 2-форма постоянного ранга 2п. Слоение Fn + r на М2" + г,
удовлетворяющее условию co|F=0, называется лагранжевым.
Для лагранжевых слоений имеют смысл обычные понятия
теории слоений: бордантность, конкордантность, индуциру-
емость (последнее предполагает трансверсальность отображения
распределению Кегсо). Обозначим Ker со буквой А", нормальное
расслоение TM\F—символом v(F). Необходимые сведения из
теории слоений см. в книге [291 ].
2. Лемма, а) Распределение К интегрируемо и KcF; б)
в каждой малой окрестности форма со задает в многообразии
слоев МIК структуру симплектического многообразия с лагран-
жевым слоением F\K; в) v(F)* = F\K\ г) форма со принадлежит
идеалу \-форм, задающих слоение.
3. Замечание. Итак, локально лагранжево слоение (М, F,
со) изоморфно произведению r-мерного пространства на р-
расслоение (q = const) в карте Дарбу U2", в которой a> = dp л dq.
Для лагранжевых слоений имеется аналог теоремы Ботта.
4. Предложение. Одночлены от вещественных классов
Понтрягина расслоения v(F) и класса формы [со] е Н2 (М; R),
имеющие степень больше 2 codim F, равны нулю.
5. Определение. Пусть на многообразии М существует
такая невырожденная 1-форма X, что @ = dX и Кег^ трансвер-
сально К. В этом случае лагранжево слоение называется
колежандровым. Обозначим распределение Ker^f)K буквой L.
6. Лемма, а) Распределение L интегрируемо; б) в каждой
достаточно малой окрестности форма X задает в многообразии
M/L контактную форму, характеристики которой касаются
слоения F\L; в) Ff]KerX\L — лагранжево подрасслоение симплек-
тического расслоения KerX\L; г) распределение Ff]KerX. интег-
рируемо.
7. Замечание. Локально, тем самым, колежандрово сло-
ение изоморфно произведению (г — 1 )-мерного пространства на
(р, корасслоение (g = const) в карте Дарбу t/2n+ с X=pdq — du.

S 62. ХАРАКТЕРИСТИЧЕСКИЕ КЛАССЫ 397
8. Конструкция. Оснащенное слоение F коразмерности
п задает на многообразии ^„-структуру и характеристические
классы F отвечают элементам группы Я* (УУ„). Для лагранже-
вых слоений роль Wn играет алгебра Gn формальных векторных
полей в R2", сохраняющих форму a> = dpAdq, и лагранжево
/ьслоение; для колежандровых слоений роль Wn играет алгебра
G„ векторных полей в R2n+1, сохраняющих форму \=pdq — du,
и (р, «)-слоение. Обозначим символом Fn модуль формальных
рядов в R", на котором Wn действует дифференцированием Ли,
и символом М„ — его фактормодуль по постоянным функциям.
9. Предложение, а) Алгебра Ли Gn порождена полями
п „ п ^ . *,
— lPj~±-, (817)
a Gn — полями V(f) и
б) Имеем точные последовательности 0^>Mn->Gn^>lVn^>0,
0-+Fn-+Gn^>Wn--+Q, где вложения i: Mn-+Gn и у. Fn-^Gn заданы
формулами i(g)=U{g\ j(h)=W(h).
10. Конструкция. Построение С„-структуры по оснащенному
лагранжеву слоению F повторяет известную конструкцию для
Wn со следующими изменениями: рассматриваются многооб-
разия 5,-, состоящие из /-струй субмерсий М на карту Дарбу
U2", отображающих слои F в слои /^-расслоения, и определя-
ющие симплектоморфизмы M/K^U2". Расслоение Sl^>S0 гомо-
топически эквивалентно расслоению реперов в v(F)->M
и rS0O = Gn, что позволяет определить С„-значную 1-форму на
многообразии М.
Более геометрическое описание Gn-структуры таково. Фик-
сируем в каждой точке хеМ лагранжеву трансверсаль
Тх к F (т. е. со | Тх = 0) и отождествим все Тх с R". Для близкой
точки у площадка Ту задается в М/K=T*R" как график
дифференциала производящей функции gy, а слои F определяют
росток диффеоморфизма <ру: R=Tx^Ty — R", близкий к тож-
дественному. Дифференциал отображения y-*(gy, <pv) задает на
М 1-форму со значениями в Mn+Wn = Gn.
Аналогичным образом колежандрово слоение задает
С„-структуру (трансверсаль задается как 1-график функции
в JlRl).

398 ГЛ. 11 ХАРАКТЕРИСТИЧЕСКИЕ КЛАССЫ
11. Замечание Итак, характеристические классы оснащен-
ных лагранжевых и-колежандровых слоений отвечают элемен-
там групп когомологий H'(Gn) и Я*(С„). Опишем эти группы.
Обозначим символом Y. прообраз 2и-остова базы в произведе-
нии универсального ^(«(-расслоения на тривиальное расслоение
BUA)->BUA), а символом Zn — прообраз 2л-остова базы
в универсальном U(w) x иA)-расслоении.
12. Теорема. Имеют место изоморфизмы
H-{Gn)^H'(Yn), H'{Gn)^H'{Zn). (820)
Доказательство. Так же как и в случае алгебры Ли Wn,
надо применить спектральную последовательность Серра — Хох-
шильда к подалгебре gl (п) a Gn.
13. Следствие. Пространство когомологий H'(Gn) при
2 порождено степенями некоторого двумерного класса.
Этому классу отвечает класс когомологий 2-формы со. При
j^2n выполняется равенство Hi(Gn) = 0.
14. Конструкция. Рассмотрим подробнее случай п=\. Про-
странство Н' (С„) имеет одну двумерную и две трехмерные
образующие. Прямая конструкция соответствующих классов
такова. Пусть лагранжево слоение коразмерности 1 задано
1-формой а. Тогда da = a л т| и ю = ал р. Трехмерные харак-
теристические классы — это класс Годбийона — Вея \г\ л dr\]
и [со л г)]. Для колежандровых слоений коразмерности 1 харак-
теристические классы таковы: [X л dX\, [r\ л dr\\, \r\ л dX\,
[X л г) л dr\], [X л г) л dX].
15. Пример. Примером колежандрова слоения коразмер-
ности 1 является известное орициклическое слоение на поверх-
ности рода g, g^2, с метрикой постоянной отрицательной
кривизны. В этом случае класс [л л dX] кратен классу Год-
бийона— Вея.
16. Пример. Обозначим буквой Р группу гиперболических
поворотов и параллельных переносов плоскости. Базис инвари-
антных 1-форм составляют формы al5 a2, a3 с ?/а1 = а3ла1,
da.2 = а2 л а3 и da3 = 0. Эти формы опускаются на компактный
фактор по дискретной подгруппе, т. е. на Р/к. Форма at задает
там слоение, лагранжевое относительно 2-формы со = а1ла2.
Класс Годбийона — Вея этого слоения равен нулю, а класс
[со л т|] = [at л a2 л а3] Ф 0.
Существование колежандровых слоений накладывает ограни-
чения на топологию многообразия.
17. Предложение. На трехмерных замкнутых многооб-
разиях с конечной фундаментальной группой не существует
колежандровых слоений.
Доказательство. Характеристическое векторное поле
бездивергентно, поэтому предложение вытекает из теоремы 18.

§ 63. ОБОБЩЕННЫЕ КЛАССЫ МАСЛОВА 399
18. Теорема. Бездивергентное векторное поле v на замкну-
том трехмерном многообразии с конечной фундаментальной
группой не включается в слоение коразмерности один.
Доказательство. Пусть слоение существует. По теореме
Новикова оно имеет рибовскую компоненту. По теореме
Пуанкаре о возвращении в открытом рибовском полнотории
найдется такая малая окрестность U точки х, в которую
траектория точки х возвращается бесконечно много раз. На
слое FX^R2 существует такая ограниченная область V, что
(F\V)f]U=0 и поле v, касающееся Fx, за конечное время
покидает V. Поэтому траектория не может возвращаться в U.
19. Замечание. Доказанная теорема верна и в дискретном
случае, поле при этом заменяется на диффеоморфизм, со-
храняющий объем и переводящий каждый слой слоения в себя.
20. Замечание. Результаты, изложенные в этом параграфе,
получены С. Л. Табачниковым. Доказательство теоремы 18
указано В. Л. Гинзбургом.
§ 63. Обобщенные классы Маслова лагранжевых
подмногообразий и симплектические связности
1. Изучение минимальных лагранжевых поверхностей в кэле-
ровых многообразиях М2п было начато Харви и Лоусоном
[380] для случая M2n = R2" = C" со стандартной кэлеровой
структурой. Они обнаружили, что любая минимальная лагран-
жева поверхность LcR2" является глобально минимальной
(следовательно, и устойчивой). Известно, что' лагранжево
подмногообразие в симплектическом пространстве R2" (а также
в некоторых других кэлеровых многообразиях М2п) обладает
топологическим инвариантом — индексом Маслова и, более
общо, характеристическими классами а; Маслова — Арнольда,
см. [169], [6], [290], [152]. А. Т. Фоменко сформулировал
гипотезу о том, что для многих кэлеровых многообразий
у минимальных лагранжевых подмногообразий характеристи-
ческие классы Маслова — Арнольда должны быть нулевыми.
Эта гипотеза была доказана им и Ле Хонг Ваном [86], [159]
для случая M2n = R2". Она вытекает из общего критерия
минимальности Ф-лагранжевых подмногообразий в эрмитовых
многообразиях [158]. А. Т. Фоменко выдвинул гипотезу, что
«разумно определенные» характеристические классы (аналоги
классов Маслова) для минимальных лагранжевых подмногооб-
разий в симплектических многообразиях значительного класса
(с естественными римановыми метриками, согласованными
с симплектическими структурами) должны быть равны нулю.
2. Конструкция. Если N—лагранжево подмногообразие
стандартного симплектического пространства R2", то сопостав-
ление с точкой xeN перенесенного в начало координат

400 ГЛ. и. ХАРАКТЕРИСТИЧЕСКИЕ КЛАССЫ
касательного пространства TXN определяет отображение
/: N-» LG* многообразия N в лагранжев грассманиан LGJ,
которое позволяет определить характеристические классы лаг-
ранжевых подмногообразий. Мы обобщим эту конструкцию на
случай лагранжевых подмногообразий. Другое определение
индекса Маслова лагранжева подмногообразия в произвольном
симплектическом многообразии дано в работе [10], см. также
[368], [447]—[451], [161], [120].
Построенное отображение /: N^> LG* индуцирует отоб-
ражение /*: Я* (LG*)-> Я* (N) в когомологиях, и каждый
класс когомологий осеН* (LG*) определяет характеристический
класс /*(<х)еН* (N) лагранжева подмногообразия N<=R2".
3. Напомним определение выделенного класса когомологий
цеЯ1 (LGJJ), который называется классом Маслова. Пусть
det: U («) -> 51—отображение, ставящее каждому преобразова-
нию его определитель. Поскольку det (О (л)) = {+ 1} = 5°, то
определено отображение det2: U («)/О (п) -» S1, являющееся
расслоением со слоем SU(«)/SO(«). На окружности S1 рассмот-
рим дифференциальную форму dz/lniz, класс когомологий
которой порождает Я1 E1; R). Тогда на U(«)/O(n) определена
дифференциальная форма (det2)* (dz/2niz). Пространство LG*
можно отождествить с U («)/О (л), это отождествление зависит
от выбора эрмитовой метрики и лагранжева подпространства,
см. § 17. Имеет место следующее утверждение.
4. Теорема. Определенный в п. Ъ класс когомологий
|i= [(det2)* (dz/2niz)] не зависит от элементов произвола,
участвующих в его определении.
Доказательство см., например, в [74].
5. Пусть NcR2" — лагранжево подмногообразие и у — кри-
вая на N. Ей отвечает кривая, составленная из лагранжевых
подпространств X (t)=TyinN. Если у — замкнутая кривая, то
определено число
I§(dt2)* (821),
I§(det).
В действительности мы определили элемент из Н1 (N; Z). Он
называется классом Арнольда—Маслова для лагранжева под-
многообразия N, см. [74].
6. Пусть М—гладкое многообразие, а со — симплектическая
структура на Т*М. Каждое касательное пространство Tz (T*M),
zeT*M, является симплектическим векторным пространством,
и в нем можно взять лагранжево подпространство V,,
касательное к вертикали, т. е. состоящее из таких касательных
векторов t,, что dnzi, = 0, где буквой п обозначена стандартная
проекция я: Т*М -> М. Выбор римановой метрики на М ин-
дуцирует положительно определенное скалярное произведение

§ 63 ОБОБЩЕННЫЕ КЛАССЫ МАСЛОВА 401
на Vz, позволяющее отождествить LG (Тг{Т*М)) с U («)/О (л).
Значит, (det2)* (dzjlniz)— корректно определенная дифференци-
альная форма на расслоении LG (Т*М), где LG (Т*М) —
расслоение над Т*М, у которого слой над точкой z состоит из
всех лагранжевых подпространств в TZ{T*M). Если N—
лагранжево подмногообразие в Т*М, то для любой кривой у на
N определена естественным образом кривая на LG (Т*М).
В этом случае, воспользовавшись (821), определим целое число;
таким образом, получим элемент из Н1 (N; Z), который
называется классом Арнольда — Маслова подмногообразия N.
Этот класс не зависит от выбора римановой метрики.
7. Определение. Пусть (М1п, со)— почти симплектическое
многообразие, т. е. гладкое многообразие М2п размерности 2л,
снабженное невырожденной 2-формой со. Связность Гд на М2п
называется почти симплектической связностью (или связностью,
согласованной с со), если Vco = 0.
Связностей, согласованных с симплектической структурой,
бесконечно много. Они изучались в работах [56], [147]—[149],
[318], [326], [381], [420], [476], [477], [508], [512], [514], [515].
8. Конструкция почти симплектических связностей. Пусть
V0 — произвольная связность на М. Положим
9 (* Y) = \ Г t (V>) (Y, ?,.,) Щ- ? (V» (У, ?,-) еЛ (822)
Z Li=l i=l J
где (Et, Ер), i=\,...,n, i* = i + n,— произвольный локальный
симплектический базис на М, т.е. со (Eh ?}) = со (?,., ?^.) = 0,
со (Eh Ej.)= — со (?;., Е/) = Би. Легко видеть, что 0 характеризует-
ся равенством со @ (A', Y), Z) = - (V^co) (Y, Z), что доказывает
независимость определения 0 от выбора симплектического
базиса. Непосредственное вычисление показывает, что V\Y=
= V$K+0 (X, Y) — почти симплектическая связность.
Если есть другая связность VA-J'=Vx Y+A (X, Y), то равенст-
во Vco = 0 имеет место тогда и только тогда, когда
со (Л (X, Y), Z) + (o(Y,A (X, Z)) = 0. Положим В(Х, Y, Z) =
= w(A(X, Y), Z), тогда Vco = O эквивалентно свойству симмет-
рии В{Х, Y, Z) = B(X, Z, Y).
Обратно, пусть имеется произвольное тензорное поле
В (X, Y, Z), удовлетворяющее соотношению В (X, Y, Z) =
= В(Х, Z, Y). Тогда В(Х, Y, Z) = co (A (X, Y), Z) можно решить
относительно A w построить почти симплектическую связность
VxF=Vx Y+A (X, Y). В качестве такого решения можно взять
А (X, Y)= t B{X, Y, Ег.) Е,- ? В(Х, Y, Е{) Е,.. (823)

402 ГЛ. II. ХАРАКТЕРИСТИЧЕСКИЕ КЛАССЫ
Итак, для почти симплектических связностей на многообразии
М имеем формулу Vx K=V? Y+Q (X, Y) + A(X, Y).
9. Лемма. Многообразие (М, со) допускает почти симплек-
тическую связность без кручения тогда и только тогда, когда
dco = O, т. е. (М, со)— симплектическое многообразие.
10. Определение. Почти симплектическая связность с ну-
левым кручением называется симплектической связностью.
11. Предложение. Пусть М—(почти) симплектическое
многообразие, на котором симплектически действует группа Ли
Р (т. е. g*co = co для каждого диффеоморфизма geP). Тогда
М имеет Р-инвариантную (почти) симплектическую связность
тогда и только тогда, когда М допускает Р-инвариантную
аффинную связность.
12. Определение. Пусть R (X, Y) Z= VxVyZ-VyVxZ-
-W{Xiy]Z—тензор кривизны. По аналогии с римановым случа-
ем определим симплектический тензор кривизны S(XX, Х2, Х3,
X4) = a(R(X3,X4)X2,X1).
13. Предложение. Симплектический тензор кривизны
S обладает следующими симметриями:
S(XU Х2, Х3, X4)=-S(XU X2, Х4, Хъ), (824)
S(XU Х2, Х3, X4) + S{XU Хъ, Х4, Х2) +
+ S(XU X4, Х2, Х3) = 0, (825)
S(XU X2, Хъ, X4) = S(X2, Xu Х3, Х4). (826)
14. Определение. Тензор Риччи а (X, Y) определяется
обычной формулой
п
о(Х, Y) = tr(V->R(V, X) Г)= X E'(R(EhX)Y), (827)
i= I
где Et — симплектический базис, а г' — дуальный кобазис, т. е.
?'(?,¦)=§;••
15. Лемма. Тензор Риччи симплектической связности сим-
метричен.
16. Пример. Основной пример симплектической связности —
связность Леви — Чивита на кэлеровом многообразии М с мет-
рикой g и комплексной структурой J. Симплектическая струк-
тура со определена равенством со (A', Y) = g (X, JY). Далее,
S{XU Х2, Х3, X4) = R(JXU Х2, Х3, ХА) и о(Х, Y) = r(X, Г), где
R — риманов тензор кривизны, а г — тензор Риччи метрики g.
За дальнейшей информацией о симплектическом тензоре
кривизны отсылаем читателя к работам И. Вайсмана.
17. Конструкция. Излагаемая ниже конструкция характери-
стических классов, обобщающих классы Маслова, принадлежит
В.В.Трофимову [260]—[262]. На симплектическом многооб-

8 63. ОБОБЩЕННЫЕ КЛАССЫ МАСЛОВА 403
разии (М2п, со) рассмотрим связность Гд, согласованную
с симплектической структурой со. Обозначим С (х0) множество
путей, начинающихся и кончающихся в точке хоеМ2". Опера-
ция параллельного переноса вдоль путей уеС(х0) порождает
группу НХо(М2п) линейных преобразований пространства
ТХдМ . Эта группа называется группой голономии данной
связности Гд. Поскольку связность Гд согласована с симплек-
тической структурой со, то группа Нх (Л/2") переводит лагран-
жево подпространство в ТХоМ2" в лагранжево подпространство,
т.е. имеем действие группы голономии НХо(М2") на лагран-
жевом грассманиане ЬС„. Поэтому можно определить приведен-
ный лаграпжев грассманиан HL (Tx M2") = LG^jHXo (M2n).
Предположим теперь, что N"<^M2n — лагранжево подмного-
образие симплектического многообразия М . Перенесем каса-
тельное пространство TXN вдоль произвольного пути у (?),
O^f^l, параллельно относительно симплектической связности
Гд в точку xoeN, причем путь у соединяет точку x = y@)eN
с точкой хо = у(\). В итоге получим подпространство xy(TxN)E
eLG (TXgM2n), которое естественно зависит от выбора пути у.
Подпространство ху (TXN) является лагранжевым, так как
связность Гд согласована с симплектической структурой со.
Возникает отображение/,,: tV-> LG (TXgM2n). Если взять другой
путь р, соединяющий точку х= р @) с х0 = Р A), то подпростран-
ство z$(TxN) отличается от xy(TxN) на некоторое преобразова-
ние из группы голономии Нх (М ), т. е. имеется корректно
определенное отображение/: N-> HL (TXgM2n) лагранжева под-
многообразия N в приведенный грассманиан HL (TXqM2").
Отображение / порождает индуцированное отображение
/*: Н* (HL (TXoM2n))~*H*(N) в когомологиях. Если аеН*
(HL (Тх М2")), то определен характеристический класс
a (N)=f* (a)eH* (N) лагранжева подмногообразия N<^M2n.
18. Определение. Пусть М2п—симплектическое многооб-
разие. NcM2"—лагранжево подмногообразие. Тогда каждый
класс когомологий ае Н* (HL (ТХоМ2п)) приведенного грас-
сманиана HL (TXQM2n) (относительно некоторой симплектиче-
ской связности) определяет естественный характеристический
класс a (N)eH* (N) типа Маслова лагранжева подмногообразия
N^M2n.
19. Замечание. Симплектические связности определены
с точностью до преобразования п) = 2~1 (х) — содТ^со51'), где
x'j—произвольная тензорная форма, см., например, [508]. При
таких деформациях группа голономии, вообще говоря, меняет-
ся. Например, верхняя полусфера 5+ =Lx2+y2 + z2= I, z>0}
с формой площади и диск D2 = {x2+y2< 1} с формой площади
симплектически диффеоморфны. Стандартные связности на
диске и на сфере являются симплектическими. Однако их
группы голономии различны: НХд (D2) = {e}, но НХо E){}
26*

404 гл || ХАРАКТЕРИСТИЧЕСКИЕ КЛАССЫ
20. Теорема (В.В.Трофимов [262]). Пусть на симплек-
тическом многообразии М выбрана симплектическая связность
с группой голономии G. Тогда каждый класс когомологий
аеН* (LGJJTX M2n)jG) приведенного лагранжева грассманиана
LG (TXqM n)jQ однозначно определяет характеристический
класс a(N)eH*(N) лагранжева подмногообразия N^M2n.
21. Замечание. В общем случае группа голономии есть
полная симплектическая группа. Она действует транзитивно на
лагранжевом грассманиане (см. § 17), и, следовательно, приве-
денный лагранжев грассманиан в этом случае тривиален.
Другой крайний случай связан с классическими классами в R2".
В этом случае группа голономии G = HXq(R2") тривиальна, т. е.
G=RW и приведенный грассманиан есть "лагранжев грассманиан
LGn. При увеличении группы голономии G приведенный
грассманиан HLn уменьшается пока в случае общей связности
не превратится в точку. Итак, запас характеристических классов
лагранжевых подмногообразий измеряется группой голономии
симплектической связности. Классификацию групп голономии
многообразий с аффинной связностью см. в работе М. Берже
[320] или в [495].
22. Частный случай. Предположим, что связность, согласо-
ванная с симплектической структурой, плоская и многообразие
М " односвязно. Тогда группа голономии HXq(M2") действует
на лагранжевом грассманиане тривиально и приведенный
грассманиан HL(TX M2n) совпадает с лагранжевым грассманиа-
ном LG(TXom2")° Известно, что H-(LG(TXoM2"); Z2) =
= Z2 [wb ..., wn ]/(wj, ..., w2). Поэтому характеристические клас-
сы Маслова лагранжевых подмногообразий плоских односвяз-
ных симплектических многообразий принимают значения
в к°ль?е Г&2 lwu...,wn]/(w2,...,w2))<=H*(N;Z2).
?5. Конструкция. Пусть на симплектическом многообразии
М " задан полный инволютивный набор функций F={j\, ...,/„}.
Совместные Поверхности уровня N={j\ =c1, ...,/„} являются
лагранжевыми подмногообразиями, связные компактные ком-'
поненты которых диффеоморфны торам Т", см. [8], [102].
В этом случае можно применить предыдущую конструкцию
к N и получить характеристические классы a (F)e л (wu ..., ws)
полного чнволютивного семейства F, здесь
л (vvb ..., w's)—-внешняя алгебра над wb ..., ws.
24. Замечание. Алгебра Ли группы голономии в силу
классической теоремы Амброузера, Зингера [126] определяется
в терминах тензора кривизны, поэтому фактически харак-
теристические классы лагранжевых подмногообразий описыва-
ются тензором кривизны симплектической связности. Грубо
говоря, чем «больше» кривизны, тем «меньше» приведенный
лагранжев грассманиан, а следовательно, тем меньше харак-
теристических классов. Для модельных примеров 5+ и D2

§ 63 ОБОБЩЕННЫЕ КЛАССЫ МАСЛОВА 405
имеем HL (S + )={pt}, HL(D2) = Sl. Пространство S2+ имеет
постоянную ненулевую кривизну, а кривизна диска D2 равна
нулю (относительно стандартных связностей). Геодезические
линии в обоих примерах имеют нулевой индекс (в соответствии
с гипотезой А. Т. Фоменко), так как в первом случае тривиаль-
ны когомологии приведенного лагранжева грассманиана, а во
втором — тривиально отображение /: N-* LG (ГХо?J) = 5'1.
25. Теорема. Пусть М—кэлерово многообразие, N—впол-
не геодезическое лагранжево подмногообразие. Тогда все харак-
теристические классы типа Маслова a (N) подмногообразия
N<= M равны нулю.
Доказательство. Действительно, если gi}—кэлерова
структура на М, то связность, согласованная с gti, дает
аффинную связность, одновременно риманову и симплектичес-
кую. Поэтому распределение касательных плоскостей TXN,
xeN, на N дает параллельное распределение относительно
симплектической связности. Следовательно, отображение
/: N^>LG(TXqM) тривиально, и поэтому все классы типа
Маслова равны нулю.
26. Обобщение. Конструкция характеристических классов,
изложенная выше, обобщается на лагранжевы подрасслоения
в векторных расслоениях с симплектической структурой. Пред-
положим, что в векторном расслоении р: Е-+В в каждом слое
р ~1 (х) задана симплектическая структура Ш;; (х), гладко завися-
щая от точки хеВ базы В. Пусть п: Х^В—такое локально
тривиальное подрасслоение в Е, Х<=Е, что все слои к'1 (Ь)
являются лагранжевыми подмногообразиями в слоях рас-
слоения р: Е-> В. Зададим в расслоении р: Е -»В связность Г'ак,
согласованную с кососимметрическим скалярным произведени-
ем <utj(x). Тогда касательное пространство Tx(n~l (b))<=p~i (b)
к слою я (Ь) сначала параллельно сдвигаем в начало
координат Oepl(b), а затем, используя связность Г'ак, это
пространство параллельно переносим в фиксированный слой
р (Ьо), ЬоеВ. Получаем корректно определенное отображе-
ние /: X^LG(pl (bo))IG, которое позволяет определить
характеристические классы а (я) =/* (а) е Н* (X), где
аеН* (LG(/?~1 (bo))/G) — произвольный класс когомологий при-
веденного лагранжева грассманиана LG(/>*1 (bo))/G в слое
Р1 (Ьо), ЬоеВ, G = Hbo(p) — группа голономии связности rj,t.
В случае касательного расслоения р = ТМ к симплектическому
многообразию М получим характеристические классы, описан-
ные выше.
27. На лагранжевом подмногообразии в T'W, лагранжево
изотопном нулевому сечению, определена целозначная функция,
сопоставляющая точке общего положения индекс Маслова пути
из этой точки на бесконечность. Наша цель — описать нули этой
функции.

406 ГЛ !! ХАРАКТКРИСТИЧкСКИК КЛАССЫ
28. Определение. Пусть М—связное гладкое многооб-
разие без края, Ncz T*M—лагранжево подмногообразие, изо-
топное нулевому сечению в классе лагранжевых подмногооб-
разий, совпадающих с ним вне компакта. Индексом регулярной
точки проекции N ^ М называется индекс Маслова ориен-
тированного пути на N, соединяющего эту точку с отмеченной.
29. Определение. Производящим семейством лагранжевой
иммерсии /: N^>T*M называется такая гладкая функция
(.v, q) -> S (л-, «у), S: R" х М -* R, что: 1) Sx. R'xM-.R" трансвер-
сально к [0}cR"; 2) i(N) = {(p, a)eT*M\Sx(x, q) = 0, p = Sq{x, q)-
для некоторого .veR"}.
Производящее семейство называется квадратичным на бес-
конечности, если для любой точки цеМ функция ./,(.*) =
= S(x, <у), /ч: R" -> R. совпадает вне некоторого шара с невыро-
жденной квадратичной формой.
30. Теорема (А. Б. Гивенталь [73]). При подходящем выбо-
ре отмеченной точки прообраз каждого регулярного значения
проекции N -> М содержит точку индекса нуль.
Доказательство теоремы 30 вытекает из следующей глубо-
кой теоремы 31 симплектической топологии (подробности см.
в работе [73]).
31. Теорема (Сикорава [494]). Лагранжево подмногооб-
разие Ncz T*M, совпадающее с нулевым сечением вне компакта
и гамильтоново, изотопное ему, можно задать производящим
семейством, квадратичным на бесконечности.
32. Замечание. Гамильтонова изотопия задается семей-
ством симплектоморфизмов, определяемых глобальным гамиль-
тонианом с компактным носителем.
§ 64. Вполне интегрируемая гамильтонова система,
торы Лиувилля которой имеют нетривиальные
индексы Арнольда — Маслова
1. В этом параграфе мы построим примеры вполне интег-
рируемых систем, для которых инварианты, определенные в п. 6
§ 63, отличны от нуля. Эти результаты принадлежат
3. Тевдорадзе.
2. Обозначения. Рассмотрим пример сферического маятника.
Для него фазовое пространство — это кокасательное расслоение
к двумерной сфере 52 = {xeR3| x\ + х\ + х\ = 1}. Пользуясь
римановой метрикой на S2, отождествим T*S2 с касательным
расслоением TS2. Гамильтониан системы имеет вид Е(х, v) =
= 2~1 <г, v}+x3, xeS2, veTxS2, <x, i>> = 0. Кинетический мо-
мент относительно оси х3 имеет вид I (x, v) = (Qx, v), где
/о -1 о\
B= 1 0 о , т.е. I{x, v) =
\о о о/

<j 64. ВПОЛНЕ ИНТЕГРИРУЕМАЯ СИСТЕМА 407
3. В точках (х, v) e TS2, где выполняются соотношения
dvy = 0, (828)
(829)
= 0, (830)
функции Е и / функционально зависимы. Пусть е3 = @, 0, 1).
Тогда точками, где имеет место функциональная зависимость,
являются х=±е3, v = 0 и v = a.-Qx, l+a2x3 = 0, л'з=±1. Они
соответствуют горизонтальному действию на сфере, т. е.
— 1 <.v3<0, || и || =A -xjI12 (-x3)~112. Соответствующие син-
гулярные значения отображения /(/, Е):
/=@, ±1), f=U-a~\ 1а2-^оГ2\ (831)
Действительно, поскольку v = a ( — х2, хи 0), то
(832)
E=l-<v, и>
Если а стремится к +1, то (831) стремится к @, —1)- При
имеем Qx=?0, т.е. х^±е3 и мы можем ввести полярные
координаты xl =sincp cosG, x2 = sin9sin0 и x3=cos<P, где 0е
6R/2itZ, сре(О, я). Риманова метрика имеет вид ds2 = dq>2 +
+ sin2(p dQ . Если Р1=д/д(р, P2 = d/8Q, то соответствующие
координаты на T'S2 обозначим ср, 0, ру, рг. Каноническая
1-форма на T'S2 имеет вид a.=p1dq>+p2dQ. Эта форма
с помощью указанной римановой метрики переписывается на
TS2 в виде p = sin29-0^0 + фй?ф, где ср, 0, ф, 0 — координаты на
TS2 (если X=ai~ + a2^-eTS2, то ф(Х) =
Симплектическая форма на TS2 принимает вид
ш = й?ф л d<p+ sin2<p -0 dq> л dQ + sm2q> dQ л dQ. (834)
В этих координатах функции Е и 7 выражаются следующим
образом:
7=0 sin2 ф, (835)
?-=2-102sin> + 2^42+cos9 = 2-42+^((p)> (836)
где
Ц ^ (837)
2 sin

408
ГЛ И. ХАРАКТЕРИСТИЧЕСКИЕ КЛАССЫ
— эффективный потенциал. Из (834)—(836) следуют равенства
sgrad /=-,
sgrad ?=ф
А + Л Sin2cp-e2
ов \2
\ д <Ь9 sin 2ф д
+ 8Шф —г — - ;—- '-г.
у оф sin ф с9
(838)
(839)
Если отождествить плоскость (ф, ф) с пространством /= const,
факторизованным по орбитам sgrad/ @-окружностям), то наша
система индуцирует на этой плоскости систему с гамильтониа-
ном Е, см. (833), (836). Редуцированная
симплектическая форма на (ф, ф) принима-
ет вид й?ф Л(/ф. Особые точки редуцирован-
ной системы задаются соотношениями
ф = 0, I2 (втф) со8ф + 8тф = 0. (840)
Рис. 88
Для редуцированной системы существует
единственная особая точка, и так как
Е -> + оо при ф -> 0, ф -* я или | ф | -> оо, то
эта точка является точкой глобального
минимума Е. Отсюда вытекает, что образ
отображения / задается соотношениями
/=а-а, ?>i<x2--a~2
(рис.88).
4. Фиксируя G0, ?0)eR2, /От^0, мы получим гладкую кри-
вую, диффеоморфную окружности
= |(Ф, Ф)е(О, n)xR\Eo = {-4>2+VIo
(841)
Для (ф, ф)еу! из (835), (836) найдем 0, 0е [0, 2л] фиксировано.
Обозначим у2 окружность, получающуюся, если фиксированы
ф, ф, 0 и 0 пробегает отрезок [0, 2л]. Гомотопические классы
окружностей у1 и у2 являются базисом для Hl(f~1(IQhE0)).
Вычислим индекс для тора
T2=/-l{I0,F0),
(842)
5. Теорема C. Тевдорадзе). Имеет место равенство <хТ2 =
= B,2)EZ@Z = W1G'2=r1(/o,?o); Z), где /о#0.
Доказательство. Рассмотрим окружность у2 в TS2,
которая определяется соотношениями ф = фо^0, ф = фо,
0 = 0О7^О> 0е [0, 2я]. Построим в явном виде отображение
Р: Т2 -» LG (TS2) и вычислим интеграл (821). Из формул (838),

§ 64. ВПОЛНЕ ИНТЕГРИРУЕМАЯ СИСТЕМА
409
(839) вытекает, что
i) (e) = fe (Фо, 0- Фо, во), Фо ~ (Фо, 9, Фо, во) +
ё0 ^ (фо, б, Фо, <эо)+ло — (фо, е, ф0,90)+50 ~. (фо,
Си С?ф Си
где
1 .
э, Фо, ео)\
о — - sin2(p0 'бо + ^пфо,
(843)
(844)
On—
sin 2фо-фо-9о
(845)
Окружность изотопна окружности, для которой фо = 0. Заметим,
что у2е TSZ+ —D2 xR2, где S2+—верхняя полусфера. Поскольку
LG {TS\) = D2 xR2 xLG (R4), то мы ограничимся рассмотрени-
ем LG (R4). Индекс не зависит от выбора метрики на S2,
д д
поэтому можно считать, что —г ортогонально — относительно
метрики. Отображение Р тогда принимает вид
(846)
{АофО в силу (840)). Из (846) следует, что Р(Уг) (9) определяет-
ся вектором е = д/д(р и точкой 0 на окружности у2 (рис. 89).
е=
Рис. 89
Рис. 90
Если в
R4 фиксируем лагранжеву плоскость (е, е0), где
= ~ @ = 0), то Р(у2) @) =
В силу (840) имеем /(у2) = 2.
Рассмотрим окружность ух в плоскости (ф, ф), над которой
расслоение опять тривиально. Поскольку 0 = //8т2ф, то

410 ГЛ. П. ХАРАКТЕРИСТИЧЕСКИЕ КЛАССЫ
— = —^-^ Если t—параметр на кривой у, то гауссово
дв /sin2«p dq> f f F f> J
отображение Р принимает вид
(x(t)) + A(x(t))±(x(t))), (847)
где A(x(t)) = 2~i sin2q>(x (/)) • 62 (x (t)) + sin<p (x (t)). Снова отоб-
ражение P(Yi) определено вектором e = d/dQ и точкой на кри-
вой х (?) (рис. 90). Непосредственное вычисление дает равенство
/(Yj) = 2. Окончательно получаем требуемое равенство
аг2 = B, 2)eZ©Z = H1(/-1(/0, ?0); Z), где /0*0. Теорема до-
казана.

Приложение. НЕРЕШЕННЫЕ ЗАДАЧИ
На семинаре «Современные геометрические методы» был сформирован
список задач, представляющих интерес с точки зрения развития идей и тем,
затронутых в книге. Он является результатом совместного обсуждения всеми
участниками семинара. Здесь мы частично воспроизводим его.
1. Две скобки Пуассона называются согласованными, если любая их
линейная комбинация с постоянными коэффициентами снова является скобкой
Пуассона. Имеется ли какой-нибудь аналог теоремы Дарбу для таких скобок,
т. е. сутцествует ли локальная система координат, в которой обе скобки имеют
простой вид? Рассмотреть простейшие ситуации.
2. Пусть на симплектическом многообразии задана пара коммутирующих
функций Аи/ Если функции независимы, то справедлива теорема Лиувилля
и можно определить переменные «действие — угол». Пусть пара функций
Аи/ имеет боттовскую особенность. Что остается от теоремы Лиувилля, могут
ли быть определены аналоги переменных «действие — угол»?
3. Понятие боттовости хорошо определено на изоэнергетической поверх-
ности. Дать определение боттовских особенностей в целом на симплектическом
многообразии МЛ (сначала локально). Дать определение боттовости полного
инволютивного набора функций на симплектическом многообразии М2п
в целом.
4. Является ли боттовость условием общего положения? Более точно, пусть
/—первый интеграл гамильтоновой системы i = sgradA, на изоэнергетической
поверхности 23 = {xeA/4|A(x) = const}. Можно ли мало возмутить гамильтони-
ан с сохранением интегрируемости (или возмутить симплектическую структуру)
так, чтобы новый первый интеграл был боттовским? Справедливо ли
утверждение для А/4.
5. Пусть дана интегрируемая гамильтонова система x = sgradhx на А/4
с дополнительным первым интегралом / Рассмотрим отображение моментов
F={h,f): M4->R2 и бифуркационную диаграмму Z = {F(x)\rkdF(x)<2}. В силу
теоремы Лиувилля на множестве F~1(K\2.), где K = lmF, могут быть
определены переменные действия, которые являются функциями от h и /
si=sl(h,f), S2 = sz(h,f). Поэтому линии уровня переменных действия могут
быть нарисованы на множестве К\1,. Требуется нарисовать качественную
картину их поведения, выбрав в качестве циклов на торах Лиувилля циклы,
пришедшие с ?.
6. Пусть А—алгебра Горенштейна (например, алгебра инвариантов связной
полупростой группы Ли). Тогда ее минимальная свободная резольвента
обладает следующим свойством симметрии: если s—длина этой резольвенты,
то ранги г-го и (s—i)-ro свободных модулей в этой резольвенте совпадают для
всех i. Обобщить алгоритм (г) на тензорные произведения L®A алгебры Ли
L и алгебры Горенштейна А.
7. Можно ли продолжить действие функтора (/) с алгебр Ли на
симплектические многообразия? Более точно, пусть М—симплектическое
многообразие, на котором в пространстве С °° (М) выделена конечномерная
подалгебра F, удовлетворяющая условиям некоммутативной теоремы Лиувил-
ля. Существует ли симплектическое многообразие N, которое «канонически»

412 ПРИЛОЖЕНИЕ НЕРЕШЕННЫЕ ЗАДАЧИ
строится по М, с алгеброй Ли функций (() (F), удовлетворяющей некоммутатив-
ной теореме Лиувилля уже автоматически.
8. Дать классификацию 5-представлений полупростых групп Ли. Выяснить
вопрос о полной интегрируемости полученных гамильтоновых систем.
9. Построить в явном виде секционные операторы для всех конечномерных
представлений полупростых алгебр Ли. Выяснить вопрос о гамильтоновости
полученных уравнений, а также вопрос о полной интегрируемости.
10. Выписать в явном виде через 8-функции римановых поверхностей
решения уравнений Эйлера х — {С(х), х] на пространстве П(С)* для полупростых
алгебр Ли G.
11. Задачи о допустимом виде бифуркационных диаграмм. Пусть /,
h — коммутирующие функции на компактном симплектическом многообразии
Af4, P. Af4-»R2— отображение моментов. Пусть особенности отображения
моментов устроены максимально просто: это либо минимаксные боттовские
окружности, либо невырожденные точки типа «центр — центр». Тогда образ
отображения моментов диффеоморфен либо кольцу, либо многоугольнику.
Могут ли быть дырки в образе F(M*) в общем случае (кроме кольца; этот
случай, по-видимому, является исключительным)? Может ли бифуркационная
диаграмма содержать петли?
12. Известно, что образ отображения моментов при действии тора является
многоугольником. Верно ли обратное утверждение (при условии, что сторонам
отвечают минимаксные боттовские окружности, а вершинам—невырожденные
точки типа «центр — центр»). Описать четырехмерные симплектические много-
образия, допускающие гамильтоновы действия тора Т2. Описать изоэнер-
гетические поверхности, допускающие гамильтоиовы действия тора Г2.
13. Пусть задана система кусочно гладких кривых EcR2, и мы
интересуемся возможностью ее реализации в виде бифуркационной диаграммы
отображения момента некоторой интегрируемой системы. Как показывают
примеры, вообще говоря, этого сделать нельзя. Рассмотрим окрестность [/(?)
множества 2 в R2. Может ли быть реализована эта окрестность, т. е. существует
ли некомпактное многообразие Af и пара коммутирующих на нем функций/,
h таких, что ImF=C/(S) и ?—настоящая бифуркационная диаграмма?
14. Пусть М*=Т2х [0, 1]х [0, 1], /, g—параметры на отрезках [0,1]
и [0, 1]. Пусть на М, = Т^х [0, 1]х [0, е] и М2=Т2х [0, 1 ] х [1-е, 1] заданы
симплектические структуры о^ и со2 соответственно такие, что {/, g}i=0
и {/> #Ь = 0. Известно (Браилов А. В.), что если косые градиенты имеют
одинаковую ориентацию на торах в смысле двух скобок, то можно продолжить
симплектические структуры со,, со, в единую симплектическую структуру со на
Af4 с сохранением условия {/, g}=0. Пусть теперь Af4 = 7x[0, 1]х5\ где
[0, 1]х5' — кольцо. Пусть симплектические структуры <Oi и со2 заданы на
множествах Г2 х [0, е]х5' и Т2 х [1— е, 1] xSl соответственно, причем
/ и g коммутируют (здесь fug параметры на [0, 1 ] и S'). Определить
необходимые и достаточные условия сшивания этих структур в единую
структуру со на Af4.
15. Вариационные задачи на симплектическом многообразии (Af2", со).
Хорошо известно, что на М2" можно определить почти комплексную структуру
J, J2=— id, согласованную с со, т.е. такую J, что со (JX, J Y) = со (X, Y)
и g(X, У) = со(ДГ, JY)—риманова метрика. Напомним явную конструкцию для J.
На Af2" зададим произвольную метрику к и определим оператор А:
ТХМ2"^ТХМ2" равенством со(Х, Y) = k(AX, У) для любых X, YeTxM2".
Оператор (—А2) является положительно определенным самосопряженным
оператором относительно скалярного произведения к, т.е. к(—А2Х, У) =
~к(Х, —A2Y) и к(-А2Х, Х)>0, AV0. В этой ситуации определен оператор
(—Л2I'2. Тогда /=(—А2)~112А — искомая почти комплексная структура.
Обозначим через J(M2", со) пространство почти комплексных структур,
согласованных с со.
а) Пусть NkczM2"—подмногообразие в Af2", vol—форма объема иа Nk
для метрики g(X, Y) \ ц = со (X, JY) \ N. На пространстве J(M2",e>) рассмотрим

ПРИЛОЖЕНИЕ НЕРЕШЕННЫЕ ЗАДАЧИ 413
функционал V= J vol. Найти его критические точки, построив соответствующий
JV
формализм. Какие свойства функционала V отражают лагранжевость подмного-
образия №
б) На пространстве У(М2", со) можно рассмотреть функционал Янга —
Миллса
JM= J ItFa*F,
Mb
где F—форма кривизны, а * — оператор Ходжа для метрики ш(Х, JY),
JeJ(M2n, to). Найти его критические точки. Выяснить их связь с уравнениями
Янга — Миллса d*F=0 и условием автодуальности *F=Fa ил ... лш и антиав-
тодуальности *F=— Fa юл ... ло). Разобрать случай кэлеровых многообразий.
В этой ситуации естественно возникает задача построения пространства
модулей.
в) Фиксируем некоторую почти комплексную структуру УеУ(М2", ш).
Рассмотрим функционал V(N) из п. а. Найти его критические точки!
Справедлива ли гипотеза Фоменко еб обращении в ноль классов Маслова
критического подмногообразия. Рассмотреть отдельно кэлеров случай и орбиты
коприсоединенного представления компактных групп Ли.
г) В работе М. Gromov, Pseudoholomorphic curves in symplectic manifolds//
Invent. Math.— 1985.— V. 82.— P. 307—347 доказаны теоремы существования
J-голоморфных кривых и показано, что они являются минимальными.
Вычислить для них обобщенные классы Маслова.
16. Вычислить классы Маслова торов Лиувилля для классических вполне
интегрируемых гамильтоновых систем, например, для трех классических случаев
движения твердого тела, закрепленного в одной точке.
17. Вычислить обобщенные классы Маслова торов Лиувилля для многомер-
ного обобщения уравнений движения твердого тела на случай полупростых
алгебр Ли (секционные операторы <\>a,b,D).
18. Выяснить возможность перенесения результатов с тензорных расшире-
ний на случай расширений вида Tor'(G, A).
19. Обобщить конструкцию Ле Нгок Тьеуена на случай оператора П такого,
что Q* = id.
20. Изучить расширения G ® А, удовлетворяющие условиям
21. Выяснить связь перестроек торов Лиувилля с вещественными частями
комплексных перестроек в особых точках.
22. Проанализировать, какие методы построения функций в инволюции
дают боттовские интегралы. Указать эффективный критерий боттовости.
23. Дать регулярный способ построения согласованных скобок Пуассона.
24. Существует ли вложенное (но не иммерсированное) компактное
лагранжево подмногообразие в 7"*R", классы Маслова которого равны нулю
(проблема М. Аудин)?
25. Построить аналог теории уравнений Эйлера для других классов алгебр
(например, для коммутативных алгебр).
26. Один из простейших многомерных интегрируемых случаев — это аналог
уравнения движения твердого тела на компактных алгебрах Ли (так называемая
компактная серия секционных операторов). Интегрируемость связана здесь
с наличием пары согласованных скобок Пуассона, а в этой ситуации первые
интегралы обладают рядом хороших свойств. Простейший пример в этой
серии — уравнения Эйлера на алгебре Ли suC). Орбиты компактны и шестимер-
ны. Образ отображения моментов — это некоторая фигура в R3, ограниченная
кусками бифуркационной диаграммы. Внутри фигуры нет никаких перегородок
(это следствие общей теории), но могут быть одномерные куски. Задача состоит

414 ПРИЛОЖЕНИЕ. НЕРЕШЕННЫЕ ЗАДАЧИ
в полном исследовании этого случая. Какая связь имеется между точками типа
«фокус—фокус» и одномерными кусками бифуркационной диаграммы?
27. Рассмотрим уравнения движения 4-мерного твердого тела на алгебре Ли
so D). Топологическая структура этого случая полностью исследована
А. А. Ошемковым. Известно, что множество критических точек отображения
моментов совпадает с объединением множества сингулярных элементов
некоторых алгебр Ли, отвечающих скобкам из семейства согласованных скобок
Пуассона. Эти алгебры Ли разбиваются на несколько принципиально различ-
ных типов. Найтн связь с бифуркационной диаграммой, т. е. охарактеризовать
бифуркационную диаграмму в терминах семейства алгебр Ли.
28. Установить связь теории Фоменко с теорией Вальдхаузена.
29. Можно ли дать определение и построить теорию разложения на
зейфертовы компоненты в неботтовском случае?
30. Пусть на Q3 задано лиувиллево слоение. Пусть это слоение
естественным образом продолжено на M4 = g3x/. Доказать, что на М4 может
быть задана симплектическая структура таким образом, что гамильтонова
система t) = sgrad/j (где h — параметр отрезка I) была интегрируема и соответст-
вующее лиувиллево слоение совпадало бы с наперед заданным.
31. Пусть Q3 фиксировано. Какие условия накладывает топология Q1 на
граф и на метки. Рассмотреть случай, когда g3 простое: сфера S3, тор Г3,
произведение S2xS\ проективное пространство RPi.
32. В примерах из механики метки очень простые. В чем причина этого?
Что отвечает за простоту или сложность меток?
33. Можно дать два определения резонансной системы: а) система
резонансная, если все траектории замкнуты; б) система резонансная, если
существует дополнительный интеграл. Какова связь между этими определени-
ями? Исследовать два случая: на изоэнергетической поверхности Q 3 и на всем
симплектическом многообразии М4.
34. Пусть Qi — глобальное расслоение Зейферта без особых слоев, т. е. это
обычное локально тривиальное расслоение над двумерной поверхностью Р2 со
слоем окружности S1. Известны 4 типа таких расслоений. Какие из них
возникают в задачах механики и математической физики (Лагранж, Кеплер,
Не3, ...)?
35. Пусть Q2—произвольное слоение Зейферта. Реализовать это слоение
как слоение на траектории интегрируемой резонансной гамильтоновой системы.
36. Разобраться, что происходит с теорией топологической классификации
при малом возмущении интегрируемой гамильтоновой системы. Выявить связь
с КАМ-теорией.
37. Пусть имеется интегрируемая гамильтонова система на М2°=Т*Р, где
Р—группа Ли. Имеется стандартная процедура редукции для таких систем,
позволяющая понизить порядок. Рассмотрим систему на (М2к, &) после
понижения порядка. Как связаны между собой инварианты этих двух систем?
38. Имеется теория бордизмов интегрируемых гамильтоновых систем,
построенная А. Т. Фоменко и А. В. Болсиновым. В рамках этой теории имеются
следующие задачи. Пусть g3— произвольное трехмерное многообразие. Извес-
тно, что Q3xl—симплектическое многообразие. Существует ли вложение Q3
в компактное симплектическое многообразие? Может ли Q3 служить краем
симплектического многообразия М4, если ?>3е{//}?
39. Пусть Q2e{H}. Существует ли компактное симплектическое многооб-
разие М с интегрируемой гамильтоновой системой r = sgrad/j такой, что
Q3 — изоэнергетическая поверхность? Может ли g3 быть краем симплектиче-
ского многообразия М4 с интегрируемой системой u = sgrad/i такой, что
63 {M4|/() }?
6 {|() }
40. Пусть (М2", <о)—симплектическое многообразие. Определим симплек-
тический класс /-мерного объема Х.'(Л/2")еНот(л2,(Л/2"), R), /=1, ..., и,
равенством
Х'(М2")(а)= j /*(юл... лю),

ПРИЛОЖЕНИЕ. НЕРЕШЕННЫЕ ЗАДАЧИ 415
где/: S2'->M2"— представитель класса аея2,(А/.2"). Вычислить Х'(М2")для
известных примеров симплектических многообразий.
41. Пусть TV"—лагранжево подмногообразие в симплектическом многооб-
разии (М2". ш). Определим относительный симплектический класс г'-мерного
объема Х'(М , N")eHom(n2i(M2", N"), R). ;'=1, ..., л, равенством
Х'(М2п, 7V)(a) = | /* (со л... л со),
О 2, V Y '
где/: (?J'. 5/J') -»(М2", Л'") — представитель класса aen2i(M2", N"). Вычис-
лить эти классы для торов Лиувилля известных вполне интегрируемых
гамильтоновых систем, например, на орбитах присоединенного представления
компактных групп Ли. Имеется ли связь между инвариантами Х'(М2", N")
и классами Маслова? В случае четырехмерного симплектического многообразия
(Мл, со) для торов Лиувилля Т2 вполне интегрируемой гамильтоновой системы
на М* найти связь между "к'(Мл, Т2) и инвариантом Фоменко.

СПИСОК ЛИТЕРАТУРЫ
1. АбловицМ., СигурХ. Солитоны и метол обратной задачи.— М.:
Мир, 1987.
2. А бра ров Д. Л. Топологические препятствия к существованию условно-
линейны)! интегралов,, Вестн. МГУ. Сер. 1. Математика, механика.—
1984.—№ 6.—С. 72—75.
3. Андреев Е. М.. Винберг Э. Б., Элашвили А. Г. Орбиты наибольшей
размерности полупростых линейных групп Ли 'Функцией, анализ и его
прил.—1961,—Т. 1, № 4.—С. 3—7.
4. Аносов Д. В. Геодезические потоки на замкнутых многообразиях
отрицательной кривизны/'Тр. МИАН СССР им. В. А. Стеклова.—
1967.— Т. 90.—С. 3—209.
5. Аносов Д. В. О типичных свойствах замкнутых геодезических /Изв. АН
СССР. Сер. мат.—1982.—Т. 46, № 4.—С. 675—709.
6. Арнольд В. И. О характеристическом классе, входящем в условие
квантования, Функцион. анализ и его прил.— 1967.— Т. 1, № 1.— С. 1 —14.
7. Арнольд В. И. Гамильтоновость уравнений Эйлера динамики твердого
тела в идеальной жидкости'/УМН.— 1969.—Т. 24. № 3.— С. 225—226.
8. Арнольд В. И. Математические методы классической механики.— М.:
Наука, 1974.
9. Арнольд В. И., Варченко А. Н., Гусейн-Заде С. М. Особенности
дифференцируемых отображений: Классификация критических точек, ка-
устик и волновых фронтов.— М.: Наука, 1982.
10. Арнольд В. И., Гивенталь А. Б. Симплектическая геометрия/, Совре-
менные проблемы математики. Фундаментальные направления.— 1985.—
Т. 4.—С. 7—139.
11. Архангельский А. А. Вполне интегрируемые гамильтоновы системы
на труппе треугольных матриц//Мат. сб.— 1979.— Т. 108, № 1.— С. 134—
142.
12. Архангельский Ю. А. Аналитическая динамика.— М.: Наука, 1987.
13. Бабич М. В., Б о бен к о А. И., Матвеев В. Б. Решения нелинейных
уравнений, интегрируемых методом обратной задачи в тэта-функциях
Якоби, и симметрии алгебраических кривых//Изв. АН СССР. Сер. мат.—
1985.—Т. 49, № 3.—С. 511—529.
14. Балинский А. А.. Новиков С. П. Скобки Пуассона гидродинамиче-
ского типа, фробениусовы алгебры и алгебры Ли//ДАН СССР.— 1985.—
Т. 283, № 5.—С. 1036—1039.
15. Барбашов Б. М., Нестеренко В. В. Геометрический анализ нелиней-
ных уравнений в теории релятивистской струны//Физика элементарных
частиц и атомного ядра.— 1984.— Т. 15, вып. 5.— С. 1032—1072.
16. Белавин А. А., Дринфсльд В. Г. О решениях классического уравнения
Янга — Бакстера для простых алгебр Ли//Функцион. анализ и его
прил.—1982.—Т. 16. № 3.—С. 1—29.

СПИСОК ЛИТЕРАТУРЫ 417
17. БелоколосЕ. Д. Задачи Пайерлса — Фрелиха и конечнозоиные потенци-
алы I, Н//Теорет. и мат. физика.—1981.—Т. 48, № 1.—С. 60—69.
18. Беляев А. В. О движении многомерного тела с закрепленной точкой
в поле силы тяжести//Мат. сб.—1981.—Т. 114, № 3.—С. 465—470.
19. Беляев А. В. О движении и-мерного твердого тела с группой симметрии
SO(k)<g)SO(N—k) в поле с линейным потенциалом. Инварианты коприсо-
единенного представления некоторых алгебр Ли//ДАН СССР.—1985.—
Т. 282, № 5—С. 1038—1042.
20. Беляев А. В. Инварианты коприсоединенного представления алгебр Ли
вида 1)фК//Анализ на многообразиях и дифференциальные уравнения.
Воронеж: Изд-во ВГУ, 1986.—С. 139—145.
21. Березин Ф. А. Несколько замечаний об ассоциативной оболочке алгебры
Ли//Функцнон. анализ и его прил.—1967.— Т. 1, № 2.— С. 1 —14.
22. Березин Ф. А. Метод вторичного квантования.— М.: Наука, 1986.
23. Березин Ф. А., Голо В. Л., Путко Б. А. Редукция киральной
суперсимметричной ст-модели//Вестн. МГУ. Сер. 1, Математика, меха-
ника.—1982,—№ 3.—С. 16—19.
24. Березин Ф. А., Переломов А. М. Теоретико-групповая интерпретация
уравнений Кортевега—де Фриза//Функцион. анализ и его прил.—1980.—
Т. 14, № 2.—С. 50—51.
25. Бессе А. Л. Многообразия с замкнутыми геодезическими.—М.:
Мир, 1981.
26. Бляшке В. Введение в дифференциальную геометрию.—М.: Гостехиздат,
1957.
27. Бобенко А. И. Об интегрировании уравнений Эйлера на еC) и soD)//
Функцион. анализ и его прил.—1985.—Т. 19, № 6.— С. 553—564.
28. Бобенко А. И. Уравнения Эйлера на алгебрах гC) и soD). Изоморфизм
интегрируемых случаев//Функцион. анализ и его прил.—1986.— Т. 20,
№ 1.—С. 64—65.
29. Богоявленский О. И. Методы качественной теории динамических
систем в астрофизике и газовой динамике.— М.: Наука 1980.
30. Богоявленский О. И. Новые алгебраические конструкции уравнений
Эйлера//ДАН СССР.—1983.—Т. 268, № 2.—С. 277—280.
31. Богоявленский О. И. Интегрируемые уравнения Эйлера, связанные
с фильтрациями алгебр Ли//Мат. сб.—1983.—Т. 121, № 2.—С. 233—242.
32. Богоявленский О. И. Динамика твердого тела с п эллипсоидальными
полостями, заполненными магнитной жидкостью//ДАН СССР.— 1983.—
Т. 272, № 6.—С. 1364—1367.
33. Богоявленский О. И. Интегрируемые уравнения Эйлера на алгебрах
Ли, возникающие в задачах математической физики//Изв. АН СССР. Сер.
мат.—1984.—Т. 48, № 5.—С. 883—938.
34. Богоявленский О. И. Периодические решения в модели вращения
пульсара//ДАН СССР.—1984.—Т. 276, № 2.—С. 343—347.
35. Богоявленский О. И. Интегрируемые случаи динамики твердого тела
и интегрируемые системы на сферах 5"//Изв. АН СССР. Сер. мат.—
1985.—Т. 49, № 5.—С. 899—915.
36. Богоявленский О. И. Некоторые интегрируемые случаи уравнений
Эйлера//ДАН СССР.—1986.—Т. 287, № 5 —С. 1105—1108.
37. Богоявленский О. И., Ивах Г. Ф. Топологический анализ интегриру-
емых случаев В. А. Стеклова//УМН —1985—Т. 40, № 4.—С. 145—146.
38. Болотин С. В. Неинтегрируемость задачи п центров при и>2//Вестн.
МГУ. Сер. 1, Математика, механика.— 1984.—№ 3.— С. 65—68.
39. Б о леи нов А. В. Вполне интегрируемые системы на сжатиях алгебр
Ли//Тр. семинара по векторному и тензорному анализу.—М.: Изд-во МГУ,
1985.—Вып. 22 —С. 8—16.
40. Болсинов А. В. Новые примеры вполне интегрируемых систем на
алгебрах Ли//Геометрия, дифференциальные уравнения и механика.—М.:
Изд-во МГУ, 1986.—С. 54—58.

418 СПИСОК ЛИТЕРАТУРЫ
41. Болсинов А. В., Матвеев С. В., Фоменко А. Т. Топологическая
классификация интегрируемых гамильтоновых систем с двумя степенями
свободы. Список систем малой сложности//УМН.— 1990.— Т. 45, № 2.—
С. 49—77.
42. Болсинов А. В. Инволютивные семейства функций на некоторых
алгебрах Ли//Современные вопросы механики и технологии машиност-
роения—М.: ВИНИТИ, 1986 —С. 57.
43. Болсинов А. ВО полноте инволютивного семейства функций, построен-
ного методом сдвига аргумента//Бакинская Международная топологичес-
кая конференция.— Баку: Изд-во Коммунист.— 1987.— С. 49.
44. Болсинов А. В. Некоторые свойства интегрируемых систем, связанных
с компактными группами Ли//Всесоюз. конф. по геометрии «в целом».—
Новосибирск: Изд-во НГУ, 1987,—С. 15.
45. Болсинов А. В. Инволютивные семейства функций на двойственных
пространствах к алгебрам Ли тпа С+К//УМН.—1987.—Т. 42, № 6.—
С. 183—184.
46. Болсииов А. В. О полноте семейств функций в инволюции, связанных
с согласованными скобками Пуассона//Тр. семинара по векторному
и тензорному анализу.—М.: Изд-во МГУ, 1988. Вып. 23.— С. 18—
38.
47. Браилов А. В. Инволютивные наборы на алгебрах Ли и расширения
кольца скаляров//Вестн. МГУ. Сер. 1, Математика, механика.—1983.—
№ 1.—С. 47—51.
48. Браилов А. В. Некоторые случаи полной интегрируемости уравне-
ний Эйлера и приложения//ДАН СССР —1983—Т. 268, № 5—С. 1043—
1046.
49. Браилов А. В. Полная интегрируемость некоторых геодезических
потоков и интегрируемые системы с некомму тирующими интегралами//
ДАН СССР.—1983.—Т. 271, № 2.—С. 273—276.
50. Браилов А. В. Серия вполне интегрируемых гамильтоновых систем на
полупрямом произведении soMx R"//Геометрия и топология в гло-
бальных нелинейных задачах.— Воронеж: Изд-во ВГУ, 1984.— С. 145—
148.
51. Браилов А. В. Полная интегрируемость с иекоммутирующими интег-
ралами некоторых уравнений Эйлера//Применение топологии в современ-
ном анализе.— Воронеж: Изд-во ВГУ, 1985.— С. 22—41.
52. Браилов А. В. Некоторые конструкции полных семейств функций,
находящихся в инволюции//Тр. семинара по векторному и тензорному
анализу—М.: Изд-во МГУ, 1985.—Вып. 22.—С. 17—24.
53. Браилов А. В. Построение вполне интегрируемых геодезических потоков
на компактных симметрических пространствах//Изв. АН СССР. Сер.
мат.—1986.—Т. 50, № 4.—С. 661—674.
54. Браилов А. В., Фоменко А. Т. Топология интегральных многообразий
вполне интегрируемых гамильтоновых систем//Мат. сб.— 1987.—Т. 133,
№ 3.—С. 375—385.
55. Бур баки Н. Группы и алгебры Ли. Группы Кокстера и системы
Титса, группы, порожденные отражениями, системы корней.—М.:
Мир, 1972.
56. Буслаев В. С, Налимова Е. А. Формула следа в лагранжевой
механике//Теорет. и мат. физика.— 1984.— Т. 61, № 1.— С. 52—63.
57. Веселое А. П. О гамильтоновом формализме для уравнения Новикова —
Кричевера коммутации двух операторов//функцион. анализ и его прил.—
1979.—Т. 13, № 1.—С. 1—7.
58. Веселое А. П. Конечнозонные потенциалы и интегрируемые системы на
сфере с квадратичным потенциалом //Функцией, анализ и его прил.—
1980.—Т. 14, № 1—С. 48—50.

СПИСОК ЛИТЕРАТУРЫ 419
59. Веселое А. П. Уравнение Ландау — Лифщица и интегрируемые системы
классической механики//ДАН СССР.—Т. 270, № 5.—С. 1094—1097.
60. Веселое А. П. Об условиях интегрируемости уравнений Эйлера на
воD)//ДАН СССР.—1983.—Т. 270, № 6—С. 1298—1300.
61. Веселое А. П., Новиков С. П. Конечнозонные двумерные периодичес-
кие операторы Шрёдингера: явные формулы и эволюционные уравнения//
ДАН СССР.—1984.—Т. 279, № 1.—С. 20—24.
62. Веселое А. П., Новиков С. П. Скобки Пуассона и компактные
торы//Тр. МИАН СССР им. В. А. Стеклова —1984—Т. 165.—С. 49—
61.
63. Веселова Л. Е. О динамике тела с эллипсоидальной полостью,
наполненной жидкостью//Вестн. МГУ. Сер. 1 Математика, механика.—
1985.—№ 3.—С. 64—67.
64. Винберг Э. Б. О некоторых коммутативных подалгебрах универсальной
обертывающей алгебры//Изв. АН СССР. Сер. мат.—1990.—Т. 56, № 1 —
С. 891 — 1021.
65. Винберг Э. Б., Онищик А. Л. Семинар по группам Ли и алгебраиче-
ским группам.— М.: Наука 1988.
66. Виноградов А. М., Купершмидт Б. А. Структура гамильтоновой
механики//УМН.—1987— Т. 42, № 4.—С. 175—236.
67. Вишик С. В., Должанский Ф. В. Аналоги уравнений Эйлера —
Пуассона и магнитной гидродинамики, связанные с группами Ли//ДАН
СССР.—Т. 238, № 5.—С. 1032—1035.
68. Владимиров В. С, Волович И. В. Локальные и нелокальные токи для*
нелинейных уравнений//Теорет. и мат. физика.—1985.— Т. 62, № 1.—
С. 3—29.
69. Гайдуков Е. В. Асимптотические геодезические на римановом многооб-
разии, не гомеоморфном сфере //ДАН СССР.—1986.—Т. 169, № 5 —
С. 999—1001.
70. Гельфанд И. М., Дикий Л. А. Дробные степени операторов и гамиль-
тоновы системы//функцион. анализ и его прил.—1976.—Т. 10, № 4.—
С. 13—29.
71. Гельфанд И. М., Дикий Л. А. Интегрируемые нелинейные уравнения
и теорема Лиувилля//Функцион. анализ и его прил.—1979.— Т. 13,
№ 1.—С. 8—20.
72. Гельфанд И. М., Дорфман И. Я. Гамильтоновы операторы и связан-
ные с ними алгебраические структуры//Функцион. анализ и его прил.—
1979.—Т. 13, № 4.—С. 13—30.
73. Гивенталь А. Б. Глобальные свойства индекса Маслова и теория
Морса//Функцион. анализ и его прил.—1988.— Т. 22, № 2.—
С. 69—70.
74. Гийемин В., Стернберг С. Геометрические асимптотики.—М.:
Мир, 1981.
75. Гледзер Е. Б., Должанский Ф. С, Обухов А. М. Системы
гидродинамического типа и их приложения.— М.: Наука 1981.
76. Годбийон К. Дифференциальная геометрия и аналитическая механика.—
М.: Мир, 1973.
77. Голо В. Л. Геометрические идеи в теории сверхтекучего гелия-
3//Топологические и геометрические методы в математической физике.—
Воронеж: Изд-во ВГУ, 1983—С. 26—41.
78. Голод П. И. Гамильтоновы системы, связанные с анизотропными
алгебрами Ли и высшие уравнения Ландау—Лифшица//ДАН УССР.—
1980—Сер. А, ]* 5—С. 5—8.
79. Голубев В. В. Лекции по интегрированию уравнений движения тяжелого
твердого тела около неподвижной точки.—М.: Гостехиздат, 1953.
80. Горр Г. В., Кудряшова Л. В., Степанова Л. А. Классические задачи
динамики твердого тела.— Киев: Наукова думка, 1978.
81. Гото М., Гроссханс Ф. Полупростые алгебры Ли.—М.: Мир, 1981.

420 СПИСОК ЛИТЕРАТУРЫ
82. Гриффите Ф., Харрис Дж. Принципы алгебраической геометрии.—
Т. 1, 2—М.: Мир, 1982.
83. Гурвиц А., Курант Р. Теория функций.— М.: Наука, 1968.
84. Гуревич Г. Б. Основы алгебраической теории инвариантов.—М.: Гос-
техиздат, 1948.
85. Дао Чонг Тхи. Интегрируемость уравнений Эйлера на однородных
симплектических многообразиях//Мат. сб.— 1978.— Т. 106, № 2.— С. 154—
161.
86. Дао Чоиг Тхи, Фоменко А. Т. Минимальные поверхности и проблема
Плато.—М.: Наука 1987.
87. Дикий Л. А. Замечание о гамильтоновых системах, связанных с группой
вращений/,'Функцион. анализ и его прил.— 1972.— Т. 6. № 4.— С. 83 —
84.
88. Диксмье Ж. Универсальные обертывающие алгебры.—М.: Мир, 1978.
89. Дирак Л. М. Обобщенная гамильтонова динамика/'Вариационные прин-
ципы механики.—М.: Физматгиз, 1959.
90. Дирак П. Лекции по квантовой механике.—М.: Мир, 1968.
91. Дирак П. Принципы квантовой механики.— М.; Наука, 1979.
92. Дринфельд В. Г. О постоянных квазиклассических решениях уравнения
Яига —Бакстера/,'ДАН СССР.—1983.—Т. 273, № 3.—С. 667—671.
93. Дринфельд В. Г. Гамильтоновы структуры на группах Ли, биалгебры
Ли и геометрический смысл классических уравнений Янга — Бакстера/,
ДАН СССР — 1983— Т. 268, № 2.—С. 285—287.
94. Дринфельд В. Г. Квантовые группы'/Дифференциальная геометрия,
группы Ли и механика VIII. Зап. научн. сем. ЛОМИ АН СССР.—
1986.—Т. 155,—С. 18 — 49.
95. Дринфельд В. Г., Соколов В. В. Уравнения типа Кортевега — де
Фриза и простые алгебры Ли//ДАН СССР.—1981—Т. 259, № 1.—
С. 11 — 16.
96. Дрюма В. С. Об аналитическом решении двумерного уравнения
Кортевега —де Фриза/'Письма в ЖЭТФ — 1974— Т. 19 № 12.—С. 219—
225.
97. Дубровин Б. А. Вполне интегрируемые гамильтоновы системы, связан-
ные с матричными операторами, и абелевы многообразия //Функцион.
анализ и его прил.—1977.—Т. 11, № 4.—С. 28—41.
98. Дубровин Б. А. Тэта-функции и нелинейные уравнения/,'УМН.—
1981.—Т. 36, № 2.—С. 11—80.
99. Дубровин Б. А. Матричные конечнозонные операторы/'Итоги науки
и техники. Современные проблемы математики.—М.: ВИНИТИ, 1983.—
Т. 23.—С. 33—78.
100. Дубровин Б. А., Матвеев В. Б., Новиков С. П. Нелинейные
уравнения типа Кортевега — де Фриза, конечнозонные линейные операторы
и абелевы многообразия'/УМН —1976.—Т. 31, № 1.—С. 55—136.
101. Дубровин Б. А.. Новиков С. П. О скобках Пуассона гидродинамиче-
ского типа//ДАН СССР.—1984.—Т. 279, № 2.—С. 294—297.
102. Дубровин Б. А., Новиков С. П., Фоменко А. Т. Современная
геометрия.— 2-е изд.— М.: Наука 1986.
103. Дубровин Б. А., Новиков С. П., Фоменко А. Т. Современная
геометрия. Методы теории гомологии.— М.: Наука 1984.
104. Захаров В. Е., Манаков С. В., Новиков С. П., Питаевский Л. П.
Теория солитонов. Метод обратной задачи / Под общей ред.
С. П. Новикова.—М.: Наука 1980.
105. Захаров В. Е., Фаддеев Л. Д. Уравнение Кортевега—де Фриза —
вполне интегрируемая гамильтонова система//Функцион. анализ и его
прил.—1971.—Т. 5, № 4—С. 18—27.
106. Захаров В. Е., Шабат А. Б. Точная теория двумерной самофокусировки
и одномерной автомодуляции волн в нелинейных средах//ЖЭТФ.—
1971.—Т. 61, № 1.—С. 118—134.

СПИСОК ЛИТЕРАТУРЫ 421
107. Зельманов Е. И. Об одном классе локальных трансляционно инвариант-
ных алгебр Ли//ДАН СССР.—1987.—Т. 292, № 6 —С. 1294—1297.
108. Зенков Д. В., Козлов В. В. Геометрическое представление Пуансо
в динамике многомерного твердого тела//Тр. семинара по векторно-
му и тензорному анализу.—М.: Иэд-во МГУ, 1988.— Вып. 23.—
С. 202—204.
109. Зиглии С. Л. Расщепление сепаратрис, ветвление решений и несущест-
вование интеграла в динамике твердого тела//Тр. Московск. мат. о-ва.—
1980.—Т. 41.—С. 287—303.
110. Зиглин С. Л. Ветвление решений и несуществование первых интегралов
в гамильтоновой механике 1//Функцион. анализ и его прил.— 1982.— Т. 16,
№ 3.—С. 30—41.
111. Зиглин С. Л. Ветвление решений и несуществование первых интегралов
в гамильтоновой механике П//Функцион. анализ и его прил.—1983.—
Т. 17, № 1.—С. 8—23.
112. Ибрагимов Н. X. Группы преобразований в математической физике.—
М.: Наука 1983.
ИЗ. Иванова Т. А. Об уравнениях Эйлера в моделях теоретической
физики//Мат. заметки.—1992.—Т. 52, в. 2.—С. 43—51.
114. И тс А. Р. «Изомонодромные» решения уравнений нулевой кривизны//Изв.
АН СССР. Сер. мат.—1985.—Т. 49, № 3.—С. 530—565.
115. И тс А. Р.. Энольский В. 3. О динамике системы Калоджеро — Мозера
и редукции гиперэллиптических интегралов к эллиптическим интегралам//
Функцион. анализ и его прил.— 1986.— Т. 20, № 1.— С. 75—76.
116. Калоджеро Ф., Дегасперис А. Спектральные преобразования и соли-
тоны.—М.: Мир, 1985.
117. Кантор И. Л., Персиц Д. Б. О замкнутых пучках линейных скобок
Пуассона//1Х Всесоюзная геометрическая конференция.— Кишинев: Шти-
инца, 1988.—С. 141.
118. Карасев М. В. Условия квантования Маслова в высших когомологиях
и аналогов объектов теории Ли для канонических расслоений симплек-
тических многообразий/МИЭМ.—М.: 1981—Деп. в ВИНИТИ, № 1092—
82, 1093—82.
119. Карасев М. В. Аналоги объектов теории групп Ли для нелинейных скобок
Пуассона//Изв. АН СССР. Сер. мат.—1986 —Т. 50, № 3—С. 508—
538.
120. Карасев М. В., Маслов В. П. Нелинейные скобки Пуассона. Геометрия
и квантование.— М.: Наука, 1991.
121. Карасев М. В., Маслов 3- П. Асимптотическое и геометрическое
кваитование//УМН.—1984.—Т. 39, № 6.—С. 115—173.
122. Картан Э. Интегральные инварианты.— М.; Л.: Гостехиздат, 1940.
123. Кириллов А. А. Локальные алгебры Ли//УМН.—1976.—Т. 31, № 4.—
С. 57—76.
124. Кириллов А. А. Элементы теории представлений.— М.: Наука, 1978.
125. Клингенберг В. Лекции о замкнутых геодезических.— М.: Мир, 1982.
126. Кобаяси Ш., Номидзу К. Основы дифференциальной геометрии. Т. 1,
2.—М.: Наука, 1981.
127. Козлов В. В. Несуществование дополнительного аналитического интег-
рала в задаче о движении несимметричного тяжелого твердого тела вокруг
неподвижной точки//Вестн. МГУ. Сер. 1, Математика, механика.—
1975.—№ 1.—С. 105—110.
128. Козлов В. В. Расщепление сепаратрис возмущенной задачи Эйлера —
Пуансо//Вестн. МГУ. Сер. 1, Математика, механика.— 1976.— № 6.— С.
99—104.
129. К о з л о в ВВ. Методы качественного анализа в динамике твердого
тела.—М.: Изд-во МГУ, 1980.
130. Козлов В. В. Две интегрируемые задачи классической динамики//Вестн.
МГУ. Сер. 1, Математика, механика.—1981.—№ 4.—С. 80—84.

422 СПИСОК ЛИТЕРАТУРЫ
131. Козлов В. В. Интегрируемость и неинтегрируемость в гамильтоновой
механике//УМН —1983.—Т. 38, № 1.—С. 3—67.
132. Козлов В. В. Интегрируемые случаи задачи о движении точки по
трехмерной сфере в силовом поле с потенциалом четвертой степени//Вестн.
МГУ. Сер. 1, Математика, механика —1985—№ 3.—С. 93—95.
133. Козлов В. В., Колесников Н. Н. Об интегрируемости гамильтоновых
систем//Вестн. МГУ. Сер. 1, Математика, механика.— 1979.—№ 6.— С.
88—91.
134. Козлов В. В., Онищеико Д. А. Неинтегрируемость уравнений Кир-
хгофа//ДАН СССР — 1982— Т. 266, № 6.—С. 1298—1300.
135. Колесников Н. Н. Натуральные системы с разрешимой группой
симметрии//Вестн. МГУ. Сер. 1, Математика, механика.— 1978.—№ 5.—
С. 99—103.
136. Колокольцев В. Н. Геодезические потоки на двумерных многообразиях
с дополнительным полиномиальным по скоростям первым интегралом//
Изв. АН СССР. Сер. мат.—1982.—№ 5.—С. 994—1010.
137. Колокольцев В. Н. Новые примеры многообразий с замкнутыми
геодезическими//Вестн. МГУ. Сер. 1, Математика, механика.—1984.—
№ 4.—С. 80—82.
138. Кричевер И. М. Методы алгебраической геометрии в теории нелинейных
уравнений//УМН.—1977.—Т. 32, № 6.—С. 183—208.
139. Кричевер И. М. Алгебраические кривые и нелинейные разностные
уравнения//УМН.—1978.—Т. 33, № 4.—С. 215—216.
140. Кричевер И. М. Нелинейные уравнения и эллиптические кривые//Итоги
науки и техники. Современные проблемы математики.— М.: ВИНИТИ,
1983.—Т. 23.—С. 79—136.
141. Кричевер И. М., Новиков СП. Голоморфные расслоения над
римановыми поверхностями и уравнение Кадомцева — Петвиашвили (КП)
1//Функцион. анализ и его прил.— 1978.— Т. 12, № 4.— С. 41—52.
142. Кронрод А. С. О функциях двух переменных//УМН.—1950.— Т. 5,
№ 1.—С. 24—134.
143. Кулиш П. П., Склянин Е. К. О решениях уравнения Янга — Бакстера//
Зап. науч. семинаров ЛОМИ АН СССР —1980—Т. 95.—С. 129—160.
144. Лаке П. Д. Интегралы нелинейных уравнений эволюции и уединенные
волны//Математика.— 1969.— Т. 13, № 5.—С. 128—150.
145. Ландау Л. Д., Лифшиц Е. М. Механика.— М.: Наука, 1968.
146. Лебедев Д. Р., Маиин Ю. И. Гамильтонов оператор Гельфанда —
Дикого и коприсоедииенное представление группы Вольтерра//Функцион.
анализ и его прил.—1979.—Т. 13, № 4.—С. 40—46.
147. Левин Ю. И. Об аффинных связностях, присоединенных к кососиммет-
рическому тензору//ДАН СССР.—1959.—Т. 128, № 4 —С. 668—671.
148. Лемлейн В. Г. О пространствах симметричной почти симплектической
связности//ДАН СССР.—1957.—Т. 115, № 4.—С. 655—658.
149. Лемлейн В. Г. Тензор кривизны и некоторые типы пространств
симметричной почти симплектической связности//ДАН СССР.— 1957.— Т.
117, № 5.—С. 755—758.
150. Ле Нгок Тьеуен. Коммутативные наборы функций на орбитах общего
положения конечномерных алгебр Ли//УМН — 1983—Т. 38, № 1—С.
179—180.
151. Ле Нгок Тьеуен. Полные инволютивные наборы функций на расшире-
ниях алгебр Ли, связанных с алгебрами Фробениуса//Тр. семинара по
векторному и тензорному анализу.— М.: Изд-во МГУ 1985.— Вып. 22.— С.
69—106.
152. Лере Ж. Лаграижев анализ и квантовая механика.— М.: Мир, 1981.
153. Лерман Л. М., Уманский Я. Л. Структура пуассоновского действия
на четырехмерном симплектическом многообразии//Методы качественной
теории дифференциальных уравнений.— Горький: Изд-во ГГУ, 1982.— С.
3—19.

СПИСОК ЛИТЕРАТУРЫ 423
154. Лерман Л. М., Умаиский Я. Л. Необходимые условия существования
гетероклинических траекторий в интегрируемой гамильтоновой системе
с двумя степенями свободы//УМН —1983.— Т. 38, № 5.—С. 195—196.
155. Лерман Л. М., Уманский Я. Л. Интегрируемые гамильтоновы системы
и пуассоновские действия//Методы качественной теории дифференциаль-
ных уравнений.— Горький: Изд-во ГГУ, 1984.— С. 126—139.
156. Лерман Л. М, Уманский Я. Л. О гладких канонических заменах
переменных//Методы качественной теории дифференциальных уравне-
ний—Горький: Изд-во ГГУ, 1984.—С. 140—147.
157. Л е Хонг Ван. Абсолютно минимальные поверхности и калибровки на
орбитах присоединенного представления классических групп Ли//ДАН
СССР—Т. 298, № 6.—С. 1308—1311.
158. Ле Хонг Ван, Фоменко А. Т. Критерий минимальности лагранжевых
подмногообразий в кэлеровых многообразиях//Мат. заметки.— 1987.— Т.
42, № 4.—С. 559—571.
159. Ле Хонг Ван, Фоменко А. Т. Лагранжевы многообразия и индекс
Маслова в теории минимальных поверхностей//ДАН СССР.— 1988.— Т.
299, № 1.—С. 42—45.
160. Л о ос О. Симметрические пространства.— М.: Наука, 1985.
161. Лосик М. В. О характеристических классах структур на многообразиях//
Функцион. анализ и его прил.— 1987.— Т. 21, № 3.— С. 38—52.
162. Лунев В. В. Гидродинамическая аналогия задачи о движении твердого
тела с неподвижной точкой в поле сил Лоренца//ДАН СССР.— 1984.— Т.
276, № 2.—С. 351—355.
163. Лэмб Дж. Элементы теории солитонов.— М.: Мир, 1983.
164. Мамфорд Д. Лекции о тэта-функциях.— М.: Мир, 1988.
165. Мзнаков С. В. Замечание об интегрировании уравнений Эйлера динами-
ки «-мерного твердого тела//Функцион. анализ и его прил.— 1976.— Т. 10
№ 4.—С. 93—94.
166. Манин Ю. И. Матричные солитоиы и расслоения над кривыми с осо-
бенностями//Функцион. анализ и его прил.—1978.— Т. 12, № 4.—
С. 53—63.
167. Манин Ю. И. Алгебраические аспекты нелинейных дифференциальных
уравнений //Современные проблемы математики. Итоги науки и техники.—
М.: ВИНИТИ, 1978.—Т. П.—С. 5—152.
168. Манин Ю. И. Калибровочные поля и комплексная геометрия.— М.:
Наука, 1984.
169. Маслов В. П. Теория возмущений и асимптотические методы.— М.:
Изд-во МГУ, 1965.
170. Маслов В. П. Асимптотические методы решения псевдодифференциаль-
ных уравнений.— М.: Наука, 1987.
171. Матвеев С. В., Фоменко А. Т. Изоэнергетические поверхности гамиль-
тоновых систем, перечисление трехмерных многообразий в порядке
возрастания их сложности и вычисление объемов замкнутых гиперболичес-
ких миогообразий//УМН.—1988.—Т. 43, № 1.—С. 5—22.
172. Матвеев СВ., Фоменко А. Т. Алгоритмические и компьютерные
методы в трехмерной топологии.— М.: Изд-во МГУ, 1991.
173. Матвеев С. В., Фоменко А. Т., Шарко В. В. Круглые функции Морса
и изоэнергетические поверхности интегрируемых гамильтоновых систем//
Мат. заметки.—1988.—Т. 43, № 3.—С. 325—345.
174. Мещеряков М. В. Замечание о динамических системах на полупростых
алгебрах Ли//Вестн. МГУ. Сер. 1, Математика, механика.—1980.—
№ 6.—С. 17—19.
175. Мещеряков М. В. Интегрирование уравнений геодезических левоинвари-
антных метрик на полупростых группах Ли с помощью специальных
функций//Мат. сб.—1982.—Т. 117, № 4.—С. 481—493.
176. Мещеряков М. В. О характеристическом свойстве тензора инерции
многомерного твердого тела//УМН.—1983.—Т. 38, № 5.— С. 201—202.

424 СПИСОК ЛИТЕРАТУРЫ
177. Мещеряков М. В. Решение уравнений Эйлера на особых орбитах
простых групп Ли//Геометрия и топология в глобальных нелинейных
задачах — Воронеж: Изд-во ВГУ, 1984.—С. 158—162.
178. Мещеряков М. В. Несколько замечаний о гамильтоиовых потоках на
однородных пространствах//УМН.— 1985.— Т. 40, № 3.—С. 215—216.
179. Миллер У. Симметрия и разделение переменных.— М.: Мир, 1981.
180. Милнор Дж. Теория Морса.—М.: Мир, 1971.
181. Милнор Дж., Сташеф Дж. Характеристические классы.— М.: Мир, 1979.
182. Митропольский Ю. А., Боголюбов Н. Н., Прикарпатский А. К..
Самойленко В. Г. Интегрируемые динамические системы: спектральные
и дифференциально-геометрические аспекты.— Киев: Наукова думка, 1987.
183. Мищенко А. С. Интегралы геодезических потоков на группах Ли,"
Функцион. анализ и его прил.— 1970.— Т. 4, № 3.— С. 73—78.
184. Мищенко А. С. Интегрирование геодезических потоков на симметричес-
ких пространствах//Мат. заметки.— 1982.— Т. 31, № 2.— С. 257—262.
185. Мищенко А. С. Интегрирование геодезических потоков на симметричес-
ких пространствах//Труды семинара по векторному и тензорному анали-
зу.—1983.—Вып. 21.—С. 13—22.
186. Мищенко А. С, Фоменко А. Т. Об интегрировании уравнений Эйлера
на полупростых алгебрах Ли//ДАН СССР.—1976.—Т. 231, № 3.—С.
536—538.
187. Мищенко А. С, Фоменко А. Т. Обобщенный метод Лиувилля интег-
рирования гамильтоновых систем//Функцион. анализ и его прил.—
1987.—Т. 12, № 2.—С. 46—56.
188. Мищенко А. С, Фоменко А. Т. Уравнения Эйлера на конечномерных
группах Ли//Изв. АН СССР. Сер. мат.—1978.—Т. 42, № 2.—С. 396—415.
189. Мищенко А. С, Фоменко А. Т. Интегрируемость уравнений Эйлера на
полупростых алгебрах Ли//Труды семинара по векторному и тензорному
анализу.—М.: Изд-во МГУ, 1979.—Вып. 19.—С. 3—94.
190. Мищенко А. С, Фоменко А. Т. Курс дифференциальной геометрии
и топологии.— М.: Изд-во МГУ, 1980.
191. Мищенко А. С, Фоменко А. Т. Интегрирование гамильтоновых систем
с некоммутативными симметриями//Труды семинара по векторному
и тензорному анализу.— М.: Изд-во МГУ, 1981.— Вып. 20.— С. 5—54.
192. Мозер М. Некоторые аспекты интегрируемых гамильтоновых систем//
УМН.—1981.—Т. 36, № 6.—С. 109—151.
193. Моисеев Н. Н.. Румянцев В. В. Динамика тела с полостями, содер-
жащими жидкость.— М.: Наука, 1965.
194. Нехорошее Н. Н. О переменных действие — угол и их обобщения/, Тр.
Московск. мат. о-ва.—1972.—Т. 26.—С. 181 — 198.
195. Николенко Н. В. О полной интегрируемости нелинейного уравнения
Шрёдингера//Функцион. анализ и его прил.— 1977.— Т. 10, № 3.—С.
55—69.
196. Новиков С. П. Периодическая задача Кортевега — де Фриза 1//Функци-
он. анализ и его прил.— 1974.—Т. 8, № 3.— С. 54—66.
197. Новиков С. П. Гамильтоиов формализм и многозначный аналог теории
Морса//УМН.—1982.—Т. 37, № 5.—С. 3—49.
198. Новиков С. П. Вариационные методы и периодические решения уравне-
ния типа Кирхгофа П//Фуикцион. анализ и его прил.—1982.— Т. 15,
№ 4.—С. 3—49.
199. Новиков С. П. Двумерные операторы Шрёдингера//Итоги науки и тех-
ники. Современные проблемы математики.—М.: ВИНИТИ, 1983.—
Т. 23.—С. 3—32.
200. Новиков СП., Гриневич П. Г. О спектральной теории коммутиру-
ющих операторов ранга 2 с периодическими коэффициентами//Функцион.
анализ и его прил.— 1982.—Т. 16, № 1.— С. 23—26.
201. Новиков С. П., Фоменко А. Т. Элементы дифференциальной геометрии
и топологии.— М.: Наука, 1987.

СПИСОК ЛИТЕРАТУРЫ 425
202. Новиков С. П., Шмельцер И. Периодические решения уравнения
Кирхгофа свободного движения твердого тела и идеальной жидкости
и расширенная теория Люстерника—Шнирельмаиа — Морса (ЛМШ) 1//
Функцией, анализ и его прил.—1981.—Т. 15, № 3.—С. 54—66.
203. О л вер П. Приложения групп Ли к дифференциальным уравнениям.—
М.: Мир, 1989.
204. Ольшанецгий М. А., Переломов A.M. Явные решения некоторых
вполне интегрируемых гамильтоновых систем//Функцион. анализ и его
прил.—1977.—Т. 11, № 1.—С. 75—76.
205. Ольшанецкий М. А., Переломов А. М. Цепочка Тоды как редуциро-
ванная система//Теорет. и мат. физика.—1980.— Т. 45, № 1.— С. 3—18.
206. Ольшанецкий М. А., Переломов А. М., Рейман А. Г., Семенов-
Тян-Шанский М. А. Интегрируемые системы И//Итоги науки и тех-
ники. Фундаментальные направления.—М.: ВИНИТИ, 1987.— Т. 16.—
С. 86—227.
207. ОшемковА. А. Боттовские интегралы некоторых интегрируемых гамиль-
тоновых систем//Геометрия, дифференциальные уравнения и механика.—
М.: Изд-во МГУ, 1986.—С. 115—117.
208. ОшемковА. А. Топология изоэнергетических поверхностей и бифуркаци-
онная диаграмма интегрируемых случаев динамики твердого тела на so
D)//УМН —1987—Т. 42, № 6—С. 199—200.
209. Ошемков А. А. Описание изоэиергетических поверхностей некоторых
интегрируемых гамильтоновых систем с двумя степенями свободы//Тр.
семинара по векторному и тензорному анализу.— Вып. 23.— М.: Изд-во
МГУ, 1988.—Вып. 23.—С. 122—132.
210. Павленко Ю. Г. Гамильтоновы методы в электродинамике и в кван-
товой механике.— М.: Изд-во МГУ, 1985.
211. Павленко Ю. Г. Задачи по теоретической механике.— М.: Изд-во
МГУ, 1988.
212. Певцова Т. А. Симплектическая структура орбит коприсоединенного
представления алгебр Ли типа ?|x|G//MaT. сб.—1984.—Т. 123, № 2.—
С. 276—286.
213. Переломов A.M. Несколько замечаний об интегрировании уравнений
твердого тела в идеальной жидкости//Функцион. анализ и его прил.—
1981.—Т. 15, № 2.—С. 83—85.
214. Переломов А. М. Решения типа инстантонов в киральных моделях//
УФН.—1981.—Т. 134, ]* 4 —С. 577—609.
215. Переломов А. М. Представление Лакса для систем типа С. Ковалев-
ской//функцион. анализ и его прил.—1982.—Т. 16, № 2.—С. 80—81.
216. Пидкуйко С. И., Степин А. М. О решении одного дифференциально-
функционального уравнения//Функцион. анализ и его прил.— 1976.— Т. 10,
№ 2.—С. 84—85.
217. Пидкуйко СИ., Степин A.M. Полиномиальные интегралы гамиль-
тоновых систем//ДАН СССР.—1978.—Т. 293, № 1.—С. 719—812.
218. Погосян Т. И. Построение бифуркационных множеств в одной задаче
динамики твердого тела//Изв. АН СССР: МТТ —1980— Т. 12.—С. 9—16.
219. Погосян Т. И. Критические интегральные поверхности в задаче Клебша//
Изв. АН СССР: МТТ.—1983— Т. 16 — С. 19—24.
220. Погосян Т. И., Харламов М. П. Бифуркационное множество и интег-
ральные многообразия задачи о движении твердого тела в линейном поле
СИЛ//ПММ — 1979.— Т. 43, № 3.—С. 419—428.
221. Погосян Т. И., Харламов М. П. Области возможности движения
в некоторых механических системах//ПММ.—1981.— Т. 45, № 4.—
С. 605—610.
222. Попов В. Л. Классификация спиноров размерности четырнадцать//Тр.
Московск. мат. о-ва —1978.—Т. 37.—С. 173—217.
223. Потемкин Г. В. О скобках Пуассона дифференциально-геометрического
типа//ДАН СССР.— 1986— Т. 286, ]* 1—С. 39—42.

426 СПИСОК ЛИТЕРАТУРЫ
224. Пуанкаре А. Новые методы небесной механики//Избранные труды.
Т. 1—М.: Наука, 1971.
225. Пуанкаре А. О проблеме трех тел и об уравнениях динамики/,'
Избранные труды. Т. 2.— М.: Наука, 1972.
226. Раджараман Р. Солитоны и инстантоны в квантовой теории поля.— М.:
Мир, 1985.
227. Рашевский П. К. Геометрическая теория уравнений в частных производ-
ных.— М.; Л.; Гостехиздат, 1947.
228. Рейман А. Г. Интегрируемые системы, связанные с градуированными
алгебрами Ли//3ап. науч. семинаров ЛОМИ АН СССР.— 1980.—Т. 95.—
С. 3—54.
229. Рейман А. Г. Орбитная интерпретация гамильтоновых систем типа
ангармонического осциллятора//Зап. науч. семинаров ЛОМИ АН СССР.—
1986.—Т. 155.—С. 187—189.
230. Рейман А. Г., Семенов-Тян-Шанский М. А. Алгебры токов и нели-
нейные уравнения в частных производных//ДАН СССР—1980.— Т. 251,
№ 6— С. 1310—1314.
231. Рейман А. Г., Семенов-Тян-Шанский М. А., Френкель ИИ.
Градуированные алгебры Ли и вполне интегрируемые системы//ДАН
СССР.—1979—Т. 247, № 4 — С. 802—805.
232. Семенов-Тян-Шанский М. А. Что такое классическая /--матрица?//
Функцион. анализ и его прил.— 1983.—Т. 17, № 4.— С. 17—33.
233. Семенов-Тян-Шанский М. А. Пуассоновы группы и одевающие
преобразования//Зап. науч. семинаров ЛОМИ АН СССР.—1986.—
Т. 150.—С. 119—141.
234. Склянин Е. К. О некоторых алгебраических структурах, связанных
с уравнениями Янга — Бакстера//Функцион. анализ и его прил.—1982.—
Т. 16, № 4—С. 27—34.—Т. 17, № 4.—С. 34—48.
235. Смей л С. Топология и механика//УМН.—1972 —Т 27, № 2 —
С. 77—133.
236. Солитоны/Под ред. Р. Буллафа, Ф. Кодри.— М.: Мир, 1983.
237. Стеклов В. А. О движении твердого тела в жидкости.— Харьков, 1983.
238. Степин А. М. Интегрируемые гамильтоновы системы. I: Методы
интегрирования гамильтоновых систем. II: Серии интегрируемых сис-
тем//Качественные методы исследования нелинейных дифференциаль-
ных уравнений и нелинейных колебаний.— Киев: Ин-т математики АН
УССР, 1981.
239. Стернберг С. Лекции по дифференциальной геометрии.— М.: Мир, 1970.
240. Тарасов В. О., Тахтаджян Л. А., Фаддеев Л. Л. Локальные
гамильтонианы для моделей на решетке//ТМФ.— 1983.—Т 57 № 2 — С
163—181.
241. Татаринов Я. В. Портреты классических интегралов задачи о вращении
твердого тела вокруг неподвижной точки//Вестн. МГУ. Сер. 1, Математи-
ка, механика —1974.—№ 6 —С. 99—105.
242. Татаринов Я. В. Геометрический формализм классической динамики;
канонические первообразные//Вестн. МГУ. Сер. 1, Математика меха-
ника.—1983—№ 4 —С. 85—95.
243. Татаринов Я. В. Лекции по классической динамике — М' Изд-во
МГУ, 1984.
244. Татаринов Я. В. Разделяющиеся переменные и новые топологические
явления в голономных и неголономных системах//Труды семинара по
векторному и тензорному анализу.— М.: Изд-во МГУ, 1988.— Вып. 23.—
С. 160—174.
245. Тахтаджян Л. А., Фаддеев Л. Д. Гамильтонов подход в теории
солитонов.— М.: Наука, 1986.
246. Трофимов В. В. Уравнения Эйлера на борелевских подалгебрах полу-
простых алгебр Ли//Изв. АН СССР. Сер. мат.—1979.—Т. 43, № 3.—
С. 160—174.

СПИСОК ЛИТЕРАТУРЫ 427
247. Трофимов В. В. О полной интегрируемости уравнений Эйлера на
борелевских подалгебрах простых алгебр Ли//Тез. докл. 7-й Всесоюз.
геометрической конф. по современным проблемам геометрии.— Минск,
1979.—С. 201.
248. Трофимов В. В. Уравнения Эйлера на конечномерных разрешимых
группах Ли//Изв. АН СССР. Сер. мат.—1980.—Т. 44, № 5.—С 1191 —
1199.
249. Трофимов В. В. Конечномерные представления алгебр Ли и вполне
интегрируемые системы//Мат. сб.— 1980.—Т. 11, № 4.—С. 610—621.
250. Трофимов В. В. Теоретико-групповая интерпретация уравнений магнит-
ной гидродинамики идеально проводящей жидкости//Нелинейные колеба-
ния и теория управления.— Ижевск, 1981.— № 3.— С. 118—124.
251. Трофимов В. В. Вполне интегрируемые геодезические потоки левоин-
вариантных метрик на группах Ли, связанные с коммутативными
градуированными алгебрами с двойственностью Пуанкаре;/ДАН СССР.—
1982.—Т. 263, № 4.—С. 812—816.
252. Трофимов В. В. Первые интегралы приближений Галеркина уравне-
ний магнитной гидродинамики//Некоторые вопросы прикладной матема-
тики и программного обеспечения ЭВМ.— М.: Изд-во МГУ 1982.—
С. 7—8.
253. Трофимов В. В. Расширения алгебр Ли и гамильтоновы системы//Изв.
АН СССР. Сер. мат.—1983.—Т. 47, № 6.—С. 1303—1321.
254. Трофимов В. В. Коммутативные градуированные алгебры с двойствен-
ностью Пуанкаре и гамильтоновы системы//Топологические и геомет-
рические методы в математической физике.— Воронеж: Изд-во ВГУ,
1983.—С. 128—132.
255. Трофимов В. В. О вполне интегрируемых геодезических потоках на
группе движений евклидова пространства//Некоторые вопросы математики
и механики.— М.: Изд-во МГУ, 1983.— С. 8—9.
256. Трофимов В. В. Методика построения 5'-представлений//Вестн. МГУ.
Сер. 1, Математика, механика.— 1984.—№ 1.— С. 3—9.
257. Трофимов В. В. Группа голономии и обобщенные классы Маслова
подмногообразий в пространствах аффинной связности//Мат. заметки.—
1991.—Т. 49, № 2.— С. 113—123.
258. Трофимов В. В. Плоские симметрические пространства с некомпакт-
ными группами движений и гамильтоиовы системы//Тр. семинара по
векторному и тензорному анализу.— Вып. 22.— М.: Изд-во МГУ, 1985.—
Вып. 22.—С. 162—174.
259. Трофимов В. В. Деформации интегрируемых систем//Анализ на много-
образиях и дифференциальные уравнения.— Воронеж: Изд-во ВГУ, 1986.—
С. 156—164.
260. Трофимов В. В. Геометрические инварианты вполне интегрируемых
систем//Тез. докл. Всесоюз. конф. по геометрии «в целом».— Новосибирск,
1987.—С. 121.
261. Трофимов В. В. Индекс Маслова лагранжевых подмногообразий сим-
плектических многообразий//Тр. семинара по векторному и тензорному
анализу.—М.: Изд-во МГУ, 1988.— Вып. 23.—С. 190—194.
262. Трофимов В. В. Симплектические связности, индекс Маслова и гипотеза
Фоменко//ДАН СССР.—1989.—Т. 304, №6.— :. 1302—1305.
263. Трофимов В. В. Введение в геометрию многообразий с симметриями.—
М.: Изд-во МГУ, 1989.
264. Трофимов В. В., Фоменко А. Т. Методика построения гамильтоновых
потоков на симметрических пространствах и интегрируемость некоторых
гидродинамических систем//ДАН СССР.—1980.—Т. 254, № 6.—С. 1349—
1353.
265. Трофимов В. В., Фоменко А. Т. О реализации механических систем на
орбитах разрешимых алгебр Ли//Изв. АН СССР. МТТ—1981.— № 3 —
С. 163.

428 СПИСОК ЛИТЕРАТУРЫ
266. Трофимов В. В., Фоменко А. Т. Групповые неинвариаитные симплек-
тические структуры и гамильтоновы потоки на симметрических простран-
ствах//Труды семинара по векторному и тензорному анализу.— М.: Изд-во
МГУ, 1983.—Вып. 21— С. 23—83.
267. Трофимов В. В., Фоменко А. Т. Динамические системы на орбитах
линейных представлений групп Ли и полная интегрируемость некоторых
гидродинамических систем//Функцион. анализ и его прил.—1983.—Т. 17,
№ 1—С. 31—39.
268. Трофимов В. В., Фоменко А. Т. Интегрируемость по Лиувиллю
гамильтоновых систем на алгебрах Ли//УМН.—1984.—Т. 39, № 2.—
С. 3—56.
269. Трофимов В. В., Фоменко А. Т. Геометрия скобок Пуассона и методы
интегрирования по Лиувиллю систем на симметрических пространствах//
Итоги науки и техники. Новейшие достижения.— М.: ВИНИТИ, 1986.—
Т. 29—С. 3—108.
270. Трофимов В. В., Фоменко А. Т. Геометрические и алгебраические
механизмы интегрируемости гамильтоновых систем на однородных про-
странствах и алгебрах Ли//Итоги науки и техники. Фундаментальные
направления.—М.: ВИНИТИ, 1987.—Т. 16.—С. 227—299.
271. Тюрина Ю. А. О функциональной независимости двух семейств гамиль-
тонианов на С2//Труды семинара по векторному и тензорному анализу.—
М.: Изд-во МГУ, 1988.—Вып. 23.—С. 195—198.
272. Фоменко А. Т. Групповые симплектические структуры на однородных
пространствах//ДАН СССР.—1980.—Т. 253, № 5.—С. 1062—1067.
273. Фоменко А. Т. Алгебраическая структура некоторых классов вполне
интегрируемых гамильтоновых систем на алгебрах Ли //Геометрическая
теория функций и топология.— Киев: Ии-т математики АН УССР,
1981.—С. 85—126.
274. Фоменко А. Т. О симплектических структурах и интегрируемых системах
на симметрических пространствах//Мат. сб.—1981.— Т. 115, № 2.—
С. 263—280.
275. Фоменко А. Т. Вариационные методы в топологии.— М.: Наука, 1982.
276. Фоменко А. Т. Алгебраические свойства некоторых интегрируемых
гамильтоновых систем//Тез. докл. Ленинградской междунар. топологиче-
ской конф.—Ленинград, 1982.— С. 46.
277. Фоменко А. Т. Полная интегрируемость некоторых классических гамиль-
тоновых систем//Моногенные функции и отображения.— Киев: Ин-т
математики АН УССР, 1982.—С. 3—19.
278. Фоменко А. Т. Алгебраическая структура некоторых интегрируемых
гамильтоновых систем//Топологические и геометрические методы в мате-
матической физике.— Воронеж: ВГУ, 1983.— С. 84—110.
279. Фоменко А. Т. Дифференциальная геометрия и топология.— М.: Изд-во
МГУ, 1983.
280. Фоменко А. Т. Симметрические пространства и интегрирование некото-
рых гамильтоновых систем // Приложение к книге: Лоос О. Симметричес-
кие пространства.—М.: Наука, 1985.—С. 183—201.
281. Фоменко А. Т. Топология трехмерных многообразий и интегрируемые
механические гамильтоновы системы // V Тираспольский симпоз. по общей
топологии и ее приложениям.— Кишинев, 1985.— С. 235—237.
282. Фоменко А. Т. Теория Морса интегрируемых гамильтоновых систем//
ДАН СССР.—1986.—Т. 287, № 5—С. 1071 — 1075.
283. Фоменко А. Т. Топология поверхностей постоянной энергии интегриру-
емых гамильтоновых систем и препятствия к интегрируемости//Изв. АН
СССР. Сер. мат.—1986.—Т. 50, № 6.—С. 1276—1307.
284. Фоменко А. Т. Качественная теория интегрируемых систем, клас-
сификация изоэнергетических поверхностей и бифуркаций торов Лиувилля
при критических значениях энергии//Геометрия и теория особенностей
в нелинейных уравнениях.— Воронеж: Изд-во ВГУ, 1987.— С. 118—139.

СПИСОК ЛИТЕРАТУРЫ
429
285. Фоменко А. Т. Топологические инварианты гамильтоновых систем,
интегрируемых по Лиувиллю//Функцион. анализ и его прил.—1988.—
Т. 22, № 4.—С. 38—51.
286. Фоменко А. Т. Симплектическая геометрия.— М.: Изд-во МГУ, 1988.
287. Фоменко А. Т., Цишанг X. О топологии трехмерных многообразий,
возникающих в гамильтоновой механике//ДАН СССР.—1987.— Т. 294,
№ 2.—С. 283—287.
288. Фоменко А. Т., Цишанг X. О типичных топологических свойствах
интегрируемых гамильтоновых систем//Изв. АН СССР. Сер. мат.—
1988.—Т. 52, № 2.—С. 378—407.
289. Фоменко А. Т., Шарко В. В. Точные круглые функции Морса,
неравенства типа Морса и интегралы гамильтоновых систем // Глобальный
анализ и нелинейные уравнения.— Воронеж: Изд-во ВГУ, 1988.— С. 92—
107.
290. Фукс Д. Б. О характеристических классах Маслова—Арнольда//ДАН
СССР.—1968.—Т. 178, № 2.—С. 303—306.
291. Фукс Д. Б. Когомологии бесконечномерных алгебр Ли.— М.: Наука, 1984.
292. Харламов М. П. Топологический анализ классических интегрируемых
систем в динамике твердого тела//ДАН СССР.— 1983.— Т. 273.— № 6.—
С. 1322—1325.
293. Хелгасон С. Дифференциальная геометрия и симметрические простран-
ства.—М.: Мир, 1964.
294. Цишанг X., Фогт Э., Колдевай Д. Поверхности и разрывные
группы.— М.: Наука, 1988.
295. Чередник И. В. Об условиях вещественности в «конечнозонном интег-
рировании»//ДАН СССР.—1980.—Т. 252, № 5—С. 1104—1108.
296. Швая К. Геометрия орбит коприсоединенного представления некоторых
групп Ли//Тр. семинара по векторному и тензорному анализу.— М.:
Изд-во МГУ, 1988.—Вып. 23.—С. 199—201.
297. Элашвили А. Г. Канонический вид и стационарные подалгебры точек
общего положения для простых линейных групп Ли//Функцион. анализ
и его прил.—1972 —Т. 6, № 1.—С. 51—62.
298. Элашвили А. Г. Фробениусовы алгебры Ли//Функцион. анализ и его
прил —1982.—Т. 16, № 4.—С. 94—95.
299. Якоби К. Лекции по динамике.—М.; Л.: ГТТИ, 1933.
300. Ablowitz M. A., Chakravarty S., Clarkson P. A. Reduction of self-dual
Gang — Mills fields and classical systems//Pys. Rev. Lett.—1990.— V. 65,
№ 9.—P. 1085—1087.
301. Abraham R., Marsden J. Foundation of mechanics.— Reading (Mass.):
Addison-Wesley, 1978.
302. Adler M. Some finite-dimensional systems and their scattering behavoir//
Comm. Math. Physics —1977 —V. 55.—P. 112—162.
303. Adler M. On a trace functional for formal pseudodifferential operators and the
symplectic structure for Korteweg—de Vries type equation//Invent. Math.—
1979—V. 50.—P. 219—248.
304. Adler M. On a trace functional for pseudodifferentia! operators and the
Hamiltonian structure of Korteweg — de Vries type equation//Lecture Notes in
Math.—1979.—V. 755.—P. 1 — 16.
305. Adler M., van Moerbeke P. Completely integrable systems, Euclidean Lie
algebras and curves//Adv. Math.—1980.—V. 3, № 3.—P. 267—317.
306. Adler M., van Moerbeke P. Linearization of Hamiltonian systems. Jakoby
varieties and representation theory//Adv. Math.—1980.—V. 38, № 3.—
P. 318—379.
307. Adler M., van Moerbeke P. The algebraic integrability of geodesic flow on
SOD)//Invent. Math.—1982.—V. 67.—P. 297—331.
308. Adler M., van Moerbeke P. Kowalewski's asymptotic method, Kac —
Moody Lie algebras and regularization//Comm. Math. Phys.—1982.—
V. 83.—P. 83—106.

430 СПИСОК ЛИТЕРАТУРЫ
309. Adler M., van Moerbeke P. Geodesic flow on SOD) and the integra-
tion of quadrics//Proc. Nat. Acad. Sci. USA —1984 —V. 81—P. 4613—
4616.
310. Adler M., Moser J. On a class of polinomials connected with
the Korteweg— de Vries equation//Comm. Math. Phys.— 1978.— V. 61.—
P. 1—30.
311. Airault H., McKean HP., Moser J. Rational and elliptic solution of the
Korteweg—de Vries equation and related many body problem//Comm. Pure
Appl. Math.—1977.—V. 30, № 1.—P. 95—148.
312. Arnold V. Sur la geometrie differentielle des groupes de Lie de dimension
infinite et ses applications a l'hydrodynamiques des fluides pur faits//Ann. Inst.
Fourier.—1966.—V. 16, № 1—P. 319—361.
313. Atiyah M. F. Convexity and commuting Hamiltonians//Bull. London Math.
Soc—1982.—V. 14.—P. 1 — 15.
314. Atiyah M. F. Angular momentum, convex polyhedra and algebraic geometry//
Proc. Edinburgh Math. Soc. Ser. 2.—1983.—V. 26.—P. 121 —133.
315. Atiyah M. F., Bott R. The moment map and equivariant cohomology//
Topology.—1984.—V. 23, № 1.—P. 1—28.
316. At kin С J. A note on the algebra of Poisson brackets//Math. Proc.
Cambridge Phil. Soc—1984.—V. 96, № 1.—P. 45—60.
317. Avez A., Lichnerowicz A., Diaz-Miranda A. Sur l'algebre des
automorphismes infinitesimaux d'une variete symplectique//J. Diff. Ge-
ometry.—1974.—V. 9, № 1.—P. 1—40.
318. BayenF., FlatoM., FronsdalC, Lichnerowicz A., SternheimerD.
Deformation theory and quantization//Ann. Phys.— 1978.— V. Ill, № 1.—
P. 61 — 151.
319. Berezin F. A., Perelomov A. M. Group-theoretical interpretation of the
Korteweg—de Vries type equations//Comm. Math. Phys.—1986.— V. 74,
№ 2.—P. 129—140.
320. Berger M. Sur les groupes d'holonomie homogene des varietes a connexion
affine et des varietes riemanniens//Bull. Soc. Math. France.—1955.—
V. 83.—P. 279—330.
321. Bogoyavlensky O. J. On perturbation of periodic Toda lattice//Comm.
Math. Phys.—1976—V. 51.—P. 201—209.
322. Bogoyavlensky O. J. A completely integrable problem of classical
mechanics//Comm. Math. Phys —1984.—V. 1.—P. 265—269.
323. Bogoyavlensky O. J. Integrable Euler equations of SOD) and their physical
applications//Comm. Math. Phys.—1984,—V. 93.—P. 417—436.
324. Borho W., Gabriel P., Rentschler R. Primideal in Einhullenden
auflosbaren Lie-Algebren//Lecture Notes in Math.— 1973.— V. 357.— P. 117—
136.
325. Bott R. Non-degenerate critical manifolds//Ann. Math. Ser. 2.—1954.—V. 60,
№ 2.—P. 248—261.
326. Biichner K. Affinzusammenhange in symplektischen Raume//Sitzungsber.
Bayer. Akad. Wiss. Math.-naturwiss. Kl,—1977.—S. 13—52.
327. Burchnall J. L., Chaundy T. W. Commutative ordinary differential
operators//Proc. London Math. Soc. Ser. 2.—1923.—V. 21, № 6 —P. 420—
440,—Proc. Roy. Soc. London (A).—1928.—V. 118.—P. 557—593,—Proc.
Roy. Soc. London (A).—1931.—V. 134.—P. 471—485.
328. Calogero F. Solution of the one-dimensional л-body problems with guadratic
and/or inversely guadratic pair potentials//J. Math. Phys.— 1971.— V. 12.—
P. 419—436.
329. Channell P. J., Scovel С Symplectic integration of Hamiltonian systems//
Los Alamos (USA): Los Alamos National Laboratory, 1988.— Preprint
LA-UR-88-1828.
330. Chuschill R. C, KumesM., RodD. L. On averaging reduction, and
symmetry in Hamiltonian systems//J. Diff. Equations.— 1983.—V. 49, № 3.—
P. 359—414.

СПИСОК ЛИТЕРАТУРЫ 431
331. ConleyC, ZehnderE. Morse-type index theory for flows and periodic
solutions for Hamiltonian equations/'/Comm. Pure. Appl. Math.—1984.—V. 37,
№ 2.—P. 207—255.
332. Date E., Jimba M., Kashiwara M., Miwa T. Operator approach lo the
Kadomtsev— Petviashvili equation. Transformation groups for solution equa-
tions III//J. Phys. Soc. Japan.— 1981.— V. 50.— P. 3806—3812.
333. DateE., JimboM., К a shiwara M., MiwaT. A new hierarchy of
solution of KP-type. Transformation groups for solution equations IV//
Physics.—1982.—V. 4D.—P. 343—365.
334. DateE, JimboM., KashiwaraM., MiwaT. Transformation groups for
solution equations. Euclidean Lie algebras and reduction of the KP
hierarchy//Publ. RIMS, Kyoto University.— 1982.— V. 18.—'P. 1077—1110.
335. DateE., Jimbo M., Kashiwara M., MiwaT. Transformation groups for
solution equations//Proc. RIMS symposium.— 1983.— P. 39—120.
336. DateE., JimboM., KashiwaraM., MiwaT. Landau — Lifschitz equa-
tion solutions, quasi-periodic solutions and infinite-dimensional Lie algebras//
J. Phys. A —1983.—V. 16 —P. 221—236.
337. Deift P., Lund F., Trubowitz E. Non-linear wave equations and constrained
harmonic motion//Comm. Math. Phys.—1980.—V. 74, № 2.—P. 141 —188.
338. DicksonL. E. Differential equations from the group standpoint//Ann.
Math.—1924.—V. 25, № 4.—P. 287—378.
339. Dixmier J,, Duflo M., Vergne M. Sur la representation coadjointe d'une
algebre de Lie//Compositio Math.—1974.—V. 29, № 3.—P. 309—323.
340. Duflo M., Vergne M. Une propriete de la representation coadjointe d'une
algebre de Lie//C.r. Acad. Sci. Paris —1969—V. 268—P. 583—585.
341. Duistermaat J. J. On global action — angle coordination//Comm. Pure
Appl. Math.—1980.—V. 33, № 6.—P. 687—706.
342. Duistermaat J. J., HeckmanG. On the variation in the cohomology of
the symplectic form of the reduced phase space//Invent. Math.—1982.—V. 69,
№ 2.—P. 259—268.
343. EbinD. Integrability of perfect fluid motion//Comm. Pure Appl. Math.—
1983.—V. 36, № 1.—P. 37—54.
344. EbinD., MarsdenJ. Groups of diffeomorphisms and the motion of an
incompressible fluid//Ann. Math,—1970—V. 92.—P. 102—163.
345. Ekelendl. A perturbation theory near convex Hamiltonian systems//J. Diff.
Equations.—1983—V. 50, № 3.—P. 407—440.
346. FlaschkaH. Toda lattice I, II//Progr. Theor. Phys.—1974,—V. 51 —
P. 703—716.—Phys. Rev,—1974,—B9,—P. 1924—1925.
347. FlaschkaH., Newell A. C, RatiuT. Kac—Moody Lie algebras and
soliton equations//Physica D.— 1983.— V. 9, № 3.— P. 300—332.
348. Flat о М., LichnerowiczA. Cohomologie des representations definies par
la derivation de Lie et la valeur dans les formes de l'algebre de Lie des chaps de
vecteurs d'une variete differentiable premiers espaces de cohomologie applica-
tions//C.r. Acad. Sci. Paris.—1986.—V. 291.—P. 331—335.
349. FomenkoA. T. The integrability of some Hamiltonian systems//Ann. global
analisis geometry.— 1983.— V. 1, № 2.— P. 1 —10.
350. FomenkoA. T. Algebraic structure of certain integrable Hamiltonian
systems//Lecture Notes in Math.—1984.—V. 1108.—P. 103—127.
351. FomenkoA. T. Algebraic properties of some integrable Hamiltonian
systems//Lecture Notes in Math.—1984.—V. 1060,—P. 246—257.
352. FomenkoA. T. New topological invariant of integrable Hamiltonian//Baku.
International Topological Conference. Abstracts, part 2.—1987.— P. 316.
353. FomenkoA. Т., Trofimov V. V. Integrable systems on Lie algebras
and symmetric spaces.— London; New Jork: Gordon and Breach science
publischers, 1988.
354. FordyA., Wojciechowski S., Marshalll. A family of integrable
quartic potentials related to symmetric spaces//Phys. Lett.— 1986.— V. 113 A.—
P. 395—400.

432 СПИСОК ЛИТЕРАТУРЫ
355. Frenkell. В. Representations of affine Lie algebras, Hecke modular forms
and Korteweg—de Vries type equations//Lecture Notes in Math.— 1982.—
V. 933—P. 71 — 110.
356. Fuchssteiner B. The Lie algebra structure of non-linear evolution equations
admitting infinite-dimensional abelian symmetry groups//Progr. Theor. Phys.—
1981.—V. 65.—№ 3—P. 861—876.
357. Fuchssteiner B. The Lie algebra structure of degenrgate Hamiltonian
and bi-Hamiltonian systems//Progr. Theor. Phys.—1982.— V. 68, №4.—
P. 1082—1104.
358. Gardner C. S. Korteweg—de Vries equation and generalization I. The
Korteweg—de Vries equation as a Hamiltonian system//J. Math. Phys.—
1971.—V. 12, № 8—P. 1548—1551.
359. Gardner С S., Green J., Kruskal M., Miura R. A method for solving
the Korteweg—de Vries equation//Phys. Rev. Lett.—1967.—V. 19.—
P. 1095—1098.
360. Gardner С S., GreenJ.M., KruskalM., MiuraR. Korteweg—de
Vries equation and generalization VI. Method for exact solution//Comm. Pure
Appl. Math.—1974.—V. 27.—P. 97—133.
361. GattiV., ViniberghiE. Spinors of 13-dimensional space//Adv. Math.—
1978.—V. 30, № 2—P. 137—155.
362. GibbonsJ. G., HolmD. D., KupershmidtB. Gauge-invariant Poisson
brackets for chromohydrodynamics//Phys. Letters.—1982.— V. 90 A, № 6.
363. GoloV. L. Non-linear regimes in spin dynamics of superfluid 3He//Lett.
Math. Phys.—1981.—V. 5.—P. 155—159.
364. Goodman R., W a 11 а с h N. R. Classical and quantum-mechanical systems of
Toda lattice type I//Comm. Math. Phys.—1982—V. 83—P. 355—386.
365. Goodman R., WallachN. Classical and quantum-mechanical systems of
Toda lattice type II//Comm. Math. Phys.—V. 94.—P. 177—217.
366. Go tay M. M., LashofR., SniatyckiJ., WeinsteinA. Closed forms on
symplectic fibre bundles//Comm. Math. Helv —1983—V. 58—P. 617—621.
367. GrangierG. Recherche d'orbites periodiques d'un champ hamiltonien en
presence d'un potentiel vecteurs//C. r. Acad. Sci. Paris.—1983.— V. 297,
№ 8— P. 489—492.
368. Grifoke J. Classe de Maslov pour les fibres quaternioniens//C. r. Acad. Sci.
Paris.—1984 —V. 299, № 1— P. 29—39.
369. GromovM. A topological technique for construction of solutions of
differential equations and inequalities, v. 2//Acta congr. Intern. Math. (Nice,
1970).—Paris: Gauthier-Villars, 1971—P. 221—225.
370. GuilleminV., SternbergS. The moment map and collective motion//
Ann. Phys.—1980.—V. 127—P. 220—253.
371. GuilleminV., SternbergS. Geometric quantization and multiplicities of
group representations//Invent. Math.—1982.— V. 67, № 3.— P. 515—538.
372. Guillemin V., SternbergS. Convexity properties of the moment mapping//
Invent. Math.—1982.—V. 67, № 3.—P. 491—513.
373. Guillemin V., SternbergS. Multiplicity-free spaces//J. Diff. Geometry.—
1984—V. 19, № 1— P. 31—56.
374. GuilleminV., SternbergS. Symplectic techniques in physics.— L.; N. Y.;
Cambridge: Cambridge University press, 1984.
375. Guillemin V., SternbergS. Convexity properties of the moment mapping
II//Invent. Math —1984.—V. 77, № 3— P. 533—546.
376. HaefligerA. Lecture on a theorem on Gromov//Lecture Notes in Math.—
1971.—V. 209.—P. 128—141.
377. Hahn P. Haar measure grouppoids//Trans. Amer. Math. Soc.—1978.—
V. 242, № 1—P. 1—33.
378. Haine L. Geodesic flow on SOD) and abelian surfaces//Math. Ann.—
1983.—V. 263, № 4.—P. 435—472.
379. Haine L. The algebraic completely integrability of geodesies flow on
SO(n)//Comm. Math. Phys —1984—V. 94, № 2.—P. 271—287.

СПИСОК ЛИТЕРАТУРЫ 433
380. Harvey R., Lawson H. В. Calibrated geometry//Acta Math.— 1982
V. 148.— P. 47—157.
381. Hess H. Connections on symplectic manifolds and geometric quantization//
Lecture Notes in Math.—1980.—V. 836 —P. 153—166.
382. Holm D., Kupershmidt B. A. Poisson structures of superfluids//Phys
Lett —1982.—V. 91 A.—P. 425—430.
383. Holm D., Kupershmidt B. A. Poisson brackets and Clebsch representa-
tions for magnetohydrodynamics, multifluid plasmas and ellasticity // Physica—
1983—V. 6 D— P. 347—363.
384. Holm D., Kupershmidt B. A. Non-canonical Hamiltonian formulation of
magnetohydrodynamics//Physica.—1983.—V. 7 D— P. 330—333.
385. Iacob A., Sternberg S. Coadjoint structures, solitons and integrability//
Lecture Notes in Phys.— 1980.— V. 120.
386. Igusa J. A classification of spinors up to dimension twelve//Amer. J.
Math —1970.—V. 92, № 4 —P. 997—1028.
387. InozemtsevV. I., Meshcheryakov D. V. Extention of the class of
integrable dynamical systems connected with semi-simple Lie algebras // Lett.
Math. Phys.—1985.—V. 9.—P. 13—18.
388. Jim bo M. Theory of т-functions in integrable systems//Lecture Notes in
Phys.—1982.—V. 153.—P. 232—237.
389. Kac V. G. Infinite-dimensional Lie algebras.— Boston, Basel; Stuttgart:
Birhauser, 1983.— Progress in Mathematics.— V. 44.
390. Kac V. G., Peterson D. H. Infinite-dimensional Lie algebras, theta
functions and modular forms//Adv. Math.— 1983.— V. 50.
391. К a 1 n i n s E. G., M i 11 e г W., W i n t e r n i t z P. The group OD), separation
of variables and the hydrogen atom//J. Appl. Math.—1976.— V. 30, №4.—
P. 630—664.
392. К a m a 1 i n S. A., Perelomov A. M. Construction of canonical coordinates
on polarized coadjoint orbits of Lie groups // Comm. Math. Phys.—1985.—
V. 97.—P. 553—568.
393. Kazhdan D., Kostant В., Sternberg S. Hamiltonian group actions
and dynamical systems of Calogero type//Comm. Pure Appl. Math.—
1978—V. 31, № 4.—P. 481—507.
394. К i r w a n F. Convexity properties of the moment mapping III // Invent.
Math.—1984.—V. 77, № 3.—P. 547—552.
395. К пор F., Littelmann P. Der Crad erzeugender Funktionen von
Invarianten ringer // Preprint.— 1986.
396. Knorrer H. Geodesies on the ellipsoid//Invent. Math.—1980.— V. 59,
№2 —P. 119—143.
397. Kobayashi O., Yoshioka A., Maeda Y., Omori H. The theory of
infinite-dimensional Lie groups and its applications//Acta Appl. Math.—
1985.—V. 3.—P. 71 — 106.
398. Kostant B. On differential geometry and homogeneous spaces.— Proc. Nat.
Acad. Sci. USA —1956—V. 42, № 5.—P. 258—261.
399. Kostant B. On convexity, the Weil group and the Iwasawa decompo-
sition//Ann. Sci. Ec. Norm. Sup. Ser. 4 —1973.—V. 6, № 4— P. 413—
455.
400. Kostant B. The solution to a generalized Toda lattice and representation
theory //Adv. Math —1979.— V. 34, № 3—P. 195—338.
401. Kostant B. Poisson commutativity and generalized periodic Toda lattice//
Lecture Notes in Math.—1982—V. 905.—P. 12—28.
402. К r a m e r M. Spharische Untergruppen in kompakten zuzammenhangenden Lie
Gruppen//Composite Math.—1979.—V. 38, № 2.—P. 129—153.
403. Kruskal M. D. The Korteweg — de Vries equation and related evolution
equations// Lecture Notes in Math.—1974.— V. 15.—P. 61—83.
404. К u m m e r M. On the construction of the reduced phase space of
a Hamiltonian system with symmetry//Indiana Univ. Math. J.—1981.— V. 30,
№2.—P. 281—291.

434 СПИСОК ЛИТЕРАТУРЫ
405. Kupershmidt В. A. Geometry of jet bundles and the structure of
Lagrangian and Hamiltonian formalisms // Lecture Notes in Math.— 1980.—
V. 775.—P. 162—218.
406. Kupershmidt B. A. On the nature of the Gardner transformation//J.
Math. Phys.—1981.—V. 22.—P. 449—451.
407. Kupershmidt B. A. Korteweg—de Vries surfaces and Bucklund curves//J.
Math. Phys.—1982.—V. 23,—P. 1427—1432.
408. Kupershmidt B. On algebraic models of dynamical systems//Lett. Math.
Phys.—1982.—V. 6.—P. 85—89.
409. Kupershmidt B. A. On dual spaces of differential Lie algebras//
Physica.— 1983.— V. 7 D — P. 334—337.
410. Kupershmidt B. A. Deformations of integrable systems ,7 Proc. Roy. Irish
Academy, sec. A.—1983.—V. 83, № 1.— P. 45—74.
411. Kupershmidt B. A. Discrete Lax equations and differential-difference
calculus // Asterisque.— 1985.— № 123.
412. Kupershmidt B. A., Ratiu T. Canonical maps between sem-direct
products with applications//Comm. Math. Phys.—1983.— V. 90.— P. 235—
250.
413. К u p e r s h m i d t B. A. Modifying Lax equations and the second Hamiltonian
structure // Invent. Math,—1981.—V. 62, № 3.—P. 403—436.
414. Lacomba E. Mechanical systems with symmetry on homogeneous spaces//
Trans. Amer. Math. Soc—1973.—V. 185.—P. 477—491.
415. Langlois M. Contribution a l'etude du mouvement du coups rigide
a N dimensions auto d'un point fixe//Theses presentee a la faculte des sciences
de l'universite de Besancon—Besencon, 1971.
416. Lax P. D. Integrals of non-linear equations and solitary waves//Comm. Pure
Appl. Math — 1968— V. 21, № 5—P. 467—490.
417. Lax P. D. Periodic solutions of Korteweg — de Vries equations//Comm. Pure
Appl. Math.—1975.—V. 28.—P. 141 — 188.
418. Leznev A. N., Saveliev M. V. Two-dimensional exactly and
completely integrably dynamical systems//Comm. Math. Phys.—1983.—
V. 89.—P. 59—75.
419. Liber man P., Marie С. М. Symplectic geometry and analytical
mechanics.— Dordrecht: D. Reidel Publishing Сотр., 1987.
420. Lichnerowicz A. Deformations of algebras assaciated with a sympelectic
manifold.//Diff. Geom. Phys.—1983.—V. 3,— P. 69—84.
421. Lojasiewicz S. Triangulation of semi-analytic sets//Ann. Scuola Normale
Superiore Pisa Ser. 3 — 1964.— V. 13, № 4.—P. 449—474.
422. Lose о L. Integrability in mechanique celeste//J. Mechanique.— 1974.— V. 13,
№ 2.—P. 197—223.
423. MacLane S. Hamiltonian mechanics and geometry//Amer. Math.
Monthly.—1970.—V. 77.—P. 570—585.
424. Magri F. A symple model of the integrable Hamiltonian equation //J. Math.
Phys —1978—V. 19,—P. 1156—1162.
425. Magri F. A geometrical approach to the non-linear solvable equations//
Lecture Notes in Phys.—1980.—V. 120.—P. 233—263.
426. MarsdenJ. A group-theoretic approach to the equations of plasma
physics//Canad. Math. Bull,—1982.—V. 25, № 2.—P. 129—142.
427. MarsdenJ. E., Morrison P. J. Non-canonical Hamiltonian field theory
and reduced MHD//Contemp. Math —1984—V. 28—P. 133—150.
428. MarsdenJ. E., R a t i u T. S. Hamiltonian systems with symmetry, fluid and
plasma dynamics.— University of California, Berkeley and Canta Cruz,
1988.
429. MarsdenJ., Ratiu Т., WeinsteinA. Reduction and Hamiltonian
structures on duals of semi-direct product Lie algebras//Contemp. Math.—
1984 —V. 28—P. 55—100.
430. MarsdenJ., Ratiu T, WeinsteinA. Semi-direct product and reduction
in mechanics//Trans. Amer. Math. Soc.— 1984.— V. 281, № 1.— P. 147—178.

СПИСОК ЛИТЕРАТУРЫ 435
431. MarsdenJ., WeinsteinA. Reduction of manifolds with symmetry// Rep.
Math. Phys —1974.—V. 5, № 1.—p. 121 —130.
432. MarsdenJ. E., WeinsteinA. The Hamiltonian structure of the Max-
well—Vlasov equations//Physica.— 1982.— V. 7 D.—P. 394—406.
433. MarsdenJ., WeinsteinA. Coadjoint orbits, vertices and Clebsch
variables for incompressible fluids//Physica.—1983.—V. 7 D.— P. 305—323.
434. McDuffD. Examples of simply-connected symplectic non-Kahlerian mani-
folds//J. Diff. Geom.—1984.—V. 20, № 1.—P. 267—277.
435. McKay W. J., Patera J. Tables of dimensions, indices and branching
rules for representatins of simple Lie algebras.— Marses Dekker, Inc.
1981.
436. McKeanH. P. Integrable systems and algebraic curves, I//Global Analy-
sis.—Lecture Notes in Math.—1979.—V. 755.—P. 83—200.
437. McKeanH. P., van MoerbekeP. The spectrum of Hill's equation /
/Invent. Math.—1975.—V. 30,—P. 217—274.
438. McKeanH. P., TrubowitzE. Hill's operator and hyperelliptic function
theory in the presence of infmetely many branch points//Comm. Pure Appl.
Math.—1977.—V. 29.—P. 143—226.
439. M e d i n a A. Structure ortogonale sur une algebre de Lie et structure de
Lie—Poisson associee//Seminaire de Geometrie differentielle, 1983—1984.—
Universite des Sciences et Techniques du Languedoc.—1985.—P. 113—121.
440. M i 1 n о r J. Curvature of left invariant metrics on Lie groups//Adv.
Math —1976.—V. 21.—P. 293—329.
441. MischenkoA. S., FomenkoA. T. Symplectic Lie group action // Lecture
Notes in Math.—1979—V. 763,—P. 504—539.
442. van MoerbekeP. The spectrum of Jacobi matrices//Invent. Math.—
1976—V. 37.—P. 45—81.
443. van MoerbekeP., MumfordD. The spectrum of difference operators
and algebraice curves//Acta Math.—1979.—V. 143,—P. 93—154.
444. M о 1 i n о P. Structure transverse aux orbites de la representation coadjointe: la
cas des orbites reductives//Seminaire de Geometrie differentielle, 1983—1984.—
Universite des Sciences et Techniques du Languedoc.— P. 55—62.
445. Montgomery R., MarsdenJ., RatiuT. Gauged Lie—Poisson struc-
tures//Contemp. Math.—1984.—V. 28.—P. 101 — 114.
446. Moody B. A new class of Lie algebras//J. Algebra.—1968.— V. 10.—
P. 211—230.
447. MorvanJ. M. Calsses de Maslov d'une immersion lagrangienne et mini-
malite//C. r. Acad. Sci. Paris —1981.—V. 292, Ser. 1—P. 633—636.
448. MorvanJ. M. Quelques invariants topologiques en geometrie symplectique//
Ann. Inst. Henri Poincare —1983.— V. 38, № 4.—P. 364—370.
449. MorvanJ. M. Sur la transversalite de deux champs de plans lagrangiens//
С r. Acad. Sci. Paris —1983.—V. 296, Ser. 1.—P. 997—1000.
450. MorvanJ. M. Obstructions a la transversalite de deux champs de plans
lagrangiens. Travaux en cours//Seminaire Sand — Rhodanien en Geometrie,
II.—Paris: Hermann, 1984.—P. 55—72.
451. MorvanJ. M., NiglioL. Classes de Maslov d'ordres superieurs//
С. г. Acad. Sci. Paris.—1985.— V. 300, № 9—P. 271—274.
452. MoserJ. On the volume elements on a manifolds//Trans. Amer. Math.
Soc—1965.—V. 120, № 2.—P. 286—294.
453. MoserJ. Three integrable Hamiltonian systems connected with isospectral
deformations//Adv. Math.—1975—V. 16, № 2.—P. 197—220.
454. MoserJ. Geometry of quadrics and spectral theory//Chern. Symposium.—
1979—P. 147—188.
455. MoserJ. Various aspect of integrable Hamiltonian systems//Dynamical
systems. Progress in Math —1980 —P. 233—289.
456. MoserJ. On examples of a Schoredinger equation with almost periodic
potential and nowhere dense spectrum//Comment. Math. Helv.—1981.— V. 56,
№ 2,—P. 198—224.

436 СПИСОК ЛИТЕРАТУРЫ
457. MulaseM. Algebraic geometry of soliton equations//Proc. Jap. Acad.
A.—1983.—V. 59, № 6 —P. 258—288.
458. MulaseM. Cohomology structure in soluton equations and Jacobian
varieties//J. Diff. Geom —1984.—V, 19, № 2— P. 403—430.
459. MumfordD. An algebro-geometric construction of commuting operators and
of solution to the Toda lattice equation and related non-linear equations // Proc.
Intern. Symp. on Algebraic Geometry.— Kyoto, 1977.— P. 115—153.
460. N a r a si m h am M., RamananS. Existence of universal connections//
Amer. J. Math.—1961—V. 83—P. 563—572.
461. NessL. A stratification of the null cone via the moment map//Amer. J.
Math.—1984,—V. 106, № 6—P. 1281 — 1325.
462. Neumann С De problemate quidam mecanic quod ad primam integralium
ultraellipicorum classem revocatur//J. reine angew. Math.— 1859.— V. 56.—
P. 46—63.
463. О k a s s a E. Prolongements des champs de vecteurs a des varietes//C. r. Acad.
Sci. Paris —1985—V. 300, № 6 —P. 173—176.
464. О k a s s a E. Prolongement des champs de vecteurs a des varietes de
points proches//Ann. Fac. Sci. Toulouse Math.—1986—1987,—V. 8, № 3.—
P. 349—366.
465. Olshanetsky M. A., Perelomov A.M. Completely integrable Hamil-
tonian systems connected with semi-simple Lie algebras//Invent. Math.—
1976—V. 37, № 2— P. 93—108.
466. Olshanetsky M. A., Perelomov A. M. Explicit solutions of the
classical generalized Toda models//Invent. Math.— 1979.— V. 56.— P. 261 —
269.
467. Olshanetsky M. A., Perelomov A.M. Quantum integbrable systems
related to Lie algebras//Phys. Reports,— 1983,— V. 94,—P. 313—404.
468. Orlik P., Vogt E., Zieschang H. Zur Topologie gefasserter dreidimen-
sionaler Mannigfaltigkeiten//Topology.— 1967.— V. 6, № 1.— P. 49—65.
469. Oshemkov A. A. The phase topology of some integrable Hamiltonian
systems on SO (я)// Бакинская междунар. топологическая конф. Ч. 2:
Тезисы / Математический ин-т АН СССР им. В. А. Стеклова; Ин-т матема-
тики и механики АН Азерб. ССР.— Баку, 1987.— С. 230.
470. Patera J.. Sharp R. Т., Winternitz P., Zassenhaus H. Invariant
of real low dimension Lie algebras //J. Math. Phys.—1976 —V. 17, №6.—P.
986—994.
471. Perelomov A. M. The simple relation between certain dynamical systems//
Comm. Math. Phys.—1978.—V. 63—P. 9—11.
472. Perelomov A.M. Lax representation for the systems of S. Kowalevski
type//Comm. Math. Phys.—1981.—V. 81—P. 239—241.
473. Perroud M. The fundamental invariants of homogeneous classical groups//
J. Math. Phys.—1983—V. 24, № 6.—P. 1381 — 1391.
474. Peterson D. H. Affine Lie algebras and theta functions // Lecture Notes in
Math —1982 —V. 933 —P. 166—175.
475. Pohlmeyer K. Integrable Hamiltonian systems with interaction through
quadratic constrains//Comm. Math. Phys.—1976.— V. 46.— P. 267—273.
476. R a d u M., V a s i 1 O. Almost cosymplectic and conformal almost cosymplectic
connections, I//Rev. Roumaine Math. Pures Appl.—1971.— V. 16, № 6.— P.
893—902.
477. R a d u M., V a s i 1 O. Almost cosymplectic and conformal almost cosymplectic
connections, II//Rev. Roumaine Math. Pures Appl.— 1971.— V. 16, № 6.— P.
903—912.
478. Rais M. La representation'coadjointe du groupe affine//Ann. Inst. Fourier.-—
1978.—V. 28, № 1.—P. 207—237.
479. Rais M. L'indice des produits semi-directs ?x(S//C. r. Acad. Sci.
Paris —1978.—V. 287, № 4._p. 195—197. *
480. Ratiu T. Involution theorem//Lecture Notes in Math.— 1980.—V. 775.—P.
219—257.

СПИСОК ЛИТЕРАТУРЫ 437
481. Rat iu Т. The motion of the free n-dimensional rigid body//Indiana Univ.
Math. J —1980.—V. 29, № 4—P. 609—629.
482. R a t i u Т., The C. Neumann problem as a completely integrable system on
an adjoint orbit//Trans. Amer. Math. Soc.—1981,—V. 264 № 2—P
321—329.
483. Ratiu T. Euler—Poisson equations on Lie algebras and the JV-dimensional
heavy rigid body//Amer. J. Math —1982,—V. 103, № 3— P. 409—448.
484. Ratiu Т., van MoerbekeP. The Lagrange ridgid body motion//
Ann. Inst. Fourier —1982.—V. 32, № 1— P. 211—234.
485. Renault J. A grouppoint approach to C*-algebras//Lecture Notes in
Math,—1980 —V. 793 —P. 1 — 160.
486. RentschlerR., VergneM. Sur le semi-centre du corps enveloppant d'une
algebre de Lie//Ann. Sci. Ec. Norm. Super.—1973.—V. 6.—P. 380—405.
487. Rey m an A. G., Semenov-Tian-Shansky M. A. Reduction of
Hamiltonian systems, affine Lie algebras and Lax equations//Invent. Math.—
1979.—V. 54, № 1—P. 81 — 100.
488. Reyman A. G., Semenov-Tian-Shansky M. A. Reduction of
Hamiltonian systems, affine Lie algebras and Lax equations//Invent. Math.—
1981.—V. 63, № 3,—P. 423—432.
489. Reyman A. G., Semenov-Tian-Shansky M. A. A new integrable
case of the motion of the 4-dimensional rigid body//Comm. Math.
Phys.— 1986— V. 105,—P. 461—472.
490. Reyman A. G., Semenov-Tian-Shansky M. A. Lax representation
with a spectral parametre for the S. Kowalevski type and its generalizations//
Lett. Math. Phys.—1987.—V. 14 —P. 55—61.
491. Samir Saad. Representation co-adjointe et ideaux primitifs pour une classe
d'algebre de Lie//Theses presentees a l'Universite de Poitiers U.E.R. des Sci.
Foundamentales et Appliquees.— 1977.
492. S а г 1 e t W. Contribution to the study of symmetries, first integrals and the
inverse problem in theoretical mechanics//Acad. Analecta.—1987.— V. 49,
№ 1.—P. 27—57.
493. SchoutenJ. A. Klassifizierreng der alternierenden Grossen dritten Grades in
7 Dimensiofcen//Rend. Circ. Mat. Palermo.—1931.
494. S i с о r a w J. С Sur les immersions lagrangiennes dans un fibre contangent
admettant une phase generatric global//С. г. Acad. Sci. Paris.—1986.—V. 302,
№ 3.—P. 119—122.
495. Simons J. On transitivity of holonomy systems//Ann. Math-—1962.— V.
76.—P. 213—234.
496. Sourian J. M. Geometrie simplectique et physique mathematique.— Paris,
1975.
497. Sternberg S. Symplectic homogeneuos spaces//Trans. Amer. Math. Soc.—
1975.—V. 212,—P. 113—130.
498. Sutherland B. Exact results for a quantum many body problem in one
dimension//Phys. Rev.—1971—V. A4 — P. 2019—2021.
499. S у m e s W. W. Systems of Toda type, inverse spectral problems and
representations theory//Invent. Math.—1980.—V. 59.—P. 13—51.
500. Symes W. W. Hamiltonian group actions and integrable systems//Physica.—
1980,—V. Dl— P. 339—374.
501. Takiff S. J. Rings of invariant polynomials for a class of Lie algebras//
Trans. Amer. Math. Soc —1971.—V. 160.—P. 249—262.
502. Thimm A. Integrable geodesic flows on homogeneous spaces//Ergod. Theory.
Dyn. Syst—1981.—V. 1, № 4.—P. 495—517.
503. Tischler D. Closed 2-forms and embedding theorem for symplectic
manifolds//J. Diff. Geom.—1977.—V. 12—P. 229—235.
504. Tits J. Sur les constantes de structure et le theoreme d'existence des algebres
de Lie semi-simples//Publ. Math. Paris.—1966—V. 31.—P. 21—58.
505. Thompson G. Polynomial constants of motion in flat space//J. Math.
Phys —1984 —V. 25, № 12.—P. 3474—3478.

438 СПИСОК ЛИТЕРАТУРЫ
506. Thurston W. Some simple examples of symplectic manifolds//Proc. Amer.
Math. Soc.—1976.—V. 55— P. 467—468.
507. Toda M, Wave propagation in anharmonic lattices//J. Phys. Soc. Japan.—
1967 —V. 23,—P. 501—506.
508. Tondcur Ph. Affine Zusammenhange auf Mannigfaltigkeiten mit fast
symplektischer Strukture//Comm. Math. Helv —1961.— V. 36, № 1—P.
234—244.
509. Topological classification of integrabte systems//Advances in Soviet Math.—
1991—V. 6.—P. 1—345 (American Math. Society).
510. Trofimov V. V. On the geometric properties of the complete commutative
set of functions on symplectic manifold //' Бакинская Международная тополо-
гическая конференция. Часть 2: Тезисы.— Баку: Математический ин-т АН
СССР им. В. А. Стеклова, ин-т математики и механики АН Азерб.
ССР —1987.—С. 297.
511. Trofimov V. V. Connections on Manifolds and new characteristic
classes//Acta Applicandae Mathematicae.—1991.—V. 22.— P. 283—312.
512. Vaisman J. Symplectic geometry and secondary characteristic classes.—
Boston, Basel, Stuttgart: Birkhauser, 1987. '
513. Vergne M. La structure de Poisson sur l'algebre symetrique d'une algebre de
Lie nilpotente//Bull. Soc. Math. France.—1972,—V. 100, № 3,—P. 301—335.
514. Vey J. Deformation du crochet de Poisson sur les varietes symplectiques//C. r.
Acad. Sci. Paris.—1975.—V. 280.—P. 725—727.
515. Vey J. Deformation du crochet de Poisson sur une variete symplectique//
Comm. Math. Helv —1975—V. 50, № 4.—P. 421—454.
516. Waldhausen F. Eine Klasse von 3-dimensionalen Mannigfaltigkeiten,
I//Invent. Math —1967,— V. 33, № 4,—P. 88—117.
517. Ward R. S. Multy-dimensional integrable systems//Lect. Notes Rhys.—
1987.—V. 280 —P. 106—116.
518. Weil A. Theorie des points proches sur les varietes differentiables//Coll.
Geom. Diff. Strasbourg —1953.—P. 111 — 117. •
519. Weinstein A. Symplectic manifolds and their Lagrangian submanifolds//
Adv. Math.—1971—V. 6.—P. 329—346.
520. Weinstein A. On the volume of manifolds all of whose geodesies are
closed//J. Diff. Geom —1974 —V. 9 —P. 513—517.
521. Weinstein A. Lectures on sumplectic manifolds//CBMS Conf. Scries,
№ 27. Amer. Math. Soc, 1977.
522. Weinstein A. Flat bundeles and symplectic manifolds//Adv. Math.—
1980.—V. 37.—P. 239—250.
523. Weinstein A. Symplectic geometry//Bull. Amer. Math. Soc.— 1981.—V.
5—P. 1 — 13.
524. Weinstein A. The local structure of Poisson manifolds //J. Diff. Geom.—
1983.—V. 18, № 3_p. 523—557.
525. Weinstein A. Symplectic gruppoids and Poisson manifolds//Bull. Amer.
Math. Soc.—1987.—V. 16, № 1.
526. Wilson G. Commuting flows and conservation laws for Lax equations // Proc.
Cambridge Phil. Soc.—1979.—V. 86.—P. 131 — 143.
527. Wilson G. The modified Lax and two-dimensional Toda lattice equations
associated with simple Lie algebras//Ergod. Theory Dyn. Syst.—1981.— V.
1—P. 361—380.
528. Wojciechowsky S. Involutive set of integrals for completele integrable
many body problems with pair interections//Lett. Nuovo Cimento.— 1977.— V.
18.—P. 103—107.
529. Z i e s с h a n g H., V о g t E., С о 1 d e w а у Н. D. Surfaces and planar discon-
tinuous groups//Lecture Notes in Math.—1980.— V. 835.

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Алгебра кватернионов 93, п. 23
— Ли 55, п. 1
абелева 56, п. 4
Z,-градуированная 208, п. 2
группы Ли 75, п. 4
двойная 222, п. 1
—:— интегрируемая 179, п. 2
коммутативная 56, п. 4
полупростая 56, п. 12
разрешимая 56, п. 9
редуггивиая 56, п. 12
симметрическая 232, п. 1
совершенная 281, п. 7
сохраняющая скалярное произ-
ведение 56, п. 13
— самосопряженная 220, п. 30
— с двойственностью Пуанкаре 214,
п. 6
— Фробениуса 220, п. 28
алгоритм (f) 212, п. 3
— (ft) 215, п. 9
аналог уравнения движения твердого
тела 275, п. 2
аннулятор ковектора 84, п. 34
Базис Вейля 84, п. 33
— Гельфанда — Цетлина 323, п. 23
— симплектический 86, п. 6
Вложение динамической системы в ал-
гебру Ли 160, п. 19
волчок Лагранжа 303, п. 14
— полностью симметричный 303,
п. 14
время в уравнении Гамильтона—Яко-
би 147, п. 6
вставка 391, п. 24
вырождение предельное 385, п. 9
Гамильтониан 112, п. 7
— неориентируемый 386, п. 12
— нерезонаисный 349, п. 2; 363, п. 38
— ориентируемый 386, п. 12
геодезическая 119, п. 7
гессиан 325, п. 2
гомоморфизм алгебр Ли 56, п. 6
— касательный 76, п. 11
— накрывающий 185, п. 3
градиент косой 112, п. 9
грассманиан лагранжев вещественный
96, п. 3
приведенный 403, п. 17
граф редуцированный 371, п. 11
группа голономии 403, п. 17
— диффеоморфизмов однопараметри-
ческая 58, п. 21
локальная 58, п. 23
порожденная векторным
полем 59, п. 25
— Ли 75, п. 1
— Гамильтона—Ли 195, п. 27
— пуассонова 195, п. 27
— симметрии гамнльтоиовой систе-
мы 185, п. 5
— симплеггическая вещественная 86,
п. 1
компактная 94, п. 25
комплексная 88, п. 8
группоид симплектический 191, п. 2
группы пуассоновы сопряженные 196,
п. 32
Движение условно периодическое 169,
п. 10
действие 147, п. 6
— гамильтоново 184, п. 3
— группоида 193, п. 14
— группы Ли 76, п. 7
— коприсоединенное псевдогруппы
Ли 195, п. 21
— по Гамильтону 38, п. 1
— присоединенное 76, п. 12
— пуассоиово псевдогруппы Ли 194,
п. 15
— свободное от кратностей 308, п. 9
— строго симплектическое 184, п. 3
диаграмма бифуркационная 378, п. 2
— сепаратрисиая 336, п. 9; 354, п. 15
диаграмма сепаратрисная входящая
336, п. 9

440
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
диаграмма сепаратрисная исходящая
336, п. 9
дифференциал абсолютный 119, п. 4
дополнение косоортогональное 85, п. 2
Задача вариационная с подвижными
концами 40, п. 3
— Гамильтона—Якоби 149, п. 14
— Неймана 124, п. 25
Значение критическое 378, п. 2
Идеал 56, п. 3
изотопия гамильтонова 406, п. 32
импульс 21, п. 2; 147, п. 6
инвариант 78, п. 19; 81, п. 26
— интегральный 43, п. 1
абсолютный 43, п. 1
относительный 43, п. 1
полного порядка 43, п. 1
Пуанкаре—Картана 45, п. 5
— коприсоединенного представления
78, п. 19
— меченый 372, п. 11
— топологический интегрируемого га-
мильтониана 351, п. 9
изоэнергетический 355, п. 19
меченый 372, п. 11; 377,
п. 23
полный 355, п. 19
//-инвариант канонический 221, п. 4
инварианты сходные 222, п. 5
инволюция антикомплексная 100,
п. 13
— Картана 233, п. 7
индекс алгебры Ли 84, п. 34; 251, п. 12
— критической точки 325, п. 5
вырожденной 326, п. 17
— представления 251, п. 12
— регулярной точки проекции 406,
п. 28
— ручки 327, п. 13
интеграл 24, п. 1
— боттовский 334, п. 4
ориентируемый 336, п. 10
неориентируемый 336, п. 10
— момента количества движения 35,
п. 14
— первый 24, п. 1
— полный 62, п. 1
— тривиальный геометрический 35,
п. 14
— циклический 19, п. 7
— энергии 35, п. 14
— Якоби 19, п. 8
Кватернион 93, п. 23
— сопряженный 93, п. 23
— чисто мнимый 93, п. 23
кернфункция Бергмана 109, п. 28
класс Арнольда—Маслова 400, п. 5;
401, п. 6
— Годбийона —Вея 398, п. 14
— когомологический диагональный
215, п. 11
— Маслова 400, п. 3
— многообразий (Н) 345, п. 41
(Q) 345, п. 41
(S) 345, п. 41
(W) 345, п. 41
— характеристический типа Маслова
403, п. 18
лагранжева подрасслоения
405, п. 26
полного инволютивного
семейства 404, п. 23
количество движения 12, п. 4
коммутатор векторных полей 60, п. 29
компонента седловая 353, п. 14
координаты в уравнении Гамильто-
на—Якоби 147, п. 6
— лагранжевы 16, п. 1
корень алгебры Ли 82, п. 30
положительный 83, п. 32
простой 83, п. 32
кривая интегральная 57, п. 20
Линия толстая 374, п. 16
— тонкая 274, п. 16
— узлов 33, п. 9
Матрица Гесса 325, п. 2
метрика отображения моментов 305,
п. 2
— Фубини — Штуди 108, п. 23
многообразие кэлерово 107, п. 20
— лагранжево грассманово вещест-
венное 96, п. 3
комплексное 96, п. 3
— пуассоново 157, п. 1
— редуцированное 372, п. 11
— симплектическое 102, п. 1
— точек //-значных 111, п. 36
— Тёрстона 109, п. 29
многообразия пуассоновы взаимно
полярные 193, п. 12
множество бифуркационное 378, п. 2
множитель Якоби последний 29, п. 10
модуль кватерниона 93, п. 23
момент внешних сил главный 15, п. 12
— инерции 30, п. 1
осевой 30, п. 1
относительно оси 31, п. 4
полярный 30, п. 1
центральный 31, п. 3
центробежный 30, п. 1
— количества движения 14, п. 9

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
441
Набор коммутативный 319, п. 8
— разделяющий 319, п. 8
Область ограниченная 108, п. 26
овал 356, п. 22; 368, п. 4
ограничение 113, п. 17
окружность толстая 374, п. 16
— тонкая 374, п. 16
оператор Ли 126, п. 1
— отвечающий базисному вектору
79, п. 20
— секционный 261, п. 2
канонический 262, п. 2
операция приклейки ручки 327, п. 13
— сдвига аргумента 197, п. 2
орбита точки 58, п. 21; 77, п. 14
ось инерции главная 31, п. 6
отображение изотропное 147, п. 7
— моментов 185, п. 4; 194, п. 19
— симплектическое 154, п. 2
— экспоненциальное 76, п. 9
Пара гамильтонова 207, п. 1
— пуассонова 207, п. 1
— сферическая 309, п. 15
переменные действие—угол 171, п. 17
перемещение возможное И, п. 1
— действительное 11, п. 1
перестройка симплектического много-
образия 110, п. 31
перестройки торов Лиувилля канони-
ческие 344, п. 37
плоскость вещественная лагранжева
100, п. 15
поверхность интегральная 385, п. 10
подалгебра 55, п. 3
— Картана 82, п. 29
— конечного типа 317, п. 3
— сферическая 309, п. 15
подгруппа изотропии 77, п. 14
— однопараметрическая 75, п. 5
— стационарная 77, п. 14
— сферическая 309, п. 15
подмногообразие лагранжево 147, п. 7
подмножество алгебраическое в СР"
108, п. 24
поднятие 185, п. 3
подпространство изотропное 85, п. 3
— коизотропное 85, п. 3
— коммутативное 317, п. 1
главное 321, п. 14
— лагранжево 85, п. 3
— симплектическое 85, п. 3
подъем функции 203, п. 1
поле векторное левоинвариантное
75, п. 2
правоинвариантное 75, п. 2
— гамильтоново 112, п. 7
поле гамильтоново локально 112,
п. 6
— параллельное 119, п. 7
— полное 59, п. 25
полноторие 340, п. 31
— диссипативное 380, п. 6
— расслоенное типа (а, Ь) 351, п. 9
положение общее для перестроек
385, п. 10
полуинвариант 79, п. 19
поток геодезический 118, п. 2
представление алгебры Ли коприсо-
единенное 76, п. 12
присоединенное 76, п. 12
— группы Ли 76, п. 10
коприсоединенное 76, п. 12
присоединенное 76, п. 12
— изотропии 189, п. 21
представления эквивалентные 77, п. 15
5-представление группы Ли 201, п. 10
преобразование каноническое 48, п. 1;
145, п. 1
унивалентное 49, п. 4
— Лежандра 23, п. 7
— симплектическое вещественное 86,
п. 1
комплексное 88, п. 8
приклейка ручки 327, п. 13
торической 387, п. 20
принцип Гамильтона 38, п. 1
— поглощения 149, п. 14
— Якоби 41, п. 3
произведение внутреннее 111, п. 1
— тензорное 212, п. 1
производная ковариантная 119, п. 4
пространство кэлерово 93, п. 19
положительное 93, п. 21
— линзовое 338, п. 17
— симметрическое 263, п. 3
максимального ранга 267, п. 14
— симплектическое 84, п. 1
— фазовое над пуассоновым много-
образием 191, п. 5
Р-пространство симплектическое 184,
п. 1
однородное 184, п. 1
псевдогруппа Ли 191, п. 2
соответствующая пуассонову
многообразию 191, п. 2
пучок лиев 237, п. 1
замкнутый 241, п. 12
неприводимый 241, п. 12
Радикал 56, п. 11
разложение гамильтоново 344, п. 36
— корневое 82, п. 30
— топологическое 344, п. 36
размерость лиева пучка 237, п. 1

442
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
размерность ручки 327, п. 13
ранг алгебры Ли 83, п. 31
— компактной группы Ли 267, п. 14
— симметрического пространства 266,
п. 14
— скобки Пуассона 158, п. 4
— фундаментальной группы 339,
п. 22
расслоение пуассоиово 191, п. 5
расширение алгебры Ли 249, п. 3
— несущественное 251, п. 9
— существенное 251, п. 9
— универсальное 251, п. 11
расширения эквивалентные 250, п. 7
реализация. гамильтонова векторного
поля 160, п. 17
— пуассонова многообразия 159, п. 15
— системы 160, п. 18
редукция 176, п. 15
решение уравнения Гамильтона —
Якоби 148, п. 14
род системы 358, п. 26
ручка 327, п. 13
— торнческая 387, п. 19
ряд канонический 321, п. 19
— подчиненный 321, п. 16
— регулярный 321, п. 15
ряды канонически эквивалентные 322,
п. 20
Связность аффинная 118, п, 3
согласованная с метрикой 119,
п. 5
— почти симплектическая 401, п. 7
— симплектическая 402, п. 10
— согласованная с формой 401, п. 7
связь 113, п. 17
— голономная 11, п. 1
— идеальная 12, п. 2
сдвиг аргумента 197, п. 2
— левый 75, п. 1
— правый 75, п. 1
седло неориентированное 341, п. 31
торическое 381, п. 6
•— ориентированное 340, п. 31
торическое 381, п. 6
семейство полное 159, п. 9
инволютивное 163, п. 1
— производящее для лагранжевой
иммерсии 406, п. 29
квадратичное на беско-
нечности 406, п. 29
— решений невырожденное «-параме-
трическое 164, п. 4
сепаратриса 354, п. 15
серия секционных операторов ком-
пактная 276, п. 4; 278, п. 12
комплексная полупростая 275,
п. 2; 278, п. 11
серия секционных операторов нор-
мальная 276, п. 6; 278,
п. 13
сжатие алгебры Лн 209, п. 3
сила 21, п. 2
— потенциальная 16, п. 16
снмплектоморфизм 145, п. 1
система координат каноническая 117,
п. 25
— типа Калоджеро—Сазерленда 310,
п. 20
— уравнений боттовская 334, п. 4
вполне интегрируемая 163, п. 1
алгебраическая 292, п. 12
в коммутативном смысле
172, п. 4
в некоммутативном смыс-
ле 172, п. 4
полная 71, п. 7
— функций канонически сопряженная
170, п. 14
полная инволютивная 163, п. 1
системы гамильтоновые эквивалент-
ные геометрически 364, п. 38
топологически 364, п. 38
скобка Березина 138, п. 13
— инвариантная 196, п. 30
— Пуассона 51, п. I; 113, п. 11;
157, п. 1
фундаментальная 51, п. 3
e-скобка Березина 208, п. 6
Д-скобка 222, п. 1
скобки Пуассона согласованные 206,
п. 1
скорость лагранжева 16, п. 1
слоение колежандрово 396, п. 5
— лагранжево 396, п. 1
слой симплектическнй 158, п. 7
случай Ковалевской 35, п. 14
— Лагранжа обобщенный 302, п. 12
— Лагранжа — Пуассона 35, п. 14
— Эйлера — Пуансо 35, п. 14
сокращение разложения многообразия
391, п. 24
степень вырождения критической точ-
ки 325, п. 2
структура комплексная 92, п. 18
— пуассонова 157, п. %1
— симплектическая 102, п. 1
каноническая на орбитах 135,
п. 2
связности 107, п. 18
сумма полупрямая 251, п. 9
Тензор структурный 55, п. 2
— кривизны симплектический 402,
п. 12
— Рнччи 402, п. 14

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
443
тор максимальный 267, п. 14
точка Л-значная 111, п. 36
— критическая 325, п. 1; 378, п. 2
вырожденная 325, п. 2
невырожденная 325, п. 2
— регулярная 378, п. 2
траектория устойчивая 335, п. 7
Угол нутации 33, п. 9
— прецессии 33, п. 9
— собственного вращения 33, п. 9
— Эйлера 33, п. 9
уравнение Гамильтона каноническое
40, п. 2
— Гамильтона—Якоби 49, п. 5; 148,
п. 14
стационарное 147, п. 6
— движения триплета 144, п. 13
— Лагранжа второго рода 18, п. 3;
21, п. 2
— Эйлера 140, п. 1
— Якобн 42, п. 4
уравнения Лагранжа 21, п. 2
— Пуассона кинематические 34, п. 11
— Эйлера динамические 34, п. 12
кинематические 33, п. 10
уровень критический невырожденный
328, п. 16
Л/-условие 222, п. 6
Форма Киллинга 82, п. 27
— Кириллова 135, п. 2
— связности универсальная 106, п. 17
— симплектическая 84, п. 1; 102, п. 1
— целочисленная 155, п. 7
функции в инволюции 113, п. 13;
159, п. 9
функции функционально зависимые
24, п. 2
функция боттовская 334, п. 5
— Гамильтона 147, п. 6
— Казимира 158, п. 4
— коллективная 309, п. 10
— Лагранжа 18, п. 5
— Морса 325, п. 3
— производящая 112, п. 7
— Рауса 41, п. 3
— центральная 158, п. 4
функции сходные 222, п. 5
Центр алгебры Ли 56, п. 7
— масс 13, п. 7
цилиндр 340, п. 31; 381, п. 6
Частота условно периодического дви-
жения 169, п. 10
часть кватерниона вещественная 93,
п. 23
мнимая 93, п. 23
число степеней свободы 16, п. 1
Штаны 341, п. 31
Элемент Казимира 319, п. 6
— регулярный 82, п. 29
— слабо регулярный 253, п. 16
элементы коммутирующие 317, п. 1
эллипсоид инерции 31, п. 6
энергия системы 21, п. 4
кинетическая 15, п. 14
Ядро гомоморфизма 56, п. 6
— кососимметрической билинейной
формы 85, п. 3
якобиан 24, п. 2

ОГЛАВЛЕНИЕ
Введение
ЧАСТЬ 1
ЭЛЕМЕНТАРНЫЕ АЛГЕБРО-ГЕОМЕТРИЧЕСКИЕ СВОЙСТВА
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 11
Глава 1. Краткий экскурс в классическую механику 11
§ I. Принцип Даламбера—Лагранжа 11
§ 2. Уравнения Лагранжа второго рода 16
§ 3. Уравнения Гамильтона 20
§ 4. Первые интегралы дифференциальных уравнений 23
§ 5. Динамика твердого тела 29
§ 6. Вариационные принципы в механике 38
§ 7. Интегральные инварианты 42
§ 8. Канонические преобразования 48
§ 9. Скобки Пуассона 51
Глава 2. Интегрирование канонических систем 55
§ 10. Алгебра Ли векторных полей 55
§ 11. Теорема Якоби 62
§ 12. Теорема Лиувилля 67
§ 13. Теорема Ли 70
§ 14. Дополнительные сведения из теории групп Ли и алгебр Ли 75
Глава 3. Снмплектическая геометрия в линейном пространстве 84
§ 15. Симплектические пространства 84
§16. Группы симплектических преобразований линейного пространства 86
§ 17. Лагранжев грассманиан 95
Глава 4. Снмплектнческая геометрия 102
§ 18. Симплектические многообразия 102
§ 19. Гамильтоновы векторные поля 111
§ 20. Геодезические потоки 118
§ 21. Алгебра Ли функций Гамильтона 126
§ 22. Снмплектическая структура на орбитах коприсоединенного пред-
ставления группы Ли 134
§ 23. Уравнения Эйлера 139
§ 24. Канонические преобразования 145
§ 25. Теорема Дарбу 150
§ 26. Вложения симплектических многообразий 153
§ 27. Пуассоновы многообразия 157

ОГЛАВЛЕНИЕ 445
ЧАСТЬ 2
АЛГЕБРАИЧЕСКИЕ СВОЙСТВА ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ
Глава 5. Гамильтоновы системы с симметриямн. Симплектические дейст-
вия групп Ли на симплектических многообразиях 163
§ 28. Вполне интегрируемы^ гамильтоновы системы 163
§ 29. Структура вполне интегрируемых гамильтоновых систем 166
§ 30. Некоммутативное интегрирование гамильтоновых систем 171
§ 31. Интегрируемые алгебры Ли 179
§ 32. Симплектнческие действия групп Ли 184
§ 33. Редукция гамильтоновых систем с симметриями и псевдогруппы Ли 190
Глава 6. Методы построения функций в инволюции иа орбитах коприсоеди-
нениого представления групп Ли 197
§ 34. Метод сдвига аргумента 197
§ 35. Метод построения коммутативных наборов функций по цепочкам
подалгебр 203
§ 36. Семейства функций в инволюции, связанные с согласованными
скобками Пуассона 206
§ 37. Сжатия алгебр Ли 208
§ 38. Метод тензорных расширений алгебр Ли 212
§ 39. Метод сходных функций 221
§ 40. Метод Я-матрицы 222
Глава 7. Полнота инволютивиых наборов функций 223
§ 41. Критерий полноты 223
§ 42. Полнота семейств функций, построенных методом сдвига аргумента 229
§ 43. Функции в инволюции на симметрических алгебрах Ли 232
§ 44. Скобки Пуассона, связанные с лиевыми пучками 237
§ 45. Инволютивные семейства функций на полупрямых суммах 249
Глава 8. Секционные операторы 261
§ 46. Динамические системы и симплектические структуры, порождаемые
секционными операторами 261
§ 47. Секционные операторы для коприсоединенного представления
и вполне интегрируемые системы 267
§ 48. Основные примеры секционных операторов 274
§ 49. Бигамильтоновость уравнений Эйлера 278
Глава 9. Полная интегрируемость по Лиувиллю некоторых гамильтоиовых
систем иа алгебрах Ли 281
§ 50. Уравнения Эйлера на алгебрах Ли, возникающие в задачах матема-
тической физики 281
§ 51. Уравнения Эйлера на полупростых алгебрах Ли 288
§ 52. Уравнения Эйлера на разрешимых алгебрах Ли 294
§ 53. Уравнения Эйлера на неразрешимых алгебрах Ли с нетривиальным
радикалом : 299
§ 54. Интегрируемые системы и симметрические пространства 304
§ 55. Коммутативные подалгебры универсальной обертывающей алгебры 316
ЧАСТЬ 3
ГЕОМЕТРИЧЕСКИЕ И ТОПОЛОГИЧЕСКИЕ СВОЙСТВА
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Глава 10. Качественная топологическая теория интегрируемых систем на
симплектяческнх многообразиях 325
S 56. Элементы теории Морса 325

446 ОГЛАВЛЕНИЕ
§ 57. Классификация трехмерных поверхностей постоянной энергии
интегрируемых систем 333
§ 58. Граф, естественно связанный с интегрируемой гамильтоновой систе-
мой 346
§ 59. Новый топологический инвариант гамильтоновых систем дифферен-
циальных уравнений, интегрируемых по Лиувиллю 349
§ 60. Построение меченого инварианта интегрируемых систем 366
§ 61. Классификация перестроек торов Лиувилля на многомерных симп-
лектических многообразиях в окрестности бифуркационной диа-
граммы отображения моментов 378
Глава 11. Характеристические классы 396
§ 62. Характеристические классы лагранжевых слоений 396
§ 63. Обобщенные классы Маслова лагранжевых подмногообразий
и симгшектические связности 399
§ 64. Вполне интегрируемая гамильтонова система, торы Лиувилля
которой имеют нетривиальные индексы Арнольда — Маслова 406
Приложение. Нерешенные задачи 411
Список литературы 416
Предметный указатель 439