Г. ФИЛИПС
ДИФЕРЕИЦИАЛЬНЫЕ
УРАВНЕНИЯ
ПЕРЕВОД ПОД РЕДАКЦИЕЙ
И С ДОПОЛНЕНИЯМИ ПРОФ. А. Я. ХИНЧИНА
ИЗДАНИЕ ВТОРОЕ
ГОСУДАГСТВЕННОЕ
ТЕХНИКО-ТЕОРЕТИ ЧЕСКОЕ ИЗДАТЕЛЬСТВО
Москва —1932 — Ленинград

Читатель! Сообщите отзыв об этой книге
(вшш замечания о ее недостатках и
желательных изменениях в следующем издании)
по адресу: Москва, Ильинка, проезд им.
Владимирова, д. 4, Государственное технико-
теоретическое издательство (в секцию
организационно-массовой работы).
Редактор ГТТИ А. Юшкевич. Техредактор А. Архангельский. Ревиз. корректор М. К. Сатал.чин.
Издание сдано в набор 9/1 1932 г., подписано к печати 14/Ш, вышло в csei в алреое в количестве
25 000 эчз.).
Книга отпечатана в Москве в 1-й „Образцовой" типографии ОГИЗ (заказ 83). Печатных листов
в книге 5, типографских знаков в листе 62 .00. Огиз № 36. Статфирмат 62 X 94. Уполномоченный
Главлита № В-6389.
1-я типография Отза РСФСР „Образцовая". Москва, Валовая, 2<5.

ОТ ИЗДАТЕЛЬСТВА.
Настоящее второе издание воспроизводит без изменений первое,
выпущенное в 1925 г. Государственным издательством.
ОТ РЕДАКТОРА ПЕРЕВОДА.
Русское издание этой книги отличается от американского, тем, что
для большинства задач в конце книги указаны более или менее
подробные решения. Все задачи проверены, и замеченные в них недочеты
.исправлены. Все меры переведены в метрические. Наконец, я позволил себе
в двух-трех случаях, где это мне казалось полезным, сопроводить текст
краткими примечаниями.
АЛ А. Хинчин.
Москва,
19 апреля 1924 г.
ПРЕДИСЛОВИЕ АВТОРА.
Настоящая книга имеет целью, с одной стороны, научить читателя
решать наиболее обычно. встречающиеся типы диференциальных
уравнений; с другой стороны, она должна дать изучающему ряд твердых
навыков в решении такого рода задач, где ему самому приходится
составлять те диреренциальные уравнения/ к решению которых сводится
проблема. Ради этой последней цели я включил в текст некоторые
сведения из механики и физики, необходимые для решения предлагаемых
задач.
Самые задачи заимствованы мною из различных источников, среди
которых я упомяну курс анализа проф. Е *В. Wilson и собрание
математических сведений для химиков, составленное проф. W. К. Lewis и
F. L. Hitchcock.
tr * ,ля ч Г* Филипс.
Кэмбридж (Macca4vceTC),
15 февраля 1922.
I*

бГЛАВЛЕНИЁ.
Стр.
От издательства и от редактора перевода •. . /ТТ . . . . • 3
Предисловие автора —•
Глава первая. Уравнения первого порядка. Случай, когда
переменные разделяются.
1. Определения 5
2. Раздечение переменных* * —
3. Различные формы решений 6
4. Соотношения, содержащие производные 7
5. Определение постоянных 8
6. Соотношения, содержащие диференциалы 10
7. Истечение воды из отверстия 11
8. Уравнение сплошности 12
9. Распространение теплоты 13
10. Процессы второго порядка 15
Задачи • . 1э
Глава вторая. Другие типы уравнений первого порядка:
11. Уравнения в полных диференциалах 20
12. Интегрирующий множитель 21
13. Линейные уравнения 22
14. Уравнения, приводимые к линейным 23
15. Однородные уравнения • 24
16. Замена переменных 26
17. Системы ураьнений 27
Задачи 29
Глава третья^ Некоторые типы уравнений второго порядка.
18. Уравнения, непосредственно интегрируемые 31
19. Уравнения, не содержащие у ;• —
20. Уравнения, не содержащие х . 32
21. Изгибание балок 34
22. Равновесие каната • 35
2 ч Прямолинейное движение материальной точки 37
24. Движение центра тяжести . 39
25. Криволинейное движение в плоскости —
26. Вращение вокруг неподвижной оси 43
27. Соединение поступательного движения и врящения 44
Задачи г 46
Глава четвертая. Линейные уравнения с постоянными
коэфицпентами.
28. Уравнения высших порядков 49
29. Линейные уравнения с постоянными коэфициентами —
30. Однородные уравнения 51
31. Неоднородные уравне «ия 53
32. Системы линейных уравнений 5S
33. Колебательное движение . 57
Задачи 59
Ответы и решения 61

ГЛАВА ПЕРВАЯ.
УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА. СЛУЧАЙ, КОГДА ПЕРЕМЕННЫЕ
РАЗДЕЛЯЮ IСЯ,
1. Определения. В настоящей главе мы4 будем рассматривать
проблемы, в которых участвуют две переменных величины, причем одна из них
является функцией от другой.
^Часто случается, что постановка проблемы дает возможность
составить уравнение, содержащее диференциалы или производные данных
переменных.
Такого рода уравнение называется диференциальнымуравне*
ни ем. Так, уравнения
(х2 -f у2) dx -f 2 ху dy = 0
и
dx2 dx
суть д* ференциальные уравнения.
Решением данного диференциального уравнения называется всякое
соотношение между переменными, обладающее тем свойством, что если
из этого соотношения мы определим производные (или диференциалы) и .
подставим их в данное диференциальное уравнение, то последнее обра»
тится в тождество.
Так, соотношение
У = х* — 2х (1),
есть решение второго из написанных уравнений; ибо, подставляя в «это ,
урарнение х2 — 2х вместо у, мы обратим его в тождество.
Уравнение, содержащее производные (или диференциалы) не выше
'первого порядка, называется уравнением первого порядка. Вообще
порядком диференциального уравнения мы называем порядок наивысшей'
из производных (или диференциалов), встречающихся в данном ура* *
1внении.
2. Разделение переменных. Если диференциальное уравнение имеет
вид:
f1(x)dx+f2(y)dy^0f (2a)
где первое слагаемое „левой части содержит только х и dx, а второе —
только у и dy, то говорят, что переменные разделяются. Решение
такого уравнения, получаемое непосредственно интеграцией, есть
J/, (х) dx -f J/, (у) dy ^ с, (2Ь)
где с &$тъ постоянная интеграции,

ГЛАВА I. УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
Так как каждая интеграция должна совершаться по одному только
переменному, то в случае, когда переменные не разделяются, мы этим
путем не получим решения данного уравнения. Так, например, в случае
уравнения
£аУ + (1 —y)dx = 0
мы не можем найти решения непосредственной интеграцией, ибо,
например, член х dy не допускает интеграции. Однако делением мы легко
приводим это уравнение к виду:
t^- + --0, (2с)
1—у 1 х
в. котором переменные разделяются Отсюда мы находим решение
In* — In (1 —у) —с.
Вообще в уравнении типа
Mdx-{-Ndy = 0
переменные могут быть разделены, если каждая из функций Му N
зависит только от одного из переменных, или яв яется произведением
множителей, каждый из которых зависит только о г одного из переменных.
3. Различные формы решений. Полученное нами решение •
lnx — ln(l—y)=c (За)
может быть написано в виде:
In = с9
откуда
х с
1— у~е ~
При этом, так как и есть произвольное постоянное, то и k есть
произвольное постоянное. Поэтому решение может быть также написано в
виде:
х=с(\—у), (ЗЬ)
где с — произвольное постоянное. Мы также можем написать его в виде:
1—у==«, (Зс)
или еще
у — 1=сх. (3d)
Каждое из соотношений (За), (ЗЬ), (Зс) и (3d) может служить
решением уравнения (2с); но, раз меется, с в этих соотношениях имеет
различное значение, так что мы не имеем права одновременно
пользоваться двумя из них.
Пример. Решить уравнение
(1 -j-JC*) dy — xydx = 0.

СООТНОШЕНИЯ, СОДЕРЖАЩИЕ ПРОИЗВОДНЫЕ
Разделяя переменные, приводим уравнение к виду:
dy х dx
У~Г+Т2_ '
откуда
\ъу —~- In (1 -f- л2) = const,
или, так как всякое постоянное есть логарифм некоторого другого
постоянного, то
lny-^-ln(l-{-x2) = \nc,
откуда
у = с/\+х*.
Это решение может быть записано иначе в одном из следующих
видов:
Упражнения.
Решить уравнения:
1. Xg х sin2 у dx -f cos2 x ctgy dy = 0.
2. (xy* + x) dx + (y -— л:2у\ dy = 0.
3. (л/2 + x)dx + (x*y — y)dy = 0.
dx
4. Соотношения, содержащие производные. Во многих случаях
бывает, что некоторые из количеств, встречающихся в данной задаче,
представляют собою производные; всякое уравнение, удовлетворяющееся этими
количествами, будет тогда уравнением, содержащим производные, т. е.
диференциальным уравнением.
Пусть, например, наклон кривой в какой-либо ее точке задается как
функция координат х, у этой точки. Так как этот, наклон характери-
dy
зуется величиной —-, то мы можем найти искомую кривую, решая ди-
ференциальное уравнение вида:
£=№, л
Далее, пусть известно, что скорость движущейся частицы есть данная
функция от пройденного пути 5 и времени t. Мы приходим тогда к ди-
ференциальному уравнению
ds л *

8
ГЛАВА I. УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
Вообще, если быстрота изменения некоторой величины х есть
данная функция от х и от времени t, то мы получаем:
dx
dt
=/(*, t).
5. Определение постоянных. Так как постоянная интеграции может
принимать какое угодно значение, то данное диференциальное уравнение
имеет бесчисленное множество решений. Но обычно дело обстоит так,
что нам заранее известна некоторая пара соответствующих друг дру"у
значений независимого переменного и функции. Подставляя э*и значения
в найденное решение, мы определим величину постоянной и получим уже
вполне определенное решение.
Во многих случаях относительно производной известно только, что
она пропорциональна некоюрой данной функции f(xf у). В таком
случае мы получаем диференциальное уравнение вида:
где k — неизвестная постоянная величина. Если при этом нам известны
две пары (хг, ул) и (х2, у2) соответственных значений функции и
независимого переменного, то обе постоянные, k и "с, могут быть найдены
подстановкою этих значений в найденное общее решение.
Таким образом постановка
задачи естественно распадается на
две части. Во-первых, задаются
условия, имеющие место в любое
время или в любой точке. Эти
условия определяют собою
диференциальное уравнение. Во-вторых,
задаются условия, выполняющиеся
лишь в определенных точках иди
в определенные моменты времени.
Эти условия служат для
определения постоянных.
Пример 1. Найти кривую,
проходящую через точку *(2, 3) и
обладающую тем свойством, что
отрезок любой ее касательной,
заключенный между координатными осями, делится пополам в точке
касания (черт. 1).
Пусть Р(х>у) есть середина касательной А В, по условию
находящаяся в точке касания. Тогда, в силу подобия треугольников, мы имеем:
ОА = 2у, ОВ = 2х.
Угловой коэфициент касательной в точке Р(х} у) есть
dy OA у
dx
OB
х

ОПРЕДЕЛЕНИЕ ПОСТОЯННЫХ
9
Это соотношение может быть написано так:
dx , dy
х ' у
в качестве решения мы получаем: !
ху = с.
Так как кривая должна проходить через точку (2, 3), то мы должны
иметь
2.3 = *;
следовательно, уравнение искомой кривой есть
ху=6.
Пример 2. Закон распада радия состоит в том, что скорость
распада пропорциональна наличному количеству радия. Известно, что половина
первоначального запаса распадается по истечении 1600 лет. Найти, какой
процент окяжется распавшимся по истечении 100 лет.
Пусть R есть количество нераспавшегося радия в момент времени t.
dR
Скорость распада измеряется величиною —. Так как она пропорцио-
с**
нальна R, то мы имеем:
dt *К
где k — величина постоянная. Отсюда
— = kdt,
и, следовательно,
\nR-kt-\-c.
Пусть первоначальный запас радия есть /?0. Подставляя £ = 0,
R = R0t мы находим:
1П/?0=:С.
Подставляя найденное значение сг получаем:
При *=1600,
Отсюда
и, следовательно,
1п£ = А/.
In 4-= 1600 А,
In 2
Ю00*

10 ГЛАВА I. УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
Поэтому при /==100 мы будем иметь
100 = —0,0433,
ш* = -.1п2
откуда
1Ьи0
~*= 0,958,
#0
Это показывает, что по истечении 100 лет 95,8°/0 первоначального
запаса сохранится, и, следовательно, 4 2°/0 распаде!ся.
6 Соотношения, содержащие диференциалы. < )бычно бывает легче
установить соотношения между первыми диференциалами переменных,
нежели между самими переменными. Это происходит вследствие того, ч\о,
оперируя с диференциалами, мы можем делать допущения, упрощающие
задачу и вместе с тем не отражающиеся на результатах. Так, например,
поскольку мы рассматриваем только первые диференциалы, небольшой
участок кривой в соседстве какой-либо точки мы можем считать
прямолинейным, а небольшой участок поверхности — плоским, в течение
небольшого промежутка времени dt мы м <жем рассматривать движение
материальной точки, как равномерное, и всякий физический процесс, как
протекающий с неизменною скоростью. Такого рода допущения не
отражаются на правильности результата по той причине, что отношение ди-
ференциалов по определению является пределом отношения приращений;
но по мере того как приращения стремятся к нулю, сделанные нами
допущения выполняются со все большею степенью точности,
неограниченно приближаясь к полной истинности.
Этот способ устанавливать соотношения между диференциалами
приближенным путем часто назыьают диференциальным методом. Как мы
указывали, способ этот при-
П меняется только к диферен-
yS циалам (или производным)
/р первого порядка
Соотношение, содержащее вторые про-
изнодные, вообще говоря,
не может быть найдено
точным, если мы малый участок
кривой считаем
прямолинейным или малую часть
физического процесса
рассматриваем, как протекающую
с постоянною скоростью.
Пример 1. Какую форму
должно иметь зеркало, чтобы
все световые лучи, выходящие из ланной точки /% после отражения
пересекались в другой данной точке F9 (черт. 2)?
Прежде всего, зеркало должно иметь форму поверхности вращения.
В самом деле, в противном случае лучи, выходящие из точки F и
лежащие в некоторой плоскости, проходящей через прямую FF\ после отра-
Черт. 2.

ИСТЕЧЕНИЕ ВОДЫ ИЗ ОТВЕРСТИЯ
1!
жения выходили бы из этой плоскости1 и не могли бы проходить через
точку F'.
Пусть PQ есть какая-либо бесконечно малая дуга. Пусть QS есть
дуга, имеющая центром точку F, a QR—дуга, имеющая центром
точку F\ Мы будем рассматривать треугольники PQS и PQR как
прямолинейные; эти треугольники имеют общую гипотенузу PQ. В силу того,
что угол падения раьён углу отражения, мы получаем:
Следовательно, треугольники равны между собою, и мы имеем:
PS = PR, (6a)
Положим FP — r, F'P = r\ При переходе от Р к Q приращение
величины г есть
dr=PS,
а приращение гг есть
tf/=— PR.
Таким образом равенство (ба) дает нам:
dr = — dr\
откуда /
г + г' = const. . (6b)
Итак, всякая плоскость, содержащая прямую FF9, пересекает зеркало
по эллипсу, имеющему точки F и F1 своими фокусами.
Пример 2. Сумма в 100 руб. помещена в 5°/0 годовых, причем по
условию приращение исчисляется непрерывно (в каждый момент). Через
сколько лет наращенный капитал составит 200 руб.?
Пусть по истечении t лет наращ нный капитал равен А В течение
короткого промежутка времени dt приращение величины А определяется
формулой
dA = 0,05 A dt.
Интегрируя в пределах от 100 до 200, мы получим:
200
t
dA л л_ л
— = 0,05 t
100
i
9
О
откуда '
^=0-^51пГ00 = 13'9леТ-
7. Истечение воды из отверстия. Если бы не происходило потери
энергии, то скорость, с которою вода вытекала из отверстия,
расположенного на расстоянии h по вертикали ниже свободной поверхности,
* Ибо только для поверхности вращения с осью FF' все нормали проходят
через прямую FF\
Прим. пер*

i ■
12
ГЛАВА I. УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
равнялась бы скорости свободно падающего тела, прошедшего путь А,
т. е.
В силу трения и условий, связанных с формою сосуда, эта скорость
в среднем равна
v = c\/r2^ht
где в обычных условиях можно принять приблизительно
с = 0,6.
Пример. В какое время вода,
заполняющая полусферическую чашу диаметра
2 м (черт. 3), вытечет из нее через
круглое отверстие радиуса 0,1 лс9 вырезанное
на дне чаши?
Пусть h есть высота воды в момент
времени t, и
Черт. 3. г = "|Л— (Д — hf
—^радиус круга, образуемого ее свободной поверхностью. Масса воды,
вытекающая-из сосуда в промежуток времени dt% образует цилиндр, высота
которого есть vdt, а основание — круг радиуса 0,1 м. Объем этой массы
есть, следовательно,
*(го)%
dt.
Вследствие этого истечения в с .суде освобождается от воды слой,
приближенно имеющий форму цилиндра, высота которого есть — dh% a
радиус основания г, и, следовательно, объем
— яг2^А = я(Л2 — 2h)dh.
Таким образом мы пслучаем:
г(А2 — 2h)dh = n Iг?Xvdt;
гс«
0,6 |/2<Л
100
dt.
Разделяя переменные, мы находим:
о
t= 37 J \(h* — 2h 2)^ = 35,2
сек.
8. Уравнение сплошности. Если какое-либо вещество, участвующее
в данном физическом процессе, не создается и не уничтожается в
течение этого процесса, то количество этого вещества, помещающееся в
данном объеме, может измениться лишь в том случае, если что-либо
войдет в данный объем или, обратно, выйдет из него через его границу^

РАСПРОСТРАНЕНИЕ ТЕПЛОТЫ J3
Очевидное в этом случае соотношение
приращение = приходу — убыль
называют уравнением сплошности. Если это уравнение составлено в
диференциальном виде, то мы получаем диференциальное уравнение,
позволяющее исследовать изменение количества данного вещества в данном
объеме.
Мы называем концентрацией с данного вещества количество его,
заключающееся в единице объема. Если концентрация равномерна, то
количество вещества в объеме v равно cv.
Пример. В резервуаре объема 100 л находится рассол, содержащий
10 кг растворенной соли. В резервуар втекает вода со скоростью 3 л
в 1 мин., и смесь вытекает из резервуара с такою же скоростью,
причем концентрация поддерживается равномерной (например, посредством
перемешивания). Сколько соли останется в резервуаре по истечении
1 час? *
Пусть количество соли, находящееся в резервуаре по истечении t мин./
есть х. Тогда концентрация будет:
. с=Шкгт1л'
В течение промежутка времени dtt 3df л воды вливаются в резервуар
и bdt л смеси, содержащих dcdt кг соли, вытекают. Отсюда изменение
количества соли в резервуаре характеризуется соотношением
dx=* — 3cdt — — — dt.
100
Количество соли, остающейся в резервуаре по истечении 1 час,
определится поэтому из соотношения
откуда
и, следовательно,
Jf--£b
10 О
Ш^—1,8
х= 1,654 кг.
9. Распространение теплоты. Если на каждой из поверхностей,
ограничивающих какое-либо тело, поддерживать постоянную температуру, то
тело по истечении некоторого времени приходит в стационарное
состояние, при котором температура различна в различных точках тела, но
в каждой отдельной точке не изменяется уже более с течением времени.
Часто бывает, что температура 7* является функцией только одной коор-

14
ГЛАВА 1. УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
динаты, например' х \ В силу закона Ньютона, * в этом случае
скорость, с которою теплота распространяется через площадку Л,
перпендикулярную к оси лг-ов, равна:
где k есть постоянная величина, называемая теплопроводностью данного
вещества. (
Если мы представим себе теперь ряд площадок А таких, что поток
теплоты, пересекаюи.ий одну из них, пересекает и каждую из остальных,
то уравнение сплошности может быть написано в виде:
= const.
(9b)
Если при этом А нам известно как функция от х, то мы получаем
диференциальное уравнение (Ьа), позволяющее определить Г, как
функцию от х. Подставляя в
найденное решение значения х и
Т на двух поверхностях
границы тела, мы определим
величину Q и постоянную инте-
, грации.
Пример. Полый железный
(&=0,14) шар (черт. 4),
имеющий внутренний радиус б см,
а внешний 10 сму находится в
стационарном тепловом
состоянии, причем температура на
внутренней его поверхности
постоянно равна 200° С, а на
внешней 20° С. Найти
температуру на расстоянии г от
центра и количество теплоты, ко-
ЧерТф 4. торое в 1 сек. шар отдает
наружу.
Из соображений симметрии мы можем считать, что теплота
распространяется радиально. На расстоянии г от центра, площадь, через
которую протекает теплота, есть площадь поверхности шара:
А = 4пг2.
Так как между отдельными сферическими поверхностями количество
теплоты остается неизменным, то через две любые поверхности прите%ает
одно и то же количество теплоты; поэтому уравнения (9) дают нам:
— 4л kr2 -— = Q = const.
dr
* То-есть все точки тела, для которых х имеет одно и то же зна ;ение, имеют
одну и ту же температуру.
Прим. пер.

ПРОЦЕССЫ ВТОРОГО ПОРЯДКА
15
Разделяя переменные и интегрируя, мы получаем:
4ттАГ = ^- + с.
г '
Подставляя Г=20, г = 10 и 7=200, г=6, мы находим:
2700
с = — ЮООтгё, Q=10 800ttA, T= 250.
г
Для скорости теплоиспускаиия шара мы получаем:
Q= 10 800п& =4750 кал в 1 сек.
10. Процессы второго порядка. Если мы имеем дело с задачей, в
которой участвуют две независимых переменных величины, х и у, то часто
бывает, что некоторая третья величина, z, пропорциональна как величине
х, так и величине у. Это надо понижать так, что при у постоянном г
пропорционально х, и при х постоянном г пропорционально у. Оба
обстоятельства можно выразить посредством одного соотношения
г = kxy.
Так, например, скорость растворения какого-либо вещества
пропорциональна наличному количеству х нерастворенного вещества, и в то же
время пропорциональна разности между концентрацией с данного
вещества в данный момент и его концентрацией s в насыщенном растворе.
Таким образом мы имеем:
^ = kx(s— с). (10а)
То обстоятельство, что полное количество данного вещества
(растворенного и нерастворенного) остается неизменным в течение процесса,
дает нам уравнение сплош .ости, позволяющее выразить с через х, и,
следовательно, -1- становится функцией второй степени от х. Такого
йг
рода процесс, в котором скорость изменения какой-либо величины х
выражается, как функция второй степени от х, называется процессом
втор ого порядка
Пример. Из некоторого (химически недеятельного) вещества добывают
серу, растворяя ее в бензоле. Найдено, что, пользуясь весьма большим
количеством бензола, удается в течение 42 мин. извлечь половину всего
наличного количества серы. Найти, сколько серы можно растворить в
течение 6 час, если в данном веществе содержатся 6 г серы и если взято
100 г бензола — количество, KOTjpoe при насыщении растворяет 11 г
серы.
Пусть £ есть количество серы остающейся нерастворениой в момент
времени /. Концентрация серы в насыщенном растворе есть
8 = —- г серы на 1 г бензола.

16 •
ГЛАВА I. УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
Для определения х мы поэтому получаем диференциальное уравнение
^ = ftx(0,H —с). (10Ь)
Если взять весьма большое количество бензола, то с становится исче-
зающе малым, и мы получаем:
dx
■=£=**.0,11.
at
А так как при атом в течение 42 мин. растворяется половина
наличной серы, то
42
jf-wuj*
о
откуда
£ = — 0,15.
Если бензола имеется 100 г, то, так как количество растворенной
серы есть б — ху мы имеем:
С~ 100 '
Поэтому уравнение (ЮЬ) мы можем написать в виде:
dx
откуда
= -0,15* (о,11 -Ц„£) —0,0016*(5 + *).
х 360
(—^-тт = — 0,0015 [ dt
и, следовательно,
откуда
11л:
1П6^+5) = -2'7'
;е = 0,19г.
Это и есть количество серы, остающейся нерастворенной по истече-
нии 6 час.
Задачи*
1. Найти уравнение кривой, для которой отрезок касательной между точкой
касания и осью jc-ob делится пополам в точке пе»ч сечения с осью у-ов.
2. Найти крив\ю, проходящую через точку (2, 0) и таиую, что о резок
касательной ме*ду точкой касания и осью у ов имеет постоянную длину 2.
3 В культуре пивных дрожж й быстрота прироста действующего фермента
пропорциональна наличному его количеству. Если это количество удваиьается в
течение I час, то во сколько раз увеличится оно в течение 2*/а ча*\?

ЗАДАЧИ
17
" 4. Активность некоторого радиоактивного отложения пропорциональна
скорости своего уменьшения. Найти зависимость этой активности от времени, если
известно, что в течение 4 дней она уменьшилась вдвое.
5. Замедляющее действие трения на лиск, вращающийся в жидкости,
пропорционально угловой скорости вращения. Найти зависимость этой угловой
скорости от времени, если и^ьестно, что диск, начавши вращаться со скоростью 100
об/мин по истечении 1 мин. вращается со с ко i остью 60 об/мин.
6. В силу закона Ньютона, скорость охлаждения какого-либо тела в
воздухе пропорциональна разности между температурой тела и температурой
воздуха. Если температура возд>ха равна гО°С и тело в течение 20 мин охлаждается
от 1( 0 до 60°, то через сколько времени температура его понизится до 30°?
7. Некоюрое вещество преобразуется в другое вещество со ско остью,
пропорциональной количеству непреобразоьачного вещества. Если количество
первого есть 31,4 г по истечении 1 час и 9,7 г по истечении 3 час, то определить:
1) сколько вещества было в начале процесса и 2) через сколько времени после
начала процесса остане.ся лишь 1°/0 первоначального количества.
8. Доказать, что для тяжелой жидкости, вращающейся около вертикальной
оси, свободная поверхность имеет форму параболоида вращения. (Пользоваться
тем, что равнодействующая силы тяжести и центробежной силы нормальна к
поверхности.)
9. Найти кривую, обладающую следующим свойством: если через любую ее
точку провести прямые параллельно осям координат до встречи с этими осями,
то площадь полученного п шмоугольника делится кривою на две части, одна из
когопых вдвое больше другой.
10. Найти форму зеркала, отражающего все лучи, выходящие из одной
данной точки, параллельно одному и тому же направлению. (Принять за начало
координат источник света и за направление оси *-ов — направление отраженных
лучей. Пользоваться в качестве переменных координатою х и полярною коорди-
наюю г.)
11. гЬйти форму зеркала, отражающего пучок лучей, стремящихся сойтись
вводной точке, так, что после отражения все лучи пересекаклся в некоторой
другой точке.
12. Некто имеет возможность скопить ежедневно 5 руб. и помещает
непрерывно свои сбережения из 6<70 сложных годовых. Через сколько времени он
будет иметь 2)000 руб.?
13. Ежегодный доход некоторого лица составляет s руб. Если оно помещает
свои доходы непрерывно из 6% сложных годовых, то через сколько времени
годовой прирост накопившегося капитала составит s руб.?
14. Э астичный шн^р длины / под действием натягивающей силы F получает
прирашеше длкны klFt где &—постоянная величина. На скочько увеличится
длина шнура под действиемвего собстаенного веса ш, если подвесить шнур за
один конец?
15. Та же задача при условии, что к нижнему концу шнура подвешен груз
веса Р.
16. Допустим, что в вертикальном воздушном столбе давление на каждом
уровне обусловлено давлением вышележащих слоев. Найти зависимость давления
от "ысоты, если известно, чго на уровне моря это давление равно 1 кг на 1 см*
и 0,92 кг на 1 см2 на высоте 500 м. (Пользоваться законом Бойля-Мариотта,
в силу которого пчотность газа пропорциональна давлению.)
17. Если движение воздуха от одного уровня к другому совершается
адиабатически, т. ve. при этом теплота не приобретается и не теряется, то
p = Ajp*, n ==1,4,
где р — давление, р — плотность и k — постоянная. Допуская адиабатический
характер распространения воздуха, найти высоту атмосферы, если на уровне моря
плотность воздуха составляет 0,0013 г на 1 см*, а давление 1 кг на 1 см\
13. Коэфициент трения между воротом и лежащим на нем ремнем равен р.
Показать, что между натяжениями Г4 и Г2 в концах ремня существует
зависимость
Г2=7>*,
Где а есть угловое расстояние концов ремня.
2 Филипс. Дпфсфевциадыше уравнения.

18 ' ГЛАВА I. УРАВНЕНИЯ ПЕРВОГО ШРЯДКА
19. При больших скоростях центробежная сила уравновешивается давлением
ремня на ворот. HaftiH зависимость между нагяжениями в концах ремия, если
скорость равна с, а вес единицы длины ремня равен w.
!l0. Конец вертикального вала радиуса а поддерживается плоской подпоркой.
При новой (неиЗношснной) подпорке все ее части испытывают одинаковое
давление р г на 1 см*. Вычислить полную работу трения при одном обороте вала,
допуская, что коэфициент трения равен р.
С течением времени подпорка изнашивается у краев несколько более, нежели
у центра. В конечном счете давление распределяется так, что дальнейшее
изнашивание становится одинаковым во всех точках подпорки. Допуская, что
изнашивание в данной точке пропорционально работе трения, отнесенной к единице
площади, помещенной в данной точке, найти закон распределения давления и
показать, что работа трения при одном обороте вала в случае изношенной
подпорки составляет % аналогичной работы в случае новой подпорки.
21. Допуская, что плошость воды, находящейся под давлением р г на
1 см* равна 0,9 (1 + 0,00000005/?) г на 1 см\ показать, что поверхность океана
глубины 7500 м лежит на 96 м ниже, чем если бы вода была несжимаема.
22. Цилиндрический резервуар с вертикальною осью имеет 6 м высоты и
4 м в диаметре. Во сколько времени вода, заполняющая резервуар, вытечет из
него через круглое отверстие радиуса 4/*2 м> сделанного в дне?
23. Та же задача в предположении, что ось цилиндра горизонтальна.
24. Два вертикальных резервуара, каждый нз которых имеет 4 %м высоты и
4 м в диаметре, поставлены рядом и соединены у дна короткой круглой трубкой
диаметра % м. Если вначале один резервуар наполнен водою, а другой — пуст,
то по истечении какого времени вода будет находиться в них на одном уровне?
Принимается, что скорость протекания воды через трубку определяется как
скорость воды, вытекающей из отверстия под тем же давлением.
25. В резервуар глубины 4 м, имеющий в поперечном сечении квадрат со
стороною 6 м, втекает вода со скоростью 10 м* в 1 мин. В какое время
резервуар-будет наполнен, если в то же время вода вытекает из него через
квадратное отверстие стороною в *д2 м% имеющееся в дне?
26. Найти время, в течение которого вся вода вытекает из конической
воронки, если известно, что половина воды вытекает в 2 мин.
27. Вертикально стоящий резервуар имеет в дне небольшую течь. Предпола*
гая, что скорость истечения воды пропорциональна давлению, найти в какое время
вытечет половина воды, если известно, что Vio ee вытекла в течение первых суток.
Ь8. Резервуар содержит 10Э л рассола, содержащего 10 кг растворенной
соли. Вода вливается в резервуар со скоростью 3 л в 1 мин., и смесь вытекает
из него со скоростью 2 л в 1 мин., причем концентрация поддерживается
равномерной посредством перемешивания. Сколько соли содержит резервуар по
истечении 1 час?
29. Дно резервуара, вместимость которого 300 Л, покрыто смесью соли и
нерастворимого вещества. Допуская, что скорость растворения соли
пропорциональна разности между концентрацией в данный момент и концентрацией
насыщенного раствора (1 кг соли на 3 кг воды), и что данное количество чистой воды
растворяет */з кг соли в I мин., найги, сколько соли будет содержать раствор
по истечении 1 час.
30. Во фляжку вместимостью 1 л по одной трубке втекает кислород, и смесь
его с содержавшимся во фаяяке воздухом вытекает через другую трубку
Допуская, что концентрация остается равномерной и что воздух содержит 21%
кислорода, наЙ1И, каков будет процент кислорода во фляжке после того, как сквозь
нее протече! 5 л газа.
31. После собрания воз!ух в зале вместимостью 10 800 м* содержит 0,12%
С02 Сколько мг воздуха, содержащего 0,01% С02, надо ежеминутно доставлять
в зал, чтобы по истечении 10 мич. содержание углекислоты в нем было 0,05%?
32. Человек в среднем дышит 18 раз в 1 мин., выдыхая каждый раз 2000 см*
воздуха, содержащего 4% С02. Какой процент углекислоты будет содержать по
истечении шлучаса воздух аудитории вместимостью 40Э мг, если в ней
находятся 50 человек, и если вентиляторы доставляют в 1 мин. 40 л*3 свежего
воздуха? (Свежий воздух содержит 0,04% С02.)
33. В то товое помещение вместимостью 10 000 м* втекает через вентиляторы
в 1 мин. 1000 м* свежего воздуха, содержащего 0.04% С02. В 9 час. утра в

ЗАДАЧИ
19
помещение входят служащие, и через полчке* со ержание С02 в возтухе повы-
maeicfl ло 0,lz%. Какой процент С02 можно ожидать в воздухе к 2 час. дня?
34. Кирпичная стена (£ = 00015) имее! 30 см толщины. Найти, как зависит
температура от расстояния точки от наружного края стены, если тем -ерагура
равна 2j° на внутренней и 0° на внешней понерчносги С1ены. НаЙ1и т кже
количество тепла, которое стена (на 1 м*) отдает наружу в течение суток.
35. Паропроюдная труба диаметром 20 см защищена покровом из магнезии
толщиною 10 см (&^0,''00i7) Допуская, что труба имеет темпе агуру 160°С, а
внешняя поверхность покрова 30° С, найти распределение температуры внутри
покрова, а также количество тепла, отдаваемого трубою наружу в течение суток
на протяжении 1 м
66. Проволока, сопротивление которой составляет 0,1 ома на 1 см длины,
помещена внутри цилин фической цементной грубки внутреннего радиуса 0,5 см
и внешнего радиуса 1 см Пропуская через? провочоку ток в 5 ампер, нашли,
что разность температур внутренней и ьнешней поверхности трубки составляет
125° С. Найти теплопроводюсть цемента.
37. Количество свега, абсорбируемого при прохождении через тонкий слой
воаы, пропорционально толщине слоя и ьоличеству сгета, падающего на его
поверхность. Если при прохождении через слой то ицины Зм абсо )бируется
половина первоначального количества света, то какая чалъ этого количества дойдет
до глубины 30 м?
33 Влага, содержащаяся в пористом веществе, испаряется в окружающее
пространство со скоростью, пропорциональной количеству влаги в данном
веществе, а также пропорциональной разности между впажно^тью ок ужающего
воздуха и В1ажн01тью воздуха насыщенного. Некоторое коли .ество вещества,
содержащее 3 кг влаги, было помещено в комнате вместимостью 100 л*3, воздух которой
первоначально имел влажность 25° 0 Насыщенный воздух при той же
температуре соде жит 0,12 кг влаги на 1 л*3. Если в течение первых суток вещество
потеряло половину своей влаги, то сколько влаги в нем останется по истечении
вторых суток?
39. В течение какого времени вещество (в задаче 38) потеряет РО*/о своей
влаги, если влажность 25°/0 окружающего воздуха поддерживать постоянной пря
помощи вентиляции?
40. Некото ое количество нерастворимого вещества содержит в своих порах
10 кг com Подвергая его действию 90 л воды, нашли, что в течение 1 час.
растворилась половина содержавшейся в нем соли. Сколько соли ра творилось бы
в течение того же времени, если бы ко шчество ноды было уивоено? Скорость
растворения пропорциональна количеству нераствореннои соли и разности между
концентрацией раствора в данный момент и концентрацией насыщенного раствора
(1 кг на 5 л).
41. Некоторое количество нерастворимого вещества, содержащее в своих
порах 2 кг соли, подвергается действию 30 л воды. Через 5 мин. I кг соли
растворяется. Через сколько времени растворится 99% первоначального количества
соли?
2»

ГЛАВА ВТОРАЯ.
ДРУГИЕ ТИПЫ УРАВНЕНИЙ ПЕРВОГО ПОРЯДКА.
11. Уравнения в полных диференциалах. Уравнение
Mdx-\~Ndy = 0 (11a)
называется уравнением в полных диференциалах, если существует
функции и, для которой
du = Mdx-\-Ndy. (lib)
В этом случае уравнение (Па) может быть написано так:
и, следовательно, его решение будет:
и = с.
В диференциальном исчислении доказывается, что выражение Mdx-\~
-\-Ndy является полным диференциалом тогда и только тогда, если
■*"*" (11с)
Чтобы определить, буяет ли данное уравнение уравнением в полных
диференциалях, мы должны поэтому найти эти частные производные и
посмотреть, будут ли они равны между собою.
Чтобы решить уравнение, необходимо найти функцию и, полным
диференциалом которой является выражение Mdx-\-Ndy. Часто бывает,
что члены уравнения удается соединить в группы, каждая из которых
представляет собою полный диференциал.
Тогда мы находим функцию и, интегрируя каждую группу в
отдельности, и соединяя затем результаты.
Если этого не удается сделать, то решение можно найти, отправляясь
от того обстоятельства, что
ди ял
. ох
Считая у постоянным и интегрируя, мы находим:
u = [Mtdx + f{y):
где постоянная интеграции может зависеть от у.

интонирующий множигьль 21
Эта функция /(у) может быть определена, если диференциал
функции и приравнять выражению Mdx + Ndy Так как при этом d/(y)
содержит только члены, зависящие от одного у, то обычно функцию
/(У) удается найти, интегрируя те члены выражения Ndy,
которые не содержат х. Однако бывают исключительные случаи,
когда этот путь не приводит к правильному результату; поэтому,
полученный ответ следует проверять диференцированием.
Пример 1. (x-\*y)dx -|-(2y-j-.*;)dj/ = 0. Это уравнение можно
написать в виде:
х dx -f- 2y dx -f- (У dx -f- x dy) = 0.
* Следовательно, это есть уравнение в полных диференциалах, и его
решение будет:
*2 + 2y2-f 2ху=ес.
Пример 2. еУйх-\-(хеУ — 2y)dy = 0.
Здесь;
дМ д •
—-тш — 0У = е?9
ду ду
Так как эти производные оказались' равными, то данное уравнение
есть уравнение в полных диференциалах. Поэтому
u={eydx = xey + f(y),
da = e^dx + \хе> + /'( y)]dy,
где f (у) есть производная функции /(у). Сравнивая полученное
выражение с данным уравнением, мы находим:
Лу) = -2у,
откуда
Решением будет соотношение
хеУ — у* = &
Функцию t(y) мы могли бы найти прямо интегрированием
выражения — 2у dy, представляющего собою ту часть выражения
(xey — 2y)dy%
которая не зависит от х.
12. Интегрирующий множитель. Если уразнение
Mdx + Ndy = Q
не есть уравнение в полных диференциалах, то оно всегда может быть
сделано таковым посредством умножения на некоторый множитель, над*

22 ГЛАВА II. ДРУГИЕ ТИПЫ УРАВНЕНИЙ ПЕРВОГО ПОРЯДКА
лежащим образом подобранный. Такого рода множитель называется
интегрирующим множителем.
Так, например, уравнение
, у (1 + ху) dx — х dy = 0
не является уравнением в полных диференциалах.
Но, написав его в виде:
ydx — xdy -\-xy2 dx = 0
и деля на д/*, мы получаем:
У*-**у+хахшв0.
Оба члена суть полные диференциалы, и мы получаем решение в виде:
у ' 2
1
Выражение -г является в данном случае интегрирующим множителем.
Хотя всякое уравнение вида Мdx-\-Ndy*=aO имеет интегрирующие
множители, но не существует общего метода для отыскания этих
множителей.
13. Линейные уравнения. Диференциальное уравнение вида
g + Py = Q, (13а)
где Р и Q суть функции от х или постоянные величины, называется
линейным. Таким образом линейное уравнение есть уравнение первой
степени относительно одного из переменных (в данном случае у) и его
производной. Коэфициентами могут служить какие угодно функции
другого переменного.
Если уравнение написано в виде (13а), то выражение
[Pdx
является для него интегрирующим множителем; в самом деле, по
умножении на это выражение уравнение принимает вид:
[pdxdy , ГР*х „ fР** л
dx ' ^
Левая часть есть производная выражения
[pdx
yeJ
Таким образом решением данного уравнения будет:
Iм* _ [nJPdx
ye"
jW"*+* (13b)

УРАВНЕНИЯ, ПРИВОДИМЫЕ К ЛИНЕЙНЫМ 23
Пример 1.
dx ' х
а+ь=*>-
В данном случае
[pdx= \~-dx = 21nx = lnx*.
Поэтому
[Pdr f .
Интегрирующим множителем является, следовательно, х2. Умножая на
х2 и переходя к диференциалам, мы получаем:
x2dy-\- 2xydx = x*dx.
Решение будет:
x2y = jx* + c.
Пример 2.
(1 -f у2) dx — (ху +у-\~у3) dy=*0.
Это есть уравнение первой степени относительно х и dx* Разделяя
на (1 -\-y2)dy9 мы приведем его к виду:
dx у
Ty~r±J2*~*y'
В данном случае Р есть функция от уу и
vi+y
Умножая на это выражение, мы приводим уравнение к виду:
dx xydy ydy
откуда
7П^~'л+>,+*
или
x=l+y* + cVl+y*.
14. Уравнения, приводимые к линейным. Уравнение вида
Q+Py = Qy», (14)

24 ГЛАВА II. ДРУГИЕ ТИПЫ УРАВНЕНИЙ ПЕРВОГО ПОРЯДКА
где Р и Q суть функции от х, приводится к линейному уравнению
заменою переменного. Деля его на уп9 мы получаем:
Если мы примем
yl~nss=U
в качестве нового зависимого переменного, то уравнение приводится
к виду:
1 — ndx ;
т. е. к линейному уравнению.
Пример.
dy , J2 = у*
dx'T" хУ л*'
Деля на j/3, мы получаем: *
Положим:
Тогда
l=V~*
откуда
<£к ; у dxf
_zdy l^du
У dx*** 2 dx%
Подставляя в данное уравнение, находим:
2dx~T~xU x*'
или
Это есть линейное уравнение, решением которого служит
соотношение
"-«* + "*•
или, так как и—у~%,
1 * • *
15. Однородные уравнения. Функция /(лг, j/) называется однородной
функцией измерения #, если при любом t,

ОДНОРОДНЫЕ УРАВНЕНИЯ ' 25
Так, Y*2-\~y2 есть однородная функция первого измерения, ибо:
\fx4* -f уЧ* = tV*2 + У2.
Легко убедиться, что многочлен, все члены которого имеют одно и
то же измерение я, есть однородная функция измерения я.
Диференциальное уравнение
Mdx + Ndy = 0 (15)
называется однородным, если М и N суть однородные функции одного
и того же изменения. Для того, чтобы решить однородное
диференциальное уравнение, достаточно положить
y = vx,
или
x=vy.
Получающееся при этом новое уравнение будет уравнением с
разделяющимися переменными.
Пример 1. -*
Это есть однородное уравнение первого измерения. Полагая y = vxf
мы приведем его к виду:
откуда.
\V^Xd\~ VX~ Vx2-tv2x2t
dx '
В этом уравнении переменные легко разделяются, и мы получаем
решение
x = c(v^Yl^^).
Заменяя v его значением —, мы после элементарных преобразований
получаем:
Пример 2.
»(2)'+я»*-,-а
dx
Разрешая относительно производной, мы находим:
dy — х-\г\/~хг *■ у2
dx~ у
откуда
ydy + xdxm* ±yx* -f- у* dx.

26
ГЛАВА II. ДРУГИЕ ТИПЫ УРАВНЕНИЙ ПЕРВОГО ПОРЯДКА
Это есть однородное уравнение первого измерения. Однако в данном
случае проще разделить обе части на \fx2-\-y2, и затем интегрировать
непосредственно. Мы получаем:
xdx+ydy
—. = ±dx.
ух* -j-y'
откуда
Ух*-]-у2 = с±:х1
или
у _ съ 4- 2сх.
Так как с можно давать по желанию положительные и отрицательные
значения, то все решения даются соотношением
У* = С* + 2СХ.
16. Замена переменных. Мы решали однородные уравнения, полагая
У
X
и принимая v в качестве нового переменного. Иногда удается привести
уравнение к более простому виду, принимая некоторую функцию от х
и у за новое переменное, или принимая некоторые две функции от х
и у за новые переменные.
Если известно только само диференциальное уравнение, т© часто
оказывается удобным принять за новое переменное какое-либо
выражение, встречающееся в этом уравнении. Так, часто бывает, что перемеы-
dy
иое у встречается только в комбинациях у2 и у -j-. Полагая
dу 1 du
мы получаем более простое уравнение.
Если уравнение получено при решении какой-либо задачи, то удобно
бывает ввести в качестве нового переменного какую-либо из величин,
имеющих важное значение в данной задаче. Так, при решении задачи
о форме зеркала (6) мы ввели в качестве переменных расстояния от двух
точек, имеющих в этой задаче существенно важное значение.
Пример.
Положим х—у~и. Тогда:
dy dii
dx dx9
и наше уравнение принимает вид:
*('-£)--■

СИСТЕМЫ УРАВНЕНИЙ 27
или
dx
Переменные разделяются; решением будет соотношение
откуда
: — 1П - \- С.
2 лг — у -f a '
17. Системы уравнений. Часто приходится иметь дело с двумя дифб-
ренциальными уравнениями
dx dv
д=-№*у)> ^j—AC*.J0. (16)
содержащими две зависимых переменных величины х и у и их
производные по одному и тому же независимому переменному /. Иногда удается
получить алгебраическую комбинацию этих уравнений, содержащую только
одно зависимое переменное, х или у, или какую-либо комбинацию их.
Тогда мы решаем новое уравнение и, чтобы получить полное решение,
подставляем результат в одно из данных уравнений.
Пример 1.
-^ktix-yy, Tt=k2y.
Второе уравнение содержит лишь одно зависимое переменное у. Его
решением будет:
Подставляя это в первое уравнение, мы получаем:
— это есть линейное уравнение; решением его будет:
х = с2е*1* — 1 \ «V.
Пример 2.
dy dx 0
• ш=х~у> ш=2у-
Умножая первое уравнение на постоянную величину я, второе — на
постоянную величину b и складывая результаты, мы получаем:
— (ау + Ьх) = ах\(2Ь- а)у.

28
ГЛАВА 11. ДРУГИЬ ГИЛЫ УРАЬНЕьИИ ПЕРВОГО ПОРЯДКА
Чтобы правая часть этого уравнения отличалась лишь постоянным
множителем от скобки, стоящей в левой части, нужно, чтобы было
а 2Ь — а
Ь а
В частности, это выполняется при # = £=1, и
2£-(У + *) = *+Л
откуда
х-\-у = сге*.
Подставляя выражение
х—сге*—у (17)
в первое уравнение, мы получаем:
— это есть линейное уравнение, решением которого будет:
Подставляя это в соотношение (17), находим?
2
Упражнения.
Решить следующие диференциальные уравнения:
1. (.i** f Ixy — ybdx -H*3 — 2xy— ty)dy»1k
2. x% + y-A
3. (X* + )P)dx + 2xydy=sQ.
4 (x* +y2)dx-~2xydy=zQ.
5 ydx + (x + y)dy = 0.
6. ydx — (x+y)dy = Q.
7. *rfy-r-yd.* = y2d*.
9. *£-**«* .
ia *2rf*~~ 2ду=гЗу.
li. (2xy* — y)dx+xdy = 0.
13. (JC* — I)9*' dy + (Jfi + 3*^}/**—1) <f*3S:0
14. yeydx=*{jP + 2x9>)dy-

ЗАДАЧИ 2Э
15. (хуеу +y*)dx — jfleydy=:Q.
16. %+У = х*.
17. *% — Зу + ^У^О.
18. д: г/jc Н- jf rf>r = д: г/^у —j/ rfjc.
19. (ху* — х) dx + {у + xyi tfy = 0.
20. xdy — у dx-z=Yx*-\- y*dx.
21. (sinx + y) dy + (ycos_x_--x*)dx=zO.
22. л: dy -?y dx = x У x* + y* dx.
23. (1 -f jc2) rfy + (jcy — *2) d* = 0.
24. j/rfjc = (yt — *)rfy.
25# ^^+^2ctgJf = cos^.
26. {x + у — I)dx + (2x + 2y — 3) dy=*0.
27. 3y* j£->»=**.
с
» (£)'-<*+»2+"=°-
31. (2* + 3jp —l)dr-t-(4x + 6;y —5)rfy«a
32. (3y + 3*y + **> dx = (a* -f- 2дсу, dy.
M- df+x=e > m *•
35. £ = ,-2,. 6*-,-*
36. «J-J + J«-*t ff+>—"*
Задачи.
1. Пользуясь прямоугольными координатами, найти фопму зеркала,
отражающего параллельно данному направлению все лучи, выходящие и* данной точки.
2. Допустим, что в примере, помещенном в § 8 1екста, i ытекающая жидкость
протекает через второй резервуар вместимостью 100 л, первоначально
наполненный чистой водой. Сколько соли будет содержать этот второй резервуар по
истечет и 1 час?
3. Обозначая через / силу тока, мы знаем, что электродвижущая сила при
сопротивлении R равна Rit а при самоиндукции L равна L —. Допуская, что
к катушке сопротивления R и самоиндукции L приложена электродвижущая
сила е, изменяющаяся со временем по закону
* = £sin(atf),
где Е и <к> — постоянные величины, найти силу тока / в момент tt если /=0
При *:г=0.
4. Две катушки, сопротивления которых суть /?, и /?2, а самоиндукции
L{ и L2, сое шнены параллельно. Сила тока, получаемого ими совместно,
выражается законом
/=/sin (<*>/).

ЬО ГЛАВА II. ДРУГИЕ ТИПЫ УРАВНЕНИЙ ПЕРВОГО ПОРЯДКА
Найти силу тока в каждом кольие в отдельности и электродвижущую силу
всей системы, допуская, что при * = 0 сила обоих токов равна нулю.
5. Цилиндр, наполненный газом вращается око.«о своей оси с постоянной
угловой скоростью <*>. В конце движение становится стационарным, и вся масса
газа вращается как твердое тело. На основании закона БоЙля-Мариотта и
принимая во внимание центробежную силу, найти закон связывающий давление газа
в данной точке с ее расстоянием от оси.
6 В некоторой химической реакции вещество с разлагается на два вещества,
х и у, причем скорое«ь образования каждого из продуктов разложения
пропорциональна наличному количеству вещества с. Найти зависимо ть х и у от
времени, если в начале процесса £=1, дг = 0, j/ = 0f а по истечении 1 час.
1 1 3
' = "2' Х = -8^ = Т
7. В некоторой химической реакции вещество х преобразуется в вещество
у со скоростью, пропорциональной наличному количеству х\ в то же время
образовавшееся вещество у посредством обратной реакции переходит в вещее\ но х со
скоростью, пропорциональной наличному количеству у. Химический анализ дал
такие результаты:
/ = 0, 3, со
*=10, 6, 5,5
y = Qt 4, 4,5.
Найти зависимость х и у от времени.
8. Преобразование радиоактивных веществ происходит со скоростью,
пропорциональной наличному количеству данного вещее«ва RaB преобразуется в RaC
с такою скоростью, что половина количества RdB оказывается преобразованной
по истечении 27 мин. В свою очередь, половина данного количества RaC
преобразуется в другое вещество в течение' 19,5 мин. Принимая первоначальное коти-
че тво RaB за единицу, найти, какие количества RaB и RaC мы будем иметь по
истечении 1 час.
9. Переходя из среды с коэфициентом преломления р в другую среду
с коэфициентом преломления р', свет преломляется по закону
ц' ^sina
~ц sine"
где в и 0' суть угол падения и угол преломления. Согласно теории Эйнштейна,
гравитационное поле Солнца отклоняет световой луч так, как если бы это была
среда с коэфициентом преломления
где а — постоянная величина, а г—расстояние до центра Солниа. Найти путь
светового луча
10 Допустим, что бактерии размножаются пропорционально их наличному
количес1ву, но в то же время вырабатывают яд, истребляющий их
пропорционально кожчеству яда и пропорционально количеству бактерий. Далее, допустим,
что скорость выработки яда пропорциональна наличному котичеству бактерий.
Показать, что число бактерий сначала возрастает до некоторого наибольшего
значения, а затем убывает до нуля, и в момент t дается формулой
Nss 4Л—
[еы+е-м]*'.
где М—наибольшее число бактерий, и время / измеряется от того момента*
когда N=-M.

ГЛАВА ТРЕТЬЯ.
НЕКОТОРЫЕ ТИПЫ УРАВНЕНИЙ ВТОРОГО ПОРЯДКА.
18. Уравнения непосредственно интегрируемые» Уравнение вида
g-/M (18)
может быть решено непосредственно двумя последовательными интеграциями.
Первая интеграция дает:
Следующая интеграция дает общее решение в виде:
y = ){yWdx} dx + cix + c*-
19. Уравнения, не содержащие у. Разрешая такое уравнение
относительно второй производной, мы приведем его к виду:
2F->(*ii)- <19a)
Примем в качестве нового переменного
р-%- <19ь>
Тогда
&у dp
dx*~ dx '
а потому уравнение (19а) принимает вид:
— это есть уравнение первого порядка, решение которого имеет вид:
p=*F(x. сг),
где сл — постоянная интеграции.

32 ГЛАВА III. НЕКОТОРЫЕ ТИПЫ УРАВНЕНИЙ ВТОРОГО ПОРЯДКА
Подставляя вместо р его значение (19Ь), мы получаем:
dy
откуда
Пример.
<'+*>£+£-•
dy
Обозначая -— через р% мы получаем:
— это есть уравнение первого порядка с разделяющимися переменными.
Решением его будет:
(1+х)р = сг.
Заменяя р его значением -~- и разделяя переменные, мы находим:
ах
. слйх
откуда *
J> —0,111(1+*) + *,.
20. Уравнения, не содержащие х. Такое уравнение может быть
приведено к виду:
%—/(Л Р\ (20а)
где
*-£. (20Ь)
Вторую производную мы можем преобразовать так:
d^y__dp _dp_ d^_ dp-
dx*—dx-dy ' dx"p7ym (20C)
Таким образом уравнение (20а) приводится к виду:
Это есть уравнение первого порядка, которое мы можем решить
относительно р. Заменяя затем р его значением ~-, мы снова полу-

УРАВНЕНИЯ, НЕ СОДЕРЖАЩИЕ X
33
чаем уравнение первого порядка, связывающее у и х. Это уравнение
легко решается, так как в нем переменные всегда разделяются.
Пример.
ydx*y dx^\dx) '
Обозначая -— через р, мы получаем:
<Ру _ dp
dx* ~Pdy'
и данное уравнение приводится в виду:
УР%=У'Р+Р-
Разделяя на р, получаем:
Это есть линейное уравнение первого порядка, решением которого
является соотношение \
Р
откуда
и, следовательно,
%=У(У + 'г)>
х==[ /У lln-f- + ^. (20d)
При решении этого п имера мы делили обе части уравнения на р.
Законность этого вытекает из того, что соотношение
р = 0 -
дало бы нам:
у = *, (20е)
т. е. решени^, содержащее лишь одно произвольное постоянное, в то
время как лы ищем общее решение, содержащее два произвольных
постоянных. Следует отметить, что соотношение (20е) есть решение
данного диференциального уравнения, и притом такое, которое мы не могли
бы получить из общего решения (2ld), давая то или иное значение
одному из постоянных. Такое решение называется особым и в некоторых
задачах имеет важное значение.
Упражнения.
Решить следующие диференциальные уравнения:
1 л*?У-1+х2
d^y dy

34 ГЛАВА Ш. НЕКОТОРЫЕ ТИПЫ УРАВНЕНИЙ ВТОРОГО ПОРЯДКА
<Ру
dx*
=.у.
g + ^o.
d*s
~di*
db
dt*
8. x
d*y
~dx*
■+(2)'
•.c*+i)S-^+^S+*+2eft
»»S-+(£)'•
И. лг2^ + ^- = 1.
rfy 1
19 ** ?!
^' dl*^**'
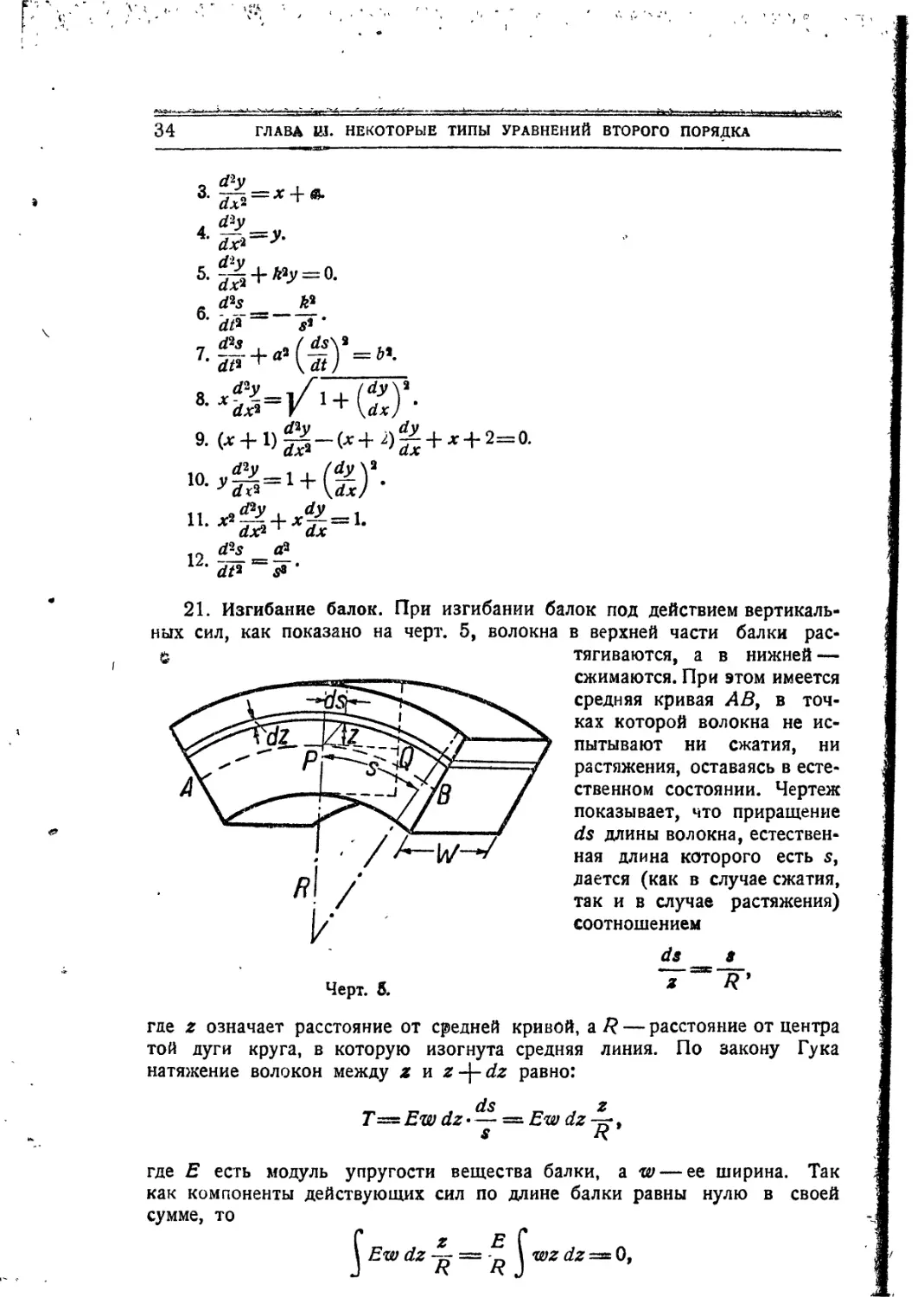
21. Изгибание балок. При изгибании балок под действием
вертикальных сил, как показано на черт. 5, волокна в верхней части балки рас-
$ тягиваются, а в нижней —
сжимаются. При этом имеется
средняя кривая АВ, в
точках которой волокна не
испытывают ни сжатия, ни
растяжения, оставаясь в
естественном состоянии. Чертеж
показывает, что приращение
ds длины волокна,
естественная длина которого есть s,
дается (как в случае сжатия,
так и в случав растяжения)
соотношением
Черт. б.
z
где z означает расстояние от средней кривой, а/? — расстояние от центра
той дуги круга, в которую изогнута средняя линия. По закону Гука
натяжение волокон между z и z-\-dz равно:
T~Ewdz— = #а/fife —,
s f\
где Е есть модуль упругости вещества балки, aw — ее ширина. Так
как компоненты действующих сил по длине балки равны нулю в своей
сумме, то
I Ew dz-p — p \wzdz=*£ О,

ИЗГИБА ИЕ ВАЛОК
откуда следует, что средняя линия проходит через центры тяжести всех
поперечных сечений балки. Момент полного натяжения относительно
перпендикулярной к балке оси PQ равен:
М*
41
wz2dz = ~,
Н
(21а)
где / есть момент инерции площади поперечного сечения относительно
той же оси 1
Пусть (х. у) суть координаты точки Р, причем х мы считаем
измеряющимся вдоль балки. Так как кривизна в обычных случаях весьма
мала, то угловой коэфициент -£- близок к нулю, так что приближенно
d2y
dx*
1
212
НШ
'dx*
Поэтому соотношение (21а) может быть написано в виде!
dx%
(21b)
Величина М, называемая изгибающим моментом балки, должна быть
равна моменту, относительно точки Я, всех сил, приложенных по одну
сторону этой точки, причем моменты сил, направленных кверху, мы
считаем положительными, а моменты сил, направленных вниз,
отрицательными. Чтобы найти форму изогнутой балки, мы должны найти
зависимость М от х и затем решить диференциальное уравнение (2lb). Мы
будем рассматривать только такие задачи, где балка состоит из
однородного вещества и имеет по всей длине одно и то же поперечное сечение.
В этих условиях величины Е и / являются постоянными.
Пример. Найти изгибание балки
длины 2/ с неподвижными концами
при нагрузке, равной w на единицу
длины балки.
Возьмем начало координат в
середине балки. Так как полна нагрузка
равна 2lw, то каждая' из подпорок,
на которых лежат концы балки,
производит давление lw, направленное
кверху. Рассмотрим силы, приложенные вправо от точки Р (черт. 6).
В конце балки мы имеем давление iw, направленное кверху. Его момент*
относительно точки Р равен wl \l—л:)
Другою силой, приложенной к отрезку РА, является нагрузка w (I — х)
этого отрезка. Так как мы предположили, что нагрузка равномерна, то
Черт. в.
* Если предположить это сечение однородным с поверхностной плотностью 1.
Пркм. пер.
3*

36 ГЛАВА III. НЕКОТОРЫЕ ТИПЫ УРАВНЕНИЙ ВТОРОГО ПОРЯДКА
действие этой силы можно заменить., действием силы той же величины,
приложенной к центру тяжести отрезка РА, отстоящему на расстоянии
-~(/— х) от точки Р. Момент этой силы есть — w (/— х) • — (/ — х).
Полный момент всех этих сил относительно точки Р поэтому равен:
w „ _ 1
M = wl (1-х)-
(/-*)*:
.w (P — x*).
Наше диференциальное уравнение поэтому принимает вид:
Первая интеграция дает:
Так как в середине направление балки горизонтально, то при дг = 0,
dx
откуда сг == 0.
Вторая интеграция дает:
1 /Як* . х*у
EIy=tw[-f-~i)+c»
причем £2 = 0, так как балка проходит через начало координат.
Уравнение той кривой, форму которой принимает из01нутая балка,
есть поэтому
1 /Рх* х*\ '
Ely--
\ 2
12
Наибольшее уклонение ^балки от прямолинейной формы
У =
5wl4
2AEI
мы получаем, подставляя х = 1 в» найденное уравнение.
Эта величина обычно называется и з-
гибанием или прогибом балки.
22. Равновесие каната. Пусть ABC
(черт. 7) есть канат, совершенно гибкий,
укрепленный в точках Л и С и
могущий иметь какую угодно нагрузку в
других точках. Возьмем ось #-ов
расположенной горизонтально, а ось у-оз
так, чтобы она проходила через самую
Черт. 7. низкую точку В каната. Рассмотрим

ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ • М '37
часть каната, заключенную менаду точкой В и произвольной точкой
р (х, у) каната. Эта выделенная нами часть должна находиться в
равновесии под действием следующих трех сил:
1) горизонтального натяжения Н, приложенного к точке В и
производимого частью АВ каната;
2) натяжения 7, приложенного к точке Р, направленного по
касательной в точке Р и производимого частью PC каната; ч
3) силы, направленной книзу, равной нагрузке W части ВР каната.
Сумма горизонтальных составляющих этих сил, направленных вправо,
должна в случае равновесия быть равна сумме составляющих,
направленных влево. Точно так же сумма вертикальных составляющих,
направленных кверху, должна равняться сумме составляющих, направленных книзу.
Таким образом
7* cos ер = //,
7sin<j>=lF.
Почленное деление этих уравнений дает:
(22а)
dv W
*»-<£-*• (22Ь)
Так как И есть величина постоянная, то это уравнение допускает
непосредственную интеграцию, KaKv скоро нам известна зависимость W
от х. Бывают случаи, когда W нам неизвестно, но его производная по х
может быть найдена. В таком случае* для определения фигуры равновесия
мы можем пользоваться уравнением
dx% H dx
Решение содержит в себе постоянную величину Н. Мы можем
определить ее, пользуясь известными нам координатами . точки В и концов
каната.
23. Прямолинейное движение материальной точки. Если
равнодействующая всех сил, приложенных к материальной точке массы /я, есть Z7,
то ускорение а этой точки определяется соотношением
F=ma. (23а)
Если точка движется прямолинейно и если s означает ее расстояние
от некоторой неподвижной точки, взятой на траектории, то скорость
движущейся точки определяется формулой
. = |. (23Ь)
а ускорение:
dv d*$ /oq.n
в-лв5?- (23с)
При этом величину s мы можем измерять в любом из двух
направлений траектории; но мы должны считать положительным то направле-

33 ГЛАВА III. НЕкОТОРь.Е ТИПЫ УРАВНЕНИЙ ВТОРОЮ ПОРЯДКА
ние, в котором s возрастает. Величины Z7, v и а будут положительными
или отрицательными, смотря по тому, совпадает ли направление той или
другой из них с положительным и отрицательным направлением
траектории.
Пример Если тело не слишком быстро погружается в жидкость, то
сопротивление приблизительно пропорционально скорости. Найти закон
движения тяжелой материальной точки, погружающейся в жидкость без
начальной скорости
Пусть в течение t сек. точка проходит путь s, который мы будем
считать положительным книзу. Если т есть масса точки и
g—ускорение силы тяжести, то вес точки будет mg, и эта величина будет
положи е 1ььой, ибо сила тяжести направлена вниз. Сопротивление,
направлен ое кверху и пропорциональное скорости, будет равно —kv.
Равнодействующая сил, приложенных к точке, будет поэтому
F=*mg — kv.
Уравнение (23а) в этом случае принимает вид:
dv '
mg— kv= ma-= т —.
я»
Разделяя переменные и интегрируя, мы получаем:
\n(mg— &&) = — t-\-c.
Так как г> = 0 при f=»0, то:
\n(mg) = e.
Вычитая это равенство почленно из предыдущего, мы находим:
ds
Так как v = , то, интегрируя, получаем отсюда:
dt
m2g _.*. t
mgt—ks = ье т +*.
А 1ак как 5 = 0 при *=0, то:
e~ k *
вследствие чего окончательно получаем:
т
n2g ( -h-t \ mo

КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ В ПЛОСКОСТИ
3St
24. Движение центра тяжести. Если М есть полная масса данного
тела или системы тел, a F—равнодействующая всех приложенных к нему
сил, то уравнение
F=Ma (24)
определяет ускорение а его центра тяжести. Другими словеми, центр
тяжести движется, как материальная точка, в которой сосредоточена вся
масса тела и к которой приложены все действующие на тело силы.
Если все точки тела движутся в одном и том же направлении и с
одною и тою же скоростью, то уравнением (24) определяется ускорение
любой точки тела. Если все ючки какой-либо системы (например цепи)
движутся по одному и тому же пути и с одинаковой скоростью и если
F означает составляющую действующих сил по направлению пути, то
уравнением (24) определяется ускорение вдоль траектории.
25. Криволинейное дзижение в плоскости. Если материальная точка
массы т движе»ся как угодно в плоскости или в пространстве, то
соотношение
F=ma
сохраняется; но в этом случае F и а представляют гобою векторы, т. е,
вместе с определенной величиною имею^ и определенное направление.
Чтобы получить соотношение, содержащее количества (а не векторы),
следует рассматривать проекции этих векторов на какое-либо
направление. Так, если проекция лектора F на какую-нибудь ось есть Fx, а
проекция вектора а на ту же ось есть а , то:
Fx*=max.
Допустим, что точка движется в плоскости, и обозначим чер°з х и
у ее прямоугольные координаты. Компоненты ускорения по координатным
осям будут:
<Рх d*y
a*~l№ И a*~"dW
Обозначая компоненты силы по тем же осям через F и
Fy, мы
получим закон движ.ния точки, решая систему диференциальных уравнений
т
d*x
dt*
*F«
т
d*y
№
= FW
(25a)
В задачах, где сила,
действующая на т чку, всегда проходит через
некоторую неподвижную т чку,
бывает иногда более удобно
пользоваться полярной системой координат
с полюсом в этой неподвижной
точке. Обозначая ч.рез Р
движущуюся точку (черт. 8), мы можем
ускорение а этой точи разложить
на две составляющих, из которых
одна, аг, направлена по радиусу-
вектору ОР, а другая, ае» пеРпен-
Черт. 8.

40 ГЛАВА III. НЕКОТОРЫЕ ТИПЫ УРАВНЕНИИ ВТОРОГО ПОРЯДКА-
дикулярна к нему. Веаичины эих составляющих определяются
выражениями
°'=Л'
(dQ\* 1 d ( 9dQ\ ,л-
U)' в«=,7лГл)' (25b)
' 'Обозначая компоненты по тем же направлениям силы, действующей
на точку, через Fr и Fb> мы найдем закон движения точки, решая
систему дифер-.нциальных уравнений
mar = F ]
Для доказательства соотношений (25Ь) следует положить
jt=rcos6, ^ = rsin0
(25с)
и вычислить выражения производных
а
у dt2
(25d)
через г, 8 и их производные по t. Выражения (25d) суть компоненты
ускорения по осям ОХ и OY. Затем для получения аг достаточно сложить
проекции векторов ах и ау на направление О А Подобным же образом
для нахождения аь достаточно взять сумму проекций этих векторов на
прямую, перпендикулярную к ОР.
Пример I. Если электрон, заряд которого равен ef движется со
скоростью v в магнитном поле напряжения //, то он подвергается действию
отклоняющей силы, величина которой есть:
F=±vH*nb
с т> с
где с — скорость распространения света, а ср — угол между направлениями
v и Н (черт. 9). Направление этой силы перпендикулярно к плоскости
векторов v и Н и таково, что правое
вращение1 около вектора F на угол ср
переводит вектор v в направление
вектора Н. Пусть электрон выходит из
начала координат (черт, 10) с начальной
скоростью v0) направленной по оси лг-ов.
Мы поставим себе задачу найти закон
движения электрона, предполагая, что
напряжение магнитного поля Н постоянно и
направлено перпендикулярно к плоскости
Черт. 9. XOY. Так как при таком условии сила,
1 Правым вращением называется такое, при котором человек, стоящий вдоль
оси вращения, головою в ее положительную сторону, видит предметы
перемещающимися от правой своей руки к левой. Прим. пер.

Ъ*гу>^
КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ.В ПЛОСКОСТИ
действующая на электрон, лежит в плоскости XOY, то электо
время остается в этой плоскости. Следовательно, <р = 90° и У Н ВСе
■vH.
Составляющие скорости по осям ОХ и OY суть:
dx dy
dt' dt'
Так как сила F перпендикулярна к скорости v и по величине равна
— vH, то ее слагающие по тем же осям суть:
с
е н^У. е Hdx
с dt с dt
(легко усмотреть из чертежа, что
знаки поставлены те, какие действительно
нужны). Уравнения движения поэтому
получают вид:
m
d*x
eHdy
dt*
с dt f
dly eH dx
m dt* ~~7 dt%
Черт. 10.
Непосредственная интеграция этих уравнений дает:
m
dt
eH -
с
dy eH
причем постоянные интеграции определены с таким расчетом, чтобы при
лг = 0, у —0 мы имели:
dx dy
dt
dt
что соответствует начальным условиям задачи (при / = 0), Деля почленно
ьторое уравнение на первое, мы находим:
dy eHx
dx crnv0 — eHy"
Освобождая от знаменателей и интегрируя, получаем:
еН(х2 -{- у2) — 2 cmvny = 0;

42 ГЛАВА Ш. НЕКОТОРЫЕ ТИПЫ УРАВНЕНИЙ ВТОРОГО ПОРЯ ,КА
cmv,
о
постоянная интеграции равна нулю вследствие того, что у = 0 при х = 0.
Таким образом электрон движется по кругу радиуса
У
.//■
Черт. 11.
г dt V Л/
Пример 2. Материальная точка
массы т притягивается полюсом
с силою, равной —у-, где k —
постоянная, а г — расстояние
движущейся точки от полюса.
Найти закон движения,
допуская, что координаты начального
положения суть (а, 0) (в
прямоугольной системе, начало которой
лежит в полюсе) и что начальная
скорость v0 >—
перпендикулярна к оси *-ов (черт. 11).
Диференциальные уравнения
движения в полярных координатах
суть:
Непосредственная интеграция второго из этих уравнений дает;
В начальный момент
Следовательно,
r dt Cl
dQ
d<d
c, = av0n di
avn
Подставляя это в первое уравнение, мы находим:
аЧ\ — k*
dt*
dr ji
или, гкм.ножая на -г? "*,
dt
dr d*r
— • — dt-
dt*
2«2
axv
k*
dt
dr.
откуда
(dr ,s
(it) ■
'a2v*-
•>(?-;).

щ
ВРАЩЕНИЕ ВОКРУГ НЕПОДВИЖНОЙ ОСИ
43,
причем постоянная интеграции взяга в соответствии с начальными
условиями, т. е. так, что .7=0 при г=а. Деля это соотношение почлен-
dt
но на уравнение
мы получаем:
/ ddy atvl
dr\* a?vl — №
w -
аЧ
Г2 (/* _ а*).
Решая это уравнение и определяя постоянную интеграции так, чтобы
иметь г=а при 0=0, мы, в конце концов, получгем уравнение
траектории в виде:
:asec
Va4l
№
avn
■0
26. Вращение вокруг неподвижной оси.
Пусть данное тело (черт. 12) вращается вокруг
оси, проходящей через точку О
перпендикулярно плоскости А О В. Положение тела может
быть определено величиною угла в между
неподвижной прямой ОА и прямой 08, неизменно
связанной с телом. Узловою скоростью
вращения будет в таком случае величина
09 =»
dd
dt !
(2Ga)
Черт. 12.
а угловым ускорением:
d<a
Hi"'
dP '
(26b)
Пусть F есть сила, лежащая в плоскости ОАВ и приложенная к
телу в точке Р. Момент этой силы относительно оси вращения есть
где / означает нормальное расстояние силы PF от точки О При этом
момент будет положительным, егли сила F стремится увеличить угол 0
Угловое ускорение а удовлетворяет уравнению
Г=/а,
*26с)
где / есть момент инерции данного тела относительно оси вращения, а
Т—равнодействующий момент относительно той же оси всех приложенных
к телу сил. Это соотношение аналогично уравнению (24), причем момент
инерции играет роль массы, а равнодействующий момент — роль силы.

44
ГЛАВА III. НЕКОТОРЫЕ ТИПЫ УРАВНЕНИЙ ВТОРОГО ПОРЯДКА
27. Соединение поступательного движения и вращения. Рассмотрим
движение твердого тела , м-^ссы /И, предполагая, что центр тяжести тела
остается в неподвижной плоскости, и в то же время тело вращается
около оси, перпендикулярной к этой плоскости. В рассматриваемых нами
задачах ось вращения всегда будет осью симметрии данного тела, а
приложенные к телу силы будут расположены в данной неподвижной
плоскости. В этом случае ось вращения неизменно остается
перпендикулярной к этой плоскости.
Движение центра тяжести определяется векториальным соотношением
а вращение — соотношением:
F=Ma.
Т=1а.
(27а)
(27Ь)
В случае, когда мы имеш дело с системой, состоящей из двух или
более твердых тел и движ щейся только что описанным образом, мы
получаем для каждого тела в отдельности
соотношение вида (27а) и соотношение вида
(27Ь). При этом F означает
равнодействующую всех сил, приложенных к данному телу.
Иногда бывает невозможно непосредственно
определить силу взаимодействия между
отдельными телами, входящими в систему.
Обозначая эту неизвестную силу какой-либо
буквой, мы затем убедимся, что число получаемых
нами соотношений позволяет определить как
ускорения, так и эти неизвестные заранее силы.
Пример L Цилиндр массы М и радиуса
г вращается вокруг своей оси. Веревка, к
которой подвешен груз массы ms обернута
вокруг цилиндра (черт. 13). Найти угол, на
который повернется цилиндр по истечении
t сек., если первоначально он находится в
состоянии покоя.
Обозначим через F натяжение веревки.
Момент его относительно оси цилиндра есть
T=*Fr.
Черт. 13.
Момент инерции цилиндра равен:
1
/=— Мг\
Уравнение (26с) получает вид:
--Mr2a = Fr,
или
— Mr a = F.
О)

СОЕДИНЕНИЕ ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ И ВРАЩЕНИЯ 45
На груз т действуют сила Ft направленная кверху, и сила тяжести
mg, направленная книзу. Ускорение а этого груза поэтому
удовлетворяет соотношению
ma = mg—F. (2)
Если в течение t сек. цилиндр поворачивается на угол в, а груз т
опускается на расстояние s, то
откуда
dt*~r dt* '
или
а —га. (3)
Из соотношений (1), (2) и (3) мы получаем:
_ 2mg _ дЩ
а~(М-\-2т)г~ dt2*
Следовательно,
_ mgfi
{М-\-2т)г*
Пример 2. Шар массы N1 и
радиуса г катится вниз по наклонной
плоскости, образующей угол <р с
горизонтам (черт 14). Допуская, что
коэфициент трения равен ja и что
благодаря большому наклону имеет
место скольжение, найти угловое
ускорение шара относительно
горизонтальной оси, проходящей через
его центр тяжести.
Действующая на шар сила
тяжести может быть разложена на две
составляющих
/?=Afgpsincj) и P=M£coscp,
из которых первая параллельна, а вторая перпендикулярна к данной
наклонной плоскости. Сила трения равна:
liP=iiMg coscp,
а момент ее есть:
T—pMgr cos ср.
Момент инерции шара равен:
5
Черт. 14.

46 ГЛАВА III. НЕКОТОРЫЕ ТИПЫ УРАВНЕНИЙ ВТОРОГО ПОРЯДКА
Следовательно,
2
JX Mgr cos cp = -F M&a,
о
откуда
5 jx^coscp
д _ -. .
2г
Задачи.
1. Банка длины 2/ лежит концами на подставках; к середине ее подвешен
груз W\ найти изги ание, пренебрегая весом балки.
2. Найти изгибание балки, гориз .нтально укрепленной одним концом и
несущей груз W на другом конае. Длина балки равна /; весом ее пренебрегаем.
3. Балка укреплена, как в задаче 2, но нагрузка ее равномерна и равна w
на единицу длины. Найти изгибание
4. Най1и изгибание балки, которая концами и серединою лежит на
подпорках, при равномерной нагрузке w на единицу длины.
5. Найти изгибание балки, один конец которой укреплен горизонтально, а
другой лежит на по шорке, при равномерной нагрузке w на единицу длины.
6. Найти изгибание балки, оба конца которой укреплены горизонтально при
равномерной нагрузке w на единицу длины.
7. Вертикальная коюнна длины /, нижний конец которой неподвижно
укреплен, поддерживает своим верхним концом груз Я, под действием которого этот
верхний конец отклонился на рассюяние а <т своего положения на вертикали.
Найти изгибающий момент и форму изогнутой колонны. Подставляя координаты
верхнего конца, убедиться, что наибольший груз, который может выдержать ко-
лонна, есть Р = f — J EL
8. Та же задьча, но при допущении, что концы колонны остаются на одной
вертикали, причем и у нижнего конца колонна может отклониться от
вертикального направления.
9. Канат висячего моста нагружен равномерно, так что на единицу
горизонтального р ссгояния приходится часть моста веса w. Пренебрегая весом каната,
найти его форму.
10. В различных точках гибкой нити подрешены стержни с одинаковыми
поперечными сечениями, но различной длины Нижние концы этих стержней
расположены по горизонтальной прямой. Лопуская, что благодаря частому
расположению стержней нагрузка может считаться непрерывною, найти фигуру равновесия
нити.
П. Найти форму равновесия каната с укрепленными концами, принимаемую
им по! ,1ействи**м собст енной тяжести.
12. Вес 1 км телеграфной пронолоки составляет 40 кг Если укрепленные
кочцы проволоки находятся на расст янии 120 м% а середина опустилась на
3 м, то как велико горизонтальное натяжение в нижней точке проволоки?
13. Арка железнодорожного моста поддерживает горизонтальное полотно
дороги. Как Bi должна быть фор^а арки, для того чтобы в каждой ее точке
действие дорожного полотна свидилось к равнодействующей, направленной по
касательной?
14. Материальная точка массы т движется по прямой линии к центру,
прилги
тягивающему ее с силою -у, где г означает расстояние точки от центра. Если
движение начинается с состояния покоя при г=д, найти время, по истечении
которого точка достигнет центра
15. Могорная л >дка весом 300 кг движется прямолинейно с начальною
скоростью 16 м\сек Допустим, что сопротивление годы пропорционально скорости
лодки и равно 10 кг при скорости I м\сек. Какое расстояние пройдет лодка,
прежде чем ее скорость станет 8 м\сек, и в на^ое время она пройдет это
расстояние?

ЗАДАЧИ 47
16. Материальная точка массы т движется прямолинейно, приближаясь к
центру, отталкивающему4ее с силою, равной №тг, гле г—расстояние точки от
центра. Если движение начинается на рассюьнии а от центра с начальною
скоростью ka, то показать, что точка, неограниченно п{.иближаясь к центру, никогда
его не достигнет.
17. Найти скорость, которую приобретет при падении на землю тело,
падающее с бесконечно большой высоты под действием притяжения земли, обратно
пропорционального квадрату расстояния точки от центра земли.
18. Найти время, нужное телу для того, чтобы упасть на землю с высоты
400000 км (приблизительное расстояние луны от центра земли), если эта
высота исчисляется от центра земли и если радиус земли есть приблизительно
6400 км.
19 Допустим, земля просверлена насквозь дырою, проходящей через центр.
Камень, упавший в дыру, притягивается центром с силой, прямо
пропорциональной расстоянию между ними. Во сколько времени камень пролетит сквозь всю
землю?
20. Тяжелое тело скользит по шероховатой наклонной плоскости, причем
угол наклона равен а, а коэфициент трения ц. Найти закон движения, если
начальная скорость равна нулю
21. Найти закон движения тела, свободно падающего без начальной
скорости, допуская, что сопротивление воздуха пропорционально квадрату скорости и
что скорость имеет своим пределом величину 75 м/сек.
22. Материальная точка брошена вертикально кверху с начальной скоростью #0.
Допуская, что сопрошвление воздуха равно kv\ найти скорость, с которою точка
упадет обратно на землю.
23. Ufnb длины 6 м соскальзывает вниз со стола без трения. Если движение
начинается с момента, когда 1 м цепи свисает, то во сколько времени
соскользнет вся цепь?
24. Та же задача, если цепь висит на крюке, причем при начале движения
по одну сторону длина цепи составляет 8 м, а по другую — 10 м
25. Задача 24, п^и условии, что имеется сила трения, равная весу 1 м цепи.
26. Снаряд вылет «ет из орудия со скоростью 800 м\сек под углом 45° к
горизонту. Найти, пренебрегая сопр01Ивлением воздуха, наибольшую высоту, на
которую п снимается снаряд, и место его падения.
27. Снаряд вылетает из орудия со скоростью vQ под углом а к горизонту.
Найти уравнения движения, предполагая, что сопротивление воздуха равно kv,
где v—скорость, a k — постоянная.
28. Материальная точка притягивается центром, находящимся в начале
координат, с силой, пропорциональной расстоянию. Движение начинается из точки
(а, 0) с начальной скоростью vQp перпендикулярной к оси *-ов. Найти
траекторию.
29. Та же задача в предположении, что точка отталкивается центром по
тому же закону. *
30 Электрон движется в магнитном поле постоянного напряжения Н. Найти
траекторию, если начальная скорость v0 образует угол а с направлением
магнитного поля. (Указ .ния: см. пример 1, стр. .0.)
31. Доказать соотношения (25Ь).
32. Найти орбиту планеты массы м% предполагая, что она притягивается солн-
цем с силою —, где г— расстояние от солнца. Пусть г0 и v0 суть расстояние
от солнца и скорость в момент, когда планета ближе всего к солнцу.
33. Найти орбиту кометы, обозначая через /*0 ее наименьшее расстояние от
солнца и допуская, что на бесконечно удаленном расстоянии скорость обращается
в нуль.
34 Материальная точка массы т притягивается началом координат с силою
&т __ ч
—J- . Найти траекторию, предполагая, что движение начинается с положения
k
(а, 0), с начальною скоростью Щ = rs=, перпендикулярной к оси лг-ов.
35. Круглый диск радиуса а, погруженный в жидкость, вращается около оси,
проходящей через его центр перпендикулярно к его плоскости. Сопротивление

48 ГЛАВА III. НЕКОТОРЫЕ ТИПЫ УРАВНЕНИЙ ВТОРОГО ПОРЯДКА
происходящее от трения, равно kv на единицу площади в каждой точке диска,
причем v есть скорость данной- точки, и k — постоянная. Найти закон движения
при начальной угловой скор сти wQ, допуская, что момент силы трения,
обусловленной осью, равен постоянной величине /С.
36. Шар радиуса г катится со скольжением по наклонной плоскости. Найти
путь, пройденный в течение / сек. центром шара, если угол наклона равен ? и
начальная скорость равна нулю.
37. Бильярдный шар начинает движение со скоростью v0 без вращения.
Найти, в течение какого времени будет продолжаться скольжение, если коэфициент ♦
трения равен ц.
38. Цилиндр массы М и радиуса г катится по поверхности стола. Обернутая
вокруг цилиндра веревка Горизонтально проходит через неподвижный блок, и
к другому концу ее подвешен груз массы т, опускающийся вертикально. Найти
ускорение центра тяжести цилиндра.
39. Та же задача в предположении, что веревка привязана к оси цилиндра.
40. Клинообразный чурбан 'массы Mf с углом наклона в 45°, скользит без
трения по поверхности стола под действием груза массы т, который в свою
очередь скользит без трения по наклонной плоскости чурбана. Найти закон
движения чурбана, если вначале оба тела находятся в покое.

* ГЛАВА ЧЕТВЕРТАЯ.
ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЗФИЦИЕНТАМИ.
28. Уравнения высших порядков. При решении диференциального
уравнения порядка п нам в простейшем случае приходится произвести п
интеграции.
Отсюда понятно, что общее решение уравнения порядка п должно
содержать п постоянных интеграции.
Эти постоянные интеграции называются независимыми между
собою, если они входят в решение таким образом, что мы не можем,
заменяя какую-либо комбинацию' двух или вообще нескольких из них
новой постоянной, уменьшить таким путем их общее число. Так, например,
соотношение
у = сг& + с2 + с3 (28)
на первый взгляд содержит три постоянных. Но, полагая
мы приводим его к виду:
у = с1х2-\-с.
Дальнейшее уменьшение числа постоянных невозможно. Поэтому мы
говорим, что соотношение (28) содержит Лве независимых постоянных.
Когда мы имеем диференциальное уравнение вида
<Py__4[dn~'iy dy
dxn
то можно показать, если функция/—алгебраическая, что это уравнение
имеет только одно решение, содержащее п независимых постоянных
интеграции.
Это решение называется общим.
Всякое решение, которое мы получим из общего, давая постоянным
интеграции какие-либо определенные значения, называется частным
решением.
Некоторые диференциальные уравнения имеют решения, содержащие
менее, нежели п независимых постоянных и в то же врем? не
являющиеся частными решениями. Такие решения называются особыми.
Они представляют, главным образом, теоретический интерес, и потому
мы в дальнейшем не будем на них останавливаться.
29. Линейные уравнения с постоянными коэфициентами.
Диференциальное уравнение вида
dny . dn^1y . . dу , _, ч ,_л ч
4 Филипс. Дпферонциальные уравнения.

9
50 ГЛАВА IV. ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФИЦИЕНТАМИ
называется линейным; этим хотят сказать, что оно есть уравнение
первой степень относительно одного из переменных (в данном случае у)
и его производных. Если при этом коэфициенты а19 ...,ап постоянны,
то мы имеем линейное уравнение с постоянными коэфициентами. Этот
тип уравнений является одним из самых важных в практических
приложениях.
4
' При исследовании этих уравнений удобно символ операции — заме-
нять более коротким символом D. Так, мы будем писать Dy вместо
dy _ d2y
j-% D2y вместо -j~ и т. д.
Уравнение (29а) тогда примет вид:
ф" + аф"-*+...+ ап_ф + an)y -/(*). (29b)
Смысл этого соотношения в том, что, производя над переменным у
операцию, выраженную символом:
D" + a1D"~'L+...+ aa_lD + an, (29с)
мы в результате получаем / (х). Операция, выражаемая символом (29с),
состоит в том, что мы у диференцируем п раз, п—1 раз и т. д.,
помножаем результаты соответственно на 1, аг, а2,... и складываем их
между собою.
Данное диференциальное уравнение мы сопоставим с алгебраическим
уравнением
^+V*~1+---+*«-i'' + a* = 0> (29<0
ямеюшим те же самые коэфициенты, что и данное уравнение (29а), но
правая часть которого есть нуль. Обозначая корни этого
вспомогательного уравнения через rv г8>.«., тп> мы можем написать
многочлен (29с) в виде:
(/)-/-,) (Z)-r2)...(D-r„),
вследствие чего уравнение (29Ь) принимает вид:
(D-гг)(D — r2)...(D-rn) у =/(*). (29е)
Производя над у операцию D—rv мы получаем:
Производя над этим символом в свою очередь операцию (D — г2),
мы находим:
(Z)-r2)(D-r1)y = (D-r!!)(g-V)=g— (,1 + ,2)g + w.
Тот же самый результат мы получили бы, если бы прямо произвели над
у операцию
ф - г,) ф - г„) . D* - (г, + rt) D + V,.

ОДНОРОДНЫЕ УРАВНЕНИЯ
Подобным же образом легко убедиться, что, производя над у все п
операций (D — г,), (D — г2), .., (D — гп) в каком угодно порядке, мы
получим тот же результат, как если бы произвели одну операцию (29с),
являюшуюся их произведением Следует отметить, что все это
справедливо только при условии, что г19 г2,... постоянны. Если бы они были
переменны, то даже соотношение
было бы, вообще говоря, неверно.
30. Однородные уравнения. Линейное уравнение называется
однородным, если правая часть его равна нулю.
Чюбы решить такое уравнение
(D-> + a1D»-i+:..+ an_1D + an)y^0, (30а)
мы разложим символ операции на множители, т. е. напишем уравнение
в виде:
. (D—r,)(D —r,)...(D—Ojr —0.
Функция
у=сге?**
удовлетворяет этому уравнению; в самом деле,
(D — гг) сгег*х = с^е?* — г^е?** = 0,
а следовательно, и
(D-rn){D — rn_1)...{D--rB)iD — r2)(D-r1)cle**-*
= (D-rn)...(D-r2) 0 = 0.
Подобным же образом каждая функция вида
y = c2tr*x> У = свег**,...
представляет собою одно из решений данного уравнения.
Наконец, функция
у = Cyf* + c2er'x +... + <?/«« (ЗОЬ)
также есть решение данного уравнения, ибо результат операции,
произведенной над этой функцией, равен сумме результатов той же операции,
произведенной над функциями
сгеГ*х, с2ег*х,...,
т. е. равен нулю.
Если все корни rv r2,..., гп различны между собою, то можно
показать, что постоянные cv £2,..., сп, входящие в соотношение (ЗОЬ),
независимы, и, следовательно, соотношение (ЗОЬ) есть общее решение
уравнгния^ (ЗЭа).
Если же два из этих корней, например гл и г2, равны между собою,
то выражение
cxeix -f c2er*x = (<?j -{- с2) &*
4*

52 ГЛАВА IV. ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЗФИЦИЕНТАМИ
содержит только одну постоянную сг -f- cv а потому соотношение (ЗОЬ)
содержит менее, нежели л, постоянных, независимых между собою. Но
в этом случае функция xeriX также служит решением данного уравнения;
в самом деле,
(D — г,) хег*х = ггхег1* -\- еГ* — глхет*=ег*х,
откуда
(D — гл) (D — г2) xer*x = (£> — ra)2 xer*x = (D — гг) er*x = 0.
Поэтому при
часть общего решения, соответствующая этим двум корням, может быть
написана в виде:
В более общем случае, когда
часть общего решения, соответствующая этим корням, принимает вид:
(^i+V + ... + cmxm-iy*. (30с)
Если коэфициенты av я2,..., ал суть действительные числа, то
мнимые корни вспомогательного уравнения соединяются в сопряженные
между собою пары; например, если t
то выражения слет*х и с2ег*х в этом случае становятся мнимыми; но в
большинстве задач сумма их оказывается действительной. Можно прямо
заменить их другими выражениями, не заключающими никакой мнимости.
Пользуясь написанными для гл и г2 выражениями, мы находим, что
(Z)-r1)(D-ri) = (D-o)» + p;
но легко показать, что
[(D — а)2 + ф\*** sin $х = 0,
[ (D — а)2 + И • ^ cos [J* = 0.
Поэтому функция
еах[сг cos pjc + с2 sin рд:] (30d)
также будет решением данного уравнения. Поэтому мы можем принять
эту функцию, в к >торой а и $ действительны, за часть общего
решения, соответствующую паре корней
Г = OLzb P*.
Чтобы решить диференциальноеуравнение

НЕОДНОРОДНЫЕ УРАВНЕНИЯ
53 е
обозначим через rlf г2,..., гп корни вспомогательного
уравнения
Если эти корни действительны и различны между,*,
собою, то общее решение есть
у = сгеГ1Х + с2ег*х -{-...+ сяегп*.
Если т из этих корней, например rv ^2,...,гт, равны
между собою, то соответствующая часть общего
решения принимает вид:
(сг+с2х + с3х* + ...+V*-i)^.
Наконец, часть общего решения, соответствующая
паре сопряженных мнимых корней r=a±$i, имеет вид:
еах [сг cos $x -j- c2-sin [5д?].
Пример 1.
Мы можем иначе записать это уравнение в виде
(D2 — D — 2) j/ = 0.
Корни вспомогательного уравнения г2 — г — 2 = 0 суть—1 и 2.
Поэтому общим решением будет:
у=:с1е~х-\-с2е2х.
Пример 2.
Корни вспомогательного уравнения rz-\-r2 — 5г-|-3 = 0 суть 1, 1
й — 3. Часть общего решения, соответствующая двум корням, равным
единице, есть (с2 + с2х) ех. *
Следовательно, общим решением будет:
У — (ci + С2Х)е* + V3*-
Пример 3.
(D* + 2D + 2)y = 0.
Корни вспомогательного уравнения суть —1 Ч- /.
Поэтому а = —1, (J = l, и общее решение принимает вид:
у = е~х [сг cos х-\- с2 sin *].
31. Неоднородные уравнения. Пусть у = и есть общее решение
уравнения

/
ч) §4 ГЛАВА IV. ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФИЦИЕНТАМИ
и пусть, с другой стороны, у = v есть какое-нибудь решение
уравнения
(/у+ei-D,"1+...+eJl.i о+0-v=/W; (31)
в таком случае функция
y = u-\-v (32)
даст решение уравнения (31); в самом деле, производя операцию
над функцией щ мы получаем нуль; а производя ту же операцию над
функцией v9 получаем/(jc). Наконец, соотношение y = u-\-v содержит
п независимых постоянных и, следовательно, является общим решением
уравнения (31).
Слагаемое и называется дополнительной функцией, а
слагаемое v — частным интегралом. Чтобы решить неоднородное
уравнение вида (31), надо, следовательно, сначала решить однородное
уравнение с тою же левою частью, а затем прибавить к его общему
решению какое-либо решение уравнения неодноролного.
Отыскивание частного интефала часто может быть выполнено при
помощи одного из нижеперечисленных правил:
1. Если f(x) — axn-\-bxn'~1-\-...-i-p, то следует положить
у = Ахп + Вхп-*+...-\-Р;
если при этом f(x) делится на хт, то следует положить
Подходящий подбор коэфициентов всегда удается.
2. Если f(x) = ceax, то следует положить
у = Ае**т
Однако, если а есть /^-кратный корень вспомогательного уравнения;.
то следует положить
у = Ахтеах.
3. Когда f(x)~Kacos$x-\-bsm$x, то следует положить
, y = Aco$$x+{-Bsm$x;
однако, если cosfLt и ship* встречаются в числе членов
дополнительной функции, то следует положить
у s=s х [A cos $x -f- В sin §x].
4. Если f(x) = aeaxcos$x-\-beaxsm (5лг, то следует положить
у = Аеах cos $х + Веах sin jbr,
если же члены e**cos[}x и eaxs\n$x встречаются в доиол^тельнрЙ!
функции, то следует положить
у = Хеах [A cos $x -f- В sin (U]

НЕОДНОРОДНЫЕ УРАВНЕНИЯ 55
., , а _ _ _____
Если f(x) содержит члены различных типов из числа рассмотренных
нами, то следует положить у равным сумме соответствующих
выражений. Подставляя таким образом выражение у в данное уравнение? мы
производим все указанные действия и определяем оставшиеся
неизвестными коэфициенты А, £,... с таким расчетом, чтобы уравнение
удовлетворилось.
Общий принцип всех указанных правил состоит в том, что мы
полагаем у равным некоторой линейной комбинации с неопределенными
коэфициентами из всех членов, входящих в выражение функции f(x).
Исключения из этого общего принципа становятся необходимы лишь
тогда, когда некоторые из этих членов входят в состав дополнительной
функции.
Пример 1.
% + «-»* + *■
Частным интегралом, очевидно, будет:
y=i(2x + 3).
С другой стороны, общее решение уравнения
есть
у =- сг cos 2х -{- с2 sin 2x.
Следовательно, общим решение л первоначального уравнения будет:
' 1
у -г с2 cos 2x -|- c2 sin 2х-\~ — (2х -{- 3).
Пример 2.
(D* + dD + 2)y=*=2 + ex.
Положим
у = А-\-Ве*.
Подставляя это выражение в данное уравнение, находим:
2А-\г6Ве* — 2-\-е*.
Следовательно,
2Л=:2, 6S=1
и
AJrBe*=\Jr~e*.
Таким образом общим решением данного уравнения будет;
1
б
у = 1 -|- _- е* -f- V~* + c2e~U'

56 ГЛАВА IV. ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФИЦИЕНТАМИ
Пример 3.
d*y d2y
dx* ' dx2
= хй
Корни вспомогательного уравнения суть 0, 0 и —1. Таким образом
нуль является двойным корнем; поэтому мы полагаем
у = х2(Ах2 + Вх-\-С).
Подставляя в данное уравнение, получаем:
12Ах* + (24А-\-6В)х 4-6£ + 2C = *2,
откуда
или
12Л = 1, 24Л+65 = 0, 6£-f 2С = 0,
Л = Г2' *—4' С=1'
Общее решение есть поэтому (
V=l2*4 — з'^ + ^ + с, + <V* + V*
32. Системы линейных уравнений. Мы будем рассматривать
исключительно системы линейных уравнений с постоянными коэфициентами,
содержащих одно независимое переменное и столько зависимых, сколько
имеется уравнений. При этом мы можем исключить все зависимые
переменные кроме одного, пользуясь процессом, аналогичным исключению
неизвестных из алгебраических линейных уравнений. Единственное
оставшееся зависимое переменное тогда удовлетворяет некоторому линейному
диференциальному уравнению. Решивши это уравнение и подставляя его
решение в другие уравнения, мы последовательно определим и все
другие зависимые переменные.
Если возможно, то следует вести решение так, чтобы, по отыскании
первого зависимого переменного, остальные могли быть найдены без
помощи интеграции. В случаях, когда это не удается, получаемые
постоянные ишеграции могут оказаться не вполне произвольными. Тогда следует
подставить все найденные решения в данные уравнения и таким путем
определить те соотношения, которыми должны быть связаны постоянные
интеграции.
Пример.
d*x о /
s _*,-„.
Обозначая символ операции — короче через Д мы можем представить
данные уравнения в виде:
(D2 — 3)лг— у = е'%
— 2х-{- Dy =q? Q.

КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ
57
Помножая первое уравнение на 2, а второе на D2 — 3, мы получаем:
2(D2 — 3)лг —2у = 2е',
_2(D2 — 3)*-HD2 — 3)Dy = 0.
Складывая эти уравнения почленно, находим:
(£з_ 3D — 2)^ = 2^.
Это есть линейное уравнение с одним зависимым переменным;
решением его будет:
У = (*i + V)*"' + *з*2'—| Л
Подставляя это выражение во второе из данных уравнений, находим:
х = I Dy = I [(с, - с,) - с,<] е-' + V» _ I еК
Упражнения.
i.^-^=o. i5.g_^=^.
dx2 dx dx* ^ ,
4. ^ + , = 0. 18. pL 4%L + 3y = **4nx.
dx* v * dx2 dx *
5.^-2^-3^ = 0. 19. ^-9jr = ^cos*
dx3 dx* dx dx* ■*
dx* $ y dx1 ' dx*
'.g-'2 + * = °- 21.g + 2*+,-..+ ~
H. g-*=*. S-+^=cos^-
l^S+4g + ^x + ^ g + g-L
33. Колебательное движение. Если мы слегка выведем какое-нибудь
тело из положения устойчивого равновесия, то оно, будучи
предоставлено самому себе, будет совершать колебания около положения
равновесия.

68 ГЛАВА IV. ЛИНЕЙНЫЕ УРАВ iEHHfl С ПОСТОЯННЫМИ КОЭФИЦИЕНТАМИ
Пренебрегая сопротивлением среды, мы обычно получаем диферен-
циальное уравнение движения в виде:
Решение этого уравнения может быть написано в виде:
х = A cos (Arf-f 6), (33а)
где А и в — постоянные. Такое движение называется
гармоническим. А называется его амплитудою, а 6 — его фазою. При
полном колебании (взад и вперед) угол kt-\-Q возрастает на 360° или 2тт.
Поэтому период полного колебания есть:
2тт
Т~ к *
Если мы учитываем сопротивление среды, принимая его
пропорциональным скорости, то диференаиальное уравнение движения принимает
вид:
d*x i dx « и л
Решение такого уравнения имеет вид:
х = Ае~** cos ф + в). (ЗЗЬ)
\ Если в момент t тело находится в крайнем положении, то амплитуда
предшествующего колебания есть Ae~at.
Таким образом амплитуда колебаний уменьшается с течением времени.
В некоторых случаях диференциальное уравнение движения
принимает вид: ^
Это уравнение ~— не линейное. Его можно сделать линейным, заменяя
sine Ч£резч в. При малых значениях в такая замена не вызывает
ощутительной ошибки. Так, при в = 5°
sin в = 0,08716,
в = 0,0&7^7,
т. е. погрешность не превышает -^-г величины угла. Даже при 8=10°
Ы)\)
ошибка составляет всего около 0,5%-
Пример.
Маятник^ состоящий из небольшого тела массы т, привешенного
к нити длины /, качается в среде, сопротивление которой
пропорционально скорости (черт. 15). Найти пери д колебания.

ЗАДАЧИ
59
Момент веса маятника относительно точки привеса есть — mglsinQ-
знак отрицателен потому, что при положительном угле 6 момент
стремится уменьшить этот угол. Скорость точки т есть
v = l
Следовательно, величина сопротивления среды есть Ы —.
dt
Момент же этого сопротивления есть —Ы—гг*1\
at
он отрицателен при положительных значениях
-гг-, вследствие чего мы и ставим знак —
near
ред его выражением.
Наконец, момент инерции маятника есть ml2.
Поэтому общее уравнение
/—- = 7
а*
в нашем случае принимает вид:
ml2 -775- = — mgl sin 0 — kl2 —-.
at* at
Заменяя sin в через в, мы получаем:
f& k_d_B g_
dp r m dt* I
Черт. 15.
Решение этого уравнения имеет вид:
kt
% = Ае
2т
COS
['/*
&2
4«*
+ а1
и, следовательно, период колебания равен
2тг
V
g
k*
I
4т*
Задачи.
1. Привести выражение х ~ с{ cos kt + c2 sin kt к виду
х = A cos (kt + e).
Найти формулы, выражающие Лив через, с4 и £2-
2. Привести выр жение x — e-a^CiCostyt + c2sin Щ к виду (ЗЗЬ).
3. Сила, натягивают\я пружину, прополшоналын увеличению ее длины
и равна i кгУ когда длина увеличивается на 1 см. К пружине подвешен груз
ьеса 2 к?. Найти период колебательного движения, которое получит этот 1руз,
если его слегка оттянуть книзу и затем отпустить.

60 ГЛАВА IV. ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФИЦИЕНТАМИ
4. Горизонтальный диск радиуса а и массы М висит на проволоке,
прикрепленной к его центру. Если повернуть диск около вертикальной оси, проходящей
через его центр, на угол 6, то момент кручения проволоки равен Т= kb>
Обнаружено, что диск, будучи повернут на малый угол и зате'м отпущен, совершает
п колебаний в 1 сек. Найти величину постоянной k.
5. Цилиндрический чурбан радиуса 3 м и веса 81 кг стоит вертикально
в воде. Вес 1 л воды равен 1 кг. Найти период колебания, которое получится,
если немного приподнять чурбан и затем отпустить его.
6. Два одинаковых груза подвешены к концу пружины. Найти движение,
которое получит один из этих грузов, если другой оборвется.
7. Тело совершает 90 кол/мин, амплитуда колебания уменьшается вдвое
в течение 15 сек.; найти диференциальное уравнение движения.
8. Тело веса 10 кг подвергается действию упругой силы, стремящейся
вернуть его к положению устойчивого равновесия. Сила пропорциональна смещению
и равна 2 кг при смещении в 1 ^. Сопротивление среды пропорционально
скорости. Амплитуда после трех колебаний уменьшаем в 10 раз. Найти период
колебания.
9. Стержень длины 2/ находится в горизонтальном положении, будучи
подвешен концами к двум шнурам длины /. Найти период колебания, если стержень
повернут на небольшой угол около вертикальной. оси, проходящей через его
середину, и :-атем отпущен.
10. Стержень длины 2/ лежит горизонтально на поверхности цилиндра
радиуса а, перпендикулярно к оси цилиндра, касаясь его сьоею серединою. Если
его слегка толкнуть в вертикальном направлении, он получит колебательное
движение. Найти период колебания.
11. Если емкость конденсатора обозначить через С, то электродвижущая
сила имеет выражение
где /—сила тока. Найти зависимость силы тока от времени в катушке,
подверженной действию постоянной электродвижущей силы Е, если
сопротивление катушки равно /?, величина самоиндукции — L и емкость — С и если
/==A/tfl=s0 при * = 0 (см. задачу 3, стр. 29).
12. Проволока длины / и массы т неподвижно закреплена одним концом
и вращается в горизонтальной плоскости. Найти, на сколько увеличится ее длина
под действием центробежной силы, если под действием силы F, приложенной
к свободному концу, проволока увеличивает свою длину на величину klF.
13. Горизонтальная трубка вращается около вертикальной оси с постоянной
угловой скоростью <о. Шар, помещенный внутри трубки, скользит по ней без
трения. Найти закон его движения, если в начальный момент он находится на
оси вращения и имеет скорость v0 вдоль трубки.
14. Материальная точка массы т притягивается каждым из двух центров
с силою, пропорциональной расстоянию. Множитель пропорциональности равен k.
Расстояние между центрами равно 2Ь. В начальный момент точка находится на
линии соединения центров на расстоянии с от ее середины. Начальная скорость
равна нулю. Найти закон движения.
15. В условиях задачи 14 начальная скорость равна v0 и направлена
перпендикулярно к прямой, соединяющей центры. Найти траекторию.
16. Если ток силы / течет в проводнике сопротивления /?, то разность
потенциалов равна //?. Если электродвижущая сила Е приложена к участку
проводника с величиною утечки G, то потеря силы тока на этом участке равна EG.
Если сопротивление кабеля равно г на единицу длины, а утечка — g на единицу
длины, то каковы должны быть сила тока и электродвижущая сила на одном
конце участка длины / для того, чтобы на другом конце они соответственно
равнялись /0 и Е07
17. Груз веса 4 кг привешен к пружине и увеличивает ее длину на 1 см.
Найти закон движения, которое получит этот груз, если верхнему концу
пружины придать гармоническое движение, закон которого y = $in(Yl00gt), где у
измеряется по вертикали,

ОТВЕТЫ И РЕШЕНИЯ.
Страница 7.
1. tg2jC — Ctg2j/ = C. С
2. l+j,« = *(l-r«). 5* ^^З^Т
3. л:2у2 + *2 _ j,2 — ,. * L
4. v + д = с sin jc. б. х = с . ч
У
Страницы 16—19.
1. Диференциальное уравнение
2xf=y,
dx '
откуда j/2 = ex.
2. Диференциальное уравнение
откуда
, = l*^ + 2In(Iz2£zi?).
3. Диференциальное уравнение — = &* дает нам
в силу начальных условий & = 1п2, а потому по истечении 2'/2 час.
х =2-i лг0 = 5,бблг0.
dR
4. Диференциальное уравнение —- = &/? дает нам
^ = **'
ь „ . In 2
причем в силу начальных условии & = j-, откуда
/г=/?ов-ад733#.
з\<
5. со = 100 ( -=- j об/мин. (Способ решения, как в предыдущей задаче.)
6. Диференциа
начальных условий:
6. Диференциальное уравнение задачи есть — = k(T—20), откуда в
t
1 \20
/ 1 Y
Г-20 = 80 (У'
при Г =30. / = 60 мин. = 1 чао.

62 ОТВЕТЫ И РЕШЕНИЯ
7. 1) 56,5 г. 2) 7,84 час Способ решения — как в предыдущей задаче.
8. Принимая ось вращения за ось j/-ob и обозначая через <о угловую
скорость вращения, получаем для плоского осевого сечения искомой поверхности
диференциальное уравнение
&dx
9. Парабола. Ибо диференциальное уравнение задачи есть
х dy = 2у йк.
10. Параболоид вращения. Диференциальное уравнение
dx — 4r = 0.
11. Гиперболоид вращения. Диференциальное уравнение
dr — Лг* = 0.
12. Около 10 лет. Диференциальное уравнение задачи есть
**-(1вю+1и)л
13. Около ПУа лет. Решение подобно задаче 12.
14. Обозначая через 5 удлинение шнура первоначальной длины х, получаем:
•» .
ds = kdxW——, $ = 0 при л: = 0.
откуда, при дг = /
s = i klW.
15.
(p+iw)
kl.
16. Диференциальное уравнение задачи есть:
dp = — kp dh,
откуда
/? = *-0,00016Л.
17. Диференциальное уравнение задачи есть
пп
dp=z — £--dh.
kn
Высота атмосферы равна 26,923 км.
18. Диференциальное уравнение задачи есть
dT=\iTda.
19. Диференциальное уравнение задачи есть
"-К'--?)*
g
откуда
g h
4
20. Работа трения равна ~ тёсАрр в случае новой подпорки и т&а*у.р — в слу-
о
чае изношенной.

-i-n. if i Г. if-i«"
>-■». л.^> Jf,ft|
ОТВЕТЫ И РЕШЕНИЯ gg
21. Диференциалькое уравнение задачи есть
dp r= — 0,9(1 + 0,00000005/?) rf/i,
где h — вьгота данной массы воды над дном океана.
22. 17,7 мин Решение по схеме § 7 текста (стр. 12).
23 18,5 мин. \
24 7,27 мин.
25. 14,7 мин. Диференциачьное уравнение задачи есть
26. 4,6 мин.
27. 6,6 дней. Диференциалькое уравнение задачи есть
dh = — khdt.
28. 3,9 кг Диференциальное уравнение задачи есть
29. 18Д т. Диференциальное уравнение задачи есть
dt"~*V6 ЗООГ
30. 99,5 °/0. Обозначая через х количество протекшего газа, через ^ —
наличное количество кислорода, имеем:
dy — dx~-ydx.
31. Около 1500 м*. Обозначая через с искомую величину, через у —
количество углекислоты в данный момент, имеем: s:'
*=<(одом-^)л
32. 0,17о/0.
33. 0,124%.
2
34. 7*= -~-л~, 864 000 кал. Решение по схеме § 9 текста (стр. 14).
35. Т =592 -187,6 In rt около 1731000 кал.
36. 0,0005.
37-ЙШ"
38. 0,82 кг. Диференциальное уравнение задачи есть
39. 3 суток.
40. 5,2 кг. Диференциальное уравнение задачи есть
dt RX\ 90 3 J'
41. 32,2 мин.
Страницы 28—29.
1. л з + jfiy _ хуъ — j/3 — с. 7. у (1 + сх) =1.
2. л* == Зху + с. Q ebx
4. Ж*—У*г=СЛГ. ^
5. 2jcy +.у2 =»л 9. 3> = - (СЛГЗ~~ *
^ * , 'Л 3
,у ^ 10. у=сх*е *,

ч
64 ОТВЕТЫ И РЕШЕНИЯ
х 2
И. у = —■ . 25. jy2 = -=■ sin x -f- с cosec2 х.
* х* — с 3
12. y + a = esinx. 26. х + 2у + \п(х + у — 2) = л
£ 27. у* = сех — л: — 1.
13. ** + 4у (х*- 1)2 =л .281/-^а 1
14. лг = .у2(* —*->0- ' у—~2 2с'
15. еУ +\пх = с. 29.у = се* или y = c + -jx*-
16. i = л: + 4" + '***• За еЧХ ~ 2^+' — л"
■У ,/ N 31. A: + 2^ + 31n(2jc + 3j/-7) = ^
П. х* = у( --хТ + с). о __£_
W / 32. (х + у)* = схЗе *+У.
18. ln(^-t-^) = 2tg-^ + c. 33. x^^et + cf-t,
20. у=±х*-^. 34. х= *,*-'+с^+1,
11 < ^ = ^-' — ^+1.
21. j/sinAr+-Tj;2 *3 = ,. i i
« J d 35. y=Cie* +c2e*\
22. у—^х^х+с — е-х-с]. L* lf
2 х=4с{е2 +3c2e2.
23. (2j/ — x) V1 + *» = 36. * = <.,*-* + ^-з/,
= С — In (X + J/ 1 -\- X% у = C4£- > + C£2*~3> ~j- cos t.
24. j/4 = 4jcy + с
Страницы 29— 30.
1. Параболоид вращения. Принимая источник света за начало координат
и данное направление за направление оси л>ов, получаем однородное уравнение
(л: — Ух* + у*) dy=zy dx.
2. Зкг. Диференциальное уравнение (линейное) задачи есть
dx = (0,3<?~ о.оз t — 0,03 л:) dt.
3. i= ——т^~^ f# sin ®t"— L® cos wfl + L® e L I •
Диференциальное уравнение (линейное) задачи есть *
#/+ L~t^E sin (o)0.
4. *i = ^2 _Д ^ Г (##2 + ^2<«>2) sin tot + со (Ig/? - R2L) (cos ю* — 7 7 ' A j
где
5. rp~c(e2 — 1), где ^и ft-постоянные.
1 3
6. лг = —(1 — 2-0» ^ = -^ (1 — 2-0. Диференциальные уравнения:
£ = *(1_х-„. |=/(!_,_,).
7. _у = 4,5 (1 — ^-0,7324 о, л: = 10 — _у. Диференциальные уравнения:

ОТВЕТЫ И РЕШЕНИЯ *<\ \ • 65
6. £ = 0,214, С=0,249. Диференциальные /равнения: ?
d-— — kB —'—kB — lC " * '
rf - **' Л —** /с-
10. Диференциальные уравнения (Г—количество яда): ' ''','*
**# кг/ t-л ^7" иг
-=Ы{а-ЬГ), ъ=сЫ,
где л, &, £ — постоянные. *
Страницы 33—34.
I ■ • .
2. jy^ln^ + ^-J-**' Ч ■
3. у = ~-(х + а)*+.с<х+с* .
5. д> = с{ cos (Ъ: -Ь с2). , ч *
■6. gAi4-g* = Т^(c{s-h 2fe*) + -^Д^sin-i f ^ "*~ fe*^ t если Ci<:<k . -
9. j/ = jc + с&е* + £2-
10. ^ = y(**4*-b£i-f-£?-*,*-*,), - _
11. .y = -~- On л:)* -f c{ In д: + ^.
12. CiS*=:a*+(ctt + c&.
Страницы 46—48.
1. Принимая за начало координат середину балки, получаем для точки балки *
<. абсциссою х момент -x-W(l — х). Отсюда диференциальное уравнение
фигуры изгибания есть * ' - *
dУ
Интегрируя и принимая во внимание, что jf=^- = 0 при х = 0,' находим:
f/^I^-i^)
1 Wl*
Наибольшее изгибание (при x = t) равно -^- -щ-.
2. Принимая за начало координат неподвижную точку балки, мы для точки Р
с абсциссою х находим:
Af = — W(l — x)t
и, следовательно,
dx*''
* Ф н я н и с. Диференциальные уравнения.

66
* ОТВЕТЫ И РЕШЕНИЯ
I
dy л л
Интегрируя и принимая во внимание, что у=~-=0 при х = 0, находим:
EIy = ±w(j*-lx*y
1 U7/3
Наибольшее изгибание, при х = /, равно -5- -vnr •
3. Способ решения как в предшествующих задачах. Диференциальное
уравнение -
-откуда
£/у = — |1 (6^2 — 4/JC» + *«).
Наибольшее изгибание, при лг = /, есть ^.р.
4. Примем за начало координат середину балки и исследуем изгибание
правой половины ее. Начальные условия будут: 1) при ^ = 0, .у = 0, -±-=0; 2) при
А" = /, j/ = Q (если обозначить длину балки через 21). Обозначая через klW
неизвестную реакцию правой подпорки, мы для изгибающего момента относительно
точки с абсциссою х получим выражение
M = klW(l — л:) — уС — х)\
и, следовательно,
Интегрируя и определяя Л и обе постоянные интеграции из трех начальных
условий, мы найдем: w
Ely = ~ (— 3/2дг2 + 5/л:3 _ 2л-*).
5. Обозначая через / длину балки и принимая за начало координат
неподвижно укрепленный конец ее, мы видим, что действующие силы и начальные
условия те же, что в предшествующей задаче. Поэтому весь ход решения и ответ
сохраняются.
6. Примем за начало координат середину балки и обозначим ее длину
через 21. Укрепленный конец испытывает реакцию, сводящуюся к силе lw,
направленной кверху, и к паре, которая нам неизвестна, но момент которой ц
относительно точки с абсциссою х есть величина постоянная. Поэтому
М = — f- (/— .*)« ^ */(/—*) + \ь
и, следовательно, ~
*/^ = " ('--*)* + »/(/-*) + !*.
Начальные условия суть: 1) y=j-=Q при jc = 0 и 2) ^ = 0 придг=£
Интегрируя и определяя постоянные, находим:
7. Принимая за начало нижний конец колонны и за ось л*ч>в вертикальную
dy
прямую и полагая р = ■— , получаем:
при начальных условиях: ^ = 0, ~ =0, при лг = 0.

ОТВЕТЫ И РЕШЕНИЯ (ft
После первой интеграции получаем:
откуда
1Ер* = Р{2ау — у*1 *
тйу
у ш.
Интегрируя, находим:
VlEu£ = VPVtoy-)fi.-
У
= «(l—сое j/ jgXj.
л
Покуда колонна выдерживает груз, мы должны иметь х = / при у = а, что дает.
'Л \2
Р = /£
(*)'
8. Способ решения аналогичен предыдущему
v2
— (т)"
9. Решение по схеме § 22, текста (стр. 37). Уравнение (22Ь), если принять за
" начало середину каната, дает:
<1у wx
dx~~ H *
откуда
— wx%
1. е. парабола.
10. Принимая ось лг-ов горизонтальной, и ось у-ов проходящей через
середину нити, имеем:
d*y_ dp _ 1 d\V__
~d&~~P dy — ~H dx—ky'
где P=^f- и к — постоянная величина (ибо W пропорционально площади кри-
» волинейной трапеции, ограниченной сверху линией нити). Отсюда
если у —а при * = 0, то £=-- ка\ отсюда
или
интегрируя, находим:
11. Обозначая через w вес единицы длины каната и через s его длину,
считаемую от нижней точки, мы в данном случае имеем:
W=swf
и, следовательно,
dp* __ djy_ __wds^ шу 2-
dx~~~dx;>~~h'dx~~ НУ ~т~Рь
Интегрируя, находим:
5»

66
ОТЫ'ТЫ м ГЬШЬПУ\>
12. Величину, на которую проволока опускается посредине, мы можем
выразить при помощи формуль? решения задачи 11 так:
3 м=ум — yi^Y С*80 с 4- *-*»« —2) = j- (**>' — *- 30^2== i800c
(приблизительно), откуда
до
Но постоянная с имеет значение —; в данном случае до— вес 1 м
проволоки— есть 0,04 яз, а потому:
//=24 кг.
13. Применяя метод § 22 текста (стр. 37) и беря ось дт-ов горизонтально,
.зидим, что W пропорционально х, вследствие чего искомая форма есть парабола*
14. Диференциальное уравнение задачи есть
d*r №
интегрируя и пользуясь начальными данными, находим:
—.? Г rdr —аХ
~~ k J У а*— г* "" k '
о
15. Диференциальное уравнение задачи есть
300г/гг 1Л .^dx
— - = —10©==— 10 7f
g dt dt9
откуда, пользуясь начальными данными, получим:
£Г=480 —ЗОсг,
при tr = 8 это дает (приблизительно)
дг = 25 м.
Лля отыскания времени, полагаем # = ^т и интегрируем еще раз. Ответ
приблизительно,
г = 2,1 сек.
16. Диференциальное уравнение задачи есть
Интегрируя и пользуясь начальными данными, находим:
—/и
г=ае ,
откуда видно, что г стремится к нулю при неограниченном возрастании L
17. Диференциальное уравнение задачи есть
л* -~ г*;
считая радиус земли за 6350 км, имеем Л = ^6350* км. Интегрируя, находим:

ОТВЕТЫ И РЕШЕНИЯ
6Й
где с=0, ибо v = 0 при r=oo; поэтому
-- =]/"2#-Ь,ЗоО= 11,15 лгл* сек (приблизительно).
, . 18. Диференциальное уравнение то же, что в задаче 17, причем k =s g (6400)4.
Начальные условия: при * = 0, с = 0, г=400 000» А Полагая 6400 = а,
находим, интегрируя
а после второй интеграции:
откуда, замечая, что
—О-зГК-'УЪ
находим:
JQQ122 час.
d2r &
19. Диференциальное уравнение = — &2г, где Л8 = ~qq, дает после
интеграции и подстановки начальных значений
t = - сек S5r 42,3 мин.
k *
20. Так как сила трения направлена противоположно движению и
пропорциональна нормальной реакции, то:
d*s
^8 = £(sina — jxcosa),
откуда
s= -у g(sin a — jxcos a) A
21. Диференцильное уравнение движения есть
d*s dv „ ,0 лч
откуда
1 t 1 —«9
*.
1
так как v = 7b м/сек при /=оо, то'& = ==, и * можем принять равной нулю
Отсюда
rfS ^75—* 75
"вгв7о-т2—гг;
^75-|-^ 75
интегрируя еше раз, находим:

70 ОТВЕТЫ И РЕШЕНИЯ
или, так как $ = 0_при t=Qf
& У 7 '
22. Диференгциальное уравнение движения, когда тело движется вверх, есть
d~s dv , 9
mdt*=mvJs = -mg-kV
при 5 = 0, vz=zVb поэтому интеграция дает
s-~2kn kv* + mg'
При v = 0 получаем налбольшую высоту
т Г kv%\
Затем начинается опускание по закону
mv -г = — mg 4- kv*»
as
Интегрируя и пользуясь начальными данными, находим величину скорости
при падении:
23. Диференциальное уравнение движения есть
начальные данные: s=l при * = 0 и #=-0; представляя
d*s __ rft;
dt^ ~~ V ds
и интегрируя, находим;
Щз + У^-Ц^}/'^,
откуда, при 5 = 6,
' = |/|1п(6 + У35).
24. Диференциальное уравнение движения есть
18^1=^-^(18-*),
или
начальные условия: s =■ 10 при р = 0; интегрируя, находим:
Vg •

ОТВЕТЫ И РЕШЕНИЯ
71
25. Диференциальиое уравнение движения есть
Решая, как в задачах 23 и 24, находим:
*==-jLin{l7 + 4|/T8}.
У g
26. Принимая за начало координат точку начала движения и проводя ось jc-ob
горизонтально в сторону движения, а ось ,у-ов вертикально кверху, мы имеем:
ач ^у_^_а
~dt*~ ' dti~~ §'
при начальных данных: х = у = 0, -- = ^ = 800• cos 45°, при t = 0.
Отсюда, полагая 800«cos45° = a, находим:
x = atf y = — jLfi + at.
Наибольшее значение у принимает при / = --, когда
g
у = 2~^z 16,3 км.
Точку падения получим, замечая, что у = 0 при /= —;< когда
2л* ее
ЛГ = - =5: 65 КЛ£. ч
27. Выбирая расположение осей, как в задаче 26, мы получаем:
d*x udx d*y .dy
л dx dv
при следующих начальных данных: х~у = 0, — = v0 cos a, — = i/0 sin а при
• w* tit
£ = 0. Интегрируя, находим:
mvn cos a f , — — < \
^^(toeSina+ni^l— « «'j-T^t
28. Проекции силы притяжения на оси суть — №х и — №у. Поэтому
при следующих начальных данных: x = at y~Q, -£ = 0, ^~=i>0 при Ы0.
Интегрируя, находим:
тг. е. эллипс.

72
ОТВЕТЫ И РЕШЕНИИ
29. Диференциалькые уравнения движения суть:
d*x Le d*y
начальные условия те же, что в задаче 28. Интегрируя, находим:
т.е. траектория есть гипербола.
30. Пусть электрон выходит нз начала координат. Примем ось дг-ов
параллельной направлению магнитного поля и выберем ось jy-ов так, чтобы вектор %
лежал в координатной плоскости (ху). Обозначая через X, У и Z проекции
действующей силы на координатные оси, будем иметь:
Отсюда
~~~ .' "— с di* ~~ с dt *
d?x
."St**0*
d*y __eHdz
Ш dt*~~ q dt1
d*z eftdZ.
m dP~~~ T dt '
Начальные данные таковы:
dz л dx dy
Интегрируя, находим: ^ *
eN(y2 + z*) — emv0 sin iz = 0,
X = t/0 cos ctf,
т. е. траекторией будет винтовая линия с осью, параллельной направлению
магнитного поля.
32. Принимая центр солнца за полюс, получаем уравнения движения в
полярных координатах:
W/У /* ' г dt\ dt)
d*r
db'
- ^9
Второе из них (на основании начальных условии r~- = t/0 при r=r0) дает
^ Ло£в
dt г2 '
Подставляя это в первое уравнение, помножаем его на .- dt, интегрируем
и замечаем, что -^==0 при r = /o. Находим:
деля это уравнение на возведенное в квадрат предшествующее уравнение,
получаем соотношение, определяющее ( fl J . Извлекая корни, интегрируя и
пользуясь начальными данными, находим окончательно
— а=г --—- -f- ( 5—г 1 COS A,
[го rfuf ) '
т. е. траектория есть коническое сечение, имеющее центр солнца одним из фокусов»

ОТВЕТЫ И РЕШЕНИЯ
7£
33. Тот же прием, как в предшествующей задаче, дает нам здесь
<dr\* 2k с? ,
с
(!
Из начальных условий si = Q при r—rQ и при г = оо. Отсюда, *2 = 0,*ia = 2Лг,_
и, следовательно,
<dr\*__2k 2krp
М)~~ г г* '
с другой стороны,
V dtj г* ~~ г* '
Деля почленно, извлекая корни, интегрируя и пользуясь начальными данными;.,
находим:
2гп
г==
1 -h cos и •
т. е. траектория есть парабола с фокусом в центре солнца. .ф7
34. Тот же прием, как в предшествующих задачах. Начальные данные*
dr Л tfO k
/■=д --- = 0, г ..== •=_ при * = 0.
7 dt ' dt а^\Г2
Уравнение траектории
r=acos0.
та* ' * ' гч
35. Момент инерции диска равен —тр*, где т — его масса- Элементарны иv
момент силы тления есть —kr---r-rdrd%t где г dr d<? — элемент площади диска;,
полный момент есть поэтому
2т: <2
ЛГ, Г 9J k* Adb
и и
Учитывая еще трение оси, находим диференциальное уравнение движения*
•2 Л*~~ 2 й dt *'
Начальные данные суть: е = 0, ^ = <*>o при г = 0. Интегрируя, находим:
36. Пишем уравнение моментов от!юсительно точки соприкосновения шар*
и плоскости. Момент инерции шара относительно этой точки есть
Следовательно, **$
,tm 7 9<т . %
Если обозначить через 5 путь, пройденный центром тяжести шара в течение
t сек., то аз_ d*
dt ~r~dt*
d*s dW 5 .
dIf = rdt* = TZsma>

/
74 ОТВЕТЫ И РЕШЕНИЯ
откуда 5
:14
S^^gttsitKL
37. Уравнение моментов дает при вращении
•откуда
~dt ~~ 2r '
•при скольжении мы имеем:
d*s ds _
В момент, когда скольжение кончается,
ds_ db ^
$г. е.
откуда
t-Ъ..
bg
38. Уравнение моментов относительно мгновенной оси вращения цилиндра
дает: ,
где Р — натяжение веревки, и, следовательно,
mg — F = ma,
где а—ускорение груза т9 или, что то же, верхней точки цилиндра. При этом
а = 2га,
следовательно,
ЗМга = -у Л£д = 4Z7 = 4(mg — та),
откуда ускорение центра тяжести
а 4mg
2 Ш + 6т
39. Тем же приемом получаем для ускорения центра тяжести выражение
Img
ЗУИ -г 2т »
40. Примем направление горизонтального основания чурбака за ось .r-ов, а
ось у-ов возьмем вертикально кверху. Допустим, что груз скользит слева направо.
Обозначая через s абсциссу нижней точки наклонной плоскости, а через хну —
координаты груза т, обозначая, далее, неизвестную силу взаимодействия обоих
«тел, направленную по нормали к наклонной плоскости, через F9 получаем:
т -тггг = г cos 45 ,
at*
т —j- = Fcos 45° — mg.

ОТВЕТЫ И РЕШЕНИЯ 75
Но в каждый момент x + y = s, ^"b^f =:^*»
откуда
2Af 4-/я
4/И -г 2*я
Страница 57.
1. у = С{ 4* £2**-
2. .у == г4£* 4- ^~Sjf-
3. .у = (*! + <**)***.
4. j/ = ££ cos jc 4- ^2 sin x.
5. j; = ^ 4-1^""*"* *+- ^з*3*-
6. у = £4#* 4- tf^r* 4- c$ sin л: 4- cx cos *.
7. y=ex \ct cos jc 4- ^2 sin дг].
S. y^e^^Xyicosy~ xj + c2sin \^-*)J
9. jf = (c4 + c^x 4- ^з-*2)*"*-
0. зг = 2 — x 4- tf^os л: 4- £2 sin *•
1. у = ске** + с*-** — ^х* — -*-.
2. j; = <?4#* —s- (sin л: 4- cos лг).
3. у = сй + С1В* — у** — х-
4. з, = Г1*-*4-^-«*4-^др_Л4-_*и.
5. y = ciea* + ctf-**+
2a
xe'
ax
6- У = (<?i 4- «~ ) sin ад: 4- r2 cos ад;.
7. <y = <r1**+/"T |^2cos(^-^ at) 4-^2sin (X~ xJj~^-5.
8. j; = с te* 4- ^г*3* — у е2* sin др.
9. у = ^ез* _p c2^-^ 4- 37 <?з*(6 sin jc — cos x).
20. у = ct + c*x 4- czx* 4- c4*-* -f j^^- (4 cos 4дг — sin 4дг).
21. y=(cl + CiX+-fxAe-x + ~ex.
22. y — c^t + Cze-t—1, x — eg* —'C&-* — I.
2 <. у = <?4 cos * 4- £2 sin /, л: = (ct 4-£2) cos * 4- (£2 — C\) sin /.
24. д; = c{e-* 4- ^"4 .У = eie^t -t- 3^~3/ 4- cos t
25. д; = с&* 4- л»*""' 4- £3 cos t-\-c^ sin /, 3/ = c^e* 4-c2<?-r — сг cos t — c4sin t»
26. x = ^4-^4-<?,** — y/3 + ^
>f = ^ - (^ + 2c3)t-±(c2 - 1);*- -i*P + ^ <*-''•
Страницы 59—60.
1. A cos^kt 4- в) = A cos б cos &f — A sin в sin kt = £{ cos &/ 4- c2 sin ££
откуда
A cos в = Cj. —- A sin 0 = c%

76
ОТВЕТЫ И РЕШЕНИЯ
и, следовательно,
А = j/V + сД 0 = arc tg (— Й.).
2. Путь решения тот же, что в задаче 1.
3. В состоянии покоя груз в 2 кг увеличивает длину пружины на 0,02 м>
Поэтому, обозначая через х координату груза, отсчи!Ываемую вни$ по вертикали,
от той точки, где находится груз в состоянии покоя, мы получаем:
fg = 2-*(* + 0.02); •
в силу условий задачи k =100, и, следовательно,
0 + 50^=0.
Общее решение этого уравнения есть *
.* = A cos \V50gt + е},
а, следовательно, период колебания равен:
iTbQg 5 r g
4. Так как момент инерции диска относительно оси вращения есть у-
2 dt**
2
то диференциальное уравнение моментов дает: —~~ -^ + ДО = 0.
Решая уравнение, находим период колебания
1
1ак как по условию задачи этот период равен —, то находим:
5. Обозначим через х вертикальную координату центра тяжести чурбана,
отсчитываемую от положения равновесия. По закону Архимеда, равнодействующая
сил, приложенных к чурбану, по величине и по знаку равна:
— «• (33). х-1000 am — 9tu> 1000 кг.
Следовательно,
81 сРх п/чл_ .
— -т^-+ 9000л* = 0.
g at1
Интегрируя, находим период колебания \^
6. Пусть увеличение длины пружины под действием одного груза в
состоянии покоя равно а, и масса груза есть г/и Обозначим через х координату груза,
отсчитываемую по вертикали ог положения равновесия. Тогда
где, очевидно,
Q

ОТЬЫ'ы И ИЬШКмИИ
77
и, следовательно,
dt* ~" а *"
Обшее решение есть
л:= /1 cos (j/^f ^ Н-«) -
Начальные условия дают: д: = л.
--- = 0 при / = 0,
отсюда
д=0, Л=д, и x = acos(y ^-Л.
7. Пусть движепие характеризуется законом
x^Ae-atcosQt + b).
По заданию /ss-r-ss-^-, откуда
£=3*.
Далее,
* 2»
откудя lnJ2
*~* 15*
Диференцируя дважды закон движения, исключая А и 9 и производя вы*
яисления, находим:
5 + 0,092^+88,8^ = 0.
8. Предполагая закон движения в той же форме, как в задаче 7, мы находим
диференцированием
С другой стороны, в силу условий задачи,
gdt*+Kdt + <« — «■
ea + j!»=|.. (I)
Сравнивая, находим:
С другой стороны,
откуда
?
Решая уравнения (I) и (II), находим (5, а следовательно, и
Т = ~ = — 1/ ~ • V\&i)* 4- in* 10
V
9. Уравнение моментов относительно оси вращения есть
з да'

78 ОТВЕТЫ И РЕШЕНИЯ
Заменяя sin & через 0, находим:
dt*^ I U'
откуда
10. Обозначая через 6 угол поворота стержня я пренебрегая малыми
величинами порядка б2, находим для момента инерции стержня относительно
мгновенной оси вращения
т/2
3 '
причем момент сил относительно той же сси есть (с тою же степенью точности)
— agnfi. Составляя дифереьииальное уравнение моментов, находим период
колебания &
11. Мы имеем:
или, диференцируя,
Общее решение есть
Н<
V3ag
dt + Ri+L*=E
Td4i ndi , 1 . л
dt* dt с
... т^,л
i^Ae 21'cos I 2L ^ ' '
Пользуясь начальными данными: * = J idt~0, L ^ = Е при / = 0, опреде-
ляем А и б и находим:
умс — нч^
12. Обозначая через х расстояние какой-либо точки проволоки от
укрепленного конца в положении покоя и через у то же расстояние в состоянии
вращения, мы замечаем, что центробежная сила элемента dx, равна w?y'\Ldx, где у.—
масса единицы длины проволоки, вызывает увеличение длины проволоки, равное
dy — dx. Отсюда
dy — dx — k-y.^ypdx = 02y2 dx,
где
6 = со \rk]i.
Отсюда
. _ dy
йХ~~ 1 + 02^/2'
9 6jtr = arctgey-bC,
где С=0, ибо y = Q при х = 0. Таким образом
Замечая, что ц/~-/я, при д: = /наводим величину растяжения
\ ушю г

ОТВЕТЫ И РЕШЕНИЯ 79>
13. Диференциальное уравнение движения есть
dt* r\
Л йг
Начальные данные: г===0, ^ = ^о при f = 0. Интегрируя, находим:
r — ^le*»* + e- *"П.
2 to ' J
14. Диференциальное уравнение движения есть (если начало координат взяты
в середине расстояния между центрами,) ,
т^ = к{Ь — дг)— Л (* + лг)=г — 2кх.
i
Начальные данные: х = с, ^т==0 при г = 0. Интегрируя, находим:
: = *СОв{|/^*}.
15. Диференциальные уравнения движения (подобно задаче 14) суть:
dlx
mw = -2kxt
Начальные данные: jy=r-^=:0, л:—г, Tt~Vf> ПрИ r=s°' ИитегРиРУя» находима
, = СС08 {/]£*},
y=v«V Tksm\V тЧ'
Отсюда
Х2 .У»-2*
т. е. эллипс
16. Диференциальные уравнения задачи суть:
откуда
*<* = &*-
Начальные данные суть: г = /0. £ = £0 при /=0. Интегрируя, находим:
i-i(4-*/I)^+-i(*+a/I)^n"».
и аналогичное выражение для Е.
17. Обозначая через х вертикальную координату груза, считаемую от
положения покоя, имеем:
4 &х *, л

бО * ОТВЕТЫ И РЕШЕНИЯ
где / — длина пружины в естественном состоянии и /? = 400, как легко видеть
из начальных условий. Отсюда
^ + 1 ОО^л: = 100^ sin С]/1Щ t) + \001g.
Это — неоднородное линейное уравнение, причем первый член правой части
входит, как легко видеть, и в дополнительную функцию. Поэтому частный интеграл
мы должны искать в виде:
t (A cos T^lOOg t + В sin У I00g t).
Таким образом окончательное решение будет содержать член, амплитуда которого
неограниченно возрастает с течением времени.