В
ы
с
ш
е
е
п
р
о
ф
е
с
с
и
о
н
а
л
ь
н
о
е
о
б
р
а
з
о
в
а
н
и
е
Е. Г. Ипполитов
A. В. Артемов
B. В. Батраков
ФИЗИЧЕСКАЯ
ХИМИЯ

ВЫ СШ ЕЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАНИЕ
Е. Г. ИППОЛИТОВ, А. В . АРТЕМОВ, В . В . БАТРАКОВ
ФИЗИЧЕСКАЯ
ХИМИЯ
Под редакцией Е. Г. ИППОЛИТОВА
Допущено
Учебно-методическим объединением
по специальностям педагогического образования
в качестве учебника для студентов высших учебных заведений,
обучающихся по специальности 032300 «Химия»
Москва
ACADEMA
2005

УДК 544(075.8)
ББК 24.5я73
И76
Рецензенты:
чл.-корр. РАН, д -р хим. наук А.Д . Изотов;
д-р хим. наук, профессор М. П. Коротеев
Ипполитов Е. Г.
И76 Физическая химия: Учебник для студ. высш. учеб, заведе­
ний / Е. Г. Ипполитов, А. В. Артемов, В. В. Батраков; Под ред.
Е. Г. Ипполитова.
—
М.: Издательский центр «Академия»,
2005.-448с.
ISBN 5-7695-1456-6
Рассмотрены основные положения теории химической термодинами­
ки, равновесия в гомогенных и гетерогенных системах, химической кине­
тики и катализа, электрохимии.
Для студентов высших педагогических учебных заведений.
УДК 544(075.8)
ББК 24.5я73
Учебное издание
Ипполитов Евгений Георгиевич,
Артемов Арсений Валерьевич,
Батраков Валерий Владимирович
Физическая химия
Учебник
Редактор Н. В. Шувалова
Технический редактор Е.Ф .Коржуева
Компьютерная верстка: Т.А. Клименко
Корректоры Л. В. Гаврилина, А. 77. Сизова, В, М. Малек
Изд. No A-1253-I. Подписано в печать 03.03.2005. Формат 60 * 90/16.
Гарнитура «Таймс». Печать офсетная. Бумага тип. No 2. Уел. печ. л. 28,0.
Тираж 5100 экз. Заказ No 14508.
Издательский центр «Академия».
Санитарно-эпидемиологическое заключение No 77.99.02.953.Д.004796.07.2004.
117342, Москва, ул. Бутлерова, 17-Б, к. 360. Тел./факс: (095)330-1092, 334-8337.
Отпечатано на Саратовском полиграфическом комбинате.
410004, г. Саратов, ул. Чернышевского, 59.
Оригинал-макет данного издания является собственностью
Издательского центра «Академия*, и его воспроизведение любым способом
без согласия правообладателя запрещается
© Ипполитов Е. Г., Артемов А. В., Батраков В. В., 2005
© Издательский центр «Академия», 2005
ISBN 5-7695-1456-6

СПИСОК СОКРАЩЕНИЙ
АН
АЦ
АсОН
Ац
АЧ
АсгО
БН
Bz
г
ГМФА
ВигО
ДМА
ДМБ
ДМСО
ДМФ
Et-Ac
{...]
ДЧ
ацетонитрил
ппэ
ацетонитрил АсОН
уксусная кислота
ацетон
EtAc
акцепторное число
ЕЮН
уксусный ангидрид
ж
бензонитрил
kat
бензол
МеОАс
газ
МеОН
гексаметилфосфо-
НМ
этиленамин
НЭ
дибутиловый
N-МП
эфир
диметилацетамид
N-МФ
диметилбутанон
ПК
диметилсульфоксид
Прд
диметилформамид
Р-Р
этилацетат
т
концентрация
ТГФ
концентрация
ФА
начальная
ХИТ
донорное число
поверхность
потенциальной
энергии
этилацетат
этанол
жидкое
катализатор
метилацетат
метанол
нитрометан
нитроэтан
М-метил-2 -пирро-
лидон
N-метилформамид
пропиленкарбонат
пропиленкарбонат
раствор
твердое
тетрагидрофуран
формамид
химический
источник тока

ПРЕДИСЛОВИЕ
Изучение физической химии имеет фундаментальное значе­
ние для подготовки грамотного химика. Как нельзя считать че­
ловека грамотным, если он не знает орфографии, так нельзя
считать грамотным химиком специалиста, не знающего основ
физической химии. Однако курс физической химии д л я студен­
тов педагогических вузов должен быть построен иначе, чем для
студентов технических вузов, так к а к учитель должен иметь бо­
лее широкое представление о проявлении законов физической
химии в явлениях природы и в повседневной жизни человека.
Учитель средней школы, лицея или колледжа должен обла­
дать достаточными знаниями, чтобы грамотно ответить на во­
просы учеников о естественно-научных законах, управляющих
миром космоса, миром минералов, миром живых существ, а без
знания физической химии невозможно дать грамотные ответы
на вопросы учеников: будут ли реагировать данные вещества и
с какой скоростью, будет ли выделяться или поглощаться тепло
в результате химической реакции и в каком количестве, какие
химические процессы будут происходить в растворе или распла­
ве при прохождении электрического тока и т. п. Физическая хи­
мия — количественная наука, используя законы физической хи­
мии можно получить количественные ответы на вопросы о том,
сколько может получиться продуктов реакции, какую часть теп­
ловой энергии можно использовать д ля получения работы с по­
мощью тепловой машины, как используется энергия пищи для
совершения работы в живых организмах, как произвести разде­
ление смесей на индивидуальные вещества, под действием какой
силы происходит обмен веществ меж ду биологической клеткой
и окружающей ее средой, с какой скоростью можно провести
реакцию при данной температуре, как очистить металлы с по­
мощью электрического тока и многие другие вопросы.

ВВЕДЕНИЕ
Название и определение физической химии впервые было д а­
но в 1752 г. М. В. Ломоносовым: «Физическая химия — наука,
которая должна на основании положений и опытов физических
объяснить причину того, что происходит через химические опе­
рации в сложных телах».
М. В. Ломоносов впервые сформулировал такж е и фундамен­
тальные принципы, как основы для развития физической химии:
• принцип сохранения энергии и материи;
• кинетическая природа теплоты и понятие о «наибольшей и
последней степени холода»;
• невозможность перехода теплоты от более холодного тел а к
более горячему.
Впервые преподавание физической химии в России было вве­
дено М. В. Ломоносовым, однако лишь в 1860 г. Н. Н. Бекетовым
была организована первая в России кафедра физической хи­
мии в Харьковском университете. Современная физическая хи­
мия создана трудами многих талантливых ученых всего мира.
A. Лавуазье и П. Лаплас (Франция) изучали теплоемкость ве­
ществ и тепловые эф ф екты реакций, Г. И. Гесс (Россия) создал
термохимию как учение о тепловых эф ф е кта х химических ре­
акций. К .Ш ееле (Швеция) открыл адсорбцию газов твердыми
телами. Г. Дэви (Англия) и Л.Тенар (Франция) обнаружили су­
ществование каталитических реакций, Й. Берцелиус (Швеция)
и Ю. Либих впервые попытались объяснить явление катализа.
B. Н. Ипатьев (Россия) заложил основы представлений о гетеро­
генном катализе и о роли хемосорбции в катализе, Н. Н. Семенов
развил теорию цепных реакций.
Ж . Гей-Люссак, Э. Мариотт, Р. Бойль, Б. П. Клапейрон (Фран­
ция), Дж. Дальтон (Англия), А. Авогадро (Италия) открыли га­
зовые законы, заложив основы молекулярно-атомистического
представления о материи.
Становление и развитие учения о равновесии в системах обя­
зано С. Карно (Франция), Р. Клаузиусу (Германия), У. Томсону
(Англия), которые создали теорию тепловых машин — в аж ­
нейший раздел термодинамики. Д. Гиббс (США), Я. Вант-Гофф
(Нидерланды), Г. И. Гесс, В. Нернст (Германия), Д. И. Менделеев
5

(Россия) разработали приложение термодинамики к химическим
процессам и создали химическую термодинамику. К. Гульдберг
и П.В ааге сформулировали закон действующих масс.
У истоков теории химической кинетики стояли Л. Вильгельми,
М. Бертло и Пиан де Сен-Жиль. Я. Вант-Гофф сформулировал
основные законы формальной химической кинетики, В. Оствальд
рассмотрел явление автокатализа и сопряженных химических
реакций, которые были развиты далее Н. А. Шиловым. С. Арре­
ниус ввел понятие об активных молекулах и энергии активации.
Н. Н. Семенов развил теорию цепных реакций.
Появление электрохимии как р азде л а физической химии от­
носят к концу XVIII в. и связывают с открытиями Л. Гальвани,
наблюдавшим воздействие электрического тока на мышцу ля­
гушки и А. Вольта, который создал первый химический источ­
ник тока — гальваническую батарею — «вольтов столб». Г. Дэви
впервые провел электролиз расплавленных натриевой и калие­
вой щелочей и получил металлический натрий и калий. В. В. Пет­
ров (Россия) получил электрическую дугу, а К. И. Гротгус (Рос­
сия) заложил основы теории электролиза. М. Фарадей (Англия)
сформулировал количественные законы электролиза, Б . С. Якоби
(Россия) откр ыл явление гальванопластики. С. Аррениус (Шве­
ция) создал теорию электролитической диссоциации, развитие
электрохимической кинетики во многом обязано А. Н. Фрумкину.
К началу XX в. физическая химия полностью определилась
как наука, изучающая химическую термодинамику (термохи­
мию и учение о химическом и фазовом равновесии), химическую
кинетику и электрохимию.

ГЛАВА 1
ХИМИЧЕСКАЯ ТЕРМОДИНАМИКА
1.1. ТЕРМОДИНАМИКА
Начиная курс химической термодинамики, попытаемся дать
определение той науки, которая носит это название, и рассмот­
реть терминологию, которая используется в термодинамике.
Раздел физики, изучающий взаимные превращения меж­
ду различными видами энергии, называют термодина­
микой.
Раздел термодинамики, изучающий обмен энергией и
массой между химическими системами, называют химиче­
ской термодинамикой.
§ 1. Системы
Одно из основных понятий термодинамики — термодинами­
ческая система (ТС). В отличие от физики, которая изучает вза­
имодействия физических тел, и от химии, которая изучает вза­
имодействия веществ, термодинамика изучает системы.
Любую часть реального физического мира, отделенную
от внешней среды границами, реальными или мысленными,
назовем системой.
Термодинамическая система. Назовем термодинамической си­
стемой систему, в которой происходит обмен массой или энерги­
ей между телами или группами тел, составляющих систему.
Изолированная система. Системы, отграниченные от внеш­
ней среды границами, непроницаемыми ни д л я вещества, ни д л я
энергии, называют изолированными.
Закры тая система. Системы, отграниченные от внешней сре­
ды границами, проницаемыми для энергии, но непроницаемыми
для вещества, называют закрытыми системами.
7

Открытая система. Системы, отграниченные от внешней сре­
ды границами, проницаемыми и д л я энергии и д л я вещества,
называют открытыми системами.
Системы могут быть гомогенными или гетерогенными в за­
висимости от числа фаз.
Часть системы, отграниченная поверхностью раздела,
причем во всех точках имеющая одно и то же значение
интенсивных параметров при отсутствии внешнего воздей­
ствия, называется фазой.
Система, состоящая только из одной фазы, называется
гомогенной системой.
Пример гомогенной системы —газ или раствор, заполняющий
полностью сосуд.
Гетерогенной системой называется система, которая со­
держит более чем одну фазу.
Пример гетерогенной системы — сосуд, заполненный раство­
ром не полностью. Такая система состоит из жидкой фазы и
насыщенного п ара над жидкостью.
§2. Параметры системы
Состояние системы определяется ее параметрами состояния.
В качестве параметров состояния могут выступать объем, давле­
ние, температура, концентрация, внутренняя энергия и т. п. Од­
нако термодинамика не включает в качестве параметра время,
так как она рассматривает только равновесные состояния тер­
модинамических систем и не рассматривает вопросы о скоростях
достижения равновесия. Если все параметры системы остаются
постоянными во времени и в пространстве, то состояние систе­
мы называют равновесным или стационарным. Из перечислен­
ных параметров системы не все являются независимыми. Общи­
ми независимыми параметрами состояния являются объем, дав­
ление, температура и концентрация. Все остальные параметры
могут быть рассчитаны из них. На практике термодинамические
процессы проводят при неизменности того или иного параметра.
При расчетах всегда можно принять один или два параметра по­
стоянными, поэтому в термодинамике часто используют уравне­
ния в частных производных. Все параметры состояния подраз­
деляются по своим свойствам на две группы.
Параметры, значения которых для всей системы равны
сумме значений этих параметров для частей этой системы,
называются экстенсивными (например, объем).
8

Величина экстенсивных параметров зависит от общего коли­
чества вещества системы.
Параметры, значения которых д л я всех частей системы
выравниваются, называются интенсивными (например, тем­
пература) .
Величина интенсивных параметров не зависит от общего ко­
личества вещества системы. Экстенсивный параметр, отнесен­
ный к единице количества вещества, массы или объема, превра­
щается в интенсивный параметр, например, объем — экстенсив­
ный параметр, молярный объем — интенсивный параметр.
Равновесным состоянием термодинамической системы
называют такое состояние, при котором в системе отсут­
ствуют односторонние потоки вещества и энергии, а интен­
сивные параметры одинаковы во всех точках системы.
Поступательное изменение состояния системы в резуль­
тате изменения параметров вследствие взаимодействия с
окружающей средой или другой системой называют термо­
динамическим процессом.
Частным случаем термодинамических процессов является хи­
мический процесс.
Термодинамический процесс, при котором изменяется со­
став системы или структура веществ, составляющих ее, или
внутренняя организация вещества в системе, называется хи­
мическим процессом или химической реакцией.
Уравнения, связывающие независимые параметры, назы­
ваются уравнениями состояния.
Дл я любого термодинамического уравнения состояния д о л ж ­
но соблюдаться соотношение:
Известно только одно уравнение состояния — это уравнение
Клапейрона—Менделеева д ля идеального газа:
pV =nRT,
(1.1)
где п — число молей газа; R — газовая постоянная, равная
8,134Дж/(моль *К).
9

В идеальном газе отсутствует потенциальная энергия
межмолекулярного взаимодействия. Полная энергия иде­
ального га за определяется кинетической энергией его мо­
лекул.
Величина, прямо пропорциональная средней кинетиче­
ской энергии молекул идеального газа, называется темпе­
ратурой.
Реальные газы отличаются от идеального газа, но при боль­
шом разряжении и высокой температуре эти отличия становятся
пренебрежимо малы, так что уравнение (1.1) определяет состо­
яние реальных газов с приемлемой точностью да ж е при ком­
натной температуре. Уравнения состояния для реальных газов
неизвестны, так как в реальных газах молекулы не бесконечно
малы и отталкиваются друг от друга, а значит, они обладают не
только кинетической, но и потенциальной энергией.
§3. Внутренняя энергия
Любая термодинамическая система является совокупностью
огромного числа частиц (молекул, атомов, электронов и т. д.).
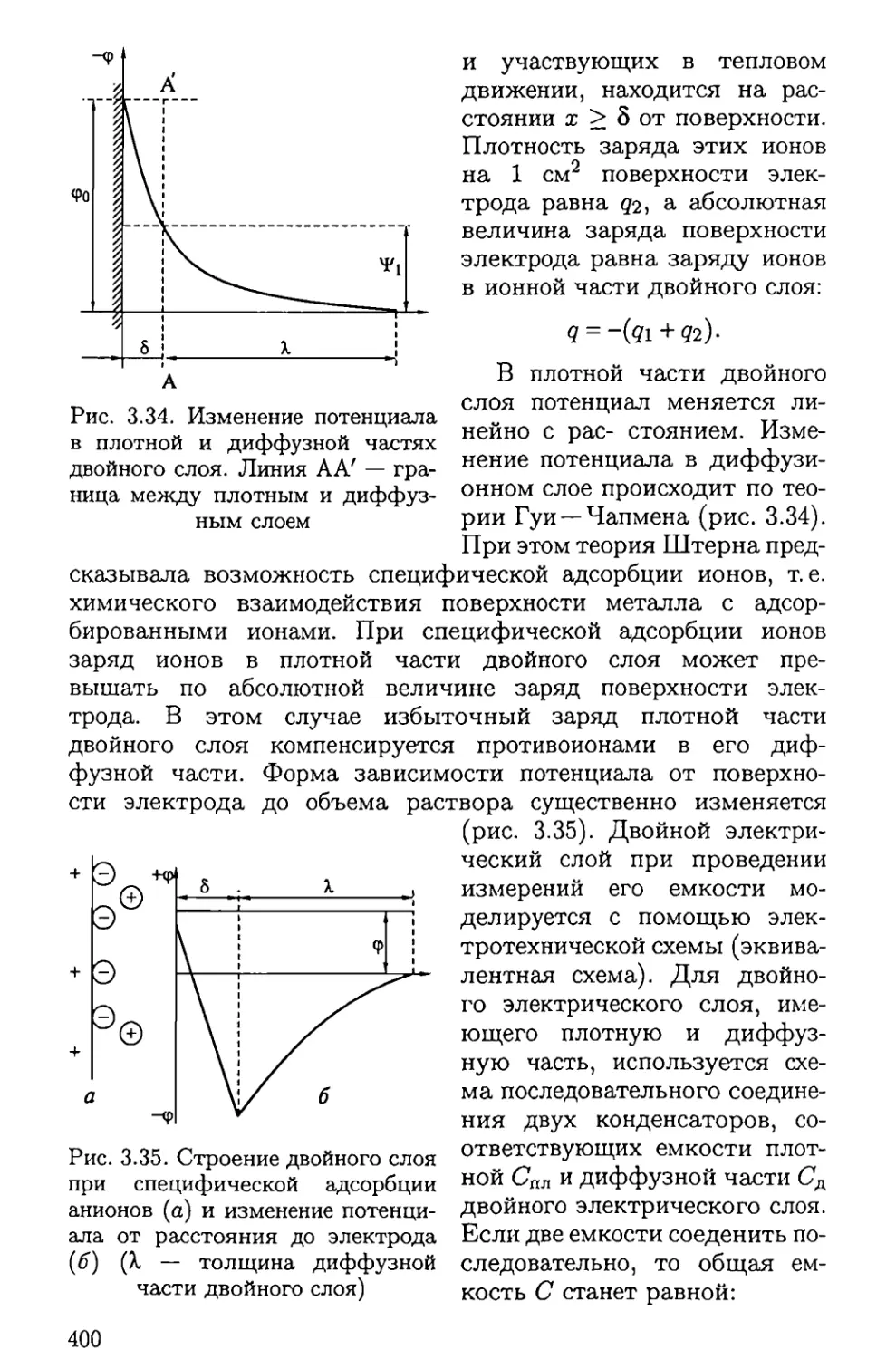
Все частицы системы находятся в движении и, следовательно,
обладают кинетической энергией, а такж е частицы взаимодей­
ствуют друг с другом, т. е. обладают и потенциальной энергией
(за исключением виртуальной системы, представляющей собой
идеальный газ). Таким образом, любая система обладает некой
внутренней энергией.
Внутренняя энергия U системы — это сумма кинетиче­
ской и потенциальной энергий всех ее частиц.
Вычислить абсолютное значение внутренней энергии невоз­
можно, так как нужно знать энергию молекул, энергию состав­
ляющих молекулы атомов, электронов и ядер, энергию нуклонов
в ядрах и т.д . до бесконечности. Но термодинамика основыва­
ется на аксиоме.
Внутренняя энергия системы является функцией состоя­
ния системы.
В математике дается следующее определение функции состо­
яния.
Функцией состояния называется такая действительная
непрерывная функция Ф = /(x ,y ,z ) , которая обладает сле­
дующими свойствами:
10

1) изменение функции состояния с изменением аргумен­
тов зависит лишь от начальных и конечных значений аргу­
ментов и не зависит от их промежуточных значений;
2) функция состояния — это функция точки: интеграл
по контуру дифференциала функции состояния равен нулю,
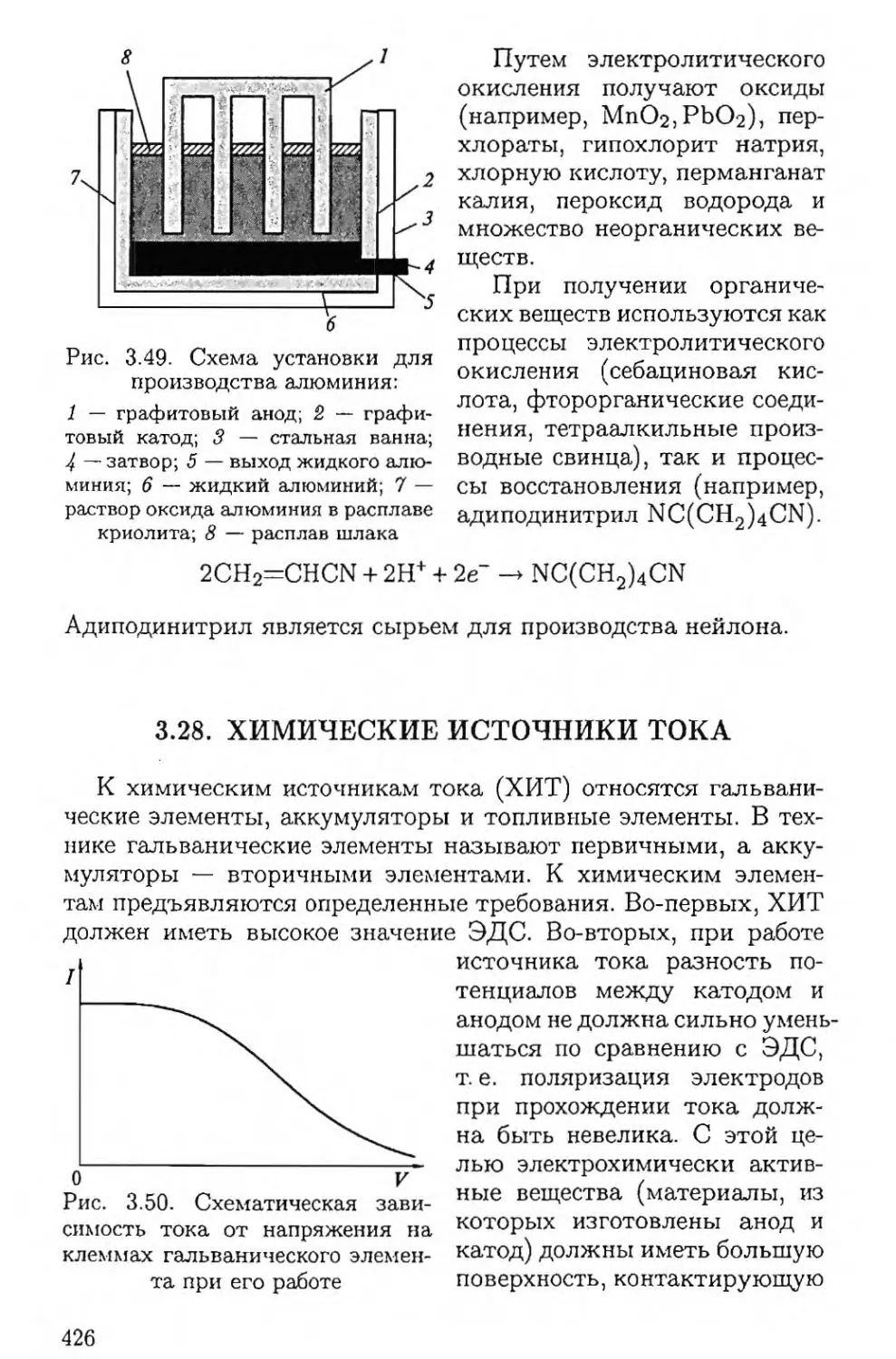
т. е.
Ф=0;
3) от всякой функции состояния можно взять полный
дифференциал, т. е.:
dU
- (SMSIMS) dz.
В изолированной системе внутренняя энергия всегда посто­
янна. Изменение внутренней энергии системы U как функции
состояния при переходе из равновесного состояния 1 в равновес­
ное состояние 2 можно представить разностью:
AU =U2-Ui.
При этом принимают з а нулевое значение внутренней энергии
значение ее при некоторых условиях, названных стандартными.
Условия, при которых температура равна 298,15 К и дав­
ление равно 1 атм, называются стандартными условиями*.
Если состоянию 1 отвечают стандартные условия и система
переходит из состояния 1 в состояние 2, то U\ = 0 и U2= A t/.
§4. Теплота и работа
При переходе термодинамической системы из состояния 1 в
состояние 2 система может обмениваться с другими системами
или с окружающей средой энергией, если система закрытая, и
(или) энергией и веществом, если она открытая. Обмен энергией
может осуществляться в двух формах:
обмен в виде энергии молекул, передаваемой хаотично;
обмен в виде организованного движения частей системы.
Обмен энергией м ежду системами в виде энергии моле­
кул, передаваемой хаотично, является обменом теплотой.
Обмен энергией в виде организованного движения частей
системы является обменом работой.
*1 атм = 1,01325- 105 Па.
11

Следует отметить, что ни теплота, ни работа не являются
видами энергии, они относятся лишь к обмену энергией и при­
ложимы не к системе, а к процессу переноса энергии при пе­
реходе из состояния 1 в состояние 2. Поэтому было бы оши­
бочно говорить, что система обладает теплотой или работой.
Система обладает внутренней энергией и может лишь обмени­
ваться со средой и теплотой, и работой, либо только теплотой и
работой.
Закрытую систему, которая не может обмениваться теп­
лотой, но может обмениваться работой, называют адиаба­
тической системой.
Рассматривая обмен системы энергией с внешней средой, необ­
ходимо условиться о знаках изменения энергии системы при об­
мене, так как энергия может поступать в систему или уходить
из системы. Условие знаков, принятое в термодинамике, состоит
в следующем.
Если энергия системы при переходе ее из состояния 1 в со­
стояние 2 возрастает, то Д Q > 0, если же уменьшается, то
Д Q < 0. Поэтому, если при обмене энергией в форме тепло­
ты теплота переходит из окружающей среды и поглощается
системой, то энергия системы возрастает, и A Q > 0, если
же теплота, напротив, выделяется системой и рассеивается
всреде,тоAQ<0.
Дл я обмена работой в термодинамике принято обратное пра­
вило.
Если из системы уходит энергия в виде работы, т. е. система
совершает работу против внешних сил, то Д W > 0 положи­
тельно, а если внешняя сила совершает работу над систе­
мой, то A W принимается отрицательной A W < 0.
В противоположность обмену энергией, обмен веществом меж­
ду системой и средой протекает лишь в единственной форме, и
знак работы, производимой при обмене веществом, положите­
лен, т. е. совпадает со знаком теплоты. Теория термодинамики,
и в том числе химической термодинамики, основывается на че­
тырех фундаментальных законах.
12

1.2. НУЛЕВОЙ И ПЕРВЫЙ ЗАКОНЫ
ТЕРМОДИНАМИКИ
Термодинамика основывается на четырех фундаментальных
законах природы. Фундаментальные законы постулируются на
основе наблюдений и опыта человеческой деятельности. Начнем
рассмотрение законов термодинамики с нулевого закона.
Нулевой закон термодинамики формулируется так.
Если две системы находятся в тепловом равновесии с тре­
тьей системой, то они состоят в тепловом равновесии.
На нулевом законе термодинамики основывается измерение
такого важного параметра как температура. Температура систе­
мы может быть измерена лишь с помощью другой системы, на­
ходящейся в равновесии с первой, и при этом зависимость изме­
нения какого-либо свойства этой второй системы с изменением
температуры известна. Пример — ртутный термометр, расши­
рение столбика ртути в котором прокалибровано по известным
процессам, протекающим при постоянной температуре.
Если система не находится в состоянии равновесия, то в ней
долж ны протекать процессы, приводящие ее в состояние равно­
весия. Рассмотрим процесс перехода системы из равновесного
состояния 1 в равновесное состояние 2. Д л я примера возьмем
простую систему в виде цилиндра с поршнем, в цилиндр по­
местим цинковый и медный электроды, которые подключим к
маленькому электромоторчику, а к
стенке цилиндра прикрепим термо­
метр (рис. 1.1).
Впрыснем под поршень раствор
соляной кислоты. Цинк в кислоте
начнет растворяться, образуя рас­
твор хлорида цинка и водород. В
то ж е время термометр укажет, что
раствор нагревается, при этом пор­
шень под давлением выделившего­
ся водорода поднимется, а в цепи
появится электрический ток, и вал
моторчика начнет вращаться. Таким
образом, переход системы из состо­
яния 1, когда в ней присутствуют
цинк и раствор кислоты, в равновес­
ное состояние 2, когда весь цинк рас-
поршень; 3—термометр;
^ —моторчик
13

творится, и раствор кислоты превратится в раствор хлорида
цинка, сопровождается нагреванием раствора, совершением ра­
боты против внешнего давления и совершением работы по пе­
реносу зарядов между электродами, в результате чего в цепи,
включающей моторчик, возникает электрический ток. Следова­
тельно, изменение внутренней энергии системы при переходе ее
из состояния 1 в состояние 2 в нашем опыте пошло на выделение
теплоты и совершение работы против внешних сил. М атемати­
чески это можно представить уравнением:
dU=8Q-bW
(1.2)
с учетом знаков теплоты и работы. Уравнение (1.2) является ма­
тематическим выражением первого закона термодинамики для
закрытых систем.
В любом процессе величина бесконечно малого приращ е­
ния внутренней энергии dU системы — это алгебраическая
сумма бесконечно малых приращений теплоты 5Q и рабо­
ты 81У, которыми система обменялась с внешней средой в
этом процессе.
Если сделать уравнение (1.2) явным по отношению к 8Q, то
первому закону термодинамики можно дать еще одну формули­
ровку.
Сообщенная системе теплота расходуется на приращение
внутренней энергии либо на совершение работы, либо на то
и другое.
Внутренняя энергия — это функция состояния и обознача­
ется в уравнении (1.2) как дифференциал, напротив, теплота и
работа не являю тся функциями состояния, поэтому бесконечно
малые их приращения в уравнении обозначены как 8. К а к ви­
дим, приращения теплоты и работы не являются дифференциа­
лами, но их сумма является дифференциалом. В этом, а также
в том, что энергия может передаваться только в виде теплоты и
работы, и ни в какой другой форме, и заключается физический
смысл первого закона.
В открытых системах может происходить обмен теплотой, ра­
ботой и веществом. Пусть система состоит из п \ молей веще­
ства 1,П2молей вещества 2, и т.д., и из
молей вещества /с,
и пусть при переходе системы из состояния 1 в состояние 2 при
постоянном объеме или при постоянном давлении она обменяла
dn\ молей вещества 1, dn2 молей вещества 2 и т.д ., и d n молей
14

вещества к. Очевидно, что с изменением числа молей какого-
либо вещества в системе изменяется и ее внутренняя энергия.
Каж дое прибавление числа молей требует совершения работы,
которая увеличивает внутреннюю энергию системы. Поскольку
единица dn — моль, а единица энергии — джоуль, то для согла­
сования единиц необходим коэффициент пропорциональности.
Обозначим его р. Тогда изменение внутренней энергии системы
при переходе ее из состояния 1 в состояние 2 будет равно
dU=dQ—dW+ pidn\+\i2dn2+ **■+p^dn^,
или
.
к
dU=5Q-5W +^2\iidn.
(1.3)
1=1
Если количество вещества г в системе возрастает, то drti счи­
тается положительным {dn > 0) и, наоборот, т. е. условия
знаков совпадают с условиями знаков изменения теплоты.
Уравнение (1.3) математически выражает первый закон тер­
модинамики для открытых систем.
§ 1. Обмен работой
Работа W — это перемещение макроскопической массы под
действием силы. Мерой количества работы служ ит произведе­
ние силы F на величину перемещения dl, т. е. 5И^ = Fdl. В за­
висимости от вида силы F существуют разные виды работы.
Например, работа против силы тяжести bW = mgdh. Следова­
тельно,
/12
W=Jmgdh=mg{h2- h\).
/и
Работа расширения газа, если / — внешняя сила, действу­
ющая на единицу площади поршня; S — поверхность поршня,
равна F = fs. Поэтому bW =fSdl =fdV. Следовательно,
W=
v2
fdV.
vi
Работа образования новой поверхности, например при раз­
мельчении вещества, определяется силой поверхностного натя-
15

жения с , растягивающей поверхность на единицу длины пери­
метра поверхности L. Вся сила, действующая на поверхность
F = f L . Если смещение периметра поверхности равно d l, то
dW = aLdl = GdS. Следовательно,
s2
W=J
5,
Работа переноса заряда q в электрическом поле с разностью
потенциалов A V равна 8W = A Vd q. Следовательно,
<72г
<71
Обобщая, можно написать общие уравнения:
Y'dy,
I
W= Y'dy.
j/i
Если видов работы то нужно суммировать их все по всем к:
bW=^Y'dy.
1=1
(1.4)
Здесь У ' — обобщенная сила; dy — бесконечно малое изменение
обобщенной координаты, причем во всех рассмотренных случа­
ях Y ' — сила внешняя, в общем, не равная соответствующим
параметрам системы.
Рассмотрим модель системы, которая показана на рис. 1.2 , а.
Невесомый поршень разделяет
цилиндр. Под поршнем идеаль­
ный газ, над поршнем ваку­
ум. Внешняя сила / , действу­
ющая на поршень, равна нулю
( / = 0). Поршень удержива­
ется запором L Освободим за­
пор 1. Под давлением газа пор­
шень поднимется до запора 2 и
переместится на dl. Работа рас-
Рис. 1.2. Работа сжатия:
ттг
Г-,т. тт л г»
а - против внешней силы; б - шиРения
при равновесном процессе
поэтому
= 0. (рис. 1.2,о).
-
2
1
16

Пустьтеперь/ >р,тогдаW=fdV< pdV,ноесли/бу­
дет отличаться от р лишь на бесконечно малую величину dp, то
/ = р, и работа расширения будет равна площади под гипер­
болой (p-V) (рис. 1 .2,6): W = JpdV. Но не ясно, при каких
условиях в уравнении работы внешняя сила / становится рав­
ной параметру системы р.
§2. Равновесный процесс
Видоизменим нашу модель: пусть в том же цилиндре (рис. 1.3)
давление газа уравновешивается гирями. Если мы начнем сни­
мать гири, то будет происходить расширение газа, как показа­
но схематически на графике зависимости (/-У) (рис. 1.4, а).
Видно, что расширение происходит скачками. В результате объ­
ем растет по ломаной линии а, Ь, с, d, е, / , р, h. Теперь, если будем
ставить назад гири, то объем будет уменьшаться по ломаной ли­
нии а, б, в, г, д, ж , з, и. Видно, что работа, которая равна площади
под ломаными линиями при расширении, больше по абсолютной
величине, но так как она отрицательна, то она меньше, чем ра­
бота, отвечающая гиперболе, проведенной через точки соедине­
ния прямоугольников, а при сжатии работа меньше по абсолют­
ной величине. Уменьшим наши грузики. Очевидно, что тогда эта
разница станет меньше, так как стороны заштрихованных пря­
моугольников станут меньше (рис. 1.4, б). Представим себе, что
грузики стали бесконечно малы. Тогда прямоугольники станут
точками, через которые можно провести гиперболу p V = const
(см. рис. 1.2 , 6 ), т. е. при этом выполняется условие равновесно­
го процесса / = р, процесс стал равновесным, а работа макси­
мальной.
Процесс, при котором можно заменить в термодинами­
ческих уравнениях внешнюю силу на соответствующий па­
раметр системы — это некий нереальный гипотетический
процесс, называемый равновесным процессом.
Особенности, характеризующие равновесный процесс:
1) внешняя обобщенная сила в любой момент лишь бесконеч­
но мало отличается от соответствующего параметра состояния
системы;
2) скорость процесса бесконечно мала;
3) работа максимальна и выражается через параметры состо­
яния;
17

2
1
4) реальный переход из одно­
го состояния в другое заменяет­
ся бесконечным набором проме­
ж уточны х состояний равновесия.
Д л я равновесного процесса Y 1
в общем уравнении работы (1.4)
можно заменить обобщенным па­
раметром состояния системы Y :
к
bW=^Ydy.
(1.5)
1=1
Рис. 1.3. Модель для изучения
сжатия газа под действием си­
лы тяжести
Проведем расчет работы рас­
ширения в различных процессах.
1.
Изохорный процесс. V = const
(рис. 1.5, а). Работа расширения равновесного процесса при этом
условии будет равна
V2
W=pdV.
Pi
Но так как V = const, dV = 0, следовательно, W = 0. На рис.
1.5, а мы видим отрезок прямой, под которым площадь р авн а 0.
Работа расширения при изохорном процессе не совершается.
2. Изобарный процесс, р = const.
W= PdV,
откуда
W =p{V2-Vi).
18

Рг
p;
P\
а
б
Рис. 1.5. Работа в различных процессах (пояснение в тексте)
На рис. 1.5, б мы видим площадь прямоугольника под прямой
v =f(p).
3. Изотермический процесс. Т = const.
V2
Гdv
Vo
=
RT— = ЯГ1п-£.
JV
Vi
Vi
График этого уравнения был дан на рис. 1 .2 ,5 , площадь под
кривой V = /(Т ). К ак видим, работа действительно зависит от
пути перехода системы из состояния 1 в состояние 2.
§ 3. Обмен теплотой. Энтальпия
1.
Пусть единственным видом работы, которая совершается
в системе, будет работа расширения. Тогда первый закон термо­
динамики можно вы разить уравнением:
5Q = dU +pdV.
2. Пусть система переходит из состояния 1 в состояние 2 при
V = const (процесс изохорный). Тогда dV = 0, 8Q = dU, Qy = U.
При изохорном процессе изменение т еплоты системы п р и­
обретает свойства дифференциала и не зависит от пути про­
цесса.
3. Пусть система переходит из состояния 1 в состояние 2 при
О2
v2
*
Г
р = const (процесс изобарный). Тогда ДQ = dU + pdV, откуда
иУ
v,
AQP=p(V2-V 1)+AU =(U2+pV2)- (Ui +pVi).
19

Введем обозначение
(1.6)
H=U+pV
и назовем функцию Н в уравнении (1*6) энтальпией.
Функция состояния, которая при постоянном давлении
равна сумме внутренней энергии и работы расширения, на­
зывается энтальпией.
Энтальпия — функция состояния, так как она является сум­
мой других функций состояния, поэтому
Qp=H2-H x=AH
dQp = dH.
(1.7)
Уравнение (1.7) является термодинамическим выражением за­
кона Гесса.
При изобарном процессе изменение теплоты системы ста­
новится дифференциалом и не зависит от пути процесса.
Это не значит, что Qp стала функцией состояния, та к как
теплота не является функцией.
§4. Теплоемкость
Если система поглотит теплоту, то ее температура повысится
(при отсутствии фазовых превращений).
Пусть в результате перехода системы из состояния 1 в со­
стояние 2 температура системы повысилась от Т\ до Т2, Ко­
личество поглощенной теплоты пропорционально повышению
температуры:
Q=c(T2-T1).
Средняя теплоемкость системы определяется к ак отно­
шение теплоты, сообщенной системе в результате перехода
из состояния 1 с температурой Т\ в состояние 2 с темпера­
турой Т2) к разности температур.
Истинная теплоемкость определяется как предел:
Q
dQ
с-lim———=
ДГ-о Т2- Т\ dT
( 1.8)
Теплоемкость системы определяется как производная
теплоты по абсолютной температуре.
20

Далее под термином «теплоемкость» будет подразумеваться
истинная теплоемкость (уравнение (1.8)). Теплоемкость пропор­
циональна массе вещества, поэтому различаю т удельную тепло-
dH
dH
емкость с = ——тп и молярную теплоемкость с =
М.
аТ
аТ
Численное значение теплоемкости зависит от условий проте­
кания процесса. При изобарном процессе dQp = d H , поэтому
dH
Ср~ dT'
При изохорном процессе dQy = dU и, повторяя рассуждения,
получим:
dQy dU
°V=~dT=dT'
Теперь первый закон можно записать в форме:
dU = cydT-pdV
приV=constи
dU = CpdT-pdV
при р = const, если из всех работ совершается только работа
расширения.
Рассмотрим соотношение между Ср и су. Д л я изохорного про-
dU
dH
цесса су ~
—
, тогда как для изобарного процесса Ср =
=
dT
dT
dUdV^
=
+p— .
Для конденсированных систем су ^ Ср, так как
dT dT
объем конденсированных систем меняется пренебрежимо мало
по сравнению с неконденсированными системами и dV = 0. Д л я
1 моля идеального газа pV = R T , причем мы условились, что
dV
р = const. Следовательно, pdV = RdT)р— = R и
Ср—су =R.
(1.9)
Уравнение (1.9) явл яется иллюстрацией зависимости теплоты
от пути перехода системы из состояния 1 в состояние 2.
§ 5. Расчеты теплоемкости
Теплоемкость идеального одноатомного газа может быть вы­
числена по изменению его внутренней энергии. Так как потенци­
альная энергия молекул идеального газа равна 0, то U = Екин. Из
21

молекулярно-кинетической теории идеального газа следует, что
3
кинетическая энергия моля идального газа равна Е кин =
L*
Поэтому U = - i? T . Следовательно,
Cl/ dT 2к>
3
су = - •8,31 = 12,5 ДжДмоль •К),
3
5
Ср=-R+R=-R =20,8ДжДмоль•К).
Z
Z
Рассмотрим теплоемкость двухатомного идеального газа. В ме­
ханике называют числом степеней свободы движущегося тела
число простейших видов движения, на которые может бы ть раз­
ложено данное сложное движение. Известна теорема о равно­
мерном распределении энергии по степеням свободы.
Представим молекулу двухатомного газа в виде гантели. По­
ступательное движение у гантели имеет три степени свободы по
трем осям координат. Вращательное движение также разлагает­
ся на три степени свободы по трем осям координат. Но гантель
имеет на одну степень свободы меньше, так как вращение вдоль
общей оси не имеет момента инерции, и энергия такого враще­
ния равна нулю. Поэтому движение молекул двухатомного газа
имеет лишь пять, а не шесть степеней свободы. У одноатомного
газа атомы имеют лишь три степени свободы, и на к аж дую сте­
пень свободы приходится Е кин = ^ R T . Следовательно, на пять
степеней свободы молекулы двухатомного идеального га за при-
5
5
7
ходитсявсумме Ек„н=-RT.Поэтому су =-R иСр=-Я, т.е.
Li
Li
Li
5
су = - R =20,8 ДжДмоль-К) и Ср =29 Дж/(моль-К).
Li
В твердом кристаллическом теле атомы располагаются в уз­
лах кристаллической решетки. Они не могут перемещаться, так
как отталкиваются от соседних атомов. Поэтому они постоянно
колеблются около положения равновесия.
Частица, совершающая гармонические колебания у по­
ложения равновесия под влиянием квазиупругой силы F ,
называется гармоничным осциллятором.
Из теории колебаний нам известно, что кинетическая энергия
осциллятора равна его потенциальной энергии:
£кин=и.
22

Колебания атома можно разложить по трем осям координат,
следовательно, колебательное движение атома имеет три степе­
ни свободы. Каждой из трех степеней свободы колебаний атома
отвечает - R T кинетической энергии. Полная энергия будет рав­
на сумме кинетической и потенциальной энергий:
U=EKHH+U=^RT =3RT
И
Су =3R =25Дж/(моль*К).
(1*10)
Уравнение (1.10) выполняется достаточно точно лишь при вы­
соких температурах. Это Закон Пти —Дюлонга.
Атомная теплоемкость кристаллов простых веществ при­
близительно равна 25 Дж/(моль*К).
Су жСр - 25Дж/(моль*К).
При низких температурах начинает играть уже заметную
роль квантово-механическая природа атомов, и внутренняя энер­
гия становится меньше 3R T . Это учитывает уравнение Эйн­
штейна:
U=3RT
hv/{kT)
ehv/{kT) __ i >
dU
поэтому выражение С у = — можно представить в следующем
dT
виде:
Су=т
g/iv/(кТ) [/jV/ (кТ)]2
(ем7(*г)-1)2 ’
( 1.11)
где к — постоянная Больцмана; к =
N — число Авогадро. При
Т ^ 0 и Су ^ 0; 0 = кч/к — характеристическая температура
Дебая.
Отношение кванта к константе Больцмана называют ха­
рактеристической температурой Дебая.
Величины характеристической температуры для многих твер­
дых веществ приведены в справочниках. Д л я трехмерного тела
теплоемкость при низких температурах можно вычислить по за ­
кону кубов Дебая:
Су=3R
ту
в)'
23

При низких температурах теплоемкость при постоянном
объеме приблизительно равна произведению утроенной га­
зовой постоянной и куба отношения абсолютной температу­
ры к характеристической температуре.
Теплоемкости огромного числа веществ измерены и приво­
дятся в справочниках в виде зависимостей от температуры,
представленной так называемыми вириальными уравнениями:
С =CLQ+0,1Т +CL2T 2 + а~2Т~2.
(1.12)
При этом указано, в каком интервале значений температуры
уравнение (1.12) действительно.
1.3. ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ
§ 1. Процессы
Процессы, происходящие в системах, могут быть обратимыми
и необратимыми.
Обратимым процессом называют такой равновесный
процесс, после которого можно вернуть систему в исходное
состояние, и при этом ни в системе, ни в окружающей среде
не останется никаких следов от протекавшего процесса.
Работа, совершаемая при обратимом процессе максимальна,
как при равновесном процессе.
Если процесс в системе происходит без вмешательства со
стороны внешней среды, то такой процесс называют само­
произвольным процессом.
Самопроизвольные процессы могут быть обратимы и необратимы.
Процесс, который протекает лишь при вмешательстве со
стороны внешней среды путем передачи системе энергии
или вещества, называется произвольным процессом.
Так как в реальных условиях невозможно избежать потерь энер­
гии на преодоление сил трения и нагревание системы, то поня­
тие обратимого процесса является абстракцией, но это понятие
24

необходимо дл я приближенного приложения термодинамики к
реальным процессам.
§ 2. Прямой и обратный процессы
Наш жизненный опыт показывает, что прямой и обратный
процессы неравноценны. Так, например, теплота передается са­
мопроизвольно от горячего тела к холодному, но для того что­
бы теплоту передать от холодного тела к горячему, необходимо
совершить работу, т. е. это уже произвольный процесс. В техни­
ке передача теплоты от более холодного тела к более горячему
совершается в специальных машинах — холодильниках, или ре­
фрижераторах. В абсорбционных холодильниках для этого рас­
ходуется тепло, в электромеханических совершается работа по
перекачке хладоагента.
Другой пример: пусть в сосуде в виде гантели с краном посе­
редине газ занимает объем одного шара. Если открыть кран, то
газ самопроизвольно расширится и займет объем обоих шаров,
но чтобы сконцентрировать газ вновь в одном из шаров гантели,
придется произвести работу.
Пример химического процесса: д ва сосуда, из которых один
наполнен аммиаком, другой — хлористым водородом, соединя­
ются посредством закрытого крана. Если кран открыть, то са­
мопроизвольно образуется дым из твердого хлорида аммония,
тогда как для обратного разделения хлорида аммония на амми­
ак и хлористый водород необходимо подвести к системе теплоту
и совершить работу по разделению газов.
Таких примеров можно привести неограниченное число.
Обобщение этих наблюдений было сделано почти одновременно
несколькими исследователями, которые дали следующие част­
ные формулировки второго закона термодинамики.
М. В. Ломоносов первым высказал принцип о невозможно­
сти передачи тепла от холодного тела к горячему. Значитель­
но позже R Клаузиус сформулировал этот принцип следующим
образом.
Никакая совокупность каких-либо процессов не может
сводится к передаче теплоты от холодного тела к горячему,
тогда как передача теплоты от горячего тел а к холодному —
естественный самопроизвольный процесс.
У. Томсон из наблюдений при сверлении пушек сформулиро­
вал еще один принцип.
25

Никакая совокупность каких-либо процессов не может
сводиться только к превращению теплоты в работу, тогда
как превращение работы в теплоту может быть естествен­
ным результатом процессов.
В. Оствальд д ал следующую формулировку:
Вечный двигатель второго рода, т. е. такая машина, ко­
то рая производила бы работу только за счет поглощения
теплоты из окружающей среды без передачи части тепла
холодильнику, невозможен.
Поскольку прямой и обратный процессы неравноценны, то
должна существовать такая функция состояния, которая опре­
деляет направление самопроизвольного процесса.
§ 3. Принцип К. Каратеодори
Пусть система переходит из состояния 1 в состояние 2 с по­
глощением теплоты. Предположим, что систему можно вернуть
обратно в состояние 1 другим путем — адиабатически без отда­
чи части энергии в виде теплоты (рис. 1.6). В таком случае для
прямого пути
Q=AU +WU
а д ля обратного пути
Q=-AU+W2,
в результате циклического процесса получаем:
Q=W2+Wi.
Так как Q > 0, то получается, что единственным результатом
прохождения циклического процесса является превращение всей
26

теплоты в работу, что невозможно. Следовательно, вернуться в
первоначальное состояние 1 система не может без потери части
теплоты. Поэтому состояние системы должно характеризовать­
ся некой функцией состояния S = f(Q ), которая изменяется при
прямом процессе и которую невозможно привести к первона­
чальному состоянию без передачи части теплоты.
1.4. ЭНТРОПИЯ. ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ
Рассмотрим, какова до лж на быть эта функция. Все законы
термодинамики относятся лишь к большому множеству частиц,
так как параметры системы — температура и давление — явля­
ются проявлением среднего действия огромного числа молекул.
Температура газа определяется средней кинетической энергией
его молекул. Давление газа — суммарный эфф ек т от ударов мо­
лекул газа о стенку. Внутренняя энергия, энтальпия и другие
функции системы зависят от давления и температуры, т. е. от па­
раметров, выражающихся через статистические, вероятностные
законы. Температура, давление и объем являю тся параметрами,
характеризующими макросостояние системы. Если эти парамет­
ры не изменяются во времени сколь угодно долго, то система
находится в равновесии, и на макроуровне в ней не происходят
никакие процессы. Однако не так обстоит дело на микроуровне.
Молекулы, из которых состоит система, находятся в непрерыв­
ном движении, и каждое энергетическое состояние системы ха­
рактеризуется своим статистическим распределением молекул
по скоростям и импульсам. Если мы знаем закон такого распре­
деления, то можем вычислить параметры и термодинамические
функции макросистемы, исходя из микросостояний ее молекул.
§1. Термодинамическая вероятность
Число различных микросостояний системы, которое со­
ответствует данному ее макросостоянию, называется термо­
динамической вероятностью W *.
Так к ак число молекул макросистемы очень велико, то термо­
динамическая вероятность является очень большой величиной и
всегда положительна. Д л я описания состояния системы необхо­
димо знать не только импульсы молекул, но и их расположение
Не путать с математической вероятностью!
27

в пространстве. Если система представляет собой газ с парамет­
рами р, V^T, то мгновенное состояние одноатомной молекулы
может быть определено шестью координатами: тремя простран­
ственными координатами x , y , z и тремя компонентами импульса
PxiPy^Pz- Поэтому мгновенное состояние молекулы может быть
полностью определено в шестимерном фазовом пространстве в
виде точки с соответствующими координатами.
Шестимерное пространство, в котором располагается
точка, определяющая данное мгновенное состояние молеку­
лы, называется фазовым пространством.
Если шесть координат молекулы в фазовом пространстве
принимают значения f+ df, то молекула занимает фазовую ячей­
ку объема фазового пространства d x dy dz dpx dpy dpz . Пусть чис­
ло молекул, находящихся в данном фазовом пространстве, рав­
но TV*, тогда фазовое пространство можно разбить на фазовые
ячейки, в которых будет размещаться какое-то число молекул, у
которых к аж да я из шести координат одинакова. Число молекул
в каждой ячейке обозначим как iVi, N2, • • • , JVfc.
§2. Уравнение Больцмана
Статистика, которую разработал Людвиг Больцман, основана
на следующих постулатах:
молекулы не имеют меток;
перемещение молекул в одной фазовой ячейке не образует
нового макросостояния;
все размещения молекул в фазовом пространстве равнове­
роятны;
данное распределение молекул по фазовым ячейкам обра­
зует данное макросостояние;
перестановка двух молекул в двух ячейках соответствует
появлению нового макросостояния.
Для примера возьмем три одинаковые молекулы а, Ь, с в фа­
зовом пространстве, разделенном на три фазовые ячейки.
Размещение трех молекул в одной из
трех фазовых ячеек
Номер ячейки
1
23
Одно мпкросостояние,
соответствующее дан­
ному макросостоянию
abc
28

Если все молекулы распределены в одной ячейке, то термоди­
намическая вероятность W = 1, поскольку перестановки внутри
ячейки не изменяют термодинамическую вероятность. Так как
фазовых ячеек 3, то молекулы могут, таким образом, размещать­
ся в одной из трех фазовы х ячеек*. Итак, всего одно микросо­
стояние возможно в данной системе с термодинамической веро­
ятностью W = 1.
Теперь предположим, что две молекулы находятся в одной
фазовой ячейке, а тре тья находится во второй фазовой ячейке,
третья фазовая ячейка при этом пуста. В этом случае термоди­
намическая вероятность W = 3, так как между тремя ячейка­
ми можно сделать три перестановки молекул, причем каждому
микросостоянию будет отвечать три макросостояния системы.
Размещение 2 + 1 молекул в трех
фазовых ячейках
Номер ячейки
1
23
Три микросостояния, со-
ответствующие данному
макросостоянию
аЪ
с
—
ас
Ь—
Ьса
—
При распределении по одной частице в фазовой ячейке тер­
модинамическая вероятность W = б, так как может произойти
6 различных размещений молекул по фазовым ячейкам и при
этом каждому такому размещению (микросостоянию системы)
соответствует одно макросостояние.
Размещение 1 + 1 + 1 молекул в трех
фазовы х ячейках
Номер ячейки
123
Шесть микросостояний, со-
ответствующие данному мак-
росостоянию
а
Ъс
а
с
Ь
Ъса
Ъас
с
bа
с
а
Ь
Итак, наибольшая термодинамическая вероятность систе­
мы достигается при равномерном распределении молекул по фа­
зовым ячейкам. Чтобы рассчитать термодинамическую вероят­
ность системы из N молекул, нужно число всех перестановок
*Стромберг Ф. Г., Сснченко Д .П . Физическая химия.
—
М.: Высш. щк., 1999.
29

по п фазовым ячейкам разделить на число размещений моле­
кул по фазовым ячейкам. В результате получаем уравнение для
термодинамической вероятности:
(1.13)
Из уравнения (1.13) видно, что термодинамическая вероятность
является очень большой величиной. Так, например, если N = 15
и п = 3, то W = 7 ,6 -105. В одном моле газа заключено 6,022-1023
молекул, поэтому термодинамическая вероятность д л я такого
числа молекул огромна. Второй закон термодинамики основы­
вается на постулате:
Каждая предоставленная самой себе изолированная система
стремится перейти в наиболее вероятное состояние, т. е. тер­
модинамическая вероятность изолированной системы стремит­
ся к максимуму.
Л. Больцман доказал, что существует функция состояния, на­
зываемая энтропией и определяющаяся термодинамической ве­
роятностью системы:
S = klnW.
(1.14)
§3. Приведенная теплота
Уравнение (1.14) выражает энтропию через термодинамиче­
скую вероятность, но как же энтропия может быть выражена
через параметры системы? Если в системе совершается только
работа расширения, то согласно первому закону термодинамики
5Q= cydT +pdV.
Дл я одного моля идеального газа из уравнения состояния имеем
соотношение: р / Т = R / V . Подставив значение р, получим:
dV
bQ=cvdT+BT—
.
Разделим обе части последнего уравнения на Т:
dT
AV
=cv—+r—>
cyd\nT + ДсИпИ.
Из определения полного дифференциала следует, что для то­
го чтобы в уравнении 8/ = adx + bdy функция 5/ была полным
30

дифференциалом d /, необходимо и достаточно, чтобы выполня­
лось равенство частных производных:
да\ _/дЬ\
ду)х~ \дх)у
5Q
Следовательно, д л я того чтобы величина — , которую на­
зываю т приведенной теплотой, была полным дифференциалом,
необходимо и достаточно, чтобы выполнялось равенство част-
ных производных:
..
тг
=
7——-
.
Но это условие как
VdlnV7T \д\пТ)р
раз и выполняется: так как су = const дл я идеального газа при
m
„
(дсу\
n(dR\п
Т=const,такжекакиR=const,то
ту
=0и
_
=0.
\dlnVJT
\д\пТ;р
Следовательно,
/ дсу \ _(dR\_
{dlnv)T~{d\nт ) ~ ■
Значит, приведенная теплота —— это функция состояния, ко­
торая запрещает возврат системы в исходное состояние без пе­
редачи системой некоторого количества тепла окружающей сре­
де или другой, более холодной системе. Э та функция получила
обозначение Sи была названа энтропией, так что
(1.15)
Уравнение (1.15) представляет математическую формулиров­
ку второго закона термодинамики.
о
5Q
Энтропия — это приведенная теплота
которая явля­
ется функцией состояния и которая запрещает возврат си­
стемы из равновесного состояния в исходное неравновесное
состояние без передачи части тепла окружающей среде.
§ 4. Объединенное уравнение термодинамики
Рассмотрим энтропию изолированной системы. Для обрати­
мых процессов в изолированной системе dQ = 0 , поэтому d S = О
и S = const. Д л я обратимых процессов в изолированной систе­
ме второй закон термодинамики выступает как закон о суще-
ствовании и сохранении энтропии.
31

Если обратимый процесс протекает в неизолированной систе­
ме, то энтропия системы может меняться, но тогда меняется и
энтропия окружающей среды, а суммарная энтропия всех тел,
участвующих в обратимом процессе, остается постоянной.
Если химическая система изолирована, то это не значит, что
энтропия ее не может возрастать, так как в ней может проте­
кать самопроизвольный химический процесс. Поэтому дл я х и ­
мической изолированной системы энтропия может быть непо­
стоянной. Т а ка я система не обменивается с окружающей средой
ни энергией, ни веществом, но в ней может протекать самопро­
извольный химический процесс, и вследствие этого энтропия си­
стемы будет расти. Прохождение процесса в изолированной хи­
мической системе приводит к производству энтропии до тех пор,
пока энтропия не станет постоянной, и состояние системы до­
стигнет равновесия. Если при этом система недостаточно изоли­
рована, то часть произведенной энтропии будет передана окру­
жающей среде. В таком случае, ка к же рассчитать изменение
энтропии, произошедшее в результате самопроизвольного хими­
ческого процесса? Для этого необходимо включить в систему те
объекты среды, которые обменялись с системой энергией или ве­
ществом, и, таким образом, отграничить новую более обширную
изолированную систему, д л я которой можно рассчитать измене­
ние энтропии при самопроизвольном химическом процессе.
Из (1.15) следует, что bQ = T d S . Подставив это выражение в
(1.2), можно составить объединенное уравнение термодинамики:
dU=TdS-bW,
(1.16)
учитывающее и первый, и второй законы термодинамики для
закрытых систем
§ 5. Критерии равновесия и прохождения самопроизвольного
процесса в изолированной системе
Если в системе совершается только работа расширения, то
уравнение (1.16) примет вид:
dU=TdS-pdV.
(1.17)
Итак,
_
dU+bW
dS = ------у
------ ■
Анализ уравнения (1.17) позволяет ответить на вопросы: при ка­
ком условии система находится в равновесии и при каком усло­
вии в системе должен протекать самопроизвольный необрати­
мый процесс.
32

Пусть в изолированной системе произошел необратимый про­
цесс. Так как 8W0ep > 5ЖНеоб, то
dSHeQ6 >
dU+bW
dSHeoe >
Если система изолирована, то 8Q = 0, следовательно
dSHeоб > 0.
(1.18)
Уравнение (1.18) представляет критерий прохождения самопро­
извольного процесса в изолированной системе. Критерий равно­
весия в изолированной системе определяется уравнением:
dS =0.
(1.19)
Итак, второй закон термодинамики может быть сформулирован
следующим образом:
Существует функция состояния S', названная энтропией,
которая определяет состояние равновесия или направление
протекания самопроизвольного процесса. В изолированной
системе при любом обратимом процессе энтропия постоян­
на, т. е. d S = 0, а при любом необратимом процессе энтропия
возрастает, т. е. d S > 0.
Математически это значит, что для изолированной системы
dS>0.
(1.20)
Из уравнения (1.20) следует, что объединенное уравнение д ля
обратимых и необратимых процессов будет иметь вид:
dU <TdS-bW.
Если имеет место только работа расширения, то
dU<TdS-pdV.
§6. Расчет энтропии в изолированных системах
Размерность энтропии в СИ ДжД м оль ■К). Вычислить из­
менение энтропии возможно только д л я обратимых процессов.
Дл я этого нужно интегрировать уравнение
AS=
Jта
Ti
Рассмотрим расчет д л я различного вида систем:
2 Ипполитов
33

адиабатный процесс: 8Q = 0 и A S = 0;
5Q
изотермический процесс: Г = const, A S = — ; фазовый пе­
реход;
изобарный процесс: dQp = CpdT или А Н = CpdT и
AS=
Та
Та
гdQp_ fCpdT
Т"JТ'
г,
г,
Если интервал температур невелик, то Ср « const и
Д5=ср1п^.
Если температурный интервал велик, то находим из справоч­
ника вириальное уравнение зависимости Ср от температуры:
ср= +о>\Т+
+ cl-^T
Подставив это значение под знак интеграла, получим сумму ин­
тегралов:
Га
Д5= J '£(а0+а1Т+а2Т2+а.2Т-2)^ .
Тх
Расчет с использованием ЭВМ можно быстро произвести,
предварительно составив небольшую программу, которая поз­
волит рассчитывать энтропию при разных температурах и раз­
ных Ср\
для изохорного процесса
dU
ТI
cydT
Т’
при изобарном процессе 5Q = dU + pdV (при отсутствии дру­
гого вида работ, кроме работы расширения), поэтому
А*-|!
Т,
Г,
ii
Г,
pdV
Т‘
Пусть рассматриваемая система — идеальный газ. Тогда Т =
т,
V,
34

Если температурный интервал невелик, то с у & const и после
интегрирования
j.
у
AS=cyln^+Rln-l.
11
VI
Если су
const, то, подставив значение с у из вириально-
го уравнения теплоемкости, получим уравнение, подобное тому,
которое было получено д л я изобарного процесса. После состав­
ления несложной программы расчет A S с применением ЭВМ не
составит большого труда.
§7. Фундаментальное уравнение термодинамики
Дл я обратимых процессов в открытых системах обобщенное
уравнение будет иметь вид:
I
к
dU=TdS + YjdVj+
■
(1.21)
j=1
1=1
Уравнение (1 .2 1) называется фундаментальным уравнением
термодинамики.
Второе слагаемое в нем представляет сумму всех видов р а­
бот против всех сил, действующих на систему; третье слагаемое
представляет изменение внутренней энергии при прохождении
химических процессов или при каком-либо другом обмене мас­
сой системы с окружающей средой. Д ля необратимых процессов
фундаментальное уравнение обращается в неравенство:
I
к
dU<TdS+Y,Yjdyj+^М «г-
(1-22)
j=1
i=1
§8. Критерий равновесия или прохождения самопроизвольного
процесса в химической системе
Дл я изолированных систем с химическими реакциями
^2\idnJ0,
так ка к число молей веществ может меняться вследствие реак­
ции. Поэтому и для изолированных химических систем необхо­
димо применять фундаментальное уравнение, хотя в них нет об­
мена веществом с окружающей средой. Если система адиабатна
и при равновесии Т = const и р = const, то из фундаментального
уравнения следует:
к
^|lidn;=0 .
(1.23)
1=1
35

Уравнение (1.23) является критерием равновесия в адиабатно­
изобарной химической системе, а значит, и равновесия химиче­
ской реакции при Т = const и р = const.
Если система изолирована и при равновесии Т = const и
V = const, то критерий равновесия будет тот же.
§9. Химический потенциал
Рассмотрим физический смысл коэффициента (I в уравне­
нии (1.3). Этот коэффициент назван химическим потенциалом.
Пусть внутренняя энергия системы будет функцией, завися­
щей от ряда параметров, в том числе и от числа молей i веществ:
U=f(S,Т,V,s,q,т,П2, ... ,гц).
Полным дифференциалом этой функции будет:
AU (-)
*8
\ d S )туР,У,з,Я, ъ
*(S.
(—)
dV
\dV J TyS,SyP,q,4 j
•
\ ° S J TySyPyVyqyUi
*(Э,
(&L\
dn, y(dU\
U n J T,KlS,9,
\dn2)7
\ д щ ] T,S,s,q,n,^
uTli.
i
dT+
S,p,V,s,q,nj
dp+
Т, s,Vyq, tij
+
dn2 +
(1.24)
Сравнивая уравнение (1.24) с фундаментальным уравнением
(1.21), получим
\ д щ ) SyзлУ%ц%п&
(1.25)
Уравнение (1.25) определяет ф изический смысл химического по­
тенциала.
Химический потенциал — это частная производная от
внутренней энергии по числу молей вещества при условии,
что все другие параметры системы, остаются постоянными,
а изменение количества данного вещества мало по сравне­
нию с его общим количеством в системе.
36

1.5. ПОСТУЛАТ ПЛАНКА
Планк сформулировал следующий постулат.
Энтропия идеального кристалла при тем пературе абсолют­
ного нуля равна 07т. е. S
—
►0 при Т —►0.
Идеальным кристаллом называется кристалл, в котором
все атомы располагаются строго в узлах кристаллической
решетки, все узлы за ня ты атомами, молекулами или иона­
ми данного соединения и примеси другого сорта атомов, мо­
лекул или ионов отсутствуют.
Хотя реальные кристаллы отличаются от идеальных, посколь­
ку д а ж е в тщательно очищенном веществе, все же, присутствуют
примеси, и кристаллическая решетка кристаллов всегда имеет
деф екты , тем не менее энтропия высокочистых кристаллов при
температуре, очень близкой к абсолютной, пренебрежимо мало
отличается от нуля. Постулат Планка определяет начало отсчета
энтропии, поэтому энтропия является единственной термодина­
мической функцией, абсолютное значение которой определено.
§1 . Экспериментальное определение энтропии
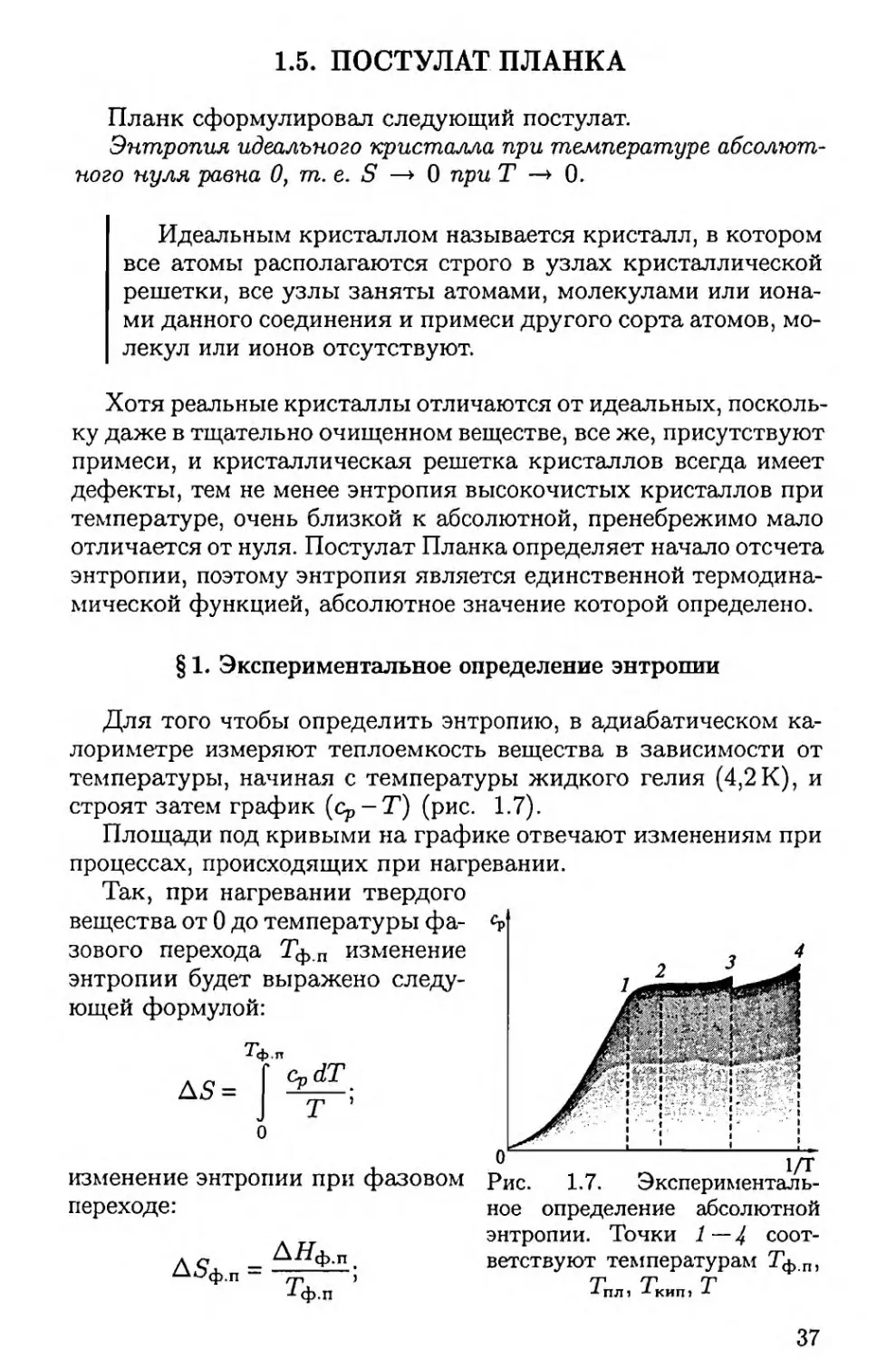
Дл я того чтобы определить энтропию, в адиабатическом ка­
лориметре измеряют теплоемкость вещества в зависимости от
температуры, начиная с температуры жидкого гелия (4,2К), и
строят затем график (ср -Т ) (рис. 1.7).
Площади под кривыми на графике отвечают изменениям при
процессах, происходящих при нагревании.
Так, при нагревании твердого
вещества от 0 до температуры ф а­
зового перехода Тф.п изменение
энтропии будет выражено следу­
ющей формулой:
с
.
■
&
<
—
Т’
з
О
! j ......Г
|
AS=
изменение энтропии при фазовом
переходе:
дс
_
.
АЬф.п -
,
-*ф.п
u
_
i/T
Рис. 1.7. Эксперименталь­
ное определение абсолютной
энтропии. Точки 1 —4 соот­
ветствуют температурам 7ф п,
37

при дальнейшем нагревании вещества до температуры плавле­
ния получим приращение энтропии:
Д5=
CpdT
Т;
Тф.П
изменение энтропии в результате плавления будет равно:
_
АЯПЛ,
нагревание расплава от температуры плавления до температуры
кипения приведет к изменению энтропии:
Д5=
' (^dT
JТ’
в результате кипения изменение энтропии:
АС*
_
Д^КИП
£**ЭКИП— rp )
- *кип
дальнейшее нагревание газа от температуры кипения до темпе­
ратуры Т приведет к возрастанию энтропии:
AS=1
Суммарное изменение энтропии при нагревании вещества от О
до Т будет равно сумме всех перечисленных изменений энтропии
и будет представлять абсолютное значение энтропии при тем­
пературе Т. Таким образом, в отличие от всех других термо­
динамических функций состояния мы можем определить или
рассчитать не только относительное, но и абсолютное значе­
ние энтропии. Итак, абсолютная энтропия вещества равна сум­
ме энтропий его агрегатных состояний и фазовы х переходов:
Гф.п
тпл
=+}
О
Тф.П
^кип
Ткип
ДЯПЛ f CpdT
ДЯкип f CpdT
~Т^~ J ~т~
~т^Г J
5=0+
CpdT ДЯФ,
1ф .п
38

§2. Цикл Карно
Важнейшей проблемой, стоящей перед человечеством, я вл я­
ется проблема использования тепловой энергии д л я совершения
работы, т. е. проблема создания тепловых машин. Вопрос о том,
какое максимально возможное количество работы может совер­
шить тепловая машина, поставил и получил на него ответ фран ­
цузский ученый С. Карно. Рассмотрим простейшее устройство
для совершения работы под действием теплоты. Представим се­
бе цилиндр, наполненный газом и закрытый поршнем. Если на­
греть газ в цилиндре, то поршень поднимется и будет совершена
работа против силы внешнего давления, равная работе расши­
рения. Однако это устройство еще не машина. Тепловая машина
до лж на совершать работу не однократно, а многократно. Д л я
этого необходимо охладить газ в цилиндре, тогда поршень вновь
опустится и совершит работу, а вся система придет в первона­
чальное состояние, совершив циклический процесс.
Процесс, при котором система, претерпевая ряд измене­
ний, возвращается в исходное состояние, называется цикли­
ческим процессом или циклом.
Дл я циклического процесса суммарное изменение любой функ­
ции состояния равно нулю. В тепловой машине должен происхо­
дить циклический процесс, чтобы она могла непрерывно совер­
шать работу. Какова же максимальная работа, которую может
совершить машина за один цикл, потребив теплоту Q?
Коэффициент полезного действия (к.гг.д.) машины Г| —
это отношение наибольшей возможной работы W , соверша­
емой за один цикл, к полученной системой теплоте Q.
W
"■g-
<L26>
Из второго закона термодинамики следует, что все тепло, по­
требляемое системой, не может быть использовано для произ­
водства работы, поэтому из (1.26) следует, что всегда Г| < 1.
Рассмотрим некий циклический процесс в координатах S и Т
(рис. 1.8, а). Точка на этой диаграмме отвечает состоянию систе­
мы, линия —обратимому процессу, а замкнутая линия — циклу.
В точке Н изменение внутренней энергии до и после прохожде­
ния циклического процесса равно 0:
AU=odU=0,
39

Рис. 1 .8. Произвольный обратимый цикл (а) и цикл Карно (б)
поэтому в цикле сумма всех теплот равна сумме всех работ:
6Q=W =TdS.
Теплота, полученная системой при переходе ее из точки Н
через точку Е в точку F равна
5(F)
Qi= [TdS.
S(H)
Теплота, отдаваемая системой при переходе ее из точки F в точ­
ку Н через точку G равна
5(Я)
Q2= [TdS.
S(F)
Теплоты Qi и Q2 не равны, так как зависят от пути перехо­
да системы: Qi равна площади HEFLKH, a Q2 равна площади
HEFGH, и при этом Qi положительно, a Q2 отрицательно.
Цикл, изображенный на рис. 1 .8, б, состоит из двух адиабати­
ческих и двух изотермических процессов: процессы НЕ и FG —
изотермические, процессы HG и FE — адиабатические. В ре­
зультате изотермического процесса при переходе из точки Н в
точку Е происходит возрастание энтропии от Si до S2 и при
этом совершается работа. При адиабатическом процессе энтро­
пия остается постоянной, а температура понижается от Т\ до Т2.
Далее система отдает теплоту окружающей среде, и ее энтропия
понижается от S2 до Si. Наконец, система адиабатически нагре­
вается от температуры Т2 до Т\.
Работа, произведенная системой в результате циклического
процесса, равна площади HEFG:
W=(T1-T2)(S2-S1).
40

Теплота, полученная системой, равна площади HEFLKGH:
Q=Tl(S2-S1).
Следовательно,
WT2-Ti
л
Qт2
Коэффициент полезного действия тепловой машины все­
гда меньше единицы и зависит только от разности темпера­
тур рабочего тела Т\ и холодильника Т2.
Отсюда вывод: чтобы повысить коэффициент полезного дей­
ствия тепловой машины, необходимо увеличить разность тем­
ператур рабочего тела и холодильника, но температура холо­
дильника равна температуре окружающей среды, которая близ­
ка к комнатной. Поэтому на практике идут по пути повыше­
ния температуры рабочего тела. Если температура пара в паро­
возном котле достигает лишь 573 К, то к. п .д . паровоза соглас­
но (1.27) не может быть выше 100(573 - 298)/573 = 48%, тогда
как к. п .д . тепловой электростанции, у которой температура па­
ра достигает 1273 К, может быть значительно выше: 100(1273-
- 298)/1273 = 75%. Еще более высокий к .п .д . может иметь дви­
гатель внутреннего сгорания, например автомобилей, в котором
температура рабочих газов достигает 1700 К. В последнее вре­
мя был построен МГД-генератор, в котором рабочим телом слу­
жит плазма температурой 4000 К и выше. Поэтому к. п .д . МГД-
генераторов может достигать 100(4000 —298)/4000 = 95%. Повы­
шение к .п .д . тепловых машин решает задачу экономии энерго­
носителей и капитальных вложений.
Любой другой цикл не позволяет получить к .п .д . выше, чем
к. п .д . цикла Карно, так как вокруг любого другого цикла мож­
но описать цикл Карно, а площадь описывающей фигуры всегда
больше площади вписанной.
Цикл Карно определяет максимальный к .п .д . тепловой ма­
шины, в которой процессы протекают обратимо. В действитель­
ности, условия полной обратимости процессов трудно создать.
Поэтому к.п .д . реальных тепловых машин значительно ниже.
Например, к .п .д . паровоза не превышает 8%.
§3. Суммы по состояниям и расчет энтропии
Как говорилось выше, энтропия определяется термодинами­
ческой вероятностью. При протекании необратимых процессов
(1.27)
41

в изолированной системе энтропия системы стремится к мак­
симуму. Энтропия — экстенсивный параметр, так как при объ­
единении систем энтропии их складываются. В теории вероятно­
сти известно,что вероятность события, слагающегося из несколь­
ких событий, равна произведению вероятностей каждого из этих
событий. Таким образом, при сложении энтропий нескольких
систем общая энтропия получающейся сложной системы будет
равна
S=Sl+S2+S3+---+Si=f(Wi)f(W2)f{W3)+ •••+f(Wi).
Следовательно, при сложении нескольких систем энтропия
общей системы будет равна
S=kln(WiW2W3+•••+Wi)=
= *(lnWi+InW2+InW3+ •••+ InWi)= к^ InWi.
Если рассматривать изолированную систему, содержащую
1 моль идеального газа, то
N2, N3 ,... , Ni молекулы газа бу­
дут иметь Ei, £2, £3 ,..., £i энергии, причем энергия отдельных
молекул принимает только дискретные значения.
Статистическая термодинамика для внутренней энергии си­
стемы дает следующее уравнение:
а-28)
Суммой по состояниям называют функцию
Ал.
Q=E e_fcr-
(1.29)
1=1
Пусть энергии молекул е* складываются из энергии поступатель­
ного, вращательного, колебательного и электронного движения:
= £п+ев+£к+£э-
Каждому виду движения будет отвечать соответствующая сум­
ма по состояниям в соответствии с (1.29) так, что:
С
Е
в
£
Qi- е"£т +е~Ет + е“£т +е“Ег.
Каждая из сумм по состояниям вычисляется отдельно. Д ля рас­
чета энтропии статистическая термодинамика дает следующее
уравнение:
42

S=kNiaQ+¥;.
Так как все остальные термодинамические функции могут
быть выражены через энтропию и внутреннюю энергию, то все
они могут быть выражены через сумму по состояниям. Д ля од­
ноатомных и двухатомных газов термодинамические функции,
таким образом, могут быть рассчитаны достаточно точно. Д л я
многих газообразных молекул удается рассчитать такие свой­
ства к а к оптические спектры, что позволяет идентифицировать
различные вещества.
1.6 . ТЕРМОДИНАМИКА ОТКРЫТЫХ СИСТЕМ.
ТЕРМОДИНАМИЧЕСКИЕ ПОТЕНЦИАЛЫ
§ 1 . Свободная энергия
В общем случае работа, совершаемая в результате прохожде­
ния в системе процесса, состоит из работы расширения и работы
против каких-либо других сил.
Всякая работа за исключением работы расширения на­
зывается полезной работой.
Итак, суммарная работа является суммой всех видов работ:
bW =bW'+pdV.
При обратимом процессе
TdS =dU+bW =dU+SW'+pdV,
отсюда
= dU-TdS+pdV.
(1.30)
ПриТ =constир=const:
-bW* =d{U-TS+pV).
Введем обозначение:
G=U -TS+pV=H -TS.
(1.31)
Функция G в уравнении (1.31) — это функция состояния,
так как все входящие в нее величины являются функциями
состояния.
43

Функция состояния, равная при изобарно-изотермичес­
ких условиях разности энтальпии и энтропии, умноженной
на абсолютную температуру, называется свободной энерги­
ей Гиббса.
Из уравнений (1.30) и (1.31) следует:
G=-W '.
Полезная работа, совершаемая при изобарно-изотерми­
ческих условиях, равна убыли свободной энергии Гиббса.
Если полезная работа совершается при Т = const и V = const, то
в уравнении полезной работы dV будет равно 0, и получим:
- 5W':=dU-TdS =d(U-TS).
(1.32)
Введем обозначение:
с
о
h
l
и
(1.33)
Из уравнений (1.32) и (1.33) следует:
-W'=G
(1.34)
и
-W'=А.
(1.35)
Полезная работа, совершаемая при изохорно-изотерми-
ческих условиях, равна убыли свободной энергии Гельм­
гольца.
В уравнении (1.33) А — это функция состояния, так как все
входящие в нее величины являю тся функциями состояния. Ее
называют свободной энергией Гельмгольца.
Свободной энергией Гельмгольца называется функция
состояния, равная разности внутренней энергии и энтропии,
умноженной на абсолютную температуру при изохорно-
изотермических условиях.
Физический смысл этих функций будет рассмотрен далее.
§2. Критерии равновесия или прохождения самопроизвольного
процесса в открытых системах
Продифференцируем уравнение (1.31) дл я свободной энергии
Гиббса:
dG=dU-TdS-SdT +pdV+Vdp.
44

Подставим в это выражение значение dU = T d S —pdV:
dG=TdS-pdV-TdS-SdT+pdl/+Уф.
После сокращений получим:
dG=-SdT+Vdp.
(1.36)
При T = const и р = const система находится в равновесии, и из
уравнения (1.36) получим:
dG =0.
(1.37)
Дифференцированием уравнения (1.33) и подстановкой в него
значения dU получим д ля dA уравнение:
dA=-SdT-pdV.
(1.38)
При Т = const и V = const система находится в равновесии и
dA =0.
(1.39)
Уравнения (1.37) и (1.39) даю т условия равновесия в закрытых
системах при р = const и V = const соответственно. Если система
открытая, то
i
dG= -S dT +Vdp+'f2 Ikdrii.
(1.40)
г=1
При равновесии в системе dG = 0, а Т = const, р = const по
условию. Следовательно, из уравнения (1.40) получим:
г
£)Мпм=0.
(1.41)
г=1
Уравнение (1.41) представляет условие равновесия в открытой
системе, в том числе и в системе, в которой имеется химическое
равновесие. Если в системе совершается помимо работы расши­
рения еще и полезная работа, то из (1.34) следует:
dG=-m\
а из (1.35) следует:
dA=-
При необратимом процессе:
5^ 'еобр<5WUP,
45

(1.42)
поэтому из уравнения (1.36) получим:
dG<-SdT-pdV.
Из уравнения (1.42) при Г = const и р = const получим:
dG< 0.
(1.43)
Неравенство (1.43) дает критерий прохождения самопроизволь­
ного процесса в изобарно-изотермической системе.
Повторяя рассуждения д л я свободной энергии Гельмгольца
при необратимом процессе, получим:
dA<-SdT-pdV.
(1.44)
Из неравенства (1.44) при Т = const n V = const получим:
dA<0.
(1.45)
Неравенство (1.45) дает критерий прохождения самопроиз­
вольного процесса в изохорно-изотермической системе. Анало­
гично д л я необратимых процессов в открытых системах получим:
t
dG< -Sdt +Vdp +Vidni.
(1.46)
1=1
Из неравенства (1.46) при Т = const и = const получим:
1
£М»Ч<0.
(1.47)
1=1
Неравенство (1.47) дает критерий д л я прохождения в системе
самопроизвольного химического процесса при изобарно-изотер­
мических условиях.
Следовательно, для того чтобы ответить на вопрос, возмо­
жен ли самопроизвольный процесс в системе, необходимо
рассчитать свободную энергию. Если система находится под
постоянным давлением (например, атмосферным) и при по­
стоянной температуре, и если свободная энергия будет от­
рицательна, то самопроизвольный процесс возможен; если
свободная энергия равна нулю, то система находится в рав­
новесии; и, наконец, если свободная энергия положительна,
то самопроизвольный процесс невозможен.
46

Если система находится при постоянной температуре и имеет
постоянный объем (например, объем автоклава), то самопроиз­
вольный процесс в ней может протекать при условии:
i
dA< -Sdt-pdV + ^ liidrii.
(1-48)
i=1
Из уравнения (1.48) при Т = const и V = const получим:
г
0.
(1.49)
i-1
Уравнение (1.49) дает критерий прохождения самопроизвольно­
го химического процесса при изохорно-изотермических условиях.
Следовательно, д л я того чтобы ответить на вопрос, возмо­
жен ли самопроизвольный процесс в системе при изохорно-
изотермических условиях, нужно рассчитать свободную
энергию Гельмгольца, и если dA < 0, самопроизвольный
процесс возможен, если dA = 0, реакция не пойдет, так как
система находится в состоянии равновесия, а при dA > 0
возможен лишь произвольный процесс.
§3. Расчет свободной энергии
Так как в уравнение свободной энергии входит внутренняя
энергия, то вычислить абсолютное значение свободной энергии
невозможно, поэтому вычисляют изменение свободной энергии
при стандартных условиях A G^gg. Д ля этого используют урав­
нение (1.31) или уравнение (1.33), так как изменение свободной
энергии зависит только от начального и конечного равновесно­
го состояния системы, то изменение свободной энергии отвечает
уравнениям:
AG =АН -TAS]
(1.50)
АА=AU -TAS.
(1.51)
или соответственно:
АН =AG-TAS,
(1.52)
AU =AA +TAS.
(1.53)
Таким образом, дл я того чтобы рассчитать изменение свобод­
ной энергии при стандартных условиях, рассчитывают измене­
ния энтальпии и энтропии при стандартных условиях. Затем по
47

уравнению (1.50) или (1.51) рассчитывают изменение свободной
энергии Гиббса при V = const и Т = const или свободной энергии
Гельмгольца при V = const и Т = const соответственно.
§ 4. Физический смысл свободной энергии
Уравнения (1.52) и (1.53) определяют физический смысл сво­
бодной энергии Гиббса и свободной энергии Гельмгольца. Так
какAG=-W7,то
АН=-W9+TAS.
При р = const АН - Qpyпоэтому
Qp=-W '+TAS.
Если к системе подводится теплота Qp>то она расходуется на
совершение полезной работы лишь частично.
Часть энергии, переданной системе в виде теплоты, ко­
торая может быть использована непосредственно д л я совер­
шения работы, называется свободной энергией.
Часть переданной системе теплоты идет на возрастание энтро­
пии. Эта часть подводимой теплоты не может быть использована
для совершения работы.
Часть энергии, переданной системе в виде теплоты, кото­
рая идет на возрастание энтропии, не может быть свободно
использована для совершения работы, поэтому она называ­
ется связанной энергией.
В справочниках приводятся значения AG^gg для большого
числа веществ, поэтому изменения свободной энергии Гиббса
при прохождении химической реакции можно вычислять по стан­
дартным свободным энергиям образования так же, как и измене­
ние энтальпий химических реакций. Однако надо помнить, что
свободные энергии образования простых веществ не равны 0.
Вопрос. Можно ли всю энергию химической реакции ис­
пользовать непосредственно д л я совершения работы?
Ответ 1. Невозможно, если энергию химической реакции
вначале получаем в виде теплоты, например, путем сжигания
водорода в кислороде.
Ответ 2. Можно, если построить такую машину, в которой
свободная энергия химической реакции не переходит в теплоту, а
48

непосредственно расходуется на совершение работы. Примером
может быть топливный элемент, в котором реакция водорода
и кислорода протекает на электродах, разделенных мембраной.
В этой машине вся энергия химической реакции используется
для совершения работы (если пренебречь потерями на сопро­
тивление в цепи). В живых организмах протекают циклические
процессы, в результате которых химическая энергия питатель­
ных веществ используется в виде свободной энергии, что предот­
вращ ает перегрев организмов. Этот же принцип используется в
технике: например, потенциальная энергия воды на гидростан­
циях может быть использована полностью д л я производства ра­
боты в виде свободной энергии, солнечная энергия, поглощае­
мая солнечными батареями, электроэнергия аккумулятора так­
же используются полностью. Разумеется, полное использование
свободной энергии во всех этих устройствах возможно лишь в
принципе. В действительности часть энергии неизбежно расхо­
дуется на преодоление сил трения и переходит в теплоту.
§5. Характеристические функции
Рассмотрим свободную энергию Гиббса как функцию от д ав ­
ления и температуры:
G = f(T,p),
а энергию Гельмгольца, как функцию от температуры и объема
л =ф(т,п
Полные дифференциалы этих функций можно выразить в част­
ных производных:
dG=
(1.54)
И
(1.55)
С другой стороны, согласно уравнению (1.36) clG = - S d T + Vdp
и согласно (1.38) dA = - S dT -pdV. Сравнивая эти уравнения с
уравнениями (1.54) и (1.55) приходим к выводу, что
=-S и
дС
др
=V;
т
р
49

)=-S и
V
дА
dVv~ -p-
Рассмотрим внутреннюю энергию как функцию энтропии н
объема, а энтальпию — как функцию энтропии и давления:
U = у (5, V) и Н = ф(5,р). Выразим их полные дифференциа­
лы в частных производных:
du-{^);,s+(Mldv’
(1-м)
(157)
Сдругой стороны, Н = U +pdV, следовательно, dH = dU +pdV+
+Vdp и после подстановки U получим dH ~ TdS-pdV+pdV+Vdp.
После сокращении
dH=TdS+Vdp.
(1.58)
Сравнивая уравнения (1.17) и (1.58) с (1.5G) и (1.57), получаем:
ди
\dS
)=Т и
V
dU\
ду)ГР
(дН_
К"
Р
дН
дрК-
s
Частные производные свободной энергии Гиббса по темпера­
туре и давлению равны параметрам - 5 и V, частные производ­
ные свободной энергии Гельмгольца по температуре и объему
равны параметрам S и -р . частные производные свободной энер­
гии по энтропии и объему равны параметрам Т и V , частные
производные энтальпии равны параметрам 5 и -р .
Функции, частные производные которых по какому-либо
из параметров равны другому параметру, называются ха­
рактеристическими функциями.
Пользуясь этим свойством характеристических функции,
можно рассчитывать соответствующие параметры системы. На­
пример, если да н а свободная энергия Гиббса в виде уравнения,
зависящего от температуры, а нужно рассчитать энтропию, до­
статочно продифференцировать заданное уравнение по темпе­
ратуре. В связи с характеристическими свойствами этих функ­
ции их назы ваю т термодинамическими потенциалами: свобод-
50

ную энергию Гиббса называют изобарно-изотермическим потен­
циалом, свободную энергию Гельмгольца называют изохорно-
изотермическим потенциалом.
§ 6. Температурная зависимость свободной энергии
Преобразуя уравнение (1.31) для рачета изменения энергии
Гиббса получим:
AG=AH-TAS.
Так как значение изменения энтропии равно - A S =
то
AG =AH +T
dAG
З Т р,TLi
dAG
дТ р,гц
(1.59)
Тем же путем дл я изменения свободной энергии Гельмгольца
получим:
АА=AU+Т
dAU\
No )v,
(1.60)
Уравнения (1.59) и (1.60) называют уравнениями Гиббса—Гельм­
гольца. Они определяют зависимость свободной энергии от тем­
пературы. Чтобы получить зависимость свободной энергии от
температуры в явном виде, нужно проинтегрировать уравне­
ния (1.59) и (1.60). Д л я этого необходимо разделить переменные.
Сделаем явным это уравнение относительно А Н :
- АН=-AG+T
fdAG\
{дТ)'
\
/ Р)П{
Пусть р = const и щ = 1, тогда можно переписать это уравне­
ние в виде:
-дя=-дс+т(^).
Разделим обе части этого уравнения на Г 2 и умножим на d T :
АН No -AGdT +TdAG
dT= —
Т2
Т2
Правая часть этого уравнения представляет собой производную
от функции / = ~jT- Следовательно,
d
AG
Т
АН
~W
dT.
51

Теперь переменные разделены, и можно провести интегриро­
вание. Получим:
AG=-T^^dT-JT,
(1.61)
где J — постоянная интегрирования. Если температура посто­
янна (стандартная) Т = 298 К, то dT = 0 и AG^gg = 298J, от­
кудаJ=
получим:
АСу>98
298 ‘
Подставив это значение J в уравнение (1.61),
AG=-T
'АН
dT- Д^298гр
298 ‘
(1.62)
Если температурный интервал невелик, то величину А Н в
уравнении (1.62) можно считать постоянной и ее можно вынести
за знак интеграла, после чего интегрирование не представляет
труда, если ж е А Н нельзя считать постоянной, то нужно под­
ставить ее выражение по закону Кирхгоффа, воспользовавшись
вириальными уравнениями д л я теплоемкостей из справочника,
и затем интегрировать полученную сумму интегралов.
Если реакция проходит при постоянном объеме, то, повторив
приведенные выше рассуждения, получим уравнение д л я зави­
симости свободной энергии Гельмгольца от температуры:
ДА=-т\^ dT+Mfir.
(1.63)
JТ2
298
v
'
В качестве конкретного примера рассмотрим реакцию диссоци­
ации димера диоксида азота:
N204*=» 2N02
Если в стеклянном сосуде, выполненном в виде гантели, со­
здать вакуум, заполнить диоксидом азота и запаять, то в нем
установится химическое равновесие в соответствии с уравнением
диссоциации. Мы будем видеть, что газ окрашен в светло-бурый
цвет. Рассчитаем свободную энергию диссоциации димера при
стандартных условиях. По справочнику* находим:
Д (7298(мо2) = 52,29 кДж/моль;
A G 298(N3o 4) = 99,68 кДж/моль.
Краткий справочник физико-химических величин/Под ред. Ф. Ф. Равеля н
Ф. М. Пономаревой. — СПб.: Специальная литература, 1999 г.
52

Отсюда
Дб?298(х.р) - Ю4 580 - 99 680 = 4900 Дж/моль.
Мы нашли свободную энергию Гиббса, но нам нужна свобод­
ная энергия Гельмгольца, т а к как в нашей системе постоянен
объем, а давление меняется вследствие диссоциации. Свободную
энергию Гельмгольца можно рассчитать по уравнению:
ДЛ=AG-AnRT,
где А п — разность стехиометрических коэффициентов продукта
реакции и исходного вещества в данном случае Д п = 2 - 1 = 1.
Подставив численные значения, получим:
ДЛ298(х.р) = 4900 -1 -8 ,314 *298Дж/моль = 2422 Дж/моль.
Свободная энергия положительна, однако диссоциация все же
происходит, что и показывает опыт. Это значит, что вопрос о
том, пойдет или не пойдет самопроизвольно химическая реак­
ция (в данном случае диссоциация), вообще говоря, некоррек­
тен. Мы можем задаваться вопросом лишь о том, находится ли
система в состоянии равновесия, и если нет, то в какую сторо­
ну будет сдвинуто равновесие реакции. Положительное значение
свободной энергии говорит лишь о том, что данная реакция при
стандартных условиях сдвинута в сторону димеризации диокси­
д а азота. Посмотрим, как сдвинется равновесие в этой реакции
при температуре 398К (100°С). Рассчитаем значение А А при
398 К по уравнению (1.62):
дл=-т
ГAU
Т2
dT+
298 '
Находим в том же справочнике:
A-^298(N0 2) = 34190 Дж/моль;
Д£/2°98= 34190 + 0,5ЯГ = 35428Дж/моль;
^■^298(n2o4) = 13300 Дж/моль;
Дt/2°98= 13300+ 2RT = 18255Дж/моль.
Откуда
Аи2Щх.Р) = I8255 “ 35428 = -17173 Дж/моль.
53

Подставив его значение в уравнение при Т = 298 К, получим:
Так как температурный интервал невелик, примем A U постоян­
ной и проинтегрируем. Откуда
Итак, при повышении температуры на 100 °С свободная энер­
гия Гельмгольца становится отрицательной, что говорит о том,
что равновесие резко сдвигается в сторону диссоциации. В этом
легко убедиться, если один шар гантели с диоксидом азота на­
греть в кипящей воде. Цвет газа в нагретом шаре становится
темно-бурым, а в холодном шаре остается светло-бурым.
§ 7. Химические потенциалы компонентов систем
Рассмотрим системы, в которых происходят химические про­
цессы. Пусть система представляет собой 1 моль идеального га­
за. При Т = const и р = const химический потенциал определяет­
ся уравнением:
поэтому при п = 1 моль:
Химический потенциал 1 мо ля чистого вещества при по­
стоянном давлении и постоянной температуре равен свобод­
ной энергии Гиббса одного моля этого вещества.
Пусть в системе, представляющей собой идеальный газ, Т = const,
а р изменяется на dp. Тогда в уравнении (1.36) SdT = 0 и
где V — объем 1 моля чистого вещества; с — постоянная инте­
грирования. При р = const, dp = 0 и JL1= с, поэтому:
АА = -22 935Дж/моль.
d\it = Vdp,
откуда:
54

где (1° — значение химического потенциала при стандартных
условиях. Подставим значение V из уравнения состояния иде­
ального газа: V = R T / р и проинтегрируем полученное уравнение:
ц=ц°+RTlnp.
При стандартных условиях Т = 298 К и р = 1 атм, следовательно,
1пр = 0, а |! = |1°, где (И° — стандартный химический потенциал.
р2
При изменении давления от р\ до р2 |LL2—M
-
i = -RTln —. Пусть
Pi
система представляет собой смесь идеальных газов. Так как в
идеальном газе частицы не взаимодействуют между собой, то
давление смеси идеальных газов равно сумме парциальных да в­
лений всех газов смеси: Р =
Поэтому химический потен­
циал 2-го газа будет равен:
Щ = lii+RT In Pi.
Пусть система представляет собой реальный газ. Тогда уравне­
ние состояния идеального газа не применимо, но так как дл я ре­
альных газов уравнение состояния неизвестно, необходимо обра­
титься к эмпирическим уравнениям, учитывающим потенциаль­
ную энергию межмолекулярного взаимодействия в реальных га­
зах. Например, можно использовать уравнение Ван-дер-Ваальса:
[т+Тп)0'-ъ) =вт.
Здесь Ъ учитывает, что объем молекул имеет конечную величи­
ну, а — влияние потенциальной энергии молекул на давление
газа. Величины а и Ь определяются из опытов по сжимаемости
газа, и д л я многих газов приведены в справочниках. Д ля того
чтобы получить уравнение д л я химического потенциала, нуж­
но преобразовать это уравнение в явное по отношению к объе­
му и подставить значение объема под интеграл Vdp. Понятно,
какое сложное уравнение получится для интегрирования, к то­
му же оно будет содержать эмпирические коэффициенты а и Ъ.
Г. Льюис предложил другой путь для учета влияния отклоне­
ний реальных газов от уравнения состояния идеального газа. Он
предложил просто вводить эмпирическую поправку в уравнение
для химического потенциала идеального газа, заменив давление
величиной
/=ур,
которую он назвал фугитивностью, или летучестью газа, а у —
коэффициентом летучести.
55

Коэффициентом летучести (фугитивности) называется
эмпирический множитель
на который умножается дав­
ление г а за и который подбирается таким, чтобы д л я реаль­
ного г аза можно было использовать уравнение химического
потенциала для идеального газа. Произведение коэффици­
ента летучести (фугитивности) на давление газа называют
летучестью или фугитивностью данного газа / .
Тогда
dii=RTdlnf
и
р=ц°+ЯГ1п/,
причем JX0 — стандартный химический потенциал реального газа.
Дл я смеси реальных газов
Mi = Hi+i£Tln/i,
где р? — стандартный химический потенциал г-го га за в сме­
си газов. Общее давление смеси реальных газов будет равно:
г
Р=
Поэтому химический потенциал г-ro га за будет
г=1
равен:
п
^ = М*+ЯГInуда,
гдеу= “
—
коэффициент летучести г-го газа. Коэффициент
Pi
летучести может быть определен различными методами, здесь
рассмотрим метод, основанный на измерении сжимаемости ре­
альных газов.
Пусть объем 1 моля газа при давлении р отличается от объ­
ема идеального газа при том ж е давлении на величину а , т. е.
RT
пусть ВТ/р =V -а . Тогда V = ----+а для реального газа при
Р
Т = const. Если реальный газ в состоянии 1 имел очень низкое
давление p i, то его свойства близки к идеальному газу. Если же
он обратимо и изотермически сжимается до давления р 2 , то его
химический потенциал изменяется от Цх до рг, и изменение хи­
мического потенциала вследствие перехода газа из состояния 1
в состояние 2 будет равно:
2
2
2
М1-Ц1=|ф =| ^~ dp+adaj =RTIn^ +1ada,
56

HO|I2 = Д° + ЯГ1пур2)) аЦ1 = Ц°+ RT\npi, поэтому JI2~{Xi=
= RTIn—+RTInу.Откуда
Pi
Iny =
(1.64)
Пользуясь уравнением (1.64), можно эмпирически определить
величину а , если измерить давление газа при переходе системы
из состояния 1 в состояние 2 ,3 и т. д. Д л я этого нужно построить
график в координатах (сс-р), измерить площадь под полученной
кривой и поделить величину площади на R T .
Теперь рассмотрим химические потенциалы в системе с веще­
ством в конденсированном состоянии. Конденсированная ф а з а
находится в равновесии с насыщенным паром. Так как химиче­
ский потенциал — параметр интенсивный, то во всех частях си­
стемы он одинаков. Действительно, равновесию между конден­
сированным веществом и паром отвечают условия равновесия в
химических системах:
i
^2M«i=0.
t=i
Пусть в этой системе dn молей г-го вещества переходит из кон­
денсированной фазы в пар. Д л я конденсированной фазы с^пцконд)
имеет отрицательное значение, для паровой ф азы — положи­
тельное:
^'г(пар) ——^'{(конд) •
При равновесии
Ц1(пар)^^г(пар) “ Ш(конд)^1(конд)
ИЛИ
Цг(пар)^г(пар) 1^г(конд)^г(конд) О
d71i(Pi(nap) —М'г(конд)) = 0*
Но drii не может быть равно 0, следовательно:
М'(пар) ~ М'(конд) •
Химический потенциал вещества в конденсированной си­
стеме определяется давлением насыщенного пара над ней.
Поэтому
М'(конд)““М* + ЛПпр(пар)
57

если пар можно считать идеальным газом, или летучестью на­
сыщенного пара; если пар нельзя рассматривать как идеальный
газ:
М^конд) = М*
/(пар)■
Пусть конденсированная система состоит из г веществ. Тогда
пар над ней насыщен по всем г веществам, и химический по­
тенциал каждого из них определяется парциальным давлением
пара этого вещества (если пар близок к идеальному газу):
М'г(конд) = М' +
1п Рг(пар)
или парциальной летучестью (уели пар отличается от идеально­
го газа):
Цг(конд)=Ц +RT In/{(пар)•
Однако это уравнение действительно лишь д л я тех систем, в
которых не образуется растворов.
Пусть конденсированная система представляет собой идеаль­
ный раствор.
Раствор, у которого давление пара при всех концентраци­
ях отвечает уравнению Рауля, называется идеальным рас­
твором.
Дл я идеального раствора давление насыщенного пара
растворенного г-го комонента Pi равно мольной доле этого
комонента в растворе, помноженной на давление насыщен­
ного пара над индивидуальным г-м веществом
Таким образом:
Pi = XiPi,
(1.65)
где Xi — мольная доля г-го вещества в растворе. Уравнение (1.65)
было названо уравнением Рауля.
Мольная доля г-го вещества в растворе равна отношению
числа молей этого вещества к сумме чисел молей всех j
веществ в растворе, включая и растворитель:
з
xi =Щ/^2,Пу
j=l
При равновесии в системе Ц(раств) = М-(пар)>следовательно:
Щ(раств)=Ц ^RT1п,Р»= Ц +RT1п(ЖьР()
58

Дг(раств) *“ Ц "bR T lnpi^nap) + R T In X{.
Ho R T In pi (nap) = const, так как давление пара индивидуального
вещества зависит только от температуры. Обозначим
Тогда
—
fi + i2Tlnpi(nap).
\ii = \s%+RTlnxi,
где
— стандартный потенциал данного вещества в растворе.
Если давление пара над раствором отклоняется существенно от
закона Рауля, то химические потенциалы такого реального рас­
твора будут отличаться от потенциалов, рассчитанных дл я иде­
ального раствора. В таком случае поступают так же, как и дл я
газовых систем: вместо мольной доли в уравнения химических
потенциалов ставят активности а, которые берутся равными
a = jiXi.
(1.66)
Коэффициентом активности называют эмпирический
множитель у к мольной доле данного компонента в рас­
творе, который позволяет для реального раствора исполь­
зовать уравнение химического потенциала д л я идеального
раствора. Произведение коэффициента активности на моль­
ную долю компонента раствора называют активностью дан ­
ного компонента а.
Химический потенциал г-того компонента в растворе согласно
(1.66) будет равен
14=|х-+RTInсц=ц-+RTln(YiXi).
(1.67)
Полученные уравнения д л я химических потенциалов в различ­
ных системах в дальнейшем будут использоваться для описания
химических равновесий фазо вы х равновесий в гетерогенных си­
стемах и равновесий в растворах.
1.7.ТРЕТИЙзакон термодинамики
Изменение свободной энергии Гиббса определяется уравне­
нием
AG=AH-TAS.
При Т « ОAG становится равным АН. В координатах (АН —Т)
и (AG —Т) кривые AG= f(T) иАН =\|/(Т) при Т =0 сходят­
ся в одной точке (рис. 1 .9 , б). Однако через одну точку может
59

АН,
AG
Рис. 1.9. К теореме Нернста: а — кривые АН = /(Т) и AG = ср(Т)
(пунктир), б —кривые А Н = /(Т) и AG = <р(!Г)
проходить бесчисленное множество кривых, но лишь одна кри­
вая свободной энергии определяет равновесие в системе. К ак же
определить эту кривую? Первый и второй законы термодинами­
ки не позволяют решить эту задачу.
В.Нернст сделал предположение, что кривые AG = /(Т) и
А Н = \|/(Т) не только сходятся в одной точке при температуре
ОК, но и имеют общую касательную в этой точке (рис. 1.9, а),
так что:
(ЭАН\
fdAG\
lim ,
.
т-оVдТ)
(1.68)
Поскольку
то
Ле
(dAG\
^
-
Ы);
lim AS =0.
г—о
(1.69)
Это означает, что в любом химическом процессе при абсолют­
ном нуле энтропия системы не меняется и остается равной нулю.
Уравнение (1.68) представляет третий закон термодинамики, ко­
торый является следствием уравнения Больцмана (1.14).
При температуре абсолютного нуля равны не только из­
менения свободной энергии и энтальпии, но равны и их про­
изводные по температуре, т. е. функции /( Т ) и vj/(T) имеют
общую касательную в исходной точке.
Следствием третьего закона термодинамики является посту-
Т-Г
о \дАН
лат Планка: если S =
, то lim Ср = 0, который позволяет
Iо1
т-+о
60

рассчитывать абсолютные энтропии. Из третьего закона термо­
динамики следует, что
температура абсолютного п ул я недостижима.
Наконец, третий закон термодинамики утверждает, что суще­
ствует только одна кривая (АG —Т), которая определяет равно­
весие в системе, а значит, и химическое равновесие в химической
системе.
1.8. ПРИЛОЖЕНИЕ ЗАКОНОВ ТЕРМОДИНАМИКИ
К ХИМИЧЕСКИМ СИСТЕМАМ. ТЕРМОХИМИЯ
Процессы, происходящие в химических системах, сопровож­
даются выделением или поглощением теплоты. Количество вы­
делившейся или поглощенной теплоты в ходе реакции называют
тепловым эффектом химической реакции.
Учение о тепловых эф фектах химических реакций назы­
вается термохимией.
Реакции в термохимии подразделяются на экзотермические и
эндотермические. По термодинамическим условиям знаков теп­
ловой эфф ек т экзотермической реакции отрицателен. Различ­
ные химические реакции протекают либо при постоянном объ­
еме, например, в автоклаве, либо при постоянном атмосферном
давлении. При этом температура обычно поддерживается посто­
янной.
Тепловой эфф ект изохорной реакции: Q y = A U и не зависит
от пути прохождения реакции.
Тепловой эффект изобарной реакции: Qp = А Н и не зависит
от пути прохождения реакции.
Г. Гесс эмпирически установил основной закон термохимии
применительно к химическим системам.
Если система из данного состояния изохорно-изотерми-
чески или изобарно-изотермически переходит в результате
химических реакций, протекающих различными путями, в
одно и то же конечное состояние, то суммарный тепловой
эф ф е к т реакции, проходящей разными путями, одинаков.
Как видим, закон Гесса является следствием первого закона
термодинамики.
61

§ 1. Теплоты образования, сгорания
Тепловые эф ф екты химических реакций, проходящих при по­
стоянном давлении, равны изменению энтальпии системы в ре­
зультате прохождения химической реакции. Тепловые эфф екты
химических реакций, проходящих при постоянном объеме, рав­
ны изменению внутренней энергии системы в результате про­
хождения химической реакции.
Так как мы не можем знать абсолютное значение внутрен­
ней энергии, то для расчетов приходится использовать значения
внутренних энергий исходных веществ и продуктов реакций при
стандартных условиях. Поскольку энтальпия представляет со­
бой сумму внутренней энергии и работы расширения, мы не мо­
жем знать абсолютных значений энтальпий исходных веществ и
продуктов реакции, поэтому приходится использовать значения
энтальпий исходных веществ и продуктов реакций при стандарт­
ных условиях, т. е. при температуре 298 К и давлении 1 атм.
Тепловой эфф ект реакции простых веществ при стан­
дартны х условиях с образованием соединения называют
стандартной теплотой образования данного соединения.
Например, стандартная теплота образования жидкой воды из
газообразного водорода и кислорода равна тепловому эффекту
реакции
Стандартные теплоты образования обозначаются как Д Я 293.
Стандартные теплоты образования простых веществ принима­
ются за 0 . Стандартные теплоты образования большого числа
веществ приведены в справочниках. По ним можно вычислить
тепловые эф ф екты многих тысяч химических реакций. Алго­
ритм д л я вычисления энтальпий химических реакций по закону
Гесса можно представить в общем виде уравнением:
где V* — стехиометрические коэффициенты, обозначения «прод»
и «исх» относятся к продуктам реакции и исходным веществам
соответственно. Стандартные теплоты сгорания главным обра­
зом органических веществ, приведенные в справочниках, поз-
Н2(г) + ^ 0 2(г) = Н20(ж) (ДЯ = -286 кДж/моль).
62

воляют рассчитать изменение внутренней энергии в результате
химической реакции по алгоритму:
|Е^дс,эдj -('Е 'ЪАЦ&Л . (1.71)
/
V 1—1
/ исх
прод
исх
Практическая ценность закона Гесса состоит в том, что он дает
возможность рассчитать тепловые эффекты химических реак­
ций, которые экспериментально не поддаются измерению. Д л я
этого данную химическую реакцию нужно заменить алгебраиче­
ской суммой химических реакций, тепловые эф ф е кты которых
известны или могут быть измерены. Например, тепловой эф­
фек т химической реакции образования оксида углерода опреде­
лить трудно, но можно его вычислить, исходя из трех уравнений
и используя уравнение (1.70),
(1)
C(T)+io2(r)=CO(r)
А Нх>
(2)
С(т) +0 2(г) = С02(г)
АЯЬ
(3)
С0(г) + ^02(г) =С02(г)
дя2.
Теплота первой из этих реакций А Н Х рассчитывается пу­
тем алгебраического вычитания третьего уравнения из второго:
АНХ = Д#1 - Д #2- Как видим, в термохимии химическую ре­
акцию описывают термохимическим уравнением, в котором ука^
зываю тся не только исходные и получающиеся вещества, но и их
агрегатные состояния: (г) — газ, (т) — твердое, (ж) — жидкое.
Если дан тепловой эфф ек т химической реакции при посто­
янном объеме, а нужно узнать тепловой эффект этой реакции
при постоянном давлении, то необходимо воспользоваться урав­
нением
AH =AU +AnRT.
(1.72)
Уравнение (1.72) получается из уравнения А Н = AU + p A V и
уравнения состояния идеального газа pV = A n R T . Здесь А п —
изменение числа молей веществ в результате химической реак­
ции. Так как изменения объемов веществ в конденсированном
состоянии пренебрежимо малы, то нужно учитывать изменение
чисел молей только газообразных веществ.
§2. Энергия кристаллической решетки
Другой пример использования закона Гесса — расчет энергии
кристаллической решетки. В грубом приближении кристаллы
63

солей можно принимать как кристаллические решетки, постро­
енные из разноименно зар яженны х ионов. Например, в кристал­
ле NaCl кристаллическая решетка построена из катионов Na+
и анионов СГ. Энергия связи в таком кристалле определяется
кулоновским взаимодействием ионов, которое уравновешивается
отталкиванием электронных оболочек ионов при сближении на
некоторое расстояние tq. Энергию ионной кристаллической ре­
шетки измерить не удается, но можно рассчитать ее по закону
Гесса.
Стандартной молярной энтальпией кристаллической ре­
шетки называется изменение энтальпии при образовании
одного моля кристаллического ионного соединения из га­
зообразных ионов при стандартных условиях.
Например, образование ионной кристаллической решетки NaCl
из простых тел, находящихся в их стандартных состояниях, мож­
но представить следующими реакциями:
1. Na(TB) —> Na(r), ДЯаТМа = +108 кДж/моль (энтальпия
атомизации натрия);
2. Na(r) —►Na+(r) + e“ ,
Д #ИМа =+495 кДж/моль (энтальпия
ионизации натрия);
3.
- С12(г) —> С1(г), Д # аТс1 = +122 кДж/моль (энтальпия
Zi
атомизации хлора);
4.С1(г)+е~ —
* СГ(г), ДЯсрс, = -360 кДж/моль (энтальпия
сродства к электрону);
5. Na+(r) + СГ(г) —>Na+Cr(T), АНХ кДж/моль (энтальпия
ионной кристаллической решетки).
Энтальпия образования хлорида натрия:
Na(i) + I c b —>NaCl(T), ДЯСбр= -411 кДж/моль.
Z
Составим общее уравнение дл я расчета А Н Х по закону Гесса:
ДЯ0бр=ДЯдтл. +ДЯИ^ +ДЯаТс|+ДЯсрс,+АНХ,
откуда
ДНх =[(-411)-(1-8+495+122- 360)]= -776кДж/моль.
Такова энергия кристаллической решетки дл я ионной модели
кристалла. Энергия кристаллической решетки реального кри­
сталла нам неизвестна, так как в ионной модели не учитывается
64

некоторая ковалентность связи и используются ионизационные
потенциалы и сродство к электрону при образовании газообраз­
ных ионов, тогда как в кристалле они несколько иные.
§3. Энтальпии сольватации ионов в растворах
Теперь рассмотрим энтальпии растворения и гидратации. Из
опыта мы знаем, что при растворении различных веществ в дру­
гих веществах часто наблюдается нагревание или охлаждение
системы, т. е. происходит изменение энтальпии.
Изменение энтальпии, происходящее при растворении
одного моля вещества в определенном растворителе с обра­
зованием бесконечно разбавленного раствора, называется
энтальпией растворения или теплотой растворения.
Например, если какой-либо ионный кристалл, скажем NaCl,
растворяется в воде, то должно произойти разрушение кристал­
лической решетки, для чего требуется затратить энергию, рав­
ную энергии ионной кристаллической решетки с обратным зна­
ком. Переходя в раствор, ионы сольватируются. Энтальпия соль­
ватации отрицательна. В сумме процесс может быть как экзо­
термическим, так и эндотермическим. Например, для хлорида
натр ия энтальпия растворения отвечает уравнению
Na+C1_(TB) + aq —>Na+(pacTB) 4- СГ(раств)
Д#раств = + 4 кДж/мОЛЬ.
Величина энтальпии гидратации получается из закона Гесса:
Сделав это уравнение явным по энтальпии гидратации и подста­
вив численные значения, получим:
Общая энергия гидратации складывается из энергий гидрата­
ции катионов и анионов. Д л я отнесения частей гидратации к от­
дельным ионам сравнивают энтальпии гидратации соединений,
имеющих общий ион, и сравнивают их с энтальпией гидратации
иона водорода -1075 кД ж/м о л ь . Следует отметить, что суще­
ствуют несколько различающиеся шкалы гидратации ионов, что
объясняется некоторой условностью разделения общей гидрата­
ции на гидратации ионов.
гидр*
ДЯГГИДРыаС! = [(+4) + (-776)] = -772 кДж/моль.
3 Иппол итов
65

§4. Энергии связей
Энергией связи называют энтальпии разложения соеди­
нения на элементы.
Например:
поглощается энергия 1666 кД ж/м о л ь . На каждую связь прихо­
дится 1666/4 = 416 кДж/моль. Энергия связи С—Н принимает­
ся равной 416 кДж/моль. В этане присутствуют 6 С—Н -связей и
1 С—С -связь, при его диссоциации поглощается 2854 кД ж . Вы­
читая сумму энергий 6 С—-Н-связей, получаем д л я С—С -связи
энергию Е = 2854 - 6 •416 = 358 кДж. Также можно найти энер­
гию связи С = С в этилене и т.д . В справочниках имеются таб­
лицы энергий связей, по которым можно приближенно рассчи­
тать теплоты химических реакций и теплоты образования мно­
гих главным образом органических веществ по уравнению:
Энтальпии химических реакций зависят от температуры. Зная
энтальпии образования веществ при стандартных условиях, мож­
но вычислить энтальпию химической реакции при стандартных
условиях, и наоборот. Но как вычислить энтальпию при темпе­
ратуре Г?
Разделим уравнения тепловых эфф ектов химических реак­
ций на dT.
Н2О=2Н+О,
АН = 458,0 кДж/моль.
При диссоциации метана на элементы:
СН4 = 4Н(г) + С(т)
ДЯ°т = ^ 2 ДЯ°исс(разорванные связи)-
-
^ 2 Д Я (образовавшиеся связи).
§5. Закон Кирхгофа
и
dQv dAH
dT
dT
dQv dAU
dT
dT
прод
прод
исх
бб

(здесь индекс к относится к исходным веществам, а индекс j к
продуктам реакции соответственно). Но
dAU
dT
-
Су
и
Подставим эти значения:
dQv
~W
=(Ev*Cv0
и
dAH
dT ~cp-
( E vJCv0
\ *—*
/ прод
dQp
прод
dT,
[(Ev^ n^ 4 E v‘<*.L] ^
dT \A '"/ прод
Проинтегрируем эти уравнения от Т\ до Т2
т2
т2
IdQv=Jf(Ev*'*.)ira. -
(Ev«),
Тх
Ti
т2
т2^
dQp =
Тх
Тх
Будем считать V* в правой сумме положительным, а в левой —
отрицательным, так что Х > = E v* - I У з и соответственно
Ev<-ЕVj-
Тогда можно эти уравнения записать в
сокращенной форме:
т2
(Qv)t2“ (Qv)ti = (53
dT
(1-73)
Тх
и
т2
(Qp)t2“ (Qp)ti = | (5 3 ^ ViCpO
Тх
Уравнения (1.73) и (1.74) являются математическими выраже­
ниями закона Кирхгоффа о зависимости тепловых эффектов хи­
мических реакций от температуры.
Температурный коэффициент теплового эффекта реак­
ции dQ /dT равен разности суммарной теплоемкости реаги­
рующих веществ, умноженной на их стехиометрические ко­
эффициенты, в конечном и начальном состоянии.
67

Достаточно составить простую программу по этим алгоритмам
и с помощью ЭВМ легко вычислить энтальпии химических ре­
акций при различных температурах, используя справочные дан­
ные по стандартным теплотам образования и теплоемкостям ис­
ходных веществ и продуктов реакций. Из уравнения Кирхгофа
следует, что влияние температуры на тепловые эф ф екты хими­
ческих реакций может быть как отрицательным, так и поло­
жительным, так как оно зависит только от изменения теплоем­
костей исходных веществ и продуктов реакции с температурой.
Теоретически рассчитать зависимость теплоемкости от темпера­
туры мы пока не можем, поэтому приходится пользоваться эм­
пирическими данными, которые получаются в результате очень
тщательных и длительных измерений в адиабатических калори­
метрах при разных температурах, начиная с температуры жид­
кого гелия. В результате такого колоссального труда накоплены
данные справочников по теплоемкостям, с помощью которых ин­
женеры рассчитывают технологические процессы и аппараты, а
исследователи используют эти данны е при калориметрических
расчетах.
§ 6. Калориметрия
Калориметрией называют методы определения теплоты
с помощью калориметров.
Калориметром называют теплоизолированный аппарат,
используемый для измерения количества тепловой энергии,
высвобождаемой или поглощаемой в результате какого-либо
процесса.
В калориметре определяют тепловые эффекты химических
реакций, ф азо вы х переходов, горения, растворения, комплексо-
образования, а такж е теплоемкости различных веществ и мате­
риалов. На рис. 1.10 представлен калориметр с калориметриче­
ской бомбой. Он представляет собой герметично закрывающ ий­
ся сосуд, окруженный водяной оболочкой, теплоизолированной
снаружи. В сосуд помещается металлическая калориметриче­
ская бомба с исследуемым образцом точно определенной массы,
накачивается кислород до давления порядка 25 атм и помеща­
ется запальное устройство, поджигаемое электрической искрой.
Образец воспламеняется и сгорает, выделяющаяся теплота го­
рения нагревает бомбу, теплота бомбы в калориметре передает­
ся воде. Произошедшее повышение температуры воды регистри­
руется. По изменению температуры воды рассчитывают тепло-
68

Рис. 1.10. Калориметр с калориметрической бомбой
ту сгорания. Предварительно устанавливается постоянная кало­
риметра по сжиганию стандартного вещества или посредством
подачи электрической энергии на сопротивление, помещенное в
бомбу.
§ 7. Процессы обмена в живых организмах
Все живые организмы потребляют энергию солнца. Расти­
тельный мир использует солнечную энергию для фотосинтеза,
минуя превращение энергии солнца в теплоту. Вся поглощенная
лучистая энергия в растениях идет на производство работы —
синтез аминокислот, углеводов и липидов, и на строительство
полупроницаемых мембран, которыми являются оболочки рас­
тительных клеток.
Вещества, которые потребляются растениями из окружаю­
щей среды — диоксид углерода, вода, кислород и минеральные
вещества, главным образом азот, фосфор, калий, магний каль­
ций и микроэлементы.
Животные организмы не создают необходимых для жизни
веществ, а потребляют вещества, созданные растениями в виде
69

Таблица 1.1
Калорийность продуктов питания
Продукт
кДж/г
Продукт
кДж/г
Кабачки сырые
0,92
Мясо куриное, сырое
9,54
Пиво
1,29
Белый хлеб
9,91
Апельсины
1,50
Мясо говяжье, сырое
11,07
Яблоки
1,96
Рис
15,36
Рыба белая
3,22
Сахар
16,80
Картофель
3,69
Сыр сорта «Чеддер»
16,82
Яйца
6,12
Орехи, арахис
23,64
Мороженое
6,98
Сливочное масло
30,41
Спирт этиловый
29,00
Жиры
38,00
пищи, и кислород воздуха. В организмах животных и человека
пища разлагается на простые составные части — аминокисло­
ты, углеводы, фосфолипиды, из которых затем строятся новые
белки, гликоген и жиры.
Таким образом, энергия большей части потребляемой пищи
идет на совершение работы по созданию строительных веществ,
которые необходимы для строительства новых животных кле­
ток, необходимых для роста, и взамен отжившим и подвергшим­
ся разложению.
Весь этот процесс требует совершения огромной работы по
поддержанию жизни в телах животных. Меньшая доля энергии
пищи идет на обеспечение мышечной работы, причем природой
были найдены пути для непосредственного использования хими­
ческой энергии в виде свободной энергии д л я совершения меха­
нической работы в организмах.
В организмах теплокровных животных часть энергии пищи
идет на обеспечение работы термостата, поддерживающего за­
данную температуру тела с точностью до десятых долей граду­
са. Поэтому важное значение имеет калорийность потребляемой
пищи, т. е. теплота сгорания, которая определяется с помощью
калориметра.
Взрослому человеку необходимо 7000 —12000 кД ж в сутки.
Избыток энергии потребляемой пищи может приводить к ожи­
рению, длительный недостаток — к дистрофии.
В табл. 1.1 приведены результаты калориметрического опре­
деления энергетической ценности некоторых пищевых про­
дуктов.
70

1.9. ХИМИЧЕСКОЕ РАВНОВЕСИЕ.
ЗАКОН ДЕЙСТВУЮЩИХ МАСС
Так как согласно третьему закону термодинамики только од­
на кривая AG = /(Т ) определяет химическое равновесие в систе­
ме, то, определив эту кривую, можно получить уравнение д л я
расчета равновесия в системе при температуре Т, а значит, и
выход продуктов химической реакции.
Числ а молей <1щ участвующих в реакции веществ связаны с
их стехиометрическими коэффициентами. Если мы наблюдаем
химическую реакцию
V1A+V2B ^ ViC+v2D
то достаточно задать лишь три коэффициента V*, а четвертый
может быть рассчитан из условия стехиометрии. Если в реак­
цию вступило dni молей вещества А, то число молей вещества В,
вступившего в реакцию, будет равно: dn2 = -dniiy^/v^). Так как
вещества А и В расходуются при химической реакции, то они
до лж ны убывать, и изменение чисел их молей будут отрицатель­
ными величинами, напротив, количества продуктов реакции С и
D при прохождении реакции растут, и изменения их чисел молей
Vi
V2
положительны и равны: dn$ = dn\ — и dn± = dn 1— . Рассмотрим
vi
vi
более общую систему:
V'lV'l +Ф^2 + •••+ Ф'-v'- + Ф-v'
+Ф2У2+•-*+VjVj+ФiVi.
г
Число исходных веществ определяется суммой Е Х Ф - , а число
г=1
г
продуктов реакции — суммой E v^ - Следовательно, реакция
г=1
определяется уравнением:
Е*м=Еф*^-
г=1
1=1
Условие химического равновесия в этой системе будет опреде­
ляться уравнением
dn\Vi
~vT
dni
Е^=о.
t=2
71

E^Vi=0
(1.75)
i
причем д л я всех исходных веществ V* отрицательны, а д л я всех
продуктов реакции —положительны. В (1.75) заложен в неявной
форме основной закон химического равновесия — закон действу­
ющих масс.
В школьном курсе химии с этим законом знакомят учащих­
ся, к сожалению, лишь в конце учебы, поэтому у них создается
твердое убеждение, что химия — наука качественная и при ее
изучении все нужно просто запоминать, заучивать, тогда как
ничто не препятствует начинать изучение химии с количествен­
ных законов, как начинают изучение физики с количественных
законов Ньютона.
Вывод закона действующих масс, который излагают в школь­
ных учебниках, основан на кинетических представлениях о ско­
ростях прямой и обратной реакций. Однако равенство скоростей
прямой и обратной реакций при равновесии в системе является
следствием за ко на действующих масс, поэтому вывод этого фун­
даментального д ля химии закона следует давать, основываясь
на законах термодинамики.
Пусть химическая система состоит из идеальных газов. Тогда
jll{ = ц9 + Т?Т1пр;, где pi — парциальное давление г -го идеального
газа в системе. Подставив это значение (1* в уравнение (1.75),
получим:
Так как Т = const по условию, то правая часть уравнения (1.76)
является постоянной величиной, которую обозначим как In К р:
Е ViM?+Е ViRT InPi =J2
+E ДТln
Pi =°-
Отсюда
(1.76)
= const =InKp.
RT
Тогда
(1.77)
72

Так как V{ исходных веществ отрицательны, а V* продуктов ре­
акции положительны, то при потенцировании уравнения (1.77)
получим:
UvVi
llPvi
(1.78)
Кр=
П$/
где п обозначает произведение, например,
IK
Г2
•Руг
Уравнение (1.78) представляет математическое выражение зако­
на действующих масс.
Отношение действующих масс продуктов реакции к дей­
ствующим массам исходных веществ при постоянной темпе­
ратуре — это величина постоянная.
Действующей массой в химической реакции называет­
ся произведение концентраций компонентов (исходных ве­
ществ или продуктов реакции) в степенях, равных сте­
хиометрическим коэффициентам, причем стехиометриче­
ские коэффициенты продуктов реакции берутся положи­
тельными, а стехиометрические коэффициенты исходных
веществ — отрицательными. Д ля реальных систем концен­
трации заменяются летучестями или активностями.
Константа К в уравнении закона действующих масс на­
зывается константой равновесия химической реакции.
Если концентрации газов выражаются через объемные концен-
щ
л/
RT
pi
трации,тоС{=—,атаккакV=щ----,тос*=—
—. Подставив
V
pi
RT
это значение pi в уравнение (1-78) получим:
Значит,
Кс = (ЯГ)£
V-
П4
КС=КР-(RT)^Vi,
где У > = У > пр - У уисх. Численное значение константы рав­
новесия определяется соответствующим уравнением химической
реакции. Например, если реакция задается уравнением
ЗН2+ N2Ь? 2NH3
73

то
ы_Pnh3
КР~“з
Ph3^ n2
Если же реакция задается уравнением
2NH3^3H2+N2
то константа равновесия будет обратной:
г, _ Рн,Рмд
т. е.
zst _______
РPnhs’
к, =±_
Кр К’
Если эта ж е реакция задается уравнением
NH3^ H 2+iN2
то и константа равновесия будет численно иной:
3/2 1/2
^// _ РнаPw,
Р PNHs
и в этом случае
§1. Константы равновесия для неконденсированных систем
Если система состоит из реальных газов, то
щ =ц?+ЯГ1пП =ц?+ЯГIn(YiPi).
Если подставим это значение в уравнение (1.78) и повторим на­
ши рассуждения, то получим
к_ш
=ш
.
м
/_ П/£ ПРф'.
ПУф; ’
т. е.
Kj =КрКу.
Пусть система представляет собой идеальный раствор. Тогда
Щ=Ц?+ЯГInа*.
74

Подставив это значение J1* в уравнение (1.78) и повторив рас­
суждения, получим
Кх=
П^ф,.
п4‘
Выразим содержание компонентов системы через их объемные
концентрации с* =
где V — объем. Мольная доля г-го компо-
, где п° — число молей растворителя,
нента равна
=
Щ
no+E«i
для разбавленного раствора по +
щ&поиХ{= —,Xi-Ci—
'
по
пи
Тогда
сUJ
гг*5'
/v\Vi
Так как при заданном объеме I —
— постоянная, то ее можно
W
объединить с константой равновесия, и тогда
Кс=
_
м
П4/
§2. Константы равновесия для конденсированных систем
Пусть система представляет собой реальный раствор. Тогда
Щ= Ц®+ RTlnOi =
+ RTlnyxi
и константа равновесия К а будет равна
„
_
П<Ш*.
^о. ~
~__
у/ v/)
т. е.
ка=кхкт
Наконец, рассмотрим равновесие в гетерогенной конденсиро­
ванной химической системе. Для такой системы
щ = ц? + ЯГ1пр{пар,
если пар близок к идеальному газу и
Hi = ^ + JtTla/inap,
75

если пар г-го компонента отличен от идеального газа. Подставив
значение |м в уравнение (1.78) и, повторив рассуждения, полу­
чим:
Kf=
ПУфгп
Прф* П у1\
Значит, дл я конденсированной химической системы констан­
та равновесия включает только давления насыщенного пара ком­
понентов с измеримым давлением пара, количества веществ, не
обладающих измеримым давлением пара, могут быть какими
угодно, если эти вещества не образуют растворов, как в жидких,
так и в твердых фазах, существующих в системе при данной тем­
пературе. Если растворы образуются, то химические потенциа­
лы растворенных веществ и растворителя будут определяться
их давлением пара над раствором. Мы рассмотрели все основ­
ные типы систем и вывели д л я них уравнения констант равно­
весия. Рассмотрим теперь влияние общего давления на равно­
весие. Д л я этого выразим концентрации газов в системе через
мольные доли: Х{ = Подставив значение pi из этого уравне­
ния в уравнение(1.78) для К х , получим:
^=
(1.79)
П хф';.
Влияние общего давления на выход продуктов реакции соглас­
но (1.79) определяется знаком
если эта сумма положи­
тельна, то с повышением общего давления выход продуктов ре­
акции уменьшается, если сумма отрицательна, то с ростом об­
щего давления выход продуктов реакции увеличивается. Если
же У > = 0, то общее давление не влияет на выход продуктов
реакции.
Рассмотрим несколько примеров:
Н2(г) +12(г)^2Н1(г)
Е»<= 2 - 1 - 1 =0. Выход йодистого водорода не зависит от
общего давления в системе.
Н2(г) + 12(г) U 2Н1(тв)
y^Vj = 0 —1 - 1 = - 2 . Выход йодистого водорода растет с ростом
общего давления в системе.
3H2(r) + N2(r) Ь* 2NH3(r)
76

$ > = 2 -3 -1 = - 2 . Выход аммиака увеличивается с повышением
общего давления в системе
NH4C1(tb) ±=> НС1(г) + NH3(r)
У = 2 - 0 = 2. Диссоциация хлорида аммония уменьшается с
ростом общего давления в системе.
Fe203(TB) + ^Н2(г) ^ 2FcO(tb) + ^Н20(г)
У \г = 3/2 - 3/2 = 0. Выход оксида железа не изменяется с ро­
стом общего давления в системе. Рассматривая влияние измене­
ний парциальных давлений на равновесие, можно отметить, что
рост парциального давления продукта реакции приводит к сдви­
гу равновесия влево (к исходным веществам), и наоборот. Таким
образом, пользуясь законом действующих масс, можно не только
сказать, как будет сдвигаться равновесие при действии общего
давления или парциальных давлений компонентов (что можно
установить по принципу Ле-Ш ателье), но и можно рассчитать
выход продуктов реакции, если известна константа равновесия,
что используется, например в количественном анализе.
§ 3. Изотерма химической реакции
Если в системе протекает самопроизвольный процесс, то этот
процесс будет протекать до тех пор, пока не установится рав­
новесие в системе, т. е. пока свободная энергия не станет равна
нулю. Только тогда будет иметь место равенство
i
5Z^dni=0.
1=1
Но до тех пор, пока в системе происходит самопроизвольный
процесс, имеет место неравенство
i
^ 2\iidm <о.
i=l
t
Однако при равновесии в системе У
i=1
i
AGx.p=^^Vj.
i=1
=
=ои
i=l
(1.80)
77

Пусть система состоит из идеальных газов. Тогда |i* = |x°+RT In pi.
Подставив значение |Tj в (1.80), получим:
AGx.p = ^ 2 ^v<+ЩRTVi1п^ ‘
Но—
= In К р. Поэтому
И,!
AGx.p=-ВТInKp+Y^ВТInPi'■
После потенцирования получим:
AGxp =-R TlnKp+RT^S^- .
(1.81)
ПPv;
Уравнение (1.81) было названо изотермой химической реак­
ции Вант-Гоффа. Оно дает возможность вычислить свободную
энергию химической реакции и определить направление само­
произвольного химического процесса в системе. Д л я этого нуж­
но знать константу равновесия и парциальные давления компо­
нентов в системе. Если A G окажется отрицательным, то равно­
весие должно смещаться в сторону образования продуктов реак­
ции, если Д G положительно — то в сторону исходных веществ, а
если Д G = 0, то система находится в равновесии. При стандарт­
ных условиях (Т = 298К; р - 1атм) Inр± = 0. В таком случае
Д(? = -298Я1пЯр.
(1.82)
Уравнение (1.82) называется изотермой химической реакции при
стандартных условиях. При температуре Т будем иметь
AG
Kp=e~RTm
(1.83)
Логарифм константы равновесия химической реакции
при стандартных условиях равен изменению свободной
энергии Гиббса химической реакции с отрицательным зна­
ком, деленному на произведение газовой постоянной и аб­
солютной температуры.
Как рассчитать свободные энергии химических реакций, было
рассмотрено выше. З ная Д(7х.р при стандартных условиях,
можно рассчитать константу равновесия. Зн ая константу
равновесия, можно рассчитать выход продукта реакции при
78

стандартных условиях. Рассмотрим д л я примера реакцию
диссоциации димера диоксида азота:
N20 4(r) *=> 2N02(r)
Ранее свободная энергия этой реакции при стандартных услови­
ях была рассчитана и оказалась положительной и равной А А =
= 2422 кал/моль. Рассчитаем константу равновесия К р при стан­
дартных условиях:
2422
2422
Кр = е" я г = е'8.314-298 - е-°-9776 = о, 376.
Пусть в сосуде, имеющем форму гантели, газ находится под ат­
мосферным давлением и пусть вначале сосуд был заполнен диме­
ром диоксида азота путем конденсации его в откачанный сосуд
при температуре жидкого азота 77,35 К. При этой температуре
диссоциация димера ничтожно мала. Пусть было взято по молей
димера. После приобретения сосудом стандартной температуры
и достижения равновесия образовалось 2хпо молей N 0 2. Тогда
в газовой смеси осталось (1 - x )uq молей димера. Всего в сосуде
при равновесии содержится (1 - х + 2х)по = (1 +х)по молей обо­
их газов. Следовательно, мольная доля димера в равновесной
(1-х)п0
2хп0
тт
смеси газов будет равна ------ -— , а мономера —---- -— .
Что-
(1 + х)по
(1 + х)по
бы рассчитать парциальные давления обоих газов в равновесной
смеси, нужно мольные доли их умножить на общее давление Р :
(2х)2
(1-х)
р"°-=
а
= (П Т)Р-Значит
КрО
Г298(х.р)
[(2х)2/(1 + х)2]Р2_ 4х2
[(1-х )/(1+х)]Р =(1-х2)
(1.84)
Решение этого квадратного уравнения при Р = 1 атм дает
х = 0,316. Если димера было взято столько, чтобы в со­
суде при стандартной температуре создалось давление, рав­
ное 1 атм, то парциальное давление мономера в равновес­
ной смеси газов при стандартной температуре будет равно
2х 2-0,316
^
=
_
= 0 ,480 атм, т. е. 48%, а парциальное давление
1+х
1,316
димера 0,520 атм (52%). Если в сосуде давление равно 0,1 атм,
то, решая уравнение (1.84), получим х = 0 ,696, и парциальное
давление мономера в смеси газов будет равно 0,082 атм, т. е. 82 %,
а димера, 18%. При давлении в сосуде 10 атм получим для х
79

значение 0,0965, и парциальное давление мономера будет рав­
но 1,76атм (17,6%), а димера — 82,4%. Таким образом, с по­
вышением общего давления содержание мономера в смеси газов
уменьшается. Итак, расчет показал, что, хотя при стандартных
условиях свободная энергия Гиббса для реакции диссоциации
положительна, все же димер диссоциирует, что и было видно
при демонстрации гантели, заполненной диоксидом азота: газ в
гантели не был совершенно бесцветен, хотя равновесие сдвину­
то в сторону димеризации. Рассчитав константу равновесия при
стандартных условиях, мы рассчитали выход продукта реакции
при этих условиях. Однако на практике химические реакции
проводят обычно не при стандартных условиях, а при темпера­
туре Т и, возможно, при давлении р, ибо приходится учитывать
кинетические факторы. При стандартных условиях редко быва­
ет, чтобы скорости реакций были удовлетворительны. Поэтому
прибегают к повышению давления или температуры, или обоих
параметров. Рассмотрим влияние температуры на диссоциацию
димера. Ранее была рассчитана свободная энергия Гельмголь­
ца для реакции диссоциации димера диоксида азота при темпе­
ратуре 398 К, которая оказалась равной А = -22 935 Дж/моль
(см. с. 54). Подставив величину А в уравнение (1.83), получим
значение
= 1023. Используя эту константу равновесия в
уравнении (1.84), получим парциальное давление мономера при
температуре 398 К, равное 0, 996. Итак, повышение температуры
на 100 °С привело к почти полной диссоциации димера (на 98 %),
что мы и наблюдали при демонстрации нагретого в кипящей во­
де шара гантели, который стал темно-бурым. Однако д а ж е при
отрицательном значении свободной энергии Гиббса 2 % димера
все еще присутствует в смеси газов. Мы использовали д л я рас­
чета свободную энергию Гельмгольца, рассчитанную д л я темпе­
ратуры Т .
§ 4. Изобара химической реакции
Из уравнения (1.83) изобары химической реакции и уравне­
ния зависимости свободной энергии от температуры можно по­
лучить интегральное уравнение зависимости константы равно­
весия от температуры
-Т
4АН
dT-JT=-RTInК.
Разделив это уравнение на - Т , получим при р = const:
1пАГ =
'АН
RT2
dT +J.
(1.85)
80

Уравнение (1.85) называют уравнением изобары химической ре­
акции.
Зависимость константы равновесия химической реакции
от температуры определяется отношением энтальпии хими­
ческой реакции к произведению газовой константы и тем­
пературы.
Если зависимость энтальпии химической реакции от температу-
АЯ
ры невелика, то величину
R
можно принять за постоянную,
которую можно вынести з а знак интеграла. Тогда
АН
InК =
RT2
+J.
Дифференциальной формой уравнения (1.85) будет уравнение
„
г,
АЯ
dinК -
Если известна температура Т, то можно взять определенный
интеграл от стандартной температуры до заданной температу­
ры Т:
Если А Н нельзя принять постоянной, то ее значение при тем­
пературе Т нужно рассчитать по закону Кирхгофа и поставить
под знак интеграла. Так к ак теплоемкости при этом необходимо
взять из справочника в виде вириальных уравнений, то полу­
чим сумму интегралов. При использовании персональной ЭВМ,
составив небольшую программу, можно довольно быстро рас­
считывать константы равновесия химических реакций при р аз­
личных температурах и далее рассчитывать зависимость выхода
продукта от температуры.
1.10. РАВНОВЕСИЕ В ГЕТЕРОГЕННЫХ СИСТЕМАХ
§1. Правило фаз Гиббса
Рассмотрим равновесие в гетерогенных системах. Гетероген­
ные системы содержат по меньшей мере 2 фазы . Только конден­
сированные системы бывают гетерогенными. Газовые системы,
81

состоящие из смеси различных газов, не расслаиваются. Кон­
денсированная система состоит по крайней мере из одной кон­
денсированной ф азы и из насыщенного пара над ней. Конечно,
можно налить жидкость в сосуд так, чтобы весь объем сосуда
был заполнен ею, тогда система будет однофазной. Но в общем
случае над жидкостью будет насыщенный пар, и система будет
по меньшей мере двухфазной. Система может содержать и твер­
дые фазы, и жидкие, так что предела числу фаз в системах в
общем нет. Во всякой гетерогенной системе, находящейся в со­
стоянии равновесия, все фазы должны находиться в равновесии
друг с другом. Например, жидкая фаза должна находиться в
равновесии с насыщенным паром, твердое вещество, р астворя­
ющееся в жидкости, должно находиться в равновесии с жидкой
фазой и с паром.
Равновесие, которое устанавливается между фазами при
физических процессах перехода веществ из одной фазы в
другую, называется фазовым равновесием.
Наша за д ач а состоит в том, чтобы найти количественный за­
кон, управляющий равновесием между фазами при изменении
параметров системы.
Процессы, при которых устанавливаются новые ф азо вы е рав­
новесия в системах —это фазовые переходы (полиморфные пре­
вращения) твердых веществ, плавление или затвердевание, ки­
пение или конденсация, переход в закритическое состояние, на­
конец, растворение и осаждение.
Введем несколько определений.
Фазой называется часть системы, отграниченная физи­
ческими поверхностями раздела, причем все интенсивные
параметры фазы такие же, как и для всей системы при от­
сутствии внешнего воздействия.
Вещества, из которых состоит химическая система, на­
зываю тся компонентами системы.
В системе, состоящей из карбоната кальция, например, суще­
ствует равновесие
СаСОз *=>СаО + С02
В этой системе три компонента: карбонат кальция, оксид каль­
ция и диоксид углерода. Однако их соотношение определяется
стехиометрией реакции. Поэтому независимых компонентов, ко-
82

торых достаточно д л я одновременного существования всех трех
фаз в этой системе, только два, так как третий компонент может
быть вычислен по уравнению реакции.
Числом независимых компонентов называется число ве­
ществ в системе, достаточное для образования всех ф аз дан­
ной системы. Чтобы вычислить число независимых компо­
нентов в системе, нужно из числа всех компонентов системы
вычесть число уравнений, их связывающих.
Так, в приведенном примере число компонентов 3, а число неза­
висимых компонентов 2 (три компонента минус одно уравнение).
В системе
NH4C1^NH3+HC1
помимо уравнения реакции существует равенство в соотноше­
нии компонентов: [NH3] = [НС1]. Поэтому число компонентов в
этой системе равно 1. В дальнейших рассуждениях под назва­
нием «компонент» будет подразумеваться только независимый
компонент. Рассмотрим д л я примера уравнение
z = f(xty).
Если параметры х и у заданы, то z, независимо от нашего жела­
ния, определен, но если один из параметров, например у, не за­
дан, то у нас появляется возможность произвольно варьировать
его. В этом случае у нас появляется степень свободы в избрании
одного из аргументов.
Число степеней свободы / системы —это число независи­
мых термодинамических параметров, которые можно про­
извольно менять в некоторых пределах без изменения числа
фаз в системе.
По числу степеней свободы системы подразделяют
на нонвариантные (0 степеней свободы), моновариантные
(1 степень свободы), бивариантные (2 степени свободы)
ит.д.
Известно, что, если д л я полного описания системы требуется
за дать п параметров, то число степеней свободы
/=n-iV,
(1.86)
где N — число уравнений, связывающих параметры. Таким об­
разом, чтобы узнать число степеней свободы, нужно определить
п и N в уравнении (1.86).
83

Пусть задана система, состоящая из Ф фаз и К независимых
компонентов. Состав каждой ф азы определяется концентраци­
ей. Очевидно, что достаточно знать ( К - 1) число концентраций,
так как концентрация одного из компонентов может быть опре­
делена как разность х* = 1 ~
. Общее число концентраций
для Ф фаз равно Ф(К - 1). Кроме концентраций система опре­
деляется еще некоторым числом интенсивных параметров га, к
числу которых относится температура, давление, электрические
поля, поверхностное натяжение и др. Д л я всех ф аз эти парамет­
ры в состоянии равновесия системы одинаковы, согласно опреде­
лению фазы. Следовательно, общее число параметров, которое
нужно для описания системы, будет равно: п = (К - 1)Ф + га, по­
скольку концентрации также являю тся параметрами системы.
При равновесии химические потенциалы каждого независимого
компонента во всех фазах одинаковы:
цв‘=ц*=р* =...
Общее число так их уравнений будет равно N = К(Ф-1). Подста­
вим значения п и N вуравнение (1.86): / = (К-1)Ф + т-(Ф -1)К,
т. е.
/=к-Ф+т.
(1.87)
Уравнение (1.87) называют правилом ф аз Гиббса.
Число степеней свободы системы равно числу независи­
мых компонентов минус число ф аз плюс число параметров
системы.
В большинстве случаев система определяется лишь дву мя ин­
тенсивными параметрами: температурой и давлением. Поэтому,
как правило, га = 2 и
/=К-Ф+2.
Правило ф аз Гиббса имеет такое же значение для фазового рав­
новесия, как закон действующих масс дл я химического равнове­
сия в системах.
§2. Уравнение Клаузиуса —Клапейрона
Если система обладает степенью свободы, то до некоторого
предела можно менять произвольно один из параметров, при
этом число ф а з не будет меняться. При этом каждый раз будет
устанавливаться новое фазовое равновесие, и химические потен­
циалы г-го компонента изменятся во всех фазах на одну и ту же
84

величинуф*,такчтофа‘ = фр‘=
= ... , где а,(3,у,...
—
различные фазы. Пусть из фазы а в фазу Р перешел только г-й
компонент. Так как д л я одного моля ф = dG, то
ф“*= -SadT+Vadp
фр' =-S^dT+V^dp.
Ноф а‘= фр‘, следовательно, -SadT+Vadp=—S^dT+Урф.
Отсюда
5р-5 “ (dp\
уР-У<*
dT
При щ = 1 (однокомпонентная система) получаем уравнение
Клаузиуса —Клапейрона:
dp_AS
dT=AV‘
(1.88)
A J-T
При прохождении в системе фазового перехода A S = — — —
. От-
- *ф.п
сюда зависимость температуры фазового перехода от давления
определяется уравнением:
аГф,п _ ГФ.ПАУ
dp
АЯф.п
(1.89)
РАВНОВЕСИЕ В ОДНОКОМПОНЕНТНЫХ СИСТЕМАХ
§3. Фазовая диаграмма воды
На рис. 1.11 представлена фазовая диаграмма воды. На этой
диаграмме при не очень высоких давлениях имеется три по­
ля, которым отвечают бивариантные состояния системы. Поля
разграничены тремя кривыми ОА , ОС и ОВ, которым отвеча­
ют моновариантные состояния системы. На диаграмме имеют­
ся две нонвариантные точки О и С. Линия ОС — кривая рав­
новесия «жидкость —пар», т. е. кривая кипения воды или кон­
денсации пара. Линия ОА — кривая равновесия «пар —твердая
фаза», т. е. кривая возгонки льда или кристаллизации пара. Ли­
ния О В — кривая равновесия «жидкость —твердая фаза», т. е.
плавления льда или замерзания воды. Линии, разделяющие по­
ля на фазовой диаграмме, определяются уравнением Клаузи­
уса-Клапейрона, так как в любой точке кривой фазового пре­
вращения тангенс угла наклона касательной к оси температур
85

будет равен т^ у В одно-
компонентной системе состоя­
ние каждой фазы определяет­
ся параметрами р, V , Т . Поэто­
му каждая точка на диаграм­
мах (р—Г), (V—Т), (р—V') соот­
ветствует определенному состо­
янию системы. Если ф а за одна,
то по правилу фаз Гиббса си­
стема бивариантна / = 1 - 1+
+2 = 2. Значит, в некоторых
пределах можно изменять про­
извольно оба параметра, не из­
меняя число ф а з. Бивариантное состояние системы представля­
ется на диаграмме полем. Если фазы две, например вода и пар,
то система моновариантна, так как / = 1 -2+2 = 1. На диаграмме
моновариантным состояниям системы отвечают линии равнове­
сия двух ф аз. В моновариантной системе можно произвольно
менять только один параметр и до определенных пределов чис­
ло ф аз при этом остается неизменным. Наконец, если ф а зы три
(например, вода, пар и лед), то система нонвариантна, та к как
/ = 1 - 3 + 2 = 0. Нонвариантное состояние однокомпонентной
системы представляется на диаграмме точкой. В нонвариант-
ном состоянии системы все параметры заданы и ни один из них
невозможно изменить, не изменив число фаз. Более трех фаз
в равновесной однокомпонентной системе не может существо­
вать.
Каждая линия на диаграмме дает зависимость температуры
соответствующего фазового перехода от давления. Естествен­
но, что температура кипения растет с ростом давления, но не
беспредельно. Кривая ОС оканчивается точкой С в отличие от
двух других кривых. Эта замечательная точка называется кри­
тической точкой. Она появляется на диаграмме вследствие до­
стижения системой критического состояния, при котором плот­
ность жидкой фазы и плотность пар а становятся одинаковыми.
Это состояние впервые заметил Д . И. Менделеев, который на­
блюдал исчезновение мениска, разделяющего жидкость и пар,
при повышении давления в запаянной стеклянной ампуле с жид­
костью. С истема в закритическом состоянии становится гомо­
генной. Примером закритического состояния вещества является
воздух, состоящий из смеси газов, находящихся в закритическом
состоянии (кислород, азот, благородные газы). Газ, находящий­
ся в закритическом состоянии, невозможно сконденсировать под
Рис. 1.11. Фазовая диаграмма
воды
86

воздействием любого давления, поэтому газ необходимо охла­
дить ниже критической температуры, и только тогда при повы­
шении давления его можно сконденсировать.
Критической точке отвечают определенные критические па­
раметры Ткр, рКр, VKp, которые являются специфическими д ля
каждого вещества. Критические параметры связаны с термоди­
намическими свойствами вещества, например с летучестью, и
приводятся в справочниках. Рассмотрим, что будет происходить
с системой, если в точке / , расположенной на диаграмме при
давлении р\ и температуре Т\ (точку / назовем фигуративной
точкой), будем изменять давление и температуру. Поскольку в
этой точке система однофазна (лед), то по правилу фаз она би-
вариантна. Следовательно, можно изменять в некоторых преде­
лах температуру и давление, не изменяя числа ф аз в системе.
Однако, если мы повысим температуру до Т2, не изменяя давле­
ние, то точка / сместится на кривую ОВ. Это кривая равновесия
«жидкость —твердая фаза», следовательно, при температуре Т\
и давлении р\ в системе появляется вторая ф а за — жидкость. По
правилу фаз система становится моновариантной, и мы уже не
можем произвольно менять оба параметра системы, так как при
этом точка вновь окажется на одном из двух полей, отвечающих
бивариантному состоянию системы. Напротив, мы можем про­
извольно менять один из параметров, и при этом число ф аз не
будет меняться, а фигуративная точка будет при этом передви­
гаться по кривой ОВ до тех пор, пока она не достигнет тройной
точки О, В этой точке система становится трехфазной (лед, во­
да, пар). По правилу ф аз в однокомпонентной системе с тремя
фазами нет степеней свободы. Точка О — нонвариантная точка.
Изменение любого из двух параметров должно вести к исчезно­
вению одной из трех ф аз в системе, а изменение сразу двух пара­
метров — к исчезновению двух фаз в системе. Поэтому, напри­
мер, при понижении давления лед возгоняется в паровую фазу,
не плавясь, и наоборот, пар, конденсируясь при низких темпера­
турах, образует иней, что мы наблюдаем в природе в холодные
времена года. Используем уравнение Клаузиуса —Клайперона
для расчета давления насыщенного пара. Д л я этого его нужно
проинтегрировать. Можно выполнить интегрирование дл я той
части фазовой диаграммы, которая ниже критической точки.
При этих условиях объем пара во много раз превосходит объем
жидкости, поэтому объемом жидкости можно пренебречь. После
преобразований уравнение (1.89) можно привести к виду:
dp _Д.//ф-п
~ dT~TV^'
87

кг
Если пар близок к идеальному газу, то V^ap = ----- .
Подставив
Рпар
это значение в уравнение (1.90) получим:
dT.
(1.91)
Рпар
ilJ
После интегрирования уравнения (1.91) получим:
АЯфп
lnPnap —С
L
RT
(1.92)
В координатах (1 пр - —) полученное уравнение (1.92) — это урав­
нение прямой, причем тангенс у гл а наклона этой прямой к оси
абсцисс равен
а постоянная С равна отрезку, который
R
отсекает прямая на оси ординат (рис. 1.12).
Следовательно, уравнение Клаузиуса—Клапейрона (1.91) поз­
воляет рассчитать теплоту парообразования из эксперименталь­
ных данных давления пара, измеренного при различных темпе­
ратурах. Эти данные получены д л я огромного числа веществ,
которые можно нагреть без разложения, причем давление па­
ра над ними поддается измерению. В справочниках эти данные
приводятся в виде уравнений с численными значениями посто­
янных С и энтальпий парообразования.
Если давления пара для жидкой фазы и для твердой фа­
зы даны в виде зависимости от температуры, то л егко могут
быть рассчитаны координаты тройной точки. Д л я этого нуж­
но приравнять давление пара, так как и для жидкой фазы, и
для твердой оно одинаково в тройной точке. Обратим внима­
ние на то, что на фазовой диаграмме воды кривая равновесия
«лед —вода» наклонена в сторону оси давления. Лишь незначи­
тельное число веществ имеет такое же изменение температуры
Рис. 1.12. Давление пара над веществом
88

плавления с изменением давления. Наклон этой кривой мож­
но рассчитать, если воспользоваться уравнением Клаузиуса—
Клапейрона (1.88), и тогда станет ясна причина такого стран­
ного поведения кривой плавления льда. Наклон этой кривой з а­
висит от знака A V = Уж—Улед. Известно из жизненных наблюде­
ний, что объем л ьда больше, чем объем воды. Буты ль, наполнен­
ная водой, лопается при замерзании воды, по этой же причине
лед плавает на поверхности воды, защищая водоемы от промер­
зания до дна, и тем спасает живые организмы от вымерзания.
Значит, A V для воды отрицательно, и температура плавления
льда должна возрастать с давлением. Подобно воде при затвер­
девании также расширяются некоторые сплавы, например брон­
за и чугун. Именно это свойство чугуна и бронзы обеспечива­
ет заполнение всех неровностей формы д л я л ить я и поэтому из
этих сплавов можно изготавливать различные художественные
изделия, которые столь высоко ценятся.
§4. Фазовая диаграмма серы
На рис. 1.13 представлена фазовая диаграмма серы. Она со­
стоит из четырех полей: поле насыщенного пара Snap> поле серы
ромбической S(pOM6.), поле серы моноклинной S(MOH.), серы ж и д­
кой Бж . Кривая D A отвечает равновесию S(pOM6.) *=> пар, кри­
вая А В отвечает равновесию между твердыми фазами S(p0M6.) ^
^ S(MOH.), кривая А С отвечает равновесию S(MOH.) ^ пар, кривая
С В отвечает фазовому равновесию S(MOH<)T ^ $(мон.)ж и кривая
CF отвечает фазовому равновесию Бж Snap- Диаграмма име­
ет три нонвариантные точки, в которых в равновесии находятся
три фазы: точка О — тройная точка, S(pOM6.) ,S(MOH.)> пар; точка
С — S(M0H.), жидкость, пар; точка В — S(pOM6.)> S(MOH.), жидкость.
Точка F — критическая точка. На примере этой диаграммы мы
Рис. 1.13. Фазовая диаграмма серы
89

можем убедиться, что каждой полиморфной форме на фазовой
диаграмме отвечает поле, так как каждая полиморфная форма
представляет собой новую фазу, обладающую собственным дав­
лением пара.
§5. Фазовые переходы в твердых компонентах
Фазовые переходы твердых веществ определяются давлени­
ем пара над ними. Из диаграммы видно, что давление пара над
ромбической серой ниже, чем над моноклинной серой, но над
обеими полиморфными формами серы давление пара ниже, чем
в тройной точке, отвечающей плавлению серы. Легко объяснить,
почему давление пара определяет полиморфные превращения,
так как фазовый переход можно рассматривать как химическое
равновесие, причем константа равновесия этого процесса зави­
сит лишь от соотношения давления пара над обеими фазами:
К-
Р (S(moh.))
Р(5(ромб.))
На диаграмме серы давление пара обеих полиморфных форм
ниже давления пара в точке плавления, поэтому фазовый пере­
ход S(pOM6.) >S(MOH.) обратим.
Обратимый фазовый переход, при котором давление па­
ра обеих полиморфных форм ниже давления пара в точке
плавления, называется энантиотропным переходом.
Иначе обстоит дело, когда давление пара второй ф азы выше,
чем давление пара в точке плавления, как это видно из рис. 1Л4.
Точка О фазового перехо­
д а полиморфных модификаций
расположена выше температу­
ры их плавления (тройные точ­
ки 0 \ и Ог). Кривая равнове­
сия «жидкость —пар» D D 1рас­
положена ниже точки О пере­
сечения кривых АА! и ВВ* рав­
новесия двух полиморфных мо­
дификаций с паром. На участ­
ке кривой АО\ устойчива a -мо­
дификация, так как в области
Рис. 1.14. Морфотропный фазо- ее существования давление па-
вый переход
ра [i-модификации выше, чем
90

давление пара ос-модификации, и выше, чем давление пара над
жидкостью. Поэтому метастабильная p-модификация самопро­
извольно превращается в стабильную сс-модификацию. Обрат­
ный переход невозможен из-за того, что плавление а-модифи-
кации заканчивается при более низкой температуре, чем темпе­
ратура а —►(5-фазового перехода. Обычный пример морфотроп-
ного фазового перехода — это превращение белого ф осфора в
красный. Белый фосфор самопроизвольно переходит в красный
при хранении, тогда как красный фосфор не переходит в белый
самопроизвольно. Чтобы получить белый фосфор, нужно прове­
сти возгонку красного ф осф ора и охладить пары. Давление па­
ра белого фосфора во всей области ее существования в твердом
виде выше, чем давление пара над красным фосфором. Поэто­
му самопроизвольное превращение возможно лишь для белого
фосфора в красный, но не наоборот.
Необратимый фазовый переход, при котором давление
пар а одной из полиморфных форм выше, чем давление па­
ра в точке плавления, называется морфотропным фазовым
переходом.
Необходимо также различать для твердых веществ фазовые
переходы первого и второго рода.
Фазовым переходом первого
переход, при котором
)rAS¥0
"
рода называется фазовый
Примерами фазовых переходов первого рода являются поли­
морфные превращения, плавление, кипение.
Фазовым переходом второго рода называют такой фа-
fAG\ л /AG\
зовый переход, при котором — -
=0,
----
=0,но
\/р
\Р)т
fd2AG\
\дТ2) Т
=|^0и
fd2AG\ ^ 0.
При фазовом переходе второго рода Ср с повышением темпе­
ратуры, начиная с температуры твердого гелия, обнаруживает-
91

ся при Т = 2,2 К так называе­
мый X переход, как представле­
но на рис. 1.15. Сначала тепло­
емкость резко возрастает, а вы­
ше 2,2 К также резко падает. Пе­
реход металлов, сплавов, кера­
мик в сверхпроводящее состоя­
ние, переход железа из ферро­
магнитного состояния в нефер­
ромагнитное, переходы, связан­
ные с замораживанием или воз­
никновением вращения отдель­
ных фрагментов высокомолекулярных или координационных со­
единений — все это примеры ф азовы х переходов второго рода.
Так, в кристаллической решетке медного купороса CuSC>4 •Н2О
молекулы воды вращаются при комнатной температуре. Ес­
ли медный купорос охлаждать, то при некоторой температуре
часть молекул воды перестают вращаться, и теплоемкость мед­
ного купороса при этой температуре резко возрастает вследствие
фазового перехода второго рода.
Рис. 1 .15. Теплоемкость гелия
1.11. РАВНОВЕСИЕ В МНОГОКОМПОНЕНТНЫХ
СИСТЕМАХ. ХИМИЧЕСКИЕ ПРОЦЕССЫ
РАЗДЕЛЕНИЯ
ФИЗИКО-ХИМИЧЕСКИЙ АНАЛИЗ
Изучение фазовых диаграмм многокомпонентных систем яв­
ляется важной проблемой при поиске новых сплавов и в техно­
логии синтеза, разделения, очистки веществ.
Учение о фазовых равновесиях в многокомпонент­
ных системах, изучаемых с помощью диаграмм «состав —
свойство», называется физико-химическим анализом.
Можно изучать различные свойства систем в зависимости от
состава, например, плотность, вязкость и др. Результаты иссле­
дований наносятся на диаграмму «состав —свойство», на кото­
рой фазовые равновесия в системе отражаются в виде геометри­
ческих образов. Таким образом, физико-химический анализ ис­
пользует геометрические преобразования вместо аналитических,
92

которые используются при изучении химического равновесия в
системах.
В основе физико-химического анализа л еж а т два геометри­
ческих принципа: принцип непрерывности и принцип соответ­
ствия.
При непрерывном изменении состава системы непрерыв­
но изменяются и ее свойства.
Каждому из фазовы х превращений в системе соответ­
ствует собственный геометрический образ на диаграмме
«состав —свойство».
Физико-химический анализ был основан и развит в России
академиком Н. С. Курнаковым, который создал школу, успешно
развивающую работы в этой области. Изучение фазовых равно­
весий в многокомпонентных системах дает базовые данные д л я
разработки новых сплавов д л я машиностроения, авиации, кос­
мической и оборонной техники, а также технологических разра­
боток при переработке минерального сырья.
1.12. РАВНОВЕСИЕ В ДВУХКОМПОНЕНТНЫХ
СИСТЕМАХ
В двухкомпонентных системах параметрами, определяющи­
ми фазовое равновесие, являются температура, объем, давление
и концентрация одного из компонентов. В большинстве случа­
ев системы изучаются при постоянном давлении (атмосферном).
Если давления пара компонентов пренебрежимо малы, то и из­
менения объема в конденсированной системе пренебрежимо ма­
лы, поэтому диаграммы двухкомпонентных систем на плоскости
можно представить в координатах «состав—давление» или «со­
став —температура».
§1. Простая эвтектическая система
Рассмотрим температуры плавления в двухкомпонентных си­
стемах в зависимости от состава. Так как температуры плавле­
ния изучаются обычно при постоянном атмосферном давлении,
то правило фаз для этого случая содержит всего один некон­
центрационный параметр: / = К - Ф + 1. Пусть компоненты в
двухкомпонентной системе в жидком состоянии полностью сме­
шиваются. Приготовим составы, содержащие возрастающие кон-
93

центрации компонента В в смеси с компонентом А: например, О,
20, 40, 60, 80, и 100% компонента В.
Наполним тигель компонентом А, погрузим в него термопару
и будем нагревать тигель до полного расплавления компонен­
та А, и далее нагреем расплав до некоторой температуры, более
высокой, чем температура плавления. Затем начнем медленно
охлаждать расплав, отмечая температуру через определенные
промежутки времени. Термопара покажет нам постепенное сни­
жение температуры, пока она не достигнет температуры затвер­
девания ТА.
При этой температуре будет наблюдаться площадка на кри­
вой охлаждения (рис. 1.16), так как при затвердевании выде­
ляется теплота фазового перехода, которая компенсирует поте­
рю теплоты образцом. К огда весь расплав застынет, темпера­
тура вновь начнет снижаться. Наполним тигель первым соста­
вом, содержащим, например, 20 мол. % вещества В, расплавим
эту смесь, немного перегреем и начнем также охлаждать, отме­
чая температуру через определенные промежутки времени. При
некоторой температуре Т\ на кривой охлаждения будет наблю­
даться уже не площадка, а наклонная кривая с точкой переги­
ба, которая появляется вследствие кристаллизации вещества А,
но площадка на кривой охлаждения уже не появляется, так как
кристаллизация компонента А снижает его содержание в рас­
плаве и изменяет температуру затвердевания, поэтому затвер-
Т
94

девание расплава не будет протекать при постоянной темпера­
туре, к ак в случае чистого вещества. Дальнейшее охлаждение
расплава будет протекать до тех пор, пока мы не достигнем тем­
пературы Те , при которой весь расплав затвердеет и на кривой
охлаждения появится площадка. Третий состав смеси, допустим,
даст кривую охлаждения, не имеющую перегибов, а имеющую
только площадку при той же температуре, как и кривая охла­
ждения второго состава. Кривая охлаждения четвертого соста­
ва будет похожа на кривую охлаждения второго состава и, на­
конец, кривая охлаждения чистого компонента В будет иметь
площадку при температуре Тв, которая отвечает температуре
плавления компонента В. Теперь спроецируем все точки переги­
ба и площадки на кривых охлаждения на рисунок, на котором
отложена по оси ординат температура, а по оси абсцисс — состав
системы (см. рис. 1.17). Получим диаграмму плавкости системы
А —В. Диаграмма состоит из четырех бивариантных полей: по­
ле I — расплав, поле II — расплав + твердый компонент А; поле
III — расплав + твердый компонент В; поле IV — твердый ком­
понент А 4- эвтектика: поле V — твердый компонент В + эвтек­
тика. Поля отграничены моновариантными кривыми.
Мелкокристаллическая смесь компонентов, затвердева­
ющая при постоянной температуре, называется эвтектиче­
ской смесью или эвтектикой.
Линии на диаграмме, отвечающие появлению твердой
фазы при охлаждении расплава или исчезновению твердой
фазы при его нагревании, называются кривыми ликвидуса.
Линии на диаграмме, соответствующие исчезновению
жидкой фазы при охлаждении расплава или появлению
жидкой фазы при его нагревании, называются кривыми со-
лидуса.
Нанесем на диаграмму три фигуративные точки: Д , / 2, / 3.
Рассмотрим фазовые превращения состава, который отвечает
точке /1 при понижении температуры. Точка /1 располагается
на поле I, которое занято расплавом, т. е. одной жидкой фазой.
Если компоненты системы имеют ничтожное давление пара, то
его можно принять постоянным. В таком случае будет меняться
лишь один неконцентрационный параметр — температура. Д л я
такого случая правило ф а з Гиббса будет отвечать уравнению
/ = К —Ф + 1. Поэтому число степеней свободы на однофазном
поле будет равно / = 2 - 1 + 1 = 2. Следовательно, состояние
системы, обозначенное полем, бивариантно. При изменении до
95

некоторого предела и состава и температуры число ф а з в фигу­
ративных точках, расположенных на поле I диаграммы, не будет
меняться. Поэтому при понижении температуры фигуративная
точка f i будет опускаться, а число фаз при этом будет оста­
ваться равным единице до тех пор, пока фигуративная точка f\
не достигнет кривой Т&Е при температуре Т\. Здесь начина­
ет кристаллизоваться компонент А в точке /{. Система стано­
вится двухфазной, число степеней свободы становится равным
/ = 2 - 2 + 1 = 1. Следовательно, кривым на диаграмме плавко­
сти отвечает моновариантное состояние системы. Поэтому далее
можно менять лишь один параметр системы: либо температуру,
либо концентрацию. При дальнейшем понижении температуры
должен продолжать выделяться из расплава компонент А, и со­
став расплава будет изменяться в соответствии с кривой А Е ,
которую называют кривой ликвидуса. Поле II, таким образом,
является двухфазным полем, в котором система моновариантна.
Количество кристаллов, выделившихся из расплава при охла­
ждении системы до температуры
можно рассчитать по пра­
вилу рычага. Д л я этого проведем через точку f " на поле II пря­
мую, параллельную оси составов. Получим отрезок, ограничен­
ный осью температур и кривой А Е . Точка / " делит этот отрезок
на две части. Вся длина отрезка отвечает общей массе расплава
и кристаллов т о , причем
то=mi+m2,
(1.93)
где m i — масса расплава; m 2 — масса кристаллов компонента
А. Величина m i обратно пропорциональна отрезку / j x, а вели­
чина m 2 обратно пропорциональна отрезку / { у. Поэтому
m2_fix
/iV
Уравнение (1-94) представляет правило рычага
Прямая, проведенная через точку на двухфазном поле
параллельно оси составов, разделяется данной точкой так,
что количества той и другой фазы обратно пропорциональ­
ны отрезкам на прямой.
Уравнения (1.93) и (1*94) представляют систему линейных
уравнений, р еш ая которую можно определить массу кристаллов
и массу расплава при температуре Ti. При дальнейшем охла­
ждении фигуративная точка /1 будет опускаться далее до тех
пор, пока не достигнет прямой C D , проходящей через точку Е .
(1.94)
96

При температуре Те исчезает жидкая фаза. Весь расплав закри-
сталлизовывается, превращаясь в мелкокристаллическую смесь
компонентов А и В.
Реакция, при которой расплав нонвариантно кристалли­
зуется, образуя эвтектическую смесь компонентов, называ­
ется эвтектической реакцией:расплавэвтектика (А+В).
Следовательно, поле IV является двухфазным полем, в пре­
делах которого система остается моновариантной, тогда как ли­
ния CD является нонвариантной прямой, так как при этой тем­
пературе в системе присутствует три фазы: кристаллы компо­
нента А, кристаллы компонента В и жидкость. Массы кристал­
лов можно рассчитать по правилу рычага. Эвтектическая пря­
мая CD совпадает с кривой солидуса. Рассмотрим процесс охла­
ждения расплава, имеющего состав фигуративной точки / 2 . До
тех пор пока эта фигуративная точка будет находиться в пре­
делах однофазного поля I, система, имеющая состав этой фигу­
ративной точки, будет оставаться бивариантной. Но как только
точка /2 попадет в точку Е, из расплава начнут кристаллизо­
ваться компоненты А и В, система станет трехфазной (твердый
компонент А, твердый компонент В и жидкость) и нонвариант­
ной / = 2-3+1 = 0. Точка Е —нонвариантная эвтектическая точ­
ка, через которую проходит нонвариантная эвтектическая пря­
мая CD. Если затвердевший сплав, имеющий состав эвтекти­
ческой точки, разрезать и срез отполировать, то под микроско­
пом будет видно, что сплав состоит из очень мелких кристалли­
ков обеих фаз, перемешанных друг с другом, как это видно на
рис. 1.17, а.
Если же рассмотреть срез сплава, затвердевшего на нон­
вариантной прямой, проходящей через эвтектическую точку,
Рис. 1 .17. Микрофотографии срезов сплавов в системе Ni — Р:
а — эвтектика Ni —ГчЧзР 19 ат.%, б—заэвтектический сплав Ni —Р 21,8 ат.%,
в — кристаллы No зР на фоне эвтектики
4 Илполито»
97

то будут видны более крупные кристаллы одной из фаз, ко­
торые отделены мелкокристаллической эвтектической смесью
(рис. 1.17, б). Таким образом, петрография (микроскопическое
изучение шлифов) помогает разобраться в фазовых равновеси­
ях в системах.
Нонвариантная точка на диаграмме плавкости, в кото­
рой происходит затвердевание смеси с исчезновением жид­
кой фазы при кристаллизации смеси или появление жид­
кой фазы при плавлении смеси, называется эвтектической
точкой.
Рассмотрим процесс охлаж дения расплава, имеющего состав
фигуративной точки / 3 . Э та фигуративная точка находится так­
же на однофазном поле, где система бивариантна. Можно ме­
нять и состав, и температуру, не изменяя числа ф аз. При охла­
ждении точка будет опускаться до кривой Е В . При температу­
ре Т3 из расплава начнет кристаллизоваться компонент В. Далее
все будет происходить так же, как и для фигуративной точки Д.
Системы, подобные рассмотренной системе А —В, являются
простыми эвтектическими системами. Координаты эвтектиче­
ской точки нам не пришлось выяснять, поскольку они опреде­
лились тем, что одна из кривых охлаждения, изображенных на
рис. 1.16 случайно прошла через эвтектическую точку. Однако
на практике редко бывает так, чтобы один из заданных составов
точно совпал с эвтектическим составом. К ак же определяют ко­
ординаты эвтектической точки? Если приглядеться к рис. 1.16,
то можно заметить, что длина площадок, отвечающих затверде­
ванию эвтектических смесей на кривых охлаждения, изменяется
таким образом, что их протяженность растет при приближении
к эвтектической точке. Если длины этих площадок нанести вер­
тикально под эвтектической прямой и соединить их концы ли­
ниями, то получим треугольник, который изображен на рис. 1.16
под эвтектической прямой.
Треугольник, построенный на диаграмме плавкости под
нонвариантной кривой путем соединения конечных точек
вертикально отложенных площадок эвтектического затвер­
девания или полиморфного превращения на кривых «тем­
пература-время», называется треугольником Таммана.
Вершина треугольника Таммана находится на одной прямой
с эвтектической точкой. Следовательно, построив треугольник
Таммана, легко найти координаты эвтектической точки.
98

§ 2. Системы с непрерывными твердыми растворами
Пусть система состоит из компонентов, смешивающихся во
всех отношениях как в жидком, так и в твердом виде, т. е. в
системе образуются твердые растворы. Многие не представля­
ют, что твердые вещества могут образовывать между собой рас­
творы, однако в природе твердые растворы встречаются весьма
часто.
На рис. 1.18 представлена диаграмма «серебро —золото», по­
строенная как проекция точек перелома на кривых «температу­
ра плавления —время».
На кривых затвердевания смесей отсутствуют площадки. З а­
твердевание смесей происходит не при постоянной температуре,
так ка к при затвердевании состав расплава постоянно меняется
вследствие выделения кристаллов твердого раствора и расплав
обогащается более тугоплавким компонентом. Поэтому на диа­
грамму проецируют точки ликвидуса и солидуса. В результате
получается диаграмма, которая состоит из трех полей, разгра­
ниченных двумя кривыми, из них верхняя — кривая ликвидуса,
ниж няя — кривая солидуса. Согласно принципу соответствия
равновесию «жидкость —твердое» соответствует определенный
геометрический образ — двухфазное поле, разделяющее одно­
фазные поля жидких растворов и твердых растворов. В фигура­
тивной точке f i в поле жидкой фазы система однофазна и бива-
Рис. 1.18. Фазовая диаграмма системы «серебро —золото»
99

риантна. При охлаждении расплава фигуративная точка будет
опускаться до кривой ликвидуса. В этот момент начнет кристал­
лизоваться твердый раствор — сплав, называемый электроном.
В этой области система моновариантна, и можно менять лишь
один параметр, а второй будет изменяться в соответствии с кри­
вой ликвидуса. Массу твердого электрона и расплава при тем­
пературе Т\ можно рассчитать по правилу рычага. Дальнейшее
охлаждение расплава приведет фигуративную точку на кривую
солндуса, где жидкая ф аза исчезает. Система ниже кривой со-
лидуса становится вновь однофазной, так как состоит из твер­
дого раствора серебра в золоте, или наоборот. Системы, в кото­
рых компоненты неограниченно растворимы как в жидкой, так
и в твердой фазе, встречаются нечасто. Поэтому можно считать,
что Архимеду повезло, когда он решал задачу о содержании се­
ребра в золотой короне по измерению плотности, ибо она могла
быть изготовлена и из сплава, плотность которого изменялась
бы нелинейно, а растворимость компонентов в твердом виде бы­
ла бы ограниченной. Например, существуют системы, у которых
на кривых ликвидуса и солидуса наблюдаются экстремумы, как
это видно из рис. 1.19, а и б . В экстремальных точках составы
жидкой и твердой фаз совпадают. Н а рис. 1.20 схематически дана
диаграмма второго вида д л я системы с ограниченными тверды­
ми растворами. В этой системе один из твердых растворов устой­
чив лишь до определенной температуры. Фигуративная точка
/1 при охлаждении системы попадает на кривую ликвидуса в
точку / [ при температуре Т \. При этой температуре из распла­
ва начинают выделяться кристаллы твердых растворов (3. При
дальнейшем охлаждении твердых растворов р меняется по кри­
вой C F , а состав жидкости — по кривой Т С . При температуре Тп
Рис. 1.19. Диаграммы с твердыми растворами:
а — с максимумом; б—с минимумом
100

т
Рис. 1.20. Диаграмма с твердыми растворами перитектического типа
в точке /{ становится устойчивым твердый раствор а , поэтому
при данной температуре начинают выпадать его кристаллы, а
кристаллы твердого раствора Р растворяются. Нонвариантная
прямая CF отвечает окончанию кристаллизации твердого рас­
твора а в соответствии с перитектической реакцией:
(ж) + тв.р .(Р) тв.р .(а)
(1.95)
Перитектической реакцией называется реакция твердой
фазы с расплавом, в результате которой кристаллизуется
другая твердая фаза.
Таким образом, твердый раствор Р реагирует с расплавом и
в конце концов исчезает, а система в точке / " становится вновь
бивариантной и состоит из одной фазы а . На кривых охлажде­
ния при температуре Тп должны наблюдаться площадки, так
как перитектическая прямая CF — нонвариантная прямая. При
дальнейшем охлаждении фигуративная точка попадает на кри­
вую распада твердого раствора а в точку
Система стано­
вится вновь двухфазной и моновариантной, та к как образуется
эвтектика, состоящая из а и Р твердых растворов.
§3. Эвтектические системы с ограниченными твердыми
растворами
Пусть компоненты системы неограниченно растворимы в рас­
плаве, но лишь ограниченно растворимы в твердых фазах. В та-
101

ком случае на диаграмме будут обязательно поля твердых рас­
творов компонента В в компоненте А и твердых растворов ком­
понента А в компоненте В, как это видно на рис. 1.21, где пред­
ставлена диаграмма «олово —свинец».
Фигуративная точка f \ из однофазного бивариантного поля
жидкости при охлаждении расплава попадает на кривую лик­
видуса Е В в точку f[. Здесь из расплава кристаллизуется твер­
дый раствор олова в свинце. Далее фигуративная точка попа­
дает на твердый раствор олова в свинце. Далее фигуративная
точка попадает на двухфазное поле ЕС В жидкой фазы и твер­
дых растворов. Массу твердых растворов и жидкой фазы мож­
но рассчитать по правилу рычага. При дальнейшем охлаждении
системы фигуративная точка опустится до кривой солидуса СВ
в точку
где исчезает жидкая фаза и остается только одна
фаза — твердый раствор олова в свинце. Система становится
вновь бивариантной. Наконец, при дальнейшем охлаждении си­
стемы фигуративная точка попадает на кривую CG в точку
где происходит частичный распад твердого раствора. При этом
выделяются кристаллы эвтектики. Кривая распада твердых рас­
творов зависит от температуры: концентрация твердых раство­
ров с понижением температуры падает, как это видно из рисун-
Рис. 1.21. Фазовая диаграмма эвтектического типа с ограниченными
твердыми растворами (система Sn —Pb)
102

ка. Фигуративная точка /2 при охлаждении системы попадает
также на кривую ликвидуса в точку
и затем в двухфазную
область жидкой фазы и твердых растворов олова в свинце, а
при дальнейшем охлаждении фигуративная то чка попадает на
эвтектическую прямую DC в точку / 2, где жидкая фаза исчеза­
ет, и остается только двухфазная область эвтектики, состоящая
из двух твердых растворов: раствора свинца в олове и раствора
олова в свинце.
§4. Системы с химическим соединением
Пусть в системе образуется химическое соединение, которое
не разлагается при температуре плавления и не образует твер­
дых растворов с компонентами системы. На рис. 1.22 представ­
лены кривые охлаждения дл я этой системы и их проекции на
систему «состав —температура плавления». В этой системе при
небольшом содержании компонента В кривые охлаждения по­
хожи на те, которые наблюдались д ля простой эвтектической
системы, но при некоторой концентрации компонента В можно
наблюдать кривую охлаждения, подобную той, которая получа­
ется при плавлении чистого соединения: наблюдается всего одна
площадка на кривой охлаждения и не наблюдается эвтектиче­
ских площадок. При дальнейшем добавлении компонента В на
Рис. 1.22. Диаграмма системы с конгруэнтно плавящимся соединением
103

кривых охлаждения наблюдаются вновь изломы и эвтектиче­
ские площадки, но при другой температуре, чем эвтектические
площадки, наблюдавшиеся при небольшом содержании компо­
нента В.
Система, полученная путем проецирования точек, в кото­
рых происходят фазовые превращения, на систему «состав —
температура плавления», составлена как бы из двух эвтектиче­
ских систем: системы А —АВ и системы АВ —В и имеет 5 нонва-
риантных точек: точка плавления компонента А, эвтектическая
точка £?i, точка плавления соединения АВ (дистектическая точ­
ка), эвтектическая точка Е 2 и то чка плавления компонента В.
Нонвариантная точка плавления химического соедине­
ния на диаграмме плавкости называется дистектической
точкой.
В дистектической точке С две фазы: жидкая фаза и кристал­
лы соединения АВ. По правилу ф аз выходит, что система в точке
С моновариантна. В то же время температура плавления хими­
ческого соединения — нонвариант. Так в чем же дело? Если пра­
вило ф аз расходится с нашими наблюдениями, то где-то кроется
ошибка в наших рассуждениях. Все дело в том, что в точке С
уменьшается число независимых компонентов, та к к ак появля­
ется новая связь между ними, из-за того, что налагается допол­
нительное условие: состав расплава и состав кристаллов стано­
вятся одинаковыми. Учитывая это условие, в точке С оказыва­
ется только один независимый компонент. Следовательно, число
степенейсвободы вточкеСравно 0 :/ =1-2+1=0(один ком­
понент и две фазы: жидкая ф аза и кристаллы компонента АВ).
Так как эту систему можно рассматривать как две объединенные
двухкомпонентные системы: систему А —АВ и систему АВ —В,
то все отношения, какие были в эвтектической системе А —В, бу­
дут существовать и в обеих системах. Остается пояснить, како­
му фазовому превращению отвечает прямая А —В на диаграм­
ме. Треугольник Таммана показывает, что наиболее протяжен­
ная площадка на кривых охлаждения соответствующих составов
совпадает с составом, содержащим 100% соединения В. Следо­
вательно, это — фазовое превращение компонента В, т. е. его
полиморфное превращение. Д иаграммы всех систем, в том чис­
ле и рассмотренных выше, д олж ны удовлетворять двум прин­
ципам физико-химического а нал иза: принципу непрерывности и
принципу соответствия. Бл аго даря принципу соответствия мы
должны ожидать, что всякий раз, как устанавливается новое
фазовое равновесие в системе, на диаграмме должен появить-
104

ся новый геометрический образ: точка, линия или поле или же,
для трехмерных систем, поверхность. В рассмотренной системе
с дистектикой на диаграмме появляется нонвариантная точка,
отвечающая плавлению или затвердеванию соединения, плавя­
щегося без разложения или, как говорят в физико-химическом
анализе, плавящегося конгруэнтно.
Соединение, которое плавится без разложения, называ­
ется конгруэнтно плавящимся соединением, а соединение,
которое плавится с разложением, называется инконгруэнт-
но плавящимся.
§ 5. Системы с соединением перитектического типа
На рис. 1.23 представлена диаграмма системы с инконгру-
энтно плавящимся соединением. На кривой охлаждения имеется
площадка, но при проецировании ее на диаграмму мы получа­
ем лишь излом на кривой ликвидуса, но не максимум, как это
было в системе с конгруэнтно плавящимся соединением. Фигу­
ративная точка fi из бивариантного поля расплава при охла­
ждении системы попадает на кривую ликвидуса при температу­
ре Т\. Здесь начинает кристаллизоваться компонент В. Состав
расплава при дальнейшем охлаждении системы изменяется по
кривой ликвидуса до температуры Тф.п - В точке /{' наблюда­
ется площадка на кривой охлаждения. Треугольник Таммана
Рис. 1.23. Диаграмма с инконгруэнтно плавящимся соединением
105

показывает, что эта остановка отвечает фазовому превращению
компонента В.
При дальнейшем охлаждении системы ф игуративная точка
попадает на нонвариантную прямую Гп в точку /{" при темпе­
ратуре Гпл, при которой происходит перитектическая реакция:
пВ + расплав
AmBn
(1.96)
При нагревании соединения AmBn выше температуры Тпл
равновесие перитектической реакции (1.96) будет смещаться в
сторону образования расплава и кристаллов компонента В. Как
видим, в отличие от эвтектической реакции, при которой рас­
плав образует при замерзании две твердые фазы, при перитек­
тической реакции одна ф а за растворяется в расплаве, а кри­
сталлизуется из него другая ф аза. Перитектическая реакция так
же, как и эвтектическая, обусловливает появление на диаграмме
нонвариантной прямой при перитектической температуре Тпл,
поэтому на кривых охлаждения наблюдаются площадки, пока
не закончится перитектическая реакция и не растворится вся
ранее выпавшая фаза В, температура остается постоянной, рав­
ной Тпл, но когда последние кристаллы компонента В растворят­
ся, система из трехфазной становится двухфазной, содержащей
жидкую ф а зу и кристаллы соединения AmBn , и, следовательно,
моновариантной. При понижении температуры состав расплава
изменяется по кривой ликвидуса, а состав твердой ф азы остает­
ся постоянным. Когда же фигуративная точка достигнет эвтек­
тической прямой, система станет трехфазной: кристаллы соеди­
нения AmBn, жидкая фаза и соединение А, а при дальнейшем
охлаждении жидкость исчезает и фигуративная точка попадает
в двухфазное поле эвтектической смеси.
§ 6. Закон постоянства состава
Пусть конгруэнтно плавящееся соединение АШВП в системе
образует твердые растворы с компонентами А и В (рис. 1.24). То­
гда по принципу соответствия твердые растворы долж ны быть
представлены на диаграмме полем. Диаграмма на рис. 1.24 ана­
логична диаграмме системы с конгруэнтно плавящимся химиче­
ским соединением (см. рис.1.23), но соединение АШВПна рис. 1.24
имеет поле существования твердых растворов, причем соедине­
нию AmBn отвечает острый максимум на кривой ликвидуса.
Напротив, диаграмма, изображенная на рис. 1.25 отличается
тем, что максимум, отвечающий образованию соединения AmBn ,
очень пологий. Как можно объяснить это различие? Острый
106

т
Те,
Рис. 1.24. Диаграмма системы, имеющая сингулярную точку
максимум на диаграмме в области образования соединения озна­
чает, что соединение не диссоциирует ни в твердой фазе, ни в
расплаве. Пологий максимум означает, что соединение диссо­
циирует в жидкой фазе. Но могут ли быть такие системы, в
которых с повышением температуры соединение диссоциирует
и в жидкой, и в твердой фазе? На этот вопрос ответ был дан
Н. С. Курнаковым: в том случае, когда соединение диссоциирует
в твердой фазе, его состав переменный.
Тв
Тег
Рис. 1.25. Диаграмма системы, не имеющая сингулярной точки
107

Закон постоянства состава преподается в средней школе как
общий закон химии. Однако в споре К.Бертолле и Ж . Пруста в
общем был прав К. Бертолле, который утверждал, что состав со­
единения зависит от соотношения взятых исходных веществ и от
условий прохождения реакции. Д л я частного случая газовых си­
стем был абсолютно прав Ж . Пруст, который и д а л первую фор­
мулировку закона постоянства состава. Но если в общем случае
состав соединений может зависеть от условий их получения, то
что же мы называем химическим соединением? Многие считают,
что постоянство состава — это критерий, достаточный д л я того,
чтобы мы считали полученное вещество химическим соединени­
ем. В действительности существует огромное число химических
соединений, состав которых переменен. Это многочисленные ми­
нералы, шлаки и т. п. Каков же критерий, который бы мог быть
положен в основу определения химического соединения? На диа­
грамме, представленной на рис.1.24 имеется острый максимум
на кривой ликвидуса. В точке максимума можно провести бес­
численное множество касательных.
Точка на кривой, к которой можно провести бесчислен­
ное множество касательных, называется в геометрии сингу­
лярной точкой.
Только наличие на диаграмме «состав —свойство» сингу­
лярной точки подтверждает существование соединения по­
стоянного состава (дальтонида).
Таким образом, постоянство состава является следствием, а
не доказательством наличия соединения постоянного состава.
Если соединение на диаграмме плавкости имеет пологий макси­
мум, к которому можно провести только одну касательную, как
это видно на рис. 1.25, то на основании измерения только одного
свойства, в данном случае температуры плавления, невозмож­
но сказать, постоянен состав соединения или переменен. Нужно
провести исследование изменения других свойств от состава, на­
пример дифракции рентгеновских лучей, твердости, плотности,
вязкости и др. и, если выявится сингулярная точка при изме­
нении хотя бы одного из этих свойств с изменением состава, то
можно сделать заключение, что данное соединение имеет посто­
янный состав, отвечающий сингулярной точке. Если сингуляр­
ная точка не обнаруживается, то невозможно сделать однознач­
ный вывод. В этом случае, может быть, избранные нами свой­
ства недостаточно чувствительны к изменению состава, чтобы
сингулярная точка могла проявиться, или же сингулярной точ­
ки вообще нет, и соединение имеет переменный состав. Часто
108

при исследовании фазового состава прибегают к методу рент­
генофазового анализа, который основан на том, что рентгенов­
ские лучи отражаются от кристалла по закону Брегга—Вульфа:
sin 0 = пХ) где п — целое число; X — длина волны рентгенов­
ских лучей; d —расстояние между двумя плоскостями, которые
образуются атомами, находящимися в узлах кристаллической
решетки.
Наименьший полиэдр кристаллической решетки, повто­
рением которого в трех измерениях можно построить всю
решетку, называется элементарной ячейкой.
Элементарная ячейка характеризуется своими параметрами:
длиной ребер, которые обозначаются как а, 6 и с, и углами меж­
ду гранями а , (3 и у. В зависимости от симметрии элементарной
ячейки для ее описания используют от одного до шести пара­
метров. Соединение постоянного состава имеет постоянные па­
раметры элементарной ячейки, однако если оно образует твер­
дые растворы с компонентами системы, то параметры твердых
растворов монотонно изменяются, чаще всего линейно. Если об­
наруживается точка перегиба или экстремумы в изменении па­
раметров, то это и есть сингулярная точка, а это значит, что
состав соединения постоянен и отвечает сингулярной точке. Та­
ким образом, рентгенофазовый метод дополняет метод плавко­
сти. Однако не все ф азы в системах кристаллические, некото­
рые могут быть рентгеноаморфны, и в этом случае не удается
получить однозначный ответ на вопрос о постоянстве состава
соединения.
Соединения постоянного состава получили название
«дальтониды», а соединения переменного состава получили
название «бертоллиды».
Итак, в конденсированных системах могут образовываться
химические соединения как постоянного состава (дальтониды),
так и переменного состава (бертоллиды), и критерием посто­
янства состава является обнаружение на диаграмме «состав —
свойство» сингулярной точки. При отсутствии на диаграммах
«состав —свойство» сингулярных точек невозможно однознач­
ное заключение о постоянстве состава химического соединения
в конденсированной системе. Далее для примера рассмотрим две
двухкомпонентные системы, которые помогут объяснить встре­
чающиеся в жизни и в технологии явления: принцип работы ле­
дяной бани, а также закалку и отжиг стали.
109

§7. Примеры реальных систем
Система Н2О —NaCl. Э та система дана на рис. 1.26. На диа­
грамме можно видеть образование инконгруэнтно плавящегося
кристаллогидрата состава NaCl • Н2О, который образуется при
температуре 273 К. Выше этой температуры соединение разла­
гается на Н2О и NaCl. Точка О на диаграмме отвечает темпе­
ратуре замерзания воды 273,15 К при атмосферном давлении.
Точка Е — эвтектика, состоящая из льда, кристаллов дигид­
рата хлорида натрия и насыщенного раствора хлорида натрия.
Содержание твердого хлорида н атр ия в эвтектической точке со­
ставляет 22,4 %, температура эвтектической точки равна 251,9 К
(-21 ,2 °С). Поскольку при эвтектической температуре в системе
три фазы , то система нонвариантна.
При нагревании эвтектическая температура будет поддержи­
ваться до тех пор, пока в системе будут существовать тр и фазы.
Это используется для приготовления соляной бани. Когда лед
и соль смешиваются, система становится неравновесной и само­
произвольно переходит в равновесное трехфазное состояние, в
результате чего температура смеси понижается до температуры
эвтектики 251,9 К. Точка С на диаграмме — перитектическая.
Если бы соединение плавилось конгруэнтно, то это происходи­
ло бы в точке D \ но максимум плавления соединения мнимый,
Рис. 1.26. Диаграмма системы «хлорид натрия —вода»
110

так ка к это соединение разлагается по перитектической реакции
при более низкой температуре по перитектической прямой. В по­
ле E C D G существуют две фазы: насыщенный раствор хлорида
натрия в воде и кристаллы дигидрата хлорида натрия. Из диа­
граммы видно, что растворимость хлорида натрия в воде слабо
зависит от температуры, поэтому очистка хлорида натрия путем
перекристаллизации невыгодна. В технике д л я этого прибегают
к осаждению хлорида натрия при насыщении раствора хлори­
стым водородом.
Система Fe —С. На рис. 1.27 представлена часть системы «же­
лезо-углерод» до содержания углерода 5%. Сплавы, содержа­
щие до 1,7% углерода, называют сталями, а содержащие 1,7 —
4,3 % углерода — серым чугуном. Сплавы с содержанием углеро­
да свыше 4,3% называют черным чугуном. Кривая АВ на этой
диаграмме отвечает кристаллизации твердого раствора 5, кри­
вая В С — кристаллизации твердого раствора у и кривая CD —
кристаллизации карбида ж елеза РезС, названного цементитом.
Эти тр и кривые пересекаются в двух нонвариантных точках В
и С. Перитектическая то чк а В располагается при температуре
1763 К и содержании 0,7% углерода. Эвтектическая точка С от-
Рис. 1.27. Диаграмма системы «железо —углерод»
111

вечает температуре 1403 К и составу 4,3% углерода. Предельная
растворимость углерода в 5-Fe р авна примерно 0,8 %. Э то т твер­
дый раствор, реагируя с жидкой фазой по перитектической ре­
акции, образует твердый раствор у-состава точки J. Поле A H N
твердого раствора 8 ограничено сверху кривой солидуса А Н , а
снизу — кривой H N превращения «твердый раствор 8 —►твер­
дый раствор у». Поле твердого раствора у, называемого аусте­
нитом, ограничено сверху кривой J N окончания превращения
8 у и кривой солидуса J E . Точке Е отвечает предельная рас­
творимость (1,7%) углерода в y-Fe при эвтектической темпера­
туре. Снизу поле твердого раствора у ограничено кривыми на­
чала распада твердого раствора у (аустенита) GS и ES> которые
пересекаются в точке S при содержании углерода 0,83% и тем­
пературе 996 К. Это температура эвтектоидного превращения.
Ниже эвтектоидной температуры устойчивы a -железо (феррит)
и карбид железа (цементит). а -Ж елезо растворяет около 0,04%
углерода при эвтектической температуре. Поле этого твердого
раствора ограничено сверху кривой GP конца эвтектоидного
превращения, а снизу — кривой P D распада твердого раство­
ра углерода в a-Fe. Структура малоуглеродистой стали выше
996 К отвечает аустениту (твердый раствор углерода в y-Fe). При
быстром охлаждении путем погружения в воду или в масло эта
сталь образует смесь y-Fe с карбидом железа (мартенсит). Эта
смесь чрезвычайно твердая, но очень хрупкая (закалка стали),
при ее нагревании при 573—773 К часть y-Fe переходит в a-Fe,
которое, в отличие от y-Fe, мягкое и вязкое (отпуск стали). Со­
четание твердых свойств смеси y-Fe + РезС с высокой вязкостью
a-Fe дает возможность получать стальные изделия, обладающие
высокой твердостью и невысокой хрупкостью. В этом сущность
закалки стали. Зная диаграмму хотя бы в общих чертах, мы на­
деемся, учитель найдет возможность объяснить ученикам, поче­
му сталь закаливают и затем отпускают. Закаленная сталь при
нагревании до красного каления и медленном охлаждении те­
ряет твердость вследствие перехода всего y-Fe в мягкое a-Fe, а
растворенный углерод частично выделяется в виде графита, и
сталь теряет свою твердость (отж иг стали). Такие свойства ма­
лоуглеродистой стали используют на практике. Вначале из ото­
жженной стали готовят изделие, что сделать не трудно, та к как
отожженная сталь легко обрабатывается, а после этого сталь за­
каливают и отпускают, придавая ей нужную твердость.
Чугун обладает тем же редким свойством расширяться при
затвердевании, как и вода. Кроме того, серый чугун очень тверд.
Эти свойства чугуна используются д л я художественного литья.
В России имелось несколько центров художественного литья,
112

славившихся своими мастерами и художниками. Изумительные
чугунные решетки, которыми украшен Санкт-Петербург, могут
слу жить примером использования чугуна д л я этих целей. Сталь
является основным конструкционным материалом в строитель­
стве (несущие конструкции делаются из стали или железобето­
на, содержащего до 30% стали), в машиностроении, при изго­
товлении инструментов и оружия. Поэтому производство стали
достигает сотен миллионов тонн в год и связано с огромными
выбросами в атмосферу пыли и газов, что ведет к масштабному
загрязнению окружающей среды. Главным источником за гр яз­
нения является доменный процесс, который представляет неиз­
бежную ступень в двухступенчатом производстве стали. Чугун
более легкоплавок, чем чистое железо, что позволяет использо­
вать каменный уголь вместо древесного угля. Ранее, до XVII в.,
сталь производилась из криничного железа, которое получалось
путем восстановления железной руды при использовании дре­
весного угля. Криничное железо представляло собой смесь кри­
сталлического железа и шлака. Для удаления шлака криничное
железо подвергалось длительной ковке при температуре белого
каления. При этом шлак выжимался, и получался монолитный
кусок железа, из которого ковались нужные изделия. При этой
ковке железо посыпалось углем, который растворялся в желе­
зе, и получалось стальное изделие. Ясно, что технология прямо­
го восстановления железной руды до ж елеза менее вредна д ля
окружающей среды.
В последние десятилетия в технологии стали вновь начали
использовать прямое восстановление железной руды, так как
дл я достижения высокой температуры стало возможно пользо­
ваться природным газом и воздухом, обогащенным кислородом.
Это в корне изменило экологическую обстановку в сталелитей­
ных регионах, таких как Рурская область в Германии. В нашей
стране эта технология используется на Липецком металлургиче­
ском комбинате.
§8. Равновесие в трехкомпонентных системах
Когда система состоит из трех компонентов, то конденсиро­
ванная система имеет пять параметров. Д л я построения диа­
граммы необходимо отложить на плоскости составов три компо­
нента. Далее приходится рассматривать частные случаи, когда
давление или температура постоянны, тогда переменные давле­
ние или температуру можно отложить на ординате. Так можно
изобразить, например, плавкость в тройной системе. Д л я ото-
113

с
бражения составов трехкомпонентной системы на плоскости удоб­
но пользоваться треугольником Гиббса (рис. 1.28).
Равносторонний треугольник с сеткой координат, па­
раллельных сторонам треугольника, называется треуголь­
ником Гиббса. Вершины треугольника Гиббса отвечают
100%-му содержанию одного из трех компонентов. Про­
тивоположная данной вершине сторона треугольника от­
вечает 0 %-й концентрации компонента, отвечающего этой
вершине.
Рис. 1.29. Фазовая диаграмма тройной системы
114

Любая точка на плоскости треугольника однозначно опреде­
ляет состав системы. Например, точке / отвечает следующий
состав: 50% компонента В, 2 0 % компонента С и 30% компо­
нента А. Д ля того,чтобы можно было отложить значения тем­
пературы, прибегают к трехмерному изображению диаграммы.
Для этого на сторонах треугольника Гиббса строят трехгран­
ную призму, как показано на рис. 1.29. На ее гранях строят­
ся соответствующие двухкомпонентные системы. Эвтектики на
диаграммах двухкомпонентных систем проецируются на осно­
вание треугольника составов, через полученные точки проходят
проекции ребер пересечения трехфазных поверхностей, которые,
пересекаясь на треугольнике составов, дают проекцию тройной
эвтектической точки на треугольнике составов. В этой эвтекти­
ческой точке четыре ф азы: три компонента и расплав. Это нон-
вариантная точка.
Если и температура, и давление постоянны, и хотя бы один из
компонентов при данной температуре — жидкость, то тройная
система представляет собой диаграмму растворимости. Пусть
жидкостью будет вода с двумя другими компонентами — две
соли с одноименным анионом (если анионы будут разные, то си­
стема уж е становится четырехкомпонентной). На рис. 1.30 пред­
ставлена простая эвтоническая система с водой в качестве рас­
творителя.
Вершины треугольника отвечают чистым компонентам. Точ­
ка А дае т растворимость соли АХ в насыщенном растворе со­
ли ВХ, а точка В — растворимость соли ВХ в насыщенном рас-
вх
Рис. 1.30. Простая эвтоническая трехкомпонентная система
115

творе соли АХ. Кривая растворимости А Е показывает раство­
римость соли АХ при изменении содержания в растворе соли
ВХ, кривая B E дает растворимость соли ВХ при изменении со­
держания соли АХ в растворе. Поле А ЕВ — вода — однофаз­
ное поле растворов, насыщенных солями АХ и ВХ. Поле АХ —
А—Е
—
двухфазное поле, состоящее из раствора обеих солей и
твердой соли АХ, поле ВХ —В
—Е
—
двухфазное поле, состоя­
щее из раствора обеих солей и кристаллов соли ВХ. Поле АХ —
Е —ВХ
— трехфазное поле, содержащее насыщенный раствор и
кристаллы двух солей. В точке Е — три фазы (эвтоника). Если
соли образуют гидраты, то на плоскости треугольника в согла­
сии с принципом соответствия появятся поля кристаллизации
гидратов и соответствующие эвтонические точки, как это видно
на рис. 1.31, где дана диаграмма растворимости с образованием
гидрата одной из двух солей; кривая А Е отвечает кристаллиза­
ции гидрата.
Прямые, проходящие через точки, отвечающие составу
жидкой фазы и твердой фазы, называются лучами Скрей-
немакерса.
Лучи Скрейнемакерса на диаграмме от кривой А Е концен­
трируются в точке D на стороне «вода —соль АХ». Они прохо­
дят через аналитически определенные составы жидкой (на кри­
вой А Е) и твердой фазы, выделенной из насыщенного раствора.
Точка D определяет состав гидрата (см. рис. 1.31).
ВХ
Рис. 1.31. Растворимость в тройной системе с образованием гидрата
116

вх
Рис. 1.32. Растворимость в тройной системе образованием двойной
соли
Если в подобной системе образуется безводная двойная соль,
то лучи Скрейнемакерса будут сходиться в точке на стороне
АХ —ВХ треугольника, как показано на рис. 1.32, а если в си­
стеме образуется гидрат двойной соли, то лучи Скрейнемакерса
будут сходиться на поле (рис. 1.33).
Разумеется, и для тройных систем возможны более сложные
случаи образования твердых растворов или соединений, раство-
вх
Рис. 1.33. Растворимость в тройной системе с образованием гидрата
двойной соля
117

ряющихся в воде с разложением (инконгруэнтно растворимых).
Однако мы не будем рассматривать эти типы систем, ограни­
чившись их упоминанием. К числу систем с инконгруэнтно рас­
творимым соединением относится система Н2О —M gC^ —КС1.
В этой системе образуется карналлит — гидрат двойного соеди­
нения состава КС1 ■MgCb ■6Н2О. Богатейшие залежи карнал­
лита имеются у нас в стране в районе г. Соликамска и служат
источником д л я производства калийных удобрений. Технология
переработки карналлита с получением хлорида калия и хлорида
магния была разработана Н. С. Курнаковым на основе физико­
химического анализа растворимости в трехкомпонентной систе­
ме. Добываемый карналлит растворяется в воде, и вследствие
разложения его донная ф аза представляет собой хлорид калия,
а в растворе накапливается хлорид магния. Получить карнал­
лит из раствора в этой системе можно только при избытке в
растворе хлорида магния, поэтому после отделения выпавшего
из раствора хлорида калия раствор упаривают и выделяют из
него карналлит. Маточник после этого упаривают, и из него кри­
сталлизуется гидрат хлорида магния. Полученный из раствора
карналлит вновь разлагают, растворяя в воде. Таким методом
получают хлорид калия и хлорид магния из карналлита. Хло­
рид калия идет на удобрения, а из хлорида магния получают
металлический магний электролизом.
1.13. РАВНОВЕСИЕ В РАСТВОРАХ
§ 1. Идеальные растворы
Рассмотрим свойства гомогенных жидких растворов в состо­
янии термодинамического равновесия. Две научные школы, за­
нимавшиеся изучением растворов, развили два взгляда на фи­
зическую химию растворов. Одна физическая школа (Я. Вант-
Гофф, С. Аррениус, В. Оствальд) развивала физический подход
в теории растворов и исключала химическую специфику вза­
имодействий между молекулами, образующими раствор, опи­
раясь на термодинамику и молекулярно-кинетическую теорию.
Д. И. Менделеев, который основал химическую школу изучения
растворов, полагал, что в растворе молекулы компонентов об­
разуют диссоциирующие соединения. Взгляды Д. И. Менделеева
оказались наиболее близко отражающими действительность, но
из-за отсутствия возможности точного математического описа­
ния химического взаимодействия приходится рассматривать спе-
118

цифические особенности каждого раствора в зависимости от со­
става, что не позволяет построить общую количественную хи­
мическую модель дл я описания растворов. С другой стороны,
физический подход отвлекается от специфических свойств ком­
понентов в растворе и потому не в состоянии д а ть математи­
ческое описание концентрированных растворов. Все физические
теории относятся только к разбавленным растворам, в которых
химическое взаимодействие еще невелико и может быть учте­
но коэффициентами активности. Итак, термодинамика раство­
ров может быть развита и применима лишь для разбавленных
растворов. Но что значит разбавленные растворы? Этот термин
подразумевает деление компонентов раствора на растворитель и
растворенные вещества, хотя, конечно, все компоненты раствора
равнозначны. Однако в разбавленных растворах масса раство­
рителя в объеме значительно преобладает над массой раство­
ренных веществ. Известны различные способы выражения со­
става раствора, т. е. концентрации растворенного вещества. Вы­
ражение концентрации в виде молярных долей мы уже рассмат­
ривали. Д л я растворов, содержащих один растворенный компо­
нент (бинарные растворы), мольные доли связаны уравнениями:
ГЦ
712
х\-
, Х2 = ---------и х\ + Х2 = 1. Для разбавленных рас­
ти + П2------- П1+П2
творов, в которых различаются растворитель и растворенный
компонент, удобно использовать понятие молярности (количе­
ство молей в 1 л раствора): с*
Щ
V
где V — объем раствора.
Молярность зависит от температуры, так как включает объем,
который определяется температурой раствора. В отличие от мо­
лярности, моляльность (количество молей в 1000 г раствора) не
*
Ю00 щ
зависит от объема и определяется уравнением тп* = -------- . Кон­
центрации, выраженные в различных единицах, можно взаимно
пересчитывать, причем в уравнение для пересчета входит плот­
ность раствора: С2 = —
—
Х2иС2=
М\
1000
m 2. Плотность разбавлен-
ных растворов пренебрежимо мало отличается от плотности рас­
творителя, поэтому концентрации молярные и моляльные при­
близительно совпадают при комнатной температуре.
§ 2. Закон Рауля
Выше мы уже использовали закон Рауля при выводе уравне­
ния д л я химических потенциалов компонентов идеального рас-
119

твора. Остановимся подробнее на его анализе. Напомним, что
математически закон Рауля выражается простым уравнением:
Pi = XiP°.
В идеальном растворе парциальное давление пара г-го
компонента Рг при всех концентрациях (0 < Xi < 1) пропор­
ционально его молярной доле в жидкой фазе
причем ко­
эф ф ициент пропорциональности равен давлению насыщен­
ного пара
над индивидуальным компонентом.
Раствор, давление пара над которым соответствует зако­
ну Рауля для всех концентраций компонентов, называется
идеальным раствором.
В отличие от идеального газа в идеальном растворе молекулы
не могут не взаимодействовать д руг с другом, так как находятся
на близком расстоянии, поэтому потенциальная энергия молекул
в идеальном растворе не может быть равной нулю, но средняя
потенциальная энергия каждой молекулы идеального раствора
равна средней потенциальной энергии каждой молекулы в соот­
ветствующем чистом жидком компоненте. Потенциальную энер­
гию молекул непосредственно нечем измерить, поэтому исполь­
зуют давление пара компонента, с которым непосредственно свя­
зана его свободная энергия Гиббса, т. е. химический потенциал.
На рис. 1.34 можно видеть зависимость общего давления и дав­
ления насыщенного пара компонентов идеального раствора от
его состава.
Реальные растворы лишь при предельном разбавлении до­
статочно точно описываются законом Рауля. При повышении
концентрации растворенных ком­
понентов наблюдаются отклоне­
ния от закона Рауля, причем эти
отклонения могут бы ть положи­
тельными или отрицательными,
как это видно на рис. 1.35, а) б.
Все же реальные растворы
удается с достаточной точно­
стью описать с помощью зако­
на Рауля, если воспользоваться
активностями компонентов вме­
сто мольных долей. В растворах
с положительными отклонения­
ми от закона Рауля средняя по­
тенциальная энергия молекул по
абсолютному значению меньше,
Рис. 1.34. Общее давление пара
(пунктир) и парциальные давле­
ния паров компонентов для иде­
ального раствора
120

Рис. 1.35. Положительные (а) и отрицательные (б) отклонения от за­
кона Рауля
чем в чистых компонентах, а при отрицательных отклонени­
ях она больше, чем в чистых компонентах. В идеальных рас­
творах они одинаковы, поэтому очень близки к идеальным рас­
творам, например, растворы тяжелой воды в воде: Н2О —D2O.
В растворах с положительными отклонениями взаимодействие
молекул растворенного компонента друг с другом выше, чем
взаимодействие их с молекулами растворителя, так что мож­
но предполагать образование ассоциатов молекул растворенно­
го вещества, как, например, в растворах спирта в воде. В систе­
мах с отрицательными отклонениями от закона Рауля образу­
ются соединения между молекулами растворителя и растворен­
ного компонента, как, например, раствор хлористого водорода в
воде.
§ 3. Парциальные молярные величины
Раствор представляет собой гомогенную систему, состояние
которой определяется ее параметрами. Можно ли рассматривать
экстенсивные параметры раствора как сумму соответствующих
параметров, относящихся к каждому компоненту раствора? Оче­
видно, что каждое экстенсивное свойство в таком случае д о л ж ­
но быть суммой экстенсивных свойств компонентов раствора,
по определению. Однако из нашего жизненного опыта мы зн а­
ем, что объем раствора не всегда равен сумме объемов компо­
нентов. Так, сумма объемов спирта и воды не равна объему по­
лучающегося из них раствора, а заметно меньше. Следователь­
но, экстенсивные свойства, в общем, зависят от состава раство­
ра. Чтобы найти эту зависимость, необходимо соответствующий
экстенсивный параметр продифференцировать по числу молей
компонента. Если компонентов раствора г, то по всем г компо-
121

нентам. Пусть параметр системы Ф является функцией темпе­
ратуры, давления и числа молей:
Полный дифференциал в таком случае можно вы разить через
сумму частных производных:
Функция у* в уравнении (1.98) называется парциальным моляр­
ным значением Ф для г-го компонента.
Парциальное молярное значение \j/i компонента Ф для
г-го компонента равно изменению параметра Ф системы при
изменении числа молей г-го компонента йщ при условии,
что температура, давление и числа молей остальных ком­
понентов остаются постоянными при постоянном давлении
и температуре.
При Т = const и р = const из уравнения (1.98) имеем:
=
5
Z(
d
n
<
=
ИV*d ni-
(!•")
х VC/n‘/V',p,r,njTS
i
Из уравнения (1.99) следует, что парциальные молярные вели­
чины \j>i являются интенсивными параметрами. Проинтегрируем
уравнение (1.99) при постоянных щ :
Ф=Ф(Т,р,У,ni,n2)... ,гц).
Введем обозначение
(1.98)
*о
(1.100)
122

Уравнение (1.100) показывает, что, если заменить молярные ве­
личины парциальными молярными величинами, то через их сум­
му можно выразить значения параметров растворов. Ранее было
показано, что химический потенциал равен частной производной:
Hi=
(1.101)
Из (1.101) следует, что gi — парциальная молярная свободная
энергия Гиббса. Таким образом, для химического потенциала
можно дать более короткое определение:
Химический потенциал — это парциальная молярная
свободная энергия Гиббса.
Точно так же
Л
/0<Л
А так как
J=-,->>то
(*2Л
-ё.
\дТдщ)т и
„
{No\
где Si —парциальная молярная энтропия. Далее, так как —- I =
\dpj
=V,то
( 9,2(3 )
\дрдщ)т
где Vi — парциальный молярный объем.
§4. Уравнение Гиббса—Дюгема
Зададимся вопросом, ка к выразить химический потенциал
одного компонента раствора через химический потенциал вто­
рого компонента. Так как dG - -SdT +Vdp +
то при
T = const и р = const для бинарного раствора
dG = \iidni +Ц2^2-
(1.102)
После интегрирования (1.102) при постоянных значениях хи­
мических потенциалов получим: G = (Liini +Ц2^2* Если химиче­
ские потенциалы становятся переменными, то
dG = jiidni +\l2dn2 +nid\l\ +П2ф,2*
(1.103)
123

Сравнивая уравнение (1.102) с уравнением (1.103), заключаем,
что nidfii+П2Ф2=0 и
фх= —
ф2.
(1.104)
711
Уравнение (1.104) называют уравнением Г иббса—Дюгема. Оно
имеет такое же важное значение д л я равновесия в растворах, как
уравнение действующих масс д л я химического равновесия и пра­
вило ф аз Гиббса для фазового равновесия. Используя это урав­
нение можно рассчитать химический потенциал растворенного
компонента, если известны число молей и химический потенциал
растворителя. Если раствор не идеальный, то химический потен­
циал г-го компонента равен (i* = р|+ДТ lnyiXi = \l\+RT In а*. Про­
дифференцируем это уравнение при постоянной температуре:
d\li = RTd In
= R Tdlnai.
(1.105)
Подставив в (1.105) значение d\Xi из уравнения (1.104), получим:
nidlnai =-П2<Ша2
или dlnai =
сЛп<22- Так как х* ------- ^
-----
,то
П1
+
dlnai = —— dlna2
X!
или nidlnyiXi +П2сПпу2^2 = 0, но так как хг = 1 - Хх, то
nidlnji +nidlnxi +ri2dlnY2-nd\nx2 = 0.
После сокращений получаем:
TlirflnYi = П2Й1пу2
или
Х2
dlnyi = -----«Ппуг*
XI
Так как парциальные давления пара компонентов раствора
непосредственно связаны с химическими потенциалами, то мож­
но рассчитать парциальное давление пара одного компонента,
если известно парциальное давление пара другого компонента,
поскольку
= |i? + RTinpi, то ф* = RTd lnp*. Подставив это
значение ф * в уравнение (1.104) получим уравнение Гиббса—
Дюгема—Маргулиса:
d\npx= -—1пр2= -—dlnp2.
(1.106)
Til
Xi
По уравнению (1.106) вычисляются парциальные давления ком­
понентов двухкомпонентного раствора.
124

РАЗБАВЛЕННЫЕ РАСТВОРЫ
§ 5. Закон Генри
Если растворы бесконечно разбавлены, т. е. такие растворы,
мольная доля растворителя которых бесконечно близка к 1, то
молекулы растворенного вещества в среднем находятся на таком
отдалении друг от друга, что в ближайшем окружении их нахо­
дятся только молекулы растворителя, поэтому средние потенци­
альные энергии молекул растворенного вещества зависят толь­
ко от взаимодействия его молекул с молекулами растворителя и
не зависят от концентрации растворенного вещества. Следова­
тельно, средняя потенциальная энергия молекул растворенного
компонента постоянна, но не равна таковой в чистом компонен­
те. Вследствие этого энтальпия разбавления бесконечно разбав-
dAH л
ленного раствора равна нулю: ^
= 0, и поэтому парциальное
давление насыщенного п ара растворенного компонента пропор­
ционально его концентрации:
Р2 =кх2.
(1.107)
Уравнение (1.107) называется законом Генри.
В бесконечно разбавленных растворах парциальное д а в ­
ление насыщенного п ар а растворенного компонента пропор­
ционально его концентрации.
Постоянную к в уравнении (1.107) принято называть коэффи­
циентом Генри, а само это уравнение — уравнением Генри. Ко­
эффициент Генри может быть как больше, так меньше давления
насыщенного пара над чистым компонентом. Напротив, давле­
ние пара растворителя над бесконечно разбавленным раствором
описывается законом Рауля. Законом Генри удобно пользовать­
ся при рассмотрении растворимости мало растворимых газов в
жидкостях.
§ 6. Растворимость
Количество компонента, которое растворилось в жидко­
сти с образованием насыщенного раствора, называют рас­
творимостью.
125

Насыщенным раствором данного компонента называется
равновесная гетерогенная система, состоящая из раствора и
не растворившейся при данной температуре ф азы взятого
компонента.
Процесс растворения можно рассматривать как химическую
реакцию, а растворимость — ка к химическое равновесие, уста­
новившееся между твердым веществом А и раствором:
А + жидкость ^ раствор
Тогда растворимость будет определяться константой равновесия:
_
а раств
&тв
Если раствор насыщен, то масса твердого вещества постоянна
и не влияет н а величину константы равновесия. Поэтому для
насыщенного раствора
К = а<раств*
Если растворимость твердого вещества мала, то а раств - Трасте и
К —араств*
Зависимость константы равновесия от температуры определяет­
ся уравнением:
dlnK=^dT,
следовательно,
сИпхг
RT2
АН
dT.
(1.108)
^расти -
Уравнение (1.108) называют уравнением Шредера. А Н 2 — эн­
тальпия растворения, т. е. теплота, которая выделяется или по­
глощается при растворении компонента в насыщенном растворе.
Так как температурный интервал невелик, то теплоту растворе­
ния можно считать постоянной. Если уравнение Шредера про­
интегрировать, то получим
Inж,раств
ДЯ2
RT
+С.
(1.109)
Уравнение (1.109) используется для расчета растворимости
в зависимости от температуры. В координатах ^1п х — ^
оно
126

Рис. 1 .36 . Растворимость в жидкой фазе в зависимости от температуры
представляет собой прямую, тангенс угла наклона которой к оси
абсцисс равен
(рис. 1.36).
Энтальпия растворения складывается из двух слагаемых: А Н
плавления и А Н смешения. В идеальных растворах энтальпия
растворения равна энтальпии плавления, но в реальных раство­
рах они могут быть не равны. Если энтальпия плавления все­
гда отрицательна, то энтальпия смешения может быть как от­
рицательной, так и положительной. Поэтому энтальпия раство­
рения д л я реальных растворов может быть как положительной
так и отрицательной. Так, при растворении поваренной соли в
воде раствор охлаждается, а при растворении безводного хлори­
да кальция раствор нагревается, так как при этом образуются
гидраты хлорида кальция.
§7. Эбулиоскопия и криоскопия
Рассмотрим, как влияет на температуру кипения растворите­
ля растворение в нем нелетучего вещества. На диаграмме одно­
компонентной системы, которую схематично представляет рис.
1.37, отметим температуру кипения растворителя при давлении
1 атм, Т кии.
Точка D на кривой равновесия «жидкость —пар» — это точ­
ка кипения при давлении 1 атм. В точке О на кривой равнове­
сия «жидкость —твердое» жидкость затвердевает при темпера­
туре То. Если же в жидкости растворен второй компонент, то
давление насыщенного пара раствора будет ниже давления па­
ра чистого растворителя, та к как оно будет равно парциально­
му давлению пара. По закону Рауля, парциальное давление пара
127

ниже общего давления, которое остается равным 1 атм. Но если
давление пара растворителя стало ниже, то температура кипе­
ния его будет выше, так как оно будет кипеть лишь тогда, когда
давление пара над ним достигнет 1 атм. Поэтому температура
кипения переместится в точку Ti, и точкой кипения раствора
станет то чк а D\. Если твердые растворы в системе не образуют­
ся, то кривая равновесия «жидкость —пар» останется той же.
В соответствии со смещением точки кипения сместится и нонва-
риантная точка из точки О в точку Oi, и температура замерза­
ния раствора Т\ станет ниже температуры замерзания чистого
растворителя. Поэтому следствием из закона Рауля является то,
что при одном и том же давлении раствор нелетучего компо­
нента ки п и т при более высокой температуре, а затвердевает
при более низкой, чем чистый растворитель.
Изучение повышения температуры кипения при раство­
рении данного компонента называют эбулиоскопией, а по­
нижение точки замерзания растворителя при растворении
данного компонента называю т криоскопией.
В разбавленных растворах понижение температуры затвер­
девания АТзахв пропорционально концентрации в единицах мо-
ляльности (м о л ь /1000 г растворителя):
А7^атв —К тп,2’
Если раствор ОДНОМОЛЯЛЬНЫЙ, ТО ГП2 = 1 и АТзатв = К , где К —
моляльное понижение температуры затвердевания или криоско-
пическая константа данного растворителя. Интегрируя уравне­
ние Шредера, получаем:
Рис. 1.37. Влияние растворения второго компонента на давление пара
и температуру замерзания растворителя
128

(1.110)
Inж} =
АЯПЛТр- Т\
R TqT\'
Рассматриваемые растворы очень разбавленные, т. е. х -z мало,
поэтому можно упростить уравнение (1.110): известно, что если
хмало,то1п(1-ж)и -х, поэтомуln^i =(l-£2)~
-жг, далее
Tj « То, иTiTq« Tq и , наконец,То-Т\ = ДТэахв. Получим
_
_
^ Ш2Л/1 ^ АЯПЛАТозатв
Ж2* юоо "
1Щ’
откуда
Д^затв “
ДУьатв-^1
1000ДЯПЛ 2‘
Следовательно, криоскопическая константа может быть вы­
числена по уравнению:
к_RTLtbM1
1000ДЯпл ‘
Криоскопическая константа имеет специфическое значение
дл я каждого растворителя, например:
Растворитель
Криоскопическая константа К
Вода .....................................................1,86
Б е н з о л ............................................... 5,146
Уксусная кислота ............................. 3,81
Ф е н о л .................................................. 6,81
Кам ф ара ............................................ 37,7
Криоскопическая константа не зависит от свойств растворен­
ного вещества. Основываясь на законе Рауля и уравнении К л а ­
узи у са —Клайперона, тем же путем можно получить уравнение
дл я повышения точки кипения раствора по сравнению с чистым
растворителем:
1000ДЯ„„ 2
Так как Д Я Э= Е т ^, где Е —эбулиоскопическая константа, то
ее значение может быть вычислено по уравнению (1.112)
Г _ ■^^Окип-^1
1000ДЯИСП‘
(1. 112)
Эбулиоскопическая константа имеет специфическую величи­
ну для каждого растворителя, например:
5 Ипполитов
129

Растворитель
Эбулиоскопическал константа Е
В о д а ...................................................0,514
Б е н з о л ................................................. 2,64
Уксусная кислота ............................. 2,93
Т о л у о л ................................................. 3,37
Нафталин ........................................... 5,65
Эбулиоскопия и криоскопия используются д л я определения
молекулярной массы растворимых веществ. Д л я определения
криоскопической и эбулиоскопической констант используют ве­
щества с известной молекулярной массой. В этих измерениях
существенное значение имеет условие, чтобы навеска растворяе­
мого вещества была достаточно мала, и раствор был сильно раз­
бавленным, но чтобы навеска бы ла достаточна для того, чтобы
можно было измерить изменение температуры с требуемой точ­
ностью.
§8. Осмотическое давление
Некоторые из твердых веществ могут в тонких пленках или
пластинах избирательно пропускать молекулы некоторых ве­
ществ. Например, тонкая палладиевая фольга в нагретом со­
стоянии легко пропускает водород, но не пропускает другие га­
зы. Многие пленки, извлеченные из животных или раститель­
ных организмов (например, рыбий пузырь, оболочки клеток),
пропускают молекулы воды и непроницаемы д л я растворенных
компонентов.
Перегородки в растворе, избирательно проницаемые для
одних компонентов р аствора и непроницаемые д л я других,
называются полупроницаемыми мембранами.
Когда такая мембрана разделяет раствор и воду, молекулы
воды проникают через нее в раствор.
Процесс переноса вещества из раствора через полупро­
ницаемую мембрану называется осмосом.
Объяснение явления осмоса можно найти с помощью законов
термодинамики. Пусть раствор и чистый растворитель находят­
ся в сосуде, разделенном мембраной, пропускающей молекулы
воды, но не пропускающей молекулы растворенного компонента,
причем обе части системы находятся под одинаковым внешним
давлением, к ак это показано на рис. 1.38.
130

Химический потенциал чи­
стой воды отличается от хи­
мического потенциала воды в
растворе. Химический потенци­
ал — это парциальная моляр­
ная свободная энергия Гиббса,
поэтому он зависит от внешнего
давления р. С ростом внешнего
давления химический потенци­
ал увеличивается. Если хими­
ческие потенциалы воды по обе
стороны полупроницаемой пе­
регородки неодинаковы, то си­
стема неравновесна, и в ней
должен протекать самопроизвольный процесс в сторону вырав­
нивания химических потенциалов воды. Вследствие этого вода
будет переходить в раствор через полупроницаемую перегородку
в ту часть системы, которая заполнена раствором, и уровень во­
ды в этой части системы будет повышаться. Тем самым создает­
ся гидростатическое давление тс*, которое изменяет химический
потенциал раствора, уменьшая разницу химических потенциа­
лов по обе стороны полупроницаемой перегородки. В конце кон­
цов, гидростатическое давление выровняет значения химических
потенциалов по обе стороны мембраны, и в системе наступит
равновесие. Давление к * называется осмотическим давлением, а
явление, которое показано на рисунке, называется осмосом. Вы­
ясним, как химический потенциал компонента раствора зависит
от внешнего давления. Химический потенциал — это парциаль­
ная молярная свободная энергия Гиббса:
Рис. 1.38. Модель осмометра:
1 — раствор; 2 — растворитель; 3 —
мембрана
^
(<9п;)Р)Т)
Продифференцируем это уравнение по давлению Р:
дщ=d2G
_
_
дР~дРдщ~дщ~Щ’
где V{ — парциальный молярный объем г-го компонента. Итак,
d p , = VidP. Проинтегрируем это уравнение от
дор
м(Р)
J d\li
ц(р°)
dP.
Ро
131

Получим:
Ц*(Р) = Щ(ро) + V i (Р-ро).
Химический потенциал чистого растворителя при p i равен Ц,, а
при Р будет p i(P). Следовательно,
ц(Р)=lxf(T)+RTInai+щ(Р-P0).
Поэтому
р?(Т) = ц?(Т) +RT InС! +true,
так как Р —р0 = я*. С учетом сказанного получим величину
осмотического давления:
ВТ. ,
.
щ = - — \п(Yixi).
v\
Если раствор идеален, то у = 1
В разбавленном растворе
Л2
1п(1-Х2) « -Х2 ~ ---- ,
Щ
поэтому
_
ВТ 712 __ВТп2
щП1
V
712
но — = с2. Окончательно получаем уравнение Вант-Гоффа:
Hi=RTc2.
(1.113)
В идеальных разбавленных растворах осмотическое давление
определяется законом (1.113), подобным закону состояния иде­
ального газа.
Осмос играет важную роль в природе и технике. Стенки жи­
вотных и растительных клеток представляют полупроницаемые
оболочки, называемые биологическими мембранами. Через эти
мембраны происходит обмен веществ с окружающей клетку лим­
фой под влиянием осмоса. Осмотическое давление может быть
настолько значительным, что обеспечивает в совокупности с ка­
пиллярными силами подъем сока в растениях и деревьях от кор­
ней к листьям. Листья испаряют воду и синтезируют сахара,
концентрация растворенных веществ в них повышается по срав­
нению с концентрацией почвенных растворов, в результате это­
го и создается осмотическое давление. Консервирование ягод и
132

фруктов с помощью сахара (варка варенья) такж е приводит к
удалению излишней влаги из ягод и фруктов благодаря осмосу.
Людям с повышенным артериальным давлением не рекоменду­
ется есть соленое, так как повышение концентрации соли в кро­
ви приводит к поступлению воды в кровь через биологические
мембраны, что ведет к повышению артериального давления.
Полупроницаемые мембраны все более широко начинают при­
меняться в технике разделения и очистки веществ, так как зза­
тра ты энергии на мембранные процессы гораздо ниже, чем на
ректификацию или экстракцию.
Так как осмотический процесс — обратимый процесс, то, ис­
пользуя внешнее давление на раствор, можно достигнуть его
концентрирования и получения пресной воды из морской. Д л я
этого трубы, снабженные на концах керамическими полупрони­
цаемыми мембранами, погружают в море мембраной вниз на
большую глубину. Под действием высокого гидростатического
давления пресная вода из морской воды проникает через мем­
брану внутрь трубы, откуда она откачивается и используется
для орошения. Огромные площади сельскохозяйственных уго­
дий созданы с использованием опресненной таким образом воды
в арабских странах. Так арабские страны использовали доходы
от продажи нефти, чтобы обеспечить себя продовольствием.
Измерив осмотическое давление в разбавленном растворе,
можно определить молекулярную массу растворенного компо­
нента, так как концентрация разбавленных растворов может
быть выражена в единицах моляльности. Осмотический метод
используют при определении молекулярной массы высокомоле­
кулярных соединений.
СИСТЕМЫ ИЗ ВЗАИМНО РАСТВОРИМЫХ ЖИДКОСТЕЙ
§9. Законы Коновалова
Пусть система представляет собой систему из двух жидких
компонентов, смешивающихся во всех отношениях. Обозначим
через х \ молярную долю г-го компонента в растворе, а через у\
молярную долю i -го компонента в паре над раствором. Суммар-
Р2
Р2
ное давление пара равно: Р =Pi+P2 и У2 = — =
-------- . Подста-
Р Р1+Р2
внм значения парциальных давлений из закона Рауля:
Х2
У2=
Х2 Р2
х\Рх + Х2Р2
Р°
(1-Я2)-Л + Я2
Рг
133

Из этого уравнения следует,что у 2 = Х2 при
.
Если
же Р? 7^ Р2> то и 2/2 7^ ^2, т*е* в общем случае молярная до­
ля компонента в паре не равна его молярной доле в раство­
ре. Кроме того, уравнение показывает, что с ростом мольной
доли компонента в растворе растет и его мольная доля в па-
dp2
ре, значит, всегда - — > 0. Подставим в уравнение Гиббса—
ах2
Дюгема—Маргулиса значения парциальных давлений компо­
нентов из уравнения Рауля:
х2
dinpi -------dlnp2 ,
Xl
т. e.
Откуда
dpi
Pi
dpi=—
X2 dp2
Xl P2
X2 Pi
dp2.
(1-X2)P2
Теперь выразим dpi через общее давление Р: dpi = dP —ф 2, то
dp2-
dP= '-2ȣ+1dp2=
Х2 1-У2 !х
.
Xl Р2
.
1-12 3/2
Разделим обе части этого уравнения на dx2:
dP
dX2
*2 1~У2
1-Х2 У2
+1
dp2
dX2
(1.114)
dp2
Так как всегда - — > 0 в уравнении (1.114), то эта величина на
ах2
dP
знак —— не влияет, так что в том случае, когда общее давление
ах2
пара растет с добавлением компонента х2, т. е. когда
dPп
^
>0'
то
*2 1 —3/2
+1 >0.
1-Х2 у2
Это значит, что х2 < у2, т.е . пар богаче компонентом х2, чем
раствор, если же
dP

то
S2 1~У2 х
1-Х2 У2
<0
И х 2 > У2, Т. е. пар беднее компонентом
чем раствор. Наконец,
если
dP
dx2
то и Х2 = 2/2, т. е. концентрация компонента Х2 в паре и жидко­
сти остается одинаковой. М. И. Коновалов на основании эмпири­
ческих данных сформулировал законы разделения компонентов
кипящего раствора:
Первый закон Коновалова: насыщенный пар над раство­
ром богаче тем компонентом, увеличение концентрации ко­
торого в системе повышает общее давление пара.
Второй закон Коновалова: если давление насыщенного
пара над раствором Р = f(x 2) имеет при неком х 2 экстре­
мальную точку, то в этой точке состав жидкого раствора и
равновесного пара одинаковы.
Математически это значит:
dP
первый закон Коновалова: если - — > 0, то Xi > 2/1, если
dxi
dPn
—
<0,тоXi<уи
dPп
второй закон Коновалова: если - — = 0, то
= у\.
dxi
Законы Коновалова являются основой для расчета процес­
сов разделения смесей путем перегонки и ректификации. Это —
процессы получения различ­
ных душистых веществ, спир­
тов, лекарственных препара­
тов, а главное, процессы пере­
гонки нефти. Рассмотрим тем­
пературу кипения в системе,
представляющей собой бинар­
ный раствор. Пусть компо­
нент А имеет при давлении
1 атм температуру кипения Тд,
_
Л
а второй компонент В кипит Рис. 1.39. Зависимость температу-
гт1 п
Ры кипения от состава в системе
при температуре Tr . Посколь-
^
к
о
из дВух неограниченно раствори-
ку компоненты смешиваются
мых жидкостей
135

во всех отношениях как в жидкой, так и в парообразной фазе,
то, по принципу соответствия, на диаграмме «температура ки­
пения-состав» должно существовать три поля: поле пара, поле
жидкой фазы и двухфазное поле, разделяющее однофазные по­
ля. На рис. 1.39 схематически д ана диаграмма такой системы.
Можно проследить за ф азовы ми превращениями при равно­
весном охлаждении системы. Фигуративная точк а / находит­
ся в однофазном и бивариантном поле пара. При охлаждении
системы точка / будет опускаться, и при этом число фаз не
будет меняться, пока точка / не окажется на верхней кривой
Та —Тв в точке
Это —кривая конденсации, так как в ней при
температуре Тз появляется вторая ф а з а —жидкий раствор. При
дальнейшем охлаждении до температуры Т\ точка / попадает
в моновариантную двухфазную область, состоящую из жидко­
го раствора и пара. Состав жидкого раствора будет изменяться
по верхней кривой Та—Тв , так что состав пара в соответствии
с первым законом Коновалова будет обогащен компонентом В
и конденсат будет отвечать по составу точке у 2 на оси соста­
вов. Таким образом, в результате первой перегонки из раствора,
имевшего состав
получился раствор состава у 2 , более богатый
компонентом В.
Если раствор при конденсации паров при температуре Т2,
вновь подвергнуть нагреванию до кипения, то пар будет иметь
состав, еще более богатый компонентом В. Повторяя перегонку
сконденсированных паров с отбором все новых фракций конден­
сата, можно полностью разделить компоненты и получить чи­
стые вещества А и В. На рис. 1.40, а, б представлены диаграммы
систем, в которых наблюдается образование азеотропов. В точ­
ке С состав п а р а и жидкости одинаков в соответствии с вторым
законом Коновалова. Раствор в точке С кипит при постоянной
температуре Т ^ .
Рис. 1.40. Системы с максимумом температуры кипения (а) и с мини­
мумом температуры кипения (6)
136

Состав раствора, который кипит при постоянной темпе­
ратуре при данном давлении и в соответствии с вторым за­
коном Коновалова образует пар, не отличающийся по соста­
ву от раствора, называется азеотропом.
По этой причине разделить компоненты А и В перегонкой невоз­
можно. Можно лишь получить чистый компонент А, если рас­
твор имел состав более бедный компонентом В, чем состав азео­
тропа, или получить чистый компонент В, если состав раство­
ра содержал больше компонента В, чем состав азеотропа. В ку­
бовом растворе будет накапливаться азеотроп (если диаграмма
имеет максимум температуры кипения), который разделить на
компоненты перегонкой невозможно. Однако у некоторых азео­
тропов меняется состав при перегонке под давлением или в ва­
кууме. В некоторых системах при изменении давления, при ко­
тором совершается перегонка, азеотроп исчезает, и тогда стано­
вится возможным разделить раствор путем перегонки.
§ 10. Ректификация
Отбирал фракции конденсата при перегонке и подвергая их
повторной и n -кратной перегонке, можно разделить компонен­
ты раствора. При этом коэффициент разделения может быть
Х\У2 „
вычислен по уравнению (Х2 = ----- . Если отклонения от закона
Х2У1
р*2
Рауля у раствора невелики, то (Х2 ~
- к . Однако такая фрак-
Я
ционированная перегонка очень трудоемка и малоэффективна.
Поэтому на практике используют приборы и установки, позво­
ляющие ускорить процесс разделения и обладающие необходи­
мой мощностью. В лабораторной практике объемы перегоняе­
мых смесей невелики, а температуры кипения компонентов раз­
личаются значительно, та к как растворителями при синтезах
органических веществ обычно служат более или менее низкоки-
пящие жидкости, такие как спирт, бензол, эфир, ацетон, а по­
лучают чаще всего значительно более высококипящие продук­
ты реакций. Поэтому разделение таких компонентов достаточно
полно может быть осуществлено в простом приборчике, называ­
емом дефлегматором, который представлен на рис. 1.41, а. Это
стеклянная трубка с вмятинами, расположенными по всей длине
трубки. Трубка снабжена термометром и вставляется плотно в
перегонную колбу. Через отвод пары поступают в холодильник
и далее в приемник. При нагревании перегонной колбы до кипе-
137

а
б
Рис. 1.41. Дефлегматор (а) и ректификационная колонна (б)
ния жидкости пары начинают поступать снизу в дефлегматор и,
конденсируясь на вмятинах, образуют на конце их капли жидко­
сти. Эти капли жидкости контактируют с поступающим паром и
находятся в равновесии с ним. При этом каж дая капля обогаща­
ется менее летучим компонентом и обедняется более летучим в
соответствии с законом Коновалова. Поэтому по высоте дефлег­
матора создается градиент температуры так, что термометр на
выходе из дефлегматора показывает температуру кипения более
низкокипящей фракции. Таким образом, капли на вмятинах де­
флегматора играют роль фракционных колбочек: накапливаю­
щийся в них более высококипящий компонент переполняет кап­
ли, и избыток жидкости стекает назад в колбу. Вверх идет поток
насыщенного более летучим компонентом пара, а вниз стекает
поток обогащенной более высококипящим компонентом жидко­
сти, которую называют флегмой. Нужную фракцию конденсата
отбирают, задавая определенный интервал температуры пара гго
термометру.
Разделение многокомпонентной системы на отдельные
компоненты, кипящие при различной температуре, с ис­
пользованием аппаратов, в которых автоматически осу­
ществляется дробная перегонка или дробная возгонка, на­
зывается ректификацией.
В технике, конечно, применяются более совершенные уста­
новки, которые называются ректификационными колоннами.
Важнейший процесс разделения, который связан с процессом
ректификации — это перегонка нефти. Нефть представляет со-
138

бой раствор углеводородов различного молекулярного состава и
поэтому кипящих при различных температурах. На рис. 1.41, б
представлен схематический разрез ректификационной колонны,
которая служит для ректификации различных растворов, в том
числе и ректификации нефти. Нефть нагревается до кипения в
кубе, и пары подаются в ректификационную колонну, которая
представляет собой цилиндр, заполненный тарелочками. Таре­
лочки поставлены друг на друга и каждая из них контактиру­
ет с насыщенным паром точно так же, как капли жидкости,
сконденсированные в дефлегматоре. Вниз стекает поток ф лег­
мы, вверх поднимается насыщенный пар. Температура колон­
ны падает снизу вверх, причем поддерживается определенный
градиент температуры. Н а выходе из колонны поставлен д а т­
чик температуры, по которому отбирается фракци я нефти, ки­
пящая в нужном интервале температур. Так, например, в ин­
тервале 80 —100 °С отбирается петролейный эф ир, в интервале
100—150 °С — бензин, в интервале 150 —200 °С — керосин, в
интервале 200 —300 °С — масла, а в перегонном кубе остается
мазут, который сжигается в топках котлов электростанций.
§ 11. Расслаивание жидкостей
Пусть две жидкости лишь ограниченно растворимы друг в
друге. На рис. 1.42, а представлена диаграмма «вода—фенол».
На ней видна кривая растворимости в зависимости от темпера­
туры, имеющая вид купола. При повышении температуры рас­
творимость фенола в воде, так же, как и воды в феноле, растет
до определенной температуры Ткрит.. Это верхняя критическая
мы «вода —никотин» (б)
139

точка растворимости двух жидкостей. При дальнейшем повыше­
нии температуры жидкости неограниченно смешиваются, и си­
стема становится однофазной. Растворимость при заданной тем­
пературе Т\ может быть определена по «методу рычага». Так,
при температуре Т\ на рис. 1.42, а смесь общего состава, отвеча­
ющего точке М , содержит раствор воды в феноле m 2 и раствор
фенола в воде т \ в соотношении:
ВМ _ т2фенол
AM mi вода
Чаще всего с понижением температуры взаимная раствори­
мость жидкостей падает до температуры Т„.крит.-
Эта темпера­
тура отвечает нижней критической точке растворения, если еще
не происходит затвердевания в системе. Ниже этой температуры
жидкости вновь смешиваются во всех отношениях.
На р ис.1.42, 6 представлен пример системы, у которой наблю­
даются и верхняя критическая температура, и ниж няя критиче­
ская температура растворения.
Температура, выше которой происходит неограничен­
ное растворение (смешивание) двух жидкостей, называется
верхней критической точкой растворения, а температура,
ниже которой происходит неограниченное взаимное раство­
рение (смешивание) двух жидкостей, называется нижней
критической точкой растворения.
Для предотвращения расслоения в растворах иногда добавля­
ют третий компонент, который предотвращает расслоение, так
как ф азовы е равновесия в полученной трехкомпонентной систе­
ме отличаются от таковых в первоначальной двухкомпонентной
системе. На этом основано действие добавок к бензину, предот­
вращающих расслоение бензина и воды, которая может попасть
в бензин по тем или иным причинам.
§12. Закон распределения Нернста
Если в системе происходит расслаивание и в ней присутству­
ет третий компонент (например, пусть в системе «вода —тетра­
хлорид углерода» присутствует йод), то встает вопрос, в каком
отношении этот третий компонент в равновесной системе рас­
пределится между двумя ж идкими фазами. Обозначим рассла­
ивающиеся фазы в системе как a -фаза и p-фаза. Химические
потенциалы третьего компонента в каждой из этих ф а з будут
140

равны: |х“ = Цз(а)+RTIn'Уз'жд;(A3= р!^ + RTInУ3Х3. При рав­
новесии в системе р®=Р3ир^а^= р ^\ так как они являются
химическим потенциалом чистого третьего компонента. Отсюда
ДТIn73X3 = ДПпУз^з и
7зхз = Тз^з*
ИЛИ
*3_Уз
Так как коэффициенты активности мало отличаются от 1, а
их отношение также близко к 1, то
^|=Д«const.
(1.115)
х3
Константу К в уравнении (1.115) называют коэффициентом рас­
пределения, а уравнение (1.115) получило название закона рас­
пределения Нернста.
Третий компонент в системе из двух ограниченно раство­
римых жидкостей при достижении равновесия распределя­
ется в соотношении, определяемом коэффициентом распре­
деления.
Если бы обе фазы были близки к идеальным растворам, то ко­
эффициенты активности были равны 1 и коэффициент распре­
деления также был равен 1. Но в этом случае в системе не про­
исходило бы расслоения. В том случае, когда третье вещество в
водном растворе диссоциирует, необходимо учитывать константу
диссоциации К о , так как недиссоциированного третьего веще­
ства будет меньше. Тогда константа распределения будет равна:
К=
х
2
3
х\Кв
Если третий компонент ассоциирован в водном растворе, на­
пример по реакции АВ -А 2В2, то необходимо учитывать кон­
станту ассоциации:
К=
Т\К2
^З^асс
Из этих уравнений можно определить константы диссоциации
или ассоциации вещества.
141

§ 13. Экстракция
Закон распределения Нернста леж ит в основе важного техно­
логического процесса разделения веществ — экстракции.
Экстракцией называют извлечение растворенного веще­
ства при помощи другого растворителя (экстрагента), рас­
слаивающегося с первым.
С помощью экстракции выделяю т различные лекарственные
препараты, цветные и редкие металлы, например, цирконий,
уран и др. Экстракция преимущественно применяется при из­
влечении нужных компонентов из водного раствора, а в каче­
стве экстрагентов используют органические растворители, не
смешивающиеся с водой. Так как органические экстрагенты до­
роги, то в целях экономии экстрагентов целесообразно вести экс­
тракцию малым объемом экстрагента, но многократно повторяя
ее. Практически экстрагент циркулирует в двух колоннах, на­
битых насадкой для увеличения поверхности соприкосновения
водной и органической фаз. Одна колонна служит д л я экстрак­
ции, вторая —д л я реэкстракции из органической фазы экстраги­
руемого вещества. Для реэкстракции вновь используют водные
растворы, повышая растворимость экстрагируемого вещества в
водной фазе путем изменения pH или добавления каких-то ве­
ществ, образующих нестойкие соединения с экстрагируемым ве­
ществом. Если начальная масса третьего компонента была т о ,
а после первой экстракции органической фазой в водной фазе
осталась масса третьего компонента m i, a Vi и V2 — объемы экс­
трагента и водного раствора соответственно, то при равновесии
_
т0-m i Vi
т\ V2
откуда
mi=m°v,+Kv2-
(U16)
Если экстракция повторяется п раз, то в органическую фазу из
(V\\п
водного раствора перейдет т , = т о I 77— 7777" I экстрагируе-
\V'i +К Vi)
мого вещества. Задаваясь нужным коэффициентом извлечения
можно рассчитать по уравнению (1.116) число необходимых по­
следовательных экстракций п. Легко показать, что использова­
ние суммарного объема экстрагента при однократной экстрак-
142

ции менее эффективно, так как в этом случае в органическую
фазу из водного раствора перейдет m i = то
+KnV^)экс~
трагируемого вещества. В технике многократную экстракцию
заменяют противотоком: снизу подают органическую фазу, свер­
ху — водный раствор. В этом случае раствор вступает в сопри­
косновение каждый раз с ненасыщенным по третьему компонен­
ту экстрагентом.
§ 14. Перегонка с водяным паром
В органическом синтезе получают множество соединений, тем­
пература кипения которых настолько высока, что перегонка их
в целях выделения из реакционной смеси и очистки невозмож­
на, так как соединение разлагается до достижения температуры
кипения. Характерный пример — выделение и очистка анили­
на, получаемого восстановлением нитробензола (реакция Зини­
на). Температура кипения анилина при стандартном давлении
составляет 469 К. При этой температуре анилин уже начинает
разлагаться. Можно очистить анилин перегонкой в вакууме, но
как выделить его из реакционной смеси? Дл я этого используют
перегонку с водяным паром.
На рис. 1.43 представлена диаграмма, на которой нанесены
давление пара над раствором с ограниченно растворимыми ком­
понентами. Давлению водяного пара отвечает точка раствора
Cl
02
Рис. 1.43. Давление пара в системе с двумя ограниченно растворимыми
жидкостями
143

анилина в воде состава х \ и раствора воды в анилине состава х \
Парциальное давление водяного пар а падает до значений #2^2 ,
а парциальное давление пара анилина понижается до значения
AijBi . Таким образом, если в смесь подавать водяной пар, то при
температуре 98,6 °С будет отгоняться смесь паров воды и анили­
на, которая после конденсации разделится на два слоя, и слой
анилина можно отделить и высушить, а слой воды, содержащей
анилин, можно подвергнуть повторной перегонке с паром. Рас­
считать количества отгоняемого компонента с паром можно по
уравнению:
m2=
Р2М2
PiMi
mi,
(1.117)
где mi и р\ — масса и парциальное давление пара перегоняемой
водяной фазы.
1.14 .
АДСОРБЦИЯ
§1. Закон адсорбции Гиббса
У поверхности раздела двух ф а з системы происходит са­
мопроизвольное изменение концентрации третьего компонента.
Этот процесс называется адсорбционным процессом или адсорб­
цией. Все адсорбционные процессы осуществляются с понижени­
ем свободной энергии. Д. Гиббс д а л следующую формулировку
понятия адсорбции:
Адсорбцией какого-либо компонента на границе раздела
двух ф аз называется разность между фактическим количе­
ством этого компонента в системе и тем его количеством,
которое было бы в системе, если бы концентрации в обеих
сосуществующих ф азах были постоянны вплоть до некото­
рой геометрической поверхности, разделяющей их.
Адсорбция обозначается буквой Г и может быть как положи­
тельной, так и отрицательной. Размерность адсорбции м о ль/м2.
Д. Гиббс вывел уравнение адсорбции как функции поверхност­
ного натяжения а и концентрации компонента в одной из фаз.
Рассмотрим систему, состоящую из двух компонентов 1 и 2 и
двух фаз а и р, которые разделены поверхностью раздела с пло­
щадью 5 . Обозначим число молей каждого компонента в каж­
дой из фаз через n“, nj, n“,
Пусть начальное число молей в
системе было равно n j и
соответственно. По определению
144

n?-n?-n§
„
n§-n?-n§
Г‘ = ------ S ------ ■ Г2 = ------ S ------ ■
Свободная энергия Гиббса для ф аз а и Р будет выражаться
уравнениями:
сЮ*= -5°rfT+Vadp+didn't+
dG9= -S^dT+V*dp+M n? +^2dn\\
dG° = -S°dT+V°dp+odS+Mn?+Mn°-
Уравнениями Гиббса—Дюгема, исходя из этих уравнений сво­
бодной энергии Гиббса, будут:
п“ф1+п®фг=0;
(1)
т1^с£цх + n^djx^ = 0;
(2)
sda+П1Ф1+п°фг = 0.
(3)
Сложим д ва первых уравнения и вычтем полученную сумму
из третьего уравнения, получим:
-dc=
_
'п
о_„о_„Р
пт-п
ТЬл .
ТЬеу 71о 72.0
—
фх +—---^ -----1ф2=Гхфх+Г2Ф2.
Если система представляет собой твердое тело и газ над ним,
то в объеме твердого те л а газ нерастворим, и поэтому химиче­
ский потенциал твердого т е л а (фаза 1) остается постоянным в
объеме. Следовательно, ф х = 0 и
Ф = -Г2ф2-
(1.118)
Уравнение (1.118) получило название уравнения адсорбции
Гиббса. Можно показать, что оно является общим для систем
разного рода.
Например, химический потенциал реального раствора опре­
деляется уравнением |1 = |Хо+ -RTIn а, откуда ф = KTd In а. Под­
ставив это значение ф в уравнение адсорбции Гиббса, получим:
ВТ da
Тем же путем получим д л я реального газа уравнение адсорб­
ции в виде:
г=-Л^£
КГdf
145

Дл я разбавленных растворов а ~ с, где с — концентрация
раствора, и в этом случае
Г
сdc
RT dc
Наконец, д л я разреженного газа, близкого к идеальному,
г_
Рdo
RT dp'
Различные вещества имеют различные адсорбционные свой­
ства в растворах. Если поверхностное натяжение о уменьшает-
da
ся с ростом концентрации растворенного вещества, т. е.
—
<О,
ас
то вещество называют поверхностно активным, если ж е с кон­
центрацией поверхностное натяжение растет, то такое вещество
называют поверхностно инактивным.
§2. Физическая и химическая адсорбция
Величина адсорбции зависит от взаимодействия м еж ду сор­
бентом и сорбируемым веществом. Адсорбцию р азделяю т на фи­
зическую и химическую. Физическая адсорбция обусловлена не­
направленными межмолекулярными силами (силы Ван-дер-Ва-
альса). Это взаимодействие не зависит от температуры и суще­
ствует в любых системах. Силы физической адсорбции адди­
тивны (предполагается, что сила взаимодействия меж ду двумя
молекулами не зависит от присутствия других молекул). Чем
выше поверхность адсорбента, тем он более активен. Пористые
адсорбенты поэтому более активны и проявляют более высокую
адсорбционную емкость. Если сорбент содержит полярные мо­
лекулы, то взаимодействие его с адсорбируемым веществом обу­
словлено не только силами Ван-дер-Ваальса, но и индукционны­
ми силами, возникающими вследствие индуцирования диполей
в молекулах адсорбируемого вещества. Эти силы имеют направ­
ленность и не аддитивны. Если полярны и поверхностные груп­
пы адсорбента, и молекулы адсорбируемого вещества, то между
диполями молекул возникают силы ориентационного взаимодей­
ствия диполей наряду с индукционным взаимодействием и си­
лами Ван-дер-Ваальса. Чаще всего энергия взаимодействия вы­
ражается суммой всех перечисленных взаимодействий. Теплота
физической адсорбции не превышает 20 кДж/моль.
Химическая адсорбция проявляется, когда молекулы ад­
сорбируемого вещества вступают в химическую реакцию с
146

поверхностью адсорбента. Теплота химической адсорбции в
5 —10 раз превышает теплоту физической адсорбции и составля­
ет 100 —200 кД ж/м о л ь. Но скорость химической адсорбции го­
раздо ниже скорости физической адсорбции. Вот почему в про­
тивогазах используется главным образом физическая адсорб­
ция. Большинство применяемых адсорбентов обладают как ф и­
зической, так и химической адсорбцией, так как возрастание
концентрации адсорбируемого вещества на поверхности адсор­
бента вследствие физической адсорбции приводит к ускорению
химической адсорбции. Большое разнообразие сил адсорбции не
позволяет пока построить единую теорию, которая дала бы воз­
можность составить общее математическое описание всех про­
цессов адсорбции.
Процессы адсорбции в целях разделения широко используют­
ся в технике для разделения газообразных смесей и разделения
компонентов в жидких растворах. В радиохимии адсорбция из
растворов используется д л я выделения и концентрирования ра­
диоактивных изотопов. Хорошо известный пример — противо­
газ, в котором ОВ адсорбируются на активированном угле. Ис­
пользование адсорбционных методов все более широко начинает
применяться дл я обогащения воздуха кислородом, что необхо­
димо в металлургии.
Наиболее важное значение процессы адсорбции приобрели д л я
разделения компонентов раствора. Рассматривая адсорбцию из
растворов, различают молекулярную адсорбцию и адсорбцию
ионов. При молекулярной адсорбции в системе три вещества:
адсорбент и два компонента. Адсорбируемость компонентов рас­
твора определяется взаимодействием всех трех веществ друг с
другом. Правило Ребиндера:
Из раствора адсорбируется преимущественно тот компо­
ненту полярность которого промежуточная между полярно­
с т я м и адсорбента и растворителя.
Полярный адсорбент, например силикагель, хорошо адсорби­
рует менее полярные вещества из неполярного растворителя, то­
гда как полярные вещества лучше адсорбируются неполярным
адсорбентом, например активированным углем, из такого поляр­
ного растворителя, как вода. Чем больше разница в полярностях
адсорбента и растворителя, тем слабее растворитель конкуриру­
ет за адсорбционные места в адсорбенте. Чем больше разность в
полярностях растворителя и растворенного вещества, тем луч­
ше протекает адсорбция растворенного вещества. Поскольку с
увеличением разности в полярностях растворенного вещества и
растворителя растворимость падает, то при уменьшении раство­
римости адсорбция растворенного вещества улучшается. Поэто-
147

му, например, полярные органические вещества из воды лучше
адсорбируются активированным углем, а из спирта — силика­
гелем. Д л я тщательной очистки воды необходимо использовать
последовательную обработку ее активированным углем и сили­
кагелем д л я удаления органических примесей, после чего нужно
применить еще и очистку с использованием ионитов.
§ 3. Иониты
Ионная адсорбция происходит из растворов, в которых рас­
творенное вещество диссоциирует на ионы. При этом адсорбция
протекает как под действием физических сил, так и благодаря
кулоновскому взаимодействию анионов или катионов с адсорбен­
том. Д л я проявления кулоновских сил взаимодействия необходи­
мо, чтобы на поверхности адсорбента имелись функциональные
группы, которые в растворе диссоциируют. Например, уголь не
обладает ионнообменными свойствами, но после сульфирования
на поверхности его образуются сульфогруппы, которые диссо­
циируют в растворе, отдавая протоны и приобретая отрицатель­
ный заряд. Основные закономерности адсорбции ионов связаны
с их свойствами: зарядом, размерами, сольватируемостью. Ионы
более высоко заряженные и большего радиуса вытесняют ионы
меньшего заряда и меньшего радиуса. В водных растворах по
способности к адсорбции ионы образуют так называемые лио­
тропные ряды или ряды Гофмейстера:
Li+< Na+< К+< Rb+<Cs+
Mg2+< Ca2+< Sr2+< Ba2+< Ra2+
СГ<ВГ<NO3<I"<NCS“
При добавлении в систему других ионов, заряженных одноимен­
но с адсорбированными ионами, в системе устанавливается рав­
новесие, при котором адсорбент обменивает эквивалентную часть
первоначально адсорбированных ионов на добавленные. Этот
процесс назы ваю т ионным обменом.
Адсорбенты, обменивающие ионы в растворе, называют
ионообменниками или ионитами.
Иониты, обменивающие катионы, называются катиони­
тами, а обменивающие анионы — анионитами.
Катиониты могут обменивать катионы на ионы водорода, ста­
новясь нерастворимыми кислотами, и, как правило, сильными
148

кислотами. Они содержат, чаще всего, сульфогруппы —S O 3 H,
карбоксильные —СООН или фенильные —СбЩОН. Аниониты
же могут обменивать анионы на гидроксилы и становятся нерас­
творимыми сильными основаниями, содержащими ионообмен­
ные группы, которые обладают основным характером, как, на­
пример, замещенные аммониевые основания. При этом всегда
необходимо помнить, что количества обмениваемых ионов стро­
го эквивалентны.
Важнейшая характеристика ионита — его полная обмен­
ная емкость (максимальные количества обмениваемых ионов в
м г-эк в/г ионита). Емкость ионитов зависит от их структуры,
температуры раствора, концентрации раствора и его pH. Наи­
большая емкость из известных ионитов — 10 мг-экв/г ионита.
Адсорбция и ионный обмен играют важную роль в приро­
де. Глины и минералы цеолиты являются адсорбентами воды и
ионообменниками и хотя их ионная емкость невелика, но огром­
ные массы этих минералов приводят к обмену огромных коли­
честв минеральных веществ, способных к ионной диссоциации.
Благодаря этим процессам поддерживается определенный хими­
ческий состав природных вод. Ввиду своей слоистой структуры
глины могут адсорбировать огромные количества воды, моле­
кулы которой внедряются (интеркалируются) между алюмоси­
ликатными слоями глин. Это приводит к сглаживанию процес­
сов потери воды почвами, что предохраняет растения от засу­
хи. С другой стороны, глины под действием воды и оснований
становятся пластичными, что имеет важное значение для произ­
водства керамики и ф арфор а. Природными ионитами являются
так ж е гуминовые кислоты, которые образуются в почвах как
промежуточные продукты разложения растительных и живот­
ных остатков. Гуминовые кислоты определяют ионнообменные
процессы, происходящие в почвах. Плодородие почв поэтому за­
висит от содержания в них гумуса. Поддержание и наращивание
содержания гумуса в почвах является важной агрохимической
задачей.
Различные удобрения по-разному адсорбируются почвами. На­
пример, ионы калия надолго задерживаются в глинистых поч­
вах, тогда как хлор не задерживается глинами и легко вымыва­
ется. Поэтому хлористый калий на суглинистых почвах вносят
под зиму, так как к весне почвы освобождаются от вредных д л я
растений ионов хлора. На песчаных почвах это уже не удается,
так как калий не адсорбируется песком и легко вымывается. По­
этому на песчаных почвах используются калийные удобрения, не
содержащие хлора, которые вносятся весной. В быту, в технике и
в химической технологии применяются в качестве адсорбентов
149

активированный уголь, силикагель и органические ионообмен­
ные смолы. Очистка воды д л я получения сверхчистых полупро­
водников или в бытовых целях осуществляется пропусканием ее
через различные адсорбенты: последовательно через активиро­
ванный уголь и силикагель для удаления органических приме­
сей, затем последовательно через катионит и анионит д л я уда­
ления ионов. В бытовых целях важ но удалить из воды катионы
кальция, магния, железа дл я умягчения воды и катионы тяже­
лых металлов, которые все без исключения ядовиты. Это дости­
гается пропусканием воды через катионит, зар яж енны й ионами
натрия (путем предварительного пропускания через катионит
раствора поваренной соли). Многие технологические процессы
включают разделительные процессы с применением адсорбен­
тов и ионитов. Например, производство сахара, лекарственных
веществ и многие другие. Наконец, технология редких и радио­
активных элементов обязательно включает процессы разделе­
ния, концентрирования и очистки с использованием адсорбентов
и ионитов.
§4. Хроматография
На основе законов адсорбции был разработан такой метод
разделения, как хроматография.
Разделение компонентов подвижной фазы при ее движе­
нии вдоль другой, неподвижной фазы, за счет их различно­
го распределения между обеими фазами называется хрома­
тографией.
Хроматографический метод разделения веществ был откры т рус­
ским ученым М. С. Цветом. Он впервые обнаружил, что если
ввести в колонку, наполненную оксидом алюминия, раствор, со­
держащий различные растительные пигменты, то по мере про­
хождения раствора отдельные пигменты адсорбируются по опре­
деленным зонам колонки и окрашивают эти зоны в различные
цвета. Хроматография используется теперь в аналитической хи­
мии д л я разделения сложных смесей и определения компонен­
тов, в биохимии —для выделения различных белковых тел, нук­
леиновых кислот и биологически активных веществ (витамины,
гормоны и др.) , в химической технологии —для выделения ред­
ких элементов из растворов и разделения элементов (например,
редкоземельных элементов). При этом применяются различные
физико-химические методы идентификации и анализа разделен­
ных веществ, а не только цвет получающихся зон. Поэтому тер-
150

мин «хроматография» несколько устарел, так ка к и бесцветные
вещества могут разделяться и определяться хроматографиче­
ски. Различают хроматографию разного рода в зависимости от
агрегатного состояния участвующих ф аз. При газовой хрома­
тографии подвижная ф аза — газ, неподвижная — твердое те­
ло. Это молекулярно-адсорбционный вид хроматографии. При
газо-жидкостной хроматографии подвижная ф а за — газ, непо­
движная — высококипящая жидкость. Разделение происходит
благодаря разной растворимости различных газов в жидкости
(распределительная хроматография). При жидкостной хромато­
графии обе фазы представляют собой жидкости. Механизм так­
же распределительный. Широкое применение находит бумаж­
ная хроматография, при которой неподвижная ф а за представ­
ляет собой особым образом приготовленную гидрофильную или
гидрофобную бумагу. Раствор разделяемых веществ наносится
на бумагу в виде капли. При растекании капли содержащие­
ся в ней вещества разделяются но зонам благодаря адсорбции
и капиллярным силам. Тонкослойная хроматография использу­
ет разделение компонентов на тонкодисперсных порошках, за ­
крепленных на непористых пластинах. В научных исследовани­
ях хроматография используется для разделения сложных сме­
сей, идентификации и очистки веществ, а такж е как метод быст­
рого и удобного контроля химического взаимодействия веществ
и изучения их физико-химических свойств (определение теплот
комплексообразования, коэффициентов активности и т. п.).
Контрольные вопросы
1 . Ч то называют термодинамической системой?
2. К ак различаются системы?
3. По каким свойствам различаются параметры?
4. Чем отличается равновесное состояние системы?
5. Какую функцию называют функцией состояния?
6. К ак вычисляется изменение внутренней энергии?
7. Чем отличается работа от теплоты?
8.Почему работа и теплота не являются функциями состояния?
9. Ч то определяет нулевой закон термодинамики?
10. Каков физический смысл первого закона термодинамики?
1 1 . Чем отличается первый закон термодинамики для открытых
систем?
12. При каких условиях работа и теплота становятся дифференци­
алами?
13. Какие следствия вытекают из того, что внутренняя энергия и
энтальпия являются функциями состояния?
14. Каковы отличительные свойства равновесного процесса?
151

15. Д ля чего необходимо понятие равновесного процесса?
16. К ак различаются теплоемкости одноатомных и двухатомных
газов?
17. Что такое характеристическая температура Дебая?
18. Чем отличается обратимый процесс от равновесного?
19. Почему многие процессы протекают самопроизвольно лишь в
одну сторону, но не обратно?
20. Почему из всех термодинамических функций лишь для энтро­
пии можно получить или рассчитать абсолютное значение?
2 1 . К ак рассчитать свободную энергию Гиббса, зная свободную
энергию Гельмгольца?
22. Почему энергию Гиббса называют свободной энергией?
23. Дом неожиданно развалился. Следует ли работу разрушения
дома называть полезной работой с точки зрения термодинамики?
24. Что нужно сделать, чтобы всю энергию сгорания метана ис­
пользовать для совершения работы?
25. К акие химические реакции в термодинамике называю т экзо­
термическими?
26. К ак рассчитать энтальпию химической реакции, зн ая ее внут­
реннюю энергию?
27. Зависит ли теплоемкость от температуры?
28. Чем отличается теплота образования от энергии связи?
29. Как рассчитать тепловой эффект химической реакции при за­
данной температуре?
30. Недостаточно сухое сено при небрежном скирдовании иногда
самовоспламеняется. В чем причина самовозгорания?
31. По правилам пожарной безопасности промасленая ветошь не
должна разбрасываться в рабочем помещении или храниться. Почему?
32. В ж ивых организмах непрерывно совершается работа, связан­
ная с обменом веществ, причем энергию для совершения работы ор­
ганизм черпает из энергии окисления съедаемой пищи. Почему орга­
низмы при этом не перегреваются?
33. Какой вид будет иметь закон действующих масс для реакции
диссоциации известняка?
34. Синтез аммиака проводят при высоком давлении. Почему?
35. Какими законами определяются химическое равновесие и фа­
зовое равновесие в системах?
36. Какое значение имеет свойство воды расширяться при замер­
зании для жизни на земле?
37. Почему для художественного литья используют бронзу или чу­
гун, а не какие-либо другие сплавы?
38. Д ля чего используется физико-химический анализ?
39. На каких принципах основан геометрический анализ диаграмм?
40. Какой закон термодинамики лежит в основе физико-химичес­
кого анализа?
41. Какова диаграмма эвтектической системы?
42. Что представляет собой эвтектический сплав? Как эвтектиче­
ский сплав выглядит под микроскопом?
152

43. Какие нонвариантные точки могут быть на диаграммах двух­
компонентных систем?
44. К ак определяют координаты эвтектической точки?
45. К ак различаются эвтектическая реакция и перитектическая ре­
акция?
46. Как выглядит диаграмма системы с непрерывными твердыми
растворами?
47. Как проявляются на диаграмме твердые растворы с ограничен­
ной растворимостью?
48. Что представляют собой твердые растворы? Как твердый рас­
твор выгладит под микроскопом?
49. К ак проявляется на диаграмме образование химического со­
единения, плавящегося без разложения?
50. Как отличить на диаграмме перитектическую реакцию от по­
лиморфного превращения компонента системы?
51. Какую точку на диаграмме называют сингулярной точкой?
52. В чем суть спора К. Бертолле и Ж . Пруста, и прав ли оказался
кто-либо из них?
53.0 чем говорит наличие в системе сингулярной точки?
54.0 чем говорит отсутствие на диаграмме сингулярных точек?
55. Д л я каких систем закон постоянства состава абсолютно верен?
56. Что называют дальтонидами и что бертоллидами?
57. Почему в ледяной бане длительное время поддерживается тем­
пература -21 °С?
58. К ак закаливают сталь?
59. Чем обусловлена твердость закаленной стали?
60. Зачем нужен отпуск стали?
61. Какие процессы происходят в стали при ее закалке, отпуске и
отжиге?
62. Почему художественные решетки отливают из чугуна, а не из
стали?
63. Как построить треугольник Гиббса?
64. К ак можно представить на диаграмме плавкость в тройной си­
стеме?
65. К ак строятся лучи Скрейнемакерса на диаграмме растворимо­
сти тройной системы?
66. К ак определяют состав соединения на диаграмме растворимо­
сти тройной системы?
67. Почему реальные растворы отклоняются от закона Рауля?
68. При каком условии все растворы практич ески идеальны?
69. Как рассчитать коэффициент активности по диаграмме «со­
став —парциальное давление пара растворенного компонента»?
70. Чем отличается парциальная молярная энтропия от молярной
энтропии?
71. По какому закону происходит разделение редкоземельных эле­
ментов при применении фракционной кристаллизации?
72. Какое море покрывается льдом при более низкой температу­
ре — Черное или Балтийское и почему?
153

73. Радиоактивный изотоп стронция при поступлении в организм
накапливается в костных тканях. Почему? С каким законом это свя­
зано?
74. Как определяют теплоты растворения?
75. Каким образом деревья предохраняют себя от морозов при окон­
чании вегетационного периода?
76. Почему сок поднимается по стволу дерева?
77. Почему пить дистиллированную воду вредно?
78. Почему в противогазе используют уголь, а не силикагель?
79. Почему в саду на песчаных почвах полезно вносить в почву
глину, а на глинистых —песок и торф?
80. Почему лёссовые и черноземные почвы столь плодородны?
81. Каким образом очищает кровь искусственная почка?
82. Как очистить воду от загрязнения фенолом?
83. Как очистить воду от загрязнения тяжелыми металлами?

ГЛABA 2
ХИМИЧЕСКАЯ КИНЕТИКА И КАТАЛИЗ
2.1. ФОРМАЛЬНАЯ КИНЕТИКА
Введение
Химическая кинетика — раздел физической химии, изучаю­
щий скорости химических реакций. Химическая кинетика изу­
чает законы протекания химических реакций во времени, меха­
низмы протекания химических реакций, влияние условий на ско­
рость химических реакций и влияние различных веществ на ско­
рость химических реакций. Химическая кинетика распространя­
ется на все химические науки, включая неорганическую, органи­
ческую химию, биохимию, химию материалов, химическую тех­
нологию. Методы кинетических исследований используют д л я
изучения механизмов химических реакций, которые позволяют
раскры ть законы взаимодействия компонентов системы через
промежуточные реакции. Математический аппарат химической
кинетики служит основой д л я расчетов химических аппаратов и
моделирования химико-технологических процессов. Проектиро­
вание химических предприятий невозможно без данных химиче­
ской кинетики.
Большой вклад в становление и развитие химической ки­
нетики внесли школы российских физико-химиков: впервые
В. Н. Ипатьев исследовал скорости химических реакций при вы­
соких давлениях, Н. И. Кобозев предложил модель промежуточ­
ных ансамблей, Н. Н. Семенов создал теорию цепных разветв­
ленных реакций, Г. К. Боресков развил кинетику каталитиче­
ских процессов, Н. М. Эмануэль —кинетику биохимических про­
цессов.
Давно было замечено, что некоторые вещества ускоряют или
замедляют химические реакции. Это явление было названо хи­
мическим катализом. Ныне химический катализ является мощ­
ным средством химических исследований и технологических раз­
работок химических производств.
Основное уравнение химической кинетики — закон действую­
щих масс —дает возможность математического описания кине-
155

тики различны х процессов без непосредственного рассмотрения
их химической природы и механизма. Раздел химической кине­
тики, посвященный этой задаче, называется формальной кине­
тикой.
§1. Скорость химических реакций
На скорость химической реакции оказывают влияние усло­
вия ее протекания (природа реагирующих веществ, их фазо­
вое состояние, текущие концентрации исходных веществ и про­
дуктов реакции, присутствие и концентрации посторонних ве­
ществ, температура, давление, радиация, длительность проте­
кания предшествующего процесса и др. Развитие современной
химической промышленности, основанной на процессах гетеро­
генного катализа, горения, взрыва и других явлениях, базиру­
ется в первую очередь на достижениях химической кинетики.
Поэтому кинетический подход является неотъемлемой методо­
логической основой современной химии. Предметом химической
кинетики является:
описание закономерностей протекания химических процессов;
расш ифровка их механизма, включающего в себя как элемен­
тарные стадии, так и макроскопические факторы, связанные с
явлениями переноса вещества;
вычисление скорости протекания химических процессов, рас­
чет реакторов и обеспечение расчетными данными промышлен­
ного проектирования технологических процессов и аппаратов
для них.
Разовое единичное взаимодействие молекул в химиче­
ской системе называют элементарным актом.
Множество одинаковых элементарных актов называют
элементарной стадией химической реакции.
Последовательность элементарных стадий, по которым
протекает химическая реакция, называется ее механизмом.
Химические процессы обычно осуществляются д ву м я спосо­
бами:
статическим — в замкнутых закрытых реакторах при посто­
янном объеме, например: газ в закрытом сосуде, объем жидко­
сти при реакции в растворах (рис. 2.1.). При проведении реакции
в за кр ы ты х условиях основными параметрами, влияющими на
ход реакции, являются температура, начальные концентрации
реагентов, константа скорости химической реакции к и продол­
жительность процесса;
156

—р
Вход
теплоносителя j_
t—
СО
Выход
теплоносителя
Рис. 2.1. Замкнутый закрытый реактор
динамическим — в проточных или так называемых открытых
реакторах, когда поток реагирующих веществ протекает при по­
стоянном давлении через реакционное пространство (рис. 2.2).
Различают детальный механизм химического процесса, т. е.
последовательность элементарных актов (одностадийных реак­
ций), и стадийный механизм как совокупность химических и
макроскопических стадий (подвод реагирующих веществ, т. е.
диффузия к зоне реакции, адсорбция или растворение, собствен­
но реакция, отвод продуктов и т.д .) . Протекание всей совокуп­
ности стадий представляет собой химический процесс. Законо­
мерности кинетики химических процессов существенно зависят
от фазового состава системы. Поэтому различают:
химические процессы, протекающие в однородной среде, т. е.
в пределах одной (жидкой, газообразной) фазы . Они называ­
ются гомогенными. Здесь сферой реакции является весь объем
системы;
химические процессы, протекающие в многофазных системах.
Они называются гетерогенными. В данных случаях сферой ре­
акции обычно является поверхность (граница) раздела фаз.
В соответствии с этим химическую кинетику можно разде­
лить на три части:
Теплоноситель
i
Выход
— - -- ------ -- - 1 продуктов
реакции
ТТеплоноситель
Примеры осуществления химической реакции в открытых
условиях:
а — в реакторе смешения; б — в реакторе вытеснения
157

с
Рис. 2.3. Изменение концентраций
реагента А и продукта Р в ходе ре­
акции А —►Р
1) кинетика гомогенных ре­
акций;
2) кинетика гетерогенных
реакций, протекающих обычно
на поверхности раздела фаз;
3) кинетика твердофазных
(топохимических) реакций.
Понятие скорости химиче­
ской реакции легче всего по­
казать на примере практиче­
ски необратимой химической
реакции
АР
где А — исходный реагент; Р — продукт реакции; к — коэф­
фициент пропорциональности, называемый константой скорости
реакции. Этой реакции соответствуют кривые зависимости кон­
центрации исходного реагента [А] и продукта реакции [Р] от вре­
мени t ([А] = cp(t), [Р] = ф'(£)) (рис. 2.3).
Средняя скорость v химической реакции в интервале времени
Ti - Т2 может быть определена как
„
_
[АЬ-[А], _д[А]
ср_ TJ-T ,
'
Дт■
Поскольку [А]2 < [A]i, то vcp по реагенту А будет отрицательной.
Это значит, что в ходе реакции концентрация исходного реа­
гента падает, а значение г>ср по продукту реакции Р будет поло­
жительной величиной, поскольку в ходе реакции Р возрастает:
РЬ-РЬ
T2-ti
В общем случае скорость химической реакции определяется
как отношение:
Это — дифференциальное уравнение скорости реакции. Гра­
фически скорость химической реакции в момент времени т = т*
равна тангенсу угла а наклона касательной к кинетической кри­
вой в точке М (см. рис. 2.3).
158

С другой стороны, скорость той же химической реакции мож­
но выразить через концентрацию продукта реакции Р:
Здесь необходимо обратить внимание на одно важное обстоя­
тельство: скорость реакции может быть однозначно определена
по скорости превращения (расходования или образования) лю­
бого из участвующих в реакции веществ. Основными парамет­
рами химической реакции, влияющими на ее скорость, являются
температура и концентрации реагирующих веществ.
Скорость химической реакции v определяется как изме­
нение количества исходного реагента, реагирующего в еди­
ницу времени в единице объема, или как изменение количе­
ства продукта реакции в единице объема и в единицу вре­
мени, или как изменение концентрации вещества в единицу
времени.
Поэтому скорость химической реакции обычно выражается чис­
лом молей п данного вещества, расходующегося (или образую­
щегося) в единицу времени в единице объема. Обычная размер­
ность скорости химической реакции в зависимости от избранной
системы единиц (моль *л -1
- с-1) или [моль • (м3)-1 ■ч-1] и т. п.
Другой тип уравнений, используемых в химической кинетике, —
интегральные уравнения скорости:
Концентрация = ф(время).
Интегральное уравнение скорости химической реакции получа­
ют в результате решения дифференциальных уравнений. Полу­
чение совокупности интегральных и дифференциальных уравне­
ний скоростей химических реакций составляет основную задачу
кинетических исследований химических процессов, которая со­
стоит из следующей последовательности основных стадий:
Экспериментальное определение зависимостей «концентра­
ция = ср (время)» и построение соответствующих графиков.
I
Предложение кинетической схемы протекания химической
реакции, например А —* Р
I
159

Составление кинетической модели процесса в виде системы
дифференциальных уравнений скорости реакции и балан­
совых уравнений, например, д л я реакции А —>Р
= ~ксА
= +кср
= Сд-Ср (еслиСр=0)
_ ____ ____ __ ____ __ ____ ____ _
i __________________________
Решение системы уравнений и получение уравнений скоро­
стей в интегральной форме, например, д л я реакции А —> Р
<* = <&(!-«Г*)
I
Нахождение технологических параметров процесса, напри­
мер, продолжительности, обеспечивающей заданную кон­
центрацию продукта, и др.
' dcа
dx
< dcp
dx
СА
2.2 . СКОРОСТЬ ХИМИЧЕСКОЙ РЕАКЦИИ
Основным законом химической кинетики являе тся закон дей­
ствующих масс (К.Гульдберг и П. Вааге, 1867 г.): скорость эле­
ментарной химической реакции, протекающей при постоянной
температуре в гомогенной среде пропорциональна произведению
концентраций реагирующих веществ в степени их стехиометри­
ческих коэффициентов.
Дл я реакции, идущей в одну стадию и написанной в общем
виде как
nA+mB pC+qD
и = /ссдСз, или v = fc[A]n[B]m.
При анализе этих уравнений необходимо обратить внимание
на следующее:
160

если реакция практически необратима, то ее скорость опре­
деляется только концентрацией исходных веществ и не зависит
от концентрации продуктов реакции;
коэффициент пропорциональности к называется константой
скорости химической реакции.
Константа скорости химической реакции зависит от темпера­
туры и природы реагирующих веществ, но не зависит от кон­
центрации компонентов и поэтому ее иногда называют удельной
скоростью. Размерность к можно получить из следующего урав­
нения:
Размерность к =
моль •л-1 •с”1
(моль • л -1 *с_1)п(моль *л -1 • с_1)ш
/МОЛЬ\ 1-п-т
\л•с/
§ 1. Порядок реакции
Показатели степени в уравнении размерности константы
скорости п и т называют парциальными (или частными)
порядками реакции: порядок п по компоненту А, порядок
т по компоненту В и т. д.
Сумма парциальных порядков п + т + • • * дает полный
или общий порядок реакции.
На практике парциальные порядки реакции определяют с по­
мощью метода изоляции, согласно которому все реагенты, кро­
ме одного, наприхмер А, берутся в таком большом избытке, что
концентрации избыточных реагентов (или реагента) остаются
практически постоянными в ходе реакции, и поэтому могут быть
включены в константу скорости; это дает новую, эффективную
константу скорости к*\
v =k’[A]n.
(2.1)
Тогда говорят, что реакция проходит в условиях псевдо-п-го по­
рядка. Существует несколько методов д л я получения численно­
го значения п. Например, уравнение (2.1) представляют в лога­
рифмической форме:
Inv = nln[A]+Inк'.
Построив гр аф ик зависимости In г? от In [А], получают пря­
мую, тангенс угла наклона которой соответствует п. Точно так
же можно найти порядок реакции по всем остальным реагентам,
6 Илполитоп
161

делал каждый из них по очереди тем компонентом, который при­
сутствует в пренебрежимо малой концентрации. Очевидно, что
в случае анализа элементарной реакции парциальные порядки
реакции дол ж ны иметь целочисленные значения. Если в ходе
определения парциальных порядков реакций их значение оказа­
лось дробной величиной, то это свидетельствует, преж де всего,
о неэлементарности данной реакции и протекании ее по несколь­
ким путям. Примером такой реакции может служ ить кислотная
бензидиновая перегруппировка N, N'-ди арил гидразинов:
СН3
СН3
NH2-NH2
н+
СНз
СН3
н+
+nh2
nh2
Скорость реакции, по которой происходит исчезновение орто-
гидразотолуола (Hz), имеет вид:
v = fc[Hz][H+]1’6.
Дробный порядок по отношению к иону водорода связан с
тем, что орто-гидразотолуол перегруппировывается в кислой
среде одновременно по двум путям, один из которых соответ­
ствует реакции первого порядка, а другой —* реакции второго
порядка:
v = fci[Hz][H+] + A:2[Hz][H+]2.
Поэтому порядок реакции, равный 1,6, является общим или
усредненным порядком, отражающим относительный вклад
каждого из двух путей. Дробные порядки появляются также в
тех случаях, когда фактическая концентрация компонента, фи­
гурирующ ая в уравнении скорости, отличается от аналитиче­
ски определяемой концентрации. Например, имеется равновесие
между частицами мономера и димера, и при разных скоростях в
реакции участвуют либо только одна, либо обе частицы. Время
от времени парциальные порядки обнаруживаются по отноше­
нию к Н+ в катализируемых кислотами реакциях. Причина за­
ключается в том, что не все водородные ионы принимают уча­
стие в реакциях. В этом случае вместо концентрации ионов во­
дорода следует использовать функцию кислотности.
162

Помимо дробных порядков реакций существуют случаи, ко­
гда зависимость скорости от концентрации в начале реакции от­
личается от зависимости на более поздних стадиях. Для таких
случаев введены представления о порядке относительно концен­
трации («концентрационный» порядок) и порядке относительно
времени («временной» порядок). Наконец, известны реакции пе­
ременного порядка, т. е. реакции, общий порядок которых изме­
няется в ходе процесса.
§2. Молекулярность реакции
Число молекул, вступающих в единичный элементарный
ак т химического взаимодействия, происходящего в резуль­
тате одноразового столкновения молекул, называется моле-
кулярностью химической реакции.
Поэтому молекулярность реакции не может быть нецелочислен­
ной. Известны только мономолекулярные, бимолекулярные и,
как редкое исключение, тримолекулярные реакции. Примером
мономолекулярной реакции может служить распад оксида азо­
та^):
N2O5—NO2+NO+О2
Порядок реакции, будучи результатом взаимоналожения кине­
тических закономерностей (и молекулярностей) отдельных ее
стадий, может быть и нецелочисленным, и не совпадать ни с сум­
мой стехиометрических коэффициентов химического уравнения
реакции, ни с молекулярностью отдельных ее элементарных ста­
дий. Порядок реакции о тр аж ает суммарную кинетическую зави­
симость скорости всей многостадийной реакции от концентра­
ции реагирующих веществ, а молекулярность — механизм эле­
ментарных стадий сложного процесса. Поэтому порядок реакции
совпадает с ее молекулярностью лишь д л я простых по механиз­
му реакций. Может показаться, что д л я нахождения молеку­
лярноеTM реакции достаточно знать коэффициенты в уравнении
процесса. Однако сам процесс может складываться из различ­
ных элементарных стадий, происходящих последовательно или
параллельно. В этом случае уравнение химической реакции от­
раж ает лишь суммарный эффект этих взаимодействий. Напри­
мер, из уравнения
А+2В=АВ2
следует, что в реакции участвуют три молекулы реагента, т. е.
она является тримолекулярной. В действительности может ока-
163

заться, что образование продукта идет по стадиям, т. е. состоит
из последовательных элементарных актов. Например,
А+В=АВ
стадия 1
и
АВ+В=АВ2
стадия 2
Каж дая из стадий является, очевидно, бимолекулярной, при­
чем скорость химической реакции определяется скоростью наи­
более медленной стадии. Иными словами, самая медленная ста­
дия определяет скорость протекания всего процесса. Таким об­
разом, приведенная реакция является не тримолекулярной, а
бимолекулярной. Как бимолекулярная реакция, та к и тримо-
лекулярная могут протекать по стадиям, молекулярность кото­
рых может быть различна. В качестве примера можно привести
процесс разложения оксида азота(У), описываемый уравнением
2N2O5 = 4NC>2+ 02- Эта реакция осуществляется в две стадии:
N2O5=N2O3+О2
N2O3+ N2O5 = 4NO2
Первая стадия — мономолекулярна, а вторая — бимолекулярна.
Дл я подобных реакций лимитирующей стадией, к а к правило,
является мономолекулярная:
АВ—А+В
за которой следует быстрая реакция А или В со вторым реа­
гентом:
А+С—АС или В+С—ВС
Тримолекулярных реакций известно немного, так как малове­
роятно, чтобы в элементарном акте реакции участвовало одно­
временно три частицы. В качестве примера рассмотрим реакцию
образования озона в присутствии азота: O2+O+N2 = O3+N2. Роль
молекулы азота заключается в поглощении избытка выделяю­
щейся энергии, которая может вызвать распад образовавшейся
молекулы Оз на О2 и О. По этой реакции происходит образо­
вание озона в стратосфере и формирование «озонового слоя»,
защищающего все живое на Земле от жесткого ультрафиолето­
вого излучения.
2.3. МЕТОДЫ ФОРМАЛЬНОЙ КИНЕТИКИ
Элементарные реакции бываю т реакциями первого порядка,
например внутримолекулярные перегруппировки или реакции
164

разложения, а чаще всего реакциями второго порядка, когда
молекулярное взаимодействие между двумя частицами прямо
приводит к продукту. Большинство химических реакций можно
представить как те или иные комбинации элементарных реак­
ций. Обычно различают следующие простые комбинации:
1) параллельные реакции (конкурирующие и одновременные);
2) последовательные реакции или последовательность реакций;
3) обратимые реакции.
Реакцию, при которой реагент подвергается превраще­
нию по двум или нескольким путям независимо и одновре­
менно, называют параллельной.
Реакцию, при которой продукт, образующийся в преды­
дущей стадии, является реагентом в последующей стадии,
называют последовательной.
Реакция, протекающая в две стадии, и обе ее стадии про­
ходят в противоположном направлении с соизмеримой ве­
роятностью, называют обратимой реакцией.
Наконец, существуют сложные реакции, сочетающие в себе
два или все три названных типа, например последовательно­
параллельная реакция.
§ 1. Простая реакция первого порядка
В качестве примеров реакций первого порядка можно при­
вести: превращение ацетохлоранилина C6H5NCICOCH3 в пара-
хлорацетоанилид CIC6H4NHCOCH3, а такж е реакции термиче­
ского распада многих сложных молекул, например: азометана,
оксида азота(У), разложения диметилового эф ира и др.
Формализованная запись простой реакции первого порядка
имеет вид:
аЛр
Изменение во времени концентраций А и Р д л я реакции первого
порядка дано на рис. 2.4.
Скорость простой реакции первого порядка прямо пропорци­
ональна концентрации [А]:
^~ЧА]-
<*•*>
Интегрирование этого дифференциального уравнения
ДА] _
[А]
165

концентраций А и Р в реакции для реакции первого порядка
первого порядка А —►Р
А —►Р
приводит к уравнению:
ln[A] = ln[A]0 -fcx
(2.3)
или
|А] = [А)ое“**,
(2.4)
где [А]о — начальная концентрация А . Это уравнение показы­
вает, что в реакции первого порядка расходование реагента во
времени происходит экспоненциально. По уравнению (2.3) зави­
симость 1п[А] от х является линейной с наклоном, равным - к
(знак «минус» указывает на уменьшение [А] во времени). Это
означает, что для разных [А]о мы получим параллельные пря­
мые в полулогарифмических координатах 1п[А] - т (рис. 2.5).
Единица измерения константы скорости первого п орядка име­
ет размерность (время)”1, обычно это с"1:
моль
л•с
моль
Уравнение д л я продукта реакции нетрудно получить из уравне­
ния (2.4) замещением [А] на [А]о -[Р]:
[Р] = [А]0(1
Кинетическая кривая первого порядка инвариантна при линей­
ном преобразовании концентрации. Это можно показать путем
/моль\
/?ч/моль\
.
(Т7И*>К-)' откуда к=
.(
166

простой операции замещения [А] на пропорциональную величи­
ну п[А] в уравнении:
d(n iAD
dz
= -кп[А].
Поскольку величина п постоянна, ее можно вынести за знак
дифференциала:
ndr-^- = -fcn[A]
dz
и затем сократить. Это означает, что кинетическое уравнение
остается неизменным при умножении [А] на какую-либо посто­
янную величину. Из этого свойства вытекают важны е следствия.
Дл я оценки к вместо концентрации можно использовать лю­
бую другую, пропорциональную ей величину, например, спек­
тральную поглощательную способность, электропроводность,
объем раствора, пошедшего на титрование и т, п. Логарифм та­
кой величины такж е меняется линейно во времени, и тангенс
угла наклона прямой соответствует - к . В соответствии с (2.3)
можно записать:
ln[Ai] = ln[A]o -frti;
1п[А2] = 1п[А]о -&Т2-
При [А]о = const, объединяя эти два уравнения, получаем:
A In[А] = -/сДт
или
LJ
Д1п[А]_
Дт
к'
т. е. относительные скорости реакции не зависят от концентра­
ции; они выражаются через время достижения концентрации ре­
агента, соответствующей некоторой доле первоначальной вели­
чины, т. е. через время относительного превращения. Например,
период полупревращения Т]у2 *“ это время, за которое концен­
трация реагента снизилась до - первоначальной величины:
In2
откуда
к=
In2
х 1/2
Это уравнение часто используется для расчета к простой реак­
ции первого порядка.
167

[А]оI
[А]02
[А]0|
[А] оз
Как видно из рис. 2.6 каса­
тельные к кривым зависимо­
сти (с — т) в точках, соответ­
ствующих разным значениям
начальных концентраций, пе­
ресекаются в одной точке Ti
на абсциссе т. Касательная в
точке начальной концентрации
представляет начальную ско­
рость vq:
Рис. 2.6. Касательные к кривым
зависимости (с —т) первого поряд­
ка в точках, соответствующих на­
чальным концентрациям
Отсюда
1
L1
Tl=7- и к=—
к
Ti
и, таким образом, величина Ti не зависит от начальной концен­
трации. Изменение концентрации продукта реакции Р во време­
ни может быть описано дифференциальным уравнением:
В случае, если в течение реакции второго порядка
А+В —►...
или более высокого порядка
Ан-В+С—►
концентрации всех компонентов кроме одного поддерживаются
постоянными, то такая реакция описывается уравнением перво­
го порядка по расходуемому компоненту и называется реакцией
псевдопервого порядка. Так, например, инверсия тростникового
сахара в водных растворах
происходит в условиях значительного избытка воды, поэтому
при постоянной ее концентрации оказывается реакцией псевдо­
первого порядка по сахару:
С12Н12О11 + Н2О —► 2СбНх20б
168

§2. Простая реакция второго порядка
Простая реакция второго порядка может протекать по двум
кинетическим схемам:
2АЛр
и
к
Ai+A2-^P
к
В случае протекания реакции по первой схеме 2А —►Р (мно­
житель 2 появляется потому, что в каждом элементарном акте
удаляются две молекулы А) уравнение скорости имеет вид:
Интегрирование этого уравнения приводит к выражению
1
1“*
(2.5)
(А] [А]о =2А:Т-
1
Это уравнение представляет прямые в координатах (т^ - ~
т)
(рис. 2.7). Тангенсы углов наклона отвечают константам скоро­
сти к. Единицу измерения константы скорости второго порядка
можно вывести из соотношения:
моль , моль2
= к ------- ,
л•с
л
откуда может быть получена размерность константы скорости
реакции:
(моль\
л
к=
^мольhz\ \моль •с/
эль2\
л2)
Константу скорости можно вы­
числить, подставляя экспери­
ментальные значения [А] при
разных значениях времени т в
преобразованное уравнение:
[А|0 - [А]
2|А]о[А|т’
имея в виду, что к постоянна.
Однако подстановку или чис­
ленный метод следует приме­
нять только в том случае, если
-1/(2ЧА]о2>
Рис. 2.7. График реакции второго
порядка 2А —>Р
169

предварительно установлено, что реакция действительно явля­
ется реакцией второго порядка, иначе небольшие отклонения мо­
гут быть интерпретированы к ак ошибки эксперимента. Уже из
графического представления легко определить возможную кри­
визну, которая должна указывать на более сложный характер
реакции. Период полупревращения для А получают после под-
[А1п
становки
вместо [А] в уравнение (2.5):
2
_
1
Tl/2 ~
Таким образом, в отличие от кинетики первого п орядка период
полупревращения в реакции второго порядка меняется в зависи­
мости от начальной концентрации. Больший интерес представ­
ляет второй тип простой реакции второго порядка:
Ai+A2-^P
Этот случай необходимо рассмотреть в разных условиях.
1. Начальные концентрации равны: [Ai]o = [Аг]о- Э тот случай
математически сводится к первому типу, но тогда вместо 2к в
предыдущих уравнениях, например в (2.5), в нашем случае по­
является просто к. Поэтому наклон графика зависимости щ
1
или |д —j от тнепосредственно д а е т константу скорости второго
порядка:
_J:_____
-_-
[Ai] [Ai]o
2. Один из реагентов берется в большом избытке, т а к что его
концентрация остается практически постоянной в ходе реакции.
Допустим,что [Аг]о [Ai ]o5то гд а уравнение скорости
® = *([А,]о-[Р])([А2]„ -[Р])
(2.6)
упрощается и принимает вид:
® =М(А,]о-[Р]),
(2-7)
где &эф — эффективная константа скорости, равная
А^Ф = Л:[А2]о
(2.8)
(здесь пренебрегают величиной [Р] по сравнению с существенно
большим значением [A^lo)-
170

Уравнение (2.7) представляет собой уравнение скорости пер­
вого порядка. Поэтому говорят, что реакция происходит в усло­
ви я х псевдопервого порядка (по отношению к А). Тогда д л я по­
лучения величины А;Эф применимы все методы кинетики реакции
первого порядка. Поскольку константа скорости первого поряд­
ка не зависит от концентрации, изменение концентрации реаген­
та Ai, взятого в недостатке, не может влиять на &эф. Согласно
уравнению (2.8) А;эф линейно возрастает с увеличением [А2]о- По
этому выражению и определяют к. Д л я получения четкого под­
тверждения случая простой реакции второго порядка необхо­
димо, чтобы обратное соотношение концентраций [Ai]o > [Аг]о
давало те же самые константы скорости псевдопервого порядка.
3. Третий метод пригоден для случая, когда [Ai]o = [Аг]о т*е.
когда начальные концентрации реагентов и неодинаковы, и не
соответствуют условиям псевдопервого порядка. Интегрирова­
ние уравнения(2.6) по частям и оценка постоянной интегрирова­
ния по начальным условиям при [Аг]о > [Ai]o дают:
График отношения левой части уравнения к т представля­
ет прямую с наклоном, равным fc. Если величина к постоянна
дл я нескольких различных начальных концентраций, то это слу­
ж и т доказательством протекания реакции первого порядка по
отношению к каждому из двух реагентов. Очевидно, что урав­
нение (2.9) неприменимо в тех случаях, когда начальные кон­
центрации равны. Примером простых реакций второго порядка
являю тся реакции этерификации:
Дифференциальные уравнения для реагентов и продуктов име­
ют вид:
(2.9)
СНзСООН + С2Н5ОН -» СН3СООС2Н5 + Н20
и омыления эфира:
СН3СООС2Н5 + Н20 + NaOH -♦ CH3COONa + С2Н5ОН
§3. Две параллельные реакции первого порядка
171

(2.10)
^ U -fa +fcMA],
(2.11)
t'-MA,.
(2.12)
Первое уравнение можно прямо записать в интегральной форме
по аналогии с уравнениями, полученными дл я простой реакции
первого порядка
[А] = [А]ое-(*1+*’>т.
(2.13)
Деление (2.11) на (2.12) дает
d[Pi] _ ki
d[P2] h ‘
Из условия, что в начальный момент в реакции присутствовал
только реагент A, a [Pi]o = [Р2]о = 0> можно записать:
[Pi] = *1
[Р2] к2
(2.14)
Таким образом, отношение концентраций продуктов зависит
только от отношения констант скоростей. Подставляя уравне­
ние (2.13) в уравнение материального баланса
[А]0= [A] + [Pi]+ [P2],
получаем
[Р1]+[Р2]=[А]о(l-e
-
°=^).
Комбинируя уравнения, находим
|Pll=*^fe|Alo(1"e'<
‘'*‘,)')'
(2Л5)
и
И=
(2.16)
На рис. 2 .8 показано изменение концентрации реагента и про­
дуктов для произвольных значений ki и к2. Д л я определения
172

каждой из констант нужно ис­
ключить из (2.15) и (2.16) вы­
ражение в круглых скобках, ис­
пользовав (2.13) соответственно:
|Pil =((A|o-[Al)j^fjj
и
[Р2] = ([А]0-[А]) к2
к\+/С2
График зависимости [Pi] и
[Р2] от ([А]о - [А]) представляет
собой прямую, проходящую че-
Рис. 2.8. Зависимость концен­
трации с от времени т для двух
параллельных реакций первого
порядка
рез начало координат, с тангенсами углов наклона
*1
к>2
к\+/^2
соответственно. Далее, как видно из уравнения (2.14),
к1+/ь2
график зависимости [Pi] от [Р2] также является прямой, про­
ходящей через начало координат, с тангенсом угла накло-
на
Последние два граф ика могут служить признаком парал-
к2
лельных реакций первого порядка. Аналогичным образом такие
же методы применимы и к большему числу параллельных реак­
ций.
Примерами параллельных реакций является образование сме­
си орто-, мета- и пара-нитробензойных кислот при нитровании
бензойной кислоты или термический распад бертолетовой соли:
КС1+02
KCIO4 + KCI
§ 4. Последовательные реакции
Последовательность двух реакций первого порядка с необра­
тимой первой стадией
А-^В-^Р
173

Реагент А превращается в продукт Р через промежуточный про­
дукт В. Кинетический анализ зависит от соотношения реакци­
онной способности А и В. Различают следующие три случая.
1. fci &2, т. е. промежуточный продукт гораздо менее реак­
ционноспособен, чем исходный реагент. Первая стадия практиче­
ски завершается до того, как начинается вторая стадия, поэтому
каждую ф азу процесса можно рассматривать как простую реак­
цию первого порядка (рис. 2.9, а). Тогда из зависимостей In [А]
и ln([P]oo - [Р]) от т получают соответственно к \ и fo.
2. fci &2. Вторая стадия очень быстро следует з а первой,
поэтому в любой момент времени [В] < [А] и [В] <£: [Р]. Это
видно из рис. 2.9, б для случая, когда 20к\ = fo. Следовательно,
уравнение материального баланса
|А]о= [А]+[В]+[Р]
упрощается, так как мы вполне можем пренебречь концентра­
цией промежуточного продукта:
[А]о= [А]+[Р]
Если продифференцировать по времени оба предыдущие урав­
нения, то можно получить:
0=d[A]+^
+ d[P]
у»
dz
dz
dz
d[A] , ___
dx
dx'
(2.17)
Следовательно,
d[B]
dx
= 0, т. e. в ходе реакции концентрация В
остается постоянной по отношению к изменениям [А] и [PJ. Урав­
нение (2.17) свидетельствует о том, что образование конечно­
го продукта Р определяется законом скорости реакции А —►В,
Рис. 2.9. Кривые зависимости концентрации с от времени т для после­
довательности двух реакций первого порядка: а — при к = 20^; б —
при 20fci = &2
174

которая является лимитирующей, или определяющей скорость,
стадией. Таким образом, поведение и реагента А, и продукта Р
описывается простой кривой первого порядка.
Очевидно, что д л я того, чтобы кинетически определить ре­
акционноспособный промежуточный продукт, необходимо рас­
сматривать ранние стадии реакции. Итак, для случая 2 при рас­
смотрении последовательности двух реакций первого порядка
можно показать, что и скорость расходования реагента А, и ско­
рость накопления продукта Р описываются кинетическими за­
кономерностями д л я простой реакции первого порядка. Поэто­
му значение к\ можно получить либо из зависимости [А] = ф(т),
либо из зависимости [Р] = <р(т), как это было сделано выше для
простой реакции первого порядка.
3.
Рассмотрим наиболее интересный случай, когда к\ =
т. е. когда различия в реакционной способности А и В незна­
чительны. В этом случае система дифференциальных уравне­
ний, которые определяют превращения всех участников реак­
ции, имеет вид:
d[А]_
dx
dx
= -*ilA],
= k1[A]-k2[B],
m
dx
= *2[B].
(2.18)
Дл я концентрации А интегрированием получаем обычное вы­
ражение для реакции первого порядка:
[А] = [A]0e-fclT.
Это выражение подставим в (2.18):
® + fc2[B] = fc1[A]0e-fe‘t .
В результате интегрирования этого уравнения получим:
iBi=h ^ iAio(e"‘" ' e"‘” )'
(2л9)
Концентрация Р определяется из уравнения материального
баланса
[Р]=[А]о- [А]- [В].
После объединения уравнений и проведения соответствующих
преобразований получим д л я концентрации продукта реакции [Р]
[Р]=[А]о 1-
&2~ к\
(кге^-кхе^)
(2.20)
175

с
Рис. 2.10. Кривые зависимости
концентрации с от времени т для
последовательности двух реакций
первого порядка при к\ = 2/^
а = 1п([А]0- [Р]) от времени х для
последовательности двух реакций
первого порядка
На рис. 2.10 представлена зависимость концентрации продук­
та реакции от времени д л я последовательности двух реакций
первого порядка при к\ = 2А?2. К ак видно из рисунка, кривая
[В] = ф(т) проходит через максимум. Время х, необходимое для
достижения максимальной концентрации ([В]тах), составляет:
_Ч1 )
(2.21)
Значение х из (2.21) подставляют в уравнение (2.19) и получают
величину [В]щах- Когда константы скоростей равны: к \ - Л:2, ка­
сательная к кривой [А] при х = 0 пересекает абсциссу в точке, со-
1
ответствующей - = хтах.
К
Таким образом, если известно &i,to по
уравнению (2.21) можно приблизительно оценить величину к2.
Кривая [Р ~ ср(х)] имеет точку перегиба вблизи [В]тах, что и
определяет S-образную форму кривой.
К концу реакции уравнение(2.20) сводится к выражению
Отсутствие в этом уравнении слагаемого fc2e“fclt объясняется тем,
что к концу реакции первая ее часть, связанная с расходовани­
ем [А], практически исчерпана. В логарифмической форме это
уравнение будет иметь вид:
1п([А]0 - [Р]) = In[А]о + In
-
к 2х.
По этой зависимости, построив гр аф ик
1п([А]0 -[Р])~<|>(т),
176

как это показано на рис. 2.11, определяют константы ki и А:2. К ак
пример последовательной реакции можно рассматривать реак­
цию омыления эфиров двухосновных кислот:
С2Н5СОО— СН2-С Н 2— СООС2Н5
+NaOH
- С 2Н5ОН
+ NaOH
- С 2Н5ОН
+ NaOH
- С 2Н5ОН
С2Н5СОО— СН2-СН2— COONa-
COONa— СН2-СН2— COONa
+NaOH
- С 2Н5ОН
§ 5. Обратимая реакция первого порядка
Обратимой реакции первого порядка соответствует кинетиче­
ская схема
^
А.
>Р
К
В этой схеме к+ и к - означают константы скорости прямой и
обратной реакций соответственно. Уравнение скорости д л я этой
реакции имеет вид:
-rf[A] _ d[Р]
dx
dx
= А:+[А]-А _[Р]
(2.22)
и при достижении равновесия, т. е. при х —►оо, принимает вид
Vtx, —/u+fAJoo ^-[Р]оо —0.
Вводя константу равновесия К , получаем
—
=Р1°°_гг
к-
[А]оо
Отсюда с учетом, что [Р]оо = [А]о - [А]оо, следует
|A|o°=t^E|A)o'
<2'23)
1р1“ =Е Т Е|А1»'
Теперь заменим [Р] в уравнении (2.22) на ([А]о - [А]) и после
преобразования получим:
^
= -(к* +*:_)([А]-
|А]0) .
177

Второй сомножитель в скобках согласно уравнению (2.23) про­
сто равен [А]оо- Следовательно,
4£1=-(*,+*.)([а]-[а ы .
Проинтегрировав это уравнение, получим:
1 [А] [А]°° __ _/7 , jLV-
П[А]0- [А]оо (А+
’
ИЛИ
[А| = [А]«, + (|А]0 -[А|„)в(-* -**->*.
График (In
А-[А], ■т) дает прямую с тангенсом угла на-
|А]о - |А]е
клона -(fc++fc_) (рис. 2.12). С использованием изложенного выше
метода получается сумма констант скоростей прямой и обратной
реакций. Разделение этих констант достигается с помощью кон­
станты равновесия.
Дл я обратимой реакции первого порядка можно рассмотреть
начальные скорости обратимого процесса (рис. 2.13). Значение
абсциссы
дл я точек пересечения касательных в начальном и
конечном участках кривой находят по выражению:
vo = [Alo-JAloo = (fc++ М([А]о _ [А]оо))
откуда
т=
(fc++ fc_)‘
л
Рис. 2.12. График полулогарифмической зависимости для обратимой
[А] - [AU
реакции первого порядка: 1пф =In yrj—ттт^-\ tga =-(к+ + fc_)
[AJo —[AJoo
178

Рис. 2.13. Касательные к кривым зависимости ( с - т ) для обратимой
реакции первого порядка
Касательная к начальному участку кривой при %= 0 пересе­
кает абсциссу в точке Т2:
t*=No
= MA]o-* -[P]o.
^2
Поскольку в начале реакции присутствует только А, второе
произведение равно нулю и
Очевидно, ни Ti, ни Т2 не зависят от начальной концентрации,
что хорошо видно из рис. 2.13. В особом случае, когда констан­
ты к равны, [А]оо = [А]о/2, по­
лучим Ti = l/2fc, Т2 = 1/к. На
рис. 2.14 показана зависимость
скорости от концентрации д л я
различных начальных концен­
траций. Тангенсы углов накло­
на прямых, проходящих через
абсциссу, равны сумме к+ + к-.
Линия, соединяющая точки на­
чальных скоростей, представ­
ляет собой проходящую через
начало координат прямую с
тангенсом угла наклона /;+. Та­
ким образом, с помощью приве­
денных выше преобразований и
Рис. 2.14. Зависимость скорости v
от концентрации [А] для обрати­
мой реакции первого порядка
179

графических построений можно определить константы скоро­
стей прямой и обратной реакций в случае изучения кинетики
обратимой реакции первого порядка.
§6. Метод наименьших квадратов
Графический метод поиска кинетических параметров хими­
ческих реакций может быть заменен аналитическим методом,
особенно в тех случаях, когда преобразованное уравнение линей­
но. Этот математический метод получил название метода наи­
меньших квадратов. Суть этого метода заключается в следую­
щем. Пусть имеется большой массив экспериментальных дан­
ных, в котором каждому значению независимой переменной Х{
соответствует свое значение зависимой переменной yi . Если су­
ществует т а к ая функция ср(тг), которая описывает взаимосвязь
между и у{) то параметры этой функции таковы, что
N
^2(Уг ~ Ф(xi))2 = Ф = min,
t=l
где N — число экспериментальных данных. Если ср(тг) линейна,
то функцию Ф можно записать в виде:
N
ф= ^ 2 [у*~ (а+Ьх»)]2= min •
i=l
Из условия экстремума (минимума) функции Ф следует, что
дФп
дФп
и зГ0;
дФ
да
дФ
~дЬ
N
N
=2ЛГа-2^^+26^х» =0;
(2.24)
t=l
i=l
N
N
N
=2Ь^х?-2
Xjj/i+2а^ х»=0.
(2.25)
t=i
t=i
i=i
Реш ая систему уравнений (2.24, 2.25) относительно о и Ь, можно
показать, что
N
N
а-
-------
izl—
180

и
N
N
N
N^2xiyi-J2yiT,xi
г=1
i=l i-1
N
N
t=l
t=l
§ 7. Обратимая реакция второго порядка
Обратимой реакции второго порядка соответствует кинетиче­
ская схема
Различают следующие дв а случая для описания кинетических
закономерностей этой реакции.
1. Оба исходных вещества присутствуют в стехиометрическом
соотношении. Тогда задача упрощается и математически сводит­
ся к реакции одного реагента:
Так как в любой момент времени Pi и Р 2 образуются в равных
концентрациях, т. е. [Pi] = [Р2] = [Р], уравнение (2.26) можно
записать в виде
Ai+А2< —Р1+Р2
к2
Уравнение скорости д л я этой реакции имеет вид:
= *+[А1][А2] - М Р 1][Р2].
(2-26)
[Ai]0 = [А2]о = [А]о или [Ai] = [А2] = [А].
-
^ =МА]2-МР]2-
(2.27)
нение (2.27), получим:
d[А]
dx
181

После преобразования последнее уравнение легко интегрируется:
[А1
Г __________ W
[А]. ([А]-[А]оо)([А] +
[А]о[А]оо .
[A]0-2[A]J
[А]о([А]р - 2[А]оо)
+J ([А]0 - [А]оо)2
о
В результате интегрирования получим:
[А]о —2[А]оо . {[А]оо[А]/([А]0 -2[А ]оо)} + [А]_ 2[А]0[А]
[А]о
[А] - [А]о©
[A]0 -[A]c* +
Второе логарифмическое слагаемое линейно зависит от време­
ни, причем тангенс угла наклона прямой равен множителю т.
Прямая отсекает от ординаты отрезок, равный первому лога­
рифмическому слагаемому (рис. 2 .15). Как и в случае обратимой
реакции первого порядка, угловой коэффициент касательной в
начальном участке кривой ([А]—т) позволяет оценить константы
скорости. И з выражения
Vo= No
= fc+[A]2-* _[P]o
при [Р]о = 0 находится Тг:
1
(МА]о)‘
Рис. 2.15. График полулогарифмической зависимости для обрати-
{[А]оо[А]/([А]0- 2[А]оо)} + [А]
мой реакции второго порядка: ln<p = In
2[А]о[А]
tga =
[А]о ~ [А]
[А] - [А]с
00 Ан-; 1п0= [А]° 21А]о°
[А]о
182

Значение абсциссы (tx) дл я точки пересечения касательных в на­
чальном и конечном участках кривой получают из выражения
_
[А]о - [А]оо
или
Vo = fc+[A]i) - А
_[Р]о,
откуда
Ti= у/щ. (\Д^ + \/k^j [А]0.
С точки зрения кинетики очень интересен случай, когда к+ =
=к- =к.Тогда[Р]оо=[А]то=
и уравнение (2.27) можно
записать в виде
<([А]_
dx
= 2*[А]0([А]-[А]оо).
Вводя новую переменную [А7] = [А] - [А]оо, получим:
4А]
dx
= *эф[А'].
Это означает, что реакция подчиняется закону скорости первого
порядка, но /сэф зависит от начальной концентрации А, т. е. А^ф
меняется дл я разных наборов равных концентраций Ai и А2.
2. Этот случай более сложный, и он встречается только то­
гда, когда невозможно подобрать условия, соответствующие слу­
чаю 1. Интегрирование общего уравнения скорости (2.26) дает:
1 , ([Ai]o - [Ai]oq)([Ai]- [Ai]qo+ Q) _ ,
_i \_
Q n ({A1]-{A1]<X))([A1}o-[Al}00+Q) ^
и
Q = Y Z l ^ K ^[A2]o - [Ai]o)2+ 4[A1]o[A2]oK,
гдe* 'E '
Примером обратимой реакции второго порядка является жид­
кофазное пероксидирование уксусной кислоты СН3СООН рас­
твором пероксида водорода с образованием СН3СОООН, т. е.
перуксусной кислоты. Рассмотрим на этом примере порядок оцен­
ки экспериментальных кинетических результатов и получение
кинетической модели процесса. На рис. 2.16 приведены типич­
ные кривые накопления перуксусной кислоты и расходования
183

пероксида водорода в ходе жидкофазного пероксидирования ук­
сусной кислоты. Как видно из этого рисунка, обе эти кинетиче­
ские кривые имеют две четко выраженные области I и II. В обла­
сти I происходит расходование пероксида водорода и накопление
перуксусной кислоты:
СНзСООН + Н20 2 СНзСОООН + Н20
В области II устанавливается равновесие между исходными
веществами и продуктами реакции:
СНзСООН + Н20 2 £ СНзСОООН + Н20
Вначале рассмотрим область I, д л я которой справедливо следу­
ющее выражение для константы равновесия:
[СН3С000Н]-|Н20|-
[СН,СООП]-|НгОг]- '
'
'
Для нахождения К преобразуем уравнение (2.28) с учетом урав­
нений материального баланса к виду:
_
[СНзСОООН]* [Н20]* _
[СНзСООН]* [Н20 2]*
[СНзСОООН]* ([Н2О]0 + [СНзСОООН]*)
" ([СНзСООН]0 - [СНзСОООН]*) ([Н2О2]0 - [СНзСОООН]*) ’
или
1 _ ([СН3СООН]о - [СН3СОООН]*)([Н2О2]0 - [СНзСОООН]*)
к
[СН3С0ООН]*([Н2О]0 + [СНзСОООН]*)
(2.29)
Рис. 2.16. Кинетические кривые расходования Н20 2 и накопления
СНзСООН в ходе жидкофазного пероксидирования уксусной кислоты
(Т=308К)
184

Далее, предполагая, что [Н20]* = [Н20]о + [СНзСОООН]* та
та [Н2О]0, уравнение (2.29) можно переписать в виде:
1 _ ([СН3СООН]0 -[СНзСОООН]*)([Н2О2]0 -[С Н 3СОООН]*)
К~
[СНзСОООН]*
[Н2О]0
[СН3СООН]0 1 Г[Н2О2]0 [СНзСОООН]*
.[СНзСОООН]* J l [H2O]0
[Н2О]0
или
1 _ [СН3СООН]о [Н20 2]о
К [СНзСОООН]* [Н2О]0
(2.30)
/ [Н2О2]0 + [СН3СООН]0N [СНзСОООН]*
V
([Н2О]0
)+ [н2о]0
•
Рассчитанные по уравнению (2.30) численные значения К
дл я различных исходных концентраций реагентов приведены в
табл. 2.1. Как видно из этих данных, экспериментально опре­
деленное значение константы равновесия является практически
постоянной величиной, д аж е при сделанном допущении о том,
что [Н20]* = [Н20]о + [СНзСОООН]* « [Н20]о и изменяется в до­
статочно узком интервале значений от 1,21 до 1,43 (Кср = 1,29)
при изменении начальных условий в широких пределах: началь­
ная концентрация Н20 2 изменялась от 35 до 65% масс.
Попытка описать кинетические закономерности процесса, про­
текающие в I области, необратимой реакцией второго порядка:
СНзСООН + Н20 2 Л СНзСОООН + Н20
(2.31)
Таблица 2.1
Исходные и равновесные концентрации в реакции пероксидирования
уксусной кислоты
Исходные концентрации
реагентов и продуктов, моль/л
Равновесные концентрации
реагентов и продуктов, моль/л
К
[А|о [В|о [H2O 2I0
[H2OI0
[А] [В] [н2о 2] [НгО]
0
2,5
10,29
27,78
0,74 1,76
9,55
28,52
1,22
0
2,5
13,24
22,22
1,10 1,40
12,14
23,32
1,44
0
2,5
16,18
16,67
1,30 1,20
14,88
17,97
1,21
0
2,5
19,12
11,11
1,68 0 ,52
17,44
12,79
1,31
Примечание. А - СНзСОООН; В - СНзСООН.
185

не привела к положительным результатам по следующим при­
чинам. Приведенной схеме (2.31) протекания предполагаемой
необратимой реакции должно было соответствовать кинетиче­
ское уравнение:
klX~ [СНзСОООН]0 - [Н2О]0 х
[Н2О2]0 ([СН3СОООН]0 - [СНзСОООН]) W
х
[СН3СОООН]0 ([Н2О2]0 - [СНзСОООН]) х
в соответствии с которым в координатах:
[Н2О2]0 ([СН3СОООН]0 - [СНзСОООН])
х
[СН3СОООН]0 ([Н2О2]0 - [СНзСОООН])
должна была наблюдаться прямолинейная зависимость во всей
области I рассматриваемой реакции. В действительности это­
го не происходило, и прямолинейная зависимость в этих ко­
ординатах наблюдалась лишь на начальных стадиях процесса
(т < 60 ч), в то время как продолжительность I области реак­
ции обычно была не менее 200 ч в выбранных условиях ведения
процесса (308К).
Это говорит о том, что необходима обработка полученных
экспериментальных данных с обязательным учетом обратимо­
сти реакции д аж е на начальных стадиях процесса:
fci
СНзСООН+Н202^=^СН3С000Н+н2о
к2
Кинетические закономерности д л я этой обратимой реакции вто­
рого порядка соответственно д ол ж ны описываться уравнением:
Таблица 2.2
Расчетные значения Q и а
Концентрации, моль/л
Q
а
к \ ■105,
л/(мин- моль)
к2■Ю5,
л/(мин- моль)
[В]о [Н2О 2]0 |Н2О]0
2,5
10,29
8,0
51,902 0,042
3,24
2,50
2,5
13,24
10,4
64,757 0,042
2,20
1,70
2,5
16,28
13,46
77,554 0,034
3,63
2,80
2,5
19,12
15,85
90,382 0,035
3,63
2,80
Примечание. В
— СНзСООН.
186

1 lM([H2O2]0-[H 2O2]*)([H2O2]-[H 2O2]*+Q) _
Q ([H2O2] - [H20 2]‘ )([H20 2]o - [H20 2]* +Q) K1 2> ’
(2.32)
где
Q=
\ / t f 2([СН3СООН]0 - [Н2О2]0)2 + 4[Н2О2]0[СНзСООН]0А'.
К—1
Уравнение (2.32) можно существенно упростить и привести к
виду, удобному для обработки на ЭВМ:
f ([Н20 2]- [Н20 2]*+Q)) .
.
Г ([Н202]- [H2o2]*) / к2{
ГА6
([Н20 2]о - [Н20 2]*)
((Н20 2]о - [Н20 2]* + Q)
Численные значения Q и а для соответствующих кинетиче­
ских опытов приведены в табл. 2.2.
При обработке экспериментальных данных использовали зна­
чения [Н2О2]*, определенные экспериментально. К ак видно из
приведенных в табл. 2.2 данных, значения к\ и &2, рассчитанные
по экспериментальным данным с использованием модели обра­
тимой реакции второго порядка, имеют близкие значения д л я
всей серии кинетических исследований (средние значения этих
констант оказались равными: к\ср = 3,175 моль • л -1 ■мин-1 и
&2ср = 2 ,45 моль • л -1 • мин-1), что говорит о правильности выбо­
ра кинетической модели д л я описания процесса жидкофазного
пероксидирования уксусной кислоты пероксидом водорода.
§8. Обратимая реакция смешанного порядка
Обратимой реакции смешанного (первого и второго) порядка
соответствуют две кинетические схемы:
А^р1+р2
и
Ai+А2£+Р
Второй случай достаточно распространен и известен как обра­
тимое образование комплекса. Оба типа реакций можно считать
одинаковой системой, реагирующей в противоположных направ­
лениях.
187

Рассмотрим случай I:
к-
Ai=tPi+P2
к+
Скорость образования продукта выражается уравнением
4*1 __
dx
= -А:+[А]+ М[А]о-[А])2.
(2.33)
Учитывая, что при равновесии
fct [A]00 = M[A]-[A]oo)2,
уравнение (2.33) можно проинтегрировать и получить выраже­
ние
|А]о([А1-[А1оо) |А]о + [А]ев
[A]g- [AJlAJoo (А]о - [А]оо * '
Далее по зависимости In
А,
~
ф(х) (рис. 2 .17), зная
lAJo [AJlAJoo
значения [А]о и [А]оо, можно определить fc+.
Рассмотрим случай II:
к.
А\+А2< —Р
fc+
Для этой реакции
[A.HA2]-fe-|Pl
реакции смешанного (первого и второго) порядков:
Inm- In
“ [А]оо).
[А]о + [А]оо ,
(A|g-[A][A)oo'‘^-1АИАй‘*
188

или
(2.34)
4 ? = M[Ai]o'- [Р])([А2]о- [Р])- МР].
Учитывая, что при равновесии
*+([Ai]0 - [Р]оо)([А]0 -[Р]оо) = к-{Р]оо,
уравнение (2.34) можно проинтегрировать и получить:
,
(Ploo-lPDIAiloM o
|Pfc-[Ai]o[A2]0
|Plce(|Ai]o(A2]0 - [ P ] TO[P])
(Pico
Система упрощается, если один из исходных реагентов берут в
большом избытке. Так, при [А2]о > [Ах]о
к'+ = А:_[А2]о- Уравнение (2.35) соответствует дифференциально­
му уравнению для обратимой реакции первого порядка. Поэтому
гр афик зависимости величины ln([Ai] - [Ai]oo) от времени дает
сумму А:++ fc_ как эффективную константу скорости А;эф.
Во второй серии экспериментов определяют концентрацию
избыточного реагента при поддержании постоянной концентра­
ции [Ai]o- Зная величины [А]о и [А]оо, можно определить к+ и
построить график кэф в зависимости от [А2], представляющий
собой прямую с угловым коэффициентом k+i отсекающую на ор­
динате отрезок, равный
Тот факт, что прямая не проходит
через начало координат, свидетельствует о наличии обратной ре­
акции.
В случае простой кинетики второго порядка или в том случае,
когда обратной реакцией можно пренебречь, прямая проходит
через начало координат. Уравнение
удобно использовать д ля расчета К с помощью графика зависи­
мую, проходящую через начало координат, с тангенсом угла на­
клона, равным К .
Дальнейшим подтверждением обратимости реакции является
то, что [Aijoo возрастает при увеличении [А2]о или то, что [Р]оо}
не достигает величины [Ai]o-
(2.35)
= [Ai]q- [Ai]oq
к-
[Ai]oo[A2]o
мости
([Ai]o-[Ai]oo)
[Al]oo
от [А2]о* График представляет собой пря-
189

§ 9. Последовательность дв у х реакций первого порядка
с обратимой первой стадией
Таким реакциям соответствует следующая кинетическая схема:
к+
Совокупность дифференциальных уравнений, отвечающая этой
кинетической модели, имеет вид:
^l= -fc+[A]+MB],
® =МА]-(*-+*2)[В],
(2.36)
d[P]
dx
= *2[В].
В общем случае результатом интегрирования этих дифференци­
альных уравнений при [В]о = [Р]о = 0 являются уравнения:
[А] =
{(гг - fc+)e-rit - (гх - Л+)е_ГзТ},
(2.37)
Г2-Г1
[В] =
-
e_r2t),
(2.38)
Г2“ Г1
[Р] = [А]0[1----——e_rit + ———е_Г2Т),
(2.39)
\ г2-П
Г2-П
J
где
п Л [(Л++к. +к2)+у/(к* +к. +к2)2~4к+к2],
(2.40)
гг = ^ [(fc++к- +к2)~ у/(к+ +к-+fo)2-
.
(2.41)
В общем случае для этой кинетической модели время тта х , соот­
ветствующее достижению максимальной концентрации [В], опре­
деляется по уравнению
■Wx= —-— In—.
(2.42)
Г1 —Г2 г2
Эти алгебраические уравнения упрощаются, если одна из стадий
процесса явл яется лимитирующей. Возможны д в а основных ва­
рианта, характеризующие последовательность из двух реакций
первого порядка с обратимой первой стадией.
190

Случай I: к++ fc_ &2. Путем соответствующих преобразова­
ний можно показать, что
.
:к
к.л
(2.43)
Используя основное условие для рассматриваемого случая А;++
к
к-
+ А:_ &2, будем считать, что
~
~
0. На основе приближе-
«2
к2
ние \/1 -х = 1 - —окончательно получим: r\ = k<i и Г2= к+.
Подставляя эти значения в уравнения (2.37) — (2.43), получим:
[А]=[А]0е-Ч [В]~0, [Р]=[А]0-[А].
Таким образом, в случае I изменение концентраций А и Р во
времени следует закону скорости первого порядка, что позволяет
оценить величину к+. Интересен случай, когда промежуточное
соединение реагирует с другим исходным реагентом (А2):
А!
к+
и при этом к++к-
/с2[А]2. Е с л и В очень реакционноспособен,
можно применить приближение Боденштейна—Семенова:
Я =0 =МАх]-(^ +А2[А2])[В].
Тогда [В] =
**[Ai]
г . Если это уравнение д л я В подставить в
А:_+ Л:2[А2]
уравнение скорости изменения концентрации реагента [Аг], то
получим:
ад ЧЁ)|А-»Аг|
*'ЧеМ'
к>2
Теперь если 1 <С —[А2], то
/С_
d[A2]
dx
^+[Ai].
В этом частном случае реакция имеет нулевой порядок по А2.
191

Случай II: к++ к-
к2. Если А превращается в В в быстрой
и обратимой стадии, а конечный продукт образуется медленно:
/
ч_
кч,
^„
А<
' (бы стро) В --------►(медленно)Р,
b
то А и В связаны константой равновесия следующим образом:
[В]
f-т-г = К . После дифференцирования этого уравнения по времени
[AJ
получим:
*Ш=кт.
(2.44)
dx
dx
Уравнением материального баланса для этой реакции будет:
[А]о = [А] + [В] + [Р], после его дифференцирования по времени
получим:
л d[A] d(B] d[Р]
0=-т^+-т^+-т^.
(2.45)
dx
dx
dx
Объединим уравнения (2.44) и (2.45):
„
.
„
«-в
.
Подставляя последнее выражение в уравнение (2.36), получаем:
т
_
«».в,_
w
А
1+ л"1*31 1+ А’|А|'
Интегрирование этого уравнения в пределах от [А]о = [A]j$ ([A]j$ —
равновесная концентрация, которая по условию устанавливает­
ся быстро, т. е. при х = 0) до [А] при х = х приводит, аналогично
простой реакции первого порядка, к уравнению:
м=
[А]
к2К
1+к х'
Это уравнение можно преобразовать, используя соотношения
и
Откуда
[А]; = 1А1° - 1А1°
К
|А|г=н Ь ?|А|°'
|А|=ТТ^|А|<,е^ ’^
'
192

а[В]=ЛГ[А],т.е.
И =j^lAloe
И, наконец, используя соотношение [Ао] = [А]+[В] + [Р], получаем
[Р] = [А]о
Здесь рассмотрены наиболее типичные реакции первого и вто­
рого порядков. На практике сталкиваются с реакциями, которые
представляют собой комбинации рассмотренных выше, что зна­
чительно усложняет расчеты констант скоростей. Однако, ис­
пользуя рассмотренные выше приемы, все же удается в боль­
шинстве случаев разрешить возникающие проблемы и рассчи­
тать константы скоростей реально происходящих реакций.
§10. Кинетика сопряженных реакций
Реакции, в которых происходит ускорение одной реакции
з а счет протекания другой реакции, называются сопряжен­
ными реакциями.
Термин «сопряженные реакции» был введен В. Оствальдом в
1900 г. В общем виде схему сопряженных реакций можно пред­
ставить в следующем виде:
А + В —+ Продукты (первичная реакция)
А + С —* Продукты (вторичная реакция)
Всего в реакции участвуют не менее трех веществ, из которых
вещество А, участвующее в обеих реакциях, называется акто­
ром; вещество В, участие которого в первичной реакции индуци­
руется протеканием вторичной реакции, называют индуктором,
а вещество С — акцептором. Количественной характеристикой
сопряженных реакций является коэффициент (или фактор) ин­
дукции:
j__^акт_П(С)
Я'инд 71(B)
где п акт и пинд — число молей прореагировавших акцептора и
индуктора соответственно. Сопряженные реакции весьма рас­
пространены, особенно в живы х организмах. Однако очень часто
7 Иплолитоп
193

их трудно отличить от катали­
тических реакций, о которых
речь будет идти ниже. Сопря­
женные реакции отличаются от
каталитических расходованием
индуктора, тогда как при ката­
лизе промежуточные соедине­
ния или комплексы разрушают­
ся с регенерацией катализато­
ра. Поэтому коэффициент ин­
дукции при катализе постоян­
но растет и в пределе стремит­
ся к бесконечности. В случае же
сопряженных реакций фактор
индукции стремится к опреде­
ленному пределу, соответству­
ющему условиям, когда индук­
тор образует промежуточный продукт, целиком входящий во
взаимодействие с акцептором.
В качестве примера на рис. 2.18 приведена зависимость фак­
тора индукции I n от отношения концентраций акцептора и ин­
дуктора в сопряженной реакции окисления бромноватой кисло­
той (актор) сернистой (индуктор) и мышьяковистой (акцептор)
кислот:
НВгОз + SC>3_
—
» (первичный процесс)
НВгОз + AS2O3 —►(вторичный процесс)
Приведенную выше схему сопряженных реакций можно рассмот­
реть в предположении, что индуктор действует каталитически
на реакцию актора с акцептором и одновременно исчезает по
независимой реакции с тем же актором. В этом случае, приняв
обе реакции за процессы второго порядка, можно получить сле­
дующие кинетические уравнения:
—
(J[акцептор] = ^
[акцептор] [актор]_
dx
In
Рис. 2.18. Зависимость фактора
индукции I n от отношения кон­
центраций актора (AI2O3) и ин­
дуктора (SO2)
- d[kat\
dx
k2 [kat\ [актор].
В этом случае величина, эквивалентная фактору индукции, вы­
разится как
In=
акто]р]о
[kat] о
/
кг
~— [kat}o
1-е *2
V
194

Очевидно, что в этом случае величина I n может бесконечно воз-
[актор]0 „
растать с увеличением соотношения .
— . Примерами сопря-
[kat\o
женных реакций могут служить окислительные процессы в ж и д­
кой фазе, например, окисление индиго в изатин, протекающее
сопряженно с самопроизвольным окислением бензальдегида:
С6Н5СНО + 0 2 —►■■• (первичная реакция)
Индиго + 0 2 —► ** (вторичная реакция)
В этих реакциях промежуточным активным окислителем яв­
ляется пероксид бензоила. Наибольшее значение коэффициента
индукции для подобных реакций равно единице — кислород рас­
пределяется поровну между индуктором и акцептором. В неко­
торых случаях возможен переход индукционного процесса в ка­
талитический, когда промежуточный продукт, который связы­
вает первичный и вторичный процессы, образуется индуктором
и когда в условиях процесса происходит его регенерация.
Дл я некоторых сопряженных реакций характерно явление са­
моиндукции, связанное с возрастанием концентрации индукто­
ра в ходе процесса. Обязательным свойством самоиндуктивных
процессов является начальное ускорение реакции и прохождение
ее скорости через максимальное значение. Согласно Н. А. Шилову
самоиндуктивный процесс можно представить в виде следующей
Схемы:
А+В-* А7+В7
А7+ В —►А"
А77+ В —►А7+ В
В соответствии с этой схемой исходные вещества первона­
чально образуют некоторые продукты А' и В7. Д алее продукт А7
взаимодействует с одним из исходных веществ, д а вая новое про­
межуточное соединение А77. Новый промежуточный продукт при
взаимодействии с другим исходным веществом восстанавливает
первый продукт, т. е. А7 (при этом считается, что первая стадия
процесса: А + В —>А7+ В7 протекает наиболее медленно).
К числу самоиндуктивных процессов относится подробно изу­
ченная реакция окисления мышьяковистой кислоты бромнова-
той кислотой:
2НВгОз + 3AS2O3 —►2HBr + 3AS2O5
НВгОз + НВг -> НВг02+ НВгО
4НВг + НВгО + НВг02 -> ЗВг2 + ЗН20
2Вг2 + As2C>3 + 2Н20 —►AS2O5 + 4НВг
(очень медленная реакция)
(медленная реакция)
(быстрая реакция)
(быстрая реакция)
195

Кинетические уравнения самоиндуктивных процессов обыч­
но совпадают с уравнениями дл я автокаталитических реакций.
Так, если д л я вышеприведенной схемы через а обозначить кон­
центрацию бромноватой кислоты, а восстановленное ее количе­
ство обозначить через х, то скорость этой реакции будет равна:
dx
v=—=к:та-х,
dx
причем скорость реакции имеет максимум при х = —
. Таккакв
такой форме уравнение неудобно для экспериментальной про-
верки(если х = 0, то v = 0, и реакция не может начаться),
то практически используется формула, которая получается при
учете заранее добавленной к реагирующей смеси бромистоводо­
родной кислоты в количестве Ь. Тогда скорость выражается со­
отношением
v=
= k(b+x)(a-x),
dx
которое при интегрировании д а ет выражение
1
а(Ь+х)
х(а+Ь) Ь(а-х)'
Эти уравнения совпадают с аналогичными уравнениями для ав­
токатализа конечным продуктом.
2.4 . СКОРОСТИ РЕАКЦИЙ В ПОТОКЕ
Методы расчета скоростей химических реакций в реакторах
периодического действия с кратной загрузкой исходных веществ
используются в малотоннажных производствах. Это синтез ле­
карственных и ароматических веществ, получение редких эле­
ментов и др.
Крупнотоннажные химические процессы проходят обычно в
проточных реакторах различного типа с регулируемой темпера­
турой и давлением. К числу так их процессов относится синтез
аммиака, крекинг нефтепродуктов, контактный способ получе­
ния серной кислоты, синтез каучука, нитрование и галоидиро-
вание и многие другие производства.
Реакции в потоке разделяются по режимам проведения на две
большие группы:
1) режим идеального вытеснения;
2) режим идеального перемешивания.
196

Режим идеального вытесне­
ния осуществляется в трубча­
тых реакторах при отсутствии
продольного и поперечного пе­
ремешивания, тогда как ре­
жим идеального перемешива­
ния отличается тем, что реа­
гирующие вещества перемеши­
ваются настолько интенсивно,
что в любой точке реактора
концентрации всех реагирую­
щих веществ равны их концен­
трациям на выходе из реакто­
ра. Строгая реализация этих
идеальных режимов недости­
жима, но в производстве стре­
мятся приблизиться к этим ре­
жимам.
На рис. 2.19 представлено изменение числа молей вещества,
реагирующего за единицу времени вдоль реактора, длиной Z,
причем число молей вещества А*, подаваемых в начало реак­
ционной зоны в единицу времени обозначено к ак поА*.
Общие кинетические уравнения химических реакций в потоке
можно получить, пользуясь методами гидродинамики. Уравнения
применимы к реакциям тех же типов, какие были рассмотрены
дл я процессов периодического действия. При этом вводится по­
нятие стационарного состояния.
Состояние в потоке, устанавливающееся при постоянстве
количества исходных веществ, характеризующееся тем, что
концентрации в каждом данном сечении со временем не из­
меняются, называется стационарным состоянием.
Общий вывод уравнения для скорости химической реакции
в режиме идеального вытеснения в потоке в трубчатом реакто­
ре довольно сложен и дается в курсах д л я химиков-технологов,
но уравнение д л я стационарного состояния довольно простое и
имеет вид:
рdl = dV,
где р — площадь сечения потока; I — длина; V — объем про­
странства, где протекает реакция.
Д л я режима идеального перемешивания в стационарном со­
стоянии уравнение д л я скорости химической реакции выражает-
nAi
О
I
Рис. 2.19. Изменение числа молей
па{реагирующего вещества вдоль
длины I реактора в режимах:
1— идеального вытеснения; 2—иде­
ального перемешивания
197

Рис. 2.20. Зависимость числа молей вещества па<, выходящего из ре­
актора в единицу времени от длины I реактора при одинаковых ско­
ростях подачи и одинаковых температурах:
1—режим идеального вытеснения; 2 —режим идеального перемешивания
ся через объемную скорость ввода веществ Vi и скорость отбора
веществ на выходе из реактора У%:
_
С0кУ\ - СкУъ
V
V*
где соа<— концентрация вещества А{ на входе в реактор; сд< —
концентрация его на выходе из реактора; Vp — объем реагиру­
ющей смеси, который при стационарном состоянии постоянен.
Эти общие уравнения для двух режимов используются для всех
видов обратимых и необратимых реакций как в гомогенных, так
и в гетерогенных системах.
Отклонения от идеальных режимов приходится учитывать
введением эмпирических поправок. На практике реакторы иде­
ального перемешивания целесообразно соединять последователь­
но, тогда можно получить выход продуктов, близкий к режиму
идеального вытеснения (рис. 2.20).
2.5 . КИНЕТИКА ТОПОХИМИЧЕСКИХ РЕАКЦИИ
Топохимическими называются реакции, проходящие на
поверхности твердых ф а з и распространяющиеся в объем
твердой фазы посредством диффузии.
К топохимическим реакциям относятся прежде всего реак­
ции, происходящие с участием твердого тела. Кинетика про­
цессов с участием твердых веществ существенно отличается от
198

кинетики реакций, протекающих в других фазах. Ее особенно­
сти обусловлены прежде всего пространственной локализацией
реакции. Процессы переноса в твердом теле протекают крайне
медленно. Твердое тело в химической реакции обычно прояв­
ляет свойства системы «с памятью»: вносимые самой реакци­
ей изменения реакционной способности «фиксируются» и вли­
яют на дальнейший ход реакции. Этот эф ф ек т обычно предпо­
лагает нестационарное протекание реакции, что влечет за собой
необходимость применения специальных методов кинетического
анализа. Приемы такого анализа будут рассмотрены на примере
реакции газа с твердым телом. В основе изучения кинетических
закономерностей химических реакций с участием твердого тела
л еж ит предположение, которое основано на концепции о лока­
лизации протекающей реакции в области поверхности раздела
твердых фаз (реагента и продукта реакции), характеризующей­
ся повышенной реакционной способностью. При контакте газо­
образного или жидкого компонента с поверхностью твердого ре­
агента в начале процесса твердый продукт отсутствует (а следо­
вательно, отсутствует и поверхность раздела твердых фаз), ре­
акция протекает с весьма малой скоростью (индукционный пери­
од). Если при реакции с газом образуются нелетучие продукты
реакции, а при реакции в жидкости продукты реакции нераство­
римы, то со временем на поверхности твердого тела образуются
ядра (зародыши) новой фазы.
Ядро фазы твердого продукта — это совокупность ча­
стиц твердого продукта с его собственной кристаллической
структурой, отличной от структуры твердого реагента.
При появлении ядер продукта реакции возникает поверхность
раздела твердых ф аз. Ядра быстро растут. Скорость реакции
возрастает со временем, что обусловлено как возникновением
новых ядер, так и (главным образом) ростом уже образовав­
шихся, при котором растет и поверхность раздела твердых ф аз
(рис. 2.21.) Поверхность раздела растет до тех пор, пока рас­
тущие ядра не соприкоснутся и не начнут перекрываться друг
другом. Скорость реакции проходит через максимум, следуя за
изменениями поверхности раздела твердых ф аз. Завершаются
эти процессы образованием сплошного слоя твердого продукта.
При этом наблюдаемая скорость реакции уменьшается часто в
более сильной степени, чем поверхность раздела, в связи с появ­
лением дополнительной медленной стадии —диффузии реагиру­
ющего газа или жидкости через слой твердого продукта. Поэто­
му наблюдаемая скорость реакции с участием твердых веществ
199

Газовая фаза
изменяется во времени по до-
:
вольно сложному экстремаль-
Рис. 2.21. Модель сечения твер-
твердого продукта ре-
дого реагента с растущими сфе- акции, изменением во време-
рическими ядрами твердого про- ни размеров реакционного про­
факторов. Наблюдаемая кинетическая кривая такой реакции со­
держит информацию о совокупности процессов различного ти­
па, д л я описания которых требуются разные модели. Молеку­
лярные объемы твердых ф аз реагента и продукта в общем слу­
чае различны, поэтому реакция в «доядерный» период и само
образование ядер должны сопровождаться существенной дефор­
мацией кристаллической решетки твердого реагента. В связи с
этим очевидно, что образование ядер фазы твердого продукта
должно происходить в тех местах поверхности, где энергетиче­
ские затраты минимальны. Такими местами могут являться раз­
личного рода дефекты поверхности, выходы дислокаций на по­
верхность кристалла и другие места. Поскольку концентрация
этих мест ограничена, возникли представления о потенциаль­
ных центрах образования ядер новой фазы, постепенно исчер­
пывающихся по мере протекания реакции. Такие представления
с кинетических позиций требуют учета уменьшения количества
потенциальных центров в ходе реакции в результате их погло­
щения растущими ядрами, что дополнительно усложняет кине­
тические модели процесса. Д л я изучения кинетики образования
ядер фазы твердого продукта предположим, что на поверхности
твердого те л а имеются потенциальные центры ядрообразования,
концентрация zo, которых изменяется за счет процесса образо­
вания ядер. Д л я упрощения будем рассматривать процесс обра­
зования ядер новой фазы только для реакции в системе «газ —
твердое тело». Обозначим удельную скорость (на один потенци­
альный центр) образования ядер ууд = k 'f(c r). Скорость образо­
вания ядер будет равна
где N — число ядер; S — поверхность раздела ф аз при на­
чальном условии Nq = 0. Интегрирование уравнения (2.47) лег­
ко осуществить, если ууд не зависит от времени. Поскольку ууд
по определению является функцией концентраций газообразных
ному закону, характер кото­
рого определяется особенностя­
ми процесса образования ядер
дукта
странства — поверхности разде­
ла твердых фаз и рядом других
(2.47)
200

компонентов реакционной смеси и температуры, указанное усло­
вие выполняется, если реакцию проводить изотермически и при
постоянном составе газовой смеси. В этом случае, интегрируя
(2.47), получим:
N=z0S
Тогда д л я скорости образования ядер будем иметь:
dN
dx
= t/w2dSe^.
(2.48)
(2.49)
Уравнение (2.49) называют экспоненциальным законом обра­
зования ядер. Оно описывает кинетику процесса для довольно
широкого круга экспериментально изученных систем. Другим
уравнением кинетики образования ядер фазы твердого продук­
та является «степенной закон», имеющий вид:
dN
dx
= ахЬ
где а и 6 — константы. Уравнения экспоненциального и степен­
ного законов являются основными уравнениями кинетики обра­
зования ядер, несмотря на наличие значительного числа дру­
гих, иногда более строгих. Н а основе экспоненциальной или сте­
пенной функции, имея в распоряжении д в а варьируемых пара­
метра, практически можно описать почти любую эксперимен­
тальную кривую. В рамках изложенных выше представлений
наблюдаемая скорость реакции с участием твердого вещества
определяется главным образом процессами на поверхности ра з­
дела твердых фаз. З ад а ча кинетического описания такой систе­
мы должна включать динамику образования и изменения этой
поверхности. Прямые экспериментальные измерения показыва­
ют, что скорость роста поверхности раздела твердых фаз в про­
цессе образования ядер новой фазы постоянна, за исключени­
ем краткого начального периода, которым можно пренебречь
при кинетическом описании. В ряде случаев кинетическая мо­
дель топохимических реакций может быть относительно про­
стой. Так обстоит дело, например, если я д р а возникают прак­
тически мгновенно в начале реакции. В таких случаях экспе­
риментальные данные описываются более простыми уравнени­
ями. Приближенные уравнения указанного типа получили зн а­
чительное распространение. Рассмотрим некоторые из наиболее
употребляющихся простых уравнений. Довольно часто применя­
ется уравнение, впервые предложенное А. Н. Колмогоровым д л я
201

процессов кристаллизации и используемое в кинетике реакций с
участием твердых веществ под названием уравнения Ерофеева,
х—\
—
е
-кхп
где х — степень превращения; к и п — константы. Основное до­
пущение при использовании данного уравнения — одинаковые
вероятности реакции д л я всех частиц исходного твердого тела
(вероятность реакции вводится к ак степенная ф унк ц ия време­
ни). Поскольку кинетическая кривая реакции с участием твер­
дых веществ часто качественно имитирует кинетическую кри­
вую автокаталитической реакции, могут быть использованы и
соответствующие кинетические уравнения автокаталитических
процессов, например уравнения вида:
dx
dx
= кх{1—я).
Помимо приведенных выше существует еще много вариантов
упрощенных моделей. Из них наиболее общими описаниями яв­
ляются уравнения, предложенные С. 3. Рогинским и Е. И. Шульц.
Первое из них относится к начальному периоду реакции — пе­
риоду роста скорости. Представим себе, что все я д р а возникли
в начале реакции. Тогда в дальнейшем кинетика реакции бу­
дет определяться только их ростом и перекрыванием. Отсечем
начальный период реакции, когда перекрыванием яд ер можно
пренебречь (степень превращения твердого реагента в этот пе­
риод составляет « 0,3). Д л я ядер сферической, кубической и
других ф орм наблюдаемая скорость реакции будет пропорцио­
нальна поверхности раздела ф аз, т. е. квадрату радиуса, а коли­
чество превращенного вещества п п — объему ядер, т. е. кубу ра­
диуса. Тогда д л я каждого отдельного растущего ядра, а значит,
и дл я всех яд ер наблюдаемая скорость реакции пропорциональ­
на количеству превращенного вещества в степени
о
dnn _
з
—г
ьИп '
dx
(2.50)
Величина к в уравнении (2.50) описывается выражением
к=
'18хМ2
—
2 УУЛ’
(2.51)
где р — плотность; М — молярная масса твердого продукта ре­
акции. Второе уравнение Рогинского —Шульц относится к ки­
нетике реакции в период снижения ее наблюдаемой скорости.
202

Если считать, что на каждом кристалле твердого реагента обра­
зовался сплошной слой твердого продукта и что скорость реак­
ции по-прежнему пропорциональна поверхности, то эта поверх­
ность сокращается по мере «сжатия» реагента, т. е. по мере ре­
акции. Для кристалла сферической формы аналогично уравне­
нию (2.50) можно записать:
~
= к:(а-п)§,
(2.52)
ах
где а — начальное количество твердого реагента; и — текущее
количество превращенного твердого реагента. Уравнение (2.52)
известно под названием «уравнение сжимающейся сферы». По­
сле интегрирования (2.52) получим:
I
I
аз -(а-п)з =кх.
(2.53)
1
Разделив обе части равенства на а з, придем к выражению:
1-(1-х)5 =*4,
которое часто успешно применяется д ля описания кинетики ре­
акций с участием твердых веществ на участке снижения скоро­
сти реакции. Широкая применимость этого уравнения связана с
тем, что такая же зависимость будет наблюдаться для кристал­
ла любой формы, лишь бы эта форма не изменялась по мере
роста слоя продукта и «сжатия» исходного кристалла. При этом
значение к в уравнениях(2.52) и (2.53) определяется выражени­
ем (2.51). Реакции газа с поверхностью могут быть самостоя­
тельным процессом в случае, когда по тем или иным причинам
реакция не может проникнуть в объем твердого тела. Почти все
стадии гетерогенно-каталитического процесса представляют со­
бой различные реакции газа с поверхностью твердого тела. Эти
же реакции выступают как гетерогенные стадии в газофазных
радикально-цепных процессах. При контакте газа с поверхно­
стью начальная скорость реакции пропорциональна концентра­
ции реакционноспособных частиц на поверхности и вероятности
реакции отдельной частицы. Затем скорость реакции снижается
по мере расходования реакционноспособных частиц и образова­
ния кластеров до значений, определяющихся исчезновением де­
фектов с поверхности за счет их диффузии в объем твердого
тела, и остается близкой к стационарной (или нулевой, если об­
мен с объемом отсутствует). С образованием ядер твердой фазы
продукта начальный период реакции завершается, и наблюдает­
ся период возрастания скорости, что характерно д ля «объемной»
реакции.
203

На рис. 2.22 представлена кинетика восстановления С112О ок­
сидом углерода. Нисходящая кривая отвечает процессам обра­
зования дефектов и кластеров дефектов на поверхности окси­
да, стационарный участок соответствует диффузионному обме­
ну между поверхностью и объемом С112О, а восходящая ветвь
соответствует началу образования и роста ядер ф азы твердого
продукта. До начала роста скорости реакция протекает без об­
разования ф а з в гомогенной области. Существует еще два ти­
па кинетических кривых взаимодействия газа с поверхностью
твердого тела. Если образования ядер фазы твердого продукта
по тем или иным причинам не происходит, реакция остается в
гомогенной области. Такую картину можно наблюдать, напри­
мер, д л я оксидов цинка, ванадия. Возможен также случай, ко­
гда реакция не проникает в подповерхностные слои, что чаще
всего обусловлено диффузионным торможением (времена реак­
ции существенно меньше времен диффузии при восстановлении
специально приготовленного оксида железа). В этом случае в
пределах поверхности монослоя может быть реализована пол­
ная кинетическая картина реакции газа с твердым телом: обра­
зование дефектов и кластеров дефектов, образование ядер фазы
твердого продукта, их рост и слияние в сплошной слой твердого
продукта. При этом на поверхностях твердых ф аз образуются
наномерные по толщине новые фазы .
На рис. 2.23 представлена зависимость скорости гетероген­
ного восстановления оксида железа оксидом углерода от сте­
пени восстановления поверхности, демонстрирующая кинетику
Рис. 2.22. Кинетическая кри­
вая начальной стадии восстанов­
ления С112О оксидом углерода
(7,5 мол. % в Не)
Рис. 2.23. Кинетика восстановле­
ния при температуре 453 К по­
верхности оксида железа оксидом
углерода (3 мол. % в Не)
204

реакции в случае образования фаз наномерной толщины на по­
верхности твердого реагента. После минимума скорости реакции
наблюдается рост скорости до максимума и затем снижение, и
все это в то время, когда реакция едва захватывает половину
поверхности. Кинетику реакций газов с поверхностью твердых
тел можно проиллюстрировать приведенными выше частными
случаями восстановления оксидов. Восстановление может быть
представлено следующей совокупностью процессов: 1) образова­
ние кислородной вакансии при удалении кислорода; 2) ее «зале­
чивание» («возвращение кислорода»), если в системе есть окис­
литель; 3) исчезновение вакансии за счет ее диффузии в объем
твердого тела (удобно говорить о диффузии вакансий, не забы­
вая при этом, что на самом деле происходит д иффузия иона
кислорода из объема на поверхность — соответственно вакансия
«проваливается» в объем). Если окислителя в системе нет, то
процесс ограничивается образованием вакансий и их диффузи­
ей в объем твердого тела. Напишем уравнение баланса вакансий
на поверхности:
noS^ =v-г/; 0(0)=0,
ат
(2.54)
где по — число частиц (например, ионов кислорода в оксиде) на
единице поверхности; 0 — безразмерная концентрация вакансий
в до л ях от no; v — скорость химической реакции; v f — скорость
диффузионного «стока» вакансий в объем.
Если кинетика изучается с помощью импульсного метода, ко­
гда между импульсами, проходящими за время т, протекает неко­
торое время t ) в течение которого диффузионный обмен продол­
жается, а реакция — нет, то вместо уравнения (2.54) следует
записать:
по5— = г>- г>'у,
(2.55)
(г+т)
где у = —- — с тем же начальным условием, т. е. 0(0) = 0. Оче­
видно, что наблюдаемая скорость образования вакансий — ско­
рость химической реакции — должна быть пропорциональна ко­
личеству оставшихся ионов кислорода
v = ^уД(1" 0)по5,
(2.56)
где v отнесена к одной вакансии, т. е. представляет собой веро­
ятность реакции вакансии з а единицу времени.
Уравнение дл я скорости диффузионного обмена между по­
верхностью и объемом твердого тела (т. е. скорость «стока» ва-
205

кансий) значительно сложнее, чем уравнение диф фузии , пред­
лагаемое д л я этой задачи.
Уравнение диффузии применимо, когда времена процесса до­
статочно велики, чтобы он захваты вал статистическое количе­
ство слоев в направлении диффузии. В нашем случае можно го­
ворить о переходе вакансии в смежный второй слой, в третий,
быть может, в десятый, но никак не в миллионный, тем более
что в обычных катализаторах, например, таких слоев от поры
до поры всего несколько десятков.
Следовательно, необходимо найти такой эквивалент, который
позволит оценить скорость «стока» вакансий вместо уравнения
диффузии. Д л я упрощения примем, что во втором слое коли­
чество вакансий настолько мало, что их концентрацию можно
считать равной нулю. Чтобы получить скорость «стока» вакан­
сий в объем, вероятность перехода вакансии из первого слоя во
второй (а она равна удельной скорости диффузии) необходимо
умножить на число вакансий и на нормировочный множитель
uqS, т. е.
v ' = v'yA0Qn0S.
(2.57)
Теперь, подставляя (2.56) и (2.57) в (2.55), получим уравнение,
содержащее только одну зависящую от времени величину 0:
§=^д(1-0)-^удТ0-
(2-58)
Интегрируя (2.58), после несложных преобразований найдем
е=—
—
Г1 _ е-Кд+Кд-')!
%ц+уууД 1-
-
I
ИЛИ
0-
_
_
Ъя__ Г1_ е-(иУДгЧд(<+т))1
иУД+ Т^УД \-
J
Подставляя значение 0 в (2.56), получим выражение для на-
блюдаемой скорости реакции
v=
^уд
vy* + yv:
d*
уд + Ууде
■(куд+уг)' )t)
(2.59)
При х = 0 уравнение (2.59) дает начальную скорость реакции
vq = vyan 0S,
и окончательно получаем
г>уд = vq
Уьуя + ^УД1“Кд+ГО*
уи'д + и.УД
(2.60)
206

Т=423КРсо=4кПа
Уравнение (2.60) можно та кж е
преобразовать к параметриче­
ской форме, в которой его удоб­
но применять дл я сопоставле­
ния с экспериментальными д ан ­
ными
п_
Уууа
,
х
^УД+У^уд
(2 61)
V0-V
\•j
^(ья+ууудУ
Применимость
уравнения
(2.61) д л я описания кинетики
реакции восстановления окси­
да меди СиО иллюстрирует
рис. 2.24. Из уравнения (2.61)
могут быть найдены значения
удельной скорости реакции (на один центр поверхности) и
характеристика диффузионной проницаемости поверхностного
слоя твердого реагента.
§ 1. Твердофазные реакции
Твердофазными реакциями называют топохимические
реакции, в которых как исходные вещества, так и продукты
реакции являются твердыми веществами.
Твердофазные реакции используются при получении керамиче­
ских материалов, материалов для электронной техники, защит­
ных, упрочняющих и жаропрочных покрытий. Твердофазные
реакции происходят в гетерофазных системах, которыми явля­
ются как исходные вещества, так и продукты реакции и про­
текают, как правило, через множество промежуточных реакций
с образованием нестойких соединений. Так как в твердом теле
все составляющие их частицы (молекулы или атомы и ионы)
связаны химическими связями по всему кристаллу, то число ча­
стиц, вступающих в элементарный химический акт, огромно из-
за кооперативного воздействия. Поэтому скорости химических
реакций определяются энергией связей между множеством ча­
стиц. Свободная энергия, как известно — это алгебраическая
сумма энтальпии и энтропийного терма. Часто именно измене­
ние энтропии является движущей причиной реакций твердых
Рис. 2.24. Применимость уравне­
ния (2.61) к описанию кинетики
восстановления поверхности ок­
сида меди(П) оксидом углерода
207

фаз. Так, например, изменение энтальпии и энтропийного тер­
ма при стандартных условиях д л я реакции Fe0 +Fe203 —►Fe304
составляют 23 кДж/моль и 6,5 кДж/моль соответственно. При
этом следует учитывать, что с повышением температуры энтро­
пийный терм возрастает быстрее, чем энтальпия. Твердофазные
реакции — реакции топохимические, так как реакционные зо­
ны в них локализованы на их поверхностях со всеми вытекаю­
щими отсюда последствиями, которые были рассмотрены выше,
т. е. с образованием ядер продуктов реакции и их диффузии в
глубь твердой фазы. Поэтому скорость диффузии определяет в
основном скорость реакции. При смыкании ядер на поверхности
с образованием плотной пленки диффузия замедляется и может
практически прекратиться. В результате скорость реакции па­
дает практически до нуля.
Начальная скорость реакции твердых ф аз сильно зависит от
величины их поверхностей. Поэтому перед проведением реак­
ции исходные фазы должны быть тонко размолоты, перемеша­
ны и спрессованы. Когда ж е наступает остановка в прохождении
реакции по причине затруднения диффузии, приходится прибе­
гать к повторному размолу и прессованию. Последовательным
повторением этих операций удается реакцию довести до получе­
ния достаточно чистого продукта реакции.
Может быть много типов твердофазных химических реакций
с образованием одного или нескольких твердых продуктов, с об­
разованием твердых продуктов с выделением газов и др. Реак­
ции могут быть практически необратимыми и обратимыми. По­
этому кинетика твердофазных реакций сложна и еще недоста­
точно разработана. Д ля количественной оценки вводят понятие
Ni
степени превращения щ = —---- , где Ni и iV tHCx — число молей
^мисх
г-го исходного реагента соответственно в начале взаимодействия
и к моменту времени т. На рис. 2.25 представлены примерные
кинетические кривые с участием одного твердофазного реаген­
та или продукта. В самом начале скорость реакции мала (ин­
дукционный период), далее скорость резко возрастает и прохо­
дит через максимум в точке к и затем снижается практически
до нуля, т а к что зависимость степени превращения о т времени
имеет S-образный характер. Индукционный период обусловлен
стартовыми изменениями системы: переориентацией частиц на
поверхностях, искажениями кристаллической решетки под дей­
ствием активации частиц, диффузией вдоль поверхности и т. п.,
что ведет к улучшению контакта между реагирующими части­
цами и образованию многоцентровых связей и увеличению ре-
208

Рис. 2.25. Степень твердофазного превращения как функция време­
ни (а); и степень твердофазного превращения как функция производ­
ной степени превращения по времени (б)
акционной зоны. Период роста скорости определяется образова­
нием и ростом ядер продуктов реакции в реакционной зоне на
поверхности. При этом могут образовываться твердые раство­
ры^ которые затем распадаются с образованием ядер продуктов
реакции. Далее скорость реакции снижается в связи с тем, что
растущие ядра продуктов реакции сливаются и закрывают по­
верхность исходной фазы , затрудняя диффузию вглубь.
Теория твердофазных реакций была разработана Е. Вагнером
и В. Шоттки. Они рассматривали реакцию Ат + Вт = Ст в пред­
положении, что исходные фазы и продукт реакции имеют пре­
имущественно ионный характер связи. Поскольку реальные кри­
сталлы содержат вакантные катионные и анионные узлы (дис­
локации) вследствие некоторого отклонения от стехиометрии, а
такж е вследствие наличия разного рода примесей, поверхность
кристалла можно рассматривать как сплошную дислокацию. На­
личие дислокаций создает возможности д л я миграции ионов в
ближайшие междоузлия и вакантные узлы. При отсутствии внеш­
него воздействия электрических и магнитных полей миграция
происходит беспорядочно подобно броуновскому движению. При
этом постулируются следующие условия:
скорость реакции лимитируется диффузией ионов через слой
образующегося продукта;
слой продукта компактен и содержащиеся в нем неравновес­
ные дефекты (дислокации, границы ядер) не вносят определяю­
щего вклада в подвижность ионов;
реакции на границе ф а з протекают значительно быстрее, чем
процессы диффузии через слой продукта. Поэтому на грани-
209

цах ф аз устанавливается локальное термодинамическое равно­
весие;
отдельные ионы движутся в реакционном слое независимо
друг от друга, так что в любом поперечном слое сохраняется
электронейтральность.
Поток ионов г-го вида в единицу времени через единицу по­
верхности реакционного слоя выражается уравнением:
_
DiCiZi di\i
*
RTdx’
где Di — коэффициент диффузии г-х ионов; с* — их концентра­
ция; Zi — з а р яд г-ro иона; Т|; — электрохимический потенциал
г-х ионов. Очевидно, что образование продукта реакции проис­
ходит на обеих границах ф аз, что объясняется противодиффу-
зией ионов в обе фазы. В этом случае толщина реакционного
слоя Д х определяется уравнением:
Ах2=2kxAVx,
где Д V — относительное увеличение объема продукта реакции
при переносе одного моля ионов; х — время; кх — константа ско­
рости реакции. Несмотря на грубые приближения, теория Ваг­
нера—Ш оттки позволяет рассчитывать константы скорости с
достаточной точностью. В табл. 2.3 приведены рассчитанные
и экспериментальные константы скорости реакций образования
никелевой и кобальтовой шпинелей из оксидов.
Однако эта теория не может объяснить многие наблюдаемые
факты. Так, например, скорости твердофазных реакций резко
возрастают в момент полиморфного превращения одной из ис­
ходных ф аз (эффект Хедвалла).
Известно, что a -модификация оксида алюминия реагирует с
оксидом магния лишь выше 1723 К, тогда как у-оксид алюминия
реагирует при более низкой температуре, так как при нагрева­
нии он переходит в корунд, и в момент перестройки кристалли­
ческой решетки образуется множество дислокаций и происходит
большое увеличение поверхности. В то же время у-модификация
Таблица 2.3
Экспериментальные и рассчитанные константы скорости реакций
кх,см2/с
NiO + O 2O3 —►ЭДСггСЦ СоО + СГ2О3 —►С0СГ2О4
Эксперимент
Расчет
5.7 -
1<Г12
3.8 -
Ю” 12
6,7 -Ю'11
7,5- 10"11
210

оксида алюминия, полученная различными методами, сильно
отличается по скорости реакции с оксидом магния. Например
у-АЬОз, полученный из гидроксида, реагирует медленнее, чем
Y-AI2O3, полученный прокаливанием алюмоаммонийных квас­
цов. Такая зависимость скоростей тведофазных реакций от пре­
дыстории образования исходной фазы не может быть объяснена
в примитивной модели В агнер а—Шоттки.
Приближение об ионном характере связи в твердых оксидах
слишком упрощенное. В действительности необходимо учиты­
вать квантово-химические представления о химической связи.
И взаимодействие, и миграцию атомов в кристаллической ре­
шетке следует рассматривать через промежуточное образова­
ние многоцентровых связей, образующихся вследствие актива­
ции атомов и молекул. Расчет может быть проведен на примере
кластера достаточно представительного размера, чтобы его гра­
ницы не вносили существенных погрешностей при расчете.
Рассмотренные закономерности относятся к медленным твер­
дофазным реакциям, скорость которых определяется диффузи­
ей частиц с поверхности ф а з в объем. Однако существуют слу­
чаи, когда твердофазная реакция быстро проходит до конца - за
время всего от долей секунды до нескольких десятков минут. Та­
кие реакции относят к быстротекущим твердофазным химиче­
ским реакциям. Очевидно, что механизм распространения таких
реакций по поверхности ф а з и затем в их объем иной. Повыше­
ние скорости реакции связано с уменьшением времени релакса­
ции трансформационных и транспортных процессов на всех эта­
пах взаимодействия. В. В. Гусаров предложил модель механиз­
мов быстрых твердофазных химических реакций, основанную
на представлении об образовании между поверхностями реаги­
рующих фаз двухмерной жидкой эвтектики (двухмерные авто­
номные фазы). Переход твердофазной реакции в область быст­
рой реакции определяется температурой плавления двухмерной
автономной фазы Тд(э) :
2д(э) УГ(э)>
где Т(э) — температура плавления автономной фазы («эвтекти­
ческая температура»); у — параметр, зависящий от типа соеди­
нения. В табл. 2.4 приведены значения параметра у для некото­
рых оксидов.
Таким образом, термодинамические свойства постулируемых
автономных двумерных ф аз должны существенно отличаться
от их трехмерных аналогов, в том числе температуры плавле­
ния двухмерных автономных фаз, и, по-видимому, должны быть
211

Таблица 2.4
Экспериментальные и
рассчитанные значения
параметра у для некоторых
оксидов
существенно ниже. Транспорт
реагентов в подобных системах
происходит путем распростра­
нения двухмерной автономной
фазы по поверхностям зерен ре­
агирующих фаз, а также по
трещинам и порам в объеме зе­
рен. При этом количество двух­
мерной автономной ф азы вос­
полняется за счет транспорта
материала зерен реагирующих
фаз. Значительное влияние на
скорость транспорта двухмер­
ных автономных ф аз должны
иметь такж е капиллярные силы, приводящие к расклиниваю­
щему действию и к расширению трещин в зернах реагирующих
фаз.
Вещество
Ypac
УЭК
Н20
0,65 0,66
ВО,,5
0,78 0,74
АЮ,,5
0,65 0,69
SiC>2
0,75 0,70
FeO,,5
0,54 0,62
2.6 . БЫСТРЫЕ РЕАКЦИИ И РЕЛАКСАЦИЯ
К быстрым реакциям относятся прежде всего многочислен­
ные реакции между ионами в растворах, которые, как ранее счи­
талось, протекают «мгновенно». Быстрые реакции характери­
зуются высокими значениями констант скоростей: д л я реакций
первого порядка к = 102 ... 108 с-1 и выше; для реакций второго
порядка к = 102 . .. Ю10л-моль"1*с“1. Энергии активации быстрых
реакций очень малы и обычно составляют 10 —14 кД ж/моль.
Для описания быстрых реакций может быть использован аппа­
рат теории столкновений. В качестве примеров быстрых реакций
в растворах можно привести рекомбинацию ионов гидроксила и
гидроксония в водном растворе:
Н30 ++ ОН" —>2Н20
или взаимодействие иона Fe3+ с роданид-ионом NCS':
Fe3+-f 3NCS“ —>Fe(NCS)3
Константа скорости последней реакции превышает 104 л-моль"1 х
х с " 1. Высокие скорости рассматриваемых процессов встречали
определенные инструментальные затруднения при количествен­
ной оценке кинетических параметров этих процессов. Однако в
последнее время были разработаны методы исследований, поз­
воляющие значительно расширить диапазон измеряемых скоро­
стей реакций. В ряде случаев может быть использован эффект
212

замедления реакции с понижением температуры. Известны из­
мерения скоростей в растворах при температурах до 159 К, когда
реакция протекает в 106 раз медленнее, чем при 298 К. Низкие
температуры могут быть использованы и в сочетании с другими
методами исследования, такими как флеш фотолиз, ЯМР, ЭПР
и др. Из специальных методов для быстрых реакций эфф ек­
тивными оказались различные струевые методы: методы непре­
рывной струи, ускоренной струи и остановленной струи. Напри­
мер, методами остановленной и ускоренной струи была измерена
скорость разложения пероксида водорода ферментом каталазой
(к = 5 ■107л • моль"1 • с-1). К кинетическим методам исследова­
ния быстрых реакций относится так называемый релаксацион­
ный метод, суть которого заключается в следующем. Если на
систему, находящуюся в равновесии, оказывать какое-либо до­
статочно резкое воздействие (например, путем изменения темпе­
ратуры или давления), то система перейдет в новое равновесное
состояние. Время этого перехода зависит от скоростей прямой и
обратной реакций.
Самопроизвольный возврат системы в первоначальное
равновесное состояние после импульсного воздействия на
нее внешней силы называется релаксацией, а время возвра­
т а системы в первоначальное равновесное состояние назы­
вается временем релаксации.
Время релаксации связано с константами скоростей реакций.
Рассмотрим обратимую реакцию первого порядка
*1
Пусть в системе установилось равновесие, характеризующееся
концентрациями [А*] и [В*]. Затем резко изменились условия
для протекания реакции. З а время х система перешла в новое
равновесное состояние [А**] и [В**]. В момент наблюдения х те­
кущие концентрации [А] и [В] пока еще отличаются от новых
равновесных концентраций на величину х :
я = [А]- [А**]=[В**]- [В].
Скорость прямой реакции, ведущей к новому состоянию рав­
новесия, в момент времени т, определяется соотношением
dx
^[AJ-^B].
(2.62)
213

В новом состоянии равновесия скорость прямой и обратной
реакций станут равны:
А;1[А"]-МВ**] = 0.
(2.63)
Объединяя уравнения (2.62) и (2.63), можно показать, что
^ =(к\+к2)х.
(2-64)
ах
В результате интегрирования уравнения (2.64) с учетом того,
чток=к\+
получим
х = хое~кх.
(2.65)
Уравнение (2.65) описывает процесс установления нового равно­
весия в системе. В нем хо означает отклонение от равновесных
концентраций непосредственно после изменения первоначаль­
ных условий. Скорость установления нового равновесия опре­
деляется константой /с, являющейся суммой констант скорости
X1
прямой и обратной реакций. Когда кх = 1, то — =
т. е. раз-
хо
е
ность между текущими и равновесными концентрациями умень­
шилась в е раз. Этот промежуток времени т и есть время релак­
сации. Очевидно, что
т-1 =к =к\+/С2,
т. е. время релаксации является величиной, обратной сумме кон­
стант скоростей.
По численному значению величина х близка к времени полу­
превращения Xi/2) так как
^
= fct1/2 = ln2 = 0,693.
X
Известно такж е, что обратная величина константы скорости ре­
акции первого порядка равна средней продолжительности жиз­
ни реагирующих молекул в данны х условиях. Поэтому, вводя
средние продолжительности ж изни молекул А и В, получаем:
Рассмотрим теперь более сложную реакцию смешанного по­
рядка — второго порядка в прямом направлении и первого по­
рядка в обратном:
к2
A +B-t
----- >С
ki
214

Исходные равновесные концентрации веществ обозначим как [А]*,
[В]* и [С]*. Равновесные концентрации, соответствующие новым
резко измененным условиям, обозначим соответственно как [А**],
[В**] и [С**]. Так же как и в предыдущем случае при рассмотре­
нии обратимой реакции первого порядка, в некоторый наблюда­
емый момент времени т после изменения условий текущие дей­
ствительные концентрации А, В и С отличаются от новых рав­
новесных концентраций на величину гг:
х = [А]-[А-] = [В]-[ВН = [С*1-[С].
Наблюдаемая скорость реакции в этот момент выражается как
-
^адм-чс].
В условиях нового равновесия скорости прямой и обратной ре­
акций равны, т. е.
ki [А**] [В**] - [С**] = 0.
Объединяя полученные уравнения и пренебрегая величиной х 2
ввиду ее малости, можно показать,что
dx
dx
M [A*1 + [B**])+fc2 х.
(2.66)
Поскольку дл я данного конкретного эксперимента величины [А**]
и [В**| постоянны, то вся величина в квадратных скобках урав­
нения (2.66) постоянна и может рассматриваться в некотором
приближении как константа скорости первого порядка (fc) урав­
нения, описывающего приближение системы к равновесию. В та­
ком случае по аналогии с предыдущим время релаксации опре­
деляется как обратная величина к:
х~1 = к = к1([А**] +[В**\)+к2.
Д л я определения констант скорости к\ и к 2 необходимо экспери­
ментально найти значение х дл я ряда концентраций ([А**] + [В**])
и вычислить константы из получаемой линейной зависимости.
З ад а ч а упрощается, если равновесие сильно сдвинуто в сторону
продуктов реакции, например при реакции нейтрализации:
.
к2
Н30++0Н-^=±2Н20
h
215

В таком случае константа Л:2 пренебрежимо мала и уравнение
для записи времени релаксации упрощается:
<■' = *!«А"]-|В”]).
При практическом применении релаксационных методов исполь­
зуют различную технику эксперимента.
В методе температурного скачка резко изменяют темпера­
туру раствора путем разряда конденсатора, заряженного до на­
пряжения ~ 100 кВ. Используя этот прием удается повысить тем­
пературу раствора на 2 .. .10 ° за 10-6 с. За дальнейшим установ­
лением равновесия следят с помощью различных методов: реги­
стрируя изменение электропроводности или ф иксируя фотомет­
рически изменение окраски реагирующих веществ или добав­
ленного индикатора и другими достаточно быстрыми методами,
такими как флешфотолиз, ЭПР, ЯМР.
В методе электрического и мп ульса используют внешнее элек­
трическое поле для резкого увеличения степени диссоциации
слабого электролита. Можно та к ж е использовать метод погло­
щения ультразвуковых колебаний, метод флеш фотолиза, ЭПР-
и ЯМР-методы. В качестве примера можно привести получен­
ные различными методами скорости одной из самых быстрых
реакций — реакции рекомбинации ионов гидроксония и гидрок­
сила. Для этой реакции к2 <£Lк\, поэтому
jk-
_______
i_______
1 т([0Н-] + [Н30 +]Г
Значение к \, определенное различными упомянутыми методами,
составляет 109 ... 1011 л •моль”1 •с”1. Ранее уже говорилось, что
кинетика многих быстрых реакций может быть описана форму­
лой, известной из простой теории столкновений в бимолекуляр­
ных реакциях:
Е
к—Z0e кг,
где Zo — частотный множитель, который равен ~ 3 • 1011 л х
х моль”1-с"1; Е —энергия активации. Реакция оказывается быст­
рой именно из-за малого значения Е (~ 10... 16 кД ж *моль”1).
Ниже приведены значения А:, вычисленные при различны х Е при
298 Кпоформуле к=10йexp(- ^ji)
Е, кДж-моль-1 ....... 67,2 60 48 33,6 19,2 (0)
к, л -моль-1
-с -1
10 102 104 106 108 1011
216

Константы скорости порядка Ю10л*моль-1* с-1 могут быть ин­
терпретированы как предельные, определяемые частотой встреч
молекул реагирующих веществ в результате диффузии. В рас­
творе, содержащем незаряженные частицы, в соответствии с з а ­
коном диффузии Фика число столкновений частиц А и В в 1 мл
за1сравно
v = 4я(£>а+ ^в)(^А +гв)папв,
где v — скорость реакции, равная числу столкновений и выра­
жаемая числом молекул, реагирующих в 1 мл за 1 с; Da и Db —
коэффициенты диффузии Da и Db молекул; га и г в — ради­
усы этих молекул; па и п в - числа молей молекул А и В со­
ответственно. Очевидно, что множитель, стоящий перед произ­
ведением чисел молей, представляет собой константу скорости
реакции (ко)> которая лимитируется диффузией:
ко=4ti(Z)a+Db)(га+Лв)
[мл*молекул-1
•с-1],
или в другой размерности:
= ^ООО(Da+-°в)(Га+Гв) [л 'моль_1 •с_1]•
Используя уравнение С то к са —Эйнштейна д л я коэффициентов
диффузии:
п
_
кТ
А
бЛГПГА И
в
бгслгв’
можно показать, что
к _ 2NAkT (гА+ гв)2_ 2кТ (гА+гв)2
D 3000т]
та^в
3000г|
та?в
[л•моль1*сх].
Полученное уравнение можно упростить, если принять, что г а =
= гв (т. е. различие в радиусах несущественно при проводимых
расчетах). Тогда
ОО'Т"»
к° = 3000л [Л'М0Ль1'С~Ч •
(2-67)
В соответствии с уравнением (2.67) константа скорости реак­
ции, лимитируемая диффузией, должна быть обратно пропор­
циональна вязкости растворителя, а энергия активации д о л ж ­
на совпадать с энергией активации вязкого течения, т. е. быть
малой величиной по сравнению с энергиями активации обыч­
ных реакций. Это приблизительно соответствует экспериментам.
Так, в воде при температуре 298 К вязкость Т| — 0,01 пуаз и
217

ко = 0,7* 1010 л •моль-1 •с"1, а в бензоле и хлороформе ко равны
соответственно 0,95 -Ю10 и 1,05 • Ю10л ■моль-1 *с-1 . Эти значения
близки к наблюдаемым на опыте значениям д л я очень быстрых
реакций незаряженных частиц. Так, например, константа скоро­
сти рекомбинации атомов иода имеет в различных растворите­
лях величину примерно Ю10 л • моль-1 • с-1 .
Если реагирующие частицы А и В представляют собой ио­
ны, то выражение для константы скорости реакции, лимити­
руемой диффузией, дополняется сомножителем, учитывающим
действие электростатических сил:
кр=
8RT 5
3000л е5- ! ’
с
^ве2
„
„
гдео= ———;е—зарядэлектрона;Z\кZq—кратностьза-
а
рядов ионов; е —диэлектрическая проницаемость растворителя;
а — расстояние сближения ионов (га + гв)> необходимое д ля ре­
акции.
2.7. ФОТОХИМИЧЕСКИЕ РЕАКЦИИ
Кванты видимого и ультрафиолетового света могут погло­
щаться электронными орбиталями атомов и молекул, что при­
водит к их возбуждению или д а ж е диссоциации на атомы или
радикалы.
Реакции, иницируемые квантами света, называются фо­
тохимическими реакциями.
Продукты фотохимической реакции могут накапливаться в кон­
центрациях, которые превышают термодинамически равновес­
ные. Образовавшиеся возбужденные продукты фотохимической
реакции могут вступать в химическое взаимодействие с други­
ми молекулами. Если фотохимическая реакция является лими­
тирующей стадией процесса, то скорость реакции не зависит или
слабо зависит от температуры.
Фотохимические реакции являю тся основой существования
жизни на Земле, так как свободная энергия солнечного излу­
чения преобразуется растениями в химическую работу по полу­
чению углеводов из диоксида углерода и воды.
Процесс фотохимического синтеза углеводов из диоксида
углерода и воды с участием хлорофилла растений называ­
ется фотосинтезом.
218

Фотосинтез —сложный многостадийный процесс, идущий под
действием света и катализируемый хлорофиллом и ферментами
растения. Его суммарную реакцию можно представить следую­
щей схемой:
6СО2 + 6Н2О = СбН^Об + 6O2
Энергия фотовозбужденных продуктов может рассеиваться в
виде света, если молекулы не успевают вступить в химическую
реакцию или если продукты химической реакции также полу­
чаются в возбужденном состоянии и не могут передать энергию
другим частицам или стенкам реактора.
Излучение света в результате химических реакций или в
результате отдачи энергии возбужденными молекулами или
атомами называется люминесценцией.
Испускание света фотовозбужденными молекулами или
атомами в результате их дезактивации называется флюо­
ресценцией.
Но некоторые молекулы и атомы при фотовозбуждении могут
переходить в метастабильное состояние и накапливаться в тече­
ние длительного времени (до одной секунды) и затем высвечи­
ваться, переходя в стабильное состояние.
Испускание света при переходе молекул и атомов из ме-
тастабильного состояния в стабильное называется фосфо­
ресценцией.
Фосфоресценция л еж ит в основе лазерного излучения. Неко­
торые химические реакции могут сопровождаться испусканием
света, если в результате химической реакции получаются про­
дукты в возбужденном или метастабильном состоянии. Это яв­
ление используется в мощных газовых лазерах (лазерное оружие)
Испускание света возбужденными или метастабильными
продуктами химической реакции называется хемилюминес­
ценцией.
§ 1. Законы фотохимических реакций
1. Фотохимическую реакцию могут вызывать лишь те из кван­
тов, которые могут поглощаться молекулами и атомами данной
химической системы.
219

2. Энергия, поглощающаяся в единицу времени, определяется
уравнением Ламберта—Вера:
I =Iq- Д ых = Л)(1- e_fcnI),
где / — толщина облученного слоя; п — число поглощающих мо­
лекул в единице объема; к — молекулярный коэффициент по­
глощения.
3. Количество продукта фотохимической реакции, образую­
щегося в единицу времени, пропорционально величине погло­
щенной световой энергии.
4. Скорость фотохимической реакции определяется уравне­
нием Вант-Гоффа:
dn_ I
~ dx~kh»'
5. Каждый поглощенный квант активирует одну молекулу.
Этот закон получил название «принцип фотохимической экви­
валентности Эйнштейна».
Отношение числа прореагировавших молекул к числу по­
глощенных квантов у называется квантовым выходом.
Отсюда скорость фотохимической реакции определяется урав­
нением:
<2-68>
Уравнение (2.68) — основное уравнение фотохимической кине­
тики. Первичные процессы всегда подчиняются принципу фото­
химической эквивалентности, но квантовый выход может быть
как равным, так и отличным от принципа эквивалентности. Это
объясняется тем, что фотовозбуждение может быть не един­
ственной стадией в механизме химического процесса, в частно­
сти, может происходить и дезактивация части фотовозбужден-
ных частиц.
Важнейшее применение фотохимии в технологии — фотогра­
фия. В фотографии используется фотохимическая чувствитель­
ность галогенидов серебра. Известно, что на свету галогениды
серебра быстро темнеют вследствие фотохимического разложе­
ния по схеме
AgCl+/iv —»Ag+
220

Отражаемый от объекта фотографирования свет, попадая на
фоточувствительную эмульсию, нанесенную на фотопленку, вы­
зывает фоторазложение галогенида серебра, содержащегося в
эмульсии. В результате на пленке получается скрытое изобра­
жение объекта, так как по принципу соответствия в результа­
те фотореакции зародыши металлического серебра выделяются
пропорционально интенсивности света, отраженного от объекта.
Далее экспонированная пленка подвергается процессу проявле­
ния, при котором используются химические восстановители д л я
восстановления серебра. При этом зародыши металлического се­
ребра, образовавшиеся при облучении, растут з а счет восстанов­
ленного серебра, и скрытое изображение на пленке становится
видимым. Далее необходимо удалить остатки галогенида сереб­
ра из эмульсии, чтобы прервать фотохимическую чувствитель­
ность фотопленки. Это достигается с помощью раствора тио­
сульфата натрия, в котором галогенид серебра растворяется бла­
годаря образованию растворимого комплекса серебра с ионами
тиосульфата:
AgCl + 2(S203)2-
- » [Ag(S20 3)2)]3_ + C r
Изображение фиксируется в виде негатива на фотопленке. З а ­
тем негатив облучается на просвет и переносится на фотобумагу
или на фотопленку. В результате этого светлые участки на нега­
тиве становятся темными на позитиве, поэтому на позитиве по­
сле его проявления появляется реальное изображение объекта.
Первоначальный фотографический процесс требовал слиш­
ком длительных экспозиий, так как фоточувствительность эмуль­
сий была мала. Это не позволяло фотографировать движущиеся
объекты. Повышение чувствительности было достигнуто путем
использования сенсибилизаторов.
Фотосенсибилизацией называется повышение фоточув­
ствительности фотоматериалов посредством добавления ве­
ществ, обладающих высоким фотовозбуждением и способ­
ных передавать возбуждение фотоматериалам.
В настоящее время фоточувствительность фотопленок удает­
ся повысить в тысячи раз и довести необходимое время экспози­
ции до миллисекунд. Это позволило использовать фотографию
для получения изображений очень короткоживущих объектов в
научных исследованиях и применить фотографию к быстро дви­
жущимся объектам, что привело к созданию кинематографии.
221

2.8 . МЕХАНОХИМИЧЕСКИЕ РЕАКЦИИ
При сверхтонком измельчении твердых веществ в специаль­
ных мельницах, называемых планетарными, происходит колос­
сальное увеличение поверхности частиц. Однако этим не исчер­
пываются наблюдаемые физико-химические явления. К о гд а раз­
меры частиц становятся соизмеримыми с элементарной ячейкой
(наноразмерные частицы), наблюдается кардинальное измене­
ние физико-химических свойств вещества (повышение раствори­
мости, аморфизация и др.) . Химическая активность сверхтон-
коизмельченного вещества резко повышается, возрастаю т ско­
рости химических реакций как между твердыми веществами,
так и между твердыми и жидкими фазами. В результате про­
исходят глубокие химические изменения состава и структуры
веществ.
Процесс сверхтонкого измельчения является не только про­
цессом увеличения поверхности, но и увеличением поверхност­
ной энергии, приводящей к изменению свободной энергии вслед­
ствие совершаемой работы.
Следовательно, с некоторого предела размеров частиц даль­
нейшее измельчение является уж е химическим процессом. По­
этому энергия, расходуемая на сверхтонкое измельчение (работа
измельчения), - dA = dG (известно, что полезная работа про­
водится за счет убыли свободной энергии системы, а в данном
случае работа имеет отрицательный знак, так как совершается
внешней средой). Поэтому изменение свободной энергии являет­
ся суммой дву х величин:
dG = —d ^A\физ + А2хим)*
При обычном измельчении (до величины частиц примерно де­
сять микрометров) в основном производится физическая работа,
и изменение свободной энергии незначительно.
При более тонком измельчении, наоборот, ф изи чес ка я рабо­
та пренебрежимо мала по сравнению с работой химической, и
изменение свободной энергии становится значительным.
Например, при сверхтонком измельчении известняка проис­
ходит его диссоциация:
СаС03 —>СаО + СО2
Использование измельчительных аппаратов специальной кон­
струкции (планетарные мельницы, струйные мельницы, вибра­
ционные мельницы, дезинтеграторы,) открывает большие воз­
можности в исследовании твердофазных химических реакций.
222

Кинетика механохимических реакций еще недостаточно разра­
ботана. Обсуждаются лишь механизмы, приводящие к химиче­
ским изменениям. В настоящее время исследователи сходятся
на следующих представлениях о механизме механохимических
реакций.
При измельчении происходит сильный местный разогрев на
контактах трущихся тел. Вследствие малой теплопроводности
твердых неметаллических тел тепло не успевает отводиться в
глубь тела, что может приводить к сублимации вещества и ак­
тивации его частиц.
В результате активации может происходить распад частиц
твердого тела с переходом электронов с одних молекулярных
орбиталей на другие, сопровождающийся испусканием квантов
электромагнитного излучения (триболюминесценция) или даже
гомолитический разрыв химических связей с образованием ак­
тивных радикалов. Излучение квантов света приводит к возбуж­
дению соседних атомов или молекул и к их активации. Поэто­
му качественным отличием механохимических превращений от
термических превращений является сходство механохимических
реакций с фотохимическими и радиационными. Это отличие ме­
ханохимических реакций позволяет использовать их для специ­
фических способов синтеза или разделения веществ.
Сверхтонкое измельчение находит применение при получении
высококачественных вяжущих веществ, д л я извлечения с помо­
щью горячих растворов редких щелочных элементов. Различные
сульфиды при сверхтонком измельчении в водной среде вступа­
ют в окислительно-восстановительные реакции.
Конечными продуктами этих реакций являю тся водород и
сульфат-ион, а катион в сульфиде может выделиться в виде ме­
та лл а или перейти в сульфат. Закисное железо при сверхтон­
ком измельчении с водой окисляется до оксида железа(Ш) и
при этом выделяется водород. Нитраты щелочных металлов при
сверхтонком измельчении разлагаются до нитритов.
Поскольку при взаимодействии твердых тел в условиях сверх­
тонкого измельчения поверхности твердых ф аз постоянно обнов­
ляются, то д иффузия перестает быть лимитирующей стадией
химического процесса, и скорость реакции определяется скоро­
стью взаимодействия на границах фаз. Образующиеся на по­
верхности фаз ядра продукта реакции не успевают занять всю
поверхность и образовать плотную пленку, поэтому диффузия
пренебрежимо мала.
Таким образом, скорость механохимических процессов резко
зависит от степени измельчения и особенно возрастает при при­
ближении частиц к наноразмерам.
223

2.9 . ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ
ОТ ТЕМПЕРАТУРЫ
Кинетические закономерности химических реакций были рас­
смотрены в предыдущем разделе в изотермических условиях.
Из опыта нам известно, что скорость реакции растет с повы­
шением температуры. Известно правило Вант-Гоффа, опреде­
ляющее влияние температуры на скорость химической реакции:
скорость химической реакции возрастает в 2 —3 раза при повы­
шении температуры на 10°. Математическое выражение правила
Вант-Гоффа имеет вид:
или
Vu
vt2
и-и
=У10
t2~t\
=Y10,
где у — температурный коэффициент (коэффициент Вант-Гоф­
фа), принимающий значения от 2 до 3;
и vt2 — скорости хи­
мической реакции при температурах t\ и соответственно; т*, и
Zt2 —продолжительность химической реакции при температурах
t\ и t 2 соответственно. Несмотря на несомненную практическую
значимость, правило Вант-Гоффа грубо приближенное, так как
температурный коэффициент Вант-Гоффа зависит от темпера­
туры.
§ 1. Энергия активации
С. Аррениус на основе статистики Больцмана получил урав­
нение, определяющее зависимость скорости реакции от темпера­
туры, которое называют уравнением Аррениуса:
Еа
v=Ze ят,
или д л я константы скорости химической реакции:
_
ЕЛ
к=АеRT,
в логарифмической форме:
\пк =\пА-
Еа_
RT’
где величину А называют частотным фактором или предэкспо-
ненциальным множителем или ж е множителем Аррениуса; Еа —
энергия активации.
224

Координата реакции
Рис. 2.26. Изменение энергии активации химической реакции при обра­
зовании промежуточного активированного комплекса А в реакции
А —>Р
Минимальная энергия, которую необходимо сообщить
взаимодействующим частицам д л я перевода их в активи­
рованное состояние, называется энергией активации.
Физический смысл величины Е а можно понять на примере
реакции А —►Р, которая проходит через промежуточное образо­
вание активированного состояния реагента А* (рис. 2.26):
к-
к
Ат=^А*—
к+
На практике энергию активации определяют графически по за ­
висимости скорости или константы скорости реакции от темпе­
ратуры. При построении графика зависимости к от Т в аррени-
усовских координатах, т. е. (lnfc ~
—
), величина Е а может быть
рассчитана по величине тангенса угла наклона прямой (рис. 2.27).
Д л я объяснения физического смысла уравнения Аррениуса
обычно используют теорию активированного комплекса и тео­
рию столкновений. В соответствии с этой теорией элементарная
реакция протекает непрерывно от начального состояния и прохо­
дит через переходное состояние, которому отвечает максималь­
ная энергия.
Гипотетическое возбужденное переходное состояние, че­
рез которое проходит элементарная реакция и характери­
зующееся максимальной энергией, назы вается переходным
комплексом.
8 Ипполитои
225

Рис. 2.27. Зависимость константы
скорости реакции от температуры
в аррениусовских координатах
Часто термины «переход­
ное состояние» и «активиро­
ванный комплекс» использу­
ются как синонимы. Измене­
ние энергии в ходе реакции
можно представить диаграм­
мой энергии (рис. 2.28).
Разность молярных энталь­
пий начального и конечного со­
стояний дает энтальпию реак­
ции АЯ °, а разность молярных
энтальпий начального и пере­
ходного состояний отвечает эн­
тальпии активации А Н^. На
абсциссе отложена координата
реакции, которая представляет
собой глубину протекания реакции. Координата энергии отра­
жает термодинамические свойства реагирующей системы, т. е.
средние изменения энергии частиц. Активированный комплекс
находится в равновесии с исходными реагентами. Д л я элемен­
тарной реакции второго порядка
Ai+A2-^P
промежуточное образование активированного комплекса соот­
ветствует схеме
A1+A2^(AiA2)^-^P
Для этой реакции константу скорости можно записать как
к=
где К 7 — константа равновесия, К 7 = ^
j - Константу ско­
рости k j можно рассматривать как частоту распада активиро­
ванного комплекса, благодаря которой образуется продукт. Г. Эй-
,
(квТ)
ринг предложил считать /су= — - — , отсюда
к=
(2.69)
h
где кв и h — постоянные Больцмана и Планка соответственно.
Константа равновесия связана с изменением свободной энергии
Гиббса:
- R TlnK*=AG¥.
(2.70)
226

Свободную энергию активации
A можновыразить через эн­
тальпию и энтропию актива­
ции, т. е.
AG*=AH*-TAS*.
(2.71)
Подстановка (2.70) и (2.71) в
(2.69) приводит к уравнению
Эйринга
,
квТ AST
к=-=—еRекг,
п
Рис. 2.28. Диаграмма изменения
энергии в ходе химической ре­
акции
или в логарифмической форме:
In&=In
+1пГ+
h
R
АН*
RT’
(2.72)
которую удобно преобразовать к виду
,
к,квAS*АН*
In—=In—h—
------
—
—.
Т
hR
RT
(2.73)
Д л я нахождения величины А Н * строят зависимость In — от
АН*
—и
получают прямую с тангенсом угла наклона, равным---- —
Т
R
Зн а я эту величину, из уравнения (2.73) находят Д5^, используя
различные наборы значений к и Т.
2.10. МЕХАНИЗМЫ ЭЛЕМЕНТАРНЫХ АКТОВ
Механизм химической реакции — это совокупность элемен­
тарных стадий, ведущих к продуктам реакций. Элементарные
стадии определяются статистической совокупностью элементар­
ных актов. Поэтому механизмы элементарных актов леж ат в
основе механизмов химических реакций. Химические реакции,
в которые вступает неисчислимое разнообразие химических ве­
ществ, могут протекать лишь через ограниченный набор элемен­
тарных актов. Совокупность элементарных актов можно подраз­
делить на реакции обмена XY+Z —>X+ZY; реакции диссоциации
и рекомбинации X++ Y" *=+XY или XY ^ X + Y; реакции изоме­
ризации: цис-, транс-изомеризация, циклизация и т. п.; реакции
227

рацимации d-C(ABCD) + Z-C(ABCD) рацемат-С(АВСБ); реак­
ции переноса электрона Х + Y —>Х++ Y- ; реакции протонизации
АсН+X—►Ас"+ХН+.
Рассмотрим теорию элементарного акта в сконденсирован­
ных системах. Молекулы, находящиеся в газе или в паре, при
движении сталкиваются друг с другом, в результате чего меня­
ются их энергии. Изменение энергии может передаваться элек­
тронам, вследствие чего молекулы переходят в возбужденное со­
стояние. Возбужденные молекулы могут релаксировать путем
излучения или же вступать в химическое взаимодействие с дру­
гими молекулами.
Если температура системы достаточно высока, то можно пред­
ставить химическую реакцию, например АВ + С —>АС + В, иду­
щую через диссоциацию молекулы АВ. Энергии атомизации мо­
лекул обычно составляют 200 —400 кД ж/моль, поэтому такой
механизм реакции возможен лиш ь при высоких температурах.
При умеренных температурах энергия активации не достига­
ется. Однако реакции происходят, и, следовательно, механизм
элементарных актов в этом случае не диссоциативный. Поэтому
для протекания реакций в этих случаях необходимо столкнове­
ние реагирующих частиц. Такое столкновение возможно лишь в
неконденсированных системах.
§1. Теория столкновений
Согласно теории столкновений реагирующие молекулы рас­
сматривают как жесткие шары, не обладающие силами при­
тяжения друг к другу. Считается, что реакция двух молекул
происходит только при их столкновении и что скорость реак­
ции зависит от частоты столкновений Z. Д ля того, чтобы после
столкновения двух молекул могла произойти химическая реак­
ция, необходимо, чтобы энергия соударяющихся молекул была
равна (или больше) энергии активации Е. В соответствии с рас­
пределением энергии Больцмана доля молекул п*, обладающих
необходимой энергией, определяется как
71*
Л-
—
= е“ят.
п
Но д л я того, чтобы столкновение могло привести к химическим
изменениям, молекулы в момент, столкновения до л ж ны быть
благоприятным образом ориентированы в пространстве. Отно­
сительное число столкновений, при которых молекулы облада­
ют подходящей ориентацией, определяется ф актором вероятно-
228

сти Р , называемым такж е стерическим фактором. Тогда кон­
станта скорости может быть выражена как
в
к = PZe~KT.
Число столкновений Z на один кубический сантиметр в се­
кунду между разными молекулами Ai и А2 можно вывести из
законов статистической механики:
Z=
N
1000
(га1+ га2)2
8кв Т
где N a — число Авогадро; га, и гд2 — радиусы реагентов; р —
(mA.rriAj „
приведенная масса, р = 7-------------- г; Z измеряется в л • моль х
(7TIAi
)
х с ' 1. Для мономолекулярных реакций частотный фактор не яв­
ляется частотой столкновений, а принимает вид средней коле­
бательной частоты, которую можно принять равной
квТ
h
. По­
следнее отношение входит в уравнение (2.69), выведенное в тео­
рии активированного комплекса. Представляет определенный ин­
терес провести сравнение соответствующих коэффициентов и
попытаться выяснить физический смысл аррениусовских пара­
метров. Рассмотрим зависимости между величинами Е а, А Н ^
и Е . Д л я этого уравнение (2.72) продифференцируем по темпе­
ратуре:
1
~Т+
Аналогично можно показать, что
d(lnfc)
dT
d(\nk)
dT
1
~2T+
АН*
(2.74)
RT2'
Е
RT2'
(2.75)
Сравнивая каждое из выражений (2.74) и (2.75) с ранее полу­
ченными уравнениями, можно показать, что
Еа=АН*+ВТ=Е+)-RT.
£
После замены АН на Еа- RT, а Е на Еа- ^РТи, проведя со­
ответствующие подстановки, получим выражение для аррениу-
совского множителя:
А=
еквТ ДS!
—F—ея =V^pz.
(2.76)
229

§ 2. Физический смысл энтропии активации
Энтропия активации связана со стерическим фактором. Это
следует из закона Больцмана S = кв In W. Если записать его для
перехода начального состояния i в активированное состояние У,
то получим
где Wy и Wi — термодинамические вероятности активированного
и начального состояний соответственно. Преобразуя последнее
уравнение, приходим к величине Р:
выражающей вероятность того, что при столкновении частицы
имеют такую ориентацию, которая необходима дл я протекания
реакции. Стерический фактор, равный единице, должен соответ­
ствовать нулевой энтропии активации. Это наблюдается в слу­
чае элементарной реакции первого порядка, где молекулярная
ориентация не имеет значения. Чем больше молекул, участву­
ющих в образовании активированного комплекса, тем большую
роль до л ж на играть их ориентация. Таким образом, мы получа­
ем Р < 1 и отрицательную энтропию активации.
Однако вместе с другими данными значение A S ^ д а е т исклю­
чительно полезные сведения о природе активированного ком­
плекса.
Известно, что чем сильнее связь или связи, подлежащие раз­
рыву, тем выше Еа. Такая зависимость действительно была най­
дена д ля некоторых экзотермических газофазных реакций. Бы­
ли также получены некоторые эмпирические корреляции между
Еа и энтальпией реакции дл я экзотермических реакций в гомо­
логических рядах:
Еа=аАН+с,
где а и с — эмпирические константы. Это уравнение может быть
справедливо для реакций, экзотермичность которых линейно свя­
зана с энергией рвущихся связей. Это означает, что образую­
щиеся связи лишь незначительно различаются по энергии. Для
§ 3. Физический смысл энергии активации
230

кДж
энергий активации типичны величины от 50 до 80 ------ . Д л я
моль
быстротечных реакций энергии активации могут иметь значения
кДж
и меньше 50 ------ . Процессы, контролируемые диффузией, ха-
моль
рактеризуются низкой энергией активации. Очень высокие зна­
чения Е а должны появляться в тех случаях, когда в лимитиру­
ющей стадии реакции образуются высокореакционноспособные
промежуточные соединения, например радикалы.
§4. Туннельные эффекты
При рассмотрении механизмов и элементарных стадий с при­
менением теории переходных состояний, как было рассмотрено
выше, постулируется, что д л я того, чтобы осуществился элемен­
тарный акт химического взаимодействия, необходимым услови­
ем является переход частицы А в активированное переходное
состояние А*:
AU[А*]->Р
т. е. частица должна в результате этого перехода преодолеть энер­
гетический барьер, который определяется энергией активации.
Если величина этого энергетического барьера д л я данных усло­
вий достаточно велика, то переход в активированное состоя­
ние не должен происходить, и реакция не происходит (экспери­
ментально мы не долж ны обнаруживать в реакционной системе
продукты реакции). В действительности существует достаточно
большое число химических реакций, в которых при наличии вы­
сокого энергетического бар ьера в реакционной системе обнару­
живаю тся продукты реакции, которые не могли бы образоваться
только в предположении протекания реакции через активиро­
ванное переходное состояние.
Одним из примеров таких реакций является процесс полиме­
ризации формальдегида при гелиевых температурах (~ 6 К):
Н(ОСН2)+ + ОСН2 Л H(OCH2)„OCHj
Константа скорости этой реакции оказалась равной к = 1 ,6 х
х Ю2 с-1 и не зависит от температуры в пределах 4 —12К. Ес­
ли д л я этой реакции при тех же температурах использовать
обычное аррениусовское приближение, то средняя продолжи­
тельность элементарного а к та составила бы Ю100 лет. Объясне­
ние высокой константы скорости этого процесса при низких тем­
пературах можно найти, если вспомнить, что молекулы являют­
ся квантово-химическими системами и их взаимодействие при
231

низких температурах необходимо рассматривать с привлечением
квантовой химии. Что приводит к выводу о том, что взаимодей­
ствие молекул может происходить путем «просачивания» сквозь
потенциальный барьер. Этот эф ф ект был назван туннельным
эффектом. Его можно представить следующей схемой:
Туннелирование
Ар.[А*] Р
В процессе туннелирования участвуют все атомы молеку­
лы. Поскольку квантовые эф ф екты становятся преобладающи­
ми лишь при низких температурах, то явления туннелирования
в чистом виде можно изучать лишь при низких температурах,
однако и при более высоких температурах туннельный эффект
может та к ж е проявляться, хотя и в незначительной степени. По­
этому и в данных условиях при длительном времени в реакци­
онной системе обнаруживаются следы продукта реакции. Для
расчета константы скорости реакции с учетом действия тун­
нельного эф ф е к та квантово-механическим путем получено урав­
нение:
к=
кБТ
W(E) exp -
Е
кБТ
dE,
(2.77)
где W ( E ) — вероятность преодоления частицей туннельного ба­
рьера. Уравнение (2.77) с учетом частоты колебаний V в потенци­
альной яме и энергетической составляющей (импульса) частицы
внутри потенциальной ямы может быть приведено к виду:
к~
кБТJехрI~hS^
Е
АъТ
dE,
(2.78)
где S (E ) учитывает энергетическую составляющую (импульс)
частицы внутри потенциальной ямы и носит вероятностный ха­
рактер. Уравнение (2.78) описывает не только туннельную кон­
станту скорости реакции, но и константу скорости реакции по
аррениусовскому типу. Кроме того, оно учитывает и надба-
рьерное отражение, которое обусловлено квантовомеханически­
ми причинами. Даже если частица обладает энергией, превы­
шающей потенциальный барьер, вероятность преодоления по­
тенциального барьера 0 ^ 1 , та к как существует вероятность
отражения частицы. Величина а носит название сечения вза­
имодействия и может быть вычислена квантово-химическими
методами. Сечение взаимодействия говорит о том, что столк­
новение молекул нельзя рассматривать подобно столкновению
232

бильярдных шаров, так к а к молекулы, как квантово-механичес­
кие системы, могут уж е взаимодействовать, находясь на неко­
тором расстоянии друг от друга и, напротив, при сближении на
более близкое расстояние начинают действовать силы отталки­
вания электронных оболочек, и молекулы расходятся.
Как видно из модели туннельного эффекта, строгий расчет
констант скорости реакций требует квантово-механического под­
хода. Химическая реакция связана с перестройкой электронно­
го окружения ядер атомов и их перемещением. Поэтому дл я
рассмотрения столь сложных процессов приходится прибегать
к приближению Б орна —Оппенгеймера, которое предлагает рас­
сматривать две подсистемы: подсистему ядер атомов и подсисте­
му электронов. Поскольку масса подсистемы электронов мала по
сравнению с подсистемой ядер, то подсистему электронов рас­
сматривают как быструю, а подсистему ядер — как медленную.
Таким образом, можно рассматривать по отдельности движение
ядер и движение электронов. Быстрая электронная система лег­
ко реагирует на перемещение ядер и ее состояние определяется
ядерной конфигурацией. С другой стороны, электронная под­
система более чувствительна к окружению соседних атомов и
молекул и быстрее, чем ядра, изменяет свое состояние. Потен­
циальная энергия системы атомов целиком зависит от их распо­
ложения. Любому расположению ядер соответствует определен­
ное значение потенциальной энергии системы. Графически это
вы раж ает поверхность потенциальной энергии (ППЭ), по кото­
рой перемещаются ядра атомов. Любая ядерная конфигурация
изображается точкой на ППЭ в многомерном пространстве. На­
ряду с устойчивым электронным состоянием, которое облада­
ет нижним уровнем потенциальной энергии, атомы и молекулы
могут находиться и в возбужденных состояниях, которым от­
вечают свои ППЭ. ППЭ основных состояний и возбужденных
состояний могут пересекаться, и молекула может переходить с
одной ППЭ на другую, что связано с изменением электронного
состояния системы. Перекрывание ППЭ двух и более молекул
приводит к сильному взаимодействию, что может вести к об­
разованию новой ППЭ, т. е. к элементарному акту химической
реакции. Поэтому при теоретических расчетах прежде всего вы­
числяют вид ППЭ, откуда и оценивают величину потенциаль­
ного барьера, разделяющего долину исходных веществ и долину
продуктов реакции.
Дл я определения ППЭ используются квантово-механические
методы расчета, которые достаточно сложны и выходят за рам­
ки данного курса физической химии. Очень часто задача описа­
ния ППЭ решается полуэмпирическими методами.
233

Если ППЭ известна, т. е. известны все возможные электрон­
ные состояния для данной химической системы частиц, то мож­
но рассматривать два возможных варианта.
1. Пусть возможные электронные состояния (термы) исход­
ных веществ (Xi) и продуктов реакции (Х2) различаю тся значи­
тельно. При определенных условиях эти два терма смешивают­
ся и образуют некоторую обобщенную ППЭ, на которой и пе­
ремещается воображаемая точка, которая представляет собой
локальное приближение химической системы. Условия смеши­
вания термов могут быть получены в результате решения урав­
нения Шредингера.
2. Возможен второй вариант, когда взаимодействие между
термами невелико. В этом случае термы не смешиваются, и дви­
жение воображаемой точки может происходить как по терму ис­
ходных веществ (Xi), так и по терму продуктов реакции (Х2).
Решение, которое позволяет рассчитать вероятность перехода
системы с одного терма на другой, дается квантовомеханиче­
ской моделью Ландау и Зингера. Графической иллюстрацией
этого варианта может являться так называемый «гарпунный ме­
ханизм», сопровождающий, например, процесс взаимодействия
атома металла с молекулой галогена Hal:
М + На12 —►MHal + Hal
«Гарпунный механизм» предполагает перенос электрона с атома
металла на молекулу галогена и образование промежуточного
ионного переходного комплекса:
е~
М+ На1я —>М+ НаЬ—►М++ Halj
терм Xi
терм Х2
Кулоновское взаимодействие образовавшихся ионов приводит к
образованию промежуточного комплекса [JVTHal^]:
М + НаЬ -> [M+Halg] <- М++ НаГ;
(2.79)
терм Xi
терм Х2
который тотчас распадается:
[M+Hals]—>М +НаГ + На1
Если ППЭ д л я термов Xi и Х2 пересекаются, то в области пе­
ресечения термов становится возможен переход от неполярного
к ионному состоянию реагентов, т. е. перескок электрона, кото­
рый является как бы гарпуном для сближения атома металла
и молекулы галогена под действием кулоновского притяжения.
234

Вероятность такого процесса может быть оценена с позиций мо­
дели Ландау —Зингера.
Подобным же образом можно представить механизмы эле­
ментарных актов при окислении субстратов молекулярным кис­
лородом. Окисление по схеме
Ft+О2—►RO+—О
требует диссоциации молекулы кислорода на атомы. Энтальпия
атомизации при этом равна 247,5 кД ж/моль. Поэтому взаимо­
действие по диссоциативному механизму может осуществлять­
ся лишь при высоких температурах. При стандартных условиях
и умеренно повышенных температурах взаимодействие проис­
ходит по схеме, подобной рассмотренной выше (2.79). При этом
молекула кислорода принимает электрон и образует переходный
супероксидный комплекс по схеме:
R+O2-> [R+Os] <- R++О2
(2.80)
терм Xi
терм Х2
Переходный супероксидный комплекс тотчас разлагается и об­
разует пероксид:
[R+C>2] ^
r2o2Д о2
Образовавшийся пероксид далее может разлагаться с образова­
нием оксида:
R2O2 ► R2O+ ~02
Техническое получение пероксида водорода химическим мето­
дом основано на окислении кислородом этилгидрохинона или
изопропанола, которое происходит при температурах, близких к
стандартной температуре и, вероятно, протекает по приведенно­
му выше механизму.
§ 5. Теории элементарных актов в растворах
Хотя теория столкновений была развита д л я газофазных ре­
акций, тем не менее, д л я большого числа реакций второго по­
ряд к а в растворах экспериментально определенные константы
скорости близки к константам, предсказанным этой теорией.
Однако в конденсированной жидкой фазе растворенные мо­
лекулы не могут непосредственно сталкиваться, так как они раз­
делены молекулами растворителя. Поэтому элементарный ак т в
растворе происходит более сложными путями. Д л я построения
теорий элементарных актов в этом случае приходится прибегать
235

к квантово-механическим представлениям о взаимодействии мо­
лекул.
На общей величине A S ^ сказывается различие в степени соль­
ватации, т. е. в степени взаимодействия с растворителем при пе­
реходе от начального состояния к активированному комплексу,
поэтому величину A S ^ можно рассматривать как сумму внеш­
него (за счет сольватации) и внутреннего (за счет истинной ре­
акции) вкладов:
Д5^=Д5^еакц+Д ^ольв.
Чем сильнее связаны молекулы растворителя, тем больше они
ориентированны и тем больше ограничена их свобода. Потеря
поступательных и вращательных степеней свободы в связанных
молекулах растворителя д о л ж н а приводить к понижению эн­
тропии. Присутствие активированного комплекса, более сильно
сольватированного по сравнению с исходными веществами, бу­
дет сдвигать А 5^ в сторону более отрицательных значений, и
наоборот. Поэтому изменение энтропии за счет ра зли чия в сте­
пени сольватации может компенсировать энтропию активации
самой реакции. Экспериментальные значения A S ^ не позволя­
ют сделать определенных выводов о молекулярности измеряе­
мой стадии реакции.
§ 6. Формы аррениусовских графиков
В растворах в небольших интервалах температур, обычно ис­
пользуемых д л я изучения скоростей, связанные с температурой
изменения энергии активации и предэкспоненциального множи­
теля настолько незначительны, что элементарная реакция пред­
ставляется практически прямой линией в аррениусовских коор­
динатах ^1п к ~
—
У Иногда небольшие отклонения от линейно­
сти могут быть замаскированы разбросом экспериментальных
точек. Нелинейный характер аррениусовой зависимости указы­
вает на то, что измеряемая константа скорости является слож­
ной и относится к более чем одной стадии реакции. Темпера­
турная зависимость дает тем больше информации, чем больше
температурный интервал эксперимента. Практически д л я опре­
деления нелинейности, связанной с более сложным характером
изучаемой константы скорости, достаточно проводить измере­
ния в интервале 30 —40° С. Нелинейность аррениусовского гра­
фика можно показать на примере последовательной реакции:
Ai^ В
-
^
Р
к*
236

т
Рис. 2.29. Аррениусовский график для реакции с эффективной кон-
,
к2К
стантой скорости, отвечающей уравнению /с3ф = -— —:
1+К
гг
,
\
£о+|ДЯ0|
1 — АН положительна (эндотермическая реакция): tgai = ---------- -------- ;
К
Е
Е
tgPi=—
— АН0отрицательна (экзотермическая реакция): tgct2 = —
R
R
Еа- |ДЯ°|
tgP a -------- д -----
Дл я этой реакции эффективная константа скорости определяет­
ся как
к2К
1+К '
Имеются два предельных случая:
_
Еп±АН°
а)К«С1.Тогдакэф=к2К=const•е
к г . Таким образом,
эффективная энергия активации состоит из энергии активации
второй стадии реакции и теплоты предшествующего равновесия.
Зн а к «±» означает, что равновесие может быть либо эндотерми­
ческим (-) , либо экзотермическим (+);
_ЕЛ
б) К > 1. Тогда кэф = к2 = const • е яг. Из-за температур­
ной зависимости к в определенном интервале температур слу­
чай (а) переходит в случай (б), и аррениусовский график тогда
становится нелинейным из-за того, что при изменении темпе­
ратуры лимитирующая стадия меняется. На рис. 2.29 показа­
ны эти возможные варианты. Кривые 1 и 2 относятся к кон­
стантам скорости эндотермической и экзотермической реакций
соответственно.
§ 7. Реакции замещения
Эти реакции подразделяют на два типа:
1) замещение одного лиганда на другой;
237

2) замещение одного центрального атома на другой.
Эти механизмы реакций обозначают как S m и S e соответ­
ственно. Индексы показывают нуклеофильное и электрофиль­
ное замещение. Нуклеофильный реагент предоставляет электро­
ны атомным ядрам в реакции. Электрофильный приобретает
электроны от нуклеофильного реагента:
Y+М-Х
->М—Y+X (SN)
М'+М-Х М'-Х+М
(Se )
В координационных соединениях центральный атом — электро­
фильный реагент, а лиганды — нуклеофильные реагенты.
Согласно определению, все восстанавливающие агенты явля­
ются нуклеофильными реагентами, а все окислители — электро­
фильными. Однако эта терминология не универсальна и при­
менение подобных терминов ограничивается теми реагентами,
которые частично отдают или присоединяют пару электронов.
При таком ограничении терминологии эти термины стали сино­
нимами оснований и кислот соответственно в самом широком
значении этих понятий, которое придал им Б. Льюис. Следова­
тельно, реакции замещения включают фундаментальную реак­
цию кислотно-основного взаимодействия
А+:В^А:В
(2.81)
Прямая реакция (2.81) называется реакцией координации, а об­
ратная — реакцией гетеролитической, или ионной, диссоциации.
Второй тип разрыва химической связи называют гомолитиче-
ской диссоциацией или реакцией диссоциации с образованием
свободных радикалов
А:В—►А+В
Механизм реакции замещения более сложен, чем представле­
но уравнением (2.81). Можно предположить, по крайней мере,
два фундаментально различных механизма. Это ассоциативный
и диссоциативный механизмы, которые были обозначены S n 2
(или Se2) и 5дг1 (или Sei)> В реакции Se2 ступенью, опреде­
ляющей скорость, является бимолекулярная реакция, в которой
один нуклеофильный реагент замещается другим:
Y+М—X
—
>Y -•М •••X —►Y—М+X
В реакции Spj7 происходит замещение электрофильных реаген­
тов, и переходное состояние записывается в виде:
М---Х---М'*
При этих бимолекулярных процессах координационное число
иона металла или лиганда в переходном состоянии увеличивает­
ся на единицу. По-видимому, при этом возникает довольно опре­
деленная стереохимическая ориентация всех лигандов.
238

Реакции Sjv2 и S e 2 происходят по двухступенчатому механиз­
му, в котором первой ступенью является медленная мономоле-
кулярная гетеролитическая диссоциация
М-Х^М +Х
з а ней следуют быстрые реакции координации М или X со вто­
рым реагентом:
М+Y->М—Y
Х+М' ->М'-Х
При этом координационные числа лиганда и иона металла.умень­
шаются на единицу в реакции, которая определяет скорость.
Более того, на этой ступени реакции образуется интермедиат с
уменьшенным координационным числом.
Однако можно представить и другие механизмы реакций за­
мещения. Это так называемый четырехцентровый механизм, при
котором два комплекса «кислота—основание» одновременно об­
мениваются группами
Д
м—х +у—м'
—
^м:' ':м '—
-
m-y+x—м'
N/
Y
Процесс происходит без выталкивания группы X или Y в рас­
твор в виде свободных ионов или молекул. Такой механизм мо­
ж ет быть в тех случаях, когда X и Y в свободном виде очень
неустойчивы, когда связь М—X или М'—Y сильно ковалентна и
затрудняет диссоциацию на ионы, когда растворитель является
неполярным (или отсутствует) и, следовательно, X и Y не могут
быть стабилизированы сольватацией. Д л я реализации механиз­
ма необходимо, чтобы М и X, М' и Y могли увеличить коорди­
национное число на единицу. Вероятно, это может происходить
з а счет потери слабо удерживаемых молекул растворителя.
Следует заметить, что реакция может одновременно проте­
кать по механизмам 5дг2 и S e2, причем X может как отталки­
ваться от иона металла, та к и притягиваться к нему. Если учесть
влияние растворителя на стабилизацию X, когда он свободен, то
все реакции происходят по механизму S e 2-
Четырехцентровые механизмы были обнаружены или посту­
лированы для многих реакций в органической химии. Полага­
ют, что реакции замещения для металлоорганических соедине­
ний Li, Be, Mg, В, Al, Hg, Zn, Cd, Tl, Si и Sn происходят по че­
тырехцентровому механизму. Возможно, что галогениды этих и
239

других металлов в неполярных растворителях реагируют таким
же способом. Например, обменная реакция
R2Hg + HgCl2 ->2RHgCl,
вероятно, происходит по четырехцентровому механизму:
Яч
R-Hg Hg -Cl
2.11 . ВЛИЯНИЕ РАСТВОРИТЕЛЯ НА СКОРОСТЬ
ХИМИЧЕСКОЙ РЕАКЦИИ
При проведении реакции в растворе может существенно из­
меняться ее скорость за счет влияния процессов сольватации на
кинетику реакции. Это может бы ть объяснено следующими при­
чинами.
1. Свободная энергия иона сильно уменьшается при переходе
от газообразного состояния к раствору, а сам переход способ­
ствует стабилизации иона.
2. Перенос ионов в растворителях также сопровождается из­
менением свободной энергии. Изменение свободной энергии воз­
растает с увеличением заряда иона. Чем меньше размер и боль­
ше заряд иона, тем сильнее он сольватирован.
3. Изменение свободной энергии происходит и при переносе в
растворителе незаряженных полярных частиц, хотя в этом слу­
чае оно и менее выражено. Чем выше полярность молекулы, тем
чувствительнее она к сольватации.
4. Относительное понижение свободной энергии растворен­
ных веществ при переносе из газовой фазы в растворитель обыч­
но уменьшается в ряду
Ионы > Полярные молекулы > Неполярные молекулы
Однако ион необязательно более способен к сольватации, чем
нейтральная молекула, поскольку поверхностный зар яд иона мо­
жет быть меньше, чем поверхностный заряд электронообогащен­
ного или электронодефицитного центра диполя.
Скорость реакции может увеличиваться при переходе в среду
с большей сольватирующей способностью:
если нейтральные молекулы образуют высокополярный акти­
вированный комплекс, например, при гетеролизе ковалентных
связей;
240

два иона с зарядами одного знака движутся вместе. Тогда
увеличение скорости происходит благодаря концентрации зар я­
да. Например, двухвалентный ион, как правило, более чувстви­
телен к переносу растворителем, чем д ва одновалентных иона.
Первым свойством растворителя, использованным для кор­
реляции с данными о скорости реакции, была диэлектрическая
проницаемость е. Диэлектрическая проницаемость связана с по­
казателем преломления света п соотношением:
Температурный коэффициент показателя преломления зависит
от плотности среды d. В поисках не зависящего от температуры
выражения, К. Лоренц и Г. Лорентц теоретически вывели зави­
симость
(п2-1) 1
(п2+2)d
= const,
называемую удельной рефракцией. Умножая ее на молекуляр­
ную массу М, получают молярную рефракцию R:
(п2-1) М
(п2+2) d
’
где R — мера электронной поляризуемости. Если п 2 заменить на
£, то получим уравнение Клаузиуса —Мосотти:
(£-1)М
(е+2)d
Величину Р называют молярной поляризуемостью. Обе величи­
ны R и Р измеряют в единицах см3 • м о л ь'1. При рассмотрении
влияния величины £ на кинетические параметры химической ре­
акции чаще всего употребляются две функции: - и так называ­
емая функция Кирквуда:
(е-1)
Борн предположил, что сво-
(2е+1)
бодная энергия иона д о л ж на меняться обратно пропорционально
диэлектрической проницаемости среды. Это привело к следую­
щему уравнению д ля константы скорости элементарной реакций
между двумя ионами:
In
const Г-
ко
\г
где к и к о ~ константы скорости соответственно в среде с диэлек­
трической проницаемостью £ и с бесконечно большой диэлектри­
ческой проницаемостью (т. е. в отсутствие электростатических
241

сил). Графическая зависимость
In А; от - должна представлять
£
собой прямую. Положительный
тангенс угла наклона этой кри­
вой, равный const с положи­
тельным знаком, должен ука­
зывать на то, что активиро­
ванный комплекс менее сольва-
тирован, чем реагенты, и на­
оборот.
Позднее Кирквудом была
развита теория влияния ди­
электрической проницаемости среды на свободную энергию по­
лярной молекулы, а из этой теории было выведено уравнение
для расчета константы скорости элементарной реакции между
двумя диполями:
,
к
(£-1)
In — = const-------Г,
ко
(2£+1)
Рис. 2.30. Зависимость между
константой скорости реакции
нитробензола с пиперидином и
диэлектрическими
свойствами
растворителя
где к0 снова относится к стандартному состоянию с бесконечно
большой £.
График зависимости In А; от
(е-1)
представляет собой пря-
(2£+1)
мую линию. Нетрудно показать, что последняя зависимость ли­
нейна и в координатах (In /с — —).
В качестве примера на рис. 2.30 приведена зависимость меж­
ду константой скорости реакции взаимодействия пара-нитро-
фторбензола с пиперидином и диэлектрическими свойствами
растворителя.
Помимо диэлектрической проницаемости двумя другими важ­
нейшими свойствами растворителя являются донорная (нуклео­
фильная, основная, катионсольватирующая) способность и ак­
цепторная (электрофильная, кислотная, анионсольватирующая)
способность, которые позволяют рассматривать взаимодействия
типа «растворенное вещество —растворитель» как кислотно-ос­
новные реакции в самом широком смысле этого слова. Харак­
теристикой донорной и акцепторной способности является до­
норное число (ДЧ) и акцепторное число (АЧ). Эталонными со­
единениями д л я такого донорно-акцепторного подхода являют­
ся пентахлорид сурьмы и триэтилфосфиноксид. Д л я эталонных
веществ механизм взаимодействия с растворителем может быть
представлен следующей схемой:
242

Cl pi
Донорный
растворитель
Cl Cl
Et
Et—P =0
I
Et
Акцепторный
растворитель
Донорное число (ДЧ) показывает способность растворителя
поделить свою электронную пару с подходящим акцептором (от­
д а т ь электроны); оно определяется как отрицательная величи­
на, равная энтальпии образования аддукта эталонной кислоты
SbCls с молекулой растворителя в сильно разбавленном раство­
ре 1,2-дихлорэтана. Растворители, характеризующиеся наличи­
ем донорного числа, называют донорными растворителями. Ак­
цепторное число (АЧ) измеряет способность растворителя по­
делить электронную пару, принадлежащую подходящему доно­
ру (принять электроны). Это число выводится из химических
сдвигов фосфора в спектрах ЯМР, регистрируемых для EtsPO
в различных растворителях. В произвольно выбранной шка­
ле АЧ за нулевое значение принят химический сдвиг в гексане,
цена деления соответствует
сдвига аддукта EtsPO •SbCls
в 1,2-дихлорэтане. Растворители, характеризующиеся наличием
акцепторного числа, называют акцепторными растворителями.
Пользуясь этими числами, зависимость скорости реакции от рас­
творителя можно представить уравнением:
где ко — константа скорости в эталонном растворителе; consti и
const2 — коэффициенты чувствительности скорости рассматри­
ваемой реакции к акцепторным и донорным свойствам раство­
рителя. Уравнение (2.82 ) можно записать и в другом виде:
где const3 — логарифм константы скорости реакции в некоорди­
нирующем растворителе. Положительные коэффициенты чув­
ствительности указывают на то, что реакция ускоряется при уве­
личении ДЧ и АЧ, и наоборот.
(2.82)
Ink = constx^4) +const2(A4)+const3,
(2.83)
243

Корреляции по приведенным выше уравнениям (2.82) и (2.83)
проявлялись в достаточно большом числе кинетических исследо­
ваний и были установлены с применением статистического ана­
лиза экспериментальных данных. Учет влияния растворителей
на кинетические параметры химических реакций связан с дву­
мя трудностями: во-первых, с высокоструктурированными или
ассоциированными растворителями и, во-вторых, с растворите­
лями, имеющими низкую диэлектрическую проницаемость.
1. Высокострурированные растворители. В этих раствори­
телях (вода, спирты, формамид и т. п.) SbCls и E t3PO сильнее
сольватируются, чем все другие рассмотренные модельные суб­
страты. Это объясняется следующим образом.
Высокоорганизованные структуры возникают в том случае,
когда растворитель обладает выраженными донорными или ак­
цепторными свойствами, т. е. молекулы растворителя вовлека­
ются в донорно-акцепторное взаимодействие друг с другом. Это
особенно характерно для растворителей, молекулы которых со­
держат кислые атомы водорода. Такие растворители отлича­
ются наличием водородных связей, их называют протонными
в противоположность апротонным растворителям. Протонные
растворители могут действовать как доноры или акцепторы, ес­
ли не разорваны связи между молекулами растворителя, а сте­
пень разры ва связей зависит в свою очередь от донорной или
акцепторной силы растворенного вещества. Следовательно, хи­
мические координирующие свойства протонных растворителей
не постоянны, а являются функцией комплементарных свойств
растворенного вещества. Таким образом, донорные и акцептор­
ные числа д л я структурированных растворителей долж ны быть
выше, чем это можно предсказать по другим индексам: части­
цы с низкой полярностью очень слабо сольватируются в высо­
коструктурированных растворителях.
2. Растворители с низкой диэлектрической проницаемостью.
Помимо сложностей, связанных с высокоструктурированными
растворителями, есть и другая причина заметных отклонений от
указанных выше корреляций - низкая диэлектрическая прони­
цаемость растворителей. Д л я таких растворителей диэлектриче­
ская проницаемость не превышает 10. В последние годы начали
различать электростатическую и координационно-химическую
сольватацию. Свободную энергию сольватации рассматривают
как сумму двух членов. Один из них отвечает донорно-акцептор­
ным взаимодействиям между растворенным веществом и рас­
творителем, находящимся в непосредственной близости от рас­
творенного вещества (ближнее взаимодействие или взаимодей­
ствие по типу водородных связей, специфическая сольватация).
244

Другой член не учитывает взаимодействия в этой сфере, а свя­
зан с диэлектрической поляризацией растворителя (дальнее вза­
имодействие, неспецифическая сольватация).
Одновременный учет влияния е, АЧ и Д Ч на кинетические
параметры реакции может быть осуществлен с помощью регрес­
сионного уравнения:
lg е = 0,0711(АЧ) + 0,0054(ДЧ) + 0,2581.
(2.84)
На рис. 2.31 представлена диаграмма дл я серии реакций соль­
ватации в зависимости от диэлектрических и донорных свойств
растворителей.
Таблица 2.5
Экспериментальные и рассчитанные значения £ для различных
растворителей
Растворитель
£Р
£э
Растворитель
еР
Сэ
Анизол
6,9
4,3 М-метил-2 -пиролидон
25,2 33,0
Анилин
42,3
6,9 Нитробензол
18,2 34,8
Ацетон
22,2 20,7 Нитрометан
45,3 36,7
Ацетонитрил
47,1 36,0 Нитроэтан
25,6 28,5
Ацетофенон
17,9 17,4 З-Пентанон
П ,4 16,6
Бензилцианид
25,1 18,7 Пипередин
8,1
5,8
Бензол
3,7
2,3 Пиридин
20,4 12,3
Бензонитрил
20,2 25,2 Пропиленкарбонат
55,0 65,0
Бромбензол
6,9
5,4 Пропионитрил
29,7 27,2
Бутанон
17,9 17,9 Сероуглерод
2,5 2,6
Гексаметилфосфо-
21,8 29,6 Сульфолан
50,5 43,3
триамид
Тетрагидрофуран
8,4
7,5
Гексан
1Д
1,9 Тетраметилмочевина
20,7 23,4
Дибутиловый эфир
3,5
зд
Толуол
3,3 2,4
Диметил ацетамид
29,7 37,8 Три-н -бутилф о сф ат
14,0
7,9
3,3-Диметил бутанон
П,7 13,2 Триметилфосфат
32,1 20,6
Диметилсульфоксид 47,1 46,7 Триэтиламин
5,3 2,4
Диметил формамид
34,6 36,7 Уксусный ангидрид
29,3 20,7
Диметоксиэтан
9,5
7,2 Хлорбензол
6,9 5,6
1,4-Диоксан
6,0
2,2 Хлороформ
9,3 4,7
Дихлорметан
14,5
8,9 Циклогексан
1,8 2,0
1,2-Дихлорэтан
17,4 10,1 Циклогексанон
16,9 18,3
Диэтиламин
7,9
3,7 Четыреххлористый
2,3
2,2
Диэтиловый эфир
4,5
4,2
углерод
Ксилол
2,8
2,3 Эпихлоргидрин
15,0 22,6
Мети лацетат
12,9
6,7 Этилацетат
8,6 6,0
245

-In*
4
6-
10
12
ДМСО"
ДМФ*
ДМА
НМ^/иАН
н£»бн
ДМБУ^Ьганон
3-ГГентангон
^Г&^Утгф
ЕЮАс/Тлим
гАнизол
■Ви20
0246810
[0,0827(ДЧ) + 5,21 (lge)]
Рис. 2.31. Корреляционная диа-
грамма для серии реакций, учиты­
вающая диэлектрические и донор­
ные свойства растворителя
В табл. 2.5 приведены дан­
ные по сопоставлению значе­
ний экспериментальных и рас­
четных значений 8, опреде­
ленных с помощью уравне­
ния (2.84) для различных рас­
творителей. Достоинством это­
го уравнения, несомненно, яв­
ляется то, что с его помо­
щью можно одновременно при­
менять оба подхода: и основан­
ный на диэлектрической про­
ницаемости, и основанный на
эмпирических параметрах. Та­
ким образом, диэлектрическая
проницаемость является хоро­
шим ориентиром для изучения влияния растворителя на те ре­
акции, которые в основном контролируются акцепторными свой­
ствами растворителя.
На рис. 2.32 приведены некоторые экспериментальные дан­
ные, касающиеся влияния перечисленных выше основных
свойств растворителя на кинетические характеристики некото­
рых реакций.
Часто удобнее оказывается использовать корреляции, кото­
рые основаны на акцепторных числах, а не на диэлектриче­
ских функциях, так как они
всегда дают лучшее совпаде­
ние. В качестве примера, по­
казывающего учет корреляций
при расчете кинетических па­
раметров, на рис. 2.32 и 2.33
приведены диаграммы для се­
рии реакций. В этом слу­
чае диэлектрическая функция
учитывает дополнительный до­
норный эфф ект растворите­
ля. Помимо диэлектрической
проницаемости и донорной и
акцепторной способности рас­
творителя изменение скорости
реакции может б ы ть вызва­
но добавлением солей. Воз­
никающие при этом эффек­
ты обычно подразделяют на
Рис. 2.32. Соотношение между
константами скорости первого по­
рядка для сольволиза пара-ме-
токсинеофилтозилата и акцеп­
торными числами растворителей
(высокоструктурированные рас­
творители отмечены знаком «А»)
246

две категории. К первой от­
носятся изменения активности
ионов или полярных молекул.
Этот эффект называют первич­
ным^ чтобы отличить его от
вторичного солевого эффекта,
обусловленного тем, что ионная
сила раствора влияет на истин­
ную концентрацию ионов, об­
разующихся при диссоциации
слабых электролитов. Хорошо
известным примером является
замедление реакции, катализи­
руемой кислотой или основа­
нием под действием соли, что
связано с подавлением иони­
зации каталитической кислоты
или основания. Оба солевых
э ф ф е к т а описываются в рамках электростатических представ­
лений с помощью уравнений, выведенных Н. Бренстедом и
Дж . Бьеррумом. Все эти уравнения основаны на теории Дебая —
Гюккеля и сводятся к простому общему виду:
Рис. 2.33. Зависимость константы
скорости второго порядка для ре­
акции замещения фтора в пара-
нитробензоле азид-ионом от ак­
цепторных чисел (высокострук­
турированные растворители от­
мечены знаком «<]»)
In
= const •y/ly
ко
(2.85)
который считается справедливым для разбавленных растворов
концентрацией не выше 1СГ2 М. Здесь I — ионная сила системы,
а ко — константа скорости при нулевой ионной силе. В соответ­
ствии с теорией Дебая —Гюккеля активность иона определяет­
ся не только его зарядом и радиусом, но еще и его донорными
и акцепторными свойствами. Если исходить из простого утвер­
ждения, что катионы — это акцепторы, а анионы —доноры, то
солевые эффекты очень хорошо согласуются с представлениями
о химических координационных эф фектах растворителя. Отсю­
д а вытекают основные следствия:
1) ионы электролита проявляют донорные и акцепторные свой­
ства в большей (или сравнимой) степени, чем истинные реаген­
ты. Следовательно, компоненты электролита будут конкуриро­
вать с реагентом при сольватации;
2) удаление молекул растворителя из внешней сольватной
оболочки реагентов может привести к изменению их активности.
В случае структурированных растворителей добавление элек­
тро лита может изменить структуру раствора и, следовательно,
его координирующие свойства. Ионы электролита проявляют
247

донорные и акцепторные свойства в большей (или сравнимой)
степени, чем молекулы растворителя. Поэтому и те и другие
могут конкурировать з а присоединение к истинным реагентам
(координация во внешней оболочке в отличие от сольватации во
внешней оболочке). Образование ионных ассоциатов и комплек­
сов во внешней оболочке может привести к резкому изменению
активности. Последовательное вытеснение молекул растворите­
ля конкурирующими молекулами, действующими к а к лиганды,
характерно д л я координационных сфер катионов переходных
металлов. Рассмотренные закономерности влияния растворите­
лей на скорости химических реакций в растворах имеют каче­
ственный характер. К сожалению, количественная теория этой
проблемы еще не разработана.
2.12 . КАТАЛИЗ
ВВЕДЕНИЕ
Явление ускорения химической реакции веществом, не прини­
мающим в ней видимого участия, не входящим в состав ее про­
дуктов и остающимся после нее химически неизменным, наблю­
дал в 702 г. араб Абу Муса Джариб на примере получения эфира
из спирта в присутствии серной кислоты. В 1771 г. Пармантье от­
крыл явление осахаривания крахмала кислотами. В 1796 г. была
открыта дегидрогенизация спирта на металлах, а в 1797 г. —де­
гидратация спирта на глинах, на основе которой более столетия
спустя С. В. Лебедев получил первый в мире синтетический кау­
чук. Д ж. Пристли наблюдал каталитическое окисление водорода
и дегидрирование спирта, а Л .Теннар в 1810 —1825 гг. осуще­
ствил разложение аммиака и пероксида водорода на металлах.
Г. Дэви и Н.Доберейнер открыли переходящее в горение окис­
ление водорода на губчатой платине («огниво Доберейнера») и
саморазогрев (до красного каления) металлов в смеси воздуха
с горючими газами, положив начало гетерогенному окислитель­
ному катализу. В 1825 г. М. Фарадей осуществил синтез аммиака
из элементов. В попытках теоретического осмысления накапли­
вающихся ф актов И. Берцелиус сформулировал представление
о «каталитической силе», лежащей в основе явлений катали­
за. Э. Митчерлих ввел представление о «контактном действии».
Ю. Либих р азвивал механические представления о расщеплении
реагирующих молекул на острых пиках поверхности катализато­
ра. Завершением второго начального этапа явилось определение
В. Оствальда: «Катализатором является вещество, которое, не
248

участвуя в конечных продуктах реакции, изменяет ее скорость».
Это определение сыграло свою позитивную роль в становлении
науки о катализе как об одном из сложнейших и важнейших яв­
лений химии. Современные формулировки понятий «катализ»,
«катализатор» базируются на представлениях о протекании хи­
мических реакций через переходное состояние с образованием
активированного комплекса.
Катализатором называется вещество, которое изменяет
скорость химической реакции посредством вхождения в со­
став активированного комплекса, но не входящее в состав
продуктов реакции.
Важнейшим термодинамическим следствием из этого опреде­
ления катализа является то, что катализатор не влияет на по­
ложение равновесия катализируемой реакции. Отсюда следует,
что в условиях равновесия катализатор в равной степени уско­
ряет ка к прямую, так и обратную реакции и обеспечивает более
быстрое достижение равновесия.
Под неизменяемостью катализатора следует понимать неиз­
менность лишь его химической природы, т. е. неизменность со­
става. Физическое же его состояние (например, дисперсность)
может сильно изменяться в течение реакции, поскольку поверх­
ностные атомы, участвуя в переходном состоянии, могут отры­
ваться от кристаллической решетки. Так, оксид марганца(1У),
катализирующий распад пероксида водорода, превращается в
мелкий порошок. Платиновые сетки, на которых аммиак окисля­
ется до оксидов азота, разрушаются, превращаясь в мельчайшую
пыль. Дисперсность многих катализаторов падает, их удельная
поверхность уменьшается, что приводит к падению их каталити­
ческой активности («старение» катализаторов).
К концу XIX в. катализ занял важное место в химической
промышленности (синтез серной кислоты, окисление аммиака,
синтез анилина, гидрирование жиров, угля, тяжелых жидких
углеводородов и т.д .) , а в XX в. стал ее основой. Сюда отно­
сятся окрытый Э. Фишером синтез углеводородов из диоксида
углерода и водорода, разработанная Ф. Габером технология син­
теза аммиака, бурное развитие нефтехимических процессов, ос­
новы которых заложил В. Н. Ипатьев (каталитический крекинг,
облагораживание бензинов, изомеризация и окисление углево­
дородов, гидратация этилена — синтез спирта, получение синте­
тических каучуков, полимеризационные процессы и т.д .) . Осу­
ществляемые в основном на твердых катализаторах каталитиче­
ские процессы обеспечивают в настоящее время получение около
249

90% всей продукции химической и нефтехимической промыш­
ленности.
§ 1. Свойства и техническое назначение катализаторов
Важным свойством катализаторов является их селективность.
Особенность катализаторов вести реакцию в одном опре­
деленном направлении называется селективностью (избира­
тельностью) их действия.
По своему каталитическому действию катализаторы подраз­
деляются на катализаторы положительного катализа и катали­
заторы отрицательного катализа.
Ускорение реакции называется положительным катали­
зом или просто катализом.
Замедление или прекращение реакции в присутствии не
расходующегося в реакции вещества называется отрица­
тельным катализом.
Общей основой каталитического действия является:
1) снижение энергетических барьеров и облегчение построе­
ния переходного состояния, т. е. влияние на механизм и энерге­
тику процесса, приводящее к снижению энергии активации;
2) снижение энтропии активации в результате повышения ве­
роятности переходного состояния вследствие оптимизации про­
странственной его конфигурации и взаимной ориентации вхо­
дящих в него участников реакции на катализаторе (матричный
эффект). Это явление особенно широко распространено в био­
логических процессах, катализируемых ферментами, а также в
катализе на комплексах.
Нахождение пути реакции с наименьшей энергией активации,
а также поэтапная ее разбивка на два (или несколько) меньших
барьера являются типичными случаями каталитического уско­
рения реакций. Отсюда проистекает распространенное представ­
ление о роли промежуточных соединений в катализе, послужив­
шее первой научной трактовкой его механизма. Каталитическое
протекание реакции сопровождается снижением энергии акти­
вации (Е) как в прямом, так и в обратном направлении. При
этом разность энергий активации в обоих направлениях равна
тепловому эф ф ек ту реакции:
Е2-Ег=АН.
На энергию активации образования активированного комплек­
са оказывают влияние энергии связей, трансформирующиеся при
250

реакции. Это проявляется в эмпирическом соотношении, най­
денном Н. Бренстедом и М. Поляни и получившем название «со­
отношение линейности», которое связывает линейной зависимо­
стью энергию активации Е и теплоту химической реакции А Н :
Е=Ео±аАН
АЕ =±аДЯ,
где Е и а — постоянные д л я ряда сходных катализаторов опре­
деленной реакции или д л я ряда сходных реакций на одном и том
же катализаторе. Знаки «минус» и «плюс» отвечают экзотерми­
ческим и эндотермическим реакциям соответственно.
В зависимости от агрегатного состояния катализатора и ре­
акционной среды, включающей в себя субстрат (реагирующее
вещество), различают следующие типы катализа:
1) гомогенный, когда и субстрат, и катализатор находятся в
одной фазе (газ, жидкость) и система гомогенна;
2) микрогетерогенный, когда и субстрат, и катализатор на­
ходятся в одной (обычно жидкой) фазе, но катализатор макро-
молекулярен или состоит из частиц коллоидных размеров, не
выделяющихся в отдельную фазу. Сюда относится катализ на
коллоидных металлах, а такж е огромной важности раздел био­
катализа —ферментативный катализ. Важную роль здесь также
играют процессы комплексообразования на макромолекулярном
уровне;
3) гетерогенный, когда катализатор и субстрат находятся в
разны х фазах: обычно катализатор твердый, а реагирующие ве­
щества — газ или жидкость, причем процесс протекает на по­
верхности катализатора. Это наиболее распространенный и ва ж ­
ный дл я промышленности тип каталитических процессов.
Подобно обычным химическим реакциям, каталитические ре­
акции могут протекать по двум основным механизмам: гомо-
литическому и гетеролитическому. Реакции, сопровождающие­
ся разрывом некоторых существующих и образованием новых
электронных пар, называются гомолитическими. Они протека­
ют с образованием (участием) незаряженных частиц (свободных
радикалов), обладающих свободными валентностями атомов. Го-
молитический разрыв связи с образованием свободных радика­
лов может быть показан на следующей схеме:
А : В—>А*+Вв
Гетеролитический разры в связей с образованием ионов может
быть представлен следующей схемой:
А :В—>А“+В+
251

При гетеролитическом процессе разрыв двухэлектронной хими­
ческой связи идет без разры ва электронной пары посредством
перехода обоих электронов на атомную орбиту одного из ато­
мов, т. е. с образованием ионов. Образованию ионов способствует
высокая диэлектрическая проницаемость среды, поэтому обыч­
но ионные механизмы оказы ваю тся энергетически выгодными в
растворах. Гетеролитические окислительно-восстановительные
реакции связаны с передачей электрона. Поэтому различаю т три
основных ти па механизма катализа:
1) кислотно-основной (крекинг, гидролиз, омыление, этери­
фикация и др.);
2) катализ, связанный с передачей зарядов по электронодо-
норно-акцепторным механизмам, например, окислительно-вос­
становительные процессы на металлических и полупроводнико­
вых катализаторах (гидрирование и дегидрирование, окисление
и т. п.);
3) катал из посредством комплексообразования.
§2. Гомогенный катализ
Катализ в газовой фазе можно представить как образова­
ние промежуточных соединений, распадающихся с образовани­
ем продуктов с последующей регенерацией катализатора. Про­
цесс образования промежуточного соединения считается быст­
рым, достигающим равновесия, а распад его выступает как ли­
митирующая стадия реакции:
Быстро
А+kat<
=
[А-• - kat]—
Промежуточный
комплекс
Медленно
В+kat
Однако С. Хиншельвуд показал, что таких реакций практиче­
ски не существует и что в действительности имеют место цеп­
ные реакции, в которых роль катализатора играют переносчики,
способствующие образованию активных промежуточных соеди­
нений. Примером является окисление СО, прекращающееся (как
и ряд других окислительных процессов) в результате глубокой
1
осушки смеси СО + О2. Реакция СО + -02протекает при участии
Z
воды с промежуточным образованием водорода:
С0+Н20 ^ С02+Н2
Н2 + ~02 *=» Н2О ИТ.Д.
252

Водород действительно был обнаружен в продуктах этой ре-
•
акции. В окислении водорода играет важную роль радикал ОН,
обнаруженный спектроскопически. Таким образом, здесь имеет
место не катализ в собственном смысле этого слова (ускорение
реакции благодаря вхождению катализатора в активированный
комплекс), а ускорение процесса по механизмам сопряженных
реакций. Возможны и иные механизмы, например местное ак­
тивирование. Возможно ускорение реакции переносом энергии с
катализатора на субстрат, когда образование связи при присо­
единении катализатора к сложной молекуле снижает прочность
соседних связей и облегчает их разрыв или миграцию. Чаще все­
го это фотокатализ, т. е. сенсибилизация связей. Однако это —
не катализ в строгом смысле. Это не ускорение идущей реак­
ции, а принудительное ее осуществление за счет притока энергии
извне. Увеличивать скорость реакции может ускорение переда­
чи энергии при столкновениях вследствие увеличения их числа.
Так, примесь водорода ускоряет процесс термического распада
эфиров вследствие большей подвижности молекул водорода и
увеличения благодаря этому числа столкновений. Это также вы­
ходит з а рамки катализа. Может показаться, что случаем газо­
вого катализа является получение серной кислоты нитрозным
методом. Однако эта реакция проходит в жидкой фазе с образо­
ванием нитрозилсерной кислоты.
Гораздо большее значение имеет гомогенный катализ в ж ид­
кой фазе: в растворе. Здесь катализаторами служат в боль­
шинстве случаев ионы. Поэтому понятно, что первое место з а ­
нимает ион Н+, т. е. НзО+ как наиболее мощный деформатор-
поляризатор, обладающий максимальной величиной напряжен-
е
ности поля - и наибольшей подвижностью в растворе. По этим
г
же причинам мощным катализатором являю тся и гидроксид-
ион ы ОН". С действием этих двух ионов и связан в первую
очередь кислотно-основной катализ в растворах. Примерами яв­
ляю тся гидролиз сложных эфиров и многочисленные реакции
окисления и восстановления в растворах. В соответствии с со­
временными представлениями:
катализатор — это вещество, способное переводить реа­
гирующее вещество в реакционноспособное состояние, пред­
ставляющее собой активный комплекс, неустойчивый из-за
повышенной потенциальной энергии.
1. Первая стадия процесса —образование промежуточного со­
единения — является обратимым и относительно быстрым про­
цессом.
253

2. Неустойчивый активный комплекс распадается относитель­
но медленно. Этот процесс представляет собой лимитирующую
стадию процесса. При этом образуются продукты реакции и ре­
генерируется катализатор.
3. Общая скорость процесса пропорциональна концентрации
активного комплекса.
Лимитирующей стадией химического процесса называ­
ют самую медленную стадию, которая и определяет общую
скорость процесса.
Примеры каталитического действия в растворах многочис­
ленны, и многие из них находят практическое применение в
аналитической химии: например, окисление щавелевой кисло­
ты перманганатом калия; катализатором являются ионы Мп2+
в присутствии H2 SO 4 . Механизм гомогенного катализа может
включать в себя как молекулярные, так и ионные промежу­
точные соединения. Снижение энергии активации вызывается
уменьшением энергии связи соседних атомов при взаимодействии
с катализатором, что облегчает разрыв связей соседних атомов
и их перегруппировку.
Рассмотрим основные закономерности гомогенно-каталитичес­
ких реакций. Одним из наиболее часто встречающихся случаев
в практике исследования гомогеннокаталитических реакций яв­
ляется каталитическая реакция второго порядка:
Ai+А2
kat ^
----- >Р
Эта реакция протекает в две стадии через образование проме­
жуточного комплекса одного из реагентов с катализатором:
к-
Ai+kat <
>[Ai ■•■kat]
к+
[Ai ■•■kat] + A2
>P+kat
Очевидно, что [kat] <C [Ai] + [А2]. Другой формой записи может
быть:
k-.[kat\
АЛ
В ^2[А2]*Р +kat
Дифференциальными кинетическими уравнениями процесса бу­
дут:
= -fc+[Ai][kat] k-[A\kat])
254

d[Ai fcat]
dx
d[A2]
dx
m
dx
= fc+[Ai] [feat] - (к- + Zc2[A2])[AiA:af],
= -&2[A2][Ai&a£],
= A:2[A2][Aifcat].
Концентрация [Ai fcat] не может быть больше [kat}o, она прене­
брежимо мала по сравнению с [Ai] и [Аг]. К [Ai&af] применимо
dfAifcatl
приближение Боденштейна—Семенова---- —— = 0, откуда
[Ai fcat] =
к+
А:_+ /с2[А2]
dx
[Ai] [fcat].
(2.86)
Объединяя это уравнение с уравнением материального баланса
по катализатору [fcat]o = [hat] + [Ai kat\ получим:
[feat] = -
[A:at] о
+ {fc+/(^+ + ^2[A2])}[Ai]
Пользуясь этим выражением, можно привести уравнение (2.86)
к виду:
г*
= {Mfc- +*2[A2])}Mo[A1]
1 1 J 1+{к+/(к- +к2[А2})}[^) '
После подстановки данного уравнения в приведенные выше д и ф­
ференциальные уравнения можно видеть, что зависимость к а ж ­
дой из концентраций [Ах], [А2] и [Р] от времени дается одним и
тем ж е выражением скорости:
t
<f[A,|
<j[Aj d[P]
dx
dx dx
_
{k+k 2[ M }/(k- + k2[A2})}[kat}0[Ai
(2.87)
1 + {k+/(k- + k2[A2])}[Ai]
Кривые ([Ai] — т) и ([A2] — т) могут различаться по форме в
зависимости от того, какая стадия реакции является лимитиру­
ющей и какой из реагентов присутствует в избытке. Существует
несколько характерных случаев протекания этой гомогенной ка­
талитической реакции.
Случай I: к 2[А2] k+[kat\о +
Поскольку лимитирующей
стадией является образование промежуточного комплекса, ско­
рость не должна зависеть от [А2]. Это легко показать математи­
чески, не учитывая величину к - ) пренебрежимо малую по срав­
нению с ^[Аг], а также величину
МАх
fc2[A2]
, пренебрежимо малую
255

Рис. 2.34. Изменение концентрации [Ai] и [А2] во времени д л я данных
значений [А]о и [kat]о при условии:
[А2] k+[kat]o:
а,б—[А2]>[Ai];в, г —[А2]<[Ai]
по сравнению с единицей. Тогда уравнение (2.87) сводится к
уравнению
v = fc+[fcat]0[Ai] = fc3*[Ai].
(2.88)
Последнее представляет закон скорости второго порядка: пер­
вого порядка по отношению к каждому из компонентов [kat] и
[Ai] или, поскольку [kat]o постоянна, — уравнение псевдоперво­
го порядка. Следует иметь в виду, что уравнение (2.88) спра­
ведливо только в таких условиях эксперимента, при которых
[А2]о > [Ai]o, потому что при обратной ситуации [А2] снижается
до нуля, и к концу реакции условие fc2[A2] k+[kat]о больше не
выполняется. Поэтому весьма важ но знать, какой из реагентов
добавляется в избытке.
Случай 1а: [А2]о > [Ai]o- Убывание [Ai] происходит по экс­
поненциальной зависимости (рис. 2.34, а). Зависимость [А2] от
времени дублирует соответствующую зависимость д л я [Ai] и по­
тому имитирует реакцию первого порядка по А2. Однако кривая
не меняется при различных начальных концентрациях [А2], т. е.
при изменении концентрации [А2]о - [А 2]оо, равной [Ai]o, как по-
256

казано на рис. 2.34, б . Это служит доказательством нулевого
порядка реакции по А2.
Случай 16: [A^Jo < [Ai]o- При недостатке реагента А2 полу­
чают только части экспоненциальных кривых. Если взять при
этом точно такое же [Ai]o, к ак в случае 1а, то получатся части
соответствующих верхних кривых рис. 2.34, в и 2.34, г. Откло­
нение от экспоненциальной зависимости начинает проявлять­
ся, когда [А2] приближается к значению, при котором условие
/с2[А2] k+[kat]о больше не выполняется. Это означает, что в
данный момент лимитирующая стадия сдвигается от образова­
ния промежуточного компонента к следующей стадии: AifcatH-
+А2—>Р+kat.
Случай II: /г2[А2] k+[kat]+k~. Лимитирующей является ста­
дия A\kat +A2 —> Р + kat. Не учитывая величину &2[А2], пре­
небрежимо малую по сравнению с fc_, и используя соотношение
к+
К = — , можно упростить уравнение (2.87) до
k2K[kat]o[Ai][A2]
1 + К[А\]
(2.89)
Анализ этого уравнения зависит от положения равновесия при
образовании комплекса: Ai + kat A\kat.
Случай Па: К[А\] 1. Т ак как равновесие сильно сдвинуто
в сторону образования исходных веществ, уравнение (2.89) при­
нимает вид:
v = k2K[kat\o[Ai\[A2] = fc^[Ai][A2].
(2.90)
Как видно, общий порядок уравнения равен 3. Порядок по ка ж ­
дому из компонентов А, А2 и [kat] равен 1. Поскольку величина
[kat] о постоянна, уравнение может подчиняться закону псевдо­
второго порядка. Зная эффективную константу скорости
кэф = k2K[kat] о,
можно найти к2К у используя различные концентрации катали­
затора. В случае На разделение величины к2К невозможно, и
нельзя сказать, какое из исходных веществ активируется ката­
лизатором.
Случай Нб: К[А\] 1. Катализатор практически полностью
связан с Ai и уравнение (2.89) становится законом скорости вто­
рого или псевдопервого порядка:
v = k2[kat] о[А2] = кэф[А2].
Для этого уравнения при условии [А2]о > [Ai]o уменьшение
[Ai] во времени линейно ( t g a = k2[kat]o[A2]) до тех пор, по­
ка К[ Ai] ~Э> 1. Из зависимости t g a от [А2]о получают величи­
ну k 2 [kat]o. К концу реакции, когда A[Ai] ~ 1, она больше не
9 Ипполито»
257

соответствует нулевому порядку, а становится реакцией перво­
го порядка по Ai согласно уравнению (2.90). Применяя условия
псевдопервого порядка [А^о ^ [Ai]o, можно оценить величину
кэф - k 2 K[kat]o[A2 ]o. Варьируя [kat\o} можно определить К и fo.
Случай III: К[А{\ ~ 1. Довольно редкий случай, когда кон­
станта равновесия ни мала, ни велика, д л я того чтобы можно
было у простить уравнение (2.87). Тогда полезно привести выра­
жение
КМ=
к+
—
-----
к новой псевдоконстанте. Введем величину
[к- + [A2J)
(к- + ^2)
---- - ------
(величину, обратную приведенной выше) и обо-
к+
значим ее как функцию Михаэлиса
так как она не постоян­
на, а зависит от А2. Используя это обозначение, уравнение (2.87)
можно переписать в виде:
fo^V[fcQ*]o|Ai][A2]
I + A’mMAi]
или
_
Aj2[fcai]o[Ai][A2]
V
Км + [А,]
(2.91)
где [Ai] не обнаруживает простой зависимости от времени. Лю­
бое из этих уравнений можно непосредственно использовать при
большом избытке Aj и при условии, что К м лишь незначитель­
но меняется в ходе реакции. В этих условиях скорость меняется
линейно с концентрацией А2:
d[A2]
dx
—
&эф[А2],
где
&эф —
A:2[A:ai]o[Ai]o
К'м +[Ai]o '
Таким образом, кэф линейно растет с [feat]о, но стремится к
предельному значению при увеличении [Ai]o- Зависимость кэф
от [Ai]o становится линейной при обращении обеих координат,
т. е. при использовании преобразований Л айнуивера—Берка:
1_1
к^~а[А^Ь
+Р»
гдеа =
К\м
-;Р=
. В обратном случае, т. е. при условии
k 2 [kat\о’ к fc2[fcaf]o
[А2]о [A^]q, уравнение (2.91) принимает вид:
258

(2.92)
<^[Ах]_&2[&п£]о[А2]о г * л
~ ~ dT~ К'м+[Ах]1lJ-
На ранних стадиях реакции, когда [Ai] > К ‘м , концентрация
[Ai] линейно уменьшается (нулевой порядок по Ai). В дальней­
шем, когда [Ах] < К м , реакция имеет первый порядок по [Ах].
При [Ах] > К'м скорость определяется стадией A \k a t+ A 2 —►Р +
+ hat. Рассмотрим теперь зависимость начальных скоростей г>о
от концентраций [Ai]o, [A^Jo и [kat]о. При низких исходных кон­
центрациях Ах скорость линейно зависит от [Ах]о согласно урав­
нению (2.92) до тех пор, пока [Ах]о < К 'м :
А?2[ ] о[А2]о[А1]о
‘Vo = --------- JP---------- *
КМ
При [Ах]0 > К'м скорость vo достигает максимальной величины
(рис. 2.35, а) в соответствии с уравнением
^О(тах) &2[^^]о[А2]0'
Аналогичная кривая получается при построении зависимости v
от [Ах]. В отличие от Ах зависимость скорости от [А2]о и от [kat\о
линейна для целого интервала концентраций. Проинтегрируем
уравнение (2.92):
In
М - ц>тах= *2[Aw/]0[A2]o
tga = MMoIMo
[Ailo
[Arf
С=^м ^ [ M o[A2]o
k.
Рис. 2 .35. Общаятрактовка реакции Ах---------
tga2=-
1
L = “ ^2[Мо[А2]о
[A\kat\ —•Л2>P+kat при
k+kat
условии [А2]о > [Ах]0:
а—зависимость начальной скорости реакции от концентрации [Ai];б — так
называемый график Генри
259

[Ai]
[Aijo
к'м +lAi]
[Ai]
d[Ai] = - k 2 [kat]o[M]o dx.
о
Получим в результате интегрирования:
КмInjL-y- +([Ai]- [Ai]o) -
- k 2 [kat]o[A2 \oX
iA iJo
или
_
T/r’-l1\i fa 1
iy'-l [A l]o “ [Al]
- ------- ---- ------- --- ------
K m k2[kat]o[A2]o ~ K M ---------------- --------------------•
x
x
Так называемый график Генри, построенный как функция
b([Ai]o/[A!]) [Ai]0 - [Ai]
ln([Ai]o/[A i])
[P]
---- -
—
—
—
от-—-----
—
-
или — -------------- от — представ-
х
х
х/
х
ляет собой прямую с наклоном, равным К \Это означает, что
для разных значений [Ai]o получится одна линия. С другой сто­
роны, при варьировании [kat\o и [А2]о получаются параллель­
ные прямые при условии, что К'м практически постоянна в ходе
реакции. Пересечение их с ординатой и абсциссой д а е т соответ­
ственно величины i f ^ 1fc2[fca£]o[A2]o и А;2[feat]о[А^]о (рис. 2.35, б).
§3. Гомогенная каталитическая реакция первого порядка
Гомогенной каталитической реакции первого по рядк а соот­
ветствует кинетическая схема
или, более детально,
А+kat < yAkat
Р+kat
k+
Подобные реакции известны как реакции Михаэлиса —Ментен.
Они обычно встречаются в процессах, катализируемых фермен­
тами. Им отвечает уравнение Михаэлиса —Ментен:
d[А] = d[Р] = k2[kai\0K ^ l [A] = k2[kat]0[А]
dx dx
1+ К'м1[А]
Км+[А]
Анализ уравнения Михаэлиса —Ментен проводится описанными
выше методами и приемами.
260

§4. Ингибирование катализатора
Как отмечалось выше, действие катализатора заключается
прежде всего в обратимом образовании комплекса с реагентом.
Это означает, что катализатор должен быть способен к образова­
нию координационных связей. Однако случай, когда весь добав­
ленный катализатор распределен между свободным состоянием
и активным комплексом «катализатор —реагент», т. е. [kat]о =
= [kat]+[Akat], встречается редко. Исключение составляют «клас­
сические» реакции, катализируемые кислотами и основаниями.
Реакции такого типа относительно просты по той причине, что
ионные процессы протекают с большими скоростями. Например:
[Н30]++ А ^ [АН]++ Н20
Другим важным типом катализаторов являю тся металлоком­
плексные катализаторы, к которым относится и большинство
ферментов. Они отличаются от кислотно-основных катализато­
ров д ву мя существенными моментами.
1. Скорости обратной реакции, т. е. перехода промежуточно­
го комплекса в исходное состояние, и реального превращения в
конечный продукт соизмеримы, так что упростить приведенные
выше математические уравнения часто не удается.
2. Сродство катализатора к реагенту так велико, что образо­
вание любых комплексов с другими компонентами реагирующей
системы, особенно с продуктами реакции, приведет к уменьше­
нию каталитической активности.
Вероятно также, что катализатор может одновременно обра­
зовывать с реагентом как активный, так и неактивный промежу­
точный комплекс или, что активный промежуточный комплекс
способен связать следующую молекулу реагента и при этом об­
разовать менее активный или совсем неактивный комплекс. Та­
кие усложняющие факторы приводят к так называемому инги­
бированию катализатора, и их необходимо принимать во внима­
ние. Это указывает на то, что реакции, отвечающие простой ки­
нетике Михаэлиса —Ментен, являются скорее исключением, чем
правилом.
Рассмотрим случай, допустив образование других комплексов
с катализатором, например:
Кг
kat+Р< )katP
К2
Aj+Aikat < )AikatAi
Кг
Ai+katP7 )AikatP
261

и т.д., где К\,7^2)
соответвующие константы равновесия.
Составим уравнение материального баланса д л я катализатора
[kat]о= [kat\+[Aikat]+[featP]+[AikatAi]+••• ,
(2.93)
где [kat] — концентрация свободного катализатора, a Ai • ■*kat —
активный промежуточный комплекс. Если предположить, что
во всех рассмотренных случаях равновесие достигнуто полно­
стью, то уравнение (2.93) можно записать, используя выраже­
ния д л я соответствующих констант равновесия:
[kat]о = [kat] +K j^ [kat][Ai] + K\ [kat][P]+
+ K2K tf[kat][Ai]2+K3Ki[kat][Ax][P]+ •••
или
M o = [kat](l +К'й1[Ax]+К г[P]+
+ K2K'^ [Ax]2+KZKX[Ax][P]+ •••).
Выражение в скобках называют функцией закомплексован­
ности катализатора с компонентами реакционной смеси и обо­
значают F . Эта функция является отношением общей концен­
трации катализатора к концентрации катализатора в свободном
состоянии. Обратную ей величину — называют коэффициен-
F
том активности катализатора. Используя обозначение F , урав­
нение (2.12) можно записать в виде:
[Ах]М=K^ k<f 0^ 1.
Г
Используя это выражение, получаем самое общее уравнение ско­
рости д л я реакции типа (2.12), катализируемой комплексом ме­
талла:
<*[Ai]_ d[A2] _ <ДР _> 2АГУМо[Аг][А2]
dx
dx dx
F
Это уравнение можно преобразовать к виду:
_
Ааку Мо[Ах][А2]
v
i+a:^[Ai]+af ’
где AF — мера ингибирования катализатора. В отсутствие ин­
гибирования A F равно нулю. Д л я того, чтобы определить со­
ответствующие константы, удобно провести измерения в таких
262

условиях эксперимента, при которых [Аг]о > [Ai]o- Тогда схема
реакции сводится к схеме типа Михаэлиса —Ментен, в которой
К м — реальная константа при данной величине [А2]о- Рассмот­
рим случай, когда A F = 0. В соответствии с кинетикой Михаэли­
с а —Ментен зависимость v от [Ai] имеет форму гиперболы. Она
преобразуется в прямую, если взять обратные величины каждой
из частей уравнения (2.94), т. е. провести уже упомянутое выше
преобразование Лайнуивера —Берка:
1_
1________ 1_
1
V
k2K ’j^[kat] o[A 2]o [A i ] k2[kat]о[А2]о
(2.95)
Тогда в координатах
-
~
\v
1
[Ai]
зависимость (2.95) полу­
чается в виде прямой с угловым коэффициентом, равным
/т
.
г,— .
.,
, ч. Пересечение прямой с ординатой и с абсцис-
(к2К£[Ш \о[А2]о)
сой позволяет получить величины ——т
-
—п
гж. . и К’м1.Оче-
(А:2(Ш ]о[А2]о)
м
видно, что графики любой зависимости — от
[Aijo
по данным
11
нескольких экспериментов и зависимости - от 7-—г по данным
V
[A i]
одного эксперимента будут совпадать друг с другом. Этот ре­
зультат служит подтверждением отсутствия ингибирования ка­
тал иза то р а продуктом. Механизмы различных типов ингибиро­
вания хорошо исследованы д л я ферментативных реакций. Вве­
денные при этом обозначения используются и д л я металлоком­
плексного катализа. Прежде всего следует различать обратимое
и необратимое ингибирование.
§5. Обратимое ингибирование
Существует несколько типов обратимого ингибирования.
Тип I: конкурентное ингибирование. Молекулы ингибитора,
которыми могут быть чужеродные частицы (In ) или продукт
реакции Р, и молекулы реагента Ai, конкурируют между собой
за присоединение к активному центру катализатора.
Тип 1а: ингибитором является чужеродная частица, концен­
трация которой не зависит от времени:
In +kat < )[Inkat]
263

1
(2.96)
AF =K1[In\,
1+K\\In\
v
fc2[A2]o(fca*]o k2K'ML[kat}o[A2 ]o [A i]'
„
,
1111
Графики зависимостей — от г . п и
—
от т—^-
[Ai]o
[Ai]
представляют
собой прямые, тангенсы угла наклона которых увеличиваются с
ростом [/га]. Все прямые, отвечающие различным концентраци-
1
ям ингибитора, пересекают ординату в одной точке
-1
(fc2[A:at]o[A2]o)’
, как это можно
а абсциссу пересекают в точках —,
.
т,fr1N
Км (1+Кг[1п})
видеть на рис. 2.36.
Тип 16: ингибитором явл яется продукт реакции Р:
Кг
Р+hat< 1Рkat
Поскольку [In] = [Ai]o - [Ai], уравнение (2.96) принимает вид
1
v
A:2[A:at]o[A2]o
(1- КмКг)+К'м{1+Кг[Ах]о)^
Тип II: неконкурентное ингибирование. К атал и зато р имеет не
один, а несколько центров, способных к комплексообразованию.
Активный промежуточный комплекс сам может присоединиться
к молекуле ингибитора, д а в а я неактивный комплекс
Aikat-bln'
К2
AikatIn
В этом случае
A F = К 2К'м1\1п\[кг].
Тип На: ингибитором является чужеродная частица:
1
v
А:2[Ш]о[А2]о
1 + К 2[1п]+К'м
[Ai]
рд.
1111
1рафики зависимости — от г, , и - от т— г
vo
[Ai]o v
[AiJ
бой прямые, пересекающие ординату в точке (1+
представляют со-
К 2[1п]
),
(fc2[fcoi]0[A2]o)
а абсциссу в точке - K j ^ { l +k2[In\). При использовании различ­
ных концентраций ингибитора получают параллельные прямые.
264

Рис. 2.36. График Лайнуивера —
Берка для конкурентного ингиби­
рования чужеродной частицей In
при [1п\ 1 < [1п}2 < [In]3
Рис. 2.37. График Лайнуиве­
ра —Берка для неконкурентно­
го ингибирования продуктом при
[Ai]oi < [Ai ]02 < [Ai ]q3
Тип 116: ингибитором является продукт реакции:
1
V
1
k2[kat\о[А2]о
1+ ^2[Ai]0- ^ 2[Ai]+ К ы
Нетрудно заметить, что график Лайнуивера —Берка в этом слу­
чае нелинеен, но становится линейным на последних стадиях
реакции, т. е. когда практически весь реагент Ai израсходован.
Прямые части графиков д л я различных величин [Ai]o парал­
лельны, их угловой коэффициент, как видно на рис. 2.37, равен
k2[kat] о[А2]о
Чисто неконкурентное игибирование наблюдается очень ред­
ко, та к как сам ингибитор может присоединяться к активному
центру катализатора. Это приводит к комбинации конкурентно­
го и неконкурентного ингибирования, так называемому «пере­
крестному ингибированию».
Тип III: перекрестное ингибирование. Этот тип ингибирова­
ния объединяет типы I и II. Различают три ситуации, в кото­
рых ингибитором является чужеродная частица, продукт реак­
ции или сам реагент. Последний случай называют «ингибирова­
ние реагентом»
Тип Ша: ингибитором является чужеродная частица. В таком
случае
AF =K1[In] +K2K ,Ml[In][Ах],
1
v
1
А;2[Ш ]о[А2]о
1+к2[1п\+ ^ м (1+ а:1[/п])|2-| -
265

График зависимости в координатах Лайнуивера—Берка пред­
ставляет прямую, тангенс угла наклона которой соответству-
К'м {1 +К\[1п\)
ет величине —^~г,—,, г . ,— .
Эта прямая пересекает ординату
в точке
fc2[fcoi]o[A2]o
1+ К2\1п
К'йЧ1 + К 2[1п])
, а абсциссу в точке
k2 [kat]o[A2]o’
1+ Ki[In\
Тип II16: продукт реакции действует как ингибитор:
J 1+ к 2[Ai]o - К'МКХ- К2[Ai] +Км(1+АГ1[А1]о)|Ту
V
k2[kat]o[A2]o
Тип Шв: ингибирование реагентом. Активный промежуточ­
ный комплекс связывает еще одну молекулу реагента, что при­
водит к образованию неактивного комплекса:
к2
Aikat + Ai AikatAi
^
k2[kat]0[А2]о
Рис. 2.38. Ингибирование реагентом. Пунктирная линия в области (а)
относится к реакции без ингибирования реагентом; два варианта (6, в)
,
11
построения графика зависимости — от т—г или от A J
[Ах]
266

В этом случае
AF =K2Kj?[Ах]2-
Дл я этого случая уравнение скорости имеет вид:
k2K'^[kat] ojA^otA!]
* 1+К ‘^ [А 1}+К2К'м1[М]2
(2.97)
или, через преобразование Лайнуивера—Берка:
1
v k2\kat) о[А2]о(-1 + К м
1
га
+ АДАх]).
(2.98)
Благо даря квадратичному члену в знаменателе уравнения (2.97)
кр ивая скорости может проходить через максимум во время
уменьшения [Ai] от начального значения до нуля (рис. 2.38,
а). Дальнейший ход кривой зависит от того, ло ж атся ли экспе­
риментальные точки на восходящую ветвь кривой, как обычно
(слева от пика на рисунке), или на нисходящую.
Имеются две возможности построения гр аф и к а по уравне­
нии от [Ах]. Оба графика пред-
нию (2.98): зависимость - о т 7—т
v
[Ах]
ставляю т собой кривые, переходящие в прямую, к ак показано на
рис. 2.38, бив. График зависимости двух обратных величин ли­
неен до тех пор, пока АДАх] 1, тогда как график зависимости
1
К~1
-
от [Ах] сохраняет линейность в области, где м
1.
V
[Ах]
§6. Необратимое ингибирование
Необратимое ингибирование или отравление катализатора
обычно рассматривают, вклю чая в кинетику реакцию отравле­
ния катализатора, являющуюся реакцией первого порядка:
kata ^ kati
и
[kata] - [kat]oe~kiZ
где подстрочные индексы а и г указывают на активный и дез­
активированный катализатор. Рассмотрим в качестве примера
учет реакции отравления катализатора в кинетической схеме:
Ai fe [AxA;af]fc^ ] P + A;<rf.
fc+[fcat]
267

Для случая Па, когда К[А\] 1, имеем
= k 2K [A 2][A1}[kat]0e-ki\
аХ
При условии [А2]о > [Ai]o его можно записать как
_
k
dz
~
Л
’
где А:эф = k 2 K [A 2 ]o[kat]o- После интегрирования получаем
-
ini ^
=- (if)(e'‘" -i)-
(2-99)
При х —►оо получим:
_1 [A-i ]qq _ &эф
[Ai]0 h
или
ln[A1]oo = in[A1]0 - ^
.
(2Л00)
Для графического представления данных уравнение (2.99) мож­
но преобразовать к виду:
-
,ni
или, подставляя (2.100), к виду:
ln[Ai] -ln[Ai]oo = Д ln[Ai] = ( ^ ) e"fciT.
С помощью последнего уравнения можно определить кон­
станты, как показано на рис. 2.39.
268

АВТОКАТАЛИТИЧЕСКИЕ РЕАКЦИИ
Автокаталитической называют реакцию, при которой
продукт действует как катализатор и которую можно рас­
сматривать как необратимое ускорение в противополож­
ность необратимому ингибированию.
§ 7. Автокаталитическая реакция первого порядка
Схема реакции имеет вид:
А-^Р
а уравнение скорости:
»=
® = ЫА|[Р) =ЧА](|А|„ - (А]).
Оно подразумевает, что реакция не будет иметь места в отсут­
ствие небольших следов продукта [Р]о, которые должны иници­
ировать реакцию. Поэтому
v = kc[А]([Р]о + [А]0-[А]).
(2.101)
Одновременно существует возможность протекания реакции
по некаталитическому пути:
ко
А:
*с[Р]
(2.102)
В этом случае дифференциальное уравнение принимает вид:
y=[A]{fco + A:c([A]o-[A])}.
(2.103)
Введем новую величину q, тогда оба уравнения (2.103) и (2.101)
можно записать в общем виде:
v = &с[А](<7+ [А]0 - [А]),
(2.104)
ко
где q равно [Р]о и — соответственно д л я схем (2.12) и (2.102).
Кс
Интегрирование этого уравнения дает выражение
[А]о
[А] = ([А0] +q) [А0] + де"М[А|о+4)т ‘
(2.105)
269

Ему соответствуют S-образные кривые, подобные кинетиче­
ским кривым для последовательных реакций. Уравнение (2.105)
упрощается на более поздних стадиях реакции, когда экспонен­
циальный член в знаменателе изменяется до величин, много боль­
ших [А]о- Тогда
[А] = No ([А]о+ ф-МНо+Ф
9
или в логарифмической форме:
In [А] = In [А1° ([А]о + 9) - fcc([A]o + 9)т.
Q
Графическая зависимость In [А] от %представляет собой кри­
вую, переходящую в прямую с отрицательным угловым коэффи­
циентом, равным /сс([А]о +д) (рис. 2.40, а). То, что угловой коэф­
фициент — это линейная функция [А]о, легко понять, так как на
последних стадиях реакции концентрация продукта тем больше,
чем больше было [А]о. Зависимость углового коэффициента от
[А]о используют не только для оценки констант, но и д л я того,
чтобы отличить одну схему от другой. В случае чисто автока-
талитической реакции результирующая прямая проходит через
начало координат и ее наклон равен кс. Если ж е одновремен­
но происходят и каталитическая, и некаталитическая реакции,
то прямая пересекает ординату в точке ко, и при этом угловой
коэффициент также равен /сс.
а
б
Рис. 2.40. Автокаталитическая реакция первого порядка (пояснение в
тексте)
270

Другим методом является прямое сравнение кривых ([А] —т)
из серии измерений, при которых изначально добавляют различ­
ные количества продукта, а начальную концентрацию понижают
на такую же величину, т. е. [P]oi +[A]oi = [А]о и т.д . (рис. 2.40, б).
В любой момент начальная скорость должна возрастать с уве­
личением [Р]о, но степень этого возрастания будет зависеть от
относительного вклада каждого из двух путей. В случае чисто
автокаталитической реакции каждую кривую можно совместить
с первоначальной кривой (т. е. с кривой д ля [Р]о = 0) таким об­
разом, что начало координат сдвинется в направлении кинети­
ческой кривой, как показано стрелками на рис. 2.40, б. Рассмот­
рим теперь изменение скорости в ходе реакции. S-образная фор­
ма кинетических кривых свидетельствует о том, что скорость
реакции проходит через максимум, находящийся в точке пере­
гиба кривой. Д л я того чтобы определить положение максимума,
преобразуем уравнение (2.104) в квадратное уравнение
v=кс
Максимальная скорость достигается, когда правый из квадрат­
ных членов становится равным нулю, поэтому:
^шах —кс
[А]о +<?\ 2
( 2. 106)
В этот момент концентрация реагента А снижается до величины
[А]^
_
[А]о Я
22’
Если q очень мало, то максимум скорости соответствует мо­
менту, когда половина исходного вещества уже превратилась в
продукт реакции. В случае большого q максимум скорости, т. е.
то чка перегиба на кривой ([А]—т), сдвинут в сторону меньшей
глубины превращения. Н а рис. 2.41 показано соотношение меж­
ду г» и [А] для трех произвольно выбранных значений q. Опреде­
лим начальные и конечные угловые коэффициенты на графике
(г»—[А]). Дифференцирование (2.106) по [А] дает
dv
= kcq + fcc[A]o - 2fcc[A).
Тогда начальный наклон (когда [А] = [А]о) будет
271

а конечный наклон будет (когда [А] = 0):
^
= M[AJo+«).
§8. Гетерогенный катализ
Гетерогенный катализ приобрел важное значение в химиче­
ской промышленности. Важнейшие химические производства,
такие как синтез аммиака, получение серного ангидрида при
синтезе серной кислоты невозможны без использования гете­
рогенного катализа. Широкое применение гетерогенный ката­
лиз находит в производстве органических веществ и материалов.
С его помощью осуществляют процессы дегидрирования (полу­
чение бутадиена, изопрена, стирола для синтеза каучуков):
- СН2-СН3 -СН=СН2+Н2
и гидрирования различных веществ, например, синтез циклогек­
сана, спиртов, аминов:
RCOOH - ^ 2 RCH2OH
ArN02+- ^ 2ArNH2+Н20
Важное место катализ занимает и в проведении многих про­
цессов окисления, например, при получении окиси этилена, ма­
леинового и фталевого ангидрида:
Рис. 2.41. Изменение скорости v в зависимости от концентрации в ав-
токаталитической реакции первого порядка при q\ < g2 <
272

сн2=сн2+|о2-»сн2—сн2
о
а та к ж е окислительного аммонолиза, как, например синтез ак­
рилонитрила:
СН2=СН-СН3+NH3+ 1,502 -> CH2=CHCN +3H20
Перечисленные реакции относятся к гомолитическим, одна­
ко гетерогенный катализ применяется и д л я гетеролитических
(ионных) процессов: гидратации и дегидратации, алкилирова­
ния, этерификации (синтез этанола, простых эфиров, ненасы­
щенных веществ, аминов):
СН2=СН2^ о * СН3-СН2ОН; 2R0H -* R0R +H20
- СНОН-СН3^^ -СН=СН2;ROH+NH3-►RNH2+H20
При прочих равных условиях преимущества гетерогенного
катализа перед гомогенным состоят в малом расходе катали­
затора на единицу количества продукта, снижении или полном
устранении токсичных сточных вод и расхода реагентов на про­
мывку реакционной массы. Это обусловлено тем, что гетероген­
ный катализатор, находясь в твердом состоянии, легко отделяет­
ся от реакционной массы или вообще не уносится. Кроме того,
нередко уменьшается коррозия аппаратуры, снижаются капи­
тальные затраты и т. д.
По способу осуществления гетерогенно-каталитические про­
цессы можно подразделить на процессы:
со стационарным (неподвижным) катализатором, где он ис­
пользуется в виде достаточно крупных гранул (3 —10 мм);
с подвижным катализатором (диспергированным, псевдоожи­
женным или плавающим), когда он применяется в измельченном
виде и способен перемещаться под влиянием потока реагентов.
В свою очередь, каж дый из этих процессов можно осуществ­
лять в газовой или жидкой фазе, причем в последнем случае
нередко реализуется более сложный гетерогенный гетерофазный
процесс (например, жидкофазное окисление и дегидрирование).
273

§ 9. Гетерогенные катализаторы
В соответствии с механизмом протекающих реакций гетеро­
генные катализаторы подразделяют на следующие три группы:
1) ионные, под влиянием которых протекают реакции с ион­
ным механизмом;
2) электронные, катализирующие гомолитические реакции;
3) бифункциональные, совмещающие ионный и электронный
катализ.
К гетерогенным катализаторам ионных реакций относятся
следующие.
1. Кислотно-основные катализаторы:
оксиды некоторых металлов, преж де всего, AI2O3, W2O3, ТЮ2
и ДР-;
природные и синтетические (А120з)т(8Ю 2)п(Н20)р алюмо­
силикаты, а такж е средние и кислые соли: Саз(РС>4)2, СаНР04,
MgHP0 4;
протонные и апротонные кислоты на носителях Н3РО4 на
AI2O3 или кизельгуре, BF3 на А2О3, гетерополикислоты и ионо­
обменные смолы, обычно представляющие собой сульфирован­
ные нерастворимые полимеры сетчатой (сшитой) структуры , на­
пример, сополимер стирола с бутадиеном-1,3 или дивинилбен-
золом, фенол-формальдегидный полимер, в приповерхностные
ароматические ядра которых введены сульфокислотные группы:
\сн—
(O t-so2oh
2. Комплексообразующие соли переходных металлов на раз­
личных носителях: C112CI2, HgCl2, PdCh+CuCb, CuC=CCu, NiCb-
Широкое распространение в качестве катализаторов комплексо­
образующие соли переходных металлов получили в процессах
окисления углеводородов.
Гетерогенные катализаторы гомолитических реакций всегда
являются электронными проводниками или полупроводниками;
обычно они глубоко окрашены и включают следующие группы
веществ:
1) переходные металлы первой подгруппы (Си, Ag) и VIII груп­
пы (Fe, Ni, Со, P t, Pd) периодической системы Д. И. Менделеева;
2) оксиды металлов MgO, ZnO, CuO, Fe203, СГ2О3, WO3,
M0O3, V2O5, сульфиды WS3, M0S3 и смеси, содержащие основ-
274

ной оксид с небольшими добавками других (модифицированные
оксидные катализаторы);
3) сложные оксидные и сульфидные катализаторы с соизме­
римым соотношением компонентов, а такж е соли-полупроводни­
ки: хромиты СиО •Сг20 з, ZnO •Сг20 3, вольфраматы СоО •WO3,
молибдаты В120з • М0О3, NiS ■М0О3, ванадаты и др.
В химической промышленности катализаторы на основе ме­
таллов (кроме Ag) применяются в процессах гидрирования; дл я
этих ж е процессов используются и сложные катализаторы. Д л я
реакций дегидрирования применяют главным образом оксиды
(MgO, ZnO, Fe203, Сг20 з), а дл я процессов окисления — такие
оксиды как (CuO, V205), а также вольфраматы, молибдаты и
Ag. В реакциях гидрирования наиболее активны P t и Pd, мень­
ше Ni; еще более мягким действием обладают Fe, Со и Си. При
окислении и дегидрировании P t, Pd и Ni способствуют слишком
глубокому превращению реагентов; это же относится и к хроми­
там. Мягкими катализаторами неполного окисления являются
CuO, V20 5, вольфраматы, молибдаты. Оксиды и сульфиды мо­
либдена и вольфрама нечувствительны к отравлению сернисты­
ми соединениями, чем объясняется их широкое распространение
при переработке нефтепродуктов. Между двумя предыдущими
типами катализатора не существует резкой границы, некоторые
из них способны ускорять и ионные, и гомолитические реакции.
Сравнительную способность их к разным типам катализа мож­
но, например, оценить по активности в реакции разложения эта­
нола, складывающегося из его дегидратации и дегидрирования:
УСН2=СН2+Н20
СН3-С Н 2ОН
4 СН3-СНО +Н2
Относительная доля продукта дегидратации от общего коли­
чества разложившегося этанола при катализе разными оксидами
изменяется так:
А203ЛУ03 ..... 98,5
М о2Оз .... -----23,0
ThO............ . . .100,0
ZrO .........
-
-
-
-
-
-
-
45,0
С г 20 з .............. . . . 91,0
Бе20 з .........
------- 14,0
S i 0 2 ................... . . . 84,0
v 2o 5 .......... .... 9,0
т ю 2 .............. ... 63,0
ZnO.........
___ 5,0
Из приведенных данных следует, что некоторые оксиды явл я­
ются бифункциональными катализаторами. Бифункционально-
275

сти катализатора можно также достичь, используя смеси окси­
дов разного типа. Лучшим примером является система ZnO на
AI2O3, успешно применявшаяся д л я синтеза бутадиена из эта­
нола, где одновременно протекают ионные и гомолитические ре­
акции. В последнее время нашли важное применение бифунк­
циональные катализаторы, состоящие из носителя кислотного
типа ( A I 2 O 3 , алюмосиликаты) с нанесенным на него металлом-
катализатором гомолитических реакций (Pt, Pd). Так, при ката­
литическом риформинге нефтепродуктов кроме СГ2О3 широко
используют P t на AI2O3 (платформинг).
Гетерогенные катализаторы долж ны удовлетворять опреде­
ленным требованиям, основные из которых:
1) высокая каталитическая активность;
2) достаточно большая селективность (избирательность) в от­
ношении целевой реакции;
3) простота получения и воспроизводимость всех свойств ка­
тализатора;
4) высокая механическая прочность к сжатию, удару и исти­
ранию;
5) достаточная стабильность всех свойств катализатора на
протяжении его службы и способность к их восстановлению при
том или ином методе регенерации;
6) небольшие экономические затраты на катализатор при про­
изводстве единицы продукции.
Обеспечение этих требований достигается, главным образом,
при разработке состава катализатора и способа его получения.
Гетерогенные катализаторы сравнительно редко применяются в
виде индивидуальных веществ и часто содержат различные до­
бавки — модификаторы. Цели их введения очень разнообраз­
ны: повышение активности катализатора (промоторы), избира­
тельности и стабильности работы, улучшение механических или
структурных свойств. Фазовые и структурные модификаторы
стабилизируют соответственно активную фазу твердого катали­
затора или пористую структуру его поверхности. Так, в медь-
хромитных катализаторах гидрирования окись хрома препят­
ствует восстановлению окиси меди с превращением ее в неак­
тивную форму. Добавление уже 1 % AI2O3 к железному ката­
лизатору сильно увеличивает его поверхность, препятствуя спе­
канию и закрытию пор и т. д. Некоторые модификаторы суще­
ственно повышают стабильность работы катализатора или силь­
но изменяют характер его каталитической активности. Напри­
мер, добавка щелочей к цинк-оксидному катализатору д л я син­
теза метанола ведет к образованию высших спиртов, от этого
же существенно зависит работа кобальтового катализатора при
276

получении синтина и т.д . К числу модификаторов можно отне­
сти и носители (трегеры), особенно часто применяемые в случае
дорогостоящих металлических катализаторов (P t, Pd, Ni, Со).
Роль носителей состоит в повышении активнсти поверхности,
увеличении термостойкости и механической прочности катали­
за то р а и т.д . В качестве носителей используют алюмосиликаты,
оксиды алюминия, хрома или кремния, активированный уголь,
пемзу, кизельгур и другие природные и синтетические матери­
алы. Их влияние на каталитические свойства можно иллюстри­
ровать таким примером: дегидрирование метил циклопентана на
платине, нанесенной на активированный уголь, ведет к образо­
ванию метилциклопентена и пентадиена, а при дегидрировании
на P t —AI2O3 образуются бензол и циклогексан. В других слу­
чаях носители изменяют активность и избирательность катали­
за то ра и т.д . Следовательно, роль носителя как модификатора
свойств катализатора может быть очень большой, и его выбор
является существенным при создании (оптимального) катализа­
то ра д л я данного процесса.
Большое влияние на свойства катализатора оказывает метод
его получения. Поскольку химическая реакция протекает на по­
верхности, в большинстве случаев очень важно получить ката­
лизатор с максимально развитой поверхностью, т. е. с большим
количеством пор. Р азличаю т следующие промышленные ката­
лизаторы:
1) осажденные (солевые, оксидные) — монолитные, таблети-
рованные или порошкообразные формованные;
2) катализаторы на носителях (солевые, оксидные, металли­
ческие) — зерненые, таблетированные, формованные;
3) природные (силикаты и алюмосиликаты);
4) плавленые (металлические и оксидные), в том числе ме­
таллы в виде проволочных сеток, спиралей и т.д .;
5) скелетные (металлические).
Все способы получения катализаторов делятся на мокрые и
сухие, из которых наиболее распространен первый. Он состоит в
осаждении активной основы катализатора в виде геля из водного
раствора соли под действием различных осадителей, например:
A1(N0 3)3+ ЗШ4ОН -» А1(ОН)3+ 3NH4NO3
Путем соосаждения двух или более гидроокисей из смеси солей
легко готовить промотированные, смешанные или солевые ката­
лизаторы. Этим же способом получают синтетические носители.
На свойства катализатора влияет как выбор используемых
реагентов, так и степень их чистоты. Активность и пористая
структура катализатора (или носителя) существенно зависят от
277

температуры и скорости осаждения, концентрации растворов,
времени созревания осадка, pH среды и т.д . Структура ката­
лизатора зависит и от последующей обработки геля, состоящей
в его отмывке от посторонних ионов, фильтровании, сушке и
прокаливании. При некоторых из этих операций и происходит
образование пор за счет выщелачивания примесей и удаления
влаги.
Катализаторы на носителях готовят методом пропитки. Обыч­
но носитель в заранее приданной ему форме пропитывают не­
сколько р аз водным раствором соли или другим веществом, по­
ка не будет достигнуто нужное содержание компонентов, после
чего следует фильтрование и при необходимости с уш ка и про­
каливание. Если активным началом катализатора является ок­
сид металла, пропитку ведут термически нестабильными соля­
ми или их смесями (нитраты, оксалаты, аммониевые соли кис­
лот данного металла), которые при последующем прокаливании
превращаются в оксиды. В случае металлических катализаторов
на носителях эти оксиды восстанавливают затем водородом до
свободного металла.
Менее распространены сухие методы приготовления катали­
заторов. Таким путем получают, например плавленые катализа­
торы (оксидные и металлические). К сухим методам относится и
получение диспергированных катализаторов путем термическо­
го разложения их солей.
Особую группу составляют очень активные скелетные ка­
тализаторы, из которых чаще всего применяется так называ­
емый никель Ренея. Несмотря на ряд недостатков (пирофор­
ность, недолговечность, дороговизна), они широко используют­
ся в лабораториях и производствах небольшой мощности. Ни­
кель Ренея получают путем выщелачивания щелочным раство­
ром никель-алюминиевого сплава (чаще всего в соотношении
50: 50), используя избыток горячего едкого натра. Таким путем
удаляется почти весь алюминий и остается очень пористая губ­
чатая (скелетная) масса никеля, которую из-за ее пирофорно­
сти нужно хранить под слоем инертной жидкости. Более пер­
спективен катализатор Бага, получаемый неполным выщелачи­
ванием алю миния (только с поверхностного слоя). В отличие от
никеля Ренея он способен к регенерации путем повторного вы­
щелачивания более глубоких слоев. Гетерогенные катализаторы
характеризуются рядом физических свойств. Фракционный со­
став зерен катализатора определяют ситовым и седиментацион-
ным анализом, фазовый состав рентгенофазовым и электронно­
микроскопическим методами. Важной характеристикой являет­
ся удельная поверхность, отнесенная к единице количества ка-
278

тализатора. Ее находят адсорбционным путем или газохрома­
тографическим способом. Средний радиус пор вычисляют де­
лением удвоенного удельного объема пор, определяемого по ис­
тинной и кажущейся пористости катализатора, н а удельную по­
верхность. Наконец, имеет значение и распределение пор по р а­
диусам, которые находят при капиллярной конденсации какого-
либо вещества, начинающейся при тем более низком давлении,
чем меньше радиус пор. Подробная методика определения ф и­
зических характеристик катализаторов изложена в специальных
руководствах. Здесь следует лишь подчеркнуть, что знание этих
характеристик необходимо при каждой исследовательской рабо­
те и они обязательно содержатся в паспорте промышленного ка­
тализатора.
§10. Теории гетерогенного катализа
Первая из теорий гетерогенного катализа состояла в пред­
положении об образовании промежуточных соединений реаген­
тов с катализатором — гидридов металлов при гидрировании,
высших оксидов при окислении и т.д . Эти промежуточные со­
единения во многих слу чаях не были впоследствии обнаруже­
ны, и такая точка зрения имеет сейчас все меньшее распростра­
нение. Однако ее нельзя полностью исключить, поскольку об­
разование промежуточных соединений иногда является вполне
достоверным. Так, при разложении муравьиной кислоты на ме­
таллических катализаторах спектральным анализом обнаруже­
ны соответствующие соли, причем активность катализатора ока­
зывается связанной с теплотой образования солей. На рис. 2.42
эта зависимость изображена для активности, выраженной че­
рез температуру, обеспечивающую равную степень превращения
муравьиной кислоты з а одинаковое время (чем ниже темпера­
тура, тем выше активность катализатора). Исходя из этих дан­
ных можно полагать, что распад молекулы муравьиной кислоты
происходит через образование ее соли, причем металлы в левой
части кривой мало способны к образованию соли, а в правой, на­
оборот, дают слишком прочные поверхностные соединения. Наи­
более высокая активность достигается д л я металлов с теплотой
образования формиата ~ 335 кДж/моль.
Наиболее распространены различные адсорбционные теории
гетерогенного катализа. В их основе л ежит представление о пер­
воначальной адсорбции реагентов на поверхности катализато­
ра. При физической адсорбции, вызываемой силами Ван-дер-
Ваальса и сопровождающейся лишь небольшим выделением теп-
279

ла (8 —21 кДж/моль), активирования реагентов практически не
происходит. В отличие от этого, активированная адсорбция со­
провождается значительным выделением тепла (84 кД ж/м о л ь и
более) и требует преодоления некоторого активационного барье­
ра, что свидетельствует о достаточно глубоком взаимодействии
реагента с поверхностью к а та ли зато ра (хемосорбция). Следова­
тельно, при физической адсорбции связь реагента с катализа­
тором можно изобразить как А • • ■ka t, а при хемосорбции как
A* —hat, где А* — активированная молекула реагента или об­
разовавшаяся из нее реакционноспособная частица, связанная
с активным центром поверхности. В отношении механизма ак­
тивирования реагента на активном центре наиболее ясен гете­
рогенный катализ ионных реакций, близкий к соответствующим
гомогенным процессам. Так, катализаторы кислотного типа име­
ют значительные кислотность ho и функцию кислотности Щ,
Они дезактивируются основаниями (NaOH, NH3, амины), при­
чем по количеству адсорбированного аммиака и дифференци­
альной теплоте его адсорбции можно определить количество ак­
тивных центров и их распределение по энергии сорбции и актив­
ности.
Для протонных гетерогенных катализаторов, например Н3РО4,
на носителях, ионообменных смол и других, речь может идти
только о протонных (бренстедовских) активных центрах, тогда
как на оксидных и солевых катализаторах имеются апротонные
(льюисовские) активные центры, появляющиеся з а счет дефици­
та электронов на атомах, например, на атомах А1. Льюисовские
центры могут, однако, превращаться в протонные активные цен­
тры за счет сорбции влаги, всегда остающейся в катализаторе
или присутствующей в реакционной смеси:
Рис. 2.42. Зависимость температуры разложения муравьиной кислоты
от энергии образования формиатов
280

Рис. 2.43. Зависимость скорости дегидратации изопропанола от функ­
ции кислотности гетерогенного катализатора:
1— алюмосиликат; 2 — алюмоцирконат; 3 —фосфорная кислота; 4 —ме­
тафосфор ная кислота на силикагеле
I
—
А1+Н20 -
I-
-А1-
I
-о
н5+
н6+
Относительное количество активных центров разного типа з а ­
висит от ряда факторов, в том числе от температуры прокали­
вания катализатора. Определяющая роль именно кислотных а к­
тивных центров при ионном катализе доказывается тем, что ак­
тивность таких катализаторов коррелирует с их кислотностью,
рассчитанной по видоизмененному уравнению Бренстеда:
lgк=P-аЯ0.
На рис. 2.43 показано изменение активности катализатора
при дегидратации изопропилового спирта; такие же зависимо­
сти найдены и для ряда других реакций.
Наконец, прямым спектроскопическим методом установлено
образование ионов карбония на поверхности. Все это дает ос­
нование полагать, что гетерогенный кислотный катализ, как и
гомогенный, протекает через образование я-комплексов и затем
ионов карбония:
—
А1-—ОН + СН2= CHR
—
А1+ ROH
I
♦—А1— О — CHR— СН3
■»— Ai— о;
R+
Н
281

Последние далее расщепляются, изомеризуются или взаимо­
действуют со вторым реагентом. При этом ионы карбония не вы­
ходят в объем и их превращения происходят только на поверхно­
сти катализатора. Значительно больше неясностей имеется при
гетерогенном катализе гомолитических реакций. А. А. Баландин
в своей мультиплетной теории подчеркнул значение геометри­
ческого соответствия в строении кристаллической решетки ка­
тализатора и молекулы реагента. Согласно его теории, молеку­
ла реагента адсорбируется на двух или более активных центрах
(дуплете, квадруплете, в общем случае — на мультиплете) с та­
ким их расположением, чтобы наилучшим образом способство­
вать синхронно протекающим разры ву прежних и образованию
новых связей. Реакция дегидрирования на дуплете изображает­
ся таким образом:
kat
II
-с—с-
II
н
н
kat
II
—
с=с-
+н-н
-
kat
II
—
с=с-
+н2
Действительно, удалось найти корреляции между активно­
стью катализатора и межатомными расстояниями в его кристал­
лической решетке, например, на рис. 2.44 графически изображе­
на корреляция для реакции гидрирования этилена.
Помимо принципа геометрического соответствия А. А. Балан­
диным был предложен так называемый «принцип энергетиче­
ского соответствия», который поясняет роль энергетического
фактора в гетерогенном катализе.
Рис. 2.44. Корреляция между активностью катализатора и межатом­
ными расстояниями в его кристаллической решетке при гидрировании
этилена
282

A
D
А ------------ D
A katkat®
kat~^s^r»-*kat
kat'^s^r^kat
В
С
В --------------------- C
Промежуточный
комплекс
Рис. 2.45. Образование и разложение промежуточного мультиплетного
комплекса
Рассмотрим каталитическую обменную реакцию
AB+CD-^AD+BC
которая протекает путем адсорбции на мультиплете через обра­
зование промежуточного мультиплетного комплекса (рис. 2.45).
В соответствии с мультиплетной теорией первой стадией этой ре­
акции является разрыв связей и взаимодействие образовавшихся
частиц с адсорбционными центрами катализатора, приводящее
к образованию мультиплетного комплекса:
АВ-
kat
►А-•■•kat + В •••kat
CD-
kat
►С-■•kat +D •■■kat
В этом случае теплота образования промежуточного мульти­
плетного комплекса будет суммой:
Е\= -QaB- QcD+Оа-Ш +QB-kat+QС-kat+Qu-kat=
=-Qab- Qcd + 2,
где q= QA-kat+QB-kat +Qc-kat +QD-Ш
- С помощью аналогич­
ных рассуждений можно легко показать,что д л я заключитель­
ной стадии процесса — р аспада промежуточного комплекса:
A---kat+D---kat^±> AD
B---fcai + C-*-jfea<^=^BC
тепловой эфф ект процесса выражается соотношением
Е2 =Qad+Яьс ~ Я-
283

Общий тепловой эффект процесса в этом случае может быть
выражен соотношением
Е=Ei+Е2=-Qab ~Qcd+Qad+Qbc«
Тогда д л я протекания экзотермического процесса (0 < Е) оче­
видным условием для данного катализатора является соотно­
шение
Qab +Qcd<Qad +Qbc
и, наоборот, д л я эндотермического процесса (0 > Е )
Qab+Qcd > Qad+Qbc-
Другие теории гетерогенного катал иза основаны на одното­
чечной хемосорбции реагентов. М. В. Волькенштейн д л я объяс­
нения гетерогенного катализа гомолитических реакций исполь­
зует зонную теорию полупроводников и рассматривает актив­
ные центры гетерогенного катализатора как локальные уровни
энергии нейтрального, донорного (свободный электрон) или ак­
цепторного (дырка) типа. При этом адсорбированные частицы
также считаются примесями или дефектами решетки, вызываю­
щими появление соответствующих примесных уровней энергий.
В результате взаимодействия частиц с активным центром ге­
терогенного катализатора образуются поверхностные радикалы
или ион-радикалы, связанные с поверхностью слабой одноэлек­
тронной или сильной двухэлектронной связью, например:
Jfcai+CH2=CH2-> Ш -СН2-СН2
Более перспективная теория электронного катал иза основы­
вается на строении электронных орбиталей атомов металлов в
кристаллической решетке катализатора. В большинстве случаев
это атомы переходных металлов, с неполностью заполненными
электронными орбиталями. В результате перекрывания 5-, р- и
d-орбиталей в кристаллах ^-переходных элементов образуются
сложные валентные зоны, при этом часть связей осуществляется
за счет неспаренных d-электронов, что характеризуется процен­
том d-состояния. Оказалось, что во многих реакциях каталити­
ческая активность коррелирует с увеличением процента d-состо­
яния, как это изображено на рис. 2.46 для гидрирования этилена.
Вместе с тем от процента d-состояния зависит радиус атома или
иона, что позволяет объяснить и влияние геометрического ф ак­
тора в электронном катализе, а та к как d-орбитали переходных
металлов или их ионов обладают высокой способностью к ком-
плексообразованию, механизм сорбции и активирования реаген­
та можно объяснить образованием донорно-акцепторной связи
284

с активным центром. Для ка­
тализаторов, которые имеют
обобщенную зону проводимо­
сти или достаточно высокую
электропроводность по меха­
низму перезарядки ионов, связь
осуществляется путем «затя­
гивания» электронов реагента
в решетку катализатора. Это
может произойти д ля ненасы­
щенных веществ, образующих
я-комплексы, а соответствую­
щие катализаторы называют
я-активирующими:
kat + О2 kat—О—О—
Рис. 2.46. Зависимость скорости
гидрирования этилена от процен­
та d-состояния в металлах
В других случаях сорбция происходит за счет окислительно­
восстановительного превращения
R3CH + Men+ -» R3C-M e(n~1)++ Н+
и такие катализаторы называют G-активирующими. Ввиду от­
сутствия в них обобщенной зоны проводимости следующая за
сорбцией передача электрона второму реагенту осуществляется
по механизму перезарядки ионов или за счет туннельного эф­
фекта. Так как в последних случаях важную роль играет рас­
стояние между атомами решетки, то и здесь может наблюдать­
ся корреляция каталитической активности с геометрическими
факторами. Образование я- и a -комплексов зависит от акцеп­
торной способности атома или иона катализатора, на которую
значительное влияние оказывает смешение с другими вещества­
ми или добавление даже небольших количеств модификаторов.
При этом акцепторная способность прямо связана с работой вы­
хода электрона, чем можно объяснить корреляцию с этой вели­
чиной каталитической активности или селективности различных
контактов.
Наконец, ясна и роль каталитических ядов, которые при элек­
тронном катализе все принадлежат к типу веществ, способных
к образованию прочных донорно-акцепторных связей с d-орби­
талями переходных металлов (соединения Р, As, S, Se, Те; ио­
ны Hg, Pb, Bi, Sn; молекулы с ненасыщенными связями — СО,
HCN и др.). Эти яды блокируют активные центры поверхно­
сти или меняют в нежелательную сторону акцепторные свой-
285

ства кристалла, причем отравление особенно сильно проявля­
ется для металлических катализаторов, поскольку оксидные и
солевые катализаторы уже имеют такое количество примесей,
что добавление новых не оказывает на них столь значительно­
го эф ф екта. Таким образом, наиболее вероятно, что на актив­
ных центрах электронных катализаторов образуются связанные
с ними донорно-акцепторными связями атомы, радикалы или
ион-радикалы. И, действительно, экспериментально обнаруже­
но, что молекула водорода диссоциирует на металлах с обра­
зованием атомов; в некоторых слу ча ях доказано и образование
адсорбированных радикалов. Дальнейшее их превращение при
достаточно сильном активировании может состоять в непосред­
ственном распаде или во взаимодействии с другой молекулой,
вылетающей из объема или физически адсорбированной. При
недостаточном активировании может потребоваться взаимодей­
ствие со свободным активным центром поверхности или активи­
рование и второго реагента. Некоторые примеры механизма го-
молитических реакций гидрирования—дегидрирования и окис­
ления можно представить таким образом:
kat+С=С
I|
+Н2+kat
kat—С—С—<
-С —С —Н+kat—H*=*2kat+ Н—С—С—Н
kat+02^ kat-О
-О
-
+RH;+fc- >kat-0 - 0 -R +kat-E
kat—OH+kat—OR ит.д.
kat +O2
kat—О —О-
CH2
+сн2=сн2
kat—О —О-
СН2
kat—02+ СН2~СН2
Ъ
§11. Основы кинетики гетерогенно-каталитических реакций
В общем случае гетерогенно-каталитический процесс проте­
кает через р яд последовательных стадий, существенно различа­
ющихся по механизму:
1)
диффузия реагентов из потока к внешней поверхности зер­
на катализатора;
286

2) диффузия реагентов к внутренней поверхности зерна ка­
тализатора (к порам);
3) адсорбция реагентов на поверхности;
4) собственно химическая реакция;
5) диффузия продуктов с внутренней поверхности зерна ка­
тализатора;
6) десорбция продуктов реакции с поверхности катализатора;
7) диффузия продуктов с внешней поверхности зерна в поток.
Любая из этих стадий может оказаться самой медленной (ли­
митирующей) и, следовательно, определяющей скорость процес­
са в целом. Кинетические закономерности, таким образом, мо­
гут контролироваться законами как диффузии или адсорбции,
так и химической кинетики, а в промежуточных случаях — их
совокупностью. Это ставит кинетику гетерогенного катализа в
несколько обособленное положение по сравнению с гомогенным
катализом.
Принято различать кинетически и диффузионно контролиру­
емые (или просто кинетические и диффузионные) области про­
текания гетерогенно-каталитических процессов. В первых из них
общую скорость процесса определяет собственно химическая ре­
акция (или хемосорбция реагентов), во вторых — диффузия ре­
агентов. Более детально различают четыре основные области.
1) внегинедиффузионная1в которой скорость процесса в целом
определяется скоростью диффузии реагентов из потока к внеш­
ней поверхности зерна катализатора (или диффузии продуктов
от нее в поток);
2) внутридиффузионная) когда лимитирует диффузия реа­
гентов от внешней поверхности зерна катализатора к внутренней
его поверхности (или наоборот — для продуктов реакции);
3) внегинекипетическая, лимитируемая самой химической ре­
акцией на внешней поверхности зерна катализатора. Это, оче­
видно, возможно, если ее скорость значительно превосходит ско­
рость внутренней диффузии (стадии 2 или 6), но значительно
меньше скорости внешней диффузии (стадии 1 или 7);
4) внутрикипетическая, когда скорость процесса определяет­
ся скоростью химической реакции, причем последняя протекает
и на внутренней поверхности зерна катализатора, что возмож­
но, когда химическая реакция идет значительно медленнее, и на
внешней, а также на внутренней диффузией.
Строгие границы между этими областями отсутствуют, они
перекрываются так называемыми переходными областями, в ко­
торых сочетаются закономерности разных областей.
Аналогом закона действующих масс, применяемым д л я го­
могенных реакций, выступает при гетерогенном катализе закон
287

действующих поверхностей, согласно которому скорость хими­
ческой реакции пропорциональна двухмерной (поверхностной)
концентрации реагентов тц (в м о л ь /м 2). При мономолекулярных
реакциях лимитирующая стадия может состоять в превращении
вещества на одном активном центре поверхности катализатора
или во взаимодействии вещества со свободным, смежным с ним
активным центром. Этим двум механизмам соответствуют такие
кинетические уравнения:
Vs=
Vs=
где vs и ks —скорости и их константы, отнесенные к единице по­
верхности катализатора; Т]о —поверхностная концентрация сво­
бодных активных центров.
При бимолекулярных реакциях (например, А 4- Y
—
> или
А + А —>) также возможны два основных механизма:
сорбируются оба реагента, взаимодействующие д руг с другом
в активированном состоянии:
vs = &5ЛаЛу
Vs=М а*
сорбируется только один из реагентов (А), активирование ко­
торого достаточно для реакции с налетающими из объема моле­
кулами второго реагента (Y):
vs=M a[Y],
где [Y] — концентрация реагента в объеме.
Поскольку величина работающей поверхности катализатора
часто неизвестна, удобнее относить скорость и ее константу к
единице массы катализатора (но не насыпного объема, который
зависит от плотности упаковки и степени измельчения зерен).
Если на единице поверхности катализатора имеется п актив­
ных центров, каждый из которых способен адсорбировать одну
молекулу реагента, то делением п на число Авогадро получим
максимальную сорбционную способность единицы поверхности
катализатора —, выраженную в моль/м . В действительности
адсорбированным веществом за н я т а не вся поверхность (или не
все активные центры), а только некоторая часть 0 (в долях еди­
ницы). Тогда концентрация вещества, моль/м2, на единице по­
верхности будет равна
Пг.
288

а при ее умножении на удельную поверхность катализатора
S (в м2/г) получим концентрацию сорбированного вещества в
расчете на единицу массы катализатора (в м о л ь/г). Следова­
тельно, скорость реакции, отнесенная к единице массы катали­
затора, составит:
= vsS =kYii^SQi'j
П
где —S
—
сорбционная емкость единицы количества катализа­
тора в моль/г; к — истинная константа скорости гетерогенно­
каталитической реакции, отнесенная к единице количества ка­
тализатора. Поскольку —и S постоянны, их можно ввести в
константу скорости, а д л я последующего вывода кинетических
уравнений использовать выражение:
v = А/П(йе<Г = *"ПеГ*.
(2.107)
До л я занятой веществом поверхности (0*) экспериментально
не определяется, и ее необходимо заменить на концентрации в
объеме реагентов А*, (или на парциальные давления pi). Д ля
этого применяют разные способы (использование изотерм ад­
сорбции, методы стационарных концентраций, линейных после­
довательностей, маршрутов и др.) .
КИНЕТИЧЕСКАЯ ОБЛАСТЬ ГЕТЕРОГЕННОГО КАТАЛИЗА
§ 12. Использование изотерм адсорбции
Когда химическая реакция на поверхности протекает значи­
тельно медленнее других стадий (включая адсорбцию и десорб­
цию вещества), можно считать, что успевает установиться ад­
сорбционное равновесие. Тогда для выражения поверхностных
концентраций веществ через их концентрации (или парциаль­
ные давления) в объеме можно воспользоваться изотермами ад­
сорбции. Наиболее распространенной из них является изотерма
Лэнгмюра, справедливая д л я мономолекулярного адсорбцион­
ного слоя на энергетически однородной поверхности:
MAil
’
1+ ЕМА,]1
где bi —адсорбционные коэффициенты; Y^biAi — сумма произ­
ведений адсорбционного коэффициента на концентрацию д л я
10 Ипполитов
289

всех компонентов реакционной массы. Подставляя величины 0*
в уравнение (2.107), находим зависимость скорости от концен­
траций или парциальных давлений реагентов. Рассмотрим по­
лучаемые при этом зависимости д л я нескольких типичны х при­
меров.
Мономолекулярная реакция: А —» В 4- Z. Д л я нее при лими­
тирующей стадии превращения на одном активном центре полу­
чим:
v=ква=
&а &а [А]
1+ &а[А] + 6В[В]+6Z[Z]
_
и
[А]
КэФ1+6а[А]+ЫВ]+Ы2]'
(2.108)
При малом заполнении поверхности, т. е. при низких концен­
трациях или низких адсорбционных коэффициентах (область
изотермы Генри), всеми слагаемыми в знаменателе (2.108) мож­
но пренебречь по сравнению с единицей, что дает:
v —kbA[А] —А;эф[А].
В этой области наблюдаемый порядок совпадает с молекулярно-
стью реакции, которая описывается простым кинетическим урав­
нением. Д л я начальных скоростей или при слабой адсорбции
продуктов можно пренебречь слагаемыми знаменателя д л я В и Z:
v —kbA-— ^
л
— Т^ТТТ*
А1+Ьа[А] ^ф1+Ьа[А]
Это уравнение дает переменный и дробный наблюдаемый по­
рядок реакции по веществу А. Однако дл я мономолекулярных
реакций более типичен другой случай, когда ввиду большей ос­
новности или ненасыщенности один из продуктов реакции ад­
сорбируется сильнее (например, вода при дегидратации, олефин
или диен при дегидрировании или крекинге):
,
[А]
v
эф 1 + ьА[А]+г>в[в]'
В пределе слагаемое Ьа [А\ может вообще выпасть из уравнения,
а при сильной адсорбции продукта В и высокой его концентра­
ции иногда можно пренебречь и единицей. Д л я всех вариантов
уравнения типично характерное д л я многих реакций гетероген­
ного к а тал и за самоторможение процесса образующимися про­
дуктами, ведущее к прогрессивному снижению скорости не толь­
ко из-за уменьшения концентрации реагента, но и из-за увеличе­
ния концентрации продуктов. Уравнению (2.109) подчиняются,
290

например, процессы дегидрирования н-бутана в н-бутилен, н-бу-
тилена в бутадиен-1,3, спиртов в альдегиды и кетоны, алкилбен-
золов в стирол и его гомологи, процессы дегидратации спиртов с
образованием олефинов и др. При лимитирующей стадии взаи­
модействия сорбированного вещества со свободными активными
центрами их долю можно определить по уравнению:
л
1_ S [Aj]
1
°
1+E 6j[Aj]~1+ЕЭДА,-]‘
Тогда скорость реакции составит:
,,-Hin -
*МА]
,
[А]
"
° А' (1+EMAj])2" ^(ТТЁМАЖ'
В кинетическом уравнении появляется квадрат знаменателя. Та­
кой тип зависимости был найден для некоторых процессов де­
гидрирования.
Бимолекулярная реакция: А + Y —►В. При необходимости хе­
мосорбции обоих реагентов поверхностную концентрацию к а ж ­
дого из них находят из изотермы адсорбции Лэнгмюра, а при
их умножении получают кинетическое уравнение с квадратом
знаменателя:
, - м Аеу- *VMA|IV
(1+ЕМА)1)
—
&эф"
[A] [Y]
'(1+6a [A] +6y[Y]+6b[B])2'
Если ж е один из реагентов налетает из объема, имеем:
-,-1-П IY1- *‘А[А]т _
t>-W A[Y]-
-
—
&эф
E^j[Aj'j
[А] [Y]
( 2. 110)
1+Ьа[А]+6у[У]+6в[В]-
При заметной адсорбции продукта здесь такж е наблюдается са­
моторможение реакции, при сорбции реагентов — переменная и
дробная зависимость скорости от их концентраций. В области
изотермы Генри пренебрежение всеми слагаемыми знаменателя
по сравнению с единицей дает:
v =А:эф[A][Y].
291

Уравнениям (2.109) и (2.110) подчиняется, например, гидри­
рование олефинов, карбонильных соединений, ароматических уг­
леводородов. Ввиду сильной адсорбции исходного реагента ино­
гда можно пренебречь всеми слагаемыми у знаменателя кроме
Ьа [А], что соответствует нулевому порядку по этому веществу:
В более сложном виде аналогичные зависимости наблюда­
ются и при гетерогенно-каталитическом окислении парафинов,
олефинов, ароматических соединений. Во всех этих уравнени­
ях эффективные константы скорости включают адсорбционные
коэффициенты, температурная зависимость которых связана с
теплотой адсорбции X:
Ь{— 0е^ >
поэтому зависимость скорости гетерогенно-каталитической ре­
акции от температуры является сложной. В простейшем случае
(область изотермы Генри) имеем:
- Е,эф
-£и
^эф - &эф,ое RT = kb^by = кое RT бддеятby,o^RT •
Откуда:
Еэф = Еист—Ха ~~^у •
Теплота адсорбции нередко бывает очень значительной, и ко­
гда она больше истинной энергии активации химической реак­
ции, скорость может даж е падать с повышением температуры.
Из-за высокой теплоты адсорбции ненасыщенных веществ на­
блюдаемая энергия активации реакций гидрирования невели­
ка —всего 30 —55 кД ж/моль. Наоборот, при дегидрировании ху­
же сорбирующихся насыщенных соединений она достигает 125 —
170 кДж/моль.
§ 13. Влияние адсорбции
Когда адсорбция или десорбция реагентов и разны е стадии
химической реакции на поверхности катализатора сравнимы по
скорости, д л я построения кинетических моделей часто использу­
ют метод стационарных поверхностных концентраций. Возь­
мем для примера двухстадийную обратимую реакцию
A+0 * = ±(x)+z
k-i
X+Y<===±()+В
к-2
292

где () и (X) — соответственно свободный активный центр и сор­
бированная промежуточная частица X. Доли занятой ими по­
верхности при отсутствии сорбции других веществ равны ( 1 - 0 )
и 0, а соответствующие поверхности равны ( 1 - 0 ) 5 и 0 5 . При­
меняя метод стационарности, получим
=ki[А](1- 0)5- k -i[Z]05- k2[Y]05+к-2[В](1- 0)5 =О,
ах
h[A] +k .2[B]
к\[А]+k-i[Z]+ [Y]+к-г[В]’
fc_i[Z] + fc2 [Y]
к\ [А] + к-\ [Z] + &2[Y] + к-2[В]
и
v=V2-v-2 =ВД05-Ь2[В](1-0)5=
A:i[A] -hA:_![Z] + A:2[Y] + /с_2[В] ’
где величину поверхности можно внести в константы скорости.
Если вторая стадия необратима, из уравнения исчезают слага­
емые, содержащие константу 2- Значительное распростране­
ние получил способ построения кинетических моделей по мето­
ду Хоугена—Уотсона, являющийся разновидностью метода ста­
ционарных концентраций. С его помощью можно оценить роль
адсорбции и десорбции при достаточно быстрых реакциях на по­
верхности. Очевидно, что скорость адсорбции вещества г равна
произведению константы скорости адсорбции, концентрации ве­
щества в объеме и свободной поверхности катализатора:
Vi — [А-г]0()5.
Скорость десорбции аналогично равна:
v~i —к—{025.
При равновесии эти скорости равны, и константа адсорбционно­
го равновесия (адсорбционный коэффициент) bi составит:
^__ki_0|
к-i [Ai]0o '
Отсюда при адсорбционном равновесии имеем:
0г - МАг]0О>
=0°^
293

00
=1-£в‘=1-в°1>1А‘1'т7гщг
Химическая реакция происходит з а счет взаимодействия адсор­
бированной молекулы со смежным свободным активным цен­
тром или другой адсорбированной молекулой. К аж д ы й актив­
ный центр окружен четырьмя, шестью или, в общем случае,
т активными центрами, и тогда до ля смежных центров соста­
вит:
0А;О=у0А0О,
0A,Y
=
^"0А0У*
В соответствии с этим скорость реакции равна:
ктп
V= кВА'° = ^ " 0А0° = кэф(1+^Ьг[А{])^
тЛ
kmn
[А][Y]
*=
у-
— вдву - ^ (1+S6j|Ail)2 -
Если же адсорбированная молекула превращается на одном ак­
тивном центре, то:
[А]
V=квА=кэф
1 + Х)МАг]
Эти уравнения соответствуют кинетической области катализа
и они аналогичны уравнениям Л энгмю ра—Хиншельвуда. Если
лимитирующей стадией явл яется стадия адсорбции исходного
реагента А, общая скорость реакции равна разности скоростей
его адсорбции и десорбции:
V=VA-V-A=
[А]0о5 - k -A$AS.
В этом случае при обратимой реакции из-за ее сравнительно вы­
сокой скорости должно установиться равновесие между поверх­
ностными концентрациями веществ, причем дл я всех реагентов
кроме А можно принять, что их поверхностные концентрации
находятся в сорбционном равновесии с концентрациями в объе­
ме. Это позволяет найти неизвестную величину 0. Так, д ля ре­
акций А + Y ^ В + Z поверхностная константа равновесия K s
находится в таком соотношении с объемной константой К :
_
0B0z _ Ьв[B]bz[Z] _ £>b &z -г,
в” 0А0у"ЬА[А]Ьу[У]"Му *
Отсюда
294

а _ 0b0z&a6y _ а [В][Z]6д
a~0yввъ2к~*° [Ж ’
0o=l-^ 0i=1-0o
+ by[Y] + Ьв[В] + fcz[Z]) ,
1+|В|у]]бА^ +MY]+No ]+ьNo
Подставляя эти выражения в уравнение скорости, получим:
v =А:д[А]0о5- k -\Q\S =
*а*([А]- TM )
1+ ^1?!?А+Ьу[У] + 6в[В]+bz[Z]
т
v = /с_в[В]0в5~ /св [В]0о =
‘bS(|a|'^ M
^ '|b|
1+^ P
^
+ 6a |A1+6v[Y] + 62[Z]
Оба выведенные уравнения, в которых в константу скорости
вводится удельная поверхность 5, отличаются от предыдущих
отсутствием в знаменателе концентрации вещества, лимитиру­
ющего скорость процесса, и наличием там члена, включающе­
го концентрации остальных веществ и адсорбционный коэф фи­
циент вещества, сорбция которого лимитирует общую скорость.
Уравнения могут быть преобразованы и дл я обратимых реакций
другой стехиометрии: А^=>В; А*=;В+Z; A+Y Ь;Вит.д .,а так­
же д л я необратимых процессов. Они получили распространение
дл я математического описания ряда важных реакций, напри­
мер дегидрирования бутилена, окисления углеводородов, синте­
за фосгена. Известны некоторые характерные черты, отличаю­
щие внутрикинетическую область гетерогенного катализа (в том
числе и область адсорбции) от других. В этом случае реакция
имеет наиболее высокую наблюдаемую энергию активации, так
как наложение диффузионных влияний из-за их малой зависи­
мости от температуры всегда ведет к снижению энергетическо­
го барьера. Во внутрикинетической области работают все поры
катализатора, и так как их поверхность преобладает по сравне­
нию с внешней, скорость процесса не зависит от размера зерен
катализатора, но сильно увеличивается при росте его удельной
поверхности. Следовательно, если данная реакция протекает во
295

внутрикинетической области, д л я нее наиболее подходят ката­
лизаторы со сравнительно крупными зернами (что снижает со­
противление слоя катализатора) и развитой поверхностью мик-
ропор. Очевидно, что внутрикинетическая область характеризу­
ется наиболее высокой производительностью катал изатора. По­
следний работает при этом в умеренном температурном режи­
ме, без перегрева поверхности зерен, так как при нелимитирую­
щей скорости диффузии теплопередача, имеющая диффузион­
ный механизм, происходит быстрее химической реакции. Поэто­
му внутрикинетическая область со всех точек зрения является
наиболее предпочтительной при гетерогенном катализе.
§ 14. Ферментативный катализ
Катализ коллоидными системами относится к микрогетеро-
генному катализу и имеет некоторые специфические черты, ко­
торые отличают его как от гомогенного катализа, так и от ге­
терогенного. Наиболее важными коллоидными каталитически­
ми системами являются координационные соединения некото­
рых металлов с высокомолекулярными белковыми молекулами.
Такие катализаторы получили название ферментов (энзимов).
Их также называют биологическими катализаторами или био­
катализаторами. Без их действия большинство биохимических
реакций протекало бы слишком медленно, что препятствовало
бы нормальному функционированию живого организма.
§ 15. Свойства ферментов
Размер ферментов. Молекулярная масса ферментов достига­
ет 105- 1 0 7, поэтому в водных системах молекулы ферментов
обладают свойствами коллоидных частиц.
Селективность ферментов. Ферменты могут характеризовать­
ся различной специфичностью. Ферменты с низкой степенью
специфичности катализируют сравнительно широкий круг био­
химических реакций. В отличие от этого ферменты с высокой
степенью специфичности способны катализировать только огра­
ниченный круг реакций. Например, ферменты из группы ли­
паз характеризуются сравнительно низкой степенью специфич­
ности. Они катализируют гидролиз большинства сложных эфи­
ров. В отличие от этого фермент (5-гликозидаза очень специфи­
чен. Он катализирует гидролиз (3-гликозидов, но не а-гликозидов.
Другим примером очень специфичного фермента является уре-
аза. Этот фермент обнаруживается в соевых бобах. Он катали-
296

зирует гидролиз мочевины (карбамида):
CO(NH2)2+ н 20 -> С02+2NH3
Однако этот фермент не катализирует гидролиз замещенных мо­
чевин. Вообще говоря ф ерменты обладают высокой селективно­
стью, и каждый из них способен катализировать только одну
специфическую реакцию или реакцию одного типа.
Эффективность ферментов. Некоторые ферменты обладают
высокой эффективностью да ж е в очень небольших количествах.
Такая высокая эффективность объясняется тем, что молекулы
ферментов в процессе своей каталитической активности непре­
рывно регенерируют. Типичная молекула фермента может реге­
нерировать миллионы раз за минуту. Примером может служить
фермент реннин, вырабатываемый слизистой оболочкой сычуга
(отдела желудка ж вачных). Реннин используется в сыроделии.
Он способен вызывать коагуляцию (свертывание) белков молока
в количествах, в миллионы раз превышающих его собственную
массу. Другой пример высокой эффективности ферментов д а ­
ет каталаза. Одна молекула этого фермента при 0° разлагает за
секунду около 50000 молекул пероксида водорода:
2Н202—►2Н20+02
Действие каталазы на пероксид водорода заключается в
снижении энергии активации этой реакции приблизительно от
75 кДж/моль до 21 кДж/моль, тогда как коллоидная платина
понижает энергию активации только до 50 кД ж/моль. Фермен­
ты обладают наибольшей активностью при температуре челове­
ческого тела, т. е. приблизительно при температуре 307 К. При
повышении температуры до 323 —333 К они разрушаются и по­
этому теряют активность, к ак это видно из рис. 2.47.
Рис. 2 .47. Зависимость скорости реакции от температуры для обычной
ферментативной реакции
297

Отравление ферментов. Ферменты очень чувствительны к при
сутствию каталитических ядов. Например, в процессе сбражива­
ния (ферментации) сахаров в спирт происходит отравление эта­
нолом тех ферментов, которые содержатся в дрожжах, и если
концентрация этанола превышает 15,5%, ферментация прекра­
щается. Поэтому с помощью одного лишь процесса ферментации
обычно не удается получать вино или пиво с концентрацией эта­
нола выше 15,5%.
§ 16. Механизм действия ферментов
В 1902 г. У. Генри выдвинул предположение, что действие
ферментов заключается в образовании комплекса с молекулой
субстрата, которое представляет собой обратимый процесс. Ком­
плекс «фермент —субстрат» соответствует промежуточному со­
единению или переходному состоянию в теории промежуточных
соединений. Затем этот комплекс распадается и регенерирует
фермент. Э то т процесс описывается уравнением Михаэлиса —
Ментен:
E+S^ES-*E +P
где Е — фермент; S — субстрат; ES — комплекс; Р — продукт
реакции.
Согласно существующим воззрениям, молекула субстрата свя­
зывается с активным центром на поверхности фермента. Ак­
тивность этого центра повышается в присутствии витаминов
и некоторых минеральных веществ. За активность ферментов
особенно ответственны различны е микроэлементы, в частности
d-переходные металлы, как, например, медь, марганец, желе­
зо и никель. Активность некоторых ферментов очень зависит
от наличия коферментов. Коферментами являются относитель­
но небольшие органические молекулы, которые связываются с
активными центрами фермента. Роль таких коферментов часто
выполняют витамины группы В.
§ 17. Роль ферментов в биологических процессах
Ферменты играют важную роль в протекании химических ре­
акций, которые осуществляются в биологических системах. На­
пример, в человеческом организме ежесекундно осуществляют­
ся тысячи ферментативных химических реакций. Кроме того,
ферменты играют важную роль и в проведении многих техно­
логических процессов. Они используются, например, в процес­
сах приготовления пищи, в производстве пищевых продуктов и
298

налитков (хлеба, кваса, пива, вина и др.) , фармацевтических
препаратов, моющих средств, текстильных изделий, кожи и бу­
маги.
Ферменты в пищеварительной системе человека. В пищевари­
тельной системе происходит превращение питательных веществ,
таких к ак белки, углеводы и жиры, в продукты, способные легко
усваиваться клетками живого организма. Эти превращения то­
же происходят с участием ферментов. Например, фермент ами­
лаза, который содержится в выделениях слюнных желез и тон­
кого кишечника, помогает превращению к р ах мал а в мальтозу.
Затем мальтоза превращается в глюкозу в тонком кишечнике с
помощью другого фермента — мальтазы. В желудке и тонком
кишечнике такие ферменты, как пепсин и трипсин, превращают
белки в пептиды. Затем эти пептиды превращаются в тонком
кишечнике в аминокислоты под действием ферментов, которые
называются пептидазами. В тонком кишечнике содержится еще
один фермент —липаза. Он гидролизует жиры (липиды), обра­
зованные жирными кислотами.
Метаболические процессы. Так называются химические об­
менные процессы, протекающие в живых клетках. Типичная ж и ­
вая клетка состоит из ядра, окруженного цитоплазмой. Клетка
ограничена клеточной мембраной. Цитоплазма участвует в про­
цессе обмена веществ, используя и запасая энергию питательных
веществ и образуя соединения, необходимые д л я функциониро­
вания других клеток. Одним из ферментов, которые обнаружи­
ваются в цитоплазме, является цитохромоксидаза. Цитохромы -
разновидность белков, которые содержат железо в форме гема.
Вместе с такими ферментами, как цитохромоксидаза, они игра­
ют важную роль в процессе дыхания. Эта роль заключается в
окислении питательных веществ и запасании энергии. Цитохро­
моксидаза содержит микроэлемент медь, в отсутствие которого
невозможен эффективный обмен веществ в организме. В расти­
тельных клетках цитохромы находятся в хлоропластах, которые
играют важную роль в фотосинтезе.
Болезни, связанные с недостатком или избытком ферментов в
организме. Некоторые заболевания вызываются недостаточным
или избыточным содержанием ферментов. Например, наслед­
ственное заболевание фенилкетонурия обусловлено недостаточ­
ным содержанием в организме фермента фениламиногидрокси-
лазы. Э то заболевание приводит к накоплению в организме вред­
ных соединений, которые вызывают разрушение клеток мозга и
замедление умственного развития. Чтобы предотвратить разру­
шение клеток мозга, больным фенилкетонурией необходимо при­
держиваться диеты с низким содержанием аминокислоты фе-
299

нилаланина. Заболевание альбинизм, связанное с недостатком в
организме фермента тирозиназы, проявляется в отсутствии пиг­
мента в кожных покровах. В обоих рассмотренных случаях недо­
статок фермента обусловлен генетической мутацией.
Сердечные приступы могут приводить к значительному по­
вышению уровня концентрации ферментов в крови. Это обуслов­
лено просачиванием ферментов из клеток разрушенной сердеч­
ной ткани.
Ферменты используются д л я лечения некоторых заболева­
ний, например, таких, как сердечная недостаточность. Нередко
сердечные приступы вызываются тромбами крови, образующи­
мися в коронарной артерии. Современный способ лечения та­
кого заболевания основан на растворении тромбов с помощью
фермента стрептокиназы, вводимой непосредственно в сердце.
Проферменты. Эти вещества известны также под названием
«зимогены». Они представляют собой образующиеся в организ­
ме растений и животных некаталитические вещества, которые
превращаются в ферменты по мере необходимости. Например, в
крови человека содержится протромбин, который при необходи­
мости превращается в тромбин — фермент свертывания крови.
Он катализирует превращение растворимого белка фибриноге­
на, содержащегося в крови, в нерастворимый белок фибрин.
§18. Ферментация (брожение)
Химические процессы, при которы х под воздействием опреде­
ленных микроорганизмов, таких, как дрожжи и некоторые бак­
терии, из сахара получают этиловый спирт и другие продукты,
называются процессами брожения. Ферментация глюкозы с об­
разованием этанола может быть описана уравнением
СбН120 6 -> 2С2Н5ОН + 2С02
Этот процесс имеет сложный механизм. Одним из его глав­
ных интермедиатов является 2-оксопропановая (пировиноград-
ная) кислота:
О
II
сн3—С — соон
Процесс состоит из 12 стадий, причем для протекания каждой
стадии необходим специфический фермент. Зи маза — один из 12
(или близкого к этому числу) ферментов, обнаруживаемых в
типичных дрожжах.
300

Промышленное получение этанола может осуществляться пу­
тем ферментации тростникового сахара с последующей перегон­
кой. Тростниковый сахар содержит приблизительно 50% саха­
розы С12Н22О11. Перед ферментацией сахарный сироп, который
называется патокой, разбавляют водой. В процессе фермента­
ции сахароза превращается в глюкозу и фруктозу. Этот процесс
катализируется ферментом инвертазой.
Пиво получают путем ферментации солода. Солод получа­
ют из хлебных злаков, обычно ячменя. Крахмал, содержащий­
ся в солоде, превращается в мальтозу под действием фермента
диастазы. Затем другой фермент, содержащийся в дрожжах, —
мальтаза, —катализирует превращение мальтозы в глюкозу. Д л я
придания пиву специфического вкуса добавляю т хмель. Освет­
ление пива осуществляется с помощью фермента папаина, кото­
рый гидролизует белки, обусловливающие наличие мути в пиве.
В процессе получения вин превращение сахаров, содержащих­
ся в виноградном соке, в этанол осуществляется благодаря нали­
чию в кожице виноградин природных дрож жей. Иногда в вино­
градный сок добавляют также культурные дрожжи. Если фер­
ментацию проводить до полного завершения, получается сухое
вино. Если ферментация приостанавливается преждевременно,
получается более сладкое вино.
Винодельческие дро ж ж и обладают способностью ферменти­
ровать сахара лишь до тех пор, пока не образуется раствор, со­
держащий 15,5% этанола по объему. Природные дрожжи позво­
л яю т проводить ферментацию лишь до получения растворов с
содержанием этанола до 5,5% по объему. Пленочные дрожжи,
как, например, те, которые используются д л я получения шерри,
позволяют проводить ферментацию вплоть до получения рас­
твора, содержащего 20 % этанола по объему. И з-за того, что рас­
творы, содержащие более 15,5% этанола, подавляют действие
ферментов в дрожж ах, получение крепленых алкогольных на­
питков требует проведения перегонки. Химическая промышлен­
ность все более широко использует ферменты, иммобилизован­
ные на твердых носителях, чаще всего на целлюлозе. В качестве
примера можно привести процесс инверсии глюкозы в фруктозу,
который проводится на иммобилизованном ферменте инвертазе.
Глюкоза производится из крахмала в огромных количествах, но
она обладает менее сладким вкусом, чем сахар. Напротив, фрук­
тоза в три раза слаще сахара, поэтому получение ее из глюкозы
является важным технологическим процессом. На производстве
растворы глюкозы пропускаются через набивку с иммобилизо­
ванной инвертазой. Миллионы тонн фруктозного сиропа исполь­
зуются при производстве прохладительных напитков и в конди­
терской промышленности.
301

2.13. КИНЕТИКА ЦЕПНЫХ РЕАКЦИЙ
ОБРАЗОВАНИЕ И ОБРЫВ ЦЕПЕЙ ПРИ ХИМИЧЕСКИХ
РЕАКЦИЯХ
В некоторых фотохимических реакциях квантовый выход мо­
жет стремиться к бесконечности и реакция носит взрывной ха­
рактер. Происходит это вследствие того, что фотовозбужденные
частицы взаимодействуют с другими частицами и возбуждают
их. Число активных частиц в газе быстро возрастает в резуль­
тате образования цепей в соответствии со схемой:
CI2+/iv->Cl+Cl
Поглощение кванта света молекулой хлора приводит к гомо-
литическому разрыву ковалентной связи и образованию интер­
медиатов, которые представляют собой атомы хлора с неспарен­
ными электронами.
Атом или группу атомов, обладающих неспаренным
электроном, называют радикалом.
Самоподдерживающаяся химическая реакция, при ко­
торой первоначально появляющиеся продукты принимают
участие в образовании новых продуктов, называется цепной
реакцией.
В свою очередь радикалы хлора играют роль активных ча­
стиц, которые порождают развитие цепного процесса:
С1+Н2—►НС1+Н и Н+С12 НС1+С1
и т.д . (стадия развития цепи). В результате образуется непре­
рывный цепной процесс, который протекает благодаря использо­
ванию химической энергии реакции д л я активирования все боль­
шего числа частиц. Поэтому цепные реакции протекают обычно
с высокой скоростью и могут приводить к взрыву. Цепные реак­
ции проходят тр и главные стадии:
инициирование (зарождение) активных частиц (интермедиа­
тов), которые могут представлять собой атомы, ионы, молекулы
или радикалы;
развитие цепи, когда интермедиаты реагируют с исходными
реагентами и образуют новые интермедиаты и конечные про­
дукты;
обрыв цепи вследствие гибели интермедиатов.
Иницирование может проходить под действием света или дру­
гого излучения, под действием тепловой энергии или анионов,
под действием катализаторов.
302

Активированный комплекс
(переходное состояние)
Стадия развития в цепных
реакциях может проходить мно­
гократно, что приводит к об­
разованию большого числа ко­
нечных и промежуточных про­
дуктов. После обрыва цепи ре­
акция прекращается. Г ибель
интермедиатов может происхо­
дить самопроизвольно, на стен­
ках реактора или под дей­
ствием ингибиторов. Потенци­
альная энергия в зависимости
от координаты реакции обнару­
ж ивает минимум, отвечающий
образованию интермедиата (рис. 2.48). Возбужденными части­
цами (интермедиатами) могут быть возбужденные молекулы,
атомы или радикалы. Наряду с реакциями зарождения и раз­
вития цепи могут происходить реакции обрыва цепей:
С1+С1^С12
Координата реакции
Рис. 2.48. Изменение потенци­
альной энергии при прохождении
цепной реакции
Н+Н->Н2
Н + С1->НС1
При этом получающиеся возбужденные молекулы должны пере­
д а т ь избыточную энергию какой-либо другой частице или стенке
реактора, иначе они вновь продиссоциируют.
Число элементарных реакций от зарождения цепи до ее
обрыва называется длиной цепи V.
Длина цепи определяется уравнением:
v
v=----,
mriQ
где v —скорость реакции; т — число активных частиц, образую­
щихся при зарождении цепи; по —число ежесекундно протекаю­
щих элементарных реакций зарождения цепи. Поэтому скорость
цепных реакций сильно зависит от объема и формы реактора,
та к как обрыв цепей происходит на его стенках. Обрыв цепей
происходит также вследствие гибели активных частиц на ато­
мах других газов (например, инертных).
Когда в результате развития цепи один элементарный
а к т порождает больше чем одну активную частицу, то цепь
называется разветвленной.
303

Скорость цепного процесса с разветвленными цепями нарастает
лавинообразно до исчерпания реагента. Примером разветвлен­
ного цепного процесса является окисление водорода кислородом:
Н2+О2 20Н
(1)
Н+Н02 (2)
2Н+М (3)
■О+Оз (4)
>(зарождение цепи)
он +н2->н2о +н
н+о2^он +о
б+н2^он +н
.
1
Н+стенка —>-Н2
Z
н+02+м-+н62+м
НО2+ стенка —» -НгО + -О2 (10)
>(обрыв цепи)
Если обозначить вероятность разветвления цепи через а , ве­
роятность ее обрыва через р, а время жизни звена цепи как Ат,
то число разветвлений будет равно х = — , а число обрывов
р
Т
цепей будет равно у = —
.
Если в единицу времени в единице
Дт
объема возникает п активных центров, то п х — число разветвле­
ний и пу — число обрывов цепей. Д л я скорости возникновения
активных центров в единице объема получим уравнение
dn
—
= п0+(т- у)п
dt
или в интегральной форме:
п0
п=
Х-у L
Скорость реакции будет равна
п
по
v=
Дт (х-у)Ат
Если х > у, то скорость реакции быстро и неограниченно растет
по экспоненциальному закону:
v = AeBt,
где А и В — константы, причем В пропорционально (х —у ).
304

§ 1. Горение
Быстро текущая реакция, приводящая к выделению теп­
ловой энергии и света, называется горением.
Если в реагирующей системе скорость образования интермеди­
атов vi выше, чем скорость их гибели г^, то реакция самоуско-
ряется и переходит в цепное горение и далее во взрыв; гц и г>2
по-разному зависят от давления. Граница области, где возмо­
жен цепной взрыв, определяется равенством v± = V2 . Д л я при­
веденной реакции водорода с кислородом скорость зарождения
цепи v \ пропорциональна произведению концентраций водорода
и кислорода, а значит, пропорциональна к вадрату общего давле­
ния Р 2. Скорость обрыва цепей г?2 складывается из обрыва цепей
на стенках реактора, которая пропорциональна общему давле­
нию Р , и из обрыва цепей в объеме газа, которая пропорциональ­
на кубу общего давления Р 3. Поэтому зависимость скорости ре­
акции от давления описывается уравнением В Р 2-С Р - А Р г = О
или АР2-ВР +С =0. Коэффициенты А)В и С зависят от тем­
пературы. Корнями этого уравнения будут
которые определяют нижнюю и верхнюю границы взрыва со­
ответственно (рис. 2.49). Верхняя граница определяется обры-
Рис. 2.49. Пределы взрыва при Рис. 2.50. Полуостров взрыва при
цепной реакции
цепной реакции
305

вом цепей в объеме, а нижняя граница — обрывом цепей на
стенке. Из рис. 2.49 видно, что существуют пределы темпера­
туры, при которой взрыв не происходит ни при каких давле­
ниях. При Т > Ткр нижняя ветвь кривой п отвечает нижнему
пределу взры ва при сравнительно малых давлениях. Верхняя
кривая 771 отвечает верхнему пределу, который более сильно за­
висит от температуры. Кривой д отвечает тепловой взрыв. На
рис. 2.50 представлена экспериментальная кривая, обозначаю­
щая полуостров взрыва д л я реакции водорода с кислородом.
В жидкой фазе цепные реакции можно рассмотреть на при­
мере окисления углеводородов растворенным кислородом. В на­
чальном периоде окисления свободные радикалы образуются при
окислении кислородом углеводорода:
Радикал R присоединяет молекулу кислорода и превращается
в пероксидный радикал RO2, который затем отрывает от моле­
кулы углеводорода атом водорода и образует гидропероксид и
свободный радикал R, который продолжает цепь. Обрыв цепей
происходит в результате взаимодействия двух радикалов. В си­
стеме накапливается гидропероксид, молекулы которого также
могут распадаться на радикалы по схеме:
Это приводит к вырожденному разветвлению цепей. В общем
виде механизм цепного окисления углеводородов можно пред­
ставить схемой:
§2. Цепные реакции в жидкой фазе
rh,o2 R
ROOH^RO +OH
R
R +02—►RO2
r62+rh-^rooh+r
ROOH —>RO + OH
R+R —»R—R
R02+R-> R-OO
-R
RO2+R02—*2ROR+02
(0)} (зарождение цепей)
(3) } (вырожденное разветвление)
(4) |
(5) > (обрыв цепей)
(6>,
306

Свободные радикалы быстро гибнут по реакциям (5) и (6).
Поэтому в системе быстро устанавливается кинетически равно­
весная концентрация этих радикалов, при которой скорость об­
разования vi и скорость гибели радикалов г>2 становятся рав­
ными, а состояние реакции стационарным. М. Боденштейн и
Н. Н. Семенов показали, что при стационарных концентрациях
радикалов их производные равны нулю:
d[R] _ d[RO]2
dx
dx
= 0. Если
концентрация кислорода велика, то [RO2] [R], и обрыв це­
пей в этом случае происходит преимущественно по реакции (6).
В таком случае
v\ —^[RCb]2
и
[ro2]=
VI
h'
Поэтому скорость окисления углеводорода будет равна
v = к\[RH][R02]= кг[КК\х1 ±.
V
( 2. 111)
На рис. 2.51 дана скорость окисления этиллинолеата в зависимо­
сти от концентрации. Из уравнения (2.111) следует, что скорость
окисления пропорциональна концентрации, и коэффициент про­
порциональности в свою очередь пропорционален квадратному
корню из скорости инициирования цепей. Если инициирование
вызывается облучением, то ско­
рость инициирования цепей
пропорциональна интенсивно­
сти света /, что и подтвержда­
ется экспериментом.
На рис. 2.52 дана зави­
симость скорости поглощения
кислорода при окислении тет-
ралина от концентрации кис­
лорода. Из рисунка видно, что
скорость окисления углеводо­
родов зависит от концентрации
кислорода, а значит, от давле­
ния кислорода над системой.
С увеличением концентрации
(парциального давления) кис­
лорода скорость быстро растет,
но после некоторой предельной
Рис. 2.51. Зависимость скорости
окисления v этиллинолеата, ини­
циированного пероксидом бензо­
ила, от концентрации этиллино­
леата
307

концентрации скорость погло­
щения кислорода замедляется
и далее изменяется незначи­
тельно. Это объясняется тем,
что характер реакции окисле­
ния цепной. Если концентра­
ция кислорода мала, то ре­
акции зарождения цепей (1)
протекают медленно по срав­
нению с реакцией (2). Тогда
•
•
[R] » [RO2], И обрыв цепей
в таком случае идет по схе­
ме (4). Лимитирующ ей стади­
ей является стадия (1). По этой
причине с ростом концентра­
ции кислорода скорость окис­
ления возрастает и если кон­
центрация растворенного кислорода велика, то окисление про-
•
•
текает быстро, [R] [RO2], обрыв цепей происходит в основном
по реакции (6), и скорость окисления становится независимой от
концентрации растворенного кислорода. Лимитирующей стади­
ей становится стадия (2). Таким образом, скорости цепных реак­
ций можно в некоторых пределах регулировать, создавая усло­
вия д л я возрастания или падения скорости иницирования цепей.
В газовых цепных реакциях можно также управлять скоростью
реакции с помощью общего давления и температуры, как пока­
зывает полуостров воспламенения, а также добавлением инерт­
ных газов, которые регулируют развитие цепей вследствие гибе­
ли радикалов при столкновении с атомами инертных газов. На
стадии развития цепей управление цепными реакциями можно
осуществлять с помощью катализаторов и ингибиторов. Приме­
ром использования катализаторов в реакциях окисления орга­
нических веществ пероксидом водорода является использование
реактива Фентона в кислых водных растворах. При добавлении
к раствору пероксида водорода соли двухвалентного ж е леза про­
исходит зарождение и развитие цепей по схеме:
Н2О2+Fe2+ -*• НО +Fe3++НО"
Fe3* + НО2 ^ Fe02H2+
Fe02H2+ -*• Fe2++ Н02
Обрыв цепей может происходить с выделением кислорода:
308
Рис. 2.52. Зависимость скорости
поглощения кислорода при окис­
лении тетралина от концентрации
кислорода

Fe3++ HO2 —►Fe2++ O2 + H+
или путем окисления органических веществ.
При окислении углеводородов кислородом в жидкой фазе ин­
гибиторами цепной реакции являются фенолы и ароматические
амины. Механизм ингибирования реакции в этом случае за кл ю ­
чается в том, что развитие радикалов тормозится благодаря ре­
акции активных радикалов с фенолами с образованием менее
активных феноксильных радикалов по схеме:
Ri
Ri
Свободный электрон в феноксильном радикале делокализует­
ся на ароматическом кольце. Феноксильные радикалы не участ­
вуют в окислительном процессе, поэтому скорость окисления па­
дает. Ингибиторы в цепных реакциях окисления углеводородов,
альдегидов, растительных масел и других легко окисляющихся
соединений используются, главным образом, дл я предотвраще­
ния их окисления.
Контрольные вопросы
I . Что изучает химическая кинетика?
2. Что является предметом химической кинетики?
3. Какими основными двумя способами осуществляются химиче­
ские процессы?
4. Что такое скорость химической реакции?
5. Что такое порядок химической реакции?
6. В чем различие между порядком химической реакции и ее мо-
лекулярностью?
7. Перечислите основные кинетические типы химических реакций.
8.Приведите кинетические кривые для необратимой реакции пер­
вого порядка. В каких координатах уравнение для этой реакции ста­
новится линейным?
9. Что такое константа скорости химической реакции? Каков ее
физический смысл?
10. Что такое период полупревращения и каков его физический
смысл?
II. Приведите кинетические кривые для необратимой реакции вто­
рого.порядка. Какова линейная форма кинетического уравнения для
этой реакции?
309

12. Приведите кинетические кривые для последовательных реак­
ций. Каковы методы графического нахождения параметров этих ре­
акций?
13. Приведите кинетические кривые для обратимой реакции пер­
вого порядка. Какова линейная форма кинетического уравнения для
этой реакции? В чем ее отличие от аналогичной формы для необрати­
мой реакции первого порядка?
14. С какой целью применяют метод наименьших квадратов?
15. На какие две большие группы разделяются по режимам прове­
дения реакции в потоке?
16. Что называют стационарным состоянием в потоке?
17. Что понимают под топохимическими реакциями?
18. Приведите примеры твердофазных реакций.
19. Приведите примеры фотохимических реакций. В чем разли­
чие между реакциями фотосинтеза, люминесценции, флюоресценции,
фосфоресценции, хемилюминесценции?
20. Приведите примеры механохимических реакций.
21. Дайте определение понятия «энергия активации» и «активиро­
ванный комплекс».
22. Что такое энтропия и энергия активации? Каков физический
смысл этих параметров?
23. В чем заключается влияние растворителя на скорость химиче­
ской реакции?
24. Что понимают под катализом?
25. В чем заключается различие между гомогенным и гетероген­
ным катализом?
26. Что понимают под ингибитором катализатора?
27. Перечислите основные типы гетерогенных катализаторов.
28. Дайте характеристику основным теориям гетерогенного ката­
лиза.
29. В чем заключается влияние адсорбции на скорость гетерогенно­
каталитической реакции?
30. Дайте характеристику процессам, которые проходят с участием
ферментативных катализаторов.
31. Приведите основные типы механизмов химических реакций.
32. Дайте определение цепным процессам. Каковы особенности ки­
нетики цепных процессов?

ГЛАВАЗ
ЭЛЕКТРОХИМИЯ
ВВЕДЕНИЕ
Электрохимия явл яе тся частью физической химии, однако
перечислить проблемы, которые изучает электрохимия доволь­
но трудно, настолько широк их круг.
Электрохимия — раздел физической химии, изучаю­
щий физико-химические свойства ионных систем (раство­
ры, расплавы, твердые электролиты), а также явления и
процессы на границе двух фаз (весьма часто «электрод—
электролит») с участием заряженных частиц — электронов
и ионов.
Об электрохимических явлениях, по-видимому, было извест­
но уж е в древности. Удивительное открытие было сделано ар­
хеологами при раскопках парфянского поселения, которое су­
ществовало в Месопотамии 2200 лет назад. Б ы л обнаружен гли­
няный горшок, в который были погружены две металлические
пластины — медная и железная. Ученые пришли к выводу, что
это было ничем иным, ка к электрохимическим источником то­
ка одноразового действия. Скорее всего это устройство имело
какое-то культовое назначение. Все же появление электрохимии
как раздела физической химии относят к концу XVIII в. и связы­
вают с открытиями Л. Гальвани и А. Вольта. Врач Л. Гальвани,
работая в Болонском университете в Италии, наблюдал сокра­
щение мышц лягушки при контакте с парой металлов —железа и
меди, лягушка была подвешена на медном крючке на железных
перилах балкона. При контакте мышц лягуш ки с балконом бед­
ное животное содрогалось, что, по мнению исследователя, было
связано с наличием животного электричества в теле лягушки.
Ранее такое явление наблюдалось при контакте мышц с источни­
ком статического электричества — электрической машиной. Р а­
ботами Л. Гальвани заинтересовался его соотечественник ф изик
А. Вольта. Он пришел к выводу, что источник электричества —
это контакт двух разнородных металлов. В 1799 г. он создал
311

первый химический источник то к а — гальваническую батарею
«вольтов столб», состоящую из чередующихся медных и цинко­
вых пластин, между которыми помещались кусочки сукна, про­
питанные, например серной кислотой. Ток от такого столба при
сближении обоих концов проволоки вызывал искры. Наполеон
Бонапарт, будучи в то время консулом Франции, заинтересовал­
ся опытами А. Вольта и способствовал учреждению в Париже
«Гальванического общества», целью которого было содействие
и поощрение исследований гальванических явлений. Вольтов
столб ученые начали использовать д л я проведения электролиза.
В 1807 г. английский ученый Х.Дэви впервые провел элек­
тролиз расплавленных натриевой и калиевой щелочей и полу­
чил металлический натрий и калий. Позднее им были получены
барий, кальций, стронций и магний. Основополагающими были
работы М. Фарадея, который в 1832 —1839 гг. сформулировал
количественные законы электролиза. Явление переноса электри­
чества через растворы было исследовано И. Гитторфом в 50-х гг.
XIX в. Продолжались опыты по созданию новых химических
источников тока (Дж. Даниэль, Б . С. Якоби, У. Гров, Р. Бунзен,
П. Р. Багратион).
Важным этапом электрохимии было развитие представлений
о природе электропроводности электролитов. В 1805 г. была
предложена первая теория электропроводности. Согласно этим
представлениям молекулы воды состоят из пар разноименно за­
ряженных частиц водорода и кислорода. В электрическом по­
ле положительно заряженные частицы водорода, перескакивая
с одной молекулы воды на другую, движутся к отрицательному
полюсу — катоду, а отрицательно заряженные частицы кисло­
рода — к аноду. На электродах происходит их р а зр яд — на като­
де выделяется водород, на аноде — кислород. Впоследствии эта
теория бы ла отвергнута. Однако в дальнейшем некоторые по­
ложения ее — эстафетный механизм — были использованы для
объяснения аномально высокой скорости перемещения ионов во­
дорода и гидроксид-ионов.
В 1887 г. шведский ученый С. Аррениус сформулировал тео­
рию электролитической диссоциации, сыгравшую важ ную роль
при объяснении электропроводности электролитов и многих фи­
зико-химических явлений. Все же теория электролитической дис­
социации С. Аррениуса имела определенные недостатки, та к как
она не учиты вала взаимодействия между ионами и молекулами
растворителя. Большой вклад в развитие электрохимии внесли
также работы В. Оствальда и В. Нернста. В 1891 г. И. А. Каблуков
ввел представление о сольватации ионов, что позволило связать
теорию С. Аррениуса с гидратной теорией растворов Д . И. Мен-
312

делеева (1868). Однако химическая школа в теории растворов
не могла дать количественных выводов. В 20-х гг. XX в. элек­
тролитическая теория С. Аррениуса была дополнена П. Дебаем
и Э.Хюккелем, предложившими полуэмпирические подходы к
учету взаимодействия между сольватированными ионами. Это
позволило распространить теорию диссоциации на среднераз-
бавленные растворы.
Основанные на полученных фундаментальных знаниях р аз­
вивались направления прикладного характера. В 1844 г. П. Р. Б а­
гратион изобрел сухой элемент — родоначальник применяемых
ныне сухих батарей. В 1859 г. Г. Планте, используя идею ака­
демика Петербургской Академии Б. С. Якоби об аккумулирова­
нии электрической энергии, изобрел свинцовый аккумулятор.
В 1865 г. Ж .Лекланш е создал элемент, представляющий пару
электродов Zn —Мп02, который в настоящее время выпускает­
ся миллиардами штук. Н ачал а развиваться гальванотехника —
нанесение металлических гальванических покрытий на поверх­
ность изделия (катод) при электролизе раствора. Родоначальни­
ком этого направления был Б. С. Якоби.
В 1885 г. американский химик М. Холл и одновременно и неза­
висимо от него французский металлург П. Эру разработали ме­
тод получения алюминия из раствора глинозема в расплавлен­
ном криолите с помощью электролиза. Метод Х о л л а —Эру сде­
лал возможным получение алюминия промышленным способом.
Так начала развиваться электрометаллургия.
Дальнейшее развитие электрохимии связано с работами по
изучению строения границы «электрод—раствор» и кинетики
электрохимических реакций. Первая модель строения двойного
электрического слоя — модель плоского электрического конден­
сатора —была предложена Г. Л. Гельмгольцем в 1853 г. Развитие
модельных представлений о двойном электрическом слое нашло
в работах Ж . Гуи, Д . Чепмена и О. Штерна.
Закономерности электрохимических процессов изучались в
работах Р. А. Колли (1878), Ю. Тафеля (1905) и позднее Т. Фоль-
мера, Т. Эрдей-Груза, А. Н. Фрумкина, К. Феттера, Дж. Бокриса,
В. Е. Конуэя, Я. М. Колотыркина и др. Дальнейшее продолже­
ние исторических изысканий не имеет смысла, так как многие
представления упомянутых исследовавателей и результаты бо­
лее поздних работ составляют основу современной электрохимии
и будут изложены в основной части раздела.
В чем же заключается различие между химическими и элек­
трохимическими реакциями и что привело к выделению элек­
трохимии в отдельный раздел физической химии? Рассмотрим
две окислительно-восстановительные реакции:
313

н2+^о2=н2о
И
2FeCl3 + SnCl2 i=i 2FeCl2 + SnCl4
Одно из веществ в обеих реакциях является восстановителем
(Н2, S11CI2), т. е. донором электронов, тогда как другое (О2,
ЁеС1з) является окислителем, т. е. акцептором электронов. При
хаотическом движении частицы восстановителя и окислителя
подходят вплотную друг к другу, вследствие чего становится
возможным переход электрона от одной частицы на другую, т. е.
для того, чтобы прошел окислительно-восстановительный эле­
ментарный акт, должен иметь место непосредственный контакт
между реагирующими частицами. Переходы электронов от од­
ной молекулы или иона к другой молекуле или иону могут совер­
шаться в любых точках реакционного пространства при наличии
у частиц запаса энергии большего или равного энергии актива­
ции процесса. При этом будет происходить изменение энергети­
ческого состояния частиц, которое сопровождается выделением
или поглощением теплоты. Так протекают химические реакции.
Приведенные выше реакции можно осуществлять т а к ж е элек­
трохимическим путем, изменяя механизм процесса. Д л я этого
необходимо составить гетерогенную систему состоящую из про­
водников I и II рода, например, использовать окислитель и вос­
становитель, разделенные мембраной, проницаемой д л я ионов, и
инертные электроды (например из платины) в качестве передат­
чиков электронов от восстановителя к окислителю. Схема такого
устройства представлена на рис. 3.1. Первый электрод помещен
в раствор восстановителя, а
второй — в раствор окисли­
теля. Д ля того чтобы раство­
ры не перемешивались, их раз­
деляет мембрана. Если соеди­
нить два платиновых электро­
д а металлическими проводни­
ками через потенциометр, то
можно убедиться, что меж­
ду электродами возникает раз­
ность потенциалов. Т а к а я гете­
рогенная система представля­
ет собой замкнутую электриче­
скую цепь. Если в нее вклю-
Рис. 3.1. Схема электрохимиче- чить вместо потенциометра ам-
ской системы
перметр, то обнаружится, что
314

в цепи протекает электрический ток. На электродах создается
разность потенциалов, под действием которой в цепи происходит
перенос электрических зарядов, т. е. совершается работа. Д ля
первой реакции частицы восстановителя (растворенного и ад­
сорбированного водорода) передают электроны платине (анод)
и окисляются, а на втором платиновом электроде (катод) части­
цы окислителя присоединяют электроны и восстанавливаются.
Дл я первой реакции:
Анод(Р0 : Н2- 2е“ —►2Н+
KaTOA(Pt) : \ о 2+2Н++2е~ -> Н20
Дл я второй реакции:
Анод(Р1) : Sn2+- 2е“ -> Sn4+
KaTCw(Pt) : 2Fe3++ 2е“ -» 2Fe2+
Электрод, на котором протекают реакции окисления, на­
зывается анодом.
Электрод, на котором протекают реакции восстановле­
ния, называется катодом.
При суммировании реакций, протекающих на аноде и катоде,
при условии равенства числа электронов, отданных восстано­
вителем и принятых окислителем, получим приведенные выше
реакции, выразив их в молекулярной форме. В рассмотренных
слу чаях энергия химической реакции переходит в значительной
степени в электрическую энергию. При этом частицы восстано­
вителя движутся к аноду, а частицы окислителя — к катоду.
Продукты реакции движ утся в обратном направлении в объем
раствора. Весьма важным фактором, влияющим на скорость ре­
акции при постоянной температуре и давлении, является скачок
потенциала, возникающий между электродом и раствором, вели­
чина которого влияет на энергию активации и, следовательно,
на скорость реакции. Если во внешнюю цепь рассматриваемой
схемы (см. рис. 3.1) включить источник постоянного тока, то,
регулируя его напряжение, можно изменять скорости реакций,
протекающих на аноде и катоде за счет изменения скачка потен­
циала на границе «электрод—раствор». При изменении поляр­
ности внешнего источника тока можно направить реакции на
электродах в обратную сторону. В этих случаях электрохими­
ческая цепь работает к ак электролизер. В отсутствии внешнего
источника тока электрохимическая цепь (см. рис. 3.1) представ­
л яет собой гальванический элемент.
315

Устройство, превращающее энергию химической реакции
в электрическую энергию, называется гальваническим эле­
ментом.
Следует отметить, что в качестве электролита можно исполь­
зовать расплавы солей и оксидов или твердые электролиты, а
в качестве электродов полупроводниковые материалы или гра­
фит. Таким образом, при протекании электрохимических реак­
ций происходит превращение вещества на аноде и катоде. Ко­
личества окисленного и восстановленного веществ подчиняются
законам Фарадея. При этом в электролите наблюдается направ­
ленное движение катионов и анионов под действием электриче­
ского поля между катодом и анодом.
Кратко остановимся на проблемах и перспективах развития
электрохимии. Это развитие водородной энергетики, т. е. исполь­
зование водорода как горючего и сырья д л я химической про­
мышленности, источника электроэнергии в автономных систе­
мах: водород в значительной мере будет получаться в резуль­
тате электролиза воды с использованием атомных электростан­
ций; применение топливных элементов как источников питания
в электромобилях; создание новых более эф ф ективны х топлив­
ных элементов; применение электрохимии в металлургии для
получения алюминия, магния, натрия; получение ти та на с ис­
пользованием магния или н ат ри я в качестве восстановителя, ко­
торые получают предварительно электролизом. Электрохими­
ческая переработка сернистых руд позволит ликвидировать вы­
брос сернистого газа в атмосферу. Более широкое развитие элек­
тросинтеза, получение хлора, фтора, органических соединений.
Более широкое применение и создание новых электрохимиче­
ских преобразователей информации (счетчики времени, датчики
давления, датчики сигналов, индикаторы на ж идких кристал­
лах и другие устройства). Расширение и модернизация электро­
химической размерной обработки металлов и сплавов. Проведе­
ние дальнейших исследований в области коррозии металлов и
сплавов. Особое направление, которое в настоящее вр емя пред­
ставляется теоретическим, должно сыграть решающую роль в
будущей судьбе электрохимии. Это биоэлектрохимия, электро­
химия процессов в живом организме, так как многие биологи­
ческие процессы, будь то усвоение и использование энергии пи­
щи, распространение нервного импульса, восприятие зрительно­
го образа, включают в себя звенья, очень сходные с электрохи­
мическими явлениями.
Краткое изложение проблем и задач электрохимии не может
включить всех направлений теоретических и прикладных иссле-
316

дований в области электрохимии. Поэтому можно закончить вве­
дение словами академика А. Н. Фрумкина: «Идей, которые тре­
буют развития мыслей, которые ж дут воплощения, нехоженых
путей, которые могут привести к интереснейшим открытиям, в
электрохимии бесконечно много».
3.1. ЭЛЕКТРОХИМИЯ РАСТВОРОВ
Первые наблюдения в области электрохимии были связаны
с явлениями, вызываемыми переносом электрического заряда.
Поэтому сначала остановимся кратко на классификации веществ,
проводящих в той или иной мере и на не проводящих электри­
ческий ток.
Системы, проводящие электрический ток, называются
проводниками, а не проводящие электрический ток назы­
ваются изоляторами.
Однако четкой границы между проводниками и изоляторами
нет.
Проводники, электропроводность которых обусловлена
переносом электронов, называются проводниками первого
рода.
В большинстве случаев в качестве электродов используются
металлы, а в качестве электролита — растворы, расплавы со­
лей. Металлы относятся к проводникам первого рода. Д л я них
характерна высокая концентрация свободных электронов. У ме­
таллов отсутствует запрещенная зона д л я перехода электронов
из валентной зоны в зону проводимости. Достаточно наложить
на концы металла минимальную разность потенциалов, чтобы
электроны начали передвигаться в электрическом поле, созда­
вая в металлическом проводнике электрический ток. Электро­
сопротивление металлов растет с температурой из-за усиления
колебаний положительно заряженных ионов в кристаллической
решетке и торможения направленного движ ения электронов по­
ложительно заряженными ионами.
Электронопроводящие проводники, в которых существу­
ет запрещенная зона, которую электроны должны преодо­
леть под действием кванта энергии, чтобы перейти в зону
проводимости, называются полупроводниками.
317

В отличие от металлов, в полупроводнике при абсолютном
нуле отсутствуют свободные электроны, все электроны находят­
ся в валентной зоне, но сообщение энергии извне приводит к
тому, что часть электронов активируется и приобретает способ­
ность преодолеть потенциальный барьер, который называется
запрещенной зоной и перейти в зону проводимости. При этом
на месте электрона, перешедшего в зону проводимости, возни­
кает положительно заряженная дырка, которая также участвует
в переносе зарядов. Ширина запрещенной зоны в полупрводни-
ках может регулироваться путем добавления примесей, которые
могут быть как донорами, так и акцепторами электронов.
У изоляторов ширина запрещенной зоны значительно боль­
ше, чем у полупроводников. В типичном полупроводнике — гер­
мании — ширина запрещенной зоны составляет 0,67 эВ, а для
такого изолятора, как алмаз, она равна 5,6 эВ. Принято, что гра­
ница между полупроводником с естественной проводимостью и
изолятором л е ж и т при значении запрещенной зоны около 1 эВ.
Полупроводники, содержащие примеси-доноры, отдаю­
щие электроны в зону проводимости, называются полупро­
водниками п-типа.
Например, при легировании полупроводника германия элемен­
тами V группы, имеющими большее число валентных электро­
нов, электроны переходят в зону проводимости.
Полупроводники, которые содержат примеси-акцепторы,
захватывающие электроны из валентной зоны и создающие
«дырки», называются полупроводниками р-типа.
Примером полупроводников p-типа является германий, легиро­
ванный атомами элементов III группы.
Активирование электронов в полупроводниках может проис­
ходить за счет энергии фотонов или под действием температу­
ры. Поэтому электропроводность полупроводников возрастает с
ростом температуры. При температуре абсолютного нуля полу­
проводник становится изолятором.
Проводник, электропроводность которого обусловле­
на переносом зарядов ионами, называются проводниками
II рода.
К электропроводящим системам ионного типа относятся ионо­
содержащие растворы и расплавы. Электропроводность раство-
318

ров зависит от концентрации и подвижности ионов в растворе.
Сольватация ионов приводит к уменьшению электропроводно­
сти. При отсутствии сольватации электропроводность раство­
ров растет с уменьшением размеров ионов, что связано с уве­
личением подвижности ионов. Наибольшей подвижностью обла­
дают в водных растворах ионы водорода и гидроксила. Поэто­
му электропроводность растворов кислот и щелочей превышает
электропроводность солей. Электропроводность расплавов со­
лей значительно превышает электропроводность растворов, так
как концентрация ионов в расплавах выше, чем в растворах.
Существуют такж е твердые ионопроводящие системы. Подвиж­
ность ионов в твердых электролитах связана с наличием дефек­
тов в кристаллических решетках таких систем. Ионы за счет теп­
ловых флуктуаций могут переходить в межузельное простран­
ство кристаллической решетки и далее перемещаться от одного
межузельного пространства к другому. Чем больше по разме­
ру межузельное пространство по сравнению с перемещающими­
ся ионами, тем выше электропроводность твердого электролита.
Вакансии, которые возникают в узлах кристаллической решетки
при переходах ионов в междуузлия, такж е участвуют в перено­
се зарядов, так как соседние ионы решетки могут перемещаться
по вакансиям. Следует отметить, что в твердых электролитах в
определенном интервале температур перенос зарядов осуществ­
ляется только катионами, например NaCl, AgCl, или анионами
(РЬСЬ, ВаСЬ). Синтезированные до сих пор твердые электроли­
ты имеют высокую электропроводность лишь при повышенных
температурах, и при повышении температуры их электропро­
водность быстро растет.
Системы, полностью теряющие омическое сопротивление
при понижении температуры ниже некоторого порога, на­
зываются сверхпроводниками.
При исследовании проводимости некоторых металлов и сплавов
при низких температурах (жидкий гелий) было установлено, что
существует порог температуры, ниже которой металл, например
медь или ртуть, теряет сопротивление прохождению электриче­
ского тока и становится сверхпроводником. Благодаря откры­
тию сверхпроводимости некоторых металлических сплавов бы­
ли созданы электромагниты с очень высокой напряженностью
магнитного поля для изготовления ЯМР-спектрографов и то­
мографов, которые открыли новые возможности для безболез­
ненной диагностики патологии мозга и других органов человека
и животных. Явление сверхпроводимости обычно связывают с
319

открытием Д ж . Беднори и К. Мюллером сверхпроводящей кера­
мики в 1986 г* Керамика состояла из оксидов меди, бария и лан­
тана и переходила в сверхпроводящее состояние уже при 30 К.
В связи с этим начались интенсивные поиски сверхпроводящих
систем. В настоящее время синтезированы сверхпроводники с
порогом температуры 135 К (жидкий азот)
3.2 . ТЕОРИЯ ЭЛЕКТРОЛИТИЧЕСКОЙ
ДИССОЦИАЦИИ
М. Фарадей разделил вещества на электролиты и неэлектро­
литы. Электролиты в растворах или расплавах проводят элек­
трических ток. Это — кислоты, щелочи и соли, которые, как он
считал, только под действием электрического тока распадаются
на ионы — катионы и анионы.
При изучении влияния концентрации растворенного вещества
на упругость пара над раствором, температуру кипения и за­
мерзания растворов, осмотическое давление были установлены
удивительные факты — электролиты вели себя так, как будто в
растворе было большее количество вещества. Понижение упру­
гости пара, повышение температуры кипения и понижение тем­
пературы замерзания, возрастание осмотического давления для
электролитов были значительно большими, чем это следовало
из законов Ф. Рауля и опытов по измерению осмотического дав­
ления (тс). Я . Вант-Гофф ввел эмпирическую поправку на более
высокую активность электролитов, которая носит название ко­
эффициента Вант-Гоффа или изотонического коэффициента г:
АДксп = ^ДДеор>
^эксп = З'Ятеор-
Величина поправки зависела от концентрации раствора и уве­
личивалась с разбавлением раствора.
В 1883 г. С. Аррениус предложил первую количественную тео­
рию, кото рая смогла объяснить с достаточным приближением
физико-химические свойства растворов электролитов. Можно
было выделить три основных положения.
1. При растворении веществ-электролитов последние распа­
даются на ионы (катионы и анионы), которые являются пере­
носчиками электричества.
Процесс распада вещества на ионы называется процессом
электролитической диссоциации.
320

2. Ионы ведут себя подобно молекулам идеального газа.
3. Диссоциации подвергается только часть вещества, которая
определяется степенью диссоциации (а).
4. Между недиссоциированными молекулами и ионами уста­
навливается динамическое равновесие в полном соответствии с
законом действующих масс. При разбавлении раствора с —> О,
а —>1.
Отношение числа молекул, подвергшихся диссоциации, к
общему числу молекул растворенного вещества называется
степенью диссоциации а .
а=
N ДИС
Разделив числитель и знаменатель уравнения на произведение
(ЛГд • V), где N J4 — число Авогадро; V — объем раствора ве­
щества, л, можно получить связь с концентрацией раствора с,
моль/л:
а=^
.
(3.1)
С
Между а и изотоническим коэффициентом г имеется связь. По
физическому смыслу величина i указывает, во сколько раз уве­
личилась концентрация частиц в растворе после диссоциации
молекул. При концентрации раствора с доля молекул а диссо­
циирует на п ионов, и общая концентрация частиц в растворе
определяется как сумма концентраций недиссоциированных мо­
лекул (с-ас) и ионов:
гс = (1-а)с +пас.
В явном виде а будет выражена следующим образом:
При бесконечном разбавлении а = 1 и i = га, т. е. осмотическое
давление раствора увеличивается в п раз. Определяя опытным
путем ДТ или к можно вычислить г и по уравнению (3.2) рассчи­
тать а. Рассмотрим равновесие, устанавливающееся при диссо­
циации бинарного электролита, например, при диссоциации ук­
сусной кислоты:
а=
г-1
гг-1*
СНзСООН Н++ СНзСОО"
Константа диссоциации К дис может быть выражена в следую­
щей форме:
11 Ипполито»
321

_
[НЧ[СНзСОО-]
дис
[СНзСООН] ■
Если концентрация растворенной кислоты равна с, то а с - кон­
центрация кислоты, подвергнувшейся диссоциации, т. е.
ас = [Н+] = [СН3СОСГ].
Концентрация недиссоциированных молекул кислоты равна:
с-ас=(1-а)с.
Подставив в (3.3) величины равновесной концентрации, получим:
к
-
Лдис" 1 -а
(3.4)
Степень диссоциации можно рассчитать, решив квадратное урав­
нение:
а=
+ 4Кдксс - К)
2с
Если вещество является слабым электролитом и в небольшой
степени диссоциирует на ионы 1 - а ^ 1, то уравнение (3.4) упро­
щается:
^дис —а с.
Тогда
а=
К:ДИС
(3.5)
Уравнение (3.5) применимо только в области не очень низких
концентраций электролита. Если выразить с через объем рас­
твора V, который занимает 1 моль вещества, то с = — . Заменив
с на это выражение в уравнении (3.4), получим:
от
ктле=(1_а)у
(3.6)
Уравнения (3.4) и (3.6) были выведены В. Оствальдом и полу­
чили название закона разведения.
Следует отметить, что уравнения (3.4) и (3.6) применимы для
растворов симметричных бинарных электролитов, т. е. когда мо­
лекула вещества диссоциирует на один катион и один анион. Для
несимметричных электролитов оба уравнения усложняются.
Теория электролитической диссоциации развивалась также в
работах П. И. Вальдена, Л. В. Писаржевского и др.
322

Теория Аррениуса успешно используется д л я описания рав­
новесий слабых электролитов в аналитической химии в количе­
ственном анализе. Однако при достаточно высоких концентра­
циях электролита наблюдается зависимость К АИС от концентра­
ции, особенно для сильных электролитов, дл я которых а = 1
или близка к этой величине. Недостатки теории электролитиче­
ской диссоциации заклю чались в том, что теорией игнорирова­
лось взаимодействие ионов с молекулами растворителя (явление
сольватации), а также взаимодействие между ионами. Теория не
дава ла объяснения причин диссоциации электролитов в раство­
ре. Кроме того, вещества с ионной связью, например NaCl, CsF
и другие, уже в твердом состоянии находятся в кристалличе­
ской решетке в виде ионов и являются не молекулами, а некими
структурными единицами, суммарный зар яд ионов у которых,
как и у молекулы, равен нулю. Поэтому при растворении ве­
ществ с ионной связью в растворе могут существовать только
ионы, а не молекулы, и уравнения (3.4) и (3.6) не применимы
для описания поведения сильных электролитов. Учет влияния
природы растворителя и ионного взаимодействия с использова­
нием эмпирических коэффициентов был предложен П. Дебаем и
Э. Хюккелем, что позволило им развить теорию сильных элек­
тролитов для разбавленных растворов.
3.3 . СОЛЬВАТАЦИЯ ИОНОВ
Д. И. Менделеев в своих работах подвергал критике теорию
электролитической диссоциации. Так, в «Основах химии» он пи­
сал, что С. Аррениус не учитывал роль химического взаимодей­
ствия растворенного вещества с растворителем. Вода, являясь
одним из наиболее распространенных растворителей, обладает
ближним порядком, т. е. представляет собой легко деформируе­
мую кристаллическую структуру за счет межмолекулярных во­
дородных связей и образует трехмерную решетку. К аж д ая мо­
лекула воды связана с четырьмя соседними и образует прибли­
зительно тетраэдрическую структуру. При наличии ионов в рас­
творе, имеющих электронное строение благородного газа, катион
или анион создает искажение трехмерной решетки, воздействуя
на диполи молекул воды. Под действием сил электростатическо­
го притяжения между диполями воды и ионом последний прочно
связывается с ближайшим окружением из молекул воды, струк-
тура растворителя искажается — диполи воды деформируются
из-за ион-дипольного взаимодействия. Ориентирующее влияние
электрического поля иона распространяется з а границу первой
323

гидратной сферы,что приводит к нарушению структуры раство­
рителя.
Окружение иона молекулами растворителя в результа­
те ион-дипольного взаимодействия называется сольватаци­
ей ионов.
Частный случай сольватации применительно к водным
растворам называется гидратацией ионов.
С ростом концентрации электролита увеличивается д о ля раство­
рителя с искаженной трехмерной сеткой. Деформируется также
ион. Таким образом, ионы в растворе окружены молекулами во­
ды, которые постоянно могут меняться местами с окружающими
молекулами воды, создавая трансляционное движение молекул
воды и пространственное передвижение иона, что обусловливает
многие свойства ионных растворов, например теплопроводность.
При наличии электрического поля происходит ориентация дви­
жения ионов по полю. Б л агодаря уплотнению молекул раство­
рителя вокруг иона процесс гидратации (сольватации), как пра­
вило, сопровождается сжатием раствора.
Например, один моль NaCl при растворении в воде с образо­
ванием насыщенного раствора при температуре 298,1 К вызыва­
ет уменьшение объема на 5,64 см3:
NaCl(T) + 8,986Н20 (ж ) —►NaCl(Hac.p)
26,87см3 162,32 см3
183,55 см3
Такое уменьшение объема чистой воды будет происходить под
давлением в 893 атм. (90451 кП а). Этот пример свидетельствует
о существовании больших сил притяжения между ионами соли
и воды.
Число окружающих ион молекул растворителя называ­
ется (сольватным) гидратны м числом иона.
Для молекул с ковалентной полярной связью разрушение связи
происходит з а счет взаимодействия молекул вещества с молеку­
лами воды, например, д л я соляной кислоты:
НС1+Н20и Н30++сг
Образовавшийся ион гидроксония и ион хлора дополнитель­
но гидратируются молекулами воды (ион-дипольное взаимодей­
ствие). Таким образом, при образовании раствора соляной кис­
лоты разрывается полярная ковалентная связь в молекуле НС1,
энергия связи в которой составляет 432 кД ж/м оль. Гидратация
324

ионов обеспечивает устойчивость растворов электролитов. При
избытке молекул растворителя кроме первичной гидратации на­
блюдается вторичная гидратация (т. е. образование второго слоя
из молекул воды). Однако прочность связи воды во втором слое
на порядок ниже, чем при первичной гидратации, вследствие
значительного снижения напряженности электрического поля,
создаваемого ионом.
Число молекул, окружающих ион, зависит от температуры
раствора. При увеличении теплового движения часть молекул
растворителя отрывается от гидратной оболочки комплекса «ион-
растворитель». В то же время такое же число молекул раствори­
те л я будет присоединяться к другому гидратированному иону.
Гидратное число явл яется статистическим и уменьшается с ро­
стом температуры раствора. Гидратное число возрастают с ро­
стом заряда иона (z) и уменьшением его размера (г) пропорцио-
z2
нально отношению —т
. Ионы с меньшим кристаллографическим
радиусом лучше гидратируются, чем ионы, имеющие такой же
зар яд, но больший размер. Последнее подтверждается меньшей
подвижностью ионов лития (почти в два раза) по сравнению с
подвижностью ионов калия в водных растворах. Ион-дипольное
взаимодействие может носить не только электростатический ха­
рактер. Между ионами и молекулами воды часто наблюдается
возникновение более прочных химических связей, что приводит
к образованию кристаллогидратов, например, Na2S04 ■IOH2O,
CaS04 •2Н2О и др.
Да ж е если не все молекулы координируются катионом, то
часть молекул воды участвует в образовании кристалла за счет
водородных связей. В кристаллогидрате C11SO4 • 5Н2О четыре
молекулы воды координируются ионом Си2+, образуя комплекс­
ный ион, а пятая молекула удерживается в кристалле за счет
водородных связей с двумя координируемыми молекулами воды
и двум я сульфат-ионами.
н2о Н20
о
325

Некоторые кристаллогидраты вообще не существуют без во­
ды, так как молекулы растворителя стабилизируют структуру
кристалла, заполняя пустоты меж ду ионами большого размера,
например, FeSiF6 •6Н2О, Na4XeOe • 8Н20 . Энтальпия сольвата­
ции ионов близка по абсолютной величине энергии кристалли­
ческой решетки. Однако эти величины имеют противоположные
знаки.
3.4 . ЭНЕРГИЯ ИОННОЙ КРИСТАЛЛИЧЕСКОЙ
РЕШЕТКИ
Ранее давалось определение энтальпии ионной кристалли­
ческой решетки. Там же приводился термохимический расчет
энергии кристаллической решетки по закону Гесса. Расчет энер­
гии кристаллической решетки в ионной модели был выполнен
впервые М. Борном и М. Ланде. К ак в теории газов отталкива­
ются от модели идеального газа, а в теории растворов — от моде­
ли идеального раствора, так при рассмотрении ионных кристал­
лов исходят из модели идеального ионного кристалла. При этом
постулируется следующее строение идеального ионного кристал­
ла:
1) ионный кристалл состоит из противоположно заряженны х
ионов;
2) взаимодействие ионов целиком определяется законом Ку­
лона и объемами ионов;
3) ионы сферические и несжимаемые;
4) м ежду газообразными ионами и ионами в идеальном ион­
ном кристалле нет различия;
5) зар яд ы ионов сконцентрированы в их центрах.
Рассмотрим энергию пары газообразных ионов К + и А", ко­
торые расположены на расстоянии г друг от друга. По закону
Кулона, энергия взаимодействия между ионами с зарядами z + и
z" равна:
4ле0Г ’
где единица заряда е = 1, 6 ■10~15 Кл; £о —диэлектрическая про­
ницаемость в вакууме. Поскольку z+ и z~ имеют противополож­
ные знаки, то энергия притяжения имеет отрицательное значе­
ние (рис. 3.2). В кристаллической решетке взаимодействие меж­
ду парой ионов усложняется, так как следует учитывать влияние
соседних ионов. Эти взаимодействия учитываются на основе за­
кона Кулона константой Маделунга А . С учетом этой константы
326

Е
Рис. 3 .2, Энергия притяжения
между парой свободныхионов:
1 — суммарная энергия взаимодей­
ствия; 2 — энергия отталкивания;
3 — энергия притяжения
Рис. 3.3. Кулоновское взаимодей­
ствие ионов в кристалле типа
NaCl:
® —центральный ион Na+; о — ионы
Na+;®—ионыСГ
энергия притяжения пары ионов в кристалле равна:
Az*z~e2
—
■.
у 4тггот
Значение константы Маделунга определяется типом решетки.
Дл я кристалла NaCl рассмотрим ион Na+, который находится в
центре фрагмента кубической решетки (отмечен крестиком на
рис. 3.3). Ближайшие соседи иона — 6С1" в центрах граней (от­
мечены черными кружочками), каждый из которых находит­
ся на одинаковом расстоянии от центрального иона. Расстоя­
ние определяется размерами ионов. Следующие ближайшие со­
седи — 12 ионов Na+ все расположены по кр аям элементарной
ячейки. Затем следуют более дальние соседи — 8 ионов С1 и т. д.
В результате константа Маделунга дл я первых трех слоев сосе­
дей будет выражена следующим образом:
Л=6-
12_ 8
Величина А представляет собой значение сходящегося ряда,
и влиянием более дальних ионов можно пренебречь. Как видно
из табл. 3.1, значение константы Маделунга не зависит от за р я­
д а и радиуса ионов и определяется только геометрией кристал­
ла. В кристаллической решетке все силы притяжения уравнове­
шиваются силами отталкивания, так как при сближении ионов,
327

Таблица 3.1
Константы Маделунга для распространенных структурных типов
кристаллов
Тип структуры
кристалла
Координационное
число
Константа
Маделунга, А
катиона
аниона
Хлорид натрия
6
6
1,74756
Хлорид калия
8
8
1,76267
Сфалерит
4
8
1,63806
Вюрцит
4
4
1,64132
Флюорит
8
4
2,51939
Рутил
6
3
2,408
Корунд
6
4
4,1719
имеющих определенный размер, между их электронными обла­
ками возникают силы отталкивания, которые резко возрастают
при дальнейшем сближении ионов (см. рис. 3.2, кр ивая 2). По
М. Борну, энергия отталкивания определяется выражением:
(3.7)
где В — константа. Значения показателя п в уравнении (3.7) мо­
гут быть получены из экспериментальных данных о сжимаемо­
сти, т. е. из значений предельного сопротивления, которое ока­
зывают ионы при их сближении. Общая энергия решетки может
быть выражена для 1 моля вещества следующим образом:
JJ—£ПР £от—
ANAZ+z~e2 N ^ B
4яеот
гп’
(3.8)
где N A — число Авогадро. Минимум энергии (см. рис. 3.2, кри­
вая 1 ) соответствует условию:
dU_ о
_
ANAz+z~e2 _ nNAB
dr
4я£ог2
r n+1
Из этого условия можно найти константу В:
В=-
A z +z~e2r n~1
4явоп
(3.9)
Подставив выражение (3.9) в уравнение (3.8) получим общую
энергию, соответствующую равновесному состоянию решетки
328

Таблица 3.2
Значения показателя п
Электронная конфигурация
иона
п
Электронная конфигурация
иона
п
Не
5 Кг, Ag*
10
Ne
7 Хе, Аи+
12
Аг, Си+
9
(см. рис. 3.2, минимум кривой 7), для расстояния между иона-
МИ Го.
или
ANAz*z~e2 ANAz+z~e2
4те0г0
U0=
U0=
ANAz+z'e2
4я£ого
4ТГ£о 7'о П
1--
п
(3.10)
Уравнение Борна —Ланде (3.10) позволяет рассчитать общую
энергию решетки ионного соединения. Д л я расчета Щ следу­
ет только выбрать величину А (см. табл. 3.1), соответствую­
щую определенной структуре кристалла, и расстояние го, кото­
рое определяется рентгеноструктурным анализом. Значение п
зависит от размера иона, так как ионы с бблыним радиусом
имеют относительно высокую электронную плотность и, сле­
довательно, большие значения тг. Д л я этого используют обоб­
щенные значения п, предложенные Л. Полингом (табл. 3.2). По
уравнению (ЗЛО) можно рассчитать энергию кристаллической
решетки NaCl. Согласно расчетам Щ = - 755,2 кДж/моль. Рас­
считанная величина отличается от экспериментального значе­
ния -770 кД ж/м оль на 2%. Последнее позволяет использовать
расчетные значения Uq при отсутствии экспериментальных д ан ­
ных. Следует отметить, что при этом расчете не учитывались
силы неэлектростатического характера (доля ковалентной свя­
зи), дисперсионные силы. Вообще ионная модель кристалличе­
ской решетки является грубым приближением, так как ионы в
кристалле не идентичны гипотетическим газообразным ионам.
3.5. ЭНЕРГИЯ СОЛЬВАТАЦИИ
Энергия сольватации —это энергия, которая выделяется
при перенесении 1 моля ионов из вакуума в растворитель
(например, воду) и образовании бесконечно разбавленного
раствора.
329

При этом предполагается,
что при расчете энергии соль­
ватации не учитывается элек­
тростатическое взаимодействие
ионов при введении последу­
ющих ионов, так как раствор
бесконечно разбавлен. В этой
связи, чтобы раствор оставал­
ся электронейтральным, в рас­
творитель необходимо вводить
такое же количество противо­
ионов и считать, что рассмат­
риваются очень разбавленные растворы, в которых кулоновское
взаимодействие между ионами равно нулю. Согласно модели,
предложенной М. Борном, ион представляет собой ш арик ради­
уса г, заряженный положительно или отрицательно, а раство­
ритель — это сплошная изотропная среда с диэлектрической по­
стоянной £о (рис. 3.4).
Перенос иона из вакуума в растворитель разбивается на три
этапа:
1) нейтрализация заряда шарика-иона;
2) перенос незаряженного шарика из вакуума в растворитель;
3) заряжение шарика в растворителе с образованием исход­
ного иона (см. рис. 3.4).
При этом предполагается, что работа А 2 = 0. Работу заряже­
ния сферы можно рассчитать, мысленно представив, что заряд
малыми порциями dq переносится из бесконечности на поверх­
ность шарика. Работа dA, которая совершается при создании до­
бавочного заряда dq на поверхности сферы, заряд которой уже
равен qy выражается соотношением:
©—
о
°
1
1
1
1
<
1
1
1
;© -s
-
^
Chv_
-
Рис. 3.4. Модель для расчета эн­
тальпии сольватации иона
dA=
Qdg
4я£ог "
Обратная работа — работа разряжения шарика с зарядом q бу­
дет иметь противоположный знак. Суммарная работа, затрачи­
ваемая на перезаряжение поверхности сферы от q до 0 в вакууме
(£о = 1), будет равна:
Ai=
(£)*
Работа заряжения нейтральной частицы (шарик) до заряда q
положительно заряженного иона в растворителе с диэлектриче­
ской проницаемостью £:
330

Таблица 3.3
Зависимость растворимости KI от природы растворителя
Растворитель
fс
е
Растворимость KI, %
СН3СООС2Н5
20 6,00
0,00012
Н-С4Н90Н
20 17,7
0,20
СНзОН
25 32,63
14,97
н2о
25 78,3
59,8
Свободная энергия сольватации для 1 моля вещества, учитывая
число Авогадро и равенство q = z+e, будет равна:
дс* =
-
^ёН)-
<з-п >
Уравнение (3.11), известное как уравнение Борна, получено в
достаточно грубом приближении (ион —заряженная сфера, рас­
творитель — непрерывная изотропная среда с диэлектрической
проницаемостью е). Однако оно дает возможность правильно
оценить порядок величины A G S.
Из уравнения (3.11) такж е следует, что с ростом е среды
энергия сольватации (дл я водных растворов гидратации) ионов
солей увеличивается. Последнее должно приводить к увеличе­
нию растворимости солей. Подтверждением этому служат дан­
ные табл. 3.3.
3.6. ЭНТАЛЬПИЯ СОЛЬВАТАЦИИ СОЛИ
Расчет энтальпии сольватации соли (теплоты сольватации)
A H S1 по закону Гесса, на примере соли NaCl был дан ранее.
Определить отдельно A # s; Na+ и А # 5; с г не представляется воз­
можным. Предполагается, что А Я 5; NaCl (теплота сольватации)
является аддитивной величиной:
АЯ5; NaCl =
Na++ АН3] СГ-
Приведенное уравнение можно полагать справедливым, так как
разности теплот гидратации солей с общим катионом или общим
анионом равны постоянной величине, что подтверждается д л я
галоидных солей щелочных металлов, например:
A#s; NaF - A HSjKF = 83,6 кДж/мОЛЬ,
331

Atfs; NaCl “ Atf5;KC1 = 83,6кДж/моль,
АЯ5;NaF- ДЯ, NaCl = 71,06 кДж/моль,
AHs-kf
-
АЯ, kci = 71,06 кДж/моль.
Таким образом, учитывая энергию ионной кристаллической ре­
шетки, получим:
АЯз;NaCl=Uq+A#s,p,
где A Hs p — энтальпия растворения 1 моля соли.
Для расчета AHs; NaCl берутся рассчитанные по уравне­
нию (ЗЛО) значения Uo и экспериментально найденная величина
Д Я 5)Р. Энтальпии гидратации д л я хлоридов щелочных металлов
приводятся в табл. 3.4.
Как отмечалось выше, при растворении веществ с ковалент­
ной связью д л я вычисления Щ используют энергию диссоциа­
ции 1 моля вещества с образованием ионов в газообразном состо­
янии. Энтальпии сольватации отдельных ионов можно рассчи­
тать, используя некоторые модельные представления. Д ж . Бер­
нал и Р. Фаулер предположили, что поскольку валентности и
кристаллохимические радиусы ионов К+ и F “ одинаковы, то теп­
лоты гидратации для них такж е должны быть одинаковыми.
Теплоты гидратации могут быть получены делением опытной
теплоты гидратации KF пополам. Однако F “ обладает большей
гидрофильностью, чем ион К+, и теплота гидратации F -иона
должна быть больше теплоты гидратации иона калия. Послед­
нее связано с тем, что диполи молекулы воды располагаются во­
круг катионов и анионов по-разному. Из-за несимметричности
диполя воды энергия гидратации анионов несколько больше по
сравнению с таковой для катионов, так как молекулы воды бли­
же подходят к аниону. Учитывая это различие в гидратации ка­
тионов и анионов, К. П. Мищенко (1947) предложил считать рав­
ными между собой теплоты гидратации ионов Cs+ и I", обладаю-
Таблица 3.4
Энтальпии гидратации хлоридов щелочных металлов, кДж/м оль и,
величины, используемые для их получения
Соль
Uono yp. (3.10) u,T29, ДHs,„
AHS.NaCl
LiCl
- 843,5
- 847,3
- 35,9
-883,2
NaCl
-773,3
-775,4
5,4
-770
KCI
- 707,3
- 708,9
18,4
-690,5
RbCl
-682,5
-683,0
18,8
-664,2
332

щих неодинаковыми размерами. Радиус иона I” на 0,055 нм боль­
ше радиуса иона Cs+. Это различие должно компенсировать р аз­
ницу теплот гидратации между катионами и анионами, т. е. д л я
большего по размеру иона I ' теплота гидратации будет такой
же как и для Cs+. Разделив пополам теплоту гидратации соли
Csl, и тем самым рассчитав теплоты гидратации ионов Cs+ и
Г", в дальнейшем можно рассчитать теплоты гидратации дру­
гих ионов, используя принцип аддитивности (см. уравнение в
начале п.3.6). Следует отметить, что имеются и другие подхо­
ды д л я расчета теплот гидратации ионов. Поэтому разные авто­
ры предлагают различные шкалы теплот гидратации ионов, но
все они основаны на несколько произвольном делении энталь­
пий гидратации солей на составляющие энтальпии гидратации
ионов. Истинная же гидратация ионов нам неизвестна и можно
считать гидратации ионов, приводимые различными авторами,
лишь приближенными величинами.
3.7. ЭНТРОПИЯ СОЛЬВАТАЦИИ ИОНОВ
К а к отмечалось выше, при растворении соединений, распада­
ющихся на ионы, увеличивается упорядоченность растворителя,
о чем свидетельствует уменьшение объема раствора и уменьше­
ние диэлектрической постоянной раствора с увеличением кон­
центрации растворенного вещества. Эти явления связаны с явле­
нием сольватации. Энтропия, характеризующая степень неупо­
рядоченности в системе, при растворении вещества-электролита
до л ж на уменьшаться. Стандартная энтропия сольватации мо­
ж е т быть определена ка к разность энтропии иона в растворе и
в вакууме:
Стандартное состояние газа из ионов данного вида соответствует
давлению 1 атм при Т = 293 К, а в жидкой фазе активность иона
должна быть равна единице при Т = 293 К. Однако опытным
путем может быть определена суммарная энтропия сольватации
1 моля вещества:
ASs =
AHS-AG S
Дл я того, чтобы рассчитать энтропию сольватации отдельных
ионов, следует прибегнуть к различным допущениям, как и в
случае расчета энтальпии сольватации отдельных ионов.
Как следует из данны х табл. 3.5, энтропии гидратации имеют
отрицательный знак, что указывает на увеличение упорядочен-
333

Таблица 3.5
Энтальпии, свободные энергии и энтропии гидратации
Соль
-AHS}кДж/моль
- AG3yкДж/моль
- ASs,Дж/(моль •К)
LiF
1025
925
336
NaF
911
825
289
KF
827
752
252
RbF
806
730
255
CsF
782
698
282
ности структуры воды из-за ориентирующего действия ионов на
ближайшие молекулы растворителя.
3.8. АКТИВНОСТЬ И КОЭФФИЦИЕНТ АКТИВНОСТИ
Расчет константы диссоциации по закону разведения Остваль­
да (3.6) показывает, что даж е д л я слабых электролитов при бо­
лее высоких концентрациях наблюдается зависимость констан­
ты диссоциации от концентрации электролита, что можно ви­
деть на примере уксусной кислоты:
с(сн 3соон)> м о л ь / л ............0,001 0,02 0,1
0,2
Кснзсоон ■Ю5, моль/л.. .1,751 1,740 1,700 1,653
Еще больш ая зависимость константы диссоциации от концен­
трации наблюдается для сильных электролитов, если полагать,
что их диссоциация также протекает обратимо:
сксь моль/л .. .0,0001 0,001 0,01
0,1
К Кси моль/л. . .0,0128 0,0456 0,1510 0,5349
Такая зависимость связана с тем, что С. Аррениус не учи­
тывал взаимодействия между частицами (ионами, молекулами)
в растворе. Согласно представлениям Н. Льюиса закон разведе­
ния будет выполнен, если вместо концентрации ионов и моле­
кул ввести понятие активной концентрации (активность). Зна­
чения активностей а выбираются так, чтобы соблюдался закон
действующих масс, и константа диссоциации не зависела бы от
концентрации электролита. Существуют три способа выраже­
ния активностей, которые отвечают трем способам выражения
количественного состава растворов:
для молярной концентрации
334

&М—Ум )
(3.12)
д л я моляльной концентрации
а7п~ 7mCm5
(3.13)
д л я мольной доли
(3.14)
&N=7NCN,
где ум, 7m и удг — коэффициенты активностей соответственно
д л я разных выражений концентрации раствора. Коэффициент
активности является величиной, учитывающей силы взаимодей­
ствия между частицами.
Следует помнить, что молярная концентрация (см) определя­
ется числом молей растворенного вещества в 1 л раствора, мо-
л яльная концентрация выражается числом молей растворенного
вещества в 1 кг растворителя, мольная доля N определяется от­
ношением числа молей данного компонента к суммарному числу
молей растворителя и всех растворенных веществ. Физический
смысл коэффициента активности можно установить следующим
образом. Химический потенциал электролита при концентрации
1 моль/л в растворе равен:
\i=li0T +RTlnaM=\i0T+RT\nc +RT\nyMl
(3.15)
где ро (Т) — стандартное значение химического потенциала при
а - 1. Отличие реальных растворов от идеальных заключается в
третьем слагаемом Я Т1пум. Это выражение представляет собой
максимальную работу переноса 1 моля электролита из идеаль­
ного в реальный раствор. Химический потенциал соли р(КА)
связан с химическими потенциалами катионов и анионов. При
диссоциации соли
Kv+Av_
-> v+KZ++V-AZ~
Ц(К) = v+n++ v_jx_.
Определить коэффициент активности и, следовательно, актив­
ность для одного вида ионов из опытных данных не представля­
ется возможным. Уравнения, которые можно использовать д л я
нахождения активностей, содержат, по крайней мере, произведе­
ние активностей всех ионов данного электролита. Поэтому вво­
дится понятие о средней активности, которая представляет со­
бой среднее геометрическое активностей ионов, из которых со­
стоит данный электролит. Д л я электролита, распадающегося на
v+ катионов и v_ анионов, средняя активность будет равна:
аср =
Дл я бинарного электролита выражение упрощается:
335

Q'c p —у/ Qf+(L—’
Таким образом, выражение д л я среднего коэффициента актив­
ности в общем виде:
Выражения подобного же вида можно получить д л я других ви­
дов концентраций. Следует отметить, что в сильно разбавлен­
ных растворах величины коэффициентов активности для раз­
ных выражений концентраций растворов становятся достаточно
близкими. В этом случае одно и то же значение коэффициен­
та активности может быть использовано д л я всех приведенных
выше способов выражения концентрации:
Yep-Ум=Ут-Jn•
При дальнейшем разбавлении растворов
Yep=Ym=Ут = Ytv->1.
В этом случае ион-ионное взаимодействие стремится к нулю, и
раствор приобретает идеальные свойства. Казалось бы, состоя­
ние бесконечно разбавленного раствора можно было бы принять
за стандартное. Однако величина концентрации бесконечно раз­
бавленного раствора является неопределенной. Поэтому за стан­
дартное состояние выбирается состояние воображаемого раство­
ра, в котором концентрация, активность и коэффициент актив­
ности были бы равны единице. При этом предполагается, что
ион-ионное взаимодействие равно нулю. Представляет интерес
установить связь между средними коэффициентами активности
для различных шкал концентрации. Такую связь можно устано­
вить, исходя из положения, что химический потенциал раство­
ренного вещества не зависит от способа вы ражения концентра­
ции. В этом случае
где ро и Мо — плотность и молярная масса растворителя.
Н. Льюисом было установлено, что в области низких концен­
траций средние коэффициенты активности не зависят от при­
роды электролита, а зависят от их заряда и общей концентра­
ции всех присутствующих в растворе электролитов и зарядов
Yep= v+VYrY-v-.
Для бинарного электролита
Yep=у/ъТ-
Yep=Ym
Yw = Ym(l + 0, OOlvMom),
и
336

их ионов. Н. Льюис и М. Рендалл ввели понятие ионной силы
раствора / , которая определяется как полусумма произведений
концентрации ионов на квадраты их зарядов:
I=
(3.16)
где Ci и Z{ — концентрация и заряд г-го иона. Д л я 1,1-валентного
электролита ионная сила совпадает с величиной концентрации,
а д л я других типов электролитов I больше концентрации. Так,
например, для электролита ВаСЬ (с, моль/л), который полно­
стью диссоциирует на ионы, ионная сила будет равна:
/ = 0,5[с-22+2с(-1)2]=Зс.
Кроме того, было установлено, что в разбавленных растворах
сильных электролитов между коэффициентом активности элек­
трол ита и ионной силой раствора существует соотношение:
lgYep= -Az+z-Vl,
(3.17)
,
e2N A
/ Site2NA ,
гдеЛ = 4,6ДГ61000у ioooifc^ k ~ константаБольцмана;NA-
число Авогадро; 8 — диэлектрическая постоянная; е — зар яд
электрона; z — заряд иона. Для водных растворов при 298 К
А = 0,5085 ~ 0, 5, и выражение (3.17) приобретает вид:
lgYep = -0, bz+z-\fl.
Из последнего соотношения следует, что электролиты с одина­
ковым произведением
(одинаковый тип электролита) обла­
даю т одним и тем же коэффициентом активности при одинако­
вой ионной силе раствора. Следует отметить, что приведенные
выше соотношения были получены до создания теории сильных
электролитов П. Дебаем и Э.Хюккелем.
3.9. ТЕОРИЯ СИЛЬНЫХ ЭЛЕКТРОЛИТОВ
ДЕБАЯ —ХЮККЕЛЯ
Теория для разбавленных растворов сильных электролитов
была создана П. Дебаем и Э.Хюккелем в 1923 г. Электростати­
ческая теория электролитов основана на представлении о пол­
ной диссоциации сильных электролитов. При этом между иона­
ми существуют силы притяжения (для ионов с разноименным
337

а
@б
зарядом) и силы отталкива­
ния (для одноименных ионов),
определяемые законом Кулона.
Последнее приводит к тому, что
ионы располагаются такж е упо­
рядоченно, как в кристалличе-
Рис. 3.5. Модель строения раство- сксш решетке. Вокруг иона, вы-
ров сильных электролитов Дебая бранного в качестве централь-
и Хюккеля (пояснение в тексте) но го, располагаются в качестве
тивоположного заряда. Однако такое расположение в значитель­
ной мере нарушается тепловым движением ионов. Поэтому во­
круг центрального иона образуется ионная атмосфера сфериче­
ской формы, содержащая предпочтительно ионы противополож­
ного знака по отношению к центральному иону. Такая модель
имеет статистическую природу (рис. 3.5, а). Выбор центрально­
го иона является условным, т. е. каждый ион можно рассматри­
вать в качестве центрального и входящего в то же время в состав
ионной атмосферы других ионов. При выводе основных уравне­
ний П. Дебай и Э.Хюккель сделали следующие допущения:
1) взаимодействие между ионами было заменено более про­
стым взаимодействием иона с ионной атмосферой;
2) дискретные заряды ионов внутри ионных атмосфер были
заменены непрерывным полем; плотность заряда в каждом эле­
менте объема поля пропорциональна избыточной концентрации
ионов противоположного зн ака по отношению к центральному
иону;
3) предполагается, что центральный ион представляет собой
точечный заряд.
Локальная концентрация ионов в ионной атмосфере опреде­
ляется уравнением Больцмана:
где Ci —средняя концентрация г-х ионов в объеме раствора; Е —
потенциальная энергия г-го электрона в данной точке ионной
атмосферы; Zi — валентность иона; е — заряд электрона; Ф —
электростатический потенциал в данной точке ионной атмосфе­
ры; к — константа Больцмана; Т — абсолютная температура.
Дл я разбавленных растворов можно допустить, что энергия
теплового движения превышает потенциальную энергию ионов,
т. е. квТ
Z{eФ. Тогда экспоненциальный множитель уравнения
(3.18) можно разложить в ряд, ограничившись первыми двумя
членами:
ближайших соседей ионы про-
_
Е
ci=секг=се
(3.18)
338

Ci-C
I квТ)
Дл я ионов с противоположным зарядом по отношению к заряду
центрального иона множитель (1 --——-) > 1. В первом случае за-
квТ
ряд имеет знак «-», а во втором —знак заряда «+» такой же, как
у центрального иона. Локальная плотность заряда в данной точ­
ке ионной атмосферы при учете знака за р яд а ионов будет равна:
Р=“
С-г-еЫд
1000
e4NA
‘ ЮООЛвТ
2Г_еФ\ c+z+eNA
квТ )
1000
2е2ФN a
V квт]
(3.19)
(c+Z+ + C-Z3)= -
Ж0квТЛ
где I — ионная сила раствора, выражение дл я которой было по­
лучено ранее (уравнение 3.16). Множитель 1000 в знаменателе
означает, что расчет плотности заряда ведется на 1 см3 раство­
ра, а концентрация с измеряется количеством вещества в 1 л
раствора.
Из раздела электростатики курса физики следует, что потен­
циал связан с плотностью заряда и диэлектрической постоянной
е уравнением Пуассона:
2т 47Ф
У2*=-—
.
где у — оператор Лапласа, являющийся сокращенной формой
записи:
(3.20)
у2Ф=
д2Ф д2Ф дЧ
+
дх2 ду2 dz2 ’
т. е. V 2^ является суммой вторых частных производных потен­
циала по декартовым координатам в данной точке пространства.
Комбинируя уравнения (3.20) и (3.19), получим:
v2*=[
( 8ne2NAI \
Ф.
\1000&бТ£)
Выражение для квадратного корня обратной величины множи-
1000кв Т£
теля grc 2 j\j i имеет размерность длины, которая отождествля­
ется с радиусом ионной атмосферы, как видно на рис. 3.5, б.
1
X
Ж0квТе
&ne2N AI '
(3.21)
Оценка радиуса ионной атмосферы по уравнению (3.21) показы­
вает, что он может меняться в зависимости от / , Т и 8 от десятых
339

Рис. З.б. Коэффициент активности в разбавленных растворах ряда
1,1-валентных электролитов. Пунктир —расчет по Дебаю и Хюккелю
долей до нескольких нанометров (1СГ9м). Величина среднего ко­
эффициента активности по теории Дебая —Хюккеля выражает­
ся уравнением (3.17).
Теория правильно передает зависимость коэффициентов ак­
тивности в разбавленных растворах (с < 0,01 моль/л) от ва­
лентного типа электролита и температуры. Однако с увеличе­
нием концентрации расхождение между теорией и опытом ста­
новится существенным (рис. 3.6), что связано со следующими
причинами.
1. Уравнение Пуассона, лежащее в основе теории Дебая —
Хюккеля, предполагает, что за р я д ионов в ионной атмосфере
размазан (т. е. не является дискретным). Последнее справедли­
во только д л я разбавленных растворов, когда размером ионов
можно пренебречь.
2. Применение уравнения Больцмана с условием, что к вТ >
ze Ф допустима только д ля разбавленных растворов.
3. Теория не учитывает уменьшение диэлектрической прони­
цаемости раствора по сравнению с чистым растворителем. На
самом деле диполи растворителя ориентируются по полю, созда­
ваемому ионами (эффект диэлектрического насыщения). В раз­
бавленных растворах нарушение структуры растворителя иона­
ми невелико и этой долей растворителя можно пренебречь.
С целью расширения области выполнения теории Дебая —
Хюккеля вводится поправка — вместо % записывается выраже­
ние
X
1+а%'
где а — диаметр иона:
340

(3.22)
.
A sfl
Y±1
rf
1+axvl
Выражение (3.22) дл я 1,1-валентного электрона расширяет гра­
ницу применения теории до концентраций 0,1 —0,5 моль/л. В бо-
лее концентрированных растворах следует принять во внимание
взаимодействие ионов с молекулами растворителя и возможное
комплексообразование, приводящее к объединению ионов с обра­
зованием ионных пар, тройников и т.д . Э .Хюккель предложил
ввести дополнительное слагаемое:
А\П
!gY± =
+BI'
(3-23)
1+a%VI
где В — эмпирический коэффициент, зависящий от природы
электролита и растворителя.
Используя уравнение (3.23) можно объяснить сложную зави­
симость растворимости малорастворимого электролита под дей­
ствием другого электролита, не имеющего общего с ним иона.
Д л я упрощения рассмотрим электролит, образованный 1,1-ва­
лентными ионами.
КА(тв) ^К ++А"
Дл я насыщенного раствора можно выразить константу равновесия:
к,
_
ак ад
акА
Поскольку акА — величина постоянная, обозначим К'а
=К,
где К — произведение активностей ионов малорастворимого элек­
тролита.
К = акад = cYkcaYa-
Принимая во внимание, что согласно теории Дебая —Хюккеля
Yk = Ya = Y>а ск = ад = 5, где S —растворимость вещества,
получим:
00
K =S2Y2.
Прологарифмируем выражение (3.24) и подставим Igy из (3.23).
В результате получим:
lgS =
InК AVI
2 1+axVI
(3.25)
В разбавленных растворах величиной о%\/7 -С 1 можно прене­
бречь. Кроме того, A \ / I 3> B I и выражение (3.25) приобретает
вид:
341

\gS=l^£ - +Ay/i.
Таким образом, растворимость малорастворимого вещества
в разбавленных растворах возрастает с ростом ионной силы.
Однако при более высоких концентрациях, когда I > 0, 5 . . Л ,
вторым слагаемым можно пренебречь по сравнению с третьим
в уравнении (3.25), и растворимость будет уменьшаться с ро­
стом ионной силы раствора. Т ак ая зависимость показана на
рис. 3.7.
Рост растворимости малорастворимого соединения с ро­
стом ионной силы раствора называется эффектом всалива-
ния. Уменьшение растворимости малорастворимого соеди­
нения с ростом ионной силы раствора называется эффектом
высаливания.
Эффекты всаливания и высаливания наблюдаются также для
аминокислот, которые в водных растворах являются биполяр­
ными ионами +НзМ—R —СОСГ. Зависимость растворимости ряда
белков, которые, как известно, построены из аминокислот, пред­
ставлена на рис. 3.8. Видно,что, варьируя ионную силу раствора
сульфата аммония, можно разделить смесь белков и выделить
каждый белок по отдельности методом высаливания.
Рис. 3.7. Эффекты высаливания
и всаливания на примере гемогло­
бина в зависимости от ионной си­
лы раствора:
1 - NaCl; 2 - KCL; 3 - (NH4)2S04;
4 —Na2S04
Рис. 3.8. Растворимость белков в
зависимости от ионной силы рас­
твора:
1 — фибриноген; 2 — гемоглобин;
3 — псевдоглобин; 4 ~ сывороточ­
ный альбумин; 5 —миоглобин
342

3.10. АССОЦИАЦИЯ ИОНОВ
Теория сильных электролитов Дебая —Хюккеля постулирует,
что сильные электролиты в растворе полностью диссоциирова­
ны. Однако ряд экспериментальных фактов свидетельствуют о
том, что ионы в растворах таких электролитов образуют ионные
пары з а счет электростатического взаимодействия:
К++ А~ = К+А~
к
_
г а-]
асс [К+][А-]'
Константу равновесия этой реакции называют константой ассо­
циации. С ростом концентрации электролита число ионных пар
увеличивается. При образовании ионных пар возможно разру­
шение сольватной оболочки ионов, и ионы могут непосредствен­
но притягиваться друг к другу.
Ассоциация зависит от размера и заряда ионов (табл. 3.6).
С ростом заряда ионов число ассоциатов заметно возрастает.
Дл я симметричных электролитов ионные пары электрически
нейтральны и не участвуют в процессе переноса электричества
при электролизе. Существует некоторая критическая концен­
трация электролита (скр), для которой энергия взаимодействия
притяжения между ионами в ионной паре равна энергии теп­
лового движения. При концентрации электролита большей, чем
скр, идет преимущественно образование ионных пар, а при кон­
центрации меньшей, чем с, идет в большей степени распад ион­
ных пар.
Следует отметить, что образование ионных пар и тройни­
ков типа (К+А“К+) или (А~К+А~) и более сложных ассоциатов
увеличивается с уменьшением диэлектрической проницаемости
растворителя (табл. 3.7). В растворителях с низкой диэлектри­
ческой проницаемостью электролит в основном присутствует в
форме ассоциатов даже при небольших концентрациях, и ни од­
но вещество не обладает свойствами сильного электролита.
Таблица 3.6
Логарифм константы ассоциации lg К &сс для некоторых пар ионов
при 25 *С
Ионы
Li+
Na+
тг
Са2+
Fe3+
ОН’
- 0,08
-0,7
0,8
1,30
12,0
F"
—
—
0,4
1,0
6,04
sol~
0,6
0,7
1,4
2,28
—
343

Таблица 3.7
Кинетика ассоциации дл я NaBrC>3 в смесях «диоксан —вода»
в зависимости от величины диэлектрической проницаемости
Содержание
диоксана, %
е
Късс
Содержание
диоксана, %
Е -Касс
0
78,48 0,50
35
48,91 2,10
10
70,33 0 ,68
40
44,54 2,73
20
61,86 0 ,90
50
35,85 6,87
30
53,28 1,33
55
31,53 11,8
3.11. ЭЛЕКТРОПРОВОДНОСТЬ РАСТВОРОВ
Ионы в растворе движутся хаотично, подчиняясь законам
броуновского движения. При наложении электрического поля в
растворе электролита движение ионов упорядочивается, и на­
правление их движения совпадает с направлением электриче­
ского поля. Катионы движ утся к катоду, который соединяется
с отрицательным полюсом источника тока, а анионы — к аноду,
соединенному с положительным полюсом источника тока. Как и
для проводников первого рода (металлы) растворы электролита
(проводники второго рода) подчиня­
ются закону Ома: сила то ка i связана
с напряженностью электрического
поля Е следующим соотношением:
г=!=ХД
(3.26)
V
гдеЕ-
V — напряжение меж­
ду двумя параллельными электро­
дами, находящимися на расстоянии I
друг от друга; р — удельное сопро­
тивление раствора, т. е. сопротивле­
ние электрическому току, создавае­
мое 1 м3 раствора, который поме­
щен между электродами с площадью
1 м2 каждый. Величина %, обратная
удельному сопротивлению раствора,
называется удельной электропровод­
ностью. Размерность р и % можно
Рис. 3.9. Ячейка для изме­
рения электропроводности
344

определить из выражения для
сопротивления Д, которое про­
порционально длине проводни­
ка и обратно пропорционально
площади его сечения:
Принимая, что Д = 1 Ом,
I=1м,S =1м2,рвыража­
ется в Ом* м, а следователь­
но, % — Ом-1*м-1 = См • м-1*.
Электропроводность раствора
обычно определяется по его
сопротивлению при прохожде­
нии переменного тока малой
амплитуды через электроли­
тическую ячейку специальной
конструкции, которая показа­
на на рис. 3.9. Постоянный ток для измерений не применяет­
ся, та к как из-за направленной миграции ионов в электрическое
поле возникает различие в концентрации ионов в электролите,
вызывающее их диффузию. Кроме того, у поверхности электро­
дов могут накапливаться продукты электролиза, которые так­
ж е осложняют проведение измерений. Измерение сопротивле­
ния растворов проводится с помощью моста переменного ток а
(мост Уитстона), принципиальная схема которого приводится на
рис. ЗЛО.
От генератора Г (источник напряжения) подается перемен­
ное напряжение достаточно высокой частоты на диагональ мо­
ста АС. В другую диагональ BD включен «нулевой» прибор
(это может быть осциллограф или чувствительный вибрацион­
ный телефон, или гальванометр). При прохождении тока через
точку А ток разветвляется и идет в точки В и Д затем возвра­
щается через точку С к генератору. Изменяя сопротивление Дз,
достигают такого значения сопротивления, когда падение напря­
жения между точками В и D равно нулю, что определяется с
помощью подключенного нулевого прибора. Падение напряже­
ния на участках АВ и AD и соответственно ВС и DC будет
одинаковым, т. е. i\R \ = i%Rx и i\R 2 = ггДз- Ток через диагональ
моста будет равен нулю. Разделив эти уравнения одно на другое,
получим:
По определению, См •м-1
— проводимость проводника, в котором проходит ток
силой 1 А при напряжении на концах проводника 1 В (1 См = Ом-1).
Рис. 3.10. Принципиальная схема
моста для измерения сопротивле­
ния раствора:
Ri и Я2 — постоянные сопротивле­
ния; Дз — переменное сопротивле­
ние; Rx — сопротивление ячейки с
раствором
345

Ri_Rx
i?2 Rs
Зная величины
и /?з, нетрудно рассчитать R Следует
помнить, что форма и положение электродов в ячейке-электро­
лизере д ол ж ны быть во всех измерениях постоянны. Поверх­
ность электродов должна быть большой, что достигается пред­
варительным осаждением на электроды (обычно из платины)
электролитического осадка платины, имеющего развитую по­
верхность. Если расстояние меж ду электродами равно Z, а пло­
щадь поверхности каждого из них £, то удельная электропро­
водность % может быть рассчитана из уравнения:
Rx =l/(xS)ft
(3.27)
где / — ф ак тор , зависящий о т геометрических особенностей
ячейки. Ф ормула (3.27) д л я удобства записывается в виде:
к
Х= р">
-iCx
где к — коэффициент пропорциональности, или константа ячей­
ки. Константа к определяется по электропроводности стандарт­
ного 0,02н КС1 раствора (используются табличные данные) из
уравнения
Л = %Якс1.
Кроме удельной электропроводности используется понятие эк­
вивалентной электропроводности X.
Эквивалентная электропроводность представляет собой
электропроводность р аствора электролита, заключенного
между двумя параллельными электродами, отстоящими
друг от дуга на расстоянии 1 м и имеющими такую площадь,
что объем раствора между электродами равен объему, со­
держ ащ ему 1 моль-экв растворенного вещества (рис. 3.11).
Связь меж ду эквивалентной электропроводностью и удель­
ной электропроводностью для 1,1-валентного электролита дает­
ся формулой:
X
с - 1000*
Поскольку с измеряется в моль-экв/л, а % относится к объе­
му 1 м3, то д л я согласования размерности единиц объема сле­
дует выразить 1 л в м3 . Этим объясняется наличие числово­
го коэффициента в уравнении (3.28). Поэтому эквивалентная
346

электропроводность имеет раз-
м2
9
мерность —---------------- = м^ ■
Ом • моль-экв
См/моль-экв.
Удельная электропроводность
растворов зависит от природы
ионов в растворе и растет с
ростом концентрации раствора,
т. е. с ростом числа ионов в
единице объема раствора. Од­
нако с ростом концентрации
растворенного вещества умень­
ш ается степень диссоциации в
случае слабых электролитов и
растет взаимодействие между
ионами в случае сильных-элек­
тролитов (коэффициент актив­
ности становится меньше), ко­
торое приводит к последующе­
му снижению электропроводно­
сти (рис. 3.12).
Рис. 3.11. Схема, поясняющая
определение эквивалентной элек­
тропроводности:
1,2 —электроды; площадь каждо­
го электрода численно равна объе­
му раствора V, в котором находит­
ся 1 моль-экв растворенного ком­
понента
При уменьшении концентрации раствора удельная электро­
проводность понижается, а эквивалентная электропроводность,
напротив, растет, так к ак возрастает площадь электродов и
увеличивается объем раствора,
содержащего моль-эквивалент
вещества, и X стремится к
предельной величине Xqq при
бесконечном разбавлении, как
видно на рис. 3.13. Д л я слабых
электролитов степень диссоци­
ации а связана с X следующим
соотношением:
Х = аХоо.
(3.29)
При постоянной темпера­
туре раствора и постоянной
напряженности электрическо­
го поля ионы движутся с по­
стоянной скоростью, т а к как
на частицы действуют уравно­
вешенные силы — движущие
силы, вызванные внешним по­
лем, и силы торможения. При
О
5
10
15
С, моль/л
Рис. 3.12. Удельная электропро­
водность
347

движении ионы испытывают
тормозящее действие окружаю­
щей среды, которую можно вы­
разить с помощью закона Сток­
са. Предполагается, если гидра­
тированный ион имеет форму
шара радиусом г, сила тормо­
жения равна:
Рис.
/торм ~ 67СТ|TV,
(3.30)
3.13. Эквивалентная элек­
тропроводность
где Г| — вязкость среды (раствора); v — скорость движения ча­
стицы. Д вижущ ая сила определяется напряженностью поля Е и
зарядом иона ze:
Eze = бкцгу.
(3.31)
После преобразования получим:
(3.32)
Е 67ГГ| г
к
V
Величина — представляет собой скорость движ ения иона во
Е
внешнем поле с напряженностью 1 В/м и называется абсолют­
ной скоростью (подвижностью) иона. Как следует из уравне­
ния (3.32), скорость движения иона зависит от его заряда, ради­
уса и вязкости среды. Введем обозначения: абсолютная подвиж­
ность катионов £/+, а анионов LL. Тогда скорость их движения
в электрическом поле с напряженностью Е будет соответствен­
но равна U+E и U-E , м/с. Установим связь между эквивалент­
ной электропроводностью и подвижностью ионов. С этой целью
предположим, что ионы бинарного электролита движ утся в ци­
линдрической трубе с поперечным сечением 1 м2 (рис. 3 .14).Чис­
ло катионов, пересекающих поперечное сечение трубы в единицу
времени, равно их количеству, находящемуся в объеме цилиндра
с поперечным сечением 1 м2 и длиной, численно равной скорости
движения ионов. Объем цилиндра для катионов будет U+E, м3, а
д л я анионов СЛ-Е, м3 (см.
рис. 3.14). Предполагая, что
молекула растворенного веще­
ства (или структурная едини­
ца, если между катионами и
анионами существует ионная
связь) диссоциирует на v+ ка­
тионов и v_ анионов, то в
1 м3 раствора будет содер­
жаться lOOOacv +Na катионов и
к+-
ии
U+E
UJE
Рис. 3.14. Модель для расчета пе­
реноса электричества ионами в
растворе
348

1000occv_./Va анионов. В объеме U+E) м3, число катионов будет
составлять WOOclcv+Na U+E, а в объеме U-E число анионов бу­
дет равно IOOOolcV-Na U-Е . Если заряд катиона равен z+y а заряд
аниона z_, то получим количество электричества, переносимое
катионами и анионами через цилиндр сечением 1 м2 в 1 с. Вели­
чина тока будет равна:
г = W00acNAeE(v+z+U+ + v_z_EL).
(3.33)
Так как перенос электричества осуществляется частицами с про­
тивоположными по знаку зарядами, то общее количество элек­
тричества складывается из двух противоположных зарядов, как
следует из уравнения (3.33). Величина е — элементарный элек­
трический заряд. Так как молекула (структурная единица) яв­
л яется электронейтральной частицей, то при диссоциации:
V+z+ = v_z_ = vz.
(3.34)
Величина vz характеризует число моль-эквивалентов в одном
моле вещества. Так, например, для соли ZnCl2 v+ = 1, z+ = 2,
v_ = 2, z_ = 1 и vz = 2. Следовательно, в 1 моле вещества ZnC^
содержится 2 моль-экв. Так как eNA = F (число Фарадея), то
уравнение (3.33) при учете (3.34) принимает вид:
%= 1000аcvzFE(U++ EL).
(3.35)
Комбинируя уравнения (3.26) и (3.35), получим выражение д л я
удельной электропроводности:
X= m0acvzF(U++EL).
(3.36)
Д л я упрощения примем, что рассматривается поведение 1,1-
валентного электролита. Тогда v z = 1, и при комбинировании
уравнений (3.28) и (3.36) получим выражение для эквивалент­
ной электропроводности:
A, = aF(E/+ + EL).
(3.37)
Произведение FU называется эквивалентной электропроводно­
стью (подвижностью) катиона FU+ и аниона FU- .
Поэтому урав­
нение (3.37) примет вид:
А, —a(Lf + A^).
(3.38)
При бесконечном разбавлении раствора a = 1 и уравнение
(3.38) для предельной эквивалентной электропроводности будет
выраж аться следующим образом:
=
+
(3.39)
349

где A/j! и
—
эквивалентные электропроводности или подвиж­
ности катиона и аниона при бесконечном разведении. Подста­
вив уравнение (3.39) в (3.38), получим уравнение (3.29). Урав­
нения (3.38) и (3.39) являются математическим выражением за­
кона Кольрауша, физическая сущность которого заключается в
том, что катионы и анионы электролита переносят электриче­
ский ток независимо друг от друга. Бесконечно разбавленный
раствор фактически является растворителем и его вязкость Т|
равна вязкости растворителя Г|о- С учетом этого уравнение (3.32)
для катиона и аниона будет иметь следующий вид:
z+e
6ТСГ|оГ+ ’
£/_ =
z^e
6ЛТ|оГ_ *
(3.40)
Подставив выражение (3.40) в (3.37) и полагая, что в бесконеч­
но разбавленном растворе l - l ' -валентного электролита а = 1,
получим:
eF
eF
eF(11
---------- b --------
—------
[—ч
----
6ЯГ|оГ+
6ЛГ|оГ_
6ЯГ|о \г+
г_
(3.41)
Если предположить, что г+иг_в первом приближении не за­
висят от природы растворителя, то из уравнения (3.41) следует,
что для разных растворителей
^ооПо ~ const.
(3.42)
Уравнение (3.42) называется правилом Вальдена —Писаржев-
ского. С ростом температуры электропроводность растворов,
как правило, возрастает, так к а к снижается вязкость раство­
рителя и уменьшаются размеры гидратированных катионов и
анионов. В первом приближении электропроводность возраста­
ет, следуя линейной зависимости:
-
^18[1 +
-
18)],
где Xt и Л-is — эквивалентная электропроводность при темпе­
ратурах t и 18° С соответственно. Приведенные выше форму­
лы в основном относятся к слабым электролитам. Теория элек­
тропроводности растворов сильных электролитов бы л а развита
П. Дебаем и Л. Онзагером. В растворах сильных электролитов
при движении иона в электрическом иоле кроме силы трения,
вызываемой вязкой средой, тормозят движение иона электрофо­
ретическая сила Fe и релаксационная сила Fr . Поэтому к урав­
нению (3.31) прибавляются еще д в а слагаемых:
Eze = 6яг|гг;+Fe+Fr.
350

Электрофоретическое торможение иона обусловлено тем, что
при наложении внешнего электрического поля противополож­
но заряженная ионная атмосфера, окружающая ион, движется
в противоположном направлении. При этом ионы ионной атмо­
сферы увлекают с собой частично молекулы растворителя, кото­
рые их сольватируют. В этом случае центральный ион движется
в растворителе, который перемещается вместе с ионной атмо­
сферой в противоположном направлении. Причиной появления
релаксационного торможения (релаксационной силы) является
нарушение симметрии ионного облака, окружающего централь­
ный ион, так как ионы ионной атмосферы движутся в обрат­
ном направлении из-за их противоположного по знаку заряда.
В результате нарушения симметрии центры положительного и
отрицательного заряда не совпадают и между ними возникает
электростатическое взаимодействие притяжения, которое допол­
нительно тормозит движение иона (Fe). Учет этих дополнитель­
ных эффектов П. Дебаем и Л. Онзагером позволил связать экви­
валентную электропроводность с ионной силой. Д л я бинарного
электролита:
А,= Xqq+В\/7,
где Хоо — эквивалентная электропроводность при бесконечном
разведении, когда I = 0, / — ионная сила раствора; В —коэффи­
циент, который может быть рассчитан по теории сильных элек­
тролитов. Однако, соответствие экспериментальной и рассчитан­
ной электропроводности наблюдается в области концентраций,
не превышающих 0,02н. В более концентрированных растворах
д л я соответствия теории и эксперимента вводятся эмпирические
поправки.
При значительном напряжении между электродами появля­
ется новый эффект, который заключается в следующем: при со­
здании электростатических полей с очень высокой напряженно­
стью (миллионы вольт на метр) ион движется настолько быстро,
что вокруг него не успевает образовываться ионная атмосфера.
Эквивалентная электропроводность резко возрастает (эффект
Вина). При наложении электрического поля высокой частоты
(прохождение переменного тока высокой частоты) ион колеб­
лется относительно центра ионной атмосферы с небольшой ам­
плитудой. В этом случае релаксационный эфф ект, связанный с
несимметричностью ионной атмосферы по отношению к иону,
практически не возникает, что также приводит к росту эквива­
лентной электропроводности (эффект Д ебая — Фолькенгагена).
Однако возрастание электропроводности не столь значитель­
но, так как электростатический эффект сохраняется. Как уже
351

Таблица 3.8
Подвижность ионов при бесконечном разведении в водных растворах,
см2/моль-экв, и эффективные радиусы ионов, нм, при 291,1 К
Катион
и?•ю4
7+
Анион
и?•104
Г-
Н+
316,6
0,0253
ОН"
176,6
0,01443
Li+
33,3
0,236
F"
46,7
0,1675
Na+
43,4
0,180
СГ
65,4
0,120
К+
64,4
0,121
Вг"
67,4
0,116
Rb+
67,5
0,116
I"
67,4
0,116
Mg2+
45,5
0,1725
NO;
61,7
0,127
Са2+
51,3
0,153
sol
68
0,115
отмечалось выше, электропроводность растворов зависит от при­
роды ионов. К ак видно из табл. 3.8, анионы более подвижны по
сравнению с катионами. Последнее связано с более низкой вели­
чиной эффективного радиуса д л я анионов в растворе по Стоксу
(уравнение (3.30)). Подвижность значительно больше д л я ионов
Н+ и ОН". Аномальное поведение этих ионов объясняется их осо­
бым (эстафетным) механизмом движения.
В водных растворах ион водорода находится в виде гидрати­
рованного иона гидроксония Н зО+ к ориентированной соответ­
ствующим образом ближайшей молекуле воды:
Гни
1
н
Нч
л1
V
/
V
/
О—н
+О
-*
О+н—о
[н/
J
н/
4hJ
Аналогично для иона ОН предлагается следующий эстафет­
ный механизм:
Н-0
- Н +[0Н]~
Рис. 3.15. График титрования
сильной кислоты (НС1) сильным
основанием (NaOH)
•[онр+н-о -н
Так как атом водорода связан
в молекуле воды более проч­
но, чем в ионе [НэО]+, то по­
движность [ОН]- иона оказы­
вается несколько ниже. Сле­
дует отметить, что приведен­
ная схема не отражает величи­
ны валентных углов в молеку­
ле воды и иона гидроксония.
Известно, что валентный угол
НОН в ионе [Н30 ]+ равен 118°,
352

тогда как в молекуле воды он равен 104,5°. Значительно боль­
ш ая подвижность дл я ионов Н+ и ОН” по сравнению с другими
ионами используется при кислотно-основном титровании. О хо­
де титрования судят по изменению электропроводности раство­
ра (кондуктометрическое титрование). В точке, отвечающей эк­
вивалентности V3KB раствор приобретает минимальную электро­
проводность, так как суммарная концентрация ионов [Н30 ]+ и
ОН” будет наименьшей (рис. 3.15).
3.12 . ЧИСЛА ПЕРЕНОСА
При прохождении электрического тока через раствор элек­
тролита на катоде и на аноде соответственно протекают процес­
сы восстановления и окисления. В противном случае, если пре­
вращение веществ (ионов) на электродах не происходит, то при
наложении постоянного напряжения между электродами ток
быстро падает до нуля. В начальный момент времени катионы
движ утся к катоду, и в катодном пространстве появляется неко­
торый избыток катионов, а в анодном — избыток анионов. Эти
частицы создают электрическое поле противоположной направ­
ленности, компенсирующее действие внешнего электрического
поля. Поэтому необходимым условием прохождения тока через
раствор или расплав электролита является протекание электро­
химических реакций на катоде и аноде, т. е. при прохождении то­
ка происходит электролиз раствора или расплава. Законы элек­
тр о л иза были сформулированы М. Фарадеем. Объединенный за­
кон М. Фарадея может быть выражен следующим образом:
_
mF
mF
Q= ——
или It=
МЭ1
(3.43)
где Q — количество электричества, протекающего через элек­
тролит, Кл, пропорциональное числу химических эквивалентов
вещества (иона), которое подверглось электролизу.
Количество электричества, которое затрачивается на
электролиз 1 моль-экв вещества, называется числом Фара­
дея.
Число Фарадея равно F = 96485 Кл/моль-экв. При прохож­
дении через раствор электролита тока I доли тока, переносимого
катионами и анионами, называются числами переноса:
U
I-
7’
12 Иплолитои
353

При этом I =i++L*.
Используя связь подвижностей ионов U+ и [/_ с величиной
тока (уравнение (3.33)), получим:
t
v+z+U+
t
V-zJJ-
+ V+Z+U++V-Z -U -'
~
v+z+U++V-z -U -'
Выражение д л я чисел переноса упрощается, если учесть соотно­
шение (3.34):
ц.
=
К
и-
=
I
+C/++CL^+
"
[/++[/_ А*+^ ’
Таким образом, числа переноса зависят от подвижности ионов, и
доля тока, в котором участвуют ионы определенного вида, зави­
сит от их подвижности. Следует отметить, что перенос электри­
чества осуществляется всеми ионами, находящимися в растворе,
а не только теми, которые участвуют в электрохимических реак­
циях на электродах. Часто основными переносчиками являются
одни частицы, а участвуют в реакциях на электродах другие.
Так, при электролизе нейтрального раствора Na2S04 на элек­
тродах разряжаю тся молекулы воды. Концентрация ионов Н+ и
ОН“ , получающихся при диссоциации молекул воды, настолько
мала, что их участием в переносе электричества в электролите
можно пренебречь.
Рассмотрим один из методов определения чисел переноса —
метод Гитторфа. Согласно методу Гитторфа числа переноса опре­
деляют по изменению концентрации раствора у поверхности элек­
тродов. Главным условием применения этого метода является
отсутствие побочных процессов на электродах.
Пусть электролизер разделен двумя пористыми перегородка­
ми (рис. 3.16). До начала прохождения постоянного то к а через
раствор концентрация электролита одинакова во всем объеме
электролизера. Предположим, что через раствор прошел один
*Молярная масса эквивалента вещества для окислительно-восстановительной
реакции зависит от числа электронов, принимающих участие в реакции восста­
новления на катоде или окисления на аноде. Например, при восстановлении на
катоде ионов Си2+ + 2е~
—
►Си, Л/экн =
? где п _ число электронов, присоеди­
нившихся к катиону. Следует помнить, что поскольку сила тока на катоде равна
силе тока на аноде, то число электронов п для катодной и анодной реакции долж­
но быть равно. При электролизе водного раствора Na2S04 на катоде идет процесс:
2Н20+2е-
—
>Н2+ 2 0 Н", а на аноде из инертного материала: Н2 0- 2е“ —►^С>2+2Н+.
Суммарная реакция электролиза молекул воды: Н2О —►Нг + ^ 0 2 . Молярная масса
для эквивалента Н2О будет равна:
МцQ
ЧквН20 = 22
= 9 г/моль-экв.
354

I
II
III
Рис. 3 .16. Электролизер для определения чисел переноса по методу
Гитторфа:
I — катодное пространство; II — средняя часть; III — ан одн ое пространство
фарадей электричества, и на электродах выделились по 1 моль-
экв продуктов электролиза. Время прохождения тока должно
быть таким, чтобы в средней части II электролизера концен­
трация электролита осталась неизменной. В катодном простран­
стве I 1 моль-экв катионов выделился на катоде, t+ катионов
поступило из отделения II. Убыль концентрации в отделении I
равна: 1 —t+ = £_ моль-экв. Уменьшение концентрации анионов
в пространстве I равно
Следовательно, в отделении I умень­
шилась концентрация вещества на £_, моль-экв. В анодном про­
странстве III 1 моль-экв анионов разрядился;
моль-экв анио­
нов поступило из отделения II. Убыль концентрации анионов в
отделении III равна 1 —t -
—t+ моль-экв. Уменьшение концентра­
ции катионов, перешедших из отделения III в отделение II, равно
t+ моль-экв. Следовательно, в отделении III концентрация веще­
ства уменьшилась на t+ моль-экв. В отделении II концентрация
катионов и анионов не изменилась, так как £+, моль-экв, катио­
нов из отделения II перешло в отделение I, и такое же количество
моль-экв катионов поступило в отделение II из отделения III.
К такому же выводу можно прийти относительно концентрации
анионов отделения II. Следовательно, концентрация вещества не
изменилась в отделении II, уменьшилась на
моль-экв, в ка­
тодном и на t+, моль-экв, в анодном пространствах. Можно та к ­
же заметить, что несмотря на различие в скоростях движения
катионов и анионов в отделениях электролизера не происходит
нарушения электронейтральности раствора. В общем виде связь
чисел переноса ионов с изменением концентрации электролита
в катодном (Дек) и анодном (Дед) пространствах определяется
следующим соотношением:
Дек_t-
ДсА U'
355

Принимая во внимание, что t+ + t- = 1, можно определить числа
переноса:
t
Аса
t
Аск
Дек+Аса*
Аск + Аса
Итак, аналитическое определение изменения концентрации элек­
тролита в отделениях I и III позволяет рассчитать числа пере­
носа ионов.
До настоящего времени развита теория сильных электроли­
тов только д л я разбавленных растворов. При переходе к более
концентрированным растворам д л я описания свойств растворов
используются поправки эмпирического или полуэмпирического
происхождения. Теория сильных электролитов д л я концентри­
рованных растворов пока не создана, хотя интенсивно ведутся
исследования свойств и строения концентрированных растворов.
При этом используются методы математического моделирова­
ния (модельные представления о структуре раство ра — модели
решеточная, ячеечная, свободного объема и др.) . Р а сче т свойств
растворов на основе предполагаемых моделей и сравнения их
со свойствами реальных растворов позволяют выявить наиболее
подходящие модели. Широко применяются методы молекуляр­
ной динамики и Монте-Карло. С другой стороны, наряду с клас­
сическими методами (измерение осмотического давления, давле­
ния пар а н ад раствором, проведение криоскопических и эбулио-
скопических измерений и т. п.) интенсивно р азвиваю тся различ­
ные спектроскопические методы, позволяющие определять ди­
электрическую проницаемость, оценивать размеры ассоциатов и
их форму, числа сольватации, энергию водородных связей, стро­
ение координационных комплексов «ион —растворитель», опре­
делять расстояние между атомами в сольватах и ионных па­
рах. Исследования проводят в замороженных растворах или ис­
следуют структуру твердых кристаллогидратов, д л я того что­
бы иметь более глубокие представления о процессах, протекаю­
щих в растворах. Так, ядерный магнитный резонанс (частоты
107-1Сг Гц) позволяет изучать ассоциацию ионов, подвижность
ионов, числа сольватации. Электронный спиновой и парамагнит­
ный резонанс (частоты до 1011 Гц) позволяет исследовать во­
дородные связи. ЯМР -спектроскопия обычно применяется при
исследовании растворов с низкой температурой, т. е. в условиях
снижения характерных частот релаксации молекул растворите­
ля. Кроме того, необходимо создать условия, препятствующие
обмену атомами с изучаемыми ядрами. Например, протонный
ядерный резонанс изучается преимущественно в органических
растворителях. Ядерный магнитный резонанс в твердых телах
356

менее информативен из-за диполь-дипольного взаимодействия,
приводящего к уширению резонансного поглощения. Д л я при­
менения метода ЯМР яд р а атомов изучаемых ионов и молекул
должны обладать некоторым магнитным моментом. Частоты,
используемые в ЯМР-спектроскопии, позволяют изучать неко­
торые усредненные состояния частиц, так как частоты недоста­
точно велики. Широко применяются методы оптической коле­
бательной спектроскопии — инфракрасная (ИК) и рамановская
(К Р), которые позволяют изучать изменения дипольных момен­
тов в результате колебания частиц, изменение поляризуемости
молекул, ионов. Методы оптической колебательной спектроско­
пии позволяют фиксировать состояние частиц в реальном вре­
мени их жизни благодаря более высоким частотам излучения
(1013- 1 0 14 Гц). С помощью рамановской спектроскопии изучают
колебания в молекулах сольватных оболочек. В последнее вре­
мя д л я изучения свойств растворов и ассоциатов применяются
спектроскопические методы, позволяющие одновременно комби­
нировать излучения высокой и низкой частоты.
3.13. ПРЕДСТАВЛЕНИЯ О МЕЖФАЗНОМ СКАЧКЕ
ПОТЕНЦИАЛОВ
При контакте двух ф а з на границе между ними возникает
разность потенциалов, которая появляется в результате частич­
ного перехода заряженных частиц (электронов, ионов) через гра­
ницу раздела или адсорбции дипольных молекул или ионов на
границе фаз. Упорядоченное распределение положительных и
отрицательных зарядов вдоль границы контактирующих ф аз не
нарушает электронейтральности всей системы в целом. Однако
одна из фаз может содержать избыток положительных или от­
рицательных зарядов, а в другой фазе соответственно имеется
избыток зарядов противоположного знака. З ар яд ы сосредотачи­
ваются в приповерхностных слоях ф аз или в случае адсорбции
дипольных молекул, например на границе «жидкость —воздух»,
молекулы растворителя ориентируются определенным образом,
так что к поверхности раздела они оказываются обращенными
определенными концами диполей (рис. 3.17, а).
На границе металла с вакуумом такж е возникает двойной
электрический слой. Электронный газ, окружающий ионный
остов кристаллической решетки металла, выходит на небольшое
расстояние из металла (электронный хвост) и на границе «ме­
талл-вакуум» происходит разделение заряда и возникает ска-
357

чок потенциала (рис. 3.17, б). При контакте металла с раствором
его соли в зависимости от концентрации раствора поверхность
металла может заряжаться или отрицательно, или положитель­
но в зависимости от того, какой процесс шел с большей скоро­
стью на границе «металл—раствор» до установления равнове­
сия: ионизация металла, т. е. переход катионов металла в рас­
твор с накоплением в поверхностном слое металла электронов и
приобретением поверхностью отрицательного заряда:
Me ►Me + 77,б(поверХНОСТЬ)
или разряд катионов металла, который уменьшает отрицатель­
ный заряд поверхности и может даж е сообщить ей положитель­
ный заряд:
Men+ + пе —>Me
Через некоторое время устанавливается электрохимическое рав­
новесие, при котором скорости прямого и обратного процесса бу­
дут равны (рис. 3.17, в). Если система состоит из двух жидких
фаз, разделенных полупроницаемой мембраной, т. е. проницае­
мой для одного вида ионов и непроницаемой дл я другого вида.
Воздух
+++++++++++
Раствор
а
Й
S
+
+
+
+
+
+
+
б
+
+
+
+
+
+
+
в
Раствор
КС1
Мембрана
си
о
А<
г
Рис. 3.17. Примеры возникновения скачков потенциалов на границе
двух фаз:
а — «воздух —раствор»; б — «металл— вакуум»; в — «металл —раствор»;
г —мембранный потенциал
358

Например, с одной стороны мембраны имеется раствор КС1, а с
другой — раствор соли с большими по размеру катионами, на­
пример (C4Hg)4N+, и теми же анионами (RC1). Часть катионов
К+ перейдет из первого раствора во второй через мембрану. Вто­
рой раствор, содержащий катионы тетрабутиламмония, получит
положительный заряд, а раствор с противоположной стороны
мембраны будет иметь эквивалентный зар яд противоположно­
го зн ак а (рис. 3.18, г). Можно привести другие примеры обра­
зования двойного электрического слоя на границе фаз. Многие
из них будут рассмотрены в дальнейшем более подробно. Таким
образом, на границе контактирующих ф а з возникает двойной
электрический слой, который можно уподобить положительной
и отрицательной обкладкам конденсатора. Из изложенного сле­
дует, что механизм образования двойного электрического слоя
может быть различным.
3.14 . ТЕРМОДИНАМИКА ЭЛЕКТРОХИМИЧЕСКИХ
СИСТЕМ
Электродом называется электрохимическая система, со­
стоящая, по меньшей мере, из двух ф аз, одна из которых
является проводником первого рода (металл, полупровод­
ники), а другая — второго рода (раствор, расплав, твердый
электролит).
Такую систему называют также полуэлементом. Если два элек­
трода имеют общий электролит или их электролиты контак­
тирую т друг с другом, то образуется гальванический элемент
(электролитическая ячейка). Можно измерить напряжение, воз­
никающее между электродами. Следует отметить, что д л я пра­
вильного измерения напряжения необходимо, чтобы конечные
металлические ф азы были одинаковы, т. е. состояли из одного
металла. Такая цепь называется правильно разомкнутой цепью
(рис. 3.18). При практических измерениях напряжения между
электродами гальванического элемента одинаковый состав ме­
таллических проводников достигается автоматически, так как
клеммы измерительного прибора всегда сделаны из одинаково­
го металла или сплава (медь, латунь, и т. п.).
При отсутствии тока в цепи гальванического элемента
измеряемое напряжение между электродами носит название
«электродвижущая сила» (ЭДС).
359

Раствор
электролита
тжщж
Электролит
ц*WWM
ш
А1
А11
Дер1*
раствор Аф раствор
1---------------------
Рис. 3.18. Схема простейшей электрохимической ячейки и распределе­
ние уровня потенциалов в ней
На рис. 3.18 видно, что измеряемое напряжение складывает­
ся, по крайней мере, из трех межфазных скачков потенциала.
В ячейке используется д л я обоих электродов один электролит.
Абсолютная величина межфазного скачка потенциала
назы вается гальвани-потенциалом.
Гальвани-потенциал измерить нельзя и его невозможно рассчи­
тать с достаточной достоверностью. Контактная разность по­
тенциалов между двумя разнородными металлами определяет­
ся различием в потенциальной энергии электронов в этих ме­
таллах. При установлении равновесия между электронами двух
контактирующих металлов гальвани-потенциал определяется как
разность химических потенциалов электрона в обеих ф азах. Од­
нако химический потенциал электрона измерить нельзя. Д ля то­
го чтобы понять природу гальвани-потенциала, введем, следуя
Е. Гуггенгейму, понятие электрохимического потенциала:
£г = Ш+ Zieф,
(3.44)
где щ — химический потенциал г-го компонента;
—
заряд
частицы; ф — электрохимический потенциал фазы.
360

Электрохимический потенциал — это работа переноса
электрически заряженной частицы из бесконечно удален­
ной точки в вакууме с потенциалом, равным 0, в данную
фазу.
При перенесении 1 моля г-го компонента выражение (3.44)
приобретает вид:
й = Щ+ 2*в#Аф=Ц*+ 2{^ф,
(3.45)
где величины Д; и р* — электрохимический и химический потен­
циалы, относящиеся к 1 молю г-го компонента. При установле­
нии электронного равновесия на границе двух металлов:
Д* = Д*1 или Pg+ zFiр1= Pg1+ zF(pu ,
(3.46)
где (p1 и срп — внутренние потенциалы I и II металлов. Так как z
электрона равен -1 , то выражение (3.46) может быть представ­
лено:
„п
,л
где A(p|j — гальвани-потенциал на границе Мец — Мej. Так как
в цепи три скачка гальвани-потенциала (см. рис. 3.18), то ЭДС
цепи будет равна:
Е = Дф!1+ A(pPacTB+ Дф[>аств.
Если включить между металлическими проводниками I и
II третий металлический проводник Мець то согласно закону
Вольта разность потенциалов Е на концах цепи не изменится.
В самом деле, поместив в правой части цепи между металла­
ми II и I металл III при установлении равновесия на границах,
будем иметь:
Й=Де1, ЙП=Д".
т-е- Ае=Д"
(3-47)
При сравнении равенств (3.47) и (3.46) видно, что суммарный
гальвани-потенциал д л я цепи из трех металлов останется таким
же, как и для двух металлов Mr и Мц. Если предположить, что
в гальваническом элементе протекает ток бесконечно малой ве­
личины, то равновесия, установившиеся на границах ф аз, не на­
рушаются. Величина джоулева тепла, выделяющегося при про­
хождении тока по проводникам, равна нулю. Можно сказать, что
в электрохимической системе при Т = const термодинамически
обратимо протекает окислительно-восстановительный процесс:
ViА\ + v2А2+ ... ViAi ViА!х+V2A'2 + • • • + у[А[ (3.48)
361

где V{ — стехиометрические коэффициенты; Ai — вещества. При
протекании процесса восстановитель отдает, а окислитель при­
нимает 2 электронов. Приведенное уравнение является обобщен­
ным дл я электрохимических реакций, протекающих на границах
«электрод —раствор». Гальванический элемент вы полняет рабо­
ту, равную изменению энергии Гиббса, взятой с обратным зна­
ком:
^ т« = -ДС =ЛГ(1пЛГ-5^1п^*),
(3.49)
где К — константа равновесия; а* — активность г-го компонента.
Напомним, что второе слагаемое уравнения (3.49) явл яе тся сум­
мой натуральных логарифмов активностей продуктов реакции
за вычетом суммы логарифмов активностей исходных веществ
с учетом стехиометрических коэффициентов v*. Д л я обратимо­
го процесса электрическая работа переноса заряда z e N \ в цепи
гальванического элемента с ЭДС, имеющей значение Е , будет
равна работе химической реакции:
Amiix= -AG =zFE.
(3.50)
Подставив уравнение (3.50) в уравнение (3.49) получим:
Г>гр
Е=— (1пК-^^).
(3.51)
Применительно к разбавленным растворам активность компо­
нентов реакции можно заменить на концентрацию:
Т>гр
Е= -(1пК-^^П
(3-52)
Из уравнений (3.51) и (3.52) следует, что, зная концентрации (ак­
тивность) компонентов реакции и измерив ЭДС гальванического
элемента, можно рассчитать константу равновесия К . Проведем
сравнение уравнения (3.50) с уравнением Гиббса—Гельмгольца,
которое было рассмотрено ранее:
Amtx=-£iG=-AH-T ^^j .
(3.53)
Для этого продифференцируем уравнение (3.50) по температуре
при постоянном давлении р = const:
дЕ
дТv
(3.54)
362

(3.55)
Комбинируя уравнения (3.50), (3.53) и (3.54), получим:
zFE= -АН+zFT
дЕ
дТр
Из уравнения (3.55) следует, что электрическая работа будет
равна тепловому эфф е кту реакции в гальваническом элементе,
когда температурный коэффициент ЭДС гальванического эле­
мента будет равен нулю, т. е. когда
элемента в явном виде:
дЕ'
дТ
| = 0. Выразим ЭДС
р
Из уравнения (3.56) следует, что при положительном знаке пер­
вого и второго слагаемых электрическая работа, произведенная
гальваническим элементом, больше теплового эф ф ек та реакции
в гальваническом элементе А Н . Если температурный коэф фи­
циент ЭДС имеет отрицательный знак, то электрическая работа
будет меньше теплового эффекта. При протекании эндотерми­
ческой реакции (А Н > 0) гальванический элемент также может
служ ить источником электрической энергии. Например, в галь­
ваническом элементе, составленном из хлор-серебряного и кало­
мельного электродов*:
(-)Ag,AgCI|HCl|Hg2Cl2,Hg(+)
Протекает реакция
Ag+^Hg2Cl2= AgCl+Hg
Элемент имеет ЭДС 0,0465 В при Т = 298 К и работает за счет
тепла, заимствованного из окружающей среды. Температурный
коэффициент имеет положительное значение 3,39 ■10"4 В/гр ад .
Из уравнения (3.56) можно рассчитать изменение энтальпии при
протекании реакции, т. е. тепловой эфф ект реакции:
АН=(Т§ -E ^zF=(298•3.39•10"4-
- 0 ,0465) •96500 5,3 •103 Дж/моль.
'Устройства этих электродов будут рассмотрены позднее.
363

В рассмотренном гальваническом элементе протекает эндо­
термическая реакция. При работе гальванический элемент бу­
дет охлаждаться. Комбинируя уравнение (3.54) с соотношени­
ем, вытекающим из известного выражения для энергии Гиббса:
(8AG
,
,
-
Д £, можно установить связь между температур-
V^ /Р
ным коэффициентом ЭДС гальванического элемента и измене­
нием энтропии:
Следовательно, температурный коэффициент ЭДС характери­
зует изменение энтропии при протекании реакции.
3.15 . РАВНОВЕСНЫЙ ПОТЕНЦИАЛ
Если металл поместить в раствор его соли, то на границе меж­
ду металлом и раствором начинают протекать процессы окисле­
ния zM —►Мp++ze~ и восстановления Мр++пе“ —►М. При проте­
кании первого процесса поверхность металла заряж ается отри­
цательно, та к как электроны при окислении атома металла и пе­
реходе его в раствор остаются на поверхности металла. Дальней­
ший процесс окисления постепенно начинает затормаживаться,
так как поверхность металла приобретает отрицательный заряд,
и работа отры ва катиона от отрицательно заряженной поверхно­
сти возрастает. Переход иона металла в раствор сопровождается
сольватацией. В то же время процесс восстановления сольвати-
рованного иона М*+ приводит к уменьшению отрицательного за­
ряда или увеличению положительного заряда, поверхности ме­
талла, так как при восстановлении катион забирает электроны
с поверхности металла и осаждается в виде атома на поверх­
ности металла. По мере восстановления катиона металла заряд
поверхности становится более положительным и процесс восста­
новления затормаживается.
Преобладание процесса окисления или восстановления зави­
сит в значительной мере от концентрации катионов металла в
растворе. Если концентрация катионов в растворе большая, то
можно полагать, что вначале после погружения электрода в рас­
твор будет протекать в большей степени процесс восстановле­
ния. Если ж е концентрация соли данного металла в растворе
мала, то в начальный момент погружения металла в раствор
будет преобладать процесс окисления. Через некоторое время
устанавливается динамическое равновесие: М^ -\-ze~
М. Пря­
мой и обратный процессы в приведенном уравнении связаны с
364

переносом заряда через границу «электрод —раствор». Поэтому
скорости процессов выражаются в единицах плотности тока:
I
>0=5 ,
где 1 — сила тока; S — поверхность электрода.
Плотность тока измеряется в А/с м 2. Однако часто она при­
водится в литературе в мА/см2.
Ток, идущий на восстановление (в данном случае на вос­
становление катиона Mz+), называется катодным током (г^),
а ток, идущий на окисление (в данном случае на окисление
атомов М), называется анодным током (га).
При равновесном потенциале:
~
~
“ ^0)
где го — ток обмена. При наличии равновесия масса электрода
не изменяется во времени. Ток обмена зависит от природы эл ек­
трода, концентрации ионов Мг+, температуры и давления (если в
равновесии участвуют газообразные вещества). При установле­
нии равновесия поверхность металла зар яж ается положительно
или отрицательно. В растворе на границе с металлом накаплива­
ется заряд, равный по абсолютной величине зар яду поверхности
металла, но противоположный по знаку, в результате возникает
электрическое поле, которому соответствует определенный ска­
чок электрического потенциала между металлом и раствором.
Скачок потенциала, который возникает при установле­
нии равновесия О х + ze~ ^ Red на границе «электрод —
раствор», называется равновесным потенциалом.
В рассматриваемом случае — это равновесие между ионами М2+
и металлом М. Заряд поверхности металла и, следовательно,
скачок потенциала можно изменять при изменении концентра­
ции ионов металла в растворе. Предположим, что поверхность
металла имеет отрицательный заряд. Если увеличивать кон­
центрацию Mz+, то указанное равновесие нарушится. Ускорится
процесс восстановления, и равновесие, по закону действующих
масс, сместится вправо. При этом часть отрицательного за р яд а
будет нейтрализоваться ионами Mz+, которые будут р а зр яж ать ­
ся и образовывать нейтральные атомы. Можно подобрать такие
концентрации ионов Mz+, что заряд поверхности металла будет
равен нулю.
365

Раствор с концентрацией соли металла, при которой за­
ряд поверхности металла равен нулю, называется нулевым
раствором.
Это название было дано в свое время В. Нернстом. При положи­
тельном заряде поверхности металла нужно уменьшать концен­
трацию ионов в растворе, чтобы уменьшить заряд. Равновесие
М(раств) + z e ~ ^ М будет смещаться по закону действующих
масс в левую сторону, поэтому с большей скоростью пойдет про­
цесс ионизации металла, и заряд поверхности будет уменьшать­
ся. При этом скачок между металлом и раствором та к ж е будет
снижаться.
Абсолютную величину равновесного потенциала н ельзя изме­
рить и нельзя рассчитать, так как он представляет собой меж­
фазный потенциал, т. е. гальвани-потенциал. Поэтому равновес­
ный потенциал измеряется относительно равновесного потенциа­
ла другой окислительно-восстановительной системы. В качестве
такого эл ектрода сравнения в основном используется водород­
ный электрод. Описание водородного электрода более подробно
будет рассмотрено позднее. Однако следует отметить, что водо­
родному электроду соответствует равновесие между ионами Н+ и
молекулярным водородом, которое устанавливается на границе
«металл (пл ати на )—раствор». Платина хорошо адсорбирует во­
дород из раствора, который насыщается молекулярным водоро­
дом, а в качестве раствора используется водный раствор сильной
кислоты (например, НС1). На поверхности платины молекуляр­
ный водород может переходить в атомарный водород и между
ними устанавливается равновесие:
2HfpaCTB.)+2e^2H^H2(Pt)
Платина является инертным электродом и играет роль посред­
ника между молекулярным водородом и ионом водорода, т. е.
платина отдает электроны иону Н+ при его восстановлении и
забирает электроны у атома водорода при его окислении. На
границе между платиной и раствором также образуется двой­
ной электрический слой, как и при рассмотрении равновесия
«металл —ион металла». Д л я правильно разомкнутого элемен­
та, состоящего из металла, погруженного в раствор его соли,
и водородного электрода, ЭДС выражается уравнением (3.52).
Проанализируем его более детально. При активности исходных
и конечных компонентов реакции, равной 1, ЭДС цепи будет
равна:

(3.57)
Уравнение (3.52) будет иметь следующий вид:
КГ\^
v.
Е=Е°~ - рZlInai’’
где все стехиометрические коэффициенты исходных веществ
Vi < 0, а стехиометрические коэффициенты продуктов реакции
Vi > 0. Уравнение (3.57) д л я ЭДС электрохимической цепи на­
зы вается уравнением Нернста. Рассмотрим применение урав­
нения (3.57) к конкретному примеру окислительно-восстанови­
тельной реакции. Составим гальванический элемент из цинко­
вого электрода, помещенного в раствор его соли ZnCl2, и водо­
родного электрода
(-) |Zn | ZnCl2 11НС11 Н2(Pt) (+).
В этом гальваническом элементе самопроизвольно будет проте­
кать реакция
Zn(T) + 2Н(раств.) - Zn(pacTB) + Н2(г)
На цинковом электроде при работе гальванического элемента бу­
дет в основном протекать процесс окисления Z n -2 e —►Z n ^ acTB
а на водородном электроде — процесс восстановления 2Н|раств ^+
+2e^H2(Pt).
Электроны будут перемещаться от цинкового электрода в на­
правлении к водородному электроду (рис. 3.19). Если сила тока
в гальваническом элементе бесконечно мала, то равновесия, су­
ществующие на границе ф аз, в элементе не будут нарушаться.
Тогда дл я химического равновесия в рассматриваемом гальва­
ническом элементе можно выразить константу равновесия:
К'=
(3.58)
Активность конденсированных ф аз, являющихся чистыми ве­
ществами, постоянна, т. е. a z n = const. Это положение справедли­
во д л я молекул растворителей (например, Н20 ) или малораство­
римых веществ (солей, оксидов, гидроксидов). Если выразить
активность молекулярного водорода через парциальное давле­
ние, то уравнение (3.58) приобретает вид:
к _ QZn2^H2
367

Рис. 3.19. Схема гальванического элемента:
1 — цинковый электрод; 2 — водородный электрод; 3 — соединительный
сосуд; 4 — солевой мостик (соединительный сосуд и отвод от водородного
электрода заполнены раствором электролита)
Используя уравнение (3.57), ЭДС гальванического элемента мож­
но выразить следующим образом:
л
_
RT,
а„+
Е=Е0-—Ь^-рН2,
21 a Zn2+
где цифра 2 в коэффициенте второго слагаемого отвечает числу
электронов, принимающих участие в окислительно-восстанови­
тельной реакции. Контактный скачок потенциала между цин­
ком и платиной входит в значение Eq. Д л я упрощения предпо­
лагается, что диффузионный потенциал на границе растворов
ZnCl2 и НС1 отсутствует*. К ак было отмечено раньше, равно­
весный потенциал электрода зависит от концентрации потенци-
алопределяющих ионов. Д л я измерения ЭДС используется стан­
дартный водородный электрод, д л я которого а щ = 1 моль/л,
Рн2 = 1 аTM (101,3 кПа) и температура 298 К. При этих условиях:
Е=Е° - — (2InaH+- Inafn- \прВг)=E°+— InaZn2+. (3.59)
Такое упрощение выражения для ЭДС связано с тем, что In ащ и
1прн2 равны нулю. Иными словами стандартный (нормальный)
равновесный потенциал водородного электрода принимается
Имеются специальные приемы, позволяющие значительно снизить диффузи­
онный потенциал и пренебречь его влиянием на ЭДС гальванического элемента.
Этот вопрос будет рассмотрен позднее.
368

Таблица 3.9
Стандартные электродные потенциалы в водных растворах
при температуре 298 К и давлении 1 атм
Электрод
Полуреакция
£°, В
Li+/L i
Li++ e~
Li
-3,045
К*/К
K++e"£?К
- 2,925
Ва2+/В а
Ba2++2e“ ^ Ba
-2,90
Са27Са
Ca2+ + 2e" i=; Ca
-2,87
Na+/Na
Na++e"
Na
- 2,714
Mg'"/Mg
Mg2* + 2e~
Mg
-2,37
А13+/А 1
Al3++3e' i=iA1
-1,70
Mn2+/M n
Mn2++2e~ £*Mn
- 1,18
Zn2+/Z n
Zn2++ 2e” t=: Zn
- 0,763
Cr3+/C r
Cr3 + 3e“
Cr
-0,74
PbS04/Pb
PbS04+2e"t;Pb+SOf
- 0,356
Fe2+/F e
Fe2++ 2e‘ J=r Fe
- 0,440
Cd2+/C d
Cd2++2e“ =? Cd
- 0,403
Ni2t/Ni
Ni2++ 2e~
Ni
- 0,250
Sn2+/Sn
Sn2++2e~ ^ Sn
-0,136
Pb2t/Pb
Pb2++ 2e~*=?Pb
-0,126
H+/H 2
2H++ 2e_
H2
0,000
Sn4+/S n2+
Sn4+ + It *=? Sn2+
0,15
Cu27Cu+
Cu2++e~U Cu+
0,123
Hg2Cl2/Hg
Hg2Cl2 + 2e-2Hg+2Cr
0,2676
AgCl/Ag
AgCl +e“ U kg+СГ
0,222
Cu27Cu
Cu2+ + 2e~
Cu
0,337
02/0H-
0 2+2H20 +4e'40H-
0,401
h/l
I2+2e“
2Г
0,5355
MnOj/Mn02
Mn04+2H20 +3e“t? Mn02+40H-
0,60
C6H40 2/C6H4(0H )2
хинон/гидрохинон
C6H40 2+2H++2e U C6H4(OH)2
0,699
Fe3+/F e2+
Fe3+ + e~t=i Fe2+
0,771
Ag+/Ag
Ag++ e" *=; Ag
0,799
Hg27Hg
Hg2*+ 2e-t3 Hgr
0,92
СЮ'/СГ
С1СГ+H20 +2e" t;Cr +20H'
0,88
Br2/Br~
Вг2 + 2e“
2Br"
1,065
02/H20
02+4H++4e~ ^ 2H20
1,229
Cr20f/C r3+
Cr20 2- + 14H++6e“ Ш2Cr3++ 7H20
1,33
ch/cr
Cl2+2e‘ £5 2СГ
1,359
Pb02/Pb2*
Pb02+4H++2e‘
Pb2++2H20
1,456
Mn07Mn2+
Mn04+8H++5e”
Mn++ 4H20
1,51
PbO2/PbS04
Pb02+4H++S04‘+2e" £3
1=* PbS04+4H20
1,685
Fa/F-
F2+2e" ^ 2F“
2,87
369

равным нулю. Хотя следует иметь в виду, что истинная абсо­
лютная величина потенциала водородного электрода неизвестна.
Равновесные потенциалы других окислительно-восстановитель­
ных систем приводят в таблицах относительно потенциала во­
дородного электрода. При этом значения равновесных потенци­
алов приводятся в стандартных условиях, т. е. активности ионов,
принимающих участие в равновесии, равны 1, давление 1 атм,
температура 298 К. Некоторые значения стандартных равновес­
ных потенциалов приведены в табл. 3.9.
Электродным потенциалом называется электродвижу­
щая сила гальванического элемента, составленного из двух
электродов, потенциал одного из которых подлежит опреде­
лению, а потенциал другого принимается условно равным
нулю — стандартный или нормальный водородный элек­
трод.
В дальнейшем под понятием «равновесный потенциал» будем
подразумевать равновесный потенциал находящейся в равнове­
сии окислительно-восстановительной полуреакции:
Ох+ze~
Red
Выражение д л я равновесного потенциала в обобщенной форме
будет иметь вид:
3.16. ПРАВИЛА ЗАПИСИ ЭДС И ЭЛЕКТРОДНЫХ
ПОТЕНЦИАЛОВ ЭЛЕКТРОХИМИЧЕСКИХ
СИСТЕМ
Международный союз по чистой и прикладной электрохимии
в 1953 г. д ал рекомендации по записи полуреакций и обозначе­
ний электрохимических систем. Электрохимическая система за­
писывается следующим образом: сначала записывается символ
металла, из которого сделан электрод, затем раствор, находя­
щийся с ним в контакте, далее раствор, который находится в
контакте с другим электродом, и затем символ металла второ­
го электрода. Символ металла отделяют от раствора вертикаль­
ной чертой, контакт между растворами разделяют двум я верти­
кальными черточками, если между растворами устранен скачок
диффузионного потенциала, или одной пунктирной линией, если
370

диффузионный потенциал не устранен. При обозначении гал ьва­
нического элемента слева записывается отрицательный электрод
(с более отрицательным потенциалом), а справа — положитель­
ный электрод. Д л я медно-цинкового гальванического элемента
эта запись будет выглядеть следующим образом:
(-)Z n|Z nC l2||CuCl2 |Cu(+)
Если диффузионный потенциал не устранен, то
(-)Zn | ZnCl2 i CuCl2 | Cu(+)
Дл я того, чтобы подчеркнуть, что цепь правильно разомкнута,
можно записать:
(-)Си | Zn | ZnCl21| CuCl2 | Cu(+)
или
(-)Zn | ZnCl2 11CuCl2 | Cu | Zn(+)
Величина ЭДС гальванического элемента положительна, и д л я
ее расчета из величины потенциала правого электрода нужно
вычесть величину потенциала левого электрода. Д ля концентра­
ционной цепи, состоящей из электродов одного металла, и рас­
творов разной концентрации, если концентрации известны, то
запись проводится с указанием концентраций:
Ag| AgN03|| AgN03|Ag
ci
c2
Если на электроде имеется малорастворимая соль или оксид,
то формула малорастворимого соединения записывается перед
металлом-электродом и отделяется запятой:
(-)Cd ICdCl2 IIКС11AgCl, Ag(+)
Величина равновесного электродного потенциала определяется
как ЭДС электрохимической цепи, в которой справа располо­
жен данный электрод, а слева стандартный водородный элек­
трод, потенциал которого условно принимается равным нулю.
При этом считается, что диффузионный потенциал предполага­
ется устраненным. Д л я такой цепи ЭДС вычисляется по урав­
нению:
Е = -Еправ "" ■Е'Н2/Н +#
Отдельные полуэлементы (электрод в растворе его соли) запи­
сываются в подстрочниках в следующем порядке: сначала пи­
шется символ потенциалопределяющего иона в растворе, затем
символ металла электрода или другого вещества:
Cu2+/C u; СГ/С12; СГ/AgCl, Ag
371

Электродный процесс записывается таким образом, что его ре­
зультатом является превращение окисленной формы в восста­
новленную:
Ох+ze~ ^ Red
3.17. КЛАССИФИКАЦИЯ ЭЛЕКТРОДОВ
Тип электрода определяется химической природой окислен­
ных и восстановленных частиц, участвующих в электродном
процессе.
§ 1. Электроды первого рода
К этой группе относятся металлические и амальгамные элек­
троды, находящиеся в равновесии с катионами металлов, опреде­
ляющих потенциал электрода, электроды газовые, а такж е ани­
онные электроды, на которых устанавливается равновесие меж­
ду электронейтральными частицами и анионами. Рассмотрим
систему
Cd2++2e“ ^C d
дл я которой равновесный потенциал равен (см. уравнение (3.59)):
_
о
RT
ECd2+/Cd- ^Cd27Cd+ ~2РlnaCd2+
где ^ c d 2+/Cd ~ стандартный электродный потенциал при аса += 1-
Активные концентрации обычно выражаются в молях вещества
на 1 кг растворителя. При низких концентрациях раствора ак­
тивную концентрацию можно заменить на см (мо ль /л). Амаль­
гамные электроды представляют собой растворы ряд а металлов
(Tl, In, Zn, Ag, Au и др.) в ртути. При этом на равновесный
потенциал электрода влияет не только концентрация ионов ме­
талла в растворе, но и концентрация его в ртути. Например, для
амальгамы серебра Ag++ е~ ^ Ag(Hg)
р
_
рО
.
RT1
a Ag+
b Ag7Ag(Hg) - ^AgVAg(Hg) + ~ Y in aAg(Hg) *
Из этого уравнения следует, что с ростом концентрации ионов
Ag+ в растворе равновесный потенциал будет увеличиваться,
что ранее было отмечено при обсуждении электрохимического
равновесия д л я полуреакции с позиции принципа Ле-Шателье.
При увеличении концентрации амальгамы равновесный потен­
циал системы будет уменьшаться.
372

Водородный электрод. Наиболее известным газовым электро­
дом является водородный электрод:
2Н++2е" ^ 2НЬтН2
Водородный электрод является лучшим электродом сравнения
благодаря высокой воспроизводимости величины равновесного
потенциала. Электрод можно использовать в большом д и апа ­
зоне температур и pH раствора.
Табличные данные равновесных потенциалов д л я других окис­
лительно-восстановительных систем даются в справочных из­
даниях относительно стандартного (нормального) водородного
электрода.
Водородный электрод представляет собой платиновый элек­
трод, помещенный на 2/з в раствор НС1 или H2SO4 с Gh+ = 1.
В раствор продувается водород, тщательно очищенный от кис­
лорода и других примесей (мышьяка, серы, ртути и др.). Метал­
лический проводник адсорбирует водород, который непосред­
ственно участвует в электрохимическом равновесии. Платино­
вый электрод обычно используется в виде пластины или прово­
лочки, впаянной в стеклянный держатель. Платина играет роль
проводника и катализатора, ускоряющего установление элек­
тродного равновесия между молекулярным водородом и ионами
Н+ в растворе. Д л я увеличения поверхности и повышения ка­
талитической активности платиновый электрод предварительно
подвергается платинированию,
т. е. получению тонкодисперс­
ного осадка платины (плати­
новая чернь) с помощью элек­
тролиза. Потенциал водородно­
го электрода в водородной шка­
ле равен ЭДС элемента, состав­
ленного из этого водородного
электрода (рн2> а н+) и стан­
дартного водородного электро-
да (рн2= 1атм, ан+= 1)- Эту ве­
личину можно рассчитать, ис-
пользуя химическую реакцию,
протекающую в элементе:
^ Н2(1 атм) + Н+(ан+) ->•
2 Н2(р нз) + Н+(ан* = 1),
где предполагается, что исход-
ная активность (ан+) > 1 и в
Рис. 3.20. Потенциал-рН-диа-
грамма для кислородного (а) и
водородного (б) электронов
373

результате реакции происходит восстановление ионов Н+ на изу­
чаемом электроде и окисление молекулярного водорода на стан­
дартном электроде. Также предполагается, что реакция проте­
кает бесконечно медленно и поэтому равновесия меж ду водоро­
дом и ионами Н+ на исследуемом электроде и стандартном элек­
троде не нарушаются. Д л я такого элемента ЭДС при учете, что
■®н+/н 2 принимается равным нулю, будет равна:
▼-I
_
RT, Рн2_ RT
RT
£н*/н2- -2F1пЖ ~"2F1прНг ^
ан+-
После подстановки численных значений постоянных Т (298 К), R
(8,313 Дж/моль) и F(96 500 Кл /моль) и перевода натуральных
логарифмов в десятичные (введя дополнительный множитель
2,303), получим выражение
#н +/н2 = -0,02951gpH2+0,0591 lgan+.
Имея в виду, что pH = - lg а н +, окончательно получим:
Днун2= “ 0 ,0591рН - 0,0295 lgрн2.
Из последнего выражения следует, что при уменьшении концен­
трации ионов Н+ на порядок потенциал водородного электрода
понижается на 0,0591 В, а при увеличении парциального дав­
ления газообразного водорода (рн2) на порядок равновесный по­
тенциал уменьшается на 0,0295 В (рис. 3.20). Поскольку водород­
ный электрод насыщается при атмосферных условиях, то изме­
нения атмосферного давления, строго говоря, влияю т на вели­
чину равновесного потенциала. Однако эти изменения невелики
и ими можно пренебречь. При изменении атмосферного давле­
ния от 95,97 кП а до 106,6 кП а равновесный потенциал умень­
шается на 0,00133 В. Водородный электрод можно использовать
для измерения pH раствора. К недостаткам водородного элек­
трода следует отнести высокие требования к чистоте водорода
и электролита.
Кислородный электрод. В отличие от водородного кислород­
ный электрод практически необратим. Значения потенциала элек­
трода были получены расчетным путем. Для кислых и щелоч­
ных растворов можно написать д в а уравнения полуреакций, про­
текающих на инертном электроде:
02+4Н++4е~^2Н20
02+2Н20+4е~
40Н“
374

В термодинамическом отношении оба уравнения равнозначны,
так как концентрации ионов Н+ и ОН" связаны соотношением:
ан+аон- = K W)
где К ю — ионное произведение воды. Поэтому д л я определения
зависимости равновесного потенциала от pH раствора можно ис­
пользовать то или другое уравнение. Результаты расчета будут
одинаковыми. При использовании первой полуреакции:
E q2/ h2o
грО
трО
■^СЬ/НгО
RT]/4
\
+ 4J 1п(ан+ро2) =
ЯГ,
RT
+ — \пан^+ — ро2,
(3.60)
где £ ° , 2/ н20 — стандартный (нормальный) потенциал кислород-
ного электрода при ац+ = 1 (рН= 0) и ро2 = 1 атм (101,3 кПа).
Стандартный равновесный потенциал кислородного электрода
равен 1,229 В. Преобразуя уравнение (3.60) с учетом pH = -lgaH+>
будем иметь:
Ео2/к2о = 1,229-0 ,0591рН+0,0148ро2•
(3.61)
Таким образом, зависимость равновесного потенциала от pH рас­
твора представляет прямую линию с тангенсом угла наклона
- 0 ,0591 В на единицу pH (см. рис. 3.20). Если pH = 14, то актив­
ная концентрация аон- = 1- Из уравнения (3.61) следует, что при
pH = 14 и ро = 1 атм равновесный потенциал £‘о2/он' = 0,401 В.
При уменьшении давления кислорода на порядок равновес­
ный потенциал уменьшается примерно на 0,015 В. В качестве
примера электрода первого рода, обратимого по аниону, мож ­
но привести теллур, помещенный в раствор, содержащий его
анионы:
2Те+2е~UТе^
RT
Ете/Те]- =
-®Те/ТеТ ~ ~^р ^n a Tel"i
^Те/Те^ = “ 0,84В.
Хлорный электрод. К обратимым по аниону электродам пер­
вого рода можно отнести хлорный электрод:
С12+2е" ^ 2СГ
В качестве адсорбирующего хлор металлического проводника
используют платину, которая играет такую ж е роль, как и в
375

случае с водородным электродом. Равновесный потенциал элек­
трода:
Ech/cv ~ Еси/сг +
1пРсь “
Inaci-
RT
RT.
Хлорный электрод ведет себя ка к обратимый. Однако в неко­
торой степени равновесие осложняется небольшой коррозией пла­
тины и протеканием побочной реакции хлора с водой:
С12+ Н20 *=+НСЮ + НС1
Равновесие может быть смещено в левую сторону при подкисле­
нии раствора и им можно пренебречь. Хлорный электрод при­
меняется к ак электрод сравнения в расплавах хлоридов солей.
В этом случае платиновый электрод заменяется на более инерт­
ный графитовый электрод.
§2. Электроды второго рода
К электродам второго рода относятся металлические электро­
ды, поверхность которых п окры та малорастворимой солью или
гидратированным оксидом. Такой электрод погружается в рас­
твор, содержащий анион малорастворимой соли или ионы О Н '
дл я оксида. Электроды обратимы по отношению к указанным
ионам:
МА+ze~ = М+Аг'
£Л-/мл,м =2&7ма.М+ ^ 1 п^
.
Активности металла и твердой фазы МА являются постоянными
и принимаются равными единице, тогда:
р
_
рО
^А=-/МА,М -
VMA,М-
—р
inаА-~ ■
Величины равновесных потенциалов электродов второго рода
хорошо воспроизводимы. Поэтому некоторые из них использу­
ются в качестве стандартных электродов сравнения. Наиболее
широко используются каломельный, хлор-серебряный, ртутно­
сульфатный и ртутно-оксидный электроды.
Каломельный электрод. Представляет собой стеклянный со­
суд, на дно которого помещается очищенная ртуть таким обра­
зом, чтобы токоотвод — платиновая проволочка — был полно­
стью погружен в ртуть (рис. 3.21). На поверхность рту ти наносят
слой каломельной пасты (Hg2Cl2). Затем в полуэлемент залива­
ют раствор КС1. Схематически каломельный электрод можно
записать:
Cr/Hg2Cl2, Hg
376

7
Рис. 3.21. Каломельный электрод:
1 — ртуть; 2 — платиновая проволока; 3 — каломель; 4 — стеклянная труб­
ка; 5 — раствор КС1; 6 — трубка для заливания растворов; 7 — медная
проволока; 8 — пробка; 9 — стеклянный сифон
На электроде устанавливается равновесие:
Hg2Cl2 + 2е~
2Hg + 2СГ
Равновесный потенциал электрода определяет концентрация ани­
онов СГ. В зависимости от концентрации раствора используют­
ся насыщенный, молярный и децимолярный каломельные элек­
троды. По водородному электроду равновесные потенциалы рав­
ны 0,2438 В (насыщенный), 0,2828 В (молярный) 0,3365 В (де­
цимолярный) . Д л я насыщенного каломельного электрода потен­
циал более устойчив, так как не меняется концентрация ионов
СГ. Децимолярный электрод имеет низкий температурный ко­
эффициент.
Хлор-серебряный электрод. Этот электрод является полуэле-
ментом СГ/AgCl, Ag. Н а электроде устанавливается равновесие:
AgCl + е~
Ag+СГ
F
-
F°
Inп
■С'СГ/AgCl, A g - ■
“ СГ/AgCl, A g
~JTln аСГ
-^cr/AgCi, A g = 0)23655 B.
377

Хлор-серебряный электрод имеет постоянный хорошо воспроиз­
водимый потенциал и широко используется как вспомогатель­
ный электрод д л я измерения потенциала.
Ртутно-сульфатный электрод. Этот электрод представляет по-
луэлемент S04_/Hg2S0 4 , Hg
Hg2S04+ 2е“
2Hg+SO^
_
о
ЛТ
■£'S057Hg2so1,Hg - E soi-/nS2so4,Hg“ “pTInasoj-;
E so24-/ng2so4, Hg = 0 .61515 B.
Электрод применяется как вспомогательный для измерения по­
тенциалов в растворах серной кислоты.
Ртутно-оксидный электрод. Этот электрод является полуэле-
ментом OH“/HgO, Hg
HgO+Н20 +2е“ = Hg+20Н"
RT
^O H7Hgo,Hg= ^oH-/Hgo,Hg“ “p " 1паон-;
^OH'/HgO.Hg = 0982 B.
Используется обычно как вспомогательный электрод при ис­
следованиях в щелочных растворах. Следует отметить, что по­
следние д в а электрода сравнения имеют определенные недостат­
ки — равновесный потенциал устанавливается до двух дней, вос­
производимость потенциала хуже, чем у хлор-серебряного и ка­
ломельного электродов.
§3. Электроды третьего рода
Металлический электрод находится в контакте с парой труд­
норастворимых солей: одна — соль данного металла, а вторая с
тем же самым анионом, что и первая соль, но с другим катионом,
и раствор, который содержит катион второй соли, например,
СаС12 | Са(СОО)2, РЬ(СОО)2, РЬ
Нерастворимые соли — оксалаты кальция и свинца. В этом по-
луэлементе осуществляется равновесие:
РЬ(СОО)2+ Са2+ + 2е~ ±5 РЬ + Са(СОО)2
При работе электрохимической цепи происходит превращение
менее растворимой соли РЬ(СОО)2 (ПР = 3,5 • 10- п ) в более
378

растворимую соль С а(СОО)2 (ПР = 2 ,57 ■1СГ9)*. Потенциал
такого электрода в конечном счете определяется активностью
ионов Са2+ в растворе. Если разобраться в этом вопросе бо­
лее детально, то потенциал свинца определяется активностью
РЬ2+, а активность Р Ь2+ — произведением растворимости соли
РЬ(СОО)2 и активностью ионов оксалата (СОО)2~, а активность
иона (СОО)2 — произведением растворимости Са(СОО)2 и а к ­
тивностью ионов Са2+ в соответствии со следующей схемой:
Е-
.ЕрЬ2 +/рь +
1пПРрь(соо)а-
RT
- fm np,Са(СОО)2
RT.
2F
RT.
InаСаг*= Е +— InоСа2..
Такой электрод использовался для потенциометрического
определения ионов Са2+. Однако электроды третьего рода в
большей степени представляют теоретический интерес. Более
широкое использование находят окислительно-восстановитель­
ные электроды.
§ 4. Окислительно-восстановительные электроды
Окислительно-восстановительные электроды или редокс-элек­
троды представляют собой благородные металлы (платина, зо­
лото, ртуть), погруженные в раствор, содержащий окисленную и
восстановленную формы вещества. Электроды из благородных
металлов непосредственно не принимают участия в электрохи­
мическом равновесии, а только являются передатчиками элек­
тронов от восстановленной к окисленной форме, или наоборот.
Различаю т простые редокс-электроды, на которых происходит
только изменение зар яд а ионов. В качестве примера простого
редокс-электрода можно привести:
Се4++2е'±5Се2+
Равновесные потенциалы такой системы определяются отноше­
нием активностей окисленной и восстановленной форм ионов в
соответствии с уравнением Нернста (3.57):
RT
ЕСе4+/Се*+ “ ^Се4+/Се2++ ~^р 1п
а4+
Се
а Се2+
В сложных редокс-системах кроме ионов одного элемента в рав­
новесии участвуют другие частицы (молекулы воды, ионы Н+,
ОН” и др.):
ПР — произведение растворимости при температуре 298 К.
379

Сг20?" + 14Н+ + бе"
?Cr20?-/Cr3+- Д°Сг50?-/Сг3
5 2Сг3+ + 7Н20
Л Г . QCr2o?-QH^
6FШ а2г3+
Величина равновесного потенциала редокс-систем характеризу­
ет окислительно-восстановительные свойства раствора. Чем от­
рицательнее значение равновесного потенциала, тем сильнее вы­
ражены восстановительные свойства раствора, и наоборот, чем
положительнее значение равновесного потенциала, тем сильнее
проявляются окислительные свойства раствора. Комбинируя не­
сколько окислительно-восстановительных равновесий, д л я кото­
рых известны стандартные потенциалы, можно рассчитать рав­
новесный потенциал трудноосуществимой реакции. Р ас чет про­
водится на основании правила Лютера. Оно заключается в том,
что если система переходит из одного состояния в другое обра­
тимо при постоянной температуре, то изменение энергии Гиббса
AG не зависит от путей перехода. Например, при контакте же­
лезного электрода с раствором, содержащим ионы Fe2+ и Fe3+,
на границах могут протекать три реакции:
1)
Fe2++ 2е“ = Fe
2)
Fe3++ Зе“ = Fe
3)
Fe3++ е~ = Fe2+
Ек*/ъ =-0,440В;
■£?.••/?. = 7Bi
-
®Fe37Fe2+ “ 771 В.
Рассчитаем равновесный потенциал второй реакции. Переход от
Fe до Fe3+ может быть осуществлен двумя путями:
Тогда
AGi +ДС»ти = AGii;
АС?,= ~ ziFE^/Fe] AGU= -z2FE°F^ /Fe,
(3.62)
AGin = -zzFEF^/Fe2+.
Подставив число электронов каждой реакции в уравнение (3.62),
получим:
2FFpe2+/Fe ^^Fe3+/Fe2+_ 3FE®e*+/Fe.
Проведя перестановку и сокращения, получим:
380

_
^Fe27Fe+^F<
'
3
'Fe3+/F e2+ _ 2(-0 ,44)+0,771
3
= -0,036 B.
Реакцию (2) действительно трудно осуществить, так как на же­
лезном электроде параллельно будет протекать реакция Fe +
+ 2Fe3+ = 3Fe2+.
На границе двух растворов с неодинаковым составом воз­
никает разность потенциалов, которая называется д и ф фу­
зионным потенциалом.
Причиной возникновения разности потенциалов в этом слу­
чае является разная подвижность ионов. Д л я упрощения возь­
мем растворы одного состава, но разной концентрации, напри­
мер раствор ZnS0 4 . Ионы Zn2+ и SO2- будут диффундировать
из более концентрированного раствора в раствор с меньшей кон­
центрацией. Подвижность ионов SO2”, окруженных гидратной
(сольватной) оболочкой, выше, чем у гидратированных ионов
Zn2+ из-за меньшего размера гидратированных ионов SO4- . Боль­
шая скорость движения ионов SO2” приводит к появлению скач­
ка потенциала на границе между растворами. В разбавленном
растворе на границе будет выше концентрация ионов SO^” , а в
концентрированном — избыток положительных ионов. Возника­
ющий скачок потенциала с одной стороны будет тормозить д а л ь ­
нейшее движение SO4” с более высокой скоростью и ускорять
движение Zn2+ в возникшем электрическом поле на границе рас­
творов. При некотором скачке потенциала скорость движения
катионов и анионов выравнивается и значение диффузионного
потенциала становится стационарным. Граница, на которой воз­
ник двойной электрический слой, будет по мере диффузии ча­
стиц перемещаться в направлении разбавленного раствора. Тео­
рия диффузионного потенциала развивалась М. Планком (1890)
и П. Гендерсоном (1907). Уравнения, связывающие подвижность
ионов и диффузионный потенциал, достаточно громоздки. Од­
нако уравнение упрощается для диффузионного потенциала на
границе двух растворов одного и того же электролита с разной
концентрацией:
3.18. ДИФФУЗИОННЫЙ ПОТЕНЦИАЛ
(3.63)
381

где U+и U—
— подвижность катионов и анионов; а\ и a<z — средние
активности соли в обоих растворах. При низких концентрациях
в уравнении (3.63) активность можно заменить на концентра­
ции с\ и С2 - Если в контакте находятся растворы 1,1-валентных
электролитов с одинаковым анионом и равной концентрацией,
например КС1 (1) и NaCl (2),
^
2,303AT U1++ U-
Е«‘ —
Принимая во внимание, что эквивалентная электрическая про­
водимость связана с подвижностью X = (U+ + U-)F, уравнение
(3.64) принимает вид:
^
2,303 ДТ Xi
Е>= —
—
>ет2
Это уравнение называется формулой Льюиса—Саржента. При
достаточно большой разнице в подвижности ионов Е д достигает
сравнительно больших значений, которыми нельзя пренебрегать
при измерении ЭДС гальванического элемента. Так, например,
для границы растворов 0,1М НС1||0,1М КС1 Ед = - 0 ,0331 В,
а д ля границы 0,1М КС1||0,1М NaCl, для которой подвижность
ионов К + и Na+ отличаются гораздо меньше, чем дл я ионов Н+ и
К+, величина Ея = -0 ,0064 В. Диффузионный потенциал возни­
кает при неравновесном процессе диффузии, и поэтому он необ­
ратим. Можно резко уменьшить диффузионный потенциал, ес­
ли между двум я растворами включить солевой мостик, т. е. по­
местить переходную трубку, заполненную концентрированным
раствором соли с близкими по величине подвижностями ионов
(КС1, NH4NO3). При помещении между растворами солевого мо­
стика появляются две границы между растворами, например,
раствор 1 —КС1(1) и раствор 2 —КС1(2). На каждой из возника­
ющих границ значения Ед меньше, так как близки подвижности
катиона и аниона концентрированного раствора, а возникающие
диффузионные потенциалы на новых границах, как правило, об­
ратны по знаку. Таким образом, можно пренебречь влиянием
диффузионного потенциала на общую величину ЭДС гальвани­
ческого элемента.
3-19. МЕМБРАННЫЕ ПОТЕНЦИАЛЫ
Рассмотрим случай, когда меж ду растворами находится по­
лупроницаемая мембрана, совершенно не проницаемая д л я неко­
торых ионов. Схема полупроницаемой мембраны, разделяющей
382

растворы I и II приведены на
рис. 3.22. В растворе I на­
ходятся две соли К А и RA.
При этом органический кати­
он R+ (например, тетрабутил-
аммоний) вследствие большо­
го размера не в состоянии про­
никнуть через мембрану. Рас­
твор II содержит только соль
КА. Сольватированные (гид­
ратированные) ионы К+ и А~
и молекулы растворителя мо­
гут беспрепятственно прони­
кать через мембрану до то­
го момента, когда между рас­
творами не установится элек­
трохимическое равновесие. Из
условия электронейтральности растворов I и II следует:
с|+схк+=с!.; с*1=с1}=с,
(3.65)
где c+ , cr+ и с_ концентрации катионов и анионов, индексы I
или II указывают на принадлежность ионов к тому или другому
раствору, с — равновесная концентрация электролита во втором
растворе. При установлении равновесия примем, что часть ионов
К+ ушла из первого раствора во второй. Как следует из равенств
в(3.65)cL>с;ис!^сгк .Врезультатес!>с!1,ас\<с*1.Итак,
вследствие разности в концентрациях ионов возникает разность
потенциалов между растворами.
Разность потенциалов между границами полупроницае­
мой мембраны, разделяющей два раствора, один из которых
содержит ионы, не проходящие через мембрану, называется
мембранной (донановой) разностью потенциалов.
Выведем уравнения д л я мембранного потенциала. При уста­
новлении равновесия меж ду растворами электрохимические по­
тенциалы катионов и анионов будут равны:
=Д+; Д-=Д-*
Развернув выражения д л я электрохимических потенциалов, бу­
дем иметь:
+ Ftp1= ц.*1+ Fcp11,
(3.66)
|il - F(pr = jxL1- F(pn ,
(3.67)
383
Рис. 3.22. Схематическое изо­
бражение мембраны, разделяю­
щей раствор I состава КА + RA и
раствор II состава КА

где Ц.+, |il, |Х+ и (ll1 — химические потенциалы ионов; ф1 и ф11 —
внутренние потенциалы растворов I и II соответственно. Сложив
уравнения (3.66) и (3.67), получим:
|4+Л =Р-++ц".
Выразив химические потенциалы через активную концентрацию
ионов в растворе получим:
|4(0)+RTInа\+ц1(0)+RTInal =
= |i+(0)+RTInal1+p”(0)+RTIna” .
Так как стандартные химические потенциалы не зависят от того,
в каком растворе находится ион, т. е.
^ (0)= ^ I(0); nI(0) = MiI(0),
(3.68)
то после проведения преобразования будем иметь:
1тт_1IIлI
Ina+a_ = Inа+а_ .
После потенцирования:
или
О?
а:
и
at
(3.69)
Донановую (мембранную) разность потенциалов можно полу­
чить, используя уравнения (3.66) или (3.67) и (3.69). Химические
потенциалы в уравнениях (3.66) или (3.67) можно вы разить че­
рез активны е концентрации ионов. Тогда, имея в виду равенства
(3.68), получим:
Л(0)+RTInа\+iV =|1+1(0)+RTInau +Ftyjj,
PT лП
Ед=ф1-фп= — ln-^.
(3.70)
г
a\
Подставив уравнение (3.69) в (3.70), выразим через активные
концентрации анионов:
DT> Л
=
(З-71)
Дл я низких концентраций растворов можно заменить актив­
ность на концентрации:
41
„и
(3.72)
384

(3.73)
Комбинируя (3.72) и (3.65), получим:
гс2
с_=
-у+CR.
с!
Реш ая квадратное уравнение (3.73), найдем
2
(3.74)
Подставив (3.74) в (3.71) и имея в виду а! = с£, а!1 = с]} = с,
получим:
„
ЯГ,
-Бд- -рг1п
Еслиcr>с,то
гЧ
(2*Л
1.2с/
RT
■—=Г ш
CR
F
С
+1
Дл я измерения мембранного потенциала составляют элемент с
полупроницаемой мембраной, разделяющей растворы I и II:
Ag,AgCl|Насыщенный RC1:раствор , | раствор п :Насыщенный
раствор
м
раствор
KCl|AgCl, Ag
Строго говоря ЭДС элемента равна сумме мембранного и
двух диффузионных потенциалов. Однако вкладом последних
можно пренебречь, так к а к в жидкостном соединении использу­
ется насыщенный раствор KCL
§1. Биологические мембраны
Биологические клетки живых организмов отделены от меж­
клеточной среды мембранами с различной степенью проница­
емости для разных веществ и ионов. Состав мембран зависит
от их типа и функций. Основными составляющими веществами
мембран являются липиды и белки.
Согласно М. Даниэлю и И. Доусону мембрана представляет
собой бимолекулярный слой фосфолипидов, к а к правило, это
глицериды высокомолекулярных жирных кислот. Ж ирные кис­
лоты в фосфолипидах связаны с каким-либо этаноламином, на­
пример с холином. Молекулы липидов ориентированы таким об­
разом, что их гидрофобные части — углеводородные хвосты —
направлены внутрь мембраны, а полярные группы — в приле­
гающий водный раствор клетки или межклеточной жидкости
(рис. 3.23). На обеих поверхностях мембраны адсорбирован слой
13 Ипполитон
385

белков. Молекулярная масса белков колеблется от 5000 и до
250 000. Клеточные мембраны многофункциональны. Кроме от­
деления клеток от межклеточной жидкости и создания архитек­
туры клетки через мембраны переносятся питательные вещества
(благодаря осмосу) и ионы, благодаря разности потенциалов на
границе «мембрана—раствор». Таким образом, мембраны созда­
ют градиент концентрации некоторых веществ и ионов.
Разность потенциалов, возникающая в биологических
объектах между цитоплазмой и межклеточной жидкостью,
называется биоэлектрическим потенциалом.
Несмотря на малую толщину (4 —10 нм) мембраны при ну­
левом мембранном потенциале имеют огромное сопротивление:
108— Ю10 О м -см 2. Поверхность мембраны возрастает при до­
бавлении гидрофобных (липофильных) ионов. Кроме просто­
го транспорта гидрофобных ионов через мембрану происходит
ионофорный перенос. Ионофорный перенос осуществляется ком­
плексными ионами между молекулами, имеющими циклическую
структуру и неорганическими катионами. На внешней поверхно­
сти мембраны обычно располагаю тся алкильные группы. Внут­
ренняя полость такой молекулы имеет полярные группы,
например, карбонильные. Внут­
ренняя часть циклической мо­
лекулы образует комплекс с
катионом щелочного металла.
Неполярное внешнее окруже­
ние такого комплекса облегча­
ет его растворение и транс­
порт в малополярных раство­
рителях. Типичным предста­
вителем таких ионофоров яв­
ляется валиномицин — цик­
лический депсипептид с 36-
членным кольцом из чере­
дующихся аминокислот и а-
оксикислот (рис. 3.24).
Катион щелочного металла
полностью экранирован внеш­
ней липофильной частью ва-
дель
структуры биологической линомицина. Комплекс хоро-
мембраны:
шо растворяется в мембранах
1 —фосфолипиды; 2 —слой белков
биологических клеток. Такой
Рис. 3.23. Схематическая мо-
386

комплекс более устойчив с
ионами К+ и менее устойчив
с катионами Li+ и Na+. Кати­
оны Li+ и Na+ легко входят в
полость валиномицина, одна­
ко их высокая энергия гидра­
тации резко понижает устой­
чивость комплекса по сравне­
нию с калиевым комплексом,
из-за того, что энергия гидра­
тации иона калия значитель­
но меньше, чем ионов лития
или натрия. Другим механиз­
мом переноса ионов через мем­
брану является перемещение
их по трансмембранным ка­
налам. Такие каналы обычно
образуют две спиралевидные
молекулы грамицидина А — пептида, состоящего из 15 амино­
кислот. Длина спиралевидной молекулы грамицидина А равна
половине толщины мембраны. Две спирали, соприкасаясь свои­
ми концами, образуют трансмембранный ионный канал. Внеш­
няя поверхность такого к анала обладает липофильными свой­
ствами. Структура канала должна быть достаточно подвиж­
ной д л я обеспечения необходимых изменений формы витков при
прохождении ионов. Внутренняя часть спиралевидного канала
в отсутствие электрического поля «перегорожена» водородны­
ми связями между С = 0 и NH-группами разных аминокислот.
При повышении напряженности электрического поля водород­
ные связи разрываются и ионы могут проходить через канал,
что приводит к значительному увеличению электропроводности
мембраны. Некоторые вещества, относящиеся к антибиотикам
пол ненового ряда могут образовывать в мембранах поры. Через
эти поры могут проникать различные катионы, молекулы воды,
молекулы неэлектролитов. Таким образом, антибиотики нару­
шают селективность мембраны по отношению к различным ве­
ществам и ионам. Н екоторая селективность сохраняется только
для аминов.
Функционирование ж ивых клеток зависит от присутствия
и концентрации ионов в клетке и в межклеточной жидкости.
Динамическое равновесие между входом и выходом ионов из
клетки, устанавливающееся благодаря мембранам, позволяет со­
хранить постоянство количественного и качественного состава
ионов. В то же время концентрации ионов внутри клетки и во
D-Изовале-
Валиномицин
Рис. 3.24. Структура молекулы
валиномицина
387

внеклеточном пространстве су­
щественно различаются, что
приводит к возникновению мем­
бранного потенциала. Ионы
Na+ и К+ играют очень важ­
ную роль в биологических про­
цессах. Внутри клеток кон­
центрация ионов к ал ия обыч­
но выше концентрации ионов
натрия. Межклеточная жид­
кость мышцы лягушки обычно
содержит 120 ммоль/л ионов
Na+ и 2,5 ммоль/л ионов К+,
а внутри клеток концентрация
ионов Na+ 9,2 ммоль/л, ионов
К+ 140 ммоль/л.
Нервная клетка (нейрон)
представляет собой звездо­
образное тело, внутри которо­
го находится ядро (рис. 3.25).
От клетки отходят отростки
(дендриты) и более длинные
ответвления (аксоны). Дендри­
ты передают возбуждение к нейрону, а аксоны — на перефирию.
Аксоны защищены миелиновой оболочкой, состоящей из смеси
липидов и белков. Участки, не защищенные оболочкой называ­
ются перехватами Ранвье. Отростки заполнены цитоплазмой.
Особенно важную роль играют ионы натрия и калия при
функционировании нервной системы. Состав жидкости в ак­
соне значительно отличается от состава межклеточной жидко­
сти. Например, аксон кальмара содержит 50 ммоль/л ионов на­
трия и 400 ммоль/л ионов калия, 40 —50 ммоль/л ионов хлора,
в межклеточной жидкости содержится 460 ммоль/л ионов на­
трия, 10 ммоль/л ионов калия и 54 ммоль/л ионов хлора. При
нахождении клетки в состоянии покоя на мембране аксона уста­
навливается потенциал покоя А Е М = Е вн - Е вяеш ~
-70мВ.
Теория мембранных потенциалов покоя была сформулирована
М. Гольдманом, А. Ходжкиным, К. Хаксли и Б. Катцем. Если
предположить, что мембранный потенциал покоя определяется
только ионами калия, натия и хлора, то в отсутствие протека­
ния электрического тока поток катионов через мембрану (сум­
марный переносимый заряд) равен потоку ионов хлора:
wi/iilllll)ll)ihini
Волокна поперечно полосатой мышцы
Рис. 3 .25. Структура двигатель­
ной нервной клетки лягушки
^Na++ ^К+ = ^СГ-
(3.75)
388

Полагая, что коэффициенты переноса а = (5 =
можно выра­
зить поток этих ионов через мембрану следующим образом:
_
AEMF
^Na+ “ ^Na+CNa£иеще 2 R T - ^Na+CNa£He
2R.T
(3.76)
JO
о
AEyF
iK+= кк+сК1яеше 2ят - % +ск;не «т ,
(3.77)
*сг = ^ с г сС1;неше 2яг - / сС1-сС1-в>1е
AEmF
2RT
(3.78)
Подставив уравнения (3.76), (3.77) и (3.78) в (3.75), получим вы­
ражение для мембранного потенциала:
А„ ЯГ,
Л£м= -р 1п
+кк+сК„сш+kcr^l„
.
^NatCN^H+
*СК« + ^СГсС1;неш
(3.79)
где ki — константы скорости реакции соответствующих ионов,
которые можно идентифицировать с проницаемостями мембран
дл я этих ионов. Уравнение (3.79) достаточно хорошо согласу­
ется с экспериментальным значением мембранного потенциала.
При этом можно предположить, что проницаемость дл я ионов
калия выше, чем для ионов натрия и ионов хлора. Проницае­
мость мембраны д л я других ионов пренебрежимо мала. Уравне­
ние (3.79) практически повторяет уравнение Гольдмана (3.80), в
котором константы скорости процессов заменены на проницае­
мости мембраны Р,f д ля соответствующих катионов:
АЕт-
RT
In
-Рка+ОчХнеш + Р К+СК„сш + Р С1-ССЦ»
-
^Na+CNa£u+ ^K+CK+,f+ ^СГсС1;неш .
(3.80)
Такой перенос ионов через
мембрану (пассивный тр анс­
порт) должен приводить к по­
нижению содержания ионов
калия и увеличению содержа­
ния ионов натрия во внутри­
клеточном пространстве и з-за
разности концентраций ионов
в межклеточном и внутри­
клеточном пространстве. При
этом мембранный потенциал
покоя должен изменяться. Од­
нако этого не происходит, так
как изменению состава раство­
ра препятствует обратный ак­
тивный транспорт. Ионы калия
Снаружи_ Мембрана Внутри
IДиффузия
I Активный
К+<
_
транспорт
Na\ KMfNa\ К*-
АТФаза lv АТФаза
. Активный
Iтранспорт
Диффузия
Рис. 3.26. Схема транспорта ионов
калия и натрия через мембрану
389

возвращаются в клеточную жид­
кость, а ионы натрия в меж­
клеточное пространство за счет
фермента Na+, К +-АТФазы. Пе­
ренос ионов натрия и калия
от меньшей концентрации к
большей сопровождается по­
треблением свободной энергии
химической реакции, напри­
мер, гидролиза богатых энер­
гией фосфатных связей в мо­
лекулах аденозинтрифосфата
(АТФ) с образованием аденоозиндифосфата (АДФ):
АТФаза
АТФ+Н20<
АДФ + Н2РО4+ Н+
Переносчик ионов натрия и калия АТФаза называется натрие­
вым насосом. Схема, поясняющая направление потоков катионов
натрия и калия представлена на рис. 3.26.
При возбуждении нерва резко возрастает проводимость мем­
браны для ионов натрия и калия. Проницаемость ионов на­
трия внутрь клетки на краткий промежуток времени становит­
ся большей, чем проницаемость ионов калия из внутриклеточ­
ной жидкости в направлении межклеточной жидкости. При этом
мембранный потенциал резко возрастает: Д £ д = Е вн - Е внеш ~
~
5 0 ... 70 мВ и, следовательно, изменение скачка потенциала
относительно потенциала покоя составляет 120 —140 мВ. Ве­
личину А Е Д называют потенциалом действия (рис. 3.27). Кон­
центрация ионов калия в клетке становится практически рав­
ной 0. После этого включается механизм активного транспор­
та, и концентрация ионов натрия и калия в клетке и в межкле­
точной ж идкости восстанавливается до концентраций, которые
соответствуют потенциалу покоя. Электрический ток, генери­
руемый потенциалом действия, направляется через тело нейро­
на к периферийному участку, д л я которого проводимость для
ионов натрия и калия и состав жидкости соответствует потен­
циалу покоя.
аЕ,
Рис. 3.27. Схематическое изобра­
жение изменения скачка потенци­
ала на мембране при возбуждении
клетки
3.20. ИОНОСЕЛЕКТИВНЫЕ ЭЛЕКТРОДЫ
Ионоселективные электроды — это вид аналитических
датчиков, основу которых составляют полупроницаемые
мембраны и которые обладают повышенной избирательно­
стью к определенному типу ионов.
390

Активность анализируемого иона определяется по величине ЭДС
между ионоселективным электродом и электродом сравнения.
Различаю т ионоселективные электроды на основе твердых мемб­
ран с фиксированными ионами и жидких мембран.
Стеклянный электрод. Данный электрод (рис. 3.28) относит­
ся к ионоселективным электродам с твердой мембраной. Обыч­
но этим электродом измеряют pH раствора. Основу конструк­
ции электрода составляет стеклянная трубка, на конце которой
выдута тонкая мембрана в виде шарика. Внутрь трубки с шари­
ком помещают стандартный раствор с определенным значением
pH (обычно применяют раствор соляной кислоты определенной
концентрации). В качестве токоотвода во внутренний раствор
помещается серебряный электрод, покрытый слоем соли AgCl.
В некоторых конструкциях вставляется еще стеклянная защит­
ная трубка. Стеклянный электрод и электрод сравнения поме­
щаются в исследуемый раствор. Потенциал стеклянного эл ек­
трода относительно электрода сравнения определяет формула:
„
„
ЯГ,
Е —Еоч——Inащ•
Г
6
Константу Е о устанавливают пу­
тем калибровки по буферным
растворам, pH которых известен.
Мембрана стеклянного электро­
да должна обладать высоким
омическим сопротивлением. По­
этому для измерения ЭДС эле­
мента «стеклянный электрод—
электрод сравнения» применяют­
ся приборы с высокоомным вы­
ходом (pH-метры или иономет-
ры). В настоящее время стек­
лянный электрод рассматрива­
ют, ка к электрод с ионообмен­
ной мембраной. Стекло представ­
ляет собой силикатную структу­
ру, внутри которой относитель- Рис. 3.28. Стеклянный элек-
но высока подвижность катио-
трод:
НОВ щелочных металлов. Н а по- 1
—
защитная трубка для шарико-
верхности стекла, контактирую- вого стеклянного электрода; 2 —
щей с раствором катионы щелоч- внутр®иний хлорсеребряный элек-
ных металлов могут обменивать- ная трубка. 4 _ внутренний рас_
ся на другие катионы, главным твор соляной кислоты; 5 — стек-
образом на ионы водорода:
лянная мембрана; 6 — пробки
391

Na+(стекло) + H+(p) = Н+(стекло) + Na+(p)
Учитывая, что с внутренней стороны стеклянной мембраны со­
став раствора остается постоянным, то постоянным будет скачок
потенциала во внутренней части стеклянного электрода. Поэто­
му в дальнейшем приведенное выше равновесие рассматривает­
ся только на внешней стороне мембраны. Принимал, что число
мест, которые могут занять ионы Na+nH + на поверхности мемб­
раны постоянно, будем полагать, что сумма активностей ионов
в стекле та к ж е является постоянной величиной:
fl>Na+ ^Н+ =
(3.81)
Тогда константа для приведенного выше равновесия будет вы­
ражаться:
ан+ама+
i\^
a Na+aH+
(3.82)
Комбинируя (3.81) и (3.82) получим:
<2Н+ aNa++Как
Ка
(3.83)
Подставим выражение (3.83) в общее уравнение (3.70) д л я по­
тенциала мембранного электрода:
ftNa++ Кац*
Ка
или
RT
Ест = Eq+ -рГ ln(aNa++ Кац*),
(3.84)
гдеЕо=
In К а. Уравнение (3.84) впервые было выведено
Б. П. Никольским. Анализ уравнения (3.84) показывает, что при
К ан+ а ^ а+, что выполняется для кислых и нейтральных рас­
творов, получим:
Ест=
^
Inан+= Я?■-^
РН.
(3.85)
В щелочных растворах, когда а>га+ Кац*
RT
Ест= Ei н—— Inа^о*.
(3.86)
г
Из уравнений (3.85) и (3.86) следует, что в кислых и нейтраль­
ных растворах стеклянный электрод является селективным по
392

отношению к ионам Н+. В ще­
лочных растворах на ход за­
висимости Ест—pH оказыва­
ет влияние концентрация ионов
Na+ и в области более концен­
трированных щелочных рас­
творов стеклянный электрод
становится селективным по от­
ношению к катиону щелочно­
го раствора и его потенциал
не зависит от pH (рис. 3.29).
Как видно из рисунка, зна­
чительное влияние на зависи­
мость (Е ст—pH) проявляется в
основном для катионов с меньшим радиусом. Наибольшая ще­
лочная ошибка наблюдается в растворах гидроксидов лития и
натрия. Катионы больших размеров меньше влияют на потен­
циал стеклянного электрода. Поэтому при изготовлении мембра­
ны из литиевого стекла щелочная ошибка наименьшая. Однако
растворимость литиевых стекол в щелочных растворах выше,
чем натриевых стекол. Введение в состав стекл а оксидов алю­
миния и бора увеличивает его катионную функцию. Созданы се­
лективные стеклянные электроды при помощи которых можно
определять активную концентрацию Na+, К+, NHJ, Т1+ и дру­
гих (работы Б. П. Никольского, М.М. Шульца, Д ж . Эйзенмана).
Качество ионоселективных электродов определяется коэффици­
ентом электродной селективности.
Избирательность определения активности исследуемого
иона при избытке в растворе других ионов называется ко­
эффициентом электродной селективности.
Известны и другие ионоселективные электроды. Хлор-, бром- и
иодселективные электроды изготавливают на основе галогени­
дов серебра, нанесенных на поверхность серебряного электрода.
Электрод, изготовленный на основе Ag2S используется для опре­
деления S2", Ag+, Hg2+. Электроды на основе смеси сульфидов
двухвалентных металлов и Ag2S применяют д л я определения
активности Pb2+, Cu2+, Cd2+ в растворах. В качестве ионоселек­
тивны х электродов используются также полимерные мембраны,
содержащие ионогенные группы.
Ионоселективные электроды создаются такж е на базе ж ид­
ких мембран. Ж идкие мембраны делают на базе раствора ионо-
обменника в подходящем растворителе. Приготовленным
Рис. 3.29. Зависимость потенциа­
ла стеклянного электрода от pH
раствора:
1- Li+;2- Na+;3- К+;4“Rb+;
5 —Cs+
393

Рис. 3.30. Схема ионоселектив­
ного электрода с жидкой мемб­
раной:
1 — хлорсеребряный электрод;
2 — внутренний раствор; 3 — рас­
твор ионообменника; 4 ~ корпус;
5 — мембрана
раствором пропитывают пори­
стую пластинку, изготовленную
из стекла или полимера (те­
флон, поливинилхлорид и др.).
Пластинка закрепляется на кон­
це трубочки. Растворитель дол­
жен обладать достаточно боль­
шой вязкостью и не смешиваться
с водой. Теория ионоселективных
электродов с жидкой мембраной
достаточно сложна. С помощью
ж идких мембранных электродов
определяют ионы Са2+, Mg2+, ряд
анионов. Схема ионоселективно­
го электрода с жидкой мембраной
дана на рис. 3.30.
В последнее время получа­
ют распространение ферментные
электроды или биоэлектрохими-
ческие сенсоры. Известно, что
ферменты обладают очень высо­
кой специфичностью. Некоторые
ферменты могут катализировать реакцию превращения только
одного вещества на фоне избытка большого количества других
веществ, близкой химической природы. Если при реакции из­
меняется pH среды, то можно использовать рН-чувствительные
электроды (например, стеклянный), покрытые тонкой плен­
кой геля, содержащего фермент, катализирующий превраще­
ние данного вещества. По изменению ЭДС элемента «стек­
лянный э л е к т р о д —электрод сравнения» количественно опреде­
ляют содержание данного вещества, которое в процессе пре­
вращения меняет pH среды. Ферменты встраивают также в
полимерные мембраны, нанесенные на поверхности электро­
дов. Более устойчивы ферменты, если они иммибилизованы
на фосфолипидные* и липосомные мембраны (биосенсоры)**.
Биосенсоры используются в медицине и для контроля каче­
ства продуктов питания. Ферментные биосенсоры позволяют
определять важные компоненты биологических систем (глю­
коза, нуклеиновые кислоты, углекислый газ, ионы аммония
и др.).
Липиды — жироподобные вещества, фосфолипиды — липиды, содержащие
эфиры фосфорной кислоты.
** Биосенсоры состоят из нескольких липидных белков.
394

3.21. ДВОЙНОЙ ЭЛЕКТРИЧЕСКИЙ СЛОЙ
К а к было отмечено ранее, на границе двух ф аз возникает
двойной электрический слой. Строение двойного электрическо­
го слоя влияет на адсорбцию поверхностно-активных веществ
и ионов, а также на скорость процессов, протекающих на гра­
нице двух фаз. Наиболее изучено строение двойного электриче­
ского слоя на границе «металлический эл е к тр од —раствор», так
как многие важные технологические процессы идут на у казан­
ной границе (электроосаждение металлов, электросинтез, рабо­
та химических источников тока, коррозия металлов и др.) . Д л я
протекания процесса на электроде необходимо, чтобы заряжен­
ная частица (ион) проходила бы через двойной слой в направ­
лении к электроду или в обратном направлении. Поэтому двой­
ной электрический слой влияет на закономерности протекания
электрохимических реакций. Как уже обсуждалось ранее, при
погружении металлического электрода в раствор его соли проте­
кают обменные процессы между атомами и катионами металла,
в результате которых на границе «электрод—раствор» на по­
верхности металла возникает положительный или отрицатель­
ный заряд, а со стороны раствора у границы контакта возникает
равный по абсолютной величине, но противоположный по зна­
ку зар яд , создаваемый анионами или соответственно катионами
раствора.
Изменяя концентрацию катионов металла в растворе можно
изменять заряд электрода и скачок потенциала между метал­
лом и раствором. Другим способом изменения заряда электрода
и скачка потенциала на границе «электрод —раствор», является
присоединение электрода к источнику постоянного тока, к ко­
торому также присоединен другой вспомогательный электрод.
Изменяя напряжение на электродах можно создавать опреде­
ленный заряд на исследуемом электроде. При этом, как пра­
вило, кроме изменения за р яд а на обоих электродах протекают
окислительно-восстановительные реакции: на электроде, соеди­
ненном с отрицательным полюсом батареи (катод) протекает
процесс (или процессы) восстановления, а на другом электро­
де, соединенном с положительным полюсом батареи (анод) идет
процесс окисления.
Электроды, у которых в широком интервале потенциа­
лов при определенных условиях электрический ток затр а­
чивается только на изменение зар яда электрода, называют­
ся идеально поляризуемыми электродами.
395

Таков, например ртутный электрод. Ртутный электрод имеет
дополнительные особенности, которые позволили использовать
его, как эталон при изучении строения двойного электрического
слоя — однородную и легко обновляемую поверхность. Послед­
нее очень важно, так как примеси, которые могут появиться в
растворе, в особенности органические вещества, влияют на стро­
ение двойного электрического слоя. Если использовать уравне­
ние д л я изотермы адсорбции Гиббса применительно к ртутному
электроду, то можно после ряда преобразований получить соот­
ношение меж ду поверхностным натяжением ртути и ее зарядом:
do
q ~ rf<p*
где (р — разность потенциалов между измеряемым потенциа­
лом Е и потенциалом незаряженной поверхности
электрода:
ср = Е - Е ^ у Потенциалы Е и 2?(0) измеряют относительно элек­
трода сравнения. Уравнение (3.87) выполняется при постоянном
составе раствора и постоянной температуры и носит название
уравнения Липпмана (1875). Зависимость поверхностного натя­
жения ртути от потенциала электрода (ропределяется так назы­
ваемой электрокапиллярной кривой, которая представляет со­
бой перевернутую параболу (рис. 3.31).
Потенциал, отвечающий максимуму поверхностного на­
тяжения металла, соответствует q = 0 и называется потен­
циалом нулевого заряда, ср(0).
Наклон касательной, проведенной для кривой ( а - (р) соот­
ветствует за р яду поверхности ртути на границе с раствором.
Как видно из рисунка, при смещении потенциала электрода в
отрицательную область потенциалов поверхность рту ти приоб­
ретает отрицательный заряд, величина которого возрастает при
дальнейшем уменьшении потенциала. При смещении потенци­
ала ртути в положительную область потенциалов относитель­
но потенциала нулевого зар яда возрастает положительный за­
ряд поверхности ртути, о чем свидетельствует увеличение на­
клона касательной. На рис. 3.31 приведена кривая 2, отобража­
ющая зависимость заряда поверхности (точнее плотности заря­
да К л/м2) от потенциала. Дифференцируя заряд по потенциа­
лу, получим значение емкости двойного электрического слоя на
границе «ртуть —раствор» при заданном потенциале (так назы­
ваемая дифференциаьная емкость). Возвращаясь к уравнению
(3.87), получим:
_
dq_ d2o
dcp
g?(p2 ’
396

т. е. емкость двойного электриче­
ского слоя — это вторая про­
изводная поверхностного натяже­
ния по потенциалу. Схематиче­
ское изображение электрокапил-
лярной кривой и зависимость ем­
кости двойного электрического
слоя от потенциала приведены на
рис. 3.32. Как видно из этого ри­
сунка, зависимость (С7—<р) име­
ет сложную форму. Д л я объясне­
ния такого рода зависимости при­
влекаются модельные представ­
ления о двойном электрическом
слое. Впервые теория строения
двойного слоя была предложена
Г. Гельмгольцем в 1853 г. Соглас­
но этой модели двойной электри­
ческий слой состоит из двух слоев
зарядов. Один слой зарядов рас­
полагается в плоскости поверхно- Рис. 3.31. Электрокапилляр-
сти металла. Другой слой проти- пая кривая (а — q )(l) и кривая
воположных по знаку зарядов на- «плотность заряда q — потен-
ходится в растворе на расстоянии,
циал а» (2)
близком к размеру диаметра молекулы воды от первого слоя. З а­
ряды в обоих слоях равномерно размыты вдоль плоскости гра­
ницы «металл —раствор». Плоскости, в которых располагаются
центры зарядов, можно уподобить плоскостям конденсатора, ем­
кость которого согласно представлениям электростатики может
быть выражена следующим соотношением:
C=4i5'
(3.88)
где е — диэлектрическая проницаемость; 8 — толщина двойного
электрического слоя. Емкость связана с плотностью заряда q по­
верхности металла и разностью потенциалов ф на границе «ме­
талл-раствор» соотношением:
£
шга q=
(3.89)
С=-
<р
"
4я8
Комбинируя уравнения (3.89) и (3.87), после интегрирования по­
лучим зависимость поверхностного натяжения (в общем случае
поверхностной работы) от потенциала:
° =0тах-8^ф2’
397

“ф
Рис.
где о т ах — константа интегриро­
вания. При<р=0, т.е. при по­
тенциале нулевого за р яд а (п.н.з.)
G = Стах- При смещении потен­
циала ртутного электрода в об­
ласть положительных или отри­
цательных потенциалов относи­
тельно п.н.з. поверхностное на­
тяжение ртути снижается, что
находится в качественном согла­
сии с рис. 3.31. Таким образом,
теория Гельмгольца находится в
качественном согласии с экспе­
риментальными данными. Одна­
ко, по теории Гельмгольца, за­
висимость заряда от потенциала
должна быть линейной, что про­
тиворечило форме кривой «заряд —потенциал», представленной
на рис. 3.31.
В результате хаотического теплового движения молекул рас­
творителя и ионов в растворе, а такж е электростатического от­
талкивания одноименно заряженных ионов, ионная обкладка
конденсатора приобретает д иффузное (размытое) строение, т. е.
часть сольватированных ионов отходит непосредственно от по­
верхности электрода вглубь раствора на некоторое расстояние.
Распределение ионов подчиняется уравнению Больцмана. Д ля
1,1-зарядного электролита концентрация катионов будет равна:
3.32. Электрокапилляр-
ная кривая:
1 — зависимость дифференци­
альной емкости от потенциала;
2—зависимость двойного слоя от
потенциала
с+=с+е
Fyx
"ВТ
а анионов:
~,
с_=с°екг,
где \\fx — потенциал в диффузной части двойного слоя на рас­
стоянии х от поверхности электрода; с° — концентрация в объ­
еме раствора. При отрицательном заряде поверхности \|/ имеет
отрицательный знак.
На рис. 3.33 приведено распределение концентрации ионов в
таком случае. Из рисунка видно, что концентрация ионов, ко­
торые заряж ены противоположно заряду поверхности металла,
уменьшается по мере удаления от поверхности. С другой сто­
роны, концентрация ионов, имеющих заряд того же знака, что
и заряд поверхности, увеличивается, и на каком-то расстоянии
от электрода концентрации катионов и анионов выравнивают­
ся и соответствуют распределению ионов в объеме раствора. За­
штрихованная часть на рисунке, выраженная в единицах заряда
398

(с+ - cJ)zF, представляет со­
бой заряд ионной части двой­
ного слоя. Толщина диффуз­
ной части двойного слоя умень­
шается с ростом отрицательно­
го или положительного заряда
электрода. С другой стороны,
с ростом температуры раство­
ра хаотическое движение моле­
кул и ионов усиливается и д иф­
фузная часть двойного слоя уве­
личивается. Эти представления
были развиты Г. Гуи (1910) и
Д. Чапменом (1913). Таким об­
разом заряд поверхности элек­
трода электростатически притя­
гивает ионы противоположного знака и отталкивает одноимен­
ные. Упорядоченному расположению ионов, вызываемому элек­
тростатическим взаимодействием с электродом, препятствует
тепловое движение. Подобная картина наблюдается в раство­
рах электролитов при образовании ионной атмосферы вокруг
иона противоположного знака. Эффективный радиус ионной ат­
мосферы, который определялся как величина i также увели-
А/
чивается с разбавлением раствора и ростом температуры (см.
уравнение (3.21)). Д иффузн а я часть двойного слоя подобна по
строению ионной атмосфере. Теория Гуи —Чапмена достаточно
хорошо описывала свойства двойного электрического слоя в ра з­
бавленных растворах. Однако теория рассматривала ионы, как
частицы точечного размера, т. е. ионы могли подходить к по­
верхности на бесконечно близкое расстояние, как это видно из
рис. 3.33. На самом деле ионы не могут приблизиться к электро­
ду на расстояние меньшее их размера.
Дальнейшее развитие представлений о строении двойного слоя
было развито О. Штерном (1924). Теория Ш терна сочетала пред­
ставления Гельмгольца и положения теории Гуи —Чапмена. По
Штерну, часть ионов противоположных по знаку заряда поверх­
ности электрода непосредственно подходит к электроду и обра­
зует плотную часть ионного слоя (слой Гельмгольца). Центры
этих ионов удалены на расстояние 5, равное среднему радиусу
ионов. Плотность зарядов в слое Гельмгольца р авна q\. Потенци­
ал раствора на расстоянии 5 будет равен некой величине \|/i (пси-
прим-потенциал). Часть ионов, находящихся в диффузном слое
Рис. 3 .33 . Распределение концен­
трации ионов у отрицательно за­
ряженного электрода по теории
Гуи —Чапмена
399

и участвующих в тепловом
движении, находится на рас­
стоянии х > 5 от поверхности.
Плотность заряда этих ионов
на 1 см2 поверхности элек­
трода равна q2 ) а абсолютная
величина за р яд а поверхности
электрода равна заряду ионов
в ионной части двойного слоя:
9 = -(91 +92)-
Рис. 3.34. Изменение потенциала
в плотной и диффузной частях
двойного слоя. Линия АА' — гра­
ница между плотным и диффуз­
ным слоем
В плотной части двойного
слоя потенциал меняется ли­
нейно с рас- стоянием. Изме­
нение потенциала в диффузи­
онном слое происходит по тео­
рии Гуи —Чапмена (рис. 3.34).
При этом теория Ш терна пред­
сказы вала возможность специфической адсорбции ионов, т. е.
химического взаимодействия поверхности металла с адсор­
бированными ионами. При специфической адсорбции ионов
заряд ионов в плотной части двойного слоя может пре­
вышать по абсолютной величине заряд поверхности элек­
трода. В этом случае избыточный заряд плотной части
двойного слоя компенсируется противоионами в его диф­
фузной части. Форма зависимости потенциала от поверхно­
сти электрода до объема раствора существенно изменяется
(рис. 3.35). Двойной электри-
+э
э
+э
э
Рис. 3.35. Строение двойного слоя
при специфической адсорбции
анионов (а) и изменение потенци­
ала от расстояния до электрода
(6) (X, — толщина диффузной
части двойного слоя)
ческий слой при проведении
измерений его емкости мо­
делируется с помощью элек­
тротехнической схемы (эквива­
лентная схема). Для двойно­
го электрического слоя, име­
ющего плотную и диффуз­
ную часть, используется схе­
м а последовательного соедине­
ния двух конденсаторов, со­
ответствующих емкости плот­
ной Спп и диффузной части Ся
двойного электрического слоя.
Если две емкости соеденить по­
следовательно, то общая ем­
кость С станет равной:
400

1_1J_
c~C„„+CA
Приведя правую часть соотношения (3.90) к общему знаменате­
лю и выразив общую емкость С в явном виде, получим:
С=
Сплс д
Сил+Сд
(3.91)
Как было отмечено ранее, при снижении заряд а электрода про­
исходит расширение диффузной части двойного слоя (особенно
в разбавленных растворах), что соответствует увеличению рас­
стояния между обкладками конденсатора как модели емкости
диффузной части двойного слоя. Последнее приводит к суще­
ственному уменьшению Сл , согласно уравнению (3.88), если рас­
стояние между обкладками конденсатора 8 будет увеличивать­
ся. В этом случае Сил
СА и из уравнения (3.91) следует, что
С ~ Сд, т. е. емкость равна емкости диффузной части двойного
слоя. Диффузная часть двой­
ного слоя наиболее размы­
т а (т. е. пластины конденсато­
ра, моделирующего диффуз­
ную часть, раздвинуты) и Сд
минимальна, и, следователь­
но, С имеет минимум при
потенциале нулевого заряд а
(п.н .з .) электрода (q = 0)
(рис. 3.36). Более высокая ем­
кость при положительных по­
тенциалах относительно п.н.з.
(~ 40 мкф/см2) объясняет­
ся тем, что расстояние меж­
ду электродом и центрами за­
ряда анионов примерно в два
раза меньше, чем расстояние
между электродом и центрами
зарядов катионов, адсорбиру­
ющихся при более отрицатель­
ных потенциалах.
Таким образом, по мини­
муму емкости, измеренной в
разбавленных растворах мож­
но определять величину п.н.з.,
которая зависит от природы
металла. В справочниках име-
С, мкф/см2
ДО)=-0,2В
Рис. 3.36. Зависимость емкости
ртутного электрода от потенциала
в растворах КС1 (потенциал изме­
рен по стандартному водородному
электроду):
1-0,1М;2-0,01М;3-0,001М
401

ются таблицы значений п.н.з. д л я разных металлов, которые из­
мерены относительно стандартного (нормального)водородного
электрода.
Снижение емкости такж е наблюдается при адсорбции орга­
нических веществ, так как молекулы органических веществ уве­
личивают расстояние между поверхностью электрода и ионной
частью двойного электрического слоя (рис. 3.37), а также умень­
шается диэлектрическая постоянная £.
Измерение емкости двойного слоя может производиться с по­
мощью мостовой схемы. В этом случае в одно из плеч к пе­
ременному сопротивлению последовательно присоединяется пе­
ременная емкость. Переменным сопротивлением измеряется со­
противление раствора между электродами (исследуемым и вспо­
могательным), а значение скомпенсированной емкости отвеча­
ет емкости двойного слоя дл я идеально поляризуемого электро­
да. Представления о строении двойного слоя получили развитие
в дальнейших работах А. Н. Фрумкина, О. А. Есина, Д . Грэма,
Р. Парсона, Б . Б . Дамаскина, Б . М. Графова, М. А. Воротынцева,
Г. А. Тедорадзе, О. А. Петрия и др.
В отличие от металла внутри полупроводников концентра­
ция носителей заряда очень низка, а его диэлектрическая по­
стоянная имеет конечное значение. Согласно зонной теории в
полупроводниках имеется два вида носителей тока — электро­
ны в зоне проводимости (п) и
дырки (р) в валентной зоне:
по=Ро-
Концентрация этих частиц за­
висит от природы полупровод­
ника. Электрону следует сооб­
щить энергию д ля перехода из
валентной зоны в зону прово­
димости. Величина этой энер­
гии определяется шириной за­
прещенной зоны, которая зави­
сит от природы вещества. Обыч­
но концентрация электронов (ды­
рок) составляет примерно 1Сг3 —
10х° частиц/см3. В металличе­
ских электродах концентрация
электронов значительно выше и
составляет ~ 1022 частиц/см3.
Весь заряд на металлическом
0
-
)
0 (Г~
О
-)
О(+-)
О<+-)
О(+-)
ОО*--)
Рис. 3.37. Схема строения
двойного слоя при адсорбции
полярных молекул органи­
ческого вещества. Справа
от линии (плоскость заряда)
условный заряд поверхности
402

электроде сконцентрирован в
поверхностном слое порядка
10-8 см. В полупроводнике за­
ряды, компенсирующие за р яд
ионной части двойного слоя,
распределяются на расстоянии
1СГ4 см. Эта величина на один-
два порядка больше по срав­
нению с толщиной диффуз­
ной ионной части двойного
слоя (рис. 3.38). Распределение
электронов и дырок в полупро­
водниках зависит от величины
Рис. 3.38. Схема распределения
потенциала на границе «полупро­
водник —раствор»
потенциала в поле двойного электрического слоя и подчиня­
ется тем же закономерностям, что и распределение ионов 1,1-
валентного электролита в диффузной части двойного слоя по
теории Гуи —Чапмена:
Fyx
RT;
Fyx
Рх=РоеRT.
Общая плотность за ряд а на 1 см2 полупроводника равна:
Я= -2Лл/nosh
,
гдеА=
гЛТ
2к
; — падение потенциала в ф а зе полупроводни­
ка. Скачок потенциала на границе «поверхность полупроводни­
к а —раствор» определяется из соотношения
=
+V1 +V2.
Эквивалентной электрической моделью границы «полупро­
водник-раствор» является цепь из трех последовательно со­
единенных конденсаторов, которые соответствуют емкости Cs в
самом полупроводнике, емкости С\ плотной части двойного слоя
и емкости С2 его диффузной части. Таким образом, в согласии
с теорией электрических цепей общая емкость на границе «по­
лупроводник-раствор» будет равна:
i_=j_ i_
С~ Cs+C~1+C^'
Из-за низкой концентрации электронов в полупроводнике ве­
личина Cs является малой по сравнению с С\ и С^- Обычно
403

С3 —0 ,0 1 ... 1 мкФ/см2. Поэтому емкость на границе «полупро­
водник-раствор» будет равна:
С~С3.
(3.92)
Из соотношения (3.92) следует, что состав раствора мало влияет
на величину емкости границы «полупроводник —раствор».
3.22. ОСНОВЫ ЭЛЕКТРОХИМИЧЕСКОЙ КИНЕТИКИ
Раздел электрохимии, изучающий скорость и механизм
электрохимических реакций, называется электрохимиче­
ской кинетикой.
В предыдущем разделе рассматривались электродные потен­
циалы в электрохимических системах в равновесных условиях,
когда величина тока в гальваническом элементе при измерении
ЭДС была равна нулю. Однако в реальных условиях при проте­
кании электрического тока при работе гальванического элемен­
та или электролизе равновесия нарушаются, и энергия хими­
ческой реакции не равна электрической энергии. Согласно вто­
рому началу термодинамики работа химической реакции пол­
ностью превращается в электрическую только при протекании
обратимых процессов. При электролизе затраченная электриче­
ская энергия больше, чем энергия протекающей химической ре­
акции на катоде и аноде. Последнее связано с тем, что часть
электрической энергии превращается в тепловую при прохожде­
нии тока через раствор и, кроме того, происходит отклонение по­
тенциала электродов (катода и анода) от равновесных значений.
Превышение потенциала электрода над равновесным
значением при прохождении электрического то к а называют
поляризацией или перенапряжением процесса.
Поляризация будет увеличиваться при увеличении плотности
тока, т. е. силы тока, приходящегося на единицу площади элек­
трода. При протекании электрохимической реакции на катоде
или аноде можно выделить несколько стадий: подвод ионов (ве­
щества) к электроду, ра зряд ионов с присоединением электро­
нов (катод) или с потерей электронов (анод) и отвод продуктов
реакции от электрода в глубь раствора. Последняя стадия мо­
жет быть видоизменена: осаждение металла на катоде, образо­
вание оксида на металлическом аноде, выделение газообразных
404

продуктов на катоде или аноде. Процессы могут быть осложне­
ны протеканием химических реакций в растворе, предшествую­
щих стадии разряда. Рассмотрим более простые случаи, когда
скорость процесса тормозится скоростью диффузии, т. е. скоро­
стью подвода вещества к электроду, или когда скорость процес­
са лимитируется непосредственно скоростью разряда частицы
на электроде, а скорость подвода вещества к электроду намного
больше скорости разряда.
3.23. ДИФФУЗИОННАЯ КИНЕТИКА
Диффузионная кинетика —раздел электрохимии, изуча­
ющий скорость доставки реагирующих частиц (ионов, моле­
кул) из раствора к поверхности электрода или отвода про­
дуктов реакции от электрода в глубь раствора и их распре­
деление.
Величина отклонения потенциала электрода от равновес­
ного значения из-за уменьшения концентрации реагирую­
щего иона или вещества в приэлектродном пространстве на­
зывается концентрационной поляризацией или концентра­
ционным перенапряжением.
При быстром разр яде ионов на электроде концентрация их
в приэлектродном пространстве уменьшается и пополняется за
счет диффузии ионов из раствора. Скорость реакции измеря­
ется в величинах плотности тока, А /м2 или мА/см2. Помимо
диффузии ионы могут перемещаться к электроду под действи­
ем электрического поля, создаваемого омическим падением на­
пряжения (разностью потенциалов) в электролите (явление м и ­
грации). Чтобы избежать этого осложнения, измерение скорости
диффузии проводится в присутствии индифферентного электро­
лита, т. е. электролита, ионы которого не участвуют в реакции,
но являются основными переносчиками электрического за р яд а
через раствор.
Перемещение заряженных частиц в электрическом поле,
которое создается по причине омического падения напряже­
ния при прохождении через раствор электрического тока,
называется миграцией.
Другим осложнением при изучении диффузии частиц явл я­
ется конвекция электролита. В результате изменения плотно­
сти раствора в приэлектродном пространстве при протекании
электрохимической реакции или неравномерном разогревании
405

Си
Со
/
О
/
*
Р ис. 3.39. Схема ячейки и распре­
деление концентрации реагирую­
щего вещества или иона, напри­
мер ионов Си2+, в диффузионном
слое при стационарной диффузии
Ф
электролита при прохождении
электрического тока, а так-
.
>щц. }Щ ж е возможном выделении пу-
Л
Щ*
зырьков газа с поверхности
электрода, происходит пере­
мешивание раствора. Конвек­
цию можно вызвать искус­
ственным путем, перемешивая
электролит. В этом случае об­
ласть диффузионного слоя со­
кращается, поступление реаги­
рующего вещества к электро­
д у увеличивается, и то к реак­
ции возрастает. Следует отме­
тить, что даже при искусствен­
ном перемешивании часть слоя
жидкости, находящегося в приэлектродном пространстве, не во­
влекается в конвективное движение. В этой области перенос ве­
щества подчиняется законам диффузии. Можно создать усло­
вия, когда явлением конвекции можно также пренебречь.
На рис. 3.39 представлена схема ячейки, в которой мож­
но исследовать диффузионные процессы. Рассмотрим конкрет­
ный пример — электроосаждение меди на катоде из раствора
Cu(N0 3 )2 + KNO3 . В левой части ячейки находится капилляр, в
торец которого плотно вставлен медный электрод. Электрод по­
мещен таким образом, что не происходит затекания электроли­
та между стенками капилляра и боковой поверхностью медного
электрода. В капиллярной трубке будет локализоваться д иффу­
зионный слой. Другим концом капиллярная трубка припаяна
к широкой цилиндрической части ячейки, в которой находится
второй электрод (анод) и производится интенсивное перемеши­
вание раствора. Таким образом у этого конца капилляра, кон­
центрация ионов Си2+ остается постоянной и равной концентра­
ции раствора с. Избыток индифферентного электролита (KNO3)
и наличие капилляра препятствуют влиянию миграции и кон­
векции на процесс диффузии.
В данном случае диффузионный слой растягивается на всю
длину I капиллярной трубки, и концентрация ионов Си2+ рав­
номерно уменьшается до величины сх у поверхности медного
электрода. Распределение концентрации Си2+ вдоль капилляра
представлено на рис. 3.39. Поток диффузии вещества (иона) че­
рез единицу площади сечения трубки в единицу времени соглас­
но первому закону Фика в несколько упрощенной форме опре­
деляется уравнением:
406

_
„dc
dc
dx
где D — коэффициент диффузии (в данном случае C ir+);
изменение концентрации (градиент концентрации) в точке, на­
ходящейся на расстоянии х от электрода. Предполагается, что
диффузия идет только по оси т, т. е. перпендикулярно к поверх­
ности электрода. К ак уже отмечалось выше, скорость реакции в
электрохимии измеряется в единицах плотности тока. В соответ­
ствии с законом Фарадея получим в приэлектродном простран­
стве (х = 0):
dc
г= nF(IA)x=o =nFD—
.
ах
Диффузионный ток — это ток, величина которого опре­
деляется скоростью транспорта реагирующего вещества
(иона) к поверхности электрода.
Если предположить, что катодный ток, т. е. ток, проходящий
через катод, имеет положительное значение, то при равномерном
падении концентрации реагирующего вещества вдоль капилляра
длиной I
dc
со Сх
—
=const=—-—
.
dx
l
Тогда ток диффузии будет равен
i=n
F
D
(3.93)
При увеличении плотности тока на электроде разность cq~ cx
возрастает, и концентрация иона у поверхности электрода пада­
ет до 0 (сх = 0). В системе возникает предельный ток, определя­
емый соотношением
inp=n
F
D
(3.94)
Разделив уравнение (3.93) на уравнение (3.94), получим после
некоторых преобразований:
сх __^
i
Со
Znp
Выразив в явном виде величину тока, имеем
г=гпр 1
Со
(3.95)
407

Следует отметить, что не нужно путать два понятия — диффу­
зионный слой и диффузный слой.
Диффузионным слоем называют слой жидкости у по­
верхности электрода, в котором наблюдается изменение
концентрации реагирующего вещества или продуктов реак­
ции из-за медленной стадии подвода вещества к электроду
или отвода продуктов реакции вглубь раствора.
Диффузны м слоем называют часть двойного электри­
ческого слоя, представляющего объем, в котором располо-
гаются ионы, частично компенсирующие за ряд электрода,
но из-за теплового движения не входящие в плотную часть
двойного электрического слоя.
Ионы притягиваются к электроду за счет электростатиче­
ского взаимодействия, но несколько удаляются от плотной ча­
сти двойного слоя из-за теплового движения гидратированных
ионов и молекул растворителя. Толщина диффузного слоя на
несколько порядков меньше толщины диффузионного слоя. По­
рядок толщины диффузного слоя составляет обычно дл я не
очень низких концентраций 1—10 нм, а толщина диффузион­
ного слоя 10“2 —10~3 см.
Свяжем величину диффузионного тока с потенциалом элек­
трода. Так к а к скорость электрохимической реакции очень высо­
ка, т. е. р а зр яд иона (вещества) на электроде происходит быстро,
то потенциал электрода будет определяться приповерхностной
концентрацией иона Си2+. В этом случае, по уравнению Нернста,
г,
^
яг,
Е —Е$+ ——InCz,
zF
где z = 2 для C u2+. В отсутствие электрического тока:
ЕСТ
Ер=Ев+—~
In со-
zF
Различие в концентрациях в приэлектродном слое при протека­
нии электрического тока вызывает изменение потенциала элек­
трода:

Подставив уравнение (3.95) в
получим:
(3 97)
Из уравнения (3.97) следует,
чтоприг=О,АЕ=0,апри
максимальном предельном токе
г= гпр,АЕ —♦оо. Как уже было
отмечено, А Е является концен­
трационной поляризацией или
концентрационным перенапря­
жением. Величина предельного
тока будет возрастать с увели­
чением концентрации р азр яж а­
ющегося иона (вещества), при
перемешивании раствора (уменьшается толщина диффузионно­
го слоя I), а также с ростом температуры раствора, так как
при этом увеличивается коэффициент диффузии ионов. Коли­
чественная связь между предельным диффузионным током и
концентрацией ионов в растворе (уравнение (3.94)) лежит в ос­
нове полярографического метода количественного и качествен­
ного анализа.
Полярографический метод с капающим ртутным электро­
дом был предложен Я. Гейровским в 1922 г. Ртутный капельный
электрод представляет собой длинный узкий капилляр, через
который вытекает ртуть в раствор. На конце капилляра образу­
ются и отрываются небольшие капли ртути (диаметр 1 —2 мм).
Поляризация капельного электрода осуществляется по отноше-
Рис. 3.41. Зависимость тока электрохимической реакции от времени
на капельном ртутном электроде:
1 — измерения с помощью осциллографа; 2 — измерения с помощью галь­
ванометра с большим периодом собственных колебаний; 7ср — средний ток;
т — период жизни капли
Рис. 3.40. Схема электролитиче­
ской ячейки для проведения по­
лярографических измерений:
АК — аккумулятор; К — ртутный
капельный электрод; Р — раствор;
А — ртутный анод; т А — миллиам­
перметр
409

нию к вспомогательному ртутному электроду большой площади,
расположенному на дне ячейки. При постоянном потенциале ка­
пельного электрода (рис. 3.40) с ростом ртутной капли будет
возрастать ток, так как увеличивается поверхность капли. При
отрыве капли ток падает практически до нуля и затем опять
начинает расти. На рис. 3.41 дана зависимость тока от времени
роста капли (т — период жизни капли). Измеряемый то к с помо­
щью гальванометра с большим периодом собственных колебаний
представляет собой некоторый средний ток / ср. Так как площадь
вспомогательного электрода в 100 —500 раз больше ртутной кап­
ли, то при достаточно высокой концентрации индифферентного
электролита и малом расстоянии между электродами изменение
напряжения, подаваемого на полярографическую ячейку, при­
водит к изменению потенциала практически только капельного
электрода. Зависимость тока от потенциала называется поля­
ризационной кривой. При более точных измерениях потенциал
ртутной капли измеряется относительно электрода сравнения.
Теория капающего ртутного электрода достаточно сложна, так
как кроме изменения тока во времени при росте капли нужно
учесть встречное движение поверхности капли к фро нту диф­
фузии. Не останавливаясь на детальном анализе изменения тока
при росте капли, приведем конечные уравнения:
ГГX?/^1
ЛТ/ПрI
Е=Е0+— 1п— +
—
\п
zFD0zF
I
= E1/2
д т /пр-/
+— In—S -
-
-,
zF
I’
(3.98)
^
^
RTDr
где Ei/2~ Eq-\
---- —
In —-----потенциал полуволны, который xa-
zF
Dо
рактеризует природу разряжаемого иона (вещества) д л я реак­
ции: Ох + ze ^ Red. Если коэффициенты диффузии Ох и Red
близки по величине, то Е ±/2 —Do, т. е. соответствует стандартно­
му равновесному потенциалу окислительно-восстановительной
системы. Иными словами Е г/2 характеризует природу разр яж а­
ющейся частицы. Из уравнения (3.98) выразим ток в явном виде:
I=Yfp,
(3.99)
z F(E-El/2)
гдеР=е
RT . Уравнение (3.99) называется уравнением по­
лярографической волны Гейровского —Ильковича. Форма ноля-
рограммы приведена на рис. 3.42. По величине предельного тока
410

на полярограмме можно опре­
делить концентрацию анализи­
руемого иона (вещества).
Дл я количественного опре­
деления концентрации получа­
ют несколько полярограмм в
растворах с разными известны­
ми концентрациями (рис. 3.43,
а), на основе которых строят
калибровочную кривую «пре­
дельный ток —концентрация »
(рис. 3.43, б). Затем, измерив
поляризационную кривую в рас­
творе с неизвестной концентра­
цией иона (вещества) по вели­
чине предельного тока и калибровочной кривой, определя­
ют неизвестную концентрацию Сх - В современной поляро­
графии применяются такж е твердые вращающиеся и стаци­
онарные металлические (серебро, золото, платина и др.) и
углеродные электроды. Н иж няя граница определяемых кон­
центраций составляет 1СГ5 • ••10“6 М. Эта граница лимитиру­
ется током заряжения двойного электрического слоя и раз­
рядом примесей. Типичная полярограмма, приведенная на
рис. 3.44, показывает возможность количественного и ка­
чественного определения состава раствора при одновремен­
ном присутствии нескольких катионов. Составлены специаль-
Т
Рис. 3.42. Идеальная форма по­
дпрограммы после введения по­
правки на ток заряжения:
/пр — предельный диффузионный
ток; Ei/2 — потенциал полуволны
а
б
Рис. 3.43. Идеальные подпрограммы для разных концентраций разря­
жающегося катиона (а) и калибровочная кривая (б)
411

ные таблицы, в которых при­
ведены потенциалы полуволн
{Ei/ 2) для неорганических и ор­
ганических ионов и веществ. Ис­
пользуя эти таблицы, по потен­
циалу полуволны неизвестно­
го вещества (иона) можно сра­
зу определить качественный со­
став раствора.
В настоящее время поля­
рографический метод получил
широкое развитие: появились
различные модификации мето­
да, связанные с различными ре­
жимами поляризации электро­
да, предварительным накопле­
нием (осаждением) изучаемого вещества на электроде, услови­
ями перемешивания раствора и т. п. Это дало возможность ис­
пользовать данный метод не только для качественного, но и для
количественного определения многих неорганических и органи­
ческих ионов в растворах.
1,5 ЕуВнас кэ
Рис. 3.44. Полярограммы раство­
ра, содержащего 1 0 _3 моль-экв/л
Pb2+, Cd2*, Zn2\ Мп2+ в при­
сутствии индифферентного элек­
тролита 1 М КС1
3.24. ЭЛЕКТРОХИМИЧЕСКАЯ КИНЕТИКА
Рассмотрим другой крайний случай протекания электрохи­
мической реакции на электроде, когда скорость процесса лими­
тируется непосредственно р азрядом или ионизацией вещества
(иона) на границе «электрод—раствор» и в целом определяет
скорость электрохимического процесса. В этом случае строение
двойного электрического слоя оказывает существенное влияние
на скорость процесса. Теория, к оторая описывает кинетические
закономерности переноса заряженных частиц через границу раз­
дела «электрод—раствор», носит название теории замедленного
разряда.
Изменение потенциала электрода относительно равно­
весного потенциала при протекании тока, обусловленное
медленностью стадии разряда-ионизации, называется элек­
трохимической поляризацией или перенапряжением разря-
Да (Л)-
Рассмотрим применение теории к реакции на электроде пер­
вого рода д л я системы «металл —ион металла» в растворе:
412

Mz++ze^M
Соответственно скорость прямой реакции (катодного восстанов­
ления) будет равна:
—
Е
гк= кгс е
~
Ш
(3.100)
а обратной анодной реакции:
—
Е
ia=k2e
~
(3.101)
где гк и га —плотности тока; Е а —энергия активации катодной
и анодной реакции; с — концентрация иона M z+ в приэлектрод-
ном слое. При высокой концентрации индифферентного элек­
тролита щ будет близок к нулю, щ — потенциал соответствует
потенциалу раствора на расстоянии, равном радиусу иона, мак­
симально приближенного к плоскости электрода. Примем это
упрощающее расчеты допущение. Тогда концентрации ионов в
приэлектродном слое и объеме раствора одинаковы. Концентра­
ция атомов металла (или активность) в уравнении (3.101) яв л я­
ется постоянной и входит в константу к2. Потенциал электрода
влияет на энергию активации реакции. При прохождении катод­
ного тока от внешнего источника тока через электрод потенциал
электрода смещается на величину А Е ) которая, как было опре­
делено, является перенапряжением реакции:
АЕ =т]=Ер -Е .
Полагают, что перенапряжение катодного процесса имеет по­
ложительное значение. При этом энергия активации катодного
процесса уменьшается на величину a z F r \, а анодного процесса
увеличивается на РzFv[. Величины аир—коэффициенты пе­
реноса, а + Р = 1. Коэффициенты переноса характеризуют до­
лю влияния потенциала электрода на энергию активации катод­
ного и соответственно анодного процессов. Уравнения (3.100) и
(3.101) будут иметь вид:
(zM*.
ik=k1ce\Kr кг),
(3.102)
(-Е . ftmFN
ia=k2ce\RT RT).
(3.103)
ПриЕ=ЕрвеличинаГ|=0итокиik=га=го,гдего—ток
обмена. Тогда уравнения (3.102) и (3.103) примут вид:
(3.104)
azr\F
гк-гоеft
413

ia—
RT■
(3.105)
Из уравнений (3.104) и (3.105) следует, что с ростом перенапря­
жения катодного процесса возрастает катодный ток и снижается
анодный ток. Ток, протекающий через электрод равен:
azr\F pzr|F\
i=ik-ia=io(e кг —e~RT J.
RT
(3.106)
При низких значениях T| , когда | Т| |< -=г , т. е. при Т| < 0,025 В.
Г
Экспоненты можно разложить в р яд и, ограничившись двумя
первыми слагаемыми ряда, получим*:
или
.
.
zF
,=,0яг,>
КГi
Г| « ———.
zF iq
(3.107)
(3.108)
Как это видно из уравнения (3.108), при низких перенапряже­
ниях т| линейно растет с ростом тока. Уравнение (3.108) напо­
минает закон Ома. В этом случае величина
RT
rp
_______
zFiо
называется сопротивлением разряда-ионизации. Используя урав­
нение (3.108), можно определить та к обмена по наклону зависи­
мости Г| —г. При прохождении внешнего тока г перенапряжение
при г = const будет тем меньше, чем больше ток обмена. Обыч­
но электроды сравнения, относительно которых измеряется по­
тенциал электрода, имеют большие токи обмена. При высоких
RT
значениях Т| » —— можно пренебречь вторым слагаемым урав-
zF
нения (3.106):
(3.109)
i=гоеRT,
Известно, что показательная функция разлагается в ряд:
е'*
хх*х°
х11
■1+—+ —+ —+•-■ч--- .
1!2!3!
п!
При малых значениях х у т. е. когда |rj| < -р - , можно ограничиться первыми двумя
членами ряда:
«2ЧГ
otzi]F
PzbF
еяг ~1+•
еЯТ
1--
ВТ’
ВТ
Подставив эти выражения в уравнение (3.106) и имея в виду, что a + p = 1, получим
уравнение (3.107).
414

Прологарифмировав уравнение (3.109) и выразив в явном ви­
де перенапряжение, получим:
Г|= -
2,зоздг
azF
lgг0+
2 ,303ДГ
аzF
lg г.
Введя обозначения а = —
303RT
azF
lgг0иb=
2,303R T
-------—
— , получим:
azF’J
Т|=а+bigг.
(3.110)
Уравнение (3.110) впервые было получено И. Тафелем (1905)
при изучении реакции выделения водорода и носит название
уравнения Тафеля. Константа а зависит от природы реакции,
природы электрода, состава раствора и температуры, а констан­
та b зависит от числа электронов, принимающих участие в ре­
акции, и от температуры. Если учесть, что реакция протекает
в более разбавленных растворах, то скачок потенциала в плот­
ной части двойного слоя, где находится центр разряжающейся
частицы, будет равен <р—vjfi, и уравнение д ля тока (3.106) бу­
дет иметь более сложную форму, особенно если учесть, что при
разряде частиц возможна адсорбция на поверхности продуктов
(промежуточных частиц) реакции.
Типичная схема д л я измерения зависимости потенциала элек­
трода от плотности тока (поляризационные кривые) дана на
Ei
Рис. 3.45. Схема электролитической ячейки для измерения поляриза­
ционных кривых:
А — аккумулятор; Р — переменное напряжение; РЭ — рабочий электрод;
В.Э
—
вспомогательный электрод; ЭС — электрод сравнения; Ai и Аг —
миллиамперметры; Е 2 — потенциал рабочего электрода относительно элек­
трода сравнения
415

рис. 3.45. На схеме конструк­
ция ячейки упрощена. Обыч­
но поляризационные измерения
проводятся без доступа возду­
ха в атмосфере инертного газа,
так как наличие в растворе кис­
лорода приводит к искажению
катодных кривых из-за восста­
новления кислорода. В анодной
области присутствие кислорода
может привести к пассивации
металла. Кислород может так­
ж е влиять на величину потен­
циала электрода в отсутствие
внешнего тока, если то к обме­
на на электроде имеет неболь­
шую величину. Следует отме­
тить, что измерение потенциала
электрода проводится относи­
тельно электрода сравнения, а
не относительно вспомогатель­
ного электрода. При этом носик
сифона от электрода сравнения
(капилляр Лугина) должен быть подведен как можно ближе
к поверхности рабочего электрода, чтобы падение напряжения
между электродом сравнения и рабочим электродом было бы
минимальным. Падение напряжения вызвано прохождением то­
ка через раствор между вспомогательным и рабочим электрода­
ми. Катодное и анодное пространства обычно разделены стек­
лянной пористой диафрагмой или стеклянным краном.
Поляризационная кривая — это зависимость потенциала
(перенапряжения) рабочего электрода от плотности тока,
проходящего через электрод.
Рабочий электрод — это исследуемый электрод, обычно
металлический.
Вспомогательным электродом называется электрод, ко­
торый используется д л я изменения потенциала рабочего
электрода за счет протекания тока от внешнего источника
напряжения.
Последний электрод играет вспомогательную роль. Обычно
изготовляется из платины. На рис. 3.46 приведена типичная по­
ляризационная кривая. Пунктиром на рисунке обозначен
кривая для медленной ста­
дии «разряд—ионизация» при
а = (3 = 0,5. Величина \\f\ прини­
мается равной нулю
416

воображаемый ход кривой в от­
сутствие обратного процесса. Из
рисунка видно, что при низких
значениях перенапряжения за­
висимость (г—Т|) имеет линей­
ный характер, как было отмече­
но ранее. Часто поляризацион­
ные кривые строят в полулога­
рифмических координатах, как
показано на рис. 3.47, дл я опре­
деления тока обмена и констант
а и Ь (см. уравнение (3.110)).
При достаточно высоком пере­
напряжении зависимости лога­
рифма катодного ( г ) и анодно­
кривая «разряд^ионизация» в
полулогарифмических коорди­
натах при а = р = 0,5. Величина
\|/i принимается равной нулю
го ( г ) процессов от перенапря­
жения носят линейный характер, и экстраполяция их до значе­
ния Г| = 0 дает величину логарифма тока обмена (го).
3.25 . ВЫДЕЛЕНИЕ ВОДОРОДА ПРИ КАТОДНОЙ
ПОЛЯРИЗАЦИИ
Одной из наиболее изученных электрохимических реакций
является реакция выделения водорода, так как это наиболее рас­
пространенный процесс при катодной поляризации электрода.
В зависимости от природы металла скорости отдельных стадий
реакции могут меняться. В растворе кислоты на электроде воз­
можны следующие процессы.
1. Р азряд иона водорода с образованием адсорбированного
атомарного водорода на электроде:
Н30++е~ —
►Надс + Н20
2. Ионизация адсорбированного атомарного водорода (обрат­
ная реакция):
Надс + Н20 —►Н30 ++ е
3. Электрохимическая десорбция атома водорода
Надс+ Н30++ е" —►Н2+Н20
4. Рекомбинация атомарного водорода на поверхности элек­
трода
Надс "ЬНадс ►Н2
14 Ипполитов
417

Дл я упрощения вопроса пренебрежем обратными стадиями
электрохимической десорбции и рекомбинации. Наиболее рас­
пространены две теории, описывающие реакцию выделения во­
дорода.
По теории замедленного р а зр яд а медленной лимитирующей
стадией является первая стадия. Теория замедленного разряда
была сформулирована М. Фольмером и Т. Эрдей-Грузом. В даль­
нейшем теория была развита благодаря работам А. Н. Фрумкина
(1933), который учел влияние строения двойного электрического
слоя на скорость реакции. Согласно этой теории скорость про­
цесса определяется скоростью реакции первой стадии на поверх­
ности не занятой атомарным водородом:
aFr|
iA=ki(l -0)сн+еВТ ,
где 0 — степень заполнения поверхности адсорбированным ато­
марным водородом; сн+ — концентрация ионов водорода у по­
верхности электрода, которая д л я концентрированных раство­
ров (\|/i = 0) будет равна объемной концентрации*; к - константа
скорости реакции, имеющая размерность А /(с м 2 ■м о л ь/л) или
мА/(см2-моль/л). При достаточно высоком перенапряжении вы­
деления водорода (г|) обратной реакцией можно пренебречь. Ес­
ли удаление происходит по механизму электрохимической де­
сорбции, то общая величина тока будет равна
ctF,r\
г=2к\(1-0)сн+е ВТ ,
так как на протекание стадии (3) затрачивается еще один элек­
трон, и поэтому величина то ка удваивается. Адсорбция атомар­
ного водорода облегчает протекание стадии (1), так как при этом
уменьшается энергия активации реакции. Величина энергии ад­
сорбции атомарного водорода включена в константу к \ . Метал­
лы, хорошо адсорбирующие водород, катализируют процесс раз­
ряда, и реакция ускоряется. Так, например, на платиновом элек­
троде перенапряжение водорода значительно ниже, чем на ртут­
ном или свинцовом электродах при одинаковой плотности тока.
Это обстоятельство связано с тем, что энергия адсорбции водо­
рода на платине гораздо выше, чем на ртути и свинце.
*В общем случае в разбавленных растворах приповерхностная концентрация
ViF
ионов Н+ равна сн+5 = сц*е пт , где у i —потенциал в плоскости плотной части
двойного электрического слоя относительно потенциала раствора, который прини­
мается равным нулю; сн+ — объемная концентрация. Знак минус показывает, что
при отрицательном значении потенциала \\f\ концентрация ионов Н+ у поверхности
электрода выше, чем в объеме раствора.
418

Электродные реакции, в которых при данном перенапря­
жении участвуют хемосорбированные частицы, называются
электрокаталитическими процессами.
Для электрокаталитических реакций с участием хемосорбиро­
ванных частиц (например, атомов водорода) характерна весь­
ма значительная зависимость скорости реакции от материала
электрода. В большинстве случаев скорость хемосорбции обыч­
но меньше скорости физической адсорбции. Однако хемосорб­
ция может протекать и достаточно быстро, как, например, при
адсорбции атомарного водорода на платине. Повышение энер­
гии адсорбции водорода сказывается и на величине тока обмена.
При Г| = 0, т. е. при равновесном потенциале Е р\
io=4=
CLFEp
PF£P
k\(l - 0)cH+e~ яг
=к2е юг .
(3.111)
Выразив E p в явном виде из уравнения (3.111), получим зависи­
мость равновесного потенциала водородного электрода от кон­
центрации (активности) ионов водорода. Некоторые данные по
току обмена для разряда ионов НзО+для различных электродов
в растворах НС1 или H2SO4 приведены ниже.
Ток обмена для различных электродов в растворах соляной
или серной кислоты (0,1М)
Электрод
H g...........
Z n ...........
A g...........
Си ...........
Fe............
P t ...........
io, А/см2
7 •КГ13
5 *10"11
1 *КГ8
1,5 •10“7
3 •КГ6
>0,1
Как видно из таблицы, наибольший ток обмена наблюдает­
ся у платины. Поэтому платину используют в качестве инерт­
ного электрода для водородного электрода сравнения. Следует
отметить, что степень покрытия поверхности металла водоро­
дом 0 увеличивается с возрастанием энергии адсорбции, вслед­
ствие этого доля свободной поверхности, на которой происходит
разряд, уменьшается. Поэтому с ростом энергии адсорбции пе­
ренапряжение водорода сначала снижается и возрастает го, что
и наблюдается при переходе от ртути к платине. На Mo, W,
419

и некоторых других металлах энергия адсорбции водорода ста­
новится еще выше и резко сокращается доля поверхности, на
которой идет разряд ионов НзО+. При этом ток обмена начина­
ет уменьшаться. При увеличении энергии адсорбции атомарно­
го водорода скорость реакции р азряд а иона возрастает, а ско­
рость электрохимической десорбции (стадия 3) или рекомбина­
ции (стадия 4) замедляется. При достаточно высокой энергии
адсорбции атомарного водорода лимитирующей стадией реак­
ции выделения водорода может стать реакция электрохимиче­
ской десорбции (механизм Гейровского) или реакция рекомби­
нации (механизм Тафеля). Скорость стадии электрохимической
десорбции будет определяться уравнением:
ctF
is = /сз0Сн+еЯТ .
При лимитирующей стадии (3) общая сила тока, протекающего
через электрод, будет равна:
aF
гз = 2А:з0сн+е Я Т т1.
Коэффициент 2 появляется вследствие того, что на образование
атомарного водорода по стадии (1) затрачивается один электрон,
и так как i\ = гз, ток удваивается. Если лимитирующей стадией
является рекомбинация атомов водорода на поверхности элек­
трода, то
0
ч=М
.
(3.112)
Между ионами водорода в растворе и атомарным адсорбиро­
ванным водородом устанавливается равновесие, так как стадии
« разряда—ионизации» протекают очень быстро по сравнению
со стадией рекомбинации:
2Н++2е~^2Наде Н2
Равновесный потенциал этой обратимой стадии определяется
уравнением Нернста:
„
„ВТ,[Н+]2 .ВТ,[Н+]
Ер-Е°+2FПЩ* ~Ер+У ПЩ ’
где [Но] — равновесная концентрация атомарного водорода на
по-верхности металла в отсутствие внешнего тока. При прохож­
дении электрического тока приведенное выше равновесие не на­
рушается, та к как ток обмена значительно выше, чем скорость
стадии рекомбинации. При этом увеличивается концентрация
атомарного водорода [Н7] и, следовательно, изменяется величина
равновесного потенциала:
EL=Е°+
ЯГш
F
[Н'] ’
420

Тогда перенапряжение процесса
„-RO-F'^lnEL:®:
4
р
р
F
[Но]
F
кг, [н'1 кг, е
“ ГР 1п|ЩГ"Р V
InЫ
И
где 0 = тД—Ц , [Н пред] — концентрация атомарного водорода
[-П
-
пред]
на поверхности электрода при предельном заполнении поверх­
ности. Выразив 0 в явном виде:
е = e0e1'F/Rr
и подставив в уравнение (3.112), получим
*4=
(3.113)
Наклон зависимости Т аф ел я (ЗЛЮ) при переходе от механиз­
ма замедленного р азряда к механизму рекомбинации уменьша­
ется в четыре раза. В то ж е время д л я большинства металлов
коэффициент b зависимости Тафеля составляет 0,116 —0,120 В,
что указывает на замедленность стадии разряда или электрохи­
мической десорбции. В настоящее время разработан квантово­
механический подход д л я описания кинетических закономерно­
стей реакции.
Следует отметить, что как и для химических каталитических
реакций, для электрокаталитических процессов имеются яды —
вещества (ионы), адсорбция или электроосаждение которых на
поверхности металла замедляет (ингибирует) процесс. Так, на­
пример, ионы ртути, ионы трехвалентного мышьяка, цианид-
ионы уменьшают концентрацию атомов водорода на платине и
снижают скорость выделения водорода.
Если рассматривать восстановление или окисление данного
вещества или иона на электродах в общем виде, то при ма­
лых плотностях тока, когда скорость электрохимической реак­
ции мала, концентрация разряжающихся частиц в приэлектрод-
ном слое остается практически такой же, как и в объеме рас­
твора. Д иффузия электроактивных частиц из глубины раство­
ра успевает пополнить убыль разряжающихся частиц и пере­
нести образующиеся в результате электрохимической реакции
вещества в глубь раствора. При более высокой поляризации
скорость электрохимической реакции возрастает, и диффузион­
ный процесс не в состоянии полностью компенсировать убыль
421

электроактивного
вещества.
В этом случае происходит обед­
нение приэлектродного слоя ак­
тивным веществом, и электро­
химическая реакция протека­
ет в смешанном диффузионно­
кинетическом режиме — скоро­
сти электрохимического разря­
да и диффузии вещества соиз­
меримы.
В случае анодного раство­
рения металла у поверхности
электрода происходит пересы­
щение раствора, так как ско­
рость диффузионного процес­
са становится меньше скорости электрохимического процесса.
В определенных условиях пересыщение может достигать доста­
точно больших значений, и на поверхности выпадает осадок со­
ли или основания. В результате концентрационных изменений у
поверхности электрода потенциал катода становится более отри­
цательным, а потенциал анода приобретает более положитель­
ное значение. При увеличении поляризации происходит дальней­
шее возрастание плотности тока, и скорость электрохимического
разряда будет существенно больше скорости диффузии. В этом
случае скорость процесса будет определять скорость подвода ве­
щества к электроду. Приповерхностная концентрация р а зр яж а ­
ющегося вещества будет равна нулю, так как все подводимое за
счет д иф фузи и вещество (ионы) будет полностью подвергаться
электрохимическому разряду. Поэтому поляризационную кри­
вую на рис. 3.48 можно разбить на три участка: участок А В —
соответствует электрохимической кинетике, и ток реакции экс­
поненциально зависит от потенциала (перенапряжения), участок
В С соответствует смешанной кинетике, участок CD соответ­
ствует диффузионной кинетике.
-Е
Рис. 3.48. Схема катодной поля­
ризации кривой:
ЛВ — область электрохимической
кинетики; ВС — область смешан­
ной кинетики; CD — область диф­
фузионной кинетики
3.26. НЕКОТОРЫЕ АСПЕКТЫ ПРИКЛАДНОЙ
ЭЛЕКТРОХИМИИ
Электролиз — самый мощный из всех известных окислительно­
восстановительных процессов. При электролизе на катоде полу­
чаются продукты восстановления, а на аноде — прдукты окисле­
ния. В качестве материалов дл я катодов применяют ртуть, сви-
422

нец, медь, никель, а дл я изготовления анодов используют пла­
тину, графит, никель, оксиды металлов (оксид свинца(1У), ок­
сид марганца(1У) и др.) В последнее время широко применяют­
ся оксидные рутениево-титановые аноды (ОРТА), которые пред­
ставляют собой электроды из титана, покрытые активной мас­
сой, состоящей из оксидов рутения и титана. Практика показала,
что такие электроды являю тся весьма устойчивыми при анодной
поляризации. Электрохимические процессы на электродах под­
чиняются законам Фарадея. Напомним физический смысл этих
законов.
1. Количество моль-эквивалентов вещества, восстановленно­
го или окисленного при электролизе, прямо пропорционально
количеству электричества, прошедшего через раствор, расплав
или твердый электролит.
2. Масса веществ, выделенных одним и тем ж е количеством
электричества, пропорциональна молярным массам эквивален­
тов восстановленных (окисленных) веществ.
Объединенный закон Ф арадея может быть представлен урав­
нением:
г-,
Q=It=
V
М,’
где Q — количество прошедшего электричества, Кл; / — сила
тока, A; t — время электролиза, с; т — масса вещества, г; Мэ —
молярная масса эквивалента (г - моль-экв-1); F — число Фара­
дея (Кл •моль-экв-1). Число Фарадея равно 96487 Кл • моль-экв“
или округленно 96 500 Кл • моль-экв"1. Физический смысл ве­
личины F — количество электричества, которое должно быть
пропущено через электролит для выделения или разложения
1 моль-экв вещества, что соответствует прохождению через
металлическую часть цепи электролизера 1 моля электронов.
Каж ды й электрон или однозарядный ион (ионная часть це­
пи электролизера) переносит количество электричества, рав­
ное 1,6 • 10"19Кл. Один моль электронов (однозарядных ионов),
как известно, содержит число частиц, равное числу Авогадро
N a = 6,022 • 1023. Следовательно, 1 моль электронов (однозаряд­
ных ионов) перенесет количество электричества 1, 6 -10“19-6 , 022х
х1023 = 96 497 Кл.
3.27. ПОЛУЧЕНИЕ ВЕЩЕСТВ С ПОМОЩЬЮ
ЭЛЕКТРОЛИЗА
Если в растворе имеется несколько видов катионов, напри­
мер, Ag+, Н+, Fe2+, то, как правило, в первую очередь на като-
423

де будут восстанавливаться катионы, которым соответствует бо­
лее положительный равновесный потенциал, т. е. сначала будут
восстанавливаться катионы Ag+, затем Н+ и, наконец, Fe2+. При
протекании процессов на аноде в первую очередь будут окис­
ляться ионы или нейтральные частицы, имеющие более отри­
цательный равновесный потенциал. Например, при наличии в
растворе анионов I" и В Г окислению будут подвергаться снача­
ла ионы I- , а затем ионы Вг“ . При достаточно близких равно­
весных потенциалах ионов или нейтральных частиц на катоде
могут восстанавливаться одновременно несколько видов частиц,
например Со2+ и Ni2+. Если обратиться к анодным реакциям, то
наиболее важно рассмотреть р азр яд ионов СГ и молекул воды:
2СГ С12 + 2е"
2Н20 —>0 2+ 4Н++ 4е~
В нейтральных растворах равновесные потенциалы этих реак­
ций достаточно близки по величине. При низких концентраци­
ях ионов СГ на аноде идет преимущественное выделение кис­
лорода. При высоких концентрациях СГ равновесный потенци­
ал системы 2СГ/С12 смещается в область более отрицательных
значений и весь анодный ток расходуется на выделение хлора.
Следует отметить, что преобладание того или иного процесса на
аноде, строго говоря, зависит также от материала электрода и
величины перенапряжения процесса. На катоде могут восстанав­
ливаться так ж е молекулы и анионы. Так, при наличии в водном
растворе катионов щелочных и щелочноземельных металлов или
аммония идет восстановление молекул растворителя:
2Н20 4- 2е“ —►20Н~ + Н2
Широко применяется в практике восстановление комплексных
анионов серебра, золота, цинка и ряда других металлов. При
восстановлении на поверхности ка то д а образуется тонкий плот­
ный блестящий осадок:
[Ag(CN)']+e-^ Ag+2CN“
[Au(CN)"] + e“ -> Au + 2CN"
Эти процессы широко применяются в гальванотехнике д л я се­
ребрения или золочения изделий. Н а аноде такж е могут окис­
ляться молекулы растворителя (например, воды) или молекулы
других веществ, а также катионы и анионы:
Н20-2е-^ Г)2+2Н+
Z
424

Fe2+ - e-
—
►Fe3+
При замене инертного анода на достаточно активный металл
(например Си, Zn, Pb, А1 и др.) при анодной поляризации проис­
ходит растворение металла (электролиз с растворимым анодом).
Этот процесс часто используется при рафинировании металлов.
Так, при получении более чистой меди в электролит, содержа­
щий сульфат меди, помещают пластину из чистой меди (катод),
а другой электрод(анод) из черновой меди. В процессе электро­
л и за загрязненный металл растворяется, и ионы Си2+ под дей­
ствием электрического то к а перемещаются от анода к катоду, и
на катоде осаждается очищенная медь:
Си- 2е~ —
>Си2+ анод
Си2++ 2е~ —
►Си катод
Примеси, имеющиеся в черновом металле обычно скапливаются
на дне электролизера (электролитической ванны) в виде шла­
ма и затем удаляются. Эти примеси содержат золото, серебро,
селен, теллур и др. редкие элементы. Поэтому шлам электро­
литических ванн является ценным сырьем д л я получения этих
элементов.
Электролитическим рафинированием называют процесс,
при котором черновой металл растворяется на аноде элек­
тролитической ванны и осаждается на катоде в очищенном
виде.
Электролизом раствора боксита (AI2O3) в расплаве криоли­
та (Na3AlFe) получают алюминий. В расплаве криолита оксид
алюминия диссоциирует по схеме:
АЬ03 *=>А10++АЮ2
На катоде происходит выделение алюминия. По мере расхода ок­
сида алюминия в расплав добавляются новые порции боксита.
Схема установки д л я производства алюминия д а н а на рис. 3.49.
В качестве анода, на котором происходит выделение кислоро­
да, используется графит, который постепенно выгорает. Поэтому
графитовый анод постепенно погружается в расплав электролита.
Электролизом расплавов гидроксидов и солей получают ще­
лочные и щелочноземельные металлы. Из расплава карналлита
(КС1 ■MgCl2 ■6Н20 ), предварительно обезвоженного, получают
металлический магний. Электролизом расплавов солей получа­
ют бериллий, титан, а такж е молекулярный фтор.
425

Рис. 3.49. Схема установки для
производства алюминия:
1 — графитовый анод; 2 — графи­
товый катод; 3 — стальная ванна;
4 —затвор; 5 — выход жидкого алю­
миния; 6 — жидкий алюминий; 7 —
раствор оксида алюминия в расплаве
криолита; 8 — расплав шлака
Путем электролитического
окисления получают оксиды
(например, М пС^РЬОг), пер­
хлораты, гипохлорит натрия,
хлорную кислоту, перманганат
калия, пероксид водорода и
множество неорганических ве­
ществ.
При получении органиче­
ских веществ используются как
процессы электролитического
окисления (себациновая кис­
лота, фторорганические соеди­
нения, тетраалкильные произ­
водные свинца), та к и процес­
сы восстановления (например,
адиподинитрил NC(CH2)4 CN).
2CH2=CHCN + 2Н++ 2е" - » NC(CH2)4CN
Адиподинитрил является сырьем д л я производства нейлона.
3.28. ХИМИЧЕСКИЕ ИСТОЧНИКИ ТОКА
К химическим источникам тока (ХИТ) относятся гальвани­
ческие элементы, аккумуляторы и топливные элементы. В тех­
нике гальванические элементы называют первичными, а акку­
муляторы — вторичными элементами. К химическим элемен­
там предъявляются определенные требования. Во-первых, ХИТ
должен иметь высокое значение ЭДС. Во-вторых, при работе
источника тока разность по­
тенциалов между катодом и
анодом не должна сильно умень­
шаться по сравнению с ЭДС,
т. е. поляризация электродов
при прохождении тока долж­
на быть невелика. С этой це­
лью электрохимически актив-
Рис. 3.50. Схематическая зави- ные вещества (материалы, из
симость тока от напряжения на которых изготовлены анод и
клеммах гальванического элемен- катод) должны иметь большую
та при его работе
поверхность, контактирующую
426

с электролитом. В этом случае
при одной и той же силе тока I
плотность тока на электродах
с развитой поверхностью будет
меньше и поляризация элек­
трода будет ниже. Кроме то­
го, сопротивление электроли­
та (внутреннее сопротивление
источника тока) должно быть
по возможности невелико. По­
этому применяются электроли­
ты с высокой электропроводно­
стью, а катод и анод распола­
гаются друг относительно друга на близком расстоянии. Напря­
жение на клеммах источника тока определяется следующим со­
отношением:
У=ЕК-Е ъ -ДИом,
Рис. 3.51. Схематическая кривая
разряда гальванического элемента
где Е к и Е а — потенциалы катода и анода соответственно;
AVOM= I R — омическое падение напряжения в электролите при
прохождении тока / ; R — внутреннее сопротивление. Выразив
силу то ка / , проходящего через источник тока, получим:
Дк-Да V
R
R‘
(3.114)
Из уравнения (3.114) следует, что чем больше ток дает ХИТ, тем
меньше будет напряжение на его клеммах V (рис. 3.50). Следует
отметить, что разность Е к —Е а также будет убывать.
В-третьих, ХИТ должен иметь большую удельную емкость,
т. е. количество электричества на единицу массы или объема ис­
точника тока. После расхода основной массы электроактивных
веществ на аноде и катоде напряжение, подаваемое от ХИТ, рез­
ко уменьшается. Типичная кривая разряда гальванического эле­
мента приведена на рис. 3.51.
В-четвертых, ХИТ долж ен обладать высокой удельной мощ­
ностью, т. е. при достаточно высоком напряжении (И) давать
большую силу тока. Наконец, электроды ХИТ должны иметь
низкий саморазряд, т. е. при разомкнутой цепи ХИТ в течение
длительного времени дол ж ны сохранять высокую удельную ем­
кость. Известно, что при хранении источника то ка в заряженном
состоянии происходит уменьшение массы электроактивных ве­
ществ из-за разрушения электродов в результате коррозии элек­
тродов или по другим причинам.
427

§ 1. Гальванические элементы
Гальванические элементы или первичные элементы —
это устройства, превращающие энергию химической реак­
ции в электрическую энергию.
Гальванические элементы представляют собой источники то­
ка одноразового действия, т. е. после того, как израсходованы
электроактивные вещества, гальванические элементы теряю т ра­
ботоспособность. По окончании работы гальванического элемен­
та потенциалы электродов заметно сближаются. Следует отме­
тить, что при работе химического источника тока процесс вос­
становления протекает на электроде (катод) с более положитель­
ным потенциалом, а процесс окисления на электроде (анод), име­
ющем более отрицательный потенциал. Одним из классических
гальванических элементов является элемент Якоби —Даниэля:
(-) Zn |Z11SO411C 11SO41Cu(+)
При работе гальванического элемента происходит окисление ак­
тивного м етал л а Zn, имеющего более отрицательный равновес­
ный потенциал д л я системы:
Zn2++2е i=?Zn; Е®= -0,76 В;
а процесс восстановления протекает на менее активном металле,
имеющем положительный потенциал для системы:
Си2++2е" ^5 Си; Е$ =0,34 В.
Таким образом на электродах протекают реакции:
Zn —>Zn2+ + 2е”
Cu2+ + 2е- —>Си
Согласно уравнению Нернста равновесные потенциалы выража­
ются следующими соотношениями:
„
Ы)
2 ,303ДТ
-kpZnW/Zn ^Pzn/Zn**- +
2F
£ OZn2+’
(3.115)
„
„0
2 ,303ДТ
^PCu2+/Cu “ ^PCu/Cu2+ + 2jP lg aCu2+‘
(3.116)
Равновесные потенциалы (3.115) и (3.116) измерены относитель­
но потенциала стандартного водородного электрода. Д л я цепи
ЭДС будет равна:
F=
-
F0
+ 2>303Д Г QCu*+
•kpcu’vcu
Pzn^/zn+
2F
lgа7,п1* '
428

Рис. 3 .52. Схема медно-цинкового
элемента:
А — амперметр; R — нагрузка; Р —
рубильник
Проанализируем более подроб­
но процессы, протекающие на
электродах.
Цинковая пластина, поме­
щенная в раствор ее соли (по-
луэлемент), имеет более от­
рицательный равновесный по­
тенциал по сравнению с мед­
ным электродом, помещенным
в раствор соли меди (вто­
рой полуэлемент). Полуэле-
менты соединены электроли­
тическим мостиком с кра­
ном, который заполнен раство­
ром электролита (раствор соли
цинка и меди) (рис. 3.52). Благодаря солевому мостику рас­
творы цинкового и медного полуэлементов не перемешивают­
ся. Во внешней цепи электроды из цинка и меди соединяют­
ся медным проводом с нагрузкой R (переменное сопротивле­
ние), амперметром и рубильником Р. При разомкнутой цепи на
границе «медь —раствор соли
меди и цинка —раствор соли
цинка» устанавливается равно­
весие между металлом и кати­
оном металла в растворе. Ве­
личины равновесных потенци­
алов определяются уравнения­
ми (3.115) и (3.116). При замы­
кании цепи равновесия нару­
шаются, и в металлической ча­
сти цепи электроны будут дви­
гаться в электрическом поле в
направлении к более положи­
тельному потенциалу от цин­
кового электрода к медному.
Дл я пополнения убыли элек­
тронов равновесие д л я цин­
кового электрода будет сме­
щаться в левую сторону, т. е.
скорость полуреакции окис­
ления увеличивается, а ско­
рость полуреакции восстанов­
ления уменьшается. На медном
электроде происходит восста-
(-)
Рис.
3.53 .
Сухой
элемент
Лекланше:
1 — герметизирующее уплотнение
из смолы; 2 — графитовый катод
с металлическиим колпачком; 3 —
МпСЬ с углем; 4 — паста из смеси
NH4CI и ZnCh; 5 — анод из цинка
429

Таблица 3.10
Некоторые первичные элементы
Элемент
Материал
электрода
Схема электродной
реакции
Основные
компоненты
электролита
Лекланше
(К) активный
графит + Мп02
(К) Мп02 -*Мп203-Н20 26%NH4C1
(А) амальгами­
рованный Zn
(A) Zn—>Zn(NH3) f
8,8% ZnCl2
Хлор-се­
(К) Ag + AgCl
(К) AgCl -» Ag
Раствор
ребряный
(A) Mg
(A) Mg
MgCl2
NaCl, зали­
вается перед
включением
Лаланда
(К)CuO+Си
(А) амальгами­
рованный Zn
(К) CuO -> Си
(A) Zn — Zn(OH)f
20% NaOH
новление ионов Си2+, и электроны, приходящие от цинкового
электрода связываются с ионами Си . Химическая реакция,
протекающая в гальваническом элементе, в ионной форме будет
иметь вид:
0
„
Zn + Cu2+ —>Zn2++ Си
а в молекулярной форме:
Zn+CUSO4 Си+ZnS
04
Для такого элемента ЭДС при концентрации солей 1 моль/л
равна примерно 1,1 В. Создано большое количество разнообраз­
ных гальванических элементов. Некоторые из них представлены
в табл. 3.10. В настоящее время в продаже встречаются разно­
образные гальванические элементы (батареи), но наиболее рас­
пространен сухой элемент Лекланш е, показанный на рис. 3.53.
Анодом этого элемента служит его оболочка, выполненная из
цинка, а катодом — графитовый стержень, который окружен
слоем из диоксида марганца и угля.
Электролитом служит паста из хлорида аммония и воды с
добавкой вяжущего вещества. Напряжение на клеммах сухого
элемента от 1,2 до 1,5 В. На электродах элемента Лекланше про­
текают реакции:
на аноде
Zn(T)—»Zn2+(pacTBop)
+ 2е“
на катоде
2МпС>2(т) + 2NH4(раствор) + 2е” —>
—
>МП2О3(т) + 2NH3(раствор) + Н2О
430

Суммарная реакция:
2Zii(t) + 2Мп0 2 (т) + 2NH4(раствор) —>
—
>2п2+(раствор) + Мп2 0 з(т) + 2NH3(раствор) + Н2 0 (ж)
Во многих современных гальванических элементах в качестве
анода применяется литий. В этом случае в качестве электролита
используются органические апротонные растворители, распла­
вы солей или твердые электролиты. В качестве материала д л я
катода применяются углеродные материалы, сульфиды или ок­
сиды металлов. В литиевых элементах ЭДС достигает 3 —4 В.
Они обладают высокой удельной емкостью и небольшим весом.
Так, например, в элементе
(—)Li|LiPF6, апротонныйрастворитель, |М0 2 |графит(+)
при его работе будет протекать химическая реакция:
х\Л + МО2 —*1лхМ02
Из большого количества гальванических элементов остановим­
ся еще на одном, который не используется как источник тока,
3
Рис. 3.54. Элемент Вестона:
1 — ртуть; 2 — пастообразная масса; 3 — герметизирующие пробки; 4 ~
насыщенный раствор; 5 — амальгама кадмия
431

а служит эталоном постоянного напряжения. Это — элемент
Вестона. Элемент Вестона представляет собой стеклянный со­
суд, в нижнюю часть которого впаяны платиновые проволочки
в качестве токоотводов (рис. 3.54). Н а дно одного полуэлемен-
та налита ртуть, над которой помещается пастообразная смесь
из CdSQ* и Hg2S0 4 . В другой полуэлемент помещается амаль­
гама кадмия состава 12,5% Cd и 87,5% Hg. Сосуд заполняет­
ся насыщенным водным раствором сульфата кадмия и твердым
CdS04 ■2, 67Н2О. Полуэлементы герметизируются специальны­
ми пробками. Элемент Вестона можно представить в виде:
(-)H g ,Cd|CdS04(насыщ., )Hg2S04(TB .)|H g(+)
Благодаря высоким токам обмена н а электродах величина ЭДС
элемента Вестона хорошо воспроизводится и остается постоян­
ной многие годы. При 20°С она равна 1,01830 В. При работе
элемента протекает реакция
Cd(Hg) + Hg2+ -» 2Hg + Cd2+
Элемент Вестона используется как устройство д л я калибровки
приборов (например, потенциометров). В зависимости от тем­
пературы окружающей среды ЭДС элемента может изменяться
согласно формуле:
Е = 1,01830 - 4, 06 ■10_5(£- 20) - 9 ,5 ■10_7(i - 20)2+1 ■10"8(t - 20)3.
§ 2. Аккумуляторы
Аккумуляторы (вторичные элементы) — это регенериру­
емые гальванические элементы многоразового использова­
ния.
Аккумулятор, как и гальванический элемент, работает до тех
пор, пока не будет использована большая часть электроактив-
ных веществ. Затем аккумулятор подсоединяют к источнику по­
стоянного тока и заряжают, т. е. регенерируют электрохимиче­
ски активные вещества на катоде и аноде. Электрод, который
был катодом при работе гальванического элемента, соединяют с
положительным полюсом, а другой электрод —с отрицательным
полюсом внешнего источника тока. При заряде аккумулятора
на первом электроде окисляется вещество, которое восстанови­
лось при работе аккумулятора как химического источника тока,
а на другом электроде идет восстановление окисленного веще­
ства. Процессы заряда и разряда составляют цикл работы ак­
кумулятора. Хорошие аккумуляторы могут выдерживать около
432

тысячи циклов. Первый акку­
мулятор (свинцовый) был изо­
бретен французом Г. Планте в
1860 г. В усовершенствованном
виде он используется до сих пор
дл я запуска двигателей внут­
реннего сгорания в автомоби­
лях. Схематически он показан
на рис. 3.55. В качестве катода в
этом аккумуляторе используют
электрод из свинца, сделанный
в виде решетки с запрессован­
ным Р Ь 02. Анод изготовлен из
губчатого свинца, а электроли­
том служит 30 %-й раствор сер­
ной кислоты в воде. Гальвани­
ческая цепь может быть пред­
ставлена в следующем виде:
(-)Pb|H2S04|Pb02,Pb(+)
ЭДС аккумулятора 2 В. При работе аккумулятора протекают
следующие процессы:
на катоде PbS04+2Н++2е” —
*Pb+H2S04
на аноде Pb+S04~-
2е“ —►PbS04
При зарядке аккумулятора на электродах протекают процессы:
на катоде PbS04+ 2Н+4*2е~ —
>Pb+H2S04
на аноде
PbS04+2Н20 - 2е~ —
>Pb02+H2S04+2Н+
Суммарное уравнение химической реакции, протекающей при
разряде и заряде аккумулятора:
+
Рис. 3.55. Свинцовый аккуму­
лятор:
1—катод — пластина из свинца, по­
крытая РЬСЬ; 2 — раствор серной
кислоты; 3—анод — пластина из РЬ
Таблица 3.11
Некоторые вторичные элементы (аккумуляторы)
Элемент
Материал электрода
Схема электродной
реакции
Основные
компоненты
электролита
Эдисона
(К)No+No203-пН20
(A) Fe
(К) Ni20 3- н20 -♦
-»No0 •тпН20
(A) Fe - Fe(OH)2
21% КОН +
+ 5% LiOH
Серебряно­
цинковый
(К)Ag+Ag202
(A) Zn
(К) Ag202 —* Ag20
Ag20 -> Ag
(A) Zn —►ZnO •ПН2О
Раствор
КОН(нас.),
Zn(OH)2
433

заряд
Pb02+2H2S04+Pb*
2PbS04+2H20 +364 кДж
разряд
Нужно отметить, что свинцовые аккумуляторы в начале XX в.
широко применялись в электромобилях. В 1900 г. электромоби­
лей было примерно в д ва р аза больше, чем машин с бензиновым
мотором. В 90-х г. XIX в. в Санкт-Петербурге ходил электро­
омнибус конструкции И. В. Романова. Омнибус двигался с помо­
щью свинцовых аккумуляторов и мог перевозить 17 пассажиров.
Некоторые из других аккумуляторов представлены в табл. 3.11.
Топливные элементы — это гальванические элементы, в
которых электроактивные вещества подаются к электродам
непрерывно в течение всего времени их работы.
В самом простом случае в качестве восстановителя может
быть использован водород, а в качестве окислителя — кислород.
Газы подаются внутрь пористого электрода. Топливный элемент
схематически представлен на рис. 3.56. Пористые электроды из­
готавливаются обычно из графита, никеля или платины, в состав
которых вводятся катализирующие добавки. На катод подается
под давлением кислород, а на анод — водород. При работе топ­
ливного элемента протекают реакции:
В общем виде химическая р еакция в топливном элементе:
Топливный элемент с емкостями для реагентов и реге­
нерирующими вспомогательными устройствами назы вают
электрохимическим генератором.
В качестве восстановителя в топливных элементах применя­
ется такж е гидразин, метиловый спирт. Предполагается в да ль ­
нейшем использовать угольный порошок, метан и другие угле­
водороды, играющие роль восстановителя, а воздух — в каче­
стве окислителя. В электрохимических генераторах электроли­
том служат растворы кислот и щелочей с высокой электропро­
водностью. Известны также высокотемпературные топливные
§3. Топливные элементы
на аноде
на катоде
1о2+2Н++2е~ —
>Н20
/
Н2 - 2е~ —>2Н+
434

Рис. 3-56. Схема топливного элемента:
1 — подача кислорода; 2 — подача топлива; 3 — водородный электрод;
4 — кислородный электрод; 5 — насос для перекачивания электролита; 6 —
ячейка для регенерации электролита; 7 — клапан для выпуска воды; 8 —
трубопроводы для электролита
Таблица 3.12
Некоторые топливные элементы
Элемент
Материал
электрода
Схема электродной
реакции
Основные
компоненты
электролита
Кислородо­
водородный
(К) Ni Опорист.+ Ag
(A) N inop„CT.+ Ni
о2—но2
(А)Н2-> Н+
6Мкон
С органическим
топливом
(К) Pt
(A) Pt
(К) о2-* но2
(A) C„Hre+2-» С 02
СНзОН - С02
Н3Р04
H2S04
435

элементы, в которых электролитами являются расплавы щело­
чей и солей. Несомненным достоинством электрохимических ге­
нераторов является длительная непрерывная работа и меньший
вес на единицу мощности по сравнению со свинцовыми акку­
муляторами. Однако электроды из каталитически-активных ме­
таллов платины и никеля легко отравляются ядами, и их актив­
ность резко снижается. В последнее время рассматривается воз­
можность применения ферментов в качестве катализаторов, ко­
торые обладают высокой селективностью и менее чувствитель­
ны к действию каталитических ядов.
В качестве катализаторов восстановления кислорода могут
применяться цитохромоксидаза, лактаза, а д ля окисления водо­
рода —гидрогеназа. Некоторые типы топливных элементов при­
ведены в табл. 3.12.
3.29. КОРРОЗИЯ МЕТАЛЛОВ
Коррозией металлов называют самопроизвольное разру­
шение металлических материалов (металлов, сплавов) при
физико-химическом взаимодейстаии с окружающей средой.
Коррозия металлов — это окислительно-восстановительный
процесс, в котором восстановителем выступает металлический
материал, а окислителем — вещества из окружающей среды.
Наиболее распространенным окислителем является кислород,
ионы НзО+ в кислой среде. Различают химический и электрохи­
мический механизм коррозии, но в обоих случаях энергия Гиббса
коррозионного процесса AG kop < 0- При химическом механизме
частицы окислителя непосредственно взаимодействуют с атома­
ми металла. Процесс протекает в непроводящей электрический
ток среде, например в сухой газовой атмосфере:
3Fe + 2O2 —►РезС>4
Для электрохимического механизма коррозии, которая протека­
ет в проводящей электрический ток среде (растворы кислот, со­
лей или щелочей, морская, атмосферная, почвенная коррозия)
можно пространственно разделить процессы окисления металла
и восстановления окислителя. Например, процесс коррозии меди
в кислой среде в присутствии растворенного кислорода:
Си+2НС1+ ^02-►СиС12+Н20
436

можно представить, как результат работы гальванического эле­
мента, состоящего из медного и кислородного электродов. Если
медь поместить в раствор ее соли, например C11CI2, то между
металлом и раствором установится равновесие:
Си2++2е~ ^ Си
Величина равновесного потенциала дл я указанного случая будет
определяться уравнением Нернста (3.57). Д л я упрощения при­
мем, что активная концентрация ионов Си2+ равна 1 м оль/л,
тогда равновесный потенциал данной системы C u/C u2+ будет
определяться величиной стандартного равновесного потенциа­
л а Е Си2+/Си = 0,34 В. Другой полуэлемент будет представлять
кислородный электрод, д л я которого на инертном электроде —
платине — будет осуществляться равновесие:
^02+2Н++2е-^Н20
Z
В стандартных условиях £<э2/н 2о = 1,23 В. При соединении
электродов гальванического элемента возникнет электрический
ток и равновесие на медном и кислородном электродах нару­
шается. Электроны будут перемещаться от медного к кисло­
родному электроду, и медь начнет окисляться (подвергаться
коррозии), а кислород будет восстанавливаться. В этом случае
A G КОр < 0, так как известно соотношение между изменением
энергии Гиббса и ЭДС гальванического элемента Е
AG=-nFE)
где Е = £ ’о 2/ н 2 о - ECu2-»yCu = 0,89 В. Таким образом, если равно­
весный потенциал окислителя больше равновесного потенциала
металла, то коррозия будет идти. Необходимым условием кор­
розии является неравенство:
Еокислит > Ем =+/м*
(3.117)
В отсутствие кислорода в растворе кислоты (НС1, разбавленная
H2SO4) медь не будет подвергаться коррозии, т а к как £ ’н+/ н 2 <
< £cu-/C u- Неравенство (3.117) указывает только на термодина­
мическую вероятность процесса коррозии, но скорость коррозии
металлов будет определяться кинетикой катодного и анодного
процессов.
Рассмотрим растворение железа в соляной кислоте. Схема,
представленная на рис. 3.57 помогает наглядно рассмотреть этот
437

процесс. При помещении ж ел еза в раствор его соли опреде­
ленной концентрации устанавливается равновесный потенциал
^Fe2+/Fe> При КОТОрОМ
i\=ii= гои
где i i и i \ — токи (скорость) катодной Fe2++ 2e“ —►Fe и анодной
F e - 2 e “ —» Fe2+ реакции*; ioi — ток обмена. Поскольку при рав­
новесном потенциале количество атомов металла, переходящих
в раствор в единицу времени, равно количеству атомов, осаж д а­
ющихся на поверхность металла за то же время, масса металла
не изменяется во времени.
При появлении частиц окислителя, который может восста-
—
у
навливаться на железе например, ион НзО+, со скоростью г2 при
равновесном потенциале железа, равновесие нарушается. В этом
случае суммарный ток реакций восстановления i\ +г2, потребля­
ющий электроны, значительно превышает ток окисления желе­
за ii, поставляющий электроны, и потенциал ж елеза начинает
смещаться в область более положительных значений до тех пор,
пока не установится равенство катодных и анодных токов:
(3.118)
Потенциал, соответствующий равенству (3.118), называется ста­
ционарным, или потенциалом коррозии (Екор). При стационар­
ном потенциале током восстановления ионов ж елеза i\ и током
окисления водорода 22 можно пренебречь в силу их малой вели­
чины. Тогда равенство (3.118) упрощается:
^2 “ г\ —2КОр,
т. е. скорость растворения металла равна скорости выделения во­
дорода. По количеству выделившегося водорода, который мож­
но собрать в бюретку, можно определить скорость коррозии же­
леза в А/см2 или г/см2, используя объединенный закон Фарадея
и имея в виду, что протекает реакция:
Fe + 2HCl->FeCl2+ H2
При этом следует помнить, что скорость гетерогенной реакции,
в частности коррозия железа, рассчитывается на единицу по­
верхности корродирующего металла.
‘ Необходимо отметить,что механизм растворения железа в кислых средах го­
раздо сложнее. В частности, на начальном этапе на поверхности железа образуется
FeOH„c:Fe+Н20- е
—
FeOHaac + Н+.
438

В отличие от равновесного
потенциала при Е кор происхо­
дит необратимое уменьшение
массы металла при его раство­
рении, так как в реакциях вос­
становления и окисления при­
нимают участие разные части­
цы, хотя сумма катодных токов
равна сумме анодных токов.
При увеличении концентра­
ции окислителя (увеличение
концентрации НС1), как и для
химической реакции, скорость
восстановления (деполяриза­
ции) ионов НзО+ i 2 возрастает,
что приводит к смещению
Е'кор в область более положи­
тельных значений, и скорость
коррозии железа i'Kop возрас­
тает (см. пунктирную кривую
на рис. 3.57). Таким образом, меняя концентрацию окислителя
или заменяя один окислитель другим (например, О2) можно
существенно изменить потенциал коррозии металла. Потенциал
металла можно также изменить при соединении его с источ­
ником постоянного тока. При анодной поляризации потенциал
ж е л еза смещается в область более положительных значений.
При этом можно достигнуть таких значений потенциала, когда
на поверхности будет образовываться адсорбционный слой из
ионов О2’ и затем фазовая пленка оксида металла, которая
мало растворима в водных растворах:
хМ + 2/Н2О - 2уе —►МхОу + 2уН+
При образовании оксидной пленки растворение металла су­
щественно снижается, и металл переходит в пассивное состоя­
ние. Например, скорость растворения хрома в кислых средах
при переходе из активной области в пассивную уменьшается
примерно в миллион раз. Перевести металл в пассивное состо­
яние можно также действием сильного окислителя. Ж елезо в
концентрированной азотной кислоте покрывается оксидом и при
комнатной температуре находится в пассивном состоянии. Это
явление наблюдал еще М. В. Ломоносов.
В пассивном состоянии скорость растворения металла прак­
тически не зависит от потенциала (рис. 3.58), поскольку в этой
области потенциалов скорость процесса определяется скоростью
Рис. 3.57. Схема, поясняющая
установление потенциала корро­
зии Е кор и появление тока корро­
зии гкор, а также увеличение тока
коррозии при повышении концен­
трации окислителя —ионов НзО+
439

растворения оксидной пленки.
С ростом потенциала метал­
ла оксидная пленка утолщает­
ся. При этом толщина оксид­
ной пленки практически ли­
нейно возрастает с ростом по­
тенциала, состав же ее по тол­
щине неоднороден. У поверх­
ности пассивированного метал­
л а выше концентрация ионов
металла и меньше концентра­
ция ионов кислорода, что со­
ответствует более низкой сте­
пени окисления металла. На
границе «оксидная пленка —
раствор» концентрация ионов
кислорода становится выше.
Последнее можно трактовать
ка к увеличение степени окис­
ления металла*.
Рис. 3.58. Схематическое изобра­
жение анодной поляризационной
кривой. Область АВ — активное
состояние; ВС — состояние пас­
сивности; CD — состояние пере-
пассивации
Механизм перехода металла в пассивное состояние и приро­
да пассивности исследуются и в настоящее время. Замедление
растворения металла может быть также вызвано образовани­
ем малорастворимой солевой пленки (солевая пассивность). На­
пример, образование пленки Р ЬСЬ или PbSCU на свинце. Д ля
металлов, которые могут окисляться до более высоких степе­
ней окисления с образованием растворимых соединений (ионы
FeOf-, Cr2Of- и др.), оксидная пленка будет растворяться, и
металл — переходить в состояние перепассивации или в транс­
пассивное состояние (Г. В. Акимов, В. П. Батраков). В состоянии
перепассивации растворение металла подчиняется законам элек­
трохимической кинетики: зависимость скорости растворения от
потенциала может быть описана уравнением Тафеля.
Коррозия металла бывает равномерной, но может носить из­
бирательный характер, (межкристаллитная коррозия, питтинго-
вая коррозия, ножевая коррозия и т. д .) . Коррозия чистого ме­
талла, как правило, заметно ниже, чем металла с примесями.
Но если, например, железо содержит углерод, то скорость вы­
деления водорода на включениях углерода в железе (или цемен­
тите Без С) существенно возрастает, что приводит к увеличению
суммарной скорости выделения водорода (на включениях угле-
Известно, что многие оксиды металлов являются бертоллидами, т. е. вещества­
ми, состав которых является переменным и зависит от условий получения.
440

рода в железе). При этом возрастает скорость коррозии (пунк­
тирная кривая для г2 (см. рис. 3.58). При контакте разнород­
ных металлов происходит увеличение коррозии более активно­
го металла из-за наличия гальванической пары (гальваническая
коррозия). Более активный металл играет роль анода и подвер­
гается более интенсивной коррозии по сравнению с коррозией
этого металла в отсутствие электрического контакта с другим
менее активным металлом. В средах с низкой электропровод­
ностью (атмосферная коррозия или почвенная коррозия) меж­
ду металлами может возникать значительная разность потен­
циалов.
При атмосферной коррозии роль электролита выполняет тон­
кая пленка конденсированной воды на поверхности металлов, со­
держащей растворенные газы (SO2, О2, H2S) и небольшие коли­
чества соли NaCl, которая всегда присутствует в довольно боль­
ших концентрациях в атмосфере городов. При почвенной корро­
зии электролитом является почва, содержащая некоторое коли­
чество воды и кислорода (песчаные почвы) или ионы НзО+ в бо­
лотистых почвах и торфяниках. Особым видом коррозии явл я­
ется биокоррозия, которая вызывается микро- и макроорганиз­
мами, а также продуктами их жизнедеятельности, в частности
промежуточными и конечными продуктами биохимических ре­
акций (органические кислоты, NH3 , H 2 S, H 2 SO 4 и др.). Коррозия
металлов наносит большой ущерб промышленности и сельскому
хозяйству. В последнее время в нашей стране не проводилось
серьезного учета потерь от коррозии. Однако, если взять конец
70-х и начало 80-х гг. в СССР, потери металлов от коррозии, по
данны м академика Я. М. Колотыркина, составляли 25 млн т в
год. По оценкам Национального бюро стандартов США, на вос­
полнение коррозионных потерь расходуется около 40% ежегодно
производимого металла.
Выяснение механизма коррозионных процессов позволило р аз­
работать ряд эффективных методов и средств защиты металли­
ческих материалов от коррозии. Рассмотрим некоторые из них.
§ 1. Легирование металлов
Введение металла или нескольких металлов в другой ме­
талл с целью изменения его технологических свойств назы­
вается легированием.
Одним из основных металлических конструкционных материа­
лов является железо. Добавление в железо хрома и никеля, на-
441

* кор
'кор
/, А/м2
Рис. 3.59. Схема, поясняющая переход стали из активного состояния в
пассивное в присутствии включений палладия на поверхности стали:
1— скорость выделения водорода на поверхности стали; 2— то же на вклю­
чениях палладия; (г'кор) — скорость коррозии стали с включениями катали­
тически активного металла
пример, повышает его коррозионную стойкость. Полученные та ­
ким образом стали называют нержавеющими. Наиболее распро­
страненной нержавеющей сталью явл яе тся сталь Х18Н10 (18%
Сг и 10 % Ni). Э та сталь проявляет высокую коррозионную стой­
кость в атмосферных условиях и в водных средах, не содержа­
щих Cl-ионов, а также высокую жаростойкость. Высокая кор­
розионная стойкость нержавеющих сталей объясняется образо­
ванием плотного сложного по составу малорастворимого сме­
шанного оксида из Рв20з, СГ2О3 и NiO. Например, скульптура
В. Мухиной «Рабочий и колхозница», выполненная из нержаве­
ющей стали, долгое время (более 60 лет) находилась в атмосфер­
ных условиях без существенных изменений.
В ряде случаев на поверхность сталей на основе ж елеза (или
в их состав) вводится каталитически активный металл (палла­
дий), на котором скорость выделения водорода намного выше,
чем на железе, что приводит к ускорению катодного процесса и
переходу стали в пассивное состояние (Н. Д . Томашов).
На рис. 3.59 приводится схема, поясняющая этот переход.
§2. Ингибиторы коррозии
В качестве ингибиторов коррозии используются неорганиче­
ские ионы большей частью окислительного типа (NO3, СгО^- ,
442

Рис. 3.60. Схема действия ингибиторов-окислителей, переводящих ме­
талл в пассивное состояние:
1 —скорость катодного процесса в отсутствие ингибитора; 2 —то же в при­
сутствии ингибитора
М оО|" и др). В присутствии ингибирующего иона возрастает
скорость катодного процесса в результате восстановления ин­
гибирующего иона. При этом металл переходит из активного в
пассивное состояние. Схема, приведенная на рис. 3.60, поясня­
ет действие ингибиторов-окислителей. Ингибиторы-окислители,
восстанавливаясь, увеличивают катодный ток и снижают пе­
ренапряжение процесса восстановления. При этом корродиру­
ющий металл из активной области (-EKop) переходит в пассив­
ную область — коррозионный потенциал металла смещается в
область более положительных потенциалов (£^ ор). Коррозия ме­
та л л а резко снижается.
Более широкое применение в качестве ингибиторов находят
поверхностно-активные органические вещества, имеющие поляр­
ные группы (амины, спирты, альдегиды, сульфиды и др.) . По­
верхностно-активные органические вещества, адсорбируясь на
границе «металл —раствор» могут блокировать поверхность ме­
та лла и затруднять подход окислителя. Молекулы ингибиру­
ющего вещества, адсорбируясь на границе раздела «металл —
раствор» могут такж е изменять строение двойного электриче­
ского слоя, что приводит к торможению катодного или анодно­
го процессов или одновременно обоих процессов. Концентрация
ингибиторов составляет, как правило, не более 1 % массы рас­
твора. При защите металлов в замкнутых объемах применяют­
ся летучие ингибиторы — вещества с высокой упругостью пара,
имеющие функциональные группы “ ОН", - N H 2 и др.
443

§ 3. Электрохимические методы защиты
A. Протекторная защита. Известно, что при смещении потен­
циала металла в область более отрицательных значений ско­
рость коррозии металла уменьшается, и при достижении рав­
новесного потенциала металл перестает подвергаться коррозии.
Если соединить защищаемый металл с более активным метал­
лом в проводящей электрический то к среде (почва, морская во­
да), то возникает гальванический элемент. Металл более а ктив­
ный (цинк, алюминий, магниевые сплавы) начинает р азруш ать­
ся. В то же время другой металл (сталь) играет роль катода
и на его поверхности идет восстановление кислорода или дру­
гого окислителя. Таким образом, более активный металл или
сплав, имеющий более отрицательный потенциал в коррозионно­
активной среде по сравнению с защищаемым металлом, играет
роль протектора. Протекторная защ ита используется дл я защи­
ты подземных коммуникаций и корпуса кораблей.
Б. Катодная защита. Смещение потенциала защищаемого ме­
талла в область более отрицательных значений можно достиг­
нуть путем подключения защищаемого металла к отрицательно­
му полюсу источника постоянного тока, а положительный полюс
источника то ка при этом подсоединяется к ненужному куску ме­
талла (разбитая батарея отопления, обломок трубы). Происхо­
дит электролиз, при котором защищаемый металл играет роль
катода, а другой, ненужный, металл является анодом и окисля­
ется. Катодный метод защиты широко применяется при подзем­
ной защите трубопроводов. Источники постоянного тока распо­
лагаются на определенном расстоянии друг от друга вдоль трас­
сы трубопровода. Расстояние между источниками тока и раз­
ность потенциалов между катодом и анодом рассчитываются с
учетом, что потенциал защищенного трубопровода долж ен до­
стигать определенного значения, при котором металл трубопро­
вода практически не подвергается коррозии.
B. Анодная защита. Широко распространен анодный способ
защиты, когда металл защищаемой конструкции (например, ме­
таллическая емкость для хранения кислоты) переводится в пас­
сивное состояние, при котором скорость коррозии металла резко
снижается. При анодной защите защищаемый металл подклю­
чается к положительному полюсу источника постоянного тока
и при анодной поляризации металл переводится в пассивное со­
стояние. Другой вспомогательный электрод подключается к от­
рицательному полюсу источника то к а и выполняет роль катода.
Часто на практике применяются комбинированные методы
защиты.
444

Контрольные вопросы
I . Что изучает электрохимия?
2. Какие бывают проводники?
3. Чем отличаются металлы от полупроводников?
4. Что называют сверхпроводимостью?
5. Чем отличается электрохимический процесс от химического?
6. Какие физико-химические свойства растворов электролитов объ­
яснила теория электролитической диссоциации Аррениуса; перечисли­
те ее основные положения.
7. Для каких электролитов можно применить закон разведения
Оствальда?
8. Расположите Lil, Nal, RbCl, Csl в ряд по возрастанию величины
п в уравнении Борна —Ланде.
9. Что означает понятие «энергия сольватации»?
10. Как рассчитать свободную энергию и энтальпию сольватации
иона?
I I . Какова ионная сила 0,01 М раствора Na2S0 4 ?
12. Каков средний коэффициент активности 0,003 М раствора КС1?
Какая размерность коэффициента активности?
13. Каковы основные положения теории сильных электролитов Де­
бая и Хюккеля?
14. Что означают термины «удельная электропроводность» и «эк­
вивалентная электропроводность»? Как зависит удельная электропро­
водность от концентрации раствора и почему?
15. Как изменится скорость движения иона Са2+ в растворе при
увеличении напряженности электрического поля вдвое?
16. Что означает понятие «абсолютная подвижность иона»?
17. Как можно объяснить более высокую подвижность ионов И* и
ОН- по сравнению с другими ионами?
18. Что означает выражение «правильно разомкнутая цепь»?
19. Каково определение галъвани-потенциала?
20. Какие явления могут приводить к возникновению скачка элек­
трического потенциала на границе фаз? Как выразить условие равно­
весия между заряженными частицами в двухфазной системе?
21. Каково определение понятия «равновесный потенциал» на гра­
нице «металл —раствор», содержащий ионы данного металла?
22. Что означает понятие «электродный потенциал»?
23. Каких типов бывают электроды по классификации?
24. Какова природа диффузионного потенциала?
25. Каковы причины возникновения мембранного потенциала?
26. Каков будет равновесный потенциал для системы Си+ Си2+ + е",
Ес^/Си=°’337В-а£CuVCu= 520В?
27. Может ли ЭДС цепи гальванического элемента быть величиной
отрицательной?
28. Что означает понятие «стандартный равновесный потенциал
электрода»?

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Панченков Г.М ., Лебедев В.П . Химическая кинетика и ката­
лиз.
— 3-е изд.
— М.: Химия, 1985.
2. Дамаскин Б. Б ., Петрий О. Л. Основы теоретической электрохи­
мии. — М.: Высш. шк., 1978. — 239 с.
3. Дамаскин Б. Петрий О. А., Цирлина Г. А. Электрохимия.
—
М.: Химия, 2001. — 624 с.
4. Стромберг А. Г., Сенченко Д. П. Физическая химия. —М.: Высш.
шк., 1999. — 557 с.
5. Добычин Д .П ., Каданер Л. И., Серпинский В. В. и др. Физиче­
ская и коллоидная химия. —М.: Просвещение, 1986. — 463 с.
6. Краснов К. С., Воробьев 3. ЛГоднее И. Н. и др. Физическая хи­
мия / Под ред. К. С. Краснова: В 2-х т. —М.: Высш. шк., 1995. —Т. 1. —
512с. -
Т.2. -
319 с.
7. Третьяков Ю.Д . / / Соросовский образовательный журнал.
—
1999. -
No4, С. 35-39.
8. Гусаров В. В. Быстропротекающие твердофазные химические ре­
акции//ЖОХ.
-
1997. -
Т.67. -
Вып. 12, - С. 1959-1964, 1997.

ОГЛАВЛЕНИЕ
Список сокращений.................................................................. 3
Предисловие................................................ ............. .............
4
Вве д е н и е ..................................................................................
5
Глава 1. Химическая термодинамика..........................................
7
1.1. Термодинамика...............................................................
7
1.2. Нулевой и первый законы термодинамики...................... 13
1.3. Второй закон термодинамики......................................... 24
1.4. Энтропия. Второй закон термодинамики......................... 27
1.5. Постулат П л а н к а ............................................................ 37
1.6. Термодинамика открытых систем. Термодинамические
потенциалы.........................................
43
1.7. Третий закон термодинамики......................................... 59
1.8. Приложение законов термодинамики к химическим си­
стемам. Термохимия ....................................................... 61
1.9. Химическое равновесие. Закон действующих масс .... 71
1.10. Равновесие в гетерогенных системах.............................. 81
1.11. Равновесие в многокомпонентных системах. Химические
процессы р а зд е л е н и я ....................................................... 92
1.12. Равновесие в двухкомпонентных системах...................... 93
1.13. Равновесие в растворах.......................................................118
1.14. Адсорбция.......................................................................... 144
Глава 2. Химическая кинетика и катализ........................................ 155
2.1. Формальная кинетика .......................................................155
2.2. Скорость химической реакции............................................ 160
2.3. Методы формальной к и н е т и к и ......................................... 164
2.4. Скорости реакций в потоке ............................................... 196
2.5. Кинетика топохимических реакций....................................198
2.6. Быстрые реакции и релаксация......................................... 212
2.7. Фотохимические реакции.................................................... 218
2.8. Механохимические р е а к ц и и .............................................. 222
2.9. Зависимость скорости реакции
от темпер атуры .................................................................. 224
2.10. Механизмы элементарных а к т о в ...................................... 227
2.11. Влияние растворителя на скорость химической реакции 240
2.12. К атализ............................................................................... 248
2.13. Кинетика цепных р е а к ц и й ................................................. 302
Глава 3. Электрохимия.................................................................... 311
3.1. Электрохимия растворов................................................... 317
447

3.2. Теория электролитической диссоциации............................320
3.3. Сольватация и о н о в ............................................................. 323
3.4. Энергия ионной кристаллической р е ш е т к и ...................... 326
3.5. Энергия сольватации.......................................................... 329
3.6. Энтальпия сольватации соли ............................................ 331
3.7. Энтропия сольватации и о н о в ............................................ 333
3.8. Активность и коэффициент а ктивн ости............................334
3.9. Теория сильных электролитов Дебая —Х ю к к е л я ............. 337
3.10. Ассоциация и о н о в ................................................................ 343
3.11. Электропроводность р а с т в о р о в ......................................... 344
3.12. Числа п е р е н о с а ...................................................................353
3.13. Представления о межфазном скачке потенциалов .... 357
3.14. Термодинамика электрохимических с и с т е м ...................... 359
3.15. Равновесный потенциал .................................................... 364
3.16. Правила записи ЭДС й электродных потенциалов элек­
трохимических с и с т е м ....................................................... 370
3.17. Классификация э л е к т р о д о в ............................................... 372
3.18. Диффузионный потенциал.................................................. 381
3.19. Мембранные потенциалы.....................................................382
3.20. Ионоселективные электроды................
390
3.21. Двойной электрический слой ............................................ 395
3.22. Основы электрохимической к и н е т и к и .............................. 404
3.23. Диффузионная кинетика.................................................... 405
3.24. Электрохимическая к и н е т и к а ............................................ 412
3.25. Выделение водорода при катодной п о л яр и за ц и и ............. 417
3.26. Некоторые аспекты прикладной электрохимии................ 422
3.27. Получение веществ с помощью электролиза...................... 423
3.28. Химические источники т о к а ............................................... 426
3.29. Коррозия м е т а л л о в ............................................................. 436
Список л итературы .................................................. ................ 446

Welcome to site
www.twirpx.com
Annotated bibliography on
thermodynamics,
statistical physics and
physical chemistry