Author: Финтельгольц Г.М.
Tags: анализ математический анализ функциональный анализ
ISBN: 5-9221-0156-0
Year: 2003
Text
УДК 517.2
ББК 22.161
Ф65
Фихтенгольц Г. М. Курс дифференциального и интегрально-
интегрального исчисления. В 3 т. Т. I / Пред. и прим. А.А. Флоринского. — 8-е изд. —
М.: ФИЗМАТЛИТ, 2003. - 680 с. - ISBN 5-9221-0156-0.
Фундаментальный учебник по математического анализу, выдержавший
множество изданий и переведенный на ряд иностранных языков, отличается,
с одной стороны, систематичностью и строгостью изложения, а с другой —
простым языком, подробными пояснениями и многочисленными примерами,
иллюстрирующими теорию.
«Курс... » предназначен для студентов университетов, педагогических
и технических вузов и уже в течение длительного времени используется
в различных учебных заведениях в качестве одного из основных учебных
пособий. Он позволяет учащемуся не только овладеть теоретическим мате-
материалом, но и получить наиболее важные практические навыки. «Курс... »
высоко ценится математиками как уникальная коллекция различных фак-
фактов анализа, часть которых невозможно найти в других книгах на русском
языке.
Первое издание вышло в 1948 г.
Редактор: доцент матем.-механич. ф-та
Санкт-Петербургского гос. ун-та А.А. Флоринский
ISBN 5-9221-0156-0 (Т. I)
ISBN 5-9221-0155-2 © физматлит, 2001, 2003
ОГЛАВЛЕНИЕ
Предисловие редактора 11
Введение
ВЕЩЕСТВЕННЫЕ ЧИСЛА
§ 1. Область рациональных чисел
1. Предварительные замечания 13
2. Упорядочение области рациональных чисел 14
3. Сложение и вычитание рациональных чисел 15
4. Умножение и деление рациональных чисел 17
5. Аксиома Архимеда 19
§ 2. Введение иррациональных чисел. Упорядочение области вещественных
чисел
6. Определение иррационального числа 20
7. Упорядочение области вещественных чисел 23
8. Вспомогательные предложения 24
9. Представление вещественного числа бесконечной десятичной
дробью 25
10. Непрерывность области вещественных чисел 28
11. Границы числовых множеств 30
§ 3. Арифметические действия над вещественными числами
12. Определение суммы вещественных чисел 33
13. Свойства сложения 34
14. Определение произведения вещественных чисел 36
15. Свойства умножения 38
16. Заключение 40
17. Абсолютные величины 40
§ 4. Дальнейшие свойства и приложения вещественных чисел
18. Существование корня. Степень с рациональным показателем ... 41
19. Степень с любым вещественным показателем 43
20. Логарифмы 46
21. Измерение отрезков 47
4 ОГЛАВЛЕНИЕ
Глава первая
ТЕОРИЯ ПРЕДЕЛОВ
§ 1. Варианта и ее предел
22. Переменная величина, варианта 50
23. Предел варианты 54
24. Бесконечно малые величины 55
25. Примеры 57
26. Некоторые теоремы о варианте, имеющей предел 61
27. Бесконечно большие величины 63
§ 2. Теоремы о пределах, облегчающие нахождение пределов
28. Предельный переход в равенстве и неравенстве 65
29. Леммы о бесконечно малых 67
30. Арифметические операции над переменными 68
31. Неопределенные выражения 70
32. Примеры на нахождение пределов 73
33. Теорема Штольца и ее применения 78
§ 3. Монотонная варианта
34. Предел монотонной варианты 81
35. Примеры 83
36. Число е 88
37. Приближенное вычисление числа е 90
38. Лемма о вложенных промежутках 94
§ 4. Принцип сходимости. Частичные пределы
39. Принцип сходимости 96
40. Частичные последовательности и частичные пределы 99
41. Лемма Больцано - Вейерштрасса 101
42. Наибольший и наименьший пределы 103
Глава вторая
ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
§ 1. Понятие функции
43. Переменная и область ее изменения 107
44. Функциональная зависимость между переменными. Примеры ... 108
45. Определение понятия функции ПО
46. Аналитический способ задания функции 113
47. График функции 116
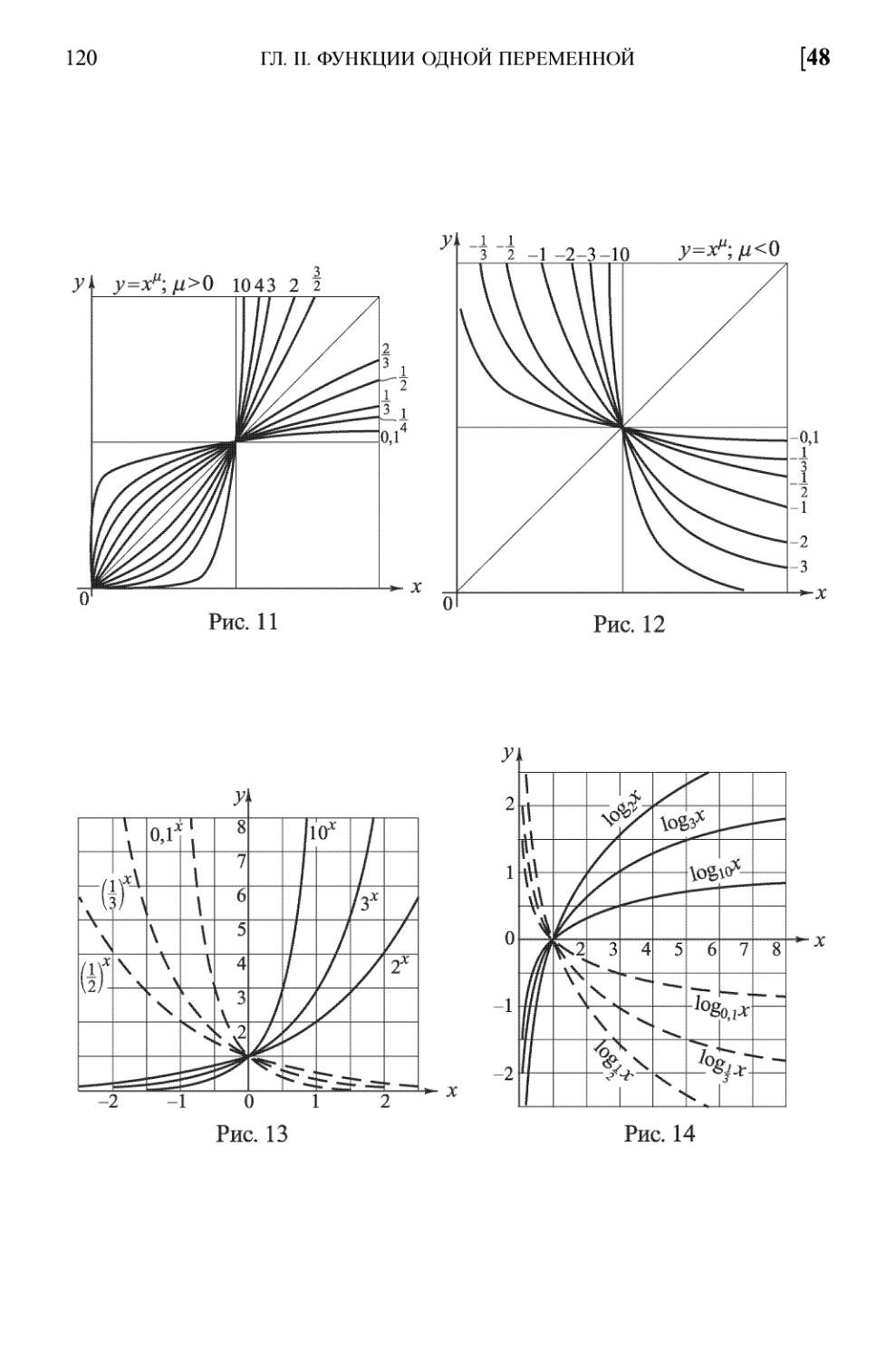
48. Важнейшие классы функций 118
49. Понятие обратной функции 124
50. Обратные тригонометрические функции 126
51. Суперпозиция функций. Заключительные замечания 131
§ 2. Предел функции
52. Определение предела функции 132
53. Сведение к случаю варианты 134
54. Примеры 137
55. Распространение теории пределов 145
56. Примеры 148
ОГЛАВЛЕНИЕ 5
57. Предел монотонной функции 151
58. Общий признак Больцано-Коши 152
59. Наибольший и наименьший пределы функции 154
§ 3. Классификация бесконечно малых и бесконечно больших величин
60. Сравнение бесконечно малых 154
61. Шкала бесконечно малых 156
62. Эквивалентные бесконечно малые 157
63. Выделение главной части 159
64. Задачи 161
65. Классификация бесконечно больших 163
§ 4. Непрерывность (и разрывы) функций
66. Определение непрерывности функции в точке 164
67. Арифметические операции над непрерывными функциями 167
68. Примеры непрерывных функций 167
69. Односторонняя непрерывность. Классификация разрывов 169
70. Примеры различных функций 171
71. Непрерывность и разрывы монотонной функции 173
72. Непрерывность элементарных функций 174
73. Суперпозиция непрерывных функций 175
74. Решение одного функционального уравнения 176
75. Функциональная характеристика показательной, логарифмической
и степенной функций 178
76. Функциональная характеристика тригонометрического и гипербо-
гиперболического косинусов 180
77. Использование непрерывности функций для вычисления пределов 182
78. Степенно-показательные выражения 185
79. Примеры 186
§ 5. Свойства непрерывных функций
80. Теорема об обращении функции в нуль 188
81. Применение к решению уравнений 190
82. Теорема о промежуточном значении 191
83. Существование обратной функции 193
84. Теорема об ограниченности функции 195
85. Наибольшее и наименьшее значения функции 196
86. Понятие равномерной непрерывности 199
87. Теорема Кантора 201
88. Лемма Бореля 202
89. Новые доказательства основных теорем 204
Глава третья
ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
§ 1. Производная и ее вычисление
90. Задача о вычислении скорости движущейся точки 208
91. Задача о проведении касательной к кривой 209
92. Определение производной 212
93. Примеры вычисления производных 216
6 ОГЛАВЛЕНИЕ
94. Производная обратной функции 219
95. Сводка формул для производных 221
96. Формула для приращения функции 222
97. Простейшие правила вычисления производных 223
98. Производная сложной функции 226
99. Примеры 227
100. Односторонние производные 234
101. Бесконечные производные 235
102. Дальнейшие примеры особых случаев 236
§ 2. Дифференциал
103. Определение дифференциала 237
104. Связь между дифференцируемостью и существованием
производной 238
105. Основные формулы и правила дифференцирования 241
106. Инвариантность формы дифференциала 242
107. Дифференциалы как источник приближенных формул 245
108. Применение дифференциалов при оценке погрешностей 247
§ 3. Основные теоремы дифференциального исчисления
109. Теорема Ферма 249
ПО. Теорема Дарбу 251
111. Теорема Ролля 252
112. Формула Лагранжа 253
113. Предел производной 256
114. Формула Коши 257
§ 4. Производные и дифференциалы высших порядков
115. Определение производных высших порядков 259
116. Общие формулы для производных любого порядка 261
117. Формула Лейбница 265
118. Примеры 267
119. Дифференциалы высших порядков 270
120. Нарушение инвариантности формы для дифференциалов высших
порядков 271
121. Параметрическое дифференцирование 273
122. Конечные разности 274
§ 5. Формула Тейлора
123. Формула Тейлора для многочлена 276
124. Разложение произвольной функции; дополнительный член в форме
Пеано 278
125. Примеры 282
126. Другие формы дополнительного члена 286
127. Приближенные формулы 289
§ 6. Интерполирование
128. Простейшая задача интерполирования. Формула Лагранжа .... 295
129. Дополнительный член формулы Лагранжа 297
130. Интерполирование с кратными узлами. Формула Эрмита 298
ОГЛАВЛЕНИЕ 7
Глава четвертая
ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ
ПРОИЗВОДНЫХ
§ 1. Изучение хода изменения функции
131. Условие постоянства функции 301
132. Условие монотонности функции 303
133. Доказательство неравенств 306
134. Максимумы и минимумы; необходимые условия 310
135. Достаточные условия. Первое правило 312
136. Примеры 314
137. Второе правило 318
138. Использование высших производных 320
139. Разыскание наибольших и наименьших значений 323
140. Задачи 324
§ 2. Выпуклые (и вогнутые) функции
141. Определение выпуклой (вогнутой) функции 329
142. Простейшие предложения о выпуклых функциях 330
143. Условия выпуклости функции 333
144. Неравенство Иенсена и его приложения 336
145. Точки перегиба 338
§ 3. Построение графиков функций
146. Постановка задачи 341
147. Схема построения графика. Примеры 342
148. Бесконечные разрывы, бесконечный промежуток. Асимптоты . . . 344
149. Примеры 348
§ 4. Раскрытие неопределенностей
150. Неопределенность вида jj 351
151. Неопределенность вида Ц 357
152. Другие виды неопределенностей 359
§ 5. Приближенное решение уравнений
153. Вводные замечания 361
154. Правило пропорциональных частей (метод хорд) 362
155. Правило Ньютона (метод касательных) 366
156. Примеры и упражнения 368
157. Комбинированный метод 373
158. Примеры и упражнения 374
Глава пятая
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
§ 1. Основные понятия
159. Функциональная зависимость между переменными. Примеры . . . 378
160. Функции двух переменных и области их определения 379
161. Арифметическое «-мерное пространство 383
8 ОГЛАВЛЕНИЕ
162. Примеры областей в ^-мерном пространстве 387
163. Общее определение открытой и замкнутой области 389
164. Функции п переменных 392
165. Предел функции нескольких переменных 395
166. Сведение к случаю варианты 397
167. Примеры 399
168. Повторные пределы 401
§ 2. Непрерывные функции
169. Непрерывность и разрывы функций нескольких переменных . . . 404
170. Операции над непрерывными функциями 406
171. Функции, непрерывные в области. Теоремы Больцано - Коши . . . 407
172. Лемма Больцано - Вейерштрасса 409
173. Теоремы Вейерштрасса 412
174. Равномерная непрерывность 413
175. Лемма Бореля 415
176. Новые доказательства основных теорем 417
§ 3. Производные и дифференциалы функций нескольких переменных
177. Частные производные и частные дифференциалы 419
178. Полное приращение функции 422
179. Полный дифференциал 426
180. Геометрическая интерпретация для случая функции двух
переменных 428
181. Производные от сложных функций 432
182. Примеры 434
183. Формула конечных приращений 436
184. Производная по заданному направлению 438
185. Инвариантность формы (первого) дифференциала 441
186. Применение полного дифференциала в приближенных
вычислениях 443
187. Однородные функции 446
188. Формула Эйлера 448
§ 4. Производные и дифференциалы высших порядков
189. Производные высших порядков 449
190. Теорема о смешанных производных 452
191. Обобщение 456
192. Производные высших порядков от сложной функции 458
193. Дифференциалы высших порядков 459
194. Дифференциалы сложных функций 464
195. Формула Тейлора 465
§ 5. Экстремумы, наибольшие и наименьшие значения
196. Экстремумы функции нескольких переменных. Необходимые
условия 468
197. Достаточные условия (случай функции двух переменных) 470
198. Достаточные условия (общий случай) 475
ОГЛАВЛЕНИЕ 9
199. Условия отсутствия экстремума 478
200. Наибольшее и наименьшее значения функции. Примеры 480
201. Задачи 484
Глава шестая
ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ
§ 1. Формальные свойства функциональных определителей
202. Определение функциональных определителей (якобианов) .... 494
203. Умножение якобианов 495
204. Умножение функциональных матриц (матриц Якоби) 497
§ 2. Неявные функции
205. Понятие неявной функции от одной переменной 500
206. Существование неявной функции 502
207. Дифференцируемость неявной функции 505
208. Неявные функции от нескольких переменных 507
209. Вычисление производных неявных функций 515
210. Примеры 519
§ 3. Некоторые приложения теории неявных функций
211. Относительные экстремумы 524
212. Метод неопределенных множителей Лагранжа 527
213. Достаточные для относительного экстремума условия 529
214. Примеры и задачи 530
215. Понятие независимости функций 535
216. Ранг матрицы Якоби 537
§ 4. Замена переменных
217. Функции одной переменной 542
218. Примеры 544
219. Функции нескольких переменных. Замена независимых
переменных 547
220. Метод вычисления дифференциалов 549
221. Общий случай замены переменных 550
222. Примеры 553
Глава седьмая
ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
К ГЕОМЕТРИИ
§ 1. Аналитическое представление кривых и поверхностей
223. Кривые на плоскости (в прямоугольных координатах) 563
224. Примеры 566
225. Кривые механического происхождения 569
226. Кривые на плоскости (в полярных координатах). Примеры .... 572
227. Поверхности и кривые в пространстве 578
228. Параметрическое представление 580
229. Примеры 582
§ 2. Касательная и касательная плоскость
230. Касательная к плоской кривой в прямоугольных координатах . . . 586
231. Примеры 588
10 ОГЛАВЛЕНИЕ
232. Касательная в полярных координатах 590
233. Примеры 591
234. Касательная к пространственной кривой. Касательная плоскость
к поверхности 593
235. Примеры 598
236. Особые точки плоских кривых 599
237. Случай параметрического задания кривой 605
§ 3. Касание кривых между собой
238. Огибающая семейства кривых 607
239. Примеры 611
240. Характеристические точки 614
241. Порядок касания двух кривых 616
242. Случай неявного задания одной из кривых 619
243. Соприкасающаяся кривая 620
244. Другой подход к соприкасающимся кривым 623
§ 4. Длина плоской кривой
245. Леммы 624
246. Направление на кривой 625
247. Длина кривой. Аддитивность длины дуги 627
248. Достаточные условия спрямляемости. Дифференциал дуги .... 629
249. Дуга в роли параметра. Положительное направление касательной 633
§ 5. Кривизна плоской кривой
250. Понятие кривизны 637
251. Круг кривизны и радиус кривизны 640
252. Примеры 642
253. Координаты центра кривизны 646
254. Определение эволюты и эвольвенты; разыскание эволюты 648
255. Свойства эволют и эвольвент 651
256. Разыскивание эвольвент 654
Дополнение
ЗАДАЧА РАСПРОСТРАНЕНИЯ ФУНКЦИЙ
257. Случай функции одной переменной 657
258. Постановка задачи для двумерного случая 659
259. Вспомогательные предложения 661
260. Основная теорема о распространении 665
261. Обобщение 666
262. Заключительные замечания 668
Алфавитный указатель 671
ПРЕДИСЛОВИЕ РЕДАКТОРА
«Курс дифференциального и интегрального исчисления» Григория Михай-
Михайловича Фихтенгольца — выдающееся произведение научно-педагогической лите-
литературы, выдержавшее множество изданий и переведенное на ряд иностранных
языков. «Курс ...» не имеет себе равных по объему охваченного фактического
материала, количеству разнообразных приложений общих теорем в геометрии, ал-
алгебре, механике, физике и технике. Многие известные современные математики
отмечают, что именно «Курс ...» Г. М. Фихтенгольца привил им в студенческие
годы вкус и любовь к математическому анализу, дал первое ясное понимание
этого предмета.
За 50 лет, прошедших после выхода первого издания «Курса . . .», его текст
практически не устарел и в настоящий момент по-прежнему может использо-
использоваться и используется студентами университетов, а также различных техниче-
технических и педагогических вузов в качестве одного из основных учебных пособий
по математическому анализу и курсу высшей математики. Более того, несмот-
несмотря на появление новых хороших учебников, аудитория читателей «Курса ...»
Г. М. Фихтенгольца за время его существования лишь расширилась и включает
сейчас учащихся ряда физико-математических лицеев, слушателей курсов повы-
повышения математической квалификации инженеров.
Высокий уровень востребованности «Курса . . .» объясняется его уникальны-
уникальными особенностями. Основной теоретический материал, вошедший в «Курс . . .», —
это классическая часть современного математического анализа, окончательно
сформировавшаяся к началу XX столетия (не содержащая теории меры и об-
общей теории множеств). Эта часть анализа преподается на первых двух курсах
университетов и входит (целиком или в значительной части) в программы всех
технических и педагогических вузов. I том «Курса . . .» включает дифференциаль-
дифференциальное исчисление одной и нескольких вещественных переменных и его основные
приложения, II том посвящен теории интеграла Римана и теории рядов, III том —
кратным, криволинейным и поверхностным интегралам, интегралу Стилтьеса, ря-
рядам и преобразованию Фурье.
Огромное количество примеров и приложений, как правило, весьма инте-
интересных, некоторые из которых найти в другой литературе на русском языке не-
невозможно, составляет одну из главных особенностей «Курса . . .», уже упомяну-
упомянутую выше.
Другая существенная особенность — доступность, подробность и обстоятель-
обстоятельность изложения материала. Значительный объем «Курса ...» не превращает-
превращается в помеху для его усвоения. Напротив, он дает возможность автору уделять
достаточное внимание мотивировкам новых определений и постановкам задач,
подробным и тщательным доказательствам основных теорем и многим другим
аспектам, облегчающим читателю понимание предмета. Вообще проблема сов-
совмещения понятности и строгости изложения (отсутствие последней приводит
12 ПРЕДИСЛОВИЕ РЕДАКТОРА
попросту к искажению математических фактов) хорошо известна любому препо-
преподавателю. Огромное педагогическое мастерство Григория Михайловича позволяет
ему на протяжении всего «Курса ...» дать множество примеров решения указан-
указанной проблемы; наряду с другими обстоятельствами это превращает «Курс ...»
в незаменимый образец для начинающего лектора и объект исследований для
специалистов по методике преподавания высшей математики.
Еще одной особенностью «Курса ...» является весьма незначительное
использование каких-либо элементов теории множеств (в том числе обозначе-
обозначений). При этом сохраняется полная строгость изложения; в целом, как и 50 лет
назад, такой подход облегчает значительной части читательской аудитории пер-
первоначальное усвоение предмета.
В новом издании «Курса ...» Г. М. Фихтенгольца, предлагаемом вниманию
читателя, устранены опечатки, обнаруженные в ряде предыдущих изданий. Кроме
того, издание снабжено краткими комментариями, относящимися к тем местам
текста (весьма немногочисленным), при работе с которыми у читателя могут
возникнуть те или иные неудобства; примечания делаются, в частности, в тех
случаях, когда используемый автором термин или оборот речи чем-либо отли-
отличаются от наиболее распространенных в настоящее время. Ответственность за
содержание примечаний целиком лежит на редакторе издания.
Редактор глубоко признателен профессору Б. М. Макарову, прочитавшему
тексты всех примечаний и высказавшему ряд ценных суждений. Хочется побла-
поблагодарить также всех сотрудников кафедры математического анализа математико-
механического факультета Санкт-Петербургского государственного университета,
обсуждавших с автором этих строк разнообразные вопросы, связанные с текстами
предыдущих изданий и идеей нового издания «Курса . . .».
Редакция заранее благодарит всех читателей, которые своими замечаниями
пожелают способствовать дальнейшему улучшению качества издания.
А. А. Флоринский
ВВЕДЕНИЕ
ВЕЩЕСТВЕННЫЕ ЧИСЛА
§ 1. Область рациональных чисел
1. Предварительные замечания. Из школьного курса читате-
читателю хорошо знакомы рациональные числа и их свойства. В то же
время, уже потребности элементарной математики приводят к не-
необходимости расширения этой числовой области. Действительно,
среди рациональных чисел не существует зачастую корней даже
из целых положительных (натуральных) чисел, например у/29 т. е.
нет такой рациональной дроби ^ {где р и q — натуральные
числа), квадрат которой был бы равен 2.
Для доказательства этого допустим противное: пусть сущест-
существует такая дробь ^, что (^) = 2. Мы вправе считать эту дробь
несократимой, т. е. р и q лишенными общих множителей. Так как
р2 = 2q2, то р есть число четное: р = 2г (г — целое) и, следова-
следовательно, q — нечетное. Подставляя вместо р его выражение, найдем:
q2 = 2r2, откуда следует, что q — четное число. Полученное про-
противоречие доказывает наше утверждение.
Одновременно с этим, если бы мы оставались в области одних
лишь рациональных чисел, в геометрии заведомо не все отрезки
могли бы быть снабжены длинами. В самом деле, рассмотрим
квадрат со стороной, равной единице длины. Его диагональ не
может иметь рациональной длины -, ибо, в противном случае,
по теореме Пифагора, квадрат этой длины был бы равен 2, что,
как мы видели, невозможно.
В настоящем введении мы ставим себе задачей расширить
область рациональных чисел, присоединив к ним числа новой при-
природы — иррациональные. Вместе с тем мы покажем, что
в расширенной области останутся справедливыми все привычные
14 ВВЕДЕНИЕ [2
свойства рациональных чисел, относящиеся к арифметическим дей-
действиям над ними и к сочетанию их с помощью знаков равен-
равенства и неравенства. Для того чтобы сделать реально возможной
проверку упомянутых свойств для расширенной числовой облас-
области, очень важно выделить наименьшее количество основных
свойств, из которых все остальные вытекали бы уже как фор-
формально-логические следствия: тогда проверке будут под-
подлежать лишь эти основные свойства.
В связи с этим мы приводим ниже перечень основных свойств
области рациональных чисел. Попутно мы на ряде примеров по-
показываем, как другие известные их свойства выводятся из основ-
основных совершенно формально. Говоря о «числах», мы здесь всегда
имеем в виду рациональные числа: буквы а, Ъ и т. д. обозначают
именно их.
2. Упорядочение области рациональных чисел. Условимся с са-
самого начала, что равные числа мы будем рассматривать как
одно и то же число в разных формах. Иными словами,
для нас понятие «равно» (=) означает «тождественно». Поэтому
мы не перечисляем свойств равных чисел.
Упорядочение рациональных чисел достигается с помощью
понятия «больше» (>), с которым связана первая группа
свойств:
11° для каждой пары чисел а и Ъ имеет место одно,
и только одно, из соотношений
а = Ь, а > Ь, Ъ > а;
12°иза>ЬиЬ>с следует а > с {транзитивное
свойство знака >);
13° если а > Ъ, то найдется также такое число с, что
а > с и с > Ъ*]
{свойство плотности).
Понятие «меньше» (<) вводится уже как производное. Именно,
говорят, что а < Ъ в том, и только в том, случае, если Ъ > а. Легко
видеть, что из а<ЬиЬ<с следует, что а < с (транзитивное
свойство знака <). Действительно, неравенства а < Ъ и Ъ < с
*) В этих условиях говорят также, что число с лежит между числами а иЬ; оче-
очевидно, таких чисел будет бесчисленное множество. {Здесь и далее звездочками
обозначены примечания автора.)
3] § 1. ОБЛАСТЬ РАЦИОНАЛЬНЫХ ЧИСЕЛ 15
равносильны, по условию, неравенствам Ъ > а и с > Ь; отсюда
следует с > а [12°] или, что то же, а < с.
Дальнейшие свойства понятия «больше», связанные с арифме-
арифметическими действиями над рациональными числами, будут указаны
ниже.
3. Сложение и вычитание рациональных чисел. Вторая
группа свойств связана со сложением, т. е. с операцией
нахождения суммы двух чисел. Для каждой пары чисел а и Ъ су-
существует (единственное) число, называемое суммой^ и J (его
обозначают а + Ь). Это понятие обладает свойствами:
111° a + b = b + a (первместительное свойство сло-
сложения);
II 2° (а + Ь) +с = а + (Ь + с) (сочетательное свойство
сложения).
Особая роль нуля характеризуется свойством:
II 3° а + 0 = а;
кроме того,
II 4° для каждого числа а существует число —а (сим-
(симметричное ему), такое, что а + (—а) = 0.
На основе этих свойств прежде всего исчерпывается вопрос
о вычитании как действии, обратном сложению. Если раз-
разностью чисел а и Ъ9 как обычно, называть такое число с, для
которого с + Ъ = а *\ то встает вопрос о существовании такого
числа и о его единственности.
Положив с = а + (-6), получим [II 2°, 1°, 4°, 3°]:
с + Ъ = [а + (-b)] +b = a+ [(-b) + Ь] =
= а+ [b + (-b)] =a+0 = a,
так что это число с удовлетворяет определению разности.
Пусть, обратно, с' есть разность чисел а и Ь9 так что с1+Ъ = а.
Прибавив к обеим частям этого равенства по (—Ъ) и преобразуя
левую часть [II 2°, 4°, 3°]:
(сг + Ъ) + (-Ъ) = с' + [Ъ + (-Ь)] = с' + 0 = с7,
заключим, что с' = а + (~Ь) = с.
*) Ввиду II 1°, это равенство, определяющее разность, можно написать и так:
Ъ + с = а.
16 ВВЕДЕНИЕ [3
Таким образом, доказаны существование и одно-
однозначность разности чисел а и Ь; обозначают ее а — Ь.
Из однозначности разности вытекает ряд следствий. Прежде
всего, из II 3° следует 0 = а — а, и мы заключаем, что, кроме
числа 0, не существует числа, которое обладало бы свойством, ана-
аналогичным II 3°. Далее, отсюда же вытекает единственность числа,
симметричного данному: — а = 0 — а.
Так как из а + (—а) = 0 следует (—а)+а = О [II 1°], то оказыва-
оказывается, что а = —(—а), т. е. числа а и —а являются взаимно сим-
симметричными. Установим еще такое свойство симметричных чисел:
для этого достаточно доказать, что
а это вытекает из II 1°, 2°, 4°, 3°.
Наконец, приведем еще одно свойство, связывающее знак > со
знаком суммы:
II 5° из а > Ъ следует а + с > Ъ + с.
Оно устанавливает право к обеим частям неравенства при-
прибавлять поровну; из него сразу следует, что неравенства а > Ъ
иа+с>Ь + с равносильны, каково бы ни было число с (дей-
(действительно, добавляя к обеим частям второго неравенства число
-с, мы получаем первое).
В частности, неравенство а > Ъ равносильно неравенствам
а — Ъ > 0 и —Ь > —а; неравенство а > 0 эквивалентно неравен-
неравенству —а < 0. Таким образом, из двух взаимно симметричных чи-
чисел а и —а одно (и только одно) будет больше нуля; его именно и
называют абсолютной величиной как числа а, так и чис-
числа —а, и обозначают символом
а\ = | — а\.
Абсолютную величину числа нуль полагают равной нулю; |0| = 0.
На свойстве II 5° основывается возможность почленного скла-
складывания неравенств: из a>bnc>d следует а + с > Ъ + d.
В самом деле, из а > Ъ следует а + с > Ъ + с; в свою очередь, из
с > d следует с + Ъ > d + Ъ или [II 1°] Ъ + с > Ъ + d, а тогда,
в силу I 2°, окончательно получаем а + с > Ъ + d.
4] § 1. ОБЛАСТЬ РАЦИОНАЛЬНЫХ ЧИСЕЛ 17
4. Умножение и деление рациональных чисел. Третья груп-
па свойств связана с умножением, т. е. с операцией нахожде-
нахождения произведения двух чисел. Для каждой пары чисел а и Ъ су-
существует (единственное) число, называемое произведением^
и Ъ (его обозначают а • Ъ или просто ab). Это понятие обладает
свойствами:
III 1° а - Ъ — Ъ - а (первместительное свойство умно-
умножения}',
III 2° (а • Ъ) • с = а • (Ъ • с) (сочетательное свойство
умножения).
Особая роль единицы характеризуется свойством:
III 3° а • 1 = а;
кроме того,
III 4° для каждого числа а, отличного от 0, сущест-
существует число ^ (обратное ему), такое, что а • ^ = 1.
Вопрос о делении как о действии, обратном умножению, ре-
решается на основе свойств умножения так же, как выше был решен
вопрос о вычитании на основе свойств сложения. Обратное число
здесь будет играть ту же роль, какую там играло симметричное
число.
Назовем частным чисел а и b (где делитель Ъ всегда пред-
предполагается отличным от 0) такое число с, что*)
с - Ъ — а.
Этому определению можно удовлетворить, положив с = а • ^,
так как [1112°, 1°, 4°, 3°]:
Обратно, если число с' удовлетворяет определению частного
чисел а и Ь9 так что с' • b = а9 то, умножив обе части этого равен-
равенства на \ и преобразуя левую часть [III 2°, 4°, 3°]:
получим, что с1 = а • \ = с.
*^ Ввиду III 1°, это равенство, определяющее частное, можно записать и так:
Ъ • с = а.
18 ВВЕДЕНИЕ [4
Таким образом, доказаны существование и одно-
однозначность частного чисел а и Ъ (при условии, что
Ъ ф 0); обозначают его а : Ъ или |.
Из однозначности частного выводим, что, кроме числа 1, нет
числа, которое обладало бы свойством, аналогичным III 3°. За-
Затем отсюда, как и выше, вытекает единственность обратного числа
(как частного 1 и а); кроме того, легко устанавливается, что чис-
ла а и ^ являются взаимно обратными.
Следующее свойство связывает оба основных арифметических
действия — умножение и сложение:
III 5° (а + b) -с = а -c + b-с {распределительное свой-
свойство умножения относительно суммы).
Отсюда легко вывести и распределительное свойство
умножения относительно разности:
(а — Ъ) - с = а - с — Ъ • с.
По определению разности, это прямо следует из того, что
{а - 6) • с + Ъ • с = [{а - Ъ) + Ъ] • с = а • с.
Применим еще свойство III 5° к доказательству того, что
6.0 = 0-6 = 0.
В самом деле [II 3°],
откуда следует 0 • Ъ = 0, а также [III 1°] Ъ • 0 = 0.
Обратно, если а-Ь = 0иЬф0, то необходимо а = 0. Дей-
Действительно, а = ?, но одновременно и 0 = | (так как 6 • 0 = 0),
а частное единственно.
Наконец, укажем свойство, связывающее знак > со знаком про-
произведения:
III 6° из а > й и с > 0 следует а • с > Ъ • с.
На этом основывается почленное перемножение неравенств
с положительными членами. Отсюда же получается, что при а > 0
и Ъ > 0 также и а • 6 > 0.
Заметим, что (—а) • b = —(а • Ь); это следует из того, что
а-Ь + (-а) -Ь = [а + (-а)} .6 = 0-6 = 0.
5] § 1. ОБЛАСТЬ РАЦИОНАЛЬНЫХ ЧИСЕЛ 19
Теперь нетрудно видеть, что если а < О, Ъ > О, так что а = —\а\,
Ъ = \Ь\, то
а-Ь = (-\а\)-\Ь\ = -(\а\-\Ь\)<0;
то же будет при а > Ъ9 Ъ < 0. Если же а < 0, Ъ < 0, то
а-Ъ= {-\а\)-{-\Ъ\) = -[\а\-{-\Ъ\)] =
= -[-(\а\-\Ь\)] = \а\.\Ь\>0.
Таким образом, мы полностью восстановили известное пра-
правило знаков при умножении, которое является логическим
следствием перечисленных свойств рациональных чисел. Иными
словами, правило знаков принудительно навязывается
нам, если мы хотим соблюдения упомянутых свойств. То лее
молено сказать (как это выяснено выше) и относительно пра-
правила умножения на 0.
Имея в своем распоряжении свойства сложения и умножения,
мы теперь могли бы доказать то свойство плотности области
рациональных чисел, которое мы сформулировали выше в числе
основных свойств [I 3°]. Именно, с помощью их можно показать,
например, что из а > Ъ следует а > ^4^- > Ъ.
5. Аксиома Архимеда. Заключим наш перечень основных
свойств рациональных чисел следующим простым и важным утвер-
утверждением, которое не вытекает из перечисленных свойств:
IV 1° каково бы ни было число с > 0, существует нату-
натуральное число /7, которое больше с {«аксиома Архимеда»).
В действительности Архимедом было высказано геометри-
геометрическое предположение, которое и известно под именем «аксиомы
Архимеда»:
если на прямой даны любые два отрезка А и В, то моле-
молено А повторить слагаемым столько раз, чтобы сумма была
больше В:
А+А-{ \-А =А-п> В.
п раз
Если перефразировать это утверждение для положительных чи-
чисел а и Ь9 то оно сведется к существованию такого натурального
числа /7, что
п раз
20 ВВЕДЕНИЕ [6
Это неравенство, если использовать уже изученные свойства раци-
рациональных чисел, оказывается равносильным такому: п > |; обозна-
обозначив частное | через с, мы и получим ту формулировку, которая
дана выше.
§ 2. Введение иррациональных чисел. Упорядочение
области вещественных чисел
6. Определение иррационального числа. ^ Множество рацио-
рациональных чисел со всеми их свойствами, перечисленными в § 1, счи-
считается данным.
Мы изложим теорию иррациональных чисел, сле-
следуя Дедекинду (R. Dedekind). В основе этой теории лежит
понятие о сечении в области рациональных чисел. Рассмотрим
разбиение множества всех рациональных чисел на два непустых
(т. е. действительно содержащих хоть по одному числу) множест-
множества^, А'. Мы будем называть такое разбиение сечением, если
выполняются условия:
1° каждое рациональное число попадает в одно, и только
в одно*\ из множеств — А или А';
2° каждое число а множества А меньше каждого числа а'
множества А'.
Множество А называется нижним классом сечения,
множество А' — верхним классом. Сечение будем обозна-
обозначать А\А'.
Из определения сечения следует, что всякое рациональное чис-
число, меньшее числа а нижнего класса, также принадлежит нижнему
классу. Аналогично, всякое рациональное число, большее числа а1
верхнего класса, и само принадлежит верхнему классу.
Пример 1. Определим А как множество всех рациональных
чисел а, удовлетворяющих неравенству а < 1, а к множеству А'
причислим все числа а\ для которых а1 ^ 1.
*' То обстоятельство, что каждое рациональное число попадает только в один
из классов, вытекает, впрочем, из требования 2°.
Другой подход к введению вещественных чисел в курсе анализа заключа-
заключается в том, что простейшие свойства всех (как рациональных, так и ирра-
иррациональных) вещественных чисел рассматриваются как аксиомы и принимаются
без доказательства. Склонный к такому подходу читатель может при чтении это-
этого параграфа сразу перейти к пп° 10 и 11. {Здесь и далее цифрой—номером
обозначены примечания редактора.)
6] § 2. ВВЕДЕНИЕ ИРРАЦИОНАЛЬНЫХ ЧИСЕЛ 21
Легко проверить, что таким образом мы действительно полу-
получим сечение. Число 1 принадлежит классу А' и является, очевид-
очевидно, в нем наименьшим числом. С другой стороны, нет наибольшего
числа в классе А, так как, какое бы число а из А мы ни взяли, всегда
можно указать рациональное число а\9 лежащее между ним и еди-
единицей, следовательно, большее а и тоже принадлежащее классу А.
Пример 2. К нижнему классу А отнесем все рациональные
числа а, меньшие или равные 1: а ^ 1; к верхнему — рациональ-
рациональные числа а\ большие 1: а' > 1.
Это также будет сечение, причем здесь в верхнем классе нет
наименьшего числа, а в нижнем есть наибольшее (именно 1).
Пример 3. Отнесем к классу А все положительные рацио-
рациональные числа а, для которых а2 < 2, число 0 и все отрицательные
рациональные числа, а к классу А' — все положительные рацио-
рациональные числа а\ для которых а1 > 2.
Как легко убедиться, мы опять получили сечение. Здесь ни
в классе А нет наибольшего числа, ни в классе А1 — наименьшего.
Докажем, например, первое из этих утверждений (второе доказы-
доказывается аналогично). Пусть а — любое положительное число клас-
класса А, тогда а2 < 2. Покажем, что можно подобрать такое целое
положительное /7, что
так что и число а + ^ будет принадлежать классу А.
Это неравенство равносильно таким:
а2 + — + -^ < 2, — + -. < 2 - а2.
Последнее неравенство и подавно будет выполнено, если п
удовлетворит неравенству ^^- < 2 —а2, для чего достаточно взять
2а + 1
п > о 2'
2 — <зг
а это всегда возможно [по «аксиоме Архимеда», IV 1°]. Итак,
каково бы ни было положительное число а из класса А, в этом же
классе А найдется большее его число; так как для чисел а ^ 0 это
утверждение непосредственно очевидно, то никакое число класса А
не является в нем наибольшим.
22 ВВЕДЕНИЕ [6
Легко понять, что не может существовать сечение, для ко-
которого одновременно в нижнем классе нашлось бы наибольшее
число ао, а в верхнем классе — наименьшее а'о. Пусть, в самом
деле, такое сечение существует. Возьмем тогда, пользуясь плот-
плотностью области рациональных чисел [I 3°], любое рациональное
число с, заключающееся между а о и а'о: а о < с < af0. Число с не
может принадлежать классу А, ибо иначе а о не было бы наиболь-
наибольшим числом в этом классе, и по аналогичной причине с не может
принадлежать классу А\ а это противоречит свойству 1° сечения,
входящему в определение этого понятия.
Таким образом, сечения могут быть только трех видов, иллю-
иллюстрируемых как раз примерами 1, 2, 3:
1) либо в нижнем классе А нет наибольшего числа, а в верхнем
классе А' есть наименьшее число г;
2) либо в нижнем классе А имеется наибольшее число г,
а в верхнем классе А' нет наименьшего;
3) либо, наконец, ни в нижнем классе нет наибольшего числа,
ни в верхнем классе — наименьшего.
В первых двух случаях мы говорим, что сечение произво-
производится рациональным числом г (которое является погранич-
пограничным между классами А и А') или что сечение определяет
рациональное число г. В примерах 1, 2 таким числом г бы-
была 1. В третьем случае пограничного числа не существует, сече-
сечение не определяет никакого рационального числа. Введем теперь
новые объекты — иррациональные числа, условившись
говорить, что всякое сечение вида 3) определяет некоторое
иррациональное число а. Это число а заменяет недоста-
недостающее пограничное число, мы как бы вставляем его между всеми
числами а класса А и всеми числами а' класса А'. В примере 3)
это вновь созданное число, как легко догадаться, и будет у/2.
Не вводя для иррациональных чисел никаких однотипных обо-
обозначений*^ мы неизменно будем связывать иррациональное чис-
число а с тем сечением А\АГ в области рациональных чисел, которое
его определяет.
Для однообразия нам часто удобно будет то же сделать и по
отношению к рациональному числу г. Но для каждого числа г су-
существует два определяющих его сечения: в обоих случаях числа
*) Речь идет о конечных обозначениях; со своего рода бесконечными
обозначениями иррациональных чисел читатель познакомится в 9. Чаще всего
индивидуально заданные иррациональные числа обозначают в зависимости от их
происхождения и роли: л/2, log 5, sin 10° и т. п.
7] § 2. ВВЕДЕНИЕ ИРРАЦИОНАЛЬНЫХ ЧИСЕЛ 23
а < г относятся к нижнему классу, числа же а' > г — к верхне-
верхнему, но само число г можно по произволу включить либо в нижний
класс (тогда г там будет наибольшим), либо в верхний (и г там бу-
будет наименьшим). Для определенности мы условимся раз навсегда,
говоря о сечении, определяющем рациональное число г, включать
это число в верхний класс.
Числа рациональные и иррациональные получили общее назва-
название вещественных (или действительных) чисел.Понятие
вещественного числа является одним из основных понятий мате-
математического анализа.
7. Упорядочение области вещественных чисел. Два ирра-
иррациональных числа а и fi, определяемых, соответственно,
сечениями А\А' и В\В', считаются равными в том, и толь-
только в том, случае, если эти сечения тождественны; впрочем,
достаточно потребовать совпадения нижних классов А и В, ибо
верхние классы А1 и В1 тогда совпадут сами собой. Это определе-
определение можно сохранить и в случае, когда числа а и /3 рациональны.
Иными словами, если два рациональных числа аир
равны, то определяющие их сечения совпадают, и, обрат-
обратно, из совпадения сечений вытекает равенство чисел а и /3.
При этом, разумеется, следует учесть условие, заключенное выше
насчет рациональных чисел. *}
Перейдем теперь к установлению понятия «больше» по отно-
отношению к вещественным числам. Для рациональных чисел
это понятие уже установлено. Для рационального числа г
и иррационального числа а понятие «больше» было, соб-
собственно, установлено в 6: именно, если а определяется сечени-
сечением А\А\ мы считаем, что а больше всех рациональных чисел, вхо-
входящих в класс А, и в то же время все числа класса А' больше а.
Пусть теперь имеем два иррациональных числа а и /3,
причем а определяется сечением А\А\ а /3 — сечением В\В'.
Мы будем считать то число большим, у которого нижний класс
больше. Точнее говоря,мы будем считать а > /3, если класс А
целиком содержит в себе класс В, не совпадая с ним. [Это
условие, очевидно, равносильно тому, что класс В1 целиком со-
содержит в себе класс А\ не совпадая с ним.] Легко проверить, что
это определение может быть сохранено и для случаев, когда
одно из чисел а, /3 или далее оба — рациональны.
*) Без этого условия, например, сечения, рассмотренные в примерах 1 и 2 [6],
оба определяли бы одно и то же число 1, не будучи тождественными.
24 ВВЕДЕНИЕ [8
Покажем, что для вещественных чисел выполняются свой-
свойства I 1° и 2°.
11° Для каждой пары {вещественных) чисел а и C имеет
место одно, и только одно, из соотношений:
а = /3, а>р, /3 > а.
Если сечение А \А\ определяющее число а, совпадает с сечени-
сечением В\В\ определяющим число /3, то а = J3. Если эти сечения не
совпадают, то либо А целиком содержит в себе В, и тогда а > /3, ли-
либо этого нет. В последнем случае существует элемент bo класса В,
попадающий в класс А'. Тогда для любого элемента а класса А
имеем а < bo. Поэтому класс В содержит класс А, не совпадая
с ним, и мы имеем /3 > а.
I 2° Из а > /3, /3 > у следует, что а > у.
Пусть числа а, /3,у (среди которых могут быть и рациональ-
рациональные) определяются сечениями А\А\ В\В\ С\С'. Если а > J3, то по
определению понятия «больше» класс А содержит в себе класс В,
не совпадая с ним. В свою очередь, раз J3 > у, класс В содержит
в себе класс С, не совпадая с ним. Следовательно, класс А целиком
содержит в себе класс С, не совпадая с ним, т. е. а > у.
Понятие «меньше» устанавливается теперь, как и в 2: мы го-
говорим, что а < /3, если J3 > а. Точно так же знак < обладает
транзитивным свойством, подобно знаку >.
8. Вспомогательные предложения. Установим теперь свойство
плотности области всех вещественных чисел (ср. I 3°); точнее,
мы докажем следующее утверждение:
Лемма 1. Каковы бы ни были два вещественных числа а
и J3, причем а > /3, всегда найдется рациональное чис-
число г, заключенное между ними: а > г > J3 (а следовательно —
бесчисленное множество таких рациональных чисел).
Так как а > J3, то нижний класс А сечения, определяющего
число а, целиком содержит в себе нижний класс В для числа /3,
не совпадая с В. Поэтому в А найдется такое рациональное чис-
число г, которое не содержится в В и, следовательно, принадлежит В';
для него
а > г ^ /3
(равенство могло бы иметь место, лишь если J3 рационально).
Но так как в А нет наибольшего числа, то, в случае надобности,
увеличив г, можно исключить равенство.
9] § 2. ВВЕДЕНИЕ ИРРАЦИОНАЛЬНЫХ ЧИСЕЛ 25
Замечание. Установив, что между вещественными числа-
числами а и /3 (если а > /3) необходимо содержится рациональное
(а не только вещественное) число, мы фактически доказали бо-
более сильное свойство области вещественных чисел, чем плотность.
В дальнейшем нам придется пользоваться этой усиленной
плотностью.
Отсюда непосредственно получается
Лемма 2. Пусть даны два вещественных числа а и fi. Если,
какое бы ни взять число е > О, числа а и fi могут быть
заключены между одними и теми же рациональными грани-
границами s и s'\
разность которых меньше е\
sr — s < e,
то числа а и /3 необходимо равны.
Доказательство будем вести от противного. Пусть, напри-
например, а > /3. По лемме 1, между а и /3 можно вставить два рацио-
рациональных числа г и г1 > г:
а > г1 > г > р.
Тогда для любых двух чисел s и s\ между которыми содержат-
содержатся а и /3, будут, очевидно, выполняться неравенства
sf > г' > г > s,
откуда
s' — s > г' — г > О,
так что разность s1 — s9 вопреки условию леммы, не может быть
сделана, например, меньшей числа е = г1 — г. Это противоречие
доказывает лемму.
9. Представление вещественного числа бесконечной десятичной
дробью. Мы имеем в виду такое представление, при котором дроб-
дробная часть (мантисса) положительна, в то время как целая часть мо-
может оказаться как положительной, так и отрицательной или нулем.
Предположим сначала, что рассматриваемое вещественное чис-
число а не является ни целым числом, ни какой-либо конечной
десятичной дробью. Станем искать его десятичные приближения.
Если оно определяется сечением А\А\ то прежде всего легко
убедиться, что в классе А найдется целое число М, а в классе
26 ВВЕДЕНИЕ [9
А' — целое же число N > М. Прибавляя к М по единице, не-
необходимо придем к таким двум последовательным целым
числам Со и Со + 1, что
Со < а < Со + 1.
При этом число Со может оказаться положительным, отрицатель-
отрицательным или нулем.
Далее, если разделить промежуток между Со и Со +1 на десять
равных частей числами
СоД; Со,2; ...; Со,9,
то а попадет в один, и только в один, из частичных промежутков и
мы придем к двум числам, разнящимся на ^ : Со,с\ и Со,с\ + ^,
для которых
Co,ci < а < Co,ci + —.
Продолжая этот процесс дальше, после определения цифр
с\, с2, ..., сп-\9 мы /7-ю цифру сп определим неравенствами
C0,cic2 .. .сп< а < Co,cic2 . .. сп + —. A)
Таким образом, в процессе нахождения десятичных приближе-
приближений числа а мы построили целое число Со и бесконечный ряд
цифр с\, с2, • • •, сп, ... Составленную из них бесконечную деся-
десятичную дробь, т. е. символ
Со,ас2...сп... B)
молено рассматривать как представление вещественного чис-
числа а.
В исключенном случае, когда а само является целым числом
или, вообще, конечной десятичной дробью, можно подоб-
подобным же образом последовательно определить число С2 и цифры
с\, с2, • • •, сп, ..., исходя из более общих, чем A), соотношений
Со, с\с2 ... сп < а < Со, с\с2 ... сп + —. Aа)
Дело в том, что в некий момент число а совпадает с одним из
концов промежутка, в который мы его заключаем, с левым или
с правым — по нашему произволу; начиная с этого момента, со-
соответственно, слева или справа в Aа) уже постоянно будет
иметь место равенство. Смотря по тому, какая из этих возмож-
9] § 2. ВВЕДЕНИЕ ИРРАЦИОНАЛЬНЫХ ЧИСЕЛ 27
ностей осуществляется, последующие цифры окажутся все нуля-
нулями или все девятками. Таким образом, на этот раз число а имеет
двоякое представление: одно — с нулем в периоде, а другое —
с девяткой в периоде, например
3,826 = 3,826000. .. = 3,825999
-3,826 = 4,174000. .. = 4,173999. .. . 2)
Пусть теперь, наоборот, по произволу задана бесконечная де-
десятичная дробь B); покажем, что всегда найдется вещественное
число а, для которого именно эта дробь и служит представлением.
С этой целью рассмотрим отрезки дроби B)
Сп=Со,с1с2...сП9 C)
которые служат как бы «приближенными значениями по недостат-
недостатку» для искомого числа, а также его «приближенные значения
по избытку»
С'п=Со,с1с2...сп + ^. D)
Нетрудно видеть, что каждое Сп меньше каждого С'т (не только при
т = /7, но и при т^п). Теперь мы следующим образом произве-
произведем сечение в области рациональных чисел: к верхнему классу А'
отнесем такие рациональные числа а\ которые больше всех Сп
(например, все числа С'п), а к нижнему А — все остальные (на-
(например, сами числа Сп). Легко проверить, что это — сечение; оно
определяет вещественное число а, которое и будет искомым.
Действительно, так как а является пограничным числом между
двумя классами, то, в частности,
а
С'п,
т. е. число а удовлетворяет всем неравенствам вида Aа). Этим
и доказано, что взятая по произволу дробь B) является представ-
представлением найденного числа.
Разность между десятичными приближениями D) и C) по из-
избытку и по недостатку, равная у^, с возрастанием п может быть
сделана меньшей любого рационального числа е > 0. Действи-
Действительно, так как натуральных чисел, не превосходящих числа ^,
2) Запись х = 4,174000 означает, что х = —4 + 0,174000.
28 ВВЕДЕНИЕ [10
существует лишь конечное число, то неравенство 10" ^ ^ или рав-
равносильное ему -^ ^ е может выполняться лишь для конечного
числа значений п; для всех же остальных будет
Это замечание, ввиду леммы 2, позволяет заключить, что число /3,
отличное от а, не может удовлетворять всем тем же неравен-
неравенствам A) или Aа), что и а, и, следовательно, имеет представление
в виде бесконечной десятичной дроби, отличное от представления
числа а.
Отсюда, в частности, следует, что представление числа, не рав-
равного никакой конечной десятичной дроби, не имеет ни нуля, ни
девятки в периоде — поскольку каждая дробь с нулем или с девят-
девяткой в периоде явно выражает конечную десятичную дробь.
Отныне читатель может представлять себе вещественные числа
как бесконечные десятичные дроби. Из школьного курса известно,
что периодическая бесконечная дробь изображает рацио-
рациональное число и, обратно, каждое рациональное число
разлагается именно в периодическую дробь. Таким обра-
образом, изображениями вновь введенных нами иррациональных
чисел служат непериодические бесконечные дроби. [Это
представление также может быть отправной точкой для построения
теории иррациональных чисел.]
Замечание. В последующем нам не раз придется пользовать-
пользоваться рациональными приближениями а и а' к вещественному числу а:
а < а < а\
разность которых произвольно мала. Для рациональ-
рационального а существование чисел а и а1 очевидно; для иррационального
же а в качестве а и а' можно было бы, например, использовать
десятичные приближения Сп и С'п при достаточно большом п.
10. Непрерывность области вещественных чисел. Обратимся
теперь к рассмотрению одного весьма важного свойства области
всех вещественных чисел, которое ее существенно отличает от об-
области чисел рациональных. Рассматривая сечение в области рацио-
рациональных чисел, мы видели, что иной раз для такого сечения в этой
области не находилось пограничного числа, про которое мож-
можно было бы сказать, что оно производит сечение. Именно
эта неполнота области рациональных чисел, наличие в ней
этих пробелов и послужили основанием для введения новых
10] § 2. ВВЕДЕНИЕ ИРРАЦИОНАЛЬНЫХ ЧИСЕЛ 29
чисел — иррациональных. Станем теперь рассматривать сечение
в области всех вещественных чисел. Под таким сечением мы пони-
понимаем разбиение этой области на два непустых множества А, Af9
при котором:
1° каждое вещественное число попадает в одно, и только
в одно*\ из множеств А, А';
2° каждое число а множества А меньше каждого числа а1
множества А'.
Возникает вопрос: всегда ли для такого сечения А \ А' найдет-
найдется — среди вещественных чисел — пограничное число, производя-
производящее это сечение, или в этой области существуют пробелы (которые
могли бы послужить основанием для введения еще новых чисел)?
Оказывается, что на деле таких пробелов нет:
Основная теорема (Дедекинда).3) Для всякого сечения А\АГ
в области вещественных чисел существует вещественное чис-
число fi, которое производит это сечение. Это число fi будет
1) либо наибольшим в нижнем классе А, 2) либо наименьшим
в верхнем классе А'.
Это свойство области вещественных чисел называют ее пол-
полнотой, атакже — непрерывностью (или сплошностью).
Доказательство. Обозначим через А множество всех ра-
рациональных чисел, принадлежащих А, а через А1 — множество
всех рациональных чисел, принадлежащих А'. Легко убе-
убедиться, что множества А и А' образуют сечение в области всех
рациональных чисел.
Это сечение А \А' определяет некоторое вещественное число /3.
Оно должно попасть в один из классов A, Af; предположим, что /3
попадает, например, в нижний класс А, и докажем, что тогда осу-
осуществляется случай 1), а именно: /3 является в классе ^4
наибольшим. В самом деле, если бы это было не так, то наш-
нашлось бы другое число од этого класса, большее /3. Вставим (опи-
(опираясь на лемму 1) между од и /3 рациональное число г:
од > г > /3;
г также принадлежит классу А и, следовательно, принадлежит
классу А. Мы пришли к противоречию: рациональное число г,
Ср. сноску на с. 20.
*)
3) Если принимать основные свойства действительных чисел без доказатель-
доказательства, а не выводить их из свойств рациональных чисел, то данную теорему
следует также рассматривать как аксиому. Ее называют аксиомой Деде-
кинда или аксиомой полноты.
30 ВВЕДЕНИЕ [11
принадлежащее нижнему классу сечения, определяющего число /3,
больше этого числа! Этим доказано наше утверждение.
Аналогичное рассуждение показывает, что если /3 попадает
в верхний класс А\ то осуществится случай 2).
Замечание. Одновременное существование в классе А наи-
наибольшего числа и в классе А' наименьшего — невозможно; это
устанавливается так же, как и для сечений в множестве рациональ-
рациональных чисел (с помощью леммы 1).
11. Границы числовых множеств. Мы используем основную
теорему [10], чтобы здесь же установить некоторые понятия, игра-
играющие важную роль в современном анализе. [Они понадобятся нам
уже при рассмотрении арифметических действий над веществен-
вещественными числами.]
Представим себе произвольное бесконечное множество
вещественных чисел, оно может быть задано любым образом. Та-
Такими множествами являются, например, множество натуральных
чисел, множество всех правильных дробей, множество всех ве-
вещественных чисел между 0и1, множество корней уравнения
sinx = |, и т. п.
Любое из чисел множества обозначим через х, так что х есть
типовое обозначение чисел множества; само же множество чи-
чисел х будем обозначать через SC = {х}.4^
Если для рассматриваемого множества {х} существует такое
число М, что все х ^ М, то будем говорить, что наше множество
ограничено сверху (числом М); само число Мв этом случае
есть верхняя граница множества {х}. Например, множест-
множество правильных дробей ограничено сверху числом 1 или любым
числом > 1; натуральный ряд сверху не ограничен.
Аналогично этому: если найдется такое число гп, что все х ^ гп,
то говорят, что множество {х} ограничено снизу (числом т),
а само число т называют нижней границей множества {х}.
Например, натуральный ряд ограничен снизу числом 1 или любым
числом < 1; множество правильных дробей ограничено снизу чис-
числом 0 или любым числом < 0.
Ограниченное сверху (снизу) множество может быть при этом
как ограничено, так и не ограничено снизу (сверху). Так, множество
' Это обозначение не предполагает, разумеется, что множество SC состоит
из одного элемента.
11] § 2. ВВЕДЕНИЕ ИРРАЦИОНАЛЬНЫХ ЧИСЕЛ 31
правильных дробей ограничено и сверху, и снизу, а натуральный
ряд ограничен снизу, но не ограничен сверху.
Если множество сверху (снизу) не ограничено, то за его
верхнюю (нижнюю) границу принимают «несобственное число»
+оо (—оо). Относительно этих «несобственных», или «бесконеч-
«бесконечных», чисел мы считаем, что
—оо < +оо и — оо < а < +оо,
каково бы ни было вещественное («конечное») число а.
Знаки +оо и — оо читаются так: «плюс бесконечность» и «минус
бесконечность».
Если множество ограничено сверху, т. е. имеет конечную верх-
верхнюю границу М, то одновременно оно имеет и бесконечное мно-
множество верхних границ (так как, например, любое число > М, оче-
очевидно, также будет верхней границей). Из всех верхних границ
особый интерес представляет наименьшая, которую мы бу-
будем называть точной верхней границей. Аналогично, если
множество ограничено снизу, то наибольшую из всех нижних
границ будем называть точной нижней границей. Так, для
множества всех правильных дробей точными границами будут
соответственно 0 и 1.
Является вопрос: всегда ли для ограниченного сверху (снизу)
множества существует точная верхняя (нижняя) граница? Дей-
Действительно, так как верхних (нижних) границ в этом случае беско-
бесконечное множество, а среди бесконечного множества чисел не всегда
найдется наименьшее или наибольшее *\ то самое существование
такого наименьшего (наибольшего) числа из всех верхних (ниж-
(нижних) границ рассматриваемого множества требует доказательства.
Теорема. Если множество SC = {х} ограничено сверху
(снизу), то оно имеет и точную верхнюю (нижнюю) гра-
границу.
Доказательство. Проведем рассуждение по отношению
к верхней границе. Рассмотрим два случая:
1° Среди чисел х множества ЭС найдется наи-
наибольшее х. Тогда все числа множества будут удовлетворять
неравенству х ^ х, т. е. х будет верхней границей для х. С дру-
другой стороны, х принадлежит SC\ следовательно, для любой верхней
границы М выполняется неравенство х < М. Отсюда заключаем,
что х есть точная верхняя граница множества ЭС.
*) Как их нет, например, среди всех правильных дробей.
32 ВВЕДЕНИЕ [11
2° Среди чисел х множества ЭС нет наибольшего.
Произведем сечение в области всех вещественных чисел сле-
следующим образом. К верхнему классу А' отнесем все верхние
границы а' множества «2Г, а к нижнему классу А — все остальные
вещественные числа а. При этом разбиении все числа х множест-
множества ЭС попадут в класс А9 ибо ни одно из них — по допущению —
не будет наибольшим. Таким образом, оба класса А, А' не пусты.
Это разбиение действительно является сечением, так как все ве-
вещественные числа распределены по классам и каждое число из
класса А' больше любого числа из класса А. По основной теореме
Дедекинда [10], должно существовать вещественное число /3,
производящее сечение. Все числа х9 как принадлежащие классу А,
не превосходят этого «пограничного» числа /3, т. е. /3 служит верх-
верхней границей для х9 следовательно, само принадлежит классу А'
и является там наименьшим. Таким образом, /3 как наименьшая из
всех верхних границ и есть искомая точная верхняя граница
множества ЭС — {х}.
Совершенно так же доказывается и вторая половина теоремы
(относящаяся к существованию точной нижней границы).
Если М* есть точная верхняя граница числового множест-
множества ЭС — {х}, то для всех х будет
х ^М*.
Возьмем теперь произвольное число а, меньшее М*. Так как
М* — наименьшая из верхних границ, то число а наверное
не будет верхней границей для множества ЭС9 т. е. найдется такое
число х' из ЭС9 что
х > а.
Этими двумя неравенствами вполне характеризуется точная верх-
верхняя граница множества SC.
Аналогично, точная нижняя граница w* множества SC ха-
характеризуется тем, что для в с е х х из SC
х^т*
и, каково бы ни было число /3, большее т*9 найдется число х11 из SC
такое, что
х" < р.
Для обозначения точной верхней границы М* и точной нижней
границы w* множества чисел SC употребляются символы
М* = sup^T = sup{x}, m* = ЫЭС = inf{x}
(по-латыни: supremum — наивысшее, infimum — наинизшее).
12] § 3. АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ 33
Отметим одно очевидное умозаключение, которое часто будет
встречаться в дальнейшем:
если все числа х некоторого множества удовлетворяют
неравенству х ^ М, то и sup{x} ^ М.
Действительно, число М оказывается одной из верхних гра-
границ множества, а потому наименьшая из всех верхних границ
его не превосходит.
Аналогично, из неравенства х^т следует, что и inf{x } ^ т.
Условимся, наконец, если множество SC = {х} не ограниче-
ограничено сверху, говорить, что его точная верхняя граница есть +оо:
sup{x} = +оо. Аналогично, если множество SC = {х} не огра-
ограничено снизу, то говорят, что его точная нижняя граница есть — оо:
inf{x} = -оо.
§ 3. Арифметические действия над вещественными
числами
12. Определение суммы вещественных чисел. Обратимся те-
теперь к установлению понятия о действиях над вещественными чис-
числами. Греческие буквы а, /3, у в последующем означают именно
вещественные числа, как рациональные, так и иррациональные.
Пусть имеем два вещественных числа а и /3. Станем рассмат-
рассматривать рациональные числа а, а' и b,b\ удовлетворяющие
неравенствам:
а < а < а1 и Ъ < E < Ъ1. A)
Суммой а + /3 чисел а и /3 назовем такое веществен-
вещественное число у, которое содержится между всеми суммами
вида а+Ъ, с одной стороны, и всеми суммами вида а' + ЪГ —
с другой:
а+Ъ<у<а' + Ъг. B)
Удостоверимся прежде всего, что такое число у существует для
любой пары вещественных чисел а, /3.
Рассмотрим множество всевозможных сумм а + Ъ. Это мно-
множество ограничено сверху, например любой суммой вида а1
Положим же [11]
у = Slip{<3 + Ь}.
Тогда а + Ъ ^ у и, в то же время, у ^ а1 + V'.
34 ВВЕДЕНИЕ [13
Так как, каковы бы ни были рациональные числа а, Ь, а', Ь\
удовлетворяющие условиям A), всегда можно числа a, b увели-
увеличить, а числа а',Ъ' уменьшить с сохранением этих условий,
то в полученных только что неравенствах, соединенных с равен-
равенствами, равенства на деле ни в одном случае быть
не может. Таким образом, число у удовлетворяет определению
суммы.
Возникает, однако, вопрос, однозначно ли сумма у — а + C
определяется неравенствами B). Для того чтобы убедиться
в единственности суммы, подберем, по замечанию в 9, рацио-
рациональные числа a, af, b, b1 так, чтобы было
а' — а < е и Ь' — Ъ < е,
где е — произвольно малое рациональное положительное число.
Отсюда
(V + Ъ1) -(а + Ъ) = (V - а) + (Ъ1 - Ъ) < 2е,
т. е. и эта разность может быть сделана сколь угодно малой *\
А тогда, по лемме 2, существует только одно число, содержа-
содержащееся между суммами а + b и а' + Ь'.
Наконец, заметим, что если числа а и /3 оба рациональны, то
их обычная сумма у = а + /3, очевидно, удовлетворяет не-
неравенствам B). Таким образом, данное выше общее определение
суммы двух вещественных чисел не противоречит старому
определению суммы двух рациональных чисел.
13. Свойства сложения. Легко удостовериться, что для вещест-
вещественных чисел сохраняются свойства:
II 1° а+ 13 =E+а;
112° {а+ 13)+у = а + (р + у);
II 3° а + 0 = а.
Докажем, например, последнее. Если рациональные числа а, а\
b9 b' таковы, что
а < а < а', Ъ < 0 < Ъ1,
то, очевидно,
а + Ъ < а < а < а < а + Ъ'.
*) Число 2е становится меньшим любого числа е > 0, если взять е < у.
13] § 3. АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ 35
Таким образом, а есть вещественное число, заключенное меж-
между числами вида а + Ъ и а' + Ь\ между которыми заключена, по
определению, и сумма а + 0. Но такое число может быть только
одно; поэтому а + 0 = а, что и требовалось доказать.
Обратимся к свойству II 4° и докажем, что для каждого ве-
вещественного числа а существует {симметричное ему)
число —а, удовлетворяющее условию а + {—а) = 0.
При этом достаточно ограничиться случаем иррациональ-
иррационального числа а.
Предполагая, что число а определяется сечением А \А\ мы опре-
определим число —а следующим образом. К нижнему классу А чис-
числа —а мы отнесем все рациональные числа —а\ где а' — любое
число класса А1\ а к верхнему классу А' этого числа отнесем все
числа —а, где а — любое число класса А. Нетрудно видеть, что
построенное разбиение есть сечение и, действительно, определя-
определяет вещественное (в данном случае — иррациональное) число: это
число обозначим —а.
Докажем теперь, что оно удовлетворяет указанному выше усло-
условию. Пользуясь самим определением числа —а, видим, что сум-
сумма а + (—а) есть единственное вещественное число, заключен-
заключенное между числами вида а — а' и а' — а, где а и а' рациональны
и а < а < а'. Но, очевидно,
а - а' < 0 < а' - а,
так что и число 0 заключено между только что упомянутыми чис-
числами. Ввиду единственности числа, обладающего этим свойством,
имеем
а + {-а) = 0,
что и требовалось доказать.
Наконец, установим свойство:
II 5° из а > /3 следует а + у > /3 + у.
Если а > /3, то между ними можно вставить два рациональных
числа 7*1 и г2'. а > г\ > г2 > 1$.
По замечанию в 9, существуют такие два рациональных чис-
числа с и с', что
С < у < С И С — С < Г\ — Г 2.
Отсюда
Г\+ С > Г2 +
36 ВВЕДЕНИЕ [14
а по определению суммы
а + у > г\ + с, г2 + с > E + у.
Сопоставляя все эти неравенства, мы и приходим к требуемому
заключению.
Таким образом, по отношению к сложению область веществен-
вещественных чисел обладает всеми основными свойствами II 1°—5°, кото-
которые в 3 были первоначально сформулированы для рациональных
чисел. Следовательно, на вещественные числа автоматически пе-
переносятся и все формально логические следствия из этих свойств.
В частности, для вещественных чисел может быть буквально
повторено все, сказанное в 3 непосредственно после изложения
II группы свойств, т. е. могут быть доказаны существование
и однозначность разности а—/3 чисел а и /3, установ-
установлено понятие абсолютной величины числа а (для которой
мы сохраняем обозначение |а|) и т. д.
14. Определение произведения вещественных чисел. Перейдем
к умножению вещественных чисел, ограничиваясь сначала по-
положительными числами. Пусть же даны два таких числа а
и J3. Мы здесь также станем рассматривать всевозможные рацио-
рациональные числа, удовлетворяющие неравенствам A), но и эти числа
предположим положительными.
Произведением а/3 двух положительных веще-
вещественных чисел а и /3 назовем такое вещественное число у,
которое содержится между всеми произведениями вида аЪ,
с одной стороны, и всеми произведениями вида а'Ъ' — с другой'.
аЪ <у < а'Ъ'. C)
Для доказательства существования такого числа у возьмем мно-
множество всевозможных произведений ab; оно ограничено сверху
любым из произведений вида а'Ъ'. Если положить
у = sup{ab},
то, конечно, аЪ ^ у, но одновременно и у ^ а'Ъ'.
Возможность увеличить числа а, Ъ и уменьшить
числа а', Ъ' (как и в случае суммы) позволяет исключить здесь
знак равенства, так что число у удовлетворяет определению произ-
произведения.
14] § 3. АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ 37
Единственность произведения вытекает из следующих со-
соображений. Подберем, по замечанию в 9, рациональные числа а, а'
и Ь, Ъ' так, чтобы было
а — а < е
и Ь' -Ь<
где е — произвольно малое рациональное положительное число.
При этом можно считать, что числа а и Ъ положительны, а числа а'
и Ъ' не превосходят, соответственно, некоторых наперед фиксиро-
фиксированных чисел а'о и Ь'о. Тогда разность
а'Ъ' -ab = а\Ъ' - Ъ) + Ъ{а' - а) < (а'о + Ь'о) • е,
т. е. также может быть сделана сколь угодно малой *\ а этого,
по лемме 2, достаточно для утверждения, что неравенствам C)
может удовлетворять только одно число у.
Если положительные числа а и /3 оба рациональны, то их
обычное произведение у = aji удовлетворяет, очевидно, нера-
неравенствам C), т. е. получается таким же и по общему определению
произведения двух вещественных чисел — противоречия нет.
Наконец, для того чтобы определить произведение произволь-
произвольной пары вещественных чисел (не обязательно положительных),
заключим следующие соглашения.
Прежде всего условимся, что
а • 0 = 0 • а = О,
каково бы ни было а.
Если же оба множителя отличны от 0, то положим в основу
обычное «правило знаков»:
а • /3 = \а\ • |/31, если а и /3 одного знака,
а • /3 = -(Н • |/3|), если а и /3 разных знаков
(что означает произведение положительных чисел |а| и |/31 —
мы уже знаем).
Эти соглашения, как мы видели в 4, в некотором смысле обяза-
обязательны для нас, если мы хотим, чтобы действия над вещественны-
вещественными числами обладали всеми основными свойствами действий над
рациональными числами.
*) Заметим, что произведение (а$ + Ь$) • е становится меньшим любого чис-
числа е > 0, если взять е < ,е h,.
38 ВВЕДЕНИЕ [15
15. Свойства умножения. Как и в случае рациональных чисел,
для любых вещественных чисел сохраняются свойства:
III 1° а-р = /5-а;
1112° (а.р).у = а.(р.у);
III 3° а • 1 = а.
Для примера докажем второе из них, начав со случая, когда все
три числа — ее, р,у — положительны. Пусть а, а1, Ъ, Ъ1, с, с' —
произвольные рациональные числа, удовлетворяющие неравен-
неравенствам
О < а < а < а', О < Ъ < J5 < Ъ', О < с < у < с'.
Тогда, по самому определению произведения двух вещественных
чисел, имеем
аЪ < afi < а'Ъ' и be < jiy < b'cr.
Пользуясь еще раз тем же определением, получим
{аЪ)с < (а/3)у < (а'Ь')с' и а{Ъс) < а(/3у) < af(bfcf).
Так как для рациональных чисел доказываемое свойство уже
известно, то вещественные числа (aj5)y и a(j5y) оказываются за-
заключенными между одними и теми же границами:
{аЬ)с = а{Ьс) и (а'Ъ')с' = a'{b'c').
Но легко показать, что за счет сближения множителей а и а\
Ъ и //, с и с1 между собой и разность произведений а'Ъ'с' — аЪс
может быть сделана сколь угодно малой (при этом можно исполь-
использовать подобное же утверждение в 14 относительно произведений
двух множителей). Отсюда, по лемме 2, и получается заключение
о равенстве чисел (аE)у и а(Eу).
Переход к случаю чисел произвольных знаков производится не-
непосредственно, если учесть лишь «правило знаков». Если же хоть
одно из чисел а, /3, у равно 0, то оба произведения обращаются в 0.
Обратимся к свойству:
III 4° для каждого вещественного числа а, отличного от
нуля, существует {обратное ему) число ^, удовлетворяющее
условию:
„.1=1.
а
Достаточно ограничиться случаем иррационального чис-
числа а. Пусть сначала а > 0.
15] § 3. АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ 39
Если а определяется сечением А \А\ то мы следующим образом
построим сечение для числа ^. К нижнему классу его А мы отнесем
все отрицательные рациональные числа и нуль, а также все числа
вида ^-, где а' — любое число класса А'; в верхний же класс А'
поместим все числа вида ^, где а — любое положительное
число класса А. Легко убедиться, что мы, таким образом, действи-
действительно получаем сечение, которое определит положительное ве-
вещественное (в данном случае — иррациональное) число; это число
обозначим ^.
Покажем, что оно удовлетворяет требуемому условию. Если
учесть построение обратного числа, то, по самому определению
произведения, число а • ^ есть единственное вещественное
число, заключенное между числами вида ^ и ^-, где а и а' —
положительные рациональные числа, удовлетворяющие неравен-
неравенствам а < а < а'. Но и число 1 заключено между упомянутыми
числами:
а а'
— < 1 < —,
а' а
следовательно, оно и является искомым произведением.
Если а < О, то полагаем
1 1
а
а\
тогда по «правилу знаков»
1 , 1
а - — = а • -—г = 1.
а \а\
После того как мы убедились, что и по отношению к умно-
умножению область вещественных чисел обладает всеми основными
свойствами III 1°—4°, ясно, что для этой области сохраняет силу
все сказанное в4о существовании и единственности
частного | чисел аир (при условии, что /3 ф 0), и т. д.
Распределительное свойство:
III 5° (а + р) -у = а-у +/3 -у
также имеет место для любых вещественных чисел, что легко дока-
доказывается для случая положительных чисел (как и свойство III 2°).
К этому случаю приводятся все остальные — путем изменения зна-
знаков обеих частей равенства или путем переноса членов из одной
40 ВВЕДЕНИЕ [17
части в другую. Исключение, впрочем, представляет случай, ког-
когда одно из чисел а, /3, у, а + /3 равно нулю; но для этого случая
равенство непосредственно очевидно.
Наконец, свойство:
III 6° из а > /3 и у > 0 следует а • у > /3 • у
проверяется без труда. Неравенство а > /3 равносильно а — J3 > 0;
тогда по «правилу знаков» и (а — /3) • у > 0. Но умножение
имеет распределительное свойство и относительно разности, так
что а - у — /3 • у > 0, а отсюда а • у > /3 • у.
16. Заключение. Остается упомянуть еще об «аксиоме Архи-
Архимед а».
IV 1° каково бы ни было вещественное число у, сущест-
существует натуральное число п, большее у.
Проверка ее легка: ведь в верхнем классе сечения С|С;, опре-
определяющего число у, найдется большее его рациональное число с7,
а для рациональных чисел этот принцип имеет место.
Теперь можно, наконец, считать установленным, что в облас-
области всех вещественных чисел полностью сохраняются
правила элементарной алгебры, относящиеся к че-
четырем арифметическим действиям и к сочетанию равенств
и неравенств.
17. Абсолютные величины. В интересах дальнейшего, присо-
присовокупим еще несколько замечаний об абсолютных величинах.
Прежде всего установим, что неравенство: \а\ < J3 (где, конеч-
конечно, /3 > 0) равносильно двойному неравенству: —/3 < а < /3.
Действительно, из \а\ < /3 следует, что одновременно а < /3
и -а < C, т. е. а > -C. Обратно, если дано, что а < C и а > -C,
то имеем одновременно: а < j3 vl — а < /3; но одно из этих чи-
чисел а, -а и есть \а\9 так что наверное \а\ < C.
Аналогично, оказываются равносильными и неравенства:
а\^ /3 и - /3 ^а < /3.
Докажем, далее, полезное неравенство:
Складывая почленно очевидные неравенства
и - |/3| ^ /3
18] § 4. ПРИЛОЖЕНИЯ ВЕЩЕСТВЕННЫХ ЧИСЕЛ 41
получим
откуда, в силу сделанного выше замечания, и вытекает требуемое
неравенство.
С помощью математической индукции оно распространяется на
случай любого числа слагаемых:
Если заменить в доказанном неравенстве /3 на — /3, то получим
\а-р\^\а\ + \р\.
Так как а = (а + /3) — /3, то \а\ ^ \а + /31 + |/3|, или
|а + /3|
Аналогично,
Н-|/
Так как одновременно и
то, очевидно,
||а|-|0
Все эти неравенства будут полезны в теории пределов.
§ 4. Дальнейшие свойства и приложения
вещественных чисел
18. Существование корня. Степень с рациональным показате-
показателем. Определение умножения (и деления) вещественных чисел
непосредственно приводит, как и обычно, к определению степени
с целым положительным (и отрицательным) показателем. Перехо-
Переходя к степени с вообще рациональным показателем, остановимся
прежде всего на вопросе о существовании корня.
Как мы помним, отсутствие в области рациональных чисел
простейших корней послужило одним из поводов к расширению
этой области; проверим же, в какой мере произведенное расшире-
расширение заполнило старые пробелы (не создав при этом новых).
Пусть а — любое вещественное число, п — натуральное число.
42 ВВЕДЕНИЕ [18
Как известно, корнем п-и степени из числа а называют такое
вещественное число |, что
Мы ограничимся случаем, когда а положительно, и будем ис-
искать положительное же |, удовлетворяющее этому соотношению,
т. е. так называемое арифметическое значение корня. Мы
докажем, что такое число | всегда существует, и притом только
одно.
Последнее утверждение относительно единственности числа |,
впрочем, сразу следует из того, что разным положительным числам
соответствуют и разные степени их: если 0 < | < |;, то |Л < Ё,'п.
Если существует такое рациональное число г, п-я степень
которого равна а, то оно и будет искомым числом |. Поэтому
впредь достаточно ограничиться предположением, что такого ра-
рационального числа нет.
Построим теперь сечение X\Xf в области всех рациональных
чисел следующим образом. К классу X отнесем все отрицатель-
отрицательные рациональные числа и нуль, а также те из положительных ра-
рациональных чисел х, для которых хп < а. К классу X' отнесем
положительные рациональные числа х\ для которых х'п > а.
Легко видеть, что классы эти не пустые и что X содержит и по-
положительные числа. Если взять, например, натуральное число т
так, чтобы было ^ < а < гп, то и подавно ^ < а < тп, так что
число ^ входит в X, а число т — в X'.
Прочие требования, предъявляемые к сечению, проверяются не-
непосредственно.
Пусть теперь | будет число, определяемое сечением X\Xf; до-
докажем, что |л = а, т. е. что | = tfa. Рассматривая |л как произве-
произведение п сомножителей, равных |, на основании определения произ-
произведения положительных вещественных чисел [14] заключаем, что
хп < Ln < х'п
если х их' суть положительные рациональные числа, для которых
О < х < | < х'.
Так как, очевидно, х принадлежит классу J, ах' — классу Х\ то,
по определению этих классов, одновременно и
хп < а < х1п.
19] § 4. ПРИЛОЖЕНИЯ ВЕЩЕСТВЕННЫХ ЧИСЕЛ 43
Но разность х' — х может быть сделана меньшей любого чис-
числа е > О [9, замечание], причем ничто не мешает считать х' мень-
меньшим некоторого наперед фиксированного числа Xq. В таком случае
разность
х'п-хп = {х1 -х)(х/п~1 +х -х'п-2 + . . . +хп~1) < е • пх'оп-\
т. е. также может быть сделана сколь угодно малой *}. Отсюда, по
лемме 2, и следует равенство чисел |л и а.
После того как доказано существование корня, обычным путем
устанавливается понятие степени с любым рациональным по-
показателем г и проверяется, что для таких степеней справедливы
обычные правила, выводимые в курсе элементарной алгебры:
(ar)r =ar-r , (а/ЗУ = аг-рг,
ar
= -^ и др-
Подчеркнем еще, что при а > 1 степень аг возрастает
с возрастанием рационального показателя г.
19. Степень с любым вещественным показателем. Обратимся
к определению степени любого вещественного (поло-
(положительного) числа а с любым вещественным по-
показателем р.
Введем в рассмотрение степени числа а
аь и аь>
с рациональными показателями Ъ и //, удовлетворяющими нера-
неравенствам
Ь < /3 < Ъ1.
Степенью числа а > 1 **) с показателем /3 называют
{и обозначают символом а@) вещественное число у, которое
*) Заметим, что число е • пх'^ становится меньшим любого числа е > О,
если взять е <
пх
71-1 '
о
**> Этим случаем можно ограничиться: при а < 1 полагаем, например,
44 ВВЕДЕНИЕ [19
содержится между степенями аь и аь :
аь < у < аъ'. A)
Легко убедиться в том, что такое число всегда существует. Дей-
Действительно, множество степеней {аь} ограничено сверху, например
любой степенью аъ . Возьмем тогда [11]
у = {}
b<j3
Для этого числа будем иметь
аь ^ у ^ аъ'.
На деле же знак равенства здесь не нужен, ввиду возможности
увеличить Ъ и уменьшить //, так что построенное число у
удовлетворяет условиям A).
Обратимся теперь к доказательству единственности числа, оп-
определяемого этими условиями.
Для этого прежде всего заметим, что лемма 2 [8] сохраняет
свою силу и в том случае, если опустить требование, чтобы чис-
числа s, sf и е были непременно рациональными; доказательство
остается то же.
Затем установим одно весьма простое, но часто полезное не-
неравенство, которое иногда связывают с именем Як. Б ер ну л ли
(Jac. Bernoulli): если п — натуральное число, большее единицы,
и у > 1, то
уп>\+п{у-\). B)
Действительно, положив у = 1 + Я, где Я > 0, по формуле бинома
Ньютона будем иметь
A+Я)" = 1+/7Я + ... ;
так как ненаписанные члены положительны, то
A+А)и> 1+иА,
что равносильно неравенству B).
Положив здесь у = а* (а > 1), получим неравенство
О)
которым мы сейчас и воспользуемся.
19] § 4. ПРИЛОЖЕНИЯ ВЕЩЕСТВЕННЫХ ЧИСЕЛ 45
Мы знаем, что числа Ъ и Ъ' можно выбрать так, чтобы раз-
разность Ъ1 - Ъ была меньше \ при любом наперед заданном нату-
натуральном п; тогда, по неравенству C),
аь> -аъ = а\аъ'-ъ - 1) < аъ (J. - А < аъ —.
V / п
Так как Ъ меньше любого (но фиксированного) Ь'о, то достаточно
взять
аь'о(а- 1)
п > - -,
е
где е — произвольно малое положительное число, чтобы было
аь> -аь <?.
В таком случае, по обобщенной выше лемме 2, между граница-
границами аь и аь не может содержаться двух различных чисел у.
Если /3 рационально, то данное выше определение возвращает
нас к обычному пониманию символа а^.
Легко проверить, что для степени с любым вещественным по-
показателем выполняются все обычные для степени правила. Остано-
Остановимся для примера на доказательстве правила сложения показате-
показателей при умножении:
Пусть b, b\ с, с1 — любые рациональные числа, для которых
Ъ < /3 < У', с < у < с\
по определению суммы [12]
Ъ + с < E + у < Ь' + с',
а по определению степени
аь < </ < аь\ ас < с? < ас> и аь+с < а^ < аь'+с'.
Перемножив почленно первые два двойных неравенства (с учетом
того, что для рациональных показателей доказываемое правило уже
известно), получим
Таким образом, два числа а^+у и а@ • ау оказываются заключен-
заключенными между границами аь+с, аь +с , которые, как легко показать,
могут быть сделаны сколь угодно близкими. Отсюда (по обобщен-
обобщенной лемме 2) и вытекает равенство этих чисел.
46 ВВЕДЕНИЕ [20
Проверим еще, что при а > 1 степень а$ возрастает с воз-
возрастанием вещественного показателя /3. Если /3 < /3, то, вставив
рациональное число г между ними: /3 < г < /3, по самому опреде-
определению степени с вещественным показателем будем иметь
оР < аг и аг < а^, откуда оР < оР.
20. Логарифмы. Пользуясь данным определением степени
с любым вещественным показателем, теперь легко установить с у -
ществование логарифма для любого положительного ве-
вещественного числа у при положительном основании а, отличном
от 1 (мы будем, например, считать а > 1).
Если существует такое рациональное число г, что
аг — у,
то г и есть искомый логарифм. Предположим же, что такого ра-
рационального числа г нет.
Тогда можно произвести сечение В\В' в области всех рацио-
рациональных чисел по следующему правилу. К классу В отнесем ра-
рациональные числа Ь9 для которых аь < у, а к классу В' — рацио-
рациональные числа //, для которых аъ > у.
Покажем, что классы В и В1 — не пустые. В силу неравен-
неравенства B)
ап > 1 + п{а - 1) > п{а - 1),
и достаточно взять
1' 1
чтобы было ап > у; такое натуральное число п относится к клас-
классу В'. В то же время имеем:
_„_ 1 1
~ ап< п{а-\у
и достаточно взять
1
п >
у(а-1У
чтобы было а~п < у и число —п попало в класс В.
Остальные требования, предъявляемые к сечению, здесь также
выполнены.
Построенное сечение В\В' определяет вещественное число /3,
которое является «пограничным» между числами обоих классов.
21] § 4. ПРИЛОЖЕНИЯ ВЕЩЕСТВЕННЫХ ЧИСЕЛ 47
По определению степени, имеем
аь < ар < аь> [Ъ < /3 < 6'),
причем а^ есть единственное число, удовлетворяющее
всем подобным неравенствам. Но для числа у имеем (по самому
построению сечения)
аь < у < аь'.
Следовательно,
ар = у и /3 = loga у;
существование логарифма доказано.
21. Измерение отрезков. Невозможность снабдить, оставаясь
в области рациональных чисел, все отрезки длинами также была
важнейшим поводом к введению иррациональных чисел. Покажем
теперь, что произведенного расширения числовой области доста-
достаточно для решения задачи измерения отрезков.
Прежде всего сформулируем самую задачу*^
Требуется с каждым прямолинейным отрезком А связать
некоторое положительное вещественное число 1(А), которое
будем называть «длиной отрезка А», так, чтобы
1) некоторый наперед выбранный отрезок Е {«эталон дли-
длины») имел длину 1: 1{Е) = 1;
2) равные отрезки имели одну и ту лее длину;
3) при сложении отрезков длина суммы всегда была равна
сумме длин складывания отрезков:
(«свойство аддитивности»).
Поставленные условия приводят к однозначному решению за-
задачи.
Из 2) и 3) следует, что q-я часть эталона должна иметь дли-
длину |; если же эта часть повторена слагаемым р раз, то полученный
отрезок, в силу 3), должен иметь длину ^. Таким образом, если от-
отрезок А соизмерим с эталоном длины и общая мера отрезков А
и Е укладывается в них, соответственно, р и q раз, то необходимо
*) Мы пользуемся здесь школьными сведениями по геометрии и не формули-
формулируем относящихся сюда аксиом.
48 ВВЕДЕНИЕ [21
Легко видеть, что это число не зависит от взятой общей ме-
меры и что если отрезкам, соизмеримым с эталоном, приписать ра-
рациональные длины по этому правилу, то для этих отрезков задача
измерения будет полностью решена.
Если отрезок А больше отрезка В, так что А = В + С, где С
есть также некоторый отрезок, то, в силу 3), должно быть:
и так как /(С) > 0, то 1(А) > 1(В). Итак, неравные отрезки должны
иметь неравные длины, а именно больший отрезок — большую дли-
ну. 1ак как каждое положительное рациональное число - являет-
является длиной некоторого отрезка, соизмеримого с эталоном длины Е,
то из сказанного, между прочим, ясно, что ни один отрезок, несо-
несоизмеримый с эталоном, не может иметь рациональную длину.
Пусть же ? будет такой отрезок, несоизмеримый с Е.
Найдется бесчисленное множество отрезков S и S\ соизмеримых
сЕи, соответственно, меньших или больших ?. *} Если обозначить
их длины через s и sf: l(S) = s9 l(Sf) = sf9 то искомая длина /(?)
должна удовлетворять неравенствам
s < /(E) <s'
**)
Если разбить все рациональные числа на два класса S и S", отне-
отнеся к нижнему классу S числа s (и кроме них — все отрицательные
числа и 0), а к верхнему классу Sf — числа s\ то получится сечение
в области рациональных чисел. Так как в нижнем классе, очевидно,
нет наибольшего числа, а в верхнем — наименьшего, то этим сече-
сечением определяется иррациональное число о, которое и будет
единственным вещественным числом, удовлетворяющим неравен-
неравенствам s < о < s'. Именно этому числу необходимо положить
равной длину /(?).
Предположим теперь, что всем отрезкам, как соизмеримым с Е,
так и несоизмеримым, приписаны длины в согласии с указанными
правилами. Выполнение условий 1), 2) очевидно. Рассмотрим два
отрезка Р, ? с длинами р = /(Р), о = /(?) и их сумму, отрезок
Т = Р + ?, длину которого обозначим через т = /(Т). Взяв любые
*) Это легко доказать, исходя из геометрической «аксиомы Архимеда», о ко-
которой уже была речь в 5.
**) Разумеется, и для длины отрезка Е, соизмеримого с Е, также выпол-
выполняются эти неравенства.
21] § 4. ПРИЛОЖЕНИЯ ВЕЩЕСТВЕННЫХ ЧИСЕЛ 49
положительные рациональные числа г, г', s, s' такие, что
г < р < rr, s < о < s1',
построим отрезки R,R\ S, Sf9 для которых именно эти числа, со-
соответственно, служат длинами. Отрезок R + S (длины г + s) будет
меньше Т, а отрезок R1 + S' (длины г1 + s1) — больше Т. Поэтому
г + s < т < г' + s1.
Но [12] единственным вещественным числом, содержащимся меж-
между числами вида г + s *) и числами г' + s', является сумма р + о.
Следовательно, т = р + а, что и требовалось доказать.
Распространение «свойства аддитивности» на случай любого
конечного числа слагаемых производится по методу математиче-
математической индукции.
Если на оси (направленной прямой) (рис. 1) выбрать на-
начальную точку О и эталон длины ОЕ, то каждой точке X этой
прямой отвечает некоторое вещественное число — ее абс-
абсцисса х, равная длине отрезка ОХ, если X лежит в положитель-
положительном направлении от О, или этой длине со знаком минус — в про-
противном случае.
Естественно встает вопрос, будет ли верно и обратное: каж-
каждое ли вещественное число х отвечает при этом некоторой
точке прямой! Вопрос этот в геометрии решается в утвердитель-
утвердительном смысле — именно с помощью аксиомы о непрерывности
прямой, устанавливающей для прямой, как множества точек, свой-
свойство, аналогичное свойству непрерывности области вещественных
чисел [10].
Таким образом, между всеми вещественными числами и точ-
точками направленной прямой (оси) можно установить взаимно од-
однозначное соответствие. Вещественные числа можно изображать
точками на оси, которую в связи в этим называют числовой
осью. Подобным изображением мы впредь постоянно будем поль-
пользоваться.
*)
Ограничение положительными числами г и s, конечно, несущественно.
ГЛАВА ПЕРВАЯ
ТЕОРИЯ ПРЕДЕЛОВ
§ 1. Варианта и ее предел
22. Переменная величина, варианта. В физике и в других на-
науках о природе читателю встречалось множество различных ве-
величин: время, длина, объем, вес и т. п. Любая из них, смотря по
обстоятельствам, принимала то различные значения, то лишь од-
одно. В первом случае мы имели дело с переменной величиной,
а во втором — с постоянной.
В математике, однако, мы отвлекаемся от физического смысла
рассматриваемой величины, интересуясь лишь числом, кото-
которым она выражается; физический смысл величины снова приобре-
приобретает важность, лишь когда занимаются приложениями математики.
Таким образом, для нас переменная величина (или короче — пере-
переменная) является отвлеченной или числовой переменной.
Ее обозначают каким-либо символом (буквой, например х), кото-
которому приписываются числовые значения.5)
^ Исходное (в историческом плане) для всего математического анализа и чрез-
чрезвычайно общее понятие переменной величины имеет скорее естественно-
естественнонаучный, чем чисто математический характер, и дать ему совершенно формальное
определение практически невозможно.
Ключевую роль в дальнейшем изложении будут играть два более специаль-
специальных типа переменных величин, определяемые строго и называемые соответ-
соответственно переменной (или, подробнее, независимой переменной)
и вариантой (или переменной типа варианты). Строгость опре-
определения указанных типов переменных величин достигается тем, что для
них дополнительно описывается процедура задания, т. е. точно указыва-
указываются условия, при которых переменная или варианта считаются заданными.
В частности, определением переменной по существу является следующий
абзац основного текста.
22] § 1. ВАРИАНТА И ЕЕ ПРЕДЕЛ 51
Переменная считается заданной, если указано множест-
множество ЭС — {х} значений, которые она может принять. Посто-
Постоянную величину (короче — постоянную) удобно рассматривать
как частный случай переменной; он отвечает предположению, что
множество ЭС — {х } состоит из одного элемента.6)
При установлении понятия предела переменной х недо-
недостаточно знать лишь, из какого числового множества ЭС получа-
получает значения эта переменная; необходимо еще знать, какие именно
значения (среди которых могут быть и повторяющиеся) и в ка-
каком порядке она принимает. Откладывая изложение вопроса о на-
направленной переменной и ее пределе, в общей постановке, до
конца следующего тома*) (когда у читателя накопится достаточ-
достаточный опыт в этой области), мы посвятим настоящую главу изуче-
изучению одного, самого простого и вместе с тем важного, частного типа
такой переменной величины.
Начнем с установления понятия числовой последователь-
последовательности. Представим себе натуральный ряд:
1, 2, 3, ..., п, ..., п , ..., A)
в котором числа расположены в порядке возрастания, так что боль-
большее число пг следует за меньшим числом п (или меньшее
число п предшествует большему числу п'). Если теперь за-
заменить в ряде A), по какому-нибудь закону, каждое натуральное
число п некоторым вещественным числом хт то получится число-
числовая последовательность:
Х\, Х2, Х$, ..., Хп, . . ., Хпг, . . ., B)
члены, или элементы, которой хп занумерованы всеми на-
натуральными числами и расположены в порядке возрас-
возрастания номеров. При п' > /7, член хп> следует за членом хп
(хп предшествует хп>) независимо от того, будет ли само чис-
число xni больше, меньше или даже равно числу хп. **)
*' См. там Дополнение: «Общая точка зрения на предел».
**) Аналогично определяется понятие последовательности точек на пря-
прямой или объектов какой-либо другой природы.
^ Таким образом, во-первых, задание (независимой) переменной
эквивалентно заданию некоторого числового множества; во-вто-
во-вторых, выражение «х — переменная» фактически равнозначно выражению «л —
типовой элемент (или произвольный элемент) числового мно-
множества». Заметим, что сказанное не следует относить к «переменным типа
варианты» (для них процедура задания описывается отдельно). По существу,
переменные только что описанного типа (т. е. независимые переменные) будут
встречаться и использоваться лишь начиная с главы П.
52 ГЛ. I. ТЕОРИЯ ПРЕДЕЛОВ [22
Переменную х, принимающую некоторую последова-
последовательность B) значений, мы — следуя М е р э (Ch. Мёгау) —
будем называть вариантой. Это и есть тот тип переменной,
рассмотрением которого мы здесь ограничиваемся.7)
В школьном курсе математики читателю встречались перемен-
переменные именно типа варианты. Ему знакома, например, последо-
последовательность вида
а, а + d, a + 2d, . . ., а + {п — l)d, . . .
1 2 з
(арифметическая прогрессия) или вида
a, aq, aq2, . . ., aqn~l, . . .
12 3 п
(геометрическая прогрессия); переменный член той и другой про-
гресии есть варианта.
В связи с определением длины окружности обычно рассмат-
рассматривается переменный периметр правильного вписанного в окруж-
окружность многоугольника, получаемого из шестиугольника последова-
последовательным удвоением числа сторон; таким образом, эта варианта
принимает последовательность значений:
7^ Хотя с точки зрения интуиции между понятиями последовательности
и варианты имеются некоторые различия, по существу эти понятия эквива-
эквивалентны. Действительно, для того чтобы зафиксировать последовательность х\, х2,
. . .,хп, . . ., как и для того, чтобы задать переменную величину х, принимающую
одно за другим значения х\,Х2, • • • ,хп, . . . 9 мы должны сделать одно и то же —
указать некоторое правило, сопоставляющее каждому натуральному значе-
значению п вполне определенное вещественное число хп (это число в зависимости
лишь от нашего желания мы можем называть далее п-м членом последовательно-
последовательности или 72-м значением варианты). Эквивалентность понятий последовательности
и варианты отражается и в обозначениях: стандартным обозначением для обоих
служит символ вида хп. Читатель может в дальнейшем безо всяких опасений
отождествлять понятия последовательности и варианты, счи-
считая эти термины взаимозаменяемыми синонимами (фиксированная варианта
отождествляется всегда с той последовательностью значений, которую она про-
пробегает). Заметим, что более универсальный термин «последовательность» рас-
распространен сейчас гораздо шире термина «варианта», который почти вышел из
употребления.
22] § 1. ВАРИАНТА И ЕЕ ПРЕДЕЛ 53
Упомянем еще о десятичном приближении (скажем, по недо-
недостатку) к у/29 со все возрастающей точностью; оно принимает
последовательность значений:
1,4; 1,41; 1,414; 1,4142; ...
12 3 4
и также представляет собой варианту.
Переменную х9 пробегающую последовательность B), часто
обозначают через хП9 отождествляя ее с переменным («общим»)
членом этой последовательности.
Иногда варианта х задается тем, что указывается непосред-
непосредственно выражение для хп; так, в случае арифметичес-
арифметической или геометрической прогрессии имеем, соответственно,
хп = а + (п — \)d или хп = aqn~l. Пользуясь этим выражением,
можно сразу вычислять любое значение варианты по заданному
его номеру, не вычисляя предыдущих значений.
Для периметра правильного вписанного многоугольника такое
общее выражение возможно лишь, если ввести число ж; вообще пе-
периметр рт правильного вписанного m-угольника дается формулой
рт = 2т R sin —.
т
В других случаях нам может быть неизвестно выражение для
общего члена хп последовательности B). Тем не менее последова-
последовательность B), а с нею и отвечающая ей варианта, считается
заданной, если мы все лее владеем правилом, по которому
может быть вычислено любое значение варианты, лишь
только известен его номер. Поэтому-то, зная правило для при-
приближенного вычисления корней, мы можем считать заданной всю
последовательность десятичных приближений к у/29 хотя выраже-
выражения для его общего члена мы не знаем.
Если варианта — в указанном смысле — задана, то этим
не только охарактеризовано все множество принимаемых ею зна-
значений в целом, но и определен порядок, в котором эти значе-
значения принимаются; каждому номеру отвечает свое значение вариан-
варианты, и из двух значений то считается следующим, номер которого
больше.
Еще раз подчеркнем, что значения варианты не должны быть
обязательно различными. Например, если задать варианту одной
из формул:
Хп — 1, Хп — ^ I) , Хп — ,
54 ГЛ. I. ТЕОРИЯ ПРЕДЕЛОВ [23
то соответствующие последовательности будут:
1,
1
1,
1
о,
1
1,
2
-1,
2
1,
2
1,
3
1,
3
0,
3
1,
4
-1,
4
1
2'
4
1,
5
1,
5
0,
5
1,
6
-1,
6
1
3'
6
В первом случае мы имеем просто постоянную величину, все «мно-
«множество» принимаемых ею значений сводится к одному. Во вто-
втором — это множество состоит из двух значений, 1 и -1, принима-
принимаемых поочередно. Наконец, в третьем случае множество значений
переменной бесконечно, но это не мешает значениям переменной
через одно равняться 0; и мы считаем, что значение 0 на пятом
месте следует не только за значением 1 на втором месте, но и за
значением 0 на первом месте.
23. Предел варианты. Читатель из школьного курса также зна-
знаком уже с этим понятием. Вот точное его определение:
Постоянное число а называется пределом варианты
х = хп, если для каждого положительного числа г, сколь
бы мало оно ни было, существует такой номер N, что все
значения хп, у которых номер п> N, удовлетворяют неравен-
неравенству
\хп - а\ < €. C)
Тот факт, что а является пределом варианты, записывают так:
Нтхя = а или limx = a
(lim есть сокращение латинского слова limes, означающего «пре-
«предел»). Говорят также, что переменная стремится к а, и пишут
хп —>> а или х —>> а.
Иной раз число а называется пределом последовательно-
последовательности B), и говорят, что эта последовательность сходится к а.
То же определение коротко может быть сформулировано так:
Число а есть предел варианты х = хт если ее значения
отличаются от а сколь угодно мало, начиная с некоторого
места.
Неравенство C), где е произвольно, и есть точная запись утвер-
утверждения, что хп от а «отличается сколь угодно мало», а номер N как
24] § 1. ВАРИАНТА И ЕЕ ПРЕДЕЛ 55
раз и указывает то «место, начиная с которого» это обстоятельство
осуществляется.
Важно дать себе отчет в том, что номер N, вообще говоря,
не может быть указан раз навсегда: он зависит от выбора
числа ?. Для того чтобы подчеркнуть это, мы иной раз вместо N
будем писать N?. При уменьшении числа ? соответствующий
номер N = 7V?, вообще говоря, увеличивается: чем большей
близости значений варианты хпк а мы требуем, тем более далекие
значения ее — в ряду B) — приходится рассматривать.
Исключение представляет тот случай, когда все значения
варианты хп равны постоянному числу а. Очевидно, что тогда
а = Нтхя, но на этот раз неравенство C) будет выполняться для
любого ? > О одновременно при всех значениях хп. *)
Неравенство C), как мы знаем [17], равносильно следующим:
—?< хп — а < е
или
а - ? < хп < а + ?\ D)
этим мы часто будем пользоваться впоследствии.
Если изобразить числа а, а ± ? и значения хп нашей вариан-
варианты точками на числовой оси [21] (рис. 2), то получится наглядное
геометрическое истолкование предела варианты. Какой бы малый
а-е
fa
х2 \ хп+1 хп I х3 хг
Рис.2
отрезок (длины 2е) с центром в точке а ни взять, все точки хП9
начиная с некоторой из них, должны попасть внутрь этого от-
отрезка (так что вне его может остаться разве лишь конечное число
этих точек). Точка, изображающая предел а, является как бы сре-
средоточием сгустка точек, изображающих значения варианты.
24. Бесконечно малые величины. Случай, когда варианта стре-
стремится к нулю: хп —»> 0, представляет особый интерес.
Варианта хт имеющая своим пределом нуль, называется
бесконечно малой величиной или просто бесконечно
малой.
*) Аналогичное обстоятельство имеет место для варианты хП9 значения кото-
которой становятся равными а, начиная с некоторого места.
56 ГЛ. I. ТЕОРИЯ ПРЕДЕЛОВ [24
Если в определении предела варианты [23] положить а = О,
то неравенство C) примет вид
хп-0\ = \хп\ < е (для п > N?).
Таким образом, данное выше определение бесконечно малой можно
подробнее сформулировать без упоминания термина «предел»:
Варианта хп называется бесконечно малой, если она
по абсолютной величине становится и остается меньшей
сколь угодно малого наперед заданного числа е > О, начиная
с некоторого места.
Не вполне удачный (исторически сложившийся) термин «беско-
«бесконечно малая» величина не должен вводить читателя в заблуждение:
ни одно в отдельности взятое значение этой величины, если оно не
нуль, не может квалифицироваться как «малое». Суть дела в том,
что это — переменная величина*}, которая лишь в процессе
своего изменения способна сделаться меньшей произвольно
взятого числа е.
Если вернуться к общему случаю варианты хт имеющей пре-
предел а, то разность
ап=хп-а
между переменной и ее пределом, очевидно, будет бесконечно ма-
малой: ведь, в силу C),
\ап\ = \хп — а\ < е (для п > N?).
Обратно, если ап есть бесконечно малая, то хп ^ а. Это при-
приводит нас к следующему утверждению:
Для того чтобы варианта хп имела своим пределом пос-
постоянное число а, необходимо и достаточно, чтобы раз-
разность между ними ап—хп- а была бесконечно малой.
В связи с этим можно было бы дать и для понятия «предел»
другое определение (равносильное старому):
Постоянное число а называется пределом варианты хп,
если разность между ними есть бесконечно малая величина.
Разумеется, если исходить из этого определения предела, то для
бесконечно малой нужно использовать второе из приведенных вы-
выше определений. Иначе получился бы порочный круг: предел опре-
определялся бы через бесконечно малую, а бесконечно малая — через
предел!
*) Исключая неинтересный случай, когда она тождественно равна нулю.
25] § 1. ВАРИАНТА И ЕЕ ПРЕДЕЛ 57
Итак, если варианта хп —>> а, то она может быть представлена
в виде
хп = а + «„,
где а„ есть бесконечно малая, и обратно, если варианта х„ допус-
допускает такое определение, то она имеет пределом а. Этим часто
пользуются на практике для установления предела переменной.
25. Примеры.
1) Рассмотрим варианты
_ 1 1 _ (-1)п+\
п п п
им отвечают такие последовательности значений:
1, -, -, -, ....
2 3 4
-1. --, --, --, ....
2 3 4
1 1 1
1. -г з' ' ••••
Все три переменные представляют собой бесконечно малые, т. е. имеют пре-
пределом 0. Действительно, для них
\ХП\ = - < ?,
П
лишь только п > \. Таким образом, в качестве N? можно, например, взять
наибольшее целое число, содержащееся в |, т. е. Е (|) .
Отметим, что первая переменная все время больше своего предела 0, вто-
вторая — все время меньше его, третья же — попеременно становится то больше,
то меньше его.
2) Если положить
п ,
п
то переменная пробегает такую последовательность значений:
3 13 13
' 2' 3' 4' 5' 6'
И в этом случае хп -л 0, так как
, 3
хп\ < -
п
для п > j, так что за N? можно принять Е (|).
*) Вообще, через Е(р) обозначается наибольшее целое число, не превосходя-
превосходящее р, или, короче, целая часть числа р; Е есть начальная буква французского
слова Entier, означающего «целый».
58 ГЛ. I. ТЕОРИЯ ПРЕДЕЛОВ [25
Мы сталкиваемся здесь с любопытной особенностью: переменная поочередно
то приближается к своему пределу 0, то удаляется от него.
3) Пусть теперь
п
с этой вариантой мы уже имели дело в конце 22. Здесь также хп —>> 0, ибо
п
лишь только п > N? = ?(§)•
Отметим, что для всех нечетных значений п переменная оказывается равной
своему пределу.
Эти простые примеры интересны тем, что они характеризуют многообразие
тех возможностей, которые охватываются данным выше определением предела
варианты. Несущественно, лежат ли значения переменной с одной стороны
от предела или нет; несущественно, приближается ли переменная с каждым
шагом к своему пределу; несущественно, наконец, достигает ли переменная
своего предела, т. е. принимает ли значения, равные пределу. Существенно лишь
то, о чем говорится в определении: переменная должна отличаться от предела
сколь угодно мало в конце концов, т. е. для достаточно далеких своих значений.
4) Возьмем более сложный пример варианты:
п2 — п + 2
3ft2 + 2ft — 4'
докажем, что ее пределом будет число -j.
С этой целью рассмотрим разность
1 — 5ft + 10
3 3Cft2 -|- 2п — 4)
и оценим ее абсолютную величину; для п > 2 имеем:
Ъп - 10 Ъп Ъп 1
-2ft-4) 3Cft2-4) 3-2ft2 ft'
так что это выражение меньше ?, если п > N? = E (j^j. Этим доказано,
что хп -л -j.
5) Определим варианту формулой
хп = а" = \/а (а > 1)
и докажем, что хп —> \.
Если воспользоваться неравенством C) в 19, то можно написать:
\хп — 11 = у/а — 1 < < ? лишь только п > N? = Е ( ).
Можно, однако, рассуждать и иначе. Неравенство
I
\хп - 1 = ап - 1 < е
25] § 1. ВАРИАНТА И ЕЕ ПРЕДЕЛ 59
равносильно такому:
" < 1о&A + е) или п >
так что оно выполняется при п > N? = Е ( ^—п+и) •
В соответствии с выбранным способом рассуждения мы пришли к раз-
различным выражениям для N?. Например, при а = 10, ? = 0,01 получаем
Ло,О1 = оШ = 900 по первому способу и Afyoi = ? @00432—) =231 — по вто-
второму. По второму способу мы получили наименьшее из возможных значений
для Л^оь ибо уже 1023Т = 1,010017. . . отличается от 1 больше, чем на ? = 0,01.
То же будет и в общем случае, ибо, как легко видеть, при
1 1
п ^ необходимо ап — 1 ^ е.
loga(l + е)
Заметим по этому поводу, что мы вовсе не заинтересованы именно в наи-
наименьшем возможном значении N?, если речь идет только об установлении
факта стремления к пределу. Должно быть гарантировано выполнение неравен-
неравенства C), начиная хоть с какого-нибудь места, далекого или близкого — безраз-
безразлично.
6) Важный пример бесконечно малой дает варианта
ап = qn, где \q\ < 1.
Для доказательства того, что ап —>> 0, рассмотрим неравенство
Ы = \q\n < e;
оно равносильно таким:
lge *}
п • lg \q\ < lge или п >
lg \q\
Таким образом, если положить (считая е < 1)
N?=E
то при п > Ne упомянутое неравенство наверное выполнится.
Аналогично, легко убедиться в том, что и варианта
Pn=A.qn,
где по-прежнему \q\ < \,aA — постоянное число, также есть бесконечно малая.
7) Рассмотрим, далее, бесконечную убывающую геометрическую прогрессию
a, aq, aq , ..., aqn~l, ... (\q\ < 1)
и поставим вопрос об определении ее суммы.
*) Под lg jc здесь (и впредь) разумеется Iog10-X- Следует иметь в виду,
что \q\ < 1 и lg \q\ < 0; поэтому при делении обеих частей неравенства на это
число знак неравенства должен быть изменен на обратный.
60 ГЛ. I. ТЕОРИЯ ПРЕДЕЛОВ [25
Под суммой бесконечной прогрессии, как известно, разумеется предел, к ко-
которому стремится сумма sn ее п членов при безграничном возрастании п. Но
а — aqn a a n
sn = — = q ,
\-q \-q \-q
так что варианта sn разнится от постоянного числа у^— на величину
ап = — yz~ • 41 •> которая, как мы только что видели, является бесконечно малой.
Следовательно, по второму определению предела, искомая сумма прогрессии
а
s = \imsn =
\-q
Таким образом, это число является суммой бесчисленного множества
членов прогрессии, что записывают так:
2 и-1 а
а + aq + aq + . . . + aq + . . . =
\-q
8) Пусть даны два числа а и Ь. Положим х$ = а, х\ = Ь, а последующие
значения варианты хп определим равенством
Хп_2+Хп_1
хп = О > 2).
Этим варианта хп, действительно, задана, так как, полагая здесь п = 2, 3, . . .,
можно последовательно найти все ее значения, до любого включительно.
Если из обеих частей написанного равенства вычесть по хп_\, то получим
хп - xn_i = -- (*„_! - хп_2) (и = 2, 3, 4, . . .).
Таким образом, в ряду разностей
х\ — хо = b — а, х2—х\, ..., хп_\ — хп_2> Xn—xn_i,
каждая (начиная со второй) получается из предыдущей умножением на — ^,
т. е. мы имеем здесь геометрическую прогрессию со знаменателем — \. Так как
сумма п ее членов есть хп — а, то, пользуясь известной нам [см. 7)] формулой
для суммы прогрессии, сразу получаем:
\\т[хп - а) = —y\ = - О - а),
1 - \~2) 5
откуда уже легко заключить, что
2. а + 2Ь
hmxn = а + -{Ь — а) = —-—.
9) Наподобие геометрической прогрессии можно рассмотреть произволь-
произвольную последовательность чисел
а\, а2, аз, . . ., ап, . . .
и, по порядку складывая их, образовать «частичные суммы»:
А\ = а\, А2 = а\-\-а2, Аз=а\+а2 + аз, ...,
Ап = а\ + <22 + . . . + ап, ...
26] § 1. ВАРИАНТА И ЕЕ ПРЕДЕЛ 61
Если, при безграничном возрастании п, Ап стремится к (конечному или беско-
бесконечному) пределу А, то это число называют суммой всех взятых чисел ап
и пишут
а\ ~Ь #2 + . . . + ап + . . . = А.
Символ в левой части этого равенства называют бесконечным рядом,
а число А — его суммой. Про ряд, имеющий конечную сумму, гово-
говорят, что он сходится.
Пусть, например, дан ряд
111 1
ГЛ + 2Л + 3^ + '" + и(и+1) +'"
Здесь
1 1 111
1 _ 1
+ 1) ~ п
так что в данном случае
/ 1\ /1 1\ /1 1 \ 1
Ап= A ) + ( )+...+ ( 1 = 1 .
V 2/ \2 ЗУ \п п+\) и+1
Очевидно, Ап —>> 1, так что предложенный ряд сходится и имеет суммой единицу.
Если ряд не имеет конечной суммы, про него говорят, что он расходится:
таков, например, ряд
26. Некоторые теоремы о варианте, имеющей предел. Пусть
варианта хп имеет предел а. При любом р < а (или q > а) легко
подобрать число г > 0 так, чтобы было
а — е > р (или а + е < q);
для этого достаточно взять ? меньшим разности а — р (или q — а).
Но, по определению предела [23], найдется такой номер N, что для
п > N будет выполняться неравенство [см. D)]
хп > а - ? (хп < а + е),
а следовательно — и подавно неравенство
хп>р (или хп < q).
1° Если варианта хп стремится к пределу а и а > р
{а < q)9 то и все значения переменной, начиная с неко-
некоторого, тоже будут >р (<q).
Это простое предложение имеет ряд полезных следствий.
2° Если варианта хп стремится к пределу а > 0 (< 0),
то и сама переменная хп > 0 (< 0), начиная с некото-
некоторого места.
62 ГЛ. I. ТЕОРИЯ ПРЕДЕЛОВ [26
Для доказательства достаточно применить предыдущее утвер-
утверждение, взяв р = О (q = 0).
Можно установить и более точный результат:
3° Если варианта хп стремится к пределу а, отличному
от нуля, то по крайней мере достаточно далекие зна-
значения хп по абсолютной величине превзойдут некоторое по-
положительное число г:
\хп\ > г > 0 {для п> N).
Действительно, при а > 0 (< 0) можно взять
0 < р < а {а < q < 0)
и положить г = р (г = \q\).
4° С другой стороны, если варианта хп имеет предел а, то
она является ограниченной, в том смысле, что все ее зна-
значения по абсолютной величине не превосходят некоторой конечной
границы:
хп\^М (М= const; /7=1,2,3,...).
Возьмем число М' > \а\9 так что — М' < а < М\ и положим
р = — М\ a q = М'. Найдется такой номер N, что для п> N будет
—М' < хп < М' или \хп\ < М'.
Это неравенство заведомо выполняется при п = N + 1, N + 2, ...,
так что ему могут не удовлетворять лишь первые N значений нашей
варианты (или некоторые из них).
Поэтому если положить М равным наибольшему из чисел
|, \х2\, ...,
то уже для всех значений хп будем иметь: \хп\ ^ М, что и тре-
требовалось доказать.
Замечания. I. Можно дать определение ограниченности по-
последовательности хп в равносильной форме, потребовав выполне-
выполнения неравенств
k^xn^g (n= 1,2,3,...),
где к и g — два конечных числа. Действительно, из этих неравенств,
если положить М равным наибольшему из чисел \к\, \g\9 следует
\хп\ ^ М; обратно, если имеет место последнее неравенство, то оно
может быть написано в форме — М ^ хп ^ М, так что — М играет
роль к,ъМ — роль g.
27] § 1. ВАРИАНТА И ЕЕ ПРЕДЕЛ 63
П. Утверждение 4° не может быть обращено: не всякая огра-
ограниченная варианта имеет предел. Если положить, например,
хп = (—l)w+1, то эта варианта, конечно, ограничена: \хп\ ^ 1, но
предела она не имеет, все время колеблясь от +1 к —1.
В заключение, опираясь на предложение 1°, докажем един-
единственность предела:
5° Варианта хп не может одновременно стремиться
к двум различным пределам.
Действительно, допустим противное: пусть одновременно
хп —> а и хп —> Ь9 причем а < Ь. Возьмем любое число г
между а и b
а < г < Ъ.
Поскольку хп —> а и а < г, найдется такой номер N\ что для
п> N' будет выполняться неравенство: хп < г. С другой стороны,
раз хп —> Ъ и Ъ > г, найдется и такой номер 7V/;, что для п > N"
окажется: хп > г. Если взять номер п большим и N\ и N", то соот-
соответствующее значение переменной хп будет одновременно и < г,
и > г, что невозможно.
Это противоречие доказывает наше утверждение.
27. Бесконечно большие величины. Бесконечно малым вели-
величинам, в некотором смысле, противопоставляются бесконечно
большие величины (илипросто бесконечно большие).
Варианта хп называется бесконечно большой, если
она по абсолютной величине становится и остается боль-
большей сколь угодно большого наперед заданного числа Е > О,
начиная с некоторого места:
\хп\ > Е {для п > Ne).
Как и в случае бесконечно малых, здесь также следует подчерк-
подчеркнуть, что ни одно в отдельности взятое значение бесконечно боль-
большой величины не может быть квалифицировано как «большое»;
мы имеем здесь дело с переменной величиной, которая лишь
в процессе своего изменения способна сделаться большей
произвольно взятого числа Е.
Примерами бесконечно больших могут служить варианты
хп = п; хп = —п; хп = ( —1)"+ п,
которые пробегают натуральный ряд чисел, но первая — со знаком плюс, вто-
вторая — со знаком минус, третья же — с чередующимися знаками.
64 ГЛ. I. ТЕОРИЯ ПРЕДЕЛОВ [27
Вот еще один пример бесконечно большой величины:
х„ = <? при |0| > 1.
Действительно, каково бы ни было Е > 0, неравенство
\Хг
= \Q\n >
выполняется, лишь только
lgE *}
п ' lg \Q\ > lgE или п > ,
igiei
так что за N^ можно взять число
Е I
Если варианта хп является бесконечно большой и (по край-
крайней мере для достаточно больших п) сохраняет определенный
знак (+ или -), то, в соответствии со знаком, говорят, что
варианта хп имеет предел +оо или -оо, и пишут:
я = +оо, хп —> +оо
или
= —сю, хп —> —сю.
Можно было бы дать для этих случаев и независимое опреде-
определение, заменив неравенство \хп\ > Е, смотря по случаю, неравен-
неравенством
хп > Е или хп < —Е,
откуда уже вытекает, соответственно, что хп > 0 или хп < 0.
Очевидно, что бесконечно большая величина хп в общем
случае характеризуется соотношением: \хп\ —>> +оэ.
Из приведенных выше примеров бесконечно больших величин, очевидно, ва-
варианта хп = п стремится к +оо, варианта хп = — п стремится к — оо. Что же
касается третьей варианты: хп = (—\)пп, то про нее нельзя сказать ни что она
стремится к +оо, ни что она стремится к — оо.
Наконец, относительно варианты хп = (У7 при Q > 1 можно сказать, что она
стремится к +оо, а при Q < —1 у нее предела нет.
С несобственными числами ±оо мы уже сталкивались в 10;
следует помнить, что их применение имеет совершенно условный
смысл, и остерегаться производить над этими «числами» арифме-
арифметические операции. Вместо +оо часто пишут просто оо.
Введение бесконечных пределов не нарушает теоремы о един-
единственности предела, установленной в предыдущем п° [см. 5°];
*} Так как \Q\ > 1, то lg \Q\ > 0.
28] § 2. ТЕОРЕМЫ О ПРЕДЕЛАХ 65
действительно, как указано было там же [4°], варианта, имеющая
конечный предел а, является ограниченной и, следовательно, никак
не может одновременно стремиться к бесконечному пределу.
В заключение упомянем о простой связи, которая существует
между бесконечно большими и бесконечно малыми величинами:
Если варианта хп является бесконечно большой, то ее
обратная величина ап — ^- будет бесконечно малой.
Возьмем любое число с > 0. Так как \хп\ —>> оо, то для числа
Е = ^ найдется такой номер N, что
\хп\ > -, лишь только п > N.
Тогда для тех же значений /7, очевидно, будет
ап\ < €,
что и доказывает наше утверждение.
Аналогично можно доказать и обратное утверждение:
Если варианта ап (не обращающаяся в 0) является беско-
бесконечно малой, то обратная для нее величина хп = ^- будет
бесконечно большой.
§ 2. Теоремы о пределах, облегчающие нахождение
пределов
28. Предельный переход в равенстве и неравенстве. Соединяя
две варианты хп и уп знаками равенства или неравенства, мы всегда
подразумеваем, что речь идет о соответствующих значениях
их, т. е. о значениях с одним и тем же номером.
1° Если две варианты хп и уп при всех их изменениях
равны: хп = уп, причем каждая из них имеет конечный предел:
Нтхя = а, 1ш\.уп = Ь,
то равны и эти пределы: а = Ъ.
Непосредственно следует из единственности предела [26, 5°].
Этой теоремой пользуются обычно в форме предельно-
предельного перехода в равенстве: из хп—уп заключают, что
66 ГЛ. I. ТЕОРИЯ ПРЕДЕЛОВ [28
2° Если для двух вариант хп, уп всегда выполняется не-
неравенство хп ^ уп, причем каждая из них имеет конечный
предел:
Нтхя = a, little = b,
то и а ^ Ъ.
Допустим противное: пусть а <Ъ. Рассуждая так же, как
и в 26, 5°, возьмем число г между а и Ъ, так что а < г < Ъ.
Тогда, с одной стороны, найдется такой номер N\ что для п > N'
будет хп < г, с другой же — найдется и такой номер Nn', что для
п > N" окажется уп > г. Если N больше обоих чисел N\ Nn\
то для номеров п> N будут одновременно выполняться оба нера-
неравенства
*п < г, уп> г, откуда хп < уп,
что противоречит предположению. Теорема доказана.
Эта теорема устанавливает допустимость предельного пе-
перехода в неравенстве (соединенном с равенством):
из хп ^ уп можно заключить, что \\тхп ^ \ш\уп.
Конечно, знак ^ всюду может быть заменен знаком ^.
Мы обращаем внимание читателя на то, что из строгого
неравенства хп> ут вообще говоря, не вытекает строгое же
неравенство limx^ > limj^, а только, по-прежнему,
Так, например, ^ > — ^ при всех /7, и тем не менее
Hm- =lim( — ) =0.
п \ п)
При установлении существования и величины предела варианты
иногда бывает полезна теорема:
3° Если для вариант хп, уп, zn всегда выполняются нера-
неравенства
%п ^ Уп ^ zn->
причем варианты хп и zn стремятся к общему пределу а:
\\тхп = limzn = a,
то и варианта уп имеет тот лее предел:
\ш\уп = а.
Зададимся произвольным е > 0. По этому е прежде всего най-
найдется такой номер N\ что при п> N'
а — г < хп < а + г.
29] § 2. ТЕОРЕМЫ О ПРЕДЕЛАХ 67
Затем найдется такой номер N", что при п > N"
а — с < zn < а + с.
Пусть N будет больше обоих чисел N' и N"; тогда, при а > N,
выполняются оба предшествующих двойных неравенства, и потому
а — е < хп ^ уп ^ zn < а + с.
Окончательно, при п > N
а — г < уп < а + г или \уп — а \ < г.
Таким образом, действительно, limj^ = a.
Из этой теоремы, в частности, следует: если при всех п
a ^yn^zn
и известно, что zn —>> а, то и уп —>> а. Впрочем, это очень легко
доказать и непосредственно.
Теоремы 1°, 2° и 3° легко распространяются и на случай бес-
бесконечных пределов.
29. Леммы о бесконечно малых. В дальнейших теоремах нам
придется рассматривать одновременно две варианты (или больше),
сочетая их между собой знаками арифметических действий. При
этом, как и выше, мы относим эти знаки к соответствующим
значениям вариант. Например, говоря о сумме двух вариант хп иут
пробегающих соответственно последовательности значений
хь х2, хз, . .., хп, ...
и
УЪ У2, УЗ, • •-, Уп,
мы имеем в виду варианту хп + уП9 принимающую последователь-
последовательность значений
, Х2+У2, *3+.УЗ, • .., Хп+уп, ...
При доказательстве теорем, относящихся к результатам ариф-
арифметических операций над переменными, важную роль будут играть
следующие две леммы о бесконечно малых.
Лемма 1. Сумма любого конечного числа бесконечно малых
есть также величина бесконечно малая.
Проведем доказательство для случая двух бесконечно ма-
малых ап и /5п (общий случай исчерпывается аналогично).
68 ГЛ. I. ТЕОРИЯ ПРЕДЕЛОВ [30
Зададимся произвольным числом ? > 0. Согласно определению
бесконечно малой, по числу ? для бесконечно малой ап найдется
такой номер N1\ что при п > N' будет
к
Точно так же и для бесконечно малой f}n найдется такой номер Nn\
что при п > N" будет
?
\Рп
<Г
Если взять натуральное число N большим обоих чисел Nf и N/f,
то при п > N одновременно выполняются оба эти неравенства,
так что
«л + Рп\ < |««| + \Рп\ < 2 + 2 = ?'
Итак, величина ап + (}П9 действительно, является бесконечно
малой.
Лемма 2. Произведение ограниченной последовательно-
последовательности хп на бесконечно малую ап есть бесконечно малая.
Пусть, для всех значений /7,
Если задано произвольное число ? > 0, то по числу ^ для беско-
бесконечно малой ап найдется такой номер N, что для п> N будет
Тогда для тех же значений /7, очевидно,
?
М
Отсюда и следует, что хп • ап есть бесконечно малая.
30. Арифметические операции над переменными. Следующие
теоремы важны в том отношении, что с их помощью во мно-
многих случаях делается ненужным восхождение всякий раз к опре-
определению понятия «предел», с разысканием по заданному е со-
соответствующего N, и т. д. Этим вычисление пределов значительно
облегчается.
1° Если варианты хп и уп имеют конечные пределы:
ап\ = \хп
?
ап\ < М- — = ?.
М
\\тхп = a, limj/^ = b,
30] § 2. ТЕОРЕМЫ О ПРЕДЕЛАХ 69
то и сумма {разность) их также имеет конечный предел,
причем
Н( ±уп) = а ±Ь.
Из условия теоремы следует, что
xn = a+an, yn = b+/3n, A)
где ап и j5n — бесконечно малые. Тогда
хп ±уп = (а ± Ъ) + (an ± J5n).
Здесь an±f3n есть бесконечно малая по лемме 1; следовательно,
пользуясь вторым определением предела, можно утверждать, что
варианта хп ±уп имеет предел, равный а ± Ь9 что и требовалось
доказать.
Эта теорема и ее доказательство переносятся на случай любого
конечного числа слагаемых.
2° Если варианты хп и уп имеют конечные пределы.
„ = a, Hmj^ = b,
то и произведение их также имеет конечный предел, и
ИтхпУп = ab.
Исходя из тех же равенств A), имеем на этот раз
Хпуп = ab + (арп + Ъап + апрп).
Выражение в скобках, в силу лемм 1 и 2, есть величина бесконечно
малая. Отсюда и следует, что варианта хпуп действительно имеет
пределом аЪ.
Эта теорема может быть распространена на случай любого ко-
конечного числа сомножителей (например, методом математической
индукции).
3° Если варианты хп и уп имеют конечные пределы:
Нтхя = a, little = b,
причем Ъ отлично от 0, то и отношение их также имеет
конечный предел, а именно
хп а
lim— = -.
Уп Ъ
70 ГЛ. I. ТЕОРИЯ ПРЕДЕЛОВ [31
Поскольку Ъ Ф 0, согласно утверждению 3° в 26, начиная с не-
некоторого места, не только уп ф 0, но даже
\Уп\ > Г > 0,
где г — постоянное число. Ограничимся теми значениями номе-
номера /7, для которых это выполняется; тогда отношение ^ заведомо
имеет смысл.
Исходя, по-прежнему, из равенств A), имеем
Уп
а
Ъ
а
~ Ъ
+
+
ап
Рп
а
Ъ
1
by»
Выражение в скобках, в силу лемм 1 и 2, есть величина бес-
бесконечно малая. Множитель же при нем, на основании сказанного
вначале, будет ограниченной переменной:
1
Ъуп
1 1
\Ъ\-\Уп\
Следовательно, по лемме 2, все произведение справа будет бес-
бесконечно малым, а оно представляет разность между вариантой ^
и числом |. Итак, предел — есть |, что и требовалось доказать.
31. Неопределенные выражения. В предыдущем п° мы рас-
рассматривали выражения
хп±уп, хпуп, — B)
Уп
и, в предположении, что варианты хп и уп стремятся к конечным
пределам (из которых, в случае частного, предел уп не должен был
равняться нулю), устанавливали пределы каждого из этих выра-
выражений.
Оставлены были без рассмотрения случаи, когда пределы пе-
переменных хп и уп (один или оба) бесконечны или — если
речь идет о частном — когда предел знаменателя нуль. Из этих
случаев мы здесь остановимся лишь на четырех, представляющих
некоторую важную и интересную особенность.
1° Рассмотрим сначала частное — и предположим, что обе
переменные хп и уп одновременно стремятся к ну-
л ю. Здесь мы впервые сталкиваемся с совсем особым обстоятель-
обстоятельством: хотя нам известны пределы хп иуп, но о пределе их отноше-
отношения— не зная самих этих вариант — никакого общего
31] § 2. ТЕОРЕМЫ О ПРЕДЕЛАХ 71
утверждения мы сделать не можем. Этот предел, в зависимо-
зависимости от частного закона изменения обеих переменных, может
иметь различные значения или далее вовсе не существовать.
Следующие простые примеры поясняют это.
Пусть, скажем, хп — \^уп — \\ обе варианты стремятся к ну-
нулю. Их отношение ^ = \ также стремится к нулю. Если
же, наоборот, положить хп — \^уп — \^^^ хотя они по-прежнему
стремятся к нулю, на этот раз их отношение — = п стремится
к оо! Взяв же любое отличное от нуля число а и построив две бес-
бесконечно малые хп = ^ куп = „--> видим, что отношение их имеет
пределом а (так как тождественно равно а).
Наконец, если хп = -—^—, уп — ^ (обе имеют пределом нуль),
то отношение— = (—1)"+1 оказывается вовсе не имею-
имеющим предела.
Таким образом, одно знание пределов вариант xnwyn в дан-
данном случае не позволяет еще судить о поведении их отно-
отношения: необходимо знать сами варианты, т. е. закон их изменения,
и непосредственно исследовать отношение —. Для того что-
чтобы характеризовать эту особенность, говорят, что, когда хп —> О
иуп —^ 0, выражение — представляет неопределенность
вида ^.
2° В случае, когда одновременно хп —> ±оо иуп —>> ±оо,
имеет место подобное же обстоятельство. Не зная самих ва-
вариант, общего утверждения о поведении их отношения сделать
нельзя. Этот факт иллюстрируется примерами, вполне аналогичны-
аналогичными приведенным в 1°:
хп = п —>> оо, Уп — п2 —> оо> — = \ —>> 0;
хп = п2 —>> оо, уп = п —)> оо, — = п —)> оо;
Уп
хп = an —)> ±00 {а фО), уп — ^^ оо> — = а —)> а;
О I ( 1 А ^~Г 1 м v г>^\ 1; 1/1 V г>^\ п О I ( 1 А М\ А
вовсе не имеет предела.
И в этом случае говорят, что выражение — представляет
неопределенность — вида Ц.
Обратимся к рассмотрению произведения хпуп-
3° Если хп стремится к нулю, в то время как уп
стремится к ±оо, то, исследуя поведение произведения хпуп->
72 ГЛ. I. ТЕОРИЯ ПРЕДЕЛОВ [31
мы сталкиваемся с такой же особенностью, как и в пунктах 1° и 2°.
Об этом свидетельствуют примеры:
хп = ^ -» 0, уп = /7 -» оо, Хду„ = I -» 0;
х„ = \ -Л 0, j;w = /72 -» оо, Хду„ = п -» оо;
^ = /7 —>> оо, Хду„ = а —>> а;
3;w = /7^OO, XWJW = (-l/^1
вовсе не имеет предела.
В связи с этим при хп —> 0 и j;w —>> оо говорят, что выраже-
выражение хпуп представляет неопределенность вида 0 • оо.
Рассмотрим, наконец, сумму хп +уп-
4° Здесь оказывается особым случай, когда хп и уп стремятся
к бесконечности разных знаков: именно в этом случае о сум-
сумме хп +уп ничего определенного сказать нельзя, не зная самих
вариант хп и уп. Различные возможности, представляющиеся
здесь, иллюстрируются примерами:
х„ = 2/7—^+оо, уп=-п^-оо, хп+уп = /7 -^+ оо;
хп = /7 —)> + оо, Уп— — 2/7 —> — оо, xw + j^w = — /7 —)> — оо;
Х^ = /7 + C —>• + ОО, уп = — /7 —>• — ОО, Л
вовсе не имеет предела.
Ввиду этого, при хп —> +сх) и j/я —)> —сю, говорят, что выраже-
выражение хп +Уп представляет неопределенность вида оо — оо.
Таким образом, поставив себе задачей определить пределы
арифметических выражений B) по пределам вариант хп куп-> из ко-
которых они составлены, мы нашли четыре случая, когда этого сде-
сделать нельзя: неопределенности вида
0 °° п *)
-, —, 0 • оо, оо — оо. ;
О оо
В этих случаях приходится, учитывая закон изменения вариант хп
иуп, непосредственно исследовать интересующее нас выра-
выражение. Подобное исследование получило название раскрытие
неопределенности. Далеко не всегда оно так просто, как
*) Конечно, символы эти лишены всякого числового смысла. Каж-
Каждый из них является лишь краткой условной характеристикой для выражений
одного из четырех типов неопределенности.
32]
§ 2. ТЕОРЕМЫ О ПРЕДЕЛАХ
73
в приведенных выше схематических примерах. Ниже мы укажем
несколько более интересных примеров этого рода.
32. Примеры на нахождение пределов.
1) Пусть р\п) многочлен с постоянными коэффициентами:
р(п) = а$п + а\п~Х + . . . + ак_\п + ак.
Поставим вопрос о пределе его. Если бы все коэффициенты этого многочле-
многочлена были положительны (отрицательны), то сразу ясно, что пределом р(п) бу-
будет +оо( — оо). Но в случае коэффициентов разных знаков одни члены стремятся
к +оо, другие к — оо, и налицо неопределенность вида оо — оо.
Для раскрытия этой неопределенности представим р{п) в виде:
/ \ к
р(п) = п
а° Н
п
ак
"Г
Так как все слагаемые в скобках, начиная со второго, при возрастании п будут
бесконечно малыми, то выражение в скобках имеет пределом uq: первый же мно-
множитель стремится к +оо. В таком случае все выражение стремится к +оо или
к — оо, в зависимости от знака а$.
Уничтожение «неопределенности» путем пре-
преобразования данного выражения (чем мы здесь
воспользовались) часто применяется для раскры-
раскрытия неопределенности.
2) Если q(n) есть такой же многочлен
q(n) =
Ъ\п
~
то частное i-H- при возрастании п представит не-
неопределенность вида §?.
Преобразуя и здесь каждый из многочленов
так, как это было сделано в 1), получим:
/ \ i a\ i \ ак
Р(п) k-l а0 +- + ••• + ^
я(п) ь0 + Ц- +... + ^ '
Второй множитель здесь имеет конечный пре-
предел т^-. Если степени обоих многочленов равны:
*)
ф
6о
к = /, таков же будет и предел отношения
При к > I первый множитель стремится к +оо,
так что рассматриваемое отношение стремится к zboo (знак — в зависимости
от знака -^). Наконец, при к < /, первый множитель, а с ним и все выражение
стремится к нулю.
3) Найти объем V треугольной пирамиды SABC (рис. 3).
Разделив высоту Н пирамиды на п равных частей, проведем через точ-
точки деления плоскости, параллельные плоскости основания. В сечении полу-
получатся треугольники, подобные основанию. Построим на них систему входящих
*) Так можно было бы получить предел ^ в примере 4), 25.
74
ГЛ. I. ТЕОРИЯ ПРЕДЕЛОВ
[32
и выходящих призм; из первых составится тело с объемом Vn, а из вторых —
тело с объемом У„9 причем, очевидно,
Уп < V < V'n.
Но разность Vfn — Уп есть не что иное, как объем нижней выходящей призмы
с основанием Q = пл. А АВС и высотой ^; итак, разность
при возрастании п, а тогда тем более стремятся к нулю и разности V — УпжУ'п — У,
т. е.
V = lim Vn = lim v'n.
Найдем теперь выражение для У!п. Мы имеем здесь тело, составленное из ряда
выходящих призм; по свойству сечений пирамиды, их основания, соответственно,
будут равны:
1 22 i2 п2
в то время как высота у всех одна и та же: Щ. Поэтому
QH n(n+ l)Bw
QH
Ш 6
так что
4) Найти площадь Q фигуры ОРМ,
образованной частью ОМ параболы
у = ах2 (а > 0), отрезком ОР оси х
и отрезком РМ (рис. 4). Разобьем отре-
отрезок ОР на п равных частей и построим на
них ряд входящих и выходящих прямоуголь-
прямоугольников. Площади Qn и Q'n составленных из
них ступенчатых фигур разнятся площадью | • у наибольшего прямоугольника.
Отсюда, как и в 3), разность Q'n — Qn —>> 0 и, так как
очевидно,
Q
= ]imQn =
* ^ Здесь мы используем известную формулу для суммы квадратов первых п
натуральных чисел.
32] § 2. ТЕОРЕМЫ О ПРЕДЕЛАХ 75
Так как высоты отдельных прямоугольников суть ординаты точек параболы,
с абсциссами
12 i n
— х, — х, ..., -х, ..., -х=х,
п п п п
и — в согласии с уравнением кривой — величина их равна, соответственно,
1 2 22 1
2 i 2
, . . ., а • —^х
П1 П1
2 2 2
а • —^ х , а • —тх , . . ., а • —^х , . . .,
2 П1 1
то для Q'n получаем выражение
,_^_а2 22 2, х__ах^_ (п+ 1)Bи + 1)
rfi п 6 rfi
Отсюда
3 2
_ , я* * • ял: xv
3 3 3
Опираясь на это, легко получить, что площадь параболического сегмен-
сегмента М1 ОМ равна ^ ху, т. е. двум третям площади описанного прямоугольника (этот
результат был известен еще Архимеду). *^
5) Доказать, что при 0 < к < 1,
lim[(w+ \)k -п] = 0.
Мы имеем здесь неопределенность вида со — со. Преобразуем, вынося пк
за скобку:
о ¦й'-'Н НИ-aW
Так как -^^ -л 0, то и подавно (п + 1)^ — пк —>> 0, что и требовалось доказать.
6) Найти предел варианты
представляющей (согласно предыдущему примеру) неопределенность вида со • 0.
Умножая и деля на сумму корней у/п + 1 + \/п, преобразуем данное выра-
выражение к неопределенности вида ^:
[у/п + 1 - у/п) [у/п + 1 + у/п) y/Tl
у/п + 1 + у/п у/п + 1 + у/п
наконец, делим числитель и знаменатель на у/п:
1
*^ Общее определение площади криволинейной фигуры будет дано лишь
в главе X (второй том); там же примененный здесь метод вычисления пло-
площади будет обобщен на другие криволинейные фигуры.
76
Очевидно,
ГЛ. I. ТЕОРИЯ ПРЕДЕЛОВ
1 <
[32
так как выражение справа стремится к 1, то это же справедливо и относительно
корня. Окончательно,
Птхп = -.
7) Найти пределы вариант:
Варианты хп и уп представляют неопределенность вида §| (так как оба кор-
корня > п, то они стремятся к оо). Преобразуем, разделив числитель и знаменатель
на п:
1
1
Уп =
Так как оба корня в знаменателе имеют пределом 1 [ср. предыдущий пример],
тохп -> 1иуп -> 1.
Выражение для zn имеет своеобразную форму: каждое слагаемое этой суммы
зависит от п, но и число их растет вместе с п.*^ Так как каждое
слагаемое меньше первого и больше последнего, то
п п
/ < zn < . т. е. хп < zn < у„.
л/п1 + п л/п1 + 1
Но (согласно уже найденному) варианты хп иуп стремятся к общему пределу 1;
следовательно — по теореме 3° [28] — к тому же пределу стремится и вари-
варианта zn.
8) Пусть дано т положительных чисел
а\9 а2, . . ., ат.
Обозначая через А наибольшее из них, доказать, что
lim ^а\ + а\ + . . . + апт = А.
Заключение это следует из очевидных неравенств
А < Ца\ + а\ + . . . + апт < А • </
[см. 25, 5)].
9) Мы видели в 27, что при а > 1 степень а" —У +оо (с возрастанием п).
Исследуем теперь поведение отношения
(при к > 0), представляющего неопределенность вида §?.
*)
Эту же особенность, впрочем, имели и выражения для Vfn и Qfn в 3), 4).
32] § 2. ТЕОРЕМЫ О ПРЕДЕЛАХ 77
Установим одно вспомогательное неравенство [ср. неравенство Бернулли
в 19]. Положив а = 1 + А, так что А > О, имеем по формуле бинома Ньютона:
яи = A + А)и = 1 + wA + V У А2 + . . . > V У А .
Так как для п > 2, очевидно, и — 1 > п, то, окончательно,
- IJ 2
: п •
При к = 1, получаем сразу
lim — = +00.
n
Так как этот результат верен при любом а > 1, то, взяв к > 1, можем
написать (по крайней мере, для достаточно больших п)
a" г (а* Г]* {ah"
ПА П
откуда п
lim — = +00 (а > 1).
Доказанный, таким образом, для к ^ 1, этот результат тем более будет
верен и для к < 1.
10) Тем же неравенством C) можно воспользоваться, чтобы установить, что
Именно, полагая в нем а = у/п9 получим
откуда
0 < <УЛ- 1 < —,
у/п
что приводит к требуемому результату.
11) Теперь мы можем установить и другой интересный предел
()
п
Здесь мы снова имеем неопределенность вида ^, ибо, как легко показать,
\ п -л +оо.
Действительно, если взять произвольное число е > 0, то, поскольку а? > 1,
для достаточно больших п будет [26, 1°]
Логарифмируя по основанию а, получим
п
откуда и следует высказанное утверждение.
78
ГЛ. I. ТЕОРИЯ ПРЕДЕЛОВ
[33
33. Теорема Штольца и ее применения. Для определения пределов неопре-
неопределенных выражений у- типа ^ часто бывает полезна следующая теорема, при-
принадлежащая Штольцу (О. Stolz).*)
Пусть варианта уп —>> +оо, причем — хотя бы начиная с некоторого
места — с возрастанием п и уп возрастает: уп-\-\ > уп- Тогда
л. %п л. %п — хп—\
lim — = lim ,
Уп Уп —Уп-\
если только существует предел справа (конечный или далее бесконечный).
Допустим сначала, что этот предел равен конечному числу /:
хп — хп—\
lim = /.
Уп -Уп-\
Тогда по любому заданному е > О найдется такой номер N, что для п > N будет
ХП—\
-I
уп —Уп-1
е
<2
? Хп ~ХП-\ ?
I- - < < /+-.
2 j/w -уп-i 2
Значит, какое бы п > N ни взять, все дроби
— XN *N+2 —-^^+1 *п-\ — хп-2
— Хп-\
yN+2—yN+l* "" Уп-\—Уп-г Уп-Уп-1
лежат между этими границами. Так как знаменатели их, ввиду возрастания уп
вместе с номером п, положительны, то между теми же границами содержится
и дробь
хп — xN
числитель которой есть сумма всех числителей написанных выше дробей, а зна-
знаменатель — сумма всех знаменателей. Итак, при п > N
<2-
Уп ~УЫ
Напишем теперь тождество (которое легко непосредственно проверить):
хп _xN — I -yN (л yN\ fxn—xN
Уп Уп
откуда
V Уп)
-I),
— -I
Уп
*N — I •УЫ
Уп
Уп — УИ
Хп ~XN
Уп ~yN
Второе слагаемое справа, как мы видели, при п > N становится < |; первое
же слагаемое, ввиду того что уп —> +оо, также будет < |, скажем, для п > N1.
*) При частном предположении уп = п мы находим эту теорему еще у Кош и
(A.L. Cauchy).
33] § 2. ТЕОРЕМЫ О ПРЕДЕЛАХ 79
Если при этом взять Nf > N, то для п > Nf, очевидно,
что и доказывает наше утверждение.
Случай бесконечного предела приводится к рассмотренному. Пусть, на-
например,
хп — хп—\
lim = +оо.
Уп -Уп-\
Отсюда, прежде всего, вытекает, что (для достаточно больших п)
Хп ~ХП-\ > уп -Уп-Ъ
следовательно, вместе с уп и хп —>> +оо, причем варианта хп возрастает с воз-
возрастанием номера п. В таком случае, доказанную теорему можно применить
к обратному отношению j1:
л- Уп л. Уп — Уп—\ г.
lim — = lim = О
Хп Хп ХП—\
(ибо здесь предел уже конечен), откуда и следует, что
lim — = +оо, что и требовалось доказать.
Уп
Обратимся снова к примерам.
12) Мы видели уже в 9), что при а > 1
lim — = +оо.
п
Этот результат с помощью теоремы Штольца получается сразу:
1- ^ л- Г П П—\\ v П (л ^\ ,
lim — = lim (a — а ) = lima 1 = +оо.
п \ a J
То же относится и к примеру 11).
13) Применим теорему Штольца к доказательству следующего интерес-
интересного предложения (Коши):
Если варианта ап имеет предел {конечный или бесконечный), то тот
ж:е предел имеет и варианта
а\ + а2 + . . . + ап
Ьп =
п
(«среднее арифметическое» первых п значений варианты ап).
Действительно, полагая в теореме Штольца
хп = а\ + а2 + . . . + я„, уп = п,
имеем:
пт Ьп = lim — = lim = hman.
Уп Уп — Уп—1
Например, если мы знаем [10)], что ^/п —>> 1, то и
1 + л/2 + v^ + . . . + ^
80 ГЛ. I. ТЕОРИЯ ПРЕДЕЛОВ [33
14) Рассмотрим теперь варианту (считая к — натуральным)
\к + 2к + ...+«*
которая представляет неопределенность вида ^?.
Полагая в теореме Штольца
лк . пк . . &
*и = 1+2+...+и, .
будем иметь
и*
\imzn = lim
Но
/ -I \А:+1 к-\-\
(п—\) = п —
к-\-\ / л\к-\-\ /т . л\ к .
и — (« — 1) =(А:+1)« +...
и [см. 2)]
\\mzn = lim — —-7
15) В заключение определим предел варианты
2к
к+\) пк к+\
представляющей в первой форме неопределенность вида со • 0, а во второй —
вида со — со. Произведя вычитание дробей, получим на этот раз неопределенное
выражение вида ^:
(к+ 1)A* + 2* + ... +пк) -
Полагая хп равным числителю этой дроби, а уп — знаменателю, применим
еще раз ту же теорему. Получим
Но
к+1 ( л\к+\л (к + I) к к_\
п -(w-1) J= п
пк-{п-\)к =
так что [см. 2)], окончательно,
w = lim
(k+\)knk~l + ... 2
34] § 3. МОНОТОННАЯ ВАРИАНТА 81
§ 3. Монотонная варианта
34. Предел монотонной варианты. Теоремы о существовании
пределов переменных, которые приводились до сих пор, имели та-
такой характер: в предположении, что для одних вариант пределы
существуют, устанавливалось существование пределов для других
вариант, так или иначе связанных с первыми. Вопрос о призна-
признаках существования конечного предела для заданной варианты,
безотносительно к другим переменным, не ставился. Оставляя ре-
решение этого вопроса в общем виде до § 4, 39-42, мы рассмотрим
здесь один простой и важный частный класс переменных, для ко-
которых он решается легко.
Вариантахп называется возрастающей, если
XI < Х2 < . . . < Хп
т. е. если из п' > п следует хпг > хп. Ее называют неубыва-
неубывающей, если
х\ О 2 < . . . ^хп
т. е. если из п' > п следует лишь xni ^ хп. Можно и в последнем
случае называть переменную возрастающей, если придать этому
термину более широкий смысл.
Аналогично устанавливается понятие об убывающей — в уз-
узком или широком смысле слова — варианте: так называется вари-
варианта, для которой, соответственно,
XI > Х2 > . . . > Хп
или
х\ ^х2 ^ . . . ^хп
так что из п1 > п следует (смотря по случаю) хп> < хп или лишь
хп> ^ хп.
Переменные всех этих типов, изменяющиеся в одном направле-
направлении, объединяются под общим названием монотонных. Обычно
о варианте говорят, что она «монотонно возрастает» или «моно-
«монотонно убывает».
По отношению к монотонным вариантам имеет место следу-
следующая — фундаментальной важности —
Теорема. Пусть дана монотонно возрастающая вариан-
варианта хп. Если она ограничена сверху.
хп^М (М= const; /7=1,2,3,...),
то необходимо имеет конечный предел, в противном лее
случае она стремится к +оо.
82 ГЛ. I. ТЕОРИЯ ПРЕДЕЛОВ [34
Точно так же, всегда имеет предел и монотонно убыва-
убывающая варианта хп. Ее предел конечен, если она ограничена
снизу:
хп ^ т {т = const; п = 1, 2, 3, . ..),
в противном Dice случае ее пределом служит —оо.
Доказательство. Ограничимся случаем возрастающей,
хотя бы в широком смысле, варианты хп (случай убывающей вари-
варианты исчерпывается аналогично).
Допустим сначала, что эта переменная ограничена сверху.
Тогда, по теореме п° 11, для множества {хп} ее значений долж-
должна существовать и (конечная) точная верхняя граница:
а = sup{xj;
как мы покажем, именно это число а и будет пределом
варианты хп.
Вспомним, действительно, характерные свойства точной верх-
верхней границы [11]. Во-первых, для всех значений п будет
хп ^ а.
Во-вторых, какое бы ни взять число г > О, найдется такой номер N,
что
xn > а — е.
Так как, ввиду монотонности нашей варианты (здесь мы впер-
впервые на это опираемся), при п > N будет хп ^ х^9 т. е. и подавно
хп > а—е,то для этих значений номера п выполняются неравенства
О ^ а — хп < е или \хп — а
< е,
откуда и следует, что Нтх„ = а.
Пусть теперь варианта хп не ограничена сверху. Тогда, сколь
велико ни было бы число Е > 0, найдется хоть одно значение нашей
переменной, которое больше Е; пусть это будет х^\ х^ > Е. Ввиду
монотонности варианты хт для п > N и подавно
а это и означает, что \ш\хп = +оо.
Легко понять, что все заключения остаются в силе и для пе-
переменной, которая, лишь начиная с некоторого места, становится
монотонной (ибо — без влияния на предел переменной — любое
число первых ее значений можно отбросить).
Обратимся к примерам применения теоремы.
35] § 3. МОНОТОННАЯ ВАРИАНТА 83
35. Примеры.
1) Рассмотрим варианту (считая с > 0)
п\
где п\ = 1 • 2 • 3 . . . п. (Она при с > 1 представляет неопределенность вида ^Л
Так как
w+ I
то, лишь только п > с — I, переменная становится убывающей; в то же время
снизу она ограничена, например нулем. Следовательно, варианта хп — по теоре-
теореме — имеет конечный предел, который мы обозначим через а.
Для того чтобы найти его, перейдем к пределу в написанном выше равенстве;
так как хп+\ пробегает ту же последовательность значений, что и хп (с точностью
до первого члена) и имеет тот же предел а, то мы получим
а = а • О,
отсюда а = 0 и, окончательно,
сп
lim — = 0.
п\
2) Считая снова с > 0, определим теперь варианту хп так:
х\ = у/с, Х2 -
и вообще
= \ с
п корней
Таким образом, хп+\ получается из хп по формуле
Хп+1 = у/С +Хп.
Ясно, что варианта хп монотонно возрастает. В то же время она ограниче-
ограничена сверху, например числом л/с + 1. Действительно, jc i = у/с меньше этого
числа; если допустить теперь, что какое-либо значение хп < \/с + 1, то и для
следующего значения получаем
xn+i < у/с + у/с + 1 < у/с + 2у/с + 1 = у/с + 1.
Таким образом, наше утверждение оправдывается по методу математической ин-
индукции.
По основной теореме, варианта хп имеет некий конечный предел а. Для
определения его перейдем к пределу в равенстве
мы получим, таким образом, что а удовлетворяет квадратному уравнению
а = с + а.
84 ГЛ. I. ТЕОРИЯ ПРЕДЕЛОВ [35
Уравнение это имеет корни разных знаков; но интересующий нас предел а не
может быть отрицательным, следовательно, равен именно положительному
корню:
л/4с + 1 + 1
а = .
3) Взяв любое xq, 0 < xq < 1, определим варианту хп рекуррентным соот-
соотношением
Хп+\ = Хп{1 — Хп).
Допустив, что 0 < хп < 1 (это условие для п = О выполнено), установим, что
О < хп < хп+х < 1.
Действительно, так как 2 — хп > 1, то хп+\ > хп; но хпB — хп) = 1 — A — хпJ,
откуда хп+\ < 1. Таким образом, индуктивно доказано, что варианта хп, моно-
монотонно возрастая, остается меньше единицы; следовательно, она имеет конечный
предел а ф 0. Переходя к пределу в рекуррентном соотношении, найдем, что
а = I. Итак, \imxn = 1.
Предоставляем читателю самому разобраться в том, что произойдет, если
взять xq вне промежутка @, 1).
Замечание. Пусть с — любое положительное число, и положимхп = суп.
Написанное выше рекуррентное соотношение заменится таким:
Уп+\ =УпB- суп).
Взяв начальное значение j/q под условием: 0 < j/q < \, получим, что уп, мо-
монотонно возрастая, будет стремиться к ^. По этой схеме на счетных машинах
и вычисляется число, обратное с.
4) Пусть даны два положительных числа а и Ь [а > Ъ). Составим их среднее
арифметическое и среднее геометрическое:
а\ = , Ъ\ =
Известно, что первое среднее больше второго; * ^ в то же время оба они содер-
содержатся между исходными числами:
а > а\ > Ъ\ > Ъ.
Для чисел а\ и Ь\ снова составим их оба средних:
ai + bi i——
B2 = , о2 = ya\b\,
причем
а\ > а2 > ^2 > Ь\,
и т. д. Если числа ап и Ъп уже определены, то ап+\ и Ьп+\ определяются по
формулам
ап + Ьп ,——
^«+1 = » Ьп+\ = уanbn
*^ Это сразу следует из неравенства
= 1 (д _ 2лМ + Ъ) = (vfr-VEJ > о (при
35] § 3. МОНОТОННАЯ ВАРИАНТА 85
и, как и выше,
ап > ап+х > Ъп+х > Ъп.
Таким образом составляются две варианты ап и Ьп, из которых первая оказы-
оказывается убывающей, а вторая — возрастающей (навстречу одна другой).
В то же время
а > ап > Ьп > Ь,
так что обе варианты ограничены и, следовательно, обе стремятся к конечным
пределам:
а = lim ап и /3 = lim Ъп.
Если в равенстве
ап + Ъп
ап+\ =
перейти к пределу, то получим
а + Р
а = , откуда а = /3.
Таким образом, обе последовательности — и средних арифметических ап,
и средних геометрических Ъп — стремятся к общему пределу \х = n(a, b); следуя
Гауссу (СЕ Gauss), его называют средним арифметико-геометри-
ческим исходных чисел а и Ь. Выражение числа ju(a, Ъ) через эти последние
покуда нам недоступно — для него требуется так называемый эллиптический
интеграл (см. второй том).
5) Отправляясь снова от двух положительных чисел а и Ь [а > Ь), на этот
раз станем последовательно составлять средние арифметические и средние гар-
ах
ап+\
а -f
1
1
ап +
2
-Ь
Ъх
Ьп
Ъх
ь2
V
lab
~ a + b'
ax+b,
2ani
а„ +
ь„
Ьп
Из известного уже нам неравенства ^^~ > л/аЬ (при а ф Ь) получаем:
a + b\2 a + b lab
> ab и, наконец, > ,
2 ) 2 а+Ь
*^ Число с называется средним гармоническим двух положительных
чисел а и Ь, если обратное ему число ^ является средним арифметическим
для обратных чисел ^ и ^:
с = 2 (л + i) ' 0ТКУДа с = Й1-
86 ГЛ. I. ТЕОРИЯ ПРЕДЕЛОВ [35
так что среднее арифметическое больше среднего гармонического; к тому же оба
средних содержатся между исходными числами. Применяя это к ап и Ьп, найдем:
ап > &п-\-\ ^ bn-\-\ ^ Ьп-
Совершенно аналогично тому, как это было сделано в предыдущем примере,
убедимся в том, что обе варианты ап и Ъп стремятся к общему пределу с, ко-
который можно было бы назвать средним арифметико-гармоническим
чисел а и Ъ.
Однако здесь предел с имеет простое выражение через а иЬ. Именно, видим,
что а\Ъ\ = ab; так как, аналогично, и ап+\Ъп+\ = anbn, то заключаем, что при
всех значениях п
anhn = ah.
Переходя здесь к пределу, получаем
с = Vab,
т. е. среднее арифметико-гармоническое двух чисел попросту есть
их среднее геометрическое.
6) Наконец, приведем более сложный пример.
Исходя из некоторого вещественного числа с, положим х\ = |, а последу-
последующие значения варианты хп определим индуктивно формулой
xn+i = - + i О)
Исследуем вопрос о пределе этой варианты при двух различных предположениях
относительно с.
Заметим, что если бы мы наперед знали, что существует конечный предел
а = limiw, B)
то найти его не составляло бы труда. Стоит лишь перейти к пределу в равен-
равенстве A), определяющем нашу варианту, чтобы получить
с а2 2
а = —| или а — 2а + с = 0.
Из этого квадратного уравнения находим
'1-е. C)
Отсюда сразу видно, что варианта хп заведомо не может иметь конечного
предела при с > 1.
(а) Предположим сначала, что 0 < с ^ 1. Тогда ясно, что хп > 0. Вычитая
из A) почленно аналогичное равенство
найдем, что
2 2
хп+1 — Хп — •
35] § 3. МОНОТОННАЯ ВАРИАНТА 87
Очевидно, Х2 > х\ = ^; а. из предыдущего равенства следует, что, лишь только
хп > хп~ъ тотчас же и хп+\ > хп. Таким образом, по методу математической
индукции устанавливается факт монотонного возрастания варианты хп.
Аналогично доказывается ограниченность (сверху) нашей варианты:
Хп < 1.
Это неравенство очевидно для п = 1; если же оно соблюдается при каком-нибудь
значении п, то будет верно и для п + 1 — в силу A). Значит, предел B) дей-
действительно существует, а тогда он выражается формулой C), и именно со знаком
минус при корне, так как предел этот не может быть больше единицы.
(б) Пусть теперь — 3 ^ с < 0. Очевидно, для всех п\
с
Хп > ~.
Покажем, что в этом случае хп < 0. Это верно при п = 1; если же допустить
справедливость этого утверждения для какого-либо значения п, то
Ы < у,
Ц
Ц- < \с\ (так как Ц- < l),
и хп+\ будет иметь знак |, т. е. будет отрицательным, что и требовалось доказать.
На этот раз варианта хп не будет монотонной. Однако если положить
в A) п = 2к и 2к — 2, а затем п = 2к-\-\и2к— \ив обоих случаях почленно
вычесть, то получим:
_ Х2к ~ х2к-2
-Х2к-1 - ^ '
_ х2к+\ ~ х2к-\
*2к
Отсюда можно индуктивно заключить, что всегда
Х2к+\ > Х2к-\ И Х2к+2 < Х2к-
Действительно, ^з > х\ = |; тогда |^з| < 1^11» ^з < ХЪ и по ВТ0Р°й из
формул D) (при к = 1) будет х4 < *2- Следовательно, |*4| > \х2\, *\ > *2>
и по первой из формул D) (при к = 2) получится х$ > х^, и т. д.
Таким образом, в рассматриваемом случае монотонными будут порознь
взятые варианты Х2к-\ и Х2к (к = \, 2, 3, ...); так как они содержатся между
конечными границами | и 0, то обе имеют конечные пределы
а = \imx2k-\> a = limjC2b
Остается показать, что а = а". С этой целью устремим значок и в A)
к бесконечности, сначала через четные значения, а затем — через нечетные. Мы
получим в пределе два соотношения:
/ с а „ с а12
E)
88 ГЛ. I. ТЕОРИЯ ПРЕДЕЛОВ [36
Вычитая, исключим с:
[а -а"){а + а" + 2) =0.
Как мы установим сейчас, если с > — 3, вторые скобки обратиться в 0 не
могут, так что необходимо а = а". Действительно, в противном случае, под-
подставляя а" = — а — 2 во второе из соотношений E), мы получили бы для а
квадратное уравнение
а'1 + 2а + D + с) = 0,
которое, именно при с > — 3, вещественных корней иметь не может.
Наконец, если с = — 3, вторые скобки обращаются в 0 одновременно с пер-
первыми, ибо в этом случае иа' = -1и/ = —1.
Итак, во всех случаях а = а". Обозначив общее значение этих пределов
через а, имеем для а выражение C), очевидно, снова со знаком минус при корне,
ибо предел отрицательной варианты хп не может быть положительным.
Изложенные примеры дают повод к следующему замечанию. Доказанная
теорема является типичной «теоремой существования»: в ней устанавливается
факт существования предела, но не дается никакого приема для его вычисления.
Тем не менее она имеет очень важное значение. С одной стороны, в теоретических
вопросах часто только существование предела представляется нужным. С другой
же стороны, во многих случаях возможность предварительно удостовериться в су-
существовании предела важна тем, что открывает пути для его фактического вычи-
вычисления. Так, в примерах 1), 2), 3), 5), 6) именно знание факта существования
предела позволило, с помощью перехода к пределу в некоторых равенствах,
установить точное значение предела.
В этом отношении особенно поучителен пример 6), (б). Ведь при с < — 3
выражение C) сохраняет смысл, но это вовсе не означает, что оно продолжа-
продолжает давать предел варианты хп; напротив, он здесь не существует: например, как
нетрудно проверить, при с = — 4 наша варианта пробегает последовательность
значений:
-2, 0, -2, 0, -2, 0, ...
и никакого предела не имеет.
В примере 4) мы выражения для предела не имеем, но, зная, что он сущест-
существует, легко можем вычислить его с любой степенью точности, ибо он содержится
между вариантами ап и Ьп, которые к нему стремятся с обеих сторон.
В следующем п° мы познакомимся с еще одним важным примером приложе-
приложения теоремы о монотонной варианте.
36. Число е. Мы используем здесь предельный переход для оп-
определения нового, до сих пор не встречавшегося нам числа.
Рассмотрим варианту
хп=[1 + -
V п
и попытаемся применить к ней теорему п° 34.
Так как с возрастанием показателя п основание степе-
степени здесь убывает, то «монотонный» характер варианты непо-
36] § 3. МОНОТОННАЯ ВАРИАНТА 89
средственно не усматривается. Для того чтобы убедиться в нем,
прибегнем к разложению по формуле бинома:
IV-i I "С"-1) 1
n) n 1 - 2 n2
п{п-\){п-2) 1 n(n-l)...(n-k+l) 1
1-2-3 и3 1-2... А: и* '
' ¦ ¦ Н
1-2...
()() F)
Если от хи перейти теперь к х^+ь т- е. увеличить /7 на единицу,
то прежде всего добавится новый, {п + 2)-й (положительный)
член, каждый же из написанных /7+1 членов увеличится, ибо
любой множитель в скобках вида 1 — ^ заменится большим
множителем 1 — ^-. Отсюда и следует, что
т. е. варианта xw оказывается возрастающей.
Теперь покажем, что она к тому же ограничена сверху.
Опустив в выражении F) все множители в скобках, мы этим уве-
увеличим его, так что
. 1 1 1
^<2 + - + - + ... + -=^.
Заменив, далее, каждый множитель в знаменателях дробей (на-
(начиная с 3) числом 2, мы еще увеличим полученное выражение,
так что, в свою очередь,
. 1 1 1
2+ + + +
Но прогрессия (начинающаяся членом ^) имеет сумму < 1, поэто-
поэтому уп < 3, а значит, и подавно хп < 3.
90 ГЛ. I. ТЕОРИЯ ПРЕДЕЛОВ [37
Отсюда уже следует, по теореме п° 34, что варианта хп имеет
конечный предел. По примеру Эйлера (L. Euler), его обозначают
всегда буквой е. Это число
имеет исключительную важность как для самого анализа, так и для
его приложений. Вот первые 15 знаков его разложения в десятич-
десятичную дробь:
е = 2,718 281828459045. ..
В следующем п° мы покажем удобный прием для приближенного
вычисления числа е9 а также попутно установим, что е есть число
иррациональное.
Некоторые свойства числа е9 которые мы установим впослед-
впоследствии [54,A3)], делают особенно выгодным выбор именно этого
числа в качестве основания для системы логарифмов. Логарифмы
по основанию е называются натуральными и обозначаются
знаком In без указания основания; в теоретических исследованиях
пользуются исключительно натуральными логарифмами *\
Упомянем, что обычные, десятичные, логарифмы связаны
с натуральными известной формулой:
lgx = lnx • М,
где М есть модуль перехода и равен
= -'- = 0,434294...;
это легко получить, если прологарифмировать по основанию 10
тождество
х=еЫх.
37. Приближенное вычисление числа е. Вернемся к равен-
равенству F). Если фиксировать к и, считая п > к, отбросить
*' Эти логарифмы иногда ошибочно называют неперовыми по имени шот-
шотландского математика Н е п е р a (J. Napier, XVI-XVII вв.) — изобретателя ло-
логарифмов. Сам Непер не имел понятия об основании системы логарифмов
(ибо строил их своеобразно, на другом принципе), но его логарифмы соответ-
соответствуют логарифмам по основанию, близкому к |. Близкое к е основание имеют
логарифмы его современника Бюрги (J. Burgi).
37] § 3. МОНОТОННАЯ ВАРИАНТА 91
все члены последней части, следующие за (к + 1)-м, то получим
неравенство
3!
к-
- 1 ч
)¦
Увеличивая здесь /7 до бесконечности, перейдем к пределу; так как
все скобки имеют пределом 1, то найдем:
О2 + + + ... + =п.
Это неравенство имеет место при любом натуральном к. Таким
образом, имеем
*п <Уп < е,
откуда ясно [в силу теоремы 3°,28], что и
Заметим попутно, что уп есть (и + 1)-я частичная сумма для беско-
бесконечного ряда [25,9)]
1 1 1
1 + Ti+2!+--- + ^ + ---'
и написанное только что предельное соотношение показывает, что е является его
суммой; говорят также, что число е разлагается в этот ряд, и пишут
Варианта уп для приближенного вычисления числа е гораз-
гораздо удобнее, чем хп. Оценим степень близости уп к е. С этой
целью рассмотрим сначала разность между любым значением уп+т
(т = 1,2, 3 ...), следующим заут и самим уп. Имеем
_ 1 1 1
Уп+т — Уп — , , -.ч, + /„ , Лч, + • • •
(/7+1)! 0 + 2)! (п + т)\
1 Г1
(и+l)! I п + 2 ' (п + 2)(п + 3)
'" + (и + 2)(и + 3)...(и + /я)|"
92 ГЛ. I. ТЕОРИЯ ПРЕДЕЛОВ [37
Если в скобках { } заменить все множители в знаменателях дробей
через п + 2, то получим неравенство
1 Г 1 1 11
" ~Уп < (^ТТ)! Г + ^+2 + (^+2)* + * * * + (/7 + 2)—Ч '
которое лишь усилится, если заменить скобки суммой беско-
бесконечной прогрессии:
1 /7 + 2
Уп+т ~Уп<
(/7+1)! /7+ Г
Сохраняя здесь п неизменным, станем увеличивать т до беско-
бесконечности; варианта уп+т (занумерованная значком т) принимает
последовательность значений
Уп+\, Уп+2, Уп+Ъ, • ..» Уп+т, • ..»
очевидно, сходящуюся к е. Поэтому получаем, в пределе,
1 /7 + 2
е
или, наконец,
п\п
Если через в обозначить отношение разности е — уп к числу ^
(оно, очевидно, содержится между 0 и 1), то можно написать также
в
е -уп = -j—.
п\п
Заменяя здесь уп его развернутым выражением, мы и придем к важ-
важной формуле:
111 1 в
1! 2! 3! п\ п\п
которая послужит отправной точкой для вычисления е. Отбра-
Отбрасывая последний, «дополнительный», член и заменяя каждый из
оставленных членов его десятичным приближением, мы и получим
приближенное значение для е.
*)
Так как (это легко проверить) (я+, 2 < ^.
37]
§ 3. МОНОТОННАЯ ВАРИАНТА
93
Поставим себе задачей с помощью формулы G) вычислить е,
скажем, с точностью до ^. Прежде всего нужно установить, каким
взять число п (которое находится в нашем распоряжении), чтобы
осуществить эту точность.
Вычисляя последовательно числа, обратные факториалам
(см. прилагаемую табличку), мы видим, что при п = 10 «допол-
«дополнительный» член формулы G) будет уже
п\п 10!-10
так что, отбрасывая его, мы делаем погреш-
погрешность, значительно меньшую поставленной
границы. Остановимся же на этом значе-
значении п. Каждый из остальных членов обра-
обратим в десятичную дробь, округляя (в за-
запас точности) на восьмом знаке так, чтобы
погрешность по абсолютной величине была
меньше половины единицы на восьмом мес-
месте, т. е. меньше j~W' ^ы свели результаты
вычислений в табличку. Рядом с приближен-
приближенным числом поставлен знак (+ или —), ука-
указывающий на знак поправки, которую
необходимо было бы прибавить для восста-
восстановления точного числа.
Итак, как мы видим, поправка на отбра-
отбрасывание дополнительного члена меньше -^.
1
2,000 000 00
- = 0,500 000 00
-} = 0,166 666 67-
- = 0,041666 67-
4!
-} = 0,008 333 33 +
- = 0,001388 89-
6!
-} = 0,000198 41 +
- = 0,000 024 80 +
8!
- = 0,000 002 76-
9!
— = 0,000 000 28-
10!
2,718 28181
Учитывая теперь еще и поправки на округление (с их знаками),
легко сообразить, что суммарная поправка к полученному прибли-
приближенному значению числа е лежит между
3 5
+
Отсюда само число е содержится между дробями
2,718 28178 и 2,718 28186,
так что можно положить
е = 2,718 281 8±о, ооо оооь
Отметим попутно, что та же формула G) может служить и для
доказательства иррациональности числа е.
94 ГЛ. I. ТЕОРИЯ ПРЕДЕЛОВ [38
Рассуждая от противного, попробуем допустить, что е равно
рациональной дроби ^; тогда, если именно для этого п написать
формулу G), будем иметь
т _ 1 1 1 в
п 1! 2! ''' п\ п\п
Умножив обе части этого равенства на п\9 по сокращении знаме-
знаменателей всех дробей, кроме последней, мы получим слева
целое число, а справа — целое число с дробью |,
что невозможно. Полученное противоречие и доказывает то, что
требовалось.
38. Лемма о вложенных промежутках. В заключение этого па-
параграфа, посвященного монотонной варианте, остановимся на со-
сопоставлении двух таких вариант, изменяющихся «навстречу» одна
другой:
Пусть даны монотонно возрастающая варианта хп и мо-
монотонно убывающая варианта ут причем всегда
хп<уп. (8)
Если их разность уп - хп стремится к О, то обе варианты
имеют общий конечный предел:
с =
Действительно, при всех значениях п имеем: уп ^у\9 а значит,
ввиду (8), и хп < у\ {п = 1, 2, 3, ...). Возрастающая перемен-
переменная хп оказывается ограниченной сверху, следовательно, она имеет
конечный предел
с = \\тхп.
Аналогично, для убывающей переменной уп будем иметь
Уп ^ лп ^ л 19
так что и она стремится к конечному пределу
с = limjv
Но, по теореме 1°,30, разность обоих пределов
с -с =lim(yn-xn),
т. е. по условию равна 0, так что с' — с\ это и требовалось доказать.
; Замена в неравенстве (8) знака < на знак ^ не нарушает справедливости
предложения.
38] § 3. МОНОТОННАЯ ВАРИАНТА 95
Доказанному утверждению можно придать другую форму, в ко-
которой оно чаще применяется.
Назовем промежутком [а,Ь] (где а < Ъ) множество всех
чисел (или, как говорят, «точек») х9 удовлетворяющих неравен-
неравенствам
а < х < Ъ.
Числа («точки») а и Ъ называются, соответственно, левым
и правым концами промежутка, а их разность Ъ — а — дли-
длиной промежутка. Нетрудно видеть, что на числовой оси проме-
промежутку отвечает отрезок (той же длины).
Условимся говорить, что промежуток [а\ Ъ1} содержится в про-
промежутке [а, Ь] или вложен в него, если все точки первого проме-
промежутка принадлежат второму или, что то же самое, если
а < а < Ь' < Ь.
Геометрический смысл этого ясен.
Пусть имеется бесконечная последовательность вложен-
вложенных один в другой промежутков
[ai,bi], [a2,b2], .. ., [an,bn],
так что каждый последующий содержится в предыдущем,
причем длины этих промежутков стремятся к 0 с возраста-
возрастанием п:
\\т(Ъп - ап) = 0.
Тогда концы ап и Ъп промежутков (с разных сторон) стре-
стремятся к общему пределу
с = liman = limbn,
который представляет единственную точку общую всем про-
промежуткам.
Это есть лишь перефразировка доказанной выше теоремы:
согласно условию,
так что левый конец ап и правый конец Ъп п-то промежутка играют
здесь роль монотонных вариант хп иуп.
96 ГЛ. I. ТЕОРИЯ ПРЕДЕЛОВ [39
Так как ап стремится к с возрастая, ъЬп — убывая, то
ап < с < Ъп (п = 1, 2, 3, .. .),
т. е. точка с, действительно, принадлежит всем нашим промежут-
промежуткам. В то же время другой, отличной от с, точки с' с тем же свой-
свойством быть не может, ибо иначе мы имели бы
Ьп — ап^ \с' — с\ > О
и длина /7-го промежутка не могла бы стремиться к 0.
Впоследствии нам не раз придется опираться на это предло-
предложение, которое мы будем называть «леммой о вложенных про-
промежутках».
§ 4. Принцип сходимости. Частичные пределы
39. Принцип сходимости. Пусть задана варианта хт пробега-
пробегающая последовательность значений
хь х2, . . ., хп, . . ., х„/, ... A)
Займемся, наконец, вопросом об общем признаке сущест-
существования конечного предела для этой варианты. Само опре-
определение предела для этой цели служить не может, ибо в нем фигу-
фигурирует уже тот предел, о существовании которого идет речь. Мы
нуждаемся в признаке, который использовал бы лишь то, что нам
дано, а именно — последовательность A) значений варианты.
Поставленную задачу решает следующая замечательная теоре-
теорема, принадлежащая чешскому математику Больцано (В. Bolzano)
и французскому математику Коши (A.L. Cauchy); ее называют
принципом сходимости Болъцано-Коши.
Теорема. Для того чтобы варианта хп вообще имела
конечный предел, необходимо и достаточно, чтобы для
каждого числа е > 0 существовал такой номер N, чтобы
неравенство
хп -хп>\ < е B)
выполнялось, лишь только п> N и п1 > N.
39] § 4. ПРИНЦИП СХОДИМОСТИ. ЧАСТИЧНЫЕ ПРЕДЕЛЫ 97
Как видит читатель, суть дела здесь в том, чтобы значения пе-
переменной между собой безгранично сближались по мере воз-
возрастания их номеров.9) Обратимся к доказательству.
Необходимость. Пусть варианта хп имеет определенный
конечный предел, скажем, а. По самому определению предела [23],
каково бы ни было число ? > О, по числу § найдется такой номер N,
что для п > N всегда имеет место неравенство
?
\хп-а < -.
Возьмем теперь любые два номера п > N и п' > N; для них
одновременно будет
\хп-а
?
- и \а-хп>
2'
откуда
? ?
\хп-хп>\ = \(хп-а) + (а-хп>)\ ^ \хп-а\ + \а-хп>\ < - + - = ?.
Этим необходимость условия доказана. Значительно труднее дока-
доказать его
Достаточность. Пусть условие теоремы выполнено; требу-
требуется установить, что тогда для варианты хп существует определен-
определенный конечный предел.
С этой целью произведем в области всех вещественных чисел
сечение по следующему правилу. В нижний класс А отнесем каж-
каждое такое вещественное число а, для которого, начиная с некото-
некоторого номера, выполняется неравенство
хп > а.
В верхний же класс А1 отнесем все остальные (т. е. не попавшие
в А) вещественные числа а'.
Прежде всего убедимся в непустоте этих классов, используя для
этого условие теоремы. Задавшись произвольным числом ? > О,
возьмем соответствующий ему (в указанном там смысле) номер N.
Если п > N и п' > N, то выполняется B), откуда
Хп> - ? < Хп < Хп> + ?. C)
Теперь мы видим, что каждое число хп> — ? (где п' > N) в от-
отдельности относится к классу А, ибо для достаточно больших п
Последовательность хп, для которой справедливо указанное в теореме усло-
условие, часто называют сходящейся в себе (распространены также термины
«фундаментальная последовательность» и «последовательность Коши»).
98 ГЛ. I. ТЕОРИЯ ПРЕДЕЛОВ [39
(именно, для п > N) хп его превосходит. С другой стороны, так как
(для тех же п) хп оказывается меньшим, чем любое из чисел вида
xni + е (при п' > N), то ни одно такое число заведомо не может
принадлежать А и, следовательно, относится к классу А!.
Правило, определяющее классы А и Af9 так сформулировано,
что из него непосредственно ясно, что каждое вещественное
число попадает в один, и только в один, из этих классов. Вместе
с тем, каждое число а (из А) меньше каждого числа а1 (из Af);
ведь, при а > а\ варианта хП9 начиная с некоторого места, пре-
превзошла бы и а\ вопреки определению чисел а''. Таким образом,
произведенное разбиение области вещественных чисел на классы
есть, действительно, сечение.
По основной теореме Дедекинда [10], существует такое ве-
вещественное число а*\ которое является пограничным между чис-
числами обоих классов:
а ^ а ^ а .
Но, как мы отметили, при любом п' > N число хп> — г есть одно
из а, а число хп> + г — одно из а'. Поэтому, в частности,
хп> — е ^ а ^ хп> + е или \а — хп/\ = \хп/ — а\ ^ ?
для любого п1 > N. По определению же предела [23], это и значит,
что
а =
Теорема доказана.10^
*)
В указанной теореме оно было обозначено через /3.
' Приведем еще одно доказательство достаточности указанного в тео-
теореме условия сходимости, не использующее понятия сечения.
Определим числа ап и Ъп равенствами: ап = inf Xk, bn = sup;^ (конечны или
бесконечны ап и Ъп — пока несущественно). Тогда ап ^ х^ ^ Ъп при к ^ п;
кроме того, ап ^ ап+\ и bn ^ Ъп+\ при любом п. По условию, для любого
е > 0 существует такое число N = N(e), что хп — хп/ < е для всех п, п > N.
Зафиксируем произвольно п > N; тогда неравенство хп < хп/ + е показыва-
показывает, что последовательность хп ограничена сверху, числа Ъп конечны при всех п
и Ъп ^ xni + е при п > N. Теперь зафиксируем п > N; поскольку хп/ ^ Ъп — е
при п > N, мы можем утверждать уже, что числа апг конечны и апг ^ Ъп — е
при п > N. Положив п = п, получим: 0 ^ Ьп — ап ^ е при п > N; тем самым,
Ъп — ап у 0. В силу первого утверждения п° 38 последовательности ап и Ъп
сходятся к некоторому общему пределу с; поскольку ап ^ хп ^ Ьп, последова-
последовательность хп также сходится к с и теорема Больцано-Коши доказана.
40] § 4. ПРИНЦИП СХОДИМОСТИ. ЧАСТИЧНЫЕ ПРЕДЕЛЫ 99
Применение этого признака мы будем не раз встречать в даль-
дальнейшем изложении.
40. Частичные последовательности и частичные пределы. Рас-
Рассмотрим теперь, наряду с последовательностью A), какую-либо
извлеченную из нее частичную последовательность (или под-
подпоследовательность)
где {щ} есть некоторая последовательность возрастающих на-
натуральных чисел:
т < п2 < т < ... <пк< nk+i < ... E)
Здесь роль номера, принимающего последовательно все нату-
натуральные значения, играет уже не /7, а к; щ же представляет собой
варианту, принимающую натуральные значения и, очевидно, стре-
стремящуюся к оо при возрастании к.
Если последовательность A) имеет определенный пре-
предел а {конечный или нет), то тот лее предел имеет и час-
частичная последовательность D).
Остановимся для примера на случае конечного а. Пусть для
заданного е > 0 нашлось такое N, что при п> N уже выполняется
неравенство:
\хп — а\ < е.
Ввиду того что щ -Л сю, существует и такое К, что при к > К
будет щ > N. Тогда, при тех же значениях к, будет выполняться
неравенство
\хщ - а\ < е,
что и доказывает наше утверждение.
[Заметим попутно, что в этом рассуждении мы не опирались
на неравенства E), т. е. не пользовались монотонностью вариан-
варианты щ. Значит, наше утверждение сохраняет силу, по какому
бы закону ни стремилась к +оо целочисленная варианта щ\
Если варианта хп не имеет предела, то это не исключает воз-
возможности существования предела для какой-либо частичной
последовательности D). Такой предел называют частичным
пределом для варианты (или последовательности) хп.
Пусть, например, хп = ( —l)w+ ; предела эта варианта не имеет. Если
же заставить п пробегать лишь одни нечетные или одни четные значения, то
100 ГЛ. I. ТЕОРИЯ ПРЕДЕЛОВ [40
частичные последовательности
*1 = 1, *3 = 1, •••» х2к-1 = 1,
и
будут иметь пределом, соответственно, 1 или — 1. Эти числа и являются час-
частичными пределами варианты хп. Аналогично, варианта хп = (— 1)w+ n имеет
частичные пределы +оо и — оо, а вариантами = тт-~ ' — частичные
пределы +оо и 0.
Легко построить примеры варианты, для которой существует бесконечное
множество различных частичных пределов; вот один из них. Зададим вариан-
варианту хп следующим правилом: если номер п написан по десятичной системе: а/3... v
(где а, /3, . . ., v — цифры), то полагаем
хп = 0, а/3... v.
Например, х\$ = 0,13, ^4035 — 0,4035 и т. д. При этом каждая конечная
десятичная дробь, между 0,1 и 1, встречается в ряду значений нашей варианты
бесконечное множество раз: например, 0,217 — на 217-м месте, а также на 2170-м,
21700-м и т. д.
Отсюда сразу следует, что каждая конечная десятичная дробь между 0,1
и 1 будет служить частичным пределом для нашей варианты. Но если взять
и любое другое вещественное число а в этих границах, то стоит лишь
представить его в виде бесконечной десятичной дроби [9]:
а = 0, с\С2. • -ск. . . (с\ ^ 1),
чтобы стало ясно, что частичная последовательность
имеет именно это число а своим пределом. Таким образом, в рассматриваемом
случае частичными пределами последовательности заполняется весь промежу-
промежуток [0,1; 1].
Всегда ли для варианты хп существуют частичные пределы?
На этот вопрос легко ответить утвердительно в случае, когда мно-
множество {хп} не ограничено. Пусть, например, оно не ограничено
сверху; тогда для каждого натурального к найдется в ряду A)
член хЩ9 больший, чем к:
Хщ>к (к =1,2,3,...)
(причем легко устроить так, чтобы номера щ возрастали вместе
с к). Частичная последовательность
X П\ 1 X П2 ' Пз ' * * * ' yik' * * * '
очевидно, будет иметь пределом +оо; это и есть частичный
предел для нашей варианты.
41] § 4. ПРИНЦИП СХОДИМОСТИ. ЧАСТИЧНЫЕ ПРЕДЕЛЫ 101
Утвердительный ответ можно дать и в случае ограниченной ва-
варианты; но это требует более тонких соображений, которые мы
приведем в следующем п°.
41. Лемма Больцано - Вейерштрасса (В. Bolzano - С. Weier-
strass). Из любой ограниченной последовательности A)
всегда молено извлечь такую частичную последователь-
последовательность D), которая сходилась бы к конечному пределу
[Эта формулировка не исключает возможности и равных чи-
чисел в составе данной последовательности, что удобно в приложе-
приложениях.]
Доказательство. Пусть все числа хп заключены между гра-
границами а и Ъ. Разделим этот промежуток [а, Ъ] пополам, тог-
тогда хоть в одной половине будет содержаться бесконечное
множество элементов данной последовательности, ибо, в про-
противном случае, и во всем промежутке [а, Ъ] этих элементов содер-
содержалось бы конечное число, что невозможно. Итак, пусть [ai,&i]
будет та из половин, которая содержит бесконечное множество чи-
чисел хп (или, если обе половины таковы, то — любая из них).
Аналогично, из промежутка [ai,&i] выделим его полови-
половину [<22, Ъ?\ — ПРИ условии, чтобы в ней содержалось бесконеч-
бесконечное множество чисел хП9 и т. д. Продолжая этот процесс до
бесконечности, на k-и стадии его выделим промежуток [ак, Ьк]9 так-
также содержащий бесконечное множество чисел хп.
Каждый из построенных промежутков (начиная со второго)
содержится в предыдущем, составляя его половину. Кроме того,
длина к-ro промежутка, равная
Ъ-а
b
стремится к нулю с возрастанием к. Применяя сюда лемму о вло-
вложенных промежутках [38], заключаем, что а^ и bk стремятся к об-
общему пределу с.
Теперь построение частичной последовательности {хщ} про-
произведем индуктивно — следующим образом. В качестве хщ возь-
возьмем любой (например, первый) из элементов хп нашей последо-
последовательности, содержащихся в [а\, Ь\]. В качестве хП2 возьмем лю-
любой (например, первый) из элементов хП9 следующих за хщ
и содержащихся в [#2, йг]> и т- Д- Вообще, в качестве хщ возь-
возьмем любой (например, первый) из элементов хП9 следующих
за ранее выделенными хщ,хП2, ... ,хщ_1 и содержащихся
в [я?, bk]. Возможность такого выбора, производимого последова-
последовательно, обусловливается именно тем, что каждый из промежутков
102 ГЛ. I. ТЕОРИЯ ПРЕДЕЛОВ [41
[а^, bk] содержит бесконечное множество чисел хп, т. е.
содержит элементы хп со сколь угодно большими номерами.
Далее, так как
®к ^ Хщ ^ bk и Итак = Итй^ = с,
то, по теореме 3°,28, и limx% = с, что и требовалось доказать.
Метод, примененный при доказательстве этой леммы и состо-
состоящий в последовательном делении пополам рассматриваемых про-
промежутков, известен под именем метода Болъцано; он часто
будет нам полезен и в других случаях.
Лемма Больцано-Вейерштрасса значительно облегча-
облегчает доказательство многих трудных теорем, как бы вбирая в се-
себя основную трудность рассуждения. Для примера докажем снова
с ее помощью принцип сходимости', мы имеем в виду доста-
достаточность содержащегося в нем условия, которая потребовала
от нас в 39 значительных усилий.
Итак, пусть условие выполнено, и по заданному г > 0 найден
такой номер N, что для п > N и п' > N имеют место неравен-
неравенства B) или C). Если п' при этом фиксировать, то из C) ясно,
что варианта хП9 во всяком случае, будет ограниченной: ее значения
для п> N содержатся между числами х„/—?их„/+?,и нетрудно
эти границы раздвинуть так, чтобы охватить и первые N значений:
Тогда, по только что доказанной теореме, можно выделить ча-
частичную последовательность {хщ}, сходящуюся к конечному пре-
пределу с:
Итхщ = с.
Покажем, что к этому пределу стремится вообще и варианта хп.
Можно выбрать к настолько большим, чтобы было
Хщ -С\< ?
и, одновременно, щ > N. Следовательно, в B) можно взять
п' = пк\
Хп Хщ\ ^ ^»
и, сопоставляя оба эти неравенства, окончательно находим
\хп — с\ < 2е (для п > N),
что и доказывает наше утверждение. *}
*) Число 2е в такой же мере «произвольно малое» число, как и е. Если угодно,
можно было сначала взять не е, а |, тогда мы здесь получили бы е. Впредь
подобных указаний мы уже делать не будем.
42] § 4. ПРИНЦИП СХОДИМОСТИ. ЧАСТИЧНЫЕ ПРЕДЕЛЫ 103
42. Наибольший и наименьший пределы. Итак, для любой варианты хп, будь
она ограничена или нет, существуют частичные пределы. Мы покажем сей-
сейчас, что среди этих частичных пределов необходимо найдутся наибольший и наи-
наименьший; они называются наибольшим и наименьшим пределами
самой варианты хп и обозначаются, соответственно, через
Теорема. Наибольший и наименьший пределы для варианты хп всегда
существуют. Их равенство есть условие, необходимое и достаточное для
существования предела варианты {в обычном смысле).*'
Доказательство. Начнем с рассмотрения вопроса о наибольшем преде-
пределе. Мы уже видели выше [40], что если варианта хп не ограничена сверху, то
из последовательности A) ее значений можно выделить такую частичную после-
последовательность {Хщ}, ЧТО
Итхч = +оо.
Таким образом, в этом случае +оо является одним из частичных пределов
варианты и, очевидно, наибольшим из всех возможных, так что
lim^w = +оо.
Предположим же теперь, что варианта хп ограничена сверху:
хп^М 0=1,2,3...).
Рассмотрим точную верхнюю границу значений хп для п > к:
Мк = ъщ{хп} = sup{*?+i, **+2, . . . } < М.
п>к
При возрастании к значение Мк может разве лишь уменьшаться, следо-
следовательно, по теореме о монотонной варианте [34], во всяком случае существует
предел (при возрастании к до бесконечности)
конечный или равный — оо.
Случай, когда этот предел есть — оо, также исчерпывается просто. Для лю-
любого Е > 0 найдется такой номер к = N, что
Mjsf < — Е;
но для п > N, очевидно, хп < М^, так что при указанных значениях п и подавно
хп < —Е.
А это означает, что существует предел (в обычном смысле)
\т\хп = —оо,
который одновременно будет и наибольшим и наименьшим.**^
*) Эта теорема, доказательство которой не использует лемму Больцано-
Вейерштрасса, перекрывает последнюю.
**) При наличии обычного предела варианты все частичные пределы с ним
совпадают [40].
104 ГЛ. I. ТЕОРИЯ ПРЕДЕЛОВ [42
Остается рассмотреть самый важный случай, когда существует конечный
предел:
\\тМк = М*;
мы покажем, что это число М* и будет искомым наибольшим пределом для ва-
варианты хп.
С этой целью установим два характерных свойства числа М*.
Если произвольно взять число е > 0, то найдется такое к = Nf, что
MN/ < М* + е; так как, при п > N1 хп < MN/, то и подавно хп < М* + е.
Итак, имеем
I свойство числа М*: каково бы ни было е > 0, существует такой
номер N1, что для всех п > N1 будет
хп < М* + е.
С другой стороны, при произвольном ?>0и любом к будет
Мк ^ М* > М - е.
Но тогда, по свойству точной верхней границы [11], среди значений хп с номе-
номерами п = к+\, к + 2, к + 3, ... найдется такое значение хп/, что и хп/ > М* — е.
Заменяя произвольно взятое к на N, сформулируем
II свойство числа М*: каковы бы ни были е > 0 и номер N, найдется
значение хп/ с номером п > N такое, что
xni > М* — е.
Подчеркнем разницу в формулировках обоих свойств. В первом случае не-
неравенство выполняется для всех значений хп сплошь, начиная с неко-
некоторого. Во втором же случае неравенству удовлетворяют лишь отдельные
значения хп, среди которых, однако, имеются значения со сколь угодно
большими номерами.
Прежде всего, опираясь на эти свойства, докажем, что число М* служит
частичным пределом для варианты хп. Для этого нужно выделить
частичную последовательность {хщ}, сходящуюся к М*.
Возьмем последовательность положительных чисел ?/ —>> 0. Положив^ = 1,
допустим, что номера
П\ = 1 < П2 < Щ < . . . < Щ — \
уже выбраны, и покажем, как выбрать щ. По I свойству для е = ?/ найдем соот-
соответствующий номер Nf = TV/, такой, что для всех п > Nt будет хп < М* + ?/.
Теперь обратимся ко II свойству, полагая по-прежнему е = ?/, а за N взяв наи-
наибольший из номеров Щ — \ и TV/; этому выбору чисел е и N и отвечает номер п = щ.
Для него, с одной стороны,
хщ > М* - е/,
с другой же, так как щ > 7V/, одновременно будет и
хщ < Af*+?/.
Отметим, кроме того, что щ > щ_\.
42] § 4. ПРИНЦИП СХОДИМОСТИ. ЧАСТИЧНЫЕ ПРЕДЕЛЫ 105
Для элементов Хщ построенной таким путем — индуктивно — последова-
последовательности будем иметь
\хП1-М*\<?, A=2,3,4,...),
так что, действительно, Хщ —> М*.
Наконец, установим, что ни один частичный предел не может
превзойти М*. В самом деле, пусть для некоторой частичной последова-
последовательности {хщ } имеем Хщ —> а, так что а есть один из частичных пределов.
По свойству I для достаточно далеких номеров (уже больших, чем Nf) будет
хщ < М* + е.
Переходя здесь к пределу, получим а ^ М* + е и, ввиду произвольности е9
окончательно,
а < М*.
Таким образом, М* действительно будет наибольшим из всех частичных
пределов, т. е.
М* = limiw.
Аналогично устанавливается существование наименьшего предела.
Не повторяя всех рассуждений, отметим следующие два обстоятельства.
Если этот наименьший предел есть +оо, то существует предел в обычном
смысле
limiw = +оо.
Если же наименьший предел есть конечное число М*,
М* = limiw,
то оно обладает свойствами, аналогичными указанным выше для М*:
I свойство числа М*: каково бы ни было е > 0, существует такой
номер Nff, что для п > Nff будет
хп > М* — е.
II свойство числа М*: каковы бы ни были е > 0 и номер N, найдется
значение хпп с номером п" > N, такое, что
хпп < М* + е.
Обратимся к доказательству заключительного утверждения теоремы. Если
существует предел в обычном смысле слова
\\тхп
(конечный или бесконечный), то все мыслимые частичные пределы с ним слива-
сливаются [40], так что необходимость высказанного условия очевидна.
Предположим теперь, что
\\тхп = \\тхп.
Если их общее значение есть +оо или —со, то, как мы видели, существует предел
варианты в обычном смысле и имеет то же значение.
106 ГЛ. I. ТЕОРИЯ ПРЕДЕЛОВ [42
Пусть, наконец, оба предела конечны:
М* =М*= а.
Тогда, сопоставляя I свойства чисел М* и М*, найдем по наперед заданному е > 0
такой номер N, что для п > N будет
а — е < хп < а + ?, т. е. \хп — а\ < е.
А это и значит, что а есть предел варианты хп в обычном смысле. Теорема до-
доказана.
Заметим, что с помощью этой теоремы совсем уж просто доказывается
достаточность условия Больцано-Коши [39]. Именно (если сохранить
прежние обозначения), из неравенств
xni — г < хп < xni + ? (для пип > N)
непосредственно усматриваем, что наибольший и наименьший пределы вариан-
варианты хп конечны и разнятся не более, чем на 2е, следовательно, ввиду про-
произвольности е, совпадают. Отсюда и вытекает существование конечного предела
в обычном смысле.
ГЛАВА ВТОРАЯ
ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
§ 1. Понятие функции
43. Переменная и область ее изменения. В 22 уже было да-
дано общее понятие о переменной. Переменная х задается мно-
множеством ЭС — {х} тех значений, которые она способна принять
(в рассматриваемом вопросе). Это множество «2Г, в котором каждое
значение х встречается по разу, называется областью изменения
переменной х. Вообще, областью изменения переменной может
служить любое числовое множество. п^
Мы уже упоминали о том, что числа геометрически истол-
истолковываются как точки на (числовой) оси. Область ЭС изменения
переменной х на этой оси изображается в виде некоторого мно-
множества точек. В связи с этим обычно сами числовые значения
переменной называют точками.
Часто приходится иметь дело с переменной /7, для которой об-
областью изменения является множество JV всех натуральных чисел.
Для варианты хп = ~ областью изменения12^ будет множест-
множество дробей вида ^ (при #2 = 1,2, 3,...) с присоединением числа 0;
для постоянной величины вся область изменения сведется к одному
числу.
Однако в анализе обычно изучаются переменные, изменяющие-
изменяющиеся, как говорят, непрерывным, или сплошным, образом: их
' Текст данного абзаца не следует, разумеется, относить к переменным типа
варианты [см. примеч. 5 и 6 на с. 50,51].
11' Область изменения варианты можно понимать и иначе, если рассматри-
рассматривать ее как частный случай области изменения функций [см. п° 45 и примеч. 14
на с. 111]. Заметим, что понятие «область изменения варианты» в дальнейшем
практически не используется.
108 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [44
прообразом являются физические величины — время, путь, прохо-
проходимый движущейся точкой, и т. п. Областью изменения подобной
переменной служит числовой промежуток. Чаще всего это
будет конечный промежуток, ограниченный двумя веществен-
вещественными числами а и Ъ (а < Ъ) — его концами, которые сами могут
быть включены в его состав или нет. В зависимости от этого мы
будем различать
замкнутый промежуток [а,Ь]: а ^ х < Ъ
(оба конца включены);
{(а, Ь] : а < х ^ Ъ
(лишь один конец включен);
открытый промежуток (а,Ь): а < х < Ъ
(ни один конец не включен).
Длиной промежутка во всех случаях называется число b — а.
Геометрическим аналогом числового промежутка является, как
легко понять, отрезок числовой оси, причем — в зависимости от
типа промежутка — и к отрезку концы его приключаются или нет.
Приходится рассматривать и бесконечные промежутки,
у которых одним из концов или обоими служат «несобственные
числа» —сю, +оо. Обозначения их аналогичны приведенным выше.
Например, (—сю, +оо) есть множество всех вещественных чисел;
(а, +оо) означает множество чисел х9 удовлетворяющих неравен-
неравенству х > а; промежуток (—сю, Ь] определяется неравенством х ^ Ъ.
Геометрически бесконечные промежутки изображаются в виде бес-
бесконечной в обе стороны прямой или луча.
44. Функциональная зависимость между переменными. При-
Примеры. Главным предметом изучения в математическом анализе
является, однако, не изменение одной переменной самой по себе,
а зависимость между двумя или несколькими переменными
при их совместном изменении. Здесь мы ограничимся прос-
простейшим случаем двух переменных.
В различных областях науки и жизни — в самой математике,
в физике, в технике — читатель не раз встречал такие совместно
изменяющиеся переменные. Они не могут одновременно при-
принимать любую пару значений (из своих областей изменения): если
одной из них (независимой переменной) придано конкрет-
конкретное значение, то этим уже определяется и значение другой (за-
(зависимой переменной или функции). Приведем несколько
примеров.
44] § 1. ПОНЯТИЕ ФУНКЦИИ 109
1) Площадь Q круга есть функция от его радиуса R; ее значение
может быть вычислено по заданному значению радиуса с помощью
известной формулы:
Q = jtR2.
2) В случае свободного падения тяжелой материальной точ-
точки — при отсутствии сопротивления — время t (с), отсчитываемое
от начала движения, и пройденный за это время путь s (м) связаны
уравнением:
2 '
где g = 9,81 ^ есть ускорение силы тяжести. Отсюда и опреде-
определяется значение s9 соответствующее взятому моменту t: пусть s
является функцией от протекшего времени t.
3) Рассмотрим некоторую массу (идеального) газа, содержащу-
содержащуюся под поршнем цилиндра. В предположении, что температура со-
сохраняется неизменной, объем V (л) и давление р (атм) этой массы
газа подчиняются закону Бойля-Мариотта:
pV = с = const.
Если произвольно изменять V, то р как функция от V будет всякий
раз однозначно определяться по формуле
с
4) Наконец, остановимся еще на зависимости давления возду-
воздуха р (атм) от высоты места к(м) над уровнем моря. В физике
выводится барометрическая формула:
P = poe~kh,
где ро — давление на уровне моря, а к — некоторая постоянная.
По этой формуле значение р как функции от h и определяется,
лишь только задано значение h.
Заметим тут же, что самый выбор независимой переменной
из числа двух рассматриваемых иногда бывает безразличен или свя-
связан с соображениями простого удобства. В большинстве же случаев
он диктуется целенаправленностью производимого иссле-
исследования.
Например, если в последнем примере связь между давлением р
и высотой h используется для того, чтобы дать возможность лет-
летчику по наблюдаемому давлению судить о достигнутой высоте, то
110 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [45
естественно обменять роли переменных и барометрическую фор-
формулу представить в виде
45. Определение понятия функции. Отвлечемся теперь, как
обычно, от физического смысла рассматриваемых величин и да-
дадим точное общее определение понятия функции — одного из
основных понятий математического анализа.
Пусть даны две переменные х и j/ с областями изменения SC
и °!/. Предположим, что по условиям вопроса переменной х мо-
может быть приписано произвольное значение из области SC без
каких-либо ограничений. Тогда переменная у называется функци-
функцией от переменной х в области ее изменения <$Г, если по некото-
некоторому правилу или закону каждому значению х из ЭС ставится
в соответствие одно определенное значение у (из *$/).
Независимая переменная х называется также аргументом
функции.
В этом определении существенны два момента: во-первых,
указание области SC изменения аргумента х (ее называют облас-
областью определения функции) и, во-вторых, установление правила
или закона соответствия между значениями х и у. [Область *? из-
изменения функции у обычно не указывается, поскольку самый закон
соответствия уже определяет множество принимаемых функцией
значении.] DJ
Можно в определении понятия функции стать на более общую
точку зрения, допуская, чтобы каждому значению х из SC отвечало
не одно, а несколько значений у (и даже бесконечное множество
их). В подобных случаях функцию называют многозначной,
в отличие от однозначной функции, определенной выше.
Впрочем, в курсе анализа, стоящем на точке зрения веществен-
вещественной переменной, избегают многозначных функций, и впредь, говоря
' Укажем еще одну общепринятую формулировку определения функции, экви-
эквивалентную приведенной выше. Функцией, заданной на множестве SC и при-
принимающей значения в множестве с?, называется произвольное правило,
сопоставляющее каждому элементу множества SC один, и только один,
элемент множества <?. Отличаясь от определения, приведенного в тексте,
лишь терминологически, последнее определение в настоящее время более рас-
распространено. [По поводу терминов «область изменения» и «множество значений»
функции см. примеч. 14 на с. 111].
45] § 1. ПОНЯТИЕ ФУНКЦИИ 111
о функции, если не оговорено противное, мы будем разуметь
однозначную функцию.
Для указания того факта, что у есть функция от х9 пишут:
y=f(x), у=ф(х), y=F(x), и т. п.*}
Буквы /, ф9 F, ... характеризуют именно то правило, по которому
получается значение у, отвечающее заданному х. Поэтому, если
одновременно рассматриваются различные функции от одного
и того же аргумента х9 связанные с различными законами
соответствия, их не следует обозначать одной и той же буквой.
Хотя именно буква «эф» (в различных алфавитах) связана со
словом «функция», но для обозначения функциональной зависимо-
зависимости, разумеется, может применяться и любая другая буква; иногда
даже повторяют ту же букву у: у = у(х).14'
В некоторых случаях пишут аргумент и в виде значка при функ-
функции, например ух. Под этот тип подходит привычное нам обозна-
обозначение варианты хт которая является (как мы теперь можем
сказать) функцией от «независимой переменной» /7, пробегающей
ряд натуральных чисел JV = {п}. Аналогично и обозначение N?
для номера N [в определении предела варианты, 23], которое под-
подчеркивает его зависимость от е9 и т. д.
Если, рассматривая функцию, скажем, у = /(х), мы хотим от-
отметить ее частное значение, которое отвечает выбранному част-
частному значению х9 равному xq9 to для обозначения его употребляют
символ: /(хо). Например, если
А) @ *()
то /A) означает численное значение функции f{x) при х — 1,
т. е. попросту число ^, аналогично, gE) означает число 2,
— число |, и т. п.
*) Произносится эта запись следующим образом: «игрек равно эф от икс»,
«игрек равно фи от икс» и т. д.
' Часто для обозначения функции в дополнение к записи у = f(x) исполь-
используют запись f\3C—± *?, где SC — область определения рассматриваемой функ-
функции, а °^/ — ее область изменения; например, запись х: ^ —>> 01 означает,
что х — варианта. Область изменения <? функции / следует отличать от
ее множества значений. Последнее состоит из тех чисел у из ^, которые
действительно отвечают некоторому значению аргументам [имеют вид;; = /(*)].
Например, если / — постоянная, тождественно равная нулю функция, то ее мно-
множество значений состоит из одного нуля (т. е. одноэлементно), областью же из-
изменения, по желанию, можно считать любое содержащее нуль множество.
112 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [45
Обратимся теперь к самому правилу, или закону, соот-
соответствия между значениями переменных, которое составляет
сущность понятия функциональной зависимости. Правило это мо-
может быть весьма разнообразной природы, поскольку оно ничем не
было ограничено.
Наиболее простым и естественным представляется осуществле-
осуществление этого правила в виде аналитического выражения
или формулы, содержащих указание на те операции или дей-
действия над постоянными числами и над значением х9 которые надо
произвести, чтобы получить соответствующее значение у. Этот
аналитический способ задания функции является наиболее
важным для математического анализа (мы еще вернемся к нему
в следующем п°). С ним читатель всего лучше знаком из школь-
школьного курса математики; наконец, именно аналитическим способом
мы пользовались в примерах, приведенных в п° 44.
Однако было бы ошибочным думать, что это — единственный
способ, которым может быть задана функция. В самой математике
нередки случаи, когда функция определяется без помощи формулы.
Такова, например, функция Е(х) — «целая часть числа х» *}. Лег-
Легко сообразить, что
ЯA) = 1, ?B,5) =2, Е(у/13) = 3, Е(-тг) = -4, и т. д.,
хотя никакой формулы, выражающей Е{х)9у нас нет.
Таковы также и многочисленные «арифметические функции»,
т. е. функции от натурального аргумента, принимающие лишь на-
натуральные же значения. В виде примера упомянем «о факториале
числа п»:
п\ = 1 • 2 • 3 ... /7,
а также о функции т(п), представляющей число делителей
ч и с л а /7, или о функции ср{п)9 указывающей, сколько в ряду
1,2,3,...,/7 имеется чисел, взаимно простых с п.
Несмотря на своеобразный характер правил, которыми задаются
эти функции, они позволяют вычислять значения функций с такой
же определенностью, как и формулы. Например, имеем:
тA0) =4, тA2) =6, тA6) = 5, ...
*) См. сноску на с. 57.
46] § 1. ПОНЯТИЕ ФУНКЦИИ 113
В естественных науках и в технике зависимость между величи-
величинами часто устанавливается экспериментально или путем наблю-
наблюдений. Например, если подвергнуть воду произвольно выбранному
давлению р(атм)9 то на опыте можно определить соответству-
соответствующую ему температуру в (°С) кипения воды: в есть функция от р.
Однако эта функциональная зависимость задается не какой-либо
формулой, а лишь таблицей, где просто сопоставлены полученные
из опыта данные. Примеры табличного способа задания
функции легко найти в любом техническом справочнике.
Наконец, упомянем еще, что в некоторых случаях — при помо-
помощи самопишущих приборов — функциональная зависимость между
физическими величинами задается непосредственно графиком.
Например, «индикаторная диаграмма», снимаемая при помощи ин-
индикатора, дает зависимость между объемом V и давлением р пара
в цилиндре работающей паровой машины; «барограмма», доставля-
доставляемая барографом, представляет суточный ход атмосферного давле-
давления, и т. п.
Мы не входим в подробности относительно табличного и гра-
графического способов задания функциональной зависимости, так как
ими в математическом анализе не приходится пользоваться.
46. Аналитический способ задания функции. Сделаем ряд
разъяснительных замечаний по поводу задания функции анали-
аналитическим выражением или формулой, которые играют
в математическом анализе исключительно важную роль.
1° Прежде всего, какие аналитические операции или
действия могут входить в эти формулы? На первом месте здесь
разумеются все изученные в элементарной алгебре и тригономет-
тригонометрии операции: арифметические действия, возвышение в степень
(и извлечение корня), логарифмирование, переход от углов к их
тригонометрическим величинам и обратно [см. ниже 48-51]. Од-
Однако, и это важно подчеркнуть, к их числу по мере развития на-
наших сведений по анализу будут присоединяться и другие операции,
в первую очередь — предельный переход, с которым читатель уже
знаком из главы I.
Таким образом, полное содержание термина «аналитическое
выражение» или «формула» будет раскрываться лишь постепенно.
2° Второе замечание относится к области определения
функции аналитическим выражением или формулой.
114 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [46
Каждое аналитическое выражение, содержащее аргумент х9
имеет, так сказать, естественную область определения: это
множество всех тех значений х9 для которых оно сохраняет
смысл, т. е. имеет вполне определенное, конечное, вещественное
значение. Разъясним это на простейших примерах.
Так, для выражения 1 2 такой областью будет все множество вещественных
чисел. Для выражения yl -i2 эта область сведется к замкнутому проме-
промежутку [—1, 1], за пределами которого значение его перестает быть веществен-
вещественным. Напротив, выражению Л—- придется в качестве естественной области
применения отнести открытый промежуток ( —1, 1), ибо на концах его зна-
знаменатель обращается в 0. Иногда область значений, для которых выражение со-
сохраняет смысл, состоит из разрозненных промежутков: для л/х2 — 1 это будут
промежутки ( —со, —1] и [1, +оо), для ^—[ — промежутки ( — со, —1), ( — 1, 1)
и A, +со), и т. д. *)
В качестве последнего примера рассмотрим сумму бесконечной геометриче-
геометрической прогрессии
\+х +х2 + ---+xn~l + ••• = lim (l+x +jc2 + ---+/7~1).
Если \x\ < 1, то, как мы знаем [25,7)], этот предел существует и имеет зна-
значение j3j. При \х\ > 1 предел либо равен +со, либо вовсе не существует.
Таким образом, для приведенного аналитического выражения естественной обла-
областью применения будет открытый промежуток ( — 1, 1).
В последующем изложении нам придется рассматривать как бо-
более сложные, так и более общие аналитические выражения, и мы
не раз будем заниматься исследованием свойств функций, задава-
задаваемых подобным выражением во всей области, где оно сохраняет
смысл, т. е. изучением самого аналитического аппарата.
Однако возможно и другое положение вещей, на что мы счита-
считаем нужным заранее обратить внимание читателя. Представим себе,
что какой-либо конкретный вопрос, в котором переменная х по
существу дела ограничена областью изменения ЭС9 привел
к рассмотрению функции f{x)9 допускающей аналитическое выра-
выражение. Хотя может случиться, что это выражение имеет смысл
и вне области ЭС9 выходить за ее пределы, разумеется, все же
нельзя. Здесь аналитическое выражение играет подчиненную, вспо-
вспомогательную роль.
* ^ Для нас, разумеется, не представляют интереса такие выражения, которые
ни при одном значении х вообще не имеют смысла.
46] § 1. ПОНЯТИЕ ФУНКЦИИ 115
Например, если, исследуя свободное падение тяжелой точки с высоты h над
поверхностью земли, мы прибегнем к формуле
[44,2)], то нелепо было бы рассматривать отрицательные значения t или значе-
значения t, большие, чем Т = д/^, ибо, как легко видеть, при t = Т точка уже упадет
V
на землю. И это несмотря на то, что само выражение Щ- сохраняет смысл для
всех вещественных t.
3° Может случиться, что функция определяется не одной и той же форму-
формулой для всех значений аргумента, но для одних — одной формулой, а для дру-
других — другой. Примером такой функции в промежутке ( — со, +оо) может слу-
служить функция, определяемая следующими тремя формулами:
f(x) = 1, если |*| > 1 (т. е. если * > 1 или х < —1),
/(*) = — 1, если |*| < 1 (т. е. если — 1 < * < 1),
и, наконец, /(*) = 0, если х = d=l.
Упомянем еще о функции Дирихле (P. G. Lejeune-Dirichlet), которая опре-
определяется так:
%(*) = 1, если х рационально,
%(*) = 0, если * иррационально.
Наконец, вместе с Кронекером (L. Kronecker) рассмотрим функцию, которую
он назвал «сигнум *» *) и обозначил через sgn^c:
sgn;\; = 1, если * > 0;
sgn;\; = — 1, если * < 0;
sgn 0 = 0.
Впрочем, не следует думать, что есть принципиальная разница между
функцией, задаваемой одной формулой для всех значений *, и функцией, опре-
определение которой использует несколько формул. Обычно функция, задаваемая не-
несколькими формулами (правда, ценой некоторого усложнения выражения), может
быть задана и одной.
Например, если привлечь операцию предельного перехода, то первая из при-
приведенных выше функций, /(*), может быть задана одной формулой (для всех х
сразу):
f{x) = Hm
х2п-\
2п +
| > 1 степень
стремится к 0 [27], так что
Действительно, при |*| > 1 степень х п -л +оо, а обратное ей выражение
lim — = lim
2" 1 1
*) По-латыни signum означает «знак».
116 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
При \х\ < 1 степень х п —>> О [25,6)], и в этом случае
= -1.
[47
х7»-!
2п
Наконец, при х = d=l будет, очевидно, х п = 1, откуда
и в пределе получается 0. Все это полностью согласуется с прежним опреде-
определением.
47. График функции. Хотя в математическом анализе функции
графически не задают, но к графической иллюстрации
функции прибегают всегда. Легкая обозримость и наглядность гра-
графика делают его незаменимым вспомогательным средством
исследования свойств функции.
Пусть в некотором промежутке SC задана функция у =/(х).
Представим себе на плоскости две взаимно перпендикулярные
оси координат — ось х и ось у. Рассмотрим пару соот-
соответствующих значений
х и у, где х взято из про-
промежутка ЭС, а у — f(x); об-
образом этой пары на плоскос-
плоскости служит точка М(х,у)9
с абсциссой х и ординатой у.
Когда переменная х изменя-
изменяется в пределах своего про-
промежутка, эта точка описыва-
описывает некоторую кривую АВ
(рис. 5), которая и является
геометрическим образом на-
нашей функции и называется
ее графиком. В этих условиях само уравнение у =/(х) на-
называют уравнением кривой^?.
Например, на рис. 6 и 7 изображены графики функций
абсцисса х
Рис.5
у = ±
и у =
у = ±л/х^ - 1;
(|*|^1)
читатель узнает в них окружность и равнобочную гипер-
гиперболу. Много других примеров графического изображения функ-
функций читатель найдет в ближайших номерах.
47]
§ 1. ПОНЯТИЕ ФУНКЦИИ
117
Рис.7
Строится график обычно по точкам.
Берут в промежутке ЭС ряд близких между собой значений х9
вычисляют по формуле у = f(x) соответствующие значе-
значения у:
х =
у =
и наносят на чертеж точки
, (Х2,У2),
Через эти точки от руки с помощью лекала проводят кривую,
которая (конечно, лишь с некоторым приближением) и дает иско-
искомый график. Чем плавнее
ход графика и чем гуще
взяты точки на нем, тем
точнее начерченная кри- У=Е(Х)
вая воспроизводит этот
график.
Следует заметить, что
хотя геометрический об- -2 -1
раз функции всегда мож-
можно себе «представить», ^~
но не всегда этот образ бу-
будет кривой в обычном, о >
интуитивном смысле. Рис. 8
118 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [48
Построим, например, график функции;; = Е(х). Так как в промежутках . . .,
[—2, —1), [—1, 0), [0, 1), [1, 2), [2, 3), ... функция сохраняет постоянные зна-
значения . . ., —2, —1, 0, 1, 2, . . ., то график будет состоять из ряда отдельных
горизонтальных отрезков, лишенных своих правых концов (рис. 8).*^
Для функции %{х) Дирихле график состоит из множества точек с ирра-
иррациональными абсциссами на осих и множества точек с рациональными
абсциссами на прямой;; = 1; его и изобразить невозможно.
48. Важнейшие классы функций. Перечислим здесь некоторые
классы функций, получивших название элементарных.
1° Целая и дробная рациональные функции.
Функция, представляемая целым относительно буквы х много-
многочленом:
у = аохп + а\хп~1 -\ Ь ап-\х + ап
(яо, ль #2, ... —постоянные), называется целой рациональ-
рациональной функцией.
Отношение двух таких многочленов:
_
а\хп~1 -\ Ь ап-\х + ап
f\rm -А- Ългт~^ -А- - - - A- h лг A-h
QA ~Г и\Л ~Г ~Г ит—\Л ~Г Um
называется дробной рациональной функцией. Она опреде-
определена для всех значений х, кроме тех, которые обращают знамена-
знаменатель в нуль.
Для примера на рис. 9 даны графики функции у = ах1 (пара-
(параболы) при различных значениях коэффициента а, а на рис. 10 —
графики функции у = ^ (равнобочные гиперболы), также
при различных значениях а.
2° Степенная функция.
Так называется функция вида
У =х",
где \х — любое постоянное вещественное число. При целом \х по-
получается рациональная функция. При \х дробном мы имеем здесь
радикал. Например, пусть т — натуральное число и
у = хт = \/х;
эта функция определена для всех значений х9 если т — нечетное,
и лишь для неотрицательных значений — при т четном (в этом
*^ Это обстоятельство символизируется стрелками, которые своими остри-
остриями указывают на точки, не принадлежащие графику.
48]
§ 1. ПОНЯТИЕ ФУНКЦИИ
119
\
\
\
/
/
1
у=ах2
\
\
\
\
\
\
/
/
/
1
I
1
\ 3
\
\
л
у
_7
7_
J
т
\ 1 2
\\\
\\\ 1
/л/
t
I
i2
1 I -3
/ \ \ 1
8
4 2
III
/
i//
///
/#/
/
/
/
\
\ '
\
-fit
\
]
/
/
/
/
/
/
/
L
\
\
\
\
[
1
1
/
1=0
2
\
V
A
i
i
4
1
8
1
8
1
4
1
2
Рис.9
Рис. 10
120
ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
[48
¦>- X
Рис. 11
У
0
¦ "з -1 -2-3-10 У=х>*\ М<0
-од
„1
1
2
-1
-2
-3
Рис. 12
У
1
аг.
¦ —
1
\
I
iJ \
\
\
ОД1
\
\
\
i
1
i
\
\
\
V \
X
8
7
6
5
4
i 3
si
/
/
/
/
/
/
/
/
k
/
/
/
2х
-2-10 1
Рис. 13
-1
-2
Рис. 14
48]
§ 1. ПОНЯТИЕ ФУНКЦИИ
121
У\
ч
\
ч
Ъж
Рис. 15
\
\
\
\
Рис. 16
122 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [48
случае мы имеем в виду арифметическое значение ради-
радикала). Наконец, если \х — иррациональное число, мы будем пред-
предполагать х > О (х = 0 допускается лишь при \х > 0).
На рис. 11 и 12 даны графики степенной функции при различ-
различных значениях /л.
3° Показательная функция, т. е. функция вида
у = ах,
где а — положительное число (отличное от единицы); х принимает
любое вещественное значение.
Графики показательной функции при различных значениях а
даны на рис. 13.
4° Логарифмическая функция, т. е. функция вида
У =1°?аХ>
где а, как и выше, — положительное число (отличное от единицы);
х принимает лишь положительные значения.
На рис. 14 даны графики этой функции при различных значе-
значениях а.
5° Тригонометрические функции:
у = sinx, у = cosx, у = tgx,
у = ctgx, у = secx, у = cscx.
Очень важно раз и навсегда усвоить, что аргументы триго-
тригонометрических функций, если их рассматривать как меры
углов, всегда выражают эти углы в радианах (поскольку
не оговорено противное). Для tgx и secx исключаются значения
вида
а для ctgx и cscx — значения вида
кж (k — целое).
Графики функций вида у = sinx (cosx) и у = tgx(ctgx) даны на
рис. 15 и 16. График синуса обычно называют синусоидой.
48]
§ 1. ПОНЯТИЕ ФУНКЦИИ
123
Иной раз, особенно в технических вопросах, представляют ин-
интерес:
6° Гиперболические функции. Так называют функции:
ех +е~х
shx =
thx =
chx =
cthx =
chx ex + e x shx ex — e x'
(гиперболический синус, косинус, тангенс, котангенс, ...);
они определены для всех значений х, исключая cthx, который теря-
теряет смысл при х = 0. Эти функ-
функции проявляют замечательную
аналогию с тригонометриче-
тригонометрическими функциями.
Ук
Рис. 17
Рис. 18
Так, имеют место формулы (обратить внимание на знаки!)
ch(x ±у) = chx • chy ± shx • shy,
sh(x ±y) = shx • chy ± chx • shy,
из которых при у = х, в частности, следует:
0 0 0 0
ch х — sh x = 1, ch 2x = ch x + sh x,
sh2x = 2shx • chx.
Например, первая из этих формул сводится к легко проверяемому
тождеству:
ех+у _|_ е-х-У ех -\- е~х еУ -\- е~У ех - е~х еУ - е~У
2 = 2 2 + 2 2 '
Так же проверяются и остальные.
Графики гиперболических функций изображены на рис. 17 и 18.
124 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [49
49. Понятие обратной функции. Прежде чем перейти к обрат-
обратным тригонометрическим функциям, сделаем пояснение относи-
относительно обратных функций вообще.
Предположим, что функция у = /(х) задана в некоторой об-
области ЭР, и пусть <? будет множеством всех значений, которые
эта функция принимает, когда х изменяется в пределах области SC.
[В нашей практике как ЭС9 так и *? обычно будут представлять
собой промежутки.]
Выберем какое-нибудь значение у = уо из области <У; тогда
в области SC необходимо найдется такое значение х = хо, при ко-
котором наша функция принимает именно значение у о, так что
Д*о) = уо;
подобных значений хо может оказаться и несколько. Таким обра-
образом, каждому значению у из *? ставится в соответствие одно или
несколько значений х; этим определяется в области *? одно-
однозначная или многозначная функциях = g(y)9 которая и на-
называется обратной для функции у = /(х).l^
Рассмотрим примеры:
1) Пусть у = ах (а > 1), где х изменяется в промежутке
iT= (—оо, +оо). Значения у заполняют промежуток °^ — (О, +оо),
причем каждому у из этого промежутка отвечает, как мы знаем [20],
ъЭС одно определенноех =logay. В этом случае обратная функ-
функция оказывается однозначной.
2) Наоборот, для функции у = х2, если х изменять в проме-
промежутке SC = (—оо, +оо), обратная функция будет двузначной:
каждому значению у из промежутка *? — [0, +оо) отвечают два
значения х = ± ^Jy из SC. Вместо этой двузначной функции обычно
рассматривают раздельно две однозначные функциих = + ^Jy
и х = —у/у («ветви» двузначной функции). Их можно порознь так-
также считать обратными для функции у = х2, в предположении лишь,
что область изменения х ограничена, соответственно, промежут-
промежутком [0, +оо) или промежутком (—оо, 0].
3) Аналогично, если взять у = chx, где областью изменения х
снова является промежуток SC = (-оо, +оо), то, решая уравнение
Лх
= у или е — 2у • ех + 1 = 0
^ Если функция, обратная для /, однозначна, то саму функцию / называют
обратимой. Часто, когда говорят об обратной функции, ее однозначность пред-
предполагают без оговорок.
49] § 1. ПОНЯТИЕ ФУНКЦИИ 125
относительно ех, найдем (приу ^ 1) два значения
откуда
Снова — двузначная функция, которая распадается на две
однозначные ветви, отвечающие порознь изменению х от О
до +оо и от —оо до 0.
4) Если же у = shx, то — при любом у — из уравнения
= у или е2х — 2у - ех — 1 = 0
2
найдем лишь одно значение для ех\
так как второе значение — с минусом при корне — как отрица-
отрицательное невозможно и должно быть отброшено. Отсюда
так что здесь обратная функция однозначна.
Заметим, что по графику функции у = f(x) легко сообразить,
будет ли обратная для нее функция х = g(y) однозначной или
нет. Первый случай представится, если любая прямая, параллель-
параллельная оси х, пересекает этот график разве лишь в одной точ-
точке. Наоборот, если некоторые из таких прямых пересекают график
в нескольких точках, обратная функция будет многозначной.
В этом случае по графику же легко разбить промежуток измене-
изменения х на части так, чтобы каждой части уже отвечала однозначная
«ветвь» этой функции. Например, по одному взгляду на парабо-
параболу (см. рис. 4), которая служит графиком функции у = х2, ясно,
что обратная ей функция двузначна и что для получения однознач-
однозначных «ветвей» достаточно раздельно рассматривать правую и левую
части этой параболы, т. е. положительные и отрицательные значе-
значения х.*)
Если функция х = g(y) является обратной для функции
у = /(х), то, очевидно, графики обеих функций совпадают. Мож-
Можно, однако, потребовать, чтобы и аргумент обратной функции
*) Ниже [83] мы вернемся еще к вопросу о существовании и однозначности
обратной функции.
126 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [50
обозначался буквой х9 т. е. вместо функции х = g(y) рассматри-
рассматривать у = g(x). Тогда лишь придется горизонтальную ось назвать
осью у, а вертикальную — осью х; график все еще останется преж-
прежним. Если же пожелать, чтобы (новая) ось х была бы, как привыч-
привычно, горизонтальной, а (новая) ось у — вертикальной, то эти оси
нужно будет переставить одну на место
* f другой, что уже изменит и график. Для
осуществления этого проще всего повер-
повернуть плоскость чертежа хОу на 180° вок-
вокруг биссектрисы первого координатного
угла (рис. 19).
Таким образом, графику = g{x) полу-
-х чается как зеркальное отражение
Рис. 19 графика у = f(x) относительно этой бис-
биссектрисы. По рис. 13 и 14, например, сра-
сразу видно, что они именно так получены один из другого. Точно так
же, исходя из высказанных соображений, легко объяснить симме-
симметричность (относительно биссектрисы) каждого из рис. 11 и 12.
50. Обратные тригонометрические функции. В дополнение
к тем классам элементарных функций, которые были упомянуты
в 48, рассмотрим теперь
7° Обратные тригонометрические функции:
у = arcsinx, у = arccosx, у = arctgx,
у = arcctgx, (у = arcsecx, у = arccscx).
Остановимся сначала на первой из них. Функция у = sinx оп-
определена в промежутке <$Г=(—оо, +оо), причем ее значения за-
заполняют сплошь промежуток *? — [—1, 1]. Параллель оси х пе-
пересекает синусоиду, т. е. график функции у = sinx (см. рис. 15)
в бесконечном множестве точек; иначе говоря, каждо-
каждому значению у из промежутка [—1, 1] отвечает бесконечное
множество значений х. Поэтому обратная функция, которую
обозначают так:
х = Arcsinj/ *},
будет (бесконечно-)многозначной.
*) Мы уже подчеркивали в свое время [48,5°], что аргумент х тригонометри-
тригонометрической функции выражает угол в радианах; разумеется, и здесь значения
обратных тригонометрических функций, если их рассматривать как меру угла
(или дуги), все выражены в радианах (в радиусах).
50]
§ 1. ПОНЯТИЕ ФУНКЦИИ
127
ш
2
Обычно рассматривают лишь одну «ветвь» этой функции, отве-
отвечающую изменению х между — ^ и ^; каждому у из [—1, 1] в этих
пределах отвечает одно значение х; его обозначают через
х = arcsin у
и называют главным значением
арксинуса.
Поворачивая синусоиду около бис-
биссектрисы первого координатного угла
(рис. 20), получаем график много-
многозначной функции у = Arcsin x; сплош-
сплошной линией выделен график главной
ветви ее j/ = arcsinx, которая одно-
однозначно определена в промежутке
[—1,1] и притом удовлетворяет нера-
неравенству
^ arcsin х ^ —,
2 2
которое характеризует ее среди других
ветвей.
Вспоминая из элементарной тригоно-
тригонометрии, как выражаются все значения
угла, имеющего данный синус, через од-
одно из этих значений, легко написать фор-
формулы, дающие все значения арксинуса:
Arcsin х = arcsin х + 2ктт
(к = 0, ±1, ±2, ...)
или
Arcsinх = Bk + \)тт - arcsinx.
Исходя из теоремы сложения для си-
синуса
sin(a + /3) = sin а • cos/3 + cos а • sin/3,
\
X
ж\
\
Рис. 20
можно получить теорему сложения для арксинуса. Именно, поло-
положим здесь а = arcsin х, /3 = arcsin у (где х и у лежат между —1
и +1); тогда
sin a =x, sin/3 =y; cos а = л/l — х2, cos/З = л/l —у2,
128 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [50
причем корни берутся со знаком плюс, так как углы а и /3, по харак-
характерному свойству главного значения арксинуса, лежат между — ^
и ^, так что косинусы их положительны. Итак,
sin(a + /3) = х у\—у2 + у у\—х2,
откуда
а + /3 = arcsin x + arcsin j/ = Arcsin (хл/\ - у2 +
Формула может быть написана проще:
arcsin х + arcsin у = arcsin (хл/l —у2 + у у\—х2 )
лишь в том случае, если и а + /3 не выходит из проме-
промежутка [—§»§]. Это условие автоматически выполняется, если
аргументы х и у (ас ними аир) имеют разные знаки. В слу-
случае же одинаковых знаков высказанное условие, как легко видеть,
равносильно такому:
х2+у2 ^ 1.
Подобные же рассуждения применимы к функции у = cosx
(-оо<х<+оо). И здесь обратная функция
у = Arccosx (—1 ^ х ^ 1)
оказывается (бесконечно-)многозначной (см. рис. 15). Для выделе-
выделения однозначной ветви ее подчиняют условию:
0 < arccosx < ж;
это есть главная ветвь арккосинуса.
Функция arccosx связана с arcsin x очевидным соотношением
ж
arccosx = — - arcsin x;
действительно, не только косинус угла ^ — arcsin x равен
sin(arcsinx) = х, но и сам угол содержится именно между 0 и ж.
Остальные значения Arccosx выражаются через главное его значе-
значение по формуле
Arccosx = 2кж ± arccosx (к = 0, ±1, ±2, ...).
Функция у = tgx определена для всех значений х9 кроме зна-
значений х = Bк +1)§ (к = 0, ±1, ±2, ...). Значения у заполняют
здесь промежуток (—оо, +оо), причем каждому у снова соответ-
50]
§ 1. ПОНЯТИЕ ФУНКЦИИ
129
ствует бесконечное множество значений х (см. рис. 16). Поэтому
обратная функциях = Arctgj/, заданная в промежутке (—сю, +оо),
будет (бесконечно-)многозначной. На рис. 21 изображен график
-з
у
/7м
У
У
Ш
2
У
О 1
Рис. 21
функции у = Arctgx, полученный поворотом на 180° вокруг бис-
биссектрисы первого координатного угла графика функции у = tgx.
За главное значение арктангенса, arctgx, принимают то из
значений этой многозначной функции, которое удовлетворяет не-
неравенствам
-- < arctgx < -.
Таким путем определяется однозначная функция — главная
ветвь арктангенса, заданная для всех значений х. Остальные
значения арктангенса, как легко показать, получаются так:
Arctgx = arctgx + ктт (к = 0, ±1, ±2, ...).
130 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [50
Теорема сложения для тангенса:
если положить а — arctg х, /3 = arctgу, дает (при ху ф 1)
так что
х + у
а + /3 = arctg х + arctg у = Arctg .
^У
И в данном случае равенство приводится к простому виду
х + у
arctg х + arctg у = arctg
I — ху
лишь если — ^ < а + /3 < f, т. е. если ху < 1.
Нетрудно установить прямую связь между функциями arctg x
и arcsinx:
х . х
arctg х = arcsm —^=^= или arcsmx = arctg
(-оо<х<+оо) \\+Х2 (
Например, если положить а = arctg х, так что tga = x, то sin a =
, причем корень берется со знаком плюс, по-
л/l+x2
тому что -f < а < f; отсюда и вытекает, что а = arcsin *
л/1+х2
Упомянем еще о функции Arctgх (—оо < х < +оо); ее глав-
главное значение определяется неравенствами
0 < arcctgx < ж
и связано с arctg х соотношением
ж
arcctgx = — - arctgх.
Остальные значения арккотангенса имеют вид
Arcctgx = arcctgx + кл {к = 0, ±1, ±2, ...).
На функциях arcscx (—оо <х^—1и1^х< +оо) и arccscx
(те же промежутки изменения) останавливаться не будем, предо-
предоставляя читателю самому в них разобраться.
51] § 1. ПОНЯТИЕ ФУНКЦИИ 131
51. Суперпозиция функций. Заключительные замечания. По-
Познакомимся с понятием суперпозиции (или наложения)
функций, которая состоит в том, что вместо аргумента данной
функции подставляется некоторая функция от другого аргумента.
Например, суперпозиция функций у = sinx и z = logy дает функ-
функцию z = log sin х; аналогично получаются и функции
и т. п.
В общем виде, предположим, что функция z = cp{y) определена
в некоторой области *? — {у}, а функция у = /(х) определена
в области ЭС — {х}, причем значения ее все содер-
содержатся в области °^. Тогда переменная z, как говорят, через
посредство у, и сама является функцией от х:
z=<p(f(x)).
По заданному х из ЭС сначала находят соответствующее ему
(по правилу, характеризуемому знаком /) значение у из ^, а затем
устанавливают соответствующее этому значению у (по правилу,
характеризуемому знаком ср) значение z; его и считают соответ-
соответствующим выбранному х. Полученная функция от функции, или
сложная функция, и есть результат суперпозиции функций /(х)
Предположение, что значения функции /(х) не выходят за пре-
пределы той области <2/, в которой определена функция q>(y)9 весьма
существенно: если его опустить, то может получиться и неле-
нелепость. Например, полагая z = lgj/, а у = sinx, мы можем рассмат-
рассматривать лишь такие значения х, для которых sinx > 0, ибо иначе
выражение lgsinx не имело бы смысла.
Мы считаем полезным здесь же подчеркнуть, что характери-
характеристика функции, как сложной, связана не с природой функцио-
функциональной зависимости z от х, а лишь со способом задания
этой зависимости. Например, пусть z = yf\ —у2 для у в [—1,1],
а у = sinx для х в [—§,§]. Тогда
z = у 1 - sin2x = cosx.
Здесь функция cosx оказалась заданной в виде сложной
функции.
Теперь, когда полностью выяснено понятие суперпозиции функ-
функций, мы можем точно охарактеризовать простейший из тех
132 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [52
классов функций, которые изучаются в анализе: это, прежде всего,
перечисленные выше элементарные функции 1°—7°, а за-
затем все те, которые из них получаются с помощью четырех ариф-
арифметических действий и суперпозиций, последовательно применен-
примененных конечное число раз. Про них говорят, что они выражаются
через элементарные в конечном виде; иногда их все также
называют элементарными.
Впоследствии, овладев более сложным аналитическим аппара-
аппаратом (бесконечные ряды, интегралы), мы познакомимся и с другими
функциями, также играющими важную роль в анализе, но уже вы-
выходящими за пределы класса элементарных функций.
§ 2. Предел функции
52. Определение предела функции. Рассмотрим числовое мно-
множество ЭС. Точка а называется точкой сгущения этого
множества, если в любой близости от а содержатся значе-
значения х из ЭС, отличные от а.
Чтобы выразить это определение в более точных терминах, вве-
введем понятие окрестности точки а\ так называется любой
открытый промежуток {а — 8, а + 8) с центром в точке а. Те-
Теперь можно сказать, что точка а будет точкой сгущения
множества ЭС, если в каждой ее окрестности содержатся
отличные от а значения х из ЭС.
Сама точка сгущения при этом может принадлежать ЭС или нет.
Пусть в области ЭС, для которой а является точкой сгущения,
задана некоторая функция f{x). Представляет интерес поведение
этой функции при приближении х к а. Говорят, что функция f(x)
имеет пределом число А при стремлении х к а {или
в точке а), если для каждого числа е > О найдется такое
число S > 0, что
\/(х) — А\ < ?, лишь только \х — а\ < S A)
(где х взято из <$Г и отлично от а)*\ Обозначают этот факт
так:
Ш/(х)=А. B)
*) Именно из того, что а есть точка сгущения для ЗС, явствует, что такие
значения х в окрестности (а — 8, а + 8) точки а наверное существуют.
52] § 2. ПРЕДЕЛ ФУНКЦИИ 133
Если область ЭС такова, что в любой близости от а, но справа
от а, найдутся отличные от а значения х из SC (в этом случае
точку а называют правой точкой сгущения для SC), то можно
специализировать только что данное определение предела функции,
ограничившись лишь значениями х > а. В этом случае предел
функции, если он существует, называется пределом функции f(x)
при стремлении х к а справа или, короче, пределом
{в точке а) справа и обозначается символом
ton f{x) или f(a+O)*K
J+0
Аналогично устанавливается понятие о левой точке сгуще-
сгущения и о пределе функции при стремлении х к а слева,
или о пределе {в точке а) слева:
lim f(x) или f(a - 0)
X—)-<2 — 0
*)
Если точка а является одновременно точкой сгущения для SC,
и правой и левой, то, как легко установить, для существования
предела B) необходимо и достаточно существование порознь
и равенство пределов справа и слева:
ton /(*) = Нт f(x)=A.
J+0 X—)-<2 — 0
При стремлении х к конечному пределу а функция может иметь
и бесконечный предел. Именно, функция f(x) имеет преде-
пределом +оо(—оо) при стремлении х к а, если для каждого
числа Е > 0 найдется такое число S > 0, что
f(x) > Е (/(х) < —Е), лишь только \х — а\ < 8 C)
(где, как и всегда, х взято из SC и отлично от а).
Запись этих фактов аналогична B):
lim f{x) = +oo (—оо).
Для рассматриваемого случая могут быть повторены сделан-
сделанные выше замечания относительно односторонних пределов справа
и слева.
Если множество ЭС — {х} содержит сколь угодно большие
(по абсолютной величине) положительные (отрицательные)
значения х, то говорят, что +оо (—оо) является точкой
сгущения для SC.
*) Если само а = 0, то вместо 0 + 0 @ — 0) пишут просто +0 (—0).
134 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [53
В этом предположении: функция f(x) при стремлении х
к +оо (—оо) имеет предел А, если, каково бы ни было чис-
число е > О, для него существует такое число А > О, что
|/(х) — А\ < е, лишь только х > А (х < —А) D)
(где х берется из «2Г). При этом пишут:
x$noof(x)=A. E)
(х—ь- — оо)
Наконец, легко перефразировать все сказанное на случай
А = +оо или —сю.
Сущность всех этих определений одна и та же: функция f(x)
должна быть сколь угодно «близка» к своему пределу А, лишь
только независимая переменная х достаточно «близка» к своему
пределу а. Но переменная «близка» к своему конечному пре-
пределу, если разность между ними (по абсолютной величине) мала,
ак бесконечному — если она сама (по абсолютной величине)
велика и притом сохраняет знак предела.
Ясно, что числа 5(Д) во всех случаях зависят от е(Е).
Заметим в заключение, что при стремлении функции f(x) к О
ее называют бесконечно малой; ее называют бесконечно
большой, если \f(x)\ стремится к оо. Если последнее обстоя-
обстоятельство имеет место при х —>> а, то говорят также, что в точке а
функция обращается в бесконечность.
53. Сведение к случаю варианты. Если рассматривать вари-
варианту как функцию от независимой переменной /7, изменяющейся
в пределах натурального ряда, то предел этой функции при п —»> оо,
как он определен в 52, очевидно, совпадает с пределом варианты,
определенным в 23 и 27 (роль А там играет N). Таким образом,
предел варианты есть частный случай предела функции.
Однако и, обратно, в некотором смысле предел функции
может быть сведен к пределу варианты.
Пусть множество ЭС — {х} имеет точку сгущения а (здесь а
может быть как конечным числом, так и бесконечностью того или
иного знака). Тогда из SC (бесчисленным множеством способов)
можно извлечь такую последовательность
Х\, Х2, Хз, ..., Хп, ... F)
значений х (отличных от а), которая имела бы своим преде-
пределом а.
53] § 2. ПРЕДЕЛ ФУНКЦИИ 135
Действительно, если а конечно, то, задавшись положитель-
положительной вариантой 8П9 стремящейся к нулю, в каждой окрестнос-
окрестности {а — 8п, а + 8п) (п = 1, 2, 3, ...) точки а найдем по точ-
точке х=хп из ЭС9 отличной от а: так как \хп — а\ < 8П9 то
хп —>> а. При а = +оо (—оо) зададимся положительной вариан-
вариантой Ап —>> +оо и для каждого Д„ найдем значение х = хп из <$Г,
для которого хп > Ап (хп < —Ап); очевидно, хп —^ +оо (-оо),
и т. д.
Последовательности F) значений аргумента отвечает последо-
последовательность значений функции
/(*i), Дх2), Д*з), ..., /(*„), ... G)
Легко усмотреть, что при наличии равенства B) эта по-
последовательность всегда имеет предел А. Остановимся для
примера на случае конечных а и А.
Если задано произвольное число е > 0, то сначала возьмем
то число 8 > 0, которое ему соответствует в силу определения
предела B). По числу 89 ввиду сходимости последовательности F)
к а, найдется [23] такой номер N9 что для п> N будет выполняться
неравенство \хп — а\ < 8, а следовательно [см. A)], и \f{xn) —А\ < г.
Этим и доказана сходимость последовательности G) к А.
Оказывается, что справедливо и обратное утверждение:
Допустим теперь, что, какую бы последователь-
последовательность F) {из SC) с пределом а ни пробегала независимая
переменная х, соответствующая последовательность G) зна-
значений функции всегда имеет предел А. Тогда это число А
будет пределом функции f(x) — в согласии с определением
в 52.
Ограничимся и здесь случаем конечных а и А. Рассуждая от
противного, предположим, что А не будет пределом функции в упо-
упомянутом смысле. Тогда для некоторого числа е > 0 уже не
существовало бы соответствующего 8; т. е., какое бы малое 8 ни
взять, всегда найдется хоть одно значение переменной х = х1 (от-
(отличное от а), для которого
\xf - а\ < 8, но тем не менее \/{xf) — А\ ^ е.
Возьмем последовательность положительных чисел {8п}, стре-
стремящихся к нулю. На основании только что сказанного, для
каждого числа 8 = 8п найдется такое значение х' = х'п9 что
\х'п — а\ < 8, но тем не менее \f(x'n) — А\ ^ е.
136 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [53
Из этих значений, таким образом, составляется некоторая по-
последовательность
X j
для которой
\х'п - а\< 8п (п= 1,2, 3, .. .);
так как 8п —> 0, то х^ —>> а.
По допущению теоремы, соответствующая последовательность
значений функции
'г), .... f{x'n), ...
должна стремиться к А, г это невозможно ввиду того, что при всех
п = 1, 2, 3, ... имеем \f(x'n) — А\ ^ е. Полученное противоречие
и доказывает наше утверждение.
Таким образом, мы в сущности приходим ко второму оп-
определению понятия предела функции, которое в 52
было выражено, так сказать, «на языке е-8». Теперь же мы можем
выразить его «на языке последовательностей», понимая равен-
равенство B) в том смысле, что для любой последовательности F),
имеющей предел а, соответствующая последовательность G)
имеет предел А.
В заключение отметим, что достаточно предположить од-
одно лишь существование предела для каждой последо-
последовательности G), отвечающей любой сходящейся к а последо-
последовательности F), чтобы отсюда уже вытекало совпадение
всех этих пределов. Действительно, допустим, что для двух по-
последовательностей:
Х\, Х2> •••' хп> ••• и Х1 ' Х2' •••' хп> •••'
стремящихся к а, имели бы
f{x'n)^A' и f{x'')^A",
где А1 ф А". Тогда, перемежая члены обеих последовательностей,
составим новую последовательность:
xl9 xx, x2, x2, . . ., xn, xn, . . .,
она, очевидно, стремится к а, поскольку для достаточно больших /7,
и х'ю и х„ отличаются от а произвольно мало. В то же время соот-
54] § 2. ПРЕДЕЛ ФУНКЦИИ 137
ветствующая последовательность значений функции:
Л*г). .... Л**). /(*?). ....
вопреки предположению, не имеет вовсе предела, так как частич-
частичные последовательности из ее членов, стоящих на четных или не-
нечетных местах, стремятся к различным пределам [40]. По-
Полученное противоречие и доказывает, что последовательности ви-
вида G) на деле стремятся все к одному и тому же пределу.
54. Примеры.
1) Докажем, что
lim ах = +оо (при а > 1).
При любом Е > 0, достаточно взять А = log^E, чтобы
х > А влекло за собой ах > Е,
что и доказывает наше утверждение. *)
Аналогично доказывается, что
lim ах = 0 (при а > 1).
х—^ — оо
Именно, каково бы ни было е > 0 {е < 1), если взять А = logfl ^ = — logfl e,
то
при х < — А необходимо ах < е.
Если же 0 < а < 1, то с помощью преобразования
—х
1
а = ( -
легко установить результаты
lim ах = 0, lim ах = +оо (при 0 < а < 1).
х—^+оо х—^ — оо
2) Установим, что при а > 1
lim к>2„;\; = +оо, lim
а
При любом заданном Е > 0, лишь только х > а , будем иметь: logfl .х > Е,
и аналогично, лишь только 0 < х < а~Е, выполняется неравенство: \oga х < — Е.
Этим и доказаны оба соотношения.
3) Имеем, далее,
Я" Я"
lim arctg^: = —, lim arctg^: = .
x—>-+oo 2 x—>¦ — оо 2
Остановимся для примера на первом пределе. При любом е > 0, достаточно
взять х > щ(Щ- — е\ чтобы было: arctgjc > ^ — е, так что
0 < arctg^: < с.
*) С более частным результатом lima" = +оо (а > 1) мы уже имели
дело в 27.
138 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [54
4) Более тонким является соотношение:
lim — = +оо (при а > 1).
—^+оо х
Вспомним, что частный случай его мы уже имели:
г а"
lim — = +00
«-5>+оо /2
[32,9)]; очевидно, одновременно будет и
ап
lim = +00.
Следовательно, по заданному Е > 0 найдется такое натуральное число N,
что при п > N выполняется неравенство
Пусть теперь х > N + 1; если положить п = Е(х), то
п > N и п ^ х < п -\- I,
так что
— > > Е,
X /2+1
что и доказывает наше утверждение.
Отсюда, как и в 32,9), легко получить
lim —г = +оо {а > 1, к > 0).
х—^+оо хК
5) Аналогично, опираясь на прежний результат [32,11)]
«—5>+оо /2
можно установить, что вообще
= 0 {а > 1),
х—>-+оо х
где * принимает любые положительные вещественные значения.
Заменяя здесь х на хк(к > 0), легко показать, что и
lim 1Щ1 =о (а > 1, к > 0).
х—>-+оо х
Действительно, если, задавшись произвольным ? > 0, взять А так, чтобы при
х > А выполнялось неравенство
то при х > А\ = А^ будет />Аи
< е.
54]
2. ПРЕДЕЛ ФУНКЦИИ
139
Если заменить здесь х на j, то полученный результат перепишется в виде
lim xk\ogax = О (а > 1, к > 0).
6) Из доказанного в 25,5) предельного соотношения
lim an = 1
можно получить более общее
Заметим, что, очевидно, и
lim
lim ax =
jc-И)
2 п = lim — = 1.
1 а»
Поэтому, каково бы ни было е > 0, можно найти такое натуральное число
, что (если, скажем, а > 1)
Если теперь
то
откуда
1 — е < а по < апо < 1 + е.
X | < ИЛИ < X < ,
по по по
--L х -L
а "о < а < апо,
1— ? < (Л* < \ ~\- ? ИЛИ |<2Х — 1 | < ?,
что и доказывает высказанное утверждение.
7) Теперь мы установим следующий (важный и для даль-
дальнейшего) результат:
lim = 1.
(8)
Предварительно, однако, нам придется
доказать некоторые полезные неравенства:
sinx < х < tgx
О < х < —).
(9)
С этой целью в круге радиуса R рас-
рассмотрим острый угол <АОВ, хор-
хорду АВ и касательную АС к окружности
в точке А (рис. 22). Тогда имеем: пло-
площадь ААОВ < площади сектора АО В < площади ЛАОС. *)
Рис. 22
*) При этом мы пользуемся теми сведениями о площадях элементарных фигур,
которые излагаются в школьном курсе.
140 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [54
Если через х обозначить радианную меру угла <АОВ, так
что длина дуги АВ выразится произведением Rx, то эти неравенства
перепишутся так:
-R2-sinx < -R2-x < -R2-tgx.
Отсюда — по сокращении на \R2 — и приходим к неравен-
неравенствам (9).
В предположении, что 0 < х < ^, разделим sinx на каждый из
членов неравенств (9). Мы получим:
откуда
Но
smx
1 > > cosx,
0 < 1 < 1 — cosx.
1 — cosx = 2 sin2 — < 2 sin — < х
[в силу (9)], так что
smx
0 < 1 < х.
Отсюда вытекает неравенство
sinx
- 1
<
которое, очевидно, сохранится и при изменении знака х9 т. е. будет
справедливо для всех х ф О, лишь только \х\ < §.
Полученное неравенство и решает вопрос. Действительно, если
по произволу задано число е > О, то за S достаточно выбрать
наименьшее из чисел е и |: при \х\ < S прежде всего
применимо это неравенство (ведь S ^ ^), а именно в силу него
(так как S < е)
sinx
<
X
По определению предела функции [52], это и означает, что
функция ^^ при стремлении х к 0 имеет пределом 1, так что
соотношение (8) оправдано.
54] § 2. ПРЕДЕЛ ФУНКЦИИ 141
7а) Предельное соотношение (8) может быть, в согласии с 53, понимаемо и
так, что, лишь только х пробегает сходящуюся к нулю последовательность {хп},
варианта ^^ будет всякий раз стремиться к 1.
Приложим это замечание к разысканию предела варианты
lim cos — • cos ^г ... cos —,
п^оо 2 22 2п
где ф — любое отличное от 0 число.
Очевидно,
ф ф 2 Ф Ф Ф
sin ф = 2 cos — • sin — = 2 cos — • cos —^ • sin — = . . .
2 2 2 22 22
ф ф ф ф
. . . = 2 cos — • cos ^r ... cos — -sin —,
2 22 2n 2n
так что интересующее нас выражение представится в виде
sin ф sin ф ^т
2п - sin §т ~ ~ф~ ' sin^'
Так как хп = ^ —>> 0, то, по сказанному выше,
llm^ = 1,
IP
и предел нашей варианты оказывается равным числу ^
8) Сейчас мы изучим также очень важный предел. Именно,
в 36 было определено число е как предел варианты
/ \\п
е= lim 1 + - . A0)
п^+оо \ п)
Теперь же мы установим более общий результат:
lim (l + -) =e, A1)
а также и
lim A + -} =е. (Па)
х^-оо \ X J
Воспользуемся на этот раз вторым определением предела
«на языке последовательностей» [53].
Прежде всего напомним, что наряду с A0) имеет место и ра-
равенство
/ I \ пк
lim A4 ) =е, A2)
V щ)
если {щ} есть произвольная последовательность натуральных чи-
чисел, растущих вместе с номером ?до бесконечности [40].
142 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [54
Пусть теперь х пробегает какую-нибудь последовательность
{%k} значений, стремящихся к +оо; можно считать даже, что
все Xk > 1. Положим щ = Е(хк)9 так что
«it < Хк < Щ + 1 И Щ -Л +ОО.
Так как при этом
1 1 1
< ^
щ + 1 Хк Щ
то
< 1 + - < 1 + -
V V
Два крайних выражения могут быть преобразованы так:
1 \ / 1 \пк
1 + -) ( )
V «it
причем, в силу A2),
а также ( 1 -\ ] —»>
V «it + 1
в то время как, очевидно,
1 +
1 + >1, 1 + ^^1;
Щ Пк+1
таким образом, оба упомянутых выражения стремятся к общему
пределу е9 а тогда и заключенное между ними выражение также
стремится к е [по теореме 3°, 28]:
/ х ук
lim Ц =е.
V )
Этим и завершается доказательство соотношения A1) «на языке
последовательностей».
Для доказательства же (Па) предположим теперь, что последо-
последовательность {хк} имеет пределом — оо (причем можно считать все
Хк < -1). Если положить хк = -уь тогда у к -> +оо (и все у к > 1).
54] § 2. ПРЕДЕЛ ФУНКЦИИ 143
Очевидно,
Ук
1
Ук-iJ V yk-i.
Так как, по доказанному, первый множитель последнего выражения
стремится к е9 второй же, очевидно, имеет пределом 1, то и выра-
выражение слева также стремится к е. Формула (Па) оправдана.
Заменим теперь в выражении A + ^)х переменную х на ^;
если придать а последовательность положительных или отрица-
отрицательных значений, стремящихся к 0 (но не равных 0), то х = ^
будет стремиться к ±оо. Поэтому формулы A1) и (Па) можно
переписать в виде
е = lim(l + a)«. A3)
Этот замечательный результат лежит в основе всех при-
приложений числа е.
9) Интересен, наконец, и пример, когда предела функции не существует:
функция sinх при стремлении х к +оо ( —оо) вовсе не имеет предела.
В отсутствии предела всего проще убедиться, стоя на «точке зрения после-
последовательностей». Достаточно заметить, что двум последовательностям
{(^-^} и {(W^J (/1=1,2,3,...)
значений х, имеющим пределом +оо, отвечают последовательности значений
функции, стремящиеся к различным пределам:
sin (in jjt = —1 —> — 1, sin f In H— jjt = 1 —> 1.
[To же можно выразить и иначе: если взять последовательность
значений х, имеющую пределом +оо, то ей отвечает последовательность значе-
значений функции:
sin (и + -\jt = (-1)" (и = 1, 2, 3, . . .),
вовсе не имеющая предела.]
Если вспомнить «колебательный» характер синусоиды, то отсутствие предела
в рассматриваемом случае станет наглядным.
Аналогично, и функция sin ^ при стремлении а к 0 (справа или слева)
предела не имеет. Это, в сущности, лишь другая форма приведенного выше
примера: стоит лишь в функции sin х заменить х на ^. Очевидно, если а пробега-
пробегает последовательность значений, приближающихся к 0 справа (слева), то х = ^
стремится к +оо( —оо), и обратно.
144
ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
[54
Напишем снова в выражении sin ^ вместо буквы а букву х (чтобы вернуться
к привычному обозначению абсциссы) и рассмотрим поучительный график
функции
у = sin - (х Ф 0),
х
ограничиваясь значениями х от 0 до -| (и от — -| до 0).
Отметим последовательно убывающие до 0 значения х:
2 12 12 12 2 1 2
jt jt 3jt 2jt 5jt 3jt Ijt Bn — \)jt гит Bп -\- \)jt
им отвечают растущие до +оо значения |:
jt 3jt 5jt Ijt
2^2 - \)jt Bn
n jt,
В промежутках между указанными значениями (при убывании х) наша функ-
функция попеременно убывает от 1 до 0 и от 0 до —1, затем возрастает от —1 до 0
и от 0 до 1, и т. д.
Таким образом, функция sin j производит бесконечное множество колебаний,
подобно функции sin х, но, в то время как для последней эти колебания распреде-
распределяются на бесконечный промежуток, здесь они все умещаются в конечном
промежутке, сгущаясь к 0.
Рис. 23
График изображен на рис. 23 (разумеется, не полностью — бесконечное мно-
множество колебаний воспроизвести невозможно!). Так как при изменении знака х
и sin j меняет знак, то левая половина графика симметрична правой относительно
начала.
10) Если (для х ф 0) рассмотреть функцию х • sin j, которая отличается
множителем х от только что изученной функции sin j, то на этот раз предел
при х —>> 0 существует:
lim х • sin — = 0,
55]
2. ПРЕДЕЛ ФУНКЦИИ
145
что сразу ясно из неравенства
При приближении х к О наша функция по-прежнему производит бесконеч-
бесконечное множество колебаний, но их амплитуда (благодаря множеству х) убывает,
стремясь к 0, чем и обеспечивается существование предела.
График функции
1
у = х • sin -
х
изображен на рис. 24; он умещается между двумя биссектрисами у = х и у = — х
координатных углов. * ^
Замечание. Мы имели ряд пределов
sin л
lim = 1,
jc-И) x
= е,
lim x sin - = О,
jc-И) х
объединенных одной особенностью: ни одна из рассматриваемых здесь функций
не определена при х = 0. Но это нисколько не мешает говорить об их
пределах при jc —>> 0, ибо, согласно точному смыслу данного в 52 определения,
как раз значение х = 0 при этом не рассматривается.
Рис. 24
Аналогично, то обстоятельство, что функция sin j не имеет смысла
при х = 0, не мешает ставить вопрос об ее пределе при х -л 0; но на этот
раз предел оказывается несуществующим.
55. Распространение теории пределов. Естественно встает воп-
вопрос о распространении теории пределов, развитой в гла-
главе I (§§ 1 и 2) применительно к случаю варианты, на рассматрива-
рассматриваемый здесь общий случай произвольной функции.
Для этого существуют два пути:
I. Прежде всего, можно перефразировать здесь изло-
изложенные там рассуждения. Мы для примера фактически
выполним это по отношению к предложению 1° в 26.
* ^ На рис. 23 и 24 для ясности пришлось по оси х взять больший масштаб, что
создает искажение.
146 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [55
Рассмотрим функцию /(х), заданную в некоторой области <$Г,
с точкой сгущения а*\
1° Если при стремлении х к а функция f(x) имеет конеч-
конечный предел А, и А > р (А < q), то для достаточно близких к а
значений х (отличных от а) и сама функция удовлетворяет
неравенству
f{x)>p (f{x)<q). A4)
Выбрав положительное число е < А — р (q — А), будем иметь
А - с > р (А + с < q).
Но, по определению предела, для этого е найдется такое 89 что,
лишь только \х—а\ < S (где х взято из SC и отлично от а), тотчас же
А - е < f(x) < А + е.
Для тех же значений х и подавно будет выполняться A4).
Читатель видит, что никаких новых идей для доказательства
привлекать не пришлось.
Отсюда непосредственно могут быть оправданы и утвержде-
утверждения 2°, 3° и 5° из 26. Например, полагая в 1° р = 0 (q = 0),
получим:
2° Если при х —)> а функция f(x) имеет конечный положи-
положительный (отрицательный) предел, то и сама функция поло-
положительна (отрицательна), по крайней мере для значений х,
достаточно близких к а, но отличных от а.
Справедливо и утверждение, аналогичное 4°, но в более узкой
форме:
4° Если при стремлении х к а функция f(x) имеет конеч-
конечный предел А, то для значений х, достаточно близ-
близких к а, функция будет ограниченной:
\f(x)\ < М1 (М1 = const, \x -a\< S).
Напомним, что первоначально и для варианты хП9 имеющей ко-
конечный предел, неравенство \хп\ < М1 было получено только для
п > N, но, так как лишь конечное число значений варианты мо-
может не удовлетворять этому неравенству, то нетрудно было, увели-
*) Число а может быть и бесконечным, но мы для определенности ограничимся
случаем конечного а.
55] § 2. ПРЕДЕЛ ФУНКЦИИ 147
чив в случае надобности М\ добиться выполнения неравенства для
всех хп. Здесь же этого, вообще говоря, сделать нельзя, ибо зна-
значений х, для которых |/(х)| > М\ может оказаться и бесконечное
множество. Например, функция f(x) = ? (для х > 0) при х -> 1
стремится к единице; очевидно, f{x) < 2, если \х — 1| < ^, однако
для всех рассматриваемых значений х функция f(x) вовсе не
будет ограниченной.
П. Переходя к другим теоремам, в которых переменные связы-
связываются знаками равенства, неравенства или арифметических дей-
действий, мы прежде всего должны оговорить, что, соединяя две или
несколько функций f(x),g(x), ... (определенных в одной и той
же области ЗГ) такими знаками, мы всегда подразумеваем, что их
значения отвечают одному и тому же значению х.
Все эти теоремы можно было бы доказать аналогичным обра-
образом наново, но — и это важно подчеркнуть — на деле нет не-
необходимости их передоказыватъ. Если, говоря о пределе функ-
функции, стоять на «точке зрения последовательностей», то, поскольку
для последовательностей теоремы доказаны, они верны и для
функций.
Для примера остановимся на теоремах 1°, 2°, 3° из 30:
Пусть в области SC (с точкой сгущения а) заданы две
функции f{x) и g(x), и при стремлении х к а обе имеют
конечные пределы
lim/(jc) = A, Hmg(x) = В.
Тогда и функции
f(x)±g(x), f(x)-g(x), ^| A5)
также имеют конечные пределы (в случае частного — в пред-
предположении, что В фО), именно
А±В, А-В, -.
В
На «языке последовательностей» данные соотношения расшиф-
расшифровываются так: если {хп} есть любая последовательность зна-
значений х из <$Г, имеющая пределом а, то
f{xn) -+А, g(xn) -+В.
148 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [56
Если к этим двум вариантам применить уже доказанные теоремы,
то получаем сразу:
\im[f{xn) ±g(xn)} =A±B, limf(xn)g(xn) = А-В,
а это (на «языке последовательностей») и выражает именно то, что
нужно было доказать. *}
Таким же образом на общий случай, рассматриваемый нами те-
теперь, автоматически переносится и все сказанное в 31 относитель-
относительно «неопределенных выражений», условно характеризуемых сим-
символами:
0 °° п
-, —, 0 • оо, сю — сю.
О оо
Как и в простейшем случае, когда мы имеем дело с функциями
натурального аргумента, здесь для «раскрытия неопределенности»
уже недостаточно знать лишь пределы функций f(x) и g(x)9 а нуж-
нужно учесть и самый закон их изменения.
Читатель легко проверит, что в примерах 4), 5) предыдущего п°
мы имели дело с неопределенностью вида ^ и 0 • оо, а в приме-
примере 7) — с неопределенностью вида jj. В следующем п° мы приве-
приведем дальнейшие примеры, уже с применением простейших теорем
теории пределов.
Мы еще вернемся к этому вопросу и в § 4 главы IV, где будут
даны общие методы раскрытия неопределенностей уже с примене-
применением дифференциального исчисления.
56. Примеры.
1) Обобщая примеры 1) и 2), 32, исследуем поведение многочлена
р(х) = ацхк + а\хк~1 + . . . + ак_\х + ак,
а затем — и частного двух таких многочленов
р{х) _ аохк + а\хк~Х + . . . + ак_\х + ак
q(x) boxl + bixl~l + . . . + bi-ix + bi
при х -Л zboo.
*) В случае частного можно было бы заметить (аналогично тому, как мы это
сделали для варианты), что для х, достаточно близких к а, знаменатель g(x) ф О,
так что дробь 1-Щг имеет смысл, по крайней мере для этих значений х.
56] § 2. ПРЕДЕЛ ФУНКЦИИ 149
Путем преобразования
к( а\ ак\
р{х) =хЧао + — + ...+ —
V х хк)
легко установить, что
lim р[х) = zbco (со — со),
причем знак предела при к четном определяется лишь знаком я о, а при к нечет-
нечетном — зависит еще и от знака х.
2) Аналогично находим, что
lim
q(x)
в зависимости от того, будет ли к > /, к = / или к < I. Знак предела (в первом
случае) устанавливается по знакам а о и bo, а также (при к — I нечетном) — по
знаку х.
3) Докажем для любого положительного рационального показателя г фор-
формулу
Начнем с простейшего случая, когда показатель есть натуральное чис-
число: г = п. По биному Ньютона
A + х)п - 1 ж + п-^±х2 + . . . + хп п(п-\) и_!
= = п + — -х + ...+х ;
12
п +
jc х 1-2
так как при * —>> 0 все члены в последней сумме, кроме первого, стремятся к О,
то, действительно, имеем
lim = п.
х^О X
Пусть теперь г = ^ (где т — натуральное), и рассмотрим выражение
X
Положим
л/ТТх -1=у, откуда х = A +у)т - 1.
Так как (считая |л| > 1)
1 - |*| < vTT^< I + |jc|. то \im лУТТх =
x-s>0
так что, вместе с х, и у —>> 0. А тогда, по предыдущему случаю,
г ^ГТ71
lim = lim
lim
у^О A +у)т — 1
*^ Ниже [77,5), (в)] она будет обобщена на случай любого вещественного по-
показателя.
150 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [56
Наконец, общий случай г = ^ исчерпывается введением той же вспомога-
вспомогательной переменной у.
A + х)™ - 1 _ A + у)п - 1 _ A + у)п - 1 у
-1 у
откуда
(i+*)?-i n
lim = -.
х^О х т
4) Найти предел
lim —.
х^О х1
С помощью той же подстановки \/\ + х — 1 = у преобразуем рассматри-
рассматриваемое выражение к виду
•У т Lv
откуда сразу ясно,
5) Предел [54,
часто используется
(а)
Очевидно,
что искомый
7)]
ДЛЯ ]
1 -
предел равен
lim
x-s>0 x
захождения других
lim -
- cos х
X2
— cos х
X2
2 sin |
X2
=
1
m- 1
2m2 '
пределов.
1
2
1
7
/sin |
так как выражение в скобках стремится к 1, то общий предел и будет ^.
tgjc — sin;\; 1
(б)
lim
х
з 2 \0
И здесь преобразование легко приводит к уже изученным пределам:
tgjc — sinjc I sinjc 1 — cosjc
x3 cos^: x x2
Заметим, что cos x —t 1 при х —t 0, как это вытекает, например, из предыдущего
результата (а).
(в) lim (secx — tgjc) = 0 @0 — 00).
Здесь удобнее перейти к переменной а = § — х; очевидно а —>> 0 при х —> f.
Имеем
1 — cos а 1 — cos a a
sec х — tg;\; = esc a — ctga = = г • • а —> 0.
sin a az sin a
57] § 2. ПРЕДЕЛ ФУНКЦИИ 151
57. Предел монотонной функции. Вопрос о самом сущест-
существовании предела функции
особенно просто решается для функций частного типа, представля-
представляющих обобщение понятия монотонной варианты [34].
Пусть функция f{x) определена в некоторой области SC = {х}.
Функция называется возрастающей (убывающей) в этой
области, если для любой пары принадлежащих ей значений
из х' > х следует /(У) > f{x) [/(У) < /(*)].
Если же
из х1 > х следует лишь /(У) ^ f{x) [/(У) < /(*)],
то функцию называют неубывающей (невозрастающей).
Иногда удобнее и в этом случае называть функцию возрастающей
(убывающей) — но в широком смысле.
Функции всех этих типов носят общее название монотон-
монотонных. Для монотонной функции имеет место теорема, вполне ана-
аналогичная той теореме о монотонной варианте, которая была уста-
установлена в 34.
Теорема. Пусть функция f{x) монотонно возрастает, хо-
хотя бы в широком смысле, в области SC, имеющей точкой
сгущения число а, большее всех значений х {оно может быть
конечным или равным +оо). Если при этом функция ограни-
ограничена сверху:
f{x) ^ М {для всех х из «2Г),
то при х —>> а функция имеет конечный предел; в противном
случае — она стремится к +оо.
Доказательство. Допустим сначала, что функция f{x)
ограничена сверху, т.е. ограничено сверху множество {/(*)} зна-
значений функции, отвечающих изменению х в области SC. Тогда для
этого множества существует [11] конечная точная верхняя гра-
граница А. Докажем, что это число А и будет искомым пределом.
Задавшись произвольным числом г > 0, по свойству точной
верхней границы, найдем такое значение х' < а, что f{x') > А — г.
Ввиду монотонности функции, для х > х' и подавно будет:
f{x) > А - с. Так как, с другой стороны, всегда f{x) ^А < А + с,
152 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [58
то для упомянутых значений х выполнится неравенство
\f(x)-A\<e.
Это и доказывает наше утверждение, стоит лишь при а ко-
конечном положить хг = а — 8 (т. е. 8 = а — х'), а при а = +оо
взять А = х1.
Если функция /(х) сверху не ограничена, то, каково бы ни бы-
было число Е, найдется такое х\ что /(V) > Е; тогда для х > х'
и подавно /(х) > Е, и т. д.
Предоставляем читателю преобразовать эту теорему для слу-
случая, когда предельное значение а меньше всех значений х, равно
как и для случая монотонно убывающей функции.
Легко усмотреть, что теорема о монотонной варианте в 34 есть
просто частный случай этой теоремы. Независимой переменной
там был значок /7, областью изменения которого служил натураль-
натуральный ряд JV = {п}, с точкой сгущения +оо.
В последующем нам чаще придется в качестве области 5Г,
в которой рассматривается функция /(х), встречать сплошной
промежуток [а1, а), где а1 < а и а — конечное число или +оо,
либо же — промежуток (а, а\ где а1 > а и а — конечное число
или —сю.
58. Общий признак Больцано-Коши. Перейдем теперь к рас-
рассмотрению общего случая — функции /(х), заданной в области
SC = {х}, для которой а служит точкой сгущения. Для сущест-
существования конечного предела этой функции при стремлении х
к а может быть установлен такой же признак, как и в случае ва-
варианты [39]. Формулировку его мы дадим параллельно для случая
конечного а и для случая а = +оо.
Теорема. Для того чтобы функция /(х) при стремле-
стремлении х к а имела конечный предел, необходимо и достаточно,
чтобы для каждого числа е > 0 существовало такое чис-
число 8 > О (А > 0), чтобы неравенство
\f{x)-f{x')\<e
выполнялось, лишь только
\х — а\ < 8 и \х' — а\ < 8 (х > А и х1 > А).
Доказательство проведем в предположении, что а — ко-
конечное число.
58] § 2. ПРЕДЕЛ ФУНКЦИИ 153
Необходимость. Пусть существует конечный предел
Ш/(х)=А.
Тогда по заданному г > О найдется такое 8 > О, что
\f{x)-A\<?-,
если только \х — а\ < 8. Пусть и \хг — а\ < 8, так что и
\А - f{x')\ < ?-.
Отсюда получаем
|Д*)-Д*'I = \[f(x)-A} + [A-f(x')]\ < |/(x)-J| + M-/(x')| < e,
в предположении, что одновременно
\х — а\ < 8 и |х; — <я| < 8.
Достаточность может быть установлена с помощью рассу-
рассуждений, вполне аналогичных тем, которые были применены в слу-
случае варианты [39]. Проще, однако, не повторяя этих рассуждений,
попросту свести вопрос к уже рассмотренному случаю. Путь для
этого нам открывает второе определение понятия предела
функции «на языке последовательностей» [53].
Итак, пусть условие, сформулированное в теореме, выполне-
выполнено, и по произвольно взятому е > О установлено соответству-
соответствующее 8 > 0.
Если {хп} есть любая последовательность значений х из «2Г,
сходящаяся к а, то, по определению предела последовательности,
найдется такой номер N, что для п > N будет: \хп—а \ < 8. Возьмем,
наряду с /7, и другой номер п' > N, так что одновременно
хп - а
< 8 и \хпг — а\ < 8.
Тогда, в силу самого выбора числа 8,
Это неравенство, таким образом, выполняется при единственном
требовании, чтобы оба номера п и пг были > N. Это означает, что
для варианты f(xn) (п = 1, 2, 3, ...) выполняется условие п° 39
и, следовательно, последовательность
/(*i), Дх2), ..., /(*„), ...
имеет конечный предел.
154 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [60
Мы видели в 53 (см. замечание в конце), что этого уже доста-
достаточно, чтобы последний предел был одним и тем же, как бы ни
выбирать последовательность {хп}, сходящуюся к а; этот предел
и будет пределом функции, существование которого надлежало до-
доказать.
[Легко вывести достаточность высказанного условия и из тео-
теоремы Больцано-Вейерштрасса — наподобие того, как это
сделано для варианты в конце 41.]
59. Наибольший и наименьший пределы функции. Даже при отсутствии
определенного предела функции f(x) при стремлении х к а, для отдельных по-
последовательностей значений хп —>> а предел
lim f(xn)
все же может существовать; его называют частичным пределом функции.
Например, для функции sin х при х —> d= оо (или для sin j при х —> 0) эти
частичные пределы заполняют весь промежуток от —1 до +1.
Среди частичных пределов функции найдется как наибольший, так
и наименьший; их обозначают так:
lim f[x) и lim f[x).
х^-а х^-а
Равенство наибольшего и наименьшего пределов есть условие, необходи-
необходимое и достаточное для существования определенного предела функции,
в обычном смысле слова.
Мы ограничимся формулировкой этой теоремы, не приводя доказательства.
Оно может быть выполнено в том же порядке идей, что и в 42.
§ 3. Классификация бесконечно малых и бесконечно
больших величин
60. Сравнение бесконечно малых. Предположим, что в каком-
либо исследовании одновременно рассматривается ряд бесконечно
малых величин:
а, /3,у, ...,
которые, вообще говоря, будут функциями от одной и той же пе-
переменной, скажем, х9 стремящейся к конечному или бесконечному
пределу а.
Во многих случаях представляет интерес сравнение назван-
названных бесконечно малых между собой по характеру их приближе-
приближения к нулю. В основу сравнения двух бесконечно малых а и /3
60] § 3. КЛАССИФИКАЦИЯ БЕСКОНЕЧНО МАЛЫХ 155
кладется поведение их отношения *\ На этот счет установим два
соглашения:
I. Если отношение -{ас ним и |) имеет конечный
и отличный от нуля предел, то бесконечно малые а
и /3 считаются величинами одного порядка.
П. Если Dice отношение ^ само оказывается бесконеч-
бесконечно малым {а обратное отношение | — бесконечно боль-
большим), то бесконечно малая /3 считается величиной высшего
порядка, чем бесконечно малая а, и одновременно бесконечно
малая а будет низшего порядка, чем бесконечно малая р.
Например, если а = х —>> О, то по сравнению с этой бесконечно
малой одного порядка с нею будут бесконечно малые
sin х, tg x, у/\ + х — 1,
ибо, как мы знаем [54,7); 56,3)],
- 1 1
lim = 1, lim -
х—^0 х х—^0 х т
Наоборот, бесконечно малые
у
tgx — sinx A)
будут, очевидно, высшего порядка, чем х [56,4); 5), (а) и (б)].
Конечно, может случиться, что отношение двух бесконечно малых не стре-
стремится ни к какому пределу; например, если взять [см. 54,9) и 10)]
1
а = х и /3 = jc sin —,
х
то их отношение, равное sin j, при х —ь 0 предела не имеет. В таком случае
говорят, что две бесконечно малые не сравнимы между собой.
Заметим, что если бесконечно малая J3 оказывается высшего
порядка, чем бесконечно малая а, то этот факт записывают так:
Р = о{а).
Например, можно писать:
1 — cosx = o{x), tgx — sinx = o{x), и т. п.
Таким образом, символ о{а) служит общим обозначением для
бесконечно малой высшего порядка, чем а. Этим удобным обозна-
обозначением мы впредь будем пользоваться.
*) Мы будем считать, что переменная, на которую мы делим, не обращается
в 0, по крайней мере для значений х, достаточно близких к а.
156 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [61
61. Шкала бесконечно малых. Иной раз встречается надоб-
надобность в более точной сравнительной характеристике поведения бес-
бесконечно малых, в выражении их порядков числами. В этом
случае, прежде всего, в качестве своего рода «эталона» выбирают
одну из фигурирующих в данном исследовании бесконечно малых
(скажем, а); ее называют основной. Конечно, выбор основ-
основной бесконечно малой в известной мере произволен, но обычно
берут простейшую из всех. Если рассматриваемые величины, как
предположили, являются функциями от х и становятся бесконечно
малыми при стремлении х к а, то в зависимости от того, будет ли а
нулем, конечным и отличным от нуля числом или бесконечностью,
естественно за основную бесконечно малую взять, соответственно
1
х, х — а, —.
х
Далее, из степеней основной бесконечно малой а (мы будем
считать а > 0) с различными положительными показателя-
показателями, ak9 составляют как бы шкалу для оценки бесконечно малых
более сложной природы. *)
III. Уславливаются считать бесконечно малую /3 величиной
к-го порядка {относительно основной бесконечно ма-
малой а), если C и ак (к > 0) будут величинами одного порядка,
т. е. если отношение -^ имеет конечный и отличный от нуля предел.
Теперь, например, можно, не довольствуясь утверждением, что бесконечно
малые A) (при jc —)> 0) будут величинами высшего порядка, чем а = х, ска-
сказать точно, что первые две из них суть бесконечно малые второго порядка,
а последняя — третьего порядка относительно а = х, ибо [56,4); 5), (а) и (б)]
\/\ + х — 1 — 1-х т — 1 1 — cos х 1
lim = - , lim = -,
х^О xl 2ml x^O xl 2
\%х — sin.* I
lim = -.
х^О х5 2
Чтобы взять более сложный пример, рассмотрим выражение
при .х —>- +оо оно будет бесконечно малым, что становится ясным, если пред-
представить его в виде
1 1
/ TT/^T"T7-/~\ T">TTTT/^T4L ТТТГ\ TTtATT 1г "--^ П Т"> С± ТТТТТТТТТ^ГО SV
видеть, что при k > 0 величина а будет бесконечно малой одновре-
одновременно с а.
62]
§ 3. КЛАССИФИКАЦИЯ БЕСКОНЕЧНО МАЛЫХ
157
Продолжая это преобразование, найдем:
1
(лЛ + 1 + у/х) (у/х + у/х - 1) (лЛ - 1 + у/х + 1)
Полагая а = ^, теперь уже нетрудно сообразить, что
lim —г- = lim
Х^+°° «5 ^^+оо (д/jc + 1 -f
- 1) Ых - 1 + Vjc + 1
Таким образом, здесь порядок выражается числом \.
Не следует думать, конечно, что для всякой бесконечно малой /3 (даже
сравнимой со всеми степенями ак) может быть установлен определенный
порядок. Любопытные примеры, относящиеся сюда, можно получить из формул,
установленных в 54,4) и 5) (при а > 1 и к > 0):
х—>-+оо х
Прежде всего, отсюда
lim —г = +оо,
lim — = 0,
+ ax
lim
х—>-+оо
lim
B)
Заменив теперь здесь х на j и положив еще в первом из этих соотношений а = \,
0 < с < 1, мы получим:
lim —г- = 0, lim
= оо.
Таким образом, бесконечно малая сх @ < с < 1) будет высшего по-
порядка, чем все степени;^ (&> 0), в то время как бесконечно малая ^~
(а > 1) оказывается низшего порядка, чем все эти степени.
logax
62. Эквивалентные бесконечно малые. Остановимся теперь на
одном особенно важном частном случае бесконечно малых одного
порядка.
IV. Будем называть бесконечно малые а и fi эквива-
эквивалентными {в знаках: а ~ /3), если их разность у = /3 — а
оказывается величиной высшего порядка, чем каждая из
*) Повсюду здесь мы пользуемся тем, что lim
в 56,3) (для корня любой степени т).
- z = 1; это было доказано
158 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [62
бесконечно малых а и /3:
у = о(а) и у =
Впрочем, достаточно потребовать, чтобы у была высшего поряд-
порядка, чем одна из этих бесконечно малых, потому что, если, на-
например, у высшего порядка, чем а, то она будет также высшего
у
порядка, чем /3. Действительно, из того, что lim - = 0, следует,
что и
у_
lim У- = lim —^— = lim —^ = 0.
Рассмотрим две эквивалентные бесконечно малые а и /3, так
что /3 = а + у, где у = о(а). Если приближенно положить
/i = a*\ то — по мере уменьшения обеих величин — стремится
к нулю не только абсолютная погрешность от этой замены,
представляемая величиной |у|, но и относительная погрешность,
У
равная
Иными словами, при достаточно малых значени-
значениях а и $ можно со сколько угодно большой относительной
точностью положить /3 = а. На этом основана, при приближен-
приближенных выкладках, замена сложных бесконечно малых эквивалентны-
эквивалентными им простыми.
Установим полезный критерий эквивалентности двух бесконеч-
бесконечно малых, который в сущности дает второе определение
этого понятия, равносильное ранее данному:
Для того чтобы две бесконечно малые а и C были экви-
эквивалентны, необходимо и достаточно, чтобы было
lim? = l.
а
Пусть сперва выполняется это соотношение, так что
*=?-!-> 0.
а
Тогда
у = E — а = S • а
будет величиной высшего порядка, чем а, ибо
lim- = lim E = 0.
а
*^ Знак = означает приближенное равенство.
63] § 3. КЛАССИФИКАЦИЯ БЕСКОНЕЧНО МАЛЫХ 159
Обратно, пусть теперь аир эквивалентны, т. е. у = /3 — а
есть бесконечно малая высшего порядка, чем а. Вследствие этого
имеем
1 = - ->> 0, откуда > 1,
а а а
что и требовалось доказать.
С помощью этого критерия, например, сразу видно, что при jc —^ 0 бесконеч-
бесконечно малые sinх и tgx эквивалентны х9 а \/\ + х — 1 эквивалентно ^ х. Отсюда —
приближенные формулы:
sin х = х, tg x = х,
в частности
Доказанное свойство эквивалентных бесконечно малых приводит к использо-
использованию их при раскрытии неопределенности вида §, т. е. при разыскании предела
отношения двух бесконечно малых -. Каждая из них при этом может быть
заменена, без влияния на существование и величину предела, любой экви-
эквивалентной ей бесконечно малой.
Действительно, если а ~ а и /3 ~ /3, т. е.
lim — = 1 и lim -=- = 1,
а /3
то отношение
(L = JL. A. ii.
а /3 а а
отличающееся от отношения -=- множителями, стремящимися к единице, имеет
предел одновременно с ним (и притом тот же).
Если удастся выбрать а и /3 достаточно простыми, то это может сразу зна-
значительно упростить задачу; например,
Л. ^/l+x+x 1 \
lim = lim —
i2
lim .
sin2jc x-s>0 2х 4
Из доказанного вытекает также, что dee бесконечно малые,
эквивалентные третьей, эквивалентны между собой.
63. Выделение главной части. Если выбрана основная беско-
бесконечно малая а, то простейшими бесконечно малыми естествен-
естественно считать величины вида с • ak9 где с — постоянный коэффициент
и k > 0. Пусть бесконечно малая /5 будет ?-го порядка относитель-
относительно а, т. е.
В
hm-г =с,
ак
160 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [63
где с — конечное и отличное от нуля число. Тогда
Hmг = 1,
сак
и бесконечно малые /3 исак оказываются эквивалентными: /3 ~ сак.
Эта простейшая бесконечно малая сак, эквивалент-
эквивалентная данной бесконечно малой fi, называется ее главной
частью {или главным членом).
Пользуясь установленными выше результатами, кроме уже указанных прос-
простых примеров, легко выделить главные части выражений:
1 2 • 1 3
1 — cosх rsj — х , tgл: — sini ~ -i .
Здесь х —>> 0, и именно а = х является основной бесконечно малой.
Наконец, если х —> +оо и за основную принята бесконечно малая а = ^,
то имеем также
Все эти результаты снова приводят к приближенным формулам.
Пусть /3 rsj cak, т. е. /3 = сак + у, где у = о(ак). Можно представить себе,
что из бесконечно малой у снова выделен главный член: у = с''а +<5, где к' > к,
а 8 = о(а ), и т. д.
Например, если положить (считая х -Л 0):
то, как мы уже имели [56,4)],
у m — \
Нт -^ =
2
так что главная часть у есть — ^j- * . Отсюда
, 1 т — 1 j j
'1+x -1 = —x z-^-x +o(x).
В частности,
Этот процесс последовательного выделения из бесконечно малой простейших
бесконечно малых все возрастающих порядков можно продолжать и дальше.
Мы ограничиваемся в настоящем параграфе установлением об-
общих понятий, иллюстрируя их лишь немногими примерами. В по-
последующем мы укажем систематический прием как для
построения главной части данной бесконечно малой величины, так
и для дальнейшего выделения из нее простейших бесконечно ма-
малых, о котором только что шла речь [см. 104,124] .
64]
§ 3. КЛАССИФИКАЦИЯ БЕСКОНЕЧНО МАЛЫХ
161
В заключение остановимся еще на таком вопросе: если для двух
бесконечно малых E и у известны их главные члены сак и с'ак ,
что можно сказать о главном члене их суммы /3 + у?
При к ф к' главным членом ее, очевидно, будет тот из чле-
членов сак и с'ак , в котором показатель меньше. Пусть теперь к = kf;
тогда главной частью для /3 + у явится сумма (с + с')ак —
в предположении, однако, что с + с' ф 0. В случае
же, когда оба главных члена взаимно уничтожаются, сумма /3 + у
оказывается бесконечно малой высшего порядка, чем каждое из
слагаемых.
Так будет, например, при х —>> 0 для бесконечно малых
Если выделить в них еще следующие члены:
+о(х)
2
= -х--х
Z
2
у = --х - -х
Z о
то ясно, что
так что /3 + у будет бесконечно малой второго порядка, а ее главный член
равен —\х2.
64. Задачи. Для иллюстрации изложенных соображений приведем несколько
задач, в которых они используются.
1) Пусть прямолинейное расстояние на местности измеряется с помощью
мерной рейки длины 1м. Так как фактически рейка прикладывается не точно
вдоль измеряемой прямой, то результат измерения оказывается несколько больше
Рис. 25
истинной длины. Сделаем самое невыгодное предположение, именно, что
рейка прикладывается зигзагом, так что ее концы отстоят от прямой пооче-
поочередно то в одну, то в другую сторону на расстояние Я м (рис. 25). Требуется
оценить погрешность.
При однократном прикладывании рейки абсолютная погрешность равна раз-
разности между длиной / рейки и ее проекцией на измеряемую прямую; проекция
же эта будет:
162 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
Воспользовавшись приближенной формулой
[64
1
= 1 + -х
при х = — -уу- (что оправдано, ввиду малости величины Я относительно /), заме-
заменим выражение для проекции следующим:
i2
/ 1-
2Х1
р Г1' i
В таком случае, упомянутая погрешность есть ^—, а относительная по-
2/L2
грешность, очевидно, будет —. Та же относительная погрешность сохранится и
при многократном прикладывании рейки.
Если для этой погрешности установлена граница 8, т. е. должно быть — < 8,
то отсюда Я < /W -.
Например, при измерении двухметровой рейкой (/ = 2) для достижения от-
относительной точности в 0,001 достаточно, чтобы уклонение Я не превосходило
2л/0^005 = 0,045 л* = 4,5 см.
Рис. 26
2) Найти формулу для длины / открытого ремня, надетого на данную пару
шкивов радиусов R и г, с расстоянием d между центрами (рис. 26).
Из чертежа имеем
- = АС + Сс + са.
Но АС = R (т? -\- а^9 с а = ^ (§ — «), где через а обозначены равные углы
<ВОС и <Ьос; а из AODo
Сс =Do= л/d2 - (R - гJ.
т(Д + г) + 2а(Я - г) + 2у^2 - (R - гJ.
Таким образом,
65]
§ 3. КЛАССИФИКАЦИЯ БЕСКОНЕЧНО МАЛЫХ
163
Для упрощения этой формулы вспомним, что
OD R-r
= sma =
— в предположении, что R — г мало относительно d. В том же предположении
После подстановки этих значений и преобразований, получим окончательную
формулу:
l = Jt{R + r) + 2d+^—^-
d
3) При разбивке дуг окружностей на местности имеет значение следующая
задача: найти отношение стрелы / = DB дуги ABC окружности к стреле
f\ = D\B\ половины АВ\В этой дуги (рис. 27).
Если положить радиус окружности равным г, <АОВ = <р, то <АОВ\ = ^ и
f = DB = r(l - coscp),
fl=r (l- cos |J .
Таким образом, искомое отношение равно
/ 1 — cosq>
Т\ ~ 1 - cos f
Выражение это слишком сложно, чтобы им удобно было пользоваться на прак-
практике. Найдем его предел при ср —>> 0 (ибо для достаточно малых ср это выраже-
выражение можно приближенно заменить его пре-
пределом). С этой целью заменяем числитель
и знаменатель их главными частями и сра-
сразу находим:
lim — = lim 2 2 = 4.
Итак, для дуг, соответствующих не-
небольшому центральному углу, приближенно
можно считать, что стрела полудуги вчет-
вчетверо меньше стрелы дуги. Это позволя-
позволяет последовательно строить промежуточные
точки дуги, для которой даны концы и се-
середина.
65. Классификация бесконечно больших. Заметим, что для бес-
бесконечно больших величин может быть развита подобная же клас-
классификация. Как и в 60, будем считать рассматриваемые бесконечно
большие величины функциями от одной и той же переменной х9
которые стремятся к +оо, когда х стремится к а.
164 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [66
I. Две бесконечно большие у и z считаются величинами
одного порядка, если их отношение -{ас ним и у-) имеет
конечный и отличный от нуля предел.
П. Если dice отношение - само становится бесконеч-
бесконечно большим {а обратное отношение у- — бесконечно малым),
то z считается бесконечно большой величиной высшего по-
порядка, чем у, и, одновременно, у будет бесконечно большой
низшего порядка, чем z.
В случае когда отношение - ни к какому пределу не стремится,
бесконечно большие у и z будут несравнимы.
При одновременном рассматривании ряда бесконечно больших
величин, одну из них (скажем,у) выбирают в качестве основной
и с ее степенями сравнивают остальные бесконечно большие. На-
Например, если (как мы предположили выше) все они суть функции
от х и стремятся к +оо при х —»> а, то в качестве основной бес-
бесконечно большой обыкновенно берут |х|, если а = ±оо, -г-^ —
при а конечном.
III. Бесконечно большая z называется величиной k-го по-
порядка {относительно основной бесконечно боль-
большой у), если z и ук будут одного порядка, т. е. если отноше-
отношение -^ имеет конечный и отличный от нуля предел.
Мы не станем приводить здесь примеров, ибо их легко получить, заменив рас-
рассмотренные выше бесконечно малые величины обратными им. Упомянем только
о том, что бесконечно большая ах (а > 1) при х —> +оо будет высшего
порядка, а бесконечно большая logfl;\; (а > 1) — низшего порядка,
чем любая степень х (с положительными показателем к); это следует из фор-
формул B), 61.
§ 4. Непрерывность (и разрывы) функций
66. Определение непрерывности функции в точке. С понятием
предела функции тесно связано другое важное понятие математи-
математического анализа — понятие непрерывности функции.
Рассмотрим функцию /(х), определенную в некоторой облас-
области ЭС — {х}, для которой хо является точкой сгущения; при
этом пусть сама точка хо принадлежит области
определения функции, так что в этой точке функция имеет
определенное значение
66] § 4. НЕПРЕРЫВНОСТЬ (И РАЗРЫВЫ) ФУНКЦИЙ 165
Когда устанавливалось понятие о пределе функции при стрем-
стремлении х к хо [52,53]
lim Дх),
неоднократно подчеркивалось, что значения хо переменная х не
принимает; это значение могло даже не принадлежать области
определения функции, а если и принадлежало, то значение /(хо)
при образовании упомянутого предела не учитывалось.
Однако особую важность имеет именно случай, когда
(x)=/(xo). A)
Говорят, что функция f(x) непрерывна при значении х = хо
(или в точке х = хо), если выполняется это соотношение;
если лее оно нарушено, то говорят, что при этом значении
(или в этой точке) функция имеет разрыв. *}
В случае непрерывности функции f(x) в точке хо (и, очевид-
очевидно, только в этом случае), при вычислении предела функции /(х)
при х —»> хо становится безразличным, будет ли х в своем
стремлении к хо принимать, в частности, и значение хо или нет.
Определение непрерывности функции можно сформулировать
в других терминах. Переход от значения хо к другому значе-
значению х можно себе представить так, что значению хо придано
приращение Ахо = х — хо**\ Новое значение функции
у = /(х) = /(хо + Ахо) разнится от старого у о = /(хо) на при-
приращение
А^о = /(*) - ГЫ = /(хо + Ах0) - Л^о).
Для того чтобы функция /(х) была непрерывна в точке хо, необ-
необходимо и достаточно, чтобы ее приращение Ауо в этой точке стре-
стремилось к 0 вместе с приращением Ах о независимой переменной.
Иными словами: непрерывная функция характеризуется тем,
*^ Эта терминология связана с интуитивным представлением о непрерыв-
непрерывности и разрывах кривой: функция непрерывна, если непрерывен ее график, точки
разрыва функции отвечают точкам разрыва графика. На деле, однако, понятие не-
непрерывности для кривой само требует обоснования, и простейший путь
к нему лежит как раз через непрерывность функций!
**) В анализе принято приращения величин х, у, t, ... обозначать через Ах,
Ay, At, . . . Эти обозначения надлежит рассматривать как цельные символы,
не отделяя А от х, и т. п.
166 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [66
что бесконечно малому приращению аргумента отвечает бес-
бесконечно малое Dice приращение функции.
Возвращаясь к основному определению A), раскроем его со-
содержание «на языке e-S» [52]. Смысл непрерывности функции /(х)
в точке хо сводится к следующему: каково бы ни было число
е > О, для него найдется такое число S > О, что неравенство
\х — хо\ < S влечет за собой |/(х) — /(хо)| < г.
Последнее неравенство, таким образом, должно выполняться
в достаточно малой окрестности (хо — S, хо + S) точки хо-
Наконец, «на языке последовательностей» непрерывность вы-
выразится так: какую бы последовательность значений х из ЭС\
Х\, Х2, -.., Хп, ...,
сходящуюся к хо, ни взять, соответствующая последователь-
последовательность значений функции
f(xi), Дх2), ..., /(*„), ...
сходится к /(хо).
Замечание. Пусть точка х =хо, служащая точкой сгуще-
сгущения для области ЭР, в которой определена функция /(х), сама
области SC не принадлежит, так что в этой точке функция не
определена. Если, однако, существует конечный предел
lim Дх),
то стоит лишь дополнить определение функции, положив /(хо) рав-
равным этому пределу, чтобы функция оказалась непрерывной
ивточкех=хо. Это в подобных случаях мы обычно
и будем впредь подразумевать.
Наоборот, если упомянутый предел не существует, то —
несмотря на то что в самой точке х = хо функция не определена —
все же говорят, что функция в этой точке терпит разрыв: она будет
иметь здесь разрыв, какое бы значение дополнительно ни приписать
функции при х = хо-
Обычно мы будем в дальнейшем рассматривать функции, опре-
определенные в промежутке ЭС\ все его точки являются его точками
сгущения, так что по отношению к любой из них можно ставить
вопрос о непрерывности. Для упрощения речи, уславливаются го-
говорить, что функция непрерывна в промежутке «2Г, если она
непрерывна в каждой точке промежутка в отдельности.
67] § 4. НЕПРЕРЫВНОСТЬ (И РАЗРЫВЫ) ФУНКЦИЙ 167
67. Арифметические операции над непрерывными функция-
функциями. Прежде чем перейти к примерам непрерывных функций,
установим следующее простое предложение, которое позволит лег-
легко расширить их число.
Теорема. Если две функции f(x) и g(x) определены в одном
и том лее промежутке SC и обе непрерывны в точке хо, то
в той Dice точке будут непрерывны и функции
f(x)±g(x), f(x)-g(x), Ш,
последняя — при условии, что g(xo) Ф 0.
Это непосредственно вытекает из теорем о пределе суммы, раз-
разности, произведения и частного двух функций, имеющих порознь
пределы [55].
Остановимся для примера на частном двух функций. Предпо-
Предположение о непрерывности функций f(x) и g(x) в точке хо равно-
равносильно наличию равенств
lim f{x) = Дх0), Ит g(x) = g(x0).
X—rXQ X—rXQ
Но отсюда, по теореме о пределе частного (так как предел знаме-
знаменателя не нуль), имеем:
1т,
пт
= ,
g(x) g(x0)
а это равенство и означает, что функция чч- непрерывна в точке хо-
68. Примеры непрерывных функций.
1° Целая и дробная рациональные функции.
Функция /(х)=х, очевидно, непрерывна во всем промежутке
(—сю, +оо): если хп —)> хо, то f{xn) = хп —)> хо = /(хо). Точно так
же непрерывна и функция, сводящаяся тождественно к постоянной.
Отсюда, на основании теоремы предыдущего п°, вытекает уже
непрерывность любого одночленного выражения
т раз
.х
как произведения непрерывных функций, а затем — и много-
многочлена (целой рациональной функции)
а\хп~1 + . . . + ап-\х
как суммы непрерывных функций. Во всех упомянутых случаях
непрерывность имеет место во всем промежутке (—сю, +оо).
168 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [68
Очевидно, наконец, что и частное двух многочленов (дроб-
(дробная рациональная функция):
аохп + а\хп~1 + . . . + ап-\х + ап
Ьохт + bxxm~l + ...+ Ьт-\х + Ьт
также будет непрерывно при каждом значении х, кроме тех, кото-
которые обращают знаменатель в нуль.
2° Показательная функция. Докажем непрерывность
показательной функции ах при любом значении х = хо, иными сло-
словами, установим, что
lim ах =ахо.
х—)-хо
[При этом достаточно ограничиться предположением: а > 1.]
Мы видели в 54,6), что
Птах = 1.
Так как 1 есть как раз значение а0 нашей функции, то это равенство
и выражает непрерывность показательной функции в точке х = 0.
Отсюда уже легко перейти к любой точке; действительно,
ах -ах°=
но при х —»> хо, очевидно, х —хо —» 0, так что — по доказанному —
что и требовалось доказать.
3° Гиперболические функции. Их непрерывность, по
уже упоминавшейся теореме, непосредственно вытекает из дока-
доказанной непрерывности показательной функции, ибо все они рацио-
рационально выражаются через функцию ех.
4° Тригонометрические функции. Остановимся сна-
сначала на функции sinx. Она также непрерывна при любом значении
х = хо, т. е. имеет место равенство
lim sinx = sinxo-
х^х0
Для доказательства заметим, что из неравенства
sinx < х,
установленного в 54, (9), для 0 < х < f, легко вывести, что нера-
неравенство
I sinxl
х|
69]
§ 4. НЕПРЕРЫВНОСТЬ (И РАЗРЫВЫ) ФУНКЦИЙ
справедливо уже для всех значений х (для
следует из того, что | sinx| ^ 1). Далее, имеем:
169
? > 1 ЭТО
sinx — smxo = 2 sin
х -
COS
так что
sinx - sinxol = 2 •
sin
x -
X +XQ
~2~'
х +х0
COS
sm
x -xq
\x -
и, окончательно,
sinx —
\x — xq|,
B)
каковы бы ни были значения х и хо-
Если задано любое е > О, то положим S = е; при \х — хо\ < S
будет
| sinx — sinxo| < ?,
что и доказывает непрерывность sinx. Аналогично устанавливается
и непрерывность функции cosx также при любом значении х.
Отсюда, по теореме предыдущего п°, вытекает уже непрерыв-
непрерывность функций
sinx I cosx I
tgx = , secx = , ctgx =
cscx =
cosx cosx sinx sinx
Исключение представляют для первых двух — значения вида
Bк + l)f, обращающие cosx в 0, для последних двух — значе-
значения вида ктт, обращающие sinx в 0.
69. Односторонняя непрерывность. Классификация разры-
разрывов. Выше с помощью равенства A) мы определили понятие не-
непрерывности функции /(х) в точке хо- При этом, вычисляя пре-
предел A), мы могли приближать х к хо и справа, и слева. Устано-
Установим теперь понятие об односторонней непрерывности, или
одностороннем разрыве, функции в данной точке.
Говорят, что функция /(х) непрерывна в точке хо справа
{слева), если выполняется предельное соотношение:
f(x)=f(xo)
\f(xo-O)= Hm f(x)=f(x0)].
x^xq—0
C)
170 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [69
Если же то или другое из этих соотношений не осуществляется,
то функция /(х) имеет в точке хо разрыв, соответственно,
справа или слева.
По отношению к левому (правому) концу промежутка 5С*\
в котором функция определена, может идти речь, очевидно, только
о непрерывности или разрыве справа (слева). Если же хо есть
внутренняя точка промежутка «2Г, т. е. не совпадает ни с од-
одним из его концов, то для того чтобы выполнялось равенство A),
выражающее непрерывность функции в точке хо в обычном смыс-
смысле, необходимо и достаточно, чтобы имели место сразу оба равен-
равенства C) [52]. Иными словами, непрерывность функции в точ-
точке хо равносильна ее непрерывности в этой точке одновре-
одновременно справа и слева.
Остановимся подробнее на вопросе о непрерывности и разрыве
функции /(х) в точке хо, скажем, справа. Предполагая, что функ-
функция /(х) в некотором промежутке [хо,хо + h] {h > 0) справа от
этой точки определена, видим, что для непрерывности не-
необходимо и достаточно, во-первых, чтобы существовал конечный
предел /(хо + 0) функции /(х) при стремлении х к хо справа, и,
во-вторых, чтобы этот предел был равен значению /(хо) функции
в точке хо-
Поэтому легко дать себе отчет в том, при каких обстоятель-
обстоятельствах для функции /(х) в точке хо справа появляется разрыв.
Может случиться, что хотя конечный предел /(хо + 0) и сущест-
существует, но он не равен значению /(хо); такой разрыв называют
обыкновенным или разрывом первого рода**}. Но мо-
может быть и так, что предел /(хо + 0) бесконечен или его вовсе нет;
тогда говорят о разрыве второго рода.
В следующем п° мы приведем примеры этих разрывов.
Замечание. Если в точке х = хо функция /(х) не определе-
определена [см. замечание в 66], то восстановить непрерывность функции
в этой точке можно лишь, если существуют оба конечных предела
/(хо + 0), /(хо - 0) и равны между собой.
Если какой-либо из этих пределов бесконечен или вовсе не су-
существует, то говорят о наличии разрыва второго рода с соот-
соответствующей стороны.
*^ Предполагая, что этот конец есть число конечное.
**) В этом случае говорят также, что функция f(x) в точке хо справа имеет
скачок, по величине равный /(xq + 0) — /(xq).
70] § 4. НЕПРЕРЫВНОСТЬ (И РАЗРЫВЫ) ФУНКЦИЙ 171
70. Примеры различных функций.
1) Рассмотрим функцию у = Е(х) (график ее представлен на рис. 8). Если
xq — не целое число и Е(х$) = т, т. е. т < х$ < т + 1, то и для всех значений х
в промежутке (т, т + 1) будет Е[х) = т, так что непрерывность функции в
точке х о непосредственно ясна.
Иначе обстоит дело, если хо равно целому числу т. Справа в этой точке
будет иметь место непрерывность, ибо правее х = т, именно для значений х
в (т, т + 1) будет Е(х) = т, так что и Е(т + 0) = т = Е(т). Наоборот,
левее х = т, для значений jc в (т — 1, т), очевидно, Е(х) = т — 1; отсюда
и ?(т — 0) = m — 1, что не равно значению Е(т), и слева в точке х = т
функция имеет обыкновенный разрыв или скачок!
2) Возьмем функцию, рассмотренную в 46:
у = /0) = lim
х2п-\
оо х2п + 1
(ее график дан на рис. 28). Она имеет обыкновенные разрывы в точках х = d=l
и справа и слева, ибо:
Д±1) =
3) Для функции
+1
... 1 ( ,., Рис. 28
/(л) = -j (при ^с ^0)
точка л: = 0 есть точка разрыва второго рода — с обеих сторон; именно в ней
функция и справа и слева обращается в оо:
/(+0) = lim — = +оо, /(-0) = lim — = -оо.
x^+Ojcj х^-0 х5
4) Функция
f(x) = sin - (при х ф 0),
х
рассмотренная в 54,9), в точке х = 0 имеет разрыв второго рода с обеих сторон,
так как не существует вовсе предела этой функции при стремлении х к 0
ни справа, ни слева.
5) Наоборот, если взять функцию [54,10)]
f(x) = х • sin — (при х ф 0),
х
для которой, как мы видели, существует предел
Um/(*)=0,
то, положив — согласно замечанию п° 66 — /@) = 0, мы восстановим непре-
непрерывность и при х = 0.
172
ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
[70
6) Определим две функции равенствами:
ЛО) = а* (а> 1), f2(x) = arctg -
х
для х Ф 0 и сверх того положим f\ @) = /2 @) = 0.
Для первой из них имеем:
/l(+0) = lim a1 = lim а = +оо,
/l(—0) = lim a1 = lim a = 0,
*->¦—0 z-^-00
так что в точке х = 0 справа — разрыв второго рода, а слева — непрерывность.
Для второй же —
/2(+0) = lim arctg- = lim arctgz = —,
x-s>+0 jc z-^+oo 2
/2(-0) = -f.
и в точке * = 0 — с обеих сторон скачки. Графики этих функций даны на рис. 29
и 30.
у=ах
+1
-Л -3 -2 -1
0 1
У'
ж
2
-4 -3 -2 -1
\у=arctg-
0 12 3 4
Рис. 29
Рис. 30
7) Вспомним еще о функции Дирихле [46]:
%{х) = 1, если * рационально.
%{х) = 0, если ^с иррационально.
Так как в любой близости от рациональной точки найдутся точки иррацио-
иррациональные, и наоборот, то каково бы ни было х$ в промежутке ( —оо, +оо), предела
х(х) при х —t xq не существует, так что в каждой точке налицо разрыв второго
рода (с обеих сторон).
8) Определим, наконец, в промежутке [0, 1] функцию f(x) так: если х
рационально и выражается несократимой дробью |, то f[x) = |; для х
иррационального положим f[x) = 0.*^ Мы утверждаем, что в каждой
рациональной точке функция имеет обыкновенные разрывы, в то время как в ка-
каждой иррациональной точке она непрерывна.
Действительно, пусть ^о будет любая точка в рассматриваемом промежутке.
Если задаться произвольным числом е > 0, то существует лишь конечное
*)
Эту функцию рассматривал Риман (В. Riemann).
71] § 4. НЕПРЕРЫВНОСТЬ (И РАЗРЫВЫ) ФУНКЦИЙ 173
число натуральных чисел q, не превосходящих ?, а значит, в промежутке най-
найдется лишь конечное число рациональных точек ^, для которых /(^) = ^ ^ ?•
Точку xq можно окружить такой окрестностью (х$ — 8, xq + 8), чтобы в нее не
попала ни одна из этих точек (кроме, быть может, самой точки х$). Тогда, лишь
только \х — xq\ < 8 (х ф xq), будет ли х рационально или нет, во всяком случае
|/(.х)| < г. Значит, для любой точки хо существуют
f(x0 + 0) = f(x0 - 0) = 0.
Если хо есть иррациональная точка, то и /(xq) = 0, т. е. в этой точке функция
непрерывна; если же xq рационально, то /(xq) отлично от 0, и налицо разрыв
(обыкновенный) с обеих сторон.
71. Непрерывность и разрывы монотонной функции. Рассмот-
Рассмотрим функцию /(х), которая — при изменении х в промежут-
промежутке 5Г*) — монотонно возрастает (убывает), хотя бы в широком
смысле [57]. По отношению к таким функциям имеет место следу-
следующая теорема:
1° Монотонно возрастающая {убывающая) функция /(х)
может иметь в SC разве лишь разрывы первого рода, т. е.
скачки.
Возьмем любую точку хо промежутка <$Г, и пусть она не явля-
является левым концом этого промежутка. Рассматривая ту часть про-
промежутка, которая лежит влево от хо, применим к ней теорему из 57
о пределе монотонной функции; поскольку для х < хо, очевидно,
/(х) ^ /(хо), то существует конечный предел
Д*о-О)= lim ЯхКДхо).
х—)а:о—0
Если он совпадает со значением /(хо), то слева в точке хо
функция непрерывна; в противном случае — налицо скачок.
Аналогично убеждаемся в том, что в каждой точке хо проме-
промежутка SC (не служащей правым его концом) справа тоже имеет
место либо непрерывность, либо скачок.
С помощью доказанной теоремы легко установить критерий не-
непрерывности монотонной функции, удобный на практике:
2° Если значения монотонно возрастающей {убывающей)
в промежутке ЭС функции /(х) содержатся в промежутке <?
и сплошь заполняют его {так что каждое значение у
*) Этот промежуток может быть как конечным, так и бесконечным замкнутым
или открытым (с одного или с обоих концов).
174 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [72
из °^ принимается функцией хоть раз), то эта функция не-
непрерывна в ЭС. *)
Попробуем допустить, что в какой-нибудь точке хо из SC функ-
функция /(х) имеет разрыв, например слева; как мы видели, этот
разрыв может быть только скачком. В этом случае существует пре-
предел /(хо — 0), но он меньше значения /(хо). Так как для х < хо
будет /(х) < /(х0 - 0), а для х > х0, очевидно, /(х) ^ /(х0),
то функция не может принимать значений у, лежащих между
числами /(хо — 0) и /(хо), принадлежащими промежутку °^. Это
противоречит условию теоремы; значит, на деле функция /(х) раз-
разрывов не имеет.
В следующем п° читатель найдет ряд примеров приложения
этой полезной теоремы.
72. Непрерывность элементарных функций. Для ряда элемен-
элементарных функций непрерывность была доказана под видом примеров
в 68. Пользуясь теоремой 2° предыдущего номера, легко, прежде
всего, наново установить непрерывность функции ах или sinx.
Функция у = ах {а > 1) монотонно возрастает при измене-
изменении х в промежутке SC' = (—оо, +оо). Ее значения положительны
и заполняют весь промежуток *? — @, +оо), что видно из сущест-
существования логарифмах = log^j/ для любого у > 0 [20]. Следователь-
Следовательно, показательная функция непрерывна при любом значении х.
Аналогично, непрерывность функции у = sinx, скажем, при из-
изменении х в промежутке ЭС — [—§,§], вытекает из ее монотон-
монотонности в этом промежутке, да еще из того факта (устанавливаемого
геометрически), что при этом она принимает каждое значение меж-
между —1 и +1. То же относится и к любому промежутку вида
Однако более интересны для нас новые результаты, ко-
которые так же легко могут быть получены применением названной
теоремы. Продолжим перечисление основных элементарных функ-
функций, начатое в 68.
5° Логарифмическая функция: у =logax (a > 0,
а ф 1). Ограничиваясь случаем а > 1, видим, что эта функция
* ^ Условие, чтобы значения f(x) заполняли сплошной промежуток ^, выска-
высказано здесь как достаточное для непрерывности монотонной функции; впо-
впоследствии [82] мы убедимся, что оно является и необходимым.
73] § 4. НЕПРЕРЫВНОСТЬ (И РАЗРЫВЫ) ФУНКЦИЙ 175
возрастает при изменении х в промежутке ЭС — (О, +оо). К то-
тому же она, очевидно, принимает любое значение у из промежут-
промежутка *? = (—оо, +оо), именно, для х = ау. Отсюда — ее непре-
непрерывность.
6° Степенная функция: у = х^ (/л ^ 0), при возраста-
возрастании х от 0 до +оо возрастает, если \х > 0, и убывает, если \х < 0.
При этом она принимает любое положительное значение у
(для х = j/'7), следовательно, и она непрерывна. *)
Наконец, упомянем
7° Обратные тригонометрические функции:
у = arcsinx, j/ = arccosx, у = arctgx, у = arcctgx.
Первые две непрерывны в промежутке [—1, +1], а последние —
в промежутке (—сю, +оо). Доказательство предоставляем чита-
читателю.
Резюмируя, можно сказать, таким образом, что основные эле-
элементарные функции оказываются непрерывными во всех точ-
точках, где они имеют смысл (т.е. в соответствующих естест-
естественных областях их определения).
73. Суперпозиция непрерывных функций. Обширные классы
непрерывных функций могут быть построены с помощью суперпо-
суперпозиции [51] функций, непрерывность которых уже известна.
В основе этого лежит следующая
Теорема. Пусть функция (р(у) определена в промежутке *?,
а функция f{x) — в промежутке SC, причем значения послед-
последней функции не выходят за пределы *?, когда х изменяется
в SC. Если f{x) непрерывна в точке хо из SC, a q>(y) непре-
непрерывна в соответствующей точке у о = /(хо) из *?, то
и сложная функция q>(f{x)) будет непрерывна в точке хо.
Доказательство. Зададимся произвольным числом е > 0.
Так как ср{у) непрерывна при у = у о, то по с найдется такое о > 0,
что
из \у ~Уъ\ < ° следует \(р{у) — ф(уо)\ < ?•
*) Если /i > 0, то значение 0 включается как в промежуток изменения х,
так и в промежуток изменения у; при \л < 0 значение Оне включается. Далее,
если \i — целое число ±« или дробное d=-c нечетным знаменателем, то
степень х можно рассматривать и для х < 0; непрерывность ее для этих значений
устанавливается аналогично.
176 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [74
С другой стороны, ввиду непрерывности f(x) при х = хо, по о
найдется такое S > О, что
из \х -хо\<8 следует \f(x) - f(xo)\ = I/O) -уъ\< о.
По самому выбору числа о отсюда следует, далее,
) - я>Ы\ = 1ф№)) - я>(/Ы)\ < е.
Этим «на языке e-S» и доказана непрерывность функции
в точке хо.
Например, если степенную функцию х^ (х > 0) представить
в виде сложной функции:
которая получается от суперпозиции логарифмической и показа-
показательной функций, то из непрерывности последних двух функций
уже будет вытекать непрерывность степенной функции.
74. Решение одного функционального уравнения. Для облегчения изложе-
изложения в ближайшем п°, займемся сейчас следующей задачей (которая представляет
и самостоятельный интерес):
Найти все непрерывные в промежутке (—со,+оо) функции f(x),
удовлетворяющие условию
f(x+y)=f(x)+f(y), (A)
каковы бы ни были значения х и у.
Уравнение (А) является простейшим примером так называемых функцио-
функциональных уравнений, формулирующих некое свойство искомой функции, по
которому она и должна быть найдена. Наша задача состоит в разыскании всех
непрерывных решений уравнения (А).
Легко видеть, что линейные однородные функции вида
f[x) = сх (с = const) (a)
удовлетворяют этому уравнению:
с(х -\- у) = сх -\- су.
Но весь вопрос именно в том, будут ли они единственными непрерывными
функциями, имеющими свойства (А).
Для того чтобы установить, что это действительно так, предположим, что
некоторая непрерывная функция f(x) уравнению (А) удовлетворяет, и по-
покажем, что тогда она необходимо имеет вид (а).
Прежде всего, с помощью метода математической индукции легко обобщить
соотношение (А) на случай любого числа (= п) слагаемых:
п
f{7T7^~~T^)=f{x) + f{y) + ... + f{z). D)
74] § 4. НЕПРЕРЫВНОСТЬ (И РАЗРЫВЫ) ФУНКЦИЙ 177
Действительно, если допустить верность его для какого-либо числа п ^ 2 слага-
слагаемых, то оно окажется верным и для п + 1 слагаемых:
f(x+y + ...+z+u)=f(x+y + ... +z)+f(u) = [f(x) + . . .
Полагая в D) х = у = . . . = z, найдем:
f(nx) = n ¦ fix). E)
Заменив здесь х на \ х, мы получим
л)
п
а затем, если подставить тх (т — натуральное) вместо х и использовать преды-
предыдущее равенство, придем к соотношению
() F)
п
Положим теперь в основном уравнении (А) х = у = 0; получим
ДО) = 2/@), так что ДО) = 0. G)
Если же взять у = —л:, то, с учетом G), найдем:
/(-*) = -/(*).
так что функция f[x) меняет знак при изменении знака х. А тогда из E) и F)
легко вывести:
f(-nx) = -Дих) = -п ¦ f{x) (8)
и, аналогично, вообще
\ п J п
Полученные соотношения E)-(9) могут быть объединены в равенстве
firx)=r-f(x),
справедливом для любого вещественного значения х, каково бы ни было ра-
рациональное число г.
Если взять здесь х = 1 и обозначить /A) через с, то получим
f(r) = сг.
Таким образом, мы, собственно говоря, установили уже вид функции /, но пока
лишь для рациональных значений аргумента. При этом мы использовали
только тот факт, что функция удовлетворяет условию (А), и не опирались на ее
непрерывность.
Пусть теперь р будет любое иррациональное значение аргумента. Легко
построить стремящуюся к нему последовательность рациональных чисел
(можно, например, взять отрезки соответствующей бесконечной десятичной дро-
дроби). Мы только что видели, что
ГЫ = сг„ (и = 1, 2, 3, ...).
178 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [75
Перейдем здесь к пределу при п —>> +оо; справа мы получим ср, слева же,
именно ввиду предположенной непрерывности функции /, получится
ton /Ы = f(P),
так что, окончательно,
/О) = ср.
Таким образом, действительно, наша функция при всех вещественных значе-
значениях аргумента выражается формулой (а). Эта формула дает самое общее реше-
решение уравнения (А) в непрерывных функциях.
75. Функциональная характеристика показательной, логарифмической и сте-
степенной функций.
1° Если
f(x)=ax (a>0), (б)
то, каковы бы ни были два вещественных числа х и у, всегда имеет место ра-
равенство
А* + у) =/(*)•№< (Б)
выражающее общеизвестное правило умножения степеней:
х-\-у х у
а у = а • а.
Оказывается, что функциональным свойством (Б), вместе со свойством не-
непрерывности, показательная функция определяется вполне. Точнее говоря:
единственной функцией, определенной и непрерывной во всем про-
промежутке (—оо, +оо) и удовлетворяющей в нем условию (Б), является
показательная функция (если не считать функции, тождественно равной 0).
Иными словами, формула (б) — за указанным исключением — дает самое
общее решение функционального уравнения (Б) в непрерывных функ-
функциях.
Для доказательства этого рассмотрим произвольную функцию f(x)9 опреде-
определенную и непрерывную при всех х и удовлетворяющую условию (Б). Исклю-
Исключается тривиальный случай, когда f{x) = 0.
Итак, при некотором значении х = xq эта функция отлична от 0. Полагая
в (Б) у = xq — х, получим
отсюда ясно, что f(x) отлична от 0 при всяком jc. Больше того, заменяя
в (Б) х и у через |, найдем:
так что f(x) всегда строго положительна.
Пользуясь этим, прологарифмируем равенство (Б), например, по натураль-
натуральному основанию е:
lnf(x+y)=\nf(X)+\nf(y).
Если положить
ф) = lnf(x).
75] § 4. НЕПРЕРЫВНОСТЬ (И РАЗРЫВЫ) ФУНКЦИЙ 179
то в лице q>(x) мы будем иметь функцию, непрерывную (как результат суперпо-
суперпозиции непрерывных функций [73]) и удовлетворяющую условию:
аналогичному (А). В таком случае, как мы установили, необходимо
ф(х) = 1п/(л) + сх (с = const),
откуда наконец
Л\ СХ X
х)=е =а
(если положить а = ес), что и требовалось доказать.
2° Если
f(x)=\ogax (*>0,я^1), (в)
то при любых положительных значениях х и у будет
f{xy) = f{x) + f{y). (В)
Это есть запись правила логарифмирования произведения:
^gaxy = \ogax +\ogay.
И здесь это равенство, совместно с непрерывностью, вполне характеризует
именно логарифмическую функцию:
единственной функцией, определенной и непрерывной в промежутке
(О, +оо) и удовлетворяющей в нем условию (В), является логарифмиче-
логарифмическая функция (за тем же исключением), так что формула (в) дает самое общее
решение функционального уравнения (В) в непрерывных функциях.
Для доказательства возьмем произвольную функцию f(x), непрерывную для
х > О и удовлетворяющую этому уравнению. Введем новую переменную |, изме-
изменяющуюся в промежутке ( — со, +оо), и положим
х=еК <pD)=f(e4),
откуда
| = Ых, f{x) = cpilnx).
Непрерывная (в силу 73) функция <р(|) удовлетворяет условию [см. (В)]
<рD + ц)= Де|+") = fie4 ¦ е") = fie4) + f(e4) = <рЦ) + 4>{п)
типа (А). Значит,
ф(?,) = с?, и f{x)=c-\nx.
Если исключить случай с = 0 (тогда f(x) = 0), то полученный результат может
быть написан и в виде
где а = е с. Этим все доказано.
3° Наконец, обратимся к функции
/(*)=*", (г)
которая, очевидно, удовлетворяет функциональному уравнению
А*у) = /(*) ¦ /(у) (г)
(при любых положительных х и у), ибо
180 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [76
Уравнение это, в соединении с непрерывностью, в данном случае также
характеризует степенную функцию в том смысле, что
единственной функцией, определенной и непрерывной в промежутке
@, +оо) и удовлетворяющей в нем условию (Г), является степенная функ-
функция (за обычным исключением).
В самом деле, если дана непрерывная для х > 0 функция f(x), удовле-
удовлетворяющая условию (Г), то прибегнем к той же подстановке, что и в 2°. Тогда
функция <р(!) будет удовлетворять условию [см. (Г)]
<РD + П)= f(e4+") = f(e4 ¦ е") = Де1) • Де") = <рф ¦ <p(i)
типа (Б). Мы уже знаем, что тогда (если исключить тривиальный случай)
*>(!)= а1 (а>0).
Отсюда
Л\ lnx и,
х)=а = х^
(если положить \i = In а), что и требовалось доказать.
76. Функциональная характеристика тригонометрического и гиперболическо-
гиперболического косинусов.
4° Если
f(x) = cos ax или chax (a ^ 0), (д)
то, при любых вещественных значениях х и у, удовлетворяется соотношение
f(y+*)+f(y-x)=2f(x)-f(y). (Д)
Это с легкостью вытекает из теоремы сложения для обоих косинусов:
cos(y d= x) = cos x - cosy d= sin л: • sin;;,
ch(y d= x) = chx • chj/ d= shjc • sh;;
[48,6°]. Функциональное уравнение (Д), вместе с требованием не-
непрерывности функции, и на этот раз полностью характеризует оба косинуса:
единственными функциями, определенными и непрерывными в проме-
промежутке (—оо, +оо) и удовлетворяющими в нем условию (Д), являются три-
тригонометрический и гиперболический косинусы (д) (если, как и выше, не счи-
считать функции, тождественно равной нулю).
Итак, пусть f(x) будет непрерывная для всех х функция, удовлетворяющая
условию (Д). Полагая х = 0 и принимая за j/ какое-либо из значений, для которых
/(у) ф 0, заключаем, что
ДО) = 1. A0)
При у = 0 в таком случае получается
/(-*) = /(*), (и)
так что функция f(x) оказывается четной.
Поскольку непрерывная функция f(x) при х = 0 будет положительна, то
найдется такое, скажем, положительное число с, что f[x) будет положительна
во всем промежутке [0, с]. В дальнейшем исследование пойдет по разным
путям в зависимости от того, будет ли (а) /(с) ^ 1 или (/3) /(с) > 1. Займемся
сначала случаем (а).
76] § 4. НЕПРЕРЫВНОСТЬ (И РАЗРЫВЫ) ФУНКЦИЙ 181
Так как 0 < /(с) ^ 1, то найдется такое 0 @ ^ 0 < ^), что
/(c) = cos0. A2)
Приведя затем основное соотношение (Д) к виду:
f(y +х) =2f(x) • f(y) - f(y -х),
станем в нем последовательно полагать
х = с, у = с;
х = с, _у — 2с;
.х = с, _у — Зс;
и т. д. Мы получим [с учетом A0) и A2)]
/Bс) =2cos20- I = cos 20,
/(Зс) = 2 cos 0 • cos 20 - cos 0 = cos 30,
/Dc) = 2 cos 0 • cos 30 - cos 20 = cos 40,
и т. д. Пользуясь методом математической индукции, легко докажем для любого
натурального т формулу
f (тс) = cos тв. A3)
Если же в (Д) положить х = у = ^ с, то получим [снова с учетом A0)
и A2)]:
[/(r)]2=/@)t/(c)=i±i^=[co4i
так как f(x) остается положительной между 0 и с, а функция cos.* — между 0
и 0, то, извлекая положительные корни в обеих частях, придем к равенству:
Совершенно так же, полагая в (Д) х = у = А с, найдем, что
и т. д. Так, последовательно (математическая индукция!), получим и общее соот-
соотношение
f(—c]=cos — e (w= 1,2, 3, ...)• A4)
Наконец, повторяя тот процесс, с помощью которого мы, отправляясь от A2),
пришли к A3), мы из A4) придем к равенству
/ т \ т
/ — с = cos — 0.
J \2n ) 2п
Итак, для положительных значений х вида ^ имеем:
f(cx) = cos вх. A5)
Но так как любое положительное число х можно представить как предел зна-
значений этого вида, то, с помощью предельного перехода (и опираясь на непре-
непрерывность функций f(x) и cosjc), установим справедливость формулы A5) для
182 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [77
всех х > 0. Для х < 0 она будет верна в силу A1), а для х = 0 — в силу A0).
Если заменить вA5)^на|и положить ^ = а, то и получим окончательно:
/(*) = COS Я*.
В случае (/3) имеем: /(с) > 1; тогда найдется такое в, что
/(с) = chfl.
Повторяя дословно все проведенные только что рассуждения и опираясь на соот-
соотношения для гиперболического косинуса, совпадающие по форме с соответству-
соответствующими соотношениями для тригонометрического косинуса, мы для рассматрива-
рассматриваемого случая найдем, что
/(*) = chax (a > 0).
При а = 0 по обеим формулам получили бы: f[x) = 1.
Функциональные уравнения (А), (Б), (В), (Г) и (Д) впервые были рассмот-
рассмотрены К о ш и, который и дал их решения в непрерывных функциях.
77. Использование непрерывности функций для вычисления пределов. Не-
Непрерывность функций многообразно может быть использована при вычислении
пределов. *) Примерам этого рода мы посвящаем настоящий номер.
1) Имеем, при любом вещественном х9
П;
Действительно, рассматриваемое выражение (считая х Ф 0) можно представить
в виде
1 + -
п
Так как | —>> 0, то варианта в квадратных скобках стремится к е [54, A3)], а тог-
тогда — ввиду непрерывности степенной функции (здесь х = const) — все
выражение имеет пределом ех.
2) Найти предел
lim <^ у/(х + а\)(х + а2) . . . (х + я^) — х \ (со — со),
где а\, B2, . . ., ак суть данные постоянные числа.
Воспользуемся тождеством
куда подставим
У = y(x+ai)...(x+ak) и z=x.
*^ Фактически мы иной раз это делали и раньше; так, в примере 3), 56, мы
попутно установили непрерывность ^/х при х = 1 и использовали ее, а в приме-
примере 5), (б), так же поступили по отношению к cosjc при х = 0.
77] § 4. НЕПРЕРЫВНОСТЬ (И РАЗРЫВЫ) ФУНКЦИЙ 183
Тогда рассматриваемое выражение представится последовательно в виде
(х + сц) . . . (х + ак) -хк
+х
При .х —>* +оо подкоренное выражение стремится к 1, следовательно, сам корень
имеет пределом л/Т =1 — ввиду непрерывности корня как частного случая
степенной функции. Так как многочлен (к — 1)-й степени (от корня), стоящий
в знаменателе, также есть непрерывная функция, то знаменатель стремится к к,
а предел всей дроби будет
а\ + а2 + . . . + ак
к '
3) Вернемся к предложению в 33,13). Пусть ап > О и ап —>> я; ограничим-
ограничимся пока допущением, что 0 < а < +оо. Применим упомянутое предложение
к последовательности {lnaw}.
Так как \пап —>> In я (в силу непрерывности логарифмической функ-
функции), то
г л . r lnai+ ...+1па„
limIn tfa\ . . . ап = lim = In a.
n
В таком случае — по непрерывности показательной функции —
С помощью пределов 1) и 2), 54, этот результат распространяется и на случай
а = 0 и а = +оо.
Таким образом, мы получаем следующее преобразование упомянутого пред-
предложения:
Если положительная варианта ап имеет предел {конечный или нет),
то тот же предел имеет и варианта
bn = \/ci\ • a2 . . . an.
4) Применив это предложение к последовательности
а2 яз ап ап+1
а\, —, —, ..., , ,
а\ а2 ап-\ ап
придем к интересному следствию:
lim ^fa^ = lim ¦
ап
в предположении лишь, что существует второй из этих пределов.
Найдем для примера предел
п/~\
Л. vn\
lim .
п
184 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [77
п\
Полагая ап = —, будем иметь
пп
Значит, и искомый предел есть -.
е
5) Установим ряд важных пределов, которые понадобятся
нам в следующей главе:
• logfl(l + <*) _л (О
а - 1
(б) lim = In a
а
A + аУ-1
(в) lim = /л
Имеем
logfl(l
а
так как выражение, стоящее справа под знаком логарифма, при
а —>> 0 стремится к е [54, A3)], то (по непрерывности логариф-
логарифмической функции) его логарифм стремится к \oga е, что и тре-
требовалось доказать.
Отметим частный случай доказанной формулы, когда речь идет
о натуральном логарифме {а = е):
1пA+а) _
а—И) а
В простоте этого результата и коренятся, по существу, те
преимущества, которые представляет натуральная система лога-
логарифмов.
Обращаясь к формуле (б), положим аа — 1 = /3; тогда при а —»> О
(по непрерывности показательной функции) и /3 —>> 0.
Имеем, далее, а = loga A + /3), так что, если воспользоваться
уже доказанным результатом:
lim = lim = = 1пя,
a^o a /^ologa(l+/3) logae
что и требовалось доказать.
78] § 4. НЕПРЕРЫВНОСТЬ (И РАЗРЫВЫ) ФУНКЦИЙ 185
Если, в частности, взять а = ^ (п = 1, 2, 3, ...), то получится
интересная формула:
lim п(</а - 1) =Ыа (оо-0).
Наконец, для доказательства формулы (в), положим
A + а)и — 1 = /3; при а —>> 0 (по непрерывности степенной
функции) будет и /3 —>> 0. Логарифмируя равенство A+а)и = 1+/3,
получим, что
\х - 1пA + а) = 1пA + /3).
С помощью этого соотношения преобразуем данное нам выраже-
выражение так:
{\ + аУ-\_р_ /3 1пA + а)
а а 1пA + Р) а '
По доказанному, оба отношения
Р 1пA + а)
- C) а
стремятся к 1, так что все произведение имеет пределом \х9 что
и требовалось доказать.
Предел, рассмотренный в 56,3), получается отсюда как частный
случай при \х — г.
78. Степенно-показательные выражения. Рассмотрим теперь
степенно-показательное выражение uv9 где и и v являются
функциями от одной и той же переменной х9 с областью измене-
изменения ЭС9 имеющей точку сгущения хо; в частности, это могут быть
две варианты ип и vn.
Пусть существуют конечные пределы:
lim и — а и lim v = b,
х—)а:о х—)а:о
причем а > 0. Требуется найти предел выражения uv.
Представим его в виде
uv = ev'lnu.
Функции v и In и имеют пределы
lim v = b, lim Inu = In a
x^^xq x—)a:o
186 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [79
(здесь использована непрерывность логарифмической функ-
функции), так что
lim vlnu = blna.
х—^х0
Отсюда — по непрерывности показательной функции —
окончательно:
lim uv = еЬЛпа = ab.
х—^х0
Предел выражения uv можно установить и в других случаях,
когда известен предел с произведения vlnu — ко-
конечный или бесконечный. При конечном с искомый предел будет,
очевидно, ес\ если же с = — оо или +оо, то этот предел, соответ-
соответственно, будет 0 или +оо [54,1)].
Самое же определение предела с — lim{t> In и) — лишь по за-
заданным пределам а и b — возможно всегда, кроме случаев, когда
это произведение (при х —>> хо) представляет неопределенность ви-
вида сю • 0. Легко сообразить, что исключительные случаи отвечают
таким комбинациям значений а и Ь:
а = 1, Ъ = ±оо;
а = 0, 6 = 0;
а = +оо, Ъ = 0.
В этих случаях говорят, что выражение uv представляет неопре-
неопределенность вида 1°°, 0°, оо°*} (смотря по случаю). Для решения
вопроса о пределе выражения uv здесь мало знать лишь пределы
функций и и v9 а нужно непосредственно учесть закон, по кото-
которому они стремятся к своим пределам.
Варианта (l + ^) , при п —> оо, или более общее выражение A + а)", при
а —>> 0, имеющие пределом е, дают пример неопределенности вида 1°°. Выше,
в 77,4), мы рассматривали варианту а ^ = (^r)w, представляющую неопре-
неопределенность вида 0 . Наконец, в 32,10), выражение у/п тоже было неопределен-
неопределенным — вида оо°.
Приведем еще несколько примеров на раскрытие неопределенностей новых
видов.
79. Примеры.
1) Найти lim (In*)* (oo°).
*) Относительно самих этих символов можно было бы повторить сказанное
в сноске на с. 72.
79] § 4. НЕПРЕРЫВНОСТЬ (И РАЗРЫВЫ) ФУНКЦИЙ 187
Обозначая данное выражение через у, имеем [54,2) и 5)]
ln(ln*) In (In*) In* f°°\
* In* * \oo/ '
так что у —>> e = 1.
2) Найти lim *smx @°).
jc-И)
Здесь [54,7) и 5I
L J n sin*
lnj/ = sin* • In* = • * In* —>> 0,
*
следовательно, опять;; —>> 1.
3) Пример 1),76, легко теперь следующим образом обобщить: если ва-
варианта хп —>> х (где * — конечное число), то
lim ( 1 -\—-
«-5>+оо \ п
Для доказательства достаточно представить предложенное выражение в виде
w "I *w
7I =
основание степени стремится здесь к е, показатель же — к *.
4) К этому можно привести и пример:
lim (cos-+Asin-V = еЯх A°°).
п^+оо \ п П/
Полагая выражение в скобках равным 1 + ^f, имеем
[* * 1 sin j- I — cos jr
cos 1 + Я sin — = Я* — — * — —> Я*,
n n\ I I
и т. д.
5) Аналогично исчерпывается пример (a, b > 0)
lim
Здесь
так что, на основании одного частного следствия из формулы 5), (б), 77,
хп —>> — (In a + In Ъ) = In л/ab,
и искомый предел, действительно, оказывается равным е n = y/ab.
6) Наконец, рассмотрим предел
1 - Лт .1
2 cos — J-
Hm(cos*)sm2x = lim l2sin
x^O x^o[V 2 J
Читатель видит, что в случае неопределенности вида 1°° удобно приводить
дело непосредственно к е.
Как уже указывалось, общие методы раскрытия неопределенностей всех
видов будут даны в главе IV [§4].
188
ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
§ 5. Свойства непрерывных функций
[80
80. Теорема об обращении функции в нуль. Займемся теперь
изучением основных свойств функции, непрерывной в некотором
промежутке. Интересные и сами по себе, эти свойства в дальней-
дальнейшем изложении часто будут служить основой для различных умо-
умозаключений.
Начнем со следующей простой теоремы, принадлежащей
Больцано (В. Bolzano) и Коши (A.L. Cauchy).
Первая теорема Болъцано-Коши. Пусть функция f{x) оп-
определена и непрерывна в замкнутом промежутке [а,Ь] и на
концах этого промежутка принимает значения разных
знаков. Тогда между а и Ъ необходимо найдется точка с,
в которой функция обращается в нуль:
/(с) = 0 {а < с < Ъ).
Теорема имеет очень простой геометрический смысл: если не-
непрерывная кривая переходит с одной стороны оси х на другую, то
она пересекает эту ось (рис. 31).
Л«)<0
Рис.31
1-е доказательство мы проведем по методу Больца-
Больцано [41] — последовательным делением промежутка. Для опреде-
определенности положим, что f(a) < 0, a f(b) > 0. Разделим промежу-
промежуток [а, Ь] пополам точкой ^^. Может случиться, что функция f(x)
обратится в нуль в этой точке, тогда теорема доказана: можно по-
положить с = ^^. Пусть же f(a^-) ф 0; тогда на концах одного из
промежутков [a, q^-]9 \^y~, b] функция будет принимать значения
разных знаков (и притом отрицательное значение на левом
конце и положительное — на правом). Обозначив этот промежуток
через [йь&1], имеем
/(ai) < 0, f{bx) > 0.
80] § 5. СВОЙСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ 189
Разделим пополам промежуток [ai,&i] и снова отбросим тот
случай, когда f(x) обращается в нуль в середине а1^ * этого про-
промежутка, ибо тогда теорема доказана. Обозначим через [#2, Ъ?\ ту
из половин промежутка, для которой
/(а2) < 0, f(b2) > 0.
Продолжим этот процесс построения промежутков. При этом
либо мы после конечного числа шагов наткнемся в качестве точки
деления на точку, где функция обращается в нуль, — и доказатель-
доказательство теоремы завершится, — либо получим бесконечную после-
последовательность вложенных один в другой промежутков. Остановим-
Остановимся на этом последнем случае. Тогда для /7-го промежутка [ап, Ъп]
(п = 1, 2, 3, ...) будем иметь
f(an) < О, f(bn) > О, A)
причем длина его, очевидно, равна
Ьп-ап = —^г. B)
Построенная последовательность промежутков удовлетворяет
условиям леммы о вложенных промежутках [38], ибо,
ввиду B), lim(bn - ап) = 0; поэтому существует точка с из проме-
промежутка [а,Ь]9 для которой
liman = limbn = с.
Покажем, что именно эта точка удовлетворяет требованию тео-
теоремы.
Переходя к пределу в неравенствах A) и используя при этом
непрерывность функции (в частности, в точке х = с), полу-
получим, что одновременно
/(с) = limf{an) < 0 и Дс)=Шп/Fя)^0,
так что, действительно, /(с) = 0. Теорема доказана.
Мы дадим ниже второе доказательство теоремы Коши, по-
построенное на другой идее. Предпошлем ему следующее очевидное
предположение:
Лемма. Если функция f(x) непрерывна в точке х = хо
и значение /(хо) отлично от 0, то для всех достаточно
близких к хо значений х функция f(x) сохраняет тот же
знак, какой она имеет в точке xq.
190 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [81
Это вытекает из утверждения 2° в 55, I, причем в данном слу-
случае роль предела А функции (именно ввиду непрерывности)
играет /Оо).
П-е доказательство. Рассмотрим все те точки х = х
промежутка [а, Ь]9 для которых fix) < 0. К их числу, например,
относятся точка а и (в силу леммы) близлежащие к ней точки.
Множество {х} ограничено сверху числом Ъ. Положим теперь
с — sup {х} [11]; мы утверждаем, что /(с) = 0.
Действительно, допустим противное; тогда либо /(с) < 0, либо
/(с) > 0. Если бы было /(с) < 0 (тогда заведомо с < Ъ, ибо нам
дано, что f(b) > 0), то — по лемме — и правее с нашлись
бы значения х, для которых fix) < 0, а это противоречило бы
определению с как верхней границы для {х}. Если же было
бы /(с) > 0, то — снова на основании леммы — имели бы fix) > 0
и вблизи с слева, именно — в некотором достаточно малом
промежутке (с — 8, с], а тогда там вовсе не было бы значений х, что
также невозможно, ибо с, по определению, есть точная верхняя
граница для {х }.
Теорема доказана.
Заметим, что требование непрерывности функции fix)
в замкнутом промежутке [а, Ь] существенно: функция, имеющая
разрыв хоть в одной точке, может перейти от отрицательного зна-
значения к положительному и не обращаясь в 0. Так будет, например,
с функцией /(х) = Е{х) — ^, которая нигде не принимает значе-
значения 0, хотя /@) = —^, а /A) = \ (скачок при х = 1).
81. Применение к решению уравнений. Доказанная теорема имеет приме-
применение при решении уравнений.
Прежде всего, с ее помощью устанавливается существование кор-
корней. Например, для всех очевиден корень х = 4 уравнения
2х = 4х,
но труднее заметить существование еще одного корня. А между тем, функция
fix) = 2х — Ах при х = 0 принимает значение /@) = 1 > 0, а при х = \ —
значение / (^) = л/2 — 2 < 0, следовательно (так как она непрерывна), обраща-
обращается в 0 в некоторой точке между 0 и ^.
Другой пример: рассмотрим, вообще, алгебраическое уравнение нечетной
степени (с вещественными коэффициентами)
fix) = аох п+ + а\х " + •••+ а2пх + «2и+1 = 0.
При достаточно больших по абсолютной величине значениях х многочлен имеет
знак старшего члена, т. е. при положительном х — знак а$, а при отрицатель-
отрицательном х — обратный знак. Так как многочлен есть непрерывная функция, то, меняя
82] § 5. СВОЙСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ 191
знак, он в промежуточной точке необходимо обращается в 0. Отсюда: всякое
алгебраическое уравнение нечетной степени (с вещественными коэффици-
коэффициентами) имеет по крайней мере один вещественный корень.
Теоремой К о ш и можно пользоваться не только для установления сущест-
существования корня, но и для приближенного его вычисления. Поясним это примером.
Пусть f(x) = х4 — х — 1. Так как /A) = —1, /B) = 13, то многочлен имеет
корень между 1 и 2. Разделим этот промежуток [1,2] на 10 равных частей
точками 1,1; 1,2; 1,3; ... и станем последовательно вычислять:
/A,1) = -0,63 . . .; /A,2) = -0,12 . . .; /A,3) = +0,55 . . .; ...
Видим, что корень содержится между 1,2 и 1,3. Разделив и этот промежуток
на 10 частей, найдем:
/A,21) = -0,06 . . .; /A,22) = -0,004. . .; /A,23) = +0,058 . . .; ...
Теперь ясно, что корень лежит между 1,22 и 1,23; таким образом, мы уже зна-
знаем значение корня с точностью до 0,01 и т. д. * ^ В свете этих замечаний интересно
сопоставить изложенные выше два доказательства одной и той же теоремы. Вто-
Второе из них является только «доказательством существования» корня уравнения
f(x) = 0, ничего не говоря о том, как корень найти. Первое же намечает опреде-
определенный путь к реальному вычислению корня: путем последовательного деления
промежутка пополам (чем мы для простоты ограничились) можно в действи-
действительности заключить искомый корень в промежуток произвольно малой длины,
т. е. вычислить этот корень с произвольной степенью точности.
82. Теорема о промежуточном значении. Доказанная в 80
теорема непосредственно обобщается следующим образом:
Вторая теорема Болъцано-Коши. Пусть функция f(x) оп-
определена и непрерывна в некотором промежутке SC {замк-
{замкнутом или нет, конечном или лее бесконечном). Если в двух
точках х — а и х — Ъ (а < Ъ) этого промежутка функция
принимает неравные значения
f(a)=A и f(b)=B,
то, каково бы ни было число С, лежащее между А и В,
найдется такая точка х — с между а и Ъ, что
f(c)=C**K
*) Впрочем, практически этот путь невыгоден. В главе IV (§5) будут указаны
гораздо более эффективные приемы.
**) Очевидно, что первая теорема Больцано-Коши есть частный случай
этой: если А и В — разных знаков, то в качестве С можно взять и 0.
192 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [82
Доказательство. Будем считать, например,
А < В, так что А < С < В.
Рассмотрим в промежутке [а, Ь] вспомогательную функцию
ср(х) = /(х) — С. Эта функция непрерывна в промежутке [а, Ь]
и на концах его имеет разные знаки:
ф) = /(а) -С=А-С<0, <р{Ь) = f{b) -C = B-C>0.
Тогда, по первой теореме Больцано-Коши, между а и b най-
найдется точка х = с, для которой ср(с) = 0, т. е.
/(с)-С = 0 или f(c)=C,
что и требовалось доказать.
Мы установили, таким образом, важное свойство функции /(х),
непрерывной в промежутке: переходя от одного своего значения
к другому, функция хоть раз принимает, в качестве значения,
каждое промежуточное число.
Иными словами это свойство можно выразить и так: значения,
принимаемые непрерывной функцией f(x), когда х изменя-
изменяется в каком-либо промежутке SC, сами также заполняют
сплошь некоторый промежуток *?.
Действительно, пусть
/и = inf {/(*)}, M=sup{/(x)}*>
и у о есть произвольное число между т и М:
т < у о < М.
Необходимо найдутся такие значения функции у\ = f(x\)
и у2 = f{x2) (x\ и Х2 взяты из промежутка 5Г), что
это вытекает из самого определения точных границ числового
множества. Но тогда, по доказанной теореме, существует меж-
между xi и Х2 такое значение х = хо (очевидно, также принадлежа-
принадлежащее «2Г), что /(хо) в точности равно у о', следовательно, это число
входит в множество °^.
* ^ Напоминаем читателю, что если множество {f(x)} не ограничено сверху
(снизу), то мы условились в 11 полагать М = +оо (т = — оо).
83] § 5. СВОЙСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ 193
Таким образом, *? представляет собой промежуток с кон-
концами т и М (которые сами могут ему принадлежать или нет —
смотря по случаю [ср. 84]).
Мы видели в 71,2°, что в случае монотонной функции упомя-
упомянутое свойство, обратно, влечет за собой непрерывность. Однако
не следует думать, что так будет всегда; легко построить заведо-
заведомо разрывные функции, которые все же этим свойством обладают.
Например, значения функции [70, 4)]:
Д*) = яп- {хфЪ), Д0) = 0,
X
когда х изменяется в каком-либо промежутке, содержащем точку
разрывах = 0, заполняют сплошь промежуток [—1, +1].
83. Существование обратной функции. Применим изученные
в предыдущем п° свойства непрерывной функции к установлению,
при некоторых предположениях, существования однозначной
обратной функции и ее непрерывности [ср. 49].
Теорема. Пусть функция у = f{x) определена, монотонно
возрастает {убывает) *} и непрерывна в некотором проме-
промежутке ЭС. Тогда в соответствующем промежутке °^ зна-
значений этой функции существует однозначная обратная
функция х = g(y), также монотонно возрастающая {убываю-
{убывающая) и непрерывная.
Доказательство. Ограничимся случаем возрастающей
функции. Мы видели выше, что значения непрерывной функ-
функции f{x) заполняют сплошь некоторый промежуток ^, так что
для каждого значения у о из этого промежутка найдется хоть
одно такое значение хо (из «2Г), что
/Оо) =уо-
Но ввиду монотонности этой функции такое значение может най-
найтись только одно: если х\ > или < хо, то, соответственно,
и/Oi) > или < /(хо).
Сопоставляя именно это значение хо произвольно взятому у о
из *$/, мы получим однозначную функцию
х =g(y),
обратную для функции у = f{x).
В строгом смысле слова (это здесь существенно).
194
ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
[83
У-
Легко видеть, что эта функция g(y)9 подобно /(х), также моно-
монотонно возрастает. Пусть
у'<у" и x'=g(y'), x" = g(y");
тогда, по самому определению функции g(y)9 одновременно
/=/(*') и y" = f{x").
Если бы было х1 > х/;, то, в силу возрастания функции /(х), было
бы и у1 > у", что противоречит условию. Не может быть их7 = х/;,
ибо тогда было бы и yf = у", что также противоречит условию.
Итак, возможно только неравенство х' < х", так что g(y)9 действи-
действительно, возрастает.
Наконец, чтобы доказать непрерывность функции х = g{y)9
достаточно сослаться на теорему в 71, 2°, условия которой вы-
выполнены: названная функция монотонна, и ее значения, очевидно,
заполняют сплошь промежуток SC. *) Все утверждения теоре-
теоремы геометрически оче-
очевидны, их легко «прочи-
«прочитать» по рис. 32.
С помощью доказан-
доказанной теоремы можно на-
наново установить ряд уже
известных нам результа-
результатов.
Если применить ее
к функции хп (п — на-
х туральное число) в про-
промежутке SC = [0, +оо),
то придем к существо-
существованию и непрерывности
(арифметического) корня х = tfy для у в <? = [0, +оо). Исхо-
Исходя из функции у = ах в промежутке SC = (—оо, +оо), докажем
существование и непрерывность логарифма х = log^j в проме-
промежутке *? = @, +оо). Наконец, рассматривая функции у = sinx
и у — tgx, первую — в промежутке ЭС\ — [-§, §], а вторую —
в открытом промежутке ЗСъ — (— §, §), убедимся в существовании
и непрерывности обратных им функций х = arcsinj и х = arctgj,
соответственно, в промежутках °!/\ = [— 1, +1] и ^2 = (—сю, +оэ).
Рис. 32
*) Какое бы х из J ни взять, стоит лишь положить у = /(х), чтобы для
этого у функция g(y) имела своим значением именно взятое х.
84] § 5. СВОЙСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ 195
[При этом предполагается, что предварительно уже доказа-
доказана непрерывность функций хп9 ах, sinx, tgx — без ссылки на
существование обратных им функций (иначе получился бы
порочный круг). Такие доказательства и были даны в 68; соображе-
соображения же п° 72, очевидно, здесь непригодны.]
Рассмотрим еще такой пример.
Пусть для х из SC = ( —оо, +оо)
у = х — е • sin.*, где 0 < е < 1. C)
Легко показать, что эта функция будет монотонно возрастающей (в узком смыс-
смысле). Именно, если х" > х' nyf9yff — соответствующие значения у, то
У — у = [X — X ) — ?(SlIlJf — SillJK ).
Но [см. B), 68]
sin*" — sin*'] < x" — х',
откуда и следует, что
// / г, II I
у — у > О, т. е. у > у .
Применив к этому случаю теорему, убеждаемся в том, что и х является
однозначной функцией от у, и т. д.
Приведенный пример представляет интерес тем, что соприкасается с одной
задачей теоретической астрономии. Уравнение
Е = M+?-sinE (За)
есть знаменитое уравнение Кеплера, которое связывает среднюю ано-
аномалию М планеты с ее эксцентрической аномалией Е (е есть эксцентриситет
планетной орбиты). Мы доказали, таким образом, что, каково бы ни было значение
средней аномалии, уравнение Кеплера, действительно, однозначно определяет
значение эксцентрической аномалии.
84. Теорема об ограниченности функции. Если функция f(x)
определена (следовательно, принимает конечные значения) для
всех значений х в некотором конечном промежутке, то это не вле-
влечет за собой с необходимостью ограниченности функции,
т. е. ограниченности множества {/(*)} принимаемых ею значений.
Например, пусть функция f(x) определена так:
f{x) = -, если 0 < х < 1, и ДО) = 0.
Функция эта принимает только конечные значения, но она не огра-
ограничена, ибо при приближении х к 0 может принимать сколь угодно
большие значения. Заметим попутно, что в полуоткрытом проме-
промежутке @, 1] она непрерывна, но в точке х = 0 имеет разрыв.
Иначе обстоит дело с функциями, непрерывными в замк-
замкнутом промежутке.
196 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [85
Первая теорема Вейерштрасса. Если функция /(х) опреде-
определена и непрерывна в замкнутом промежутке [а, Ь], то она
ограничена, т. е. существуют такие постоянные и конечные
числа т и М, что
т ^ /(х) ^ М при а ^ х ^ Ъ.
Доказательство поведем от противного: допустим, что
функция /(х) при изменении х в промежутке [а, Ь] оказывается
неограниченной.
В таком случае для каждого натурального числа п найдется
в промежутке [а, Ь] такое значение х = хП9 что
\f(x ) I > n D)
\J \лп)\ ^ п- V v
По лемме Больцано-Вейерштрасса [41], из после-
последовательности {хп} можно извлечь частичную последователь-
последовательность {хщ}, сходящуюся к конечному пределу:
хщ -л хо (при к -л +оо),
причем, очевидно, а ^ хо ^ Ь. Вследствие непрерывности функции
в точке хо, тогда должно быть и
/(хщ) -»/(хо),
а это невозможно, так как из D) следует, что
Полученное противоречие и доказывает теорему.
85. Наибольшее и наименьшее значения функции. Мы знаем,
что бесконечное числовое множество, даже ограниченное, мо-
может не иметь в своем составе наибольшего (наименьшего)
элемента. Если функция /(х) оп-
* ределена и даже ограничена в не-
некотором промежутке изменениях,
то в составе множества ее зна-
^х чений {/(х)} может не оказать-
оказаться наибольшего (наимень-
Рис. 33 шего). В этом случае точная
верхняя (нижняя) граница значе-
значений функции f(x) не достигается в названном промежутке.
Так будет обстоять дело, например, с функцией
f(x)=x-E(x)
(график ее представлен на рис. 33). При изменении х в любом про-
промежутке [О, Ь] (Ъ ^ 1), точной верхней границей значений функ-
85] § 5. СВОЙСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ 197
ции будет 1, но она не достигается, так что наибольшего значения
функция не имеет.
Читателю, вероятно, ясна связь этого обстоятельства с нали-
наличием у рассматриваемой функции разрывов при натуральных
значениях х. Действительно, для непрерывных в замкну-
замкнутом промежутке функций имеет место:
Вторая теорема Вейерштрасса. Если функция /(х) опре-
определена и непрерывна в замкнутом промежутке [а,Ь], то
она достигает в этом промежутке своих точных верхней
и нижней границ.
Иными словами, в промежутке [а, Ь] найдутся такие точки
х = хо и х —х\, что значения /(хо) и f{x\) будут, соответ-
соответственно, наибольшим и наименьшим из всех значений
функции /(х).
1-е доказательство. Положим
M=sup{/(x)};
по предыдущей теореме, это число — конечное. Предположим (во-
(вопреки тому, что нужно доказать), что всегда /(х) < М, т. е. что гра-
граница М не достигается. В таком случае, можно рассмотреть вспо-
вспомогательную функцию
Так как, по предположению, знаменатель здесь в нуль не обраща-
обращается, то эта функция будет непрерывна, а следовательно (по пре-
предыдущей теореме) ограничена: ср(х) ^ \х (/л > 0). Но отсюда легко
получить, что тогда
т. е. число М — -, меньшее, чем М, оказывается верхней гра-
границей для множества значений функции /(х), чего быть не может,
ибо М есть точная верхняя граница этого множества. По-
Полученное противоречие доказывает теорему: в промежутке [а, Ь]
найдется такое значение хо, что /(хо) = М будет наибольшим
из всех значений /(х).
Аналогично может быть доказано утверждение и относительно
наименьшего значения.
198 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [85
II-е доказательство. Можно и здесь исходить из леммы
Больцано-Вейерштрасса [41]. Ограничимся утверждением
о наибольшем значении. Если, как и только что,
M=sup{/(x)},
то, по свойству точной верхней границы [11], для любого п
найдется такое х = хп в [а, Ь]9 что
f(Xn)>M-1-. E)
Тогда из последовательности {хп} может быть извлечена час-
частичная последовательность {хщ}, сходящаяся к некоторому значе-
значению хо из [а,Ь]: хщ —»> хо, так что, ввиду непрерывности функции, и
/Ы ->Д*о).
В то же время из E) имеем
/(хщ) > М и, в пределе, /(х0) ^ М.
Щ
Но /(хо) не может быть больше верхней границы М множества
значений функции, и следовательно,
/(хо) = М,
что и требовалось доказать.
Отметим, что оба приведенные доказательства суть чистые «до-
«доказательства существования». Средств для вычисления, например,
значения х = хо никаких не дано. Впоследствии [в главе IV, § 1],
правда, при более тяжелых предположениях относительно функ-
функции, мы научимся фактически находить значения независимой пере-
переменной, доставляющие функции наибольшее или наименьшее зна-
значения.
Если функция /(х), при изменении х в каком-либо промежут-
промежутке «2Г, ограничена, то ее колебанием в этом промежутке назы-
называется разность
со = М — т.
Иначе можно определить колебание со как точную верхнюю
границу множества всевозможных разностей f(x") — /(х;), где х'
их" принимают независимо одно от другого произвольные значе-
значения в промежутке ЗС\
со= sup {/(*")-/(*')}¦
х7, х" из дС
86]
§ 5. СВОЙСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ
199
Когда речь идет о непрерывной функции f(x) в замк-
замкнутом конечном промежутке ЭС — [а, Ь]9 то, как следует из до-
доказанной теоремы, колебанием будет попросту разность меж-
между наибольшим и наименьшим значениями функции
в этом промежутке.
В этом случае промежуток *? значений функции есть
замкнутый промежуток [т,М]9 и колебание дает его длину.
86. Понятие равномерной непрерывности. Если функция f(x)
определена в некотором промежутке SC (замкнутом или нет, ко-
конечном или бесконечном) и непрерывна в точке хо этого проме-
промежутка, то
lim f{x) = /(хо)
или [«на языке е-8»9 66]: для каждого числа е > О найдется
такое число 8 > О, что
\х — хо| < <5 влечет за собой \/(х) -/(хо)| < ?-
Предположим теперь, что функция f(x) непрерывна во всем
промежутке ЭС9 т. е. непрерывна в каждой точке хо этого проме-
промежутка. Тогда для каждой точки хо из ЭС в отдельности по
заданному г найдется 8,
соответствующее ему в
упомянутом выше смыс-
смысле. При изменении хо
в пределах ЭС9 даже если
е неизменно, число 89 во-
вообще говоря, будет ме-
меняться. Одного взгляда
на рис. 34 достаточно,
чтобы убедиться в том,
что число 5, пригодное
на участке, где функция
изменяется медленно
(график представляет
пологую кривую), мо-
может оказаться слишком большим для участка быстрого изменения
функции (где график круто поднимается или опускается). Иными
словами, число 8 вообще зависит не только от г, но и от хо.
Если бы речь шла о конечном числе значений хо (при
неизменном г), то из конечного числа соответствующих им чисел 8
200 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [86
можно было бы выбрать наименьшее, и это последнее годилось бы,
очевидно, и для всех рассматриваемых точек хо одновременно.
Но по отношению к бесконечному множеству значенийхо,
содержащихся в промежутке «2Г, так уже рассуждать нельзя: им
(при постоянном е) соответствует бесконечное множество чисел 8,
среди которых могут найтись и сколь угодно малые. Таким обра-
образом, по отношению к функции /(х), непрерывной в промежутке «2Г,
встает вопрос: существует ли, при заданном е9 такое 89 которое го-
годилось бы для всех точек хо из этого промежутка?
Если для каждого числа е > 0 найдется такое число S > 0,
что
\
\х —
< о влечет за содой \j(x) — j(xo)\ <
где бы в пределах рассматриваемого промежутка SC ни
лежали точки хо и х, то функцию /(х) называют
равномерно непрерывной в промежутке 30.
В этом случае число 8 оказывается зависящим только от е и мо-
может быть указано до выбора точки хо: 8 годится для всех хо
одновременно.
Равномерная непрерывность означает, что во всех частях про-
промежутка достаточна одна и та же степень близости двух значений
аргумента, чтобы добиться заданной степени близости соответству-
соответствующих значений функции.
Можно показать на примере, что непрерывность функции
во всех точках промежутка не влечет необходимо за собой ее
равномерной непрерывности в этом промежутке. Пусть, напри-
например, /(х) = sin^ для х, содержащихся между 0 и -|, исключая 0.
В этом случае область изменения х есть незамкнутый проме-
промежуток @, ^],ив каждой его точке функция непрерывна. Положим
теперь хо = пп+1)ж9 х ~ mi (где п — любое натуральное число);
тогда
/(хо) = sinB/7 + 1) — = ±1, /(х) = sin/7jr = 0,
так что
несмотря на то что |х -хо| = „^h+iw с В03Растанием п может быть
сделано сколь угодно малым. Здесь при г = 1 нельзя найти 8, кото-
которое годилось бы одновременно для всех точек хо в @, -|], хотя для
каждого отдельного значения хо, ввиду непрерывности функции,
такое 8 существует!
87] § 5. СВОЙСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ 201
Весьма замечательно, что в замкнутом промежутке [а, Ь]
аналогичного положения вещей быть уже не может, как явствует
из следующей теоремы, принадлежащей Кантору (G. Cantor).
87. Теорема Кантора. Если функция /(х) определена и не-
непрерывна в замкнутом промежутке [а,Ь], то она и рав-
равномерно непрерывна в этом промежутке.
Доказательство поведем от противного. Пусть для некото-
некоторого определенного числа г > 0 не существует такого числа
8 > 0, о котором идет речь в определении равномерной непрерыв-
непрерывности. В таком случае, какое бы число 8 > 0 ни взять, найдутся
в промежутке [а, Ь] такие два значения Xq их7, что
|х; — x'q\ < 8, и тем не менее \f{xf) — /(^о)| ^ ?•
Возьмем теперь последовательность {8п} положительных чисел
так, что 8п —>> 0.
В силу сказанного, для каждого 8п найдутся в [а,Ь] зна-
значения Xq и jcW (они играют роль Xq и х'), такие, что
(при п = 1,2, 3, ...)
\х(п' — Xq | < 8п, и тем не менее \/(х^) — /(xq) \ ^ ?•
По лемме Больцано-Вейерштрасса [41] из ограничен-
ограниченной последовательности {х М } можно извлечь частичную последо-
последовательность, сходящуюся к некоторой точке хо промежутка [а,Ь].
Для того чтобы не осложнять обозначений, будем считать, что уже
сама последовательность {х^} сходится к хо-
Так как х^> - Xq —»> 0 (ибо |х^ - Xq | < 8П9 а 8п —>> 0), то
одновременно и последовательность {xq } сходится к хо- Тогда,
ввиду непрерывности функции в точке хо, должно быть
И f( X ) ~
так что
а это противоречит тому, что при всех значениях п
Теорема доказана.
202 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [88
Из доказанной теоремы непосредственно вытекает такое след-
следствие, которое ниже будет нам полезно:
Следствие. Пусть функция f(x) определена и непрерывна
в замкнутом промежутке [а,Ь]. Тогда по заданному е > 0
найдется такое S > 0, что если промежуток произвольно
разбить на частичные промежутки с длинами, меньшими 8,
то в каждом из них колебание функции f{x) будет меньше с.
Действительно, если, по заданному ?, в качестве 8 взять число,
о котором говорится в определении равномерной непрерывности,
то в частичном промежутке с длиной, меньшей 8, разность меж-
между любыми двумя значениями функции будет по абсолютной ве-
величине меньше е. В частности, это справедливо и относительно
наибольшего и наименьшего из этих значений, разность
которых и дает колебание функции в упомянутом частичном про-
промежутке [85].
88. Лемма Бореля. Мы докажем сейчас одно интересное вспо-
вспомогательное утверждение, которое — подобно лемме Боль-
цано-Вейерштрасса — может быть полезно при проведе-
проведении многих тонких рассуждений; оно принадлежит Борелю
(Е. Borel).
Рассмотрим, наряду с промежутком [а, Ь]9 еще некоторую сис-
систему ? открытых промежутков а9 которая может быть как ко-
конечной, так и бесконечной. Условимся говорить, что система!!
покрывает промежуток [а, Ъ] (или что этот промежуток покры-
покрывается системой ?, и т. п.), если для каждой точки х промежут-
промежутка [а, Ъ] найдется в ? промежуток <т, содержащий ее. Этот способ
речи облегчит нам формулировку и доказательство упомянутого
утверждения.
Лемма Бореля. Если замкнутый промежуток [а,Ь] по-
покрывается бесконечной системой ? = {о} открытых про-
промежутков, то из нее всегда молено выделить конечную
подсистему
?* = {Gь <72, . . . , 0У,},
которая также покрывает весь промежуток [а, Ь].
1-е доказательство поведем от противного, применив ме-
метод Больцано [41]. Допустим же, что промежуток [а, Ь] не мо-
может быть покрыт конечным числом промежутков о из ?. Разделим
промежуток [а, Ь] пополам. Тогда хоть одна из половин его тоже
не может быть покрыта конечным числом о\ действительно, если
88] § 5. СВОЙСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ 203
бы одна из них могла быть покрыта промежутками о\, о2, ..., от
(из S), а другая — промежутками crw+i, от+2, ..., оп (из S), то из
всех этих промежутков составилась бы конечная система S*, по-
покрывающая уже весь промежуток [а, Ь]9 вопреки допущению. Обо-
Обозначим через [а\, Ь\] ту половину промежутка, которая не покры-
покрывается конечным числом о (если же обе таковы, то — любую из
них). Этот промежуток снова разделим пополам и обозначим че-
через [#2, йг] ту из его половин, которую нельзя покрыть конечным
ЧИСЛОМ G, И Т. Д.
Продолжая этот процесс неограниченно, мы получим бес-
бесконечную последовательность вложенных промежутков [ап, Ьп]
(п = 1, 2, 3, ...), каждый из которых составляет половину пред-
предшествующего. Промежутки эти все выбираются так,
что ни один из них не покрывается конечным
числом промежутков а. По лемме о вложенных промежут-
промежутках [38], существует общая им всем точка с, к которой стремятся
концы аП9 Ъп.
Эта точка с, как и всякая точка промежутка [а,Ь]9 лежит в од-
одном из промежутков <т, скажем, в &о = (а, /3), так что а < с < р.
Но варианты ап и ЪП9 стремящиеся к с, начиная с некоторого но-
номера будут сами содержаться между а и C [26, 1°], так что опре-
определяемый ими промежуток [ап, Ьп] окажется покрытым всего лишь
одним промежутком о"о, вопреки самому выбору этих промежут-
промежутков [ап, Ьп]. Полученное противоречие и доказывает лемму.
Приведем еще одно доказательство, построенное на новой идее;
она принадлежит Лебегу (Н. Lebesgue).
II-е доказательство. Рассмотрим точки х* промежут-
промежутка [а,Ь]9 обладающие тем свойством, что промежуток [а,х*] по-
покрывается конечным числом промежутков а. Такие точки х*9 во-
вообще, найдутся: так как, например, точка а лежит в одном из о", то
и все близлежащие к ней точки содержатся в этом о и, следова-
следовательно, оказываются точками х *.
Нашей задачей является установить, что и точка Ъ принадлежит
к числу точек х*.
Так как все х* < Ъ9 то существует [11] и
sup{x*} = с < 6.
Как и всякая точка промежутка [а, Ь]9 с принадлежит некото-
некоторому со = (а, /3), а < с < р. Но, по свойству точной верхней
границы, найдется х%9 такое, что а < х$ < с. Промежуток [a, Xq]
204 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [89
покрывается конечным числом промежутков о (по самому
определению точек х*); если к этим промежуткам присоединить
еще лишь один промежуток со, то покроется и весь промежу-
промежуток [а, с], так что с есть одна из точек х*.
Вместе с тем ясно, что с не может быть < Ъ9 ибо иначе между с
и /3 нашлись бы еще точки х*9 вопреки определению числа с как
верхней границы всех х*. Таким образом, необходимо b = с;
значит, Ъ есть одно из х*9 т. е. промежуток [а, Ь] покрывается ко-
конечным числом промежутков а9 что и требовалось доказать.
Заметим, что для справедливости заключения леммы в равной
мере существенно как предположение о замкнутости основ-
основного промежутка [а,Ь]9 так и предположение о том, что промежут-
промежутки а, составляющие систему S, — открытые. Например, система
открытых промежутков
- -) (- -) (- -) (- -
2' 2) ' \49 4/ ' V8' 8У ' "¦¦' \2п' 2п
покрывает промежуток @,1], но из них нельзя выделить
конечной подсистемы с тем же свойством. Аналогично, система
замкнутых промежутков
-}. [- -1. [-.
2 ' 2'4 4'
2» _ 1 2"+1 - 1
и [1,2]
покрывает промежуток [0,2], но и здесь выделение конечной
подсистемы невозможно.
89. Новые доказательства основных теорем. Покажем теперь,
как лемма Б о р е л я может быть использована для доказательства
основных теорем о непрерывных функциях Больцано-Коши,
Вейерштрасса и Кантора.
1° 1-я теорема Болъцано-Коши [80]. На этот раз дока-
доказывать ее будем от противного. Допустим, что — при соблюде-
соблюдении предположения теоремы — все же ни в одной точке функ-
функция f{x) не обращается в нуль. Тогда, по лемме п° 80, каждую
точку х1 промежутка [а, Ь] можно окружить такой окрестностью
о' — {х1 - S', х1 + ?'), что в ее пределах *} f{x) сохраняет опреде-
определенный знак.
*^ То есть в общей части этой окрестности и промежутка [а, Ь], в котором х
только и может изменяться.
89] § 5. СВОЙСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ 205
Бесконечная система Т, = {а} этих окрестностей покрывает,
таким образом, весь данный промежуток [а, Ь]. Тогда, по лемме
Б орел я, для этого оказывается достаточно уже конечного
числа упомянутых окрестностей, образующих систему S*.
Левый конец а нашего промежутка принадлежит одной из
окрестностей этой системы S*, скажем, окрестности о\ = {х\ — 8\,
х\ + 8\). Ее правый конец х\ + 8\9 в свою очередь, принадлежит
xl ! X2 \ ^~? v Г"' Xn .'
Рис. 35
окрестности о2 — {x2 — 82, X2 + 82) из S*, точка X2 + 82 содержит-
содержится в окрестности о"з = (хз — 5з, хз + #з) из S*, и т. д. (рис. 35).
После конечного числа шагов, передвигаясь направо, мы придем к
окрестности оп = (хп — 8п,хп + 8п) из S*, заключающей в себе уже
правый конец Ъ данного промежутка. Если бы S* содержала еще
какие-либо другие промежутки, кроме
О, О, О? •••» O"w» F)
то их, очевидно, можно было бы просто опустить.
В окрестности о\ функция /(х) сохраняет определенный знак,
именно знак /(а). Но ив^ функция имеет определенный знак,
который должен тоже совпадать со знаком /(а), поскольку о\
и о взаимно налегают. Так же убеждаемся в том, что тот же
знак функция сохраняет и в следующей по порядку окрестности оз,
налегающей на G2, и т. д. В конце концов, придем к заключению,
что и в последней окрестности оп функция имеет знак /(а), так
что и f{b) совпадает по знаку с /(а), а это уже противоречит
предположению. Теорема доказана.
2° 1-я теорема Бейерштрасса [84]. Ввиду непрерывно-
непрерывности функции /(х), какую бы точку х промежутка [а, Ь] ни взять,
задавшись числом е > 0, можно окружить эту точку столь малой
окрестностью о1 = (х; — 8\ xf+Sf), чтобы для всех принадлежащих
ей значений х выполнялись неравенства
или
f(x')-e<f(x)<f(x')+e.
206 ГЛ. П. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ [89
Таким образом, в пределах каждой такой окрестности функция f(x)
заведомо ограничена: снизу — числом /(V) — ?, а сверху — чис-
числом /(V) + ?.
Читателю ясно, что и здесь к бесконечной системе S окрестно-
окрестностей, обладающих указанным свойством, надлежит применить лем-
лемму Б орел я. Из нее следует, что найдется в S конечное число
окрестностей F), также в совокупности покрывающих весь проме-
промежуток [а,Ь]. Если
mi ^ f(x) ^ М\ в о"ь
^2 < /0) <:М2 В 02,
тп < /0) < тп в Gп,
то, взяв в качестве т наименьшее из чисел т\9 Ш29 ..., тП9 а в ка-
качестве М — наибольшее из чисел М\9 Mi9 ..., М„, очевидно, будем
иметь
т < /0) < М
во всем промежутке [а,Ь]9 что и требовалось доказать.
3° Теорема Кантора [87]. Зададимся произвольным числом
е > 0. На этот раз каждую точку хг промежутка [а, Ъ] окружим
такой окрестностью а' = (V - S\xf + Я7), чтобы в ее пределах
выполнялось неравенство
Если хо также есть точка этой окрестности, то одновременно и
Таким образом, для любых точекхихоизо будем иметь
\Ax)-f(xo)\<e.
Стянем каждую окрестность о1 вдвое, сохраняя ее центр,
т. е. вместо о1 рассмотрим окрестность
<7'=[Х'--,Х' + -).
Из этих окрестностей также составится система S, покрывающая
промежуток [л, i], и именно к ней мы применим лемму Б орел я.
89] § 5. СВОЙСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ 207
Промежуток [а,Ь] покроется конечным числом промежутков
из S:
~о\ = (xj - -j-,Xi + -j-j (z = 1,2, ...,/7).
Пусть теперь 8 будет наименьшим из всех чисел у, и хо, х —
любые две точки нашего промежутка, удовлетворяющие условию:
|х-хо|<<5. G)
Точка хо должна принадлежать одной из выделенных окрестно-
окрестностей, например окрестности
о 2~» х*о "¦ 2~
так что |хо ~^/0| < ~Y'
Так как 8 ^ -у, то, ввиду G), |х — хо| < -у, откуда
|х — xz-0| < 8j09 т. е. точка х (а подавно — и точка хо) принадле-
принадлежит той первоначально взятой окрестности
стягиванием которой получена окрестность о7^. В таком случае,
по свойству всех первоначально взятых окрестностей,
Поскольку S было выбрано вне зависимости от положения точ-
точки хо, равномерная непрерывность функции f{x) доказана.
Как видно из приведенных рассуждений, лемма Боре ля
с успехом прилагается в тех случаях, когда «локальное» свойство,
связанное с окрестностью отдельной точки, подлежит распростра-
распространению на весь рассматриваемый промежуток.
ГЛАВА ТРЕТЬЯ
ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
§ 1. Производная и ее вычисление
90. Задача о вычислении скорости движущейся точки. Начнем
с частного примера, именно, рассмотрим свободное падение (в пу-
пустоте — чтобы не учитывать сопротивления воздуха) тяжелой ма-
материальной точки.
Если время t (с) отсчитывается от начала падения,
то пройденный за это время путь s (м), по известной
формуле, выразится так:
* = р. а)
>м
где g = 9,81 (;§). Исходя из этого, требуется опре-
определить скорость v движения точки в данный
момент t, когда точка находится в положении М
(рис. 36).
Придадим переменной t некоторое приращение At
и рассмотрим момент t + At, когда точка будет в по-
Рис. 36 ложенииМь Приращение ММ\ пути за промежуток
времени At обозначим через As. Подставляя в A) t + At вме-
вместо t, получим для нового значения пути выражение
s + As = | (t + AtJ,
откуда
Разделив As на At, мы получим среднюю скорость падения
точки на участке ММ\\
91] § 1. ПРОИЗВОДНАЯ И ЕЕ ВЫЧИСЛЕНИЕ 209
Как видим, эта скорость меняется вместе с изменением At,
тем лучше характеризуя состояние падающей точки в момент t,
чем меньше промежуток At, протекший после этого момента.
Скоростью v точки в момент времени t называют
предел, к которому стремится средняя скорость г;ср. за про-
промежуток At, когда At стремится к 0.
В нашем случае, очевидно,
2
Аналогично вычисляется скорость г; и в общем случае прямо-
прямолинейного движения точки. Положение точки определяется ее рас-
расстоянием s, отсчитываемым от некоторой начальной точки О; это
расстояние и называется пройденным путем. Время t отсчи-
тывается от некоторого начального момента, причем не обязатель-
обязательно, чтобы в этот момент точка находилась в О. Движение счита-
считается вполне заданным, когда известно уравнение движения:
s = f(t)9 из которого положение точки определяется для любого
момента времени; в рассмотренном примере такую роль играло
уравнение A).
Для определения скорости v в данный момент t пришлось бы,
как и выше, придать t приращение At, этому отвечает увеличение
пути s на As. Отношение
выразит среднюю скорость v cp .за промежуток At. Истинная
же скорость v в момент t получится отсюда предельным переходом:
v = lim vcv = lim ——.
P' At^O A^
Мы рассмотрим ниже другую важную задачу, приводящую к по-
подобной же предельной операции.
91. Задача о проведении касательной к кривой. Пусть дана
кривая (К) (рис. 37) и на ней точка М; обратимся к установлению
самого понятия касательной к кривой в ее точке М.
В школьном курсе касательную к окружности опре-
определяют как «прямую, имеющую с кривой лишь одну общую точ-
точку». Но это определение имеет частный характер, не вскрывая
существа дела. Если попытаться применить его, например, к пара-
параболе у = ах2 (рис. 38, а), то в начале координат О обе коорди-
координатные оси подошли бы под это определение; между тем, — как,
210
ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
[91
вероятно, непосредственно ясно и читателю, — на деле лишь ось х
служит касательной к параболе в точке О\
Мы дадим сейчас общее определение касательной. Возьмем
на кривой (К) (рис. 37), кроме точки М, еще точку М\ и про-
проведем секущую ММ\. Ког-
Когда точка М\ будет перемещаться
вдоль кривой, эта секущая будет
вращаться вокруг точки М.
Касательной к кри-
кривой (К) в точке М называет-
называется предельное положе-
положение МТ секущей ММ\, когда
Рис. 37
точка М\, двигаясь вдоль кри-
кривой, стремится к совпадению с М. [Смысл этого определения
состоит в том, что угол <М\МТ становится сколь угодно малым,
лишь только достаточно мала хорда ММ\]
Применим для примера это определение к параболе у = ах2,
в любой ее точке М(х,у). Так как касательная проходит через
эту точку, то для уточнения ее положения достаточно знать еще ее
угловой коэффициент. Мы и поставим себе задачей найти угловой
коэффициент tg а касательной к точке М.
ОТ Т Р
Рис. 38
Придав абсциссе х приращение Ах, от точки М кривой перей-
перейдем к точке М\ с абсциссой х + Ах и ординатой
у + Ау =а(х + АхJ
(рис. 38,а). Угловой коэффициент tgср секущей ММ\ опреде-
определится из прямоугольного треугольника MNM\. В нем катет MN
91] § 1. ПРОИЗВОДНАЯ И ЕЕ ВЫЧИСЛЕНИЕ 211
равен приращению абсциссы Ах, а катет NM\9 очевидно, есть со-
соответствующее приращение ординаты
Ау = аBх -Ах + Ах2),
так что
Ау
tg ер = —— = lax + а • Ах.
Ах
Для получения углового коэффициента касательной, как легко
понять, нужно перейти здесь к пределу при Ах —>> 0. Мы приходим
таким образом к результату:
tea = lira (lax + а • Ах) = lax.
[Заметим попутно, что отсюда вытекает удобный прием для
фактического построения касательной к параболе. Именно, из тре-
треугольника МРТ (рис. 38,6), отрезок
ТР= у = ах2 = х 9
tg a lax 1'
так что Т есть середина отрезка ОР. Итак, для того что-
чтобы получить касательную к параболе в ее точке М, достаточно
разделить пополам отрезок ОР и середину его соединить с точ-
точкой М]
В случае любой кривой, с уравнением
У=/(х),
угловой коэффициент касательной устанавливается подобным же
образом. Приращению Ах абсциссы отвечает приращение Ау ор-
ординаты, и отношение
Ду
Ах
выражает угловой коэффициент секущей, tg<p. Угловой же ко-
коэффициент касательной получается отсюда путем перехода к пре-
пределу при Ах —)> 0:
Ау
tga= Hm tgcz) = lim .
A^O A^O Ax
212 ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ [92
92. Определение производной. Сопоставляя операции, кото-
которые мы осуществляли при решении рассмотренных выше фунда-
фундаментальных задач, легко усмотреть, что в обоих случаях — если
отвлечься от различия в истолковании переменных — по суще-
существу делалось одно и то же: приращение функции делилось на при-
приращение независимой переменной и затем вычислялся предел их
отношения. Таким путем мы и приходим к основному понятию диф-
дифференциального исчисления — к понятию производной.
Пусть функция у = /(х) определена в промежутке SC. Исходя
из некоторого значения х = хо независимой переменной, прида-
придадим ему приращение Ах ^ 0, не выводящее его из промежутка «2Г,
так что и новое значение хо + Ах принадлежит этому промежут-
промежутку. Тогда значение у = /(хо) функции заменится новым значением
у + Ау = /(хо + Ах), т. е. получит приращение
Aj = ДДхо) = Д*о + Ах) - Дх0).
Предел отношения приращения функции Ау к вызвавшему
его приращению независимой переменной Ах, при стремле-
стремлении Ах к О, т. е.
Ш ? = Нт
Ах Дх^О
и называется производной функции у = /(х) по незави-
независимой переменной х, при данном ее значении (или в данной
точке) х = хо-
Таким образом, производная при данном значении
х = хо — если существует — есть определенное число^; если
же производная существует во всем промежутке «2Г, т. е. при каж-
каждом значении х в этом промежутке, то она является функцией
от х.
Пользуясь только что введенным понятием, сказанное в 90
о скорости движущейся точки можно резюмировать так:
Скорость v есть производная от пройденного пути s
по времени t.
Если слово «скорость» понимать в более общем смысле, то
можно было бы производную всегда трактовать, как некую «ско-
«скорость». Именно, имея функцию у от независимой переменной х,
*) Пока мы ограничиваемся случаем, когда упомянутый выше предел
конечен [см. 101].
92] § 1. ПРОИЗВОДНАЯ И ЕЕ ВЫЧИСЛЕНИЕ 213
можно поставить вопрос о скорости изменения перемен-
переменной у по сравнению с переменной х (при данном зна-
значении последней).
Если приращение Ах, приданное х, влечет за собой прираще-
приращение Ау для у9 то, по аналогии с 90, средней скоростью
изменения у по сравнению с х9 при изменении х на величину Ах,
можно считать отношение
Ау
"«* = Д^
Скоростью лее изменения у при данном значении х естест-
естественно назвать предел этого отношения при стремлении
Ах /сО:
Ау
v = lim vcv = lim ——,
Дх^О Р' Дх^О Ах
lim
Дх^О Ах
т. е. как раз — производную от у по х.
В 91 мы рассматривали кривую, заданную уравнением у = /(х),
и решили вопрос о проведении касательной к ней в за-
заданной точке. Теперь мы можем сформулировать полученный нами
результат так:
Угловой коэффициент tga касательной есть производная
от ординаты у по абсциссе х.
Это геометрическое истолкование производной ча-
часто бывает полезным.
Приведем в дополнение к рассмотренным выше еще несколько
примеров, выявляющих роль понятия производной.
Если скорость движения v не постоянна и сама изменяется с те-
течением времени t\ v = f{t)9 то рассматривают ускорение —
«скорость изменения скорости».
Именно, если приращению времени At отвечает приращение
скорости Af, то отношение
Av
выразит среднее ускорение за промежуток времени At9
а предел его даст ускорение движения в данный момент времени:
а = lim acv = lim ——.
p' At^o At
Таким образом, ускорение есть производная от скорости по
времени.
214 ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ [92
Обратимся к учению о теплоте — и с помощью производ-
производной установим понятие теплоемкости тела при данной
температуре.
Обозначим входящие в вопрос физические величины следу-
следующим образом: в — температура (в градусах Цельсия), W — коли-
количество тепла (в калориях), которое нужно сообщить телу, при на-
нагревании его от 0 до в°С. Ясно, что W есть функция от в\ W = /(9).
Придадим в некоторое приращение Ав, тогда W также получит
приращение AW. Средняя теплоемкость при нагревании
от0° до (9 + Ав)° будет
_ AW
Сср- " ~Ав'
Но так как, вообще говоря, при изменении Ав эта средняя тепло-
теплоемкость меняется, мы не можем принять ее за теплоемкость
при данной температуре в. Для получения последней нуж-
нужно перейти к пределу:
с = lim сср = lim ——-.
р Дб>^о Ав
Итак, можно сказать, что теплоемкость тела есть производ-
производная от количества тепла по температуре.
Наконец, возьмем пример из учения об электричестве: уста-
установим понятие о силе переменного тока в данный
момент.
Обозначим через t время (в секундах), отсчитываемое от неко-
некоторого начального момента, а через Q — количество электричества
(в кулонах), протекавшего за это время через поперечное сечение
цепи. Очевидно, что Q есть функция от t\ Q = f(t). Повторив пре-
предыдущие рассуждения, получим, что средняя сила тока за
промежуток времени At будет
/ -AQ
а сила тока в данный момент выразится пределом
ДО
/= lim /CD = lim ——,
p' A/^0 At
т. е. сила тока есть производная от количества протекшего
электричества по времени.
92] § 1. ПРОИЗВОДНАЯ И ЕЕ ВЫЧИСЛЕНИЕ 215
Все эти применения производной (число которых легко было
бы увеличить) с достаточной яркостью обнаруживают тот факт,
что понятие производной существенным образом связано
с основными понятиями из различных областей знания.
Вычисление производных, изучение и использование их свойств
и составляет главный предмет дифференциального исчисления.
Для обозначения производной употребляют различные сим-
символы:
3? или ^^*} Лейбниц (G.W. Leibniz);
у' или f'(xo) Лагранж (J.L. Lagrange);
Dy или Df(x о) К о ш и (A. L. Cauchy).
Мы будем пользоваться преимущественно простыми обозначе-
обозначениями Лагранж а. Если применяют функциональное обозначе-
обозначение (см. второй столбец), то буква хо в скобках указывает именно
то значение независимой переменной, при котором берется произ-
производная. Наконец, заметим, что в случаях, когда может возникнуть
сомнение относительно переменной, по которой взята производ-
производная (по сравнению с которой устанавливается «скорость изменения
функции»), эта переменная указывается в виде значка внизу:
у'Х9 /х(х0)9 Dxy, Dxf(x0),
причем значок х не связан с тем частным значением хо независи-
независимой переменной, при котором берется производная.
[В некотором смысле, можно сказать, что цельные символы
j-9 / или fx, Df или Dxf
играют роль функциональных обозначений для произ-
производной функции.]
Запишем теперь, пользуясь введенными для обозначения про-
производных символами, некоторые из полученных выше результатов.
Для скорости движения имеем:
ds ,
v = — или v = st,
*^ Пока мы рассматриваем обозначения Лейбница как цельные символы;
ниже [104] мы увидим, что их можно рассматривать и как дроби.
216 ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ [93
а для ускорения
dv ,
а = — или а = vt.
Аналогично, угловой коэффициент касательной к кривой
у = /(х) напишется так:
dy ,
tg a = — или tg а = ух, и т. п.
93. Примеры вычисления производных. В качестве примеров
вычислим производные для ряда элементарных функций:
1° Отметим, прежде всего, очевидные результаты: если у = с =
= const, то Ау = 0, каково бы ни было Ах, так что у' = 0; если
же у = х, то Ау = Ах и у1 = 1.
2° Пусть теперь j/ = х", где п — натуральное число.
Придадим х приращение Ах *); тогда новое значение у будет
у + Ау = (х + Ах)" = хп + ях"-1 • Ах + ^ ~ ^ х"-2 • Ах2 +. . .,
так что
Ау = пх"-х • Дх + !<^_!1х«-2 . Дх2 + _
Ах 1 • 2
Так как при Ах —>> 0 все слагаемые, кроме первого, стремятся
к нулю, то
/= Hm ^ = m»-\
Д
3° Если у = j, то у + Aj/ = х+дх, так что
1 1 -Ах
х + Ах х х(х + Ах)'
Ау _ 1
Ах ~~ х(х + Ах)'
* ^ Если производная вычисляется при любом значении аргумента, то обык-
обыкновенно его обозначают той же буквой, что и аргумент, без каких-либо значков
при нем.
93] § 1. ПРОИЗВОДНАЯ И ЕЕ ВЫЧИСЛЕНИЕ 217
Отсюда
Дх^О Ах X2
При этом предполагается, конечно, х ф 0.
4° Рассмотрим функцию у = v^ (при х > 0). Имеем:
j/ + Aj/ = Vx + Ax,
Ах
Ay = \Jx + Ax - y/x =
/x + Ax + v-*'
Av 1
Ах у/х + Ах +
наконец, пользуясь непрерывностью корня, получим
, у &У
у = hm -— =
Ах 2л/х'
Все эти результаты содержатся как частные случаи в следу-
следующем.
5° Степенная функция: у = х^ (где \х — любое вещест-
вещественное число). Область изменения х зависит от \х\ она была указана
в 48, 2°. Имеем (при х ф 0)
Ax^-x^
= А1_1
Ax Ax й* '
X
Если воспользоваться пределом, вычисленным в 77 [5), (в)], то по-
получим
у' = lim —— = их^~ *К
Ах^О Ах
В частности,
если у = - =х~!, то у' = (-1) -х~2 = —;
X X'
г- 1 ,1_1
если у = л/х =х2, то у = -х 2 =
2
*^ Если /i > 1, то при х = 0 легко непосредственно получить значение произ-
производной: у' = 0.
218 ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ [93
6° Показательная функция: у = ах (а > О,
—оо < х < +оо). Здесь
д ах+Ах _ах Ах _
— = аХ
Ах Ах Ах
Воспользовавшись пределом, вычисленным в 77 [5), (б)], найдем:
В частности,
Ау
у = lim —— = ах • In a.
Дх^О Ах
если у = ех, то и у' = ех.
Итак, скорость возрастания показательной функции (при а > 1)
пропорциональна значению самой функции: чем большего значения
функция уже достигла, тем быстрее в этот момент она растет. Это
дает точную характеристику роста показательной функции, о кото-
котором мы имели уже случай говорить [ср. 65].
7° Логарифмическая функция: у = logax @ < а ф 1,
О < х < +оо). В этом случае
Аз/ = 1оёа(х + Ах) - 1оёах = 1 1оёа A + ^)
= =
Ах Ах х А*
х
Воспользуемся пределом, вычисленным в 77 [5), (а)]:
/= lim ^ =
АО Ах
В частности, для натурального логарифма получается ис-
исключительно простой результат:
при у = lnx имеем у' = —.
х
Это дает (хотя, по существу, и не новое) основание для предпоч-
предпочтения, которое оказывается натуральным логарифмам при теорети-
теоретических исследованиях.
То обстоятельство, что скорость возрастания логарифмической
функции (при а > 1) обратно пропорциональна значению аргумен-
аргумента и, оставаясь положительной, стремится к нулю при безгранич-
безграничном возрастании аргумента, хорошо согласуется со сказанным по
этому поводу раньше [65].
94] § 1. ПРОИЗВОДНАЯ И ЕЕ ВЫЧИСЛЕНИЕ 219
8° Тригонометрические функции. Пусть j/= sinx,
тогда
Av sin(x + Ах) - sinx sin 4^
Пользуясь непрерывностью функции cosx и известным [54, (8)]
пределом lim ^^ = 1, получим
а—И) а
у' = Нт —— = cosx *}.
Ах^О Ах
Аналогично найдем:
если у = cosx, то у1 = -sinx.
В случае у = tgx имеем
sin(x+Ax) _ 2ii?^
^ _ tg(x + Ax) -tgX _ cos(x+Ax) cosx _
Ax ~~ Ax ~~ Ax ~~
sin(x + Ax) • cosx - cos(x + Ax) • sinx
Ax • cosx • cos(x + Ax)
sin Ax 1
Ax cosx • cos(x + Ax)'
Отсюда, как и выше,
у1 = lim —- = —z— = sec2x.
д*—И) Ax coszx
Аналогично,
/ 1 2
если у = ctgx, то у = ^— = — esc x.
sin х
94. Производная обратной функции. Прежде чем заняться вы-
вычислением производных от обратных тригонометрических функ-
функций, докажем следующую общую теорему.
*^ Отметим, что эта формула обязана своей простотой тому, что угол изме-
измеряется в радианах. Если бы мы стали измерять х, например, в градусах,
предел отношения синуса к углу был бы равен не единице, а, как легко видеть,
^щ, и тогда мы имели бы
(sin*)' = Tfo
220
ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
[94
Теорема. Пусть 1) функция /(х) удовлетворяет условиям
теоремы п° 83 о существовании обратной функции, 2) в точ-
точке хо имеет конечную и отличную от нуля производ-
производную /;(хо). Тогда для обратной функции g(y) в соответ-
соответствующей точке у о = /(хо) также существует производная,
равная __L_
Доказательство. Придадим значению у = у о произволь-
произвольное приращение Ду, тогда соответственное приращение Ах полу-
получит и функция х = g(y). Заметим, что при Ау ф 0, ввиду одно-
однозначности самой функции у = /(х), и Ах ф 0. Имеем
Ах
1
Ах
Если теперь Ay —»> 0 по любому закону, то — в силу непрерыв-
непрерывности функции х = g(y) — и приращение Ах —»> 0. Но тогда
знаменатель правой части написанного равенства стремится к пре-
пределу /(хо ф 0), следовательно, существует предел для левой части,
равный обратной величине
ут^гт; он и представляет со-
собой производную gf(yo).
Итак, имеем простую
формулу:
У-
Уо
oyf
х0
Ст ™
Легко выяснить ее гео-
геометрический смысл.
Мы знаем, что производная у'х есть тангенс угла а, образованного
касательной к графику функции у = /(х) с осью х. Но обратная
функция х = g(y) имеет тот же график, лишь независимая пере-
переменная для нее откладывается по оси у. Поэтому производная х'у
равна тангенсу угла /3, составленного той же касательной с осью у
(рис. 39). Таким образом, выведенная формула сводится к извест-
известному соотношению
tga
связывающему тангенсы двух углов а и /3, сумма которых равна f.
95] § 1. ПРОИЗВОДНАЯ И ЕЕ ВЫЧИСЛЕНИЕ 221
Положим для примера у = ах. Обратной для нее функцией
будет х = logay. Так как (см. 6°) у'х = ах • In а, то, по нашей фор-
формуле,
х' = l = l =l0g^,
у у'х ах Лпа у
в согласии с 7°.
Переходя теперь к вычислению производных от обратных три-
тригонометрических функций, мы для удобства обменяем ролями пе-
переменные х и у, переписав доказанную формулу в виде
ху
9° Обратные тригонометрические функции. Рас-
Рассмотрим функцию у = arcsinx (-1 < х < 1), причем —§<>><§.
Она является обратной для функции х = sinj, имеющей для ука-
указанных значений у положительную производную х' = cos у.
В таком случае существует также производная ух и равна, по нашей
формуле,
,11 1 1
ху
корень мы берем со знаком плюс, так как cos у > 0.
Мы исключили значения х = ±1, ибо для соответствующих
значений у = ±| производная х'у = cosj = 0.
Функция у = arctgx (—оо < х < +оо) служит обратной для
функции х = tgj/. По нашей формуле,
,11 1 1
Vv = -г =
x^ sec2j/ l+tg2j/ l+x7
Аналогично можно получить:
для у = arccosx у1 =
для у = arcctgx у — 2
1 ~т~ X
95. Сводка формул для производных. Сделаем сводку всех вы-
выведенных нами формул:
1. у =с у1 = 0
2. у =х у' = 1
222
3.
4.
5.
6.
7.
8.
9
10.
11.
12.
13.
ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
j/ =Х^
у = фс
у = ах
у = ех
У - 1оёа х
у = lnx
у = sinx
у = cosx
У -tgx
j — ctgx
у arcsinx
у arccosx
у = arctgx
у = arcctgx
у'
у'
у'
у'
у'
у1
у'
у'
у'
у'
у'
у'
у'
у'
у'
= и^~1
= ах -Ыа
= е*
1°ё<2 е
X
= 1
= COSX
= - sinx
2 !
coszx
sin х
1
1
1
~ 1+х2
1
~ 1+х2
[96
96. Формула для приращения функции. Докажем здесь два
простых утверждения, имеющих приложения в дальнейшем.
Пусть функция у = /(х) определена в промежутке SC. Исходя
из определенного значения х = хо из этого промежутка, обозначим
через Ах ^ 0 произвольное приращение х, подчиненное лишь тому
ограничению, чтобы точка хо + Ах не вышла за пределы SC. Тогда
соответствующим приращением функции будет
Aj = ДДхо) = f(x0 + Ах) - Дх0).
1° Если функция у = /(х) в точке хо имеет {конечную) про-
производную у'х = //(хо)? то приращение функции может быть
представлено в виде
ДДхо) = /(хо) -Ах+а-Ах B)
97] § 1. ПРОИЗВОДНАЯ И ЕЕ ВЫЧИСЛЕНИЕ 223
или, короче,
Ау = ух • Ах + а • Ах, Bа)
гд? а есть величина, зависящая от Ах и вместе с ним стре-
стремящаяся к нулю.
Так как, по самому определению производной, при Ах —»> О
Ах
то, полагая
Ду
видим, что иачО. Определяя отсюда Ау, придем к формуле Bа).
Так как величина а • Ах (при Ах —>> 0) будет бесконечно малой
высшего порядка, чем Ах, то, употребляя введенное в 60 обозна-
обозначение, можно наши формулы переписать в виде
C)
или
Ау =ух • Ах + о(Ах). (За)
Замечание. До сих пор мы считали Ах ^ 0; величина а и не
определена была при Ах = 0. Когда мы говорили, что а —>> 0 при
Ах —)> 0, то (как обычно) предполагали, что Ах стремится к 0
по любому закону, но не принимая нулевого значения.
Положим теперь а = 0 при Ах = 0; тогда, разумеется, форму-
формула B) сохранится и при Ах = 0. Кроме того, соотношение а —>> 0
при Ах —)> 0 можно понимать и в более широком смысле, чем рань-
раньше, не исключая для Ах возможности стремиться к 0, принимая
в числе прочих и нулевые значения.
Из доказанных формул непосредственно вытекает:
2° Если функция у = /(х) в точке хо имеет (конечную) про-
производную, то в этой точке функция необходимо непрерывна.
Действительно, из Bа) ясно, что соотношение Ах —>> 0 влечет
за собой Ау —)> 0.
97. Простейшие правила вычисления производных. В преды-
предыдущих пп° мы вычислили производные для элементарных функций.
Здесь и в следующем п° мы установим ряд простых правил, с по-
помощью которых станет возможным вычисление производной для
любой функции, составленной из элементарных при посредстве ко-
конечного числа арифметических действий и суперпозиций [51].
224 ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ [97
I. Пусть функция и = ср{х) имеет {в определенной точке х)
производную и'. Докажем, что и функция у — си [с — const) так-
также имеет производную {в той dice точке), и вычислим ее.
Если независимая переменная х получит приращение Ах, то
функция и получит приращение Аи, перейдя от исходного зна-
значения и к значению и + Аи. Новое значение функции у будет
у + Ау = с(и + Аи).
Отсюда Ау = с • Аи и
lim —— = с • lim —— = с - и .
Дх^О Ах Дх^О Ах
Итак, производная существует и равна
у' = (С • и)' = С • U1.
Эта формула выражает такое правило: постоянный мно-
множитель может быть вынесен за знак производной.
П. Пусть функции и = ср(х), v = гр(х) имеют (в определен-
определенной точке) производные и\ г/. Докажем, что функция у = u±v
также имеет производную (в той лее точке), и вычислим ее.
Придадим х приращение Ах; тогда и, v и у получат, соответ-
соответственно, приращения Аи, Av и Ау. Их новые значения и + Аи,
v + Av и у + Ау связаны тем же соотношением:
у + Ау = {и + Аи) ±(v + Av).
Отсюда
Av Аи Av
Ay = Аи ± Av, -г- = — ± —
* Ах Ах Ах
и
Ау Аи Av , ,
lim —— = lim —— ± lim —— = и ± v ,
Ax^O Ax Ax^O Ax Ax^O Ax
так что производная у' существует и равна
у' = {и ± v)f = и' ± г/.
Этот результат легко может быть распространен на любое чис-
число слагаемых (и притом — тем же методом).
III. При тех Dice предположениях относительно функ-
функций и, v, докажем, что функция у = и - v также имеет произ-
производную, и найдем ее.
97] § 1. ПРОИЗВОДНАЯ И ЕЕ ВЫЧИСЛЕНИЕ 225
Приращению Ах отвечают, как и выше, приращения Аи, Av
и Ау; при этом у + Ау = (и + Au)(v + Af), так что
Ду = Aw • v + м • Аг; + Аи • Аг;
и
Ау Аи Av Аи
-^- = -—-v + u--— + -—
Ах Ах Ах Ах
Так как при Ах —>> 0, в силу 96, 2°, и At» —>> 0, то
Ау л. Аи Av , ,
lim —- = lim —- - v + и - lim —- = и • v + м • v ,
АО Ах Ах^О Ах Ах^О Ах
т. е. существует производная у' и равна
у' = (и-v)' = u -v + u-v'.
Если ^ = uvw, причем u',v', w' существуют, то
у' = \{uv) - w]f = {uv)f - w + {uv) - w = uvw + uv'w +
Легко сообразить, что для случая п сомножителей будем иметь
аналогично:
п
[ uvw . . . s ] = u'vw . . . s + uv'w . . . s + uvw'. . . s + . . .
. .. +uvw. ../. D)
Для того чтобы доказать это, воспользуемся методом математиче-
математической индукции. Предположим, что формула D) верна для некото-
некоторого числа п сомножителей, и установим ее справедливость для
/7+1 сомножителей:
[uvw . .. st] = [( uvw . .. s ) • t] = (uvw .. . s)' -1 + {uvw .. . s) -1';
если производную (uvw ... s)' развернуть по формуле D), то при-
придем к формуле
[uvw . . . st]' = u'vw . . .st + uv'w . . . st + . . .
. . . + ш;м;. . . ?;7 + ш;м;. . . st',
совершенно аналогичной D). Так как в верности формулы D) при
/7 = 2 и 3 мы убедились непосредственно, то эта формула верна
при любом п.
IV. Наконец, если и, v удовлетворяют прежним предполо-
предположениям и, кроме того, v отлично от нуля, то мы докажем, что
функция у = jy также имеет производную, и найдем ее.
226 ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ [98
При тех же обозначениях, что и выше, имеем
и + Аи
так что
Аи • v — и • Av
Av =
v(v
_
Ах v(v + Av)
Устремляя здесь Ах к нулю (причем одновременно и А г; —>> 0),
убеждаемся в существовании производной
ur - v — и - vr
98. Производная сложной функции. Теперь мы можем уста-
установить весьма важное при практическом нахождении производных
правило, позволяющее вычислить производную сложной функции,
если известны производные составляющих функций.
V. Пусть 1) функция и = ср{х) имеет в некоторой точке хо
производную и'х = ф'(хо)9 2) функция у = /(и) имеет в соот-
соответствующей точке щ — ср(хо) производную у 'и = /'(щ). Тогда
сложная функция у — f(cp(x)) в упомянутой точке хо также
будет иметь производную, равную произведению производных
функций f(u) и ср{х):
/ ))-ф/ы *>
или, короче,
Ух =Уи'их-
Для доказательства придадим хо произвольное приращение Ах;
пусть Аи — соответствующее приращение функции и = ф(х) и, на-
наконец, Ау — приращение функции у = /(и), вызванное прираще-
приращением Аи. Воспользуемся соотношением Bа), которое, заменяя х
на и, перепишем в виде
Ау = у'и • Аи + а • Аи
*^ Подчеркнем, что символ ffu(q)(xo)) означает производную функции f{u) по
ее аргументу и (а не по х), при значении щ = cp(xq) этого аргумента.
99] § 1. ПРОИЗВОДНАЯ И ЕЕ ВЫЧИСЛЕНИЕ 227
(а зависит от Аи и вместе с ним стремится к нулю). Разделив его
почленно на Ах, получим
Ау _ , Аи Аи
Если Ах устремить к нулю, то будет стремиться к нулю и Аи
[96, 2°], а тогда, как мы знаем, будет также стремиться к нулю
зависящая от Аи величина а. Следовательно, существует предел
lim —- = у • lim —- = уи • их,
который и представляет собою искомую производную ух.
Замечание. Здесь сказывается полезность замечания в 96 от-
относительно величины а при Ах = 0: покуда Ах есть приращение
независимой переменной, мы могли предполагать его от-
отличным от нуля, но когда Ах заменено приращением функции
и = ф(х), то даже при Ах ф 0 мы уже не вправе считать, что
АифО.
99. Примеры. *) Сначала приведем несколько примеров приложения пра-
правил I-IV.
1) Рассмотрим многочлен:
у = аохп + а\хп~ + . . . + ап_2х + ^п-\х + ап-
По правилу II, а затем I, будем иметь
у' = (аох"У + (atx"-1)' + ... + (а„-2х2У + К-1*)' + Ы' =
/ п\1 . / п—\\/ , , / 2\/ . / \/ . / \/
= ао(х ) +а\(х )+...+ ап_2(х ) + an-i(x) + (ап) .
Использовав же формулы 1, 2, 3, 95, окончательно получим
у' = паохп~1 + (и — 1)<21^"~2 + . . . + 2ап_2х + ««-1-
2) у = Bх2 - 5х + 1) • ех. По правилу III,
у' = Bх2 -5х + 1)' • ех + Bх2 - 5х + 1) • (вх);.
Опираясь на предьщущий пример и формулу 4, 95, найдем:
у' = Dх - 5) • ех + Bjc2 - 5jc + 1) • ех = Bл1 - х - 4) • ех.
*) Буквами jc, з^» w? y ниже обозначены переменные, а другими буквами —
постоянные величины.
228 ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ [99
* + ъ
-^ . По правилу IV,
, (ах + Ъ)'(х2 + 1) - (ах + Ъ)(х2 + 1)'
ах + Ъ
3) у = —г . По правилу
(*2
-я*2 -2bx + a
(*2 + IJ (*2 + IJ
4) Вычислим снова производную функции у = tg*, исходя из формулы
у = . Пользуясь правилом IV [и формулами 6, 7, 95] получим
cos*
, (sin*)' • cos* — sin* • (cos*)' cos * + sin * 1
У — ~~ ~~
COS2 X COS2 X COS2 X
[cp. 8, 95].
^sin^ + cos^c
5) j/ = . Здесь приходится пользоваться сначала правилом IV,
х cos;\; — sin^:
а затем правилами II и III [и формулами 6, 7, 95]:
, (х sin;\; + cosxY(x cos^: — sin^:) — (x sin^: + cos^:)(^: cos^: — sin*)'
(x cos* — sin*J
* cos * • (* cos * — sin *) — (* sin * + cos *) • (—* sin *) *
(* cos* — sin*J (* cos* — sin*J '
Вычисление производных числителя и знаменателя мы произвели, не расчле-
расчленяя его на отдельные шаги. Путем упражнения необходимо добиться того, чтобы
вообще писать производные сразу.
Примеры на вычисление производных сложных функций:
6) Пусть;; = In sin*, иначе говоря, у =\пи, где и = sin*.
По правилу V, у' = у' • и' Производная у' = (In и)' = - [формула 5]
и
должна быть взята при и = sin*. Таким образом,
ух = • (sin*) = = ctg*. формула 61
sin* sin*
7) у = у 1 + *2, т. е. у = у/п, где и = 1 + * ; по правилу V,
[формула 3; пример 1]
у = е , т. е. _у = е , где г/ = * ;
^ = е*2 ¦ (х2)' = 2х ¦ ех\ [V; 4 и 3]
Конечно, в отдельном выписывании составляющих функций на деле нет
надобности.
9) у = sin ax;
у'х = cos ах • (ах)' = а • cos ax. [V; 7, 1, 2]
99] § 1. ПРОИЗВОДНАЯ И ЕЕ ВЫЧИСЛЕНИЕ 229
10)>; = (*2+* + 1)й;
ух = п(х2 + х + I)" 2
= пBх + \)(х2 + х + I)
11) з^ = 2smx;
12) j/ = arctg -;
n-l
1п2-
+ 1);
COS X
=
[V;
з,
пример
[V; 4,
1]
6]
Случай сложной функции, полученной в результате нескольких суперпози-
суперпозиций, исчерпывается последовательным применением правила V:
13) у = фё-х; тогда
V 2 ^ (!) [V;3]
secV'U*) = [V; 8]
sec
14) у = esm *; в этом случае
ух =esm2* - (sin2-)' = [у; 41
[V; 3]
sin2 ! 1 1 / 1 \ ;
= е х • 2 sin - • cos - ( - ) = [V; 6]
х х \х / х
= -±-sm--eW?. [V; 3]
XZ X
Дадим еще несколько примеров на применение всех правил:
ех - е~х
\5)у = shjc = ;
/ = \ [(ехУх ~ (е~хУх] = е~±^— = chx.
Наоборот, если у = chjc, то у' = shjc. Наконец, как и в 4), легко получить:
если у = th;\; = , то у' = ——,
, 1
если у = cth^:, то у = —=—.
230
ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
[99
/
Ух =
16) у =
1
= .(* + л/^ + ТУ =¦
1 + -
Тот же результат можно получить и из других соображений. Мы видели
в 49, 4), что функция у = \п(х + \Д2 + 1) является обратной для функции
х = shj/; поэтому [94; пример 15; 48, 6°]
1 1
\1)у =
18) у = - arctg -^-р (-1 < х < 1);
У =2"
\-{\-х2)-х-{-Ъ)
19) у =
/
У =
1
/ах + Ь - \/Ь - ас
In —. . (мы предполагаем: о — ас > 0);
/Ь — ас у/ах + Ь + у/Ь^ас
1
g
/b — ас \_y/ax+b — y/b — ac y/ax + b + y/b — ac
1
arctg \\ (здесь предположено: ас — Ъ > 0);
1
2\)y =
- arcsm
ас — Ъ 2\/ах + Ъ (х + с)\/ах + Ъ
a sin х -\- b
(w<«-f
~ <х < |j;
a cos * • (a + b sin^:) — (a sin;\; + b) • b cos;\; 1
(a + Z?sinjcJ a + 6 sin*'
§ 1. ПРОИЗВОДНАЯ И ЕЕ ВЫЧИСЛЕНИЕ 231
1
Ъ + a sin.* — \/Ъ2 — а2 •
b2 - a2 \_b + a sin* - \/b2 - a2
b sin*
23) В виде упражнения исследуем еще вопрос о производной степенно-
показательного выражения у = uv (v > 0), где и и v суть функции от *,
имеющие в данной точке производные и , v'.
Прологарифмировав равенство;; = uv, получим
Inj/ = v - \пи. E)
Таким образом, выражение для;; можно переписать в виде;; = ev nu, откуда уже
ясно, что производная у' существует. Самое же вычисление ее проще осущест-
осуществить, приравнивая производные по х от обеих частей равенства E). При этом мы
используем правила V и III (помня о том, что и, v и у суть функции от х). Мы
получим
1 , , , ^ 1 ,
— - у = v • ти -\- v • — • и ,
у и
откуда
У =У\
или, подставляя вместо у его выражение,
F)
Эта формула впервые была установлена Лейбницем и И. Бернулли
(Johann Bernoulli).
Например,
если у = xsmx, то у'х = *smx (^ + cos*
24) Предполагая, что функция /(*) имеет производную /'(*), написать вы-
выражения производных для функций
(a) sin/M, (б) е^хК (в) lnf(x)
по *, и для функций
(г)/(sin0, (д)Де'). (е)/AпО
по t.
Ответ: (a) cos/(*) •/'(*); (б) е/(х) • /'(*); (в) L^l;
(г) /(sinO . cost; (д) f\el) • г1; (е) f'Qnt) • J.
По поводу последних трех примеров (г), (д), (е) обращаем внимание читателя на
то, что символ /;(. . .) означает производную по аргументу *,от которого за-
зависит функция /(*), но при значении этого аргумента, соответственно, * = sint,
е\ \nt, уже зависящем от t. [Ср. сноску на с. 226.]
232
ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
[99
25) Функция f(x), определенная в симметричном относительно 0 промежут-
промежутке, называется четной, если f(—x) = f(x), и нечетной, если f(—x) = —f(x).
[Примерами четных функций могут служить четные степени х2, х4, . . .,
а также cosjc, chx; примеры нечетных функций: нечетные степени
х, х3, . . ., sin.*, shjc.]
Доказать, что производная четной функции (если существует) сама явля-
является нечетной функцией, а производная нечетной функции сама будет
четной.
26) Вычислить производную для функции у = \n\x\ при х ^ 0.
При х > 0, очевидно, у' = -; покажем, что та же формула сохраняется
х
и при х < 0. Действительно, вычисляя производную для функции
у = In 1*1 =ln(-jc)
как сложной функции, будем иметь
и в этом случае.
27) Рассмотрим кривую;; = ял" {п > 0).
Угловой коэффициент касательной к ней в некоторой ее точке (х,у)
будет [91-92]:
tg а = J/ =
и-1
По рис. 40 видно, что отрезок ТР (так на-
называемая подкасательная) равен
ТР =
ах
tga
хп—\
X
п
Это обстоятельство делает легким самое по-
построение касательной. [Обобщение результа-
результата п° 91.]
28) Для кривой (цепная линия)
подобным же образом,
у = а • ch — (а > 0),
a = у = sh -.
На этот раз определим (считая х > 0)
1
cos a =
так что у • cos а = а. Если из основания D ординаты у = ?)М (рис. 41) опу-
опустить перпендикуляр DS на касательную МТ, то отрезок DS окажется равным а.
99]
§ 1. ПРОИЗВОДНАЯ И ЕЕ ВЫЧИСЛЕНИЕ
233
Отсюда снова вытекает простой способ построения касательной к рассматри-
рассматриваемой кривой: на ординате DM, как на диаметре, строят полуокружность и из
точки D делают засечку S радиусом а:
прямая MS и будет касательной.
29) Пусть материальная точка ко-
колеблется по оси около некоторого сред-
среднего положения по закону
s = А • sin(cot + а) (А, со > 0).
Такое колебание носит название гармо-
гармонического: А — его амплитуда, со — час-
частота, а — начальная фаза.
Взяв производную от пути s по вре-
Т О
D
N
Рис. 41
мени t, найдем скорость движения:
v = Ао) • cos(cot + а).
Наибольшей величины ±Асо скорость
достигает в моменты, когда s = 0, т. е.
точка проходит через среднее положение. Наоборот, когда точка находится в наи-
наибольшем удалении от этого среднего положения (s = =L4), скорость v = 0.
Производная от и по ^:
а = — Ао) • sia(cot + a)
даст нам ускорение, с которым движется точка; очевидно,
Отсюда, если ввести массу m движущейся точки, то, по закону Ньютона, си-
сила F, под действием которой происходит гармоническое колебание, выразится так:
F = —та) • s.
Как видим, она всегда направлена к среднему положению (ибо имеет знак, обрат-
обратный знаку s) и пропорциональна удалению точки от него.
30) Движение, происходящее по закону
-ы
s = Ae sincot (A, k, со > 0),
-Ы
называется затухающим колебанием, ибо наличие множителя е заставляет
точку, хоть и колеблясь около среднего положения, все же стремиться к совпаде-
совпадению с ним:
lim s = 0.
В этом случае
v = s't = Ae l (со - cos cot — k • sin cot)
a = v't = —Ae (со • sin cot + 2cok • cos cot — k • sin cot).
Вводя в скобках еще члены ±к -sin cot, после очевидных преобразований получим
а = — Ае~ \(со +к ) sin cot-\-2к (со • cos cot — к- sin cot)] = — (со -\-k)-s—2k-v.
234
ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
[100
Сила, под действием которой происходит подобное движение, равна
F = -(со2 + к2)т • s - 2кт • v.
Мы видим, что она слагается из двух сил: 1) из силы, пропорциональной расстоя-
расстоянию точки от среднего положения и направленной к этому среднему положению
(как и в случае гармонического колебания), и 2) из тормозящей движение
силы, пропорциональной скорости и направленной обратно скорости.
100. Односторонние производные. Обратимся, в заключение,
к обзору ряда особых случаев, которые могут представить-
представиться в отношении производных. Начнем с установления понятия об
односторонних производных. Если рассматриваемое значе-
значение х является одним из концов
того промежутка 5Г, в котором
определена функция у = /(х),
то при вычислении предела от-
отношения д? приходится ограни-
ограничиться приближением Ах к ну-
х лю лишь справа (когда речь
идет о левом конце промежут-
промежутка) или слева (для правого
о
м
Рис. 42
конца). В этом случае говорят
об односторонней производной, справа или слева. В соот-
соответствующих точках график функции имеет одностороннюю
касательную.
Может случиться, что и для внутренней точки х существуют
лишь односторонние пределы отношения -^ (при Ах —>> +0
или Ах —>> — 0), не равные между собой; их также называют
односторонними производными. Для графика функции в соот-
соответствующей точке будут существовать лишь односторонние
касательные, составляющие угол; точка будет угловой (рис. 42).
В качестве примера рассмотрим функцию;; = f(x) = \x\. Исходя из значе-
значения х = 0, будем иметь
4У = ДО + Ах) - ДО) = f(Ax) = \Ax
Если Ах > 0, то
Ау = Ах,
4у
lim —- = 1.
Ах
Если же Ах < 0, то
Ау = —Ах,
Ау
lim — = -1.
Ах^О Ах
Начало координат является угловой точкой для графика этой функции, состоящей
из биссектрис первого и второго координатных углов.
101]
§ 1. ПРОИЗВОДНАЯ И ЕЕ ВЫЧИСЛЕНИЕ
235
101. Бесконечные производные. Если отношение приращений
д? при Ах —>> 0 стремится к +оо(—оо), то это несобственное число
также называют производной (и обозначают как обычно). Анало-
Аналогично устанавливается понятие об односторонней бесконеч-
бесконечной производной. Геометрическое истолкование производной как
углового коэффициента касательной распространяется и на этот
случай; но здесь — касательная оказывается параллельной оси у
(рис. 43, а, б, в, г).
у и
О
Рис. 43
В случаях (а) и (б) эта производная равна, соответственно,
+оо и —оо (обе односторонние производные совпадают по зна-
знаку); в случаях же (в) и (г) односторонние производные разнятся
знаками.
Пусть, например, f\(x) = xi; при х Ф 0 формула 3, 95 дает
3 Зхз
но она неприложима при х = 0. В этой точке вычислим производную исходя
непосредственно из ее определения; составив отношение
Ах Ах д^1
видим, что его пределом при Ах —>> 0 будет +оо. Аналогично убеждаемся, что
для функции f2(x) =jc3 прих = 0 производная слева равна — оо, а справа +оо.
Пользуясь расширением понятия производной, можно допол-
дополнить теорему п° 94 о производной обратной функции указанием,
что и в тех случаях, когда /;(^о) равна 0 или ±оо, производная
обратной функции gf(yo) существует и равна, соответственно, ±оо
или 0. Например, так как функция sinx при х = ±^ имеет произ-
производную cos (=fcf) = 0, то для обратной функции arcsinj при у = ±1
существует бесконечная производная (именно, +оо).
236 ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ [102
102. Дальнейшие примеры особых случаев.
1° Примеры несуществования производной. Уже функция;; = |*| в точке
х = 0 [см. 100] не имеет обычной, двусторонней, производной. Но интерес-
интереснее пример функции
f{x) = х • sin - (при х ф 0), ДО) = 0,
X
непрерывной и при х = 0 [70, 5)], но не имеющей в этой точке даже односторон-
односторонних производных. Действительно, отношение
ДО + А*)-ДО) ДА*) ^J
= = ^
Ах Ах Ах
не стремится ни к какому пределу при Ах —>> ±0.
По графику этой функции (см. рис. 24) легко усмотреть, что секущая ОМ\,
исходящая из начальной точки О, не имеет предельного положения при стремле-
стремлении М\ к О, так что касательной к кривой в начальной точке нет (даже односто-
односторонней).
Впоследствии (во втором томе) мы познакомимся с замечательным примером
функции, непрерывной при всех значениях аргумента, но ни при одном из них не
имеющей производной.
2° Примеры разрывов производной. Если для данной функции у = f(x)
существует конечная производная у' = f'{x) в каждой точке некоторого проме-
промежутка SC, то эта производная, в свою очередь, представляет собой в SC функцию
от х. В многочисленных примерах, которые нам до сих пор встречались, эта функ-
функция сама оказывалась непрерывной. Однако это может быть и не так. Рассмотрим,
например, функцию
fix) = х2 • sin - (при х ф 0), ДО) = 0.
х
Если х Ф 0, то ее производная вычисляется обычными методами:
f\x) = 2x • sin cos -,
х х
но полученный результат неприложим при х = 0. Обращаясь в этом случае
непосредственно к самому определению понятия производной, будем иметь
/'@) = lim /@ + А^)-/@) = lim Дх • sm -L=0.
Ах^О Ах Ах^О Ах
Вместе с тем ясно, что fix) при х —>> 0 не стремится ни к какому пределу, так
что при х = 0 функция f\x) имеет разрыв.
То же справедливо и для любой функции
fix) = ха • sin - (при х ф 0), ДО) = 0,
X
если только 2 > а > 1.
В этих примерах разрывы производной оказываются второго рода.
Это — не случайность: ниже [113] мы увидим, что разрывов первого рода, т. е.
скачков, производная иметь не может.
103] § 2. ДИФФЕРЕНЦИАЛ 237
§ 2. Дифференциал
103. Определение дифференциала. Пусть имеем функцию
у — /(х), определенную в некотором промежутке SC и непрерыв-
непрерывную в рассматриваемой точке хо- Тогда приращению Ах аргумента
отвечает приращение
Ау = ДДхо) = /(хо + Ах) - /(хо),
бесконечно малое вместе с Ах. Большую важность имеет вопрос:
существует ли для Ау такая линейная относительно Ах бес-
бесконечно малая А-Ах (А = const), что их разность оказывается,
по сравнению с Ах, бесконечно малой высшего порядка:
Ау = А-Ах+о(Ах). A)
При А ф 0 наличие равенства A) показывает, что бесконечно
малая А • Ах эквивалентна бесконечно малой Ау и, значит, служит
для последней ее главной частью, если за основную бесконеч-
бесконечно малую взята Ах [62,63].
Если равенство A) выполняется, то функция у — /(х)
называется дифференцируемой (при данном значении
х = хо), само лее выражение А • Ах называется диффе-
дифференциалом функции и обозначается символом dy или df(xo).
[В последнем случае в скобках указывается исходное значе-
значение х Ч]
Еще раз повторяем, что дифференциал функции характе-
характеризуется двумя свойствами: (а) он представляет линей-
линейную (однородную) функцию от приращения Ах аргумента
и (б) разнится от приращения функции на величину, кото-
которая при Ах —>> 0 является бесконечно малой порядка высшего,
чем Дх.16^
* ^ Здесь df как единый символ играет роль функционального обозначения.
' Пункты (а) и (б), выделенные курсивом, составляют вместе развернутую
форму определения дифференциала функции / в фиксированной точке ^о- Под-
Подчеркнем, что областью определения функции dy = df(xo) служит (как и для
всякой линейной функции) вся вещественная прямая 01. Это означает, что
каждому вещественному числу Ах отвечает определенное значение диффе-
дифференциала dy; оно выражается через Ах формулой dy = А • Ах, где число А
представляет собой угловой коэффициент линейной функции dy.
238 ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ [104
Рассмотрим примеры.
1) Площадь Q круга радиуса г задается формулой Q = жг2.
Если радиус г увеличить на Аг, то соответствующее приращение
AQ величины Q будет площадью кругового кольца, содержащего-
содержащегося между концентрическими окружностями радиусов г и г + Аг.
Из выражения
AQ = ж{г + АгJ - жг2 = 2жг • Аг + ж{АгJ
сразу усматриваем, что главной частью AQ при Аг —»> 0 будет
2жг • Аг; это и есть дифференциал, dQ. Геометрически он вы-
выражает площадь прямоугольника (полученного как бы «выпрямле-
«выпрямлением» кольца) с основанием, равным длине окружности 2яг, и вы-
высотой Аг.
2) Аналогично, для объема V = | жг3 шара радиуса г, при уве-
увеличении радиуса на Аг, получается приращение
AV = ^ л(г + АгK - ^лг3 = 4жг2 • Аг +4лг • (АгJ + ^ л(АгK,
главной частью которого при Аг —>> 0, очевидно, будет
б/К = 4жг2 • Аг. Это — объем плоского слоя с основанием, равным
поверхности шара 4лт2, и с высотой Аг; в подобный слой как бы
«распластывается» слой, содержащийся между двумя концентри-
концентрическими шаровыми поверхностями радиусов г иг + Аг.
3) Наконец, рассмотрим свободное падение материальной точ-
точки по закону s = ^-. За промежуток времени At, от t до t + A^,
движущаяся точка пройдет путь
При А^ —»> 0 его главной частью будет ds = gt • At. Вспомнив, что
скорость в момент t будет v = gt [90], видим, что дифференциал
пути (приближенно заменяющий приращение пути) вычисляется
как путь, пройденный точкой, которая в течение всего промежутка
времени At двигалась бы именно с этой скоростью.
104. Связь между дифференцируемостью и существованием
производной. Легко установить теперь справедливость следующего
утверждения:
Для того чтобы функция у =/(х) в точке хо была диф-
дифференцируема, необходимо и достаточно, чтобы для нее
104] § 2. ДИФФЕРЕНЦИАЛ 239
в этой точке существовала конечная производная у' = /;(хо).
При выполнении этого условия равенство A) имеет место
при значении постоянной А, равном именно этой производной:
Ay =y'xAx + о(Ах). (la)
Необходимость. Если выполняется A), то отсюда
Ау _ о(Ах)
Ах Ах
так что, устремляя Ах к 0, действительно, получаем
Ау ,
-^- у'
Ах
Ау ,
A =lim-^- = у'
Ах х
Достаточность сразу вытекает из 96, 1° [см. там (За)].
Итак, дифференциал функции у = /(х) всегда равен *}
dy=y'x-Ax. B)
Подчеркнем здесь же, что под Ах в этом выражении мы разуме-
разумеем произвольное приращение независимой переменной, т. е.
произвольное число (которое часто удобно бывает считать не зави-
зависящим от х). При этом вовсе не обязательно предполагать
Ах бесконечно малой; но если Ах —>> 0, то дифференциал dy
также будет бесконечно малой, и именно (при у'х ф 0) — главной
частью бесконечно малого приращения функции Ау. Это и дает
основание приближенно полагать
Ay=dy, C)
с тем большей точностью, чем меньше Ах. Мы вернемся к рас-
рассмотрению приближенного равенства C) в 107.
Чтобы истолковать геометрически дифференциал dy и его
связь с приращением Ау функции у = /(х), рассмотрим график
этой функции (рис. 44). Значением х аргумента и у функции опре-
определится точка М на кривой. Проведем в этой точке кривой каса-
касательную МТ; как мы уже видели [92], ее угловой коэффициент, tg a,
*) Легко проверить, что именно так и составлялся дифференциал во всех слу-
случаях, рассмотренных в предыдущем п°. Например, в случае 1), имеем: Q = жг ,
Qfr = 2жг, dQ = 2жг • Аг, и т. д.
240
ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
[104
равен производной ух. Если абсциссе х придать приращение Ах,
то ордината кривой у получит приращение Ay = NM\. В то же
время ордината касательной
получит приращение NK. Вы-
Вычисляя NK как катет прямо-
прямоугольного треугольника MNK,
найдем:
NK = MN - tg a =
= y'x-Ax=dy.
Итак, в то время как
Ау есть приращение ордина-
ординаты кривой, dy является соот-
соответственным приращением ординаты касательной.
В заключение остановимся на самой независимой пе-
переменной х: ее дифференциалом называют именно прираще-
приращение Ах, т. е. условно полагают
dx = Ax.17) D)
Если отождествить дифференциал независимой перемен-
переменной х с дифференциалом функции у =х (в этом — тоже
своего рода соглашение!), то формулу D) можно и доказать,
ссылаясь на B): dx = х'х • Ах = 1 • Ах = Ах.
Учитывая D), можно теперь переписать формулу B) в виде
dy=y'x-dx E)
— так ее обычно и пишут.18^
17)
Формула D) подразумевает, что dx является функцией от аргумента Ах.
Более точно, dx — линейная функция от Ах с угловым коэффициентом 1.
Обратим здесь внимание читателя на некоторые особенности использования
обозначения dy. Это (традиционное и удобное) обозначение обладает некоторой
неполнотой: оно не содержит указания на то, в какой точке х берется дифферен-
дифференциал функции. Соответственно, значение dy фактически оказывается зависящим
от двух параметров: точки х, в которой рассматривается дифференциал, и при-
приращения Ах, т. е. dy = dy(x, Ax). Когда значение одного из этих параметров
фиксировано, то dy становится функцией другого параметра. До сих пор исполь-
использовалась лишь одна интерпретация символа dy — как функции от Ах. Однако
вторая интерпретация того же символа — как функции от х при фиксированном
Ах — столь же важна (она существенно используется, например, при определе-
определении дифференциалов высших порядков).
105] § 2. ДИФФЕРЕНЦИАЛ 241
Отсюда получается
У* = -г, F)
/ dy
~dx'
так что выражение, которое мы раньше рассматривали как
цельный символ, теперь можно трактовать как д р о б ь. То об-
обстоятельство, что слева здесь стоит вполне определенное число,
в то время как справа мы имеем отношение двух неопределенных
чисел dy и dx (ведь dx = Ах произвольно), не должно смущать
читателя: числа dx и dy изменяются пропорционально, при-
причем производная у'х как раз является коэффициентом пропорцио-
пропорциональности.
Понятие дифференциала и самый термин «дифференциал» *)
принадлежат Лейбницу, который не дал, однако, точного опреде-
определения этого понятия. Наряду с дифференциалами, Лейбниц рас-
рассматривал и «дифференциальные частные», т. е. частные двух диф-
дифференциалов, что равносильно нашим производным; однако имен-
именно дифференциал был для Лейбница первоначальным понятием.
Со времени К о ш и, который своей теорией пределов создал фунда-
фундамент для всего анализа и впервые отчетливо определил производ-
производную как предел, стало обычным отправляться именно от производ-
производной, а понятие дифференциала строить уже на основе производной.
105. Основные формулы и правила дифференцирования. Вы-
Вычисление дифференциалов функций носит название дифферен-
дифференцирования*5^. Так как дифференциал dy лишь множителем dx
отличается от производной у'Х9 то по таблице производных для эле-
элементарных функций [95] легко составить таблицу дифференциалов
для них:
1. у = с dy = 0
2. у = х^ dy = \ix^~x - dx
*^ От латинского слова differentia, означающего «разность».
**) Впрочем, тем же термином обычно обозначают и вычисление производных,
для которого на русском языке нет особого термина. В большинстве иностран-
иностранных языков для обозначения этих операций существуют два различных термина;
например, по-французски различают «derivation» и «differentiation».
242 ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ [106
3. у = ах dy = ах -Ыа • dx
dy = ex - dx
4.
5.
6.
7.
8.
9.
10.
II.
12.
у = е
У = loga x
у — lnx
у — sinx
J = COSX
У =tgx
J = ctgx
у — arcsinx
у — arccosx
у — arctgx
у — arcctgx
dy = cos -dx
dy — — sinx • dx
dy = sec2 x - dx = -Щ—
s cos2 x
dy — - esc2 x - dx = - -т^г-
sin x
4y = —#4
Правила дифференцирования^ выглядят так:
I. d(cu) = с - du,
II. d{u ±v)=du± dv,
III. d{uv) = и - dv + v - du,
^r -, / u \ v - du — и - dv
IV. d - = —
v J v2
Все они легко получаются из соответствующих правил для про-
производных. Докажем, например, два последних:
d{u - v) = (и - v)r - dx = (V • v + и - v')dx =
= v - (и - dx) + и - (г/ • dx) = v - du + и - dv,
v - (uf - dx) — и - (г/ • б/х) v - du — и - dv
=
106. Инвариантность формы дифференциала. Правило диф-
дифференцирования сложной функции приведет нас к одному замеча-
замечательному и важному свойству дифференциала.
*) Если речь идет именно о вычислении дифференциалов.
106] § 2. ДИФФЕРЕНЦИАЛ 243
Пусть функции у = /(х) их = cp(t) таковы, что из них может
быть составлена сложная функция: у = /(<рG)). Если существу-
существуют производные у'х и х\9 то — по правилу V [98] — существует
и производная
у',=Ух-х'г G)
Дифференциал dy9 если х считать независимой переменной,
выразится по формуле E). Перейдем теперь к независимой пе-
переменной t; в этом предположении имеем другое выражение для
дифференциала:
dy = y\ • dt.
Заменяя, однако, производную у[ ее выражением G) и замечая, что
x'fdt есть дифференциала как функции от t9 окончательно получим:
dy = у'х - x'tdt = ух - dx,
т. е. вернемся к прежней форме дифференциала!
Таким образом, мы видим, что форма дифференциала
может быть сохранена далее в том случае, если прежняя
независимая переменная заменена новой. Мы всегда имеем пра-
право писать дифференциалу в форме E), будет ли х независимой
переменной или нет; разница лишь в том, что, если за независи-
независимую переменную выбрано t9 то dx означает не произвольное при-
приращение Ах, а дифференциал х как функции от t. Это свойство
и называют инвариантностью формы дифференциала.
Так как из формулы E) непосредственно получается форму-
формула F), выражающая производную ух через дифференциалы dx
и dy9 то и последняя формула сохраняет силу, по какой бы
независимой переменной (конечно, одной и той же в обо-
обоих случаях) ни были вычислены названные дифференциалы.
Пусть, например, у = у/1 — х2 (—1 <х < 1), так что
Положим теперь х = sin 7 (—^ < t < f). Тогда у = у 1 — sin2/^ =
= cos t9 и мы будем иметь: dx = cos t • dt9 dy = — sin t • dt. Легко
проверить, что формула
, —smt-dt sin t
у = =
x cos t • dt cos t
дает лишь другое выражение для вычисленной выше производной.
244 ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ [106
Этим обстоятельством особенно удобно пользоваться в слу-
случаях, когда зависимость у от х не задана непосредствен-
непосредственно, а вместо этого задана зависимость обеих переменных х и у
от некоторой третьей, вспомогательной, переменной (называемой
параметром):
x=q>{t), y = №- (8)
Предполагая, что обе эти функции имеют производные и что для
первой из них существует обратная функция t = 6(х)9 имеющая
производную [83, 94], легко видеть, что тогда и у оказывается функ-
функцией от х:
у = ф(в(х))=/(х), (9)
для которой также существует производная. Вычисление этой про-
производной может быть выполнено по указанному выше правилу:
Ух dx
х dx x'fdt x't <p'(t)'
не восстанавливая непосредственной зависимо-
зависимости у от х.
Например, если х = sinf, у = cos^ (-f < t < f), то произ-
производную у'х можно определить, как это сделано выше, не пользуясь
вовсе зависимостью у = у/1 — х2.
Если рассматривать х и у как прямоугольные координаты точ-
точки на плоскости, то уравнения (8) каждому значению парамет-
параметра t ставят в соответствие некоторую точку, которая с изменени-
изменением t описывает кривую на плоскости. Уравнения (8) называются
параметрическими уравнениями этой кривой.
В случае параметрического задания кривой, формула A0) по-
позволяет непосредственно по уравнениям установить угловой ко-
коэффициент касательной, не переходя к заданию кривой уравнени-
уравнением (9); именно, ,
tg«=77- (И)
xt
Замечание. Возможность выражать производную через диф-
дифференциалы, взятые по любой переменной, в частности, приводит
к тому, что формулы
dy I dy dy du
dx 4* ' dx du dx'
dy
выражающие в лейбницевых обозначениях правила дифференциро-
дифференцирования обратной функции и сложной функции, становятся просты-
простыми алгебраическими тождествами (поскольку все дифференциалы
107] § 2. ДИФФЕРЕНЦИАЛ 245
здесь могут быть взяты по одной и той же переменной). Не следу-
следует думать, впрочем, что этим дан новый вывод названных формул:
прежде всего, здесь не доказывалось существование произ-
производных слева, главное же — мы существенно пользовались инва-
инвариантностью формы дифференциала, которая сама есть следствие
правила V.
107. Дифференциалы как источник приближенных формул.
Мы видели, что при Ах —»> 0 дифференциал dy функции у (если
только у'х ф 0) представляет собой главную часть бесконеч-
бесконечно малого приращения функции Ау. Таким образом, Ay ~ dy,
так что
&y=dy, C)
или подробнее
ДДхо) = Д*о + Ах) - Дх0) =/'(*о) • Ах (За)
с точностью до бесконечно малой высшего порядка, чем Ах. Это
значит [62], что относительная погрешность этого равенства
становится сколь угодно малой при достаточно малом Ах.
Рассмотрим простой пример: пусть у = х3. Тогда
Ду = (*о + А*K -*о = Зхо • Ах + 3*о • Ах2 + Ах3,
и линейной частью Ау (как мы это выше установили в общем ви-
виде), действительно, является дифференциал dy = 3xq-Ax =y'x-Ax.
Положим конкретно хо = 2,3; если взять Ах = 0,1, то бу-
будем иметь Ау = 2,43 - 2,33 = 1,657 и dy = 3 • 2,32 • 0,1 = 1,587,
так что погрешность от замены первого числа вторым бу-
будет 0,070, а относительная погрешность превысит 4%.
При Ах = 0,01 получим Ау = 0,159391 и dy = 0,1587, что да-
дает относительную погрешность, уже меньшую 0,5%; при
Ах = 0,001 — относительная погрешность меньше 0,05%,
и т. д.
Подобное же обстоятельство может быть и непосредственно
усмотрено из рис. 44, дающего геометрическое истолкование диф-
дифференциала. На графике видно, что при уменьшении Ах мы, дей-
действительно, все с большей относительной точностью можем
заменять приращение ординаты кривой приращением ординаты ка-
касательной.
Выгода замены приращения функции Ау ее дифференциа-
дифференциалом dy состоит, как ясно читателю, в том, что dy зависит от Ах
линейно, в то время как Ау представляет собой обыкновенно
более сложную функцию от Ах.
246 ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ [107
Если положить Ах = х — хо и хо + Ах = х, то равенство (За)
примет вид
f(x)-f(xo)=ff(xo)-(x-xo)
или
f(x)=f(xo)+f'(xo)-(x-xo).
По этой формуле, для значений х, близких к хо, функция /(х)
приближенно заменяется линейной функцией. Геометрически
это соответствует замене участка кривой у = /(х), примыка-
примыкающего к точке (хо,/(хо)), отрезком касательной к кривой
в этой точке:
(ср. рис. 44). Взяв для простоты хо = 0 и ограничиваясь малыми
значениями х, будем иметь приближенную формулу:
Дх)=/@)+/'@)-х.
Отсюда, подставляя вместо f(x) различные элементарные функции, легко
получить ряд формул:
(l+jc)^ = l+/ijc, в частности
ех = \+х, Ы(\+х)=х, sin;\;=;\;, tg;\; =х, и т. п.
(из которых многие нам уже известны).
Приведем примеры приближенных формул другого типа, также имеющих сво-
своим источником равенство C).
1) Если длину тяжелой нити (провода, каната, ремня), подвешенной за оба
конца, обозначить через 2 s, пролет — через 2/, а стрелу провеса — через
/ (рис. 45), то для вычисления
s часто пользуются (приближен-
(приближенной) формулой
Рис.45 n r \
Величину / здесь будем считать
независимой переменной, a s —
функцией от /. Требуется установить связь между изменением As длины s и из-
изменением А/ стрелы провеса /.
Заменяя As на ds, получим
4 / 3 /
As = --j-Af, откуда А/= -•-• As.
Если, например, учесть изменение длины провода от изменения температуры или
нагрузки, то отсюда можно предусмотреть и изменение стрелы провеса.
* ^ Действительно, уравнение прямой с угловым коэффициентом к, проходящей
через точку (xq,yo), будете = уо~\-к(х —xq);b случае касательной здесь следует
положить у о = f(xo), к = f\x0).
108]
§ 2. ДИФФЕРЕНЦИАЛ
247
2) Известно, что круговой ток (рис. 46) действует на единицу так называ-
называемого «магнитного заряда», помещенную на его оси на расстоянии х от центра О,
с силой
к
Рис. 46
где к — постоянный коэффициент, а —
радиус. Найти выражение для силы, с ка-
какой круговой ток будет действовать на маг-
магнит NS длины Ах, расположенный по оси
тока. При этом будем считать, что в полю-
полюсе N сосредоточен положительный «магнитный заряд» т, а в полюсе S — равный
ему отрицательный «магнитный заряд» —т.
Общая сила F действия тока на магнит выразится так:
F =
km
km
= — km • А
1
(а2+х2J [а2 + (х + АхJ}2
Заменяя приращение функции (в предположении, что Ах мало) ее дифференци-
дифференциалом, получим
1
F= - km- d
(а2+х2J
= Ък • тАх •
(а2 +х2J
108. Применение дифференциалов при оценке погрешностей. Особенно
удобно и естественно использовать понятие дифференциала в приближенных вы-
вычислениях при оценке погрешностей. Пусть, например, величину х мы измеряем
или вычисляем непосредственно, а зависящую от нее величину у определя-
определяем по формуле:;; = f(x). При измерении величиных обыкновенно вкрадыва-
вкрадывается погрешность, Ах, которая влечет за собою погрешность А;; для величины;;.
Ввиду малой величины этих погрешностей, полагают
Ау =у'х • Ах,
т. е. заменяют приращение дифференциалом. Пусть 8х будет максимальной
абсолютной погрешностью величины х: \Ах\ < 8х (в обычных условиях по-
подобная граница погрешности при измерении известна). Тогда, очевидно,
за максимальную абсолютную погрешность (границу погрешности) для у
можно принять
8у = \у'х\-8х. A2)
1) Пусть, например, для определения объема шара сначала (с помощью штан-
штангенциркуля, толщемера, микрометра и т. п.) непосредственно измеряют диа-
диаметр D шара, а затем объем V вычисляют по формуле
V=-D\
Так как VfD = ^ D , то в этом случае, в силу A2),
у = -D- 8D.
248 ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ [108
Разделив это равенство на предыдущее, получим
V D '
так что (максимальная) относительная погрешность вычисленного значения
объема оказывается втрое большей, чем (максимальная) относительная погреш-
погрешность измеренного значения диаметра.
2) Если число х, для которого вычисляется его десятичный логарифм
у = log х, получено с некоторой погрешностью, то это отразится на логариф-
логарифме, создавая и в нем погрешность.
Здесь у'х = Ц- (М= 0,4343), так что, по формуле A2),
8х
8У = 0,4343 • —.
х
Таким образом, (максимальная) абсолютная погрешность логарифма просто
определяется по (максимальной) относительной погрешности самого числа,
и обратно.
Этот результат имеет многообразные применения. Например, с его помощью
можно составить себе представление о точности обыкновенной логарифмической
линейки, со шкалой 25 см = 250 мм. При отсчете или установке визира можно
ошибиться, примерно, на 0,1 мм в ту или другую сторону, что отвечает погреш-
погрешности в логарифме
Sy = 55 = 0'0004
Отсюда, по нашей формуле,
8х 0,0004
— = = 0,00092 .. . = 0,001.
х 0,4343
Относительная точность отсчетов во всех частях шкалы одна и та же!
3) При вычислении угла ср по логарифмо-тригонометрическим таблицам
встает вопрос, какими таблицами выгоднее пользоваться — таблицами синусов
или тангенсов. Положим
ух = lgsinp и у2 = lgtgp
и будем считать максимальные погрешности 8у\ и 8у2 равными (скажем, полови-
половине последнего знака мантиссы). Если обозначить соответствующие максимальные
погрешности в угле ср через 8\ср и 82д), то, как и выше, получим:
8у\ =
так что
Таким образом, оказывается, что при одинаковых ошибках в логарифме та-
таблица тангенсов дает меньшую погрешность в угле, чем таблица синусов, и, стало
быть, является более выгодной. *'
м
sing)
52<
sq) • 8\(р,
p = 8\q> -
Sy2
cos cp
M
tg<p
< 8\q>.
sec cp
*) При этих выкладках мы предполагали углы выраженными в радианах, но
результаты, очевидно, справедливы безотносительно к тому, какой единицей из-
измеряются углы.
109]
3. ОСНОВНЫЕ ТЕОРЕМЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ 249
( Rx У
8у=
\а — х / х
4) В качестве последнего примера рассмотрим вопрос о точности измере-
измерения неизвестного сопротивления у с помощью мостика Уитстона (рис. 47).
При этом подвижной контакт D передвигается по градуированной линейке АС
до тех пор, пока гальванометр G не покажет отсутствие тока. Сопротивление у
определяется по формуле
у = —, A3)
а — х
где а = АС, х = AD, R — известное сопротивление ветви ВС.
По формуле A2) получается:
aR
= т ТТ ' Sx>
(а -хJ
если разделить почленно это равенство на равенство A3), то получим выражение
(максимальной) относительной погреш-
погрешности для у:
8у а • 8х
у х(а — х)
Так как знаменатель х(а — х) достигает
своего наибольшего значения при
х = | *\ а погрешность 8х при изме-
измерении единицы длины можно считать не
зависящей от х, то наименьшее зна-
значение для относительной погрешности
достигается именно при х = f. Поэто-
D
Рис. 47
му обыкновенно, для получения возмож-
возможно точного результата, сопротивление R (с помощью магазина сопротивлений)
устанавливается с таким расчетом, чтобы ток исчезал при положении контакта D,
возможно более близком к середине линейки АС.
§ 3. Основные теоремы дифференциального исчисления
109. Теорема Ферма. Знание производной f'(x) некоторой
функции f(x) часто позволяет делать заключение и о поведении
самой функции f(x). Вопросам этого рода и будут, в сущности,
посвящены настоящий параграф и следующие за ним.
*) Из
очевидного неравенства
непосредственно получаем
х(а -х)
что и доказывает наше утверждение.
250 ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ [109
Предварительно докажем простую лемму.
Лемма. Пусть функция /(х) имеет конечную производную
в точке хо. Если эта производная /'(хо) > 0 [/'(хо) < 0], то
для значений х, достаточно близких к хо справа, будет
/(х) > /(хо) [/(х) < /(хо)], а для значений х, достаточно
близких к хо слева, будет /(х) < /(хо) [/(х) > /(хо)].
Иными словами этот факт выражают так: функция /(х)
в точке хо возрастает [убывает]. Если имеется в виду одно-
односторонняя производная, например справа, то сохраняет силу лишь
утверждение о значениях х9 лежащих справа от хо.
Доказательство. По определению производной,
X — Хо
Если f'(xo) > 0 (ограничимся этим случаем), то, в силу 55,2°,
найдется такая окрестность (хо — S, хо + 8) точки хо, в которой
(при х ф хо)
f{x)-f{xp) ^ 0
х -хо
Пусть сначала хо < х < хо + 8, так что х — хо > 0; из пре-
предыдущего неравенства следует тогда, что f(x) — f{xo) > 0, т. е.
f(x) > /(хо). Если же хо — 8 < х < хо и х — хо < 0, то, очевид-
очевидно, и /(х) — /(хо) < 0, т. е. /(х) < /(хо). Лемма доказана.
Теорема Ферма (P. Fermat). Пусть функция /(х) опреде-
определена в некотором промежутке 37 и во внутренней точке
с этого промежутка принимает наибольшее {наименьшее)
значение. Если существует двусторонняя конечная производ-
производная f [с) в этой точке, то необходимо f [с) — 0. *)
Доказательство. Пусть для определенности /(х) прини-
принимает наибольшее значение в точке с. Предположение, что
f'(c) ф 0, приводит к противоречию: либо f [с) > 0, и тогда
(по лемме) /(х) > /(с), если х > с и достаточно близко к с, либо
/'(с) < 0, и тогда /(х) > /(с), если х < с и достаточно близко к с.
В обоих случаях /(с) не может быть наибольшим значением функ-
функции /(х) в промежутке ЭС. Полученное противоречие и доказывает
теорему.
*) Это утверждение, разумеется, воспроизводит лишь сущность того приема,
который применял Ферма для разыскания наибольших и наименьших значений
функции (Ферма не располагал понятием производной).
110]
3. ОСНОВНЫЕ ТЕОРЕМЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ 251
Вспомним [91,92] геометрическое истолкование производной
yf = ff(x) как углового коэффициента касательной к кривой
у — f{x). Обращение в нуль производной f'(c) геометрически
означает, что в соответствующей точке этой кривой касательная
параллельна оси х. Рисунок 48 делает это обстоятельство совер-
совершенно наглядным.
В доказательстве существенно было использовано пред-
предположение, что с является внутренней точкой промежутка, так как
нам пришлось рассматривать и точки х справа от с, и точки х
слева от с. Без этого предположения теорема перестала бы быть
верной: если функция f(x) определена в замкнутом промежутке
и достигает своего наибольшего (наименьшего) значения на одном
из концов этого промежутка, то производная f'(x) на этом конце
У\
О а
с
Рис. 48
Рис. 49
(если существует) может и не быть нулем. Предоставляем читате-
читателю подыскать соответствующий пример; геометрически этот факт
иллюстрируется рисунком 49.
В качестве приложения теоремы Ферма докажем одну лю-
любопытную теорему о производной функции.
110. Теорема Дарбу (D. Darboux). Если функция f(x) име-
имеет конечную производную в промежутке [а, Ь] *\ то функ-
функция f'{x) принимает, в качестве значения, каждое промежу-
промежуточное число между f'(a) и f'(b).
Доказательство. Сперва предположим, что f'(a) и f'{b)
имеют разные знаки, например, что /f(a) > 0, a f (Ь) < 0, и до-
докажем существование точки с между а и Ь9 в которой производ-
производная обращается в нуль. В самом деле, из существования конечной
*) При этом мы считаем, что в точке а существует производная справа,
а в точке Ь — производная слева. Они в дальнейшем обозначаются просто /;(а)
252 ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ [111
производной f'{x) следует непрерывность функции f(x) [96,2°],
а тогда, по 2-й теореме Вейерштрасса [85], f(x) принимает
в некоторой точке с свое наибольшее значение. Эта точка с не
может совпадать ни с а, ни с Ъ, так как, согласно лемме, f(x)
больше /(а) вблизи точки а (справа) и больше f(b) вблизи
точки Ъ (слева). Итак, а < с < Ъ. Тогда, по теореме Ферма,
получаем f'(c) = 0.
Переходя к общему случаю, возьмем любое число С, за-
заключенное между f'(a) и f'(b); пусть, для определенно-
определенности, f'(a) > С > f'(b). Рассмотрим вспомогательную функ-
функцию ср(х) = f(x) — Сх; она непрерывна и имеет производную
ф/(х)=//(х)-Св промежутке [а,Ь].
Так как ср'(а) = f'(a) - С > 0, а ср'{Ъ) = f'{b) - С < 0, то, по
доказанному, существует такая точка с {а < с < Ь)9 в которой
(р\с) = f\c) - С = 0, т. е. /'(с) = С.
Доказанная теорема имеет большое сходство со 2-й теоремой
Коши [82], согласно которой всякая непрерывная функция пере-
переходит от одного значения к другому, лишь переходя через все про-
промежуточные числа. Однако теорема Дарбу отнюдь не является
следствием теоремы Коши, так как производная f\x) непрерыв-
непрерывной функции сама может и не быть непрерывной функцией.
111. Теорема Ролля. В основе многих теорем и формул
дифференциального исчисления и его приложений лежит следу-
следующая простая, но важная теорема, связываемая с именем Ролля
(М. Rolle) Ч
Теорема Ролля. Пусть 1) функция f(x) определена и непре-
непрерывна в замкнутом промежутке [а, Ь]; 2) существует конеч-
конечная производная f'(x), no крайней мере в открытом проме-
промежутке (а, Ь); 3) на концах промежутка функция принимает
равные значения: f{a) = f(b).
Тогда между а и Ъ найдется такая точка с (а < с <Ъ),
что f'{c)= 0.
Доказательство. f{x) непрерывна в замкнутом промежут-
промежутке [а,Ь] и потому, по 2-й теореме Вейерштрасса [85], при-
принимает в этом промежутке как свое наибольшее значение М, так
и свое наименьшее значение т.
* ^ В действительности Р о л л ь высказал это утверждение лишь для много-
многочленов.
112]
3. ОСНОВНЫЕ ТЕОРЕМЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ 253
Рассмотрим два случая:
1. М = т. Тогда f(x) в промежутке [а, Ь] сохраняет постоянное
значение: в самом деле, неравенство т ^ f(x) ^Мв этом случае
дает f(x) = М при всех х; поэтому f'(x) = 0 во всем промежутке,
так что в качестве с можно взять любую точку из (а,Ь).
2. М > т. Мы знаем, что оба эти значения функцией дости-
достигаются, но так как f(a) = f(b)9 то хоть одно из них достигается
в некоторой точке с между а и Ь. В таком случае из теоремы
Ферма следует, что производная f\c) в этой точке обращается
в нуль. Теорема доказана.
На геометрическом языке теорема Ролля означает следую-
следующее: если крайние ординаты кривой у = f(x) равны, то на кривой
найдется точка, где касательная параллельна оси х (рис. 50).
Обращаем внимание на то, что непрерывность функции f(x)
в замкнутом промежутке [а,Ь] и существование производной
во всем открытом промежутке (а, Ъ) существенны для вер-
верности заключения теоремы. Функ-
Функция f(x) = х — Е(х) удовлетворяет
в промежутке [0, 1] всем услови-
условиям теоремы, за исключением того,
что имеет разрыв при х = 1, а про-
производная f'(x) = 1 везде в @, 1).
Функция, определяемая равенства-
равенствами f(x) = х при 0 ^ х ^ \ и
f(x) = 1 — х при \ ^ х ^ 1, также
удовлетворяет всем условиям в том
же промежутке, исключая лишь то
обстоятельство, что при х — \ не существует (двусторонней) про-
производной; в то же время производная f\x) равна +1 в левой по-
половине промежутка и — 1 в правой.
Точно так же существенно и условие 3) теоремы: функция
f(x) = х в промежутке [0, 1] удовлетворяет всем условиям тео-
теоремы, кроме условия 3), а ее производная f'(x) = 1 повсюду.
Чертежи предоставляем читателю.
112. Формула Лагранжа. Обратимся к непосредственным
следствиям теоремы Ролля.
Теорема Лагранжа. Пусть 1) f(x) определена и непре-
непрерывна в замкнутом промежутке [а, Ь], 2) существует ко-
конечная производная f\x), no крайней мере в открытом
254
ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
[112
промежутке (а,й).*) Тогда между а и Ъ найдется такая
точка с (а < с < Ъ), что для нее выполняется равенство
№-f{a)
Ъ-а
A)
Доказательство. Введем вспомогательную функцию, опре-
определив ее в промежутке [а, Ъ] равенством:
Эта функция удовлетворяет всем условиям теоремы Р о л л я. В са-
самом деле, она непрерывна в [а, Ь]9 так как представляет собой раз-
разность между непрерывной функцией f(x) и линейной функцией.
В промежутке (а, Ь) она имеет определенную конечную производ-
производную, равную
v/ J v/ Ъ-а
Наконец, непосредственной подстановкой убеждаемся в том, что
F(a) = F{b) = 0, т. е. F{x) принимает равные значения на концах
промежутка.
Следовательно, к функции F(x) можно применить теорему
Рол ля и утверждать существование в (а, Ъ) такой точки с, что
F'(c) = 0. Таким образом,
Ъ-а
откуда
f\c) =
№-f{a)
Ъ-а '
Рис. 51
что и требовалось доказать.
Доказанную теорему называют также теоремой о сред-
среднем значении (в дифференциальном исчислении).
Теорема Рол ля является частным случаем теоремы Лаг-
ранжа; замечания относительно условий 1) и 2) теоремы, сде-
сделанные выше, сохраняют свою силу и здесь.
*) Конечно, непрерывность функции f(x) в (а,Ь), предположенная в 1), уже
следует из 2), но мы ни здесь, ни в последующем не ставим себе целью расчленять
условие теоремы на взаимно независимые предположения.
112] § 3. ОСНОВНЫЕ ТЕОРЕМЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ 255
Обращаясь к геометрическому истолкованию теоремы Лаг-
ранжа (рис. 51), заметим, что отношение
f{b)-f{a)
Ъ-а АС
есть угловой коэффициент секущей АВ, а /'(с) есть угловой коэф-
коэффициент касательной к кривой у = /(х) в точке с абсциссой х = с.
Таким образом, утверждение теоремы Лагранжа равносильно
следующему: на дуге АВ всегда найдется по крайней мере одна
точка М, в которой касательная параллельна хорде АВ.
Доказанная формула
f(O)=/'(c) или f(b)-f(a)=f'(c).(b-a)
носит название формулы Лагранжа или формулы ко-
конечных приращений. Она, очевидно, сохраняет силу и для
случая а > Ъ.
Возьмем любое значение хо в промежутке [а,Ь] и придадим
ему приращение Ах ^ 0, не выводящее его за пределы промежут-
промежутка. Применим формулу Лагранжа к промежутку [хо,хо + Ах]
при Ах > 0 или к промежутку [xq + Ax, xq] при Ах < 0. Число с,
заключенное в этом случае между хо и хо + Ах, можно предста-
представить так:
с =хо + в • Ах, где О<0<1*}.
Тогда формула Лагранжа примет вид
или
ДДхо) = Д*о + Ах) - Дхо) = /4*0 + в Ах) • Ах. B)
@ < в < 1)
Это равенство, дающее точное выражение для приращения функ-
функции при любом конечном приращении Ах аргумента, естествен-
естественно противопоставляется приближенному равенству [107, (За)]:
ДДхо) = Я*о + Ах) - /(хо) =/'(*о) • Ах,
*) Иногда говорят, что в есть «правильная дробь»; не следует только думать,
что речь идет о рациональной дроби — число в может оказаться и иррацио-
иррациональным.
256 ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ [113
относительная погрешность которого стремится к нулю лишь при
бесконечно малом Ах. Отсюда проистекает и самое название «фор-
«формула конечных приращений».
К невыгоде формулы Лагранжа — в ней фигурирует неиз-
неизвестное нам число в *) (или с). Это не мешает, однако, многообраз-
многообразным применениям этой формулы в анализе.
113. Предел производной. Полезный пример такого примене-
применения дает следующее замечание. Предположим, что функция /(х)
непрерывна в промежутке [xq, хо + Н] (Н > 0) и имеет конечную
производную /'(х) для х > хо. Если существует (конечный
или нет) предел
lim f'(x)=K,
х)х+О
то такова же будет и производная в точке хо
справа. Действительно, при 0< Ах ^ Н имеем Aа). Если
Ах —»> 0, то — ввиду ограниченности величины в — аргумент про-
производной хо + 9Ах стремится к пределу К, что и требовалось до-
доказать. Аналогичное утверждение устанавливается и для левосто-
левосторонней окрестности точки хо-
Рассмотрим в качестве примера функцию
f(x) = х arcsin^: + у 1 — х2
в промежутке [—1, 1]. Если —1 < х < 1, то по обычным правилам дифференци-
дифференциального исчисления легко найти:
f'(x) = arcsin^: -\i
При х -Л 1 — 0 [х —>> — 1 + 0) эта производная, очевидно, стремится к пределу
§ (—§); значит, и при х = d=l существуют (односторонние) производные
Часто сделанное замечание применяется при следующих обсто-
обстоятельствах: из того факта, что найденное для производной выраже-
выражение стремится к +оо (—сю) при приближении х к хо с той
или другой стороны, делается заключение, что в самой точ-
точке хо соответствующая односторонняя производная равна
+оо (—оо).
*) Лишь в немногих случаях мы можем его установить; например, для квадра-
квадратичной функции f(x) = ах + Ъх + с, как легко проверить, имеем в = \.
114] § 3. ОСНОВНЫЕ ТЕОРЕМЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ 257
1 2
Например, если вернуться к функциям /i (х) = х з и /2 (х) = х з,
которые мы рассматривали в п° 101, то для них (при х ^ 0) имеем:
/i() A> /2() A
Зх з Зх з
Так как первое из этих выражений при х —>> ±0 стремится к +оо,
а второе при х —>> +0 или при х —>> — 0 имеет, соответственно, пре-
пределы +оо или —сю, то заключаем, что для /i(x) в точке х = 0
существует двусторонняя производная: +оо, в то время как для
/2(л) в этой точке существуют лишь односторонние производные:
+оо справа и — оо слева.
Из сказанного вытекает также, что если конечная производ-
производная /;(х) существует в некотором промежутке, то она представляет
собою функцию, которая не может иметь обыкновенных разрывов
или скачков: в каждой точке она либо непрерывна, либо имеет раз-
разрыв 2-го рода [ср. 102,2°].
114. Формула Коши. Формула конечных приращений обоб-
обобщается следующим образом:
Теорема Коши. Пусть 1) функции /(х) и g(x) непрерыв-
непрерывны в замкнутом промежутке [а,Ь]; 2) существуют конечные
производные f'{x) и g/(x), по крайней мере в открытом про-
промежутке (а, Ъ); 3) g/(x) Ф 0 в промежутке (а,Ь).
Тогда между а и Ъ найдется такая точка с (а < с < Ъ),
что
f{b)-f{a) Ас)
g(b)-g{a) g>{Cy {)
Эта формула носит название формулы Коши.
Доказательство. Установим сперва, что знаменатель левой
части нашего равенства не равен нулю, так как в противном слу-
случае выражение это не имело бы смысла. Если бы было g{b) = g(a)9
то, по теореме Ролля, производная gf(x) в некоторой промежу-
промежуточной точке была бы равна нулю, что противоречит условию 3);
значит, g(b) ф g(a).
Рассмотрим теперь вспомогательную функцию
F{x) = fix) ~ /(«)
Эта функция удовлетворяет всем условиям теоремы Ролля. В са-
самом деле, F(x) непрерывна в [а, Ь]9 так как непрерывны /(х)
258 ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ [114
и g(x); производная F'(x) существует в (а, Ь)9 именно, она равна
Наконец, прямой подстановкой убеждаемся, что F{a) = F(b) = 0.
Вследствие этого в промежутке (а, Ь) существует такая точка с,
что F'(c) = 0. Иначе говоря,
Пс)
f{C) g(b)-g(a)
ИЛИ
П) g{b)-g{a) g[Ch
Разделив на gf(c) [это возможно, так как gf(c) ф 0], получаем
требуемое равенство.
Ясно, что теорема Лагранжа является частным случаем
теоремы К о ш и. Для получения формулы конечных приращений
из формулы Коши следует положить g{x) =x. Теорему Коши
называют обобщенной теоремой о среднем значении
(в дифференциальном исчислении).
Геометрическая иллюстрация теоремы Коши — та же, что
и для теоремы Лагранжа. Чтобы читателю легче было это
усмотреть, перейдем к другим обозначениям: х заменим на t,
а функции обозначим через q>(t) и ip(t). Если t изменяется в про-
промежутке [«,/?], то формула Коши напишется так:
m щ <„<,<« D)
Рассмотрим теперь кривую, заданную параметрическими
уравнениями
x = <p(t), y = № (a^t^p). E)
Тогда левая часть формулы и здесь выражает угловой коэффициент
хорды, соединяющей концы дуги этой кривой, а правая — угловой
коэффициент касательной в некоторой внутренней точке дуги, от-
отвечающей t = у [106, A1)].
Замечание. Эти соображения подсказывают мысль о воз-
возможности вывести формулу Коши из формулы Лагранжа.
Суть этого вывода в том, что вместо параметрической зависимо-
зависимости E) устанавливают непосредственную зависимость: у =/(х),
и тогда формула D) оказывается равнозначащей с A).
115] § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 259
§ 4. Производные и дифференциалы высших порядков
115. Определение производных высших порядков. Если функ-
функция у = f(x) имеет конечную производную у' = f'{x) в некотором
промежутке «2Г, так что эта последняя сама представляет новую
функцию от х, то может случиться, что эта функция в некоторой
точке хо из «2Г, в свою очередь, имеет производную, конечную или
нет. Ее называют производной второго порядка или
второй производной функции у = f(x) в упомянутой точке
и обозначают одним из символов
у", 1*у.
Так, например, мы видели в 92, что скорость v движения точки
равна производной от пройденного точкой пути s по времени t:
у = ^-? ускорение же а есть производная от скорости v по времени:
а = 4jL. Значит, ускорение является второй производной от
пути по времени: а = ^f.
Аналогично, если функция у = f(x) имеет конечную вторую
производную в целом промежутке ЭС (т. е. в каждой точке этого
промежутка), то ее производная, конечная или нет, в какой-либо
точкехо из <$Гназывается производной третьего порядка
или третьей производной функции у = f(x) в этой точке,
и обозначается так:
„, з1;.
Подобным же образом от третьей производной переходим к чет-
четвертой и т. д. Если предположить, что понятие (п — 1)-й производ-
производной уже определено и что (п — 1)-я производная существует и ко-
конечна в промежутке «2Г, то ее производная в некоторой точке хо
этого промежутка называется производной п-то порядка
или /7-й производной от исходной функции у = f(x); для
обозначения ее применяют символы:
Иной раз — при пользовании обозначениями Лагранжа или
К о ш и — может возникнуть надобность в указании переменной, по
260 ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ [115
которой берется производная; тогда ее пишут в виде значка внизу:
у% D\,y, $>(xo), и т. п.,
причем х2,х3,... есть условная сокращенная запись вместо
хх, ххх, ... Например, можно написать: а = s.
[Читателю ясно, что и здесь цельные символы
^, /*) или f%\ Dnf или Dnxnf
можно рассматривать как функциональные обозначения.]
Таким образом, мы определили понятие /7-й производной, как
говорят, индуктивно, переходя по порядку от первой произ-
производной к последующим. Соотношение, определяющее /7-ю произ-
производную:
называют также рекуррентным (или «возвратным»), поскольку оно
«возвращает» нас от /7-й к {п — 1)-й производной.
Самое вычисление производных п-то порядка, при численно задан-
заданному производится по известным уже читателю правилам и формулам. Напри-
Например, если
1 4 1 3 „ 2 4 1
у = — х х + 2х -\— х ,
У 2 6 3 2
то
у' = 2х3 - -jc2 + 4jc + -, у" = 6х2 -х+4,
т 1О л IV 1О
у = Izjc — 1, у = 12,
так что все последующие производные равны тождественно 0. Или пусть
у = ы(х + \Д2 + 1);
тогда
/ 1 // X fff АХ 1
У = , л У =
v- +i О2+ 1I' (jc2 +1M'
что читателю легко проверить самостоятельно.
Заметим, что по отношению к производным высших порядков
так же, индуктивно, можно установить понятие односторонней
производной [ср. 100]. Если функция у = f(x) определена лишь
в некотором промежутке «2Г, то, говоря о производной любого по-
порядка на конце его, всегда имеют в виду именно односторон-
одностороннюю производную.
116] § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 261
116. Общие формулы для производных любого порядка. Итак,
для того чтобы вычислить /7-ю производную от какой-либо функ-
функции, вообще говоря, нужно предварительно вычислить производ-
производные всех предшествующих порядков. Однако в ряде случаев уда-
удается установить такое общее выражение для /7-й производной,
которое зависит непосредственно от п и не содержит более обозна-
обозначений предшествующих производных.
При выводе таких общих выражений иногда бывают полезны
формулы:
(см)**) = с • i/71), {и ± v){n) = г№ ± г/"),
обобщающие на случай высших производных известные читателю
правила I и II п° 97. Их легко получить последовательным приме-
применением этих правил.
1) Рассмотрим сначала степенную функцию у = х^9 где \х —
любое вещественное число. Имеем последовательно:
у1 = ^~\ у" =
Легко усмотреть отсюда и общий закон:
но, строго говоря, он еще подлежит доказательству. Для этого вос-
воспользуемся методом математической индукции. Допустив, что для
некоторого значения п эта формула верна, продифференцируем ее
еще раз. Мы придем к результату:
1) . . . (И - П
- п + l)
так что наша формула оказывается верной для (п + 1)-й производ-
производной, если была верна для /7-й. Отсюда и следует ее справедливость
при всех натуральных значениях п.
Если, например, взять \х = — 1, то получим
262 ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ [116
а при /i = — i
1 „
И Т. П.
Когда само /i есть натуральное число т, то m-я производ-
производная от хт будет уже постоянным числом т\, а все следующие —
нулями. Отсюда ясно, что и для целого многочлена степени т име-
имеет место аналогичное обстоятельство.
2) Для несколько более общего выражения
у = (а + ЪхУ {а, Ъ — const)
столь же легко найдем:
В частности, получается, как и выше,
» (-l)nn]bn
а + Ъх) (а+Ьх)п+1'
\{п) _ (-l)nBn-l)\\bn
) ~ 2( Ь)/ Ъ'
/а+Ъх) 2п(а + Ьх)пл/а +Ъх
3) Пусть теперь у = lnx. Прежде всего, имеем
/ = (In*)' = \.
Возьмем отсюда производную (п — 1)-го порядка по соответ-
соответствующей формуле из 1), заменив в ней п на п — 1; мы и получим
тогда
4) Если у = ах, то
у' = ах-\па, у" = ахAпаJ, ...
*^ Символом п\\ обозначают произведение натуральных чисел, не превосходя-
превосходящих пи одной с ним четности, так что, например,
7!! = 1 • 3 • 5 • 7, 10!! = 2 • 4 • 6 • 8 • 10.
116] § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 263
Общая формула
легко доказывается по методу математической индукции.
В частности, очевидно,
5) Положим у = sinx; тогда
у1 — cosx, у11 — - sinx, у111 — - cosx,
IV • V
у = sinx, у = cosx, . ..
На этом пути найти требуемое общее выражение для /7-й производ-
производной трудно. Но дело сразу упрощается, если переписать формулу
для первой производной в виде у1 = sin (х + f); становится ясным,
что при каждом дифференцировании к аргументу будет прибавлять-
прибавляться ^, так что
( • \(п) • ( , Л\
к } \ 2)
Аналогично получается и формула
^ = cos(x +п - —\
6) Рассмотрим функцию;; = —= =-. Представив ее в виде
х1 — а1
1 1
2а\х — а х + а
мы получаем возможность использовать пример 2) (и общие правила, указанные
вначале). Окончательно,
1 \М (-l
2а
1 1
- а)п+1
а)п+1 (х + «
7) В случае функции у = еах sin Z?^ мы употребим более искусственный при-
прием. Именно, имеем
у' = аеах sin foe + beax cosbx;
если ввести вспомогательный угол ф, определяемый условиями
Ь а
264 ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ [116
то выражение для первой производной можно переписать в виде:
у' = у а2 + Ъ2 • еах • (sinbx • cos cp + cosbx • sin<p) =
= л/а2 + b2 • еах • sin(bx + ф).
Повторяя дифференцирование, легко установить общий закон
yW = [а + b J • еах • sm(bx + пер)
и обосновать его по методу математической индукции.
8) Остановимся еще на функции у = arctg x. Поставим себе сначала задачей
выразить у(п' через у. Так как х = tgy, то
1 2 ¦ ( , я
у = у = cos у = cosy • sin (у -\
Дифференцируя вторично по х (и помня, что у есть функция от х), получим
у" = — siny • sin fу -\ j + cosy • cos fу -\ J • у =
= cos у • cos f 2y -\ j = cos у • sin 2 f у -\ j .
Следующее дифференцирование дает
у'" = [-2siny • cosy • sin2 (у + -J +2cos2y • cos2 (y + -jj • yf =
= 2 cos у • cos f 3y + 2 • — J = 2 cos у • sin 3 f у -\ J .
Общая формула:
yW = (n — l)!cos"y - sinniy -\ J
оправдывается по методу математической индукции.
Если (при х > 0) ввести угол
1 jt
z = arctg — = у,
х 2
то эта формула может быть переписана так:
y(w) = (и - 1)! w • sinn(jr - z)
или, наконец,
f™\ „л 1 1
• sin n arctg —.
9) Установим в заключение, в виде упражнения, формулу
I
Dn(xn~leh = (-1)п-Ц- (п= 1,2, 3...).
117] § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 265
Справедливость ее при п = 1 и п = 2 проверяется непосредственно. Допустим те-
теперь, что она верна для всех значений п вплоть до некоторого п ^ 2,
и докажем, что тогда она сохранит верность и при замене п на я + 1 *\ С этой
целью рассмотрим выражение
Пользуясь нашим допущением, можно переписать это выражение так:
Dn+l (xneh = n • (-ir-^т - D [(-If-1—1 = (-1Г+1^
что и требовалось доказать.
Итак, формула верна для всех натуральных значений п.
117. Формула Лейбница. Как мы заметили в начале преды-
предыдущего п°, правила I и 11,97, непосредственно переносятся и на
случай производных любого порядка. Сложнее обстоит дело с пра-
правилом III, относящимся к дифференцированию произведения.
Предположим, что функции и, v от х имеют каждая в отдельно-
отдельности производные до /7-го порядка включительно: докажем, что тогда
их произведение у = uv также имеет /7-ю производную, и найдем
ее выражение.
Станем, применяя правило III, последовательно дифференциро-
дифференцировать это произведение; мы найдем:
у' = u'v + ш/, у" = u"v + 2u'vf + uv",
у'" = umv + Зг/V + Ъи'у" + uv'", . . .
Легко подметить закон, по которому построены все эти форму-
формулы: правые части их напоминают разложение степеней бинома:
и + v9 (и + vJ, (и + г;K, ..., лишь вместо степеней и, v стоят
производные соответствующих порядков. Сходство станет более
полным, если в полученных формулах вместо и, v писать и^\ v^\
Распространяя этот закон на случай любого /7, придем к общей
* ^ Обращаем внимание читателя на эту своеобразную форму применения мето-
метода математической индукции; в действительности (см. текст ниже) мы используем
справедливость нашей формулы для п и для п — \.
266 ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ [117
формуле *);
/=0
Для доказательства ее справедливости прибегнем снова к мето-
методу математической индукции. Допустим, что при некотором значе-
значении п она верна. Если для функций и, v существуют и (п + 1)-е про-
производные, то можно еще раз продифференцировать по х; мы по-
получим:
/=0 i=0 i=0
Объединим теперь слагаемые обеих последних сумм, содержа-
содержащие одинаковые произведения производных функций и и v (сумма
порядков производных в таком произведении, как легко видеть, рав-
равна всегда /7+1). Произведение u^n+1^v^ входит только в первую
сумму (при / = 0); коэффициент его в этой сумме есть С^ = 1.
Точно так же u^v^1^ входит только во вторую сумму (в слага-
слагаемое с номером i = п)9 с коэффициентом С% = 1. Все осталь-
остальные произведения, входящие в эти суммы, имеют вид u^n+1~k^v^k\
причем 1 ^ к ^ п. Каждое такое произведение встретится как
в первой сумме (слагаемое с номером i = к)9 так и во второй
сумме (слагаемое с номером г = к — 1). Сумма соответствующих
коэффициентов будет Скп +С^~1. Но, как известно,
*^ Символ J2 означает сумму однотипных слагаемых. Когда слагаемые эти
зависят от одного значка, меняющегося в определенных границах, то эти границы
и указываются (снизу и сверху). Например,
J2ai — а0
i=0
к=\
118] § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 267
Таким образом, окончательно находим:
k=l
и+1
Мы получили для jAw+1) выражение, вполне аналогичное выра-
выражению A) (только п заменялось числом /7 + 1); этим и доказана
справедливость формулы A) для всех натуральных значений п.
Установленная формула носит название формулы Ле й б ниц а.
Она часто бывает полезна при выводе общих выражений для
/7-й производной.
Заметим, что такую же формулу можно было бы установить
и для /7-й производной произведения нескольких сомножи-
сомножителей у = uv. . Л\ она имеет сходство с разложением степени
многочлена {и + v + ... + t)n.
118. Примеры.
1) Найдем при помощи формулы Лейбница A) производную
Положим v = х2, и = cos ax. Тогда
(к) к
и> ' = a cos ( ах + к
¦!)¦
Г ~ II ~ III IV г*
v = 2x, v =2, v = v =...=0.
Таким образом, в формуле A) все слагаемые, кроме трех первых, равны нулю,
и мы получаем:
М<5°) = х2 • а50 • cos(a* + 50 . |) + ^ . 2х • а"9 • cos (ах + 49 . |
50-49 48 /
+ -р-^- • 2 • а48 • cos^jc + 48
-J =
= а48 [B450 - а2х2) cos ах - Шах • sin ах].
2) Возвращаясь к примеру 7), 116, теперь мы может получить общее выра-
выражение для п-й производной функции
у = еах • sinbx
268
ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
[118
непосредственно по формуле Лейбница:
О?)
У = е
ах\ ¦ и ( п п[п-\) „_2 2 \
sin for (я —-—а Ъ + ...J +
+ cos bx I na
/i-l,
•¦)]•
1 -2-3
3) Найдем выражение для (п + 1)-й производной функции у = arcsinjc.
Имеем, прежде всего,
так что, по формуле Лейбница,
„+1 =
1
1
О+7
О^7
О+7
М
О^7
О+7
(/1-1)
л(л - 1) / 1
1 -2
1 -2-3
1+JC
п-Ъ)
(и-2)
О^7
/Г^Гх
Если теперь к вычислению последовательных производных от J-— и J^—
применить формулы, полученные в 116,2), то придем к результату
^2 - 1)!!
2я - 3)!! 1!!
п(п - 1)
-х)
{In- 5)!!3!!
Ь2 A+jc)"-2A -xJ
4) Требуется найти значения всех последовательных производных функции
у = arctg^: при х = 0.
Так как j/ = j-^, toj/A + х2) = 1. Возьмем я-ю производную от обеих
частей этого равенства (пользуясь формулой Лейбница):
Положим здесь х = 0; если значение производных при х = 0 отмечать значками 0
внизу, то получим:
(«+1) _ _ / _ i\ 0-1)
При jf = 0 производная у" = —
2х
2
обращается в 0: у" = 0. Из найден-
ного соотношения ясно, что всегда у^ = 0. Что же касается производных
нечетного порядка, то имеем для них рекуррентную формулу:
Принимая во внимание, что^о = 1, получаем отсюда:
yBm+l) = {_1ГBтI
118] § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 269
Тот же результат можно было бы получить и из общей формулы приме-
примера 8), 116.
5) То же — для функции у = arcsin^c.
Указание. Формулу Лейбница применить к соотношению:
A-х2).у"-х-у'=0.
Ответ: у$т) = О, у^т~1) = I2 • З2 . . . Bт - IJ = [Bт - I)!!]2. Этот
результат из общих выражений в 3) получается не столь просто.
6) Многочлены Лежандра. В заключение остановимся на важных много-
многочленах, носящих имя Лежандра (А.М. Legendre). Они определяются равен-
равенствами
Хп{х)=сп К ^п } (/1=1,2,3,...),
где постоянным коэффициентом сп придаются те или иные значения в зависимо-
зависимости от соображений удобства.
Прежде всего убедимся в том, что многочлен Хп[х) (степени п) имеет п
различных вещественных корней, которые все содержатся между —1 и +1. Для
простоты положим пока сп = 1.
Легко видеть, что многочлен (х2 — \)п = (х — \)п • (х + \)п и его п — 1
последовательных производных обращаются в нуль при х = d=l. Тогда первая ее
производная, по теореме Ролля [111], будет иметь корень и между —1 и +1;
по той же теореме, вторая производная будет иметь два корня между —1 и +1,
и т. д., вплоть до {п— 1)-й производной, которая, помимо корней —1 и +1, будет
между ними иметь еще п — 1 корней. Применив к ней еще раз теорему Ролля,
придем к требуемому заключению.
Сохраняя коэффициенты сп = 1, определим теперь значения многочлена
Хп(х) при х = ±1.
По формуле Лейбница, рассматривая степень (х — \)п как произведение
(х + \)п на (х — \)п, можно написать:
dxn dx dxn~
Так как все слагаемые, начиная со второго, содержат множитель х — 1 и, следо-
следовательно, обращаются в 0 при х = 1, то очевидно: Хп(\) = 2п • п\.
Аналогично получаем: Хп{ — \) = ( — 1)" • 2п • п\.
Если в формуле, дающей общее определение многочлена Лежандра Хп(х),
положить, в частности,
1
то получится многочлен, который чаще всего встречается; именно его мы будем
впредь всегда обозначать через Рп(х). Он характеризуется тем, что в точках
х = \ и х = — 1 принимает значения
270 ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ [119
С помощью формулы Лейбница легко установить далее, что многочлены
Лежандра Хп(х) удовлетворяют следующему соотношению:
О2 - 1)Х" + 2х • Х'п - п(п + \)Хп = 0,
которое играет важную роль в теории этих многочленов.
В самом деле, полагая у = (х — \)п, имеем
1 ^ /2-1 \п—1 /2 л\ I п.
у = 2пх • (х — 1) , так что (х — 1) • у = 2пх • у.
Возьмем теперь (п + 1)-е производные от обеих частей последнего равенства;
по формуле Лейбница,
Отсюда
(,2 _ 1)у(п+2) + ^(„+1) _ и(и + l)y(n) = Q
и, по умножении на сп, получается доказываемое соотношение.
119. Дифференциалы высших порядков. Обратимся теперь
к дифференциалам высших порядков; они также определяются ин-
индуктивно. Дифференциалом второго порядка или вторым
дифференциалом функции у = /(х) в некоторой точке назы-
называется дифференциал в этой точке от ее (первого) дифференциала;
в обозначениях
d2y=d{dy).
Дифференциалом третьего порядка или третьим
дифференциалом называется дифференциал от второго диф-
дифференциала:
d3y =d(d2y).
Вообще, дифференциалом /7-го порядка или п-м диф-
дифференциалом функции у = f(x) называется дифференциал
от ее (п - 1)-го дифференциала:
dny=d(dn-ly).l9)
19' Подчеркнем, что в формулах d2y = d{dy) и dny = d(dn ly) все диф-
дифференциалы рассматриваются как функции от х при фиксированном Ах; это
необходимо, чтобы повторное дифференцирование стало возможным. Отметим
[ср. примеч. 18 на с. 240], что, когда Ах фиксировано, dy является функцией
от х, a dx — постоянным числом, причем dy = y'x • dx. Это позволяет говорить
о дифференцируемости функции dy как функции он и находить от нее произ-
производную и значение дифференциала (отвечающее тому же значению Ах), поль-
пользуясь простейшими правилами дифференцирования: (dy)f = (у'х • dx)' = у" • dx;
d(dy) = (dy)'x • dx = y'x' • (dx)\ и т. д.
120] § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 271
Если пользоваться функциональным обозначением, то последо-
последовательные дифференциалы могут быть обозначены так:
d2f(x0), d3f(x0), ..., dnf(x0), ...,
причем получается возможность указать то частное значение
х = хо, при котором дифференциалы берутся.
При вычислении дифференциалов высших порядков очень важ-
важно помнить, что dx есть произвольное и не зависящее от j
число, которое при дифференцировании по х надлежит рассмат-
рассматривать как постоянный множитель. В таком случае, будем
иметь (все время — предполагая существование соответствующих
производных):
d2y = d(dy) = d{y' • dx) = dy1 • dx = (/' • dx) • dx = y" • dx2,
d3y = d(d2y) = d{y"'dx2) = dy"'dx2 = {y'"'dx)'dx2 =y'"-dx3 *},
и т. д. Легко угадываемый общий закон
доказывается методом математической индукции. Из него следует,
что
(п) _ йПУ
так что отныне этот символ можно рассматривать как дробь.
Воспользовавшись равенством B), легко теперь преобразовать
формулу Лейбница к дифференциалам. Достаточно умножить
обе части ее на dxn9 чтобы получить
dn(uv) = Y^CJ^u • cfv (d°u = и, d°v = v).
i=0
Сам Лейбниц установил свою формулу именно для дифферен-
дифференциалов.
120. Нарушение инвариантности формы для дифференциа-
дифференциалов высших порядков. Вспоминая, что (первый) дифференци-
дифференциал функции обладает свойством инвариантности формы,
естественно поставить вопрос, обладают ли подобным свойством
*^ Под dx , dx , . . . и т. п. всегда разумеются степени от дифференциа-
дифференциала: (dx) , (dx)i , . . . Дифференциал от степени будет обозначаться так: d(x ),
272 ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ [120
дифференциалы высших порядков. Покажем, например, что уже
второй дифференциал этим свойством не обладает.
Итак, пусть у = f(x) и х = q>(t)9 так что у можно рассмат-
рассматривать как сложную функцию от t: у = f{cp{t)). Ее (первый)
дифференциал по t можно написать в форме dy = y'x -dx9 где
dx = x't - dt есть функция от t. Вычисляем второй дифференци-
дифференциал по t: d2y = d{y'x -dx) = dy'x -dx +y'x -d(dx). Дифференциал dy'x
можно, снова пользуясь инвариантностью формы (первого) диффе-
дифференциала, взять в форме dy'x = у • dx, так что окончательно
d2y=yfxf2-dx2+yx-d2x, C)
в то время как при независимой переменной х второй дифферен-
дифференциал имел вид d2y = у -dx2. Конечно, выражение C) для d2y
является более общим: если, в частности, х есть независимая
переменная, то d2x = 0 — и остается один лишь первый член.
Возьмем пример. Пусть;; = х , так что, покуда х — независимая пере-
переменная:
dy = 2xdx, d у = 2dx .
Положим теперь х = t2; тогда у = t4, и
dy = 4t3dt, d2y = \2t2dt2.
Новое выражение для dy может быть получено и из старого, если туда подставить
х = t , dx = 2tdt. Иначе обстоит дело с dry. сделав такую же подстановку,
мы получим St dt вместо \2t dt . Если же продифференцировать равенство
dy = 2xdx по t, считая х функцией от t, то, наподобие C), придем к формуле
d2y = 2dx2 + 2xd2x.
Подставив сюда х = t , dx = 2tdt, d x = 2dt , получим уже правильный резуль-
результат: \2t2dt2.
Итак, если х перестает быть независимой переменной, то диф-
дифференциал второго порядка d2y выражается через дифференциа-
дифференциалы х двучленной формулой C). Для дифференциалов третье-
третьего и дальнейших порядков число добавочных (при переходе к но-
новой независимой переменной) членов еще возрастет. В соответ-
соответствии с этим в выражениях высших производных у, у'"ъ, ... через
дифференциалы
уже нельзя дифференциалы брать по любой переменной, но
лишь по переменной х.
121] § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 273
121. Параметрическое дифференцирование. Можно, впрочем,
написать выражения производных по х и через дифференциалы,
взятые по любой переменной t, но они будут гораздо сложнее.
Именно, считая все ниже написанные дифферен-
дифференциалы взятыми по t, имеем последовательно
^\ dx-d2y-d2x-dy
d)
-, -, di^\ dx-dy-
, = dy_ „ = dy_, = a\dx) = dxi
Ух dx' У%1 (dx)x dx dx
т. e.
„ dx • d2y — d2x • dy
y =;
затем,
dx'd2y-d2x-c
dx
dx3(dx- d3y-d3x- dy)-3dx2-d2x(dx- d2y-d2x- dy)
_ dx^_
~ dx
и окончательно:
//; dx(dx - d3y — d3x • dy) — 3d2x(dx • d2y — d2x • dy)
и т.д. Формулы E), F), ... являются наиболее общими;
если в них считать х независимой переменной, то d2x, d3x
обратятся в нуль — и мы вернемся к формулам D).
Полученные нами формулы для производных у по х осущест-
осуществляют так называемое параметрическое дифференциро-
дифференцирование. Если х и у заданы в функции от параметра t:
x=<p(t), y=ip(t),
то, как мы видели в 106, при известных условиях этим определяет-
определяется и у как функция от х: у = f(x). При наличии последовательных
производных отх и^по/ существуют соответствующие производ-
производные от у по х и выражаются выведенными выше формулами.
Иногда удобнее иметь выражение производных у по х через
производные же (а не дифференциалы) от х и у по t. Их лег-
легко получить из дифференциальных выражений, разделив числитель
274 ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ [122
и знаменатель, соответственно, на dt,dt3,dt5, ... Таким путем
придем к формулам:
~di f \~dt)
аналогично:
и т. д.
122. Конечные разности. Пусть функция f(x) определена в некотором про-
промежутке SC и все значения х, которые будут встречаться, считаются принадлежа-
принадлежащими этому промежутку. Фиксировав некоторое приращение Ах переменной х
(мы будем предполагать, для определенности, Ах > 0, хотя ничто не мешало бы
рассматривать и Ах < 0), положим
Af(x) = fix + Ах) - fix)
и назовем это выражение первой разностью нашей функции. Второй раз-
разностью называется первая разность от первой разности:
А2/0) = A[Af(x)] = Af(x + Ax)-Af(x) = /0 + 2Ajc)-2/0 + Ajc)+/0).
Высшие разности определяются индуктивно:
Anf(x) = A[An~lf(x)}.
Впрочем, для п-й разности может быть установлена и формула
п
Anf(x) = ^(-\)lClnf(x + ~п^1Ах) = f(x + пАх) -
i=0
f(x + n — \Ax) + — -f(x + n — 2Ajc) — . . . + ( — l)nf(x),
выражающая эту разность непосредственно через значения самой функции f(x)
в равноотстоящих точках
х, х + Ах, х + 2 Ах, . . ., х + п Ах.
Эта формула легко доказывается по методу математической индукции, что может
быть предоставлено читателю.
Сопоставим теперь эти конечные разности с производными и дифферен-
дифференциалами.
Предположим, что функция f[x) имеет п—\ непрерывных производных
J \х)> J \х)> • • •» / \х)
в замкнутом промежутке [xq, xq + пАх] и конечную п-ю производную /^ (х), по
крайней мере в открытом промежутке (xq, XQ-\-nAx). Тогда имеет место формула
л"/0о) = /n\in) • Ах11, где ^0 < in < xq + пАх. G)
122] § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 275
При п = 1 дело сводится к формуле конечных приращений, которая является
простейшим частным случаем формулы G). Намереваясь провести доказатель-
доказательство нашего утверждения по методу математической индукции, мы допустим спра-
справедливость измененной формулы G), получаемой при замене пшп—\, разумеет-
разумеется, при соответственно измененных предположениях, и докажем G) при сделан-
сделанных предположениях. Из них следует, что для функции Af(x) = f(x-\-Ax) —f(x)
в промежутке [xq, xq + п — \Ах] с избытком выполняются условия применимости
измененной формулы G), и мы можем записать
A"-l[Af(x0)] = Anf(x0) = Ц{п-1)A,-1+Ь<)-/-п-1\Ь-1)] ¦ Ах"-1, (8)
где xq < ?и—1 < xq -\- п — \Ах. Применяя к правой части этого равенства фор-
формулу конечных приращений *\ получим непосредственно формулу G), причем
*0 < |и-1 < in < in-\ + Ax < xq + nAx.
Заметим, что если производная /^ (х) существует также в точке xq и притом
непрерывна в этой точке, то из соотношения G) при Ах —>> 0 (тогда |w -^ xq)
следует, что
Г Ч*о) = lim л п • (9)
А^О Ахп
л п
Ахп
Впрочем, эта интересная формула, устанавливающая возможность получения
п-й производной с помощью лишь одного предельного перехода, справедлива
при единственном предположении, что эта производная существует именно в точ-
точке xq. Это значит, что в некоторой окрестности точки jcо существуют
производные
/(*). /"(*)..... Z"-1^)
и, следовательно, при достаточно малом Ах может быть применена фор-
формула (8). Ввиду существования производной /^(*о)» воспользовавшись форму-
формулой B) п° 96, можем написать
где а и /3 зависят от Ах и вместе с ним стремятся к нулю. Отсюда и из (8)
вытекает**^:
где у — новая бесконечно малая. Наконец, деля это равенство почленно на Ахп
и переходя к пределу при Ах -л 0, придем к формуле (9).
Подчеркнем, что она имеет место лишь в предположении, что су-
существует производная f (xq). Предел справа может существовать
*) На что мы имеем право, так как функция рп 1\х) непрерывна в промежут-
промежутке [!и_ь ?и—1 + Ах], а внутри него имеет конечную производную /^(х).
**) Учитывая, что 0 < |w_i — xq < (n — \)Ах (при Ах > 0).
276 ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ [123
и тогда, когда этой производной нет. *) Рассмотрим, например, функцию, опре-
определенную так:
f{x) = х3 • sin - 0 ф 0), ДО) = 0,
х
взяв xq = 0. Для нее существует первая производная
/'(*) = Зх2 • sin - - х • cos - 0 ф 0), /@) = 0,
X X
но нет в точке 0 второй производной, ибо отношение
/'@) ЗА*2 • sin ^-Ax-cos ^
sin ± _ cos
А
3 ^ sin cos
Ах Ах Ах Ах
при Ах —у 0 предела не имеет. В то же время выражение
А2/@) _ ДО + 2Ajc) - 2/@ + Ajc) + ДО) _
Ajc2
sin Л- - 2А^3 • sin J- 1
^?* 8A i
1 1
*- = 8Ajc • sin 2Ajc -sin у 0.
2A A
== 8Ajc • sin2Ajc -sin
Ajc2 2Ajc Ajc
§ 5. Формула Тейлора
123. Формула Тейлора для многочлена. Если р(х) есть много-
многочлен степени п\
pipe) = ао + tfi* + <Я2Х2 + <яз*3 + .. . + апхп, A)
то, последовательно дифференцируя его п раз:
j^;(x) = а\ + 2 • <Я2Х + 3 • <2зх2 + .. . + п • апхп~1,
р"(х) = 1 • 2 • а2 + 2 • 3 • а3х + .. . + in - \)п • ^х",
//"(*) = 1 • 2 • 3 • аз + • • • + (л - 2)(л - \)п • а^71,
pW(jc) = 1-2-3... и-а,,
и полагая во всех этих формулах х = 0, найдем выражения
коэффициентов многочлена через значения самого
*) Так что формула (9) отнюдь не дает нового определения самого понятия
п-и производной, равносильного старому!
123] § 5. ФОРМУЛА ТЕЙЛОРА 277
многочлена и его производных при х = 0
ао=,«». в1 = Ш. .2 = ^,
//"(О) ' р(«)@)
а3 = ^-, .... а« = —Г-
Подставим эти значения коэффициентов в A):
1 + 1+^1+... + ^1,B)
Эта формула отличается от A) записью коэффициентов.
Вместо того чтобы разлагать многочлен по степеням х9 можно
было бы взять его разложение по степеням х — xq9 где хо есть
некоторое постоянное частное значение х:
р(х) = А0 +А\(х -хо) +А2(х -хоJ +
+ Аъ(х - хоK + ... +Ап(х - хо)п. C)
Полагая х — хо = |, р(х) = р(хо + |) = РD)9 для коэффициентов
многочлена
РD) =A0+Ali+ A2i2 + АЪ? + ..
имеем, по доказанному, выражения:
Рш@) ()'
3!
Но
_
«—
так что
Р@)=р(х0), Р'(О)=р'(хо), Р"(О)=р"(хо),...
Ао = р(х0), Ах = —^т-А А2 = 1 ',
1! 2!
А р'"Ы . р{
А3 A
т. е. коэффициенты разложения C) оказались выра-
выраженными через значения самого многочлена и его
производных при x=xq.
278 ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ [124
Подставим в C) выражения D):
Формула E), так же как и ее частный (при хо = 0) случай B), на-
называется формулой Тейлора. (В. Taylor). *) Известно, какие
важные применения она имеет в алгебре.
Сделаем (полезное для дальнейшего) очевидное замечание,
что если многочлен р(х) представлен в виде
р{х) = со+—- (х-хо) + — (*-*оJ+^- (х-
то необходимо
124. Разложение произвольной функции; дополнительный член
в форме Пеано. Обратимся теперь к рассмотрению произволь-
произвольной функции /(х), вообще не являющейся многочленом. Предпо-
Предположим, что для нее в некоторой точке хо существуют производные
всех порядков до /7-го включительно. Это значит, точнее говоря,
что функция определена и имеет производные всех порядков до
{п — 1)-го включительно:
f{x), f'{x), /'"(*), .... /"-1}M
в некотором промежутке [а, Ь]9 содержащем точку хо, и, кроме
того, имеет производную /7-го порядка /^ (хо) в самой точке хо **^
Тогда, по образцу E), и для функции f(x) может быть составлен
многочлен
Согласно предшествующему замечанию, этот многочлен и
его производные (до/7-й включительно) в точке хо име-
*^ Впрочем, формулу B) часто называют формулой Маклорена
(С. Maclaurin).
**) Если точка х о является одним из концов промежутка [а,/?], то, говоря
о производных в этой точке, мы имеем в виду односторонние производные.
124] § 5. ФОРМУЛА ТЕЙЛОРА 279
ют те же значения, что и функция f(x) и ее про-
производные.
Но на этот раз, если только f(x) не есть целый многочлен
/7-й степени, уже нельзя утверждать равенства f(x) = р(х). Много-
Многочлен/?(х) дает лишь некоторое приближение функции/(х).
Поэтому особый интерес приобретает изучение разности
r{x)=f{x)-p{x). G)
Установим прежде всего, что при х —»> хо эта разность пред-
представляет собой бесконечно малую порядка выше п-го (по срав-
сравнению с х -хо):
ф)=о«х-хоГ). (8)
По свойству многочлена р(х)9 для функции г(х), очевидно, бу-
будут иметь место равенства
фо) = г'(х0) = г"(х0) = ...= rW(xo) = 0. (9)
Мы сейчас установим общее утверждение: если для ка-
какой-либо функции г(х), имеющей в точке хо производные
до п-го порядка включительно, выполняются условия (9), то
имеет место соотношение (8).
Доказательство проведем по методу математической индукции.
При /7=1 это утверждение имеет вид: если функция г(х), име-
имеющая в точке хо производную (первого порядка), удовлетво-
удовлетворяет условиям
г(хо)=г/(хо)=О,
то
г(х) = о(х -х0).
Его справедливость проверяется непосредственно:
г Г(Х) г г(х)-г(х0) ,, , А
lim ——^ — lim —^ —- = г (хо) = 0.
^х0 х Хо х^х0 х Хо
Предположим теперь, что сформулированное выше утвер-
утверждение справедливо для какого-либо п ^ 1, и докажем, что
оно остается верным и при замене п на п + 1, т. е. что: если для
какой-либо функции г(х), имеющей в точке хо про-
производные до (п + \)-го порядка включительно, выполняются
условия
фо) = г'(х0) = г"(*о) = ... = гпЫ = Ап+Х\хо) = 0, (9*)
то
+1). (8*)
280 ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ [124
Из (9*) усматриваем, что функция г'(х) удовлетворяет услови-
условиям типа (9), а значит, для нее по предложенному уже имеем:
г'(х)=о((х-х0у).
Но, по формуле конечных приращений [112],
г{х) = г(х) -г(хо) =г\с) • (х -хо),
где с содержится между хо и х; так как \с — хо| < \х — хо|, то
г'(с) = о ((с-*оГ) = 0 ((*-*„)"),
и мы окончательно приходим к (8*), что и требовалось доказать.
Таким образом, наше утверждение оправдано для любого нату-
натурального /7, и для разности G) действительно выполняется соотно-
соотношение (8). Принимая во внимание F), мы получаем формулу
A0)
которая от формулы E) для многочлена разнится наличием
дополнительного члена (8). В указанной форме дополни-
дополнительный член был дан Пеан о (G. Реапо). Формула A0) и называ-
называется формулой Тейлора с дополнительным членом в форме
Пеано.
Доказанная формула является естественным обобщением фор-
формулы C) п° 96, которую можно написать так:
f{x) = Д*о) +/'(*<>)(* -*о) + о{х -х0);
она отвечает /7=1. Там функция /(х), с точностью до бесконечно
малой порядка выше первого, представлялась в виде линейной
функции, здесь же мы представляем ее целым многочленом
/7-й степени, но уже с точностью до бесконечно малой порядка
выше /7-го.
Легко показать, что такое представление функции f{x) един-
единственно, т. е. что если имеем одновременно вблизи хо
f{x) =Ao+Alix-xo)+A2ix-xoJ + ...+Anix-xo)n+oiix -xo)n)
fix) =A'0+A[ix-xo)+A'2ix-xoJ+...+A'nix-x0)n+oiix -xo)n),
124] § 5. ФОРМУЛА ТЕЙЛОРА 281
то необходимо
A0=Af0, Ai=A[, ..., An=Atn.
Действительно, из тождества
А0+Ах(х -хо)+А2(х -хоJ + ... +Ап(х -xo)n=Afo +
+ А[(х - х0) + А'2(х - х0J + . .. + А'п(х - хо)п + о ((х - хо)п)
при х —>> хо сразу получаем Ао = А'о. Уничтожив эти члены и деля
их на х — хо, получим:
Ах +А2(х - х0) + ... +Ап(х - хо)^1) =
= А[ +А'2{х -х0) + ... +А'п(х -хоГ +о((х -хоГ),
откуда, аналогично, А\ = А[,ит. д.
Иногда удобно формулу A0) применять в другой форме. До-
Дополнительный член г(х) можно представить так:
г(х) = — (х -хо)",
где а зависит от х и стремится к 0 вместе с х -хо- Подставляя это
выражение, получим
AOa)
Далее, перенося в формуле A0) /(хо) налево и полагая
х — хо = Ах, можно переписать ее в виде
^ ¦ Ах2 + ...
. A06)
В этой форме она еще ближе к формуле C) п° 96:
Af(x0)=f\xQ)-Ax+o(Ax).
Последняя выделяет лишь один главный член из бесконечно ма-
малого приращения функции А/(хо) — считая, как всегда, Ах за
основную бесконечно малую, в то время как в формуле A06) вы-
выписаны члены всех порядков до /7-го включительно, причем все они
являются простейшими бесконечно малыми в смысле п° 63.
282 ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ [125
С точностью до дополнительного члена, таким образом, при-
приращение функции разложено по степеням прира-
приращения независимой переменной.
Наконец, вспоминая, что
f'(xo)-Ax=df(xo), f
мы можем переписать A06) в такой форме:
ДДхо) = df(x0) + ^ d2f{x0) + ... + ^dnf{x0) + o(Axn).
Отсюда видим, что (при Ах —>> 0) последовательные дифференциа-
дифференциалы представляют собой, с точностью до факториалов в знаменате-
знаменателе, именно простейшие бесконечно малые члены соответственных
порядков в разложении бесконечно малого приращения функции.
125. Примеры. Всего проще выглядит формула Тейлора,
если хо = 0*):
К этому частному случаю всегда можно свести дело, взяв х — хо
за новую независимую переменную.
Рассмотрим в виде примера некоторые конкретные разложения
по этой формуле для элементарных функций.
1) Пусть f{x) = ex; тогда f^k\x) = ex при любом к = 1,2,
3, ... Так как в этом случае /@) = 1, /^@) = 1, то, по форму-
ле A1), 2
е* = 1 + - + - + ... + - + ф-).
2) Если f{x) = sinx, то f^k\x) = sin [x + к |), так что
ДО) = 0, /2т\0) = sin mn = 0,
у{2т-1)(о) = sin (mn - f) = (-l)^ (w = 1, 2, 3, ...).
Поэтому, положив в формуле A1) п = 2т, имеем
r3 r5 r2m— 1
+...+AГ
*) И эту формулу связывают с именем Маклорена [см. сноску *) на с. 278].
125] § 5. ФОРМУЛА ТЕЙЛОРА 283
3) Аналогично, при Дх) = cosx: f^k\x) = cosuc + к — j;
ДО) = 1, /2™)@) = (-l)w, /(^-^(O) =0 (m = 1, 2, 3, ...).
Таким образом (если взять п = 2т + 1):
г 4 r 2m
4) Рассмотрим теперь степенную функцию хт, где т — не на-
натуральное число и не нуль. В этом случае при х —»> 0 либо сама
функция (если т < 0), либо ее производные (начиная с некоторого
порядка, при п> т) бесконечно возрастают. Следователь-
Следовательно, здесь уже нельзя брать хо = 0.
Возьмем хо = 1, т. е. станем разлагать хт по степеням х — 1.
Впрочем, как уже упоминалось, можно ввести в качестве новой
переменной х — 1; мы ее по-прежнему будем обозначать через х
и станем разлагать функцию A +х)т по степеням х.
Как мы знаем [116, 2)],
/*)(*) = /и(/и - 1). . . (т - к + 1)A +х)т~\
так что
ДО) = 1, /W@) =m(m- 1)...(т-к+1).
Разложение имеет вид
х™ 772 (#2 — 1) о
(l+x)w = l+mx+ y V +
В частности, например, при п — 2 yl т — —I, \, —\ будем иметь
-; = 1-Х +Х2 +о(х2),
1 +х
х х + о(х2),
у/1 +х 2 8
Первое из этих разложений очень легко получается элементарно —
дополнительный член здесь просто равен ^. Второе же и третье
потребовали бы более длинных выкладок [ср. 63].
284 ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ [125
5) Если перейти к логарифмической функции lnx, которая стре-
стремится к —оо при х —>> +0, то, как и в предыдущем примере, мы
предпочтем рассматривать функцию /(х) = 1пA+х)и разлагать
ее по степеням х.
Тогда [116, 3)]
Д0) = 0, «
Отсюда
л
6) Пусть теперь f(x) = arctgx. Мы имели в 118, 4) значения
ее производных при х = 0:
/2™)@) = 0, /2т~1)@) = (-lI*^ - 2)!,
так что ее разложение представится в виде
arctgx =х-у + у-... + (-
Х2т— 1
7) Для функции /(х) = tgx закон образования коэффициентов
в формуле Тейлора сложен. Тем не менее несколько первых
членов ее написать нетрудно. Так как, например,
w/ ч ! гп( ч 0 sinx ,„ l+2sin2x
fix) — ——, / (х) = 2—=—, / (х) = 2 j ,
J v J cos2x J v y cos3x 7 v J cos4x
.IV/ л о • 2 + sin2x
/lv(x) = 8smx ^ ,
то
Д0)=0, /@) = 1, Г@)=0, ///;@)=2, /IV@)=0,
так что
x3
tgx =x + — +o(x4).
*)
Под О! мы, как всегда, разумеем 1.
125] § 5. ФОРМУЛА ТЕЙЛОРА 285
Пользуясь известными разложениями, можно, уже не вычисляя производных,
непосредственно писать разложения и для более сложных функций. Например,
предыдущая формула могла бы быть получена из разложений для sin x и cos x.
Приведем новые примеры; при этом все степени х, до назначенной включительно,
мы будем точно учитывать, а более высокие степени (не выписывая их) будем
сразу включать в дополнительный член.
8) Написать разложение функции esmx до х . В силу 1),
esinx = 1 + sin* + - sin2* + - sin3 x + o(*3)*};
2 6
но, по 2),
sin х = х х + о(х ),
6
так что
= 1 + (х - -х3) + -х2 + -*3 + о(*3).
\ 6 / 2 6
Член cjc исчезает и, окончательно,
х + 0(х ).
Аналогично,
etgx - 1 * -*2 -*3 of*3)
- +* + 2*+2*+о(*).
9) Написать разложение функции In cos* до члена с *6. Согласно 5),
In cos* = ln[l + (cos* —1)] =
При этом, ввиду 3),
отсюда
\_ 2 J_ 4 J_ б\ _}_(}_ 4 J_
2^ 24* 720* У 2V4* 24'
или — после приведения —
In cos* = --Х1 - —х4 - —х6 + о(х6).
Аналогично,
1п(* + \Л+*2 ) =х - -хJ + — *э + о(*э)
*^ Следовало бы написать о (sin *), но, ввиду эквивалентности бесконечно
малых * и sin*, это все равно что о(х ).
**) Так как A — cos*) одного порядка с * [61], то o((cos* — 1) ) в то же
время есть о(х ).
286 ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ [126
Все эти разложения, полученные без непосредственного использования фор-
формулы Тейлора, могли бы, конечно, быть получены и по этой формуле, и при-
притом — в точности с теми же коэффициентами, ввиду установленной выше един-
единственности подобного разложения функции.
Замечание. Так как рассмотренные здесь функции имели
в окрестности точки х = О производные всех порядков, то мы ни-
ничем не были стеснены в выборе числа п в формуле A1), т. е. могли
продолжать разложения этих функций вплоть до любой степени х.
126. Другие формы дополнительного члена. Формула Тей-
Тейлора с дополнительным членом в форме Пеан о имеет мно-
многообразные приложения (см. следующую главу); но все они, так
сказать, «локального» характера, т. е. относятся к самой точке хо.
Если в них иной раз и идет речь о других значениях х, то эти зна-
значения предполагаются «достаточно близкими» к хо и наперед не
могут быть взяты по произволу.
Между тем естественно попытаться использовать много-
многочлен/?(х) как приближение к функции /(х), с помощью
которого она и может быть вычислена с нужной степенью точности.
Для того чтобы многочлен р(х) был пригоден для этой ро-
роли, необходимо иметь возможность оценивать разность G) для
данного х. В этом случае форма Пеан о, характеризующая
лишь стремление г(х) к 0 при х —>> 0, служить не может. Она
не позволяет устанавливать, для каких значений х многочлен р(х)
воспроизводит функцию /(х) с наперед указанной степенью точно-
точности; ничего не говорит она также о том, как можно было бы — при
данном х — воздействовать на величину дополнительного члена
г(х) = гп(х) за счет увеличения и*), и т. д.
Поэтому мы обратимся к выводу других форм дополни-
дополнительного члена гп(х). Для определенности будем рассматривать
промежуток [хо, хо + Я] (Я > 0) вправо от точки хо и будем счи-
считать функцию /(х) определенной в этом промежутке; случай, когда
функция задана в промежутке [хо - Я, хо], исчерпывается анало-
аналогично.
На этот раз сделаем более тяжелые предположения, именно,
допустим, что во всем промежутке [хо,хо + Я] существуют и не-
*) Нужно помнить, что дополнительный член г(х) зависит, вообще говоря,
от п, для подчеркивания этого обстоятельства мы и будем впредь обозначать
его через гп(х).
126] § 5. ФОРМУЛА ТЕЙЛОРА 287
прерывны первые п производных:
f(x), f'(x), f"(x), .... /")(х)
и кроме того, по крайней мере в открытом промежутке (хо, хо+Н)9
существует и конечна (п + 1)-я производная
Отметим, что, ввиду F) и G),
гя{х) = f(x) -
Фиксируем теперь любое значение х из промежутка [хо,хо+Н]9
и по образцу правой части формулы A2), заменяя постоян-
постоянное число хо на переменную z, составим новую, вспомогательную
функцию:
<p(z)=f{x)-f{z) - Щ- (х -z) - ^1 (х -zJ - . ..
причем независимую переменную z считаем изменяющейся в про-
промежутке [хо,х]. В этом промежутке функция q>(z) непрерывна
и принимает на концах его значения [см. A2)]:
<р(*о) =гп(х), (р(х) = 0.
Кроме того, в промежутке (xq,x) существует производная
cp'iz) = -f{z) - \f^L (x -z)-f{
или, после упрощения,
288 ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ [126
Возьмем теперь произвольную функцию ip(z)9 непрерывную
в промежутке [хо,х] и имеющую не обращающуюся в нуль про-
производную i/)'(z)9 по крайней мере в открытом промежутке (хо, х).
К функциям q>(z) и ip(z) применим формулу Коши [114]:
ф) -фр) = <р'(с)
где
хо < с < х или с = хо + 9{х — хо) (О < в < 1).
Так как
ф) = 0, ф0) = rn(x), <p'{c) = -J п{К } (х - с)\
то
п[Х) -
ф'{с) п\ [Х С) •
Теперь, если подставлять вместо ip(z) любые удовлетворяющие
поставленным условиям функции, мы получим различные формы
дополнительного члена гп(х).
Пусть ip(z) = (х — z)p, где р > 0. Имеем:
tp'(z) = -p(x-z)P-1 (xo<z<x).
Очевидно, эта функция удовлетворяет поставленным требованиям.
Поэтому
П(с)
Так как с = хо + 0(х — хо)9 то х—с=х— хо — 0(х — хо) =
= A — 9){х — хо), и окончательно:
Это выражение называется дополнительным членом
в форме Шлемильха и Роша (О.Schlomilch-Roche).
127] § 5. ФОРМУЛА ТЕЙЛОРА 289
Из него, придавая р конкретные значения, можно получать бо-
более частные формы дополнительного члена. Положив р = п + 1,
получим дополнительный член в форме Лагранжа:
который выглядит особенно просто. Он напоминает следующий
очередной член формулы Тейлора, лишь вместо того, чтобы
вычислить (п + 1)-ю производную в точке хо, эту производную бе-
берут для некоторого среднего (между хо и х) значения с.
Формула Тейлора с дополнительным членом в форме Ла-
Лагранжа, таким образом, имеет вид
Если перенести в ней член f(xo) налево, то легко усмотреть в ней
прямое обобщение формулы конечных приращений [112], которую
можно написать так:
f(x)-f(xo)=f\c).(x-xo).
Хотя охотнее всего пользуются дополнительным членом имен-
именно в форме Лагранжа, ввиду ее простоты, все же в отдель-
отдельных случаях эта форма оказывается непригодной для оценки до-
дополнительного члена, и приходится прибегать к другим формам,
менее простым. Из них упомянем здесь о дополнительном
члене в форме Кош и, который получается из общей формы
Шлемильха и Роша при р = 1:
127. Приближенные формулы. Положим, для простоты, в фор-
формуле A3) хо = 0, а вместо с станем писать вх, где 0 < в < 1:
и! + (и+1)! ' [ '
290 ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ [127
Если отбросить здесь дополнительный член, то получится при-
приближенная формула:
заменяющая функцию сложной природы целым многочленом. Но
на этот раз мы в состоянии оценить погрешность этой
формулы, ибо она как раз и равна (по абсолютной величине) от-
отброшенному члену. Например, если (п+ 1)-я производная (по край-
крайней мере, при изменении аргумента между Оих) ограничена по
абсолютной величине числом М, то
, ,, Mxm+l
Для примеров обратимся к элементарным функциям. Нам
нет надобности повторять выкладки п° 125, лишь дополнительный
член мы будем писать в новой форме.
1) Положим f(x) = ex. Приближенная формула:
хх хп
вх = 1 + - + - + ... + —;
1! 2! п\
так как дополнительный член здесь
то, например, при х > О погрешность оценивается так:
К(х)|<ех--^—.
В частности, если х — 1,
11 1
6 ~ +1! + 2! + "' + Й!'
3
Vn{l)\<
Подобной формулой мы уже пользовались в 37 для прибли-
приближенного вычисления числа е, но оценка дополнительного члена,
полученная другим путем, там была более точной.
127] § 5. ФОРМУЛА ТЕЙЛОРА 291
2) Взяв /(х) = sinx, получим
Г3 Г5
л л
sinx = х- — + — -...+ (-\у
3! ' 5! '¦¦ ' v > Bm — 1)!*
В этом случае дополнительный член:
Bm + 1)!
и погрешность оценивается легко:
"^ {1т + 1)!'
В частности, если мы довольствуемся одним членом и полагаем
sinx = х,
то для того, чтобы погрешность была меньше, скажем, чем 0,001,
достаточно взять (считая х > 0)
х3
— < 0,001
6
или
х < 0,1817,
что примерно равно 10°. При пользовании двучленной формулой
sinx = х ——,
6
для достижения той же точности уже достаточно взять
х^_
120 <
или
х < 0,6544 (= 37,5°);
если же ограничиться углами х < 0,4129 (= 23,5°), то погрешность
будет даже < 0,0001, и т. д.
Мы видим, что с увеличением числа членов многочлена
Тейлора он все с большей точностью и на большем протяже-
протяжении воспроизводит исходную функцию. Этот факт наглядно иллю-
иллюстрируется рис. 52, а, где наряду с графиком функции у = sinx
представлены графики многочленов
х3 х3 х5
292
ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
[127
а)
у=тпх
Рис. 52
3) Аналогично, для /(х) = cosx имеем
г2 г4
_+_
причем
так что
B/Я + 2)!'
B1И + 2)!'
127] § 5. ФОРМУЛА ТЕЙЛОРА
Например, для формулы
293
cosx = 1 ——
погрешность
и заведомо будет, скажем, < 0,0001 для х < 0,2213 (= 13°),
и т. п. На рис. 52, б представлены для сравнения графики функции
у = cosx и графики последовательных многочленов
х2 х2 х4
у = 1, у = 1 ——, у = 1 —— + —, и т. д.
Мы обращаем внимание читателя на существенное продвиже-
продвижение вперед по сравнению с формулами пп° 62, 63, 107: теперь мы
умеем устанавливать границы погрешности и располагаем
формулами любой точности.
Укажем еще, что формула Тейлора является источником для построения
приближенных формул совершенно иного типа.
4) В качестве первого примера остановимся на формуле Гюйгенса
(Ch. Huygens) для приближенного спрямления дуги окружности, малой по срав-
сравнению с радиусом.
а)
\
\
¦—
d
х /
б)
X /
Рис. 53
Пусть s — длина дуги, d — соответствующая ей хорда, а 8 — хорда, со-
соответствующая половине дуги (рис. 53, а). Поставим себе задачей представить s
возможно точнее приближенной формулой вида s = Ad + В8, где А, В —
коэффициенты, подлежащие определению.
294 ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ [127
Если г — радиус окружности, а 2х — центральный угол, соответствующий
дуге s, то имеем
d = 2r • sinx =
2r (x - - х3 + — х5) @ < в' < 1)
V 6 120 /
и, аналогично, заменяя х на |,
S = 2rsmX-=2r(iX-^ + ^) @ <*»<!).
Отсюда
' L
в то время как s = 2rx. Естественно выбрать А и В так, чтобы было
А+-В = 1, -А + —В = 0,
ибо тогда разница между левой и правой частями рассматриваемой формулы бу-
будет лишь в членах, содержащих х . Для коэффициентов Аи В получаем значения
А = — -j,i? = !,H формула принимает вид
88 -d 28 - d
s = — = 2S+—.
Ее погрешность А, как легко видеть, оценивается так:
~5
Например, при центральном угле в 30°, т. е. х = у^, имеем, согласно этой
оценке, | А| < г • 0,000007; в действительности s = г • 0,523599 . . ., а по формуле
Гюйгенса получается s = г • 0,523593 . . ., так что расхождение не превосходит
установленной границы.
5) Для той же цели П.Л. Чебышёв дал следующее правило: дуга при-
приближенно равна сумме равных сторон равнобедренного треугольника, по-
построенного на хорде и имеющего высотой \ ^ стрелки (рис. 53,6).
Положим пока h = yf; ниже выяснится, что, полагая у = J ^, мы действи-
действительно получаем — в некотором смысле — наилучшее приближение.
Как мы видели только что,
-d = г • sinх = г(х х3 Н х5} @ < в\ < 1);
аналогично,
* = yf = yr(l ~ cosx) = yrQx2 - ^*4) (O<02< 1).
128] § 6. ИНТЕРПОЛИРОВАНИЕ 295
Обозначая через s * сумму сторон равнобедренного треугольника, о которой упо-
упоминается в правиле Ч е б ы ш ё в а, имеем
Теперь, именно для того, чтобы уничтожить под корнем член с х , положим его
коэффициент равным 0, откуда и находим у =
Для оценки погрешности перепишем выражение для s* в виде
s* = 2гхл/1+Ах4, A5)
причем выражение А окажется содержащим вторую и четвертую степени х. Пред-
Предполагая х < т?, будем иметь: х < 2,5, х < 6,5, а тогда для А получится оценка
\А\ < 0,06, так что \А\х4 < 0,4.
Обозначив для удобства Ах через у, по формуле конечных приращений [112]
будем иметь
У
@ < в < 1).
zy I -t- vy
Последняя дробь оценивается так:
Сопоставляя выражение A5) для s* с только что полученными результатами,
видим, что
s = s + р, где |р| < 0,\гх .
Порядок погрешности тот же, что и в формуле Гюйгенса.
Мы вернемся к формуле Тейлора с дополнительным членом
в главе XI второго тома, посвященной бесконечным рядам; там эта
формула будет играть весьма важную роль.
§ 6. Интерполирование
128. Простейшая задача интерполирования. Формула Лагран-
жа. Представим себе, что для некоторой функции /(х), опреде-
определенной в промежутке [а,Ь]9 вычислены т + 1 ее значений в точках
хо, х\, ..., хт промежутка:
Дхо), A*i), .-., f(xn) A)
и требуется по этим значениям вычислить значение f(x)
при каком-либо новом значении х.
296 ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ [128
В этом и состоит простейшая задача интерполирова-
интерполирования. Конечно, в такой постановке вопроса содержится много не-
неопределенного. Обычно задачу понимают так: ищется целый мно-
многочлен L(x) наинизшей степени, который в заданных точках xt
(/ = 0, 1, ..., т)9 называемых узлами интерполирования, прини-
принимает те же значения/(х,), что и функция/(х), и приближенно
полагают для любого х из [а,Ь]:
f(x)=L(x). B)
Подобное приближенное равенство называется интерполяционной
формулой. Итак, надлежит прежде всего найти интерполяцион-
интерполяционную формулу, а затем — при определенных предположениях отно-
относительно функции /(х)— оценить погрешность приближенной
формулы B).
Для разыскания многочлена L(x)9 удовлетворяющего условиям
L(x,)=f(x,) (/ = 0,1,...,/я), C)
удобно ввести многочлены т-й степени
_ (х -Хр) . . . (х -Xk-l)(x -Xfc+l). . . (Х ~Хт)
(Xk
которые, соответственно значку, принимают значение 1 прих = Xk
и обращаются в 0 при х = Xj9 если / ф к. Теперь ясно, что много-
многочлен
т
ВД = ?/(**)'*(*) D)
к=0
удовлетворяет всем условиям C). Степень этого многочлена не
выше т9 и стало быть, условиями C) он определяется однозначно,
его называют интерполяционным многочленом Лагранжа,
а приближенное равенство B) — интерполяционной формулой
Лагранжа.
Заметим, что многочлен lk(x) можно написать более сжато,
если ввести выражение
(о{х) = 0 -хо)(х -х\).. . (х -хт),
обращающееся в 0 как раз в узлах интерполированияхо,х\, .. .,хт.
Именно, очевидно,
(х -х0).. . (х -xk-i)(x -Xk+\). ..(х-хт) = ——— (х фхк),
X Хк
129] § 6. ИНТЕРПОЛИРОВАНИЕ 297
а
(Xk-Xo). • • (Xk - Xk-l)(Xk - Xk+l) . • • (Xk-Xm) =
= lim —^- = lim —-^ —- = со
X — Xk x^xk X — Xk
Таким образом,
и L{x) =
-Xk)
129. Дополнительный член формулы Лагранжа. Обратимся
теперь к оценке разности f(x) — L(x)9 где х есть любое фик-
фиксированное значение в промежутке [а, Ь]9 отличное от узлов
интерполирования. Предположим, что функция f(z) в этом
промежутке имеет производные всех порядков до (т + \)-го
включительно.
Какова бы ни была постоянная К, функция
<p{z) = f[z) - L[z) - К • <o[z)
тоже имеет т + 1 производных и к тому же обращается в 0 в уз-
узлах Xj (i = 0, 1, ..., т). Мы выберем теперь постоянную К так,
чтобы и при z = х было ф(х) = 0, т. е. положим
(так как хфх\9 то со(х)фО). По теореме Ролля [111],
в т+\ промежутках между т+2 корнями х, xq,x\, ... ,хт функции
cp(z) найдется т + \ различных корней ее производной q>'(z). При-
Применяя снова теорему Ролля к функции cp'(z) икт промежуткам
между ее т + 1 корнями, установим существование т различных
корней второй производной q>n{z)9 и т. д. Продолжая это рассу-
рассуждение, на {т + 1)-м его шаге придем к существованию корня |
{т + 1)-й производной <p(w+1)(z), так что
= 0 (a<4<b). F)
Но L^m+l\z) = 0, ибо степень многочлена L(z) не выше т9
a a)(m+l\z) = (т + 1)! Учитывая определение вспомогательной
функции #)(z), имеем
cp(m+l\z) = f<m+l\z) - К - (т + 1I
298 ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ [130
так что из F) получается, что
Окончательно, из E) находим:
/(х)=Ь(х) + 1-^-тЩсо(х) (а<4<Ъ). G)
Это — интерполяционная формула Лагранжа с дополни-
дополнительным членом. В отличие от B), она является точной!
Замечание. Если в промежутке [а, Ь]
то, так как в этом промежутке \co(z)\ < (b-a)m+l, получаем такую
оценку для погрешности формулы B):
Правая часть при т —>> оо стремится к нулю лишь для очень узкого
класса функций f(x); например, это будет иметь место для та-
таких функций, которые в [а,Ь] дифференцируемы любое число раз,
причем все их производные ограничены одной постоянной М.
В этом случае по мере возрастания числа узлов интерполиро-
интерполирования и независимо от закона, по которому выбираются
эти узлы, погрешность формулы B) будет равномерно стремить-
стремиться к нулю. Как доказал Марцинкевич (J. Marcinkiewicz), для
каждой отдельно взятой непрерывной функции можно достигнуть
такого же эффекта путем надлежащего выбора последовательных
систем узлов. Но — по теореме Фабера (G. Faber) — не су-
существует такого закона выбора узлов, который годился бы в этом
смысле для всех непрерывных функций одновременно. В подроб-
подробности относительно этих и им подобных вопросов мы здесь входить
не имеем возможности.
130. Интерполирование с кратными узлами. Формула Эрми-
та. Можно поставить более общую задачу интерполирования,
задав в узлах xq,x\, ... ,хт, кроме значений самой функции /(х),
130] § 6. ИНТЕРПОЛИРОВАНИЕ 299
также и значения последовательных ее производных:
Дх0), Г /)
/(*»), f'(xm), ..., /*">(*„,),,
(8)
где по,п\, ... ,пт — неотрицательные целые числа. Общее число
этих условий равно
(щ + 1) + (/71 + 1) + ... + (пт + 1)=N.
Задачу вычисления значения функции f(x) при любом отличном от
узлов значении х из [а, Ь] — с использованием всех данных (8) —
мы, подобно простейшему случаю, будем понимать так. Ищется
многочлен Н(х) наинизшей степени, который в каждом узле Xj9
вместе со своими производными до порядка щ включительно, при-
принимает те же значения, что и сама функция f[x) и ее соответствую-
соответствующие производные, а затем приближенно полагают
Дх)=Я(х). (9)
Узлы Xj называются узлами интерполирования, соответственно
кратности пг¦ + 1.
Можно доказать существование и единственность многочле-
многочлена Н(х) степени не выше N — 1, удовлетворяющего всем постав-
поставленным условиям. Его называют интерполяционным многочле-
многочленом Эрмита, а формулу (9) — интерполяционной формулой
Эрмита (Ch. Hermite).
Если все nt положить равными нулю, то мы вернемся к форму-
формуле Лагранжа B). Мы встречались и с другим частным случаем
формулы Эр мит а: возьмем один лишь узел хо, но кратности /7+1,
т. е. от многочлена не выше /7-й степени, Г(х), потребуем, чтобы
в точке хо его значение и значения п его производных совпадали,
соответственно, со значениями самой функции f(x) и ее производ-
производных. Мы знаем, что этим требованиям удовлетворяет многочлен
Тейлора [124, F)]
Таким образом, приближенная формула
/(*) = Т(х)
[ср. п° 127] также является частным случаем интерполяционной
формулы Э р м и т а.
300 ГЛ. III. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ [130
Дополнительный член формулы (9), восстанавливающий ее
точность, выводится с помощью рассуждений, аналогичных приве-
приведенным в предыдущем номере. Рассмотрим многочлен N-и степени
ОД = (z -xo)n°+\z -х,Г+1 ...{z -xmy»+l
и положим для а ^ z ^ Ъ
фB) = f(z) - H{z) - К • ft(z), где К = const.
Если предположить, что функция /(z) в промежутке [а, Ь] имеет
N последовательных производных, то это будет справедливо и для
<E>(z). Фиксируя значение z = x9 отличное от узлов, мы выберем
постоянную К так:
при таком выборе функция <?(z) обращается в 0 и при z = х.
Всего она будет иметь N + 1 корней, если каждый корень считать
столько раз, какова его кратность *\ Применяя последовательно
теорему Ролля, как и выше (с тем лишь усложнением, что каж-
каждый кратный корень функции Ф(^) еще в течение нескольких
шагов будет фигурировать и как корень ее последовательных про-
производных), окончательно придем к утверждению, что в некоторой
точке | обратится в 0 производная Ф^'(г). Отсюда
и ввиду A0)
Дх)=Н(х) + ^Р-П(х). (П)
Это и есть интерполяционная формула Эрмита с дополни-
дополнительным членом.
Формула Лагранжа с дополнительным членом [G)] являет-
является ее частным случаем. Точно так же, взяв единственный узел хо
кратности /7+1, мы как частный случай формулы A1) получим фор-
формулу Тейлора с дополнительным членом в форме Лагранжа
[126, A3)].
*) Мы распространяем понятие кратности корня, привычное для читателя
по отношению к целому многочлену, на любую функцию Ф(^): число а называ-
называется ее корнем р-и кратности, если а обращает в 0, вместе с Ф(г), и р — lee
производных.
ГЛАВА ЧЕТВЕРТАЯ
ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ
ПРОИЗВОДНЫХ
§ 1. Изучение хода изменения функции
131. Условие постоянства функции. При изучении хода изме-
изменения функции на первом месте появляется вопрос об условиях,
при которых функция сохраняет в данном промежутке постоянное
значение или изменяется в нем монотонно [57].
Теорема 1. Пусть функция /(х) определена и непрерывна
в промежутке ЭС^ и имеет внутри него конечную произ-
производную f'{x). Для того чтобы /(х) была в ЭС постоянной,
необходимо и достаточно условие
f\x) — О внутри ЭС.
Необходимость условия очевидна: из /(х) = const следует
f'(x) = 0. Докажем теперь обратное.
Достаточность. Пусть условие выполнено. Фиксируем не-
некоторую точку хо из промежутка SC и возьмем любую другую
его точку х. Для промежутка [хо, х] или [х, хо] удовлетворены все
условия теоремы Лагранжа [112], следовательно, можем напи-
написать
где с содержится между хо их и, значит, заведомо лежит
внутри SC. Но по предположению f\c) = 0, так что для всех х
из^Г
/(х) =/(хо) = const,
и наше утверждение доказано.
В интегральном исчислении важное приложение найдет выте-
вытекающее отсюда простое предложение.
*)
Промежуток SC может быть замкнутым или нет, конечным или бесконечным.
302 ГЛ. IV. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ [131
Следствие. Если две функции f(x) и g(x) определены и не-
непрерывны в промежутке ЭС и внутри него имеют конечные
производные f'(x), g?(x), причем
/' (х) = g (х) (внутри ЭС),
то эти функции во всем промежутке ЭС разнятся лишь на
постоянную'.
f(x)=g(x)+C (С = const).
Для доказательства достаточно применить теорему к разности
f(x) —g(x)\ так как ее производная f'(x) -gf(x) внутри ЭС сводится
к 0, то сама разность будет постоянной.
Особенности пользования этой теоремой выясним на примерах.
1) Рассмотрим две функции
х / ч
arctg^: и arcsin — ( — со < х < +оо).
Так как производная второй из них
D arcsin
" 1+JC2
совпадает с производной первой функции, то эти функции во всем промежутке
от —со до +со разнятся на постоянную:
X
arctg х = arcsin —-^=^= + С.
л/1 +х2
Для определения значения этой постоянной можно, например, положить здесь
х = 0; так как при этом арктангенс и арксинус оба обратятся в 0, то и С должно
быть нулем. Итак, мы доказали тождество
х
arctg^c = arcsin —-^=^= ( — со < х < +оо),
которое, впрочем, в 50 было выведено из элементарных соображений.
2) Предлагается аналогично доказать, что
arcsinх = arctg —-^=^= ( — 1 < х < 1).
л/1 — х2
3) Рассмотрим теперь функции
1 2х
arctgх и -arctg-
2 1 — xz
Легко проверить, что их производные совпадают во всех точках х, исключая
х = ±1 (где вторая из функций теряет смысл). Поэтому тождество
1 2х
- arctg г- = arctg x + С
2 1-х1
132] § 1. ИЗУЧЕНИЕ ХОДА ИЗМЕНЕНИЯ ФУНКЦИИ 303
оказывается установленным лишь для каждого из промежутков
в отдельности. Любопытно, что и значения постоянной С для этих проме-
промежутков будут различными. Для первого из них С = 0 (в чем убеждаемся, пола-
полагая х = 0), а для двух других имеем, соответственно, С = § или С = — § (что
легко усмотреть, если, например, устремить х к — со или +оо).
Все эти соотношения также могут быть доказаны элементарно.
Замечание. Значение теоремы 1 проявляется в теорети-
теоретических исследованиях и вообще в тех случаях, когда функция
задана так, что из ее определения непосредственно не вытекает,
что она сохраняет постоянное значение. Подобные случаи нам не
раз встретятся в дальнейшем.
132. Условие монотонности функции. Выясним теперь, как по
производной функции можно судить о возрастании (убывании) са-
самой функции в данном промежутке. Остановимся сначала на случае
функции, монотонно возрастающей в широком с м ы с л е, т. е. не
убывающей (или монотонно убывающей в широком смысле,
т. е. не возрастающей) [57].
Теорема 2. Пусть функция /(х) определена и непрерывна
в промежутке ЭС и внутри него имеет конечную произ-
производную f'{x). Для того чтобы /(х) была в ЭС монотонно
возрастающей {убывающей) в широком смысле, необходимо
и достаточно условие
/'(х)^О (^0) внутри 5Г.*}
Необходимость. Если /(х) монотонно возрастает, хотя бы
в широком смысле, то, взяв х внутри ЭС и придав ему приращение
Ах > 0, будем иметь:
!/w, >о,
и в пределе, при Ах —>> 0, получим /;(х) ^ 0.
Достаточность. Пусть теперь, обратно, дано, что /;(х) ^ О
внутри SC. Возьмем два значения х1 и х11 {х1 < х") из промежут-
промежутка ЭС и к функции /(х) в промежутке [х;, х"\ применим формулу
*) Хотя формулируем теоремы мы параллельно и для возрастающих, и для
убывающих функций, но при доказательстве ограничиваемся лишь случаем воз-
возрастания.
304 ГЛ. IV. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ [132
Лагранжа:
/(*") - /{х') = f (с) ¦ (*" - *') (х'<с< х").
Так как /'(с) ^ 0, то
и функция f(x) будет возрастающей, по крайней мере в широком
смысле.
До сих пор для функции f(x) не была исключена возможность
сохранять в некоторых промежутках и постоянные значения, а для
ее производной — обращаться в этих промежутках тождественно
в 0. Если мы эту возможность исключим, то придем к случаю
возрастания (или убывания) в строгом смысле.
Теорема 3. При сохранении тех же предположений отно-
относительно непрерывности функции f(x) и существования ее
производной f (х), для того чтобы f(x) была монотонно воз-
растающй {убывающей) в строгом смысле, необходимы и дос-
достаточны условия:
1) /'(*) ^ 0 (^ 0) для х внутри ЭО\
2) f'(x) не обращается тождественно в 0 ни в каком
промежутке, составляющем часть SC.
Необходимость. Если f(x) возрастает в промежутке «2Г, то
по теореме 2 имеем f'(x) ^ 0, так что условие 1) выполняется. Вы-
Выполняется и условие 2), так как если бы производная обращалась
в 0 в некотором промежутке сплошь, то по теореме 1 в нем f(x)
была бы постоянной, что противоречило бы предположению.
Достаточность. Пусть выполняются условия 1), 2) теоре-
теоремы. Тогда, в силу теоремы 2, функция f(x) является, во всяком слу-
случае, неубывающей. Если взять в SC два значения х' и х" (V < х"),
то будем иметь не только
/(*')</(*"). A)
но и
Ах') ^ Ах) ^ Ах") для х в [х',х"\. B)
Докажем, что знак равенства в A) на деле осуществиться не
может. Если бы было /(V) = /(V7), то, ввиду B), получили бы
Ах') = Ах) = Ах") для х в [х',х"]г
т. е. функция f(x) была бы постоянной в промежутке [х\ х"] и мы
имели бы /'(х) = 0 в этом промежутке сплошь, вопреки уело-
132]
§ 1. ИЗУЧЕНИЕ ХОДА ИЗМЕНЕНИЯ ФУНКЦИИ
305
х1 < х"
вию 2). Итак,
fix') < fix") при
т. е. функция f(x) возрастает в строгом смысле . Этим теорема
доказана.
Установленная связь между знаком производной и направ-
направлением изменения функции геометрически совершенно оче-
очевидна, если вспомнить [91,92], что производная представляет со-
собой угловой коэффициент касательной к графику функции. Знак
а)У-
О
б) У\
о
Рис. 54
этого углового коэффициента показывает, наклонена ли касатель-
касательная вверх или вниз, а с нею — идет ли вверх или вниз и сама
кривая (рис. 54).
Однако в отдельных точках касательная при этом может ока-
оказаться и горизонтальной, т. е. производная — даже в строгом смыс-
смысле — возрастающей (убывающей) функции может для отдельных
значений х обращаться в 0.
Примеры.
1) Простейший пример последнего обстоятельства доставляет функция
f(x) = х : она возрастает, и тем не менее производная ее f\x) = Ъх при
х = 0 обращается в 0.
2) Аналогично, возрастающей будет и функция
f(x) = х — sin.*,
ибо ее производная
f'(x) = 1 — cos х
не отрицательна, обращаясь в 0 для значений х = 2ктт (к = 0, ±1, =Ь2, . . .).
3) Наконец, чтобы показать, что для возрастающей функции производная
может даже в конечном промежутке обращаться вО бесконечное мно-
множество раз, рассмотрим функцию
i /@) = 0.
для х > 0,
306 ГЛ. IV. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ [133
Очевидно,
дт+о/(,) = о,
так что наша функция непрерывна и при х = 0. Имеем, для х > 0:
/'(*) = е81"*1-- • (l - cos j) • ^ > 0,
причем эта производная обращается в 0 при х = -^ (к = 1, 2, 3, . . .).
Заметим, что
0 < /'(*) < 2е • ^- ->> 0 при jc ->> +0,
отсюда [113] и/'(О) = 0.
Можно построить примеры возрастающих (убывающих) функ-
функций, для которых точки, где производная обращается в 0, распреде-
распределены еще более сложным образом. Однако подобные случаи встре-
встречаются редко, и для практических целей обычно пользуются та-
таким достаточным признаком: если производная f'{x) > 0
(< 0) повсюду, исключая разве лишь конечное число значе-
значений х, то функция f{x) будет возрастающей {убывающей).
Этот признак очень удобен в приложениях.
Для примера рассмотрим функцию f(x) = ( 1 Н— ) при х > 0 и докажем,
Достаточно доказать, ч
x) =ln/(jc)=jcpn(jc
что она возрастает. Достаточно доказать, что возрастает ее логарифм
Имеем
g\x) = рп(* + 1)-1п]
J jc + 1
Так как, по формуле конечных приращений [112],
In (х + 1) — \пх = -, где х < | < х + 1,
то g (х) > 0: g(x) возрастает, что и требуется доказать.
133. Доказательство неравенств. Изложенный простой критерий монотон-
монотонности успешно применяется к доказательству неравенств.
1) Докажем, что для 0 < х < ^ имеем
2
sin х > — х.
Пусть f(x) = {О < х ^ j). Производная
будет отрицательна, так как х < tgx. Значит, функция f(x) убывает
и /0) >/(f) = hесли ° < х < f •
133] § 1. ИЗУЧЕНИЕ ХОДА ИЗМЕНЕНИЯ ФУНКЦИИ 307
2) Функция f(x) = cos x — 1 + 2 х обращается при х = 0 в нуль. Ее произ-
производная, при х > 0,
/ (х) = — sin х + х > 0 (ибо sin х < х).
Значит, функция /(jc) для х ^ 0 оказывается возрастающей, и при jc > 0 будет
/(*) > /@) = 0, т. е.
COS.X > 1 X .
Отсюда, аналогично, при х > 0 получим, что
sinjc > jc х ,
6
и т. д.
3) Доказать, что при 0 < х < § будет
1 з
tg X > X ~\ X .
3
Для этого достаточно установить, что для указанных х производная функции
tg;\; — х — \х\ равная sec х — 1 — х , положительна, т. е. что tg х — х > 0,
а это приводит к известному неравенству tgx > x [54, (9)].
4) Так как функция f(x) = Ых — х (х > 0) имеет производную
fif \_]_ _л /> 0 при 0 < jc < 1,
X
то функция эта возрастает, пока х изменяется в промежутке @, 1], и убывает
в промежутке [1, +оо). Отсюда ясно, что /A) = —1 будет наибольшим значе-
значением функции, так что для х > 0
Ых < х — 1.
5) Рассмотрим еще функцию f(x) = ха —ах для х ^ 0 (предполагая
0 < а < 1). Имеем
f'M - n(ra~l - Л />° ПРИ 0<к1,
< 0 при х > 1,
и — аналогично 4) — заключим, что для х > 0
jca - ах < 1 - а. C)
Полученное простое неравенство является источником для вывода ряда клас-
классических неравенств. В связи с этим полезно представить его еще и в других
формах.
Полагая х = f, где а и Ъ — произвольные положительные числа, и обозна-
обозначая 1 — а через /3, приведем C) к виду
aabP ^аа+ /ЗЬ. (За)
(а,Ь,а,р>0;а+р=1)
308 ГЛ. IV. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ [133
Иногда вводят числа к = ^ > 1 и &; = А > 1, так что к' = ^^у. Заменяя
ответстве
-я*+ — ^. C6)
/с /с
в предыдущем неравенстве а и Ь, соответственно через ак и Ък , получим
6) Прежде всего, неравенство (За) можно распространить на случай любо-
любого числа перемножаемых степеней. От двух к трем переход осуществляется так
(с двукратным применением неравенства (За)):
аа + (В + ) Ь
/ /3 у \
< аа + (/3 + у) ( Ъ -\ с ) = аа + /ЗЬ + ус,
так что окончательно
aabPcy < aa+pb + yc.
(а,Ь,с,а,/3,у>0; а-\-/3-\-у=1)
Аналогично можно было бы совершить и переход от п к п + 1 и доказать —
по методу математической индукции — общее неравенство, которое (в изменен-
измененных обозначениях) имеет вид:
\^ q2a2 + . . . + qnan-
{a\,...,an, qi,...,qn>0; qi+...+qn=l)
Взамен qi можно ввести произвольные числа pt > 0, полагая qi = ——, так что
Yp
сумма ^2qt = 1. Неравенство напишется так:
При р\ = р2 = . . . = рп = 1 мы придем к известному неравенству
. а\ + а2 + . . . + ап f л
Уаха2. . .а„ < , Dа)
устанавливающему, что среднее геометрическое ряда положительных чисел
не превосходит их среднего арифметического. Таким образом, неравенство D)
является естественным обобщением этого классического утверждения.
7) Обратимся к доказательству так называемого неравенства Коши-Гель-
д е р а (A. L. Cauchy - О. Holder)
i=\ i=\ i=\
(aibi>0; кк*>1; ? + p = l)
Кош и установил это неравенство для частного случая к = к1 = 2:
Ъ]. Eа)
\
а1 \
<¦=!
133] § 1. ИЗУЧЕНИЕ ХОДА ИЗМЕНЕНИЯ ФУНКЦИИ 309
Предположим сначала, что
п п
V~^ к V~^ к'
так что подлежащее доказательству неравенство примет вид
п
i=\
Положим в неравенстве C6) поочередно а = я/, Ъ = bi (i = 1, 2, . . ., п) и про-
просуммируем все полученные неравенства; учитывая условие F), придем к требуе-
требуемому результату.
Общий случай приводится к рассмотренному частному, если взамен чи-
чисел at, bt ввести числа
аг ,, bi
а\ =
7=1 7=1
для которых уже выполняются условия типа F). По доказанному
а это равносильно E).
8) Из неравенства Коши-Гельдера сразу получается еще одно важное
неравенство, носящее имя Минковского (Н. Minkowski)
{±y{±y {±y G)
1 = 1 1 = 1 1 = 1
(ahbj>O;k>\)
Очевидно, п
i=\ i=\ i=\
Если к каждой из последних двух сумм применить неравенство E), то получимн
}{
1=1 1=1
}№}}{
1=1 1=1 } 1=1
и, наконец, сократив на последний множитель, придем к G).
*) Напомним, что j- + -р- = 1.
310 ГЛ. IV. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ [134
У\
134. Максимумы и минимумы; необходимые условия. Если
функция Дх), определенная и непрерывная в промежутке [а, Ь]9
не является в нем монотонной, то найдутся такие части [а, /3] про-
промежутка [а, Ь]9 в которых наибольшее или наименьшее значение
достигается функцией во
внутренней точке, т. е.
между а и /3. На графи-
графике функции (рис. 55) таким
промежуткам соответству-
соответствуют характерные горбы или
впадины.
Говорят, что функция
f(x) имеет в точке хо
максимум (или мини-
минимум) *\ если эту точку молено окружить такой окрестно-
окрестностью (xo-S,xo + S), содержащейся в промежутке, где задана
функция, что для всех ее точек х выполняется неравенство
(или Дх)^/(хо)).
Иными словами, точка хо доставляет функции f(x) мак-
максимум (минимум), если значение Дхо) оказывается наибольшим
(наименьшим) из значений, принимаемых функцией в некоторой
(хотя бы малой) окрестности этой точки. Отметим, что самое опре-
определение максимума (минимума) предполагает, что функция задана
по обе стороны от точки хо.
Если существует такая окрестность, в пределах которой
(при х ф хо) выполняется строгое неравенство
/(*) < Д*о)
(или Дх)>Дх0)),
то говорят, что функция имеет в точке хо собственный, или
строгий, максимум (минимум), в противном случае — несоб-
несобственный, или нестрогий.
Если функция имеет максимумы в точках хо и х\9 то, приме-
применяя к промежутку [xq,xi] 2-ю теорему Вейерштрасса [85],
*) По-латыни слова maximum и minimum означают «наибольшее» и «наимень-
«наименьшее» (значение).
134] § 1. ИЗУЧЕНИЕ ХОДА ИЗМЕНЕНИЯ ФУНКЦИИ 311
видим, что наименьшего своего значения в этом промежутке функ-
функция достигает в некоторой точке Х2 между хо и^1 и имеет там
минимум. Аналогично, между двумя минимумами непременно
найдется максимум. В том простейшем (и на практике — важней-
важнейшем) случае, когда функция имеет вообще лишь конечное число
максимумов и минимумов, они попросту чередуются.
Заметим, что для обозначения максимума или минимума су-
существует и объединяющий их термин — экстремум*).
Поставим задачу о разыскании всех значений аргумента, до-
доставляющих функции экстремум. При решении ее основную роль
будет играть производная.
Предположим сначала, что для функции f(x) в промежут-
промежутке (а,Ь) существует конечная производная. Если в точке хо функ-
функция имеет экстремум, то, применяя к промежутку (хо — 8,xq + 8)9
о котором была речь выше, теорему Ферма [109], заключаем, что
/'(хо) =0: в этом состоит необходимое условие экстрему-
экстремума. Экстремум следует искать только в тех точках, где производная
равна нулю; такие точки будем называть стационарными**).
Не следует думать, однако, что каждая стационарная точка до-
доставляет функции экстремум: указанное только что необходимое
условие не является достаточным. Мы видели, например, в 132, 1),
что для функции х3 производная Зх2 обращается в нуль при х = 0,
но в этой точке функция не имеет экстремума: она все время воз-
возрастает.
Если расширить класс рассматриваемых функций f(x) и допус-
допустить, что в отдельных точках двусторонней конечной производной
не существует, то не исключена возможность того, что экстремум
придется на какую-либо из таких точек: ведь теорема Ферма
утверждает равенство f'{x) = 0 лишь в предположении, что
существует двусторонняя конечная производная! Например, функ-
функция хз, очевидно, имеет минимум при х = 0, в то время как
в этой точке ее производная слева равна —сю, а справа +оо [101];
точно так же в точке х = 0 имеет минимум функция |х|, хотя
двусторонней производной для нее в этой точке нет [100]. Следо-
Следовательно, и точки, в которых не существует двусторонней конеч-
конечной производной, также могут доставлять функции экстремум. Но,
*) Латинское extremum, что означает «крайнее» (значение).
**) В них изменение функции как бы «приостанавливается»: скорость этого
изменения [92] обращается в нуль.
312 ГЛ. IV. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ [135
разумеется, и в этом случае также не может быть гарантировано
наличие экстремума во всех таких точках. Примерами могут слу-
служить функции у = х з и у = х • sin j (с дополнительным условием:
у = 0 при х = 0). Первая из них имеет бесконечную производ-
производную в точке х = 0 [101], вторая же вовсе не имеет производной
в этой точке [102, 1°], но точка х = 0 не доставляет экстремума ни
той, ни другой функции (ибо в любой ее окрестности обе функции
принимают и положительные и отрицательные значения).
135. Достаточные условия. Первое правило. Итак, если точ-
точка хо есть стационарная точка для функции /(х) или если в этой
точке не существует для нее двусторонней конечной производной,
то точка хо представляется, так сказать, лишь «подозрительной»
по экстремуму и подлежит дальнейшему испытанию.
Это испытание состоит в проверке достаточных условий
для существования экстремума, которые мы сейчас установим.
Предположим, что в некоторой окрестности (хо — S, хо + S)
точки хо (по крайней мере для i/io) существует конечная про-
производная f'(x) и как слева от хо, так и справа от хо (в отдельности)
сохраняет определенный знак. Тогда возможны следую-
следующие три случая:
I. f'(x) > 0 при х < хо и /;(х) < 0 при х > хо, т. е. про-
производная f'(x) при переходе через точку хо меняет знак
плюс на минус. В этом случае, в промежутке [хо - S, хо] функ-
функция /(х) возрастает, а в промежутке [хо, хо + S] убывает [132], так
что значение /(хо) будет наибольшим в промежутке [xq — S, хо + ?],
т. е. в точке хо функция имеет собственный максимум.
П. /;(х) < 0 при х < хо и f'{x) > 0 при х > хо, т. е. произ-
производная f'{x) при переходе через точку хо меняет знак минус
на плюс. В этом случае аналогично убеждаемся, что в точке хо
функция имеет собственный минимум.
III. f'{x) > 0 как при х < хо, так и при х > хо, либо же
/;(х) < 0 и слева и справа от хо, т. е. при переходе через хо /;(х)
не меняет знака. Тогда функция либо все время возрастает, либо
все время убывает; в любой близости от хо с одной стороны найдут-
найдутся точки х, в которых /(х) < /(хо), а с другой — точки х, в кото-
которых/(х) > /(хо), так что в точкехо никакого экстремума нет.
Графическая иллюстрация простейших возможностей дана
на рис. 56, а, 6, в.
135]
§ 1. ИЗУЧЕНИЕ ХОДА ИЗМЕНЕНИЯ ФУНКЦИИ
313
Итак, мы получаем первое правило для испытания «подо-
«подозрительного» значениях о: подставляя в производную f'{x) сна-
сначала х < хо, а затем х > хо, устанавливаем знак производной
О
б) У
о
мин.
1
i
макс.
х0
Xq
)У-
о
мин.
Y
л-
макс.
Xq
X 1
>"Х
х0
Рис. 56
вблизи от точки хо слева и справа от нее; если при этом
производная f'{x) меняет знак плюс на минус, то налицо
максимум, если меняет знак минус на плюс, то — минимум;
если лее знака не меняет, то экстремума вовсе нет.
Это правило полностью решает вопрос в том случае, когда
в промежутке (а, Ь), как это обычно бывает, всего лишь конеч-
конечное число стационарных точек или точек, где отсутствует конечная
производная:
а < х\ < Х2 < .. . < Xk < %к+\ < .. . < хп < Ъ. (8)
Именно, тогда, прежде всего, в любом промежутке
(а,х\), (xi,x2), . .., (xk,Xk+i), ..., (xn,b)
существует конечная производная f\x) и, кроме того, в каждом
таком промежутке ff(x) сохраняет постоянный
знак. Действительно, если бы ff(x) меняла знак, например, в про-
промежутке (хк,Хк+\)9 то, по теореме Дарбу [110], она обращалась
бы в нуль в некоторой точке между хк и Хк+\9 что невозмож-
невозможно, поскольку все корни производной уже содержатся в ряду
точек (8).
314 ГЛ. IV. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ [136
Последнее замечание бывает полезно в некоторых случаях на
практике: знак производной f'{x) во всем промежутке (х^, *?+i)
определится, если вычислить значение (или даже только устано-
установить знак) ее в одной какой-либо точке этого промежутка.
136. Примеры.
1) Найти экстремумы функции f(x) = (х + 2) (х — 1) .
Ее производная всегда существует и конечна:
/'(*) = 2(jc + 2)(* - IK + 3(х + 2J(х - IJ = (х+ 2)(х - 1JE* + 4).
Корнями производной (стационарными точками) будут:
4
xi = -2, х2 = -- = -0,8, jc3 = 1.
Этими значениями весь промежуток ( —оо, +оо) разбивается на следующие
части:
(-оо, -2), (-2, -0,8), (-0,8, 1), A, +оо).
Для определения знака производной в этих промежутках можно, воспользо-
воспользовавшись сделанным выше замечанием, установить его для конкретных значений,
например для — 3, — 1, 0 и 2. Определяя знаки отдельных множителей, для всей
производной получаем следующие знаки:
в промежутке ( —оо, —2) (
в промежутке (-2, -0,8) (+)(+)(-) = -
в промежутке (-0,8, 1) (+)(+)(+) = +
в промежутке A, +оо) (+)(+)(+) — +
Отсюда ясно, что при х = — 2 функция f{x) имеет максимум, при х = —0,8
она имеет минимум, а при х = 1 экстремума вовсе нет.
Однако обычно поступают иначе, не подставляя в производную конкретных
значений. Начнем с х = —2. Произведение двух последних множителей про-
производной (х — 1) и 5х +4 при х = — 2 имеет знак минус, следовательно
(по непрерывности), сохраняет тот же знак и вблизи этой точки (как слева,
так и справа). Множитель же х + 2, когда х9 возрастая, проходит через зна-
значение —2, меняет знак минус на плюс, так что производная меняет знак плюс
на минус, и функция имеет максимум. При х = — ^ (и вблизи этого значе-
значения) первые два множителя производной имеют знак плюс; последний же мно-
множитель 5х + 4 (а с ним и вся производная) при прохождении через это значение
меняет знак минус на плюс; функция здесь имеет минимум. Наконец, при пе-
переходе через значение х = 1 не только первый и третий множители сохраняют
знак, но и второй множитель также, ибо квадрат всегда положителен; экстремума
здесь нет.
Зная точки х, доставляющие нашей функции экстремальные значения,
легко вычислить теперь и сами эти значения: максимум /(—2) = 0 и минимум
136]
§ 1. ИЗУЧЕНИЕ ХОДА ИЗМЕНЕНИЯ ФУНКЦИИ
315
На рис. 57 дан график, иллюстрирующий изменение этой
/(—0,8) = — 8,40.
функции. *)
2) Найти экстремумы функции f(x) = sin3 х + cos3 x.
Ввиду того что функция имеет период 2ж, достаточно ограничиться теми зна-
значениями х, которые содержатся в промежутке [0, 2ж]. Производная этой функции
существует везде:
f'{x) = 3 sin x • cos x — 3 cos x -mix =
= 3 sinx • cosx • (sinx — cos.*).
Корни производной (стационарные точки)
в этом случае будут:
0, -, -,
5тт Ътт
-, - Bя).
При переходе через * = 0 множитель sin * ме-
меняет знак минус на плюс, а вся производная
меняет знак плюс на минус, ибо последние два
множителя сохраняют вблизи * = 0 знак ми-
минус; налицо максимум. Множитель sin* — cos*,
обращающийся в нуль при * = J, при пе-
переходе через эту точку меняет знак минус на
плюс. То же будет и с производной, так как
первые два множителя положительны; следова-
следовательно, здесь будет минимум. Аналогично ис-
исследуются и остальные стационарные точки:
все они поочередно доставляют функции мак-
максимумы и минимумы. Подставляя их в выра-
выражение функции, получим сами максимальные
и минимальные значения:
максимумы: ДО) = fBjv) = 1, /(§) = 1, /|
минимумы: /(f) = ^=0,71, f{pt) = -1, /|
График функции представлен на рис. 58 [ср. 147, 1)].
Рис. 57
= -ут= -0,71,
= -1.
0,5
^vj = sin3x+cos3x
Ъш
рж 2W
4
Рис. 58
* ^ Здесь и в следующих примерах изменение функции мы иллюстрируем гра-
графиками, но самый вопрос о построении графиков будет подробно рассмотрен
лишь в § 3 [см., в частности, 149,3)].
316 ГЛ. IV. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ [136
3) Найти экстремумы функции f(x) = xi — (х — 1)з.
На этот раз конечная производная
f(x) -1Х-ЬЛ(Х2_ п-5 .ъ-1. ^-')"-¦
существует везде, исключая точки х = 0 и х d= 1.
При приближении х к этим значениям (с обеих сторон) производная стре-
стремится к zboo.
У\
Для определения корней производной, приравниваем нулю ее числитель; мы
найдем х = =Ь-^. Итак, «подозрительными» по экстремуму будут точки:
-1. -± о. ±. +1.
При jc = 0 (и вблизи этой точки) числитель и второй множитель знаменателя
имеют знак плюс. Множитель же jc з знаменателя меняет знак минус на плюс,
производная — тоже: минимум. При х = -4= и (вблизи) знаменатель сохраняет
знак плюс. Числитель же, имея в виду значения х, близкие к А=, перепишем
так: A — х2)з — х2; он обращается в нуль при х = Д=, с уменьшением х —
увеличивается, а с увеличением — уменьшается, так что меняет знак плюс на
минус, и налицо максимум. То же и при х = —\=. При переходе через х = 1
множитель (х1 — 1)з" в знаменателе, который обращается в этой точке в нуль,
не меняет знака; это же справедливо и для производной, так что при х = 1
экстремума нет. То же и при х = — 1.
Итак, максимумы / ( =Ь-^= ) = л/4= 1,59, а минимум /@) = 1.
График функции дан на рис. 59 [ср. 149, 4)].
4) Затухающие колебания. Пусть движение точки происходит по сле-
следующему закону:
s = Ae~ f sin cot,
где s — пройденный путь (отсчитываемый от начального положения), a t — вре-
время (отсчитываемое от начального момента). Будем считать все постоянные А, к,
со, а также переменную t — положительными. Выясним вид графика этой зависи-
136]
§ 1. ИЗУЧЕНИЕ ХОДА ИЗМЕНЕНИЯ ФУНКЦИИ
317
мости; его интересно сопоставить с уже знакомой нам синусоидой s = A sin cot.
Так как е > О, то, очевидно, оба графика пересекают ось х в одних и тех
же точках t = п ^ (п = 1,2,3,...). Заметим, что функция s = A sin cot имеет
попеременно максимумы и минимумы в точках t = (п + ^) ^, где обращается
в нуль ее производная sf = Aco cos cot. Составим производную для заданной
функции [ср. 99, 30)]:
-~ t(со • cos cot — к • sin cot) =
-ktf о)
s = Ae
= A •
: COS COt —
sm cot
Вводя вспомогательный угол q> под условиями:
со к
Vсо2 + к2
перепишем выражение производной в виде
Она обращается в нуль в точках
\ 2; со со
и так как косинус, проходя через нуль, меняет знак, то легко сообразить, что
при этих значениях наша функция, действительно, имеет максимумы при п чет-
четных и минимумы при п нечетных. По сравнению с синусоидой произошло
смещение экстремальных точек влево на ?.
Нетрудно проверить, что все максимумы будут положительны, а миниму-
минимумы — отрицательны. Если величину п-то экстремума обозначить через Ап, то
так что размахи убывают в геометрической прогрессии.
График (для простого частного случая) представлен на рис. 60. Движение
подобного типа носит название затухающего колебания.
318 ГЛ. IV. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ [137
Замечание. В большинстве представляющихся на практике случаев изло-
изложенного в предыдущем п° правила оказывается вполне достаточно для исследова-
исследования «подозрительных» значений. Однако следует дать себе отчет в том, что могут
быть случаи, где оно неприложимо: это будет тогда, когда в любой близости от
испытуемой точки содержится бесконечное множество других подобных же то-
точек, и производная не сохраняет определенного знака с той или
с другой стороны от этой точки.
Рассмотрим для примера функцию, определяемую равенствами:
/0) = х2 • sin - (при х ф 0) и ДО) = 0.
X
Мы уже знаем, что она при х = 0 имеет производную /'(О) = 0 [102, 2°]. Од-
Однако в любой близости от стационарной точки х = 0 как слева, так и справа
производная
f'(x) = 2x • sin cos -
х х
бесконечное множество раз меняет знак. Здесь в точкех = 0 нет экстремума.
Если же определить функцию так:
f(x) =x2(l + sin -\ при х ф 0, ДО) = 0,
то она обнаруживает такую же особенность, но на этот раз при х = 0, очевидно,
будет минимум. Правило в обоих случаях неприложимо.
137. Второе правило. При разыскании экстремумов исследова-
исследование знака производной вблизи испытуемой точки можно заменить
исследованием знака второй производной в самой этой точке;
покажем это.
Итак, пусть функция f{x) не только имеет производную f {х)
в окрестности точки хо, но и вторую производную в самой точ-
точке хо: //;(хо). Точка хо — стационарная, т. е. /'(хо) = 0. Если
//;(хо) > 0, то, по лемме п° 109, функция f'(x) в точке х =хо
возрастает, т. е. вблизи точки хо слева f'(x) < /'(хо) = 0,
а справа f'(x) > /'(хо) = 0. Таким образом, производная /'(х)
меняет знак минус на плюс и, следовательно, /(х) имеет
в точке х =хо минимум. Если //;(хо) < 0, то f'(x) в точке
х =хо убывает, меняя знак плюс на минус, так что налицо
максимум.
Таким образом, можно сформулировать второе правило для
испытания «подозрительного» значения х$. подставляем хо во
вторую производную //;(х); если //;(хо) > 0, то функция име-
имеет минимум, если лее /"(^о) < 0, то — максимум.
137]
§ 1. ИЗУЧЕНИЕ ХОДА ИЗМЕНЕНИЯ ФУНКЦИИ
319
Это правило имеет, вообще говоря, более узкий круг примене-
применения; оно, например, явно неприложимо к тем точкам, где не сущест-
существует конечной первой производной (ибо там и речи быть не может
о второй). В тех случаях, когда вторая производная обращается в
нуль, правило также ничего не дает. Решение вопроса зависит тогда
от поведения высших производных [см. следующий п°].
Если пожелать приложить это правило к примеру 2), то нужно вычислить
вторую производную:
f"(x) = 6sin;\; cos;\;(cos;\; + sin.*) — 3 (sin x + cos x).
При x = 0 Bjt), j, ж, Щ- первое слагаемое обращается в нуль и знак f"(x)
противоположен знаку f(x) = sin3 x + cos3 х; это будет минус для х = 0 Bjt), ^
(здесь максимумы) и плюс для х = ж и Щ- (здесь минимумы). Для х = f и ^f,
ввиду равенства sinx = cosx, f"{x) сведется к 6 sin x, так что в первой из этих
точек знак второй производной будет плюс (минимум), а во второй — минус
(максимум).
Вот новый пример: найти экстремумы функции f(x) =
х1 - 5х + 6
-6 -4 -2 0 2 4 6
Рис. 61
8 10 12 14 16
Производная f'{x) = 5 х( 2 ,2 обращается в нуль вместе с числителем;
ее корни будут х\ = \ — л/2= — 0,41ил:2 = 1 + л/2 = 2,41. Дифференцируем
производную снова как произведение:
причем точками заменен член, содержащий множитель х2 — 2х — 1 и нам не
нужный, ибо для тех значений х, которые мы собираемся подставлять, он
заведомо нуль. Легко видеть, что f"(x\) < 0, a f"(x2) > 0, следовательно,
значение f{x\) = 7,04 есть максимум, a f{x2) = — 0,03 — минимум.
График функции дан на рис. 61 [см. 149, 5)].
320 ГЛ. IV. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ [138
Наконец, рассмотрим еще такую задачу геометрического содержания:
найти экстремальные значения для расстояния г от данной (на плоскости) точ-
точки Р(|, г\) до точек М(х,у) кривой (К), заданной своим уравнением: у = f(x)
(рис. 62).
у\ \Р Вместо функции г можно
рассмотреть функцию
и=г2 =
о
Рис. 62
где;; = /(*). Приравнивая ну-
нулю производную:
их = х - | + (у - Л) 'Ух>
видим, что для того, чтобы
точка М(х,у) на кривой (К)
доставляла экстремум рассто-
расстоянию г, необходимо выполне-
выполнение условия:
i-x+y'x(r1-y)=0.
Иными словами, точка
|, г\) должна лежать на прямой
X-x+y'x(Y-y)=0,
проведенной через точку М(х,у) кривой перпендикулярно к касательной*^; ее
называют нормалью к кривой.
Допустим же, что точка Р(|, г\) действительно лежит на нормали к кри-
кривой (К) в точке М(х, у); будет ли расстояние РМ экстремумом? Решение этого
вопроса зависит от знака второй производной:
их2 = I +УХ + (у - П) -УХ2-
Это выражение обращается в нуль (предполагая у ф 0) лишь в точке С с ко-
, l+y'2 l+v'2
ординатами:
для нее вопрос остается открытым. Точка С отделяет на нормали те точки Р, для
которых и" < 0, и расстояние РМ будет максимумом, от тех точек Р, для
которых и" > 0, и это расстояние есть минимум.
Впоследствии [243,253] мы увидим, что эта пограничная точка С на
нормали замечательна во многих отношениях.
138. Использование высших производных. Мы видели, что
если /;(хо) = 0 и //;(хо) > 0, то функция f(x) достигает в точке хо
минимума; если же /'(хо) = 0 и /;/(хо) < 0, то функция имеет
*) Ее угловой коэффициент —\- обратен по величине и по знаку угловому
коэффициенту ух касательной.
138] § 1. ИЗУЧЕНИЕ ХОДА ИЗМЕНЕНИЯ ФУНКЦИИ 321
в этой точке максимум. Случай, когда и /;(хо) = О и //;(*o) = О,
был оставлен нами неисследованным.
Предположим теперь, что функция /(х) имеет в точке
х = хо п последовательных производных, причем все они, вплоть
до (п - 1)-й, в этой точке обращаются в нуль:
/'(хо) = ГЫ = ¦ ¦ ¦ = /И-!)Ы = о,
между тем как /^(хо) ф 0. Разложим приращение /(х) - /(хо)
функции /(х) по степеням разности х — хо по формуле Тейлора
с дополнительным членом в форме Пеан о [124, A0а)]. Так как
все производные порядков меньших, чем /7, равны в точке хо ну-
нулю, то
/0) - Д*о) = -^ (х - хо)п.
Вследствие того что а —»> 0 при х —»> хо, при достаточной
близости х к хо знак суммы в числителе будет совпадать со зна-
знаком /М(хо) как для х < хо, так и для х > хо- Рассмотрим два
случая.
\° п — нечетное число: п = 2к + 1. При переходе от
значений х, меньших, чем хо, к значениям, большим, чем хо, выра-
выражение (х — хо)" изменит знак на обратный, а так как знак первого
множителя при этом не меняется, то и знак разности /(х) — /(хо)
изменится. Таким образом, в точке хо функция /(х) не может иметь
экстремума, ибо вблизи этой точки принимает значения как мень-
меньшие, так и большие, чем /(хо).
2° п — четное число: п = 2к. В этом случае разность
/(х) — /(хо) не меняет знака при переходе от х, меньших, чем хо,
к большим, так как (х—хо)">О при всех х. Очевидно, вблизи хо
как слева, так и справа знак разности /(х) — /(хо) совпадает со
знаком числа /^(хо). Значит, если /^(хо) > 0, то /(х) > /(хо)
вблизи точки хо, и в точке хо функция /(х) имеет (собственный)
минимум; если же /^(хо) < 0, то функция имеет (собственный)
максимум.
Отсюда получаем такое правило:
Если первая из производных, не обращающихся в точ-
точке хо в нуль, есть производная нечетного порядка, функция
не имеет в точках хо ни максимума, ни минимума. Если
322 ГЛ. IV. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ [138
такой производной является производная четного порядка,
функция в точке хо имеет максимум или минимум, смот-
смотря по тому, будет ли эта производная отрицательна или
положительна.
Например, для функции f(x) = ех + е ~х + 2 cos х точка х = О является
стационарной, так как в этой точке обращается в нуль производная
Далее:
/"(*) = ех + е~х - 2cosjc, /"@) = 0;
/'"(*) =ех - е~х + 2sin*, /'"(О) = 0;
/iv(jc) = ех + е~х + 2 cos *, /IV@) = 4.
Так как в нуль не обратилась первая производная четного порядка, то
налицо экстремум, а именно минимум, ибо / @) > 0.
Замечание. Хотя выведенный выше критерий решает вопрос об экстре-
экстремуме в весьма широком классе случаев, но, теоретически говоря, он все же не
является всеобъемлющим: функция, не будучи тождественно постоянной, может
иметь в окрестности испытуемой точки производные всех порядков, которые, од-
однако, в этой точке все зараз обращаются в нуль.
В качестве примера рассмотрим (вместе с Кош и) следующую функцию:
/(*) = е~Ь- (при х ф 0), /@) = 0.
При х ф 0 она имеет производные всех порядков:
X5 \ JC4 Х° J
и, вообще,
/п\х) = Р„(^У е~^ (и =1,2,3,...), (9)
где Pn(z) есть многочлен (степени Ъп). В общности этого закона легко убедиться
по методу математической индукции.
Установим теперь, что и в точке х = 0 для нашей функции существуют
производные всех порядков, причем все равны нулю. Действи-
Действительно, прежде всего,
™-™=±-^0 при ,-><>•>.
х
*) Напомним, что ez при z —>> +00 будет бесконечно большой высшего по-
порядка, чем любая степень z , т. е. lim |j- = 0 [65]. Здесь роль z играет -^
(при jc —>> 0).
139]
§ 1. ИЗУЧЕНИЕ ХОДА ИЗМЕНЕНИЯ ФУНКЦИИ
323
так что /'(О) = 0. Допустим, что доказываемое утверждение верно для всех
производных до п-то порядка включительно. Тогда [см. (9)]
0 при jc —^ 0,
поскольку числитель представляет собой сумму членов вида фп- Значит,
и /(w+1)@) = 0. По методу математической индукции утверждение оправдано
полностью.
Хотя непосредственно ясно, что данная функция при х = 0 имеет
минимум, но установить этот факт с помощью рассмотрения ее последовательных
производных в этой точке — не удалось бы.
139. Разыскание наибольших и наименьших значений. Пусть
функция f(x) определена и непрерывна в конечном замкнутом про-
промежутке [а, Ь]. До сих пор мы интересовались лишь ее макси-
максимумами и минимумами, теперь же поставим вопрос о разыска-
разыскании наибольшего и наименьшего из всех значений,
которые она принимает в этом промежутке; *) по 2-й теореме
Вейерштрасса [85], такие наибольшие и наименьшие значения
существуют. Остановимся для определенности на наибольшем
значении.
Если оно достигается в некоторой точке между а и Ь9 то
это одновременно будет одним из максимумов (очевидно, наи-
наибольшим); но наибольшее значение может достигаться и на одном
из концов промежутка, а или Ъ
(рис. 63). Таким образом, нуж-
нужно сравнить между собой все
максимумы функции f{x) и ее
граничные значения f(a)
и f(b); наибольшее из этих чи-
чисел и будет наибольшим из всех
значений функции f(x) в [а, Ь].
Аналогично разыскивается и
наименьшее значение функции.
Пусть, например, разыскиваются наибольшее и наименьшее значения функ-
функции f(x) = sin x + cos х в промежутке [—f, ^]; два максимума, равных 1,
II
Рис. 63
*' Таким образом, мы сохраняем за термином максимум его «локальный»
смысл (наибольшее значение в непосредственной окрестности соот-
соответствующей точки) и отличаем его от наибольшего значения функции
во всем рассматриваемом промежутке.
То же относится к минимуму и наименьшему значению функции.
324 ГЛ. IV. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ [140
Рис. 64
больше граничных значений / (— f) =/(x) = 0> следовательно, 1 и бу-
будет наибольшим значением функции в указанном промежутке. Минимум, рав-
равный 0,7. . ., больше граничных значений, так что наименьшим значением
будет 0. Для промежутка [f, ^] в качестве наибольшего значения при-
пришлось бы взять больший из двух максимумов 1 и —0,7. . ., достигаемых
при х = j и Щ-, ибо на концах принимаются значения / ( ^) = 0,7. . .
и /(^) = —1, меньшие, чем 1. Наи-
Наименьшее значение достигается на правом
конце, в то же время, при х = ж, совпа-
совпадая с минимумом.
Если желают избежать исследования
на максимум или минимум, то можно по-
поступить иначе. Нужно лишь вычислить
значения функции во всех «подозритель-
«подозрительных» по экстремуму точках и сравнить их
с граничными значениями f[a) и f(b);
наибольшее и наименьшее из этих чи-
чисел, очевидно, и будут наибольшим и наи-
наименьшим из всех значений функции.
Например, для промежутка [—f, ^] сравниваем значения /@) = 1,
/(f) = 0,7 . . ., /(§) = 1 с граничными /(—f) = /(х) = 0, а для промежут-
промежутка [f, ^] сравниваем числа /(§) = 1, /(я*) = — 1, /(х) = ~^,7 ... с гранич-
граничными значениями /(f) = —0,7 ... и /(^) = — 1.
Замечание. В прикладных задачах чаще всего встречается простой слу-
случай, когда между а и Ъ оказывается лишь одна «подозрительная»точка xq.
Если в этой точке функция имеет максимум (минимум), то без сравнения с гра-
граничными значениями ясно, что это и будет наибольшее (наименьшее) значение
функции в промежутке (см. рис. 64). Часто в подобных случаях оказывается бо-
более простым произвести исследование на максимум и минимум, чем вычислять
и сравнивать частные значения функции (особенно если в состав ее выражения
входят буквенные постоянные).
Важно подчеркнуть, что сказанное приложимо в полной мере и к откры-
открытому промежутку {а, Ь), а также к бесконечному промежутку.
140. Задачи. Изложим теперь, в виде примеров, ряд задач из разных об-
областей, решение которых приводится именно к разысканию наибольшего или
наименьшего значения функции. Впрочем, чаще всего интерес представляют не
столько сами эти значения, сколько те точки (те значения аргумента), которые
доставляют их функции.
1) Из квадратного листа жести со стороною я, вырезая по углам равные
квадраты и сгибая края (рис. 65), составляют прямоугольную открытую коробку.
Как получить коробку наибольшей вместимости?
Если сторону вырезаемого квадрата обозначить через х, то объем у коробки
выразится так:;; = х(а — 2х) , причемх изменяется в промежутке [0, |]. Вопрос
привелся к нахождению наибольшего значения функции у в этом промежутке.
140]
§ 1. ИЗУЧЕНИЕ ХОДА ИЗМЕНЕНИЯ ФУНКЦИИ
325
Так как производная у' = (а — 2х)(а — 6х) между 0и^ имеет единствен-
единственный корень х = |, то, убедившись в том, что это значение доставляет функции
максимум, одновременно получаем и искомое наибольшее значение. Или иначе:
при х = | имеем у = ^т~, в то время как граничные значения у равны 0; следо-
следовательно, при х = |, действительно, получается наибольшее значение для;;.
Рис. 65
Рис. 66
2) Дано бревно с круглым сечением диаметра d. Требуется обтесать его
так, чтобы получилась балка с прямоугольным сечением наибольшей проч-
прочности.
Указание. В сопротивлении материалов устанавливается, что прочность
прямоугольной балки пропорциональна произведению bh , где b — основание
прямоугольника в сечении балки, a h — его высота.
Так как h = d — b , то речь идет о наибольшем значении для выражения
у = bh2 = bid2 — b2), причем «независимая переменная» b изменяется в проме-
промежутке @, d).
Производная у' = d — ЪЬ обращается в нуль лишь однажды внутри этого
промежутка, в точке b = -4=. Вторая производная j/; = — 6b < 0, следовательно,
в указанной точке достигается максимум, а с ним и наибольшее значение.
При b = -4= будет h = dJ^, так что d : h : b = л/3 : л/2 : 1. Из рис. 66
видно, как построить требуемый прямоугольник (диаметр разделен на три рав-
равные части, в точках деления восстановлены перпендикуляры). В строительном
деле обычно предписывается отношение h : Ъ = 7 : 5; это и есть приближенное
значение л/2 = 1,4 . . .
3) Вокруг полушара радиуса г описать прямой круговой конус наимень-
наименьшего объема; при этом предполагается, что основания полушара и конуса
лежат в одной плоскости и концентричны (рис. 67).
Здесь нужно еще рационально выбрать независимую переменную; пусть ею
будет угол ср при вершине конуса. При обозначениях чертежа будем иметь
R = ^—, h = ^—, так что объем конуса
1 j i тгг
v = - JtRzh =
cosz ср • sin ср
Для того чтобы объем v имел наименьшее значение, очевидно, нужно, чтобы
выражение у = cos q> sin <p, стоящее в знаменателе, получило свое наибольшее
326 ГЛ. IV. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ [140
значение, при изменении ср в промежутке @, ^). Имеем
у = —2 cos ср • sin ср + cos ср = 2 cos <
tg <
);
между Ои ^ производная обращается в нуль лишь при tg ср = -4=, ср = arctg -4=
(что отвечает 35° 15/52//), меняя при этом знак плюс на минус. Этот угол достав-
доставляет выражению у наибольшее значение, а объему v — наименьшее.
R
Рис 67
Рис. 68
4) Груз веса G, лежащий на горизонтальной плоскости, должен быть сдвинут
приложенной к нему силой (рис. 68). Под каким углом к горизонту — при на-
наличии трения — надлежит приложить эту силу, чтобы величина ее F была
наименьшей? Коэффициент трения \i дан.
Указание. Трение считается пропорциональным силе, прижимающей те-
тело к плоскости (закон Кулона), и направлено против движения. Множитель
пропорциональности \л и есть «коэффициент трения».
Определим силу F, которая соответствует данному углу в. Разлагая ее по
горизонтальному и вертикальному направлениям, получим для составляющих ве-
величины F-cos в и F-sin в. Сила, прижимающая тело к плоскости, будет G—F-sin в,
так что, по закону Кулона, трение R = jj(G — F • sin в); горизонтальная состав-
составляющая F • cos в тянущей силы F как раз и должна уравновешивать его трение:
F • cos в = \х • (G - F • sin в),
откуда
F=
cos в + /i sin в
Речь идет о разыскании наименьшего значения этой функции — или
наибольшего значения функции у = cos# + \x sin# — при изменении в
в промежутке [0, § ]. Производная у'в = \х cos в — sin# обращается в нуль, если
tgO = ц или в = arctg/i; этот угол в называется «углом трения». Так как
у1'2 = — /i sin в — cos в < 0, то прилагать силу под углом трения оказывает-
оказывается наиболее выгодно. Например, если нужно сдвинуть камень по деревянному
настилу, то ц = 0,4 и в = 22°.
5) Известно, что стоимость плавания судна в течение часа выражается в руб-
рублях эмпирической формулой а + bv , где а и b — постоянные, ко-
которые должны быть установлены отдельно для каждого судна, аи — скорость
140] § 1. ИЗУЧЕНИЕ ХОДА ИЗМЕНЕНИЯ ФУНКЦИИ 327
судна в узлах (узел =1,85 км/ч). *^ При какой скорости («экономической») судно
покроет любое расстояние с наименьшими затратами?
На покрытие 1 км потребуется j^v часа? соответствУюшие затраты выразят-
выразятся формулой
1 3\ 1 / 2 а
1,85и '° + ^ ' ~ 1^85 V + и
Приравнивая нулю производную выражения у = bv1 + ^, получим j/^ =
= 2Zw — -^- = 0, откуда v = у^. Так как у = 2Ь + Щ > 0, то при най-
найденном значении v затраты действительно
достигают наименьшей величины. в)
Численный пример: а = 40, b = 0,01, Щ
v = л^2000 = 12,6 (узлов).
6) Пусть электрическая лампочка может
передвигаться (например, на блоке) по вер-
вертикальной прямой О В (рис. 69). На каком
расстоянии от горизонтальной плоскости ОА
ее следует поместить, чтобы в точке А этой б- ^ vo-
плоскости получить наибольшую осве-
щенность? Рис. 69
Указание. Освещенность J пропорци-
пропорциональна ътф и обратно пропорциональна квадрату расстояния г = АВ, т. е.
ЪШф
J = с • —г-,
rz
где с зависит от силы света лампочки.
Если за независимую переменную выбрать h = OB, то
h
\Г
J = с • т @ < h < +оо).
Далее, производная
, а — 2h
обращается в нуль при h = -^= = 0,7а, меняя знак при переходе через это значе-
значение с плюса на минус. Это и есть наивыгоднейшее расстояние.
Можно выбрать за независимую переменную угол д>; тогда
с 2
s
с 2
J = — • cos cp sin q>,
а1
cos ф а1
и дело сводится к разысканию наибольшего значения для функции у = cos ф sin ф
в промежутке @, ^). Но мы уже знаем [см. задачу 3)], что это наибольшее
значение достигается при угле ф$, для которого tgфo = -у=- Для расстояния h
получаем прежнее значение a tg<po = A=.
*)
В этой формуле постоянная часть расхода а относится к амортизации и к со-
содержанию команды, а второй член bv — к стоимости топлива.
328 ГЛ. IV. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ [140
7) Из точки А, находящейся на железнодорожной магистрали АВ (рис. 70),
грузовой поток направляется в точку С, отстоящую на расстоянии
СВ = / от линии железной дороги. Стоимость провоза весовой единицы на едини-
единицу расстояния есть а — по железной дороге и /3 — при гужевой транспортировке.
К какой точке М следует провести шоссе МС, чтобы провоз груза из А в С (по
линии АМС) был возможно дешевле?
При обозначениях чертежа стоимость провоза весовой единицы груза — при
произвольном положении точки М — оказывается равной
Имеем
yr =
.*2 + l2
Если к ^ 1 (a ^ /3), то это выражение сохраняет знак минус, не обра-
обращаясь вовсе в нуль. Функция у убывает с возрастанием х от 0 до d
и, очевидно, достигает своего наименьшего значения при х = d. В этом случае
всего выгоднее начинать шоссе непосредственно у точки А.
То же справедливо и при к < 1, если только одновременно
Действительно, при к < 1 вы-
выражение
имеет единственный корень
kl
М'
Рис. 70 „
Но при сделанном предположе-
предположении этот корень оказывается ле-
лежащим вне допустимого для х промежутка изменения (или на конце его), так
что внутри промежутка производная ух оказывается отрицательной.
Лишь в том случае, если упомянутый корень будет < d, это значение х опре-
определяет положение точки М между А и В, при котором расходы по перевозке
будут наименьшими.
Замечание. Пользуемся случаем обратить внимание читателя на следу-
следующее обстоятельство. При разыскании наибольшего или наименьшего значения
функции для определенного промежутка изменения аргумента легко может ока-
оказаться, что внутри этого промежутка вовсе нет корней производной (или дру-
других «подозрительных» значений). Это свидетельствует о том, что в рассматривае-
рассматриваемом промежутке функция оказывается монотонно возрастающей или убывающей
и, следовательно, достигает как наибольшего, так и наименьшего своего значения
на концах промежутка.
В последней задаче при определенных соотношениях между входящими в нее
величинами как раз и осуществляется подобное положение.
141] § 2. ВЫПУКЛЫЕ (И ВОГНУТЫЕ) ФУНКЦИИ 329
§ 2. Выпуклые (и вогнутые) функции
141. Определение выпуклой (вогнутой) функции. После клас-
класса монотонных функций, возрастающих или убывающих,
выделяется класс так называемых выпуклых или вогнутых
функций.
Функция f{x), определенная и непрерывная в проме-
промежутке 5С*\ называется выпуклой {выпуклой вниз), если
для любых точек х\ и Х2 из SC {х\ ^ х2) выполняется нера-
неравенство
f{q\x\ + q2x2) < q\ • f{x\) + q2 • f(x2), A)
каковы бы ни были положительные числа q\ и q2, в сумме
дающие единицу. Функция называется вогнутой {выпуклой
вверх), если — вместо A) — имеем
ГЫх+Ягхг) > qx • /(*i) + qi • f(x2). **} (la)
Очевидно, что если функция f{x) выпукла (вогнута), то функ-
функция —f{x) оказывается вогнутой (выпуклой), и наоборот. Это про-
простое замечание позволит нам во многих случаях ограничиваться
изучением лишь выпуклых функций.
Приведенное определение выпуклой функции имеет простой
геометрический смысл. Прежде всего отметим, что выражение
х =q\xi+q2x2 {x\<x2), B)
при наложенных на q\ и q2 условиях, содержится между х\ и х2;
обратно, каждое число х9 которое содержится между х\ и х2, мо-
может быть единственным образом представлено в указанной форме,
с коэффициентами
х2 — х х — х\ /л ч
q\ = — и q2 = -. Bа)
x2-xi x2-xi
* ^ Здесь SC снова может быть замкнутым или нет, конечным или бесконечным.
**) Понятие выпуклой (вогнутой) функции было введено Иенсеном
(J.L. W. V. Jensen), который исходил, однако, из более частного соотношения,
чем A) [или Aа)], именно:
s (xl+x2\ / /(*l)+/(*2).
J \ 2 ) ^ 2
&)
оно отвечает q\ = q2 = \. В случае непрерывных функций, которыми мы
ограничиваемся, его определение равносильно данному в тексте.
330 ГЛ. IV. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ [142
Если рассмотреть график функции f(x) (рис. 71) и его дугу
между точками
А() и
где уi = f(x\)9 у2 = /(xi), то в левой части неравенства A) —
при коэффициентах Bа) — мы имеем ординату точки А дуги А\А2
с абсциссой х. В правой же части
у* этого неравенства стоит ордина-
ордината точки В хорды
У =
X -Х\
У\-\ У2 C)
Х2~Х\
с той же абсциссой. Таким обра-
образом, выпуклая функция ха-
характеризуется тем, что все
точки любой дуги ее графи-
графика лежат под соответству-
соответствующей хордой или на ней. [В случае вогнутой функции вместо
«под» следовало бы сказать «над».] Одновременно с самой функци-
функцией/(х) выпуклой (вогнутой) называют и кривую у = f(x).
Тривиальным примером выпуклой (и — одновременно — вогнутой) функ-
функции служит линейная функция f(x) = ах + Ъ\ для нее соотношение A)
выполняется всегда со знаком равенства. Выпуклой функцией будет и функ-
функция f(x) = х , что легко проверить непосредственно по определению:
(ЯХ + 4*) qx + 4* + 44(* x) < 4* + 4*
41*1
если q
ниже.
> 0, q\-\-qi — 1- Другие примеры выпуклых функций читатель найдет
142. Простейшие предложения о выпуклых функциях.
1°. Произведение выпуклой функции на положительную по-
постоянную есть выпуклая функция.
2°. Сумма двух или нескольких выпуклых функций тоже
выпукла.
В обоих случаях доказательство сразу получается из опреде-
определения.
Замечание. Произведение двух выпуклых функций может
не оказаться выпуклой функцией. Пример тому будет дан ниже
(в сноске на с. 335).
3°. Если ср{и) есть выпуклая и притом возрастающая
функция, аи — f{x) также выпукла, то и сложная функ-
функция q>(f(x)) будет выпуклой.
142]
§ 2. ВЫПУКЛЫЕ (И ВОГНУТЫЕ) ФУНКЦИИ
331
Действительно, ввиду выпуклости / [см. A)] и возрастания ср
имеем
<Р
q> {q\ • /Oi)
/O2)),
а в силу выпуклости ср последнее выражение не превосхо-
превосходит q\ • q> (f(x\)) + q2 - ф (f(x2))9 так что окончательно получаем
неравенство
<Р (Д?1*1 + ^2^2)) < q\ •
которое и представляет собой соотношение типа A) для функ-
функции ф(/0)).
Предлагаем читателю доказать аналогичные утверждения, со-
содержащиеся в таблице:
ф(и)
выпукла, убывает
вогнута, возрастает
вогнута, убывает
u = f(x)
вогнута
вогнута
выпукла
выпукла
вогнута
вогнута
4°. Если у = f(x) и х = g(y) суть однозначные взаим-
взаимно обратные функции {в соответствующих промежутках),
то одновременно
giy)
выпукла, возрастает
выпукла, убывает
вогнута, убывает
вогнута, возрастает
выпукла, убывает
вогнута, убывает
Пусть, например, в первой строке из предположения относи-
относительно / мы хотим вывести заключение относительно g. Положим
f(x\)=yi, /O2) =^2,так что xi =g(yi), x2=g(y2)-
Имеем, по основному неравенству A),
f(q\x\ + q2X2) < q\ • f(x\) + q2 • f{x2) =q\y\+ q2y2.
Так как, по теореме об обратной функции [83], функция g(y) также
будет возрастающей, то
g(qiyi +qiy2) > g(f(q\x\ +q2x2)) =q\ -g(yi) +q2
что и доказывает вогнутость функции g [см. (la)]. *}
*^ Все сформулированные в таблице утверждения очевидны из чертежа.
332 ГЛ. IV. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ [142
5°. Выпуклая в промежутке ЭС функция Дх), отличная
от постоянной, не может достигать наибольшего значе-
значения внутри этого промежутка.
Допустим противное: пусть функция достигает наибольшего
значения во внутренней точке хо промежутка. Так как функция
отлична от постоянной, то эту точку можно заключить в такой
промежуток (х 1, х 2):
XI < Х0 < Х2,
чтобы хоть на одном из концов значение функции было строго
меньше, чем в точке хо- Пусть, скажем,
/(*!)< Д*0), Д*2КД*0).
Полагая хо = q\x\ + q2%2-> умножим обе части первого неравенства
на q\9 а второго на q2 и сложим. Мы получим
q\ - /(*i) + qi - Д*2) < Д*о) = /(?i*i + <?2*2),
что противоречит выпуклости функции /. Этим наше утверждение
доказано.
6°. Если промежуток [xi,X2], где х\ < Х2, содержится
в промежутке 37, в котором функция Дх) выпукла, то соот-
соотношение A) выполняется либо всегда со знаком равенства,
либо всегда со знаком неравенства.
Возвращаясь к обозначениям на рис. 71, геометрически это
можно выразить так: дуга А\А2 либо сливается с хордой А\А2,
либо лее {за исключением концов) вся лежит под хордой.
Для доказательства рассмотрим линейную функцию C),
которая в точках xi и Х2 принимает те же значения, что и функ-
функция Дх); для краткости обозначим эту функцию через /(х). Раз-
Разность
ф(х)=Дх)-/(х)=Дх) + [-/(х)],
ввиду выпуклости функций / и —/, тоже будет выпуклой [2°]. Тог-
Тогда либо ф(х) = 0 в промежутке [х\, хг], либо этого нет. В первом
случае Дх) = /(х) в этом промежутке, т. е. дуга сливается
с хордой, и соотношение A) выполняется всегда со знаком ра-
равенства. Во втором случае во всем промежутке (х\,Х2) должно
быть ср{х) < 0, ибо, если бы функция ф принимала в этом про-
промежутке и неотрицательные значения, то она достигала бы своего
наибольшего в промежутке [xi,x2] значения внутри этого про-
промежутка, что для отличной от постоянной выпуклой функции не-
невозможно [5°]. Итак, внутри промежутка Дх) < /(х) кривая лежит
143]
§ 2. ВЫПУКЛЫЕ (И ВОГНУТЫЕ) ФУНКЦИИ
333
под хордой, и соотношение A) выполняется всегда со знаком
неравенства.
Если для любого промежутка [х\9Х2], х\ <Х2, содержа-
содержащегося в SC, соотношение A) выполняется со знаком неравен-
неравенства, мы будем функцию f{x) называть строго выпуклой.
Аналогично устанавливается понятие строго вогнутой функ-
функции. Эта терминология применяется одновременно и к кри-
кривой у = f{x).
143. Условия выпуклости функции. Учитывая B) и Bа), мож-
можно основное неравенство A) переписать так:
или — более симметрично —
(x2-x)f(Xl) + (*i -x2)f(x) + (x-Xl)f(x2) > 0. D)
Наконец, это условие может быть записано и с помощью опреде-
определителя:
1 хх f{xx)
1 х f{x)
1 Х2 f(x2)
E)
Во всех случаях предполагается, что х содержится между х\ и Х2\
для определенности будем впредь считать х\ < Х2- Заметим, по-
попутно, что условие выпуклости функции в форме E) получает не-
непосредственное геометрическое истолкование, если вспомнить, что
написанный определитель выражает удвоенную площадь /\A\AA2
(рис. 72) с плюсом именно тогда, когда
треугольник положительно ориенти-
ориентирован, т. е. периметр его А\—А—А2 описы-
описывается против часовой стрелки.
Отметим особо, что если речь идет о
строгой выпуклости, то во всех этих
условиях знак равенства должен быть
исключен.
Удобные для проверки условия выпук-
выпуклости функции f(x) получаются, если привлечь ее производные.
Теорема 1. Пусть функция f{x) определена и непрерывна
в промежутке ЭС и имеет в нем конечную производную f'{x).
У'
о
А
У\
/
У
2
Уг
Рис. 72
334 ГЛ. IV. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ [143
Для того чтобы f(x) была выпуклой в ЭС, необходимо и до-
достаточно, чтобы ее производная /''(х) возрастала (в широком
смысле).
Необходимость. Пусть функция f(x) выпукла. Предпола-
Предполагая х\ < х < Х2, перепишем условие D) в виде:
f(x)-f(xг) ^ Ах2)-Ах)
X — Х\ ^ Х2 — X
Если теперь устремить здесь х к х\ или к х2, то в пределе, соот-
соответственно, получим
/'(*>) < /(Х2)-/(Х1) Gа)
Х2 Х\
f(x2) > /(X2)"/(Xl), G6)
Х2 — Х\
откуда f'{x\) < ff{x2), так что функция f'{x) действительно ока-
оказывается возрастающей (в широком смысле).
Достаточность. Предположим теперь выполнение этого
последнего условия. Для доказательства неравенства F) применим
к каждой из его частей формулу конечных приращений [112]
причем xi < |i < х < ?,2 < Х2- Так как, по предположению,
/4li) ^ /412), то соотношение F), действительно, имеет место,
а из него можно восстановить соотношение D), обусловливающее
выпуклость функции f(x).
Теорема 2. Пусть функция f(x) определена и непрерывна
вместе со своей производной f'(x) в промежутке SC и имеет
внутри него конечную вторую производную f"{x). Для вы-
выпуклости функции f{x) в SC необходимо и достаточно, чтобы
внутри SC было
f"{x) > 0. (8)
В связи с предыдущей теоремой, достаточно применить к функ-
функции f'(x) теорему 2 в п° 132.
*) В интересах последующего подчеркнем, что при выводе неравенств Gа)
и G6) использовано было только существование производной, соответственно,
в точке х\ или Х2-
143]
§ 2. ВЫПУКЛЫЕ (И ВОГНУТЫЕ) ФУНКЦИИ
335
(8*)
Для вогнутости функции аналогично получается условие
/"(*) < 0.
Таким образом, требование
/"(*)> 0 (<0) (9)
заведомо обеспечивает строгую выпуклость (вогнутость),
ибо исключает возможность для функции f(x) быть линейной в ка-
каком бы то ни было промежутке [142,6°].
Теперь сразу облегчается построение любого числа примеров как выпуклых,
так и вогнутых функций:
1) Функция ах (а > 0, а ф 1) является выпуклой в промежутке
(-оо, +оо), так как (Vе)" = ах • (ЫаJ > 0;
2) функция Ых вогнута в промежутке @, +оо), ибо (Ых)" = —\ < 0
[ср. 142,4°];
3) для функции х • Ых (в том же промежутке) вторая производная ^ > 0,
и функция выпукла;
4) для функции хг (в том же промежутке) вторая производная равна
г {г — \)хг~ : отсюда видно, что при г > 1 и г < 0 функция выпукла,
а при 0< г < 1 — вогнута*^, и т. д.
Во всех этих примерах фактически имела место строгая выпуклость или
вогнутость.
В заключение мы укажем еще одну важную геометрическую
характеристику выпуклой функции f(x). При этом вместо хор-
хорды графика функции у = /(х),
которую мы рассматривали
в п° 141, здесь мы привлечем
к рассмотрению касатель-
касательную в любой точке графика
(рис. 73).
Теорема 3. Пусть функция
f{x) определена и непрерыв-
непрерывна в промежутке ЭС и име-
em в нем конечную произ-
производную f'{x). Для выпукло-
выпуклости функции f{x) необходи-
необходимо и достаточно, чтобы ее график всеми точками лежал
над любой своей касательной {или на ней).
х0
Рис. 73
*) Этот пример дает возможность — попутно — показать, что произведение
двух выпуклых функций может не быть выпуклой функцией; так, функция —х з
2
выпукла, в то время как ее квадрат, т. е. функциях з оказывается вогнутой.
336 ГЛ. IV. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ [144
Необходимость. Касательная к кривой у = f(x) в точ-
точке Ао(хо, /(хо)) имеет угловой коэффициент /;(хо). Уравнение
касательной напишется так:
Надлежит показать, что выпуклость функции /(х) влечет, для лю-
любых точек хо и х из «2Г, неравенство
f(x)>f(xo)+f'(xo)(x-xo). (Ю)
Оно равносильно двум таким
f'(xo)^f{x)lf{xo) для х>х0 (Па)
X X Q
для х<х0, A16)
х — хо
а эти неравенства совпадают, соответственно, с неравенствами Gа)
и G6), полученными при доказательстве теоремы 1 (именно в пред-
предположении выпуклости функции), если в первом из них поло-
положить Х2 = X, Х\ = Хо, а ВО ВТОрОМ Х2 = Хо, Х\ = X.
Достаточность. Предположим, наоборот, что выполняется
неравенство A0) или — что то же — неравенства (Па) и A16).
Тогда по ним можно восстановить неравенства Gа) и G6), отку-
откуда следует, что f {х\) ^ /;(х2), так что производная /;(х) будет
возрастающей функцией. Это же, в свою очередь, как мы знаем
(теорема 1) влечет за собой выпуклость функции /(х).
Замечание. Обращаем внимание читателя на то, что фак-
фактически (см. сноску на с. 334) необходимость неравен-
неравенства A0) — для данного хои произвольного i/io — доказана
в предположении лишь существования производной /'(^о) в самой
точке хо-
144. Неравенство Иенсена и его приложения. Согласно определению выпу-
выпуклой функции [см. A)], имеем
q\ • /Ol) + qi • f[x2).
Можно доказать, что для выпуклой функции имеет место более общее неравен-
неравенство (которое связывают с именем Иенсена):
• • • + qnxn) < q\ ' /Ol) + 42 ' f(x2) + . . . + qn - f(xn)9 A2)
каковы бы ни были значения х\,х2, . . . ,хп из основного промежутка ЗС.
Для п = 2 оно, как мы знаем, верно; допустив теперь, что оно верно для какого-
144] § 2. ВЫПУКЛЫЕ (И ВОГНУТЫЕ) ФУНКЦИИ 337
либо натурального числа п ^ 2, докажем, что оно верно и для п + 1, т. е.
что, взяв п + 1 значений jci, . . ., ;*w» *и+1 из «^ и п + 1 положительных чисел
#1, . . ., qn, <37?+ь сумма которых равна единице, будем иметь
Д?1*1 + . . .+qnxn+qn+lXn+l) < tfl'/(*l) + . • .+^/i'/(^/i)+^/i+l-/(^/i+l). A3)
С этой целью заменим слева сумму двух последних слагаемых qnxn + qn+\xn+\
одним слагаемым
/ ч/ Чп ,
\Яп + tf/i+l) ; х» Н
\qn+qn+\ qn
это дает возможность воспользоваться неравенством A2) и установить, что вы-
выражение в A3) слева не превосходит суммы
(qn
Остается лишь применить к значению функции в последнем слагаемом основное
неравенство A), чтобы прийти к A3). Таким образом — по методу математиче-
математической индукции — неравенство A2) полностью оправдано.
Обычно, вместо множителей gz, сумма которых равна единице, вводят про-
произвольные положительные числа р\. Полагая в неравенстве A2)
р\ + . . . + рп
приведем его к виду
В случае вогнутой функции /, очевидно, знак неравенства нужно изменить
на обратный.
Выбирая различными способами функцию /, можно получать важные кон-
конкретные неравенства — и притом все из одного источника! Приведем примеры.
1) Пусть f(x) = х , где х > 0, к > 1 (выпуклая функция). Имеем
Еа ) " Еа
или
Заменяя здесь pi на Ь- , а хг^ на g{ , приведем к уже известному нам неравен-
ству Коши-Гельдера
к-\
[ср. 133,E)].
338 ГЛ. IV. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ [145
2) Полагая f(x) = Ых, где х > О (вогнутая функция), получим
л
ln
2^ Pi 1^ Pi
Отсюда, потенцируя, тоже придем к уже встречавшемуся неравенству
[ср. 133,D)].
3) Наконец, возьмем f[x) = х Лпх, гдех > О (выпуклая функция). Тогда
окажется, что
Умножая на J^ pi и потенцируя, получим неравенство
В частности, положив здесь р\ = j-, будем иметь
Если распространить понятие среднего гармонического**^ на случай
нескольких чисел, то неравенство это можно сформулировать так: среднее гар-
гармоническое ряда положительных чисел не превосходит их среднего геомет-
геометрического.
145. Точки перегиба. При построении графиков функций (чему
будет посвящен следующий параграф) представляют интерес так
называемые точки перегиба кривой у = f(x).
Точку M(xo,f(xo)) кривой называют ее точкой пере-
перегиба, если она отделяет участок кривой, где функция f(x)
выпукла (выпукла вниз), от участка, где эта функция вогнута
(выпукла вверх) (рис. 74).
Если предположить, что в рассматриваемом промежутке функ-
функция f(x) имеет конечную производную, то эта производная,
по теореме 2, возрастает в некоторой окрестности [хо - S, хо]
слева от хо и убывает в окрестности [хо,хо + <5] справа, или
наоборот — убывает слева и возрастает справа. В первом
*^ Наподобие того, как J^ означает сумму, знак Y[ означает произве-
произведение.
**) См. сноску на с. 85.
145]
§ 2. ВЫПУКЛЫЕ (И ВОГНУТЫЕ) ФУНКЦИИ
339
случае f'{x) имеет при х = хо максимум, а во втором — мини-
минимум. Если допустить еще существование конечной второй произ-
производной f"(x) хотя бы только при х = хо, то необходимо
/"(*о)=О[ср.134].
У1
о
а)
Рис. 74
Это условие //;(хо) =0 играет такую же роль в отношении то-
точек перегиба, какую играло условие /;(хо) = 0 при разыскании
экстремумов функции /(х): оно необходимо, но не достаточ-
достаточно. В последнем легко убедиться на примере — пусть /(х) = х4,
тогда f"{x) = \2х2 ^ 0 в промежутке (—оо, +оо), так что, по тео-
теореме 2, функция /(х) выпукла во всем этом промежутке, хотя
f"{x) обращается в нуль в точке х = 0.
Если вторая производная f"(x) существует везде внутри рас-
рассматриваемого промежутка, то абсциссы точек перегиба следу-
следует искать среди корней этой производной. Но каждый ко-
корень хо подлежит испытанию. Пусть в некоторых окрестностях
[хо - S, хо) и (хо, хо + S] слева и справа от хо производная f"(x)
сохраняет определенный знак. Тогда для распознавания
точки перегиба можно дать такое правило: если при перехо-
переходе через значение х = хо производная f"(x) меняет знак,
то налицо перегиб, если лее знака не меняет, то перегиба
нет [ср. 135].
Отметим, что при этом на участках кривой, отделенных точ-
точкой (хо, /(^о))? кривая оказывается строго выпуклой на одном
и строго вогнутой на другом.
Рассмотрим, для примера, функцию f(x) = sin^c; для нее f"(x) = — sin^c
обращается в нуль в точкахх = ктт (к — целое), меняя при этом знак. Сле-
Следовательно, все точки синусоиды, лежащие на оси х, являются точками перегиба;
легко видеть, что в промежутках Bт — \jt, 2тл) синусоида выпукла (выпукла
вниз), а в промежутках Bтж, 2т + \л) она вогнута (выпукла вверх).
340 ГЛ. IV. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ [145
Можно было бы, как мы это сделали в п° 138 при разыскании
экстремумов функции, привлечь и высшие производные в испыту-
испытуемой точке хо, для которой //;(хо) = 0. Таким путем получается
правило: если первая из производных {выше второго порядка),
не обращающихся в точке хо в нуль, есть производная нечет-
нечетного порядка, то налицо перегиб; если лее такой производной
является производная четного порядка, то перегиба нет.
В заключение укажем замечательное свойство кривой у = /(х)
относительно касательной к ней в точке перегиба (если такая ка-
касательная существует): кривая переходит в этой точке с одной
стороны касательной на другую, т. е. кривая и касательная
взаимно пересекаются (см. рис. 74).
Это обстоятельство очевидно, если касательная вертикальна
(ср. рис. 43, а и б). Обратимся к случаю наклонной или горизон-
горизонтальной касательной, предполагая существование конечной про-
производной /;(хо). Допустим для определенности, что левее точ-
точки перегиба, для хо — ? ^ х < хо, кривая выпукла, а правее, для
хо < х ^ хо + S, кривая вогнута (это отвечает рис. 74,6). В этом
случае установим, что для х < хо кривая лежит над касатель-
касательной (или на ней), а для х>хо — под касательной (или на ней),
т. е. что
/(х) ^ /(х0) + /'(*<))(* -х0), если х < х0,
и
/(х) ^ /(х0) + /'(хо)(х -х0), если х > х0.
Но первое из этих неравенств совпадает с неравенст-
неравенством A0) [143] (следует иметь в виду замечание, там же). Вто-
Второе есть аналог неравенства A0) для вогнутой функции.
Замечание. Часто именно это свойство кривой принимают
просто за определение точки перегиба. Такое определение
вовсе не равносильно данному выше. Кривая, прежде
всего, может не иметь касательной в точке перегиба, так что второе
определение окажется неприложимым. Может случиться обратное:
кривая пересекает касательную в точке, которая не отделяет вы-
выпуклого участка кривой от вогнутого, и первое определение не-
приложимо. Таковы кривые на рис. 43, в и г; но интереснее кривая
у = х5A + sin2 j) при х ф 0, у = 0 при х = 0, которая в начале
координат касается оси х и пересекает ее; здесь существует даже
непрерывная вторая производная, но она бесчисленное множество
раз меняет знак вблизи точки х = 0 как слева, так и справа от нее.
146] § 3. ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ 341
§ 3. Построение графиков функций
146. Постановка задачи. Во всеоружии методов дифференци-
дифференциального исчисления вернемся к вопросу о построении графи-
графиков функций [ср. 47]. Пусть сначала требуется построить гра-
график непрерывной в конечном промежутке [а, Ь] функции у = f(x).
При этом сейчас основной целью для нас является возможно точ-
точная характеристика самого хода изменения функции;точ-
функции;точность отдельных ординат интересует нас в меньшей степени.
Обычно применяемый прием построения «по точкам» [47], взя-
взятым более или менее густо, но случайно и без отношения
к (неизвестным наперед) особенностям графика, непригоден. Он,
прежде всего, требует вычисления большого числа координат, что
практически неудобно. Но главное в другом: он непригоден
принципиально, потому что именно ввиду случайности вычи-
вычисляемых ординат он все же не обеспечивает достижения постав-
поставленной цели.
Предположим теперь, что функция у = f(x) вообще имеет ко-
конечную производную у1 = ff(x); исключение может представиться
лишь в конечном числе отдельных точек, где производная оказы-
оказывается бесконечной — определенного знака или разных зна-
знаков справа и слева. Тогда методы дифференциального исчисления
дают возможность установить некоторое число «опорных» точек,
характерных именно для данного графика, по кото-
которым график строится уже с достаточной точностью.
Прежде всего мы имеем здесь в виду поворотные точ-
точки графика, т. е. вершины его горбов и впадин, отвечающие
экстремальным значениям функции [134-138]. Впрочем, к ним сле-
следует присоединить все вообще точки, где касательная горизонталь-
горизонтальна или вертикальна, даже если они не отвечают экстремумам функ-
функции. Разумеется, должны быть отмечены и концы графика.
Когда упомянутые только что точки нанесены на чертеж (а чис-
число их обычно невелико), этого, собственно, уже достаточно для
построения графика.
Построенный подобным образом график уже довольно полно
отображает ход изменения функции, точно отмечая промежутки ее
возрастания и убывания, а также точки, где скорость изменения
функции падает до нуля {у' = 0) или возрастает до бесконечно-
бесконечности {у1 = ±оо).
342 ГЛ. IV. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ [147
Можно достигнуть дальнейшего уточнения графика, если
учесть его выпуклость (выпуклость вниз) или вогнутость
(выпуклость вверх) на отдельных участках и положение отделя-
отделяющих их точек перегиба [143,145].
147. Схема построения графика. Примеры. Итак, пусть функ-
функция у = f{x) в рассматриваемом промежутке [я, Ъ] дважды диф-
дифференцируема, исключая отдельные точки, в которых производ-
производная у' = f'(x) имеет бесконечное значение, определенного знака
с обеих сторон или разных знаков справа и слева.
Тогда для построения графика функции у = f(x) надлежит вы-
выполнить следующее:
1) определить значения х9 для которых производная у' = f (х)
равна нулю или бесконечности, и подвергнуть их исследованию на
экстремум;
2) определить значения х9 для которых вторая производ-
производная у11 = f"(x) равна нулю, и подвергнуть их исследованию на
перегиб;
3) вычислить значения самой функции у = f{x)9 отвечающие
всем этим значениям х9 а также концам а и Ъ рассматриваемого
промежутка.
Результаты удобно расположить в виде таблицы [см. ниже при-
примеры], с непременным указанием особенности вычисленной
точки графика: максимум, минимум^ у' = 0, у' = +оо или —оо,
у' = ±оо или =роо *\ перегиб.
Иногда к названным точкам графика при желании присоединя-
присоединяют еще и некоторые другие, например точки пересечения графика
с осями.
После нанесения на чертеж всех вычисленных точек через них
проводят самый график, учитывая при этом все упомянутые их
особенности.
Мы имеем в виду, конечно, обычный в практике постро-
построения графиков случай, когда первая производная обращается
в О (или в ±оо) или вторая производная обращается в 0 —
лишь в конечном числе точек. Тогда в промежутках между
ними график идет все время вверх или все время вниз, а также
оказывается выпуклым, вниз или вверх.
*) Так мы условно будем отмечать тот факт, что производная слева есть +оо,
а справа — оо, или наоборот.
147]
§ 3. ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ
343
Вычисления и проведение кривой упрощаются, если функция не
изменяет своего значения при изменении знака х (четная функ-
функция), так что график симметричен относительно вер-
вертикальной оси. Аналогичную услугу может оказать и сим-
симметрия относительно начала координат, которая ана-
аналитически выражается в том, что функция при изменении знака х
также лишь меняет знак (нечетная функция).
Примеры.
1) В 136, 2) мы уже исследовали поведение функции
у = sin *
s
cos *;
с помощью ее производной мы установили значения *, доставляющие функ-
функции экстремумы, а также вычислили и сами экстремальные значения функции.
При этом, ввиду периодичности функции, мы ограничились промежутком [0, 2тг]
изменения х. График функции также достаточно построить для этого промежутка.
Теперь нам нужно найти корни второй производной. Если представить ее
в виде
9 / 2\
yff = -(sin* + cos*) (sin 2x 1,
то легко видеть, что первый множитель в скобках обращается в 0 при * = 'Щ- =
= 2,36 и ^ = 5,50, а второй — при х = 0,36 B1°), 1,21F9°), 3,51B01°)
и 4,35 B49°); во всех случаях знак;/' меняется, так что налицо перегиб.
Составляем таблицу:
X
у
0
1
(/ = 0)
макс.
X
у
0,36
0,86
перегиб
3,51
-0,86
перегиб
0,78
0,71
(/ = 0) MUH.
3,94
-0,71
{у1 = 0) макс.
1,21
0,86
перегиб
4,35
-0,86
перегиб
1,57
1
{у' = 0) макс.
4,71
-1
{у' = 0) MUH.
2,36
0
перегиб
5,50
0
перегиб
3,14
-1
{у' = 0) MUH.
6,28
1
{у1 = 0) макс.
По этой таблице и построен график, изображенный на рис. 58.
Замечание. Читатель должен иметь в виду, что приводимые в книге чер-
чертежи, ввиду малого масштаба, не полностью используют те точные данные, ко-
которые получены вычислением. Рекомендуется повторить эти чертежи в большом
масштабе.
2) Рассмотрим функцию
у = sin * + sin 2x.
Она не только периодична, но и нечетна. Это позволяет сократить еще про-
промежуток изменения *, сведя его к [0, я*].
В этом промежутке производная
у' = cos* + 2cos2* = 4cos * + cos* — 2
344 ГЛ. IV. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ [148
обращается в 0, если cos.* = g , т. е. при х = 0,94 E4°) и 2,57 A47°). Так
как вторая производная
у11 = — sin.* — 4 sin 2x = — sin;\;(l + 8cos;\;)
при первом из этих значений, очевидно, отрицательная, то она доставляет функ-
функции максимум; аналогично, при втором значении имеем минимум.
Сама вторая производная обращается в 0 вместе с sinjc при х = 0
или х = ж = 3,14, а также вместе с множителем в скобках при х = 1,70 (97°) —
во всех случаях меняя знак (перегиб).
Таблица:
X
У
0
0
перегиб
0,94
1,76
{у' = 0) макс.
1,70
0,74
перегиб
2,09
0
2,57
-0,37
(/ = 0) MUH.
3,14
0
перегиб
К указанным выше значениям х мы присоединили здесь еще значе-
значение х = |л* = 2,09 A20°), при которому = 0 (график пересекает осъх). График,
'-ъ
X
Рис. 75
построенный по этим точкам, изображен на рис. 75; для промежутка [—ж, 0] он
получается двойным перекладыванием: вокруг оси у, а затем — вокруг оси х.
148. Бесконечные разрывы, бесконечный промежуток. Асимп-
Асимптоты. Полезно расширить класс рассматриваемых функций
в двух направлениях. Во-первых, мы допустим теперь для функ-
функции у = f(x) возможность обращаться в бесконечность
для отдельных значений х. Это значит: если хо есть одно из таких
значений, что, при приближении х к хо с той или с другой стороны,
f(x) стремится к +оо или к — оо. Во-вторых, нас может интересо-
интересовать поведение функции и в бесконечном промежутке.
Так как размеры чертежа, разумеется, конечны, то в обоих этих
случаях приходится довольствоваться частью всего графика. За пре-
148]
§ 3. ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ
345
О
делами чертежа стараются оставить такие части графика, о виде
которых легко наперед составить себе представление исходя из то-
того, что начерчено.
Остановимся на случае бесконечного разрыва функции, ска-
скажем, при х = хо- При приближении х к хо с одной сторо-
стороны функция стремится к бесконечности (того или иного зна-
знака) монотонно — если,
по крайней мере в конечной
части промежутка, производ-
производная у1 = f'(x) лишь конечное
число раз меняет знак. С раз-
разных сторон от хо (если хо не
есть конец промежутка) функ-
функция может иметь пределы
и разных знаков. Во всяком
случае, график будет безгра-
безгранично приближаться, уходя
в бесконечность, к верти-
вертикальной прямой х=хо
в верхней или в нижней его
части, смотря по знаку беско-
бесконечного предела. Эта пря-
прямая позволяет отчетливо представить себе вид
графика и за пределами чертежа (рис. 76). Примера-
Примерами могут служить и уже известные нам графики функций у = |
при х = 0 (см. рис. 10), у = tgx при х = Bк + l)f (см. рис. 16),
у = logax при х = 0 (см. рис. 14).
В случае бесконечного (в одну сторону или в обе) промежутка,
подобную же услугу иногда оказывает горизонтальная или
наклонная прямая, к которой график приближается безгранич-
безгранично. В связи с этим, дадим следующее общее определение.
Пусть имеем кривую, ветвь которой в том или ином направ-
направлении удаляется в бесконечность. Если расстояние S от точки
кривой до некоторой определенной прямой по мере удаления
точки в бесконечность стремится к нулю, то эта прямая
называется асимптотой кривой.
Только что мы имели дело с вертикальными асимптотами;
теперь займемся асимптотами горизонтальными и наклон-
наклонными — все время для кривой, заданной уравнением у = /(х).
Рис. 76
346 ГЛ. IV. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ [148
Примеры горизонтальных асимптот нам уже встречались:
для кривой у = ^ — прямая у = 0 при х —>> ±оо (см. рис. 10),
для кривой у = arctgx — прямые .у = § и 3; = ~§> соот-
соответственно, при х —>> +оо и х —>> —сю (см. рис. 21), для кри-
кривой у = ах — прямая у = 0 при х —>> — оо, если а > 1 и
при х —>> +сх), если а < 1 (см. рис. 13).
Для того чтобы, например, при х —>> +оо, прямая 7 = й служи-
служила асимптотой для кривой у = /(х), очевидно (рис. 77), необ-
необходимо и достаточно, чтобы было
lim S = lim [у — ЪI = 0
или
lim у = lim f(x) =
Таким образом, вопрос о горизонтальной асимптоте сводится
попросту к вопросу об этом пределе.
у.
\
о
:У=Лх)
Рис. 77
Рис. 78
Отдельно нужно искать подобный предел и при х —>> — оо; при
этом (как, например, в случае кривой у = arctgx) может получить-
получиться и другая асимптота.
Переходя к наклонным асимптотам, упомянем, что при-
примерами их могут служить известные читателю из аналитической
геометрии асимптоты у = ±|х гиперболы
2 2
Х__У_ _ ,
a2 b2~
или
A)
(см. также рис. 7).
Предположим теперь, что кривая у =/(х) имеет наклон-
наклонную асимптоту
Y = ах + Ь B)
(рис. 78), скажем, со стороны положительной части оси х. Так как
разность ординат \у — Y\ лишь постоянным множителем (равным
148] § 3. ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ 347
косинусу угла между асимптотой и осью х) разнится от расстоя-
расстояния ?, то при х —>> +оо одновременно с S должна стремиться к нулю
и эта разность:
lim (у -ах -b) = 0. C)
Разделив на х, получим отсюда:
lim - = а; D)
^+оо х
кроме того, равенство C) непосредственно дает
-aX)=b. E)
Итак, для того чтобы прямая B) была асимптотой для данной
кривой, необходимо выполнение условий D) и E). Обрат-
Обратное рассуждение легко покажет и их достаточность. Воп-
Вопрос здесь свелся к последовательному разысканию пределов D)
и E), которыми уже и определятся коэффициенты уравнения
прямой B).
Разумеется, для х —»> — оо нужно повторить все исследование.
Например, в случае гиперболы A), считая х —»> +оо, имеем
V —\— I Л / V ^ /ТГ ^ V I
затем,
аЪ
+ VxT-a2
и мы приходим к известным уже нам асимптотам:
V = ±— X.
а
Возвращаясь к задаче о проведении графика функции, теперь
мы добавим к сказанному в предыдущем п° в пунктах 1),2),3),
что следует еще:
4) определить значения х, обращающие функцию у = f(x)
в бесконечность, с учетом знака, и построить соответствующие вер-
вертикальные асимптоты;
5) найти горизональную или наклонную асимптоту графика
(и притом отдельно при х —»> +оо и при х —»> -оо, если проме-
промежуток бесконечен в обе стороны).
Обратимся снова к примерам.
348 ГЛ. IV. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ [149
149. Примеры.
3) Вернемся к функции
у = (х+2J(х - IK,
для которой мы уже искали экстремумы в 136,1). Эта функция сохраняет непре-
непрерывность при — оо < х < +оо. При х —t zboo не только;;, ной j стремится
к оо, так что асимптот нет.
Рассмотрим дополнительно вторую производную
у" = 20 - 1)A(к2 + \6х + 1).
Она обращается в 0 при х = 1; —0,07; —1,53, меняя при этом знак (перегиб).
Составим таблицу:
X
У
-2
0
{у' = 0) макс.
-1,53
-3,58
перегиб
-0,8
-8,40
(/ = 0) MUH.
-0,07
-4,56
перегиб
0
-4
1
0
{у' = 0) перегиб
График мы уже имели на рис. 57.
4) Пусть 2 i
у = х? — (х —1K
[см. 136,3)]. Функция сохраняет непрерывность в промежутке ( — оо, +оо).
Представив ее в виде
1
У = ~~4 2 1 Г'
JC3 +JC3(JC2 - 1K + (х2 - 1K
легко установить, что j/ —>> 0 при х —>> zboo, так что график нашей функции имеет
асимптотой ось jc (и направо и налево). Вторая производная у" не имеет корней;
перегибы будут лишь в точках, где производная у' обращается в бесконечность.
Ввиду четности функции — симметрия относительно оси j/.
Таблица:
X
У
— оо
0
-1
1
/ = +оо
-0,71
1,59
{уг = 0) макс.
0
1
у' = ±оо мин.
0,71
1,59
{у' = 0) тиа/<-с.
1
1
у' = —оо
+ ОО
0
График — на рис. 59.
[см. 137].
+
Непрерывна в ( — оо, +оо). При х —>> zboo, очевидно, limj/ = 1: горизон-
горизонтальная асимптота. Вторая производная
(г2 + IP
обращается в нуль при х = — 1; 2 + л/3 = 2,41 и 2 — л/3 = 0,27, меняя знак
(перегиб).
149]
§ 3. ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ
349
Таблица:
X
У
X
У
— оо
1
2
0
-10
1,55
2,41
-0,03
{у1 = 0) MUH.
-5
2,15
3
0
-1
6
перегиб
3,73
0,08
перегиб
-0,41
7,04
{у1 = 0) макс.
5
0,23
0
6
10
0,55
0,27
4,40
перегиб
+ ОО
1
График — на рис. 61. Небольшой масштаб здесь мешает отчетливости черте-
чертежа, особенно в промежутке изменения х от 2 до 5; эта часть графика представлена
в увеличенном масштабе.
Дадим теперь ряд новых при- У
меров.
(х -
6)у = )
(х + ij- "I Jf^ X
Функция обращается в беско- -10 -8 -6 -4 -2 0f% 4 6 8 ШХ
нечность ( — оо) при х = — 1. Так
как при х —>> zboo имеем
У_
х
1,
у — х =
-5,
то кривая имеет асимптоту: Y=х — 5.
Вычислим производные:
.У =
5)
IK
/у
у
/
——v
\
\
к
-ю-
-12-
-14-
-16-
-18-
Рис. 79
(X + 1L '
Первая обращается в нуль прих = 1 (перегиб) иприте = — 5 (максимум); других
точек перегиба нет. По таблице:
X
У
-10
-16,4
-5
-13,5
{у' = 0) макс.
-3
-16
-1
— оо
0
-1
1
0
{у' = 0) перегиб
5
1,78
10
6,05
строим график, с учетом асимптоты (рис. 79).
{а > 0).
По этой формуле функция получает вещественные значения, лишь если х ^ 0
или х > а; при х = а функция обращается в бесконечность.
350 ГЛ. IV. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ [149
Считая х > а, имеем при х —t +oo
у -х =
у
X
X
у х
X
-
а
—>>
а
1,
а
х —~а 2'
/х — а
так что, со стороны положительных х9 кривая приближается к асимптоте
у = х +1. Аналогично получается со стороны отрицательных х другая асимптота
Производная
у = - •
У
Х2{х-\а)
(х - аJ
обращается в нуль при х = \а, меняя знак
минус на плюс (минимум). Она обращается
в нуль и при х = 0, но это — конец проме-
промежутка (— оо, 0], в котором мы функцию рас-
рассматриваем, и об экстремуме здесь не может
быть и речи.
Рис. 80
Рис. 81
Вторая производная:
II 1 4 а Х
У = у ' (х -аK'
она > 0 и при х < 0, и при х > а, так что кривая всегда выпукла (вниз). Вычислив
еще ординату;; = 2,60а, отвечающую х = \а, мы имеем уже достаточно данных
для построения графика (рис. 80).
(а > 0).
Переменная х может изменяться лишь в промежутке @, а]; при х = 0 функ-
функция обращается в бесконечность.
150] § 4. РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ 351
Производная
, а3+2х3 1 /х у
oxzy 2 \у х,
всегда отрицательна, так что функция убывает. При х = а производная у1 = — оо.
Вторая производная
„ 1,
У = ~\У ~ХУ )\^2 2
2 V;\;z j/z
обращается в нуль, меняя знак, лишь при у = х = -^= = 0,63а (перегиб); при
V4
этом, очевидно, ^' = — 1. График представлен на рис. 81.
§ 4. Раскрытие неопределенностей
150. Неопределенность вида jj. Мы применим теперь по-
понятие производной и доказанные в §§3, 5 предшествующей гла-
главы теоремы для раскрытия неопределенностей. По-
Последующие теоремы 1-4 в основном принадлежат Лопиталю
(G.F. de PHospitale) и И. Бернулли (Joh. Bernoulli). Высказан-
Высказанное в них правило обычно называют правилом Лопиталя.
Сначала мы займемся основным случаем неопределенности вида jj,
т. е. исследуем вопрос о пределе отношения двух функций f(x)
и g(x)9 стремящихся к нулю (при определенном предельном пере-
переходе х —»> а).
Начнем с простой теоремы, непосредственно использующей са-
самое понятие производной.
Теорема 1. Пусты 1) функции f(x) и g(x) определены в про-
промежутке [а, Ь], 2) lim f(x) = 0, lim g{x) = 0, 3) существуют
конечные производные ff{a) и g/(a), причем g/(a) ф 0. Тогда
Доказательство. Существование конечных производных
f'(a) и gf(a) обеспечивает непрерывность функций f(x) и g{x)
в точке а. В силу 2) имеем: f{a) = lim f(x) = 0 и g{a) =
= lim g(x) = 0. Ввиду того что gf(a) Ф 0, по лемме п° 109,
g{x) ф 0 для значений х9 достаточно близких к а; ими мы и огра-
ограничимся, так что отношение 44 имеет смысл.
&\х)
352 ГЛ. IV. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ [150
Теперь это отношение можно переписать в виде
г( \ г( \ г( \ f(x)~f(a)
Я*) = Л*) ~ /О) = х-а
g(x) g(x)-g(a) s{x)-g{a) '
Переходя здесь к пределу при х —>> а9 и получим требуемый ре-
результат.
Примеры.
1) Найти предел
lim
\п(е -х)+х - Г
По теореме он равен вычисленному при х = 0 отношению производных
2 2е
1 -
х=0 х ~ ё
1 - i е - 1
2) Найти предел
Он равен
В том случае, когда одновременно /f(a) = 0, gf(a) =0, мож-
можно воспользоваться следующим обобщением теоремы 1, привлека-
привлекающим к рассмотрению производные высших порядков:
Теорема 2. Пусть: 1) функции f{x) и g{x) определены в про-
промежутке [а, Ь], 2) lim f(x) = 0, lim g(x) =0, 3) в промежут-
промежутке [a, b] существуют конечные производные всех порядков
до (п-\)-го включительно f'{x), f"{x), ..., f^n~l\x), g/(x),
g"(x), ... ,g(n~l\x), 4) при x = а они все обращаются в 0,
5) существуют конечные производные f^n\a) и g^n\a), при-
причем g(n\a) ф0. Тогда
=
g(x) g(")(a)'
Доказательство. Приложим к каждой из функций /(х),
g(x) в промежутке [а, х] (а < х ^ Ь) формулу Тейлора с допол-
дополнительным членом в форме Пеан о [см. 124, A0а)]. Ввиду 2), 3)
150] § 4. РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ
и 4), получим
353
где а и /3 —»> 0 при х —»> а.
Второе из этих равенств, вследствие условия g^n\a) Ф 0, преж-
прежде всего показывает, что g{x) отлично от нуля, по крайней мере для
значений х, достаточно близких к а. Если этими значениями огра-
ограничиться, то отношение чЧ имеет смысл.
Тогда из написанных равенств непосредственно и получается
требуемый результат:
lim
f{x)
= lim
Пример.
3) Найти предел
lim
-2*
x — sin.*
Здесь имеем:
f(x) =ex - e~x - 2x,
f'{x) = ex + e^ - 2,
g@) = 0;
gf@) = 0;
g"@) = 0;
/@) = 0; g(x) = x - sin*,
/'(O) = 0; g;(^) = 1 - cos*,
/"(*) = e- _ e-, //(о) = 0; /;(^) = sin*,
///;(*) = ex + e^, ///;@) = 2; g'"M = cos*, g'"@) = 1.
Следовательно, искомый предел равен 2.
Хотя в большинстве случаев для раскрытия неопределенности
вида ^ уже достаточно доказанных теорем, но на практике обычно
удобнее следующая.
Теорема 3. Пусть: 1) функции f(x) и g(x) определены в про-
промежутке (а, Ъ], 2) lim f{x) = 0, lim g{x) =0, 3) в промежут-
промежутке (a, b] существуют конечные производные f'(x) и gf(x),
причем gf(x) ф 0, и наконец, 4) существует {конечный или
нет) предел
Тогда и
g(x)
354 ГЛ. IV. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ [150
Доказательство. Дополним определение функций f(x)
и g(x)9 положив их при х = а равными нулю: f(a) = g{a) = 0. *)
Тогда эти функции окажутся непрерывными во всем замкнутом
промежутке [а, Ь]: их значения в точке а совпадают с пределами
при х —>> а [ввиду 2)], а в прочих точках непрерывность вытекает
из существования конечных производных [см. 3)]. Применяя тео-
теорему Коши [114], получим
f{x) =f{x)-f{a) =f'{c)
g(x) g(x)~g(a) g*(c)'
где a < с < x. To обстоятельство, что g(x) ф 0, т. e. g[x) ф g(a)9
есть следствие предположения: gf(x) ф 0, как это было установле-
установлено при выводе формулы Коши.
Когда х —>> а9 очевидно, ис-Уа, так что, в силу 4),
что и требовалось доказать.
Таким образом, доказанная теорема сводит предел отношения
функций к пределу отношения производных, если последний
существует. Часто оказывается, что нахождение предела отно-
отношения производных проще и может быть осуществлено элементар-
элементарными приемами.
Пример.
4) Найти предел
tgjc -х
lim
x — sinjc
Отношение производных последовательно упрощается:
глт — 1 1 1 — cos2 х 1 + cos х
coszx
1 — COS.X COS2 X 1 — COS.X COS2 X
при х -л 0 оно, очевидно, стремится к 2. Таков же будет, согласно теореме,
и искомый предел.
Теорема 1 в этом случае была бы неприложима, ибо при х = 0 производ-
производные числителя и знаменателя обе равны 0. Что же касается теоремы 2, то хотя
с ее помощью задача могла бы быть разрешена, но для этого потребовалось бы
(в чем легко убедиться) вычислить три последовательные производные от задан-
заданных функций.
*) Конечно, можно было бы просто предположить заранее функции определен-
определенными и непрерывными при х = а; но в приложениях иной раз удобнее формули-
формулировка условий теоремы, данная в тексте (см., например, теорему 3*).
150] § 4. РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ 355
Обращаем внимание читателя на то, что здесь и отношение производных
снова представило неопределенность вида jj, но раскрыть эту неопределенность
оказалось возможным путем элементарных преобразований. В других случаях мо-
может понадобиться применить теорему повторно. Важно подчеркнуть, что при
этом допустимы всякие упрощения получаемых выражений,
сокращение общих множителей, использование уже извест-
известных пределов и т. п. [Всего этого делать нельзя, если применяется теоре-
теорема 2] В следующем примере теорема 3 применяется последовательно три раза;
после первого мы сокращаем на ех, а после второго — отбрасываем множитель ех
в знаменателе (ибо он стремится к 1). Этим выкладки упрощаются.
Примеры.
5) lim
_ 2е2х + 2ех
(е* - IK
7хр:
lim
2хе2х + е2х + хех + ех - 4е2х + 2ех
3(ех - IJ
2хех - Зех + 3 + х 1 2хех + 2ех - Зех
= lim = - lim
Ъ( IJ 3
= lim
Ъ(ех - IJ 3 х^О 2{ех - \)ех
1 -ех + 2хех + 1 1 2хех + ех 1
= - lim = - lim
6 х 1 6
lim lim .
6 х^О ех — 1 6 х^О ех 6
1 х - A +jc)ln(l +
6) lim ^—-!¦ -= lim(l
Так как первый множитель справа стремится к е, то достаточно заняться
вторым множителем. С помощью двукратного применения теоремы 3 найдем, что
предел его равен — ^,
е
Ответ: .
Теорема 3 легко распространяется на случай, когда аргумент х
стремится к бесконечному пределу: а = ±оо (этого, разумеется,
нельзя сделать в отношении теорем 1 и 2). Именно, имеет место,
например,
Теорема 3*. Пусть: 1) функции f{x) и g{x) определе-
определены в промежутке [с, +оо), где с > О, 2) lim f\x) = 0,
lim g(x) = 0, 3) существуют в промежутке [с, +оо) конеч-
конечные производные f'{x) и gf(x), причем gf(x) ф 0, и, наконец,
4) существует {конечный или нет) предел
lim ц \ = К.
Тогда и
lim 44 =к-
356 ГЛ. IV. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ [150
Доказательство. Преобразуем переменную х по формуле
х = j9 t = j. Тогда если х —>> +оо, то t —> 0, и обратно. Ввиду 2),
имеем
lim /f-1 =0, lim gf-^) =0,
а в силу 4),
/"'(I)
К функциям /(j) и g( j) от новой переменной f можно приме-
применить теорему 3, что даст нам *}
а тогда и
lim
X-
что и требовалось доказать.
Замечание. Иногда при раскрытии неопределенностей рас-
рассматриваемого вида можно обойтись формально без приме-
применения указанных выше теорем, используя разложения функций
по формуле Тейлора [124-125]. Пусть х —>> 0 (к этому случаю
всегда можно свести дело). Если с помощью известных разложений
удается выделить из числителя и знаменателя главные члены:
f{x) = ахп + о(хп), g(x) = Ъхт + о(хт),
то становится сразу ясен предел дроби ^м-: он равен нулю, |
или ±оо, смотря по тому, будет ли п больше, равно или мень-
меньше т**\ [Ср. 62,63.]
Так, в примере 1) имеем, заменяя функции ех, е~х и
Ы(е -х) - 1 = In A - |) несколькими первыми членами их разло-
разложений:
lim , '' г '-1.^ — iim _ _—!_!_!—
е- Г
* ^ Функции /(}) и^(|) мы дифференцируем по t как сложные функции.
**) В последнем случае знак бесконечности нетрудно сообразить по знакам а
и Ь, а также (в случае нечетности разности т — п) по знаку х.
151] § 4. РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ 357
Аналогично в примере 4):
(x + ? + ...)-X ^ +
^ =
- (х - ? + ...)
Предлагается, в виде упражнения, тем же методом решить приме-
примеры 3) и 5).
151. Неопределенность вида ^. Обратимся к рассмотрению
неопределенных выражений вида Ц, т. е. исследуем вопрос о пре-
пределе отношения двух функций f(x) и g(x)9 стремящихся к +оо
(прих —»> а).
Покажем, что в этом случае применимо то же правило Ло-
питаля: следующая теорема есть простая перефразировка тео-
теоремы 3.
Теорема 4. Пусть: 1) функции f(x) и g{x) определены
в промежутке (а, Ь], 2) lim f(x) = +оо, lim g(x) = +оо,
3) существуют в промежутке (а, Ь] конечные производ-
производные f'{x) и gf(x), причем gf(x) ф 0, и, наконец, 4) существует
{конечный или нет) предел
Тогда и
1ипЩ=К.
Доказательство. Рассмотрим сначала случай конечного К.
Так как производная gf(x) не обращается в нуль, то, по теоре-
теореме Дарбу [110], она сохраняет знак, и функция g(x) изменяется
монотонно [132]. Из 2) тогда ясно, что gf(x) < 0 и g(x) с убыва-
убыванием х, монотонно возрастая, стремится к +оо. Можно считать,
что всегда g(x) > 0.
Задавшись произвольным числом е > 0, в силу условия 4), най-
найдем такое ц > 0, что при а < х < а + ц будет
-к
358 ГЛ. IV. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ [151
Положим для краткости а + ц — хо и возьмем х между а и
К промежутку [х,хо] применим формулу Коши^:
Д*)-Д*о) Г {с)
где х < с < х
g(x)-g(x0)
о, следовательно,
-к
Напишем теперь тождество (которое легко непосредственно
проверить):
№
Ф)
откуда
-К =
f(xo)-K-g(xo)
Л*)
-К
Ф)
f(xo)-K-g(xo)
[ ф) \
Ф)
Д*)-Д*о)
Ф) -Фо)
f(x)-f(xo)
-К
g(x) -g(x0)
-К
Второе слагаемое справа для х < xq = а + ц будет меньше |,
в силу A). Ввиду того же, что g{x) —>¦ +оо при х —> а, первое
слагаемое при этом стремится к нулю, и найдется такое 8 > О
(можно считать 8 < т]), что для а < х < а + 8 первое слагаемое
тоже станет меньше |. Для указанных значений х будем иметь
тогда
-к
< е,
что и доказывает требуемое утверждение. **)
В том случае, когда К = +оо (заведомо f (х) ф 0, по крайней
мере вблизи а), имеем, меняя ролями / и g9
„ Ф)
2% Ш
= 0, так что и
= 0,
откуда, наконец,
= +оо,
*^ В этом — существенное отличие от доказательства теоремы 3: здесь нель-
нельзя применить формулу Кош и к промежутку [а, х], ибо, как бы ни определять
функции f[x) и g[x) в точке а, ввиду 2), из них не получить функций, непрерыв-
непрерывных в этой точке.
**) Подчеркнем, что в нашем рассуждении мы фактически не пользовались пред-
предположением, что lim/(jc) = +00 [ср. доказательство теоремы Штольца в 33].
152] § 4. РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ 359
так как (по крайней мере вблизи а), очевидно, и f(x) > О
ия(х)>0.*>
Отметим, что доказательство без существенных изменений рас-
распространяется и на случай а = — оо. Точно так же теорема могла
бы быть доказана и для промежутка [Ь, а) {Ъ < а) как при конеч-
конечном а, так и при а = +оо. Таким образом, на случай бесконечного
предела аргумента теорема 4 распространяется автоматически.
В виде примера легко получить уже известные нам пределы:
7) lim = lim —х-—.- = lim = 0 (если \л > 0).
х—>-+оо х^ х—>-+оо jJLX^ х—>-+оо jJLX^
х12 ах^~1
8) lim — = lim — {а > 1, \х > 0).
х^+оо ах х^+оо ах -Ыа
Если \л > 1, то справа снова имеем неопределенность того же типа ^;
но, продолжая этот процесс и повторно применяя теорему 4, в конце концов
получим в числителе степень с отрицательным (или нулевым) показателем. По-
Поэтому, во всяком случае,
lim — = 0.
х
Сделаем общее замечание относительно теорем 3 C*) и 4.
В них устанавливается предел отношения функций в предполо-
предположении, что существует предел отношения производных. Но обра-
обращение этих теорем недопустимо, и первый предел может сущест-
существовать при отсутствии второго.
Например, существует предел
х + sinx / sinx\
lim = lim (Ц =1,
^+oo x x—^+oo \ X '
sinx / sini1
= lim (Ц
X x—^+00 \ x
хотя отношение производных, равное 1 + cosx, предела при
х —>> +оо не имеет.
152. Другие виды неопределенностей. Предыдущие теоремы
относились к неопределенности вида jj и Ц.
Если имеем неопределенность вида 0 • оо, то ее можно привести
к виду ^ или Ц и тогда воспользоваться правилом Лопиталя.
Пусть
Jim f{x) = 0, Jim g(x) = +оо.
Тогда имеем
*)
Случай К = — оо при предположениях теоремы невозможен.
360 ГЛ. IV. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ [152
Второе из этих выражений представляет при х —>> а неопределен-
неопределенность вида 0, третье — неопределенность вида Ц.
Пример.
\пх - Xй*
9) lim (хи • \пх) = lim = lim * г = lim =0
х^+0 х^+0 X~V х^+0 -1ЛХ-^~1 х^+0 -ц
(мы считаем /i > 0).
К виду ^ или Ц всегда можно привести и неопределенности
вида сю — сю. Пусть имеем выражение /(х) — g(x)9 причем
lim f{x) = +оо, lim g{x) = +oo.
Тогда можно произвести, например, следующее преобразование,
сводящее это выражение к неопределенности вида ^:
fix) g{x) f{x) ' g{x)
Часто, впрочем, того же удается достигнуть проще.
Пример.
/ 2 1 \ -х2 * cos2jc — sin2jc
10) lim I ctg x г ) = llm 9 5 H0
.x • cos ^c — sin x x • cos^c + sin^c x • cos^c — sin^c
х2 • sin2x x x • sin2x
предел первого множителя находится элементарно:
х • cos х + sin x / sin x \
lim = lim cos;\; -\ = 2,
x-s>0 x jc->-0\ x /
а ко второму применяем теорему 3:
х • cos;\; — sin;\; — х • sin;\;
lim ^ = lim
r\ 11111 r\
sin x x -^0 sin x + 2x • sin x • cos x
-1 1
= lim
mx +2cosjc 3
Таким образом, искомый предел равен — |.
В случае неопределенных выражений вида 1°°, 0°, оо° реко-
рекомендуется эти выражения предварительно прологарифмировать.
Пусть у = [f(x)]g^; тогда Ыу = g(x) -ln/(x). Предел Ыу
представляет собой неопределенность уже изученного типа 0 • оо.
Допустим, что одним из указанных выше приемов удается най-
найти lim Ыу, который оказывается равным конечному числу к, +оо
или —сю. Тогда lim у, соответственно, будет ек9 +оо или 0.
153] § 5. ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ 361
Примеры.
11) Пусть
/Sin*\ l-cosx
у = {—) ¦
Требуется найти lim;; при * —>> 0 (неопределенность вида: 1°°).
Если считать * > 0 (этим предположением, ввиду четности функции;;, мож-
можно ограничиться), то
In sin * — In *
1 — cos*
Применяя теорему 3 (и используя уже найденный в предыдущем примере резуль-
результат), получим:
г ШТ-х- у *• cos*-sin* 1
lim lnj; = lim -^^ — = lim = = ,
x^O x^O sin* x^O *-sinz* 3
откуда
lim у = е
I2)y=(^ -arctg*
~e 3 " y-'
При * —>> +oo это выражение представляет неопределенность вида 0 . Имеем
lnj; = ^
In*
По правилу Лопиталя:
1 # 1
lim lnj/ = lim
arctg* — ^
1 ~"
х 2
= lim -—-т-^— = lim = — 1,
так что lim у = -.
x—^+oo e
§ 5. Приближенное решение уравнений
153. Вводные замечания. Займемся теперь задачей о нахождении корней
данной функции /(*), т. е. корней уравнения
/(*) = о. A)
Впрочем, решать эту задачу мы будем в предположении, что интересующий нас
корень | изолирован, т.е. что найден содержащий его промежуток [а, Ь\.
а < | < Ь,
в котором других корней нет.
362 ЕЛ. IV. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ [154
Если, сверх того, на концах промежутка функция f(x) имеет значения f{a)
и f(b) разных знаков, то, как это было разъяснено в п° 81, в связи с применением
1 -й теоремы Больцано-Коши, последовательно деля на части промежуток,
содержащий корень, и определяя знак функции f(x) в точках деления, можно
произвольно сужать этот промежуток и тем осуществлять приближенное вычи-
вычисление корня. Однако этот прием, несмотря на его принципиальную простоту, на
практике часто оказывается непригодным, ибо требует слишком большого коли-
количества вычислений. В настоящем параграфе читатель познакомится с простейши-
простейшими приемами приближенного вычисления (изолированного) корня уравнения A),
которые более систематически и более быстро ведут к цели. При этом мы снова
будем иметь случай использовать основные понятия и методы дифференциально-
дифференциального исчисления.
Мы будем всегда предполагать выполнение следующих условий:
1) функция f(x) в промежутке [а, Ь] непрерывна вместе со своими
производными f'(x) и fff(x);
2) значения f{a) и f[b) функции на концах промежутка имеют разные
знаки: f{a) • f(b) < 0;
3) обе производные f'(x) и f"(x) сохраняют каждая определенный
знак во всем промежутке [а, Ь].
Из непрерывности функции f(x) и условия 2) следует, что между а иЬ содер-
содержится корень | уравнения A) [80]. Так как производная ff(x) сохраняет знак [3)],
то f(x) в промежутке [а, Ь] возрастает или убывает и, следовательно, обращается
в 0 лишь однажды: корень | изолирован.
Условие 3) геометрически означает, что кривая у = f[x) не только идет
в одном направлении — все время вверх или все время вниз, смотря по зна-
знаку f(x) [132], — но к тому же (строго) выпукла вниз или вверх, смотря по зна-
знаку f"(x) [143]. На рис. 82 изображены четыре возможных случая, отвечающих
различным комбинациям знаков f'(x) и /"(*),
В алгебре устанавливается, что при вычислении (вещественных) корней
алгебраических уравнений всегда может быть создано такое положение ве-
вещей, при котором выполняются условия 1), 2), 3), так что эти условия принципи-
принципиально не ограничивают приложимости излагаемых ниже приемов. Этого нельзя
сказать по отношению к трансцендентным (т. е. неалгебраическим) урав-
уравнениям. Однако на практике поставленные ограничения мало стеснительны, так
как в большинстве случаев высказанные условия выполняются.
154. Правило пропорциональных частей (метод хорд). Если промежу-
промежуток [а, Ь] достаточно мал, то с известным приближением можно считать, что —
при изменении х в его пределах — приращение функции f(x) пропорцио-
пропорционально приращению аргумента. Обозначая через | корень функции, имеем,
в частности,
Д|)-/(а) _j-a
f(b)-f(a) Ь-а
откуда с учетом того, что /(!) = 0,
(Ь-а)- f(a)
| = а- л*)-/(«г
154]
§ 5. ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ
363
Таким образом, за приближенное значение корня здесь принимается число
{Ъ-а)- Да)
х\=а — ——. B)
f{b) - f(a)
Это выражение, очевидно, можно представить и в такой форме:
(Ь-а). f(b)
Xi=b~ f{b)-fia)' B)
Изложенное правило получения приближенного значения корня и называет-
называется правилом пропорциональности частей *\ Оно допускает простое геомет-
Рис. 82
рическое истолкование. Заменим дугу ММ1 кривой (рис. 82) — хордой ММ1.
Уравнение последней может быть написано, например, в виде
У ~
7
о — а
C)
Наше правило, по существу, сводится к тому, что вместо точки А пересечения
кривой с осью х определяется точка D пересечения с осью х этой хорды.
*) В старину его называли «правилом ложного положения» (regula falsi), ибо
оно основано на предположении, которое, строго говоря, не отвечает действи-
действительности.
364 ГЛ. IV. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ [154
Действительно, полагая в C) у = 0, для абсциссы х\ точки D получаем именно
выражение B).
В связи с этим правило пропорциональных частей называют также методом
хорд.
Обратимся теперь к исследованию вопроса о положении точки х \ по отно-
отношению к корню |. Непосредственно ясно, что точка х\ лежит между а и Ь, но
с какой стороны от | ?
Так как в случаях I и II (III и IV) мы имеем дело с выпуклой вниз (вверх)
функцией, то кривая ММ1 лежит под (над) хордой ММ\ т. е.
(х-а) (а<х<Ь). D)
(>) Ъ - а
Полагая здесь х = х \, непосредственно получаем
/(*!)< О,
(>)
так что f(x 1) всегда имеет знак, противоположный знаку //;(х). Отсюда, наконец,
заключаем, что в случаях I w IV значение х \ лежит между а и |, в случаях
же II и III — между | и Ъ.
Ограничиваясь случаями I и IV, применим снова наше правило, на этот раз
к промежутку [х\, Ь]; заменяя в B) а на х\, получим новое приближенное
значение корня |:
содержащееся, по доказанному, между х\ и |. Этот процесс можно продолжать
неопределенно и построить последовательность все возрастающих прибли-
приближенных значений
а < х\ < Х2 < - - - < Хп < Хп+1 <...<!•
При этом любые два последовательных значения хп и хп+\ связаны формулой,
аналогичной B):
f{b) - f{xn)
Покажем, что, с возрастанием п,хп —t |. В самом деле, монотонно возраста-
возрастающая, но ограниченная (например, числом |) переменная хп должна стремиться
к некоторому конечному пределу а < |. Если перейти к пределу в равенстве E),
используя при этом непрерывность функции f(x), то получим, что
(Ь-а)- f(a) _
fib) ~ /(«)
откуда f(a) = 0. Так как других корней уравнения A), кроме |, в промежут-
промежутке [а, Ь] нет, то а = | *\
* ^ Сходимость процесса можно установить и без предположения, относящегося
ко второй производной, но тогда не исключена возможность того, что точки хп
переходят с одной стороны от корня на другую.
154]
§ 5. ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ
365
Рис. 83 иллюстрирует постепенное приближение точек D\, D2, . . . пересе-
пересечения последовательных хорд с осью х к искомой точке А.
Легко понять, что в случаях II или III повторное применение правила при-
приведет к последовательности убывающих приближенных значений
Ь > Х\ > Х2 > - - - > Хп > Хп+\ >...>!,
стремящихся к корню | справа.
Таким образом, во всех случаях, применив достаточное число раз указанное
выше правило, можно вычислить корень | с любой степенью точности.
При этом, впрочем, остается открытым вопрос, как оценить точность
уже вычисленного при-
приближенного значениями. J "L ^ *~oMf
Для решения его применим
к разности f(xn) — /(|) формулу
конечных приращений [112]:
/Ы = /(*„) - /(I) =
= (Xn-4).f'(c)
Отсюда
f'{cY
Рис. 83
если обозначить через т наи-
наименьшее значение |/;(л:)| в рассматриваемом промежутке (которое можно раз
навсегда вычислить наперед), то получим оценку:
1/Ы1
<
F)
Так по самой величине f(xn) оказывается возможным судить о близости хп
к корню!
Рассмотрим пример. Уравнение
х3 - 2х2 - Ах - 1 = О
имеет корень между 3 и 4, ибо, если через f(x) обозначить левую его часть
/C) = -10 < 0, /D) = 9 > 0.
Поставим себе задачей вычислить этот корень с точностью до 0,01. В промежут-
промежутке [3,4] обе производные
/'(*) = Зх2 -Ах -4 и f'\x) = 6х - А
сохраняют знак плюс (случай I); наименьшее значение первой из них будет
т = 11.
Имеем:
х1=3-
Л3)
=3+^ =
19
366 ГЛ. IV. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ [155
округляя, положим х\ = 3,52. Так как /C,52) = —2,246592, то, по неравен-
неравенству F), требуемой точности еще нет. Продолжаем:
0,48 • /C,52) L07836416
XI = 3,52 = 3,52 -\ = 3,52 + 0,09. . .
2 /D)-/C,52) 11,246592
или, округляя, Х2 = 3,61. Вычислив /C,61) = —0,458319 и пользуясь неравен-
неравенством F), снова видим, что цель еще не достигнута. Наконец,
Округляя, положим х$ = 3,63. Так как мы округлили «в сторону корня», то мог-
могли и перескочить через него; что этого не произошло, видно по знаку числа
/C,63) = —0,041653. На этот раз, по неравенству F),
0 041
|*з - II = ! -*з < ' и'" < 0,004.
Таким образом,
3,630 < | < 3,634,
т. е. | = 3,63+о,оо4-
Этим примером мы ограничимся, так как метод хорд все же мало эффек-
эффективен; ему следует предпочесть метод касательных, к которому мы и пе-
переходим.
155. Правило Ньютона (метод касательных). Вернемся к прежним пред-
предположениям относительно функции f(x) [153]; искомый корень | этой функции
изолирован в промежутке [а, Ъ\. а < | < Ъ. Отправляясь от какого-нибудь из
концов этого промежутка, например от Ь, напишем формулу Тейлора с до-
дополнительным членом в форме Лагранжа:
о = f(i) = № + f'(b) ¦а-ь)+1- f"(c) -d-bJ D<c< b). G)
Отбрасывая дополнительный член, приближенно можно положить
f(b)+f'(b)-D-b)=0,
откуда
Таким путем мы приходим к приближенному значению корня |:
т
Получение этого значения можно наглядно истолковать и геометрически. Рас-
Рассмотрим касательную к кривой у = f(x) в точке М1, с абсциссой Ъ. Ее урав-
уравнение имеет вид
y-f{b)=f'{b)-{x-b).
Полагая здесь;; = 0, найдем абсциссу точки Tf пересечения касательной с осью х;
она в точности совпадает с (8). Значит, суть дела в приближенной замене дуги
кривой MMf — касательной к ней в одном из ее концов (см. рис. 82).
155] § 5. ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ 367
Это правило, носящее имя Ньютона, называется также методом каса-
касательных.
Встает, однако, вопрос, где лежит значение х[, получаемое по формуле (8).
Ведь тот же рис. 82 показывает, что точка пересечения касательной с осью х
может лежать даже вне рассматриваемого промежутка! Мы докажем, что, если
значение f[b) — одного знака с f"(x) (т. е. в случаях I и IV), х[ лежит
между | и Ъ.
Действительно, так как f[b) и f'(b) — одного знака, то из (8) непосред-
непосредственно ясно, что х[ < Ъ. С другой стороны, из G) и (8) следует:
Но f"(x) в рассматриваемых случаях имеет одинаковый знак с ff(x), следова-
следовательно, | < х[. Окончательно: | < х[ < Ъ.
Аналогично, если исходить из точки а и касательную к кривой провести
в конце М (с абсциссой а), то, взамен (8), получим приближенное значение
/ /О) ,Q*x
*1=в-7ч^ (8)
Относительно вычисленного по этой формуле значения можно установить, как
и выше: если значение f{a) — одного знака с f"(x) (т. е. в случаях II и III),
х[ лежит между а и |.
Таким образом, для каждого из четырех возможных случаев указано,
с какого конца гарантирована успешность приближения к корню по правилу
Ньютона. Повторное применение его дает в случаях I и IV последовательность
убывающих значений:
Ъ > х[ > х'2 > . . . > х'п > х'п+1 >...>!,
а в случаях II и III — последовательность возрастающих значений:
а < х^ < х2 < . . . < хп < xn+i <...<!,
причем вычисление последующего значения по предыдущему всегда производится
по формуле
/ _ Г f(Xn)
ХХ
И здесь легко доказать, что хп —> |. Монотонная и ограниченная пере-
пере'п имеет конечный предел /3; переходя же к пределу в A0), с учетом
непрерывности обеих функций f(x) и /;(jc), найдем:
^=0, откуда /08) = 0 и /3 = |.
Рис. 84 иллюстрирует приближение к точке А со стороны точек Т\, Т2, . . .
пересечения последовательных касательных с осью х.
Таким образом, и правило Ньютона, повторно примененное, позволяет вы-
вычислить корень | с любой степенью точности. При этом точность уже
вычисленного приближенного значения оценивается, как и выше, по фор-
формуле F).
368 ГЛ. IV. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ [156
Чтобы охарактеризовать скорость убывания разностей хп — |, вернемся
к формуле (9); заменим в ней Ъ через х'ю а х[ — через х^^:
ХП+\
2 Г(х'п)
Обозначая через М наибольшее значение \f"(x)\ в заданном промежутке [а, Ь]
(и сохраняя за т его прежнее значение), отсюда легко получить теперь:
|4+1-!К^.|4-!12- (П)
Поскольку справа стоит квадрат, этим обеспечено весьма быстрое приближе-
приближение х'п к | (по крайней мере, начиная с некоторого места), что и делает метод
касательных одним из самых эффективных методов приближенного вычисления
корня.
О
Рис. 84
Неравенство A1) выполняет еще одну функцию. Если точность вычисленно-
вычисленного значения хп уже оценена, например с помощью неравенства F), то неравен-
неравенство A1) позволяет наперед оценить точность еще невычисленного значе-
значения х'п+1. Это может оказаться полезным при решении вопроса о том, на каком
знаке целесообразно его округлить.
Обратимся к примерам. Их решение, разумеется, предполагает использова-
использование всех вспомогательных средств вычисления, какие имеются под рукой, как то:
таблиц степеней и корней, таблиц умножения, арифмометра, логарифмических
и логарифмотригонометрических таблиц, натуральных таблиц тригонометриче-
тригонометрических величин, таблиц для перевода градусной меры углов в радианную, и т. п.
156. Примеры и упражнения. В этом п° мы будем пользоваться исключи-
исключительно методом касательных.
1) Вычислить с точностью до 0,01 корень уравнения
х3 - 2х2 - Ах - 1 = 0,
зная, что он содержится в промежутке C,4) [ср. 154].
156]
§ 5. ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ
369
Имеем:
/(*) = х3 - 2х2 - Ах - 7, /C) = -10 < 0, /D) = +9 > О,
/'(*) = Ъх2 - Ах - А > 0, /"(*) = 6х - А > 0 (при 3 < х < 4)
(случай I); наименьшее значение |/(*)| есть т = 11.
Отправляемся от того из концов заданного промежутка Ь = 4, для которого
знак функции f(x) совпадает со знаком f"(х). По формуле (8)
'.=4-^^=4- — =4-0,32...;
1 f АЛ 98
28
округляя, положим ^с^ = 4 — 0,3 = 3,7. Так как/(^^) = /C,7) = 1,473, то, по не-
неравенству F), х[ — | < ^Р < 0,14, т. е. достигнутая точность недостаточна.
Далее,
4 = 3,7-/^ = 3,7-1^ = 3,7-0,066..,
2 /'C,7) 22,27
положим, х'2 = 3,7 - 0,066 = 3,634. На этот раз f(x'2) = /C,634) = 0,042
так что, в силу F), х2 — | < -у^— < 0,004. Поэтому 3,630 < | < 3,634
и | = 3,63 с требуемой точностью.
[Получение этого же результата в 154 по методу хорд потребовало трех
шагов.]
2) Для второго примера предложим себе решить уравнение
х • \gx = 1.
Воспользуемся этим случаем, чтобы пояснить читателю, как графическое
изображение функций может служить
для предварительной ориентировки в рас-
расположении корней уравнения. Значение х,
удовлетворяющее уравнению
очевидно, представляет абсциссу точки пе-
пересечения кривых
1
у = \gx и у = -.
х
Рис. 85
Даже грубое их изображение (рис. 85) сра-
сразу показывает, что искомый корень ле-
лежит между 2 и 3. Это легко теперь проверить и вычислением, ибо, полагая
f(x) = х • \gx — 1, имеем
/B) = -0,39793 . . . < 0,
/C) = 0,43136... > 0.
Вычислим упомянутый корень с точностью до 0,0001.
370 ГЛ. IV. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ [156
Очевидно, при 2
/'(*) =
>0,
/"(*) = ^ > о
X
(случай I); можно положить т = 0,7.
Так как именно /C) имеет тот же знак, что и fff(x)9 то, по формуле (8),
/C) „ 0,43136...
= 3-
= 3 -
= 3 - 0,473 . . .;
/'C) " 0,91141...
положим х[ = 3 - 0,47 = 2,53. Имеем f{x[) = /B,53) = 0,019894. . ., так что
х[ -|< Щ^< 0,03. Далее,
х\ = 2,53 -
/B,53)
= 2,53 -
0,019894...
= 2,53 - 0,02375. .
/;B,53) '"" 0,83741...
возьмем х'2 = 2,53 — 0,0237 = 2,5063. Оценим, по неравенству F), погрешность:
/B,5063) = 0,000096
0,000096 . . .
х'2 =
< 0,0002,
т. е. 2,5061 < | < 2,5063. В таком случае имеем, с уже
требуемой точностью,
| = 2,5O62±o,oooi-
[На деле 2,5062 является избыточным приближенным
значением для |, ибо /B,5062) > 0.]
3) Вернемся к уравнению
2х = 4х,
о котором уже была речь в 81. Мы видели там, что
между 0 и 0,5 заключен корень этого уравнения. Это об-
обстоятельство также легко было бы заметить с помощью
графиков функций у = 2х и у = 4х; на рис. 86 ясно
видно, что эти кривые кроме точки с абсциссой 4 пере-
пересекаются еще в некоторой точке с абсциссой | между 0
и 0,5. Предложим себе вычислить этот корень с точно-
точностью до 0,00001.
Имеем для 0 ^ х ^0,5
/(*) = 2х - 4х, f'{x) = 2х • In2 - 4 < 0,
/"(*) =2X -1п22> 0
(случай II). Здесь т = 4 - \Д\п2 > 3, М = л/2 In2 2 <
< 0,7, ^ < 0,12. Так как /@) = 1 имеет одинаковый
знак с f/f(x), то начинаем с а = 0. В силу F), погрешность этого приближенного
значения < -j, а тогда, в силу A1), можно наперед оценить погрешность:
?-х[< 0,12- - < 0,014.
156]
§ 5. ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ
371
Поэтому вычисленное по формуле (8*) значение
х\ = = = 0,30. . .
1 1п2-4 3,306852...
округляем на втором знаке: х[ = 0,30. Пользуясь значением /@,30) =
= 0,031144. . ., по неравенству F), точнее оцениваем погрешность:
, 0,031144
4-х[< -?— < 0,011,
а тогда, по A1),
| - х2 < 0,12 • 0,000121 < 0,000015,
так что приближаемся к требуемой точности. Следующее приближение:
4 = 0,30 -
2
= 0,30
= 0,309897 ...
0,30 +
0,8533643 ... - 4 3,1466356 ...
округляем на пятом знаке «в сторону корня» х2 = 0,30990. Так как
/@,30990) = 0,000021 ... > 0, то это значение все же меньше корня. Погреш-
Погрешность же его, в силу F), на деле оказывается
, 0,000022
| - х2 < < 0,00001,
так что, окончательно,
4) Уравнение
= О,ЗО99О±о,оооо1-
имеет бесчисленное множество корней. Это можно сразу усмотреть из рис. 87 —
по бесчисленному множеству точек пересечения графика тангенса у = tg x с пря-
прямой у = х. Предложим себе вы-
вычислить наименьший поло-
положительный корень этого уравне-
уравнения, который содержится между Щ-
и 2-.
Так как при х = Щ- тангенс об-
обращается в бесконечность, то пред-
предложенное уравнение удобнее пред-
представить в виде f[x) = sin л: —
—х • cos л: = 0.
Имеем:
Рис. 87
x • соъх < 0 (случай IV).
f'(x) = x • mix < 0, m > 2,7; f"(x) = sin.*
Начинаем с b = Щ- = 4,7123889. . .; получим
x\ = — = 4,7123889... - 0,2122066. . .
1 2 3?r
372 ГЛ. IV. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ [156
Здесь мы сталкиваемся со следующим обстоятельством: в таблицах тригономет-
тригонометрических величин (и их логарифмов) углы указываются в градусах, минутах и се-
секундах; поэтому округление поправки 0,2122066 . . . нам удобнее делать именно
в этих единицах. Мы возьмем 12° 10/, что отвечает несколько большему чис-
числу 0,21223484 . . . (округление в «сторону корня»), так что
х[ =4,5000406... B57°50;).
Далее,
f(x[) = - cos 12° 10' + 4,5000406 ...» sin 12° 10' = -0,0291274
/ / / 0,03
/Vi) = -4,398962. . .; x[ - | < -^— < 0,012.
Продолжаем:
0 029127'4
x'2 = 4,5000406 ... - — = 4,5000406 ... - 0,0066214. . .;
округляем поправку до 0,0066177 . . . B2;45/;) и берем
xf2 = 4,4934229. . . B57°27/15//).
Так как f(x'2) = -0,000059 . . ., то
, 0,00006
х'2 - | < < 0,0000223.
Таким образом,
4,4934006. . . < | < 4,4934229
и можно положить
| = 4,4934+о,ооооз.
5) Сила метода Ньютона особенно проявляется, когда промежуток, содер-
содержащий корень, достаточно сужен. Вычислим в заключение с большой точностью,
скажем, до -Д^-¦> корень уравнения х —2л — 5 = 0, исходя из промежутка B; 2,1),
в котором он содержится.
Здесь:
/(*) = х3 - 2х - 5, /B) = -1 < 0, /B,1) = 0,061 > 0,
/'(*) = Зх2 -2 > 0, f"{x) = 6х > 0 (при 2<jc<2,1).
(случай I). Легко подсчитать, что т = 10, М < 12,6, так что
^ < 0,63.
2т
Начинаем с Ъ = 2,1. По формуле F): Ъ - | < ^р < 0,0061. Теперь,
пользуясь неравенством A1), мы заранее подсчитаем, какой точности можно
ждать от;^:
x[-i< 0,63 • 0,00612 < 0,000024.
Поэтому число
^=24-^=2,1-^=2,1-0,00543...
1 /'BЛ) п23
157] § 5. ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ 373
округляем «в сторону корня» на пятом знаке: х[ = 2,1 — 0,00544 = 2,09456. Так
как/Oi) = /B,09456) = 0,000095078690816, то теперь, по формуле F), можно
точнее оценить погрешность:
/1-i<0'0001°095-< 0.000Q1.
Переходя к х2 и снова прибегнув к A1), подсчитаем наперед:
х2 - | < 0,63 • 0,000012 = 0,000000000063.
Поэтому число
= 2Ш56 _ 0,000095078690816 = _ 5Ш16
2 11,1615447808
округленное на одиннадцатом знаке: х2 = 2,09456 — 0,00000851841 =
= 2,09455148159, все же отличается от искомого корня меньше, чем
на 0,00000000007. Итак,
2,09455148152 < | < 2,09455148159,
т. е. | = 2,0945514815 ^
157. Комбинированный метод. Этот метод состоит в одновременном исполь-
использовании как метода касательных, так и метода хорд.
Для определения предположим, что мы имеем дело со случаем I. Прибли-
Приближенные значения х\ и х[ вычислим, как и выше, пользуясь формулами B) и (8):
_ __ (b-a)-f(a) , f(b).
1W' Xl-b~7WY
тогда, по доказанному,
а < х\ < | < х[ < Ъ.
При следующем же шаге мы попросту заменяем в этих формулах а и Ъ через х \
X2~Xl~ fW-A*i) ' 2" Х~ЖУ
Этот процесс может быть продолжен неопределенно; имея два приближенных зна-
значения хп их'п, между которыми содержится корень |, мы переходим к следующей
паре приближенных значений по формулам:
_ (х'п -ХП) • f[xn) , _ , _ f(x'n)
Xn+l~Xn no-fM ' Хп+1~Хп гиг
Вторая из них тождественна с A0); первая же существенно отличается от E)
тем, что точка Ъ заменяется здесь точкой хп, все более и более близкой
к |. Если неравенство D) — для рассматриваемого случая — переписать в виде
х — а Ъ — а
f{x) - f(a) > f(b) - f(a)
и положить в нем а = хп их = х'п, то легко усмотреть, что упомянутая замена Ъ
на х'п способствует лишь более быстрому приближению хп к искомому
корню (геометрически это очевидно!).
374 ГЛ. IV. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ [158
Таким образом, при комбинированном методе мы получаем одновременно
недостаточные и избыточные приближенные значения корня, которые стремят-
стремятся к нему с разных сторон. В случаях I и IV хп стремится к | слева, а^ —
справа; в случаях же II и III, очевидно, будет наоборот. Величина \х'п — хп \
непосредственно позволяет судить о качестве достигнутого приближения —
в этом удобство комбинированного метода.
Применение его осветим примерами.
158. Примеры и упражнения. Здесь предполагается пользование лишь ком-
комбинированным методом.
1) Найти три вещественных корня уравнения
/0) = 2х3 - х2 - 1х + 5 = О
с точностью до 0,001.
Грубый график функции у = f(x) помогает найти промежутки, в которых
содержатся эти корни:
-2 < |i < -1, 0 < |2 < 1, 1 < !з < 2;
проверить это легко по изменению знака функции.
(а) В промежутке [—2, —1]
/'(*) = 6х2 - 2х - 7 > 0, f"(x) = \2х - 2 < 0
(случай III). Так как /(—2) = — 1 < 0, /( — 1) = 9 > 0, то правило Ньютона
надлежит применять к левым концам промежутков. Имеем: /;(—2) = 21 и
xi = -1 = -1,9.
9-(-1)
Округляя значение х[ в сторону уменьшения, получим число —1,96 < Ё,\. Если
же округлить его в сторону увеличения, т. е. в сторону корня, то получим чис-
число — 1,95; но /(—1,95) = 0,01775 > 0, т. е. в этом случае мы перескочили через
корень. Это обстоятельство выгодно для нас, ибо дает возможность сузить про-
промежуток, содержащий корень, и, отбросив прежнее значение х \, положить
х[ = -1,96, xi = -1,95.
Далее, имеем:
/(-1,96) = -0,180672, /(-1,96) = 19,9696,
х'2 = -1,96 + °'180672 = -1,96 + 0,00904. . . = -1,95095 . ..,
х2 = -1,95 0!0^0!01775— = _ 0(Ю89 = _1 95089 . . .
0,01775 + 0,180672
Поскольку |i должно быть заключено между этими границами, то ясно, что
!i = -l,95O9±o,ooi
(так что требуемая точность превзойдена!).
158] § 5. ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ 375
(б) В промежутке [0, 1] первая производная f'(x) сохраняет знак минус, но
вторая производная f"{x) меняет знак, обращаясь в нуль в точке х = |. Это
обстоятельство заставляет предварительно еще сузить промежуток. Испытывая
значения х = 0,5, получаем: /@,5) = 1,5 > 0; так как /A) = — 1 < 0, то ?,2 со-
содержится внутри промежутка [0,5, 1], где f"(x) сохраняет знак плюс (случай II).
И здесь правило Ньютона применяем к левым концам. Имеем:
х[ = 0,5 + — = 0,7307 = 0,74, хх = 1 = 0,80.
6,5 2,5
Округление х[ в сторону корня не привело к перескакиванию через корень,
ибо /@,74) = 0,082848 > 0. Наконец,
0,01296
х2 = 0,80 = 0,756 . . .,
0,298848
так что 0,755 . . . < |2 < 0,756 . . ., и можно положить
|2 = O,756±o,ooi-
(в) В промежутке [1,2] вторая производная сохраняет знак плюс, но первая
производная меняет знак, обращаясь в 0 при
1 + V43 .
х = = 1,26.
6
Испытываем 1,5: /A,5) = —1, в то время как/B) = 3, так что 1,5 < |з < 2;
f'(x) в этом промежутке имеет знак плюс (случай I). Имеем:
jci = 1,5+1 = 1,6, xi =2-1 = 1,7;
через корень и здесь не перескочили, ибо /A,7) = 0,036. Наконец,
0,0568
х2 = i?6 + = 1,6 + 0,094. . . = 1,694
0,604
, 0,036
х7 = 1,7 = 1,7 - 0,005 . . . = 1,694
6,94
так что и |з = l,694+o,ooi-
Замечание. Так как сумма корней, по известной теореме алгебры, должна
равняться 0,5, то этим можно воспользоваться для проверки.
2) Уравнение
/(*) = х4 - Зх2 + 75jc - 10 000 = 0
имеет два вещественных корня: один — между —11 и —10, а другой — между
9 и 10. Вычислить их с точностью до 0,00001.
(а) В промежутке [—11, —10]
/'(*) = 4х3 - 6х + 75 < 0, f'\x) = \2х2 - 6 > 0
376 ГЛ. IV. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ [158
(случай II). Получаем:
3453
Х1 = ~Ю~Ш = ~10'23 ¦ ¦ ¦ = ~
в первом случае мы округлили в сторону корня, но через него не перескочили.
Далее,
25 27984
(то же замечание). Наконец,
х\ = -10,262+ 4>334569118736 = _ю,262+0,0010354. . . = -10,2609645
3 4186,137218912
jc3 = -10,260- 0'00807038048 = _ю,260-0,0009642. . . = -10,2609642.
8,369759358736
так что
!i = -lO,26O964_o,oooooi
(даже с большей точностью, чем требовалось).
(б) В промежутке [9, 10] /'(*) > 0 и /"(*) > 0 (случай I). Здесь:
= 9
3007
= 9 + 0,869. . . = 9,87 (в сторону корня!).
х[ = 10 - -^- = 10 - 0,112. . . = 9,89;
х>2 = 9'89 -
= 9'89 - 0,003993 ... = 9,886006...
V
О S
2-
так что, очевидно, I2 = 9,886OO±o,ooooi-
3) Рассмотрим уравнение
f(x) = х • sinjc - 0,5 = 0.
^y=smx Построив графики функций у= sin x
^ж Иу = -2- (рис. 88), видим, что они пере-
пересекаются в бесчисленном множестве то-
точек, так что наше уравнение имеет бес-
бесчисленное множество корней. По графи-
графику видно также, что наименьший положи-
положительный корень | близок к 0,7; поставим
себе задачей вычислить его с точностью
до 0,000001. [Здесь следует иметь в виду
замечание об округлении в долях градуса, которое было сделано по поводу
задачи 4) в 156.]
гис. бб
158] § 5. ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ 377
Подставляя в функцию f(x) значения
а = 0,6981317... D0°)
и
Ь = 0,7853982... D5°),
получаем в первом случае отрицательный результат, а во втором — положитель-
положительный, значит, а < | < Ъ. Обе производные ff(x)9 f"(x) в этом промежутке имеют
знак плюс (случай I).
Схема вычислений:
XI = 0,6981317 . . . + 0,0419512 . . .,
х[ = 0,7853982 ... - 0,0438510 . . .;
первую поправку «округляем» до 0,0418879... B°24;), а вторую — до
0,0439231 . . . B°31;), так что окончательно
xi = 0,7400196 . . . D2°24;), х[ = 0,7414741 . . . D2°29;).
Далее,
х2 = 0,7400196. . . + 0,0008211 . . . = 0,7408407. . .,
х'2 = 0,7414741 ... - 0,0006329. . . = 0,7408412
откуда и получаем с требуемой точностью:
| = 0,740841 ±о,оооооо5-
4) В заключение вернемся к уравнению
/0) =х4 -х - 1 = 0.
Мы видели в 81, что оно имеет корень | между а = 1,22 и Ь = 1,23. Установить,
какую точность в определении этого корня дает всего лишь двукратное примене-
применение комбинированного метода.
Схема вычислений (случай I):
0,0000466544
0,05886641 = =
1 6,443468
0,00000005533760598398
х2 = 1,2207 + = 1,22074407
2 ' 0,001255538012096
, 0,0009788499821761
х7 = 1,2209 = 1,2207441 . . .
2 6,279478581316
Таким образом,
| = l,22O7441±o,ooooooi.
ГЛАВА ПЯТАЯ
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
§ 1. Основные понятия
159. Функциональная зависимость между переменными. При-
Примеры. До сих пор мы изучали совместное изменение двух пе-
переменных, из которых одна зависела от другой: значением
независимой переменной уже вполне определялось значение
зависимой переменной или функции. В науке и в жизни нередки,
однако, случаи, когда независимых переменных оказыва-
оказывается несколько, и для определения значения функции необходимо
предварительно установить значения, совместно принимаемые все-
всеми этими независимыми переменными.
1) Так, например, объем V кругового цилиндра есть функция
от радиуса R его основания и от высоты Н; зависимость между
этими переменными выражается формулой
V = jtR2H,
которая дает возможность, зная значение независимых пере-
переменных R иЯ, установить соответствующее значение V.
Объем V усеченного конуса, очевидно, является функцией о т
трех независимых переменных — радиусов R и г обоих его осно-
оснований и высоты Н, по формуле
2) По закону Ома, напряжение V в цепи электрического тока
связано с сопротивлением R цепи и с силой тока / зависимостью
V = RL Если V и R считать данными, то отсюда определится / как
функция от V vl R\
"I-
160] § 1. ОСНОВНЫЕ ПОНЯТИЯ 379
3) Пусть температура массы газа, находящегося под поршнем
цилиндра, не постоянна; тогда объем V и давление р одного моля
газа связаны с ее (абсолютной) температурой Т так называемой
формулой Клапейрона:
PV = RT (Л = const).
Отсюда, считая, например, V и Т независимыми перемен-
переменными, функцию р можно выразить через них так:
RT
4) Изучая физическое состояние какого-нибудь тела, часто при-
приходится наблюдать изменение его свойств от точки к точке. Таковы:
плотность, температура, электрический потенциал и т. п. Все эти
величины суть «функции точки» или, если угодно, функции от ко-
координат x,y,z точки. Если физическое состояние тела меняется
во времени, то к этим независимым переменным присоединяется
еще и время, t. В этом случае мы имеем дело с функциями от
четырех независимых переменных.
Число подобных примеров читатель и сам может произвольно
увеличить.
Уточнение понятия функции в случае нескольких независимых
переменных начнем с простейшего случая, когда этих перемен-
переменных две.
160. Функции двух переменных и области их определения. Го-
Говоря об изменении двух независимых переменных х и у9 мы долж-
должны всякий раз указывать, какие пары значений (х,у) они
могут принимать совместно; множество <Ж этих пар и бу-
будет областью изменения переменных х,у.
Самое определение понятия функции дается в тех же выра-
выражениях, что и для случая одной независимой переменной:
Переменная z (с областью изменения Z) называется
функцией независимых переменных х,у в мно-
множестве <Ж, если каждой паре (х,у) их значений из <Ж — по
некоторому правилу или закону — ставится в соответствие
одно определенное значение z {из Z).2^
' Это определение можно перефразировать, используя вместо словосочетания
«значение переменной» термин «точка множества». Мы сделаем это сразу для
функции п переменных [см. примеч. 21 на с. 393].
380 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [160
Здесь имеется в виду однозначная функция; легко распро-
распространить это определение и на случай многозначной функции.
Множество ^#, о котором выше шла речь, и есть область
определения функции. Сами переменныех,у — по отношению
к их функции z — называются ее аргументами. Функциональ-
Функциональная зависимость между z и х,у обозначается, аналогично случаю
одной независимой переменной, так:
z=f(x,y), z = cp(x,y), z=z(x,y), и т. п.
Если пара (хо,уо) взята из ^#, то f(xo,yo) означает то частное
(числовое) значение функции /(х,у), которое она принимает,
когда X =Х0,У = Jo-
Приведем несколько примеров функций, заданных аналитически — форму-
формулами, с указанием их областей определения. Формулы:
1) z = ху,
2)z=,2+/
определяют функции для всех пар (х,у) без исключения. Формулы:
3) z = у7
4) г = 7^
7^- х1 - у1
годятся (если мы хотим иметь дело с конечными вещественными значениями z)
лишь для тех пар (х,у), которые удовлетворяют, соответственно, неравенству
х2 +У2 < 1 или х2 +у2 < 1.
Формулой:
5) z = arcsin —\- arcsin —
а Ъ
функция определена для тех значений х и у, которые порознь удовлетворяют
неравенствам
—а ^ х ^ а, —Ъ ^у ^Ъ.
Во всех этих случаях мы указывали наиболее широкую — естествен-
естественную [46,2°] — область применения формулы.
Рассмотрим теперь такой пример.
6) Пусть стороны треугольника произвольно изменяются, с тем лишь ограни-
ограничением, что периметр его сохраняет постоянную величину 2р. Если две стороны
его обозначить через х и у, то третья сторона будет 2р — х —у, так что тре-
треугольник вполне определяется сторонами х и у. Как зависит от них площадь z
треугольника?
По формуле Г е р о н а эта площадь выразится так:
z = у/р{р - х){р - у)(х +у - р).
Что же касается области определения^ этой функции, то она обусловли-
обусловливается, на этот раз, тем конкретным вопросом, который привел к рассмотрению
160]
§ 1. ОСНОВНЫЕ ПОНЯТИЯ
381
функции. Так как длина каждой стороны треугольника есть положительное число,
меньшее полупериметра, то должны выполняться неравенства
0 < х < р, 0 < у < р, х +у > р;
они и характеризуют область *Ж. *)
Таким образом, в то время как для функции одной перемен-
переменной стандартной областью изменения аргумента являлся (конеч-
(конечный или бесконечный) промежуток, в случае функции двух пе-
переменных мы уже сталкиваемся с большим разнообразием и слож-
сложностью возможных (и естественных) областей изменения аргумен-
аргументов.
Рассмотрение этих областей значительно облегчается их гео-
геометрической интерпретацией. Если взять на плоскости две взаим-
взаимно перпендикулярные оси и обычным образом откладывать на них
значения х и j/, то, как известно, каждой парой (х,у) однозначно
определяется точка на плоскости, имеющая эти значения своими
координатами, и обратно.
Тогда для характеристики тех пар (х,у)9 для которых опреде-
определена функция, проще всего указать, какая фигура на плоскости хОу
заполняется соответствующими точками.
Так, говорят, что функции 1) и 2) определены во всей плоскости,
функции 3) и 4) — в круге, соответственно, замкнутом (т.е. включающем
окружность) или открытом (без окружности) (рис. 89); функция 5) определена
в прямоугольнике (рис. 90); наконец, функция 6) рассматривается в откры-
открытом треугольнике (рис. 91).
Рис. 89
Рис. 90
Рис. 91
Эта геометрическая интерпретация настолько удобна, что обыч-
обычно самые пары чисел (х,у) называют «точками», а множество
*) Несмотря на то что полученная формула сама по себе сохраняет смысл
и в более широкой области, например для х > р и у > р.
382
ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[160
таких «точек», отвечающее тем или иным геометрическим обра-
образам, называют по имени этих образов. Так, множество «точек», или
пар, (х,у)9 для которых выполняются неравенства
а ^ х ^ Ь, с ^ у ^ d,
есть «прямоугольник», измерения которого равны Ъ — a nd — c; его
будем обозначать символом [a,b;c,d\9 сходным с обозначением
промежутка. Множество «точек» или пар (х,у)9 удовлетворяющих
неравенству
2 22
есть «круг» радиуса г, с центром в «точке» (а, /3), и т. п.
Рис. 92
Наподобие того, как функция у = f(x) геометрически иллюст-
иллюстрировалась своим графиком [47], можно геометрически истол-
истолковать и уравнение z =f(x,y). Возьмем в пространстве прямо-
прямоугольную систему координатных осей x,y,z; изобразим на плос-
плоскости ху область ^Ж изменения переменных х и у9 наконец, в каж-
каждой точке *Ж(х,у) этой области восставим перпендикуляр к плос-
плоскости ху и отложим на нем значение z =f(x,y). Геометриче-
Геометрическое место полученных таким образом точек и явится своего рода
пространственным графиком нашей функции. Это будет,
вообще говоря, некоторая поверхность; в свою очередь, равенство
z = f(x,y) называется уравнением поверхности.
161]
§ 1. ОСНОВНЫЕ ПОНЯТИЯ
383
Для примера на рис. 92, 93 и 94 изображены геометрические
образы функций:
z = ху, z=x
z = д/l — х2 — у2.
Первый из них представляет собой гиперболический пара-
параболоид, второй — параболоид вращения, а третий —
полусферу.
Рис. 93
Рис. 94
В заключение упомянем, что иногда приходится рассматривать
переменную хт,т значения которой занумерованы двумя нату-
натуральными значками тип (каждый из которых, независимо от дру-
другого, пробегает натуральный ряд чисел). Такая переменная пред-
представляет собой, в некотором смысле, обобщение варианты хп.
Можно положить, например,
т\п\
mz + n
2'
и т. п.
По сути дела, значки тип следует рассматривать как не-
независимые переменные, а переменную хт^п — как функцию от
них. Область изменения независимых переменных в данном случае
геометрически иллюстрируется своеобразной точечной квадратной
сеткой в первом координатном угле.
161. Арифметическое я-мерное пространство. Переходя
к функциям от п независимых переменных (при /7^3), мы снача-
сначала остановимся на системах совместных значений этих пере-
переменных.
384 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [161
В случае /7 = 3 такая система из трех чисел (х,у, z), как ясно
читателю, еще может быть геометрически истолкована как точка
пространства, а множество таких троек — как часть про-
пространства или геометрическое тело. Но при п > 3 возможно-
возможности непосредственной геометрической интерпретации уже нет, вви-
ввиду отсутствия у нас интуиции пространства с числом измерений,
большим трех.
Тем не менее, желая распространить геометрические методы
(оказавшиеся плодотворными для функций двух и трех перемен-
переменных) и на теорию функций большего числа переменных, в анализе
вводят понятие /7-мерного «пространства» и при п > 3.
Назовем (/7-мерной) «точкой» систему из п вещественных чи-
чисел: М(х\, Х2, ..., хп) *); сами числахь Х2, ..., хп являются к о ор-
динатами этой «точки» М. Множество всех мыслимых /7-мерных
«точек» составляет /7-мерное «пространство» (которое ино-
иногда называют арифметическим).
Целесообразно ввести понятие «расстояния» ММ' между двумя
(/7-мерными) «точками»
2, ...,*„) и
Подражая известной из аналитической геометрии формуле, пола-
полагают
MM' = MM =
- xiJ + (*2 - *2J + • • • + « - *пJ1 A)
при /7 = 2 или 3 это «расстояние» совпадает с обычным расстоя-
расстоянием между двумя соответственными геометрическими точками.
Если взять еще одну «точку»
*) Имея дело с неопределенным числом переменных, представляется удобным
обозначать их не различными буквами, но одной и той же буквой, лишь с раз-
различными номерами. Таким образом, Х[ означает (вразрез с прежней практикой)
не z-e значение некоей переменной, а саму z-ю переменную, которая сама по себе
принимает различные значения.
161]
§ 1. ОСНОВНЫЕ ПОНЯТИЯ
385
то, как можно доказать, для «расстояний» ММ1, М'М" и ММ" вы-
выполняется неравенство
ММ" < ММ' + ММ",
B)
напоминающее известную теорему геометрии: «сторона треуголь-
треугольника не превосходит суммы двух других сторон».
Действительно, для любого набора вещественных чисел
яь <Я2, ..., ап и Ь\, Й2> • • • ,Ьп имеет место неравенство *}
\
Если положить здесь
\
Е*?-
то
at =
хг -х
xt хг,
получим
\
п
1=1
7 //
^ 1
= 1
п
1=1
/
/¦'
,2,
так что
• • -, п),
-х,J +
\
а,+Ъ,=х'/-
п
1 = 1
что равносильно B). Таким образом, существенное свойство рас-
расстояния оказывается налицо и в нашем «пространстве».
В /7-мерном «пространстве» можно рассматривать и непрерыв-
непрерывные «кривые».
*) Это неравенство есть не что иное, как частный случай уже встретившегося
нам неравенства Минковского [133, G)] при к = 2. Если возвести обе части
его в квадрат и опустить в обеих частях равные члены, то оно сведется к тоже
известному неравенству Кош и [133, Eа)]. Приведем совершенно элементарное
доказательство этого последнего неравенства, а вместе с тем — и неравенства
в тексте.
Квадратный трехчлен
f>,x + Ъ,J = J2a2-X2 + iJZ^b, -х + ? b2,
i=\ i=\ i=\ i=\
очевидно, не принимает отрицательных значений. В таком случае он не может
иметь двух различных вещественных корней, и выражение
п п ( п >,2
i=\ i=\ 4=1 )
должно быть неотрицательным, а это равносильно неравенству К о ш и.
386 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [161
Известно [106], что уравнения
х =<p(t), у =i/>(t),
где q>(t) и xj){t) суть функции от параметра t9 непрерывные в не-
некотором промежутке [tf, t'% выражают на плоскости непрерывную
кривую. Аналогично, но лишь с помощью трех непрерывных функ-
функций:
выражается непрерывная кривая в (обыкновенном) пространстве.
Подражая этому, рассмотрим теперь п непрерывных функций от t
ХХ = <pX{t)9 Х2 = <P2(t), . . . , Хп = <pn{t) {t' ^t^ t").
Тогда множество «точек»
{(pi{t),(p2{t),...,(pn(t)),
получаемых при различных значениях параметра t9 и составля-
составляет непрерывную «кривую» в /7-мерном «пространстве». Положив
х\ = Ф1(О, ..., х'п = cpn{t')- х'{ = n(t"), ..., х'; = q>n{t"),
можно сказать, что эта «кривая» соединяет «точки»
М'(х\,...,х'п) и М"{х'(,...,х'^).
В этом случае, когда все функции ф\,...,(рп оказываются
линейными, «кривая» переходит в «прямую»:
здесь коэффициенты а\, ..., ап предполагаются не обращающими-
обращающимися зараз в 0, a t изменяется от — оо до +оо. Будем считать «точки»
ее следующими одна за другой в порядке возрастания пара-
параметра; если tr < t < t/f, то из соответствующих «точек» М\ М, Мп
именно «точка» М лежит между двумя другими, так как следует
за М' и предшествует М". При этих условиях, как легко показать,
расстояния между ними удовлетворяют соотношению:
М'М" = М'М + ММ",
что является характерным для прямой в обычном пространстве.
Уравнения «прямой», проходящей через две заданные «точки»
МЧх\,...,х'п) и М"{х'{,...,х''),
162] § 1. ОСНОВНЫЕ ПОНЯТИЯ 387
очевидно, могут быть написаны в виде:
xi=x[+ t(x" - х[), . . ., хп = х'п + t(x" - х'п)
( — (X) < t < + О<о),
причем сами «точки» М' и М" получаются отсюда при t = 0 и 1.
Если же изменять t только от 0 до 1, то получится «прямолинейный
отрезок», соединяющий эти «точки».
«Кривая», состоящая из конечного числа «прямолинейных от-
отрезков», называется «ломаной».
162. Примеры областей в я-мерном пространстве. Обратимся
теперь к рассмотрению некоторых примеров «тел» и «областей»
в /7-мерном «пространстве».
1) Множество «точек» М(х\,Х2, • • •, хп)9 координаты которых
независимо одна от другой удовлетворяют неравенствам
ai^xi^bi, Я2О2О2, . .., ап < хп < Ьп,
называется (/7-мерным) «прямоугольным параллелепипедом» и
обозначается так:
[a\,bi; a2,b2; ...; an,bn].
При /7 = 2 отсюда, в частности, получается тот «прямоугольник»,
о котором уже была речь в п°160; трехмерному «параллелепипеду»
отвечает в пространстве обыкновенный прямоугольный параллеле-
параллелепипед.
Если в написанных соотношениях исключить равенство:
a\<xi<bi, a2<x2<b2, . .., ап < хп < Ьп,
то этим определится открытый «прямоугольный парал-
параллелепипед»
(a\,bi; a2,b2; ...; an,bn),
в отличие от которого рассмотренный выше называется замкну-
тым*1 Разности Ь\ — а\9 Ь2 — #2? • • • ¦» Ьп — ап называют измере-
измерениями обоих параллелепипедов, а точку
'а\+Ь\ п2 + Ъ2 ап +
— их центром.
*' Можно рассматривать также и бесконечный «параллелепипед», для
которого определяющие его промежутки (или некоторые из них) оказываются
бесконечными.
Говоря об ^-мерном «параллелепипеде», если не сделано оговорок, мы всегда
будем иметь в виду конечный «параллелепипед».
388
ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[162
Окрестностью «точки» Мо(х®,х2, ... ,х„) называется лю-
любой открытый «параллелепипед»:
.;х°п-8п, х°п + 8п) C)
io\ чаще всего это будет
(8\, 82, ..., 8п > 0) с центром в точке
«куб»:
;" - 8, х" + 8; х2 -8, х2 + 8; .
...; х°п-8, x°n +
(8 > 0), все измерения которого равны B8).
2) Рассмотрим множество «точек» М(х\,Х2, .. -,хп)9 коорди-
координаты которых удовлетворяют неравенствам
х2
0).
При /7 = 2 соответствующим этому множеству геометрическим
образом будет равно-
равнобедренный прямоуголь-
прямоугольный треугольник, а при
/7 = 3 — тетраэдр
(рис. 95). В общем слу-
случае его называют симп-
симплексом^ (именно —
замкнутым, в отли-
чх чие от открытого,
который получится, если
в написанных соотноше-
соотношениях исключить равен-
равенство).
3) Наконец, множество «точек» М(х\,х2, ... ,хп), определя-
определяемое неравенством
(х\ — х\J + (х2 — х2J + . . . + (хп — х^J ^ г2 (или < г2),
если Мо(х\, х2, ..., х®) есть постоянная «точка», а г — постоянное
положительное число, образует замкнутую (или открытую)
/7-мерную «сферу» радиуса г, с центром в «точке» Мо. Иными сло-
словами, «сфера» есть множество «точек» М, «расстояние» которых
*) По-латыни simplex означает «простой»: симплекс представляет собой,
действительно, простейшее многогранное «тело», с наименьшим возможным для
данного пространства числом граней.
163] § 1. ОСНОВНЫЕ ПОНЯТИЯ 389
от некоторой постоянной «точки» Мо не превосходит (или мень-
меньше) г. Само собой ясно, что этой «сфере» при п = 2 отвечает круг
[ср. 150], а при /7 = 3 — обыкновенная сфера.
Открытую «сферу» любого радиуса г > 0 с центром в точке
Мо(х^, ... ,х%) можно также рассматривать как окрестность
этой точки; в отличие от той («параллелепипедальной») окрест-
окрестности, которую мы ввели раньше, эту окрестность будем называть
«сферической». Полезно раз навсегда дать себе отчет в том, что
если «точка» Мо окружена окрестностью одного из указанных двух
типов, то ее можно окружить и окрестностью второго типа так,
чтобы эта окрестность содержалась в первой.
Пусть сначала задан «параллелепипед» C) с центром в «точ-
«точке» Мо. Достаточно взять открытую «сферу» с тем же центром
и радиусом г, меньшим всех St (z = 1, 2, ..., /7), чтобы эта сфера
уже содержалась в названном «параллелепипеде». Действительно,
для любой «точки» М(х\,Х2, • • • ,хп) этой «сферы» будем иметь
(при каждом / = 1,2,..., п)\
\х- -
к=\
или
х^ -St <xt <х° + й,
так что эта точка принадлежит заданному «параллелепипеду».
Обратно, если задана «сфера» радиуса г с центром в Мо,
то «параллелепипед» C) в ней содержится, например, при
Si = 82 = ... = 8п = -у=. Это следует из того, что любая «точка»
М(х\, Х2, ..., хп) этого «параллелепипеда» отстоит от «точки» Мо
на «расстояние»
ММ0 =
\
к=\
\
к=\
и, следовательно, принадлежит заданной «сфере».
163. Общее определение открытой и замкнутой области. На-
Назовем «точку» М'(х[9х'29 ... 9х'п) внутренней «точкой» мно-
множества ^Ж (в /7-мерном «пространстве»), если она принадлежит
множеству ^# вместе с некоторой достаточно малой ее окрестно-
окрестностью.
390 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [163
Из утверждения, доказанного в конце предыдущего п°, следу-
следует с очевидностью, что безразлично, какого типа окрестнос-
окрестности здесь иметь в виду — «параллелепипедальные» или «сфери-
«сферические».
Для открытого «прямоугольного параллелепипеда»
(ai,bi;...;an,bn) D)
каждая его «точка» является внутренней. Действительно, если
а\ <х\<Ъ\, . . ., ап < х'п < Ьп,
то легко найти такое 8 > 0, чтобы было
а\ < х[ — 8 < х[ + 8 < Ь\, .. ., ап < х'п — 8 < х'п + 8 < Ъп.
Аналогично, в случае открытой «сферы» радиуса г с цен-
центром в «точке» Мо, каждая принадлежащая ей «точка» М' также
является для нее внутренней. Если взять р так, что
0 < р < г - М'Мо,
и описать вокруг М' «сферу» этим радиусом р, то она целиком
будет содержаться в исходной «сфере»: лишь только ММ' < р9
тотчас же [160, B)]
ММ0 ^ ММ' + М'М0 < Р + М'М0 < г,
так что «точка» М принадлежит исходной «сфере».
Такое же заключение можно сделать и об открытом симп-
симплексе:
xi > 0, . .., хп > 0, х\ + .. . +хп < h (А > 0).
Подобного рода множество, целиком состоящее из внут-
внутренних «точек», будем называть открытой «областью».
Таким образом, открытый «прямоугольный параллелепипед»,
открытая «сфера», открытый симплекс — служат примерами от-
открытых «областей».
Обобщим теперь понятие точки сгущения [52] на случай мно-
множества ^Ж в /7-мерном «пространстве». «Точка» Мо называется
«точкой сгущения» множества *М, если в каждой ее
окрестности (и снова — безразлично, какого типа) содержится
хоть одна «точка» множества ^Ж, отличная от Мо.
«Точки сгущения» для открытой «области», не принадлежащей
ей, называются пограничными «точками» этой «области». По-
Пограничные «точки» в их совокупности образуют «границу области».
163] § 1. ОСНОВНЫЕ ПОНЯТИЯ 391
Открытая «область» вместе с «границей» ее называется
замкнутой «областью».
Нетрудно видеть, что для открытого «параллелепипеда» D) по-
пограничными будут «точки» М(х\, ..., хп)9 для которых
а\ <*i < Ь\, ..., ап ^хп < Ьп,
причем хоть в одном случае имеет место именно равенство.
Точно так же, для рассмотренной выше открытой «сферы» по-
пограничными будут «точки» М9 для которых в точности ММо = г.
Наконец, для открытого симплекса E) пограничными являются
«точки» М(х\, ..., хп)9 удовлетворяющие соотношениям:
xi ^ 0, ..., хп ^ 0, xi + ... +хп < h,
причем хоть однажды осуществляется равенство.
Таким образом, замкнутый «прямоугольный параллелепипед»,
замкнутая «сфера» и замкнутый симплекс дают примеры замкну-
замкнутых «областей».
Впредь, говоря об «области», открытой или замкнутой, мы все-
всегда будем иметь в виду «область» в указанном здесь специальном
смысле.
Установим теперь, что замкнутой «области» принадлежат
уже все ее «точки» сгущения.
Пусть даны замкнутая «область» & и «точка» Мо _вне ее.
Докажем, что тогда Мо не будет «точкой» сгущения для &.
Замкнутая «область» & получается из некоторой открытой
«области» & путем присоединения к ней ее «границы» S. Оче-
Очевидно, Мо не является «точкой» сгущения для &\ следовательно,
Мо можно окружить такой открытой «сферой», чтобы в ней во-
вовсе не содержалось «точек» из @1. Но тогда в ней не может быть
и «точек» из ё\ ведь, если бы какая-нибудь «точка» М' из $ в нее
попала, то в ней содержалась бы целиком и некоторая окрестность
«точки» М\ и в этой окрестности не было бы ни одной точки из @9
вопреки определению «точки сгущения» и множества $ как «гра-
«границы». Итак, в упомянутой «сфере» нет «точек» из &)9 что и дока-
доказывает наше утверждение.
Вообще «точечное» множество *М9 содержащее все свои «точ-
«точки» сгущения, называют замкнутым. Таким образом, замкнутая
«область» есть частный случай замкнутого множества.
Введем еще ряд терминов. Множество «точек» ^Ж называет-
называется ограниченным, если оно целиком содержится в некотором
«прямоугольном параллелепипеде».
392
ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[164
«Область» называется связной, если любые ее две «точки»
можно соединить «ломаной», лежащей всеми своими «точками»
в «области». На рис. 96 представлено для иллюстрации несколько
связных областей на плос-
плоскости.
Ограниченная и связная
«область» в /7-мерном «про-
«пространстве» (открытая или
замкнутая) есть, в некото-
некотором смысле, аналог конеч-
конечного промежутка (соответ-
(соответственно, открытого или
замкнутого). Читатель ви-
видит, однако, насколько
усложняется картина при
переходе к /7-мерным (при
/7^2) образцам. Простым
и однотипным промежуткам, границей которых служат всего лишь
две точки, здесь противопоставляется огромное многообразие
«областей» со сложными «границами».
Все изложенное в последних пп° можно рассматривать как уста-
установление лишь некоего геометрического языка; с этим
не связано (при п > 3) никаких реальных геометрических
представлений. Однако полезно подчеркнуть, что на деле /7-мерное
арифметическое пространство является лишь первым шагом к тем
в высшей степени плодотворным обобщениям понятия про-
пространства, которые лежат в основе многих более высоких частей
современного анализа.
Рис. 96
*)
164. Функции п переменных. Пусть имеем п перемен-
переменных ii, X2, • • •, хП9 совместные значения которых могут выбирать-
выбираться произвольно из некоторого множества <Ж точек /7-мерного про-
пространства: эти переменные называются независимыми. Опре-
Определение функции и все сказанное по поводу него для случая двух
независимых переменных [160] непосредственно переносится и на
рассматриваемый случай, так что нет надобности на этом останав-
останавливаться.
*) Мы помещали в кавычках все геометрические термины, которые употребля-
употреблялись в смысле, отличном от обычного: «точка», «расстояние», «область», и т. п.
Впредь мы этого делать уже не будем.
164] § 1. ОСНОВНЫЕ ПОНЯТИЯ 393
Если точку (х\,Х2, ... ,хп) обозначить через М, то функ-
функцию и = f(x\,X2, ... ,хп) от этих переменных иногда называют
функцией точки Ми обозначают тем же знаком: и = /(М).21^
Предположим теперь, что в некотором множестве ?Р точек
m-мерного пространства (где т не связано с п) заданы п функций
от т переменных t\, t2, ..., tm\
2,...,tm), . .., xn = q>n(ti,t2,...,tm) E)
или, короче,
xi=q>i(P), ..., xn = q>n(P), Ea)
где Р означает точку (t\9t2, ..., tm) w-мерного пространства. Допу-
Допустим, сверх того, что, когда точкаP(t\, t2, ..., tm) изменяется в пре-
пределах множества ЗР9 соответствующая ей /7-мерная точка М9 с ко-
координатами E) [или Eа)], не выходит за пределы /7-мерного мно-
множества *М9 где определена функция и = f(x\, Х2, • • •, хп) = f(M).
Тогда переменную и можно рассматривать как сложную
функцию от независимых переменных t\, /2, ... ,tm (в множест-
множестве^)— через посредство переменных х\, ... ,хп:
h,t2, . . .,tm), . . ., q>n(h,t2, . . ^tm))\
и является функцией от функций ср\, ..., срп. [Ср. 51.]
' Здесь уместно заметить, что более распространенная сейчас форма опре-
определения функции (приведенная в примеч. 13 на с. ПО) тем и удобна, что при
переходе к функциям п переменных остается без изменений: функцией, задан-
заданной на множестве SC и принимающей значения в (числовом) множестве *?,
называется произвольное правило, сопоставляющее каждой точке х мно-
множества SC одну, и только одну, строго определенную точку множества °^/.
Область SC определения функции может быть промежутком на прямой или облас-
областью ^-мерного пространства — и мы говорим, соответственно, о функции одной
или п вещественных переменных.
' Словосочетание «функция от функций» как синоним выражения «сложная
функция» довольно распространено в бытовой математической речи, однако это
словосочетание все же двусмысленно. Действительно, область определения су-
суперпозиции совпадает с областью определения функций q>\, . . ., фп, т. е. является
некоторым множеством значений переменных t\, . . ., Тт. Выражение же «функ-
«функция от функций», созвучное с выражением «функция от х», наводит на мысль, что
рассматривается функция, заданная на множестве других функций. Такие объекты
действительно рассматриваются и изучаются в функциональном анализе и вари-
вариационном исчислении под названием функционалов. Сказанное объясняет,
394 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [164
Самый процесс определения сложной функции по функциям
Фь ..., срп и функции / называется (как в простейшем случае функ-
функций одной переменной) суперпозицией.
Класс функций нескольких переменных, с которыми непосред-
непосредственно приходится иметь дело на первых порах, очень невелик. По
существу, он строится с помощью суперпозиций на элементарных
функциях одной переменной [48,50] и на следующих функциях
двух переменных:
z — х ±у, z — ху, z — — и z — ху,
У
т. е. на четырех арифметических операциях и на так называемой
степенио-показательной функции.
Арифметические операции, повторно примененные, исходя из
независимых переменных х\9Х2, • • • 9хп и постоянных, приводят,
прежде всего, к многочленам *);
, Х2-> • • • 9 %п) = / J
^v\,V2,...,vnXi %2 ' ' ' хп
V\,V2,...,Vn
(целая рациональная функция) и к частным двух таких мно-
многочленов
У{Х\,Х2, . . . ,Хп) —
(дробная рациональная функция).
Привлечение элементарных функций одной переменной приво-
приводит к таким, например, функциям:
ф(х,у, z, t) = smxy + smyz + sinzt + sintx,
и т. п.
Те замечания, которые были сделаны в 46 по поводу аналитиче-
аналитического задания функций одной переменной, могут быть повторены
и здесь.
в частности, почему термин «функция от функций» в настоящем курсе лишь
упоминается, но практически не используется.
*) Мы знаем, что знак Е означает сумму однотипных слагаемых. Здесь мы
имеем более сложный случай, когда слагаемые зависят от нескольких значков.
165] § 1. ОСНОВНЫЕ ПОНЯТИЯ 395
165. Предел функции нескольких переменных. Предположим,
что функция f(x\, ..., хп) определена в некотором точечном мно-
множестве ^#, допускающем точку сгущения Мо(а\, <Я2> • • • > #и).
Аналогично определению предела функции от одной перемен-
переменной, говорят, что функция f(x\, ..., хп) имеет пределом число А
при стремлении переменных х\, ..., хп, соответствен-
соответственно, к а\, ..., ап, если для каждого числа г > О найдется такое
число S > О, что
|/0ь ...,хп)-А\<?,
лишь только
\х\ - а\\ < S, . . ., \хп - ап\ < S.
При этом точка (х\, ..., хп) предполагается взятой из <Ж и от-
отличной от (<2i,..., ап). Итак, неравенство для функции должно
выполняться во всех точках множества ^#, лежащих в достаточно
малой окрестности
(а\ -8,а\+8;...;ап- S,an + 8)
точки Мо, но исключая саму эту точку (если она принадлежит *Ж).
Обозначают предел функции так:
А = lim /(хь ...,хп). F)
В геометрических терминах, вводя для точек (х\, ... ,хп)
и (а\, ..., ап) обозначения М и Мо, можно было бы перефразиро-
перефразировать приведенное определение так: число А называется пределом
функции f(M) при стремлении точки М к Мо (или —
в точке Мо), если для каждого числа е > 0 существует
такое число г > 0, что
\/(М)-А\<г,
лишь только расстояние М§М < г.
Как и выше, точка М предполагается взятой из ^#, но отлич-
отличной от Мо. Таким образом, неравенство для функции должно вы-
выполняться во всех точках множества ^#, лежащих в достаточно
малой сферической окрестности точки Мо, за исключением
самой этой точки.
396 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [165
Обозначение предела функции также можно приспособить
к этому определению:
А = Jim ДМ). F*)
Из замечания п° 161 об окрестностях разных типов непосред-
непосредственно ясна тождественность обоих приведенных определений.
Аналогично устанавливается понятие о бесконечном пределе
функции. В случае А = +оо или —оо, неравенство
|/0ь ...,хп)-А\<е
лишь заменяется, соответственно, неравенством вида
/Оь ...,*„)> Е
или
/Оь ...,хп)< -Е,
где Е есть произвольное наперед взятое положительное число.
Упомянем в заключение о случае, когда некоторые из неза-
независимых переменных х\, ... ,хп стремятся к бесконечным
пределам.
Можно было бы распространить понятие точки сгущения
Мо(а\, ..., ап) области *М и на тот случай, когда все координаты
этой точки (или некоторые из них) бесконечны. *)
Например, точка (+оо, ..., +оо) является для <Ж точкой
сгущения, если в этой области найдутся точки со сколь угод-
угодно большими (положительными) координатами.
В этом предположении, говорят, что функция /Оь ..., хп)
имеет пределом число А при стремлении всех переменных
х\,Х2, • • • ,хп к +оо, если для каждого числа е > 0 сущест-
существует такое число А > 0, что
|/(хьх2, . . . ,х„) -А\ < с,
лишь только
xi > А, х2 > А, ..., хп > А.
В обозначениях:
А= lim /(xi, • • .,хп).
*) В этом случае точка Mq называется несобственной.
166] § 1. ОСНОВНЫЕ ПОНЯТИЯ 397
В частности, возвращаясь к переменной хт,П9 о которой была
речь в конце п° 160, говорят, что эта переменная при безгра-
безграничном возрастании обоих номеров тип имеет пределом А,
если для каждого е > 0 найдется такой номер N, что
\хт,п — А\ < е при т > N, п> N.
Записывают это так:
А = lim хтп или просто А =
„.
Легко понять, как трактуется случай, когда А = +оо или — оо.
166. Сведение к случаю варианты. Рассмотрим в /7-мерном
пространстве последовательность точек
Мы будем говорить, что эта последовательность сходится к пре-
предельной точке Мо(а\, ..., ап)9 если, при к —»> +оо, расстояние
М0Мк -+ 0. G)
Вместо этого можно было бы потребовать, чтобы координаты
точки Мк порознь стремились к соответствующим координатам
точки Mq9 т. е. чтобы было
х?^аи ..., хР^а„. (8)
Равносильность обоих определений, собственно, вытекает из
доказанного в 161 утверждения об окрестностях двух типов. Дей-
Действительно, условие G) означает, что, каково бы ни было число
г > 0, точка Мк при достаточно большом к удовлетворяет нера-
неравенству
ЩЩ < г,
т. е. попадает в (открытую) сферу радиуса г с центром в точке Мо;
требование же (8) имеет тот смысл, что, каково бы ни было число
S > 0, названная точка — снова при достаточно большом к —
удовлетворяет неравенствам
1*1 —а\\<8, ..., \хкп — ап\<8,
т. е. содержится в (открытом) параллелепипеде
(ai-8,a\+8; ...; ап - 8, ап + 8)
с центром в той же точке.
398 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [166
Пусть теперь точка Мо(а\, ..., ап) является точкой сгу-
сгущения некоторого множества ^Ж в /7-мерном пространстве. Тогда
из <Ж всегда можно извлечь такую последовательность отличных
отМо точек: {М^}, которая сходилась бы к Мо как к предельной
точке.
Для доказательства зададимся положительной вариантой г к -л 0.
По определению точки сгущения [162], в каждой сферической
окрестности точки Мо, радиуса г^, найдется (отличная от Мо) точка
Мк множества <Ж. Последовательность {М^}, очевидно, и будет
искомой.
Теперь можно сформулировать такое условие, необходимое
и достаточное для существования предельного равенства F)
[или F*)]: если извлечь из <Ж последовательность {М^} от-
отличных от Мо точек, сходящуюся к Мо, то числовая по-
последовательность {/(Mk)}, состоящая из соответствующих
значений функции, всегда сходится к А.
Необходимость. Пусть имеет место F*), и по заданному
е > 0 найдено соответствующее ему г > 0, в согласии с опре-
определением предыдущего п°. Если последовательность точек
сходится к Мо, то — для достаточно больших к — будет
< Г,
а это влечет за собой неравенство
\f(Mk)-A\<e,
которое и показывает, что /(М^) —>> А.
Достаточность. Предположим теперь, что выполняется вы-
высказанное выше условие. Для того чтобы доказать наличие равен-
равенства F*) в соответствии с определением предыдущего п°, допу-
допустим противное тому, что содержится в этом определении. Тогда
для некоторого числа е > 0 уже не существует соответству-
соответствующего г, т. е., какое бы число г > 0 ни взять, всегда в ^# найдется
такая (отличная от Мо) точка М;, что одновременно
М0М'<г, но
Взяв положительную варианту г^ -л 0, станем за г поочеред-
поочередно брать числа г^\ для каждого г^ найдется, по сказанному, своя
(отличная от Мо) точка Myt, для которой
М0Мк<гь но
167] § 1. ОСНОВНЫЕ ПОНЯТИЯ 399
Построенная таким образом последовательность точек
сходится к Мо, и в то же время числовая последовательность
{/(Мк)} не может иметь пределом А, вопреки условию. Это про-
противоречие и доказывает наше утверждение.
Читателю ясно, что высказанное условие дает другую фор-
форму (на «языке последовательностей») определения предела функ-
функции.
Таким образом, и для функции нескольких переменных удается
вопрос о пределе функции свести к вопросу о пределе варианты
[ср. 53]. Этот результат легко распространить и на случай, когда
числа А, а\, ..., ат или некоторые из них, бесконечны.
Указанное обстоятельство позволяет распространить на новый
тип предела все основные понятия и предположения развитой в гла-
главе I теории пределов — наподобие того, как это было сделано в 55
для предела функции от одной независимой переменной.
167. Примеры.
1) Пользуясь теоремой о пределе произведения, прежде всего,
легко показать, что
lim Cx\l ...xvnn =Cav'..avn\
где С, а\, ..., an — любые вещественные, a v\, ..., vn — неотрица-
неотрицательные целые числа. Отсюда, если через Р(х\, ..., хп) обозначить
целую рациональную функцию [163]:
Р(х\, .. ., хп) = 2_^ CVu^^Vnxl ...xnn,
v\,...,vn
по теореме о сумме, получается также
lim P(xi, ...,xn) =P(au ...,ап).
Аналогично для дробной рациональной функции [163]
i^\x\, . . . ,xn) —
по теореме о пределе частного,
lim Q(x\, ...,xn) = Q{a\, . .., an),
i-tai
конечно, лишь при условии, что знаменатель в точке (а\, ..., ап)
в 0 не обращается.
400 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [167
2) Рассмотрим степенно-показательную функцию ху при х > 0
и произвольном у. Тогда, если а > 0 и Ъ — любое вещественное
число, будем иметь
limx^ =ab.
Действительно, если взять любые варианты хп —> а и уп —>> Ъ9
то [ср. 78]
хУп =еУпЛпхп _+еЬ.Ыа =аЬ^
а это — на «языке последовательностей» — и устанавливает тре-
требуемый результат.
3) Пусть о вариантах хп и уп известно, что они имеют пределы,
соответственно, а и Ъ9 и ставится вопрос о пределе составленного
из них выражения
хп±ут хп-уп, — или хупп.
Уп
Для случая так называемых неопределенных выражений, условно
характеризуемых символами:
оо-оо, 0-оо, % -, 1°°, 0°, оо°,
0 оо
как мы знаем [31,78], предел может вовсе не существовать, а если
существует, то может — при тех же а и Ъ — иметь различные зна-
значения, в зависимости от частного закона изменения вариант хп и уп.
Если вспомнить определение предела функции двух незави-
независимых переменных на «языке последовательностей», то станет яс-
ясно, что упомянутые типы «неопределенностей» связаны с фактом
несуществования следующих пределов:
X X
lim (x -у), lim (x -v), lim -, lim -,
^+оо х^О х^Оу х^±оо у
О ±
lim xy, lim xy, lim xy.
x—tl х^-0 +
4) Поставим вопрос о пределе:
ху
lim
+у2
[Функция здесь определена на всей плоскости за исключением именно точки
*=0,;у =0.]
168]
§ 1. ОСНОВНЫЕ ПОНЯТИЯ
401
Если взять две частичные последовательности точек
¦
очевидно, сходящиеся к точке @, 0), то окажется, что при всех к
Отсюда уже следует, что упомянутого предела не существует.
Предлагается аналогично убедиться в том, что не существует предела
2 2
v х -у
lim —z т.
5) Наоборот, существует предел
lim . У . = 0.
2 2
Это сразу вытекает из неравенства
Точно так же доказывается, что и
lim
= О-
168. Повторные пределы. Кроме рассмотренного выше пре-
предела функции f(x 1, Х2, ..., хп) при одновременном стрем-
стремлении всех аргументов к их пределам, приходится иметь дело
и с пределами другого рода, получаемыми в результате ряда
последовательных предельных переходов по каждому аргу-
аргументу в отдельности, в том или ином порядке. Первый предел на-
называется п-к ратным (или двойным, тройным, и т. д. —
при п = 2, 3, ...), а последний — повторным.
Ограничимся для простоты случаем функции двух переменных
f(x,y). Допустим к тому же, что область <Ж изменения перемен-
переменных х,у такова, что х (независимо от^) может принимать
любое значение в некотором множестве 5Г, для которого а слу-
служит точкой сгущения, но ему не принадлежит, и, аналогично, у
(независимо отх) изменяется в множестве ^ сне принадле-
принадлежащей ему точкой сгущения Ъ. Такую область ^Ж можно было бы
символически обозначить как SC х^/. Например,
(а,а+Н; Ь, Ъ + К) = (а, а + Я) х (b,b+K).
402 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [168
Если при любом фиксированном у из *? существует для
функции f(x,y) (которая оказывается функцией лишь от х) пре-
предел при х —>> а, то этот предел, вообще говоря, будет зависеть от
наперед фиксированного у:
Затем можно поставить вопрос о пределе функции д>{у) при у —>> Ъ
lim q>{y) = lim lim f(x,y)
— это и будет один из двух повторных пределов. Другой получится,
если предельные переходы произвести в обратном порядке:
lim lim f(x,y).
Не следует думать, что повторные пределы эти необходимо равны. Если,
например, в области *Ж @, +оо; 0, +оо) положить
х -У+*2+У2
1) А*,У) =
;
х +У
и взять а = Ь = 0, то получим:
ср(у) = \imf(x9y) =y -I, Hm ф(у) = lim \imf(x,y) = -1,
x-s>0 j^^O j^^Ox^O
в то время как
ф(х) = \imf(x,y) =x + l, \imj(x) = lim M
Может случиться также, что один из повторных пределов существует, а дру-
другой — нет. Так будет, например, для функций:
х sin - + у
2)f(x,y) = х—^ или
х+у
3) f(x,y) = х • sin —;
У
в обоих случаях здесь существует повторный предел lim lim /, но нет повторного
.y-s>0x-s>0
предела lim lim / (а в последнем примере — нет даже простого предела lim /).
s0s0 s0
Эти простые примеры показывают, насколько осторожным нуж-
нужно быть при перестановке двух предельных перехо-
переходов по разным переменным: не раз ошибочные умоза-
умозаключения проистекали именно от такой незаконной перестановки.
В то же время многие важные вопросы анализа связаны именно
с перестановкой предельных переходов, но, разумеется, всякий раз
дозволительность перестановки должна быть особо обоснована.
168] § 1. ОСНОВНЫЕ ПОНЯТИЯ 403
Один из путей к такому обоснованию открывает следующая те-
теорема, которая в то же время устанавливает связь между двойными
и повторными пределами:
Теорема. Если 1) существует {конечный или нет) двой-
двойной предел
и 2) при любом у из <? существует {конечный) простой
предел по х
Я>{у) =\xmaf(x,y),
то существует повторный предел
lim ср{у) = lim lim f(x,y)
y^Ъ у^Ьх^а
и равен двойному.
Докажем это для случая конечных А9 а и Ъ. Согласно опреде-
определению п° 163, по заданному е > 0 найдется такое 8 > 0, что
\f(x,y)-A\<e, (9)
лишь только \х — а\ < S и \у — Ъ\ < 8 [причем х берется из «2Г,
а у из (?\. Фиксируем теперь у так, чтобы выполнялось неравенство
\у - Ъ\ < 8, и перейдем в (9) к пределу, устремив х к а. Так как,
ввиду 2), f(x,y) при этом стремится к пределу q>(y)9 то получим
Вспоминая, что у здесь есть любое число из *У9 подчиненное
лишь условию \у — Ь\ < 89 приходим к заключению, что
А = lim q>(y) = Hm lim f{x,y),
У^Ъ y^bx^a
что и требовалось доказать.
Если, наряду с условиями 1) и 2), при любом х из SC существует
(конечный) простой предел по у
гр{х) = Umf(x,y)9
у^-Ъ
то, как следует из уже доказанного, если х и у обменять ролями,
существует также и второй повторный предел
lim гр{х) = lim lim f(x,y)
х—)># х^ау^-Ъ
и равен тому же числу А: в этом случае оба повторных
предела равны.
404 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [169
Из доказанной теоремы сразу ясно, что в примерах 1) и 2)
двойной предел не существует (почему?). В этом легко убедиться
и непосредственно.
В примере 3), наоборот, двойной предел существует: из нера-
неравенства
. 1
• sin —
у
усматриваем, что он равен 0. Этот пример показывает, что усло-
условие 1) теоремы не влечет за собой условия 2).
Не следует думать, однако, что существование двойного преде-
предела необходимо для равенства повторных: в примере 4) пре-
предыдущего п° оба повторных предела существуют и равны 0, хотя
двойного предела нет.
§ 2. Непрерывные функции
169. Непрерывность и разрывы функций нескольких перемен-
переменных. Пусть функция f(x\, ..., хп) определена в некотором мно-
множестве <Ж точек /7-мерного пространства, и Мг(х[, ..., х'п) есть
точка сгущения этого множества, принадлежащая самому
множеству.
Говорят, что функция f(x\, .. .,хп) непрерывна в точке
Vj, ..., х'п), если имеет место равенство
lim/ f(xl9...9xn)=f(x'l9...9x'n); A)
в противном Dice случае — функция терпит разрыв в точ-
точке Мг.
На «языке г-8» непрерывность функции в точке М' выразится
так [165]: по любому заданному г > 0 должно найтись такое
8 > 0, что
\f(Xl,...,xn)-f(x[,...,x'n)\<e, B)
лишь только
|*i-*i|<5, ..., \хп-х'п\<8; C)
или иначе: по е > 0 должно найтись такое г > 0, что
\f(M)-f(M')\<?,
лишь только расстояние
ММ' < г.
169] § 2. НЕПРЕРЫВНЫЕ ФУНКЦИИ 405
При этом точка М(х\, ..., хп) предполагается принадлежащей
множеству *Ж9 в частности же, может совпасть и с точкой М'.
Именно ввиду того, что предел функции в точке М' равен значению
функции в этой точке, обычное требование, чтобы М была отлична
от М\ здесь становится ненужным.
Рассматривая разностих\ — х[, ... ,хп—х'п как приращения
Ах[, ..., Ах'п независимых переменных, а разность
— как приращение функции, можно сказать (как в случае
функций одной переменной), что функция непрерывна, если
бесконечно малым приращениям независимых переменных от-
отвечает бесконечно малое же приращение функции.
Определенная выше непрерывность функции в точке М1 есть,
так сказать, непрерывность по всей совокупности пере-
переменных х\, ..., хп. Если она имеет место, то одновременно и
lim f(xl9x'29 ...,x'n) =f(x/l,x/2,...,x/n),
lim f(x1,x2,x'3, .. .,x'n) = f(x[,x'2,x'3, .. .,x'n),
xx^xx
x2^xf2
и т. п., ибо здесь мы осуществляем лишь частные законы при-
приближения М к М'. Иными словами, функция оказывается непрерыв-
непрерывной в отдельности по каждой переменной Xj9 по каждой
паре переменных Xj,Xj9 и т. д.
С примерами непрерывных функций мы уже сталкивались. Так,
в 166, 1) была установлена непрерывность целой и дробной
рациональной функций от п аргументов во всех точках /7-мер-
/7-мерного пространства (для дробной функции — за исключением тех
точек, которые обращают ее знаменатель в 0). Там же, в 2), бы-
была доказана непрерывность степенно-показательной функ-
функции ху для всех точек правой полуплоскости (х > 0).
Если вновь рассмотреть функцию
определенную этой формулой во всей плоскости, кроме начальной точки, и по-
положить дополнительно: /@, 0) = 0, то получим пример разрыва. Он имеет
место именно в начальной точке, так как [167, 4)] при х —>> 0, у —>> 0 для функции
предела не существует.
406 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [170
Здесь мы сталкиваемся с таким интересным обстоятельством. Рассмотренная
функция f(x,y), хотя и не является непрерывной в точке @, 0) по обеим пере-
переменным зараз, тем не менее будет непрерывна в этой точке как по х, так
и по _у в отдельности; это следует из того, что f(x, 0) = f@,y) = 0.
Впрочем, сказанное перестает быть удивительным, если сообразить, что, говоря
о непрерывности по х и по у в отдельности, мы учитываем лишь приближение
к точке @, 0) вдоль по оси х или по оси у, оставляя в стороне бесчисленное
множество других законов приближения.
Если для функции /(М) при стремлении МкМ' вовсе не существует
определенного конечного предела
lim f(M),
мм' к J
то говорят, что в точке Mf функция имеет разрыв, даже в том случае, когда в самой
точке М1 функция не определена [ср. замечание в 66].
Точки разрыва функции могут быть не только изолированными, как в преды-
предыдущем примере, но и заполнять собою линии, поверхности и т. п. Так, функции
двух переменных
х2-у2' х2+у2-\
имеют разрывы: первая — вдоль прямых;; = due, а вторая — вдоль окружности
х + у =1. Для функций трех переменных
x+y+z 1
ху — z х2 -\- у2 — z2
разрывы заполняют в первом случае гиперболический параболоид z = ху, а во
втором — конус z = х + у .
170. Операции над непрерывными функциями. Легко сфор-
сформулировать и доказать теорему о непрерывности суммы, разности,
произведения, частного двух непрерывных функций [ср. 67]; предо-
предоставляем это читателю.
Мы остановимся лишь на теореме о суперпозиции не-
непрерывных функций. Как и в п° 164, мы предположим, что кроме
функции и = f(x\, ... ,хп)9 заданной в множестве <Ж /7-мерных
точек М(х\, ..., хп)9 нам даны еще п функций
х\ = q>i(h, . . .,tm), ..., xn = q>n(ti,...,tm) D)
в некотором множестве ЗР m-мерных точек P(t\, ..., tm)9 причем
точка М с координатами D) не выходит за пределы упомянутого
множества *М.
Теорема. Если функции q>j(P) (/' = 1,...,и) все не-
непрерывны в точке P'(t[, ..., t'm) из ЗР, а функция f(M)
непрерывна в соответствующей точке М1 {х[, ..., х'п)
171] § 2. НЕПРЕРЫВНЫЕ ФУНКЦИИ
с координатами
407
то и сложная функция
и = f(q>i(h, . . ., tm), . . ., q>n(ti, . . ., fw)) =
будет непрерывна в точке Р1.
Действительно, сначала по е > 0 определится число 5 > 0,
такое, что из C) следует B) (ввиду непрерывности функции /).
Затем по числу 8 (ввиду непрерывности функций q>\, ..., q>n) най-
найдется число ц > 0 такое, что неравенства
\ti-t[\<ri, ..., \tm-tfm\<t] E)
влекут за собой неравенства
-x[\ =
\хп-х'п\ = \q>n(tu...9tm) -<pn(t'l9...,t'm)\ <
Но тогда, при наличии E), будет также
|/(хь ...,xn)-f(x\,...,x'n)\ =
— \f{<P\{t\, ..., tm), ..., (pn(t\, ..., tm)) -
[, .. .,Q, .. .,cpn{t[, .. .,
S.
что и доказывает наше утверждение.
171. Функции, непрерывные в области. Теоремы Больцано-
Коши. Мы будем говорить, что функция f(x\, ..., хп) непрерыв-
непрерывна в некотором множестве <Ж точек п-мерного пространст-
пространства, если она непрерывна в каждой точке этого множества,
которая является для него точкой сгущения. Впредь, как пра-
правило, мы ограничимся случаем, когда множество <Ж представляет
собой открытую или замкнутую область [163], наподобие того,
как непрерывные функции одной переменной мы рассматривали
в промежутке.
Обращаемся теперь к изучению свойств функции нескольких
переменных, непрерывной в некоторой области /7-мерного про-
пространства. Они вполне аналогичны свойствам функции одной пе-
переменной, непрерывной в промежутке (гл. II, § 5).
При изложении мы лишь для краткости ограничимся случаем
двух независимых переменных. Перенесение на общий случай
408 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [171
производится непосредственно и не представляет труда. Впрочем,
некоторые замечания по этому поводу будут сделаны попутно.
Сформулируем теперь теорему, аналогичную 1-й теореме
Больцано-Коши для функции одной переменной [80].
Теорема. Пусть функция f(x,y) определена и непрерыв-
непрерывна в некоторой связной области &. Если в двух точках
МК^сь^о) и М\(х\,у\) этой области функция принимает зна-
значения разных знаков:
o) < 0, /Оь>ч) > 0,
У\
О
то в этой области найдется и точка M'ix'^y1), в которой
функция обращается в нуль: f{x'', j/) = 0.
Доказательство мы построим на сведении к случаю функ-
функции одной независимой переменной.
Ввиду связности области ^, точки Мо и М\ можно соединить
ломаной, всеми точками лежа-
лежащей в & (рис. 97). Если последова-
последовательно перебирать вершины лома-
ломаной, то либо окажется, что в какой-
либо из них функция обращается
в 0 — и тогда теорема доказана, ли-
либо этого не будет. В последнем слу-
, х чае найдется такая сторона ло-
ломаной, на концах которой функция
Рмг Q7
принимает значения разных знаков.
Изменив обозначения точек, будем
считать, что Мо и М\ как раз и являются концами этой стороны.
Ее уравнения имеют вид [161]:
х =х0 +t(x\ -х0), У =.Уо +t(yi -yo) @ < t < 1).
Если точка М(х,у) передвигается именно вдоль этой стороны, то
наша первоначальная функция f(x,y) превращается в сложную
функцию одной переменной t\
F{t) = /(*o + t(xx -хо), уо + Пух -yo)) (Q^t^ 1),
очевидно, непрерывную (по теореме предшествующего п°), ввиду
непрерывности как функции f(x,y)9 так и линейных функций от t,
подставленных вместо ее аргументов. Но для F(t) имеем:
F(O)=f(xo,yo) < 0, F(l) = f(xuyi) > 0.
172] § 2. НЕПРЕРЫВНЫЕ ФУНКЦИИ 409
Применяя к функции F(t) одной переменной уже доказанную
в п° 80 теорему, заключаем, что F(t') = 0 при некотором значе-
значении t' между 0 и 1. Вспоминая определение функции F(t)9 имеем
таким образом
f(xo+tf(xi -хо), yo + tf(yi-yo)) =0.
Точка Af (*',/), где х' = х0 + t'(x\ -х0), у' =Уо + t'{y\ -у0)
и является искомой.
Отсюда вытекает, как и в 82, 2-я теорема Больцано-Коши,
которая, впрочем, могла бы быть получена и сразу.
Читатель видит, что переход к пространству п измерений (при
п > 2) не создает никаких затруднений, ибо в /7-мерной связной
области точки также могут быть соединены «ломаной» и вопрос
сведется к рассмотрению ее стороны, вдоль которой функция будет
зависеть от одного параметра, и т. д.
172. Лемма Больцано - Вейерштрасса. Для дальнейшего изло-
изложения нам понадобится обобщение леммы Больцано-Вейер-
ш т р а с с а [41] на случай последовательности точек в пространстве
любого числа измерений; как всегда, мы ограничимся «плоским»
случаем.
Лемма. Из любой ограниченной последовательности
точек
. .., Мп(хп,уп), ...
всегда можно извлечь такую частичную последовательность
МП1(хП1,уП1), МП2(хП2,уП2), ..., Mnk(xnk,ynk), ...
которая сходилась бы к предельной точке.
1-е доказательство мы проведем, перенеся на рассматри-
рассматриваемый случай рассуждение, которым мы пользовались в «линей-
«линейном» случае [41].
Ввиду ограниченности данной последовательности точек,
найдется такой (конечный) прямоугольник [a,b;c,d\9 в котором
она целиком содержится. Разделим как промежуток [а, Ъ] значе-
значений х, так и промежуток [с, d] значений у пополам:
li±?\, \i±lj
410
ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[172
Комбинируя каждую из половин первого промежутка с каждой
из половин второго, мы получим четыре прямоугольника:
(I)
(III)
a + b
a + b
d
с +.
(П)
(IV)
a + b с
„ ,b; c, —
а +Ъ
разлагается основной
2 ' ' 2
прямоугольник
[a,b;c,d]
на которые
(рис. 98).
Хоть в одной из этих частей будет содержаться бесконечное
множество точек данной последовательности, ибо, в против-
противном случае, и во всем прямоугольнике их содержалось бы лишь
конечное число, что невозможно. Пусть [а\, b\;c\, d\] будет тот
из прямоугольников (I), (II), (III), (IV), в котором содержится
бесконечное множество точек нашей последовательности
(или один из таких
прямоугольников, если
их несколько).
Полученный прямо-
прямоугольник снова разло-
разложим на четыре мень-
меньших прямоугольника
и возьмем тот из них,
в котором содержится
бесконечное мно-
множество точек дан-
данной последовательно-
c+d
О
III
I
IV
II
а+Ь
2
Рис. 98
сти; обозначим его че-
через [а2,Ь2;с2,с12\.
Этот процесс последовательного дробления прямоугольников
мы представляем себе продолжающимся до бесконечности. На к-й
стадии его мы выберем прямоугольник [яь Ъь\ сk, dk] под условием,
что в нем содержится бесконечное множество точек Мп.
Измерения этого прямоугольника
Ьк-ак =
b-a
d-c
стремятся к 0 при к —> +оо.
Применим теперь в отдельности к последовательности проме-
промежутков {[ак, Ьк]} значений х и к последовательности промежутков
172] § 2. НЕПРЕРЫВНЫЕ ФУНКЦИИ 411
{[с к, dk]} значений у лемму о вложенных промежутках [38]. Из нее
следует, что концы промежутков а^ и bk, а также с к и dk стремятся,
соответственно, к общим пределам:
lim а к = lim Ък — х и lim с к = lim dk = у. F)
Можно сказать, что последовательность прямоугольников {[ак, Ък\
с к, dk}} «стягивается» в точку M(Y,y).
Теперь, взяв в качестве Мщ любую точку нашей последователь-
последовательности, попадающую в прямоугольник [а\, b\;c\, d\], мы станем за-
затем поочередно выделять точки МП2, Мщ, ..., выбирая — в общем
случае — в качестве Мщ(хщ,ущ) любую точку последовательно-
последовательности, следующую за ранее выбранными и содержащуюся
в к-м прямоугольнике [ак, Ък\ с к, dk]. Это сделать можно именно по-
потому, что каждый из прямоугольников содержит бесконечное
множество точек Мп.
Так как
а к < *пк ^Ьк и ск < уПк < d^
то, ввиду F),
lim хщ = х, lim ущ = у,
так что выделенная частичная последовательность {Мщ} сходится
к точке М(х,у) как к предельной [166].
II-е доказательство. Проще, однако, поступить иначе, ис-
использовав теорему, уже доказанную в 41 для случая линейной по-
последовательности. Если точки нашей последовательности содер-
содержатся в конечном прямоугольнике [a, b;c,d\9 то
а ^хп^Ь, с ^yn^d (для п = 1, 2, 3, . ..).
Применив теорему п° 41 сначала к последовательности {хп},
выделим частичную последовательность {хщ}, сходящуюся к неко-
некоторому пределу х. Таким образом, для частичной последователь-
последовательности точек
первые координаты уже имеют предел. Вторично применим упо-
упомянутую теорему к последовательности вторых координат {ущ}
и выделим такую частичную последовательность {ущ }, которая
412 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [173
тоже стремится к некоторому пределу у. Тогда, очевидно, частич-
частичная последовательность точек
\xnkl» Ущх )» \хпк2» Ущ2 )»•••» \хпкт »JVw^ )» • • •
будет стремиться к предельной точке (х, j7).
Заметим и здесь, что оба рассуждения легко переносятся на слу-
случай пространства п > 2 измерений. В первом из них, например,
изменяется только число частей, на которые распадается заданная
прямоугольная область, если разделить пополам каждый из опре-
определяющих ее промежутков; в общем случае этих промежутков бу-
будет /7, а частей — всего 2п.
173. Теоремы Вейерштрасса. С помощью доказанной теоремы
прежде всего может быть установлена для функций двух перемен-
переменных 1-я теорема Вейерштрасса:
Теорема. Если функция f(x,y) определена и непрерывна
в ограниченной замкнутой области @*\ то функция
ограничена, т. е. все ее значения содержатся между двумя
конечными границами:
т <:f(x,y) < М.
Доказательство (от противного) вполне аналогично рас-
рассуждению п° 84. Пусть функция f(x,y) при изменении (х,у) в @1
оказывается неограниченной. Тогда для любого п найдется
в & такая точка Мп(хп,уп)9 что
\f{xn9yn)\>n. G)
По теореме п° 172, из ограниченной последовательности {Мп}
можно извлечь частичную последовательность {Мщ}, сходящуюся
к предельной точке М(х, у).
Отметим, что эта точка М необходимо принадлежит области &.
Действительно, в противном случае точки Мщ все были бы от нее
отличны, и точка М была бы точкой сгущения области ^,
ей не принадлежащей, что невозможно ввиду замкнутости облас-
области ^ [см. 163]. _
Вследствие непрерывности функции в точке М должно быть
/(Мщ) = /(хщ,ущ) -> ДМ) = f(x9y)9
а это находится в противоречии с G).
*)
Которая, на этот раз, может быть и несвязной.
174] § 2. НЕПРЕРЫВНЫЕ ФУНКЦИИ 413
2-я теорема Вейерштрасса формулируется и доказывается
(с ссылкой на предыдущую теорему) совершенно так же, как и в 85.
Заметим, что без существенных изменений в рассуждениях —
обе теоремы Вейерштрасса переносятся и на случай, когда
функция непрерывна в любом ограниченном замк-
замкнутом множестве <Ж (хотя бы и не представляющем собой
области).
Как и в случае функции одной переменной, для функции f(x9у)9
определенной и ограниченной в множестве *Ж9 разность меж-
между точными верхней и нижней границами значений функции в *Ж
называется ее колебанием в этом множестве. Если *Ж ограни-
ограничено и замкнуто (в частности, если *М есть ограниченная замкну-
замкнутая область), и функция / в нем непрерывна, то колебание есть
попросту разность между наибольшим и наименьшим ее значения-
значениями.
174. Равномерная непрерывность. Мы знаем, что непрерыв-
непрерывность функции f(x,y) в определенной точке (хо,^о) мно-
множества *Ж9 где функция задана, на «языке е-8» выражается так:
по любому е > О должно найтись такое 8 > О, что неравенство
\f(x>y) ~
выполняется для всякой точки (х,у) из ^#, лишь только
\х -хо\ < 8, \у -уо\ < 8.
Пусть теперь функция f(x,y) непрерывна во всем мно-
множестве <Ж\ тогда возникает вопрос, можно ли по данному е > О
найти такое 8 > О, которое годилось бы — в указанном смыс-
смысле — для всех точек (хо,уо) из <Ж одновременно. Если
это возможно (при любом е)9 то говорят, что функция в ^Ж
равномерно непрерывна.
Теорема Кантора. Если функция f(x,y) непрерывна в ог-
ограниченной замкнутой области <2), то она будет и рав-
равномерно непрерывна в <2).
Доказательство поведем от противного. Допустим, что для
некоторого числа е > 0 не существует числа 8 > 0, которое
годилось бы одновременно для всех точек (хо,.уо) области &.
Возьмем последовательность стремящихся к 0 положительных
чисел
8\ > 82 > ... > 8п > ... > 0, 8п —»> 0.
414 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [174
Так как ни одно из чисел 8п не может годиться — в указанном
смысле — одновременно для всех точек (хо, у о) области 319 то для
каждого 8п найдется в 3) такая конкретная точка {хп,уп)9 для кото-
которой 8п не годится. Это значит, что существует в 3) точка (х'п,у'п)9
для которой
\х'п -хп\ < 8п, \у'п -уп\ < 8п,
и тем не менее
Из ограниченной последовательности точек {(хп,уп)}9 по тео-
теореме Больцано-Вейерштрасса, извлечем такую частичную
последовательность {(хПк,уПк)}9 что хПк —^ х9 уПк —^ у, причем пре-
предельная точка (х,у) необходимо принадлежит области 31 (ввиду
ее замкнутости).
Так как, далее,
\ХЩ ХЩ Щ> \У Щ Ущ пк
и, при возрастании к9 щ -л +оэ и 8Пк —»> 0, то
так что и
Ввиду непрерывности функции f(x,y) в точке (х,у)9 принад-
принадлежащей области &9 мы должны иметь как
так и
откуда
Л^.^-Л^.^) ^°'
что оказывается в противоречии с неравенством (8). Теорема до-
доказана.
Для формулировки вытекающего отсюда следствия нам понадо-
понадобится понятие диаметра точечного множества: так называется
точная верхняя граница расстояний между любыми двумя точками
множества.
Следствие. Если функция f(x,y) непрерывна в ограничен-
ограниченной замкнутой области &, то по данному г > 0 найдется
175] § 2. НЕПРЕРЫВНЫЕ ФУНКЦИИ 415
такое 8 > О, что, на какие бы частичные замкнутые же об-
области &\, ..., &п с диаметрами, меньшими 8, ни разбить эту
область,^ колебание функции в каждой части в отдельности
будет меньше е.
Достаточно за 8 взять то число, о котором говорится в опреде-
определении равномерной непрерывности. Если диаметр частичной об-
области Slj меньше 8, то расстояние любых двух ее точек (х,у)
и (хо,уо) меньше 8: J{x - хоJ + (у -уоJ < 8. Отсюда и по-
подавно \х —хо\ < 8 и \у —уо\ < 8, так что \f(x,y) — f(xo,yo)\ < ?-
Если эти точки выбрать так, чтобы f(x,y) и f(xo,yo) были соот-
соответственно, наибольшим и наименьшим из значений функции в об-
области @19 то и получим требуемое утверждение.
Легко видеть, что доказанная теорема без изменений переносит-
переносится (подобно теоремам Вейерштрасса) на случай функции,
непрерывной в любом ограниченном замкнутом
множестве *М.
175. Лемма Бореля. Полезное предложение, доказанное в 88,
может быть обобщено на многомерный случай.
Пусть имеем систему S открытых областей о на плос-
плоскости; если каждая точка множества <Ж содержится хоть в од-
одной из этих областей о", то будем говорить, что система S
покрывает множество ^Ж.
Лемма Бореля. Если ограниченное замкнутое множество
<Ж точек плоскости покрывается бесконечной системой
S = {а} открытых областей, то из нее всегда молено выде-
выделить конечную подсистему
которая также покрывает все множество ^Ж.
Доказательство (от противного). Допустим, что множест-
множество <Ж не может быть покрыто конечным числом областей о
из S.
Ввиду ограниченности множества ^#, оно содержится в неко-
некотором прямоугольнике [a, b;c, d]. Разделив каждый из двух проме-
промежутков [а, Ь] и [с, d] пополам, мы разложим этот прямоугольник,
как и при доказательстве леммы Больцано-Вейерштрас-
са [172], на четыре прямоугольника. Вместе с тем и множество ^#
*) Эти частичные области могут иметь общими лишь пограничные точки.
416 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [175
разложится на части, содержащиеся соответственно в этих частич-
частичных прямоугольниках; частей, впрочем, может оказаться и меньше
четырех, если какой-либо прямоугольник не содержит вовсе точек
множества *М. Хоть одна из этих частей (скажем, ^#i), в свою
очередь, не может быть покрыта конечным числом областей о
(ибо в противном случае все множество ^#, вопреки предположе-
предположению, было бы покрыто конечным числом областей о). Тот из
частичных прямоугольников, который содержит именно часть *M\
множества *М, обозначим через [а\, b\;c\,d\].
Этот прямоугольник снова разложим на четыре прямоугольни-
прямоугольника. Хотя бы один из них — обозначим его через [#2, ^2?<?2> d?\ —
содержит часть ^#2 множества ^#, которая не может быть покрыта
конечным числом областей а.
Продолжая этот процесс до бесконечности, на к-и стадии его мы
придем к прямоугольнику [а к, bk\Ck, dk], содержащему такую часть
^Жк множества ^#, которая не может быть покрыта конечным
числом областей о.
Как и в 172, мы заключим отсюда, что прямоугольники [а^, bk\
Ck.dk] «стягиваются» в точку (х, j7), так что
lim cik = lim bk = 3c", lim с к = lim dk = у.
Эта точка М(х, у) принадлежит множеству *М. Действительно,
какую бы окрестность (х — S, х + S;у — S, у + S) точки М ни взять,
для достаточно больших к будет
х — 8 < ak < bk <х + 8, у — 8 < Ck < dk <y + 8,
так что в упомянутую окрестность попадает часть ^Mk множест-
множества <Ж (по самому выбору ее, наверное содержащая бесконечное
множество точек). Следовательно, точка М является точкой
сгущения для множества ^Ж и должна ему принадлежать, ввиду
его замкнутости.
В таком случае, точка М содержится в одной из областей о",
скажем, в a§.
Так как &о есть открытая область, то в нее входит и неко-
некоторая окрестность
(х-89х+8;у-8,у + 8)
этой точки. Как и только что, легко показать, что в эту окрест-
окрестность целиком попадет, при достаточно большом к, прямоугольник
176] § 2. НЕПРЕРЫВНЫЕ ФУНКЦИИ 417
[а к, Ьк'9 с к, dk]93,c ним — и содержащаяся в нем часть ^Ж^ множест-
множества ^Ж. Таким образом, все множество ^Ж^ покрывается одной
областью со, между тем как выбирали его мы так, чтобы оно не
могло быть покрыто никаким конечным числом областей о.
Полученное противоречие и доказывает лемму.
В тех применениях леммы Б о р е л я, которые читатель най-
найдет в следующем п° и в других частях курса, в качестве множест-
множества <Ж будет фигурировать обыкновенно замкнутая область.
Но иной раз придется применять ее и к другим замкнутым мно-
множествам, например к непрерывной кривой.
176. Новые доказательства основных теорем.
1° 1-я теорема Вейерштрасса. Функция f(x,y) предпо-
предположена непрерывной в ограниченной замкнутой области @. Сле-
Следовательно, каждую точку (х',у') этой области можно окружить
такой окрестностью о1', что в ее пределах (если через е обозначено
наперед взятое число)
\f(x,y)-f(x',y')\<e
ИЛИ
f(x',y')-e<f(x,y)<f(x',y') + e.
Таким образом, в области о' функция оказывается ограничен-
ограниченной.
Применяя лемму Боре ля к системе Т, = {а'} этих окрест-
окрестностей, можно выделить из S конечное число окрестностей
о"ь о, ..., от которые в совокупности покрывают всю область &.
Если
mt ^ f(x, у) ^ Mt в о (/ = 1,2, ...,«),
то, взяв в качестве т наименьшее из rrij, а в качестве М — наи-
наибольшее из Mj9 будем иметь в <%!
т ^f(x,y) < М,
что и требовалось доказать.
2° Теорема Кантора. Задавшись произвольным числом
е > 0, каждую точку (х',у') окружим такой окрестностью
а' = {х'-8'9х' + 8'\ y'-S\y' + S'),
что для любой принадлежащей ей точки (х,у) (из @!) будет
1А*,дО-/(*',/)!<§.
418 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [176
Если (хо,уо) есть другая подобная же точка, так что и
то в результате
\f(x,y)-f(xo,yo)\<?. (9)
Заменим каждый прямоугольник о1 вчетверо меньшим прямо-
прямоугольником, с тем же центром,
/ ( . 8' 8' . 8' 8'
Система S = {о'} этих открытых прямоугольников покрывает
область &. По лемме Б орел я, из нее выделяем конечную
систему прямоугольников
\Xi 2'X' 2' Vi 2'yi 2
с тем же свойством. Наконец, обозначим через 8 наименьшее
из всех чисел ^.
Пусть (х,у) и (хо,уо) — любые две точки области Si, для
которых
\х-хо\<8, \y-yo\<8. A0)
Точка (хо,уо) принадлежит одной из окрестностей Wj9 напри-
например окрестности
Jo | Jo . ^о i ^о
2 1 "^ lQ ~Т~ г* ? У IQ г* 1 У IQ ~Т~ г*
Z Z Z
так что
Ь'0^! <
я я я
Из A0), так как 8 < -^-, следует, что |х -хо| < -^ и [у — >>о| < -f-.
Отсюда
|х -xi0\ < 8iQ9 \y -yio\ < 8iQ9
и точки (х,у)9 (хо,уо) обе оказываются лежащими в одной
из первоначально определенных окрестностей
(xi0 -8io,xio +8io; yio -8io,yio+8io),
а тогда, по доказанному, для них выполняется (9).
Итак, удалось по г > 0 выбрать 8 > 0 независимо от по-
положения точки (хо, jo)? чем и доказано, что функция f(x,y) рав-
равномерно непрерывна.
177] § 3. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ 419
§ 3. Производные и дифференциалы функций
нескольких переменных
177. Частные производные и частные дифференциалы. Для
упрощения записи и изложения мы ограничимся случаем функций
от трех переменных; все дальнейшее, однако, справедливо и для
функций любого числа переменных.
Итак, пусть в некоторой (открытой) области ^ имеем функ-
функцию и = /(x,j/, z); возьмем точку Мо(хо,уо, zo) в этой области.
Если мы припишем у и z постоянные значения у о и zo и будем
изменять х, то и и будет функцией от одной переменной х (в ок-
окрестности хо); можно поставить вопрос о вычислении ее производ-
производной в точке х = хо. Придадим этому значению хо приращение Ах,
тогда функция получит приращение
Ахи = Axf(xo,yo,zo) = /0o + Ax,yo,zo) - f(xo,yo,zo),
которое можно было бы назвать ее частным приращением
(по х), поскольку оно вызвано изменением значения лишь одной
переменной. По самому определению производной, она представ-
представляет собой предел
г Ахи г
lim —— = lim
А
= lim .
Ах Ах^О Ах
Эта производная называется частной производной функции
f(x,y,z) по х в точке (хо,уо, zo).
Как видим, в этом определении не все координаты равноправны,
так как у о и zo наперед фиксированы, а х меняется, стремясь к хо-
Частную производную обозначают одним из символов:
ди df(xo,yo,zo) *) , ,
; и f(xoyozo)' Du D
Заметим, что буква х внизу в этих обозначениях лишь указы-
указывает, по какой из переменных берется производная, и не связана
с тем, в какой точке (xo,yo,zo) мы производную вычисляем. **)
*) Я к о б и (С. G. Jacobi) предложил пользоваться круглым д (вместо прямо-
прямого d) в обозначении именно частной производной.
**^ И здесь цельные символы -g^, ffx, Dxf можно рассматривать как функ-
функциональные обозначения для частной производной по х. Подобных при-
примечаний впредь мы повторять уже не станем.
420 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [177
Аналогично, считая х nz постоянными, а у переменным, можно
рассматривать предел
= Нш
Ay Ау^О Ay
Предел этот называется частной производной функции
f(x,y,z) по у б точке (xo,yo,zo) и обозначается символами,
аналогичными предыдущим:
ди
Q, 7; uy, fy(xo,yo,zo), Dyu, Dyf(xo,yo,zo)-
Точно так же определяется и частная производная функции
f(x,y,z) no z в точке (xo,yo,zo).
Само вычисление частной производной по существу не
представляет ничего нового по сравнению с вычислением обык-
обыкновенной производной.
Примеры.
1) Пусть и = ху (х > 0); частные производные этой функции будут:
ди у_х ди у
дх ду
Первая из них вычисляется как производная степенной функции от х (при
у = const), а вторая — как производная показательной функции от у (при
х = const).
х
2) Если и = arctg -, то
у
ди у ди х
n 9 i 9 ' n 9 i 9 '
дх xz-\-yz ду xz-\-yz
X
3) Для и = —z г т- имеем
*z +yz +zz
ди у + z — х ди —2ху ди —2xz
4) nycTbz =y-f(x —у ), где f(u)—произвольная функция (имеющая
производную). Показать, что для z всегда выполняется соотношение:
I dz 1 dz _ z
х дх У ду yz
какова бы ни была функция /.
177] § 3. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ 421
По правилу дифференцирования сложной функции (означая штрихом произ-
производную по и) имеем
— =у - /С*2 -у2) -2х = 2ху - /С*2 -у2)>
дх
|1 =/(**-/)-2у2./'(*2-Л
ду
и отсюда
1 3z I 3z ,2 2ч . 1 г( 2 2ч о .// 2 2ч z
-• —Н — =2у-/(* -;у)Н f(x -y)-2y-f{x -y) = —
х дх у ду у yz
5) Сторона а треугольника определяется по двум другим сторонам Ь, с и за-
заключенному между ними углу а так:
а = у Ь2 + с2 — 2Ьс • cos a,
Тогда
За Ъ — с • cos а Ъ — с • cos а За 6с • sin a
cf у/?z + cz — 2/?c • cosa " oa a
6) Известная из физики формула Клапейрона pV = RT (где
R = const) выражает связь между объемом V, давлением р и абсолютной темпе-
температурой Т одного моля идеального газа и определяет одну из величин р, V, Т как
функцию двух других. Если р, V — независимые переменные, а Г — функция от
них: Т = —, то
R
дТ _ V дТ _ р
~др ~ R' ~dV ~ R'
Если роль независимых играют переменные р и Г, а V — функция от них:
RT
V = —, то
Р
dV RT dV R
dp p2 ' дТ р
RT
Пусть, наконец, V и Т — независимые переменные, р — функция от них: р = —;
V
тогда
dp _ RT dp _ R
~dV ~ ~У2' ЗГ ~ V'
Отсюда, между прочим, получается важное в термодинамике соотношение
dp dV дТ RT R V RT
Заметим, что обозначения Якоби частных производных (с круглыми 3)
следует рассматривать только как цельные символы, а не как частные или дро-
дроби. Полученное только что соотношение с особенной ясностью подчеркивает это
существенное различие в характере обозначений обыкновенных и частных произ-
производных: если бы выписанные в левой части производные были обыкновенными, то
можно было бы их рассматривать как частные одних и тех же дифференциалов,
и по сокращении мы получили бы 1, вместо — 1; здесь же, как мы видим, этого
делать нельзя.
422 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [178
Произведение частной производной |^ на произвольное прира-
приращение Ах называется частным дифференциалом по х функ-
функции и; его обозначают символом
dxu= — -Ax.23)
дх
Если и здесь под дифференциалом dx независимой переменной х
разуметь приращение Дх 24\ то предыдущая формула напишется
так:
dxu= — -dx.
ox
Аналогично,
dyu= -—- dy, dzu= — • dz.
ду dz
Таким образом, мы видим, что можно было бы и частные про-
производные представить в виде дробей
dxu dyu dzu
dx' dy dz'
но при непременном условии указывать, по какой переменной бе-
берется дифференциал.
178. Полное приращение функции. Если, исходя из значе-
значений х = хо, у =уо-> z=zo независимых переменных, придать
23 ^ Как и в случае одной переменной, частный дифференциал dxu функции и,
взятой в фиксированной точке (xq, yo, zq), очевидно является линейной функцией
от аргумента Ах; число их • Ах есть значение dxu(Ax) этого дифференциала,
отвечающее значению Ах. Если же (xQ,yo, zq) не фиксировать, то значение dxu
оказывается зависящим от (в данном случае) четырех аргументов: х, у, z, Ax.
Подробная запись этой зависимости имеет вид:
dxu = dxu(x,y, z, Ax) = их(х,у, z) • Ах.
Определением дифференциала dx независимой переменной х, таким обра-
образом, служит равенство dx = Ах. Это равенство показывает, во-первых, что значе-
значение dx является линейной функцией аргумента Ах (с угловым коэффициентом 1),
и во-вторых, что значение dx не зависит от аргументов х, у, z. В частности, если
Ах фиксировано, то dx представляет собой «постоянное число». В то же са-
самое время dxu при фиксированном Ах является функцией от х, у, z; имея в виду
именно это обстоятельство, иногда говорят, что дифференциал независимой пе-
переменной постоянен, а дифференциал функции — переменен.
178] § 3. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ 423
всем трем некоторые приращения Ах, Ду, Az, то функция
и = f(x,y, z) получит приращение
Аи = Af(xo,yo,zo) =f(xo+Ax,yo+Ay,zo+Az)-f(xo,yo,zo),
которое называется полным приращением функции.
В случае функции у = /(х) от одной переменной, в предполо-
предположении существования в точке хо (конечной) производной /;(хо)>
для приращения функции имеет место формула [96, B)]
Ау = Д/(х0) = /'(*<>) -Ах+а-Ах,
где а зависит от Ах и а —»> 0 при Ах —»> 0.
Мы имеем в виду установить аналогичную формулу для прира-
приращения функции и = f(x,y, z):
Д^ = Д/(х0, 3><ь zo) =
+ f'z (хо, jo, ^o) • Az + a • Дх + р • Ду + у Az, A)
где а, /3, у зависят от Дх, Ду, Az и вместе с ними стремятся
к нулю. Однако на этот раз придется наложить на функцию более
тяжелые ограничения.
Теорема. Если частные производные f'x(x,y,z), f'y(x,y,z),
ffz(x,y,z) существуют не только в точке (хо,.уо,^о),
но и в некоторой ее окрестности, и кроме того непрерывны
(как функции от х, у, z) в этой точке, то имеет место
формула A).
Для доказательства представим полное приращение функ-
функции Аи в виде:
Аи=
+ [/(*<>, У о + Aj/, z0 + Az) - /(хо, у о, zo + Az)} +
+ [Д*<ь У о, ?о + Az) - /(х0, у о,
Каждая из этих разностей представляет частное прираще-
приращение функции лишь по одной переменной. Так как мы предполо-
предположили существование частных производных в окрестности точки
(яо» .Уо» zo)? то — при достаточной малости Дх, Ау9 Az — к этим
разностям по отдельности можно применить формулу конечных
424 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [178
приращений [112] *); мы получим
Аи = f'x(x0 + 9 Ах,у0 + Ay, z0 + Az) • Ах +
+ /у (*<ь у о + 0i Ay,zo + Az)-Ay+ffz(xo, .уо,^о + 02 Az)-Az.
Если положить здесь:
f'x(x0 + в Ах, уо + Ду, z0 + Az) = /i(xo,^o, *o) + «,
/^(ЬЛ) + вгАу, z0 + Az) = f'y(xo,yo, z0) + ^8,
Л (^0,^0,^0 + 92Az) = f'z(xo,yo,zo) +y,
то придем к выражению A) для Аи. При Ах —>> 0, Aj —> 0,
Az —»> 0 аргументы производных в левых частях этих равенств
стремятся к хо, уо-> ?о (ибо в, в\9 в2 — правильные дроби), следо-
следовательно, сами производные, ввиду предположенной не-
непрерывности их для этих значений переменных,
стремятся к производным в правых частях, а величины а, /3, у —
к нулю. Этим и завершается доказательство.
Доказанная теорема дает возможность, между прочим, устано-
установить, что из существования и непрерывности в данной точке
частных производных вытекает непрерывность в этой точке
самой функции; действительно, если Ах —»> 0, Ау —»> 0, Az —»> 0,
то, очевидно, и Аи —»> 0.
Для того чтобы формулу A) можно было написать в более ком-
компактной форме, введем в рассмотрение выражение:
р = у Ах2 + Ay2 + Az2
— расстояние между точками
(хо,.У(ь^о) и (хо + Ах,^о + Ду, zo + Az).
Пользуясь им, можем написать:
( Ах Ay Az\
а • Ах + р • Ау +у • Az = [а Ь/3-^- + у ) • р.
\ Р Р Р )
*' Если взять, например, первую разность, то ее можно рассматривать как при-
приращение функции f(x,yo + Ay, zq + Az) от одной переменной х, отвечающее
переходу от j =.%о?к-х = xq + Ах. Производная по х от этой функции,
т. е. ffx(x,yo + Ay, zq + Az), по предположению, существует для всех значе-
значений х в промежутке [xq, xq + Ах], так что формула конечных приращений при-
применима, и т. д.
178] § 3. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ 425
Обозначив выражение, стоящее в скобках, через ?, будем иметь
а • Ах + р • Ау + у • Az = ? • р,
где е зависит от Ах, Ду, Az и стремится к нулю, если Ах —»> О,
Ау —»> 0, Az —»> 0 или, короче, если р —»> 0. Итак, формулу A)
можно теперь переписать в виде:
Аи = Af(xo,yo,zo) =f'x(xo,yo,zo) • А* + /?(*<ьЗ><ь*о) • 4у +
+ f'z(xo,yo,zo)-&z+?-p, B)
где г —»> 0 при р —»> 0. Величина с-р, очевидно, может быть записана
как о(р) (если распространить введенное в 60 обозначение и на
случай функций нескольких переменных).
Заметим, что в нашем рассуждении не был формально исклю-
исключен случай, когда приращения Ах, Ay, Az порознь или даже все
сразу равны 0. Таким образом, говоря о предельных соотношениях
а ^ 0, ? -» 0, у ^ 0, е ^ 0
при Ах —)> 0, Ау —)> 0, Az —)> 0, мы понимаем их в широком смысле
и не исключаем для этих приращений возможности в процессе их
изменения обращаться в нуль. [Ср. аналогичное замечание в 96.]
При доказательстве предыдущей теоремы мы потребовали от функции не-
нескольких переменных больше, чем в случае функции одной переменной. Для того
чтобы показать, что без соблюдения этих требований формула A) или B) здесь
могла бы оказаться и неприложимой, рассмотрим в заключение следующий
пример (где для простоты мы имеем дело всего лишь с двумя независимыми
переменными).
Определим функцию f(x,y) равенствами:
f(x,y) = -^^ (если х2 +у2 > 0), ДО, 0) = 0.
х1 +у2
Эта функция непрерывна на всей плоскости; для точки @, 0) это следует
из 167, E). Далее, существуют частные производные по х nnoj; также на всей
плоскости. При х -\-у > 0, очевидно,
, Ъуъ , х\х2-уг)
Г*(*'У)= {Х2 +3,2J' Гу^У)= {х2+у2J-
В начальной же точке имеем: f'x @,0) = f' @,0) = 0; это непосредствен-
непосредственно вытекает, по самому определению частных производных, из того, что
f(x, 0) = f@,y) = 0. Легко показать, что в точке @, 0) непрерывность про-
производных нарушается (для первой из них достаточно, например, положить
426 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [179
Формула вида A) или B) для нашей функции в точке @, 0) не имеет места.
В самом деле, если допустить противное, то было бы
где е —>> 0 при Ах —>> 0 и А;; —>> 0. Положив, в частности, А;; = Ах > 0,
имели бы
- Ах = ? • л/2 • Ах, откуда е = ——,
2 2л/2
и е не стремилось бы к нулю при Ах —>> 0, что противоречит допущению.
Аналогичную особенность в точке @, 0) проявляет и функция
Предоставляем читателю разобраться в этом.
179. Полный дифференциал. В случае функции у = /(х) од-
одной переменной, мы рассматривали в 103 вопрос о представимости
ее приращения Ау = Д/(хо) = /(хо + Ах) — /(хо) в виде
Д/(х0) = А • Ах + о(Дх) 04 = const). C)
Оказалось [104], что для возможности такого представления не-
необходимо и достаточно, чтобы существовала в точкех =хо
конечная производная /;(хо)> причем написанное равенство осуще-
осуществляется именно при А = /;(хо). Линейную часть
А • Ах = /;(х0) • Ах = у'х • Ах
приращения функции мы и называли ее дифференциалом, dy.
Переходя к функции нескольких, например трех, переменных:
f(x,y,z)9 определенной в некоторой (скажем, открытой) облас-
области @19 естественно поставить аналогичный вопрос о представимости
приращения
Аи =
в виде
ДДхо,Уо,?о) = А • Ах + В • Ау + С • Az + о(р), D)
где ^,5иС — постоянные, ар = \/Ах2 + Ay2 + Az2.
Как и в 103, легко показать, что если имеет место разложе-
разложение D), то в точке (хо,уо,?о) существуют частные производные
по каждой из переменных, причем
179] § 3. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ 427
Действительно, например, полагая в D) Ay = Az = 0 и Ах ф О,
получим
/(х + Ахр, у о, z0) - f(xp,yo, zp) _
Ах "Л+ Ах '
откуда и следует, что существует
Ax,yo,zo) -f(xo,yo,zo)
— =A.
Таким образом, соотношение D) всегда осуществляется только
в виде
+ f'z(xo,yo,z0)-Az+o(p) E)
или — в более короткой записи —
Au = u'x-Ax+u'y-Ay+u'z-Az+ o(p). E*)
Однако, в то время как в случае функции одной переменной
существования производной ух = /;(хо) в рассматриваемой точке
было уже и достаточно для наличия соотношения C), в нашем
случае существование частных производных
их =/?(*<ьЗ><ь*о), и'у =/у(хо,уо,*о), uz =f'z(xo,yo,zo)
их
еще не обеспечивает разложения D). Для случая функции двух
переменных мы это видели на примере в предыдущем п°. Там же,
в теореме, были указаны достаточные условия для выполне-
выполнения соотношения D): это — существование частных производных
в окрестности точки (хо,.У(ь^о) и их непрерывность
в этой точке. Впрочем, легко показать, что эти условия отнюдь не
необходимы для формулы E) или E*). Это, собственно говоря,
следует уже из того, что для функции одной переменной (которую,
если угодно, можно рассматривать и как функцию от любого числа
переменных) подобные условия не необходимы.
При наличии формулы E) функция f(x,y,z) называется
дифференцируемой в точке (хо,.У(ь^о) и (только в этом
случае!) выражение
их -Ax+uy-Ay + uz-Az =f'x(xo,yo,zo) • Ах +
т. е. линейная часть приращения функции, называется
ее {полным) дифференциалом и обозначается символом du
или df(xo,yo,zo)-
428 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [180
В случае функции нескольких переменных утверждение: «функ-
«функция дифференцируема» в данной точке, как видим, уже не равно-
равнозначаще с утверждением: «функция имеет частные производные по
всем переменным» в этой точке, но означает нечто большее.
Впрочем, мы обычно будем предполагать существование и не-
непрерывность частных производных, а это уже перекрывает
дифференцируемость.
Под дифференциалами независимых переменных dx9 dy, dz
уславливаются разуметь произвольные приращения Ах, Ду,
Az; *) поэтому можно написать:
df(xo,yo,zo) = ffx (*<ьЗ><ь*о) 'dx +
+ /?(*<ьЗ><ь*о) -dy +f'z(xo,yo,zo) 'dz
или
du — ux - dx + uy - dy + uz - dz.
Полный дифференциал оказывается равным сумме част-
частных дифференциалов [177].25^
180. Геометрическая интерпретация для случая функции двух
переменных. Желая дать геометрическое истолкование сказанно-
сказанному выше, аналогичное геометрическому истолкованию производ-
производной и дифференциала функции одной переменной [91,104], вернем-
вернемся к понятию касательной к кривой Ж в данной на ней точке М$.
Мы определили касательную М$Т (рис. 99) как предельное по-
положение секущей MqM при стремлении MqM к нулю [91].
*^Если отождествить дифференциал независимой переменной х
с дифференциалом х, как функции от независимых переменных х, у, z, то,
по общей формуле, можно написать
dx = х'х • Ах + х'у • /\у + x'z • Az = 1 • Ах + 0 • А;; + 0 • Az = Ах,
тогда равенство dx = Ах оказывается доказанным.
' Таким образом, полный дифференциал du функции и в фиксированной точке
(xq, уо, zq) является (линейной) функцией трех аргументов: Ах, Ay, Az; в це-
целом же значение du зависит от шести аргументов: du = du(x, у, z, Ax, Ay, Az).
Фиксируя приращения Ах, Ay, Az (и тем самым превращая в постоянные числа
dx, dy, dz), мы можем рассматривать полный дифференциал du функции и как
функцию (лишь) аргументов x,y,z. Именно так поступают при определении
дифференциала 2-го порядка du функции и, а также и в ряде других случаев.
180]
§ 3. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
429
Очевидно, можно дать и такое, равносильное этому, опреде-
определение:
Прямая МоТ называется касательной к кривой Ж
в точке Мо на ней, если расстояние МР переменной точ-
точки М кривой Ж от прямой МоТ, при
стремлении расстояния МоМ к нулю,
является бесконечно малой высшего
порядка, чем МоМ (т. е. если отношение
МР/МоМ при этом стремится к нулю *)).
Рассмотрим теперь некоторую поверх-
поверхность с? и на ней точку Мо (рис. 100).
Аналогично определению касательной
прямой, дадим определение касательной
плоскости:
Плоскость MqK называется касательной
Рис. 99
тъю к поверхности S в точке
плоскос-
на ней, если рассто-
расстояние МР переменной
точки М поверхнос-
поверхности S от этой плос-
плоскости, при стремле-
стремлении расстояния МоМ
к нулю, является бес-
бесконечно малой выс-
высшего порядка, чем
МоМ (т. е. если отноше-
отношение МР/МоМ при этом
стремится к нулю).
Пусть [159] поверх-
поверхность задана уравнени-
уравнением z = f(x,y) в прямо-
прямоугольных координатах.
Возьмем на ней точ-
точку Мо(хо,уо,*о) [где
zo = f(xo,yo)] и исследуем, при каких условиях плоскость ЗР^
проходящая через точку Мо и имеющая уравнение
Z-zo=A(X-xo)+B(Y-yo), F)
удовлетворяет этому определению.
Рис. 100
*) А это значит, что стремится к нулю sin<p, а с ним и угол ср между секу-
секущей MqM и прямой MqT (см. рис. 99).
430 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [180
Проведем ML параллельно оси z (см. рис. 100) и из Мо опу-
опустим на ML перпендикуляр M$N. Так как отрезок МК отличается
от МР постоянным множителем (не равным нулю), то вместо отно-
отношения МР/ММо можно рассматривать отношение МК/ММц. По-
Покажем теперь, что, не меняя по существу определения касательной
плоскости, можно, наконец, заменить здесь расстояние г =
отрезком р =
Если при М —>> Мо стремится к нулю отношение МК/р, то это
тем более верно для отношения МК/r, ибо г > р. Предполо-
Предположим теперь, что МК/r стремится к нулю, и уста-
установим, что тогда стремится к нулю и МК/р. Для
этого достаточно доказать, что при М —»> Мо отношение - остается
ограниченным.
Отрезок МК, с точностью до знака, равен выражению
z -Z = z -z0 -A{x -хо) -В(у -уо)
или, если ввести обозначения
х -хо = Ах, у -уо = Ay, z -z0 = Az = Af(xo,yo),
— выражению
Az - (ААх +ВАу).
Ввиду сделанного предположения, по крайней мере для точек М9
достаточно близких к Mq9 будем иметь
1 1
|Az-(.4A;c+?A>0| < -г = - у/Ах2 + Ay2 + Az2,
так что
Р ' ' Р ' ' Р 2 V V Р
или (усиливая неравенство)
Отсюда
Р )
180]
§ 3. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
431
а следовательно,
<2(\А\
что и требовалось доказать.
Таким образом, плоскость F) будет касательной к поверхности
в том, и только в том, случае, если отношение
Az - (А Ах +ВАу)
м
стремится к нулю вместе с р, т. е. если имеет место разложение
Az = Af(xo,yo) = А-Ах+В-Ау + о(р)
[ср. D)].
Мы приходим к окончательному заключению: для того
чтобы поверхность z=f(x,y) в точке Мо(хо,.уо,^о), где
zo = f(xo,yo), имела касательную плоскость *\ необходи-
необходимо и достаточно, чтобы
при х = хо, у = уо Функ-
Функция f(x,y) была диффе-
дифференцируема.
Так как при выполнении
этого условия коэффициен-
коэффициенты А и В необходимо рав-
равны частным производным
fx(xo,yo) и fy(xo,yo)9 то
касательная плоскость вы-
выразится уравнением
Z-z0 =
Рис. 101
Обычно значков при х9 у, z не пишут; тогда уравнение каса-
касательной плоскости принимает вид
Z-z=fx[x,y) ¦ (X-x)+f'Jx,y) • (Y-y).
G)
*) Имеется в виду плоскость, не параллельная оси z.
432 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [181
Нетрудно видеть, что если пересечь поверхность и касательную
к ней плоскость любой плоскостью, параллельной оси z и проходя-
проходящей через точку Мо, то в сечении с первой получается некоторая
кривая, а в сечении со второй — касательная к ней прямая *\
В частности, в сечении поверхности плоскостями Y = у о
и Х = хо получатся кривые, угловые коэффициенты **} которых
соответственно равны:
f'x(xo,yo) и f'y(xo,yo).
На рис. 101 отрезки К\М\9 К2М2 и КМ представляют частные
и полное приращения функции, а отрезки K\N\9 K2N2 и KN — част-
частные и полный ее дифференциалы [ср. п° 104 и рис. 44].
181. Производные от сложных функций. Пусть имеем функ-
функцию
u = f(x,y,z),
определенную в (открытой) области @19 причем каждая из пере-
переменных х9у9 z в свою очередь является функцией от переменной t
в некотором промежутке:
x=<p(t), y=ip(t), z=x(t).
Пусть, кроме того, при изменении t точки (х,у, z) не выходят
за пределы области <%!.
Подставив значения х, у и z в функцию /, получим сложную
функцию:
Предположим, что и имеет по х9 у и z непрерывные частные
производные ufx9 и' u'z ***) и что х[9 у[ и z't существуют. Тогда можно
доказать существование производной сложной функции и вместе
с тем вычислить ее.
Действительно, придадим переменной t некоторое прираще-
приращение At, тогда х, у и z получат соответственные приращения Ах,
Ау и Az, функция же и получит приращение Аи.
*^ Ниже [234] будет рассмотрен более общий вопрос о касательных к любым
кривым, проведенным по поверхности через данную точку.
**) Легко сообразить, по отношению к каким координатным системам вычисля-
вычисляются эти угловые коэффициенты.
***) Собственно говоря, достаточно предположить дифференцируемость функ-
функции и = f(x,y, z).
181] § 3. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ 433
Представив приращение и в форме A) (это мы можем сделать,
так как предположили существование непрерывных частных
производных их9 и'у9 uz)9 получим
Аи = их • Ах + и'у • Ау + щ • Az + а • Ах + /3 • Ау + у • Az,
где a, fi,y —>> О при Ах, Ду, Az —»> 0. Разделив обе части равенства
на А/1, будем иметь
Аи , Ах , Ay , Az Дх Ay Az
Устремим теперь приращение Д^ к нулю; тогда Дх, Ay, Az будут
стремиться к нулю, так как функции х, у и z от t непрерывны (мы
предположили существование производных x^^nz^a потому а,
/3, у также будут стремиться к нулю. В пределе получим:
i/t = i/x.x't + rfy.y't + iJz.z't. (8)
Видим, что при сделанных предположениях производная слож-
сложной функции действительно существует. Если воспользоваться диф-
дифференциальным обозначением, то формулу (8) можно записать так:
du ди dx ди dy ди dz
Теперь рассмотрим тот случай, когда х, у и z зависят не от
одной переменной t, а от нескольких переменных; например,
x=q>(t,v), y = ip(t,v), z=x(t,v).
Кроме существования и непрерывности частных производных
функции /(х,у, z) *\ мы предполагаем здесь существование про-
производных от функций х, у, z по t и v.
После подстановки функций <р, гр и % в функцию / мы будем
иметь некоторую функцию от двух переменных t и l>, и возника-
возникает вопрос о существовании и вычислении частных производных и[
и u'v. Но этот случай не отличается существенно от уже изучен-
изученного, ибо при вычислении частной производной функции от двух
переменных мы одну из переменных фиксируем, и у нас остается
функция только от одной переменной. Следовательно, для этого
случая формула (8) остается без изменения, а формулу (9) нужно
*) См. сноску ***) на с. 432.
434 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [182
переписать в виде:
ди ди дх ди ду ди dz
~dt~~dx'~dt+~dy"dt+~d^'~dt' ^ '
182. Примеры.
1) Рассмотрим степенно-показательную функцию
Положив х = (p(t),y = ip(t) и продифференцировав по только что выведен-
выведенному правилу дифференцирования сложной функции, получим известную уже нам
формулу Г.В. Лейбница и И. Бернулли:
и[ = у • ху~1 • х[ + ху • \пх • у[.
Раньше мы установили ее (в других обозначениях) с помощью искусственного
приема [99, 23)].
2) Пусть и = f(x,y,z) имеет непрерывные частные производные, и вмес-
вместо х, у и z подставлено:
х = Ц - f, у = $ - 4, z = | - ц.
Тогда
ди ди ди ди ди ди ди ди ди
<9| ду dz' дц дх dz' д?, дх ду
3) Если (при тех же предположениях относительно функции /), сохра-
сохраняя х независимой переменной, положить
у = у(х) и z = z(x),
где функции у(х), z(x) дифференцируемы по х, то и, как сложная функция от х,
будет иметь производную:
du ди ди dy ди dz
dx дх ду dx dz dx
или
^=f'x(X,y(X),z(x))+f'y(X,y(X),z(x))-y'(x)+f'z(x,y(X),z(x))-z'(x).
dx y
Здесь само х играет роль переменной t в формуле (8).
4) Если же обе переменные х, у оставить независимыми, а вместо z под-
подставить функцию
z=z{X,y),
имеющую частные производные по х и по j, то для сложной функции
и = / (х, у, z(x, у)) будем иметь:
— = f'x (x,y,z(x,y)) +f'z (x,y,z(x,y)) -zfx(x,y),
дх
— = f'y (x,y,z(x,y)) +f'z (x,y,z(x,y)) -Zy(x,y).
182] § 3. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ 435
5) В качестве дальнейшего примера применения формулы (9) рассмотрим
вопрос о дифференцировании определителя
А =
а\\ а и ... a i
a 2i а22 ... ai
ап\ ап2 ... апп
в предположении, что элементы его а^ (/, к = 1, 2, ...,«) суть функции от
некоторого параметра ^, для которых существуют производные по t: -^р.
Вспоминая разложение определителя по элементам к-то столбца
А = A\k • a\k + A2k - а2к + • • • + Alk • alk + . . . + Апк • ank,
где алгебраические дополнения А\к, . . ., ^«А: элемента аг^ не содержат, приходим
к заключению, что
В таком случае, по формуле (9),
dt ^^ dalk dt dt
k=\ i=l lk k=\ i=l
n
Заметим, что сумма J^ Ajk • -^ дает разложение определителя, отлича-
i=\
ющегося от данного лишь тем, что элементы его &-го столбца заменены их про-
производными по t. Отсюда правило: производная определителя А равна сумме п
определителей, получающихся из А заменой, поочередно, элементов его 1-го,
2-го, . . ., п-го столбца производными.
Формула (8) сходна с формулой ut = ux -х\ для случая функции и от одной
переменной jc. Подчеркнем, однако, снова разницу в условиях, при которых
были выведены эти формулы. Если и зависит от одной переменной, то достаточ-
достаточно было предположить существование производной их; в случае же нескольких пе-
переменных — мы вынуждены были предположить еще и непрерывность производ-
производных их, и , . . . Следующие примеры показывают, что одного существования
этих производных для действительности формулы (8), вообще, недостаточно.
6) Определим функцию и = f(x,y), полагая:
f{x, у) = * У (при х2 +у2 > 0), ДО, 0) = 0.
х1 +yz
Эта функция, как мы видели, имеет частные производные во всех точках, не ис-
исключая и начальной @, 0), причем
/>,0)= 0, /;@,0)=0;
заметим, что именно в этой точке производные терпят разрыв.
Если ввести новую переменную t, положив х = t и у = t, то получим слож-
сложную функцию от t. По формуле (8) производная этой функции при t = 0 была
бы равна
и = их • xt + и • yt = 0.
436 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [183
Но, с другой стороны, если на деле подставить значения х и у в данную
функцию и = f(x, у), получим
U = -z т- = - t.
t2 + t2 2
Продифференцировав теперь непосредственно по t, будем иметь ut = ^ при
любом значении t, значит, и при t = 0.
Оказывается, что формула (8) в данном случае неприменима.
7) Поведение функции и = f(x,y), определяемой равенствами
4iZ *2+/>о), /(о,о) = о,
JCZ+J/Z
в точке @, 0) вполне аналогично. Взяв здесь х = у = t, получим сложную функ-
функцию и = jf5, которая при t = 0 имеет бесконечные односторонние произ-
производные. Если же положить: х = t, a
4 1
у = t3 sin - при ^ ф 0, _у = 0 при t = 0,
то сложная функция, определяемая равенствами:
f • sin f
и = = при t Ф 0, г/ = 0 при /^ = 0,
1 i - ¦ 2 1
1 -И з • smz }
при /^ = 0 никакой производной иметь не будет.
183. Формула конечных приращений. Пусть функция /(х,y,z)
определена и непрерывна в замкнутой области 31 и имеет не-
непрерывные частные производные ffx9fy9fz внутри этой области
(т. е. во всякой внутренней ее точке). Рассмотрим две точки
из 31
Щ(хо,уо,го) и М\(хо + Ах, jo + Ay, z0 + Az),
которые можно соединить прямолинейным отрезком МоМ\9 цели-
целиком лежащим в области 3).
Тогда имеет место формула:
- Ах, jo + Ay, z0
= /хОо + 0Ах,уо + 9Ау, z0 + 0Az) • Ах +
+ f'y(...).Ay+f'z(...).Az (O<0<1), A0)
вполне аналогичная известной формуле конечных прира-
приращений для функции одной переменной [112, B)].
Для доказательства ее положим в функции f(x,y, z)
х =xo+t-Ax, у =yo+t • Ay, z=zo + t-Az A1)
183] § 3. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ 437
(при 0 ^ / ^ 1), т. е. рассмотрим нашу функцию именно в точках
прямолинейного отрезка М§М\. Сложная функция от t
F(t) = /Оо +1 • Ах, у о +1 • Ay, z0 +1 • Az)
непрерывна во всем промежутке [0, 1] [170], а внутри него имеет
производную, которая, по формуле (8), равна
F\t) =ffx(xo + t-Ax,yo+t-Ay,zo + t-Az) -Ax +
+ /;(.. .).Ay+f'z(...).Az,
ибо из A1)
dx dy dz
— = Ах, -f = Ay, — = Az.
dt dt dt
Применим к функции F(t) в промежутке [0, 1] форму-
формулу B) п° 112:
F\e) @<в< 1).
Если заметить, что, по определению функции F(t)9
- F@) = f(x0 + Ax,yo + Ay, z0 + Az) - f(xo,yo, z0),
и подставить вместо производной F'F) только что найденное вы-
выражение (при t = в), то и придем к формуле A0).
В качестве простого примера приложения доказанной формулы
упомянем следующее предложение:
Если функция f(x,y,z), непрерывная в замкнутой и связ-
связной области <3, внутри области имеет частные производные,
равные 0:
f'x=f'y=f'z = o,
то эта функция во всей области & сводится к постоянной'.
f = const.
Пусть Мо(хо, yo,zo) и М(х, у, z) будут любые две точки облас-
области @. Ввиду предположенной связности @9 эти точки можно со-
соединить ломаной, не выходящей за пределы @. Если М\(х\,у\, z\)
есть следующая за Мо вершина ломаной, то, положив в A1)
хо + Ах =х\9 уо + Ау =у\9 zo + Az = z\9 сразу получим
438
ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[184
переходя так последовательно от вершины к вершине, окончатель-
окончательно найдем:
f(x,y,z) =f(xo,yo,zo),
что и требовалось доказать.
184. Производная по заданному направлению. Частные произ-
производные функции f(M) = f(x, у, z) по х9 по у, по z выражают «ско-
«скорость изменения» функции по направлению координатных осей.
Например, f'x есть «скорость изменения» функции по х: точка
предполагается перемещающейся лишь по параллели оси х. Меж-
Между тем, во многих физиче-
физических вопросах может пред-
представить интерес также «ско-
«скорость изменения» функции
f(M) и по другим направле-
направлениям. Так будет, например,
в случае, если дано поле
температуры, т. е. если
задана температура
f(M) в каждой точке М рас-
рассматриваемого тела. Законы
распределения и перемеще-
у г ния тепла существенно за-
Рис. 102 висят от скорости падения
(или роста) температуры по
всем направлениям. Уточним понятие «скорости изменения» или
производной функции по любому заданному направлению.
Здесь мы также будем иметь случай применить формулу (9).
Пусть функция f{M) определена в некоторой (открытой) облас-
области. Рассмотрим любую точку М)(хо, ^o»zo) этой области и лю-
любую направленную прямую (ось) /, проходящую через эту точку
(рис. 102).
Пусть М(х ,y,z) — какая-нибудь другая точка этой оси, М$М —
длина отрезка между Мо и М9 взятая с надлежащим знаком, именно:
со знаком плюс, если направление М$М совпадает с направлением
оси /, и со знаком минус — в противном случае.
Пусть М неограниченно приближается к Mq. Предел
lim
f{M) - /(Mq)
MqM
184] § 3. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ 439
называется производной от функции f{M) no на-
направлению I (или вдоль оси /) и обозначается следующим об-
образом:
dl dl
Эта производная характеризует «скорость изменения» функции
в точке Мо по направлению /.
В частности, как упоминалось, и обычные частные производ-
производные Ц-, j-, |j тоже можно рассматривать как производные «по
направлению».
Предположим теперь, что функция /(x,j/, z) имеет в рас-
рассматриваемой области непрерывные частные производные.*}
Пусть ось / образует с осями координат углы а, /3, у. Докажем,
что при сделанных предположениях производная по направлению /
существует и выражается формулой
д
Для доказательства заметим, что если положить М§М = t, то
будем иметь
х — xq = t - cos а, у — у о = t - cos /3, z — zq = t • cos y.
Таким образом, вдоль оси / координаты х, у, z можно рассмат-
рассматривать как функции t\
х = хо + t - cosa, j =^0 + t - cos^, z = zo + z1 • cosy, A3)
а функцию /(M) = f(x,y, z) — как сложную функцию q>(t) от /^.
При этом точке Mo соответствует значение t, равное нулю.
Таким образом, имеем:
dl
если только существует производная q>f@). Но производная cp\t)
при сделанных предположениях существует и выражается по фор-
формуле (9) следующим образом:
, =<9/ dx_ д? <&__>?? ^_
СРК) дх' dt ду' dt dz' dt'
*) См. сноску ***) на с. 432.
440 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [184
Используя формулы A3), получаем
// ч д/ д/ д/
<р @ = тг- -cosa + тг- - C0SP + т~ - cosy>
дх ду dz
откуда и следует наше утверждение.
Зададимся теперь вопросом: по какому направлению функция
в данной точке будет всего быстрее возрастать! Конечно,
этот вопрос имеет смысл лишь в том случае, если производные
д/(хо,уо^о) , df(xo,yo,zo)
а = Б ' Ъ = Б ' с =
д д
дх ду dz
не равны одновременно нулю (ибо иначе — производная по любому
направлению была бы нулем).
В этом предположении прибегнем к преобразованию выраже-
выражения A2):
а - cos а + Ъ • cos /3 + с • cos у —
а
= л/а2 + Ъ2 + с2 • ( • cos а + • cos E + • cos у
Дроби в скобках можно рассматривать как направляющие косинусы
некоторого направления g:
а „ Ъ с
——= = COS Я, —== — COS/i, —== — COSV,
и тогда мы получим
л/а2 + Ъ2 + с2 - (cos Я • cos a + cos \х • cos E + cos v • cos у).
Если, наконец, через (g, /) обозначить угол между направлениями g
и /, то по известной формуле аналитической геометрии получим:
^ ,f). A5)
Теперь ясно, что, если / отождествляется с g9 эта производная
достигнет наибольшего значения:
Вектор g9 имеющий проекции A4) на оси координат, указы-
указывает направление наиболее быстрого возрастания функции, а его
185] § 3. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ 441
длина | g | дает величину соответствующей производной. Этот век-
вектор называют градиентом функции f{M) = f(x,y,z).
Переписав формулу A5) в виде
легко усмотреть, что вектор, который получится, если на направле-
направлении / отложить отрезок |?, представляет собой попросту проекцию
градиента на это направление.
185. Инвариантность формы (первого) дифференциала. Пусть
функция и = f(x,y,z) имеет непрерывные частные производ-
производные их9 и' u'z^ причем х, j/, z, в свою очередь, являются функциями
от новых переменных t и v\
x=q>(t,v), y=i/>(t,v), z=x(t,v),
также имеющими непрерывные же частные производные xft9 x'v, yft9
y'v, z't9 z'v. Тогда [181] не только существуют производные от слож-
сложной функции и по t и v9 но эти производные также непрерывны по t
и v9 как это легко усмотреть из (8).
Если бы х, у9 z были независимыми переменными, то, как мы
знаем, (полный) дифференциал функции и был бы равен
du = их - dx + и' - dy + uz - dz.
В данном же случае и зависит — через посредство х9у9 z — от
переменных t и v. Следовательно, по отношению к этим перемен-
переменным, дифференциал напишется так:
du = u't - dt + u'v - dv.
Но, в силу (8),
u[ = ux -x't+u'y -y't+uz -z't
и, аналогично,
uv =u'x-x'v+uy -y'v+u'z -z'v.
ux
Подставив эти значения в выражение для du9 будем иметь:
du = (ux -x't + Uy -y't + u'z • z't) • dt + (u'x 'x'v + uy -y'v + u'z • z'v) • dv.
Перегруппируем члены следующим образом:
du = ux-(x[-dt+x'v-dv)+Uy-{y[-dt+y'v-dv)+uz-(z't-dt+z'v-dv).
442 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [185
Нетрудно видеть, что выражения, стоящие в скобках, суть не
что иное, как дифференциалы функций х9 у, z (от и и v)9 так
что мы можем написать:
du — их - dx + и'у - dy + uz - dz.
Мы пришли к той же самой форме дифференциала, что
и в случае, когда х9 у, z были независимыми переменными (но
смысл символов dx9 dy, dz здесь, конечно, уже другой).
Итак, для функций нескольких переменных имеет место
инвариантность формы {первого) дифференциала, как
и для функций одной переменной. *)
Может случиться, что х9 у и z будут зависеть от различных
переменных, например,
x=q>(t), y=ip(t,w), z=%{y,w).
В таком случае мы всегда можем считать, что
х = q>i(t, v, w), у = ipi(t, v, w), z = xi(t, v, w),
и все предыдущие рассуждения будут применимы и к этому случаю.
Следствия. Для случая, когда х и у были функциями одной
переменной, мы имели следующие формулы:
d{cx) = с - dx, d(x ±y) = dx ± dy, d(xy) = у • dx + х • dy,
у - dx — х - dy
<-) =
У2
Эти формулы верны и в том случае, когда х и у
являются функциями любого числа переменных,
т. е. когда
х = q>(t, v, ...), у = i/>(t, v, ...).
Докажем, например, последнюю формулу.
Для этого примем сначала х и у за независимые переменные;
тогда
у - dx — х - dy
{(-) = -• dx . dy = — 0
\yJ у у1 у1
*) Отметим, что то же заключение справедливо и при одном предположении
дифференцируемости всех рассматриваемых функций. Чтобы убедиться
в этом, достаточно показать, что результатом суперпозиции дифференцируемых
функций будет также дифференцируемая функция.
186] § 3. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ 443
Видим, что при этом предположении дифференциал имеет тот
же вид, что и для функций х иу одной переменной. На основании
же инвариантности формы дифференциала можно утверждать, что
эта формула справедлива и в том случае, когда х и у являются
функциями любого числа переменных.
Доказанное свойство полного дифференциала и следствия из него позволяют
упрощать вычисление дифференциалов, например:
х 1 (х \ у • dx — х • dy
1) d arctg — = у ' d[ — ) — 9 2 '
2) d
x (x2 + y2 + z2)dx - x • d(x2 + y2 + z2)
x2+y2+z2 (x2+y2+z2J
(y + z — x )dx — 2xy - dy — 2xz
(x2+y2 + z2J
Так как коэффициентами при дифференциалах независимых переменных
являются соответствующие частные производные, то отсюда сразу же
получаются и значения этих последних. Например, для u = arctg - имеем непо-
непосредственно
ди у ди х
а для и =
X
х2 + у2
ди
дх
дх х2 -\
ТТО ПЛАТИЛ f
y2+z2-
ди
^У2'
сразу
9
X
ду
ди
ду
2xz
Х2 +
(*24
у2'
2ху
-y2+z2J
dz (x2+y2+z2J
[ср. 2) и 3), 177].
186. Применение полного дифференциала в приближенных вычислениях.
Аналогично дифференциалу функции от одной переменной [108] и полный диф-
дифференциал функции от нескольких переменных с успехом применяются в прибли-
приближенных вычислениях при оценке погрешностей. Пусть, например, мы имеем функ-
функцию и = f(x,y), причем, определяя значения х и у, мы допускаем погрешности,
скажем, Ах и Ау. Тогда и значение и, вычисленное по неточным значениям аргу-
аргументов, также получится с погрешностью Аи = f(x-\-Ax, у + Ay) —f(x,y). Речь
идет об оценке этой погрешности, если известны оценки погрешностей Ах
и Ау.
Заменяя (приближенно) приращение функции ее дифференциалом (что
оправдано лишь при достаточно малых значениях Ах и Ау), получим
Аи = ^ • Ах + ^ • Ау. A6)
дх ду
444
ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[186
Здесь и погрешности Ах, Ду, и коэффициенты при них могут быть как положи-
положительными, так и отрицательными; заменяя те и другие их абсолютными величи-
величинами, придем к неравенству
|Аи
1АИ-
Если через 8и, 8х, 8у обозначить максимальные абсолютные погреш-
погрешности (или границы для абсолютных погрешностей), то можно, очевидно,
принять
8и = —
ди
~дх
• 8х +
ди
~ду
A7)
Приведем примеры.
1) Прежде всего, с помощью выведенных формул легко установить обычные
в практике приближенных вычислений правила. Пусть и = ху (где х > О,
у > 0), так что du = у dx + x dy; заменяя дифференциалы приращениями, по-
получим Аи = у • Ах + х • Ау [см. A6)] или, переходя к границам погрешнос-
погрешностей [см. A7)]:
8и = у • 8х + х • 8у.
Деля обе части этого равенства на и = ху, придем к окончательной формуле
8и 8х 8у
и х у
A8)
выражающей такое правило: (максимальная) относительная погрешность
произведения равна сумме (максимальных) относительных погрешностей
сомножителей.
Можно было бы поступить проще — сначала прологарифмировать формулу
и = х • у, а затем продифференцировать:
du dx dy *)
ти = тх + mj/, — = 1 , и т. д.
и х у
х
Если и = —, то по этому методу найдем
у
du dx dy
In г/ = \nx — \ny, — = ;
и x у
переходя к абсолютным величинам и к максимальным погрешностям, мы получим
снова формулу A8). Таким образом (максимальная) относительная погреш-
погрешность частного равна сумме (максимальных) относительных погрешностей
делимого и делителя.
2) Частное применение находит исчисление погрешностей в топографии,
главным образом при вычислении не измеренных непосредственно элементов тре-
треугольника — по измеренным его элементам. Приведем примеры из этой области.
* ^ Обращаем внимание читателя на то, что дифференциал In и мы вычисляем
так, как если бы и была независимой переменной, хотя на деле она является
функцией от х и у [175]. Это замечание следует иметь в виду и ниже.
186]
§ 3. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
445
Пусть в прямоугольном треугольнике ABC (рис. 103) катет АВ = Ъ и при-
прилежащий угол <ВАС = а измерены; второй же катет а вычисляется по формуле:
а = b • tga. Как отражаются на значении а погрешности при измерении b и а?
Рис. 104
Дифференцируя, получим
da = tg а • db
так что и
8а = tg а • 8Ь
da,
8а.
Пусть, например, измерения привели к результатам:
Ь = 121,56л* ± 0,05 л*, <а = 25°2l'4O" ± 12",
так что
а = 51,62м.
Определяя по нашей формуле 8а, положим в ней 8Ь = 0,05, а 8а = 206265"
(ведь 8а нужно выразить в радианах, а один радиан равен именно 60 ' ^ 36° =
= 206265"). Мы получим
\- 8а = 0,0087,
12"
tga-8b = 0,0237, -
cosza
так что, округляя, можно считать 8а = 0,04. Итак, а = 51,62 м d= 0,04 л/.
3) Найдем погрешность при определении стороны а косоугольного треуголь-
треугольника ABC (рис. 104) по формуле
а = л/b2 + с2 — 2Ьс • cos а.
Пользуясь результатами примера 5), п° 177, можно по формуле A7) сразу напи-
написать:
b — с • cos а с — b • cos a be • sin a
8а = • 8b -\ • 8с -\ • 8а.
Из чертежа же имеем непосредственно:
b — с • cos а = а • cosy, с — b • cos a = а • cos/3, be - sina = а - ha,
где ha есть высота треугольника, опущенная из вершины А. Таким образом ока-
оказывается, что
8а = cos у • 8Ъ + cos /3 • 8с + ha • 8а;
по этой формуле легко судить о влиянии на 8а отдельных погрешностей 8Ь, 8с, 8а.
446 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [187
187. Однородные функции. Как известно, однородными мно-
многочленами называются многочлены, состоящие из членов одного
и того же измерения. Например, выражение
Ъх2 - 2ху + Ъу2
есть однородный многочлен второй степени. Если умножить здесь х
и у на некоторый множитель t9 то весь многочлен приобретет мно-
множитель t во второй степени. Подобное обстоятельство имеет место
для любого однородного многочлена.
Однако и функции более сложной природы могут обладать та-
таким же свойством; если взять, например, выражение
х -у
то и оно приобретает множитель t2 при умножении обоих аргу-
аргументов х и у на t9 уподобляясь в этом отношении однородному
многочлену второй степени. Подобную функцию естественно так-
также назвать однородной функцией второй степени.
Дадим общее определение:
Функция f(x\, ..., хп) от п аргументов, определен-
определенная в области <3, называется однородной функцией
т-й степени, если при умножении всех ее аргументов на
множитель t функция приобретает этот же множитель
в т-й степени, т. е если тождественно выполняется равенство
f(txu .. .,txn) =Г • f(xu .. .,хп). A9)
Для простоты мы ограничимся предположением, что х\, ..., хп
и t здесь принимают лишь положительные значения. Область &)9
в которой мы рассматриваем функцию /, вместе с любой своей
точкой М(х\, ..., хп) предполагается содержащей и все точки вида
Mt(tx\, ..., txn) при t > 0, т. е. весь луч, исходящий из начальной
точки и проходящий через точку М.
Степень однородности т может быть любым вещественным
числом; так, например, функция
X X
хп -sin—Yyn • cos-
У У
является однородной функцией степени л от аргументов х иу.
187] § 3. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ 447
Постараемся теперь получить общее выражение одно-
однородной функции степени т.
Пусть сперва f(x\, ..., хп) есть однородная функция нуле-
нулевой степени; тогда
f(tXi,tX2, . . .,tXn) =f(xi,X2, • • .,Хп).
Положив t = —, получим
f(x\, Х2, • • • , Хп) = / 1, —,...,—
V xi xi
Если ввести функцию от п — 1 аргументов:
то окажется, что
J\X\,X2,... ,Хп) = ф [ —, . . .
\Х\ Х\
Итак, всякая однородная функция нулевой степени представляет-
представляется в виде функции отношений всех аргументов к одному из них.
Обратное, очевидно, также верно, так что предшествующее равен-
равенство дает общее выражение однородной функции ну-
нулевой степени.
Если f(x\,X2, .. .,хп) есть однородная функция rn-и степени
(и только в этом случае), отношение ее к х™ будет однородной
функцией нулевой степени, так что
f(xi,X2, . . . ,Хи) (Х2 Хп
xf =(PW"-^
Таким образом, мы получаем общий вид однородной
функции степени т\
2, ..., хп) = х р
\Х\ Х\
Пример.
х -у у у- - 1
448 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [188
188. Формула Эйлера. Предположим теперь, что однородная
(степени т) функция f(x,y,z) *) имеет в (открытой) области @1
непрерывные частные производные по всем аргументам. Фикси-
Фиксируя по произволу точку (xo,yo,zo) из @9 в силу основного тож-
тождества A9), будем иметь для любого t > 0:
/(tao, ty0, tz0) = tm • /(x0,yo, zo).
Продифференцируем теперь это равенство по t: левую часть
равенства — по правилу дифференцирования сложной функции **},
правую — просто как степенную функцию. Получим
f'x (tx0, tyo, tz0) -xo+fy (tx0, tyo, tz0) -yo+fz (tx0, tyo, tz0) • z0 =
= mtm~l -f{xO9yo9zo).
Если положить здесь t = 1, то придем к следующей формуле:
= т
Таким образом, для любой точки (х,у, z) имеет место равенство
f'x(x,y,z)-x+f'y(x,y,z)-y+f'z(x,y,z)-z=m-f(x,y,z). B0)
Это равенство носит название формулы Эйлера (L. Euler).
Мы видели, что этому равенству удовлетворяет любая однород-
однородная функция степени т9 имеющая непрерывные частные производ-
производные. Покажем теперь, что и обратно — каждая функция, непрерыв-
непрерывная вместе со своими частными производными и удовлетворяющая
равенству Эйлера B0), необходимо является однородной функ-
функцией степени т.
Действительно, пусть f(x,y,z) будет такой функцией. Фикси-
Фиксируя по произволу значения хо9 у о, ^о? рассмотрим следующую функ-
функцию от t (при t > 0):
=
*) Лишь для упрощения письма мы ограничиваемся здесь случаем трех пере-
переменных.
**)
Именно для того, чтобы иметь право применить это правило, мы и предпо-
предположили непрерывность частных производных [181].
189] § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 449
Она определена и непрерывна при всех t > 0. Вычислив ее произ-
производную cp\t) по правилу дифференцирования дроби, получим также
дробь, числитель которой равен
(f'x(txo, tyo, tz0) -xo+fy(txo, tyo, tz0) -yo +
+ ffz(txo,tyo,tzo) -z0) -t-m-f(txo,tyo,tzo).
Заменив в формуле Эйлера B0) х9 у, z на txo, tyo, tzo,
видим, что этот числитель обращается в нуль, так что q>'{t) = 0
и ф(/) = с = const (при t > 0). Чтобы определить постоянную с,
положим t = 1 в равенстве, определяющем q>(t). Получим, что
с =f(xo,yo,zo)-
Итак,
/(tap, ty0, tz0)
^W = jik
или
f(txo,tyo,tzo) =tm -
что и требовалось доказать.
Можно сказать, что формула Эйлера в такой же мере харак-
характеризует однородную функцию степени т9 как и основное равен-
равенство A9).
§ 4. Производные и дифференциалы высших порядков
189. Производные высших порядков. Если функция
и = f(x,y, z) *) имеет в некоторой (открытой) области @ част-
частную производную по одной из переменных, то названная про-
производная, сама являясь функцией от x,y,z9 может в свою оче-
очередь в некоторой точке (xo,yo,zo) иметь частные производные по
той же или по любой другой переменной. Для исходной функции
и = f(x,y, z) эти последние производные будут частными произ-
производными второго порядка (или вторыми частными про-
производными).
*) Мы и здесь для простоты письма ограничиваемся случаем функции от трех
переменных.
450 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [189
Если первая производная была взята, например, по х, то ее
производные по х, у, z обозначаются так:
д2и
дх2 ~ дх2
д2и d2f(xo,yo,zo) д2и
дх ду дх ду дх dz дх dz
или
Ux2 = /х2(хо,УО,*о),
иху =fxy(x0,y0,Z0), u"z =f"z(xo,yo,ZO).*)
Аналогичным образом определяются производные 3-го, 4-го
и т. д. порядков (третьи, четвертые, ... производные).
Общее определение частной производной /7-го порядка может
быть дано индуктивно.
Заметим, что частная производная высшего порядка, взятая
по различным переменным, например
д2и д2и д4и
дх ду ' ду дх ' дх ду dz2 '
называется смешанной частной производной.
Примеры.
1)
2)
Пусть и =
Мы имели
4 i 7
х у z ; тогда:
их =
< =
ш
uxyz =
Uy'xx =
U"xy =
уже [177"
ди
дх
3x4y2z2,
2x4y3z,
24x3y2z,
36x2y2z2
24xVz,
| частные
у
х2+у2'
<у =
v =
t/Jx =
с =
tfxxz =
U%x =
производные
ди
ду
I2x3y2z2,
\2xVz2,
Sx3y3z,
12x2y2z,
12x2y2z,
llx2y2z.
для функц
X
x2+y2'
*) Разумеется, дифференциальные обозначения следует рассматривать как
цельные символы. Квадрат дх в знаменателе заменяет условно дх дх и указывает
на дифференцирование дваждыпо!; точно так же значок х внизу заменяет хх.
Это нужно иметь в виду и дальше.
189] § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 451
вычислим теперь дальнейшие производные:
д2и _ д ( у \ Ъу
~дх2 ~ ~дх~
д2и д
дхду ду \х2 +у2
д2и д ( х
ду дх дх
д2и _ д
'ду2 ~ ~ду
д3и д
дх2 ду ду
д3и д
2 2
х —у
(х2+у2
Ъу
\ бху2
бху —
г
1
г
-2х3
дудх2 дх \(х2+у2J
и т. д.
3) Для функции и = -—^^^=^^^ = [х2 + у2 + z2) 5 имеем последова-
у/х2 +у2 +z2
тельно: _ .
ди /22 2\ — §
д2и ,2/2.2. 2\-j ( 2 . 2 . 2\-\
аналогичные выражения получим и для |-|, ^-%. Сложив их, убедимся, что
функция и удовлетворяет уравнению:
д2и д2и д2и
=
4) Пусть у = f(x + at) + cp(x — at), где а = const, a f(u), cp(u) — две
произвольные функции, имеющие первую и вторую производные. Показать,
что j/ удовлетворяет уравнению —¦%¦ = а • —\, каковы бы ни были функции /и ср.
Пользуясь правилами дифференцирования сложной функции, находим * ^:
/ = /'(* + at) + <р'(х - at), -4 = f"(x + at) + <р"(х - at),
дх дх1
¦j- = f'(x +at)-a + cp\x - at) • (-а),
ot
—j = f"{x + at) • a1 + cp"{x - at) • (-aJ = a2 • —j,
dtl dxl
что и требовалось доказать.
*) Штрихи в обозначениях ff,q>',... означают производные по аргументу и
функций f(u), ф{и).
452 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [190
5) Доказать, что выражение
где ср и гр — произвольные функции (имеющие первую и вторую производ-
производные), удовлетворяет уравнению
х2 Э^+2х d2z | 2 d2z
дх2 дхду ду2
Имеем:
д* (У\ У , (У\ У ,t (У\
Тх=Л-х)--х'(р Ы"^^ Ы'
dz , (у\ 1 I (У\
дх2 х3 \х) х3 \х) х4 \х) '
У п (у\ 1 ,'(У\ У ," (У\
52^ 1 „ (у\ \ „ /у\
—- = - • ср 1-1-1 ^ ' г I ~ ) »
dyz х \х J xz \x J
d2z
dy
:лед
действительно получаем 0.
умножая последние три производные, соответственно, на х , 2ху, у и складывая,
190. Теорема о смешанных производных. При рассмотрении
примеров 1) и 2) бросается в глаза совпадение смешанных про-
производных, взятых по одним и тем же переменным, но в разном
порядке.
Нужно сразу же отметить, что это вовсе не вытекает с необхо-
необходимостью из определения смешанных производных, так что
существуют случаи, когда упомянутого совпадения нет.
Для примера рассмотрим функцию
f(x9y)=xyJLrZy (прих2+у2>0), Д0,0) = 0.
х1 +у2
Имеем
Придав х частное значение, равное нулю, будем иметь при любом у (в том числе
и при;; = 0): ffx@,y) = —у. Продифференцировав эту функцию по j/, получим
fxy@,y) = — 1. Отсюда следует, в частности, что в точке @, 0) будем иметь
190] § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 453
Вычислив таким же образом f1' в точке @, 0), получим
/"*@,0) = 1.
Итак, для рассматриваемой функции /^@, 0) ф /"х@, 0).
Тем не менее, подмеченное на примерах совпадение смешанных
производных, отличающихся лишь порядком дифференцирований,
не случайно: оно имеет место в широком классе случаев — при
соблюдении определенных условий. Начнем со следующей простой
теоремы.
Теорема. Предположим, что 1) f(x,y) определена в {откры-
{открытой) области &), 2) в этой области существуют первые
производные /х и f'y, а также вторые смешанные произ-
производные fxy и ffjx и, наконец, 3) эти последние производные fxy
и f' как функции х и у непрерывны в некоторой точ-
точке (хо,.уо) области &. Тогда в этой точке
fZy(xo,yo)=f"Axo,yo). A)
Доказательство. Рассмотрим выражение
w _ f(xp + h, у о + к) - f(xp + h, у о) - f(xp, у о + к) + f(xp, у о)
~ hk '
где h, к отличны от нуля, например положительны, и притом на-
настолько малы, что в <%! содержится весь прямоугольник [хо, хо + h;
Jo? У о + к]; такими мы их фиксируем до конца рассуждения.
Введем теперь вспомогательную функцию от х:
которая в промежутке [хо, хо + /z], в силу 2), имеет производную
и, следовательно, непрерывна. С помощью этой функции выраже-
выражение W, которое равно
B)
454 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [190
можно переписать в виде:
= q>(xo + h) -фрр)
h
Так как для функции ср(х) в промежутке [хо, xo + h] выполняют-
выполняются все условия теоремы Лагранжа [112], то мы можем, по фор-
формуле конечных приращений, преобразовать выражение W так:
= f'xjxo + eh>yo + k)- /xQo + 9h,y0) ,Q<e<l\
К
Пользуясь существованием второй производной fxy(x,y)9 сно-
снова применим формулу конечных приращений, на этот раз — к функ-
функции от у: fx(xo + Oh,у) в промежутке [уо>.Уо + к]. Окончательно
получим
W = f"y(xo + 6h,yo + 0\k) (O<0, 0i<l). C)
Но выражение W содержит х и у, с одной стороны, и h и к —
с другой, одинаковым образом. Поэтому можно обменять их роли
и, введя вспомогательную функцию
,/ ч = f(xo + h,y) -f(xo,y)
путем аналогичных рассуждений получить результат:
W = f>;x(xo + 92h,yo + 93k) @<92,93<\). D)
Из сопоставления C) и D), находим:
ffxfy(x0 + 9h,y0 + 0i*) = /;х(х0 + 02h,y0 + 93k).
Устремив теперь кикк нулю, перейдем в этом равенстве к пределу.
Ввиду ограниченности множителей в, 6\, 02, #з? аргументы и спра-
справа и слева стремятся, соответственно, к хо, уо- А тогда, в силу 3),
окончательно и получим
fxy (х о > J о) = /^х (х о»J о), что и требовалось доказать.
Таким образом, непрерывные смешанные производные /х
и ffjx всегда равны.
190] § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 455
В приведенном выше примере эти производные
не имеют вовсе предела при jc —> 0,у —> 0 и, следовательно, в точке @,0) терпят
разрыв: к этому случаю наша теорема, естественно, неприложима.
Интересно поставить в связь вопрос о равенстве A) с вопро-
вопросом о повторных пределах, рассмотренным в п° 168. Если предпо-
предположить существование первых производных, то, написав выраже-
выражение W в виде B), легко усмотреть, что
lim W = — (h = const) E)
и, аналогично,
Тогда, по самому определению производной,
jhmfmlF, F)
f'(xo,yo) =
Таким образом, вопрос о существовании и равенстве смешанных
производных тождественен с вопросом о существовании и равен-
равенстве повторных пределов для выражения W (зависящего
от h и к).
Это замечание позволяет следующим образом усилить до-
доказанную теорему.
Предположим, помимо существования первых производных,
существование лишь одной из смешанных производных, напри-
например f"y(x,y), в окрестности точки (хо,уо) (исключая далее
саму эту точку). Пусть, далее, существует конечный предел
Отсюда уже вытекает существование в точке (хо,.уо) обеих
смешанных производных и равенство A).*)
*) Это предложение принадлежит Шварцу (Н. A. Schwarz).
456 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [191
Действительно, исходя из сделанных предположений можно,
как и выше, прийти к равенству C), а затем, пользуясь существо-
существованием предела функции fx'y{x,y) в точке (хо,уо)9 установить су-
существование двойного предела при одновременном стрем-
стремлении h и к к нулю.
Но простые пределы E) и E*), по предположению, су-
существуют: тогда, по теореме п° 168, существуют также повтор-
повторные пределы F) и F*) и равны двойному. А это и значит,
что существуют и равны между собой производные /хУ(хо>Уо)
191. Обобщение. Обратимся, наконец, к доказательству о б -
щей теоремы о смешанных производных:
Теорема. Пусть функция и = f(x\, Х2, • • • ,хп) от п пере-
переменных определена в {открытой) п-мерной области & и име-
имеет в этой области всевозможные частные производные до
{к — \)-го порядка включительно и смешанные производ-
производные к-го порядка, причем все эти производные непрерыв-
непрерывны в УЯ.
При этих условиях значение любой к-й смешанной про-
производной не зависит от того порядка, в котором произво-
производятся последовательные дифференцирования.
Доказательство. Для к = 2 теорема уже доказана, так что,
например,
д2и д2и
Действительно, чтобы свести этот случай к первой теоре-
теореме, достаточно заметить, что при вычислении этих производных
можно всем прочим переменным (кроме xt и Xj) приписать по-
постоянные значения, причем названные производные, непрерывные
по всей совокупности переменных, будут непрерывны и по пе-
переменным Xj и Xj9 при фиксировании остальных. Пусть теперь
к> 2.
Докажем сначала нашу теорему для того случая, когда при вы-
вычислении производной ?-го порядка произведена перестановка
191] § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 457
только между двумя последовательными дифференцирова-
дифференцированиями, т. е. докажем справедливость равенства
дки
dxh dxi2 . . . dxih dxih+l . . . dxh
G)
dxh dxh . . . dxih+l dxh . . . dxh
[Здесь z'i, /2, ..., ih, ih+i> • • • ¦» h есть некоторое размещение
из п знаков 1, 2, ... п по к, с возможными повторениями.]
Произведя последовательно необходимые для вычисления
этих производных дифференцирования, видим, что производ-
производные (h — 1)-го порядка в обоих случаях одинаковы. Применив к ним
уже доказанную для к = 2 теорему, получим, что и производ-
производные (А + 1)-го порядка равны. Дальше же в обоих случаях нужно
производить одинаковые операции, которые и приведут к одинако-
одинаковым результатам.
Итак, равенство G), действительно, справедливо, и теорема для
этого случая доказана. Но так как всякая перестановка элементов
может быть достигнута рядом перестановок двух последо-
последовательных элементов, то теорема доказана и в общем случае:
при условии непрерывности соответствующих производных, всегда
можно переставлять между собою дифференцирования по различ-
различным переменным.
Непрерывность производных мы впредь всегда будем предпо-
предполагать, так что для нас порядок последовательных дифференци-
дифференцирований будет безразличен. Это дает нам право впредь при обо-
обозначении смешанной производной собирать вместе дифференци-
дифференцирования по одной и той же переменной. Если и есть функция
от х\, Х2, ..., хП9 то мы будем писать такую производную в виде
дки
где а\ + «2 + • • • + ап — к; если же и есть функция от х, у, ..., z,
то — в виде
дки
дха
где а + /3 + ...+у=к. Отдельные «показатели» а\, «2» • • •» ап
или а, /3, ... ,у могут быть и нулями: наличие дифференциала
458 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [192
с «показателем» 0 означает отсутствие на деле дифферен-
дифференцирования по соответствующей переменной.
192. Производные высших порядков от сложной функции.
Пусть имеем функцию
и = f(xi,x2, • • .,*„),
где х\,х2, ... ,хП9 в свою очередь, суть функции от перемен-
переменных^,^, '",tm:
Xf =<Pi(tut29...9tm) (/ = 1,2, ...,/7).
Относительно функций f и срг предположим, что они
имеют непрерывные частные производные по всем перемен-
переменным до k-го порядка включительно. Рассматривая и как сложную
функцию от переменных t\, t2, ... ,tm:
U = F(t\, t2, • • • , tm) = /(фь ф2, • • • , Фп),
докажем, что сложная функция имеет также все производные
до k-го порядка включительно, и притом непрерывные.
Точнее говоря, мы будем доказывать следующее предложение:
каждая производная k-то порядка функции F су-
существует и составляется из производных функ-
функции / (по ее аргументам х\, х2, ..., хп) и функций срг (по их
аргументам t\, t2, ... 9tm)9 порядка не выше k-т о, путем
умножений и сложений.
Доказательство будем вести по методу математической ин-
индукции. Для к = 1 это утверждение справедливо; оно следует
из выведенной ранее формулы для производной сложной функ-
функции [181].
Предположим, что теорема верна для производных всех по-
порядков, низших, чем к; докажем, что она верна и для производ-
производных ?-го порядка. Каждая к-я производная получается из некото-
некоторой (к - 1)-й посредством дифференцирования по одному из tj.
Представим себе производную {к — 1)-го порядка. Она по пред-
предположению получается из производных функций / и cpt по пере-
переменным х и t порядков не выше к — \ путем умножений и сло-
сложений, т. е. представляет собой сумму произведений упомянутых
производных. Дифференцируя по tj любое из этих произведений,
мы должны по очереди дифференцировать каждый из множителей.
Если этот множитель есть производная порядка не выше к — 1 от
одной из функций ф, то в результате дифференцирования его мы
193] § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 459
получим производную той же функции порядка не выше к. Если
же это будет производная порядка не выше к — 1 функции /, то,
рассматривая эту производную как сложную функцию от перемен-
переменных t и дифференцируя ее по tj9 мы заменим ее известной суммой
произведений. *)
В результате, для рассматриваемой производной к-то порядка
получится, очевидно, выражение как раз указанного вида, что и до-
доказывает наше утверждение.
Непрерывность производных сложной функции F вытекает из
самого способа составления их из производных /и q>u поскольку
последние предположены непрерывными.
193. Дифференциалы высших порядков. Пусть в области &
задана некоторая функция и = f(x\, Х2, • • •, хп)9 имеющая непре-
непрерывные частные производные первого порядка. Тогда, как мы знаем,
(полным) дифференциалом du называется следующее выражение:
ди ди ди
du = -—dx\ + -—dx2 + . . . + -—dxn,
oxi 0x2 oxn
где dx\, ..., dxn — произвольные приращения независимых пере-
переменных JC l, . . . , Хп.
Мы видим, что du также является некоторой функцией
otxi,X2,...,xw. Если предположить существование непрерывных
частных производных второго порядка для и9 то du будет иметь не-
непрерывные частные производные первого порядка, и можно гово-
говорить о (полном) дифференциале от этого дифференциала du9 d{du)9
который называется дифференциалом второго порядка
(или вторым дифференциалом) от и; он обозначается сим-
символом d2u.
Важно подчеркнуть, что приращения dx\, dx2, ..., dxn при
этом рассматриваются как постоянные и остаются одними
и теми Dice при переходе от одного дифференциала к следу-
следующему. 26'
*^ Именно предположение о непрерывности всех производных функций/
и обеспечивает право пользоваться известным нам правилом для вычисления про-
производных от сложной функции [181].
26^ Фиксация одних и тех же значений приращений переменных во всех диффе-
дифференциалах весьма существенна. Она позволяет считать все дифференциалы функ-
функциями аргументов х\,Х2, • • • ,хп; это необходимо, чтобы повторно дифференци-
дифференцировать их [см. примеч. 25 на с. 428].
460 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [193
Таким образом, если воспользоваться правилами дифференци-
дифференцирования из п° 185, будем иметь
d2u = d(du) = d — dx i + — dx2 + ... + — dxn) =
\ox\ 0x2 oxn J
или, раскрывая,
i2 fd2u 7 д2и 1 д2и \ 7
^w= hrT^Xl + ^—Б^^Х2 + --- + ^——dxn)-dxi
\dxf дх\дх2 дх\дхп J
д2и 1 д2и 1 д2и 1
—dx\ + ~^dx2 + . . . + —dxn
x 9 дхдх
d2u 1 d2u 1 d2u 1 \ 1
^ + * + • • • + ir^ydxn ) -dxn
82U
^ ам 7 7 , a^ 7 7
+ 2 ^xi^2 + 2 ^1^3 + • • • +
OX I 0X2 OX I OX3
n-\ dxn.
+ 2<ix2^X3 + . . . + 2
0x20x3 охп-\дхп
Аналогично определяется дифференциал третьего по-
порядка, d3u, и т. д. Вообще, если дифференциал (к — 1)-го поряд-
порядка dk~lu уже определен, то дифференциал ?-го поряд-
к a dku определяется как (полный) дифференциал от дифференци-
дифференциала (к — 1)-го порядка*^
dku = d(dk~lu).
Если для функции и существуют непрерывные частные произ-
производные всех порядков до ?-го порядка включительно, то существо-
существование этого ?-го дифференциала обеспечено. Но развернутые вы-
выражения последовательных дифференциалов становятся все более
и более сложными. В целях упрощения их записи прибегают к сле-
следующему приему.
*) Легко установить понятие и о частных дифференциалах любого порядка;
на этом останавливаться не будем.
193] § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 461
Прежде всего, в выражении первого дифференциала условно
«вынесем букву и за скобки»; тогда его символически можно
будет записать следующим образом:
du = ( -—dx\ + -—dx2 + . . . + -—dxn) -и.
\3x\ 3x2 3xn J
Теперь замечаем, что если в выражении для второго диффе-
дифференциала также «вынести и за скобки», то остающееся в скобках
выражение формально представляет в раскрытом виде квадрат
выражения
-—dx\ + -—dx2 + . .. + -—dxn;
Зх\ 3x2 охп
поэтому второй дифференциал символически можно запи-
записать так:
72 ( д 7 Э 7 Э 7 V
d и = dx\ -\ dx2 + . . . Н dxn • и.
\дх\ 3x2 дхп )
Аналогично можно записать третий дифференциал, и т. д. Это
правило — общее: при всяком к будем иметь символическое
равенство
dxl + dx2 + ... + dxn) и, (8)
ах\ 0X2 vXn J
которое можно понимать так: сначала многочлен, стоящий в скоб-
скобках, формально возводится по правилам алгебры в степень,
затем все полученные члены «умножаются» на и (которое дописы-
дописывается в числителях при дк)9 и только после этого всем символам
возвращается их значение как производных и дифференциалов.
Мы видели, что это правило верно при к — 1,2; поэтому до-
достаточно показать, что если оно верно для dku9 то оно будет также
верно и для dk+lu.
Допустив, что этот закон для dku выполняется, будем иметь
в развернутом виде:
2> дх, дх2 дхп
где суммирование распространяется на всевозможные группы не-
неотрицательных целых чисел а\, «2» • • •» ат удовлетворяющих усло-
условию а\ + <Х2 + ... + ctn = к9 а
с - ш
суть «полиномиальные» коэффициенты.
462 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [193
В предположении, что существуют непрерывные производные
(к + 1)-го порядка, продифференцируем предыдущую формулу;
мы получим
Г Як+1и
rfk+\ \^r J ° иd
Очевидно, то же самое мы могли бы получить, формально
перемножив символические выражения:
п
( д 1 д 1 д 1
х — dx\ + -— dx2 + ... + -z— dxn
\дх\ 0X2 oxn
и потом приписав и. Но это «произведение» есть не что иное, как
д 1 д 1 д 1 к
-—dxi + -—dx2 + ... +-—dxn
OX I 0X2 OXn
/ д 1 д 1 д 1 \
x — dxx + -— dx2+ ... + — dxn =
\ax\ 0X2 oxn J
( д 1 д 1 д 1
= -— dx\ + -— dx2 + ... + t— dxn
\OX\ 0X2 vXn
так что
dk+lu= (—dxi + —dx2 + ... + —dxn) -и,
\ОХ\ 0X2 vXn J
что и требовалось доказать.
Из предыдущих рассуждений видим, что к-й дифференциал
является однородным целым27^ многочленом степени к,
или, как говорят, является формой к-й степени относитель-
относительно дифференциалов независимых переменных, коэффициентами
' Термин «целый» по отношению к многочлену подчеркивает, что в его
записи фигурируют лишь целые степени независимых переменных.
193] § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 463
при которых служат частные производные к-то порядка, умножен-
умноженные на целочисленные постоянные («полиномиальные» коэффи-
коэффициенты).
Например, если и = f(x,y)9 то
7? д2и 7 9 ^ д2и 7 7 д2и 7 9
d2d 2 + 2dd + d 2
x + 2dxdy + ^
дх ду dyz
3и = -^ dx3 + Зл й?х2^/у +
д3 дх2 ду
-4
дх ду5 ду4
и т. д. Положив конкретно и = arctg -, будем иметь
ydx—xdy 2 2х^(б/у2 — б/х2) + 2{х2 — y2)dx dy
(Л 1Л — ^ ^ . (Л1Л —
2+2
(X2+J2J
A8ху2 - 6x3)dx2dy
(х2
- \Sx2y)dx dy2 + Bx3 -
з _
и и —
и т.д.
Сложность выражения для дифференциала возрастает с увели-
увеличением числа переменных. Если и = fix, у, z), то, скажем, третий
дифференциал d3u в развернутом виде таков:
3m= — Jx + — dy + — dz) M=-TJx3 + -T
\3jc 3j dz ) дх5 ду5
dx2dy + 3
= Jz + 3Tdxdy + 3
dz5 дх1 ду дх ду
464 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [194
194. Дифференциалы сложных функций. Пусть мы теперь
имеем сложную функцию:
u = f(xi,x2, . . .,*„),
где, в свою очередь,
xt = q>i(tu t2,..., tm) (z = 1, 2, . . ., n).
В этом случае первый дифференциал может быть сохранен
в прежнем виде:
ди ди ди
du = -—dx\ + -—dx2 + . . . + -—dxn
oxi ox2 oxn
[на основании инвариантности формы первого дифференциа-
дифференциала, 185]. Но здесь уже dx\, ..., dxn являются дифференциалами
не независимых переменных, а функций и, следовательно, сами бу-
будут функциями, и могут не быть постоянными28', как
в предыдущем случае.
Вычислив теперь второй дифференциал нашей функции, бу-
будем иметь [если воспользоваться правилами дифференцирова-
дифференцирования п° 185]:
/J , д 7 д 7 \2
= -—dx\ + -—dx2 + . . . + -—dxn
\дх\ дх2 охп
ди о ди о ди 9
+ — • d2xi + -— d2x2 + ... + -—. d2xn.
oxi ox2 oxn
Мы видим, что для дифференциала порядка выше первого ин-
инвариантность формы вообще не имеет места.
Рассмотрим теперь частный случай, когда х\,х2, ... ,хп
являются линейными функциями от t\, t2, ... 9tm, т. е. когда
х, = а\\ + a\2)t2 + . . . + a\m)tm + Eг (/ = 1,2,..., п),
где cij и /3i — постоянные.
28 ^ См. примеч. 24 на с. 422.
195] § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 465
В этом случае будем иметь
dxf = a\l)dtx + .. . + a\m)dtm = a\l)Atx + .. . + a\m) Atm = Ax,.
Мы видим, что все первые дифференциалы функций х\, Х2, ...
..., хп в этом случае постоянны, не зависят от t\, t2, ..., tm;
следовательно, применимы без изменений выкладки п° 193. От-
Отсюда вытекает, что, в случае замены независимых перемен-
переменных х\,Х2, • • • ,хп линейными функциями от новых пе-
переменных t\, /2, ..., tm, могут быть сохранены прежние
выражения даже для дифференциалов высших порядков.
В них дифференциалы dx\, dx2, ..., dxn совпадают с приращения-
приращениями Ахь Ах2, ..., Ахт но эти приращения не произвольны, а обус-
обусловливаются приращениями At\9 At2, ..., Atm.
Это простое и важное замечание (принадлежащее К о ш и) мы
используем непосредственно в следующем п°.
195. Формула Тейлора. Мы уже знаем [126,A3)], что функ-
функция F(t)9 при условии существования ее п + 1 первых произ-
производных, может быть следующим образом разложена по формуле
Тейлора:
F{t)=F{to)+F'{to)-{t-to) +
+ ^ F"(t0) ¦ (t - t0J + ... + ^ F^ (t0) ¦ (t - to)" +
+ ^^ f("+1) (to + e(t -10)) • (t - to)n+x (о < в < i)
(дополнительный член взят в форме Лагранжа). Эту формулу,
положив
t - t0 = At = dt, F(t) - F(t0) =
можно переписать так:
AF(^o) = dF(t0) + ^ d2F(t0) + ... + ^ dnF(t0) +
+ T^ydn+lF(to + 6-At) @ < в < 1).
При этом важно подчеркнуть, что величина dt, входящая в раз-
различных степенях в выражения дифференциалов справа, в точ-
точности равна тому приращению At, которое фигурирует
в приращении функции слева.
466 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [195
Именно в последней форме формула Тейлора распростра-
распространяется и на случай функции от нескольких переменных.
Для упрощения письма ограничимся функцией f(x,y) двух пе-
переменных.
Предположим, что в окрестности некоторой определенной точ-
точки (хо,уо) эта функция имеет непрерывные производные всех по-
порядков до (п + 1)-го включительно. Придадим хо и у о некоторые
приращения Ах и Ау так, чтобы прямолинейный отрезок, соеди-
соединяющий точки (хо,уо) и (хо + Ах, у о + Ду), не вышел за пределы
рассматриваемой окрестности точки (хо,уо).
Требуется доказать, что при сделанных предположениях отно-
относительно функции f(x,y) справедливо следующее равенство:
Ay) -f(xo,yo) =
= df(xo,yo) + ^d2f(xo,yo) + ... + ^
^l О<0<1), (9)
причем фигурирующие справа в различных степенях дифферен-
дифференциалы dx и dy равны именно тем приращениям Ах и Ау неза-
независимых переменных, которые породили приращение функции
слева.
Для доказательства [как и в п° 183] введем в рассмотрение но-
новую независимую переменную t9 положив
x=xo+t-Ax, y=yo + t-Ay @<f<l). A0)
Подставив эти значения х и у в функцию f(x9y)9 получим
сложную функцию от одной переменной t:
F{t) = Дх0 +t-Ax,yo+t- Ay).
Мы уже знаем, что введенные нами в рассмотрение формулы A0)
геометрически выражают прямолинейный отрезок, соединяющий
точки Мо(хо,уо) и М(*о + Д*,.Уо + Ау).
Теперь мы видим, что вместо приращения
= f{xо + Ах,уо + Ay) - f(xo,yo)
195] § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 467
мы можем рассматривать приращение вспомогательной функции:
AF@)=F(l)-F@),
так как оба приращения равны. Но F(t) является функцией от од-
одной переменной и имеет [192] п + 1 непрерывных производных;
следовательно, применив к ней уже выведенную ранее формулу
Тейлора, получим
- F@) = dF@) + ^ d2F@) + ...+-. dnF(O) +
1 dn+lF{d) @<в< 1); A1)
(n+1)!
при этом дифференциал dt9 входящий в различных степенях справа,
равен Д* = 1 — 0 = 1.
Теперь, пользуясь тем, что при линейной замене перемен-
переменных свойство инвариантности формы имеет место и для высших
дифференциалов, можем написать, что
dF(O)=f'x(xo,yo)-dx+f'y(xo,yo)-dy=df(xo,yo),
d2F@) = ffj2(xo,yo) • dx2 + 2ffJy(xo,yo) • dxdy +
+ fy2(xo,yo) • dy2 = d2f(xo,yo),
и т. д. Наконец, для (п + 1)-го дифференциала будем иметь
dn+lFF) = dn+lf(x0 + в Ах, у о + ОАу).
Важно отметить, что здесь дифференциалы dx и dy ничем не
отличаются от ранее взятых приращений Ах и Ау. Дейст-
Действительно,
dx = Ах • dt = Ax, dy = Ay - dt = Ay.
Подставив все это в разложение A1), мы и придем к требуемо-
требуемому разложению (9).
Читатель должен дать себе отчет в том, что, хотя в дифференци-
дифференциальной форме формула Тейлора для случая функции нескольких
переменных имеет такой же простой вид, как и для случая функ-
функции одной переменной, — в развернутом виде она гораздо слож-
сложнее. Вот как выглядят первые три ее члена даже для функции лишь
468 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [196
двух переменных:
/(хо + Ах,уо + Ay) -f(xo,yo) =
= [fx(*o,yo) ¦ A* +f'y(xo,yo)^y] +
^ [f">(*o,yo) • Ах3 + 3/%у(хо,уо) ¦ Ах2Ay +
2(хо, у о) ¦ AxAy2+f^(xo,yo) ¦ Ду3] + • • •
Формула (9) имеет место и при /7 = 0; этот частный случай мы
уже рассматривали в 183.
§ 5. Экстремумы, наибольшие и наименьшие значения
196. Экстремумы функции нескольких переменных. Необходи-
Необходимые условия. Пусть функция
U =
определена в области @) и {х\,х\, ... ,х^) будет внутренней
точкой этой области.
Говорят, что функция f(x\, Х2, .. ., хп) 6 точке (х^, х\, . .., х%)
имеет максимум (минимум), если ее можно окружить
такой окрестностью
(jc?-5,jc? + 5; x°2-S,x°2 + S; ...; х°п - S,x°n + 5),
чтобы для всех точек этой окрестности выполнялось нера-
неравенство
Если эту окрестность можно взять настолько малой, чтобы знак
равенства был исключен, т. е. чтобы в каждой точке ее, кроме самой
точки (х^,Х2,...,х^), выполнялось строгое неравенство
196] § 5. ЭКСТРЕМУМЫ, НАИБОЛЬШИЕ И НАИМЕНЬШИЕ ЗНАЧЕНИЯ 469
то говорят, что в точке (х\,х\, ... ,х„) имеет место собствен-
собственный максимум (минимум); в противном случае, максимум (мини-
(минимум) называется несобственным.
Для обозначения максимума и минимума употребляется и об-
общий термин — экстремум.
Предположим, что наша функция в некоторой точке (хJ, х\, ...
..., х„) имеет экстремум.
Покажем, что е с л и в этой точке существуют (конечные) част-
частные производные:
то все эти частные производные равны нулю, так что обращение
в нуль частных производных первого порядка является не-
необходимым условием существования экстремума.
С этой целью положим х2 = х%, ..., хп = х%9 сохраняя х\ пере-
переменным; тогда у нас получится функция от одной переменной х \:
Так как мы предположили, что в точке (х^х^,...,^) сущест-
существует экстремум (для определенности — пусть это будет макси-
максимум), то, в частности, отсюда следует, что в некоторой окрестнос-
окрестности (xj —8,x(( + S) точки xi = х ^ необходимо должно выполняться
неравенство
/Yr r° r0>l < f(r° r° г0>!
/Vx Х х) ^ /VXX х)
так что упомянутая выше функция одной переменной в точке
х i = х 5 будет иметь максимум, а отсюда по теореме Ферма [109]
следует, что
ff /Y0 r0 r0\ _ 0
/xilxl>x2> • • -'X«J — U-
Таким же образом можно показать, что в точке (х^х^, ... ,х^)
и остальные частные производные также равны нулю.
Итак, «подозрительными» по экстремуму являются те точки,
в которых частные производные первого порядка все обращаются
470 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [197
в нуль; их координаты можно найти, решив систему уравнений *)
ffXl(xi,x2, . . .,х„) = 0, '
f'X2(xi,x2, ...,*„)= 0,
A)
fXn(xi,X2,...,Xn) = 0.,
Как и в случае функции одной переменной, подобные точки
называют стационарными.
Замечания. I. Необходимое условие существования экстре-
экстремума в случае дифференцируемой функции кратко можно записать
еще так:
df(xi,x2, ...,*„)= 0,
так как если f'Xl = f'X2 = ... = f'Xn = 0, то, каковы бы ни были
dx\9 dx2, ..., dxn9 всегда
df(xi,x2, . . .,хп) = fXl -dx\ +fX2 -dx2 + . . . +fxn -dxn = 0.
И обратно: если в данной точке тождественно выполняется это
условие, то ввиду произвольности dx\9 dx2, ..., dxn про-
производные fXl9 fXl9 ..., fXn порознь равны нулю.
П. Обычно рассматриваемая функция f(x\,x2, ... ,хп) имеет
(конечные) частные производные во всей области, и тогда точки,
доставляющие функции экстремумы, следует искать лишь среди
стационарных точек. Однако встречаются случаи, когда в от-
отдельных точках некоторые частные производные имеют бесконеч-
бесконечные значения или вовсе не существуют (в то время как остальные
равны 0). Подобные точки, собственно, тоже следует причислить
к «подозрительным» по экстремуму, наряду со стационарными точ-
точками [см. ниже: 201, 6)].
197. Достаточные условия (случай функции двух перемен-
переменных). Как и в случае функции одной переменной, в стационарной
точке вовсе не обеспечено наличие экстремума. Если для примера
*^ Для случая функции двух переменных z = f(x,y) — в предположении
ее дифференцируемости — условия
f'x{x,y)=Q, f'y(x,y)=0
допускают простое геометрическое толкование: касательная плоскость
[см. 180,F)] к поверхности z = f(x,y) в ее точке, отвечающей экстре-
экстремуму, должна быть параллельна плоскости ху.
197] § 5. ЭКСТРЕМУМЫ, НАИБОЛЬШИЕ И НАИМЕНЬШИЕ ЗНАЧЕНИЯ 471
взять простую функцию z — ху9 то для нее z'x = у и z' = х обра-
обращаются одновременно в 0 в единственной — начальной — точ-
точке @, 0), в которой z = 0. В то же время непосредственно яс-
ясно, что в любой окрестности этой точки функция принимает как
положительные, так и отрицательные значения, и экстремума нет.
На рис. 92 изображена поверхность (гиперболический параболо-
параболоид), выражаемая уравнением z = xy; вблизи начальной точки она
имеет седлообразную форму, изгибаясь в одной вертикальной
плоскости вверх, а в другой — вниз.
Таким образом, встает вопрос об условиях, достаточных
для существования (или отсутствия) экстремума в стационарной
точке, т. е. о том исследовании, которому эта точка должна быть
дополнительно подвергнута.
Мы рассмотрим сначала случай функции двух перемен-
переменных f(x,y). Предположим, что эта функция определена, непрерыв-
непрерывна и имеет непрерывные частные производные первого и второго
порядков в окрестности некоторой точки (хо,уо)9 которая является
стационарной, т. е. удовлетворяет условиям
fx(xo,yo)=O, f'y(xo,yo)=O. (la)
Чтобы установить, действительно ли наша функция имеет в точ-
точке (хо,уо) экстремум или нет, естественно обратиться к рассмотре-
рассмотрению разности
A = f(x,y)-f(xo,yo).
Разложим ее по формуле Тейлора [195], ограничиваясь двумя
членами. Впрочем, так как точка (хо,уо) предположена стационар-
стационарной, то первый член исчезает, и мы будем иметь просто
А = !{/? • Ах2 + 2f% ¦ Ах Ay + /;2 • Ау2}. B)
При этом роль приращений Ах, Ау играют разности х—хо,у—уо
и производные все вычислены в некоторой точке
(хо + вАх,уо + вАу) @< в < 1).
Введем в рассмотрение значения этих производных в самой ис-
испытуемой точке:
C)
472 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
И ПОЛОЖИМ
[197
9Ау) = ап + «и,
"i(. ..)=a22
D)
так что, ввиду непрерывности вторых производных,
все а -л О при Ах —>> 0, Ау -л 0.
Разность А напишется в виде:
Д = - |#п Ах2 + 2а\21АхАу + а22Ау2 +
¦аи Ах2 + 2ai2AxAj/
Как мы установим, поведение разности А существенно зависит от
знака выражения а\\а22 — а\2.
Для облегчения рассуждений введем «полярные координаты»,
взяв за полюс исходную точ-
точку (*(ь.Уо) и проведя через нее
полярную ось параллельно
оси х (рис. 105). Пусть р —
= л/Ах2 + А^2 есть расстояние
между точками (хо,.уо) и (x,j/),
а ф означает угол, составленный
соединяющим их отрезком с по-
поХ0 X
Рис. 105
лярной осью, так что
Ах = р cos ф, Ау = р sin ф.
Тогда интересующая нас разность А напишется так:
А = -z-jtfn cos2 q> + 2а \2 cos q> sin q> + a22sin2 cp +
+ an cos ф + 2ai2cos<psin<p + a22sin cp>.
1° Пусть, сначала, аца22 - a\2 > 0.
В этом случае аца22 > 0, так что а\\ Ф 0, и первый трех-
трехчлен в скобках {... } может быть представлен в виде:
Ч- E)
197] § 5. ЭКСТРЕМУМЫ, НАИБОЛЬШИЕ И НАИМЕНЬШИЕ ЗНАЧЕНИЯ 473
Отсюда ясно, что выражение в скобках [... ] всегда положитель-
положительно, так что упомянутый трехчлен при всех значе-
значениях ср, не обращаясь в нуль, сохраняет знак ко-
коэффициента а\\. Его абсолютная величина как непрерывная
в промежутке [0,2л] функция от ср имеет (очевидно, положи-
положительное) наименьшее значение т [85]:
а\\ cos2 ср + 2аи cos ср sin ср + #22 sin2 ф| ^ т > 0.
С другой стороны, если обратиться ко второму трехчлену
в скобках {...}, то, ввиду D),
\а\\ cos2<p + 2ai2cos<psin<p + a22sin2</)| ^ \ct\\\ + 2\ап\ + \ct2i\ < m
сразу для всех ср, если только р (а с ним и Ах, Ау) достаточно ма-
мало. Но тогда все выражение в скобках {...}, а значит и разность А,
будет сохранять тот же знак, что и первый из трехчленов, т. е.
знак а\\.
Итак, если а ц > 0, то и А > 0, т. е. функция в рассматриваемой
точке (хо,.уо) имеет минимум, а при а\\ < 0 будет и А < 0,
т. е. налицо максимум.
2° Предположим теперь, что а\\п22 — а^2 < 0.
Остановимся на случае, когда а ц ф 0, тогда можно и здесь
использовать преобразование E). При ср = ср\ = 0 выражение
в скобках [... ] будет положительно, ибо сведется к а\х. На-
Наоборот, если определить ср = ср2 из условия
а\\ cosqJ + аи sin<p2 = 0 (sin<p2 ф 0),
то это выражение сведется к (<яц<Я22 - ^12) s^2 Я>2 и будет отри-
отрицательно. При достаточно малом р второй трехчлен в скоб-
скобках {... } как при ср = фь так и при ср = ср2, будет сколь угодно
мал, и знак А определится знаком первого трехчлена. Таким
образом, в любой близости от рассматриваемой точки (хо,.уо) на
лучах, определяемых углами ср = ср\ и ср = ср2, разность А будет
иметь значения противоположных знаков. Следовательно, в этой
точке экстремума быть не может.
Если а и = 0 и первый трехчлен в скобках {... } сведется к
2а i2 cos ф sin ф + B22 sin ср = sin ср • {2а и cos ф + <222 sin ф),
то, пользуясь тем, что наверное аи ф 0, можно определить угол
ср\ ф 0 так, что
22| • I sinфх
474 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [197
Тогда при ср = ср\ и ср = q>2 = —ср\ упомянутый трехчлен будет
иметь противоположные знаки, и рассуждение завершается, как
и выше.
Итак, если аца22 — а\2 > 0, то в испытуемой стацио-
стационарной точке (хо,.уо) функция f(x,y) имеет экстремум,
именно, собственный максимум при ац < О и собствен-
собственный минимум при ац > 0. Если же а\\п22 — а\2 < 0, то
экстремума нет.
В случае же а ц а22 - а\2 = 0 для решения вопроса приходится
привлекать высшие производные; этот «сомнительный» случай мы
оставим в стороне.
Примеры.
1) Исследуем на максимум и минимум функцию
2 2
z = ^- + y— (p>0,q>0).
2р 2q
Вычислим частные производные:
, _ х_ г _У_
Zx~ p Zy~ q
Отсюда сразу видим, что единственной стационарной точкой является начало
координат @, 0).
Вычислив а и, а\2 и а22, получим
1 1
ап = -, а и = 0, а22 = -',
р q
отсюда а и а 22 — я 12 > 0. Следовательно, в точке @, 0) функции z имеет мини-
минимум; впрочем, это ясно и непосредственно.
Геометрическим образом нашей функции будет эллиптический пара-
параболоид с вершиной в начальной точке (ср. рис. 93).
х2 у2
2)z = — -y- (p>0,q>0);
2р 2q
= - z = --
Р У q
И здесь видим, что стационарной точкой является @, 0).
Вычисляем
ап = -, а и = 0, а22 = --;
р q
отсюда а\\п22 ~ а\2 < 0. Следовательно, экстремума нет.
Геометрически мы здесь имеем дело с гиперболическим парабо-
параболоидом, вершина которого — в начале координат.
3) z = у2 + х4 или z = у2 + х3; в обоих случаях стационарной является
точка @, 0) и в ней <2ц<222 ~ ^12 = ®-
Наш критерий не дает ответа; при этом, в первом случае, как непосредственно
видно, налицо минимум, а во втором — экстремума вовсе нет.
198] § 5. ЭКСТРЕМУМЫ, НАИБОЛЬШИЕ И НАИМЕНЬШИЕ ЗНАЧЕНИЯ 475
Замечание. Результаты настоящего п° впоследствии [236]
окажутся тесно связанными с геометрическим вопросом о пове-
поведении кривой вблизи ее «особой» точки.
198. Достаточные условия (общий случай). Обратимся теперь
к рассмотрению общего случая. Пусть функция /(xi,X2, ... ,хп)
определена, непрерывна и имеет непрерывные производные перво-
первого и второго порядков в окрестности некоторой стационарной
точки (х^,Х2,...,х^). Разлагая разность
A = f(xl9X29...9xn)-f(x0l9x029...9x0n)
по формуле Тейлора, получим, как и выше,
+ 2fi[X3 • Дх1 Ахз + ... + 2fl_xXn • Ахп^Ахп) =
_ 1 Л „
*иъ=\ ХгХк
где Axj = xt — х®; производные все вычислены в некоторой точке
Введем и здесь значения
fxiXk(x^9 х%, • • •, х%) = atk (/, А: = 1, 2, . . ., п), F)
так что
fx'ixk(x\ + 0Д*Ь ...,*? + 0Ах„) = a/it + «/it, *}
и
a,i -» 0 при Axi -)> 0, ..., Ах„ -)> 0. G)
Теперь интересующее нас выражение А можно написать в виде
- !/V V 1
^7 fr—1 7^—1 ^
На первом месте в скобках здесь стоит второй дифферен-
дифференциал функции / в рассматриваемой точке; он представляет собой
*} Ясно, что а1к = ак1 (и alk = akl).
476
ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[198
однородный многочлен второй степени или, как говорят, квадра-
квадратичную форму от переменных Ах\, ..., Ахп. *) От свойств
этой квадратичной формы, как мы увидим, и зави-
зависит решение интересующего нас вопроса.
В высшей алгебре квадратичную форму
(9)
i,k=l
от переменных у\, ... ,уп называют определенной положитель-
положительной (отрицательной), если она имеет положительные
(отрицательные) значения при всех значениях аргументов, не
равных одновременно нулю. Так, например, форма
6yi + Ъу\ + 14уз + 4yiy2 - 8у\уз - ЬгУъ
будет определенной положительной. Это становится ясным, если
представить ее в виде
Byi - Зу3J + 2(yi + у2 +уъ? + 3(у2 ~Уъ?.
Мы не имеем возможности вдаваться здесь по этому пово-
поводу в подробности. Ограничимся упоминанием о принадлежащем
Сильвестру (J.J. Sylvester) необходимом и достаточном условии
для того, чтобы форма (9) была определенной и положительной.
Оно выражается цепью неравенств:
ап > О,
ап
аг\
Я31
аи
Я 22
^32
ап
ап
> О,
а \п
**)
ап\ ап2
*' Вторая сумма имеет сходный вид, но в ней и коэффициенты сами суть функ-
функции от тех же переменных.
**) Обращаем внимание на то, что член cytyk (i ф к) встречается в сумме (9)
дважды, так что а^ = а^ есть половина коэффициента при;;ty^. Для нашего
примера условие легко проверяется, если учесть, что
а\\ = 6, «22 = 5, «зз = 14,
а\2 = а2\ = 2, d\i = «31 = —4, «23 = ^32 = ~1-
198] § 5. ЭКСТРЕМУМЫ, НАИБОЛЬШИЕ И НАИМЕНЬШИЕ ЗНАЧЕНИЯ 477
Так как определенная отрицательная форма с изменением знака
всех ее членов переходит в определенную положительную, и обрат-
обратно, то отсюда легко найти и характеристику отрицательной фор-
формы: она дается цепью неравенств, которая получается из написан-
написанной выше изменением смысла неравенств через одно (начиная
с первого).
Пользуясь этими понятиями, сформулируем достаточные для
существования экстремума условия:
Если второй дифференциал, т. е. квадратичная форма
п
Y, aikAxiAxk A0)
i,k=l
со значениями F) коэффициентов оказывается определен-
определенной по л о лейте лън ой {отрицательной) формой, то
в испытуемой точке {х\, ... ,х%) будет собственный минимум
{максимум).
Для доказательства введем расстояние
р = ^Ах\ + ...+Ах2п
между точками (х5, ..., х%) и (х\, ..., хп). Вынося в (8) за скоб-
скобку р1 и полагая
/ = 1,2,...,и),
перепишем выражение для А в виде
2 г п п n
Л Р / V" at i V" ? ? \
Z\ = —-< ^^ uikSiSk + ^2_^ aikbibk (•
^i,k=2 i,k=l *
Числа |,- зараз не обращаются в нуль, поэтому, если фор-
форма A0) — положительная, первая сумма в скобках в форму-
формуле A1) имеет всегда положительный знак. Больше того, так как
Е!г2 = 1, A2)
1=1
то найдется такое постоянное положительное число w, что
при всех возможных значениях |z- будет
п
Е
i,k=l
a ikiiik ^ гп.
478 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [199
Действительно, эта сумма представляет непрерывную функцию от
аргументов |z- во всем пространстве, в частности же — ив мно-
множестве *М тех точек (|ь ..., |„), которые удовлетворяют соотно-
соотношению A2) («сферическая поверхность»). Но множество это, как
нетрудно видеть, замкнуто, т. е. содержит все свои точки сгущения;
а тогда, по теореме Вейерштрасса [173, см. замечание после ее
доказательства], названная сумма будет иметь в *М и наимень-
наименьшее значение т9 необходимо положительное (как и все ее значе-
значения в ьЖ).
С другой стороны, ввиду G) вторая сумма в A1) для достаточ-
достаточно малых р, очевидно, будет по абсолютной величине уже мень-
меньше т9 так что вся скобка окажется положительной. Итак, в до-
достаточно малой сфере, с центром в точке (х^, ..., х%)9 разность А
будет положительна, откуда и явствует, что в названной точке функ-
функция /(ii, ..., хп) имеет собственный минимум.
Аналогично исчерпывается и случай, когда форма A0) будет
определенной, но отрицательной.
199. Условия отсутствия экстремума. Квадратичная форма (9)
называется неопределенной, если она способна принимать значе-
значения противоположных знаков. Такова, например, форма
бу? +у\ + Уз + 8J>iJ>2 - %У\Уъ - 2-У2УЗ.
Действительно, например, ее значение равно +6 при у\ — 1,
У2 =УЗ = 0 И -1 При у\ = 19у2 = -19уз = 0.
Теперь мы можем дополнить доказанное в предыдущем п° пред-
предложение следующим образом:
Если квадратичная форма A0) будет неопределенной,
то в испытуемой точке (х\, ..., х%) заведомо нет экстремума.
Пусть при Axj = hi (i = 1,2,..., п) форма A0) принимает
положительное значение:
п
Е
i,k=l
aikhihk > 0, A3)
L
а при Axj —hi (z = 1, 2, ..., n) — отрицательное:
n
У а^^^ < 0.
i,k=l
199] § 5. ЭКСТРЕМУМЫ, НАИБОЛЬШИЕ И НАИМЕНЬШИЕ ЗНАЧЕНИЯ 479
Положим сначала
Axj=hjt при гфО (/ = 1,2, ...,«),
что отвечает передвижению вдоль по прямой, соединяющей
точки (xj, ..., х„) и (xj + йь ..., х^ + Aw)- Тогда, вынося в (8)
за скобки t2, получаем для этого случая
^V 7^—1 У 7^—1 ^
^2
2 ' ¦ ' " i,k=l
Первая сумма в скобках есть определенное положитель-
положительное число, ввиду A3). Что же касается второй суммы, то ее
коэффициенты стремятся к 0 при t —>> 0, ибо при этом, очевидно,
и все Axj —>> 0. Значит, при достаточно малом t, выражение в фи-
фигурных скобках (а с ним и вся разность А) становится поло-
положительным, т. е. в точках упомянутой выше прямой, достаточно
близких к (х^, ..., х^), будет
С другой же стороны, если взять
Axi=hjt при t ф 0 (/ = 1,2, ...,«),
т. е. передвигаться вдоль другой прямой, соединяющей точку
(xj, ..., x*J) с точкой (xj+Ai, ..., x%+hn)9 то в ее точках, достаточ-
достаточно близких к (х^, ..., х^) (т. е. отвечающих достаточно малому t)9
окажется
Этим доказано, что в испытуемой точке не может быть ни мак-
максимума, ни минимума.
Может случиться, что форма (9), не будучи способна прини-
принимать значения разных знаков, все же не является определенной,
ибо обращается в 0 не только при нулевых значениях аргументов:
в этом случае форму называют полуопределенной. Это относится,
например, к форме:
у\ +у\ +у\ + 2У\У2 + 2у\уз + 2у2Уз = (у\ +У2 +узJ;
отрицательных значений она не принимает, но в 0 обращается вся-
всякий раз, когда
У\ +У2 +УЪ = 0,
скажем, при у\ — у2 = \ и ^з = — 1.
480 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [200
Случай, когда форма A0) оказывается полуопределен-
полуопределенной, есть «сомнительный» случай. В зависимости от поведения
высших производных, в этом случае может быть экстремум, мо-
может его и не быть. В частности, высшие производные должны быть
привлечены и тогда, когда все производные второго порядка в ис-
испытуемой точке обращаются в 0.
Исследованием «сомнительного» случая мы заниматься не
будем.
Замечание. Для функции f(x) одной переменной фор-
форма A0) сводится к одному члену
где хо — испытуемая точка. Эта «форма», очевидно, является опре-
определенной — положительной при //;(*о) > 0 и отрицательной при
//;(хо) < 0. Таким образом, признак п° 137 есть частный случай
изложенного в 198.
Переходя к случаю функции f(x,y) двух переменных, заметим,
что и результат п° 197 также содержится в том, что было установле-
установлено в 198 и 199. Легко усмотреть, что попутно в 197 было доказано,
что форма
а и Ах2 + 2а и Ах Ау + аъгАу1
в случае, если а\\a2i - а\г > 0? будет определенной (положи-
(положительной при а и > 0 и отрицательной при а\\ < 0), в случае же,
если а\\п22 - а\2 < 0, — неопределенной.
200. Наибольшее и наименьшее значения функции. Приме-
Примеры. Пусть функция и = f(x\, X2, • • •, хп) определена и непрерывна
в некоторой ограниченной замкнутой области 3) и, за ис-
исключением, быть может, отдельных точек, имеет в этой области ко-
конечные частные производные. По теореме Вейерштрасса [173],
в этой области найдется точка (х^х^, — -,х%)9 в которой функ-
функция получает наибольшее (наименьшее) из всех значений.
Если точка (х^, х^, • • •, х%) лежит внутри области 319 то в ней
функция, очевидно, имеет максимум (минимум), так что в этом
случае интересующая нас точка наверное содержится среди «по-
«подозрительных» по экстремуму точек. Однако своего наибольшего
(наименьшего) значения функция и может достигать и на границе
области. Поэтому, для того чтобы найти наибольшее {наи-
{наименьшее) значение функции и = f(x\, ..., хп) в области 3),
нужно найти все внутренние точки, «подозрительные» по
200] § 5. ЭКСТРЕМУМЫ, НАИБОЛЬШИЕ И НАИМЕНЬШИЕ ЗНАЧЕНИЯ 481
экстремуму, вычислить значения функции в них и сравнить
со значениями функции в пограничных точках области: наи-
наибольшее {наименьшее) из этих значений и будет наибольшим
{наименьшим) значением функции во всей области.
Поясним сказанное примерами.
у t
1) Пусть требуется найти наибольшее значение ~
функции
и = sinx + sin;; — sinfx -\-у)
в треугольнике, ограниченном осью х, осью у и прямой
х + у = 2ж (рис. 106).
Имеем
их = cos* - cosO +j/), uy= cosy - cos(>
Внутри области производные обращаются в нуль
в единственной точке C^j-, ^f), в которой и = Щ^-. Так как на границе об-
области, т. е. на прямых х = 0, у = 0 их +^ = 2ж, наша функция равна 0,
то, очевидно, найденная выше точка {^у, ^у) и доставляет функции наибольшее
значение.
2) Найти наибольшее и наименьшее значения функции
и = а2х2 + Ь2у2 + А2 - (ах2 + by2 + cz2J
2 2 2л
при условии, что переменные х, у, z связаны зависимостью х + у + z =1
(и а > Ъ > с > 0). Определив отсюда z и подставив его выражение в и, придем
к функции
и = (а2 - с2)х2 + (Ъ2 - с2)у2 + с2 - [(а - с)х2 + (Ь - с)у2 + с]2
от двух независимых переменных х, у в круге х -\-у ^ 1.
Производные
их = 2х(а - с){(а + с) - 2[(а - с)х2 + {Ъ - с)у2 + с]},
и'у = 2у(Ъ - с){(Ъ + с) - 2[(а - с)х2 + {Ъ - с)у2 + с]}
одновременно обращаются в нуль в точках
A) х=у=0 (и = 0), B) х=0, У = ±^
C) * = ±^=> У=<>
Теперь надлежит обратиться к границе области, т. е. к окружности
х + у = 1. Определяя отсюда;; и подставляя его выражение в и, получим
функцию одной переменной х
и= (а2 - Ъ2)х2 + Ъ2 - [{а - Ъ)х2 + Ь}2
в промежутке [—1, 1]. Внутри этого промежутка производная
их =2{а -ЪJх(\ -2х2)
482 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [200
обращается в нуль при
D) х=0 (и = 0) и E) * = ±;^=
Наконец, вспомним о концах рассматриваемого промежутка
F) х = ±1 (и = 0).
Итак, подлежат сравнению значения
и= 0; i(fc -сJ; X-{a-cf; l- (а - ЬJ;
из них наименьшим будет 0, а наибольшим |(а — с) . Это и будут искомые наи-
наименьшее и наибольшее значения функции, которые достигаются, соответственно,
в точках
@, 0, ±1), @, ±1,0), (±1,0,0) и (±-L 0, ±4=
V v 2 V 2
Вообще, в случае функции двух переменных и = f(x,y), область обычно
оказывается ограниченной кривою (или несколькими кривыми). Вдоль этой
кривой (или каждой из кривых, если их несколько) переменные х, у либо зависят
одна от другой, либо обе зависят от одного параметра, так что на границе
наша функция и = f{x,y) оказывается зависящей от одной переменной, и ее
наибольшее (наименьшее) значение находится уже методами п° 139. Если, ска-
скажем, кривая задана параметрическими уравнениями:
х = q>(t), У = *p(t),
где t изменяется в промежутке [to, T], то на этой кривой наша функция будет
(сложной) функцией от V.
для которой наибольшее (наименьшее) значение найти мы умеем.
3) Найти наибольшее значение для произведения
и = xyzt
неотрицательных чисел х, у, z, t, при условии, что сумма их сохраняет постоян-
постоянную величину:
х +у +z +t = Ac.
Покажем, что наибольшее для и значение получится, когда множители все
равны: х = у =z = t = с. * ^
Определив t из данного условия: t = Ас — х — у — z, подставим в и это
выражение:
и = xyz{Ac — х —у — z).
Мы имеем здесь функцию из трех независимых переменных х, у, z в трех-
трехмерной области, определяемой условиями
х ^0, у ^ 0, z^0, х +у + z < 4с.
*) Мы лишь для определенности взяли число сомножителей равным четырем;
результат будет тот же для любого числа сомножителей.
200] § 5. ЭКСТРЕМУМЫ, НАИБОЛЬШИЕ И НАИМЕНЬШИЕ ЗНАЧЕНИЯ 483
Геометрически эта область представляется в виде тетраэдра, ограниченного
плоскостями х = 0, у = 0, z = 0, х + у + z = 4с.
Вычисляем производные и приравниваем их нулю:
— = yzDc - 2х -у - z) = 0, — = zxDc - х - 2у - z) = 0,
дх ду
— = ХуDс - х - у - 2z) = 0.
dz
Внутри области уравнения эти удовлетворяются лишь в точкех = у = z = с,
в которой и = с . Так как на границе области и = 0, то в найденной точке,
действительно, достигается для функции наибольшее значение.
Утверждение наше доказано (ибо при х = у = z = с также и t = с). *^
Вообще, в случае функции трех переменных и = f(x,y,z)9 область огра-
ограничивается поверхностью (или рядом поверхностей). Вдоль такой поверхности
переменные х, у, z зависят от двух параметров (ими могут служить и две из
этих переменных, как, например, только что: z = 4с — х —у). Тогда и функция и
будет зависеть только от двух параметров, так что определение наибольше-
наибольшего (наименьшего) значения ее на границе является уже более простой задачей,
о которой шла речь выше. И т. д.
Если функция и = f(x\, X2, . . ., хп) задана лишь в открытой (или нео-
неограниченной) области ЯЯ, то уже нельзя заранее утверждать, что она достигает
в области своего наибольшего (наименьшего) значения. Тем не менее такое зна-
значение в отдельных случаях может и существовать; мы поясним на примере, как
в этом можно удостовериться.
4) Найти наименьшее значение для суммы
и = х + у + z + t
положительных чисел х, у, z, t, при условии, что произведение их сохраняет
постоянную величину
xyzt = с4.
Покажем, что наименьшее значение для и получится, когда слагаемые все
равны: х = у = z = t = с. **^
с4
Определим t\ t = , подставим это выражение в и:
XV
и = х + у + z -\ .
xyz
*) Из сказанного следует, что произведение положительных чисел xyzt, сумма
которых равна 4с, не превосходит с , так что
т.е. среднее геометрическое не превосходит среднего ариф-
арифметического. Этот результат, справедливый для любого количества рассмат-
рассматриваемых чисел, нам уже известен [133, Dа)].
**) И здесь число слагаемых может быть любым [ср. сноску на с. 482].
484 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [201
Нам нужно отыскать наименьшее значение для этой функции трех переменных х,
у, z, в области, определяемой неравенствами х > 0, у > 0, z > 0, т. е. в первом
координатном октанте, открытом и безграничном.
Попробуем применить прежний метод: если в области есть точка, где наша
функция достигает наименьшего значения, то эта точка, как и прежде, должна
быть в числе стационарных. Имеем
с4 с4 с4
4 = 1--^-= 0, i/=l--?_= 0, i4 = l--i_ = 0;
xzyz y xyzz xyzz
отсюда х = у = z = с, чему отвечает t = с; при этом и = Ас.
Как теперь проверить, что это значение, действительно, будет наимень-
наименьшим?
Ясно, что при приближении к пограничным плоскостям х = 0, у = 0, z = 0,
равно как и при удалении в бесконечность, наша функция и бесконечно возрас-
возрастает. Найденную точку можно окружить кубом [е, Е;е, Е;е, Е], взяв Е > 0 на-
настолько большим, а е > 0 настолько малым, чтобы вне этого куба и на его
поверхности было и > Ас. Но в кубе, как в замкнутой и ограниченной об-
области, функция и должна иметь наименьшее значение; теперь уже ясно, что это
значение достигается именно в найденной выше точке и что оно будет наимень-
наименьшим и для всей первоначальной области, что и требуется доказать.
Замечание. В примерах 1), 3), 4) внутри рассматриваемой области суще-
существовала одна лишь «подозрительная» точка. Можно было бы удостовериться,
что в ней налицо максимум (или минимум). Однако — в отличие от того, что
было отмечено для случая функции одной переменной [см. замечание в 139], —
здесь из этого одного нельзя было бы сделать заключение, что мы имеем
дело с наибольшим {наименьшим) значением функции в области.
Следующий простой пример показывает, что подобное заключение в действи-
действительности может привести к неверному результату. Рассмотрим в прямоугольни-
прямоугольнике [—5, 5; —1, 1] функцию
и = х —Ах + 2ху — у .
Ее производные
их = Зх — Ъх + 2у, иу = 2х — 2у
в пределах области обращаются в нуль лишь в точке @, 0). Как легко убедиться
с помощью критерия п° 197, в ней функция имеет максимум (равный 0).
Однако значение это не будет наибольшим в области, ибо, например, в точ-
точке E, 0) функция и = 25.
Вследствие этого, в случае функции нескольких переменных — при разыска-
разыскании наибольшего или наименьшего значения функции в области — исследование
на максимум и минимум оказывается практически ненужным.
201. Задачи. Многие задачи — как из области математики, так и из других
областей науки и техники — приводят к вопросу о нахождении наибольшего или
наименьшего значения некоторой функции.
Решение задач 1)-4) связано с уже рассмотренными в предыдущем п° при-
примерами.
201] § 5. ЭКСТРЕМУМЫ, НАИБОЛЬШИЕ И НАИМЕНЬШИЕ ЗНАЧЕНИЯ 485
1) Среди всех вписанных в данный круг радиуса R треугольников найти тот,
площадь которого наибольшая (рис. 107).
Если через х, у, z обозначить центральные углы, опирающиеся на стороны
треугольника, то они связаны зависимостью
х + у + z = 2jt,
откуда
z = 2тт — х — у.
Площадь треугольника Р через них выражается так:
Р = - R2 • sinjc + - R2 • sinj/ + - R2 • sinz =
= -R2 • (sinjc + sin;; - sin(* +y)). Рис-
Область изменения переменных х и у здесь определяется условиями: х ^ 0,
у ^ 0, х + у ^ 2ж. Нужно найти те значения переменных, которые сообщают
выражению в скобках наибольшую величину.
Мы уже знаем [200, пример 1)], что это будутх = у = 3^, так что hz = у:
получается равно-
получается равносторонний треугольник.
2) Среди всех треугольников данного периметра 2р найти тот, площадь ко-
которого Р наибольшая.
Пусть х,у, z означают стороны треугольника; тогда по формуле Гер он а
P= y/p(p-x)(p-y)(p-z).
Можно было бы, подставив сюда z = 2р — х —у, преобразовать Р к виду
Р =
и искать наибольшее значение этой функции в треугольной области, о которой
уже была речь в 160,6).
Мы поступим иначе: задача сводится к нахождению наибольшего значения
для произведения положительных чисел
и = {р - х){р - у){р - z)
— при условии, что их сумма постоянна:
(Р ~ х) + (р - у) + (р - z) = Ър - 2р = р.
А мы уже знаем [200, пример 3)], что для этого все множители должны быть
равны, так что х = у = z = -j-. Снова получается равносторонний
треугольник.
3) Среди вписанных в данный эллипсоид
2 2 2
х у z
^+ &2 +^2 = !
прямоугольных параллелепипедов (с ребрами, параллельными его осям) найти
тот, который имеет наибольший объем.
486 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [201
Если через х, у, z обозначить координаты той из вершин, которая лежит
в первом координатном трехгранном угле, то объем v = 8xyz. Вместо v можно
рассмотреть величину
v2 х2 у2 z2
а2 Ь2 С2>
ибо они, очевидно, достигают своих наибольших значений при одних и тех же х,
y,z. По отношению же к и вопрос снова приводится к примеру 3) предыдущего п°.
Ответ:
х2 у2 z2 1 а Ъ с
—z = т = т = -, так что х = —=, у = —=, z = —=.
а2 Ъ2 с2 3 л/3 л/3 л/3
4) Предположим, что какой-нибудь газ (например, воздух) сжимается в пор-
поршневом компрессоре от атмосферного давления ро до давления р > pq.
Работа, затрачиваемая при этом на сжатие 1 моля газа, выразится так:
здесь R есть «газовая постоянная», Го — абсолютная температура газа до сжа-
сжатия, а у есть некоторое число (> 1), зависящее от конструкции компрессора.
Работа А, очевидно, тем меньше, чем меньше начальная температура Т$. При
больших степенях сжатия, когда экономия в затрачиваемой работе представляет
важность, разбивают весь процесс сжатия на несколько ступеней, в промежут-
промежутках подвергая охлаждению сжатый (и нагревающийся вместе с тем) газ. Пусть,
например, мы имеем трехступенчатый компрессор, с двумя промежу-
промежуточными холодильниками, в которых температура доводится снова до Т$. Если
обозначить через р\ и р^ давления в конце первой и второй ступеней, то общая
работа сжатия теперь будет
Тогда возникает вопрос, как при заданных ро, р, Tq выбрать промежуточные
давления р\ и р2 с таким расчетом, чтобы величина затрачиваемой работы была
наименьшей.
Если отбросить постоянный множитель и постоянные слагаемые, которые не
влияют на искомые величины р\ и р2, то дело сведется к исследованию выражения
Так как произведение
(-)
\P2J
у-\
У
у-\ / ^ у-\_ / ^ у-\_
(ЕЛ~ (Е1\~г (^-\~г - (Р-\
\Ро) \Pl) ' \P2J ~ \Po)
сохраняет постоянную величину, то, воспользовавшись примером 4), 200, сра-
сразу видим, что сумма и достигает своего наименьшего значения тогда, когда все
201] § 5. ЭКСТРЕМУМЫ, НАИБОЛЬШИЕ И НАИМЕНЬШИЕ ЗНАЧЕНИЯ 487
слагаемые равны:
или
(EL
у—1
у—1
у—1
EL - El - L.
Р0 ~ Р\ ~ Р2'
так что последовательные давления составляют геометрическую прогрессию.
Отсюда
Pi = \/Ро'Р>
5) На плоскости дан треугольник со сторонами а, Ь, с (рис. 108); на нем мож-
можно построить бесчисленное множество пирамид с данной высотой h. Требуется
из них найти ту, которая имеет наименьшую боковую поверхность S.
Вопрос сводится к нахождению
проекции М вершины пирамиды. По-
Положение ее определяется величинами
трех перпендикуляров х,у, z, опущен-
опущенных, соответственно, на стороны а, Ь,
с. Каждому перпендикуляру мы при-
приписываем знак плюс, если точка лежит
с той же стороны, что и сам треуголь-
треугольник, и знак минус в противном случае.
Величины х, у, z связаны соотношени-
соотношением (Р означает площадь треугольника)
откуда
by + cz = 2Р,
2Р - ах - by
Рис. 108
Интересующая нас боковая поверхность S выразится теперь так:
где z должно быть заменено найденным выражением; областью изменения
независимых переменных х, у является вся плоскость ху. Имеем
2S' =
откуда х = у = z.
¦ h2 л/у2 + h2 ^Jz2 + h2
Соответствующая точка М есть центр вписанного в треугольник круга.
Что этим значениям х и у отвечает наименьшее значение для S, легко пока-
показать, как в примере 4) предыдущего п°, опираясь на то, что — при безграничном
возрастании х или у — и S растет до бесконечности.
488
ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[201
6) Пусть даны на плоскости три точки М\(а\, Ь\), М^а^, ^2)? ^/3(^3» ^з)?
не лежащие на одной прямой. Требуется найти в этой плоскости такую точку,
чтобы сумма ее расстояний до данных точек была наименьшей.
Взяв любую точку М(х,у), положим
Pi = V(x - aiJ + (у -
Тогда исследованию подлежит функция
(» = 1, 2, 3).
Для нее существуют — везде, кроме данных точек, — частные произ-
производные
ди v-^ x ~ ai V~^
— = > = > cos#/,
дх ^ pi 7 '
ди v-^ У —
/
M3(a3,b3)
Рис. 109
°У Pi
где Of означает угол прямой М(М с осью х.
«Подозрительными» по экстремуму точками являются, таким образом, преж-
прежде всего точки М\, М2 и М3, в которых производных нет, а затем та точка Mq (мы
увидим, что она не всегда существует), в которой производные зараз обращают-
обращаются в 0. Так как при бесконечном возраста-
возрастании х или у наша функция и, очевидно, так-
также бесконечно растет, то наименьшего зна-
значения она достигает в одной из упомянутых
точек.
Чтобы разыскать стационарную точку
Mq, приравняем нулю обе частные производ-
производные; это даст нам условия:
cos в\ + cos 62 + cos 6>з = 0,
sin в\ + sin 62 + sin 6>з = 0.
Умножим первое на sin 62, а второе на cos 62 и вычтем; мы получим
sin@i - 02) = sin(#2 - 0з), откуда в\ - в2 = в2 - в3.
Аналогично найдем, что
Таким образом, углы между прямыми M\Mq, M2M0, M3Mq, взятыми попарно,
все должны быть равны ^, и точка Mq получается в пересечении дуг величи-
величиной =?. радиан, построенных на сторонах треугольника М1М2М3.
Если в этом треугольнике нет угла, большего или рав-
равного ^у, то названные дуги, действительно, пересекаются внутри треугольника
и определяют точку Mq, из которой стороны его видны под углами, равными 3^
(рис. 109). В этом случае надлежит сравнить значения, которые и получает в на-
названных четырех точках. Мы докажем, что значение и в стационарной точке Mq
будет меньше других (а значит, и вообще наименьшим). Действительно, по «тео-
«теореме косинусов»
мхм\ =
' моМ2 >
201] § 5. ЭКСТРЕМУМЫ, НАИБОЛЬШИЕ И НАИМЕНЬШИЕ ЗНАЧЕНИЯ 489
м0м2 + -
Аналогично,
1
2
Складывая, получим
М\М2 + М\МЪ > М0М\ + М0М2
т. е.
«(Mi) > и(М0).
Очевидно, точка М\ здесь может быть заменена точкой М2 или Mi,, что завершает
доказательство.
Иначе обстоит дело, если один из углов треугольника М\М2М^
равен или больше 'Щ-. Тогда стационарной точки вовсе не существует
и наименьшее значение функции и доставляется одной из данных точек М\, М2,
Мз — именно той, которая служит вершиной тупого угла.
Любопытной особенностью этой задачи является именно то, что в ней прихо-
приходится кроме стационарной точки считаться и с точками, в которых производных
не существует [ср. 196, замечание II].
7) Обобщим задачу 1): станем искать вписанный в данный круг (радиуса R)
(п + 1)-угольник с наибольшей площадью Р.
Обозначим через х\,х2, . . ., хп, хп+\ центральные углы, которые опираются
на стороны многоугольника; тогда
откуда
хп+х = 2ж - (х\ +х2 + . . . +хп).
Площадь Р равна
1 2 1 2 1 2 1 2
Р = - R • sin^i -\— R • sin^2 + . . . Н— R • sin;\;w -\— R • sinjcw+i;
если подставить вместо хп+\ его выражение, то вопрос сведется к разысканию
наибольшего значения для функции
+ sinBjr — (x\ + x2 + . . . -\-xn)j,
причем область & изменения независимых переменных х\,х2, . . . ,хп определя-
определяется неравенством
х\ ^ 0, х2 ^ 0, . . ., хп ^ 0, х\ + х2 + . . . + хп < 2тг,
т. е. представляет собой ^-мерный симплекс [162].
По общему правилу вычисляем производные и приравниваем их нулю:
+х2 + . . . +хп) = 0,
cosxn — cos(^i +x2 + . . . + хп) = 0;
490 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [201
единственной внутренней точкой области, в которой выполняются эти усло-
условия, будет точка
2л- / 2л-
тогда и
" п + 1 V "^ n + L
ей отвечает и = (и + 1) sin j^pj".
Для того чтобы доказать, что это действительно будет наибольшим значени-
значением и, воспользуемся методом математической индукции. При п = 2 наше утвер-
утверждение уже установлено в примере 1) предыдущего п°. Допустим, что оно верно
для случая п слагаемых синусов (так что для их суммы наибольшим значением
будет п • sin ^), и докажем верность его и для нашей суммы п + 1 синусов.
Согласно общим указаниям, сделанным выше, надлежит сравнить значение
{п + 1) sin -^Y со значениями, которые функция принимает на границе области @.
Возьмем, например, «грань симплекса» хп = 0; на ней и будет функцией лишь
от п — 1 переменных:
и, по допущению, наибольшим значением здесь будет п • sin ^. То же можно
установить и для других «граней». Но так как
2ж . 2тт * \
п • sin — < (и + 1) • sin , ;
п п + 1
то наше утверждение доказано. Наибольшую площадь будет иметь правиль-
правильный многоугольник.
8) Рассмотрим электрическую питательную сеть с параллельным
включением. На рис. 110 представлена схема сети, причем А и В — зажимы источ-
источника тока, а Р\, Р2, . . ., Рп — приемники тока, потребляющие, соответственно,
токи i\, i2, . - -, in- Требуется, при наперед заданном допустимом общем падении
потенциала в цепи 2е, определить сечения проводов так, чтобы на всю магистраль
пошло наименьшее количество меди.
AJ^A®A2®A3 An® Ап
Рис. ПО
Очевидно, достаточно ограничиться рассмотрением одного из проводов, ска-
скажем, ААп, так как другой провод находится в совершенно аналогичных условиях.
Обозначим через 1\, /2, ...,/« длины частей АА\, А\А2, . . ., Ап_\Ап (в м), через
*^ Это обстоятельство следует из того, что функция ^Ур. монотонно убывает
при возрастании z от 0 до ж [см. 133, 1)].
201] § 5. ЭКСТРЕМУМЫ, НАИБОЛЬШИЕ И НАИМЕНЬШИЕ ЗНАЧЕНИЯ 491
q\, q2, . . ., qn — площади их поперечных сечений (в мм ). Тогда выражение
= кЯ1 + hqi + ...+lnqn
как раз и представит объем всей затраченной меди (в см ); для него нам нуж-
нужно добиться наименьшей величины, принимая во внимание, что общее падение
потенциала в проводе ААп должно равняться е.
Легко подсчитать, какие токи J\,J2,...,Jn будут протекать в отрез-
отрезках АА\, А\А2, . . ., Ап_\Ап цепи:
J\ = h + h + • • • + in, h = h + • • • + in, • -, Jn = in-
Если обозначить через р сопротивление медной проволоки длиной в 1 м и с се-
сечением в \мм , то сопротивления этих отрезков будут
ph ph pin
r\ = , r2 = , ..., rn = ,
q\ qi qn
так что соответствующие падения потенциала в этих отрезках, согласно закону
Ома, выразятся так:
т pl\J\
T phh т
\ \\ е2 = r2Ji = , - - -, еп = rnJn =
q\ qi qn
Чтобы избежать сложных выкладок, мы, вместо переменных q\, q2, . . ., qn,
введем именно эти величины е\, е2, . . ., еп, связанные простым условием
е\ + е2 + • • • + еп-\ + еп = е, откуда еп = е — е\ — е2 — . . . — еп_\.
Тогда, в свою очередь,
pl\J\ phJl plnJn
q\ = , qi= q
e\ e2 en e — e\ — e2 — . . . — en_\
e\ en_\ e — e\ — . . . — en_\
причем область изменения независимых переменных е\, е2, . . ., еп_\ опре-
определяется неравенствами
е\ > 0, е2 > 0, . . ., еп_\ > 0, е\ + е2 + . . . + еп_\ < е
(открытый симплекс).
Приравнивая нулю производные и по всем переменным, получим систему
уравнений
(е - е\ - . . . - еп_\У
/2 г /2 т
ln-\Jn-\ V^ _ q
откуда (снова вводя еп)
/2 т /2 т /2 т
~о^ ~ ~ ~
е\
492 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [201
Удобно обозначить общую величину всех этих отношений через 4у (Я > 0). Тогда
ei = MiyJJi, e2 =
причем Я легко определяется из условия е\ + е2 + . . . + еп = е
Я =
НуР\-
Так как, при приближении точки (е\, е2, . . ., еп_\) к границе области, и рас-
растет до бесконечности, то найденные значения е\, е2, . . ., еп_\(еп) действительно
доставляют функции и наименьшее значение.
Наконец, возвращаясь к нашим основным переменным q\, q2, . . ., qn, на-
находим
Ф 0. A4)
A A A
так что наивыгоднейшие сечения проводов оказываются пропорциональными кор-
корням квадратным из соответствующих сил тока.
9) Метод наименьших квадратов. Так называется очень распростра-
распространенный метод обработки наблюдений, суть которого заключается в следующем.
Пусть требуется определить значения трех*^ величин х, у, z, если для них
установлено п > 3 линейных уравнений
djX + hiy + C[Z = dj (i = 1, 2, . . ., п),
причем некоторые из коэффициентов at, bj9 cz, di получены опытным путем и из-
известны лишь по приближению. При этом мы предположим, что хоть какие-нибудь
три из этих уравнений имеют определитель, отличный от нуля; например, пусть
а\ Ь\ с\
а2 Ъ2 с2
а3 Ъъ с3
Однако вычисленные из первых трех уравнений значения х, у, z, вообще
говоря, не будут точно удовлетворять остальным (либо ввиду неизбежных по-
погрешностей в коэффициентах уравнений, либо вследствие того, что сами равен-
равенства оказываются лишь приближенными). Не имея оснований предпочесть одни
уравнения другим и считаясь с неизбежностью погрешностей
какие бы ни брать значения х, у, z, стараются достичь лишь того, чтобы сумма
квадратов этих погрешностей
п п
W = ^ ^ = ^Ы + biy + C,Z - dif
i=\ i=\
была наименьшей (отсюда и название метода). Иными словами, наилучше
согласующимися с результатами опыта считаются те значения х, у, z, которые
доставляют наименьшую величину функции W = W(x, у, z).
*}Мы
ограничиваемся тремя величинами лишь для простоты письма.
201] § 5. ЭКСТРЕМУМЫ, НАИБОЛЬШИЕ И НАИМЕНЬШИЕ ЗНАЧЕНИЯ 493
По общему правилу, чтобы найти эти значения, приравниваем нулю произ-
производные от W по х, у, z:
п
2SS^al[alx + bty + ctz — dt) = О,
n
n
2 7 сЛа[Х -\- biy -\- CfZ — df) = 0.
Гаусс (С. F. Gauss) ввел другие обозначения сумм однотипных слагаемых,
разнящихся лишь указателями; именно, он пишет
п п
[аа] вместо \ at, [ab] вместо \ я/Ь/, и т. п.
i=\ i=\
В обозначениях Гаусса полученные для определения значений х, у, z
уравнения перепишутся так:
[аа]х + [ab]y + [ac]z = [ad],
[ba]x + [bb]y + [bc]z = [bd],
[ca]x + [cb]y + [cc]z = [cd];
их называют нормальными уравнениями.
Для того чтобы быть уверенными, что этими уравнениями однозначно опре-
определятся значения х, у, z, нужно установить, что определитель системы отличен
от нуля. Но, по известной теореме алгебры, квадрат этого определителя представ-
представляется в виде
[аа\
[Ьа]
Ы
[ab]
№
[сЬ]
[ас]
[be]
[ее]
= ?
аг
ак
причем суммирование распространяется на всевозможные сочетания (/, j, к)
из п значков 1, 2, . . ., п по три. Так как из всех определителей справа, по нашему
предположению, хоть один отличен от нуля, то отсюда и следует, что определитель
слева также не нуль.
Остается еще убедиться в том, что определяемые из нормальных уравнений
значения переменных действительно доставляют функции W наименьшее значе-
значение. Для этого достаточно, например, установить, что вне сферы достаточно боль-
большого радиуса W будет сколь угодно велико.
С этой целью рассмотрим значения первых трех скобок в выражении W
Ъ\у + c\z — d\ = mi, п2Х + b^y + cjz —
а\х
= M2,
C3Z
Ввиду A4), через эти значения, в свою очередь, линейно выражаются, с вполне
определенными постоянными коэффициентами, и х, у, z, так что, пока все три
величины mi, M2, Щ остаются ограниченными, ограниченными необходимо будут
сами х,у, z. Отсюда уже ясно, что при бесконечном возрастании г = х -\-у -\-z
также растет до бесконечности и щ -\- щ -\- щ (а следовательно, и W).
ГЛАВА ШЕСТАЯ
ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ;
ИХ ПРИЛОЖЕНИЯ
§ 1. Формальные свойства функциональных
определителей
202. Определение функциональных определителей (якобиа-
(якобианов). В настоящей главе (равно как и в других частях курса) важ-
важным формальным орудием исследования для нас явятся особого
рода определители, составленные из частных производных.
Изучим предварительно основные их свойства.
Пусть даны п функций от п переменных
У2 =
Уп =
A)
которые определены в некоторой /7-мерной области <%! и имеют
в ней непрерывные частные производные по всем переменным. Со-
Составим из этих производных определитель
ду\ ду\
дх\ дх2
дх\ дх2
дуп дуп
дх\ дх2
дхп
дхп
дуп
дхп
Этот определитель называется обычно функциональным опре-
определителем Якоб и или якобианом системы A) — по имени не-
немецкого математика Якоби (С. G. J. Jacobi), впервые изучившего его
203] § 1. ФОРМАЛЬНЫЕ СВОЙСТВА ФУНКЦИОНАЛЬНЫХ ОПРЕДЕЛИТЕЛЕЙ 495
свойства и применения. *) Обозначают его для краткости символом
У2, - - -,Уп)
D{x\, x2, . . . ,xn)'
сходным с обозначением производной. Якобиан имеет ряд свойств,
подобных свойствам обыкновенной производной.
203. Умножение якобианов. Кроме системы функций A), возь-
возьмем систему функций
= q>i(h,t2,
B)
хп =
определенных и имеющих непрерывные частные производные в об-
области ^. Пусть при изменении точки (t\, t2, ..., tn) в ?Р со-
соответствующая точка (х\, Х2, ..., хп) не выходит из области <%!,
так что у\,у2, • • • ,Уп можно рассматривать как сложные функции
от t\, t2, ..., tn через посредство х\, х2, ..., хп.
Умножим теперь якобиан системы A) на якобиан системы B):
дх 1 дх 1 дх 1
dt2
dtn
дхп дхп дхп
tx dt2 '" dtn
Из теории определителей нам известна теорема об умножении
определителей, выражающаяся формулой
п\\ CL\2 . . . CL\n
а2\ ^22 • • • а2п
ЯпХ ап2 • • • Япп
Ь\\ Ъ\2 ... Ь\п
Ъ2\ Ъ22 ... Ъ2п
Ъп\ ЪП2 ... Ъпп
=
С\\ С \2 ... С in
С2\ С22 ... С2п
Сп\ СП2 ... Спп
где общий элемент последнего определителя такой:
ai2b2k + .. . + ainbnk
*^ В науку якобианы были введены одновременно с Якоби и М.В. Остро-
Остроградским.
496 ГЛ. VI. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ [203
[умножение по правилу «строка на столбец»]. Применяя эту фор-
формулу к функциональным определителям, получим
3*1
дхп
д_У2
дхп
дхп
dt2
дх2
dtn
дх2
дхп дхп дхп
dt\ dt2 dtn
ду\ дх\ ду\ дхп
дх\ dt\ дхп dt\
ду2 дх\ ду2 дхп
дх\ dt\ дхп dt\
дуп дх\ дуп дхп
ду\ дх\ ду\ дхп
дх\ dtn " ' дхп dtn
ду2 дх\ ду2 дхп
дх\ dtn дхп dtn
дуп дх\ дуп дхп
дх\ dtn дхп dtn
Замечая, что, по формуле для производной сложной функции,
общий элемент этого определителя есть
/, дхп дуг
'"
дхп dtk dtk
мы можем последний определитель переписать в виде
ду\
~дГх
ik
дуп
dti
ду\
dt2
^h
дуп
dt2
Yn
dtn
дуп
~dh
Доказанное только что первое свойство якобиана в крат-
кратких обозначениях можно переписать так:
1,У2, - - -,Уп) D(xi,x2, • • .,х„) D(yi,y2, • • .,уп)
х2,..., хп) D(tu t2,..., tn) D(tu t2,..., tn)
-¦ C)
204] § 1. ФОРМАЛЬНЫЕ СВОЙСТВА ФУНКЦИОНАЛЬНЫХ ОПРЕДЕЛИТЕЛЕЙ 497
Если бы имели одну функцию у от х9 где х есть функция от t9 то
получили бы известную формулу для производной сложной функ-
функции:
- ^ = -?¦;
= -?¦; таким образом, выведенное свойство якобианов
является обобщением формулы для производной сложной функции.
Отметим особо тот случай, когда переменные t\, t2, ..., tn тож-
тождественны с у\,у2, • • • ,Ут так что система функций B) есть ре-
результат обращения системы A)*}. Тогда полученное соотно-
соотношение сведется к следующему:
,У2, • • -,Уп) D(xi,x2, • • .,хп)
или
,Х2, • • -,Хп) D(y\,y2, • • -,Уп)
VI, . . . , У л) 1
= 1
Р(Х1,Х2,...,Х„) '
D)
В этом виде оно напоминает формулу для производной обратной
функции.
204. Умножение функциональных матриц (матриц Якоби).
Пусть имеется т функций у\,у2, • • • ,Ут от п (п > т) перемен-
переменных jc 1, Х2, • • •, хп:
У\ =
У2 =
т =fm(xi,X2, . . . ,Х„),
причем, в свою очередь, переменные х\, Х2, • • •, хп являются функ-
функциями от т переменных t\, ^2, ... ,tm:
1 = q>i(h,t2, .. .Л/и),
Предполагая в обоих случаях существование непрерывных
частных производных, постараемся найти выражение для якобиа-
якобиана у\, у2, • • • , Ут Как фуНКЦИЙ ОТ t\, t2, . . . , tm.
*^ Самую возможность такого обращения мы здесь допускаем. См. следу-
следующий параграф.
498 ГЛ. VI. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ [204
В теории определителей устанавливается общая теорема
об умножении матриц (для которой использованная выше
теорема об умножении определителей является частным случаем).
Рассмотрим две матрицы (таблицы)
(ап аи ... а\п\
я 21 а22 ... а2п
\ат\
. . . атп)
и
(п > т).
фп\
Их произведением является квадратная матрица
\ сп
С21 С22
\Ст\ Ст2 . . .
элементы которой вычисляются по формулам
Cik — ацЪ\к + ааЪгк + • • • + Qi
ацх ац2 . . . ацт
ацх a^h - - - a2im
ami\ amii • • • amim
Ъ\х\ bix2 ... bjim
bi2l bi22 . . . bj2m
b\n\ bim2 . . . bimm
Соответствующий этой матрице определитель равен сумме
Е
распространяющейся на всевозможные сочетания (z'i, /2, ..., im)
из п значков 1, 2, ..., п по т.
Применив этот результат к функциональным матрицам
(или матрицам Якоби)
дух дух\ (дхх дхх дх\\
дх2
^Х~2
\дхх
дхп
дхп
дут
~дх~)
\,
дх2 дх2
dtx dt2
дхп_ дхп_
dt2
dtn
дхп
204] § 1. ФОРМАЛЬНЫЕ СВОЙСТВА ФУНКЦИОНАЛЬНЫХ ОПРЕДЕЛИТЕЛЕЙ 499
мы получим
ду\ дх\
ду2 дх\
ду\ дхп ду\ дх\ ду\ дхп
дхп dt\ дх\ dtm дхп dtm
ду2 дхп ду2 дх\ ду2 дхп
дхп dt\ дх\ dtm дхп dtm
... +
дУт д*п
дУт дх\
дх\ dt\ дхп
ду\ ду\
дхп дх12
дУт дх\
дх\ dtm
дут дхп
дхп dtm
?
ду\
дх12
дх1п
дх12
dtm
дх12
dtm
dt\ dt2
dtm
п дх12 дх1т
Если снова вспомнить формулу для производной сложной функции,
то определитель в левой части этого равенства перепишется так:
ду\ ду\ ду\
dt\ dt2 " ' dtm
дГХ
ti dt2 "' dtm
В кратких обозначениях полученный результат имеет вид
,У2, - - -,Ут)
'Л' У "\1\ 1 E)
V» 1
у
f^ D(xh,xi29...9xim) D(tut2,...,tm)
•> 4i • • ••> im)
где сумма распространяется на всевозможные сочетания из п
значков 1, 2, ..., п по т.
При т = 1 доказанная формула переходит в известную форму-
формулу для дифференцирования сложной функции (через посредство
нескольких промежуточных переменных):
dy y-^ ду dxj
~dt ~ ^~dx~t ' ~df
и, таким образом, является ее обобщением.
500 ГЛ. VI. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ [205
Отметим частный случай нашей формулы, который получается
при п = 3 и т = 2:
D(xi,x2)
=
D(ti,t2) ~ D(xux2) D(tut2)
Р(уиУ2) D(x2,x3) D(yuy2) D(x3,xi)
^ D(x2,x3) ' D(tl9t2) D(x3,xx) ' D(tl9t2) ' l ;
Эта формула находит себе особенно частое применение.
Мы установили ряд формальных свойств якобианов, анало-
аналогичных свойствам обыкновенных производных; к ним примыкает
и формула, которую мы выведем в одном из ближайших п° [210,8)].
Но более глубокая аналогия между производными и якобиана-
якобианами обнаруживается по той роли, которую они играют в теории
неявных функций (см. следующий параграф), и, особенно,
в вопросе о замене переменных в двойных, тройных
и, вообще, кратных интегралах (в третьем томе).
§ 2. Неявные функции
205. Понятие неявной функции от одной переменной. Предпо-
Предположим, что значения двух переменныхх иу связаны между собой
уравнением, которое, если все члены его перенести налево, в об-
общем случае имеет вид
F(x,y)=0. A)
Здесь F(x,y) есть функция двух переменных, заданная в какой-
либо области. Если для каждого значения х — в некотором про-
промежутке — существует одно или несколько значений у, которые
совместно с х удовлетворяют уравнению A), то этим определяет-
определяется, однозначная или многозначная, функция у = /(х), для которой
равенство
F(x,f(x)) = 0 B)
имеет место уже тождественно относительно х.
Возьмем, например, уравнение
205] § 2. НЕЯВНЫЕ ФУНКЦИИ 501
оно, очевидно, определяет у как двузначную функцию от х
в промежутке [—а, а], именно
И если вместо у подставить в уравнение Aа) эту функцию, то по-
получится тождество.
Здесь удалось найти для у очень простое аналитическое выра-
выражение через х, даже в элементарных функциях. Так обстоит дело
далеко не всегда. Если взять уравнение
у — х — ?sinj/ = 0 @ < е < 1),
которое нам уже встречалось [при других лишь обозначениях пе-
переменных, 83], то мы знаем, что этим уравнением у определяется
как однозначная функция от х, хотя в конечном виде она через
элементарные функции и не выражается.
Функция у = /(х) называется неявной, если она задана при
посредстве неразрешенного (относительно у) уравне-
уравнения A); она становится явной, если рассматривается непосред-
непосредственная зависимость j; oti. Читателю ясно, что эти терми-
термины характеризуют лишь способ задания функции у =/(х) и не
имеют отношения к ее природе. [Строго говоря, противопоставле-
противопоставление неявного и явного задания функции с полной четкос-
четкостью возможно лишь, если под явным заданием разуметь явное
аналитическое задание; если же, в качестве явного, допускать
задание с помощью любого правила [45], то задание функции у отх
с помощью уравнения A) ничем не хуже всякого другого.]
В простейшем случае, когда уравнение A) — алгебраическое,
т. е. когда функция F(x,y) есть целый относительно х и у много-
многочлен, определяемая им неявная функция у от х (вообще мно-
многозначная) называется алгебраической. Если степень уравне-
уравнения (относительноу) не выше четырех, то алгебраическая функция
допускает явное выражение в радикалах, при степени выше че-
четырех такое выражение возможно лишь в виде исключения.
Сейчас нас будет интересовать лишь вопрос о сущест-
существовании и однозначности «неявной» функции {рав-
{равно как и о других ее свойствах), независимо от возможно-
возможности представить ее в «явном» виде аналитической форму-
формулой. Впрочем, в этой постановке вопрос для нас не нов; с част-
частным случаем его мы имели дело, когда речь шла о существовании
502 ГЛ. VI. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ [206
и о свойствах обратной функции, и уравнением
У-/(х)=0
переменная х определялась как «неявная» функция от у.
Поучительна геометрическая трактовка указанного вопроса.
Уравнение A), при известных условиях, выражает кривую на плос-
плоскости [например, уравнение Aа), как известно, выражает эллипс
(рис. 111)]; в этом случае оно называется неявным уравне-
уравнением кривой. Вопрос заключается в том, может ли кривая A)
(или ее часть) быть выражена обычным уравнением вида у = /(х),
с однозначной функцией справа; геометрически это означа-
означает, что кривая (или ее часть) пересекается прямой, параллельной
оси у, лишь в одной точке.
Если мы желаем иметь однозначную функцию, то, как видно
на примере того же эллипса, нужно ограничить не только область
изменения х, ной область изменения у.
Мы будем говорить, для краткости, что в прямоугольнике
(a,b; c,d) уравнение A) определяет у как однознач-
однозначную функцию от х, если при каж-
у\ ^ | дом значении х в промежутке {а, Ъ)
уравнение A) имеет один, и только
один, корень у в промежутке (c,d).
Обычно нас будет интересовать опре-
определенная точка (хо,уо)9 удовлетворяющая
уравнению A) (лежащая на кривой), и в
роли упомянутого прямоугольника будет
фигурировать окрестность этой точ-
точки. Так, например, в случае эллипса (см. рис. 111), очевидно, можно
утверждать, что уравнение Aа) определяет ординатур как одно-
однозначную функцию от абсциссы х в достаточно малой окрестности
любой точки эллипса, кроме вершин его А, А' на большой оси.
206. Существование неявной функции. Теперь установим усло-
условия, обеспечивающие существование однозначной и непрерывной
неявной функции.
Теорема 1. Предположим, что
1) функция F(x,y) определена и непрерывна в некотором
прям оуголънике
@=[х0- А, х0 + А;у0- А', у о + А7]
с центром в точке (хо,уо)'9
206]
§ 2. НЕЯВНЫЕ ФУНКЦИИ
503
2) F(x,y) в этой точке обращается в нуль: F(xo,yo) = 0;
3) при постоянном х функция F(x,y) монотонно возрас-
возрастает (или монотонно убывает) с возрастанием у.
Тогда
а) в некоторой окрестности точки (хо,уо) уравнение A)
определяет у как однозначную функцию от х: у =/(х);
б) при х=хо эта функция принимает значение jo-
/Оо) =Уо1 наконец,
в) функция f(x) непрерывна.
Доказательство. Станем передвигаться вдоль вертика-
вертикали, проходящей через точку Мо(хо,уо) (рис. 112), т. е. фиксируем
х = хо; тогда рассматриваемая функция F(x,y) сведется к функ-
функции F(xo,y) от одной переменной у. В силу 2), она при у =уо
у-
Уо
У
Oft
/
/
/
'Г/Л
'////,
У///
У///
Л;\А
У////
у////,
¦
У////,
У////'
л
в2
У/.
У/.
Р
У/у
1
/
/
хо+А"
Рис. 112
обращается в 0. В то же время по условию 3) функция F(xo,y)
возрастает вместе с у, так что для у < у о ее значение меньше
нуля, а для у > у о — больше нуля. В частности, следовательно,
она будет иметь значения разных знаков в точках ^0(^0^0 — Д;)
и Во(хо,уо + А7), именно
F(A0) = F(jc0, У о ~ А7) < 0, F(B0) = F(jc0, Jo + А7) > 0.
Перейдем теперь к горизонтальным прямым, проходящим че-
через эти точки Ао и Во, т. е. фиксируем на этот раз у = у о - А7
или j=3;o + A7. Получатся две функции от одной пе-
переменной х: F(x,yo — А7) и F(x,yo + А7), которые, как
мы видели, при х = хо имеют: первая — отрицательное значе-
значение, а вторая — положительное. Но по условию 1) эти функции
504 ГЛ. VI. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ [206
непрерывны*), а потому найдется некоторая окрестность (хо — So,
%о + $о) точки хо @ < So ^ А), в которой обе функции сохраняют
свой знак [80, лемма], так что при хо — So < х < хо + So
F(x,y0 - А') < 0, F(x,y0 + А7) > 0.
Иными словами, на нижнем и верхнем основаниях исходного пря-
прямоугольника вдоль отрезков А\А2 и В\В2 длины 2So с центрами
в точках Ао и Во заданная функция F(x, у) имеет отрицательные
значения на первом и положительные — на втором.
Фиксируем в промежутке (хо - So,xo + So) любое значение
х = х и рассмотрим вертикальный отрезок, соединяющий
точки А(х, у о — А7) и В(рс,уо + А7). Вдоль него наша функция
снова сведется к функции Fix, у) от одной переменной у. Так как
она, в силу 1), непрерывна*) и, как сказано, на концах промежутка
\уо — А'9уо + А7] имеет значения разных знаков:
F(A) = Fix, у о - А7) < 0, F(B) = Fix, у о + А7) > 0,
то, по теореме Больцано-Коши [80], при некотором значении
у = у, содержащемся между у о - А7 и у о + А7, эта функция F(x, у)
обращается в нуль:
F(x9y)=0.
И здесь из условия 3) следует, что при у ^ у будем иметь, соответ-
соответственно, F{x,у) ^ 0, так что у есть единственное значение у
в промежутке (уо - А\уо + Af), которое совместно сх=х удо-
удовлетворяет уравнению A). На каждом вертикальном отрезке А В
найдется только одна точка Mix, у), обращающая левую часть
уравнения в нуль.
Таким образом, в окрестности
(х0 - So, х0 + So; уо - А7, у0 + А7)
точки (хо, уо) уравнение A), действительно, опре-
определяет у как однозначную функцию отх:^=/(х)-
В то же время предыдущее рассуждение, ввиду 2), показывает
также, что f{xo) = уо- Именно, из того что F(xo, у о) = 0, усматри-
усматриваем, что jo и есть то единственное значение у в промежутке
*) Мы предположили непрерывность функции F(x,y) по совокупности пере-
переменных х,у; но в таком случае она будет непрерывна и по каждой переменной
в отдельности.
207] § 2. НЕЯВНЫЕ ФУНКЦИИ 505
(уо ~~ А'9уо + А7), которое совместно с х = хо удовлетворяет
уравнению A).
Остается лишь установить непрерывность функции у = /(х)
в промежутке (хо - <So>*o + So). Для точки х =хо это получа-
получается непосредственно из предыдущего рассуждения, которое при-
ложимо и к любому меньшему прямоугольнику с центром в точ-
точке Мо(хо,уо). Заменив число А7 любым числом е < А7, мы нашли
бы, как и выше, такое S ^ <5о, чтобы для любого х из промежутка
(хо — S,xo + S) соответствующее ему единственное значе-
значение у, которое совместно с х удовлетворяет уравнению A), оказа-
оказалось именно междууо — е иуо + е. Таким образом, при \х — хо\ < S
имели бы
\f(x)-yo\ = \f(x)-f(xo)\<e,
что и доказывает непрерывность функции /(х) в точке х = хо-
Доказательство для любой точки х = х аналогично доказатель-
доказательству для х = хо- Точка М(х, у), где у = fix), удовлетворяет таким
же условиям, как и точка Мо(хо,.уо)? ибо F(jc,y) = 0. Поэтому,
как и выше, в окрестности точки M(Y,y) уравнением A) перемен-
переменная у определяется как однозначная функция от х, непре-
непрерывная в точке х = х. Но, именно ввиду однозначности, эта функ-
функция совпадает с /(х), и тем устанавливается непрерывность /(х)
при х = х.
Мы доказали теорему существования неявной функ-
функции, не задаваясь вопросом о вычислении ее значений или
об ее аналитическом представлении; этим мы займемся
в главе XII.
Доказанная теорема, очевидно, является обобщением теоре-
теоремы п° 83.
207. Дифференцируемость неявной функции. Теперь мы уси-
усилим предположения относительно функции F(x,y) и тогда полу-
получим возможность установить и существование производной для
функции у = /(х).
Теорема 2. Предположим, что
1) функция F(x,y) определена и непрерывна в прямо-
прямоугольнике
@=[х0- А, х0 + А; у о - А7, у0 + А7]
с центром в точке (хо,.уо);
506 ГЛ. VI. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ [207
2) частные производные F% и Fy существуют и непрерыв-
непрерывны в &;
3) F(x,y) в точке (хо,уо) обращается в нулъ:Р(хо,уо) = 0;
наконец,
4) производная Fy(xo,yo) отлична от нуля.
Тогда выполняются заключения а), б), в) теоремы 1 и, кро-
кроме того,
г) функция /(х) имеет непрерывную производную.
Доказательство (рис. 113). Пусть, например, Fy(xо,уо) > 0;
так как производная Fy(x,y)9B силу 2), непрерывна, то можно по-
построить такой квадрат:
[х0 - S\ х0 + 8'9 уо - 8', у0 + S'} (8' < А и А7),
чтобы для всех его точек было: F'(x9y) > 0. *) Тогда для это-
этого квадрата выполнены все условия теоремы 1: монотонность
У'
Уо
\
\
Рис. 113
функции F(x,y) no ^, при x = const, вытекает именно из того,
что Fy > 0 [132]. Следовательно, заключения а), б), в) можно счи-
считать оправданными.
Переходя к доказательству утверждения г), будем под у ра-
разуметь именно ту неявную функцию у = /(х), которая опреде-
определяется уравнением A) и тождественно ему удовлетворяет. При-
Придадим х приращение Ах; наращенному значению х + Ах бу-
будет соответствовать значение у + Ay = f(x + Ах), вместе с ним
*) Ибо и для функции нескольких переменных справедливо утверждение, ана-
аналогичное лемме п° 80 для функции одной переменной.
208] § 2. НЕЯВНЫЕ ФУНКЦИИ 507
удовлетворяющее уравнению A): F(x + Ах, у + Ау) = 0. Оче-
Очевидно, и приращение
AF(x,y) = F(x + Ах, у + Ау) -F(x,y) = 0.
Представив AF по формуле A) п° 178, получим
0 = AF(x,y) =Fx(x,y) -Ax + F^(x,y) -Ay +aAx + /ЗАу,
где аир зависят от Ах, Ау и стремятся к нулю, когда Ах и Ау
одновременно стремятся к нулю. Отсюда
Ау_ _ F^(x,y)+a
Ах ~ F;(x,j/)+/3*
Устремим к нулю Ах; в силу установленной уже непрерыв-
непрерывности функции у =/(х) [см. в)], при этом Ау также стремится
к нулю, а потому и а —>> 0, /3 —>> 0. Так как Fy ф 0, то существует
предел правой части, а следовательно, существует и производная у
по х:
Подставляя /(х) вместо j, будем иметь
так как в числителе и в знаменателе имеем непрерывные функции
от непрерывных же функций и знаменатель не обращается в нуль,
то отсюда ясно, что f'{x) — также непрерывная функция. Теорема
доказана.
Замечательно, что по свойствам функции F(x,j/), кото-
которая нам дана непосредственно, мы можем судить о свойствах
функции у =/(х), для которой непосредственного задания мы
не имеем.
208. Неявные функции от нескольких переменных. Аналогич-
Аналогично уравнению A) можно рассматривать и уравнение с большим
числом переменных
F(xi,x2, ...,xn,y)=0. D)
При известных условиях этим уравнением у определяется как «не-
«неявная» функция от п переменных хь Х2, ..., хп:
у =/(хьх2, . . .,*„),
508 ГЛ. VI. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ [208
которая, вообще говоря, будет многозначной. Если подставить ее
вместо у, то будем иметь
F(xi,x2, • • •, хп, /Оь х2, • • •, хп)) = 0
уже тождественно относительно х\, х2, ..., хп.
Мы будем говорить, что в (п + I)-мерном параллелепипеде
(а\,Ь\; п2,Ъ2\ ...; an,bn; c,d)
уравнение D) определяет у как однозначную функцию от
хь х2, ..., хп, если для любой точки (х\, х2, ..., хп), содер-
содержащейся в п-мерном параллелепипеде
(а\,Ъ\\ п2,Ъ2\ ...; ап,Ьп),
уравнение D) имеет один, и только один, корень у в проме-
промежутке (с, d).
В роли такого параллелепипеда обычно будет фигурировать
окрестность интересующей нас точки (х\, х\, ..., х%).
Сформулируем теперь относящуюся к уравнению D) теорему.
Теорема 3. Предположим, что
1) функция F(x\, ..., хп,у) определена и непрерывна
в {п + I)-мерном параллелепипеде
®=\хо1-Аих°1+ Д1; ...;х°п- Ап, х°п + Ап; у0 - А', у0 + Д'1
с центром в точке (х®, ..., х%, у о);
2) частные производные F^, ..., F^n, Fy существуют и не-
непрерывны в <3\
3) функция F в точке {х\, ..., х%, у о) обращается в нуль;
и, наконец,
4) производная Fy в этой точке не равна нулю.
Тогда
а) в некоторой окрестности точки (х^, .. .,х%,уо) уравне-
уравнение D) определяет у как однозначную функцию от х\, ..., хп:
у =f(xu...,**);
б) при х\ = Xj, ..., хп = х® эта функция принимает зна-
значение у о: /О?,..., xl) = у о;
в) функция f(x\, ..., хп) непрерывна по совокупности своих
аргументов и
г) имеет непрерывные лее частные производные fxv ... ,fXn.
208] § 2. НЕЯВНЫЕ ФУНКЦИИ 509
На доказательстве мы останавливаться не будем, так как оно
совершенно аналогично доказательству теорем 1 и 2.
Наконец, в самом общем случае может быть дана система из т
уравнений с п + т переменными
, .. .,хп;уи .. .,ут) = 0, ]
...,xn;yi,.. .,ym) = 0,
Fm(xi, ...,xn;yi,.. .,ym) = 0.,
E)
Здесь речь идет об определении этой системы т переменных
у 1, ..., ут как «неявных» функций от п переменныхх\,х2, ... ,хп:
У\ =
так что при подстановке в E) получаются тождества
. . ,х„), . . .,q>m(xi, . . .,х„)) = 0,
.. .,хп)) = 0.
Говорят, что б (п + т)-мерном параллелепипеде
{а\,Ъ\\ ...; an,bn; c\,d\\ ...; cm,dm)
система E) определяет yi,...,ym как однозначные
функции от х 1, ..., хп, если для каждой точки (х\, ..., хп)
б п-мерном параллелепипеде
{аи Ъ\\ ...; ап, Ъп)
система уравнений E) имеет одну, и только одну, систему
решений у и ... ,ут, принадлежащую т-мерному параллелепи-
параллелепипеду
{cud\\ ...; cm,dm).
Мы видели, что в вопросе о существовании однозначной неяв-
неявной функции, определяемой одним уравнением A) или D), ре-
решающую роль играло требование, чтобы в рассматриваемой точ-
точке, удовлетворяющей уравнению, не обращалась в нуль производ-
производная Fy — именно по той переменной, которая подлежит опреде-
определению как неявная функция. В вопросе же о существовании од-
однозначных неявных функций у и ... ,ут, определяемых системой
510 ГЛ. VI. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ [208
уравнений E), к которому мы сейчас переходим, аналогичную роль
будет играть якобиан от функций, стоящих в левых частях, по
переменным у \, ..., ут:
J =
D(FU
D(yu
...,Fm)
¦¦¦,Ут)
ду\
dF2
dyi
9Fm-\
dyi
dFm
ду\
dF2
ду2
dFm-l
dFm
ду2
dF2 dF2
дут-l дут
dFm-\ dFm-\
дут-l dym
dFm dFm
dym-\ дут
F)
Теорема 4. Предположим, что
1) все функции F\, ..., Fm определены и непрерывны
в (п + т)-мерном прямоугольном параллелепипеде
& = [х1 - Аь х°2 + Аь ...; х°п - АП9 х°п + Ап;
с центром в точке {х\, ..., х%; у\, ..., у^);
2) существуют и непрерывны в & частные производные
от этих функций по всем аргументам;
3) точка (х\, ... 9у%) удовлетворяет системе E);
4) якобиан J [см. F)] в этой точке отличен от нуля.
Тогда
а) в некоторой окрестности точки (х^,...,у%) система
уравнений E) определяет у\, ... ,ут как однозначные функции
от х\, ...,хп:
У\ =/lOb • • .,Хп), . . ., ут-\ =fm-l(xi, . . .,Хп),
Ут =fm(xi, • • чХп)',
б) при х\ = Xj, ... ,хп = х® эти функции принимают, со-
со,ym_i
ответственно, значения у\
/l(*?,...,*°)=J?, ..., fm-l(x°l9...9X°n)=y0m_l9
0 r0\ _ 0.
i, . . . ,Xn) — ym9
208] § 2. НЕЯВНЫЕ ФУНКЦИИ 511
в) функции /i, ..., fm непрерывны и
г) имеют непрерывные лее частные производные по всем
аргументам.
Доказательство поведем по методу математической ин-
индукции. При т = 1, когда система сводится к одному уравнению,
теорема верна (это — теорема 3). Допустим теперь, что теоре-
теорема верна для случая, когда система состоит из т — 1 уравнений
и речь идет об определении т — 1 неявных функций, и докажем ее
для системы из т уравнений.
Поскольку якобиан J в точке {х®, ..., у^) отличен от нуля, в по-
последнем столбце его хоть один элемент в этой точке также не равен
нулю; пусть, например,
Э/Ь(х°,...,у°)
ду
В таком случае, по теореме 3, последнее уравнение сис-
системы E) — в некоторой окрестности ^* точки
(х®, .. .,у%) — определяет ут как однозначную функцию от осталь-
остальных аргументов
ут = ф(хи .. .,хп;уи .. .,ym-i), G)
так что тождественно (относительно этих аргументов) имеем
Fm(xu . .. ,xn;yi, .. .,ут-и q>(xu .. .,ym-i)) = 0. (8)
Эта функция q> непрерывна и имеет непрерывные частные произ-
производные; кроме того,
<р(хо1,....хоя;у1...,уоя_1)=у°я. (9)
Важно подчеркнуть, что, поскольку мы ограничива-
ограничиваемся впредь упомянутой окрестностью 31*9 уравнение
Fm(xu .. .,хп;уи .. .,ут) = 0
равносильно уравнению G): в пределах ^* ему удовлетво-
удовлетворяют одни и те же системы значений переменных х\,...,хп;
Заменяя последнее из уравнений E) этим уравнением G)
и подставляя функцию ср вместо ут в остальные уравнения сис-
системы E), мы получим новую систему уже из т — 1 уравнений
512 ГЛ. VI. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ [208
с п + т — 1 переменными
Ф\(х\,...,хп\у\,.. .,ym-i) = 0, >
Ф2(х\, .. ,,xn;yi, .. .,ут-\) = 0, I
Фт-iOb • • -,xn;yi, .. .,ут-\) = 0, ,
где для сокращения положено (при j = 1, 2, ..., т — 1)
ФуОь • • -,хп;у\,.. .,ут-\) =
ь • • -,Ут-\))- (И)
Если выходить за пределы окрестности ^*, то сис-
система E) оказывается равносильной системе A0) с добавле-
добавлением уравнения G). Поэтому если нам удастся доказать, что систе-
системой A0) в достаточно малой окрестности d* точки {х\, ... ,y^_i)
т — \ переменных у\, ... ,ут-\ определяются как однозначные
функции от х 1, ..., хп:
yi=fl(xi,---,Xn), . .., ym-l=fm-l(xi,...,Xn), A2)
то, в силу G), и переменная ут определится как такая однозначная
функция:
Ут =fm(xi, ...,Xn) =
= q>(xi, .. .,xn;fi(xi, .. .,хп), .. .,fm-i(xi, .. .,хп)), A2а)
и заключение а) будет полностью оправдано. *}
Обратимся же к системе A0) и покажем, что в окрестнос-
окрестности точки (х^, ..., y®m_l) для нее выполняются условия, аналогич-
аналогичные 1), 2), 3), 4). Справедливость первых двух непосредственно
вытекает из свойств функций Fj и <р, ввиду A1). Точно так же
условие 3), в связи с A1) и (9), дает нам (для j = 1, ..., т - 1)
*^ Поясним, что (п + т — 1)-мерный (открытый) параллелепипед d* предпо-
предполагается настолько малым, чтобы определяющие его промежутки содержались
в соответствующих промежутках, определяющих {п + т)-мерный параллелепи-
параллелепипед <3)*. Та окрестность точки (х\, . . . ,у^), о которой упоминается в заключе-
заключении а), и определится всеми промежутками, связанными с <i*, с присоединением
к ним последнего из промежутков, связанных с ^'.
208]
§ 2. НЕЯВНЫЕ ФУНКЦИИ
513
Остается лишь рассмотреть якобиан (аналогичный J)
J* =
дФх
дух
дФ2
дух
дФт-1
дух
дФх
дФ2
ду2
дФт_х
ду2
дФХ
дУт-1
дФ2
дУт-1
дУт-1
и убедиться в том, что он отличен от нуля в точке (х^, ... ,y^_i).
С этой целью преобразуем определитель J, прибавляя к элементам
первых его т — \ столбцов элементы m-го столбца, умноженные,
соответственно, на j^-,д
д<
д :
J =
dF{
ду\
dF2
dyi
dFm-,
дух
dFm
дух
+
1
1
1
1
+
dFx
dF2
дут
dFm_x
дут
дер
дер
дух
дер
дер
дух
dFx
dF2
дУт-1
dFm_x
дУт-1
дУт-\
1
dF2
, dFm_x
, dFm
дер dFx
дер dF2
дУт-1 дУт
дер dFm_x
дУт-1 дУт
дер dFm
дут_х дут
Если считать здесь ут = ср{х\, ... ,ym-i)9 то все элементы, кро-
кроме находящихся в последней строке и в последнем столбце, бу-
будут представлять собой частные производные от функций Ф7
(по у\, ... ,ут-\). Именно, ввиду A1), дифференцируя Ф7 как
сложную функцию по yi, ... ,ут-\ [пользуясь правилом п° 181],
получим для j = 1, . .., т - 1
дФ
J _
дер
дФ
ду\ дух дут дух
дУт-1
дер
ду
С другой стороны, если продифференцировать по у\, .. .,ут-\
тождество (8) *}, то окажется, что
dFm
дух дут дух
дср_ _
д
dFm
dFm дер
дут-1 ду>
= 0.
*^ Ведь если (сложная) функция, стоящая в (8) слева, тождественно равна ну-
нулю, то и производные ее по любому аргументу — также нули.
514 ГЛ. VI. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ [208
Таким образом, элементы в последней строке (кроме последнего)
все равны нулю. Окончательно
J =
C/V 1
д Ф 1
ду\
0
дУт-1
дФ2
дУт-1
ЭФт-1
0
dF2
Эут
dFm_x
Разложив этот определитель по элементам последней строки,
придем к результату
Положим, наконец, здесь х\ = х\, ..., ут-\ = у^т_\\ тогда
ут = q>(x\, ... ,ут_\), в силу (9), обратится в у^т. Так как в этом
случае, по условию 4), J отлично от нуля, то не может быть нулем
и J*, что и требовалось доказать.
Для системы A0), содержащей т — 1 уравнений, наша теорема
предположена верной. Следовательно, система эта в окрестности
точки {х\, ..., у®т_х) определяет однозначные функции A2), не-
непрерывные и имеющие непрерывные производные; кроме того, эти
функции удовлетворяют и требованию б):
Л(хЧ,...,х°я)=уЧ,
/я-1(хо1,...,хон)=У°я_1. A3)
Отсюда следует, что т-я функция A2а) также непрерывна и име-
имеет непрерывные производные, и, наконец, принимая во внимание
A3) и (9):
• • • >хю J\\x\* - - - >xl)> • • • »
Теорема доказана.
Замечание. Мы обращаем внимание читателя на локаль-
локальный характер всех теорем существования неявных функций: речь
идет все время лишь о некоторой окрестности рассматри-
рассматриваемой точки. Но и в таком виде эти теоремы полезны; например,
209] § 2. НЕЯВНЫЕ ФУНКЦИИ 515
читатель увидит это в главе VII, где при изучении свойств
геометрического образа в данной его точке совершенно
достаточно ограничиться непосредственной ее окрестностью.
209. Вычисление производных неявных функций. Ход рассуж-
рассуждений, с помощью которых устанавливались теоремы существова-
существования неявных функций, в общем случае не давал представления о са-
самом способе вычисления производных (первого порядка)
от неявных функций. О производных высшего порядка и вовсе не
было речи. Теперь на этих важных вопросах мы остановимся спе-
специально.
Начнем с простейшего случая, когда дано уравнение A). Бу-
Будем считать выполненными, в окрестности рассматриваемой точки,
условия теоремы 2; существенную роль в дальнейшем будет играть
требование Fy ф 0.
Покажем простой прием для вычисления производной ух
(если существование ее наперед известно). Мы знаем, что
если неявную функцию у = f(x) подставить в уравнение A), то
оно обратится в тождество [см. B), 205]. Итак, если под у разу-
разуметь именно эту функцию от х, то левая часть равенства A),
F(x,y)9 представит собой сложную функцию от х9 которая
тождественно равна нулю. Тогда и производная ее по х так-
также есть нуль. Если продифференцировать эту функцию по прави-
правилу п° 181, то получим
%(х,у)+1$(х,у)-у'х=0,*> A4)
откуда (так как F' ф 0)
, __Fx(x,y).
Ух~ F'(x,yY
мы пришли к уже известной нам формуле [ср. C), 206].
Теперь можем пойти дальше. Если функция F(x,y) име-
имеет непрерывные производные второго порядка, то выражение,
стоящее в формуле A5) справа, может быть продифференцировано
по х, следовательно, существует и производная от у'х, т. е. вторая
производная у, от неявной функции у. Выполняя дифференци-
дифференцирование и подставляя всякий раз вместо ух ее выражение A5),
* ^ Собственно, такого же типа рассуждение мы уже проводили выше [ср. сноску
на с. 513].
516 ГЛ. VI. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ [209
найдем
(рп + F", • V ) • F1 - (F">> +F" • V ) • Ff
ff к1 xy * 1 yi Ух) 1х к1 х2 * xy Ух) 1y
/7/3
У
отсюда же видим, что вторая производная будет непрерывной функ-
функций от х.
Если функция F(x,y) имеет непрерывные производные
третьего порядка, то, очевидно, существует и третья про-
производная от неявной функции: у'"ъ\ ее выражение снова может
быть получено непосредственным дифференцированием выраже-
выражения для у9 и т. д. С помощью математической индукции легко
доказать, что существование непрерывных производных функ-
функций F(x,y) до k-го порядка (к > 1) включительно обеспечива-
обеспечивает и существование {непрерывной) производной k-го порядка
от неявной функции.
После того как, таким образом, самый факт существования по-
последовательных производных от неявной функции установлен, вы-
вычисление их проще производить путем повторного дифференциро-
дифференцирования тождества A4), с учетом того, что у есть функция от х. На-
Например, первое же дифференцирование этого тождества даст нам
F*+K 'Ух + (Ку +^" 'Ух) -Ух+К -j/'2 = 0, A6)
откуда [ведь Fy ф 0]
У
подставив вместо ух его выражение A5), вернемся к уже найден-
найденному выражению для у9 и т. д.
Аналогично обстоит дело и в случае уравнения D) с большим
числом переменных. Здесь предполагаем выполненными условия
теоремы 3. Если под у разуметь неявную функцию, определяемую
уравнением D), то D) превращается в тождество. Фиксируя
значения Х2, ..., хп и рассматривая у как функцию лишь от х\9
продифференцируем это тождество по х\\
Fx
Кх +Fy -уXl = °> откуда ухх = -Т7-;
У
209] § 2. НЕЯВНЫЕ ФУНКЦИИ 517
точно так же получим
Ух2 = Ъ> •••> з4 = -%> ит.д.
У У
Если нужны все производные первого, второго, ... поряд-
порядка, то проще сразу вычислять dy, d2y, ... Продифференцируем
же наше тождество полным образом, т. е. приравняем ну-
нулю полный дифференциал от его левой части [используя при этом
инвариантность формы первого дифференциала, 185]:
dF l dF l dF l dF 1
— dxx + —dx2+ ... + —dxn + —dy= 0,
дх\ 0X2 охп ду
так что
dF dF
- jrdx
ду ду
В то же время
ду -, ду ,
dy = -^-dxi+... + -^-dxn.
дх\ дхп
Ввиду произвольности dx\, ..., dxn, отсюда ясно, что
~ dF ^ dF
^}L-_?L ду _ -^
— dF > * * •' p)r ~ dF >
как мы и получили выше.
Дифференцируя еще раз, получим
\d2F 1 d2F 1 d2F 1 1 1 dF j2
l—^dxi + ... + -—— dxn + -——dy\dx\ + . .. + —d у = О
loxf дх\дхп дх\ду \ ду
и определим d2y, что приведет нас к выражениям для
d2y d2y d2y
dx2' dx\dx2* dx\'
и т. д. Мы видим, что во всех этих выкладках основную роль играет
условие, что
„, dF , „
518 ГЛ. VI. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ [209
Перейдем теперь к рассмотрению системы уравнений E). Бу-
Будем предполагать, что в окрестности взятой точки выполняются
условия теоремы 4. Снова обращаем внимание на роль, которую
будет играть требование J ф 0.
Мы знаем, что неявные функции у\, ... ,ут имеют частные
производные по х\, ..., хп. Самое вычисление их произво-
производится дифференцированием тождеств, которые получаются из E),
если под у\, ... ,ут разуметь именно упомянутые неявные функ-
функции. Дифференцирование по х\9 например, дает
' dF\_ №\_ <ty± , dFi дут _
дх\ ду\ дх\ '*' дут дх\
dFm_dy)_ dFm дут _
д д д д
дх\ ду\ дх\ дут дх\
Это — система линейных уравнений относительно неизвестных
|^,...,§^, с отличным от нуля определителем
Отсюда
D(Fu...,Fm)
Diyu
D(FU
D{yi,...,ym)
Аналогичные выражения получаются и для производных
ОТ ух, . . .,ут ПОХ2, . . . ,Х„.
Если функции F\, ..., Fm имеют непрерывные частные про-
производные второго порядка, то правые части всех полученных
формул имеют (непрерывные) производные по всем аргументам,
следовательно, существуют (непрерывные) вторые производные
от неявных функций. Вообще (как это легко доказать индуктивно)
существование для функций Fx, ..., Fm непрерывных производ-
производных до k-го порядка включительно влечет за собой существо-
существование и непрерывность всех производных k-го порядка и для
неявных функций.
Вычисление производных от неявных функций и в об-
общем случае также производится либо дифференцированием тож-
тождеств E) по тем или другим переменным, либо дифференциро-
дифференцированием их полным образом. Получаемая для определения
210] § 2. НЕЯВНЫЕ ФУНКЦИИ 519
производных или дифференциалов система линейных уравне-
уравнений своим определением всегда имеет отличный от нуля якобиан J.
Эти замечания станут более ясными на примерах.
210. Примеры.
1) Пусть у связано с х уравнением
In xjx1 +y2 = arctg -.
х
Дифференцируя последовательно по х (причем у считаем функцией от i), по-
получим
х +уу* ху1 -у , ,
—* т = ^ о или х + уу = ху —у,
х + У х + У
затем
-, . /2 . // //
1 + У +УУ = ху ;
и т. д. Из первого уравнения находим
/ х +у
У = ,
х — У
из второго (если подставить найденное значение у')
y
х-у (x-yf
и т. д.
2) Дано уравнение
F(x,y)=x + у — Ъаху = 0.
Требуется найти экстремумы определяемой им неявной функции у от х.
Имеем здесь
^ = 3(х2 - ay), F'y = 3(у2 - ах).
Ввиду A5), для того чтобы было у'х = 0, должно выполняться равенство F^. = 0.
Решая совместно уравнения F = 0 и F^. = 0, найдем две пары соответственных
значений х и у.
^=0, 3^ = 0 и х = ал/2, у = ал/А.
Но в первой точке обращается в нуль и F , так что мы не можем утверждать,
что в ее окрестности наше уравнение определяет у как однозначную функцию
от х; поэтому точку @,0) оставляем в стороне.
Во второй точке F1 = За \П > 0, и к ней приложима теорема 2. Чтобы убе-
убедиться в наличии экстремума, вычислим j/'2 ПРИ х — а v^ проще всего исходить
из A6), полагая тдму'х = 0;
*> Это — не общее выражение для у\ оно годится лишь в интересующей нас
точке (ал/2, а\/4).
520 ГЛ. VI. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ [210
Так как Fn2 = 6х > 0 при х = а\/29 то у < 0, и налицо максимум.
3) Пусть неявная функция z от х, у определяется уравнением
Л .,2 2
Х1 У- fl-i
а2 + b2 + с2
Имеем последовательно
х dx у dy z dz ex су
— + '—f + — = 0, dz = dx--fdy,
a1 bl cl alz blz
так что
о 2 о 2
<9z с jf 3z су
dx a^z' ду h^z
Затем
dx1 dy1 dz1 zd2z
— + -^Г + — + —2- = 0,
я2 bl cl cl
откуда (если воспользоваться известным уже выражением для dz)
сА\(х2 z2\dx2 Ъу (у2 z2\dy2
что дает нам
d2z с4 (х1 z2\ d2z с4ху
Эх2 a2z^\a2 с2)' дхду a2b2z^'
d2z с4 ^2 ~2
Т. Д.
dy2 bhl \b2 c2y
4) Пусть z определяется, как функция от х и у, из уравнения
z = х + у • cp(z).
Предполагая 1 —у • ср''(z) 7^ 0? доказать, что
<9z
<9jc 1
dz
~ду ~
1
— у • cp'iz)
dx
dz
' ду
Имеем
q>{z)
откуда и вытекает требуемое.
5) Пусть из уравнения
у = хф) + (/-(z)
переменная z определяется как неявная функция от х и у. Предполагая
х • ср'(z) -\- \p'(z) ф 0, установить, что эта функция удовлетворяет дифферен-
дифференциальному уравнению
d2z /dz\2 dz dz d2z d2z /dz\2
Jx2 ' \~dyJ ~ ~dx ' ~dy ' dxdy + ~dyl ' \~d~x) ~
210]
§ 2. НЕЯВНЫЕ ФУНКЦИИ
521
г • q — 2pq • s + t • p = 0,
где для краткости положено
dz
дх
dz
ду Я'
d2z
дх2 ~
Последовательно дифференцируя по х и
и, далее,
2q>'(z)-p +
<p'(z)-q-\
-[*
Г'
<р'
п
я>
' Я>
1
[z) -\- гр (
(') + *'
'(') + *
'(*) + *
z)] ¦ р =
1 ( \Л 2
(z) • ч
по
0,
+
+
+
У>
[*
[X
Г'
d2z
дхду
получим
[х ¦ <p'{z)
¦ <p\z) +
¦ <p'{z) +
¦ <p'(z) +
d2z
S> ду2
-\- гр (z)l •
гр (z)l • r
q =
= 0,
= 0,
= 0.
~2pq
Сложив последние три равенства, предварительно умноженные на q , —2pq,
р , и придем к требуемому соотношению.
6) Пусть дана система
х +у
и = а, х2 +у2 +z2 + и2 = Ь2, х3 +у3 +z3 + и3 = с3,
определяющая у, z, и как функции от х. Имеем
-,./././ Л . /. /. / Л 2.2/.2/.2/ Л
1 + 3^ +z + и =0, jv: Ч-З^З7 +^ +ww =0, ^с + у у + z z -\- и и =0.
Предполагая определитель
1 1 1
У z и = (z - у)(и - у)(и - z)
у z и
не равным нулю, имеем отсюда
{z-x){u-x)
У =--, г; г, и т. д.
7) Пусть переменные ^с, з^, z связаны с переменными г, 6, ф соотношениями
х = г • cos 0 cos ф, j/ = г • sin 0 cos cp, z = г • sin <p,
где 0 < г < +оо, — ^ < в < §, — § < <р < f. Якобиан
cos 0 cos <p —r sin 0 cos <p —r cos 0 sin <p
г, в,
sin ^ cos <p r cos 0 cos <p —r sin 0 sin <p
0
г cos<p
= г cos <р > 0.
522 ГЛ. VI. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ [210
Упомянутые соотношения определяют г, в, ср как функции от х,у, z. Для
вычисления производных этих функций продифференцируем эти соотношения
полным образом:
cos в cos ср dr —r • sin в cos ср d6 — г • cos в sin ср dcp = dx,
sin в cos cp dr + г • cos в cos cp d6 — г • sin 0 sin cp dcp = dy,
sing) dr -\- r • cos<p <i<p = dz.
Отсюда определим <ir, d6 vl dcp\
r2 • cos 0 cos2 ф r2 • sin 0 cos2 ф r2 • sincp cos ю
dr = dx H dy H dz,
J J У J
r • sin в г • cos в
d6 = dx H dy,
J J У
r • cos в sin cp cos <p r • sin 0 sin <p cos <p r • cos cp
dcp = d!x dy H dz.
* J J У J
Этим, собственно, уже и найдены интересующие нас производные (если учесть
указанное выше значение J):
дг дг дг
— = cos в cos ср, — = sin в cos ср, — = sin ср,
дх ду dz
дв sine дв cose дв
— = , — = , — = 0,
дх г • cos ср ду г • cos ср dz
дер cose sinср дер sine sinср дер cosq>
дх г ' ду г ' dz r
Предложенные уравнения легко решить относительно г, в, ср\
г = ух2 -\-у2 + z2, в = arctg —, ср = arctg —-^^^^=.
* л/х2+у2
Это дает возможность вычислить все эти производные и тем проверить найденные
результаты.
8) В качестве заключительного примера на дифференцирование
неявных функций выведем еще одну формулу, снова подчеркива-
подчеркивающую аналогию между якобианом системы функций и производной
одной функции.
Пусть дана система п уравнений с 2п переменными:
Fi(xi,x2, • • .,х„; yi,y2, - - -,Уп) =0 (/ = 1,2, .. .,п).
Предполагая якобиан
отличным от нуля, рассмотрим у\,у2, • • • ,Уп к^к функции
от х\,Х2, • • • ,хП9 определяемые этой системой уравнений и,
210]
§ 2. НЕЯВНЫЕ ФУНКЦИИ
523
следовательно, обращающие их в тождества. Дифференцируя эти
тождества по каждому х7, результаты можем представить в виде
1 = —I _1± -\ 1 Л + .. . -| L -УЦ-
dxj ду\ dxj ду2 dxj дуп dxj
Определитель, составленный из левых частей этих равенств, есть
v ' D(xux2,...,xny
определитель же, составленный из правых частей, очевидно, пред-
представляет собой произведение определителей
[см. 203, C)]. Отсюда получается формула
D(xi9...9Xn) ^ ^ D{Fu..,Fn) -
являющаяся аналогом формулы A5).
Если уравнения даны в виде, разрешенном относитель-
нохьх2, .. .,хп:
xi — Ф/(УЬ ^2» • • • ,Уп) (/ = 1, 2, . . . , п),
то под рассмотренный случай это подойдет, если положить
Fj = q>j —Xi. Так как здесь |^- = — 1 или 0, смотря по тому, бу-
будет ли z = j или z ф у, то числитель сведется к
=(-1)и,
о ... -1
и формула примет вид
1,-..,Уп) 1
-1
0
0
0 .
-1
0
0
0
.. -1
D(xl,...,Xn) D(xL...,Xn) •
Этот результат нам уже знаком [203, D)].
524 ГЛ. VI. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ [211
§ 3. Некоторые приложения теории неявных функций
211. Относительные экстремумы. Рассмотрим вопрос об экс-
экстремуме функции /(ii, ..., хп+т) от п + т переменных в предпо-
предположении, что эти переменные подчинены еще т уравнениям
связи
=0 (/ = 1,2, . . .,
A)
Мы уточним понятие о таком относительном экстремуме
и укажем приемы для его разыскания.
Говорят, что в точке Мо(х\, ... ,х„+т), удовлетворя-
удовлетворяющей уравнениям связи, функция f(x\, ... ,хп+т) име-
имеет относительный максимум {минимум), если неравен-
неравенство
f
О)
выполняется в некоторой окрестности точки Мо для всех ее
точек (х\, ... ,хп+т), удовлетворяющих уравнениям
связи.
Мы будем предполагать, что как функция /, так и функция Ф,-
имеют в окрестности рассматриваемой точки непрерывные част-
частные производные по всем аргументам. Пусть, далее, в точке Мо
отличен от нуля хоть один из определителей т-го поряд-
порядка, составленных из матрицы частных производных *)
дФ\ дФ\ дФ\ дФ\
i
B)
дх\
дФ2
дх\
ЭФпг
дх„
дФ2
дх„
ЭФпг
эф2
дхп+1
ЭФпг
1 дхп+т
эф2
дхп+т
дФт
дхп
дхп
+т
например, определитель
?>(Фь ..., Фм)
(xn+\, . . ., хп+т
дФ2
дхп+1 '
дФт
дФ2
дхп-\-т
дФт
C)
В этом случае говорят, что матрица B) имеет (в точке Mq) ранг т.
211] § 3. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ТЕОРИИ НЕЯВНЫХ ФУНКЦИЙ 525
Тогда, если ограничиться достаточно малой окрестностью точ-
точки Мо, по теореме 4 система A) равносильна системе вида
Xn+i=(Pi(xi,...,xn), ..., xn+m = q>m(xi,...,xn), D)
где ф\, .. .,фт суть неявные функции, определяемые систе-
системой A). Иными словами, требование, чтобы значения пере-
переменных ii,... ,хп,хп+\, ... ,хп+т удовлетворяли уравнениям
связи A), можно заменить предположением, что переменные
Хи+ь • • •» Хп+т представляют собой функции D) от ii, ..., хп.
Таким образом, вопрос об относительном экстремуме
для функции /(ii,...,iw+w) от п + т переменных в точке
)+, ..., х^+т) сводится к вопросу об обыкновен-
обыкновенном (абсолютном) экстремуме для сложной функции от п пе-
переменных
f(x\, ...,хп; ф\(хи .. .,*„), .. .,фт(хи .. .,*„)) E)
в точке Ро(х((, ... ,х%).
Эти соображения указывают и на реальный путь для нахож-
нахождения точки, доставляющей относительный экстремум функции
f(x\, ..., хп+т)\ если мы умеем фактически разрешить уравнения
связи, например относительно переменных х^+ъ ..., хп+т, и найти
явные выражения для функций D), то дело сводится к нахож-
нахождению абсолютного экстремума для сложной функции E). Соб-
Собственно говоря, мы так именно и поступали в ряде ранее ре-
решенных задач [200, 201], например, когда мы искали наимень-
наименьшее значение для суммы х + у + z + t при условии xyzt = с4,
и т. п.
Укажем теперь другой путь для нахождения точки Мо
(х j, ... ,х%+т)9 не предполагая, что мы имеем явные выражения
для (неявных) функций D), хотя существованием этих функций
мы будем пользоваться и здесь.
Итак, пусть в точке Мо функция f{xi, ..., хп+т) имеет отно-
относительный экстремум или — что то же — сложная функция E)
в точке Ро имеет экстремум абсолютный. Тогда, по замеча-
замечанию I п° 196, в этой точке должен обращаться в нуль ее диффе-
дифференциал и притом — тождественно относительно дифференциа-
дифференциалов независимых переменных dx\, ...dxn. По инвариант-
инвариантности формы первого дифференциала [185], это условие можно
526 ГЛ. VI. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ [211
записать так:
п-\-т о г
2_^ dxj = 0, F)
7 = 1 J
где под dxn+\, ..., dxn+m разумеются дифференциалы функции D)
в точке Ро, в то время как частные производные вычислены в точ-
точке Мо, ибо (как явствует из теоремы 4)
Из F) нельзя, конечно, заключить о равенстве нулю коэф-
коэффициентов при дифференциалах, так как не все эти диффе-
дифференциалы произвольны. Для того чтобы свести дело к произвольно
выбираемым дифференциалам, т. е. к дифференциалам dx \, ..., dxn
независимых переменных, мы постараемся исключить отсюда
дифференциалы dxn+\, ..., dxn+m переменных зависимых. Это
легко сделать, если продифференцировать полным образом
уравнения связи A), разумея под хп+\, ..., хп+т функции D) *}:
П+т дФг
^2, —" dxj =0 (/ = 1, 2, .. ., т). (8)
7 = 1 J
Здесь, как и выше, ввиду G), частные производные вычислены
в точке Мо. Так как, по предположению, определитель C) в этой
точке — не нуль, то dxn+\, ..., dxn+m могут быть отсюда линей-
линейно выражены через dx\, ..., dxn. Если эти выражения подставить
в F), то получится равенство вида
A\dx\ + . . . +Andxn = 0,
где А\, ... ,Ап означают п выражений, рациональных относитель-
относительно частных производных функций Ф7, и здесь взятых в точке Мо.
Так как в этом равенстве фигурируют только дифференциалы
dx\, ..., dxn независимых переменных, то в точке Мо имеем
Вместе с уравнениями связи это дает п + т уравнений для опреде-
определения неизвестных х\, ..., хп+т.
*) Точнее говоря, мы дифференцируем те тождества, которые получаются
из уравнения A), если вместо хп-\.\, . . ., хп+т в них подставить неявные функ-
функции D). Подобный способ речи мы будем применять и впредь.
212] § 3. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ТЕОРИИ НЕЯВНЫХ ФУНКЦИЙ 527
Конечно, мы установили лишь необходимые условия для
экстремальной точки М^{х\, ..., х„+т). Но и в таком виде усло-
условия могут быть полезны даже для разыскания наибольшего (или
наименьшего) значения функции / при условиях A), если по ха-
характеру вопроса наперед ясно, что внутри рассматриваемой облас-
области должна существовать точка, где это наибольшее (наименьшее)
значение достигается, или если такое допущение сделано в поряд-
порядке наведения, с тем чтобы найденную точку апробировать другими
соображениями. Примеры приведены ниже, в 214.
212. Метод неопределенных множителей Лагранжа. В изло-
изложенном выше способе нарушается симметрия в отношении пере-
переменных: часть из них трактуется как независимые, часть — как
зависимые, одни дифференциалы исключаются, другие — сохраня-
сохраняются. Иногда это влечет за собой усложнение выкладок. Л а г р а н ж
предложил метод, при котором все переменные сохраняют одина-
одинаковую роль.
Умножим равенства (8), соответственно, на произвольные пока
(«неопределенные») множители Хг [г — 1, 2, ..., т) и результаты
почленно сложим с F). Мы получим равенство
f(f ^ (9)
~{\dxj dxj dxj )
где по-прежнему dxn+\, ..., dxn+m означают дифференциалы неяв-
неявных функций D) (в рассуждении мы пока сохраняем нерав-
неравноправие переменных); производные вычислены в точке М$.
Выберем теперь значения множителей Хг¦ = Xf (z = 1, ..., т)
так, чтобы обращались в нуль именно коэффициенты при зави-
зависимых дифференциалах dxn+\, ..., dxn+m\
-=0 A0)
(j = n+ 1, . . ., m).
Это сделать можно, поскольку определитель C) системы линейных
уравнений, получающейся для определения Аь А2, ..., AW5 отличен
от нуля. При выбранных значениях множителей равенство (9) при-
примет вид
528 ГЛ. VI. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ [212
Здесь мы снова имеем дело лишь с дифференциалами независи-
независимых переменных, поэтому коэффициенты при них должны быть
нулями, т. е. наряду с A0) имеем и
Итак, для определения п + т неизвестных х\, .. ,,хп+т, да
еще т множителей Аь ..., Aw, имеем столько же уравнений, имен-
именно, т уравнений связи и п + т уравнений
~ \- h ' т h ... + Aw • -— = 0
oXj oXj axj
(j = 1,2, ...,n + m)
[см. A0) и A0*)].
Для того чтобы облегчить выписывание этих уравнений, обык-
обыкновенно вводят вспомогательную функцию
тогда упомянутые уравнения могут быть записаны в виде
^ = 0 G = 1,2,. ..,п + т). A1)
Они выглядят так же, как и условия обыкновенного экстремума
для функции F. Это следует рассматривать лишь как указание,
облегчающее запоминание.
И метод Лагранжа приводит к необходимым условиям.
В остальном здесь может быть повторено то, что было сказано
в конце предыдущего номера.
Замечание. В изложенной теории существенную роль сы-
сыграло предположение о ранге матрицы B), которым
мы воспользовались трижды. При решении задач одним из указан-
указанных методов — для уверенности в том, что не пропущена ни одна
точка, доставляющая функции относительный экстремум, — следо-
следовало бы предварительно установить, что упомянутое предположе-
предположение выполняется на деле во всех точках рассматриваемой области,
удовлетворяющих уравнениям связи. В простых случаях мы будем
предоставлять это читателю.
213] § 3. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ТЕОРИИ НЕЯВНЫХ ФУНКЦИЙ 529
213. Достаточные для относительного экстремума условия. По
этому поводу мы ограничимся немногими замечаниями. Пред-
Предположим существование и непрерывность вторых производ-
производных для функций / и Ф7 (у = 1, 2, ..., т). Пусть теперь точка
Мо(х5, ..., Хп+т), совместно с множителями А^, ..., А^, удовле-
удовлетворяет установленным выше необходимым условиям.
Вопрос о наличии в этой точке (относительного) экстремума
зависит, как и в 198, от знака разности
А = /(хь ..., хп+т) - /(*?, ..., х°п+т),
с той лишь существенной оговоркой, что и точка (х\, ... ,хп+т)
удовлетворяет уравнениям связи A) или — что то же — D). Легко
понять, что для таких точек приращение функции / может
быть заменено приращением функции F (где все множители А/ мы
считали равными А,0):
А = F(xu .. ., хп+т) - F(x°l9 .. ., х°п+т).
Ввиду того что в точке Мо выполняются условия A1) — в этом-то
и состоит выгода перехода к функции F, — это приращение, по
формуле Тейлора, может быть записано так [ср. 198, (8)]:
= -\
n+m n+m
А = -\ Y^ AjkAxjAxk + ^
j,k=l
где
и cijk —> 0, если Axi —)> 0, ..., Axn —)> 0 [остальные приращения
Дхя+ъ ...» A^«+w при этом сами собой будут бесконечно малыми
по непрерывности функций D)].
Если заменить здесь все приращения Ах7 соответствующими
дифференциалами dxj9 то по отношению к независимым пе-
переменным это вообще ничего не изменит; что же касается за-
зависимых переменных, то произведенная замена вызовет лишь
необходимость поставить вместо коэффициентов ад другие беско-
бесконечно малые /Зд:
1 г п+т
А = -| Yl 4Jkdxjdxk +
n+m n+m
j,k=l
530 ГЛ. VI. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ [214
Переход к дифференциалам выгоден потому, что дифференциалы
зависимых и независимых переменных связаны системой линей-
линейных соотношений (8). Так как определитель C) в точке Мо, по
предположению, — не нуль, то отсюда зависимые дифференциа-
дифференциалы выразятся линейно через независимые. Подставив их выраже-
выражения в А, мы, вместо первой суммы, получим квадратичную
форму относительно дифференциалов dx\, ..., dxn.
А теперь, так же как и в 198 и 199, можно показать, что: если
эта форма будет определенной и притом положи-
положительной {отрицательной), то в испытуемой точке
будет относительный минимум {максимум): если же форма
оказывается неопределенной, то относительного экс-
экстремума нет.
Впрочем, практическое значение этого критерия невелико
[ср. замечание в 200].
Перейдем к примерам и задачам.
214. Примеры и задачи.
1) Пусть требуется найти экстремум функции / = х -\-у + z -\-t при условии
Ф = xyzt — с = 0; область изменения переменных определяется неравенствами
х > 0, у > 0, z > 0, t > 0. Мы уже решали эту задачу в 200,4), фактически вы-
выражая t из последнего условия. Теперь, дифференцируя это равенство полным
образом, найдем
dx dy dz dt fdx dy dz\
1 1 1 = 0, откуда dt = -t[ 1 1 ).
xyzt \ x у z J
Исключая dt из равенства df = dx + dy + dz + dt = 0, придем к результату
1 - -)dx + (l - -)dy + (l - -)dz = 0,
x J \ у J \ z J
который, ввиду произвольности dx, dy и dz, распадается на три:
1 - - = 0, 1 - - = 0, 1 - - = 0,
х у z
так что x=y=z=t = c.
Применяя к той же задаче метод Лагранжа, введем вспомогательную
функцию
F = х +у +z +t + Xxyzt *)
и составим условия:
F'x = 1 + Xyzt = 0, . . ., F( = 1 + Xxyz = 0,
откуда
yzt = xzt = xyt = xyz, так что х = у = z = t = с
*) Если вспомнить роль этой функции, то станет ясно, что постоянное слага-
слагаемое в составе Ф здесь может быть опущено без вреда.
214] § 3. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ТЕОРИИ НЕЯВНЫХ ФУНКЦИЙ 531
Для того чтобы воспользоваться результатом предыдущего п°, вычислим
Я = —j и рассмотрим функцию
ху zt
F =x +y +z +t —.
Ее второй дифференциал (в точке x=y=z = t = c) будет
d2F = (dxdy + dxdz + dxdt + dydz + dydt + dzdt).
с
Дифференцируя уравнения связи (все в той же точке), получим
dx + dy + dz + dt = 0.
Если определить отсюда dt и подставить в предыдущее выражение, то оконча-
окончательно найдем
--[dxdy + dxdz + dydz - {dx + dy + dzJ] =
= - \(dx +dy + dzJ + dx2 + dy2 + dz2].
с L J
Так как эта форма, очевидно, определенная и положительная, то в найденной
точке будет относительный минимум.
[Отсюда, однако, нельзя сделать заключение, что этот минимум будет и наи-
наименьшим значением функции f = x-\-y-\-z-\-t при указанной связи между
значениями ее аргументов; ср. 200,4)].
2) Станем вновь [ср. 200,2)] искать наименьшее и наибольшее значения
функции
2 2 . ,2 2 . 2 2 , 2 . , 2 . 2ч2
и = а х + b у + с z — (ах + by + cz )
(а > Ь > с > 0)
при наличии связи:
2,2.2 ,
X +у +Z = 1,
т. е. на сферической поверхности, выраженной этим уравнением. * ^
С этой целью сначала найдем по методу Лагранжа все относительные
экстремумы функции. Вспомогательная функция
F = а2х2 + Ь2у2 + А2 - (ах2 + by2 + cz2J + Х(х2 + / + z2)
приводит к условиям:
*[(я2 + Я) - 2а[ах2 + 6у2 + cz2)] = 0,
y[(b2 + Я) - 2%jc2 + by2 + cz2)] = 0,
z[(c2 + Я) - 2с(я*2 + by2 + cz2)] = 0,
*) Ввиду того что эта поверхность представляет замкнутое ограниченное мно-
множество, существование на ней точек, где функция принимает наименьшее и наи-
наибольшее значения, вытекает из теоремы Вейерштрасса [см. замечание в кон-
конце п° 173].
532 ГЛ. VI. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ [214
к которым надлежит присоединить еще уравнение связи. Отсюда
A) х = О, у = О, z = ±1 (и = 0);
B) х = 0, у = ±h z = 0 (и = 0);
C) jc = ±1, j/ = 0, z = 0 (и = 0);
D) х = 0, j; = ±^, z = ±.-±5 (м = !(* - сJ);
E) * = ±4-, 3^ = 0, z = ±-L (,= !(.-сJ);
Выбирая из указанных в скобках значений и наименьшее и наибольшее, мы и при-
придем к решению задачи [ср. 200,2)].
3) Вернемся к задаче о наивыгоднейших сечениях проводов в электрической
сети с параллельным включением [201,8)]. Сохраняя принятые там обозначения,
будем искать экстремум функции
f(qi, q2, ..., qn) = hq\
при условии, что
,, ч PhJ\ . Phh . .
Ф(#1, q2, • • -, qn) = 1 \~ • • • H
при этом мы не станем даже вводить, взамен q\, q^, . . ., qn, Другие перемен-
переменные, как сделали это выше, ибо нашими новыми методами задача и так решается
просто.
Итак, дифференцируя полным образом уравнение Ф = 0, получим
затем следующее выражение для дифференциала dqn\
Подставляя его в равенство df=l\dq\ + ... + ln-\dqn_\ + lndqn = 0, придем
к результату:
Jn Ч\
Так как dq\, . . ., <i^w_i уже произвольны,29^ то коэффициенты при них порознь
нули, откуда
2 2 2 2
Я
J\ J2 Jn-\ Jn
. . ., qn = Ял/Х- A2)
29) См. примеч. 30 на с. 549.
214] § 3. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ТЕОРИИ НЕЯВНЫХ ФУНКЦИЙ 533
Множитель пропорциональности Я легко определить из уравнения связи:
п
i=\
Если применить метод Лагранжа, то нужно построить вспомогательную
функцию*^
F(^i, ^2, • • •, #0 = hq\ + ... + lnqn + ?i h ... + -
и приравнять нулю ее производные:
3Z7 Л, Г 3Z7 Л, х
dq\ q^ ' ' dqn q%
откуда снова получаем A2), и т. д.
4) В качестве более сложного примера рассмотрим такую задачу: трехосный
эллипсоид ^ + ^т + Ц = \(а>Ь>с) пересечен плоскостью lx + my + nz = О,
Q и С
проходящей через его центр; требуется определить полуоси получающегося в се-
сечении эллипса. Иными словами, нужно найти экстремальные значения функции
г = х + у -\- z , если переменные подчинены указанным выше двум урав-
уравнениям связи.
Метод исключения зависимых дифференциалов [211] здесь приводит к слож-
сложным выкладкам; поэтому мы сразу прибегнем к методу Лагранжа.
Для того чтобы убедиться, что ранг матрицы
[а* # сЛ
\1 т п )
равен 2 во всех точках пересечения эллипсоида с плоскостью,**^ допустим
противное. Из обращения в 0 всех определителей второго порядка следует
пропорциональность элементов верхней и нижней строк; но тогда равенство
1х + ту + nz = 0 влечет за собой ^Ц- + тт + ^т = 0, что невозможно.
J а2 Ъ2 с2
Составив вспомогательную функцию
/2 2 Z2\
F(x,y,z) =х2 +у2 +z2 + Я ( — + У- + — ) +2fi(lx +my + nz),
\az bz cz J
приравняем нулю ее производные:
*+Я-^-+^/ = 0, у + А- ^- +jjm = 0, z + А- Дг + fin = 0. A3)
а1 Ъ1 с1
Умножая эти уравнения, соответственно, на х, у, z и складывая, получим (с уче-
учетом уравнений связи), что Я = —г .
*) «Неопределенный множитель» мы для удобства берем в форме Аи вклю-
включаем в него постоянную р.
**) См. замечание в 212.
534 ГЛ. VI. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ [214
Если предположить, для определенности, что ни одно из чисел /, т, п не
равно нулю, то из A3) можно усмотреть, что г не равно ни я, ни Ь, ни с. Тогда
уравнения A3) перепишутся в виде:
la1
mbl
Отсюда легко найти ^ ас ним и х, у, z; но минуя это, можно, сложив эти
равенства, предварительно умноженные на /, т, п, получить уравнение
72 2 2г2
la то
п2с2
Ъ1 — г1
= 0,
откуда непосредственно и определяются интересующие нас два экстремальных
значения г .
Так как существование этих экстремальных значений наперед известно, то
здесь, таким образом, получается полное решение вопроса.
5) Наконец, предложим себе найти наименьшее и наибольшее значения квад-
квадратичной формы
f(x\, X2, . . ., хп) = ^2 alkxtxk (alk = akl)
i,k=l
при условии
(х\,Х2, . . .,Хп) =
,2 - 1 *)
A4)
Составим функцию
F(x\, X2, . . ., хк
Исключая х\, Х2, . .
1 dF
1 dF
^7— = «21
2 дх2
1 и г
Л агранжа
,) =/(^1,^2, --^Хп)
., хп из условий
\ — X) • х\ -\- а 12 • Х2 4
•^1 + («22-Я) -*24
-Х(х\+х
-...+«!«
- . . . + «2и
- (апп — Я)
•хп = 0,
•хп = 0,
•хп = 0,
придем к уравнению п-и степени
ап -Я
«22 -
апп — Я
A5)
A6)
относительно Я. Если Я есть один из его корней, то системе A5) линейных
уравнений можно удовлетворить значениями х\, Х2, . . ., хп, ис сплошь равны-
равными нулю; умножив их на надлежащий множитель, можно добиться и выполнения
*)
Здесь можно сделать замечание, аналогичное сноске**^ на с. 531.
215] § 3. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ТЕОРИИ НЕЯВНЫХ ФУНКЦИЙ 535
условия A4). Однако определение этих значений не представляет для нас инте-
интереса, ибо, как увидим, вопрос о наименьшем и наибольшем значениях функции /
решается и без них.
Действительно, умножая равенства A5), соответственно, на х\,х2, . . .,хп
и почленно складывая, придем к равенству
/(*!,*2, • • -,хп) — к(хх + х2 + . . . +хп) = О
или, в силу A4),
f(x\,x2, . . . ,хп) = Я.
Таким образом, если Я удовлетворяет уравнению A6), то значение функции /
в соответствующей точке (х\,х2, . . •, хп) и равно самому Я.
Мы приходим к изящному результату: искомые наименьшее и наибольшее
значения функции /, при соблюдении условия A4), совпадают с наименьшим
и наибольшим из (вещественных) корней *^ уравнения A6).
215. Понятие независимости функций. Рассмотрим систему
функций
У\ =/l(*b*2, • • -,Хп),
У2=/2(хиХ2,...,Хп)9
Ут =fm(xi,X2, • • -,Хп
определенных и непрерывных, вместе со своими частными произ-
производными, в некоторой /7-мерной открытой области &.
Рассмотрим случай, когда значение одной из них, например^,
однозначно определяется совокупностью тех значений, которые
принимают остальные функции
(уI, ...,yj-i,yj+i, ...,ym).
Точнее говоря, если So есть множество таких {т — 1) -мерных точек,
отвечающих всевозможным точкам (хь...,хи) в®, то предпола-
предполагается, что в So будет иметь место функциональная зависимость
Уу =ф(уи . ..,^-ь^+ь ••-,Ут), A8)
причем это равенство оказывается тождеством относитель-
относительно х в <%!, если вместо всех yt подставить функции A7) **\ Тог-
Тогда говорят, что в области <%! функция уу зависит от
остальных. Впрочем, для того чтобы иметь возможность при-
применять дифференциальное исчисление, мы включим в определение
*)
Впрочем, можно доказать, что все корни этого уравнения будут вещест-
вещественными.
**)
Существенно, что функция ср в числе своих непосредственных аргу-
аргументов не содержит х.
536 ГЛ. VI. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ [215
еще требование, чтобы функция ср была определена и непрерывна
со своими частными производными в некоторой открытой облас-
области S {т — 1)-мерного пространства, содержащей множество до-
довели, в частности, одна из функций A7), j/y, сводится к постоян-
постоянной, то она явно будет зависеть от остальных: здесь можно просто
положить ср = const. Функции у\,у2, • • • ,Ут называются вообще
зависимыми в области @9 если одна из них (все равно какая)
зависит от остальных.
Примеры.
1) Если положить
\У\ =
-х2
2
то нетрудно проверить, что во всем ^-мерном пространстве будет выполняться
тождество
\
У2 =у\ -
2) Аналогично, для функций
КУЗ = [XX + I) [х
имеем тождественно (в трехмерном пространстве)
УЗ =У\ ~У\У2 +У2-
Все это — зависимые функции.
Если ни в области @9 ни в какой-либо частичной, в ней содер-
содержащейся, области не имеет место тождество вида A8), то функции
УьУ2, • • •»Ут называют независимыми в области @.
Ответ на вопрос о независимости функций дает рассмотрение
так называемой матрицы Якоб и, составленной из частных
производных этих функций по всем независимым переменным:
П_ ду\ \
с2 дхп
дх\
дут дуг
\dxi дх:
дхп/
A9)
216] § 3. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ТЕОРИИ НЕЯВНЫХ ФУНКЦИЙ 537
Предполагая п^ т, прежде всего имеем такую теорему:
Теорема 1. Если хоть один определитель т-го порядка, со-
составленный из элементов матрицы A9), отличен от нуля
в области &, то в этой области функции у\,у2, • • • ,Ут не-
независимы.
Доказательство. Пусть
дх\ дх2 дхт
B0)
дут дут
дх\ дх2 дхт
Если бы неравным нулю был не этот, а какой-нибудь другой
определитель, то, изменив нумерацию переменных, можно было
бы свести вопрос к случаю B0).
Доказательство теоремы будем вести от противного. Предполо-
Предположим, что одна из функций, например ут, выражается через осталь-
остальные, так что
Ут = ф(у1,У2, • • -,Ут-\), B1)
хотя бы в некоторой части &о области @1.
Продифференцировав это тождество по каждой из переменных
хг: (/ = 1, ..., т)9 мы получим ряд тождеств (в @Iq) вида
дугп _ дугпду]_ дугпду^ дут дут-\
dxi дул dxi дуо dxi дут—л dxi
A = 1,2,...,»!).
Мы видим, что элементы последней строки определителя B0)
получаются путем сложения соответственных элементов пер-
первых т — 1 строк, умноженных предварительно на множители
тр2-, ..., ддут . Такой определитель, как известно, равен нулю. Это
противоречит условию теоремы. Полученное противоречие дока-
доказывает невозможность равенства B1).
216. Ранг матрицы Якоби. Переходя к общему случаю, введем
следующее определение. Назовем рангом матрицы Якоби A9)
(в области @1) наивысший из порядков определителей, образо-
образованных из элементов этой матрицы и не обращающихся в нуль
тождественно в^. Может, конечно, случиться, что все эле-
элементы матрицы A9) тождественно обращаются в нуль; тогда го-
говорят, что ранг матрицы есть 0; но этот случай не представляет
538 ГЛ. VI. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ [216
интереса, ибо здесь попросту все функции у\,у2, • • • ,ут сводят-
сводятся к постоянным [183]. Если ранг матрицы A9) есть \х ^ 1, то
существует хотя бы один определитель /i-ro порядка, составленный
из элементов матрицы (это, конечно, предполагает rn ^ jj и п ^ jj)
и не равный в ^ тождественно нулю, в то время как все определи-
определители порядка выше \х (если таковые имеются) тождественно равны
нулю. Говорят, что ранг \х достигается в некоторой точке об-
области, если упомянутый определитель ^-го порядка именно в этой
точке отличен от нуля.
Теорема 2. Пусть ранг матрицы Як оби в области &
есть и > 1 и достигается он в точке
этой области. Тогда в некоторой окрестности &о названной
точки \х функций из числа наших т {именно те, производные
которых входят в определитель \х-го порядка, не равный нулю
в точке Мо) будут независимы, а остальные от них зависят.
Доказательство. Без умаления общности можно предполо-
предположить, что в точке Мо отличен от нуля именно определитель
D(yu ---чУр)
D(xl9...,:
дх\
3*1
дх\
ду\ ду\
дх2 дх^
ду2 ду2
дх2 дх^
0X2 vXu
=
дх\
д/2
дх\
дх\
дЛ
дх2
д/2
дх~2
дх2
df\
~дх^
df2
дхк
~дх~
B2)
Ввиду непрерывности частных производных, то же будет и в не-
некоторой окрестности упомянутой точки, и, следовательно, по тео-
теореме 1, функции у\,у2, • • • ,Уц будут в этой окрестности незави-
независимы.
Обозначим теперь через у\, у\, - - -, у^ значения этих функ-
функций в точке Мо. На основании теоремы 4 п° 208 в некотором
{п + /л)-мерном параллелепипеде
B3)
216] § 3. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ТЕОРИИ НЕЯВНЫХ ФУНКЦИЙ 539
первые \х из уравнений A7)
i, ...,xn)-yi=0,y
B4)
определяют xi,X2,...,x^ как однозначные функции от остальных
переменных yi, ... ^у^^х^+х, ... ,хП9 фигурирующих в этих урав-
уравнениях
B5)
В упомянутой области системы уравнений B4)
и B5) оказываются вполне равносильными, т.е.
удовлетворяются одними и теми же значениями переменных
xi,..., хт и у\,у2, • • • ,Уп- Из самой теоремы, на которую мы
опирались, следует, что если вместо xi,X2, ...,^ подставить
в B4) функции B5), то получатся тождества относительно
У\, • • • ,У'/л> х/и+\, ... ,хп. Но для нас сейчас важно и другое: если
вместо у\, ... ,уИ подставить в B5) функции /ь /2, ..., /И,
то получатся тождества относительно переменных
х\,Х2, ... ,хп — по крайней мере в некоторой окрестности точки
Мо(х^, х%, • • •, х%). Именно, достаточно выбрать эту окрестность
^о = (*? - Д}, х? + 8[; х°2 - S'2,x°2 + S/2;...;x°n- S'n,x°n + S'n)
так, чтобы было
0<S[^Su 0<S'2^S2, ..., 0 < 8fn ^ Sn
и, кроме того, чтобы для ее точек значения у\,у2, • • •, JV опре-
определяемые из B4), т.е. значения /ь /2, ..., /^, отличались от
^1,^2» • • • ^У% соответственно, меньше, чем на Аь А2, ..., А^. *)
Действительно, тогда точка (х\,х2, ..., хп;у\,у2, ... ,уп) попадет
в ^о? и одновременно с равенствами B4) должны выполняться
и равенства B5).
*) Это можно осуществить ввиду непрерывности функций f\, /2, . . ., /]ц, при-
принимающих в точке Мо значения у\, у2, . . ., у^
540 ГЛ. VI. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ [216
Возьмем теперь (если т> \х) любую из остальных функ-
функций A7), например .у^+ь и докажем, что она зависит от первых \х
функций у\,у2, • • • ,У/и- Если в равенство j^+i = /^+i(xi, ..., хп)
вместо хь ..., Хц подставить функции B5), то .у^+1 представится
в виде (сложной) функции от у\, ...,j^;x^+i, ..., хп\
..,**). B6)
На основании сделанного выше замечания, если в это равен-
равенство вместо у \,у2, • • • ,Уji,y 1л+\ подставить, соответственно, функ-
функции /ь /2, ..., fju, fju+i, то оно удовлетворится тождественно
относительно х-ов в области <%Sq.
Для того чтобы убедиться в зависимости функцииy^+i от
функцийу\,у2, • • • ,У/и, остается лишь доказать, что функция i^+i
в B7) на деле аргументов х^+ь ..., хп не содержит. С этой
целью достаточно установить, что — тождественно относительно
У и • • -,Ур',Хр+1, ...,хп — будет:
дхп
[ср. п° 183]. Остановимся для примера на первом равенстве; осталь-
остальные доказываются аналогично.
Продифференцируем по x^+i уравнения B4), считая хь ..., х^
функциями B5) оту\, ..., j;^, х^+ь ..., хп; мы получим равенства:
д<Р1 , , dfi dcp/j dfi
— = U?
Ы
+ ... + —-^ + ^ = 0, B7)
линейные относительно величин ^
dq)\
Из этих \л линейных равенств как следствие выте-
вытекает (ц + 1)-е линейное равенство
'" 9х 9x 9x
3x^+1 '" 9х^ 9x^+1
216] § 3. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ТЕОРИИ НЕЯВНЫХ ФУНКЦИЙ 541
потому что определитель (/i + 1)-го порядка, составленный из
коэффициентов при упомянутых величинах и из свободных членов
во всех \х + 1 равенствах B7) и B7*), т.е. определитель:
dfl
дх\
dfl
дх\
аи
дх\
df/j+l
дх\
dfl
dfl
dx,
аи
дхц
dxy.
d j 1
uX n-\-l
dfl
dx,+l
dh
дхИ+1
тождественно равен нулю [ведь ранг матрицы A9) есть /л].
Но левая часть равенства B7*), по самому определению B6) функ-
„ dFu+i rj, r
ции /^+ь представляет производную дхИ . 1аким образом, вви-
ввиду B7*), эта производная действительно равна нулю.
Итак, в функции F^+i аргументы х^+ь ..., хп могут быть опу-
опущены: уjj+i зависит лишь оту\, ..., у^ что и требовалось доказать.
В примере 1), 215, матрица Якоб и имеет вид
/1 1 ... 1 \
I 2х\ 2x2 • • • 2хп I .
Если к элементам третьей строки прибавить, соответственно, элементы второй,
умноженные на ^, то получится строка, состоящая (подобно первой) из равных
элементов. Отсюда ясно уже, что все определители третьего порядка — нули. Ранг
матрицы равен двум, и действительно — две функции из трех независимы,
а третья зависит от этих двух.
Аналогично сказанное применяется и к примеру 2), 215.
В заключение заметим, что возможны случаи, когда в одной части рассмат-
рассматриваемой области имеет место одна зависимость между функциями, а в другой
осуществляется другая зависимость, или же функции оказываются независимыми,
и т. п.
3) Пусть, например, функции^! иу2 от двух независимых переменных х\, Х2
определяются на плоскости х\Х2 следующими равенствами:
2 3
0, [х\х\,
У1 = л
0, [0,
если
если
xi ^ О,
х^ < 0.
если jc 1 ^ 0,
если jc 1 < 0,
Легко проверить, что эти функции непрерывны вместе со своими производными
на всей плоскости.
В данном случае ранг матрицы Я к о б и равен двум для первого коорди-
координатного угла, единице — для второго и четвертого углов и, наконец, нулю —
для третьего. Лишь в первом координатном угле функции независимы.
542 ЕЛ. VI. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ [217
§ 4. Замена переменных
217. Функции одной переменной. Цель этого параграфа — дать представле-
представление о формальном процессе замены переменных. Поэтому мы не будем
здесь отвлекать внимание выяснением всех условий, при которых производимые
манипуляции законны (что к тому же и не представляет никаких трудностей).
Значительная часть содержания настоящего параграфа могла бы быть изложе-
изложена и раньше; однако нам казалось целесообразным сосредоточить весь материал,
связанный с заменой переменных, в одном месте.
Пусть дано некоторое выражение
содержащее независимую переменную х, функцию от нее у и ряд производных
от у по х до некоторого порядка. Иной раз требуется перейти в подобном выра-
выражении к новым переменным — независимой t и функции от нее и, с которыми
старые переменные х и у связаны определенными соотношениями (носящи-
(носящими название формул преобразования). Точнее говоря, требуется представить W
в функции от t, и и производных от и по t.
Такая замена переменных обычно мотивируется либо особым интере-
интересом, который представляют в рассматриваемом вопросе переменные t и и, либо
тем упрощением, которое эта замена вносит в само выражение W.
Остановимся сначала на случае, когда заменяется лишь независимая пере-
переменная и дана формула преобразования, непосредственно связывающая х с новой
независимой переменной t.
Предположим, что эта формула преобразования разрешена относительно х:
х = cp(t). A)
Если j/ есть функция от х, то через посредство х она является и функцией от t. Мы
имели уже в 121 формулы, выражающие производные от у no x через производные
от х и у по t: /
у1* = %
B)
г'3
t
III
Ух* =
Так как xft, x, x'$, . . . можно считать известными функциями от t [они
получаются из A) дифференцированием], то остается лишь подставить в W
вместо у'х, у11 2, . . . эти выражения их через t, yft, y, . . .
Если формула преобразования дана в неразрешенном относительно х виде:
Ф(*,0 = 0. C)
то задача по существу решается так же, лишь производные х\, х, . . . вычисля-
вычисляются по правилам дифференцирования неявных функций. *)
*) Впрочем, при этом может оказаться, что в окончательном выражении W еще
останется х; его придется исключать при помощи C).
217] § 4. ЗАМЕНА ПЕРЕМЕННЫХ 543
Переходя к общему случаю, когда заменяются обе переменные, предположим,
что формулы преобразования разрешены относительно старых переменных:
x=q>(t,u), y=ip(t,u). D)
Если у связано функциональной зависимостью с х, то отсюда и будет связано
зависимостью с t, а тогда, в силу D), х иу окажутся сложными функциями от t.
По правилу дифференцирования сложных функций, будем иметь
х[ = q>[ + cpfuut, y\ = \p't + \p'uut\
4 = rt + 2Ф;>; + Ф>;2 + у'у;,, у»г = *» +... + *щ;...
Обращаем внимание читателя на то, что через x't,y't и т. п. мы обозначаем
«полные» производные от х и у по t, т. е. с учетом и зависимости и от t; наобо-
наоборот, q>ft, ipft, . . . означают производные по t лишь постольку, поскольку t входит
в функции ср, гр, . . . в качестве одного из двух аргументов.
Подставив эти выражения в формулы B), найдем выражения производных
от у по х через t, и и производные от и по t, и т. д.
Если формулы преобразования не разрешены относительно х и у:
Ф(х,у, t, и) = 0, Ф(х,у, t, и) = 0, E)
то производные xft,yft,xf2,yff2, . . . вычисляются отсюда по правилам дифферен-
дифференцирования неявных функций. Например, дифференцируя E) по t (причем не толь-
только х и у, но и и считается функцией от t), получим уравнения
ф>; + ф>; + ф; + ф>; = о, *;*; + ф>; + *; + ф>; = о,
из которых найдутся x't, yft, и т. д.
В том частном случае, когда формулы преобразования разрешены относи-
относительно новых переменных:
t = a(x,y), и = р(х,у), F)
можно, прежде всего, пользоваться изложенным только что общим методом. На-
Например, дифференцируя формулы F) по t (причем х,у,и считаем функциями
от t), получим
1 ii.ii i ni i , ni i
1 = axxt + ayyv щ = Cxxt + pyyt,
откуда
и, наконец,
, aYut — .
Ух =
Проще, однако, в этом случае поступить так, как если бы проделывали
обратный переход от переменных t, и к переменным х,у. Продифферен-
Продифференцировав формулы F) по х (считая;; функцией от х)9 получим
tx =ах+ avyx,
544 ГЛ. VI. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ [218
откуда для ух получается то же выражение, что и выше.
И здесь мы различаем производные tx, их, ах, /Зх: первые означают «полные»
производные по х, с учетом и зависимости у от х, а вторые считаются с х лишь
как с одним из двух аргументов функций а, /3.
Заметим, что переход от переменных х, у к переменным t, и по формулам F)
может быть истолкован геометрически как некоторое точечное преобра-
преобразование плоскости (или ее части): если х, у рассматривать как координаты
некоторой точки М плоскости, a t, и — как координаты некоторой точки Р, то
преобразование переводит точку М в точку Р. Возьмем затем какую-либо кри-
кривую Ж на плоскости, с уравнением у = f(x); этой функциональной зависимости
между х и у отвечает некоторая зависимость между t и и: и = g(t), которая
также определяет на плоскости некоторую кривую «2Г. Итак, в рассматриваемом
преобразовании кривая Ж переходит в кривую же «2Г. Если в точке М первой кри-
кривой провести касательную с угловым коэффициентом yft, то в соответствующей
точке Р вторая кривая будет иметь касательную с угловым коэффициентом ut, ко-
который определяется по формуле G). Таким образом, по координатам точки М на
кривой Ж и угловому коэффициенту касательной в М однозначно определя-
определяются как координаты соответствующей точки Р на преобразованной кривой «2Г, так
и угловой коэффициент касательной в Р. Поэтому если через точку М провести
две кривые, касающиеся в этой точке, то преобразованные кривые будут также ка-
касаться в соответствующей точке Р. Рассматриваемое точечное преобразование
плоскости сохраняет касание [ср. ниже пример 5)].
218. Примеры.
1) Пусть дано уравнение х2ух2 + хух + у = 0; преобразовать его, полагая
х = еК
По формулам B), имеем
/ —tii —it / и i\
Ух=е -yt> yxi=e -(yt2-yt)>
и уравнение примет более простой вид:
у',2+у = о.
2) Преобразовать выражение
w y
полагая х = t — у.
Под общую схему это преобразование подойдет, если написать х = t — и,
у = и. По формулам B),
w *да-*&'-/(*;+у,'J
W+y',K
С другой стороны, формула преобразования дает x't = \—y't\ подставляя, найдем
окончательно W = у — у'г
218]
§ 4. ЗАМЕНА ПЕРЕМЕННЫХ
545
3) Перестановка ролей переменных. Предположим, что незави-
независимая переменная х и функция от нее у обмениваются ролями; под общую схе-
схему это преобразование подойдет, если положить х = и, у = t. Поставим себе
задачей выразить производные от у по х через производные от х по у. Сно-
Снова прибегаем к формулам B), заменяя t через у. Если учесть, что у' = 1
(и у = у"ъ = • • • = 0), то сразу получим
о // 2
1
Ух = -V. УХ2 = -
V
/ ///
~хуху3
Например, выражение W = у'ху"ъ ~
Х
У'"
если применить к нему это пре-
У
%
образование, получит вид W = —=тт-
ху
4) Переход к полярным координатам. Еслих,у рассматривать как
прямоугольные координаты точки, то уравнение у = f[x) выразит кривую. Часто
бывает полезно перейти к полярным координатам г, в, выражая кривую
ее полярным уравнением г = g@). Тогда, естественно, представляет-
представляется необходимость, исходя из выражений различных геометрических элементов
кривой через х,у,у'х,у, . . ., получить соответствующие выражения их че-
через в, Г, Гд, Г*'2, . . .
Формулы преобразования в этом
случае, как известно, имеют вид
х = г cos в, у = г sin в. Дифферен-
Дифференцируя их по в (причем учитываем,
что г есть функция от в), получим
хв = гв cos в — г sin в,
у'в = г'в sin в + г cos в;
x"Ql = г02 cos в — 2г'в sin в — г cos в,
ув2 = гв2 sin в + 2гв cos в — г sin в,
Рис. 114
Отсюда, по формулам B), найдем (подставляя в вместо t):
1
Ух =
rfn sin в + г cos в
// _
У х^
гв2
г' cos0 — r sin# ' J'хл (г'в cos^ — г sin^K '
Таким образом, например, угловой коэффициент касательной будет
, г п sin в + г cos в
tga = v = -j ;
г'в cos в — г sin в
тангенс угла со, образованного касательной с продолженным радиусом-вектором
(рис. 114),
= tg(a - 0) =
tga - tgв
хух -у
546 ГЛ. VI. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ [218
теперь выразится простой формулой
в связи с чем при полярном задании кривой положение касательной предпочитают
определять именно углом со.
Рассмотрим еще выражение
представляющее, как увидим ниже [в п° 251], важный геометрический элемент
кривой («радиус кривизны»). Если подставить сюда найденные выше выражения
для ух и у> то после упрощений получим
R =
- rr>>2
5) Преобразование Лежандра. Поставленную в предыдущем п° за-
задачу замены переменных можно обобщить, допустив присутствие произ-
производных уже в формулах преобразования. Мы ограничимся одним примером
этого рода:
t=yx, и = х-ух-у;
это преобразование называется преобразованием Лежандра.
Продифференцируем вторую формулу преобразования по х, рассматривая
слева и как функцию от х через посредство t (зависимость t от х дается первой
формулой):
i it i , Hi и
Щ'Ух2=Ух+Х'Ух2-Ух=Х' УХ2-
Отсюда (в предположении, что у ф 0) и м[ = v. Таким образом, если
учесть и обе формулы преобразования, имеем
х = ut, у = t • ut — и,
чем выявляется взаимность преобразования: t,u,ut выражаются через х,
у, ух совершенно так же, как последние величины выражаются через первые.
Дифференцируя подобным же образом по х формулу ut = x, получим
// " л //1
ut2 -yx2 = 1, откуда ух2 = —.
uf2
Дальнейшее дифференцирование дает
ЩЪ ' УХ2 + Щ2 - ухъ = 0, так что ух3 = --—,
Ut2
и т. д. 1
Заметим, что если преобразование Лежандра истолковать геометрически
как преобразование плоскости, то оно отнюдь не будет точечным преобра-
преобразованием. Для определения координат t, и точки Р недостаточно знать координа-
координаты х, у точки М, но нужен и угловой коэффициент ух касательной в этой точке
219] § 4. ЗАМЕНА ПЕРЕМЕННЫХ 547
к рассматриваемой кривой;; = f(x). Тем не менее, кривая преобразуется здесь
снова в кривую, и касание сохраняется*^.
219. Функции нескольких переменных. Замена независимых переменных.
Перейдем теперь к задаче о преобразовании выражения
dx ду дх2 дхду
содержащего, кроме независимых переменных х, у, . . . и функции от hhxz, также
частные производные z по ее аргументам, до определенного порядка.
По тем же мотивам, что и в простейшем случае, рассмотренном выше, и здесь
может понадобиться перейти к новым переменным, которые со старыми
связаны с помощью формул преобразования. Если обозначить новые незави-
независимые переменные через t, и, . . ., а функцию от них — через v, то задача
состоит в том, чтобы выразить W через t, и, . . ., v и через производные от v
по ее аргументам. Очевидно, достаточно научиться делать это по отношению
к старым производным ||, Щ, . . ., |^§, -?rjj;, . . . Для простоты письма мы
будем предполагать, что независимых переменных всего две: старые х и у, а но-
новые t и и.
Начнем и здесь с того случая, когда заменяются лишь независимые пере-
переменные, и формулы преобразования непосредственно связывают старые перемен-
переменные х, у с новыми t, и.
Предположим, что формулы преобразования разрешены относительно старых
переменных:
x = <p(t,u), y = ip(t,u). (8)
Рассматривая z как сложную функцию от t и и через посредство х и j/, по правилу
дифференцирования сложных функций получим:
dz дх dz ду dz dz дх dz ду dz
dt dt дх dt ду' ди ди дх ди ду
Таким образом, для определения старых производных || и Щ мы имеем систе-
систему линейных уравнений; отсюда старые производные линейно выразятся через
новые:
dz dz dz dz dz dz
— =A VB—, —=C VD—. A0)
dx dt du dy dt du
При этом важно отметить, что коэффициенты А, В, С, D составляются из произ-
производных функций ср, гр, фигурирующих в формулах (8), но вовсе не зависят
от z.
*^ Подобные преобразования, сохраняющие касание, играют важную роль
в различных областях геометрии и анализа. Они носят название касательных
преобразований, или преобразований прикосновения. Точечные
преобразования и преобразования Лежандра являются лишь частными при-
примерами их.
548 ГЛ. VI. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ [219
Это замечание позволяет применить формулы A0) к производным ||, Щ
(вместо z). Таким путем, например, для |^§ получится выражение
д2^
dx2 dx\dx) dt\dx) du\dx
_ / d2z d2z dA dz dB dz\
~ \ dt2 dtdu dt dt dt du)
( d2z d2z dA dz dB dz\
+ B(A b?^-H 1 ).
V dtdu du1 du dt du du/
Применяя A0) к производным второго порядка (вместо z), можно получить вы-
выражения для производных третьего порядка, и т. д.
Если формулы преобразования разрешены относительно новых переменных:
t = a(x,y), u = p(x,y),
то удобнее прибегнуть к обратному методу, т. е. рассматривать z как
сложную функцию отх, у через посредство t, и и дифференцировать ее по старым
переменным. Это сразу приведет нас к формулам типа A0):
dz _ dt dz du dz dz _ dt dz du dz
dx dx dt dx du' dy dy dt dy du
На этот раз коэффициенты
dt du dt du
A D S~~i ТЛ
/i — , D — , \-s — , LJ —
dx dx dy dy
будут функциями от ;\;,j/, но также не зависят от z.
Применяя повторно формулы A1), можно и здесь получить выражения даль-
дальнейших производных. Например,
d2z _ d / dz dz\ _ dA dz dB dz d /dz\ d /dz\ _
dx2 ~ dx \ dt du) ~ dx dt dx du dx\dt) dx \du) ~
dA dz dB dz / d2z d2z \ / d2z d2z
\
dx dt dx du \ dt2 dtdu) \ dtdu du
Наконец, в общем случае, при произвольных формулах преобразования
Ф(х,у, t, и) = 0, ^(x,y,t,u) =0, A2)
можно пользоваться как прямым, так и обратным методом, вычисляя частные
производные
dx dx dy dy dt dt du du
dt' du' dt' du' dx' dy' dx' dy
по правилам дифференцирования неявных функций.
* ^ Здесь уместно сделать замечание, аналогичное замечанию на с. 542. Так как
выражения старых производных через новые содержат х, у, то после подстановки
этих выражений в W может оказаться необходимым еще исключать х, у с помо-
помощью формул преобразования. Читатель легко заметит и в дальнейшем случаи,
сходные с этим.
220] § 4. ЗАМЕНА ПЕРЕМЕННЫХ 549
220. Метод вычисления дифференциалов. Укажем теперь и другой метод
для выражения старых производных через новые, особенно удобный, если в W
входят не отдельные производные, но все производные данного порядка. Это —
метод вычисления полных дифференциалов. Он также может быть
представлен в двух формах, в зависимости от того, считаются ли t и и или х и у
независимыми переменными.
Пусть сначала независимыми будут t и и, все дифференциалы берутся имен-
именно по этим переменным (прямой метод). Дифференцируя полным образом
формулы преобразования A2), можно выразить dx и dy линейно через dt и du:
dx=adt + f3du, dy = у dt + S du; A3)
затем, дифференцируя эти формулы, представим d x и d у виде однородных мно-
многочленов второй степени относительно dt и du:
d2x = edt1 + f dtdu + t] du2, d2y = в dt2 + i dt du + xdu2, A4)
и т. д. Коэффициенты a, ft, . . ., i, x суть известные функции от х, у, t и и.
Представим теперь dz двояко (пользуясь инвариантностью формы дифферен-
дифференциала):
dz dz dz dz
dz = — dx Л dy Л dt Л du. A5)
dx dy dt du
Если вместо dx и dy подставить их выражения A3) и приравнять коэффициенты
при dt и du в обеих частях равенства *^, то получатся линейные уравнения
dz dz dz dz dz dz
a by— = — и P \-S— = —,
dx dy dt dx dy du
из которых определятся производные || и Щ.
Аналогично, можно представить двояко d z (помня о том, что независимыми
переменными являются не х и у, a t и и):
9 и Z 9 U Z и Z 9 и Z 9 и Z 9
Л = —^dx + 2 dx dy -\ у dy -\ d х -\ dy =
dx1 dx dy dy1 dx dy
d2z 9 d2z d2z 9
= -Г + 2 dtdu+ -^ du. A6)
dt2 dtdu du2 v J
Подставив вместо dx, dy, d x и d у их выражения A3) и A4), приравняем ко-
коэффициенты при dt , dt du и du в обеих частях равенства* \ Это дает нам
2 2 2
систему трех линейных уравнений для определения производных
я2
z
я2
(так как ||, |^- уже известны), и т. д.
|, , ^-\
*) Напомним, что равенство Adt -\-B du = Afdt -\- Bfdu может иметь место для
произвольных30^ dt и du лишь в том случае, если А = Af и В = Bf.
**) Равенство Adt2 + В dtdu + С du2 = A'dt2 + В'dt du + С'du2 может иметь
место для произвольных30^ dt и du лишь при А = Af,B = Bf, С = С1.
' В рассматриваемом равенстве и правая и левая части являются функция-
функциями. Из равенства двух функций всегда следует равенство значений этих функций
при любых фиксированных значениях аргументов. (Поэтому практически в лю-
550 ГЛ. VI. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ [221
Более простым в осуществлении является обратный метод, при котором
независимыми переменными считаются .х и j/, так что все дифференциалы берутся
на этот раз по этим переменным.
Последовательным дифференцированием из формул преобразования A2) мы
получаем здесь
dt = adx + bdy, du = с dx + d dy, A7)
d2t = edx2 + fdxdy + gdy2, d2u = hdx2 + idxdy +jdy2, A8)
и т. д. И здесь коэффициенты а, Ь, . . ., i, j суть известные функции от х, у, t и и.
Если в A5) вместо dt и du подставить их выражения A7) и приравнять ко-
коэффициенты при dx и dy в обеих частях равенства, то непосредственно
получим
dz dz dz dz dz dz
— =a he—, — =b bd—.
dx dt du dy dt du
Взамен A6) в настоящем случае будем иметь
П2 П2 П2
л d z 2 ~ d z d z 2
d z = —dx + 2 —— dxdy + —^dy =
dxz dx dy dyz
2 2 d2z i 2 dz j2 dz
d1 dZ
i 2 dz j2 dz j2
du1 +—dZt+— dlu.
d d
= —dt + 2 —— dtdu+—2 du +—dt+—
dtz dt du duz dt du
Подстановка выражений A7), A8) и приравнивание коэффициентов при dx2,
dx dy и dy2 в обеих частях равенства непосредственно приведут к вы-
Я2 Я2 Я2
числению производных ^-4, -^-, ^-4, и т. д.
г дх1 дх ду ду1
221. Общий случай замены переменных. Обратимся, наконец, к общему
случаю, когда заменяются и независимые переменные, и функция. Пусть формулы
преобразования разрешены относительно старых переменных:
х = cp{t, и, v), у = ip(t, и, v), z = %(t, и, v). A9)
Если z есть функция от х и у. z = f(x, у), то, подставляя сюда вместо х, у и z их
выражения через t, и, v, получим зависимость между последними переменными,
так что v будет функцией от t и и.
Считая независимыми переменными t и и (прямой метод), az — функ-
функцией от них через посредство х и у, как и выше, получим равенства (9), а из
них A0). Но здесь под ff» • • •» |§ разумеются «полные» частные производные
от х,у, z no t или и, получаемые из A9) с учетом того обстоятельства, что v
сама зависит от t и и:
dx dep dep dv dz dx dx dv
dt dt dv dt ' ' du du dv du
Коэффициенты A, B,C, D содержат не только t, и, v, но и производные |^, |^;
последние входят рациональным образом. Последовательное применение
формул A0) и здесь приведет к выражениям для вторых производных, и т. д.
бом верном равенстве, содержащем дифференциалы независимых переменных,
эти дифференциалы можно при желании считать и произвольными фиксирован-
фиксированными числами.)
221] § 4. ЗАМЕНА ПЕРЕМЕННЫХ 551
Если формулы преобразования разрешены относительно новых переменных:
t = a(x,y,z), u = /3(x,y,z), v = y(x,y,z), B0)
то обычно прибегают к обратному методу, т. е. считают независимыми
переменными х и у. Имеем
dv dv dt dv du dv dv dt dv du
dx dt dx du dx ' dy dt dy du dy
Вместо f?,• • •, fr; сюда нужно подставить их выражения, получаемые дифферен-
дифференцированием по х и по у формул B0), с учетом того, что z есть функция от х иу:
dt _ da da dz dv _ dy dy dz
dx dx dz dx' ' dy dy dz dy
Таким путем получаются линейные относительно |f и ff уравнения, из ко-
которых эти производные легко выражаются через х, у, z, |j и |^.
Вычисление дальнейших производных проще всего выполнить так: дифферен-
дифференцируем полученное для || (или |^) выражение снова по х (по у), рассматривая
производные |j и |^ как функции от х и у через посредство t и и, и т. д.
В случае формул преобразования общего вида
А(х,у, z,t, и, v) = 0, В (х,у, z, t, и, v) = 0, 1
F(x,y,z, t, и, v) = 0, J
можно пользоваться любым из этих методов с применением правил дифференци-
дифференцирования неявных функций.
Для решения рассматриваемой общей задачи замены переменных применим
и метод вычисления полных дифференциалов. Мы ограничимся
изложением той его формы, которая связана с предположением, что независимы-
независимыми являются старые переменные х иу (обратный метод), так что по этим
переменным и берутся все дифференциалы.
Последовательным дифференцированием, исходя из формул B1), можно най-
найти выражения
dt = a\dx + a^dy + а^ dz,
du = bxdx + b2 dy + b3 dz, J> B2)
dv = сi dx + C2 dy + C3 dz;
d2t = d\ dx2 + d2 dx dy + d3 dy2 + d4 dx dz +
+ d5 dy dz + d6 dz2 + a3 d2z,
d2u = e\ dx2 + . . . + e6 dz2 + b3 d2z,
2 2 2 2
d v = /i dx + . . . + fedz + c3d z;
Если в равенство
dv dv
dv = — dt Л du
dt du
B3)
|^f
552 ГЛ. VI. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ [221
подставить вместо dt, du и dv их выражения B2), то получим
с\ dx + С2 dy + сз dz = —(а\ dx + а^ dy + «з fife) Н (&i dx -\-bidy -\- Ъ^ dz),
dt du
откуда
dz =Adx +B dy, B4)
где А, В рациональным образом содержат производные |^ и |^. Сопо-
Сопоставляя это с формулой
<7Z OZ
dz = — шс Н firy,
видим, что
dz dz
— =Л, —=В.
дх ду
Возьмем теперь равенство (t и и не являются независимыми перемен-
переменными)
dlv = -тГ + 2 —- dtdu+—2 du1 +—dZt+— dzu
dt1 dt du du1 dt du
и подставим сюда вместо dt, du, d t, d u, d v их выражения B2) и B3), а затем
и fife, заменив его выражением B4). Из полученного равенства определится d z:
d2z =Cdx2 + 2Ddxdy+Edy2,
tj\qC,D,E рациональным образом содержат производные |^, |^, |^
-?-%-, т~у- Сопоставляя с формулой
д2 р2 р2
d2z = —jdx2 + 2 ——- dxdy + —j dy2,
dxz dx dy dyz
приходим к результату
— -С —-D —-Е
dx2 dx dy ' dy2
и т. д.
Задаче преобразования переменных и здесь можно придать геометрический
смысл. Если переменные (x,y,z) и (t,u,v) рассматривать как координаты то-
точек М и Р пространства, то формулы преобразования, например в форме B0),
относят каждой точке М некоторую точку Р, т. е. характеризуют точечное
преобразование пространства (или его части). Зависимости между ;\;,j/
и z отвечает зависимость между t, и и v, так что каждая поверхность S преобра-
преобразуется при этом в некоторую поверхность 2Г.
Мы видели, что значениями х, у, z, || и Щ однозначно определяются значе-
значения t, и, v, |^ и |^. Вспоминая уравнение касательной плоскости [180, F)]:
Z-z=aJ.(X-X)+BJ-(r-y),
dx dy
отсюда легко заключить, что двум касающимся в точке М поверхностям S\ и с>2
отвечают в рассматриваемом преобразовании две поверхности &\ и ^2, также
касающиеся в точке Р. Точечное преобразование пространства сохраняет
касание [ср. ниже пример 7)].
222] § 4. ЗАМЕНА ПЕРЕМЕННЫХ 553
222. Примеры.
1) Переход к полярным координатам. Пусть z есть функция
точки на плоскости z = /(М). Обыкновенно положение точки определяется ее
прямоугольными координатами (х,у), так что z является функцией от перемен-
переменных jc и j/. Часто, однако, оказывается более удобным характеризовать положение
точки полярными координатами г, в, и тогда возникает необходимость преобра-
преобразования к новым переменным. Проделаем этот переход различными методами.
Прямой метод: независимыми переменными считаются г, в. Исходя из
формул преобразования
х = г cos в, у = г sin в,
по образцу формул A0) имеем
откуда
dz dz dz dz dz dz
— = cos e h sm e —, — = — r sm в \- r cos в —,
dr dx dy d6 dx dy
dz dz sine dz dz dz cose dz t ч
— = cose , — = sine 1 , B5)
dx dr r d6 dy dr r d6 K J
так что выражения cose, —^Я, sine, ^^ играют здесь роль коэффициен-
коэффициентов А, В, С, D. Затем,
<92z d ( dz sine dz\ sine d ( dz sine dz \
—r = cose— cose- — — cose- — =
dxz dr \ dr r d6/ r d6 \ dr r d6/
2 <92z 2sine cose <92z sin2 в d2z 2sine cose dz sin2 в dz
= cos e —T 1—= т н ^ 1 .
drz r dr d6 rz d6z rz d6 r dr
Аналогично находим
<92z 2 <92z 2sine cose d2z
—- = sm e —r- -\ \-
dyz drz r dr d6
и т. д.
Обратный метод: независимыми переменными считаютсях, у. Для того
чтобы воспользоваться формулами A1), нужно знать производные |j, |j, Щ9 Щ.
Их можно найти, разрешив предварительно уравнения, связывающие старые пере-
переменные с новыми, относительно последних. Но можно воспользоваться методами
дифференцирования неявных функций, не разрешая уравнений. Если продиффе-
продифференцировать формулы преобразования по х и по у, считая г и в функциями от х
и у, то получим
dr d6 dr d6
1 = cos e r sin e —, 0 = sin e h r cos e —
dx dx dx dx
cos2 6
ld2z
dOz
2 sin e cos e
r2
dz
dO
+
cos2
r
в
dz
dr
Отсюда
dr d6 dr d6
0 = cos e r sm e —, 1 = sm e \- r cos в —.
dy dy dy dy
dr d6 sine dr d6 cose
— = cose, — = , — = sine, — =
dx dx r dy dy r
и — по формулам A1) — мы возвращаемся к выражениям B5), и т. д.
554 ГЛ. VI. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ [222
Метод вычисления дифференциалов. Пусть, как и только что,
независимыми переменными будут х, у.
Дифференцируем полным образом формулы преобразования
dx = cos 6 dr — г sin 6 d6, dy = sin 6 dr + r cos 6 d6;
отсюда
— sin 6 dx + cos 6 dy
dr = cos 6 dx + sin 6 dy, d6 = ,
r
так что
dz dz ( dz sine dz\ ( dz cose dz\
dz = —dr + —dO= cose- — )dx+ sine — + —)dy,
dr d6 \ dr r 86/ \ dr r 86/
что снова приводит к выражениям B5).
Вторичное дифференцирование формул для dr и d6 дает:
2 sin2 6dx2 -2 sin в cos 6 dx dy + cos2 6 dy2
dzr = - sin e d6 dx + cos 6 d6 dy = —,
r
2 —r (cos e dx + sin 6 dy) d6 — (cos 6 dy — sin 6 dx) dr
2 sin e cos e <ix2 - 2(cos2 e - sin2 e) dx dy -2 sin e cos e <iy2
Тогда для А будем иметь:
82z 82z
^^е +
Л = т^ + 2^^е + 1^е + Л + /е =
<9rz 3r 86 86l dr 86
( i 82z 2 sine cose <92z sin2 6 82z sin2 6 dz
= cos e —^ —— + —^- —^ + — +
у 8rz r dr 86 rz 86Z r dr
2 sine cose dz\ о / ч / 2
+ -2 — J dx2 + 2 (...) dx dy + (...) ф2,
откуда для вторых производных |-|, . . . получатся те же выражения, что и выше.
Рассмотрим, для примера, выражения
/dz\2 /dz\2 d2z d2z
W\ = ( —) +( —), W2=^-\ т.
V3jc/ V3;;/ 3jc2 3;;2
С помощью найденных формул они преобразуются так:
dz\2
3r/ r
/dz\2 I /dz\2 d2z 1 <92z 1 dz
=Ь" +~ \u ' ^2= ^T + ~^2 + "^"'
l\d6/ dr1 rl d6l r dr
2) Переход к сферическим координатам. В пространстве роль,
аналогичную полярным координатам на плоскости, играют так называемые сфе-
сферические координаты р, ф, е, с которыми прямоугольные координа-
координаты х, у, z связаны с помощью формул
х = р sin q> cos е, у = р sin <p sin 6, z=pcoscp.
222] § 4. ЗАМЕНА ПЕРЕМЕННЫХ 555
Пусть требуется преобразовать к переменным р, q>, в выражения
ди\2 (ди\2 (ди\2 д2и д2и д2и
/ Vdy/ \dz/ <9;\;z ду1 dzz
где г/ есть некоторая функция точки в пространстве.
Если преобразование произвести в два приема, полагая сначала х = г cos в,
у = г sin в (и оставляя z неизменным), а затем z = р cos<p, г = р sin<p (остав-
(оставляя 0 неизменным), то можно будет воспользоваться результатами примера 1).
Например, для второго выражения имеем
д2и д2и д2и 1 д2и 1 ди
д2и д2и\ 1 д2и 1 ди
Выражение в скобках, на основании того же примера 1), перепишется так:
д2и 1 д2и 1 ди
др2 р2 дер2 р др'
наконец,
ди ди cosq> ди
— = sin ср 1 .
дг dp p дер
Подставляя все это, окончательно найдем
д и 1 д и 1 д и \ ди ctg cp ди
др р дер п sin ф дО р др р дер
Аналогично,
w. -(ди\21 х (ди\21 х (ди ~
3) Показать, что выражения W\ и Wi сохраняют свою форму при любом
преобразовании прямоугольных координат в прямоугольные же
х = а\х + 6ц/ + ciz, у = Я2-Х + /?23^ + C2Z, z = «з^ + b^y + C3Z,
где коэффициенты а, Ь, с удовлетворяют известным соотношениям
1 при i = j,
О при i ф j.
Метод вычисления дифференциалов. Считая;\;,j/, z независимыми
переменными, имеем
/ 2 /
dx = a\ dx -\- Ъ\ dy -\- c\ dz, d x =0,
<iy = ci2 dx -\- b2 dy -\- C2 dz, d у = 0,
dz = B3 dx -\- Ьз dy -\- C3 dz, d z = 0.
556 ГЛ. VI. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ [222
Тогда
du = —- (а\ dx + b\dy + c\ dz) +
dx'
du du
+ ^т («2 dx + b2dy + с2 dz) + —- (я3 dx + b^dy + c3 dz),
dy' dz'
откуда
— = a\ -—
5* дх'
— = c\ h с г h C'x ;
dz dx' dy' dz'
возводя в квадрат и складывая, в силу B6), получим
du
dy'
du
du
du
du
du
du
1 ЗУ +
du
du
2з7 +
du
3 ~dz~'
Затем,
d м = ——r {a\dx +bidy + c\dz) +
dx'1
d2u
+ 2 — (a\ dx + b\ dy + c\ dz) • (a2 dx + b2dy + C2 dz) + . . .
Выражение И^ есть сумма коэффициентов при dx , dy и dz ; с помощью B6)
нетрудно установить, что
П2 о2 П2
3 м 3 м 3 м
4) Преобразовать уравнение
2 d2w 2 д2^ 2 52^ д1™ d2w d2w
х —г- + з^ —5" + z —т + У2 1" zx 1" ХУ
dx1 dy1 dz1 dy dz dz dx
г + з^ 5 + z т + У21 zx1 ХУ= °
dx1 dy1 dz1 dy dz dz dx dx dy
к новым переменным t, и, v по формулам х = uv, у = vt, z = tu.
Прямой метод. Считая независимыми переменными t, и, v, будем иметь
dw dw dw dw dw dw dw dw dw
— = — v -\ м, — = — v -\ t, — = — м -\ t.
dt dy dz du dx dz dv dx dy
Отсюда
dw 1 dw 1 dw 1 dw
x — = t V -u V -v —,
dx 2 dt 2 du 2 dv
dw 1 dw 1 dw 1 dw
у — = — t — — — и 1 v —,
У dy 2 dt 2 du 2 dv
dw 1 dw 1 dw 1 dw
z — = — t 1 м v —.
dz 2 dt 2 du 2 dv
222] § 4. ЗАМЕНА ПЕРЕМЕННЫХ 557
Далее,
2 д2т д ( дт \ д ( 1 dm I dm I dm \
dxz dx \ dx / dx \ 2 dt 2 ди 2 dv /
1 м2 1 o2 1 o2 1 o2
\ 2 д W \ 2 д U) 1 2 d W 1 <9lt>
- f 7Г- + ~ U г- + - t> r- + - UV ¦
1 d w 1 5 u> 3 dw \ dw \ dw
v t tu 1 t и v ,
2 dvdt 2 dtdu 4 dt 4 du 4 dv
d2w d ( dw\ d /1 dw I dw 1 dw
(
d ( dw\ d /1 dw I dw 1 dw\
= z — у — = z — ( — t и 1 v — =
dzVdyJ dz\2 dt 2 du 2 dv)
yz z у
dydz dzVdy
\ 2 д W 1 2 d W 1 2 d W 1 d W
1 dw 1 dw 1 dw
+ -t и v —,
4 dt 4 du 4 dv
и т. д. Сложив все подобные выражения (и отбросив числовой множитель), полу-
получим преобразованное уравнение в виде
2 d W 2 д w 2 д W
dt1 du1 dv1
До сих пор заменялись лишь независимые переменные; приведем примеры,
где замене подвергается и функция.
2 dz 2 dz 2
5) Преобразовать уравнение х \- у — = z , полагая
dx dy
t t
x = t, у =
\+tu \+tv
Прямой метод. Независимые переменные: t, и. Дифференцируем тре-
третью из формул преобразования по t и по и, рассматривая переменные z и v как
функции от t, и (первую — через посредство х, у):
dz
dx
Отсюда
dz
1
dy A
dz
dx
Преобразованное
1
+ tuJ
1 /
(\+tvJ V
уравнение
1 -Г2
A+f
1 /2
после
~dt
dv
dt
dz
dy (
dv\
du)'
сокращения
dt
2
dz
dy
будет
(H
A 4
иметь
A
-tu)
-tv)
вид:
2
2
2
^J
du
dv
du
Решим ту же задачу иначе.
Обратный метод. Выразим из формул преобразования новые перемен-
переменные через старые:
11 11
t = х, и = , v =
ух z х
558 ГЛ. VI. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ [222
и будем считать независимыми переменными х,у. Дифференцируя третью фор-
формулу по х и по у (v зависит от них через посредство t, и), найдем:
\ dz 1 dv dv 1 1 dz dv 1
dz _ 2/ 1 dv 1 dv\ dz _ z2 dv
dx~Z \x2 dt x2 du)9 dy ~ y2 du
6) Выражение
d2z d2z d2z
W = -^ -2-
dx2 dx dy dy2
преобразовать к переменным t=x-\-y,u=^,v = j.
Метод вычисления дифференциалов. Независимые перемен-
переменные: х,у. Дифференцируем формулы преобразования:
у \ z \
dt = dx + dy, du = r- dx -\— dy, dv = ~ dx -\— dz.
X1 X X1 X
Если v рассматривать как функцию от х, у через посредство t,u,ro дифференци-
дифференциал dv напишется так:
dv dv dv . dv ( у 1
dv = — dt + — du = — (dx + dy) + —[ ^dx + -dy
dt du dt du\ xl x
Сопоставляя два выражения для dv, находим
z dv dv (у \
dz = - dx +x — (dx+dy)-\ dx + dy .
x dt du\x J
Составим теперь вторые дифференциалы от новых переменных:
? ? 2у о 2
d t = 0, d и = —г dx т dx dy,
х5 xl
d2v = -4г dx dz + Ц dx2 + - d2z.
X1 X5 X
С другой стороны,
dlv =—dtz + 2 —— dtdu^-j du1 +—dlt+— dlu =
dt1 dt du du1 dt du
dtz dt du
d2v ( у 1 \2 dv fly
dv fly 2 2 \
5m \^:j ^z /
222] § 4. ЗАМЕНА ПЕРЕМЕННЫХ 559
Приравнивая оба выражения для d v и заменяя dz полученным выше его
выражением, придем к равенству, из которого определится d2z:
j dx Гz dv dv / у \~\ 2z
d z = 2 — - dx + x — (dx + dy) H fibc + (
jc |jc dt du\x
fc(rfx + фJ + 2 ^(Л + dy) (-^
dtl dt du \ xl
d2v ( у 7 1 \2 dv fly 7 2 2
ди\х5 xz
Отсюда можно определить производные |^f, ^j^j, j\ как коэффициенты
при fibf , Idx dy, dy . Но нужный нам результат можно получить проще, заметив,
что d z переходит в W, если взять dx = 1, dy = — 1. Таким путем находим:
(
Лз ди2 t ди2'
7) Преобразование Лежандра. Наподобие 5),218, мы и здесь при-
приведем преобразование Лежандра как пример более общего преобразования,
когда уже формулы, связывающие старые и новые переменные, содержат произ-
производные. Положим
dz dz dz dz
dx dy dx dy
Разумея tiorz некоторую определенную функцию отх иу: z = f(x, у), будем
предполагать ее такой, что
D(x,y) dx1 dy1
Дифференцируя третью из формул преобразования по х и по у (причем v
рассматриваем как функцию от х, у через посредство t, и), получим
dv d2z dv d2z d2z d2z
dt dx2 du dx dy dx2 dx dy'
dv d2z dv d2z d2z d2z
1 = x \- у ,
dt dx dy du dy2 dx dy dy2'
откуда
dv dv dv dv
x = —, У = —> так что и z=t — + u- v, B8)
dt du dt du
т. е. преобразование имеет взаимный характер.
Дифференцируя первые две из полученных формул B8) сначала по х, а затем
по у, придем к уравнениям
_ d2v d2z d2v d2z _ d2v d2z d2v d2z
~ dt2 dx2 dtdu dxdy' ~ dt du dx2 du2 dx dy
и
d2v d2z d2v d2z d2v d2z d2v d2z
~ dt2 dxdy dtdu dy2' ~ dtdu dx dy du2 dy2'
560 ГЛ. VI. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ [222
Так как [203, D)]
_ d2v d2v / d2v \2 _ D(x,y) _ 1
~~ dt2 du2 \dtdu) ~ D(t,u) ~ J
0,
то из этих уравнений
дх2 '
ди1
I
д z = wL
дхду I '
d2z
I
Если х, у, z nt, и, v трактовать как координаты некоторых точек пространст-
пространства, то преобразование Лежандра можно рассматривать как преобразование
пространства (но не точечное). Поверхность, характеризуемая зависимостью меж-
между z их,у, переходит при этом в поверхность, определяемую зависимостью меж-
между v и t, и. Так как t, и, v, |j, |j зависят только от х, у, z, |§, Щ, то преобразо-
преобразование Лежандра сохраняет касание*^.
8) Легко обобщить преобразование Лежандра на случай пространства
любого числа измерений. Пусть, скажем, z есть функция от х\, Х2, • • •, хп. По-
Положим
,,-?¦ (.-1.2 .)
dxt
dz
здесь v есть новая функция от новых переменных t\, t2, - - -, tn.
Будем предполагать и здесь определитель
J =
d2z
dx2
дх2 дх\
d2z
дхп дх\
d2z
дх\ дх2
d2z
dx2.
d2z
дх„дх2
d2z
дх\дхп
дх2 дхп
d2z
Эх2
отличным от нуля.
Продифференцируем формулу, определяющую v, по х^ (рассматривая при
этом v как функцию от х\, . . ., хп через посредство t\, . . ., tn)\
Edv д z
dtt dxi дхь-
д z
xi дхь-
Ввиду J ф 0, отсюда следует
dv
— =xt (i = 1, ..., w).
at
*)
Сюда также относится сноска на с. 547.
222]
§ 4. ЗАМЕНА ПЕРЕМЕННЫХ
561
Таким образом, и
dv
-¦-!>?
V,
к
так что в общем случае преобразование также имеет взаимный характер.
9) Наконец, рассмотрим еще один пример преобразования, представляющий
некоторое своеобразие. Пусть
q>(u\, . . ., ип;х\, . . .,хп)
будет функция от 2п переменных, однородная 2-й степени относи-
относительно переменных х\, . . . ,хп. Предполагая определитель
Н =
д ср
д ср
дх2дхх
д2ср
дхп дх\
д2ср
дх\ дх2
д2ср
дх2
д2ср
дхп дх2
д2ср
дх\дхп
д2ср
дх2 дхп
д2ср
дх2
отличным от нуля, положим
д(р
и введем t\, . . ., tn в качестве новых независимых переменных вместо х\, .
Тогда функция ср преобразуется в некоторую функцию
. ., хп.
, . . ., un;t\, . . ., tn).
Доказать, что
дщ дщ
Дифференцируя ср = гр похь рассматривая гр как функцию от х\,
через посредство t\, . . ., tn\
д(р
дгр dzcp
i=l
С другой стороны, производная -^- будет однородной функцией пер-
первой степени относительно переменных х\,...,хп. Тогда по формуле
Эйлера [188]
дер
дхк
д2ср
Сопоставляя полученные два разложения для ^-, ввиду// ф 0, заключаем о спра-
справедливости соотношений (а).
562 ГЛ. VI. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ [222
Дифференцируя же по щ, получим
п о
дер dip ^-^ dip д ср
дщ дщ ^-^ ди дхь дщ
к=\
Но ^L, очевидно, однородная функция второй степени относитель-
относительно^!, • • • >хп. Снова применяя формулу Эйлера, видим, что последняя сумма
дает нам
Ед /д<р\ _ д<р
dxfc \дщ / дщ
к=\
Отсюда и следуют соотношения (б).
ГЛАВА СЕДЬМАЯ
ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
К ГЕОМЕТРИИ
§ 1. Аналитическое представление кривых и поверхностей
223. Кривые на плоскости (в прямоугольных координатах).
В настоящей главе мы остановимся на некоторых приложениях
изученных понятий, фактов и методов дифференциального исчис-
исчисления к геометрии. [С немногими из них мы сталкивались уже вы-
выше, в пп° 91, 141, 143, 145, 148, 180]
Мы считаем полезным предварительно напомнить читателю
различные способы аналитического представления кривых и по-
поверхностей; этому посвящен § 1. Оговорим наперед, что функции,
о которых будет идти речь в этой главе, как правило, предполага-
предполагаются непрерывными и имеющими непрерывные же
производные по своим аргументам; в случае надобности, мы
будем требовать существования и непрерывности и дальнейших
производных.
Начнем с плоских кривых, причем в основу положим не-
некоторую прямоугольную систему координат Ох у.
Выше мы не раз рассматривали уравнение вида
у = /0) или х = g(y) A)
и изучали соответствующую ему кривую [47, 91, 146 и след.]. Тако-
Такого рода задание кривой, когда одна из текущих координат ее точки
представляется в виде (однозначной) явной функции от дру-
другой координаты, мы будем называть явным заданием (или пред-
представлением) кривой. Оно обладает простотой и наглядностью; как
увидим, всякое другое задание — в некотором смысле —
может быть сведено к этому.
564 ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [223
В связи с теорией неявных функций нам приходилось также
говорить о неявном задании кривой, т. е. о представлении кри-
войуравнением вида
F(x,y) = 0, B)
не разрешенным ни относительно х9 ни относительно у [205
и след.]. Такое уравнение носит название неявного уравнения
кривой.
Из теорем о существовании неявной функции [205,206] следует,
что если в точке (хо, у о) кривой выполнено условие
О или Ffa
то, по крайней мере в некоторой окрестности этой точки, кривая
может быть представлена явным уравнением A) того или другого
вида (причем фигурирующая в нем функция / или g непрерывна
вместе со своей производной).
Таким образом, только точки (хо,уо) кривой, для которых вы-
выполняются сразу оба условия
f;(xo,jo) = O, f;(xo,jo)=O, C)
могут иметь ту особенность, что в их окрестности кривая не
пред ставима явным уравнением (ни того, ни другого вида). Точки
кривой, удовлетворяющие уравнениям C), и называют особыми.
Ниже [236] мы займемся вопросом о поведении кривой B)
вблизи особой точки. Но, как правило, особые точки будут исклю-
исключаться из рассмотрения, и мы будем изучать кривую лишь в ок-
окрестности ее о б ы к н о в е н н о й (т. е. неособой) точки.
Наконец, в предыдущем изложении не раз упоминалось о том,
что уравнения вида
x=<p(t), y=№> D)
устанавливающие зависимость текущих координат точки от неко-
некоторого параметра t9 также определяют кривую на плоскос-
плоскости [см., например, 106]. Подобные уравнения называют пара-
параметрическими; они дают параметрическое представле-
представление кривой.
Рассмотрим точку (хо,уо)9 определяемую значением t = to па-
параметра, и предположим, что при t — to будет cpf{to) ф 0. Тогда
и вблизи этого значения t производная x't = q>'{t) — по непрерыв-
непрерывности — будет сохранять тот же знак; функция х = cp{t) оказы-
оказывается монотонной [132]. При этих условиях, в силу 83 и 94,
можно t рассматривать как однозначную функцию от х: t = в{х)9
223] § 1. АНАЛИТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ КРИВЫХ 565
непрерывную и имеющую непрерывную же производную. Подста-
Подставив эту функцию вместо t в выражение для у, установим непосред-
непосредственную зависимость у от х\
У = Ф(в(х))=/(х),
где — снова — функция / непрерывна вместе со своей производ-
производной; таким образом, мы выразим явным уравнением по крайней
мере участок кривой, примыкающий к взятой точке. Аналогичное
заключение можно сделать, если даже (//(/о) = 0, но ^;(/о) ф О,
с той единственной разницей, что получится явное уравнение дру-
другого вида: х = g(y).
Лишь в том случае, когда одновременно
= O и у'( = ф'(ь) = 0, E)
кривая в окрестности рассматриваемой точки может оказаться не
пред ставимой явным уравнением; такую точку будем называть
особой.
В 237 мы остановимся вкратце на виде кривой D) вблизи
особой точки, но, как правило, и здесь мы будем изучать лишь
обыкновенные точки.
Важно теперь оговориться, что все сказанное выше об обыкно-
обыкновенной точке (хо, уо)-> т- е. такой, для которой не выполняются усло-
условия E), предполагает еще, что эта точка получается только
при одном значении параметра t = to (т. е., как говорят,
является простой точкой). Если бы, наоборот, точка (хо,уо)
была кратной и отвечала, например, двум различным значени-
значениям параметра t = to и t = t\9 то в ней, вообще говоря, пересекались
бы два участка кривой: один, определяемый значениями t9 близки-
близкими к /о, а другой — значениями t9 близкими к t\. В этом случае
всю кривую в окрестности данной точки опять-таки нельзя было бы
представить явным уравнением. Таким образом, кратные точки
также по существу следует относить к особым*).
Подведем итоги сказанному. Мы не пытались дать геометриче-
геометрическую характеристику понятия кривой: для нас кривая есть гео-
геометрическое место точек, удовлетворяющих аналитическому
*) Есть, впрочем, один случай, когда точку, получающуюся дважды, все же не
считают кратной: это будет тогда, когда точка отвечает двум крайним значе-
значениям параметра и в ней кривая замыкается. В примере окружности
х = а • cos в, у = а • sin в @ < в < lit)
это будет точка, определяемая значениями в = 0 и в = 2jt.
566 ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [224
соотношению вида A), B) или D), — в предположении непре-
непрерывности встречающихся в них функций и их производных. Правда,
геометрические образы, определяемые этими различными способа-
способами, в целом могут значительно разниться по своему облику, но
в малом, в окрестности обыкновенной (а в случае параме-
параметрического задания и простой) точки, все они уподобляются тем
простейшим образам, которые задаются уравнениями вида A).
224. Примеры. Сделаем обзор наичаще встречающихся кривых (многие из
них, впрочем, уже знакомы читателю из аналитической геометрии).
1) Цепная линия (см. рис. 41). Ее уравнение
а , х _х. х
у = —(еа + е а = a ch -.
2 v J a
По такой линии устанавливается в равновесии гибкая и нерастяжимая тяжелая
нить (цепь, провод и т. п.), подвешенная за оба конца.
Форма кривой вблизи вершины А (см. рис. 41) напоминает параболу, но
при удалении от вершины кривая круче устремляется в бесконечность. Отре-
Отрезок ОА = а определяет точнее ее форму — чем а меньше, тем кривая круче. То
расположение кривой, которое изображено на чертеже, вовсе не обязательно, но
оно позволяет придать уравнению кривой наиболее простой вид.
2) Эллипс, отнесенный к осям симметрии, имеет уравнение
Поскольку сумма квадратов величин | и ? должна равняться единице, естест-
естественно принять их, соответственно, за косинус и синус некоторого угла t. Это
приводит к обычному параметрическому представлению эллипса:
х = a cos t, у = Ъ sin ^;
при изменении t от 0 до 2тт эллипс описывается против часовой стрелки начиная
от конца А(а, 0) большой оси.
Можно было бы, разумеется, использовать и какие-либо другие выражения,
сумма квадратов которых равна единице, и положить, например,
1-й2 2и
у = Ъ т,
1 + и2
где и изменяется от — оо до +оо. Так как при и —>> zboo имеем х —t —а, у —>> 0,
то можно считать условно, что точка А;(—а, 0) получается при и = zboo.
Аналогично для случая гиперболы:
а2 Ь2
вспоминая известное соотношение, связывающее гиперболические косинус
и синус, можно положить
x=acht, y = bsht ( — oo<t<-\-oo).
224]
1. АНАЛИТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ КРИВЫХ
567
Другое представление той же кривой:
1 + и2 , 2и
( —оо < и < +оо;
=Ь1).
Читателю рекомендуется во всех случаях дать себе от-
отчет в передвижении точки по кривой при изменении па-
параметра.
3) Полукубическая парабола (рис. 115)
у2 -сх3 = 0 (с > 0).
Здесь особой точкой служит начало @,0).
Если решить уравнение относительно у, то получим
явные уравнения двух симметричных ветвей кривой
у = ±л/с~х~1 = ±Vc~xi. ^ ' Х
Так как у' = 0 при х = 0 для обеих ветвей, то
в начале они обе касаются оси х, и налицо острие
[точка возврата, см. 236].
4) Астроида (рис. 116)
Это уравнение, собственно говоря, не подходит
под тот тип, которым мы условились ограничиться: Рис. 115
в каждой из точек (±я, 0) и @, ±я) одна из част-
частных производных левой части уравнения обращается
в оо. Впрочем, нетрудно, освободив уравнение кривой от иррациональностей,
представить его в виде
((х2+у2)-а2K+27а2Х2у2 = 0.
При этом представлении указанные точки как раз и будут особыми.
Из уравнения кривой видно, что кривая ле-
лежит в круге х -\-у = а и симметрична относи-
относительно обеих осей; ограничимся поэтому первым
квадрантом. Разрешая уравнение относительно;;:
( ~ -\Ъ
у V /
х и дифференцируя:
у =—{а3—х3J-х 3,
видим, что при х = 0 касательная вертикаль-
вертикальна, а при х = а — горизонтальна. Отсюда сле-
Рис. 116 дует, что во всех четырех особых точках будут
острия (точки возврата).
Желая получить параметрическое представление астроиды, используем то,
что — в силу уравнения кривой — сумма квадратов выражении у^) и у^)
должна равняться единице. Положив их равными cos/^ и sirU, придем к таким
568
ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[224
параметрическим уравнениям:
х = a cos t, у = a sin t @
;2*r).
Так как производные
.Xf = —За cos fsinf, _yr = 3a sin ^cos^
обе обращаются в 0 при t = 0 Bjt), ^, jt, Д^, то этим значениям параметра
отвечают особые точки — те же, что и выше.
5) Декартов лист (рис. 117)
х3 +у3 - Заху = 0*} (а > 0).
Особой точкой служит начало координат @, 0): в нем кривая сама себя
пересекает. Кривая имеет асимптоту х -\- у + а = 0 как при х -л +оо, так и при
Чтобы убедиться в этом, разде-
разделим уравнение почленно на х :
)
КХ / XX
Отсюда, прежде всего, можно заклю-
заключить, что, скажем, при \х\ > За, 1^
остается ограниченным, а тогда уже
ясно, что при х —>> zboo отношение
j —>> — 1. С другой стороны, урав-
уравнение дает нам
Заху
у+х =
х2 — ху +у2
Рис. 117
так что при х —>> zboo будет j^ + * —>- — л. Этим наше утверждение и оправда-
оправдано [148].
Вводя в качестве параметра отношение t = j и подставляя в уравнение
кривой;; = ta, легко получить параметрическое представление:
3at
3atz
( —оо < t < +оо;
t3 + Г г3 + 1
При f —>> zboo обе координаты стремятся к 0; можно считать, что начальная
точка @,0) получается как при t = 0, так и при t = zboo. При изменении t
от — оо до —1 точка (х,у), исходя из начала, вдоль правой ветви удаляется
в бесконечность. При изменении t от — 1 до 0 наша точка из бесконечности вдоль
левой ветви возвращается к началу. Наконец, при возрастании t от 0 до +оо точка
описывает (против часовой стрелки) петлю.
*) См.пример 2), 210. Точка А (ал/2, ял/?), отвечающая максимуму у как
функции от х, отмечена на чертеже.
225]
§ 1. АНАЛИТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ КРИВЫХ
569
225. Кривые механического происхождения. Продолжая перечень примеров,
рассмотрим еще некоторые кривые механического происхождения, полученные
путем качения одних кривых по другим.
6) Циклоида. Вообразим, что по прямой Ох (рис. 118) слева направо ка-
катится без скольжения круг радиуса а с центром в А. Кривая, описываемая
У\
Н
при этом любой точкой окружности, и называется циклоидой. Проследим,
например, путь точки О за время одного оборота круга.
Рассмотрим катящийся круг в новом положении. Точкой касания служит уже
другая точка N; таким образом, по прямой точка касания переместилась на рас-
расстояние ON. В то же время точка О переместилась в положение М, пройдя по
окружности круга путь NM. Так как качение происходит без скольжения,
то эти пути равны:
NM= ON.
Если выбрать теперь в качестве параметра, определяющего положение точки,
угол t = <NDM, на который успел повернуться радиус, имевший в начале качения
вертикальное положение АО, то координаты х и у точки М выразятся следующим
образом:
х = OF = ON - FN = NM - MG = at - a sint,
у = FM = NG = ND - GD = a - a cost.
Итак, параметрические уравнения циклоиды имеют вид:
х = a(t — sin^), у = а{\ — cost) @ < t < 2jv).
При изменении t от —со до + со получится кривая, состоящая из бесчисленного
множества таких ветвей, какая изображена на рис. 118.
Так как производные
х[ = а{\ — cost), y't = a s'mt
одновременно обращаются в 0 при t = ктт (к = 0, d=l, d=2, . . .), то этим значе-
значениям отвечают особые точки кривой. Но [106, A0)]
, y't sint t
Ух — ~1 — ~л — Ct§ ~'
x't \ — cost 2
так что например при t —>> d=0 (или при х —>> ±0) производная ух будет стре-
стремиться к zbco; ясно, что в начальной точке (равно как и в других особых точках)
касательная вертикальна: здесь налицо острие [точка возврата, 237].
570
ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[225
7) Эпи- и гипоциклоида. Если один круг без скольжения катится
извне по другому кругу, то кривая, описываемая произвольной точкой окруж-
окружности подвижного круга, называется эпициклоидой. В случае же качения
изнутри мы имеем дело с гипоцик-
гипоциклоидой. Остановимся на выводе уравнений
первой из этих кривых.
Возьмем начало координат в центре О
неподвижного круга, а ось х проведем че-
через то положение А интересущей нас точки,
в котором она является точкой касания обо-
обоих кругов (рис. 119). Когда подвижный круг
перейдет в новое положение, указанное на
чертеже, точка А перейдет в М. Геометри-
Геометрическое место точек М нам и надлежит опре-
определить.
Обозначим через а радиус неподвижно-
неподвижного круга, а через та — радиус катящего-
катящегося круга. Выберем за параметр здесь угол
t = <хМСВ между радиусом СМ, соединя-
соединяющим центр катящегося круга с интересую-
интересующей нас точкой на его окружности, и радиусом СВ, проведенным в точку касания.
В начале движения пусть этот угол равен 0.
Прежде всего посмотрим, в чем здесь проявляется отсутствие сколь-
скольжения. Дуга АВ, пройденная точкой касания по неподвижной окружности,
должна равняться дуге MB, пройденной точкой касания по катящейся окруж-
окружности:
а • <АОВ = та • <МСВ = mat, откуда <АОВ = mt.
Выразим теперь координаты х и у точки М через t. Имеем:
х = OG = ОЕ + ЕМ = {а + та) cos mt + та sin <FCM;
У
[
fynt ^
| > >, Y"
С-Г i
Рис. 119
но
так что
<FCM = <5CM - «ЭСЕ и <ОС? = mt,
<FCM= (I
sin <FCM = - cos(l + m)t.
Окончательно
^ = а (A + w) cos mt — т cos(l + w)r).
Подобным же образом найдем
у = a ((I -\- m) sin mt — т sin(l + m)t^.
Эти уравнения дают параметрическое представление эпициклоиды.
Когда катящийся круг снова придет в соприкосновение с неподвижным кру-
кругом в той же своей точке, что и в начале движения (т. е. при t = 2jt), точка М
закончит одну ветвь кривой. При дальнейшем качении она будет описывать сле-
следующую ветвь, подобную первой, и т. д.
225]
§ 1. АНАЛИТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ КРИВЫХ
571
Производные
xt = —т(т + \)a(sinmt — sin(l
y't = m(m
— cos(l
обращаются одновременно в 0 при t = 2kж (где к = 0, d=l, d=2, . . .), т. е. всякий
раз, когда рассматриваемая на подвижном круге точка становится точкой касания.
Соответствующие точки кривой будут особыми — точками возврата.
Эпициклоиды
Гипоциклоиды
Рис. 120
В случае гипоциклоиды подобным же образом получаются такие пара-
параметрические уравнения:
х = а (A — т) cos mt + т cos(l — m)i},
у = я(—A — т) smmt -\- m sin(l — m)i].
Здесь т также означает отношение радиуса катящегося круга к радиусу неподвиж-
неподвижного. Легко заметить, что эти уравнения получаются из уравнений эпициклоиды
заменой т на —т.
На рис. 120 изображены эпициклоиды, соответствующие т = 1, 2, -j, и ги-
гипоциклоиды, соответствующие w = ^ и |. В последней читатель узнает аст-
аст^
роиду
*^
*) Если в уравнениях гипоциклоиды положить т = | и заменить /^ на —4/, то
и получатся уравнения, приведенные в 4).
572
ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[226
8) Эвольвента круга. Представим себе, что на круг, описанный из цен-
центра О радиусом я, навернута по часовой стрелке нить; пусть конец нити при-
приходится в точке А. Станем нить развертывать (против часовой стрелки), сма-
сматывая с круга и все время натяги-
натягивая ее за конец. Кривая, описывае-
описываемая при этом концом нити, называет-
называется эвольвентой круга [ср. ни-
ниже 254, 246].
Возьмем начало координат
в центре О (рис. 121) и проведем
ось х через точку А. Когда будет смо-
смотана часть АВ нити, она займет поло-
положение ВМ, располагаясь по касатель-
касательной к кругу, а точка А перейдет в М.
Итак, АВ = ВМ. В качестве пара-
параметра введем угол t = <AOB между
радиусами О А и ОВ. Координаты х,
у точки М выразятся следующим об-
образом:
Рис.121 x=DC-DO = BF-DO =
= BMsin <BMC - OB cos <DOB;
но ВМ = АВ = at, а углы <ВМС и <DOB равны тт — t, так что
х = at sin(jr — t) — a cos(jv — t) = a {t sin t + cos t).
Далее,
у =CM=CF + FM=DB +FM =
= OB sin <DOB + BMcos <BMC = a(sint - t cost).
Таким образом, наша кривая представляется следующими параметрическими
уравнениями:
х = a (t sin t + cos t), у = a (sin t — t cos i).
Единственная особая точка отвечает значению t = 0, при котором обра-
обращаются в 0 обе производные
xt = at cost, yt = atsint.
Предлагаем читателю убедиться в том, что та же кривая получится, если
катить прямую (без скольжения) по кругу и рассмотреть траекторию какой-
либо точки прямой.
226. Кривые на плоскости (в полярных координатах). Приме-
Примеры. Во многих случаях оказывается проще представлять кривые их
полярными уравнениями, устанавливающими зависимость
между текущими полярными координатами г, в точек кривой. По-
Полярный угол в мы отсчитываем от полярной оси, считая его поло-
положительным против часовой стрелки. Полярный радиус-вектор г мы
будем брать как положительным, так и отрицательным; в первом
226]
§ 1. АНАЛИТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ КРИВЫХ
573
случае его откладывают в направлении, определяемом углом 0, а во
втором — в противоположном направлении.
Как в случае прямоугольных координат, и здесь зависимость
между г и в может быть задана в явной, неявной или параметри-
параметрической форме. Мы ограничимся, преимущественно, простейшим
случаем, когда кривая представляется явным уравнением вида
г = f(9).
Если перейти к прямоугольным координатам, взяв, как обычно,
полюс за начало, а полярную ось — за ось х9 то уравнения
х = г cos в = /(в) cos в, у = г sin в = /(в) sin в
дадут параметрическое представление нашей кривой, причем
роль параметра здесь будет играть полярный угол в. [Полученные
\
ч
здесь функции от 0, вместе с /, непрерывны и имеют непрерывные
производные.]
Формулы
- г
у'в =
показывают, что особая точка [в смысле п° 223] может встре-
встретиться лишь в том случае, если г = rf0 = 0.
Обратимся к примерам.
1) Архимедова спираль: г = ав (рис. 122).
574
ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[226
Кривую можно рассматривать как траекторию точки, равномерно движущей-
движущейся по лучу, исходящему из полюса, в то время как этот луч равномерно вращается
вокруг полюса.
Для построения ряда точек А, В, С, D, ... кривой отложим по вертикали
ОА = а • §, а затем возьмем ОВ = 2ОА, ОС = ЗОА, OD = 4ОА, и т.д., ибо
им отвечают углы 2 |, 3 |, 4|, и т. д. Изменяя угол в от 0 до оо, получим бес-
бесконечное множество витков кривой OABCD, DEFGH, . . .; расстояния соседних
витков, считая по лучу, равны 2тта.
Можно углу в придавать и отрицательные значения, от 0 до — оо. Тогда
получится вторая часть кривой OAB'CD1. . ., намеченная пунктиром; она сим-
симметрична первой.
Заметим, что уравнение г = ав + Ъ также выражает архимедову спи-
спираль: если повернуть полярную ось на угол а = — ^, то это уравнение приве-
приведется к виду г = ав.
2) Гиперболическая спираль: г = — (рис. 123).
6
При возрастании угла в до бесконечности радиус-вектор стремится к нулю,
а точка кривой стремится к совпадению с полюсом (никогда его не достигая);
Рис. 123
в этих условиях полюс называется асимптотической точкой кривой.
Кривая бесчисленное множество раз заворачивается вокруг полюса.
Если на луче в = f отложить отрезок О А = ^ и взять АВ = \ОА,
ОС = \ OB, OD = \ ОС, . . ., то точки А, В, С, D, . . ., очевидно, лежат на
кривой.
Угол в может принимать и отрицательные значения. При изменении в от О
до — оо, как и в случае архимедовой спирали, получается вторая часть кривой
А'ВС'Df. . ., симметричная с первой; она и здесь намечена пунктиром.
Для уточнения формы кривой в бесконечности рассмотрим вертикальное рас-
расстояние точки кривой до полярной оси у = г sinO = а ^-. При t —>> ±оо
или — что то же — при в —>> d=0 имеем limj/ = а. Таким образом, прямая, про-
проведенная параллельно полярной оси на расстоянии а от нее, служит для кривой
асимптотой.
226]
§ 1. АНАЛИТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ КРИВЫХ
575
3) Логарифмическая спираль: г = ае (рис. 124).
Если угол в возрастает (или убывает) в арифметической прогрессии, то
г возрастает (убывает) в геометрической прогрессии. Отложим на полярной
оси отрезок ОА = а, а на вертикали к ней — отрезок О В = ает 2; обе точ-
точки А, В принадлежат нашей кривой. Если построить теперь прямоугольную ло-
ломаную ABCDE. . ., то из подобия треугольников нетрудно заключить, что от-
отрезки ОА, ОВ, ОС, OD, ОЕ, . . . образуют геометрическую прогрессию со
знаменателем ет^; так как соответствующие углы суть 0, j, 2 • j, 3 • j
и т. д., то, очевидно, все точки С, D, Е, ... также лежат на рассматриваемой
спирали.
Когда угол в растет от 0 до +оо, точка делает бесчисленное множество
оборотов вокруг полюса, быстро удаляясь от него в бесконечность; расстояния
между витками уже не равны. Угол в может принимать и отрицательные значения;
Рис. 124
множество раз заворачивается вокруг полюса, безгранично к нему приближаясь
(но никогда не достигая, см. часть АВ'СD''Ег... на рис. 124); полюс является
асимптотической точкой кривой.
Отметим, наконец, что, поворачивая полярную ось вокруг полюса, можно
добиться уничтожения множителя а и привести уравнение логарифмической спи-
спирали к простейшему виду: г = етв.
4) Улитки: г = a cos# + Ъ (рис. 125).
Происхождение этих кривых можно себе представить так. Возьмем окруж-
окружность диаметра а. Если выбрать полюс О лежащим на самой окружности, а по-
полярную ось провести через центр С, то для любой точки М окружности, очевидно,
будет г = a cos в. Это и есть полярное уравнение окружности. Если изменять
здесь угол в от 0 до 2jt, то переменная точка дважды опишет окружность
(против часовой стрелки).
Если удлинить теперь все радиусы-векторы ОМ1 окружности на постоянный
отрезок MfМ = Ъ (Ъ > 0), то из построенных таким путем точек М составится
576
ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[226
новая кривая, которая и носит общее название улитки. Ее полярное уравнение,
очевидно, будет г = a cos в + Ъ.
Проще всего обстоит дело, если Ъ > я, ибо тогда радиус-вектор все-
всегда положителен и кривая окружает полюс со всех сторон (рис. 125, а). При
Ъ < а кривая проходит через полюс и, сама себя пересекая, образует внут-
внутреннюю петлю, как на рис. 125, б. Для определения углов в, при которых пе-
переменная точка проходит через полюс, полагаем г = 0 в уравнении кривой.
Мы получаем уравнение cos# = — |, которое имеет решение именно потому,
что Ь < а.
М'М=Ъ=а
MfM=b<a
Рис. 125
Особенно интересен промежуточный тип кривой, отвечающий случаю, когда
b = а. Здесь полюс лежит на кривой (в = ж), но петли нет; кривая изображена на
рис. 125,в. Сразу бросается в глаза тождество этой кривой с кардиоидой, рас-
рассмотренной выше, как частный случай эпициклоиды (см. рис. 120). Представ-
Представляем читателю убедиться в этом.
226]
§ 1. АНАЛИТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ КРИВЫХ
577
5) Лемниската Бернулли: г = 2а cos26 (рис. 126).
Эту кривую можно определить как геометрическое место точек М, для кото-
которых произведение их расстояний р = FM и р = F1 М до двух данных точек F
и Ff, отстоящих одна от другой на расстоянии 2а, есть постоянная величина а . *)
,-S
Рис. 126
При обозначениях рис. 126 из треугольников OMF и OMF1 имеем
2ar cos 6,
2 2,2
р = г + а
так что, по определению,
Л'2
/2 2 2
= г + B — 2<2Г COS 0,
= (г2 + а2J - 4я2г2 cos2 6 = а4,
откуда после элементарных преобразований получим
г2 = 2а2 соъ26.
Это и есть полярное уравнение лемнискаты.
Так как левая, а с ней и правая часть этого уравнения не могут принимать
отрицательных значений, то угол в может изменяться лишь в таких промежутках,
для которых cos 26 ^ 0. Это будут промежутки
/ял (Ътт Ътт\ (lit \
@,-), (—, —), (—,2л-).
V 4/ V 4 4 ) V 4 )
Вся кривая расположится в двух вертикальных углах между прямыми SS
и ТТ, проведенными под углами j и ^ к полярной оси (см. рис. 126). Она сама
себя пересекает в полюсе, которому отвечают в = f, ^f, ^р, ^р
Если обычным образом перейти к прямоугольным координатам, то легко по-
получить такое (неявное) уравнение лемнискаты:
2\2
J
2/ 2
= 2а (х -
*"> При указанном соотношении между расстоянием FF1 и постоянной вели-
величиной произведения ppf, очевидно, середина О отрезка FFf принадлежит кривой
(р = р = а). Иначе обстоит дело, если рр = Ъ , где Ъ ф а, тогда получаются
так называемые овалы Кассини.
578 ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [227
227. Поверхности и кривые в пространстве. Мы не предпо-
предполагаем здесь углубляться в приложения дифференциального ис-
исчисления к геометрии в пространстве, оставляя эти вопросы для
специального курса дифференциальной геометрии. Поэтому в от-
отношении пространственных образов мы ограничимся лишь тем, что
необходимо для дальнейших частей самого курса анализа.
Как и выше (напомним это еще раз), все рассматриваемые
функции будем предполагать непрерывными и имеющими
непрерывные производные по своим аргументам.
Будем исходить из прямоугольной системы координатных
осей Oxyz. Нам приходилось уже говорить о том, что поверхность
в пространстве может быть выражена уравнением между текущими
координатами вида
z=f(x,y) F)
[см., например, 160]. Такое уравнение, равно как и аналогичные
ему х = g(y, z) и у = h(z, x), мы будем называть явным урав-
уравнением поверхности.
К этому простейшему случаю, в известном смысле, сво-
сводятся и другие способы задания поверхности.
Часто случается, что поверхность выражается уравнением вида
F(x,y,z)=0, G)
не разрешенным относительно той или иной координаты (неяв-
(неявное задание). Если в точке (хо,уо, zo), ему удовлетворяющей,
хоть одна из частных производных F^(xo,yo, zo), Fy(xo,yo9zo)9
^(^Cbjo^o) отлична от 0, то в окрестности этой точки по-
поверхность пред ставима явным уравнением того или ино-
иного типа. Действительно, если, например, F^(xo,yo^o) ф 0, то,
по теореме 3 п° 208, по крайней мере в окрестности рас-
рассматриваемой точки, уравнение определяет z как однознач-
однозначную функцию от х и у: z=f(x,y) (и притом — не-
непрерывную вместе со своими производными по обоим аргу-
аргументам).
Таким образом, исключение может представиться лишь в осо-
особой точке поверхности, удовлетворяющей сразу трем условиям:
F'x = 0, F' = 0, F'z = 0.
227] § 1. АНАЛИТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ КРИВЫХ 579
Уравнение
F(x,y) = 0, (8)
не содержащее вовсе одной из координат, также может быть ис-
истолковано как уравнение поверхности. Именно, на плоскос-
плоскости ху оно выражает кривую; если на ней, как на направляю-
направляющей, построить цилиндрическую поверхность с образующи-
образующими, параллельными оси z, то все точки этой поверхности, и только
они, будут удовлетворять рассматриваемому уравнению [поскольку
z в него не входит и ничем не стеснено].
Аналогично истолковываются уравнения вида G(y,z) = 0 или
H(z,x) = 0.
Обратимся теперь к кривым в пространстве. Простей-
Простейшим способом задания кривой в пространстве является тот, когда
две текущие координаты, например у и z, задаются в виде функций
от третьей, х:
y=f(x), z=g(x). (9)
Подобный способ есть естественный аналог явного задания кри-
кривой на плоскости. И здесь уравнения указанного типа можно было
бы называть явными уравнениями кривой.
Как и в случае плоской кривой, к явному заданию, в основном,
сводятся и другие аналитические представления простран-
пространственной кривой.
Каждое из уравнений (9) может быть истолковано либо как
уравнение проекции нашей кривой на координатную плоскость, со-
соответственно, ху или xz9 либо как уравнение проектирующего
цилиндра [см. (8)] с образующими, параллельными, соответ-
соответственно, оси z или оси у.
Более общий способ задания пространственной кривой состоит
в том, чтобы рассматривать ее как пересечение двух поверхностей
вообще. Если эти поверхности выражаются каждая одним из ниже-
нижеследующих уравнений
F(x,y,z)=0, G(x,y,z) = 0, A0)
то совокупность обоих уравнений дает аналитическое представле-
представление кривой пересечения. Уравнения A0) называют неявными
уравнениями кривой.
580 ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [228
Составим матрицу из частных производных от функций F и G
(?' F' F'
U 4 4
Пусть какой-нибудь из определителей этой матрицы, например
к
отличен от 0 в рассматриваемой точке. Тогда на основании теоре-
теоремы 4 п° 208 в окрестности этой точки уравнения A0) могут быть
заменены уравнениями типа (9) [причем фигурирующие в этих
уравнениях функции снова оказываются непрерывными вместе со
своими производными].
Таким образом, возможность сведения к простейшему способу
задания перестает быть обеспеченной лишь в окрестности такой
точки кривой (ее называют особой), где все три определителя
матрицы A1) одновременно обращаются в нуль.
228. Параметрическое представление. Перейдем, наконец,
к параметрическому заданию поверхностей и кривых в простран-
пространстве, причем на этот раз начнем с кривых. Подобно тому, как
мы это делали на плоскости, координаты переменной точки про-
пространственной кривой можно задать в функции от некото-
некоторой вспомогательной переменной — параметра — t:
x = cp{t), y=i/>(t), z=X(t), A2)
с тем чтобы при изменении параметра t точка, координаты которой
даются этими уравнениями, описывала рассматриваемую кривую
[в случае явного задания (9) роль параметра играло само х].
Если для взятой точки кривой хоть одна из производных x't9 y't9
z't отлична от 0, то — как и в случае плоской кривой — легко в ок-
окрестности этой точки перейти от параметрического к явному
заданию. Лишь в окрестности особой точки, где все эти произ-
производные — нули, нельзя гарантировать такую возможность.
Как и в случае плоской кривой, к числу особых следует от-
отнести и так называемые кратные точки, т. е. точки, получаемые
при двух или большем числе значений параметра. *)
*) См. сноску на с. 565.
228] § 1. АНАЛИТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ КРИВЫХ 581
Обратимся к параметрическому представлению по-
поверхностей.
На этот раз определение положения точки на поверхности по-
потребует двух параметров [в случае явного задания F) роль этих
параметров играли две из координат: х иу]. Пусть имеем урав-
уравнения
х = ф(и, у), у = гр(и, у), z = %(и, t>), (^)
где (и, у) изменяется в замкнутой области А. Составим матрицу
(< а х'и\ A4)
и предположим, что для и = щ и у = vq отличен от 0 хоть один
из определителей этой матрицы; например, пусть
Фу
.
Тогда, переписав первые два из уравнений A3) в виде
ф(и, у) — х = 0, гр(и, у) — у = О,
на основании теоремы 4 п° 208 можем утверждать, что этой сис-
системой двух уравнений с четырьмя переменными и9 v9 х9 у (если
ограничиться значениями их, близкими к интересующим нас) пе-
переменные и9 у определяются как однозначные функции от х9 у:
и = g(x,y), у = h(x,y),
непрерывные со своими производными. Наконец, подставляя эти
выражения и и у в третье из уравнений A3), придем к обычному
представлению поверхности явным уравнением
где и функция / непрерывна и имеет непрерывные производные.
Лишь в том случае, если все три определителя матрицы A4) од-
одновременно обращаются в 0 (соответствующая точка поверхности
будет особой), такое представление может оказаться неосущест-
неосуществимым.
Читателю ясно, что в связи с параметрическим представлением
поверхности так же может быть установлено понятие о простой
582 ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [229
и кратной точках поверхности: первая получается лишь при од-
одной системе значений (и, v) параметров, а вторая, по меньшей ме-
мере, при двух*\
Возвращаясь к параметрическим уравнениям A3) поверхнос-
поверхности, фиксируем в них значение одного из параметров: например,
положим и = щ. Тогда получатся, очевидно, уравнения некоторой
кривой
х =ф(щ,ь), у =ф(щ,у), z =х(щ,у),
всеми точками лежащей на поверхности. Изменяя значение щ, по-
получим целое семейство таких «кривых (и)». Аналогично, фик-
фиксируя значение v = vq9 получим также кривую на нашей поверх-
поверхности
х = ф(и, vo), у=гр(и, vo), z=x(u,vo);
из таких «кривых (и)» также составляется целое семейство.
Так как значения ииу можно рассматривать как координаты
точек на поверхности, то эти линии называют координатными
линиями поверхности. Если точка поверхности простая,
т. е. получается лишь при одной системе значений (и, v) параме-
параметров, то через нее проходит по одной координатной линии из ка-
каждого семейства.
Обозревая различные способы аналитического представления
поверхностей [см. F), G) и A3)] и пространственных кривых [(9),
A0) и A2)], мы могли бы повторить сказанное в конце п° 223.
В окрестности обыкновенной (и простой) точки дело сво-
сводится к наглядному случаю явного задания.
229. Примеры.
1) Кривая Вивиани. Так называется кривая пересечения поверхностей
сферы и прямого цилиндра, для которого направляющей служит окружность, по-
построенная на радиусе сферы, как на диаметре (рис. 127). Пусть радиус сферы
есть R; если расположить оси, как указано на рисунке, то уравнения сферы и ци-
цилиндра, соответственно, будут
x2+y2+z2=R2,
х2 +у2 = Rx.
Совокупность их и определяет нашу кривую.
*^ Отметим, что в случае замкнутой поверхности (т. е. поверхности, не
имеющей контура, например сферической), ее точки заведомо не могут быть
поставлены в взаимно однозначное соответствие точкам плоской области А на
плоскости uv. В этом случае наличие кратных точек неизбежно при любом пара-
параметрическом задании.
229]
1. АНАЛИТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ КРИВЫХ
583
Кривая имеет вид изогнутой восьмерки; в точке (R, О, 0) она сама себя пере-
пересекает, так что эта точка — заведомо особая. Это подтверждается и вычисле-
вычислением. Матрица
2х 2у
- R 2у 0
имеет определители
2у 2z
2у О
= -4vz,
2z
0
2х
2х -R
= Axz - 2Rz,
2х
2х -R
2у
2у
которые все вместе обращаются в 0 именно в этой точке.
Кривую В и в и а н и можно представить и параметрически, например так:
2
х = R sin t, у = R sin t cos t, z = R cos t.
Действительно, нетрудно проверить, что эти выражения тождественно удо-
удовлетворяют неявным уравнениям кривой и что при изменении параметра t, ска-
скажем, от 0 до 2ж, полностью описывается
вся кривая. Точка (R, О, 0) получается два- Zl
жды — при t = j vLt = ^,т. е. является
кратной, как и следовало ожидать.
Рис. 127
Рис. 128
2) Есть случаи, когда параметрическое представление естественно вытека-
вытекает из самого происхождения кривой. Рассмотрим, в виде примера, винтовую
линию. Происхождение ее можно себе представить следующим образом. Пусть
некоторая точка М, находившаяся первоначально в А (рис. 128), вращается рав-
равномерно вокруг оси z (скажем, по часовой стрелке) и одновременно участвует
в равномерном же поступательном движении параллельно этой оси (допустим,
в положительном направлении). Траектория точки М и называется винтовой
л и н и е й. За параметр, определяющий положение точки М, можно принять угол t,
составляемый с осью х проекцией ОР отрезка ОМ. Координаты х и у точки М бу-
будут те же, что и у точки Р, так что х = a cos t и у = a sin t, где а есть радиус опи-
описываемой точкой Р окружности. Что же касается вертикального перемещения z,
584
ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[229
то оно растет пропорционально углу поворота t (ибо поступательное и враща-
вращательное движения оба происходят равномерно), т. е. z = ct. Окончательное па-
параметрические уравнения винтовой линии будут
x=acost, y=asint, z = ct. A5)
Полученная винтовая линия называется левой; при правой системе коор-
координатных осей те же уравнения выражали бы правую винтовую линию.
Легко исключить из уравнений A5) параметр t и перейти к явному заданию;
например, найдя t из последнего уравнения и подставив его в выражение в первые
два, получим
х = a cos -, у = a sin -.
с с
3) Рассмотрим сферическую поверхность радиуса R с центром в начале
координат (рис. 129). Ее неявное уравнение будет, как известно,
Желая получить ее обычное параметрическое представление, прове-
проведем «экваториальное» сечение AKAf, а через «полюсы» Р, Р1 и рассматривае-
рассматриваемую точку М — «меридиан» РМКР1. Положение точки М на сфере может быть
определено углами ср = <РОМ и в = <АОК. Имеем z = NM = R cos ср. Затем
ON = R sin q>, а через ON координаты х
и у (те же для М, что и для N) выразят-
выразятся так: х = ON cos в, у = CW sin 0. Со-
Собирая все эти результаты, окончательно
параметрические уравнения поверхнос-
поверхности сферы получим в виде:
х = R sin ф cos в,
у = R sin ф sin в,
z = R cos <p,
причем угол ф достаточно изменять от О
до ж, а угол в — от 0 до 2тт.
Однако соответствие между точка-
точками сферической поверхности и точками
прямоугольника [0, ж; 0, 2jv] на плоскости фв не будет взаимно однозначным*^:
значения в = 0 и в = 2тт приводят к одним и тем же точкам поверхности и,
кроме того, при ф = 0 {ср = л"), каково бы ни было значение О,
получается одна лишь точка — полюс Р{РГ).
Если ф заменить углом Я = § — ф, изменяющимся от — ^ до §, а 0 менять
между —л" и л", то мы придем к обычным географическим координатам:
широте и долготе.
Для матрицы частных производных
/ R cos ф cos 0 Рсоъф sin 0 — Я sin ф\
О J
Рис. 129
*)
Ср. сноску на с. 582.
229]
1. АНАЛИТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ КРИВЫХ
585
все определители
R sin q> cos в, R sin q> sin в, R sin q> cos cp
обращаются вместе в нуль при ср = 0 и ср = ж. Однако очевидно, что оба «полю-
«полюса» представляют особенность только применительно к этому аналитическому
представлению сферы.
Легко видеть, что одно семейство координатных линий на сфере составится
из меридианов (в = const), а другое — из параллельных кругов
(<р = const).
4) Можно обобщить предыдущий пример следующим образом. Пусть в плос-
плоскости xz задана кривая (образующая) своими параметрическими уравнениями
х = <р(и), z = ф(и), A6)
причем ср(и) ^ 0. Станем вращать ее, как твердое тело, вокруг оси z (рис. 130).
Если через v обозначить угол поворота, то уравнения получаемой поверх-
поверхности вращения напишутся в виде
х = ср{и) cos и, у = ср{и) sin и, z = гр(и) @ ^ v ^ 2тт).
Если в плоскости xz взять полуокружность
х = R sin и, z = R cos и
и ее вращать вокруг оси z, то параметрическое представление образуемой та-
таким путем сферической поверхности мы получим (с точностью до обозначений)
в прежнем виде.
Предоставляем читателю убедиться в том, что особыми точками для поверх-
поверхности вращения могут быть лишь точки на оси вращения либо же точки, полу-
полученные при вращении из особых точек образующей.
Координатными линиями и здесь служат различные положения образующей
(меридианы) и параллельные круги.
5) Если к вращательному движению кривой A6) присоединить еще
поступательное — параллельно оси вра-
вращения, то (предполагая оба движения про-
происходящими равномерно) получим общую
винтовую поверхность
х = ср{и) cos и, у = ср{и) sin и,
z = гр(и) + cv.
Возьмем, в частности, в качестве образу-
образующей положительную часть оси х:
х = и, z = 0 (и ^ 0).
Подвергнув ее винтовому движению, придем
к обыкновенной винтовой поверх-
поверхности
х = и cos v,
z = cv.
у = и sin v,
Для общей винтовой поверхности одно
семейство координатных линий состоит из различных положений образующей
(у = const), а другое — из винтовых линий (и = const).
586 ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [230
§ 2. Касательная и касательная плоскость
230. Касательная к плоской кривой в прямоугольных коорди-
координатах. Понятие касательной нам уже встречалось не раз
[см., например, 91]. Кривая, за-
заданная явным уравнением
У=/(х),
где / — непрерывная функция
с непрерывной производной,
в каждой своей точке (х,у)
имеет касательную, угловой ко-
коэффициент которой tga выра-
х жается формулой
О
р
Рис. 131
N
tga=y'x=f'(x).
Таким образом, уравнение касательной имеет вид
Y-y=y'x(X-x). A)
Здесь (как и ниже) X, Y означают текущие координаты, а х, у —
координаты точки касания.
Легко получить и уравнения нормали, т. е. прямой, прохо-
проходящей через точку касания перпендикулярно к касательной:
Y-v = -\(X-
ИЛИ
X-x+y'x(Y-y) = 0. B)
В связи с касательной и нормалью рассматривают некото-
некоторые отрезки — именно, отрезки ТМ и MN и их проекции ТР
и PN на ось х (рис. 131). Последние называются, соответствен-
соответственно, подкасательной и поднормалью и обозначаются че-
через sbt (subtangens) и sbn (subnormal). Полагая в уравнениях A)
и B) Y = 0, легко вычислить, что
sbt = TP= —,
Ух
C)
Тогда из треугольников МРТ и MPN определятся и длины отрез-
отрезков касательной и нормали
= TM =
= MN =
D)
230] § 2. КАСАТЕЛЬНАЯ И КАСАТЕЛЬНАЯ ПЛОСКОСТЬ 587
В случае неявного задания кривой
F(x,y) = 0,
в окрестности ее обыкновенной точки М(х,у) можно пред-
представить себе кривую выраженной явным уравнением. Если в точ-
точке М, например, F^(x, у) ф 0, то кривая выразится уравнением вида
у = /(х), где функция / непрерывна и имеет непрерывную произ-
производную. Отсюда ясно, что для кривой существует в точке М каса-
касательная, и ее уравнение может быть представлено в форме A). Но
мы знаем [209, A5)], что в этом случае
подставляя, после простых преобразований получим вполне сим-
симметричное относительно х иу уравнение касательной
Fl(x,y)(X-x)+Fl(x,y)(Y-y) = O. E)
К тому же результату придем и в случае, если F' = 0 в точ-
точке М9 но FJ. ф 0. Лишь в особой точке это уравнение теряет
смысл, и относительно касательной, без дополнительного исследо-
исследования [236], здесь ничего сказать нельзя.
Уравнение нормали для рассматриваемого случая, очевидно,
будет таково:
F;(x,y)(X-x)-Fl(x,y)(Y-y)=0.
Наконец, предположим, что кривая задана параметрически:
x=<p(t), y =
Мы видели, что, если cp'{t) ф 0, касательная к кривой существует
и имеет угловой коэффициент
4- F)
xt
[106, A1)]. Уравнение касательной может быть написано так:
г-у = %<?-,) ^? ^
x
588
ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[231
В последней форме уравнение годится и для случая, когда
х[ = 0, но у\
0
*\
Лишь в особой точке, где и х[ = О
и у[ = 0, уравнение теряет смысл, и вопрос о касательной остает-
остается открытым [237].
Иногда удобно, умножив оба знаменателя на множитель dt9 пи-
писать уравнение касательной в виде
Х-х Y-y
dx
dy
G)
231. Примеры.
1) Парабола:;; = 2рх. Дифференцируя это равенство (считая;; функци-
функцией отх), получимуух = р. Таким образом [см. C)], поднормаль параболы
есть постоянная величина. Отсюда вытекает простой способ построения
нормали (а с ней и касательной) к параболе. По формуле D), для отрезка нормали
к параболе имеем выражение
У1 ч
х у
2) Эллипс: —г-Н—? = 1
az bz
(рис. 132). По формуле E),
имеем такое уравнение каса-
касательной:
Учитывая само уравнение
эллипса, можно последнее урав-
уравнение переписать в более про-
простом виде
хХ yY _
Полагая здесь 7 = 0, най-
2
дем X = ^-. Таким образом, точка Т пересечения касательной с осью х не
зависит ни от j;, ни от Ь. Касательные к различным эллипсам, отвечаю-
отвечающим различным значениям Ь, в их точках, имеющих абсциссу х, все проходят
через одну и ту же точку Т на оси х. Так как при Ь = а получается окруж-
Рис. 132
*) При этом, как всегда уславливаются в аналитической геометрии, если в про-
пропорции
Х 1
один из последующих членов есть 0, то это означает просто, что равен 0 и соот-
соответствующий предыдущий член.
231] § 2. КАСАТЕЛЬНАЯ И КАСАТЕЛЬНАЯ ПЛОСКОСТЬ 589
ность, для которой касательная строится просто, то точка Т сразу определяется,
и это приводит к простому способу построения касательной к эллипсу, ясному
из рис. 132. *}
Легко определить длину отрезка нормали для эллипса:
Ь4х2 + а4у2
Такое же выражение получается и в случае гиперболы ^ — р- = 1.
3) Астроида: *з + уз = «з (см. рис. 116). Уравнение касательной
Ц)-Ц
с помощью самого уравнения кривой может быть преобразовано к виду
X Y 2 X Y
= «3 или Н 2~
~Т "I г = «3 или 2 t
хз уз а^хз y
Последнее уравнение есть «уравнение в отрезках». Следовательно, касатель-
касательная отсекает на осях отрезки «з^з жаъуъ. Отсюда легко получить одно интерес-
интересное свойство астроиды. Обозначив через г длину отрезка касательной между
осями, имеем
1 4 2 4 2 ?
г = «3jc3 + а?>уъ = а
и
г = а = const.
Таким образом, оси симметрии астроиды на всех касательных
отсекают равные отрезки.
4) Циклоида (см. рис. 118):
х = a(t — sin t), у = a (I — cost)
Мы имели уже [в 225, 6)] равенство у'х = ctg j, т. е.
t fjvt\
ctg 2 =tg V2" ~ 2/ '
и можно принять а = ^ — ^.
Вспомним (см. рис. 118), что Г = <MDN, так что <MEN = ?. Если про-
продолжить прямую ЕМ до пересечения в Г с осью х, то <ЕТх = § — ^ = а.
Следовательно, прямая ME, соединяющая точку циклоиды с высшей точкой ка-
катящегося круга (в соответствующем положении), и будет касательной. Отсюда
ясно, что прямая MN будет нормалью.
Впоследствии нам полезно будет выражение для отрезка п нормали, которое
легко получить из прямоугольного треугольника MEN. Именно,
п = MN = 2а sin -.
* ^ Это свойство касательных к эллипсу непосредственно связано с тем фактом,
что эллипс можно рассматривать как ортогональную проекцию некоего круга
(радиуса а), лежащего в наклонной плоскости.
590 ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [232
5) Эпициклоида (см. рис. 119):
х = а (A + т) cos mt — т cos(l + m)t),
у = а ((\ -\- т) sin mt — wsin(l + m)i\
Написав выражения для производных х[ жу\ в виде
xt = 2ат{\ + т) sin - cosf т -\— )t,
y't = 2ат{\ + т) sin - sinf т -\— )t,
найдем, что
y't ( 1 \
tga = ф =tg(m+-)t.
Отсюда а = (т + ^) t.
Если соединить (см. рис. 119) точку D с М, то эта прямая составит с осью х
как раз такой угол:
<xTD = <DOT + <ODT = mt + -.
Следовательно, ?)Г есть касательная в точке М, a MB будет нормалью.
6) Эвольвента круга (см. рис. 121):
х = a (t sin t + cos ^), _y = a (sin f — f cos ^)
Здесь
откуда a = ^
Таким образом, касательная МГ параллельна радиусу ОВ, и 5М есть нормаль
к нашей кривой.
Замечание. Результаты примеров 4), 5), 6) можно было бы получить без
всяких выкладок, исходя из кинематических соображений. При качении
одной кривой по другой точка касания служит всякий раз мгновенным центром
для движущейся фигуры, так что нормаль к траектории любой ее точки проходит
через эту точку касания.
232. Касательная в полярных координатах. Если кривая зада-
задана полярным уравнением г = /@), то, переходя обычным образом
к прямоугольным координатам, получаем параметрическое пред-
представление кривой в виде
х = г cos в = /(в) cos в,
у = г sin0 = /@)sin0,
причем роль параметра здесь играет в.
233]
§ 2. КАСАТЕЛЬНАЯ И КАСАТЕЛЬНАЯ ПЛОСКОСТЬ
591
В таком случае, по общей формуле F),
в
r'e cos 9 — г sin в
Однако, если кривая исследуется в полярных координатах,
обычно положение касательной определяют не углом а с по-
полярной осью, а углом со с продолженным радиусом-вектором
(рис. 114 и 133). Мы имели
уже [218, 4)] простую формулу Д^ \
Точно так же вместо от-
отрезков t, n, sbt, sbn, о которых
была речь в 230, здесь рас-
рассматривают другие отрезки. _
Проведя через полюс О ось,
перпендикулярную к радиусу-
вектору (эта ось вращается
при перемещении точки), про-
продолжают касательную и нор-
нормаль до пересечения с ней, со-
соответственно, в точках Т и N.
Тогда отрезки ТМ и MN назы-
называются полярными отрез-
отрезками касательной и нормали,
а их проекции ТО и ON на упомянутую ось — полярными под-
касательной и поднормалью. Обозначать их будем, как и прежде, но
помещая внизу в виде значка букву р. Легко получить, используя
формулу (8):
г
sbtp = ТО = rtgco = —, sbrip = ON = г ctgco = rfe,
а отсюда уже
= TM=-
re
r2 +r
/2
= MN = л/г2
233. Примеры.
1) Архимедова спираль: г = ав (см. рис. 122).
Так как г'в = а, то sbnp = а = const. Это позволяет сразу устанавливать
положение точки N, а с ней — нормали и касательной.
Заметим, что tgco = в, так что при в —>> оо и tgw —>> со, т. е. угол &>
стремится к прямому.
592
ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[233
2) Гиперболическая спираль: г = ^ (см. рис. 123).
На этот раз r'e = —3^9 sbtp = — а = const, что также облегчает очевидным
образом построение касательной.
3) Логарифмическая спираль: г = ае (рис. 134).
Имеем г'в = таетв, так что tg&> = ^ = const, и сам угол о) = const. Та-
Таким образом, логарифмическая спираль обладает тем замечательным свойством,
что угол между радиусом-вектором и касательной сохраняет постоянную вели-
величину. Иными словами, логарифмическая спираль пересекает все
свои радиусы-векторы под постоянным углом. Этим свойством она
Рис. 134
Рис. 135
напоминает окружность, которая также пересекает радиусы-векторы, исходящие
из центра, под постоянным (именно под прямым) углом. [Впрочем, и окружность
можно рассматривать как частный случай логарифмической спирали, отвечающей
т = 0]
4) Улитки: г = a cos0 + Ъ (рис. 135).
Отметим, что sbnp = r'e = —amiв оказывается не зависящей от Ъ. Таким
образом, если взять лежащие на одном луче (из полюса) точки различных улиток,
отвечающих различным значениям Ь, то для всех этих точек полярная поднормаль
будет общая, т. е. точка N — одна и та же. Но при Ъ = 0 получается окружность,
для которой построение нормали очевидно; тогда легко построить нормаль и для
любой из улиток (см. рис. 135). Из треугольника MON вычисляется полярная
нормаль:
пр = V'a2 + 2abcos6 + b2.
Особенно просто выражение полярной нормали для кардиоиды*) (Ь = а):
в
nD = 2а cos —.
*) Именно этот частный случай и изображен на рис. 135.
234] § 2. КАСАТЕЛЬНАЯ И КАСАТЕЛЬНАЯ ПЛОСКОСТЬ 593
5) Лемниската: г = 2а cos26 (см. рис. 126).
Дифференцируем это равенство, считая г функцией от 6; получим
гг'в = -2a2sm26.
Разделив почленно эти два равенства, ввиду (8), найдем
\%(o=^r = -ctg20,
гв
откуда со = 26 + j. Обозначая через а и /3 углы наклона касательной и нормали,
имеем
Р = а - -, а = а) + 6 = 36+-,
следовательно, /3 = 36: угол наклона нормали к лемнискате равен
утроенному полярному углу точки касания. Это дает простой прием
построения нормали.
234. Касательная к пространственной кривой. Касательная
плоскость к поверхности.
1° В случае пространственной кривой, определение касатель-
касательной остается буквально то же, что и для плоской кривой [91]. Огра-
Ограничимся здесь предположением, что кривая задана парамет-
параметрически:
x=<p(t), y=*l>(t), z=X(t).
Возьмем определенное значение t и, тем самым, определенную
точку M(x,y,z) на кривой; пусть это будет обыкновенная
и простая точка [223]. Придадим t приращение At, тогда нара-
наращенному значению t + At параметра будет отвечать другая точка
М\ (х + Ах, у + Ду, z + Az). Уравнения секущей ММ\ будут иметь
вид
Х-х _Y -у _ Z-z
Ах ~ Ay ~ Az '
где X, 7, Z — текущие координаты. Геометрический смысл этих
уравнений не изменится, если мы все знаменатели разделим на А^:
Х-х _Y -у _ Z-z
Ах ~ Aj^_ ~~ Az *
At At At
Если эти уравнения в пределе, при At —> 0, сохраняют опре-
определенный смысл, то этим будет установлено существование
предельного положения секущей, т. е. касательной.
594 ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [234
(9)
Но в пределе мы получаем
Х-х Y-у Z-z
и эти уравнения, действительно, выражают прямую, поскольку
не все знаменатели — нули. Таким образом, в каждой обык-
обыкновенной точке кривой касательная существует и выражается
этими уравнениями. Для особой точки вопрос о касательной
остается открытым.
Замечание. Мы переходили к пределу в уравнениях секущей
при At —»> 0; покажем, что это равносильно предположению,
что ММ\ -л 0. Ввиду непрерывности функций q>, i/>, %, из At —»> 0
следует, что и
ММ\ = у Ах2 + Ay2 + Az2 -> 0.
Для доказательства обратного заключения зададимся произволь-
произвольным числом е > 0. Так как ММ\ есть непрерывная функция от At,
то при | At\ ^ е эта функция имеет наименьшее значение 8, очевид-
очевидно, положительное (так как взятая точка предположена простой,
т. е. не получается ни при каком значении параметра, отличном
от t). В таком случае
при ММ\ < 8 необходимо \At\ < с,
что и требовалось доказать.
Иногда уравнения (9) удобно писать в виде
Х-х _ Y -у _ Z-z
dx dy dz
который получается из (9) умножением всех знаменателей на dt.
Если через а, р,у обозначать углы, составленные касательной
с осями координат, то направляющие косинусы cos a, cos/3, cosy
выразятся так:
cos a = f cos/3 =
/
cosy = ¦
Выбор определенного знака перед радикалом отвечает выбору
определенного направления касательной.
234] § 2. КАСАТЕЛЬНАЯ И КАСАТЕЛЬНАЯ ПЛОСКОСТЬ 595
Вопрос о касательной к кривой, заданной неявными уравнени-
уравнениями F(x,y, z) = 0 и G(x,y, z) = 0, мы рассмотрим ниже, в 3°.
2° Пусть поверхность задана явным уравнением z = f(x,y).
Мы в 180 дали определение касательной плоскости и,
в предположении дифференцируемости функции f(x,y) *\ нашли
уравнение этой плоскости [180, F)]:
Z-z=f'x(x,y)(X-x)+fy(x,y)(Y-y).
Обыкновенно обозначают
-=fx(x,y)=p, -=fy(x,y)=q
и пишут уравнение касательной плоскости так:
Z-z=p(X-x)+q(Y-y). A0)
Если cos Я, cos /i, cos v суть направляющие косинусы нормали
к поверхности (так называют перпендикуляр к касательной плос-
плоскости в точке касания), то для них имеем выражения
cosv = —; A1)
±Vl+P2 + <72
двойной знак перед радикалом отвечает двум противоположным
направлениям нормали.
Проведем теперь по поверхности через рассматриваемую точку
произвольную кривую
x = <p(t), y=ip(t), z=X(t),
так что тождественно относительно t будет
Дифференцируем это тождество по t [181]:
X'(t)=pq)'(t)+qip'(t).
Возьмем касательную к кривой в рассматриваемой неособой
точке в форме (9). Если, наконец, в предыдущем равенстве за-
заменить производные q>f,i/>f, %' пропорциональными им, в силу (9),
*) Мы здесь предполагаем существование и непрерывность частных производ-
производных, следовательно, дифференцируемость налицо [179].
596 ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [234
разностями X — х9 Y — у, Z — z, то придем к A0). Таким об-
образом, касательная (9) всеми точками лежит в касательной плос-
плоскости A0).31^ Мы можем, следовательно, теперь определить каса-
касательную плоскость к поверхности в заданной на ней точке
как такую плоскость, в которой лежат касательные ко всем
кривым, проведенным по поверхности через эту точку. *}
Если поверхность задана неявным уравнением F(x,y,z) = 09
то, предполагая F/ / 0 в рассматриваемой точке, в окрест-
окрестности ее можно выразить поверхность и явным уравнением
z = f(x,y)9 так что существование касательной плоскости обес-
обеспечено. Так как в этом случае
р ~ ~дх ~ ~?у q ~ ~ду ~ ~?у
то, подставляя эти значения ри q в уравнение A0), легко преобра-
преобразуем его к виду
Fi(x9y9z)(X-x)+F;(x9y9z)(Y-y)+F^x9y9z)(Z-z)=0. A2)
Очевидно, в таком же виде представится уравнение касатель-
касательной плоскости и в случае, если Ffz = 0, но какая-нибудь из двух
других производных F?, Fy отлична от 0. Лишь в особой точ-
точке это уравнение теряет смысл (и вопрос о касательной плоскости
остается открытым).
3° Теперь легко сообразить, как найти касательную к кривой,
заданной двумя неявными уравнениями:
F(x9y,z)=09 G(x9y9z) = 09
т. е. представляющей пересечение двух соответствующих поверх-
поверхностей. Если рассматриваемая на кривой точка — обыкновенная, то
в ее окрестности кривая может быть выражена и явными уравнени-
уравнениями [227], так что существование касательной обеспечено. Эта ка-
касательная, очевидно, лежит в пересечении касательных плоскостей
к упомянутым двум поверхностям и, следовательно, выражается
*) Частично об этом уже была речь в 180.
^ Можно проверить также, что касательные к лежащим на поверхности и пе-
переходящим через х^ кривым заполняют всю касательную плоскость к поверх-
поверхности.
234] § 2. КАСАТЕЛЬНАЯ И КАСАТЕЛЬНАЯ ПЛОСКОСТЬ 597
уравнениями
Л х) А у) zK \ A3)
[Так как в обыкновенной точке для матрицы коэффициентов хоть
один из определителей отличен от 0, то этими уравнениями, дей-
действительно, определится прямая.]
4° Возвращаясь к поверхности, перейдем, наконец, к случаю,
когда она выражается параметрическими уравнениями:
x=q>(u,v), y = r/)(u,v), z=x(u,v).
Снова ограничиваемся обыкновенной (и простой) точ-
точкой; так как [228] в ее окрестности поверхность может быть выра-
выражена и явным уравнением, то существование касательной плос-
плоскости обеспечено. Уравнение ее может быть написано в виде
А(Х - х) + B(Y - у) + C(Z - z) = 0, A4)
где коэффициенты А, В, С еще подлежат определению.
Если в уравнениях поверхности закрепить за v значение, отве-
отвечающее выбранной точке, то получатся уравнения координатной
линии [«кривой (f)»], проходящей через эту точку. Касательная
к этой кривой в указанной точке выразится уравнениями [см. (9)]
Х-х _ Y -у _ Z-z
Y1 ~ V1 ~ 71 '
ли Уи ^и
Аналогично, фиксируя щ получим координатную линию другого
семейства, проходящую через данную точку [«кривую (и)»] и име-
имеющую в ней касательную
Х-х _ Y -у _ Z-z
Av Уу Av
Так как обе эти касательные должны лежать в касательной плос-
плоскости A4), то выполняются условия
Ax'u + By'u+Cz'u = 0,
Ax'v+By'v+Cz'v=0.
В таком случае коэффициенты А, В, С должны быть пропорцио-
пропорциональны определителям матрицы
598
ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[235
Обыкновенно полагают их равными этим определителям:
А =
в =
с =
у
и
V У V
У V ZV
Теперь уравнение касательной плоскости проще всего написать
с помощью определителя:
Х-х Y-y Z-z
У'и
= 0;
A6)
xv Уу zv
в обыкновенной точке оно действительно выражает плоскость.
Направляющие косинусы нормали будут
А В
cos Я =
с
cosv =
A7)
235. Примеры.
1) Рассмотрим винтовую линию (см. рис. 128):
х = a cost, у = asint, z = ct.
В этом случае
х\ = —a sirU, y\ = a cos^, z\ = с,
и уравнения касательной имеют вид
Х-х _Y -у _ Z-z
—asint a cost с
Направляющие косинусы касательной
a sin t
cos a = — -
cos/3 =
a cos t
cosy =
/<2z + cz \J az + cz
Отметим, что cosy = const, следовательно, и у = const. Если представить
себе винтовую линию навернутой на прямой круглый цилиндр, то можно сказать,
что винтовая линия пересекает все образующие этого цилиндра под постоянным
углом *).
2) Эллипсоид:
*2 , у2 , z1 ,
*) Если поверхность цилиндра разрезать по образующей и развернуть, то вин-
винтовая линия превратится в прямую, которая все вертикали, естественно, пересе-
пересекает под одним и тем же углом. Это соображение делает предыдущий результат
совершенно очевидным.
236] § 2. КАСАТЕЛЬНАЯ И КАСАТЕЛЬНАЯ ПЛОСКОСТЬ 599
Касательная плоскость получается по формуле A2), с учетом самого урав-
уравнения эллипсоида:
хХ yY zZ
3) Конус (второго порядка):
а2 + Ь2 С2~ °-
Касательная плоскость:
хХ yY zZ _
В вершине @, 0, 0) конуса, которая является особой точкой, это уравнение
теряет смысл, и касательной плоскости нет.
4) Кривая Вивиани (см. рис. 127):
х2 +у2 +z2 =R2, х2 +у2 =Rx.
Касательная выражается уравнениями [см. A3)]
xX + yY + zZ = R2, Bх -R)X+2yY = Rx.
Эти уравнения перестают выражать прямую лишь в особой точке (R, 0, 0).
5) Винтовая поверхность:
х = г/cos и, у = г/sin и, z = cv.
По формуле A6), уравнение касательной плоскости будет
X-х Y -у Z-z
cos v sin v 0
—г/sin t> ucosv с
= 0.
С учетом уравнений поверхности это уравнение может быть упрощено так:
sin v • X — cos v • Y -\— • Z = uv.
с
236. Особые точки плоских кривых. Здесь мы остановимся по-
подробнее на поведении кривой, заданной неявным уравнением
F(x,y) =0,
вблизи ее особой точки (хо,уо). Не имея в виду исчерпать этот
вопрос, мы хотим лишь познакомить читателя с главными типами
особых точек. При этом функцию F мы предполагаем непрерывной
и имеющей непрерывные производные первых двух порядков. Без
умаления общности, можно считать хо = 0, у о = 0; это отвеча-
отвечает просто переносу начала координат в испытуемую точку. Итак,
имеем
f(o, о) = о, f;(o, о) = о, f/(o, о) = о.
600 ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [236
Введем обозначения
а 11 = F? @, 0), а 12 = F'Jy @,0), а22 = F1^ @,0).
Предполагая, что из чисел ац, аи, а 22 хоть одно — не нуль, мы
станем классифицировать представляющиеся возможности в зави-
зависимости от знака выражения <яц<Я22 — <я22. Исследования на-
настоящего п° теснейшим образом примыкают к ис-
исследованиям п° 197.
1° апа22 — ci\2 > ®-
В этом случае, как мы знаем, функция F(x,y) имеет в на-
начальной точке экстремум. Значит, в достаточно малой окрестности
этой точки F > 0 или F < 0 (исключая самую начальную точ-
точку, где функция обращается в 0). Иначе говоря, в упомянутой
окрестности нет ни одной точки нашей кривой, кро-
кроме начальной: эта последняя оказывается изолированной точкой
кривой.
Примеры, иллюстрирующие рассматриваемый случай:
х2+у2 = 0 или {х2+у2){х +у - 1) = 0.
Начальная точка принадлежит обеим кривым и для обеих явля-
является изолированной. Но, в то время как первая вся состоит
из одной точки, вторая, кроме нее, содержит еще прямую х +у = 1,
не проходящую через начало.
2° апа22 — ®2\2 < 0-
Как и в 197, в окрестности начальной точки можно представить
F(x,y) в следующем виде:
{ +2а\2ху+а22У + ацх + 2а\2ху
где
все а —»> 0 при х —»> 0, у —»> 0,
или, если ввести полярные координаты р, q>\
2
F(x,y) = —jan cos2 ср + 2aи coscp sincp + <322sin2<p +
+ a\\ cos2 ф + 2a\2 cos ф sincp + ^22 sin2 ф \.
В рассматриваемом случае, если предположить еще а 22 ф 0,
трехчлен an+2a\2t + a22t2 имеет различные вещественные корни
236]
§ 2. КАСАТЕЛЬНАЯ И КАСАТЕЛЬНАЯ ПЛОСКОСТЬ
601
h, h (t\ < t^) и разлагается на множители #22(/ — t\){t — t?). Поло-
Положим, ср\ = arctg/^, Ф2 = arctg^? так что t\ = tgcpi, ti — tgф2- Те-
Теперь легко преобразовать первый трехчлен в скобках {... } к виду
а\\ cos2 q> +
cosф sinф +
A8)
Отсюда становится ясным, что прямые, проведенные через нача-
начало под углами ф1 и ф2 к оси х — будем для краткости называть
их прямыми (<pi) и (ф2), — делят плоскость на две угловые облас-
области, в одной из которых упомянутый трехчлен сохраняет знак плюс,
а в другой — знак минус *) (рис. 136).
Заключим теперь прямые (ф\) и {ср2) внутрь двух сколь угод-
угодно узких угловых областей — двух пар вертикальных углов, со-
содержащихся, соответственно, между прямыми {ср\ — г) и {ср\ + е)
или (ф2 — е) и (д>2 + ?) (эти углы на рис. 136 заштрихованы).
Взяв круг достаточно малого радиуса г? вокруг начала, можно
утверждать, что — по выделении упомянутых углов — он разо-
разобьется на две угловые области,
в каждой из которых уже са-
сама функция F(x,y) сохраняет
определенный знак: в одной —
плюс, а в другой — минус (см.
рис. 136). Действительно, так
как при изменении угла вне
промежутков (ср\ - е, щ + е)
Рис. 136
и (ф2-?, q>2 + z) трехчлен A8)
не обращается в 0, то он оста-
остается по абсолютной величине
большим некоторого положи-
положительного числа т?. С другой
стороны, при достаточно ма-
малом р выражение ац cos2 q> + 2a\2 cos q> sin q> + ^22 sin q> по абсо-
абсолютной величине будет меньше т?. Отсюда и следует наше утвер-
утверждение [ср. рассуждение в 197, 1°].
Рассмотрим теперь два заштрихованных вертикально располо-
расположенных сектора круга, например те, которые ограничены прямы-
прямыми (ф1 - е) и (q>i+e). Так как на этих прямых функция имеет
*^ Этим мы несколько углубляем сказанное в 197, 2°: там нам достаточно было
констатировать наличие двух прямых, на которых трехчлен имеет разные знаки.
602 ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [236
противоположные знаки, то на каждой вертикали, пере-
пересекающей упомянутые секторы, найдется точка,
в которой F(x,y) обращается в 0, т.е. точка нашей
кривой. Это следует из известного свойства непрерывной функ-
функции [80], если применить его к функции F(x,y) от у (при фикси-
фиксированном х).*}
Таким образом, внутри каждой пары заштрихованных секторов
расположена ветвь кривой, проходящая через начало, в то время
как вне их, в пределах круга, точек кривой нет. Ввиду произволь-
произвольности ?, ясно, что в начале эти ветви касаются, соответственно,
прямых (<pi) и (фг).
Правда, остался открытым еще вопрос, единственна ли та точ-
точка на упомянутой вертикали, в которой F(x,y) = 0. Если бы их
нашлось две, то, по теореме Ролля [111], между ними
на той же вертикали нашлась бы точка, в которой было бы
F'(x, у) = 0. Итак, единственность будет установлена, если мы
докажем, что по крайней мере в достаточной близости к началу
такое равенство невозможно.
Допустим противное. Тогда будем иметь Fy(xn, yn) = 0 для
некоторой последовательности точек {(хп,уп)}9 где хп —>> 0
и Уп_ _^ tgcpi = t\. Применим к функции Fl(x, у) формулу ко-
Xyi У ^ '
нечных приращений [183, A0)]:
= F'Jy(впхп, епУп) ¦ хп + Ffi{епхп, впУп) -у„ @ < в„ < 1)
или
F"y@nxn, впУп) + F(enxn, епУп) ¦ ^ = 0.
Хп
Переходя здесь к пределу, получим окончательно аи + #22^1 = 0
или t\ — — I12-, что неверно: такое значение t\ могло бы иметь лишь
в том случае, если бы корни трехчлена ац + 2а ut + <Я22^2 были
равными.
Из сказанного попутно вытекает, что, в достаточной близости
к началу, ни одна точка упомянутых двух ветвей, кроме самой на-
начальной, уже не будет особой.
Аналогично исчерпывается и случай, когда а22 = 0, но ац ф 0
или а и = #22 = 0, но а и ф 0; отметим лишь, что в последнем
случае роль прямых (ср\) и {ср2) играют оси координат.
*)
Ср. доказательство теоремы 1 [206] о существовании неявной функции.
236]
§ 2. КАСАТЕЛЬНАЯ И КАСАТЕЛЬНАЯ ПЛОСКОСТЬ
603
Итак, при сделанном предположении аца22 — а\2 < 0 точ-
точка @, 0) оказывается двойной точкой кривой: в ней пересекаются
две ветви кривой, каждая из которых в этой точке имеет свою каса-
касательную. Угловые коэффициенты этих касательных определяются
всегда из уравнения ац + 2ant + <222t2 = 0; лишь если #22 = 0?
следует считать, что, кроме конечного корня, оно имеет корнем
и бесконечность.
Примерами могут служить уже знакомые нам кривые
(х2 + у2J + 2а2(у2 - х2) = 0 (лемниската, рис.126),
х3 + у3 - Ъаху — 0 (декартов лист, рис.117),
для которых начало и будет двойной точкой. В первом случае име-
имеем а и = —4а2, а и = 0, #22 = 4<я2, t\ = 1, /2 = — 1? так что каса-
касательными в начале служат биссек-
биссектрисы координатных углов. Во вто-
втором: а\\ = #22 = 0, а\2 = —За,
tx — 0, t2 = 00, и касательными
служат оси координат.
апа22-а
2 _
12
= 0.
Рис. 137
Допустим и здесь, что а22 ф 0.
Квадратный трехчлен а \ \ + 2а ut +
+<Я22^2 в этом случае имеет двой-
двойной корень t\ — — ^п. Пола-
Полагая, как и выше, ср\ = arctg/^, про-
проведем через начало прямую под
этим углом ср\ и оси х. Заклю-
Заключим ее в угловую область между
прямыми (ф1 - е) и (ф1 + е) (на
рис. 137 она заштрихована). С по-
помощью соображений, сходных с примененными выше, можно уста-
установить, что вне заштрихованной области, но в достаточной близо-
близости к началу, функция F(x,y) сохраняет определенный знак,
один и тот же с обеих сторон: плюс или минус, в зависимости от
того, будет ли <Я22 > 0 или <222 < 0- Теперь на прямых (ср\ ±е) функ-
функция имеет одинаковые знаки, и применять теорему Коши
нельзя.
Мы не будем углубляться в исследование этого случая, требу-
требующего более сложных рассуждений, с привлечением высших про-
производных. Ограничимся указанием на основные возможности, ко-
которые здесь представляются.
604
ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[236
а) Вблизи начальной точки, кроме нее самой, нет точек кривой:
изолированная точка (как в случае 1°).
Примеры.
х4+у2 =
или
Для обеих «кривых» начало является изолированной точкой.
б) В обоих заштрихованных вертикальных углах (в достаточной
близости к началу) на каждой вертикали лежат по две точки
нашей кривой, через начало проходят две ветви кривой, имеющие
в ней общую касательную (ср\); двойная точка (как и в случае 2°).
Пример.
4 2 п i 2
х —у =0, т. е. у = dzjc
— две параболы, в начальной точке касающиеся оси х.
в) В одном из заштрихованных углов вовсе нет точек кривой,
а в другом — две ветви, которые как бы заканчиваются в началь-
начальной точке, имея в ней общую касательную (q>\).
Здесь мы имеем дело с новым типом особой
точки — с точкой возврата (или точкой за-
заострения). В зависимости от того, лежат ли
обе встречающиеся в ней ветви по разные сто-
стороны от общей касательной или по одну сто-
сторону, различают точки возврата первого и
второго рода.
Примером кривой, имеющей в начале
точку возврата первого рода, может служить
кривая
о
/-*з =
Рже. 138 (полукубическая парабола, рис. 115).
Более редкий случай точки возврата второго рода проиллюстриру-
проиллюстрируем таким примером:
х5-(у-х2J = 0
или
у =х2±х2л/х (х
Обе ветви в начальной точке касаются оси х, располагаясь (по край-
крайней мере вблизи начала) над нею (рис. 138).
237] § 2. КАСАТЕЛЬНАЯ И КАСАТЕЛЬНАЯ ПЛОСКОСТЬ 605
Если а и = а \2 = #22 = 0, то приходится рассматривать произ-
производные высших порядков. В этом случае возможны и более слож-
сложные типы особых точек {тройные или, вообще, п-кратные точки,
и т. д.).
237. Случай параметрического задания кривой. Скажем еще
несколько слов об особых точках плоских кривых, заданных па-
параметрическими уравнениями
х =<p(t), y = ip(t).
Пусть при t = to имеем
x'o = <p'(to)=O и у'0 =
но из производных второго порядка x'q и j/q пусть хоть одна, на-
например Xq, отлична от нуля.
Проведем секущую через точки (хо,уо) и (х>у) кривой, от-
отвечающие значениям to и t параметра. Ее уравнение может быть
написано так:
X -хр _ Y -ур
х-х0 у-уо'
Но по формуле Тейлора [с дополнительным членом в форме
Пеан о, 124, A0а)], так как х'о = у'о = 0, имеем
О + )( J
где аи /3 стремятся к 0 при t —>> /о- Подставляя, перепишем уравне-
уравнение секущей, после сокращения обоих знаменателей на \{t — toJ,
в следующем виде:
Х-х0 Y-y0
хо+а
Здесь можно перейти к пределу при t —> to*\ и таким путем
получается уравнение касательной:
Ц^ = Ц^ или У-у0 = Уф(Х-Х0). A9)
х0
*^ См. замечание в 234, которое приложимо и здесь, если рассматриваемую
точку считать простой.
606 ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [237
Мы предположили х[( / 0; пусть, например, х$ > 0. Тог-
Тогда функция х = q>(t) при t = to имеет (собственный) мини-
минимум [137], т. е. х > хо при зна-
У \ ^^ чениях t, близких к to (как при
^^ t < to, так и при t > to). Таким
образом, в точке (хо,уо) смы-
смыкаются две ветви кривой, отве-
отвечающие t < to и t > to; они
имеют общую (наклонную или
-й ¦ > х горизонтальную) касательную,
Рис 139 и °^е Расположены вправо
от вертикали х = хо- Иными
словами, налицо точка возвра-
возврата (рис. 139). Это — основной случай особой точки для кривой,
заданной параметрически.
Легко пойти несколько дальше в этом исследовании, чтобы
установить, какого рода будет эта точка возврата. С этой це-
целью привлечем третьи производные, и приращения х —хо^у —уо
напишем в виде
х-хо = -x%(t - toJ + - К" + a){t- to)\
где а и ji снова стремятся к 0 при t —>> to.
Вычислим, пользуясь уравнением A9), ординату Y точки
касательной с абсциссой х; мы получим
Составим, наконец, разность ординат Y и у, отвечающих одной
и той же абсциссе х\
'' Хг
6
где через у обозначена снова некоторая бесконечно малая
при t —>> to.
Теперь, если только х'^у^ —х'оУо' Ф 0 (что обыкновенно и вы-
выполняется), ясно, что разность Y — у будет разных знаков
238] § 3. КАСАНИЕ КРИВЫХ МЕЖДУ СОБОЙ 607
при t < to и t > to, т. е. для тех двух ветвей кривой, которые встре-
встречаются в точке (хо,уо) (в предположении, конечно, что мы огра-
ограничиваемся значениями t, достаточно близкими к to). Ветви распо-
располагаются по разные стороны от касательной, и мы устанавливаем
точку возврата первого рода.
Примеры подобных особенностей встречались нам уже не раз,
циклоида, эпи- или гипоциклоида, эвольвента круга — все имеют
такие точки возврата (см. рис. 118-121).
Может оказаться, в исключительном случае, что х^у^—х^у^ =
= 0; тогда разложение Y — у по степеням t — to начнется с чет-
четвертой или более высокой степени этого двучлена. Если степень
эта четная, то рассматриваемая особая точка будет точкой воз-
возврата второго рода.
§ 3. Касание кривых между собой
238. Огибающая семейства кривых. Если две кривые имеют
общую точку Мо и — в этой точке — общую касательную, то
говорят, что кривые касаются в точке Мо. Настоящий
параграф посвящен некоторым вопросам, связанным с касанием
плоских кривых.
Приступая к рассмотрению огибающей семейства кри-
кривых, остановимся сначала на самом понятии семейства кривых.
Нам уже не раз приходилось встречаться с уравнениями кривых,
в которые, кроме текущих координат х и у переменной точки, вхо-
входит еще один или несколько параметров. В случае одного
параметра, скажем, а, уравнение имеет вид
F(x,y,a) = 0. A)
Левая часть является функцией трех переменных, из которых пе-
переменную а мы иначе называем лишь потому, что она играет осо-
особую роль: для получения конкретной кривой значение параметра а
должно быть фиксировано. При изменении этого значения, обыч-
обычно в пределах некоторого промежутка, будут получаться, вообще
говоря, различные (по форме или расположению) кривые.
Совокупность всех этих кривых и называют семейством
кривых с одним параметром, а уравнение A)— уравнением
семейства.
608 ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [238
Иногда случается, что для подобного семейства кривых сущест-
существует кривая, которая касается каждой кривой семейства
в одной или нескольких точках и притом вся состоит из
этих точек касания (рис. 140). Такая кривая носит название
огибающей данного семейства. Мы покажем сейчас, как уста-
установить, существует ли огибающая, и как найти ее в случае сущест-
существования.
С этой целью допустим сначала, что огибающая существует.
Для простоты предположим, что речь идет об огибающей (точ-
(точнее — ветви огибающей), которая каждой кривой семейства каса-
касается в одной точке. Тогда координаты этой точки касания одно-
однозначно определяются указанием кривой семейства, т. е. значением
параметра а:
х=ф(а), у = гр(а). B)
Поскольку огибающая вся состоит из точек касания, эти уравнения
и дают параметрическое представление огибающей.
Рис. 140
Мы предполагаем существование и непрерывность
частных производных функции F и производных функций ср и гр.
Точка B) лежит на кривой A), определяемой тем же значением
параметра а, так что имеет место такое тождество относитель-
относительно а\
F(<p(a),il>(a)9a)=0. C)
Продифференцировав его полным образом по а, получим
[181, 185] *)
F'xdx + F^dy+F^da = 0, D)
причем производные вычислены при указанных в C) значениях ар-
аргументов, a dx и dy означают дифференциалы функций B).
* ^ Здесь, между прочим, мы используем и непрерывность частных производных
функции F.
238] § 3. КАСАНИЕ КРИВЫХ МЕЖДУ СОБОЙ 609
Теперь постараемся аналитически выразить тот факт, что оги-
огибающая касается в точке B) кривой A). Касательная к кри-
кривой A) [см. 230, E)]
F^X-x)+F;(Y-y)=0 E)
и к кривой B) [230, G)]
Х-х Y-у
dx dv
F)
должны совпасть. Условие совпадения этих прямых можно напи-
написать в виде
Fidx+F^dy = 0. G)
При этом, как и выше, под х и у мы разумеем их значения B),
а под dx и dy — дифференциалы функций B).
Заметим, что уравнения E) и F) действительно выражают ка-
касательные к кривым лишь в предположении, что рассматриваемая
точка не будет для них особой. Тем не менее равенство G)
имеет место даже в том случае, если эта точка
будет особой для той или другой кривой.
Сопоставляя G) с D) и учитывая, что da — произвольное чис-
число, найдем, что Ffa = 0 или в развернутом виде:
FXa),^(a),a)=0. (8)
Тождества C) и (8) показывают, что функции B), нам неиз-
неизвестные, должны тождественно относительно а удовлетворять сис-
системе уравнений
F(x,y, a) = 0, Fa(x,y, a) = 0. (9)
Итак, если огибающая существует, ее параметрические урав-
уравнения B) получаются как решения относительно х и у системы (9).
В том случае, когда эта система при переменном а вообще не
допускает решений в виде функций от а, положение вещей ясно:
огибающей вовсе нет. Предположим же теперь, что в ре-
результате решения системы (9) получены уравнения B), выража-
выражающие кривую без особых точек. *} Будет ли эта кривая огибающей
нашего семейства кривых?
*) При наличии отдельных особых точек ограничимся промежутком изменения
параметра, не содержащим критических его значений.
610 ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [238
Так как функции B) удовлетворяют уравнениям (9), то выпол-
выполняются тождества C) и (8). Дифференцируя первое из них, по-
получим D), а сопоставляя это с (8), придем к равенству G). Если
точка B) (ни при одном а) не будет особой на соответствующей
кривой A), так что уравнение E) действительно выражает каса-
касательную к названной кривой, то равенство G) обусловливает сов-
совпадение этой касательной с касательной F) к кривой B). В этом
случае кривая B) на самом деле будет огибающей
семейства.
В частности, это можно гарантировать, если, например, кривые
данного семейства вовсе лишены особых точек.
Наоборот, если такие особые точки имеются и при изменении а
геометрическое место их образует кривую B), то соответствую-
соответствующие ей функции ср и гр необходимо удовлетворяют системе (9),*)
хотя в этом случае кривая может не быть огибающей.
Итак, при наличии особых точек кривая B), полученная в ре-
результате решения системы (9), подлежит еще проверке: она мо-
может быть огибающей, может быть геометрическим местом особых
точек на кривых семейства или, наконец, частью — огибающей,
частью же — таким геометрическим местом.
Обыкновенно при разыскании огибающей не останавливаются
на системе уравнений (9), но идут дальше — исключают из
них а. Иными словами, получают соотношение вида
Ф(х,у) = 0, (Ю)
уже не содержащее а и представляющее собой условие, необходи-
необходимое и достаточное для того, чтобы для пары значений х, у нашлось
такое значение а, которое совместно с ними удовлетворяло обоим
уравнениям (9).
Все точки кривой B), полученной решением системы (9),
должны удовлетворять уравнению A0). Поэтому, если это послед-
последнее уравнение не выражает никакой кривой, то сразу ясно, что оги-
огибающей нет. Если же уравнение A0) выражает кривую (ее называ-
называют дискриминантной кривой семейства), то она, как вы-
выше, подлежит проверке. В ее составе должна оказаться огибающая
(если она существует), но должно быть и геометрическое место
особых точек (если таковые налицо). Кроме того, здесь есть еще
*) Для них выполняется C), значит, и D). Затем имеет место G), как выше
упоминалось в тексте; сопоставляя с D), приходим к (8).
239]
3. КАСАНИЕ КРИВЫХ МЕЖДУ СОБОЙ
611
одна неприятная возможность, которую следует исключить провер-
проверкой: именно, в состав дискриминантной кривой может попросту
входить одна или несколько частных кривых семейства. Так будет
в том случае, когда бесконечному множеству точек дис-
дискриминантной кривой отвечает одно и то же значение а, совместно
с ними удовлетворяющее уравнениям (9)*\
Все сказанное всего лучше выяснится на примерах.
239. Примеры.
1) Найти огибающую для семейства окружностей:
(х — а) + у = г (г = const)
(рис. 141).
Дифференцируем по а: —2{х—а) = 0. Исключая я, получим^ —г = 0 или
у = d=r: две прямые, параллельные оси х, которые, очевидно, составляют
огибающую**^.
1 1 1 1 %
\ \ \ \ d
Ч 7Лч >С ^'ч
Гу y'V
1 - - J * - - "т
\ S®>\ :
\f
rr:
) j
Рис. 141
Рис. 142
2) Найти огибающую различных положений прямой, скользящей двумя точ-
точками, находящимися друг от друга на постоянном расстоянии а, по осям коорди-
координат (рис. 142).
*) Если оперировать непосредственно уравнениями (9), то такая возможность
исключается, потому что уравнения пытаются решить при заведомо перемен-
переменном а.
**' Если уравнение семейства взять в виде
х — a d=
то результат дифференцирования по а будет — 1 = 0; из невозможности этого
равенства, казалось бы, вытекает заключение об отсутствии огибающей. Такое за-
заключение, однако, было бы неверно, так как вся изложенная теория предполагает
существование и непрерывность частных производных от левой части уравнения
семейства, а здесь (именно при j/ = d=r) конечной производной по j/ нет.
612
ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[239
Взяв за параметр угол 0, составленный перпендикуляром к движущейся пря-
прямой с осью х, уравнение прямой можно написать в виде:
х у
sin 0 cos 0
= а.
Дифференцируем по 0
х
~— cos 0 Н
sin2 0
cos2 0
Иначе это можно написать так:
sin 0 = О или
У
sin30
cosJ0
sin
2 0 cos2 0
sin2
cos
2 0
откуда x = a sin3 0, j/ = a cos3 0.
Читатель узнает в этих уравнениях параметрическое представление аст-
астроиды [224, 4) : t = § — 0], которая в данном случае и является огибающей.
С этим свойством астроиды мы уже однажды сталкивались [231, 3)].
3) Во многих случаях огибающая как бы ограничивает («огибает»)
часть плоскости, занятую кривыми се-
У\
у=(х-аJ
мейства. Что это не всегда так, показы-
показывает пример:
(рис. 143).
Рис. 143
Рис. 144
Здесь огибающей служит ось х, пересекающая все кривые семейства.
Аналогичное обстоятельство проявляется и в следующем, более сложном при-
примере.
4) Найти огибающую семейства парабол:
у = а (х — а) .
Сопоставляя это уравнение с уравнением
2а(х - аJ - 2а2(х - а) = 2а(х - а)(х - 2а) = О,
получим либо х = а (у = 0), либо х = 2а (у = а ), так что дискриминантная
кривая состоит из прямой;; = 0 и кривой 16у = х . Первая касается всех парабол
239] § 3. КАСАНИЕ КРИВЫХ МЕЖДУ СОБОЙ 613
в вершинах. Вторая имеет с каждой параболой три общие точки: касается
ее при х = 2а и пересекает при х = — 2а d= 2ал/2.
5) Рассмотрим эллипс:
- + у--\
а2 + Ъ2~
Станем искать огибающую семейства окружностей, построенных, как на диа-
диаметрах, на хордах эллипса, параллельных оси j/ (рис. 144).
Приняв за параметр абсциссу t центра окружности, напишем уравнение этого
семейства в виде:
Fix,у, t) = (x- tf + у2-^(а2- t2) = О,
причем t изменяется в промежутке [—а, а]. Имеем
, 2b a
Ft = —2(x — t) -\ =- t = 0, откуда t = —z ~x.
az az + bz
Подставив это значение t в уравнение F = 0, мы получим уравнение огибающей
в следующем виде:
ах \2 , 2 Ь1 (_г
a2 + b2 ) a
или, после преобразований:
Мы пришли к эллипсу с теми же осями симметрии, что и данный.
Любопытно отметить, что этот эллипс касается не всех окружностей
семейства. Это обстоятельство легко усмотреть, если не исключать t из уравне-
уравнений F = 0 и F/ = 0, а выразить из них х и у через t:
a2 + b2 f _±b_ i 4_,2 + b2 2
a2 ' a2
Действительно, отсюда сразу видно, что выражение для у может быть веществен-
вещественным лишь при \t\ < ,а2 2. Значит, только для части семейства окружнос-
окружностей, соответствующей указанным значениям t, существует огибающая.
Этот поучительный пример показывает, что параметрическое задание огиба-
огибающей может оказаться более выгодным, потому что из него легче усмотреть, для
какой части данного семейства огибающая действительно существует.
6) Для семейства концентрических окружностей:
9 9 х
х +у = а (я ^ 0)
огибающей нет: дифференцирование по а сразу приводит к невозможному равен-
равенству 0=1.
7) Рассмотрим два семейства полукубических парабол:
(а) (у-аJ-х3 =0
(б) у2-(х- аK = 0
(рис. 145). Дискриминантная кривая будет: (а) х = 0; (б) у = 0, и в обоих
случаях является носительницей особых точек. Но в случае (б) она все же одно-
одновременно будет огибающей; в случае (а) огибающей нет.
614
ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[240
8) Более сложный пример такого же типа дает другое семейство по л у ку-
кубических парабол:
(у-аJ-(х- аK = 0
(рис. 146). Здесь дискриминантная кривая распадается на две прямые: у = х
и у = х — yj. Первая является лишь геометрическим местом особых точек,
а вторая будет огибающей.
а)ку
*- х
Рис. 145
Рис. 146
9) Наконец, рассмотрим семейство прямых:
4A +t)x =t2y.
Если продифференцировать по t: 4x = 2ty и исключить t из обоих уравнений,
то получим, как результат исключения:
х(х +у) = 0.
Это уравнение представляет две прямые: х = 0 и у = —х, которые входят
в состав данного пучка (при t = Ои/ = —2). Ни одна из них не является ни
огибающей, ни носительницей особых точек. Огибающей в этом случае нет.
Этот пример иллюстрирует указанную нами ранее возможность того, что
уравнение A0) представит не огибающую, а одну или несколько кривых семей-
семейства. Если бы мы, не исключая t, попытались выразить х и у через t при
переменном t, то это оказалось бы невозможным.
240. Характеристические точки. С понятием огибающей тесно
связано другое интересное геометрическое понятие — характе-
характеристических точек.
Возьмем одну из кривых семейства
F(x,y,a) =0,
определяемую значением а параметра. Придадим а некоторое при-
приращение Аа; значению а + Аа параметра будет отвечать другая
240] § 3. КАСАНИЕ КРИВЫХ МЕЖДУ СОБОЙ 615
кривая семейства
F(x,y, a + Аа) = 0,
«близкая» к первой.
Может случиться, что при достаточно малом Аа обе кривые пе-
пересекаются в одной или в нескольких точках. При стремлении Аа
к нулю эти точки пересечения будут каким-то образом перемещать-
перемещаться по первой кривой. Если при этом какая-либо из точек пересе-
пересечения стремится к определенному предельному положению, то эту
(а)
Рис. 147
предельную точку называют характеристической точкой
на исходной кривой (рис. 147). [Обращаем внимание читателя на
то, что характеристическая точка связана не только с той кривой,
на которой лежит, но и со всем семейством. Говорить о характе-
характеристической точке для отдельно заданной кривой было бы лишено
смысла.]
Точка пересечения упомянутых выше кривых должна удовле-
удовлетворять системе уравнений
F(x,y, а) = 0, F(x,y, а + Аа) = О
или равносильной ей системе
F(x,y,a)=0, — д^
616 ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [241
Устремив здесь Аа к нулю, мы придем к уже знакомой нам
системе (9):
F(x9y9a)=09 F^(x9y9a)=09
которой, таким образом, при заданном а, и должны удовлетворять
координаты характеристической точки.
Точнее говоря, если сохранить за х и у значения координат точ-
точки пересечения, то вместо A1) [применяя формулу Лагранжа]
можно написать:
F{x9y9a) = 0, Fl(x9y9 а + вАа) = 0 @ < в < 1).
Если при Аа —»> 0 координаты х, у имеют соответственно преде-
пределы jc,y9 то, переходя в написанных равенствах к пределу, ввиду
непрерывности функций F и Fj, легко убедиться в том, что коор-
координаты х, у характеристической точки, действительно, удовлетво-
удовлетворяют системе уравнений (9).
Допустим теперь, что характеристические точки существуют на
каждой кривой семейства. Тогда можно поставить вопрос о гео-
геометрическом месте характеристических точек.
Если это место представляет собой кривую вида B), то функ-
функции cp(a),ip(a), фигурирующие в ее уравнениях, должны удовле-
удовлетворять системе (9), а значит — получаться в числе решений этой
системы относительно х,у. Точно так же все точки упомянуто-
упомянутого геометрического места удовлетворяют и уравнению A0), т. е.
это место необходимо входит в состав дискриминантной
кривой.
Из сказанного ясно, что геометрическое место характеристиче-
характеристических точек, если существует, представляет собой (полностью или
по частям) либо огибающую, либо носительницу особых точек.
Легко убедиться в том, что в примерах 1), 2), 4), 5) предыду-
предыдущего п° геометрическое место характеристических точек совпада-
совпадает с огибающей. Это в некотором смысле — общий случай. Но
вот в примере 7), (а) это геометрическое место служит лишь но-
носительницей особых точек, а в примерах 3) и 7), (б) вовсе нет пе-
пересечения между кривыми (хотя огибающая существует).
241. Порядок касания двух кривых. Рассмотрим две кривые,
касающиеся в точке М$.
Если кривые заданы явными уравнениями у = f(x) и
Y = g(x) и Мо имеет абсциссу xq9 to совпадение ординат и угловых
241] § 3. КАСАНИЕ КРИВЫХ МЕЖДУ СОБОЙ
коэффициентов касательных может быть записано так:
617
Для характеристики близости рассматриваемых кривых в ок-
окрестности точки Мо возьмем точки М и т на этих кри-
кривых (рис. 148) с абсциссой х и установим порядок бесконечно ма-
малого отрезка
тМ= Y -у = g{x) - f{x) = ср{х)
относительно основной бесконечно малой х—х^.Если
этот порядок равен п + 1 {или больше, чем /7+1), то го-
говорят, что кривые в точ-
точке Мо имеют порядок ка-
сания п {или выше, чем п).
Мы видели, что при нали-
наличии касания всегда
ф(*о) = g(xo) - /Оо) = О,
cp'{xo)=g'{xo)-f'{xo)=O.
Рис. 148
Пусть в точке xq для функ-
функций f{x) и g{x) существуют производные всех порядков до
{п + 1)-го включительно, причем
f"(xo)=g"(xo),
так что
О величине производных f^n+1\xo) и g^n+1\xo) пока ника-
никаких предположений не делаем. Применяя к функции ср(х)
формулу Тейлора с дополнительным членом в форме
Пеано [124, A0а)]:
A2)
тМ
ВИДИМ, ЧТО
lim
618 ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [241
Таким образом, если f(n+l\xo) ф g^n+l\xo), T0 кривые имеют
касание /7-го порядка, если же /^+1)(*о) = g^+14*o)> T0 порядок
касания будет выше п. Отсюда (в предположении существования
всех упоминаемых производных) следует:
Для того чтобы в точке с абсциссой хо кривые у = f(x)
и Y = g(x) имели касание п-го порядка, необходимо и доста-
достаточно, чтобы выполнялись условия
/(*„)= g(*o), /'(*<>) =g'(*o), .... /я)(*о)=*Г(и)(*о), A3)
A4)
[Если последнее неравенство не установлено, то можно лишь
утверждать, что порядок касания не ниже п.]
Для случая, когда порядок касания точно равен /7, из A2) непо-
непосредственно вытекает, что при п четном кривые, касаясь
в точке Мо, взаимно пересекают одна другую, при п
же нечетном этого нет.
Замечание. В свете выведенных условий мы вернемся вновь
к самому определению порядка касания. Это определение ка-
кажущимся образом связано с выбором координатной системы. На
деле же порядок касания двух кривых от этого выбора не
зависит (лишь бы только ось у не была параллельна общей каса-
касательной), так что установленное понятие является действительно
геометрическим.
Если повернуть координатную систему на произвольный угол а,
то новые координаты х, у выразятся через старые xjc помощью
известных формул преобразования:
х = х cos а + у sin а, у = — х sin a + у cos a.
Пусть в старой системе координат дана кривая у =/(х); если
в предыдущих уравнениях под у разуметь именно эту функцию, то
они дадут параметрическое представление кривой в новой
системе, схв роли параметра. Очевидно, производные
dx dy . dy . dy
-— = cos a + — sin a, — = — sin a + — cos a
dx dx dx dx
одновременно в О обратиться не могут, так что в новом представ-
представлении ни одна точка не будет особой, а тогда ясно, что первая
из этих производных — не 0 в интересующей нас точке [ибо иначе
242] § 3. КАСАНИЕ КРИВЫХ МЕЖДУ СОБОЙ 619
касательная к кривой в этой точке была бы параллельна оси у].
Следовательно, в ее окрестности кривая выразится и в новой сис-
системе явным уравнением у = fix).
Теперь легко видеть, что [ср. 121]
dy _ - sin a + |? cosa d2y _ ¦?$
dx cosa + $L sin a ' dx2 (C0Sa + &L sin aK '
и вообще
^7 _ /dy d2y dky
где Rk есть символ рациональной функции. Отсюда ясно, что как
только для двух функций у от х выполняются равенства A3),
то для двух соответствующих функций у от х выполняются
аналогичные равенства. Точно так же — при наличии A3) — из не-
неравенства A4) вытекает такое же неравенство для новых функций,
ибо — в противном случае — обратное преобразование привело
бы нас, взамен неравенства A4), тоже к равенству.
Этим и завершается доказательство высказанного утверждения.
242. Случай неявного задания одной из кривых. Рассмотрим
теперь случай, когда вторая кривая задана неявным уравнением
G(x,y) = 0. A5)
Пусть рассматриваемая точка Мо(хо, у о) не является для этой кри-
кривой особой, а именно пусть Gfy(xo,yo) Ф 0. Тогда в окрест-
окрестности этой точки уравнение A5) определяет однозначную функ-
функцию у = g(x)9 и для установления порядка касания могут быть
использованы уже известные условия A3) [и A4)].
Но так как явного выражения функции g(x) в этом случае мы
не имеем, то было бы удобнее выразить эти условия в такой форме,
которая использовала бы лишь данную функцию G.
С этой целью вспоминаем, что значения функции g(x) и ее
производных gf(x), gf'ix),..., g(n\x) последовательно и притом
однозначно определяются уравнением A5) и теми уравнени-
уравнениями, которые получаются из него дифференцированием по х, если
620 ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [243
иоду разуметь g(x) [209]:
G(x,g(x))=0, G'x{x, g{x)) + G'v(x, g(x))g'(x) = 0,
;2 + 2G"g\x) + G[g'(x)}2 + G'g"{x) = 0.
— n *)
Поэтому если (при x = xo) в этих равенствах везде вме-
вместо g(xo),gf(xo), ... ,g(n\xo) подставить, соответственно, /(хо),
/;(хо), ..., /^(хо)? то получатся условия
G(x0, /Ы) = 0, G'x(x0, f(x0)) + С'у{х0, f(xo))f'(xo) = 0,
2 = o,
^
которые совершенно равносильны условиям A3).
Для того чтобы представить их в более обозримой форме, вве-
введем обозначение
Ф(х) = О(х,/(х)). A6)
Тогда условия эти перепишутся так:
Ф(х0) = 0, Ф;(х0) =0, ..., Ф(^(хо) = 0. A7)
Итак, при соблюдении условий A7) {в точке с абсциссой
кривая A5) будет иметь с кривой у = f(x) касание порядка
не ниже п. Нетрудно сообразить, что этот порядок точно п,
если сверх того
Ф^+^о^О. A8)
243. Соприкасающаяся кривая. Предположим теперь, что вме-
вместо кривой A5) нам дано семейство кривых с п + 1 пара-
параметрами
и-Н
G(x9y9a9b9...,l) = 0. A9)
*) В каждом уравнении подчеркнута именно та величина, которая из него
однозначно определяется, если уже определены предшествующие ей вели-
величины. Это относится и к приводимой ниже системе уравнений.
243] § 3. КАСАНИЕ КРИВЫХ МЕЖДУ СОБОЙ 621
Теперь естественно поставить вопрос, можно ли, распоряжаясь
значениями параметров, выбрать из этого семейства такую кри-
кривую, которая с данной кривой у =/(х) в определенной ее точ-
точке Мо (х о, f{x о)) имела бы наивысший возможный (для данного
семейства) порядок касания.
Подобная кривая и носит название соприкасающейся
с данной кривой в точке Мо. [Точнее было бы сказать: соприка-
соприкасающейся кривой из такого-то семейства, ибо для
отдельно взятой кривой A5) этот термин не имеет смысла.]
Для разыскания соприкасающейся кривой введем обозначение,
аналогичное A6):
и напишем ряд условий, вроде A7):
Ф(х0, а, Ь, ...,/) = О, Ф'х(х0, а, Ь, ...,/)= О, ... 1
..., Ф$>(хо,а,Ь9...91)=О. J
Мы имеем здесь систему из /7+1 уравнений с /7+1 неиз-
неизвестными а, Ь, ..., /. Обычно эта система однозначно опре-
определяет систему значений параметров, и таким путем находится
соприкасающаяся кривая, имеющая порядок касания не
ниже /7.
При этом обычно оказывается, что
так что порядок точно равен п. Такое положение вещей (при п+1
параметрах) считается нормальным.
В тех же исключительных точках, где дополнительно выполня-
выполняется и равенство
Ф{??\х0,а,Ь,...,1) = 0, B1)
говорят о пересоприкасании. Эти точки можно найти, если
равенства B0) и B1) вместе рассматривать как систему из
/7 + 2 уравненийс /7 + 2 неизвестными хо, а, Ь, ...,/•
Примеры.
1) Соприкасающаяся прямая. Семейство прямых выражается уравнением
у = ах + Ъ
с двумя параметрами. Поэтому наибольший порядок касания, который удается
установить в общем случае, будет первый.
622 ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [243
Здесь имеем:
Ф(х, а, Ъ) = у — ах — Ь, Фх(х,а,Ь)=у —а,
Фх2(х,а,Ь) =у ,
если под у разуметь f{x). Отмечая ноликами значения y,yf,yff, отвечающие
выбранному значению х = х$, для определения параметров а и Ъ получим урав-
уравнения
УО — ахо — Ъ = 0, j/q — а = 0.
Отсюда а = у'ц и Ъ = уо — у'^хц. Подставляя эти значения в уравнение прямой,
придем к уравнению
у =уо+у'о(х -*о)»
в котором читатель без труда узнает уравнение касательной.
Итак, соприкасающейся прямой является касательная.
Порядок касания, вообще говоря, как указывалось, будет первый. Он повы-
повышается в тех отдельных точках, где выполняется дополнительное условие у§ = 0
(например, в точках перегиба).
2) Соприкасающийся круг *'. Семейство окружностей выражается уравне-
уравнением
(х - if + (у - цJ = R2
с тремя параметрами |, ц и R. Наивысший порядок касания вообще будет
второй.
Так как здесь, если снова под у разуметь f(x),
Ф(х, |, I/, R) = (х - |J + (у - пJ - R2,
то параметры определяются из уравнений
(*о - IJ + (уо - лJ = R\
*о - I + (уо - ч)у'о = О,
1 +у'о + (Уо - ч)у'о = 0-
Из двух последних (в предположении, что j/q ф 0) находим координаты
центра:
B2)
а тогда из первого получится радиус
По этим элементам и устанавливается соприкасающийся круг.
*) В этом контексте слово круг привычным образом употребляется в смысле
окружность.
244] § 3. КАСАНИЕ КРИВЫХ МЕЖДУ СОБОЙ 623
По сказанному в п° 241, как правило, касательная не пересекает кривой, а со-
соприкасающийся круг, наоборот, пересекает ее. Исключение может представиться
лишь в точках, где порядок касания повышается против нормального.
244. Другой подход к соприкасающимся кривым. Пусть да-
даны кривая у = /(х) и семейство кривых A9) с п + 1 парамет-
параметрами. Возьмем на кривой произвольные п + 1 точек с абсцисса-
абсциссами ii, х2, ..., хп+\. Для того чтобы кривая семейства через эти
точки проходила, должны выполняться /7 + 1 условий:
Ф(хь а, Ь, ...,/)= О, Ф(х2, а, Ь, ...,/)= О, . ..
...,Ф(хп+иа,Ь, ...,/) =0.
Обычно отсюда значения параметров определяются однозначно;
обозначим их через а, Ъ, ... ,Т.
Предположим теперь, что когда взятые /7+1 точек по произ-
произвольному закону стремятся к некоторой определенной точке кри-
кривой с абсциссой хо, то и значения параметров а, Ъ, ..., / стремятся
к определенным пределам а, Ъ, ...,/. Можно считать, что прохо-
проходящая через упомянутые точки кривая семейства, перемещаясь или
деформируясь, стремится к предельной кривой.
Для того чтобы ее найти, станем рассуждать так. Функция от х
Ф(х,а,Ь,...,Т)
обращается в 0 для /7+1 значений х\ х\ < Х2 < ... < хп+1-
Тогда, по теореме Ролля [111], первая производная обратится в 0
для /7 значений х[ < х'2 < ... < х'п9 вторая — для /7—1 значе-
значений: х'[ < х'2 < ... < х„_19 ..., (/7 — 1)-я — для двух значений:
0?-1) (л-1) (л)
х\ < х\ и> наконеЦ? ^"я — Для некоторого значениях\ , при
этом все упомянутые значения лежат между х\ изд.
Таким образом, имеет место /7+1 равенств:
Ф(хь а,Ь, • • •, Т) = 0, Ф^О;, а, Ь, .. ., Г) = 0,
Ф%2(х'{, а,Ь, • • •, 7) = 0, . .., Ф$(х<?\ а,Ь, . .., О = 0.
Если теперь одновременно х\ —)> хо9 Х2 —> ^о? • • •» ^л+i ~^ ^о? то
а —> а, Ъ -л Ъ9 ..., / —> / и, очевидно, также х^ —>> хо, х7/ —> хо, ...,
Xj —> хо- Переходя к пределу в написанных выше равенствах, мы
вернемся к уже знакомой нам системе B0), определявшей сопри-
соприкасающуюся кривую.
624 ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [245
Итак, если существует предельное положение для кривой
семейства, проходящей через п + 1 точек данной кривой, то
эта предельная кривая и будет соприкасающейся.
В связи с этим иногда говорят (не слишком строго, но образно),
что соприкасающаяся кривая — из семейства с п + 1 параметра-
параметрами — есть «кривая, проходящая через п + 1 бесконечно близких
точек» данной кривой. В частности, касательная проходит через
две бесконечно близкие точки кривой, а соприкасающийся круг —
через три.
§ 4. Длина плоской кривой*)
245. Леммы. Рассмотрим (незамкнутую или замкнутую) пло-
плоскую кривую АВ, заданную параметрически уравнениями:
x=<p(t), у=И<) (fo^t^T), A)
где функции q> и гр здесь пока предполагаются лишь непре-
непрерывными. Пусть кратных точек на кривой нет, так что каж-
каждая точка получается лишь при одном значении параметра t (за
исключением — если кривая замкнута — совпадающих концов кри-
кривой). **} При этих предположениях кривую будем называть непре-
непрерывной простой кривой.
Имея в виду установить для такой кривой понятие длины,
мы начнем с некоторых вспомогательных предложений. Пусть
to ^ tr < tn ^ Г, и значениям параметра tr и t" отвечают точ-
точки М1 и М".
Лемма 1. Для любого S > О найдется такое ц > 0, что
при t" -t' <ц длина хорды ММ11 < S.
Действительно, ввиду (равномерной) непрерывности функ-
функций ср и xj) из A), по 8 найдется такое ц > 0, что при \t" —1'\ < r\
будет одновременно
\(p(t")-<p{t>)\<-j=, \rp(t")-rp(t>)\<^=
*) Хотя этот вопрос по существу относится к интегральному исчислению,
но мы в некоторой части начинаем его изложение уже здесь, так как в следующем
параграфе нам понадобятся и понятие длины дуги кривой и его свойства. Самое
вычисление длины дуги кривой мы откладываем до второго тома.
**) См. сноску на с. 565.
246] § 4. ДЛИНА ПЛОСКОЙ КРИВОЙ 625
а тем самым
М'М" = y/[<p(t") - cp(t')}2 + Щ") - ip(t')}2 < 8.
Имеет место также
Лемма 2. В случае незамкнутой кривой для любого
е > О существует такое 8 > О, что, лишь только длина хорды
М'М" < 8, тотчас же разность t" — t' значений параметра,
соответствующих ее концам, будет < г.
Допустим противное; тогда для некоторого г > О,
при любом 8 > О, найдутся такие две точки M'(t')
и M"(t")9 что М'М" < 8 и в то же время t" -t'^e. Взяв по-
последовательность {8п}9 сходящуюся к 0, и полагая поочередно
8 = 8п {п = 1, 2, 3, ...), придем к двум последовательностям точек
)} и {<(#)}> Для которых
ЩЩ<8п, но %-t'n^e (/7=1,2,3,...).
По лемме Больцано-Вейерштрасса [41], без умаления
общности, можно предположить, что при этом
(этого легко добиться, переходя — в случае надобности — к ча-
частичным последовательностям). Очевидно,
f* -f ^e,
так что t* ф t**. В то же время для соответствующих точек М*
и М** имеем М*М** = 0, т. е. эти точки должны совпасть, что
невозможно, так как кривая не имеет кратных точек и не замкнута.
Полученное противоречие завершает доказательство.
Для замкнутой кривой утверждение леммы оказывается
неверным: хорда М'М" может быть сколь угодно малой и при до-
достаточной близости t' к to, a t" к Т.
246. Направление на кривой. Будем считать, что точка А от-
отвечает значению параметра t = to, а точка В — значению t = Г,
и называть^ начальной, &В конечной точкой кривой. Вооб-
Вообще, расположим точки Мкривой по возрастанию параметра t,
т. е. из двух отличных от А и В точек ту будем считать следующей,
которая отвечает большему значению параметра. Таким образом
определяется «направление на кривой». Однако формально
это определение поставлено в зависимость от частного пара-
параметрического представления A). Покажем, что на деле понятие
626 ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [246
направления на кривой не зависит от конкретного способа за-
задания кривой.
Начнем с более простого случая незамкнутой кривой.
Если незамкнутая кривая АВ, наряду с представлени-
представлением A), имеет и представление (также без кратных точек)
х=<р*(и), у = Г(и) (uo^u^U), A*)
где функции ср* и гр* по-прежнему непрерывны, и значе-
значению и — щ отвечает точка А, а значению u — U — точка В,
то оба представления определяют на кривой одно и то же
направление.
Каждому значению t отвечает некоторая точка кривой, кото-
которая в свою очередь однозначно определяет значение и; обратно,
каждому и отвечает одно определенное значение t. Таким обра-
образом, и оказывается однозначной функцией от t: и — co(t)9 которая
к тому же при изменении t между to и Т принимает каждое
свое значение лишь однажды. В частности, co(to) = щ
и (о{Т) = U.
По лемме 1, двум достаточно близким значениям t отвечают
сколь угодно близкие точки кривой, а тогда — по лемме 2 — им
отвечают и сколь угодно близкие значения и9 т. е. функция и = co(t)
оказывается непрерывной.
Отсюда можно заключить, что эта функция будет монотонно
возрастающей (в узком смысле). Действительно, если бы при
to < t' < t" имели и' = oo(t') > и" = oo(t") > щ — co(to)9 то — по
известному свойству непрерывной функции [82] — между font'
нашлось бы значение t'n\ для которого o)(t'") = ип\ так что значе-
значение и" принималось бы функцией и = co(t) дважды (при t = t"
и t = t'"), вопреки тому, что было доказано выше.
Теперь, раз установлено, что и = co(t) возрастает вместе с t9
уже ясно, что расположение точек по возрастанию параметра t
совершенно равносильно расположению их по возрастанию пара-
параметра и.
Это направление, которое можно было бы назвать направле-
направлением на кривой от точки А к точке В, оказывается, таким
образом, вполне геометрическим понятием.
Аналогично, заменяя, скажем, t на —t' и располагая точки по
возрастанию параметра t\ установим понятие о направлении на
кривой от точки В к точке А; его, очевидно, молено получить
247] § 4. ДЛИНА ПЛОСКОЙ КРИВОЙ 627
таксисе, располагая точки по убыванию параметра t. Ко-
Конечно, и это направление не зависит от частного выбора
представления кривой.
Обратимся, наконец, к вопросу о направлении на замкнутой
кривой. Возьмем на ней по произволу две (отличные от А) точ-
точки С иД и пусть им соответствуют значения параметра t = t\
и t = t2 > t\9 так что в том расположении, которое было выше
установлено с помощью параметра t, точка D следует за С.
Можно показать, что всякое направление на кривой, определенное
любым параметрическим представлением, но сохраняющее этот по-
порядок точек СиД совпадает с прежним. Действительно, если зна-
значениям t = t$ и t = Г*, где to < tl < t\ и t2 < Т* < Г, отвечают
точки А* и ?*, то для (незамкнутой) дуги А*В* подобное заклю-
заключение вытекает из предыдущего; но так как t$ может быть взято
сколь угодно близко к /о, а Г* — к Г, то оно справедливо и для
всей кривой.
Таким образом, можно говорить о направлении от А через С
и D к А как не зависящем от выбора параметрического представ-
представления кривой. Аналогично устанавливается понятие о направлении
от А через D и С к А.
247. Длина кривой. Аддитивность длины дуги. Будем исходить
из представления A) кривой АВ и направления на ней, определя-
определяемого возрастанием параметра t. Возьмем на кривой ряд точек
А=М0, Ми М2, ..., Ми М-+ь ..., Мп=В B)
так, чтобы они шли в указанном направлении, отвечая
возрастающим значениям параметра
to < h < t2 < ... < U< ti+\ < ... <tn. C)
Соединяя эти точки последовательно прямолинейными отрез-
отрезками (рис. 149), мы получим л ом а -
ную МоМ\... Мп_\Мп, вписан-
вписанную в кривую АВ. Напомним, что
в предыдущем п° выяснена независи-
независимость понятия направления, а с ним
и понятия вписанной лома- _л
ной — от частного выбора парамет-
рического задания A).
628 ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [247
Длиной кривой АВ называется точная верхняя грани-
граница S для множества периметров р всевозможных вписанных
в кривую ломаных:
S = sup{p}.
Если это число S конечно, то кривая называется спрям-
спрямляемой.^
Из определения длины кривой следует, что периметр любой
вписанной в кривую АВ ломаной не превосходит длины S кри-
кривой: в частности, это относится и к длине хорды АВ, соединяющей
начальную и конечную точки кривой.
Возьмем теперь на кривой АВ точку С между А и В так,
что она отвечает значению t = /", промежуточному между to и Т:
t0 < t < Т.
Если кривая АВ спрямляема, то спрямляемы порознь и ду-
дуги АС и СВ. Обратно, из спрямляемости этих дуг вытекает
спрямляемость всей кривой АВ. Обозначая длины дуг АВ, АС
и СВ, соответственно, через S, Sf и S", будем иметь при этом
S = S'+S". D)
Для доказательства предположим сначала спрямляемость кри-
кривой АВ и впишем произвольные ломаные с периметрами р'
и р"9 соответственно, в дуги АС и СВ. Из этих ломаных, взятых
вместе, составится ломаная с периметром
вписанная в кривую АВ. Так как р ^ S, т. е.
А/а, E)
то, очевидно, и порознь
р' < S и р" < S.
* ^ Обращаем внимание читателя на важность уточнения понятий направ-
направления на кривой и вписанной ломаной. Если бы точки М/ можно было
брать где попало, то граница S всегда была бы +оо.
248] § 4. ДЛИНА ПЛОСКОЙ КРИВОЙ 629
Таким образом, множества {//} и {р"} ограничены сверху
{S — конечно!), и дуги АС, С В спрямляемы, ибо имеют конеч-
конечные длины
S" = sup{//}, S" = sup{/?"}.
По свойству точных верхних границ [11], периметры рг
и р" — независимо один от другого — могут быть взяты сколь
угодно близкими к своим границам S'
и S". Поэтому из E) с помощью пре-
предельного перехода получаем:
S" + S" ^ S. F)
I в
Пусть теперь дано, что спрям-
ляемы дуги АС и СВ. Впишем
произвольную ломаную, с пери- f рис 15q
метром р9 в кривую АВ. Если точка С
входит в состав вершин ломаной, то последняя непосредственно
распадается на две ломаные, с периметрами р1 и р", вписанные,
соответственно, в дуги АС и СВ. Если же С не оказалась вер-
вершиной взятой ломаной, то мы дополнительно введем эту
точку в состав вершин, от чего периметр ломаной может лишь
увеличиться (рис. 150); новая ломаная, как угодно, распадется
на две. Во всяком случае, имеем
р^р'+р" tZtS' + S".
Множество {р} ограничено сверху (S" и S" конечны), и кри-
кривая АВ спрямляема, причем ее длина
Наконец, из сопоставления этого неравенства с F), приходим
к требуемому равенству D).
Таким образом, введенное выше понятие длины дуги кривой
обладает свойством аддитивности [ср. 21,3)].
Доказанное предположение легко распространяется на случай
любого числа частичных дуг.
248. Достаточные условия спрямляемости. Дифференциал ду-
дуги. До сих пор мы рассматривали общий случай непрерыв-
непрерывной простой кривой A). Желая дать удобные достаточные
630 ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [248
условия ее спрямляемости*) и изучить дальнейшие свойства
длины дуги, мы вернемся к обычным в этой главе предположениям
о существовании непрерывных производных q>'(t)
и ip'(t). Докажем, что при сделанных предположениях кри-
кривая A) спрямляема.
Рассмотрим ломаную с вершинами в точках B), определяемых
значениями параметра C). Координатами точки Mt будут
хг = <р(и) и yi = ip(ti) (/ = 0,1,2,..., и).
Тогда периметр р ломаной запишется так:
л-1
Р= Y1 V (**+1 -**"J + 0'/+1 -УгJ'
Но, по формуле конечных приращений [112],
{tt < Ti,Ti < tt + 1),
так что, окончательно,
p = E >/[<р'Ы2 + [Ф'Ш2 ¦ (t,+i - n). (?)
i=0
Если через LnL обозначить, соответственно, наибольшие зна-
значения функций |ф;@1 и 1^401 в промежутке [to, Г], то из G) не-
нетрудно получить оценку:
L2+L2-(T-t0). (8)
Множество {р} оказывается ограниченным сверху, значит, кривая
имеет конечную длину S, т. е. спрямляема, что и требовалось до-
доказать.
Так как S = sup{/?}, то из (8) попутно получаем и оценку для S
сверху:
L2+L2.(T-t0), (9)
которая нам сейчас понадобится. Впрочем, нам нужна будет и оцен-
оценка снизу; если ввести наименьшие значения / и 7 функций
*) Самые общие условия спрямляемости (необходимые и достаточные!) чита-
читатель найдет в третьем томе.
248] § 4. ДЛИНА ПЛОСКОЙ КРИВОЙ 631
|<//G)| и \ip'(t)\ в промежутке [to, Т], то из G), аналогично (8), най-
найдем, что
а тогда тем более
Если изменить /, ас ним вместе и положение точки M(t) на
кривой, то длина переменной дуги AM окажется функцией
от параметра t; мы будем обо-
обозначать ее через щ^
s=s(t).
Придадим переменной t положи-
положительное приращение At: точ-
точка М переместится вдоль по кри- А
вой, по направлению к В, в поло- Рис. 151
жение М' (рис. 151). Величина s
получит положительное же приращение As, равное длине
дуги ММ1 (по аддитивности длины дуги, доказанной в пре-
предыдущем п°). Таким образом, функция s{t) оказывается возраста-
возрастающей.
Рассмотрим теперь, вместо промежутка [to, T], промежуток
[/о» to + At] и применим к дуге ММ', длины As, оценки (9) и (9*):
ф2 + l2 - At < As $
но здесь под / и L G и L) мы вправе разуметь наименьшее и наиболь-
наибольшее значения функции |ф;@1 A^@1) Уже в промежутке [t, t + At].
Отсюда
и, так как — по непрерывности производных — при At —> 0 оба
числа / и L —)> |ф;@1' а °^а числа 7 и L —>> ^'(Ol? T0 °ба корня
в предшествующем неравенстве стремятся к общему пределу
Следовательно, к тому же пределу стремится и отношение ^;
как легко видеть, это справедливо и для At < 0. Итак, имеем
632 ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [248
окончательно: длина переменной дуги s = s(t) оказывает-
оказывается дифференцируемой функцией от параметра t; ее
производная по параметру выражается формулой:
s>(t) = lim ^± =
At^O At
или, короче,
' • (Ю)
Если возвести это равенство в квадрат и умножить почленно
на dt2, то получим замечательную по простоте формулу
ds2 = dx2 + dy2, A1)
которая к тому же обладает геометрической наглядностью. На
рис. 152 в (криволинейном) прямоугольном треугольнике MNM\
«катетами» служат приращения координат точки М: MN = Ах,
NM\ = Ду, а «гипотенузой» — дуга ММ\ = As, которая явля-
является приращением дуги AM = s. Оказывается, что если не для
самих приращений, то для их глав-
главных частей — дифференциалов —
имеет место своеобразная «теорема
Пифагора».
Полезно отметить частные слу-
случаи важной формулы A0), отвечаю-
щие различным частным типам зада-
рис 152 ния кРивой. Так, если кривая задана
явным уравнением в декартовых
координатах у = /(х), то в роли «параметра» оказывается х9 ду-
дуга s зависит от х\ s = s(x)9 и формула A0) принимает вид
4 = у]\ +У'Х2- (Юа)
Если же кривая задана полярным уравнением г = g(9)9 то это, как
мы знаем, равносильно заданию ее параметрическими урав-
уравнениями
х = г cos в, у —г sin в,
где параметром будет в; дуга на этот раз будет функцией от в\
s = s@). Так как, очевидно,
х'е = r'e cos в — г sin в,
у'в = r
249] § 4. ДЛИНА ПЛОСКОЙ КРИВОЙ 633
то
и формула A0) преобразуется так:
,2+г2. A06)
Часто представляется удобным взять в качестве начальной
точки А для отсчета дуг не один из концов дуги, а какую-
либо внутреннюю точку ее. В этом случае естественно дуги, от-
откладываемые от нее в направлении возрастания параметра, считать
положительными, а в другом — отрицательными и, соответственно
этому, длину дуги в первом случае снабжать знаком плюс, а во вто-
втором — знаком минус. Вот эту величину s дуги со знаком
мы для краткости будет называть просто дугой. Формулы A0),
A1), A0а), A06) имеют место во всех случаях.
[Заметим, что если положительное направление для отсчета дуг
выбирать не в сторону возрастания параметра, как это делается
обычно, а в сторону его убывания, то в формулах A0), A0а), A06)
пришлось бы перед радикалом поставить знак минус]
249. Дуга в роли параметра. Положительное направление каса-
касательной. Так как переменная дуга s = s(t) является непрерывной
монотонно возрастающей функцией от параметра t9 то и послед-
последний, в свою очередь, может быть рассматриваем как однозначная
и непрерывная функция от s: t = co(s)9 где s изменяется от 0 до
длины S всей рассматриваемой кривой [83]. Подставляя это выра-
выражение t в уравнения A), мы получим текущие координаты х и у
выраженными в функции от s:
х = q>(eo(s)) = Ф(я),
Несомненно, дуга s9 играющая роль «криволинейной абсциссы»
точки М9 является самым естественным параметром для опреде-
определения ее положения.
Заметим, что начальная точка А для отсчета дуг может быть взя-
взята и не на одном из концов рассматриваемой дуги кривой; тогда, как
это разъяснено выше, дуга s может принимать как положительные,
так и отрицательные значения.
634 ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [249
Пусть точкаМкривой — в представлении A) — будет обык-
обыкновенной, так что [см. A0)]
s't = y/x',2+y't2>0;
тогда [94] для соответствующего значения s (и вблизи него) су-
существует и непрерывная производная
t's=co'(s) =
а следовательно, существуют и непрерывные производные
Из основной формулы A1), считая, что все дифференциалы
взяты, например, по s9 получим,
Таким образом, если точка М была обыкновенной в прежнем пред-
представлении A) кривой, то она наверное будет обыкновенной и при
переходе к параметру s. Формула A2), далее, позволяет устано-
установить следующее полезное утверждение:
Пусть М — обыкновенная точка кривой. Если че-
через М\ обозначить переменную точку той же кривой, то при
стремлении М\ к М отношение длины хорды ММ\ к длине
дуги ММ\ будет стремиться к единице*^.
= 1. A3)
ММ\
Примем дугу за параметр, и пусть точка М отвечает значению s
дуги, а точка М\ — значению s + As. Их координаты пусть будут,
соответственно, х,у их + Ах, у + Ду. Тогда
а ММ\ = л/Дх2 + Ау2,
* ^ Для простоты мы пишем ММ\ — вместо «длина отрезка ММ\», и ММ\ —
вместо «длина дуги ММ\».
249]
§ 4. ДЛИНА ПЛОСКОЙ КРИВОЙ
635
так что
ММ\
\/Ах2 +
\As
Ay2
\(Ах\2
(АуJ
У\
Ау
Переходя справа к пределу при As —> 0, в силу A2), получаем
требуемый результат.
До сих пор мы определяли положение касательной к кривой
в (обыкновенной) точке М — ее угловым коэффициен-
коэффициентом tga, не различая двух противоположных направлений на
самой касательной: tg а для обоих
один и тот же. В некоторых иссле-
исследованиях, однако, представляется
необходимым фиксировать одно
из этих направлений.
Представим себе, что на кри-
кривой выбраны начальная точка
и определенное направление для
отсчета дуг; возьмем именно дугу
за параметр, определяющий поло-
положение точки на кривой.
Пусть точке М, о которой бы-
была речь, отвечает дуга s. Если придать s положительное при-
приращение As, то дуга s + As определит новую точку М\9 лежащую
отМв сторону возрастания дуг. Секущую направим от М
к Mi, и угол, составленный именно этим направлением секущей
с положительным направлением оси х, обозначим через /3. Про-
Проектируя отрезок ММ\ на оси координат (рис. 153), по известной
теореме из теории проекций, получим
ир.хММ\ = Ах = ММ\ cos/3,
= Ay = ММ\ sin/3,
б?
В
Рис. 153
откуда
cos/3 =
sin/З =
ММХ г ММХ
Так как ММ\ — As, то эти равенства можно переписать так:
Ах ММХ
А у ММ\
A4)
636 ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [249
Будем называть положительным то направление ка-
касательной, которое идет в сторону возрастания дуг;
точнее говоря, оно определяется как предельное положение при
As —> 0 для луча ММ\, направленного так, как это разъяснено
выше. Если угол положительного направления касательной
с положительным направлением оси х обозначить через а, то из
A4) получим в пределе, с учетом A3),
dx . dy
cos а = —, sin а = —. A5)
ds ds
Эти формулы определяют угол а уже с точностью до 2кп
(к — целое), следовательно, действительно фиксируют одно из
двух возможных направлений касательной, именно — положи-
положительное.
Замечание. Все сказанное в пп° 245-249 по поводу плоских
кривых переносится без существенных изменений на случай прост-
пространственной кривой:
x=<p(t), у = ф(?), z=X(t) (to^t^T). (I*)
Понятие длины кривой устанавливается в тех же терминах,
что и в п° 247. При наличии у функций ср, гр, % непрерывных про-
производных — длина конечна, и кривая спрямляема. Длина пе-
переменной дуги (от начальной точки кривой до переменной точки,
отвечающей параметру t)
s=s(t)
дифференцируема по t, причем ее производная по t выражается
формулой
Отсюда получается формула для дифференциала дуги:
ds2=dx2+dy2+dz2. A1*)
В случае отсутствия особых точек [228], можно перейти к тако-
такому параметрическому представлению кривой, в котором роль па-
параметра играет сама дуга s. Наконец, устанавливается понятие по-
положительного направления касательной, направляющие косинусы
которого даются формулами:
dx dy dz / *х
cosa = —, cos/3 = —, cosy = —. A5 )
ds ds ds
250] § 5. КРИВИЗНА ПЛОСКОЙ КРИВОЙ 637
§ 5. Кривизна плоской кривой
250. Понятие кривизны. Пусть снова дана простая кривая
x=q>(t), y=№ (to^t^T)9 A)
где на этот раз функции ср игр предполагаются непрерывными вме-
вместе со своими производными первого и второго порядка.
Рассмотрим дугу этой кривой, без особых точек.
Если в каждой ее точке провести касательную (скажем, в поло-
положительном направлении), то вследствие «искривленности» кривой
эта касательная с перемещением точки касания будет вращаться;
этим кривая существенно отличается от прямой, для которой
касательная (совпадающая с ней) сохраняет одно и то же направ-
направление для всех точек.
Важным элементом, характеризующим течение кривой, явля-
является «степень искривленности», или «кривизна», ее в различных
точках; эту кривизну можно выразить числом.
Пусть ММ\ (рис. 154) есть дуга кривой; рассмотрим касатель-
касательные МТ иМ\Т\, проведенные (в положительном направлении) в ко-
конечных точках этой дуги.
Естественно кривизну кривой характеризовать углом поворо-
поворота касательной, рассчитанным на единицу длины дуги, т. е. от-
отношением ^, где угол со из-
измеряется в радианах, а дли-
длина о — в выбранных еди-
единицах длины. Это отноше-
отношение называют средней
кривизной дуги кривой.
На различных участках "' р
кривой средняя кривизна ее
будет, вообще говоря, раз-
различной. Существует, впрочем, (единственная) кривая, для которой
средняя кривизна везде одинакова: это окружность*).
Действительно, для нее имеем (рис. 155)
со со 1
о какой бы дуге окружности ни шла речь.
Не считая, разумеется, прямой, для которой кривизна всегда нуль.
638
ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[250
рис
От понятия средней кривизны дуги ММ\ перейдем к по-
понятию кривизны в точке.
Кр ив изной кривой в точке М называется предел, к кото-
которому стремится средняя кривизна дуги ММ\, когда точка М\
вдоль по кривой стремится к М.
Обозначив кривизну кривой в данной
точке буквой к, будем иметь
к = lim —.
Для окружности, очевидно, к = -^, т. е.
кривизна окружности есть величина,
обратная радиусу окружности.
Замечание. Понятия средней кривиз-
кривизны и кривизны в данной точке совершен-
совершенно аналогичны понятиям средней скорости
и скорости в данный момент для движущей-
движущейся точки. Можно сказать, что средняя кривизна характеризует сред-
среднюю скорость изменения направления касательной на некоторой
дуге, а кривизна в точке — истинную скорость изменения этого
направления, приуроченную к данной точке.
Обратимся теперь к выводу аналитического выражения для
кривизны, по которому ее можно было бы вычислять исходя
из параметрического за-
задания кривой.
Предположим снача-
сначала, что в роли параметра
фигурирует дуга. Как мы
знаем [249], такое пред-
представление всегда осу-
осуществимо, если ограни-
ограничиться дугой кривой, где
_х нет особых точек.
Возьмем на этом
участке кривой точку М
(заведомо не особую),
и пусть ей отвечает значение s дуги. Придав s произвольное прира-
приращение As, получим другую точку M\{s + As) (рис. 156). Прира-
Приращение Да угла наклона касательной при переходе от М к М\ даст
угол со между обеими касательными: со = Да.
У\
А
а+Аа
Рис. 156
250] § 5. КРИВИЗНА ПЛОСКОЙ КРИВОЙ 639
Так как о =^As9 то средняя кривизна будет равна ^.
Устремив ММ\ = As к нулю, для кривизны кривой в точке М
получим выражение
Да da /ЛЧ
к= lim — = — B)
A^o As ds
Важно отметить, впрочем, что эта формула верна лишь с точ-
точностью до знака, так как кривизна, по нашему определению,
есть число неотрицательное, а справа может получиться и отрица-
отрицательный результат.
Дело в том, что как Да, так и As могут быть отрицательными,
так что, строго говоря, следовало бы писать: со = |Да|, о — \As
и, наконец,
Это замечание следует иметь в виду и впредь.
Для того чтобы придать формуле B) вид, удобный для непо-
непосредственного вычисления (а вместе с тем установить самое су-
существование кривизны), обратимся к произвольному параметриче-
параметрическому заданию кривой A).
Так как рассматриваемая точка M(t) не является особой,
и х'2 +у'2 > 0, то без умаления общности можно считать, что
именно х\ = q>'(t) ф 0.
Перепишем теперь формулу B) иначе:
dt -jL st
Но s't — yXf2 +yl2 [248, A0)], остается лишь найти a't. Так как
[Ю6, (И)]
+ у\ „ ^у\
Подставив в C) значения s't и a't9 придем к окончательной формуле:
Эта формула вполне пригодна для вычисления, ибо все фигуриру-
фигурирующие в ней производные легко вычисляются по параметрическим
уравнениям кривой.
640
ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[251
Если кривая задана явным уравнением у = /(х), то эта формула
принимает вид
к= У>. Eа)
Наконец, если дано полярное уравнение кривой: г = g{9)9 то, как
обычно, можно перейти к параметрическому представлению в пря-
прямоугольных координатах, принимая за параметр 9. Тогда с помо-
помощью E) получим
+ К2 - гг>>>
к =
E6)
251. Круг кривизны и радиус кривизны. Во многих исследова-
исследованиях представляется удобным приближенно заменить кривую вбли-
вблизи рассматриваемой точки — окружностью, имеющей ту же кри-
кривизну, что и кривая в этой точке.
Мы будем называть кругом *)
кривизны кривой в данной на ней
точке М — круг, который:
1) касается кривой в точке М;
2) направлен выпуклостью вбли-
вблизи этой точки в ту лее сторону,
что и кривая'^
3) имеет ту лее кривизну, что
и кривая в точке М (рис. 157).
Центр С круга кривизны называет-
называется просто центром кривизны,
а радиус этого круга — радиусом
кривизны (кривой в данной точке).
Из определения круга кривизны яв-
явствует, что центр кривизны всегда ле-
лежит на нормали к кривой в рассматриваемой точке со стороны
вогнутости (т. е. со стороны, обратной той, куда направлена выпу-
выпуклость кривой). Если кривизну кривой в данной точке обозначить
через к, то, вспоминая [250], что для окружности имели формулу:
Рис. 157
*)
32)
Сюда также относится замечание, сделанное в сноске на с. 622.
Пункт 2), строго говоря, нуждается в более точной формулировке. Читатель
может найти ее на с. 648.
251]
§ 5. КРИВИЗНА ПЛОСКОЙ КРИВОЙ
641
теперь для радиуса кривизны, очевидно, будем иметь
Пользуясь различными выражениями, введенными в предыду-
предыдущем п° для кривизны, мы можем сразу же написать ряд формул
для радиуса кривизны:
ds
к ~ 1~>
R =
R =
A+jfI
F)
G)
Ga)
R =
+ 2r'e2 -
G6)
которые и применяются в соответственных случаях.
Из всех формул радиус кривизны получается со знаком, как
и выше — кривизна. Однако здесь мы не станем отбрасывать знак,
а постараемся установить его геометрический смысл.
С этой целью введем понятие о положительном направле-
направлении нормали к кривой. Мы разъяснили уже в 249, что на каса-
касательной положительным считается направление в сторону возрас-
возрастания дуг. На нормали же
мы за положительное выбе-
выберем такое направление, что-
чтобы оно относительно (поло-
(положительно направленной) ка-
касательной было так же ори-
ориентировано, как ось у отно-
относительно оси х. Например,
при обычном расположении
этих осей нормаль должна
составлять с касательной О\
угол +^ против часовой
стрелки.
Теперь, рассматривая радиус кривизны R = МС как направлен-
направленный отрезок, лежащий на нормали, естественно приписывать ему
знак плюс, если он откладывается по нормали в положительном
направлении, и знак минус — в противном случае. Так, на рис. 158
Рис. 158
642 ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [252
в случае кривой I радиус кривизны будет иметь знак плюс, а в слу-
случае кривой II — знак минус.
Мы утверждаем, что знак радиуса кривизны, получаемый по лю-
любой из выведенных выше формул, в точности соответствует только
что данному определению. При этом, однако, важно подчеркнуть,
что во всех случаях положительное направление отсчета дуг пред-
предполагается соответствующим возрастанию параметра G, х или в).
Убедиться в сказанном проще для случая явного задания кри-
кривой: здесь (рис. 158) касательная направлена направо, следова-
следовательно, нормаль — вверх. Если у > 0 (как в рассматриваемой
точке, так и — по непрерывности — вблизи нее), то кривая здесь
выпукла вниз [143], и радиус кривизны R положителен; таким он
и получается по формуле Gа). Наоборот, при уп2 < О кривая вы-
выпукла вверх, радиус R отрицателен, что и в этом случае вполне
соответствует формуле Gа).
То же можно показать и для других формул.
252. Примеры.
1) Цепная линия (рис. 41):
у = a ch —.
а
В этом случае [ср. 99, 28)]
а а9
с другой стороны,
// 1 , х у
у 2 = -ch - = —.
я а а1
Поэтому [см. Gа)]
Так как то же выражение, как нетрудно видеть, имеет и отрезок нормали
п = MN, то приходим к такому способу построения центра кривизны С: отре-
отрезок нормали MN (см. рис. 41) нужно отложить по нормали же, но в обратную
(положительную) сторону.
2) Астроида (рис. 116):
Производные;;^. иу можно найти, не разрешая уравнения, по методу диф-
дифференцирования неявных функций:
х~з +y~^yf = 0 или х^у' +з^з — О,
откуда
1
У = - -
252] § 5. КРИВИЗНА ПЛОСКОЙ КРИВОЙ 643
откуда
2 2
у = ^г
J7 = т
Ъхуъ у
Подставляя значения у' и у" в формулу Gа), получим
R = Ъ(аху)%.
3) Циклоида (рис. 118):
х = a(t — sint), j/ = a (I — cost).
Так как [231, 4)] а = ^ — ^, то da = — jdt;c другой же стороны, как легко
вычислить,
x't = а(\ — cost), y't = asint, x't + y't = 4a sin -,
так что
т. e. ds = 2a sin - dt.
В таком случае для вычисления R можно воспользоваться основной формулой F):
ds 2a sin I dt t
R = — = г^— = —4a sin -.
da -\dt 2
Если вспомнить выведенное нами в 231, 4) выражение для отрезка нормали п,
то окажется, что
R = -2п.
Отсюда — построение центра кривизны С, ясное из чертежа.
4) Эвольвента круга (рис. 121):
х = a (cos t + t sin t), у = a (sin t — t cost).
Здесь a = t [231, 6)], так что da = dt. С другой стороны,
xt = й^ cos ^, yt = fltf sin /^, xt -\- yt -\- a t ;
отсюда
s^ = я*, ds = я* <#.
Поэтому также получаем просто
ds
R = — = at = MB.
da
Таким образом, точка касания В (точка схода нити с круга) и будет центром кри-
кривизны для траектории концаМнити. Геометрическим местом центров
кривизны нашей кривой оказывается исходный круг.
[Здесь мы сталкиваемся с частным осуществлением одного факта, который
в общем виде будет рассмотрен нами ниже, в 255.]
5) Логарифмическая спираль (рис. 134):
тв
г = ае .
644 ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [252
Имеем v'q = mr, г = т г. Подставляя это в формулу G6), найдем:
R = г2 + 2т2г2 - т2г2
Но т = ctg&> [233, 3)], так что выражение для R можно написать в виде
г
R =
sin &>
а тогда непосредственно из чертежа ясно, что полярный отрезок нормали
Пр = NM. Следовательно, центром кривизны будет точка N; это дает легкий
способ построения центра кривизны для логарифмической спирали.
6) Кардиоида (рис. 135):
г = а{\ + cos0).
Здесь г'в = —я sin 0, г02 = — a cos0. Легко посчитать, что
г + г'в = 4а cos -;
остается еще вычислить
п
г'в — гг'^2 = а A + cos0) = 2a cos -,
а тогда, по формуле G6), сразу получаем
4 в
R=-3acos-.
Вспоминая [233, 4)] выражение полярного отрезка нормали для кардиоиды,
видим, что
7) Лемниската (рис. 126):
2 2 2
г = 2а cos 26.
Мы видели в 233, 5), что в этом случае а = 36 + ^, так что <ia = 3d6.
Но тогда, по формуле F), сразу получаем
ds 1 , 1 fZ " 1 2а2
Так как нормаль к лемнискате мы строить умеем, то отсюда получается и спо-
способ построения центра кривизны.
8) Парабола:
у2 = 2рх.
Пользуясь здесь методами дифференцирования неявных функций, найдем по-
последовательно
УУх = Р> УУ"г +У? = °' откуда у3у = -р2.
Теперь, по формуле Gа),
у уъух1 -р2
252] § 5. КРИВИЗНА ПЛОСКОЙ КРИВОЙ 645
Вспоминая [231, 1)], что отрезок нормали п = у у2 + р2, получаем
з
*=-?¦
9) Эллипс и гипербола:
Дифференцируем это равенство дважды:
откУда
уу' , Ъ х
° откУда уут;
далее,
// О ,2 3 // ^ / х | З7 \ °
УУХ2 = Т^Ух ' ИЛИ З7 ^v-2 = К \ ^у ± -рг ] = т.
х я2 х а2 уа2 /?2у а2
Как и только что, отсюда
Мы имели уже [231, 2)] для этого случая выражение отрезка нормали
Известно, что как для эллипса, так и для гиперболы полупараметр р выра-
выражается так: р = ^-. Поэтому и здесь для ^ получается то же окончательное
выражение, что и для параболы.
Для всех трех конических сечений радиус кривизны ока-
оказывается пропорционален кубу отрезка нормали.
10) В заключение скажем несколько слов об одном практическом вопросе,
в котором как раз и используется существенно изменение кривизны вдоль
кривой: речь идет о так называемых переходных кривых, применяемых
при разбивке железнодорожных закруглений.
Как устанавливается в механике, при движении материальной точки по кри-
кривой развивается центробежная сила, величина которой определяется формулой
F= mv2
~ R '
где т — масса точки, v — ее скорость, а R — радиус кривизны кривой в рас-
рассматриваемой ее точке.
Если бы прямолинейная часть железнодорожного пути непосредственно при-
примыкала к закруглению, разбитому по дуге круга (рис. 159, а), то при переходе
на это закругление центробежная сила возникала бы мгновенно, создавая резкий
и сильный толчок, вредный для подвижного состава и для верхнего строения пути.
646
ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[253
Для избежания этого прямолинейную часть пути сопрягают с круговой с помо-
помощью некоей переходной кривой (рис. 159,6). Вдоль нее радиус кривизны
постепенно убывает от бесконечного значения — в точке стыка с прямоли-
прямолинейной частью — до величины радиуса круга — в точке стыка с круговой дугой,
и соответственно этому постепенно нарастает центробежная сила.
В качестве переходной кривой чаще всего используется кубическая
парабола;; = щ. В этом случае, очевидно, имеем
х3 х
1 л 11 л
У = ^-» У = -»
2q q
так что для радиуса кривизны получается выражение
При х = 0 имеем у' = 0 и R = со, наша кривая в начале координат касается
оси х и имеет нулевую кривизну * ^.
Иногда в роли переходной кривой применяется и лемниската.
253. Координаты центра кривизны. Выведем теперь форму-
формулы для координат центра кривизны. Будем обозначать координаты
рассматриваемой точки М кривой через х и у, а координаты отве-
отвечающего ей центра кривизны С — через | и ц.
Радиус кривизны R = МС (см. рис. 158) лежит на оси — имен-
именно на направленной нормали, которая с осью х составляет угол
а + ^. Проектируя отрезок МС поочередно на ось х и на ось у,
*) Методами дифференциального исчисления [134, 135] легко установить, что
выражение для R убывает лишь до х = 0,946^/q, где оно имеет минимум 1,390^/q.
Только эта часть кривой и используется на практике.
253] § 5. КРИВИЗНА ПЛОСКОЙ КРИВОЙ 647
по основной теореме теории проекций будем иметь
| —х = Rcosia + — J = -i?sina,
ц — у = i?sin(a + — J = i?cosa.
Отсюда для координат центра кривизны получаем:
ц = у +i?cosa. j
Используя выведенные нами раньше формулы [251, F);
249'A5I я
ds dx . dy
R — ——, cos a = ——, sin a = ——,
da ds ds
только что полученные выражения можно переписать в виде:
Л ' (9)
da
Если кривая задана параметрическими уравнениями A), то,
вспомнив выражение D) для a't, легко преобразовать формулы (9)
следующим образом:
х'2 +у/2
I = х ГТ, 7Г~ГУ^
/2 I /2
A0)
Как видим, | и /у здесь выражены в функции от того же параметра t,
что и х, у.
В случае кривой, заданной явным уравнением у = /(х), фор-
формулы A0) принимают частный вид:
Формулы A0) можно применить и в том случае, если кривая
задана полярным уравнением г = g(9)9 выбирая, как обычно, за па-
параметр угол в.
Если сопоставить только что полученные формулы A0а) с фор-
формулами для пограничной точки на нормали, найденными при
648 ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [254
решении задачи п° 137 (рис. 62), то убедимся в том, что упомя-
упомянутая пограничная точка совпадает с центром кривизны.
Еще более важный результат получится, если сопоставить фор-
формулы A0а) и Gа) с формулами B2) и B3) п° 243: круг кривизны
кривой в данной точке есть не что иное, как соприкаса-
соприкасающийся круг. Иными словами [244], круг кривизны представля-
представляет собой предельное положение круга, проходящего через три
точки кривой, которые стремятся к совпадению с данной.
Этот результат, конечно, можно было предвидеть: в случае ка-
касания второго порядка между данной кривой и окружностью,
ординатами две ее производные yfx ny/f2 имеют в данной точке
одни и те же значения для обеих кривых, так что для них совпа-
совпадают в этой точке направления выпуклости и величины
кривизны, зависящие только от упомянутых производных.
254. Определение эволюты и эвольвенты; разыскание эволю-
эволюты. Если точка М(х,у) перемещается вдоль данной кривой, то со-
соответствующий ей центр кривизны С(?,,г]), вообще говоря, также
описывает некоторую кривую. Геометрическое место центров
кривизны данной кривой называется ее эволютой. Обратно,
исходная кривая по отношению к своей эволюте называется
ее эвольвентой.
Формулы A0) или A0а) предыдущего п°, выражающие коор-
координаты |, ц центра кривизны С через параметр t (или х), можно
рассматривать как уже готовые параметрические уравне-
уравнения эволюты. Иногда представляется выгодным исключить из
них параметр и выразить эволюту неявным уравнением
F(|, г]) = 0.
Примеры.
1) Найти эволюту параболы у = 2рх. Пользуясь полученными вы-
выше [252, 8)] результатами:
/ 3 // 2
УУх = А У Ух2 = -Р '
по формулам A0а) находим координаты центра кривизны:
I = х - уух з пХ = х Н = 3* + р = — + р,
У3УХ2 Р 2р
У2 + (УУХJ У / 2 2ч У3
ц = у -\- у —— =у -(у -\-р ) = -
у*у" Р Р
254]
§ 5. КРИВИЗНА ПЛОСКОЙ КРИВОЙ
649
Итак, параметрические уравнения эволюты параболы (где у — в роли пара-
параметра) будут
2р р2
Исключая из этих уравнений у, получим
откуда, наконец,
1 " 21р УЬ F> •
Мы видим, что эволютой параболы является полукубическая парабола
(рис. 160).
У\
Рис. 160
Рис. 161
2) Найти эволюту эллипса х = a cost, у = b sint.
Имеем
xt = — я sirU, xt2 = — a cost, yt = boost, yt2 = —bsint.
Подставляя это в формулу A0), получим
= a cos t —
b cos t(a2 sin21 + Z?2 cos21) a2 — b2 _ 3
cos t,
7] = --
sin t.
Таково параметрическое представление эволюты эллипса. Исключив t, полу-
получим уравнение этой кривой в неявном виде:
= J (где с2 = а2 - Ъ2).
Кривая напоминает собой астроиду и получается из нее путем вытягивания
по вертикальному направлению (рис. 161).
650
ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[254
Аналогично, но лишь с помощью гиперболических функций (вместо триго-
тригонометрических), и для гиперболы -^ — ^ = 1 получается эволюта
(я|K -
= J
(где с2 = а2 + Ъ2).
3) Найти эволюту астроиды jcз -\-уЪ =
Мы имели уже в п° 252, 2):
;=-©'¦
Ух =
У.х.2 =
Подставив это в формулы A0а), после упрощений получим
| = х + Зх 3;/ 3 9 ц = у + Зх 3;; 3 .
Из этих уравнений, совместно с уравнением самой астроиды, следующим образом
можно исключить х и у:
Если повернуть оси координат на 45°, то но-
новые координаты |i, Гц выразятся через старые |,
ц по формулам
так что в новой координатной системе уравнение
х искомой эволюты получит вид
Мы узнаем в этом снова уравнение астроиды.
Таким образом, эволютой астроиды служит
Рис. 162 астроида же вдвое больших размеров, с осями,
повернутыми на 45° по сравнению с прежним по-
положением (рис. 162).
4) Найти эволюту циклоиды х = a(t — siru), у = а{\ — cost).
Так как мы знаем [231, 4)], что для циклоиды:
ж t 1
то удобнее воспользоваться формулами (9). Подставив в них это значение da,
получим
?=x+2y't, r]=y-2x[
или
| = a(t + siru), 7] = — а{\ — cost).
Положив t = r — jt, полученные параметрические уравнения перепишем
в виде
| = — jra + а (г — sinr), /i = —2а + а{\ — cos г).
255] § 5. КРИВИЗНА ПЛОСКОЙ КРИВОЙ 651
Отсюда ясно, что эволюта циклоиды есть циклоида, конгруэнтная с данной,
но смещенная на отрезок ж а влево (параллельно оси х, в отрицательном на-
направлении) и на отрезок 2а вниз (параллельно оси у, тоже в отрицательном
направлении).
Представляем читателю убедиться в том, что эволюта эпи- или гипоциклоиды
также конгруэнтна с исходной кривой и получается из нее простым поворотом.
5) Найти эволюту логарифмической спирали г = ает .
Геометрическое построение центра кривизны, указанное в 252, 5), позволяет
с легкостью установить его полярные координаты г\ жд\. Именно (см. рис. 134),
ri = rip = r ctg со = тг, в\ = в -\ .
Исключая г и в из этих уравнений и уравнения самой спирали, получим
уравнение эволюты
/w(#i-f) тв\
г\ = тае v i 2/ — а\е .
Повернув полярную ось на надлежащий угол, можно отождествить это урав-
уравнение с исходным; таким образом, эволюта логарифмической спирали есть такая
же спираль, получающаяся из исходной поворотом вокруг полюса.
К построению эвольвент для заданной кривой мы вернемся после
того, как изучим некоторые свойства эволют и эвольвент.
255. Свойства эволют и эвольвент. Мы имели параметрическое
представление эволюты в виде (8)
? = х — Rsina, ц — у + R cos a,
считая х,у, R,a функциями от параметра. Предположим теперь
существование (непрерывных) третьих производных от х и у
по параметру*); тогда выражение (8) можно продифференциро-
продифференцировать:
d? = dx - R cos a da - dR sin a,
dt] = dy - R sin a da + dR cos a.
Принимая во внимание, что
R cos ada = -——da = dx,
da ds
R sin ada = — — da = dy,
da ds
окончательно получим
d? = -sinadR, dr\ = cos a dR. A1)
* ^ Напомним, что в R уже входят вторые производные.
652 ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [255
Ограничимся теперь рассмотрением такого участка кривой,
на котором R не обращается ни в нуль, ни в бесконечность и, кро-
кроме того, dR не обращается в нуль. Этим исключена возможность
особых точек как на данной кривой, так и на ее эволюте. Так как
dR ф О, то радиус кривизны R изменяется монотонно: либо возрас-
возрастает, либо убывает.
Деля одну на другую формулы A1), найдем:
drj 1 1
_=_ctga=__=_f,
так что угловые коэффициенты касательных к эволюте и к эволь-
эвольвенте обратны по величине и по знаку, а сами касательные — вза-
взаимно перпендикулярны. Итак:
1° Нормаль к эвольвенте служит {в центре кривизны)
касательной к эволюте.
Возьмем семейство нормалей к эвольвенте; оно зависит от од-
одного параметра (например, от того, которым определяется положе-
положение точки на данной кривой). Из доказанного ясно, что эволюта
является огибающей для этого семейства нормалей.
Для упражнения предлагаем читателю убедиться в этом же дру-
другим путем: исходя из уравнения нормалей
(где параметр t содержится в x,y,xft,yft)9 методами п° 238 найти
огибающую и установить ее совпадение с эволютой A0). Можно
доказать также, что центр кривизны есть характеристическая
точка на нормали, т. е. предельное положение точки пересечения
данной нормали с бесконечно близкой к ней.
Перейдем теперь к рассмотрению дуги о на эволюте. Возводя
равенства (И) в квадрат и складывая, найдем — с учетом форму-
формулы A1), 248, для дифференциала дуги —
do1 = df + dt]2 = dR2,
откуда
da = ±dR A2)
или (ведь dR ф 0)
dR
255]
§ 5. КРИВИЗНА ПЛОСКОЙ КРИВОЙ
653
Так как это отношение есть непрерывная функция от пара-
параметра, которая не может перескакивать от значения — 1 к зна-
значению + 1 (не проходя промежуточных значений), то она на всем
участке равна одному из этих чисел. Иными словами, в правой
части равенства A2) на всем участке фигурирует один и тот
же знак, плюс или минус.
Знак этот зависит от выбора направления для отсчета дуг
на эволюте. Если выбрать его так, чтобы дуга о возрастала вме-
вместе с радиусом кривизны R, то в формуле A2) нужно взять плюс;
если же дуга о возрастает в том направлении, которому отвечает
убывание R, то будет минус.
Сделаем первое из этих допущений; тогда
dR = da, откуда R — а = с = const,
A3)
и мы получаем, что
2° радиус кривизны разнится от дуги эволюты на величину
постоянную.
Таким образом, разность радиусов кривизны в двух точках
эвольвенты равна дуге эволюты между соответствующими цен-
центрами кривизны. Отсюда, меж-
ду прочим, вытекает любопыт-
ный способ спрямления дуги
на эволюте.
Доказанное свойство эво-
эволюты допускает изящное ме-
механическое истолкование. Для
того чтобы облегчить его изло-
изложение, допустим, что радиус
кривизны R, который (не обра-
обращаясь в 0) сохраняет на всем
рассматриваемом участке один
и тот же знак, будет везде по-
положительным; этого можно до-
добиться выбором надлежащего
направления для отсчета дуг
на эвольвенте. Далее, отсчиты-
отсчитывая дугу на эвольвенте от той точки Р9 которой отвечает наимень-
наименьший радиус кривизны, будем иметь и о > 0. В этих условиях и пос-
постоянная с, фигурирующая в равенстве A3), также положительна.
Рис. 163
654 ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [256
Представим себе теперь, что на эволюту навернута гибкая нера-
нерастяжимая нить, от конца Q (рис. 163) к началу Р; она сходит
с эволюты в начальной точке Р по касательной и обрывается на рас-
расстоянии с от Р в соответствующей точке А эвольвенты. Станем нить
развертывать, сматывая с эволюты, но сохраняя ее в натянутом со-
состоянии. Пусть QNM будет произвольное ее положение; так как NM
больше РА = с как раз на длину дуги PN = а9 то NM и есть радиус
кривизны R, т. е. точка ? лежит на эвольвенте.
Итак: эвольвента может быть описана путем разворачи-
разворачивания нити, предварительно навернутой на эволюту *\ Иначе
можно сказать, что эвольвента есть траектория точки А пря-
прямой АР, описываемая ею, когда прямая катится по эволюте
без скольжения.
В заключение выведем еще формулу для радиуса кривиз-
кривизны р эволюты. Обозначив через /3 угол, составленный каса-
касательной к эволюте с осью х9 имеем, очевидно:
Р = а±—, так что dp = da, A4)
Поэтому [см. A3) и A4)]
_ do _ dR _ ds dR _ dR
Нужно помнить, что эта формула предполагает, что о растет
вместе с R; в противном случае следовало бы в правой части по-
поставить минус.
Если же считать, что о растет вместе с s9 то формулу можно
написать в виде
dR
p=R
А ' A6)
объединяя, таким образом, случай ^ > О (R возрастает вместе с s)
и случай ^ < О (R убывает в возрастанием s).
256. Разыскивание эвольвент. Мы видим, что каждая эволь-
эвольвента может быть восстановлена по всей эволюте с помощью раз-
разворачивания навернутой на эволюту нити или — что по существу
то же — путем качения прямой по эволюте (без скольжения).
*) Отсюда, собственно, ведут свое происхождение и самые термины эволюта
и эвольвента, означающие «развертка» и «развертывающая».
256]
§ 5. КРИВИЗНА ПЛОСКОЙ КРИВОЙ
655
Докажем теперь обратное утверждение: если прямая катит-
катится {без скольжения) по данной кривой, то траектория любой
ее точки служит для данной кривой эвольвентой. [Таким об-
образом, каждая кривая имеет бесчисленное множество эвольвент.]
Пусть кривая PN (рис. 164) задана параметрически уравне-
уравнениями
причем ср и xj) имеют непрерывные производные до второго по-
порядка; допустим также, что на рассматриваемом участке кривой
нет кратных и вообще особых точек. Дугу а кривой будем отсчи-
отсчитывать от точки Р.
Рис. 164
На касательной в точке Р9 направленной в сторону возраста-
возрастания дуг, возьмем произвольную точку А, расстояние которой от Р
(с учетом знака) обозначим через с, и проследим ее траекторию
при качении прямой РА (без скольжения) по данной кривой. При
новом положении прямой, когда точкой касания станет N, точка Р
перейдет в S, а А — в М; очевидно,
SN = PN = о", так что NM = с — о.
656 ГЛ. VII. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [256
Если координаты точек N и М обозначить, соответственно, че-
через (|, г\) и (х9у)9 а угол между прямой SN и осью х — через /3,
то, проектируя отрезок NM на оси, нетрудно получить:
х = | + (с - о) cos/3, у = ц + (с - о) sin/3. A7)
Эти уравнения и дают параметрическое представление искомой
траектории.
Дифференцируя их, найдем
dx = di - cos/3 do - (с - a) sin/3df3,
dy = dt] - sinfida + (c - a) cos/3 d/3.
Так как [см. 249, A5)]
cos/3 = ^, sin/3 = %L, A8)
do do
то эти результаты упрощаются:
dx = -(с - о) sin/3<i/3, б/у = (с — а) cos/3df3.
Исключим случаи, когда dji = 0 или о = с *); тогда, разделив по-
почленно эти формулы, получим
dy 1
t t/3
Отсюда уже ясно, что касательные к обеим кривым взаимно
перпендикулярны, так что данная кривая действительно является
огибающей для семейства нормалей к построенной кривой, т. е. ее
эволютой. Значит, построенная кривая служит для данной эволь-
эвольвентой, что и требовалось доказать.
Примером получения эвольвенты указанным путем может
служить уже рассмотренная выше эвольвента круга [225, 8);
ср. 252, 4)].
*) Им отвечают особые точки на построенной кривой.
ДОПОЛНЕНИЕ
ЗАДАЧА РАСПРОСТРАНЕНИЯ ФУНКЦИЙ
257. Случай функции одной переменной. Рассмотрим функ-
функцию /(х), определенную в некотором (конечном или бесконечном)
промежутке 30 или — более обще — в области 30, состоящей из ко-
конечного числа отдельных таких промежутков. Если функция f{x)
непрерывна в 37 и имеет в этой области непрерывные лее
производные до п-го порядка включительно {п ^ 1), то гово-
говорят, что она в области 30 принадлежит классу Сп.
Отметим при этом, что если конец какого-либо из промежутков
включен в его состав, то по отношению к этой точке имеются в виду
односторонние производные*).
Пусть же функция f(x) в некоторой области 30, не охватыва-
охватывающей всей числовой оси, принадлежит классу Сп {п = 1, 2, 3, ...).
Предположим, что в какой-либо области 30*, налегающей
на 30, существует функция /*(х), тоже класса Сп, которая в об-
общей части областей 30 и 30* совпадает с f(x); тогда эта функ-
функция /* осуществляет распространение функции f на 30*
с сохранением класса.
Всегда ли возможно такое распространение функций на более
широкую область? На этот вопрос отвечает следующая
Теорема. Любую функцию f(x) класса Сп (п = 1, 2, 3, ...)
в замкнутой**] области 30 можно распространить на всю
числовую ось 30* = (-оо, +оо) с сохранением класса.
Покажем, что здесь распространение осуществляется просто
с помощью целых многочленов. С этой целью сделаем пред-
предварительно следующие замечания.
*' Или — что в данных условиях означает то же самое — предельные
значения для производных, при приближении к названному концу со стороны
самого промежутка.
**) То есть состоящей из одного или нескольких замкнутых промежутков
вида [а, Ь], [а, +оо), ( —оо, Ь].
658 ДОПОЛНЕНИЕ [257
Как мы видели в 123, многочлен п-и степени
р(х)=со + С-±(Х-а) + Ц(х-аJ + ... + С-^(х-аУ A)
в точке х = а, вместе со своими п производными, принимает, со-
соответственно, именно значения со, с\, с2, ..., сп.
Пусть, далее, требуется построить такой многочлен, кото-
который, удовлетворяя по-прежнему условиям, относящимся к точ-
точке х = а, кроме того, принимал бы, вместе со своими п производ-
производными, в некоторой другой точке х = /5 наперед заданные значения
do, d\, d2, ..., dn. Возьмем искомый многочлен в виде
р(х) + (х-а)"+1ф), B)
где р(х) есть многочлен A), а многочлен /7-й степени q(x)
еще подлежит определению. Как бы ни выбирать q(x)9 много-
многочлен B) в точке х = а во всяком случае удовлетворяет постав-
поставленным условиям. Продифференцируем многочлен B) последо-
последовательно п раз и подставим в этот многочлен и его производ-
производные х = /3; приравняв полученные выражения, соответственно,
do, d\, d2, ..., dm мы придем к системе линейных уравнений отно-
относительно q(P), qf(P), q"(P), • • •, 9^(/0> из которых эти значения
последовательно и определятся. По ним же, пользуясь формулой,
аналогичной A), уже нетрудно восстановить q{x). [Ср. 130.]
Обратимся теперь к доказательству высказанного утверждения.
Пусть, в общем случае, область SC состоит из замкнутых проме-
промежутков ЗС^{к = 1, 2, ..., т)9 перенумерованных слева направо. По-
Полагая в этих промежутках функцию /* = /, дополним ее опреде-
определение следующим образом. Если левый конец а\ промежутка ЗС\
есть конечное число, то для х < а\ положим /* равной многочлену
вида A), при
со = Лаг), cx=f"(a{)9 ..., cn=/n\ai).
Аналогично распространяется функция / и направо от SCm^ если
только правый конец Ът этого промежутка есть конечное число.
Наконец, для промежутка (&#, ак+\)(к = 1, 2, ..., т — 1), отделяю-
отделяющего ЗСъ от <%+ь отождествим /* с таким многочленом, который
вместе со своими п производными в обеих точках х = Ьк и х = аь+\
принимает те же значения, что и функция / и ее производные. Не-
Нетрудно видеть, что определенная так функция /* и осуществляет
требуемое распространение на всю область SC* — (—оо, +оо).
258] ЗАДАЧА РАСПРОСТРАНЕНИЯ ФУНКЦИЙ 659
258. Постановка задачи для двумерного случая. Положение
вещей сразу усложняется при переходе к функциям нескольких пе-
переменных. Мы ограничимся в дальнейшем случаем функции двух
переменных. Результаты, которые для этого случая будут установ-
установлены, переносятся и на общий случай любого числа переменных.
Мы будем рассматривать области ^Ж в двумерном про-
пространстве, разумея под этим либо открытую область, либо же
открытую с присоединением к ней части ее границы «2Т или же всей
границы (в последнем случае область будет замкнутой).
При распространении на рассматриваемый случай определе-
определения функций класса Сп(п ^ 1) мы сталкиваемся с своеобраз-
своеобразным затруднением. Дело в том, что в точке, лежащей на грани-
границе «2Т области, может оказаться просто неприложимым са-
самое определение частной производной того или иного типа. На-
Например, если область *Ж есть замкнутый круг х2 + у2 ^ 1, то
в точках @, ±1) нельзя говорить о частной производной по х, ибо
при у = ±1 значению х = О нельзя придать никакого приращения,
чтобы сразу же не выйти за пределы области, где задана функ-
функция; аналогично, в точках (±1,0) не имеет смысла частная произ-
производная по у.
Говоря о частной производной (определенного порядка и ти-
типа) , непрерывной в области ^#, мы условимся в граничной
точке Мо области разуметь под этой производной^ лишь
предельное значение, к которому стремится одноимен-
одноименная производная, вычисленная во внутренней точке М, при
стремлении М к Мо — независимо от того, будет ли оно на деле
играть роль производной или нет.
Из дальнейшего изложения впоследствии выяснится, что упо-
упомянутое предельное значение — в широком классе случа-
случаев — будет вместе с тем и настоящей производной, если только
положение точки Мо относительно области позволяет вообще го-
говорить о производной рассматриваемого типа. Впрочем, для про-
простейшего случая прямоугольной области мы этот факт
установим уже сейчас.
Итак, пусть функция f(x,y) непрерывна вместе со все-
всеми своими производными, до /7-го (/7^1) порядка включитель-
включительно, в некотором прямоугольнике ^#, и точка Мо(хо,уо) лежит
*)
Сохраняя при этом для нее обычное обозначение.
660
ДОПОЛНЕНИЕ
[258
на отрезке прямой у = у о, служащем границей этого прямоуголь-
прямоугольника (рис. 165) и входящем в его состав.
Начнем с производной f 9 для которой вопрос исчерпывается
просто. По формуле Лагран-
жа [112], отношение приращений
-f(xo,yo)
Мо
@< в< 1),
и при к —>> 0 стремится именно
к предельному значению
fy(xo,yo)9 которое таким обра-
образом оказывается и производной в собственном смысле 33^ [ср. 113].
Что же касается производной f'x9 то соответствующее ей отноше-
отношение приращений само может быть рассмотрено как предел:
-f(xo,yo)
-f(xo,yo
7
П к^О П
Но последнее выражение, снова по формуле Лагранжа, пре-
преобразуется к виду
/ро + /г, у о + к) - /ро, у о + к) _ ,
/z х
@< 0< 1).
При /г —^ О, А: —^ 0 оно стремится к предельному зна-
значению /х(хо,уо). По теореме же п° 168, ввиду существования
простого предела при к —> 0, этот двойной предел служит
в то же время и повторным пределом:
f' (х ) = lim lim = ^*° + ^У^+к)~ Л^о> У о + ^) =
' /7^0А:^0 /z
= lim
-f(xp,yo)
А
так что и здесь число /^(^о^о)? определенное лишь как предель-
предельное значение производной, является настоящей производной. Ска-
Сказанное последовательно переносится и на производные высших по-
порядков.
33)
Точнее, односторонней производной.
259] ЗАДАЧА РАСПРОСТРАНЕНИЯ ФУНКЦИЙ 661
Итак, заключенное выше условие позволяет теперь говорить
о непрерывных производных в любой области ^#, как бы ни бы-
были расположены по отношению к этой области ее граничные точ-
точки (включенные в ее состав). Функция f(x,y) принадлежит
классу Сп(п ^ 1) в двумерной области <Ж, если она в <Ж
непрерывна и имеет непрерывные же производные всех
типов и всех порядков до п-го включительно. Пусть область *М
не охватывает всей плоскости; если в какой-либо области ^#*,
налегающей на ^#, существует функция /*, тоже класса Сп,
которая в общей части областей <Ж и <Ж* совпадает с /, то мы бу-
будем говорить, что она дает распространение функции f на ^Ж*,
с сохранением класса. Естественно и здесь поставить воп-
вопрос: всегда ли возможно такое распространение на более широкую
область, в частности на всю плоскость? Как мы покажем, на этот
вопрос для замкнутой области <Ж можно ответить утверди-
утвердительно, если только ее контур удовлетворяет некоторым простым
условиям. Впрочем, для облегчения изложения мы будем всегда
предполагать область ^Ж ограниченной, хотя окончательное утвер-
утверждение верно и для неограниченной области.
Излагаемые результаты в основном принадлежат Уитнею
(Н. Whitney) и Хестинсу (М.R. Hestenes).
259. Вспомогательные предложения. Для облегчения доказа-
доказательства основной теоремы установим предварительно некоторые
леммы.
Лемма 1. Пусть функция ср{и, v) будет класса Сп(п ^ 1)
в области ЗР, определяемой неравенствами*^
а < и < Ъ, 0 ^ г; < Д.
Тогда существует распространение ср* функции ср, с сохране-
сохранением класса, на весь прямоугольник
SP* = (a,b;-A, А).
Определим /7+1 чисел Аь А2, ..., Aw+i из следующей систе-
системы/7+1 линейных уравнений:
4Уа2 + ... + (--|тУ*»н = 1 C)
= 0, 1,2, ...,/7).
*) Промежуток (а, Ь) может быть и бесконечным; точно так же и положитель-
положительное число А может равняться +оо.
662 ДОПОЛНЕНИЕ [259
Выполнить это можно, так как определителем системы является
так называемый определитель Вандермонда для неравных
между собой чисел — 1, — \, ..., — ^к-, который, как известно, от-
отличен от 0.
Определим теперь в SP* функцию q>*(u,v)9 полагая ф*(и, у) =
= ср(и, v) для v ^ 0 и
q>*(u, v) = Х\ф{и, -v) + Х2ф(и, -- у) + ...
¦Хп+\ф(и, -——-у) D)
для у < 0. Если г^о есть произвольное значение и из (а, Ь)9 то,
прежде всего,
Ф*(и, у) = (Ai + Я2 + ... + Aw+i)<p(w<b 0) = <р(м0, 0),
в силу первого из условий C), отвечающего к = 0. Этим уста-
установлена непрерывность функции <р* в тех точках прямо-
прямоугольника ^*, которые лежат на прямой у = 0; непрерывность
ее в остальных точках ^* очевидна. Обратимся теперь к вопросу
о существовании и непрерывности производных функций <р* в ^*;
и здесь рассмотрения требуют лишь точки прямой у = 0. Для всех
производных
мы установим предельное равенство
и,ц) = э'+Уио, о)
ди1дук ди1дук '
С этой целью продифференцируем равенство D) i раз по и9 а затем
к раз по у(у < 0):
a'+V(«.«>)_, ,u, д'+кф,-у) ,
и перейдем к пределу при и ^ щ vl у ^ — 0. В результате, в силу
равенства C), мы и получим F).
259] ЗАДАЧА РАСПРОСТРАНЕНИЯ ФУНКЦИЙ 663
Таким образом, существование единого предельного зна-
значения для любой производной E) как со стороны v > О, так
и со стороны v < О — обеспечено. Больше того, если за значение
производной E) в точках прямой v = О принять это ее предельное
значение, то получится непрерывная во всем ЗР* функция. Но точка
(щ, 0) является для SP* внутренней точкой, и здесь нам нужна
была бы производная в собственном смысле. В этом отношении
мы имеем возможность сослаться на доказанное в предыдущем п°:
упомянутое предельное значение будет в то же время и настоящей
производной.
Функция ф* и осуществляет искомое распространение функ-
функции ср на ^*.
Лемма 2. Пусть функция f(x,y) будет класса Сп в некото-
некоторой ограниченной открытой области ^#*}. Если каждую точ-
точку границы ? этой области молено окружить окрестностью,
в пределах которой допустимо распространение функции f
с сохранением класса, то такое распространение возможно
и на всю плоскость $.
Для любой точки М замкнутой области <Ж = <Ж + i?34'
найдется **} либо окрестность, в которой функция / определена
и принадлежит классу Сп, либо же окрестность, на которую / мо-
может быть распространена с сохранением класса. Эту окрестность
можно взять, например, в виде открытого круга W = Ж{М, Ъг)
с центром М и радиусом Ъг. Таким образом, вся замкнутая
область ^# покрывается не только системой ^? состоящей из этих
кругов о7, но и системой J2-> состоящей из кругов а = Ж{М,г}
с втрое меньшими радиусами.
Так как область ^#, а с нею и ^# ограничены, то к данно-
данному случаю применима лемма Боре ля [175], и <Ж покроется
конечной системой
/ J — {о"Ь а2, - - - •> &т}>
т
извлеченной из J2- Здесь
Тг) (/ = 1,2,...,/и);
*) Мы не предполагаем этой области даже связной и пока ничего не говорим
о виде ее границы.
**) В зависимости от того, принадлежит ли М открытой области ^Ж или грани-
границе SE.
Здесь знак плюс означает объединение двух множеств.
664 ДОПОЛНЕНИЕ [259
одновременно будем рассматривать и круги
о[ = Ж{Ми 2гг), о1' = Ж{Ми Ъгг).
Легко построить функцию hj(M) = hj(x,y) класса Сп в S, та-
такую, что
ht{M) = О в а и ht{M) = 1 в g - о[ (/ = 1,2,..., /и).
Можно, например, определить — методами п° 257 — функцию h(t)
класса Сп во всем промежутке — оо < t < +00 так, чтобы было
h(t) = 0 для К 1 и h(t) = 1 для t ^ 2,
затем положить
С помощью функций А,- составим функции
Я1 =НХ(М) = l-/zi,
Я, = Я,(М) = AiA2 ... A,-_iA - hi) A < i ^ m);
они также принадлежат классу Сп в $. Очевидно,
Hj = 0 в о-/ (для всех j > i), G)
Ht = 0 в ^ - а/, (8)
ибо в Gt обращается в нуль множитель А,-, а в $ — о\ — множи-
множитель 1 — А/. Так как
#1 + Я2+ ... + Щ = A - hi) + Ai(l - А2) + ...
... + AiA2 ... Ai_i(l - hi) = 1 - AiA2 ... hi9
то
#i+#2 + ...+#i- = l в а,-, (9)
потому что там обращается в нуль множитель А,-.
Пусть теперь ф; в сг/; совпадает с функцией / или с ее распрост-
распространением, о котором упоминалось выше, а вне о[' пусть срг = /
в точках ^Ж и = 0 в прочих точках. Функция cptHi обращается
в нуль в S — о\ [см. (8)] и, очевидно, во всей плоскости $ принад-
принадлежит классу Сп. Положим, наконец, во всех точках $
7=1
Этим равенством функция /* определяется во всей плоскости
и притом оказывается функцией класса Сп.
260]
ЗАДАЧА РАСПРОСТРАНЕНИЯ ФУНКЦИЙ
665
Возьмем любую точку М из *Ж\ она принадлежит некоторому
кругу Of. Так как все q>j(M) = f(M) и, кроме того, в этой точ-
точке [ввиду (9) и G)]
Н\ + Я2 + ... + Щ = 1, a Hj• = 0 для у > /,
то f*(M) = f(M). Таким образом, функция /* и есть искомая.
260. Основная теорема о распространении. Теперь мы в со-
состоянии доказать и для случая функции двух переменных теорему
о распространении, но налагая ограничения на контур области.
Условимся называть гладкой кривой класса Сп{п ^ 1) про-
простую кривую без особых точек, выражаемую уравнениями
x=<p(t)9 у=ф(*)> (Ю)
где t изменяется в некотором промежутке 2Г9 в предположении,
что функции q>, гр принадлежат в этом промежутке классу Сп.
Теорема 1. Если функция f(x,y) принадлежит классу Сп
(и ^ 1) в ограниченной замкнутой области ^Ж, контур кото-
которой !? состоит из одной или нескольких {непересекающихся)
гладких кривых, тоже класса Сп, то эта функция может
быть распространена на всю плоскость $ с сохранением
класса.
Пусть Мо(хо,уо) есть произвольная точка контура «2Г; для про-
простоты будем считать хо = у о = 0. Эта точка лежит на одной
из кривых, входящих в состав i?, и является обыкновенной
a) yi б)
Рис. 166
ее точкой. В таком случае, без умаления общности, можно допус-
допустить, что в окрестности точки Мо кривая выражается явным урав-
уравнением у = g(x)9 где g — также класса Сп9 и что область ^Ж ле-
лежит вверх от нее, т.е. (вблизи Mq) определяется неравенством
y>g(x) (Рис- 166,а).
Произведем преобразование переменных, полагая
х = и, у = g{u) + v.
666
ДОПОЛНЕНИЕ
[261
Функция f(x,y) при этом перейдет в функцию
q>(u,v) =f(u,g(u) +v),
которая оказывается класса Сп вблизи точки и = v = 0, именно,
для v ^ О (рис. 166,6). Тогда, по лемме 1, функцию q> можно
распространить с сохранением класса и на значения v < О (все
время ограничивалась точками, достаточно близкими к начальной).
Если это распространение осуществляется функцией q>*(u, v)9 то,
возвращаясь к старым переменным, легко видеть, что функция
f*(x,y)=cp*(x,y-g(x))
дает распространение функции / на некоторую окрестность точ-
точки М$.
На основании леммы 2 мы можем заключить теперь, что функ-
функция /, действительно, допускает распространение, с сохранением
класса, на всю плоскость $.
261. Обобщение. Однако полученный результат для практиче-
практических надобностей все же недостаточен, поскольку часто приходится
иметь дело с областями, контуры которых имеют «угловые точки».
Условимся называть кусочно-гладкой кривой класса Сп кривую,
состоящую из нескольких гладких дуг класса Сп, примыкающих
одна к другой под углами (не равными ни 0, ни я).
Теорема 2. Заключение теоремы 1 сохраняется, если кон-
контур ? области <Ж состоит из одной или нескольких непере-
непересекающихся кус очно-гладких кривых класса Сп.
Мы уже видели, что любую точ-
точку контура cS?, не являющуюся угло-
угловой, можно окружить окрестностью,
в пределах которой допустимо рас-
распространение функции / с сохра-
сохранением класса. Докажем теперь то
же относительно угловой точки
Рис. 167
И здесь снова можно принять
xq = уо = 0; можно, не нарушая общности, предположить также,
что смыкающиеся в начале дуги имеют в этой точке касательные,
из которых одна совпадает с положительной частью оси х, а другая
идет к ней под углом (рис. 167). В таком случае в достаточной
261] ЗАДАЧА РАСПРОСТРАНЕНИЯ ФУНКЦИЙ 667
близости к началу эти дуги выражаются, соответственно, уравне-
уравнениями
y=g(x) и х=й(у),
причем ^@) = 0; функции g и h принадлежат обе классу Сп.
Прибегнем к замене переменных
x=u + h(v), y=g(u)+v. A1)
Так как якобиан этих функций
в точке и = v = 0 обращается в 1, то система (И) в окрестности
нулевых значений всех аргументов допускает однозначное обра-
обращение:
и = Л(х,у), ь = ц(х,у), A2)
причем функции Я, /л также оказываются класса Сп [209].
При v = 0 и и ^ 0 из A1) получаем у = g{x) и х ^ 0, так что
положительной части оси и отвечает первая из названных дуг; ана-
аналогично убеждаемся в том, что положительной части оси у отве-
отвечает вторая из дуг.
Очевидно, при этом преобразовании две угловые области, на ко-
которые этими дугами делится окрестность начальной точки на
плоскости ху9 отвечают тем двум — «входящему» и «выходя-
«выходящему» — прямым углам, на которые положительными частями
осей и и v делится на плоскости uv окрестность начальной точ-
точки (рис. 168, а и б).
Подставляя в функцию /выражения A1), получим преобразо-
преобразованную функцию
q>(u, v) = f{u + h(v), g(u) + v),
определенную и принадлежащую классу Сп в том или другом —
смотря по случаю — из упомянутых только что прямых углов.
Если речь идет о «выходящем» угле (рис. 168, а), то, по лем-
лемме 1, сначала функцию ср распространяют на IV координатный
угол, а затем полученную функцию (меняя роли и и у) распро-
распространяют уже на II и III углы, т. е. на полную окрестность начала.
Сложнее обстоит дело, если речь идет о «входящем» угле
(рис. 168,6). В этом случае поступают так. Прежде всего, опи-
опираясь на лемму 1 (но меняя знак и), распространяют функцию ср
668
ДОПОЛНЕНИЕ
[262
с левой полуплоскости на правую*) и получают, таким обра-
образом, функцию ср\ — в полной окрестности начала. Затем рассматри-
рассматривают функцию гр = ф — (pi в нижней полуплоскости и, пользу-
пользуясь указанным при до-
доказательстве леммы 1
методом, распростра-
распространяют ее на верхнюю
полуплоскость, что да-
дает функцию xj)\ — уже
в полной окрестности
начала. Но в III угле
ipi = гр = ср - ср\ = О,
а тогда, по самому ха-
характеру упомянутого метода, ясно, что гр\ = 0 и во II угле. Если
положить теперь в окрестности начала <р* = гр\ + ф\9 то во II
и III углах гр\ = 0 и ф\ = ф, так что и <р* = ф, и в IV угле
хрх = \р = ф — фЪ и опять-таки <р* = (ф - ф\) + ф\ = ф. Таким об-
образом, построенная функция <р* дает распространение ф на полную
окрестность начала.
С помощью обратного преобразования A2) к старым перемен-
переменным получается и распространение
Рис. 168
функции /. Доказательство завершается, как и в теореме 1, ссыл-
ссылкой на лемму 2.
262. Заключительные замечания. Доказанная теорема о рас-
распространении функций имеет многообразные приложения. Мы
ограничимся здесь указанием на обобщение с ее помощью ряда
локальных, т. е. связанных с окрестностью определенной точ-
точки, формул и теорем анализа — на случай, когда упомянутая точка
лежит на границе рассматриваемой области, а не внутри
нее, как обычно предполагается.
Пусть, например, в замкнутой области ^#, ограниченной
контуром Z (рассмотренного выше типа), определена функ-
функция z — f(x,y), непрерывная вместе со своими производны-
производными f'x и ff. Тогда, если только точка (хо,уо) лежит
внутри J#, имеет место известная [178] формула для полного
*) Все время имея в виду лишь точки, близлежащие к началу.
262] ЗАДАЧА РАСПРОСТРАНЕНИЯ ФУНКЦИЙ 669
приращения функции:
Az = /(х0 + Ax, jo + Ay) - f(xo,yo) =
A3)
где а и /3 стремятся к нулю вместе с Ах и Ау. Рассуждения, приве-
приведенные для доказательства этой формулы, вообще неприложимы,
когда точка (хо,.уо) оказывается лежащей на контуре. А между
тем формула верна и для этого случая, если толь-
только связать Ах и Ау условием, чтобы точка (хо + Ах, у о + Ау)
не выходила за пределы ^Ж. В этом легко убедиться, если напи-
написать сначала формулу для функции /*, дающей распространение /
на всю плоскость, а затем — ограничиваясь, как указано, точками
области <Ж — вернуться к исходной функции /.
Во всех случаях, когда в основе умозаключений лежала форму-
формула A3), мы получаем теперь существенное дополнение к прежним
результатам.
Так, при сделанных относительно функции / предположениях
она оказывается дифференцируемой [179] не только во внут-
внутренних точках области ^#, но и в точках ее границы. Для поверх-
поверхности, выражаемой уравнением z = f(x,y)9 мы получаем возмож-
возможность говорить о касательной плоскости [180] даже в точ-
точках ее контура.
На рассмотренной формуле, как мы знаем, основано также пра-
правило дифференцирования сложной функции [181].
Если функции
x=<p(t), y=i>(t) (to^t^T) A4)
имеют производные, и точки (cp(t), \j){t)) лежат все внутри об-
области ^#, то для сложной функции z = f(cp(t), ip(t)) мы имели
формулу
Теперь она распространяется и на случай, когда «кривая» A4) под-
подходит вплотную к контуру области J#, и т. д., и т. п.
Не входя в подробности, укажем еще один важный пример.
Пусть имеем систему функций
х = ср(и, v), у = гр(и, у), A5)
непрерывных вместе со своими производными в некоторой замкну-
замкнутой области <Р на плоскости иу, с контуром Ж^ и пусть в некоторой
670 ДОПОЛНЕНИЕ [262
точке (щ, i>o) этой области якобиан
D(u,v)
отличен от 0. Если точка (щ,уо) лежит внутри ЗР^ то, по
теореме 4 п° 208, система функций A5) допускает обращение,
так что в окрестности точки (хо,уо)> где
х0 =
Уо =
переменные и, v выражаются однозначными функциями от пере-
переменных х,у: is \ ( \ /k*n
и = Л(х,у), v = ц(х,у), A5 )
непрерывными вместе со своими производными в упомянутой ок-
окрестности. Таким образом, ограничиваясь значениями u,v,x,y9 до-
достаточно близкими, соответственно, к щ, vo, xo,yo> можно сказать,
что соотношения A5) и A5*) совершенно равносильны. Этим мы
пользовались, например, при доказательстве утверждения, что по-
поверхность
X = ф(и, V),
у = гр(и, v),
z =x(u,v),
где (и, v) изменяется в области <Р9 вблизи ее обыкновенной
точки Мо (отвечающей и = щ, у = vq) может быть выражена
явным уравнением [228]. Но к точкам контура поверхности наши
рассуждения были неприложимы, ибо в плоскости uv точка (щ, vq)
не могла лежать на контуре Ж области ЗР.
Теперь же, воспользовавшись распространениями <р* и ^* функ-
функций q> и i/>9 мы можем обобщить результат, относящийся к обра-
обращению системы функций, и на случай, когда точка (щ, vo) лежит
на контуре Ж. Примыкающей к точке (щ, vo) части области !Р
отвечает на плоскости ху некоторая примыкающая к точке (хо,уо)
область, в пределах которой все же обращение допустимо.
Соответственным образом дополняется и упомянутый геомет-
геометрический результат.
Приведенных примеров достаточно для того, чтобы читатель
уяснил себе важность доказанных теорем как для самого мате-
математического анализа, так и для его приложений. Другие примеры
применения теорем о распространении функций читатель найдет
в последующих томах.
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Абсолютная величина 16, 36, 40
Абсолютный экстремум 525
Алгебраическая функция 501
Аналитический способ задания функции
112, 113
Аналитическое выражение функции 113
— представление кривых 563, 579
поверхностей 578
Аномалия (эксцентрическая) планеты
195
Аргумент функции ПО, 380
Арифметическое значение корня
(радикала) 42, 122
— пространство 384
Арксинус, арккосинус и т. д. 126
Архимед 75
Архимеда аксиома 19, 40
Архимедова спираль 573, 591
Асимптота 345
Асимптотическая точка 574, 575
Астроида 567, 571, 589, 612, 642, 649,
650
Барометрическая формула 109
Бернулли, Иоанн 231, 351
— , Яков 44
— лемниската 577, 593, 644, 646
Бесконечная десятичная дробь 25
— производная 235
Бесконечно большая величина 63, 134
, классификация 163
, порядок 164
— малая величина 55, 134
высшего порядка [обозначение
о{а)} 155
, классификация 154
, леммы 67
, порядок 156
, эквивалентность 157
Бесконечность (+оо, — оо) 31, 64
Бесконечный промежуток 108, 344
— разрыв 345
Бойля—Мариотта закон 109
Больцано 96
— метод 102
Больцано—Вейерштрасса лемма 101,
409
Больцано—Коши теоремы 1-я и 2-я 188,
191, 204, 409
условие 96, 152
Бореля лемма 202, 415
Варианта 52, 383
— возрастающая (неубывающая) 81
— , имеющая предел 61
— как функция значка 111
— монотонная 81
— ограниченная 62
— убывающая (невозрастающая) 81
Вейерштрасса—Больцано лемма 101,
409
— теоремы 1-я и 2-я 196, 197, 205, 412,
413, 417
Вертикальная асимптота 345
Верхняя граница числового множества
30
точная 31
Вещественные числа 23
, вычитание 36
, деление 39
, десятичное приближение 25
, непрерывность области 28
, плотность (усиленная) области
25
, равенство 23
, сложение 33
, умножение 36
, упорядочение области 23
Вивиани кривая 582, 599
Винтовая линия 583, 598
— поверхность 585, 599
Вложенные промежутки, лемма 96
Внутренняя точка множества 389
672
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Вогнутые (выпуклые вверх) функции
или кривые 329
, условия вогнутости 335
— строго функции или кривые 333
Возврата точка 604, 606
Возрастающая варианта 81
— функция 151
Вращения поверхность 585
Выпуклые (выпуклые вниз) функции
или кривые 329
, условия выпуклости 333,
334
— строго функции или кривые 333
Высшего порядка бесконечно малые
[обозначение о(а)] 155
дифференциалы 270
функции нескольких
переменных 459
производные 259, 261
, связь с конечными
разностями 275
частные 450
1 армоническое колебание 233
Гаусс 85, 493
Гельдера—Коши неравенство 308, 337
Географические координаты 584
Геометрическое истолкование
дифференциала 239
полного дифференциала 432
производной 213
Гипербола 566, 645, 650
— равнобочная 116, 118
Гиперболическая спираль 592
Гиперболические синус, косинус и т. д.
123
— функции, непрерывность 168
обратные 124, 125
, производные 229
Гипоциклоида 570
Главная ветвь (главное значение)
арксинуса, арккосинуса и т. д.
127-130
— часть (главный член) бесконечно
малой 160
Гладкая кривая 665
Горизонтальная асимптота 345
Градиент функции 441
Граница области 390
— числового множества (верхняя,
нижняя) 30-33
Граница числового множества точная 31
График функции 116
, построение 341
пространственный 382
Гюйгенса формула 293
Дарбу теорема 251
Движения уравнение 209
Двойная точка кривой 603
Двойной предел функции 401
Двух переменных функция 379
Дедекинд 20
Дедекинда основная теорема 29
Действительные числа,
см. Вещественные числа
Декартов лист 568, 603
Десятичное приближение
вещественного числа 25
Десятичные логарифмы 90
Диаметр точечного множества 414
Дирихле функция 115, 118, 172
Дискриминантная кривая 610, 616
Дифференциал 237, 241
— 2-го, 3-го, п-то порядка 270
— , геометрическое истолкование 239
— дуги 629, 636
— , инвариантность формы 242
— полный 427
2-го, 3-го, п-то порядка 459, 460
, геометрическое истолкование
432
, инвариантность формы 441
, метод вычисления (при замене
переменных) 549
— , применение к приближенным
вычислениям 245-247, 443
— частный 422, 460
Дифференцирование 241
— параметрическое 273
— , правила 241, 442
Дифференцируемая функция 237, 427
Дифференцируемость неявной функции
505
Длина отрезков 47
— плоской кривой 628
, аддитивность 629
— пространственной кривой 636
Дополнительный член формулы
Лагранжа 297
Тейлора 280, 288, 289, 465
Эрмита 300
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
673
Дробная рациональная функция 118
, непрерывность 167
нескольких переменных 394
в (число) 90, 168
е, иррациональность 93
е, приближенное вычисление 93
Единица 17, 38
Зависимые функции 536
Замена переменных 542
Замкнутая область 391
— сфера 391
Замкнутое множество 391
Замкнутый параллелепипед 391
— промежуток 108
— симплекс 391
Заострения точка 604
Затухающее колебание 233, 316
Знаков правило (при умножении) 19, 37
Иенсен 329
Иенсена неравенство 336
Измерение отрезков 47
Изолированная точка кривой 600, 604
Инвариантность формы дифференциала
242, 441
Интерполирование 296
Интерполирования узлы 296
кратные 299
Интерполяционная формула Лагранжа
295
, дополнительный член 298
Эрмита 299
, дополнительный член 300
Иррациональные числа 22
Кантора теорема 201, 206, 413, 417
Кардиоида 571, 576, 592
Касание кривых 607
, порядок 617
Касательная 210, 235, 432, 586, 593,
596, 622
— односторонняя 234
— , отрезок 586
— , — полярный 591
— плоскость 429, 596
Касательная, положительное
направление 636
Касательное преобразование 544, 547,
552, 560
Касательных метод (приближенного
решения уравнений) 366
Кассини овал 577
Квадратичная форма 476
, наибольшее и наименьшее
значения 534
неопределенная 478
определенная 476
полуопределенная 479
Кеплера уравнение 195
Клапейрона формула 379, 421
Класс гладкой кривой 665
Классификация бесконечно больших 163
малых 154
Классы функций 118
Колебание гармоническое 233
— затухающее 233, 316
— функции 198, 413
Комбинированный метод
(приближенного решения
уравнений) 373
Компрессор 486
Конечные разности 274
Конечных приращений формула 255,
436
Конус 2-го порядка 599
Координатные линии (поверхности) 582
Координаты «-мерной точки 384
Корень из вещественного числа,
существование 41
— уравнения, приближенное
вычисление 191, 361
(функции), существование 190
Косеканс 122
Косинус 122
— гиперболический 123
, функциональная характеристика
180
— , функциональная характеристика 180
Котангенс 122
— гиперболический 123
Коши 78, 79, 96, 215
Коши—Больцано теоремы 1-я и 2-я 188,
191, 204, 409
условие 96, 152
— форма дополнительного члена 289
— формула 257
Кратная точка кривой 565, 580, 603, 605
674
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Кривизна 637
— , круг 640
— , радиус 640
— средняя 637
— , центр 640
Кривые, см. соответствующее
название
— в пространстве 579, 580
— в «-мерном пространстве 386
— на плоскости 563, 569, 572
— переходные 645
Кронекер 115
Куб «-мерный 388
Кусочно-гладкая кривая 666
Минковского неравенство 309
Многозначная функция ПО, 125, 380,
500, 508
Множество точек замкнутое 391
ограниченное 391
— числовое, ограниченное сверху,
снизу 30
Множители неопределенные, метод 527
Модуль перехода от натуральных
логарифмов к десятичным 90
Монотонная варианта 81
— функция 151
, непрерывность, разрывы 173
Монотонности функции условие 303
Лагранж 215, 289, 527
Лагранжа интерполяционная формула
295
, дополнительный член 298
— теорема, формула 253, 255
— форма дополнительного члена 289,
465
Лебег 203
Лежандра многочлены 269
Лежандра преобразование 546, 559, 560
Лейбниц 215, 241, 271
Лейбница формула 267, 271
Лемниската Бернулли 577, 593, 644, 646
Логарифм, существование 46
— десятичный 59, 90
— натуральный (или неперов) 90
, переход к десятичному 90
Логарифмическая спираль 575, 592, 643,
651
— функция 122
, непрерывность 174, 194
, производная 218, 221
, функциональная характеристика
179
Ломаная (в «-мерном пространстве) 387
Лопиталя правило 351, 357
Маклорена формула 278, 282
Максимум, см. Экстремум
Матрица функциональная (Якоби) 498,
536
, ранг 524, 528, 537
Матрицы умножения 497
Мерэ 52
Минимум, см. Экстремум
И переменных функция 392
«-кратная точка кривой 605
«-кратный предел 401
«-мерная сфера 388, 391
«-мерное пространство 384
«-мерный параллелепипед 387, 391
«-мерный симплекс 388, 391
Наибольшее значение функции 197, 323
нескольких переменных 480
Наибольший предел варианты 103
функции 154
Наименьшее значение функции 197, 323
нескольких переменных 480
Наименьший предел варианты 103
функции 154
Наименьших квадратов метод 492
Наклонная асимптота 346
Наложение функций 131
Направление на кривой 625
Натуральный логарифм 90
Независимость функций 536
Независимые переменные 108, 378, 379,
392
Неопределенности раскрытие 72, 351
— вида g 71,351
--?71,357
0 • оо 72, 359
оо - оо 72, 360
1°°,00, оо° 186,360
Неопределенные множители, метод 527
Непер, неперовы логарифмы 90
Непрерывность области вещественных
чисел 28
— прямой 49
— функции в области 407
в промежутке 166
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
675
Непрерывность функции в точке 165,
404
односторонняя 169
равномерная 199, 413
Непрерывные функции, операции над
ними 167, 406
, свойства 188-207, 407-418
, суперпозиция 131, 406
Неравенства, доказательство 139, 306,
337
Неравенство Иенсена 336
— Коши 308, 385
— Коши-Гельдера 308, 337
— Минковского 309
Несобственные числа (точки) 31, 64,
396
Неявные функции 500, 507
, вычисление производных 515
, существование и свойства 502,
505, 507
Нижняя граница числового множества
30
, точная 31
Нормаль к кривой 586
, отрезок 586
, — полярный 591
поверхности 595, 598
Ньютона метод (приближенного
решения уравнений) 366
Область в «-мерном пространстве 390
— замкнутая 391
— изменения переменной (переменных)
ПО, 379
— определения функции ПО, 380
— открытая 390
— связная 392
Обратная функция 124
, непрерывность 193
, производная 219
, существование 193
Обратные тригонометрические функции
126
, непрерывность 175, 194
, производные 221
Обыкновенная точка (кривой или
поверхности) 564, 565, 582
Овалы Кассини 577
Огибающая семейства кривых 608
Ограниченная варианта 62
Ограниченное множество точечное 391
Ограниченное множество числовое 30
Ограниченность непрерывной функции,
теоремы 196, 206, 412, 417
Однозначная функция ПО, 380
Однородная функция 446
Односторонние непрерывность и
разрывы функции 169
Односторонняя касательная 234
— производная 234
высшего порядка 260
Окрестность точки 132
«-мерная 388, 389
Определитель, производная 435
— функциональный (Якоби) 494
Особая точка (кривой или поверхности)
564, 565, 578, 580, 594, 596, 599
двойная 603
изолированная 600
кратная 565, 580, 603, 605
Остроградский 495
Открытая область 390
— сфера 388, 390
Открытый параллелепипед 387, 390
— промежуток 108
— симплекс 388, 390
Относительная погрешность 158, 245,
444
Относительный экстремум 524
Отрезок, измерение 47
— касательной, нормали 586
, — полярный 591
Оценка погрешностей 247, 443
Парабола 74, 118, 588, 612, 644, 648
Параболоид вращения 383
Параллелепипед «-мерный 387
Параметр 244, 564
Параметрическое дифференцирование
273
— представление кривой 244, 564, 573
в пространстве 580
поверхности 581
Пеано форма дополнительного члена
280
Перегиба точка 338
Переменная 51, 107
— независимая 108, 392
Переменных замена 542
Переместительное свойство сложения,
умножения 15, 17, 34, 38
676
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Перестановка дифференцирований 453,
456
— предельных переходов 403, 455
Переходные кривые 645
Периодическая десятичная дробь 28
Поверхность 382, 579, 581
— вращения 585
Повторный предел функции нескольких
переменных 401
Пограничная точка 390
Погрешность абсолютная,
относительная 158, 245, 248, 444
Подкасательная 232, 586
— полярная 591
Поднормаль 586
— полярная 591
Подпоследовательность 99
Показательная функция 122
, непрерывность 168, 174
, производная 218
, функциональная характеристика
178
Полное приращение функции 422
Полный дифференциал 426, 443
высшего порядка 459, 462
, геометрическая интерпретация
432
, инвариантность формы 441
, применения к приближенным
вычислениям 443
Полукубическая парабола 567, 604, 613,
649
Полуоткрытый промежуток 108
Полярная подкасательная, поднормаль
591
Полярное уравнение кривой 572
Полярные координаты 553, 572
Полярный отрезок касательной,
нормали 591
Порядок бесконечно большой величины
164
малой величины 156
— дифференциала 270
— касания кривых 617
— производной 259
Последовательность 52
Постоянства функции условие 301
Правило, см. соответствующее
название
Предел варианты 54, 56
бесконечный 64
, единственность 63
Предел варианты монотонной 81
наибольший, наименьший 103
частичный 99
— отношения 69
— произведения 69
— производной 256
— разности 69
— суммы 69
— функции 132-134
монотонной 151
наибольший, наименьший 154
нескольких переменных 395, 398
повторный 401
частичный 154
Предельный переход в равенстве,
в неравенстве 65
Преобразование Лежандра 546, 559, 560
— точечное (плоскости, пространства)
544, 552
Приближенное решение уравнения 361
Приближенные вычисления,
применение дифференциала 245,
247, 443
Приближенные формулы 159, 162, 245,
289-295
Приращение переменной 165
— функции, формула 222
нескольких переменных полное,
формула 423
частное 419
Приращений конечных формула 255,
436
Произведение вариант, предел 69, 71
— функций, предел 147, 148
, непрерывность 167, 406
, производная и дифференциал
224, 242, 265, 271, 442
— чисел 17, 36
Производная 212, см. также название
функции
— бесконечная 235
— высшего порядка 259
, связь с конечными
разностями 275
— , геометрическое истолкование 213
— , несуществование 236
— односторонняя 234
— по заданному направлению 438
— , правила вычисления 223
— , разрыв 236
— частная 419
высшего порядка 449
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
677
Промежуток 95
— замкнутый, полуоткрытый, открытый,
конечный, бесконечный 108
Промежуточное значение, теорема 191
Пропорциональных частей правило 362
Простая точка (кривой или
поверхности) 566, 582
Пространственный график функции 382
Пространство «-мерное
(арифметическое) 384
Прямая в «-мерном пространстве 386
Равномерная непрерывность функции
199, 413
Радикал, арифметическое значение 42,
122
Радиус кривизны 640
Разность вариант и т. д., см. Сумма
— чисел 15, 36
Разрыв производной 236
— функции 165
монотонной 173
, обыкновенный, 1-го и 2-го рода
170
нескольких переменных 404
Ранг матрицы 524, 528, 537
Раскрытие неопределенностей 72, 351
Распределительное свойство умножения
18,39
Распространение функций 657
Расстояние между точками в «-мерном
пространстве 384
Рациональная функция 118
, непрерывность 167
нескольких переменных 394
, непрерывность 399, 405
Рациональные числа, вычитание 15
, деление 17
, плотность 14
, сложение 15
, умножение 17
, упорядочение 14
Риман 172
Ролля теорема 252
Роша и Шлемильха форма
дополнительного члена 288
Связи уравнения 524
Связная область 392
Сгущения точка 132, 133, 390
Секанс 122
Семейство кривых 607
Сечение в числовой области 20, 28
Сигнум (функция) 115
Сила тока 214
Сильвестр 476
Симплекс «-мерный 388, 391
Синус 122
— гиперболический 123
— , предел отношения к дуге 139
Синусоида 118, 339
Скорость в данный момент 209, 213
— движения точки 208
— средняя 208
Сложная функция 131, 393
, непрерывность 175
, производные и дифференциалы
226, 243, 272, 432, 441, 464, 465
Смешанные производные, теорема 452
Соприкасающаяся кривая 620
— прямая 621
Соприкасающийся круг 622, 640
Сочетательное свойство сложения,
умножения 15, 17, 34, 38
Сравнение бесконечно малых 154
Среднее арифметико-гармоническое 86
— арифметико-геометрическое 85
— арифметическое 308, 483
— гармоническое 85, 338
— геометрическое 85, 308, 338, 483
— значение, обобщенная теорема 258
, теорема 254
Средняя кривизна 637
— скорость 208, 213
Стационарная точка 311, 470
Степенная функция 118
, непрерывность 175
, производная 217
, функциональная характеристика
178
Степенно-показательная функция (двух
переменных) 394
, дифференцирование 420
, непрерывность 405
, предел 400
Степенно-показательное выражение,
предел 185
, производная 231, 434
Степень с вещественным показателем
43
Сумма вариант, предел 69, 72
— функций, непрерывность 167, 406
678
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Сумма функций, предел 147, 148
, производная и дифференциал
224, 242, 261, 442
— чисел 15, 33
Суперпозиция функций 131, 394, 406
Сфера 383
— «-мерная 388, 390
Сферические координаты 554
Сходимости принцип 96, 152
Функциональное уравнение 176,
178-180
Функциональный определитель 494
Функция 110, см. также название
функции
— , исследование 301
— нескольких переменных 379, 392
— от функции (или от функций) 131,
393
Табличный способ задания функции
113
Тангенс 122
— гиперболический 123
Тейлора формула 276, 280, 289, 466
Тело геометрическое 384
Теплоемкость 214
Точка, см. соответствующее
название
Точки функции 393
Точная граница (верхняя, нижняя) 31
Тригонометрические функции 122
, непрерывность 168
, производные 219
Тройная точка 605
Тройной предел 401
У бывающая варианта 81
— функция 151
Угловая точка 234
Узлы интерполирования 296
кратные 299
Уитней 661
Улитка 575, 592
Уравнение кривой 116, 258, 564, 572,
579, 580
— поверхности 382, 579, 581
— , приближенное решение 190, 361
— , существование корней 191
Ускорение 213, 259
Ферма теорема 250
Форма квадратичная 476
Формула 112, 113, см. также
соответствующее название
Функциональная зависимость 108, 378
— матрица 497, 536
Характеристическая точка на кривой
614
Хестинс 661
Ход изменения функции 301
Хорд метод приближенного решения
уравнений 362
Целая рациональная функция 118
, непрерывность 167
нескольких переменных 394
, непрерывность 399, 405
— часть числа [Е(р)\ 57
Центр кривизны 640, 646
Цепная линия 232, 566, 642
Циклоида 569, 589, 643, 650
Цилиндр проектирующий 579
Частичная последовательность 99
Частичный предел варианты 99
функции 154
Частная производная 419
высшего порядка 450
Частное вариант, предел 69, 70
— значение функции 111
— приращение 419
— функций, непрерывность 167, 406
, предел 147, 148
, производная и дифференциал
225, 242, 442
— чисел 17
Частный дифференциал 422, 460
Чебышёва формула 294
Числа, см. Рациональные,
Иррациональные, Вещественные
числа
Числовая ось 49
— последовательность 51
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
679
Шварц 455
Шлемильха и Роша форма
дополнительного члена 288
Штольца теорема 78
Эвольвента 648, 652-654
— круга 572, 590, 643
Эволюта 648, 652-654
Эйлер 90
Эйлера формула 448
Эквивалентные бесконечно малые
величины (знак ^) 157
Экстремум (максимум, минимум)
311
— , правила отыскания 311, 312, 318,
321
— собственный, несобственный 310
Экстремум функции нескольких
переменных 468
абсолютный 525
относительный 524
Электрическая сеть 490, 532
Элементарные функции 118
, непрерывность 174
, производные 216, 221, 261-263
Эллипс 502, 566, 588, 613, 645, 649
Эллипсоид 598
Эпициклоида 570, 590
Эрмита интерполяционная формула 299
, дополнительный член 300
Якоби 419
— матрица 497, 536
— определитель (якобиан) 494
Учебное издание
ФИХТЕНГОЛЬЦ Григорий Михайлович
КУРС ДИФФЕРЕНЦИАЛЬНОГО И ИНТЕГРАЛЬНОГО
ИСЧИСЛЕНИЯ
В 3 томах
Том I
Редактор А.А. Флоринский
Выпускающий редактор О.М. Рощиненко
Оформление обложки А.А. Логунова
ЛР №071930 от 06.07.99. Подписано в печать 23.10.03.
Формат 60x90/16. Бумага офсетная. Печать офсетная.
Усл. печ. л. 42,5. Уч.-изд. л. 39,89. Заказ №
Издательская фирма «Физико-математическая литература»
МАИК «Наука/Интерпериодика»
117997, Москва, ул. Профсоюзная, 90
E-mail: fizmat@maik.ru
Отпечатано с диапозитивов
в ОАО «Чебоксарская типография № 1»
428019, г. Чебоксары, пр. И. Яковлева, 15
ISBN 5-9221-0156-0
9 785922 '101561