Ж<€.сМоЪено$
СУ? ■ ^О
по
УЧПЕЛГИЗ • 1 Q4Q

П. С. МОДЕНОВ
СБОРНИК ЗАДАЧ
по
ДИФФЕРЕНЦИАЛЬНОЙ
ГЕОМЕТРИИ
Допущен
Министерством висшгго образования СССР
в качествг учебного пособия
для педагогических институтов и
государственных университетов
ГОСУДАРСТВЕННОЕ
УЧЕБНО-ПЕДАГОГИЧЕСКОЕ ИЗДАТЕЛЬСТВО
МИНИСТЕРСТВА ПРОСВЕЩЕНИЯ РСФСР
МСХ: К У А 1949

ПРЕДИСЛОВИЕ
Настоящий сборник составлен для физико-математических
факультетов педагогических институтов. Я считаю, что его можно
использовать и студентам механико-математических, физических и физико-
математических факультетов университетов. Задачи, помещённые в
сборнике, предлагались мною на практических занятиях, которыми я
руководил с 1932 г. на физическом факультете Московского ордена Ленина
государственного университета им. М. В. Ломоносова. Имея в виду
в основном будущего учителя, я стремился разнообразить задачи и со
стороны их содержания и со стороны-методов решения. Так, например,
в сборник включены задачи, связанные со смежными дисциплинами:
с математическим анализом, физикой, теоретической механикой (задачи,
связанные с движением материальной точки под действием
центральной силы, движение электрона в магнитном поле, задачи о рулеттах,
о равновесии нити, задачи о каустике, некоторые вопросы
плоскопараллельного движения и т. д.). Таких задач сравнительно немного,
но они укажут будущему учителю на возможные приложения
дифференциальной геометрии к теоретическим вопросам смежных
дисциплин. Что касается методов решения, то в решениях задач
преобладают в основном аналитические решения (что соответствует
современному преподаванию дифференциальной геометрии). Однако
к некоторым задачам даны и синтетические решения. Эти решения
построены всегда на базе известных читателю фактов из курса
математики и никогда не базируются на туманных инфинитезимальных
соображениях.
Мне кажется, что синтетические методы решения помогут
установить связь между отдельными фактами курса и тем самым будут
способствовать более глубокому его усвоению.
Большая часть задач относится к линии (плоской и
пространственной); мы не имеем в нашей учебной литературе специального достаточно
полного сборника задач по этому разделу в духе современного
преподавания теории линий (а именно, с широким использованием формул
Френе). Что касается задач на поверхности, то дополнительно к
настоящему сборнику я в первую очередь рекомендовал бы «Сборник
задач по высшей геометрии» (Житомирский, Львовский, Милинский,
ч. II), в котором раздел теории поверхностей представлен весьма
полно (рамки задачника выходят за пределы программы пединститутов
и, пожалуй, университетов).
* 3

К большинству задач даны указания и решения, к части задач —
только ответы. Задачи расклассифицированы по степени трудности.
Задачи повышенной степени трудности отмечены знаком *, задачи
наиболее трудные — знаком **.
Для решения части задач необходимо знакомство с
дифференциальными уравнениями; учитывая, место последнего курса в учебном плане
пединститутов, я во всех таких случаях даю в указаниях решение
соответствующего дифференциального уравнения. *
Наконец, часть задач (например, часть задач на огибающие) имеет
аффинно-дифференциальный характер. В решениях этих задач
используется понятие аффинного преобразования и его свойств.
При составлении настоящего сборника мною использованы
следующие учебники:
Б ю ш г е н с, Дифференциальная геометрия.
Дубнов, Основы векторного исчисления.
Житомирский, Львовский, Милинский, Сборник задач
по высшей геометрии.
Гюнтер и Кузьмин, Сборник задач по высшей математике.
Рашевский, Курс дифференциальной геометрии.
Бляшке, Дифференциальная геометрия.
Милинский, Дифференциальная геометрия.
Шифф, Сборник задач по выешей математике.
Я выражаю глубокую благодарность редактору сборника проф. Нор-
дену А. П. за просмотр и исправления, внесённые в рукопись, за
указания и советы, а также проф. Маркушевичу А. И. и С. И.
Новоселову за просмотр рукописи и за сделанные замечания. Чертежи
к задачам выполнены Н. А. Атабековым; ему я также выражаю
благодарность за хорошее исполнение чертежей и за помощь,
оказанную им при их гТасчётах.
Москва, 23 октября 1948 г.
Моденов П. С.

ГЛАВА 1
ВЕКТОР-ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА
Указания
Пусть каждому числу t из некоторого множества Щ чисел
поставлен в соответствие вектор г. Тогда говорят, что на множестве
9М задана вектор-функция скалярного аргумента, и указанную
зависимость записывают в виде:
r=r{t).
Множество Ш называется областью определения вектор-функции г (t).
Мы будем предполагать далее, что множество Ш является сегментом
[а, Ь\ или интервалом (а, Ь) (или полуинтервалом).
Функция r(t) называется непрерывной в точке ^=^0, если она
определена в некоторой окрестности этого значения t = tQ и если
для любого е^>0 найдётся &^>0 такое, что \.r(t) — г(/0)|<е при
всех ty удовлетворяющих неравенству \t—101 <^ 8.
Если функции r(t), p(0, JR(t), \{t) непрерывны при /=*0, то
при том же значении t будут непрерывны следующие функции:
И, r-fp, г — р, Хг, гр, гХр, И, [rp], rpR.
Если r = r{f) и t = t(s), причём функция t(s) непрерывна при
s = s0, а функция r(t) непрерывна при / = /(s0), то сложная функция
r{t(s)} непрерывна при s = s0.
Замечание. Мы будем широко пользоваться двумя операциями
над векторами ориентированной плоскости: псевдоскалярным
произведением гХр и п'оворотом вектора на -f- 90°, [г].
Псевдоскалярным произведением двух векторов г и р, лежащих
в ориентированной плоскости, в случае, если они неколлинеарны,
называется число, абсолютная величина которого равна площади
параллелограма, построенного на векторах г и р, отложенных от
произвольной точки плоскости. Это число положительно, если репер
г, р — правый, и отрицательно, если этот репер левый. Если векторы г
и р коллинеарны, то по определению гХр = 0. В координатах:
гХр= Л у где г={а, Ь) и р = {с, d}. Вектор, полученный из
5

данного вектора г поворотом на -f- 90°, мы будем обозначать так: [г].
В координатах (в декартовой прямоугольной системе координат):
И = {—ft, a}*).
Мы будем говорить, что вектор а является пределом вектор-
функиии r = r(t) в точке t=tQ, если вектор-функция г (t) определена
в окрестности t=t0, кроме, быть может, этого значения t = tQ, и если
для любого е ^> 0 найдётся 8 ^> 0 такое, что | г (/) — а | <^ е при всех
t^zt0i удовлетворяющих неравенству \t — £0|<Сй-
Если вектор-функция r(t) имеет предел а в точке t = tQt то мы
будем писать:
lim г (f) = a.
Пусть функции r(f), р(0» #(0 и ^(t) имеют пределы вточке* = *§.
Тогда в той же точке имеют пределы следующие функции:
И. Г + Р» г— Р. Хг> ГР> гХр, И, [rpl, гр#,
причём:
Jim |r| = | limr|,
lim (г -f- p) = Hm г -f- lim p,
lim (r— p)= Hm r— lim p,
lim (Xr) = lim X lim r,
t— to t— t$ t= t$
lim (rp) = lim г Hm p,
lim (r X p) = Hm г X lim P>
lim [r] = [limr],
t=t0 t=t0
lim [rp] = [lim г limp],
t=t0 , t = t0 t±=t0
lim (rpR) = lim r lim p lim /?.
*=/<, *=*0 t = t0 t = t<>
Если функция t=t(s) имеет предел в точке s = s0, а функция г(/)
имеет предел а в точке £ = /(.s0), то функция r{t(s)\ имеет предел,
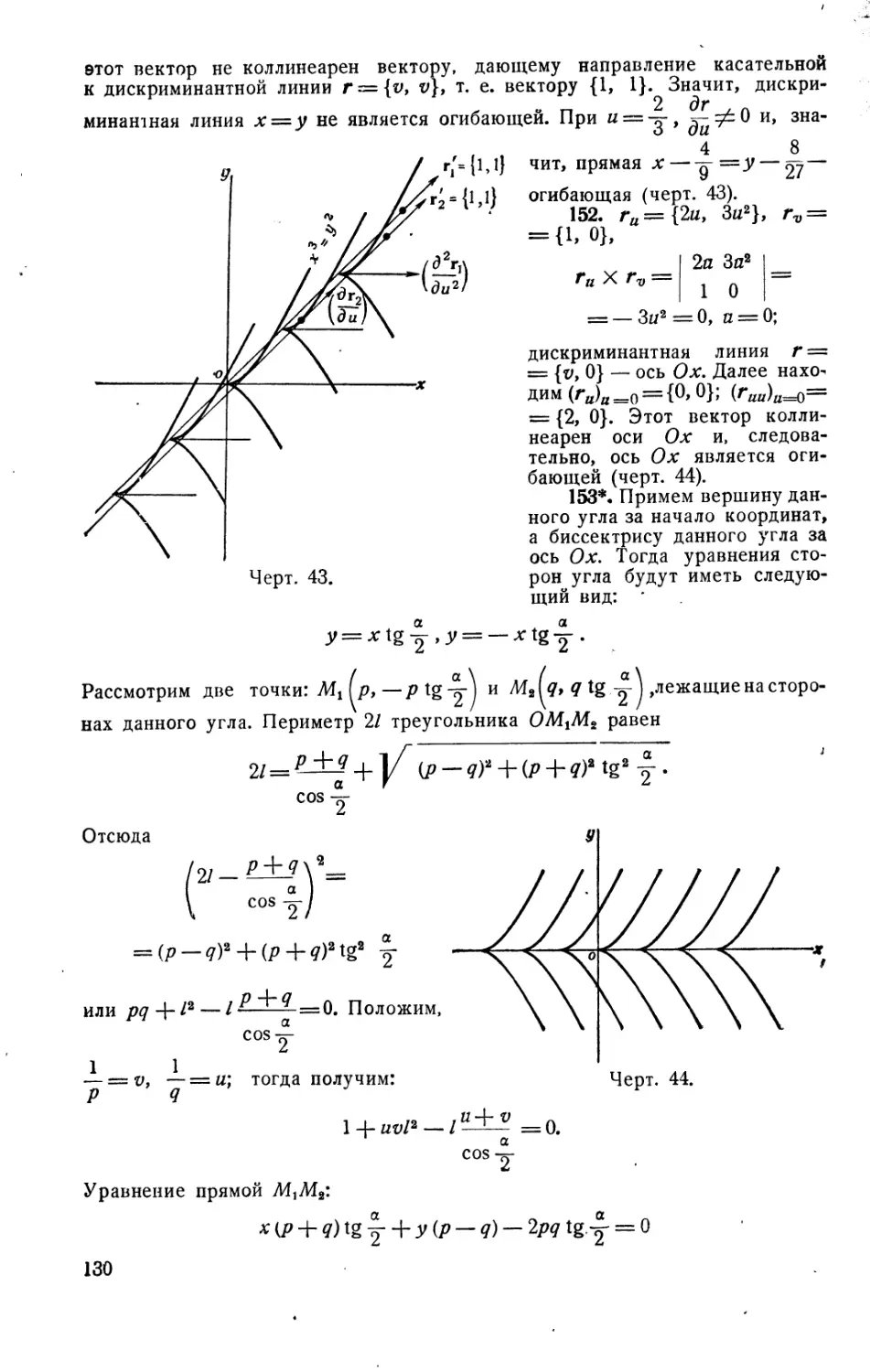
равный а в точке s = s0.
Производной вектор-функции r(t) в точке t=tQ называется
следующий предел:
lim r(i)-r(t0)
t—t0 r —ro
*) См. Дубнов Я. С, Основы векторного исчисления, ГТТИ, 1939 г., ч. I;
Бахвалов С. В., Моденов П. С, Пархоменко А. С., Сборник
задач по аналитической геометрии, Гостехиздат, 1948 г.
6

Производную функции r(t) будем обозначать так: г\ Аналогично
вводится понятие производных высших порядков: г ', г'",...
Если вектор-функция r(f) имеет при t = t0 производные до
порядка az —|— 1 включительно, то имеет место формула Тейлора с
остаточным членом в форме Пеано:
• r(0 = r(f0) + (f-^0)r'(^o) + (-^1r"(g + ...+ ••'
где
^=7^Т17Г^я+,)^) + *Ь ит«=о.
Если откладывать значения вектор-функции г (t) от фиксированной
точки О:
OM = r(t\
то множество всех точек М, соответствующих всем значениям t из
области определения функции r(t), называется годографом вектор-
функции r{t).
Если вектор-функция r = r(t) определена и имеет производную
г' (t) на сегменте [а, Ь], причём эта производная не обращается в нуль
при всех t из этого сегмента, то годограф вектор-функции r = r(t)
есть гладкая линия.
Если вектор-функция г (t) определена и имеет производную на
сегменте [а, Ь], причём в некоторой точке t = tu, а<^0<^&,
производная г' (t0) отлична от нуля: г' (t0) ф О, то вектор г (^0) коллинеарен
касательной к годографу вектор-функции г (t) в точке,
соответствующей значению t = tQ. Если же при t = t9 мы имеем:
г (*,) = г" (*,) =... = г<* - »(*,) == О, r<*> (*,) ф О,
то вектор r{k)(t0) коллинеарен указанной касательной.
Если каждой паре чисел (щ v) из некоторого множества 9Й пар
чисел поставлен в соответствие вектор г, то говорят, что на
множестве Ш задана вектор-функция r = r(u, .v) двух аргументов и, v.
Множество Ш мы чаще всего будем предполагать «прямоугольником»:
Пределы
t. r(u-\- /iu,v) — r(u,v)
urn :
и
г г (ц, р -f- &р) — г (и, р)
aJ=o д*
называются соответственно частными производными от вектор-функции
г (w, г/) по и и v и обозначаются так:
7

Понятие дифференцируемой функции двух аргументов
устанавливается аналогично тому, как это делается в курсах математического
анализа.
§ 1. Вектор-функция скалярного аргумента
U Найти производные по t от следующих функций: г2, г'3, г'у^г",
[rr"]t rr"r"\ if[rr]*, -/г* (г = r(t); штрихом обозначено
дифференцирование по f).
2. Доказать, что если в некотором интервале (tu ^2), | г | = const,
то г _[_/*'• Выяснить геометрический смысл этого утверждения. Верно
ли обратное положение?
3. Доказать, что если в некотором интервале (tu t%) вектор-
функция r = r(t) имеет производную, равную нулю: г' = 0 при всех
t^(tu /2), то*в этом интервале г = const. Верно ли обратное
положение?
4. Обозначим через ср угол от вектора а до единичного вектора
г° ориентированной плоскости. Доказать, что
5. Полагая г=гг° (|г° | = 1) и считая, что r = r{f) есть закон
движения точки, найти скорость v = г' и ускорение w = r" в
полярных координатах; найти также v и w.
6. Можно ли утверждать, что
1) k'l=H', ■
2) rr' = rr'?
7. Доказать, что если в пространстве движутся две материальные .
точки, расстояние между которыми постоянно, то проекции
скоростей этих точек на направление прямой, их соединяющей, — равны.
8. Отрезок постоянной длины скользит своими концами по двум
линиям г —г (и) и р= p(v). Найти направление касательной к линии,
описываемой серединой отрезка.
9. Плоская линия С задана уравнением r = r{t). Функция r(t)
определена и непрерывна на сегменте [а, Ь]. Точки М1(а) и Ж2 (Ь)
лежат по разные стороны от некоторой прямой /. Доказать, что линия
С пересекает прямую /.
10. Вектор-функцият(^) определена на сегменте [tu t9], непрерывна
на нём и имеет отличную от нуля производную г' (t) в интервале
(tXi /2), причём r(t1) = r(t2J. Применить к функции аг(а =*= const)
теорему Ролля и дать геометрическое истолкование результата.
11. Вектор-функция r(t) определена и имеет отличную от нуля
производную на сегменте [tlf tfj. Векторы r(tx) и r(t2) неколлинеарны.
Применить к функции r(t) r(tt) r(t^) теорему Ролля и истолковать
результат геометрически.
12. Плоская линия задана уравнением r = r(t)\ функция r{t)
определена на сегменте [tu t%], при разных значениях t из этого
8

сегмента функция принимает разные значения и имеет производную
в интервале (tl9 tq), причём г'(^)^0 при всех t£(tu t%). Доказать,
что существует точка М(£), ii(tltt%)9 касательная в которой к
данной линии параллельна хорде, проходящей через точки Mx(tx) и
13. Пусть Fx и F2— фокусы эллипса, а М — произвольная точка,
лежащая на этом эллипсе. Положим FxM — ru F2yM=r2, РгГ% = к;
тогда rx = k -\- г2, гх-\- г2 = 2а (а — большая полуось эллипса). Исходя
из этих соотношений и считая, что rt = rx (t) есть вёкторно-параметри-
ческое уравнение эллипса, найти способ построения нормали к ч
эллипсу.
14. Доказать, что если пучок лучей, выходящих из точки Fu
после отражения от линии С собирается в точке F2, то линия есть
эллипс с фокусами Fx и F2.
15. Решить задачу, аналогичную задаче 13 для гиперболы.
16. Пучок лучей с центром Fx после отражения от линии С
остаётся пучком расходящихся лучей с центром F%. Доказать, что
линия С—гипербола.
17. Какое заключение можно сделать о двух семействах эллипсов
и гипербол с общими фокусами, если исходить из результатов задач
13 и 15?
18. Применяя метод решения задач 13 и 15, указать на способ
построения нормали к овалу Кассини rxr^ = const.
19. Принимая за начало радиусов-векторов фокус параболы, можно
записать её уравнение в виде
где i—вектор коллинеарной её оси ([ i\ = 1). Считая г = г(t), найти
способ построения нормали и касательной к параболе.
20. Доказать, что если пучок лучей, отразившись от линии,
становится пучком параллельных лучей, то линия—парабола. \
21. Полагая r = {rcoscpcos6, r sin ф cos 6, г sin 6}, где г, <р, 0 —
полярно-сферические координаты точки в пространстве (ср — долгота,
6 — широта). Найти скорость г', модуль скорости |г'|, ускорение г"
и модуль ускорения | г" | в полярно-сферической, системе координат.
22. Найти в полярно-сферической системе координа-f скорость v
и модуль этой скорости для точки, движущейся по поверхности шара
радиуса г.
23. Точка движется по поверхности сферы так, что пересекает
все меридианы под одним и тем же углом L Найти соотношение
между широтой и долготой движущейся точки.
24. Полагая r={rcoscp, r sin9, z\y где г, ср, z — полярно-цилиндри-*
ческие координаты точки, найти скорость г, модуль скорости |г' |,
ускорение г" и модуль ускорения | г" | в полярно-цилиндрической
системе координат.
25. Точка движется по поверхности круглого цилиндра, пересекая
все его образующие под одним и "тем же углом X. Найти
соотношение между широтой ср и «высотой» z движущейся точки.
9

26. Имеет ли место для вектор-функции скалярного аргумента
формула Тейлора с остаточным членом в интегральной форме?
27. Вектор-функция r = r{f) определена в интервале (tlt t^) и имеет
в этом интервале производные до третьего порядка включительно.
Пусть s — s(t) — монотонная, непрерывная и трижды
дифференцируемая функция от t в интервале (tlt t%), a t==t(s) — обратная,
функция. Произвести замену аргумента в следующих выражениях:
г', г", г"\ г\ [г'г"], г'Хг", r'r"r"\
[r'[r"r']]9 Зг"(г'Хг") —r'(r'XO;
штрихом обозначены производные по t.
28. Дана вектор-функция двух аргументов: r = r(u, v). Произвести
* * WW
замену аргументов: и = и(и, v),v = v(u, v) в следующих
выражениях:
1) \дЛд±\
2) {^LdL^L\ (д2гдг дг\ ( д*г дгдг\*
\ди2~ди dv) \dv2du dv) \ dudv du dv) *
29. Исходя из закона Ньютона F—ma (F—сила, т — масса,
а — ускорение) движения материальной точки, вывести соотношение:
где v—скорость, r = r(t) — закон движения материальной точки.
30. Пусть r = r(t) — закон движения материальной точки. Назовём
[гг'] = а секториальной скоростью точки относительно выбранного
начала радиусов-векторов. Доказать, что если эта секториальная
скорость постоянна, то сила, под влиянием которой движется точка,—
центральная, и обратно: если сила центральная, то секториальная
скорость относительно центра — постоянна.
31. Количеством движения материальной точки называется
произведение её массы на скорость. Моментом количества движения
материальной точки М относительно точки Q называется векторное
произведение радиуса-вектора ОМ = г точки М на количество движения.
Моментом силы F относительно точки О называется векторное
произведение радиуса-вектора точки М приложения силы на эту силу.
Доказать, что производная по времени от момента количества
движения точки относительно какой-либо точки равна мохменту силы
относительно той же точки.
32. Доказать, что производная по времени от секториальной
скорости равна моменту ускорения относительно той же точки.
33. Точка движется по плоскости. Назовём секториальной
скоростью точки относительно начала радиусов-векторов — произведение
г X f'• Найти выражение секториальной скорости в полярных
координатах.
10

34.* Доказать, что если на некотором сегменте [tu t2] вектор-
функция г (t) непрерывна вместе со своей производной г, причём
г || г', но г' ф О и г^О, то годограф вектор-функции r — r(t) есть
отрезок прямой линии.
35.* Доказать, что если на некотором сегменте [tu t^] вектор-
функция r = r(t) непрерывна вместе со своими двумя первыми
производными г и г", если эти производные отличны от нуля при
всех t£[tu t2] и если они коллинеарны: г' || г" при всех t£[tl9 t%]9
то годографом вектор-функции r = r(t) является отрезок прямой
линии. Дать кинематическую интерпретацию.
36.* Плоская линия задана уравнением: г = {ф(0, ^р(ОЬ При
каком условии это уравнение определяет прямую линию?
37.* Найти функцию г = г (ср), зная, что это уравнение в полярных
координатах на плоскости определяет прямую линию.
38. Линия задана уравнением
Найти необходимое условие точек перегиба (г' X *"" = 0)- Как будет
выглядеть достаточное условие точки перегиба
r'Xr" = 0,r'Xr'V0?
39. Плоская линия определяется уравнением r — r(t); функция
r(t) определена, непрерывна и дважды дифференцируема на сегменте
[а, Ь], причём
Г' X г" 1
(Г*2)8/* =^ = COnSt;
Доказать, что уравнение r — r{t\ определяет окружность.
40*. Доказать, что если годограф вектор-функции r = r(t),
определённой и имеющей производные до четвёртого порядка на сегменте
[tu t2], является сферической линией (т. е. этот годограф расположен
на сфере), причём векторы г\ г", г'" неколлинеарны при всех
1 t [tu t%], то:
1) радиус-вектор центра этой сферы определяется соотношением
а = у^тт \{г'г) [г"г"'] + (г'2 + rr") [r"Y] + (3/-V" + гг'") [гУ]};
2) вектор-функция r(t) удовлетворяет соотношению
(г VV) (Зг"2 + 4гУ" + гг™) + (г'г) (r'r'"r™) +
4- (г'2 + гг") (г'V>IV) + (Зг'г" + гг'") (г'г" г™) = 0.
41. Вектор-функция г = г (t) определена на сегменте [tx t%] и
имеет на этом сегменте непрерывные производные г\ г", г'"; при
всех t(i[tl t%] эти производные компланарны, но г' Мт". Доказать,
что годограф вектор-функции r = r(t) есть плоская линия. Верно ли
обратное положение?
42. Доказать, что точка под действием центральной силы
описывает плоскую траекторию.
11 .

43. Линия задана уравнением r = r(t). Вектор-функция r(t)
определена и имеет производную на сегменте [tl9 t%]. В некоторой
точке t0, tl<^t0<^t2 имеем: г' (t0) ф 0. Доказать, что существует
такая окрестность числа tQ, что для всех / из этой окрестности»
меньших, чем tQ, вектор Ar = r(t) — r(t0) образует с вектором г (t0)
тупой угол, а для всех t из этой окрестности, больших /0, — острый.
44. Плоская линия задана уравнением r = r(t). Функция r(t)
определена и дважды дифференцируема на сегменте [а, Ь], причём г'
неколлинеарно г". Доказать, что в достаточно малой окрестности
точки A40(t0), a<^tQ<^b мы имеем:
кЧ'о) X г'Чдаг'('о) X М > о-
45 *. Плоско-параллельное движение на плоскости задано законами
движения r = rx{t)y r = r2(t) концов твёрдого стержня. Найти
уравнение неподвижной центроиды (произвольная точка центроиды
является точкой пересечения прямых, проходящих через концы
стержня перпендикулярно к направлениям скоростей его концов).
46 *. Подвижной центроидой в плоско-параллельном движении
называется множество мгновенных центров вращения относительно
движущегося стержня (см. предыдущую задачу). Составить.уравнение
подвижной центроиды.
47 *. Доказать, что линейная скорость v точки в любом
плоскопараллельном движении определяется соотношением *? = а>[г], где
г—радиус-вектор рассматриваемой точки М (R) относительно
мгновенного центра вращения (см. задачи 45, 46). Выразить ш через
rY и г2, а также найти скорость v точки М (R).
48. На материальную точку М действует ньютонианская сила
с центром притяжения О. Пусть г—радиус-вектор точки Ж. Тогда
единичный вектор, имеющий то же направление, равен —. Так как
k
модуль ньютонианской силы равен -g-(£^>0), а сила F направлена
от Ж к О, то
Р r_k_ kr ,
с другой стороны, по закону Ньютона F^=ar" (a. = cons/, r" —
ускорение), значит дифференциальное уравнение движения точки таково;
г" = —£(*>0).
Исходя из этого соотношения, доказать, что точка движется по
линии второго порядка.
49 *. Рассмотрим движение материальной точки под действием
центральной силы: F=Fr°. На основании результата задачи 42
движение будет происходить в некоторой определённой плоскости.
Составить уравнение движения в этой плоскости в полярных
координатах и составить дифференциальное уравнение траектории в
полярных координатах (формула Бине).
12

Рассмотреть случаи ньютонианской силы
50 *. Движение электрона в постоянном магнитном поле
определяется следующим дифференциальным уравнением:
г" = [г7/], H = const.
Доказать, что траектория — винтовая линия.
51 *. Дифференциальное уравнение движения электрона в поле
магнитного полюса имеет вид:
r''' = ^-[rr1(X=.const).
Доказать, что траектория есть геодезическая линия круглого конуса.
52 *. Найти линии, определяемые дифференциальным уравнением
г' = [<ог].
53 *. Найти линии, определяемые дифференциальным уравнением
г' = [е[ге]]9
где е — постоянный единичный вектор.
54 *. Найти линии, определяемые дифференциальным уравнением
r' = ae-j- [er],
где
а = const, e = const.
55 *. Найти линии, определяемые дифференциальным уравнением
г' = ^^е — г (re),
где
е== const и |е| = 1.
56*. Пусть r = rl(t) и r = r%(t) — законы движения двух точек
твёрдого тела, имеющего одну неподвижную точку, которая принята
за начало радиусов-векторов. Найти угловую скорость <о
произвольной точки М(г) движущегося тела в произвольный момент времени»
57 *. Свободное движение твёрдого тела задано законами
движения r = rt(t)t r = rq(t), r = r%(t) трёх его точек, не лежащих на
одной прямой. Скорость v любой точки тела слагается из мгновенной
линейной скорости, вызываемой вращением тела около некоторой
оси, и мгновенной скорости скольжения вдоль мгновенной оси
вращения. Найти мгновенную угловую скорость to, скорость
скольжения вдоль мгновенной оси вращения и уравнение мгновенной оси
вращения.
58**. Плоская; линия задана уравнением r = r(t), где функция
r(t) определена и имеет непрерывную производную на сегменте
[*i, 1а]. Рассмотрим какую-нибудь точку М (t9) этой линии, в которой
13

производная г'(/0) не равна нулю: г'(/0)^0. Пусть
М0К—произвольная прямая, проходящая через точку М0 и отличная от
касательной в точке М0 к рассматриваемой линии. Доказать, что
существует интервал (t0— 8, t0-\-b) такой, что любая прямая,
параллельная прямой М0К, пересекает дугу данной линии, соответствующую
данному интервалу, не более чем в одной точке.
69**. Линия задана уравнением r = r(t)\ функция г (t)
определена и дважды дифференцируема на сегменте [tl9 t2]. В некоторой
точке М0 (t0) имеем г (t0) ^ г" (t0). Доказать, что. существует такая
окрестность (t0 — 8, t0 -j- 8), что касательная к линии в точке М0
имеет с дугой линии, соответствующей интервалу (t0 — 8, t0 -j--8),
только одну общую точку Ж0.
60**. Плоская линия задана уравнением r = r(t)\ функция r(t)
определена, дважды дифференцируема на сегменте [а, Ь] и при
разных значениях t£ [a, Ь] принимает разные значения. Будем эту линию
называть выпуклой, если треугольник с вершинами Mr{tx), M2(t2)f
Мъ (td) имеет вполне определённую ориентацию при любом выборе
*ь ^2> *ъ таких, что a^t1<^t2<^t9^b. Доказать, что линия
выпуклая, если г' Хг"^0 ПРИ всех ^6 [ау Ь] и если существует
по крайней мере четыре прямых различных направлений, которым не
параллельна ни одна из касательных к данной линии.
61 **. Плоская линия задана уравнением r = r(t). Функция r(t)
определена и имеет непрерывные производные г' и г" на сегменте
[а, Ь\\ г' и г" неколлинеарны при всех ££ [а, Ь]. Доказать, что
если t0 — любое число из интервала (а, #), то
1) любая прямая, параллельная касательной к линии в точке MQy
расположенная по определённую сторону от касательной на
достаточно близком расстоянии от касательной, пересекает дугу данной
линии, соответствующей некоторому интервалу (t0 — 8, ^0~|~^)>
в двух различных точках.
2) Существует интервал (—/г, h) такой, что любая прямая,
проходящая через точку М0 и наклонённая к касательной в точке М0
на угол <р"£(—/г, К) (ср ф 0), пересекает дугу линии,
соответствующую интервалу (tQ— 8, £0-{-8), только в одной точке (не считая
точки Ж0).
62**. Линия задана уравнением r — r(t). Функция r(t)
определена и имеет непрерывные производные г' и г" на сегменте [а, Ь].
Пусть в некоторой точке М0(£0), а<^0<С^ мы имеем
г' (*о)Х г" (/0) Ф0.
Доказать, что существует окрестность (t0 — 8, t0 -f- 8) такая, что
дуга линии r=^r(t)t ей соответствующая, может быть задана
полярным уравнением г=г(ср).
63**. Плоская линия определена уравнением r = r(t). Функция
r(t) определена и имеет непрерывные производные г' и г" на
сегменте [а, Ь]. В некоторой точке M0(t0), t0£ (а, b) векторы г'
и г" неколлинеарны: г'(t0) % г" (t0). Доказать, что в некоторой
14

окрестности (t0 — 8, ^0 -f- 8) числа tQ функция г (/) и соответствующая
ей дуга С линии обладают следующими свойствами:
1) r'(t)Xr"(t)^0 при всех t(. (*0 —8, *0 + 8).
2) Треугольник Мх Ж2 Ж3 с вершинами Мх (tt)9 М2 (/2), Мъ (/3),
где t0 — 8=^:^ <С^2<^з ^*о + &> имеет вполне определённую
ориентацию независимо от выбора tu t%, tb (лишь бы эти числа
удовлетворяли указанным выше неравенствам).
3) Любая прямая пересекает дугу линии С не более чем в двух
точках.
64**. Плоская линия задана уравнением r = r(t)\ функция г (/)
определена, при' разных значениях t принимает разные значения и
дважды дифференцируема на сегменте [а, Ь]. Пусть точки Мх (tx),
М2(£2), М3(£3), a^^^t^^tz^b лежат на одной прямой и
существуют по крайней мере два направления, которым не параллельна
касательная. Доказать, ' что в интервале (а, Ь) существует число Е
такое, что векторы г' (£) и г" (£) коллинеарны.
55**. Плоская линия задана уравнением r = r(t). Функция r(t)
определена и дважды дифференцируема на сегменте [а, Ь], причём
г'(О X f" (0 т^ О ПРИ всех *i (а> ^)- Существуют по крайней % мере
два направления, которых не имеет касательная к данной линии.
Доказать, что любая прямая пересекает данную линию не более чем
в двух точках.
66**. Плоская линия задана уравнением r = r(t). Функция г(t)
определена и дважды дифференцируема на сегменте [а, Ь], причём
г' X г" сохраняет знак на указанном сегменте.
Кроме того, существует направление, которого не имеет ни одна
из касательных к данной линии. Доказать, что г' (tx) X г' (t%) имеет
определённый знак при условии
a^ti^t^-s^b.

ГЛАВА II
плоская линия -
Уравнение касательной к плоской линии r = r(t) пишется так:
если г' ф 0 и
если »
г' = г" = ... = И*-1) = 0, rW ф о.
В параметрической форме:
Х=х + \х\
У=У + *У'.
В более общем случае:
X = x+lx<k\
Уравнение нормали:
R = r + l[r']
или
(/? — г)г' = 0;
в координатах:
(*_^*' + (7--.у)/ = о,
или в более общем случае:
(Я —/■)/<*> = 0.
Если из точки О опустить перпендикуляры на касательные к линии С,
то их основания образуют, вообще говоря, линлю, называемую
подэрой линии С относительно точки О. Антиподэрой линии С
относительно точки О называется линия, подэра которой
относительно точки О есть линия С.
Если плоская линия задана уравнением r = r(t)y то для
построения её можно придерживаться следующей последовательности
действий:
16

I. Находим корни уравнения r"Xr" = 0. Пусть t = t9 — одия
из таких корней. Если ,
r'(«=r"(^) = .... = r(ft-»(/o) = 0, r<fe)(^0)^0,
r<*> (/,) X г <*+1> (/,) = rO» (t0) X И*+2> (*„) =.. .=/•<*> (*,) X И*-») (*в)=0,
и если:
1) k — нечётное,1 5 — чётное, то точка М (t0) — обыкновенная;
2) k — нечётное, s — нечётное; точка M(t0) — точка перегиба;
3)„ £ — чётное, s — нечётное, точка М (t0) — точка возврата
первого рода;
4) k — чётное, S-— чётное; точка M(tQ) — точка возврата
второго рода.
При всех остальных значениях t будем иметь г' X г" "Ф 0; все
точки линии, соответствующие значениям t, при которых rr X f" H^
обращается в нуль — обыкновенные (k=l9 s = 2).
II. Значения.^, соответствующие точкам, в которых линия вогнута
«вверх» (т. е. в сторону вектора у):
х'(х'у"— х'У)>0;
условие вогнутости «вправо» (т. е. в сторону вектора /):
у'(х'у"— УУ)<0.
III. Точки пересечения линии с, осями координат найдём,
разрешая уравнения x(t) = 0 (из этого уравнения найдём значения t,
соответствующие точкам пересечения линии с осью Оу) и y(t) = 0
(отсюда найдём значения t, соответствующие точкам пересечения
линии с осью Ох).
IV. Если х' ф 0, у' = 0, то в точке М (t) касательная параллельна
оси Ох, а если х = 0, у' Ф 0, то оси Оу.
V. Если lim^ = oo и если lim Z =k. (число!), lim (у — kx) = bt
t=t0 t t=t0 x t=t0
то прямая y = kx-\-b является асимптотой данной линии. Если
lim у= со и \\тх = т, то прямая х = т есть асимптота данной линии.
t—t§ t=tQ *
VI. Иногда выгодно произвести замену параметра, перейти
к полярным координатам. Полезно обратить внимание, если это
имеет место, на периодичность функции r{t) или на её
ограниченность, на периодичность или ограниченность функций x(t)y у (t)
и т. д.
Наконец, для бодее точного вычерчивания графика полезно
построить ряд обыкновенных точек линии, соответствующих
различным значениям t.
Алгебраической линией называется линия, определяемая
уравнением:
2 П. С. Моденов * 17

где F(x, у)— целая рациональная функция от ^ и у. Для
построения и исследования алгебраической линии следует иметь в виду
следующее:
— 1) Абсциссы точек пересечения линии с осью Ох определяются
из уравнения:
F(x, 0) = 0.
2) Ординаты точек пересечения линии с осью Оу определяются
из уравнения:
F(0, у) = 0.
3) В точках, координаты которых удовлетворяют условию
касательная параллельна оси Ох.
4) В точках, координаты которых удовлетворяют условию
dF п п n dF n
касательная параллельна оси Оу.
5) Координаты особых точек удовлетворяют соотношениям:
„ п OF п dF
причём для исследования характера точки (л;0, у0), координаты
которой удовлетворяют указанным соотношениям, можем поступить
так: разложить функцию F(x, у) по степеням х— х0 и у—у0.
Пусть
F (х, у) = 1 [(* — хл) ш + (у — уо) -fyjf7 (л:,, у о) -г
+ (T^i)![^-^)^ + 0'-v„)|rjfe+,F(^) у„) +
н- +
где k ^ 2. Рассмотрим первую неисчезающую форму:
[(x — xo)j^ + (У — У о) -^ ] *F G*o. У о)
относительно х — х0 и у—yQ. Эта форма разлагается в
произведение множителей вида
а(х — х0)+$(у—у0).
Пусть р — число множителей линейно-независимых с действительными
коэфициентами, имеющих нечётную кратность, a q —число указанных
множителей с действительными коэфициентами (q^p). Тогда через
18

точку (л;0, д>0) проходит не менее р и не более q простых
аналитических дуг *), касательные к которым получим, приравнивая нулю
формы а (х — х0) -\- |3 (у —у0) с действительными коэфициентами.
6) Если в некоторой точке выполнены условия: F(x0, у0) = 0
^7С*о> Уъ)Р'хх(Хь> y0) — 2F'x(x0f y0)F'v(x0t у0) ^С*о> .Уо)+
+ F% (xQ, y0) F'y'y (xQi y0) = 0,
F? (*o, Л) F'xxx (x0> Уо) — ър? (xo> У о) F'x C*0> У о) F'xxy (*0> У о) +
+ 3F; (xq, yQ) F'J (x0, y0) F'Jyy (x0i y0) — F'/ (x0, yj Fv'v'y (x0, y0) Ф 0,
причём F'x(x0, y0) и Fy(x0i y0) одновременно не равны нулю, то
точка (х0, у0)— точка перегиба,
7) В точках линии, где выполнено условие
Д = /\,
F
1 XX
F
XX
FY
F
1 XV
F
1 vv
/-•„
F*
fv
0
>o
линия вогнута „«вверх», а в точках, где А <^ 0, — «вниз».*
8) Необходимое и достаточное условие вогнутости «вправо:
F F F
1 XX g XV X
F F F
Г VX Г VV V
>0.
9) Пусть Fn(x,у) — форма наивысшей степени, входящая в состав
F (х, у). Пусть ku £2,...— простые корни уравнения F (1, &) = 0.
Тогда уравнения
^Fn(hk)
— уравнения асимптот; Fh_x{x, у) — форма степени п — 1, входящая
в состав F(x, у). Если уравнение FH(x> 1) = 0 имеет простой
нулевой корень, то уравнение
. , /V,(0,1)
= 0
*
определяет асимптоту, параллельную оси Оу.
В каждом отдельном случае применимы и другие соображения,
например: если F (х, у) — функция чётная относительно у, то линия
симметрична относительно оси Ох, а если она чётная относительно х,
то линия симметрична относительно оси Оу. Если F(x, у) — нечёт-
.*) Если функция г (t) разлагается в окрестности любой точки интервала
(а, Ь) в ряд Тейлора, т. е.
. r(t) = r(t0) + r'(t0)(t-t0)+^r"(t0)(t-t0r + ... + ~№
(сумма ряда определяется так же, как и в курсах математического анализа),
то говорят, что уравнение r = r{t) определяет аналитическую линию.
* 19

дх^
ди
дх
dv
ду
ди
ду
dv
ная (или чётная) функция по обоим аргументам, то линия
симметрична относительно начала координат; если F(x,y) — симметричная
^функция, то линия F (х>у) = 0 симметрична относительно прямой х=у.
Иногда удаётся разрешить уравнение относительно у или х9
иногда выгодно перейти к параметрическим уравнениям, к полярному
уравнению, произвести то или иное аффинное преобразование,
упрощающее уравнение F(x, y) = 0, и т. д.
Многие из соображений, указанных для построения
алгебраических линий, без всякого изменения переносятся и на любые линии,
заданные уравнением:
F(xty) = 0.
Дискриминантная линия семейства линий, заданных уравнением:
r = r(u) v)
(v — параметр линии в семействе, и — параметр точки на линии
семейства) определяется так: составляем уравнение
ди ' dv
или
= 0.
Если эту зависимость между а и v представить в виде:
u=u(t)} v = v(t)
или v=f(ii) или u = cp(v), то уравнение
r = r\n{t\v{t)\
или t = r{utf(u)} или г = г{ 9 (/£>)> v} и есть уравнение дискрими-
нантной линии. Если при и = и (t), v = v(t) частная производная ^~
не обращается тождественно в нуль, то дискриминантная линия —
огибающая. Если же указанная функция от t тождественно равна
нулю, то надо найти первую не обращающую тождественно в нуль
dkr
производную -г-£ при u = u(t), v = v(t) и сравнить полученный
вектор с производной г', взятой из уравнения дискриминантной линии.
Если
(—\ II '
то дискриминантная линия — огибающая, а если
(д*г\ ^ ,
то дискриминантная линия — не огибающая.
20

' Если семейство линии задано уравнением
F(xt уу г0 = 0,
то множество точек плоскости, координаты которых удовлетворяют
уравнениям:
F(x,y, v) = 0,d~ = 0,
называют также дискриминантной линией. Если в точках дискрими-
нантной линии частные производные
dF dF
ох ду
одновременно в нуль не обращаются, то дискриминантная линия
является ргибающей данного семейства линий.
Если две линии имеют общую точку (х0, у0), одна из линий
определена уравнением
F(x, у) = 0,
другая — уравнениями
x = x(t), v = y(0.
если точке (х0, v0) соответствует значение параметра /=/п и если
9('о) = 9'('о) = ф''('о) = ••• =9{/г)(*о) = 0, Ф^ + 'Ч'о^О,
где
9(t) = F{x(t)4 у(/)},
то в данной точке линии имеют соприкосновение &-го порядка.
Кривизна линии определяется соотношением:
_ |х'у" — х"у'\ _ \г' х г"|
Уравнением - %
или уравнениями:
Х = х — у'—пг
, х'* 4- V'8
v . ' X* + V'*
7 ' ху' —х'у
определяется эволюта данной линии r = r(t). •
Дуга (или криволинейная абсцисса, или натуральный параметр)
линии r = r(t) определяется соотношением:
t' t
21

ФормулУ
dt
ds = m>
dn .
выражающие производные от единичного касательного вектора t и
единичного нормального вектора п по натуральному параметру,
называются формулами Френе. Они играют основную роль при изу-
чении дифференциальных свойств плоских линий.
Соотношение
f(R, s) = o
или
/(*, s) = 0,
связывающее кривизну и дугу, называется натуральным уравнением
линии. Если на линии фиксирована точка и направление отсчёта
натурального параметра, то линия имеет вполне определённое
натуральное уравнение независимо от её положения на плоскости, и
*обратно: если дано уравнение /(х, s) = О, то на плоскости имеется
множество линий, конгруентных (т. е. наложимых друг на друга) и
таких, что начало отсчёта и направление отсчёта дуги также
совместятся при наложении линий.
Для отыскания параметрических уравнений линий по её
натуральному уравнению /(х, s) = 0 следует решить систему
дифференциальных уравнений v
da_
dx
— = cos a,
ds '
dy
5 = S1De'
где a — угол от единичного вектора оси Ох до единичного вектора /,
касательного к данной линии в произвольной точке. Если x = x(s),
то из первого соотношения найдём a = a(s)t а тогда два последних
определят х и у в функции 5. Возможно решение и с произвольным
параметром.
§ 1. Касательная и нормаль
67. Составить уравнение касательной и нормали к следующим
линиям:
1) г = \acost, bsint} (эллипс),
2) г={т(' + т)» у(^—у)} (гипербола),
3) A* = {acos3/, asin3* [ (астроида),
4) r=\a(t — sin;), a(l—cos t) } (циклоида),
22
i

5) r = {i-**-l*4, 1^ + |>}в точке t = 09
• 6) r = {acpcoscp, a^sin^} (спираль Архимеда).
68. Составить уравнение касательных и нормалей к следующим
линиям:
1) х*(х-\-у) — а1(х — у) = 0 в точке (0,0),
2) 2х% — jcV— Ъх-\-у + 7 = 0 в точке (1, —2).
69. Может ли касательная к кубической параболе у = хъ
составлять с осью Ох тупой угол?
70. В какой точке касательная к параболе у = х* образует
с осью Ох угол в 45°?
71. В каких точках с одной и той же абсциссой касательные
к линиям у = х* и у = хь параллельны?
72. Найти касательную к параболе у = х2, параллельную прямой
у = \х — 5.
73. Через фокус параболы проведена хорда, перпендикулярная
оси параболы. Доказать, что касательные к параболе, проведённые
в точках пересечения этой хорды с параболой, —
взаимно-перпендикулярны.
74. Составить уравнения касательных к линии
, - 1
у = х
* X
в точках пересечения её с осью Ох.
75. Составить уравнение нормали к линии
х*у — х*-{-Зх — 6 = 0
в точке с абсциссой х = 3.
76. Доказать, что только одна нормаль линии у = хп (п — целое
положительное число) проходит через начало координат.
77. Под каким углом пересекаются линии
х*-\-у* = 8, у* = 2х?
78. Под каким углом пересекаются линии
д^ + У' = 8*. j," = jiL?
79. Под каким углом пересекаются линии
^ = 4у, у = ^?
80. Доказать, что длина отрезка касательной к астроиде
111
хъ -f-y3 =a3 *
заключённого между осями координат, равна а.
81. Доказать следующий способ построения касательной к цеп-
X X '
ной линии у = — {еа-^-е а ): на ординате MN точки /VI, как на
23

диаметре, строим полуокружность, обращенную выпуклостью к оси
ординат; находим на этой полуокружности точку Р такую, что .
NP=a; прямая MP — касательная к цепной линии в точке М.
*82. Доказать, что отрезок касательной к трактриссе
у = -0\п хг у а*— х*, ■
заключённый между осью Оу и точкой касания, имеет длину,
равную а.
83. Доказать, что линия у == ekx sin mx касается каждой, из линий, •
y = ekx и у = — екх во всех общих с ними точках.
84.. Доказать, что. для любой точки М равносторонней
гиперболы х* — у* = а* отрезок нормали от точки Ж .до точки пересече- .
* ния с осью Ох равен отрезку ОМ.
85. Доказать, что для параболы r=asec-97> сумма углов,
образованных* касательной с радиусом-вектором и с полярной осью,,
равна 180°. Использовать это свойство для геометрического способа ' •
построения касательной к параболе." •
86. Доказать, что параболы r=.asec2 ~ и г— a cosec2 -^
ортогональны^
87. Доказать, что кардиоиды:
г=а (1 -f- COS9), r=a{\—coscp)
ортогональны. ;
88. Линия задана параметрическими уравнениями
"r=r(t), 9 = 9(0
в полярных координатах. Найти тангенс угла между касательной, w
радиусом-вектором точки касания.
89. Доказать, что нормаль к циклоиде в произвольной её точке М
проходит через точку касания Р „производящего круга" с прямой,
по которой катится этот круг. .
90. Плоская линия С в точке М0 имеет касательную. Пусть-
М^М^-—секущая, проходящая через точки Мх и Ж2 линии. Можно*
ли утверждать, что предельное положение прямой МХМ^ при
условии, . что точки Mj и Ж2 неограниченно приближаются по линии С .
к точке Ж0, есть касательная к линии С в точке М0?
91. Если на продолжениях радиусов-векторов линии С отложить,
отрезок заданной длины, то концы отложенных отрезков опишут
линию, называемую конхоидой линии С Составить уравнение
конхоиды С* линии С и найти вектор, 'определяющий касательную»
к линии С*. .^
92*. Составить уравнение линии, из точек которой данная
парабола видна под данным углом а. Рассмотреть случай а = -^-.
24 .'•*'■■

• 93**. Найти линию, обладающую тем свойством, что касательные,
•проведённые из любой точки этой линии к линия второго порядка
апх* -f- 2апху -f- а2<^у2 -\- 2ахх ~\- 2а%у -\- а = О,
образуют угол ср. Рассмотреть частные случаи:
1) линия задана каноническим уравнением;
. 2) ор = 90°.
94. Плоская линия задана уравнением r = r(t)\ функция г (ty
определена на сегменте [а, Ь]. При некотором значении t £ (а, Ь)
имеют место соотношения:
г1 (<,) = /■"(*«)= ... =г(*-0(<в) = о,г<*)С<0)^0.
Доказать, что вектор г(/е)(/0), коллинеарный касательной ■ к линии
в точке М0, направлен в сторону роста параметра, т.е. r(fe)(Y0) Дг^>0
-при всех t, больших t0 и достаточно близких к t0.
95*'*. Назовём" линией взаимно-однозначный и непрерывный образ
отрезка. Касательной / к линии С в точке уИ0 назовём прямую,
проходящую через точку М0 и обладающую следующим свойством:
если через точку Ж0 провести две различные прямые аир,
отличные от прямой /, то все точки некоторой части дуги линии в
окрестности точки М0 (кроме самой точки Ж0) попадут внутрь той пары
вертикальных углов, образованных прямыми а и (3, -в которых
проходит прямая /.
1) Доказать, что если линия С в точке М0. имеет касательную,
то только одну.
2) Что означает фраза:, «линия С " в точке М0 не имеет каса-
.тельной»? *
3) Доказать, что если линия С задана уравнением r = r(i), где
функция г {t) определена на сегменте [а, Ь\ и при значении t = t0£ (a,b)
имеют место соотношения: . / .
(в частности г' (t0) Ф 0), то линия С в точке Ж0 (t0) имеет
касательную и эта касательная коллинеарна вектору r{k)(t0).
4).Доказать, что касательной к линии в начале координат
{jc2 sin — , ■ если х Ф 0,
О, если л: = 0,
. является ось Ох.
5) Доказать, что линия, определяемая уравнением
\ х sin —, если х Ф 0
У = \ х
I 0, если х = 0,
в начале координат, не имеет касательной.
96. Пусть Ж Г—касательная к линии С в точке М. Доказать,
что если произвести любое аффинное преобразование, то образ М Т*
25

касательной будет касаться образа С линии С в точке М' (М' —
образ /И). Применить это положение к построению касательной
к эллипсу.
97. Плрская линия задана уравнением r = r{t)\ функция r(t)
определена в окрестности точки t = t0, причём
rVn)=r"(t0)= ... =r<*-'>(*0) = 0, /**>(*0)*0,
• • • =** (t0) X П*-*> (t0) = 0, r<*> (*0) X i**> (t0) ф 0.
Доказать следующее положение:
Расположение линии С в
достаточно малой окрестности
точки М0 относительно
касательной к линии С в точке М0
k
нечётное
нечётное
чётное
чётное
s
чётное
нечётное
нечётное
чётное
по одну сторону
переходит с одной
стороны на другую
переходит с одной
стороны на другую
по одну сторону
Расположение линии С в
достаточно малой окрестности
точки М0 относительно любой
прямой, проходящей через
точку Mq и отличной от
касательной к линии С в точке М9
переходит с одной
стороны на другую
переходит с одной
стороны на другую
по одну сторону
по одну сторону
3 а м е ч aja и е. . Мы будем говорить, что линия С в точке М0
расположена по одну сторону от прямой v, проходящей через
точку Ж0, если все точки дуги линии С в достаточно малой
окрестности точки Ж0, за исключением самой точки М0, расположены по
одну сторону от прямой v. Мы будем говорить, что» линия С в точке
М0 переходит с одной стороны прямой v на другую, если все точки
линии в достаточно малой левой окрестности точки М0, за
исключением самой точки Ж0, расположены по одну сторону от прямой.v,
а все точки достаточно малой правой окрестности точки Ж0, за
исключением самой точки Ж0, расположены по другую сторону от
прямой v.
§ 2. Точки перегиба. Выпуклость и вогнутость
98. Найти точки перегиба линии
у = jc4 — 12х3 + 48х2 — 50.
99. Доказать, что линия
У =
х+\
имеет три точки перегиба, расположенные на одной прямой.
100. Доказать, что если линия задана уравнением у—/(х) и
в точках х = хи х = х2(х1<^х%) функция f (х) принимает
экстремальные значения, то существует Е, xl<^t<dx2 такое, что точка
(£. /(0) является точкой перегиба данной линии. Функция,/(л:) имеет
.26

производные /' (х), /" (х), причем /" (х) обращается в нуль на
рассматриваемом сегменте в конечном числе точек.
101. Доказать, что точки перегиба линии
sin х
v=—
лежат на линии
y(jf4 _|_4) = 4.
102. Найти* точки перегиба линии
х = sin t, у = cos 2t.
103. Найти точки перегиба линии
х = ес, y — sint.
104. Найти точки перегиба улитки:
r=a +ft c'oscp (а>0, ft>0, а ф Ъ, афЩ.
105. Плоская линия задана уравнением r=r(t); функция r(t)
определена и дважды дифференцируема* на сегменте [я, Ь]у причём
г' Хг" ^ Ф °^е производные г' и г" непрерывны на сегменте [а, Ь].
Пусть а — произвольный, отличный от нуля вектор. Отложим его
от точки M0(t0) данной линии.
1) При каком необходимом и достаточном условии конец
отложенного вектора упадёт в сторону вогнутости данной линии в точке Ж0,
т. е. в ту полуплоскость от касательной к данной линии в точке Л40,
где расположена достаточно малая часть дуги данной линии в
окрестности точки Ж0.
2) Рассмотреть частные случаи выпуклости и вогнутости по
отношению к масштабным векторам i и у.
3) Дать ответы на поставленные выше вопросы в том случае,
если линия задана уравнением y=f(x).
106. Плоская линия задана уравнением r = r(t)\ функция r(t)
определена и дважды дифференцируема на сегменте [а, Ь], причём
г'у^г'фО при всех tt(a, b). Доказать, что единичный вектор
нормали к линии, направленный в сторону её вогнутости,
определяется соотношением:
[гг1 (г' х г")
п [ г' | | г' х г" |
107. Исследовать вогнутость линии y = s\nx «вверх» и «вниз»-
108. Плоская линия задана уравнением r = r(t); функция г (t)
определена на сегменте [а, Ь]. При некотором значении £0ё(а, Ь)
имеем: г (/0) = г" (*0)=... = И* - »(*0) = 0, r^(t0) Ф 0,
= rm (t0) X ^_1) (*о) = 0, И*> (*0) X ^ (*о) т* 0. причём 5 —чётное.
При каком необходимом и достаточном условии конец вектора
27

а, отложенного от точки М0 (/0), упадёт- в сторону вогнутости
данной линии? Рассмотреть случай, * когда линия задана уравнением
y^f(x\ причём f(x)^09f"(x)=f"'(x) = . • .=/(*)<^-» = 0,
/(•*) (х) ф О и 5 — чётное. .'
109. Плоская линия задана уравнением r = r(t); функция r(t)
определена и имеет непрерывные производные г и г" на сегменте
[а, Ь] причём/г' Хг" 7^ 0 при всех Ц [а, Ь]. Пусть
/—произвольная прямая, не проходящая через точку М (t) данной линии, МР_]_1У
точка Р лежит на прямой /. Будем говорить, что линия С в точке М
выпукла к прямой /, если точка Р лежит со стороны выпуклости
линии С в точке М.
1) При каком необходимом и достаточном условии данная
линия С выпукла к прямой /, заданной уравнением
р = р04-на?
2) Рассмотреть, частные случаи:
a) линия С задана уравнением у =/(х), причём/ '(х)Ф 0,/" (х)ф 0;
b) прямая / — ось Ох;
c) прямая /—ось Оу.
ПО. Исследовать выпуклость и .вогнутость синусоиды у = sin x
к осям Ох и Оу.
111. Как изменятся выводы задачи 1Q9, если прямая / задана
уравнением
Ах-±-Ву-{-С=0?
.112. Линия задана уравнением F (x, y) = Q, При каком
необходимом и достаточном условии, эта линия в точке (х, у) вогнута
в сторону вектора а, „вверх", „вниз", к оси Ох, к оси Ov?
113. При каком необходимом и достаточном условии линия,
определяемая уравнением F (ху у) = 0, вогнута к прямой
A* + £y + C = 0?
114. Линия задана уравнением у—.f (х), где функция f(x)
определена на сегменте [а, Ь] и имеет в каждой точке этого сегмента
производную порядка &^2, отличную от нуля. Доказать, что на
линии нет точек возврата. Как отыскать точки перегиба?
115. Пусть линия задана уравнением у=/(х),'гд.е функция f (х)
определена на сегменте [а, Ь\ и имеет в каждой точке этого
сегмента производную . порядка k ^ 2, отличную от нуля, . причём эта
функция определяется уравнением F (х, у) = 0 и в окрестности
исследуемой точки (jc0, у0) функция F (х, у) дважды
дифференцируема; кроме того, F (х0, у0) == 0, F'x (х0у у0) или F[> (x0, у0) Ф 0, и
точка (х0, у0) — точка перегиба; тогда F'y2 (х^, y0)Fxx(x{h у0)~
— 2Fx(x0y y0)F;(x0, y0)Fxy(x0, у«)-\-Рх2(х0У y0)Fyy(x0f У0) = 0
(необходимый признак точки перегиба).
116. Пусть линия задана уравнением у =/(*), где функция /(х)
определена на сегменте [а, Ь\ и имеет на этом сегменте
производив '." .

ные до третьего порядка включительно. Пусть эта функция f(x)
находится из уравнения F (х, у) = 0, где функция F(x, у) трижды
дифференцируема в окрестности точки (х0, у0), причём F(x0, y0) = 0,
но Р'х (х0, у0) или F'y (x0, у0) ф 0. Предположим, что
Fy2 (*о> У о) F*x (х9,у0) — ^Fx (*e> y0) F'y (x0 y0) F*y (xQt у0) -f
+ Р'х (xQ9у0) Fyy (х0,у0)=0, Fy (x0, y0)F'xxx W Л) —
— Зр;2(д;0, у0) F'x(x0, y0)Fxxy (x0, уй) +
+ Щ С*0» Л) F*2 (x99 y0) FXyy (x0i y0) — Fx (x0; y0) F'yyy (x0, у0) ф 0.
Тогда точка (х0, у0) является точкой перегиба линии.
§ 3, Исследование и построение линий
117. Исследовать линию r = {t* -\-t—б, f1 -f- St — 4} на особые
точки, на выпуклость и вогнутость: а) „вправо", Ь) „вверх", с) к оси
Ox, d) к оси Оу.
Найти точки пересечения линии с осями координат, точки, в
которых касательная параллельна оси Ох, оси Оу и т. д. Построить
линию.
118. Исследовать линию ^={^2, tl-\~tb}' в целом. Построить её.
{Ы- 5/3 1
'YjTJT~ > ТХТм в целом-
Построить её.
120. Исследовать линию
r={axt*+blt-\-cu a/> + V + ^b
121. Исследовать линию,
и построить её график.
{2 -1-12 t ^
гтг& > * ~Ь m* г •
123. Исследовать линию-
U2 + i > *2 + i j\
124. Исследовать линию
r=^{— 5t*-\-2t\ — 3^ + 2/3},
125. Исследовать линию /
_ f t — t* t2 — t*\
r— Yi + t* ' \ + t*lm
Записать уравнение этой линии в неявном виде, а также в
полярных координатах.
126.-Исследовать линию
. I /—'1 ' i* — 1 /•
29

127. Исследовать линию
i(t + 2f (*-2)Ч
I / + 1 > t—lf'
128. Исследовать линию
r—I l—/» ' \—t* Г
129. Найти асимптоты следующих линий:
,1>j'=c+(^'
2} v3 — oft jc3
-3) y*(x*+\) = x*(x*— 1),
4) У*=г6х24-хв,
5) 2з/(х+1)*2 = л:3,
6) Jcy2 + x*y = a3
7) y(*2 — 3^ + 2^2) = jc3-
8) л:(д:2+У) = аУ,
9) (**_у8)«_2а*(.*+.у)*
10) (jc2
► 11) 2jc4
У*)ч = д*(х*-{-у*)9
3ax* + a3,
-2£2(* — y)2 = 0f
x*y -f x2^2 — jcy3 — .y4 — 8x3 -f- If у —
— 8jcy2 + 2y3 + 8jc2-f 8У— 4 = 0,
12) бл3^ + 5* V — 6*y8 -f 12x3 — 6x*y — 2xy* -f
+ 12.У3 — 32x2 + Uxy — 16y2 — 16* + 48.У + 79
= 0.
130. Найти асимптоты следующих линий, заданных уравнениями
в полярных координатах:
1) гср = а (гиперболическая спираль),
2) r29 = a2 („жезл"), -
3) r = a sec 29.
131. Исследовать следующие алгебраические линии и построить
их:
1) jc6 — х4 + у* = о,
2) л;3 — 27(jt — Л2 = 0,
3) jc3—v2+l=0,
4) xk — v4 — 4х2у = 0,
5) х44-^4 —2ху = 0,
6) х44-У — х2— у9 = 0,
7) *34-У3 — 3*у = 0,
8) ^-^4з/3 = 0,
9) у54--*4— ху* = 0,
Ю) х4 — 6х*у 4- 25У — 16х2 = 0.
11) у2 (х2 — 4) 4- (**4- 4j/ — 4)* = 0.
§ 4. Подэры
132. Найти подэру эллипса относительно его центра.
133. Найти подэру гиперболы относительно её центра.
134. Найти подэру параболы относительно её фокуса.
135. Найти подэру эллипса относительно его фокуса.
136. Найти подэру гиперболы относительно её фокуса.
30

137. Составить уравнение подэры линии
ап^Ьп
относительно .начала координат.
138*. Доказать, что уравнение подэры линии г=>(/)
относительно начала радиусов-векторов можно записать в виде:
р = (т) п
или
где п — единичный вектор нормали данной линии.
139. Составить уравнение подэры линии y=f(x) относительно
начала координат.
140*. Доказать, что уравнение антиподэры линии г = r(t) можно
записать в виде: *
•1) Р^-лИ.
2) Р^+^И,
где t—единичный вектор касательной, a n=[t].
х^ v^
141. Составить уравнение антиподэры эллипса -, -f- ^ = 1
относительно его фокуса.
142. Найти антиподэру гиперболы относительно её центра.
143. Найти антиподэру параболы относительно её вершины.
144. Составить уравнение антиподэры линии y=f{x)
относительно начала координат.
145. Найти антиподэру эллипса относительно его центра.
§ 5. Огибающие
146. Найти огибающую семейства прямых, соединяющих концы
пар сопряжённых диаметров эллипса.
147. Найти огибающую семейства прямых, отсекающих от
сторон прямого угла треугольник неизменной площади.
148. На эллипсе берутся пары точек таких, что, соединив их с
центром эллипса, получим эллиптический сектор заданной площади 5*
Найти огибающую семейства прямых, проходящих через указанные
пары точек.
149. Найти огибающую семейства прямых, отсекающих от
данной параболы сегменты данной площади.
150. Из данной точки под разными углами к горизонту с одной
и той же (по модулю!) начальной скоростью выбрасываются
материальные точки. Найти огибающую траекторий (парабола
безопасности).
31

151. Найти огибающую семейства линий
(и — параметр точки на линии семейства, v — параметр линии в
семействе).
152. Найти огибающую семейства линий:
г= {и2 -\-v, и3},
(и — параметр точки на линии семейства, v — параметр линии
в семействе).
153*. Найти огибаюпхую семейства прямых, отсекающих от
сторон данного угла треугольник данного периметра.
154. Найти огибающую семейства окружностей, построенных,
как на диаметрах, на параллельных хордах некоторой- окружности.'
155. Произвольный радиус окружности проектируется на два её
взаимно-перпендикулярных диаметра и на проекциях,' как на
полуосях, строится эллипс. Найти огибающую построенного семейства,
эллипсов.
156*. Произвольный радиус-вектор эллипса проектируется по
направлению двух каких-нибудь его сопряжённых диаметров на эти
диаметры и на проекциях, как на сопряжённых полудиаметрах,
строится эллипс. Найти огибающую построенного семейства эллипсов. ,
157. Пусть О — центр симметрии равносторонней 'гиперболы, а
М — произвольная точка, лежащая на гиперболе. Отрезок ОМ
проектируется на асимптоты гиперболы, и на проекциях, как на
полуосях, строятся эллипсы. Найти огибающую построенного семейства
эллипсов. .
158*. Пусть О — центр гиперболы, а УН — произвольная её точка.
Проведём через точку М прямые, параллельные асимптотам
гиперболы, которые отсекут на асимптотах отрезки ОР и OQ. Построим
на отрезках ОР и OQ, как на сопряжённых полудиаметрах, эллипс.
Найти огибающую построенного семейства эллипсов.
159. Найти огибающую скоростей точек прямолинейного стержня
при мгновенном вращении этого стержня вокруг неподвижной точки-.
160. Найти огибающую скоростей точек окружности при
мгновенном вращении её вокруг точки, лежащей внутри окружности.
161. Найти огибающую различных .положений диаметра окруж- "
яости, катящейся без скольжения по прямой.
162*. Найти огибающую скоростей точек стержня произвольной
формы при мгновенном вращений этого стержня вокруг некоторой
точки.
163. Рассмотрим окружность С и внутри этой окружности —
точку F. Будем перегибать окружность так, чтобы „перегнутая"
часть дуги окружности проходила бы через точку F; найти
огибающую „линий сгиба" (прямые линии).
164. Даны две концентрические окружности радиусов а и Ь.
Строится семейство окружностей, центры которых расположены на
окружности радиуса Ъ, а радиусы равны а. Строится второе семей- «
.32

ство окружностей, центры которых расположены на окружности
радиуса а, а радиусы равны Ь. Доказать, что оба семейства
окружностей имеют одну и ту же огибающую и найти эту огибающую.
. 165. Отрезок неизменной длины / скользит своими концами по
двум взаимно-перпендикулярным прямым. Найти огибающую
семейства прямых, на которых расположены отрезки.
166. Найти огибающую семейства эллипсов, имеющих общие
главные оси и заданную сумму полуосей. *
167. На зеркало, имеющее сферическую форму, падает пучок
параллельных лучей. Найти огибающую отражённых лучей (каустика).
168. Найти огибающую семейства эллипсов, имеющих заданную
площадь и общие главные оси.
169. Найти огибающую семейства эллипсов, имеющих заданную
площадь и два общих сопряжённых диаметра.
170. Найти огибающую семейства окружностей, проходящих
через вершину параболы х* = 2ру и имеющих центры на этой
параболе.
171 *. Найти огибающую семейства окружностей, имеющих центры
на эллипсе и проходящих через один из его фокусов.
172*. Найти огибающую семейства окружностей радиуса а с
центрами на линии r = r(v).
173*. Найти огибающую нормалей линий г = г (v).
Вектор-функция r(v) определена, непрерывна и дважды дифференцируема на
сегменте [а, Ь]. В каждой точке этого сегмента г и г" неколлинеарны.
174. Найти огибающую семейства прямых, каждая из которых
проходит через основания перпендикуляров, опущенных из
произвольной точки параболы на её ось симметрии, и касательную в
вершине.
175. Найти огибающую лучей, отражённых от окружности, если
светящаяся точка находится на окружности.
176*. На радиусах-векторах линии r = r(v)f как на диаметрах,
построены окружности. Доказать, что огибающая этого семейства
окружностей есть подэра данной линии относительно начала
радиусов-векторов.
177*. Составить уравнение огибающей семейства нормалей к
данной линии, взяв уравнение семейства в виде:
(#— г)г' = 0.
178. Найти огибающую семейства окружностей, построенных, как
на диаметрах, на хордах параболы и проходящих через её фокус.
179. Прямая вращается с^ постоянной угловой скоростью вокруг
точки, равномерно движущейся по прямой. Найти огибающую.
180. Найти огибающую семейства окружностей, построенных на
фокальных радиусах-векторах данного эллипса.
181. Найти огибающую семейства окружностей, построенных,
как на диаметрах, на фокальных радиусах-векторах данной гиперболы.
182. Найти .огибающую семейства окружностей, построенных,
как на диаметрах, на фокальных радиусах-векторах данной параболы.
3 П. С. Моденов 33

183. Найти огибающую семейства прямых, отсекающих от двух
взаимно-перпендикулярных прямых Ява отрезка, сумма длин которых
задана.
184*. В одной плоскости-расположены две оси координат Охи
Оу. Найти огибающую семейства прямых, каждая из которых
проходит через точки М и М'у лежащие соответственно на осях Ох и
Оу и имеющие равные координаты:
М(х\ М'(у), х=у.
185*. Найти огибающую семейства прямых, проходящих через
точки М и М двух окружностей—таких, что разность дуг О'М' и
ОМ — одна и та же для всех прямых семейства.
§ 6. Соприкосновение плоских линий
186. Вершиной линии называется точка, стационарная для радиуса
соприкасающейся окружности (в частности точка локального
экстремума радиуса соприкасающейся окружности). Найти вершину линии
у = \пх. *
187. Найти соприкасающуюся окружность равносторонней
гиперболы ху=1, радиус которой имеет минимальное значение.
188. Вычислить радиус соприкасающейся окружности в произ^
вольной точке линии второго порядка:
апх* -f 2anxy -f- а22У* -f ^а\х + 2а2У + а = 0.
189. Пусть М — точка циклоиды, а Р соответствующая точка
«производящего круга»; продолжим отрезок MP на расстояние
РС=МР\ доказать, что С — центр соприкасающейся окружности
циклоиды в точке Ж.
190*. Доказать, что при аффинном сдвиге плоскости относитель- у
но касательной МТ к линии С в точке М мы получим новую
линию С, имеющую* в точке М ту же соприкасающуюся окружность.
19Г*. Исследовать изменение соприкасающейся окружности в
точке М линии С при аффинном сжатии этой линии к касательной
МТ, проведённой к линии С в точке М.
192. Пользуясь результатом предыдущей задачи, найти
построением центры соприкасающихся окружностей для эллипса в его
вершинах.
193*. Пользуясь результатом задач 190 и 192, найти
построение центра соприкасающейся окружности в произвольной точке
эллипса.
194. Вычислить радиус соприкасающейся окружности гиперболы.
х% v8
~—4s=l в ее вершине и дать геометрический способ построения
центра соприкасающейся окружности. Рассмотреть частный случай
равносторонней гиперболы х*—у* = а*.
34

195*. Найти геометрический способ построения центра
соприкасающейся окружности в произвольной точке гиперболы.
196. Вычислить радиус соприкасающейся окружности параболы
в её вершине и дать геометрический способ построения центра
соприкасающейся окружности.
197 *. Дать геометрический способ построения центра
соприкасающейся окружности в произвольной точке параболы.
198*. Линия С дана уравнением r = r(t)\ вектор-функция r(t)
определена и трижды дифференцируема на сегменте [а, Ь], причём
г'^г'фО при всех ti [а, Ь]. Назовём вектор v = 3r"(r'XO —
— г'(г.' X г") вектором аффинной нормали линии С в точке Мг
Доказать, что если этот вектор не перпендикулярен касательной к \
линии С в точке Ж0, то соприкасающаяся окружность линии С в
точке Ж0 пересекает линию С.
199*. Доказать, что если линия С задана уравнением r = r(f),
функция r(t) имеет производные до четвёртого порядка
включительно на сегменте [а, Ь], причём в точке М0 выполнены следующие
условия:
ГоХ^о'^0, r'v=0,
V = ЗГо' (Го X Го) — Го (Го X П"\
(го X го) (4г0 г0' + Зг0'2) — (го X rf) г02 ф О,
то соприкасающаяся окружность не пересекает линии С в
достаточно малой окрестности точки М0.
200*. Пусть линия С задана уравнением r = r(t)\ функция r(t)
определена и имеет производные до третьего порядка включительно
на сегменте [а, £], причём г' X г" Ф 0 ПРИ всех id [а, Ь]. Пусть R —
радиус соприкасающейся окружности линии С в точке М. Доказать,
что если —ф0, то линия С в точке М пересекает соприкасающуюся
окружность.
201. Найти вектор аффинной нормали
v = 3r"(r'XO— r'(r'Xr")
для следующих линий:
1) r={acost9 bsint} (эллипс),
2) г==={х('+4)' х(*—г)} (гипеРбола^
3) у = ах* (парабола),
4) у = \пх
и определитьх расположение соприкасающейся^ окружности
относительно линии в каждом случае.
202. Доказать, что окружность (х— с£?-\-(У — я)3 <г = 0 и
парабола j/" Ъх-\- j/ Зу = 2 -\f а имеют в точке (-^-9 4)
соприкосновение третьего порядка.
35

203. Дана полуокружность АКВ, имеющая центр в точке (а, 0)
и радиус г. Соединить начало координат О и В параболой так, чтобы
окружность и парабола в точке В имели бы соприкосновение
наивысшего порядка (см. чертёж 85 к, ответу этой задачи).
204. Найти гиперболу, касающуюся вершиной линии у = 1 —cos*
в начале координат и имеющую наивысший порядок
соприкосновения.
205. Найти эллипс, касающийся вершиной циклоиды
r={l(t — sin/), X (1—cos/)} и имеющий в точке касания
наивысший порядок соприкосновения.
206. Линия у=/(х) касается оси Ох в начале координат.
Функция y=zf(x) при х = 0 имеет производные первого и второго
порядка. Составить уравнение параболы, касающейся данной линии в
начале координат и имеющей наивысший порядок - соприкосновения.
207. Составить уравнение параболы, касающейся вершиной
косинусоиды y = cosx в точке (0,1) и имеющей наивысший порядок
соприкосновения. Определить этот порядок соприкосновения.
208*. Составить уравнение параболы, касающейся линии у = \пх
в точке (1,0) и имеющей в этой точке с данной линией
соприкосновение наивысшего порядка. Определить этот порядок.
209. Доказать, что линии y = sinx и Y = xi—-^ -\- х имеют
в начале координат соприкосновение третьего порядка.
210. Найти линию у = а0-^- ахх-\- а^х* -)- ...-j- anxn, имеющую с
данной линией y=f(x) в точке (0, /(0)) соприкосновение п-го
порядка.
211**. Найти линию, на которой расположены фокусы парабол,
касающихся данной линии в данной точке и имеющих в этой точке
с данной линией соприкосновение второго порядка.
212**. Уравнение всякой параболы, проходящей через начало
радиусов-векторов, можно записать в виде:
• (гХя)2 + 2гХ* = 0,
где а -ff д. Исходя из этого уравнения, составить уравнение
соприкасающейся параболы к линии r = r(t) в данной на ней точке,
считая, что эта точка является началом радиусов-векторов. Функция г (t),
определена и трижды дифференцируема на сегменте [а, Ь\ и
г'У^г'ф'О при всех ti [а, Ь].
213**. Пусть линия r — r(t) проходит через начало радиусов-
векторов; функция r(t) определена и имеет производные до четвёр- ,
того порядка включительно на сегменте [а, Ь\. Рассмотрим
уравнение линии второго порядка
аЛ1х* -j- а^ху -f- а^у* -j- 2atx -f- 2a^y = 0,
также проходящей через начало координат. Это' уравнение можно
переписать так:
х(апх-{- а12у) -f у (апх -f- а22у) + 2 (ахх + а^у) = 0
36

или г Ф г -f- 2аг = 0, где Фг — линейная вектор-функция вектора
г={х, у\, Фг=\апх~\-а1гу, апх~\-а^). Исходя из уравнения
гФг-\-2аг=0 линии второго порядка, найти линию второго порядка,
имеющую с данной в начале радиуров-векторов соприкосновение
наивысшего порядка.
214. Как определить характер соприкасающейся линии второго
порядка в произвольной точке линии у=/(х)? Функция f(x)
определена, непрерывна и имеет производные до четвёртого порядка на
сегменте [а, Ь]; при этом /' (х) ф 0.
215. Определить типы соприкасающейся линии второго порядка
в произвольной точке следующих линий:
l)y = sinx (синусоида),
• 2) у = \пх,
3) у = — (гипербола),
4) у = хпу где п zfz 0 и п ~ф. 1,
X X
5) у = у (еа -\-е а) (цепная линия).
216. Определить тип соприкасающейся линии второго порядка
в произвольной точке следующих линий:
1) r = {a(t — sin*), a (I-.— cos*)} (циклоида),
2) r=\a (cost -|-*sin*), a (sin*—*cos^)}
(эвольвента окружности), *
3)r={^i"°cos^*'Й^8!п^^'(клотойда)- •
217. Линия задана уравнением г = г (ф) в полярных координатах.
Определить тип соприкасающейся линии второго порядка для этой
линии в произвольной её точке.
218. Определить тип соприкасающейся линии второго порядка
в произвольной точке спирали Архимеда: г=ау.
219. Определить тип соприкасающейся линии второго порядка
в произвольной точке кардиоиды r=a (1-f-cos9).
220*. Составить уравнение линии, которую образуют центры
соприкасающихся линий второго порядка для линии, заданной
уравнением г = г(*); функция г(*) определена и имеет производные, до
четвёртого порядка включительно на сегменте [а, Ь]; при этом
г'Хг'фО.
221*. Найти огибающую аффинных нормалей* линии r^=r(t).
Функция г (*) определена и имеет производные до четвёртого порядка
включительно на сегменте [а, Ъ\,
222*. Доказать, что производная от радиуса-вектора
р=г+-рзг?^г'1
* Аффинной нормалью линии С в точке М называется прямая,
проходящая через точку М и имеющая направление вектора аффинной нормали
•линии С в точке М (см. задачу 198).
37

центра соприкасающейся окружности линии r = r(t) определяется
соотношением:
<= [f] ;(г«)8/« у
223**. Плоская линия задана уравнением r = r(f). Функция r(t)
определена на сегменте [а, Ь] и имеет на этом сегменте производные
до третьего порядка включительно.. Кроме того, во всех точках этого
сегмента г' у^ г' ^Ь 0 и радиус соприкасающейся окружности является
монотонной функцией от L Доказать, что из двух любых
соприкасающихся окружностей одна вложена в другую.
224. Составить уравнение соприкасающейся линии второго порядка
для линии, заданной уравнением y = f(x).
225. Составить уравнение соприкасающейся линии второго порядка
для цепной линии
в её вершине, т. е. в точке (0, а).
226. Найти линию, аффинные нормали которой имеют неизменное
направление.
227*. Доказать, что центры линий . второго порядка, имеющих
с данной линией в данной точке соприкосновение третьего порядка,
расположены на аффинной нормали линии в рассматриваемой точке.
228. Составить4 уравнение параболы, ось которой параллельна:
1) оси Ох, 2) оси Оу, и которая с окружностью х*-\-у*^Ь имеет
в точке (1,2) соприкосновение второго порядка.
229*. Найти линию, на которой располагаются центры
равносторонних гипербол, имеющих в данной точке с данной линией
соприкосновение второго порядка.
230*. Линия y=f(x) касается оси Ох в начале координат.
Составить уравнение равнобочной гиперболы, проходящей через начало
координат и имеющей с данной линией в данной точке
соприкосновение третьего порядка.
231**. Назовём касательной окружностью к линии С в точке М
окружность, касающуюся в точке М касательной МТ к линии С
в точке М. Соприкасающейся окружностью линии С в точке М
назовём касательную окружность 5 (радиуса R) к линии С в точке Ж,
обладающую следующим свойством: если провести две любые
касательные окружности к линии С в точке М — одну радиуса Ri<^R,
другую радиуса R%^>R и расположенные по ту жб сторону от
касательной, что и окружность S, то достаточно малая-часть дуги
линии С в окрестности точки М будет лежать вне окружности радиуса
/?t и внутри окружности радиуса /?2 (точка М исключается!). Исходя
из этого определения, доказать:
1) единственность (т. е. доказать, что если в точке М линия С
имеет соприкасающуюся окружность, то только одну);
38

' 2) найти координаты центра соприкасающейся окружности и её
радиус, предполагая, что уравнение линии задано в векторно-пара-
метрическом виде: r = r(t)\ функция r(t) определена и имеет
производные г' и г" на сегменте [а, Ь], причём г' Xг" Ф О ПРИ всех
К [я, Ь]\
3) доказать, что прямая линия в любой своей точке не имеет
соприкасающейся окружности;
4) доказать, что линия у = \/xg в начале координат не имеет
соприкасающейся окружности;
5) доказать, что любая линия С в точке перегиба и в точке
возврата первого рода не имеет соприкасающейся окружности.
§ 7. Кривизна
232. Вычислить радиусы кривизны следующих линий:
1) y = sinx в вершине (синусоида),
2) х = а (1 -j- m) cos mt — am cos (1 -\- m) t,
y = a(l -\-m) sin mt — am sin (1 -\-m)t (эпициклоида),
x
3) у ==a ch— (цепная линия),
4) х*у2 — (аА— у*)ф+у? (конхоида),
5) г2 = a* cos 2cp (лемниската),
6) г=а(1-\-coscp) (кардиоида),
7) г = аф (спираль Архимеда),
8) r=\ttcos* ty a sin8*} (астроида).
233. Найти кривизну гиперболы ху = 4 в точке (2,2).
234. Найти кривизну параболы у* = Sx в точке (-g-, 3) .
235. Найти кривизну линии (у — х)* = х* в начале координат.
236. Найти кривизну следующих линий:
1) у = — In cosx,
2) х=Ы*, y=3t — t* при /=1,
3) х = a (cos t-\-tsint)t у = а (sin / — t cos t) при t = у,
4) х = а(2 cos t— cos2t), y = a(2sin t — sin 2t).
237. Доказать, что радиус кривизны параболы х* = 2ру равен
где а — угол касательной к параболе с осью Ох.
cos* a
238. В каждой точке некоторой линии задана производная ~ =
= ф(х, У)- Вычислить радиус кривизны линии в произвольной точке.
239. Линия,задана уравнением F(x9 y) = 0. Вычислить её радиус
кривизны в произвольной точке.
240. По какой формуле следует вычислять радиус кривизны линии,
заданной уравнением в полярных координатах: г=г(ф)?
241. По какой формуле следует вычислить радиус кривизны линии,
заданной параметрическими уравнениями r=r(t), ф = ф(£) в
полярных координатах?
39

242. Найти кривизну следующих линий, заданных в полярных
координатах:
1) г=аф,
2) r=acpk,
3) r=a,v в точке ср = 0.
243. Доказать, что кривизна лемнискаты: г2 = о} cos 2ф
пропорциональна г.
244. Вершиной линии называется точка, в которой кривизна
принимает экстремальное значение; найти вершины следующих линий:
1) /1+/^=/а,
2) у = е*,
3) r=asm3y.
245. Задано поле: р = {Х(х, у), Y (х, у)} векторов, касательных
к линиям однопараметрического семейства (дифференциальное
уравнение семейства: Xdy— Ydx = 0). Найти радиус кривизны линии
семейства; проходящей через точку (х, у).
246*. Найти радиус-вектор р центра касательной окружности
к линии r = r(t) в точке М (t), проходящей через точку Мх {t -f- iU)y
и найти lim р. В заданной точке г Xг" Ф О-
д* = о
247**. Решить предыдущую задачу, предполагая, что в точке М
имеют место соотношения:
г' = г" =... = г<* - 1>= 0, г<*> ф 0. "
248**. Доказать, что если линия задана уравнением y=f(x) и
в некоторой точке /" (х) — 0, то в этой точке не существует
соприкасающейся окружности в смысле предыдущей задачи (если 2k = sf
то соприкасающейся окружностью будем называть окружность, центр
которой совпадает концом вектора
(г(к)Г^ (2k)! [г{%
fik) х ^2k) 2 (k \f
отложенного от точки М). ^
249*. Плоская линия задана уравнением r = r(t)\ функция r(f}
определена и имеет непрерывные производные г' и г" на сегменте
[а, Ь]. Найти острый угол со между касательными к линии в точках
М (t) и М (t -\- M) и доказать, что
,. «> \Г' X Г"\
(х — кривизна линии в точке М).
250. Плоская линия задана уравнением г = /•(/); функция r(t)
определена и дважды дифференцируема на сегменте [a, h);
производные г' и г" непрерывны на этом сегменте и г' X г" Ф 0- Условимся
40

считать, что данная линия в точке имеет правую ориентацию, если
репер г',г" —правый (т. е. если г' X /"" ^> 0), и левую в противном случае.
Будем называть ориентированной кривизной х данной линии в точке М
число, абсолютная величина которого равна кривизне линии в точке М
и которое положительно, если линия в точке М имеет правую
ориентацию, и отрицательно в противном случае; если кривизна линии С
в точке М равна нулю, то условимся считать х = 0. Найти формулу,
определяющую ориентированную кривизну х данной линии. Дать
различные геометрические интерпретации понятия ориентации линии
в данной точке. Какой вид принимает формула для ориентированной
кривизны, если линия задана уравнением y=f(x) (функция f(x)
определена, непрерывна и дважды дифференцируема на сегменте [а,Ь ])?
251. Плоская линия задана уравнением r = r(t)\ функция r(t)
определена и имеет производные г, г", г'" на сегменте [а, Ь], причём
в некоторой точке М0 (t0) имеем:
r'(t0)Xr"(t0) = 0f гЧ*о)Хг"'(*о)^0.
При каком необходимом и достаточном условии линия С имеет при
t<^t0 правую ориентацию, а при t^>t0 — левую (имеется в виду
достаточно малая окрестность значения t = t0)?
252. Найти ориентированную кривизну линий:
1) r=={a(t — sin/), a(l—cos^)},
2) r = {t\ П
3) y = s'mx,
4) y=\nx,
5)y=ach^.
§ 8. Эволюта и эвольвента
253. Составить уравнения эволют следующих линий и сделать
чертежи:
1) r=\acost, bsint} (эллипс),
2) г = {х, ах2} (парабола),
з) г=а [*+т) • i [*- т)} (™пеРб°ла).
4) у = sin х (синусоида),
5) у = \пх,
6)jy = e*
7) r=a(l-(-COS9) (кардиоида),
8) r={a(t — sin/), a(l—cqsf)} (Циклоида),
9) r={acos3£, asin3^} (астроида),
x
10) у = a ch — (цепная линия),
11) (jc2+y)2 — аЦх*— у*) = 0 (лемниската).
254. Линия задана полярным уравнением г= г(ф). Составить"
уравнения её эволюты.
41

255. Составить уравнения эволюты линии, заданной
параметрическими уравнениями r=r(t)y cp — cp'(t) в полярных координатах.
256*. Составить уравнение эволюты линии
о
257. Составить уравнение круга кривизны для линии
С*2+У)-*— 2ау* = 0
в точке (а, а).
258. Доказать, что эволюта логарифмической спирали г =а* есть
та же спираль, но повёрнутая на некоторый угол вокруг полюса.
Можно ли подобрать а так, чтобы эволюта.совпала с данной линией?
259. Найти длину всей эволюты эллипса с полуосями а и Ь.
260. Составить уравнение эволюты спирали Архимеда г = аср.
261**. Исследовать число нормалей, которые можно провести из
точки Р(х0, у0) к эллипсу ^4-|г=1-
262**. Исследовать число нормалей, которые можно провести из
х2 у2
данной точки Я(лг0, у0) к гиперболе -^—-—-=1.
263**. Исследовать число нормалей, которые можно провести из
данной точки 'к параболе.
264. Сколько нормалей из данной точки плоскости можно
провести к эвольвенте окружности?
265. Исследовать число нормалей, которые можно провести из
данной точки к кардиоиде.
^266**. Найти радиус-вектор точки пересечения нормалей к линии
r = r(t) в двух её точках M(t) и M(t-\-kt) и затем найти limp.
Функция r(t) определена и дважды дифференцируема на сегменте
[а, £],. причём г'у^г"ф0 при всех t£ [а, Ь].
267. Составить уравнение эвольвент окружности.
268. Найти эвольвенты параболы х2 = 2ру.
269. Найти эвольвенту цепной линии, проходящую через вершину
цепной линии
r={alntg(! + 4),<sb}.
270. Найти эвольвенты спирали Архимеда г = щ.
§ 9. Длина дуги
271. Вычислить дугу следующих линий:
1 l)y = ach~9
2) у = х8'*,
3) У = х\
42

S4) y = \nx,
5) r = a (1 -j-coscp),
6) r=\a(t — sint), a (I — cos/)},
^7) r=\a(cost-^-tsint), a (sin/— /cos/)},
8) r = jy (2 cos / + cos 2/), -j (2 sin / + sin 2/)},
9) r={acos3/, a sin3/},
11) r=la (In ctg у — cos Л , a sin /1
272**. Найти lim ' Ar,lA""'As| ,
273. Найти предел при As = 0 отношения расстояния 8 от точки
М' (s -f- As) линии до касательной к этой линии в точке М (s) к квадрату
дуги ММ'.
274. Найти длину дуги циссоиды у2 (а — х) = хг от начала
координат до какой-нибудь её точки (х, у).
275. Найти длину дуги одного завитка спирали Архимеда г=ау.
276. Доказать, что для цепной линии у = a ch — проекция
ординаты каждой, её точки на касательную в этой точке равна длине дуги,
отсчитанной от вершины (0, а).
277. Найти длину дуги линии:
X = —/' (a) sin а —/" (a) Cos a,
у =f (a) cos a —f (a) sin a.
§ 10. Натуральные уравнения
278. Составить натуральные уравнения линий, указанных в
задаче 271.
279. Найти параметрические уравнения линий, зная их
натуральные уравнения:
3) Rs = a\
44)/? = a+f,
5) s2 + 9/?2=16a2,
6) $■ + #*= 16a*f
v 7) /?« = 2as,
8) #*-fa« = a«* a.
S2
280*. Зная натуральное уравнение /? = a -( цепной линии,
составить натуральное уравнение её эволюты.
43

281*. Знал натуральное уравнение следующих линий, составить
натуральное уравнение эволют этих линий:
1) R = as (логарифмическая спираль),
52 R2
2) -ji + £2 = ! (эпициклоида),
3) Rs=a2 (клотоида),
4) s2-f 9/?2=16а2 (улитка),
5) s2 *\-R2 = 16а* (циклоида),
6) /?2 = 2as (эвольвента окружности),
7) /?2 -\- а2 = а*е а (трактрисса).
dR '
282*. Исходя из соотношений р = /?--, o = R, связывающих
радиус кривизны р эволюты и её дугу а с радиусом кривизны R
эвольвенты и её дугой s (см. № 297), составить натуральное уравнение
эвольвенты по натуральному уравнению эволюты:
1) р = С (окружность),
с2
2) р = а-| (цепная линия),
3) р2 -f- a2 = а2 (циклоида),
4) р = а<з (логарифмическая спираль),
5) ро = а2 (клотоида).
283. Дано натуральное уравнение линии: а=/(р). Составить
натуральной уравнение её эвольвенты.
284. Дана линия a2-j-p2 = £a (трактрисса). Исходя из
результата предыдущей задачи, составить натуральное уравнение её эволюты.
285*. Составить натуральное уравнение второй эвольвенты
окружности.
286*. Найти линию r = r(s), эволютой которой является линия
?=[г].
287**. Составить натуральное уравнение линии r = r(s)y для
которой эволюта определяется уравнением р == [г] -f-t.
288**. Дано натуральное уравнение s = s(x) линии. Составить
натуральное уравнение линии p = f-\-an, «параллельной» данной,
считая, что 1 — ах ^> 0.
§ 11. Применение формул Френе
289**. Взяв уравнение эвольвенты линии r=r(s) в виде p = r — st,
доказать, что эвольвента встречает эволюту точкой возврата первого
рода.
290**. Если в некоторой точке эвольвенты радиус кривизны R
dR d2R
отличен от нуля: R z/z 0, затем -г- = 0, но —г-^ -ф 0„ то этой точке на
эволюте соответствует точка возврата первого рода.
44

291**. Пусть в некоторой точке эвольвенты *0 = 0, ia ф О* (точка
перегиба). Доказать, что нормаль к эвольвенте в этой точке служит
асимптотой эволюты.
292**. Доказать, что если в некоторой точке эволюты х0 = 0>
i0^0 (точка перегиба) и если этой точке эволюты r = r(s)
соответствует точка на эвольвенте р = г — st, в которой s = sQ-tQ, то
эта точка является точкой возврата второго рода.
293*. Эвольвента встречает эволюту в точке перегиба последней.
Доказать, что эта точка встречи является точкой перегиба и
эвольвенты.
294**. Доказать, что точке. перегиба линии (х0 = 0, щ ф 0)
соответствует на, её подэре точка возврата первого рода.
295*. Исследовать особые точки линии р = г -j— an(a = const),
«параллельной» линии r = r(s).
296*. Выразить кривизну линии Съ описываемой концом
единичного касательного вектора t к линии С, через кривизну линии С.
297*. Выразить кривизну эволюты линии С через кривизну
эвольвенты.
298*. Линия задана уравнением r=r(s). Её эволюта определяется
уравнением p = r-\-Rn. Составить уравнение второй эволюты (т. е.
уравнение эволюты линии p = r-{~Rn).
299*. Составить уравнение третьей эволюты.
300*. Найти кривизну второй эволюты (см. задачу 298). /
301*. Найти радиус кривизны третьей эволюты.
302*. Дана линия r = r(s). Рассмотрим линию р = г -\- at
Доказать, что прямая, соединяющая точку Р (р) с соответствующим центром
кривизны линии r = r{s), является нормалью к линии p=p(s).
303*. Пусть М — произвольная точка линии r = r(s)y
Р—соответствующая точка её второй эволюты, Q — центр кривизны линии С
в точке М, а 5—середина отрезка MQ. Доказать, что касательная
к линии, описываемой точкой S, ортогональна прямой MP.
304*. На линии С взята точка М. Построен соответствующий
центр кривизны К и от него отложен в определённо выбранном
направлении отрезок АГР, пропорциональный (с постоянным
коэффициентом пропорциональности) радиусу кривизны линии С в точке М.
Когда точка М движется по линии С, точка Р описывает линию Сг.
Доказать, что касательная, проведённая к линии Сх в точке Р,
проходит через точку М.
305*. Пусть р — расстояние от начала радиусов-векторов до
касательной к линии С в точке М, а г—расстояние от точки О до
точки М. Доказать, что
306*. В некоторой точке линии f-—r(s) имеем: х0 ф 0, х0 ф 0.
* Точкой мы будем обозначать производные по дуге: х = —, г = —
45

Взяв уравнение соприкасающейся окружности в виде:
(р — r0 — R0noy2 = /?o, доказать, что соприкасающаяся окружность
пересекает данную линию в окрестности указанной точки.
307*. В некоторой точке линии выполнены условия: /0 ф 0, х0=0,
х0 -ф. 0 (экстремум кривизны, вершина). Доказать, что соприкасающаяся
окружность линии в этой точке не пересекает дуги линии в
достаточно малой окрестности рассматриваемой точки.
d*A dR
308*. Доказать, что если на интервале a^s^b, -г- или -г-
сохраняют знак (радиус кривизны изменяется, монотонно), то две любые
соприкасающиеся окружности вложены одна в другую.
309. На нормалях данной линии откладывается отрезок
неизменной длины (от точки линии, скажем, в сторону вогнутости).
Доказать, что линия, описываемая концом отложенного отрезка, имеет
нормаль, общую с данной линией.
310*. Дана гладкая замкнутая линия С, являющаяся
непрерывным и взаимнооднозначным образом окружности. Пусть Cj — линия,
«параллельная» и находящаяся на расстоянии а от линии С.
Выразить длину дуги линии Cj через длину дуги линии С при условии,
что ориентированная кривизна линии С удовлетворяет неравенству
1+я*>0.
311**. Выразить площадь, ограниченную линией С1 (см.
предыдущую задачу), через площадь, ограниченную линией С, через длину
линии С и через ширину полосы, ограниченной линиями С и СА.
312. Доказать, что ф/-й?х = 0.
313*. Составить уравнение соприкасающейся параболы (гХ#)2~Ь
-f- 2 (г X Ь) — 0 линии r = r(s) (начало радиусов-векторов помещено
в исследуемую точку).
314*. Найти вектор v —3r" (r X r") — r(r'Xr'") аффинной
нормали линии, заданной уравнением r = r(s).
315*. Какой- вид примет уравнение соприкасающейся параболы
(3/0jc -f- x^)2—18х03у = 0, если за масштабные векторы приняты
векторы *0 и v0 = 3xgn0 — х/0. ~ f
316*. Найти тангенсы углов, образованных касательной к линии
r = r(s) в какой-либо её точке и аффинной нормалью в той же точке.
'317*. Найти линию, в каждой точке которой, аффинная нормаль
совпадает с обычной нормалью.
318*. Найти линию, аффинная нормаль которой составляет
постоянный угол с касательной.
319**. Составить уравнение гФг-}-2аг = 0 соприкасающейся
линии второго порядка для линии, заданной уравнением r = r(s)
(начало радиусов-векторов помещено в исследуемую точку данной
линии).
320*. Какой вид примет уравнение соприкасающейся линии
второго порядка, если за координатный репер принять
46
*о> v0 = Зхбл0 — х/0.

321*. Доказать, что соприкасающаяся линия второго порядка
в данной точке линии х = х($){или R = R(s)\ будет эллипсом,
если 8 = 94 — 5x§-j-3x0x0 ;>0, гиперболой, если 8<^0, и параболой,
если 8 = 0. Доказать, что вместо указанного выше выражения можно
рассматривать следующее: 9-j-^o — 3/?0/?0.
322*. Найти линию, описываемую центрами соприкасающихся
линий второго порядка для линии r = r(s). 4
323*. Найти огибающую аффинных нормалей линии r = r(s).
324*. Будем называть эллиптической точкой линии такую её точку,
в которой соприкасающаяся линия второго порядка является эллипсом,
гиперболической, если соприкасающаяся линия второго порядка —
гипербола, и параболической, если соприкасающаяся линия —
парабола. Определить характер точек следующих линий, заданных своими
натуральными уравнениями:
s2
1) R = a-\ (цепная линия),
2) s2 + jR2=16a2 (циклоида),
3) R* = 2as (эвольвента окружности),
4) R^==as (логарифмическая спираль),
5) Rs==ai (клотоида),
6) -2+£а = 1 (эпициклоида).
325. Преобразовать выражение
(4)
326. Дано уравнение R=f(a), где R— радиус кривизны линии,
а a — угол от постоянного вектора а до касательного к линии
вектора t Составить параметрические уравнения линии.
327. Дано уравнение a=f(R) (см. предыдущую задачу).
Составить параметрические уравнения линии.
328. Даны уравнения R = R(t), a = a(£) (см. задачу 326).
Составить параметрические уравнения линии.
329. Составить параметрические уравнения линий, для которых
1) # = -V. 2)^=^4-, 3) Rs=a**f
' cos2 о' ' sin* a9 y '
4) R = aay 5) /? = asin/wa, 6) /?=asina,
7) R = p- — (см. задачу 326).
(1—е*СОааа)/8
330. Дано уравнение s = /(a), где s — дуга, а a— угол от
постоянного вектора а до вектора t, кабательного к, линии. Составить
параметрические уравнения ^инии.
331. Дано уравнение a = f(s) (см. предыдущую задачу).
Составить параметрические уравнения линии.
47

332. Даны уравнения s==s(t), a==a(t) (см. задачу 330).
Составить параметрические уравнения линии.
333. Составить параметрические уравнения линий, j для которых
1) s = aat 2) s = atga, 3) s = aea,
4) s=-Kacili 5) s = a cos ay 6) s= a cos та (см. задачу 330).
334. Пусть М — произвольная точка линии, а
Р—соответствующая точка ее подэры относительно начала О радиусов-векторов.
Обозначая через а угол от произвольного вектора е до касательного
вектора t к данной линии в точке Му а через о — дугу подэры,
доказать, что do = rdoif где г=ОМ, ' -
335*. Доказать, что нормаль к подэре в точке Р делит пополам
отрезок ОМ, где О — точка, относительно которой строится подэра,
а М — точка антиподэры, соответствующая точке Р.
336*. Если в некоторой точке М0 антиподэры х0 = 0, х0 ф 0 и
касательная к антиподэре в этой точке не проходит через ту точку,
относительно которой берётся подэра, то точке М0 антиподэры
соответствует точка возврата первого рода на подэре.
337**. По линии С (основание рулетты), заданной уравнением
r=zr(s) (s — дуга), катится без скольжения линия 2,
уравнение которой в начальном положении: р = р(о) (о — дуга). Составить
уравнение линии (рулетта), описываемой точкой М (а), неизменно
связанной с линией 2 (производящая рулетту).
338*. Решить предыдущую задачу, считая, что линия С задана
уравнением y=f(x), а линия 2 — уравнением Y = F(x); при этом
линии С и 2 касаются (в их начальном положении) в точке с
абсциссой х=±х0. Рулетта описывается точкой (а, (3). относительно
плоскости, в которой задана линия у =f (x).
339*. Доказать, что нормаль к рулетте проходит через точку
касания линий С и 2 (см. задачу 337).
340*. Парабола У = аХ* катится по оси Ох. Составить уравнение
линии, которую описывает фокус катящейся параболы.
341*. По параболе у=ах* катится парабола У =— аХ*.
Составить уравнение линии, описанной вершиной катящейся параболы.
342**. Линия 2 катится без скольжения по линии С; точка М (а),
связанная с линией 2> описывает при'этом рулетту.
Обозначая через х и k кривизны линией 2 и С в
соответствующих точках, доказать, что радиус* кривизны рулетты (в
соответствующей точке) определяется соотношением:
(k *а)\ а рI3 *-i
А=-гг—Ч- ' , ; r-,nxev—единичный вектор нормали линии У.
(k — x)|a— p|2+(a—p)v * ^
343*. Доказать, что касательная к ,рулетте в точке встречи её
с линией С, по которой катится линия 2» производящая рулетту,
является нормалью линии С.
344*. Линия 2 катится без скольжения по линии С. Пусть М0 —
точка встречи этих линий, х0 и к0 — кривизны линий 2 и С в точке Ж9.
Доказать, что если х0 ф k0 и 2х0 ф kQ, то точка М0 является точкой
48

возврата первого рода на рулетте, которую описывает точка М0
линии £ ПРИ её качении по линии С.
345**. Из начала радиусов-векторов на линию r = r(s) падает
пучок светящихся лучей. Составить уравнение огибающей
отражённых лучей (каустика).
346**. Доказать, что каустика относительно начала радиусов-
векторов для линии r = r(s) есть эволюта линии, точки которой
получаются симметричным отражением начала радиусов-векторов в
касательных к этой линии.
'347*. Какой вид примет уравнение каустики линии относительно
начала радиусов векторов, если уравнение линии дано в виде г = f (t)?
348**. Дана линия С. Рассмотрим точку О плоскости. Пусть М —
произвольная точка линии С. Построим окружность с центром
в точке М и радиусом ОМ. Доказать, что каустика линии С
относительно точки О есть эволюта огибающей указанного семейства
окружностей.
349**. На линию, заданную уравнением r = r(s), падает пучок
параллельных лучей, имеющих направление вектора е(\е\=1).
Составить уравнение огибающей лучей, отражённых от данной линии
(каустика). Рассмотреть случаи, когда линия задана уравнением r=r(f)
и когда она задана уравнением y=f(x).
350*. Составить уравнения (параметрические) каустики линии
y=f(x), если на неё падает пучок лучей, параллельных: 1) оси Ох,
2) оси Оу.
v 351*. Найти каустику для пучка лучей, перпендикулярных оси
параболы х* = 2ру-\-р*.
352**. Плоская нить находится в силовом поле; р — силовая
плотность („сила на единицу длины нити"), Т — натяжение нити.
Условием равновесия нити с закреплёнными концами является соотношение:
(которое легко разъяснить, рассматривая элемент нити и замечая,
что он находится в равновесии под действием сил: Т„—(Т-\-dT)
и pds) (см. черт. 115 к решению). Найти линию прогиба однородной
нити под действием силы тяжести.
353**. По какой линии располагается нить, находящаяся под
действием вертикальной нагрузки, равномерно распределённой по
горизонтали ?
354**. Замкнутая нить находится под действием нормально
распределённой нагрузки р, пропорциональной в каждой точке
ориентированной кривизне х линии. Доказать, что нить находится в
равновесии.
4 П. С. Моденов
49

ГЛАВА III
ПРОСТРАНСТВЕННАЯ ЛИНИЯ
Указания
Если линия задана уравнением r=zr(t), причём в исследуемой
точке векторы г и г" неколлинеарны, то:
1) уравнение касательной:
или
или
или
Х= х-\-\х,
Z=z+lz';
2) уравнение нормальной плоскости:
(/?—г)г' = 0
(Х-х) х' + (Y-y)y' + {Z-z)z":
3) уравнение бинормали:
/?=г + х'[г>"]
X=x + \(y'z' — /V),
Y=y-\-\(z'x" — z"x),
Z=z + \(x'v"—x"y');
4) уравнение соприкасающейся плоскости:
(R—r)r'r" = 0
■0;
или
X — х Y—y Z-.
х' у' £ | = 0;
х" у" г"
5) уравнение главной нормали:
/?=r+A [[r'r"]r']
50

или
X
У=у4-х( х'
Z=z-\-\i у
z' x'
z"x"
x у
x"y'
y'z'
y"z"
-У
— z'
— x
x' y'
х"у"
y'z' 1
y"z' 1
z'x' 1
z"x"
}■
}■
}■
Отметим, что вектор [[r'r"] г'] направлен в то полупространство от
спрямляющей, где расположена линия С; поэтому при определении
репера t, ny b Френе линии С в точке М надо вектор п выбирать
одинакобо направленным с вектором [[r'r"] r'].
6) уравнение спрямляющей плоскости:
(/? — r)r'[r'r"]=0
или
= 0.
Х—х
У-У
Z — z
х' у' z'
У z
y"z"
z'x'
z"x"
х'у'
х"у"
Кривизна линии вычисляется по формуле:
_ lfr'r"l!
|Г'|
или
V
y'z'
y"z"
2
г' х'
z"x"
+
х' у'
х'У
(х" -f у'2 4- 2/2)3/а
Кручение вычисляется по формуле:
О:
или в координатах*:
r'r г
X у 2"
х" у" z"
г"У"г'"
Формулы:
у' zk I2
y'V I
i = хя,
z' x'
I 2r"x" I "T I AT"yM
6 =
-оя,
выражающие производные по дуге от единичных векторов £, п, b
репера Френе через эти векторы, называются формулами Френе
\t—единичный вектор касательной, п — единичный вектор главной
нормали, направленный в то полупространство от спрямляющей
плоскости, где расположена линия, и b — единичный вектор
бинормали, b = [ttl\).
51

Соотношения: ,
% = x(s),
0 = 0 (s),
выражающие кривизну и кручение через дугу s, называются
натуральными уравнениями линии. Натуральные уравнения определяют
линию с точностью до положения в пространстве, однако отыскание
линии по её натуральным уравнениям в общем случае приводит
к дифференциальному уравнению типа Рикатти, и, следовательно,
задача отыскания параметрических уравнений линии по ее
натуральным уравнениям, вообще говоря, в квадратурах неразрешима.
Спроектируем линию С в соприкасающуюся плоскость этой линии,
взятую в точке Ж. Пусть С*— эта проекция, aS—соприкасающаяся
окружность линии С* в точке М\ тогда 5 называется
соприкасающейся окружностью к линии С в точке М. Прямая, проходящая
через центр соприкасающейся окружности 5 линии С в точке М
перпендикулярно соприкасающейся плоскости линии С в точке Ж,
называется осью кривизны линии С в точке М,-
§ 1. Касательная. Главная нормаль. Бинормаль.
Нормальная плоскость. Соприкасающаяся плоскость.
Спрямляющая плоскость. Кривизна. Кручение
355. Составить уравнения касательной к линии 2x*-\-3y'i-\-z<2 = 47i
л;2-f 2у2 = 2 в точке (—2, 1, 6).
356. Составить уравнения касательной к линии х*-{-у* = z* 9
х=у в точке (*0, уй, z0).
357. Составить уравнения касательной к линии
г ^ £ t2 1
r~ IT' 3"' 2J
в произвольной точке.
358. Составить уравнения касательной к линии, определяемой
уравнениями: y*-f-29=25, х*-\-у*=10 в точке (1, 3, 4).
359. Составить уравнение соприкасающейся плоскости каждой из
следующих линий:
1) у% = х, x*=z в точке (1, 1, 1),
2) у = 9(х), z = ay(x)-\-by
3) x* = 2az> y==2fe,
4) x* + z*=a\ у*-\-г* = Ь\
5) r={e*, e"\ t/2}.
360. Составить уравнения главной нормали и бинормали линии
у* = ху x* = z в точке (1, 1, 1).
361. Составить уравнения главной нормали и бинормали линии
r — 1-j, о", у| в произвольной точке.
52

•tit
362. Доказать, что линия r= { £*^ cos£, е^2 sin/, е^2 \ лежит на
конусе х*-\-у* = г* и пересекает его образующие под углом 45°.
363. Дана винтовая линия
г = {a cost, a sin/, bt\.
Составить уравнения касательной, нормальной плоскости, бинормали,
соприкасающейся плоскости, главной нормали, спрямляющей
плоскость. Найти векторы t, n, b репера Френе. Вычислить кривизну,
кручение.
364. Дана линия r={/, £3, t*-\-4\. Составить уравнения
касательной, нормальной плоскости, бинормали, соприкасающейся плоскости,
главной нормали и спрямляющей плоскости в точке £== I. Найти
в той • же точке кривизну и кручение, ,а также векторный репер
Френе (t, n, b).
365. Дана линия г={£2, 1—1$ t'6}. Составить уравнения
касательной, нормальной плоскости, бинормали, соприкасающейся
плоскости, главной нормали, спрямляющей плоскости в произвольной
точке и в точке * = 1. Найти векторы t, пл b в произвольной точке
и в точке *=*1. Найти кривизну и кручение в произвольной точке
и в точке t = 1.
366. Дана линия r=\sint9 cost, tgt}. Составить уравнения
касательной, нормальной плоскости, бинормали, соприкасающейся
плоскости,, главной нормали и спрямляющей плоскости в точке £=-т-»
Найти в той же точке репер 'Френе t, n, Ь, кривизну и кручение.
367. Дана линия х*-\-у* -]-z2 = 3, х*-\-у* = 2. Составить
уравнения касательной, нормальной плоскости, бинормали, соприкасающейся
плоскости, главной нормали, спрямляющей плоскости этой линии
в произвольной^ точке и в точке (1, 1, 1). Найти векторы /, п, b
репера Френе в произвольной точке и в точке (1, 1, 1). Вычислить
кривизну и кручение в произвольной точке и в точке (1, 1, 1).
368. Составить уравнения касательной прямой и нормальной
плоскости для линии, заданной пересечением двух поверхностей:
F{x.y> *) = 0f Ф(х9 у, г) = 0.
369. Линия, по которой пересекается сфера с круглым цилиндром,
в два раза меньшего радиуса, причем цилиндр проходит через
центр сферы, называется линией Вивиани. Составить уравнение
линии Вивиани в неявной и параметрической форме. Найти уравнения
касательной, нормальной плоскости, бинормали, соприкасающейся
плоскости, главной нормали, спрямляющей плоскости. Найти репер
Френе этой линии t, n, b, а также кривизну и кручение.
370. Доказать, что линия:
/■=Wa + M + *i, «МЧ-^ + с,, ^-4V+^K
плоская, и составить уравнение той плоскости, в которой она
расположена.
53

371. Вычислить кривизну и кручение линии x2 = 3jy, 2xy = 9z.
372. Найти кривизну и кручение линии х2 —у1 -\-zl — l, у1—2х-\-
-[-2-=0 в точке (1, 1, 1).
373. Вычислить кривизну и кручение линии
у^ = х, x* = z.
374. Определить кривизну и кручение линии
х2 = 2azy У = 2bz.
375. Найти кривизну и вручение следующих линий:
l)r = -U — sin£, 1—cos£, 4sin-^i,
2) r={e\ е~\ t/2],
3) r={2t, In*, f2},
4) r = {etsinty e'cost, el\,
5) r=\3t —1\ 3t\ 3* + *3},
6) r=]cos3*, sin3*, cos2t\.
376. Вывести формулы для вычисления кривизны и кручения
линии, заданной уравнениями у=у(х), z = z(x), и найти репер
Френе этой линии.
377. Доказать, что линия r = { atgt, bcost, bsint} расположена
на линейчатой поверхности второго порядка. Составить уравнение
этой поверхности и доказать, что данная линия пересекает
прямолинейные образующие одной из серии под прямыми углами.
378*. Найти линии, пересекающие прямолинейные образующие
гиперболического параболоида xy — az под прямым углом.
. 379. Линия, расположенная на сфере и пересекающая все
меридианы сферы под данным углом, называется локсодромией.
Составить уравнение локсодромии. Найти векторы £, пг b репера Френе
этой линии в произвольной точке, вычислить её кривизну и кручение.
380. Дана линия r={vcosu, v sin и, kv}, nxev = v (и).
Доказать, что эта линия расположена на конусе. Определить функцию v (и)
так, чтобы эта линия пересекала бы образующие конуса под
постоянным углом 6.
381*. В каждой точнее линии r = r(t) задан касательный вектор
7= Т(р) Ф 0. Функция г (t) определена, непрерывна и имеет
непрерывную производную г' ф 0 на сегменте [а, Ь]. Функция T(t) непрерывна
на сегменте [а, Ь]. Доказать, что на данной линии можно ввести
такую параметризацию, при которой -j = T.
382*. Назовём касательной к линии С в точке М прямую /,
проходящую через точку М и обладающую следующим свойством:
если построить любой конус второго порядка с вершиной в точке Му
внутри которого проходит прямая /, то внутрь этого конуса попадёт
достаточно малая часть дуги линии С в окрестности точки М.
Доказать, что если линия С задана уравнением r — r{t)y причём
функция г (t) определена и дифференцируема на сегменте (а, Ь) и имеет
54

в точке Ж производную г, отличную от нуля, то линия С в точке Ж
имеет касательную и эта касательная коллинеарна вектору г.
383*. Линия С задана уравнением r = r(t)\ функция r(t)
определена на сегменте [а, Ь], причём в некоторой точке этого сегмента
имеет место условие:
г'=г"= ... =r<*-i>==:0, г<*>^0.
Доказать, что линия С имеет касательную в точке Ж, и
составить её, уравнение (см. задачу 382).
384**. Линия С определена уравнением r = r(t); функция r(t)
определена на сегменте [а, Ь].^В некоторой точке Ж имеют место
соотношения
/■<*> || /ЧА+D || ... || г**-1* %/•<*>.
Далее: векторы г*5-*"1*, г(5+2), ... , г^—Х) компланарны векторам r^s)
и г(/г), но векторы г(/г), r<s), r^ — некомпланарны. Построим в точке Ж
следующие три прямые: касательную а, произвольную прямую (3,
лежащую в соприкасающейся плоскости линии С в точке Ж,
проходящую через точку Ж и отличную от касательной а, наконец —
произвольную прямую у, проходящую через точку Ж и не лежащую
в соприкасающейся плоскости. Определить расположение линии С
в окрестности точки Ж относительно репера, образованного
прямыми а, (3, у (в зависимости от чётности или нечётности чисел &, s, q).
385*. Начертить проекции линии на грани репера Френе в каждом
из восьми случаев, рассмотренных в предыдущей задаче.
386**. Линия С в точке Ж имеет касательную. Назовём
касательной плоскостью к линии С в точке Ж плоскость, проходящую
через касательную к линии С в точке Ж. Соприкасающейся*
плоскостью к линии С в точке Ж назовём касательную плоскость тс
к линии С в точке Ж, обладающую следующим свойством: каковы бы
ни были две различные касательные плоскости аир линии С в точке Ж,
отличные от плоскости тс, все точки достаточно малой части дуги
линии С в окрестности точки Ж расположены внутри той пары
вертикальных углов, образованных плоскостями а и Р; в котором
проходит плоскость тс (точка Ж исключается).
1) Доказать, что если линия С имеет в точке Ж соприкасающуюся
плоскость, то только одну.
2) Доказать, что если спроектировать линию С на какую-нибудь
плоскость так, что касательная к линии С в точке Ж спроектируется
в точку, то касательной к проекции будет проекция на ту же
плоскость— соприкасающейся плоскости.
3) Что означает фраза: «линия С в точнее Ж имеет касательную,
но не имеет соприкасающейся плоскости»?*
4) Доказать, что линия ЛВС (АВ и ВС — дуги двух
окружностей, лежащих на соседних гранях куба и касающихся ребра BD
в точке В) в точке В не имеет соприкасающейся плоскости
{см. черт. 121 в решениях).
55

5) Линия Q задана уравнением г = r (Y); некоторой точке М (t)
функция г (t) имеет производные г'и г" и эти производные неколлинеарны.
Доказать, что линия С в точке Ш имеет соприкасающуюся плоскость —
эта плоскость проходит через точку М и компланарна векторам г' и г\
387*. Линия задана уравнением r = r(t)\ функция r(f)
определена на сегменте [а, Ь]. В некоторой точке М имеют место
соотношения: г'=г"= ... =И*-1> = 0,-г<л)^0;
r(k) || г(* + 1) || _ || Г(5-1) ^ r(S\
Доказать, что линия С в точке М имеет соприкасающуюся плоскость*
и составить её уравнение (см. задачу 386).
388*. Линия С задана уравнением r = r(t); «функция r(t)
определена и непрерывна"на сегменте [а, Ь]. В некоторой точке М
функция имеет неколлинеарные производные г' и г". Найти
hm — •
[г'Дг]
f ,. ,. - единичный вектор, перпендикулярный' касательной
плоскости к линии С в точке М (t), проходящей через точку М1 (t -f- &t)~
389*. Линия С задан'а уравнением r = r(t); функция r(t)
определена на сегменте [а, Ь]. В некоторой точке М функция г (t) имеет
производные г', г", г'", прилзм эти производные некомпланарны..
Доказать, что соприкасающаяся плоскость линии С в точке М
пересекает линию С.
390*. Доказать, что если все соприкасающиеся плоскости линий
проходят через одну и ту же точку, то линия плоская.
391**. Линия С задана уравнением r = r(t)\ функция r(t)
определена на сегменте [а, Ь] и имеет на этом сегмента производные г*
и г", причём г'%г". Пусть МТ—касательная к данной линии
в точке М. Рассмотрим окружность, касающуюся прямой МТ
в точке М и проходящую через точку Мх (t-\-At) линии С. Пусть К —~
центр окружности. Найти lim MK=p- Если отложить вектор р от
точки М, то, его конец определит некоторую точку Кг Окружность^
проходящая через точку М и имеющая центр в точке Л"0, называете*
соприкасающейся окружностью данной линии в точке М.
392*. Назовём касательным круглым цилиндром линии С в точке М
круглый цилиндр, касающийся бинормали линии С в точке М.
Соприкасающимся круглым цилиндром линии С в точке М назовём
касательный круглый цилиндр П линии С в точке М, который
обладает следующим свойством: если построить два касательных круглых
цилиндра IIj и П2, касающихся цилиндра П внутренним образом, —
один (ilj) радиуса меньшего, чем радиус П, другой (П2) радиуса
большего, чем радиус Ц, то все точки части дуги линии С в
окрестности точки М будут расположены внутри цилиндра П2 и вне
цилиндра П|. Доказать, что соприкасающийся круглый цилиндр
линии С в точке М пересекает соприкасающуюся плоскость линии С
56

в точке М по соприкасающейся окружности проекции С* линии С
на соприкасающуюся плоскость.
393*. Линия С задана уравнением r = r(t); функция г (t)
определена на сегменте [а, Ь]. В некоторой точке M(t) функция r{t)
имеет производные г', г", г'", причём г % г". Найти
it
Jim
где 8 — расстояние от точки M(t -\~ Ы) линии до соприкасающейся
плоскости линии С в точке М. Рассмотреть частный случай, когда
линия задана уравнением r = r(s).
394**. Найти необходимое и достаточное условие, при котором
данное семейство прямых г = р (и)-{-\е (и) имеет огибающую, и найти
эту огибающую ( | е | = 1).
395. По какой линии пересекают касательные к обыкновенной
винтовой линии плоскость, перпендикулярную к образующим цилиндра,
на котором расположена винтовая линия?
396. При каком значении b кручение винтовой линии
r = \ a cos t, a sin t, bt\ (a = const)
имеет максимальное значение?
397. Доказать, что если в некоторой точке М линии С кручение
отлично от нуля, то соприкасающаяся плоскость линии С в точке М
пересекает линию С.
§ 2. Применение формул Френе
398. Выразить г, г, "г через ty n, b, x и о.
399. Доказать, что формулы Френе
i — ш, п = — y.t-\-oby 6 = — an
можно записать в виде:
*=((!>/], п=:[юп], b=[<ab]-
Найти вектор со (вектор . Дарбу) и выяснить его кинематический
смысл.
400. Доказать, что tbb=za.
401. Доказать, что bbb = a*( — X.
402. Доказать, что it *=х5( — V.
403**. Доказать, что если главные нормали линии образуют
постоянный угол с направлением вектора е, то
ds d a ' »
х
ds x
57

и обратно: если выполнено последнее соотношение, то главные
нормали линии образуют постоянный угол с направлением некоторого
вектора. Найти этот вектор.
404. Доказать, что если все нормальные плоскости линии содержат
вектор е, то данная линия или прямая, или плоская.
405*. Доказать, что если все соприкасающиеся плоскости линии С
(С — не прямая линия!) содержат один и тот же вектор, то линия
плоская.
406**. Доказать, что если касательная к линии образует
постоянный угол с определённым направлением .(линия откоса), то
отношение кривизны к кручению постоянно. Обратно: если отношение
кривизны к кручению для некоторой линии постоянно, то касательные
к линии образуют постоянный угол с некоторым определённым
направлением. Найти это направление.
407*. Доказать, что линия х2 = Зу, 2ху = 9z — линия откоса.
Найти вектор, с которым касательные к данной линии образуют
постоянный угол.
' 408*. Доказать ,что если спрямляющие плоскости линии содержат один
и тот же вектор, то рассматриваемая линия является линией откоса.
Доказать обратное положение и найти вектор, которому коллинеарны
все спрямляющие плоскости линии откоса.
409*. Доказать, что если бинормали неплоской линии образуют
постоянный угол с вектором е = const, то данная линия является
линией откоса, и обратно.
410*. Доказать, что годограф бинормали линии откоса —
окружность.
411*. Доказать, что если все спрямляющие плоскости проходят
через одну и ту же точку, то отношение кручения к кривизне есть^
линейная функция дуги:
— = as 4- b.
412. Доказать, что если b = const, то линия плоская.
413. Доказать, что если соприкасающиеся плоскости линии имеют
один и тот же наклон, то линия плоская.
414. Доказать, что линии откоса характеризуются соотношением:
(4)
rrr = 0.
415*. Доказать, что: 1) если различные линии имеют в
соответствующих точках общие бинормали, то они плоские; 2) главные
нормали линии С являются бинормалями линии С*. Доказать, что
х = \ (х2 -f- о2), где \ = const.
416**. Доказать, что если две линии С и С* имеют общие
главные нормали" (линии Бертрана), то кривизна и кручение линии С
(также и линии С*)ч связаны линейной зависимостью:
Хх -{- \io == 1
(Х = const, \ь = const).
58

417**. Доказать, что если кривизна и кручение линии связаны
линейной зависимостью:
Ьс -\- jkj = 1,
где X и \i — числа, отличные от нуля, то существует линия С*,
имеющая с линией С общие главные нормали.
-418. Доказать, что линия с постоянным кручением и кривизной
есть обыкновенная винтовая линия.
419. Доказать, что линия с постоянной кривизной является линией
Бертрана.
420**. Найти кратчайшее расстояние $ между двумя главными
нормалями линии r = r(s) в точках М0 (s0) и М (s) и найти
hm - -
•*«*0|s —s0|-
421**. Линия С задана уравнением r = r(s). Функция г (s)
определена на сегменте [а, Ь\ и имеет на этом сегменте производные до
четвёртого порядка включительно; г%г при всех s£ [a, b]. Найти
кратчайшее расстояние 8 между бинормалями линии С в точках M(sQ)
и М (s) и найти
lim .
s=s0 I s - s01
422**. Линия С задана уравнением r = r(s). Функция r(s)
определена на сегменте [а, Ь\ и имеет на этом сегменте производные до
четвёртого порядка включительно; при этом г % г. Найти кратчайшее
расстояние 8 между касательными к данной линии в точках Ж0 (%)
и M(s) и найти предел
lim
s=So is —sol*-
423. Выразить кривизну линии р = г (s) -f- \b(s) (к = const)
через кривизну и кручение линии r = r(s).
424**. Назовём эвольвентой неплоской линии r = r(s) линию
р = г — st. Выразить кривизну и кручение этой линии через кривизну
и кручение линии r — r(s). Доказать, что если линия r = r(s) —
линия откоса, то линия р = г — st плоская.
425*. Составить уравнение линии С*, по которой пересекаются
соприкасающаяся плоскость данной линии С в точке М0 с
касательными к этой линии С и найти кривизну линии С* веточке М0.
426**. Поверхность образована касательными к линии С.
Составить уравнение линии С*, по которой пересекается эта поверхность
с нормальной плоскостью к линий С в какой-либо её точке М0.
Доказать, что если в точке М0, xe'i£ 0, о0 ф 0, то точка М0 является
для линии С точкой возврата первого рода и касательной к линии С
в точке М0 является главная нормаль линии С в точке Л10.
427**. Дана линия С. Поверхность П образована касательными
к линии С. Линия С* получается при пересечении поверхности П
спрямляющей плоскостью линии С в какой-либо её точке Ж0. Дока-
' 59

зать, что если в точке уИ0 кривизна и кручение линии С отличны
от нуля, то точка М0 является точкой перегиба линии С*.
428**. Поверхность образована главными нормалями линии С.
Линия С* получается при пересечении этой поверхности
соприкасающейся плоскостью линии С в какой-либо её точке М0. Доказать,
' * 2 * •
что х0 =-тг х0, где х0 — кривизна линии С в точке Ж0, а х0 —
кривизна линии С* ^в той же точке.
429*. Найти lim р, где р — радиус-вектор точки пересечения
, S^Sq
нормальной плоскости в какой-либо точке M0(s0) линии r — r(s)
с главной нормалью этой линии в точке М (s).
430**. Поверхность образована главными нормалями линии С.
Линия С* получается при пересечении этой поверхности с
нормальной плоскостью линии С в какой-либо её точке Ж0. Найти кривизну
линии С* в точке Ж0*, соответствующей точке М0 (точка Ж*
определяется радиусом-вектором р0 = r0 -f- -^ — см.. предыдущую задачу).
Рассмотреть частный случай: линия С имеет постоянную кривизну.
431**. Поверхность образована бинормалями линии С. Линия С*
получается при пересечении этой поверхности соприкасающейся
плоскостью линии С в какой-либо её точке Ж0. Доказать, что
кривизны линий С и С* в точке Ж0 равны.
432*. Пусть С—пространственная линия, заданная уравнением
/v=r(s), а С*— её проекция в соприкасающуюся плоскость линии С
в какой-нибудь её точке Ж0. Найти вектор аффинной нормали линии С*
в точке Ai0.
433*. Пусть t0, n0, ^0 —репер Френе линии r=r(s) в какой-
либо её точке Ж0 (s0). Составить уравнения проекции этой линии на
. грани репера Френе и исследовать их в окрестности точки М0,
считая х0 ф 0, а0 ^ 0. *
434*. Линией С\ «параллельной» линии С, называется линия,
имеющая с линией С общие нормальные плоскости. Составить
уравнение линии С, зная p = p(s)—уравнение линии С.
435*. Доказать, что центры кривизны линии С*, «параллельной»
линии С, лежат на осях кривизны последней.
436*. Рассмотрим однопараметрическое семейство нормалей:
р (s) = г О) + \ {b (s) cos <р (s) 4~ n (s) sin 9 (s) \
линии r = r(s). Определить функцию cp(s) так, чтобы это семейство
нормалей имело бы огибающую (эволюта).
437**. Доказать, что если л^ния плоская, то лишь одна из её
эволют (см. задачу 436) плоская (именно та, которая лежит в
плоскости данной линии). Все остальные эволюты являются линиями
откоса и расположены на цилиндре, для которого направляющей
является эволюта данной линии. Точки эволюты получаются при
пересечении этого цилиндра с нормалями, которые мы получим, повернув
бинормали данной плоской линии от b к п на постоянный угол 9.
60

Найти также вектор, с которым касательная к эволюте образует
постоянный угол, а также найти этот угол. Вычислить кривизну и
кручение эволюты.
438**. Дана плоская линия С уравнением г = г($). На бинормалях
линии С в одном направлении откладываются отрезки MP, про-
<j
порциональные дуге М0 M = s. Составить уравнение линии С*,
описанной точкой Р, найти её дугу, кривизну и кручение. Доказать,
что С* — линия откоса и что она пересекает образующие цилиндра,
образованного бинормалями С под постоянным углом. Найти этот угол.
Найти репер Френе линии С* в произвольной точке и доказать,
что главная нормаль линии С* коллинеарна главной нормали линии С
в соответствующей точке. Доказать, что касательные к линии С*
пересекают плоскость линии С в точках эвольвенты последней (см. чертёж
к ответу этой задачи).
439. Доказать, что кривизна линии С в точке М0 равна кривизне
в той же точке MQ проекции С* линии С в соприкасающуюся
плоскость этой линии в точке М0. л < ч
440**. Найти кривизну и кручение эволюты:
р = г -f- Rn -\~ R ctg <p6
линии r = r(s) (см. № 436).
441**. Найти огибающую осей кривизны линии С.
442*. Найти кривизну и кручение огибающей осей кривизны
линии С. v
443*. Доказать, что если линия С есть линия откоса, то
огибающая её осей кривизна есть также линия откоса.
444*. Доказать, что сущестаует линия С*, касающаяся
мгновенных осей вращения трёхгранника Френе линии С. Составить
уравнение линии С*.
445*. Рассмотрим линию С. Пусть С* — огибающая осей кривизны
линии С. Доказа?ь, что:
1) соприкасающаяся плоскость линии С параллельна
нормальной плоскости линии С*;
2) нормальная плоскость линии С- является соприкасающейся
плоскостью линии С*.
446. Найти радиус соприкасающейся сферы линии r={t, t*tt'6)
в точке / = 0.
447*. Найти радиус соприкасающейся сферы и огибающую осей
кривизны винтовой линии Rz={aco$t, asint, bt\*
448. Найти радиус соприкасающейся сферы линий:
1) г = {е\ е'\ t/~2\,
2) r=\etsintt егcos t, е*}.
449. Доказать, что соприкасающаяся плоскость линии пересекает
соприкасающуюся сферу этой линии в той же точке по
соприкасающейся окружности.
450. Определить расположение линии относительно
соприкасающейся сферы этой линии в какой-либо её точке в окрестности этой
точки.
6L
1
/

ГЛАВА IV
ПОВЕРХНОСТЬ
Указания
Поверхность может быть задана одним из следующих способов:
1) уравнением ^
F(x, у, z) = 0;
2) уравнением
3) уравнением
r = r(u, v)
или тремя параметрическими уравнениями:
х = х(и9 v)9
z = z(u, v);
последний способ задания поверхности наиболее удобен для
исследования её дифференциально-геометрических свойств.
Касательная плоскость к поверхности, соответственно трём
способам её задания, определяется уравнением:
!> (»).<*-* о) + (^00>-Уо) + (£)о(*-*о) = 0
2) z — Zo=P(x — Xo) + q(y—yo),
p—fx(xb, y0), q=fA**, -Vo)'»
3) (R-r)rurv = 0
или
где
или
X — х У —у Z
ха Уи Z
xv yv z
= 0.
62

Если задано семейство поверхностей
F(x, у, 2, а) = 0,
то множество точек, координаты которых удовлетворяют уравнениям
при фиксированном а, называется характеристикой поверхности
семейства, соответствующей рассматриваемому значению а. Множество
всех характеристик или множествр всех точек пространства,
координаты которых удовлетворяют двум уравнениям
называется дискриминантной поверхностью.
Если в точках дискриминантной поверхности частные производные .
dF dF dF
дх9 ду9 dz
одновременно не равны нулю, то дискриминантная поверхность
является огибающей данного семейства.
Множество точек, координаты которых удовлетворяют
соотношениям
д. n 6F л &F п
называется ребром возврата данного семейства. Ребро возврата
касается всех характеристик.
Длина дуги линии u = ii(t), v = v(t)t расположенной на
поверхности г = г (и, v), определяется соотношением:
h ^
rE du% + 2F dudv + G dv\
h
где
,-J,;
■ *-'-(£)'+(£У+(£)'.
P дх дх , ду ду , gj: gg >
t — rurv — ju dv~T~da dv~T~du dv9
n ., [\dx\* , /dy\* , /<te\*
Квадрат дифференциала дуги поверхности г —г (и, v), т. е.
rfs4 = E dul + 2Z7 dudv + G dxFa
называется первой основной квадратичной формой поверхности.
Углы между двумя линиями поверхности Определяются
соотношением:
А _,_ Е du&u + F (duSv + dvhi) + Gdvbv
COS О* a = ±' .. r ■ —,
YEdu* -f- 2Fduuv + Gav* \f ЕЫ* + 2F6u6v + GSv*
63

где da, dv — дифференциалы функций а и v, взятые из уравнений
первой линии: и = их (t), v = vl (t), а Ъи, bv — дифференциалы от и и v,
взятые из уравнений второй линии: u = u2(t), v = v2(t).
Площадь части поверхности определяется двойным интегралом:
чи
EG—F* dudv.
распространённым на ооласть изменения параметров и и ti на
рассматриваемом куске поверхности.
Вторая квадратичная форма поверхности имеет- вид:
Ldu*-\-2Mduftv + Ndv\ ■
где L, М, N определяются соотношениями:
М--
N--
иц>
-mra
где т — единичный вектор нормали к поверхности. Так как
т-
V [гЛ]> '
то
L =
Г пи* 11?т)
М:
Vlrarv? '
N =
или в координатах
VlVv?
пи Уии zuu
и Уи zu
'-л У-п **
Vea — F*
М:
uv У иго zuv
'и У и zu
V У "О ZV
N=
Veg—f»
*VV Ут)Т) ZW
xu Уи zu
X-Q У-о Zrp
Пусть m — единичный вектор нормали к поверхности в точке Af.
Проведём через нормаль к поверхности в точке /И произвольную
плоскость и пусть эта плоскость рассечёт поверхность по линии С.
Нормальной кривизной называется число, равное по абсолютной
64

величине кривизне линии С в точке М; это число х положительно,
если линия С в точке М вогнута в сторону вектора т, и
отрицательно, если линия С в точке М выпукла в сторону вектора т.
Нормальная кривизна определяется соотношением
~_ Ldu2 + 2Mdudv + Ndv2
Edu2 + 2Fdudv + Odv2 '
где du и dv соответствуют направлению прямой /, по которой
рассматриваемая плоскость, проходящая через нормаль к поверхности,
рассекает касательную плоскость к поверхности; можно, например,
считать, что du, dv — координаты любого вектора, коллинеарного
прямой /, в случае если за масштабные векторы принять, векторы
Га и rv.
Если через касательную в точке М прямую к поверхности, не
имеющей асимптотического .направления, провести два сечения
поверхности: одно нормальное, другое наклонное, то проекция центра
кривизны нормального стечения на плоскость наклонного есть центр
кривизны наклонного сечения (в точке Ж) —теорема Менье.
Нормальная кривизна поверхности в данной на ней точке (не
омбилической!) достигает один раз максимума ъи другой раз
минимума х2. Эти значения нормальных кривизн поверхности в данной
точке называются -главными.
В омбилической точке нормальная кривизна имеет одно и то же
значение для любого нормального сечения. В омбилической (и только
в омбилической!) точке коэфициенты квадратичных форм (I и II) —
пропорциональны:
Е~ F~~G*
Главные кривизны щ и х2 связаны с нормальной кривизной
любого сечения соотношением:
х = Xj cos2 9 -f- х2 sin2 9»
где 9 — угол между плоскостью рассматриваемого сечения и
плоскостью сечения, при котором в сечении получаем главную
кривизну х,.
Главные кривизны определяются из соотношений!
__~ . _LN-M2
А XjX2 EQ—F* •
2Я_; ■ j _ EN-2FM + LG ,
К называется полной кривизной поверхности, а Я — средней
кривизной поверхности в рассматриваемой точке.
Если координатные линии и =\ const и v = const являются ли-*
ниями кривизны, то
дг ~ дт_ дг - dm,
ди ' * ди ' dv77~ X2 dv
5 П. С. Моденов 65

— формулы Олинде Родрига.
Форма
dm* = edu* -f- 2fdudv,-{- gdv*
называется третьей квадратичной формой поверхности; I, И, III
квадратичные формы связаны соотношением:
III —2//. II+ #.1 = 0.
Пусть tcj и тг2 — плоскости, проходящие через нормаль к поверх^
ности в точке Ж, которые дают главные нормальные сечения
поверхности, a /j и /2 — прямые, по которым эти плоскости
пересекают касательную плоскость к поверхности в точке М.
Прямые 1Х и /2 называются главными прямыми поверхности
в точке Ж, а их направления называются главными направлениями
поверхности в точке /И.
Линией кривизны поверхности называется линия, расположенная на
поверхности и обладающая тем свойством, что касательная к этой линии
в каждой точке является главной прямой поверхности в той же точке.
На всякой поверхности имеется ортогональная сеть линий кри- .х
визны. Дифференциальное уравнение этой сети:
I Eda -f- Fdv Fdu -\~ Gdv I
I Ldu -f Mdv Mdu + Ndv | = °'
Точки поверхности, в которых полная кривизна К^>0,
называются эллиптическими; в окрестности эллиптической точки поверхность
располагается по одну сторону от касательной плоскости. Точки,;
в которых К<^0У называются гиперболическими; в окрестности
гиперболической точки поверхность располагается по разные стороны
от касательной плоскости; поверхность имеет седловидную форму»
Наконец, точки, в которых К = 0, называются параболическими.
Примером параболической точки может служить любая точка
обыкновенного цилиндра. Асимптотической линией поверхности называется
линия, расположенная на поверхности и обладающая тем свойством,,
что её соприкасающаяся плоскость в любой точке является
касательной плоскостью к поверхности в той же точке.
Дифференциальное уравнение асимптотической линии поверхности
имеет вид:
Ldu* + IMdndv + Ndv* = 0.
В области эллиптических точек поверхности асимптотических
линий нет.
Геодезическое линией поверхности называется линия, главная
нормаль которой в каждой точке М совпадает с нормалью к
поверхности в той же точке. Дифференциальное уравнение
геодезических линий имеет вид:
(Edu + Fdv) (Ги 2du* + 2T{9t%dudv +
+ ГИ.ЯЛ>9) — (Fdu -f Gdv) (Fiitldu% + 2T12tldudv + TnAdv*) +
-j- {EG — F*) (dud'2v — dvd*u) = 0,
66

где \ -
J- 11,2 ruurv A„2 XT, "Г ^2 ^77 ~Г Х72 Л^">
J- 12,1 — гиг»га —
да2 dv ' dn2 <Ъ ~ d^2 dr/ J
д2ЛГ дХ , (?2У dj/ , d22 dz
" dadr/ dw * dudv да ~ дндг/ дн
и т. д.
Дифференциальное уравнение геодезических линий — второго
порядка, поэтому оно имеет единственное решение при следую-
тих начальных' данных: щ, v0, (— J0; геометрически это означает,
что через каждую точку поверхности в .данном направлении
проходит единственная геодезическая линия (под направлением на
поверхности в данной точке М мы понимаем направление любой
прямой, проходящей через точку М и лежащей в касательной
плоскости к поверхности в точке Ж). Кратчайшее расстояние двух
точек поверхности по поверхности измеряется длиной дуги
геодезической линии, проходящей через эти точки.
Геодезической кривизной линии С (в точке М), расположенной
на поверхности 5, называется кривизна в точке М ортогональной
проекции С линии С на касательную плоскость к поверхности
в точке М. Ясно, что линия С, геодезическая кривизна которой
равна в каждой точке нулю, есть геодезическая линия поверхности
и обратно.
Отметим два специальных класса поверхностей:
1) линейчатая поверхность:
где г = г(и) — данная линия, а —а (и) — вектор-функция, дающая
распределение прямолинейных образующих линейчатой поверхности;
2) развёртывающаяся поверхность — это поверхность,
образованная касательными к пространственной линии, а также любой конус
или любой цилиндр.
Линейчатая поверхность p = r-\-va будет развёртывающейся
тогда и только тогда, когда
dpada = 0.
d2r d2r d*r dm dm дг
Векторы gjjg, ш-, ^, —, — можно разложить по векторам ш ,
g- и т. Формулы, определяющие это разложение имеют вид:
шь=г" к+г^ к+Мт>
д*Г — Г 1 дг _1_ V 2 дг I л/fft
67

— деривационные формулы Гаусса и
дт ,, дг ,2 &г
да г Ои 1 dv'
дЛИ — — ^дЛ — ^^-
dv ~ °* да u*dv
— деривационные формулы Веингартена. Коэфициенты Ц определи»
ются# соотношениями:
frl _ bjig22 ~ bi&*i ft 2 _ "" ^igi8 + bi9gu
gllg22 — gl2 ' ^ l gllg22—gll '
r^e Sij и */y — коэффициенты I и II квадратичных форм.
§ 1. Составление уравнений поверхностей
451. Составить параметрические уравнения следующих поверх*
лостей: ' {
1) сфера,
2) эллипсоид,
3) однополостны^ гиперболоид,
4) двуполостные гиперболоид,
5) эллиптический параболоид,
6) гиперболический параболоид,
7) конус второго порядка,
8) эллиптический цилиндр,
9) гиперболический цилиндр,
10) параболический цилиндр.
452. Составить уравнения цилиндра, для которого линия р = р (а)
является направляющей, а образующие параллельны вектору е.
453. Составить уравнение конуса с вершиной в начале радиусов-
векторов, для которого линия р = р(и) является направляющей.
454. Составить уравнение поверхности, образованной
касательными к данной линии р = р(и).
455. Окружность радиуса а перемещается так, что её центр
движется по заданной линии p = p(s), а плоскость, в которой она
расположена, является в каждый момент нормальной плоскостью
к заданной линии. Составить уравнение поверхности, описываемой
окружностью.
456. Вокруг оси Oz вращается плоская линия x — cp(v)f z = ty(v).
Составить параметрические уравнения поверхности вращения,
выяснить характер координатной сети. Рассмотреть частный случай,
когда меридиан задан уравнением x=f.(z).
457. Вокруг оси Oz вращается окружность x = a-\-bcosv%
z = b sin v (0 <^ b <^ а). Составить уравнение поверхности вращения
(тор) и выяснить характер координатной сети.
68

458. Прямая движется поступательно с постоянной скоростью,
пересекая другую прямую под прямым углом, и одновременно
вращается равномерно вокруг этой прямой. Составить уравнение
поверхности, которую описывает движущаяся прямая (прямой геликоид).
459. Составить, уравнение поверхности, образованной главными
нормалями винтовой линии.
460. В точках линии р = р(м) задано векторное поле: е = е(и).
Составить уравнение линейчатой поверхности, для которой данная
линия является направляющей, а вектор е{и) даёт направление
образующей в соответствующей точке поверхности.
461. Составить уравнение поверхности, образованной семейством
нормалей данной линии р = р (s).
462*. Прямая движется так, что точка М пересечения её с
окружностью движется по данной окружности,, причём эта прямая
остаётся в нормальной плоскости к окружности в
соответствующей точке и поворачивается на угол, равный углу МОМ0,
который прошла точка Ж, двигаясь по окружности. Составить уравнение
поверхности, описываемой движущейся прямой, считая, что
начальным положением движущейся прямой была ось Ох, а окружность
задана уравнениями: х* -{-у* = аа, 2=0.
463. Даны две линии г = г(и) и р=р(х>). Составить уравнение
поверхнрсти, описываемой серединой отрезка, концы которого лежат
на данных линиях (поверхности переноса).
464. Составить уравнение поверхности,образовцнной вращением
. цепной линии у = ach — вокруг оси Ох (катеноид).
465. Составить уравнение поверхности, образованной вращением
трактриссы:
p = |alntgf^ + YJ — asinj, acosA
вокруг её асимптоты. Эта поверхность называется'псевдосферой.
466. Коноидом называется поверхность, образованная движением
прямой параллельно заданной плоскости (направляющей), так что
образующая пересекает заданную прямую (направляющую). Для
задания коноида надо задать направляющую прямую, направляющую
плоскость и линию, которую пересекает движущаяся прямая
(направляющая линия). Составить уравнение коноида, если даны:
направляющая плоскость yOz, направляющая прямая y=?09z = h и напра-
вляющая линия -т + т2 = 1, z = 0 (эллипс).
467. Составить уравнение коноида, для которого направляющие
прямая, плоскость и линия заданы соответственно уравнениями:
1) х = а, у = 0,
2) *=0,
3) у2 = 2/72, * = 0.
468. Цилиндроидом называется поверхность, образованная
прямыми, параллельными некоторой плоскости. Цилиндроид может
69

быть задан двумя направляющими линиями (лежащими на нём) и
направляющей плоскостью (которой параллельны образующие
цилиндроида). Составить уравнение цилиндроида, если его
направляющими являются окружности
х2 + 22 — 2ах = 0, у = 0 *
и
У + г2 — 2ау = 0, х = 0,
2l направляющей плоскостью является плоскость хОу.
469. Составить уравнение линейчатой поверхности, образующие
которой параллельны плоскости у — 2 = 0 и пересекают параболы
у* = 2рх, z=t=0 и <г2 = — 2рху у = 0.
470. Составить уравнение линейчатой поверхности, образующие
которой пересекают ось Ozy параллельны плоскости хОу и
пересекают линию xyz = a*y jfc2-|-j/2 = £2.
471. Составить уравнение линейчатой поверхности, рбразующие
которой пересекают прямую r = a-\-uby линию р = р (г>) и
перпендикулярны вектору п.
472. Составить уравнение поверхности, образованной при
вращении окружности вокруг одной из её касательных.
473. Составить уравнение линейчатой поверхности, образующие
которой параллельны плоскости хОу и пересекают два эллипса:
474. Составить уравнение линейчатой поверхности, образованной
прямыми, пересекающими линию р = {иу и2, и3}, параллельными
плоскости хОу и пересекающими ось Oz,
475. Составить уравнение поверхности, образованной прямыми,
параллельными плоскости х-\-у-\-z = 0, пересекающими ось Oz
и окружность p = {by a cos и, asinu\.
476. Составить параметрические уравнения поверхности,
образованной прямыми, пересекающими окружность jc2 -)- z2 = 1, у = 0 *и
прямые у = lf z—l и x=ly z = 0.
477. Составить уравнение поверхности, образованной
касательными к винтовой линии p = {acosv, a sin и, bv\ (развёртывающийся
геликоид). '
478. Составить уравнение конической поверхности с вершиной
в точке (0,0, — с) и направляющей
(^+У2)2 = а2(^ — у2).
479. Доказать, что касательные плоскости к поверхности ,xyz = a*
отсекают от координатных плоскостей тетраэдры равных объёмов.
480. Поверхность задана уравнением r = r(uyv). Составить
уравнение её подэры относительно начала радиусов-векторов.
481. Найти подэру эллипсоида относительно его центра.

§ 2. Касательная плоскость и нормаль
482. Доказать, что плоскости, касательные к поверхности
z = xf I — ], проходят, через одну и ту же точку.
483. Составить уравнение касательной плоскости и нормали
к геликоиду г = {г; cos и, v sin и/ ku}.
484. Составить уравнение касательной плоскости к поверхности
xyz = a}.
485. Составить уравнение касательной плоскости к поверхности
xy*-}-z'd=V2 в точке (1,2,2).
486. Доказать, что касательные плоскости к поверхности
V ХЛ~ Vy-\~ Vz — a отсекают на осях координат отрезки, сумма
котррых неизменна.
487. Доказать, что поверхности
X* ~{-У*-{-Z* = ах>
х*+у*-\-г* = $у9
x*-\-y2-\-z* = yz
попарно ортогональны.
488*. Поверхность образована касательными к линии С. Доказать,
что эта поверхность во всех точках одной и той же касательной
к линии С имеет одну и ту же касательную плоскость. ;
489*. Поверхность образована главными нормалями линии С.
Составить уравнение касательной плоскости и нормали в
произвольной точке поверхности.
490*. При каком условии линейчатая поверхность r = p(a)-f-
+ X е (и) (| £ | = 1) является конусом ? Предполагая это условие
выполненным, найти вершину конуса.
491*. Поверхность образована главными нормалями линии С.
Доказать, что в точках линии С касательная плоскость к
поверхности совпадает с соприкасающейся плоскостью линии С, т. е.
линия С—асимптотическая для указанной поверхности.
492*. Составить уравнение касательной плоскости и 'нормали
к поверхности, образованной бинормалями линии С. t
493*. Доказать, что в точках: линии С для поверхности,
образованной бинормалями этой линии, касательная плоскость к
поверхности совпадает со спрямляющей плоскостью линии С, а нормалью
к поверхности является главная нормаль линии С.
49*4*. Найти касательную плоскость и нормаль к поверхности,
образованной осями кривизны линии С.
495*. Найти касательную плоскость и нормаль к поверхности,
образованной мгновенными осями вращения трехгранника Френе.
496*. Доказать, что касательная плоскость к поверхности канала:
г = р (s) -{- v (s) cos 9 4~ ? (s)sin 9
71

параллельна касательной к линии p = p(s) в соответствующей точке,
а нормалями к поверхности являются нормали к данной линии
(v и р соответственно единичные векторы главной нормали и
бинормали линии р).
497*. Доказать, что если вокруг оси / вращается плоская
линия С (меридиан!), то нормаль MN к этой линии (расположенная
в плоскости этой линии) будет нормалью и к поверхности
вращения.
498**. Будем рассматривать поверхность как непрерывный и
взаимнооднозначный образ прямоугольника. Пусть Ж —
произвольная точка поверхности, а /я — её прообраз. Пусть существует" только
одна плоскость тс, проходящая через точку Ж, * которая обладает
следующим свойством: каков бы ни был конус второго порядка
с вершиной в точке Ж, имеющий с плоскостью тс' только одну
общую точку (именно точку Ж), некоторая часть поверхности в
окрестности точки Ж лежит вне этого конуса (под частью поверхности
в окрестности точки Ж мы понимаем образ любого круга с центром
в точке т). В таком случае плоскость тс называется касательной
плоскостью к поверхности в точке Ж, а поверхность тс в точке М
называется гладкой.
1) Исходя из этого определения, разъяснить смысл фразы:
«поверхность тс в точке Ж не имеет касательной плоскости».
2) Доказать, что если через точку Ж провести произвольную
плоскость и если она рассечёт поверхность по линии С, а
касательную плоскость по прямой /, то прямая / является касательной к
линии С в точке Ж.
3) Предполагая, что поверхность задана уравнением r = r(a,v)y
что функция r(u,v) дифференцируема в точке (u,v) и что частные
дг дг
производные ^- и -к- неколлинеарны, доказать, что данная
поверхность имеет касательную плоскость в рассматриваемой точке: это есть
ал дг дг
плоскость, проходящая через точку Ж, коллинеарная векторам ^- и -^ .
499. Поверхность образована касательными к линии С. Найти
ортогональные траектории прямолинейных образующих этой
поверхности. Найти кривизну ортогональных траекторий.
500. Пусть Ж — точка поверхности 5, а Ж' — соответствующая
точка подэры S' относительно точки О. Доказать, что нормаль
к поверхности 5' в точке Ж' делит пополам отрезок ОМ.
501. Составить дифференциальное уравнение линий, делящих
пополам углы между координатными линиями данной
поверхности.
602. Найти уравнения линий, делящих пополам углы между
координатными линиями:
1) геликоида r={ucosv, usinv, av}\
2) гиперболического параболоида r=\a (u-\-v), b (и—v), uv\.
603. Найти тройку векторов, взаимных векторам гш rv, т.
72

504. На нормалях к поверхности 5 в одном направлении
отложены отрезки постоянной длины. Концы отложенных отрезков
описывают поверхность 5*, «параллельную» поверхности S. Доказать,
что поверхности 5 и S* имеют в соответствующих точках общие
нормали.
505- Сеть линий на поверхности r = r(u,v) задана
дифференциальным уравнением
Фп du* -f- 2ф12 dudv -f- ф22 dv* = 0.
При каком условии эта сеть ортогональна?
• 506. Найти ортогональные траектории прямолинейных
образующих произвольной линейчатой поверхности г = р -|- 1е.
§ 3. Огибающая. Характеристики. Ребро возврата
507. Найти огибающую семейства поверхностей r = r(u, v, w)
{w — параметр поверхности в семействе).
508. Две параболы расположены в перпендикулярных плоскостях
и имеют общую вершину и общую касательную в вершине.
Найти огибающую. семейства плоскостей, касательных к обеим
параболам.
509. Найти огибающую семейства сфер постоянного радиуса,
центры которых расположены на. данной линии p = p(s)
(поверхность канала).
510. Найти ребро возврата семейства сфер постоянного радиуса
а, центры которых расположены на линии p = p(s).
511. Найти огибающую и ребро возврата семейства сфер pa- v
диуса а, центры которых расположены на окружности
*а+У = **, г = 0.
512. Найти огибающую и ребро возврата семейства сфер,
проходящих через начало координат, центры которых 'расположены
на линии
г={ы3, и\ и}.
i
513. Составить уравнение огибающей и рёбра возврата семейства
сфер, проходящих через начало радиусов-векторов; центры сфер
расположены на линии p = p(s).
514. Найти огибающую, характеристики и ребро возврата
семейства соприкасающихся плоскостей данной линии.
515. Найти огибающую, характеристики и ребро возврата
семейства нормальных плоскостей данной линии.
516. Найти характеристики, огибающую и ребро возврата
семейства спрямляющих плоскостей данной линии.
517. Найти характеристики, огибающую и ребро возврата
семейства плоскостей:
rn-\-D = o, n = n(u)t D — D(u\ |л| = 1.
73

§ 4. Первая и вторая квадратичные формы. Полная и средняя
кривизны
518. Вычислить первую квадратичную форму следующих
поверхностей второго порядка:
Г) r={rcosHcosx>, r sin и cos v, r sin г;} (сфера).
2) r = {a cos и cos v, b sin и cos v, с sin v} (эллипсоид).
3) r = {-J (* + -£) cos a, 4(t» + i)sinH, |(z;-i)} (одно-
полостный гиперболоид).
4) r = {a 17^7 > * Tqrf- > c Vqr^} (однополостный гиперболоид).
5) r = {f l1"-v)C0Sttj 2" t^- 7)sinMj T^ + i)} (ДВУП0Л°-
стный гиперболоид).
6) r — lv/pcosu, vifqs'mti, yi (эллиптический параболоид).
7) г = {(н-(- v)\/rpi (и — v)\/q, 2uv} (гиперболический параболоид).
8) r=\av cosu, bvsinu, cv\ (конус).
9) r={acos«, &sinw, v\ (эллиптический цилиндр).
10) r= |у(н-| ), y\u ) > v\ (гиперболический цилиндр).
11) r — {2pn*, 2pu, v\ (параболический цилиндр).
519. Вычислить первую квадратичную форму поверхности
r=p-f-(X— s) х, образованную касательными к линии p = p(s).
520. Вычислить первую квадратичную форму следующих
поверхностей :
1) г = р -f- Хе, e = const (цилиндр).
2) r — vp(s) (конус).
3) г = р (s) -j- Хе (s) (линейчатая поверхность), (| #| = 1).
4) г = р (s) -j- v (s) cos ф -j- (3 (s) sin'9 (поверхность канала).
5) r={9(?/)cosw, 9(x>)sinw, ty(v)\ (поверхность вращения).
6) г = {/ (x>) cos и, /(^)sinw, т;} (поверхность вращения).
7) r=j(a-j-£ cos х>) cos и, (a-{-b cosv)sinu, bsinv} (тор).
8) r={x>cos ut usin a, kit} (минимальный геликоид).
9) г = p (s) -)- Xv (s) (поверхность главных нормалей).
10) г = р (s) 4~ ^{3 (s) (поверхность бинормалей).
521. Найти вторую квадратичную форму поверхностей, полную
и среднюю кривизны для поверхностей, заданных в условии
задачи 518.
522. Вычислить среднюю кривизну круглого конуса, у которого
угол между осью вращения и образующей равен 0.
523. Исходи из зависимости
ill — 2/У-И -J- ДГ-I = 0
74

между I, II и III квадратичными формами, выразить коэфициенты
III квадратичной формы через коэфициенты Е, F, G, L, М, N двух
первых квадратичных форм.
524. Доказать, что для линейчатой поверхности полная кривизна
не положительна (К^О).
525. Найти главные кривизны прямого геликоида:
r={vcosu, vsinu, ku}.
526. Найти полную и среднюю кривизны гиперболического
параболоида:
, ху = az.
527. Найти линию, на которой располагаются центры главных
сечений гиперболического параболоида ху = аг для различных точек
оси Ох.
528. Чему равна полная кривизна развёртывающейся поверхности?
• 529. Вычислить среднюю кривизну развёртывающейся поверхности
г = р 00 + ^00-
530. Найти полную и среднюю кривизны поверхности,
образованной бинормалями данной линии.
531. Найти полную и среднюю кривизны поверхности,
образованной главными нормалями линии.
532. Доказать, что можно установить такое взаимооднозначное
отображение развёртывающейся поверхности на плоскости, при
котором линейные элементы имеют один и тот же вид. Какую сеть
при этом придётся ввести на плоскости?
533. Выразить кривизны координатных линий поверхности через
коэфициенты I и II квадратичных, форм этой поверхности.
534*. Принимая для I и II квадратичных форм следующие
обозначения:
I = gndu* + 2gndudv -}- gndv\
II = bndu2 -j- 2b12dudv -\- b^dv*,
доказать, что кривизны координатных линий определяются
соотношениями
*<a= COnst ^ J3/2 9
Д6 ««-coot —. ^Щ ,
g=gllg*%—gl*
535*. Выразить через коэфициенты I и II квадратичных форм и
через символы Кристоффеля кручения координатных линий
поверхности r = r(uy v).
536*. Выразить коэфициенты I и II квадратичных форм
поверхности S*9 „параллельной" поверхности S, через коэфициенты I и II
квадратичных форм поверхности 5. , .
75

537*. Выразить полную кривизну /if* поверхности S*,
«параллельной» поверхности S, через полную и среднюю кривизны
поверхности 5.
538*. Выразить среднюю кривизну Н* поверхности «S*,
«параллельной» поверхности 5, через полную кривизну К и среднюю
кривизну Н поверхности 5.
539*. Составить уравнение минимальной поверхности S*.t «парал-
лельной» поверхности S, если для поверхности S, ^ = const.
540*. Дана поверхность постоянной средней кривизны И. Нз
всех её нормалях отложены отрезки ^^ Доказать, что у построенной
таким образом поверхности, «параллельной» данной, полная кривизна
постоянна.
541*. На всех нормалях поверхности постоянной положительной
полной кривизны К отложены отрезки —— . Доказать, что средняя
кривизна построенной таким образом поверхности постоянна. Найти
эту среднюю кривизну.
542*. Поверхность S* «параллельна» поверхности 5. Доказать,
что линиям кривизны поверхности 5 соответствуют линии кривизны
поверхности «S*.
543. Доказать, что в соответствующих точках у двух
параллельных поверхностей полная и средняя кривизны связаны соотношением:
Я2 — 4/С _ Я*2 — 4/f*
К2 ~ К** "
§ 5. Теорема Менье
544. Исходя из того, что эллипс можно спроектировать в
окружность, найти радиусы кривизны эллипса в его вершине, используя
теорему Менье.
545. Через точку М поверхности проводятся всевозможные
сечения. Составить уравнение поверхности, на которой расположены
центры соприкасающихся окружностей этих сечений.
546. Какие направления на поверхности исключаются для теоремы
Менье?
547. Параболический цилиндр пересекается плоскостью,
перпендикулярной к его образующим по параболе С. Пусть М — вершина
этой параболы, а МТ—касательная к параболе в её вершине М.
На какой линии располагаются фокусы парабол, получающихся в
сечении указанного цилиндра плоскостями, проходящими через,
прямую МТ?
548. Доказать, что отрезок нормали к плоской линии С от
точки М этой линии до точки прямой /, вокруг которой вращается
линия С, равен радиусу кривизны нормального сечения поверхности
вращения плоскостью, проходящей через точку М перпендикулярно
плоскости, в которой лежит линия С и прямая /.
76

§ 6. Омбилические точки
549: Указать на геометрический, способ построения омбилических
точек поверхности вращения.
550. Синусоида у = sin х вращается вокруг оси Ох. Найти на
поверхности вращения омбилические точки.
551. Найти омбилические точки эллипсоида вращения (сжатого
или вытянутого).
552. Разность К2 — Н (К — полная кривизна поверхности, И —
средняя кривизна) называется Эйлеровой разностью. Доказать, что
Эйлерова разность обращается в нуль в омбилической и только
в омбилической точке.
553. Найти омбилические точки эллиптического параболоида
2г = |+f ^>0' q>0)-
554. Найти омбилические точки трёхосного эллипсоида
y-2 1»2 ?-2
£.+i+* = l (а>Ь>с>0).
555. Найти омбилические точки двуполостного гиперболоида
в«~£» с8
556. Найти омбилические точки поверхностей:
1) xyz = a*,
2> | + ? + F = L
§ 7. Линейчатые и развёртывающиеся поверхности
557. На нормалях к развёртывающейся поверхности r = p(s)-f-
-4-Xt(s) отложены отрезки постоянной длины. Составить уравнение
поверхности, описанной концами отложенных отрезков; доказать,
что эта'поверхность будет также развёртывающаяся и найти её ребро
возврата.
558. Пусть Р и Q — точки встречи прямолинейной образующей
развёртывающейся поверхности с линиями С и Съ расположенными
на этой поверхности. Доказать, что касательные к линиям С и Сх
в точках Я и Q лежат в одной плоскости.
559. При каком условии поверхность z=f(x, у) будет
развёртывающаяся?
560. При каком условии поверхность F(x, yy z) = Q будет
развёртывающаяся?
561*. Две плоские линии С и Сх расположены в параллельных
плоскостях. Доказать, что линейчатая поверхность, проходящая через
эти линии, будет развёртывающаяся в том и только в том случае,
77
V

когда образующая встречает линии в точках М и Мь касательные
в которых к данным линиям параллельны.
662*. Найти геометрический способ построения развёртывающейся
поверхности, проходящей через две плоские линии Си С,.
663*. Дать геометрический способ построения развёртывающейся
поверхности, проходящей через две линии С и С,.
564*. Поверхность те, образованная касательными к линии С,
развёртывающаяся. Существует ли ещё другая развёртывающаяся
поверхность, проходящая через линию С?
565*. Исходя из результата задачи 558, доказать, что геликоид,
однополостный гиперболоид и гиперболический параболоид — не
развёртывающиеся поверхности.
566**. Доказать, что проективный образ развертывающейся
поверхности есть снова развёртывающаяся поверхность.
567**. Найти развёртывающуюся поверхность, имеющую плоскую
линию кривизны (отличную от прямой!) (конусы и иилиндры
исключаем).
568**. Пусть / и /' — две прямолинейные образующие
линейчатой поверхности г = р + \е:
г = р(и) + Х*(и), ,(/)
г=р(и + Ди) + ^(й + д»)- (О
Пусть а — прямая, пересекающая ортогонально прямые / и /', Р и
Р— точки пересечения прямой а с прямыми / и /' и R—радиус-
вектор точки Я. Найти UmR = p. Точка М(р) называется централь-
Ди*=0
ной точкой образующей. Множество центральных точек образует
линию, называемую стрикционной линией данной линейчатой
поверхности или линией сжатия данной линейчатой поверхности. Составить
уравнение линии сжатия.
569**. Предел отношения кратчайшего расстояния двух
прямолинейных образующих линейчатой поверхности l(u) и /(w-j-Aw),
заданной уравнением r = p(w) -f- Уе{и), к углу между ними при
да = 0 называется параметром распределения образующих линейча-/
той поверхности. Найти параметр распределения указанной
поверхности.
570*. Найти параметр распределения и стрикшлонную линию
гиперболического параболоида:
r={(u + v)/p, (v — u)Vq9 2uv].
571*. Найти стрикиионную линию и параметр распределения
развёртывающейся поверхности.
572**. Пусть 5 — семейство прямолинейных образующих
линейчатой поверхности, а 5* — второе семейство асимптотических линий
этой поверхности. Доказать, что если взять четыре любые линии
семейства S*9 то ангармоническое отношение четырёх точек
пересечения любой прямолинейной образующей с этими линиями имеет
одно и то же значение для всех прямолинейных образующих,
78

573**. Доказать, что котангенс угла между касательными
плоскостями к линейчатой поверхности в точке М стрикционной линии и
в точке М\ находящейся на прямолинейной, образующей, проходящей
через точку М стрикционной линии и отстоящей от неё на
расстоянии 1, равен параметру распределения.
674. Найти параметр распределения и стрикционную линию
минимального геликоида.
575. Доказать, что если параметр распределения линейчатой по-„
верхности равен нулю, то поверхность развёртывающаяся.
576. Доказать, что прямой геликоид является минимальной
поверхностью.
577**. На^ти минимальную линейчатую поверхность,
образующие которой параллельны данной плоскости.
§ 8. Линии кривизны
678. Составить уравнения линий кривизны прямого геликоида
г = {v cos w, v sin к, ku}.
579. Составить дифференциальное уравнение линий кривизны
гиперболического параболоида az = xy и проинтегрировать его.
580. Составить дифференциальное уравнение линий кривизны
параболоида
r={(u-\rv)/~pi (u — v)/q, 2uv} /
и проинтегрировать его.
581. Найти, линии кривизны эллиптического параболоида.
582. Доказать, что любая линия на поверхности сферы (или на
плоскости) является линией кривизны сферы (плоскости).
583. Составить дифференциальное уравнение линий кривизны
поверхности, образованной бинормалями данной линии.
584. Составить дифференциальное уравнение линий кривизны для
поверхности, образованной главными нормалями данной линии.
585. Доказать, что сети линий кривизны поверхности 5
соответствует ортогональная сеть на поверхности S*; «параллельной» 5.
• 586**. Найти, линии кривизны развёртывающейся поверхности.
587. Найти линии кривизны поверхности вращения.
588*. 1) Доказать, что если поверхности St и 52 пересекаются
по линии С, являющейся линией кривизны на каждой из, них, то
они пересекаются под постоянным углом.
2) Доказать, что если две поверхности St и S% пересекаются
под постоянным углом и линия С является линией кривизны на
одной из них, то она будет линией кривизны и на другой.
589. Развёртывающаяся поверхность пересечена семейством
параллельных плоскостей. Доказать, что эволюты * линий сечения также
лежат на развёртывающейся поверхности.
590*. Доказать, что если сфера или плоскость пересекает
поверхность 5 под постоянным углом, то линия пересечения является
линией кривизны поверхности 5.
7$

591*. Доказать, что если сфера или плоскость пересекают
поверхность 5 по линии кривизны, то эта сфера (плоскость) пересекает
поверхность под постоянным углом.
592**. Найти геометрическим построением линии кривизны
поверхности канала.
593. Чем являются прямолинейные образующие и их
ортогональные траектории, расположенные на развёртывающемся геликоиде для
этой поверхности?
694. Доказать, что если сфера касается развёртывающейся,
поверхности, то линия касания является ортогональной траекторией
прямолинейных образующих этой поверхности.
595**. Касательные к линии касаются сферы. Доказать, что
соприкасающиеся плоскости той же линии также касаются этой
сферы.
596*. Доказать, что ребро возврата всякой развёртывающейся
поверхности, описанной около сферы, есть геодезическая линия на
конусе, проходящем через это ребро возврата с вершиной в центре
сферы.
§ 9. Асимптотические линии
597. Найти асимптотические линии: 1) гиперболического
параболоида, 2) однополостного гиперболоида.
598. Найти асимптотические линии развёртывающегося Геликоида
r={x;cosH — sin и, v sin и -j- cos и, и).
599. Найти асимптотическую сеть на прямом геликоиде.
600. Что можно сказать про асимптотическую сеть минимальной
поверхности?
601. Найти асимптотические линии произвольной линейчатой
поверхности r = $(u)-\-ve(u).
602**. Доказать, что для асимптотической линии на поверхности
о2 = — К (о — кручение, К—полная кривизна) — теорема Бельтрами
Эннепера.
603**. Доказать, что при проективном преобразовании
поверхности асимптотическая линия переходит в асимптотическую линию.
604*. Найти кручение асимптотических линий поверхности,
образованной бинормалями данной линии.
§05*. Найти кручение асимптотических линий поверхности, обра*
зованной главными нормалями данной линии.
606*. Найти асимптотические линии поверхности:
2
607**. Доказать, что кручение асимптотических линий,
проходящих через точку М поверхности, определяются соотношением
°if2 = ±/—AT,
где К — полная кривизна поверхности в точке М.
60

608*. Дана поверхность
г = { u(3v* — и* — ~\ , vibu1 — v* — 1) , 2Ц.
Найти линии кривизны и асимптотические линии этой поверхности.
Найти её полную и среднюю кривизны в каждой точке.
§ 10. Геодезические линии
609**. Найти геодезические линии развёртывающейся
поверхности.
610**. Найти геодезические линии круглого конуса х* -\-y*z=z*.
611**. Найти геодезические линии геликоида
г = {и cos v, и sin v, hu\
612**. Найти геодезические линии произвольной конической
поверхности.
613**. Доказать, что геодезическая кривизна линии u=u(s)9
v = v(s)y расположенной на поверхности г = г(и, v), вычисляемся
по формуле х^ = rrm,' где т — единичный вектор нормали к
поверхности.
614*. Найти геодезическую кривизну винтовых линий геликоида
г = [иcost/, usinv, av\.
61S*. На касательных к линии С отложены от точек касания
отрезки одной и. той же длины а. Определить геодезическую*
кривизну линии, описываемой концами отложенных отрезков.
616**. Вычислить геодезическую кривизну ортогональных
траекторий прямолинейных образующих любой линейчатой поверхности
в точках её стрикшюнной линии.
617**. Доказать, что на минимальной'поверхности сумма
квадратов кривизны и кручения геодезической линии равна — К.
618. Доказать,/ что геодезическая кривизна линии, заданной на/
поверхности r = r(u, v) уравнениями и = и(/),. v = v(t), может
быть определена соотношением
Г1Ь2н'2+2Г12,2н^+Г22,2*/'2 Tlulu^+2Vl2t,a'vf + r22$lv^
Fu' + Gv' Eu' + Fv< ___
-HIT2
a'v'
W(Eu'2 -f 2Fu'v' + Gv'2)g/*
619. Найти геодезические кривизны координатных линий.
620. Найти геодезические кривизны координатных линий в
случае, если координатная сеть поверхности ортогональна.
6 П. С. Моденов 81

ОТВЕТЫ И РЕШЕНИЯ
ГЛАВА I
§ 1., Вектор — функция скалярного аргумента.
x.zrr, irr , r xr , \rr j, rr r , y^—^ > у?'
2. r2 = const, 2rr'=0, /r' = 0. Геометрическая интерпретация: если
|r| = const, то линия r = r(t) расположена на сфере с центром в начале
радиусов-векторов; ясно, что в таком случае касательная к линии
перпендикулярна радиусу сферы (r'J_r). Обратно: если г J_r', то гг' = 0, (г2)' = 0,
г2 = const.
3. r(t) = x(t)i±y(t)j+z(t)k, r'(t)=,x'(t)i + y'{t)j + z'{t)k, откуда
л;'(£) = (), y'(t) = Q, z'(t) = 0; следовательно, х = const, у = const, 2 = const,
а потому г = const.
Обратное положение верно.
4. r° = {cos cp, sin cp} в системе координат, в которой ось Ох имеет
направление вектора а, а ось О у—направление вектора [а]. Далее находим:
dr°
— = {— sin cp, coscp}. .
5.г>=г'==(гг°)'=гт0 +rr°'= r'r° + rep' ^- = r'r°+rcp' [r°]. Таким образом,
компоненты скорости v в системе r°, [r°] соответственно равны:, vr = г'
(радиальная скорость) и tf = rep' (трансверсальная скорость):
п= Yv? + V= yVa -f r2<p'3.
Аналогично находим: w = (r" —rcp'2)r° + (2ry.+ rep") [r°],
w = y"(r" — r^Y + (2rV + ry")K
6. 1) Нет. Пример: г = {cos £, sin /}, r' = {— sin t, cos /}, | r' \ = I,
| r! = 1, | г |' = 0. 2) Да. Доказательство: r2 = г2; дифференцируя, получим
требуемое соотношение. *
7. Пусть г = rx(t) и r—r2(t) — законы движений точек; по условию
| гх — г21 = const или (rt — г2)2 = const, откуда 2 (гх — r2) (rV — г2') = 0,
аг1=а^', где 0 = ^ —г2.
8. Уравнение линии, описываемой серединой отрезка: Я = у (г + Р)>
причём "| г—р | = const. Касательная коллинеарна вектору
В последнем выражении параметры и и v не произвольны; они связаны
соотношением | г — р | = const.
82

9. Пусть Лх ~\-Ву -\-С — 0— уравнение прямой /. Тогда непрерывная на
сегменте [а, Ь] функция ср (/) = Ах (t) -f- By (t) + С имеет на концах сегмента
разные знаки. Поэтому, существует ££ (а, Ь) такое, что
?(6) = Лдг(6)+5у(6) + С = 0.
10. Найдётся £ такое,, что г'(^)1а. Геометрическая интерпретация:
годограф данной вектор-функции —
замкнутая линия; найдётся касательная к этой
линии, ортогональная любому
направлению (а).
11. Найдётся S£(/i, 4) такое, что
** (£) f(*i) ** (*s) = °- Геометрическая
интерпретация: линия г— г (t) упирается
своими концами в плоскость,
проходящую через начало радиусов-ректоров
и концы радиусов-векторов r(/i) и
г(/2); найдётся касательная к данной
линии, компланарная указанной
плоскости.
12. Вцедём систему координат
на плоскости. Разности х (t2) — х (tx)
и у (t2)—y(ti) одновременно не равны
x{t2) — x{h)^z\). югда w/;:j w,Л — -згтн,
Черт.
нулю. Пусть,
где tx < £ < 4-
например
Применение
х(М*—х(Ь) дг'(е)
теоремы Коши здесь допустимо, так как х' (/) и у' (t) одновременно
в нуль не обращаются. Из указанного соотношения и следует, что хорда
MiM2 параллельна касательной к данной линии в точке"■. Л1 (6).
13. Дифференцируя,
по * соотношения гх =
' = k+r2,
r1+ra=2e,получим fY — Гз', Г/-|-Г2' =
= 0. Но r±rx = г^,
r2V2 = r2'r2, значит г/ =
.= | г2° | = 1) и,
следовательно, Гх°Г%' + Г2°Г2 = <0
или Гх W 4- г2°) = 0,
откуда rtr_L а0 + г2°. Но
вектор г/ коллинеарен
касательной к эллипсу в
точке My значит вектор
Г!° + га° имеет
направление нормали. Таким
образом, для построения
нормали к эллипсу в точке М
надо продолжить отрезки
FtM и F2M за точку М,
на продолжениях
отложить равные отрезки MP
и MQ и- на них
построить параллелограм
(ромб!). Диагональ MR этого ромба —■» нормаль к эллипсу в точке М — делит
'пополам угол между .радиусами-векторами FtM И /yW (черт. 1).
14. Вводя обозначения предыдущей задачи, будем иметь %' (r^ -f- г2°) = 0,
. " П ^ r2 ' rt "*" г2 ч '-
г/ + A-g/ =? 0, (rt + г2)' = 0, rt + r2 = const.
15. Применяя метод решения, аналогичный методу решения задачи № 13,
Черт,
Л'Г!0 + г1'г2°'== 0, ъ'ъ*.+ г2'г2° = 0,
получим
*
соотношение г/ (г^ — г2°) = 0, т. е. /вектор rf — г2°
коллинеарен
83

нормали к гиперболе в точке М; следовательно, вектор г,° + г2° коллинеарен
касательной к гиперболе в точке М (черт. 2). .
16. Указание. Обратить ход рассуждений, данных в задаче 15.
17. Указанные семейства образуют ортогональную сеть (черт. 3).
18. г1г20 + г2г10 — вектор, нормальный к овалу Кассини в точке М. На
чертеже дано построение нормали: MP = FlM, MQ = F2M, MPRQ (черт. 4) —
параллелог^ам; MR — нормаль..
- /) == 0; зна-
1S. r = p + ri, r' = r'if — — г7=0, r°r'— r'/=0, r (г° -
чит вектор г° — / имеет направление нормали, а вектор г° + / — направление
касательной (черт. 5).
20. Указание. Обратить рассуждения предыдущей задачи.
Черт. 3.
Черт. 4.
21. v = г' = (г' cos cp cos б — г sin cp cos 9- cp'— r9'cos cp sin9, г'sin cp cos 0-f-
-f W cos ф cos 9 — r0' sin cp sin 9, r' sin 0 + r0' cos 0},
j v I = "J/V2 + r20'2 + ry2 cos29, w = r" = {(r" — rep'2 — r0'2)coscpcos0 —
— (2r'cp'+ rep") sin cp cos 0—(2r'9'+r9") cos cp sin 0 + 2r0'cp' sin <p sin 9, (r" — rep'8 —
— r6'2) sin cp cos 0 + (2rV -f rep") cos cp cos 9 — (2r'0' + r.9") sin cp sin 9 —
— 2rG'cp' cos cp sin 8, (2r'8 + r9") cos 9 + (r" — r9'2) sin 8},
w =
Г [{r- _ r?'2 __ rQ'2)2 _|_ (2rV + rep")2 + (2r'8' + r0")2] cos29 +
"1 / 4_ 2rcp' (rcp'0" — jtr'by — 2r8(cp") sin 9 cos 9 +
+ [(2r'0' + r9")2 + 4r2G'y2 + (r" — r0'2)2] sin20.
22. v = {— rep' sin cp cos 0 — r9' cos у sin 9, rep' cos cp cos 0 — r0' sin cp sin 9,
Г0' COS 9}, | V I = Г l/0'2 + COS20.cp'2
(см. задачу 21). ,
23. vr = {— rcos cp sin0, — r sin cp sin 0, r cos 0},
= r,
•—: = {— cos cp sin9, — sin cp sin 0, cos 9},
f— я)п ф cos 9 • ©' — ft' cos со sin 9, cp' cos cp cos 9 — 9'sin cd sin 9, 9'cos 6)
jA/2 + cp'2 COS20
S4
|rj|*|
: COS X.

После простых преобразований получим:
j/"e^_j_cp'aC0S2Q
=,cosX,*
db
откуда 0'2 tg2X = ф'2 cos89 или g = ctg X dcp, откуда
In
Траектория точки называется локсодромией (черт. 6).
24. v = r' = {г' cos ф — гф' sin ф, г-sin 9 + rep' cos ф, z'},
\v\ = V r'* + r*y'* + г'*,
Z0 = {(f"-^r<p'2)coscp— (2г'ф' + np")sincp,
(г" — rcp/2) sin cp -f (2rV -Ь гср") cos 9 „г")-,
= l/"(r" — гср'2>2 + (2г'ср' + гф")2 + z'\
25.
V
1*1
Черт. 5.
{— г©' sin ф, гф' соч ср, г'}
у r2y'2 + z>*
Черт. 67
*' - ~>
Уг*ч* + г*\
г'* = cos2 X (г'2 + г2ф'2), tg2X -У2 = /*2ф'2> tg X;- dz = п% 2 = гф ctg X + С,
т. е. z — линейная функция ф.
26. Да. Доказательство: r(t) — r (t0) = I г' (a) da = — \ г"(a) d (t <— а)=г
= [- Г' (a) (* - a)]f + f ' (/ - a) df (a) = r' (ta)(t -10) +
-f ^ (t- a) r" (a) da = r' (/„) (i - t0) -i j' r" (a) d (/-a)» = r'(t0) (t-Q +
+ [- -J- Г" (a) (* - a)s] ^ + -£ JJ (* - a)* dr" (a) = r' ft) (t _/J +-
+ ^ Г" (W - 4)8 + \ j*^ (/ ^ «)2 Г"' (a) da =.. .== r' (4) (< - U) +
+ о", Г" (Q (t - /.)» + -_-. Г'" ft) (/ - t0f + ... + ~ Г(») (ta) (t - ty> -H
3!
n\
+ ^J^-«)rer("+1)(«)da.
85

27. Обозначая производные по s точкой и применяя правило
дифференцирования сложной функции, будем иметь:
г =fs', г" = rs'2 + fs"\ r'" = rs'b-\- 3rs's" + rs'", f^r^s'*, [r'r"] =
= [fr] s'\ r' x r" = rx rs'\ r>"r7,> = rrrs'\ \r' [r"r']] = [r [rr]] s'\
Зг" (г' хг")- г' (r' x r'") = (3rs'2 + 3rs") г x rs'z — s'r (r x r s'4 +
+ 3r x rs'2s") = {3r (r X r) — r (r x r)} s'B.
23.
dl/ =
^r d« dr dv
or __ dr du _i_ ^r dtf
dt/'
dV
du2 =
d2r(du
ди2
ди,
+
d2r dudv , d2r(dv\2
+ 2 * .*л»л» +
dudv
dudu'
dvV drd2u dr
drd2v
дй2
d2r d2r du du
+
.+
* *
dudv
)+
d2rdvdv dr d2u
dudv'
dr d2t/
fa*dudv
+
d2r
d2r (dudv
£Jv[du dv ^ dv ди) "Г ^*2 du dv т $• dudv ^ £ dudv' dv'
__d2r /da\2
du2
d2r du dv
dvdv
+ ^ .* * /to /to + .*. l/fyj ""l~
dudv
(Prfdv)2
% \dv)
dv'-
dr d4
*dv dv dv*'
drd2u
*
du
Отсюда
[dr dr~\ [drdr\ . ,
1 * *
du dv
' dr/ du
du dv
dv dv
^rdrdr_j d*r dr dr (day „ d*r_ dr dr du dv . дЧ дг dr (dv \*y
Mdudv-Xfa d* d%\du)^ + *£&&£dadu + д1>д*и(£\ди)}А'
» - U;2 ^ Л a ^ + .• j* .* .* W №+du й/+
d2r dr<
dudv du i
Kdu2 du dv
dudv du dv
d2r dr dr dv dv
\ ■& «•
dv2 du dv
or dv djn .
Л dudv] ' .
d2r dr dr
dv2 du i
dr_ j^rdrdr(^\2 . о_^!Г_ dS^L дАд®1—~^(д^\2\ л
ov"" U, я» ,* WW + ,*i Л» ,* a^d* + A .• .• [dvj ] Л
кди2 ди dv
Положим для краткости
d2rardr
du2 du dv.
dudv du dv
dv2 du dv
d2r drdr
dudv du dv
d^rdrdj^_
dt/2 dw dt/
тогда
==Л5
/dV dr dr\ /dV dr dr\ ___ / d*r_ dr dr\2 _ .
\du2 du dv) \dv2 du dv) \dudvdudvj ~~ " .
г dr/d«+p \d«^+^^y + Tadw J -
86

.2 Г jfdttY (dv\* .(dvyldu) 9dududvdv\
~A ГЧ[ди) \dv) +\du) W ldudvdudv)
__ 02 f dudvdudv /du, dv dudv\2\ j __J
^ I du du dv dv ~*~ \du dv~* dv du) J J
l-M//2 fiii Л71/ \/Wi2 Л/7 Л*./ \f)nfin tin riti' J
xdu2dudv' xdv2dudv'
^dudv du dv}
du du
du dv
dvdv
du dv
29. F^ma, F=mr"t r'F=mr'r", Fr' = -2 m(r'2)',
dr
dt
p-(i-r)!
SO. Если о == const, то a' = [rr']'=e[/r"] = 0, откуда r" tl Л но Fllr",
значит F\\r. Обратно: если F\\r, то^ г" 11 г, значит [гг"] = 0, [ггТ=0,
[гг'] = о = const.
31. [rmv\ = [г'/wtf] + [r/wz>'] = [/razw] + [rma] = [г/7].
32. [rr'Y = [r'r'l + f/r"] = [rr"].
33. rxr'^rx(r^)' = rx<r'r° + r0^rx(^ + r?'^j = rX . ,
X (r'r° + rep'[r0]) = rV (см. задачу 4). f
34,* Положим— =Х; X(£) —непрерывная на сегменте [tl9 t2) функция,
- [w
сохраняющая определённый знак. Имеем г'—Хг=0, откуда (re J )' = 0>
- Схл Глл \ш fx<# *
/•£ J = а, r=aeJ . Так как производная от функции £J равна \eJ >
fx<#
то она сохраняет знак на сегменте [tlt /2], т. е. функция £J — монотонная
и непрерывная функция t.
35.* Применяя метод решения предыдущей задачи, будем иметь:
J . nTKvrra r==a I pJ dt-l~ h. Пппияппгшяя от I £^;
:fl£
e J d/ + b-
■ к
Производная от
j
dtf равна
fx<#
е- >> 0; значит, \eJ dt есть монотонно возрастающая функция от t на
сегменте [tlf t2]. Кинематическая интерпретация: если в любой момент
времени скорость и ускорение непрерывны, коллинеарны и отличны от' нуля,
то движение происходит по прямой линии.
36.* г> = {?', ср + ц% г" = {?", 2?' + *Р"Ь
г'Хг" = 2<р'8 —??"•
Ланное уравнение определяет прямую тогда и только тогда, когда 2ср'2 —
9 9
= Ctt + Q
dv l
окончательно ф =
у= / 1 д> гДе я и £ — числа.
87

Иг №г *
37. * г = rr°, ^ « r'r° + г [r°l, ^4 = r"r° + 2r' fr°l — гт* =* (r" — r) r»+
+ ^И.*х0-
г' г
г" — г 2г'
= 2г'2 — гг" + г2 = 0.
Полагая — = w, находим -j-^ = — = — — = o> — 2a>* — ru> 7- + r = D,
dcp ' d<p2 dy dr dy dr' dr
2o)2 wrfo)
7*~~7Jr + l ;
dp 2p , , ^ dp 2p
положим <i>2 = p, r2 = q, получим ^- = ^-f-l. Решая уравнение — = —,
dp
найдём p=Cq2. Выбираем С так, чтобы удовлетворялось уравнение -т- =
= — + 1; получим С = а (я = const). Итак: р = aq2 — ? или ш2 = яг4 —
— г2, — = rl^ar2 —1. Производя здесь подстановку — = ?, легко найдём
^ = Ci sin (9 + С2) (Q и С2 — произвольные числа).
38. г' х г" = 2? '2 — 99" = 0.
Дифференцируя это соотношение, найдём
г' х г'" = 3<ру' — ер?'" 7^ 0.
39; Рассмотрим вектор-функцию:
р-г + Я-Ш ,
l/>'2 -
находим:
р'=г' + л -#-^ =г'+
г' х г" з_ -
(Г/2) 2
-г г, х г// г/ х г/.
Итак, р = const. Таким образом, данное уравнение определяет окружность
_з -
(Г'2) 2 / Г'3 \
радиуса R = —, — с центром в точке М (р) или М ( г -\ ; — М ).
* X г \ г X Г J
,40.* Пусть а — радиус-вектор центра сферы; тогда (г — а)'(г — а) = 0,
откуда rr'=.ar'. Дифференцируя это соотношение три раза, получим:
г'2 + гг" = аг"9 Зг'г" + гг"' = аг'"9
• 3r"2+.4r'r"' + r/-(4)=ar(4).
Отсюда по формуле Гиббса находим а; подставляя а в соотношение Зг"2 +
_j_ 4г'.г"' + rr(4) = ar(4), мы получим соотношение 2), указанное в условии
задачи.
41. Обозначим через а единичный вектор, перпендикулярный трём
компланарным векторам г', г", г'". Тогда аг' = 0, ar" = 0, аг"' = 0,
оггкуд-а aV + #г" = ° или «'г' = 0 и а'г" + а/*'" == 0 или а'г" = 0;
значит, а' X г' и а' _|_ г", т. е. а\\а' и, следовательно, а = const.
Теперь из соотношения ar' = 0 находим (аг)'='0, т. е. ar— const;
следовательно, линия расположена в плоскости (перпендикулярной вектору а)..

Замечание: вектор-функция a(t) имеет производную, так как а =
\г'г '1
1 l— a по условию вектор-функция r(t) имеет производные до третьего
\ [г'г"\
порядка включительно. Обратное положение имеет место.
42. /7=Хг — тг". Дифференцируя, получим: Х'г + *г' = тгш\
следовательно, векторы г', г", г'" компланарны (см. задачу 41).
4а Дг = r(t) — г (ад = {rf (t0) + a} (t — ад, где lim а = 0. Отсюда
*== * о
Г (tQ) Дг = {г'2 (*0) + г} (t — ад, причём lim е = 0.
* = *о
44, г' (to) X Аг = г' (Л,) X {/•(*) - г (t0)} = г' (/0)"X {г' (ад (* - 4) + {г" (Q +
+ «} ВД^^^Х^'^ + е}^, Jims = 0,
г 0
{Г' (/0) X Г" (*0)} {Г' (/0) X Г" (ад +е} (*~Т/°)2 = {{А" (/в) X Г" (t0)V +
+ *l}
{t-tof
, lim т] = 0.
45.* Радиус-вектор р произвольной точки неподвижной центроиды может
быть определён одним из двух соотношений:
Р = П + 1 [г/] = г2 + jj. [/V], п — г, + X [г/] = у [г2'],
fa - rj г.'+ XI/V]/•/ = <>,
(Л-л»,1
Х = -
Л' X Г г
в координатах: р = г4 + ' . v ' >2 [Л1;
't—^ '* (^2— ^i) *а' + (Уа — У1)У27 ,. ,
С = Л1 ; ; ; ; yi ,
Х1 У 2 Х2^У\
v — л, _L (Х2 — Х^ Х2 + (У2—У1)У2 „ ,
xi Уз — х2 у±
)Тр]
(Гъ — Гх)Гъ ш
(черт. 7).
46.* Рассмотрим вектор X [г/], где
Черт. 7.
X = _lLl_—'1Г |а ; если этот вектор of-
**1 X ^*2
ложить от конца М{ стержня, то его конец упадёт в мгновенный центр
вращения. Проекции вектора X [г^ на векторы r2 — rt и [r2 — ri]
соответственно равны:
Потому уравнения подвижной центроиды:
О—rt)/y /0<^VzL?li) =- (r2 — r^r2 rx'(r2 — rx)
П'хг,' I r2 — rx i '» ^ r/xr,' |/V—/V|
или
{(x2 — лгО jy -f (y2 — 3МУ2'}
лг = -
. *i У1
•^2 — «^i У2 У1
*i' у/
Vr(^-x1)« + (y1-jfJ«

y={(Xt—Xi)xt' +(y, —yjy,'} {(Xs — X1)xl' + {yi — У1)У1'}
1 *\ *', \V(x*-Xi)2 + (y*-yif
47. * # = rt + /? = rx + Ы -f- t) [а], где a = r2' — /*i, 8 = const, vj = const
(точка М жёстко связана со стержнем); R' = rt' + ia'-\-1\ [а']. Так как
| a | = | r2 — rx I = const, то a' _L л; значит,
a' = s [a], r2' — rt' = s [r2 — rj, (ry — rt') [r/] = s [r. •— rj [rx%
(см. задачу 45). Итак:
a'=fT[aJ, [a'] = —-J-a, /?' = r,' + -|- [a] - -3. a =
с другой стороны, r = R — p — ri + ta + ri [a] —rx — X [rt'] ±=£a + *] M —*
— ЧЛ'Ь И = /г1'-т5[л]—^а, значит,/?' = y И (формула Эйлера), <° = у.
4а г" || г, [гг"] = 0, [/r']'=*[rr"]; значит, [гг<] = а = const, [a/^l =
=-^3[[rr1r]=-l3(r'^^
Итак:
^{[ar'J + X ■£} = 0, [аг') + X £ = Ъ = const.
Умножая обе части этого соотношения на г и замечая, что [аг'] г=а [г*г] =
= — л2, имеем: —д2-}-Хг=#г. Движение происходит в одной плоскости,
перпендикулярной вектору а (так как из соотношения [rrf] = а следует ar = 0).
Введём в этой плоскости полярную систему координат, совмещая полюс
с началом радиусов-векторов, и направляя полярную ось по вектору Ь.
Получим — a2 -\-lr—t?rcos ср, откуда г =. __- , линия второго
порядка.
4а* зд = (г" — г?'2) г° + (V?'+ пр") И (см. задачу 5), F=mw, Fr° =
= mw, m(r" — rep'2) = Z7, 2r'<p' + rep" = 0.
Из последнего соотношения:
—-' + ^ = 0, (lnr2 + lncp')' = 0, lnr2 + !ncp' = lnC,
1
где и = у.
Далее:
G d^ ? "~ r* d<p2 * Г2 ^з гз ~ m
\d?2^ У /яСа
90

— это и есть формула Бкнэ (дифференциальное уравнение движения точки
под действием центральной силы в полярных координатах). В случае ньюто-
нианской силы
Г2
Дифференциальное уравнение Бинэ принимает вид:
(•=п
d2u , Л
Его частное решение: и = а, а общее решение уравнения -т~г + и — " такое:.
ц = — 5= d co& 9 + Q sin ср.
Значит, окончательно: — = Сх cos ср + С2 sin ср -\- а или 1 = Ctx + Qy + а г,
1 — С,х—С2у = аг,
VQ + Cl VQ + Q ' VQ+Cl d
— коническое сечение, для которого притягивающий центр является
фокусом, а соответствующая ему директрисса определяется уравнением:
CtX + Czy—1=0.
50*. г'г"=±0, (г'2)' =*= 0, | г' | = const (движение с постоянной скоростью);
далее г"//= 0, г'Я = const; значит, направление скорости образует
неизменный угол с вектором Я (траектория — линия откоса!). Из соотношения
г" = [г'И] находим: г' = [гН] +с (с == const), [Иг'} = [Я \гЩ] + [Нс\,
{[Я \гН]\ — [сН\У = |Яг']2 ~№'а- (ЯГ')2 = const; следовательно, | [Я[гЯ]] —
— [сЯ] | = const; но -—7/а" есть вектор-проекция вектора г в плоскость,
перпендикулярную вектору Я; таким образом, проекция траектории в
указанную плоскость есть окружность (Цт^— радиус-вектор её центра],а
траектория — винтовая линия.
51*
[гП = -Ь 1г (гг']) = х гг' ^ , [rr'Y = -'х (yj,
\rr]' — l (с ] (с = const).
Умножая обе части последнего соотношения скалярно на г, получим
сг=г — уравнение прямого кругового конуса. Отменим также, чтог'г"==0,
| г' | = const, т. е. движение происходит с постоянной скоростью. Так как
г" \_г и г" JL г', а векторы г и г' определяют направление касательных
к линиям, лежащим на конусе (к образующей и к траектории), то ти имеет
направление нормали к поверхности конуса. С другой стороны, г" имеет
направление главной нормали линии С; в самом' Деле: в общем случае
направление главной нормали определяется вектором [г* [г"г']] = г"-г'2—
— г (г'г") = г" • г'2 || г" (в силу того, что (г7)2 = const, /V1 = 0).
52*. г'ю = 0, г'г = 0; значит, па = const (плоскости, перпендикулярные
вектору (а) и г2 = const (сферы с центром в начале радиусов-векторов).
Линии, определяемые дифференциальным уравнением г'= [»г],—окружности,
центры которых расположены на прямой, ироходящей через начало радиусов
91

векторов коллинеарно вектору «*, а плоскости этих окружностей
перпендикулярны к указанной'прямой.
53*. Введём декартову систему координат, располагая ось Oz коллинеарно
вектору е. Тогда [e[re]} = xi -\- yj, и указанное дифференциальное
уравнение даёт х' = х, у' =у, z' = О, откуда x = c1ety у== с2 е*, z — cs — искомые
линии — прямые, по которым пересекаются плоскости, перпендикулярные
вектору е, с плоскостями, проходящими через прямую, проведённую через
полюс О коллинеарно вектору е.
54*. Введём декартову прямоугольную систему координат, располагая
ось Oz коллинеарно вектору е. Тогда ае-\-[ег] = — yi-\*x]-\-ае9 и данное
дифференциальное уравнение принимает следующий вид: х' = — у, у' = х,
z* = д. Из соотношений х' =—у, у' = х находим хх' + УУ' = 0, х2 + у2 = Сх —
семейство круглых цилиндров, оси которых совпадают с прямой, проходящей
через начало радиусов-векторов коллинеарно вектору е. Далее:
dz,
откуда
х dy —у dx
Tz
dx
dz~~~~~
x* + y2
~ a
r = dz,
у dy x
~a' dz~~a '
xdy — ydx _ Л У
X* \ ~t~ Xi
z + C2 = a • arctg ^
— семейство прямых геликоидов, для которых осью является упомянутая
выше ось цилиндров. Интегральные линии — винтовые. Наконец, z = at + С3.
Из полученных соотношений легко выразить х, у, z через t.
55*. Введём декартову систему координат, располагая ось Oz коллинеарно
вектору е. Тогда
~ r2e-r(re) = ±(x2 + y2 + z2)e-(xi + yj + ze)z =
fc= — XZi —yZj + _ (Х2 + у2 __ 22} е>
и данное уравнение сводится к системе:
х' = — xz, y' = — yz, z' = ~L {х2 + у2 — z2).
Имеем: х'у—у'х = 0, у^С^х — семейство плоскостей, проходящих через
прямую, в свою очередь проходящую через начало радиусов-векторов
коллинеарно вектору е. Далее находим: хх'-\-уу'= — z (х2-\-у2) и, полагая
х2-{-у2 = р2, будем иметь:
-i(p«)' = -*p», *' = !
- (?2Y = — zfy z' = ^ {f - z2\ p' = - z?t
j-F- flz* . (9*-~z2)d9 + 2z9dz = 0,
(p2 — z*)dp + 2z9dz_ (?2 — z2)dp + 229dz_
{?*-z2)9 + 2z9.z ' 9(z2 + 92) ~U>
* r=C2 sin 0
второй интеграл в полярно-сферической системе координат; это
поверхности, получаемые от вращения вокруг оси Oz окружностей, касающихся '
92

оси Oz в начале координат. Указанное семейство окружностей является
интегральными линиями данного дифференциального уравнения (черт. 8).
56*, Применяя формулу Эйлера, получим r1, = (e»ri],rj = [юг2]. Из этих
соотношений следует, что ю J_ г/, <d_Lr2'> значит, ю = Х [лТУ]. Далее
находим: г/ = [X [ач'аУ] rj = Хг2 (гл') — Хг/(г1г2') = — 'кг1'(г1Г2) (так как 1^1 =
= corfst). Итак, X = -
1-
и значит ш
[г8'г/1
ГЛ /W
57*, Пусть а—радиус-вектор, перпендикулярный к искомому вектору»
и такой, что его конец лежит на мгновенной оси вращения. Дело сводится
к решению системы:
отсюда
Mn-a) -fx» = /y, [»(ra-
[(о (г, — а)] + Хю = /у,
- а)] + Хю == /У,
Далее,
■ ГЯ)] = Л' — Г>', [to (П — Г,)] = г/ — Г8',
ш^ [(г/-г8')(г1'--г8')1
(Л—Га)(гУ —Г8')
[[«(Л— а)]»]==[г>],
(rt — а) w2 — со( (rt — а)») = [г^ю],
(rj — а) (й2 — to (г^) = [г/ю],
<J Tl Z •
Черт. 8.
Уравнение мгновенной оси вращения R =
откуда X = —j— и скорость скольжения
a -^ 6 <*• Наконец, Xw8 = rx V
:Х«Й =
(Гх'гА) Ы у
— проекция
скорости точки движущегося тела на мгновенную ось вращения.
58*. Введём систему координат, принимая касательную к данной линии
в точке М0 за ось Ох, прямую М0К — за ось Оу. Тогда г'(t0) = х'(t0) i (ибо
г' (t0) || /). Так как r'(t0)z£Q, то и xl (t0)z£Q. Функция r'(t) непрерывна при
t — t0, значит, х' (t) также непрерывна при t=tQ. Пусть х' (t0)>0.
Существует окрестность (t0 — 8, *0 + <$), в которой x'(t)>Q, значит, x(t)
монотонно-возрастающая \функция t\ следовательно, . t
(to - Mo + *) ^(х & - *), х (t9 + 8)).
Любому x£(x(t0 — &), x(t0-\-b)) соответствует единственное значение
*£(*о— 8, ^о + £)> а этому значению t соответствует % единственное значение
У («.
59**. Аг = г (t) - г (t0)' = г' (t0) (t - tQ) + { г" (t0) + « }
('-'о)2,
где
lim a = 0. Отсюда [г' (*0) Аг] = { [г' (*e) r"(t0)] + s} ^~J^ , где lim s = О,
t = t0 2 t = t0
Так как [г' (/0) г" (£0)] ^ 0, то существует окрестность t0 такая, что при
всех t из этой окрестности [г' (/0) г" (t0)] + s ф О, а значит, и [г' (*0) А^] ^ О
при всех t из этой окрестности (отличных от tQ).
60**. Примем прямую MtM* за ось Ох, а за ось Оу примем любую
прямую, проходящую через точку М8, отличную от прямых MtMSt M»MS и
имеющую такое направление, какого не может иметь касательная к данной линии
(так как таких направлений по меньшей мере 4, а ось Оу не может иметь лишь
трёх направлений М^МЪ M.2MS и M8Mlt то остаётся ещё по меньшей мере
ох'но направление). Теперь находим:
|*('i)y('i) 1
A = U(*s>y('a) l
\x(ts)y(t3) 1
-|*0i)-
■x(tt) y(i%) — y(ti)\_L-
93

= {x(t2)-x(tl)}{x(tz)-x(t,)}
= (/,-«(/,-«ЛГ'(;)^(Ч)
j y(t%)—y(ti)
x{tt) — x(tx)
1 у (h) — у (t*)
x(tb) — x{t2)
1 ?'la)
X' (a)
1 1Ж
x'№
=• ft - *l) ft - *l) (P - «) X* (5) X' (!)) ;
1
r'(C)Xr"(C).
'x-(S)
Далее заметим, что t3 — tt > 0, /3 — £2 > 0, Э — a > 0,
r'(0 X r" (0 >0, ^(C)>0.
f
Производные x'(%) и лгЧ7)) одного знака, так как если бы они были -разных
знаков, то производная x'(t) обращалась бы в нуль при некотором
значении /, а это невозможно ввиду принятого расположения осей координат
(касательная не имеет ни в одной точке направления оси Оу и, значит,
х'фО при всех t^la.b}). Итак: А > 0.
61**. Пусть г'(УХг"(/0)>0. Расстояние от точки M (t) данной линии
до касательной к этой линии в точке M0(t0) определяется соотношением:
г'(Q
Отсюда
1/VS ft)
x{r(<)-r'ft)}.
do
г'ft)
dt
X r'(t):
/"'ft)
X{r'ft-r'ft)} =
V^ft) V^ft)
=тМт *"•"«•>+•"«-<•>={^Ag" +•} «-'•>•
где lim e = 0. Отсюда следует, что при всех t, достаточно близких к t6 и
tmmt*
меньших /0, имеем: -г? < 0, а при всех /, достаточно близких к / и боль-
ших *0, имеем: —тг > 0. При / = /0> о=*0, значит, существуют интервалы
(t0 — Л, /0) и (t0, tb~\-h) такие, что на первом из них 5 монотонно убывает
от 6 (/0 — h) до 0, а на втором монотонно возрастает от 0 до о (t0 -f- /г).
Предположим что о (t0 — К) > о (£0 + /г). Тогда любая прямая, ^параллельная
касательной к линии в точке MQ и находящаяся от касательной на
расстоянии, меньшем чем о(£0 + ^)> пересекает дугу линии, ' соответствующую
интервалу (tQ — Л, t0-\-h) в двух точках (при этом указанная прямая должна
быть расположена по ту же сторону от касательной, где расположена дуга
линии). 2) Примем касательную к данной линии в- точке М0 за ось Ох,
точку М0 — за начало координат, а нормаль к линии в точке Л10^за ось Оу.
94

Угол ср = arctg — от оси Ох до хорды М0М есть монотонная и непре-
х \
dy ху' — х'у
dt х2+у2
так как ■
рывная функция t в окрестности t —
t A/2\ А*2
гхг, [г', М + (г"0 + вх) т] х (г'0 + (г"0 + в,) М) г'0 х r"„ T + 5
dcp
где lim £ = 0, откуда и< видно, что -~- сохраняет знак в окрестности t=tQ
д/ = о dt
При t=t0, cp = 0. Таким образом, существует интервал (/0 — 8, /0-f-&) такой,
что соответствующий интервал значений <р, (—а, *р) отображается на
него взаимнооднозначно и непрерывно. Любая прямая, проходящая через
точку М0 и наклонённая к касательной под углом ср £ (— а, р), встречает
рассматриваемую дугу только в одной точке (не считая точки М0).
62**. Достаточно малая дуга данной линии в окрестности данной точки
М0 обладает тем свойством, что любая прямая, проходящая через точку М0,
пересекает её не более чем в одной точке (не считая точки М0); эта дуга
и может быть определена полярным уравнением, если за полюс принять
точку М0 (см^ задачу 61).
63**. 1) Функция г (t) X /*".(/) непрерывна при t~tQ, и так как
г' (t0) X г" (А,) Ф 0, то г' (t) X г" (t) ф О
ив некоторой окрестности t = t0. 2) Угол между касательными к дуге С
в точках М (/0) и M{t) определяется соотношением:
) = arc cos ■
r'(t)r'(tQ)
\r'(t)\\r'(t0)\
это непрерывная функция L Так как при tr=t0, 6== 0, то при всех ty
достаточно близких к t0, отклонение касательной к линий в точке М от
касательной . в точке М0 сколь угодно мало; теперь вопрос сведён к задаче 60
(вспомним, что в условии задачи 60 мы требовали, чтобы существовали
четыре напраэления, каких не может иметь касательная; в силу малого
отклонения касательной к дуге С в точке М от касательной в точке М0
это условие будет выполнено). 3) Из сохранения ориентации треугольника
МхМ2Мг с вершинами Мг {tt)t М2 (t2)y М3 (tz), где /0 — s < h < t2 < tz < t0 + й,
следует, что никакие три точки дуги С не лежат на одной прямой; значит,
любая прямая пересекает дугу С не более чем в двух точках.
64**. Примем прямую, на которой расположены, точки Мх (£Д M2(t2)
и Ms(ts) за ось Ох, а за ось Оу ^примем прямую, которая,не имеет
направления ни одной касательной к данной линии. Условие коллинеарности точек
Ml9 M2, M&:
jfW-jfft) y(h)-y(tt) I __,
*(*•) — *,(*■) y(h)-y(t2) I -
0 =
y(t*)-y(h)
x(t2)*
y\h)-
~x(tx)
■y (4)
x (4) — x (t2)
{x (t2) - x (h)} { x (4) - x (t2)} =
= { x (t2) - x(tt)} {x (4) - x (t2)} {x, x<
У (ft
m=
= { X (t2) - X(tx) } { X (h) - X(t2) } (p- «) -
Отсюда r'(9xr"0 = O.
65**. См. задачу 64.
г"(с)У(£)
*'2(У
95

66**. Придадим оси Оу направление, которого не имеет ни одна из
касательных. Имеем:
— *'(М *' ('2) (<, -Vi) г'(6) х г" (5), <, < 6 < 4;
— х'2 (?)
дг'(4) и л'(<2) имеют один знак, так как в противноя случае х'(i)
обращалось бы в нуль при некотором значении t, т. е. имелась бы касательная,
параллельная оси Оу. Геометрически сохранение знака^ г' (tt) X г* (*s)
означает, что касательная к линии вращается в одном направлении при
возрастании t от а до Ь.

. ГЛАВА II
§ 1. Касательная и нормаль
67. 1) Касательная Я = {a (cos/— Xsin/J, £(sin/+X cos/)} или £ cos/A"+
+ a sin / У — ab = 0\ Нормаль: R = {(a + bl) cos /, (b -\- a\) sin /} или aXsin t—
— bV cos / + (b* — a2) sin / cos / = 0. 2) Касательная R = [|- [/ + -1] -j-
+4(1-ж).-И'-1)+4('+^)}
или
нормаль
«Ч*1('+1)-4('+Я-4('->'4('-Л
ИЛИ
3) Будем рассматривать полуинтервал 0^^<2гг; если / = 0,толг = а, у=»0
в точке (а, 0) касательной является ось Ох, а нормалью—прямая х = а;
если /=-^-, то л; = 0, j; = a; касательной в точке (0, а) является ось Оу,
а нормалью — Прямая у = а; если /=тг, то лг = —л,, у-=0; касательной
в точке (—а, 0) является ось Ох, а нормалью — прямая х =— а; если
/=-=-, то л: = 0, j; = — а; касательной к линии в точке (0, —а) является
ось Оу, а нормалью — прямая у =* — д. При всех остальных значениях
/£(0,2тг) имеем: касательная Xsint-\-Y cost—д sin/cos/=^=0; нормаль:
Acos/—Ksin/-[-tf (sin2/ —coss/) = 0. 4) В точках / = 2/wr, где Л принимает
все целые значения, касательными являются-соответственно прямые x = 2kTta,
а нормалью — ось Ох. Во всех остальных точках имеем: касательная
Actgy-r+a(2-/ctg-y=:0,
нормаль
A+Kctgy —а/ = 0.
5) Касательная А—К = 0, нормаль А+^ = 0. 6) Касательная
(sincp + cp cos cp)A —(coscp — cp sin ср) К — аср8 = 0; нормаль:(cosср — ср sincp; А-+-
+ (sin cp-j-cp cos cp) F—аср = 0.
7 Л. С. Моденов . 97

68. 1) Касательная дг—-у — О, нормаль
7х —- by — 17 = 0, нормаль 5* + 1у + 9 = 0«
69. Нет.
л: -|- у = 0. 2) касательная
70.
71.
(2' 4J-
(I- 4)и(
27У'
72. 4х — у — 4 = 0.
74. 2дг—j> —2 = 0, 2х-
75. 27х—3у —79 = 0.
77. Один из углов: arc tg 3.
78. 45° и 90°.
79. arctg3. 88, tg6 = г
89. Координаты точки
у + 2 = 0.
г •
Р: лг =
а/, _у = 0. Далее надо составить
уравнение нормали к циклоиде г={а
(t — sin t)t a (I — cos t)} и
проверить, что на ней лежит точка Р.
90. Нет. Пример: рассмотрим
линию, изображённую на чертеже
и заключённую между двумя
параболами. В точке М0 эта линия,
очевидно, имеет касательную —
это общая касательная к
параболам в точке М0. Точки Мх и М2
можно выбрать сколь угодно
близкими к точке М0 и так, что
прямая МХМ2 будет отклоняться от
касательной в точке М0 на угол,
скажем, больший, чем 45°
(разумеется, при подходящем выборе
линии С). Рекомендуется построить
аналитический пример (черт. 9).
91. Уравнение конхоиды,
р = г+ -^(а = const), P' = r'-f
at! af_
Черт. 9. r r%
92*. Возьмём уравнение
параболы в виде у = ах2. Угловые коэфициенты касательных в двух точках
этой параболы k1 = 2axl, k2~2ax, а тангенс угла между \ними:
2а (х-*,)
1 + *a*xxt - 1ь • * '
С другой стороны, разрешая уравнения касательных к параболе: 2ахХ—У =
= ах2, 2аххХ—У = ах\ относительно X и У, получим:
2X=x±xv Y = axxv (2)
Из уравнений (1) и (2) находим;
tg2 а (1 + 4д2лглг1)2 = 4а2 (х — л:,)2,
tg2a(l-f 4aK)2 = 4a2{(jc-fjc1)2 — 4ххг }, >
tg2a(l + 4aK)2 = 4a2(4^2 ) — гипербола.
98

В частности, при а^=^ получаем: 1 + 4а,лмг1 = О, У===^^'-^- -
рисса данной параболы.
93**. Тангенсы углов, образованных прямыми —^ р- = О,
ляются соотношениями
_2_ , .
2«# . Д* 2 /~}2
директ-
опреде-
tg? = ±
а2 — Ь*
1
£2
Л
Л=-
1
Уравнение пары касательных, проведён-
где Л ____,., .^
ных из точки (лг0, yQ) к данной линии имеет вид:
2FQ . 2F-(xFXq + VFyo + zFHf^ О,
откуда
Ji = &^an + *wd-Fx\--Fy\ = J^b-Fx\--F%
Л = («и • 2FQ - Fx*q) (a22 . 2F0 - /%J) -(a12-2F0 - /^ /V0)* =
= Л(2^о)2-аи/7у^ 2F0-a22/yo . 2/^0 + 2alEFXQF^ 2F0.
В силу тождества
#21«22«2
«11 «12 FX
«21 «22* у
FXF'TF
находим:
и, следовательно,
Таким образом,
I ui as a
X = Л(2/у» + 2F0(78 - Л • 2F.) = Л • 2Я1,
tg«Pi,» = ±-
2y:-y..2f,
Л . 9F F 2 F
Vo
Искомое уравнение
~ (Л • 2F — /у» — Fff + 4Л2/7 ctg3 cp = О
—линия четвёртого порядка. В частности, при ер=з 90°.
J^F—F^ — F/^O
—линия второго порядка. Выражение Jt • 2F — Fx*— Ff легко
преобразовать к виду
Л (-*3 + У) — 2Atx — 2А& + /Са,
где
Ах = д2а1а — «i«22» ^а = aia12 — «2«u» %ъ = «п« "fe«22« — «? — «!•
Отсюда следует, что линия, из точек которой данная линия второго порядка
видна под прямым углом, есть окружность, если данная линия эллипс или
гипербола. Если же данная линия парабола, то указанная линия — прямая 2i4i^ +
-\-2А2у — /С2 = 0. Это уравнение определяет директриссу параболы. Его
можно записать в виде:
«И «12 X
«21 «?2 У
ах а2 1
«n«i
+
«32л2
as a

В таком виде, следовательно, может быть записано уравнение директриссы
параболы, заданной общим уравнением. Пусть теперь линия задана кано-
х2 v2
ническим уравнением: 1) -^- -)- ~ = 1; .
а*
^+у1
а2Ъ2
1 1 \2 4ctg2y/x2 . f \_
а2 Ь2) а2Ь2 [а2 •" Ь2 1)—"-
В частности, если <р = 90°, х2-\-у2 = а2-\-Ь2 — окружность.
Z) а2 Ъ2 -1'
/х2 + у2 1 1 \> 4*tgjy /л:2 У2 Л п
а?Т b2 j ~г яа£- U2 ^ У
я*£2
В частности, если <р = 9Э°, х2 -f- V2 = <*2 — Ь2\ при а"> b это уравнение
определяет окружность радиуса \^а2—Ь2 с центром — в центре гиперболы.
При а-=.Ь уравнение определяет центр гиперболы. При а < Ъ нет ни одной
пары взаимно-перпендикулярных касательных к гиперболе;
3) у = ах2;
аУ + -^) +а сХ^ 9 {у-т- ах2) = 0 -
гипербола. В
частности, при ср = 90°, ау + ~г = 0 -
•директрисса параболы.
94.
/<*> (« Д Г = И*> (*0){/« (« + «} <Ц^ :
= {(r^>(/0))2 + s}
(t-t0)k
lime = 0.
Значит, r*k) (t0) Д r> 0 при всех t, достаточно близких к t0 и больших /0.
95**. 1) Пусть / — касательная к линии С в точке М0, а /' — любая
прямая, проходящая через точку MJf отличная от прямой /. Построим
прямые а, р, а', Р', так, как указано на
чертеже 10. Тогда все точки достаточно
малой дуги линии в окрестности точки *
М0 попадут внутрь той пары
вертикальных углов, образованных прямыми аир,
где проходит прямая/,
следовательно,никакая дуга в окрестности точки М0 не
попадёт целиком внутрь той пары
вертикальных углов, образованных прямыми
а' и #', в которых проходит прямая /'.
2) Какова бы ни была прямая /,
проходящая через точку М0, найдётся пара
различных прямых аир, отличных от
прямой I, и таких, что какова бы ни была
дуга линии С в окрестности точки Мог
хотя бы одна из точек этой дуги будет
лежать внутри той пары вертикальных
углов, образованных прямыми аир, где
не проходит прямая /.
3) г (/)-г(/в)==Дг =={/*> (*.) + •}
_ где lima = 0. Проведём через
точку М0 прямую /, коллинеарную вектору r^ (t0), и отложим этот вектор
от точки М0:М^Р=/-(^(/о). Проведём через точку М0 произвольные
различные прямые а и р, отличные от прямой /. Построим окружность с центром
100
Черт. 10.

в точке Р такую, чтобы она не пересекала прямые а и ft Так как lim «= О,
то найдётся окрестность (t0 — Ь, /0 -|- $) такая, что концы векторов Ик) (t0) + «,
отложенных от точки М0, попадут внутрь построенной окружности, а значит,
концы векторов {г^(/0)+а}-гг= Дг
при всех t£(t0 — o, t0-\-b),
отложенных от точки М0, попадут внутрь той
пары вертикальных углов,
образованных прямыми о и ft где проходит
прямая /, а это и значит, что прямая /
есть касательная к линии С в точке
М0 (черт. 11).
4) Данная линия заключена
между, двумя параболами у = л:2 и
у = — л:3. Если провести две прямые
а и ft отличные от оси Ох, то внутрь
пары вертикальных углов,
образованных этими прямыми, в которых
Черт. 11.
Черт. 12.
проходит ось Ох, попадут дуги этих парабол в окрестности начала координат,
а следовательно, туда же попадёт и некоторая часть дуги нашей линии
в окрестности начала координат (черт. 12).
\
J>''\
-'•'-''^^У /
9
,.-Vj^o
'•''у/
Черт. 13.
5) Проведём через начало координат произвольную прямую /, а также
две'прямые а и g. таких, что одна из прямых у = х или у == — х не попала бы
внутрь цары вертикальных углов, образованных прямыми а и ft где проходит
прямая / (черт. 13). Пусть, например, внутрь указанной пары вертикальных
углов не попадёт прямая у = лг. На прямой у=х имеются точки данной
101

линии, сколь угодно близкие к началу координат и отличные от начала
координат; абсциссы этих точек определяются из уравнения Arsin —= дг,
где х ф О, т. е. из уравнения sin
\
• 1. Таким образом, в любой окрестности
начала координат есть точки данной линии, расположенные вне той пары
вертикальных углов, образованных прямыми а и {j, в котором проходит
прямая /.
S6. Понятие касательной (см. задачу 95) — аффинно-инвариантно.
Построение касательной к эллипсу дано на чертеже (черт. 14).
97. Вектор r^(t0) = -z коллинеарен касательной к линии С в точке М0.
Пусть v — любой вектор, не коллинеарный вектору т, а п — прямая,
проходящая через точку М0 и имеющая
направление вектора v. Находим:
Д/fe
v X Ar = v X {г(к) (/о) + *}
:(v XV+e)
, lim e = 0.
. д* = о
Т Так как vxx^O, то при всех М„
достаточно малых по модулю, знак
произведения v x Ar определяется
следующим образом: если k
нечётное, то v X Аг сохраняет
определённый знак при всех М < 0 (и доста-
. точно малых по модулю) и сохраняет
противоположный знак при всех
АГ> 0 и достаточно малых, а это как
раз и означает, что линия С в окрестности точки Мь переходит через^пря-
мую п. Если k — чётное, то v x Аг имеет определенный знак при всех А/,
достаточно малых по модулю, а это значит, что линия С в окрестности
точки М расположена по одну сторону от прямой п. Далее находим:
Черт. 14.
X Дг = /•<*> (/0) х { г<*> (*.) |f +1» + » ft)
Д/ft + l
<*+!)!
+ ••• +
+ |*-1)(^(|^Г15Г+{г«Л)+«}^} = {/<*)(«Х^>(« + .}^.
lim e = 0.
д* = о •
Остаётся повторить рассуждения, вполне аналогичные предыдущим.
§ 2. Точки перегиба. Выпуклость. Вогнутость
98. (2,62) и (4,206).
102. Данная линия не имеет точек перегиба.
103. (е
Зтс
- + ** (—1)*\
Ь ± 2,..., ± п,.
104. Точки перегиба существуют при условии 2я2 + Ь2 < ЗаЬ . Соответ-
ствующие значения ср определяются из соотношения cos<p = — '
ЪаЬ
105. 1) {г' (/„) Х г" (t0)} {r' (t0) х а] > 0;
102

. 2)kcw /(«
I -** Co) f Co)
*' Co) У Co)
*' Co) У' Co)
3)
^Co)>Q —условие вогнутости «вверх»;
УСо)<° —условие вогнутости «вправо»;
4) /" (х) [т — //' (х)] > 0, где {/, т} = а}
f (л:) > 0 — условие вогнутости «вверх»;
/Ч*)/" (•*")< 0 —условие вогнутости «вправо».
106. Данный вектор и, очевидно, имеет направление нормали к данной
линии, так как он имеет направление вектора [г']. #Остаётся доказать, что
этот вектор направлен в сторону вогнутости линии. Имеем:
г'3 (г* у г" \%
^x^^x") = |/i|rxn>0'
Накбнец, ясно, что |и| = 1.
107. У = cos л;, у' = — sin л:; у" > 0 в интервалах (— тс + 2&тс, 2&тс), где k
принимает все целые значения* На этих интервалах синусоида вогнута
вверх. Далее у9у" = — sin х cos х = — -к- sin 2х < 0 или sin 2 х > 0; решение
этого неравенства:
2Ы < 2л: < 2&тс -f тс или /гтс < х < £тс + у .
На этих и только на этих интервалах синусоида вогнута «вправо». На интер-,
[Х —к--\-къ <. х <. kit синусоида врп
108. {r<fe) С) х Дг} {/■**>'(/0) X а] > 0
валах—~- + £* < х < ^ синусоида вргнута «влево»
лг(/г) С0) > 0 — условие вогнутости «вверх»;
y(k) Со) < 0 — условие вогнутости «вправо»;
{г<*> (/в) х г<*> (*„)} {r<fe) (/0) х а} > 0.
Соответственно этому обобщаются и остальные выводы задачи № 105:
\x{k) (t0) У*Ч'о)
U(J) Со) У^ Со) |
U(/J)(4)yfe)Co)
U^Cojy^Co)!
/^ [(х) [т - If (*)]> 0; где {/, m} = a
— условие вогнутости по отношению к вектору a (s — чётное);
/^ (дг) > 0 — условие вогнутости «вверх».
f (х) /^ (дг) < 0 — условие вогнутости «вправо».
109. МР= *-~ [а]. Точка Р лежит со стороны выпуклости,
линии С в точке М, если
(г' X П (г' X —~%)Х" [«]) < 0
или
(r'X^)(/-'a)((r-p0)X«)<0.
В частности, если прямая / проходит через начало радиусов-векторов, можно
принять ро=?0, и условие принимает следующий вид:
(г' X г") (r'a) (г. X «) < 0.
103

Если прямая / является осью Ох, то это условие" принимает зид:
х'у
х" у"
х' у > 0.
Если прямая / является осью Оу, то это условие принимает вид:
I х' у' I
у' х<0
— условие выпуклости к оси Оу.
Если линия задана уравнением y=f(x), то предыдущие условия принимают
вид:
f'(x)[l + mf(x)]
х — х0у—у0
I m
<0
— условие выпуклости линии у=/(х) к прямой
х = х0 + lt,y±=y0 + mt;
/(*)/" (лг)> 0
— условие выпуклости линии y=f(x) к оси Ох;
xf(x)f'(x)<0
— условие выпуклости линии y=.f(x) к оси Оу
(черт. 15).
д, 110. уу№,= ъ'тх(— sin x) = — sin2x<0 при
всех х фЫ (k — любое целое число). Значит,
синусоида вогнута к оси Ох всюду, за
исключением точек x — kn (в которых она пересекает
ось Ох). Далее,
xf (x) f (х) = х cos х (— sin x) = — у х sin 2x.
Пусть х > 0. Тогда =- х sin 2х < 0, если sin 2 х > 0 и, значит, в интер-
тс
валах /гтс<лг<&тг4-у синусоида выпукла к оси Оу, k = 0, 1, 2,..., я,...,
а в интервалах — -~- -)- &тс < л* < &тс, £=1,2,..., /г,... вогнута к оси Оу.
Если л: < 0, то условие — -=- д: sin 2л: < 0 будет выполнено, если sin 2 л:<0;
значит, в интервалах —~- + kiz < д:< &тт, & = 0,— 1, — 2,..., —я,...
синусоида выпукла к оси Оу, а в интервалах
Ы < х < &тг + у, £ = — 1, — 2,..., — п,...
вогнута к оси Оу.
111. 1) Условие выпуклости к прямой / линии г = /*'(/):
(Ах + Ву + С)>0.
х' у'Л \х'у'
\х"у"\\ А В
2) Условие выпуклости к прямой / линии у=./(х):
у" (Ау'—В)(Ах + Ву + С)< 0. ,
1С4

dF dF
112. Рассматривая только точки, в которых ^ и ^- одновременно не
равны нулю, находим:
1) необходимое и достаточное условие вогнутости линии в сторону
вектора а:
* *■*• * хм * х
(lFx + mFy)
хх л ху л х
'ух 'уу * v
Fx Fy О
>о,
где {/, т) = а.
2) Необходимое и достаточное условие вогнутости «вверх»:
F F F
1 хх 1 ху 1 х
г ух *уу ^у
Fx F, О
>0.
3) Необходимое и достаточное условие вогнутости «вправо»:
'хх г ху ' х
Fyx *уу 'у
Fx Fy О
>о.
4) Необходимое и достаточное условие вогнутости к оси Ох:
ур>-
г хх Fху 'х
'УХ Fyy Fy
Fx Fy О
<o.
5) Необходимое и достаточное условие вогнутости к оси Оу:
xFx
'хх Fху Fх
г ух ''уу 'v
Fx Fv О
<0.
115. (AFx + BFy)(Ax + By + C)
F хх F ху F x
'ух Fyy г у
Fx F9 0
<0.
114. r={x,f(x)}, г' = {1,/(дг)}^0, /^>={0,/<*>(*)}, r'x/ft)= ,
значит, если k — чётное, то рассматриваемая точка обыкновенная, а если
к — нечётное, то точка перегиба.
„= „,1 F* fy (F** + Г**У') - F* F*s + fyy.?1) --
. Fv(fxx-
_ Fyfxx —
p2
Fx
ry
рхр>
F _
/ XX
' #y] Fx
F2
fF xy Fx
fy
-2FxFyF
(fyy-
Fy FXy
,v + F
Fy Г") _
+ Fl
*F.yy
/я* —
fy
10&

116. у":
отсюда
Fy Fxx — %FX Fy Fxy + F% Z7,
M:
■F3yy = F$Fxx-2FxFyFxy + F2xFT
у' xy~r' x ' yy
Дифференцируя по х, получим:
- 3 F$ (Fxy + Fyyy')y" - Fyy'" = (2Fy Fxy + 2FV Fyyy') Fxx + Fy (Fxxx +
+ Fxxyy') - 2 (Fxx + Fxy yf) Fy Fxy - 2 Fx (Fxy + Fyy y') Fxy - 2FX Fv (Fxxy +
+ Fxyyy') + (2FXFXX + 2FX
'хуУ ) *yy + F2x(FXyV +
= p- (fy Fxxx — 3Fy Fx Fxxy 4- 3Fy Fx Fxyy — Fx Fvyy).
Если у" = 0, то
/" = — Та (fy Fxxx — 3Fy Fx Fxxy 4- 3Fy Fix Fxyy — F% Fyyy)
y
и, значит, у'" ф. О (так как по условию задачи отлично от нуля выражение,
стоящее в квадратных скобках).
§ 3. Исследование и построение линий
117. г' — {2t 4- 1, 2t 4-3} ф О при всех значениях t\ г" = {2, 2},
12*4-1 2/4-3
г х г =
= — 4^0—все точки данной линии обыкновен-
Ух
Черт. 16.
ные. Линия вогнута «вверх» в точках, где (х'у" — хту')х'>0 или
— 4(2*4"1)>0 или /< — -у. Линия выпукла «вверх» при f>—~-. Ли-
3
ния вогнута «вправо» в точках, где (х'у№—х"у')у'<:0 или при /> — у.
3
Линия вогнута «влево» при t<z — -~-. Точки пересечения линии с осями
106

координат: (6, 0) при t = — 4; (0,-4) при t~ — 3; (—4,0) при /= 1 и (0,6)
при t = 2. Линия выпукла к оси Ох при t< — 4 и —-~-</<1. Линия во-
гнута к оси Ох при — 4</< — -<у и />L Линия выпукла к оси Оу
3 3
при — 3 < * < — -^ и при t > 2. Линия вогнута к оси Оу при — у <^<2
и /< — 3 (черт. 16). Исключая'параметр t из уравнений
jc = /» + "/-—6,
^ = ^ + 3^ — 4,
последовательно имеем:
■у — дг = 2/ + 2,
/==-*-(у — х —2), "
х = ~(у~х-2Г + ^(у-х-2)^6
или х2 — 2дгу + У2 — 2* — 2у — 24 = 0 (парабола).
118. r' = {2t, 4/* + 5/4}; отсюда ясно, что г' = 0 только при / = 0. Этому
значению / соответствует на данной линии точка (0, 0), являющаяся точкой
возврата второго рода, так как г" (0) = {2, 0} ^Ь 0, г'" (0) = 0, г{4) (0) = {0,24},
г" (0) х г<4) (0)
2 0
0 24
= 48^:0.
Составляем уравнение* г'Хг" = 0, которое здесь принимает вид:
2/(12/2 + 20*3) — 2(4*3-f 5*4) = 0, откуда ■*= — г^(^=0 опускаем). При
■"■■О (
этом значении * имеем г' (— р 1 ^0, г' ( —ус) X г" ( — ,-=) = 0, но
г' ( — те) X г'" (-— — ) ^0; значит, при / = — ус имеем точку перегиба
., /64 28 672 \ п ~ /п Ач n m
1 \22V 755"375) ' ^анная линия пересекает ось Ол: в точках (0, 0) и (1, 0).
В точке Л42 (9-^, ото^ касательная параллельна оси Ох.
Наконец,
Jim л: = +со, \[ту = -\-со,
t=-j-CQ / = -j-- ОО
11тл: = + 0<::>> Пту = ^— оо
£ = — оо t— — оо
(черт. 17).
119. Производная г' обращается в нуль только при ^ = 0;
г"(0)={10,0}^0, г'"(0) = {0,30},
г" (0) X г'" (0) = 300 ^0.
Точка (0,0) — точка возврата первого рода. Касательной к линии в этой
точке является ось Ох (так как г"(0) = {10,0}). Далее г' X г" = &2.
Это произведение обращается в нуль только при £ = 0. Таким образом, все
точки линии, кроме (0,0), — обыкновенные. В точке, соответствующей
значению t = |/ .—, т. е. в точке Мх (/Ш, у 72), касательная параллельна
107

оси Оу. В точке, соответствующей значению ^=1/ -^-, т. е. в точке
М2(У~12, ]/108), касательная параллельна оси Ох. В точке,
соответствующей значению /=1, т. е. в точке Мв (-у, -=-], касательная
перпендикулярна биссектрисе лг=у координатного угла. Точки, соответствующие
значениям параметрами—, симметричны относительно биссектрисы х = у
координатного угла. Линия, симметрична относительно прямой х=у (черт. 18).
120. Если ах = ^2 = ^ = ^2 = 0, то уравнение линии не определяет.
Если а1 = а2 = 0, но хотя бы одно из чисел Ь1 или Ь2 отлично от нуля, то
данное уравнение определяет прямую линию, параметрические уравнения
которой х = bx t -f- с1У у = b21 -f- с2. Пусть теперь обращается в нуль только а%
Черт. 17.
Черт. 18.
или а2. Положим а2 = 0. Тогда данное уравнение примет вид: r={aj/2 +
+ К t + cv &21 + с2}. Если здесь Ь2 ■=£ 0, то из уравнения у = £2 ^ + с2 на-
. у — с 2
ходим tz=z^———? и значит
#2
х=-ах
Ь,
•с%
+ h —т—- -{-С! — парабола.
#2
Если £2 = 0, то уравнение r={at t2 + btt-{-cuc2} определяет часть
прямой у = с2, коллинеарной оси Ох, а именно ту её часть,, которая
соответствует всем значениям x = a1t2-{'b1t-\- cu где t принимает все
действительные значени! (если, например, at > 0, то при t = — х-1-,л: принимает
минимум, равный
*rain — а^а\ 2^^С^— 4of ;
таким образом, уравнение г = {ах t2-\-b^ t-\- с19 с2} определяет часть пря-
4а с Ь2
мой у = с2, соответствующую х^—1—}^—-. Пусть теперь ^ 9^0 и a2?tQ.
Из уравнения
находим:
1С8
r={a1t2-\-b1t-\-cl9 a2t2-\-b2t + c2}
r,= {2a1t + bu 2a2t + b2y,

производная г' обращается в нуль при / =—о-*-, если — = —. Полагая
— = X, находим: Ьх = Ы19 Ь2 = *Д2,
г = {a, (t* + X/) + clf я2 (/2 + М) + с2},
у = а2 (/2 4- >i) + с„ /2 + Х/ = — (у - с2),
д2
ЛГ=г1 (У —*•) + *!
«2
— прямая линия. Однако в выражениях x = att2 -\- bt t-{-ct> у = а212 + b^t-\-c2
л- и у не могут принимать всевозможных значений. Так, например, если
аг > 0, то эти уравнения определяют часть указанной прямой, соответствую-
4fll С\ 7 Ь1 • Пусть, наконец, ^- ф ^ . Тогда г' = {2ах t +
щей значениям л:!
+ £ь 2<г2 t-\-b2}^:0 при всех /. Далее, г" = {2^, 2я2},"
г' X г":
= 2(ла£1 — atbJJbQ,
12М4-Л 2a2t + b2
| 2at 2а2
все точки линии — обыкновенные. Исключим параметр t из уравнений
x = a1t2-\-b1t-\-cly y = a2t2^-b2t-\-с2.
а2х — а1у = (bt а2 — b2 at) t-\-C!a2 — с2 alt
t^a2x — aly — (cia2 — c2 at)
bt a2~b2al ' x
Имеем:
[а2 x — at у — (сг а2 — c2 a^f
a2 x — flt у j- (gt q2 — c2 at)
У 2 (b,a2~b2alf ^"2 ' M. —Mi ^2f
у (bta2 — b2akf + a2 { (a2x — a^yf — 2 (cta2 — c2at) (a^ — ay) + {cxa2—с2ал)2}+ ,
4- b2 {bxa2 — b2ax) { a2x — aty — (c^ — с2аг) }-\-c2 (bxa2 — atb2)2 = 0,
a2 (a2x — axyf — 2a2 (сга2 — с2аг) (а^—а^) -\-у (bxa2 — b2at)2 +
+ b2 {bla2 — bgit) (a2x — atf) + const = 0.
Производя аффинное преобразование x* = a2x — a^, y'=y, получим
уравнение a2x'2 —2д2 (cta2 — с2аг) x' + (bta2 — b2at)2 y' + b2 (bta2—Ъ&г) x' -j- const =0 —
это уравнение определяет параболу. Предположим, что a2bt — а!#2>0.
Решая неравенство (г' X г") х' > 0 или лг'>0 (так как г' X г" = 2 {a2bt —
— яА) > 0) или 2at/ + #i > °> находим t > — <р- (пусть й^ > 0). При
указанных значениях t парабола вогнута «вверх». Решая неравенство у' < 0 или
2a2t -|- £2 < 0, находим £ < — s-2- (пусть а2 > 0). При этих значениях t пара-
€ола вогнута «вправо». При t<c — к^- парабола вогнута «вниз». При
/>—_ 2 парабола вогнута «влево».
121. г ={2/, 60/3 + 4(tf4}; г'=0 только при /=0.
г" = { 2, 180 ^2 4-ч160 /3 }, У (0) = { 2, 0 } ^£ 0,
г'" = { 0, 360/ + 480 *« }, г"' (0) = { 0, 0 },
г<4>4= { 0, 360 + 9601}, И4)(0) = { 0, ^360 },
12 0
г" (0) X И4)(0) =
Находим:
0 360
= 720.^: 0;
109

точка (0, 0) — точка возврата второго рода. Далее,
\2t 60/3 + 40/
Г' X Г" =
2 180/2+160/3
240/3 + 240/4 = 0;
отсюда * = —1. Далее, г'( — 1) = { —2,-20 }, г"# (—1) = {0, 120},
г'( — 1) X г'"( — 1)^0; при / =—1 имеем точку (1,7) перегиба; теперь
находим: (г' X r")x' = 240/3(/-f-l)2/> 0. Это неравенство имеет место при
всех />—1, за исключением £ = 0. Прки этих значениях t линия вогнута
«вверх». При/<— 1 линия вогнута «вниз». Решаем
неравенство (г' X г")у' <0 или 240/3 (t+ 1) tB • 20
(3-)-2/)<0, откуда—-0- <Lt<.— 1; при этих значениях
Л
I
/линия вогнута «вправо». При t <. к-и f> — 1
линия вогнута «влево». Наконец, линия пересекает
ось Ох в точках (0,0) и (-^j-, Oj (при t = ^Л
(черт. 19).
122. При / = ±: I/ -к- имеем две точки
перегиба (-_ + |/_j, В точке (2,0) касательная
параллельна оси Оу. Для значений t,
удовлетворяющих неравенства
»-Vl
</<0и/>
v\
линия вогнута «вверх», а при /<—I/— и
0< *<!/— — выпукла «вверх». Для значений
Черт. 19.
Т
*<-
линия вогнута «вправо», а
1
линия
при— I/ -о-<*< I/ -о- вогнута «влево». Для— I/ -~-</< I/
вогнута к оси Ох, а для t<. — j/~q- и * > г Т выпУкла к оси О** Для
— 1/ "о-<^<|/ "о- т линия вогнута к оси Оу. Для / < — I/ -^- и / > 1/ -тг-
выпукла к оси Оу. Наконец,
lim jc= lim лс = 1, limy = +со, limy= — со.
t==~\-oo t=—oo / = -|-00 t = —oo
Прямая* a: =1 является асимптотой данной линии. Исключая из уравнений
t
•г1+/2 гх
параметр t, получим:
123. г'Хг"=-
(х2 + у2) х — 2х2 — у2 = 0 (черт. 20).
24
/1 4- /2\2 " все точки линии обыкновенные. Линия вогнута
«вверх» в точках, для которых (г' Х'г") х'>0, т. е. />0, и вогнута «вниз»
ПО

при /<0 jc' =
8/
(1+/2)2
; при / = 0 касательная параллельна оси Оу
/4 _|_ б/2 3
[точка (— 3,0)]. Далее: у' = — .- — ; касательная параллельна, оси Ох
(I -j- 1)"
в точках, где / = :£ у 2\^3—3; при / = ± |ЛЗ линия проходит через
начало координат. Наконец,
lim х = 1, lim у = ± оа
Таким образом, линия имеет асимптоту х=1 (черт. 21).
\ • N
Черт. 20.
Черт. 21.
124.г'={ 10/(/8—1), 6/(/—1)Д; г' = 0 при / = 0 и /=L Находим:
г" = { 40?3 — 10, 12/ — б }, г"(0) = { — 10, — 6 } ф О,
/•"' = { 120/2, 12}, г'"(0)~{0,12}, г"(0) X г";(0)^0;
точка (0,0) — точка возврата первого рода. Далее,
г" (1) = {30,6 } ф 0, г"' (1) = { 120,12 }, г" (1) х г"' (1) ^ О,
точка, определяемая радиусом-вектором^ г={— 5 + 2, —3 + 2} =
= { — 3, —1 }, — также точка возврата первого рода. Приравнивая нулю
детерминант х'у" — х"у', найдём ещё одно значение / =— -^ . При этом
значении / производная г' отлична от нуля. Находим: г"' = {120/2, 12},
г' х г"1 —
Ю/* — Ю* 6/2 — 6/
120/а 12
:60/
f«—1 /_1
12/а 2
11L

При / = —£г- имеем*
'(-1KB)-
30
9^
8
3
Ф0,
значит, точка (—jg, —lj —точка перегиба. Далее: линия- вогнута «вверх»,
если
10/* — 10/ б/2 —6/
40/3—10 12/ —6
(10/*—10/) > 0
или — 600/3 (/ — I)3 (/2 + / + 1) (2/ + 1) > 0. Действительные корни левой
части в порядке возрастания — -^ , 0, 1. При / = —1 левая часть положи-
1
тельна; значит, решение неравенства /<—~-, 0</<1. Линия вогнута
«вниз» при — 9~</<0 и /:> 1. Линия вогнута «вправо» в точках, где
10/4 —10/ 6/2 — 6/
40/3 —10 12/ —6
Черт. 22.
(б/2 — 6/)<0,
откуда'— -y-<t<0 и />1.
Линия вогнута «влево» при
/< — -к и 0</<1. Линия
вогнута к оси Ох при / < — 9
и 0</<1 и *>-9"- При
I 3
— -^ < t < 0, 1 < / < _
линия выпукла к оси Ох.. При
-|<*<о,
3/
1</<
V-
.<>f!
линия вогнута к оси Оу. При /< — -^-, 0 < / < 1
1С оси Оу (черт. 22).,
125r'=(i=^^ -/*-3/* + 2/l
I (1 + /2)2 ' (1+/2)2 Г
f 2/2 —4/ —2 — 2/5 — 4/3 — 2/2 — 6/ 4- 2 1
г ~1 (1+/2)3 ' (1 + /2)3 Г .
Производная г' отлична от нуля при всех /. Далее
линия выпукла
г'хг"--
2/7 + 6/е — 2/5 + 14/* — 10/3 4- Ю/а — 6/ + 2 __ 2 (/3 + З/2 — 3/ +1)
Уравнение
(1+/2)5
/з + 3/2 — 3/+1=0
(1-Й2)3
имеет один действительный корень / = /!== — 1 —у 2 — У~~^>
соответствующий точке перегиба данной линии. В точках / = —1 :±J/2~ касательная па-
112

раллельна оси Оу. В точке £ = 0 касательная совпадает с осью Ох.
Линия вогнута «вверх» при t<tt и — "|/~2 — ^< t< ]/~2 — 1. Линия
выпукла «вверх» при tl<t< — У2 — 1 и7>|/"2 — 1. Уравнение линии в
декартовых координатах (в неявном виде): х\х* +у2) — -*у+У* =0. Линия
третьего порядка. Полярное уравнение
г = sin ср -
cos<p
Наконец,
Итлг = — 1, Нту = —-оо, Нту = + оо.
(=НЬоо £=-|-оо £ =—со
Прямая * = —1 асимптота. При t=^t2=V ^+V 2+V l—V 2 (корень
уравнения tz -f-3^—2 = 0) касательная параллельна оси Ох (черт. 23).
- 126- г' = { fz?^ > 7^~Т)Г } ^ ° при всех *, Далее:
г ~~ 1(*—1)3> (/"—1)8Г
— — 2/5 + 4/4 — 8/3 Ц- 10^g — 2ае — 2 = /34-3/-М
~ (* —1J*(*» —1)« % (*а — 1)3 '
Уравнение tz + 3* 4-1 = 0 имеет только ^ один действительный корень
^ = j/Z^_j/gp--0,32.. Эхо
значение t соответствует точке перегиба данной линии.
Касательная параллельна оси Оу при £ = 0 и t~2.
Касательная не параллельна оси Ох ни в одной точке
lim;t = — оо, limy = 0; lim;c = + 00> lira у = 0;
t = — оо tf =— оо t — -\-oo t=-\-co
ось Ох—асимптота данной линии;
limjc = —<г, limy = —оо, limv = + oo;
прямая х =э — -у — асимптота. Далее:
13
прямая у = -у •* —т — асимптота;
lim х = — оо, lim у = — оо,
Нтдг = + оо, . lim у === + °°> ч
Черт. 23.
Линия вогнута «вверх» при — I < t < tlt при 0 < t < 1 и при t > 2. Линия
выпукла «вверх» при *< — 1, ^</<0и 1<К2 (чеРгт» 24). В неявной
форме данное уравнение запишется так:
у(х-у)(1+х)-х(\+у)* = 0.
8 П. С* Моденов
ИЗ

»»•'={£+£» ih=w}' r'=0'при '=0>
2 2
-" = {(7TTF'?^}>r"(0) = {2'-2b '
r"4-(FW' -(t~iy}' г"'Ф)^{-6, -6},
г"(0)осг'"(0) =
_6^
2 -2!
— 6 —6
^0.
У
Черт. 24.
При £ = 0 имеем точку (4, —4) возврата первого рода. Касательная
параллельна оси Ох при t = 2 и параллельна оси Оу при / = — 2.
Соответствующие точки 1-^, 0] и (0, —-о-)- Далее:
9 9
Нтл- = —оо, limy = — -^7, limx = -foo, limy = —-x-;
асимптота y = -
2 '
асимтота Л" =
lim x = lim jc = -~-, lim у = — 00, lim у = + oo,
9
2 '
limjc = limy = — 00, lim x = lim у = -f- 00;
/= — 00 * = —00 / = -}-oo / = -f-oo
соответствующая асимптота у = л: — б;
г' X г" =
12/2
^0
(/2 — I)3
при t^tO. Все точки линии, кроме (4, — 4), — обыкновенные. Линия вогнута
«вверх» при /< — 2, — 1</<0и/>1. Линии выпукла «вверх», если —
2</<—1 и 0</<1 (черт. 25).
114

\t (t% 4- 3)
128. r' X r" = /i _/2\a > ПРИ ^ = ° имеем точку перегиба.
Направление касательной к линии в точке перегиба определяется вектором { 1,1 }.
Касательная параллельна оси Ох в точках, где У = 0, т. е. 2tx — 5t2 f 1=0,
откуда t = ±y — У . и Линия вогнута «вверх» при — 1<*<,0 и г>1
и вогнута «вниз» при 0<*<1, при t«
■ 1. Далее:
lim х = 0, lim^ = ~\- оо, lim^ === — оо,.
t = + oo ^ = -}-сзо t — — оо
Черт. 25.
значит, ось Оу является асимптотой линии. Для нахождения других асимп-
это угловые коэффициенты
асимптот найдём lim — = —1 и lim — = —1
.#=-1 х ,ts=i х
тот. Считая, что уравнения асимптот взяты в виде у = kx-\-b, находим b
из соотношения: # = lim [у (t) — kx(t)\, это даёт ^ = — 2, #2 — 2. Имеем
асимптоты у==— х-3-2 и у-
линии (черт. 26).
•х-\-2. Этими данными определяется вид
129. 1) х=Ь, у = с.
2) х+у = 0.
3)х±у = 0.
4) jc — у + 2 = 0.
5) х+\ = 0, х — 2у — 2 = 0.
6) х = 0, у = 0,х+у = 0.
7) х—у-\-3(Ь — а) = 0 и x = b, x = 2bf если J и 2^ не есть корни
уравнения х* — 3 ах2 + л3 = 0.
8) jc = a.
9) х —у ± я 1^2" = 0, х + у ± b У2 = 0 (произвести аффинное
преобразование х + У =Д, * — j> = К).
* 115

"10) (х — у) У2 ±д = 0, (х + У) V~2 ±л = 0 (см. предыдущую задачу).
И) х—у — 2 = 0, 2х + у — 4=0.
12) * = 2, >' = —2, 2х+3у — 4 = 0, Зл; —2у + 4 = 0.
130. 1) у = д,
2) полярная ось,
3) (* — у) j/2~ it я = 0, (л: + y)j/"2 ± а = 0.
131. 1) Точки пересечения с осью Ох: Мх (0, 0), Л12,3 (±: 1,0). Точка
пересечения с осью Оу: Mt (0, 0). Точки, в которых касательные к линии парал-
-Ь
Черт. 26.
Уб ^ 2Т/Т
•7\- 3 ' - 9 /'
точка Mt(0, 0); через особую точку проходят две дуги с общей касательной
лельны осям Ох и Оу: MAf 5, б, 7 I — ^ > — ~^Г~) ' М^3 (± 1' 0)' Особая
у = 0. Точки
* ** ( -./"9—1/33 9—l/ЗЗ-. /3+V
перегиба M8|9jl0f ц ^=t|/ —^—, ± ^—|/ ^
оо\
+1^33
7
Асимптот нет. Оси симметрии х= 0 и у = 0. Уравнения линии в
параметрической форме:
х = cos t,
у = sin f cos2 /.
Интервалы вогнутости «вверх» и «вниз»
116
/У —1/33 -,/9 —1/33
—15—<*<}/ -T2—•

у ^ 0 —- «вверх»,
<х<
/■
9 —j/33.
у ^ 0 — «вниз»,
]Лй
/9 — 1/33 1^6 л -, /"9- V&^^^Vj „^п
^ <x<-Lrp,.y>0—«вниз», 1/ j| <^<iL3~,y<0—
~ J/ 12 >
«вверх»,
У5
<лг<
у > О — «вниз»,
ZJ^^ j3> < О — «вверх», У~ < лг < \,у > О — «вниз»
1/Т
з.
1/Т
о . •
У<1 — «вверх», —1<;с<-
ут
у > 0 — «вниз», —!<*<:-
<лг<1,
V < О — «вверх» (черт. 27). 2)^Гочки пересечения с осью Ох: М1 (О, О), Л12 (27,0).
Точка пересечения с осью Оу:
Мх (0,0). Точки, в которых
касательные к линии параллельны
оси Ox: Ms (12, 4). Точек, в
которых касательные
параллельны оси Оуу нет. Особая точка
Мх (0, 0) — точка возврата
первого рода. Касательная в
особой точке у—х. Асимптот нет.
Осей симметрии нет;
уравнения линии- в параметрической
форме:
л: = 27(1—О1,
у = 27/(1—О1-
Черт. 27.
Интервалы вогнутости «вверх» и «вниз»: (—со, 1) — «вниз», (1, +оо) —
«вверх» (черт. 28). 3) Точка пересечения с осью Ох: Мх (—1,0). Точки
пересечения с осью Оу: М2 3(0, ± 1). Точки, в которых касательные к линии
Черт. 28.
Черт. Ж
параллельны оси Ох: -М2.3(0, :± 1). Точки, в которых касательные к линии
параллельны оси Оу: Мх (— 1, 0). Особых точек нет. Точки перегиба
М2>з(°> ~ *)• Асимптот нет. Ось симметрии у = 0. Уравнения линии в
параметрической форме:
л* = /я — 1,
117

Интервалы вогнутости «вверх» и «вниз»: (—оо, —1) — «вниз», (—1,0) —
«вверх», (0, 1) — «вниз», (1, 4-°°) — «вверх» (черт. 29). 4) Точка пересечения
с осью Ox: Mt (0, 0). Точка пересечения с осью Оу: Л^ (0, 0). Касательных,
параллельных осям координат, нет. Особая точка (0, 0) — тройная, касатель-
4 __
ные в особой точке х2 = 0, у = 0. Точки перегиба: М<1Ъ (± 2 т/г27, 2 |ЛЗ ).
Две асимптоты у + х-\-\1=Ъ. Ось симметрии х = 0. Уравнения линии
в параметрической форме:
___ 4/ __ 4*2
Интервалы вогнутости «вверх» и «вниз»: (—оо, — 1) — «вверх»
• —- , ~\ — «вверх», (—. , 1
уз уз; \|/з
■(--£)-
(1, + оо) — «вверх»
(черт. 30). 5) Точка пересечения с осью Ox: Mt (0,0). Точка пересечения
с осью Оу: Mt (0, 0). Точки, в
которых касательные к линии
параллельны оси 0%:
М3
Мя
"27
16
fir
-п.-г
27 ^
IB у
Черт. 30.
Точки, в которых касательные к
линии параллельны оси Оу:
*Щ- VI)■
'■ 4-fl-fl)-
Особая точка Mt (0, 0). Через особую
точку проходят две дуги. Касательные в особой точке: х = 0, у = 0. Точка
перегиба Mt (0, 0). Асимптот нет. Ось симметрии у = х. Центр симметрии
(0, 0). Уравнения линии в параметрической форме:
2/ • 2/3
*-2 ч»2
/4 У У
1+'4
Т+'4
Интервалы вогнутости «ввгерх» и «вниз»: лт > 0,1 0,1/ -^ ) — «вверх»'; х > 0,
i Г~П
п
-f-oo
лг<
0,(o,J/ ij — «вниз», лг<оЛу^-,+с
«вверх» (черт. 31). 6) Точки пересечения с осью Ох: М\у 2 (±: 1,0). Точки
пересечения с осью Оу: М3 4(0, ±1). Точки, в которых касательные
к линии параллельны оси Ох: М3 4(0, ±1),
М
5,6
*%../*$!). *,(***.-уПЩ.
Точки, в которых касательные к линии параллельны оси Оу:
м,, s (± 1,0), м9> 10 [± у 1-±f-, Щ, л|11( 12[± у 1-±-р-, - Щ-
118

Особая точка (0, 0) — изолированная.
Асимптот нет. Оси симметрии х = 0, у == 0. Центр симметрии (0,0).
Уравнения линии в параметрической форме:
х — г + Р ' у ~~ 1 + ** •
Для отыскания точек перегиба данной линии полезно заметить, что
если уравнения линии даны в виде х = х (t), у = tx (t), то г' X г" = 2х'* — хх'9
м1
мц
ц1
Jk^
, i
м?
У
й
т^
*
т^гт
^Ж
\Мд
Щ
\мп
м8
Черт. 31.
Черт. 32,
а если при этом лг==Т/"<р W (что имеет место в данном случае), то г' X г" ■■
= —!—j—I-L—. Полагая здесь ср = !■ ^-, получим:
;f_ 1 — 4 (^ — 8/е — б/4 — 8^8 + ^) _ ** — 8^ — 6^ — ^-f 1
Г Х Г 4ср (1 + ^4 U + **> (А + г*Г
Действительные корни имеет лишь уравнение
# ^ — 2(2 4- |/~~б)'2Ч- 1 =0
Отсюда
". (^|У-2 + 2 1/"в,
Ограничиваясь положительными значениями /, получим;
*+ у ==|/ 6-f-2J/ 6
/-li-jt/ 2 + 2J/ 6.
119

Рассмотрим, например, значение./, соответствующее знаку + в правой
части последнего соотношения:
Отсюда
*+|=/б + 2|/"б,
t — у=/2 + 21/"б.
—Т- = / 6 + 2^6,
fl -4 + 2^6,
1 + t* _ /б +2]/^
1 + ^~ 4 + 2|/ о '
'l'+fl 1 /б + 21^6_
l + *4~~*~ 4+2|Лб ~
- у (/вТгут- / ^Fb ) £^f
x=±i/j(/^TiT^-/^HT^)^^P>
Г * ■ 4 + 21А6
««-* L+il-f /б + 2]Лб ._
У~ "1 + ^4 4,4-2^6 ~
^ЩТ+^+У^+ЩП) /б + 21Лб_)
^ 4 + 21^6
у-± 1/4(/^+17б+/¥+Т7^)^^Р-.
К z 4 + 2^6
Имеем 4 точки перегиба:
(±1/4(/б + 2ТЛб-/2+ДУ^) /"6 + 2Fg ,
\ К ^ 4 + 2^6
Г ^ 4 + 21^6 /
Если теперь взять
'+4=/б + 21Лб,
*-|=-/ 2 + 21^6,
120

то найдём ещё 4 точки перегиба:
V\
^ 4 + 2}/*6
Таким образом, данная линия имеет 8 точек перегиба (эти точки
перегиба, на чертеже 32 не выделены).
Интервалы вогнутости «вверх» и «вниз» (укажем только для первой
четверти): ' ,
(■
(
О, у ( / 6 + 21/""6 — /2 + 2 У Ъ)) — «вниз»,
у (/■ б + 2 |Лб — /2 + 2]/" б), /}Л2—l) — «вверх»,
(/l/"2—1, у (/'б + 21/*"б + /2+21/" б)) — «вниз»,
(у(У'6 + 2|А) + / 2+2|/"б), + ooj —«вверх» (черт. 32).
Черт. 33.
Черт. 34.
7) Точка пересечения с осью Ох: Мх (О, 0). Точка пересечения с осью
Оу: Alt(0, 0). Точка, в которой касательная к линии параллельна оси
Ox: Mt \y 2, ]/4). Точка, в которой касательная к линии параллельна
оси Оу: ЛГ3(|/4,-|/Т). Особая точка: Л^ (0,0). Через особую то,чку
проходят две дуги. Касательные к линии в особой точке: х=0, у = 0. Асимп-»
тота: л; + у+1=0. Ось симметрии х — j/ = 0. Уравнения линии в
параметрической форме:
Зг З*2
х= -.
У =
1 + /з > у — 1 +1* •
Интервалы вогнутости «вверх» и «вниз»: (— оо , 1/ у)-
(1/ у, +оо j — «вниз»(черт. 33). 8) Точка пересечения с осью Ох: Мх(0,0).
-«вверх»,
121

Особая точка (0Г0).
Точка пересечения с осью Оу: Mt (0, 0), Точки, в которых касательные
■к линии параллельны оси Ox: M2t 31 ±- *-j— , -г] - Точки, в которых
касательные к линии параллельны оси Оу: Л44 5 ( ± —^—, -q-
Через особую точку проходят три дуги. Касательные в особой точке у = 0,
х—у = 0, х-\- у = 0. Точек перегиба нет. Асимптот нет. Ось симметрии
л: = 0. Уравнения линии в параметрической форме:
x — t{l—t*),
у = /2(1—/2).
«вниз»,
Интервалы вогнутости «вверх» и «вниз»: I оо^ -р— J —1
/ -^=-, —рг=г] — «вверх», [-—=у ^оо]—«вниз» (черт. 34). 9) Точка
пересечения с осью Ox: Mt <0, 0). Точка пересечения с осью Оу: Мх (0, 0).
Точка, в которой касательная
к линии параллельна оси Ох:
М2 (-J^r44,1^27T64J. Точ-
ка, в которой касательная к
линии параллелЪна_ оси О у:
xMa{^Z±,f^j. Особая
точка: Мх (0,0); через особую
точку проходят две дуги, на
одной из них особая точка
является точкой перегиба, на
другой — точкой , возврата первого
^ода. Касательные а особой
точке; jc=0, у=0. Асимптот нет.
исей симметрии нет.
Уравнение линии в параметрической
форме:
У= -7Г--
Черт. 35.
jt-l? •
Интервалы вогнутости «вверх» и «вниз»: (—оо, 0) — «вниз», (ОД) — «вверх»»
, 11, -s-) — «вниз», (~су, + оо) — «вверх» (черт. 35). 10) Точки пересечения с осью
Ох: Мх (0, 0), М% 3(± 4,0). Точка пересечения с осью Оу: Л1, (0, 0). Точки, в
которых касательные к линии параллельны оси Ox: М4^5(+. ^5",— D»
^6,7 (±: 2 |/~5~, 4). Точки, в которых касательные к линии параллельны оси
Оу: Л18 9(±:5,3). Особая точка Мх (0, 0). Через особую точку проходят две
дуги с касательными 4jcj:5y = 0. Асимптот нет. Ось симметрии jc = 0.
Уравнения линии в параметрической форме:
x~5sint,
y=3sin2/ + 2sin2/.
Исходя из параметрических уравнений линии, находим:
1
-_. (лгу\— х'У) = 6 cos* / — 12 sin / cos21 — 4 sin* /.
0
122

Полагая х'у" — *'у = 0, находим:
tg3* + 3tg*-__=0.
Решая это уравнение по формуле Кардано 1р = 3, ч q =— у), находим
единственный действительный корень
tg
отсюда
две точки перегиба:
sin / =
cos t==
1^1-1
JT2
in-i_
' /|AT6"--^ 4 + 1
Интервалы вогнутости «вверх» и «вниз
{ — -£ • агс tg ДГ 1 ) — «вверху \ arc tg
2^2 — 6|/Ч + 1
3, 3/
V 16 -У HI
: + arc tg
V2 J
^2
|/1—1 те.
|A2 Z
, ' У 4 — 1
«вверх», I it + arctg 3——
у 2
— «вниз»,
Зге
.2
Л1) ^Гочки пересечения с
осью Ох: М, 2(±2,0).
Точки пересечения с осью Оу:
М, (о, -| j и М, (0, 2). Точки, ^
в которых касательные к
линии параллельны оси Ох:
МАО, ~)иМ4(0, 2). Точек,
в которых касательные к
линии параллельны оси Оу,
нет. Особые точки М2(—2,0),
М1 (2, 0). Обе т$чки возврата
первого рода. Касательные
к линии в особых точках:
v it*—2 = 0.
Черт. 36.
123

Точки перегиба М5 6
У 5 2
Асимптот нет. Ось симметрии jc = 0.
Уравнения линии в параметрической форме
х =2 sin/,
_ 2 cos21
y~2 + cosr
Интервалы вогнутости «вверх» и «вниз»:!—9","о~
«вверх», (с
(черт. 37).
вверх», I arc sin -—— , тг -f arc sin -— ) — «вниз»
«вниз»,(-~-, arc sin J—— ) —
arc sin
1/5 3*
, -s-1 — «вверх>
§ 4. Подэра.
132. Возьмём уравнение эллипса в виде: г = {a cos ф, Ь sin ф}. Уравнение
касательной к эллипсу в произвольной его точке:
Ьх cos ф + &У sin 9 — ab = 0.
Уравнение перпендикуляра к этой касательной из начала координат:
ах sin ф — by cos 9 = 0.
Разрешая два полученных уравнения относительно х и у, получим
уравнение подэры в виде:
{ab2 cos ф a2b sin 9 1
б2 cos у -^ a* sin2 ф ' b2 cos2 ф + я2 sin2"?/ "
Исключая* ф, получим
(х2 + у2)2 = а2х2 + £2у2.
133. Возьмём уравнение
гиперболы в виде:
Hf ('+4). Н<-1)Ь
Уравнение касательной к
гиперболе:
b (t2 + \)x—a (t2 — l) у —2abt=0.
Уравнение прямой, проходящей
через начало координат (центр
гиперболы) и перпендикулярной
указанной касательной, имеет вид:
ax(t2 — l) + £y(f» + l) = 0.
Разрешая уравнения относительно х и у, получим уравнение подэры в виде;
__ \ 2ab2t(t2 + l) -.2a2bt(t* — \) \
Г ~~ [b* (t* -t- 1)* + аг (t* — if > b* (t* + if + да (/**— l)2 J
или, наконец, исключая параметр:
(л:2 + j/2)2 = л2лг2 — Ь*уК
124
Черт. 37.

134. Касательная к параболе в её вершине.
135. Окружность, описанная около эллипса.
136. Окружность, центр которой совпадает с центром гиперболы и
которая касается вершин гиперболы.
2 " 1
137. Полагая лг = a (cos cp)rt, y = b (sin <p)w, получим, уравнение подэры
в виде:
2-1
аЬг (cos tp) n
2-2
4
4-А
У =
a2/? (sin <р) п
4-1
4-1'
fc2(coscp)~ n + a2(sincp)" п ЬЦсоъуУ n+a2(siny) n
исключая <р, получим
(х*+у2)п-*=(ах)п-]+(Ьу)п-\
В частности, при п = 2 получаем подэру эллипса:
(л-2+^2)2 = а2;с2 + 62^2.
г
/>
■ ~^7
/
/х
П
Черт. 38.
Черт. 39.
138*. 1) р = In, (р — г) я = 0, (Хя — г) *г = О, X = гп, р = (гп)п (черт. 38).
. Г\1\П
г ГГ(*)ГлгГ(*)-/Ч*)] /(лг)-л-Г(х)!
1М г-[ . 1+/'«(*) > 1+ГЦх) Г
140*. 2) р = г + Иг], р' = г' + Х'[г]+.Х[г'], pV==0, rr'+ X [г'] г = 0,
Х = -
г' X г
, Р = >-
гг
г' X г
W.
1) Р = г-
г'Хг
И = г-
Frl[rl==r-S[rJ(4epT'39)-
• иг
141. Принимая точку (с, 0) за начало радиусов-векторов, можно
записать уравнение эллипса в виде:
г = { a cos <р — с, 6 sin <p }.
Ответ:
г . . &1 —с1 . . ее .
p = J <z cos ср — с — с sin2 <р, —^— sin <р -f- -г-sin 9 cos cp
125

142. Взяв уравнение гиперболы в виде:
«tt("4HK)}.
получим уравнение антиподэры в виде:
HfKK(<4)VJ).}(<-JKK)'H)b
143. Взяв уравнение параболы в -виде у = ах2, получим уравнение
антиподэры в виде:
р = 1 — 2а2х\ ^ + 3ах2\
или в неявном виде:
27Х2 —4а(Г —~-V = 0.
144 Q _ f 2xf (x) - x2f (х) + f2 (х) Г (х) f2(x)-2xf(x)f'(x)-x*}
Р "~ I / (х) - xf (х) '■ / (л) - xf (х) ]'
145. p=^i ^^p (а2 + с2 sin2 -?), ^_? (^2 _ C2 C0S2 ?) | #
§ 5. Огибающие
146. Возьмём уравнение эллипса в виде:
r={a cos cp, 6 sin ср }•
Точки (a cos ср, 6 sin ср) и \а cos (cp -f. -i* j & sinf cp + -у) или (— a sin ср> Ь cos cp)
являются концами двух его сопряжённых диаметров. Уравнение прямой,
проходящей через эти две точки, имеет вид:
Ь (sin ср —cos ср) л: — a (sin cp -|- cos cp)у -{-ab = 0.
Дифференцируя левую часть по ср и приравнивая результат нулю, будем
иметь:
Ь (cos cp -|- sin ср) х — q(coscp — sincp)j/ = 0.
Исключаем ср:
[ Ь (sin ср — cos ср) л: — a (sin cp -f- cos cp) уу -)-
+ [Ь (cos ср + sin ср) х — a (cos ср — sin у)у]2 = а2Ь2,
х2 у2
или 2#2л;2 + 2я2.у2 = аЧ2, или N2 + у^.—г = * — эллипс, гомотетичный
данному; центр гомотетии совпадает с центром эллипса; коэфициент
гомотетии равен —^ггтг (черт. 40). Найденная дискриминантная линия является
огибающей, так как частные производные по х и у от левой части данного
уравнения, т. е. b (sin cp — cos ср) и — a (sin 9 4- cos cp), одновременно в нуль не
обращаются. Другой вариант решения: пусть А — аффинное преобразование, пере-
126

водящее данный эллипс в окружность. Данное семейство прямых
преобразование А переводит в семейство прямых, на которых лежат стороны всех
квадратов, вписанных в окружность, являющуюся образом данного эллипса.
Огибающей последнего се- У1
мейства является
окружность, концентричная
указанной с радиусом р=
где #—радиус окружности,
являющейся образом
данного эллипса. Остаётся
произвести аффинное
преобразование А"1. Вместо
аффинного преобразования можно
рассматривать
параллельную проекцию, при которой
' эллипс проектируется' в
окружность.
147. Примем данные
прямые за оси координат.
Тогда уравнение
семейства примет вид: — -^^-«=1, или bx+ ay = ab, или
2sx + asy — 2fls = 0, где s —данная площадь. Дифференцируя левую часть
по л и приравнивая результат нулю, получим: ±.2ау — 2s = О, а = ± — >
Черт. 40.
2s
х±ау = 2s, ил»
Черт. 4}.
s s s
уравнение дискриминантной линии 2sx ± ^ у ч= 2 —- = 0, или 2sx ± — = (К
или ху = ± 4- — две равносторонние соасимптотические гилерболы. Так как„
12?

например, частная производная от.левой части уравнения 2sx ± а2у— 2as =
= 0 по jc равна 2s, т. е. отлична от нуля, то найденная дискриминантная
линия является огибающей. Другой вариант решения: рассмотрим какую-
нибудь касалгельнукг к гиперболе ху = С. Эта касательная отсечёт от асимптот
гиперболы треугольник, площадь которого равна s. Произведём
гиперболический поворот, принимая данные прямые за неизменяемые. В этом аффинном
преобразовании х = \Х', у = -- у', гипербола ху — С перейдёт в, себя,
касательная перейдёт в .касательную, а площадь треугольника, отсекаемого от
асимптот, сохранится, так как гиперболический поворот — преобразование
эквиаффинное (сохраняющее площади). Таким образом, если мы выберем С
так, чтобы какая-нибудь касательная отсекла от асимптот треугольник,
площадь которого равна s, то и любая другая касательная к этой гиперболе
отсечёт треугольник с площадью, равйой s; вместе с тем любая прямая,
отсекающая от асимптот треугольник с площадью s, — касательная к
гиперболе. Нетрудно видеть, что для этого надо взять С= zt-^-s (черт. 41).
148. Эллипс, гомотетичный данному, с коэфициентом гомотетии, рав-
s ..
ным cos -т , причем центр гомотетии совпадает с центром симметрии эллипса.
й х2 у2
В самом деле: преобразуем аффинно Х = х, Y=-j-y, эллипс -^ + \^ = 1
в окружность X2 + Y2 = а2. Тогда s' = ~г- s, где s — площадь прообраза, а
s' — площадь образа. Пусть L — образ прямой / семейства. Площадь соот-
ветствующего сектора окружности равна -г-. Расстояние прямой L от центра
окружности равно a cos -т. Отношение радиусов окружности, касающейся
о
всех прямых L к радиусу а окружности X2 + К2 ==а2, равно cos-г.
Производя обратное аффинное преобразование, мы получим, что семейство пря-
мых L перейдёт в данное семейство, а окружность X2 + Y2 = a2 cos2 -=•
перейдёт в эллипс, гомотетичный данному, с коэфициентом- гомотетии
s
cos -г, причем центр гомотетии совпадает с центром данного эллипса.
149. Рассмотрим параболу у = ах2 и прямую у = й(а>0,. h > 0). Эта
прямая отсекает от данной параболы сегмент, площадь s которого равна
4 1 Г~Н 1 Г $as2 I fQas2
s = -~/zl/ —; отсюда h = V -т-тт-. Таким образом, прямая^ = 1/ -ттг
отсекает от данной параболы сегмент, площадь которого равна s. Рассмотрим
аффинное преобразование
х' = х -{- X, у' = 2alx + у 4- дХ2,
где X — любое число; это аффинное преобразование называется
параболическим поворотом; в этом преобразовании рассматриваемая парабола
переходит в себя. Также переходит в себя любая парабола у = ах2 -f- с,
полученная переносом рассматриваемой в направлении оси Оу. Таким образом, оги- '
-ш/"gas2
бающей данного семейства прямых будет парабола у = ах2-\- I/ ~г^-,так
—р- касается этой параболы и отсекает от данной
параболы сегмент, площадь которого равна s. Производя указанный выше пара-
128 •' *

болический поворот, мы можем утверждать, что прямая _у = 1/
9as2
-jq-
переидёт в касательную к параболе у = ах2 -|-
16
и будет отсекать от
начальной параболы сегмент с площадью s, так как параболический поворот есть
эквиаффинное преобразование (т. е. преобразование, сохраняющее площадь).
Вместе с тем параболическим поворотом можно получить любую прямую
данного семейства (т. е. производя все параболические повороты, мы получим
все прямые, отсекающие от начальной параболы сегмент, площадь которого
равна s).
150. Параметрические уравнения линий семейства
gt2
х = v0t cos а, у = v0t sin a — ^~-
Находим:
дх
jfi = V0 COS а,
ду
: v0 sin а — gt,
дх . ду .
ч- = — vJ sin а, -^ = vJ cos а.
да ° ' да °
Приравнивая нулю якобиан п// / , получим: ^ — gt2v0 sin a = 0, откуда
Z-/ [tf <Х)
, и параметрические
gsma г г
уравнения дискриминантной
линии:
! ctg a,
V = — 74 "
J g 2g sin a
gx*
2g
—парабола с вершиной
2г/а
о
и параметром /? = —°. Дискри-
минантная линия является
огибающей, так как, например,
Черт. 42.
&=v0cosa?tQ и, значит, вектор-^ = 1^,-^1^:0 (этот вектор
определяет направление касательной к линии семейства) (черт. 42).
151. га = {2и, За2}, /ч,= {1, 1}, rttxr„ = | , л | = 2и-3и2 = 0,
1 1
a = 0, м = -^ .
При и = 0 имеем: r={t>, v}> т. е. прямая лг=у.
При и = -~- имеем: г =
.9
+ "' Т +
■•»•
т. е. прямая л:—Q-=3f —
9
"27'
При и = 0 имеем: (ги)н = 0 = {2а, 3и2}н==0={0, 0};
9 П. С. Моденов
129

этот вектор не коллинеарен вектору, дающему направление касательной
к дискриминантной линии r~{v, v], т. е. вектору {1, 1}. Значит, дискри-
2 дт
минашная линия х = у не является огибающей. При u = -j, дй^° и' зна"
4 8
г'={1,1} чит, прямая х — ~д==У — 27"~
огибающая (черт. 43).
152.
= {1,0},
Гц X Г у ==
:{2и, Зи2}, rv =
2а Зя2
1 0
= — Зг/2 = 0, я = 0;
Черт. 43.
дискриминантная линия г =
= {г/, 0} — ось Ох. Далее
находим (/я)вяо = {°> °}' (г««)и=0=
= {2, 0}. Этот вектор
коллинеарен оси Ох и,
следовательно, ось Ох является
огибающей (черт. 44).
153*. Примем вершину
данного угла за начало координат,
а биссектрису данного угла за
ось Ох. Тогда уравнения
сторон угла будут иметь
следующий вид:
Рассмотрим две точки: Mt (p, —p tg-^-j и JVlJq, q tg-y] ,лежащие на
сторонах данного угла. Периметр 2/ треугольника OMtM2 равен
21--
P±l + ]f(p--q)*+(p + q)*lg2j<
а
cosT
Отсюда
21 —
Р + ?\*-
а
cosy
= (p-?)2 + (P+<7)2tg2 у
или pq-\-P — /' =0. Положим,
cos|
1 1
— = г;, — = и: тогда получим:
Р Я
Черт. 44.
1 _|_ И1,/а __ /
н+ г>
= 0.
COS-
Уравнение прямой М^М2:
X (Р + q)tgj + у (р — q) — 2pq tg — ==Q
130

xtg^r + y)u + (•* {8Y~~Av~~2t^l" ==0*
Дифференцируя левую часть по а и приравнивая результат нулю, будем
иметь:
. a . , f . a \ dv Л
откуда
С другой стороны, дифференцируя соотношение:
cos^
по и, получим:
1+-
cos у
Подставляя сюда найденное выше значение -г- , будем иметь:
v(y — xtg-^\ + uU + xXg^) ^=°-
7 ' /cos-~-
Отсюда и из уравнения — (у — xXg-A v+ ly + xXg-^-\u — 2xg -? =0
находим:
V , a V a
/cos-^- /cos~~-
м = , , v= .
У + xXg-^ y — xXg
Подставляя эти значения и и v в соотношение
1 a
cosT
2
после упрощения получим:
*^1у+*Ч'*т)"
131

— окружность радиуса / tg -^ с центром в точке
cos-
, 0\(черт. 45 и 46).
Найденная дискриминантная линия (окружность) является огибающей, так
#1
М2(Яг <Mgf)
хЧг
Черт. 45.
Черт. 46.
как частные производные -*"tg -<^ -f-y и xXg-^y — у от левой части уравнения
семейства по и и v одновременно в нуль не обращаются*.
154. х = a cos v cos u, y = asinv + acosv sin u (черт. 47). Приравнивая
* D<x* v) *
нулю якобиан -p- ■, будем иметь:
J D(u, v) J
cos v sin u — sin v = 0, tg v = sin к.
Отсюда следует, что дискриминантная линия определена лишь для
^1 —-j- ^^^—. Далее: cos и = }/~1— tg2 ^
и уравнения дискриминантной линии:
лг = й cos г>]/~1 —-tg2 г>, у = 2а sin z/
или
х = a jAcos2 z> — sin2 #, у = 2а sin v.
Исключая v, будем иметь:
—- = cos** v — sin3 v,
а2
^ = 2sin2*, -%+fe = \
Л1
2d
— эллипс с полуосями а и а У 2.
Дискриминантная линия является огибаюшей, так
как-5-=| — a cos v sin u, acosocos к|^0
Черт. 47.
при —
155. х = a cos z> cos a, y = asinv sin н (черт. 48). Приравнивая нулю яко-
биан т^——т\ > получим:
D{a, v)'
sin2 v cos2 и — cos2 v sin2 и = 0,
sin (u -j- z>) sin (и — v) = 0,
132

v = — и, v = n — и, v = a, v = — ir-f-я.
Дискриминантная линия состоит из четырёх отрезков прямой:
х = a cos2 и, у = — a sin2 и;
х = — a cos2 а, у = a sin2 и;
х = а cos2 u> у = а sin2 и;
х =— a cos2 и, у-=.— а sin2 к
(1)
(2)
(3)
(4)
Черт. 48.
— это четыре стороны квадрата, вершинами которого служат точки
пересечения диаметров окружности с самой окружностью. Каждая из сторон
квадрата является огибающей, так как ч- ^ 0.
156*, Параллелограм, вершины которого находятся в точках
пересечения двух рассматриваемых сопряжённых диаметров с эллипсом (черт. 49).
У.казание: преобразовать аффинно заданный эллипс в окружность и
воспользоваться результатами
предыдущей задачи.
157. Две гиперболы ху == ± -~-
(если начальная гипербола задана
уравнением ху = 1) (черт. 50).
158. Две гиперболы. Указание:
преобразовать аффинно данную
гиперболу в равностороннюю (черт. 51 )#
Черт. 49.
Черт. 50.
133

циент FM равен — J~ , а угловой
159. Парабола, центр мгновенного вращения является её фокусом, данный
стержень — касательной в вершине. Это ясно из следующего свойства
параболы: подэра параболы относительно её фокуса есть касательная в вершине
параболы. Задачу можно решить и аналитически: располагая оси координат
так, как указано на чертеже 52, и полагая, что точка F (центр мгновенного
вращения) имеет координаты 0, ^-, будем иметь: М (v, 0); угловой коэфи-
коэфициент прямой семейства равен — .
2v
Уравнение прямой семейства: у =— (л: — v) или py = 2vx— 2v2. Далее:
х2
уравнение дискриминантной линии: ру = х2— 2 -j-
или х2 = 2ру. Дискриминантная линия
является огибающей (черт. 52).
160. Эллипс, большая полуось которого
равна радиусу окружности, один из фокусов
которого совпадает с мгновенным центром
вращения, а центр симметрии совпадает
с центром окружности. Это следует из
известного свойства эллипса: подэра
эллипса относительно его фокуса есть окруж-
Черт. 51.
Черт. 52.
ность, описанная около эллипса (черт. 53). Аналитическое решение:
располагая оси координат так, как указано на чертеже 53, и считая, что радиус
окружности равен а, координаты мгновенного центра вращения — с, 0,
запишем уравнение семейства в виде:
отсюда
ay sin v + (с + cl cos v) x — а2 — ас cos г; = 0,
ay cos v — а(х — с) sin v = 0,
ay sin v + a (x — c) cos v = a2 — ex.
Возводя каждое из этих уравнений в квадрат и складывая затем
полученные уравнения почленно, получаем:
а2у2 + (а2 — с2) х2 = а2 (а2 — с2)
и, полагая а2 -
-с2 = Ь2, будем иметь: а2у2 + Ъ2х2 = а2Ъ2 или —2+У
Ъ2
1
— эллипс. Эта дискриминантная линия является вместе с тем огибающей.
161. Прямая семейства проходит через точку [a(t — sin t)y a (I — cos^)]
циклоиды и точку (at, а) катящейся окружности. Уравнение прямой семейства:
х cos / — у sin t + a sin t — at cos t = 0.
134

Дифференцируя левую часть по / и приравнивая результат нулю, будем
иметь:
— х sin t — у cos t + at sin t = 0.
Из двух последних уравнений находим:
х = a (t — sin t cos t) = -^ (2* — sin 2/),
y = asin2/==%-=-(l-- cos 2/).
Этими уравнениями определяется дис-
криминантная линия, являющаяся
циклоидой, «производящей» круг, который
в два раза меньше начальной
окружности. Вместе с тем дискриминантная
линия является огибающей, так как
частные производные cos t и — sin t
по х и у от левой части уравнения
семейства одновременно в нуль не
обращаются (черт. 54).
162*. Огибающей является
антиподэра А стержня С относительно
мгновенного центра вращения. Если r = r(v)
Черт. 53.
есть уравнение линии С, то уравнение антиподэры (черт. 55)
гг'
р = Г
г' ХГ
[г] (см. № 140*).
В координатах:
£ г I **'+W' -л и ХХХ'+Ж'
Черт. 54.
Черт. 55.
163. Эллипс, один из фокусов которого совпадает
с точкой F, другой — с центром F данной окружности.
Ббльшая полуось эллипса равна радиусу данной
окружности. Это следует из того, что точки, симметричные
фокусу эллипса относительно касательной к нему,
лежат на окружности радиуса 2а с центром в другом
фокусе, а потому на хорде АВ можно построить
окружность С', проходящую через точку F, радиус которой
равен радиусу окружности С (черт. 56).
164. Уравнение обоих семейств можно записать
в виде:
г = {a cos и + Ь cos v, a sin и -{^ # sin v].
Черт. 56.
135

Черт. 57.
Черт. 53.
В одном случае v — параметр линии в семействе, и — параметр точки на
линии семейства, в другом случае наоборот. Уравнение гах /Ч, = 0 здесь
принимает вид:
I — a sin и a cos и
— bslnv bcosv
= 0
или sin (a —*■ v) = 0, откуда v — u или v = и -\- тс. Соответственно этому дис-
криминантная линия состоит из двух окружностей:
г = {(а ± b) cos и, (а ± £) sin и},
концентричных данной. Дискриминант-
ная линия является огибающей обоих
семейств, так как гиф0, rv^Q (черт.
57 и черт. 58).
165. Принимая данные взаимно
перпендикулярные прямые за оси
координат и вводя параметры и и v так,,
как указано на чертеже 59, будем иметь:
г= {(/ — и) cost;, usmv}.
Соотношение /
вид: и = / sin2 ^.
нантной линии:
Черт.
>и X rv = Q принимает
Уравнение дискрими-
г = {(/ — / sin21>) cos v,
I sin31/} или r = {/ cos31/, / sin31>} —
астроида (черт. 59). Дискриминантная
линия является огибающей, так как
Ги — { — cos v* sin v} ф 0.
166. Обозначая через / заданную
сумму полуосей, через и — одну из
полуосей, через v—«эксцентрический
угол», получим уравнение семейства
в виде: г = {(/ — и) cos z/, и sin v], и
решение в точности совпадает с
решением предыдущей задачи. Дискрими-
нантной линией является астроида:
Эта линия является огибающей, так как
r = {a cos3 v, a sin3 v}.
rv = {—(/ — и) sin v, и cos v) ф 0
(черт. 60).
136

167. Уравнение прямой семейства:
у — a sin v = Xg 2v (х — a cos v)
или
х sin 2v —у cos 2v — a sin v = 0.
Параметрические уравнения дискриминантной линии:
х= -у (2 sin v sin 2v -f- cos v cos 2v\
y=~(— 2sin v cos 2p + cos vsin 2t/)
л; = -^ (3 cos i/ — cos 3v), y = -r-(3sinv — sin 3v) — гипоциклоида.
Черт. 60. Черт. 61.
Дискриминантная линия является здесь огибающей (черт. 61).
х2 v2 v2
168. Уравнение семейства эллипсов 1- — = 1, или х2 -\ у2 — v = 0.
Zv с с v с
Отсюда —у2 — 1 = 0, v = -^~^. Уравнение огибающей: х2 + т~1 о~а==^'
или ху =■ ± у V" с (две гиперболы, черт. 62).
169. Две гиперболы, для которых заданные диаметры являются
асимптотами.
Указание: преобразовать аффинно два заданных диаметра во взаимно-
перпендикулярные прямые. Огибающая и заданное семейство даны на
чертеже 63.
170. Уравнение семейства
x* + f — 2vx — — у = 0.
Огибающая: у (х2 -\-у2) + рх2 = 0.
137
•

171*. Уравнение семейства окружностей:
(х — а cos vf -f (у — b sin vf = (— с —a cos z/)2 + b2 sin2 p
2a (л: + с) cos z/ + 2by sin z/ = x2 + y2 — c*
Дифференцируя по v обе части этого уравнения, получим:
— 2а (х + <?) sin я + 2#у cos v = 0.
Черт. 62.
Черт. 63.
Возводя оба уравнения в квадрат и складывая, будем иметь
4а2 (х + cf + 4^2У = (х2 +Г- c2f
или
4 (Ь2 + О (* + cf + 4£2у2 = (*2 + У2 — с2Ъ
W [(х + cf + у2\ = (х2 + .У2 - с*? — ^ (х + с?>
U2 [{х + с)2 + у2] = (х2 + У2 — '2 + 2слг + 2с2) (х2 +.у2 - с2 — 2сх — 2с2),
^2 -i-j^s — 2сх — Зс2 = 4£2
или (jc — с)2 +.у2 = 4я2 — окружность
радиуса 2а с центром во втором фокусе
(черт. 64).
172*. Уравнение семейства: p = r(t/) +
da
-f- a (u); имеем: ри =
du '
= [а], pv=f.
Черт. 64.
Условие рй || 9v Даёт [а] || г', т. е. а _L Л
значит а = ± у-тт а и, значит, уравнение
дискриминантной линии (которая здесь
является огибающей, так как ри = [а]фО)
Гг'1
имеет вид: р = г±а~~г1- Огибающей
являются две линии, «параллельные»
данной и «отстоящие» от данной линии
(по нормалям к данной линии) на
расстояниях а. Таким образом, данная линия и
огибающая имеют общие нормали, т. е.
138
#

являются эвольвентами одной и той же эволюты — эволюты данной линии
(черт. 65).
173*. Уравнение семейства нормалей: p — r (v)-\-u [r' (v)]. Находим:
Ри = [П Pv = r' + u [г"], Рм X р„ = 0, [г'} Х(г' + и [г" ]) = 0, [г'] X г' +
+ и [г'] X [г"] = О, — г'2 + иг' хг" = 0, и = —г——- и уравнение огибаю-
# X #
** = Г fa)
Черт. G5.
Р*РМ
Черт. 66.
щей (ри == [г'] ^ 0) имеет вид: р =■ г -f М -р ^
В координатах £ — х — у'—,„,,,> "Ц—у + х'
7- (эволюта данной линии).
тр-т- (черт. 66).
лг'у"-— х"у' ' ' ~ ' лгу'' — jC'jy
174. Парабола.
175. Кардиоида (черт. 67).
176*. Уравнение семейства окружностей R(R—г)=0 или R2 — Rr — 0.
Дифференцируя левую часть по v и приравнивая результат нулю, будем
иметь Rr== 0, откуда /? = Х[г'].
Для определения X подставим
>.[/*']• вместо R в соотношение
R* — Rr = 0, получим XV2 —
г' х г
— Хг'Хг=0, откуда Х = §— и,
г'
следовательно, уравнение огибающей
Черт. 67.
Черт. 68.
г' х т
/?== 2— М — подэра данной линии относительно начала радиусов-век-
г'
торов (черт. 68) (см. № 138*).
. 177*. (R— г)г'=0, (/? — г) г"—г'2= 0, /? — г=*Х[г'], Х[г']г"—г'2 = 0,
г' X г'
г г
Г X Г"
139

178. Прямая и окружность. Пусть (xlt yt) и (x2i у2) — концы хорды
(параболы у2 = 2рх)у проходящей через фокус. Длины FMX и FM2 соответственно
равны Xi + 'f- и х2 + -т[> значит М1М2 = х1-{- х2 -\-р. Уравнение окружности
семейства:
Х1*Г Х2 \
Ух +У* \2 fxt + x2 + py
+('-***)■-(
* Г~1 +['— Г-/ ~\ 2-
)'.
откуда в силу соотношений у2 — 2рхи у2 = 2рх2 получим: х2-\-у2 —
— (хх + х2) х — (ух + у2)у Н——2 === ~т • И3 условия коллинеарности точек
Ml>M2w f(£-,Q] находим:
xt у,
х2
р
2
У*
0
1
1
1
у\
а так как xt = -^-, х2 -
принимает вид:
А
2р
= 0,
, то уху2 — —р2. Теперь уравнение семейства
/у2 л3 \ / n2 \ Зр2
У2 — [^ + щ)х~[У1 — ^)У = -^-г Дифференцируя левую
нулю, пол
х— у = 0,
или х2
часть по ух и приравнивая результат нулю, получим:
Р2-У1
РУх
О \f V О2 V2 V2
— —^-i.==:r!L# Возводя в квадрат, получим/-^ -\-'~ = 2 + "^. Ур
откуда
нение огибающей:
П
При .*• =— ™ левая часть тождественно равна нулю, следовательно, из неё
можно выделить множитель
*+4;
сделав это, получим ещё уравнение: х2 + у2 — ~ л: = 0 или ( лг — -— 1 + у2 я
/Зр\2 - р
= (— ) —эта окружность вместе с директриссои лг = — ~у и составляет
огибающую.
179. Циклоида.
180. Окружность, описанная около данного эллипса (см. № 176* и № 135).
140

181. Окружность, центр которой
совпадает с центром симметрии
данной гиперболы и радиусом, равным
действительной полуоси гиперболы
(см. № 176* и Jfe 136).
182. Касательная к параболе в ее
вершине (см. № 176* и № 134).
183. Парабола.
184*. Не нарушая общности,
можно считать, что начало
координат на одной из прямых лежит на
другой (точка О). Рассмотрим декар-
тову систему координат хиу, в
которой точка О' служит единичной
точкой' оси Оу. Тогда уравнение прямой
семейства будет иметь вид:
:1
v ^ v + 1
(v+l)x + vy — v2—v = 0.
Черт. 69.
Дифференцируя левую часть по v и приравнивая результат нулю, получим:
V+1:
1
(х + у + 1)
и уравнение огибающей:
2х > , 2у
= 1
Черт. 70.
х + у— 1 х-^у+1
или
(аг + у)3 + 2(лг~у) + 1 = 0.
Положим х-\-у=Х, х —
— у = ^. В системе XOY
единичной точкой является
точка О'. Уравнение
огибающей в этой системе:
^2 + 2Г + 1 = 0 или Х* =
= — 2( Y 4* -у ]—парабола,
для которой прямая Y +
+ у=0 или х—У+-2" =
= 0 — касательная, а Х=0
или х-\-у = 0 — диаметр,
проходящий через точку
прикосновения (черт. 69 и
черт. 70).
185*. Располагая оси
координат так, как
указано на чертеже 71, будем
иметь:
М (a cos v, k -f- a sin v),
M' {a cos (v + ю),
— k -|- a sin (v + <u)),
141

где k — ордината точки С, a w — разность «фаз» точек М и М'. Уравнение
прямой семейства
х у 1
a cos v k-\-asinv l
acos(v-\-(d) —k-\-a sin (v-\-ы) I
= 0
или
\2'k~ 2a:sin -^- cos Iv + ^j\x — 2ay sin Iv ■-{- -j-j sin-^- -\-
-f a2 sin w — 2я& cos -~- cos (г> + -~-) ='0
или
2a sin -^- x — 2ak cos -^-) cos f v -f- -y) — 2ay sin -^ sin ( p -f- -~- j ==
= — 2kx — a2sinw.
Черт. 71.x Черт. 72.
Дифференцируя обе части этого соотношения по vy получим:
I 2a sin -у х + 2ak cos -у) sin f *> + y) — 2ау sin у cos (г; -f ■?-) = °-
Возводя два последних уравнения в квадрат и складывая почленно, будем
иметь:
2ах sin -у + 2ak cos у) + 4я2.у2 sin2 ^- = (2Ьт + a2 sin сй)2
или
Я^Ш2-^-— /И ctg2
= 1 — эллипс, если a sin -~- > £,
гипербола, если a sin -~- <с /г (черт. 71 и черт. 72).
142

§ 6. Соприкосновение плоских линий.
186. (—7= , —9"1п^)— точка>в которой ра'диус соприкасающейся
окружности линии у = In х имеет наименьшее значение.
187. Две окружности:
(*_2)« + (у-2)« = 2, (* + 2)2 + (у + 2)2 = 2.
188. R = 1(ап* + а1*У + ot)2 + (02i* + fl22y + fl2)2]2
189. Указание: вычислить координаты центра (С) соприкасающейся
окружности циклоиды в произвольной её точке, а затем координаты
середины отрезка СМ; получим at, О, т. е. координаты точки Р (черт. 73).
190*. Примем точку М за начало радиусов-векторов. Пусть г—радиус-
вектор любой' точки Р линии С. Радиус-вектор р образа Р' точки Р при
аффинном сдвиге относительно касательной к линий С в точке М
определится соотношением:
Р —r+£(rxri)r0.
Отсюда сразу находим: pi = r0; pi X pi'= ri X ri'. Кроме того: г0 = ро = 0
(черт. 74).
го
191*. J^ = *, р = г + (* — 1) (гяо) %
р' = Г' + (Х — 1) (г'Ло) 1»о», Pi = К,
р" = г" + а-1)(г"Лв)Яо,
Pi' = rj' + (X — 1) (ri' л0) n0 =
So Го]
= ri'+(*-l)-
[ra;
отсюда
Pi X Pi' = r0 X ri' +(>. — !) (Г6 X ri') = Xri x ri'
143

й значит
т. е. при аффинном сжатии плоскости к касательной с коэффициентом
сжатия X радиус соприкасающейся окружности увеличивается при сжатии и
уменьшается при растяжении (черт. 75).
(Г По) П0
192. х2 = — , /?2 = -г = х — РаДиУс соприкасающейся окружности в вер-
а
шине А2. Далее: >■! = -
вершине
а_
а п b b*
-г, ^i=zY== радиус соприкасающейся
окружности в вершине Лх. Построение: пусть F2— фокус, ^/ A2F2C2 = 90°;
тогда С2— центр соприкасающейся окружности эллипса в вершине.
Построение центра соприкасающейся окружности в вершине At: строим
окружность радиуса b с центром в точке Ах и из центра эллипса проводим
касательную к этой окружности; ТСХ _L ОАх\ Сх —центр соприкасающейся
окружности эллипса в вершине Ах (черт. 76 и черт. 77).
193*. Произведём аффинный сдвиг относительно касательной к эллипсу
в точке М такой, чтобы точка К перешла бы в точку К\ причём
№К' _L MT. Тогда данный эллипс с
сопряжёнными диаметрами МК и
АВ перейдёт в эллипс, для которого
А 'В' и МК' будут главными осями.
Если DA' > DMy то дальнейшее
построение таково: ME=DA'; /яА1ЕС^=
= 90°; С — центр соприкасающейся
окружности. Если A'D<.DMy то
построение аналогично построению
чертежа 77 задачи № 192. Наконец,
если A'D = DM, то центр соприка-
точкой D (середина отрезка МК')
сающейся
(черт. 78).
Черт. 77.
окружности совпадает с
■«•-{!('+1). К<-4)}.'-ЙЫ).|('+?)}.
г"={^ > ~ i} >r'(1)={0, b)> r"(1)={а"'
■Ь}
144
Я(1) =
(Г1 )
£2
|г'хг"| а

Геометрическое построение дано на чертеже 79. Для равносторонней
гиперболы ОА = АС (черт. 79).
195*. Пусть М — произвольная точка гиперболы. Произведём аффинный
сдвиг относительно касательной МТ к гиперболе в точке М и такой, чтобы
Черт. 78.
Черт. 79.
диаметр ОМ перешёл бы в нормаль МО' к гиперболе в точке М(00' _[_ О'М);
прямые Q'M и АВ будут иметь главные направления образа гиперболы,
О' будет центром образа, О'А и О'В — асимптоты образа, М — вершина;
значит, построив АС±_0'А, мы и попадём в центр соприкасающейся
окружности. Итак, построение: из центра гиперболы опускаем перпендикуляр 00'
на нормаль MN, соединяем точку О' с точкой Л, в которой касательная
пересекает одну из асимптот, и проводим ACj_0'A; С — центр
соприкасающейся окружности
гиперболы в точке М.
196.^=2/^^,
"-{*?}•
г-(0) = {1, 0},
r"(0)={o.i};
А
Я-|г,хг„(=а
т. е. центр
соприкасающейся окружности
удалён от вершины в два
раза дальше, чем фокус.
Отсюда способ построе-
нияг пусть М —
произвольная точка параболы:
строим МР_\_Оу, OP = OQ, проводим MQ; пусть R — точка встречи
прямой MQ с касательной к параболе в ее* вершине; строим RF J_MQ,
F—фокус, OF=FC, С — центр соприкасающейся окружности в вершине.
Заметим, что для построения соприкасающейся окружности параболы в
Черт. 80.
10 П. С. Моденов
145

ее вершине О достаточно знать ось симметрии, касательную в вершине,
и ещё одну точку М параболы (черт. 81).
197*. Произведём аффинный сдвиг относительно касательной к
параболе в точке М так, чтобы диаметр MR перешёл бы в нормаль MS. При
этом точка Р параболы перейдёт в точку Q параболы-образа, причём
PQ = RS. Для параболы-образа точка М — вершина, MS — ось симметрии.
Строим
MT = MS, TQt LA±TQ, MA = AQ
С—центр соприкасающейся окружности. Заметим, что для построения
достаточно знать точку М параболы, касательную в ней, диаметр и ещё
другую точку Р той же параболы (черт. 82).
Черт. 81.
198*. Примем точку М0 линии С за начало радиусов-векторов. Пусть р0—
радиус-вектор центра соприкасающейся окружности линии С в точке М0.
Тогда уравнение соприкасающейся окружности будет иметь вид:
(Г-Ро)2 = Р§
или г2 — 2гро=0. Функция у(г) = г*—2гр0>0 для точек М(г),
расположенных вне окружности, и меньше 0 для точек, расположенных внутри
окружности. Таким образом, надо исследовать знак функции
?« = г2(0-2г(ОРо
вблизи / = *0; имеем:
?'№ = 2/r'-2r'Po, *'('•) = 0, T?"(') = /T'' + r'2--r''Po,
1 2 2 Г'%
-о" <Р" (to) = Г'о - Г'о'Рс = гС — Г,'/ [Г0] —rrr-ZTT
& 'о* *0
Го —г0 =0,
,2
1 ?'" (t) = Зг'г"+гг- - г"' р0( 1 *•" ц„) = 3riro' - К'' К) 'V
^ ^ Л, х /•„
* и *^ *о 'о <*» * о
146

и, значит, ф (/) меняет знак при переходе t через t0, т. е. линия С в точке М0
пересекает свою соприкасающуюся окружность (черт. 83).
199*. ф (/) = г2 - 2гр0, ~ ф' (4) == 0, у ф" (/0) =* 0, 1 ф"' (/в) =
riv Л 1 m „ ч 1
= 0, 1 ?(4) Л) = „, d -„ «г! X /-J') (4/W +
+ 3r-2)-(r;xr(04))r;2}^0
и, значит, ф (t) сохраняет знак в достаточно малой окрестности t = t0, т. е.
линия С в достаточно малой окрестности точки М0 не пересекает свою
соприкасающуюся окружность — достаточно малая часть дуги линии С
в окрестности точки М0 (за исключением с дм ой точки М0) расположена
или целиком вне, или целиком внутри соприкасающейся окружности линии С
в точке М0.
,2
^U- Л — dt\ r'xr" }-
(г'2)
_L
r'2\ 2
(r' X r")2
{3r'r" (r' X r") — r'2 (r' x r"')} =
(r'2)2 (r'v)
^0
(r' X г")2 ^ Черт. 83.
(см. задачу 198).
201. 1) Для эллипса v || {— a cos t, b sin t}. Этот вектор перпендикулярен
вектору г'={—a sin/, #cos/} только в вершинах эллипса (а^Ь) и, значит,
во всех точках эллипса, кроме, быть может, его вершин, соприкасающаяся
окружность пересекает эллипс. В вершинах эллипса соприкасающаяся
окружность не пересекает эллипса (в достаточно малой окрестности вершин), так,
например, в вершине, соответствующей г = 0, имеем r'v = 0, но
(г' х г") (4 г'г'" + Зг"3) — г'2 (г' X r(4)).=ЗаЬс* 7^ 0.
2) Соприкасающаяся окружность пересекает гиперболу во всех её
точках, за исключением вершин. Вектор аффинной нормали направлен по
диаметру гиперболы, проходящему через рассматриваемую точку.
3) Если линия задана уравнением у=/(лг), то v = {—у'", Зу"*—у'у'"};
произведение r'v =ЗуУ'2 —у/2у'" — у , а выражение (г' X г") (4г'г'" 4-
_|_ Зг"2)— г'2 (г' X гЩ принимает вид: у" (4у'уш + Зу"2) — у(4) (1 + у'2). Для
параболы вектор аффинной нормали всюду коллинеарен оси; значит,
соприкасающаяся окружность пересекает параболу всюду, кроме, быть может, её
вершины. В вершине
уп (4уу" -f- Зу"2) — у<4) (1 + у'2) = 24л3 ф 0,
и, значит, парабола не пересекает своей соприкасающейся окружности.
4) Для линии у = Inх имеем: v = -j т> ~Й1> f/:=ib —L *"'v =3
1 2x2 1 f~\
= 5—. Отсюда: r'v ^ 0 при всех x, лг>0, л:^£ I/ — , т. е. во всех
точках, за исключением, быть может, точки (I/ -=■ 9 —— In 2),
соприкасающаяся окружность пересекает линию у = 1пх. В точке (1/ —, —^-ln2j
имеем: у"(4у'у'" -f-Зу"2) — у(4) (1 -\-у'*)ф 0, и, значит, в этой точке
соприкасающаяся окружность линии не пересекает.
* 147

4 4
202. Полагая в уравнении параболы х = -^- at2, найдём у = — а (1 — /)3.
Заданной точке соответствует значение * = -~-. Составляем функцию
Отсюда находим:
,(!)_,.(' )-,-(^=.,,„(^.
— соприкосновение третьего порядка (черт. 84).
203. Пусть (ах + Pv)2 + 2улг + 2Ьу = 0 — искомое уравнение.
Параметрические уравнения данной окружности: х = а + г cos /, jy = r sin *. Далее
находим:
ср (/) = [a(a + rcost)+$r sint]2 + 2? (а + г cos t) + 2 8 r sin *.
Черт. 84.
Черт. 85.
Для точки В *=0. Имеем: ? (0) == а2 (а + г)8 + 2? (а + г) == 0. Уравнения
ср' (0) = 0, ср" (0) = 0 имеют вид:
(а + г) ф -(- 8 = 0, р2г — а2 (а + г) — 7 = 0.
Отсюда:
Соответственно этому имеем два уравнения:
Так как касательная к искомой параболе в начале координат должна
составлять с осью Ох острый угол, то надо взять нижние знаки:
{x~y±±L yy-{a + r)x + 2{a+£ у = 0 (черт.
85).
148

204. Возьмем искомое уравнение в виде: ^ ' 5 = 1.
Составляя
функцию ср №
__(! —cos;c + £)2 х*
1 и приравнивая нулю её
производные (при лг = 0), получим: а2 = 3, £2 = 9. Искомое уравнение:
0> + 3)2
= 1.
9 3
Отметим, что при у = 1 из
уравнения у = 1 —cos x нахо-
дим л: =-у «з 1,57, а из урав-
: 1 ПрИ
нения
(У + 3)2 х2
9
у= 1 найдём л:
«У>1А
Здесь мы имеем
соприкосновение пятого порядка:
Черт. 86.
ср' (0) = ср" (0) = ср'" (0) = ?(4) (0) =
= ср(5) (0) = 0, ср(б) (0) ф 0 (черт. 86).
205. В системе хОу (черт. 87)
параметрические уравнения циклоиды имеют вид: x = \(t — sin t) — тсХ, у-
= X (1 + cos /). Взяв уравнение соприкасающегося эллипса в виде
Черт. 87.,
{у-Ь?
1 = 0,
исследуем функцию
1
* (0 = ^ frit-sin t)-~Tt\]* + -w[l(\+cost)--l>]*--l
в точке, соответствующей значению / = тт. Условие ср (тс) = ср' (тс) = 0
выполняется. Условие ср"(тс) = 0 даёт а2 = 4Х£. Условие ср'"(тс) = 0 выполняется.
Условие ср(4)(тг) = 0 даёт £ = ЗХ, следовательно, а2 = 12Х2 и уравнение
соприкасающегося эллипса
12 X2
СУ-ЗХ)2
9Х2
-1=0.
При у = 2Х, xc&±3,2k; значит, соприкасающийся эллипс «охватывает»
циклоиду. Условие ср<5) (к) = 0 выполняется. Наконец, ср(б) (тс) ф 0 —
соприкосновение пятого порядка.
206. y=^f"(0)xK
149

207. y = l — -^-. Соприкосновение третьего порядка.
208*. Возьмём уравнение параболы в виде:
[а(л:-1) + ЗД2+2т(д:-1) + 2^ = 0,
ср (х) = [ а (х — 1) + р 1 п х]2 + 2т (* — 1) + 2 81 п л:.
Из соотношений ср'(1) = ср"(1) = ср"/(1):=0. Легко выразить р, т и 5 через а.
Ответ: х* + 4ху + 4у2 — 20л: + 14у +19 = 0.
Соприкосновение третьего порядка.
209. Проверить условия: j; (0) = Г (0), у(0)==Г(0), у"(0) = Г' (0),
у'" (0) = У" (0), jK4) (0) ^ У(4> (0).
211**. Все касательные параболы, имеющие с данной линией в данной
точке соприкосновение второго порядка, получаются из одной такой
параболы всеми её аффинными сдвигами относительно касательной в
исследуемой точке. Пусть л:2 = 2Ry — одна из таких парабол (R — радиус
соприкасающейся окружности). Тогда параболы, полученные из данной аффинным
сдвигом относительно касательной, определяются уравнением:
(x + kyf — 2Ry = 0
или
. и kR и I . k*R
\+k*\* 2R """^^.2(1 + 6»),
Yl + k* 1 1 1/"Г+Л2
(1+Л*)2
R
Отсюда ясно, что параметр этой параболы равен р = г-, а коордй-
наты фокуса определяются из системы:
kR
х + кУ-\ + ¥ = *>
— kx -f- v -
2(1 +*2)_
Vl+b* 2(f+/fe*)8/»
или
ii. kR и , Я 1 - *2
*+^ = ГТ^' -** + *= 2TTF-
Отсюда можно найти параметрические уравнения линии, на которой
расположены фокусы. Исключая параметр, получим:
х2 -(- У2 = -н- /?У — окружность.
212**. Полагая ср (/) d= {г (^) X a}a + 2r(f) X & и, приравнивая нулю три
производные от ср в рассматриваемой точке, будем иметь:
?'(*) = 2 (г х а){г* х а)4-2г' X Ь, ср'(/0) = 2rJ х Ь = 0;
можно положить b = r'0. Тогда
— ср' (г) = (г х а) (г' х а) + rf x rj.
150

Составляя уравнения ф"(/0) = °» ?"4W = 0> будем иметь:
r'0xa = Vr'0x r0', rj' x a = JL
1 /oXri"
з VKxK'
(мы предполагаем, что rj X rj' > 0; в противном случае мы взяли бы
Ь = —Го). Далее полагаем: а = Х r£ + ц. r'Q'. Умножая обе части этого
равенства псевдоскалярно один раз на r'Q, другой раз на г'0' (слева), найдём:
Хв—£*1Г9 ^-—±—.
з(г;хг;')^' (г;хг;)^'
следовательно:
зг;' (г; х о — г; (г0 х г0") ___ v
а =
3(r0XrJ')3/2 3(г0хг0')3/з '
v == Зг0' (г0 X г0') — г0 (г0 X г0") — вектор аффинной нормали.
О т в е т: (г X v)2 + 18 (гJ X г0')3 (г X г0) = 0.
213**. Полагая ср (/) = г(t) Ф г(t) + 2ar (t), последовательно находим
— у' (t) = г' Ф г + аг1, y 91 (А>) = ar'Q = 0; значит, а ± г0. Положим а = -—[г0],
тогда ~£ <р' (t) = г'Фг + г' х г0. Далее:
-1 <р" (t) = г" Ф г + г'Фг' + г" х г0,
-L <р"' (*) = г"'Фг+ Зг"Фг' + г'" х г0,
1 <р<4) (f) = /Ч4)фГ + 4г'"фГ' + ЗГ"ФГ" + Г(4) X rj.
Составляя уравнения: <р" (/<>) = °> ?"' (А>) = °» <Р(4) Со) = °» будем иметь:
г0Фг0 = г0 х г0', г0Ф/-;' = ~ г0 х г0", 4г;''Фг; + Зг0'Фг0' + г0(4) X г0 == 0.
Но
* о А * о * о ^ ' о
значит, уравнение <р(4)(/0) = 0 принимает вид:
4 Г1 ' * ff г'0 х г0' + 4-^§1 . Iri X /Г+Зг0'Ф/Г =r0 X r0(4),
'о Х'о ' о А Г0 О
откуда
Г"(Ъ*." Jl «.' v r<4) 4--i#." yr'"-i- (ro X Го'')2
Если теперь принять векторы г0 и rJ' за масштабные векторы декартовой
системы координат, то
г = лт0 + уг0', Фг = хФг0 + уФг"
и, значит,
гФг == лг2г0Фг0 -f- 2лгуг0Фг0' + У2/*0'Фг0'
151

и искомое уравнение:
(К X г'0') х2 + ~ г'о X г£" ху +
Это уравнение упрощается, если изменить масштабный вектор оси Оу,
приняв на новую ось OY аффинную нормаль. Итак: полагая е1 = г'0, е% =
= 3ri' (г'о X Го) —Го (г0 X г^')» будем иметь
г = Л4 + Ye2 = Xr0 + Y {Зг'о' (г'0 X rj') -rj (rj X rj")b
откуда
x = X — Yr'o X ri", y = 3Yr'0Xro".
Подставляя эти выражения для х и у в уравнение, полученное выше,
после упрощений, будем иметь:
** + gk« —6rjxr;'r=o,
где
• Q = 3 (г; X К') (г0 X г(04>) - 5 (rfo X гГ)2 + 12 (г£ х rf) (г J' X К").
Таким образом, аффинная нормаль линии является диаметром
соприкасающейся линии второго порядка; последняя будет эллипсом,если Q > 0,
гиперболой, если Q < 0, и параболой, если Q = 0. Если соприкасающаяся линия
(Зг' Y г" \
0,—^——). Если
соприкасающаяся линия — парабола, то её уравнение в указанной системе (r0> v) имеет
вид: X2 — бГо Хг;Т = 0.
214. Q = 3y"y{*) -^5у'"2. Если£>0, то соприкасающаяся линия —
эллипс, если Q < 0, то гипербола, если Q = 0, то парабола (см. предыдущую
задачу).
215.1)2 = — 3sin2;c — 5 cos2 * < 0 — все точки синусоиды
гиперболические (за исключением её точек перегиба);
2
2) Q = q<-Q — все точки гиперболические;
• х
ПС*
3) Q = s^O — все точки гиперболические;
4) Q = n2 (п—1)2 (п — 2)(—2п+1) х2П-«; при я = 2 и # = y все точки
параболические. Для -~- < п < 2 все точки эллиптические. Если
я<— или /г>2, то все точки гиперболические. Начало координат
исключается из рассмотрения;
„ _х х_ - х_ х_
ЛГ~5
Значит, все точки цепной линии с ординатами меныцими, чем а I/ -^ , —
152

i 5
эллиптические, с ординатами большими, чем а I/ -^ , —гиперболические, a
две точки с ординатами ау-~ — параболические.
216. 1) Й = 2а4(1 — cos*)(2 — cos*)>0 (точки возврата исключаются).
Все точки эллиптические.
2) й = аЧ2 (4 -}- 9*а) > 0 — все точки (* = 0 исключаем) — эллиптические.
3) Q == -j-j- (9^ — 5а4). При 11 | > а 1/ -д- имеем: Q > 0 -— точки
эллиптические; при / = ±а|/— — точки параболические (две точки), при
f-g"
-g- — точки
гиперболические (черт. 88).
217. r=rr°, г' = г'г° + г [г%
г" = (г" — г) г° + 2г'[г°],
-H4r'"-4r')[r°],
о я I r' r I I г'
^ — ^ I г" — г 2г'| | у-С4) — 6^" -+-
Г I е| Г' Г I2,
4-г4г"' —4г'|—°|г'"—Зг'Зг"—г| "г
. то! r' r\\r" — r 2г' I
-Г ^ |г,/__г 2г»| • | rw _3 г' Зг" — г I "
Если Q > О, то соприкасающаяся и
линия эллипс, если £ < О, то гипер- Черт. 88.
бола, если Q = 0, то парабола.
218% Q = а4 (9ср4 4- 58<р2 4~ 120) > 0 при всех <р — все точки эллиптические.
219. &= 18а4 (1 4-cos cpH11 + Ю cos ср) > 0, все точки эллиптические
(точки возврата исключаются).
220*. R=±r + 3 Г*Г~{Зг"(г' X г") —г* (г' X г'")},
где
Q = 3 (г' X г") (г' X г(4)) — 5 (г' X г'")2 4-12 (г' X г") (г" х г'").
Эта линия связана с исходной аффинно-инвариантно («аффинная эволюта»).
221*. Уравнение аффинной нормали: jR = r-\-\v, где
v = Зг" (г' X г") — f (г' X г'").
Находим:
#' = r'4-*'v + b\
Этот вектор должен быть коллинеарен вектору v, т. е.
i
vx(r'4-b'v + Xv')==0,
откуда
v X г'
v' X v
153

и уравнение огибающей
о , v X г'
vxr' = -3(r'x г")2,
v' = Зг'" (г' х г") + 2г" (г' х г'") — г' (г" х г'") — г' (r' x г(')),
v' х v = — 12 (г" х г'") (г' X г")2 + 5 (г' X г'")2 (г' х г") —
— 3 (г' х г")2 (г' х г(4)) = — г' х r'U
Значит, окончательно:
* = r + 3-^-^v
(см. предыдущую задачу), т. е. огибающая аффинных нормалей совпадает
с линией центров соприкасающихся линий второго порядка.
222*.р = г + 7=— -,.pW+ ^ ^ -7^ +
"^ 1?"7^ I г' х г" J ~~ "^ (^i)«/, г' х г" "^
-l Jrl f(r'2)3/gy
V* I г' х г" / •
Вектор [г"] г'2 — (r'r") [r'J перпендикулярен вектору [г9] (так как скалярное
произведение этих векторов равно нулю). Значит:
[r'']r'2—(r'r")[r'] = Xr\
Умножая обе части этого равенства скалярно на г', найдём X = г" х f.
Итак:
0,_г, , r»xr> (г'2)3/* И \ (г'2)3/Ч'_
(г'2)3/2 г' х г" "*" у-^2 1 г' х г" / —
|/~ Г'2 \ Г' X Г" J "
Гг1 Г (г'2>8/2 1 '
223**. На основании предыдущего упражнения р' = -1 J. J -—-— К .
/г'2 [ r'xr" J
Так как по условию г' X г"^0, аг'Х г" является непрерывной функцией /
(ибо г' X г" имеет производную г' X А"'")» то г' X г" на данном сегменте
(г'2)3/2
сохраняет знак. Пусть, например, г' X г" > 0. Тогда ~—^—^- = /?, где Я —
/* X /*
радиус соприкасающейся окружности и, значит, p'==-yi _., Отсюда
,2 fdRY -,/-72-
р' = ( -ут 1 и, следовательно, |/ р' =
/г'2 d'
154
По условию R (t) — монотонная

функция от t, значит, производная R' на данном сегменте не меняет знака.
Пусть, например, R'^zQ. Тогда |р'| = /?'. Отсюда
Р
f |р'|Л = #(Р) — #(<?), тле а<Са<р^Ь.
Но
Итак:
f Ip'I^^IJp'
d*
= |Р(Р) —Р(«)
|р(Р)-р(«)1
■/?(«),
т. е. расстояние между центрами
соприкасающихся окружностей не больше разности их
радиусов, а это как раз и означает, что одна из
соприкасающихся окружностей вложена в дру-
. гую (черт. 89).
224. Если исследуемая точка принята за
начало координат, а за масштабные векторы
принять векторы
*i = { 1> Уо }> <?2 = { —У'о", 3yJ'2 — УоУ'о" },
то уравнение соприкасающейся линии второго
порядка запишется так:
где
Черт. 89.
0> Уо4)== ~"з • Принимая точку (0,0) за начало
координат, а за масштабные векторы ех = { 1,0 } <= /, е2 = \ 0,'— }, найдём:
225. /0 = 0, Уо' = — , У'о
*s + -r*-
г = о.
Принимая за масштабные векторы / и J, будем иметь:
Отсюда х = Х, у=—«-, Х—х, Y=.—~-t и уравнение соприкасающейся ли-
CL и
нии второго порядка принимает следующий вид:
х2 + ^ — 2ау = 0
или
£+<^-? («...о».
155

226. Уравнение искомой линии возьмём в виде y = f(x) и будем
считать, что аффинные нормали параллельны оси Оу. Так как
У" = О, У'= 2а, у' = 2ял: + Ь, у = ах2 + дх + с-— парабола.
227*. Возьмём уравнение линии в виде: у=/(лг). Пусть исследуемая
точка лежит в начале координат и пусть /'(0)=:0 (т. е. за ось Ох выбрана
касательная к данной линии в данной точке). Уравнение линии второго
порядка, проходящей через начало координат и
касающейся в начале координат оси Ох, имеет вид:
апх2 + 2а12ху + а22у2 + 2а*у = 0.
Рассмотрим функцию
ср (х) = апх2 + 2а12х/ (х) + а22Р (х) + 2a2f (x).
Условия
?'(0) = ср"(0) = ср'"(0) = 0
дают:
«и + aJo = °> За12/0' + «а/о" = 0,
и уравнение линии второго порядка принимает вид:
Центры этого семейства линий (6 — параметр) лежат
на прямой Fx = 0:
Черт. 90.
— это уравнение аффинной нормали к данной линии в начале координат
(/о = 0).
2 /7
228. (у
5 V5
,(,-
i_y__i6/ii
5 \5
')•
229*. Принимая исследуемую точку за начало координат, а касательную
в ней за ось Ох, имеем:
апх2 + 2а12ху + а22у2 + 2а^ — 0,
ср (х) = апх2 + 2а12х/ (х) + я22/2 (л:) + 2а2/ (х),
<р' (0) = 0, 9" (0) = ап + a2f0' = О/ ди + а22 = 0,
— «а/о'*2 + 2flltAT,y + я2/0'У2 + 2яаУ = °>
_*2 + 2^+у2 + -^==0, —* + 6у = 0, ег + У+47 = 0,
/о /о *
. л: л:2 , ,1
:0, ЛГ2+У + -^7=0
/О
— окружность.
1£*1
3 /Г
230*. /i'x» + ~ Цп- ху —Го'у* - 2у = 0.
156

231**. 1) Пусть S — соприкасающаяся окружность линии С в точке М.
Тогда никакая другая касательная в точке М окружность St не есть
соприкасающаяся, так как можно «окружить» окружности S и St касательными
окружностями: S', S" и S[9 S[' такими, что образовавшиеся при этом «серпы»
не будут иметь общих точек, кроме точки М. И так как достаточно малая
часть дуги линий С в окрестности точки М попадает внутрь одного из
«серпов», то никакая часть дуги,линии С в окрестности точки М не
попадёт внутрь второго серпа (черт. 91).
2) Поместим начало радиусов-векторов в исследуемую точку М. Тогда
уравнение касательной окружности запишется так: (г— Rn0)2 = R2 или
г2— 2Rrn0 = Q, где R— её радиус, а щ — единичный вектор нормали к
линии С в точке М, направленный в ту сторону от касательной, где
расположена касательная окружность. Для точек Р(г)у лежащих внутри
касательной окружности, будем иметь: г2 — 2Rrn0 < 0, а для точек, лежащих вне,
г2 — 2Rrn0>0; значит, для определения положения точек линии r = r(t)
относительно касательной окружности надо исследовать знак функции
y(t) = r2(t) — 2Rr(t)n0 вблизи t = t0 (/0 —зна- до
чение параметра, соответствующее точке М).
Имеем:
Т' (t) = 2rr' — 2Rr'n0y <p' (t0) = 0 — 2Rr'on0 = О,
ср" (*) = 2rr" + 2r'2 — 2Rr"n0,
<?"(t0) = 2r'l — 2Rr'0'n0.
Эта производная обращается в нуль при R =
г'2 г'2
= ^,?w , причём, если R < ^^ ,то <р" (*0) > 0 й,
Го П0
' К'По
значит, ср (t) > 0 при всех t, достаточно
близких к t0 и отличных от t0y т. е. достаточно Черт. 91.
малая часть дуги линии С в окрестности
точки М (за исключением самой точки М) лежит вне касательной
окружности радиуса R*
' К'щ
. Если же R > -
Г и П.
•, то <р" (*<>)< 0 и, значит, <р (t) < О
при всех t, достаточно близких к t0, т. е. достаточно малая часть дуги
линии С в окружности точки М лежит внутри касательной окружности
радиуса R >
К*
Итак, касательная окружность радиуса R = ,,° 9
Но
П п
расположенная со стороны вогнутости линии, и есть соприкасающаяся,
единичный вектор нормали к линии С, направленный в сторону её
вогнутости, определяется соотношением:
[Го1 К X Го'
Ло=-
Г'о\\г'0Х Го
(см. № 106),
значит, окончательно:
# =
/2
Го
Г'о К]
\ri\
ГоХГр- __, (r02)3^ _ f*024-y02)3/*
/"о X г0' |
г0 х г;
\Х*Уо—ХоУо\
Координаты центра соприкасающейся окружности получим (сейчас
предполагаем, что начало радиусов-векторов в произвольной точке), прибавляя
к радиусу-вектору точки М вектор Rn0:
Р_г0 + Л«„- r0 + |r,xr;,, jTft, ,* xri'i -r»+W on? •
В координатах:
*о +Уо
7) =^0 + Х'о Z
<2+у?
*аУо
'ХоУь
157

3) Любая часть прямой линии в окрестности любой её точки лежит вне
любой касательной окружности.
4) Докажем, что достаточно малая часть дуги данной линии в
окрестности х = О лежит внутри любой окружности, касающейся оси Ох в
начале координат и расположенной в области положительных ординат. В самом
деле: уравнение любой такой окружности: х2 + (У — °02 = <*2> где а > 0 или
(интересующая нас часть): »
у — аг—Уа* — **^'
где lim е = 0. Далее, К = л;4/з. Имеем:
х = 0
+•.
Y—y = xi/*-
•?ОН"Ы*т (!+■)]
и, значит, в достаточно малой окрестности нуля Y—у>0.
5) Если линия С в точке М имеет соприкасающуюся окружность, то
в силу данного определения достаточно малая часть её дуги в окрестности
точки М должна лежать по одну сторону от касательной к линии С
в точке М.
§ 7. Кривизна.
«£
4)
д (у4 _ 2£уЗ _|_ д2£2)3/9
233.
3
у*\2аЧ-
8) За | sin t cos / |.
.у*__3£у2
234. 0,128.
235. 0.
236. 1) | cos x\\ 2) -g- ;
3>а~Я; 4>
8я sin
238. /? =
(1+?2)2
0<Р . ду I
239. У? =
(/£ + /ф2
mod
^хх^ху^х
Гух*уу**у
FxFy 0
240. /? = -
(г2+г'2) 2
|2г' — rr" + r2
241. г = rr\ r'=r'r° — rep' [r°], r" = r"r° + 2r>' [r°l + rep" [r°] — rcp'V =
= (Г" _ n>2) r« + (2ry + ry") [r°], r'2 = r'2 + rV*, r' X r" =
•rep'
Гер'
2rV + rrf "
Я =
2r'V + rr'cp" — rr'Y + r2cp'3,
12r'V -f- rr'cp" — rr'u' + ry3
158

2 + <P8
2) *!* + " + *. ; 3)
,2\3/2
242. 1)
a (1 -X. ©I)8/! ' ' дср/г-i (/j2 _|_ ?ij
244. 1) («, «) 2)(-Iln2, ^);8)(^..)
1
l/l + (ln«)a
245. Решение. g = ^,g = ^z
_ d Y _\дх~*~ду X] \дх~*~ду X)
~dxX X*
-M*-"*"*-^-*-*)-
ox dy ox ay |
246
(X3 + Y*?'*
P^X[r'], p—J-A^XAr. (р-уДг)дг = 0, ХИДг = уДЛ
/Ar\.
■ 2 [г'] Дг' " 2 [г'] Дг l' ь «'Го " - д1-о 2т- х
= lita
г1* fr'l
-eVxl^ + 4) r'xr
A*2
r'2
Таким образом, точка С (конец вектора lim р> от-
ложенного от точки М данной линии) — центр
соприкасающейся окружности в данной точке
(черт. 92).
247*. р = Х[И&)]. Повторяя рассуждения,
приведённые в предыдущей задаче, получим:
Дг2 [г<*>].' •
Далее:
2 [r{k)] Дг
Черт. 92.
2r{k) х Ar = 2r(fe)xli
.(ft)
+ r'
(&!)2'
^ , ■ Js-l) M~
(k'+\)\ + -" + r (s-1)!
i* + i>v A'fe+1 ■ _l,i.-i> _^!___ +
+<^+«»^}.
Предположим, что в точке М:
r^)||r(ftH-i)||...||r(5~i)^r.
Тогда
{Гт + а}
1 _ ^rfe].
159

I случай: 2k > s. Тогда litnp = 0.
/>(feh2 (2k)l
II случай: 2k = s. Тогда lim p = ,J ' * h
м = о ^>хЛ(й!)2
III случай: 2k < s. Тогда lim p = oo.
[r(ft'j(
248**. r {x, f (x)}, r' = {1, /' (x)} ф 0, k = 1, r" = {0, /" (*)} = 0 (в дан-
ной точке). Таким образом, s^3h, значит, 2&< 5, откуда limp = oo (см.
предыдущую задачу).
г'Х (г' + Дг') I |г'Х Дг'!
249. sin со =
Отсюда «о = arc sin
Далее:
г' | - |г' + Дг' | Г
г'Х Дг'|
|г'||г' + Дг'|
г' 11 г' + Дг' | '
,. о) ,. <о Г со sin о>1
lim 'Лллл = "m ni—i = "П1 — n—: =
= lim
lim
I r' X Дг' I
I r' X r" I
lim
I , Дг'
Г Х-гт
Д/
|г'||г' + Дг'|
Дг
i Д/
250. S = *аг.
(г'2)3/2
У"
, Если данная линия имеет в точке М0,
(i+/V/2
скажем, правую ориентацию, то и во всех точках достаточно малой
окрестности точки М0(/0) Она также имеет правую ориентацию, и существует
окрестность (t0 — 8, /0 + &) такая, что репер г'(/0), Дг — правый, или же;
любой треугольник с вершинами Мг (tx\ M2 (t2), Ms (/3)i где t0 — 8 < tx <
< t2 < ts < t0 + 5 имеет правую ориентацию (см. № 60).
251. Если г'Хг'">0, то при /</0 ориентация левая, а при />/0—
правая; при г' X г'" < 0 — наоборот. В самом деле: (г' X г")' = г' X г"' и,
значит, если г' X г'" > 0, то (функция г' X г" возрастающая, а если
г' X г'" < 0, то убывающая.
252.1)- ', 1 ■ 2) б_я/а; 3) sinx
4а
111 (4 + а/а)3/*'
(1 + cos2*)
;«*lV« "'
4)
(1 + *2)3/2
; 5)
ach2 —
§ 8. Эволюта и эвольвента.
253. 1) г' = {— л sin *, £cos/}, [г'] = {-г Ь cos /, — a sin*}, r'2 = a2sin^+
+ £2cos2/, r" = {— a cos *, — Ь sin /}, г' X г" = я£.
Уравнение /? = г+ [г']
^ принимает вид:
г' X г"
/?= {д cos t, b sin /} + {— b cos ty — a sin /}
{c2 c% Л
— cos3/, ^ sin8/ J-
a2 sin8/ + 62 cos2/ __
ab ~~
160

— астроида (черт. 93).
2) R = | — 4а2 х\ ^~а + Зах*} или 27Х2 = l6a ( Y — ^ )* —
полукубическая парабола (черт.-94).
Черт. 93.
Черт. 94.
о) ° = -{g- тз > —яа—/з— fJ поскольку лиг выражаются
через * рациональйо, линия, определяемая этим уравнением —
алгебраическая (черт. 95).
Черт. 95.
4) A'=x + cosjc
1 + cos2*
sin л:
Г = -
2 cos2jc
sin л:
(черт. 95).
5) X=2x + —, К=1плг —х2 —1 (черт. 97).
6) Аг=лг — 1—е2Х, Y = ex-\-2ex (чертёж аналогичен тому, который
дан к примеру 5).
7) Векторно-параметрическое уравнение:
г = {a cos <? (1 -J- cos cp), a sin <р (1 + cos <?)}.
11 П. С. Моденов
161

Отсюда находим уравнение эволюты в виде:
R = 11- (cos cp — cos2cp + 2), ~ sin cp (1 — cos cp)|:
9
полагая X o-a = — fe У = *\ и производя замену параметра cp = ir —1%
о
получим: е = 4 cos t (1 + cos /), *i = 4 sin * (l + cos ^ "" снова кардиоида в
три раза меньше данной. Её
расположение относительно данной кардиоиды
определяется формулами преобразова-
2
ния: X— -£-л = — £, K=y) (черт.
Черт. 96.
Черт. 97.
8) R={a {t-\- sin t\ — a(\ — cos t)} т— снова циклоида (черт. 9Э).
9) R = \ -ty (3 cos t — cos 3t), -у (3 sin t -\- sin 3/ \ — эпициклоида (черт. 100).
10) R=lx — ash ^ch ~ , 2<zch-^j (черт. 101).
id UT+^) U^-^)=^-(4epT-102)-
Черт.
Черт. 99.
254. r={rcoscp, rsincp}, r'={r'coscp — rsincp, r'sin cp-[-rcoscp},
r'2 = r'2 4-, r2* f" = {r" cos cp — 2r' sin cp — r cos cp, r" sin cp -f- 2r' cos cp — r sin cp},
r' x r" = 2r'2 — rr" + r*.
Уравнения эволюты:
^ =:j r cos cp — (r sin cp -f- г cos cp) -
2r"
r sin cp -j- (r' cos cp — r sin cp) —-
rr" + ra '
ra4-r'2 l
162

Другое решение:
Г = ГЛ % = Г'Г° + Г [П % = Г"Г° + 2г' [Г°] — "* = <г" - г> г° + 2г' 1^1.
г'2 = г'2 + г2, г' X г" = I г„^_ г 2г' I = 2г'2 — гг" + га»
и уравнение эволюты принимает вид:
г2 + г'2
Л==Г + <Г'^]-Г/*)—у „ .
2г' —rr" + r2
Отсюда сразу получаются уравнения, приведённые выше.
г'2 + гУ2
255. # = г + (г' [г0] — гр'г0)
2r'V + п-'?" — rr'Y + г2?'4
256*. r=r{t).
257. 3 (х2 +у2) + 14ял; — 16ду — 4а2 = 0.
259. 4
аъ — Ьь
260. х =
Черт. 100.
я© cos ср я(ср2-|-1)
<Р2 + 2
дер sin cp
ср2 + 2
а(ср2 + 1)
sin <р,
Черт. 101.
ср2 + 2^ ср2 + 2
cos ср.
261**. Мы дадим здесь геометрическое решение этой задачи, не
являющееся вполне строгим. Преимущество этого решения
заключается в его геометрической наглядности. Так как нормаль эллипса касается
его эволюты, то вопрос сводится к подсчёту числа касательных, которые
можно провести из данной точки к эволюте эллипса. Пусть точка Р лежит
внутри криволинейного «треугольника» ОАВ (черт. 103,1). Геометрически
очевидно (вот здесь и заключена неточность рассуждения), что из точки Р,
лежащей внутри криволинейного «треугольника» ОАВ, можно провести
четыре касательных к эволюте эллипса, и следовательно, четыре нормали
к эллипсу. То же заключение имеет место, если точка Р лежит внутри
одного из криволинейных треугольников ОВС, OCD и ODA. Пусть теперь
точка Р лежит в части плоскости, ограниченной дугой АВ и
продолжениями отрезков О А и ОБ за точки А и В (черт. 103, II), причём точка Р не
лежит ни на самой дуге, ни* на указанных лучах. Тогда из точки Р можно
* 163

провести две касательные к эволюте эллипса и, следовательно, две нормали
к эллипсу. То же относится к случаям расположения точки Р в частях
плоскости, симметричных указанной относительно осей симметрии эллипса
(или осей симметрии его эволюты). Если точка Р лежит на эволюте эллипса,
но не совпадает ни с одной из её
У| точек возврата (черт. 103, III), то из
неё можно провести три
касательных к эволюте эллипса и, значит,
три нормали к эллипсу. Если точка
Р совпадает с одной из точек
возврата эволюты эллипса, то из неё
можно провести только одну
касательную к эволюте эллипса, следо-
v вательно, только одну нормаль к
эллипсу. Если точка Р лежит на
одном из отрезков О А, ОВ, ОС, OD
между граничными точками, то из неё
можно провести три касательные к
эволюте эллипса и, следовательно, три
нормали к эллипсу (черт. '103, IV).
Если точка Р совпадает с центром
симметрии эллипса, то из неё можно
провести две касательные к эволюте
эллипса и, следовательно, две
нормали к эллипсу. Наконец, если точкаР
лежит на продолжении одного из отрезков ОА, ОВ, ОС, OD за точки Л,
Ву С, D, то из неё можно провести одну касательную к эволюте эллипса и,
значит, одну нормаль к эллипсу. Итог исследования представлен на схеме
чертежа 103, где эволюта эллипса изображена в виде утолщённой линии.и
Черт. 102.
Черт. 103.
в каждой из указанных выше частей плоскости указано число нормалей,
которые можно провести к эл/шпсу из точки, находящейся в этой части.
Эллипс на этой схеме не изображён.
164

262**. Решение может быть проведено вполне аналогично решению
предыдущей задачи. Итог исследования дан на чертеже 104, на котором
изображена условно эволюта гиперболы и в соответствующих частях
плоскости указано число нормалей, которые можно провести к гиперболе из любой
точки, находящейся в рассматриваемой части плоскости.
263**. Решение может быть получено на основании геометрических
.соображений, с использованием эволюты параболы. На чертеже 105 указано
число нормалей, которое можно провести
к параболе при различных положениях
точки относительно эволюты параболы.
264. 2,1 или ни одной, в зависимости
от того, лежит ли данная точка вне, на
окружности или внутри окружности,
являющейся эволютой данной линии
(эвольвента окружности).
265. Эволюта кардиоиды — снова
кардиоида и, таким образом, вопрос сводится
к подсчёту числа касательных, которые
можно провести из данной точки к кардиоиде. Вывод: из любой точки
плоскости, лежащей вне кардиоиды-эволюты, можно провести к
кардиоиде-эвольвенте три нормали, из любой точки кардиоиды-эволюты, отличной
от точки возврата, — две нормали, из точки возврата кардиоиды-эволюты —
одну нормаль, из любой точки, лежащей внутри кардиоиды-эволюты, — одну
нормаль (черт. 106).
Черт. 104.
Черт. 105.
Черт. 106.
. 266**. p = r + \[r'] — r-{- Дг + fxfr'-f- Д/*]. Умножая обе части этого
соотношения скалярно на г' + Дг', получим:
г (г' + Дг') + X г' X Дг' = (г + Дг) (г' + Дг'),
откуда
} *__ (г'+ Дг') Дг
и, значит,
р = г-
г> х Дг'
(г' + Дг') Дг
Ш
г' х Дг'
Для перехода к пределу преобразуем это выражение так:
Дг
(?+&)
д/
И+г.
Отсюда
lim р=г+-, ,
и = о г х г
тгН
— радиус-вектор центра соприкасающейся окружности. Поэтому иногда
говорят, что центр соприкасающейся окружности в данной точке данной линии
165

есть точка пересечения нормали к линии в этой точке с нормалью в точке,
«бесконечно близкой» к рассматриваемой точке.
267. r={a cos t, a sin t},r' = {—a sin t, a cos t], у r,2 = a,
•S— = {— sin /, cos /}, Г yV2 Л.= at
Уравнение семейства эвольвент
*-' + TFi(c-J/^)
здесь принимает следующий вид:
/? = {a cos t, a sin t} -\-(С — at) {— sin t, cos /}
или в координатах:.
Х=а cos t-{-at sin t—Csint,
K = asin/ — at cos t-\- С cost (черт. 107).
Черт. 107.
Черт. 108.
268.
x^+^z^\c-t^x+^+H
У~x2
Y^
С-|-1п(* + 1^+л],
269.
— трактрисса (черт. 108).
R = \a In tg f x + "9") ~~~ a sin*' a cos4
270.
x — дер cos cp — (C + s)
у = ay sin cp — (C + s)
coscp — cp sin cp
sin cp -)- ф cos cp
где
16S
*= у l«P Kl + <P2 + In (? + VI + <f3)].

§ 9. Длина дуги
X £ _£ X
1. 1) s= £/\+y'*dx = ^(ea-e a); 2) s = J/l + /9
о о , .
= 1[(4 + 9х)2~8]; 3) s = j/l+/2^ = |x^TT"4^+4b(2~x +
271.
Ar =
4- 1^Г+^2); 4) s= J /14-/2^ = J ^ l + ** -<**' =1Л + *2 +. .
о
= 4asin|-; 6) s= Г / *'* +У* dt=4q (1—cos-£); 7) s = Г/лг'2 + у'2^ =
о и
= ^8;8)s=J/yr+7^=ysin{; 9) 5 = J/^ + /^ = |sin^
10)
S=J/l+/d^VAT+^4-I.n^^=i-^2--In(^2-l);
11) s= riAx^-f-y'2d/ = alnsin/.
[Ar| —|As] =
Д/-2 Д§2
= Иш
{Ms + Z'^+Cr + a,^3)2-!^
iAe'*(|£!+1)
= lim
д5* + г»Д|! ±(-rr+ С) ^ +/Ч?4-«) ^- +(r + «)2^ -^
""•(!« И
= lim ■
^+(-,. + С>£:+«7+.>£+<Г + .^
IAs4
+ 11
~~ \~T j) * T~ 24"
Таким образом, если * ^ О, то разность между хррлой и соответствующей ей
дуги («стягивающей») —третьего иорадка ио отношению к дуге.
167

273. ^-x.
сх~,л лГ^а — Ъх , _/-=-, "l/ 4/7 — Зл: — l/~3~ V"а — х 0
274. а I/ Ьа1/3 1п- = -—гЛ 2л.
-\f\a- Злг . гт
а у \-ауд\п = -p-i—
Г а — х |/ а (2 — 1^3 >
275. ~ [2т: V 1 + № + In (2к + Vl+Aiz*J\.
277. /(а)+/"(а).
§ 10. Натуральные уравнения
278. 1) Я = а + —;
2) (27, + 8)*=> [4 + 9^У';
4) Параметрические натуральные уравнения:
5== у 1 +д:а -f In r— ' —
или, полагая jc== tg cp, получим:
5 = sec <р + In tg —-, х = sin <p cos2 9.
5) s* + 9R2 = \6a2;%
6) s2 + #2=16a2;
7)R2=2as;
8) s2+9tf2 = ^a2;
9) /?2 + 4s2 — 6as = 0.
10) Параметрические натуральные уравнения:
s=/l + e +Tin-J^X >xs=.
2 |/"f+^2* + l ' ^i + ^Va'
_ ?£
И) /?S + a2 = a2£ О.
279. 1) S=« = ". a=-ln*««««, ^ = Cosa, ^ = sma,
С , С aa, aeaa , , . x aeaa
r= I cosads=a I cos aeu da ^= -y---r (a cos а + sin a), y = 2 -(asina—
,2^«a aeaa.
ПОЛОЖИМ
a2e /
— cos a); отсюда x2 4-y2 = , r=yx2 + y2 — , ,
. 1 п. А У Л Sin a — COS a , , , it
я = tg ф. Тогда tg 9 = — = —: j = —■ ctg (a + ф), 9 = a + ф + —,
6 . T X Sina-f-д COS a s \ i . /» т i т I 2 >
1
a = <p— ф—^, r = X- g 2 = Сё9—логарифмическая спираль.
168

2) Положим s — a sin/, R = boost, a= I %ds = I т -. acostdt = -=-,
X = I cos a ds = I cos -r- cos /d/ =— I | cos ( -r -f- *) + cos (-v- — /) Lfc =
r sin *—7—i- 4- г sin -
д — <T
sin ads =
"2" 1*+^
= ( siny costdt = ~\ sin (у+ 0 + sin (^- —') <# =
, a ( b (a + b)t b <a — b)t\
2 I a+£ £ д—£ # J
i-{- b b ,a>—b <
3) r = J J cos ^~2 ds, I sin ^-y ds > — клотоида. .
oo
4) s = atgt, R=asec*t, a = Г ^tiladt = U x= Г
& J й« cos2 £ J
Jflcos * j* i + I TC . * I f • л Г л sin t ., a
—- dt = a In tg ~г + тг \> У= \ sin a ds = I s— d/ = r — деп-
cos21 4 2 J J cos ' cos *
cos ads=s
ная линия.
5) s = 4a sin /, # = -^ д cos / и т. д.
Ответ: г = {|г (sin4/ + 2 sin2t), — j(cos4/ + 2cos2/)|.
6) s = 4д sin £, R = 4a cos /и т. д.
Ответ: г = {я (2/ + sin 20» a (2 — cos 20} — циклоида.
at2
7) 5 = -у , R = д* и т. д.
Ответ: г = {a (cos / + * s*n 0» я (sin t—* cos 0} — эвольвента окружности.
8) e a = sec £, R ■=* a tg t и т. д.
Ответ: r = <a cos t, a In tg ~ -f -^ — a sin * >
-трактрисса.
280*. Пусть a — дуга эволюты цепной линии, ар — радиус кривизны
эволюты.
Имеем a= AJ, р = RR (см. задачу 297),
или
р л 25 ао
a a 2a»
4a3 = a(p2 + 4a2).
fl2p2
4aa2
281*. 1) a = R, p=RR, a = as, p = a2s, р = дз— снова логарифмическая
спираль.
2)о=/Ь Р = ЯЯ, ^+^- = 1, ~4
/?/?
£2S
az ' £2
аар >д*р*
:0, #Я=—
£2S
2 9
■R,
Ъ% у раг "г Ьч
.^-1 £Г
£4
о2
<п о a2 л2 / a2\ a4 8 йв s . 2
1 — снова эпициклоида.
0.
169

4) l$RR+2s = 0, RR = -1., c = R, p = —|, s = -9p,
'81р2 + 9а2=16д2.
5) /?/? = — s — p, <s = R, p2 + a2 = 16л2 — снова циклоида.
6) 2/?/? = 2a, #/? = a — p — окружность.
7)2RR = —2ae atRk = — ae a=p, с = Д, с2 + я2 = д2 ( ±\
ap + a2 + a2"=Q.
282*. 1) С = Я ^, Я2 = 2Cs.
as *
, a2 „Я7? n , a2 ndR . R2 1 d(#2)
n, 1 д*и и , u + a2 da 2ds . 9 . . 25
/?- = и, находим: -^ --- = f- a = —! , —=—ъ = — , In (a2 + a) = — э
2 ds a ' a ' и +fl я a
c2 + R2 = £a— трактрисса.
3) R2fdR\2 + R2 = a2t R^=Y^-ZTR2 Ж =<te
\ dsj l ds * Ya2 — /?2
— jAa2 — /?2 = 5, a2 — R2 = s2, R2+s2 = a2-— снова циклоида.
4) /? ——=iaR, R = as — снова логарифмическая спираль.
dR
5) R -P- /? = a2, Ra = 3#2s — эвольвента клотоиды.
ds
s-
2
284. R = j — =a-\ • цепная линия.
' ^ln(a2 + s2)J a
285*. 2R* = 9as2.
286*. [r] — r + Rn; дифференцируя, получим: n = Rn, R= 1, R = s —
натуральное уравнение логарифмической спирали.
287**. 1+ /? = ** . <TS.
288**. Пусть a — дуга, а /г — радиус кривизны линии, «параллельной»
данной. Имеем:
11 k
do = (l— ar.)ds = (\ — an) s' (x) dx. Ho -£- = л, x = ■,■■■. , ,
aQ { ~* l + ak) S \ l+ak) (1 + ^)2"^S \ l + ak) (1+<,*/»•
§ 11. Применение формул Френе
289**. pr= r ~ * — st = — sx/г, р' (0) = 0, р" = — x/i — sx/г — sx/г =
= — ХП — 5/Я _[. S7t2^ р" jQj = __ хп ф 0э р'" =- _ $л __ yfr __ х|2 _ ^ _ ^ _j.
-f Л + 5 • 2x* * + sv4, p'" <0) = — 2* л + 2x**, p" (0) x P'" (0) = — ш (— 2 i«+
-r 2x2^; = 2x3 ^ 0 (чера. 109;.
170

290**. Возьмём уравнение эволюты в виде р = г + #я.
Находим:
p' = r + Rn + Rh = t + Rn — Rv.t = Rn, p'(so) = 0
(ибо R = 0 при s = s0)-
Далее:
p"==Rn + Rh = Rn--Rr.t, p"(s0) = Rn^0t р'" = #* + £*-- Ы —
-.&Л — Ы, p"f(s0) = Rn—2R*t, p"{s0)Xp'"(s0) = Rnx(Rn — 2R-x.t)=^
==__2x^29zf:0 (чеРт- 110)-
291**. Пусть р = г + Rn — уравнение эволюты.
Расстояние 6 от какой-нибудь точки до нормали к
эвольвенте в точке перегиба определяется
соотношением:
В = (р — Го) X щ = (г — г0 + Rn) хп0 = (г — г0) X
X ih + Rn X /г0 = (г — г0)Х /lo + e x Я°.
Черт. 109. Черт. ПО.
Отсюда
Цш 5== um ^^= lim^ = Urn ~xf Х "°^ ~^ Х "" =0.
S = 50 5=50 X S—So * S —So У- ' *0
С другой стороны:
lim р—со, так как lim я = /г0, a lim R = oo (черт. 111).
S = 50 5 = Sq Sf^S0
292**. Пусть r = r(s) — уравнение эволюты, а !р = г — st—уравнение
эвольвенты, причём точке эволюты, в которой х0 = 0, х0^0 соответствует
значение s = 50^=0.
Находим:
p' = r — t — si= — sy.n, p'(s0)=0, p" = —• х/г — sxn + s*2t,
р" (s0) = — s0:/0n0z£l 0, p'" = — 2in — sin+ 2x2f -j- 3sxVt + sx*h,
P"' (*o) = — 2">o«o — S0«0Л0, p" (So) X p'" (S0) = 0,
p(4)= — 2 ХЛ + 2x7 t — ЪП — S* П + s *x* + 4x7* + 2х3Л + 3x*f-f 3sxЦ -J-
+ 3s*4n + х3л + 3sx2x/i — sx4*, p<4)(s0) = — Зу0/г0 — s0y:0nQ + 3v^o.
P" (S0) X p(4>(S0) = ~ 5o*o«o X (— 3x0/*0 — S0x0П0 + 3s0ijj*0) =
= 358*8^:0 (черт. 112).
293*. Пусть r = r(s) — уравнение эволюты, а р = г — st — уравнение
эвольвенты. Находим: р' = — sx/г, р (0) = 0, р",= — ш — s:m + s*2tt p" (0) = 0,
р"' = — 2хл + 2/2* — sx/г + 3s*** + s*4 р'" (0) = — 2хоЛ0 ^ 0, р(4) = — Зхл +
+ 6*** + №"• — s*я + 4sx**+3x*f + 3s*2/ -+- 6s**'m — s%% p{4> (0) ==— Зх0Ло,
171

р''(°)Хр(4) (0) = 0, р(5) = — 3'Zn + S%xt^6*4+6*Y.t + 6*4n + 9*4n—3*4-~
— "In — s^4)n + s/ "X t + 4x it + 4sxx* + 4sx'-/ t + 4sx*£ji 4- 3-iH + 3xx* -t-
4-3x2x/2 4-3x2/4-6sx^4- 3sx2xrt 4- 6х2хЯ 4- 12sxx*JI 4- 6sx2xfl— 6sx3xf — x4* —
- 4sx*xf- sx<5> л, p<5> (0) = — 4'x 0n04- 12x^0, p'"'(0) X p(5)(0) =
= - 2*Л x (- 4 ЗГ 0л0 4- 12x§^0) = 24xg ^ 0.
294**. Уравнение подэры p=(rn) п. Отсюда находим
Pi=o, р?= — *в{(^о)л0+(Го1»о)М» pS' x р^/,=2х2(г0я0)^о.
295*. р' = (1 — ах) *, р" = х/з (1 — а-*.) — ах *. Если в данной точке х0 ф 0,
1 — ат.0ф0, т. е. R0^La, то pi x pi'=х0(1 — ахо)2:^0 и точка
обыкновенная. Пусть х0 ф 0, 1 — ах0 = 0, т. е. R0 = a, и пусть х0 -^ 0. Тогда р'0 = 0,
pi' = — а*^0фО, p"' = хя (1 — ах) — х2*(1 — ах) — 2аххя — ах*, pi" =
= — 2ах0х0я0— a%0t0, Pi' X pi" =2а2х0х2,^0—точка возврата первого рода.
Черт. 111. . Черт. 112.
29?*. Уравнение линии Сх: р = г (s) 4- * (s). Находим: р' = г 4" * = * + хЛ>
р" = i 4- *л 4-y# = *я 4- *л — *2* =—*2* 4- (* 4- *) я>
|1х|
|р'Хр"| mod I —x2 x 4-х I |*4-x84-x|
«1 =
1 1 i "
(p'2)2* (14-*2)2 (14-*2)2
297*. Уравнение эволюты: р = г 4- #я. Находим: р' ='r-{-Rn +Rh =
\P' Xp"\ __ \*R* i
ip'i3 U3l~
1
— t + Rn — R*t = Rn, p" =Rn + Rh = Rn — %Rt, xx =
\RR\ .
Отсюда R1 = \RR |.
298*. p'=r+Rn+Rh=Rn, p"=Rn-\-Rh=Rn—*Rt, p'2=£2, p' X p"=
0 R
•*R R
= %R*'> уравнение второй эволюты: /?=р4~[р']
p' X P"
;/--h
4-Яя 4- [Ля] 4±- = r 4- Ял — R'Rt
RH
172

299*. p*=r + Rn — RRt, p' = r + Rn + Rn — RH — RRt — Rn =
= -(Я2 + RR) t, p" = -(3RR + RR)t — (R* + RR) ш9 p'2 = (R* + RR)*,
p'Xp" =
гэ'2
=(#2+W*, Q=P+[P']-^pff-
(R* + RR) 0
- (3RR + RR) —(R* + RR) *J
= r+Rn-RRt-(R*+RR)n (R\+™*r ^r+Rn-RRt—Rtf* + RR)n =
*(R* + RR)
= r — RRt + R(\—R* — RR)n.
300*. Кривизна *2 второй эволюты определится соотношением (см. № 299):
IPT |#» + /?tf|s \R(R*+.RR)\ '
301*. q= r— RRt + R (1 — R3 — RR) n, q' = r -^ RH — RRt — Rn +
-\-R(\—R3 — RR)n+R(—3RR — RR)n — (l—R3 — RR)t =
= (\ — R)n, где X = # —#/?a —jW;
q"=(i — R)n — %(i — R)t,
4* = (i - ф», (вY/f = (x—/? |8,
q'Xq-' = .A(i-Ry,Rs = Ji^lr = \R(K--R)\ = \RRt + 'lRi-RR.+ R3R\.
302*. Радиус-вектор центра кривизны: р == г + Яя. Находим: р —р =
= at — Rn, p' = r — ai=t — a*n, р'(p —p) = (at — Rn)(t — a%n)^=a — a=0.
303*. Уравнение второй эволюты: p=zr-\-Rn — /?£*\ Отсюда р— г =
= R(n — Rt). Уравнение линии, описываемой точкой 5 будет q г= г + у /?я.
Отсюда ^ = ^4-^^-^=1(^ + /?/г), tf'(p-r) = 0.
304*. р = г+ #я + /?а, где a = const;^ = t+R(n + a) + R(—r.t) =
= R(n+ а) ||р —г.
305*. р = | rn |. Предположим, что г/г > 0; тогда р = га. Отсюда -/• =
= гп + гя = — rfa = — гг* = — гг% = — г — *, откуда и получаем
требуемое соотношение.
306*. Уравнение (р — г0 — R0n0f = /?02 перепишем в виде: (р — г0)2 —
— 2R0n0(p — r0) =,0 и рассмотрим функцию ср (s) = (г — r0)2 — 2R0n0(r—r0).
Имеем: ср' (5) = 2 (г — г0) * — 2Я0я0*\ ср' (s0) = 0, ср" (s) = 2 + 2*я (г— г0) —
— 2Я0я0*я, ср" (s0) = 0, ср'" (s) = 2:/я (г — Го) — 2-Л (г — г0) — 2RQn0%n +
+ 2/?0#о*2£ <р'"($о) =— 2/?0х09^0 и, значит, ср (s) меняет знак при переходе 5
через s0, а так как ср (s) есть степень точки относительно окружности, то
предложение доказано.
307*. См. решение предыдущей задачи: имеем cp'(s0)=cp"(s0) = cp'" (s0) = 0,
cp<4,(S) = 2'itl (Г — Г0) — 2*** (Г — Г0) — 4-лк* (Г — Г0) — 2*3Я (Г—Г0) — 2*2 —
— 2R0n0*n + 2R0n0Mt + 4£я0*х*+ 2/?0я0*3я, ср(4) (s0) = — 2тс§ — 2#0*0 + 2xjj =
= — ^о^о^О; значит, степень точки линии относительно соприкасающейся
окружности не меняет знака при переходе s через s0.
173

308*. p = r-\- Rn— уравнение эволюты данной линии. Имеем: p' = Rn,
Ур'2= у R2 = R (так как R сохраняет знак, то, считая R > 0, будем иметь
у R2 = i R | =R; если бы производная R меняла бы знак на интервале (я, b)t
то мы имели бы у R2 = \R | и последующие рассуждения не имели бы места).
Дуга эволюты: а = I Rds = R (s2) — R (st). Ясно, что а больше расстоя-
*i
ния MtM2 между центрами соприкасающихся окружностей данной линии
в точках"^ (st) и Ms(s2)9 т. е. MlM2< R{s2)~ RisJ, а отсюда и следует,
что одна из соприкасающихся окружностей вложена в другую.
309. p = r + an; p'r=r + ah = t~a%t=t(l~a'A)\\t
310*. Пусть r=r(s) — уравнение линии С. Уравнение линии Cj будет:
p = r — an. _
Отсюда р' = t + e*f = (1+ ex) t, VV2 = 1 + я*
(так как 1 4- я* > 0). Теперь находим длину ч
линии d; имеем:
с= I (1 +e-/)d5(/ —длина линии С) =
о
Черт. 113.
а — угол, образуемый % касательной к линии С с
неизменным направлением; если точка М
описывает линию С, то вектор t поворачивается на
угол 2тс; отсюда пределы интегрирования от 0 до
2тс (черт. 113).
311**. Если линия р = р (s) замкнута, то площадь, ею ограниченная, может
быть вычислена по формуле:
/ I
* ~ ~2 \ ^ху'~~ * -^ dS = "2" р Х р' ^'
где (0, /) — интервал изменения параметра 5. Для линии С19 «параллельной»
линии С, имеем р=г— an. Отсюда p' = t-\-a%t=(\ -\-av.)t. р х р' = (г— яя) X
X (1 4- a*) t — (l + аъ) (г X t + а) = г X *+ « + а*г X f 4-я2*- Обозначая
/
через S площадь, ограниченную линией С, будем иметь: А = -9- I r X W5 +
о
/ / /
+ уй I rfs-fyfl I rrxto + yfl2 i *ds = о + -о- в/ 4- Л% 4-
0 0 О
4--к а \ ^Х tds. Далее: d(r X п) <=ds — г X Hds. Отсюда 1 d(r X п) =
о , о
t= Г ds-~ \%rxtds. Но fd(rX/2) = 0, ибо r(0) = r(/) и п(0) = п(1);
174

1
1
значит, I -x.rXtds = l и окончательно: Л = 8+ ^-д/ + д2гс + ~ al или
о
Ь = Ъ + а1 + а2п.
312. фпЬ = ф d(r%)—ф*<*г = — ф *^г=--ф%Ш==фы5==ф<*й==0.
313*. <?(s)={r(s) х a}2 + 2r(s) х Ь, <p(so) = 0, cp'(s) = 2(r ха)(гх а)+.
+ 2гхЬ = 2(гха)(*ха) + 2*хЬ, cp'(s0) = 2*0 х Ь = 0, & = *<>, ф"(*) =
= 2 (* х а)М- 2(гха)(пх а) «4- 2хл * t0f <р"($о) = 2(*0 X а)2 —2*0 = 0,
Wo = f*o, ср"'(5)=4(^ха)7с(дха) + 2(^ха)(йха)^~2(гха)(*ха)*24-
+ 2(г х а)(л X а)х— 2*2* х t0 + 2inx t0, f (s0) =6(t0 X a) (n0 Xa)x0-
— 2xft = 0, 3y^По X а*0 =f *o> л0 • а == -g-^-. Пусть a=lt0+^n0, t0Xa=
= n = Уч >n» X а = — Х=^-4т-, а = —-T'-Sr^o+Vr«o"«o- Введём си-
О 'Xfl 'S О Xq '2
стему координат, принимая касательную за ось Ох, а нормаль — за ось Оу.
Получим r = xto + y'n0, и уравнение (г х а)2 + 2(г х Ь) = 0 примет вид:
_ _L *° т/Т"
+ 2
лгу
1 0
или
314*.
(3xfc4-*0y)2— 18xjy = 0.
» = 3г(гхг)-г(гх'г) = Зхл« — ** = 3-А?п — х £
315*. г = Xto + Kv0 = Xt0 + Г (3*2я0 — *</<>) = (*— *оП *о + 3*20K/i0,
х ^ ЛГ - х0Г, у = 3**Г, [3-л§ (* - *0Г) + х0 • 3-л§Г]2 - 18/3 . Зх*Г = 0
иди 9**X2 — 54х§Г = 0 или AT3 = 6-л0^.
316*. v = 3x2/i — i/, tgcp19= ± -?- = ±—.
317*. £v = 0, х == 0, х = const ~ окружность.
318*. /? = С, /?== Cs — натуральное уравнение логарифмической спирали.
319**. ср (5) = г (s) Ф г (s) + 2ar (s), ф = ^Фг + 2af, у ф = *Фг 4- at,
—. ф0 = af0 = 0; положим а = — щ; тогда у ф = t&r — too» у 9 = *яФг +
4" *Ф* — /I0^; у Фо = *оФ*о — *о = 0, *0ф*0 = х0, у ф* = */*Фг — *2М>Г +
+ Зхяф* + щН* — /Ш0х> у ? о = Зх0ЛоФ*о — ^о = 0, Я0Ф*0 = -д. ^-, у ср =
= х лФг — ™*Фг 4- *яФ* — 2хх*Фг -т- *3яФг — ЛФ* + З-АлФ* — 3*2*Ф* +
1 (4)
+ Зъ*пФп + П0П*г + Я0*2** + Л0*х* ~ /*<>#*> у 9о = 4VV£*o ~ 4*<&>Ф*о +
4" Зх§Л0Ф/10 + х* — х0 = 0, 4 — - 4*о + Зх2ЯоФ/г0 4- *S — *о = 0, ПоФЩ =
о х0
= з^(^ + ^-4^)=«о+з^-т|-уРавнение'ф'-2^=0
переписать так: (xto 4- У^0) Ф (xt0 + УЩ) — 2щ (xt0 4- уп0) = О
или
лг2*0Ф*о + 2ху^0Ф/1о + у*п0Фп0 — 2у = О
или
МОЖНО
175

320*. x = X - 4X у = Зх§Г, х0 (ЛГ - x0K)2 + |- J- (* — i0Y) 3xgF +
+ (^-4| + 3^)9x^-2.3.gF = 0
или X2 + (9xJ — 5*2 + 3x0x0) Г2 — 6x0K == 0.
321*. См. предыдущую задачу.
322*. Координаты центра линии X2-^bY2— 6xF = 0 таковы: ^ = 0,
Y= — . Отсюда искомое уравнение:
о
р = г+^ = г + ?*(3х2/г-х*).
323. Уравнение семейства аффинных нормалей p = r-\-l (Зх2# — %fy
l— it, ~-=t-^l(67L:Afl 3*
= t + X (5х*я — Зх3* — Щ.
Имеем: —= Зх2я — х*, ^ = t + X (бххя — Зх3* — х* — ххя) =
ак ds
Из условия ~ х ^ = 0 находим:
— х Зх2 I п
1 _ зХх3 — Хх 5Ххх | — и>
Зх Зх
9х* —5х2+3хх~~" $*
Следовательно, огибающая аффинных нормалей совпадает с линией,
описываемой центрами соприкасающихся линий второго порядка.
*324*. 1) Д = 9+/е2 — SRR (см. № 321), A = 9 + ^Y—3 (а + —\— =
= 3-??.
а1
Если |5|<а1/ -^—точки эллиптические, при 5 = ±л|/ -^
параболические (две параболические точки), при | s | > а I/ -^ — гиперболические.
2) s + RR== 0, 14-ЯЯ + Я2 = 0, Д = 9 + Я2 —3jR#==9 + jR2-3(—1 —
— R2)— 12+ 4^2 > 0 — все точки эллиптические.
3) RR = a, R2 + RR = Q, А = 9 + Я2 — 3RR = 9 +R2+ 3R2 = 9 +
. -f-4$2>0 — все точки эллиптические.
4) R = ay R = 0, Д = 9-|-а2>0— все точки эллиптические.
5)^ = -,^=^-^,^==^г, Д = 9 + ?-^- = 9- —.При|5|>
> 1/ — а — точки эллиптические, при | s | < 1/ -^ а — гиперболические, при
-Q- а — параболические (две параболические точки).
**j_ S-0 R* + RR | * -о ffS_ 62 ** д_о, ri.
— 3jR^ = 9 -|- £2 + 3 (£2 +,-£-)> 0 — все точки эллиптические.
175

325. Q = 3xx+9x« — 5i».
326. £
ds
= x = j-r-y, ds=f(a)da, лг= I cos a f (a) da, y= I sin a/ (a) da.
x = Г cos [/ (R)] Rf (R) dR, 328. x = Г cos [a (/)] /? (/) a' (/) dt,
у = J sin [/ (tf)] /?/ (#) rf/?. у = J sin [a (/)] # (/) a' (*) #.
329. 1) ;c=fllntg
- + -
У = цепная линия.
' * cos a
a
2) •y=""9cin2^ j/ = —flctg a — парабола.
2 sin2 a
3) x = -^ea (cos a + sin a)» У = у *a (sin a — cos a) — логарифмическая
спираль.
4) x=a(a sin a +cos a)> y = a(sina — a cos a) — эвольвента окружности*
5) x= щ£=Т)cos t(1 - m) a] ~ 2(1+111) cos [(1 + w) a]'
У == 2(1 — ю) sin K1 — w)aI~ 2(1+ m) Sin [(1 + w) al ~ эпициклоида
при* m < 1 и гипоциклоида при m > 1.
6) лг= — (1 — cos 2a), у = -j- (2a — sin 2a) — циклоида.
«ч p sin a Cos a t ,
7) лг— r j/ = —p—— или (1 — e2)л:2 +
1— e2 y"i_e2cos2a ' V1— e2cos*a
P2
-i~y2:=f-_~2 —эллипс, если 0<е<1, и гипербола, если £ > 1.
330. Х= I cos a/7 (a) da, у = I sin a/* (a) da.
331. x=z \ cos [/(s)] ds, y = ( sin [/(5)] ds.
332. лг = Г cos [a (t)] s' (t) dt,y = f sin [a (/)] 5' (/) dt.
333. 1) jc= д sin a/y = — a cos a — окружность.
лч « те , a
2) x = alntg j-+у
a
-у = цепная линия.
' J cos a
3) jc = -~- £a (cos a + sin a), у = ^- £ (sin a — cos a) — логарифмическая
спираль.
4) x = a (a sin a + cos a), 3; = a (sin a — a cos a) — эвольвента окружности.
5) x = — -^ (1 — cos 2a), у = — -r- (2a — sin 2a) — циклоида.
4 4 *
6) *=- 2(&ocos [(1 ~ OT) a]+w^h*)cos [(1+m) a]'
У = -2{\a-m) Sln [(1 -m)al + 2(Ь+и) sinK1 + m)a]*9ПИЦИ'клоиДа
при m<.\, гипоциклоида при m > 1.
12 11. С. Моденов 177

334. Уравнение подэры р = (гп)п. Отсюда
do = Y?2 ds = V {— (rt)x— (rn)t*}2 ds = xrds = rda.
335*. Принимая точку О за начало радиусов-векторов и считая, что
уравнение антиподэры имеет вид: r = r(s), находим уравнение подэры в виде
р = (гя)л. Имеем:
р'= -{(/*) л + (га) *}х,
[p']\\-t(rt) + (rn)n.
Уравнение нормали к подэре R = (га) п + X {/ (rt) — п (т)}. Этот радиус-
вектор коллинеарен вектору г== (rt) t + (га) n при условии
I \rt (1 — Х)га I п ыпм I X 1-Х I п
• I rt га И0 или I 1 1 1 = ^
откуда X = -^ , и, значит, /? = (га) п + -^ {t (rt) — п (га)} = у {(rt) *-p
+ (гл) л} = |Г.
336*. Уравнение подэры
р = (гл) я, р; = 0, pj' = — х0 {(г0*0) л0 + (г0л0) *0} ^ О,
9о' X Р6" = 2х$ГоЯ0 ^ °-
337**. Пусть М0 (50) или М0 (о0) — точка, в которой касаются линии С и £ в
начальном положении, тс (р) — произвольная точка линии £; тогда %М = а — р.
Обозначим через х и v единичные векторы касательной и нормали к линии Е
в точке гс(х = —, v = [x]J; координаты вектора пМ в системе х, v таковы:
(а — р)х и (а — р) v.- Поставим в соответствие точке я линии £ точку Я
линии С такую, ч^о 70отг = л5оР, т. е. о — a0 = s — s0 (или a — a0 = s0—s,
если числа a — о0 и s — s0 — числа разных знаков; в дальнейшем мы будем
считать, что эти числа одного знака, т. е. что s и о растут соответственно
от М0 к Р и от М0 к к; этого всегда можно добиться, заменяя в уравнении
r = r(s) в случае необходимости s на — s). Обозначим через t и я
единичные векторы касательной и нормали к линии С в точке p(t = j-, n~[t]\.
Рассмотрим вектор PN, имеющий в системе t, n соответственно те же
координаты, что и вектор тМ в системе х, v. Тогда уравнение рулетты
запишется так: R = r-{-PN или R = г + ((а — р)х)*-|- ({а — р) v)n, причём
здесь o=s-f-ao — so- В частности, если нужно составить уравнение рулетты,
описываемой началом радиусов-векторов, то уравнение будет иметь вид:
R — r — (pi)t — (pv)/i (черт. 114)
338*. 6 = х + Jlzt У'П(«-*> + (*"- У') (? - П
r_v , (1 + /П(^Г) + ^--П(а-^) dy Y'-dY-x*x
связаны соотношением:
dXl
л -л.
Г]/Т+75^= Г |/"i + У'2 dx.
*0
178

339*. R = г + ((a — p)<%) £ + ((a — P)v^л. Так как $ и a связаны
соотношением s —s0 = <s — o0, то, дифференцируя R no s и обозначая кривизну
линии r = r(s) через k, будем иметь:
#==(* —х) ((а — р)т)л —(* — x)((a — p)v)*_L#-r.
Черт. 114.
340*. Применяя уравнения,~указанные в решении задачи № 338
(v = aX\ Y' = 2aX, у<=0, у' = 0, <z = 0, Р = j-),
получим: £ = *-* l/i+4^^2, 1,:ь11Л + 4<ЛХ» ,
л: = Г |/"1 + fa2*2 dx=^V\+ №Х* + 1 In (2a* + V^ I + 4<*2*2),
5 = ~ In (2eX + J/ I + 4л2X2).
Полагая Л=/? (расстояние от вершины параболы до её фокуса) и исклю-
4д
А _1
чая X из уравнений £ = 6(<АГ), т)==у](^Г), получим: у\ = %(ер +е ?)
—цепная линия.
341*. Применяя уравнения, указанные в ответе к задаче № 338, и замечая,
что здесь х = Х, получаем параметрические уравнения линии в виде: *
- циссоида.
179

щ
342**, Уравнение рулетты р — г + ((а — р) х) t + ((а — р) v) n, откуда
p'=(Aj--x){((a--p)x)/t-((a--p)v)0},p''=(^-"/){((flt-p)T:)»--((ar-p)v)^ +
+ (*-*) {—n + (* — k) ((a-p)z)t + (*-k) ((a—p)v)n}.
Радиус кривизны рулетты вычислять по формуле:
343*. Воспользуемся уравнением рулетты в виде: R = r — (рт:) £ — (pv) л.
В точке встречи рулетты с линией r = r(s) имеем р = 0. Теперь легко
находим, что в этой точке /?' = 0, /?" =— (k— г.)2 п.
344*. Уравнение рулетты: R = r— (pz) t—(pv)fl.
Отсюда R0 = 0, /?;' = — (k0 — x0) л0 ф О, /?;' X fl'i' = — (k0 — x0)2 (2£0 — x0) ^ 0.
345**. Точка, симметричная полюсу относительно касательной к данной
линии в точке М (г), определится радиусом-вектором р ■== 2 (гл) л, где п —
единичный вектор нормали данной линии в точке М. Направление прямой,
симметричной ОМ относительно указанной касательной, определяется
вектором
гч— 2 (гп) п — (rt) t — (rn) n,
а направление нормали к этой прямой (ft) 1t-\-(rn)t, Уравнение
отражённого луча:
(R-r)((rt)n + (rn)t) = 0.
Дифференцируя по параметру, получим:
— гл + (# — г)(п + 2*(гп)п — 2х(г*)*) = 0.
Отсюда:
,» rw_ (m)(rt) (rn)-
(X r)t- 2.^+rn, (R-r)n- 2u* + rn '
>=r+ 2^+rn Krn)n-(rt)t}
— уравнение каустики.
346*. Вопрос сводится к отысканию эволюты линии R = 2(rri)n.
Находим:
R' = — 2у ((rt) п + (rn) t), R" = — 2* {(rt) n + (rn)t}—2*{n + 2(rn) m —
— 2 (rt) H }, /Г = 4*2r2, R x Rf = 4-х2 (m + 2*r2);
уравнение эволюты:
R=2(rn)n — 2*{(rn)n — (rt)t} 4*V2
4x2 (гл + 2%r2)
= r + 2(rn)n-r+{i;rn)n-(rt) t} rf^Xr2 =
= r + {l~ rn + lr* )«rn)n-(rt)t) = r+7K^
(см. предыдущую задачу).
г' [гЧ
347*. Указание. Положить t = - " —
|r'|* \f\-
Ответ:'
*=г+2*> х г'. + (Гг> х rr>W* W-(r*?h
348**'. Уравнение семейства окружностей (R — г)2 = г2 или R2 — 2Rr = 0.
Дифференцируя по/параметру, получим: Rt = Q; отсюда R=\n и далее:
12я2 — 2Хгас= 0, }/= 2гл; уравнение огибающей: /? = 2 (гл) л (далее — см.
решение задачи 346).
180

349**. Вектор — е 4- 2 (et) t= — (en) n + (ef) t симметричен вектору е
относительно касательной к данной линии. Вектор \et)n -\- (en) t к нему
перпендикулярен. Отсюда находим уравнение отраженного луча:
(R — r){(et)n + (en)t}=0.
Дифференцируя по параметру, будем иметь:
— еп + 2* (R — r) {(en)n — (et)t}=0.
Разрешая два последних уравнения относительно (R — r)t и (R— г)п, будем
иметь:
откуда
. R = r + ~{n(en)-t(et)}
— уравнение каустики. Если линия задана уравнением r = r (t), то, полагая
г1 _ [г']
будем иметь:
*=f + С х %{(г'х е) [Л ~ (г'е) г'}-
Если линия задана уравнением у=/(х), то
r = { x,f (х)}, г'= { 1, /(х) }, г" = {0, /»(*) }.
и, полагая е={1, т}, получим:
R = { *,/ <х)} + my,!f{x()X) Um-lf (х)) {-fix), l } -
-(^ + т/'(лг)){1;/'(х)}}
или
[w - У (гЛа р, rt (w - If (*)) (I + mf (x))
р 2/"W fW , 2t".(x) '
у_/(лг)Н 2/"(лг) 2/4^) /W
350*. 1) Х = х+У'^,Г , У=у + ^.
352**. См. черт. 115. В рассматриваемом случае силовая плотность р
постоянна. Положим Г= Tt, где £— единичный касательный вектор к нити.
Имеем:
ds ds*ds "*" ds ^"
181

Введём систему»координат, направив ось Оу коллинеарно вектору р
(вертикально!). Тогда t= { cos a, sin а }, п= { — sin а, cos а }, р = { 0, р } и из
последнего соотношения получаем:
~ п dT 1 ds
T = pRcos a, -т- = р sin а, где /? = — = —
'ds
da%
Теперь находим:
dT = p sin a ds = p sin а Rda=
Т
= 0 sin а da = Tig a da,
dr
р cos a
^- = tg a da, In Г= In С — In cos a,
С
-(Тч-dT)
cos a
и далее:
; = I cos a ds = I COS a : = I
J J p sin a J
cos a
cos2 a p sin a
С f da С , I тс , a I
= 7J"^^7lntg|T + T|'
С . J Г • Csinada С f
V= 1 SinadS= I Sin a - : = — I
J J COS2a.psina p J
sin a da
Итак:
л: = — In tg
tz a
T + T
, y =
COS45 a
pcosa
/? cos a
— цепная линия. Отметим выражение модуля натяжения Т нити через
радиус кривизны и через ординату у точки депной линии:
Т = pR cos a = pR у ,
откуда
Черт. 116.
(из соотношений Т =. и у = ).
\ cos ъ р cos a/
353** <*(Гсо8а)=0 <*(7*sina) dx
J* * ds p ds*
ds
откуда
T cos a = С, Г sin a =/>* + ?> tg a = алг + #, / = ллг + #, у = -g- ал:2 + &* + c
— парабола.
354**. Условия равновесия: ф pds = О и ф г X pds = 0 выполняются.
В самом деле: ф pds == ф kinds = Л ф df = 0, фгХ pds = ф г X &*nds =
= А? фг X dt = — k (Ь t X dr = k ф t x fds = 0 (черт. 116).
182

ГЛАВА III
§ 1. Касательная. Главная нормаль. Бинормаль. Нормальная
плоскость. Соприкасающаяся плоскость. Спрямляющая плоскость.
Кривизна. Кручение.
355. R = {— 2 + 27Х, 1+28Х, 6 + 4Х}.
356. R = {xQ + kz0i у0 + \z0t zq + 2Хлг0}-
357./? = | j + X*8, y + M2> у+X/}, если /^0; ести же / = 0, то
г' (0) = 0, г" = { З/2, 2*, 1 }, г" (0) = { 0, 0, 1} — касательной к данной линии
в точке (0, 0, 0) является ось Oz,
358. Пусть x = x(t), у = у(/), z = z (t) — параметрические уравнения
данной линии. Тогда данные уравнения обратятся в тождества, если в них х,у, z
заменить соответственно на х (t), у (t), z (t). Дифференцируя эти тождества
по U получим новые тождества уу' + zz' = 0, хх' + уу' == 0 или { 0, у, z } г' =
= 0, { х, у, 0 } г' = 0. Для данной точки: { 0, 3, 4 } г' = 0, { 1, 3, 0 } г' = 0,
откуда г' || [ { 0, 3, 4 } { 1, 3, 0 } ] = { — 12, 4, — 3}. Уравнения касательной:
лг= 1 — 12Х, у = 3 + 4Х, 2 = 4 —ЗХ.
359. 1) блг —8у — 2 + 3 = 0, 2) ay — z + b = 0, 3) ЬхХ — ауУ = Ъ
4) Ь*х*Х—а2у*У+(а2 — &) z*Z<=a*l>* (a* — b*)t 5) е-'Х—е-' Y — уТ Z+ 2*=0.
360. Главная нормаль: х=1 — 31X, у = 1 — 26Х, z = 1 + 22Х. Бинормаль:
jc=l+6X, у = 1—8Х,г=1 —X.
361. Главная нормаль:
x = ^ + l(t* + 2t)9y=^+l(l-t%z = ^-l(2t*+t).
Бинормаль: •
z4 *3 *8
x-jJ + X, у=^~2>^, z = j+kt\
t t t
362. (eVT cos *)» + (e^ sin /)* == (e^Г)8.
Далее;
_i_ JL _L JL -J-l
I/. 2 1^2 K2
183

Найдём угол между векторами г и г':
t t
ёУ 2 cos t
cos 8 = =—*■— — +
(-р=в^аС0в*-в^8в1п<)
/it j 17
eV1 sin' (yl"*/T sin t+eV^cos t+ i/тeV1
.* * . % ,2*
,L/»+_L/a
V2 V2 _Vl
— U_ — 2 , o_«.
2e^
363. Касательная:
JR =1= { a cos t — Хя sin /, д sin * + ^X cos t, b (X -f *)}.
Нормальная плоскость:
^sinf —«ycos/--£Z + £2/==0.
Бинормаль:
R =*= { a cos t-\-kb sin *, a sin t — b\ cos tt bt -f- la }.
Соприкасающаяся плоскость:
ЬХ sin t —■ ЬУ cos t-{- aZ — abt = 0.
Главная нормаль:
#= {(a + X) cos t, (a + X) sin U bt}.
Спрямляющая плоскость:
Xcost+ysint—a±=0;
t = ,- { — a sin t, a cos /, # }, n = { — cos tt — sin U 01,
& = ■ .- { b sin t, — b cos /, a }, */ = —з■ ,й-, о = —
j/> + £2 я2 + £2 a2 + £2
364. г' = {1, 3/3, 2/}, ri = {l, 3, 2}, r0={l, 1, 5}.
Касательная:
/?={1 + X, 1 + ЗХ, 5 + 2Х}.
Нормальная плоскость:
at—l + 3(y—1) + 2(2г —5) = 0
или
jc + 3y + 22—14 = 0;
r" = {0, «, 2}, rV = {0, 6, 2}Ц {0, 3, 1}, [,-г'о'НИ-З, -1, 3}.
184

Бинормаль
# = {1— ЗХ, 1-Х, 5 + ЗХ}.
Соприкасающаяся плоскость
— 3(х — 1) — (у — 1)+3(2 — 5)=0
или
Злг + у — 32 + 11=0;
IWrVl ri] II {,-11, 9, -8}.
Главная нормаль:
#={1 — 11Х, 1+9Х, 5 — 8Х}.
Спрямляющая плоскость:
11 (Х _ 1) _ 9 (у — 1) + 8 (2 — 5) = 0
или
цАГ_9у4-82-~42 = 0; *0 = ^^ -1= { 1, 3, 2 },
I го I |/ 14
я _ [КгУЩ] _ 1 » _8>
[ г^о 1 ^ l_ f Q _, яг .. __ 1 [ Кг',']
I г'оГ'о] | \Г 19
Ki3
1 3 2
0 6 2
0 6 0
*о = 7т5^4т = Т7=?{--3,.-1, 3}, *а =
= У 11L.; г'" =г'0" = {0, б, 0}, rir'0V;f =
7/14
_' 19 гт — ГоГ"Г'<> — 3
_—l^a_lrirVj, _ ш.
365. г'={2*, —1, З/2}.
Касательная:
jc = *s + 2X/, y=^l— t— X, 2 = *3 + 3)i*.
В точке / = 1:
лг=1+2Х, у = — Х, 2 = 1+ЗХ.
Нормальная плоскость:
2/(лг — /2) — (у— 1 + 0 + 3^а(2—/3) = 0.
В точке t = \\
2лг —у+ 32 — 5 = 0.
Далее:
г"=*{2, 0, 6*}, [гУ"] = {-6*, — 6*», 2}П {-&, —ЗР, 1}ф
Бинормаль:
л: = га —ЗХ*, у = 1 — t — ЗХ*2, 2 = *3+Х.
В точке /=. 1:
л: = 1 — ЗХ, у = — ЗХ, 2 = 1 + X.
Соприкасающаяся плоскость:
3/ (х — /*) + З*2 (у — 1 +1) — 2 +1* = 0.
В точке *= 1:
Злг + Зу —2—2 = 0.

Далее:
[ [r'r"] г'] И { — 9/4 + 1, 2/ + 9/8, St + 6/»}.
Главная нормаль:
лг = ^2+- Х(1 — 9t% y = l— / + Х(2/ + 9/8), 2 = /8 + X(3/-f-6/8).
В точке /== 1:
л- = 1 — 8Х, у = ИХ, 2=1+9Х.
Спрямляющая плоскость:
(1 — 9t*)(x.— *2) + (2/ + 9/3) (у - 1 + t) + (3/ + 6*»Х* — *3) = °- *
В точке /== 1:'
-^-8(лг — 1)4-11^ + 9(2— 1) = 0 /
или
<8лг — 11у — 92 + 1=0.
Далее:
^__ (2/, -1,3/4 _{2,--l,fr}.,
/ 1 + 4/2 + 9/4 ^ ° /14 '
{1—9/у, 2/ + 9/3, 3/ + 6/8}
/г = -
{-6, 11, Q } fc »{—3/,-ЗЛ 1} fc _ { — 3, — 3, 1 }
/266 jA+9f+9/4 /19
/(1 — 9/4)2 + (2t + 9/3)2 + (3/ + 6/3)2 '
_3/,
Г+
_ 1 [r'r"] | _ 2 (1+9/2 + 9/4)v* _ /19 _ гГУ"
*- |Г|8 ~~ (1+4/2 + 9/4)^ ' *°~ 7 /14 ' а~ 1гУТ
_ 3 __ 8
1 _^_ 9/2 -Н ь^/4 * а°~"1Э-
366. Касательная
Нормальная плоскость:
х— .y + 2/~2(2 — 1) = 0.
Бинормаль:
" I V 2 у 2 Г
Соприкасающаяся плоскость:
2^ + 6у+ ^Тг- 5 /Т=0.
Главная нормаль:
Спрямляющая плоскость:
7л- — у — У~2 (4г — 1) = 0.
{ 1, - 1, 2 / 2"} {-7,1, 4 У^
186

367. Пусть x=zx(t), y = y(t), 2 = z (t) — параметрические уравнения
данной линии. Подставляя в данные уравнения х (t), у (t), z (t) вместо х, yt z,
мы получим тождества относительно t; дифференцируя not эти тождества,
получим
хх' + уу' + zz' = 0, хх' + УУ' = О
или
zz' = 0, хх' + УУ' —9у
или
{О, 0, *}г'=0, {х,у, 0}г' = 0, г' || {-у, дг, 0}.
Выберем такую параметризацию, чтобы г'={—у, дг, 0} (см. задачу №381)
Далее:
Г" = {-У', х\ 0} = {-х,-у,0}, /•'" = {-*',-./, 0} = {.у,-л;,0}.
Касательная:
/? = { а: — Ху, у + Хх, -г }.,
В точке (1, 1, 1):
/?={1-Х, 1 + Х, 1}.
Нормальная плоскость:
у(Х-х)-х(У-у) = 0
или уХ — хУ = 0; Х—У = 0 (в точке (1, 1, I)). .
Далее:
[г'г"] = {0,0,дг^^} = {0, 0, 2}.
Бинормаль:
R={x, У, 2+Х};
в точке (1, 1, 1):
/?={1,1,1 + Х}.
Соприкасающаяся плоскость:
Q(X—x) + 0(y — y) + 2(Z—z) = Q или Z = * или 2=1;
далее
, [[г'г'Тг'ПИ*.^ 0}.
Главная нормаль:
R={x + \x, y+ly, z};
в точке (1, 1, 1):
Я = {1+Х, 1 + Х, 1}.
Спрямляющая плоскость:
х(Х-х) + у(У-у) = 0
или
хХ + уУ — 2 = 0;
в точке (1, 1, 1):
Х + У — 2 = 0;
,=i=^, „_Ii£JU.,«,=(o.o,,1;
(данная линия состоит из двух окружностей).
187

868. Касательная:
X=x+l
У=у + 1
Z = z+\
EL ?L
dy dz
дФ дФ
ду dz
EL ?L
dz dx
дФ дФ
dz dx
dF_ dF^
dx dy
аФ аФ
dx dy
Нормальная плоскость:
X — x У —у Z—z
dF^ dP dF^
dx dy dz
dФ дФ d<&
dx dy dz
= 0.
369. Выбирая соответствующим образом систему координат, запишем
уравнения линии Вивиани в виде:
г*2
#+р+яш = а*у (х - -|)* +У = ~
или
х* + у* + г* = а\
х2 + у2 — ах = 0.
Для составления параметрических уравнений положим
а а . а . ,
X — у = у COS /, у = у SHI t.
а2 a* t
Тогда -^ (1 + cos tf + -j- sin2 / -+- z* = a3, 2 = a sin -^ (знак можно опустить,
так как, если к / прибавить 2тс, то х и у не изменятся, а 2 изменит знак). ч
Итак:
г = {у (1 + cosf), у sin/, asinyi.
Отсюда легко находим.
Касательная:
Я=|у (l-j-cos/) — Xsin/, у sin / + X cos /, a sin -g- + X cos -7Л.
Нормальная плоскость: A'sin/—К cos/ — ZcosyssO.
Бинормаль:
# = j^(l + cos/) + X sin -^ (2 + cos/),^ 4- sin/ —X cos у (1 + cos/),
asin -~- + 2xL
188

Соприкасающаяся плоскость: \
sin-^(2 + cos^)X — cos у (14-coa/)K + 2Z—y8i0y(54-cc»O = O.
Главная нормаль:
R = |у (1 + cos /) 4- X [^- cos* L (1 + cos /) — 2 cos t),
-tysint—^ sin ^ (^ "Ь cos 0* esin-H- — XsiayL
Спрямляющая плоскость:
[— cos2 ~ (1 4- cos 0 — 2 cos fl X— i sin * (6 + cos f) Y — sin .-£• ^ +
+ |-(3 + cos^==0,
* =
-I— sin Л cos *, cos -у [
/'
1 + cos» -
-t bin у (2 + cos t), — cos у (1 + cos 0» 2J,
'—[/ 13 + 3 cosi
\ — cos2 -s- (1 4- C(>s ') — 2 cos /, —-~- sin t (6 + cos *)» — sin -~4
^
[__ cos2 4(1 + cos 0 — 2 cos t\* + -i- sin21 (6 + cos /)2 -f sin* ~
-^
13 4- 3cos t
%(14- cos2 4
12 cos -=-
a (13 4- 3 cos t)
370. r'" = 0, a = 0. Уравнение плоскости, в которой расположена нэта
линия:
ах Ъх сг — х
а2 д2 с2—у 1 = 0
л3 #з с3 —г
или
at Ьх х
а2 #з У
az Ьг z
. =
«1 *i с,
Д2 #2 С2
а3 £8 с2
371. Пусть х е= д: (/), у = у (0» 2 = 2(0-— параметрические уравнения
данной линии. Подставляя в данные уравнения х (*)> У (t), г (t) вместо х, у, zt
. получим тождества относительно t. Из этих тождеств находим:
2хх' — 3у = 0, 2у^.+2ху'— 92?'= О
или ,
^ {2х — 3,0} г' = 0, {2у, 2л: — 9'} г' = 0,
г' || [{2дг,- 3,0} {2у, 2*,- 9}) || {3, 2х, 2у} = Г.
Выберем на данной линии такую параметризацию, что (см. задачу № 381):
t = {3, 2лг, 2у} (х' = 3, у = 2лг, 2' = 2у).
189

Тогда находим:
г" = {0, 2лг', 2у'} = {0, 6, 4л:}, г'" = (0, 0, 4х'} = {0, 0, 12};
[/■У] = 6 {2у, - 2лг, 3}, |г'| = |/"9 4-4лг2 + 4у2 = }/"9+12у + 4у2 = 2у + 3,
_6|/"9 + 4лг24-4у8 _ 6
*~ (2у + 3)* ~(2у + 3)**
Далее: r'r"r'" = 18 . 12,
18-12 б n
"" Зб(9 + 4лг2 + 4)/2) (2у + 3)2 *
Отметим, что*х = о (линия откоса; см. ниже задачу 407).
372. хх* —уу' + zz* = 0, 2уу' — 2лг' +jg* = 0, (л:, — у, г} г' = О,
{-2, 2у, }}г' = 0, /•' = {1+2*, ^--2у, 2-2*},
г" = {2*\ 5 хУ — х? __ 2у', — 2х'};
г'" = {2*", 5 (х"у-ху»)у*-2уУ(х>у-ху') _ ^ _ ^
г'0 = {3, 3, 0}, ri' = {0, - 6, — 6}, rj" = {- 12, 42, 0};
1 .
Кб
373. Указание. Векторно-параметрическое уравнение данной линии
г={Л У, У4}.
Ответ:
__ 2 ]/! + Збу + 64у« == 12jf
* — |Л(1+4уа+1бу)г" "" 1 + Збу4 + Ь4ув '
374. Положим: z = t*. Тогда л: = /]/2а, у = * y2b, r={t У2а, t У2b, t2},
r'={Y2a~, У2b, 2/}, г" = {0, 0, 2}, г"' = {0, 0, 0}, \г'г"} =
:{2у2Ь, —2^2^,0}, |tr'r//]|=2Vr2 Уа~+¥, \г' \ => |/г2в"+ 2£ + 4**,
а = 0,
2}/T|Ai + * _ (a + £)Vg
О=0, / :
21^2 (а + £ + 2г)8/* (а + * + 2*/'*
(линия плоская). Уравнения пары плоскостей, в которых расположена линия:
Ъх* — ау2 = 0.
375.
n l Л/Г~77~7Г cos ^ (cos ^5)
1)У = ТК _|+Sin "2> ° = 4(d-co»f) ;
^ Л— (1+2/2)2 ' а~~ (1 -т-2/2)3 '
4; Л-~ &< ' з^'
190

6)>== 3 а==__±__.
25 sin /cos/ ' 25 sin/-cos/'
376.
j/y"8 + г "2 Ц. {y>z» __ у у)2 _, y»z'»—y'"z"
lAl+y'2^-*'3)8^ ' °~~~ y''24-2''2 + (yVr--yV)2 '
я =
"|Л+у'24-<г'а '
{— z'z" — v'y", y" — z' (y'z" — y'V), y' (y'z" — г у) + г")
У(г'г" + y'y")* + [y" — zf (y'z" — y'V)li;+ fz" + y' (yV—г'у")]2
VV*" — y'V^-t-^-f-y"8 "
377. AT = atg/, — =tg*, дгу = д<г.
Далее: r' = i fl. . , — £sin t, Ьсоь t\.
\ cos81 r
Уравнения образующих одной из серий л: = и, иу — Я2 = 0.
Вектор р={0, а, и} = {0, а, atgt} перпендикулярен этой образующей, так
как рг' = 0.
378. Уравнения образующих одной из серий х = и, ну — а.г = 0.
Вектор ^={0, а, и] = {0, а, л:} коллинеар*ен этой образующей.
Пусть r=r(t) — искомая линия. Из условия г' ±р находим: у'a -]~z'x = Q
или ау' + г' ~ — 0 или уу' + гг' = 0, откуда у2 + & = const — это семейство
круглых цилиндров, пересекающих данную поверхность по ортогональным
траекториям одного из семейства прямолинейных образующих. Точно также
находим второе семейство:
дга 4- я2 = const, *у = az
ортогональных траекторий прямолинейных образующих второго семейств».
379. Возьмём уравнение сферы в виде: r=^ {a cos v cos и, a cos v sin и, a sin f}.
Пусть tt = cp(i;) — уравнение локсодромой. Находим г', считая u = y(v); из
условия cos 6 = \^\\\\ находим S = Jofv ' °ТКуАа И ^tg 9 1П tg (Г + 5")
уравнение локсодромии. Из равенства г = a {cos t> cos и, cos и sin и, sin v],
считая и = <p (и) и учитывая, что — = —§— , находим г* и г", затем
а2 [ Х&Ъ \
[г*г"] = —— < sin и, — cos и, —-—>. Дифференцируя это соотношение по
v, получим:
cos2 6 \ cos v cos v cos2 v J
умножая скалярно этот вектор на —г", найдём
cos4 0 cos2?
(это выражение нужно знать для вычисления кручейия).
191

Ответ- t = cos 9 {— sin v cos и — sin и \g 9, — sin v sin и + cos a tg 9, cos v}9
cos 6 ( . cos и
V
i+'£5
( , cos и
{— cos и cos v + tg v sin и tg 9 tg2
\ ' б s cost/ &
COS2 If
— sin tt cos v — tg2 9 — tg v tg 9 cos u, — sin v\,
cos tf 6 & & j >
{ sin и, — cos a, - &—}
I cos v J
1/ 1 + -^
Г- ^ cos2 v
cos9 -I/ tg2fl
cos4 v
a (cos2 v + tg2 9)
380, r' = {*>' cos a — v sin и, t>' sin a -\- v cos u, kv'}; вектор {cos a, sin u, £}
определяет направление образующих. Имеем:
{cos и, sin и, /г} {г/1 cos и — v sin и, tr' sin и + г/ cos tt, Ли'} Л
/ —- ■ ' .. = cos 9,
]Л+k2 Yv*\+v'2(l+ &)
—# — ' , — = cos 9;
]Л + k2 у v2 + v'*(l+k*)
отсюда
a ctg 8
уравнение искомых линий:
и ctg. 9
r=Ce *l + {cos м, sin м, /г}.
381*. Из условия J- = T находим: ~ .- == Г,-^=~^ >z = \ -у <#.
Функция т; = т;(/), определяемая этим соотношением, непрерывна и имеет непре-
рывную производную — = —Г, сохраняющую знак на данном сегменте.
Следовательно, эта функция монотонная. Обратная функция t=t(-z) также
монотонная и дифференцируемая, причём т- = г - Теперь находим:
382*. См. решение задачи № 95. Доказательство аналогично: надо
построить вектор Лl/;C = г,, а затем сферу с центром в точке /С, целиком
умещающуюся внутри указанного конуса.
Atk
383*. Дг= -хг (r(ft)+ a), lima и далее так же, как и в предыду-
«! м=о
щей задаче.
384**. Будем говорить, что линия С в окрестности точки М расположена
по одну сторону от плоскости тс, проходящей через точку М, если
существует такая часть линии С в окрестности точки М, все точки которор (за
исключением точки М) лежат по одну сторону от плоскости тс. Будем
говорить, что линия С в окрестности точки М переходит через плоскость,
проходящую через точку М, если существует такая часть дуги линии С—«ле-
вая> окрестность точки М, все точки которой лежат по одну сторону от
плоскости тс, и если существует такая «правая» окрестность точки М, все
точки которой лежат по другую . сторону от плоскости тс; сама чточка М в
192

обоих случаях исключается из рассмотрения. Пусть плоскость те,
проходящая через точку М, компланарна векторам а и b(atf Ь). Составим
функцию ср (t) = ab {r (t) — г (*о)Ь гДе * = А> — значение параметра,
соответствующее точке М. Предположим, что ср' (t0) = ср" (t0) = ... = cp(v — ^ (£0) = О,
cpW (t0) ?± О, т. е. abr' = afcr" = ... = abr(v ~ ° = 0, afcr(v) % 0. Тогда, если
v нечётное, то линия С в окрестности точки М переходит через плоскость
те, а если v чётное, то расположена по одну сторону. Применим этот
признак соответственно к плоскостям (3, у), (т> а)> (а> f)- Так как
соприкасающаяся плоскость коллинеарна векторам r(k) и ris), а вектор г(?) не колли-
неарен векторам rik) и r(s), то векторы а, Ь, с, соответственно коллинеарные
прямым а, р, у, будут: а = Пк)у b = r{s)-\-lr{k), c = rW) + p.r(*) + vr(s).
Составляем функцию ср (f) = 6с {г (*) — г (t0)} = r(s)r(V) {r (t) — г (*„)} +
+ pr(s)r(b) {r(t)-r(t0)} + lr(k)r(D {/■(*) —г (/„)} +for(*)r(*) {r(t)-r(t0)}.
Отсюда ясно, что в точке М: ср' = <р" =... = cp(fc-i) = 0, cp(fe) ф0.
Составляем функцию ф (t) = ca {г (/) — r(*0)} = r(W) {r(t)~ r(t0)} +
+ vr(s)r(k) {r(t) — r(t0)}. Отсюда ясно, что в точке М
ф'=<]/' = ... = ф(*-1)=0, ф^^О. •
Наконец, рассмотрим функцию:
X (0 = ab {г (t) - г (t0)} = rWrW {r it) - г(*0)}.
Отсюда следует, что в точке М:
Г=='/" = ... = Х^"1)=0, XW^O.
Итог исследования приводим в следующей таблице:
k
н
•
н
н
s
Ч
ч
н
я
н
ч
ч
Линия в окрестности точки
расположена по одну сторону или
переходит через шюскость
№. т)

переходит

переходит

переходит
I (т, ^f
по одну
сторону
по одну
сторону

переходит
<<*, 3)

переходит
по одну
сторону
по одну
сторону
У^^
Черт. 117, I
jU^*^
J»
Черт. 117, II
к~—>
Р
Черт. 117,111
13 П. С. Моденов
193 •

Продолжение
k
н
ч
ч
ч
ч
J
н
н
н
ч
ч
Q
н
ч
н
н
ч
Линия в окрестности точки распо
ложена по одну сторону или пере
ходит через плоскость
(P. Y)

переходит
по одну
сторону
по одну
сторону
по одну
сторону
по одну
сторону 1
| (Y. «)

переходит

переходит

переходит
по одну
сторону
по одну
сторону
| (а, (3)

переходит
по одну
сторону

переходит

переходит
по одну
сторону
Ъ- ^
зА7\,
Р
Черт. 117, IV
1 fi V
| Черт. 117, V
!W
Черт. 117, VI
Черт. 117, VII
^А^\д
р
Черт. 117, VIII
1 194
Н. — нечётное; Ч — чётное

385. См. чертёж 118.
386**. 1) Если тс—соприкасающаяся плоскость линии С в точке М, а
щ — любая касательная плоскость линии С в точке М, отличная от
плоскости тс, то существует две пары касательных плоскостей а, р и аг, j3t та-
>
^—а
г
'N
v
^г
<
-а /5-
rv
Черт. 118.
3 \JL
Y
ких, что пары двугранных углов, образованных этими плоскостями, в
которых проходят соответственно плоскости тс и nit не имеют общих внутренних
точек (черт. 119).
2) Если касательная проектируется в точку, то соприкасающаяся
плоскость тс проектируется в прямую /. Рассмотрим две произвольные прямые а
и £,'лежащие в плоскости проекции и проходящие через проекцию М* точки
М. Через эти прямые проходят
касательные плоскости аир. Некоторая
часдь дуги линии С в окрестности точки
М попадает внутрь того двугранного
угла, образованного плоскостями аир,
^в котором проходит плоскость те;
следовательно, некоторая часть проекции С
линии С в окрестности точки ЛГ попадёт
внутрь той пары вертикальных углов,
образованных прямыми а и Ь> в
которых проходит прямая /, а это и значит,
что / касательная к проекции С линии
С в точке М' (черт. 120).
3) Какова бы ни была
касательная плоскость те линии С в точке Щ,
найдётся хотя бы одна пара
касательных плоскостей аир линии С в точке
М, отличных друг от друга и от
плоскости тс, таких, что какова бы ни была
часть дуги линии С в окрестности
линии Mt найдётся хотя бы одна точка
линии С, принадлежащая этой части, которая лежит вне той пары
вертикальных углов, образованных плоскостями а и р, в которых проходит
плоскость тс.
4) (Черт. 121). См. ответ на вопрос 3).
5) Построим плоскость тс, проходящую через точку М, компланарную
векторам г' и г". Построим две касательные плоскости аир линии С
в точке М, отличные друг от друга и от плоскости тс. Пусть МК = **"*
Черт. 119.
♦
195

Построим сферу с центром в точке К, не пересекающую плоскостей аир.
Имеем:
А/2
Дг = г'Д/ + (г" + а)-75-, Нта = 0.
При всех достаточно малых Д^ конец вектора г" + а, отложенного от точки
М, попадёт внутрь упомянутой сферы, а значит прямая, имеющая направле-
Д/2
ние вектора г'М -\- (г" + а)
проходящая через точку М, попадёт
внутрь той пары вертикальных двугранных углов, образованных плоскостями
.а и fp, в которых проходит плоскость те. Но йа указанной прямой лежит
точка М (t -\- M). Таким образом, при всех достаточно малых А^ по
абсолютной величине все точки M{t-\-kt) попадут внутрь той пары двугранных
углов, образованных плоскостями а и р, в которых
проходит плоскость те, а это, согласно определению,
означает, что плоскость те — соприкасающаяся плоскость
линии С в точке М.
А?
Черт. 121.
387*. Решение аналогично решению задачи 388. Уравнение
соприкасающейся плоскости: (R — г) r^fe)r*5) = 0 или в координатах:
X — х У—у
388*. Ответ:
в точке М.
x(s)
/*>
[r'r"]
[r'r"\ | "
,A/2
:0.
единичный вектор бинормали линии С
_ А^3
389*. \r=r'M + r"^r + (r'" + «)~т, Ит а=>0. Отсюда Аг [г'г"] =
^ 31 М = 0
А£3
= (г'г"г'" + s) -^-, lim s = 0 и, следовательно, функция ~Ar [r'r"] в доста-
0 д* = о
точно малой окрестности точки М меняет знак при изменении знака А*.
390*. Принимая точку, через которую проходят все соприкасающиеся
плоскости, за начало радиусов-векторов, ьимеем; гг7г" = 0 (тождество от-
плоская, так как её
-J"*"-
носительно t). Отсюда следует, что линия р
кручение равно 0; данная линия является годографом вектор-функции р' и,
следовательно, тоже плоская.
391**. Щ = Х [[г'Аг] г']; (X [[г'Аг] г'] — Аг)2 = Ха [[г'Аг] г']2, X [г'Аг]2 =
тАг2, ^- Т[гщ
№ _ ттт* [[г'Аг] г'] . Аг2
* ' жд — 2 [г'Аг]2
ч» мк^ЩП^г^.
М = 0
В частном случае, когда линия задана уравнением r = r(s), имеем:
Р
196
-. lim М/С == —
Д5 = 0 *

392*. См. задачу №231.
r'r'r"
393*. 8:
Ar-J^I
[r'r"] I
-^—} откуда искомый пре-
\[r'r"\\ Г
1 r'r"r'" 1 . ,
дел равен -g--, r , „-,—; в частном случае -^-х а.
6 | [г'г ] | J 6
394**. Не об х о дим ост ь. Считая X = X(и), находим: г' = р'4-Х'#4-
+ Х£'||£. Умножая обе части этого соотношения на [ее'], получим: р'ее' = 0,
'таким образом, необходимое условие
е'фО, р'ее' — О.
Достаточность. Пусть e'^iO и р'££=0. Векторы р', е, е' —
компланарны. При этом векторы е и е' неколлинеарны (ибо в противном случае
было бы £ = const). Значит, р' = & -\-f\e\ откуда г'= р'-\-\'е~\-\е'= &-{-
+ тг]^' -|- \'е + Х#' || £, и так как #' J. е, то надо положить X = — ч\. Для
определения Y) умножим обе части соотношения р' = $е -\-г\е' на #'; получим:
Р'е'
е'
р'е'
Уравнение огибающей: r = p — J-—r- <
395. Эвольвента окружности.
396. При а = Ь.
397. См. задачу № 389.
§ 2. Применение формул Френе
398. г = ty г = у-я, г = — *2£ 4- *л -f- у-су&.
399. Будем искать вектор ю в виде: о> = at + ?# + ^Ь. Находим: [&f\ =
= — р£> -f- ТЛ = /л, откуда ? = 0, у = %. Далее: [ад] = aft — у*" = — ** + а^>
о = с. Остаётся проверить последнюю формулу, имеем: [toft] = [(at + ъЬ) b] =
= — ся. Кинематический смысл: <о — мгновенная угловая скорость репера
Френе при движении точки по линии со скоростью, равной 1 (по
абсолютной величине); / , я, Ъ — скорости годографов векторов t> я, b.
400. Применить формулы Френе.
401. Применить формулы Френе.
402. Применить формулы Френе.
403**. еп = С,е (— *t + ab)= 0, et~- ^-eb = 0y em — ( —J eb + — en = 0,
x2 4- с2
eb — C—/-K»-. Дифференцируя ещё раз, получим требуемое соотношение.
Отметим, что в силу приведённых выше соотношений можно считать:
а %24-*2 . , , х2+а2 ,
Если выполнено соотношение:
' X2 4" °!
197

то этот вектор постоянный (в этом можно убедиться, определив е\ эта
производная обратится тождественно в нуль). Этот постоянный вектор е
образует с вектором п угол, косинус которого равен -=—r = const. ■
404. #£=0, х£/г = 0; отсюда или х = 0 (прямая линия), или е#=-0; если
еп — 0, то е(—уЛ -f- <sb) = 0, откуда с = 0 (линия плоская).
405*. eb = 0t о£/г = 0; отсюда с = 0, так как, если бы было с^О, то
еп = 0, £ (— •*& 4*а&) = 0, *£* = 0, £* ^ 0, значит * = 0 — прямая линия.
406**г Пусть £ = const— вектор такой, что е — — et =c = const. Тогда
£/:=0или ъеп=0; отсюда или х=0 (прямая), или еп=0. Далее е/г = Q,e(—%t-\-
4- Qb) = 0, —~ Ст. + aeb =zQ,eb = —С, С ( — ] = (&£)" = — оеп == 0; значит,
-1 = const. В частности, если о = 0, то линия плоская и касательные к ней
о
ортогональны нормали к той плоскости, в которой лежит эта линия. Обратно:
У.
пусть — = С= const. Из предыдущего следует, что е = (et) t + (en) n -f-
-|-(eb)b = Ct~) Cb = C(t-\ b). Положим поэтому в случае—== const,
е = / ~|— ft. Тогда
G
cos(e, /)=s 7===г-= const.
Нетрудно проверить, что е = const (# = 0).
X X
407*. См. задачи № 371 и № 406, — ==1. Искомый вектор: e = t-\ b =
о о
= * 4-Ь - г' | И"") ._{3, 2г,2у) 6{2у,-2*, 3}_{2у + 3,0, 2у + 3}_
"^ I г'Г I [г'г"] Г 2у + 3 "■" 6(2у + 3) - 2у + 3
=s {1, 0, 1}. Таким образом, касательные к данной линии параллельны
биссектрисе угла xOz.
408*. Пусть £ —вектор, принадлежащий всем спрямляющим плоскостям
о
некоторой линии. Тогда еп = 0, {—y.t -f- ab) e = 0, —et И be = 0.
Дифференцируя ещё раз, получим: (—) =0, откуда — = const. Отметим, что
е = (et) t + (en) n + (eb) b || — t + &• Если — = const, то,полагая e=~t + b,
с одной стороны находим еп = 0, с другой стороны е = — у.п — ся = 0,
т. е. е= const; этим доказано обратное положение. Отметим, что вектор
±-t+b\\*t + xb
есть вектор Дарбу (вектор, определяющий мгновенную ось вращения
репера Френе при движении его по линии; см. № 399).
409*. Ье = С, — <зпе = 0, пе = 0, — xet + seb = 0, et~ — С, х#я =
= (—) С или ( — ] =0 или—= const. Обратно: если — = const, то, пола-
198

гая е — —t-\-b, находим eb — const и e = — х/г— а/г=0, откуда е=const;
вектор е и здесь коллинеарен вектору Дарбу.
410*. Для линии откоса (—) = 0, а значит, , на основании
упражнения 401, bb b =0, т. е. b = b(s) — плоская линия; с другой стороны, эта
линия расположена на сфере и, значит, является окружностью.
411*. Принимая за начало радиусов-векторов точку, через которую
проходят все спрямляющие плоскости линии, получим г/г = 0. Дифференцируя
по s это соотношение, получим:
Г(_х* + ob)= 0, — xrt+ arb = 0, rt — yrb«= 0;
дифференцируя по s ещё один раз, получим: ,
о \ - . а*
2
r& j г/г = 0;
х у х
. ■ Ш"
но т = 0, значит rb~—.—гт-; отсюда —ог/г = )—г^; но г/г = 0, следо-
вательно, ( —J =0, откуда — = as4-^-
412. 6 = — о/г = 0, a = 0.
413. См. предыдущую задачу.
....(4) . х
414. ггг=ъ2(хо — xa); отсюда — = const.
о
415*. 1) Пусть r = r(s) — уравнение одной из линий. Тогда уравнение
другой: p = r-\-lb. Находим: р' = £+ Xfr— Xa/г; так как бинормаль линии
p = p(s) имеет также направление вектора Ь, то b _L р' и, значит, 6р'= 0,
откуда X = const, p' = t — Xa/г. Далее: р" = х/г — Ха'/г — Ха (— xtf + ab), и
так как р" _|_ Ь, то р"Ь = 0, откуда Ха2 = 0, т. е. а = 0 (Х^0, ибо в
противном случае линии r = r(s) и p = p(s) совпадали бы). 2) Пусть г = r(s) —
уравнение линии С; уравнение линии С*: р = г-{-\п. Находим: р' = г*-|-
+ Х/г + X (— xtf + <*Ь). Так как р' ±^Ь* = п, то р'/г^=0, откуда X = const,
и, значит, р' = (1 — Xx)i*+Xoft; далеер" =—(Xx)Y + (l—Хх)х/г-|-(Ха)'&—Ха2/г.
Так как р" _[_&* =/г, то р"/г = 0, откуда (1—Хх)х — Ха2 = 0 или х =
= X (х« +а2).
416**. Пусть r==r(s) — уравнение линии С; тогда уравнение линии С*:
р=:г + Х/г. Из условия р'_]_/г находим: Х = const; из условия
компланарности векторов р', р;', /г (р'р'7г = 0) находим: a -f- X (xa — xa ) = 0, откуда
^+xi^i==0)(-i)- + x(Ay=0)-l + x| = -,(=cons,),
Xx + {xa=l.
417**. Уравнение линии С*: р = г 4- ^я; легко проверить, что р' _L n и
что векторы /г, р', р" компланарны (в силу условия Хх 4-^ = 1), т. е. /г
является главной нормалью линии р = г 4- Х/г.
419. См. задачу № 417; положить р = 0, Х = —.
420**. Принимая точку M0(s0) за начало радиусов-векторов, имеем:
5 _ 1 /тг0/г 1
199

Пусть
rn0n = ф (s).
Находим:
ф = to0/& + га0 (— ** + °^) = toon — *rn0t 4- arn0b, ф (s0) = 0, ф = х/ш0л +
+ tn0 (— х£ -f- aft) — хг#0£ — х*я0* — *гп0 (ш) -|-
+ агп0Ь + <stnQb — <s2rn0n, ф (s0) == 2а0.
Положим далее
[*оЛ]2 = Ф(5).
Находим:
ф = 2 [п0п] [щ (- х* + aft)], ф (s0) == 0, ф = 2 [Ло (- х* + cft)]« +
+ 2 [ityi] [й0 (— xt + aft)]; ф (s0) = 2 (— х0 [л0*0] + °о [я<А>])2 =
= 2(Xoft0 + a0^o)2 = 2(x2 + a2).
Отсюда
и, следовательно,
где
1 |ф
lim
s = Sos-s0 y$ V~A + °l
s=[7^W+']]s-s-u
lim a = 0.
s=s0
421**. Пусть Л40 (s0) —начало радиусов-векторов, тогда
5^ irftpftl
V" [ W *
Полагая
rft0ft = Ф (5),
находим:
ф (S) == tft0ft — rft0«a, ф{<?0) = 0, q?(s) =
= xnft0ft — f ft0/*a — tb0n<s — rbQ (— xt + aft) a — rb0tla, ф (s0) = 2a0.
Положим
ф(з) = [&0&Р;
имеем
ф (s) = - 2 [ft0ft] [ft0/*] a, ф (so) == 0, ф (s) =
= 2 [ft0«]2 «2-2 d[ft0ft] [ft0«] - 2 [ft0ft] [ft0 (- xf + aft)] a, ф (S0) = 2a?.
Отсюда
5 r 1 1Ф (s),l .
lim : r = hm -—— r:— = 1
S - 50 I S — S0 | 5 = 50 S — S0 Yty (S),
и, следовательно,
S=(l +a)|s —S0|,
где
lim fc = 0.
5=50
422**. Пусть M0(s0) — начало радиусов-векторов. Тогда
8== \rt0t\ = \rr0r\
VWF V[r0rV '
200

Положим
• ф (s) = r'r0r, ф (s) = [r0r]2. Имеем:
9(s) = rr0r, i(s0) = Oti(s)=srrQr + rr0r, 9(s0) = 0, <p (s) = 2rr0r 4-
. (4) ... (4) (4) . (4) . (5) (4)
+ rr0r, <?(s0) = 0, ф (s) = 2rr0r +2rr0r +rr0r +rr0r, <? (s0) =
=v— ^A*o Л> ^ o*
Следовательно,
9 (s) = — ^2 ^° *"° ^ ° + aH« — s0)\
где
lim a = 0.
Далее:
ф (s) = 2 [r0 r] [r0rl, Ф (So) = 0, ф (s) = 2 fr0 r]2 +.2 [r0 г] [г0 г ]„
Ф(5о)=2[г0г0]2,
значит:
*(s)=([r0r0]2+g)(s-So)2, lim /3 = 0;
1 (
T9lWi+a|
8 = ^-===- | s- sQ \\ lim a= limp = 0;
lim -«_-!- IW«
12
4^j= = l*|a|;e=(l xla|+g)ls-8o|», lim6=0L
42o *, _ W + X*^ + (x - Xa + X2 A)2
4^' ~ (1 + XV)5 "
424**.
p'^= — Sx«, p" == S*2/ -— (-/. -(- si) Я — SxA, p"' = (s*2)' t +
+ S*3ft — (2% + Sx) П — ('Л + si) (— *f +. <J&) — (S'AQ)' Ь + S*a2#,
I P' I = I sx I, [p'p'1 = SV let + *b) и т. д.
Ответ: х* = " ' ,— , а* =. —————.— ). Если — = const, то а* = 0.
| s% | , S* (^ + с2) \ а / а .
425*. Уравнение линии С* имеет вид: р = г + Х£, где X находится из
условия р — г0_!_#0, т.е. Х =—j—- , Для вычисления кривизны линии С* в
точке М0 находим: *
р' = f + U+ Ххл = (1 +\)t+lm
и далее
р" = X* + (1 4- X) *я + Ххл 4- Ья + >■* (— ** 4- *Ь) = (X — Хх2) t 4-.
4- (* 4- 2Х* 4- **) ^ 4- ЬюЬ;
так как вектор р" при s=,s0 должен находиться в плоскости векгоров tQ и
п0, то X (s0) = 0 и значит:
• Ро = (1 + ^о) *о, Р0' = Vo 4~ (*о 4~ 2VoJ Щ>
201

откуда
I Po I = I 1 +\ 1,1 [PoPo'l I = I (1 + V>) (1"+ 2>o) I «о
* I 1 I 0\ I
и, значит, x = !—3" , ° x0. Остаётся найти X0. Имеем:
(1 + Ao)2
p"' = Tt + Хх/г + Ххл + (1 4- X) -л/г 4- (1 + X) x (— x* 4- oft) 4- Хх/г 4- Хх/г 4-
4- Xx (— x* 4- aft) + Un + Хх/г 4- Xx (— xt 4- aft) 4- (Xx)'(— xt + aft) +
4- Xx (— it — *2/г 4- aft — а2/г).
Полагая здесь s = s0 и приравнивая нулю коэфициент при ft, найдём:
ms0) =—о-, и значит:
2^
3 _ 3
: *о 7 ГТ2 —Г "4" *°
'(-т)"
(теорема Бельтрами).
426**. Уравнение линии С* имеет вид: р = г-\-М, где X определяется
из условия р — г0 _|_ *0> следовательно, X = ^т—, откуда Х0 = 0 и искомое
t*Q
уравнение:
Находим:
р' = /4- U 4- Ь/г = (1 + X) 14- Ь/г.
В точке 5 = s0 имеем:
Ро = (! 4" *в) *о + >ч)*оЯо-
Так как этот вектор должен лежать в нормальной плоскости, то 1 4~ ^о = 0>
Х0 = — 1. Далее
р" = X* 4- (* + *) *« + *** + х*л + Ь (— ** + аЬ) = $ — >*2)17+
4- (* + 2Хх 4- **) п 4- kwft, Ро' = Vo — V*o-
Этот вектор также должен лежать в нормальной плоскости; следовательно,
Х0 = 0, Х„ = 0. Далее,
р'" = (X — Xx2)Y 4- (X — Ь2) «л + (х 4- 2Хх + 3* х 4- > *)« 4-
4- (*/- 4" 2Х* + Ь-) (— ** + а&) + Ь*°& 4" * (*?*)% Ро" = (*о — 3*о) по — 2x0a0ft0 =
= — 2tt0/z0 — ^"лоао^о*
Значит, если xQ^£0, a0^0, то р'=0, р" Хр"'^0—точка Л10 — точка воз-
врата первого рода. Касательная к линии С* в точке М0 является главной
нормалью линии С. Поэтому линия С называется ребром возврата
поверхности, образованной касательными к этой линии.
427**. p=zr + \t, p' = (l + i)t + \*n, Х0 = 0, р" = XV 4-(1 4" 2Х) *я 4-
+ Хх/г 4- Хх (— *t 4- ob), >0 = — у , р; = 2- 'о, Р0' = Мо II р;, р'" ='>> 4-
4- Ххя 4- 2Ххл 4- (1 4- 2Х) г/г 4- (1 4- 2Х) х (— и 4- aft) + x in 4- X (in) 4-
4- Xx (— х*4- aft) 4- х[х(— х*4- aft)]", р^" = Хо*о — у МоМ|р;
(коэфициент при п0 должен обратиться в нуль).
202

428**. Уравнение линии С* (точка М0 принята за начало
радиусов-векторов): р —r-j-X/t; X определяется из услония: р J_ b0\ однако, как и иыше,
можно обойтись и без явного выражения X. Итак, учитывая, что р — г0 _1_ Ь0,
имеем: р' = (1 — Х-/) t -f- in + lab, p[ = tQ + X0/*o> X0 = 0, p" = (— 2Xx — X*) *+
<y— Xx2 + X — Xa2) Л + (2Xo -f \i) b, p'o' = — 2X0/o*o + (*o + >o) Щ + 2Х0а0Ь0 и
так как коэфициент при b0 должен быть равен нулю, то р' = t0, р" = (ч +
-h'iQ)n0. Для определения Х0 найдём р'" и приравняем нулю коэфициент при
Ь0. Отыскивая р"', выпишем только те слагаемые, которые содержат вектор Ь:
р" = (х — Хкг+Х — Xc2)a& + (2Xa + 3Xa + Xi')& + (. . .)t + (. . i) П, р^" =
= (^o + X0a0+2a0X0)b0-|-(. . .)* + (■ . .) п. Имеем: 3a0X0 + a0y.0 = 0,
- 1 ' 2
Х0 = — -=- х0. Значит, р" = -к- *0Яо» откуда
о о о
* \w:v
429*. р=г4-Хл. (Р—Го)^о = °Д=-"-Ьг- Имеем: lim r = r0, lim л = яа,
lim X=lim ( ^] = lim (-—-7 л ,° -ч .-)=—> следовательно, limp =
= r0 + Ron0\ соответствующая точка М (г0 +■ R0n0) — центр соприкасающейся
окружности линии С в точке М0.
• 430**. р = г + Хя; p — r0±t0, р' = (1—">[х)^ + Хл + ХсЬ, Х0 = — , р'=
*о °
= ^о + - &о> Р" = (— 2Ь — X/) t + (* — X*2 + X — Ха2) /г + (2Ха + Хс) Ь,
х0
— 2Х0*0 — X0i0=0, X0 = —т^т, Р' = — с^Яо+- Ь0. Выпишем теперь в
о о
выражении для р'" только коэфициент при векторе t:
— 2Хх — ЗХ -л — Xi — х (х — X*2 +"Х — Ха2);
в точке М0 этот коэфициент должен быть равен нулю. Это даёт: •
х2 х а2
А°~2?" Зх2^3х '
откуда
2a*\ / о0*о _ о0
*0
К' = [щ-г*1-ъ?)п° + (-~-,т+г)ь«-
Теперь находим:
3/(х§ + 4х^
* 2
В частном случае х = const, имеем: х0 = -^ х0.
203

431**. Уравнение линии С* имеет вид: р = г 4- ^Ь, Р' _!_ Ь^ отсюда
р' = t + ib — \<зп J_ b0; значит, Х0 = 0, р" = х/г — \<з п — Ха/г — Ха (— xf 4- аб) -{-
+ 1Ь — Хая, р^' = х0/|0,
;_|[р>П1_х
°~~ lo'l3 ~~ °'
I *о I
432*. Для плоской линии, заданной уравнением р = р (/), вектор аффинной
нормали определяется соотношением:
v = 3p"(p'Xp")-p'(p'Xp'"). •
Уравнение линии С* имеет вид: р = г — (rb0) Ь0. Находим: р' = t — (tb0) b0,
р" = х/г — -/ (nb0) b0, р'" = in + х (— xf + c&) — i (nb0) b0 — * ((— xf 4- Qb) b^b^
Po = '°' Po' ='*o*<» P^" = *o*o — *o'o-
Отсюда
v0 = Зх0л0х0 — fox0 = 3xj;/i0 — xof0.
433*. 1) Уравнение проекции на соприкасающуюся плоскость р = г4-М><*
где X = X(s) — такая функция от s, что р — г0 ±_ Ь0. Находим: р' = t -\-'kbot
р" = 77* 4" >А>- Р'==^о4- КК >о = °> Ро =*о> Ро = V*o 4" ><А>» ?о = ЧЩ-
Значит, точка М0 является обыкновенной для проекции С* линии С на
соприкасающуюся плоскость. Кривизна линии в точке М0 равна х0 =
_1_КО!_х
2) Уравнение проекции С** на спрямляющую плоскость: р = г 4~ *-#<>,
причём р — г01 л0; имеем:
р' = *4-^л, Ро = ^о> p" = *n + ln0, pi'=0 (так как p"J_ n), р'"=хл4-
4-х(— у^4- ^) 4- >'л0, ро'" = — хо% 4- *0*<А> р^ х р'о" = — vo7f:0 — точка
АГ0 для линии С** является точкой перегиба.
3) Уравнение проекции С*** на нормальную плоскость:
Р = г 4- Х*0> Р — r0 J_ *0. Р' = t + М0, 9[ = Or р" = х/г + М0,
р" = х0Я0 ^zf: 0, р'" = W 4- X (— r.t + а&) 4~ Мо>
Р^" = *o*o 4" *о<*о&о. [Ро'Ро'Ч = *о30*о ^- °
— точка М0 для линии С*** является точкой возврата первого рода
(черт. 122).
434*. г = р 4- С (v cos 9 4" £ s*n ?)» гДе ¥ == — | а^5> С = const.
435*. Исходя из уравнения г = р 4~ С (v cos 9 4- £ sin cp)j где ц> = — I a rfs,
найдём центр кривизны линии С*: R* = R-}-С sin у$, где /?— радиус-вектор
центра кривизны линии С, а /?* — радиус-вектор соответствующего центра
кривизны линии С*.
436*. Считая X = X(s), имеем:
р' = 14- Ч& cos cp 4- п sin ср) 4- X (6 cos ср 4- п sin ср)* || b cos cp 4- w sin <p.
204

Так как производная
(Ь cos ф + п sin <P)"
единичного вектора Ь cos ф + л sin ф к нему перпендикулярна и так как
t А_Ь cos ф + л sin ф, то для выполнения условия коллинеарности необходимо
и достаточно, чтобы
t + X (Ъ cos ф + п sin ф/ = О
или
t -\- X (— <зп cos Ф — & sin ф • ф + (— v-t + cfr) sin Ф + Л cos ф • ср) = О
(1 — Хх sin ф) £ -|г X (ф — a) cos ФЛ + X (а — ф) sin Ф& = О,
откуда
Cs 1
Ф—а=0, ф= \ cds, Х = г
J *0 * S11
sin ф
Уравнение огибающей:
р = г +'R (n + b ctg ф).
Черт. 122.
Функция 1 ads называется полным кручением "линии на интервале (s0, s).
J *0
Таким образом, если в точке М0 (s0) выбрать бинормаль (ф = 0), то в точке
М (s) нормаль п sin ф -\^Ъ cos ф должна составлять с бинормалью угол ф,
равный величине полного кручения дуги М0М. Условие ф = а будет
соблюдено, если к ф прибавить любое число. Геометрический смысл этого
обстоятельства таков: если Некоторое однопараметрическое семейство нормалей
линии имеет огибающую, то, повернув все нормали в нормальных
плоскостях на один и тот же угол; мы получим новое семейство нормалей, также
имеющее огибающую. Если определить эволюту пространственной линии как
огибающую нормалей^о полученный результат позволяет утверждать, что
всякая пространственная линия имеет бесконечное множество эволют.
205

437**. p = r + Rn + Rbctgy, p' = R (n + b ctg 9), p" = R(bctg 9 + л)—
— £xf, p'" == (— 2#x — £x) * + (7j — £x2) я + # ctg cp &, [p'p"J =
= — R2* (n ctg cp — 6), [p'p"]2 = £4x2 cosec2 cp, p'p"p"' = kz*3 ctg cp, | >' |3 =
sin cp cos cp _ _ v. л *
* sin2 cd
= # cosec cp |3, x = ■—Г7, o:
l л/г 1
л . - Пусть RR > 0; тогда -^ = tg cp —
RR <*
ь
эволюта является линией откоса. Из соотношения р' = -—(6coscp-|-/isincp)
. r Sin cp v '
ясно, что р' образует угол ср с вектором b (черт. 123 и 124).
R ctgr <р
Черт. 123.
Черт. 124.
438**. Уравнение линии С* имеет вид: p=r-fO&s- Находим:
S*= f|p'|ds= f |^ + X6|ds==sVrbfX?, p'=* + X&, р"=*=хл,[р'р"] =
= [(t+lb)xn] = *(b—}t), x==
1[p'p"]1 /i+>2_ *
" (1 + Xa)a/s 1 + X2
p"' = x/t —x2*, p'pV" = Xx3, a* =
Xx3
X*
(1 + X2) x2 1 + X2 ' a*
X '
Касательная к линии С* образует с вектором b угол 6, определяемый
соотношением:
X
cos 0 = ~- =
Далее:
** =
lb + t
р-1 |Al + X2
b — )t
. „* = [&***] ^
|Л 4- X2' j/"l + ^
[(6 - It) (lb + *)] _ \bt] - X2 ff 6] _
14. Xs 1 + л» • •
Уравнение касательной к линии С* будет: /? = г -f-^s& + ?(* + )&). Эта
касательная встречает плоскость, тс линии С в точке, в которой R — rj_b, т. е.
b{R — г) = 0. Это даёт Xs -f- 6X = 0, т. е. Е = — s, и уравнение R = г + Xs& —
— s(f + X6) или .Л = г — st — уравнение эвольвенты линии С (черт. 125).
439. Уравнение С*: р = г — (г60) 60> р' = * — (/60) &о> Р ' = *о>-
|[Р'Р"11
р" = хл — x(nb0)b0, р'' = х0л0, шиш = Хо.
lPoi ^
440**. p' = (R — Ra ctg cp) (я + b Ctg cp), p" = — x (/?V- Яа ctg cp) * + { (R —
— jRcr ctg cp)* — a ctg cp (R — iRa ctg cp)} (n + b ctg cp); отсюда [p>"] = x (# —
206

— /?з ctg cp) (b — n ctg cp). Дифференцируя по s это соотношение, получим:
[р'р'"] = {* (R — /?с ctg cp)2}* (Ь — п ctg?) + х <£ — iRa ctg cp)2 ( — а/г + xt ctg cp —
/га
■ а& ctg cp -
sin2>J = {x(^~^aCtgCp)2}* (&-«Ctgcp) + x2ctgcp(iR-
r— Rq ctg cp)2* — x(R — Ra ctg cp) a ctg cp (b — /г Ctg cp) = x2 ctg cp (R — Ractgcp)2/ 4.
+ {(x (R — Ra Ctg cp))' — x (fl — Re ctg cp)2 0 ctg cp} (b — Л Ctg cp).
Умножая обе части этого соотношения на р'\ получим:
р'р"р'" = х3 ctg cp (# -1 /?а ctg cp)3.
Теперь находим
* | [р'р"] | | х sin3 cp
R sin cp — Ra cos cp
ip'pT
x3 ctg у (R — Rz ctg cp)3 sin2?
x2 (R — #a ctg cp)4 ~~~
x cos cp sin cp x cos cp sin2 cp
R — Ra ctg cp R sin cp — Rj cos cp
Черт. 125.
441**. Уравнение оси кривизны:
р = г + /?л + ХЬ; X найдём из условия
р' || &. Находим: р' = t + Rn + R(— xt+ab) + \Ь — Хал == (£ — Ха) я +
ь ь
(X + Rq)by R — Ха = О, X = —; уравнение огибающей: р = г + Rn + - b. От-
а а
метим, что р определяет центр соприкасающейся сферы линии С.
442*. p = r + Rn+ (f )b,p'=|/?a+f|Hb = co&, где ш = Да + (у) *
p" = tob — ша/i, р'"=(в6 — 2(йа/1 — о>а/г — <оа (— xf-f-ab) = o)ax£ — (2а>а-|-<*>а)Я+
+ № — ша2) &, [рУ'] == — <А [&/г] == о>2а*, р'р"р'" = а>3а2х, | р' | ?= | о> |, х* =.
оз2 I a I
443*. Указание. См. предыдущую задачу.
444*. Вектор « Дарбу, коллинеарный мгновенной оси вращения
трёхгранника Френе, определяется соотношением a> = <st + *#• Уравнение
мгновенной оси вращения р = г +• X». Находим: р' = (1 + Ха -|~ Хс) f -р (Хх -|- Хх) Ь.
Для того чтобы было выполнено условие со || р', необходимо и достаточно»
чтобы /
откуда
1 _|_ Ха + Ха Хх + Хх
а х
=0,.
Уравнение С* имеет вид:
Р = г-
ох — ха
(а*+ *!*)..
207

445*. p = r + Rn+%b. p'={tfa + (j) }b, p" = {tfa+i j) } 6-
-{^+(7)}^ [p'P"]=^{^+(f )}V [[p'p"]p']==-{*° + (f)} ^
Отсюда
** = ± b, n* = ±.n, £>* = it £
446. г'={1, 2ДЗ*2}, r"={0,2,<6/}, r'" = {0,0,6},^=(14-4/49/4)I/2,
^ = {1,0,0}, /■;' = {0,2,0}, r;" = {0,0,6}, s'Q = l, [r'r"] = {5/2,-6^,2},
n ^ (4 + 3S/2 + 36*4)1/2 ds dt ds
\_
3 T T (144/3 + 720(l + 4/2 + 9^4)2
2" 0 + 4/2 + 9/4) (8/ + 36^3) (33/* + 36'2+ 4) — ^ T
= 2 (36;4 + 36/2 -f 4)^ .
(36^4 + 36*2 + 4) (1 + 4*2 + 9^4)~2
i?e=0 — радиус соприкасающейся сферы данной линии в данной точке равен -^ .
447*. 'Уравнение огибающей
p = r + Rn + -b.
Имеем:
а2 4- Ь2
R = ——— = const, п = {— cos t, — sin /, 0}, р = {а cos *, a sin £ bt} +
J ! {—COS^, — Sin^, 0}={— - COS^, Sin/, bt\
n ' » «2 + ^2
— винтовая линия. Радиус соприкасающейся сферы равен !— .
448. 1) (е* + е-')2у ~ + (е< — e^f. 2) 3]/ТЛ
R
449. Радиус-вектор центра соприкасающейся сферы: р = r + Rn-\— b.
45Q. Поместим полюс в исследуемую точку. Уравнение соприкасающейся
Ь
сферы примет вид: (р — а)2 = а2, где а = R0n0 -\—- Ь0. Степень <р точки М (s) '
* о0
данной линии относительно соприкасающейся сферы определится
соотношением:
9 = (г — а)2 — а2.
Находим:
.-2 <р'= *(г--а), ?; = 0, 1<р" = */1(г-«) + 1. 9"(s0) = 0.у 9'" =
=(хя + ха& — хЧ)(Г — а),— у ср^ = ко/?о + ^о=(^)о==0, 19(4>=={х|1 +
-f зс (— xt+ ab) + (ха + х'а.) & — ха£я — 2хх* — х3я} (г — а) — х2, ср(4)^0
о
{вообще говоря) и, значит, степень точек дуги данной линии в окрестности
рассматриваемой точки сохраняет знак; поэтому в окрестности данной точки М0
все точки линии расположены или внутри или вне соприкасающейся сферы
линии С в точке М0.
208

rVlABA IV
§ 1. Составление уравнений поверхностей
451. 1) Вводя географические координаты: а — долгота, v — широта,
будем иметь (черт. 126): х = г cos и cos v, у = г sin a cos vt z=rsinv или
r=r {cos и cos v, sin и cos v, sin v}; здесь 0 ^ я < 2тг, —^- ^ tf =^ -к-.
Координатные линии а = const — полумеридианы, из которых исключены «полюсы»
(т. е. точки (0, 0, it г)); координатные линии v = const ( v yfz ± -^ \ — парал*
л-ели. На чертеже 127 изображена
сфера с нанесённой на ней
координатной сетью. Конечно,
возможны и ' иные параметризации
сферы.
2) В аффинном преобразова-
v й л? b г, с
нии Х=—х, Y = — y, Z = ~z,
образом сферы х2 -\-у° + z2 = г3
X* у2 Z2
будет эллипсоид —2 + -р + -#= L
Таким образом, уравнение
эллипсоида может быть записано так:
r= {a cos a cost/, b sin и cos v, c sin v},
IIKT*,-^:
Черт. 126.
Здесь и и v — долгота и широта
прообраза точки эллипсоида (на
сфере). Эллипсоид вместе с
координатной сетью изображён на •
чертеже 128.
n 3) Рассмотрим сначала однополостный гиперболоид вращения,
полученный при вращении вокруг оси Oz гиперболы Л = -~- f t;-j J, zz=-~-[v — ^7) •
Обозначая через и долготу точки М (х, у, z), получим:
x^{v + Vjcostt' ^ = |('+F)sinB' z = i{v~i;)
или
r={i ("+!-)cosa' -i{v+i)sinu> i{v-^)}-
14 11. С. Моденов
209

Черт. 127.
Черт. 128.
210

Линии и = const — меридианы, линии v = const — параллели (из v = const
следует 2 = const). Производя аффинное сжатие Х=х, К = —-у, Z = z
к плоскости xOz, получаем уравнение
гЧт(° + т)С08И' -2-(*+^)sin"' l[v-T)}
произвольного однополостного гиперболоида. Линии и = const получаются
в сечении поверхности полуплоскостями, проходящими через ось Oz, линии
v = const получаются в сечении поверхности плоскостями,
'перпендикулярными её оси,— эллипсы. Введём ещё новую параметризацию на поверхности
однополостного гиперболоида
х?
а
У2
2 ^ Ь2 с2
Перепишем уравнение в виде:
х*
д2"
или
= 1
(I+I)(J-t)-(' + *)('4)
7 + 7--('+*). T-T-il'-f)
уравнения:
х д
«('-'*). Т-7"7('Ч)
определяют прямолинейные образующие этой
поверхности. Разрешая эти уравнения относительно х, у, 2,
получим:
Координатная сеть состоит из прямолинейных
образующих (черт. 129).
4) Рассмотрим сначала двуполостный
гиперболоид вращения, полученный от вращения гиперболы
г = {д —\— , Ь —;— , с—j— \.
[ых обра- ^
Черт. 129.
3 = -s-(ir + —), x=£(v ) вокруг оси Oz. Обозначая через и долготу
поверхности, получим:
* = 1 V ~~ ~v) C0S U' У ^ У V ~~ ~v) Sin Щ z=='^[v +
или
= {1(^-1i:)costt' y=y(*-!)sina, '-т(в + т)}-
Линии а = const — меридианы поверхности, линии v = const — параллели.
Производя аффинное сжатие Х = х, К = — у, Z=2 к плоскости xCte,
получим уравнение
гвШ°-"?)cosa' ? {v-^)sina' i{v+i>)}
211

произвольного двуполостного гиперболоида. Линии и = const получаются
при пересечении поверхности полуплоскостями, проходящими через ось Oz,
линии v = const — эллипсы, получаются в сечении
поверхности плоскостями, перпендикулярными её
оси (черт. 130)?
5) Рассмотрим сначала эллиптический
параболоид вращения, полученный от вращения
вокруг оси Ог параболы x2 = 2pz. Обозначая через
и долготу точки поверхности, получим
х = \/~р v cos и, у= ]/р v sin и, z = -^- v2
или
г = lypvcosu, ypvsin и, "9"W.
Производя аффинное сжатие X
Z — z к плоскости xOz, получим произвольный
эллиптический параболоид:
г = \v Ур cos и, v У q sin и, -=- v2 } .
Линии и = const получаются при пересечении
поверхности полуплоскостями, проходящими
через вершину поверхности (части парабол), линии
t/ = const—эллипсы, ролучающиеся в сечении поверхности плоскостями,
перпендикулярными оси Oz; и — эксцентрический угол эллипса сечения.
Координатная сеть дана на чертеже 131.
Черт. 130.
Черт. 131.
Черт. 132.
х2 у2
6) Перепишем уравнение гиперболического параболоида — = 22
в виде:
и положим:
{vp+Vq)ivp Vq Ъ
_х у __ г х у
Vp Vq~"' Vp Vq
Vp Vq ' Vp Vq
:2«;
212

Разрешая эти уравнения относительно лг, у, z, получим:
г = {(и + v) Vp, (v — и) V^y 2uv).
Координатная сеть состоит из прямолинейных образующих (черт. 132).
7) Рассмотрим сначала круглый конус, полученный от вращения вокруг
оси Oz прямой х = — г или z=>cv, x = av. Обозначая через и долготу
точки поверхности конуса, получим:
х = av cos и, у <= av sin и, z = cv
или
r={av cos и, avsina, cv}.
Линия u = const состоит из двух лучей — полупрямых, полученных в
сечении конуса полуплоскостью, проходящей через ось конуса. Линии v = const —
Черт. 133.
Черт. 134.
окружности, полученные в сечении конуса плоскостями, перпендикулярными
его оси. Производя аффинное сжатие Х — х, К = — у, Z~z к плоскости
. xOz, получим произвольный конус второго порядка:
r={avcosuy bvs'mu, cv}.
Линии rz = const — такие же, как и в случае конуса вращения (см. выше),
линии v == const получаются при сечении конуса плоскостями,
перпендикулярными его оси (черт. 133).
8) r={a 6osu,b sinrz, v}, О^и < 2тг, — оо < v < + оо. Линии и=const —
прямолинейные образующие, линии v = const—сечения плоскостями,
перпендикулярными образующим (эллипсы); и — эксцентрический угол точки
эллипса V — const, v — расстояние (ориентированное) от точки поверхности
до плоскости, в которой лежит эллипс v = 0 (черт. 134).
9) г = |-~-(нН ), -к-\и )' vf»M принимает все действительные
значения, кроме « = ©, — оо < г> < -f- оо. Линии и = const — прямолинейные
213

образующие; линии # = const — гиперболы, получающиеся при пересечении
цилиндра плоскостями, перпендикулярными к его образующим (черт. 135).
10) r={2pu2, 2pu, t/}, —оо<м<+оо, —oo<t/<-{-oo. Линии
и = const — прямолинейные образующие, линии v — const — параболы, полу-
Черт. 135.
чающиеся при пересечении поверхности плоскостями перпендикулярными
образующим (черт. 136).
452. r=p-\-ve\ координатная сеть состоит из прямолинейных
образующих (и = const) и линий v = const, получаемых переносом линии р = р(и)
вдоль образующих (черт. 137).
453. r = vp. Линии и = const — прямолинейные образующие, линии
'v = const получаются из данной всеми её гомотетиями к началу радиусов-
векторов (черт. 138).
Черт. 136. Черт. 137.
454. г = р -f- t/p\ Линии и = const — прямолинейные образующие.
Линии v = const — в случае, если |р'| = 1 (т. е. и—дуга данной
линии), получаются, если на касательных от точки касания отложить
равные отрезки.
214

455. г = р (s) + v (s) cos 9 + P (s)sin ¥• Линии s = const — окружности,
линии cp-const описываются точками движущейся окружности (черт. 139).
456. г= {<р (z/)cos и, у (v) sin и, ф (v)}. В частном случае:
г = {/(v) cos и, f(v) sin и, v}.
Линии и = const — меридианы поверхности, линии
v = const — параллели (черт. 140).
457. r=»{(a-\-b cos v) cos и, (а-\- b cos г>) sin и,
£sinz/}; линии и = const — меридианы, линии v =
= const— параллели (черт. 141).
458. Пусть в начальный момент движущаяся
прямая совпадала с осью Ох; вторая прямая, о которой
говорится в условии — ось Oz. Тогда уравнение
прямого геликоида занишется в виде
,r = {v cos ы, v sin ы, ku};
здесь v — расстояние точки геликоида от его оси
(ось Oz), и—долгота точки. Линии v = const —
винтовые линии, линии и = const — главные
нормали этих винтовых линий.
Черт. 138.
Черт. 139.
459. Если уравнение винтовой линии взять в виде:
p=z{acosuf a sin н, bu},
то вектор п;=■ {— cos и, — sin и, 0} — вектор главной нормали. Отсюда искомое
уравнение:
г = р—1п — {(а — ))cosm, (а — X) sin и, bu} = {v cos и, v sin ы, bu} —
прямой геликоид.
460. r=p + ve.
461. Г = р (s) + I {n (s) cos ? <s) + 6 (s) sin cp (s)},
где cp (s) — какая-нибудь функция от s.
Черт. 140.
Черт. 141.
462*. Нормальную плоскость к окружности р = {«cos и, a sin a, 0}
определяют векторы:
л= {cos а, sin а, 0} и {0, 0, 1}.
215

Бектор, лежащий в нормальной плоскости и наклонённый под углом и
к вектору п, будет' а = п cos и + A? sin и, поэтому уравнение искомой
поверхности
r=t {a cos its a sin и, 0} -f- va = {a cos и + v cos2 ц,
a sin и + v sin « cos и, v sin и}.
Исключая параметры и u v, находим
cos^u
х = а cos u + 2 = ctg и (a sin и + z cos и), у = a sin и + г cos и,
^ sin и & v ~ у '
у2 (^ _|_ у8) — (ду _|_ ^2 _
поверхность четвертого порядка.
463. R=^{r(u) + p(v)}.
464.
r = \v, a cos uch —- , a sin и ch — L r/ — долгота,
г/ — ориентированное расстояние
от "точки поверхности до плоскости
горлового сечения катеноида
(черт. 142).
465. г
= (a In
— a sin t, a cos £ cos и, д cos ^ sin u
(черт. 143).
466. Уравнение данной
прямой Г\ = {и, 0, Л}. Уравнение
эллипса:
r2 = {a cos v, b sin t/, 0}.
Черт. 143.
Черт. 142.
Далее:
гг — г2 = {и — a cos #, — b sin t>, /г}, и — a cos # = 0, r, — r2 = {0, — £ sin p, /z}*
Искомое уравнение:
r={acosv, bsmv, 0} + X {0, — & sin v, h} = {acosv, b (1 — X) sin vy lh}.
Исключая параметры Х и v, получим уравнение коноида в неявном виде:
('-SXi-r-S-*'
467. п = {а, 0, и], г2 = |о, г», ^J, /-,—r2 = |e, — г;, и — ~},
a-g=0, « = g,r,-r2=={a,-г», 0}, г = {о, *, 0+4*. -». 0} =
или
д2у2 == 2pz (х — а)2.
468. Параметрические уравнения данных окружностей:
гг = {а (1 + cos а), 0, а sin и}, г2 = {0, а (1 + cos v), a sin v}.
216

Находим ч -
гг — г2 = {а (1 + cos и\ — а (1 + cos v), a (sin и — sin v)}.
Имеем:
sin и — sin v = О,
откуда-.
1) v = u-\-2kr,,
2) v = тс — к + 2&тг.
В первом случае имеем:
ri-r2={a(l +COSM), -a(l + cosa), 0}||{1, — 1, 0};
таким образом получаем эллиптический цилиндр
р = {а (1 -j-% cos и), 0, a sin и} + X {1, — 1, 0} = {а (1 -f- cos и) + X, — X, а sin и}.
Во втором случае:
v — тг — и + 2/br
имеем:
г, — г2 — {а (1 + cos и), —а(\— cos и), 0},
и вторая поверхность, составляющая данный цилиндроид, определится
уравнением:
R = {а (1 -f- cos и), 0, a sin а] + X {а (1 -f- cos «), — а (1 — cos и), 0} =
= {л (1 + V) (1 + cos и\ — аХ (1 — cos и), a sin и}.
Исключая параметры X и и, получим:
24 + 22 [(дг __ у)2 _ 2д (Х ц. у)] + 4а2ху = 0.
469.^ = ^,1/. 0], г2 = {-^, 0, tj, ri-r2 = {-^-, и, -„J.
Условие коллинеарности этого вектора и плоскости у — 2 = 0 даёт
u + t/ = 0, t/ = — и, П—r2 = j—, н, и}.
Искомое уравнение: ;
r={S,a'°}+47'"'aWS(1+2^ и(1+*)-Ч-
Исключая параметры ос, получим у% — z2 = 2/?* — гиперболический
параболоид.
470. Уравнение оси Ог имеет вид: гл = {0, 0, к}, уравнение данной линии:
r2 = \b cos v, bsinv, r-9 : [.
2 I b2 cos v sin v J
Находим:
r2 —r1 = l^cosz/, 6sint/, -то = *4>
2 J I />24:os t/sin v J'
a8
m = rr : , r2 — ri = {b cos v, b sin t/, 0},
b2 cos t> sin t> ' l
Г = |о, 0,-rr ~ } + X{6costN bslnv, 0} =
I b2 cos t/ sin v \
= Jx&cost/, X^sint/,-T5 : L
i . b2 cos t/ $in v J
217

Исключая параметры \ и v, получим:
b2xyz=>aB(x2-)-y2).
471. (a + ub — р)я = 0, u = ^j^> a + ub — р =
472. Если вращать окружность х = я + я cos z/, 2 = asinfl вокруг
оси Oz, то уравнение поверхности вращения:
г = {а (1 + cos i/) cos и, а (1 + cos i/) sin и, я sin t/}.
473. Возьмём уравнение данных эллипсов в виде:
r1 = {a, bcosu, с sin и}, г2 = {—я, с cos v, bsinv},
гг — r2 = {2я, 6 cos u — с cos i/, с sin ц — # sin v}, с sin и — b sin i/ = 0,
sin v = j- sin и, cos i/ = ± -,- V b2 — c2 sin2u , rx — r2 =
= J2a, b cos u ± ~ J/^* — c2 sin2« , ol.
Искомое уравнение: /
/?= {a, bcosu, с sin u) -\-v Via, b cos a ± — jA&2 —c2sin2«, Oj-
или
/?=|я -\-2av, bcosu + vl bcosu ± -|- ~|/~62 — Am2*/ j, с sin и}-.
474. Уравнение оси Oz: p={0, 0, v}. Находим:
p — p={u, u2, uz — v}y ug-—v = 0, v = u*> p = {0, 0> us}.
Искомое уравнение:
г = р + ir (p — p) = {0, 0, и3} + v {u, .u2, 0} = {air, иЧг, и3}.
475. г = {6i/, at/ cos u, (b -\-a cos u) (I — v) + я sin и}.
476. Уравнения данных прямых р = {и, 1, 1} и />={1, t/, 0}. Уравнения
•прямой, проходящей- через 2 произвольные' точки этих прямых, имеет вид:
г={1, и, 0}+Х{и, 1, 1}.
Для точки встречи этой прямой с плоскостью xOz имеем:
v+\ = 0, l = — v, г={1, v, 0} — v[u, 1, 1}={1— uv, 0, —г;}.
Эта точка
Значит,
откуда
.
должна
лежать на окружности
х = cos ср, у = 0, z = sin ср.
1 — uv = cos cp, i/ = — sin <p,
1 — cos 9 SP
И- -!sin<p - tg2 •
218

Остаётся составить уравнения прямой, проходящей через точки l — tg — 9l,l\
и (1, — sin <р, 0); имеем:
г={1, — sin ср, 0} + ф{{1, — sin cp, 0}-|_tg-|,l, l}} =
= {l+*(~l + tg|-), -sin? — ф(1-г-яп>), -<|j.
477. г == {a (cos t/ — и sin v), a (sin v + и cos t/), & (и + **)}•
478. с2 (х2 +.у2)2 = д2 (л*2 — у2) (z + с)\
480. r* = f£'£ft[W„]. /
[rurv\
481. Взяв уравнение эллипсоида в виде:.
г = {л cos a cos v, b cos a sin vt с sin и},
получим уравнение подэры в виде:
Г ab2c2 cos и cos #
или
U2c2 cos2 a cos21/ + c2a2 cos2 и sin2 v + д2&2 sin2 и *
a2bc2 cos и sin v
b2c2 cos2 w cos2 v + с2д2 cos2 a sin21/ + я2£2 sin2 u '
я2&2с sin u
62c2 cos2 и cos21/ 4- £2Д2 cos2 и sin2 v + д2&2 sin2
u)
§ 2. Касательная плоскость и нормаль
482. р = ~ = f — — /', # = ^- = /'. Уравнение касательной плоскости
Z-*/=(/~^/')(*-*) + (K-^)/' .
или2=(/— -/'U+1T — все касательные плоскости проходят через
начало координат. Впрочем, это ясно и из того, что данное уравнение
определяет конус с вершиной в начале координат (-г — однородная функция
от л: и у).
483. Касательная плоскость:
kx sin u — ky cos u + vz — kuv = 0;
нормаль:
r= {v cos и + X& sin и, t/ sin u — Ik cos u, ku + X?}.
484. * +1 + ^- = 3.
485. x + y + z = 9. *■■•:.£
219

488*. Пусть уравнение линии С имеет вид: р =,р (s). Уравнение
поверхности: г=>р+Хт, где х — единичный вектор касательной к линии С.
Находим:
:t + X*v, ^=т, ^
5s г ' dX ' dx ds
= btf;
при s = const (т.е. в точках одной и той же касательной) этот вектор имеет
неизменное направление (ибо тогда £== const). Отсюда также следует, что
касательной плоскостью к такой поверхности во всех точках линии С является
соприкасающаяся плоскость этой линии (ребро возврата), и, значит, ребро
возврата указанной поверхности является асимптотической линией этой
поверхности.
489*. Уравнение поверхности:
r = p + b.£-, + X(_„ + «fc |=v, [!£] = (1_X*)»-X«.
Уравнение касательной плоскости:
У
(R — р — Xv) (3 — U$~ Хат) = О,
R (J — Хат) — р (0 — Хат) + Х2а = 0.
Уравнение нормали:
/?=р + Ь + е(Р_>лт).
р'#'
490**. #' -=/Ь 0, ее'р'— 0, р — —^ # = const; радиус-вектор вершины:
г=р— р-^е (см. N° 394).
491*. См. задачу № 489.
Уравнение касательной плоскости:
(/? — р — ХЗ) (v + ^t)==0
или
(/?—р) (v + Xot) = 0.
Уравнение нормали
/?=р + Хр + е (v + Хат).
493*. См. предыдущую задачу.
494*. r = p(s) + #(s)v(s) + Xp(s), ^==1:+^V +
+ /?(— x«c + ep) — Xav=£v+/frP — Xjv, ^t = P,
<ЭХ"
[нЬ<*-^
220

— значит, касательная плоскость к поверхности, образованной осями
кривизны линии С, совпадает с нормальной плоскостью к данной линии.
Нормалью является прямая} проходящая через точку оси кривизны линии С,
параллельная касательной.
> 495*. Г =• р + X (ах + *р), =- = х- + I (lz + «v + *Р — *3v) = т +
+ Х(« +i» = (l + Ь)* + Х*Р, ^=*« + Ч
M.didxJ~
- (7 -|- Хтл — Х-ла) v.
Отсюда следует, что касательной плоскостью к указанной поверхности
является спрямляющая плоскость данной линии, а нормалью к поверхности —
прямая, параллельная главной нормали данной линии.
496*. рг- = т -t1 (— хт + <#) cos cp — cv sin cp =
= (1 — -л cos cp) *c — a sin cpv + с cos cp . 0,
+ pcos
■ v sin <р -
v coscp -|- ^ sin ср.
497*. Если прямая перпендикулярна к касательным, проведённым к двум
сечениям поверхности в данной точке по разным направлениям, то она
Черт. 144.
Черт. 145.
является нормалью к поверхности. В данном случае прямая MN
перпендикулярна к касательной МТ, проведённой к меридиану в точке М, и, кроме
того, прямая MN перпендикулярна к параллели, проходящей лёрез точку М
4 (касательная к параллели (окружность!) есть прямая, перпендикулярная
плоскости чертежа) (черт. 144).
498**. 1) Или существуют несколько плоскостей, проходящих через точку
М и обладающих свойством,.указанным в определении касательной плоскости
(примером может служить поверхность, образованная вращением линии
вокруг касательной к этой линии в её точке возврата первого рода), или:
какова бы ни была плоскость it, проходящая через точку М, найдётся хотя
бы'один конус второго порядка, имеющий с плоскостью только одну общую
221

точку (точку М) и -такой, что какова бы ни была часть поверхности в
окрестности точки М, хотя бы одна точка этой части попадёт внутрь указанного
конуса (черт. 145). 2) Следствие из определения касательной, данного в за»
даче № 95. 3) Пусть
где
Дг = (г„ + «) Дн + (г, + Р) Да,
lim a = lim Р = 0.
да=о ди = о
дг>=о дт>=о
Проведём через точку М плоскость, компланарную векторам ги и rv.
Отложим эти векторы от точки М: МР=гш MQ = rv. Рассмотрим
произвольный конус второго порядка с вершиной в точке М, имеющий с данной
плоскостью только одну общую точку М
(черт. 146), а затем построим две сферы
с центрами в точках Р и Q, которые не
пересекают этого конуса. В силу того, что
пределы а и (3 в точке Ли = Дг/^= 0 равны
нулю, мы можем утверждать, что концы векто-
/£&Гр UN? 0^W\ ров ги + « и /■„ + р, отложенных от точки М>
/тШг- /\—'—чР\ попадут соответственно внутрь указанных
/ ч^у Z^N ш» Л сфер при всех Ди и Дг/, достаточно малых
по абсолютной величине. Значит их
линейная комбинация
*/" = (ги + «) Да + ОЧ, + Р) Дг;
есть такой вектор, что если его отложить от
точки М, то его конец упадёт вне конуса.
Но конец вектора Дг, отложенного от точки
Му определяет точку М! поверхности. Итак,
все точки поверхности в некоторой
окрестности точки М лежат вне указанного конуса. Остаётся доказать, что другой
плоскости, обладающей тем же свойством, не существует. В самом деле,
если мы рассмотрим любую другую плоскость, проходящую через точку Mt
то всегда можно построить конус второго порядка, внутрь которого попадёт
или точка Р, или точка Q. Пусть; например, внутрь построенного конуса
попадёт точка Р. Построим сферу с центром в точке Р, целиком
умещающуюся внутри построенного конуса; положим:
Черт. 146.
Дг = г (и + Д«> v) — г (и, v) = (ги + а) Ды
и выберем о > 0 такое, чтобы | а | < р при всех | Ди !< Ь (р — радиус сферы).
Тогда конец радиуса-вектора Дг, отложенного от точки М, попадёт внутрь
сферы при всех Дг/ =з= 0 и Дм таких, что | Ди | < 5.
499. г=р + Хх. Найдём функцию 1 = 1 (s) такую, что -т- _L **• Имеем:
^=z+U + U*. (T+iT + bv)t = 0, l + X=0, X = — 1, \=C — s.
Искомое семейство ортогональных траекторий г=р-|г(С — s)z. Кривизна
ортогональных траекторий в произвольной точке:
}Л2 + °2
*|С-«|
222

500, Уравнение поверхности 5' имеет вид: p=*(rm)m, где r=-r(u> v)—*
равнение поверхности S, а т — единичный вектор нормали к поверхности S.
аходим:
Рй = (гти) т + (га) тш pv ==^\rmv)m + (rm) m*.
Далее:
V "" 2) 9и = I(Г/П) т ~~ Т }((Г/Ий) m + (rm) m^ ~
= (га) (mur) г- у (гав) (гт) — -^ (га) (гаа) = 0.
Аналогично:
(>-£)*-<
501. Пусть u = u(t), v = v(t) — уравнение линии, делящей пополам углы
между линиями и = const, i/ = const. Вектор, касательный к этой линии: dr=
= radu-\-rvdv. Векторы ги и rv — касательные к координатным линиям,
значит:
(ruda + rvdv) ru _^_ (rudu + rvdv) rv
\r„\ ~ |r„|-
&fa + Fdv Fdu + Grit/
или
y~Edu±yGdv = 0.
502. 1) In (и + 1/""2+я2)±г/ = С.
2) (и + ya' + q'-PS») (t, + "j/V + ei + *i ) = Ci>
ц 4. j/V 4 Л8 _|_ #2 -_ c, (i> + ]/V + a2 + £2).
503 . fa = fo»*] =Gru — Frv ^ = [wfj ^Ery-Frg ^
rarvm И ' rttrT>m Я
504. Уравнение поверхности S*:
р=^г + am,
где m — единичный вектор нормали к поверхности S. Имеем*
Puz==ruJTamuy Pv = r<v + amv
Так как т единичный вектор, то та±т и tn<v± m\ значит, векторы рв и
pv компланарны с векторами ги и rsV.
ею гт dV 0V
505. Пусть -г и * корни уравнения:
fdv \2 , п di/. , Л
<Цаг/+2*»-й+*«=0;
тогда
dtf Sw ~~ сраа ' da "■" bu <p22
223

Условие ортогональности сети
Eduou -\- F{dulv + dvou) + Gdvov = О
принимает вид:
Е'Ы — 2/^12 + С?п = 0.
506ж Считая 1 = 1 (и), имеем:
откуда
X=="-JpWtt(|*|==l);
искомое уравнение:
r=p — e I p'edu.
§ 3. Огибающая. Характеристики. Ребро возврата
507. Пусть w = w(u,v) — внутреннее уравнение огибающей. Тогда
векторы, определяющие касательную плоскость к огибающей таковы:
дг_ дг dw dr . дг_ dw
du "■ dw du dv dw dv
0 dr dr
Эти векторы компланарны векторам -ч— и ^— , определяющим касательную
du dv
dr
dr dr
плоскость к поверхности в том случае, если векторы з~ > з~ и -^ ком-
dr dr dr Л
планарны, т. е. з— е- з— = 0
du dv dw
«ли
dx dy dz
du du du
dx dy dz
dv dv dv
dx dy dz
dw dw dw
= 0.
Это соотношение и определит функцию w = w(u> v). Если при этом
векторы -к- и ч— неколлинеарны, то уравнение r=r(u>v, w{uyv)) есть
уравнение огибающей. В противном случае вопрос требует дополнительного
исследования.
508. Взяв уравнение парабол в виде: у2 = 2рх, 2 = 0 и у2 = 2qzf x = Q,
получим уравнение огибающей в виде у2 = 2рх-\-2qz — параболический
цилиндр с параметром ]/~/?2 -\- q2. '
509. (R—р)2 = #2. Дифференцируя по s, получим: (R — р)т = 0. Отсюда
jR-— р = >.^ -J-^v; так как (/?— р)2 = а2, то \2-\-у.2 = а2 и-можно положить
Х = а cos<p, ]L = a sine
224

так что уравнение огибающей
/? = р + а (0 cos <p + v sin 9).
510. Ребро возврата представляет собой линию, точки которой
получаются при пересечении осей кривизны линии р = р (s) с соответствующими
сферами данного семейства сфер.
511. Уравнение семейства
(х — b cos ср)2 -\-у — b sin ср2 + *8 ~ я2 = О-
Огибающая.— тор: его уравнение получим, исключая ср из уравнений
Р=0и ^ = 0:
дер
— поверхность четвёртого порядка. Ребро возврата в случае а>Ь сводится
к двум точкам:
(0, 0, ± 1/я2 — Ъ2)
или к одной точке (0, 0, 0), если а = Ь.
512. Уравнение семейства:
x2+y2 + z2 — 2игх — 2и2у — 2uz = 0.
Огибающую найдём, исключая и из этого уравнения и( уравнения '
Зи2х -\-2uy + z = 0:
Зх [9х (х2 +у2 + z2) — 2zy]2 + 2у [9х (х2 +у2 + z2) — 2zy] — (I2xz — 4у2) +
+ z(l2xz — fy2)2 = 0.
Ребро возврата найдём, присоединяя к двум указанным выше уравнениям
ещё уравнение:
бих + 2у = 0
или
Отсюда
Зих + У = 0.
--£■
и уравнения ребра возврата:
' 27л:2 (л:2 + у2 + *2) — 4у3 +• 18у2х = 0, у2 — Здгг == 0.
Ребро возврата можно получить и в параметрической форме:
— i 2ма — 6и4 6м5 \
r~~iW + m2+ 1' 9а4 + 9и2 -[Л' 9ц* + 9и8-ИГ
513. Уравнение семейства
(г —р)» = ра
или
г2 — 2гр=0.
15 П. С. Моденов 225

Огибающая определится соотношениями:
г2 — 2гр = 0, гс = 0.
Имеем:
г = Xv + **g, (Xv + ;ig)2 - 2р (Xv + rf) = О,
X2+j*2 - 2pvX - 2pg|J. = О, (X -pv)2 + fr- pg)2 =
= (pv)2 + (pg)2, X = pv + j/V)2 + (pg)2 cos cp,
P = pg + lA(pv)2+(pg)2sin cp,
Г = (pv) v + (pg) g + "[/"(pv)2 + (pg7 (v cos cp -f g sin cp)
— уравнение огибающей. Ребро возврата определяется соотношениями:
г2 — 2гр = 0, гс = 0, rv = 0, откуда
r=2(pg)g.
514. Пусть p = p(s) — уравнение данной линии. Уравнение семейства
соприкасающихся плоскостей
(r-p)g = 0.
Дифференцируя по s, получим
(г —р)т = 0.
Характеристикой является касательная:
(г—р)Р = 0, (r-p)v = 0.
Огибающая: г = р + Хт— поверхность, образованная касательными к данной
линии. Дифференцируя соотношение
(г —p)v = 0
ещё раз, получим:
(r-p)g = 0.
Отсюда и из соотношений
(r-p)g = 0, (г —p)v = 0
имеем:
/- = Р,
т. е. ребром возврата является данная линия.
515. Характеристики: оси кривизны данной линии, огибающая —
поверхность, образованная осями кривизны. Ребро возврата — линия, описываемая
центрами соприкасающихся сфер данной линии.
516. Характеристики — оси мгновенных вращений репера Френе,
огибающая — поверхность, ими образованная. Ребро возврата — огибающая
мгновенных осей вращения репера Френе (см. задачу № 444).
517. rn' + Df = b, r=an + $n'+ X [nn']t a = rn = — D,
0 rn' D'
Уравнение огибающей:
г==_ Dn-Щ- + Х[/ш']
Л'2
(параметры и и X). Характеристики — прямые и = const
226

Ребро возврата определим, разрешая уравнения
rn + D = 0, r/*' + D' = 0, m" + D"=0
относительно г:
_(гп) \п'п,г\ + (т') [п"п] -f (тп) [пп'] =
~~~ nn'ti
_ D [п'п") + П [п"п] + D" [пп']
пп'п"
§ 4. Первая и вторая квадратичные формы. Полная и средняя
кривизны
518. 1) г2 (cos2 vdu2 + dv2\ 2) { (a2 sin2 и + b2 cos2 tt) cos2 *>с?н2 +
-f- 2 (a2 — £2) sin и cos u sin v cos vdudv + { (a2 cos2 и + b2 sin2 и) sin2 z; -(-
+ c2 cos2 о } dv2, 3) -j f v + — \ (a2 sin2 u + b2 cos2 и) d«2 +
+ ^(b2 — a2)sinucosu[v--^ dadv + {-^ ^ 1 — _ j (a2 cos2 и +
В частности, для гиперболоида вращения (а = Ь):
^+;)"-+{7('-i)v;Ki)>.
В ещё более частном случае («равносторонний» гиперболоид вращения,
а = Ь = с):
+ с2 (и2 + I)2 } <*"2 + 2 { я2 (и2 — 1) (v2 — 1) — 4£2н*> +
+ с2 (и2 + 1) (v2 + 1) } dtt<fo + { я2 (и2 ~ I)2 + 4£2н2 + с2 (и2 + I)2 } cfo2],
5) ~ (v — ~Y (a2 sin2 u + b2 cos2 и) du2 +
+ -j (b2 — a2) sinucosulv T\ dudv + j -^f 1 + -^J (a2 cos2 и +
+ ^sin2«) + ^-(l-^)2}^2.
В частности, для двуполостного гиперболоида вращения (д = #):
£(«Ч)'^М^)*+'('Ч)>Л
В ещё более частном случае («равносторонний» однополостный гиперболоид
вращения, а = Ь = с):
£(* - ~V du2 + ^ (l + -yl) dv*> 6) (Psin2и + * cos2 и) *■ <*и2 +
+ 2 (q — р) sin u cos ududv •+ (p cos2 и + q sin2 и + v2) cto3.
* 227

В частности, для эллиптического параболоида вращения (p = q):
pv2du2 + (p + v2) dv2, 7) (р + q + 4v2) du2 + 2{p — q + 4uv) dudv +
+ (P + <I + 4"2) dv2> 8) v2 (a2 sin2 и + b2 cos2 и) ,Л/8 +
-\-2(b2 — a2) v sin и cos и tfr/dt/ + (a2 cos2 и + #2 sin2 и -f- c2) dt/2.
В частности, для круглого конуса (а = Ь)\
a2v2du2 + (а2 + с2) dv2y 9) (a2 sin2 и + b2 cos2 и) dtf2 + dv2.
В частности, для круглого цилиндра
(a = b): d2du2 + dv2,
•°){т('-^+£(' + ^)> + -
В частности, для «равностороннего» гиперболического цилиндра:
т (* + if) du2 + ^ И) (1др2ц2+4/?2) d"2+dvK
519, 57 = (X_s).v, ^ = т, (^ = E = (X_s)-*, - ^ = /^0,
~)2 = G = 1, rfs2 =р (X — s)2*2ds2 + dX2.
520. 1) rfs2 + 2-zedsdl + d\2f
2) v2ds2 4- 2vzpdsdv + p2dv2,
3) fx -f X ^V rfs2 + 2* т<ЫХ + dX2,
4) { (1 — x cos <p)2 + a2 } ds2 + 2adsd? + dy\
5) cp2^2 + (cp/2 _|_ у2) dv2f
6)/W+(l+/'W,
7) (a + b cos v)2 du2 + b2dv2,
8) (v2 + £2) du2 + dv2,
9) {(1 — X*)2 + a2X2 } ds2 + rfX2,
10) (1 +X2G*) ds2 + d)2.
522, Уравнение конуса r= {и cos t/, и sin v, и ctgG},
r, ' cosO
523, e = 2HL — EK, f=2HM-KF, g = 2HN — KG.
524, Если бы было К > 0, то кривизны всех нормальных сечений
поверхности в данной точке были бы положительны, между тем среди нормальных
сечений есть сечение, дающее прямую линию, кривизна которой равна нулю
(сечение, проходящее через нормаль к поверхности и прямолинейную
образующую).
228

k
525. *i = -*2= k2 + Zf2 .
526. // = 4" (*i + *s) = • — 57-, K= *r*2 =
2 v * ' ^ ~' (д.+ ^ + y>)V. ' 'v ~ ™ - (*2 +y + a2)2 '
527. яу 4-jcz = 0, 22 — л;2 = а2.
528. 0.
529. H == c
2|X|x '
530. r=p(s) + up(s), AT =
(1 4- и2а2)2 '
7 + X3a«a U
H:
ds
531. K = ,H
(1+И2а2)0/2
U2 ("ла — на) 4- И?
[(1 — ха)2 + И2з2]2 ' 2 [(1 — mf + и2а2]3/* '
532. Линейный элемент развёртывающейся поверхности г = р (s) + Хт (s)
имеет вид: (1 -f- X2*2) ds2 4~ 2ds dX -j- d№. Рассмотрим плоскую линию p = p(s),
натуральное уравнейие которой ъ = % (s). Пусть R = p(s) + M(s) —
уравнение плоскости (t — единичный касательный вектор к линии p = p(s)). Тогда
линейный элемент плоскости будет иметь тот же вид (развёртывающаяся
поверхность может быть изогнута в плоскость).
cqq* ., I \гагии\ I I \гигит I
•»«• А-= const- '1Гц|3 - Еу% ,
гаи =«"« + Р^ + im, [rurau] *=.Э [rarJ + т [r„m] =?Wm + i [rum],
[rurUuY = Pa W* + Т»Я, T = «ree = I, гиг, = Ea + Ffi, ruarv = Fa + G?,
yry2 v*-" ««' xi *■ * a«' «/ — ш у *-" ww i» 2
»— ^н» ruurv ^и 9 v> P — П72 i у и 9~ ^ ) 9 M I '
Vw.{'
;(/=■„-i^_i-F£„ J" + EV
1 £a/*
m:
_r rl
G (f,- ^Gu)-jFGv )+G№
xj = const
Аналогично найдём
534*. Воспользуемся деривационными формулами Гаусса:
г1а = Г12Г! 4- Г|аг8 4- *iSm,
/*22 = Г|а Гх 4" Г222Г2 4" #22^,
дг д2г
гдеГ1 = ^Г'Г11==^ит'д-
Отсюда [гл,] = Г2и [гЛ] 4" *ц [^ш] = I^Vsw+Ju [^т], [iVn]^ (Г2и)2£ +
-\~ biign> отсюда находим -x.v = const. Аналогично получаем и выражение
для хи = const.
. . 229

сок* - г1^цГщ
535 * а-= const" [г1Гц]. •
Воспользуемся деривационными формулами:
г 12 = Г}ЯГ! + Г212г2 + Ьат,
г22 = Г^л + Г|2г2 + £22/я,
m1= — b\rl — b\r2i
m2 = —b\ri — blr2. .
Находим: for,,] = l/gT^m + *и |r,m], г,11 = (Г}1), Л + Г^, + (ГЬ), г2 +
+ Г^Гц + (Mi w + Ьитг = (Г1Л rt + ГЬ (Г}Л + Г?л + Ь1Хт) +
+ (ГЬ^ г2 + Т\х (1*Л + Г»Л + Ь1Ёт) + (Mi ™ +
+ Ь1Х (- *}г, - ^г.) = {(Г^), + (ТЫ + Г^Г}8 - *„*}} г, +
+ {ГЬГЬ + (ГЬ)! + ГЬГ?, - *„*«} г2 + {Г1^п + Ч А, + (Mi} m пгпгш=
= Vg?\i {Y\ibn + Г? А* + (h&Y-Vgbn {Г11Г11 + (Г?^ + ГЦ*, - bnb\].
Отсюда
_ Уёгь {Г1Л,+гу„ + (W
Vg*.. {гьи,+(г?.),+гьгь - мп
Аналогично получим:
«- const fW + Wg*
_ У>«ы {TJ Ji. 4- ОЪЬ + ГШ. - *M*J}
536*. r* = r+ am, r% = ra + ama, r% = r„ + sw„ £* = if = ^ +
+ 2aramB + a<, = £ — 2aL + ее = £ — 2aL + a2 (2//Z — EfQ;
аналогично находим:
F* = (l — a*K)F + 2a(aH—l)M, G* = (l -a2/C) G + 2a(ati— 1) ЛГ,
L* = aEK+(l—2aFi)L, M* = M-a(27H//^-/7/0, N* = N— a(2NH— GK).
К
%XJi •
538*.
53S*.
540*.
541*.
'V -
//* =
r* =
/c* =
//* =
" 1 — 2aH + я2Л:
H — aK
~ 1 — 2ati-\-a*K
= 4№ = const.
=-\Vk.
542*. Из условий /7 = 0, Л1 = 0 следует: /7* = Q, М* = 0. Кроме того,
задача допускает и не аналитическое решение; в самом деле: параллельные
поверхности имеют общие нормали, а линии кривизны на одной из них
высекаются развёртывающимися поверхностями нормалей. Отметим, что
утверждение задачи 543 содержится в здесь доказанном.
230

§ 5. Теорема Менье
545. Применить теорему Менъе. Возьмём исследуемую точку за начало
координат, а касательную плоскость к поверхности этой точки — за
плоскость хОу. Пусть z =/ (х, у) или z = у (апх2 + 2а12ху + а22у2)-{-... —
уравнение поверхности в этой системе. Тогда уравнение поверхности, о которой
говорится в условии задачи, будет иметь вид:
(*■ +У2 + **) (ваУ1 - 2а12ху + а22х*) = z(x*+ у2).
546. Асимптотические.
547. На окружности.
§ 6. Омбилические точки
549. Рассмотрим произвольную точку М меридиана: проведём плоскость
через эту точку и касательную к параллели (окружность); проведём в этой
же точке через ту же касательную нормальное сечение. Центр Р кривизны
этого сечения (главного!) по теореме Менье лежит на оси вращения. Второй
линией кривизны, проходящей через точку, является меридиан. Таким образом,
если (и только в этом случае!) центр кривизны меридиана в точке М лежит
на оси вращения, то точка М — омбилическая. Отсюда геометрический
способ построения омбилических точек поверхности: строим эволюту меридиана
и находим точки Ръ Р2, ... встречи этой эволюты с осью вращения. Пусть
Ми М2> ... — соответствующие им точки эвольвенты (меридиана). Тогда
параллели, проходящие через эти точки, состоят из омбилических точек.
550. Омбилические точки описываются вершинами синусоиды и только
этими точками.
551. Две омбилические точки — точки встречи поверхности с осью
вращения, так как ось вращения встречает эволюту эллипса, от вращения
которого получается эллипсоид только в двух точках.
552. К*-Н = хЗД -1 («! + *2)2 = \ (xi - *2)2.
553. (о,±У7(р^,"+-£^).
mi) (s^^), »(**..*»*£).
где R=\f"я4 + & + с\
§ 7. Линейчатые и развёртывающиеся поверхности
557. г = р + ^ + #!* — уравнение поверхности, «параллельной» данной.
Эта поверхность линейчатая (уравнение прямых линий 5 = const). Считая
Х=Х($), находим: -г- = z + Xx -\- Xkv — aav. Из условия -г- || х находим:
Ъ. — аа = 0, Х = — и уравнение ребра возврата: г = р+ — z-\-a§.
558. Указанные касательные лежат на плоскости, касающейся
поверхности по прямой PQ.
559. *£ ^-(^У=0.
554.
?И ?! — (
дх2 ду2 \
дх ду)
231

560.
d2F d2F d2F dF
dx2 dxdy dxdz dx
d2F d2F d2F dF
dy dz dy
d2F dF
~dz~
dy dx dy2
d2F d2F
dzdx dzdy
dF dF
dz2
dF
dz
0
= 0.
I dx dy
561*. Пусть уравнения данных линий С и Ct имеют вид: г = г(и)
и R = R(v). Положим e = r(u) — R(v). Считая v = v(u), находим
необходимое и достаточное условие того, что поверхность р = r-f- le будет
развёртывающаяся:
r'u(r-R)(r'a-R'„fu)^0
К С-
:**s-*
Отсюда — либо v = const (соответствующая поверхность при этом-
ческая), либо r'u (r — R)R'v = 0.
Значит, векторы
dr
du'
r — R и
dR
dv
компланарны, а так как линии С и Ct лежат в параллельных плоскостях, та
dr dR
— и -г- коллинеарны.
562*. Пусть / — прямая, по которой пересекаются плоскости линий С и Ct.
Из произвольной точки М прямой / проводим касательные MP и MQ
к линиям С и d. Прямая PQ, соединяющая точки касания, и будет
прямолинейной образующей, проходящей через
линии С и Cv При движении точки М
по прямой / прямая PQ опишет раз- ^^
вёртывающуюся поверхность,
проходящую через линии С и Сх (черт. 147).
Черт. 147.
Черт. 148.
563*. Пусть С* — линия, по которой пересекаются развёртывающиеся
поверхности, образованные касательными к линиям С и Съ а М — любая
точка линии С*. Проведём из точки М касательные MP и MQ к линиям С и Ct.
Прямая PQ является образующей развёртывающейся поверхности,
проходящей через линии С и С*. При движении точки М по линии С* прямая PQ
опишет развёртывающуюся поверхность, проходящую через линии С И Ci
(черт. 148).
232

564*. Да.
565*. 1) Касательная к винтовой линии, лежащей на геликоиде, не
пересекается с осью геликоида. 2) Будем рассматривать однополостный
гиперболоид как линейчатую поверхность, проходящую через горловой эллипс и
одну из прямолинейных образующих /0. Пусть Р и Q — точки встречи любой
образующей второй серии с выбранной образующей и с горловым эллипсом.
Тогда касательная к эллипсу в точке Q не пересекается с образующей.
Аналогично устанавливается неразвёртываемость гиперболического
параболоида.
566**. Развёртывающуюся поверхность можно определить как поверхность,
образованную касательными к пространственной линии (и ещё конусы
и цилиндры). Это определение проективно-инвариантно.
567**. Линиями кривизны развёртывающейся поверхности являются
ортогональные траектории прямолинейных образующих (и сами образующие).
Крушение ортогональной траектории г = р-{~ (к — s)т:
'О,
(*2 + а2)(с — s)-a
откуда — = const, т. е. ребро возврата есть линия откоса, а поверхность
образована касательными к линии откоса. Обратно: для любой поверхности,
образованной касательными к линии откоса, все линии кривизны плоские
(с*=0).
568**. Пусть гх = р (а) + \е (а) и г2 = р (м + Дм) + ре (и + Дм) — радиусы-
векторы точек Р и Р. Тогда г2 — rt \\ [е (а) е (и -f- Дм)] = [екё\,
Др-|-^£(м + Дм)— \е(и) — % \e\e\. Умножая обе части этого соотношения
скалярно на вектор [е (и -f- Дм) [£Д#]], получим:
[Дре (и + Дм)] [еЬе] — 1\е (и) е{а + Да)] [еЬе] = О
или
[Дрг (а + Дм)] \e\e\ — X \e\e\* = О,
откуда
Х =
[Др# (и -f Дм)1 \еке\
\e\e\
и следовательно:
R=p+ nip '
, fP'^J \ee'\ *
таково уравнение стрикционной линии. В частности, если вектор е —
единичный, то уравнение упрощается:
р'е'
569**. Кратчайшее расстояние между образующими
Г\ = р (и) + )е (и) и г2 = р (а + Дм) + ре (и + Дм)
равно:
|ДреД# | _
Синус угла между указанными образующими
YJelef
sin о = , . , . JA , .
/ | e | \e + Д* | -
Отсюда
233

о _\^pe^e\ -\е\ \e + ^e\
sin © [е\е^
и, значит,
« = lim —: = f тт^ .
д«=о sin© [ee'f
В частности, если вектор е — единичный, то
е'2 *
570*. Перепишем данное уравнение в виде:
r={uYI, -uV7> 0} +v{ \fj, V~q~> 2м}.
Полагая
9={uVJ> —uVT, °b e = {VJ> V~7> Щ,
найдём
P'={VJ> ~VJ,b}> e'={0, 0, 2}
и т.д.
ь_\р'ее'\е*^УЙ(р + д + №)
[ee'f p + q
Стрикционная линия определяется уравнением:
Г 2pVJ Uf~2qVJ 2u>P^]
н I /> + ? /> + ? p + ql
. (парабола).
571*. k = 0. Стрикционная линия — ребро возврата.
572**. Дифференциальное уравнение семейства «S* есть уравнение типа
Риккати.
573**. Pl==p + ief p2==9 + (i + i)e, х = -££(|*| = 1).
Находим:
дрх — о'А-\е' д-2±-е
и аналогично
Отсюда
Полагая
находим:
234
«!«• = [ер']* + (2Х +1) [*pl И'] + X (X + 1) [ее? =
р'=\е-\- \ье' -f- ^ 1^Ъ

так что
т = (е,У+ &? + &£_(в?г. №
е е' е
(o'ee'Y
-- —-г" > Ni^sl = [[ер'] [ее']] = е (ер'е'),
574. Стрикционная линия — ось геликоида. Для определения параметра
распределения возьмём уравнение геликоида в виде:
г = { О, О, Ы } + v { cos и, sin и, 0}.
. Полагая
р = { 0, 0, Хм }, £ = { cos и, sin и, 0 },
найдём:
,2
578. // = 0.
577**. Геликоид.
§ 8. Линии кривизны
578. v = ± Л ch (и — С) (С = const).
579. Цилиндры
(x + V'rfHb**) Or + l/^TTJ^C! их+>л^Ч:^=СЛ^+1^^Т7)
пересекают данную поверхность по двум семействам линии кривизны.
580. Внутренние уравнения семейств линий кривизны:
p + ? + 4a» = Ci(p + ? + 4i>") и (р + ^ + 4и2)0?+^ + 4^)==С2.
581. х2 — ^ = ™ Л ,—— ; эти гиперболические цилиндры пересекают
С рС + #
~х2 v2
эллиптический параболоид \~ — = 2z по линиям кривизны.
582. Нормали к сфере вдоль любой линии, расположенной на сфере,
образуют коническую поверхность, т. е. поверхность развёртывающуюся.
Нормали к плоскости вдоль любой линии, расположенной на плоскости,
образуют цилиндрическую поверхность, т. е. развёртывающуюся.
583. Г = р (S) + ыЗ (s), adit2 + (cil — * — -/а2 и2) du ds — с (1 + а2и2) ds* = 0.
584. г = р (s) 4- w> (s), cdtf2 + (на + и2<™ — и2*а) du ds +
+ а (2и% — и2*2 — и2а2 — 1) ds2 = 0.
585. р = г + а/и, Ри = ги + атй> р^ = rv + amv.
Отсюда р^ = а%тат^. Для линий кривизны в силу формул Родрига ти и mv
соответственно коллинеарны ги и rv, значит, Z7* = рдр^ = 0.
586**. Прямолинейные образующие и их ортогональные траектории.
587. Меридианы и параллели. Нормали к поверхности вдоль меридиана
лежат в одной плоскости (развёртывающаяся поверхность). Нормали к
поверхности вращения вдоль параллели образуют конус с вершиной на оси
вращения (или цилиндр) — также развёртывающаяся поверхность.
588*. 1) Нормали к поверхностям Sx и 52 вдоль линии С образуют
развёртывающиеся поверхности. Линия С является ортогойальной траекторией
образующих каждой из этих развёртывающихся поверхностей. Значит,
образующие одной поверхности получаются поворотом образующих другой вокруг
точек линии С на один и тот же угол.
, 235

2) Пусть С — линия кривизны по поверхности 51# Нормали к 5j здо'ль С
образуют развёртывающуюся поверхность. Нормали к S2 получаются
поворотом указанных нормалей к 5, на один и тот же угол и, значит, также
образуют развёртывающуюся поверхность.
589. Пусть / — какая-нибудь прямолинейная образующая
развёртывающейся поверхности, а г. — плоскость, касающаяся поверхности по
образующей /. Рассечём данную развёртывающуюся поверхность параллельными
плоскостями. Эти плоскости рассекут плоскость тс по параллельным прямым,
касающимся линий сечений в точках прямой /. Отсюда следует, что главные
нормали линий сечения в точках прямой / параллельны, и так как все они
пересекают прямую /, то они лежат в одной плоскости р-. Рассмотрим
огибающую семейства плоскостей р. Пусть М — точка, в которой построенная
развёртывающаяся поверхность (огибающая) встречает главную нормаль
одной из линий сечения, тогда плоскость а линии сечения рассечёт
огибающую по прямой, касательной к линии С (в точке М), по которой плоскость а
пересекает указанную развёртывающуюся поверхность. Значит, линия С —
эволюта рассматриваемого плоского сечения, и таким образом все эволюты
плоских сечений лежат на развёртывающейся поверхности — огибающей
семейства плоскостей р-.
590*. Любая линия на поверхности сферы (или на плоскости) является
линией кривизны сферы (плоскости). См. задачи № 582 и № 588.
592**. Поверхность канала есть огибающая семейства сфер постоянного
радиуса, центры которых расположены на некоторой линии С Окружность,
по которым нормальные плоскости линии С рассекают соответствующие
сферы, обладают тем свойством, что касательная плоскость к сфере и
касательная плоскость к поверхности канала совпадают. Значит, на основании
теоремы Иоахим-Шталя эти окружности и будут линиями кривизны
поверхности канала. Второе семейство линий кривизны получается в пересечении
поверхности канала с развёртывающимися поверхностями, образованными
нормалями к линии С, так как эти нормали будут и нормалями к
поверхности канала; последнее обстоятельство объясняется тем, что линия С и
линия, по которой пересекается упомянутая развёртывающаяся поверхность
с поверхностью канала, являются ортогональными траекториями
прямолинейных образующих развёртывающейся поверхности (отрезки
прямолинейных образующих развёртывающейся поверхности между двумя её
ортогональными траекториями равны).
593. Линиями кривизны. Ортогональными траекториями прямолинейных
образующих развёртывающегося геликоида являются эвольвенты винтовой
линии.
594. Линия касания на основании теоремы Иоахим-Шталя — линия
кривизны развёртывающейся поверхности, а одно из семейств линий кривизны
развёртывающейся поверхности есть семейство ортогональных траекторий
прямолинейных образующих.
595**. te = 0 (| * | = 1), et + em = 0.
Линия касания — ортогональная траектория прямолинейных образующих;
значит, et — Q, откуда еп = 0. Из условий et = Q, en = Q следует, что
вектор е перпендикулярен соприкасающейся плоскости данной линии.
596**. Соприкасающаяся плоскость ребра возврата касается сферы (см.
предыдущую задачу). Касательная же плоскость к конусу проходит через,
центр сферы и содержит касательную к ребру возврата. Значит,
касательная плоскость к конусу перпендикулярна соприкасающейся плоскости ребра
возврата в соответствующей точке/
§ 9. Асимптотические линии
597. Прямолинейные образующие.
598. и = С19 u — 2v= C2.
599. Геликоид — минимальная поверхность. Значит, асимптотическая сеть
на нём ортогональна. Одно семейство состоит из прямолинейных образую-
236

щих, другое — из винтовых линий, так как винтовая линия на прямом
геликоиде пересекают его образующие ортогонально.
600. Она ортогональна.
601. Одно семейство и — const (прямолинейные образующие). Отыскание
второго семейства сводится к интегрированию дифференциального уравнения
типа Риккати.
dv . 1 е'е'е в , 1 е"р'е-\-р"е'е , 1 р"р'е А
— 1)- _L_ 1 1—. 7J-+- - -— = О
du^ 2 е'р'е ^2 е'р'е ^2 е'ре
602**. Для асимптотической линии Ь = т,
f = **, **=-ап,№)'= * = *£■ Но lll-VJ-U+K. 1 = 0.
ds ds ' ds \ds ) I
Для асимптотической линии 11 = 0, значит, — = — ^откуда с2 = — К.
603**. Асимптотическая линия — это линия, расположенная на
поверхности и обладающая тем свойством, что касательная плоскость к
поверхности в любой её точке является соприкасающейся плоскостью линии
в той же точке. Это определение проективно-инвариантно.
604*. а
605*
1 + и2°2'
о
(\—ш)2-\-и2з2'
606*. Дифференциальное уравнение асимптотической сети:
(5u2v + v2) du2 — 2иЧи dv = 0
даёт: 1) и = const (прямолинейные образующие).
2) (5и2 v -f- v2) du — 2u3dv = 0 —дифференциальное уравнение Бернулли.
Его интеграл даёт второе семейство асимптотических:
u{v-\-u2f — c2v2 = 0.
608*. Линии кривизны и ±v = const. Асимптотическими линиями являются
координатные линии. Полная кривизна:
*—.—'—г-
3И* + За2 + -g-
Средняя кривизна И = 0 (поверхность минимальная).
§ 10. Геодезические линии.
609**. Возьмём уравнение развёртывающейся поверхности в виде:
r=p(s) + u-(s),
а уравнение геодезических линий в форме Гаусса:
2WdQ = -^ (Eudu + E^ds) + Esds — 2Fudu — Guds,
где G—угол, под которым геодезическая пересекает прямолинейную
образующую s = const: получим:
d3 = — *ds, e = c— fxds. Но tg9= g Wd* .
J b Edu f Eds
Значит,
du ' , ,
— линейное дифференциальное уравнение первого порядка (интегрируется
в квадратурах).
237

610**. Положим г= {и cos t>, и sin yy и}. Возьмём уравнение
геодезических линий в виде:
2^s(Fu + Gv)==Evu2 + 2Fvuv + Gvv\
получим: 2 (u2v)'= 0, и2 у = С. Так как ds2-=2du2 -\-u2dy2, то «W =
= С2 (2du2 + u2dv2), откуда уравнения геодезических линий:
( С cos v С sin у С \
г=\ . Сх±у' . С1±^> . d±tf I.
i sin * _ sin * sin х__ (
I 1/^2 ^2 /2 J
611**. Взять уравнение геодезических в виде:
2 ~ (Fu + Gif) = Evu2 + 2Fvuv + Gvi>2,
Cdu
3 + /i2) (и2 + h2 — C2)
612**. Возьмём уравнение конуса в виде: r = ttp(y) и будем считать,
что | р [ = 1, | р'| = 1 (t/_дуга). Применяя уравнение Гаусса, получим
уравнения геодезических линий в виде:
Г=~-~Ф Г Р(») •
sin (С — у) г v
613**. По теореме Менье радиус кривизны R линии С в точке М равен
проекции радиуса геодезической кривизны Rgi = — ] в соприкасающуюся
плоскость линии С, т. е. R = \ Rg cos G |; вектор е = [пя] — единичный вектор,
лежащий в касательной плоскости к поверхности и ортогональной линии С;
п — единичный вектор главной нормали линии С;
| cos 6 | = \еп |, %g= а | cos 91 = а | еп ] = | et\—\ttm \ = | тга
614*.
Sa'-
u2 + a2
615\ «y= « + «*'+«».
У (l+02*2)72
616**. 0.
617**. Применим вторую формулу Френе: п = — *t-{-ab.
гт « ч /dn\2 (dm\2 III , , 9
Для геодезической линии (т = п): [-*-) ==1"Т") = -т- = *2 + а2;
при # = 0 имеем: — — — Af, значит: y2-fa2 = — A;.
* \^У HPs'* IP's3
и т. д.
619.
620. Ы,-const = ^ д^Л
У EG ov
V g)u=*const |/-gg 0>U
238

ОГЛАВЛЕНИЕ
Глава I
ВЕКТОР-ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА
Стр.,
Глава II
ПЛОСКАЯ ЛИНИЯ
§ 1. Касательная и нормаль 22
§ 2. Точки перегиба. Выпуклость и вогнутость 26
§ 3. Исследование и построение линий 29
§ 4. Подэры * 30
§ 5. Огибающие 31
§ 6. Соприкосновение плоских линий 34
§ 7. Кривизна 39
§ 8. Эволюта и эвольвента 41
§ 9. Длина дуги 42
§ 10. Натуральные уравнения 43
§ 11. Применение формул Френе 44
Глава III
ПРОСТРАНСТВЕННАЯ ЛИНИЯ
§ 1. Касательная. Главная нормаль. Бинормаль. Нормальная
плоскость.. Соприкасающаяся плоскость. Спрямляющая плоскость.
Кривизна. Кручение 52
§ 2. Применение формул Френе 57
Г л а вш IV
ПОВЕРХНОСТЬ
§ 1. Составление уравнений поверхностей 68
§ 2. Касательная плоскость и нормаль 71
§ 3. Огибающая. Характеристики. Ребро возврата 73
§ 4. Первая и вторая квадратичные формы. Полная и средняя
кривизны 74
§ 5. Теорема Менье 76
§ 6. Омбилические точки 77
§ 7. Линейчатые и развёртывающиеся поверхности 77
§ 8. Линии кривизны . . . 79
§ 9. Асимптотические линии 80
§ 10. Геодезические линии 81
Ответы и решения . 82

Редактор Л. А. Борисов
Техн. редактор Н. Н. Шахова
Подписано к печати 13/VII 1949 г. А - 01247.
Печатных листов 15. Учётно-издат. листов 17,97.
Заказ JVs 102.
Отпечатано в тип. Н-38с матриц2-ой типографии
„Печатный Двор" имени А. М. Горького Глав-
полиграфиздата при Совете Министров СССР.
Лецинград, Гатчинская, 26.