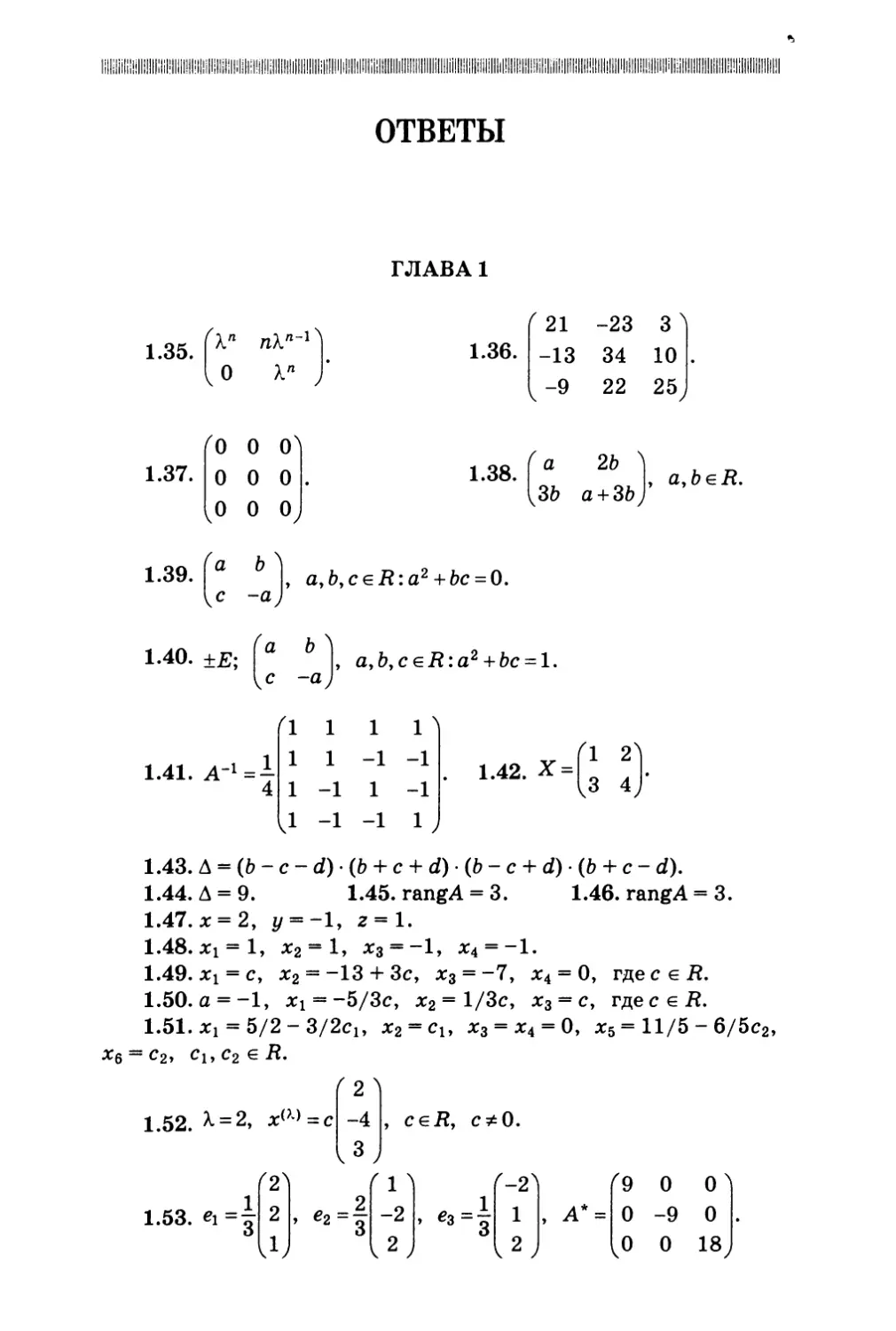И. А. Соловьев, В. В. Шевелев
А. В. Червяков, А. Ю. Репин
ПРАКТИЧЕСКОЕ РУКОВОДСТВО
К РЕШЕНИЮ ЗАДАЧ
О ВЬ СШЕЙ МАТЕМАТИКЕ
Линейная алгебра
Векторная алгебра
Аналитическая геометрия
Введение в математический анализ
Производная и ее приложения
ЛАН~ь

И. А. СОЛОВЬЕВ, В. В. ШЕВЕЛЕВ,
А. В. ЧЕРВЯКОВ, А. Ю. РЕПИН
ПРАКТИЧЕСКОЕ
РУКОВОДСТВО
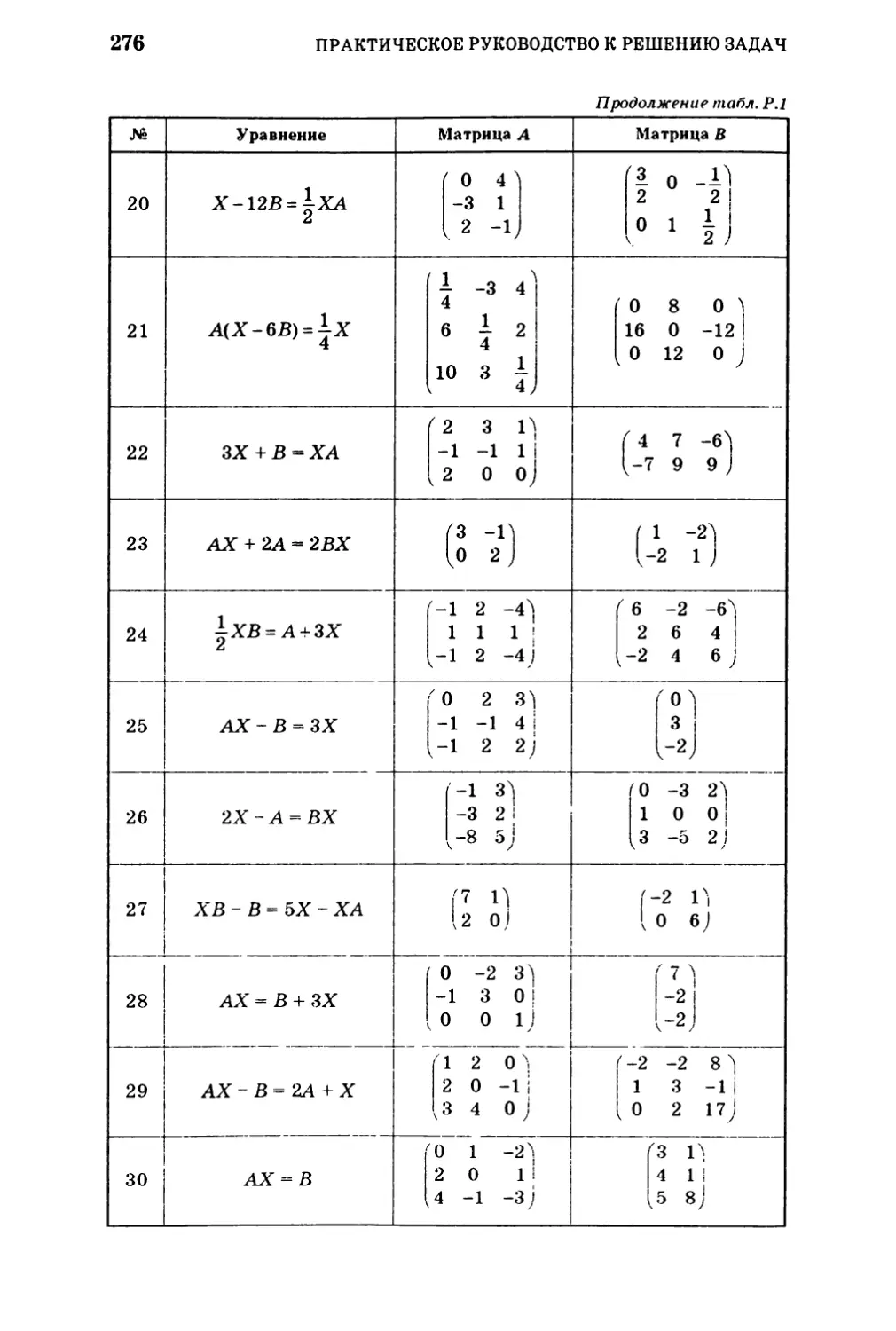
К РЕШЕНИЮ ЗАДАЧ
ПО ВЫСШЕЙ
МАТЕМАТИКЕ
ЛИНЕИНАЯ АЛГЕБРА
ВЕКТОРНАЯ АЛГЕБРА
АНАЛИТИЧЕСКАЯ
ГЕОМЕТРИЯ
ВВЕДЕНИЕ
В MATEMATN×ÅÑÊÈÈ
АНАЛИЗ
ПРОИЗВОДНАЯ
И ЕЕ ПРИЛОЖЕНИЯ
Учебное пособие
САНКТ-ПЕТЕРБУРГ - МОСКВА ° КРАСНОДАР
2007

ББК 22.1я7
С 60
С 60
IS ВХ 978-5-8114-0751-4
Учебное пособие посвящено практическому освоению теоре-
тического материала по следующим разделам высшей математи-
ки: векторная алгебра, аналитическая геометрия, элементы ли-
нейной алгебры, введение в математический анализ, дифферен-
циальное исчисление функции одной переменной.
Предлагается последовательное изучение методов решения ос-
новных задач по каждому разделу. Имеется большое количество
задач для самостоятельного решения, которые снабжены ответа-
ми. Пособие содержит расчетно-графические задания по всем рас-
смотренным темам.
В пособии излагаются основы высшей математики, поэтому
оно может быть полезным для студентов инженерных специаль-
ностей университетов, академий, технических, экономических,
финансовых, экологических и сельскохозяйственных вузов как
очной, так и заочной или дистанционной форм обучения. Расчет-
но-графические задания могут использоваться преподавателями
в качестве заданий для самостоятельной внеаудиторной работы.
Предполагается выпуск дальнейших частей учебного пособия.
ББК 22.1я7
Обложка
А. Ю. ЛАПШИН
Охраняется законом РФ об авторском праве.
Воспроизведение всей книги или любой ее части
запрещается без письменного разрешения издателя.
Любые попытки нарушения закона
будут преследоваться в судебном порядке.
© Издательство «Лань», 2007
© И. А. Соловьев, В. В. Шевелев,
А. В. Червяков, А. Ю. Репин, 2007
Ос Издательство «Лань»,
художественное оформление, 2007
Соловьев И. А., Шевелев В. В.,
Червяков А. В., Репин А. Ю.
Практическое руководство к решению задач по
высшей математике. Линейная алгебра, векторная ал-
гебра, аналитическая геометрия, введение в матема-
тический анализ, производная и ее приложения: Учеб-
ное пособие. — СПб.: Издательство «Лань» 2007.—
320 с.: ил. — (Учебники для вузов. Специальная ли-
тература).

пРедислОВие
В соответствии с Государственным образовательным стан-
дартом учебными планами всех математических, техни-
ческих, экономических и многих других специальностей
предусмотрено изучение основ высшей математики, кото-
рые затем используются в прикладных дисциплинах. Пред-
лагаемое учебное пособие предназначено в первую очередь
для студентов инженерных специальностей, оно может
быть полезно и для студентов экономических и других спе-
циальностей как очной, так и заочной и дистанционной
форм обучения.
В настоящем пособии осуществлена попытка соединить
воедино материалы, связанные с теоретическими сведения-
ми, подробными решениями типовых задач, а также задач
повышенной трудности, задач, снабженных только отве-
тами для самостоятельной работы как в аудиториях, так и
вне аудиторий. Кроме того, приведены контрольные рас-
четно-графические задания, предназначенные для само-
стоятельной внеаудиторной работы. Среди рассмотренных
задач имеется как набор основных традиционных, кото-
рые необходимы для начального освоения теоретического
материала, так и новые задачи, ранее не входившие в су-
Шествующие сборники задач.
В первой главе вводятся необходимые теоретические
сведения из линейной алгебры, рассматриваются задачи,
~вязанные с матричным исчислением, определителями,
решением систем алгебраических уравнений, элементами
линейных преобразований.

ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
Во второй главе излагаются основные понятия вектор-
ной алгебры и методы решения задач по этому разделу.
В третьей и четвертой главах подробно излагаются
приемы применения понятий векторной алгебры к реше-
нию задач аналитической геометрии на плоскости и в про-
странстве. Рассматриваются также и специфические зада-
чи этого раздела, связанные с кривыми второго порядка, а
также поверхностями.
Пятая глава посвящена применению теории пределов,
исследованию свойств непрерывных функций.
В шестой главе рассматриваются задачи, связанные с
понятием производной, а также применением этого поня-
тия к исследованию свойств функции одной переменной.
Предложены оригинальные постановки задач, связанные
с устойчивостью операции дифференцирования.
В конце учебного пособия приводится большой набор
расчетно-графических заданий, предназначенных для са-
мостоятельной работы по всем представленным разделам.
Каждое отдельное задание содержит по 30 задач.
В конце пособия представлены ответы к задачам для
аудиторной и внеаудиторной работы для самостоятельно-
го решения.
Предполагается выпуск дальнейших частей учебного
пособия.

1.1.
МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ
Определение 1.1. Матрицей размера т &g ; lt  (т х и-
цей) называется прямоугольная таблица чисел или функ-
цийа;,, где~ = 1,2, ..., m; j = 1,2, ..., и, состоящаяизстрок
и столбцов.
ап а1 ... а1„
а21 а22 ". аа
=((а;, (!.
(1.1)
ащ] ащ2 ". ащд
Здесь а;; — элементы матрицы, i—
номер строки, j — номер столбца, числа.
Нумерация строк и столбцов матрицы по-
казана на рисунке 1.1.
Определение 1.2. Размерами матри-
цы называется совокупность чисел (т; n),
первое из которых m обозначает число
Рис. 1.1
строк матрицы, а второе и — число
столбцов.
Если число строк матрицы не равняется числу столб-
цов, т. е. т w и, то матрица называется прямоугольной,
если же т = и — квадратной:
ап а2 ... а~„
а2~ а22
(1.2)
ГЛАВА 1
ЭЛЕМЕНТЫ
ЛИНЕЙНОЙ АЛГЕБРЫ
1 -э 2 -э 3 ... n
1
2
1
3
1
тп

ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
В случае квадратной матрицы (1.2) размеров (и; n) ис-
пользуется термин «матрица порядка и».
У квадратной матрицы (1.2) различают главную диа-
гональ, образуемую элементами а11, а22, ..., а„„, и побоч-
ную диагональ, образуемую элементами а1„, а2„ i ..., а„1.
Определение 1.3. Квадратная матрица, все элементы
которой, стоящие на главной диагонали, отличны от нуля,
а все остальные элементы (недиагональные) равны нулю,
называется диагональной матрицей.
Определение 1.4. Диагональная матрица, все диаго-
нальные элементы которой равны единице, называется
единичной матрицей и чаще всего обозначается буквой Е.
Таким образом,
1 0 ... 0
0 1 ... 0
0 0 ... 1
Вектором-столбцом или вектором-строкой называют-
ся матрицы, состоящие соответственно из одного столбца
или одной строки:
Х=
~=(У1 Уз "y„).
(1 З)
Xm
Очевидно это матрицы размеров (т; 1) и (1; n) соответ-
ственно.
Определение 1.5. Матрица, у которой все элементы рав-
ны нулю, называется нулевой матрицей или (нуль-матри-
цей) и обозначается символом О.
ДЕЙСТВИЯ НАД МАТРИЦАМИ
А=В, если а;,=Ь... i=1,2,...,т, j=1,2,...,n. (1.4)
Определение 1.6 (равенство матриц). Две матрицы
А = (а;,(( и В = Ilb ill считаются равными, если эти матрицы
имеют одинаковые размеры и все их соответствующие эле-
менты совпадают, т. е.

1 ЛАВА 1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
с;,=а;,+Ь;,.
(1.5)
Обозначение суммы матриц: С = А + В.
Определение 1.8. Произведением матрицы А = ~~аЦ (~ =
= 1, 2, ..., т; у = 1, 2, ..., n) на вещественное число Х назы-
ваетсяматрицаС = ll~~,ll(i = 1,2, ..., т;у = 1,2, ..., и)техже
размеров, элементы которой равны
(1.6)
с;; = Ха;, (i = 1, 2, ..., т; g = 1, 2, ..., n).
Обозначение: С = ХА или С = АХ.
Определение 1.9. Матрица В = ~~ЬД (т = 1, 2, ..., т; у = 1,
2, ..., n) называется транспонированной по отношению к
матрице А = ~~аД (i = 1, 2, ..., и; у = 1, 2, ..., т), если строки
матрицы А превращаются в столбцы матрицы В с сохране-
нием порядка их следования: b;, = а;, для всех i = 1, 2, ...,
т; j = 1, 2, ..., и. Транспонированная матрица обозначает-
ся символом Ат. Переход от матрицы А к матрице Ат назы-
вается транспонированием.
СВОЙСТВА ОПЕРАЦИЙ СЛОЖЕНИЯ МАТРИЦ
И УМНОЖЕНИЯ МАТРИЦЫ
НА ДЕЙСТВИТЕЛЬНОЕ ЧИСЛО
1. А + В = В + А — переместительное свойство.
2. (А + В) + С = А + (В + С) — сочетательное свойство.
3. ).(А+ В) = ХА + Х — распределительное свойство от-
носительно суммы матриц.
4. (Х. + р)А = ХА + рА — распределительное свойство от-
носительно суммы чисел (Х и р).
5. (Хр)А = л(рА) — сочетательное свойство относитель-
но числового множителя.
6. (g+ В)т Ат+ Вт
7. (ЛА)т = ~ Ат
8. А + О = А — сумма матрицы А и нулевой матрицы О.
&g ;. ля каж ой матр ц А существ ет противопол
ная матрица, которая удовлетворяет равенству А+ А = О.
Определение 1.7. Суммой двух матриц А = ~~аД и В = ~~ЬД
(i = 1, 2, ...; т; j = 1, 2, ..., n) одинаковых размеров (т; n)
называется матрица С = ~~сЦ (г = 1, 2, ...; т; у = 1, 2, ..., и)
тех же размеров (т; n), элементы которой равны сумме со-
ответствующих элементов матриц-слагаемых

ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
й
с;, =pa>. ~; (i =l,... т; j=l,...,
(1. 7)
т. е. элемент матрицы С вЂ” с;,, стоящий в i-й строке и j-м
столбце, равен сумме попарных произведений элементов
i-й строки матрицы А и j-ro столбца В:
c;) =~~1Ь1~ + ~;2Ь2~ + -" + ~;~Ьц~ + °" +
Отсюда следует, что А = — А, т. е. А =(( — а;, [! = — [! а,, ~!. Таким
образом, А + ( — А) = О.
Замечание. Разностью двух матриц А и В одинаковых
порядков называется такая матрица С тех же порядков,
которая в сумме с матрицей В дает матрицу А, т. е. если
В+ С =А, тоС =А — В.
Из приведенных выше определений линейных операций
над матрицами и их свойств следует, что разность двух мат-
риц А и В может быть получена по правилу С = А + ( — 1) В.
Определение 1.10. Произведением матрицы А размеров
(т; Й) на матрицу В размеров (Й; n) называется матрица
С = АВ размеров (т; п) = (т; k)(k; n), каждый элемент кото-
рой получается по правилу умножения «строка на столбец».
с» = элемент а» первой строки матрицы А, умножен-
ный на элемент b» первого столбца матрицы В, + эле-
мент а12 первой строки матрицы А, умноженный на эле-
мент Ь21 матрицы В, + ..., + элемент а» первой строки
матрицы А, умноженный на элемент b» первого столбца
матрицы В; ...;
с;, = элемент a;& t; -й стр ки матр цы А, умножен ый
элемент Ь1, у-ro столбца матрицы В, + элемент ад i-й стро-
ки матрицы А, умноженный на элемент b&g ;j j ro стол ца м
рицы В, + ..., + элемент a;A, i-й строки матрицы А, умно-
женный на элемент b& t; j ro стол ца матр цы В; .
с „= элемент а 1m-й строки матрицы А, умноженный
на элемент b>„n ro стол ца матр цы В + элем н  2
строки матрицы А, умноженный на элемент bq„n-ro столб-
ца матрицы В, + ..., + элемент а& t; -й стр ки матр цы
умноженный на элемент Ь~„п-ro столбца матрицы В.
Таким образом, элементы с;, определяются по формуле

ГJIABA 1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
СВОЙСТВА ОПЕРАЦИИ
ПЕРЕМНОЖЕНИЯ МАТРИЦ
1.(А . В) С = А (В С) — сочетательноесвойство.
2. (А+ В) С = А С + В С вЂ” распределительное свойст-
во относительно суммы матриц.
3. А . (Х В) = Х (А В) — сочетательное свойство отно-
сительно числового множителя Х.
4. А Е = Е . А = А — произведение квадратной матри-
цы А и единичной матрицы Е.
5. (А В)т = Вт . Ат
Замечание 1. По отношению к произведению двух мат-
риц переместительный закон в общем случае не выполня-
ется:
АВ w ВА.
Замечание 2. Для квадратной матрицы А ее степень и
определяется следующим образом:
А" АА ...А =Аи-' А, ne N, АО =E.
(1.8)
и раз
Каждой квадратной матрице (1.2) ставится в соответ-
ствие число, называемое определителем матрицы А и обо-
значаемое
а11 ац ... а1„
Qgy Qgg ... Qg
detA. =
(1.9)
Q y Qg ... Я~„
где числа а;, (i = 1, 2, ..., и,; у = 1, 2, ..., n) называются эле-
ментами определителя.
В записи первый индекс i о0з3нHaач~aаеeт T нНоОмМеер ~ с~тTр~оopки~, а вто-
Рои индекс j — номер столбца.
Определение 1.11. Минором М;, элемента а;, матрицы
n-ro порядка А называется определитель и-го порядка,
соответствующий той матрице, которая получается из
Замечание. Из сформулированного определения опе-
рации перемножения матриц вытекает, что матрицу А
можно умножать на матрицу В только в случае, когда чис-
ло столбцов матрицы А равно числу строк матрицы В.

10
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
матрицы А в результате вычеркивания i-й строки и j-го
столбца, на пересечении которых стоит элемент а;,. Минор
элемента обозначается обычно символом М;,. Таким образом,
а1г ... а1 1
агг °" аг) — 1
а»
аг1
M„J J=
а11 а12 ... а1,1 а 11 ... ~i 1„. (110)
а+11 а+1 г " ai+ij i ai+iJ+i -" ai+in
aÄÄÄÄ
апг ... аи~ 1
a„j+&
a„„&
А;, = ( — 1)"'M;;.
(1.11)
Определение 1.13. Определителем порядка и, соответ-
ствующим матрице А, называется число, обозначаемое
det А и вычисляемое по формуле
Таким образом, по определению
а» ад ... а1„
аг1 агг " аг
и
= ~а1,А1,.
j=l
detA =
(1.12)
Q„y айаг
а„„
Каков бы ни был номер строки i = 1, 2, ..., и или столб-
ца j = 1, 2, ..., и, определитель и-го порядка равен сумме
Минор М» для элемента а» матрицы первого порядка
А, состоящей всего из одного элемента, равен этому эле-
менту.
Определение 1.12. Алгебраическим дополнением А;,.
для элемента а;, называется минор М;, этого элемента, взя-
тый со знаком «+», если сумма индексов строки и столбца
(i + j), на пересечении которых стоит этот элемент, четная,
и со знаком « — », если сумма индексов нечетная.
Таким образом,

["ÄAÂÀ 1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
произведений элементов этой строки или этого столбца на
их алгебраические дополнения, т. е.
det A = ~а;,А„= ~а„А„.
(1.13)
СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ
1. Строки и столбцы определителя равноправны, т. е.
величина определителя не изменится, если поменять мес-
тами его строки и столбцы с сохранением порядка их сле-
дования. Эта операция называется транспонированием
определителя. В соответствии со сформулированным свой-
ством det А = det AT.
2. При перестановке местами двух строк (или двух
столбцов) определитель сохраняет свою абсолютную ве-
личину, но меняет знак на противоположный.
3. Определитель с двумя одинаковыми строками (или
столбцами) равен нулю.
4. Умножение всех элементов некоторой строки (или
некоторого столбца) определителя на число Х равносильно
умножению определителя на число Х.
5. Если все элементы какой-либо строки (или какого-
либо столбца) определителя равны нулю, то и сам опреде-
литель равен нулю.
6. Если элементы двух строк (или двух столбцов) опре-
делителя пропорциональны, то определитель равен нулю.
7. Если к элементам некоторой строки (или некоторо-
го столбца) определителя прибавить соответствующие эле-
менты другой строки (другого столбца), умноженные на
Произвольный множитель Х, то величина определителя не
изменится.
8. Сумма произведений элементов какой-либо строки
(какого-либо столбца) определителя на соответствующие
алгебраические дополнения элементов любой другой стро-
~& t; (люб го друг го столб а) ра на ну
9. Если все элементы i -й строки определителя представ-
лены в виде суммы двух слагаемых а;, = b, + с,, то опреде-
литель равен сумме двух определителей, у которых все стро-
&lt и, кр ме i и, та ие е, а  в задан ом определите

12
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
а i-я строка в одном из слагаемых состоит из элементов Ь;,
а в другом — из элементов с;.
Аналогичное свойство справедливо и для столбцов
определителя.
10. Определитель произведения двух квадратных мат-
риц равен произведению их определителей: det (А В) =
= det А det В.
Для вычисления определителя любого порядка мож-
но применять метод последовательного понижения поряд-
ка определителя. Для этого пользуются правилом раз-
ложения определителя по элементам строки или столб-
ца(1.13). Еще один способ вычисления определителей
заключается в том, чтобы с помощью элементарных пре-
образований со строками (или столбцами), прежде всего
в соответствии со свойствами 4 и 7 определителей, при-
вести определитель к виду, когда под главной диагона-
лью определителя (определяемой так же, как и для квад-
ратных матриц) все элементы равны нулю. Тогда опреде-
литель равен произведению элементов, расположенных
на главной диагонали.
При вычислении определителя последовательным по-
нижением порядка для уменьшения объема вычислитель-
ной работы целесообразно с помощью свойства 7 определи-
телей добиться обнуления части элементов какой-либо стро-
ки или какого-либо столбца определителя, что уменьшит
число алгебраических дополнений, вычисляемых в (1.13).
ОБРАТНАЯ МАТРИЦА
А А1=А1 А=Е,
(1.14)
где Š— единичная матрица тех же порядков, что и А. Мат-
рица А ' называется обратной к матрице А.
Определение 1.14. Квадратная матрица А называется
вырожденной (особенной), если определитель этой матри-
цы равен нулю, и невырожденной (неособенной) в против-
ном случае.
Определение 1.15. Для любой невырожденной матри-
цы А существует и притом единственная матрица А ' та-
кая, что

~ ЛАЦА 1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Обратная матрица определяется формулой
А11 А21 ... А
А„А2, ... Ап2
А '=
detA
(1.15)
А]п А2п .. Апл
где А;, — алгебраические дополнения элементов а;,.
Для обратной матрицы справедливы следующие ра-
венства:
1) (аА) '= — А ';
О,
2)(А.В) ~ =В '.А ~;
3) (А-~)т (Ат)
а» а2~ ... a„& t; .
а~2 а22 ... а„2 ... 0 1 0
0
0
а~„а2„... а„„... 0 0 0
Далее, с помощью элементарных преобразований над
с~роками, приводим матрицу В к виду (Е~А '), что всегда
возможно, если матрица А невырождена.
Кроме метода нахождения обратной матрицы, выте-
кающего из формулы (1.15) (метод присоединенной мат-
рицы), существует метод нахождения обратной матрицы,
называемый методом элементарных преобразований.
Определение 1.16. Элементарными преобразованиями
матрицы называются следующие преобразования:
1) перестановка строк (столбцов);
2) умножение строки (столбца) на число, отличное от
нуля;
3) прибавление к элементам строки (столбца) соответ-
ствующих элементов другой строки (столбца), предвари-
тельно умноженных на некоторое число.
Для нахождения матрицы А ' построим прямоуголь-
ную матрицу В = (А~Е) порядков (и; 2n), приписывая к мат-
рице А справа единичную матрицу Е через разделитель-
ную черту:

14
ПРАКТИЧЕСКОЕ РУКОВОДСTBO К РЕШЕНИЮ ЗАДАЧ
РАНГ МАТРИЦЫ
называются линейно зависимыми, если найдутся такие
числа Х1, Х2, ..., Х~, что справедливо равенство
Х|a;„+kqa;„+...+kqa;„, =0 (j =1,2,...,n),
Х'+л, '+...+X' „w0 (1&lt i & t; т, 1
(1.16)
Строки матрицы А называются линейно независимы-
ми, если равенство (1.16) возможно лишь в случае, когда
все числа Х~ = ~2 = ... = Xy = О.
Определение 1.17. Пусть в матрице А размеров (т; и),
выбраны произвольно k строк и k столбцов (k & t; min m; и
Элементы матрицы, стоящие на пересечении выбранных
строк и столбцов, образуют квадратную матрицу порядка
k, определитель которой называется минором М» поряд-
ка й, или минором й-го порядка матрицы А.
Определение 1.18. Рангом матрицы называется макси-
мальный порядок r отличных от нуля миноров матрицы
А, а любой минор порядка r, отличный от нуля, — базис-
ным минором. Обозначение: rang А = r. Если rang А = rang В
и размеры матриц А и В совпадают, то матрицы А и В на-
зываются эквивалентными. Обозначение: А — В.
Основными методами вычисления ранга матрицы яв-
ляются метод окаймляющих миноров и метод элементар-
ных преобразований.
Суть метода окаймляющих миноров состоит в следую-
щем. Пусть в матрице уже найден минор порядка k, отлич-
ный от нуля. Тогда далее рассматриваются лишь те мино-
ры порядка k+ 1, которые содержат в себе (т. е. окаймля-
ют) минор k-го порядка, отличный от нуля. Если все они
равны нулю, то ранг матрицы равен Й, в противном случае
среди окаймляющих миноров (k + 1)-го порядка найдется
отличный от нуля и вся процедура повторяется.
Понятие ранга матрицы тесно связано с понятием ли-
нейной независимости ее строк (столбцов).
Определение 1.19. Строки матрицы А = ~~а;,~~ (~ = 1, 2, ...,
т; j=-1,2,...,n):

1-JfABA 1. элементы линейнОЙ АлГеБРы
15
Аналогичным образом определяется линейная зависи-
мость и независимость столбцов матрицы А.
Определение 1.20. Если какая-либо строка (а~) мат-
рицы А (где (а~) = (ац, а~2, ..., а,„)) может быть представле-
на в виде
(а~) =Х,(а;,)+12(а;,)+...+Х„(ац),
(1.17)
1.2.
ЛИНЕЙНЫЕ ПРОСТРАНСТВА
Определение 1.21. Множество L элементов любой при-
роды х, у, z, ... называется линейным пространством, а
сами элементы векторами, если выполнены следующие
условия.
1. Имеется правило, в соответствии с которым любым
двум элементам х и у множества ставится в соответствие
опРеделенный элемент z этого же множества, называемый
~ÓìMî~ элементов х и у и обозначаемый z = х + у.
2. Имеется правило, в соответствии с которым любому
элементу х из множества L и любому вещественному чис-
лу л ставится в соответствие определенный элемент U того
~е множества L, называемый произведением элемента х
на число n., обозначаемый U = Х,х.
Указанные два правила подчинены следующим вось-
ми аксиомам.
+ у = у + x — коммутативность суммы (переста
вочное, переместительное свойство).
то в этом случае говорят, что указанная строка является
линейной комбинацией строк i&g ;, 2, . .,
Аналогичным образом определяется понятие линейной
комбинации столбцов. Справедлива следующая теорема о
базисном миноре.
Теорема 1.1. Базисные строчки и базисные столбцы
линейно независимы. Любая строка (либо столбец) матри-
цы А является линейной комбинацией базисных строк
(столбцов), т. е. строк (столбцов), пересекающих базисный
минор. Таким образом, ранг матрицы А: rang А = й равен
максимальному числу линейно независимых строк (столб-
цов) матрицы А.

16
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
(1. 18)
Если в левой части (1.18) все Х1, Х2, ..., Х равны нулю,
то такая линейная комбинация называется тривиальной.
Если же хотя бы один из коэффициентов линейной ком-
бинации отличен от нуля (Xy + Ц + ... + Х2 4 0), то линей-
ная комбинация называется нетривиальной.
Система векторов х1, х2, ..., х называется линейно за-
висимой, если может быть построена нетривиальная ли-
нейная комбинация этих векторов, равная нулевому век-
тору. Если же такую комбинацию нельзя построить нетри-
виальным образом, то система векторов (элементов) х1,
х2, ..., х называется линейно независимой.
Определение 1.22. Линейное пространство L называет-
ся п-мерным, если в нем имеется и линейно независимых
элементов, а любые и+ 1 элементов уже линейно зависи-
мы. Часто и-мерное линейное пространство обозначается Ь„.
2. (х + у) + z = х + (у + z) — ассоциативность суммы (со-
четательное свойство).
3. Существует нулевой элемент 0 такой, что х + 0 = х
для любого элемента х множества L.
4. Для каждого элемента х существует противополож-
ный элемент ( — х) такой, что х + ( — х) = О.
5. 1 . х = х для любого элемента х множества l. (особая
роль числового множителя 1).
6. Х(рх) = (Хр)х — ассоциативность умножения относи-
тельно числовых сомножителей Х, р.
7. Дистрибутивность умножения относительно суммы
чисел (распределительное свойство умножения относитель-
но суммы чисел Х, р):
(Х+ р)х = Хх+ рх.
8. Х(х + у) = Хх + Ху — дистрибутивность умножения
относительно суммы векторов (элементов).
Из произвольных т элементов (векторов) х„х2, ..., х
линейного пространства и вещественных чисел Х1, Х2, ...,
Х можно построить линейную комбинацию Х1х1+ Х~х~ + ... +
+ Хх = у, которая представляет некоторый элемент того
же пространства. В частности, из любых векторов х1, х2, ...,
х можно построить линейную комбинацию, равную ну-
левому вектору:
Х]х] + Х~х~ + ° + Хщхщ 0

z'„[A~A 1. элементы линейнОЙ АлГеБРы
17
х = ~y&l ; + Х Г~ +. .+ Х„
(1.19)
Коэффициенты Х„Х2, ..., Х этой линейной комбина-
ции называются координатами вектора х относительно
базиса е1, е~, ..., е„.
Разложение любого вектора х, принадлежащего L„,
единственно.
Отсюда следует, что между вектором конечномерного
линейного пространства и его координатами относитель-
но базиса этого пространства существует взаимно однознач-
ное соответствие.
1.3.
АНАЛИТИЧЕСКИЕ МЕТОДЫ
РЕШЕНИЯ СИСТЕМ ЛИНЕИНЫХ
АЛГЕБРАИЧЕСКИХ УРАВНЕНИИ
1.3.1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
Определение 1.26. Система т линейных алгебраиче-
сKHx уравнений с п неизвестными имеет вид:
+11+1 + +12&l ;2 + . + 1n +n
+21+1 + +22+2 +... + а~„х„= ~2
(1.20)
а 1х1 + а„,~х~ >+ .  а „ =
Определение 1.23. Если число линейно независимых век-
торов элементов в линейном пространстве не ограничено, то
такое линейное пространство называется бесконечномерным.
Определение 1.24. Базисом линейного пространства
называется любая конечная упорядоченная система век-
торов — элементов множества Ln, если:
а) она линейно независима;
б) каждый элемент из Л„является линейной комбина-
цией элементов этой системы.
Определение 1.25. Максимальное число линейно незави-
симых векторов элементов в системе векторов элементов на-
зывается рангом системы векторов и часто обозначается r.
Из определения базиса следует, что число векторов в
базисе равно размерности пространства и каждый вектор
х линейного и-мерного пространства Л„является линей-
ной комбинацией базисных векторов е1, е2, ..., е„:

18
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
а» а12 --- а1и
а21 а22
(1.21)
ат1 ат2 - .. ати
Определение 1.28. Расширенной матрицей системы
(1.20) называется матрица, первые т столбцов которой сов-
падают со столбцами основной матрицы системы, а послед-
ний столбец составлен из правых частей уравнений (1.20):
Ь2
а» а12 --- а1
а21 а22 - - а2
(1.22)
amp amp - - - amn bm
Система уравнений (1.20) может быть представлена в
виде одного линейного уравнения между столбцовыми мат-
рицами:
а»
а12
а1
а21
а22
ag„
(1.23)
+" +in
+ Х2
am,
am2
amp
которое есть линейное уравнение между векторами т-мер-
ного линейного пространства а&g ;, 2, . ., „,
х1 а1 + х~ а~ +... + х„а„= Ь .
(1.24)
Система называется однородной, если все Ь1 = Ь2 = ... =
= Ь = О. Если хотя бы одно из чисел Ь1, Ь2, ..., Ь отлично
от нуля, то система называется неоднородной.
Система (1.20) называется совместной, если она имеет
хотя бы одно решение, и несовместной, если ее решением
является пустое множество.
Совместная система называется определенной, если она
имеет только одно решение, и неопределенной, если она
имеет более одного решения.
Определение 1.27. Основной матрицей системы (1.20)
называется матрица вида

19
pJIABA 1. элементы линейнОЙ АлГеБРы
Отсюда следует, что вопрос о существовании решения
системы (1.20) сводится к вопросу о разложении (1.23) мат-
рицы-столбца правых частей
Ято разложение возможно только в том случае, если ранги
системы векторов
а12
а1„
а»
а22
а21
/У
э ° ° ° э
а2 =
a& t; —
gm2
©my
а12
а1Л,
а»
а22
а2Л,
а21
;b=
а2 =
° /У
э ° ° ° э ~ï
и а1 ——
ащ2
атп
rangA = rangÀ = r.
(1.25)
Однородная система всегда совместна, так как она все-
гда имеет нулевое решение, которое называется тривиаль-
ным х1 — х2 = ... — х„— О.
Если ранг г совместной системы равен числу неизвест-
нь~х и, г = и, то система будет определенной.
Ес» ранг совместной системы меньше числа неизвест-
нь~х ~ & t; п, то сист ма неопределенн я В э ом слу ае
репзения системы (1.20) выделяем любой базисный минор,
его элементы в столбцах являются коэффициентами при г
\
равны. Это положение формулируется в виде следующей
теоремы.
Теорема 1.2 (Кроиекера — Капелли). Для того чтобы
система (1.20) была совместной, необходимо и достаточно,
'~тобы ранг основной матрицы системы rang А равнялся
paHry расширенной матрицы rang À:

20
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
неизвестных, которые называются базисными неизвестны-
ми системы (1.20). Остальные и — г неизвестных называ-
ются свободными неизвестными. Выделив из заданной
системы (1.20) подсистему уравнений с г базисными не-
известными и перенеся в правую часть каждого уравне-
ния выделенной подсистемы слагаемые со свободными не-
известными, решаем последнюю, придавая произвольные
значения свободным неизвестным.
Однородная система, для которой число уравнений
меньше числа неизвестных (т & t; ), все да им ет нетри
альное решение.
Однородная система, для которой число уравнений сов-
падает с числом неизвестных (т = п), имеет нетривиаль-
ное решение при det А = 0 (r & t;
1.3.2. МЕТОД, ОСНОВАННЫЙ
НА ПРИМЕНЕНИИ ОБРАТНОЙ МАТРИЦЫ
(МАТРИЧНЫЙ МЕТОД)
А-Х=В,
(1.26)
й11 й12 ... О~1
©21 ©22 ° .. ©2
где А=
— основная матрица системы;
й 1 йл2 ... й„
Х1
~2
— век-
Х2
— вектор-столбец неизвестных; В =
хп
тор-столбец правых частей.
Уравнение (1.26) называется матричным уравнением.
Если основная матрица квадратной системы невырож-
дена, то решение этой системы можно записать с помощью
обратной матрицы так:
Любая квадратная система п уравнений (1.20) с п неиз-
вестными на основании операции перемножения матриц
может быть записана в матричном виде:

Г }А}3А 1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
21
Х=А ' В.
(1.27)
~матричное уравнение У А = В имеет решение
Y=Â -А '.
(1.28)
Матричным методом выгодно решать несколько квад-
ратных систем с одинаковой невырожденной основной мат-
рицей и разными правыми частями.
(1.2U)
Л Л
где Л1 — определитель, получающийся из Л заменой эле-
ментов первого столбца элементами столбца свободных
членов В; Л2 — заменой элементов второго столбца элемен-
тами столбца свободных членов В, ...; ˄— заменой эле-
ментов п-ro столбца элементами столбца свободных чле-
нов В.
2. Если Л = О, а хотя бы один из Л» (k = 1, 2, ..., п) отли-
чен от нуля, то система не имеет решений.
3. Если все определители Л~ = hq = ... = Л„= Л = О, то в
случае.
а) неравенства ранга основной матрицы системы рангу
расширенной матрицы rangA w rangÀ система не имеет
решений;
о) равенства ранга основной матрицы системы рангу
расширенной матрицы rangA = rangÀ = r, система имеет
бесчисленное множество решений.
1.3.4. МЕТОД ГАУССА
Метод Гаусса состоит из двух основных этапов, назы-
ваемых прямьиа ходом и обратпным ходом.
CyTb прямого хода заключается в последовательном ис-
ключении неизвестных с целью преобразования систе-
М» (1.20) к так называемому ступенчатому виду, когда
1.3.3. МЕТОД КРАМЕРА
Теорема 1.3 (Крамера).
1. Если определитель Л = det А основной матрицы квад-
ратной системы (1.26) отличен от нуля (Л w О), то система
имеет единственное решение, которое определяется фор-
мулами Крамера.

22
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
основная матрица системы имеет на главной диагонали от-
личные от нуля элементы, а под главной диагональю нахо-
дятся только нулевые элементы. Последовательное исклю-
чение неизвестных может производиться с использовани-
ем расширенной матрицы системы и тех же действий, что
и при нахождении ранга этой матрицы, описанных в раз-
деле 1.1. Рассмотрим вначале квадратную систему (1.20)
(т = и).
17ервый исаг прямого хода. Пусть элемент a» w О. Он
называется ведущим элементом на данном шаге преобра-
зований. Получим под ним одни нулевые элементы, для
этого вычтем из элементов второй строки расширенной
матрицы системы соответствующие элементы первой стро-
ки, умноженные на число <21/ lt;11 сокра
(2) — (1) 2' . Затем (3) — (1) з', ..., (т) — (1)
а» а» а»
а1г
а1„
а»
«аг1 аг1
аг1 — а» ' — агг — а1г—
а» а»
аг1
аг,„— а1
а»
Ь2 — Ь~—
аг1
а»
а„,1 а,„1 а„,1
aq — a»' — а г — а1г — ... а — а1
а» a» a»
Ь.-Ь,—
а„1
а»
В результате получим
а11 а12 ... а1
(1) (&g
0 а2 ... а2
0
° ° ° ° ° ° ° ° °
(&g ;)
0 йт2 '.. ©тт
Второй исаг прямого хода. Пусть элемент a(2 ~0. На
данном шаге он является ведущим элементом. Получим
под ним одни нулевые элементы, для этого вычтем из эле-
ментов третьей строки расширенной матрицы системы со-
ответствующие элементы второй строки, умноженные на
(&g
©32
число —, сокращенно:
(&g ;
а22

23
ГЛАВА 1. элементы линейнОЙ АлГеБРы
(1) (1) (1)
(3) — (2) .. Затем (4) — (2) —, ..., (т) — (2)
32 42 ат2
(1) (1) ' (1)
а22 а22 а22
а11
b(1)
2
О
(1) а' '
(1) (1) О32 (1) (1) 32
32 22 (д) " 3m 2m (д)
а22 а22
(1) а' '
(1) (1) т2 (1) (1) т2
m2 22 (д) ". ~тт 2m (д)
а22 а22
В результате получим
адт
(2)
О ° ° ° атт
О3(2)
т
О
Последний, (т — 1)-й шаг прямого хода.
Пусть в результате (т — 2)-го шага получена следую-
щая матрица, эквивалентная исходной расширенной мат-
рице:
(2)
аз
О О
(т — 2)
(т — 1)(т-1)
(т — 2)
т(т — 1)
b(m — 2)
т — 1
b(m — 2)
т
П усть элемент а,),,) ~0. Получим под ним нуле-
(т — 2)
вой элемент. для этого вычтем из элементов последней
~~р~ки расширенной матрицы системы соответствующие
элементы предпоследней строки, умноженные HR число
ад2
(1)
а22
адд ад 2
(1)
О а22
О О
О О
адд а12
О а22
(1)
О О
ад(т — 1)
а'"
2(m — 1)
(2)
3(т — 1)
адт
(1)
а2т
(1)
а2т
(2)
азт
~ (1)
2
О3(2)
3
адт
(1)
&lt
(m — 2)
(т — 1) т
(т-2)
а
(1)
~(1) ~(1) (~32
Зт 2т (и
а22
а('
О3(1) р (1) m2
тт 2т (ц
22
b(1)
2
~ (2)
3

24
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
(т — 2) (т — 2)
(т — 1) и т(т — 1)
а
(т-2) ' (т — 2)
(т — 1)(т — 1) (т — 1)(т — 1)
а
сокращенно:
(т-2)
(m) — (т — 1)
(т — 2)
(т — 1)(т — 1)
В результате получим
а1m
(1)
а2
а12
(1)
0 а22
а1( 1)
а' '
2(т — 1)
(2)
3(т — 1)
й(1)
2
й(2)
3
(2)
азm
0 0
(т — 2)
0 ". (m 1)(m 1)
(т — 2)
(т-1) т
(т — 1)
атт
й(т — 2)
т — 1
0
й(т — 1)
m
О 0
0
Обратиый ход начинается с записи системы, которой
соответствует итоговая расширенная матрица, полученная
в результате прямого хода:
а11х1 + адх~ +... + ац 1) xm — ~ + à~m õ,„= Ь~,
(1) (1) =й '
22 Х2 + .. Q2(т — 1)Хт-1 + а2тХт = й2
(т-2) (т — 2) у,(т — 2)
(т 1)(т 1) m 1 (m — 1) т т m 1
(т 1) (т 1)
а
Из последнего уравнения находят х, подставляют
найденное значение в предпоследнее уравнение и находят
х 1, и т. д., в первое уравнение подставляют х, х
..., х2 и находят х1.
Зажеч,ание.
1. Если какой-то из ведущих элементов оказывается
равным нулю, то ero меняют местами с одним из ненуле-
вых элементов, принадлежащим этой же строке основной
матрицы системы. Если же все элементы, принадлежащие
строке основной матрицы системы, где отыскивается ве-
дущий элемент, равны нулю, а за разделительной чертой
находится ненулевой элемент b> ' p 0, то реше ие прек
щают, так как система оказывается несовместной.

25
ГлАцА 1. элементы линейнОЙ АлГеБРы
2. Строки, целиком состоящие из нулей, удаляются.
g результате прямого хода после вычеркивания нулевых
строк появится ступенчатая матрица, у которой элементы
~„, а 2, ..., а„„отличны от нуля, а в столбцах под ними одни
нулевые элементы. Тогда обратный ход начинается с си-
стемы вида:
д11Х1+а12Х2+...+Q(n 1)(n 1)Xn 1+а(и — l)nXn+а(и 1)(„.1)Х„,1+...+а(и 1) Х =Ь1,
(1) (1) (1) (1) (1) g.(1)
22 X2 + ' + а( 1)(n — 1)Õ 1 + а(и 1) Х + а(и-1Х+1)~"1 " а( -1)
р (и-2)
и-1
(и-2) (и-2) (и — 2) (и-2)
— + а( 1)их + а( ~~„.~Х~~ +" + а
(и — 1) (и-1) (и-1)
аии Хи + аи(и„)Хи,1+... + аии, Х„,
а11Х1 + Q12X2 + ° .. + Q(n 1)( 1)Xn 1 + a(n 1)иХ = а( 1)(n+1)Xn+l —... — а( — 1)mÕ + Ь1
(1) (1) (1) (1) (1) z,(1)
+ "° + а(и 1)(„1)Х~-1 + а(„1)„хи = а(и 1Х„1)Х~~1 "- а(„1) Х~ + ~2
(и-2) + (и-2) (и-2) (и — 2) + g.(n-2)
а( 1)(„1)Х~ 1 + а(и 1)ихи = а(и 1Хи+1)Х~~1 ° ° ° а( 1) Х~ + ~„1
(и-1) (и-1) (и-1) д.(и — 1)
а„и Хи = — an(n+1)Xn+1 —... — anm Xm + bn
Далее начинается описанное выше продолжение обрат-
н«о хода метода Гаусса. Базисная неизвестная х„из послед-
Hero уравнения выражается через о„" 1) и линейную комби-
нацию свободных неизвестных. Найденное выражение для
х, затем подставляется в предпоследнее уравнение, из кото-
р«о находится х„1 и т. д., пока из первого уравнения не
бунет получено выражение базисной неизвестной х1 через
"1 и линейную комбинацию свободных неизвестных.
Если однородная система с m уравнениями и и неиз-
вестными (т & t;
Qllxl + Q12x2+... + Ql(k 1)х~ l + аухц + Ql(k 1)х~ 1+. ° ° + Qlnx„=О,
а21Х1 + а22х2+... + а2,~ 1)х~ 1+ а2~х~ + а2(~ 1)xk.1 +... + а2их„= О,
х +
( -1)1 1 а( l)2x2+...+а(д 1)(„1)Х„1+а(ц 1)kxk+а(~ 1)(д.1)Х~.1+...+Q(k 1)nxn О,
ацх1 + ak2x2 +... + Q(k)(k.l)xk 1+ а(k)kxk + a(k)(k+1)xk+1+ ... + а(ц)„х„= О,
° ° ° ° ° ° ° у
a„,
(~.1)1~1 + а(~,1 )2Х2 + ... + а(~.1)(~ 1)Xk 1+ а(~.1 )~Х~ + а(~,1)(~.1)Х~.1 +... + а(k+1)n Xq = О,
° ° ° ° ° ° ° ф
а( )1Х1 + а(„,)2Х2+... + а(„,)( 1)Х~ 1+ a(m)kXц + a(m)(k)Xk+1 +... + а(„,)иХ„= О
Неизвестные х1, х2, ..., х„являются базисными, а х„+ q,
х„+ ~, ..., х — свободными. Свободные неизвестные пере-
носятся в правые части:

26
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИК) ЗАДАЧ
приводится к треугольному виду с ненулевыми элемента-
ми (для которых номер строки, в которой они расположе-
ны, равен номеру столбца) основной матрицы системы:
611Х1+612Х2+.. +61(т — цХт — 1+Q1mXm =О,
(1) (1) (1)
Q22 Х2 + . + 2(т — ЦХт — 1 + 2тХт = О,
(т-2) (т — 2)
И(т — )(m — цХт — 1 + И(т — цтХт = Оъ
(т — ц
©тт Хт =О,
Я11Х1 + Й12Х2 + . " + Я1(~ ц Х~ 1 + Яц Х~ + Q1(&gt +ц Х +1 + . + 1л Х =
(1) (1) (1) (1) (1)
622 Х2 +... + Q2(P, 1) Х~ — 1 + Q2P, Xk + Q2(P, 1) X@+1 +... + Q2„X„= О,
(т — 2) (т — 2) (т — 2) (т — 2)
a(~»(Äцх~ 1+ а(,„1 х~ + а(,1)(„.,цх~+1+... + Q(~,)„х„= О,
(т — ц (т — ц (т — ц
а» х~ + а~(„.,цх~,1+ ... + а„„х„= О,
то ее решение можно получить следующим образом. По-
очередно столбец свободных неизвестных
Х~,1
Х~+2
хл
приравнивают столбцам единичной матрицы
1 0 0 ... 0
0 1 0 ... 0
0 0 0 ... 1
и решают получающиеся системы уравнений. В результа-
те будут получены решения, которые называются фунда-
то ее решение тривиально: х; = О, i = 1, 2, ..., m.
Если однородная система с т уравнениями и и неиз-
вестными (т & t; п) приводи с к ступенчат му в

ГЛАЦА 1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
27
,ентальной совокупностью решений (ФСР) однородной
истемы алгебраических уравнений:
хд — — с,
(2)
Х2 =С2
(2)
(и — k)
хд — — сд
(и — Й)
Х2 =С2
()
х, =с,'
()
Х2 =С2
(n — k)
Xk — — С,„
, ..., е„~ ——
Е2 =
xk„q — — О
х~+2 —— О
Xk+3
Ед=
х„=О
х„=1
хи =0
Так как сумма двух решений произвольной однород-
ной системы и произведение ее решения на любое вещест-
венное число также являются решениями этой же систе-
MbI линейных уравнений, то можно показать, что множе-
ство всех решений однородной системы образует линейное
пространство I.„k, элементами которого являются как век-
тор-столбцы е&g ;, 2, . ., «e k, а и их линей ые комбина
с произвольными множителями ад а2, ..., а„~ из области
вещественных чисел:
Х =адед+a2e2+...+a„ke„k.
(1.31)
Если неоднородная система с т уравнениями и и неиз-
вестными (т & t;
~"-')1Х1 + а(а-1)гХ2+" + а(Ь-i)(k-i)xk-1 + а(д-1)аХа + ЦЬ-1ХВ+1)~4+1 + ° ° + а(а-цпХп = ba 1,
аа1х1 + ak2z2+ ° .. + qk)(kl)xkl + qk)kxk + ц~Хц,l)xk,l +... + а(~)„х„= Ь)„
tk+i)2 2 +" а(ЫХ~-1)Х~ 1 + Цц+Ух~ + Ц~+1Х~+1)~~+1 + " + +kl)nxn = bkil ъ
° ° ° ° ° ° ° ф
а(~)1 1 а(т)2 2 + ° "+ (m)(k-1)zk-1 + ~(m)kzk + (m)(k)xk+1 + ° ° + ~(m)nxn bm
Xk — — С
(д)
< .i
х~+2 — — О
Xk+3
Xk — — С,„
(2)
х~,д — — О
Х~+2 —— 1
Xk+3
а11х1+а12хг+... +а1( 1)xk, +ацх~+а1(k„)zk,l+... +àl„x„=bl,
аг1х1 + 22Z2+ ... + аг(~ 1)zkl +Q2kxk+ аг(~.1)х,1 +... + а2„х„=Ь2,

28
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДА
1
приводится к треугольному виду с ненулевыми элемента-
ми (для которых номер строки, в которой они расположе
ны, равен номеру столбца) основной матрицы системы, а
затем члены со свободными неизвестными xk 1, х~ 2, ...,
х„переносятся в правые части, то система приобретает вид:
a»x) +a>qxq+...+ац, х ) +а)) хц Ђ” Ђ” Ђ” а) )„))х ,> — ..— а,„
(1) ~ (1) (1) (1) (1) b(1)
а22 Х2 + ° ' + а2(~ 1) xk 1 + а2~ xk = — а2(у~~1) Ху~~1 — а2п x + ~2
(т — 2) (т — 2) (m — 2) (т — 2) z.(т — 2)
а( 1)(k — 1)õk 1+ а(„„.„Х,, = — а(„— 1)(„„)õk,1 — ...— а, -1)х„+ и„—
(т — 1) (т — 1) (т — 1) д.(т — 1)
а, х~ — а„.( .1)х~.1 — ". — а,„х„+ й„
(1.32)
л
Х1
л
Х2
л
х&
л
~част. неодн.
л
х~,1 — — 0
л
х~+2 — — 0
х„=О
системы (1.32), когда все свободные неизвестные, получен-
ные в результате (т — 1)-го шага метода Гаусса, приравни-
ваются к нулю:
а»х& t; +а) х    ° +а ), х~ Ђ” 1+ l = о) al(k+1)x +   ° а
(1) =й'
а22-х2 + ° ° ° + a2(k 1)хй 1 + a2Ä xk = b2 a2(„„)xki1 ° ° ° a2„x„
(т — 2) (т — 2) ~.(т — 2) (т — 2) (т — 2)
а( — „— 1)õk 1+ à(„— „х~ — — „— — а(„— 1)(„„)õk1 —... — а(„— )„õ„,
(т — 1) ~(m — 1) (т — 1) (т — 1)
а„,„х~ — — bk а„(~,1)х~1 —... — а, „х„,
Решение этой системы находится в соответствии со сле-
дующей теоремой.
Теорема 1.4. Общее решение неоднородной системы
есть сумма частного решения

29
ГлАдА 1. элементы линейнОЙ АлГеБРы
д о~щего решения соответствующей однородной систе-
мы(1 З1):
х1 =с1
( )
х2 =с2
()
л
х1
л
х2
()
х~ — — с„
л
х&
л
х~,1
л
х~+2
л
~ОбЩЕЕ НЕОДН.
х~,1 — — 1
х~+2 =0
хй+3 = 0
+ ul
=0
=0
х„=О
х„=О
(и — k)
х1 — — с,
(и — Й)
х2 =с2
Xl — — С,
(2)
(2)
х2 =с,'
(и — k)
Xk — — ф
Xk — — ф
(2)
х~,1 — — 0
х„+2 — — 1
Xk+3
х~,1 — — 0
х~+2 — — 0
Xk+3
+...+Gk
+ +g
х„=О
х„=1
1.4.
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
(ОТОБРАЖЕНИЯ)
Определение 1.29. Отображением множества I. в мно-
~«»0 Х (или функцией Hà L со значениями в К) называ-
еТс& t; прави о, по котор му кажд му элеме ту множес
~ ставится в соответствие определенный элемент множе-
~»& t; Х. Та ое отображе ие обознач ют f  w
Если при отображении f элементу ~, принадлежаще-
'"у ~, соответствует элемент у, принадлежащий К, то эле-
мент у называют образом элемента х, а элемент х — про-
образом элемента у, и записывают это в виде у = /(х).

30
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
Ю
Отображение A. одного линейного пространства в дру-
гое называется линейным, если для любых элементов
х иу, ,принадлежащих L, и для любого вещественного чис-
ла и выполняются условия:
А(х» у) Ах+ Ау — аддитивность отображения; (1.33)
А(ддх) ~» — одноРодность отобРажениЯ. (1.34)
х1
Х2
(1.35)
Х = Х] Е1 + Х2Е2 +... + Х Е
=Х,
хп
У1
У2
(1.36)
У =У1е1+У2е2+...+У„е„=
=Y
уп
С учетом (1.33) — (1.36) образ вектора х можно предста-
вить в виде:
Ю л
у = Ах = А(х,ед + х2е2 +... + х„е„) =
= хд(Аед) + х2(Ае2) +... + х„(Ае„).
л
Вектор Ае, Й=1,2,...,и, — образ базисного вектора
е — является вектором того же пространства L„ur задает-
Ю
Определение 1.30. Линейное отображение А: l. w К
называют линейным оператором, действующим из L в К.
Если линейное пространство К совпадает с L, то линей-
ное отображение А: L -+ К называется линейным преоб-
разованием пространства L.
В тех случаях, когда К является множеством вещест-
венных чисел IR или множеством комплексных чисел С,
линейный оператор, действующий из L„s IR или из L„s С,
называется линейной формой.
При линейном отображении А: L„— + L„m вектор-про-
образ х, и вектор-образ у = Ах принадлежат одному и тому
же линейному пространству, так что каждый из них раз-
лагается по базису е1, е2, ..., е„этого пространства:

pgABA 1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
ся своими координатами ац, (i = 1, 2, ..., и; k = 1, 2, ..., и)
относительно базиса I„:
а»
ая/
л
Ае~ — — а»е1 + а2е2 +... + а„~е„=
(1.37)
a„„&
ап а12 ... а1„
а21 аы " а2
(1.38)
а 1 ад2 ... а~~
в которой сконцентрирована вся информация о содержа-
нии линейного преобразования А. Эта матрица называет-
ся матрицей линейного преобразования (оператора).
Таким образом, линейное преобразование можно задать
в матричном виде.'
Y=A. Х,
(1.39)
~де А определено (1.38), а матрицы Х и Y соответствен-
но (1.35) и (1.36).
пользуясь правилом перемножения матриц, уравне-
"ие (1 39) можно представить в виде системы линейных
уравнений
ay y xy + ay2x2 +... + а1„~:„= ру,
Q2] X] + а22~ 2 +... + а2„~
(1.40)
Q„AX( + Q„pe +... + Q„„X„= Д„.
1
11ри и = 2 и п = 3 уравнения (1.40) характеризуют ли-
НеАНое преобразование соответственно плоскости и трех-
Мерного пространства.
Определение 1.31. Упорядоченная совокупность коор-
динатных столбцов (1.37) всех образов базисных векторов
линейного пространства Ь„образуют квадратную матрицу
порядка и,

32
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
дейстВия
НАД ЛИНЕЙНЫМИ ОПЕРАТОРАМИ
(ОтОБРАжениЯми)
Ю л л
Пусть А и  — два линейных оператора, А: Ь„-+ К
В: Ь„-+ К.
Определение 1.32. Суммой операторов А и В называ-
ется линейный оператор А+ В, определяемый равенством
(А+ В)х = Ах + Вх.
Определение 1.33. Произведением линейного операто-
ра А на скаляр Х называется линейный оператор ~, опре-
деляемый равенством
ХАх = Х(Ах).
Определение 1.34. Нулевым оператором, обозначае-
мым символом 0, называется оператор, отображающий
все элементы пространства L„s нулевой элемент простран-
ства К:Ох =О.
Ю
Определение 1.35. Для каждого оператора А проти-
воположный оператор — А определяется соотношением
— А =( — 1)А.
Множество всех линейных операторов (отображений),
действующих из L„s К, с определенными выше опера-
циями суммы и умножения на скаляр и выбранным нуле-
вым и противоположным операторами образуют линейное
пространство.
Пусть А и  — линейные операторы, действующие из
L â L„, т. е. А: L„-+ L„, В: Ь„-+ L„. Произведением опе-
раторов А и В называется оператор Ах В, действующий
по правилу:
(А х В)х = А х (Вх).
При det А ~ О матрица преобразования А невырожден-
ная и линейное преобразование называется невырожденным,
причем Х определяется по формуле (1.27), в которой мат-
рицу В нужно заменить матрицей У. В этом случае невы-
рожденное линейное отображение определяет взаимно од-
нозначное отображение Х на У и У на Х.

33
ГЛАЦА 1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Справедливы следующие свойства линейных операто-
ров, действующих из Ь„в Ь„:
1. Э.(А х В) = (ХА) х В.
2. (А+ В) х С = А х С + В х C.
3. Ах(В+С) =АхВ+АхС.
4. (А х В) х С = A x (B x С).
(1.41)
Определение 1.36. Тождественным преобразованием
л
(оператором) Е называется линейное отображение (one-
Ю
ратор), действующее по правилу Ex = х.
Пусть вектор
Х1
Х = х2 — — Х1 Е1 + Х2Е2 + ХЗЕз
ХЗ
а11 а12 а1з
А= а21 а22 а2з
а31 а32 азз
вектор
У1
У2 = У1е1 + У2е2+ Узез
Уз
т. е. У=А.Х.
~Âåðeì в рассматриваемом трехмерном линейном npo-
eTðeíñòÂå новый базис (е1,е2,е3), связанный со старым,
следующими формулами перехода:
Е1 ~11Е1 + ~12Е2 + ~13Е3
Е2 ~21Е1 + ~22 Е2 + ~23 ЕЗ
е3 41е1 + 42е2 + ~133е3
(1.42)
> да матр ца А' преобразова ия вект р  в век о
в новом базисе будет иметь вид: А' = В ' x А ~ В.
заданный в базисе (е„е2,е3), преобразуется с помощью
линейного оператора A., матрица которого в данном бази-
се есть А:

34
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
1.5.
СОБСТВЕННЫЕ ЗНАЧЕНИЯ
И СОБСТВЕННЫЕ ВЕКТОРЫ
ЛИНЕЙНЫХ ОПЕРАТОРОВ
Определение 1.37. Любой ненулевой вектор х, удовле-
творяющий уравнению
Ах =Хх,
(1.43)
называется собственным вектором линейного операто-
ра А, а число Х вЂ” собственным значением линейного опе-
л
ратора А, соответствующим вектору х.
Если задан базис соответствующего линейного про-
странства L„, то уравнение (1.43) можно представить в мат-
ричном виде:
(1.44)
det(A — ХЕ) = 0.
(1.45)
Определение 1.39. Многочлен det (А — ХЕ) относитель-
но Х называется характеристическим многочленом опе-
ратора А.
В развернутом виде характеристическое уравнение (1.45)
запишется следующим образом:
адд -Х
ад 2
ад„
а~~ -Х ... а~„
а2д
(1.46)
а„д
ал2
а„„
или
Х" — с11" 1+ с21" ~ + + ( — 1)" 1с„Х + ( — 1)"с„= О. (1.47)
(А — ХЕ)х =О,
л
где А — матрица оператора А, в заданном базисе (т. е. мат-
рица порядка и) Š— единичная матрица порядка и; О—
нулевой столбец.
Определение 1.38. Матрица (А — ХЕ) называется харак-
теристической матрицей линейного оператора А.
Уравнение (1.44) представляет собой линейную однород-
ную систему уравнений, нетривиальные решения которой
являются искомыми координатами собственных векторов
и существуют только тогда, когда ранг rang (А — ХЕ) & t; и, т.
определитель

ГЛАЦА 1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
B общем случае характеристическое уравнение (1.47)
линейного оператора А имеет и действительных или ком-
плексных корней — собственных значений линейного опе-
ратора.
Для нахождения собственных векторов линейного опе-
л
ратора А, соответствующих найденным собственным зна-
чениям оператора, необходимо найденное собственное зна-
чение Х; (i = 1, 2, ..., n) подставить в уравнение (1.44):
(а11 — Х)х, + а,~х, +... + а,„х„= О,
а~,х, +(а~2 — Х)х, +... + а~„х„= О,
(1.48)
а„,х, + а„,х, +... + (а„„вЂ” Х)х„= 0.
Решив полученную однородную систему уравнений для
каждого собственного значения Х;, найдем собственные век-
торы x"& t; =( ", х~ 1, . ., x~ ~) (i 1, 2,. ., ), соответствую
этим собственным значениям.
Так как совместная система (1.48) является неопреде-
ленной, то собственные векторы находятся с точностью до
числового множителя.
1.6.
ЕВКЛИДОВЫ ПРОСТРАНСТВА
В приложениях важную роль играет понятие ортого-
нальности собственных векторов линейного оператора. Это
понятие вводится, исходя из определения их скалярного
произведения.
Определение 1.40. Линейное пространство Е называ-
eTcs евклидовым пространством, если выполнены сле-
ду~ощие условия.
1- Имеется правило, с помощью которого любым двум
элементам х и у этого пространства ставится в соответст-
~пе вещественное число, называемое скалярным произве-
дением этих элементов и обозначаемое символом (х, у).
2. Указанное правило удовлетворяет следующим четы-
рем аксиомам'.
а) (x, у) =(у,х);
б) (х+у,z)=(x,z)+(y,~)'

36
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
x = x~e~ + xaea + ". + x~ e» y = hei + gaea + ". + y„e
— разложение векторов х и у по этому базису, то скаляр-
ное произведение (х, y) может быть определено равенст-
вом (удовлетворяющим аксиомам а — г скалярного произ-
ведения):
В В
(х, у) = gga;„»,y„,
i=1 А=1
где ад — — (е;, е) — элементы матрицы А = ll~;all (i = 1, 2, ..., и;
Й=1,2, ...,и).
В формуле (1.49)
(1.49)
2i 21+2g+...+2п °
Определение 1.42. Если векторы базиса е&g ;, ~, . ., е„
парно ортогональны, т. е. (q,, е„) =О, если i w k, то такой
базис называется ортогональным.
В ортогональном базисе у матрицы А = ~~а;Д (i = 1, 2, ..., n;
k = 1, 2, ..., n) отличны от нуля только элементы на глав-
ной диагонали, остальные элементы равны нулю. Такая
матрица называется диагональной. В этом случае скаляр-
ное произведение вычисляется по формуле
(х, у) = ~а;;х;у;.
i=1
Определение 1.43. Если дополнительно к условию ор-
тогональности выполняется условие нормировки (е;, е;) =
(1.50)
в) (~.», y) = ).(», y);
г) (х, х) & t; О, е л х Ђ” ненуле ой элеме т; », х =
если х — нулевой элемент.
Определение 1.41. Два произвольных элемента х и у
евклидова пространства Я называются ортогональными,
если скалярное произведение этих элементов равно нулю.
Если скалярное произведение введено в и-мерном ли-
нейном пространстве I„, то соответствующее ему евклидо-
во пространство называется и-мерным евклидовым про-
странством Е„ (или E").
Если в E' выбран некоторый произвольный базис
8у,ea,...,8 H

ГЛАЦА 1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
37
1 (~ = 1, 2, ..., n), то базис е&g ;, ~, ", е, называе ся ортон
~аи рованы ым.
Q ортонормированном базисе скалярное произведение
равно сумме произведений соответствующих координат:
(1.51)
й-1
fq = @,..., fq —— gq — Г С f (Й = 2, 3,..., n),
(Вf)
Где Ст — — ~ ~у
(f,f )
1.7.
КВАДРАТИЧНЫЕ ФОРМЫ.
ПРИВЕДЕНИЕ К КАНОНИЧЕСКОМУ ВИДУ
УРАВНЕНИЙ КРИВЫХ
И ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
Определение 1.44. Квадратичной формой, порождае-
мой матрицей А = II< )( ( = 1, 2, . ., и  = 1, 2, . ., ), 6y
называть следующую величину:
В общем случае формой нескольких переменных назы-
ва~тся однородный многочлен от этих переменных, в соот-
ветствии со степенью которого форма может быть линей-
ной, квадратичной, кубичной и т. д.
Квадратичные формы от двух переменных и, соответ-
ственно, от трех переменных записываются следующим
Образом:
F(x~, х~) = a„x~ + 2а12х1х2 + а~~х~,
(1.52)
(х, ф ) = ~х; ф; = x]g] + хетаг +... + хл у~ °
1=1
Теорема 1.5. Во всяком п-мерном евклидовом простран-
стве Е" существует ортонормированный базис.
Любую систему линейно независимых векторов g&g ;,
..., g„n-мерного евклидового пространства Е" с помощью
процесса ортогонализации Шмидта можно преобразовать
в ортонормированный базис е1, е2, ..., е„по форм улам:

ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
F(«1 «2 «3) @11«1 @22«2 + @22«2 +
+ 2а12х1х2+ 2а1зх1хз + 2а2зх2хз
(1.53)
или в матричном виде
F(x» х2) = Х . А Х, F(x» х2, хз) = Х А. Х, (1.54)
где
Х1
«2, (1.55)
ХЗ
Х1
Х =(x„x2), Х=, Х =(х1,х2 хз) Х=
Х2
а11 а12 а13
(1.56)
а21 а22 а23 а12 а21 а13 а31 а23 а32 '
а31 а32 а33
Матрицы А и А называются симметричными. Из опре-
целения этих матриц следует, что они совпадают со свои-
ми транспонированными матрицами, т. е. А = Ат, А = Ат.
СВОЙСТВА СИММЕТРИЧНОЙ МАТРИЦЫ
F(x1, х2) = Х1«1 + Х2«2,
Р(«1, «2~ хз) = 11«1+ Х2«2 + ~1 зхз~
(1.57)
(1.58)
где Х1, Х2, Хз — собственные значения матриц соответст-
вующих форм. Для нахождения соответствующего линей-
ного преобразования, приводящего (1.52) к (1.57) и (1.53)
к (1.58), необходимо сделать следующее:
1. Собственные значения симметричной матрицы (ли-
нейного оператора, представимого симметричной матри-
цей) с действительными элементами — действительные
числа.
2. Собственные векторы симметричной матрицы (ли-
нейного оператора, представимого симметричной матри-
цей), соответствующие различным собственным значени-
ям, — ортогональны.
Квадратичные формы (1.52), (1.53) при помощи линей-
ного преобразования вида (1.39), (1.40) могут быть преоб-
разованы к каиоиическому виду, т. е. к сумме квадратов

ГлАцА 1. элементы линейнОЙ АлГеБРы
1) найти собственные векторы матриц А и А, соответ-
стцук)щие собственным значениям k&g ;, Х и 1, &g ; Хз
ТеМ нормировать эти векторы, разделив их на числа, рав-
Hz&g ;e модул м. Указан ые вект ры дол ны б ть попа
ортогональны'.
х'"=m2i+n2j т'+n'=1 (1.59)
i, j=1,2;
х =m>i п1
(>)
т;т;+и;и, =0;
х® =m>i п1 j+р
х~~~ = т2~ +п2j+pzk,
х~з) = тзю + пз] + рз
т2+n2+ р2 =1
m;m;+n;n, +р;р; =0; i, j=1,2,3;
(1.60)
2) матрицы линейного преобразования переменных за-
пишутся так:
m& t; n&
m& t;
В= В = т2 п2 р2
mQ п2
~пз пз Рз
(1.61)
а11 а12
У\У
А= detB =+1, detB =+1,
а 21 а22
а сами линейные преобразования
(1.62)
Х1 = 7И1Х1 + П1 Х2, Х2 = mg Х1 + П2Х2,
&g ; = my & t; + ny
хг = mz>>+ 2-х2
хз = ~пз-х1 + пзха + Рзхз.
(1.63)
3. Для приведения к каноническому виду общего урав-
нения кривой или поверхности второго порядка необходи-
мо квадратичную форму, входящую в это уравнение, запи-
саТ~ в каноническом виде, т. е. согласно (1.62) или (1.63);
линейные по х1, х2 или Х1, х2, хз члены уравнения преоб-
р~~уются по формулам(1.67) или (1.68), и при k; w 0 их
мо~но исключить переносом начала координат.

40
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
1.8.
РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ
1.1. Найти матрицу С = 2А+ В, если
А=( ), В=(
Замечание. Можно было решить эту задачу следующим
образом.'
С=
2 2+3.0 2.1+3.( — 5) 4 — 13
° ° ° ° ° ° °
2.3+3 ( — 1) 2.4+3 6 3 26
1.2. Даны матрицы
1)А= 3 2 3, В= — 1 2;
1 3 2
2)A=( ), В=1 О 2
Найти А В.
P е ш е н и е. В соответствии с определением операции
умножения матриц имеем:
1 1+1 ( — 1)+2 1 1 1+1 2+2 4 2 11
1) А.В= 3 1+2 ( — 1)+3 1 3.1+2 2+3 4 = 4 19;
4 1+3 ( — 1)+2 1 4 1+3 2+2 4 3 18
2 ) АВ=
1 1+1 1+3.1 1 3+1.0+1 0 1 2+1.2+3.( — 1) 5 3 1
1.1+0.1+21 13+00+20 12+02+2.( — 1) 3 3 0
1 2
1.3. Вычислить
P е ш е н и е. В соответствии с определением линейных
операций над матрицами и их свойствами имеем.

41
ЛАВА 1 ,')ЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
р е ш е н и е. Исходя из определения степени матрицы
натуральным показателем, имеем:
4 — 3 4 — 3 4 — 15 10 — 3 4 — 45 10
].4. Найти значение многочлена f(A) от матрицы А:
1 — 1
f(x) = х2 — 5х, А =
2 3
Решение. Имеем
" =(' ')'-'(' ')=(' ') (' ')-'(' ')=
=(' ')-(' ')=('-' '-:)=(: -')
1.5. Найти все матрицы, перестановочные с данной:
А=( ).
P е ш е н и е. Необходимо найти матрицу В =
удовлетворяющую условию А В = В . А, или
с d
(' ')(::)=(: ')(' ')
Перемножая матрицы, получим:
( 2а+ Зс 2b+ 3d (2a+ О За+ 4b
а+ 4с b+ 4d L 2c+ d Зс+ 4Ш
2а+ Зс = 2а+ Ь,
2Ь+ Зд = За+4Ь,
а+4с =2c+d,
b+ 4d = Зс+ 4d.
~ак как матрицы слева и справа должны быть равны,
~о в соответствии с определением равенства матриц, по-
Учим следующую систему линейных уравнений:

42
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
Откуда следует, что
Ь =Зс,
2b=3(d — а), О=Зс,
а+4с =2c+d, 2c =d — а,
Ь=Зс,
а Зс
Таким образом, В=, гдеа, с e IR.
с а+2с
w d = a+ 2с, Ь = Зс, а, с e IR.
0 1
1 2 3
1.6. Даны матрицы А =; В = 2 1
— 3 4 — 5
1 3
Найти Ат. Вт
P е ш е н и е. Транспонируем матрицы А и В.
Ат 2 4 Вт
Перемножая полученные матрицы, находим:
P е ш е н и е. Замечаем, что второй столбец определите-
ля уже содержит один нулевой элемент. Прибавим к эле-
ментам второй строки элементы первой строки, умножен-
ные на — 1, а к элементам четвертой строки — элементы
первой строки, умноженные на 5. Получим:
3 1 — 1 2
3 1 — 1 2
— 3 — 1 — 8
Ат Вт= 4 8 14
— 5 1 — 12
1.7. Вычислить определитель
3 1 — 1 2
— 3 1 4 — 5
2 0 1 — 1
3 — 5 4 — 4
( — 3 — 3) (1 — 1) (1+ 4) ( — 2 — 5)
2 0 1 — 1
(15+ 3) (5 — 5) ( — 5+ 4) (10 — 4)
— 6 0 5 — 7
2 0 1 — 1
18 0 — 1 6

43
разлагая полученный определитель по второй строке,
имеем:
— 6 5 — 7
( Ц1+2 . 1.
= — 2 °
2 1 — 1
18 — 1 6
(Затем мы вынесли сомножитель 2 первого столбца на ос-
новании свойства 4.) Далее прибавим к элементам первого
и второго столбца элементы третьего столбца определите-
ля. Получим:
— 2 — 2 — 7
— 10 — 2 — 7
2 2 7
0 0 — 1 =10 °
3 5 6
0 0 — 1
15 5 6
= — 2 5 °
0 0 — 1.
3 5 6
д= — 2.
Здесь мы вынесли множитель в первом столбце, а за-
тем общий множитель ( — 1) в первой строке. Разлагая те-
перь получившийся определитель третьего порядка по эле-
ментам второй строки, получим:
2 2
g =10 ( — 1) ( — 1)2+з =10.(10 — 6) =40.
3 5
Здесь определитель второго порядка вычислен в соот-
ветствии с его определением, по формуле
а11 а12
= ~11'Жа — ©л '+an
1.8. Вычислить определитель матрицы
wdetA=
P е ш е н и е. Используя 7-е свойство определителя, вы-
чтем из второй строки третью, из четвертой строки — со-
~)ответствующие элементы первой строки определителя,
~множенные соответственно на 3, 4, 5. Эти действия со-
кращенно будем обозначать так: (2) — (1) х 3; (3) — (1) х 4;
(4) — (1) х 5. Получим:
ГЛАц~ 1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
1 2 — 1 4
3 5 — 2 0
4 0 1 — 1
5 1 2 3
— 3 5 — 7
1 1 — 1
9 — 1 6
1 2 — 1 4
3 5 — 2 0
4 0 1 — 1
5 1 2 3

44
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
1 2
(3 — 3 1) (5-3 2)
(4 — 4 1) (Π— 4 2)
(5 — 5.1) (1 — 5 2)
деФА =
1 2 — 1 4
0 — 1 1 — 12
0 — 8 5 — 17
0 — 9 7 -17
Далее, в соответствии с введенными обозначениями,
выполним действия: (3) — (2) х 8; (4) — (2) х 9. Получаем
2 — 1 4
— 1 1 — 12
( — 8 — 8. ( — 1)} (5 — 8 1} ( — 17 — 8. ( — 12))
( — 9 — 9.( — 1}} (7 — 9 1} ( — 17 — 9.( — 12}}
1 2 — 1 4
0 — 1 1 — 12
0 0 — 3 79
0 0 — 2 91
Выполним действия: (4) — (3) х —. Имеем
2
3'
1 2 — 1 4
0 — 1 1 — 12
0 0 — 3 79
(Π— 2/3 О) (Π— 2/3 О) ( — 2 — ( — 3) 2/3) (91 — 79 2/3)
detA. =
1 2 — 1 4
0 — 1 1 — 12
0 0 — 3 79
ΠΠ— 2 115/3
Так как элементы определителя, расположенные под
его главной диагональю, равны О, то, следовательно, опре-
делитель равен произведению элементов, расположенных
на главной диагонали: detA =1 ( — 1).( — 3) =115.
115
3
1
0
detA =
(0-8. О)
(0-9 О)
— 1
( — 2 — 3-( — 1))
(1-4 (-1))
(2 — 5. ( — 1))
4
(0-3 4)
( — 1 — 4 4)
(3-5 4)

ГЛАВА 1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
45
1.9. Пользуясь свойством, состоящим в том, что опре-
~литель матрицы С = А В, которая представляет собой
произведение кв дратных матриц А и В одинаковых по-
рядков равен произведению определителей матриц А и В,
T. e. det С = det А det В, вычислить определитель матри-
— 2 3 4
— 1 — 3 5
0 4 3
0 2 8
В=
3 2 — 3
0 2 О
4 1 3
3 2 5
detA=0 2 8 =
4 1 7
=2 ( — 1)2'2 =2 (9+12) =42.
4 3
Здесь мы умножили второй столбец определителя на
( — 4), прибавили к третьему столбцу, а затем разложили
полученные значения определителя по второй строке.
Аналогично
0 9 — 6
— 2 3 4
9 — 6
=( — 1) ( — Ц"' =51.
4 3
detB =
— 1 — 3 5
0 4 3
— 1 — 3 5
0 4 3
Здесь мы умножили вторую строку на ( — 2) и прибавили
& t; П~р ой стро е а за ем разлож ли получивши ся опре
литель по первому столбцу. Перемножая полученные зна-
чения определителей, находим, что det С = 51 . 42 = 2142.
Можно убедиться легко в том, что этот же результат мы
«лучим, если найдем сначала матрицу С, перемножив
ми~рицы А и В, при этом матрица С имеет вид:
-8 23 37
С = -2 26 34,
-9 37 42
а затем вычислим det С.
<р ме мет да пониже ия поря ка определит ля (п
меР 1.7) и метода приведения к треугольному виду (при-
еР 1.8), при вычислении определителей используется
P e ш е н ие. Найдем определители матриц А и В и за-
тем перемножим их. Имеем

46
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
1 1 1
а1
2
а2
Q 2
2
аз ... а„
2 2
аз
D„=
Qn-1 Qn-1 Qn-1 аП вЂ” 1
1 2 з и
Покажем, что при любом и & t 2 определит ль Ванд
монда равен произведению всевозможных разностей а;—
— а;, где 1 & t   l ;  lt; и В са ом е е  ри и
1 1
~2
а1 а2
= а2 -а1.
Пусть утверждение доказано для определителей Ван-
дермонда порядка и — 1:
П(a; )
1<j& t;i l
где символ
а;
означает произведение элементов а;, т. е.
Докажем, что эта формула справедлива и для D„. Для это-
го из последней и-й строки вычтем (и — 1)-ю, умноженную
на а„и далее последовательно вычитаем из Й-й строки (Й—
— 1)-ю, умноженную на а,. В результате получим
метод рекуррентных соотношений. Суть метода состоит в
том, что исходный определитель D„n-го порядка выражает-
ся через определители того же типа, но более низкого поряд-
ка, т. е. по рекуррентной формуле вида: Р„= f(D„„D„
..., Р„~), справедливой для всех натуральных и, боль-
ших й. Из этого соотношения, применяя метод математи-
ческой индукции, получается формула, выражающая опре-
делитель З„через определители D„1, D„„..., З„
В качестве примера применения указанного метода
вычислим определитель Вандермонда:

ГлАцА 1. элементы линейнОЙ АлГеБРы
47
ап — а1
2
ап — ana1
а2 — а1
а2 а?а
2»
аз -а1
аз — аза1
2
D„=
0 Qï-1 — Qï-2Q Qn-1 — аи-2Q
2 2 1 3 3 1 ° ° и п 1
Qn — 1 — Qn — 2а
Далее разложим этот определитель по первому столб-
цу H вынесем из всех столбцов общие множители. В ре-
Зудьтате получим рекуррентное соотношение:
1 1
ап
а2
аз
аз
2
2
ап
Q2
2
Р„= (а2 — а,) (аз — а~)...(а„— а~).
ап — 2
п
Qn-2 Qn-2
2 3
=(а2 — а~) (аз — а,)...(а„— а,)х
а; — а;= а; — а;.
2& t; j&
1&l ;j &
1.10. Методом присоединенной матрицы найти А ', если
А= 1 2 5.
P е ш е н и е. Прежде всего вычисляем определитель
данной матрицы, чтобы убедиться в существовании обрат-
ной матрицы. Имеем
detA =
Здесь мы прибавили к элементам второй строки элемен-
ты третьей строки, умноженные предварительно на ( — 1), а
3~òåì раскрыли определитель по второй строке. Так как оп-
Ределитель данной матрицы отличен от нуля, то обратная к
° .Ф
" H матрица существует. Для построения присоединенной
1
0
0
2 5 6
1 2 5
1 2 3
2 5 6
2 5
0 0 2=( 2) =2.
1 2 3

48
матрицы находим алгебраические дополнения элементов
данной матрицы. Имеем
1 2
1 2
А =(-1)'"
1 5
1 3
А1з = (-1)"
А11 —— ( — 1)'"
=2,
= — 4,
2 5
1 2
2 6
1 3
( 1)2+3
= — 3,
— 0,
5
= — 1
2
2 6 2
= — 4 Адд — — ( — 1)з'з
1 5 1
=13 Ад~ — — ( — 1)з'2
(1)з+н
В соответствии с формулой (1.15) транспонируем мат-
рицу А*:
— 4 2 0 — 4 — 3 13
А — 3 0 1 (А )т 2 0 4
13 — 4 — 1 0 1 — 1
Тогда по формуле (1.15) имеем
1.11. Методом элементарных преобразований найти А ',
если
1 2 4
А= 2 1 5.
3 2 6
P e ш е н ие. Образуем матрицу В:
1 2 4
B=215
3 2 6
1 0 0
0 1 0 .
0 0 1
Обозначим строки матрицы В через и1, а2, аз. Произведем
над строками матрицы В следующие преобразования:
О 3 и3 3С~1 j (X3 R3 2С~2 ~
и 1 т 1 n i n
гъ m
а2 —— — — &lt 2~ .з Ђ” Ђ” Ђ” lt 3~ 1 в ” в ” †4а2+ а
3 ' 2
<iv,„, & t;v
з — 3 2 з — з .
2 5
2 3
5 6
2 3
5 6
2 5
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
-2 -3/2 13/2
А'= 1 0 — 2
0 1/2 — 1/2

49
0
0
1
1 2
-+0 1
0 1
1 0
-+0 1
0 1
1
— 1
2
2 1
3 2
Следовательно, А ' =
P е ш е н и е. Найдем А ' методом присоединенной мат-
рицы. Имеем det А = 2. Найдем алгебраические дополне-
ния элементов матрицы А. В данном случае алгебраиче-
скими дополнениями элементов матрицы будут соответст-
вующие элементы самой матрицы, взятые со знаком в
соответствии с формулой (1.11). Имеем А1, = 3, А12 = — 4,
&lt 2 gt; = Ђ” , А2 = 2. Об азуем присоеди енную м
А'=(
~транспонируем матрицу.4*:
На~одим обратную матрицу по формуле (1.15):
А-' = — [
1ддцА 1. элементы линейнОЙ АлГеБРы
B результате последовательно получаем
1 2 4 1 0 0 1 2 4 1 0
2 1 5 0 1 0 -+ 0 — 3 — 3 — 2 1
3 2 6 0 0 1 0 — 4 — 6 — 3 0
4 1 0 0 1 0 0 -2/3
1 2/3 -1/3 0 w 0 1 1 2/3
0 1/2 -1 1/2 0 1 0 1/2
0 -2/3 -2/3 1 1 0 0 — 2/3
1 2/3 -1/3 0 w 0 1 0 1/2
-1 -1/6 -2/3 1/2 0 0 1 1/6
2 2
3 3
1
2
1
6
2 1
1.12. Найти А ' для матрицы A. =
4 3
-2/3 1
— 1/3 0
— 1 1/2
-2/3 1
-1 1/2
2/3 -1/2

50
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
1.13. Методом окаймляющих миноров найти ранг мат-
рицы
2 1 2 1 2
1 1 5 — 2 3
— 1 0 — 4 4 1
3 3 8 1 9
P е ш е н и е. Минор второго порядка
2 1
=2 1— - 11=1;0,
1 1
отличный от нуля, расположен в левом верхнем углу мат-
рицы А. Минор третьего порядка
1 0 — 3
1 1 5
— 1 0 4
2 1 2
1 1 5
— 1 0 4
=4 — 3=1~0,
1 — 3
— 1 4
M3 =
окаймляющий минор М2, также отличен от нуля. Однако
оба минора четвертого порядка, окаймляющие Мз,
2 1 2 1
2 1 2 2
1 1 5 — 2
— 1 0 — 4 4
1 1 5 3
— 1 0 — 4 1
М4 =
М4 =
3 3 8 1
3 3 8 9
равны нулю. Поэтому ранг матрицы А равен 3, а базисным
минором является, например, представленный выше ми-
нор Мз.
Метод элементарных преобразований основан на том,
что элементарные преобразования матрицы не меняют ее
ранга. Используя эти преобразования, можно привести
матрицу к виду, когда все ее элементы, кроме а», а22, ...,
а„„(г & t; min m, и ), ра ны ну ю. Э о, очевид о, означа
что rang А = r. Заметим, что если матрица и-го порядка
имеет вид верхней треугольной матрицы, т. е. матрицы, у
которой все элементы под главной диагональю равны нулю,
то ее определитель равен произведению элементов, стоя-
щих на главной диагонали. Это свойство можно использо-
вать при вычислении ранга матрицы методом элементар-
ных преобразований: необходимо с их помощью привести

ГлАцА 1. элементы ЛинейнОЙ АлГеБРы
51
~атрицу к треугольной и тогда, выделив соответствующий
~пределитель, найдем, что ранг матрицы равен числу эле-
ментов главной диагонали, отличных от нуля.
1.14. Методом элементарных преобразований найти
ранг матрицы
5 7 12 48 -14
9 16 24 98 -31
14 24 25 146 -45
11 12 24 94 -25
Р е ш е н и е. Обозначим i-ю строку матрицы А симво-
лом а;. На первом этапе выполним элементарные преобра-
зования ©2 — +2 — ©3 + ©1 ©3 — ©3 — ©2 — ©1 +4 — о 4 — о 3 + О1 °
На втором этапе выполним преобразования
I1 1 1 It 1 1
©3 =ОЗ+©2,©4 =О4 О2 °
В результате получим
5 7 12 12 -7
0 — 1 0 2 0
0 0 — 1 0 3
0 0 0 0 0
H»ðåT~åì этапе мы переставили четвертую строку на
~есто третьей, а третью — на место четвертой. На четвер-
то~ц
о'" этапе мы разделили элементы четвертого и пятого
стол
~~лбцов соответственно на 4 и 2 и поменяли местами тре-
тий и четвертый столбцы. Из вида матрицы, получившей-
ся и
" П~~ле четвертого этапа преобразования, следует, что
5 7 12 48 -14
9 16 24 98 -31
14 24 25 146 -45
11 12 24 94 -25
5 7 12 48 -14
0 — 1 11 0 0
0 0 0 0 0
0 0 0 — 4 6
5 7 12 48 -14
0 — 1 11 0 0
0 1 — 11 0 0
0 0 0 0 0
5 7 12 48 -14
0 — 1 11 0 0
0 0 0 — 4 6
0 0 0 0 0

52
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
х1 + 4х2+10хз — — 1,
7х1 + 8х2 +18хз — — 2,
Зх1 + 7х2 +17хз — — 3.
P е ш е н и е. Определим ранги основной А и расширен-
ной А матриц системы:
А= 7 8 18
1 4 10 1
А= 7 8 18 2.
3 7 17 3
Начнем с расширенной матрицы. Произведем следую-
щие действия: (2) — (1) ~ 7, (3) — (1) ~ 3, получаем
1 4 10
А- 0 -20 -52
0 — 5 — 13
— 5 .
Разделим вторую строку на 4:
1 4 10
А — 0 — 5 — 13
0 — 5 — 13
— 1,25 .
Вычтем из третьей строки вторую:
1 4 10
А- 0 — 5 — 13
0 0 0
— 1,25 .
Получили, что у основной матрицы системы
1 4 10
А — 0 — 5 — 13
0 0 0
rang А = 3. Можно было бы продолжить преобразование
матрицы А, добиваясь обнуления остальных элементов мат-
рицы с различными индексами, но вряд ли это целесообраз-
но при нахождении ранга матрицы. Заметим также, что по-
лучившуюся в результате элементарных преобразований
нулевую строку можно было бы не писать при дальней-
ших преобразованиях матрицы, а просто вычеркнуть, что,
очевидно, никак не повлияет на ранг исходной матрицы.
1.15. Исследовать систему уравнений

ГлАЯА 1. элементы линейнОЙ АлГеБРы
53
всего лишь две линейно независимые строки — первая и
вторая, значит, rang А = 2. Чтобы найти ранг расширен-
ной матрицы системы, составим минор третьего порядка.'
1 4 1
=1.( — 5) ( — 1,25) = — 6,25~0,
Мз=0 5 — 125
0 0 1,25
значит, r»g A = З. 'Гак как rang A e rang A, то по теореме
Кронекера — Капелли система несовместна.
1.16. Исследовать систему уравнений
Зх1 +4х2+ Зхз — — О,
х1 — х2 + хз — — О,
х1 + Зх2 — хз — — — 2,
х1 + 2х2+ Зхз — — 2.
P е ш е н и е. Найдем ранги основной матрицы системы
и расширенной матрицы. Имеем
1 — 2 1
3 4 3
1 3 — 1
1 2 3
меняем местами
1 и 2 строки
А-
1 — 2 1
0 10 0
0 5 — 2
0 4 2
~из 2строки — (1строка) хЗ;
- из Зстроки — 1строка;
из 4 строки — 1 строка
0
0
— 2
1
1 — 2 1
2 строку разделим на 10; 0 1 0
I,4 строку разделим на 10 0 5 — 2
0 2 1
1 — 2 1 0
0 1 0 0
0 0 1 1
0 0 1 1
l
из 3 строки — (2 строка) х 5;
i из4строки — (2строка)х2
0' удаляем
0 нулевую
1 четвертую
0 строку
1 — 2 1
»з 4 строки — 0 1 0
~3 строка 0 0 1
0 0 0
1 — 2 1 0
0 1 0 0
0 0 1
3 4 3
1 — 2 1
1 3 — 1
1 2 3
0
0
— 2
2,
0
0
— 2
2
0
0
— 2
2

54
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
Полученный результат показывает, что матрица А и
расширенная матрица А имеют одинаковый ранг:
rang À = rang À = 3,
таким образом, система уравнений совместна и имеет толь-
ко одно решение.
1.17. Исследовать систему уравнений
2х~ + 2х2 + 2хз — х4 — — 1,
5х1 + 5х~ +2хз + Ох4 — — 2,
», + Зхв + хв + х4 = 1,
3Х1 +»в + Хв — Х4 = 1,
Х] + 2Х2 + ЗХв — Х4 = 1.
P е ш е н и е. Найдем ранги основной матрицы системы
и расширенной матрицы. Имеем:
1 2 3 — 1
5 5 2 0
2 3 1 1
3 2 1 — 1
2 2 2 — 1
2 2 2 — 1
5 5 2 0
2 3 1 1
3 2 1 — 1
1 2 3 — 1
меняем местами
1и 5строки
1 2
0 — 5
— 0 — 1
0 — 4
0 — 2
1
— 3
— 1 — [(4) делим на 2]—
— 2
— 1
1 2 3 — 1
0 — 5 — 13 — 5
0 — 1 — 5 — 3
0 — 2 — 4 — 1
из одинаковых
строк 4 и5
вычеркиваем
5-ю
1 2 3 — 1
0 — 1 — 5 — 3
0 — 5 — 13 — 5
0 — 2 — 4 — 1
1
— 1 (3) — (2) х 5;
— 3 (4) — (2)х2
— 1
2 и 3 переставили
местами
1 2 3 — 1
0 — 1 — 5 — 3
0 0 12 10
0 0 6 5
1 2 3 — 1
0 — 1 — 5 — 3
2 0 0 12 10
0 0 0 0
1 2 3 — 1 1
— [вычеркиваем нулевую 4-ю строку] — 0 — 1 — 5 — 3 — 1
0 0 12
(2) — (1) х 5;
(3) — (1) х 2;
(4) — (1) х 3;
(5) — (1) х 2
1 2 3
0 — 5 — 13
0 — 1 — 5
0 — 2 — 4
0 — 2 — 4
1
2
1
1
1
1
— 3
— 1
— 1
— 1
3 — 1
— 13 — 5
— 5 3
— 8 2
— 4 1
1
— 1
2
0
1
2
1
1
1
1
— 3
— 1
— 1

ГЛАЦА 1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
55
Минор третьего порядка, совпадающий с определите-
лем матрицы, эквивалентной для основной матрицы сис-
темы, отличен от нуля:
1 2 3
0 — 1 — 5 = — 12,
0 0 12
detA. =
х1 +2х2+Зхз — х4 =1,
— х2 — 5хз — Зх4 = — 1,
12хз +10х4 = — 1.
Пусть х4 = С (свободная неизвестная). Тогда из послед-
него уравнения системы получаем
хз — — — ( — 1 — 10 С).
1
12
Применяя обратный ход метода Гаусса, последователь-
но определяем остальные неизвестные х2, х1.
1.1S. Матричным способом решить систему уравнений
х1 +2х2+4хз — — 5,
2х1 + х2+5хз —— 7,
Зх1 +2х2+бхз — — 9.
P e ш е н и е. Перепишем систему в матричном виде'.
Х= В, где
2 4 х1 5
1 5,Х= х2,В= 7
2 6 хз 9
А= 2
отсюда следует, что rang А = 3. Поскольку этот же минор
входит в состав расширенной матрицы системы, имеющей
лишь три строки, то rangÀ =3 и по теореме Кронекера—
К',апелли система совместна. Так как число неизвестных
ц = 4 больше ранга основной матрицы системы, то система
неопределенна и имеет бесчисленное множество решений.
С учетом вида последней из эквивалентных матриц для рас-
ширенной матрицы системы запишем соответствующую
систему алгебраических уравнений:

56
Решение представляется в виде Х = А ' В. Обратная мат-
рица для основной матрицы системы найдена в приме-
ре 1.11, ее вид
А'=
Имеем
Х=А '.В= 0 .
1.19. Решить IIQ формулам Крамера систему уравнений
из примера 1.18.
P е ш е н и е. Определитель для основной матрицы сис-
темы вычисляется так'.
1 2 4
215=115 — 225421
2 6 3 6 3 2
= — 4+6+4 = б;
~z 0 ~з
х2 = — = — =О, хз—
Л 6 Л 6
~ó 6
х~ — — — — — — — — 1,
Л 6
Решение совпадает с тем, которое найдено матричным
способом.
1.20. Решить систему уравнений из примера 1.18 мето-
дом Гаусса.
5 2 4
7 1 5
9 2 6
1 5 4
2 7 5
3 9 6
1 2 5
2 1 7
3 2 9
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
2 2
3 3
1
2
1
б
— 1
2
2 1
3 2
1 5 7 5 7 1
= 5 ° — 2 ° +4 ° = — 20+6+ 20 =6;
2 6 9 6 9 2
=1 ° — 5 ° +4 ° = — 3+15 — 12 =0;
7 5 2 5 2 7
9 б 3 6 3 9
1 7 2 7 2 1
=1 -2. +5 =-5+6+5=6;
2 9 3 9 3 2

ГЛАВА 1. элементы линейнОЙ АлГББРы
57
решение. Имеем
5 1 2
(2) — (1) х 2;
9 Π— 4
7 (3) (1)„3 3
2 4
А=2 1 5
3 2 6
5
— 3 — [(2): ( — 3)]—
— 6
— 3
5 1 2 4
1 — [(3) — (2) х ( — 4)] — О 1 1
— 6 ΠΠ2
2 4
- О
P — 4 — 6
На этом прямой ход метода Гаусса закончен, и для про-
ведения обратного хода составляем систему, которая соот-
ветствует последней матрице, эквивалентной исходной
расширенной матрице системы:
х1 +2х2+4хз — — 5,
х2+ хз =1,
2хз — — 2.
х1 + 2х2 + хз — х4 = 1,
— х2 — 5хз — х4 = — 1,
бхз+5х4 =1.
3ðeñ~ свободное неизвестное х4, перенесем его в правые
Части, базисные неизвестные х1, х2, хз оставим в левых час-
~ц~ уравнений
х1+2х2+хз =х4+1,
— х2 — 5хз = х4 1,
бхз = — 5х4+1.
Найдем из последнего уравнения выражение хз и, под-
став
~~~ив во второе уравнение, определим х2. Имеем
5 1 5 1 1 31
хз — х4 +, х2 — 1 — 5 — х4 + — х4 — — х4 °
6 6' 6 6 6 6
Из последнего уравнения находим хз = 1, подставляя
найденное хз во второе уравнение, найдем х2 = 1 — хз = О.
Из первого уравнения найдем x& t  5 Ђ 2 х2 Ђ 4 х =
1.21. Решить методом Гаусса систему из примера 1.17.
Р е ш е н и е. В результате элементарных преобразова-
»й над расширенной матрицей системы получили в кон-
се прямого хода метода Гаусса следующую систему.'

ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
Подставим теперь хз и х2 в первое из уравнений и най-
дем х1.
1 31 5 1 1 73
х1 =-2 — — — х4 — — — х4+ — +х4+1= — + — х4.
6 6 6 6 2 6
Таким образом, ответ запишется так:
»4 ЕЯ,
1 73
Х1 = — + — Х4
2 6
1 31
Х2 = — — — Х4~
6 6
5 1
ХЗ Х4 +
6 6
1.22. Решить методом Гаусса систему уравнений из при-
мера 1.15.
P е ш е н и е. Запишем систему уравнений, соответст-
вующую окончательному виду расширенной матрицы си-
стемы из примера 1.15:
— 1,25
1 4 10
Π— 5 — 13
О О О
х1 + 4х2 + 1 Охз — — 1,
— 5' — 13хз = — 1,25,
Охз —— 1,25.
х1 + 7х2 — 8хз + 9х4 — — О,
2х1 — ЗХ2 + Зхз — 2х4 — — О,
4х1 + 11х2 — 13хз + 16х4 — — О,
7x& t; Ђ” х + х + x4 Ђ” Ђ”
P е ш е н и е. Основная матрица системы имеет вид
1 7 — 8 9
2 — 3 3 -2
4 11 -13 16
7 — 2 1 3
Нетрудно видеть, что данная система несовместна, так
как последнее уравнение неверно при любом значении хз.
1.23. Найти фундаментальную систему решений для сис-
темы уравнений и записать общее решение этой системы.

ЛАВА 1. 3лементы линейнОЙ АлГеБРы
59
ранг этой матрицы равен 2, причем минор второго по-
рядка расположенный в верхнем углу этой матрицы, не
равен кулю, а все остальные его окаймляющие миноры
уретьего порядка равны нулю. Это означает, что третье и
че~вертое уравнения системы являются следствием первых
двух. Отсюда следует, что все решения исходной системы
являются решениями следующей системы, соответствую-
,цей первым двум строкам основной матрицы системы:
х1 + 7х2 — 8хз + 9х4 — — О,
2х1 — Зх2 + Зхз — 2х4 — — О.
Х1 +7Х2 =8Хз — 9Х4
2Х1 — ЗХ2 — — — Зхз + 2х4.
Решим систему матричным способом. Обратная матри-
ца для квадратной матрицы второго порядка
А=( )
~TpoHTñà сокращенно следующим образом: переставляют-
«местами элементы на главной диагонали, а элементы на
~оброчных диагоналях меняют свой знак, полученная мат-
Рица делится на определитель прямой матрицы:
ЙеСА = =1 ( — 3) — 7 2= — 17.
1 7
2 — 3
3 7
-3 -7 17 17
— 17 — 2 1 2 1
17 17
Имеем А-' =
Далее получаем:
3 7
17 17
2 1
17 17
3 13
— ХЗ вЂ” — Х4
17 17
19 20
— ХЗ вЂ” — Х4
17 17
3десь свободные неизвестные хз и х4 следует перенести
в правые части уравнений, оставив в левых частях базис-
ные неизвестные х1 и х2.

60
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
-ХЗ
Приравнивая столбец свободных членов сначад~
Х4
1 0
к, затем к получим фундаментальную систему
13
17
20
17
0
решений
Х(~)—
Х~Ц =
Общее решение исходной однородной системы получит-
ся в виде
3 13
a.— +P
17 17
X = aX~'~ + (X~2~ = a
Здесь а и р — произвольные действительные числа.
1.24. Найти общее решение неоднородной системы
х1+ 7х2 — 8х3+ 9х4 = 4.
P е ш е н и е. Ранги основной матрицы системы и рас-
ширенной матрицы системы равны единице. Поскольку
число неизвестных равно четырем, то количество базис-
ных неизвестных равно единице (пусть базисной неизвест-
ной будет xi), а количество свободных неизвестных равно
трем (пусть свободными неизвестными будут х2, хз, х4). Пе-
репишем систему так:
x& t = Ђ” x gt; + 8 3 в ” 9х
Приравнивая столбец свободных членов
х2 1 х2 0
х = О, Жобщ.одн.) = х = 1
3 Ф 3
х4 0 х4 0
х2 0
-ХЗ
х4 1
получим фундаментальную систему решений однородной
системы х1+ 7х~ — 8х3 + 9х4 = 0:
3
17
19
17
1
0
3
17
19
17
1
0
13
17
20
17
0
19 20
a. — +P
17 17
а 1+( О
а.0+Р.1

ГЛАЦА 1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
61
— 9
0
0
1
Х(3)—
Общее решение соответствующей однородной системы:
Х(общ. одн.)
1
где С,1, а2, аз — любые действительные числа. Найдем те-
перь частное решение исходной неоднородной системы
х1+ 7х2 — 8хз + 9х4 = 4.
Для этого положим все свободные неизвестные равны-
ми нулю: х1 + 7 0 — 8 0 + 9 0 = 4. Получили, что частное
решение имеет вид
x1 — — 4
х2 — — 0
хз — — 0
х4 =0
'~(частн. неодн.)
Общее решение неоднородной системы есть сумма ее
частного решения и общего решения соответствующей од-
нородной системы:
Х(общ. неодн.) у(общ. одн.) + Х(часты. неодн.)
9 4~
0 0
+оз +
0 0
1 0
1.25. Найти общее решение неоднородной системы
х1 + 7х2 — 8хз + 9х4 — — 1,
2х1 — Зх2+Зхз — 2х4 =1,
4х& t + 1 x2 Ђ” 1 х + 1 х4 Ђ” Ђ”
7х1 — 2х2 + хз + Зх4 — — 4.
— 7
Х(1) =
1
0
0
— 7
1
0
0
1
0
0
8
0
+ С~2
1
0
8
0
1
0
0
1
0
0
0
1

62
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
P е ш е н и е. Основная матрица системы совпадает с
той, которая рассмотрена в примере 1.23. Нетрудно пока-
зать, что ранги расширенной матрицы системы и основ-
ной матрицы системы равны 2, система совместна. Систе-
ма эквивалентна следующей:
& t; x gt; + 7 2 в ” Ђ” + 8 з вЂ
2x& t; Ђ” х2 Ђ” Ђ 1 Ђ” х + 2
Общее решение соответствующей однородной системы
получено в примере 1.23, его вид таков:
3 13
а — +P.—
17 17
19 20
a. — +P
17 17
а 1+P 0
а 0+P 1
Х~общ. одн.) g,
Частное решение найдем, положив свободные неизвест-
ные равными нулю:
х1+7х2 — — 1+8 0 — 9 0=1,
2х1 — Зх2 —— 1 — 3 О+2 0=1.
С помощью обратной матрицы для основной матрицы
этой системы (она найдена в примере 1.23) получаем:
Х= =А' В=
отсюда следует, что
'~'(частн. неодн.)
3
17
19
17
1
0
13
17
20
17
0
10
17
1
17
0
0
10
17
1
17

ГлАцА 1. элементы линейнОЙ АлГеБРы
63
Следовательно,
Х(~ "'") =а
1.26. Найти координаты вектора
Х1
Х= хг
хз
если линейное преобразование, переводящее его в вектор
У= 2,
задано системой уравнений
х1+2хг+Зхз — — 1,
— Х1 + ЗХг + 4Хз — — 2,
2Х1 — ЗХг + 5Хз —— 3.
Р е ш е н и е. Найдем обратную матрицу для основной
Матрицы системы
2 — 3 5
Вычисляем определитель данной матрицы, чтобы убе-
диться в существовании обратной матрицы. Имеем
1 2 3 А11 — — 27, Аг1
Ое~А = — 1 3 4 =44~0; А1г =13, Агг
2 — 3 5 А1з = — 3 Агз
27 -19 -1
А '= — 13 — 1 — 7.
44 3 7 5
= — 19, &gt 31 Ђ” Ђ”
= — 1, Азг= — 7,
Азз =5.
«3
17
19
17
1
0
13
17
20
17
0
10
17
1
17
О
3 13 10
a — +P — +—
17 17 17
19 20 1
a. — +P. — +—
17 17 17
а 1+P 0
а0+P1

64
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
Отсюда
7
22
5
22
13
22
Х=А '.В=
Полученное решение дает координаты искомого вектора.
1.27. Дано линейное преобразование с помощью систе-
мы уравнений
g1 — — — х1+О х2+О.х3,
g2 — — О х1+1 х2+О.х3,
~~~3 0 "1+О' "2+1' "3
Найти матрицу преобразования, будет ли она вырож-
денной?
P е ш е н и е. С учетом матричной записи преобразова-
Здесь матрица преобразования
А= О 1 О
Х1 Х2
Ь~1 (122 ~123 Х2 — — 2Х2
Ь1 (132 ~133 Х3
Х2 Х3
~11 Ж2 Жз
~21 ~22 ~23
~31 ~32 ~33
Х2
Х1
Х1 + Х-З
ХЗ
имеет отличный от нуля определитель, равный произве-
дению всех элементов, расположенных на главной диаго-
нали det А = ( — 1) 1 . 1 = — 1 w О (отображение также невы-
рожденное).
1.28. Имеются линейные преобразования Ах = {х2 — х3,
х1, х1+ х3) и Вх = {х2, 2х2, х1) вектора х = {х1, х2, х3). Най-
ти отображение В (2А — В)х.
P е ш е н и е. Выпишем матрицы линейных отображе-
ний. Для этого запишем заданные отображения в матрич-
ном виде:

ГЛАЦА 1.. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
65
Перемножая матрицы в левых частях записанных мат-
ричных уравнений, получим
~111х1 + 42x2 + 43x3 х2
Ь21Х1 + Ь22Х2 + ЬЗЗХЗ вЂ” — 2Х2
~131Х1 + ~132Х2 + ~1ЗЗХЗ Х1
Ц„Х1 + а12Х2 + а1ЗХЗ Х2 — ХЗ
Я21Х1 + ~22Х2 + ~23ХЗ Х1
И31-Х1 + И32Х2 + a33X3 х1 + ХЗ
Отсюда следует, что
a12= 1,
а22= 0,
а32=0,
~12
b22 — — 2,
032=О
Таким образом, матрицы А и В имеют вид
А=1 О О, В=О 2 О.
С учетом свойств линейного преобразования найдем
матрицу искомого линейного отображения.'
В. (2А — В) = 2В А — В. В =
0 1 0 0 1 — 1 0 1 0 0 1 0 2 — 2 0
=2-020.100 — 020-020=0 — 40
1 0 0 1 0 1 1 0 0 1 0 0 1 1 — 2
1 1 2
1.29. Пусть с помощью матрицы А = 3 — 1 О про-
1 1 — 2
изводится преобразование вектора х в базисе (e1, е2, еЗ).
определить матрицу преобразования А' в базисе (e,' е' е' )
если
1 / 1
е1 — — e1 — е2+ез e2 — e, +е2 — 2ез ез = — е1 +2е2+ез °
Р е ш е н и е. Выпишем матрицу преобразования старо-
» базиса в новый:
а11= О,
a21= 1,
~31= 1
b11 О,
~21= О,
"з1= 1
~13 =
а23= О,
~зз = 1.
~13 — О,
"23= О,
~33 = О.

66
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
1 — 1 1
В= — 1 1 — 2.
— 1 2 1
Найдем обратную матрицу В ', предварительно убедив-
шись, что она не вырождена:
5 3 1
3 2 1,
— 1 — 1 0
=1~0, В '=
0 — 1 1
— 1 1 — 2
— 1 2 1
detB =
15 — 2 8
8 — 1 4
— 4 1 — 2
В' А= 3 2 1
3 — 1 0
Найдем искомую матрицу преобразования по формуле
А'=В 1 А В= 8 — 1 4 — 1 1 — 2 = 5 — 1 14 .
д'1 =(1; 1;О), g2=(2;0; 1), д=(0; 1;-2).
Решение.
f, =g, =(1;1;О),
С|г (д'г,(1)/(f1 (1) =(2'1+ О 1+ 1 О)/(1г+ 1г+ Ог) = 1,
fg = gg Сгf (2. О. 1) — 1 (1. 1 О) (1. -1 1)
Ci=(ga,fi)/(fi,fi)=(0 1+1 1+( — 2) o)/(1'+1'+О')=o,5,
C8 = (gз, Ю/Иг, fг) = (О 1+ 1 (-1)+
+ ( — 2) 1)/(1г+ ( — Ä)2+ 1г) — 1,
/г = gg — СУ~ — C)f2 = (О; 1; — 2)—
— 0,5 (1; 1; О) — (-1) (1; -1; 1) = (0,5; -0,5; -1).
[/2 /2 p)
e& t; Ђ” Ђ” (
1.30. Применяя процесс ортогонализации Шмидта, по-
строить ортонормированный базис (e&g ;, г, г) по данн
базису (gq, g2, g3):

ГЛАДА 1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
67
( Гз i3 Гз]
( /6 /6 /6]
е =6/
ез =1з/
][.31. Найти собственные значения и собственные век-
торы линейного оператора А с матрицей
A=( ].
будут ли собственные векторы ортогональны?
Р е ш е н и е. Составим характеристическое уравнение
2
= О =э (1 — Х)(2 — Х) — 6 = О w Х~ — ЗХ вЂ” 4 = О.
2 вЂ
Решая квадратное уравнение, находим собственные
значения Х1= — 1, Х~ = 4. Далее найдем собственный век-
тор, соответствующий собственному значению Х1 = — 1. Со-
ставим систему
с (1 — Х, ) х, + 2xg = О, 2х, + 2х2 —— О,
=& t; 1+ х2 Ђ” Ђ”
Зх| + (2 — Х,)х2 = О. Зх| + Зх2 — — О.
Ю т
х&l ;ц mi Ђ” m
— т
Для собственного вектора kq= 4 получаем аналогично
& t; (1 Ђ” Х~ х + х~ — Ђ” О, Ђ” х + х~
' =& t ' =&g ; З 1 в ” 2х2 Ђ”
»& t + (2 Ђ” kq xq Ђ” Ђ” О. х| Ђ” х2 Ђ” Ђ”
Положим x& t = т, д т Ђ” произволь ое действите
ное число, отличное от нуля, тогда
х&lt ~~ =т~+1, m
1,5m
»epBbIH собственный вектор, соответствующий собствен-
~orvry значению Х~, имеет вид
Положим x& t = m, д т Ђ” произволь ое действите
ное число, отличное от нуля. Собственный вектор, соот-
ветствующий собственному значению Х1, имеет вид

68
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
m
х&l ; = mi Ђ” m
— m
А= 1 — 5 1
1 1 — 2)
Будут ли собственные векторы ортогональны?
P е ш е н и е. Составим характеристическое уравнение
( — 1 — Х) 1
1 ( — 5 — Х)
1 1
=Ow Xç+8~2+14~ =Ow
( — 2 — Х)
=~ Х(Х~ + 81+ 14) = О,
отсюда получаем Х1 = О, Х2 з — — — 4+ J2.
Найдем собственный вектор, соответствующий собст-
венному значению Х1 = О, из следующей системы уравне-
ний:
( — 1 — Х~)х~+1.х2+1.хд =О,
1 х1+( — 5 — k~)xi+1.хз — — О,=э
1. х1+1.х2+( — 2 — kq)хд — — О.
— х1+х2+хз — — О,
х1 — 5х2 + хз — — О,
х1 + х2 — 2хз — — О.
Определитель этой системы равен нулю, минор, стоя-
щий в левом верхнем углу,
— 1 1
=4~0,
1 — 5
отсюда следует, что ранг основной матриць~ системы ра-
вен 2 и линейно независимыми являются только первые
Найдем скалярное произведение собственных векторов:
x&lt '&gt  ~ & t  т + ( — ) - 1 5m = в ” 0,5 2. Чтоб
были ортогональны, необходимо, чтобы их скалярное про-
изведение было равно нулю, но тогда т = О, а этого быть не
должно, так как по определению собственный вектор не
может быть нулевым, следовательно, собственные векто-
ры неортогональны.
1.32. Найти собственные значения и собственные век-
торы линейного оператора А, заданного матрицей

1.ЛАВА 1. элементы линейнОЙ АлГеВРы
69
два уравнения, при этом свободной неизвестной будет х3,
~которую перенесем в правые части уравнений:
г
— Х, +Х2 —— — Х3,
х1 — 5х2 — — — х3.
Решаем систему по правилу Крамера:
— -ХЗ
— — ХЗ
-х3 1
— 1 1 2
— хз — 5 3
— 1 1 2
х2
Х1 ——
1 — 5
1 — 5
Положим х3 = т, где т — произвольное действитель-
ное число, тогда собственный вектор
1,5т
х® = 1,5mi + 0,5ту + mk = 0,5m .
m
Найдем собственный вектор, соответствующий соб-
ственному значению ~г = — 4 —,Г2, из следующей системы
уравнений:
(3+ Я)х~ + хг + хг — — О,
X) + ( — 1 + ~/2)хг + x3 — — О,
x& t + х + 2+ 2) хг Ђ” Ђ”
Аналогично предыдущему случаю, третье уравнение
есть следствие первых двух, поэтому третье уравнение от-
брасываем и получаем следующую систему для определе-
ния координат второго собственного вектора:
(3+ ~Г2)х1 + хг — — — хг,
x& t  ( Ђ” 1+ ~ 2) хг Ђ” Ђ” Ђ”
отсюда получаем
х~~~ = 0,5+2mi + ( — 2 — 1,5~Г2)ту + mk =
( — 1 — Хг)х, +1.х, +1.хг =О,
1 х, +( — 5 — ~г)хг+1.хг =0, э
1 х1+1.хг+( — 2 — Хг)хг — — О.
0,5 j2m
( — 2 — 1,5 Г2)т

70
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
Найдем собственный вектор, соответствующий собст-
венному значению Хз = — 4+ ~2, из следующей системы
уравнений:
(3 — j2)x>+х2 хз
х& t + -1 —, 2) х + х =
х& t + х + (2 Ђ” /2 xq Ђ” Ђ”
( — 1 — Хз)х&gt +1 х +1 хз Ђ” Ђ”
1 х1+( — 5 — Хз)х~+1 х, =О,»
1 х1 + 1 х2 + ( — 2 — Хз ) хз —— О.
Третье уравнение вновь есть следствие первых двух,
поэтому третье уравнение отбрасываем и получаем следую-
щую систему для определения координат третьего собст-
венного вектора.'
(3 — ~2)х& t + х2 Ђ” Ђ” Ђ”
x& t  ( Ђ 1 Ђ” ~2 х~ — Ђ” Ђ”
отсюда получаем
0,5Г2т
(2 — 1,5 j2)m
х'з' = 0,5 ~2т&gt ' + (2 Ђ” ,5 ~2) j + m
Выясним, ортогональны ли собственные векторы. Для
этого найдем их скалярные произведения:
х'" х'~& t; =( ,5 ,5 2+ , ( Ђ” ,5 ~2 Ђ” 2)+ )т
х&lt '&gt х&lt з> =(1 5 0,5 2+0 5 ( — 1, ~2
х~2& t; х з> =( ,5 2 0, ~2 ( — 2 в ” 1 5 2) 2 — 1,5v2 + )m
F(x, у) = 5х2 + бху + 5у~ = 5х2 + Зху + Зух + 5y2,
а11= 5, а~д = а~~ = 3, а22= 5.
Соответствующая ей матрица А квадратичной формы
такова:
Таким образом, ортогональными являются только век-
торы х~'~ и х~ ~.
1.33. Привести к каноническому виду квадратичную
форму, с помощью которой определяется уравнение кри-
вой второго порядка 5x2 + бху + 5y2 — 5х — 5y = 2.
P е ш е н и е. Квадратичная форма, определяющая дан-
ное уравнение, имеет вид

71
3
5 вЂ
=0»(5 — Х) — 9=0»k& t; Ђ” Ђ” 2, X&g ; в ”
Квадратичная форма в новой системе координат Ох'у'
запишется следующим образом: F(x', у') = 2(х')~ + 8(у')2.
Найдем собственный вектор для Х1 = 2. Составляем си-
стему'.
& t; (5 Ђ” Х, ) '+ у = О, З '+ у =
'~ х'+у'=Оw у'= — х'.
Зх'+ (5 — Xq ) у' = О. Зх'+ Зу' = О.
Положим х' = т, где т — произвольное действитель-
ное число, отличное от нуля, собственный вектор, соответ-
ствующий собственному значению Х1, имеет вид
х~ц =mi — mj =
— т
Нормируем этот вектор, разделив его координаты на
модуль,
=т 2: х~ц= — i — — j=
~2 —. ~2 -.
2 2
[х~ц (=
Найдем собственный вектор для Х2 = 8. Составляем сис-
тему:
& t; (5 Ђ” Х~) '+ у = О, Ђ” Зх'+ у =
~ х' — у'=0~ у'=х'.
3Х +(5 — Xq)y'=О. Зх' — Зу'=О.
Положим х' = т, где т — произвольное действитель-
ное число, отличное от нуля, собственный вектор, соответ-
ствующий собственному значению Х2, имеет вид
т
х~@=mi +mj =
т
Нормируем этот вектор, разделив его координаты на
модуль,
ГЛАВА 1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
A=( ].
Составляем характеристическое уравнение:
j2
2
~~2
2

72
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
=т/2: х~2& t; = ~ж ~
2 2
х
Выпишем теперь матрицу линейного преобразования,
элементы которой по строкам есть координаты собствен-
ных векторов:
а само искомое линейное преобразование имеет вид
Подставим эти зависимости в исходное уравнение кри-
вой с учетом того, что квадратичная форма, входящая в
это уравнение, уже найдена:
2(х')2+8(у')2 — 5 — х' — — у' — 5 — х'+ — у' =2»
Д,Д, Л,Д,
2 2 2 2
»2(х')~+8(у')~ — 5 2x'=2.
Выделим в полученном выражении полный квадрат:
2
2 (х')2 — 2 х' + +8(у')2 =2»
,15252
2 2 4
2
х' 5 2 +4у2=1.
4
Преобразование координат
х"=х' —, у"=у'
4
означает параллельный перенос осей в новое начало коор-
динат
(5Г2 о
~2 j2
2 2
~2 ~2
2 2
х = — х' — — у', у = — х'+ — у'.
~2, j2, ~2, ~2
2 2 ' 2 2
J2
2
J2
2

ГJIABA 1. элементы линейнОЙ АлГеБРы
73
()кончательно получим следующее каноническое уравне-
ние эллипса.
(х")~ (у")~
1~ (0,5)~
1.34. Привести к каноническому виду уравнение по-
верхности
3x + 4у + 5z + 4xy — 4yz + 2x — 8у + 14z = 16.
P е ш е н и е. Квадратичная форма, определяющая дан-
ное уравнение, имеет вид
F(x, у) = Зх2 + 4у~ + 5z2 + 4ху — 4yz.
Соответствующая ей матрица А квадратичной формы
такова:
А= 2 4 — 2.
Для поиска собственных значений составляем харак-
теристическое уравнение'.
О
(5 — Х)
Будем искать корни данного уравнения среди делите-
лей свободного члена 28. Имеем, при Х1 = 1 f(X) = Хз — 1212+
+ З9л — 28 = О. Разделим многочлен:
(Хз — 1212+ 391 — 28): (Х вЂ” 1) = 1,2 — 111+ 28,
отсюда ~2 — 11& t + 2   и X = 4, Х = 7. Квадратич ая ф
~~ в новой системе координат Ох'у'z'çàïèøåòñÿ следую-
~Чим образом: F(x', у', z') = (х')2 + 4(у')' + 7(z')2. Найдем соб-
ственный вектор для ~1 = 1. Составляем систему:
(5 — 1)х'+2у'+О z'=О,
2х '+ (4 — 1) у' — 2z' = О,
0 х' — 2у'+(5 — 1)z'=О,
х'+у'= О,
2х'+ 3y' — 2z' = О,
у' — 2z' = О.
(3 — Х) 3
2 (4-Х)
Π— 2
=0~ Хз — 1212+39Õ вЂ” 28=0~

74
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИ~О ЗАДАЧ
Так как определитель системы равен нулю, а минор,
составленный из элементов первой и последней строк
1 1
=1~0,
0 1
то второе уравнение есть следствие первого и третьего урав-
нений. Свободное неизвестное здесь у', а базисные х', z'.
Отбросив второе уравнение и решая полученную систе-
му из оставшихся уравнений относительно х', z', предва-
рительно перенеся у' в правые части, получим х' = — у',
z' = 0,5у'. Полагая у' = т, где т — произвольное и отлич-
ное от нуля действительное число, найдем координаты пер-
вого собственного вектора: х~ц = — т~ + mj + 0,5mk. Анало-
гичнО для Х2 = 1 и Хз = 7 пОлучим сОбственные вектОрЫ
х~2~ =m(i+0,5j+k), х~з~ =т((+2у — 2k). Нормируем их,
разделив соответственно на модули:
(х~'&g ;I
=1,5m;
(х~2~I =m
=1,5m;
Ix&lt »l
=Зт; х&lt
Выпишем матрицу линейного преобразования и само
преобразование:
2, 2 1
х = — — х'+ — д'+ — z
3 3 3
«2 1 2
3 3 3
g= — х+ — g+ — z,
«1, 2, 2
z = — х'+ — g — — z
3 3 3
Подставим эти зависимости в заданное уравнение по-
верхности.'
(х') +4(у')~ +7(z')2+ 2 — — х'+ — у'+ — z'—
3 3 3
— 8 — х'+ — у'+ — z' + 14 — х'+ — у' — — z' = 16.
2, 1, 2, 1, 2 2
3 3 3 3 3 3
2 2 1
3 3 3
2 1 2
3 3 3
1 2 2
3 3 3
— g х~ц 2-; 2-. 1 -.
х&l ;  = Ђ i +- j+
' =~х(1)~= 3 3 3 '
- 2 х~2~ «2-. 1-. 2 -.
Х(2) =-i +- j +-Й;
[ «&l ;
х~» «1-; 2-. 2-
= — i + — j — — k.
~х< ~

ГлАцА 1. элементы линейнОЙ АлГеБРы
75
Выделим полные квадраты в полученном уравнении:
((х') — 2х'+ 1 — 1) + 4((у')2+ 2у'+ 1 — 1) +
+ 7((z')2 — 2z'+ 1 — 1) = 16.
1.9.
ЗАДАЧИ
Х 1
1.35. Вычислить
0 Х
X c R.
1.36. Найти значение многочлена f(A) от матрицы А:
2 — 4 1 .
f(x) = Зх2 — 2х+ 5, А =
3 — 5 2
1.37. Вычислить AB — ВА, где
, В=
0 0 1
0 0 7
1.38. Найти все матрицы В, перестановочные с
А=( ).
1.39. Найти все матрицы второго порядка, квадраты
~вторых равны
1.40. Найти все матрицы второго порядка, квадраты
~вторых равны
Е=( ].
формулы х" =- х' — 1, g = g + 1, 2" = 2' — 1 п03ВОляют
дроизвести параллельный перенос осей координат в новое
начало координат (1; — 1; 1). Окончательно получим сле-
дующее каноническое уравнение поверхности:
(Х) (Д) (2)
28 7 4
которое является уравнением эллипсоида.

76
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
преобразований найти
1 1 1
1 1 — 1
1 — 1 1
1 — 1 — 1
1.42. Решить матричное уравнение
1.44. Вычислить определитель, приводя матрицу к тре-
угольному виду
3 2 2
1.45. Вычислить ранг матрицы методом элементарных
преобразований
1.46. Найти ранг матрицы А методом окаймляющих
миноров
1.41. Методом элементарных
обратную матрицу для матрицы
( )х( )(
1.43. Вычислить определитель
0 b c
b 0 d
с d 0
d c b
2 3 2
2 2 3
2 2 2
25 31 17
75 94 53
75 94 54
25 32 20
1 3 5
2 — 1 — 3
5 1 — 1
7 7 9
43
132
134
48
— 1
4
7
1

ГЛАВА 1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
77
1.47. По правилу Крамера решить систему линейных
уравнений
х+у — 2z =6,
2х+ Зу — 7z =16,
5х+ 2у+ z = 16.
1.48. Методом Гаусса решить систему
2х1 + 2х2 — хз + х4 — — 4,
4х1 + Зх2 — хз + 2х4 — — 6,
8х1 + 5х2 — Зхз + 4х4 — — 12,
Зх1 + Зх2 — 2хз + 2х4 — — 6.
9х1 — Зх2 + 5хз + бх~ — — 4,
6xj — 2х2 + Зхз + 4х4 —— 5,
Зх1 — х2 + Зхз + 14х4 — — — 8.
1.50. Определить значения параметра а, при которых
система имеет нетривиальные решения, и найти их.'
2Х1 + х2+ Зхз — — О,
4х1 — х2 + 7хз —— О,
х1 + аХ2+2хз — — О.
1.51. Методом Гаусса исследовать совместность и най-
ти общее решение системы
8х1 + 12х2 — — 20,
14х1 + 21х2 — — 35,
9хз + 11х4 — — О,
16хз + 20x4 — — О,
10х5 + 11х6 — — 22,
15х5 + 18х6 — — 33.
1.52. Найти собственные числа и собственные векторы
линейного оператора, заданного матрицей
0 — 1 0
— 1 — 1 0
1.49. Исследовать совместимость и найти общее реше-
ние системы

78
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
1.53. Найти ортонормированный базис из собственных
векторов и матриц оператора в этом базисе, если в неко-
торой opTQHQpMHpoBBHHQH системе матрица оператора
имеет вид
11 2 — 8
2 2 10.
— 8 10 5
В задачах 1.54 — 1.60 определить, какие квадратичные
формы являются положительно либо отрицательно опре-
деленными:
1.54. (р = х1+ 26х2+ 10х1х2.
1.55. y = — х21 + 2х1х2 — 4х22.
1.56. y = х~ — 15х2 + 4х1х2 — 2х1х3 + бх2х3.
1. 57. (р = 1 2х1х2 — 1 2х1х3 + бх2х3 — 1 1 х1 — бх2 — бх3.
1.58. (р = 9х21 + бх22+ бх2З+ 12х1х2 — 10х~ха — 2х2х3.
1.59. q = 2х4 + х1х2 + х1х3 — 2х2х3 + 2х2х4.
1.60. (р = х1+ 4х2+ 4х3+ 8х4+ 8х2х4.
В задачах 1.61 — 1.64 написать каноническое уравнение
кривой второго порядка, определить ее тип.
1.61. 9х — 4ху + бу + 16х — 8у — 2 = О.
1.62. х — 2ху+ у — 10х — бу+ 25 = О.
1.63. 5х2+ 12ху — 22х — 12у — 19 = О.
1.64. 2х + 4ху + 5y — бх — 8у — 1 = О.

ГЛАВА 2
ВЕКТОРНАЯ АЛГЕБРА
2.1.
КООРДИНАТЫ ТОЧКИ
И ВЕКТОРА
Определение 2.1. Любую совокупность действительных
чисел (х1, х2, ..., х„) будем называть точкой, а сами чис-
ла — координатами этой точки.
Будем обозначать точки большими латинскими бук-
вами, а координаты записывать в круглых скобках: Х(х1,
Х2; ...; Х„).
Точку (О; О; ...; О) будем называть началом координат и
обозначать О.
Определение 2.2. Пусть А(а~, а2, ..., а„) и В(Ь1, Ь2, ...,
b„) — две точки. Назовем вектором АВ величину, определя-
емую следующим образом: АВ = (Ь, — aÄ bz — а~, ..., ܄— а„).
Точка А(а~, а2, ..., а„) называется. началом вектора, а точка
B(b&g ;, Ь ,' . ., „) Ђ” конц
Векторы будем так же обозначать с помощью двух боль-
ших или одной маленькой латинских букв со стрелкой
сверху, указывая их координаты в фигурных скобках:
Щ а = (а1, .а2;...; а„).
Определение 2.3. Два вектора
а = (а,; а2,..., а„) и Ь = (Ь1, Ьд, ..., Ь„}
с одним и тем же числом координат называются равными
»ом и только в том случае, если равны соответствующие
координаты а1= '01, а2 = Ь2,...., aÄ = b„.
Определение 2.4. Длиной (или модулем) вектора
а = (а,; а ° ° а } назовем величину
(а[=

80
ПРАКТИЧЕСКОЕ РУКАВ(ЯСТВО К РЕШЕНИЮ ЗАДАЧ
Определение 2.5. Вектор а = {О; О; ...; О) называется ну-
левым вектором.
Определение 2.6. Вектор { — а1, — а2,, — а„) называется
противоположным вектором по отношению к вектору
а = {а1, а2, ..., а„)
и обозначается так: — а = { — Ж вЂ” ag ". — a ).
Определение 2.7. Произведением вектора
а = {а1, аз, ..., а„)
на действительное число Х называется вектор
с = {с1, с2, ..., с„) = Ха = {Xaq, Xaq', ..., Ха„).
Определение 2.8. Векторы
a = {aq, ад,..., a„) H Ь = {g; Ь2, ...,' Ь„),
удовлетворяющие соотношению
а = {a&g ;, 2, . ., „ = Х = {g Ђ” Ђ” X &g ;, 2 в ” †Xaz .. , Ь„=
Условие коллинеарности двух векторов
а = {aq, а2, ..., а„) и Ь = {Ь~, Ь~, ..., ЬД )
в координатной форме таково:
Ь1 Ь2 ~ï
° ° °
а1 а2 а„
СВОЙСТВА ОПЕРАЦИИ
УМНОЖЕНИЯ ВЕКТОРА НА ЧИСЛО
1. ь(~„а) = (~~„) а здесь Й и Х вЂ” действительные числа. (2. 1)
2. 1.й=а. (2.2)
Определение 2.9. Назовем ортами векторы, имеющие
только одну координату, равную единице, при этом осталь-
ные координаты равны нулю:
е1 = {а, = 1; а2 =О; ...; а~ = О; ...; а„= О),
е2 — — {а, =О;а2 =1;...;a~ =О;...;а„=О),...,
(2.3)
е~ — — {а, =О; а2 =О;...; а~ =1; ...; a„=О),...,
е„= {a& t = О; a = О;. .; a gt; = ; ..;
называются коллинеарными.
Условие коллинеарности двух векторов в векторной
форме:
а =ХЬ.

81
ГДАВА 2. ВЕКТОРНАЯ АЛГЕБРА
Заметим, что длина орта равна единице: ~ е~ ~= 1.
Определение 2.10. Назовем двумерной декартовой пря-
моугольной системой координат (декартовой прямоуголь-
нои системой на плоскости) такую, которая определяется
двумя ортами i = (1; 0) и у = (О; 1), исходящими из единого
начала O(0; О), называемого началом координат. Множе-
ство концов векторов х(=x(1;0) =(x;0), где х c R, колли-
неарных орту (=(1;0), называется осью абсцисс. Множе-
ство концов векторов уу =y(0;1) =(О;у), где у е R, колли-
неарных орту у = (О; 1), называется осью ординат.
Определение 2.11. Назовем трехмерной декартовой
прямоугольной системой координат (декартовой прямо-
угольной системой координат в пространстве) такую, ко-
торая определяется тремя ортами (=(1;0;0), у =(О;1;О) и
Й = (О; О; 1), исходящими из единого начала O(0; О; О), кото-
рое называется началом координат. Множество концов век-
торов xi =x(1;0;0) =(x;0;0), гдех е R,êîëëèíåàðíûõîðòó
( = (1; О; О), называется осью абсцисс. Множество концов
векторов уу =y(0;1;0) =(О;у;О), где у е R, коллинеарных
орту у = (О; 1; p), называется осью ординат. Множество кон-
цов векторов гй =z(0;0;1) =(0;0;z), где г E R, коллинеар-
ных орту ф = (p; p; ц, называется осью аппликат.
Определение 2.12. Суммой двух векторов
а =(а~, а2,...,а„) и Ь =(Ь~,Ь~,...,Ь„)
а'+ Ь
Рис. 2.1
с одним и тем же числом координат назыв я вектор
с = (с~, с2,, с„), координаты которого удовл ряют ус-
ловиям с; = ц; + Ь;, i = 1, 2, ..., и.
В двумерной и трехмерной декартовых пря гольных
системах координат сложение векторов по ука ому спо-
собу соответствует сложению по правилу треуг ника или
(что то же самое) по правилу параллелограмм
Правило треугольника. Суммой двух ве ов а и Ь
называется вектор, идущий из начала векто в конец
вектора р при условии, что вектор
приложен к концу вектора а
(рис. 2.1).
Правило параллелограмма. Ес-
ли неколлинеарные векторы Й и о

82
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
Рис. 2.2
Рис. 2.3
А,В,
А,
в,
Рис. 2.5
Рис. 2.4
а = (a&g ;, 2, . ., „   = ( ~, 2, . .,
с одним и тем же числом координат называется вектор
с = (с„~2 с„) = а+ ( — Ь) = 1а, — Ь1, a2 — Ь2; ...; а„— Ь„).
В двумерной и трехмерной декартовых системах коор-
динат разность векторов находится по правилу треуголь-
ника (рис. 2.3).
Свойства операции нахождения суммы векторов:
1. а+Ь =Ь+а. (2.4)
2. (а+ Ь)+ с = а+(Ь+ с). (2.5)
3. а+О=а. (2.6)
4. а+( — а)=0. (2. 7)
Векторы, в двумерной и трехмерной прямоугольных
декартовых системах координат могут быть соответствен-
но представлены с помощью разложения по ортам:
а =(a„;a„) =a„i +a„j; а =(а„;а„;а,) =a„i +a„j+a,é. (2.8)
приложены к общему началу и на них построен паралле-
лограмм, то сумма а+ Ь (или Ь+ а) этих векторов представ-
ляет собой диагональ указанного параллелограмма, иду-
щую из общего начала (рис. 2.2).
Определение 2.13. Разностью векторов

83
ГЛАВА 2. ВЕКТОРНАЯ АЛГЕБРА
2.2.
ДЕЛЕНИЕ ВЕКТОРА
В ДАННОМ ОТНОШЕНИИ
Пусть вектор АВ = (܄— а„; b„— a„; Ь, — а,) задан коорди-
натами своего начала А(а„; ад, а,) и конца B(b„; b„; b,) и
пусть точка С(с„; c„; с,) расположена между точками А и
В (рис. 2.6), пусть при этом известно отношение длин век-
)АС)
'= [св[
Рис. 2.6
тогда координаты точки С(с„; c„; с,) находят по формулам:
а„+ ХЬ„а„+ ХЬ„а, + ХЬ,
(2.9)
2.3.
ПРЕОБРАЗОВАНИЯ
КООРДИНАТ
Пусть новая система координат х'О'у' получается в ре-
ЗУльтате параллельного переноса хОу в точку с новым на-
чалом координат О'(а; Ь).
Выпишем формулы для выражения старых координат
® и у точки через новые х' и у'
х=х'+a,
у = у'+b.
(2.10)
Проекцией вектора а =АВ на ось и называется вели-
чина направленного отрезка А1В1 оси и (рис. 2.4) (А1 и
д — основания перпендикуляров на ось и из точек А и Я
1
соответственно).
Координаты векторов в двумерной и трехмерной де-
картовых прямоугольных системах координат равны
проекциям этих векторов на соответствующие оси коор-
динат.
Точка А(х; у) изображается в двумерной декартовой
прямоугольной системе координат как конец вектора
Я = {х; у), если начало этого вектора фиксировано в на-
чале координат (рис. 2.5).

84
ПРАКТИЧЕСКОЕ РУКДДДДСТДД K РЕШЕНИЮ ЗАДАЧ
Новые координаты точки выражаются через старые так:
<х =х Ђ”
(2.11)
Пусть новая система координат х'О'у' получается пово-
ротом старой системы хОу на угол (p. Отметим, что угол (р
считается положительным, если поворот производится про-
тив часовой стрелки, и отрицательным, если по часовой.
Старые координаты точки выражаются через новые по
формулам:
° °
х = х'cosy — у'sing,
у = х'sing+ у'cosy.
(2.12)
х' = xcosy+ ysiny,
° ° °
у' = — xsiny+ ycosy.
(2.13)
При суперпозиции (т. е. при переносе и повороте осей в
произвольном порядке) указанных преобразований декар-
товых координат связь между ними определяется форму-
лами:
& t  = х'c sy Ђ” у'si g+
у = х'sing+ у'cosy+ о,
&
х' = (х — а) cosy+ (у — Ь) sin y,
у' = — (х — а) sin y+ (у — Ь) cos y.
(2.14)
(2.15)
2.4.
ПОЛЯРНАЯ СИСТЕМА КООРДИНАТ
И ЕЕ СВЯЗЬ
С ДЕКАРТОВОЙ СИСТЕМОЙ
Полярная система координат на плоскости задается
точкой О, называемой полюсом, лучом ОР, исходящим из
М полюса и называемым полярной
осью. Кроме того, задается мас-
v
штабная единица длины.
Ч
Полярными координатами точ-
о г ки М называются два числа: р и
у, первое из которых (полярный
радиус) р равно расстоянию точ-
Рис. 2.7
Новые координаты точки выражаются через старые по
формулам:

85
ГДАВА 2. ВЕКТОРНАЯ АЛГЕБРА
ки М от полюса, а второе (полярный угол) q — равен углу,
отсчитываемому от полярной оси против часовой стрелки
до направления ОМ. Отметим, что угол q определен с точ-
ностью до слагаемого, кратного 2z (рис. 2. 7).
2.5.
СВЯЗЬ МЕЖДУ ДЕКАРТОВЫМИ
ПРЯМОУГОЛЬНЫМИ
И ПОЛЯРНЫМИ КООРДИНАТАМИ
м„
х = pcosy,
у = psiny,
& t;
tgy = у/х.
(2.16)
М, Х
Рис. 2.8
2.6.
ЛИНЕЙНАЯ ЗАВИСИМОСТЬ
И НЕЗАВИСИМОСТЬ СИСТЕМЫ ВЕКТОРОВ
Определение 2.14. Линейной комбинацией и векторов
а, а2 а называется сумма произведений этих векто-
ров на произвольные вещественные числа Х; (i = 1, 2, ..., п),
т. е. выражение вида
1~а~ + Х2а2 +... + Х„а„. (2.17)
Определение 2.15. Система векторов а1, а2, ..., а„назы-
вается линейно зависимой, если найдутся такие вещест-
BBHHbIB числа Х1, Х2, ..., Х„, из которых хотя бы одно отлич-
но от нуля, что линейная комбинация этих векторов с
Указанными числами обращается в нулевой вектор, т. е.
Имеет место равенство
~)&l ; + ~ & t;2 + ... + Х„
° ° °
X& t; +X gt;~ . .+
(2.18)
Пусть начало декартовой прямоугольной системы ко-
ординат XOY совпадает с полюсом полярной системы, ось
ОХ совпадает по направлению с полярной осью, тогда ме-
жду декартовыми и полярными коор-
Y
динатами имеется связь, выражаемая
формулами (рис. 2.8):

86
ПРАКТИЧЕСКОЕ РУКОВОДСТВО K PEIIIEHHN ЗАДАЧ
Определение 2.15'. Система векторов а, а2, ..., а„на-
зывается линейно независимой, если равенство нулевому
вектору их линейной комбинации возможно лишь в слу-
чае, когда все числа Х1, Х~, ..., Х„равны нулю, т. е.
Х~а, +1~а~+...+Х„а„=О,
° ° ° °
~, =~, =...=~„=О.
Необходимым и достаточным условием линейной за-
висимости двух ненулевых векторов является их коллине-
арность. Векторы a, b, с называются компланарными,
если они лежат либо в одной плоскости, либо в параллель-
ных плоскостях. Необходимым и достаточным условием
линейной зависимости трех ненулевых векторов является
их компланарность. Любые три вектора на плоскости так
же, как и любые четыре вектора в пространстве, линейно
зависимы.
Условие компланарности трех векторов в трехмерном
пространстве имеет вид
а„а„а,
b„b b,
=0.
(2.19)
с„с„с,
Определение 2.16. Три линейно независимых вектора
а, Ь, с образуют базис в пространстве, если любой вектор
d может быть представлен в виде некоторой линейной ком-
бинации векторов а, b, с, т. е. если для любого вектора ~
найдутся такие вещественные числа Х, р, v, что справедли-
во равенство
d=Х а+и b+v с.
(2.20)
с =Х а+р Ь.
(2. 21)
Определение 2.17. Два лежащих в плоскости а линей-
но независимых вектора а и Ь образуют базис на этой плос-
кости, если любой лежащий в плоскости а вектор с может
быть представлен в виде линейной комбинации векторов
а и b, т. е. если для любого лежащего в плоскости а векто-
ра с найдутся такие вещественные числа Х, р, что спра-
ведливо равенство

87
ГЛАВА 2. ВЕКТОРНАЯ АЛГЕБРА
Справедливы следующие фундаментальные утверж-
дения:
° любая тройка некомпланарных векторов а, Ь и с обра-
зует базис в пространстве;
° любая пара лежащих в данной плоскости неколлине-
арных векторов а, Ь образует базис на этой плоскости.
Равенства (2.20) и (2.21) называются соответственно
разложением векторов d и с по базисам (а, Ь, с в первом
случае и а, Ь вЂ” Bo втором).
Числа Х, и, v в случае равенства (2.20) называются ко-
ординатами вектора d относительно базиса ц, b, с, в слу-
чае равенства (2.21) Х, р — координаты вектора с относи-
тельно базиса а, Ь.
Разложение по базису любого вектора единственно, т. е.
для любого вектора d его координаты относительно бази-
са определяются однозначно. Основное значение базиса
состоит в том, что линейные операции над векторами при
задании базиса становятся обычными линейными опера-
циями над числами — координатами этих векторов. Это
следует из свойства линейных операций над векторами, в
силу которых, если
dg =Х Й1+~л g+v с1, d2 =Х a~+) b2+V с2,
то
d, + dq — — (Х1 + Х2)а+ (р, + pz )b + (v& t + vq
и для любого вещественного числа t
< d~ Ђ” Ђ” (< Х )а+(1 p gt;)
2.7.
СКАЛЯРНОЕ, ВЕКТОРНОЕ
И СМЕШАННОЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
2.7.1. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
ВЕКТОРОВ И ЕГО СВОЙСТВА
Определение 2.18. Скалярным произведением двух не-
нулевых векторов называется число, равное произведению
длин этих векторов на косинус угла между ними. (Под уг-
лом между двумя векторами подразумевается тот угол,
который не превосходит ~~.) Скалярное произведение

88
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
обозначается а b. Если угол между векторами а и b ра-
вен Л(а; Ь) = y, то по определению скалярного произведе-
ния имеем
(2.22)
а ь =I а I I ь I cos cP.
Если хотя бы один вектор а или b нулевой, то скаляр
ное произведение принимается равным нулю.
ГЕОМЕТРИЧЕСКИЕ СВОЙСТВА
СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ
(2.23)
АЛГЕБРАИЧЕСКИЕ СВОЙСТВА
СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ
1. а. Ь = Ь а (переместительное свойство).
2. (Х. а)Ь = Х(а. Ь) (сочетательное относительно число-
вого множителя свойство).
3. (а+ Ь) . с = а. с + Ь с (распределительное относитель-
но суммы векторов свойство).
4. а. а & t; О, е л a Ђ” ненуле ой вект р    = 0, е
а — нулевой вектор.
ВЫРАЖЕНИЕ СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ
В ДЕКАРТОВЫХ КООРДИНАТАХ
Если два вектора а и b определены своими декартовы-
ми прямоугольными координатами
Й = (xy, gy, zy ), Ь = (x2, g2, z2),
то скалярное произведение этих векторов равно сумме по-
парных произведений их соответствующих координат, т. е.
а.b = х1 -х2+y>.у~+z&g
(2.24)
1. Необходимым и достаточным условием ортогональ-
ности двух векторов является равенство нулю их скаляр-
ного произведения.
2. Два нулевых вектора а и b составляют острый (ту-
пой) угол тогда и только тогда, когда их скалярное произ-
ведение положительно (отрицательно).
3. Из определений проекции вектора на ось и скаляр-
ного произведения двух векторов следует, что
Пр.-Ь = 'b
(а(

89
ГЛАВА 2. ВЕКТОРНАЯ АЛГЕБРА
Необходимым и достаточным условием ортогонально-
сти векторов а =1х1, у1, zq) и Ь = (х2, у2, zq) является равен-
во
(2.25)
ст
х1 х2+у~.у2+21 22 — — О.
Угол между векторами а = (х,, у,, z,) и b = {х2, у~, z2) оп-
ределяется формулой
Х1 Х2+gg.gg+21 22
cosq) =
(2.26)
Длина вектора а = (х, у, z) определяется формулой (вы-
текающей из (2.25) при а = Ь)
[а)= /а а =
(2.27)
Косинусы углов а, Р, у наклона вектора а = (х, у, z) к
осям Ох, Оу и 02 соответственно называются направляю-
щими косинусами вектора а. Из определения проекции
вектора на ось, геометрического смысла его координат сле-
дует, что
х
сова =
(а[
cosP =
g
[а[
(2.28)
2
сову =
(а[
Сумма квадратов направляющих косинусов любого век-
тора равна единице, т. е.
cos2а + cos2P + cos~y = 1.
(2.29)
2.7.2. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
ДВУХ ВЕКТОРОВ И ЕГО СВОЙСТВА
Определение 2.19. Векторным произведением ненуле-
~о~о вектора а на ненулевой вектор b называется вектор
с = а х b, удовлетворяющий следующим трем условиям.
1. Длина вектора с равна произведению длин векто-
Ров а и bна синус угла между ними, ,т. е.
с =! а . Ь Н а ) ( Ь | в1п ср.
(2.30)

ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАД®~
90
ГЕОМЕТРИЧЕСКИЕ СВОЙСТВА
ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ
1. Необходимым и достаточным условием коллинеар-
ности двух векторов является равенство нулю их вектор-
ного произведения.
2. Длина (или модуль) векторного произведения ~ а х b ~
равна площади S параллелограмма, построенного на при-
веденных к общему началу векторах а и ~. Если е — орт
векторного произведения а х о, то
ахЬ =S е.
(2.31)
Ортом произвольного ненулевого вектора с называет-
ся единичный вектор с, коллинеарный с и имеющий
одинаковоес с направление со=с/~с1
АЛГЕБРАИЧЕСКИЕ СВОЙСТВА
ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ
1. ахЬ = — Ь ха
(2.32)
(свойство антиперестановочности сомножителей).
2. (Х а) х Ь = Ха х Ь (2.33)
(сочетательное свойство относительно числового мно-
жителя Х).
2. Вектор с ортогонален ~
каждому из векторов а и b.
3. Вектор с направлен так,
что с конца вектора с поворот
первого вектора-сомножителя а
ко второму вектору-сомножите-
лю о через наименьший угол
рассматривается против часово@
стрелки. Упорядоченная тройка
Рис. 2.9
векторов а, b,с называется ле-
вой, если кратчайший поворот от а к О, наблюдаемый с с,
происходит по часовой стрелке.
Если хотя бы один вектор-сомножитель нулевой, то век-
торное произведение принимается равным нулевому век-
тору. Тройка векторов a, b, e в указанном определении на-
зывается правой (рис. 2.9).

91
ГЛА
ЛАРА 2. ВЕКТОРНАЯ АЛГЕБРА
3. (ц+ Ь) х с = ах с+ Ь х с (2.34)
(распределительное свойство относительно суммы век-
торов).
4. ц х а = 0 для любого вектора а.
(2. 35)
ВЫРАЖЕНИЕ
ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ
В ДЕКАРТОВЫХ КООРДИНАТАХ
Если два вектора а и Ь определены своими декартовы-
~д прямоугольными координатами
Й = (х1, yy zy} О = (х~,yg 2~},
~д векторное произведение этих векторов имеет вид
ахb =(y,zz — yzz>)i+(z gt; z — zzxz)у (х, ~ — x y& t;)
j й
У~ Zy —. Х1 Zy - Х1 У~
1 + & t; (2.
У2 Z 2 Х2 Z2 Х2 У2
ахо = х1 y& t;
Х2 У2 Z2
Следствие. Если два вектора
a=(x>,y> z>}~b =(
~оллинеарны, то их координаты пропорциональны, т. е.
Х1 Д~ Zy
Х2 g2 ~2
(2.38)
2.7.3. СМЕШАННОЕ
ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
И ЕГО СВОЙСТВА
Определение 2.20. Если вектор а векторно умножить
~~ вектор b, а затем получившийся в результате вектор
~ ~ & t; скаля но умнож ть на век ор с, т в результ те
"~~ается число а х Ь.с, называемое смешанным произве-
~е~НеМ трех векторов а, Ь и с.
Для запоминания формулы удобно использовать сим-
вол определителя.
Пользуясь приведенными в гл. 1 правилами вычисле-
ния определителей второго и третьего порядков, форму-
лу (2.36) можно представить в виде

92
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДЩ
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ
СМЕШАННОГО ПРОИЗВЕДЕНИЯ ТРЕХ ВЕКТОРОВ
Смешанное произведение ах Ь с равно объему парал-
лелепипеда, построенного на приведенных к общему нача-
лу векторах а, Ь и с, взятому со знаком плюс, если тройка
а, Ь, с правая, и со знаком минус, если тройка а, Ь, с левая.
Если векторы а, Ь, с компланарны, то а х Ь . с равно нулю.
Справедливо равенство
ах О.с =а.(b хс).
(2.39)
ВЫРАЖЕНИЕ СМЕШАННОГО ПРОИЗВЕДЕНИЯ
ТРЕХ ВЕКТОРОВ В ДЕКАРТОВЫХ КООРДИНАТАХ
Если три вектора а, Ь и с определены своими декарто-
выми прямоугольными координатами
Й = {х~, gy, &l ;y }  = { з, 2, ~з }  = { з, ga ~з
то смешанное произведение а - Ь ° с равняется определите-
лю, строки которого соответственно равны координатам
перемножаемых векторов, т. е.
Х1 у~ Zy
Х2 У2 22
хз Уз гз
ахЬ с=
(2.40)
Необходимым и достаточным условием компланарности
Tðåõ векторов а = {х1, у1, z~ }, b = {хз, уз, z~ }, с = {хз, уз, гз } аа-
ляется равенство нулю определителя, строками которого
служат координаты этих векторов, т. е. равенство
Х1 у, Zy
Х2 у2 Z2
Хд УЗ 2д
(2.41)
=0.
В силу (2.39) смешанное произведение векторов а, b, p
можно писать в виде а Ь с, не указывая при этом, какие
именно два вектора (первые два или последние два) пере-
множаются векторно.
Необходимым и достаточным условием компланарно-
сти трех векторов является равенство нулю их смешанно-
го произведения (cM. 2.19).

93
ГЛАВА 2. ВЕКТОРНАЯ АЛГЕБРА
2.8.
РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ
2.1. Отрезок Ав точками С(3, 4) и D(5, 6) разделен на
ури равные части. Найти координаты точек А и В.
Р е ш е н и е. Обозначим координаты точек А и В так:
А(х,, у,), В(х~, у~). Для отрезка А0 точка С является сере-
диной, потому Х = АС/CD = 1 и по формулам деления от-
резка в данном отношении (2.6) получим
х1 +Ххах х~+хд у1+ Худ у~+уд
1+1 2 1+1 2
Подставим в последние равенства координаты хс, ус,
хр~ уо:
3 = (х1+ 5)/2, 4 = (у1 + 6)/2,
откуда находим х~ = 1, у1 = 2. Точка А имеет координаты
А(1, 2).
Поскольку точка D есть середина отрезка СВ, то хд =
= (хс + х~)/2, или 5 = (3 + х~)/2, отсюда х~ = 7.
ув = (ус + y~)/2, 6 = (4 + у~)/2,
отсюда у~ = 8. Получили В(7, 8).
Ответ: А(1, 2), В(7,8).
2.2. Систему координат ХОУ вначале параллельно пе-
ренесли так, что новое начало стало находиться в точке
О'(2, 3), а затем был совершен поворот осей на угол y = 30'.
Определить новые координаты точки А, если старые коор-
динаты в системе XOY таковы: А( — 1, 5). Определить, ка-
~ие координаты имела точка В в старой системе ХОУ, если
в новой системе координат она задается так: В(4, — 2).
Решение:
а) при параллельном переносе системы координат, ко-
')Р,цинаты точки А станут такими:
& t; х~ х~ Ђ” а=-1-2=
у,~ — — у,~ — Ь=5 — 3=2,
"Р~ повороте осей на угол 30' координаты точки А преоб-
Р~зУются следующим образом.'

94
ПРАКТИЧЕСКОЕ РУКОРОДСТдО К РЕШЕНИЮ ЗАДАЧ
х„" = х„' cos y+ у.'~ sin y = ( — 3) cos 30'+ 2 sin 30' =
1+2 ГЗ 2'ГЗ вЂ” 3-0 72
2 2 2
у„" = — х„siny+ yÄ' ñosy = — ( — 3) sin 30'+ 2cos30' =
= 3.— + 2.— = 3,598;
/з
2 2
б) в системе координат XOY точка В имеет коордййаты:
хв — — хв совр — ув siny = 4сов30' — ( — 2)»n30' = 3,732;
ув = хв»ny+ ув совр = 4 sin 30 + ( — 2) сов30' = 2,464.
В системе координат XOY точка В имеет координаты:
хв —— хв + а = 3,732+ 2 = 5.732; ув = ув + b = 5,464.
P= = $25 =5;
tg y = 3/4; y = arctg 0,75 = 36'53'.
Рекомендуем самостоятельно
сделать чертеж к задаче.
От в е т. р = 5; y = arctg 0,75 =
= 36'53'.
2.4. Построить по точкам уча-
сток линии р = 0 5 у (спираль Ар-
химеда), 0 & t  &lt 27~, д вая у
ния через ч/4.
P е ш е н и е. Составим таблицу:
Рис. 2.10
5к/4 Зл/2 7ч/4 27~
л/4 ~ л/2 Зл/4
Зп/4= 7п/8= ~ и=
= 2,11 = 2,75 = 3,14
51'/8 =
= 1,96
Зл/8 = л/2 =
= 1,18 = 1,57
л/8 = л/4 =
=0,39 =0,7
р 0
0 т в е т: хА = 0,722; y& t = 3,5 8; х = 5,7 2' у = 5,4
2.3. Декартовы координаты точки А(4, 3) известны.
Найти координаты этой точки в полярной системе коор-
динат, если полюс расположен в начале координат декар-
товой системы, а полярная ось совпадает по направлению
с осью ОХ.
P е ш е н и е. Воспользуемся формулами, связывающи-
ми полярные координаты с декартовыми:

95
ГЛАВА 2. ВЕКТОРНАЯ АЛГЕБРА
(:оединив полученные точки плавной линией, постро-
им искомую кривую (рис. 2.10).
2.5. Даны точки А(1, 2, — 2) и В(3, 1, 4). Найти коорди-
наты векторов АВ и ВА; Найти ~ АВ ~ и ~ ВА ~ .
Pe øåíèå. Координаты векторов АВи ВА находят-
q~ как разности соответствующих координат конца и на-
чала векторов, т. е. разность соответствующих координат
точек А и В. Имеем, таким образом,
АВ = (3 — 1, 1 — 2, 4 — ( — 2) } = (2, — 1, 6}, т. е. AB = 2i — у + 6Й.
Очевидно, что координаты вектора ВА противополож-
ны по знаку координатам вектора АВ, т. е.
ВА = ( — 2, 1, — 6} и ВА = — 2i + J — 6Й.
Длина или модуль вектора АВ находятся по форму-
ле (2.27). Подставляя координаты вектора АВ в форму-
лу (2.27), получим:
= ~41.
= $38.
Имеем теперь по формулам (2.28):
сова =
6
38
cosP =
— 1
38
1
сову =
38
2.7. Вектор а составляет с координатными осями оди-
наковые углы. Найти его координаты, если I а I= ~ГЗ.
Очевидно, что IABI =IB+I= v4&g
2.6. Вычислить направляющие косинусы вектора А~,
если А( — 3, 2, О) и В(3, — 3, 1).
Р е ш е н и е. Направляющие косинусы вектора АВ оп-
ределяются по его координатам формулами (2.28). Нахо-
дим координаты вектора АВ так, как это было сделано в
Задаче (2.5). Имеем АВ =(3+3, — 3+2,1 — 0} =(6, — 1,1}. Мо-
дуль вектора АВ находим по формуле

ДРАКТИЦЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
96
1
сова = cosP = сову = —.
,Гз
х = ~ а ~.сова = ~/3 — =1;
]
,Гз
у = ~ а ~.cosP = <3. Ђ”
г-
,Гз
z = ( а ( сову = ~/3 — = 1.
г—
Гз
Таким образом, а = {1, 1, lj. Аналогично, в случае когда
1
сова = cosP = сову = — —,
,ГЗ'
получим, что а = { — 1, — 1 — lj.
2.8. Найти орт вектора а = {3, — 4, 12).
P е ш е н и е. В соответствии с определением орта — это
единичный вектор ао, коллинеарный с а и имеющий оди-
наковое с а направление. Имеем
аО . а
(а(
=13,
и, следовательно:
3 4 12
а
13' 13'13
2.9. Написать разложение вектора а по векторам
р = {1, 2, 4); q = {1, — 1, Ц; r = {2, 2, 4); а = { — 1, — 4, — 2) .
P е ш е н и е. Согласно (2.20) мы должны найти такие
числаХ, и, v, что
а=Х р+р-q+v.r.
P е ш е н и е. Направляющие косинуса удовлетворяют
условию (2.29), и так как углы, составляемые вектором
а с координатными осями, равны, т. е. и = P = у, то с уче-
том этого (2.29) в рассматриваемом случае примет вид:
3cos а = 1. Отсюда следует, что
1
сова = cosP = сову =+ —.
Зная направляющие косинусы и модуль вектора ~ а ~,
найдем его координаты. Имеем в первом случае-,иногда

97
ГДАВА 2. ВЕКТОРНАЯ АЛГЕБРА
Подставляем в это равенство разложение векторов
& t; p, д r по баз су i, j, k, котор ми ни зад н в усло
задачи, получим
— i — 4у — 2Й = Х (i + 2j + 4k) + p. (i — j + k) + v. (2i + 2J + 4k).
Пользуясь свойствами линейных операций над векто-
рами, заданными разложением по базису, получим из по-
следнего равенства
— ( — 4у — 2Й = (Х+ p+ 2ч)(+ (2Х вЂ” p+ 2ч)~ + (41+ p+ 4ч)Й.
Так как в левой и правой частях этого равенства записа-
ныразложенияодногоитогожевектора а побазису i, j,k,
то, следовательно, должны выполняться равенства:
1+ @+2v = — 1,
2Х-p+2v = — 4,
4Х+ р+ 4v = — 2.
Мы получили схему линейных уравнений для трех не-
известных величин Х, р, v. Решая эту систему, например,
методом Гаусса (см. гл. 1), найдем искомые величины Х,
р, v. Имеем:
— 4 — &
— 2 -+
1 1 2
2 — 1 2
4 1 4
1 1 2
0 — 3 — 2
0 0 — 2
1 1 2
0 — 3 — 2
0 — 3 — 4
— 2 .
Здесь мы на первом этапе (помеченном цифрой 1), в со-
ответствии с методом Гаусса, первую строку таблицы (т. е.
первое уравнение системы) умножили на — 2 и прибавили
ко второй строке (ко второму уравнению системы) поэле-
1ентно: первый элемент первой строки, умноженный на
— 2, сложили с первым элементом второй строки, второй эле-
мент первой строки после умножения на — 2 сложили со вто-
рым элементом второй строки и т. д. Третья строка после
1ервого этапа преобразования получена в результате умно-
>ке ия пер ой стр ки на Ђ  и сложе и с трет ей строк
На втором этапе к элементам третьей строки прибави-
ли элементы второй строки, умноженные на — 1. В полу-
чившейся таблице третья строка представляет собой со-
~ращенную запись третьего уравнения рассматриваемой

98
ДРАКТИЦЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
а = p+2q — 2ã.
2.10. Коллинеарны ли векторы а и b, построенные по
векторам р и д?
а =Зр — 4q; b =2P+q; P =(1,1,2}; q =13,1,0}.
P е ш е н и е. Для решения этой задачи можно восполь-
зоваться геометрическим свойством первого векторного
произведения, т. е. найти координаты векторов а и Ь от-
носительно базиса i, j, k, а затем вычислить их векторное
произведение. Имеем
а = 3(i + у +2Й) — 4(3i + у) = — 9i — у +6Й,
b =2(i + j+2k)+3(3i +j ) =5i +Зу+4Й.
Вычисляя векторное произведение этих векторов по
формуле (2.37), получим
j k
— — 1 6 —.— 9 6 — — 9 — 1
=i — j +k
3 4 5 4 5 3
Q&gt &
— 9 — 1 6
5 3 4
= — 22i + 66) — 22k.
Так как векторное произведение а х Ь отлично от нуле-
вого вектора, то, следовательно, векторы а и Ь неколли-
неарны.
Другое, более быстрое решение. Если а и b коллине-
арны, то координаты этих векторов пропорциональны, но
в данном случае: 3/2 w — 4/1.
2.11. Найти косинус угла между векторами АВ и АС,
где А(1, 2, 1), В(3, — 1, 7), С(7, 4, — 2).
системы, которое после проведенных нами преобразова-
ний имеет вид: — 2ч = 4, откуда получим v = — 2. Исходя из
вида второи строки таблицы, второе уравнение системы
имеет теперь вид — Зр — 2v = — 2. Откуда после подстановки
найденного значения v получим — Зр = — 2 + 2 ( — 2) = 6, или
р = 2. Наконец, подставляя найденные значения v и р в
первое уравнение системы Х = — 1 — 2v — р, получим Х = — 1+
+4 — 2=1,т.е.1=1.
Таким образом, искомое разложение имеет вид

99
ГЛАЦА 2. ВЕКТОРНАЯ АЛГЕБРА
АВ АС
cosy =
l~l (Ас(
Для нахождения cos y по этой формуле необходимо найти
координаты векторов AB и АС, имеем:
АВ = (2, — 3, 6), АС = (6, 2, — 3).
Вычисляя АВ АС,~ АВ~ и ~АС~, получим
2 6+( — 3) 2+6 ( — 3)
12
49
cosy =
2.12. Вычислить площадь параллелограмма, построен-
ного на векторах Й и Ь, длины диагоналей параллелограм-
ма, cos(a, р) и IIp;b, если
а =5p+2q,Ь = р — 3q,l р~=4~2,I ql=6 (р,q) =7~/4.
P е ш е н и е. Площадь S параллелограмма, построенно-
го на векторах а и b, равна модулю векторного произведе-
ния этих векторов. Пользуясь алгебраическими свойства-
ми векторного произведения, имеем
axb =(5p+2q)x(p — Çq) =5 рхр — 15.pxq+2 qxP — 6 qxq =
= — 15 pq — 2.рва = — 17.рва.
Здесь мы учли, что p X p = q X q' = 0 согласно алгебраи-
ческому свойству 4 векторного произведения, а также ал-
гебраическому свойству 1. Находим теперь, в соответствии
с определением модуля векторного произведения (форму-
ла (2.31)),
~=( ахЬ (=17 IPxql=17 I pl.lql si~(p,q) =17.4с~2 6 si~ — =
4
=17.4.6'42.— =17 6.4 =408.
/ j2
2
Таким образом, S = 408 (кв. ед.). Для определения
длин диагоналей параллелограмма заметим, что одна из
Д1агоналей, в соответствии с правилом параллелограмма
p e ш е н и е. Из определения скалярного произведения
(формула (2.30)) следует, что искомый косинус угла меж-
ду векторами определяется формулой

ПРАКТИЧЕСКОЕ Р~КОДОДСТДО К РЕШЕНИЮ ЗАДАЧ
сложения векторов, равна а+ b, а другая, в соответствии
с правилом вычитания, — а — Ь (см. рис. 2.2, 2 3) «ла-
дывая и вычитая векторы а и Ь, получим
а+Ь =бр — q,a — Ь =4p+5q.
Для определения длин диагоналей параллелограмма,
т. e. ~ а+ b ~ и ~ a — b ~, воспользуемся формулой (2.27). Полу-
чим:
I а+6[=
=6 5=30.
Аналогично
= 2~593.
(а — b l=
Для определения сов(а, р) воспользуемся формулой (2.22),
согласно которой
— а.р
сов(а, р) =
Вычисляем величины, входящие в правую часть этого
равенства:
а . P = (5P + 2q) . р = 5р2 + 2q . P = 5 I P l2 +2 I q I . I p I сов — =
4
~2
=5.32+2.6.4~2.— =160+48 =208.
2
)а)=
= 2~356.
Подставляя полученные результаты в формулу для
сов(а, р), получим
— 208 13
сов(а, р) =
2~356 j2 Д78

101
[' ДАВА 2. ВЕКТОРНАЯ АЛГEHPA
Найдем теперь Пр;Ь, т. е. проекцию вектора Ь на век-
тор а. Для этого необходимо вычислить величины а Ь и ~ а ~,
входящие в формулу
-а Ь
Пр.-ь =
Имеем
а Ь = (5р+ 2q)(p — Çq) = 5р' — 15р q + 2р. q — бд' =
=5(р'(~ — 13р'.д — 6(у[~=5 32 — 13 412 б †36 =
~/2
= 160 -312-216 = -368.
(а(= jci а =
= 4~89.
Таким образом,
П Ь-. 368 92
4~89 ~89
2.13. Компланарны ли векторы
а, Ь, с: а = (1, — 2, 1), Ь = (3, 1, — 2), с = (7, 14, — 13)?
1 — 2 1
1 — 2 3 — 2 3 1
— — 2) +1
14 -13 7 — 13 7 14
ахЬ e=
3 1 — 2
7 14 -13
= — 13+ 28+ 2( — 39+ 14) + 42 — 7 = 15 — 50+ 35 = О.
Так как смешанное произведение а Ь - e оказалось рав-
ным нулю, то векторы а, Ь, с компланарны.
2.14. Даны вершины тетраэдра (см. рис. 2. 11) А(2, — 1, 2),
B(5, 5, 5), С(3, 2, О), D(4, 1, 4). Вычислить: 1) объем тетра-
здра; 2) его высоту, опущенную из вершины D; 3) угол ме-
жду ребром AD и его гранью ABC'.
P е ш е н и е. Для ответа на поставленный вопрос необ-
ходимо вычислить смешанное произведение этих векто-
ров, и если оно окажется равным нулю, то это будет обо-
значать, что вектора а, Ь, с компланарны. Находим сме-
шанное произведение а. b с по формуле (2.40).

102
ПРАКТИЧЕСКОЕ >YKOBOPC B K РЕШЕ ИЮ ЗА
Е,
с,
АВ = (3, 6, 3), АС = (1, 3, — 2), AD = (2, 2, 2).
Вычисляя теперь смешанное произведение по форму-
ле (2.40), получим:
3 6 3
1 3 — 2
2 2 2
= — ~ 18 — 24+ 6 — 18+ 12 — 12 ~ = 3.
6
V=—
«1
6
2. Объем тетраэдра определяется также формулой
~=-'Яь,
3
где S — площадь основания (в рассматриваемом случае это,
очевидно, площадь треугольника АВС); h — высота пира-
миды, которую необходимо найти. Площадь S треуголь-
ника АВС находим, руководствуясь геометрическим смыс-
лом модуля векторного произведения, в соответствии с
которым
S = — [АВх АС!.
2
по формуле (2.37):
Найдем АВ>
j й
6 3
—.6 3 --.3 3 -3 6
— j +й
3 — 2 1 — 2 1 3
АВхАС=
3 — 2
= i ( — 12 — 9) — j ( — 6 — 3) + k(9 — 6) = — 21i + 9j + Çk.
Р е ш е н и е. 1. Объем тет-
/ раэдра V равен одной шестой
части объема параллелепипеда
Д г 1 АВЕСВВ1Е1С1. Объем паралле-
'С
1 лепипеда по геометрическому
h
1
° .Ф
1
своиству смешанного произве-
1
дения равен модулю смешан-
А В ного произведения, например,
Рис. 2.11 векторов АЯ, Ас, АЯ.
Таким образом, искомый объем определяется выраже-
V = — ( АВ &g ;& t; С
6
Для вычисления смешанного произведения найдем
координаты векторов АВ, АС, АЮ. Имеем

103
ГЛАВА 2. ВЕКТОРНАЯ АЛГЕБРА
Тогда, определяя модуль векторного произведения
~ AB x АС ~, находим
~.48 AC~= /441-;81-;9=А81.
Так как h = 3V/S, à S = — ~АВх АС~, то
6V
h=
(АВх АС(
Подставляя полученные выше значения V и ! АВх АС(,
найдем, что
18 6
Д31 $59
В числителе полученного выражения записан модуль
смешанного произведения векторов ~, ~ и АС, который
можно вычислять описанным выше способом, зная коорди-
наты этих векторов. Однако в этом нет необходимости, так
как вектор АВх АС мы нашли, отвечая на второй вопрос
задачи. Поэтому скалярное произведение АЛ . АВ ~ АС про-
ще найти непосредственно, через координаты перемножае-
мых векторов. Определяя модуль вектора ~ имеем
(~ АВ х АС ~ был найден во втором пункте задачи):
2 ( — 21)+2 9+2 3 3
2 ГЗ ~~31 ~177
3
отсюда (р = arcsin =13,03'.
177
sing=
3. Найдем угол между ребром АВ и гранью АВС. Это
угол у между прямой АВ и ее ортогональной проекцией на
плоскость, которой принадлежит грань АВС (рис. 2.11).
Для того чтобы найти угол &lt р, достато но на ти коси
угла iy между векторами AD и АВ х АС (рис. 2.11). Тогда,
так как y = q + +z/2 (в зависимости от того, острый или ту-
пой угол ~y), cosy = cos (q+ +z/2) = csin q. Откуда следует,
что sin (р = icos q. Причем знак « — » соответствует случаю,
когда cos y ( 0 (угол у тупой), а «+» — когда cos y & t; О
том, и другом случае sin q & t; О. ба слу ая ле ко учиты
ются соотношением sin &l ; = I os I. Учитыв я,
I ADx АВ АС( !АЮхАВ АС(
cosy =, получим sin(p =
I Аю I I АВ I I Ac I ' / АЮ ! ! АВ ! ( АС !

104
ПРАКтичеСКОе руКОц()Д(;тВО к РЕШеНИЮ ЗАДАЧ
2.9.
ЗАДАЧИ
2.15. Треугольник задан координатами своих вершин
А(1, 2); B(5, 3); С(3, — 2). Найти координаты точки пересе-
чения медиан.
2.16. Даны вершины треугольника А(2, — 4); В(4, — 5) и
С( — 4, 7). Определить середины его сторон.
2.17. Даны три вершины параллелограмма А(2, — 4);
В(4, — 2); С( — 2, 4). Определить четвертую вершину D, про-
тивоположную В.
2.18. Даны вершины треугольника А(2, 3); В(4, — 10);
С( — 4, 1). Определить длину его медианы, проведенной из
вершины В.
В задачах 2.19 — 2.21 заданы уравнения в полярной сис-
теме координат р = p((p). Получить уравнения этих линий
в декартовой системе координат.
2.19. р = 4(1 + sin (р).
2.20. р = 3(1 + cos (р).
2.21. р = 4(1 — cos <
В задачах 2.22 — 2.24 заданы уравнения линий в декар-
товой системе координат. Получить полярные уравнения
этих линий.
2.22. (х2 + у2)2 = 2уз
2.23. (х2+ у2)з = 4х4
2 24. (хз + y2)ç 9(х2 — у2)2.
2.25. Найти угол между диагоналями параллелограм-
ма, построенного на векторах a = 4i + 2у, b = — 4у + 2k.
2.26. Найти вектор х, коллинеарный вектору а = (6, 3, — 3)
и удовлетворяющий условию х а = 9.
2.27. Найти проекцию вектора а =(3/2, — 7,— 9) на ось,
составляющую с координатными осями Ох и Oz углы
а = 45', у = 60', а с осью Оу — острый угол Р.
2.28. Данытри вектора а = (1, — Х), b = (1,1), с = (2,4). Най-
ти разложение вектора х = 2а+ ЗЬ + с по базису а, Ь.
2.29. Даны четыре вектора а = (6, 3, 0), b = (3, — 3, 6),
с = (6, 6, — 3), d = (9, 21, — 21). Найти разложение каждого из
этих векторов, принимая в качестве базиса три остальных.
2.30. Даны вершины треугольника А(2, 2, — 3); В(4, 1, — 1);
С(0, — 2, 1). Определить его внешний угол при вершине А.

105
~ JIABA 2. ВЕКТОРНАЯ АЛГЕБРА
2.31. Дан треугольник с вершинами А(3, — 2, 8); В(2, О, 4);
С(8, 2, О). Найти его площадь S и высоту В&g
2.32. Вычислить площадь параллелограмма, построен-
ного на векторах
а =2p+4q,Ь =2р — 6q,где lpl=» Iql=3 m(P' q) =<
2.33. Даны три вектора а, Ь, с, удовлетворяющие усло-
вию 2а+Ь+с =О, )Ь|=4, Icl=~2. Найти ахЬ+Ь хс+ахс.
2.34. Вычислить синус угла между диагоналями парал-
лелограмма, построенного на векторах
а =i + j+й,b =2i +Çj+4й.
2.35. Показать, что (2а+ЗЬ) (а+с) x b = — 2а.b c.
2.36. Показать, что векторы
а = — 2i +6j+4й,b =2i — Çj — 4й,с = — i +4j+2й
компланарны, и разложить с по векторам а и Ь.
2.37. Показать, что точки А(1, — 2, — 3); B(0, 1, О); С(1,
2, — 1) и D(4, — 1, — 7) лежат в одной плоскости.
2.38. Показать, что объем параллелепипеда, построен-
ного на диагоналях граней данного параллелепипеда, ра-
вен удвоенному объему данного параллелепипеда.
2.39. Даны три вектора:
а =(2, — 2,6), b =(-6,6,3),с =(3, — 2,5).
Вычислить а х b c.
Ф
2.40. Доказать компланарность векторов а, Ь, с, зная,
что а.Ь+Ь-с+с а =О.
2.41. Показать, что
(а+ 3Ь вЂ” с)[(а — Ь) х (а — Ь вЂ” с)] = 4а х Ь с.
2.42. Вычислить объем параллелепипеда, построенно-
го на векторах р = а+ Ь+ с, q = а+ Ь вЂ” с, r = а — b+ c.
2.43. Вычислить объем параллелепипеда, построенно-
го на векторах а =2р — Çq+r,b =2p+2q — Çr,с =p+2q+2r,
где p, q u r — взаимно ортогональные орты.
2.44. Вычислить объем параллелепипеда, построен-
~ого на векторах а =бр+100, Ь =Çp — бо, с =4p+14q, где
Ipl=1, lql=2,(р;q) =135 .

106
ПРАКТИЧЕСКОЕ PygPgPpgyBP К РЕШЕНИЮ ЗАДАЧ
2.45. Сила F = (6, 8, — 4) приложена к точке А(2, — 1, — 2).
Определить величину и направляющие косинусы этои силы
относительно начала координат.
2.46. Даны три силы
а = (1, — 2, — 4), Ь = (2, 1, — 2), с = (-5, О, 2),
F) — — (1,2,3), Fg — — (2,3,1), Е"з — — (-4, — 3, — 2),
приложенные к одной точке. В ~числить, какую работу
производит равнодействующая э их сил, когда ее точка
приложения, двигаясь прямолинейно, перемещается из
точки А(1, 2, 1) в точку В(3, — 2, — 5).
2.49. Найти вектор х, удовлетворяющий трем уравне-
ниям: х а=а,х.Ь =P,х с =у.
2.50. Пусть а, Р, у — корни уравнения хз+ рх+ q = О.
Вычислить
у а
0 у
2.51. Доказать, что расстояние h между параллельны-
ми прямыми можно выразить формулой
г~ . г~
1г21
где r& t; Ђ” вект р, иду ий из то ки на од ой пря о в т
ку на другой прямой, а г~ — вектор, параллельный дан-
ной прямой.
2.52. Три вектора ОА,ОВ и ОС удовлетворяют усло-
вию ОА ОВ+ОВ OC+OC.OA =0. Доказать, что 1) векто-
ры ОА,OB u OC компланарны; 2) точки А, В, С лежат на
одной прямой.
приложенные к точке А( — 2, 3, — 3). Найти величину и направ-
ляющие косинусы этих сил относительно точки В(1, 2, — 2).
2.47. Вычислить работу силы F = (2, 3,4), когда точка ее
приложения перемещается по прямой из точки А(1, 1, 1) в
точку В(3, — 1, 2).
2.48. Даны три силы

ГЛАВА 3
АНАЛИТИЧЕСКАЯ
ГЕОМЕТРИЯ
НА ПЛОСКОСТИ
3.1.
ПРЯМАЯ ЛИНИЯ
(3 1)
Ах+By+ С = О.
При этом вектор, перпендикулярный прямой, носит
название нормального вектора и имеет координаты
(3.2)
й =(A;B).
К общему уравнению прямой можно прийти, записав
условие ортогональности вектора й =(А; B) и текущего
вектора PM = (х — хо, у — gp ), который определяется задан-
ной точкой прямой P(xp, 'уо) и точкой прямой М(х; у) с пе-
ременными координатами.'
А(х — хо) + В(у уо) = О,
или Ах + By + С = О, где С = — Ах() — Вур.
(3.3)
Если В ~ О, то из общего уравнения прямой (3.1) полу-
чается уравнение прямой с угловым коэффициентом
(3.4)
у = Йх + Ь, Й = — А/В, Ь = — С/В,
где k = tgpI. — угловой коэффициент, равный тангенсу угла
наклона прямой с положительным направлением оси абс-
цисс. уравнение с угловым коэффициентом не описывает
~Рямые, параллельные оси ординат.
Уравнение прямой, проходящей через данную точку
~ (xp', yp) и имеющей угловой коэффициент Й:
yp = k(x x,).
(3.5)
В декартовой системе координат на плоскости общее урав-
нение прямой имеет вид

108
ПРАКТИЧЕСКДЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
К уравнению (3.5) можно прийти, использовав форму-
лу для тангенса угла наклона прямой к оси ОХ
(3.6)
k = tgpI. = (у — уо)/(х — xp).
Каноническое уравнение прямой
(3. 7)
(у — gp)/l = (х — xp)/т
У Уо
ХО
(3.8)
1 хО
У1 Уо
Если прямая не проходит через начало координат и не
параллельна осям координат, то ее общее уравнение (3.3)
может быть преобразовано к уравнению прямой в отрезках:
х/а + у/Ь = 1, а = — С/В, Ь = — С/В.
(3.9)
Здесь а и b — проекции отрезка прямой между точка-
ми пересечения с осями координат на эти оси координат.
Нормальное уравнение прямой:
х cos а+ у sin а — р = О.
(3.10)
Параметр р — длина перпендикуляра, опущенного из
начала координат на прямую, а — угол, образованный этим
перпендикуляром с положительным направлением оси абс-
цисс. Нормальное уравнение прямой можно получить из
общего уравнения путем умножения всех его членов на
множитель
1
7
знак которого должен быть противоположен знаку С.
Параметрические уравнения прямой:
& t; о+
g =@0+m&
(3.11)
можно получить, записав условие коллинеарности векто-
ра а =(l; m), называемого направляющим вектором пря-
мой, и текущего вектора прямой PM = (х — xp , 'у — уо), опре-
деляемого точками P(xp' ,gp) и М(х; у), которые принадле-
жат прямой.
Аналогично можно получить каноническое уравнение
прямой, проходящей через две заданные точки P(xp; yp) и
Q(x&g ;, '

109
1'ЛАВА 3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
получаются из канонического уравнения (3.7) приравни-
цанием равенства отношений переменному параметру t,:
(у — уд)/t = (х — хд)/т = t.
Уравнение прямой в полярной системе координат—
(3.12)
р = р/cos(9 — а),
— kg 1+ kg
tgq =, cosy =
1+ k2ky ~~+ ~2 '~~+ ~ 2
— kg
Ытнр =
1+ 2 j+p2
(3.13)
~1 ~2~ (3.14)
~1 1/~2з (3.15)
б) общими уравнениями А1х+ В1у+ С1 = Ои А2х+ В2у+
+ С2 = 0 определяются формулами
А1 В2 — А2В1 . А1 В2 — А2В1
А1А2+ В1 В2
(3.16)
А~/А2 = В1/В2,
А1А2+ В1В2 = О;
в) каноническими уравнениями (у — у,)/t, = (х — х1)/m,
и (у — у2)/l2 = (х — х2)/т2 определяются формулами
1т2 — pm~ . L~m2 — Qm&
),~2+ т,т2
(3.17)
(3.18)
Определяется длиной перпендикуляра р, опущенного из по-
л1оса на прямую, и углом а, образованным этим перпенди-
куляром с полярной осью. Уравнение (3.12) получается из
нормального уравнения (3.10) путем подстановки в него
формул перехода от декартовых координат к полярным
(х = р cos &lt р   р in l ;р) и ко инуса ра нос и os q Ђ
= COS (P - СО$ О. + SlIl (P SlIl И.
Угол q) между двумя прямыми, а также условия парал-
лельности и перпендикулярности этих прямых в случае
задания:
а) уравнениями с угловыми коэффициентами у = kqx + Ь1
и у = Й2х + b2 имеют следующий вид:

ДРАКТРРЦ:СКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
110
(3. 19)
(3.20)
/~ ~л /~2
I~Ig+ mg~g О.
Уравнение пучка прямых, проходящих через точку
пересечения двух данных прямых, заданных
а) общими уравнениями А,х + В,у + C& t   и 2 + ~
+ С2 = О, таково
(3.21)
А,х+ В,у + С, + Х(А~х + В~у+ С~) = 0;
б) уравнениями с угловыми коэффициентами у = k~x + b,
иу = й~х+ Ь2, таково
k~x — у+ b, + X(kqx — у+ b2) = 0;
(3.22)
Расстояние от точки P(xo, уо) до прямой, заданной
а) общим уравнением Ах + By + С = О, таково
l»o+Byo+CI
/А' + B'
б) нормальным уравнением х cos а + у sin а — р = О, вы-
числяется по формуле
(3.23)
о = lxo cos а+ yo sin а — р1
(3.24)
A(xo + А) + B(y p + В) + С & t;
Геометрический смысл неравенства первой степени с
двумя неизвестными определяется следующими теоре-
мами.
Теорема 2.1. Всякая прямая Ах + By + С = О разбивает
плоскость XOY на две полуплоскости. Для координат всех
точек М(х; у), лежащих в одной полуплоскости, выполня-
ется неравенство Ах+ By + С & t; О, ля коорди ат в ех
чек другой полуплоскости справедливо противоположное
неравенство Ах + By + С & t;
Теорема 2.2. Пусть прямая задана общим уравнением
Ах+ Ву+ С = О.
Если отложить нормальный вектор М(х; у) от любой
точки P(xp' ,yp) этой прямой РМ= й, то конец М(хо+ А;
yp+ В) отложенного вектора будет находиться в положи-
тельной полуплоскости от данной прямо~, т. е.

ГР[~ЦА 3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
Теорема 2.3. При параллельном переносе прямой Ах +
+ By + С = О в направлении нормального вектора й = {А; В}
величина L(x; у) = Ах + By + С возрастает. При переносе
этой прямой в противоположном направлении L(x; у)
убывает.
3.2.
РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ
Приведенное краткое изложение теории демонстрирует
важность использования понятий векторной алгебры при
получении и исследовании уравнений прямых на плоско-
сти. В связи с этим рекомендуем перед рассмотрением ниже-
приведенных решений повторить следующие условия.
Условие коллинеарности двух векторов а = {Х~, Y~} и
Ж2» ~2}
Х~/Х2 = У~/У2,
условия ортогональности двух векторов:
а-b = Х1Х2+У1 Yg — — О.
й = {А; В} = {4; — 1}
P = (2;3)
Рис. 3.1
и текущий вектор PM = {х — 2; у — 3}.
3-й шаг. Выпишем одно из условий — ортогонально-
сти или коллинеарности, в соответствии с заданием. По
Условию задачи PM J й, поэтому воспользуемся условием
ортогональности двух векторов в координатной форме
4(х — 2) + ( — 1)(у — 3) = О.
3.1. Получить уравнение прямой на плоскости, если
известна точка Р(2; 3), через которую проходит прямая, и
вектор, перпендикулярный прямой й = {А; В} = {4; — 1}.
Решение.
1-й шаг. Сделаем схемати-
{А В) {4 1)
ческий чертеж (рис. 3.1).
2-й шаг. Выпишем коор-
динаты векторов, определяю-
Щих данный геометрический
у)
объект — прямую. Это нор-
мальный вектор прямой

112
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
4-й шаг. Произведем алгебраические преобразования,
сводящие уравнение к известному виду. Получаем общее
уравнение прямой 4х — у — 5 = 0.
3.2. Получить уравнение прямой, проходящей через
точку P( — 1; 2) и параллельной вектору а =(l; т} = (8; — 4).
Решение.
1-й шаг. Сделаем схематический чертеж (рис. 3.2).
2-й шаг. Выпишем координаты векторов, определяю-
щих данный геометрический объект — прямую. Это на-
правляющий вектор прямой а = (l; m) =(8; — 4) и текущий
вектор PM =(х+1; у — 2).
3-й шаг. Выпишем одно из условий — ортогонально-
сти или коллинеарности, в соответствии с заданием. По
условию задачи PM ~~ а, поэтому воспользуемся условием
коллинеарности двух векторов в координатной форме
(х + 1)/8 = (у — 2)/ — 4. Получаем каноническое уравнение
прямой.
3.3. Получить уравнение прямой, проходящей через две
заданные точки Pp(1; 2) и Р,(3; 2).
Решение.
1-й шаг. Сделаем схематический чертеж (рис. 3.3).
2-й шаг. Выпишем координаты векторов, определяю-
щих данный геометрический объект — прямую. Это теку-
щий вектор, лежащий на прямой РОМ = (х — 1; у — 2} и век-
тор, образованный двумя точками прямой
Ро Р1 = (3 — 1' 2 — 2) = (1' О) .
М = (х;у)
М = (х;у)
p, = (3;2)
Рис. З.З
Рис. 3.2
3-й шаг. Выпишем одно из условий — ортогонально-
сти или коллинеарности, в соответствии с заданием. По
условию задачи РОМ ~~ РОР„поэтому воспользуемся усло-
вием коллинеарности двух векторов в координатной фор-
ме (х — 1)/2 = (у — 2)/О. Получаем каноническое уравнение
прямой. Иногда в ответ рассматриваемой задачи ошибоч-

ГЛАВА 3. АНАЛИТИЧЕСКАЯ ГЕОМЕТ}'ИЯ НА ПЛОСКОСТИ
но не записывают ту часть уравнения, где встречается в
знаменателе нуль, ссылаясь на то, что на нуль делить нель-
зя. Однако уравнение (х — 1)/2 = (у — 2)/О не описывает де-
ления на нуль, здесь лишь осуществлена символическая
запись того, что текущий вектор РОМ коллинеарен векто-
ру РОР1, одна из компонент которого равна нулю.
3.4. Исходя из уравнения прямой в общем виде 3x — 4у +
+ 20 = О, преобразовать это уравнение: 1) в уравнение с уг-
ловым коэффициентом; 2) в уравнение в отрезках; 3) в урав-
нение в каноническом виде; 4) в нормальное уравнение; 5) в
параметрические уравнения; 6) в полярное уравнение.
Решение.
1) чтобы получить уравнение с угловым коэффициен-
том, решим исходное уравнение относительно у:
у= — х+5;
=3
4
2) определим отрезки, которые отсекает данная прямая
на осях координат. Полагая хо = О, получим из общего урав-
нения 3 - 0 — 4 . у() + 20 = 0 ординату точки пересечения
данной прямой с осью ОУ, уо = b = 5. Полагая y& t = О,
лучим абсциссу точки пересечения данной прямой с осью
абсцисс 3 х1 — 4 . 0 + 20 = О, х, = а = — 20/3. Подставим
найденные значения в уравнения прямой в отрезках (3.9),
получаем х Д 1.
-20/3 5
3) определим координаты двух точек, принадлежащих
данной прямой. В предыдущем пункте получены две та-
кие точки: Ро = (О; 5) и P& t  ( Ђ” 20 3; ). Теп рь запи
каноническое уравнение прямой, проходящей через две
точки (формула 3.8)
х — 0
— 20/3 — ΠΠ— 5
~ итоге получаем каноническое уравнение прямой
х «y — 5
20/3 5
4) чтобы записать нормальное уравнение прямой, со-
гласно (3.10) необходимо вычислить
=5.

114
ПРАКТИ iECKPE PygpgpggygP K РЕШЕНИЮ ЗАДАЧ
Поскольку знак коэффициента С = 20 в уравнении
Зх — 4у + 20 = 0 положителен, то нормальное уравнение
имеет вид
3 4
— х+ — у — 4=0;
5 5
5)чтобы получить параметрические уравнения, при-
равняем равенство в каноническом уравнении переменно-
му параметру t:
х «у — 5 20
20/3 5 ' 3
х =О+ — t; у =5+5t;
6) полярное уравнение прямой получим из нормального
уравнения, введя следующие обозначения: р = 4, cos а =
= — 3/5, sin а = 4/5, а = н — arcsin (4/5), отсюда р = 4/cos (y—
— н + arcsin (4/5)).
3.5. Определить угол между двумя прямыми у = 2х + 3
иу = — Зх — 8.
P е ш е н и е. Имеем Й2 = — 3, k, = 2, по формуле (3.13)
tgñð=( — 3 — 2)/(1+ 2 ( — 3)) =1,ср =arctg1= тс/4=45 .
1 1 7
у — 2= — — (х — 1) или у= — — х+ —.
3 3 3'
3.7. Найти расстояние от точки P(3; 8) до прямой (х—
— 1)/3 = (у — 2)/4.
3.6. Прямая задана уравнением с угловым коэффици-
ентом у = Зх — 4;
1) написать уравнение прямой, параллельной данной
и проходящей через точку Pp = (1; 2); 2) написать уравне-
ние прямой, перпендикулярной данной и проходящей че-
рез точку Pp = (1; 2).
Решение.
1) исходя из условия параллельности (3.14) двух пря-
мых, заданных уравнениями с угловыми коэффициента-
ми k2 = k~ = 3, получим с помощью формулы (3.5), что ис-
комое уравнение имеет вид у — 2 = 3(х — 1) или у = Зх — 1;
2) исходя из условия (3.15) перпендикулярности двух
прямых, получаем k2 = — 1/Й1 — — — 1/3. Вновь воспользовав-
шись формулой (3.5), получим

115
ГЛАВА 3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
P е ш е н и е. Преобразуем данное уравнение к общему
виду:
4(х — 1) = 3(у — 2), 4х — Зу + 2 = О.
Теперь воспользуемся формулой (3.23):
14хо — 3yo+21 14 3 — 3.8+21
Ш= = =2.
Можно было найти расстояние по-другому, с помощью
HopMBJIbHOro уравнения прямой. Составим нормальное
уравнение из полученного выше уравнения в общем виде.
Имеем.'
= — 0,8, — 0,8х+ О,бу — 0,4 = О.
сова =
3 2+ 2 ( — 3) — 4+ Х(2+ 3+ 5) = О, Х = 0,4.
Искомое уравнение получается из уравнения пучка
прямых путем подстановки в последнее найденного Х. Име-
ем Зх+ 2у — 4+ 0,4 (х — y+ 5) = О, 3,4x+ 1,6у — 2 = О.
3.9. Составить уравнения биссектрис углов между пря-
мыми 3x+4у — 8 = Ои 5x — 12у+ 1 =О.
P е ш е н и е. Если точка М(х; у) принадлежит одной из
биссектрис углов, образованных прямыми, то расстояния
от нее до прямых одинаковы. Пользуясь формулой (3.23),
можно записать
I »+4y — 81 15х — 12у+11
45~ +122
Для всех точек одной из биссектрис функции i.,(x, у) =
= 3~ + 4у — 8 и I-2(х, у) = 5х — 12y + 1 имеют одинаковые
Отсюда расстояние можно рассчитать по формуле (3. 24):
Ш = 1 — 0,8 3+ 0,6 8 — 0,41 = 2.
3.8. Составить уравнение прямой, проходящей через
точку Р(2; — 3) и точку пересечения прямых Зх + 2у — 4 = О
их — у+ 5 =О.
Решение.
Воспользуемся уравнением (3.21) пучка прямых Зх+
+ 2у — 4 + Х(х — у + 5) = О. Поскольку искомая прямая про-
ходит через точку Р(2; — 3), то, подставив координаты этой
точки в уравнение пучка прямых, найдем параметр Х:

116
ПРАКТИЧЕСКОЕ РУКОДОДСТВО К РЕШЕНИЮ ЗАДАЧ
знаки, обращаясь в нуль в точке пересечения прямых. Для
всех точек другой биссектрисы I.,(õ, у) и Lz(x, у) имеют
разные знаки (теорема 3.1). Отсюда уравнение первой бис-
сектрисы
(Зх + 4у — 8)/5 = (5х — 12у + 1)/13, 14х + 112у — 109 = О,
а уравнение другой биссектрисы
(Зх + 4у — 8)/5 = — (5х — 12у + 1)/13, 64х — 18у — 99 = О.
B(X89 y8)
Зх +
2х+ 5у — 73 = 0
C(xcy yc)
x+g+12=0
Рис. 3.4
3.10. Получить уравнения медианы, биссектрисы и вы-
соты, выходящих из вершины треугольника, которая яв-
ляется пересечением двух сторон треугольника Зх — 4у +
+ 8 = О и 12х + 5у — 73 = О, если уравнение третьей сторо-
ных+ у+ 12 =0.
P е ш е н и е. Сделаем схематический чертеж (рис. 3.4).
1. Найдем координаты вершины, из которой исходят
искомые медиана, биссектриса и высота. Для этого решим
совместно систему уравнений Зх'-4у+ 8 = О, 12х+ 5у—
— 73 = О. Из первого уравнения, умноженного на 4, вычтем
второе уравнение, получаем — 21у = -105, отсюда хд = 4,
ув = 5. Итак, искомая вершина В(4; 5). Найдем аналогич-
но координаты других вершин А и С. Из второго уравне-
ния системы уравнений Зх — 4у+ 8 = О и х+ у+ 12 = О вы-
разим х = — 12 — у и подставим в первое уравнение, получа-
ем хв = — 8, ув = — 4. Координаты вершины А( — 8; — 4). Из
второго уравнения системы 12х + 5у — 73 = О и х + у + 12 = О
вновь находим х = — 12 — у и подставляем в первое уравне-
ние. При этом получим хс = 19, ус = — 31. Координаты вер-
шины С(19; — 31).
2. Найдем середину отрезка АС. Для этого воспользу-
емся формулами деления отрезка в данном отношении

117
I.ËÀÂÀ 3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
хц = ( — 8+ 19)/2 = 5,5, у~ = ( — 4 — 31)/2 = — 17,5. Уравнение
медианы получим как уравнение прямой, проходящей че-
рез две заданные точки В и М (формула (3.8)):
(х — 4)/(5,5 — 4) = (у — 5)/( — 17,5 — 5),
(х — 4)/1,5 = (у — 5)/ — 22,5.
Упростим это уравнение, разделив все компоненты на-
правляющего вектора а =(1,5; — 22,5) на 1,5. Получим но-
вый направляющий вектор, коллинеарный а, с координа-
тами а'=(1; — 15). Уравнение искомой медианы принима-
ет вид
(х — 4)/1 = (у — 5)/ — 15.
3. Чтобы найти уравнение биссектрисы, проходящей
через вершину В, воспользуемся теоремой о том, что бис-
сектриса треугольника делит противоположную сторону
на части, пропорциональные прилежащим к ней сторонам.
С помощью формул деления отрезка в данном отноше-
нии (1.6)
-~А +~~С УА +~УС
~к= „~ уа=
где
Х = AK/КС = АВ/ВС,
получаем
5
13
АК АВ
КС ВС
Отсюда координаты основания биссектрисы, выходя-
щей из вершины В, таковы: К(х~; у~) = ( — О,о; — 11,5).
Уравнение биссектрисы получается с помощью фор-
мулы (3.8): (х — 4)/( — 0,5 — 4) = (у — 5)/( — 11,5 — 5) или (х—
— 4)/ — 4,5 = (у — 5)/ — 16,5. Разделим все компоненты направ-
ляющего вектора биссектрисы Ь =( — 4,5; — 16,5) на ( — 1,5),
получим новый направляющий вектор b'=(3;1]}, колли-
неарный прежнему, заменяя координаты b = ( — 4,5; — 16,5)
B уравнении биссектрисы, получим новое уравнение для
нее в виде (х — 4)/3 = (у — 5)/11.
4. Уравнение высоты из вершины В найдем как урав-
нение прямой, проходящей через точку В(4; 5) и па-
раллельной нормальному вектору 6 =11; 1) прямой АС.

118
IIPAKTHHECKOE РУЩ)РОДСТВО & t; РЕШЕ ИЮ ЗА
Запишем условие коллинеарности текущего вектора пря
мой ВЯ = {х — 4; у — 5} и вектора й = (1; 1}: (х 4)/1 =
= (у — 5)/1 — уравнение высоты.
3.11. Уравнение одной из сторон квадрата АВС.0 — АВ
есть х + 3y — 5 = О. Составить общее уравнение трех осталь-
В С
ных сторон квадрата, если Р( — 1; О)—
точка пересечения его диагоналей.
Р е ш е н и е. Сделаем схематический
К P
чертеж(рис. 3.5).
1. Найдем координаты точки К пе-
ресечения АВ с перпендикуляром РК,
опущенным из точки P на АВ, т. е. имею-
А
Рис. 3.5
щим текущий вектор РМ =(х+1; у — О}
и перпендикулярным прямой АВ (парал-
лельным ее нормальному вектору й = (1; 3}). Записав усло-
вие коллинеарности PM и ~, получим уравнение перпен-
дикуляра PK:
D
(*-» цд =д~3, 3x — д~ а= о.
Умножим уравнение АВ на 3 и из полученного вычтем
уравнение РК, тогда получим 10y = 18, у~ = 1,8, хк = — 0,4.
Итак, Х( — 0,4; 1,8).
2. Определим координаты точек А(хд , 'y„) и В(хв, ув).
Для этого вначале вычислим ~ХР~2:
(ХР(2 = ( — 1 — ( — 0,4))2+ (Π— 1,8)2 = 3,6.
Теперь запишем равенство квадратов расстояний
[АХ[' = /ВХ[ = /РХ['
подставив в них найденное из уравнения прямой АВ выра-
жение для х = 5 — Зу. Имеем
(5 — Зу+ 0,4)2+ (у — 1,8)2 = 3,6 10y~ — 36у+ 28,8 = 0.
хА=х1= — 2,2, gA=у1=2,4; хв=х2=1,4, ув=у2=1,2.
Итак, А( — 2,2; 2,4), B(1,4; 1,2).
Решая квадратное уравнение, получаем у1 = 2,4; у2 = 1,2.
Подставим найденные у1 и у2 в уравнение прямой АВ и по-
лучим соответствующие абсциссы точек А и В:

119
ГЛАВА 3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
3. Найдем координаты точек С и D, используя форму-
лы деления отрезка в данном отношении и то, что точка Р
есть середина АС и BD:
А+ с 1 =yÓë" +'yÓñ 0. C( 0,2. 2 4
2 ' 2
в а 1. Ув Уа 0. D( 3,4
2 ' 2
4. Уравнение прямой AD найдем из условия коллине-
арности текущего вектора этой прямой
АМ =(х+2,2; у — 2,4)
и нормального вектора прямой АВ й =(1; 3):
(х + 2,2)/1 = (у — 2,4)/3.
Преобразуем уравнение AD к общему виду: Зх — у+ 9 = О.
5. Поступая аналогично предыдущему пункту, полу-
чим уравнение ВС.
ВМ={х — 1,4;у — 1,2) ~~й =(1;3),
(х — 1,4)/1 = (у — 1,2)/3 или Зх — у — 3 = О.
6. Уравнение CD найдем как уравнение прямой, про-
ходящей через две точки (формула (3.8)):
(х — 0,2)/( — 3,4 — 0,2) = (у — ( — 2,4))/( — 1,2 — ( — 2,4)).
В знаменателях дробей в последнем равенстве можно
заменить координаты направляющего вектора а = ( — 3,6; 1,2)
на координаты коллинеарного вектора а' = ( — 3; Ц, который
получается из а делением на 1,2. Уравнение CD после
этого приобретает вид (х — 0,2)/ — 3 = (у — ( — 2,4))/1 или
х + Зу + 7 = Π— общее уравнение прямой.
3.12. Даны уравнения одной из сторон АВ ромба ABCD:
х — Зу + 10 = О, и одной из его диагоналей: х + 4у — 4 = 0.
Диагонали ромба пересекаются в точке P(0; 1). Найти урав-
нения остальных сторон ромба, расстояние от точки P до
стороны Ац и внутренние углы ромба.
P е ш е н и е. Сделаем схематический чертеж (рис. 3.6).
1. Уравнение диагонали АС получим из условия ортого-
нальности АС и BD и того, что BD проходит через точку Р,
(х — О)/1 = (y — 1)/4, 4х — у + 1 = ().

120
ПРАКТИЧЕ~;КОЕ PygPBPgPTBO К РЕШЕНИЮ ЗАДАЧ
х+ 4у—
Рис. 3.6
2. Координаты точек А и В найдем из решений соответ-
ствующих систем уравнений:
«А(7 11;39 11);
4х — у+1= О
х — Зу+10=0
х+4у — 4 =О
3. Поскольку диагонали ромба делятся точкой пересе-
чения пополам, то из формул деления отрезка в данном
отношении найдем координаты точек C(xc' yc) и D(xo' ур):
х,~ + xc 7/11+ хс у„+ ус
2 2 2
1 = с; С( — 7/11; — 17/11),
2
— 4+ хд ув + уп
2 ' 2
xB+xD
x& t; —
2
7
1 =; D(4; 0).
4. Уравнения сторон ВС, CD u AD найдем как уравне-
ния прямых, проходящих через две заданные точки (фор-
мула (3.8)):
х+4 у — 2 х+4 у — 2
— 7/11+4 — 17/11 — 2' 37/11 — 39/11'
39х+ 37у+ 82 = О.
х — 4 g — О х — 4 у
— 7/11 — 4 — 17/11 — 0' — 51/11 — 17/11'
х — 3y — 4 =О.
х — 4 у — О х — 4
7/11 — 4 39/11 — 0' — 37/11 39/11'
39х+ 37у — 156 = О.

121
p„qABA 3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
5. Расстояние от точки Р(0; 1) до прямой АВ с уравне-
ццем х — Зу+ 10 = 0 найдем следующим образом:
I 0 — 3. 1+ 10 ( 7 7~~0
Д0
б. Угол между двумя прямыми АВ и ВС определяется
из формулы (3.13):
1-39-3.37
=0,4235,
170
сов(~АВС) =
ЛАВС =115', ~ВАЛ = ~ВСЮ = 65'.
3.13. Изобразить область, описываемую системой нера-
венств
х+у — 1&l ;0 (
— х+ у — 1& t 0
у ) — 1 (АС).
АВ: х/( — 1) + у/1 = 1,
ВС: х/1 + у/1 = 1, АС: у = — 1.
Получаем треугольник АВС, внутри которого находит-
ся пробная точка 0(0; О).
Непосредственной подстановкой убеждаемся, что ко-
ординаты пробной точки удовлетворяют неравенствам
(АВ), (ВС) и (АС):
0+0 — 1&lt 0, - +О Ђ” 1 lt 0,
3.14. Найти наибольшее значение величины I.(x, у) =
2х + у внутри области, определяемой системой нера-
~енств из задачи 3.13.
Решение. Выберем в каче-
стве пробной точки такую, кото-
рая не принадлежит ни одной из
прямых, уравнения которых по-
лучаются из данных неравенств
Рис. 3.7
путем замены знаков неравенств
на равенства. Проще всего считать пробной точкой 0(0; О).
Построим упомянутые прямые, предварительно преобра-
зив их уравнения (рис. 3.7) к виду уравнений в отрезках.

122
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
3.3.
КРИВЫЕ ВТОРОГО ПОРЯДКА
Окружностпью называется геометрическое место точе~
плоскости, равноудаленных от данной точки этой же плос-
кости, называемой центром. Уравнение окружности с р®-
диусом R и центром в точке Ро(хо, 'yp) в декартовых коорди
натах записывается следующим образом (рис. 3.9):
(х — хо)'+ (у — уо)' = Ж (3.2б)
Уравнение (3.25) можно получить, записав равенство
расстояния от текущей точки окружности М(х; у) до цен
тра Р(хо; уо) радиусу R:
р e rrr e н и е. Построим прямуо
L(x, у) = — 2х + у = О, т. е. у = 2х,
и отложим нормальный вектор
этой прямой ц = {-2; Ц (рис. 3.8).
В соответствии с теоремой 3.3
при перемещении прямой у = 2~
в направлении вектора д вели-
чина L(x, у) = — 2х + у будет воз-
Рис. 3.8 растать. Самая крайняя из этих
параллельных прямых, которые
имеют хотя бы одну общую точку с областью, лежащей
внутри треугольника АВС и включающей в себя стороны тре-
угольника, есть та, что проходит через вершину А( — 2; — 1).
В данной точке L(x, у) = — 2х + у = L( — 2, — 1) = L,„=
= — 2( — 2)+( — 1) =3.
Другое решение основано на том положении, что ли-
нейная функция, имеющая общие точки с замкнутой об-
ластью в виде выпуклого многоугольника, которая описы-
вается соответствующей системой линейных неравенств,
принимает наибольшее значение либо в вершинах много-
угольника, либо на какой-то стороне многоугольника.
Таким образом, чтобы определить на большее значение
L(x, у) = — 2х + у внутри треугольника С, нужно выбрать
наибольшее из чисел L(x„, уд) = L( — 2, — 1) = 3, Ь(хв, ув) =
= L(0, 1) = 1, L(x~, ус) = L(2, — 1) = — 5. Отсюда получим тот
же результат, что и найденный выше: L,,„„= =3, это значе-
ние достигается в точке А( — 2; — 1).

123
ГЛАВА 3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
=R,
® Затем возведя обе части этого
равенства в квадрат.
При специальном выборе де-
картовой системы координат, ко-
рда начало координат совпадает с
центром окружности, уравнение
Окружности принимает вид
Уо
Х0
Рис. 3.9
&gt 2+ у =
(3.26)
Параметрические уравнения окружности, соответст-
вующие (3.26):
x=Rcos t, у =Rsint, 0 & t  &l
(3.27)
Уравнению (3.27) соответствует следующее полярное
уравнение окружности.'
p=R, 0<(р&
(3.28)
= 2a & t; е. 3.
Последовательно избавля-
ясь от радикалов и вводя обо-
значение
b~=y~ с2
'7
(3.30)
получим следующее канони-
ческое уравнение эллипса
(рис. 3.10):
х2/а2 + у2/Ь2 = 1. (3.31)
Рис. 3.10
Эллипсом называется геометрическое место точек плос-
кости, для каждой из которых сумма расстояний до двух
фиксированных точек этой же плоскости, называемых
фокусами, есть данное положительное число 2а, большее,
чем расстояние 2е между фокусами.
В специально выбранной системе декартовых коорди-
нат, когда фокусы располагаются на оси ОХ симметрично
начала координат (F&g ;( Ђ” а; ), Fz a; О ), запи ем равенс
величин, упоминаемых в определении эллипса,

124
ПРАКтяКедще руКОВОДСТВО К РеШеНиЮ ЗАДАЧ
Точки А1( — а; О), А~(а; О), В,(0; — Ь), В~(0; Ь) — называ-
ются вершинами эллипса, 0(0; О) — центром эллипса. От-
резки А,А2 = 2а и В1В2 = 2b называются соответственно
большой и малой осью эллипса. Расстояния от текущей
точки эллипса М(х; у) до его фокусов
r& t; —
ИГ2 =
называются фокальными радиусами этой точки. Отношение
е = с/а называется эксцентриситетом эллипса (е = с/а <'
Две прямые, параллельные малой оси и отстоящие от нее на
расстояние а/а, называются директрисами эллипса.
Уравнения директрис эллипса в декартовых коорди-
натах:
(3.32)
х = — с/а, х = с/а.
Для любой точки эллипса М(х; у) справедливо так на-
зываемое директориальное свойство:
rq/dq = rg/dq = е,
(3.33)
(3.35)
x= a cost, y=bsint, 0 & t  &l
Полярное уравнение эллипса (полюс находится в фо-
кусе, полярная ocb перпендикулярна директрисе и направ-
лена в сторону, противоположную направлению к ближай-
шей от этого фокуса директрисе, р — фокальный параметр,
определяемый формулой (3.34), е = с/а — эксцентриситет):
р=, 0<y& t;2 . (
1 — ecosoc
Уравнение касательной прямой к эллипсу (3.31) в точ-
~å Ро(хо' yo):
где d& t; Ђ” расстоя ие от то ки М х; у) до директр с
= — с/а; d~ — расстояние от точки М(х; у) до директрисы
х = с/а. Кроме того,
Г1 =й сх, 72=a+Ex.
Фокальным параметром р эллипса называется полови-
на хорды, проведенной через фо с параллельно малой оси,
b2
Р=
Параметрические уравнения эллипса, соответствую-
щие (3.31), имеют следующий вид:

125
PJIABA 3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
xxp/a2+ ууо/b2 = 1.
(3.37)
Прямая Ах + By + С = О касается эллипса (3.31), если
Дц2+- Bb2 — g = О.
(3.38)
Условие касания прямой у = kx + т эллипса (3.31):
й2а2+ b2 т2
(3.39)
(3.40)
=2a <
Последовательно избавляясь
от радикалов и вводя обозначение
b2 С2 д2
(3.41)
получим следующее каноническое
уравнение гиперболы (рис. 3.11):
х2/а2 — у~/b2 = 1. (3.42)
Точки А,( — а; О), А,(а; О) — дей-
ствительные вершины, В,(0; — Ь),
Рис. 3.11
Касательная к эллипсу в произвольной точке Mp(xp, yp)
является биссектрисой внешнего угла Мд треугольника
FyFgM p, имеющего своими вершинами фокусы эллипса Fg
и F2 и данную точку Ыо.
Оптическое свойство эллипса заключается в следую-
щем. Если из одного фокуса испускается луч света, то по-
сле отражения от внутренней поверхности эллипса, этот
луч пройдет через другой фокус.
Гиперболой называется геометрическое место точек
плоскости, для каждой из которых абсолютное значение
разности расстояний до двух заданных точек этой же плос-
кости, называемых фокусами, есть данное положительное
число 2а, меньшее, чем расстояние 2с между фокусами.
В специально выбранной системе декартовых коорди-
нат, когда фокусы располагаются на оси ОХ симметрично
относительно начала координат (Р1( — а; О), Fz(a; О)), запи-
HIRAM равенство величин, упоминаемых в определении эл-
липса:

126
ДРАКТИ~ЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
В2(0; Ь) — мнимые вершины гиперболы, 0(0; О) — центр
гиперболы. Отрезок А,А2 = 2а называется действительной
осью гиперболы, и В,В = 2Ь вЂ” мнимой осью гиперболы.
Расстояния от текущей точки гиперболы М(х; у) до ее фо-
кусов
r& t; —
иг2 =
у =+ — х.
b
а
(3.43)
Если оси гиперболы равны, т. е. а = b, то гипербола на-
зывается равнобочной или равносторонней, ее уравнение
имеет следующий вид:
X — у =а
(3.44)
Асимптотами равносторонней гиперболы являются
биссектрисы координатных углов. Если за оси координат
принять асимптоты равносторонней гиперболы, то ее урав-
нение примет вид
ху = а2/2.
(3.45)
Уравнения директрис гиперболы (3.42) в декартовых
координатах.
(3.46)
х =+а/е.
Для любой точки гиперболы М(х; у) справедливо так
называемое, директориальное свойство
r,/d, = г2/dq = к,
(3.47)
где d~ — расстояние от точки М(х; y) до директрисы х =
= — с/а; d2 — расстояние от точки М(х; y) po директрисы
х = с/а. Кроме того, r, = а — ех, rq = а + ех.
называются фокальными радиусами этой точки.
Отношение е = с/а называется эксцентриситетом гипер-
болы (е = с/а & t; ). ве прям е, параллель ые ма ой с
отстоящие от нее на расстоянии а/е, называются дирек-
трисами гиперболы.
Директрисы гиперболы расположены на расстоянии
d = а/вот центра. Асимптоты гиперболы имеют уравнения:

127
ГЛАВА 3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
Фокальным параметром р называется половина хорды,
проведенной через фокус перпендикулярно действитель-
ной оси'-
р = b2/à.
(3.48)
xxp/a' — yyp/b~ = 1.
(3. 51)
Прямая Ах + By + С = О касается гиперболы (3.42), если
Аа2 — Bb2 = С2
(3.52)
Условие касания прямой у = kx + т гиперболы (3.42):
P2y2 — Ь2 = т2
(3. 53).
Касательная к гиперболе в произвольной точке Mp(xp, yp)
Является биссектрисой внутреннего угла между фокаль-
~ыми радиусами точки касания.
Отрезок касательной гиперболы между асимптотами
делится в точке касания пополам.
Гиперболы, имеющие уравнения
x2/a2 - y'/b' = 1 и y'/b x /a' = 1
(3. 54)
~а~ываются сопряженными. Они имеют общие асимпто-
~ь~, действительная ось каждой из них равна мнимой оси
ЦРугой.
Параболой называется геометрическое место точек плос-
кости, для каждой из которых расстояние до некоторой
Параметрические уравнения гиперболы, соответствую-
щие (3.42), имеют следующий вид:
е'+е ' е' — е '
х=а.eht=a, y=b sht=b . (3.49)
2 ' 2
Полярное уравнение одной ветви гиперболы (полюс
находится в фокусе, полярная ось перпендикулярна ди-
ректрисе и направлена в сторону, противоположную на-
правлению к ближайшей от этого фокуса директрисе, р—
фокальный параметр, определяемый формулой (2.51),
я = с/а — эксцентриситет):
Р=
Р
0& t; y&
1 — ecosoc
Уравнение касательной прямой к гиперболе(3.42) в
точке Pp(xp' yp):

ДРАКтиЦе~;КОе РУКОВОДСТВО К РЕШениЮ 3АдА~
128
дир
Х
(3.55)
и последовательно избавляясь от радикалов, получим ка-
ноническое уравнение параболы:
у2 = Ярх,
(3.56)
Точка O(0; 0) называется вершиной параболы. Вели-
чина р называется фокальным параметром или парамет-
ром параболы. Эксцентриситет параболы принимается рав-
ным единице c = 1.
Параметрическое уравнение параболы, соответствую-
щее (3.56),
~2
y=t, х= —.
2р
Полярное уравнение параболы (полюс находится в фо-
кусе, полярная ось перпендикулярна директрисе и направ-
лена в сторону, противоположную направлению от фокуса
к директрисе, р — фокальный параметр):
р =, 0~ ~р(2т~.
1 — cosy
Касательная к параболе в точке Мр(хр, ур) имеет урав-
нение
(3.57)
(3.58)
У фиксированной точки этои
плоскости, называемой фо-
кусом, равно расстоянию до
некоторой фиксированной
О
прямой, не проходящей че-
рез фокус и называемой ди-
ректрисой.
Чтобы записать уравне-
ние параболы в канониче-
ском виде, необходимо специальным образом выбрать сис-
тему декартовых координат. Ось ОХ пусть совпадает с пер-
пендикуляром, опущенным из фокуса на директрису, начало
координат пусть будет расположено на середине этого пер-
пендикуляра. В этой системе координат (рис. 3. 12) коорди-
наты фокуса F(p/2; 0), а уравнение директрисы х = — р/2.
Записывая равенство величин, упоминаемых в опреде-
лении параболы,

129
['ËÀÂÀ 3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
(3.59)
уело = p(x + «о).
Прямая у = kx + Ь касается параболы (3. 56), если
р = 2ЬЙ.
(3.60)
Касательная к параболе в произвольной точке являет-
ся биссектрисой угла между фокальным радиусом точки
касания и диаметром, проходящим через точку касания.
Геометрический смысл неравенства второй степени
определяется следующей теоремой.
Теорема 3.4. Пусть уравнение второй степени F(x, у) = 0
определяет на плоскости некоторую кривую второго по-
рядка. Тогда вся плоскость разбивается этой кривой на об-
ласти: координаты любой точки каждой отдельной облас-
ти удовлетворяют только одному неравенству: или F(x,
у) &lt О, ли F x, у &
3.4.
РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ
(х — 1)2 — 1 + (у + 3)2 — 9 = 6, или (х — 1) + (у + 3) = 42.
Центр окружности 0(1; — 3), радиус В = 4.
3.17. Составить уравнение геометрического места то-
чек на плоскости, каждая из которых вдвое ближе к точ-
ке А(4; p), чем к точке В(1; О).
3.15. Составить уравнение окружности с центром в точ-
ке Ро(1; — 2) и радиусом R = 3.
P е ш е н и е. В соответствии с формулой (3.25) уравне-
ние окружности запишется так: (х — 1) 2 + (у + 2) 2 = 32 = 9.
3.16. Привести уравнение окружности х2 — 2х + у2+
+ 6y = 6 к каноническому виду. Определить координаты
цектра и радиус.
P е ш е н и е. Используем формулы для полного квад-
рата суммы и разности и дополним до полного квадрата
выражения
а) х2 — 2х = х2 — 2 х. 1+ 12 — 12 = (х — 1)2 — 1
б) у~+ 6у = у~ — 2. у 3+ 32 — 32 = (у+ 3)2 — 9.
Уравнение окружности можно переписать теперь сле-
дующим образом:

130
ПРАК~ИЧЕ~;~ОЕ РУКОЦОДСТВО K РЕШЕНИЮ ЗАДАЧ
P е ш е н и е. Расстояние от текущей точки М(х; g) ис-
комой кривой до точки А(4; 0) обозначим через
r& t; —
до точки В(1; О) — через
Г~ =
Из условия задачи следует, что r1 = 2г2, отсюда получаем
Возводя обе части последнего соотношения в квадрат, по-
лучим(х — 4) + у2 = 4((х — 1) + у2). Раскроемскобкиипри-
ведем подобные члены: х +у =(2~ГЗ) — уравнение ок-
ружности с центром в начале координат и радиусом 2~ГЗ.
3.18. Найти эксцентриситет, координаты фокусов и
вершин эллипса х2/25 + у~/9 = 1.
Решение. По условию а2 = 25, b2 = 9, отсюда а = 5,
b = 3. В соответствии с обозначениями на рисунке 3.10 по-
лучаем с=,(25 — 9 =4, а = 4(5 = 0,8,А, е(~5;0),В,,(0; ~8),
F& t; (~4;
3.19. Составить геометрическое место точек на плоско-
сти, отношение расстояний которых до точки F(4,5; О) и
до прямой х = 0,5 равно трем.
P е ш е н и е. Сделаем схематиче-
M(x. „1 ский чертеж (рис. 3.13).
Обозначим координаты текущей
точки искомой кривой через М(х; у).
0)
Тогда расстояние от точки М(х; у) до
прямой х = 0,5 равно di = I» — 0,51 а
расстояние от точки М(х; у) до точки
F(4,5; О) равно
х = 0,5
Рис. За13
r& t; —
Из условия задачи следует r& t = 3 1, отс
=Çl» — 0,5(.
После возведения обеих частей в квадрат и приведения по-
добных членов получим каноническое уравнение гипербо-
лы: »2/2,25 — у~/18 = 1.

ГЛАВА 3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
3.20. Составить геометрическое место точек, равноуда-
ленных от точки А(4; 1) и от оси ординат.
P е ш е н и е. Исходя из определения параболы, заклю-
чаем, что искомое геометрическое место точек — парабо-
ла. Выберем специальным образом систему координат так,
чтобы уравнение параболы имело канонический вид. На-
чало координат должно находиться на середине перпенди-
куляра, опущенного из фокуса на директрису, т. е. в точке
0'(2; 1). Координаты Х'О'Y' связаны с координатами XOY
так: х' = х — 2, у' = у — 1. Параметр р равен расстоянию от
фокуса до директрисы: р = 4. Уравнение параболы в систе-
ме координат Х'О'Y' (у')2 = 8х'. Переходя к старым коор-
динатам ХОУ, получим (у — 1)2 = 8(х — 2).
3.21. Найти параметр р, координаты фокуса и уравне-
ние директрисы параболы у2 = 2рх, если известно, что ка-
сательная к этой параболе в некоторой точке имеет сле-
дующее уравнение в отрезках: х/( — 75} + у/15 = 1.
P е ш е н и е. Преобразуем уравнение касательной к па-
раболе в точке (xo = yo2/(2р}; yo) (формула (3.59)) к виду
уравнения прямой в отрезках:
х/(-xo) + V/(P>o/ o =
Подставим в последнее соотношение абсциссу точки
касания:
x/(-yo'/(2P)) + y/(yo/2) = 1
По условию yo/2 = 15, — yo2/(2р) = — 75, отсюда yo = 30,
P = 6, уравнение директрисы х = — р/2 = — 3, а координаты
фокуса F(P/2; О) = F(3; О).
3.22. Установить, что уравнение р = 36/(4 — 5cos rp) опре-
деляет гиперболу, и найти ее полуоси.
P e ш е н и е. Разделим и числитель и знаменатель на 4.
Преобразуем данное уравнение к виду
Р=
9
5
1 — — cosy
4
Поскольку c = c/a = 5/4 & t; 1, найден ое уравне
определяет правую ветвь гиперболы. Пользуясь фор-
мулами (3.50), b2 = с — а~ и равенством, определяющим

132
ПРАКУИЧЕ~;КОЕ РУ~'„ОЦОДСТВО К РЕШЕНИЮ ЗАДАЧ
эксцентриситет, получим систему уравнений для нахож-
дения а и b. Имеем
с2 25 b2 с2 — а2
— — р= — = =9, а=16,
а2 16 a a
я= —, с=20,
5
= 12.
3.23. Составить полярное уравнение эллипса x~/a~+
+ у~/b~ = 1 при условии, что направление полярной оси сов-
падает с положительным направлением оси абсцисс, а по-
люс находится в центре эллипса.
P е ш е н и е. Подставим в уравнение эллипса вместо х и
у их выражения через полярный радиус р и угол q.
Имеем
р cos (р р sin (р b cos (р+а sin (р
а b2 а2b2
Заменим в числителе Ь на а — с и воспользуемся ос-
новным тригонометрическим тождеством
a — c cos~(p+a sin (p
cos~ y+ sin~ y = 1, р
ц 2~2
=1.
a2 — c'2 cos2 (p p2
р2 =1, — 1 — — со82(р =1
а2b2 Ь2 а2
Подставим c~ = c~/a~, тогда получим р = b~/(1 — c~ cos~ y).
3.24. В какой точке линейная функция L(x, у) = J2x — у
достигает максимума в области, описываемой неравенст-
вом х~/9+ у~/7 & t;
P е ш е н и е. Применяя теоремы 3.3 и 3.4, получим, что
максимум L(x, у) достигается в точке касания правой ка-
сательной к данному эллипсу, параллельной прямой
Г2х — у = О. Воспользуемся условием 3.39:
Й = Г2 = Г2х — 2у, а = 3, Ь = Г7; 2 9+ 7 = т~
Из двух значений m =+5 выбираем m = — 5, так как
функция L(x, у) = Г2х — у достигнет максимума в данной
области в направлении вектора й =(~Г2; — 1) на правой ка-
сательной у = Г2х — 5. Определим координаты точки каса-

133
ГЛАВА 3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ HA ПЛОСКОСТИ
сия, подставив в уравнение эллипса вместо у величину
,/2х — 5. Отсюда
(Я~ — 5}2
9 7
+ =1,
25x~ — 90~2х+162=0, wх1 — — х2 —— 1,842.
Подставим х1 в уравнение касательной и найдем у~ =
= — 1,4. При этих х, и у, линейная функция достигает сле-
дующего максимального значения:
1(1,8~2, — 1,4) = ~2.1,8. ~Г2 — ( — 1,4) = 5.
3.5.
ЗАДАЧИ
ПРЯМАЯ ЛИНИЯ
3.',25. Составить уравнение прямой, проходящей через
точку А(2; 3) перпендикулярно вектору й = ( — 2; 5).
3.26. Составить уравнение прямой, проходящей через
точку А(1; 2) параллельно вектору а = (3; О}.
3.27. Составить уравнение прямой, проходящей через
две точки А(1; 2) и В(2; 5).
3.28. Исходя из уравнения прямой в общем виде 3x+
+ 2у — 8 = О, получить уравнение: 1) с угловым коэффици-
ентом; 2} в отрезках; 3} B каноническом виде; 4} нормаль-
ное; 5} в параметрическом виде; 6} полярное.
3.29. Дана прямая 5x — бу + 7 = О. Написать уравнение
прямой: 1} параллельной данной и проходящей через точ-
ку А(8; 4); 2) перпендикулярной данной и проходящей че-
рез точку В(1; — 3).
3.30. Получить уравнение прямой, проходящей через
точку P(5; 7) и точку пересечения прямых х + 2у — 3 = 0 и
2х — у+4 =О.
3.31. Треугольник задан координатами своих вершин
А(1; 2}, В( — 3; 5} и С(4; — 1}. Составить уравнение медианы и
высоты, выходящих из вершины А.
3.32. Треугольник задан координатами своих вершин
< 1; }, В 4; 6 и С 7; 1 ). Состав ть уравне ие биссект
сы, выходящей из вершины А.

134
ПРАКУИЧЕ~;КОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
3.33. Найти точку А, симметричную точке В( — 2; 4} от-
носительно прямой Зх — 5у + 1 = О.
3.34. В параллелограмме А.ВС1Э известны уравнения
сторонЫ: 2х — у+ 4 = ОиВС: 2х — у+ 10 = О, атакжеурав-
нение диагонали АС: х + у+ 2 = О. Найти координаты вер-
шин и точки пересечения диагоналей.
3.35. Найти площадь прямоугольного треугольника с
вершиной в начале координат, две другие вершины кото-
рого являются точками пересечения прямой 2х — Зу — 6 =- О
с осями координат.
3.36. В равнобедренном треугольнике А.ВС известны
уравнения основания АС: х + 2у = О и боковой стороны АВ:
х — у+ 5 = О. Составить уравнение другой боковой сторо-
ны, если известно, что она проходит через точку D(1; 5).
3.37. Даны уравнения биссектрис двух углов треуголь-
ника x/2 + у/2 = 1 и (x + 3)/3 = (у+ 3)/1, а также коорди-
наты одной из вершин А(2; 4). Составить уравнения сто-
рон треугольника.
3.38. В треугольнике известны уравнения двух высот
(x — 1}/2 = (у — 3}/7, x = — 14t + 10, у = — 4t + 2. Зная коор-
динаты одной из вершин треугольника А(3; 4), найти урав-
нения сторон.
3.39. Составить уравнения прямых, перпендикулярных
прямой x/6 + у/2 = 1 и отстоящих от точки A(5; 4} на рас-
стояние f10 единиц длины.
3.40. Определить, находится ли точка М(1; 4} внутри
треугольника, заданного уравнениями своих сторон 2х +
+ Зу — 6 = О, 2х — Зу + 6 = О и у = — 8. Опишите область, за-
ключенную внутри треугольника, включая границы, с по-
мощью системы неравенств.
3.41. Найти наибольшее значение величины 1.(x, у) =
= Зх + 4у+ 8 внутри области, определяемой системой не-
равенств 7х — Зу+ 14 & t; О, х у Ђ” 1 & t; , 1 x — у Ђ 4
3.42. Найти наибольшее значение величины 1.(x, у) =
= ЗОх + 29у, которое она принимает внутри области, опи-
сываемой системой неравенств 2x + 5y & t; 0, 2   &l
8х+ 9у & t; 1 4  & t  ,
3.43. Стороны треугольника 3àð»» уравнениями:
a;x + Ь,у + с; = 0 (i = 1, 2, 3).

135
ГЛАВА 3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
Доказать, что площадь треугольника S можно вычис-
лить по формуле
S = g /(2~4~4~з)
где
а, Ь, с1
2
~з Оз сз
а2 b2
Л1 —— ~0,
~3 ~3
Л~ = ~0, Л~ — — ~0.
~3 ~3 ~2 ~2
3.44. Площадь трапеции равна 2, а сумма диагоналей
равна 4. Найти высоту трапеции.
КРИВЫЕ ВТОРОГО ПОРЯДКА
В задачах 3.45 — 3.47 привести уравнения кривых вто-
рого порядка к каноническому виду.
3.45. 9х2+ 4у2 — 36х+ 8у+ 5 = О.
3.46. у = х2 + 4х + 5.
3.47. 4х2 — 9y2+ 8х — 36у — 68 = О.
В задачах 3.48 — 3.50 преобразовать полярные уравне-
ния кривых второго порядка в канонические уравнения в
декартовых координатах.
3.48. р = sin q + cos q.
3.49. р = 9/(4 — 5cos <
3.50. р = 3/(2+ sing).
3.51. Асимптоты гиперболы имеют уравнения 12у+
+ +5х = О, а расстояние между фокусами равно 338. Соста-
вить каноническое уравнение гиперболы.
3.52. Составить уравнение параболы, имеющей дирек-
трису х = — 2 и фокус F(2; 4).
3.53. Составить уравнение эллипса, у которого малая
полуось а = 2, а расстояние между фокусами равно 2.
3.54. Составить уравнение эллипса, если известны ко-
ординаты его фокусов F~( — 3; О) и Fz(3; О), а также эксцен-
триситет c = 3/5.
3.55. Составить и привести к каноническому виду урав-
(ение линии, для которой Отношение расстояний от каж-
дой ее точки до точек 0(0; О) и А(0; 5) равно 9/4.

136
ДРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
3.56. Составить уравнение геометрического места то-
чек, отношение расстояния которых до данной точки
B(0; 4) и до данной прямой у — 1 = 0 равно 2.
3.57. Найти площадь треугольника, образуемого ося-
ми координат и касательной к эллипсу х /16 + у~/3 = 1 в
точке Р(2; 2,25).
3.58. Найти расстояние между двумя касательными к
эллипсу х2/24 + у~/30 = 1, параллельными прямой 2х — 4у +
+ 23=0.
3.59. Составить полярное уравнение гиперболы х2/а~—
— у2/b2 = 1 при условии, что направление полярной оси сов-
падает с положительным направлением оси абсцисс, а по-
люс находится в центре гиперболы 0(0; О).
3.60. На плоскости произвольно выбраны две точки А
и В. Найти геометрическое место точек, отстоящих от А на
расстоянии вдвое меньше, чем от В.
3.61. Каково геометрическое место фокусов парабол,
касающихся данной прямой и имеющих вершину в дан-
ной точке?
3.62. Окружность единичного радиуса катится по верх-
ней стороне положительной ветви гиперболы у = 1/х. Бу-
дет ли линия, которую описывает центр окружности, вет-
вью какой-либо гиперболы?

ГЛАВА 4
АНАЛИТИЧЕСКАЯ
ГЕОМЕТРИЯ
В ПРОСТРАНСТВЕ
4.1.
ПЛОСКОСТЬ И ПРЯМАЯ
B декартовой прямоугольной системе координат общее
уравнение плоскости имеет вид
(4.1)
Ах+By+ Cz+D= О.
При этом вектор, перпендикулярный плоскости, носит
название нормального вектора и имеет координаты
.(4.2)
й =(А, В, С).
K общему уравнению плоскости можно прийти, запи-
сав условие ортогональности вектора й = (А; В; С) и теку-
щего вектора РоМ = (х — xp, у — yp, z — го):
A(x — xp)+В(у — уо)+С(г — zp) =О
(4.3)
дАх+By+Cz+D=О, где D= — Ахц — Вуо — Czp.
х — &g ; у Ђ” y я Ђ”
m~
=0.
(4.4)
и&
mQ
Уравнение плоскости, проходящей через две данные
точки Ро (хо, yp, zp) и Р1(х1, у&g ;, , и параллель ой вект
Уравнение плоскости, проходящей через данную точ-
ку Ро(хо~ уо, zp) и параллельной двум неколлинеарным век-
торам а = (1~, т„п1 ) и Ь = (Ц, тр, n~), имеет вид с учетом ус-
ловия компланарности трех векторов — текущего вектора
РоМ = (х — xp, у — yp, z — zp) и векторов а и Ь:

ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
138
а = (1, m, n), также записывается с учетом условия компла-
нарности трех векторов:
текущего вектора—
PpM=(x — xp,у — у ~ — зо)
вектора, принадлежащего плоскости,—
PoPi =(xi — ~о У1 — Уо з1 зо)
вектора ц.—
~о У Уо ~ ~0
=0.
xy — ~о Уi — Уо ~& t; Ђ”
m u
(4.5)
Уравнение плоскости, проходящей через три данные
точки Pp(xp, gp, zp), Pi(xi, gi, zi) H Pg(xg, у~, zg), получает
ся из условия компланарности трех векторов: текущего
роМ =(x — ~о У вЂ” Уо & t; Ђ” о и д ух вектор в, принадле
ЩИХ ПЛОСКОСТИ,
PoPi =(~1 ~о у1 уо ~i ~o)»oPa =(xr ~о уз уо зз зо):
~о У Уо ~ ~0
xi — ~о У1 Уо ~i ~0
~2 ~0 У2 УО ~2 ~0
=0.
(4.6)
Нормальное уравнение плоскости имеет следующий
вид:
(4. 7)
x cos а + у cos P + z cos у — р = 0.
Параметр р — длина перпендикуляра, опущенного иа
начала координат на плоскость, cos а, cos P u cos у — на-
правляющие косинусы нормального вектора (4.2}. Нор-
мальное уравнение плоскости можно получить из общего
уравнения (4.1 п тем множения всех его членов на мно-
житель +1/ А2 + В2 + C2, знак которого должен быть про-
тивоположен знаку свободного члена В.
Если в общем уравнении плоскости (4.1) ни один из
коэффициентов А, В, С, D не равен нулю, то оно может
быть преобразовано к виду уравнения плоскости в от-
резках
x/а+у/b+ z/ñ = 1, а = — D/А, b= — 3/В, с = — D/C. (4.8)

139
ГЛАВА 4. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
Здесь а, b и с — длины отрезков, отсекаемых плоско-
стью на осях координат (считая каждый отрезок от начала
координат), взятые со знаком плюс, если соответствующая
координата пересечения положительна, и со знаком ми-
нус, если она отрицательна.
Расстояние от точки Pp(xp, yp, zp) до плоскости, за-
данной:
а) общим уравнением (4.1), вычисляется по формуле
(4.9)
d= (Ахо+Byp+Czp+D[l
б) нормальным уравнением (4.7), вычисляется по фор-
муле
d = ~xp cos a + yp cos p + zp cos 7 — ф.
(4. 10)
Г еометрический смысл неравенства первой степени с
тремя неизвестными определяется следующими теоремами.
Теорема 4.1. Всякая плоскость Ax + By + Cz + D = О раз-
бивает трехмерное пространство на два полупространства.
Для координат всех точек М(х, у, z), лежащих в одном по-
лупространстве, выполняется неравенство Ах + By + Cz +
+ D & t; О, ля коорди ат в ех то ек друг го полупростр
ства справедливо противоположное неравенство Ax + By +
+Cz+D&lt
Теорема 4.2. Пусть плоскость задана общим уравнени-
ем Ах + By + Сг + D = О. Если отложить нормальный век-
тор и = (А, В, С) от любой точки Pp(xp yp, zp) этой прямой
РОМ =й, токанецM(xp+ А, yp+ В, zp+ С) отложенноговек-
торабудет находиться B положительном полупространстве
от данной прямой, т. е. A(xp+ А) + B(yp+ В) + C(zp + С) & t;
Теорема 4.3. При параллельном переносе плоскости
&l ; + B + C     в направле ии нормальн го вект
и = (А, В, С) величина 1.(x, у, z) = Ах + By + Cz + D возрас-
~~ет. При переносе этой прямой в противоположном на-
правлении 1,(x, у, z) убывает.
Общими уравнениями прямой в пространстве называ-
®тся уравнения:
А,х+ В1у+ C&gt z+ D&g ; в ”
(4. 11)
А2х + В2у + С2г + Л2 = О,
~оторые описывают множество точек пересечения двух
"епараллельных плоскостей.

140
ДРАКТИцЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАНАЧ
Канонические уравнения прямои
Х вЂ” Xp g — gp ~à — Zp
7
Х1 — Xp gy — gp .Г1 — .Го
здесь направляющий вектор прямой имеет координаты
(4.13)
~ =(» — »о y — yp ~ — ~о).
Параметрические уравнения прямой, имеющей направ-
ляющий вектор а = (l, m, n),
х=-хо+ It g =~о+ mt ~ = zp+ и
(4.14)
получаются из канонических уравнений (4.12) приравни-
ванием равенства отношений переменному параметру t:
Х вЂ” Xp g — До Z — Zp
=t.
т и
Условия взаимного расположения плоскостей и пря-
мых, в частности условия перпендикулярности и парал-
лельности, получаются путем рассмотрения соответствую-
щих углов между векторами, которые определяют эти гео-
метрические объекты.
Уравнение пучка всех плоскостей, проходящих через
прямую пересечения двух данных плоскостей,
А1х+В1у+C~z+Dj = О и А2х+В2у+ Cgz+Dg =О,
имеет следующий вид:
(А,»+ В|у+ C,z+ D,)+ Х(А~»+ В2у+ Czz+ D2) = О. (4.15)
Расстояние от точки Р,(»,, у,, zg) до прямой, заданной
уравнениями (4.12), вычисляется по формуле
х — хо g — gp ~ — zp
m n
можно получить, записав условие коллинеарности векто-
ра а = (l, т, п), называемого направляющим вектором пря-
мой, и текущего вектора РоМ =(x — xp, у — уо, z — zp), кото-
рый определяется заданной точкой прямой Pp(xp, уо, zp) и
точкой прямой М(», у, z) c переменными координатами.
Аналогично можно получить канонические уравнения
прямой, проходящей через две заданные точки Pp(xp, yp, zp)
и Q(x&g ;, >

141
pJIABA 4. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
2 2 2
y& t; Ђ” () Z&g ; в ” () ~ Ђ” гО 1 Ђ” ХО ~ в ” () &gt
+ +
(4.16)
Расстояние между двумя прямыми
х — х1 у — у1 г — zl х — х2 у — у2 г — z2
и
m1 п1 L2 m2 n2
вычисляется по формуле
g2 У1 ~2 ~1
Х2 — Х1
11
~2
m1
П1
П2
m2
(4.17)
4.2.
РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ
4.Е Составить уравнение плоскости, которая перпен-
дикулярна вектору ц=(8,2,]) и проходит через точку
Ро(3, — 5, 4).
Р е ш е н и е. Выпишем координаты текущего вектора.
РОМ =(х — 3, y+5, z — 4). Запишем в координатной форме
Условие ортогональности векторов й и Р~М:
8(х — 3) + 2(у + 5) + 1(z — 4) = P,
8х + 2у + z — 18 = О.
4.2. Две плоскости заданы своими общими уравнениями:
5x — 4у+ z — 1 =0,
10х + 2у + 4z — 7 = О.
Многие задачи на прямую и плоскость в пространстве
решаются с учетом взаимного расположения векторов, оп-
ределяющих эти геометрические объекты, поэтому пре-
жде чем приступить к рассмотрению приведенных ниже
решений, рекомендуется повторить условия коллинеар-
ности, ортогональности двух векторов и условие компла-
нарности трех векторов.

ДРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
142
Определить величину двугранного угла между этими
плоскостями.
P е ш е н и е. Двугранный угол между плоскостями из-
меряется, как известно, линейным углом, а последний
равен углу между векторами, перпендикулярными плос-
костям. Вектор, перпендикулярный первой плоскости,
имеет координаты й1 — — (5, — 4,1), ко второй плоскости—
й2 = (10, 2, 4). Воспользуемся формулой для косинуса угла
между двумя векторами
5 10+( — 4) 2+1 4
П1 й2
cos(p =
й1 й2
— 0,69,
12
y = arccos(0,69) = 52'.
РоР1 —— (2, 4, — 2), РоР2 — — (3, 3, — 1).
Для этих векторов справедливо условие компланарности:
х — 2 у+1 z — 2
2 4 — 2 =О.
3 3 — 1
Приведем уравнение плоскости к общему виду, для чего
вычислим определитель, пользуясь правилом разложения
по элементам первой строки:
х — 2 у+1 z — 2
2 4 — 2
4 — 2 2 — 2 2 4
= (х — 2) — (у+1) + (z — 2)
3 — 1 3 — 1 3 3
3 3 — 1
= 2х — 4у — 6z+ 4 = О, х — 2у — Зг+ 2 = О.
4.4. Дано уравнение плоскости в общем виде 2x — 2у +
+ z — 20 =О.
Преобразовать это уравнение: 1) в уравнение плоско-
сти в отрезках; 2) в нормальное уравнение плоскости.
4.3. Составить уравнение плоскости, проходящей через
точки Рд(2, — 1, 2), P,(4, 3, О), Р~(5, 2, 1).
P е ш е н и е. Составим координаты текущего вектора
плоскости POM = (х — 2, у+1, z — 2) и векторов

143
УАВА 4. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
Решение.
1) вычислим величины отрезков, отсекаемых плоско-
стью на осях координат, считая от начала координат. Пола-
гая yp = О, zp = О, получим 2хо — 2. О+ Π— 20 = О, xp = 10 = а.
Пусть теперь х1 = О, г1 = О, тогда 2 Π— 2 у1 + Π— 20 = О,
y = — 10 = b. Наконец, найдем отрезок, отсекаемый плос-
костью на оси OZ, для чего положим х2 = О, у2 = О, 2 О—
— 2 О + zz — 20 = О, zz = 20 = с. Уравнение плоскости в от-
резках имеет вид
х/10 + у/( — 10) + z/20 = 1;
2) чтобы записать нормальное уравнение плоскости,
вычислим
Поскольку знак у свободного члена отрицательный, то нор-
мальное уравнение имеет вид
— 2/3 . х + 2/3 . у — 1/3 z + 20/3 = О.
4.5. Определить расстояние от точки Ро(3, — 7, 2) до плос-
кости
2х — y+ 2z+ 1 =О.
P е ш е н и е. Воспользуемся формулой (4.9)
d= ~Ахо+Byp+Czp+Di/
=(2 3 — 1.( — 7)+2 2+1(/
=6.
4.6. Прямая задана своими общими уравнениями:
3х-4y-z-1=0,
x+ 2y+ 4z — 5 = О.
Получить из этих уравнений: 1) канонические уравне-
ния; 2) параметрические уравнения; 3) найти расстояние
от точки А(3,2; 4,4; — 1) до данной прямой.
Решение.
1) найдем координаты двух точек, принадлежащих
прямой, для этого полагаем вначале zp = О и подставляем
~го в уравнение прямой:
&
Зхо — 4yp — 0 — 1 = О& t; хо Ђ”
'=~хо =2 2' уо =1 4
хо+2Уо+4.0 — 5=o, хо+2Уо =5,

ДРДКТИ iECKOE РУКОВОДСТВО К РЕШЕНИЮ ЗА„ЦАЦ
Координаты первой точки прямой равны Pp(2,2; 1,4; О).
'~еперь положим, например, z~ = 1, и аналогично над-
дем координаты второй точки прямой Р1(х1, у,, z,):
&
»& t; Ђ” у~ Ђ 1 Ђ  = О, х1 Ђ” у~ Ђ” Ђ”
'==~ x& t; Ђ” Ђ” 0 8; у~ Ђ” Ђ 0
х1+2у1+4 1 — 5=0, х1+2у1 — — 1,
тогда координаты точки Р1(0,8; 0,1; 1).
Составим координаты текущего вектора прямой
РрМ =(х — 2,2; у — 1,4; г — О)
и вектора PpPj — — ( — 1,4; — 1,3;1), принадлежащего прямой.
Запишем условие коллинеарности векторов РрМ и РОР,:
(х — 2,2)/( — 1,4) = (у — 1,4)/( — 1,3) = >
Умножая последние уравнения на ( — 0,1), получим ка-
нонические уравнения прямой в следующем виде:
(х — 2,2)/14 = (у — 1,4)/13 = z/( — 10);
2) чтобы найти параметрические уравнения прямой,
ПОЛОЖИМ
(х — 2,2)/14 = (у — 1,4)/13 = z/( — 10) = t,
х = 2,2 + 14t, у = 1,4+ 13t, z = — 10t;
3) расстояние от точки А до прямой найдем по форму-
ле (4.16). В данном случае
х1= 32, у~ =44, z& t; Ђ”
хо=2,2, уо= 1,4, ло=О,
1=14, m=13, и=-10,
~1146 у 57
J4OS
4.7. Составить уравнение прямой, проходящей череа
данную точку Ро(3, 4, 2) и перпендикулярной плоскости
8x — 4у+ 5z — 4 = О.
P e ш е н и е. Найдем координаты текущего вектора ис-
комой пРЯмой PpM =(x — 3, У вЂ” 4, z — 5). ПосколькУ пРЯмая

145
<~I BA 4. АНАЛИТИЧЕС АЯ ГЕОМЕТ И В ПРОСТРАНС
перпендикулярна плоскости, то направляющим вектором
прямой является нормальный вектор плоскости й = (8, 4, 5).
3апишем условие коллинеарности векторов РрМ ий, по-
лучим уравнение прямой:
(х — 3)/8 = (у — 4)/( — 4) = (г — 2)/5.
4.8. Составить уравнение прямой, проходящей через
точку Ро(4, — 3, 2) и параллельной данной прямой:
2х — у — z+1=0,
Зх+ 2у+ z — 8 = О.
j й
— — 1 — 1 —. 2 — 1 — 2 — 1
— у +й
2 1 3 1 3 2
й1 ~й2 ——
2 — 1 — 1
3 2 1
=i — 5j +7k,
а =(1,— 5,7) — направляющий вектор данной в условии
прямой, а значит, он является также направляющим век-
тором искомой прямой. Уравнение искомой прямой выра-
жает собой условие коллинеарности векторов а и РОМ:
(х — 4)/1 = (у + 3)/( — 5) = (z — 2)/7.
4.9. Составить уравнение плоскости, проходящей через
прямую (х =Т)/2 = (у — 3)/4 = z/( — 1) и точку Р,(1, 5, 2).
P е ш е н и е. Запишем условие компланарности трех век-
торов: текущего PpM = (х — 1, у — 3, г), вектора PpPj — — (0, 2, 2),
Щ>инадлежащ го плоскос и и направляющ го вект ра д
ной прямой а = (2, 4, — 1), параллельного данной плоскости:
х — 1 у — 3 z
0 2 2
2 2 0 2 0 2
= (х — 1) — (у — 3) + z
4 — 1 2 — 1 2 4
2 4 — 1
= — 10(х — 1)+4(у — 3) — 4г=О, 5х — 2у+2z+1=0
— искомое общее уравнение плоскости.
P е ш е н и е. Определим координаты направляющего
вектора прямой, для чего найдем векторное произведение
векторов, перпендикулярных плоскостям 2х — у — z + 1 = 0
иЗх+ 2у+ г — 8 =0. Имеем n& t; — Ђ” (2, Ђ” 1, Ђ” 1) й2 =(3,2,

ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
146
4.10. Даны координаты вершин пирамиды А1(4, 2, 5),
А2(0, 7, 2), А (О, 2 7), А (1, 5, О). Найти: 1) уравне~~е плос-
костей А1А~Аз и А,AzA~; 2) угол между ребром А,Аз H гра-
нью А1А2А4, 3) расстояние от вершины Аз до ~р»Н A1А2А4
4) кратчайшее расстояние между прямыми А~А2 и АЗА4,
5) уравнение высоты, опущенной из вершины Аз на грань
А,А,А4.
Решение.
1) уравнение плоскости А,А~Аз получим из условия ком-
планарности трех векторов'. текущего
А,М =(х — 4, у — 2, z — 5)
и двух векторов, принадлежащих данной плоскости,
А,А2 — — ( — 4,5, — 3) и А,Аз — — ( — 4, 0,2),
х — 4 у — 2 z — 5
— 4 5 — 3
5 — 3 — 4 — 3 — 4 5
= (х — 4) — (у — 2) + (z — 5)
0 2 — 4 2 — 4 0
— 4 0 2
=10x+20y+ 20z — 180 = О, x+ 2y+ 2z — 18 = 0
— искомое общее уравнение А1А2Аз. Аналогично получим
уравнение плоскости А1А2А4 из условия компланарности
трех векторов:
А1М=(х — 4,у — 2,z — 5), А,А~ =(~,5,— 3), А,А4 =( — 3,3,— 5),
х — 4 у — 2 z — 5
— 4 5 — 3
5 — 3 — 4 — 3 — 4 5
= (х — 4) — (у — 2) + (z — 5)
3 — 5 — 3 — 5 — 3 3
— 3 3 — 5
= — 16x — 11у+ Зг+ 71 = 0
— искомое общее уравнение А1А2А4,.
2) угол между ребром А~Аз и гранью А,А~А4 выразим
через угол между вектором
А1 Аз —— ( — 4, О, 2) и й = ( — 16, — 11, 3)
— нормальным вектором плоскости
й А1Ад ( — 16) ( — 4)+( — 11) О+3 2
cosy=
(й ( 1A1A31 ( — 16)~ ~-( — 11)2+-32 .,/(-4)2+-02 q2~
70
= 0,7967, (р = 41'.
386. 20

147
[ËAÂÀ 4. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
Угол между ребром А1А3 и гранью А1А2А4 y = 180'—
— 41' =- 139';
3) расстояние от вершины Аз до грани А1А2А4 вычис-
лим по формуле (4.9)
~= ~( — 16) О+( — 11) 2 — 3.7 — 61(/
=3,56;
4) чтобы найти кратчайшее расстояние между прямы-
ми А1А2 и АзА4, выпишем вначале уравнения этих прямых:
(х — 4)/( — 4) = (у — 2)/5 = (z — 5)/( — 3),
(х — О)/1 = (у — 2)/3 = (z — 7)/( — 7),
а затем воспользуемся формулой (4.17). Имеем
ZQ Zg
х2 х1 У2 У1
m~
Ц т2
п1
п2
Π— 4 2 — 2 7 — 5
— 4 5 — 3
1 3 — 7
— 4 Π2
— 4 5 -3
1 3 — 7
: 70/43,886 — 1,595;
5) уравнение высоты из вершины А4 на грань А1А2А3
Получим из условия коллинеарности текущего вектора
искомой прямой А~М = (х — 1, у — 5, г) и нормального век-
тора плоскости й =(1,2,2),
(х — 1)/1 = (у — 5)/2 = z/2.
х1= 4,
х2=0,
l~ = — 4
~2
у~ = 2, z& t =
у2 = 2, zg = 7,
m& t; 5, 1= Ђ”
т2=3, п2= — 7.

148
ДРАКУДЧЕСКОЕ РУЕОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
4.11. Составить уравнение плоскости, равноудаленной
от точек В(4, 1, О) и С(2, О, 3).
P е ш е н и е. Воспользуемся формулами расстояния ме-
жду точками и найдем координаты точки А(0, О, z), рав-
ноудаленной от двух данных точек, и приравняем величи-
ны lml = I~el.
Имеем
(АВ[=
(АС(=
17+ z2 = 4+ (3 — z)~, z = — 2/3.
— 2 х — 1. у+ 3. (z+ 2/3) =О, — 2х — у+ 3z+ 2 = О.
4.12. Найти точку пересечения прямой
(х — 2)/1 = (у — 3)/1 = (z + 1)/4
И ПЛОСКОСТИ
х+ 2у+ 3z — 10 = О.
P е ш е н и е. Выпишем параметрические уравнения дан-
ной прямой (формула (4.14)):
x=2+t, у=3+~, z= — 1+4t.
Подставим координаты точек прямой в уравнение плос-
кости:
(2+ t)+ 2(3+ t) + 3( — 1+ 4t) — 10 = О, t = 1/3.
Искомые координаты точки пересечения получаются
в результате подстановки найденного t = 1/3 в параметри-
ческие уравнения прямой
хо = 2+ t = 7/3 уо = 3+ t = 10/3 ~о = 1+ 4t = 1/3,
точка пересечения имеет координаты Р(7/3, 10/3, 1/3).
4.13. Найти координаты точки А', симметричной точ-
ке А(0, — 3, — 2) относительно прямой (x — 1)/3 = (у — 2)/
4 = (z — 5)/1.
Уравнение искомой плоскости получим из условия орто-
гональности текущего вектора плоскости АМ = (х, у, z+ 2/3)
и вектора ВС = ( — 2, — 1, 3):

149
ГЛАВА 4. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
P е ш е н и е. Составим уравнение плоскости, проходя-
щей через точку А перпендикулярно данной прямой, вос-
пользовавшись условием ортогональности текущего век-
тора АМ = (х, у+ 3, z+ 2) и направляющего вектора прямой
а =(3,4,1).
Имеем
3 х+ 4 (у+ 3) + 1 (z+ 2) = О,
Зх+ 4у+ z+ 14 =0.
Аналогично тому, как это было сделано в задаче 4. 12,
найдем координаты точки пересечения прямой и плос-
кости,
x=l+3t, y=2+4t, z=5+t,
3(1+ 3t) + 4 (2+ 4t) + (5+ t) + 14 = О, t = — 15/13,
хд = 1 + ( — 15/13) = — 2/13, уд = 2 + 4 . ( — 15/13) = — 34/13,
zz = 5 + ( — 15/13) = 50/13, P( — 32/13, — 34/13, 50/13).
С помощью формул деления отрезка в данном отноше-
нии определим координаты точки А' из условия того, что
Р есть середина отрезка АА'.
хр = (хд+ хд )/2, ур = (уд+ уд )/2, zp = (яд+ ыд )/2,
x„=-64/13, у„=-29/13, ыд = 126/13.
4.14. Найти координаты точки А', симметричной точ-
ке А(2, О, 2) относительно плоскости 4х+ бу + 4z — 50 = О.
P е ш е н и е. Составим уравнение прямой, проходящей
через точку А перпендикулярно данной плоскости:
(х — 2)/4 = (у — О)/6 = (z — 2)/4.
Приведем уравнение прямой к параметрическому виду
(х — 2)/4 = (у — О)/6 = (z — 2)/4 = t,
x=2+2t, у =3t, z=2+2t.
4 (2+ 2t) + 6 (3~) + 4 (2+ 2~) — 50 = 0
хр=4& t; gp 3, ~р
Подобно тому, как это было сделано в задаче 4. 12, най-
дем координаты точки пересечения найденной прямой и
данной плоскости:

150
IIPAKTHЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
С помощью формул деления отрезка в данном отноше-
HHH определим координаты точки А' из условия того, что
P есть середина отрезка АА'.
х~ = (х,~+ х,г)/2, ур = (у„+ у„)/2, zp = (zg+ z~)/2,
хл, = 6, у& t = 6, z lt
х'=2х, у'=2у, z'=2z.
Чтобы получить образ плоскости 2х+ Зу+ z — 3 = О,
сделаем замену
х =х'/2, у = у'/2, z =z'/2.
После этого получим
2х'+ Зу'+ z' — 6 = О.
Поскольку 2 . 2 + 3 1 + ( — 1) — 6 = О, следовательно, точ-
ка А(2, 1, — 1) принадлежит образу плоскости.
4.3.
ПОВЕРХНОСТИ
ВТОРОГО ПОРЯДКА
ЦИЛИНДРИЧЕСКИЕ ПОВЕРХНОСТИ
Цилиндрической поверхностью называется поверх-
ность, описываемая прямой (образующей), параллельной
данному направлению и пересекающей данную линию (на-
правляющую).
Если образующие параллельны оси OZ, то уравнение
цилиндрической поверхности может быть представлено
уравнением
Р(х, у) = О, или у = ((х), или х = (р(у). (4.19)
Если образующие параллельны оси o&g ;, To уравне
цилиндрической поверхности может 6bITb представлено
уравнением
4.15. Пусть Й = 2 коэффициент гомотетии с центром в
начале координат. Верно ли утверждение, что точка A(2,
1, — 1) принадлежит образу плоскости 2х + Зу + z — 3 = 0?
Решение.
Формулы преобразования подобия с коэффициентом
й = 2 имеют вид

151
ГЛАВА 4. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
G(x, z) =О, или z = r(x), или x= cp(z). (4.20)
Н(у, z) = О, или z = q(y), или у = и(г). (4.21)
ПОВЕРХНОСТЬ ВРАЩЕНИЯ
Пусть в плоскости XOZ задана своим уравнением ли-
ния F(x, у) = О. Чтобы получить уравнение поверхности,
образованной вращением этой линии вокруг оси ОХ, необ-
ходимо заменить z на + у2+ z2. Уравнение поверхности в
таком случае принимает вид Р(х, + у +z2) =О. В табли-
це 4.1 приведены различные уравнения поверхностей вра-
щения.
Таблица 4.1
ОСНОВНЫЕ ПОВЕРХНОСТИ
ВТОРОГО ПОРЯДКА
И ИХ КАНОНИЧЕСКИЕ УРАВНЕНИЯ
Сфера с центром в начале координат и радиусом R опи-
сывается уравнением
.~2+ У2 + Z2 R2
(4. 28)
Если образующие параллельны оси ОХ, то уравнение
цилиндрической поверхности может быть представлено
уравнением

ДРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
152
Эллипсоид с центром в начале координат и главными
осями, принадлежащими осям координат, описывается
уравнением
x2/ö2 + у~/Ь + z /с
(4.29)
Однополостный гиперболоид описывается уравнением
x'/à2 + y'/b~ — z2/с
(4.30)
На рисунке 4.1 показан однополостный гиперболоид
вращения относительно OZ (а = Ь).
Двуполостный гиперболоид описывается уравнением
x2/à2 + у2/b2 — z2/c2 = — 1
(4.31)
На рисунке 4.2 изображен двуполостный гиперболо-
ид вращения относительно OZ (а = Ь).
Эллиптический параболоид описывается уравнением
x2/a2 + у2/b2 = 2z
(4.32)
На рисунке 4.3 показан эллиптический гиперболоид
вращения относительно OZ (а = Ь).
Конус второго порядка описывается уравнением
х2/а2 + y2/Ь2 — z2/ñ2 = О.
(4.33)
На рисунке 4.4 изображен конус вращения относитель-
но OZ (а = Ь).
Гиперболический параболоид описывается уравне-
нием
x2/ö2 у2/Ь2 = 2z
(4.34)
Гиперболический параболоид получается движени-
ем образующей параболы z = — у2/2Ь2 по направляющей
параболе z = x2/2а2 (вершина образующей параболы
скользит по направляющей). Образующую и направляю-
щую параболы можно поменять местами. Результат бу-
дет таким же.
Геометрический смысл неравенства второй степени в
трехмерном пространстве для поверхностей (4.19) — (4.34)
определяется теоремой, аналогичной теореме 3.4, в кото-
рой слово «кривая» следует заменить на «поверхность».

НАЛИТИЧЕСКАЯ ГЕОМЕТРИ Я В ПРОСТРАНСТВЕ
ГЛ А]ЦА 4. АН
Рис. 4.3
Рис. 4.4
Рис. 4.2

154
ДРДКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
4.4.
РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ
(х')' + (y')'+ (z')' = Л'.
Поскольку центр данной сферы расположен в точке с
координатами С(1, — 1, — 1), то естественно совершить па-
раллельный перенос системы координат так, чтобы новое
начало находилось в точке С. Тогда старые координаты х,
у, z будут связаны с новыми х', у', z' следующим образом:
х' = х — 1, у' = у+ 1, z' = z+ 1.
Отсюда в старых координатах уравнение сферы имеет
вид
(x 1) +(y+ 1) +(z+ 1) =R
Чтобы найти величину радиуса, подставим в уравн~
ние сферы координаты точки А(4, 2, 2):
(4 — 1)2+(2+1)2+(2+1)2 = R2 R2 = 27, R = ß7.
4.18. Какую поверхность определяет уравнение
х2 — 2х — 3y2+ 12у + 2z2+ 12z — 11 = О?
P е ш е н и е. Выделим полные квадраты по х, у, z:
х' — 2x + 1~ — 1~ — 3(у' — 4у + 2' — 22) +
+ 2(z2 + бя + 3' — 32) — 11 = О,
(х — 1)' — 3(у — 2)' + 2(z + 3)' = 18,
(x — 1) /18 — (у — 2)2/6 + (z + 3)2/9 = 1
— уравнение однополостного гиперболоида с центро~~ ~
точке О'(1, 2, — 3).
4-16. Определить, какой геометрический образ соотвр~
ствует в пространстве уравнению х + у = 9.
P e ux e H H e. Поскольку данное уравнение не содер„щ~~
z, To 3To уравнение определяет цилиндрическую повар~
ность с образующими, параллельными оси QZ.
4.17. Сфера проходит через точку А(4, 2, 2) и имеет
центр в точке С(1, — 1, — 1). Составить ее уравнение.
Р е ш е н и е. Уравнение сферы с центром в начале ко-
ординат имеет вид

„ЛдВА 4. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
155
4.19. Какую поверхность определяет уравнение
х2+ 2х + у2 — 2у — 2z — 2 = О?
Р е ш е н и е. Выделим полные квадраты по х, у:
4
«'+»+1'-1'+ у'-2у+1'-1'-2( +1) = o
(«+ 1)2 + (у — 1)2 = 2(z + 2).
Совершим параллельный перенос системы координат
~ак, чтобы новое начало находилось в точке О'( — 1, 1, — 2),
<о да ста ые координ ты х, у z бу ут связ н с нов
~', у', z' следующим образом.'
х'=х+1, у'=у — 1, г'=z+2.
Отсюда в новых координатах уравнение поверхности
имеет вид
(х')2+ (у')2 = 2z'.
Получили каноническое уравнение эллиптического
параболоида.
4.20. Дано уравнение линии, лежащей в плоскости
ХОУ, 4«2 + pyz = 1 и координаты точки А(3/2, 1, 1). Требу-
ется: 1) составить уравнение поверхности, образованной
~ращением этой линии вокруг оси ОХ; 2) подобрать значе-
&lt @e параме р р т к, чт бы то к А леж ла на поверх
сти вращения.
Решение.
1) поскольку линия вращается вокруг оси ОХ, то для
~()мучения уравнения поверхности вращения необходимо в
®отношении 4х + ру = 1 заменить у на + . Имеем
4«z+p(+ ) =1, 4х +р(у +z~) =1;
2) подставим вместо х, у, z координаты точки А и най-
48lv[ значение параметра р:
4 (3/2)2+ р(12+ 12) = 1, р = — 4.
~равнение поверхности вращения после замены в нем
~) ~~ — 4 принимает вид
4«2 4 . (у~ + z2) = 1
Последнее можно переписать так:
у2/0,25 + z2/0,25 — х'/0,25 = — 1.

156
ДР~КТИЦЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАД~1~
Получили уравнение двуполостного гиперболоида вра-
щения.
4.21. Установить, что плоскость z — 2 = О пересекаер
эллипсоид x2/12 + у2/4 + z2/16 = 1 по эллипсу. Составить
его уравнение и найти полуоси и вершины.
P e ш е н и е. Подставим в уравнение поверхности вме-
стоя число4,
x2/12 + yz/4 + 4/16 = 1,
x2/12 + yz/4 = 3/4,
«2/3' + у'/3 = 1,
отсюда эллипс имеет полуоси а =3, Ь= j3.
4.22. Составить уравнение геометрического места то-
чек, равноудаленных от точки А( — 2, О, 0) и от плоскости
x=2.
P е ш е н и е. Приравняем расстояния от точки до плос-
кости и между двумя точками:
(1.«+0 у+О.z — 2(/
Возведем обе части равенства в квадрат:
(« — 2)' = («+ 2)'+ у'+ г' « = -(у'+ г')/3.
Если заменить x = — x', у =у', z = z', то в новых коорди-
натах уравнение примет вид канонического уравнения эл-
липтического параболоида:
2«' = ((у')2+ (z')2)/4.
t = /4/3, P( ~4/3 J4/3 J4/3),
L,,„„==L( /4/3, /4/3, ]4/3) =3 ~/4/3 =2/ /3.
4.23. В какой точке линейная функция L(«, у, г) = «+
+ у + z достигает максимума в области, описываемой не-
равенством x2+ y2+ z2 ( 4?
P е ш е н и е. При перемещении плоскости x + у + z = o
в направлении нормального вектора й =(1,1,1) функция
L(x, у, z) возрастает и достигает максимума в точке каса-
ния, которая находится на пересечении прямой x = t, у = ~
z = 1исферы«+у + z2= 4,

ГД ОВА 4. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
157
4.5.
ЗАДАЧИ
ПРЯМАЯ И ПЛОСКОСТЬ
В ПРОСТРАНСТВЕ
4.24. Составить уравнение плоскости, проходящей че-
рез точку A(1, 2, — 3) параллельно данной плоскости Зх—
— 8У+ 4z — 1 = О.
4.25. Составить уравнение плоскости, проходящей че-
рез три данные точки А(0, О, О), В(1, 4, О) и С(3, — 2, 1).
4.26. Составить уравнение плоскости, проходящей че-
рез две точки А(3, 5, 4), B(5, 8, 3) параллельно вектору
а=( — 2,4,5).
4.27. Составить уравнение прямой, проходящей через
точку А(1, 2, — 3), перпендикулярно плоскости х + 4у — 5z—
— 1= О.
4.28. Составить уравнение прямой, проходящей через
точку А(1, 2, 3) и параллельной данной прямой х = 2t — 1,
у = 4t+ 2, z = — 5t + 1.
4.29. Найти расстояние между двумя прямыми (х — 1)/2 =
= (у — 3)/3 = (г — 1)/4 и (х — 2)/2 = (у — 4)/3 = (г — 1)/1.
4.30. Две грани куба лежат на плоскостях 2x — 2у + z—
— 1 = О, 2х — 2у+ z — 5 = О. Вычислить объем куба.
4.31. В пучке плоскостей 2х — Зу+ z — 3 + Х(х+ Зу+ 2г+
+ 1) = О найти плоскость, которая: 1) проходит через точ-
ку А(1, — 2, 3); 2) параллельна оси OZ.
4.32. Составить канонические и параметрические урав-
нения прямой
х — 2y+3z — 4 =О
Зх+ 2у — 5z+4 = 0 .
4.33. Найти проекцию точки А(5, 2, — 1) на плоскость
2х — У+ 3z+ 23=0.
4.34. Найти проекцию точки А( — 1, 2, 4) на прямую (х—
1)/4 = (у — 2)/3 = z/5.
4.35. Составить уравнение общего перпендикуляра к
двум прямым (х — 2)/4 = (у + 2)/( — 2) = (z — 1)/1 и (х — 9)/8 =
= (у — 6)/4 = (z — 4)/1.
4.36. Даны две вершины треугольника А( — 4, — 1, 2) и
~(3, 5, — 16). Составить уравнения всех сторон треугольника,

158
ДРАКТИЦ:СКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
зная, что середина стороны АС лежит на оси OY, a середина
стороны ВС вЂ” на плоскости XOZ.
4.37. Вычислить объем пирамиды, ограниченной плос-
костью Зх + бу + 4z — 24 = 0 и координатными плоскостями.
4.38. Вычислить расстояние между двумя параллель-
ными плоскостями 2x — 2у + z — 14 = О и 2х — 2у + z + 1 = P.
4.39. Указать систему неравенств для области внутри
пирамиды, образованной плоскостью 2х + 3y + 6z — 12 = 0
и координатными плоскостями.
4.40. Найти наибольшее значение, которое принимает
величина L(x, у, z) = 2х + 4у + 6z + 5 в области, описывае-
мой системой неравенств х+у — z & t; О, х+ Зу Ђ  & t;
+y Ç&lt
ПОВЕРХНОСТИ
ВТОРОГО ПОРЯДКА
В задачах М 4.41 — 4.44 составить уравнения поверхно-
стей вращения данной линии вокруг данной оси. Постро-
ить поверхности.
4.41. z=e",y=p, вокругоси ОЯ.
4.42. z = 5/xz, у = О, вокруг оси OZ.
4.43. z = х, у = О, вокруг оси ОХ.
4.44. х2/9 — yz/4 = 1, z = О, 1) вокруг оси ОУ; 2) вокруг
оси ОХ.
4.45. Составить уравнение геометрического места то-
чек, равноудаленных от точки А(0, О, 3) и от плоскости
z = — 3.
4.46. Составить уравнение геометрического места то-
чек, отношение расстояний каждой из которых от точки
А(0, О, 10) и от плоскости z = — 3 равно ~/2.
4.47. Найти радиус и центр сферы х~ — 2x + у~ + 6у + z2—
— 4z = 2.
4.48. Найти наибольшую координату z на линии пере-
сечения цилиндра х + у = 4 и плоскости z + у = 1. Постро-
ить получающееся сечение.

ГЛАВА 5
ВВЕДЕНИЕ
В МАТЕМАТИЧЕСКИЙ
АНАЛИЗ
5.1.
ЭЛЕМЕНТЫ
ТЕОРИИ МНОЖЕСТВ
5.1.1. МНОЖЕСТВА
И ОПЕРАЦИИ НАД НИМИ
Множество есть исходное понятие. Множества условим-
ся обозначать большими буквами А, В, ..., Z, а элементы
множества — малыми буквами а, b, ..., z. Символ с назы-
вается символом принадлежности элемента множеству и
используется для обозначения того, что данный элемент,
например а, принадлежит данному множеству А: а с А.
Если а не принадлежит А — пишут а ~ А. Символ с: назы-
вается символом вложения одного множества в другое.
Запись А с В означает, что каждый элемент множества А
является элементом множества В. Если А с В и В с А, то
множества А и В называются равными (совпадающими) и
»о обозначается следующим образом. 'А = В. Если элемен-
ты некоторого множества В являются также элементами
множества А, то множество В называется подмножеством
®ножества А. При этом используется символ с вложения
Подмножества в множество: В с А. Нижняя черта означа-
еТ, что одним из подмножеств данного множества А явля-
ется и само множество А: А с А. Множество, не содержа-
~цее ни одного элемента, называется пустым и обозначает-
ся символом И. Для всякого множества А пустое множество
~ является подмножеством: 0 а А. Множество всех под-
множеств множества А будем обозначать P(A). Всякое не-
~устое подмножество множества А называется собствен-
~bi~ подмножеством.
Для задания множества часто используются следующие
Ц&g ;а спосо

160
IIpAKTHHECKOE РУКОВОДСТВО К РЕШЕНИЮ ЗАДу~
&g ;) непосредстве но перечисляю ся се элемен ы
= {~1, ~2, ..., а„), например А = {1, 3, ..., 2n + 1);
б) указывается свойство или свойства, объединяющие
все элементы, например А = {а = целое число, большее 3).
Множество, содержащее конечное число элементов
называется конечным, если же число элементов множест-
ва не ограничено, то оно называется бесконечным.
Пересечением (или произведением) множеств А и В на-
зывается множество Х, содержащее все общие элементы
этих множеств; пересечение множеств записывается с по-
мощью символа П:
Х= АПВ = {х: х е А и х е В).
Множества А и В называются непересекающимися,
если их пересечение пусто: А П В = О.
Объединением (или суммой) двух множеств А и В на-
зывается множество У, состоящее из элементов, при-
надлежащих по крайней мере одному из этих множеств.
Объединение множеств записывается с помощью симво-
лами:
Y= A lJB = {y: ó е А или у е В).
Разностью множеств А и В называется множество и,
элементов, состоящее из всех элементов множества А, не
являющихся элементами множества В. Разность множеств
записывается с помощью символа ~:
R=А~В={r: r е А,r е В).
Если множество А есть подмножество множества В, то
разность В~А называется дополнением А до В и обознача-
ется так: А =В~А, при этом В=AlJA.
Операции над множествами обладают следующими
свойствами:
1) коммутативностью: А U В = В U 4; А П В = В () А;
2) ассоциативностью: (А ljB) lj С = А U (В LI С); (А Л В) Л
Л С =АД(В ЛС);
3) идемпотентностью: А U А = А; А () А = А;
4) дистрибутивностью: A U (В И С) = (А lJ В) Д (А { ) С);
А И (В lj С) = (А Д В) U (А Д С).

ГЛАВА 5. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
161
5.1.2. ВЗАИМНО
ОДНОЗНАЧНОЕ СООТВЕТСТВИЕ
И ЭКВИВАЛЕНТНОСТЬ МНОЖЕСТВ
5.1.3. ПРЯМОЕ
ПРОИЗВЕДЕНИЕ МНОЖЕСТВ
ПустьимеетсядвамножестваАиВ, ипустьа е А, о е В.
Множество всех возможных пар (а, b) образует новое мно-
жество, которое называется прямым произведением мно-
жеств А и В и обозначается А - В.
5.2.
МНОЖЕСТВО
ВЕЩЕСТВЕННЫХ
(ДЕЙСТВИТЕЛЬНЫХ) ЧИСЕЛ
Различают следующие множества действительных
чисел.
1. Множество натуральных чисел N = (1, 2, 3, ..., и, ...).
2. Множество целых чисел Z = (+1, +2, +3, ..., +и, ...).
3. Множество рациональных чисел Q, т. е. чисел вида
— (g N Op p E Zð g E Z)ð
Р
Д
Q =(r: r =, p c Z, q c Z, q s 0).
P
Д
Множество всех вещественных чисел R = Q lj 1, где 1—
множество иррациональных чисел, т. е. чисел, предста-
вимых в виде бесконечной десятичной непериодической
дроби.
Если каждому элементу множества А поставлен в соот-
ветствие единственный элемент множества В и при этом
каждому элементу множества В поставлен только один
элемент множества А, то говорят, что между множествами
А и В установлено взаимно однозначное соответствие. Мно-
жества, между которыми установлено взаимно однознач-
ное соответствие, называются эквивалентными. Это обо-
значается следующим образом. 'А — В. Если два множества
эквивалентны, то говорят, что они имеют одинаковую мощ-
ность или равномощны.

162
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
5.2.1. ОСНОВНЫЕ СВОЙСТВА
ВЕЩЕСТВЕННЫХ ЧИСЕЛ
5» Р1 ' Ч2 + Р2 Ч1
— 1
Ч1 Ч2
нахождение суммы чисел называется операцией сложения.
Правило сложения вещественных чисел обладает сле-
дующими свойствами:
а) а + Ь = b + а (переместительное или коммутативное
свойство);
б) (а + Ь) + с = а + (Ь + с) (сочетательное или ассоциатив-
ное свойство);
в) существует вещественное число, обозначаемое О
(ноль), такое, что для любого вещественного числа а спра-
ведливо равенство а + 0 = а;
г) для любого вещественного числа а существует число
а' такое, что а + а' = 0; число а' называется противополож-
ным для числа а.
3. Правило образования произведения.
Любым двум вещественным числам а и b ставится в со-
ответствие вещественное число с, называемое их произве-
дением и обозначаемое символом с = а Ь.
Для рациональных чисел а = р1/qq, Ь = р2/qq их произ-
ведение определяется следующим образом:
р1 Р2
g3. ' g2
Нахождение произведения чисел называется умноже-
нием.
1. Правило сравнения.
Любые два числа связаны только одним из знаков:
о (больше), & t; (меньш ) = (равн
Econ ~ & t; b, т  & t; а  с и  g ; ,  g ; с, то а &
транзитивности знака &gt
2. Правило суммирования.
Любым двум вещественным числам а и b по опреде-
ленному правилу ставится в соответствие вещественное
число с, называемое их суммой и обозначаемое символом
с = а + Ь. Для рациональных чисел а = р,/q& t   = р2 qq
сумма определяется следующим образом.'

ГДАВА 5. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
163
Правило умножения вещественных чисел обладает
следующими свойствами:
а) а Ь = Ь а (переместительное свойство);
б) (а Ь) с = а (Ь с) (сочетательное свойство);
в) существует вещественное число, обозначаемое 1 (еди-
ницей), такое, что для любого числа а справедливо равен-
ствоа. 1 = а;
г) для любого вещественного не равного нулю числа а
существует вещественное число а' такое, что а а' = 1; чис-
ло а' называется обратным числу а.
Свойство, связывающее правила сложения и умноже-
ния вещественных чисел:
(а+ Ь) с = а с+ Ь с.
Свойства, связывающие знак «больше» со знаком сло-
жения и умножения.'
а) если а & t; Ь, то ля люб го вещественн го чи л с сп
ведливо неравенство
а+с>Ь
б) если а & t; Ь, то ля люб го вещественн го положите
ного числа с справедливо неравенство
а c&g ;b
Свойство Архимеда. Каким бы ни было вещественное
число а, можно число 1 повторить слагаемым столько раз,
что полученная сумма превзойдет а. Каждому веществен-
ному числу на числовой оси (прямой, на которой выбрана
1очка начала отсчета О, задан масштаб и указано положи-
тельное направление) соответствует определенная точка.
Абсолютная величина — модуль вещественного числа
а есть число, обозначаемое |а| и определяемое формулой
!
а, если а &gt
а =
&

— а, если а &lt
~Модуль вещественного числа обладает следующими основ-
ными свойствами:
1) al & t; О; 2) a = Ђ” l; 3  &lt la , в ” а
4) а+Ь|(lal+|Ь!; 5) |а| — Ь!| &lt |а Ђ”

ДРАКТРРЦ:СКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
164
5.2.2. ОГРАНИЧЕННЫЕ МНОЖЕСТВА
BEIg;ECTBEHHbIX ЧИСЕЛ
5.2.3. НЕКОТОРЫЕ КОНКРЕТНЫЕ
МНОЖЕСТВА
ВЕЩЕСТВЕННЫХ ЧИСЕЛ
Различают следующие множества вещественных чисел.
1. Сегмент (замкнутый отрезок или отрезок) символи-
ческая запись [а, Ь]:
[а, Ь] = (х: а & t  &l
2. Полусегмент — символическая запись [а, Ь) или (а, b]:
[а, Ь) = (х: а & t  &l
(а, b] = (х: а & t  &l
Множество вещественных чисел Х называется ограни-
ченным сверху (снизу), если существует такое веществен-
ное число М (число т), что каждый элемент х множества
Х удовлетворяет неравенству х & t М ( &g
Числа М и т называются верхней (нижней) гранью
множества Х, соответственно.
Любое ограниченное сверху (снизу) множество Х име-
ет бесконечно много верхних (нижних) граней.
Наименьшая (наибольшая) из всех верхних (нижних)
граней множества Х называется точной верхней (нижней)
гранью множества Х и обозначается, соответственно, sup Х,
inf Х (sup от латинского «supremum» (супремум) «наи-
высшее», inf от латинского «infimum» (инфимум) «наи-
меньшее»).
Данное выше определение точной верхней и точной
нижней граней чаще формулируют в другой, эквивалент-
ной форме.
Число х (число х) называется точной верхней (точной
нижней) гранью ограниченного сверху (снизу) множества
Х, если выполнены следующие условия.
1) каждый элемент х е Х удовлетворяет неравенству
х<х(х&
2) каково бы ни было вещественное число х', меньшее
х (большее х), найдется хотя бы один элемент хд & t; х' х &lt

165
[ЛАВА 5. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
3. Интервал — символическая запись (а, Ь):
(а, Ь) = (х: а & t  &l
Замечание. Сегмент, полусегмент, интервал называют-
ся промежутками.
4. Окрестность точки х — любой интервал (х — а, х + Ь),
содержащий точку х.
5. е-окрестность точки х — любой интервал (х — е, х+ я),
гдето & t;
6. Числовая (бесконечная) прямая — символическая
запись ( — ~о, +oc):
( — сс, +oo) = (х: — oo & t  <
7. Полупрямая [а, +oc) или ( — ~о, Ь]:
[а, +oo) = (х: а & t х &lt
( — oo, Ь] = (х: — ~о & t  &l
8. Открытая полупрямая (а, +ао) или (а, — ао):
(а, +oo) = (х: а & t  <
( — ~о, Ь) = (х: — ~о & t  &l
9. Расширенная прямая — множество вещественных
чисел, дополненное элементами +~ и — о, и обозначается
R. Элементы+ о и — о называются иногда бесконечно уда-
ленными точками расширенной числовой прямой.
5.2.4. СТРУКТУРА ОТКРЫТЫХ
И ЗАМКНУТЫХ МНОЖЕСТВ
НА ПРЯМОЙ
Точка х E R называется внутренней точкой множества
R, если существует некоторая е-окрестность точки х, при-
надлежащей целиком этому множеству.
Точка х E В называется предельной точкой множества
Х с: В, если в любой я-окрестности точки х найдется хотя
бы одна точка х1 множества Х, отличная от х.
Множество Х с: В называется открытым, если все точ-
ки этого множества являются внутренними.
Множество Х с В называется замкнутым, если оно со-
держит все свои предельные точки.

166
ДРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
5.З.
PCHOBHbIE
ЛОГИЧЕСКИЕ СИМВОЛЫ
Bbtezaabcea~uev наэываетСЯ предложение, отноСитЕЛь-
но которого известно, что оно или истинно или ложно.
Конъюнкцией а л b высказываний а и b называют вы-
сказывание, которое истинно тогда и только тогда, когда
оба высказывания одновременно истинны. Символ л заме-
няет в речи союз «и».
Диззюнкцией а v Ь высказываний а и Ь называют вы-
сказывание, которое ложно в том и только в том случае,
когда оба высказывания ложны, а истинно, когда хотя бы
одно из них истинно. Символ v заменяет в речи союз «или».
Импликацией а ~ b высказываний а и b называют вы-
сказывание, которое ложно тогда и только тогда, когда а
истинно, а b ложно.
Отрицанием а (или а) высказывания называется вы-
сказывание, утверждающее, что а ложно.
Эквивален~пнос~пью а &lt = gt; b высказ в н й а и b н
ется высказывание, истинное только тогда, когда оба вы-
сказывания а и b одновременно истинны или ложны. Вы-
сказывание а с=& t b означа т, т а являе ся необходи ы
достаточным условием b.
Истинному высказыванию обычно ставят в соответст-
вие логическую единицу, а ложному — логический ноль.
Результаты применения этих операций могут быть
представлены в виде таблицы истинности алгебры выска-
зываний (табл. 5.1).
Законы де Моргана: 1) отрицание конъюнкции экви-
валентно дизъюнкции отрицаний: а л Ь с=:& t  v Ь; 2) от
цание дизъюнкции эквивалентно конъюнкции отрица-
ний: аvбсФа лb.
Таблица 5.I

~ ДАВА 5. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
167
5.4.
КВАНТОРЫ
5.5.
ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
Последовательностью называется закон, сопостав-
ляющий множеству натуральных чисел N множество дей-
ствительных чисел х„. Последовательность обозначается
как {х„) или х„.
Число х~ при конкретном k называется членом (элемен-
том) последовательности, а k — его номером. Последова-
тельность {х„) называется ограниченной сверху (снизу),
если существует такое число М, что все члены последова-
тельности, начиная с некоторого номера N, удовлетворя-
ют неравенству {х„) & t М ( „&g ; М). Символ чес и это
сывается следующим образом:
(5.1)
3М, 1n c N: х„& t М ( „&g
Последовательность {х„) называется ограниченной,
если существует такое число М & t; О, то се чл ны пос
довательности, начиная с некоторого номера N, удовлетво-
ряют неравенству ~х„~ & t; М. Символиче ки то записыва
ся следующим образом:
3M: Чn c N ==& t; ~ „ &
(5.2)
Последовательность {х„) называется неограниченной
сверху (снизу), если для любого М & t 0 ( & t; О) суще
такое п, что справедливо неравенство х„& t М ( „&l ; М)
волически это записывается следующим образом:
VM & t 0 Ч &l ; О) 3« : х„&g ; М (х„&l
В математике некоторые словесные выражения пред-
ставляются с помощью символов (кванторов): 4 (квантор
всеобщности) означает «каково бы ни было», «для любо-
го»; 3 (квантор существования) означает «существует»;
символ « . '» означает группу слов «такое, что», «выполня-
ется», «удовлетворяет условию».
Отрицание под знаком ~ превращает его в знак 3, и на-
оборот, отрицание под знаком 3 превращает его в знак 'Ф.

168
дрАКТИчЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
Последовательность называется неограниченной, если
для любого М ) p существует такое и e N, что справедли-
во неравенство ~х„~ & t;
Символически это записывается следующим образом:
УМ3п е N: ~х„~ & t;
(5.4)
ЧЙ1 c N, ЧФ2 ~ N: k~ & t   g ; k w х», > х , ( », <
Последовательность (х„) называется неубывающей (не-
возрастающей), если, начиная с некоторого номера k, для
любых двух натуральных kg и kg, таких, что kg & t; g,
полняется неравенство х», & t; », ( » <
Символически это записывается следующим образом.'
b'161 c N, O'йд c N: 161 & t; Й  g ; k w х», &gt х» (х , &lt х
Возрастающие, убывающие, неубывающие и невозрас-
тающие последовательности называются монотонными,
а две первые — строго монотонными.
Число а называется пределом последовательности (х„)
при и -+ ~, если для любого сколь угодно малого я & t О
ществует такое К(е) е N, что как только начнет выполнять-
ся неравенство и & t; К( ), ста ет справедл в и неравенс
~х„— а~ & t; е. Обозначае ся пре ел последовательно
а = limx„.
И вЂ” +~
Символически это определение записывается следующим
образом:
а = limх„с& t; Ч  gt; О З (е с N Мп gt Х(е) w х †а ~&
й — + С
Проиллюстрируем геометрический смысл предела по-
следовательности. Отложим по оси абсцисс номера членов
последовательности, а по оси ординат — значения х„, и
вдоль горизонтальной прямой у = а проводим сколь угод-
но узкую полосу шириной 2å. Эта полоса разбивает все мно-
Последовательность (х„) называется строго возрастаю-
щей (строго убывающей), если начиная с некоторого но-
мера й, для любых двух натуральных й, и k2, таких, что
ky & t; g, выполняе ся неравенс во » > х , х», &
Символически это записывается следующим образом.'

169
~'ДАВА 5. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
р~сество точек последовательности на два подмножества:
одно подмножество, содержащее бесконечное число чле-
нов, начинающихся с номера К(е) + 1, будет содержаться
внутри этой полосы, другое подмножество, содержащее
конечное число первых членов до номера К(е) включитель-
но, находится вне этой полосы.
Последовательность, имеющая предел, называется схо-
дящейся, а не имеющая предела — расходящейся.
Число а не является пределом последовательности (х„)
при п — ~ с~, если3е >Отак е, чт ~ ~ 3 & t; К: х„ Ђ а
Символически это записывается следующим образом:
а w lim х„&lt -& t 3 &g ; О b É E  n &gt  : ~ х„ Ђ” а
И вЂ” +сс
Последовательность (х„) не имеет конечного предела,
если
~М & t О 3 E №. ~ „ &
(5.9)
Последовательность (x„) называется положительно бес-
конечно большой и используется обозначение lim x„=+~,
П вЂ” +~
если для любого сколь угодно большого положительного
числа М существует натуральное число n(M), такое что
начиная с номера n(M) + 1 все элементы этой последова-
тельности удовлетворяют неравенству х„& t;
Символическая запись этого определения.
limx„=+m = ЧМ&g ;0 3n(M) N: Уп>n(M) х„>
Последовательность (х„) называется отрицательно бес-
~онечно большой и используется обозначение
limx„=~wVM &l ;О 3n M) Ж: Уп &g ;п(М) = х„<
П вЂ” ~у
Последовательность (х„) называется обьединенной бес-
~сонечно большой и используется обозначение limx„=~,
lim х„= -~,
И вЂ” ~ э"-
если для любого сколь угодно большого по модулю отри-
цательного числа М существует натуральное число n(M),
такое, что начиная с номера n(M) + 1 все элементы этой
11оследовательности удовлетворяют неравенству х„& t;
Символическая запись этого определения:

170
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
если для любого сколь угодно большого положительд~г„
числа М существует натуральное число n(M), такое, что
начиная с номера n(M) + 1 все элементы этой последова.
тельности удовлетворяют неравенству [x„[ & t;
Символическая запись этого определения.
limx„=<n~b' >0 3 (M е N Мп gt; n( ) =~ х„ I&g
Il~
Положительная, отрицательная и объединенная бес~ц&g
нечно большие последовательности называются сокращен-
но бесконечно большими.
Последовательность (x„} называется положительноц
бесконечно малой, если для любого сколь угодно малого
положительного с существует такой зависящий только pz
а номер K(c), что как только начнет выполняться неравен-
ство и & t; K( ), ста ет справедл в и неравенс в  &l ;
Для описанного в данном определении предела будем ис-
пользовать следующее обозначение: lim х„=+О.
П вЂ” Ь~
Символическая запись этого определения:
lim х„=+О &lt =&g ; b c &gt  3 (c  N: п & t K( ) 0 &lt
П вЂ” +Ю
Последовательность (х„} называется отрицательной
бесконечно малой, если для любого сколь угодно малого
положительного я существует такой зависящий только от
е номер K(c), что как только начнет выполняться неравен-
ство и & t; K( ), ста ет справедл в и неравенс во Ђ  &l ;
Для описанного в данном определении предела будем ис-
пользовать обозначение
lim x„= — О.
П~ ~'-
Символическая запись этого определения:
limx„= — Ос=& t; ' > 3 ( )  Мп gt K( ) =» †c<
П~~
Последовательность (х„} называется объединенной бес
конечно малой, если для любого я & t О найде ся та ой
мер K(c), что как только начнет выполняться неравенство
n & t; K( ), ста ет справедл в и неравенс во ~ „~ «. ля
санного в данном определении предела будем использова~~
обозначение
1пп ~„= О.

РАВА 5. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
171
Символическая запись этого определения:
lim х„= 0 &lt =& t  E &gt  3 (в   : 'd n gt; (е ~~ х„
П -Ээ".
Положительная, отрицательная и объединенная беско-
~рцно малые последовательности сокращенно называют-
( q бесконечно малыми.
Подмножество {» ) последовательности {х„) называ-
ется подпоследовательностью {» )
Число а называется предельной точной (или частич-
цьсм пределом) последовательности {x„), если из последо-
вательности {x„) можно выделить подпоследовательность
{»„), сходящуюся к а.
Замечание. В окрестности предельной точки последо-
вательности {х„) содержится бесконечное число членов этой
последовательности.
Наибольший (наименьший) частичный предел число-
вой последовательности {x„) называется ее верхним (ниж-
ним) пределом и обозначается символом
lim x„(lim х„).
Иьт иьх,
ПРИЗНАКИ СУЩЕСТВОВАНИЯ
ПРЕДЕЛА ПОСЛЕДОВАТЕЛЬНОСТИ
Последовательность называется фундаментальной,
если для любого е & t 0 существ ет та ой но ер Ж( ),
для любого натурального п & t; Ж в и люб го натуральн г
выполняется неравенство
x„— х„+р & t;
Геометрический смысл фундаментальной последова-
~~льности заключается в следующем. Если все члены этой
«следовательности расположить на числовой оси, то все-
~да можно указать бесконечное число членов, расстояния
~~~&lt ду котор ми бу ут мен ше люб го напе ед заданн
"ложжтельногоо числа е.
Последовательность называется нефундаментальной,
~~~и существует я & t О так е, то ля люб го натуральн
существуют натуральные не равные друг другу n & t
"' ~ K, для которых справедливо неравенство
)х„— х) & t;

дрАКТИчЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
172
1. Критерий Коши. Для того чтобы последовательность
сходилась, необходимо и достаточно, чтобы она была фун-
даментальной.
я. для того чтобы монотонная последовательность схо-
дилась, необходима и достаточна ее ограниченность.
Следствие. Пусть дана бесконечная система отрезкод
[а1, bl], [а2, Ь2], ..., [а„, Ь„], ..., каждый последующий из
которых содержится в предыдущем, и пусть модуль раз-
ности ~bÄ â€” a J стремится к нулю при п -+ сю. Тогда сущест-
вует точка, и притом только одна, принадлежащая всем
этим отрезкам.
3. Для того чтобы последовательность была сходящей-
ся, необходимо и достаточно, чтобы она была ограничен-
ной и чтобы ее верхний и нижний пределы совпадали.
ОБЩИЕ СВОЙСТВА
СХОДЯЩИХСЯ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
1. Сходящаяся последовательность имеет только один
предел.
Замечание. Если последовательность сходится, то она
имеет только одну предельную точку.
2. Теорема Больцано — Вейерш,трасса. Из любой огра-
ниченной последовательности можно выделить сходящую-
ся подпоследовательность.
3. Из любой неограниченной последовательности
можно выделить бесконечно большую подпоследователь-
ность.
4. Из произвольной последовательности можно выде-
лить либо сходящуюся, либо бесконечно большую подпо-
следовательность.
5. Теорема о предельном переходе в неравенстве. Если
1ппх„=а и1ппу„=Ь,
и, начиная с некоторого номера, выполняются неравенства
x„& t; yÄ x &gt у )  о а & t;
Если элементы сходящейся последовательности (x„},
принадлежат отрезку [а, Ь], то ее предел также принадле-
жит этому отрезку.

ГЛАВА 5. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
173
6. Теорема о трех последовательностях. Если
limx„=а и lппуи =а,
и, начиная с некоторого номера, выполняется двойное не-
равенствохи & t  &l ; „, то li
и — +х
7. Если limx„=a и1ппу„=о, то
П вЂ” ФоО и — +сс
(5. 16)
а) lim(x„+ у„) = а + Ь,
П вЂ” Фх
б) lim(x„y„) =a. Ь,
и — +х
в) если Ь w О, то, начиная с некоторого номера, опреде-
лена последовательность (х„/y„) (т. е. существует номер
К е N такой, что для любого п ) К у„~ 0) и
lim(x„ /у„) = a/Ь.
П вЂ” +X&
(5. 18)
сВОЙстВА БескОнечнО мАлых
И БЕСКОНЕЧНО БОЛЬШИХ
ПОСЛЕДОВАТЕЛЬНОСТЕЙ
1. Неограниченная монотонная последовательность
сходится к +m, если она не убывает (возрастает), и к — сс,
если она не возрастает (убывает).
2. Если 1ппх„=+~и limy„=t~, и, начиная с некото-
П вЂ” +х П вЂ” +х
poro номера, выполняется двойное неравенство x„& t; „&l
1о lim z„= t~. Аналогично, если одновременно
limхи = — с и limуи = — ~,то limz„= — о.
3. Если последовательность (x„) — бесконечно большая
(положительная бесконечно большая, отрицательная бес-
конечно большая), то начиная с некоторого номера опре-
делена последовательность (1/x„), которая является бес-
конечно малой (положительной бесконечно малой, отри-
цательной бесконечно малой).
4. Если последовательность (х„) — бесконечно малая
(положительная бесконечно малая, отрицательная бес-
конечно малая) и для любого натурального п х„~ О, то

174
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДД1»
Если limx„=0m limy„=O, то говорят, что lim(x„/у„)
и-+оо И-+ос П ~со
содержит неопределенность типа «0/0».
Если limx„=+&lt ~~ ( ли Ђ” ~ и limy„ +~ ( ли Ђ” o ), то
варят, что lim(x„/y„) содержит неопределенность типа
Q QQ 00 &gt
последовательность (1/x„) является бесконечно большои
(положительной бесконечно большой, отрицательной Qe~
конечно большой).
5. Алгебраическая сумма конечного числа бесконечно
малых последовательностей является бесконечно малод
последовательностью.
Замечание. Для бесконечно больших последователь-
ностей в общем случае аналогичная теорема несправед-
лива.
6. Произведение бесконечно малой последовательности
на ограниченную является бесконечно малой последова-
тельностью.
7. Произведение бесконечно большой последовательно-
сти на ограниченную является бесконечно большой после-
довательностью.
8. Произведение конечного числа бесконечно малых по-
следовательностей есть бесконечно малая последователь-
ность.
9. Произведение конечного числа бесконечно больших
последовательностей есть бесконечно большая последова-
тельность.
10. Если, начиная с некоторого номера К+ 1, эле-
менты некоторой последовательности (y„) по модулю не
меньше элементов бесконечно большой последователь-
ности (х„), то последовательность (у„) — бесконечно боль-
шая.
11. Теорема Штольца. Пусть (yÄ) — возрастающая бес-
конечно большая последовательность, и пусть последова-
тельность ((х„— х„1)/(у„— у„1И сходится к предельному
значению а. Тогда последовательность (xÄ/у„) также схо-
дится к пределу а.

175
УАВА 5. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
5.6.
ФУНКЦИИ ДЕЙСТВИТЕЛЬНОГО
ПЕРЕМЕННОГО
5.6.1. ВВЕДЕНИЕ
ПОНЯТИЯ ФУНКЦИИ И ОСНОВНЫЕ
СПОСОБЫ ЗАДАНИЯ ФУНКЦИЙ
Пусть заданы два множества действительных чисел
Х с R и У с R и задано соответствие f, по которому эле-
~менту х е Х поставлен в соответствие единственный эле-
менту E У.
Символически это записывается следующим образом.
f(x) =(у = f(x) е УсR:хсX).
При этом число х е Х называют аргументом, множе-
ство Х вЂ” областью допустимых значений аргумента (об-
ластью определения или областью существования функ-
ции) и обозначают с помощью символа D(f). Число у е У,
соответствующее х е Х, называют значением функции,
множество У называют областью значения функции f u
обозначают с помощью символа R(f).
Рассмотрим множество А ~ D(f) тогда множество В =
= (у: у = f(x), х е А), называется образом подмножества А
и обозначается В = ((А). В частности, R(f) = f(D(f)).
Множество точек плоскости с декартовыми координа-
тами (х, f(x)), х е Х называют графиком функции f, опре-
деленной на множестве Х & t;
Если задана формула, указывающая последователь-
~ость математических действий, которые следует выпол-
нить с аргументом х, чтобы получить явное выражение для
у, то говорят, что функция определена явным аналитиче-
«им способом: у = f(x).
Если задано соотношение F(x, у) = О, х е Х = D(f), из
которого у находится в результате решения уравнения
F(x, у) = О, то говорят о неявном способе задания функ-
ции.
Замечание. Если для некоторого х E Х = D(f) уравне-
ние Р(», у) = p имеет несколько решений, то говорят, что
соотношение F(x, у) = О задает многозначную функцию.
Rc JIM зависимость у от X задана с помощью двух функций

ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАД Ч
176
от некоторого вспомогательного переменного ~ е Т с-д
называемого параметром,
x=9('), t,òàR.
у = y(t)
то говорят о параметрическом способе задания функции.
Если дискретному набору значений аргумента сопостав-
лен дискретный набор значений функции с помощью таб-
лицы, то говорят о табличном способе задания функции:
Алгоритмическим способом задания функции называ-
ют такой, когда задано точное предписание, определяю-
щее вычислительный процесс, начинающийся с произволь-
ного (допустимого) исходного значения X и направленный
на получение значения у.
Графическим способом задания функции называют тот,
при котором зависимость у от х определяется линией на
плоскости XOY.
Заметим, что это приближенный способ, зависящий от
масштаба и точности измерения абсциссы и ординаты от-
дельных точек графика.
Если аргумент х функции у = f(x) является функцией
другого аргумента x = w(s) c R(w), s c D(w), то говорят, что
на множестве D(w) задана сложная функция у = f(w(s)) «
зависимого аргумента 8.
Функция у = f(x) называется инзективной, если раз-
ным значениям аргумента х1 A х~ соответствуют разные
значения функции у, = f(x~) w уг = f(x2).
Если задана инъективная функция у = f(x), то уравне-
ние у = f(x) определяет обратную функцию х = f '(у).
Из определения обратной функции следует (f ') ' = 1
f ~(f(x)) = X paa b'X e Х = D(f), f(f ~(y)) = y для &g ; c R
Замечание. Графики взаимно обратных функций сим
метричны относительно биссектрисы у = х первой и тре~~
ей четверти координатной плоскости XOY.

p„q.АВА 5. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
177
5.6.2. НЕКОТОРЫЕ СВОЙСТВА
ФУНКЦИЙ
Функция у = f(x), определенная на множестве х е Х =
= D(f) ~ R, называется четной, если для b'х E Х = D(f) и
'ф( — х) E Х = D(f) выполняется равенство f( — х) = f(x).
График четной функции симметричен относительно
z(:z OY. Область допустимых значений аргумента четной
функции симметрична относительно точки x = О.
Функция у = f(x), определенная на множестве х е Х =
= D(f) ~ R, называется нечетной, если для gx е Х = D(f) и
&l ;( Ђ” х   = D f) выполняе ся равенс во f( Ђ” х = Ђ” /(
График нечетной функции симметричен относительно
начала координат — точки (О, О). Область допустимых зна-
чений аргумента нечетной функции симметрична относи-
тельно точки х = О.
Функция у = f(x), определенная на множестве х E Х =
= D(f), называется функцией общего вида (ни четной, ни
нечетной), если существует хотя бы одно значение х E Х =
= D(f), для которого одновременно выполняются два нера-
венства:
f( — х) w f(x) и f( — х) w — f(x).
Замечание. График функции общего вида не обладает
симметрией ни относительно оси ОУ, ни относительно на-
чала координат — (О, О). Область допустимых значений
аргумента функции общего вида не симметрична относи-
тельно точки х = О.
Функция у = f(x) называется ограниченной сверху, если
3М, такое, что для b'х ~ Х = D(f): у = f(x) & t;
Функция у = f(x) называется ограниченной снизу, если
3М, такое, чтодля b'х ~ X =D(f): у = f(x) & t;
Функция у = f(x) называется ограниченной, если 3M & t;
такое, что b'x ~ Х = D(f) w ~f(x)~ & t;
Верхняя (нижняя) точная грань множества R(f), являю-
щегося областью значений функции у = f(x), называется
точной верхней (точной нижней) гранью функции у = f(x).
Функция у = f(x), определенная на множестве х ~ Х =
= D(f) E Л, называется периодической, если существует
отличное от нуля положительное число Т е В, что для

178
др~цд'ИчЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДд~
4» E Х = D(f): x + T c X = D(f), х — Т е Х = D(f) и справед-
ливо равенство
f(»+- Т) = f(x — Т) = /(»).
(5.19)
Наименьшее из положительных чисел Т =с О, при кото-
ром выполняется равенство (5.19) для периодической функ-
ции у = f(») называется педиодом этой функции.
Замечание. Область допустимых значений аргумента
периодической функции представляет собой неограничен-
ное числовое множество.
Замечание. Функция у = const — периодическая, но не
имеющая периода. График периодической функции полу-
чается из графика у = f(x), построенного на отрезке (полу-
отрезке, интервале), протяженностью в один период, пу-
тем параллельного переноса графика у = f(x) в направле-
нии и против направления оси ОХ на расстояния, кратные
периоду. Если функция у = f(x) имеет период Т, то функ-
ция у = f(ax + b), где а = const & t; О  = con t, им ет пе
од Т/а.
Прямая у = ах+ b на плоскости XOY называется на-
клонной асимптотой для графика функции у = f(x) при не-
ограниченном увеличении в положительную сторону аргу-
мента х (в отрицательную сторону), если для любого поло-
жительного я & t О существ ет та ое положитель ое чи
М(е) & t О (отрицатель ое чи ло М е &l ; О , ч о как ольк
нет выполняться неравенство х & t; М е) ( < (е)),
справедливо и неравенство вир(f(x) — (ах + Ь)( & t;
Замечание. В частном случае, когда а = О, то наклон-
ная асимптота называется горизонтальной.
Геометрический смысл приведенных определений асим-
птот заключается в том, что при движении по асимптоте в
сторону от начала координат максимум отклонения точек
асимптоты от точек кривой у = f(x) стремится к нулю.
Функция у = f(x), определенная на множестве Х = D(f),
называется:
а) Возраспъающей, если для b x) E X и b»2 е Х таких
что х1 & t; 2, выполняе ся неравенс во f( , & t;
б) неубывающей, если для b'x, g Х и ~»2 е Х таких, что
x, & t; x2 выполняе ся неравенс во f( ~ >

~'ДАВА 5. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
179
в) убывающей, ((х)) ( ((хг);
г) невозрастающей, ((х,) & t; /(х
Во всех четырех случаях функция у = f(x) называется
монотонной. Возрастающие и убывающие функции назы-
ваются строго монотонными. Точка (х,„, ((х,„)) назы-
вается локальным максимумом функции у = f(x), если су-
ществует Ь-окрестность точки х,„: (х,„— о, х,„+ 5) та-
кая, что при всех х е (х,„— 5, х,„+ Ь) с D(f) и х w х,„
выполняется неравенство
f(x) & t; f(x,
Точка (x;„, f(x;„)) называется локальным миниму-
мом функции у = f(x), если существует 5-окрестность точ-
ки хт)п (хт))) б»xmin +5) такая, что при всех
хе(хп), — 5,х и+5)». D(f)и x/xmi))
(»+» f(»)+f(*2)
2 2
(5.20)
Функция у = f(x) называется строго выпуклой вниз (во-
гнутой) на интервале х е Х = D(f), если для любых двух
разных х, е (а, Ь) и хг е (а, Ь) выполняется условие
f(»)+f(»)
2
(5.21)
Геометрический смысл этих понятий заключается в
том, что на участке выпуклости вверх (выпуклости вниз)
середина любой хорды располагается под графиком у = f(x)
(над графиком у = f(x)).
Точки, в которых меняется выпуклость вверх на вы-
пуклость вниз или выпуклость вниз на выпуклость вверх,
называются точками перегиба.
выполняется неравенство f(x) & t; (х )
Если для функции у = ((х) при всех х е Х = D(f) суще-
ствует единственная точка максимума (минимума), то она
называется точкой глобального максимума (минимума).
Функция у = f(x) называется строго выпуклой вверх (вы-
пуклой) на интервале х е (а, Ь) ~ D(f), если для любых двух
разных xi E (а, Ь) и хг E (а, Ь) выполняется условие

180
ДРАКТИ iECKOE РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
5.6.3. ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
И ИХ КЛАССИФИКАЦИЯ
К основным элементарным функциям относятся у = С
(& t; Ђ” констант ), степен ая функ и   х ( c ), по
зательная функция у = а' (х, а е R, а & t; О  g ), логар
мическая функция у = log,x (x» О, а & t; О  w ), триго
метрические функции:
y=sinx, y=cosx, y=tgx, y=ctgx,
обратные тригонометрические функции:
у = arcsin х, у = arccos x, у = arctg x, у = arcctg x.
Другие элементарные функции образуются из основ-
ных с помощью арифметических операций, примененных
произвольное конечное число раз, а также с помощью су-
перпозиции с основными элементарными функциями, при-
мененной также любое конечное число раз.
Элементарные функции обычно делят на следующие
классы.
1. Многочлены (полиномы) — это функции, которые
могут быть заданы формулами вида
П
у = P(x) = g а~х~.
a=o
Если а„~ О, то число и c N называется степенью данно-
го многочлена.
2. Рациональные функции (рациональные дроби) — это
функции вида P„(x)
Q (x)
где Р„(х) и Q (x) — многочлены степеней и и т соответст-
венно.
3. Иррациональные функции — это функции, которые
могут быть заданы с помощью конечного числа рациональ-
ных функций, степенных функций с рациональными по-
казателями, которые связываются основными арифмети-
ческими действиями.
4. '1'рансцендентные функции — это функции, не являю-
щиеся иррациональными. К трансцендентным функциям
относятся все прямые и обратные тригонометрические
функции, показательная и логарифмическая функции.

181
['ЛАВА 5. ВВЕДЕНИЕ В MATEMATHÖECÊÈÉ АНАЛИЗ
5.7.
ПРЕДЕЛ ФУНКЦИИ
5.7.1. ОПРЕДЕЛЕНИЕ
ПРЕДЕЛА ФУНКЦИИ
И ЕГО ГЕОМЕТРИЧЕСКИЙ СМЫСЛ
Определение предела по Коши. Число А называется
пределом функции у = f(x) при х, стремящемся к а (обо-
значается так: x -+ а) (или в точке х = a), если для любого
сколь угодно малого я & t О существ ет та ое завися ее то
ко от а положительное число 5(а) & t; О, то ак тол ко н
нет выполняться неравенство О & t; ~x Ђ” a < 5(е), танет
ведливо и неравенство ~f(x) — А~ & t;
Символически это определение записывается следую-
щим образом:
А = lim f(x): &lt => F,(A) 3 ~(a): /( д( )) с: ,(A).
х +a
Преимущество этого определения предела по Коши за-
ключается в том, что оно вбирает в себя как приведенное
выше, так и все приведенные ниже определения.
Запишем традиционные определения пределов по Ко-
ши при x ~ +~, х — ~ — оо, х — ~ ~, а также те определения, в
которых описывается стремление f(x) к+со, f(x) к — oo и f(x)
к о в символическом виде.
А = lim f(r): &lt =& t; Oc & t;030( ) &gt 0:0< х — а[& t 5( ) )f(r)
Х вЂ” &g
Если а е D(f(x) и А = f(a), функция у = f(x) называется
непрерывной в точке x = а.
Определение предела по Коши можно сформулировать
в терминах окрестностей точки а расширенной прямой R
(к расширенной числовой прямой R добавлены две беско-
нечно удаленные точки ( — ~; +co)).
Точка А расширенной числовой прямой R называется
пределом функции у = f(x) при х, стремящемся к а (или в
точке x = а), если для любой сколь угодно малой а-окрест-
ности точки А — F,(À) существует такая проколотая 5-ок-
рестность Uq(a) точки а, размеры которой определяются
числом в, что ~Д5(а)) ~ Р,(А).
Символически это определение записывается следую-
щим образом:

182
ДРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
А = lim f (x): &lt =» ~  gt; 0 3 (c &g ; 0: Ъ х gt; (е) ~ ( х) †А
Х ~+о'
А = lim f(x): &lt =» ~  gt; 0 З (е &l ; 0: b x lt; (c) ~ f x — A
Z-+~
А=»mf(x):~bй>ОЗК е) >0:b'õ,)х) gt;У е)4 f(x) — А[
+«~ = lim f (r):&l ;» O  gt; 0 Ç (M &g ; О Ъх, х gt; (М) « ( х) — А [
+m = lim f(x): с» 'cfM & t О ÇN M & t; : ~ , х l ; N( ) w (r) &g
+«о=limf(x):с» cfM >OÇN M) >О:1 ,/х1& t; N(M) f x)&
Х~~
-«~= Ит f(x):ñ» чМ<ОЗФ М) > : ' , х & t; И(М) f x)&
Х~+Х
— ««t= lim f(x):ñ»~М<ОЗЮ М) <О:Vx, & t;N( ) w f( ) &
Х ~ — »'-'
— «« = limf(x):с»ЪМ<ОЗЖ М) >О:Ъ'х,~х & t;И( ) т f( ) &
Z~»"-
«c = lim f(x): ñ& t    gt; 0 З (М &g ; 0 ~х, х & t; Ф М) =» f x)
Х ~+~
= lim f(r):с>'cfM<ÎЗК(М)<0:'cfx,r<N(M =» f(r
Х ~-&l
~ =lim f(x):&l ;» ~Ì > 3N(Ì) gt;0:× , x> (Ì) «~ (r)
+~ = lim f(r): с&
Х-+Д
с& t; Ч  gt; 0 3 (M &g ; 0  х 0 l ; х в ” a [& t 5 M) f(
— «C = 1im f (x): с&
Х-+Д
&l ;= V  lt; О 3 (M &g ; О: Ч , О & t ( х † ( & t 5 M) w (
о = lim f(r): с&
Х -+Д
со ~М & t; 035 M & t; О: « х О &lt  х — ~ l ; 5( ) = ~ f( ) ~
Определение предела функции по Гейне. Точка А c R
называется пределом функции у = f(x) в точке x = а (при
х — & t  е ), е ли ля лю ой последовательно ти ( „) зна
ний аргумента х, стремящейся к а, элементы которой от-
личны от а, соответствующая последовательность (f(x„))
значений функции сходится к точке А. Символически
определение предела функции по Гейне записывается сле-
дующим образом:

БУЛАВА 5. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
183
А = lim f(x), А c R, а c R: «»
х-+a
«» b'(x„), (х„~ а): lim x„= а ~
и ~+«~о
w lim f(x„)=A, AcR, acR.
(5. 39)
lim f(x)=А, аcR, АcR:
х~а+О
b' E >ОЛб е) > :(0 l ;x вЂ
wJ f(x) — А (& t;
(5.40)
Определение предела слева по Коши. Число А с В на-
зывается пределом слева функции у = f(x) в точке а c R
(обозначается:
lim f(x) =А),
х~а — О
если для любого сколь угодно малого я & t 0 существ ет
кое зависящее только от а положительное число б(е) & t;
что как только начнет выполняться неравенство 0 & t; а
— x & t; б( ), ста ет справедл в и неравенс во Jf x) Ђ” А &
Символически это определение записывается следующим
образом.
lim f(x)=A, acR, AcR:
х~а-О
'с~а & t О Чб е & t; О  О & t  — x
w[ f(x) — А [& t;
(5.41)
Если А' w А, то точка х = а называется точкой разрыва
первого рода функции у = f(x).
Определения предела функции по Коши и Гейне экви-
валентны.
Определение предела справа по Коши. Число А с В на-
зывается пределом справа функции у = f(x) в точке а c R
(обозначается:
lim f(x)=A),
х~а+О
если для любого сколь угодно малого я & t 0 существ ет
кое зависящее только от а положительное число б(е) & t;
что как только начнет выполняться неравенство 0 & t; x
— а & t; б( ), ста ет справедл в и неравенс во ~f x) Ђ” А &
Символически это определение записывается следующим
образом:

184
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЦ
А slim f(x): «»
х~а
«» 3ао & t    gt   х с Х =
((О & t  х Ђ а (& t 5 л ( f( ) в ” А &g
(5.42)
Приведем отрицание определения (5.40) предела функ-
ции по Гейне.
Число А не является пределом функции у = f(x) при
х — э а, если существует сходящаяся к а последовательность
(x„) (х„е Х = D(f) и х„~ а) такая, что для соответствующей
последовательности либо lim f(x„) не существует, либо
П ~+оо
lim f(x„) существует, конечен, íî lim f(x„) ~А.
и-+н~ П ~+оО
Символическая запись этого определения:
А e lim f(x): «» 3(x„), lim x„= а,
(x„~ X = D(f) ~ x„& t; a 3 im f( „ v im ~( „ ~
Если хотя бы один из односторонних пределов не су-
ществует или равен бесконечности, то точка х = а называ-
ется точкой разрыва второго рода.
Геометрический смысл определения предела (5.22) за-
ключается в следующем.
Пусть у = f(x) монотонная функция в некоторой окре-
стности точки а. Тогда, для любого сколь угодно малого ~
путем проецирования я-окрестности оси ОУА — c & t  & t
через график функции у = f(x) на ось ОХ определяется ок-
рестность а — 51(а) & t   l ; а + ~(а). жимая а-окрес
А — е &l ;у & t А+я в т чку А при умен ше ии я, со
ствующая проецируемая на ось ОХ окрестность а — 5,(а) &
& t   l ; а + 5~(а) сжи а тся в т ч у
Приведем отрицание определения (5.22) предела функ-
ции по КОши.
Число А не является пределом функции у = f(x) при
x ~ а, если существует такое яд & t; О, то ля люб г
существует такое х с Х = D(f), что одновременно выпол-
няются два неравенства: 0 & t; Jx Ђ” а  l ; 5 и Jf( ) Ђ А~ >
волическая запись этого определения:

185
,Ллцл 5. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Функция у = f(x) не имеет конечного предела при x — & t;
сли для любого А, принадлежащего множеству действи-
ельных чисел R, существует такое ео(А) & t; О, то ля лю
„е 5 & t О 3   = D f) так е, то одновреме но выполня
я два неравенства: О & t; Ix Ђ” а  l ; 5 и If( ) Ђ А( gt; ед
~дческая запись этого определения:
limf(x) e А: е&
х — эа
с=&gt ~А еЛ3ео А) gt;0( 5& t;03x(5 cX=
((О & t I х 5) Ђ а I& t 5 ~ (I ~ х(5 ) в ” А I &
(5.44)
Ix(5) — а~ & t  и f(x( ) &
Символическая запись этого определения такова:
+~~ e lim f(x): &lt =& t 3M g ; О'Ф5 g ; О 3x(5)
(5.45)
((I x(5) — а I& t; 5 л (f(x( ) &lt
Если для некоторой последовательности (х„) значений
аргумента, принадлежащих области допустимых значений
аргумента X =D(f) функции у = f(x), при lim х„=хц су-
п ~+оо
Шествует предел lim f(x„) = А, то он называется частич-
П -++&l
~ь~м аределом функции в точке хр. Наибольший и наимень-
~ий частичные пределы в точке х( называются соответст-
венно верхним и нижним пределом функции f(x) в точке а
"обозначаются limf(x) и lim f(x).
х~а х-+а
5.7.2. ОСНОВНЫЕ ТЕОРЕМЫ О ПРЕДЕЛАХ
Предел постоянной функции равен ее значению.
Если существуют пределы lim f(x) = А, lim q(x) = В, где
'~~В,а ~В,ВеR, то
1) предел суммы или разности равен соответственно
~Уйме или разности пределов:
Функция у = f(x) не имеет предела +с~ при x -+ а, если
существует такое действительное число М & t; О, то
любого положительного 5 существует x(5), принадлежащее
области допустимых значений функции, такое, что одно-
временно справедливы два неравенства:

186
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИК) 3'&
lim(f(x)+g(x)) =limf(x)+limg(x) =А+В; (5.46}
х~а х — ~а х — ~а
2) предел произведения равен произведению пределе .
lim(f(x) g(x)) = lim f(x) . limg(x) = А В.
х-+а х~а х~а
Следствие. Постоянный множитель можно выносд~~
за знак предела.
(5.47}
lim(C f(x)) =С.limf(x), где С=const;
х~а х — ~а
3) при отличном от нуля пределе знаменателя
(5.48}
lim g(x) = В w О
х~а
предел частного равен частному от пределов.
lim(f(x)/g(x)) = lim f(x)/limg(x) = А/В;
х~а х~а х — ~а
4) если в некоторой 8-окрестности точки а (за исключе-
нием, быть может, самой точки а) заданы функции /(х),
g(x), Ь(х) и справедливо двойное неравенство ~(х) & t; ~ х
& t; h x) и, кр ме то о, существ ют рав ые пред лы ля кр
них функций этого двойного неравенства
(5.49}
lim f(x) = limb(x),
х~а х~а
то существует предел для центральной функции двойного
неравенства, равный пределу крайних функций
lim f(x) = limb(x) = limg(x);
х~а х — ~а х — ~а
5) если существуют
lim f(x) = Ь и lim F(y)
х~а у — +Ь
и в некоторой проколотой окрестности точки Ь f(x) w Ь, то
гда в точке а существует предел сложной функции F(f(x))
lim F(f(x)) = lim F(y).
х~а ~ -+Ь
5.7.3. БЕСКОНЕЧНО БОЛЬШИЕ
И БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ
<функ и  = f x) называе ся положитель ой б
нечко большой в точке x = а (при х — + а), где а c R есл"
для любого сколь угодно большого положительного '~и~
ла М & t О существ ет завися ая тол ко о М окрестно

~gA 5. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
~ЛА
187
,. (a) c Х = D(f) точки а такая, что f(x) & t М ля в
[/ф
UM(a) или
lim f(x) =+~.
х~а
(5.50)
функция у = f(x) называется отрицательной бесконеч-
„е большой в точке х = а (при х -+ а), где а c R, если для
л,оpprp сколь угодно большого по модулю отрицательного
цисла М & t 0 существ ет завися ая тол ко о М окре
ность Ум(а) с Х = D(f) точки а, такая, что f(x) & t М ля в
g c UM(a) или
(5.51)
lim f(x) = — m.
х~а
Функция у = /(х) называется объединенной бесконеч-
но большой в точке х = а (при х — ~ а), где а c R, если для
любого сколь угодно большого положительного числа M & t
еуществует зависящая только от М окрестность UM(a) c Х =
= 1)(() точки а такая, что ~/(х)~ & t М ля в е  < UM(
limf(x) =~; (5.52)
х~а
Положительная, отрицательная и объединенная беско-
нечно большие функции сокращенно называются беско-
нечно большими.
Функция у = f(x) называется положительной бесконеч-
но малой в точке х = а (при х — ~ а), где а c R, если для лю-
Оо~о сколь угодно малого я & t 0 существ ет завися ая то
~о от е проколотая 5-окрестность U> a   = D f) то к
~акая, что 0 & t; f x  lt; е дл  с х х c U;(
(5.53)
lim f(x) = — О.
х — эа
Функция у = f(x) называется объединенной бесконеч-
но
о малой в точке х = а (при х — & t; ), де R, е ли ля лю
~(:)
() ~вдоль угодно малого а & t 0 существ ет завися ая тол
lim f(x) =+О.
х — эа
Функция у = f(x) называется отрицательной бесконеч-
но малой в точке х = а (при х — э а), где а c R, если для лю-
~о~о сколь угодно малого я & t 0 существ ет завися ая то
~о от е проколотая 5-окрестность U;(a) c Х = D(f) точки а
~акая, что — е & t; ( х  lt; 0 дл  с х х с Uz(

188
ДР~КТИ~ЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАД~~
от е проколотая 3-окрестность U~(a) е Х = D(f) точки а та-
кая, что If(x)l & t е ля в е  е U; a)
(5.55)
»m f(x) = О.
х — +а
Положительная, отрицательная и объединенная беско-
нечно малая функции сокращенно называются бесконеч-
но малыми.
5.7.4. СВОЙСТВА
БЕСКОНЕЧНО МАЛЫХ
И БЕСКОНЕЧНО БОЛЬШИХ ФУНКЦИЙ
1. Если функция у = f(x) бесконечно большая при x w а,
где а E R, то функция 1/f(x) является бесконечно малои
прих~ а.
2. Если функция у = f(x) бесконечно малая при x -+ а,
где а E R, то функция 1/f(x) является бесконечно большой
при х~ а.
3. Алгебраическая сумма конечного числа бесконечно
малых функций при x -+ а, где а е R, является бесконечно
малой функцией.
Замечание. Для бесконечно больших функций в общем
случае аналогичная теорема несправедлива.
4. Произведение бесконечно малой при x -+ а (а е R)
функции на ограниченную является бесконечно малой
функцией.
5. Произведение конечного числа бесконечно больших
функций при x — & t; а, д  c R, являе ся бесконе но бо
шой функцией.
6. Произведение конечного числа бесконечно малых
функций при x -+ а, где а е R, является бесконечно малой
функцией.
7. Если функция у = f(x) имеет при x -+ а, где а c R,
предел, равный А, то (f(x) — А) есть бесконечно малая при
х~ а.
8. Если функция у = f(x) представима при x + а, где
а c R в виде f(x) = А + а(х), где а(х) — бесконечно малая
»mf(x) = А.
r-+а
9. Всякая бесконечно большая функция при x -+ а яв
ляется неограниченной.

189
Гг('~HA 5. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
5.7.5. ДВА ЗАМЕЧАТЕЛЬНЫХ
ПРЕДЕЛА
Первый замечательный предел раскрь~вает неопреде-
ленность типа «О/О»:
sinx
r — «О х
(5.56)
Второй замечательный предел раскрывает неопреде-
ленностьтипа «1»'.
lim(1+ n)'~" = lim(1+1/x)" = е =2,71828... (5 57)
и — +О Х вЂ” Ф~
Число е — иррациональное число, основание натураль-
ных логарифмов
log,x = lnx.
(5.58)
5.7.6. НЕКОТОРЫЕ СПОСОБЫ
РАСКРЫТИЯ
НЕОПРЕДЕЛЕННОСТЕЙ
1. Раскрытие неопределенности типа «~/~»при x -+ m
(x — >+~ ), ко да од зна ом пред ла находи ся отноше
степенных многочленов.
Рекомендация. Необходимо разделить и числитель, и
знаменатель на аргумент в старшей степени и воспользо-
ваться теоремами, суть которых отражена формулами
(5.46), (5.48), (5.49).
В результате получится, если и в числителе, и знаме-
нателе многочлены записаны в приведенной форме,
ах +а 1х '+...+а1х+ао
О, m(n,
а /Ь„, т= и,
т) и.
1пп
х +b„gx '+ ° ° ° +gx+bp
2. Раскрытие неопределенности типа «О/О» при x -+ а,
иногда под знаком предела находится отношение бесконеч-
но малых многочленов.
Рекомендация. Необходимо разложить многочлены в
ч1слителе и знаменателе на множители, произвести сокра-
Щение íà (x — а) и воспользоваться теоремами, суть кото-
Рмх отражена формулами (5.46), (5.48), (5.49):

190
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
а х +а,х '+...+а1х+< ,. (х Ђ” )" Р),
1im =шп
b„x +))„,х -)+ ..+b,x+b() (х — а)'Q~,(х)
О, k&gt
Р ~(а)/Q.;.(à), Й =,),
т. sign(P „(a)/Q„;(a)), Й & t;
~/0(х) + А &lt -э ~/0 х +
~eaux) + A++ з/02(х) + Аз/0(х) + А~
4. Раскрытие неопределенности типа «О/О» при х w а
(а е В), когда под знаком предела функции sin а(х), tg а(х),
arcsin а(х), arctg а(х), 1 — cos 2а(х) от бесконечно малого
аргумента а(х) при х w а (а е В).
Рекомендация. Необходимо каждую функцию допол-
нить до отношения, которое находится под знаком преде-
ла в первом замечательном пределе (5.56) (путем умноже-
ния и деления на одну и ту же величину).
5. Раскрытие неопределенности типа «1», когда под
знаком предела при х w а (а е В) можно выделить величи-
ну (f(x))«"), где lim g(x) = +~, lim f(x) = 1.
х~а к~а
Рекомендация. Необходимо представить функцию ) (х)
в виде 1 + а(х), где lim а(х) = 0, переписать выражение
х~а
(f(x))~(") в следующем виде:
(f(x))R(&g ;) ( + с((х))1/а(х))а(х)к
и воспользоваться вторым замечательным пределом (5 5'()'
3. Раскрытие неопределенности типа «О/О» при х -+ а
(а E R), когда под знаком предела находится отношение,
содержащее иррациональности.
Рекомендация. Необходимо и числитель, и знаменатель
умножить и разделить на величины, сопряженные кад&l
дой иррациональности, произвести сокращение одинако-
вых выражений и воспользоваться теоремами, суть кото-
рых отражена формулами (5.46), (5.48), (5.49). Выпишем
некоторые взаимно сопряженные иррациональности:

191
~ЛАВА 5. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
6. Раскрытие неопределенности типа «oo/oo», когда под
3яяком предела имеется отношение степенного многочле-
па к алгебраической сумме показательных функций с oc-
goâàíèÿìè, большими единицы.
Рекомендация. Необходимо вынести за скобки стар-
~дую степень х из степенного многочлена, показательную
функцию с наибольшим основанием — из алгебраической
~уммы показательных функций, воспользоваться теорема-
ми, суть которых отражена формулами (5.46), (5.48), (5.49),
и результатом задачи 5:
а х +а 1х '+...+а1х+ap
1пп
Ь„с„" + Ь„, с„", +... + g с," + bp
х (а+а 1х '+...+a,x' аох )
= lim
=О
х~~ с„"(Ь„+ Ь„,(с„, /с„) +... + Ь1(с1 /с„) + Ьо(1/c„))
а х +а 1х '+...+а1х+ао
lim
х~ Ь„1оа, х + Ь„, 1оа,, х+... + g 1 о а,„х+ bp
х (а +а 1х '+...+а1х' +апх )
= lim
ОО °
1о~, х(Ь„+(Ь„,1оа,, х+...+Ь~1о~„х+Ьп)/1о~, х)
8. Раскрытие неопределенности типа «m. P».
Рекомендация. Раскрытие неопределенности типа «о . О»
Заключается в сведении ее к неопределенности типа «oo/oo»
зли «О/О» с помощью алгебраических преобразований вы-
~~~кения под знаком предела. Пусть а c R u
lim f(x) = с~, lim g(x) = О,
7. Раскрытие неопределенности типа «oo/oo», когда под
знаком предела находится отношение многочлена по сте-
пеням х и алгебраической суммы логарифмов с основания-
ми, большими единицы.
Рекомендация. Необходимо вынести за скобки стар-
шую степень х из степенного многочлена, логарифмиче-
скую функцию с наибольшим основанием — из алгебраи-
ческой суммы логарифмических функций, воспользовать-
ся теоремами, суть которых отражена формулами (5.46),
(5.48), (5.49), и результатом задачи 5:

192
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
тогда
lim f(x) g(x) = lim f(x)/(1/g(x)).
9. Раскрытие неопределенности типа «О» .
Рекомендация. Раскрытие неопределенности типа «00„
заключается в сведении ее к неопределенности типа «oo/oo,
или «0/0» с помощью алгебраических преобразований вь1
ражения под знаком предела. Пусть а e R u
lim f(x) = О, lim g(x) = 0,
тогда
lim(f(x))~'"& t = limexp(g(x ln f( ) = limexp(g(x)/(1 ln f(x
или
lim(f(x))~i"~ = limexp(g(x)ln f(x)) = limexp(ln f(x)/(1/g(x))).
5.7.7. СРАВНЕНИЕ
БЕСКОНЕЧНО МАЛЫХ
И БЕСКОНЕЧНО БОЛЬШИХ,
ТАБЛИЦЫ ОСНОВНЫХ
ЭКВИВАЛЕНТНЫХ ВЕЛИЧИН
Функции f(x) и g(x), для которых
f(x) = 0(g(x))
Ф
(символ 0 читается «О большое»).
Символ О обладает следующими свойствами.
1 /(х) = 0(g(x))wg(x) = 0(f(x)).
Я. f(x) = 0(g(x)) n g(x) = 0(q>( )) ~( х = 0(ср(х
Функция f(x) называется бесконечно малой более вь~
сокого порядка малости по сравнению с функцией К(")
при х -+ а, если существует равный нулю предел их отно
шения.
lim f(x) = О и limg(x) = 0,
х-+а х +a
называются бесконечно малыми одного порядка при х -+ a,
если существует отличный от нуля конечный предел и~
отношения. Символически это записывают.

[ДАВА 5. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
193
Символически это записывается:
f(x) = о(д(х))
(символ о читается «о малое»)
&l ;= 31im(f(x)/g( ) =
(5.59)
(5.60)
f(x) — g(x) =& t; lim(f(x)/g( ) =
х — +а
СВОЙСТВА ЭКВИВАЛЕНТНЫХ
БЕСКОНЕЧНО МАЛЫХ ФУНКЦИЙ
1) f(x) — g(x)» (f(x) — g(x) = (f(x)) л f(x) — g(x) = o(g(x))); (5.61)
2) пусть f(x) — g(x), а функция и(г) w 0 для b'z c U(b) и
limu(z) = а, тогда f(u(z)) — g(u(z)).
г-+b
Пусть
V„(x), и =1, N
— бесконечно малые функции при x w а,
При этом функция g(x) называется бесконечно малой
более низкого порядка (соответственно f(x) называется бес-
конечно малой более высокого порядка).
Справедливы следующие теоремы.
1. Произведение любого конечного числа бесконечно
малых функций при х ~ а и отличных от нуля в некото-
рой выколотой окрестности точки а есть при х -+ а беско-
нечно малая функция более высокого порядка по сравне-
нию с каждым сомножителем.
2. Функции f(x) и g(x) называются несравнимыми бес-
конечно малыми при х -+ а, если не существует ни конеч-
ного, ни бесконечного предела их отношения. Функция f(x)
называется бесконечно малой k-го порядка малости отно-
сительно g(x) при х w а, а число Й вЂ” порядком малости,
если f(x) и (g(x))" — бесконечно малые одного порядка:
f(x) = O(g(x))".
Бесконечно малые при х w а функции f(x) и g(x) назы-
ваются эквивалентными бесконечно малыми при х-+ а,
если предел их отношения при х -+ а равен единице.
Символически это записывается:

194
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАс~
S(x) = QV~(x)
k=1
— их сумма, которая также бесконечно малая функция
при х-+ а. Если
Г„(х) = o(V,(x))
при ~~ = 2, у, то V~(õ) называется главной частью суммы
S(x) бесконечно малых функций VÄ(x).
Замечание. Если в сумме содержатся несравнимые сла-
гаемые, то их главную часть определить не удается.
Справедливы следующие свойства бесконечно малых,
для суммы которых можно выделить главную часть.
1. Если сумма
Я(х) = QV>
1=1
конечного числа бесконечно малых при х w a функций
V„(x), и = 1, N имеет главную часть V,(õ), то S(x) — V,(õ).
2. 3U>( ), то ри ' с Uz a) су
S(x) = QV(x)
й=1
бесконечно малых при х ~ а функций V„(x), и =1, N со-
храняет знак своей главной части.
ТАБЛИЦА ОСНОВНЫХ
ЭКВИВАЛЕНТНЫХ
БЕСКОНЕЧНО МАЛЫХ ФУНКЦИИ
Пусть lima(x) =О, тогда
х-+а
sin a(x) — a(x),
— 1 — а(х)/р,
arcsina(x) — a(x),
tg а(х) — a(x),
arctg а(х) — a(x),
1 — cos a(x) — а 2 (х) /2,
а"'"& t; Ђ” 1- а х) 1
»g, (1+ а(х)) — а(х) /ln a.

pglry&gt ~A 5. ВВЕДЕ И В МАТЕМАТИЧЕС ИЙ АНА
195
При раскрытии неопределенности типа «О/О» исполь-
зуется следующее утверждение, позволяющее применять
таблицу эквивалентных бесконечно малых функций.
Предел отношения двух бесконечно малых функций
~ — & t а ра ен пред лу отноше ий эквивалент ых им ве
чин, т. е.
(f(x) — и(х) лд(х) — v(x)) =& t; i =
f(x) . и(х)
х-+а g(x) х-эа v(x)
5.7.8. СРАВНЕНИЕ
БЕСКОНЕЧНО БОЛЬШИХ ФУНКЦИЙ
Функция f(x) называется бесконечно большой при
у -+ а, где a c R, если
f(x) = 0(g(x))
(символ 0 читается «О большое»).
Символ О обладает следующими свойствами:
1) f(x) = 0(g(x)) =>g x = 0(f(x
(5.63)
2) ((х) = o(g(x)) л д(х) = 0(V(x)) ~ ((х) = 0(V(x)).
х-+a х~а х~а
Функции f(x) и g(x) называются несравнимыми беско-
нечно большими при х -+ а, если не существует ни конеч-
ного, ни бесконечного предела их отношения.
Функция f(x) называется бесконечно большой более
низкого порядка роста по сравнению с функцией g(x) при
х -э а, а функция g(x) — бесконечно большой более высоко-
го порядка роста, если существует равный нулю предел их
отношения f(x)/g(x). Это эквивалентно обращению в со, +~
или — со предела отношения обратной величины f(x)/g(x).
Символически это записывается:
f(x) = v(g(x))
limf(x)=+~ или limf(x)= — ~ или limf(x)=~. (5.6Я)
х~а х — +а х~а
Две функции f(x) и g(x) называются бесконечно боль-
шими одного порядка при х — э а, где а c R, если предел их
отношения существует, конечен и отличен от нуля. Сим-
волически это записывают:

196
ДРДКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ 3AQAQ
(символ о читается «о малое» )
m 31im f(x) /g(x) = 0 v 31im f(x) /g(x) ~
Функция f(x) называется бесконечно большой k-го по-
рядка относительно g(x) при х -+ а, если f(x) и (g(x))" бес-
конечно большие одного порядка: f(x) = O(g(x))". Беско-
нечно большие при х -+ а функции f(x) и g(x) называются
эквивалентными бесконечно большими, если предел их от-
ношения при х -+ а равен единице. Символически это запи-
f(x) — g(x) сэ lim f(x)/g(x) =1.
х~а
Свойство эквивалентности для бесконечно больших
функций при х -+ а симметрично:
(5.64)
(5.65)
f(x) — g(x) сэ g(x) — f(x),
и транзитивно:
(f(x) — и(х)) ~ (и(х) — g(x)) ~ /(х) — g(x). (5 66)
Справедлива следующая теорема.
Пусть V„(x) (и = 1, N) — бесконечно большие функции
прих~а, а N
S(x) = g V„(x)
A,'=l
их сумма, которая также бесконечно большая функция при
х ~ а. Если V„(x) = o(V~(x)) при b'k = 2, N, то Г,(х) назы-
х~а
вается главной частью суммы S(x) бесконечно больших
функций V„(x).
Замечание. Если в сумме содержатся несравнимые сла-
гаемые, то их главную часть определить не удается.
Справедливы следующие свойства бесконечно малых,
для суммы которых можно выделить главную часть.
1. Если сумма
S(x) = g Г» (х)
й=1
конечного числа бесконечно больших при х -+ а функций
1"„(х) (п = 1, N) имеет главную часть V,(х), то S(x) — V,(х).
2. Сумма бесконечно большой функции x -+ а и ограни-
ченной функции эквивалентна этой бесконечно большой.

[ ДАВА 5. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
197
5.8.
РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ
ВЫЧИСЛЕНИЕ ПРЕДЕЛА
ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
5.1. Найти предел последовательности
lim
Зи — би +Зи+5
(п+ 1)~ — (п — 2)~
P e ш е н и е. Прежде всего преобразуем знаменатель
этой последовательности, используя формулы сокращен-
ного умножения:
(n + 1)~ — (п — 2)6 = ((п + 1)э — (n — 2)э)((п + 1)э + (п — 2)э) =
= 3((n + 1)2 + (п + 1)(n — 2) + (n — 2)~)((п + 1)2 — (п + 1) х
~ (п — 2) + (n — 2)~)(2п — 1) =
= 3(2п — 1)(3п~ — 3n + 3)(п~ — п + 7).
Подставим этот результат в исходный предел и разде-
лим числитель и знаменатель дроби на и5~, после этого, от-
брасывая бесконечно малые, получим требуемый предел:
3 — 6/n+ 3/n4 + 5/п5
3(2 — 1/n)(3 — 3/и+ 3/n~)(1 — 1/п+ 7/n2)
5.2. Найти предел последовательности
lim
-!Я+1
P е ш е н и е. Разделим числитель и знаменатель дроби
на и. После преобразований и отбрасывания бесконечно
малых величин получим требуемый результат:
lim
— J4n+ 1
/n — ~n+1/п
5.3. Найти предел последовательности:
lim(
— n).

198
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
Р е ш е н и е. Умножим и разделим общий член после-
+ n и используем формулу
довательности на
сокращенного умножения:
l im
п~х &
+n)
— n) (
+n)
((n+ 2)(n+ 7) — n~)
= 1пп = 1пп
и — эм n( + 1) и-Фт- и(
9n+14
+1)
9+14/п
= lim
и — ээ:(
= 9/2.
+1)
5.4. Найти предел последовательности
n!+(n+1)!
1пп
и эх (n — 1)!+ (n + 1)!
P е ш е н и е. Из определения факториала следуют про-
стые соотношения:
и. '= (и — 1)! n,(n + 1)! = (и — 1)!. п .(и + 1).
После их подстановки и сокращения общего множителя
получаетс
я
(n — 1)! n+(n — 1)! п (n+1)
lim
(и — 1)!+(и — 1)! п (и+1)
n~+2n . 1+2/п
= 1пп = lпп
n~ + п+1 1+1/п+1/п'
5.5. Найти предел последовательности
5 — 7п
2n2+2n+3
im
и 2п -2и+5
P e ш е н и е. В данном случае имеем неопределенность
&l ;( 1"
2n2+2n+3 1- 1 4n — 2
и-+~о 2n — 2n + 5 и~~ 2n — 2n + 5
(4п — 2)(5 — 7п)
2и — 2n+5 2n2 — 2n+5 (4 — 2/ и)(5/п — 7)
4п-2
2
— l jm р 2 2/n+5/n
2
4n — 2
и-~ 2ц2 — 2n+ 5
=e ~4 ~0.

ГЛАВА 5. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
199
ВЫЧИСЛЕНИЕ ПРЕДЕЛА ФУНКЦИИ
5.6. Найти предел функции
lim
Зх4 — 2x3+6х2+ х—
9х4 + 5x3 + 7х2 + x+1
Решение.
Çx4 «2хз -+6Х2+х
llm 4 3 2 llm
Зх4 — 2õç + бх2 + х — 2» . х4
9х4+5хз +7х2+ х+1 9х4+5xз + 7х2+ х+1
х4
3 — 21im — + 61im — + lim з 2 l пп 4
1 . 1 . 1 . 1
х — +с Х х — +с Х х — +о~ Х х — +о~ Х
9+ 5lim --+ 71im — 2+ lim з + lim 4
1 . 1 . 1 . 1
х-+ос Х х-+ос Х х-+с~ „'~ х-+со Х
3 — 2 ° Оtá OtO — 2 0 1
9+5.0+7.0+0+0 3
5.7. Вычислить предел
lim
1 12
х~2 2 — х 8 — хз
= lim
4+2х+ х2 — 12 . х2 t2x — 8
з
= lпп
8 — х х~2 8 — х
з
lim
1 12
х-э2 2 — х 8 — хз
(имеем неопределенность «О/О»)
(х — 2)(х+4) 2+4 1
«2 (2 — х)(4+ 2х+ х~) 4+ 4+ 4 2
5.8. Вычислить предел
Гх-1-3
1о х — 10
P е ш е н и е. Определяем с помощью подстановки х = 10
в выражение под знаком предела, что в данном случае име-
ется неопределенность типа «О/0». Раскрываем ее умно-
жением и делением на выражение, сопряженное числите-
лю дроби:
P е ш е н и е. Подстановка значения х = 2 в выражение,
стоящее под знаком предела, дает неопределенность типа
< со Ђ” ». ля ее раскры ия приве е к общ му знамена
лю указанные дроби. Имеем

200
ДРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
( Jx — 1 — 3)( Jx — 1 + 3)
lim = lim
х~» х — 10 х~» (х — 10)( Jx — 1+ 3)
= lim
х — 10
lim
1о (х — 10)( Jx — 1+ 3) » ~/х — 1+ 3 ~9+ 3 6
5.9. Вычислить предел
lim (
Х ~+»
P е ш е н и е. В данном случае мы имеем неопределен-
ность типа «сс — сс». Для ее раскрытия умножим и разде-
лим исследуемое выражение на сопряженное значение.
Получим
х~+1 — х~+
)= llm
lim (
Х -++»
ХH+»
= lim
=О.
Х ~+»
5.10. Вычислить предел
tg бх
1пп
х~о 81пЗх
P е ш е н и е. Для вычисления этого предела, представ-
ляющего собой неопределенность типа «О/О», лучше все-
го воспользоваться теоремой о замене бесконечно малых
функций эквивалентными величинами.
В соответствии с этой теоремой при х -+ О, tg бх — бх,
sin Зх — Зх. С учетом этого имеем
lim = lim — = 2.
~гмбх . бх
х-+о sin Зх х~о Зх
5.11. Вычислить предел
1+ sin2x — cos2x
llm
х~о 1 — 81п2х — cos2x
р е ш р н и е. Под знаком предела имеем неопределен-
Носп, типа «0/0». Для ее раскрытия воспользуемся известн-
ымии формулами тригонометрии:
sin 2х = 2 sin x cos х, 1 — cos 2х = 2sin2х.

201
ГЛАВА 5. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
С учетом этого получим
1+sin2x — cos2x . 2sin~ x+2sinxcosx
llm = lпп
xylol — sin2x — cos2x х~о 2sin х — 2sinxcosx
2sinx(sinx+cosx) sinx+cosx О+1
= lпп = lпп
х~о 2sinx(sin x — cosx) x~o sin x — cosx Π— 1
5.12. Вычислить предел
sin5x
lim
х~~ sin2x
P е ш е н и е. Имеем неопределенность типа «О/О». В дан-
ном случае воспользоваться таблицей эквивалентных бес-
конечно малых функций нельзя, так как аргументы sin 5х
и sin 2х при х -+ к не являются бесконечно малыми. Поэто-
му введем новую переменную х — к = t и преобразуем рас-
сматриваемый предел к новой переменной. Имеем
s jn 5х . sin(5m+ 5t) . ап(п+ 5t)
lim . =lim = lпп
х-+кsin2х ~ — +О sin(2m+ 2t) ~ — эО sin2t
sin 5t . 5t 5
= -lim = -lim — = — —.
c~o sin2t с~о 2t 2
5.13. Вычислить
lim(z — х) ctg x.
х~к
P е ш е н и е. Данный предел представляет собой не-
определенность типа «О ~ñ». Для ее раскрытия введем но-
~ую переменную к — х = t. Тогда
lim(~ — х) ctg х = limt ctg (т~ — t) = — limt ctg t = — lim = — 1.
Х--&g ; 8 Ђ” +О ~0 ~o t
5.14. Вычислить предел
lim
х-+О
P e ш е н и е. Здесь мы имеем неопределенность типа
«О/0». Для ее раскрытия заменим входящие под знак пре-
дела функции им эквивалентными.
lim
х-+О

202
IIPAKTH'IECKOE PYKOBOPCTBO K PEIIIEHHN 3APp~
Устраняем неопределенность домножением и делед~.
ем на соответствующие сопряженные иррациональност~
Имеем теперь
( ~1+ 4х — ~1 — 4х)(
(з (1+ 4х) 2 + ' 1+ 4
+фГ+4х'/1 — 44хх+ з (1 — 4х)2)
~х /~1 — 4х+ )(Д вЂ” Зх+ Jl+Зх)
(Д вЂ” Зх+~1+Зх)
(Д Зх — ~~+ Зх)
(1+ 4х — 1+ 4g)(~1 — Зх + ~1+ Зх)
= lim
х — +0(
+~31+4x~l — 4х+ )(1 — Зх — 1 — Зх)
= lim
Зх( /1 — ЗЗхх+ ~1+ Зх)
о-6x(з (1+4х)2+~~~+4х~~~ — 4х+ з (1 — 4х) )
— 4 1+1
3 1+1+1 9
5.15. Вычислить предел
lim
1 1
х~о sin 2x tg2x
5.16. Вычислить предел
mx
lim 1+—
х
P е ш е н и е. Имеем неопределенность 1". С помощью пре
образований, изложенных в разделе 5.7. 5 (п. 5), получим
тх х/Й
тй
iim i+ — =iim 1&l ; ) =е
1
х-»со х х — ~ас х/ф
P е ш е н и е. Вычисляемый предел представляет собой
неопределенность типа «с~ — с~». Для ее раскрытия приве-
дем к общему знаменателю дроби, представив предвари-
тельно 1/tg 2х в виде cos 2х/sin 2х. Получим, выполняя
указанные преобразования.
llm
1 1,. 1 cps 2x,. 1 — cos2x
= 11m = llm
к~О sin 2х tg2x х-+О sin 2x sin 2х х-+О sin 2Х
2sin~ х,. 2sin2 х,. sin x
= llm . = llm = llm
х-~О sin 2x х~О 281пх совх х-+О cosx

203
1~1~ЦА 5. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
5.17. Вычислить предел
Р е ш е н и е. Вычисление этого предела также связано
(; раскрытием неопределенности типа 1". Проведем преоб-
разования, рекомендованные в разделе 5.7.5 (пункт 5).
Имеем
3
(*3 — 1 * . ( (хз — 1)/2]
lim — 2 lim — 3
2 ~.:3 1
Е», хз 1 Е х-+1 — 1/х Е2
Здесь мы воспользовались непрерывностью компози-
ции непрерывных функций.
5.18. Вычислить предел
з
4х2 — х+1 2-"
lim
х 2х +х+1
Р е ш е н и е. Этот предел не является неопределенно-
стью, так как при
4х — х+1 х
х — + ~) — ~2,а — — х
2х2+ х+1 2 — х
Следовательно:
4х2 — х+1 2-»
lim =lim 2
х-+зс 2Х + х+ 1 х-+:с
Зх — 1
2х2+ х+1
3
lim—
Зх — 1
»m 2 =2 =О.
2х2+ х+1
5.19. Вычислить предел
lim arctg
х — +2+0 2 — х
Р е ш е н и е. При х ~ 2 — О величина 1/(2 — х) ~ im, так
~~~ условие х w 2 — О означает, что х стремится к 2 слева,
1' е. остается все время меньше 2.

204
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
Тогда arctg (1/(2 — х)) w и/2. Таким образом,
1 т~
lim arctg
х-+2 — О 2 — х
Аналогично, при х ~ 2 + О величина 1/(2 — х) w — oo, так ка
х больше 2 при указанном предельном переходе. То~д~
arctg (1/(2 — х)) w — и/2. Таким образом,
1 к
lim arctg
х — э2+О 2 — х 2
5.20. Вычислить пределы
lim
1
О+О 1+ 32/'»
Pеш ени е. Прихw О+ 0(хw+О) величина2/хw+со.
Тогда 3~~'w О. Следовательно, 1/(1+ 3~~') w О. Таким об-
разом,
lim
1
=0.
х-+О+О 1+ 32/х
Рассуждая аналогично, получим, что при х w Π— О (х w — О)
величина 2/х w — oo, тогда 3~~' w — oo, следовательно,
1/(1 + 3~~') w 1. Таким образом,
lim
1
=1.
х — +Π— Q 1+- 32/»
ИССЛЕДОВАНИЕ
НЕПРЕРЫВНОСТИ ФУНКЦИИ В ТОЧКЕ
5.21. Исследовать непрерывность функции
4х, если 0<х
f(x) =
3 — х, если 1<х
lim f(x) = lim f(x) =f(g).
х +а — О х-+а+О
В данном случае f(1) = 4х = 4.
lim f(x) = lim 4х=4; lim f(x) = lim (3 — х) =2.
1-0 »~1+0 х +1+0
P е ш е н и е. Непрерывность данной функции может на-
рушаться только в точке 1. На промежутках [0, 1) и (1, 4]
функция непрерывна. Исследуем непрерывность функции
в точке 1. Напомним, что если функция непрерывна в точ-
ке а, то должны выполняться условия

205
ГЛАВА 5. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Таким образом, нарушается условие равенства односто-
ронних пределов (т. е. предел в точке 1 не существует).
следовательно, рассматриваемая функция не является не-
~рерывной в точке 1.
5.22. Пусть
е з, если х&lt
х =
a+5x, если х&gt
При каком выборе числа а функция f(x) будет непре-
рь~вной?
P е ш е н и е. Запишем условие непрерывности функции
ц точке х = О, где она пока не является непрерывной в силу
произвольности числа а. Имеем
lim f(x) = lim f(x) = f(0).
х~Π— О х-+0+0
В данном случае
lim f(x) = lim ез' =ео =1;
х-+Π— О х-+Π— О
lim f(x) = lim (а+5х) =а;
х-+0+0 х-+Π— О
f(0) = (а+5х) ),д — — а.
Для непрерывности в точке х = 0 должно выполняться
условие а = 1.
5.23. Исследовать функцию
хз, если [x[&lt
х =
1, если ~х~&g
на непрерывность и выяснить характер точек разрыва.
Р е ш е н и е. Нарушение непрерывности в данном слу-
чае возможно в точках х = +1. Имеем в точке х = 1
lim хз =1, lim 1=1,((1)=1~
- 1-0 х-+1+0
в точке х = 1 функция непрерывна. Исследуем точку
~ = — 1. Имеем
lim f(x) = lim 1=1 lim f(x) = lim х~ = — 1; f( — 1) = — 1.
х-э-1-0 х — ~ — 1 — О х-+ — 1+О х-+ — 1+О
Таким образом, нарушается одно из условий непрерыв-
ности. Следовательно, в точке х = — 1 функция имеет раз-
Рыв 1-го рода, так как существуют, но не равны между со-
бой односторонние пределы функций в этой точке.

206
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
5.24. Исследовать функцию
5'/"
1+ 5'~"
на непрерывность и выяснить характер точек разрыва.
Р е ш е н и е. Функция определена всюду, за исключе-
нием точки х = О. Исследуем поведение функции в окрест-
ности точки х = О. Найдем односторонние пределы
51~ z
lim f(x) = lim,— =О,
zî-О zî-О 1+ 51/"
так как при х w 0 — О, т. е. слева от нуля, 1/х w — с~ =:&
5'/" -+ О.
5/" 1
lim f(x) = lim = lim =1,
о+о о+о 1+ 5'/" z-+0+0 5-'/'z + 1
sin3x 3 11щ sint 3
х — эО х х — эО
(сделана замена 3x = t).
В самой точке х = 0 функция не определена. Таким об-
разом, в точке х = 0 имеем устранимый разрыв. Он устра-
няется доопределением данной функции значением 3 в точ-
ке х = О. Новая функция
sin3x
д(х) = х
3, x=0
будет уже непрерывна в точке х = О.
так как при х w О+ 0 1/х w +~ 5 '~" w 0.
Таким образом, односторонние пределы функции в точ-
ке х = 0 существуют, но не равны между собой. Следователь-
но, в точке х = 0 функция f(x) имеет разрыв первого рода.
5.25. Исследовать функцию
sin3x
х
на непрерывность и выяснить характер точек разрыва.
P е ш е н и е. Односторонние пределы этой функции су-
ществуют и равны 3:

207
~ДАВА 5. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
2
5.26. Исследовать функцию f(x) = e ~ -'& t; на непрер
ность и выяснить характер разрыва.
Р е ш е н и е. Функция определена всюду, кроме точки
~ = 1. В этой точке односторонние пределы равны
2
lim f(x) = lim е -' =о~,
х — «1 — О х — «1 — О
так как при х w 1 — 0 — 2/(х — 1) w +~ и
2 2
е -' -+о~ lim f(x) = lim е -~ =О,
r-— «1+О х — «1+О
2
так как при х w 1 + 0 — 2/(х — 1) ~ — с~ и е ' -+ 0.
Предел слева в точке х = 1 равен бесконечности, следо-
вательно, в точке х = 1 функция
2
р х — 1
имеет разрыв второго рода.
5.27. Функция f(x) не определена при х = О. Определить
число f(0) так, чтобы f(x) была непрерывна при х = О, если
f( ) 51+X — 1
~4+ х — 2
Решение. Найдем предел f(x) вточкех = О.
Имеем
lim f(x) = lim
1+х — 1
~~î $4+õ — 2
+ ~1+ х+1)
(Я+ x — 1)(~4+ х + 2)(
= lim
о ( $4+ х — 2)(~4+ х + 2)(з (1+ х)2
(1+ х — 1)($4+ х+ 2)
= lim
-о (4+ х -4)( + ~/1+х+1)
+Я+х+1)
~4+х+2 4
~-~l~- х+1 3
= lim
х-+О
Данная функция будет непрерывной в точке х = О, если
положить f(0) = 4/3.

208
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИК) 3,Ч
5.9.
ЗАДАЧИ
ВЫЧИСЛЕНИЕ ПРЕДЕЛА
ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
2п +1
х Зп
5.31. »m
Х +X
п+3
— n)2
5.32. »m
Х вЂ” +с~)
1+ 3+ 5+... + (2п — 1)
5.38. lпп п
Х ~(~~ п+4
5.40. lim + +... +
1 1 1
2 3 3 3 (За — 1)(3n+)))
1
5.42. lпп
3 — 1
Х ~~
3~~ -+ 2
5.41. lim
4" — 2
х4" +2
(2п + 1) 4 — (Зп — 1) 4
5.30. »m
(Зп — 1)~ +(2п+1)9
5.34. »m
п&
' x~~2(n+1)! — Зп!
2(п+ 3)!+ (и+ 2)!
5.35. lпп
х~ 4(п+3)! — (и+2)!
1 1 1
1+ — + — +...+ — n
5.36. lim
3 9 3
Х~~
1+ — + — +...+ — и
4 16 4
1+ 3+ 5+... + (2п — 1)
5.37. lпп
Х ~~:) 2п
3 39. (im — + — +...+
1 1 1
х+m 2 6 пп — 1)
2пз +10п~ — 1
5п~+4п

pЛАВА 5. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
209
sin(n3 + 2)
n+1
5 44 11 1 — 2+3 — 4+...— 2
ВЫЧИСЛЕНИЕ ПРЕДЕЛА ФУНКЦИИ
5.45. »m
хз+8
х-+2 ХЗ вЂ” 4
546 1 х +3x +4+3
х~о х+2
5.47. lim
х-+2 Х вЂ” 2
4g l1 х х х+1
3 2
х~2 хз 2х2 х+- 2
5.50. 11 27х — 1
х~~ Зх + 2х — 1
551 1 х х х+1
х~1 х — 2х — х+ 2
5.52. lim
1 12
х-+2 2 — Х 8 — ХЗ
Зх+6 х — 4
з х2 — 5х+4 х2 — Зх+2
5.54. ljm, m, и — целыечисла
х" — 1
х 1xm — 1
555 1 2х — Зх +7
х-+~с хз 9Х + 2х — 4
5.56. 1. х — 2x2+3
- х2+5х+2
5 57. Г х'-2х'+Зх'+4х+2
- х6+7х5+ЗХ4+2х+9
5.58. Г 2+Зх — 4х
+ х2 — 2хз
5.43. lim
х -+х
48 1 х — бх+9
х-+3 X — 9X
з

210
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
5.59. »m 3 2 х+1
х4
х3+3x2+1
хз Х2
5.60. 11п1
х-+" 4х2 — 1 4x+ 1
(х+ 1) 5 + (х+ 2)5 +... + (х+ 10)5
5.61. 1дщ
х ~со х5+1О
5.62. lim
5.63. lim
х +x&
.3
х — э0
.3
5.64. »m
х — эО
х — 8~х
х~4 /» 2
5.67. lim
х-+0
5.69. li
о "/х+1 — 1
5.70. »m
2х+ х2
х-+0
5.71. lim
х — э2
5.72. lim(
5.73. lim(
— х)
х — ++~
5.74. lim (
— х)
х — ++со
5.75. lim(
х ~+©)
5.68. lim
h~O
5.76. lim х@~(
х~сО
5.77. 11П1 я1'14х
х-+0 Х
~/х — 2 — 3
хп х — 11

2И
~'ЛАВА 5. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
5.79. 11т
x~o sin(Px)
5х~ — агсвьп(Зх~)
5.81. 1цп
х-+О Х + Я]~СфЯХ
583. 1; 1-сов'(2х)
хо х arcsin(2x)
582 11п11
х-эО Х
sin(5x)
5.87. 1&g ;
х~~ sin(3x)
589
сов(2х)
4
5.88. lim()): — x)ctgx
1+ sin—
5.90. »m
2
х-+-л х - х
cos — cos — + з1п—
2 4 4
сов(ах2) — cos(Px~)
5.91. lцп
х-+О х4
в1п (2х) — в1п (Зу) 593 1. 2—
у 4х -9у х-.О З1П2 Х
в1п(ах )
хо sin(f3x~)
4 arcsin(2x)
5.80. lцп
х~о sin(2x)
(1 — сов х~)~ х~
5.84. lцп
ОФд х — з1п х
5.86. li
х-+- — Я
2 — +х
2
5.85. lim
1 1
о в!п(Зх) ф(Зх))

ГЛАВА 6
ПРОИЗВОДНАЯ
И ДИФФЕРЕНЦИАЛ ФУНКЦИИ
ОДНОЙ НЕЗАВИСИМОЙ
ПЕРЕМЕННОЙ
6.1.
ОПРЕДЕЛЕНИЯ ПРОИЗВОДНОЙ
И ДИФФЕРЕНЦИАЛА
Определение 6.1. Производной функции у = f(xp) в данной
фиксированной точке хо называется предел отношения
приращения функции Лу(хо) = f(xp + Лх) — f(xp) к прираще-
нию аргумента Лх = х — х( при стремлении приращения
аргумента к нулю и если такой предел существует (конеч-
ный или бесконечный):
у'(хо) = 11т
ь-о Лх
Символическое изображение производной может быть
и таким: dy/(dx), или у(х), или у (х) (здесь индекс указы-
вает, по какой переменной находится производная).
Операция нахождения производной называется диф-
ференцированием.
Геометрический смысл производной заключается в сле-
дующем. Производная f (xp) в точке (xp', f(xp)) численно
равна тангенсу того угла, который образует касательная к
кривой у = f(x) в этой точке с положительным направле-
нием оси абсцисс.
Механический смысл производной заключается в сле-
дующем. Производная пути s(t) по времени t движущейся
прямолинейно материальной точки равна мгновенной ско-
рости этой точки: s (t) = v„„„.
Определение 6.2. Пределы (конечные или бесконечные)
у' (хо) = lim, у,'(хо) = lim
~у(хо), . Лу хо
л о Лх ' ' л о Лх

213
~'ЛАВА б. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ
называются соответственно левой и правой производны-
ми функции у = f(x) в данной фиксированной точке хо.
Определение 6.3. Если функция у = f(x) имеет разрыв
первого рода в точке х(), то выражения
Лу хо
у'(хо — 0) = lim
лх-э-о Лх
Лу хо
у,'(хо+0) = lim
лх- +о Лх
называются соответственно левой и правой в расширенном
смысле производными функции у = f(x) в данной фикси-
рованной точке х().
Определение 6.4. Функция у = f(x) называется диффе-
ренцируемой в данной фиксированной точке х, если ее при-
ращение Лу(х) может быть представлено в виде Лу(х) =
= АЛх + а(Лх), где А — конечное число, а
сх(Лх)
1пп
~~0 Лх
Определение 6.5. Дифференциалом функции у = ((х) в
данной фиксированной точке х называется величина, обо-
значаемая dy(x) и определяемая следующим образом:
dy(x) = АЛх, здесь А — конечное число, АЛх — главная ли-
нейная относительно приращения аргумента Лх часть при-
ращения функции Лу(х) = АЛх + а(Лх), а
сх(Лх)
1пн
~~0 Лх
Теорема 6.1. Для того чтобы функция у = f(x) была диф-
ференцируемой в данной точке х, необходимо и достаточ-
но, чтобы она имела в этой точке конечную производную.
Следствие. В случае дифференцируемости функции
y = f(x) ее дифференциал находится по формуле dy(x) =
= у'(х)Лх. Поскольку dx = Лх, то последнее соотношение
можно переписать так: dy(x) = у'(x)dx.
Геометрический смысл дифференциала заключается в
следующем: dy(x) равен приращению ординаты касатель-
ной к кривой у = f(x) в точке (хо,' f(xp)), когда приращение
аргумента равно dx = ~х.

214
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
6.2.
ПРАВИЛА НАХОЖДЕНИЯ
ПРОИЗВОДНЫХ
И ДИФФЕРЕНЦИАЛОВ СУММЫ,
РАЗНОСТИ, ПРОИЗВЕДЕНИЯ
И ЧАСТНОГО ФУНКЦИЙ
(и(х) + v(x))' = и'(х) + v'(õ),
d(u(x) + v(x)) = du(x) + dv(x),
(6.1)
(и(х) v(x))' = и'(х) v(x) + и(х) v'(х),
d(u(x) v(x)) = v(x)du(x) + u(x)dv(x),
(6.2)
(С и(х))' = С и'(х), d(C и(х)) = С du(x).
( и(х) и (х). v(x) — и(х) v'(õ)
vx ~0,
v(x) v2(x)
их võ duõ — их dvõ
vx ~0.
v(x) v2(x)
(6.3)
Здесь предполагалось, что все производные или диф-
ференциалы, формирующие и левые, и правые части ра-
венств (6.1) — (6.3), существуют и конечны.
6.3.
ДИФФЕРЕНЦИРУЕМОСТЬ.
ПРОИЗВОДНЫЕ СЛОЖНЫХ ФУНКЦИЙ,
ОБРАТНЫХ ФУНКЦИЙ.
ТАБЛИЦА ПРОИЗВОДНЫХ
Теорема 6.2. Пусть функция х = q> t) дифференцир
ма в некоторой точке tp, а функция у = f(x) дифференци-
руема в соответствующей точке xp = (p(tp), тогда сложная
двухзвенная функция f(V(t)) дифференцируема в точке &l
и ее производная по 1 равна произведению производной
первого звена по второму с сохранением ero аргумента на
производную второго звена по t, т. е.
в частности, постоянный множитель С можно выносить за
знак производной или дифференциала

215
Теорема 6.3. Пусть функция у = f(x) строго монотонна
и непрерывна в некоторой окрестности точки хд. Пусть,
кроме того, функция у = f(x) дифференцируема в точке х0
и производная f,'(xp) w О. Тогда существует обратная функ-
ция х = /'(у), которая определена в некоторой окрестно-
сти точки gp = f(xp), дифференцируема в этой точке и име-
ет производную, равную 1/(f'(xp)).
ТАБЛИЦА ПРОИЗВОДНЫХ
(6.4)
1. (С = const)' = О.
(6.5)
(6.6)
(6.7)
(6.8)
(6.9)
(6. 10)
. х,'(t) °
sin2 (x(t))
1
8. (ctg(x(t))),' =
9. (arcsin(x(t))),' =
х,'(t) °
10. (arccos(x(t)))', =
х,'(Е).
(6.15)
1 ЛАВА 6. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ
2. ((х(Й))")', =n(x(t))" '.х,'(t),
п = const, ( Jx(t)),' = х'(t).
2 x(t)
3. (а"<' g ;)' = а'& t;'>
а = const ) О, а ~ 1, (e'(~&g ;  = e & t;"
4. (log,(x(t))),' = х'(t),
х t)lna
а = const & t; О  w 1, (ln(x(t)) ' = х'(
x(t)
5. (sin(x(t))),' = cos(x(t)) х'(t).
6. (cos(x(t))),' = — sin(x(t)) х'(t).
7. (gg(x(t)))', = х'(t).
cos2 (x(t))
(arctg(x(t)))I = х'(t).
1+ (x(t))~
12. (arcctg(x(t)))I = х'(t).
1+ (x(t))'
(6.11)
(6. 12)
(6. 13)
(6.14)

216
ДРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
(6.16)
(6.17)
13. (sh(x(t))),' = ch(x(t)) х '(t).
14. (ch(x(t))),' = sh(x(t)) х'(t).
15. (th(x(t)))', = . х'(t).
ch~(x(t))
(6.18)
16. (cth(x(t)))', = х'(t).
sh~(x(t))
(6.19)
17. (Arsh(x(t)))', =
. х,'(t)
(6.20)
18. (Arth(x(t))),' = х'(t).
1 — (x(t))2
(6.21)
6.5.
ЛОГАРИФМИЧЕСКОЕ
ДИФФЕРЕНЦИРОВАНИЕ
Если функция представляет собой произведение (или
отношение) большого количества функций или функцию
в степени функция, то удобно применять логарифмическое
дифференцирование по следующим алгоритмам.
1. Если у(х) = &l ;р "д х . <р~(х ..... q
то ln(y(x)) = т1псрд(х) + ling>z x + . + klnq&g ; (x и по
лу дифференцирования сложной функции
т
у~(х) = дрдх(х)+ (pgz(x) + ° .. + (p~z(x)~
г
y(x) e (» др~(х) др„(х)
6.4.
ИНВАРИАКТКОСТЬ ФОРМЫ
ПЕРВОГО ДИФФЕРЕНЦИАЛА
Теорема 6.4. Пусть функция х = q> t) дифференцир
ма в некоторой точке to, а функция у = f(x) дифференци-
руема в соответствующей точке хо = q>(t ), то да пер
дифференциал может быть представлен и как произведе-
ние производной по t на дифференциал по t: dy = f,'(x(t))dt,
и как произведение производной по х на дифференциал по
х: dy = f (õ)dõ. (Это свойство называется инвариантностью
формы первого дифференциала.)

217
ГЛАВА б. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ
отсюда
О,(Х) = Х(Х) - „.(Х),. ',2.(Х) О- ... О- " 02„,(Х)],
(р1 (х) (р2 (х) (р„(х)
подставляя вместо у(х) ее выражение в виде произведения
функций, получим
y'(x) — (р, (х) . (p> x) . .. (р„ х
О О2.(Х)+ М.(Х)+ "+ ОО.'.(Х)]
(р1(х) (р2 х) (р„х)
2. Если
(р,(х) (р2(х).... (р„(х)
ух =
и,(х).и2(х).... ид(х)
то 1n(y(x)) = 1п(р,(х) + 1n(pq(x) + ° ° ° + 1п(рд(х) 1пи1(х) 1пи~(х)
— ... — 1пид(х) и по правилу дифференцирования сложной
функции
у„(х) = (р1, (х) + (р2„(х) + ". + (р„„(х)—
у(х) (pq(x) (pq(x) (р„(х)
— и,', (х) — и2, (х) —... — и р„(х) 2
и,(х) ' и, х ' ид(х
отсюда
у.(х) =у(х). (р,„(х)+ (р2„(х)+...+ (р„„(х)—
(р1 (х) (р2 (х) (p„(х)
— ОЭ! (Х) — 022 (Х) —...— 202*(0))
и1 х) и2 х) ид х
( ) Vi(x) q2(x) " (рп(х) 1 ( ) 1 ( )
ид(х)'и2(х)'...'ид(х) щ(х) (р2(х)
(Х) — 0ll (Х) — 202 (Х) †...— 022,(X))
1, 1, 1 1
(p„(x) щ(х и2 х) ид(х)
3. Если y(x)=[(р,(х)12(02(~22 то1п(у(х)) = (p> x) In(p,(x)
правилу дифференцирования сложной функции
(р2 (х)
Х (Х) = ' 202*(0) 0 202*(&g ;) 10 22 (Х
у(х) (р1 х
подставляя вместо у(х) ее выражение в виде отношения
функций, получим

218
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗЩ~АЧ
отсюда
g,'(х)=х(х) .q',,(x)+qa*(x) )пф,(x)),
(р, (х)
подставляя вместо у(х) ее выражение, получим
у,'(х)=[<),(х)]~~ *~ q'„(x)+q(, х) )nq,(х
(р1 х
6.6.
ПРОИЗВОДНАЯ ФУНКЦИИ,
ЗАДАННОЙ ПАРАМЕТРИЧЕСКИ
Пусть функция задана параметрически:
х = x(t),
y=y(t) ~о <t
тоГда
у((~)
4(~)
(6.22)
6.7.
ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
ВЫСШИХ ПОРЯДКОВ
находится по одной из
следующих формул:
д~~ ~ у dy ~гд;
агу dt ~~г dt ~~г
dx2 г
dt
(6.2З)
Определение 6.6. Пусть функция у = f(r) дифференци-
руема, тогда производная от производной этой функции
называется второй производной и обозначается и вычис-
ляется: у," =(f.(х))'.
Механический смысл второй производной заключает-
ся в следующем. Вторая производная пути s(t) по времени
t движущейся прямолинейно материальной точки равн®
мгновенному ускорению этой точки: s,'(t) = а„„„.
Вторая производная от функции, заданной параметри-
чески,

219
ГЛАВА 6. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ
Определение 6.7. Пусть существует производная
(и + 1)-го порядка для функции у = f(x). Тогда дифферен-
циалом (и + 1)-го порядка называется дифференциал от
)(ифференциала и-го порядка d"+ '(f(x)) = d"(f(x)).
Если х — независимая переменная, то
d" ' '(f(x)) = f("")(x)dx.
Производные п-го порядка для основных элементарных
функций:
(а')(") = а'(1па)", а & t; О  &
(sin х)(") = sin (х + пя/2),
(cos x)(") = cos (х+ пя/2),
(х )(") = т(т — 1)(т — 2) ... (т — п + 1)x
(1nx)(") = ( — 1)" '(п — 1)I/õ".
Формула Лейбница для производной п-го порядка от
произведения функций:
(ии)" =„( )U+ — и(" ')и'+ „( 2)(,"+...+
и,, пп — 1
11 21
п(п 1) (п k+1) („„) („) („)
п1
(6.24)
6.8.
ТЕОРЕМЫ РОЛЛЯ, ЛАГРАНЖА, КОШИ
Теорема (Ролля) 6.5. Пусть выполняются условия:
а) функция у = f(x) непрерывна на отрезке [а; Ь];
б) функция у = f(x) дифференцируема на интервале (а; Ь);
в) на концах отрезка функция принимает одинаковые
значения )"(а) = )"(Ь).
Тогда существует по крайней мере одна точка с с [а; Ь],
в которой производная равна нулю f'(ñ) = О.
Теорема (Лагранжа) 6.6. Пусть выполняются условия:
а) функция у = f(x) непрерывна на отрезке [а; Ь];
б) функция у = f(x) дифференцируема на интервале (а; Ь).
Тогда существует по крайней мере одна точка с с [a; Ь],
B которой f(b) — f(a) = f,'(c)(b — a).
Теорема (Коши) 6.7. Пусть выполняются условия:
а) функции у = f(x) и у = g(x) непрерывны на отрезке
[а; Ь];

220
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗА@~
б) функции у = f(x) и у = g(x) дифференцируемы на и
тервале (а; Ь).
Тогда существует по крайней мере одна точка с е [а; ь)
"b) -" ) = Й(с)
g(b) — д(а) g„'(с)
6.9.
ПРАВИЛО ЛОПИТАЛЯ
Теорема 6.8. (правило Лопиталя для раскрытия неопре-
деленностей типа «О/О»). Пусть выполняются условия:
а) функции у = f(x) и у = g(x) определены в некоторои
окрестности точки а, где а — число или символы +~~;
б) limf(x) =О, limg(x) =0;
х-~а х-~а
в) существуют производные f„'(õ) и g (õ) в упомянутой
окрестности, за исключением, быть может, самой точки а,
причем(f.'(х))2+ (g.'(õ))2 ~ 0 при х ~ а;
г) существует конечный или бесконечный предел
fõ( )
х-+а g (Х)
Тогда справедливо равенство
f( ),. П()
х-+а g(X) х~а gz(X)
Теорема 6.9. (правило Лопиталя для раскрытия неоп-
ределенностей типа «о~/о~»). Пусть выполняются ус-
ловия:
а) lim f(x) = lim g(x) = m;
х~а х~а
б) существуют производные f„'(õ) и g„'(х) в некоторой
окрестности точки а, за исключением, быть может, самои
точки а;
в) (f,'(х)) + (g,'(х)) w 0 в упомянутой окрестности;
г) существует конечный или бесконечный предел
fõ (х)
х-+а gz(X)
Тогда справедливо равенство
/(х) . /(х)
х~а g(X) х — +а g' (Х)

221
~л &lt НА 6. ПРОИЗВОД А И ДИФФЕРЕНЦ АЛ ФУНК
6.10.
ФОРМУЛЫ ТЕИЛОРА
И МАКЛОРЕНА
Теорема 6.10 (формула Тейлора). Пусть существуют
~качения f(x), f„'(х), ..., Д" '> x) на интерв ле а; ). Пу
— любое значение из упомянутого интервала. Тогда
Справедлива формула Тейлора
f(x)=f(xp)+ " (х — xp)+ " (х — xp)~+
(и)
+...+ " о (х — xp)" +R„„(x),
и.
(6.25)
где остаточный член R„+ ~(х) может быть представлен в од-
ном из следующих видов:
а) в форме Шлемильха — Роша
( )и+1(1 Цп — рй
R„,(x)= f(x +О(х — xp)),
п&l
где р — произвольное положительное число, а Π— некото-
рое число, удовлетворяющее условию 0 & t  &
б) в форме Лагранжа
(х — xp)""
R„„(x) = f(xp+OI(х — xp)),
(и+ 1)!
где 0& t; Ђ” некото ое чис о, удовлетворяю ее усло
0 & t; e &
в) в форме Коши
В„+~ (х) = f (xp + 0g (x — xp )),
(х — xp)""(1 — О~)"
п~
f(x) = f(0)+ " х+, х~+...+ ' х" +R„„(x) (6.26)
п~
@ носит название формулы Маклорена.
&gt де 0&g ; — нек торое исло, удовлетво яющее у
0&l ;0
г) в форме Пеано В„+ ~(х) = о((х — xp)").
При xp = 0 формула Тейлора имеет следующий вид:

222
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАд,~
ТАБЛИЦА РАЗЛОЖЕНИЙ
ОСНОВНЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
ПО ФОРМУЛЕ МАКЛОРЕНА
х х2 х"
1 ° е' =1+ + +" + — +~,~(х), — o&l ;x & t;+oo
1! 2! и!
хз х5
2. з~пх=х +
!
ц 1 х2в-1
...+( — 1)" ' +RÄÄ(x), — oo & t x &l
(2и — 1)!
(6.28)
Х2 Х4
3. ~о~х=1, +
х2в
...+( — 1)" +R„,1(х), — oo &l ;x &l
(2n)!
(6.29)
4. (1+х) =1+ — х+...
1!
т(т — 1)(m — 2)... (т — и + 1)
...+ Х +
GI
+R„„(x), — 1&l ;х
(6.30)
Х2 ХЗ Х4
5. 1n(1+x) =х + +...
2 3 4
(6.31)
6.11.
УРАВНЕНИЯ КАСАТЕЛЬНОЙ
И НОРМАЛИ К ГРАФИКУ КРИВОЙ
Уравнение касательной к кривой у = f(x) в точке (xo&
f(x)), если она не параллельна оси ординат, т. е. если
f„'(õ) ~+с~, таково: у = f(xp) + f„'(xp)(x — xp). Если же каса-
тельная в точке (xp,' f(xp)) параллельна оси ординат, то ее
уравнение х = х().
Уравнение нормали (т. е. прямой, перпендикулярной
касательной) к кривой у = f(x) в точке (xp, f(xp)), если эта
нормаль не параллельна оси ординат, т. е. если f '(х) g О,
таково:

223
ГЛАВА 6. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ
у = f(xp) —, (х — xp).
1
С(хО)
ясли же нормаль в точке (xp, f(xp)) параллельна оси орди-
нат, то ее уравнение х = хд.
Определение 6.8. Углом между кривыми у = /,(х) и
у = (в(х) в их общей точке Mp(xp' gp) называется угол меж-
ду касательными к этим кривым в данной точке Mp(xp, yp).
6.12.
ИНТЕРВАЛЫ МОНОТОННОСТИ,
ЭКСТРЕМУМЫ
Определение 6.9. Функция у = f(x) называется возрас-
тающей (убывающей) на интервале (а; Ь), если для любых
х,, х2 е (а; b) е ОДЗ, удовлетворяющих неравенству х1 & t;
выполняется неравенство /(х1) о /(х2) (((х1) & t; /(х2
Теорема 6.11 (критерий возрастания или убывания
функции на интервале). Для того чтобы функция у = f(x),
имеющая конечную или бесконечную производную на ин-
тервале (а; Ь) е ОДЗ, возрастала (убывала), необходимо и
достаточно, чтобы на этом интервале выполнялись усло-
вия: а) f,'(х) ) 0(f,'(х) & t; ); б) f„' õ) необращала ьв н ль
на одном отрезке (а; р) е (а; Ь) е ОДЗ.
Определение 6.10. Функция у = f(x) имеет локаль-
ный максимум (минимум) в точке х = а, если для лю-
бых значений из окрестности этой точки, принадлежа-
щих ОДЗ, таких, что х w а, выполняется неравенство
«x) & t; ( а) (f x >
Теорема 6.12 (о необходимом условии экстремума функ-
ции). Если в точке х = а существует экстремум функции
y = f(x) то в этой точке должно выполняться одно из ус-
ловий:
а) производная в этой точке равняется нулю f,'(а) = 0;
б) производная в этой точке не существует, но функ-
ция у = f(x) в этой точке непрерывна.
Определение 6.11. Точки, которые удовлетворяют не-
обходимому условию экстремума, называются критиче-
скими точками первого рода.
Теорема 6.13 (первое достаточное условие существова-
ния точки экстремума по первой производной). Если при

224
HPAKTH×ÅÑÊÎÅ РУКОВОДСТВО К РЕШЕНИЮ ЗАДА
6.13.
НАИБОЛЬШЕЕ
И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ
НЕПРЕРЫВНОЙ ФУНКЦИИ
НА ОТРЕЗКЕ И ИНТЕРВАЛЕ
Определение 6.13. Число M(m) называется наиболь-
шим (наименьшим) значением непрерывной функции /(х)
на [а, Ь], если для Чх е [а, Ь] справедливо неравенство
f(x) & t M (f x &g
Теорема 6.16. Непрерывная на отрезке функция дос-
тигает своего наибольшего и наименьшего значений либо
на концах отрезка, либо во внутренних точках локальнь~~
экстремумов.
Определение 6.14. Наибольшим (наименьшим) значе
кием непрерывной функции f(x) на интервале (а; Ь) назо
вем значение ее глобального максимума (глобального ми
нимума), если он существует.
и
Замечание. Наибольшего или наименьшего значени"
непрерывной функции /(х) на интервале (а; Ь) может н~
существовать.
переходе слева направо через критическую точку перво „
рода первая производная меняет свой знак с плюса на ]~„
нус, то эта точка является точкой максимума, если с мин
са на плюс, то минимума.
Теорема 6.14 (второе достаточное условие существова-
ния точки экстремума по второй производной). Если вто-
рая производная имеет в критической точке первого рода
знак плюс (f" (x) &gt 0) т в э ой то ке миним м, е ли
минус (f"(õ) & t; ), т в э ой то ке Ђ” максим
Теорема 6.15 (третье достаточное условие существова-
ния точки экстремума по и-й производной). Если (и + 1)—
четное число, ~ц(а) = ~@(а) = P3~(à) = ... = f "'(à) = 0, а не-
прерывная в точке х = 0 производная P" + 1~(а) & t; О, т в т
ке х = а — минимум, если же P" ' "(а) & t; О, т в э ой то
максимум.
Определение 6.12. Наибольший (наименьший) из всех
локальных максимумов (минимумов) называется глобаль-
ным максимумом (глобальным минимумом).

[' ЛАВА б. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ
225
6.14.
ИНТЕРВАЛЫ ВЫПУКЛОСТИ,
ВОГНУТОСТИ, ТОЧКИ ПЕРЕГИБА
Определение 6.15. Функция у = f(x) называется выпук-
лой (вогнутой) на интервале (а; Ь) ~ ОДЗ, если для любых
X E (а; Ь) график линии у = f(x) располагается выше (ниже)
любой своей хорды, принадлежащей (а; P) ~ [а; Ь] или ниже
(выше) любой своей касательной на (а; P) ~ [а; Ь].
Определение 6.16. Пусть для плоской кривой у = ((х)
выполняются условия:
1) функция у = f(x) непрерывна в точке х = с;
2) в точке Р(с; f(c)) кривая имеет единственную каса-
тельную;
3) в достаточно малой окрестности точки Р(с; f(c)) кри-
вая расположена внутри одной пары вертикальных углов,
образуемых касательной и нормалью к кривой функции
у = f(x);
4) при переходе через х = с слева направо в некоторой
окрестности (с — 5; с + 5) е ОДЗ меняется выпуклость на
вогнутость или вогнутость на выпуклость, тогда точка P(c;
((с)) называется точкой перегиба функции у = f(x)
Если при х = с функция f(x) непрерывна, à f'(х) имеет
разрыв первого рода при х = с, тогда эта точка называется
угловой точкой графика функции (x).
Теорема 6.17 (о необходимом условии существования
точки перегиба). Если х = а — точка перегиба, то в этой
точке должно выполняться одно из условий:
а) вторая производная в этой точке равняется нулю
/„",(х) =О;
б) вторая производная в этой точке не существует, но
функция у = f(x) в этой точке непрерывна и в ней сущест-
вует единственная касательная к графику у = ((х).
Определение 6.17. Точки, которые удовлетворяют не-
обходимому условию существования точки перегиба, на-
зываются критическими точками второго рода.
Теорема 6.18 (первое достаточное условие существова-
ния точки перегиба по второй производной). Если в точке
х = а функция непрерывна и в ней существует касатель-
ная, а вторая производная IIpH переходе слева направо

226
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
через критическую точку меняет свой знак, то эта точ~а
является точкой перегиба.
Теорема 6.19 (второе достаточное условие существова-
ния точки перегиба по и-й производной). Если (и + 1)—
нечетное число, P "(а) = P~~(a) = ~~'(а) = ... = ~"'(а) = o,
P" + "(a) w О, то точка x = а является точкой перегиба функ-
ции у = f(x).
6.15.
ОБЩАЯ СХЕМА
ИССЛЕДОВАНИЯ ФУНКЦИЙ
И ПОСТРОЕНИЯ ГРАФИКОВ
1. Найти область допустимых значений аргумента
(ОДЗ = D(f)).
2. Исследовать на четность — нечетность.
Определение 6.18. Функция у = f(x) называется четной,
если при любых х е ОДЗ и ( — x) е ОДЗ выполняется равен-
ство f(-х) = ((х).
График четной функции симметричен относительно
оси ординат. ОДЗ четной функции симметрична относи-
тельно начала координат.
Определение 6.19. Функция у = f(x) называется нечет-
ной, если при любых х E ОДЗ и ( — х) е ОДЗ выполняется
равенство f( — х) = — ((х).
График нечетной функции симметричен относительно
начала координат. ОДЗ нечетной функции симметрична
относительно начала координат.
Определение 6.20. Функция у = f(x) называется функ-
цией общего вида, если существуют х,, х2 c D(f): — x&g
х2 е Л(Д и f(») Ф f( х1), ((х2) Ф f( х2).
3. Исследовать на периодичность.
Определение 6.21. Функция у = f(x) называется пе-
риодической, если существует такое число Т ) О, что при
всех х с ОДЗ w х+ Т с ОДЗ и выполняются равенства
f(x+ Т) = f(x).
0пределение 6.22. Наименьшее положительное числ0
;(') О, удовлетворяющее определению 6.19, называетс~
периодом функции /(х).
4. Исследовать на непрерывность и точки разрыва.

227
I'ËAÂA б. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ
Точки разрыва ищутся там, где функция не существу-
ет или меняет свое аналитическое выражение. В этих точ-
ках находятся односторонние пределы. Если они не суще-
ствуют, равны бесконечности или не совпадают, то соот-
ветственно в этих точках разрыв второго или первого рода.
Если же односторонние пределы равны друг другу, но не
совпадают со значением функции в этой точке, то в данной
точке функция имеет устранимый разрыв.
Теорема 6.20. Если в точке х = а функция у = f(x) име-
ет производную, то в этой точке функция непрерывна.
Теорема 6.21. Элементарная функция непрерывна в тех
точках, в которых она определена.
5. Исследовать на асимптоты.
Определение 6.23. Асимптотой к графику функции
у = f(x) называется прямая Ах + By + С = О, при перемеще-
нии вдоль которой от начала координат в +~ или — Ос) мак-
симум отклонения графика кривой у = f(x) от прямой Ах +
+ By + С = О стремится к нулю.
Вертикальные асимптоты ищут в точках разрыва вто-
рого рода, на краях ОДЗ и в точках, где меняется аналити-
ческое выражение функций. При этом в этих точках нахо-
дятся односторонние пределы.
Если при приближении к точке а слева или справа од-
носторонний предел обращается в бесконечность, то с со-
ответствующей стороны от х = а прямая х = а является вер-
тикальной асимптотой.
Коэффициенты k u b наклонной асимптоты у = kx+ b
находятся по формулам:
f( )
lim (((х) — kx).
Х~+~ (ИЛИ -~)
Х~+ ~(ИЛИ -~) Х
Если k = О, то асимптота называется горизонтальной.
6. Исследовать на экстремумы и найти интервалы воз-
растания и убывания.
7. Исследовать на точки перегиба и найти интервалы
выпуклости и вогнутости.
8. Найти область изменения функции, точки пересе-
чения графика с осями координат и другие характерные
точки.

228
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДА~
6.16.
КРИВИЗНА КРИВОИ
(6.32)
(6.33)
с~х2
(6.34)
Х=х
Дх2
с~х2
Определение 6.24. Угол, образованный двумя касатель-
ными, проведенными из одной точки к данной кривой, кото-
рая не пересекает саму себя, называется углом смежности.
Определение 6.25. Кривизной кривой, которая не пе-
ресекает саму себя, называется предел отношения угла
смежности Ла к длине дуги Al, стягиваемой касательны-
ми, образующими угол Ла, при стремлении длины дуги к
нулю и если такой предел существует:
К = lim —.
Ла
л~- о Al
Определение 6.26. Величина, обратная кривизне, назы-
вается радиусом кривизны.
Определение 6.27. Окружность, находящаяся в облас-
ти вогнутости кривой, имеющая в данной точке кривой
общую касательную и радиус, равный радиусу кривизны,
называется окружностью кривизны. Круг, охватываемый
этой окружностью, называется кругом кривизны. Центр
круга кривизны называется центром кривизны.
Если кривая задана уравнением в декартовой системе
координат у(х) = f(x), кривизна, радиус кривизны и центр
кривизны соответственно вычисляются по формулам:
у2р
2

229
ГЛАВА 6. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ
Если кривая задана параметрически:
то кривизна, радиус кривизны и центр кривизны соответ-
ственно вычисляются по формулам:
d~P da dP d~a
(6.35)
R(t) =
~~~3 da ~~3 d2a
(6.36)
д~2 Д~ Д~ д~2
do,
~~~3 da д2„dp
,~~2 dt ~~2
Дд д До,
Y= ~~+
d P da d~a dP
(6.37)
~~2 Д~ ~~2
Если кривая задана уравнением в полярной системе
координат р = p(y), то кривизна, радиус кривизны и центр
кривизны соответственно вычисляются по формулам:
(p(cp))~ + 2. — — p(cp) .
8р dр
дф ~~2
К—
(6.38)

230
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗА,ЦАЧ
2 3/2
(p(v))'+—
дф
(6.39)
R((p) =
(2
(p(V)) 2 + 2 — р(&lt р
cE(p
р2 + р р соя(р+ — р- ып(р
Х = pcosy
dp ' . dp (6.40)
p2 + — - p Sin q) — — — COS(P
Дд дф
У = psiny
р2+2 — р
6.17.
РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ
ПРОСТЕЙШИЕ ЗАДАЧИ
НА ВЫЧИСЛЕНИЕ ПРОИЗВОДНОЙ
6.1. Найти приращение функции Л((х0, Лх) в точке х0,
если.'
а) f(x) = jx, хд — — 1, Лх =0,21;
б) f(x) = sin х, хд = л/2, Лх = л/3.
Решен и е.
а) Af(xp, Лх) = х0 + Лх —,/х0 — — 1+0,21 — Я = 0,1.
б) Л((х0, Лх) = sin(xq + Лх) — sin хз = sin(n/2 + л/3)—
— sin(n/2) = — 0,5.
6.2. Доказать, что если f(x) = 0 и
lim =О,тоlim — = f (0).
f(x) . f(x)
х «О Х х «О Х
Решение. Имеем
f(x+ Лх)—
' х =0 — — lim
Лх~О Ьх
f(hx) — 0
= lim
л о Ьх
1(х) . f(0+ Лх) — f(0)
лх-~о Ьх
= О.
((Лх)
«~о Лх

231
ГЛАВА 6. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ
6.3. Пользуясь определением производной, найти про-
изводную функции f(x) = cosmx.
Решение.
cos(mx+ Лх) — cosx
'х =lim
Акбар Ьх
— 2sin(mx+m/2 hx)sin(m/2 Лх)
= lim
Лх-+О
= — 2 lim sin(mx+m/2 Лх) lim
sin(m/2 Лх)
Лх-+О лх~о Ьх
= 2sin(mx) (т/2). lim
sin(m/2 Лх)
= — т sin(mx).
лр (т/2 Лх)
Здесь использовался первый замечательный предел
sinu
а-+О и
6.4. Пользуясь определениями левой и правой произ-
водных функции f(x) в точке хр найти их для
HX0
f(x) =
Решение.
f+(x) = lim
Лх-++О
Ьх
= lim
Лх~+0 ЛХ
=+ lim
Лх-++О
=+1.
6.5. Исходя из определения производной, доказать, что
производная четной (нечетной) дифференцируемой функ-
ции есть функция нечетная (четная).
Решение.
f( — х+ Лх) — f( — х)
f'( — х) = lim
Лх +0 Ьх
— f(x — Лх)+ f(x)
lim = f (õ), если f( — х) = — f(x),
~~o — ( — Лх)
/(х — Лх) — f( — х)
lim— = — f (õ), если f( — х) = f(x).
Лх — +Π— Ьх

232
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
/((х + Т) + Лх) — f(x+ Т)
' х+Т) = lim
Лх-~0 Лх
f((x+ dx)+ T) — f(x+ T) . ((х+ Лх) — f(x)
Лх-+О Лх
Лх-+О Лх
ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ
С ПОМОЩЬЮ ТАБЛИЦЫ ПРОИЗВОДНЫХ
И ПРОСТЕЙШИХ ПРАВИЛ
ДИФФЕРЕНЦИРОВАНИЯ
6.7. f(x) =4х~ — — — 8~х~ +10.
х7
Решение.
5
f (õ) =(4хз — 5x 7 — 8х6 +10)'= [((x)")'= nx" ', (const)'=О] =
5
=4(х )' — 5(x 7)' — 8(х6)'+(10)'=4 Зхз ' — 5.( — 7)х 7 '—
— 8.— х6 +0=12х +35х — — х 6 =12х +
5 - -1 2 8 20 -- 2 35 20
6 3 х8 36Я
Производная определена при х е (О; +m).
6.8. f(x) =Зх2 — 4х о'+7~х~—
х4
Решение.
Перепишем функцию так:
/(х) = Зх — 4х oë+ 7х~(~ — 8х ~Л
--1 4 41
f'(õ)=3 2х2 ' — 4 ( — 0,5)x о' '+7 — хз — 8 ( — — )х 5
3 5
=бх+ 2 + 32 +14 1
jx& t 5 х» ~
Производная определена при х е (0; +сс).
6 g. /(х) = 4х1п х+ 5
cosx
6.6. Исходя из определения производной, доказать, что
производная периодической функции есть периодическая
функция.
Решение.

I'JIABA 6. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ
Решение.
Рекомендуется воспользоваться правилами дифферен-
пирования суммы, произведения и частного функций.
1
(f(x))' = Ix lnx — 5
cosx
= [(uv)' = и'v+ uv', (и/ v)' =, (х)' = 1, (е" )' = е",
0
(lnx)' = 1/х, (cosx)' = — sinx] =
(е" )'cos х — е" (cos x)' 1
=(х)'inx+ x(lnx)' — 5 = 1.1nx+ х ——
соя2х
х
-5 2 = lnx+1-5
е".cosx — е" ( — sinx) е" cosx+ е" sinx
соя2 х соя2х
ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ
СЛОЖНЫХ ФУНКЦИЙ
6.10. f(x) = sin(x2).
P е ш е н и е. Данная функция — сложная двухзвенная:
первое внешнее звено — синус, второе внутреннее звено,
аргумент первого звена — это квадратичная функция. Про-
изводная сложной функции есть производная первого зве-
на по его аргументу с сохранением этого аргумента, умно-
женная на производную второго звена по х:
(f(x))' = (sin(x2))' = cos(x2) (х )' = cos(x2) 2х.
6.] ]. f(x) = tg(2" Jx).
Решение.
(2" Jx)' = ((2")' /x+2" ( /х)') =
cos~(2" . х) cos2(2" x)
(2" ln2 vx+2" ), xs(p;+on).
cos2(2" х) 2 х
Г(х) =
Нередко допускаются такие ошибочные решения.'
1. (f(x))' = cos х 2х. Здесь в производной первого звена
не сохранен его аргумент х2.
2. f'(х) = cos 2х. Здесь производная второго звена запи-
сана на месте аргумента первого звена.

234
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
6.12. Найти производную сложной трехзвенной функ.
ЦИИ
f(x) = arcsin( jl — е" ), х & t;
Решение.
Здесь первое внешнее звено — арксинус, второе — ко
рень квадратный, третье — сумма единицы и экспоненты
Дифференцируем последовательно:
f'(õ) =
1
(j] — е )'=
1
(1 — е")' =
1
2 1 — е"
Ех Ех/2
(Π— е")= =, x&lt
2~/~ 8х 2. ех/2 jl. 8» 2~/~ 8х
6.]3. f(x) =arctg
1оОз -х
х5
Решение.
(1ояз х) 'х 1ояз х'(х )
f'(õ) =
2
1+ 1оО3 х
(Х3)2
— — х -log3x 5х
5 4
xln 3
х е (p;+<
х10
2
1+ 1оО3 х
6.14. Найти производную функции
are tg(x2 sin(1/(5x))), х ~ О,
х =
О, х=О
и вычислить ее значение в точке х0 = О.
P е ш е н и е. Найдем производные при х е О. Имеем
f'(х) = (х2 sin(1/(5x)))' =
1+(х2 sin(1/5x))2
((х2)' sin(1/(5х)) + х2 (sin(1/(5x)))') =
1+ (х sin(1/(5х)))2
(2х sin(1/(5x))+ х . cos(1/(5x)) ( — 1/(5x2))) =
1+(х2 sin(1/(5х)))2
— 2х н!п(1!(Бх)) ], х sO.
1+ (х2 sin(1/(5х)))2
° ° ° ° °
5

235
ГЛАВА 6. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ
Поскольку односторонние пределы
lim sin(1/5x)
0+0
не существуют, то не существуют и односторонние преде-
лы у f'(х) при хд = О.
Чтобы найти производную в заданной точке, восполь-
дуемся определением производной.
2
1
arctg 0+ Лх яп — — — — — — — О
5(0+ Лх)
f'(0) = lim
Лх — +О
Поскольку предел произведения ограниченной функ-
ции sin(1/(5Ëõ)) на бесконечно малую Лх равен нулю, то
получаем, что у'(О) = О.
Заметим, что исходная функция f(x) непрерывна в точ-
ке хо = О. В самом деле, функция определена как в самой
точке х0 = О, так и в некоторой ее окрестности, кроме того,
limarctg(x sin(1/(5x))) =0= f(0).
х — +О
ctg(log& t; (arccos( 2" )
6.15. f(x) =
Решени е.
(f(x))' = ((1+ х+ х2)1~з)' ctg(log>(arccos(42 )
+ (1+ х+ х2)1~з(сФд(1од7(агссоя(42")))' =
= — (1+х+х') ~~~ (1+х+х2)' ctg(log,(arccos(4~"))+
3
(О+ 1+ 2х) . ctg(log7 (arccos(42"))—
1
(1+х+х2)~
(агссоя(42"))' =
sin~(logq(arccos(42"))) arccos(42') 1п 7
1 (1+ 2х) . ctg(log7 (arccos(4~" ))
3
(1+ х+ х2)'/з
(42z )'
sin2(log7(arccos(42"))) arccos(42 ) 1п7
+(> * x ) ~  ~ (1одт(агссон(4~* )
sin~(logq(arccos(4~)))
1/3

236
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
1 (1+ 2x) ctg(log>(arccos(4'
(1+ х+ хз)'/з 1
+
sin2(log7(arccos(42"))) arccos(4з") . 1п 7
1 (1+ 2х) ctg(logq(arccos(4з"))
3
(1+ х+ хз)'уз 1
+
4»1п4 2.
в1пз(1одс(агссов(4з"))) arccos(42") ln7
ИССЛЕДОВАНИЕ НЕУСТОЙЧИВОСТИ
ОПЕРАЦИИ ДИФФЕРЕНЦИРОВАНИЯ
6.16. Показать, что при и — э Ою значения двух функций
f(x) = О и g(x) = (1/п)в1п(я/6 + 2пзх) в точке х = я становят-
ся сколь угодно близкими друг другу, в то время как мо-
дуль разности их производных в данной точке стремится к
бесконечности.
P е ш е н и е. Имеем
lim ( д(тс) — f(n)( =lim — sin(n/6+ 2пзтс) — О = lim = О.
1
2
П -+ ~'-' п~х Q п~с~ 2П
Производные имеют вид f'(õ) = О, g'(õ) = 2п . сов(п/6+
+ 2пзх), в частности
f'(я) — = О, g'(и) =2п.сов(я/6+2пзя) =n j3.
lim )д'(тс) — f '(тс)( = lim ( n~3 — О (= ~с.
ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ
С ПОМОЩЬЮ ЛОГАРИФМИЧЕСКОГО
ДИФФЕРЕНЦИРОВАНИЯ
6.17. f(x) = x3cos'x(arctg х)'ln4x(arcsin х)'о.
Решение.
ln(f(x)) = ln(x3cos'x(arctg x)~ln~x(arcsin х)'о).
(ln(f(x)))' = (31nx + 51n(cos х) + 71n(arctg х) +
+ 41n(ln х) + 101n(arcsin х))'.
1, 1 1
(f(x))'=3 — +5 ( — sinx)+7.
1 1
+
f(x) x cosx arctgx
+4 — +10.
1 1 1 1
1пх х arcsinx

237
I'JIABA 6. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ
(f(x))' = (хз cos5 x(arctg х)' ln4 x(arcsinx)'~ ) X
3.— — 5. tgx+7
1
х
arctgx 1+х2
1 j
+4 - — +10
1 1
lnx x
arcsinx
6.18. /(х) =
Решение.
(ln(f(x)))' = 41n x+ 51n(1+ х) — — ln(x+ 8) — —. ln(x — 2)
1 1
2 2
1, 4 5 1 1 1 1
f(x) х 1+х 2 х+8 2 х — 2
х~(1+х)~ 4 5 1 1 1 1
+
х 1+х 2 х+8 2 х — 2
6.19. f(x) = х".
Решение.
lnf(x) =lnx", lnf(x) =xlnx.
(ln f(x))' = (xlnx)'.
f(x)
. (f(x))' = (х)' lnx+ х. (lnx)'.
1, 1
(f(x))' = 1. lnx+ х — = ln x+ 1.
f(x) х
(f(x))'= f(x) (lnx+1) =х" (lпх+1).
ВЫЧИСЛЕНИЕ ПРОИЗВОДНОЙ ФУНКЦИИ,
ЗАДАННОЙ НЕЯВНО
6.20. Найти производную у„'(х) функции /(х, у(х)) =
= у~(х) + х~ — 1 = О, заданной неявно.
P е ш е н и е. Будем искать производную от обеих частей
равенства. Имеем (у~(х) + х~ — 1)„' = (О)„', 2 у(х) у„'(х) +
+ 2. х = 0. Здесь выражение у~(х) рассматривалось как
сложная двухзвенная функция: возведение во вторую сте-
пень — первое внешнее звено, у(х) — второе внутреннее
звено. Отсюда у„'(х) = — х/(у(х)).

238
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
6.21. Найти производную у (x) функции f(x, у(х)) =
= 1n у(х) + ctg x~ — 2x = О, заданной неявно.
Решение.
(1n у(х) + ctg x~ — 2x)' (0)'
у„'(x) 2 =О,
у(х) sin~ x~
отсюда у(х) = y(x) (2x/(sin~x~) + 2).
6.22. Найти производную y (x) функции
f(x,у(х)) = еУ'~"~ — arcsiny(x) — х — 1 = О,
заданной неявно.
P е ш е н и е. (е~ ~"& t; Ђ” arcsiny x) Ђ” x3 Ђ” 1 „ = (0)
у(х)
2у(х) у (х) е~ ~"&
Зх2 =P,
отсюда
зх2
у(х) =
2 у(х) е~ '"'
ВЫЧИСЛЕНИЕ ПРОИЗВОДНОЙ ФУНКЦИИ,
ЗАДАННОЙ ПАРАМЕТРИЧЕСКИ
6.23. Найти производную у(х) функции x(t) = t~,
(t)
Решение.
(»nt3)I З~Р
y„'х=
(t2)'
6.24. Найти производную
y(t) = arcctg t4.
Решение.
(arcctg t4)',
у„'х=
(ctg t~)',
= —.1.cos1 .
° соя~ 3 з
2t
у„'(х) функции x(t) = ctg t,
1+ ~8
3'"' . »3 ( — sin t)
— 3cost ]п3 я~в t
1
/1:Р
4~з
2t2 . сдп2 ~2
° 2t
Я1П
6.25. Найти производную у„' функции x(t) = arcsin &l
у = 3'"'
Решение.
(3сов1 )~
y„'х=
' (arcsint),'

239
1 ДАВА 6. ПРОИЗВОДНАЯ И ДИффЕРЕНЦИАЛ ФУНКЦИИ
ОПРЕДЕЛЕНИЕ КАСАТЕЛЬНОЙ И НОРМАЛИ
К ГРАФИКУ ФУНКЦИИ
fj'(õ;) — Я(х;) (2х; — 2) — ( — 2х; + 4)
tgo.; =
1+ ((х; ) Я(х; ) 1+ (2х; — 2)( — 2х; + 4)
( =1,2).
1+ (2х; — 2)( — 2х; + 4)
Имеем tg а~ = 6/7, а~ = arctg (6/7), tg а~ = — 6/7, а~ =
— arctg 6/7.
ВЫЧИСЛЕНИЕ
ПЕРВОГО ДИФФЕРЕНЦИАЛА
6.30. Найти первый дифференциал для функции
d arctg
6.26. Составить уравнения касательной и нормали к
кривой у = f(x) = 2хз — х — 4 в точке хд = 1.
P е ш е н и е. Найдем производную и вычислим ее зна-
чение и значение функции в заданной точке: f'(õ) = бх~ — 1,
((1) = — 3, f'(1) = 5.
Уравнение касательной у = — 3 + 5 (х — 1) = 5х — 8. Урав-
нение нормали у = — 3 — (1/5)(x — 1) = — 0,2х — 2,8.
6.27. Написать уравнение касательной к графику функ-
ции f(x) = (х' — 1)/5 в точке его пересечения с осью абсцисс.
P е ш е н и е. Найдем координаты точки пересечения
кривой с осью абсцисс: f(x) = (х — 1)/5 = О, хд = 1, уд = О.
В этой точке производная f„'(х) = х' равна f„'(1) = 1. Урав-
нение касательной имеет вид у = х — 1.
6.28. Определить, под каким углом график кривой
f(x) = е" — х пересекает ось ординат.
P е ш е н и е. f„'(х) = е" — 1, f„'(0) = е~ — 1 = О, отсюда угол
пересечения равен а = О'.
6.29. Найти углы, под которыми пересекаются кривые
f(x) = — х~ + 4х+ 4 и f(x) = х~ — 2х+ 4.
P е ш е н и е. Найдем абсциссу точки пересечения кри-
вых: — х + 4х+ 4 = х — 2х+ 4, х1 = О, х2 = 3. Тангенс угла
между касательными в каждой точке определяется угло-
выми коэффициентами касательных:

240
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
Решение.
v(x)du(x) — u(x)dv(x) v(x)du(x) — u(x)dv(x)
v~(x) v~(x)+u~(x)
(и(х))
6.31. Найти первый дифференциал функции у(х) =
= ез"1п (1 + х~) и вычислить его значение при х = О, dx =
= Лх=0,1.
P е ш е н и е. Первый способ, основанный на непосред-
ственном применении формулы dy(x) = у'(x)dx.
Имеем
2 езх -2х
у'(х) =Зез" 1п(1+х~)+
+х2 '
отсюда
2 езх 2х
Уу(х) = (Be~* )п(1 + х') + de.
1+х2
Второй способ основан на применении правил нахож-
дения дифференциала произведения:
dy(x) = Ш(ез")1п(1+ х~)+ ез"Ш(1п(1+ х~)) =
ЕЗх 2.1.
= Зе01п(1+ х')Шх+ dx,
1+х2
dB(0)=(Bee~)п(1-';0')+ ' 01=0.
ез02 0
1+ 02
6.32. Найти первый дифференциал функции у(х) =
arctg (1/х) и вычислить его значение при х = 1, dx =
= Лх =-0,1.
Решение.
Шу(х) =
1
. ( — 1/x~)dx =—
1+1/х'
( 0,1) =0,05.
12+1
dx,
х2+
dy(1) =

241
I'ËÀÂÀ 6. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ
6.33. Получить приближенную формулу
"Х" +АХ =ХО+
Лх
0 - 0 их.1
0
при условии хе & t; О, [ х « х
P е ш е н и е. dy(x) = Лу(х) = у(х+ Лх) — у(х), отсюда
у(х + Лх) = у(х) + у'(х)Лх.
В случае у(х) = ~х, получаем
1
п,~ 1
"х+Лх =~х+ — -х .Лх.
И
ЕСЛИ Х = Х0", тО
= хо(Я+ — Лх/х" ) = хе +
и их"
0
XO
6.34. С помощью первого дифференциала вычислить
,/25,2.
Решен ие.
f(x+ Лх) = f(x) + f '(õ) . Лх = ~/25 + . 0,2 = 5,02.
2 25
ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ
И ДИФФЕРЕНЦИАЛОВ ВЫСШИХ ПОРЯДКОВ
6.35. Найти вторую производную от функции у(х)
x~ln(1+ sin х).
Решение.
у'(х) = 2xln(1+ sin х) + х~ .
1+ sinx
) 2l (1 . ) 2x.cosx 2xcosx
1+ sinx 1+ sinx
— sinx(1+ sin x) — cos~ х
+х2. =21n 1+sinx +
(1+ sinx)~
+ Х = 41П(1+ $1ПХ) +
4х cosx z (1+»») ..... 4х.cosx — х
1+ sin x (1+ sin x)2 1+ sinx
6.36. Найти у"(х) = f(e2').
Решение.
у'(х) = f'(е~') . (е~')' = ((е2) е2 . 2,
у"(х) = f"(е~") е" 4+ f'(е~ ) . е2' 4.

242
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
6.37. Найти вторую производную у"(х) от функции
arctg (2у(х)) + у(х) — х = О, заданной неявно.
Решение.
1+ у~(х) 3+ у~(х) — 2
2 1 3+ у~(х) 3+ у~(х) 3+ у~(х)
1+ у~(х)
у'(х) =
6.38. Найти вторую производную от функции, задан-
ной параметрически x(t) = 1n t, y(t) = Р+ 2t — 3+ 7.
Решение.
gc (~~+2~ — 3)t ЗР+2 з
х,' (1n t),' 1
t
(У,'),' (3t3+2t),' 9Р+2 9 з
х,' (1nt)c 1
t
6.39. Найти первые три дифференциала функции у =
= х2 — 2х+- 3
Решение.
dy = (х~ — 2»+ 3)'dx = (2х — 2)dx,
d~y = (2х — 2)'(dx)~ = 2(dx)~,
зy = (2)'(dx)3 = 0 (dx)3 = 0.
6.40. Найти четвертый дифференциал функции у =
= хЗ] х
Решение.
dy = (хз 1n x)'dx = Зх~ . 1п х+ хз — dx = (3»~ ]n» + х~ ) . d»,
х
Уу=((31пх+1)х )'.(dx) = — х~+(31пх+1)2» .(d»p =
х
= (бх. in»+5») (dx)~,
(arctg(2y(x)) + у(х) — х) = (О),
. y'(х} + и'(х) — 1 = О,
1+ у~(х)
I
у (х)=(1)' — =2 2у'(3+у~) ~ =
я+ 2
1+у
3+ у~ 4. (1+ у~ }
(3+ 2)2 (3+ 2)з

243
1 ЛАВА 6. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ
азу=(6х1пх+5х)' (dx)3 = 61пх+бх — +5 .(dx)3 =
1
Х
= (61пх+11). (dx)3,
d4y = (61п х+ 11)' (dx)4 = —. (dx)4.
Х
6.41. Найти и-й дифференциал функции у = е~".
Решение.
dy = (е'")'. dx = 5e5"dx,
d~2&g ; = 52е'"(d )2 d~" gt;у= 5"е'
ПРИМЕНЕНИЕ ТЕОРЕМ РОЛЛЯ,
ЛАГРАНЖА, КОШИ
6.42. Удовлетворяетлифункция f(x) =1 — ~x2 наотрез-
ке х c [ — 1; 11 теореме Ролля?
P е ш е н и е. Функция непрерывна на отрезке х c [ — 1;
11, так как она элементарная и определена во всех точках
этого отрезка. На концах отрезка f( — 1) = f(1) = О. Сущест-
вует производная f'(х) =
3з/х
на интервале х c ( — 1; 1), кроме внутренней точки х = О. Не-
обходимые условия теоремы Ролля не выполнены.
6.43. Доказать, что для функции f(x) = х~ + 3 выполня-
ются все условия теоремы Лагранжа на отрезке х c [ — 1; 21.
Найти точку с, в которой справедливо равенство
f(2) — f( — 1)
2 — ( — 1)
P е ш е н и е. Функция непрерывна как элементарная,
определенная во всех точках отрезка. Производная f'(õ) =
= 2х существует и конечна во всех точках интервала
х E ( — 1; 2), все условия теоремы Лагранжа выполнены.
Имеем f(2) — f( — 1) = 2с(2 — ( — 1)), или (22 + 3) — (( — 1)2 + 3) =
= 2с(2 — ( — 1)), отсюда с = 1/2.
6.44. С помощью теоремы Лагранжа доказать спра-
ведливость неравенства (arctga — arctgb( & t; (Ь Ђ” а! ри
быхаиЬ.
P е ш е н и е. Функция f(x) = arctg х непрерывна на лю-
бом отрезке х ~ [а; b] и дифференцируема внутри него,

244
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ 3АДАЧ
значит, все условия теоремы Лагранжа выполняются дл~
этой функции, поэтому существует такая точка с с [а; b)
в которой справедливо равенство ((агсСд с)'! = ((arctg b—
— arctg а)/(Ь вЂ” а)!, или fl/(1 + с2)[ = /(arctg Ь вЂ” arctg а)/(Ь вЂ” а)!
Поскольку !1/(1 + с2)f & t 1 ри лю ых действитель ых с,
farctg а — arctg bf & t; /b Ђ”
6.45. С помощью теоремы Лагранжа доказать следую-
щее утверждение. Пусть функции f(x) и g(x) определены и
дифференцируемы при любых значениях х & t  и пу ть
полняются соотношения /(а) = ~(а), f'(õ) & t; g' х) р  &
тогда справедливо неравенство /(х) & t; ~ х) р  &
Р е ш е н и е. Составим функцию h(x) = f(x) — g(x). На
произвольном отрезке [а; х] справедлива теорема Лагран-
жа и существует некоторая точка с, в которой выполняет-
ся равенство h(x) — h(a) = h'(с)(х — а).
Поскольку Ь(а) = f(a) — д(а) = О, а'(с) = f'(ñ) — g'(ñ) & t;
х — а & t; О, то h x  gt; 0 п и х > а и f( ) & t  (x
6.46. Пусть функции a(x) и р(х) удовлетворяют следую-
щим условиям:
1) a(x) и р(х) п-кратно дифференцируемы;
2 a'~(хе) = ф~(хе), где т = О, 1, ..., п — 1;
3) a~"> x > "~( ) п и х
Тогда справедливо неравенство a(x) & t; р х) р  &g
Ре ш е н и е. Рассмотримфункцию fC" '~(х) = а'" '~(х)—
— ф" '~(х) и применим к ней теорему Лагранжа на отрезке
[хе, х]: f " '~(х) — p" '~(хе) = p"~(ñ)(õ — хе), в силу условий 2)
и 3) получаем P" '> х  gt; О п и х > хе. А алоги
доказать, что f(x) & t; О, ли a x > р(х , п и х
6.47. С помощью теоремы Лагранжа доказать неравен-
ство е" & t   1 р  &
P е ш е н и е. Составим функцию f(x) = е" — х — 1, эта
функция удовлетворяет всем условиям теоремы Лагран-
жа на любом отрезке [О; х], где О & t; х. Существ ет то к
(О «x), где справедливо равенство (е» вЂ” х — 1) — (eo — Π— 1) =
= (e' — 1)(х — О), отсюда е' — х — 1 & t О р  &
6.48. Используя постоянство производной функции
arcsin х + arccos х на отрезке х е [ — 1; 1], доказать справед-
ливость равенства arcsinx + arccos х = н/2.

245
ГЛАВА 6. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ
Решение. Имеемдля
f(x) =arcsinх+arccosх f (õ) =
=0
P е ш е н и е. Функции f(x) = sin х и g(x) = cos х диффе-
ренцируемы всюду на R, следовательно, они дифференци-
руемы и непрерывны при х с [0; и/2] и д(н/2) е g(0). В со-
ответствии с формулой теоремы Коши составим уравнение
(sin x)' а1п(п/2) — sinO y~
— с1~с = — 1, c = —.
(cosx)',, сов(п/2) — cosO 4
ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ
С ПОМОЩЬЮ ПРАВИЛА ЛОПИТАЛЯ.
НЕОПРЕДЕЛЕННОСТЬ ВИДА «О/Q»
х4 1
6.50. lim
х~1 1п х
P е ш е н и е. Проверим условия применимости прави-
ла Лопиталя: 1) имеется неопределенность
x41 0
lnx, 0'
2) функции х4 — 1 и 1п х дифференцируемы в окрестности
точки х = 1; 3) (1пх),', w О; 4) существует предел
(х4 — 1)' . 4хз
lim, = lim = lim4x4 = 4.
х~1 (1пх)' х-+1 1/х х-+1
4 1 (x4
Отсюда iim = »m, =4.
х-+1 1пх х-+1 (1nx)'
при х ~ ( — 1; 1), отсюда при х E ( — 1; 1) функция f(x) =
= arcsin х+ arccos х = const и в силу прерывности этой
функции на отрезке х c [ — 1; 1] заключаем, что f(x) =
= arcsin х + arccos х = const всюду при х c [ — 1; 1].
В точке х = 1 получаем f(1) = arcsin 1 + arccos 1 =
= const = н/2.
6.49. Доказать, что для функций f(x) = sin х ид(х) = cos x
выполняются все условия теоремы Коши на отрезке
х с [0; н/2]. Найти точку с, в которой справедливо равен-
f'(ñ) /(тс/2) — f(o)
g'(ñ) д(тс/2) — g(0)

246
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
Q.5j lim Ç
«~1 sin 2т~х
Решен и е.
я1пЗнх, . (я1пЗнх)',. Зн соя Знх 3
llm = 0 Oj=lim , = llm
x~1 я1п 2нх xwl (я1п 2нх)' x~i 2н. соя 2нх 2
НЕОПРЕДЕЛЕННОСТЬ ВИДА «со/со»
lim 1пх
х — ++о Х
Решение.
lim =(<n/ ю = l m = i = im Ђ”
lnx . (lпх)' . 1/х
х-++х Х х ++ao (Х)' х~&lt - 1 х~ л
6.53. »m —.
«~x Е
Реш ен и е.
lim — = (с~/с~) = lim = lim — = О.
х . (x) . 1
х-~х Е» (е" )' x ~ac е'
НЕОПРЕДЕЛЕННОСТЬ ВИДА «О со»
6.54. lim (х — и/2).tgx.
х-+ л/2
Решение.
х-н/2
lim (х — тс/2) tgx=(0 ~) = lim
х — +л/2 х-+л/2 Ctg Х
=(О/О)= lim, = lim
(х — тс/2)'
х — +л/2 (Ctg Х) х-ьл/2
1
1
81п2х
6.55. lim (lпх lп(х — 1)).
х +1+0
Решение.
1
zw1+0 1 ' «~1+0 1 х — ~1+0 Х вЂ” 1
1пх
х1п2 х
2ln х
= lim =(О/О) = lim — = lim 2хlпх=О.
1п2 х . х
х +1+01 1
х~1+О 1 х-+1+0
х х2
lim (lпх ln(x — 1))=(0 (~)) = lim
ln(x — 1)
= (-сю/ — oo) =
х-+1+0 х +1+0 1
1пх

247
ГЛАВА 6. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ
НЕОПРЕДЕЛЕННОСТЬ ВИДА «~о — m»
6.56. »m — — „
1 1
х — эо х
Решение.
— — = (с~ — ~о) = lim = (0/0).
1 1 е" — х — 1»
х — эо х х~о х(е — 1)
Дважды применим правило Лопиталя:
lim = lim = (0/0) =
о (х(е — 1))' ~~о е" — 1+ хе"
(е" — 1)' . е" 1
=lim, =lim
x~o(e* — 1+хе")' * ое" (х+2) 2
6.57. lim (e" — Б).
х ~+оо
Решение.
lim (е* — jx ) = (со — со) = lim е" 1 ——
х ~+~о х — ++m е"
Поскольку
lim — =(~/< )= l m = im
,Я . ( /х)' . 1
х-++~с Я + (е*)' * ' 2 /хе*
то
lim 1 — — =1
lim е" 1 — = lim е" lim 1 — — = lim е*.l=+&lt
х — +~ х — ++о". х — ++оо х-++ а
НЕОПРЕДЕЛЕННОСТЬ ВИДА «Оо,&
6.58. »m хх.
х-++О
Решение.
6.59. lim(1 — cos х)*.
х — +О
(1n х)' . 1/х
lim xlnx lim —, ~im z ijm ( — х)
П1 Xx e»-++о = Ех — ~+о(1/х)' eõ — «-' — 1/х' e» —. «о ео 1
х-++О

248
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
Решение.
lim х1п(1 — cos X)
lim(1 — cosx)* = (Оо) = е-0
х — +О
Найдем отдельно
Х Х
= — 1пп
2 2 .. «/2 х
х -2sin — cos—
= — lim2x - lim -limcos — =0.
х-эО съ 2 Х х-+О х/2-+О - Х х-+О 2
2Я1п— БП1—
2 2
Здесь использовался первый замечательный предел
lim . =1.
a~o sinu
о
Отсюда е-' О 1
НЕОПРЕДЕЛЕННОСТЬ ВИДА «1" э
6.60. lim(cosx)'/* .
х-++О
Решение.
ln cosx
lm
lim (cos x)'/" = (1 ) = е "'
х-++0
sinx
ln cos x . (1п сов ») 1. cos x 1
lim = lim = lim
x~+0 «2 x~+0 («2)' x~+0 2х 2 '
1' ( )1/х — 1/2
х-++О
1/х4
81пх
х-++0 Х
Решение.
1/ 4 ln(sin х/х)
81ПХ
lim = (1~ ) pr~+0 х4
х-++0 Х
sinx
1п 1 — cosx ' . 1 сов»
limx in(1 — cosx) =(Π(~)) =lim, =lim
х~о х~О (1/Х)' х~О 1
Х2

249
ГЛАВА 6. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ
Найдем отдельно
ctgx—
(cosxsjnх — х)'
= lim
16хз +о (16хз sin2 х)'
= lim
х — ++О
(1/2sin2x — х)' . cos2x — 1
lim = lim
x~+o (16х~ sin2 х)' +о 48х2 sin2 x t 32хп sin xcosx
281п2х
»m
x~+048x sin2 х+32хз Бц1хсоях
cosx
= »m
+048xsinx+24х2 sinх+48х2 cosx — 16хз sinx
НЕОПРЕДЕЛЕННОСТЬ ВИДА есоо~
Решение.
s1n х
1 lim ( — sinx lnx) — lim sinx/х lim x.lnx
lim : рх-++О р х — )+О х-++ΠŠ— 1 0 ЕО 1
+0 Х
inx
11д) х(п(е — 1) = (Ох) р~-"о)п(е — 1)
х ++0
lim
е 1 lim
е
— Е~+о хе» вЂ” (рО/О ) <~~o(x+1
(1n sin х — 1n х}'
1m
4 ~ 3
+о (х4)' +о 4хп
(sin x)'
1пп
x~+o (24х2 sin х + 1 6хз cos х)'
1/х4
Отсюда lim
sinx
x~+0 х
ыпх
6.62. »m—
х ++0 Х
1
6.63. lim х'"'" ц.
х — )+О
Решение.
1
(xctgx — 1}'
= lim
x~+o (4x4)'

250
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ 3АдА,
ИСПОЛЬЗОВАНИЕ ФОРМУЛ
МАКЛОРЕНА Й ТЕЙЛОРА
6.64. Разложить функцию f(x) = хз — 4x~ + 5х — 2 и„
формуле Тейлора по степеням (x+ 1), т. е. с центром раз
ложения в точке х() = — 1.
Решен и е.
f( — 1) = — 12, f'(õ) = Зх~ — Sx+ 5, f'( — 1) = 16, f"(õ) = 6х — 8,
f"( — 1) = — 14, f"'(õ) = 6, f"'( — 1) = 6, P"> õ = О, е л  &
Имеем
f(x) =хз — 4x~+5x — 2= f( — 1)+ (х+1)+ (х+1)з+
1.' 2!
— 16 — 14
+ (х+1)з+... = — 12+ — (х+1)+ (х+1)~+
3& t
+ — (х+1)з + О = — 12+16(х+1) — 7(х+1)~ +(х+1)з.
6
6
6.65. Разложить функцию f(x) = ез" по формуле Мак-
лорена.
P e ш е н и е. Воспользуемся таблицей разложения, по-
ложив и = Зх:
и~ и" Зх 9х~ 3" х"
И 2! п~ 1 2 п~
е" =1+ + +...+ — +... =1+ + +...+ +...
6.66. Разложить функцию
f(x) =
х~ — 3х+ 2
по формуле Маклорена.
Решение.
Преобразуем функцию
f(x) =
х~ — Зх+ 2 (х — 1)(х — 2) х — 2
1 1 1
2 (1 — х/2) 1 — х'
1
х — 1
воспользуемся формулой суммы для бесконечно убываю
щей геометрической прогрессии 1/(1 — и) = 1 + и + и~ + ." +
+ и," + ... и запишем

251
~g~~ÂA 6. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ
f(«) = — — 1+ + +...+ — +... +(1+х+х +...+х" +...) =
1 х Х2
2 п
4 2"
1 3 7 2 1
= — + — х+ — x +...+ 1— Х +...
2 4 8 2" +'
х2
cosx = 1 — — + R = cos0,1 = 1 — ' + R = 0,995+ R.
2! 2
Здесь погрешность вычисления определяется оценкой
Остаточного члена в форме Лагранжа
(В(= ' & t; Ђ” =0
24 24
Здесь 0 некоторое число, удовлетворяющее неравенст-
ву О & t  & t; 1. Ита , c s 0,1 = 0 995 +
6.68. С помощью формул Тейлора и Маклорена вычис-
лить пределы
sin« — х
х3
1n(l + х) — х+ х2 /2
б) &gt
х — эО :3
Решение.
(х — «~/6+ о(«~)) — х . 1 о(«~)
а) iim = llm — +
х — эО ,3 х~о 6 Х3 6'
1n(1+ х) — х+ «~ /2
lim
х — эО :3
(х — х2 /2+ хз /3+ о(хз)) — х+- «2 /2
= lim
х — эО ХЗ
о(хз)
= 1пп — +
хэо 3 Х3 3
6.67. По формуле Маклорена вычислить cos 0,1, ис-
пользуя только первые два члена разложения, и оценить
погрешность вычисления.
Решение.

252
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАцу
НАХОЖДЕНИЕ ИНТЕРВАЛОВ
MOHOTOHHOCTH И ЭКСТРЕМУМОВ ФУНКЦИИ f(x)
6.69. f(x) = 2хз — 3x2 — 12х — 1.
P е ш е н и е. Найдем f'(õ) = 6x2 — бх — 12 = 6(х+ 1)(х — 2)
f'(õ) = 0 при х = — 1 и при х = 2. Имеем при х е ( — oo; — 1) g
[] (2; +со) f (õ) & t; О и на э их интерва ах функ ия возр
тает, при х E ( — 1; 2) f'(õ) & t; О и зд сь функ ия убыва
Так как при переходе через критическую точку первог~
рода х = — 1 первая производная меняет свой знак с «+»
на « — », то в этой точке локальный максимум f,,„„( — 1) = 6.
При переходе через другую критическую точку первог~
рода х = 2 первая производная меняет свой знак с « — » на
«+», следовательно, в этой точке имеется локальный ми-
нимум /„„.„(2) = — 29.
ДОКАЗАТЕЛЬСТВО ЕДИНСТВЕННОСТИ
РЕШЕНИЯ УРАВНЕНИЯ f(x) = а
ПРИ ЛЮБОМ ЗНАЧЕНИИ ПАРАМЕТРА а
С ИСПОЛЬЗОВАНИЕМ
ПРИНЦИПА МОНОТОННОСТИ
НАХОЖДЕНИЕ НАИБОЛЬШЕГО
И НАИМЕНЬШЕГО ЗНАЧЕНИЙ ФУНКЦИИ
f(x) НА ОТРЕЗКЕ х е [а, Ь]
6.71. f (x) = — + —; х ~ [1; 6].
х 2
х
f'(õ) = — — — =О,
1 2
8 х2
Решен и е.
только один корень этого уравнения х = 4 е [1; 6]. Вычис
ляем f(4) = 1, f(1) = 2 —. f(6) = 1 —.
8 12
f„,„б(х„„б = ) = —, f„,„„(õ„,„„=4) =1.
1
6.70. f(x) = хз — 2х + 100х — 8= а.
P е ш е н и е. Найдем f'(õ) = 3x~ — 4х+ 100. Поскольку
дискриминант квадратного трехчлена отрицателен, а при
х2 положительный коэффициент, то производная f'(õ) & t;
значит, всюду на ОДЗ функция f(x) строго монотонна (воз-
растает), следовательно, каждое свое значение она прини-
мает только один раз, поэтому при любом а c ( — oo; +oo) урав-
нение f(x) = а имеет только один корень.

253
~ ЛАВА 6. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ
НАХОЖДЕНИЕ НАИБОЛЬШЕГО
И НАИМЕНЬШЕГО ЗНАЧЕНИЙ ФУНКЦИИ f(x)
НА ИНТЕРВАЛЕ Х е (а, Ь)
S(x) = х — P — х = — Px — х2,
1 1
2 2
где
0&lt х&l ;
1
2
Найдем производную и определим значение х, при кото-
ром выполняется необходимое условие существования экс-
тремума.
S'(õ) = — P — 2х, х = —, S — = —.
р р р2
2 ' 4' 4 16
Так как при
О& t; х&l ; — S'(
4
— & t  &l ; — S'(
P P
4 2
а при
P
\J
то в точке х = — имеется глобальныи максимум функции
4
Р
S(x) на интервале О & t  &l ; — и наиб льшее зн чение
4
ди достигается при х = — и равно S — = —.
P р Р2
4 4 16
6.72. f(x) = хз — 3«~ + 1; х c ( — 1; 1).
Pешение. f'(õ) = 3«~ — бх= 3« (х — 2) = О при х1 — — О,
«2 =2. Интервалу х c ( — 1; 1) принадлежит только x& t =
Имеем при х E ( — 1; p) f'(õ) & t; О и функ ия возраста т,
«c (p; 1) f'(õ) & t; p и функ ия убыва т, на интерв
х c ( — 1; 1) имеется только глобальный максимум f (õ
= О) = 1, наименьшего значения не существует.
6.73. Среди всех прямоугольников, периметр которых
равен Р, найти тот, площадь которого наибольшая. Вы-
числить эту площадь.
P е ш е н и е. Выпишем формулу для площади прямо-
угольника, введя длины сторон х и
а = — (P — 2х) = — P — х.
1 1
2 2
Площадь в этом случае есть функция вида

254
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДф~~
ДОКАЗАТЕЛЬСТВО НЕРАВЕНСТВА
НАХОЖДЕНИЕМ ГЛОБАЛЬНЫХ ЭКСТРЕМУМОВ
ИЛИ НАИБОЛЬШИХ И НАИМЕНЬШИХ
ЗНАЧЕНИЙ ФУНКЦИИ
НА ЗАДАННЫХ ОТРЕЗКАХ
РЕЩЕНИЕ УРАВНЕНИЯ f(x) = О
НАХОЖДЕНИЕМ ГЛОБАЛЬНЫХ
ЭКСТРЕМУМОВ ФУНКЦИИ f(x)
6.75. хе "— 1/е = О.
P е ш е н и е. Составим функцию f(x) = хе ", найдем ко-
рень уравнения f'(õ) = е '(1 — х) = 0 ==& t  = 1. Поскол ку
х c ( — co; 1) f'(õ) & t; О а р  с 1; + o) f' õ & t; О, то ф
f(x) имеет глобальный максимум f,„(1) = 1/е. Ответ: х = 1.
НАХОЖДЕНИЕ ИНТЕРВАЛОВ ВЫПУКЛОСТИ,
ВОГНУТОСТИ И ТОЧЕК ПЕРЕГИБА
ДЛЯ ФУНКЦИИ у = f(x)
6.76. f(x) = х~ + хз — 18x~ + 24х — 5.
P е ш е н и е. Найдем первую и вторую производные
f'(õ) = 4х~ + 3x~ — 36x + 24, f"(õ) = 12х~ + бх — 36.
Определим критические точки второго рода f"(õ) = 0
при x& t = Ђ” 2, х = 1 5. Соста им табли
6.74. Доказать неравенство х & t; 1 х р  с О; +c
Pешение. Составимфункцию f(x) = х — 1nх. Найдем
ее производную f'(õ) = 1 — 1/х. Воспользуемся необходи-
мым условием экстремума и определим критические точ-
ки первого рода, т. е. такие, в которых либо существует
f'(õ) = О, либо f'(õ) не существует, Hî f(x) в этих точках не-
прерывна. Имеем f'(õ) = 0 при х = 1.
Воспользуемся достаточным условием экстремума по
первой производной и определим интервалы знакопосто-
янства f'(õ) на ОДЗ. Имеем: при 0 & t   lt; 1 f (õ  lt;
1 & t  &l ; +~с f (õ > . В в д  ри х = функ ия и
бальный минимум f(1) = 1. Значит, всюду на ОДЗ f(x) = х—
— 1nх& t; 1

255
1 ЛАВА 6. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ
6.77. /(х) = I»2 — Зх + 2I.
Решение.
2, при — ~(х&lt
не существует при х = 1;
— 2, при х с (1, 2);
не существует при х = 2;
2, при 2&l ;х
f""(х) =
Составим таблицу:
НАХОЖДЕНИЕ АСИМПТОТ ФУНКЦИИ у = f(x)
6.78. 1(х) =
P е ш е н и е. Вертикальные асимптоты ищем на краях
области допустимых значений аргумента и в точках раз-
рыва второго рода. Имеем
lim
1 1
= — сО,
<~ -0 (х Ђ” )' (1 Ђ” 0) Ђ”
значит, при приближении к х = 1 слева график функции
устремляется к — Оо. Аналогично
lim
1 1
— = +op
1+о (х — 1)~ ((1+ О) — 1)з

256
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
при приближении к х = 1 справа график функции устрем-
ляется K +~. Вывод: х = 1 — вертикальная асимптота прц
приближении к х = 1 и слева и справа. Найдем наклонные
асимптоты:
k& t; Ђ” Ђ” i =
f(х) . 1
з
х~-~о Х х~о Х(Х вЂ” 1)
Ь1 — — lim [f(x) — kx]= lim 2 =О,
1
х~~о х~-~о (Х вЂ” 1)
у = 0 есть горизонтальная асимптота при х -+ — ~. Анало-
гично f(x)
k2 —— lim = lim =О;
х х~~ х(х — 1)~
Ь2 — — lim [f(x) — kx]= lim =О,
1
х~но x~+m (» — 1)
х2+4х+1 ( — 2 — 0)2+4( — 2 — О)+1 — 3
lim = — = +оО,
х-&gt -2 Ђ О + ( Ђ 2 Ђ” О +2 Ђ
при приближении к точке х = — 2 слева график функции
устремляется к +~, х = — 2 есть вертикальная асимптота
при х — + — 2 слева,
х2+4х+1 ( — 2+О) +4( — 2+О)+1 — 3
lim = — = — оо,
х~ 2 О х+2 ( — 2+О)+2 +О
при приближении к точке х = — 2 справа график функции
устремляется к -~, х = — 2 есть вертикальная асимптота при
х -+ — 2 справа. Найдем наклонную асимптоту при х — + — ~'
f(x) 1 х2 + 4х+ 1
х xw х(х+ 2)
Ь1 — — lim [f(x) — kx] = lim
Х ~-&lt -с Ђ”
х = lim =2,
2х+1
х-~-.~ х+ 2
у = х + 2 есть наклонная асимптота при х -+ — о. Аналогич-
но найдем
у = 0 есть горизонтальная асимптота при х -+ +~.
6.79. /( ) = х'+4х+1
х+2
P е ш е н и е. Вертикальные асимптоты ищем в точке
х= — 2:

257
ГЛАВА 6. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ
/(х) . х2+ 4х+1
~= lim = lim
x ++ х x > co х(х
Ь2 — — »m =2
2х+1
х — &gt +~ Х
и у = х+ 2 есть наклонная асимптота при х -+ +~.
6.80. Найти наклонную асимптоту функции и доказать
справедливость неравенства
f(x) =2х — — 1n е — &g ;О ри хc —; с
Зх 1 1
2 Зх Зе
P е ш е н и е. Найдем наклонную асимптоту функции
F(x) = 1n е — при х ++m:
«3х 1
2 Зх
k= lim — ln е—
Зх 1
х — ~+м 2х Зх
=3
2'
Зх 1 3 1
b= lim — ln е — — — х
+ 2 3х 2 2е'
«3 1
и у = — х — — есть наклонная асимптота при х — ++~ и кри-
2 2е
вая расположена под асимптотой. Поскольку у = 2х про-
3 1 1
ходит выше асимптоты у = — -х — — на участке x e —; + ~,
2 2е Зе
то
f(x) =2х — — 1n е — — &gt
3х 1
2 3х
ИССЛЕДОВАНИЕ СВОЙСТВ
ФУНКЦИИ у = f(x)
И ПОСТРОЕНИЕ ЕЕ ГРАФИКА
6.81. Провести исследование свойств функции
и построить ее график.
P е ш е н и е. Имеем:
1) область допустимых значений аргумента: х c ( — ~;+<
2) область изменения функции у c ( — m; +m)&
3) функция общего вида, так как у( — 2) = 2~2 w у(2) = 0;

258
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ 3AQAq
4) функция непериодическая, так как не существует
бесконечного множества ее нулевых значений, повторя~~-
щихся через период, нулевых значений всего два: при х = 0
их=2;
5) данная функция элементарная, она определена во
всех точках числовой оси, значит, она всюду непрерывна
при х c ( — < ); +&l
6) вертикальных асимптот нет, так как нет точек раз-
рыва второго рода и краев ОДЗ;
7) наклонная асимптота у = — х + 2/3 при х ~+~ и при
х-+ -~, так как
= lim
й= lim
x~+~
— ( — 1)х) =
х~ — хз+хз
b= lim(
х-++с~
2
+„~ 3'
= lim
х — &g ;
8) два экстремума: х;„= О, у;„= О и х,„= 4/3,
2з/
у„„„= — ч4.
В самом деле,
4х — Зх~
3
4 — Зх
у'(4/3) = О, у'(О) — не существует, а функция в точке х = О
непрерывна, значит, в этих точках выполняется необхо-
димое условие экстремума. При переходе слева направо
через точку х = О у'(х) меняет свой знак с « — » на «+», а при
переходе через точку х = 4/3 с «+» на « — »;
9) поскольку при х c ( — ~; О) и х с (4/3; +~) у'(х) & t; О,
на этих интервалах функция убывает. Функция возраста-
ет при х E (О; 4/3), так как на этом интервале у'(х) & t;
10) найдем вторую производную
— 3з(2з — «зр — (4 — 3 ) 4(2х — х )(4х — Зх )
3
у "(х) =
9х4/3(2 )5/3 '

259
ГЛАВА 6. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ
y"(х) ~ О при Vx c ( &lt a; 0)
Q (О; 2) Q (2;+< ). р
при х = 2 вторая производ-
ная не существует, но функ-
ция в этих точках непре-
рывна, значит, в этих точ-
ках выполняется необходи-
у = -х + 2/3
мое условие существования
точки перегиба. Исследуем
Рис. 6.1
знаки у"(х) вблизи указан-
ных точек. При Чх c ( — ~; О) () (О; 2) у"(х) & t  и знач т,
этих интервалах кривая выпукла, а точка х = 0 не являет-
ся точкой перегиба. При Чх с (2; +о~) у"(х) & t; О, знач т,
этом интервале кривая вогнута, а точка х = 2, у = 0 явля-
ется точкой перегиба. График функции представлен на ри-
сунке 6.1.
6.82. Провести исследование свойств функции
х2+2х — 1
g=
и построить ее график.
Решен ие. Имеем:
1) область допустимых значений аргумента: х c ( — &lt a;
() (о;+-);
2) область изменения функции у c ( — m; +m);
3) функция общего вида, так как
— у(х) =
х2+2х — 1
х
хз+2х — 1
х
( — х)з + 2( — х) — 1
у(-х) =
( — х)
х2 — 2х — 1
Ф
х
4) функция непериодическая, так как не существует
бесконечного множества значений х = О, повторяющихся
через период, при которых функция не существует;
5) данная функция элементарная, она определена при
х E ( — &lt K; О) () О; +о ), знач т в э их интерва ах на вс
непрерывна;
6) разрыв второго рода, так как
х2+2х — 1
х — э+О х

260
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
Из этого также следует, что х = О есть вертикальнад
асимптота при х — + +О;
7) наклонная асимптота у = х+ 2 при х -+ +с~ и при
х — э — ~о, так как
х2+2х — 1
x-++x
b= lim
х +2х — 1 . 2х — 1
х = lim =2;
Х ++crl х х — )+ос Х
8) экстремумов нет. В са-
У
мом деле, у'(х) = 1 + 1/х2 & t
Ч при всех х е ( — с~; О) U (О; +со)
и функция строго возрастает
на всей ОДЗ;
9) найдем вторую произ-
— 2 0 ~2 — 1 Х
водную. у "(х) = — 2/хз. у"(х) не
существует при х = О. На ин-
тервалах чх E ( — m; О) и Чх E
E(0; +с~) у"(х) имеет соответ-
ственно знаки «+» и « — ». На
Рис. 6.2
интервале Чх E ( — с~; О) гра-
фик кривой вогнутый, на интервале Чх е (О; +co) — вы-
пуклый. Точек перегиба нет. График функции представ-
лен на рисунке 6.2.
ОПРЕДЕЛЕНИЕ КРИВИЗНЫ,
РАДИУСА КРИВИЗНЫ И КООРДИНАТЫ
ЦЕНТРА КРИВОЙ В ДАННОЙ ТОЧКЕ
6.83. Найти кривизну, радиус кривизны и координаты
центра кривой у = 4/х в точке х = 2.
Решение.
(2
с~х2
I 8/х I
К=
х4 +16 3/2
К(2) = J2/4, R(x) = =, R(2) =2@2,
К(х) 8хз

261
ГЛАВА 6. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ
и „(а]'
=Х
d2f 8/xÇ
с~х
1+
df
dx 1+ 16/х х4 + 16
У=у+
d2f 8/хз 8х
=g+ =g+
— . (1+16/х4)
4 16
=Х+
2хз
Х=х
с~х
Х=4, У =4.
6.84. Найти кривизну, радиус кривизны и координаты
центра кривой х = a(t) = t — sin t, у = P(t) = 1 — cos t в точке
t = и/2.
Решение.
&lt 2P
dt~ ~й
К=
dD
2
— +
dt
dP сРа
&lt ~ d t ( os (1 Ђ” co t) Ђ”
- и 1
2~2
3/2
du dP
((1 — cost)~ + sinai' t)3 2
Л(й) =
d~p du сф d~u /cost(1 — cost) — вш2t/
(t2 dt dt ~~2
Л вЂ”,' =2Я.
((1+ cos t)~ + яш t) яш
cos t(1 — cos t) — яш t
((1 — cos t)2 + яш2 1)(1 — cos t)
У=у+
cost(1 — cost) — яш' t
Х=х
Х вЂ” "' = — "'+1, У вЂ” , '= — 1.
2 2 ' 2
6.85. Найти кривизну, радиус кривизны и координаты
центра кривой р = 1 — cos &l ; в то ке & t;р

262
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДЯ~Ч
Решение.
(р(ср))' + 2 — — р(ср)
dp ' сРр
(1 — cosy)~ + 2 sin~ y — (1 — cos y) cos y
((1 — cosy)~+sin ~y)' ~
(р(р))'+
др
d(p i
К=
1 — 2cos(p+ cos' (p+ 2s> i~ (р Ђ” cos p+ c s~ ( 3 Ђ” 3cos p+ 2s& t;
(1 — 2cosy+cos~y+sin~y)"' '-' (2+2сояср)" ~
Х(0) =О.
:3 2
(р(р))-'+ д-
dp 3
дф! (2+2сояср)" '
,р 3 — 3cos (p+ 2яш '(p
(р(ср))~ + 2 — Р- — p(y) Р
dp
R(y) =
R(0) =+х.
((1 — cos ср)-' + яиц ср)((1 — cos ср) cos ср+ s in y sin ср)
Х=(1-cosy cosy
(1 — cosy)~+2sin y — (1 — cosy)cosy
((1 — cos y) ~ + sin~ ср)((1 — cos y) sin y+ я пир соя y)
Y=(1 — cosy siny+
(1 — cos y)~ + 2яи]~ y — (1 — cosy) cos y
Х(0) = О, Y(0) = О.
6.18.
ЗАДАЧИ
ВЫЧИСЛЕНИЕ ПРОИЗВОДНОЙ
6.86. Найти приращение функции Af(xp, Лх), если
а) f(x) = ~х, xp = О, Лх =0,01; б) f(x) =1g х, xp = 100,
Лх = — 90; в) f(x) = 1/(х2 + х — 6), х = 1, Лх = 0,2; г) f(x) = хз,
xp = 1, Лх = 0,1.
6.87. Исходя из определения производной, доказать,
что в случае существования производной f'(xp) справедли-
во равенство
xf(xp) xpf(x)
Х вЂ” ) Х0 Х вЂ” XP
6.88. Пользуясь определениями левой и правой произ-
водных функции f(x) в точке хр найти их для f(x) = ~х—
- j i+ ix+ 1!и xp — — +l.

263
ГЛАВА 6. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ
6.89. Пользуясь определениями левой и правой произ-
водных функции f(x) в точке хр, найти их для
х, если х &lt
f(x) = и хд =1.
— х2+2х, если х &g
ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ
С ПОМОЩЬЮ ТАБЛИЦЫ ПРОИЗВОДНЫХ
И ПРОСТЕЙШИХ ПРАВИЛ
ДИФФЕРЕНЦИРОВАНИЯ
6.90. f (x) = Зх2 — 4х ~ 5 + 7~х~—
5 4
ОПРЕДЕЛЕНИЕ f-''(х0) и ~+(х0)
В ЗАДАННОЙ ТОЧКЕ х0
x — 2, если х&lt
6 106 f(x) = xp = 2.
x2 — 2х, если х & t;
О, еслих&lt
6.107. ((х) = 4 ' хд — — О.
х41nx, если х & t;
6.91. f(x) =4Гх+ —.
х2
6.92. f(x) = x4cos х.
6.93. f(x) = arctg х/1оя~х.
6.94. f(x) =5х4 — 7/х8 — 3~x3 +9.
6.95. f(x) = Зх~ — 4х о 5+ хзsin х.
6.96. f(x) = 2cos х — 7sin х.
6.97. f(x) = sin х . arctg x.
6.98. f(x) = ln х/хз.
6.99. f(x) = е (5 /arcsinх).
6.100. f(x) =1оа'з х jx tgx.
6.101. f(x) = ctg х/х9.
Вычислить значение производной функции f(x) в за-
данной точке x = а.
6.102. f(x) = х~ — 4х + 2, а = 2.
6. 103. f (x) = 4~х — Зх~ + 2, а = О.
6.104. f(x) = х — 41 а, = 1, а2=4.
6.105. f(x) = х2 — Зх+ 2), а, = 1, а2 = 3.

264
ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ
СЛОЖНЫХ ФУНКЦИИ
6.108. f(x) = агся1п~х.
6.109. f(x) = сСд(3» ~х).
1оЮЗ х
6.110. f(x) = arctg
6.111. f(x) = cos(+x).
6.112 f(x) х7 ез»
х2 — Ях
6 113 ((х) = Ф»
'F4+1
6.118. f(x) =
6.119. f(x) =
1 ( ) ~~(3 +1)
lIl~ X
ИССЛЕДОВАНИЕ
НЕУСТОЙЧИВОСТИ ОПЕРАЦИИ
ДИФФЕРЕНЦИРОВАНИЯ
Показать, что при п -+ с~ значения двух функций f(x) и
g(x) в заданной точке х = а становятся сколь угодно близ-
кими друг другу, в то время как модуль разности их произ-
водных в данной точке стремится к бесконечности.
6.121. f(x) = —, g(x) = — соя(х/4+ 2n~x), а = х.
1~2 1
и 2 ' и
6.122. f(x) =, g(x) = — arctg(1+ пзх), а =О.
2 1+х 1
и и
6.123. ((х) =
6.114. f(x) =
6.115. f(x) =
6.116. f(x) =
6.117. f(x) =
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДА~
ctg(logq (агссоя(4» ))).
2» . ctg( — 4х).
log(x~ + 2х + 9).
arctg(4x3) . ln(1 + 10х).
ar csin(2x)
х2+4
shx3 . агссоя ~х.
1
, g(x) = — 1п(е+ и'х), а = О.
и и

265
ГЛАВА 6. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ
6.124.
f(x) =, д'(х) =
tgx
fL
, a=0.
6.125.
g(x) 31+sin(nД(х — 1)) ц
1
fL
6.126. ) (х) =
6.127. f(x) = — log> 2+ arctg( (x Ђ” 2)
1
fL
1
, g(x)= — е
fL
, a=3.
6.128. f(x) =arctg
и
ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ у„'(х)
ФУНКЦИЙ f(x, у(х)) = О, ЗАДАННЫХ НЕЯВНО
6.138. ((х) =
Сд3».хз~2.arctg( jx)
1п2» 2sx
arcsin 6x. ctgx2
6.140. х =
sh2x cos(lnx)
6.129.
6.130.
6.131.
6.132.
6.133.
6.134.
6.135.
6.136.
6.137.
f( ) arcsin x ( ) 1 21+и /пх & t
(х — 2)з
g(x) = arcsin, а = 2.
fL
f(x, у(х)) = у~(х) + sin х2 — 1 = О.
f(x, у(х)) = ln у(х) — ycos x — х = О.
f(x, у(х)) = ctg у — y2sin х — 5y = О.
f(x, у(х)) = arctg у~ — у/(1 + х2) — ln у = О.
f(x, у(х)) = 7"arcsin у — 9х = О.
f(», у(х)) = »~1ó + sh y2 — 8х = О.
f(x, у(х)) = х~ — ух — 6 = О.
f(x, у(х)) = 2"~" — (х/у)х = О.
f(x, у(х)) = 3" + 3" — 3"+ ~ = О.
ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ
С ПОМОЩЬЮ ЛОГАРИФМИЧЕСКОГО
ДИФФЕРЕНЦИРОВАНИЯ
»4(1+ х)~

266
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАц
6.141. ((х) =
log~(x~+1) arccos7x.(xs+2) е»»
6.142. ((х) = х'"»
f(x) = х'Б.
6.143.
f(x) Д . агсв1п Гх
6.144.
f(x) = (cos(x3 — 2х — 5))2'.
6.145.
6 146 f(x) =(
х2+]
6.147. f(x) =(lnx)'~9»
f(x) =(arcsin(e2"))" .
6.148.
ВЫЧИСЛЕНИЕ ПЕРВЫХ
ПРОИЗВОДНЫХ ФУНКЦИИ,
ЗАДАННОЙ ПАРАМЕТРИЧЕСКИ
6.149. х = sin3t, у = cos3t.
6.150. х = lnt, у = ctgt.
х = arccos(in t), у = е' .
t+1
, у = arctgt2.
~2+2
1од~(Р+1), y=~t2+1.
tsin 2t, у = tcos 2t.
е'sin t, у = е'cos t.
a(t — sin t), у = a(1 — cos t).
6.152.
6.153.
6.154.
6.155.
6.156.
ОПРЕДЕЛЕНИЕ КАСАТЕЛЬНОЙ
И НОРМАЛИ К ГРАФИКУ ФУНКЦИИ
6.157. Составить уравнения касательной и нормали к
кривой у = 4хз + х — 4 в заданной точке х ) = 1.
6.158. Составить уравнение нормали к кривой у = х2—
— х + 1 в точке пересечения этой кривой с прямой у = 2х — 1.
6.159. На линии х = ln t, у = t2 — 8t найти точки, в кото-
рых касательная параллельна прямой у = — бх.
6.160. Под каким углом график функции у = е~~ пере-
секает прямую х = 2?

267
i'ßÀÂÀ 6. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ
6.161. Найти угол наклона к оси абсцисс касательной к
функции у = — 1/(2х2) в точке х = 1.
6.162. Найти угол, под которым пересекаются кривые
у = (х — к/2)з + 1 и у = sin х при х е [9z/10; 11к/10].
6.163. Под какими углами пересекаются нормаль к
кривой у = х2 — 2х + 1 и касательная к кривой у = — х2 + 2х,
в точке пересечения х = 1?
НАХОЖДЕНИЕ ПЕРВОГО
ДИФФЕРЕНЦИАЛА И ИСПОЛЬЗОВАНИЕ ЕГО
В ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЯХ
6.164. Найти: а) d(arcsin (и/v3)); б) d(arctg (и1п v));
в) d(2"tg(v~)); г) d
1+и
6.165. Найти первый дифференциал: а) у = хз — Зх — 1;
ctg5x
б) у = x4cos х2; в) p =
~х
6.166. Найти дифференциал функции у(х) и вычислить
его значение при заданных значениях х dx = Лх: а) у(х) =
= е~"/1n(e + Зх»), х = О, dx = Лх = 0,1; б) у(х) = cos х + xsin х,
х = к/2, dx = Лх = — 0,1; в) у(х) = 1n
dx = Лх = 0,01.
6.167. С помощью дифференциала вычислить:
а) ; б) ; в) cos 31'; г) arcsin 0,51.
— xarctgx, х = 1,
ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ
И ДИФФЕРЕНЦИАЛОВ ВЫСШИХ ПОРЯДКОВ,
ПРОИЗВОДНЫХ ВТОРОГО ПОРЯДКА
6.168. f(x) = x4sin 2х.
6.169. f(x) = х/1пх.
6.170. f(x) = 2ax
6.171. f(x) = arctg 5x.
6.172. Найти первые три дифференциала функции:
а) у = хз + 2х — 8; б) у = cos хз + 9х.
6.173. Найти 5-й дифференциал функции у = х' — 4х4 +
+ Яхз — 2х+ 5.
6.174. Найти и-й дифференциал функции у = e~»

268
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАД~А
ПРИМЕНЕНИЕ ТЕОРЕМ РОЛЛЯ,
ЛАГРАНЖА, КОШИ
6.175. Доказать, что для функции f(x) = х — хз выпол
няются все условия теоремы Ролля на отрезках х е [ — 1; P]
и х E [О; 1]. Для каждого отрезка найти точку с, в которой
справедливо равенство f'(ñ) = О.
6.176. Функция f(x) = з (х — 2)2 принимает на конца~
отрезка х е [О; 4] значения, равные ~~4. Справедлива ли
теорема Ролля для данной функции на этом отрезке?
6.177. Доказать, что для функции f(x) = ~3x4 выполня-
ются все условия теоремы Лагранжа на отрезке х е [ — 1; 1].
Найти точку с, в которой справедливо равенство
1(1) — f( 1)
1 — ( — 1)
6.178. На отрезке х е [1; 3] найти точку, в которой ка-
сательная к параболе f(x) = х~ параллельна хорде, прове-
денной через точки с абсциссами х = 1 и х = 3.
6.179. С помощью теоремы Лагранжа доказать справед-
ливость неравенств: а) )sin b — sin a) & t; )b Ђ” a) ри лю ы
b; б) )cos b — cos a) & t; )b Ђ” a) ри лю ы  и b; в х Ђ  >
— 1)приа & t; 2  & t; 1; г) х Ђ” a & t ~x Ђ а ри &g
д) 1 + 21n х & t; х2 р  & t; 0 е) х † 2/2 l ; n(1 + х п
ж) tgx & t; х+ х /2 р   l ; х
6.180. Пользуясь тем, что в заданном промежутке про-
изводная функции равна нулю, доказать справедливость
равенств:
а) 2arctgx+arcsin =к при х&gt
2х
1+х2
1 — х2
б) arccos — 2arctgx=0 при х&gt
+х2
в) sin2x = (1 — cos 2х)/2.
6.181. Доказать, что для функций f(x) = х2 + 2 и g(x) =
= хз — 1 выполняются все условия теоремы Коши на от-
резке х е [1; 2]. Найти точку с, в которой справедливо ра-
венство
('(с) ((2) — f (1)
Д'(с) g(2) — g(1) '

269
1'ЛАВА 6. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ
ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ
С ПОМОЩЬЮ ПРАВИЛА ЛОПИТАЛЯ
6.183 1. Sin10~x
z~] Е2х — ]
6.182 1. Sin14x
0 tg7x
6.185. 1,. 1п(х -3)
х~2 Х2 — ЗХ+ 2
6.184. 1. Sin X — х
х-0 tgX — Х
6.186. lim и +х 6.187. lim "'
»~~in(~/2 — arctgx) -+ 2»
6.189 lim (sin x)сд»
х-~+и/2-0
6 188. 11п1 (tg «ya»
х-++Я/2-0
6 191 1, 1+p
6.190. (im х'/х
6 193 lim(arctgx/õ)'~»
6.192 lim(sin x/õ)'~»'.
х — э0
х — ~0
ИСПОЛЬЗОВАНИЕ ФОРМУЛ
МАКЛОРЕНА И ТЕЙЛОРА
6.194. Разложить функцию f(x) = 2х4 — 5хз — Зх2 + 8х+ 4
по формуле Тейлора по степеням (х — 2).
6.195. Разложить функцию f(x) = (х2 — 2х + 3)з по фор-
муле Тейлора по степеням х.
6.196. Пользуясь разложением по формуле Маклоре-
на функции (1 + х), разложить функцию
f(x) =
по степеням х до члена, содержащего х4.
6.197. Пользуясь разложениями по формуле Маклорена
функций ln(1 + х) и sinx, разложить функцию
f(x) = $2+x
по степеням х до члена, содержащего хб.
6. 198. Разложить функцию ((х) = 1/(х2 — 4х + 3) по фор-
муле Маклорена.
6. 199. С помощью формулы Тейлора приближенно вы-
числить: а) arctg 0,8 с точностью 3,2 10 5; б) cos л/20 с точ-
ностью 10 5; в) ~5 с точностью 10 4.

270
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
6.200. Оценить погрешность приближенного вычиспе
ния по формуле Маклорена1п 1,5, если используются толь-
ко первые четыре члена разложения.
6.201. Пользуясь формулами Тейлора и Маклорена,
вычислить пределы:
1 — сон х
х эО gg 1
— х /2
г) lim
х — «О х4
— х /2
е) lim
х-+О
1 — (cosx)""
); з) lim
х — эО
3
Ех + Е-х — 2
а) lim
х — эО х2
в) lim
х2
х — «О
х+ х~ — sinxe»
д 1пп
х-+О
3
ж) lim (
НАХОЖДЕНИЕ ИНТЕРВАЛОВ МОНОТОННОСТИ
И ЭКСТРЕМУМОВ ФУНКЦИИ ((х)
6.202. f(x) = хе з".
6.203. f(x) = (2х — 1)/(х — 1)2.
6.204. f(x) = х3 — бх~+ 9х — 3.
6.203, f(x) =,(2х2 — x+ 2.
ДОКАЗАТЕЛЬСТВО ЕДИНСТВЕННОСТИ
РЕШЕНИЯ УРАВНЕНИЯ f(x) = а
ПРИ ЛЮБОМ ЗНАЧЕНИИ ПАРАМЕТРА а
С ПОМОЩЬЮ ПРИНЦИПА МОНОТОННОСТИ
6.206. f(x) = хт + х4 + 500х = а.
6207 f(x) х +х +500x25
6.208. f(x) = arctg3x + х' + 2х = а.
НАХОЖДЕНИЕ НАИБОЛЬШЕГО
И НАИМЕНЬШЕГО ЗНАЧЕНИЯ
ФУНКЦИИ ((х) НА ОТРЕЗКЕ х е [а, Ь]
6 2p9 f(x) = — х — — х — — х + 2; х е [ — 2; 4].
1 4 2 3 3
4 3 2
6 210. f(x) =acctgx — — 1пх, хх[1( )3;)3].
1
6.211. f(x) = [Зх4 — 16хз + 24х2 — 43[, х с [2; 3].
6.212. Среди всех равнобедренных треугольников с дли-
ной боковой стороны а найти тот, площадь которого наи-
большая. Вычислить эту площадь.

271
[ ЛАВА 6. ПРОИЗВОДНАЯ Я ДЯф~ф~ЯРЯНЦИАЛ ~»«g«
ДОКАЗАТЕЛЬСТВО НЕРАВЕНСТВА
НАХОЖДЕНИЕМ ГЛОБАЛЬНЫХ ЭКСТРЕМУМОВ
ИЛИ НАИБОЛЬШИХ И НАИМЕНЬШИХ
ЗНАЧЕНИЙ ФУНКЦИИ НА ЗАДАННЫХ ОТРЕЗКАХ
6.216. Доказать справедливость неравенства 1п х/х & t;
на интервале х с (О; + ю).
6.217. Доказать справедливость неравенства
( 1+ х ('~' & t
2
на интервале х с (О;+с~).
6.218. Доказать справедливость неравенства cos x ) 1—
— х2/2.
6.219. Доказать, что при х е [ — 2; 1] справедливо нера-
венство О ( Зх4+ 4хз + 1 ( 17.
6.220. Доказать, что при х е [ — 2; 1] справедливо нера-
венство — 3 ( хз — Зх2+ 1 ( 17.
РЕШЕНИЕ УРАВНЕНИЯ ((х) = О
ПУТЕМ НАХОЖДЕНИЯ
ГЛОБАЛЬНЫХ ЭКСТРЕМУМОВ ФУНКЦИИ ((х)
6.221. = — Л
6.222. х2~з — (х2 — 1)1~з = з/4.
6 223 (x+1)~~~ — (х — 1)~~~ = — ф4.
6.224. х4/4 — хз/3 — х2+ 8/3 = О.
6.213. Разность арифметической прогрессии равна наи-
меньшему значению функции f(x) = 6х2 — хз на отрезке
х с [1; 3], второй член прогрессии равен наибольшему зна-
чению данной функции на указанном отрезке. Найти сум-
му первых десяти членов прогрессии.
6.214. Из круга вырезан сектор с центральным углом а.
Из сектора свернута коническая поверхность. При каком
значении угла а объем полученного конуса будет наиболь-
шим?
6.215. Периметр равнобедренного треугольника равен
2Р. Каковы должны быть ero стороны, чтобы объем конуса,
образованного вращением этого треугольника вокруг своей
высоты, проведенной к основанию, был наибольшим?

272
ОПРЕДЕЛЕНИЕ ИНТЕРВАЛОВ
ВЫПУКЛОСТИ, ВОГНУТОСТИ
И ТОЧЕК ПЕРЕГИБА ФУНКЦИИ F(X)
6.225. f(x) = х4 — бх2+ 5. 6.226. f(x) = 4x.
6.227. f(x) =1n(1 + хх). 6.228. f(x) = 1/(1+ x2).
6.229. f(x) = 3x4 — 8х~+ бх2+ 12.
6.230. f(x) = e-™
6.231. Найти точки перегиба графика функции:
а) f(x) = — х4 х2 + 2; б) f(x) = (х — 5) ~~~ + l.
=«3
8
6.232. Найти все значения параметра а, при которы~
графики функций вогнуты на всей числовой оси:
а) f(x) = х' — ах~+ бх2 — х — 1;
б) f(x)=х'+аха+ — x~+3.
з
2
6.233. Пользуясь определением вогнутой функции, до-
казать справедливость неравенства:
а) (т~/2)х — arcsin х & t 0 р  с О; ); б х Ђ” 1 ( + 2
при х с (О; 1).
6.237. f(x) =1n х/х~.
6.239. f(x) = sin х/х.
6.242. f(x) =
6.243. f(x) = х + cos х/х.
6.245. f(x) = (хз + 3)/х2.
6.244. /(х) =
ИССЛЕДОВАНИЕ СВОЙСТВ ФУНКЦИИ
у = /(х) И ПОСТРОЕНИЕ EE ГРАФИКА
6.246. f(x) = хз — бх + 9х — 1.
6.247. f(x) = (х + 1)з/(х — 1)2
6.248. f(x) =31nx/~х.
6.249. f(x) = х — Зх + Зх~ — 5.
6.234.
6.235.
6.236.
6.238.
6.240.
6.241.
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ 3АДАс~
НАХОЖДЕНИЕ АСИМПТОТ
ДЛЯ ГРАФИКА ФУНКЦИИ у = ((х)
f(x) = хе'~'.
f(x) = (Зх~+ 3x)/(х+ 1).
f(x) = х arctg x.
Дх) 21/(х — 1)
f(x) = arcsin(4x/(1+ х4)).
f(x) = х + 2arctg х.

273
ГЛАВА 6. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ
6.251. f(x) = (х — 5)х2~'
6.253. f(x) = х4 — 2х2 + 3.
6.250. f(x) = х + 1n(x2 — 1).
6.252. f(x)
l-~х-1'
6.254. f(x) = х/(1 + х2).
6.256. f(x) = (1 — хз)/х2.
6 255 ~(х) =
6.257. f(x) = е'/(х + 1).
ОПРЕДЕЛЕНИЕ КРИВИЗНЫ,
РАДИУСА КРИВИЗНЫ
И КООРДИНАТ ЦЕНТРА КРИВОЙ
В ДАННОЙ ТОЧКЕ
6.258. Кривая задана уравнением в декартовой систе-
ме координат у = f(x), абсцисса точки х = xp.'
а) f(x) = хз + х2 — 4, xp = 0; б) f(x) = 1n(1/х), xp = 1; в) f(x) =
= sin x, xp = — — тс/2; г) f(x) = х, xp = 1.
6.259. Кривая задана параметрически:
а)х=Р, у=2Р в точке t= 1; б)х=асов t, у=Ьвш
в точке t = 0; в) х = е'sin t, у = е'cos t в точке t = 0;
г) х= Г2совз1,у= )2sin~t B Tочкet =z/4.
6.260. Кривая задана в полярной системе координат:
а) р = а(1 + cos &lt р в то ке & t;
б) р= ау вточке у = л/2;
в) р = ae4' в точке y = 1n 2.

РАСЧЕТНО-ГРАФИЧЕСКИЕ
ЗАДАНИЯ
ЗАДАЧА 1
Даны две матрицы А и В (табл. P. 1}. Найти неизвестную мат-
рицу Х, удовлетворяющую данному матричному уравнению.
Таблица P.1

275
РАСЧЕТНО-ГРАФИЧЕСКИЕ ЗАДАНИЯ
Матрица А
Матрица В
Уравнение
1 -1 2
-1 2 0
,2 -1 1
10
(Х+ А
12 (Х вЂ” В)А
XAB =
13
'-1 -2 0
2 0 3
8 — Х = ВАХ
14
-3 8 -3
1 6 — 1
3 0 3
— АХ =В+Х
3
АХ= — — Х
3
2 —, 1
3
16
0 0
(-1 2 з)
АВХ = 5А — Х
~ — 2 2
ВХ вЂ” 2А = — 'Х
2
~'2 — 1
,0 1
4Х вЂ” 15А = ABX
19
XA = — В+Х
1
2
— АХ
1
3
15 12
-3 15
3 0
4 2
-2 0
Продолжение табл. Р.1
-16 12 0
8 20 4
2 -1 1
4 3 -2
0 0 1
-1 -4
2 5,
4 -1
2 3,
1 01
0 -2,
2 1!
1 0 -1
4 3 2
о-ь al
4 0~
— 2 6
0 8
'о 4)
— 3 1
2 — 1

276
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
Продолжение табл. P.g
Матрица В
Матрица А
Уравнение
Х вЂ” 12В = — XA
2
20
1
— — 3 4
АХ= В+ ЗХ
28
— 2
АХ вЂ” В= 2Л+Х
29
30
0 4
— 3 1
2 — 1
— 1 3 0
,0 0 1
'1 2 0~
2 0 — 1
,3 4 0~
'0 1 — 2~
2 0 1~
4 — 1 — 3)
— о --'~
2 2~
1
о
— 2 — 2 g'I
1 3 — 1
0 2 17~
/
3
4 1
5 8)

277
РАСЧЕТНО-ГРАФИЧЕСКИЕ ЗАДАНИЯ
ОБРАЗЕЦ РЕШЕНИЯ ЗАДАЧИ 1
Решим следующее матричное уравнение: ЗХ + А = В (Х + 4А),
Где
1 — 1 2 3
А= 4, В= 2 0 1.
3 4 3 2
Прежде всего, раскроем скобки в правой части уравнения,
не меняя при этом порядка сомножителей.
ЗХ + А = ВХ + 4ВА.
1 0 0
Е=О 1 0
0 0 1
Пусть
— единичная матрица, тогда уравнение можно записать в сле-
дующем виде: А — 4ВА = ( — 3E)X.
Определим матрицу  — 3E:
— 1 2 3 1 0 0
 — 3E= 2 0 1 — 30 1 0=
4 3 — 2 0 0 1
— 1 2 3 3 0 0 — 4 2 3
2 0 1 — 0 3 0 = 2 — 3 1
4 3 — 2 0 0 3 4 3 — 5
Находим определитель матрицы  — 3E:
— 4 2 3
[ — ЗЕ~=
=( — 4) ( — 3).( — 5)+2 1.4 — 4.( — 3).3 — 2 2.( — 5)—
2 — 3 1
4 3 — 5
— 3.1 ( — 4) = — 60+8+18+36+20+12=34.
Так как определитель матрицы  — 3E отличен от нуля, эта
матрица имеет обратную. Найдем матрицу ( — ЗЕ) '. Для этого
найдем, прежде всего союзную матрицу:
-4 2 3 12 19 11
( — ЗЕ)'= 2 — 3 1 = 14 8 10.
4 3 -5 18 20 8
Таким образом, обратная матрица будет равна
12 19 11
( — 3E) '= — —. 14 8 10 .
24
18 20 8

278
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
Теперь определим матрицу А — 4АВ:
5 — 8 — 12
-16 -12 -7
1 0 0 — 4 8 12
Š— 4В= 0 1 0 — 8 0 4
0 0 1 16 12 8
5 — 8
А — 4АВ =(Š— 4В)А = — 8 1
-16 -12
В итоге получено простейшее матричное уравнение:
Искомая матрица Х равна
12 19 11 -63 1467
Х = —. 14 8 10 . -16 =- — 1380 .
34 34
18 20 8 -85 2134
ЗАДАЧА 2
Таблица P.2
Решить систему линейных алгебраических уравнений мето-
дом Гаусса (табл. P.2).

279
Система ура вне ний
Система уравнений
2x& t; Ђ” х + хз Ђ” Ђ”
=2,
=5,
— — 7
з =14
~х, +Зх2+х~ — -5,
2х1 + 7хг + 6x
13
14
15
16
17
18
19
21
22
23
24
РАСЧЕТНО-ГРАФИЧЕСКИЕ ЗАДАНИЯ
2Х1 — х~ + хз - х, = 1,
2х1 -х2-Зх~ =2,
l
Зх, — х;+х, = — 3,
2х1+2xz -2xz+5x~ =--6
9х~ — Зх2 + 5x
Gx& t; Ђ” 2х~+Зхз+ х =
[Зх, — х., +Зхз+14х, = — 8
Зх, — 2х2 + 5хз + х„= 20,
2х, — Зх2+хз+5х~ =14,
х, —,2õ2 — 4х~ = — 8,
x& t; Ђ” х~ Ђ” х + х = Ђ
х1 +2х~ — Зхз+5х~ =1,
х1 +3x
Зх~ -'5
2х1 -'3
х, +2x& t; Ђ” 2х.; х,
х, +Зх2 — 5х~+ Зх~ — — 3,
2х1 4х~ — 7хз + 8х~ = 5
х~ + х~ — Зхз — 4х~ = 1,
4х, +5х~ — 2х~ — х4 = 3,
Зх1 +4х.„+ хз + Зх~ — — 2
Продолжение табл. Р.2
г
q +Çx~ = — э,
+ 4х~ — — 2,
z х~ =-3,
з-'2õ~ = — 4
.~ + 5х~ — — — 1,
хз тбх1 —- 1,
х, +8х~ — — 2,
Зх, +5х~ —.х~ — 9x~ =1
5-~1 + xg — Зхз = — 6
4х1 + 2х~ — 4хз — — — 7,
2х, — 5х>+ хз Ђ” Ђ”
5x, — 2х., ~-2х; = 1
х, + х.„+ Зхз -2х, — Çõ; = 1,
2х, + 2х~ —.4хз — xq + Зх~ — — 2,
Зх1+Зх~ — . '5хз — 2х~ +Зх; =1,
2x& t + х~ Ђ” x + х
2Х~ — Х2 + Хз + 2X ~ + ЗХ~ = 2,
бх, — Зх~ + 2хз + 4х~ +5х-, = 3,
бх, — Зх& t + 4х ;+ х, +1 х =
4х1 — 2х~ —.' Хз+х~+2х; =1
х, — 2х~+Зхз — х, =1,
Зх, +5х~ — х, х~ —.2х,.; =О,
9х~ + 4х~ — 2хз х~ ~- х; = 3
х1 -4х~ — 2хз — 3x; =2,
2х1 + 9хг хз 4х~ =5,
х1 5х~ + хз — 4х~ - Зх,; = 3
x& t; Ђ” х + х + х =
4х1 — 7хг + 2хз+ х4 — — 3,
Зх1 — 5xq — х~ — Çx~ = 2

ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
Продолжение табл. Р&
ОБРАЗЕЦ РЕШЕНИЯ ЗАДАЧИ 2
Методом Гаусса найдем общее решение следующей системы
линейных алгебраических уравнений:
Прежде всего, составим расширенную матрицу системы:
Согласно алгоритму Гаусса будем приводить эту матрицу к
треугольному виду (все проводимые преобразования указаны
между матрицами).
(2Х1).
(3) — 2(1),
(4) — 3(1)
1 1 — 1 — 1
(3)+си(2),
(4)+4(2)
-1/2(2) 0
0
0
1 1
1 1
0 1
0 1
1/6(3)
(4)-(3)
0 0
0 0
0
0 0
0 0
где число в скобках — номер строки.
1 1
1 — 1
2 — 3
3 — 1
— 1 — 1
— 1 0
4 2
— 2 — 3
-1
1
0
2
6
2
1 — 2
Х1+Х2 — ХЗ = — 1,
х1 — х2 — х3 — — О,
2х1 — ЗХ2+4Х3 =2,
3х1 — х2 — 2х3 — — — 3.
1 1 — 1 — 1
1 — 1 — 1 О
2 — 3 4 2
3 — 1 — 2 — 3
1 1 — 1 — 1
0 — 2 0 1
0 — 5 6 4
0 — 4 1 0
1 — 1 — 1
1 0
2
0 1
4
0 1 — 2
1 0
1
2
— 5 6 4
— 4 1 0
— 1 — 1
0
1
2
1
1
4
0
2

РАСЧЕТНО-ГРАФИЧЕСКИЕ ЗАДАНИЯ
Однако уравнение, отвечающее последней строке получен-
ной матрицы, является противоречивым. Следовательно, рас-
сматриваемая система несовместна, т. е. не имеет решений.
ЗАДАЧА 3
Вычислить площадь параллелограмма, построенного на век-
торах а и Ь. Найти длину вектора а (табл. P.З).
Табл и.цв P.3
и
(р,q)
л/6
Зр-q
p+ 2q
л/4
Р— 2q
3p+ q
1/5
л/2
p+2q
5л/6
p+5q
1/2
Зр — 2q
Зл/4
л/3
p+3q
л/2
2Р— q
л/4
4p+q
P Ч
л/6
л/3
10
Зр+ 2Ч
P Ч
10
л/2
4Р— Ч
p+2q
л/4
12
л/3
6.
14
л/3
2р+ 3q
р — 2q
15
л/4
2Р— ЗЧ
3p+q
16
л/6
18
1/2
л/2
19
бр — q
Р+Ч
л/4
10p+q
ЗР— 2q
20
л/6
21
p+2q
1/2
22
5/2
л/2
р — 2q
p+3q
Р— 4Ч
Р+ 4Ч
2p+Çq
Зр Ч
5Р+Ч
7p — 2q
6Р— Ч
ЗР+4Ч
2p+q
р — 2q
ЗР+Ч
2Р— q
Р— 2q
p+2q
Р -ЗЧ
p+3q

282
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ 3A JAq
Продолжение табл. р д
ОБРАЗЕЦ РЕШЕНИЯ ЗАДАЧИ 3
Пусть а =3P+2q,b 2p — д, значения модулей ~р~=4,lq l=3
л
а угол между векторами (р, q) = Зл/4.
Определим площадь параллелограмма, построенного на век-
торах аио:
S= (ахЬ|=((3р+2д)х(2р — q)l =I6Pxp+4q хp — Зрхд — 2q > l
= 17q х р ~= 7 I q I.I p I в1п(р, q) = 7 3 4 = 42 Г2.
2
Найдем длину вектора а:
(а( =~аа =
ЗАДАЧА 4
Даны координаты вершин пирамиды ABCD (табл. P.4). Най-
ти объем пирамиды, площадь грани АВС и угол между ребрами
Ац и AD.
ОБРАЗЕЦ РЕШЕНИЯ ЗАДАЧИ 4
Пусть координаты вершин А, В, С и D: А(1, — 1, 2); В(2, 1, 2);
С(1, 1, 4); D(6, — 3, 8).
Введем в рассмотрение следующие векторы:
АВ(1,2, 0), АС(0,2,2), AD(5, — 2,6).

РАСЧЕТНО-ГРАФИЧЕСКИЕ ЗАДАНИЯ
Таблица P.4
(7,— 1,— 2)
(7,2,4)
( — 1,5, — 2)
1, 4)
6,0,-3)
— 5,2
1 — 1)
2, О)
(1, 2, 1)
( — 10,9, — 7)
2)
( — 1, 7, 1)
(1, -4, 6)
О, — 4)
( — 5,— 3,2)
( — 2,— 6,— 3)
( — 2,2,— 1)
,4,5)
(3, О, -3)
2, О)
(5, 2, 6)
(8,4, -9)
(1, 2, -1)
(3,2, 1)
( — 4,2,5)
— 1,2)
( — 1, 1,3)
(2, — 2,4)
( — 1, О, — 2)
1,2)
(4, 1, -2)
3, 1)
(6, 3
(2, 3, 1)
(3, 2
( — 3,6, 3)
( — 2,
16
(1, 5, -4)
— 3,4, — 7)
17
( 5
( — 1,2, -3)
(4, -1, 0)
18
7
( — 2, 1, 0)
(4, -1, 3)
19
( — 2,0,3)
20
(1, -1, 1)
(1,2, 0)
(1, — 1,2)
(О, 1, -1)
(4, 4, -2)
21
(1, 2, -1)
(1,0,2)
22
( — 3,0,1)
(2,— 2,1)
(1, О, 1)
23
25
( — 1, 2,4)
(7, -3, 1)
О,
26
(О, -3, 1)
1 5)
(3, 1, -4)
27
1
О, 1)
28
(-2, -1, -1) , '(О, 3, 2)
(2, 1, -4)
( — 3,— 5,6)
30
(2, -4, -3)
(5, -6, 0)
( — 1,3,— 3
( — 10,— 8,7)
(1, 3, 6)
( — 4,2,6
1, — 1)
(1,5, -7)
(1, 2, -3)
(3, 10, — 1)
(2, 2, 1)
2, — 3, 0)
( — 2,3,5)
(2, 5, О)
( — 1, О, 1)
( — 10,5, 8)
(3,3, 1)
( — 7, — 3,2)
(3,6, — 3)
(1, -5, -9)
(1, 2, 4)
(5, О, -6)
(4, -8, -4)
( — 2, — 1,6)
О,— 3)
( — 4,6,— 3)
( — 5,2, — 4)
( — 4,2, 1)
( — 6, — 3,6)
( — 10,6, 7)
( — 1, — 6,3)
( — 1,1,1)
(2, 1, О)
(1, -1, 2)
( — 4,7,3)
( — 5,2,— 8)

ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ 3~Ay
Объем пирамиды вычисляем по формуле
1
= — (12+20+Π— Π— О+4) =6.
6
,Цалее определим векторное произведение векторов АВ и AC:
2 0 —. 1 0 —. 1
i — у+
2 2 0 2 0
Й =4i — 2j +2@.
2
А.Вх АС =
1 2 0
0 2 2
Тогда площадь грани АВС определяем по формуле:
Smc — — — IABx ACI =—
«1 1
2 2
= J6.
Найдем угол между ребрами АВ и AD:
А.В- AD
cosy =
[АВНЛЛ[
5-4+О
1 1
Я. $65 5/13
т- е- (р=агссов
1
5 13
ЗАДАЧА 5
Заданы векторы a,b, с и р своими координатами в некото-
ром базисе (табл. P.5). Показать, что векторы а, b, с образуют
базис. Найти координаты вектора р в базисе a, b, ñ.
ОБРАЗЕЦ РЕШЕНИЯ ЗАДАЧИ 5
Пусть векторы имеют следующие координаты:
а(1,1,1), Ь(2,2,1), с(1,2,3), р( — 1,4,7).
Покажем, что векторы а, b, с образуют базис. Как известно,
в пространстве любые три некомпланарных вектора образуют
базис. Для того чтобы векторы а, Ь,c были некомпланарными
достаточно, чтобы их смешанное произведение не равнялось
нулю.
1 1 1 1
аЬ с=2 2 1=0
1 1
0 — 1 =1.
1 2 3 0 1 2
Найдем координаты вектора р в базисе а, b, с. Представим
вектор р ввиде
р =ха+уЬ+гс.
1
Гдвсо — — — I АВ. АС. AD I = — 0
1 1
6 6
5
2 0
2 2
— 2 6

285
РАСЧЕТНО-ГРАФИЧЕСКИЕ ЗАДАНИЯ
Таблица P.Ü
( — 1,2,4)
(О, -1, 2)
( — 2,4,7)
(6, 12, — 1)
(О, 1, 2)
(1, 3, О)
(1,0, 1)
(2, -1, 1)
(1, О, -1)
(13, 2, 7)
(2, -1, 3)
( — 1,2,1)
(1, 1, -1)
( — 1,7,— 4)
(2, О, 3)
10
(6, 5, — 14)
(О, -3, 2)
(2, 1, -1)
(1, 1,4)
(6,— 1,7)
(1, — 2,
— 1, 1,3)
(1, 0,4)
12
13
(1,0,5)
(3, О, 2)
( — 1, 1, 1)
(8, 1, 12)
— 3, 2, О)
(1, -1, 2)
( — 9,— 8,— 3)
(О, 1, — 2)
20
(О, 5, 1)
21
(1,0, 1)
22
(1, — 1,0)
23
( — 3,2, 5)
(2, 1,0)
(23, — 14, — 30)
24
(2, 1,0)
(1,0, 1)
,2)
25
(0,3, 1
(1,— 1,2
, О)
,2)
(1, 1,4
, 18)
(О, -2, 1)
(3, 1, -1)
, 9)
(О, 1,5)
(1,0, 1)
(3, -1, 2)
(1,— 2,0)
29
— 13)
(0,3, 1)
(2, 7,5)
(2, 1, -1)
(4,1,1)
( — 2, О, 1)
(О, 1, 1)
(1, О, 2)
(3, 1, 0)
(0,3, 2)
(2, О, -3)
(1,3, -1)
( — 1,3,2)
(0,1,— 2)
( — 1, О, 1)
(1,1,0)
(1, 2, -1)
(3, -1, 1)
(3, 2, -1)
(О, — 2, 1)
(1,— 1,1)
( — 1,2, 1)
(0,4, 1)
(3, 1, О)
(2, -1,4)
( — 1, О, 2)
(О, — 1, 1)
(1, 0,3)
(2, 5, -3)
(4, 1, 2)
(2, О, -1)
(4, 1,0)
( — 1, 1, 0)
(1,3, О)
(4, 2, 1)
(2, — 1,0)
( — 1, 1, 1)
(1, -4, 4)
( — 9,5,5)
( — 5, — 5,5)
( — 19, — 1,7)
(3, -3, 4)
(3, 3, -1)
(5, 15, О)
(2, — 1, 11)
(11, 5, -3)
(8, О, 5)
(3, 1, 8)
( — 5,9, — 13)
(-15, 5, 6)
(8, 9,4)
(3, 1,3)
( — 1, 7, 0)
(11, — 1,4)

286
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
Получаем систему линейных уравнений:
x+2y+z = — 1,
x+2y+2z = 4,
x+y+3z =7.
Решим эту систему по правилу Крамера:
— 1 2 1
4 2 2
— 1 2 1
0 10 6
1 — 1 1
1 4 2
1 — 1 1
0 5 1
7 1 3
1 2 1
1 2 2
1 1 3
0 15 10
0 8 2
1 7 3
1 2 — 1
0 0 5 =5.
0 — 1 8
1 2 — 1
1 2 4
1 1 7
ЗАДАЧА 6
Найти основание перпендикуляра, опущенного из точки А
на плоскость, проходящую через точки А1, А2, Аз, заданные свои-
ми координатами (табл. P.6).
х — 1 y — 5 z+7
— 4 1 10
= (х — 1)( — 10) — (у — 5)( — 10) +
A,М. А1А2. А1Ад ——
— 3 2 10
+ (z+ 7)( — 5) = — 10х+ 10у — 5z — 75.
Итак, уравнение искомой плоскости.'
2x — 2у + z + 15 = О.
Далее найдем уравнение прямой, проходящей через точку
А перпендикулярно найденной плоскости. Нормальный век-
тор плоскости п(2, — 2, 1) будет направляющим вектором для
ОБРАЗЕЦ РЕШЕНИЯ ЗАДАЧИ 6
Пусть координаты точек А(1, — 1, 2), А,(1, 5, — 7), А2( — 3, 6, 3),
Аз( 2 7 3).
Найдем уравнение плоскости, проходящей через точки А1,
А2, Аз. Если М(х, у, z) — произвольная точка этой плоскости, то
Be~Tîð» А,А, А,А и А,М должны быть компланарными, а зна-
чит, их смешанное произведение должно быть равно нулю.

РАСЧЕТНО-ГРАФИЧЕСКИЕ 3АДАНИЯ
287
А.,
О, — 1)
10
12
13
16
17
18
19
20
21
,— 3,7)
24
25
4, 5)
( — 13,
, О)
26
1,2)
27
( 5
28
29
30
( — 12,7, — 1)
(1, -6, -5)
( — 2,4,2)
(2, -1,4)
( — 5, — 9, 1)
(3, -2, -9)
( — 2,3,5)
( — 3,4, — 5)
(4, 3, О)
( — 21, 20, — 16)
(3, 6, 68)
(2, — 10, 8)
( — 3, 2, 7)
(5, -4, 5)
( — 12, 1,8)
(10, 1,8)
( — 3,1,8)
(10, — 8, — 7)
( — 4, — 13,6)
( — 6, 5, 5)
(2, 3, 8)
( — 5,— 4,8)
( — 3, — 7,6)
( — 3,4, — 7)
( — 1,2,— 3)
( 3,— 1,1)
(1, -1, 1)
(1,2, 0)
(1, 0,2)
(1, 2, -3)
( — 1,2,4)
(О, — 3,1)
(1,3, 0)
( — 2, — 1, — 1)
( — 3,— 5,6)
(2, -4, -3)
(1, -1, 2)
(1,3,6)
( — 4, 2, 6)
(7, 2,4)
(2, 1, 4)
( — 1,— 5,2)
(О, -1, -1)
(5, 2, О)
(2, -1, -2)
( — 2, О, — 4)
(1, 1,2)
(2,3, 1)
(1, 1, -1)
(1, 5~, — 4)
(4, -1, О)
( — 9, 1, — 2)
( — 2,0,3)
(1, -1, 2)
(1,2, — 1)
(1, О, 1)
( — 2,3, — 5)
( — 1,— 2,— 4).
( — 4, 1,2)
(4, -1,2)
(О, 3, 2)
(2, 1, -4)
(5,— 6,0)
(2, 1,2)
(2, 2, 1)
(2, -3, О)
(7, -1, -2)
(3, 5, -2)
( — 6, О, — 3)
( — 2,3,5)
(2, 5, О)
(1, 2, 1)
( — 1,7,1)
( — 5, — 3,2)
(3, О, -3)
(1,2, — 1)
( — 1,1,3)
(4, 1, -2)
(2, 3, 1)
Таблица P.6
( — 5, — 2, 0)
(2, 1, -2)
(3, -5,4)
(2, 1, -1)
(О, 1, -1)
(2, -2, 1)
( — 2,— 1,6)
( — 6, О, — 3)
(3, О, -1)
(2, -1, 5)
(3, О, 1)
(3, 1, -4)
(О, -3, -1)
( — 1,3,— 3)
(1, 1,4)
( — 1, О, 1)
(— - 10,;, 8)
( — 5, — 2, — 1)
( — 7,— 3,2)
(3, 6, -3)
(1,— 5,— 9)
(1, 2,4)
(5, О, -6)
(4, -8, -4)
( — 2, — 6, — 3)
(5, 2, 6)
(3, 2, 1)
(2, -2, 4)
(6, 3, 7)
(3, 2, 1)

ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
искомой прямой. Следовательно, каноническое уравнение пря-
мой имеет вид
х — 1 у+12 — 2
2 — 2 1
Для дальнейших вычислений удобно перейти к параметри-
ческой форме:
х =1+2t,
у = -1-2t,
2 =2+ t.
Для того чтобы найти основание перпендикуляра, определим
координаты точки пересечения найденных прямой и плоскости.
2(1+ 2t) — 2( — 1 — 2t)+(2+ t)+ 15 =0,
9t+21=0, t= — 7/3,
х = 1 + 2( — 7/3) = — 11/3,
у = — 1 — 2( — 7/3) = 11/3, z = 2 — 7/3 = — 1/3.
ЗАДАЧА 7
Вычислить пределы числовых последовательностей (табл. P.7).
Таблица P."

289
РАСЧЕТНО-ГРАФИЧЕСКИЕ ЗАДАНИЯ
Продоижеиие тай ч P.7
ОБРАЗЕЦ РЕШЕНИЯ ЗАДАЧИ 7
Вычислим предел последовательности
а 1+3+". +2п-1
п2+3
2 2
п2 . 1
п~х п2+3 п +~1+3/п2
Используя известную формулу для первых п членов ариф-
метической прогрессии, найдем, что
1+3+...+2п — 1=
1+ 2п — 1
2
-п=п .
Наша задача сводится к вычислению предела

290
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
ЗАДАЧА 8
Вычислить предел функции (табл. P.8).
Та~лица Р.Ь'
Задание
Задание
11»1
jl+ 2х — 3
x' — 7х'+15х — 9
11111
r ! x~ -4хг +21x' 18
cos3x — cpsõ
11П
х -., tg&l ;'
.,ц ~27+ х — ~~7 — х
х+ 2Д
),.„,Я.х-Л:х
1+ x sill х — cps 2x
lil11
х-«о ЯЦ1 Х
1»(1+ я!» х)
li»1
. - о si»4х
10
1 1 — cos'x
л«О 4х-
'7
12
1,.», 1- cos10x
.'J
.»«0 р
13
14
1
'J
liln 5 4
..-о cosx
х' -1
li»1
л -ь1 111 Х
16
15
1
Я
11»1(1 - 111cos х)
18
17
111х
r«0
ctg~x
11111 6-
.i-«o cos x
111 !
1111
.r«;. '~ (л -4х)г
20
19
хг -2х+1
111п
..«1 х~ — хг — х+1
1&g ;» cos5x-со
11и
sin' х
22
21
24
23
1;,и агся1112Х
о Sill 3(Х+ л)
11п
.r;. г яш(5х/2)""'
26
25
27
28
liln
sl» _#_х
11м(щ(х/4 — х})
х-во
30
29
111п "
х-е-2
соя(лх/2)
11П1
.r -е1 1 ]х
11!11
~ -«о Sl ll x
lilII
1100г х
1
1.» Зх-1 y. -&g
Зх+1
11ш(соя Jz)
.»«о
2' ' — 2
111п
о 111(1+ 4х)
2з.» Зг.»
liln
.»о х+ агся!» х'
... /х~-4 — 2
.. о ЗагсФ~х

291
РАСЧЕТНО-ГРАФИЧЕСКИЕ ЗАДАНИЯ
ОБРАЗЕЦ РЕШЕНИЯ ЗАДАЧИ 8
Найдем следующий предел:
~1+ Зх — 2
Jx — 1
Для вычисления предела проведем алгебраические преобра-
зования:
~/Г+Зх — 2 (~1+3x — 2) (~1+3x+2) (~х+1)
~х — 1 (~1+3x+2) (~х — 1) (Jr+1)
(Зх — 3) (~х+1),/х+1
(Д+Зх+2) (х — 1) Д+Зх+2
Точка xp = 1 является точкой устранимого разрыва для функ-
ции
) Л+Зх — 2
х — 1
После проведенных преобразований предел вычисляется под-
становкой х = 1:
~x — 2 . 3(~х+ 1) 6 3
Jx — 1 'Д+Зх+2 4 2
ЗАДАЧА 9
Таблица P.9
Вычислить производную от заданной функции
(табл. P.9).

292
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
Продолжение табл. P.9
ОБРАЗЕЦ РЕШЕНИЯ ЗАДАЧИ 9
Вычислим производную от функции
f(x) =
Для этого используем формулы производной от сложной
функции и производной от частного:
F,'(è) = F„'(è).è,', (и/u)'=
В нашем случае получаем:
f'(õ) = —.
1 3 — х2 (3 — х2)'.(3+х2) — (3+х2)' (3 — х2)
2 3+х2 (3+ x2)2
бх
-12х
(3+х )2
бх
1
2
(3+ х2). 9 — х'
ЗАДАЧА 10
Найти производную от функции, заданной параметрически
(табл. P.10).

293
РАСЧЕТНО-ГРАФИЧЕСКИЕ ЗАДАНИЯ
Тиблицо P.10
Задание
Задание
'r=(1-t) Р,
f (/ = 3/(2Р) — 2/ t
х = as1»
x = (2t ~ t2') /(1 t3')
у =(2t t~) j(1- t~)
у= 1-Р
r = t(1 — si» t),
,,у= tcost
(x = Зсоя1,
= '1 я111 1
х = 21»ctgt -'1,
,у = tg t+ct gt
10
г
r=-Р-:1,
12
у=Р -t-1
[x = atcost
э
у = atsi»
x= 2tg t
х = arcsi»(t/
у = агссоя(1/
fy= 2яш2 t я!и2г
x=si»t,
Iy=a
fx = ln(1 — Р),
16
~yl = t — arctgt
I
x=2'',
у=Р
x=2t — Р,
19
у=3t Ð
x = Зи1!(1+ t
у =ЗаР/(1 —,
23
\
I
r =si»
у = cos-' t
25
(x=(1 lnt)l
~ х = arctgt,
/
! y = t-' /2
'Ly =(3.2ln t)/t
27
28
fx = (t -:1)/t,
Ly =(t -1)/t
x= cost+я»Е,
у = si»2t
29
30
I
1
21
1
1
1
у = acos~ t
x =u(t — si» t),
у = a(1 — cost)
х = t(tcost — 2si»t),
у = t(tsi» t+ 2cost)
r= —,
«1) 1
t
2 4
у= — t ~ — t
1 ~ 1
2 3
Jx = a(t sin t ~ cos t),
[(/ = а(яш t — t cos t)
х = (1 — t-3'),/(Е2 - 1)
18 )
1
у=t '(t' 1)
— +—
fx=t t',
20''
fy=t' — Р
x= t' — 1,
1
22 ~
у=t
1
I
+—
! x= 1»t,
у = cos2t
!
I
(х = sin t.
i J(=1»cost
I
I

294
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
ОБРАЗЕЦ РЕШЕНИЯ ЗАДАЧИ 10
Рассмотрим параметрически заданную функцию:
В данном случае легко исключить параметр t, в самом деле
х2/4 = cos2t у2 = sin2t w х2/4 + у2 = 1
Получено уравнение эллипса. Нетрудно получить явную
функцию, которая будет двузначной:
у=+
На практике очень часто не удается исключить параметр t,
поэтому при вычислении производной у» нужно воспользовать-
ся известной формулой:
у Х = v~/vc
у» = —, = . = — — ctgt.
cost 1
y' -2sin t 2
ЗАДАЧА 11
Применяя правило Лопиталя, найти пределы следующих
функций (табл. P.11).
ОБРАЗЕЦ РЕШЕНИЯ ЗАДАЧИ 11
Найти предел.'
Для того чтобы воспользоваться правилом Лопиталя, перейдем
от неопределенности «m — m» к неопределенности «0/0»:
— 8пх
1 1 . х-81пх
» — О SlnX Х»-эО Х'SlnX
К последнему пределу уже можно применить правило Лопи-
таля:
х sinõ 1. 1 cosx 1. sin x
»- О xsinx»-+О sinx+хсо$х»-+О 2cosx — xsinx
где х = cp(t); у = y(t).
В нашем случае
&
х = 2cost,
у = sin t.
1 1
lim
»-+ Sln Х Х

295
Таблица P.11
Задание
Задание
11m
$1»' х
— Arctg x
g x— - si»x
Sl» Х вЂ” X
— е»)ctgx
1 1
()» — 1
,г» ~)1 х
1» х — COSХ
l»(tgx)
23» Згл
+ gpcsj» XÇ
lim(cos 2х)~
19
»-+о
cos jx)"'
21
23
27
28
29
РАСЧЕТНО-ГРАФИЧЕСКИЕ ЗАДАНИЯ
° l»(tg7x
11111
i о 1]](сg2x
хг —,2Х
111
-+x
111П(СОЯ Х)' '
»-+О
~ьх
11»1
г~:~ 0,5 — $11]
1»(xг — 3
]l
гхг Зх—
& t ~
»1I — '
о~ х
tg — "'."
li»l
..] 111(1 — х
~,„~ 1 — icos
' "1 — cos ~
г
1 1
х- о Хг xS11
,.1» х $1» 2х
.r o 1+ cos(x — Зл)
tgx — si»х
111П
о х(1 — соя 2х)
1 (»--,. - г)
111» tg —,
x
;.;г 2
х — $1»2х
Зхг — х
1 — si» х
CO$ X
з ° 1»$1» х
111»
, »(2х — л)г
г
jcosx — 1
111»
$1»' -2х
1 сов»
11»] ctg—
Х
2
г
З11]~ х — tg~x
linl
.r-+о х"

296
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
ЗАДАЧА 12
Найти производную и-го порядка (табл. P.12).
ОБРАЗЕЦ РЕШЕНИЯ ЗАДАЧИ 12
х — 1
Вычислим производную и-го порядка от функции 9 = »
X+1
у' = (1n [ х — 1 [ — 1n [ х+ 1 [)' =
x — 1 x+1
1 1
(х 1)2 ( ) (х+ 1)2 '
у =(-1).(-2) -(-1).( — 2).
1 1
(х — 1)з (X+ 1)3 '
у& t; " g ; = ( Ђ 1) ( Ђ” ) ... ( Ђ” и †1) . — ( Ђ 1) ( Ђ” ) ... ( Ђ” и вЂ
1 1
(х — 1)" (х+ 1)"
Тибли ци P.12

297
РАСЧЕТНО-ГРАФИЧЕСКИЕ ЗАДАНИЯ
Продолжение табл. P.12
ТМлица P.1 3
ЗАДАЧА 13
Составить уравнения касательной и нормали к данной кри-
вой в точке хц (табл. P.13).

298
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
Продолжение тибл. Р.13
ОБРАЗЕЦ РЕШЕНИЯ ЗАДАЧИ 13
Построим касательную и нормаль к графику функции
х2
у = — — 2Jx+3
2
в точке
хд — — 1: у'(х) = х — 1/ ~х, у'(1) =О.
Уравнения касательной и нормали имеют вид
В нашем случае уравнение касательной
у = у(хд) = 3/2, т. е. у — 3/2 = О.
Формула для нормали непосредственно неприменима, поэто-
му запишем уравнение нормали иначе:
у'(x<& t;) y — y x lt &gt ))  х
Теперь ясно, что уравнение нормали х — 1 = О.
у = у(хд)+ у'(хд) (х — хд), у = у(хд) — 1/(у'(хд)) (х — хд), (у'(хд) w 0).

299
РАСЧЕТНО-ГРАФИЧЕСКИЕ ЗАДАНИЯ
ЗАДАЧА 14
Найти наибольшее и наименьшее значения функций
на заданных отрезках (табл. P.14).
Т06.7МЦ0 P.14
Задание
Задание
[ — 4;2]
2; — 1/2]
2х+ 2)
1; 4]
; 3]
0; 3]
; [2;4)
у = х — 2х + 16/(х — 1) — 13;
[2' Я
х — 4 jx2+8; [ — 1;7]
24
=4xj(4+x ); [ — 4; 2)
; [ — 3;4]
26
у=
2 у
у = 8x + 4/x~ — 15; [1/2; 2]
; [ — 2;4]
у=
27
у = 2(х + 3)/(хг + 2х + 5);
[ — 5; 1]
у - х + 4х + 16/(х + 2) — 9;
[ — 1; 2]
30
29
ОБРАЗЕЦ РЕШЕНИЯ ЗАДАЧИ 14
Исследуем на экстремум функцию у = х + 1/х на отрезке
(1/2; 2]. Находим производную от изучаемой функции:
(х — 1) (х+1)
„г .г

300
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
у(1/2) = 5/2, у(2) = 5/2.
Наименьшее значение функции на отрезке [1/2; 2]:
у;„= min(y(1/2); у(1); у(2)] = у(1) = 2.
Наибольшее значение функции:
у,„= max(y(1/2); у(1); у(2)] = у(1/2) = у(2) = 5/2.
ЗАДАЧА 15
Провести полное исследование функций и построить их гра-
фик (табл. P.15).
ОБРАЗЕЦ РЕШЕНИЯ ЗАДАЧИ 15
Провести полное исследование функции и построить график:
у = х2/(х — 1)2.
1. Область определения:
Т(~йлицо Р.1о
При 1/2 « х &l ;1 у' х  l ; 0 и ф нкция уб в ет, а п и 1 &
у'(х) & t 0 Ђ” функ ия возраста т. Следователь о, то к   1
ляется точкой локального минимума — у(1) = 2.
Определяем значения функции на концах отрезка [1/2; 2]:

301
РАСЧЕТНО-ГРАФИЧЕСКИЕ ЗАДАНИЯ
2. Функция ни четка, ни нечетка, т. к. у( — х) = х2/(х+ 1)2 ~ +у(х).
3. Функция не является периодической.
4. Интервалы возрастания и убывания.
2х(х — 1)2 — х2 2(х — 1) 2(х2 — х — х2)
(х — 1)4 (х — 1)~ (х — 1)~
у' = 0 при х = 0; у' не существует при х = 1.
Функция убывает при х е ( — ~; 1) Ll (1; +сс).
Функция возрастает при х е (О; 1).
(О; О) — точка минимума.
5. Выпуклость и вогнутость кривой.
— 2((х — 1)з — х 3(х — 1)2) — 2(х — 1 — Зх) 2(2х+1)
g
(х — 1)6 (х — 1)4 (х — 1)4
у" = О при х= — 0 5; у" несуществует при х = 1.
х c ( — ~с; — О,б): у" ( 0 — кривая выпукла.
х е (1; +< ): у  0 Ђ” кри ая вогну
( — О,б; 1/9) — точка перегиба.
6. Асимптоты.'
а) вертикальные: х = 1;
б) наклонные: у = kx + b.
ii "") =k,
х — ~+~ Х
lim [f(x) — kx] = b.
х . х2
й= lim =0; b= lim =1.
x- = (х — 1)2 +«(х — 1)2
у = 1 — горизонтальная асимптота.
7. График (рис P 1)

ОТВЕТЫ
ГЛАВА 1
21 -23 3
1.36. -13 34 10 .
— 9 22 25
135 Х" n~" '
О Хп
О О О
о о о.
О О О
1.38. a, b e R
3b a+3b '
а b
1.39. а,b,с~R: a'+bc =0.
с — а
1.40. +~;;
а, b, с ~В: а~+ bс =1.
с — а
1 1 1 1
1 1 — 1 — 1
1 — 1 1 — 1
1 — 1 — 1 1
1 2
3 4
1.42. Х=
1.41. А ' =—
4
1 52 1=2, х<' gt; с Ђ” 4 ceR
3
2
1.53. е, = — 2, ег =—
«1 2
3 ' 3
1
1 — 2
1
— 2, ез =3
2 2
О О
— 9 О
О 18
А*= О
О
1.43. Л = (b — с — d) (b + с + d) (b — с + d) (b + с — d).
1.44. Л = 9. 1.45. rangA = 3. 1.46. rangA = 3.
1.47. х = 2, у = — 1, z = 1.
1.48.х~=1, х2=1, хз= — 1, х4= — 1.
1.49. х~ = с, х2= — 13+Зс, хз = — 7, х4 = О, гдес e R.
1.50. а = — 1, х~ =-5/Зс, х2= 1/3c, хз = с, гдес е R.
1.51. х~ = 5/2 — 3/2c~, х2 = c&g ;, х = х = О, 5= 1 /5 Ђ” 6/5
Х6 — С2, С~, С2 Е В.

303
ОТВЕТЫ
1.54. Положительно определенная.
1.55. Отрицательно определенная.
1.56. Общего вида.
1.57. Отрицательно определенная.
1.58. Положительно определенная.
1.59. Общего вида.
1.60. Положительно определенная.
х2
1.61. Эллипс: — + У
1.62. Парабола: у~ = 4Лх
х2 у2
1.63. Гипербола: — — — =1. 1.64. Эллипс: +
4 9
ГЛАВА 2
2.15. (3; 1).
2.16. Координаты середин сторон АВ, ВС, АС есть соответст-
венно: (3; — 4,5), (О; 1), ( — 1; 1,5).
2.17. D( — 4; 2).
2.18. 13.
2.19. х' + 2х2у2 + у~ — 8ух — 8yз — 16х = 0.
2.20. (х2+ у2 — Зх)2 = 9(х2+ у2)
2.21. (х2+ у2+4х)2 = ]6(х2+у2)
р 2sin~ у 2.23. р = 1 + соя 2(р.
2.24. р = Зсоз2 2у. 2.25. 90'.
2.26. (1; 0,5; — 0,5}. 2.27. — 5.
2.28. a+6b
d =2а — ЗЬ+с, с = — 2a+3b+d,
b =(2/3)а+(1/3)с — (1/3)d,
а =(3/2)b — (1/2)с+(1/2)d.
2.29.
2.49.
2.50.
2.30.
2.32.
2.34.
2.39.
2.43.
2.45.
2.46.
2.47.
2.48.
агссов( — 4/9). 2.31. S = 7Д, ~ BD ~= 2~21/3.
150 кв. ед. 2.33. — 9.
,]2/29. 2.36. с = (5~6)а+(1/3)b
— 42. 2.42. 4 ( а b с !.
43 куб. ед. 2.44. 0 куб. ед.
30, cos a = 1/15, cos у = 11/30.
5 j6, сова= — 1/ /6, совр= — 2/ /6, сову=1/ /6.
2.
— 46.
a(b х с)+ р(с ха)+у(а х Ь)
аЬс
О.

304
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
ГЛАВА 3
ГЛАВА 4
4.24. 3x — 8у+ 4z+ 21 = О.
4.25. 4х — у — 14z = О.
4.26. 19x — 8у+ 14z — 73 = О.
4.27. (х — 1)/1 = (у — 2)/4 = (z + 3)/( — 5).
3.25. -2х + 5у — 11 = О.
3.26. (х — 1)/3 = (у + 2)/О.
3.27. (х — 1)/1 = (у — 2)/4.
3.28. 1) у = ( — 3/2z)x + 4; 2) х/(8/3) + у/4 = 1; 3) х/2 = (у — 1)/3;
4) ( — 3/~11)x+( — 2/~11)y+8/411=0; 5) х = t+ 1, у = 4t+ 2;
6) р = (8/ Jl 1) /сов(ср+ arcsin(2/~11)).
3.29. 1) 5х — бу — 16 = 0; 2) (х — 1)/5 = (у + 3)/( — 6).
3.30. (х+ 1)/6 = (у — 2)/5.
3.31. (х — 0,5)/0,5 = (у — 2)/О; (х — 1)/6 = (у — 2)/7.
3.32. (х — 6)/5 = (у — 26/3)/( — 20/3).
3.33. А( — 2,5; 35).
3.34. А( — 2; О), В( — 6; — 2), С( — 4; — 2), D(0; 4), М( — 3; 1).
3.35. 3 ед. площади. 3.36. 7х — у — 2 = О.
3.37. 7х+у — 10 = О, х+ 7у — 6= О, х — у — 6= О.
3.38. x — у + 2 = О, 2х + 7у + 22 = О, 7х + 2у — 13 = О.
3.39. Зх — у — 1 = О, Зх — у — 21 = О.
3.40. Нет; 2х + Зу — 6 & t; lt О, х Ђ  у +  gt; О  в
3.41. L,„= 88.
3.42. L„„„= 430; x,„= 9, у,„= 8.
3.44. /2.
345. х2/4+ у~~/9 = 1, где х, = х — 2, у, = у+ 1.
3.46. у1 = х21, где x& t   + 2, у  у Ђ”
3.47. х'/9 — у2/4 = 1, где х1= х+ 1, у, = у+ 2.
3.48. х2+у2=(,/0,5)2, где х1 —— х — 0,5, у~ —— у — 0,5.
3.49. х2/16 + у2/9 = 1. 3.50. х2/4 + (у + 1)2/4 = 1.
3.51. х2/144 — у~/25 = 1. 3.52. (у — 4) = 8х.
3.53. х2/4 + y2/3 = 1 3.54. х2/25 + y2/16 = 1.
3.55. х2 + (у — 9)2 = 36. 3.56. х2/12 — у2/4 = — 1.
3.57. 3 ед. площади. 3.58. 30/~20.
3.59. р = b2/(ezcos &l ;р Ђ”
3.60. Окружность радиуса (2/3)(АВ(.
3.61. В системе координат с началом в данной точке и задан-
ной прямой x = — 1 геометрическое место точек есть парабола
у = x2 без вершины.
3.62. Нет.

305
ОТВЕТЫ
4.28. (х — 1)/2 = (у — 2)/4 = (z — 3)/( — 5).
4.29. И=3/ /117.
4.30. 8.
4.31. 1) 2х + 15y + 7z + 7 = О; 2) Зх — 9у — 7 = О.
432.х/2=(у+2)/7=z/4; х=2t, у=7t — 2, z=4t.
4.33. А'(1,4; — 7).
4.34. А(1,96; 2,72; 1,2).
4.35. х + у = О, 5х — 11y + 4z + 5 = О.
4.36. (х + 4)/7 = (у + 1)/6 = (z — 2)/( — 18); (х — 3)/1 =
= (у — 5)/( — 10) = (z + 16)/14; (х + 4)/8 =
= (у + 1)/( — 4) = (z — 2)/( — 4).
4.37. 32.
4.38. 5.
4.39. 2х+ Зу+6z — 12 & t; l ; ,  g ; , у &g
440.L,„=71 при х=О, у=3, z=9.
4.41. z=е" +~
4.42. z = 5(х' + у~).
4.43. х'+ z~ = у'
4.44. 1) (х' + у~)/9 — z~/4 = 1 — однополостный гиперболоид;
2) х~/9 — (у' + z~)/4 = 1 — двухполостный гиперболоид.
4.45. х~+ у~ = 12z.
4.46. х + у — z~ = — 50 — двухполостный гиперболоид.
4.47. (х — 1)~+(у+ 3)~+(z/2)~ =4' В=4, 0'(1; — 3; 2).
4.48. z,„= 3.
ГЛАВА 5
5.80.
5.85.
5.90.
5.93.
4.
О.
— 1
1/8.
5.28.
5.33.
5.38.
5.43.
5.48.
5.53.
5.58.
5.63.
5.68.
5.73.
5.74.
5.75.
5.76.
5.81.
5.86.
5.91.
2/3. 5.29. ~о. 5.30. 65/97. 5.31. l.
— 2. 5.34. О. 5.35. 1/2. 5.36. 9/8.
— 4. 5.39. 1. 5.40. 1/2. 5.41. 1.
О. 5.44. — 1/8. 5.45. 4. 5.46. 5.
О. 5.49. — 2/7. 5.50. 9/4. 5.51. 2/3.
О. 5.54. и/т. 5.55. 2. 5.56. ~.
2. 5.59. 1. 5.60. 1/4. 5.61. 10.
-1. 5.64. О. 5.65. 1/6. 5.66. 12.
2/3. 5.69. т/и. 5.70. — 1/4. 5.71. — 1/4.
1, если х-++~; ~, если х-+ — ~.
3/2, если х-++со; оо, если х-+ — oo.
— 1, если х ++~; 1, если х ~ — о.
3. 5.77. 4. 5.78. а/Р. 5.79. а/Р.
1. 5.82. 1/2. 5.83. 3. 5.84. 1/6.
— 1/2. 5.87. 5/3. 5.88. 1. 5.89. — 1/ j2.
(P' — а')/2. 5.92. sin(4y)/4ó.
5.32.
5.37.
5.42.
5.47.
5.52.
5.57.
5.62.
5.67.
5.72.
1/2.
1/2.
2/3.
ОС,
— 1/2.
О.
1/2.
2.
О.

306
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
ГЛАВА 6
6.86. а) hf(xp, Лх) = 0,1; 6) hf(xp, Лх) = — 1;
в) hf(xp, Лх) = — 1/21; г) hf(xp, Лх) = 0,331.
6.88. f'( — 1) = — 2, f,'( — 1) = О, f (1) = О, f,'(1) = 2.
6.89. f'(1) = 1, /,'(1) = О.
6.90. f'(õ) =15х +1 2х '3+Зх-г/3+5х 12~7
6.91. f (х) =
Зз хг
6.92. f'(õ) = 4x3cos х — х4sin х.
log& t x ar t
6.93. f'(х) 1+х х1п2 6.94. f'(õ) =20õç+
г 56 9
log22 х х 5~~хг
6 95 f'(х)=6х+ +Зх в1пх+х совх.
ХЗ
6 98
х6
5" .1п 5 arcsin х — 5" .
1 — хг
5х
6.99. f'(х) =е +е'
arcsin x
arcsin2 х
р ФДХ logÇХ 'ЙЯХ logÇХ '~Х
6.100. ~' х = + +
1п3 ~х 2~х сов х
— — 9х с1дх
в
6.101. /'(Х) = s111 13
6.102. f'(õ) = 2х — 4, f'(2) = О.
6.103. f'(õ) = — — бх, f'(О) не существует.
х
— 1, при — m<x
6.104. f'(õ) = О, не существует при х =4;
1, при 4 & t х &l
f'(1) = — 1; f'(4) не существует.
6.96. /'(Х) = — 2sin х — 7cos х. 6.97. f'(x) =cosx arcigx+ в1пх
1+ хг

307
ОТВЕТЫ
2х — 3, при — ~<х
не существует при х =1;
3 — 2х, при — ~о<х
не существует при х = 2;
2х — 3, при 2 & t х &
6.105. f'(х) =
/(1) не существует, f(3) = 3.
6.106. /(хо) = О.
6.107. f '(õo) = О.
6.108. f'(õ) =
2~/х 1 — х
6.109. f'(õ) = 3' in 3~x~ +3*
sin~(3'3 х~) 3 х
х — logs x(5x4)
х1п3
6.110. f'(õ) =
г
1+ ~О@3 х
х5
х
6.111. ~'( ) =—
sin( ~õ)
2 х
6 112 f'(x) = 7x6e3ê + 3x~e3ê
4хз
(2х — 8)~х~ +1 — (х~ — 8х)
5
6.113 /'(х) =
х — 8х
5] 4+1
(1+ 2x)ctg(logq(arccos(4~')))
1
(1+ х+ х~) з
+2
sin~(logq(arccos(4~)))
1 1
4~'(1п 4).
arccos(4~ ) ln7
6.115. f'(х)=2 ln2 ctg( — 4х)+2 . ( — 4).
sin~( — 4х)

308
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
6.116. Г(х) = (2х+2).
(x2+2x+9) ln 2
6.117. f'(õ) = (12х2) 10.
1+16х6 1+10х
2(х2 + 4) — 2х arcsin(2x)
6.118. f'(õ) =
(х2+4)2
}~хз
6.119. f'(õ) =3xschxs агссов ~х
2 х 1 — х
агссФд(Зх+1)21n х
31п2 х
агссйд(Зх+ 1) 1+ (Çx+ 1) 2
1п2 х
1п4 х
у2cosx
6.131. у (x) =
+2умпх — 5
1
sin2 у
2ху
(1+ х2)2
6.132. У (х) =
Зу
+у6 1+х2 у
6.133. у,'(х) =
7»
7" 1п у arcsin у+
1 — у~
8 — ~1 — у
6 134 у,'(х)=
+ 2chy
2 1 — у
6.136. у,'(х) = у/х.
4 5 1 1 1 1
6.138. Г(х) =
+
х 1+х 2 х+8 2 х — 2
6.129. Ух (х)
3 у х )2
6.130. у (х) = y('-ysinx)
1 — ycosx
6.135. у„'(х) =" xlny
х ylnx — х
3'(3» — 1)
6.137. " (х) = 3»(1 3 )

309
ОТВЕТЫ
3
tgÇx х2 arctg(+x)
6.139. ' х =
X
1п2 х.25"
3 3 1
+ +
~дЗх cos Зх 2х агс~д,Я
X
1 1 1 1
2 .— — 5ln2 .
1+х 2,/» lnx x
arcsin6x ctgx'
6. 140.
Х
sh2x cos(lnx)
Х
с~дх2
агся1пбх
2ch 2х sin(ln х)
Х +
sin2х' sh2x cos(lnx) х
6.141. ' х =
log>(x' 1) агссо 7х (х 2 е
Х
2х 7
Х
(х'+1)ln2 arccos7x
6.143. f'(x) =x ' +
.Б ln x 1
х х
6.142 дх) =x~„„21nõ
х
6 144 Дх) ctgx""'" ~„- 1пс1дх агсв1пх
2,Я j] — х ctgx sin2õ
Х
6.145. f'(x) =(
х — cos5x ln(x +х+7)+ — sin5x.
5
2
1 . 2х+1
3 3 х2+х+7
)sin5x
6.146. Г(х) =(
— ппв5х 1п(х' в хв 7)-.'- — в!п5х.
5 2 1
3 3 х2+х+7
2х tg9x—
сов'9х 1 (1 ) х2+1
tg29x tg9x 1пх х
х~+1
6.147. f'(õ) =(1пх)~в9"
24х
',:з+2

310
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
6.148. f'(x) =(arcsin(e2*))' х
1 2е2х
arcsin(e2*) /1
6.150. у,' = — t/sin2t.
х 3»~ inarcsin(e2*)+x3
6.149. у„' = — ctg t.
6.151. у„' =
е
2
6.153. ' = ~+~
21п2
2t(t +2)
(1+ t")(2 — Р— 2t)
vçdи — u3v2сЬ
6.164. а) dy=
6) dy=
1
° ln vdu+ — dv;
и
+и2 1п2 )
V
в) d(2'tg(v2)) =2" 1п2Сд(и2)Ни+2" dv;
cos~(v~)
~~+и, „
ctgu sn и
г) d
ctgu
Иу
6.165. а) dy = (3» — 3)dx; 6) dy = (4x3cos»~ — 2»"sin x2)dx;
5,/» ctg 5x
вш25» 2 ß
в Шу= Их.
х
е2' in(e+3x2) — е2'
е+Зх2
6.166. а) dy(x) = dx, dy(0) = 0,1;
in2(е+ 3»2)
6) dy(x) = x cos xdx, dy(x) = 0; в) dy =—
0,017с
6 154 i cos2t — 2t sin2t
sin 2t+ 2t cos2t
6.156. у,' = sin t/(1 — cos t).
6.157. Уравнение касательной у = 13x — 12. Уравнение нор-
1 14
мали у= — — х+ —.
13 13
6.158. у = 2 — x.
6.159. (О; — 7), (in 3; 15).
6.160. arctg(2/е).
6.161. а = 45'.
6.162. а = 0'.
6.163. а = 90'.

ОТВЕТЫ
6.167. а) 6,01; б) 6,99; в) J3/2 - 0,851;
2 180'
г) х/6+ 0,001 = 0,513.
6.168. f"(x) = 12x2sin 2х+ 16x~cos 2х — 4х'sin 2х.
6.169. f"(x) = +
1 2
~1 2. ~1 3.
6.170. f" (x) = 9 23'(1n22).
6.171. f"(x) =
1+ 25х2
6.172. а) dy = (Зх2+ 2)dx, d~y = 6x(dx)~, d~y = 6(dx)3;
б) dy = (( — 3/2)x2sin(2x3) + 9)dx;
d~ó = — 3(sin(2x3) + Зх"cos(2x~))(dx)~;
&lt ~ = Ђ” 18х'(cos(2 3 + 2xcos(2 ~) Ђ” Зх"sin(2x~))(dx
6.173. d'ó = 120(dx)5.
6.174. Ш("&g ; = 2ле2хф
6.175.
6.182. 2.
6.186. -2.
6.190. 1.
+ 9.
6.198. f(x) = — + — x+ — x + "+ 1 — x" +".
2 8 26 2
3 9 27 3""
6.199. а) arctg 0,8 = 0,67474;
б) cos (х/20) = 0,98769; Я = 2,236022.
6.200. 0,401 ( ln1,5 ( 0,408.
6.201. а) 1; б) 1/4; в) 0,5; г) 1/12; д) — 1/3;
е) — 1/12; ж) 1/3; з) 0,5.
6.202. f;„(3) = Зе 9, убывает при x s ( — oo; 3), возрастает при
х е (3; +oo).
6.203. f;„(3) = 5/4, убывает на интервале x s (1; 3), возрас-
тает на интервалах х е ( — oo; 1) и x s (3;+oo).
6.204. Возрастает на интервалах x E ( — oo; 1) их е (3;+oo), убы-
вает на интервале х s (1;3), f,„(1) = 1, f,„(3) = — 3.
6.205. f,„(1/4) =,/15/8, убывает при х e ( — oo; 1/4), возрас-
тает при x s (1/4; +oo).
6.176.
6.177.
6.183.
6.187.
6.191.
6.194.
6.195.
6.196.
6.197.
с1 = — е[ — 1;О], ср — — — е[0;1].
3 3
Нет, так как не существует /(2).
с = О. 6.178. x = 2. 6.181. с = 14/9.
5. 6.184. -2. 6.185. 4.
О. 6.188. 1. 6.189. 1.
е'/2 6.192. е '/6 6.193. е '~з
f(x) = 2(х — 2)' + 11(x — 2)3 + 15(x — 2)2.
f(x) = x6 — бх5 + 21x' — 44хз + 63х2 — 54х
f(x) = 1 + x2/2 — x'/8+ o(xs).
f(x) = — x2/2 — x'/12 — x6/45 + о(х7).

312
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
1 1
6.209. /наиб(хинин = 2) = 53 /наим(хнаим = 3) =
1
6.210. Наибольшее значение равно /„б = — + — ~» идостига-
ется при x„,„б = 1; наименьшее значение равно f„,„,„= 1 и дости-
гается при х„,„„=1/ JR.
6.211. f-.e = f( — 20) = 229, &lt -. f( Ђ” 1 =
6.212. Наибольшее значение площади равно Я = — a2 и дости-
2
гается при х = я/2.
2
6.213. 445. 6.214. а = я~8/3.
6.215. 0,8р; О,бр; О,бр.
6.221. х = — 1/2.
6.223. x = — 1. 6.224. x = 2.
2
6.225. На интервалах ( — ee; — 1) и (1; +ee) график функции во-
гнут, на интервале ( — 1; 1) график функции выпуклый. Значения
функции в точках перегиба f( — 1) = О, f(1) = О.
6.226. На интервале ( — ee; О) график функции вогнут, на ин-
тервале (О; +oo) график функции выпуклый. Значение функции
в точке перегиба f(0) = О.
6.227. На интервале ( — 1; 1) график функции вогнут, на ин-
тервалах ( — ~; — 1) и (1; ~ю) график функции выпуклый. Значение
функции в точках перегиба f(+1) = 1n2.
6.228. На интервале ( Я/3; Я/3) график функции выпук-
лый, на интервалах ( — ~; — ~3/3) m(J3/3;+со) график функции
вогнутый. Значение функции в точках перегиба f(+ J3/3) = 0,75.
6.229. На интервале (1/3; 1) график функции выпуклый, на
интервалах ( — ~; 1/3) и (1/3; +ee) график функции вогнутый. Зна-
чение абсцисс точек x& t = 1 3, х =
6.230. На интервале ( — J2/2; J2/2) график функции выпук-
лый, на интервалах ( — со; — ~2/2)z(42/2;+ж) график функции
вогнутый. Значение абсцисс точек х, р — — + J2/2, хр — — 1.
6.231. Значение функции в точках перегиба:
а) /(+2/3) = 44/27; б) f(5) = 1.
6.232. а) а е ( — 4; 4); б) а е ( — 2; 2).
6.234. Наклонная асимптота у = x + 1 при x -+ +~, вертикаль-
ная асимптота х = О при x -+ +О.
6.235. Наклонная асимптота у = 3x при x -++~, вертикаль-
ная асимптота x = — 1 при x -+ +О.

ОТВЕТЫ
313
6.236. Наклонные асимптоты: у = (я/2)x — 1 при х ++~о и
у = (я/2)x — 1 при x -+ — ~ю.
6.237. Вертикальная асимптота x = О при х -++О, горизон-
таЛЬНая аСИМПтОта у = О ПрИ X -++О0.
6.238. Вертикальная асимптота x = 1 при х -++О, горизон-
таЛЬНая аСИМПтОта у = О ПрИ X -++О0.
6.239. Горизонтальная асимптота у = О при x -+ +«~.
6.240. Горизонтальная асимптота у = О при x -+ +О0.
6.241. Наклонные асимптоты: у = х + к при х -+ +~ и у = x—
— упри x w — xo.
6.242. Вертикальная асимптота x = 2 при x -+ 2 + О, наклон-
ные асимптоты: у = х + 1 при х -+ +О() и у = — x — 1 при х -+ — О0.
6.243. Вертикальная асимптота x = О при х -++О, наклонная
асимптота: у = x npu x -++О0.
6.244. Наклонная асимптота у = x — 3 при х -++О0.
6.245. Вертикальная асимптота x = О при x -+ +О, наклонная
асимптота: у = х при х ~ +~с.
6.246. ОДЗ х н ( — ~; +oo); область изменения функции
у н ( — oo; +oo); функция общего вида, непериодическая, непрерыв-
ная всюду при х е ( — ~ю; +сс); асимптот нет; /,„„„= 3, х,„= 1; ин-
тервалы возрастания х н ( — ~с; 1) и х н (3; +oo); fm,„= — 1, xn»n = 3;
интервал выпуклости х е (О; 2), интервал вогнутости х е (2; +oo),
точка перегиба (2; — 2).
6.247. ОДЗ х н ( — oo; 1) Q (1; +oo); область изменения функции
х E ( — oo; +сс); функция общего вида; непериодическая; непрерыв-
ная всюду за исключением точки x = 1, в которой имеется раз-
рыв второго рода; асимптоты x = 1 и у = x + 5; в интервалах
х н ( — oo; 1) и х н (5; +oo) — возрастает, в интервале х н (1; 5)—
убывает; f,„;„= 13,5, x,„„„= 5; в интервале х н ( — oo; 1) выпукла, на
интервалах х E ( — 1; 1) и х E (1; +oo) — вогнута, точка перегиба—
( — 1; О); точки пересечения с осями координат (О; 1) и ( — 1; О).
6.248. ОДЗ х E (О; +oo); функция общего вида; непериодиче-
ская; непрерывная всюду на ОДЗ; асимптоты x = 0 и у = 0; в ин-
тервалах х E (О; е ) — возрастает, в интервале х е (e; +oo) — убы-
вает; f„„„= 6/е, x,,„„= =е~; в интервале х е ( — ~; е~~з) вогнута, на ин-
тервале х н(Я/5; ц — выпукла, точка перегиба — (ез~з; 8/е'~з);
точка пересечения с осью абсцисс (1; О).
6.249. ОДЗ х н ( — ~; +oo); функция четная; непериодическая;
непрерывная всюду на ОДЗ; асимптоты нет;
в интервале х E ( — со; 0) — убывает,
в интервале х е (О; +ao) — возрастает; f„;,„= — 5, x;„= 0;

314
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
в интервалах х E ( — 00; — 1), х E ( — Я/5; Я/5) и х E (1; +с~) — во-
гнута, на интервале хе( — 1; Я/5),хе(Л/5;1) — выпукла, абс-
циссы точек перегиба — х =+Я/5.
6.250. ОДЗ x e ( — ю; — 1) lJ (1; +~); функция общего вида; не-
периодическая; непрерывная всюду на ОДЗ; асимптоты x = +1; в
интервале х e ( — 1 — J2; О) — убывает, в интервалах х e ( — ~; — 1 — /2)
и x e (1; +со) — возрастает; f = — 1 — i/2+1п(2+2)2), x,„=
= — 1 — /2 при x e ( — ~; — 1) и x e (1; +с~) — выпукла, точек переги-
ба нет.
6.251. ОДЗ х E ( — ~; +~); функция общего вида; непериодиче-
ская; непрерывная всюду на ОДЗ; асимптот нет; в интервалах
х e ( — ~; О) и х е (2; +~) — возрастает, в интервале x e (О; 2)—
убывает; f ~„=О,x „=О, ~~; = — 3~4, x;„=2;прихе( — 1;0)и
х е (О; +~) — вогнута, точек перегиба нет.
6.252. ОДЗ х e ( — с~; О) U(0; 1]; функция общего вида; непе-
риодическая; непрерывная всюду кроме точки x = О, в точке x = 0
разрыв второго рода; горизонтальная асимптота у = О, вертикаль-
ная асимптота x = О; на интервалах х E ( — ~; О) и х E (О; 1) — убы-
вает; экстремумов нет; на интервале х E ( — ~; О) — выпукла, на
интервале x e (О; 1) — вогнута; точек перегиба нет.
6.253. ОДЗ х E ( — с~; +с~); функция четная; непериодическая;
непрерывная всюду на ОДЗ; асимптот нет;
в интервалах х E ( — ~; — 1) и х E (1; +~) — убывает, в интерва-
ле x e ( — 1; 1) — возрастает; f,„= 3, x,„= О, f;„= 2, x;„= 1; при
х e( — ю; — J3/3) иx e(J3;+со) — вогнута, при х&l ;( Ђ” 3; J3
пукла; точки перегиба: ( — Л; — Л/4), (Л; Л/4) °
6.254. ОДЗ х e ( — со; +со); функция нечетная; непериодиче-
ская; непрерывная всюду на ОДЗ; горизонтальная асимптота у = О;
в интервалах х E ( — ~; — 1) и х E (1; +~) — убывает, в интервале x e
е ( — 1; 1) — возрастает; f,„= 1, x,„= 0,5, f„;,„= — 1, x;„= — 0,5; при
x e (~; — J3) и х e ( j3/3; + ~о) — вогнута, при х е ( — ГЗ /3; ~3/3)—
выпукла; точки перегиба: хe( — ГЗ/3;22/9),х e(J3/3;22/9).
6.255. ОДЗ x e ( — oo; +~о); функция общего вида; неперио-
дическая; непрерывная всюду на ОДЗ; наклонная асимптота
у = х+ 2/3; в интервалах x e ( — ~; О) их е (4/3;+~) — убывает, в
интервалеx е (О;4/3) — возрастает; f,„= — ~4, х,„= 4/3, f;„= О,
«2з~
™"

ОТВЕТЫ
315
х,.„= 0; при х е ( — oo; О) и х & t; 2; + o) Ђ” вогну а, р  е О; 2)
выпукла; точки перегиба: (О; О), (2; О).
6.256. ДДЗ x e ( — сс; О) U (О; +~с); фУнкциЯ общего вида; непе-
риодическая; непрерывная всюду на ОДЗ; наклонная асимптота
у = x + 2/3; в интервалах х е ( — oo; О) и х е (4/3; +oo) — убывает, в
интервалех е (О;4/3) — возрастает; f,„= — ~4, x,,„„= =4/3, f„„„= 0,
2з~
x~;„= О; при х e ( — oo; О) и х е (2; +~) — вогнута, при x e (О; 2)—
выпукла; точки перегиба: (О; О), (2; О).
6.257. ОДЗ x e ( — ~с; О) () (О; +с~); функция общего вида; непе-
риодическая; непрерывная всюду на ОДЗ, кроме точки x = — 1,
где имеется разрыв второго рода; вертикальная асимптота
x = — 1, горизонтальная асимптота у = 0 при x -+ — ~; в интерва-
лах х н ( — oo; — 1) их н ( — 1; О) — убывает, в интервале х е (О;+oo)—
возрастает; f;„= О, x;„= О; при x e ( — oo; — 1) и x e ( — 1; +oo)—
вогнута.
6.258. а) К = 2, R = 1/2, Х = О, У = — 3 5;
б) К=]2/4,R=2~2, Х=З,У=2;
в) К=1,R=1,Х= — я/2, Y=O;
г) К =0,06jlO,R =5/10/3, Х = — 4, У = 1,6.
6.259. а) К =3~40/SOO,R = 20~40/3, Х = — 19, У = 26/3;
б)К=а/b2 R=b2/a, Х= 1 — b2/a, Y=O;
в) К = J2,R= J2/2, Х = 0,5, У= 0,5;
г) К = j5, R = j6/6, Х = 2, У = 2.
6.260. а) К = 3/(4a), R = 4a/3, Х = 2a/3, Y = 0;
я2 /4+ 2 а(я2 /4+ 1)з ~ 2
,R=
п(я2/4+1)3)2 ' z2/4 t2
а(я~ + 4) а(я~ + 6)
g2qg 2~8
в) К =22/4a, Л =2а /2, Х = — 2asin(ln2),
У = 4a sin (in2) — а cos (in2).

СПИСОК
ЛИТЕРАТУРЫ
1. Ильин В.А., Позняк Э. Г. Аналитическая геометрия. М.: Физмат-
лит, 2006.
2. Ильин В.А., Позняк Э. Г. Линейная алгебра. М.: Физматлит, 2006.
3. Ильин В.А., Позняк Э. Г. Основы математического анализа: В 2 т.
М.: Физматлит, 2005.
4. Кудрявцев Л.Д. Математический анализ: В 2 т. М.: Физматлит, 2006.
5. Бугров Я. С., Никольский С. М. Высшая математика: В 3 т. М.: Физ-
матлит, 2005.
6. Фихтенгольц Г. М. Курс дифференциального и интегрального ис-
числения: В 3 т. М.: Физматлит, 2006.
7. Пискунов Н. С. Дифференциальное и интегральное исчисление:
В 2 т. М.: Интеграл-Пресс. 2006.
8. Цемидович Б. П. Сборник задач и упражнений по математическо-
му анализу. М.: Физматлит, 2005.
9. ЕфимовА. В., Цемидович Б. П. Сборник задач по высшей матема-
тике для втузов: В 4 ч. М.: Физматлит. 2004.
10. Цанко П. Е., ПоповА. Г., Кожевникова Т. Я. Высшая математика
в упражнениях и задачах: В 2 т. М.: ОНИКС, 2006.
11. Кузнецов Л.А. Сборник заданий по высшей математике. М.: Выс-
шая школа, 1983.
12. Кручкович Г. И. Сборник задач по курсу высшей математики. М.:
Высшая школа, 1973.
13. Иванова И. Е. Дифференцирование функций одного переменного:
Учебник для втузов. М.: Изд-во МГТУ им. Баумана, 1998.
14. Минорский В. П. Сборник задач по высшей математике для вту-
зов. М.: Наука, 1987.
15. Каплан И.А. Практические занятия по высшей математике. Харь-
ков: Изд-во Харьковского Гос. ун-та, 1972.
16. ГусакА.А. Задачи и упражнения по высшей математике. Минск:
Высшая школа, 1973.
17. Лихолетов И. И., Мацкевич И. П. Руководство к решению задач
по высшей математике, теории вероятности и математической ста-
тистике. Минск: Высшая школа, 1969.
18. Виноградова И.А., Олехник С.П., Садовничий В.А. Задачи и уп-
ражнения по математическому анализу. М.: Изд-во МГУ, 1988.
19. Запорожец Г. И. Руководство к решению задач по математическо-
му анализу. М.: Высшая школа. 1964.

ОГЛАВЛЕНИЕ
Глава1
Элементы линейной алгебры....................
1.1. Матрицы и определители...................
1.2. Линейные пространства....................
1.3. Аналитические методы решения систем
линейных алгебраических уравнений
1.3.1. Основные определения
1.3.2. Метод, основанный на применении
обратной матрицы (матричный метод)
1.3.3. Метод Крамера....................
1.3.4. Метод Гаусса
1.4. Линейные преобразования (отображения) .....
1.5. Собственные значения и собственные векторы
линейных операторов......................
1.6. Евклидовы пространства...................
1.7. Квадратичные формы.
Приведение к каноническому виду уравнений
кривых и поверхностей второго порядка ......
1.8. Решение типовых задач....................
1 .9. Задачи ..................................
5
5
15
17
17
... 20
... 21
... 21
... 29
... 34
... 35
... 37
... 40
... 75
Глава 2
Векторная алгебра .........................
2.1. Координаты точки и вектора.............
2.2. Деление вектора в данном отношении
2.3. Преобразования координат ..............
2.4. Полярная система координат и ее связь
с декартовой системой ..................
2.5. Связь между декартовыми прямоугольными
и полярными координатами
2.6. Линейная зависимость
и независимость системы векторов........
2.7. Скалярное, векторное
и смешанное произведения векторов
... 79
... 79
... 83
... 83
............ 84
.-.......... 85
.-.......... 85
............ 87
П редисловие .......................................... 3

318
ПРАКТИЧЕСКОЕ РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
2.7. 1. Скалярное произведение векторов
Lt
и его своиства в ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° °
2.7.2. Векторное произведение двух векторов
и ero свойства............
2.7.3. Смешанное произведение векторов
%,Ф
и ero своиства.....................
2 ° 8. Решение типовых задач......
2 .9. Задачи ..................................
87
89
91
93
104
Глава 3
Аналитическая геометрия на плоскости
3. 1. Прямая линия..................
3.2. Решение типовых задач..........
3.3. Кривые второго порядка
3.4. Решение типовых задач..........
3
° ю
.э. адачи ........................
107
107
111
122
129
133
° ° ° °
° ° ° °
° ° ° °
° ° ° °
° ° ° °
° ° ° °
Глава 4
Аналитическая геометрия в пространстве
4.1. Плоскость и прямая..............
4.2. Решение типовых задач...........
4.3. Поверхности второго порядка......
4.4. Решение типовых задач...........
4 .5. Задачи .........................
137
137
141
150
154
157
° °
° °
° °
° °
° °
° °
Гла
Введ
5.1.
159
159
159
161
161
161
162
164
5.2.
164
165
166
167
168
175
5.3.
5.4.
5.5.
5.6.
175
177
180
181
5.7.
181
ва 5
ение в математический анализ ...................
Элементы теории множеств......................
5.1.1. Множества и операции над ними ..........
5.1.2. Взаимно однозначное соответствие
и эквивалентность множеств
5.1.3. Прямое произведение множеств...........
Множество вещественных (действительных) чисел...
5.2.1. Основные свойства вещественных чисел....
5.2.2. Ограниченные множества вещественных чисе
5.2.3. Некоторые конкретные
множества вещественных чисел...........
5.2.4. Структура открытых и замкнутых
множеств на прямой ....................
Основные логические символы ...................
К ванторы.....................................
Предел последовательности......................
Функции действительного переменного............
5.6.1. Введение понятия функции
и основные способы задания функций......
5.6.2. Некоторые свойства функций.............
5.6.3. Элементарные функции и их классификация
П редел функции...............................
5.7.1. Определение предела функции
и его геометрический смысл..............

319
ОГЛАВЛЕНИЕ
185
186
188
189
° °
° °
189
192
195
197
209
° °
° °
° °
° °
219
220
221
222
223
224
225
228
228
230
262
274
302
316
5.7.2. Основные теоремы о пределах
5.7.3. Бесконечно большие
и бесконечно малые функции............
5.7.4. Свойства бесконечно малых
и бесконечно больших функций..........
5.7.5. Два замечательных предела .............
5.7.6. Некоторые способы
раскрытия неопределенностей...........
5.7.7. Сравнение бесконечно малых
и бесконечно больших,
таблицы основных эквивалентных величин
5.7.8. Сравнение бесконечно больших функций ..
5.8. Решение типовых задач........................
5 .9. Задачи ......................................
Глава 6
Производная и дифференциал функции
одной независимой переменной
6.1. Определения производной и дифференциала
6.2. Правила нахождения производных
и дифференциалов суммы, разности,
произведения и частного функций...................
6.3. Дифференцируемость. Производные сложных
функций, обратных функций. Таблица производных ...
6.4. Инвариантность формы первого дифференциала .......
6.5. Логарифмическое дифференцирование...............
6.6. Производная функции, заданной параметрически......
6.7. Производные и дифференциалы высших порядков .....
6.8. Теоремы Ролля, Лагранжа, Коши ..................
6 .9. Правило Лопиталя
6.10. Формулы Тейлора и Маклорена....................
6.11. Уравнения касательной и нормали к графику кривой ..
6.12. Интервалы монотонности, экстремумы..............
6.13. Наибольшее и наименьшее значения
непрерывной функции на отрезке и интервале.........
6.14. Интервалы выпуклости, вогнутости, точки перегиба....
6.15. Общая схема исследования функций
и построения графиков...........................
6.16. Кривизна кривой................................
6.17. Решение типовых задач
6 .18. Задачи
Расчетно-графические задания
Ответы .........
Список литератур~д...
212
212
214
214
216
216
218
218

Игорь Алексеевич СОЛОВЬЕВ, Валентин Владимирович ШЕВЕЛЕВ,
Александр Викторович ЧЕРВЯКОВ, Андрей Юрьевич РЕЯИН
ПРАКТИЧЕСКОЕ РУКОВОДСТВО
К РЕШЕНИЮ ЗАДАЧ
ПО ВЫСШЕЙ МАТЕМАТИКЕ
Линейная алгебра, векторная алгебра,
аналитическая геометрия, введение
в математический анализ, производная и
ее приложения
Учебное пособие
Генеральный директор А. Л. Кноп
Директор издательства О. В. Смирнова
Художественный редактор С. Ю. Малахов
Редактор И. Л. Яновская
Корректоры А. К. Райхчин, И. А. Короткова
Подготовка иллюстраций В. В. Воскресенская
Выпускающие Н. К. Белякова, О. В. Шилнова
ЛР М 065466 от 21.10.97
Гигиенический сертификат 78.01.07.953.П.004173.04.07
от 26.04.2007 г., выдан ЦГСЭН в СПб
Издательство «ЛАНЬ»
lan@lpbl.spb.ru; www.lanbook.corn
192029, Санкт-Петербург, Общественный пер., 5.
Тел./факс: (812)567-29-35, 567-05-97, 567-92-72;
print@lpbl.spb.ru
Книги издательства «Лань»
можно приобрести в оптовых книготорговых организациях:
САНКТ-ПЕТЕРБУРГ. 000 «Лань-Трейд»
192029, Санкт-Петербург, ул. Крупской, 13,
тел./факс: (812) 567-54-93,
тел.: (812) 567-85-78, (812) 567-14-45, 567-85-82, 567-85-91;
trade®lanpbl.spb.ru
www.lanpbl.spb.ru/price.htm
МОСКВА. 000 «Лань-пресс»
109263, Москва, 7-я ул. Текстильщиков, 6/19,
тел.: (495)178-65-85; (495)740-43-16;
lanpress@ultimanet.ги; 1апргеаа@уапйех.ги
КРАСНОДАР. 000 «Лань-Юг»
350072, Краснодар, ул. Жлобы, 1/1, тел.: (861)274-10-35;
lankrd98@mail.ru
Сдано в набор 07.02.07. Подписано в печать 20.10.07.
Бумага офсетная. Гарнитура Школьная. Формат 84~108 '/З2.
Печать офсетная. Усл. и. л. 16,80. Тираж 2000 экз.
Заказ М 164.
Отпечатано с готовых диапозитивов в ООО «Первая типография»
195237, r. Санкт-Петербург, ул. Руставели, д. 13.