Н. Н. БОГОЛЮБОВ, Д. В. ШИРКОВ
КВАНТОВЫЕ ПОЛЯ
Допущено Министерством высшего
и среднего специального образования СССР
в качестве учебного пособия для студентов
физических специальностей высших учебных заведений
москва «наука»
главная редакция
физико-математической литературы
1980

22.31
Б 74
УДК 530.45
БОГОЛЮБОВ Н. Н., ШИРКОВ Д. В. Квантовые
поля, учебное пособие. — М.: Наука. Главная редак-
редакция физико-математической литературы, 1980.
В последние годы курс релятивистских квантовых
полей, являющихся основой квантовой теории ма-
материи, занял прочное место в программе физических
факультетов университетов.
Предлагаемая книга задумана как учебное посо-
пособие, предназначенное для студентов, впервые изу-
изучающих предмет, План книги следует первой поло-
половине известной монографии тех же авторов «Введе-
«Введение в теорию квантованных полей» и содержит ли-
линейное изложение теории квантовых полей, начиная
от свободных классических полей и кончая техникой
устранения расходимостей в теории возмущений.
Изложение значительно упрощено по сравнению
с упомянутой монографией. Материал каждого пара-
параграфа примерно соответствует полуторачасовой лек-
лекции, а полное содержание книги — годовому курсу.
Вынесенный в Дополнения технический материал и
наборы задач и упражнений, помещенные в конце
книги в виде семи заданий, предназначены для се-
семинарских занятий.
„„ - ■ © Издательство «Наука».
20402—0Э7 r7A,nonnnn Главная редакция
i 95-80, 1704020000 физико-математической
053@2)-80 литературы, 1980

ОГЛАВЛЕНИЕ*)
Предисловие • • ■ • 8
Некоторые обозначения . . , . '. < 9
§ 1. Частицы и поля. , 11
1.1. Частицы и их основные свойства A1). 1.2. Законы
сохранения A2). 1.3. Соответствие частица «— поле A3).
1.4. Представления группы Лоренца A4).
Глава I. Свободные классические поля 17
§ 2. Динамические инварианты полей 17
2.1. Лагранжиан A7). 2.2. Динамические инварианты. Энер-
Энергия-импульс A9). 2.3. Теорема Нётер B0). 2.4. Момент
количества движения и спин B1). 2.5. Вектор тока и заряд
B3).
§ 3. Простейшие, поля 24
3.1. Скалярное поле B4). 3.2. Импульсное представление
B5). 3.3. Векторное поле B8). 3.4. Локальный репер C1)-.
§ 4. Электромагнитное поле 32
4.1. Потенциал электромагнитного поля C2). 4.2. Калибро-
Калибровочная инвариантность и условие Лоренца C3). 4.3. Обоб-
Обобщенный лагранжиан C5). 4.4. Диагональная калибровка
C7). 4.5. Переход к локальному реперу C9).
§ 5. Поле Дирака 40
5.1. Уравнение Дирака и матрицы Дирака D0). 5.2. Лаг-
ранжев формализм D3). 5.3. Импульсное представление D4).
5.4. Разложения по спиновым состояниям D5). 5.5. Дина-
Динамические инварианты D6).
Глава П. Квантование свободных полей 49
§ 6. Квантование полей ....,,..., , 49
6.L Сущность процедуры квантования полей D9). 6.2. Кор-
Корпускулярная трактовка представления чисел заполнения
E0). 6.3. Каноническое квантование E3). 6.4. Представле-
- ния Шредингера и Гайзенберга E5). 6.5. Релятивистская
схема квантования полей E6).
*) Курсивом отмечены разделы, которые могут быть опущены при первом
чтении—см; по этому поводу Методические указания на стр, 314.
V

4 ОГЛАВЛЕНИЕ
§ 7. Перестановочные соотношения
7.1. Физический смысл частотных компонент E8). 7.2. Ам- 58
плитуда вакуума и фоковское представление F0). 7.3. Типы
перестановочных соотношений F1). 7.4. Квантование по
Ферми—Дираку и Бозе — Эйнштейну F4). 7.5. Связь спина
со статистикой. Теорема Паули F6).
§ 8. Поля с целым спином , 67
8.1. Скалярное поле F7). 8.2. Запись динамических пере-
переменных через нормальные произведения F7). 8:3. Комплекс-
Комплексное векторное поле G0). 8.4. Электромагнитное поле —
трудности квантования G2). 8.5. Электромагнитное поле —
квантование по Гупта — Блейлеру G3).
§ 9. Спинорные поля 75
9.1. Квантование поля Дирака G5). 9.2. Спи норное поле
с массой нуль G7). 9.3. Зарядовое сопряжение (81).
9.4. СРТ-теорема (83).
Глава III. Взаимодействующие поля 85
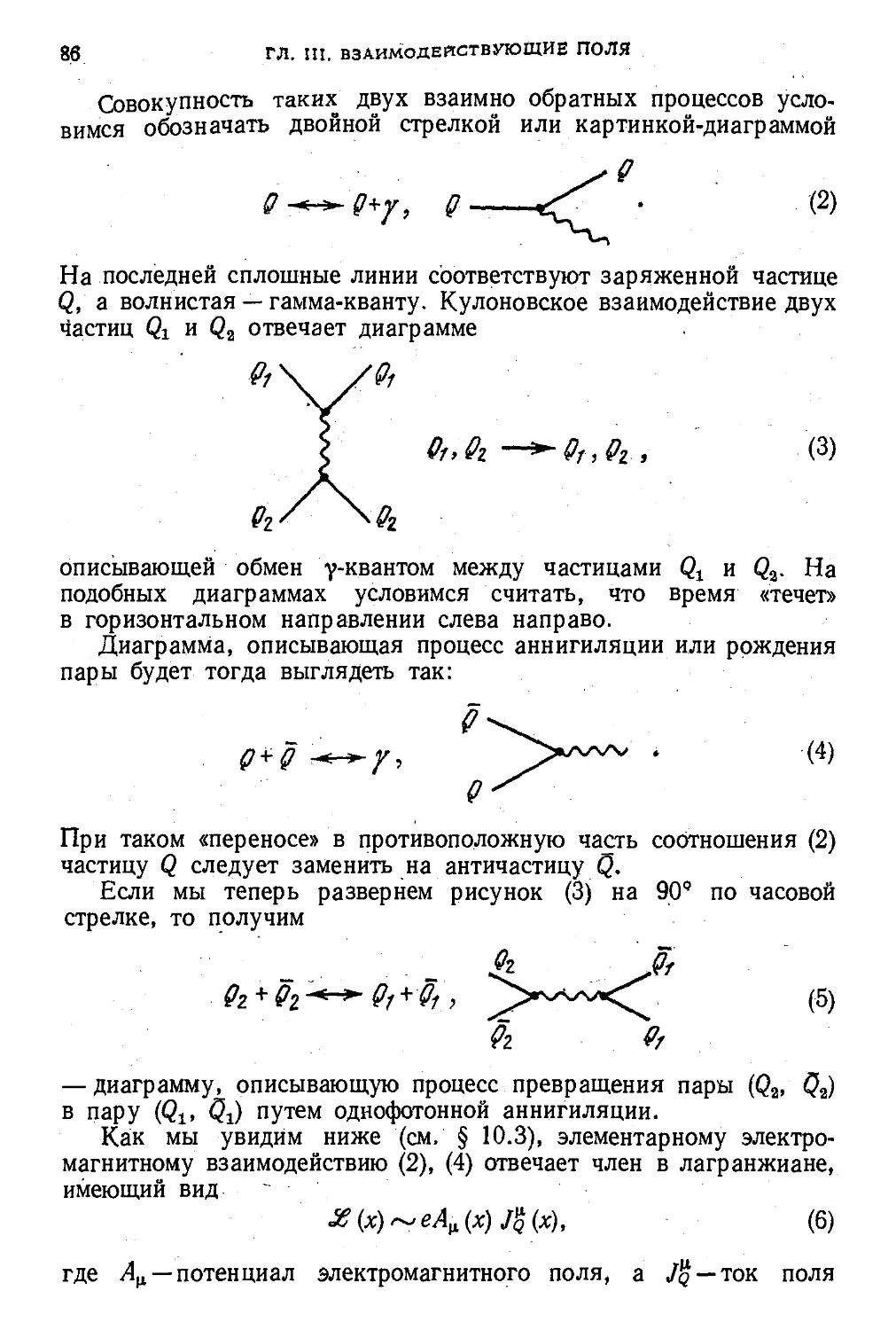
§ 10. Взаимодействие полей . .' 86
10.1. Взаимодействие частиц (85). 10.2. Лагранжианы вза-
взаимодействия (89). 10.3. Электромагнитное поле как кали-
калибровочное (92).
§ 11. Неабелевы калибровочные поля 94
11.1. Поле Янга — Миллса (94). 11.2. Калибровочное взаимо-
взаимодействие полей (96). 11.3. Спонтанное нарушение симмет-
симметрии (98). 11.4. Массивное поле Янга — Миллса A01).
§ 12. Квантовые системы со взаимодействием 103
12.1. Постановка задачи A03). 12.2. Иллюстрация A05).
12.3. Гамильтанов подход A06). 12.4. Диагоналиэация
модельных гамильтонианов A08). 12.5. Эффекты взаимодей-
взаимодействия A11).
§ 13. Модель тяокелого нуклона 112
13.1. Формулировка модели A12). 13.2. Решение в однонук-
лонном секторе A13). 13.3. Свойства однонуклонного реше-
решения A16). 13.4. Переход к локальному пределу A17).
Глава IV. Матрица рассеяния 119
§ 14. Матрица рассеяния 119
14.1. Теория возмущений A19). 14.2. Представление взаимо-
взаимодействия A21). 14.3. Матрица рассеяния A23). 14.4. Хро-
Хронологические произведения A25). 14.5. Хронологическая
экспонента A26).
§ 15. Общие свойства S-матрицы. 127
15.1. Матрица рассеяния как функционал A27). 15.2. Реля-
Релятивистская ковариантность и унитарность A29). 15.3. Усло-
Условие причинности A31). 15.4. Дифференциальное условие при-
причинности A32).
§ 16. Аксиоматическая S-матрица 134
16.1. Разложение по степеням взаимодействия A34). 16.2. Усло-
Условия на Sn A34). 16.3. Определение явного вида S2 и S3
A36). 16.4. Общий вид S (g) A37).
§ 17. Теоремы Вика 138
17.1. Приведение к нормальной форме A38). 17.2. Первая
теорема Вика A39). 17 3. Хронологические спаривания
A41). 17.4. Вторая теорема Вика A43). 17.5. Третья тео-
теорема Вика A43).

ОГЛАВЛЕНИЕ 5
Глава V. Диаграммы и правила Фейнмана . , 145
§ 18. Функция Грина свободных полей 145
18.1. Функция Грина скалярного поля A45). 18.2. Причин-
Причинная функция Грина A47). 18.3. Особенности на световом
конусе A48).
§ 19. Диаграммы Фейнмана 150
19.1- Коэффициентные функции A50). 19.2. Графическое
изображение Sn A51). 19.3. Спинорная электроЛшамика
A53). 19.4. Поле Янга—Миллса A56).
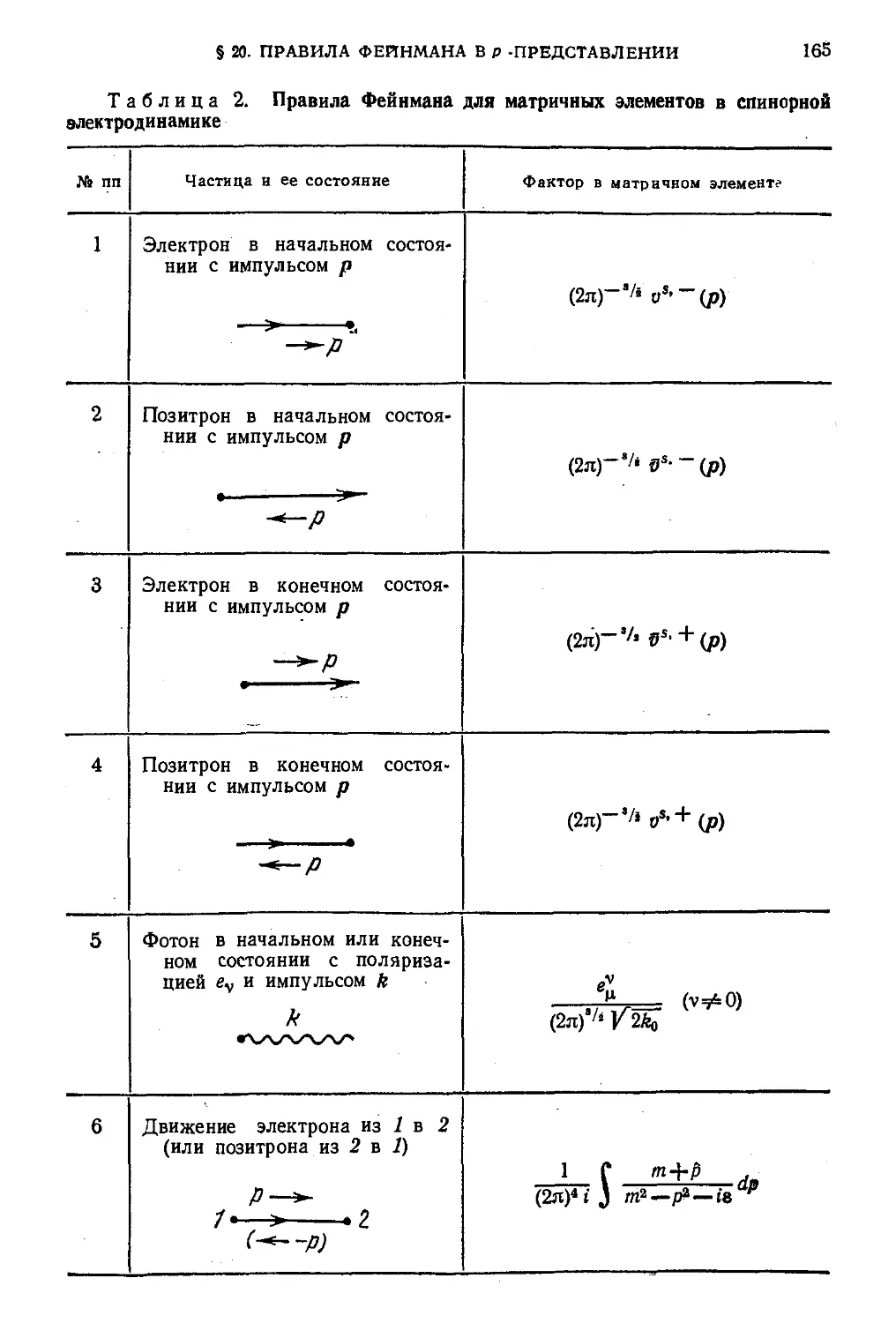
§ 20. Правила Фейнмана в р-представлении 159
20.1. Переход к импульсному представлению A59). 20.2. Пра-
Правила Фейнмана для матричных элементов A61). 20.3, Иллю-
Иллюстрация для модели ф4 A62). 20.4. Спинорная электродина-
электродинамика A64). -
§ 21. Вероятности переходов. 168
21.1. Общая структура матричных элементов A68). 21.2. Нор-
Нормировка амплитуды состояния A69). 21.3. Общая формула
для вероятности перехода A71). 21.4. Рассеяние двух частиц
A73). 21.5. Двухчастичный распад A75)
Глава VI. Вычисление интегралов и расходимости , , 176
§ 22. Техника вычисления интегралов. . 176
22.1. Интегралы по виртуальным импульсам A76). 22.2. Аль-
Альфа-представление и гауссовы квадратуры A77). 22.3. Фейн-
мановская параметризация A80). 22.4. Ультрафиолетовые
расходимости A81).
§ 23. Вспомогательные регуляризации 182
23.1. Необходимость регуляризации A82). 23.2. Регуляри-
Регуляризация Паули — Вилларса A83). 23.3. Размерная регуляриза-
регуляризация A85). 23.4. Регуляризация обрезанием A87).
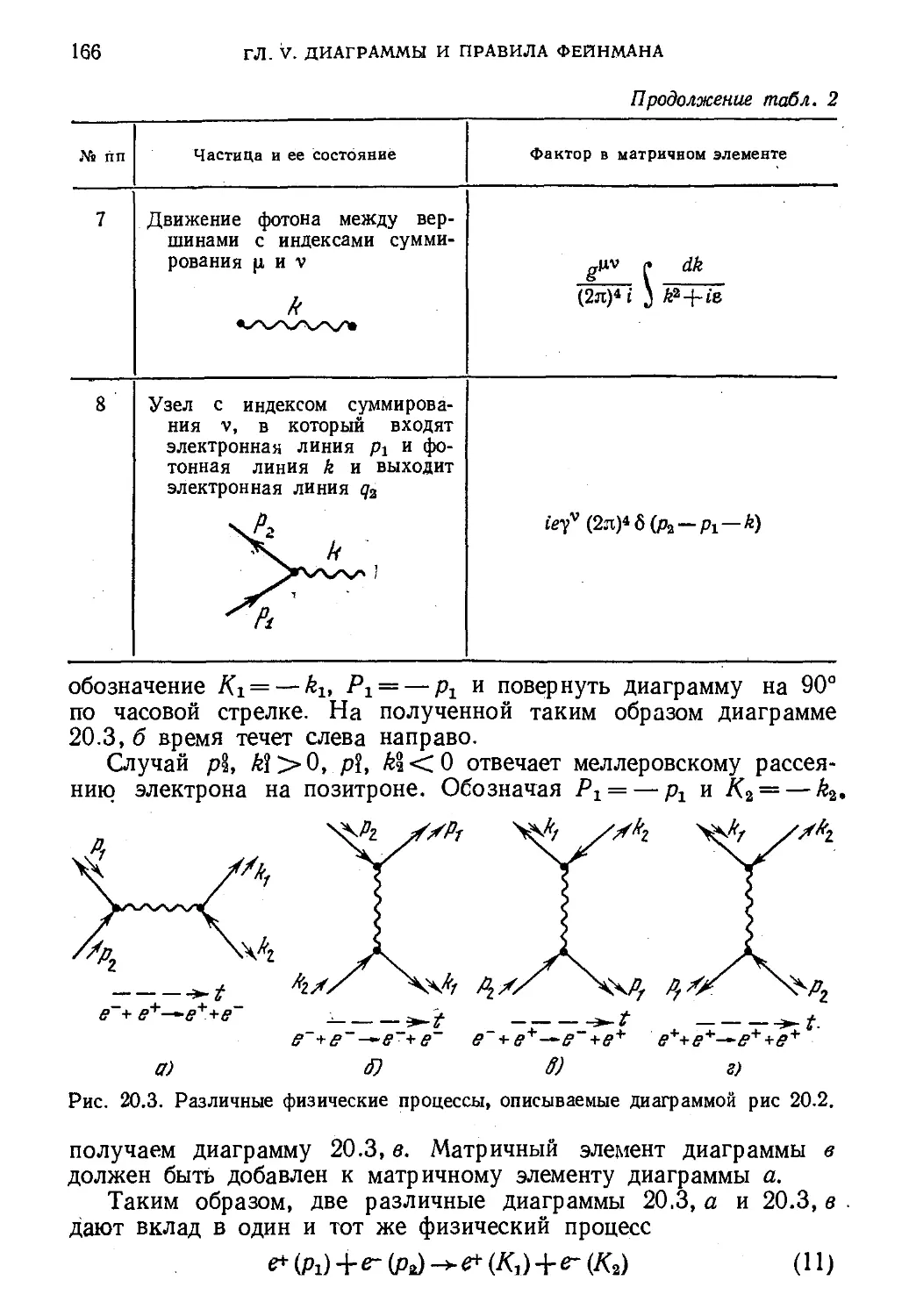
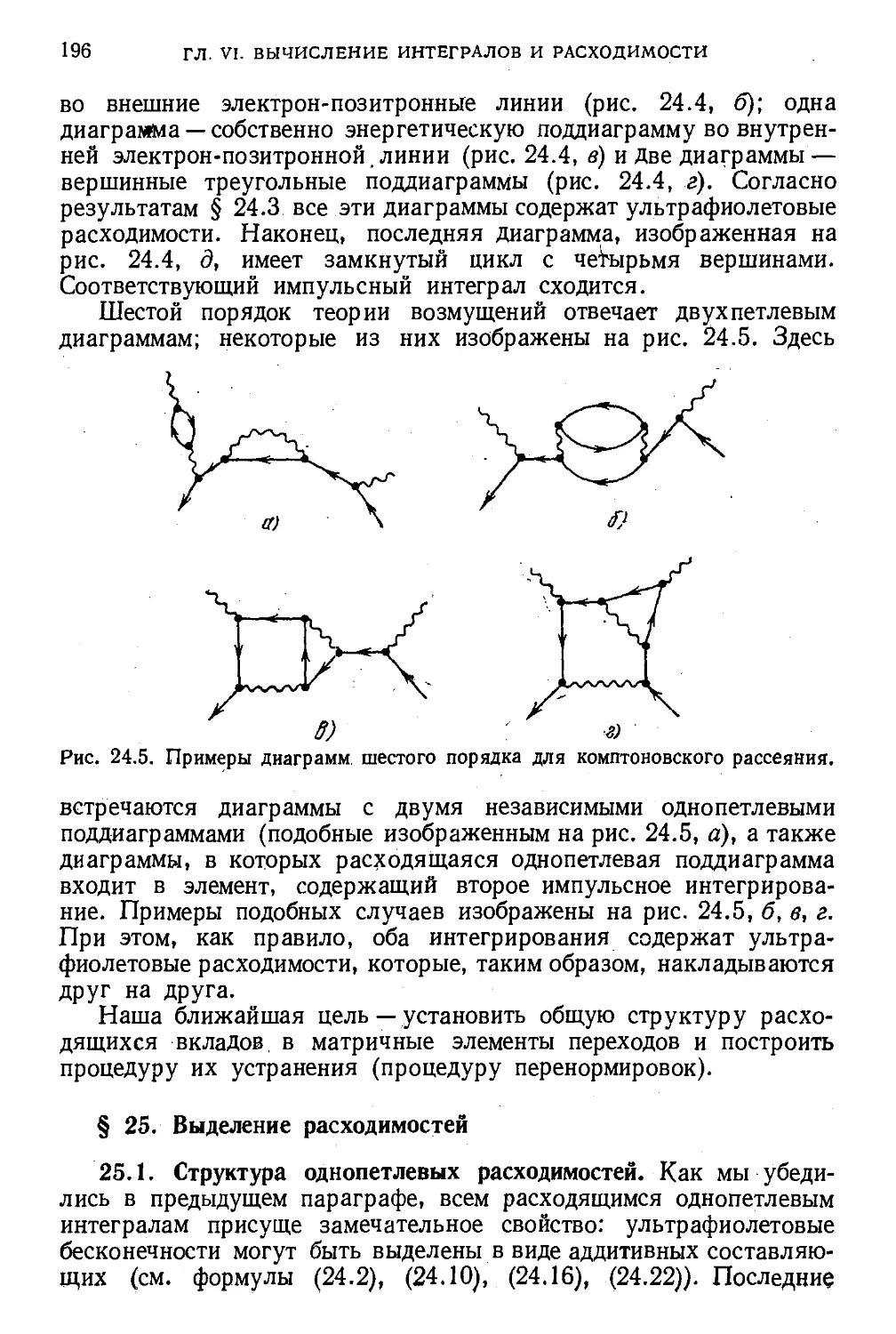
§ 24. Однопетлевые диаграммы 188
24.1. Скалярная «рыба> A88). 24.2. Собственные энергии
фотона и электрона A90). 24.3. Треугольные вершинные
диаграммы A92). 24.4. Ультрафиолетовые расходимости
в высших порядках A95).
§ 25. Выделение расходимостей , , , 196
' 25.1. Структура однопетлевых расходимостей A96).
25.2. Вклад в S-матрицу A97). 25.3. Контрчлены и пере-
перенормировки B00). 25.4. Расходимости и обобщенные функ-
функции B02).
Глава VII. Устранение расходимостей , . ; . . 204
§ 26. Общая структура расходимостей. ,.....;■ 204
26.1. Расходимости высших порядков B04). 26.2. Связь
с контрчленами и перенормировки B06). 26.3. Степень рас-
расходимости диаграмм B08). 26.4. Свойство перенормируемо-
перенормируемости B10).
§ 27. Полные функции Грина . . .... 212
27.1. Пропагаторы физических полей B12). 27.2. Высшие
функции Грина B15). 27.3. Сильносвязные многохвостки
(вертексы) B17). 27.4. Редукционные формулы B18).
§ 28. Процедура перенормировок ; 219
28.1. Перенормировка вкладов в функции Грина B19).
28.2, Теорема о перенормируемости B22). 28,3. Рецепт вычи-

6 ОГЛАВЛЕНИЕ
тания на массовой поверхности B24). 28.4. Неоднозначность
перенормировки вертекса B25).
§ 29. Перенормировки в спинорной электродинамике 226
29.1. Условие градиентной инвариантности B26). 29.2. Гра-
Градиентное преобразование фотонного пропагатора B27).
29.3. Пропагатор фотона с радиационными поправками B28).
. 29.4. Полный пропагатор электрона B31). 29.5. Вершинная
часть и тождество У орда B33).
Глава VIII. Описание реальных взаимодействий , , 236
§ 30. Электромагнитные взаимодействия 236
30.1. Спинорная электродинамика B36). 30.2. Аномальный
магнитный момент электрона B38). 30.3. Пределы спинор-
спинорной электродинамики B41).
§ 31. Слабые взаимодействия 242
31.1. Взаимодействия Ферми B42). 31.2. Структура слабого
тока B44). 31.3. Неперенормируемость и ультрафиолетовое
поведение B45). 31.4. Гипотеза промежуточного бозона
B46).
§ 32. Модель Вайнберга—Салама 247
32.1. Основные свойства B47). 32.2. Структура бозонного
сектора B48). 32.3. ФермионньЛ сектор B50). 32.4. Лаг-
Лагранжиан и квантование B52). 32.5. Физическое содержание
и экспериментальный статус B53). .
§ 33. Общая картина 254
33.1. Сильные взаимодействия B54). 33.2. Ограничения
.метода теории возмущений B55). 33.3. Другие методы кван-
квантовой теории поля B57). 33.4. Заключение B60).
Дополнение I. Изотопический формализм , . , . 261
1. Дублет нуклонов B61). 2. Триплет пионов B62).
Дополнение П. Матрицы Дирака и уравнение Дирака .....,,, 264
1. Матрицы Дирака B64). 2. Уравнение Дирака B66). 3. Транс-
Трансформационные свойства B67). 4. Нерелятивистский предел B69).
Дополнение III. Непрерывные группы . . 271
1. Общие определения B71). 2. Группы Ли B72). 3. Представле-
Представления групп Ли B75). 4. Генераторы и алгебра Ли B77).
Дополнение IV. Операторные преобразования , 279
1. Линейные непрерывные преобразования B79). 2. «Распутыва-
ние> экспонент B82). 3. Коммутаторы с оператором плотности
числа частиц п (ft) B83).
Дополнение V. Сводка сингулярных функций 283
1. Вспомогательные сингулярные функции B83). 2. Функции ска-
скалярного поля B84). 3. Функции электромагнитного, векторлого
и спинорного полей B85).
Дополнение VI. Формулы импульсного интегрирования 286
1. Альфа-представление B86). 2. Фейнмановская параметризация
B87). 3. Размерная регуляризация B88). 4. Регуляризация обре-
обрезанием B89). 5. Простейшие однопетлевые квадратуры B90).
Дополнение VII. Кинематические соотношения для вершин. . , , , . 291
1. Тройная вершина B91), 2, Четверная вершина B92),

ОГЛАВЛЕНИЕ 7
Дополнение VIII. Правила Фейнмана для полей Яига —Миллса. . . 294
1. Свободное поле группы SU B) B94). 2. Взаимодействие калиб-
калибровочного поля с полями материи B97). 3. Массивное поле Янга-
Миллса B98).
Задание «Сентябрь» к главе I , , , , 301
Задание «Октябрь» к главе П. , , 304
Задание «Ноябрь» к главе III 306
Задание «Декабрь» к главе IV 308
Задание «Февраль» к главе V , 309
Задание «Март» к главе VI. ,,.... 311
Задание «Апрель» к главе VII 312
Методические указания ......... 314
Литература. - 315
Предметный указатель. , , ....,..,,,,............ 316

ПРЕДИСЛОВИЕ
Основная цель книги состоит в том, чтобы дать студенту
физического факультета университета минимальный материал
по основам современной квантовой теории поля.
Она может оказаться достаточной как для теоретиков, специа-
специализирующихся по физике ядра, квантовой статистике и других
областях, использующих квантовополевые методы и опирающихся
на квантовые представления, так и для экспериментаторов в обла-
области ядерной физики и физики высоких энергий. Для последней
категории читателей эта книга должна быть дополнена курсом
физики частиц и их взаимодействий. В то же время ее можно
рекомендовать для первого чтения лицам, намеревающимся рабо-
работать в области квантовой теории поля и теории элементарных
взаимодействий.
Изложение построено таким образом, что оно соответствует
годовому курсу. Наш собственный опыт говорит о крайней жела-
желательности параллельных семинарских занятий. С этой целью часть
технического материала вынесена в конец книги в виде Дополне-
Дополнений. Там же помещены наборы упражнений и задач, собранные
в Задания к главам основного текста.
Авторы признательны редактору книги Д. А. Славнову, рецен-
рецензентам М. А. Брауну, Л. В. Прохорову, К. А. Тер-Мартиросяну,
а также Б. М. Барбашову, Б. В. Медведеву, А. А. Славнову и
Н. М. Шумейко за ценные замечания по рукописи книги.
р. Дубна, ноябрь 1979 Авторы

НЕКОТОРЫЕ ОБОЗНАЧЕНИЯ .
Все компоненты 4-векторов условимся выбирать действительными. 4-век-
тор а = (а°, а), состоящий из нулевой компоненты а0 и пространственного
вектора а, будем согласно традиции называть контравариантным. 4-вектором и
обозначать его компоненты верхними индексами
а" = (а<>, а\, а2, а3).
Произведение двух векторов а и Ь определим так:
Его удобно записать в виде
^ (|1,\ = 0, 1, 2,3).
ц, v
где g^v — диагональный метрический тензор,
gnv = 0 при \i¥=v, gm = \; gu = fe=to = —1-
отличающийся знаком от известного тензора Минковского. Переход от контра-
вариантных аУ к ковариантным а^ компонентам (опускание индекса) дости-
достигается с помощью метрического тензора:
т. е.
ао = а°, ak=—ak (&=1, 2, 3), а„ = (аа, —а).
Здесь и ниже мы всегда будем подразумевать суммирование по дважды
повторяющимся индексам, опуская знак суммы. Индексы суммирования по
трем пространственным компонентам обозначаются латинскими буквами, взя-
взятыми из середины алфавита:
ab = anbn = akbk = a1b1 + афг+афг,
а по всем четырем компонентам @, 1, 2, 3) — греческими:
ab = avbv^
Ц. V - .
Иногда в целях упрощения записи громоздких выражений будем оба грече-
греческих индекса помещать внизу или наверху, т. е.

ГО НЕКОТОРЫЕ ОБОЗНАЧЕНИЯ
Таким образом, наличие двух одинаковых греческих индексов в различных
множителях всегда подразумевает ковариантное суммирование независимо от
расположения этих индексов.
Индексы, относящиеся к группам внутренних симметрии (например, изо-
изотопические индексы), обозначаются, как правило, латинскими буквами, взя-
взятыми из начала алфавита (а, Ь, ...).
Символом й обозначена свертка компонент 4-вектора av с матрицами
Дирака
(J=av7v=av?v-
Для производных по ковариантным и контравариантным компонентам часто
используются сокращенные обозначения
При этом разумеется
Оператор д'Аламберз
□ =Д — д$
представим как
По всей книге используется так называемая рациональная система единиц,
в которой скорость света и постоянная Планка равны единице, т. е. с = ft = 1.
В этой системе энергия и импульс имеют размерность массы или обратной
длины, а время xo = t—размерность длины
Формулы четырехмерного преобразования Фурье, как правило, записы-
записываются в виде
f(x).~[er4"f(p)dp, F(p)~$eiP*f(x)dx.
Знак показателя экспоненты выбран из соображений соответствия его первого
слагаемого квантомеханической формуле
/ (*°, х) =/ (t,x) ~ j е~Ш7 (Е, х) dE.
Трехмерное преобразование Фурье соответственно имеет вид
Ф (х) ~ J «** ф (р) dp, ф (/>) ~ J е-1** ф {х) dx.
Исключение составляют формулы для положительно-частотных частей функций
поля и положительно-частотных частей функций Грина. Нормировочные мно-
множители фурье-преобразований (степени 2я) в различных местах книги выби-
выбираются по-разному.
Внутри каждого параграфа употребляется одинарная нумерация формул:
A), B), C), ..., которая непосредственно используется для ссылок на формулы
внутри данного параграфа. Двойная нумерация (8.21), (Д11.6) и т. д. сигна-
сигнализирует об отсылке к формуле другого параграфа. При этом первый символ
указывает номер параграфа или Дополнения (§ 8, Дополнение II), а второй —
порядковый номер формулы в нем.
Признаком библиографической ссылки является год, стоящий после фами-
фамилии автора. Например, «Медведев A977)» обозначает ссылку на книгу Б. В. Мед-
Медведева, опубликованную в 1977 г.> полное библиографическое наименование
которой приведено в списке цитированной литературы в конце книги. Исклю-
Исключение из этой системы сделано для третьего издания нашей книги «Введение
в теорию квантованных полей», которое упоминается как «Введение».

§ 1. ЧАСТИЦЫ И ПОЛЯ II
§ 1. Частицы и поля
1.1. Частицы и их основные свойства. Квантовая теория поля представ-
представляет собой физическую теорию элементарных частиц и их взаимодействий.
Она опирается на связи между релятивистскими частицами и квантовыми
полями, возникающими при квантовании классических полей. Свойства кван-
квантовых полей находятся в тесном соответствии со свойствами частиц. Поэтому
прежде всего мы перечислим основные характеристики частиц.
Важным атрибутом релятивистской частицы является ее масса покоя т.
Известное соотношение теории относительности связывает массу m с энергией
частицы £ и ее импульсом р:
В рациональной системе единиц это соотношение принимает вид
В этой системе массу можно измерять в энергетической шкале. Для массы
электрона те имеем*) те = 9,109534D7) 10-28 г = 0,5110034A4) МэВ. Масса
протона тр = 938,2796B7) МэВ ===0,94 ГэВ и т. д.
Второй существенной характеристикой частицы является ее спин (т. е.
собственный механический момент). В соответствии с общими теоремами кван-
квантовой механики спин частиц оказывается квантованным—его абсолютные
значения являются целыми кратными половины постоянной Планка
Й=А/2л= 1,0545887E7) 10-" эрг • с=6,582173 A7) • 10-22 МэВ.
Поэтому в употребляемой нами рациональной системе единиц спины элек-
электрона и протона оказываются равными половине, а спин фотона (-у-кванта) —
единице:
*e = Sp = V2. SY=1.
Третье кардинальное свойство частиц —наличие электрического заряда,
значения которого также являются квантованными. Заряды всех наблюдае-
наблюдаемых**) частиц кратны так называемому «элементарному заряду» е=4,803242( 14) х
ХЮ-Юед. СГС = 1,6021892D6) 10» кулона, равному заряду электрона. В от-
отличие от спина, квантовая природа которого совершенно ясна, дискретность
электрического заряда представляет собой волнующую загадку.
Наконец, важной характеристикой частицы является ее время жизни т.
Дело в том, что лишь немногие из частиц в свободном состоянии живут
практически бесконечно долго (т. е. являются абсолютно стабильными)'. К ним
относятся электрон е~, протон р, фотон и нейтрино v ***), а также их анти-
античастицы—позитрон е+, антипротон р и антинейтрино v. Все остальные частицы
нестабильны и по экспоненциальному закону ехр (— t/t) самопроизвольно
распадаются на другие частицы. Коэффициент т и называется временем жизни.
Например, для нейтрона, распадающегося по схеме (Р-распад)
*) Здесь и ниже мы приводим новейшие данные. Цифры в скобках пока-
показывают неопределенность в одну стандартную ошибку, выраженную в едини-
единицах последнего знака основного числа, т- е. 0,5110034A4) = 0,5110034 ±:
±0/3000014.
**) Электрические заряды кварков (гипотетических составляющих адрона)
считаются равными простым дробям (± 1/3, ± 2/3) от е. Однако в свободном
состоянии кварки не наблюдались.
*** ) Существуют по крайней мере три разновидности нейтрино: электронное
нейтрино ve, мюонное нейтрино v^ и недавно открытое т-нейтрино vt.

12 НЕКОТОРЫЕ ОБОЗНАЧЕНИЯ
время жизни оказывается равным тя = 918 A4) с=± 15,3 мин. Заряженный
пя-мезон я+ распадается на мюон и нейтрино:
со временем жизни тя+= 2,6030 B3) • 10~8 с. и т. д.
Нестабильность частиц представляет собой проявление важнейшего свой-
свойства микромира — свойства взаимопревращаемости частиц, являющегося следст-
следствием их взаимодействий. Взаимодействия частиц распадаются на четыре класса:
сильные, электромагнитные, слабые и гравитационные. Мы не будем сейчас
останавливаться подробно на свойствах взаимодействий (которые обсуждаются
ниже —в § 10). Отметим л[.;шь, что взаимодействия частиц приводят к тому,
что частицы и их совокупности, как правило, переходят в другие частицы и
их совокупности, если такие переходы не запрещены какими-либо законами
сохранения (энергии, импульса, момента количества движения, электрического
заряда, барионного заряда, странности и некоторыми другими).
Отсутствие каких-либо переходов, разрешенных известными законами
сохранения, воспринимается как указание на существование нового, еще не
известного, закона сохранения.
1.2. Законы сохранения. Вообще говоря, законы сохранения являются
следствием тех или иных симметрии, которые отражают свойство ненаблюдае-
ненаблюдаемости некоторых характеристик физических объектов. Хорошо известно, что
закон сохранения энергии в консервативных системах представляет собой
проявление симметрии относительно непрерывной операции сдвига времени.
Инвариантность относительно сдвига времени в свою очередь эквивалентна
ненаблюдаемости абсолютного времени. Другую цепочку подобного рода обра-
образуют закон сохранения четности, инвариантность относительно зеркального
отражения и условность понятий «правого» и «левого» (т. е. ненаблюдаемость
«абсолютно правого» и «абсолютно левого»).
Большая часть законов сохранения связана с непрерывными симметриями
и может быть получена из последних с помощью теоремы Истер (см. ниже
§ 2.3). Среди них следует выделить законы сохранения энергии, импульса и
момента количества движения, которые являются следствиями симметрии
физических объектов в пространстве-времени. Подобная симметрия обуслов-
обусловлена такими глубокими и общими свойствами, как ненаблюдаемость абсолют-
абсолютного времени и абсолютных пространственных координат (симметрия относи-
относительно преобразований сдвига), изотропия пространства и эквивалентность
систем координат, движущихся друг относительно друга с постоянными ско-
скоростями (симметрия относительно пространственных и лоренцевых поворотов).
Соответствующие законы сохранения являются весьма общими, характерны
для всех частиц;, выполняются во всех переходах.
В пределах точности современного эксперимента столь же универсальными
являются законы сохранения электрического заряда и барионного числа.
Этим законам сохранения также можно сопоставить уже упоминавшиеся сим-
симметрии относительно фазовых преобразований непрерывного вида. Однако
последние не имеют под собой наглядной физической основы и не связаны
со "структурой пространства—времени. Подобного рода симметрии называются
внутренними симметриями.
К классу внутренних симметрии относятся изотопическая симметрия,
а также некоторые другие (например, так называемая унитарная симметрия):
Большинство внутренних симметрии и связанных с ними сохраняющихся
величин носит приближенный характер. За только что упоминавшимися двумя
исключениями (электрический заряд и бар ионное число), соответствующие
законы сохранения выполняются в одних взаимодействиях и нарушаются
в других.
Изотопическая инвариантность (закон сохранения изотопического спина 1)
выполняется в сильных взаимодействиях и нарушается в электромагнитных
и слабых

§ Т. ЧАСТИЦЫ И ПОЛЯ
13
Закон сохранения четности (точнее — пространственной четности), связан-
связанный с симметрией волновой функции относительно операции отражения прост-
пространственных осей, выполняется в сильных и электромагнитных взаимодейст-
взаимодействиях и нарушается в слабых. Аналогично ведут себя законы сохранения
странности, а также нового квантового числа —очарования, лежащие вместе
с изотопической инвариантностью в основе унитарной симметрии. Эти свойства
подытожены в табл. 1.
Таблица 1. Свойства симметрии взаимодей-
взаимодействия и сохраняющиеся физические величины
Физические величины
Электрический заряд
Барионное число
Четность
Изоспин
Странность
Типы взаимодействия
сильные
+
+
+
электро-
магнит-
магнитные
+
+
+
слабые
(+) = сохраняется; (—)=не сохраняется.
Мы не обсуждаем здесь свойств гравитационного взаимодействия из-за его
чрезвычайно малой интенсивности. Для иллюстрации отметим, что сила гра-
гравитационного притяжения двух протонов примерно в 103? раз меньше силы
их электростатического отталкивания.-
1.3. Соответствие частица —«поле. Поле представляет собой физическую
систему с бесконечным числом степеней свободы. Понятие поля естественно
возникает при попытке отказа от представления о мгновенном действии частиц
друг на друга- на расстоянии (ньютоновское actio in distans) — представления,
противоречащего специальной теории относительности (см. Медведев A977),
ч. II, § 6, а также Вигнер A971), с. 12). Считая, что пространство между
частицами заполнено полем, мы возлагаем на поле функцию передачи возму-
возмущения с конечной скоростью от одной частицы к другой. Таким образом,
введение классического поля в физику диктуется соображениями релятивист-
релятивистской инвариантности. В теории частиц центральную роль играют релятивист-
релятивистские квантовые поля.
Квантованное волновое поле—фундаментальная физическая концепция,
в рамках которой формулируется динамика частиц и их взаимодействия. Она
позволяет описывать различные состояния системы многих частиц единым физи-
физическим объектом в обычном пространстве-времени — квантованным полем. Кван-
Квантованное поле возникает путем квантования классического поля, в результате
которого полевая функция приобретает операторный характер и выражается
через операторы рождения и уничтожения частиц. Тем самым появляется
возможность описывать важнейшее свойство мира элементарных частиц — про-
процессы их взаимного превращения.
Давно и хорошо известным примером классического поля является электро-
электромагнитное поле, отвечающее за взаимодействия электрически заряженных
частиц. Классическое описание, базирующееся на уравнениях Максвелла, при-
приводит к чисто волновым представлениям об электромагнетизме. Методически
иногда оказывается удобным рассматривать непрерывную систему —поле в виде
предела дискретной механической системы с числом степеней свободы N,

14 НЕКОТОРЫЕ ОБОЗНАЧЕНИЯ
стремящимся к бесконечности. Каждой степени свободы соответствует осцил-
осциллятор поля.
Описание корпускулярных свойств света достигается в результате проце-
процедуры квантования, в ходе' которой полю сопоставляются дискретные кванты
энергии, соответствующие различным возможным энергетическим состояниям
осцилляторов поля. Кванты электромагнитного поля—фотоны—имеют нуле-
нулевую массу покоя, не имеют электрического заряда и обладают спином, равным
единице. Последний факт соответствует поляризационным свойствам классиче-
классического поля и находит свое отражение в том, что электромагнитное поле
является многокомпонентным и описывается набором полевых функций — ком-
компонентами напряженностей электрического и магнитного полей или компонен-
компонентами потенциала Av-
Свойства полевых функций, отвечающих другим частицам, также отражают
спиновые, зарядовые и прочие дискретные характеристики соответствующих
частиц. После квантования кванты полей обычно отождествляются с частицами.
Реальному миру взаимодействующих частиц ставится в соответствие система
связанных уравнений для различных полей. После квантования выражения,
отвечающие за связь этих уравнений (лагранжиан или гамильтониан взаимо-
взаимодействия—см. ниже § 10), описывают элементарные акты взаимодействия раз-
различных частиц. Наглядную интерпретацию такие выражения получают в пра-
правилах соответствия Фейнмана (см. ниже §§ 19, 20).
Мы отложим рассмотрение аппарата взаимодействия частиц и полей и
займемся вначале изучением свойств свободных полей и их квантованием.
1.4. Представление группы Лоренца. Рассмотрим законы преобразований
полевых функций при релятивистских преобразованиях координат. Напомним
некоторые определения.
Полная (иначе—общая ортохронная) группа Лоренца состоит из однород-
однородных линейных преобразований четырех координат xv, которые оставляют инва-
инвариантными квадратичную форму
x? = XvXv=()py—&
и не меняют направления времени х°. Эта группа включает обычные прост-
пространственные повороты, лоренцевы «повороты» в плоскостях х°х1, х°х2, х°х3:
(т. е. преобразования- к системе координат, движущейся относительно исход-
исходной с постоянной скоростью), отражения пространственных осей и все произ-
произведения таких преобразований. Если добавить еще отражение оси времени, то
мы получим общую группу Лоренца.
В физике большую роль играет группа, составленная из преобразований
полной группы Лоренца и преобразований трансляции по всем четырем осям.
Она называется неоднородной группой Лоренца (или полной группой Пуан-
Пуанкаре) Инвариантность относительно этой группы мы будем называть реляти-
релятивистской инвариантностью, в отличие от лоренц-инвариантности, соответству-
соответствующей группе Лоренца.
В дальнейшем нас будут интересовать законы преобразования полевых
функций при преобразованиях координат из полной группы Пуанкаре
х-+х' = Р(а>; х), A)
где u) = (L, а) обозначает совокупность параметров, описывающих трансля-
трансляции (а) и повороты (L), причем
V %=Svtl- B)
Полевая функция и(х) представляет собой одну (однокомпонентная функ-
функция) или несколько (многокомпонентная функция) функций четырех коорди-
координат xv, заданных в каждой системе отсчета. При этом переходу от системы
отсчета х к системе х', связанной с х преобразованием B), сопоставляется
однородное линейное преобразование компонент полевых функций
и (х) -*• и' (*')=Л (о) и (х), C)

§ 1. ЧАСТИЦЫ И ПОЛЯ 15
где Л—матрица преобразования, целиком определяемая матрицей L лоренцева
преобразования B), т. е. зависящая от тех же параметров, что и L.
Подчеркнем, что преобразование C) не сводится к замене аргументов х
на х', так как описывает преобразование системы координат, а не операцию
перемещения из одной точки пространства в другую.
Каждому лоренцеву преобразованию L соответствует матрица Л^, причем
единичному элементу группы L соответствует единичная матрица Л = 1, а про-
произведению двух элементов Lt и L2 группы Лоренца соответствует произведение
Система матриц с такими свойствами в теории групп называется линейным
представлением группы. Матрицы конечного ранга Л образуют конечномерное
представление группы Лоренца. Ранг представления определяется размерностью
матриц, т. е. числом компонент и.
Поэтому возможные типы волновых функций и их законы преобразования
могут быть получены исследованием конечномерных (неприводимых) представ-
представлений группы Лоренца. Подобное исследование составляет особый раздел тео"-
рии представлений групп, результат которого сводится к следующему. Конечно-
Конечномерные представления группы Лоренца могут быть однозначными или дву-
двузначными, т. е. соответствие L-*-KL может быть однозначным или двузначным.
Важность для физики двузначных представлений обусловлено тем, что поле-
полевые функции, вообще говоря, не являются непосредственно наблюдаемыми
(в частности, поля, преобразующиеся по двузначным представлениям, всегда
входят в наблюдаемые величины в билинейных комбинациях). Неоднозначность
оператора А^ должна быть все же такова, чтобы наблюдаемые величины транс-
трансформировались вполне однозначно при любом лоренцевом преобразовании L.
Кроме того, необходимо, чтобы операторы AL были непрерывными функциями
параметров преобразования L, т. е. чтобы бесконечно малому преобразованию
системы отсчета соответствовало бесконечно малое преобразование функций
поля. Совокупность указанных требований приводит к тому, что представле-
представления группы Лоренца^ распадаются на две категории. Первая категория харак-
характеризуется однозначностью соответствия L-*-A.L и содержит однозначные так
называемые тензорные и псевдотензорные *) представления. Функции поля,
преобразующиеся по тензорным представлениям, называются тензорами (псев-
дотензорами) и в некоторых случаях могут быть наблюдаемы непосредственно
(электромагнитное поле). Во втором случае это соответствие оказывается: дву-
двузначным: L->±AL, -
Закон преобразования (псевдо) тензора N-ro ранга Т 1" 2> '" N при не-
непрерывных преобразованиях г.оординат имеет вид
rv ... vN (*')=^.- Щ^ ?V ... *N (x), D)
или, в обозначениях B),
Двузначные представления называются спинорными, а соответствующие
величины— спинорами. Закон преобразования спинорных величин имеет более
сложную структуру и для простейших спиноров приведен в Дополнении II.
Отметим лишь, что вытекающий из D) закон преобразования тензорных величин
и(х)-+и'{х') = и{х) E)
*) Различие между тензорами и псевдотензорами связано с преобразова-
преобразованиями отражения пространственных осей и рассматривается в конце параграфа.

•б НЕКОТОРЫЕ ОБОЗНАЧЕНИЯ
при преобразовании трансляции
является справедливым также и для спиноров.
Приведем теперь простейшие тензорные представления и соответствующие
им величины. Тензор нулевого ранга, при любых непрерывных преобразова-
преобразованиях трансформирующийся по закону E), является инвариантом и называется
скаляром (псевдоскаляром).
Тензор первого ранга, преобразующийся при поворотах координат по
закону
«'V(/)=LV/W=L4%W, F)
называется контравариантным вектором (псевдовектором). Связанный с ннм
ковариантный вектор
()
преобразуется по закону
и^(х')==^«ц(х). G)
Могут быть выписаны без труда соответствующие формулы для тензоров
различной вариантности второго и более высоких рангов.
Рассмотрим теперь преобразование пространственной инверсии Р, т. е.
отражения всех трех пространственных осей:
х-^х' = Рх, xj = xo> х' — — х. (8)
Законы преобразования полевых функций формулами D) не определяются
и должны быть сформулированы отдельно. В силу тождественности двукрат-
двукратного преобразования (Р2=1), вытекающей из однозначности тензорных пред-
представлений, эти законы для компонент тензоров Т'" (х) могут иметь лишь две
формы:
РТ (х) = Т {х') = Т'(Рх) = ±Т (х).
Тензор нулевого ранга, не меняющий знака при инверсии,
. Ры (*) = +«(*) (9)
называется скаляром. Во втором случае соответствующая величина, удовлет-
удовлетворяющая соотношению
Ри(х)= — и(х), ,. A0)
именуется псевдоскаляром.
Если тензор первого ранга при преобразовании Р меняет знак своих про-
пространственных компонент и не меняет знак временной:
PV°(x)=*V°(x), PV(x) = —V(x), A1)
то он называется вектором. Если же пространственные компоненты не меняют
знак, а меняет лишь временная:
PV°(x) = —V0(x), PV(x)=V(x), A2)
то он является псевдовектором (аксиальным вектором). Вообще можно описать
закон преобразования псевдотензоров формулой D), умноженной на детерминант
преобразования координат. Соотношения (9), A0) и им подобные определяют
также важное свойство четности полевых функций и соответствующих им ча-
частиц. Это свойство играет существенную роль (см. ниже § 10.2) при уста-
установлении возможных форм взаимодействия различных полей.

Глава I. СВОБОДНЫЕ КЛАССИЧЕСКИЕ ПОЛЯ
§ 2. Динамические инварианты полей
2.1. Лагранжиан. В этом параграфе мы изложим формализм,
позволяющий получать на общей основе как уравнения движения,
так и сохраняющиеся во времени величины, соответствующие
свойствам инвариантности относительно тех или иных непрерыв-
непрерывных преобразований. Такой формализм в механике систем с ко-
конечным числом степеней свободы основывается на функции Лаг-
Лагранжа и называется лагранжевым формализмом.
Функция Лагранжа L является функцией времени, зависит
от динамических переменных системы и в механике записывается
в виде суммы по всем материальным точкам системы. В случае
непрерывной системы типа волнового поля эта сумма заменяется
пространственным интегралом от плотности функции Лагранжа X:
\ х).
Эта последняя
и называется лагранжианом.
Исходным пунктом лагранжева формализма является действие
системы ©^, представляющее интеграл по времени от L:
A)
Отсюда видно, что функция Лагранжа L (t) в теории полей ока-
оказывается промежуточной и основную роль играет лагранжиан
Х(х).
Уравнения движения могут быть получены с помощью прин-
принципа наименьшего действия, который гласит, что реальное дви-
движение происходит таким образом, что действие еЛ оказывается
экстремальным, т. е. его вариация обращается в нуль. Из условия
О,

18 ГЛ. I. СВОБОДНЫЕ КЛАССИЧЕСКИЕ ПОЛЯ
полагая, что вариации функций поля 6мг исчезают на границе
объема интегрирования, с помощью интеграции по частям полу-
получаем уравнения Лагранжа—Эйлера
Перечислим кратко основные требования, налагаемые на лаг-
лагранжиан в квантовой теории поля.
Лагранжиан, во-первых, является функцией только динами-
динамических переменных, т. е. компонент полевых функций ы„(л:)иих
производных. Явной зависимости от координат х он не содержит,
поскольку такая зависимость нарушает релятивистскую инвари-
инвариантность. При этом локальность теории обеспечивается тем, что
значение лагранжиана X в точке х определяется значениями
иа(х) и конечного числа частных производных, взятых в той же
самой точке х. Такой лагранжиан называется локальным. Нали-
Наличие, например, интегральных зависимостей приводит к нелокаль-
нелокальному случаю.
Для того чтобы получить дифференциальные уравнения по-
порядка не выше второго, лагранжиан считают функцией компо-
компонент поля и и их первых производных
Х(х) = Ф(иа(х), иа:у(х)). . C)
Отметим еще, что поскольку физические свойства системы
определяются действием orf, в выражение для которого лагран-
лагранжиан входит под знаком интеграла, то соответствие оЛ -+Х не
является взаимно однозначным. Лагранжианы, отличающиеся друг
от друга полной 4-дивергенцией (от некоторого 4-вектора)
Z'(x) = Z(x) + dvF(x), D)
оказываются физически эквивалентными.
В самом деле, интеграл A) от f^v с помощью теоремы Гаус-
Гаусса — Остроградского сводится к поверхностному интегралу от F*
по трехмерной границе четырехмерного объема интегрирования.
Принимая еще во внимание, что вариации функций поля бы исче-
исчезают на этой границе, получаем, что член F?y~ не дает вклада
в физические величины.
Важными требованиями, предъявляемыми к свойствам лагран-
лагранжиана, являются его вещественность (в квантовом случае — эрми-
товость) и релятивистская инвариантность.
Вещественность лагранжиана приводит к вещественности (эрми-
товости) динамических инвариантов: энергии, .импульса, тока
и т. п. и в конечном счете к унитарности 5-матрицы.
Релятивистская инвариантность лагранжиана
X1 (х') = Ф (и'а (x')t u'a;v (х')) = Ф (иа (х), ua; v (х)) = X (х) E)

§ 2. ДИНАМИЧЕСКИЕ ИНВАРИАНТЫ ПОЛЕЙ 19
означает, что X ведет себя как (псевдо)екаляр при преобразова-
преобразованиях Пуанкаре. Поскольку бесконечно малый элемент объема
4-интегрирования в A) dx = dx°dx также является инвариантом
то мы получаем, что значение действия не меняется при преоб-
преобразованиях из группы Пуанкаре. Поэтому скалярность лагран-
лагранжиана обеспечивает инвариантность действия.
2.2. Динамические инварианты. Энергия-импульс. Это послед-
последнее свойство оказывается важным для получения так называемых
динамических инвариантов, т. е. величин, сохраняющихся во
времени. К динамическим инвариантам относятся энергия, им-
импульс, момент количества движения, а также некоторые другие
величины, сохраняющиеся в силу соответствующей инвариантно-
инвариантности действия (или лагранжиана), как, например, электрический
заряд.
В качестве примера рассмотрим 4-вектор энергии-импульса Pv.
Он может быть представлен в виде пространственного интеграла
Pv = ldxTv°(x°, х) F)
от соответствующих компонент тензора энергии-импульса, кото-
который выражается через лагранжиан соотношением
T*(x)=^£-ualv(x)-fF>X(x). G)
Независимость интегралов F) от времени л:0 является след-
следствием того, что тензор Т*1 удовлетворяет уравнению непрерыв-
непрерывности
Для того чтобы убедиться в этом, рассмотрим интеграл
dx-
Преобразуя его к поверхностному интегралу по теореме Гаусса —
Остроградского,
где а —поверхность, ограничивающая объем интегрирования,
a dojj — элемент поверхности, нормальный к оси хР, допустим, что
объем интегрирования неограниченно расширяется в пространст-
венноподобных направлениях и ограничен по времени двумя трех-
трехмерными плоскостями al(x° = t1) и а2(л:0 = /2). Предполагая еще,
что на бесконечно удаленных в пространственноподобных направ-
направлениях точках поля иа, их производные и компоненты тензора

20 ГЛ. I. СВОБОДНЫЕ КЛАССИЧЕСКИЕ ПОЛЯ
энергии-импульса равны нулю, получим из (8) и (9)
$ dxTv0(x) - $dxTv°(x) = \dxTv0(/lt x)-[dxT*°(t2, x) = 0,
что и требовалось доказать.
Покажем теперь, что уравнение непрерывности (8) является
следствием уравнений движения. Рассмотрим дивергенцию от пра-
правой части G):
дЛ*» = ~ (J^~) и: ^ + J£- ди Ш Л- д*Х.
Ц дх*\диа;ц) " диа;ц й ^ ° '
Используя уравнения движения B) и меняя порядок дифферен-
дифференцирований у.второй производной, получим
dJS дип дХ ди„. „ дХ
Подведем теперь некоторые итоги. Мы установили, что каждая
из четырех величин Pv (v = 0, I, 2, 3) сохраняется во времени
благодаря тому, что соответствующая пространственная плотность
7^° является нулевой компонентой «4-вектора» 6^ (v) ^ 7^^, удов-
удовлетворяющего уравнению непрерывности (8). Последнее вытекает
из уравнений Лагранжа—Эйлера, а также того факта, что лаг-ъ
ранжиан X зависит от координат х только через функции поля иа
и их первые производные ы; v, вследствие чего
дХ _дХ дХ д (диа
dxv диа " +5"а;ц <4WW
Как можно показать, сохранение проекции «4-вектора» Pv на
v-ю ось является следствием ковариантности лагранжиана (и ра-
равенства нулю соответствующей вариации действия) относительно
трансляции вдоль оси xv.
2.3. Теорема Нётер. Это утверждение является частным слу-
случаем так называемой теоремы Нётер, которую можно сформули-
сформулировать следующим образом.
Пусть имеет место некоторое непрерывное преобразование
координат и одновременно функций поля, зависящее от s
параметров coft {k= I, 2, ..., s):
Xv->4=M*; ю), A0)
ua(x)^u'a(x') = Ua(ub(x); со) A1)
— и обращающее в нуль вариацию действия &£ = ^ X {х) dx:
Тогда существует s динамических инвариантов Ск (т. е. со-
сохраняющихся во времени функций от полевых функций и

§ 2. ДИНАМИЧЕСКИЕ ИНВАРИАНТЫ ПОЛЕЙ 21
их производных), которые представимы в виде пространст-
пространственных интегралов
от нулевых компонент некоторых «4-векторов»
*V=4f-{ua.,»X»k-4a.,k)-Xl%(x), A3)
a: v
причем
„ =" (И)
ди
Ш-0
Мы не будем приводить здесь доказательства этой теоремы,
отослав интересующегося читателя к § 2.1 Введения.
Отметим прежде всего, что приведенные выше выражения F),
G) являются частными случаями общих выражений A2), A3),
соответствующих
XI = 81 Va.,k = 0. A5)
Значения A5) соответствуют преобразованиям
и'а (ХГ) = Ua (X),
т. е. преобразованиям трансляции всех четырех координат.
Последняя формула является законом преобразования функ-
функций поля при преобразованиях трансляции. Как видно, он оди-
одинаков для функций поля различной тензорной размерности. Под-
Подставляя значения A5) в общую, формулу A3), получаем выраже-
выражение G)) для тензора энергии-импульса. С помощью A2) приходим
к формуле F) для сохраняющегося во времени 4-вектора энер-
энергии-импульса Pv.
2.4. Момент количества движения и спин. Получим теперь
динамические инварианты, соответствующие 4-мерным лоренцевым
вращениям системы координат. Как следует из A4), достаточно
рассматривать только их инфинитезимальную форму, которая
имеет вид
A6)
где 6Lv,i — бесконечно малые параметры поворотов. Благодаря
антисимметричности величин 8Ь^ в качестве независимых пара-
параметров могут быть выбраны шесть из них:
6<»(nv) = 6Lnv при fi<v, A7)
представляющих собой бесконечно малые углы вращения в пло-
плоскости х^Ху. Таким образом, индекс k из формул A2)—A5) пред-
представляется двойным индексом (ц/у).

22 ГЛ. I, СВОБОДНЫЕ КЛАССИЧЕСКИЕ ПОЛЯ
Представляя вариацию 6л: в виде
6xv = X*6«ft= £ Х<Гб«(ра), A8)
получим с помощью A6), A7)
8xv = х» Ы^ = £ (Л? - х%°) 6со(
о(ра),
Р<ст
т. е.
д;аб?-А;рб?. ■ A9)
Бесконечно малую вариацию функций поля и'а (х1) = иа (л) + бы„ (л:),
представим в виде
8иа(х)= ^ Л*(р(Ч(хNсо(ра). B0)
Ь, р<ст
В соответствии с A.5) и A.6) для скалярного поля
л:::=о
и для векторного поля
, Р<<т.
Поэтому для векторного поля
Wa) = AVp°\(x) = ua(x)8Z-u°(x)8%. B1)
Подставляя B1) и A9) в A3), получаем тензор момента количе-
количества движения
Мх (Рв) = ЭХ ^ _ . + ^ (^PgCTt _ xagPt) _ дХ А» (рв) (л)>
B2)
Сравнивая первые два члена в правой части с G), видим, что их
можно представить в виде
/71рт-д;рГат = Л1оТ<ра). " B3)
Это выражение соответствует связи между тензорами момента
и энергии-импульса в механике точки. Поэтому величину B3)
следует отождествить с орбитальным моментом волнового поля.
В случае однокомпонентного (скалярного, псевдоскалярного) поля
весь момент сводится к орбитальному.
Для многокомпонентных полей последнее слагаемое в правой
части B2) отлично от нуля. Оно характеризует поляризационные
свойства поля и соответствует спиновому моменту поля.
Итак,

§ 2. ДИНАМИЧЕСКИЕ ИНВАРИАНТЫ ПОЛЕЙ 23
где
"ua; X
Для векторного поля с помощью B1) получаем
B4)
~-ua{x)dS\. B5)
диа ди0)
Здесь символом и обозначена частная производная по времени
от и. Тройка величин S(*3), SC1), S(li) представляет собой ком-
компоненты пространственного псевдовектора —вектора спина
$п = вптр$(тр) (П) т> р=1, 2, 3). ' B6)
2.5. Вектор тока и заряд. Наконец, в случае комплексных
полей, которые соответствуют частицам с зарядом (в простейших
случаях этот заряд —электрический), лагранжиан оказывается
инвариантным по отношению к фазовому преобразованию полевых
функций (градиентному преобразованию первого рода), не затра-
затрагивающему координат.
Поясним суть дела на примере системы, описываемой одним
комплексным полем. В силу свойства вещественности лагранжиан,
равно как и динамические величины, может зависеть от ком-
комплексного поля лишь через квадратичные формы вида иаиь, где иа
* -
и иа — взаимно комплексно-сопряженные функции или их произ-
производные. Отсюда непосредственно вытекает, что комплексные вол-
волновые функции и могут быть умножены на произвольный уни-
унитарный фазовый множитель вида exp (ice), что не приводит
к изменению квадратичной формы ии, а тем самым и к каким-
либо наблюдаемым эффектам.
*
Рассматривая и и и как линейно независимые функции, можем
поэтому записать градиентное преобразование первого рода в виде
йь-+й'ь = е-1аиь. B7)
Полагая а бесконечно малой величиной, находим
* * *
«->« + /««, «->« — /««. ■
Согласно A4) отсюда вытекает, что
%» = '«<» для всех «я,
Wb = — iub для всех иь,

24 ГЛ. I. СВОБОДНЫЕ КЛАССИЧЕСКИЕ ПОЛЯ
а также, что Х = 0. Подставляя эти соотношения в A3), прихо-
приходим к выражению, имеющему тензорную размерность вектора:
' B8)
<4:v
Этот 4-вектор подчиняется уравнению непрерывности
dvf = 0 B9)
и потому обычно отождествляется с 4-вектором тока. Простран-
Пространственный интеграл от его нулевой компоненты
\ . C0)
\4;о диЬ;о
не зависит от времени и представляет собой сохраняющуюся ха-
характеристику поля. Она отождествляется с зарядом. При этом
интеграл движения Q может описывать как электрический заряд,
так и другие сохраняющиеся характеристики, такие, как бари-
онный заряд, странность, очарование и т. п.
Как видно, системы с подобными интегралами движения опи-
описываются комплексными (в общем случае— многокомпонентными)
полями. Отметим еще, что преобразования только что рассмот-
рассмотренного типа (¥^=0, Х = 0), не затрагивающие координат, назы-
называются преобразованиями внутренних симметрии. Важными для
физики примерами внутренних симметрии являются изотопическая
симметрия и унитарная симметрия. Соответствующие им преоб-
преобразования также могут быть изучены с помощью теоремы Нётер,
что приводит к понятию сохраняющихся векторов изотопического
и унитарного спинов.
§ 3. Простейшие поля
3.1. Скалярное поле. Наиболее простым является веществен-
вещественное скалярное поле q> (*), описывающее бесспиновые частицы
одного сорта. Свободный лагранжиан этого поля выбирается сле-
следующим образом:
с тем, чтобы полученное из него уравнение движения B.2) ока-
оказалось уравнением Клейна — Гордона

§ 3. ПРОСТЕЙШИЕ ПОЛЯ 25
Здесь
— оператор д'Аламбера.
С помощью B.7) получаем из A) тензор энергии-импульса
V»(x) = V*(x)qfi»(x)-#»X. C)
Тензор момента количества движения можно получить теперь
отсюда, используя соотношение B.23). Спиновый момент равен
нулю. ,
Подставляя в C) явный вид лагранжиана A), получаем плот-
плотность энергии
r°l2)[*(Vs + mV] D)
и плотность вектора импульса
7°* = — <?•■>* (k=\, 2, 3)
3.2. Импульсное представление. В теории частиц весьма упо-
употребительным является импульсное представление. Оно, во-пер-
во-первых, более адекватно обычной физической постановке задачи,
когда частицы характеризуются своими энергиями и импульсами
(а не пространственно-временными координатами). Во-вторых, ди-
динамические переменные в этом представлении принимают более
компактную и наглядную структуру.
Итак, представим функцию поля ф(л:) в виде четырехмерного
интеграла Фурье:
$ dk = dkodk.
Условие вещественности ф (*) = ф (я) дает
Согласно B) фурье-амплитуда ф удовлетворяет уравнению
(£2 - т2) ф (£) = О
и потому представима в виде
ф (k) = /2я 8 (k2 - m2) ф (k).
Дельта-функция устанавливает связь
-Л2 = т2 E)
между частотой k0, волновым вектором k и параметром т. Как
будет показано ниже, частоту k0 следует отождествить с энергией,
а волновой вектор — с вектором импульса, вследствие чего связь
E) оказывается известным соотношением из релятивистской
механики частицы, в котором т представляет массу.

26 ГЛ. I. СВОБОДНЫЕ КЛАССИЧЕСКИЕ ПОЛЯ
Разложение Фурье принимает вид
Ф (х) = Bя)~3'2 $ dk Ь (k2 - т2) е***ф (к).
Из-за наличия под знаком интеграла б-функции интеграция
происходит не по всему 4-мерному ^-пространству, а лишь по
двум полам трехмерного гиперболоида
одна из которых целиком лежит внутри верхнего светового
конуса, а другая — внутри нижнего. Замечая еще, что указанные
полы гиперболоидов по отдельности являются лоренц-инвариант-
ными, мы приходим к следующему релятивистски инвариантному
разбиению полевой функции на два слагаемых:
*), F)
где
ф± (х) = Bя)~ w \ dk е± ч?ЫЬ* -т2) ф± {к). G)
Здесь
а б —известная разрывная функция:
о,
Функции ф+ и ф- мы будем в дальнейшем именовать соответ-
соответственно положительно-частотной и отрицательно-частотной частями
функции ф (х). Как видно, при этом знак частотности связывается
со знаком произведения kx (точнее, со знаком «временного» члена
k°x° = x° ]fk2 + /и2 в подынтегральной экспоненте). В связи с этим
заметим, что в современной литературе иногда принимают обрат-
обратный порядок обозначений, связывая «частотность» со знаком формы
kv,xVL = kx-\-kixi = — kx. Подобные обозначения ассоциируются
с привычной записью квантовомеханической волновой функции,
которая пропорциональна ехр (—iEx0), где Е — энергия.
Наш выбор обозначений связан с тем, что выражения типа ф+
в квантовой теории соответствуют рождению частиц поля,
а выражения типа „ф~ — их уничтожению. Поэтому в принятой
нами системе обозначений знаки (+) и (—) символизируют физи-
физический смысл соответствующих квантовых операторов.
Как будет показано ниже, произведенное разбиение оказывается
также весьма удобным при записи динамических величин
в импульсном представлении, поскольку последние выражаются
в виде билинейных форм по ф+ (k) и ф~ (k).

§ 3. ПРОСТЕЙШИЕ ПОЛЯ 27
Заметим, кроме того, что в соответствии с G) правила комп-
комплексного сопряжения для ф±(й) имеют вид
Выполняя в G) интеграцию по k0, получаем
' Bл)'* J Уйь Т
Здесь введены обозначения
Подставляя F) и (8) в D), получим
= \ Г00 d* = (V2) \ Ww (x)J + ™V (х)] dx =
+ m2 [Ф+ (х) Ф+ (*) + 2Ф+ (х) Ф" (л:) + Ф- (х) ф- (л:)]}.
Отметим, что все суммирования по v в этом выражении неко-
вариантные. Нетрудно показать, что слагаемые, содержащие
произведения функций ф± одинаковой частотности, не дают
вклада в динамический инвариант Р°. Так, например,
BяK
J $L ф+ (*) ф+ (- *) eu>"*° (m2 - AJ - Л2),
а так как m2 —^o+*2 = O> получаем
$ dx [(Э,Г WJ + /n2 (
Подобное соотношение имеет место и для квадратичной формы
по ф~. Поэтому
Р° = J dx агф+ (х) dv ф~ (л:) + т2ф+ (л:) ф- (л:).
Подставляя в это выражение формулу (8), с помощью аналогич-
аналогичных выкладок находим теперь
Соответствующее выражение для вектора импульса имеет вид
+(k)<p-{k), /1=1,2,3.

28 ГЛ. I. СВОБОДНЫЕ КЛАССИЧЕСКИЕ ПОЛЯ
Объединяя эти выражения, запишем их в форме, справедливой
также и в том случае, если бы в процессе всех выкладок функ-
функции ф+ и ф~ считать взаимно некоммутируемыми (т. е. не менять
их порядка):
Р* = ~ j dk k" [ф+ (к) Ф- (к) + ф-.(*) Ф+ (к)]. (9)
Теперь виден смысл нормировочных множителей, введенных
в (8). Произведения
выступают как средние плотности числа незаряженных, бесспино-
бесспиновых частиц массы т, обладающих импульсом к и энергией ]/ т2 + к2.
После квантования эти произведения превращаются в операторы,
имеющие целочисленные собственные значения.
Практически важным является поле, соответствующее пи-
мезонам (пионам). Это поле является псевдоскалярным. Тройка
пионов л+, я0, л~, отличающихся друг от друга лишь электри-
электрическим зарядом, равным 0±1, образует изотопический триплет.
Этому отвечает трехкомпонентная полевая функция ф = |ф1, ф2,
Ф3}, составляющие которой образуют вектор в трехмерном изо-
изотопическом пространстве;
Свободный лагранжиан записывается в виде
^ = у(ф;гФ!Г)-^!(фф) A0)
и представляет собой сумму выражений лагранжианов для каждой
из компонент изотопического вектора. Поэтому динамические
величины, отвечающие преобразованиям группы Пуанкаре, пред-
представляются суммами выражений, полученных в §§ 3.1 и 3.2 для
каждой из изотопических компонент.
Новая сохраняющаяся величина соответствует преобразова-
преобразованиям вращения в изотопическом пространстве и называется
вектором изотопического спина.
3.3. Векторное поле. В качестве следующего примера рас-
рассмотрим векторное поле, используемое для описания частиц со
спином 1. Это поле Uv состоит из четырех (v = 0, 1, 2, 3) ком-
компонент, которые образуют ковариантный 4-вектор, т. е. при
лоренцевых поворотах B.16) преобразуются по закону
Лагранжиан векторного поля может быть сконструирован
различными способами. Дело в том, что простейшее обобщение
лагранжиана A) в виде ковариантной суммы по компонентам
Х = -\и^№\%и»№ A1)

§ 3. ПРОСТЕЙШИЕ ПОЛЯ 29
не является единственно возможным лоренц-инвариантным выра-
выражением. К нему может быть прибавлен член, пропорциональный
A2)
который в силу B.4) эквивалентен выражению
Для того чтобы убедиться в этом, достаточно установить, что
разность выписанных выражений представима в виде 4-дивер-
генции dyF*.
Лагранжиан A1) «хорош» тем, что все динамические величины
для него являются ковариантными суммами (по ji) соответствую-
соответствующих выражений из A) для однокомпонентного поля. Однако
поскольку член, связанный с компонентой UQ, входит в такие
суммы со знаком минус-, его вклад в энергию оказывается отри-
отрицательным*. Для разрешения этой трудности на компоненты U^
налагают инвариантное дополнительное условие
d»Ull = ^-Ull(x)^(dU) = 0. A3)
Это условие уменьшает количество линейно независимых
компонент с четырех до трех и, как будет показано ниже, обеспе-
обеспечивает положительную определенность энергии векторного поля.
Оставшиеся три независимые компоненты соответствуют трем
возможным значениям проекции спина на заданную ось A, 0, —1),
т. е. описывают частицы со спином единица. Наложение допол-
дополнительного условия эквивалентно исключению частицы со спином
нуль, приводящей в этой формулировке к отрицательной энергии.
Условие A3) совместно с уравнениями движения. Более того,
путем надлежащей модификации лагранжиана A1) (добавлением
члена вида A2))
где
Н^ = д^-д^, A4)
оно может быть получено как следствие уравнений движения
djr» - m*U» = Q - m2) U* + № dvW = 0. A5)
Эти уравнения называются уравнениями Прока. Дифференцируя
их по хР, после элементарных преобразований получаем допол-
дополнительное условие A3). Таким образом, уравнения Прока экви-
эквивалентны совокупности уравнений Клейна — Гордона и условию
A3).

30 ГЛ. I. СВОБОДНЫЕ КЛАССИЧЕСКИЕ ПОЛЯ
Динамические величины, соответствующие аналогичному
лагранжиану комплексного векторного поля
X = - 1 Н^Н^ + m*UvU\ A6)
имеют вид:
тензор энергии-импульса —
Т^ = Н^и% + Нн^-ё^, A7а)
вектор тока —
Jv = i{U°Hav-HavU°), A76)
тензор спинового момента —
_ н^иа + HavV^ - U°H»V. A7в)
Для дальнейших вычислений следует разложить потенциалы на
положительно- и отрицательно-частотные части и перейти к 3-мер-
3-мерному импульсному представлению:
(и аналогично для U~).
Подставляя разложения A8) в нулевые (v = 0) компоненты
выражений A7) и выполняя интегрирование по dx, получаем
динамические величины:
Л,—-\dkkv[u»(k)U+'»(k) + U+(k)U--»(k)], A9)
Q = [dk[Ui (k) U+-»(k)-Ut(k)U--»(*)]> B0)
Sri\dk{[u+(k)xG-(k)]-[u-(k)xU+(k)]}- B1)
Принимая во внимание следующие из определений A8) усло-
условия комплексного сопряжения
видим, что вклад в правую часть A9), отвечающий ц, = 0, оказы-
оказывается отрицательным, а энергия Ро — знаконеопределенной.
Как упоминалось выше, указанная трудность снимается при
наложении дополнительных условий, которые в импульсном пред-
представлении A8) принимают вид
= 0. , B2)
В силу этих условий компоненты t/v не являются более
независимыми. Выражая с их помощью компоненты Uf через

§ 3. ПРОСТЕЙШИЕ ПОЛЯ 31
остальные:
±knU{k), Uf(k) = ^kM(k) (n = 1,2,3),
получаем для квадратичной формы, входящей под знак интеграла
в A9), следующее выражение, зависящее лишь от «пространствен-
«пространственных» компонент потенциала:
-± {kU± (к)) (k(/+ (k)). B3)
3.4. Локальный репер. Это выражение диагонализуется линей-
линейной подстановкой:
j я I та
Здесь et и е2 суть единичные векторы, ортогональные волновому
вектору к и друг другу:
(erej) = 8ij, ea = k/\k\ (i, /=1, 2, 3),
т. е. орты поперечной поляризации. Подстановка B4) представ-
представляет собой разложение векторного потенциала на продольную и
поперечную составляющие по отношению к импульсу, т. е. переход
к локальному реперу в импульсном пространстве. С помощью B4)
получаем -
Внося это выражение в A9) и B0), приходим к диагональным
выражениям для энергии-импульса и заряда, причем в новых
переменных энергия оказывается явным образом положительно
определенной:
Pv = J dk kv [at (k) arn (k) + к (k) at (*)],
Q = $ dk [at (k) an (k) - к (k) at (k)\.
Однако выражение для вклада в проекцию спина на направле-
направление вектора импульса
А53 ~ i [at (k) a$ (k) — a\al + cqat — aja$) B6)
оказывается недиагональным.
Линейная подстановка
= 4i#' «? = *? B7)
(то же для сопряженных амплитуд а^) диагонализирует это выра-

32 ГЛ. I. СВОБОДНЫЕ КЛАССИЧЕСКИЕ ПОЛЯ
жение, не нарушая диагонального вида Pv и Q:
Pv = \dk kv [к (к) Ь-п (к) + к (k) bt (к)}, B8)
Q = $ dk [bt (k) bn (k)-h(k)bt (*)], B9)
ASa~[bt(k)bT(k) — bjbt + hbZ-bZbi]. C0)
Отсюда видно, что квадратичные, комбинации амплитуд Ь± и 6+
могут рассматриваться как плотности среднего числа частиц,
обладающих определенными значениями энергии, импульса, заряда
и проекции спина на направление движения. При этом, напри-
например, величина b%(k)b$(k) представляет плотность числа частиц
с импульсом к, энергией kQ, зарядом — 1 и проекцией спина
на ось движения, равной + 1; соответственно Ь% (k) bt(k) является
плотностью числа частиц с импульсом k, энергией &,,, зарядом
— 1 и нулевой проекцией спина и т. д. Как мы убедимся ниже,
*
в связи с этим после квантования амплитуда 6J (Л) описывает
рождение частицы с энергией kg, импульсом к, зарядом +1,
проекцией спина -|-1, амплитуда b%(k) описывает ее уничтоже-
уничтожение и т. д.
Поэтому в соответствии с B4) и B7) амплитуды alt 2 отвечают
линейно поляризованным, a blf 2 — поляризованным по кругу
колебаниям.
Таким образом, комплексное векторное поле описывает поло-
положительно и отрицательно заряженные частицы с массой тфОи
тремя возможными значениями проекции вектора спина на
направление движения, равными 1, 0, — 1.
§ 4. Электромагнитное поле
4.1. Потенциал электромагнитного поля. Свободное электро-
электромагнитное поле удовлетворяет уравнениям Максвелла
rot E = — H, rot Н=Ё,
div£ = 0, div#=0.
Для более симметричного описания электромагнитного поля
вводится действительный ковариантный 4-вектор электромагнит-
электромагнитного потенциала .4v = ^0, —А) так, чтобы
Е= — gracM0 — A, H=rotA.
Компоненты «четырехмерного ротора» потенциала А образуют
известный антисимметричный тензор электромагнитного поля
Fv.y = dliAy — dyAv,, A)

§ 4. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ 33
компоненты которого связаны с компонентами векторов напряжен-
напряженности электрического и магнитного полей соотношениями
Рп— р ит — _о р (п т п 1 9 31 11\
• '- — 1 яо> ll — 2 ятР пР v » ' "— х> *"> I v /
Эту связь удобно изобразить в следующем наглядном виде:
'О — £1 — £2 _j
1 —т о
\Ез Нг —Нх
Уравнения Максвелла эквивалентны следующим уравнениям
для компонент тензора" F:-
„о. ■ <3>
Переходя в этих уравнениях otF к потенциалу Л, убеждаемся,
что вторая четверка уравнений C) является следствием опреде-
определения A) и не приводит к какому-либо уравнению для А, а пер-
первая четверка дает
- - - - - D)
— аналог уравнений Прока C.15).
Отсюда видно, что формулировка уравнений электромагнитного
поля в терминах потенциала Av действительно проста, симме-
симметрична и явно ковариантна..
4.2. Калибровочная инвариантность и условие Лоренца. Про-
Процедура введения 4-потенциала Л^, неоднозначна. Не составляет
труда убедиться, что наблюдаемые величины Е, Н, F^, а также
уравнения Максвелла, инвариантны относительно так называемого
градиентного преобразования второго рода потенциала Av:
Av(x)^Av(x) = Av(x) + dJ(x), E)
которое часто называют калибровочным.
Таким образом, потенциал Л, который не является наблюдае-
наблюдаемой величиной, оказывается неоднозначным. Входящая в правую
часть E) функция / произвольна. На нее обычно накладывают
условие гладкости.
Подобная неоднозначность означает, что динамическое описа-
описание электромагнитного поля в терминах Л содержит нефизиче-
нефизическую степень свободы, обычно ассоциируемую со значением
4-дивергенции
для которой мы ввели специальное обозначение. Требование
обращения в нуль этой величины
дА(х) = 0 F)
2 Н, Н, Боголюбов, Д. В. Ширков

34 ' ГЛ. I. СВОБОДНЫЕ КЛАССИЧЕСКИЕ ПОЛЯ
известно в теории электромагнитного поля как условие Лоренца.
Поскольку, соблюдая явную релятивистскую ковариантность, при
квантовании (см. ниже § 8.5) удовлетворить условию. Лоренца
как операторному соотношению не представляется возможным,
нам окажется полезным изучить степень свободы, выражаемую
наличием произвольной скалярной функции х (х) и обсудить ее
физический смысл.
Для этого, во-первых, отвлечемся на время от свободного
электромагнитного поля и допустим, что потенциал Av(x) не
удовлетворяет уравнению D). Можно считать, что он описывает
некоторое поле, порождаемое какими-либо внешними источниками
и, например, удовлетворяет неоднородному уравнению
где Jv — ток источников.
Во-вторых, перейдем к импульсному представлению
причем будем использовать один и тот же символ А, как для
функций, так и для фурье-образов. В этом представлении опе-
операции дифференцирования по конфигурационным переменным
(и им обратные операции) являются алгебраическими. Калибро-
Калибровочное преобразование E) принимает вид
G)
причем функция f(k) отличается мнимой единицей от фу рье-обр аза
функции f{x).
Введем проекционные операторы
plong /£ч _ Т**У /g4
Отметим, что операция (й2) в ^-представлении является инте-
интегральной и записывается в виде
где G — функция Грина для уравнения д'Аламбера, определенная
соотношением
QG(x) = -6(x). (9)
Функции Грина для уравнений свободных полей рассматри-
рассматриваются ниже в § 18. Там показано, что для однозначного опре-
определения решения уравнения (9) следует учесть граничные усло-
условия. В данном месте это обстоятельство не является существенным,
и нам окажется вполне достаточным того, что функция G удов-
удовлетворяет уравнению (9). Разложим теперь 4-потенциал А на

§ 4. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ 33
поперечную и продольную составляющие, используя проекцион-
проекционные операторы (8):
\\ -j- ./lv» ^v ^= •* VU^ У *iv ^= •* VII ^* •
Эти составляющие удовлетворяют соотношениям
kvA^{k) = Q, kvAl(k) = kA(k). A1)
Здесь удобно ввести специальное обозначение
для величины, которая с точностью до мнимой единицы совпа-
совпадает с фурье-образом функции х(х).
Из формул A0) и A1) следует, что продольная составляющая
электромагнитного поля определяется функцией |. Действительно,
При калибровочном преобразовании G) последняя преобра-
преобразуется по формуле
В то же время поперечная составляющая Л'г не испытывает
изменений при преобразовании G). Не составляет труда убедиться
также, что калибровочно-инвариантный тензор F от Л1 (от I) не
зависит. Очевидно поэтому, что степень свободы, описываемая
скалярной функцией I (k), несет в себе весь произвол, связанный
с неоднозначностью 4-потенциала А, и является нефизической.
4.3. Обобщенный лагранжиан. Уравнения движения D) могут
быть получены с помощью вариационного принципа из лагран-
лагранжиана
<^г = --^^\ ■ A2)
представляющего собой запись в терминах F известного выраже-
выражения A/2) (Е* — Н2). Нижний индекс «tr» отмечает, что лагранжиан
A2) калибровочно-инвариантен и не содержит зависимости от
продольных составляющих Л1.
Отметим, что дифференциальный оператор уравнения движе-
движения D)
пропорциональный поперечному проекционному оператору Р'г,
не имеет обратного, что затрудняет решение соответствующего
неоднородного уравнения движения. Поперечный лагранжиан ХХт
также обладает некоторой спецификой с точки зрения гамильто-
вова формализма. Напомним, что в гамильтоновой формулировке

36 ГЛ. I. СВОБОДНЫЕ КЛАССИЧЕСКИЕ ПОЛЯ
важную роль играют канонические импульсы, определяемые как
производные лагранжиана по скоростям Vi = qt, т. е. по времен-
временным производным координат системы q^ В случае системы с беско-
бесконечным числом степеней свободы — поля — в качестве обобщенных
координат выбирают полевые функции ф(лг, /) = ф(*). Поэтому
обобщенные канонические импульсы классического поля опреде-
определяются следующим образом:
Гамильтонов формализм представляет собой базу так назы-
называемого канонического квантования, которое изложено ниже
в § 6. Отсылая читателя к этому параграфу за более подробным
изложением гамильтонова формализма для полей, вернемся
к лагранжиану A2).
Выбирая за обобщенные координаты компоненты 4-потен-
циала Ау, убеждаемся элементарной выкладкой, что обобщенные
импульсы, отвечающие нулевой компоненте Ло, оказываются рав-
равными нулю:
яо(*)-/оо = О.
Иными словами, лагранжиан cS?tr не содержит зависимости от
«скорости» Ао. Лагранжианы, обладающие подобными свойствами,
иногда называются вырожденными или сингулярными. Они соот-
соответствуют системам со связями. Для описания систем со связями
используется введенная Дираком A968) обобщенная гамильтонова
динамика. В нашем случае переход к обобщенной динамике экви-
эквивалентен следующей модификации лагранжиана:
#tr-^#=-4V*v+f(M)«, A3)
где а—некоторый численный коэффициент.
Этот лагранжиан приводит к следующим уравнениям движения:
dvF„v + ад». (дА) = □ А». + A + а) д» (д А) = 0, A4)
из которых в частности следует, что продольная составляющая
электромагнитного поля удовлетворяет уравнению1 д'Аламбера
0. A5)
Отметим, что это свойство продольной составляющей сохра-
сохраняется также и в случае, когда электромагнитное поле взаимо-
взаимодействует с другими полями, т. е. когда в правой части уравне-
уравнений движения A4) стоят компоненты внешнего тока Jv, удовлет-
удовлетворяющие уравнению непрерывности dvJv = O. Таким образом,
продольная степень свободы х (х) не взаимодействует ни с попе-
поперечными составляющими Л'г, ни с другими полями.

§ 4. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ 37
Как видно, лагранжиан A3) и уравнения A4), вообще говоря,
уже не являются инвариантными относительно преобразования E).
Таким образом, можно сказать, что введение в лагранжиан члена
г^(дЛJ фиксирует калибровку. В то же время выражения A3),
A4) не меняются при специализированном калибровочном преоб-
преобразовании
A'() A() dJ(x), A6)
калибровочная функция которого подчиняется уравнению д'Алам-
бера
П/о(*) = О. A7)
Введение в лагранжиан фиксирующего калибровку члена приводит
также к тому, что оператор уравнения движения
A8)
перестает быть сингулярным, т. е. обладает обратным
4.4. Диагональная калибровка. Если фиксирующий калибровку
коэффициент d\ |:авен единице, то мы приходим к диагональным
выражениям для К и /С:
Такая калибровка называется диагональной. В этой калибровке
лагранжиан
путем интегрирования по частям может быть преобразован к виду
■4l'W. A9)
представляющему ковариантную сумму лагранжианов для каж-
каждой из компонент А^ по отдельности.
Лагранжиан A9) приводит к уравнениям движения
ПЛЛ*) = 0 " B0)
в форме уравнений д'Аламбера. Этот лагранжиан окажется наи-
наиболее удобным для квантования. По физическому содержанию
(наблюдаемые поля Е, Н) лагранжиан A9), так же как и более
общее выражение A3), эквивалентен исходному «поперечному»
лагранжиану A2).

38 ГЛ. I. СВОБОДНЫЕ КЛАССИЧЕСКИЕ ПОЛЯ
Отметим еще, что уравнения движения B0) и лагранжиан A9),
представляя собой частный случай общих соотношений A3) и A4),
являются инвариантными относительно преобразования A6).
В любой фиксированной системе отсчета функцию /0 этого преоб-
преобразования можно выбрать таким образом, чтобы нулевая компо-
компонента потенциала" Ао, удовлетворяющая свободному уравнению B0),
обратилась в нуль. Условие Лоренца принимает при этом вид
div4 = 0. ' B1)
Соответствующая калибровка называется кулоновской.
В импульсном представлении уравнение B1) выглядит сле-
следующим образом:
kA (k) = 0.
Как видно, в кулоновской калибровке электромагнитное поле
удовлетворяет условию поперечности в обычном (трехмерном)
смысле. Таким образом, несмотря на то, что электромагнитное
поле описывается 4-компонентным потенциалом, физический смысл
имеют лишь две линейно независимые компоненты, ортогональ-
ортогональные волновому вектору к. Фактическое сведение 4-компонентного
поля к двухкомпонентному, происходящее вследствие градиентной
инвариантности, тесно связано с равенством нулю массы покоя
частиц поля— фотонов. Именно в силу этого важного свойства
в уравнениях поля содержатся лишь производные от Av и воз-
возникает свойство калибровочной инвариантности электромагнитного
поля. " . ■
Из лагранжиана A9) стандартным приемом получаем:
тензор энергии-импульса
пространственные плотности 4-вектора Pv
тензор спинового момента
пространственную плотность вектора спина
S=[A(x)xA(x)].
Условие Лоренца F) следует наложить дополнительно к лагран-
жеву формализму.
Для вычисления динамических инвариантов произведем раз-
разбиение на частотные слагаемые и введем импульсное представ-

§ 4. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ 39
ление для свободного поля
4.5. Переход к локальному реперу. Для проведения диагона-
лизации в импульсном представлении B2) необходимо разложить
поле по составляющим, связанным с локальным репером. Из-за
равенства нулю массы покоя (/л = 0) преобразование C-24) должно
быть модифицировано. Представим А (к) в виде суммы попереч-
поперечных, продольной и временной составляющих
А~ (к) = е\аг (k) + elaf {k) + evar (к) + e°va£ (к). B3)
Здесь е1 (к) и е2 (k) — чисто пространственные поперечные орты,
подобные введенным в C.24), е3 = k/\ к | — продольный орт, причем
3 = 0, е1е' = дф [е'х^=е* (/, /, k= 1, 2, 3),
а е° —единичный временной 4-вектор: ^ = 6^. Легко проверить,
что преобразование B3) оставляет диагональной основную квад-
квадратичную форму
A+(k)A-v(k) = g°ea+(k)a-p(k). B4)
Внося разложение B3) в условие Лоренца, записанное по отдель-
отдельности для положительно- и отрицательно-частотных компонент,
получим два соотношения
\k\ar (k)-
Замечая, что, ввиду равенства нулю массы т, \k\ = k0; находим
отсюда
at (k) as(k) = <u(k)<% (к). B5)
Смысл полученного соотношения B5) состоит в том, что
в силу условия Лоренца плотности средних чисел «продольных»
фотонов ata» и «временных» фотонов а^аЪ равны друг другу.
Поскольку их вклады в правую часть B4) противоположны по
знаку, можно поэтому сказать, что «продольные» и «временные»
фотоны как бы «компенсируют» друг друга. Подставляя B5)
в B4), получаем
- АХ (k) Av (к) = at (к) ат (к) + at (k) ai (k).
Вычисляя далее 4-вектор энергии-импульса
/>v= 2 \dkk?at{k)crs{k), - .
s=l,2
находим, что в рассматриваемом случае, как и для векторного
поля, энергия оказывается положительно определенной лишь
в силу условия Лоренца.

40 ГЛ. I. СВОБОДНЫЕ КЛАССИЧЕСКИЕ ПОЛЯ
Определяя затем вектор спина
S=i]dk[A+ (k) X A-(k)] = i\dkгаЬсеаа%(k) a7,(k),
находим его проекцию на направление волнового вектора в виде
&S3 ~ /[at (k) oq (k) - at (к) ат (к)].
Вводя новые амплитуды Ьх и bv как в § 3, получаем для Pv и
S3 «диагональные» выражения
Pv= [dkkv[bt(k)bi(k) + bi(k)bi(k)\ B6)
AS3~[bi(k)bl(k)~bt(k)b*ik)l B7)
из которых непосредственно вытекает, что произведения
ns(k) = bf(k)b;(k) (s = l,2) B8)
могут рассматриваться как плотности средних чисел частиц с мас-
массой нуль, импульсом к, энергией | k |, обладающих проекцией
спинового момента на направление волнового вектора к, равной
-(- 1 (s= 1) и — 1 (s = 2). Фактически мы имеем дело с фотонами.
Таким образом, переход к импульсному представлению позво-
позволяет наглядно убедиться, что электромагнитное поле описывает
поперечные фотоны с двумя возможными значениями проекции
спина на направление движения.
§ 5. Поле Дирака
5.1. Уравнение Дирака и матрицы Дирака. Спинорными полями
обычно называют поля, преобразующиеся по спинорным представ-
представлениям группы Пуанкаре. Эти поля после квантования описывают
частицы с полуцелым спином (V2> 3/2, 6/2, ...). Простейшим из
спинорных полей является поле спина г/2.: Такое поле для частиц
с отличной от нуля массой покоя было введено Дираком для
описания электронов. Оно описывает также мюоны, нуклоны
(протоны и нейтроны) и некоторые гипероны. Это поле мы и
будем далее называть полем Дирака. Соответствующие уравне-
уравнения, следуя Дираку, получим путем «факторизации» оператора
Клейна — Гордона:
2
где для удобства записи использованы обычные квантовомехани-
ческие обозначения
Оператор □— т2 является квадратичным относительно произ-
производных dv и, как легко убедиться, не может быть представлен

§ 5. ПОЛЕ ДИРАКА 41
в виде произведения двух линейных по Pv сомножителей с чис=-
ленными коэффициентами. В самом деле, если по аналогии
с формулой разбиения на множители разности двух квадратов
попытаться записать его в виде
р _ т2 = (Р + т)(Р — т),
где Р — некоторая линейная комбинация операторов Pv с коэф-
коэффициентами yv:
P=Pvy\
то для этого необходимо потребовать, чтобы выполнялось соот-
соотношение
раскрывая правую часть которого, найдем условие, определяю-
определяющее коэффициенты у:
W 0)
Ввиду того, что, согласно этому условию величины yv с различ-
различными индексами антикоммутируют, они не являются числами и
могут быть выбраны в виде матриц.
С помощью этих величин оператор Клейна — Гордона может"
быть представлен в виде произведения двух коммутирующих
матричных операторов:
□ _ m2 = (iyvdv+т) A-рд# - т),
и, для того чтобы функция поля подчинялась уравнению Клейна —
Гордона
BИ 0
мы можем- потребовать, чтобы она удовлетворяла одному из
уравнений первого порядка
(iyvdv - т) г|з (х) = 0 или (iyvdv + т)Ц(х)=0.
В соответствии с традицией мы выберем в качестве уравнения
движения для спинорного поля первое из этих уравнений
> Aд-т)Ц(х) = 0, д=уЧ. B)
Уравнение B) разумеется является менее общим, нежели урав-
уравнение Клейна■— Гордона. Можно ожидать поэтому, что оно содер-
содержит более детальную информацию. Как известно, такое положе-
положение действительно имеет место, поскольку с помощью уравнения
B) Дираку впервые удалось описать спин электрона, равный г/2.
Уравнение B) называется уравнением Дирака, а матрицы yv<
определяемые соотношениями A), — матрицами Дирака*

42 ГЛ. I. СВОБОДНЫЕ КЛАССИЧЕСКИЕ ПОЛЯ
Благодаря матричному характеру дифференциального опера-
оператора уравнения Дирака функция поля г|) оказывается многоком-
многокомпонентной. Как показано в Дополнении II, в простейшем случае
поле Дирака г|э представляет собой 4-компонентный спинор, часто
изображаемый в виде столбца
который для экономии места мы будем также записывать сле-
следующим образом: ^(ih, i|V %> №■
Таким образом, одно матричное уравнение B) содержит чет-
четверку уравнений
(i?4-/n/)epifo(x) = 0 (a, p = l, 2, 3, 4).
Четыре величины yv представляют собой квадратные матрицы
четвертого ранга с матричными элементами у£р, а / — единичную
диагональную матрицу (/ар = бар)> символ которой мы будем
часто опускать. Основные свойства матриц Дирака определяются
(анти)коммутационным соотношением A) и подробно изложены
в Дополнении П. Из A) в частности вытекает, что матрицы
Дирака могут быть выбраны унитарными:
+ +
Yvyv = YvYv = /, (нет суммирования по v),
если условия эрмитова сопряжения наложить в виде
Pv* C)
Как видно, операция опускания (и поднятия) лоренцева индекса
у матриц Дирака выполняется по обычным правилам. Эрмитово
сопряженный спинор ■$ представляет собой 4-компонентную строку
* * * * *
i|) = (i|I, г|)а, i|K, ijL), элементы которой получаются из компонент \|за
комплексным сопряжением. Умножая этот спинор справа на
матрицу у0, получаем так называемый дираковски сопряженный
(далее — просто сопряженный) спинор
С учетом C) можно показать (см. Дополнение II), что сопря-
сопряженный спинор \р удовлетворяет уравнению
= O. D)
Напомним еще, что каждая из компонент спинора г|э (х) удов-
удовлетворяет уравнению Клейна —Гордона. Для того чтобы убе-
убедиться в этом, достаточно подействовать на уравнение Дирака B)

§ 5. ПОЛЕ ДИРАКА 43
■л. ■
слева оператором Лд-\-т и воспользоваться коммутационным
соотношением A)-
Отметим, что, согласно принятому обычаю, произведение грОг|э,
где 0 — некоторая матрица, подразумевает суммирование по спи-
норным индексам
и обозначает число, тогда как выражение вида Щ является
матрицей
i|n|) = А, Лар = i|)ai|)p.
5.2. Лагранжев формализм. Уравнение Дирака B) и ему
сопряженное уравнение D) могут быть получены из лагранжиана
X = (i/2) И (х) vvdvt|> - dvy (x) vvf (x)] - пЩ (х) ф (х) E)
с помощью вариационного принципа. Особенность этого лагран-
лагранжиана состоит в том, что он обращается в нуль, если входящие
в него г|3 и г|з удовлетворяют уравнениям движения.
Используя теорему Нётер, получим отсюда тензор энергии-
импульса
Т*» = (r/2) [ip (х) fd»ip (х) - д^ (х) Y*t|> (х)] F)
и вектор тока
$(( . G)
При выводе выражения F) были использованы уравнения дви-
движения.
Для вычисления тензора спина заметим, что после выполне-
выполнения суммирования по спинорным индексам формула B.24) при-
принимает вид
ST <^v> = — — Л* <^VH|> (x) - % (х) A* W ~,
дг|);т д$;х
причем входящие в нее инфинитезимальные генераторы А^, Af
с помощью формул бесконечно малых преобразований Лоренца
следующих из формул (ДП.16, 18, 20), определяются в виде
(см. Упражнение С29)
где а^ —так называемый матричный тензор спина (см. формулу
(ДП.2)). Поэтому

44 ГЛ. Г. СВОБОДНЫЕ КЛАССИЧЕСКИЕ ПОЛЯ
5.3. Импульсное представление. С учетом того, что компоненты
дираковского спинора i|)o(x) удовлетворяют уравнению Клейна —
Гордона, импульсное представление запишем в виде
i|) (х) = Bя)-'/. J dp е>р*8 (р2 - /и2) у (р),
причем амплитуда ■$ удовлетворяет уравнению Дирака в импульс-
импульсном представлении
(Напомним, чтов наших обозначениях p = vvPv)
Разлагая, как обычно, функцию поля на частотные состав-
составляющие i|) = i|)+4-i|J~ и интегрируя явно по р0, определим фор-
формулы трехмерного импульсного представления в виде
г|>± (х) = Bя)"'/. J dp г|>± (р) exp (± ipx). (9)
Здесь под знаком интеграла (и далее везде в этом параграфе)
Ро =
Спиноры ф- (р) удовлетворяют матричным уравнениям
(т±р)^(р) = 0. A0)
Соответствующие уравнения для сопряженных спиноров будут
Явный вид компонент ty£ и ijjjf зависит от представления
дираковских матриц у и может быть определен следующим обра-
образом. В силу ковариантности уравнения A0) его можно рассмат-
рассматривать в какой-либо фиксированной системе отсчета, имея в виду,
что переход к любой другой системе может быть всегда осущест-
осуществлен с помощью приведенных в Дополнении II преобразований.
Выбирая в качестве таковой систему, в которой р = 0, находим
из A0)
(V0 ± I) г|)± @) = 0.
Отсюда в стандартном представлении (ДП.5) получаем
%@)=сЛа + сЛа, yU°) = <hfl* + cft#- С12)
Здесь а, [} — спинорные индексы, а бар — символы Кронекера.
Решение для произвольного р, отличного от нуля, может
быть получено из A2) соответствующим лоренцевым преобразо-
преобразованием.
Уравнения, которым удовлетворяют 1JJ+ и г|г, могут быть
также представлены в форме

§ 5. ПОЛЕ ДИРАКА 45
в которой они отличаются друг от друга лишь знаком при р0.
Каждое из них, как только что установлено, обладает двумя
линейно независимыми решениями. Отсюда следует, что уравне-
уравнение Дирака для каждого заданного значения 4-вектора р (знак
компоненты р0 фиксирован!) обладает лишь двумя линейно неза-
независимыми .решениями.
Соответственно этому сопряженный спинор \|э при фиксирован-
фиксированном знаке Ро также обладает двумя линейно независимыми реше-
решениями. Из комплексности рассматриваемых решений уравнения
Дирака вытекает, что они описывают частицы, отличающиеся
зарядом (точнее, частицы и античастицы). Наличие двух линейно
независимых решений означает, что указанные частицы могут
находиться в двух различных состояниях, отличающихся, как
будет показано ниже, знаком проекции спина на направление
движения.
5.4. Разложения по спиновым состояниям. Обозначая норми-
нормированные (соотношения нормировки см. ниже —A6)) линейно неза-
независимые решения для ро>О, т. е. для первого из уравнений A0),
через vs'+(p), а для р„<;0, т. е. для второго из уравнений A0),
через Vs- ~(р) (s=l, 2), запишем разложения функций ^(р) по
спиновым состояниям в виде
Щ(Р)= S a±(p)v^±(p)=c^{p)v^±{p). A3)
s=1.2
Соответственно для сопряженного спинора
^±(p) = af(p)is-±(p)^*af(p)*vs-±(p)y°. A4)
Так как \|э+ и г|г представляют собой положительно- и отрица-
отрицательно-частотные части функции г|э, условия эрмитова сопряже-
сопряжения для нормированных спиноров v имеют следующий вид:
(о». ±(j[,))* = t*s. +{Р). A5)
Поэтому условия ортонормированности спиноров v можно записать
в форме
S». ± (р) о'.+(р) а 2 %.±(/>)t£ *(/>)=б".
а=1. 2, 3. 4
Путем чисто алгебраических преобразований из A5) и A6) и
уравнений Дирака можно получить ряд соотношений для квад-
квадратичных форм спиноров v и v = vy°, важнейшими из которых
являются:
условие ортонормированноети для дираковски сопряженных
спиноров
0».±(рH'.+(р) = ±^а"; A7)

46 ГЛ. I. СВОБОДНЫЕ КЛАССИЧЕСКИЕ ПОЛЯ
условие взаимной ортогональности спиноров v с аргументами,
отличающимися знаками,
■1>.±(р)хГ-±(-р) = 0; A8)
соотношения.^, я=1, 2, 3)
vs- ± (/>) (рY - PV - ^V"Vm) vr- ± (— Р) = 0.
A9)
и, наконец, формулы суммирования по спиновому индексу
B0)
5.5. Динамические инварианты. Подставляя (9), A3), A4) в F)
и интегрируя rOv no dx с учетом условий ортонормированно-
сти A6), получаем 4-вектор энергии-импульса
Pv = \dk k,[h (k) aj (k) - к (ft) at (ft)]. B1)
Принимая во внимание, что, согласно использованным опре-
делениям} законы комплексного сопряжения амплитуд импульс-
импульсного представления имеют вид (а~)* = а+, убеждаемся, что сле-
следующее из B1) выражение для. энергии
Ро = \ dkk0 [к (k)aj(k) - к (k) at (k)} B2)
не является положительно определенным. Положительная опре-
определенность энергии спинорного поля достигается лишь в кванто-
квантовой теории квантованием по Ферми —Дираку.
Переходя к вычислению вектора спина, отметим, что в стан-
стандартном представлении (ДИ.5) компоненты тензора спина а^у
могут быть выражены через матрицы а,- и ау следующим образом:
/а»° а°1 а»2 а01Ц / 0 iax ia2 Ia3\
\а3» а»1 а»а азз/ , \_ fo3 а2 — Oj 0
Поэтому, полагая в (8) т = 0 и [л, v = l, 2, 3, убеждаемся,
что пространственная плотность вектора спина выражается через
матричный вектор о:
.S-(Vi) S* (*)<*|> (*)<*?• B4)
В противоположность спинам векторного и электромагнитного
полей вектор спина B4) поля Дирака не сохраняется во времени
(что связано с отсутствием симметрии у тензора энергии-импульса).

§ 5. ПОЛЕ ДИРАКА - 47
Однако в том случае, когда функции поля i|), \|э не зависят от
некоторых из координат х°, х1, ..., можно добиться выполнения
уравнения непрерывности для отдельных компонент тензора S,
а следовательно, сохранения во времени соответствующих инте-
интегралов. Так, полагая d/dx1 = d/dxi = 0, получим
откуда следует, что проекция вектора спина на ось х2
сохраняется во времени. В импульсном представлении эта кар-
картина соответствует сохранению проекции вектора спина на на-
направление движения.
Переходя в B4) к трехмерному импульсному представлению
и выполняя интегрирование по трехмерному конфигурационному
пространству, получаем
AS ~ (V.) №.(*) <"Г (*) f Г '(*) <*Y (*) +
Ограничиваясь рассмотрением компоненты S3, воспользуемся пер-
первым из соотношений A9), которое представим в форме
*v± ДО от± (—*)=! *v± (k) [к х v] v± (— к).
В силу этого соотношения в системе отсчета, где &i = ife2 = 0,
зависящие от времени члены в S3 исчезают, и мы приходим
к выражению
AS3 - (V2) [к (к) а-г (к) р*- + (к) atxf- ~ (к) +
+ *aT(k)a+r(k)v°--(k)o3vr-+(k)l B5)
для дальнейшей конкретизации которого удобно перейти к какому-
либо частному представлению матриц Дирака. В стандартном
представлении матрица о, диагональна
Выбирая при этом нормированные спиноры в системе kx = k2 =

48
в виде
ГЛ. I. СВОБОДНЫЕ КЛАССИЧЕСКИЕ ПОЛЯ
V
1, О,
О, 1,
, о.
о
О,
О,
ko+mj '
1, 0 )\
, о, 1 )т,
B6
где Af —нормировочный множитель, равный
находим, что- выражение B5) принимает форму
* * * *_
Сравнивая выражения для энергии-импульса B1), проекции
вектора спина B7) и непосредственно вытекающего из G) выра-
выражения для заряда
Q = $.•$ (х) г|з (х) dx = J dk[at (k) aj (k) + aj (k) at (k)}, B8)
находим, что поле Дирака соответствует заряженным частицам
с возможными значениями проекции спина на заданную ось,
равными ± 1/2. Более детальная классификация возможных зна-
значений энергии-импульса, заряда и проекции спина.будет прове-
проведена после квантования (§ 9), где она получит полное и одно-
однозначное обоснование.

Глава II. КВАНТОВАНИЕ СВОБОДНЫХ ПОЛЕЙ
§ 6. Квантование полей
6.1. Сущность процедуры квантования полей. Квантование
волновых полей —процедура, по сути своей аналогичная кванто-
квантованию в нерелятивистской квантовой механике. Специфика состоит
в том, что, в отличие от физических систем с конечным числом
степеней свободы, обычно рассматриваемых в квантовой механике,
волновые поля соответствуют системам с бесконечным числом
степеней свободы. Такую систему можно рассматривать как пре-
предел системы с большим числом степеней свободы N при N-^-oo.
В обычной квантовой механике подобный пример дает система,
состоящая из большого числа частиц. Частным случаем такого
типа является система N осцилляторов. .
Важным техническим аспектом процедуры квантования полей
является представление чисел заполнения (или, как его часто
называют, — представление вторичного квантования*). Это пред-
представление наиболее лросто вводится на примере квантовомехани-
ческого осциллятора и широко используется при рассмотрении
систем из большого числа тождественных частиц. Отсылая чита-
читателя за техническими деталями к стандартным курсам квантовой
механики (см., например, Давыдов A973), § 33; Мессиа A978),
гл. XII; Елютин, Кривченков A976), гл. III, § 12; Медведев,
A977), ч. III, § 10), напомним здесь лишь логику основных рас-
рассуждений.
Гамильтониан одномерного осциллятора с единичной массой
запишем в виде
4 ). A)
Волновые функции % различных состояний осциллятора удов-
*) Термин «вторичный» как бы подразумевает наличие первичного кванто-
квантования. На самом дела квантование проводится только один раз и этот термин
оказывается дезориентирующим. Мы будем, по возможности, избегать его.

50 ГЛ. II. КВАНТОВАНИЕ СВОБОДНЫХ ПОЛЕЙ
летворяют уравнению
и могут быть получены одна из другой с помощью некоторых
операторов а и а:
. a% = Yn+l i|Vu. Щп = УпЩп-1, B)
обычно реализуемых с помощью комбинации операторов диффе-
дифференцирования и умножения на координату в переменных р и
(или) q (здесь положено Й=1), т. е. .
причем р =—id/dq, q = q в координатном представлении ир—р,
q = id/dp — B импульсном. (Здесь крышка сверху «v» обозначает
оператор.) Оператор а повышает индекс состояния на единицу
(а энергию на %<£>) и называется повышающим. Оператор а соот-
соответственно—понижающим. Основное состояние удовлетворяет
соотношению . -
0. C)
Числовые множители ~\fn +1, ~\Гп вводятся в B) из сообра-
соображений нормировки состояний (см. ниже формулу F)). .
• Из формул B) вытекает, что состояния tyn являются собствен-
собственными функциями произведений шише собственными значе-
значениями п-\-\ и п. Поэтому можно написать
+ v " + ■' v V.
аа = п+1, аа = п, п$„ = п%,
а также
Г +Л + +
[а, а\ = аа — аа= 1,
Оператор п уместно назвать оператором индекса состояния.
Гамильтониан может быть теперь представлен в виде
| E)
6.2. Корпускулярная трактовка представления чисел заполне-
заполнения. Переход к представлению чисел заполнения заключается
в том, что вместо того, чтобы задавать г|>функцию как функцию
от координат (координатное представление) или как функцию от
импульсов (импульсное представление), состояние системы харак-

§ 6. КВАНТОВАНИЕ-ПОЛЕЙ 61
теризуют числом заполнения п — номером возбужденного состоя-
состояния.
Факт линейной зависимости гамильтониана E) от оператора
числа заполнения п в осцилляторной задаче является основой
ее корпускулярной трактовки.
Условимся для этого представлять себе осциллятор, находя-
находящийся в возбужденном состоянии 1|зл(я3г1), как совокупность п
квантов возбуждения, каждый из которых имеет энергию со (т. е.
Йсо). Эквидистантность уровней, т.. е. факт линейной зависимости
энергии от числа л, приводит к важному свойству неразличимости
квантов возбуждения. В такой трактовке операторы повышения
и понижения номера возбужденного состояния а и а приобретают
смысл операторов рождения и уничтожения квантов возбуждения.
Индекс п равен теперь числу квантов возбуждения в состоянии
\|)„, а оператор п становится оператором числа квантов.
Состояние г|)„, .содержащее п квантов (частиц) может быть полу-
получено из основного состояния %, не содержащего частиц (которое
вследствие этого уместно назвать вакуумным состоянием), я-крат-
ным применением оператора рождения
Ц. (в)
Числовой множитель (п\)~'/г в этой формуле возникает в соответ-
соответствии с первой из формул B) и обеспечивает равенство норм
состояний \|)„ с различными п.
Соотношения B) —F) представляют собой формулировку
квантово-механической задачи об осцилляторе на языке представ-
представления чисел заполнения (или фоковского представления). Особо
подчеркнем, что частицы соответствуют не самому осциллятору,
а квантам его возбуждения. Частицы «возникли» в результате
обычного квантования.
Для перехода к случаю многих степеней свободы Af>l вво-
вводится набор N осцилляторов с различными частотами сой. Индекс
k пробегает N значений щ, щ, ..., aN. Гамильтониан представ-
представляется суммой •
Операторы аА, at удовлетворяют коммутационным соотноше-
соотношениям D) при совпадающих индексах k = l и коммутируют друг
с другом при 1гф1, т. е.
ак, ai] = 8kh [ak, аг] =

52 ГЛ. II КВАНТОВАНИЕ СВОБОДНЫХ ПОЛЕЙ
Произвольное состояние системы характеризуется здесь набо-
набором чисел заполнения nv щ, п3, ..., я^. Состояние
■ <7)
содержит п\ частиц 1-го сорта с энергией щ, я2 частиц 2-го
сорта с энергией <оа и т. д.
Покажем теперь, что вещественная скалярная функция поля
и(х), удовлетворяющая уравнению Клейна — Гордона,
может быть представлена в виде совокупности осцилляторов. Для
этого, во-первых, перейдем от неограниченного конфигурацион-
конфигурационного пространства к «большому кубу» с объемом V = L3 и нало-
наложим на решения уравнения условия периодичности:
u(x) = u(t, xlt х%, xa) = u(t, хг+1, х2, х3) =
= «(/, хъ x2+L, xa) = u(t, хъ х2,
Представляя и в виде суммы Фурье
получим уравнение движения для амплитуды a(t, k):
a(t,
где (о1 = /гг + /пг. Это уравнение есть не что иное, как уравнение
для осциллятора. Таким образом, амплитуда a(t, k) есть ампли-
амплитуда осциллятора с частотой (oft = (ft2 + m2)'^.
Условие периодичности в ж-пространстве приводит к дискрет-
дискретности допустимых значений импульсов:
. , ч Bя 2л 2л
к (nlt п2, п3) = |-£- nlt -j- п2, -j- n
Каждому k (n) отвечает осциллятор с энергией
Таким образом, релятивистскому полю, удовлетворяющему
уравнению Клейна — Гордона, может быть сопоставлен гамильто-
гамильтониан осцилляторного типа, в котором осцилляторы перенумеро-
перенумерованы тремя целыми числами пъ п2, па.
Переход к реальному бесконечному конфигурационному про-
пространству (L-*-oo) приводит к непрерывному импульсному

§ 6. КВАНТОВАНИЕ ПОЛЕЙ 53
пространству. При этом все суммы заменяются на интегралы
по правилу
(¥724 <*
а символ Кронекера —на дельта-функции
2^L*'-> 5 (*-*')•
С учетом изменения нормировки операторов
2ji\3/i ...
у a(k)
получаем перестановочные соотношения
+ 1
), a(q)\=0.
Формула G) в непрерывном случае сохраняет свой вид. Соот-
Соответствующие состояния содержат кванты со строго фиксирован-
фиксированными импульсами. Волновые функции этих состояний в конфи-
конфигурационном представлении отвечают плоским волнам. Поэтому
подобные состояния не имеют конечной нормы (см. задание 03).
Отметим еще, что в результате квантования (8) полевая функ-
функция u(x)=u(t, х), удовлетворяющая уравнению Клейна —Гор-
—Гордона, оказывается представленной в виде трехмерного импульс-
импульсного интеграла от линейной формы по операторам a (ft), a (k)
и, таким образом, сама становится оператором.
6.3. Каноническое квантование. Изложенная выше операторная
формулировка квантовомеханическои задачи об осцилляторе может
быть также довольно просто получена из классической задачи
об осцилляторе, изложенной с помощью канонического форма-
формализма классической механики.
В каноническом формализме основными переменными явля-
являются координаты q и сопряженные им импульсы
дХ
Гамильтониан осциллятора в переменных q, p имеет вид A).
Уравнения движения для динамической переменной А, являю-
являющейся функцией от q, p и явно не зависящей от времени, запи-
записываются в виде
4%^-М, Я}, О)

54 ГЛ. II. КВАНТОВАНИЕ СВОБОДНЫХ ПОЛЕЙ
где фигурными скобками обозначена классическая скобка Пуас-
Пуассона
г <1 dadb dadb
Поэтому, в частности,
{<7, Pl = l (П)
q = {q,H}=p, p=\p, H} = -tfq.
Из последних формул, представляющих собой канонические урав-
уравнения движения, следует, что решения могут быть разложены
на положительно- и отрицательно-частотные части:
p yf[fl-@-fl'-@], A2)
причем
Используя соотношения, обратные к A2), а также A1), полу-
получаем
,{а<->@, fl(+> (/)} = -*. . A3)
Подставляя A2) в гамильтониан A), -находим
Я = A /2) [а<+> (t) a<-> (t) + а<-> (t) tft+) @] = A /2) (аа + flfl) •
Здесь мы сохранили порядок сомножителей, следующий из A)
(эта предосторожность окажется полезной в дальнейшем при пере-
переходе к квантовому случаю), а также ввели более компактные
обозначения . •
Процедура квантования теперь может быть выполнена с по-
помощью следующего постулата канонического квантования:
Будем считать, что динамические переменные типа qt р,
а, а, так же" как и функции от них (например, гамильто-
гамильтониан Я), суть операторы, действующие на ф-функцию состоя-
состояния.
Законы взаимных перестановок этих операторов устанав-
устанавливаются по следующему «правилу соответствия»: в формулах
канонического формализма типа (9), A1), A3) классическая
скобка Пуассона A0) заменяется на квантовую скобку Пуас-
Пуассона, определенную соотношением
К *}«№.■= -^О> b\ = ^{ab-ba),
т, e.
{a, b\Ka-+\{a, b]. A4)

§ 6. КВАНТОВАНИЕ ПОЛЕЙ 55
Поэтому в квантовом случае уравнение движения (9) для опера-
операторной величины А принимает вид
<^=[Д Я], A5)
а формулы A1), A3) превращаются в коммутационные соотно-
соотношения:
[q, p] = i, [a, a] = l. A6)
С учетом последнего коммутатора гамильтониан Я может быть
записан в виде E). Таким образом, мы убеждаемся, что выше-
вышеприведенный постулат канонического квантования для осцилля-
осциллятора совершенно эквивалентен обычной формулировке квантова-
квантования, изложенной в~§ 6.1. Будучи применен к физическому полю,
он может рассматриваться как основа квантования полей. При
этом мы сразу получаем квантовую формулировку в представле-
представлении чисел заполнения.
Для дальнейшего обсуждения взаимосвязей между различными
формулировками квантования систем с большим числом степеней
свободы следует напомнить некоторые элементарные сведения из
теории представлений квантовой механики.
6.4., Представления Шредингера и Гайзенберга. Наиболее рас-
распространенным в квантовой механике является представление
Шредингера. В этом представлении эволюция системы во времени
описывается с помощью зависящей от времени волновой функции
(/ удовлетворяющей уравнению Шредингера
Здесь Я —оператор Гамильтона, соответствующий полной энергии
системы и не зависящий от времени для консервативных систем.
В представлении Шредингера динамические переменные характе-
характеризуются операторами В, не зависящими от времени явно. Их
средние значения
Б; =4@5^) A7)
могут, однако, зависеть от времени через волновые функции ij> (t\
В выражении A7) временная эволюция среднего значения дина-
динамической переменной В обусловлена ty(t). Можно перенести ее
непосредственно на оператор В. С этой целью формально про-
проинтегрируем уравнение Шредингера. Получим
= 1/(94?, A8)
где
V(t) = er<™. A9)

56 ГЛ. II. КВАНТОВАНИЕ СВОБОДНЫХ ПОЛЕЙ
С помощью A8) правую часть A7) представим в виде
5 я ф (о = $# $
причем
BH(t) = V{t)BU{t)=etH'Be-lHt. B0)
Таким образом, среднее значение Bt представлено как среднее
по функциям i|), не зависящим от времени, от оператора B0),
явно зависящего от времени. Мы пришли здесь к представлению
Гайзенберга, в котором зависимость от времени перешла с вол-
волновой функции на оператор. Дифференцируя B0) по t, получаем
уравнение движения
idI^l=[BH(t), H]. B1)
Отметим, что мы получили два различных способа описания эво-
эволюции системы во времени. Для перехода от момента 0 к моменту
/следует либо преобразовать волновую функцию г|) по формуле
A8), либо преобразовать оператор В по формуле B0).
Сравнивая . B1) с A5) заключаем, что схема канонического
квантования, описанная в § 6.2, приводит к гейзенбергову пред-
представлению для квантованных волновых полей.
В каноническом формализме время играет выделенную роль.
Поэтому может сложиться впечатление, что при использовании
этого приема в теории волновых полей релятивистская инва-
инвариантность последних оказывается под угрозой. В действитель-
действительности этого не происходит, и в результате канонического кванто-
квантования полей мы получаем выражения, обладающие надлежащей
инвариантностью. Существует, однако, еще одна схема квантова-
квантования, в которой релятивистская инвариантность сохраняется
на всех промежуточных этапах. Эта схема основана на теории
представлений, точнее на требованиях соответствия законов пре-
преобразования квантованных и классических полей при преобразо-
преобразованиях полей и координатных систем отсчета.
Эту схему, восходящую к работам Швингера конца 40-х годов,
мы назовем релятивистской схемой, и кратко изложим ее основ-
основные моменты. (Более полное изложение содержится, например,
в § 9 Введения.)
6.5. Релятивистская схема квантования полей. В результате
квантования полевые функции приобретают * операторный смысл
и линейно выражаются через операторы рождения и операторы
уничтожения частиц, между которыми устанавливаются надлежа-
надлежащие перестановочные соотношения. Эти операторы-действуют на
общую для всех полей волновую функцию Ф.
В соответствии с обычной квантовой механикой волновая
фунщия Ф полностью характеризует физическое состояние системы,

§ 6. КВАНТОВАНИЕ ПОЛЕЙ 57
описываемой квантованными волновыми полями. Подобно обыч-
обычной г|)-функции величина Ф может рассматриваться как вектор
в некотором линейном пространстве. Ввиду этого функцию Ф
называют амплитудой (или вектором) состояния.
Как и в квантовой механике, не все векторы Ф обладают
конечными нормами (например, соответствующие плоским волнам).
Однако нормы реальных физических состояний всегда могут быть
выбраны конечными. Средние значения динамических величин и
вероятности перехода выражаются через квадратичные формы от Ф.
Рассмотрим теперь трансформационные свойства векторов Ф
при преобразованиях координат и полевых функций, введенных
в §§ 1, 2 (см. формулы A.1), A.3), B.10)):
х^>~х' =Р(а>; х) и(х)-*-и'(х') = А(а)и(х).
Подобным преобразованиям соответствует некоторое преобразова-
преобразование вектора состояния, которое вследствие принципа суперпози-
суперпозиции должно быть линейным:
Ф->Ф' = £/(со)Ф B2)
и благодаря сохранению нормы унитарным:
#(сй)£/(сй) = 1. B3)
В простейшем случае преобразования трансляции и' (х) —
s=u(x — <a) оператор U имеет вид
U(u>)=exp(iPll<i>»). B4)
Экспоненциальный характер зависимости от параметров со сле-
следует из группового характера преобразования. В силу условия
унитарности B3) операторы сдвига должны быть эрмитовыми:
Яц = Рц. Отметим, что формула B4) в частном случае <ov = — 8vot
соответствует формуле A9). Оператор Рц, таким образом, является
оператором 4-импульса. Аналогом формулы B0) для операторной
полевой функции будет
u'(x) = u(x-a) = U-1(a)u(x)U(a). B5)
При бесконечно малых со преобразование амплитуды состояния
по виду совпадает с бесконечно малым преобразованием полевой
функции
u'(x) = (l+tpa)u(x). B6)
Если считать, что « — обычная волновая функция, то коэф-
коэффициенты Pv могут рассматриваться как квантовомеханические
операторы 4-импульса:
id

58 " ГЛ. II. КВАНТОВАНИЕ СВОБОДНЫХ ПОЛЕЙ
Подчеркнем, что pv — это генератор сдвига (оператор импульса)
в пространстве полевых функций и(х), a Pv —генератор сдвига
в пространстве векторов состояний Ф, т. е. в представлении
чисел заполнения или представлении вторичного квантования.
(Именно такое соответствие и послужило в свое время причиной
появления термина «вторичный».)
Выписанные формулы можно обобщить на случай общих пре-
преобразований из группы Пуанкаре x'=Lx-\-a:
+±-MiLV<i>^, Ф'=A+^а + у^«)ф. B7)
и'(x)={\+ipa + ~m(iiju{x), mllv = i(xlldv — xvdvl). B8)
Здесь т,^ —генераторы 4-мерных поворотов.
Исходя из соображений соответствия, мы будем поэтому интер-
интерпретировать Р и М в B7) как операторы 4-вектора энергии-
импульса и тензора момента количества движения соответственно.
Аналогично этому при градиентных преобразованиях функций
поля:
■ Ф ->. ф' = е'аф, ф ->q>' = е-'аф B9)
унитарный оператор преобразования
Ф' = иаФ.
имеет экспоненциальную структуру
C0)
в которой эрмитов оператор Q следует интерпретировать как
оператор заряда. В качестве основного постулата квантования
волновых полей мы примем, что эрмитовы операторы 4-вектора
энергии-импульса Р, тензора момента количества движения М,
заряда Q и т. п., являющиеся генераторами бесконечно малых
преобразований векторов состояний (см. формулы B7) и C0)),
выражаются через операторные функции полей теми же соотно-
соотношениями типа B.6, 7, 22, 30), что и в классической теории полей,
разумеется с установлением при этом надлежащего порядка опе-
операторного умножения. Этот постулат. является дальнейшим при-
применением принципа соответствия и определяет закон трансформа-
трансформации вторично квантованных амплитуд состояния.
§ 7. Перестановочные соотношения
7.1. Физический смысл частотных компонент. Рассмотрлм
соотношение F.25) для случая бесконечно малого преобразования
трансляции. Подставляя в него разложения по степеням (оц и
удерживая линейные члены, получим

§ 7. ПЕРЕСТАНОВОЧНЫЕ СООТНОШЕНИЯ 59
— четверку уравнений, обобщающих уравнение движения F.21).
Эти уравнения оказываются очень удобными для анализа частот-
частотных составляющих функций поля в импульсном представлении.
Подставляя в A) трехмерные импульсные разложения Фурье
типа C.8), D.13), E.9), получаем алгебраические операторные
уравнения
V** (*) = + ["-(*). ЛЛ- B)
Введем теперь состояние с определенным значением pv 4-вектора
энергии-импульса, описываемое амплитудой Фр:
C)
Умножая первое из уравнений B) справа на Фр, получаем
с учетом C) -
Pvu+ {к) Фр = (pv + kv) ы+ (k) Фр.
Из второго тем же способом находим
причем в обоих случаях &0 = У
Из. полученных соотношений вытекает, что выражение и+ {к) Фр
либо равно нулю, либо представляет амплитуду состояния с энер-
энергией-импульсом p + kt а и~(к)Фр есть амплитуда состояния
с энергией-импульсом p — k (либо нуль). Поскольку при этом
выполняется соотношение й2 = т2, то следует считать, что опера-
оператор и+ (к) описывает рождение частицы с массой т и 4-импуль-
сом k> а оператор и-(к) соответствует уничтожению такой же
частицы.
Подчеркнем, что это свойство частотных частей операторов
поля является совершенно общим, справедливым для полей любой
тензорной размерности, как вещественных, так и комплексных,
и не зависит от конкретного вида реализации перестановочных
соотношений (т. е. справедливо как при квантовании по Бозе —
Эйнштейну, так и при. квантовании по Ферми —Дираку— см.
ниже § 7.4).
Отметим еще, что, отправляясь от соотношения типа F.25),
для градиентных преобразований F.29), F.30)
, e~iau = U-1 (a)uU (a)
получим, приравнивая коэффициенты при членах, линейных по а:
и(х)=[и(х), Q] ы(а-) = -[ы(х), q]. D)
Уравнения D) дополняют формулы B). Из них, в частности,
следует, что операторы и (а также и частотные составляющие ы±)
являются «понижающими» по отношению к заряду системы (т. е.

60 ГЛ. II. КВАНТОВАНИЕ СВОБОДНЫХ ПОЛЕЙ
собственному значению оператора заряда Q). Сопряженные опе-
операторы и, ы± повышают собственное значение на единицу. Мы
предоставляем читателю самостоятельно провести соответствую-
соответствующие выкладки.
*
Таким образом, в случае комплексного поля оператор «+ рож-
рождает частицу с зарядом -j-1, оператор и- уничтожает частицу
с зарядом — 1 и т. д.
7.2. Амплитуда вакуума и фоковское представление. Теперь
можно естественным способом определить состояние вакуума и
установить правила построения амплитуд, соответствующих состоя-
состояниям с определенным числом различных частиц.
Рассмотрим динамическую систему, состоящую из нескольких
невзаимодействующих квантованных полей, характеризуемых опера-
операторными функциями их(*), ..., и„(х). Для удобства записи вклю-
включим в эту последовательность также и соответствующие сопря-
женные функции в тех случаях, когда щ отличаются от щ.
Определим амплитуду состояния вакуума Фо для данной дина-
динамической системы. Так как в вакууме отсутствуют частицы, то
импульс вакуума равен нулю, а энергия вакуума минимальна
(ее также можно положить равной нулю). Поскольку отрицательно-
частотные операторы и- уменьшают энергию, а энергия вакуум-
вакуумного состояния Фо минимальна, то следует положить
«Г(л;)Ф0 = 0 (i = l п) E)
при всех х. Аналогичная аргументация приводит к соотношению
Переходя к импульсному представлению, получаем соответственно
"Г(*)Ф0 = 0. F)
Соотношение F) и сопряженное ему Фоы/ (k) = 0 вместе с усло-
условием нормировки
можно считать определением вакуума свободных полей.
Амплитуда любого состояния рассматриваемой динамической
системы может быть теперь представлена с помощью введенной
выше амплитуды вакуума и операторов рождения соответствую-
соответствующих частиц. Так, амплитуда состояния, содержащего s частиц Д,...
..., /, сортов (некоторые из индексов / могут совпадать), пред-
представится выражением вида

§ 7. ПЕРЕСТАНОВОЧНЫЕ СООТНОШЕНИЯ 61
Входящие в него функции /•"<— I •••> имеют смысл обычных квантово-
механических волновых функций системы s частиц в импульсном
представлении. Амплитуда состояния, в котором присутствует
точно s частиц с заданными характеристиками /lt ..., /,, полно-
полностью описывается одной такой функцией.
В общем случае, когда число частиц не фиксировано, ампли-
амплитуда состояния характеризуется цепочкой функций Fs с различ-
различивши значениями индекса s. Суммируя по дискретным индексам jt,...
...,'./, и по s, запишем
Ф= S \F{rJ-)(..-k...)uji(k1)...ujs(ks)dk1...dksO0. (8)
Мы получили здесь фоковское представление амплитуды состояния.
Переходя к координатному представлению с помощью соотношений
■vA...x...)dx1...dxt,
, и@, х) = и (х) |„.о,
получаем вместо (8) следующее выражение для амплитуды состояния:
Ф= Ц J9,(*i **) П {«;v{0. JCv)d*v}<l>o- (9)
Входящие сюда функции <ps в нерелятивистском случае имеют
смысл обычных волновых функций в конфигурационном прост-
пространстве.
Как видно, временная зависимость из Ф выпала; это совер-
совершенно естественно, так как в выбранном нами представлении
амплитуда состояния при отсутствии взаимодействия оказывается
постоянной.
7.3. Типы перестановочных соотношений. Перейдем к установ-
установлению перестановочных соотношений между операторными волно-
волновыми функциями. В классической теории свободных полей с квад-
квадратичным лагранжианом при введении канонического формализма
полевые функции линейно выражаются через взаимно сопряжен-
сопряженные обобщенные координаты и импульсы. Классические скобки
Пуассона функций поля {«(*), и(у)} оказываются при этом неко-
некоторыми функциями от х и у (точнее, от разности х — у), не зави-
зависящими от и. Поэтому, исходя.из принципа соответствия, в кван-
квантовой теории свободных полей часто принимают, что закон пере-
перестановки операторных полевых функций имеет вид
{иа(х), иь.{у))-вв[иа(х), иь(</)] =
= «а (*) «6 (У) - «6 (У) «а (*) = Лаб (* - У)- (ЮБ)

62 ГЛ, П. КВАНТОВАНИЕ СВОБОДНЫХ ПОЛЕЙ
Это коммутационное соотношение однако оказывается слишком
жестким и не охватывает ряд физически важных случаев. Поэтому
в качестве альтернативы к A0Б) полагают, что
{иа(х), ub(y)}+ = ua(x)ub(y) + ub(y)ua(x) = Aab(x-y), A0Ф)
т. е. считают, что с-числом является не коммутатор, а антиком-
антикоммутатор двух полевых операторов.
Антикоммутативность полевых операторов., выражаемая пере-
перестановочным соотношением A0Ф) приводит к тому, что комму-
коммутаторы динамических величин, являющихся билинейными формами
полевых операторов, выражаются через перестановочные функ-
функции А. В этом смысле и следует понимать принцип соответствия
для второго случая.
Кванты полей, удовлетворяющих соотношениям A0Б), подчи-
подчиняются статистике Бозе —Эйнштейна, Соответствующие частицы
называются бозонами. Кванты полей, удовлетворяющих A0Ф),
подчиняются статистике Ферми —Дирака, а соответствующие
частицы называются фермионами.
Точный вид перестановочных функций А для любого поля
определяется уравнениями A), D) и структурой оператора энер-
энергии данного поля. Однако независимо от конкретного вида пере-
перестановочных соотношений можно показать, что перестановочная
функция свободных полей зависит лишь от разности х — у, т. е.
{иа(х), иь[у)\ = ЬаЬ{х-у). A1)
Для того чтобы установить это, рассмотрим коммутационные
соотношения A0) в импульсном представлении. Вследствие линей-
линейности формул фурье-преобразования коммутаторы или антиком-
антикоммутаторы частотных составляющих в импульсном представлении
и- (fc) также должны быть с-числами. Покажем прежде всего,
что операторы одинаковой частотности должны строго коммути-
коммутировать или антикоммутировать:
{«*(*). «?@} = О. A2)
Здесь, как и в A1), символ { } обозначает либо коммутатор,
либо антикоммутатор.
Рассмотрим амплитуду состояния Фр с определенным значе-
значением 4-импульса, удовлетворяющую уравнению C). Действуя на
нее операторами ui(k) и ut{q) в различной последовательности,
получаем новые амплитуды
которые, в соответствии с ранее установленным, удовлетворяют
уравнениям
ЛФ (

§ 7. ПЕРЕСТАНОВОЧНЫЕ СООТНОШЕНИЯ 63
Складывая и вычитая эти уравнения, находим
Если теперь допустить, что {«£, и\\ есть с-число, отличное
от нуля, то, сокращая на него, получим
т. е. придем к противоречию с исходным уравнением C). Тем
самым доказано A2). Точно таким же образом можно доказать, что
{«*(*), uf Щ = 0 при кФя. - A3)
Соотношения A2), A3) имеют простой физический смысл. Они
соответствуют тому, что акты рождения частиц любого поля не
интерферируют между собой, как не влияют друг на друга акты
уничтожения частиц, а также акты рождения и уничтожения
частиц с различными импульсами.
Если теперь положить, что в общем случае вместо нуля в пра-
правой части A3) стоит b{k — q), то в координатном представлении
мы получим соотношения A1). Отметим, что эта формула отра-
отражает трансляционную инвариантность перестановочных соотноше-
соотношений. Вполне естественно, что для ее доказательства были исполь-
использованы свойства оператора 4-вектора энергии-импульса, являю-
являющегося генератором преобразований сдвига.
Не составляет труда показать, что в случае комплексных
полей, помимо A2), всегда равны нулю также коммутаторы (анти-
(антикоммутаторы) операторов, относящихся к частицам разных заря-
зарядов, т. е.
{«+, «-} = {«+, «-} = 0. A4)
Для этого следует рассмотреть амплитуду состояния Ф? с опре-
определенным значением заряда и провести рассуждения, подобные
приведенным выше для доказательства A2). Мы предоставляем
это читателю.
Физический смысл соотношений A4) заключается во взаимной
независимости актов рождения и уничтожения частиц с различ-
различными зарядами.
Таким образом, установлено, что для любого (комплексного)
поля отличными от нуля могут быть лишь с-числа {««(/»),««(/»)}
и {««(/>),««(/>)}, т. е. (анти)коммутаторы операторов рождения
и уничтожения, относящихся к частицам с одинаковым 4-векто-
ром энергии-импульса и одинаковым зарядом Соответствующие
выражения в координатном представлении являются трансляци-
онно инвариантными:
{и±(х), и±{у)} = А±(х-у),

64 ГЛ. II. КВАНТОВАНИЕ СВОБОДНЫХ ПОЛЕЙ
а их сумма дает полную перестановочную функцию
Для определения перестановочных функций следует обратиться
к явному виду оператора 4-вектора энергии-импульса и исполь-
использовать уравнения A) и D).
7.4. Квантование по Ферми — Дираку и Бозе — Эйнштейну.
Для установления конкретного вида перестановочных соотноше-
соотношений воспользуемся теперь уравнениями A), B), причем оператор
энергии-импульса запишем в виде
*
^v = £ $ dq qv [at (q) aj (q) ± *aj (q) at (q)]. A5)
s
В соответствии с классическими выражениями C.9), C.28), D.26)
и E.21) мы выразили его через независимые амплитуды а—, а~,
*
связанные с и±, м- линейными соотношениями вида
причем коэффициенты v± являются с-числами. -
Ввиду некоммутируемости операторов а±, а- их порядок в A5)
соответствует порядку функций и и и в лагранжианах. Напом-
Напомним, что операторы а— и а- связаны условиями комплексного
(теперь эрмитового) сопряжения
Верхний знак перед вторым членом в правой части A5) отно-
относится к полям с целым спином (скалярное, векторное, электро-
электромагнитное), нижний — к полям с полуцелым спином (спинорное).
Для вывода перестановочных соотношений заметим прежде
всего, что коммутаторы операторов а± с билинейными комбина-
комбинациями a±(q)a:*:(q), входящими в правую часть A5), могут быть
представлены в виде
[a±(k), a>(q)cr(q)] =
= {а± (k), tf (q)} or (q) -а+ (q) {cr (q), a± (k)}. A6)
Здесь, как уже говорилось, символом {а, Ь] обозначен либо ком-
коммутатор, либо антикоммутатор операторов а и Ь, причем необхо-
необходимо пользоваться одним и тем же определением одновременно
в первом и во втором члене правой части.

§ 7. ПЕРЕСТАНОВОЧНЫЕ СООТНОШЕНИЯ 65
Аналогично этому
= {a±(k), a~(q)}a+(q)-Z-(q){a+(q), a±(k)}. A7)
На основании A2) и A4) имеем
[a+(k), a+(q)cr(q)] = [cr(k), *ar {q) a+{q)] = 0,
[cr (k), a+ (q) a- (q)] = {a~ (k), Z+ (q)} a~ (q), ;
[a+(*)> *cr(q)a+{q)]={a+{k), Zr{q)}a+{q).
Подставляя A5) в B), получаем теперь
(k) = \ dq<7V2] {aTa (k), at (q)} сГь (q),
b
+ k^a(k)-[dqq^ {at(k), a~b (q)}at(q),
ь
откуда следует
{a-a(k), *at(q)} = 8ab8(k-q), A8)
\at(k), a-b(q)} = + 8ab8(k-q), A9)
причем явно указанная неопределенность в знаке (±) следует
формуле A5). Таким образом, для поля каждого типа мы полу-
получили два варианта перестановочных соотношений. Требование
симметрии этих соотношений относительно замены заряда, точ-
точнее, замены частиц на античастицы
а± (k) ** с£ {К) ' B0)
однозначно определяет рецепт квантования в каждом случае. Сим-
Симметрия B0) • отражает тот факт, что выбор tмежду «основной»
функцией поля и и ее комплексно-сопряженной и есть вопрос
соглашения, и противоположный выбор w = u, w = u приводит
лишь к замене «основных» частиц на античастицы. Такая замена
сказывается на операторе заряда, который не инвариантен отно-
относительно B0), но не должна сказаться на уравнении движения A)
и выражении для 4-вектора энергии-импульса. Условия симметрии
относительно B0) также обеспечивают правильный переход от
комплексного к действительному полю: и {х) = и {х), а- (к) = а- (к).
Отметим, что преобразование вида B0) называется зарядовым
сопряжением, а соответствующая симметрия — зарядовой симмет-
симметрией (см. ниже § 9.3). Если теперь взять верхний знак в правой
части формулы A9) (что соответствует полям с целым спином),
то симметрия формул A8), A9) относительно преобразования B0)
3 Н. Н. Боголюбов, Д. В, Ширков

66 ГЛ. II. КВАНТОВАНИЕ СВОБОДНЫХ ПОЛЕЙ
приведет к тому, что символ {а, Ь\ должен пониматься как ком»
мутатор. В противном случае (нижний знак правой части фор-
формулы A9), спинорное поле) симметрия обеспечивается условием
{а, Ь} = {а,-Ь}+.
Таким образом, мы получили, что поля с целым спином кван-
квантуются по Б озе — Эйнштейну:
[a-a{k), а*Ш] = [£(*). at(q)] = 8ab8(k-q), B1)
а с полуцелым спином —по Ферми —Дираку:
К (*). at (?)}+ = {а-а (k), at (g)}+ = 8ab8 (k-q). B2)
Заметим здесь, что перестановочные соотношения фиксируют нор-
нормировку операторных полевых функций.
7.5. Связь спина со статистикой. Теорема Паули. Полученные
результаты представляют собой частный случай фундаментальной
теоремы Паули, устанавливающей связь трансформационных
свойств поля и способа его квантования (связь спина со стати-
статистикой):
Поля, описывающие частицы с целым спином, квантуются
по Бозе —Эйнштейну; поля, описывающие частицы с полу-
полуцелым спином, квантуются по Ферми—Дираку.
Теорема Паули применима к полям с произвольным (сколь
угодно высоким) спином.
В нашем доказательстве мы использовали симметрию относи-
относительно зарядового сопряжения. Однако возможны и другие пути
рассуждений. Нарушение связи спина со статистикой, устанав-
устанавливаемой теоремой Паули, приводит к ряду глубоких противо-
противоречий.
Так, если вместо B0) использовать свойство положительности
метрики в гильбертовом пространстве
то можно прийти к формулам A8), A9) только лишь из условия
A7) (см. задание 08).
В то же время квантование поля с целым спином по Ферми —
Дираку приводит к противоречию со свойствами коммутаторов
в пространстве-времени (см. задание 09).
Хорошо известная апелляция к отрицательному знаку второго
члена в операторном выражении для энергии спинорного поля
E.22) приводит к невозможности квантования этого поля по Бо-
Бозе—Эйнштейну.

§ 8. ПОЛЯ С ЦЕЛЫМ СПИНОМ 67
§ 8. Поля с целым спином -
8.1. Скалярное поле. В этом параграфе мы изложим кванто-
квантовую теорию скалярного, векторного и электромагнитного полей.
В соответствии с результатами § 7.4 коммутационные соотно-
соотношения для скалярного поля в импульсном представлении имеют
вид:
а) для действительного поля
[«Г(А), Ф+ (?)] = «<£-Я), [9=4*), Ф*@] = О; A)
б) для комплексного поля
tf ¥ b{k-q) B)
(все остальные коммутаторы равны нулю).
Переходя к координатному представлению, получаем в правых
частях вместо дельта-функций
— частотные части так называемой перестановочной функции
Паули — Йордана
D{x) = D+ (х) + D- (х) = j Bя)1 g-»*e (k°) б (^2 -m*)dk. C)
Ограничиваясь действительным полем, запишем коммутационные
соотношения для функций поля в координатном представлении:
[qr(x)t <p+(y)] = -iD-(x-y),
[Ф+ (л;), Ф- (у)] = - ^ (х-у), D)
(л;), Ф (</)] = — Ю{х-у).
Явный вид функций D± и D приведен в Дополнении'V.
Отметим здесь важное свойство функции D(x). Она равна
нулю вне светового конуса —см. ниже A8.17). Поэтому
= 0 при (х-у)*<0. E)
Это свойство называется свойством локальной коммутативности
и отражает причинную независимость событий, разделенных про-
странственноподобными интервалами.
Прежде чем записать лагранжиан и динамические переменные
для квантового случая, дадим некоторые полезные определения.
•8.2. Запись динамических переменных через нормальные про-
произведения. Введем понятие оператора, записанного в но( мальной
форме, и понятие нормального произведения операторов.
3*

68 ГЛ. II КВАНТОВАНИЕ СВОБОДНЫХ ПОЛЕЙ
Нормальной формой оператора называется такая форма, в каж-
каждом слагаемом которой все операторы рождения ы+ стоят слева
от всех операторов уничтожения и~.
Нетрудно видеть, что нормальная форма операторов является
наиболее удобной с точки зрения вычислений. Действительно,
при вычислении матричного элемента ФЛФ какого-либо опера-
оператора Л в нормальной форме необходимо лишь коммутировать
входящие в Л операторы иг со всеми а+ из амплитуды состоя-
состояния Ф и ы+ из Л со всеми <г из Фдо тех пор, пока один из и-
не подействует на Фо или один из м+ —на Фо, что даст нуль.
Рассмотрим пример: запишем в нормальной форме произведе-
произведение двух бозе-операторов и (х) и и (у). Имеем последовательно
и (х) и (у) = ы+ (*) ы+ (у) + ы+ (*) и-(у) + и- (х) ы+ (у) + и- (х) и- (у) =
= ы+ (х) ы+ (//)+«+ (х) и-(у) + ы+ (у) и- (х) + иг (х)и- (у) - /А- (х-у).
Очевидно, что в более общем случае, приводя к нормальной
форме, произведение некоторого количества операторных полевых
функций и, мы получим сумму произведений компонент ы+, и~
и перестановочных А~-функций. Общий рецепт такого приведения
рассмотрен нами ниже (§ 17) и составляет содержание первой
теоремы Вика. Все выражение в целом можно условно считать
«полиномом» по степеням Д--функций. Нулевой член этого поли-
полинома, т. е. сумма членов, вообще не содержащих А~-функций,
называется нормальным произведением исходных операторных по-
полевых функций. Нормальнее произведение можно также опреде-
определить как произведение, приведенное к нормальной форме, причем
в процессе приведения все перестановочные функции считаются
равными нулю.
Нормальное произведение операторов ult u2, ..., и„ обозна-
обозначается символом :и^щ.,. и„:. Результат последней выкладки можно
записать в виде
и (х) и (у) = :и {х) и (у):- i'A- {х-у).
Условимся теперь все динамические переменные, квадратично
зависящие от операторов с одинаковыми аргументами (такие, как
лагранжиан, энергия-импульс, ток и т. д.), записывать по опре-
определению в форме нормального произведения. Например, лагран-
лагранжиан комплексного скалярного поля будем писать в виде
Нетрудно видеть, что отсюда в силу определения амплитуды
вакуума Фо

§ 8. ПОЛЯ С ЦЕЛЫМ СПИНОМ 69
и ему сопряженного соотношения
фоф+ (х) = фо|+(х) = О
следует равенство нулю вакуумных средних всех динамических
величин. Тем самым мы автоматически исключаем все псевдофи-
псевдофизические величины типа энергии вакуума, заряда вакуума и т. д.
Очевидно также, что все законы сохранения, установленные
в классической теории, остаются верными и для квантовых выра-
выражений, записанных в нормальной форме, поскольку использован-
использованные в доказательстве теоремы Нётер алгебраические тождества
не нарушаются.
Основные динамические величины комплексного скалярного
поля запишем теперь в виде
7V* = : («Р: цФ; v + Ф; уф; ц): - fii*#. G)
/" = $dftft4qHft)qr(ft) + q>+(ft)$r(ft')]f (8)
Q =-J dft [ф* (ft) qr'(ft)+ ф+(ft) $-(*)]. (9)
Из структуры операторов Pv, Q вытекает, что $*(ft) есть опера-
оператор рождения частицы с энергией-импульсом k и зарядом +1,
ф- (ft) — оператор уничтожения той же частицы; ф+(ft) — оператор
рождения частицы с энергией-импульсом k и зарядом—l;qr(ft)—
оператор уничтожения той же частицы.
Заметим, что рассуждениями § 7, установившими смысл ча-
частотных частей функции поля ф+ и ф~, не была определена их
нормировка. Эта нормировка может теперь быть установлена с по-
помощью, выражения (8) для 4-вектора энергии-импульса. Вводя
в рассмотрение амплитуду состояния, содержащего одну скаляр-
скалярную частицу с ненормированной функцией распределения по им-
импульсам с (ft)
] A0)
вычислим среднее значение оператора Pv (8) по этому состоянию.
Выполняя коммутации операторов, получаем
<pv>x = ф^ауф^ = j с (ft) с (ft) W dkl\ | с (ft) |2 dk.
Переход к состоянию с фиксированным значением 4-импульса
может быть выполнен путем локализации функции с (ft) в малой
окрестности значения k = K (например, предельным переходом
c(ft)->-6 (ft — К)). При этом №-*•!(", и мы получаем
Таким образом, среднее значение оператора Pv по состоянию
с фиксированным значением 4-импульса Xv в точности равно Kv,

70 ГЛ. И. КВАНТОВАНИЕ СВОБОДНЫХ ПОЛЕЙ
и, следовательно, нормировка операторов ф— (Аг), <р- (k), установ-
установленная коммутационными соотношениями A), B), соответствует
нормировке выражений типа (8), (9) для динамических величин.
8.3. Комплексное векторное поле. Для установления правил
квантования 4-потенцйала векторного поля заметим, что механи-
механическое обобщение на этот случай правил квантования скалярного
поля, т. е. независимое квантование каждой компоненты потен-
потенциала Vv по образцу скалярного поля, оказывается невозможным,
поскольку такая процедура не обеспечивает положительности
среднего значения энергии и оказывается несовместной с допол-
дополнительным условием C.13). Схема квантования поэтому должна
быть связана с дополнительным условием, которое, как мы убе-
убедились в § 3, автоматически обеспечивает положительность Р°.
Там было, в частности, показано, что в результате перехода от
Uv к продольным и поперечным составляющим по формулам
C.24), C.27) 4-вектор энергии-импульса может быть выражен
через три линейно независимые амплитуды ba (k) следующим об-
образом:
\ C.28)
При такой записи классического, 4-импульса учтено дополни-
дополнительное условие C.13) и обеспечена положительность некванто-
ванного Р°. Ясно .также, что непосредственное квантование по
Бозе—Эйнштейну трех независимых амплитуд Ьа (а=1, 2, 3)
приводит к положительной определенности среднего значения опе-
оператора энергии.
Ввиду этого операторы Ьа мы подчиним следующим переста-
перестановочным соотношениям:
[Ьа {к), bt(g)]. = [ba(k), bt(g)] = 8ab8(k-q) A1)
(все остальные коммутаторы равны нулю).
Аналогичные коммутационные соотношения имеют место для
+ *+
операторов car, ссь-
Выражения для заряда и третьей проекции спина соответст-
соответственно формулам C.29), C.30) будут
A2)
А53 -~ [k (*) Ьт (k) - k (*) b* (k) - bt(k) k Ф) + bt (k) h {Щ. A3)
*
Вычисляя затем соответствующие средние, убеждаемся, что b\(k)
и Ьг (k) суть соответственно операторы рождения и уничтожения
частицы с импульсом k, зарядом +1 и проекцией спина на ось
движения +1; b$(k), b^ (k) — операторы рождения и уничтожения
частицы с импульсом к, зарядом +1 и проекцией спина, —1;

§ 8. ПОЛЯ С ЦЕЛЫМ СПИНОМ 71
bt (k) и Ьз (k) — операторы для частицы с импульсом k, зарядом
+1 и нулевой проекцией спина. Смысл операторов Ь% и Ъ~а можно
получить отсюда, применяя следующее правило:
переход от bj к Ь^ соответствует изменению знака заряда
и знака проекции спина.
Мы видим теперь, что комплексное векторное поле описывает
заряженные частицы с массой т и тремя возможными значениями
проекции спина A, 0, —1) на заданную ось. Говоря иначе,
кванты этого поля являются заряженными мезонами со спином 1
(их называют также векторными мезонами).
Амплитуды ас также имеют простой смысл. Так, амплитуды а3
соответствуют частицам с нулевой проекцией спина на направле-
направление движения, a aj и а2 описывают смеси состояний с проек-
проекциями спина 1 и —1, соответствующие линейным поляризациям.
Выпишем еще перестановочные соотношения для четырех за-
зависимых амплитуд Uv. С помощью C.24) без труда находим пере-
перестановки трех амплитуд Un (n=l, 2, 3):
[Un(k), U
Используя связь k0U0-\-knUn = 0, определяем затем коммутаторы,
содержащие Uo:
Объединяя эти выражения, получаем формулу
которая является релятивистски симметричной и совместной с до-
дополнительными условиями C.22). Переходя к координатному
представлению, находим
[U-V(x), U
Не представляет труда проверить, что полученные перестано-
перестановочные соотношения являются совместными как с уравнениями
поля, так и с дополнительными условиями. Так, действуя на обе
стороны A5) оператором Клейна — Гордона Q* — т2, приходим
к тождеству 0 = 0, так как в соответствии с C)

72 ГЛ. П. КВАНТОВАНИЕ СВОБОДНЫХ ПОЛЕЙ
8.4. Электромагнитное поле — трудности квантования. При
квантовании электромагнитного поля необходимо одновременно
удовлетворить требованиям положительности плотности энергии,
дополнительному условию Лоренца и условию поперечности. Вся
формулировка должна при этом обладать свойством релятивист-
релятивистской ковариантности.
Сходное положение мы имели при квантовании векторного
мезонного поля. Отличие состоит в том, что векторные мезоны
могут находиться в трех спиновых состояниях, а фотоны из-за
поперечности — лишь в двух, так как, в противоположность мезо-
мезонам, масса покоя фотонов равна нулю. Первое обстоятельство
приводит к тому, что компоненты потенциала электромагнитного
поля в еще большей степени, нежели у векторного поля, содер-
содержат в себе «лишние» переменные, ибо имеются четыре компоненты,
а состояний, в которых могут находиться реальные фотоны,
только два.
Второе отличие (/п = 0) делает невозможным применение
к электромагнитному полю процедуры, использованной при кван-
квантовании векторного поля. Действительно, уже квантование гипо-
гипотетического векторного поля с исчезающе малой массой, т. е.
поля, отличающегося от электромагнитного поля отсутствием
градиентного преобразования и потому трехкомпонентного, вызы-
вызывает значительные затруднения. При подобном квантовании мы
получаем бессмысленные выражения, во-первых, при диагонали-
зации энергии-импульса подстановкой C.24), а во-вторых, при
установлении перестановочных соотношений для компонент потен-
потенциала Av A4), A5) из-за присутствия исчезающе малой массы
в знаменателях указанных выражений.
Поэтому квантование электромагнитного поля проводится сле-
следующим образом. Компоненты векторного потенциала считаем не-
независимыми величинами, отказавшись тем самым от условия
Лоренца в операторной форме. Тогда по общему рецепту кван-
квантования, исходя из структуры 4-вектора энергии-импульса, вы-
выраженного через продольную, поперечные и временную компо-
компоненты Oft (к)
\ A6)
приходим к перестановочным соотношениям
№(k), <(<?)] = -£v^ (k -q). A7)
Квантование A7) позволяет рассматривать операторы а~ как
операторы рождения и уничтожения четырех независимых сортов
фотонов: двух поперечных, «продольных» и «временных». Однако
при таком квантовании возникает следующая трудность. Компо-
Компонента а0 удовлетворяет соотношению
[а; (к),

§ 8. ПОЛЯ С ЦЕЛЫМ СПИНОМ 73
сравнивая которое с G.19), видим, что операторы рождения и
уничтожения «временных» фотонов как бы поменялись местами,
что обязано отрицательному знаку члена ata^ в выражении A6).
Такое коммутационное соотношение несовместимо с предполо-
предположением о положительной определенности метрики в гильбертовом
пространстве состояний (см. задание 012).
. Указанная трудность может быть ликвидирована формальным
приемом (метод Гупта —Блейлера), основанном на том обстоя-
обстоятельстве, что эта трудность целиком обусловлена «временными»
фотонами, которые в действительности не "существуют, а их воз-
возникновение в промежуточных рассуждениях связано с переходом
от наблюдаемых величин (векторов Е и Н) к ненаблюдаемому
4-потенциалу Av, произведенным для придания теории реляти-
релятивистской симметрии и ковариантности.
8.5. Электромагнитное поле — квантование по Гупта — Блей-
леру. Отсылая читателя за подробностями к специальной лите-
литературе (Введение, § 12.2; Ахиезер, Берестецкий A969), § 5.2),
приведем сейчас лишь основную идею метода Гупта —Блейлера
и окончательные формулы.
Центральную роль здесь играет условие Лоренца. При кван-
квантовании A7) подразумевалось, что компоненты потенциала Av не-
независимы, поэтому накладывать условие Лоренца как условие на
операторы нельзя. Легко убедиться, что наложить условие Ло-
Лоренца на допустимые состояния
также невозможно, ибо такое условие противоречит, например,
определению вакуума. В самом деле, полагая Ф = Ф0, имеем
дА (х) Фо = дА+ (х) Фо = 0.
Умножая слева на Л^(у),"получаем
= щ[А1 (х) Av (у)- ig^Dt (х-у)]Ф0 = ~ tdvDt(х-у)Ф0^0.
Здесь Do — перестановочная функция частотных компонент элек-
электромагнитного поля, т. е. положительно-частотная часть переста-
перестановочной функции Do, введенной ниже в B2).
Поэтому квантовое условие Лоренца сформулируем как усло-
условие на допустимые состояния:
дА-(х)Ф = ?^М-Ф = 0, Ф(дЛ+)=О. A8)

74 ГЛ. II, КВАНТОВАНИЕ СВОБОДНЫХ ПОЛЕЙ
Ослабленное условие A8) обеспечивает выполнение условия Ло-
Лоренца для средних значений
что вполне достаточно для соответствия с классическим полем.
Как отмечалось в § 4, скалярная функция % (х) = дА(х) в рас-
рассматриваемой здесь диагональной калибровке удовлетворяет сво-
свободному уравнению D.15) даже при наличии взаимодействия
с источниками. Поэтому ослабленное условие Лоренца A8) со-
сохраняет свою форму и при включении взаимодействия квантового
электромагнитного поля с сохраняющимся током заряженных
частиц»
Переходя к импульсному представлению, в переменных ло-
локального репера и с учетом того, что ko = \k\, получаем вместо A8)
:*)=o, (i9)
где
Отсюда следует, что в допустимые состояния комбинация
а£аз — аоао вклада не дает:
*
(<4а» — Доао) = Ф (аз — <Ч) °з Ф = 0,
вследствие чего суммарный вклад в энергию и импульс допусти-
допустимых состояний от продольных и временных псевдофотонов равен
нулю.
Нетрудно убедиться, что совместные с условиями A8), A9)
допустимые состояния имеют следующую структуру:
где Ф?г, Ф"г — амплитуды реальных фотонных состояний, не со-
содержащие псевдофотонов.
Покажем теперь, что в разложении по локальному реперу
D.23) оказываются существенными лишь поперечные составляющие
At (k) = el (к) а, (к) + el (к) а2 (к).
Представим правую часть D.23) в виде
А7 (к) = А*< ~ (к) + (-щ- Svo) сц (*)Ч- Svoao (*) =
= А *' ~ (к)+НЛ (к) + 8VOF~ (к).
Здесь член ^vA = ^va5'(ft)/|A-| имеет структуру 4-градиента и может
быть исключен градиентным преобразованием, a Z7- (А?) ф == 0

S 9. СПИНОРНЫЕ ПОЛЯ
согласно A-9). Поэтому
и, следовательно,
Можно показать, что справедливо более общее утверждение
ФК (А) Ф = ФК (Air) Ф = Ф?Д (Аи) Ф?г, B1)
где К(А) — оператор, полиномиально зависящий от А, а Ф?г вве-
введено в B0).
Итак, согласно B1), среднее по допустимым состояниям от
произвольного потенциала А равно среднему от поперечного по-
потенциала Atr по реальным физическим состояниям.
Отметим еще, что последовательное проведение этой программы
требует введения индефинитной метрики в той части гильбертова
подпространства допустимых состояний, которая содержит вре-
временные псевдофотоны. Мы не имеем возможности останавливаться
на этом более подробно.
Приведем в заключение сводку формул для квантованного
электромагнитного поля в лоренцевой калибровке:
коммутатор полевых функций
[Ау(х), AVL{y)] = igvv.D<){x-y), B2)
причем
Do (х) = D (x) !m_0 = -1 Bя)-з J e">*8 @) г (*•) dk; B3)
уравнения поля
П^ = 0; B4)
условие Лоренца на допустимые состояния
-О; B5)
среднее значение 4-импульса по допустимым состояниям
У. (Й(*)о5(*)\. B6)
<J=1, 2 /
§ 9. Спинорные поля
9.1. Квантование поля Дирака. Из структуры 4-вектора энер-
энергии-импульса спинорного поля
Pv = \dkkv[at(k)a7(k)-a7(k)at(k)] E.21)
видно, что квантованию могут быть подвергнуты независимые
амплитуды as (s=l, 2).

76 ТЛ. II. КВАНТОВАНИЕ СВОБОДНЫХ ПОЛЕЙ
Как уже указывалось, ■ требование положительности среднего
значения оператора энергии Р° приводит к тому, что спинорное
поле должно быть проквантовано по Ферми —Дираку. Поэтому
фурье-амплитуды спинорного поля a?(k) следует считать опера-
операторами, удовлетворяющими перестановочным соотношениям
Ферми—Дирака:
[aj(k), at(q)]+ = [aj(k), %(Q)h = &sMk-q) A)
(все остальные антикоммутаторы равны нулю).
Перестановочные соотношения для операторов т|з (х) получим
отсюда с помощью следующих из E.9), E.13) и E.14) формул
фурье-преобразований
Ч>± (х) = Bл)-3/2 $ dk e± ""a* (k) v*< ± (k), B)
\{k)v*' ±(k) C)
и формул суммирования по спиновому индексу E.20).
Имеем
1 r>
Аналогично этому можно показать, что
Вводя обозначения
Si» (■«)'= (id+ m)afi D- (x), 5 = 5++ S;
получаем
№(*). jP(y)] = 7-S(x-y), D)
где
S(*) = (id+m)D(*) =B^j J ^**e'(A»-m«)e(A°;(^ + /n)rf*. E)
Перестановочные соотношения совместны с уравнениями поля,
так как
(id - т) S: (х) = (□ - m2) D D = 0.
Записывая лагранжиан с помощью нормального произведения:
(х)]:-т:Щ:,'- F)

S 9. СПИНОРНЫЕ ПОЛЯ 77
получаем тензор энергии-импульса
тензор плотности спина
1 1
и вектор тока _
р (х) = :тр (х) yvt|) (x):. (9)
В результате перехода к импульсному представлению по фор-
формулам B), C) соответствующие интегралы движения, согласно
E.21) и E.27), E.28), примут вид:
4-вектор энергии-импульса
a+ (A?) Ss" (A?)], A0)
заряд'
Q = \dk[at(k)aj(k)-at(k)a7(k)], A1)
проекция спина на направление движения
4 A2)
Из выражений A0) —A2) вытекает, что операторы of (ft) и
us (ft) суть соответственно операторы рождения и уничтожения
частиц с импульсом ft, энергией kQ = Y ft2 + /> зарядом +1 и
проекцией спина на направление к, равной г/г (s=l) или —х/г
(s = 2). Операторы at(k) и а7 (ft) соответствуют частицам, отли-
отличающимся от только что описанных знаком заряда (—1) и зна-
знаком проекции спина (т. е. 7г (s = 2) и —Va (s=l))-
9.2. Спинорное поле с массой нуль. Особый интерес представ-
представляет спинорное поле с массой нуль, соответствующее нейтрино.
Полагая в уравнении Дирака /га = 0, имеем
Это уравнение распадается на два независимых двухкомпонент-
ных уравнения. Для того чтобы показать это, воспользуемся тем,
что в отсутствие массового члена оператор уравнен и я_ Дирака
антикоммутирует с матрицей у5-
Вводя проекционные операторы
р ...! * V»
— — 2 '
получаем
5

78 ГЛ. И. КВАНТОВАНИЕ СВОБОДНЫХ ПОЛЕЙ
т. е. два отдельных уравнения для т|з± = Р±т|з
Щ+ = 0, /£ф_-0. ■ A3)
В стандартном представлении
3
Таким образом, каждая из функций т|з+, т|з_ содержит лишь по две
независимые компоненты и в «расщепленном» виде
может быть выражена через двухкомпонентные спиноры
Используя «расщепленную» запись (ДП.7) для матриц Дирака,
получим вместо A3)
Уравнения такого вида впервые были предложены Вейлем.
Для того чтобы уяснить физический смысл двухкомпонентных
функций фа[« = (+)> (—)]> перейдем к импульсному представ-
представлению: ■ ■ ■ . .
Уравнения Вейля принимают вид
р) = 0. A5)
Как было установлено в § 5.3 (см. E.24)), матричный век-
вектор, а описывает спин фермиона. Из уравнений A5) следует
(см. также задание 016), что спин нейтрино может быть направ-
направлен либо по направлению спина, либо наоборот. Поэтому каж-
каждая из 4-компонентных импульсных амплитуд ty± содержит лишь
одно спиновое состояние.
Значение проекции спина фермиона на направление ее
импульса (ар)/\р\ называют спиральностью. Экспериментально
установлено, что у нейтрино спин направлен антипараллельно
импульсу, т. е. спиральность нейтрино равна —1/2 (что справед-
справедливо как для электронного, так и для мюонного нейтрино). Как
будет показано ниже, функция i|x. описывает частицы с отрица-
отрицательной спиральностью, a i|?+ —с положительной.

§ 9. СПИНОРНЫЕ ПОЛЯ 79
Поэтому оператор поля для нейтрино определим следующим
образом:
v(x) = P.ty(x).
Он удовлетворяет безмассовому уравнению Дирака
idv(x) = 0
и дополнительному условию
P+vW = i±l6v(x) = 0. A6)
*
Соответствующая сопряженная функция v = vy° удовлетворяет
сопряженному уравнению
id»? (x) у^ = 0
и дополнительному условию
Лагранжиан квантованного свободного нейтринного поля записы-
записывается в виде
^ A7)
Выражения для тензора энергии-импульса и тензора плотности
спина в координатном представлении получаются из формул G),
(8) подстановкой \{х) вместо ty(x). В импульсном представлении
формула для Р* получается из A0) опусканием суммирования по
спиновому индексу:
ру. = \dpp» [а+.(/>) а- (р) + а+ {р) *а- {р)]. A8)
Отдельно рассмотрим спин нейтринного поля. Для этого будем
исходить из выражения вида E.25) для плотности вектора спина
(Vt): {«+ (Р) а- (р) у+ (р) osir (р) + а~ (р) а+ (р) v~ (p) а3ь+ (р)}:, A9)
справедливого в системе отсчета рх = р2 = 0, т. е. когда ось х3
направлена по импульсу. В этой системе нормированные спиноры,
удовлетворяющие уравнениям
и дополнительным условиям
A +v5) о± (р) = h (р) A + Y5) = 0,
могут быть выбраны в виде (имеется в виду стандартное пред-
представление матриц Дирака)

80 ГЛ. II. КВАНТОВАНИЕ СВОБОДНЫХ ПОЛЕЯ
здесь w (р) — двухкомпонентные спиноры, удовлетворяющие урав-
уравнению Вейля A5)
( Q
имеют вид
W
<*>-(!)•
Выше мы учли, что для безмассового нейтрино Ро — Рз- Очевидно
также, что
»(/>) = @, 1),
поэтому
Подставляя этот результат в A9), находим
AS3 у **:(/») <г (/>)+у **•(/>)«-(/»)■
Первый член этого выражения соответствует левовинтовому нейт-
нейтрино с отрицательной спиральностью, а второй — правовинтовому
антинейтрино. Спиральность антинейтрино равна -f 1-.
Выражение B0) соответствует формуле A2) при аг = 0, аъ = а.
Если бы вместо функции v = i|>_ мы рассмотрели функцию т|з+, то
получили бы аналог формулы A2) при я2 = 0, описывающий
частицы с положительной спиральностью и античастицы с отри-
отрицательной спиральностью.
Отметим, что при рассмотрении процессов слабых взаимодей-
взаимодействий, в которых участвуют левовинтовые нейтрино, иногда
используют следующее представление матриц Дирака (л = 1, 2, 3):
/ГоГЛГз. . B1)
Мы использовали здесь расщепленную запись через 2x2 матрицы /,
О и матрицы Паули (см. Дополнение II).
В этом представлении проекционные операторы Р+ диаго-
нальны, вследствие чего спинор с отрицательной спиральностью
имеет более простой вид
Представление B1) уместно назвать спиральным представлением
матриц Дирака. Со стандартным представлением (ДП.5), (ДП.7)

§ 9. СПИНОРНЫЕ ПОЛЯ 8'
оно связано преобразованием
г-о-то, o-^(J
9.3. Зарядовое сопряжение. Как нетрудно убедиться из фор-
формул § 2, для комплексных полей с целым спином, описывающих
заряженные частицы; преобразование
■фа(*)-*-<Й(*) = Фа(*).' 22
к новым функциям поля ф', ф' сохраняет выражения для всех
динамических величин, кроме тока и заряда, неизменными, а у Jv
и Q Меняет знак. Поэтому такое преобразование называют пре-
преобразованием сопряжения заряда или зарядовым сопряжением.
Зарядовое сопряжение спинорного поля сложнее преобразова-
преобразования B2) из-за матричного характера (многокомпонентности) спи-
норных волновых функций; это есть матричное преобразование
следующего вида:
(C-h№, B3)
для совместности которого нужно потребовать, чтобы
-GvoCVo = l. B4)
Преобразование, обратное B3), есть соответственно
Ч> (х) = GP' (х)\ \р = г^-1 = (С-Ч')т-
Мы видим, таким образом, что определенное по B3) зарядовое
сопряжение, кроме очевидного свойства тождественности двукрат-
двукратного преобразования, обладает еще свойством зеркальной сим-
симметрии, т. е. совпадает по форме с обратным.
Конкретный вид матриц С определим, потребовав, чтобы
лагранжиан свободного поля, а следовательно, и 4-вектор энер-
энергии-импульса не меняли-своего вида, а 4-вектор тока менял бы
знак, т. е. чтобы имели место соотношения
Для этого оказывается достаточным (см. задание 017) потребо-
потребовать, чтобы выполнялись два соотношения
vi|>i(*).: B5)
*К. B6)
причем % и т|з2 равны либо самой т|з, либо ее производным
и преобразуются по формулам B3).

82 гл> п. КВАНТОВАНИЕ СВОБОДНЫХ ПОЛЕЙ
Итак, рассмотрим ограничения, налагаемые на матрицу С
условиями B5) и B6). Подставляя B3) в B5), имеем
% (х) ГЖ (х): = ф (х) Cr
Учитывая антикоммутативность квантованных спиноров if' и гр',
получаем отсюда соотношение
■ . ■ т т
сравнивая которое с B5), находим первое условие, налагаемое
на матрицу С: -
или, в транспонированной форме,
C-V^Vv B7)
Аналогичным образом, подставляя B3) в B6), имеем
:Щ: = г^'С-Кир': = — :^'СС" Y:,
т
откуда находим второе условие для матрицы С: СС-1 = — 1, т. е.
С = —С. ■- B8)
Используя B8), можно записать B7) в виде
C"VC = — vv- B9)
Как нетрудно показать (см. задание 017), из формул B8), B9)
и B4) вытекает унитарность матрицы зарядового «сопряжения
СС=1. . C0)
Формулы B9) и C0) позволяют определить явный вид матрицы
С в люб®м фиксированном представлении матриц Дирака. Мы
предлагаем читателю убедиться самостоятельно, что, как в стан-
стандартном представлении (ДП.5), так и в спиральном представле-
представлении B1) матрица С равна произведению «нулевой» и «второй»
матриц Дирака, т. е.
Отметим, что в общем случае при переходе от одного пред-
представления матриц Дирака у к какому-либо иному у

$ 9. СПИНОРНЫЕ ПОЛЯ 83
новую матрицу зарядового сопряжения С получим по формуле
С = ОСО,
т
где О матрица, транспонированная по отношению к О.
Физический смысл операции зарядового сопряжения С заклю-
заключается в замене частицы на античастицу. Поэтому, например,
инвариантность относительно операции С (имеющая место для
сильных и электромагнитных взаимодействий) приводит к тому,
что если осуществляется некоторый процесс П (представляющий
собой произвольную комбинацию сильных и электромагнитных
взаимодействий), то возможен и происходит с той же вероят-
вероятностью процесс СП, отличающийся от П заменой всех частиц на
античастицы.
9.4. СЯГ-теорема. Заключая рассмотрение квантованных сво-
свободных полей, упомянем одно из важнейших утверждений локаль-
локальной квантовой теории поля — так называемую СРГ-теорему, фор-
формулирующую свойство инвариантности относительно трех дискрет-
дискретных преобразований:
— зарядового сопряжения С,
— пространственного отражения Р,
— обращения оси времени Т.
Кроме операции С, рассмотренной на предыдущих страницах,
мы сталкивались ранее с операцией Р отражения всех трех
пространственных осей координат (см. § 1 и Дополнение II).
Третья операция — обращение (или отражение) оси времени —
имеет вид
X —>■ XJ, Хо = — Xq , X === X*
В отличие от непрерывных преобразований, входящих в группу
Пуанкаре, операции Р и Т не отвечают каким-либо реальным
движениям физической системы. Они, однако, подобно операции С,
связывают друг с другом различные физические процессы.
Мы вернемся к этому вопросу в конце раздела, а пока рас-
рассмотрим эти преобразования формально. Возьмем простой пример
комплексного скалярного поля, описываемого операторами
Ф (х) == ф+ (*) + ф- (*), ф (*) = ф+ (*)
Операции Р и Т меняют знак аргумента в координатном пред-
представлении. Например,
РГФ± (х) = РГФ± (х0, х) = РФ± (- х0, х) = Ф* (-*„. - х) = Ф± (-Х),
тогда как операция С меняет частицы на античастицы:

84 ГЛ. П. КВАНТОВАНИЕ СВОБОДНЫХ ПОЛЕЙ
Поэтому
СР7\р±(л:)=Ф±(— х), СРГф±(д;) = ф±(— х).
Подобно тому как преобразованиям группы Лоренца L ставятся
в соответствие унитарные операторы UL, преобразующие опера-
операторы полей и векторы состояний (см., например, F.25)), преоб-
преобразованиям С, Р, Т в квантовом случае также сопоставляются
операторы Uq, Up, Ut- Например, для комплексного» скалярного
поля
<Рс(х) = ис1<р(х)ис = у(х),
<pp(x) = Upl<p(x)Up = q>(x0, -х)
и т. д. ■
- СРГ-теорема утверждает*), что локальный лагранжиан системы
квантовых полей, построенный по «нормальным правилам», ока-
оказывается инвариантным:
x') UTUpUc = &(х), х' = -х
относительно одновременного применения всех трех операций.
«Нормальные правила» включают правила квантования полей
в соответствии с теоремой Паули и выбор констант связи в соот-
соответствии с условием эрмитовости лагранжиана.
Обсудим теперь физические следствия СРГ-теоремы.
Операция С заменяет частицы на античастицы. Операция Р
меняет направления в 3-мерном пространстве, т. е. изменяет все
3-векторы (импульсы, компоненты электрического поля и т. п.)
на обратные. Операция Т меняет начальные состояния на конеч-
конечные и наоборот; изменяются также направления импульсов и
спинов. Поэтому из СРТ-теоремы вытекает равенство квадратов
матричных элементов процесса П и СРТП, причём процесс СРТП
получается из П заменой всех частиц на античастицы, всех спи-
спинов на обратные и перестановкой начальных и конечных состоя-
состояний. В частности, из СРГ-теоремы следуют равенства масс и
времен жизни, а также отличие лишь в знаке магнитных момен-
моментов частиц и античастиц.
*) Более точную формулировку в терминах современной аксиоматической
теории поля читатель может найти в книге Боголюбова, Логунова, Тодорова
A969), гл. 5.

Г л а в а III. ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛЯ
§ 10. Взаимодействие полей
10.1. Взаимодействие частиц. Важнейшей физической чертой
микрочастиц является их способность к взаимодействию и взаимо-
взаимопревращению. По современным представлениям все многообразие
различных видов и форм взаимодействия материи сводится
к четырем типам элементарных (или фундаментальных) взаимо-
взаимодействий между частицами:
1) гравитация,
2) электромагнетизм,
3) слабые взаимодействия,
4) сильные взаимодействия.
Гравитационное взаимодействие является универсальным. Оно
присуще всем видам материи, всем микрочастицам.
В электромагнитных взаимодействиях непосредственно участ-
участвуют электрически заряженные -частицы.
Как гравитационное, так и электромагнитное взаимодействия
являются дальнодействующими. Их интенсивность слабо убывает
на больших расстояниях (i~^r-1), вследствие чего именно эти
взаимодействия играют определяющую роль в макрофизике.
В то же время, как уже отмечалось в § 1, в микромире гра-
гравитационное взаимодействие гораздо слабее электромагнитного.
Ввиду этого мы его учитывать не будем.
Рассмотрим сначала электромагнитные взаимодействия. Хорошо
известно, что кулоновское взаимодействие двух заряженных
частиц, представляющее собой действие на расстоянии (action in
distans), есть результат взаимодействия каждой из частиц с элек-
электромагнитным полем. В результате квантования последнее описы-
описывается своими квантами— фотонами, а элементарный акт взаимо-
взаимодействия заряженной частицы Q с электромагнитным полем
выступает как акт испускания или поглощения этой частицей
у-кванта:
QQ + или Q + y-t-Q. A)

86 ГЛ. III. ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛЯ
Совокупность таких двух взаимно обратных процессов усло-
условимся обозначать двойной стрелкой или картинкой-диаграммой
B)
На последней сплошные линии соответствуют заряженной частице
Q, а волнистая — гамма-кванту. Кулоновское взаимодействие двух
частиц Qx и Q2 отвечает диаграмме
C)
описывающей обмен у-квантом между частицами Qx и Qa. На
подобных диаграммах условимся считать, что время «течет»
в горизонтальном направлении слева направо.
Диаграмма, описывающая процесс аннигиляции или рождения
пары будет тогда выглядеть так:
D)
При таком «переносе» в противоположную часть соотношения B)
частицу Q следует заменить на античастицу Q.
Если мы теперь развернем рисунок C) на 90* по часовой
стрелке, то получим
дг + д2 ^_^ д1 + gf ;
9г ■ . Ъ ..
— диаграмму, описывающую процесс превращения пары (Q2, ф2)
в пару (Qx, Qx) путем однофотонной аннигиляции.
Как мы увидим ниже (см. § 10.3), элементарному электро-
электромагнитному взаимодействию B), D) отвечает член в лагранжиане,
имеющий вид ~
, F)
где /4ц —потенциал электромагнитного поля, а /# — ток поля

§ 10. ВЗАИМОДЕЙСТВИЕ ПОЛЕЙ 8?
частиц Q. Например, для электрон-позитронов
%{х)=еА»{х)у{х)ГЪ(х). G)
Типичным примером слабого взаимодействия является р-распад
нейтрона
n^p + tr+v,, (8)
который мы изобразим графически в «более симметричном» виде:
или
Как правило, элементарные процессы слабого взаимодействия
имеют четырех-фермионную структуру, подобную (9). В качестве
второго примера приведем процесс распада мюона (р,->е^ +
e), который соответствует взаимодействию
(Ю)
/г
/
Слабые взаимодействия, описывающие процессы типа (9), A0),
в лагранжиане представлены членами, имеющими структуру
(ток х ток):
Xr^GJll{x)J^l(x), (И)
где .
/^ (х) = р (х) Ovn (х) + ve (x) (V(х) +% (х) Ovli (x) + ... A2)
— слабый ток, Ov —некоторые матрицы, G — постоянная Ферми,
а операторные полевые функции обозначены теми же символами,
что и соответствующие им частицы. Численное значение постоян-
постоянной Ферми может быть выражено соотношением, содержащим
мировые константы с, % и квадрат массы. Выбирая для этой
цели массу нуклона М, имеем
A3)
Отличная от нуля размерность постоянной Ферми в системе
% — с—Х ([G] = mr2) практически означает, что интенсивность
слабого взаимодействия существенно зависит от энергии. При
энергиях в с. ц. м. порядка 1 ГэВ (т. е. порядка массы нуклона)
интенсивность описывается числовым соотношением A3). Однако

88 ГЛ. III. ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛЯ
в области энергий 102 —103 ГэВ она возрастает до величин
порядка 1, и взаимодействие Ферми перестает быть слабым.
Сильные взаимодействия охватывают большую группу частиц,
которые обладают относительно большой массой (з* тп) и назы-
называются собирательным термином — адроны. Эти взаимодействия
являются короткодействующими
Лы~ехр(— г/гЯЛ);
они проявляются лишь на малых расстояниях, характеризуемых
радиусом действия ядерных сил
гл^~о± 1,4/= 1,4^ 1<Н» см, A4)
близким к комптоновской длине пи-мезона.
Сильные взаимодействия отвечают за ядерные силы, связы-
связывающие протоны и нейтроны в атомных ядрах. Они называются
сильными, так как в микромире приводят к большим количест-
количественным эффектам. В то же время на малых расстояниях (при
г<гяд) они велики по абсолютной величине и существенно'пре-
существенно'превосходят электромагнитные взаимодействия. Поясним эту мысль.
Существуют разные способы сравнения интенсивности различ-
различных взаимодействий. Один из них основан на сравнении энер-
энергетических эффектов. Так, электромагнитные взаимодействия
могут быть охарактеризованы энергией связи s-электрона в атоме
водорода: £9Л~10эВ.
Сильные взаимодействия ответственны за энергию связи нук-
нуклонов в ядре: £вд=^10 МэВ = 106£8Л.
Второй способ заключается в сопоставлении числовых безраз-
безразмерных характеристик, описывающих интенсивности различных
взаимодействий.
Лагранжиан электромагнитного взаимодействия поля Дирака
с электромагнитным полем G) содержит заряд электрона е, кото-
который является мерой интенсивности взаимодействия. Кулоновское
взаимодействие двух заряженных частиц пропорционально е2 и
может быть охарактеризовано безразмерной комбинацией
— так называемой постоянной тонкой структуры. Эта же самая
величина (точнее говоря, а/л~х/4зо) выступает в качестве пара-
параметра разложения в электродинамической .теории возмущений.
Поэтому принято считать, что электромагнитные взаимодействия
имеют порядок 10~2 — ЮЛ Именно такой порядок имеют относи-

§ 10. ВЗАИМОДЕЙСТВИЕ ПОЛЕЙ 89
тельные расщепления масс внутри изотопических мультиплетов:
'.~ 1,38-10-»,
Мп-Мр 939,55-938,26
Мр — 938,26
т +-т 0 139,57-134,96
"- я ~- ; -34- 10~а
т# — ' 136,96 —°Л ^ ,
которые принято относить к электромагнитным эффектам. В то
же время часто полагают, что юкавскому взаимодействию пионов
и нуклонов
A6)
соответствует член в лагранжиане
¥(x), A7)
интенсивность которого характеризуется константой связи силь.
ного взаимодействия g. Численное значение безразмерной комби-
комбинации, аналогичной постоянной тонкой структуры а, оказывается
равным
4&-14'7' 08)
т. е. не является малым по сравнению с единицей. По этой при-
причине теория возмущений не может быть использована в моделях
ядерных взаимодействий, основанных на лагранжианах подобного
типа. - .
10.2. Лагранжианы взаимодействия. При изучении системы
связанных полей, описывающей процессы взаимодействия соот-
соответствующих частиц, исходят из полного лагранжиана системы,
который обычно представляют в виде суммы
свободного лагранжиана =S?0 (являющегося суммой лагранжианов,
входящих в систему свободных полей) и лагранжиана взаимодей-
взаимодействия =S?B3. Примеры =S?B3 были представлены выше формулами
G), (И), A7).
. Сейчас мы сформулируем некоторые общие свойства, кото-
которыми должны обладать лагранжианы взаимодействия полей.
Лагранжиан =S?B3 должен, во-первых, представлять локальную
эрмитову лоренц-инвариантную конструкцию полевых функций
различных полей и их производных. Кроме того, =S?B3 должен
отражать свойства симметрии и дискретные законы сохранения,
присущие данному механизму взаимодействия.

90 ГЛ. Ш. ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛЯ
Ограничиваясь простейшими полиномиальными (точнее, поли-
полилинейными) формами, получаем, например, что взаимодействие
скалярного поля ф со спинорным полем ф при сохранении чет-
четности может быть построено по типу скаляр х скаляр: ty (х) г|э (х) ф (х)
или по типу вектор хвектор: гр (#) Yvi|> (#) Ф; v (*)•
Аналогично этому простейшая форма взаимодействия псевдо-
псевдоскалярного изовекторного поля пионов п(х) с полем нуклонов
Ч? (х), описываемая формулой A7), имеет вид псевдоскаляр х псевдо-
псевдоскаляр в конфигурационном пространстве и одновременно струк-
структуру изовектор хизовектор в изотопическом пространстве. Альтер-
Альтернативная форма, построенная по типу (псевдовектор х псевдовек-
псевдовектор) х (изовектор х изовектор), имеет, вид
¥(х)у*уЧУ(х)я;у(х) -A9)
и представляет собой так называемый «псевдовекторный» вариант
юкавского взаимодействия. Отметим здесь, что изотопическая
симметрия представляет собой пример нарушенной симметрии —
она имеет место лишь в сильных взаимодействиях. Подобно
этому симметрия относительно пространственных отражений имеет
место в сильных и электромагнитных взаимодействиях. Слабые
взаимодействия не сохраняют пространственную четность. Слабый
ток представляет собой линейную комбинацию вектора и псевдо-
псевдовектора. . .
В то же время такие свойства, как законы сохранения элек-
электрического и барионного зарядов выполняются во всех известных
взаимодействиях. Наряду с лоренц-инвариантностью они счита-
считаются абсолютными.
В соответствии с законом сохранения электрического заряда
лагранжиан должен быть инвариантным относительно фазового
преобразования комплексно-сопряженных функций поля, описы-
описывающих заряженные частицы:
ф-^е'-аф, ф-^е-к^ф, B0)
а также функций всех других полей, несущих данный заряд.
Аналогичные ограничения налагают законы сохранения бари-
барионного заряда, странности и т. д.
При введении взаимодействия полей обычно исходят из сооб-
соображений соответствия с наблюдаемыми на опыте процессами.
Такой способ рассуждений, разумеется, не имеет достаточно глу-
глубокого теоретического обоснования и может приводить к ошиб-
ошибкам. Открытым, в частности, остается вопрос о существовании
промежуточного векторного бозона, с помощью которого можно
представить 4-фермионное взаимодействие Ферми A1) как след-
следствие трилинейного взаимодействия ^(х)В^(х), где В^ — неко*
торое векторное поле, т. е., подобно переходу от формулы C)

§ 10. ВЗАИМОДЕЙСТВИЕ ПОЛЕЙ 91
к формуле B), расщепить 4-фермионный узел, изображенный
в (9), A0), и представить его в виде
Х А
В квантовой теории поля важную роль играют простые модели,
содержащие небольшое число квантованных полей, связанных
простыми по форме взаимодействиями.
Ниже мы часто будем обращаться к модели скалярного дей-
действительного поля с четверным взаимодействием, полный лагран-
лагранжиан которой имеет вид
При этом последнее слагаемое, содержащее константу связи ft,
будем рассматривать как лагранжиан взаимодействия и называть
модель B1) моделью ф4. В лагранжиане B1) поле ф можно счи-
считать как скаляром, так и псевдоскаляром. Поэтому модель ф4
близка к модели пион-пионного взаимодействия, описываемой
лагранжианом
X (х) = 1 д& (х) д"Чр (х) - <£ ф (х) y(x)-h (фф)«,. B2)
где ф —введенный в C.10) изовектор. Член взаимодействия
h (ффJ описывает одновременно несколько процессов:
B3)
Как уже было отмечено выше, никакого серьезного основания
считать взаимодействия B3) фундаментальными у нас нет.
В кварк-глюонной модели сильных взаимодействий (см. ниже § 33),
например, пион-пионные взаимодействия B3), как и пион-нуклон-
ное взаимодействие A6), A7), оказываются производными от
более фундаментального кварк-глюонного взаимодействия. Однако
кварковая модель адронов содержит серьезные трудности и еще
далека от завершения.
При таком общем неудовлетворительном состоянии вопроса
о структуре взаимодействий полей имеются, однако, довольно
глубокие соображения, позволяющие установить общую струк-

92 ГЛ. III. ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛЯ
туру электромагнитных взаимодействий, которые мы сейчас
изложим.
10.3. Электромагнитное поле как калибровочное. Отправным
моментом является своеобразное выделение электромагнитного
поля, его противопоставление остальным полям, которые будем
ниже называть полями материи.
Полевые функции электрически заряженных полей материи и
подобно квантовомеханической \|з-функции не являются наблюдае-
наблюдаемыми и в физические динамические величины входят через били-
билинейные формы по. и и и. (В противоположность этому напряжен-
напряженности электромагнитного поля непосредственно измеряемы.)
Вследствие этого функции полей материи определены с точностью
до фазового множителя. Выше (§§ 2.5 и 6.5) этот произвол
позволил ввести калибровочное преобразование вида B0) с фазой а,
не зависящей от координат, и в конечном счете получить выра-
выражения для оператора заряда.
Потребуем теперь, чтобы теория оставалась инвариантной и
в случае, когда параметр калибровочного преобразования зави-
зависит от х:
«(*)->«' (х) = е'а^и(х), «(*)->-«' (х) — е-1аМи(х), B4)
т. е. чтобы относительная фаза а(х) — а(х') в двух различных
точках пространства-времени х и х' была совершенно произ-
произвольна. Локальное фазовое преобразование B4) соответствует пред-
предположению о том, что произвол в выборе фазового множителя
у волновой функции поля материи может иметь локальный
характер.
Не составляет труда убедиться, что лагранжианы рассмотрен-
рассмотренных комплексных полей [см., например, C.16), _E.5)] не инва-
инвариантны относительно B4) в силу того, что градиенты полей,
кроме фазового множителя, получают аддитивную добавку, про-
пропорциональную градиенту функции а(х). ■
Инвариантность можно восстановить, если ввести дополни-
дополнительное векторное поле Ау, преобразующееся одновременно с B4)
по закону
Ау (х) -+ Ау (х) = Av (x) + f. v (x). B5)
При этом следует заменить все производные дуи, дуи* в лагран-
лагранжиане на оператор_ы
Dy(A)u = (dy-ieAy(x))u(x),
* # #
Dy(A)u = (dy + ieAy(x))u(x),
зависящие от А. Выражения B6) называются удлиненными или
ковариантными производными.

§ 10. ВЗАИМОДЕЙСТВИЕ ПОЛЕЙ 93
При выполнении условия а (х) = ef (х) ковариантные производ-
производные при одновременном преобразовании B4), B5) преобразуются
подобно B4), т. е. меняют фазу:
y()() ()()
# # # #
Dv (А') и' (х) = e-bf i*)Dv (А) и (х).
Кроме замены обычных производных на ковариантные, в лаг-
лагранжиан следует ввести также лагранжиан Хй свободного поля Ау:
и, и, ди, ди)^%' = %(и, и, D(A)u, б(А)и) + Х0.(А),- B8)
который в свою очередь должен быть инвариантным относи-
относительно B5). Его следует выбрать в виде D.12)
B9)
причем
Fliy = dllAy-dyAll D.1)
и поле Ау с необходимостью оказывается безмассовым. Константа е,
входящая в B6) и B7), может быть отождествлена с электри-
электрическим зарядом, а векторное поле Av— с электромагнитным полем.
Таким образом, электромагнитное воле, введенное через кова-
ковариантные производные D, D, выступает как компенсирующее
поле. Поля, компенсирующие изменение калибровки полей
материи, называют также калибровочными, полями. В силу абеле-
вого (перестановочного) характера группы, образованной пре-
преобразованиями B5), электромагнитное поле является калибро-
калибровочным абелевым полем.
Переход в свободном лагранжиане от обычных производных
к ковариантным по правилу B8), B6) приводит к появлению
взаимодействия исходного поля и с электромагнитным полем А.
Взаимодействие, введенное с помощью ковариантных произ-
производных (или, как иногда говорят, с помощью «удлинения» произ-
производных), называют также минимальным электромагнитным взаимо-
взаимодействием.
В случае спинорных полей, когда Хй линейно по производ-
производным, минимальное электромагнитное взаимодействие линейно по
полю А и имеет вид G).
Для полей с целым спином в обычной формулировке мини-
минимальное взаимодействие содержит квадратичные члены. Так,
лагранжиану комплексного скалярного поля соответствует
•S?» (х) = ie [и (х) «;v (х) - «;v (х) и (х)] А" (х) + ehi (x) и (х) А" (х) Ау (х).
C0)

94 ГЛ. III. ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛЯ
Таким образом, мы убедились, что электромагнитное поле
обеспечивает инвариантность полного лагранжиана относительно
локальных фазовых преобразований, являющихся обобщениями
«глобальных» фазовых преобразований, приводящих к сохранению
электрического заряда. Такая точка зрения устанавливает связи
между свойствами полей в пространстве-времени и так называе-
называемыми внутренними симметриями. Важнейшим примером внутрен-
внутренней симметрии, непосредственно обещающим зарядовую сим-
симметрию, является изотопическая симметрия.
Требование инвариантности относительно локально фазовых
изотопических преобразований приводит к необходимости введе*
пия нового компенсирующего векторного поля —поля Янга —
Миллса.
§ П. Неабелевы калибровочные поля
11.1. Поле Янга —Миллса. Требование инвариантности отно-
относительно локальных фазовых преобразований непрерывной группы
симметрии приводит к появлению компенсирующего векторного
поля. Впервые подобное поле для неабелевой группы изотопи-
изотопических преобразований было введено Янгом и Миллсом в 1953 г.
Впоследствии неабелевы калибровочные поля получили название
полей Янга —Миллса. В современной' физике такие поля находят
широкое применение в моделях слабых и сильных взаимодейст-
взаимодействий (см. §§ 32, 33). В этих моделях используются калибровочные
группы достаточно высоких рангов. Для облегчения изложения
здесь мы ограничимся самой простой неабелевой группой —груп-
—группой SU B) (обозначения и терминология теории непрерывных
групп объясняются в Дополнении III), которую условно будем
называть «изотопической»,- не вкладывая в этот термин опре-
определенного физического содержания.
Пусть многокомпонентная полевая функция <ра (а=1,... , А)
преобразуется по некоторому неприводимому представлению
калибровочной группы G (т. е. образует изотопический мульти-
плет). Инфинитезимальное преобразование
Фа —*" фа = фя + ig^k {Th)ab ф* (k=l, ... , К) A)
содержит К независимых действительных бесконечно малых
параметров ak, из которых для удобства дальнейшего изложения
вынесен конечный общий множитель g. Число К называется раз-
размерностью группы G. В случае A0.24) оно равно 1. Для рас-
рассматриваемой сейчас группы SU B) К = Ъ; для группы унитар-
унитарных преобразований SU C) К = 8 и т. д. Эрмитовы генераторы Tk
являются матрицами представления, к которому принадлежит
мультиплет фа. Для изодублета (А = 2) они пропорциональны
матрицам Паули хк (ср. формулу (Д1.5)), для изотриплета (Л = 3)

§ 11. НЕАБЕЛЕВЫ КАЛИБРОВОЧНЫЕ ПОЛЯ 95
матрицы Т могут быть выражены через единичный антисиммет-
антисимметричный тензор е (см. (Д1. 13)):
, Тк = tk, {tk)ab = tkab = — fekatf B)
и т. д.
Полезно отметить, что коммутаторы матриц Т произвольного
представления имеют универсальный вид
. [Tk, Tl] = — (tn)klTn = ieklnTa C)
и содержат матричные элементы матриц t так называемого при-
присоединенного представления в качестве структурных констант.
Размерность этого представления равна размерности группы —
в данном случае трем.
Формула A) с параметрами ak, не зависящими от координат,
аналогична формуле B.27) и вписывает так называемое глобаль-
глобальное калибровочное преобразование. Переходя к локальному пре-
преобразованию типа A0.24), т. е. считая, что параметры а зависят
от л; .
ак-+ак(х),
по аналогии с электродинамикой заменим обычные производные
от ф на ковариантные
ду<ра -+ (Д, (В) Ф)в = д^а - igBkv (х) (Tk)ab щ, D)
содержащие новое компенсирующее векторное поле Bv. Это поле,
в отличие от электромагнитного поля Av, имеет групповые (верх-
(верхние) индексы и преобразуется по более сложному закону
B% + {B%)' = Bav + igab{x)tbacBcy + d^a(x), E)
который, кроме «градиентного удлинения» дуа, содержит еще
изотопическое вращение. Генераторы этого вращения &x = ita
являются матрицами присоединенного представления.
Заметим, что наличие калибровочного произвола приводит
здесь к тому, что, как и в электродинамике (см. § 4.3), из четырех
компонент векторного потенциала Bv лишь две «трехмерно
поперечные» компоненты отвечают физическим степеням свободы.
С помощью формул C) теперь можно показать, что ковариант-
ная производная Dyq> при калибровочных преобразованиях A),
E) преобразуется подобно ф:
[D,(B')(p']a = [Dv(B)(p]a + igall(x)(TkU[Dy(B)if]l). F)
Аналогом электромагнитного тензора напряженности F^y оказы-
оказывается тензор
/•^ = д^Ву — д^Вр + igtkinBy^By. G)

96 гЛ. т. взаимодействующие поля
Для группы SU B) с помощью B) получаем также
f?liy = dllBv-d^Bll + g{BlixBy]. (8)
Тензор F преобразуется по присоединенному представлению
калибровочной группы
Инвариантный лагранжиан свободного поля Янга —Миллса имеет
вид
«SfYM(S) = -l/^v, A0)
близкий к лагранжиану электромагнитного поля. Однако, в отли-
отличие от выражения A0.29), в котором каждый из сомножителей F^
калибровочно инвариантен, в данном случае инвариантно лишь
все выражение A0) в целом.
Лагранжиан A0) подобно поперечному лагранжиану электро-
электродинамики D.12), A0.29) является вырожденным.. Поэтому при
квантовании его необходимо модифицировать Вытекающие из
него уравнения движения ^
нелинейны и содержат «самодействие».
Если бы мы попытались квантовать поле Янга — Миллса
с помощью метода Гупта —Блейлера, изменив лагранжиан по
рецепту D.13)
то, как можно показать, продольная функция
в этом случае удовлетворяла бы не свободному уравнению д'Алам-
бера, а нелинейному уравнению - ^
. П1а(х) + §гаЬсВьу(х)д\с» = 0. A2)
Таким образом, продольная степень свободы не «отщепляется»
от поперечных. Отсюда следует, что в процессе временной эволю-
эволюции «физические состояния», для которых справедливо (в среднем)
условие Лоренца {%) = 0, могут перейти в состояния, содержащие
отличную от нуля продольную составляющую. Поэтому метод
Гупта — Блейлера нуждается в обобщении, которое будет описано
в § 19.4,
11.2. Калибровочное взаимодействие полей. Как было показано
в § 10.3, требование инвариантности лагранжиана полей материи
относительно локальных фазовых преобразований A0.24) приво*

§ 11. НЕАБЕЛЕВЫ КАЛИБРОВОЧНЫЕ ПОЛЯ 97
дит к необходимости введения компенсирующего электромагнит-
электромагнитного поля Лц, взаимодействие с которым всех электрически
заряженных полей материи описывается единственной констан-
константой е. Преобразование A0.24) отвечает абелевой группе первого
ранга U(l).
В более сложных случаях, когда в качестве калибровочной
выступает некоторая простая неабелева группа G, условие инва-
инвариантности лагранжиана также приводит к «единообразному»
взаимодействию полей материи с калибровочным полем Bv. Таким
путем образуется некоторая совокупность полей материи (с раз-
различными спинами, электрическими зарядами и т. п.), связанных
универсальным образом с полем Bv. Члены взаимодействия, возт
никающие при удлинении производных полей материи по правилу
D), содержат ту же самую безразмерную константу связи g, что
и нелинейные составляющие поля Янга —Миллса (см. формулы
G), (8)).
Процедура построения калибровочной модели взаимодействую-
взаимодействующих полей состоит из следующих этапов:
1) Выбираем (простую) калибровочную группу G и фиксируем
набор полей материи «A)>... , «(л), преобразующихся по различ-
различным (но определенным) представлениям этой группы и описывае-
описываемых свободным лагранжианом
Хо (и, ди) = 2 А («(о. ^и@). A3)
2) Вводим компенсирующее векторное поле Ву, отвечающее
присоединенному представлению группы G, и образуем полный
лагранжиан системы (поля материи «A),..., «(„, + поле Янга —
Миллса Ву) по рецепту
%0(и, ди) + Х(и, В),
X (и, В) =Je0 (и, D (В) и) + Хум (В). A4)
В первом члене правой части производные каждого из полей u(i)
удлинены по правилу D) с Одной и той же константой g, кото-
которая также входит в ifyM- Поэтому лагранжиан X (и, В), описы-
описывающий систему взаимодействующих п + 1 полей, в случае простой
группы содержит всего лишь одну константу связи. Этот лагран-
лагранжиан инвариантен относительно одновременного калибровочного
преобразования A), E) всех входящих в него полей.
Как отмечалось в конце § 11.1, свободное калибровочное
векторное поле с необходимостью является безмассовым. Это
обстоятельство существенно ограничивает возможности использова-
использования калибровочных моделей взаимодействия полей, поскольку
в реальном мире единственным безмассовым векторным полем
является электромагнитное поле Ау, отвечающее абелевой калиб-
калибровочной группе.
4 Н. Н. Боголюбов, Д. В. Ширков

98 ГЛ. III. ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛЯ
Оказывается, однако, что существует нетривиальный способ
введения массы в калибровочное поле, взаимодействующее с неко-
некоторым скалярным полем материи. Этот способ основан на так
называемом механизме спонтанного (самопроизвольного) наруше-
нарушения симметрии, к рассмотрению которого мы сейчас перейдем.
11.3. Спонтанное нарушение симметрии. В различных главах
физики, начиная с классической механики, известны примеры
систем, демонстрирующих самопроизвольное нарушение симметрии.
Речь идет о такой системе, которая описывается выражениями
(лагранжиан, гамильтониан, уравнения"движения), обладающими
некоторой симметрией, в то время как реальное физическое
состояние системы, отвечающее частному решению уравнений
движения, этой симметрией не обладает. Подобное положение
возникает тогда, когда нижнее симметрич-
симметричное состояние не доставляет системе абсо-
абсолютный минимум энергии и является не-
неустойчивым. Реальной причиной наруше-
нарушения симметрии оказывается сколь угодно
малое несимметричное возмущение.
Простой пример дает механическая си-
система, состоящая из пустого сосуда с вы-
выпуклым дном и маленького шарика. Сосуд,
а) б) представляющий собой тело вращения,
Рис 11.1. Механическая поставим строго вертикально (относительно
система, демонстрирую- поля тяжести Земли) и точно по оси бро-
щая спонтанное наруше- сим „ него ^ерху шарик (рис 11.1, в).
ное'со^Гяние^бМонеч: Достигнув дна, шарик не удержится^ на
ное состояние. центральной выпуклости и скатится на
периферию (рис. 11.1,6). Конечное состоя-
состояние не обладает симметрией вращения. Другой пример подобного
типа являет изотропный ферромагнетик, выделенное направление
вектора намагниченности которого нарушает симметрию относи-
относительно пространственных вращений.
Обратимся теперь к скалярному классическому полю <р (х),
характеризуемому лагранжианом
X = T(d<p)-V(<p), A5)
в котором Г —кинетическая часть, зависящая лишь от компонент
градиента, а V — потенциальная функция.
Для обычного свободного скалярного поля, рассмотренного
в § 3, У (ф) представляется параболой второго порядка m2<j>2/2,
изображенной на рис. 11.2. Минимуму потенциальной функции
отвечает нулевое решение, а квантование свободного скалярного
поля, проведенное в § 8, — квантованию малых колебаний около
положения равновесия при <р = 0. -

§ 11. НЕАБЕЛЕВЫ КАЛИБРОВОЧНЫЕ ПОЛЯ "
Лагранжиан A5) обладает симметрией относительно «преобра-
«преобразования отражения» ф->- —ф и нижнее состояние ф = 0 симмет-
симметрично и устойчиво. Введение в V (ф) положительных членов вида
+ ф4 (ср. A0.21), A0.22)), описывающих самодействие поля, не
меняет этих свойств.
Для того чтобы получить спонтанное нарушение симметрии
отражения, допустим, что зависимость V от ф имеет вид четной
функции с двумя симметричными минимумами, изображенной на
рис. 11.3. Подобную зависимость можно описать двучленом
Это выражение содержит квадратичный по ф член с «отрицатель-
«отрицательным квадратом массы», что может вызвать ассоциацию с гипоте-
гипотетическими частицами—тахионами, движущимися быстрее света.
Р
Рис. 11.2. Потенциальная
функция свободного ска-
скалярного поля.
■ on Q5 '
Рис. 11.3. Потенциальная
функция модели скаляр-
скалярного поля, содержащей
спонтанное нарушение
симметрии.
Нам, однако, существенно то, что благодаря отрицательному знаку
первого слагаемого точка ф = 0 не является минимумом, а поло-
положения устойчивого равновесия располагаются в двух точках
Ф = ±ФО, фо = м./Л.
Оба нижних состояния имеют одинаковую энергию
вследствие чего соответствующая квантовая система обладает
двукратно вырожденным вакуумным состоянием.
Теперь следует выбрать одно из нижних состояний, например
+ Фо. и операцией сдвига на константу перейти к новой функции
поля:
<р (*)->-и(*) = <р (*)-%,■
что окажется удобным для изучения малых отклонений от ф0.
Получаем этим путем

100 ГЛ. III. ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛЯ
Отвлекаясь от постоянной Vo, сдвигающей лишь шкалу энер-
энергии, видим, что положительный второй член в правой части отве-
отвечает массе квантов малых колебаний, равной т = ц,уг2, а третье
и четвертое слагаемые, дающие нелинейные вклады в уравнения
движения, при малых h могут рассматриваться как возмущение,
соответствующее самодействию поля.
Заметим здесь, что преобразование поля вида
Ф (х) = const -\-" (х)
впервые было введено в квантовую физику одним из авторов .при
построении микроскопической теории сверхтекучести в 1946 г.
(см. Боголюбов A979), с: 115—131), а метод изучения квантовых
систем со спонтанно нарушенной симметрией, известный как метод
квазисредних, —в 1960—61 гг. (см. Боголюбов A979), с. 193—269).
Достаточно простое, но физически содержательное обобщение
возникает при переходе от однокомпонентного (синглетного) поля ф
к изотопическому мультиплету ф (<pJt ...., фд) и потенциалу
Дискретная симметрия отражения заменяется на непрерывную
симметрию изотопических вращений, подобную симметрии про-
пространственного вращения вокруг вертикальной оси в приведенной
иллюстрации из механики.
Минимум потенциальной энергии теперь отвечает соотношению
ФФ = Ф? = ^/Л2, A7)
определяющему (п ~ 1)-мерное многообразие в n-мерном изотопи-
изотопическом пространстве. Необходимо произвести сдвиг функции поля ф
на постоянный вектор ф0, удовлетворяющий условию A7). Не
теряя общности, выберем этот вектор в виде
Фо-(Фо. 0, .... 0), Фо =
Полагая затем
ф(*) = фо+ «(*). A8)
получим для V выражение
V (ф0 + и (х)) = VQ + № +lxhu1 (ее) + ~ ■(»»)",
не содержащее членов квадратичных по иа, и3 ип. В то же
время структура V относительно новой переменной их аналогична
однокомпонентному случаю.
Таким образом, в результате спонтанного нарушения симмет-
симметрии, выражаемого сдвигом A8), сдвинутая компонента их «при-
«приобретает» свободную массу т1 = ц. |/2, а остальные компоненты

§ 11. НЕАБЕЛЕВЫ КАЛИБРОВОЧНЫЕ ПОЛЯ ЮГ
и2, «з «л отвечают безмассовым степеням свободы (т2=т3 =
= ...т„ = 0).
Последнее свойство является непременным атрибутом спонтан-
спонтанного нарушения непрерывной симметрии, так как каждая из без-
безмассовых степеней свободы отвечает бесконечнократному вырож-
вырождению вакуумного состояния, которое в нашем случае описывается
соотношением A7). В механическом примере безмассовая степень
свободы относится к виртуальному перемещению шарика в конеч-
конечном состоянии (рис. 11.1,6) по кольцеобразному углублению дна
сосуда.
Сформулированное выше предложение об обязательном появле-
появлении безмассовых скалярных мезонов при спонтанном нарушении
непрерывной симметрии в квантовой теории поля известно под
названием теоремы Голдстоуна, а безмассовые частицы называются
голдстоуновскими бозонами. Теорема Голдстоуна является реля-
релятивистским аналогом теоремы о дальнодействии в квантовой ста-
статистике (см. Боголюбов A979), с. 193—269, особенно гл. II).
11.4. Массивное поле Янга — Мидлса. Подчеркнем, что спон-
спонтанное нарушение симметрии является нарушением симметрии
решения, а не симметрии лагранжиана. Исходный лагранжиан A4),
A6) не меняется при преобразовании сдвига на константу A8),
которое представляет лишь переход к новым независимым пере-
переменным. Это обстоятельство удается использовать для того, чтобы
ввести массу неабелева калибровочного поля, не нарушив калиб-
калибровочную симметрию лагранжиана. Такое массивное поле не может
быть свободным. Оно должно взаимодействовать со скалярным
полем, служащим инструментом спонтанного нарушения симметрии.
Пусть неабелево калибровочное поле Янга— Миллса В взаимо-
взаимодействует со скалярным полем и, преобразующимся по триплет-
ному представлению группы SU B). Предположим, что поле и
подчиняется нелинейным уравнениям, отвечающим лагранжиану
типа A5), A6):
■j?o.(e, ди) = ~дчид*и+^-ии—~{ии)\
Полный лагранжиан системы полей и-{-В на основании A4) будет
Х(т-В) = Яа(и, D(B)u) + Xym(B), - A9)
где ковариантная производная D (В) и определена согласно D).
Используя эту формулу, находим
Х(и, B) = A/2)(dvu + g[BvXu])(dvu + g[B\xu]) +
+ ^-иа-~(ииJ + ^уМ(В). B0)
Рассмотрим члены, содержащие оба поля: и и В. После
небольших упрощений их можно представить следующим образом:
(g*/2) {(By») (В*и)-(ии) (BvB4 + g([dvuxu]B»). B1)

102 ГЛ. III. ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛЯ
Выполним теперь операцию сдвига на константу для скаляр-
скалярного поля
), B2)
причем изовектор и0 направим вдоль третьей оси:
«о=Ф<Аз-
Получаем из B1) члены, квадратичные по полю Янга —Миллса
и не содержащие нового скалярного поля v:
- (£2Ф»/2) (ё^ВД - BVBV) = + ^Vv (В№ + ВЪВ$), B3)
которые следует рассматривать как массовые члены компонент В1,
В2 поля Янга —Миллса. Таким образом, эти две компоненты
приобретают массу M — g(p0- Компонента В3 осталась безмассовой.
Форма B1) после сдвига скалярного поля включает также
квадратичные члены, .содержащие как векторное, так и новые
скалярные поля:
V М {В\, <Э»1иа - ВЪ &V1) B4)
Наличие таких «перекрестных» квадратичных слагаемых, вообще
говоря, затрудняет интерпретацию безмассовых компонент скаляр-
скалярного поля vt и и2 (см. по этому поводу ниже в § 12.2). Однако
в данном случае имеется одно важное обстоятельство, приводящее
к существенному упрощению. Можно устранить перекрестные члены
путем калибровочного преобразования специального вида, фикси-
фиксировав калибровку таким образом, чтобы выполнялись условия
Oi-M = о5(*)= 0, dvB'vs(x) = 0. B5)
В результате мы получим лагранжиан, зависящий лишь от одного
скалярного поля v'a = v и векторного триплета В' = {В[, В'%, В'г):
X (и, В) = X (v, В'). B6)
Входящие в него две компоненты векторного поля В[, В'%,
согласно B2), имеют равные массы
M1 = M2 = M = g(po=g^/h, - B7)
компонента В'ъ осталась безмассовой, а скалярный бозон v обла-
обладает массой
m = "|/jn. " B8)
Таким образом, вместо исходного изотриплета безмассовых
векторных полей и триплета скалярных полей с отрицательным
квадратом массы мы получили дублет массивных векторных полей,
одно безмассовое векторное поле и один скалярный мезон с мас-
массой. Безмассовые голдстоуновские мезоны исчезли в результате
калибровочного преобразования. Этот процесс превращения без-

§ 12, КВАНТОВЫЕ СИСТЕМЫ СО ВЗАИМОДЕЙСТВИЕМ ЮЗ
массового калибровочного, поля в массивное с одновременной
«аннигиляцией» голдстоуновских мезонов называется эффектом
(или механизмом) Хиггса. Выживающий массивный скалярный
мезон именуется хиггсовым бозоном, а его поле (в данном слу-
случае v3 = v) — полем Хиггса.
Нетрудно проверить, что механизм Хиггса не изменяет число
частиц всей системы в целом. Напомним для этого, что безмас-
безмассовое 4-векторное поле (например, электромагнитное) в результате
квантования описывает две частицы. Мы будем говорить для
краткости, что оно имеет две физические степени свободы. Мас-
Массивное векторное поле имеет три степени свободы, как это сле-
следует из § 8.3.
Поэтому исходный лагранжиан B0) содержит 3x2 = 6 степе-
степеней свободы трех безмассовых векторных полей и 3x1=3 сте-
степени свободы трех скалярных полей. Итого 6 + 3 = 9 степеней
свободы. Конечный лагранжиан X (us, В) имеет 2x3 = 6 степеней
свободы двух массивных векторных полей, 1x2 = 2 степени сво-
свободы безмассовой векторной компоненты В3 и 1x1 = 1—одну
компоненту хиггсова поля v3. Итого 6 + 2+1=9 степеней сво-
свободы.
Отметим еще, что если несколько усложнить рассмотренную
модель и вместо триплета скалярных полей взять квадруплет
B-компонентный изоспинор комплексных скалярных полей), то
мы получим систему с 10 степенями свободы. В результате пре-
преобразования вида B2) возникает три голдстоуновских бозона и
все три компоненты поля Янга — Миллса приобретают массу.
Три безмассовых бозона затем будут поглощены калибровочным
преобразованием. В итоге мы получим три массивных векторных
поля и один хиггсов бозон.
Таким образом, механизм Хиггса позволяет придать массу
всем компонентам калибровочного векторного поля. Однако обя-
обязательным атрибутом модели, содержащей массивное поле Янга —
Миллса, является хиггсов бозон. Механизм Хиггса используется
при построении единых моделей слабого и электромагнитного
(«электрослабого») взаимодействия (см. ниже § 32).
§ 12. Квантовые системы со взаимодействием
12.1. Постановка задачи. При рассмотрении взаимодействия
квантованных полей можно исходить из полного лагранжиана
системы полей
F(Ui, Vuj, uh).
С помощью теоремы Нётер получаем по формулам § 2 тензор
энергии-импульса и полную энергию (гамильтониан)
Я = Я(«, \и, п). A)

104 ГЛ. Ш. ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛЯ
Ввиду того, что решения уравнений движения (в отличие от
предыдущего) нам, как правило, неизвестны, использование
4-мерных преобразований Фурье для функций поля оказывается
нецелесообразным. Вместо этого можем записать:
и(х)-и+ + и-, и±(х)«= Bn)-'/'\e+il>xa±(k, t)dk. B)
Следует отметить, что,в отличие от свободного поля, разделе-
разделение на положительно- и отрицательно-частотные части здесь может
оказаться релятивистски неинвариантным, и что величины а± не
обязательно имеют смысл операторов рождения и уничтожения ре-
реальных частиц.
Тем не менее ниже мы будем предполагать, что амплитуды а+
могут быть представлены линейной комбинацией положительны^
временных экспонент
а+(к, Ъ = £е1**м<а£ (к) C)
OS
и потому являются операторами рождения, а амплитуды от —опе-
—операторами уничтожения. Гамильтониан Я может быть теперь выра-
выражен через амплитуды а± и их производные по времени. Ввиду
того, что Я не зависит от времени, можно положить / = 0 и
перейти к амплитудам
a±(k) = a±(k, 0), d±(*)=d±(A, 0)... ■ D)
Для усхановления перестановочных соотношений теперь можно
воспользоваться каноническим квантованием и получить квантовые
уравнения движения в представлении Гайзенберга
<-^=[«, Я], " E)
а также одновременные коммутационные соотношения типа [q, p]
Подставляя B) и A) в E), мы придем к довольно сложным
нелинейным операторным соотношениям для амплитуд ^(Ar, t).
Решение этих соотношений эквивалентно решению уравнений
движения.
С другой стороны, используя F) и переходя к амплитудам D),
мы получим коммутационные соотношения вида
[ег (к), a+(q)] = 8(k-q). G)
Совокупность уравнения Шредингера, выражений для гамильто-
гамильтониана Я (и других динамических величин), записанных через не
зависящие от времени операторы D)#и коммутационных соотно-
соотношений G) представляет собой формулировку задачи в представле-
представлении Шредингера.

§ 12 КВАНТОВЫЕ СИСТЕМЫ СО ВЗАИМОДЕЙСТВИЕМ 105
Переход от одновременных коммутационных соотношений G)
к разновременным, т. е. конструктивный переход от представле-
представления Шредингера к представлению Гайзенберга, требует знания
вида временной зависимости операторов а± (т. е. явного вида
формул C)), что в свою очередь эквивалентно решению уравнений
движения. Таким образом, хотя канонические перестановочные
соотношения формально и решают задачу квантования системы взаи-
взаимодействующих полей, фактически они оказываются бедными по
физическому содержанию, так как совершенно не отражают дина-
динамики. -
12.2. Иллюстрация. Этот тезис может быть проиллюстрирован
следующей решаемой моделью:
J? = jpo(?i. /ni) + <3?o(<p2> msJ+gqVPa, (8)
где
Лагранжиан (8) может быть диагонализован путем подстановки
91 = cosa-«1+sina • и2, <p2 = i
где
Здесь подразумевается, что Am8 =m\ — т\>0, а выбор знака
корня соответствует тому, что при g->-0 и.-^-*-^ и «2->-ф2.
В результате преобразования имеем
причем новые массы могут быть представлены в виде
Проводя квантование новых свободных полей
[«*(*). «/(«/)] = — tikiDk(x- у)
и возвращаясь к исходным, получаем
i [фх (х), фх (г/)] = cos2 a • Dx (x — у) + sin2 a • D2 (к — г/),
i[f2(x), ф2(г/)}=со82аО2(х —г/) +sin2aDr(x —г/), (9)
»[ф1 (*). Ф2 («/)] = sin a cos a- {D2 (x-y)-D1 (х-у)}
— разновременные коммутационные соотношения, полностью отра-
отражающие' динамику задачи. Дифференцируя их по х° и полагая

106 гл. ш. взаимодействующие поля
затем x° = y° = t, можем получить канонические перестановочные
соотношения ^•
[Ф,(/, х), щA, у)] = 1бы8(х-у),
[<Pi(f, х), <ph(t, У)] = [%«, х), щЦ, у)]-0,
которые не содержат динамической информации, связанной со
взаимодействием полей <pi, <р2. -
Очевидно, что диагонализация лагранжиана (подобная прове-
проведенной) одновременно приводит- к явному решению уравнений
движения. Однако в реалистических моделях такое решение ока-
оказывается, как правило, невозможным.
Вместо него используют.метод теории возмущений—разлагают
искомое решение в ряд по степеням малого параметра, за кото-
который принимают константу связи. Исходное нулевое приближение
тем самым сводится к системе свободных уравнений, решения
которых нам уже известны и представляются суперпозициями
плоских волн. Такой подход является основным в сегодняшней
квантовой теории поля. Он формулируется в виде ковариантной
теории возмущений и органически связан с известными диаграм-
диаграммами Фейнмана. Его изложению посвящены следующие главы.
В методических целях представляется целесообразным рас-
рассмотреть задачу взаимодействия квантовых систем с бесконечным
числом степеней свободы в нерелятивистском приближении, исходя
из уравнения Шредингера в представлении чисел заполнения.
Такое рассмотрение позволит нам достаточно простым путем ввести
такие понятия, как перенормировка массы и волновой функции,
связанные с представлением об «облачении» частиц, обусловленном
эффектами квантового взаимодействия, а также понять физическую
природу ультрафиолетовых расходимостей локальной квантовой
теории поля.
12.3. Гамильтонов подход. Пусть имеется система N тожде-
тождественных частиц (бозонов или фермионов), связанных силами
парного взаимодействия. В представлении вторичного квантования
такая система описывается гамильтонианом
+ \г J a(ftja(q2) V (qlt q2; рх, р2)a{рх) a(/?t)dqx dq%dpx dp2. A1)
+
Здесь а, а — бозе- или ферми-операторы с заданными перестано-
перестановочными соотношениями
[a (ft), а-D)Ьг= 5 (* ~ Ф> 1а> а\ - Й а] = °- №)
Мы получили здесь, разумеется, формулировку квантовой задачи
взаимодействия в представлении Шредингера.

§ 12. КВАНТОВЫЕ СИСТЕМЫ СО ВЗАИМОДЕЙСТВИЕМ 107
Проекция оператора Я на одночастичное состояние Фх (ft) =
= a(ft) Фо будет
вследствие чего ю (ft) представляет энергию частицы с импуль-
импульсом ft. Проектируя затем Н на ЛЛ-частичное состояние, убеж-
убеждаемся, что V представляет собой энергию парного взаимодей-
взаимодействия двух частице соответствующими импульсами (см., например,
Блохинцев A976), § 118, Боголюбов A970), т. 2, с. 330-350).
формулы типа A1), A2) «хороши» тем, что они описывают
систему N частиц при произвольном, но фиксированном числе N
и явно от этого числа не зависят. Это свойство позволяет сделать
важное обобщение и отказаться от условия N — const. Для этого
достаточно так изменить функцию Н (а, а), чтобы она перестала
коммутировать с оператором полного числа частиц
N = \a{q)a{q)dq
или в случае, если система состоит из наборов, отличных друг
от-друга, но тождественных внутри каждого набора частиц, с опе-
операторами частиц соответствующих сортов Ni,
В качестве примера приведем так называемый гамильтониан
Фрёлиха
где
= 2] \Е (*)** (*)а* (*) dk + ]v(q)b (q) b (q) dq + H,, A3}
S
Нг = \ dk dk' dgVPr (ft, ft', q) as (ft) as (ft') (b (q) + b (- q)],
W(ft, ft', q) =
Здесь a, a — ферми-операторы электронов, s = ± V2 — спиновой
индекс, по которому подразумевается суммирование, о, b — бозе-
операторы фононов, Е и ю энергии электрона и фонона, g— кон-
константа связи в нормировке, принятой в теории сверхпроводимости.
Этот гамильтониан соответствует системе электронов в металле,
взаимодействующих с колебаниями кристаллической ионной
решетки. Член Нх описывает процесс возбуждения электронами
колебаний кристаллической решетки — процесс рождения кванта
этих колебаний — фонона, равно как и обратный процесс — про-
процесс поглощения фонона электроном. В соответствии с этим
гамильтониан Н?т коммутирует с оператором полного числа
электронов и не коммутирует с оператором полного числа фононов.
В такой, как мы ее называем, гамилыпоновой постановке
задача ставится следующим образом: найти собственные векторы

108 ГЛ- III. ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛЯ
состояний гамильтониана Н и отыскать его собственные значения,
соответствующие этим собственным векторам.
Если наряду с гамильтонианом Н заданы операторы других
динамических величин А (а, а, ...), то знание собственных век-
векторов позволит- получить соответствующие средние значения. Важ-
Важной величиной такого типа является импульс системы. Заметим
в этой связи, что введенные в этом разделе аргументы k,q,p...
операторов а и а пока не имеют физического смысла и отождест-
отождествлялись с импульсами частиц чисто формально Однако они при-
приобретают смысл импульсов, если определить оператор импульса
системы. Так для модели Фрёлиха
k (я = 1, 2, 3). A4)
Теперь нетрудно проверить, что
и вообще
Щ +ь (*0 ф«]=[2 /*+2 *£] (Л« (р'Щ +ь (*о ф
если
Аналогичным образом в надлежащих случаях можно ввести
операторы электрического заряда, спина и т. д.
12.4. Диагонализация модельных гамильтонианов. Процесс ре-
решения задачи в гамильтоновой постановке сводится к диагона-
лизации гамильтониана путем унитарного операторного преобра-
преобразования. Простой, точно решаемый пример дает гамильтониан так
называемой задачи «статического источника»
Я = J ш (ft) b{k) b (ft) dk + J [g (ft) b (ft) + *g (k)b (ft)] to (ft) dk. A5)
+ , *
Здесь b, b — бозе-операторы, a g(k), g(ft) — с-числовые функции,
характеризующие источник поля fe-частиц и являющиеся фурье-
образами соответствующих пространственных распределений.
Задача состоит в определении собственных функций и собст-
собственных значений уравнения Шредингера
) = Е(д)Ф(д).
Формальная операция «сдвига» переменных

§ 12. КВАНТОВЫЕ СИСТЕМЫ СО ВЗАИМОДЕЙСТВИЕМ '. Ю1Э
приводит гамильтониан A5) к диагональному виду
Я = \ to (ft) В (ft) В (ft) dk- $ to (k)\g(k) |2 dft.
Поэтому задача сводится к отысканию унитарного оператора,
осуществляющего преобразование Ь-*-В, т. е.
U-*(g)b(k)U(g) = B(k), U
С помощью стандартной техники (см. Дополнение IV) получаем
tf(g) = expjd*fc (*)£(*)-}(*)&(*)]. A6)
Для отыскания собственных функций гамильтониана Я заме-
заметим, что в терминах операторов В, В они имеют очевидную форму
WN = B(k1)...B(kN)W0, A7)
причем Yo — вакуум fi-поля:
B(k)W0 = G. A8)
Собственные значения, соответствующие A7), будут
Для того чтобы выразить состояние WN через собственные век-
векторы поля Ь, подставим в уравнения A7) и A8) формулы A6).
Умножая еще слева на U, получаем
Фм = U(g) VN = b (kj) ...b (kN) Фо,
причем состояние
®o = U(g)Vo A9)
на основании A8) удовлетворяет условию ЬФо = 0 и, очевидно,
является вакуумом 6-поля.
Рассмотрим подробнее структуру нового вакуумного вектора
x¥0 = U-1(g)QH. С этой целью приведем оператор U-1 к нормаль-
нормальному виду (см. (Д1У.1О))
t/-i (g) = Z»/. exp (- \dkg (ft) b (ft)) exp (j dq g (q) b (q)),
где
Таким образом, новый вакуум
Wo = Z1'. exp (- J dk g (ft) Mft)) Фо =

110 ГЛ. 177. ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛЯ
является суперпозицией бесконечного числа собственных состоя-
состояний гамильтониана H0 = ^ca(k)b {k)b (ft)dft.
Приведем еще без выкладок (см., впрочем, задание Н13)
решение задачи с билинейным взаимодействием двух бозе-полей
Н= 2 \<*{k)br{k)br{k)dk +
г= 1, 2
+$ g (ft) ш (ft) [h (ft) b2 (ft) + fe2 (ft) b, (k)} dk. B1)
Диагонализация достигается преобразованием
■Bl (ft) = f/ fc) fex (ft) t/ (g) == jj§ [6t (ft) - bt (ft)],
52 (*) = У -(ff) &2 (*) Uig) = 71 [6i (*) + &a (*)],
причем ' -
U (g) = exp |^= J d*[6t (*)^ (*) - bx (k) b% (*)]}. B2)
В результате получаем диагональное выражение для гамиль-
гамильтониана
r(k, g)Br(k)Br{k)dk, B3)
где
Оы(*. ?) =
Собственные значения имеют вид
НЧ{п, т) = Е(п, /и)Т(/г, т),
Е(п, т)= 2 Qi№)+ I] G, Г*»,
W (п, т) = Bt (ftx)... Bt (*„) 59+ (^)... В+ (^и) Т„,
а вакуум полей В совпадает с вакуумом полей b
bvyo=Bvyo=o.
Наконец, рассмотрим модельный гамильтониан, возникающий
в задаче о сверхтекучести:
H = \dk\(o(k)b(k)b (ft) +g(k) [b (ft) b (-k)+b (к) b (- ft)]}. B4)
Этот гамильтониан диагонализуется унитарным преобразованием
В (ft) = ch a (ft) b (к) + sh а (ft) b (— ft) = U~l (a) b (ft) U(a),
В (ft) = ch a (ft) b (ft) + sh а (к) b(—k) = U~l (a) b (ft) U (a),

§ 12. КВАНТОВЫЕ СИСТЕМЫ СО ВЗАИМОДЕЙСТВИЕМ 111
причем (ср. OUV,5.6))
In U (а) = $ dka (к) [Ь (к) Ь (— *) - Ъ (к) Ь (— *)], B5)
а а (k) находится из соотношения
2g (k) th а (к) = ю (*) - /ю2 (к) - ? (к). B6)
Основное состояние гамильтониана B4) определяется выра-
выражением
где Фо —вакуум поля Ъ. Приводя с помощью формулы (Д1У.12)
оператор (У (а) к нормальному виду, получаем
¥„ (а) = Z1/* ехр {— \ th a (k)b(k)b(— k).dk)o0, B7)
где
Z = ехр B Jdfclncha (*))..
Формула B7) содержит когерентную суперпозицию коррели-
коррелированных пар квантов первоначального поля Ь с противополож-
противоположными импульсами, т. е. таких пар, суммарный лмпульс которых
равен нулю.
12.5. Эффекты взаимодействия. Рассмотренные в предыдущем
разделе решаемые модели имеют в основном методическое зна-
значение. Правда, модель B1), аналогичная полевой модели (8),
имеет отношение к проблеме смешивания /('-мезонов (см., напри-
например, Липкин A977), гл. 7; Фейнман A978), § 10), а гамильто-
нова модель с линейным взаимодействием A5),' как указывалось,
родственна задаче фермион-бозонного взаимодействия юкавского
типа и ее решение будет использовано ниже в § 13 при анализе
однонуклонного сектора модели статического нуклона.
Здесь для нас основная ценность этих моделей заключа-
заключается в том, что полученные выше решения позволяют понять
в основных чертах физическую структуру эффектов взаимо-
взаимодействия.
Наиболее важным из них является переход к новым коорди-
координатам, к новой системе квантов возбуждения, описываемых пре-
преобразованными операторами В, В. В более реалистических моделях
точная диагонализация оказывается невозможной, однако, как
правило, ключом к приближенному решению является правиль-
правильный выбор той, наиболее физически важной части взаимодействия,
которая поддается диагонализации. Остальная часть взаимодей-
взаимодействия учитывается по теории возмущений.
Как мы убедились, в результате взаимодействия появляются
новые состояния, являющиеся (см. формулу B0)) бесконечными
суперпозициями состояний исходного гамильтониана Но. Таким

112 ГЛ. III. ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛЯ
образом, от системы векторов YN свободного гамильтониана Яо
мы переходим к системе векторов Ф# полного гамильтониана Н.
Иногда удается установить однозначное соответствие WN <-* Ф^,
и тогда имеет смысл говорить о том, что взаимодействие «одевает»
исходное «голое» состояние и превращает его в «одетое» или
«физическое» состояние Ф#. Процесс такого одевания меняет энер-
энергию кванта (в релятивистском случае —массу), а также может
приводить к изменению нормы и, как мы увидим ниже, к изме-
изменению константы взаимодействия, т. е. к эффекту экранировки.
Мы хотим напомнить здесь читателю, что эффект изменения
массы частицы под влиянием взаимодействия известен, например,
из квантовомеханической задачи движения электрона в кристалле
(см. Блохинцев A976), § 55; Давыдов A973), § 128), а экрани-
экранировка заряда, внесенного в среду, имеет место в классической
электродинамике.
Подобные эффекты изменения масс, констант связи и норм
состояний называются в квантовой теории эффектами перенорми-
перенормировок. Характерная особенность перенормировок в квантовой
теории поля связана с их сингулярным характером, обусловлен-
обусловленным локальностью взаимодействия. Разбираемая ниже модель
статического нуклона нелокальна, и при обсуждении эффектов
перенормировки мы рассмотрим переход к локальному пределу.
§ 13. Модель тяжелого нуклона
13.1. Формулировка модели. Рассмотрим задачу взаимодействия
юкавского типа между бесспиновыми легкими бозонами (мезонами)
и тяжелыми фермионами (нуклонами). Фермионы будем считать
настолько тяжелыми, что их энергия не зависит от импульса
(равна массе), а также пренебрежем возможностью переориента-
переориентации их спина (что оправдано при достаточно малых импульсах).
Вводя для мезонов бозе-операторы Ъ (к), Ъ (к), а для нуклонов
+
ферми-операторы а(р), а(р), запишем гамильтониан системы
в виде
H = H0 + Hlt A)
где
Яо = МI dp а (р) a{p) + \dkv (ft) b [к) b (k), B)
Н1 = $ dp $ dkg(k) <о (*)a(p + k)a (p) [b (к) + b (-к)]. C)
Здесь предполагается, что исходный лагранжиан мезон-нуклонного
взаимодействия нелокален:

5 13. МОДЕЛЬ ТЯЖЕЛОГО НУКЛОНА ИЗ
а формфактор F зависит лишь от модуля радиуса-вектора, при-
причем его фурье-образ связан с введенной в C) функцией g(k)
соотношением
,-s-w , - , v~, dx = gf (ft) = Bя)'/.]/2ю3(*)£г(Л), Jfe = |*|. D)
Локальному пределу F (х) = б3 (х) отвечают предельные выражения
Гамильтониан A) записан в шредингеровском представлении.
Операторы а, а удовлетворяют фермиевским перестановочным
соотношениям, а Ь, Ъ — бозевским. Член Нг описывает рождение
и уничтожение мезонов на нуклонах. Число нуклонов остается
неизменным. В отличие от обычного выражения типа ibibcp
++ +
(см. § 10.2), #! не содержит слагаемых вида aab и aab, ответ-
ответственных за рождение и аннигиляцию нуклонных пар. Поэтому
нелокальность не огранивается функцией «размазки» \Ф 1, а имеет
более глубокий характер. (Подробнее это обстоятельство рас-
рассмотрено ниже в § 15.3.) Если, однако, считать нуклоны очень
тяжелыми, т. е. M^>a(k) для всех физически существенных
импульсов, то реальные процессы рождения и аннигиляции пар
невозможны, а виртуальными эффектами этого вида мы условимся
пренебрегать, не вдаваясь в обсуждение законности такого при-
приближения. В этом смысле мы и будем ниже понимать формулу E)
как определение локального предела.
Отметим еще, что в соответствии с вышесказанным гамильто-
гамильтониан A) коммутирует с оператором полного числа нуклонов NK,
а также с оператором полного импульса
Pn=\pndpa (р)а (р) + \ kn dkb (к) Ъ {к) (п = 1, 2, 3) F)
и не коммутирует с оператором полного числа мезонов.
13.2. Решение в однонуклонном секторе. Модель статического
нуклона допускает точное решение в так называемом однонуклон-
однонуклонном секторе гильбертова пространства, состоящем из векторов "V,
удовлетворяющих соотношению
Такие состояния с фиксированным полным импульсом, равным р,
могут быть записаны в виде
]{q)<b{q), G)
где Ф(^) —вектор состояния, не содержащего нуклонов (и содер-
содержащего произвольное число мезонов), который имеет следую-

114 ГЛ. III. ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛЯ
щую структуру:
Fb(<l)®o- (8)
Здесь Фо — амплитуда вакуума, a Fb — некоторый функционал
от операторов рождения мезонов Ь с фиксированным полным
импульсом д.
Чтобы получить уравнения для мезонной амплитуды Ф,
вычислим проекцию коммутатора [а @), Я] на состояние Wp.
Имеем
[а @), Н0]Ч, = {М + $ dk ю (к) ЬЩ Ь (ft)} Ф (/>),
где введено обозначение
B(k)=g(k)co(k)[b
Таким образом, в однонуклонном секторе задача свелась к оты-
отысканию решения уравнения
р), (9)
где
W = [dkio(k)b(k)b(k)
— оператор энергии мезонов.
Для решения этого уравнения воспользуемся формулой (Д1У. 15).
Полагая в ней
п(к) = Ь(к)Ь(к), l±(k)=±g(k)e+ik*, X» = — g*(k),
получим
[rt(ft), e«*>] = — {g(fi)[b(k)+b(-k)]et** + ?{k)}e«*>, A0)
где
А (х) = [dq&*giq) [b (q)-b( -q)}
— антиэрмитов оператор.
Проверим, что решение уравнения (9) может быть записано
в виде
фМ(р) = т{р; Ь, Ь)ФО, A1)
где Фо — амплитуда мезонного вакуума, причем оператор Т имеет
следующую структуру:
т{р; b, b)=c\dxelP*eA(xh A2)

§ 13. МОДЕЛЬ ТЯЖЕЛОГО НУКЛОНА
Коммутируя Т с оператором энергии мезонов W, находим с по-
помощью A0)
\ A3)
где
$ ^j$g A4)
Принимая во внимание, что Ф0 = 0, получаем из A3)
dk В (Аг) Ф<°> (р + Аг) + ДМФ<°> (р) = 0,
Сравнивая это соотношение с (9), убеждаемся, что формулы (И),
A2) действительно дают решение уравнения (9) при условии
Таким образом, выражение A4) представляет поправку к массе
нуклона за счет взаимодействия с мезонным полем.
Набор формул G), A1), A2) дает нам явное выражение для
«одетого» однонуклонного состояния Wp'. Для его полной' конкре-
конкретизации следует определить константу с в уравнении A2), что
удобно сделать, исходя из условия нормировки
ф(°> (р) Ф(°» (/>') = S (р -р').
Подставляя в это условие представления G) и (И), находим
Используя формулу A2), с учетом антиэрмитовости оператора А
получаем в итоге интегрирования по q, x и у:
\с|2 \ dx \ dy \ dq^y-nv+p)* ф |елw-aw j 0) =
= BяK1с|2 J dxer-'P* = Bл)в |с|25 (р).
Поэтому можно положить с = Bя)~3.
Приведем еще оператор Т к нормальной форме для того,
чтобы записать правую часть формулы (И) в виде (8). Исполь-
Используя для этой цели формулу Хаусдорфа (см. (Д1У.1О)), запишем:
еА (*) _
где

1 16 ГЛ. III. ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛЯ
Собирая результаты, представим «одетое» однонуклонное состоя-
состояние в виде G)
^l^ A5)
где
Z = erL, ■ A6)
а амплитуда 47 удовлетворяет уравнению
Я47 = (М-ДМL7 A7)
и условию нормировки
4747=1. A8)
13.3. Свойства однонуклонного решения. Формула A5) пред-
представляет состояние физического нуклона 47 через бесконечную
суперпозицию состояний, содержащих один голый нуклон и про-
произвольное число мезонов.
Разлагая в ряд входящую в правую часть этой формулы опе-
операторную экспоненту, получаем после интегрирования по х
.. .} Фо. A9)
^ 2!
При этом амплитуда вероятности того, что физический нуклон
с импульсом *р находится в состоянии голого нуклона, равна
Ъч\ амплитуда вероятности того, что он «состоит» из голого
нуклона с импульсом p — q и мезона с импульсом q, равна
Z4'g(q) и т. д.
Важно отметить, что амплитуды высших слагаемых фактори-
зованы относительно импульсов мезонов. Бесконечные суперпо-
суперпозиции бозонных состояний такого типа известны под названием
когерентных состояний. Такие состояния Фког можно определить
операторным соотношением
где Р—с-число. Иными словами, когерентные состояния являются
собственными состояниями оператора уничтожения. Это свойство
имеет место как в импульсном, так и в координатном представ-
представлении. Физически важным является следующее из B0) свойство
фактор изуемости так называемых корреляционных функций поля Ь.
Именно это свойство и позволяет связать Фког с явлением опти-
оптической когерентности (см., например, Клаудер, Сударшан A970),
гл. 7).
Нетрудно показать, что амплитуда 47' описывает нижнее
состояние в однонуклонном секторе. Заметим для этого, что дей-

§ 13. МОДЕЛЬ ТЯЖЕЛОГО НУКЛОНА 1'7
ствие оператора уничтожения на эту амплитуду дает
&(ftL7' = -g(ftL7L*. B1)
что при k — О переходит в B0). Отсюда видно, что амплитуда
Wp' удовлетворяет условию
(здесь мы воспользовались обозначением из § 12.4). Таким обра-
образом, оператор уничтожения «одетого» кванта поля Ь действительно
аннигилирует амплитуду Wp'. Верхний индекс @) теперь приоб-
приобретает ясный смысл.
Представляет интерес построить бозе-возбуждения ^состояния
Wp'. Простейшее из этих состояний отвечает системе мезон + нук-
нуклон. Ищем такое состояние Wp"(k) с полным импульсом р\-к
в виде
Не составляет большого труда убедиться (см. задание HI7), что
это выражение при c(k) = g(k) является собственным вектором
гамильтониана, т. е.
(к), B2)
где
^ B3)
Любопытно отметить, что роль оператора рождения физического
мезона здесь играет выражение
h, B4)
где 1 ь — оператор, увеличивающий импульс на k, т. е. опреде-
определенный соотношением
Видно также, что формула B0) может быть переписана в виде
В(к)Чр = 0, B5)
где
-k. B6)
Заметим еще, что из того установленного выше факта, что
выражение B3), описывающее физическое состояние мезон ■+■ нук-
нуклон, является собственным вектором гамильтониана, непосред-
непосредственно следует отсутствие рассеяния мезона на нуклоне в рас-
рассматриваемой модели.
13.4. Переход к локальному пределу. Рассмотрим свойства полу-
полученного решения при переходе к локальному пределу E). Этот

1 18 ГЛ. III. ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛЯ
предел оказывается сингулярным. Для того чтобы изучить струк-
структуру возникающих сингулярностей, введем вспомогательный пара-
параметр Л, характеризующий «степень размазывания» формфактора
f(k). С этой целью определим формфактор следующим образом:
е-**/2л*; jfe-|ft|. B7)
Параметр Л играет роль импульса обрезания в импульсном пред-
представлении. В координатном представлении длина гА — Н/А харак-
характеризует область нелокальности нуклона. Для перехода к локаль-
локальному пределу следует устремить Л к со. Для дальнейшего обсуж-
обсуждения нам потребуются два интеграла
в которых мы использовали релятивистское выражение энергии
мезонов с массой ц. В пределе Л^>ц получаем
AAf~£-A, Lc*-£,b£. - B8)
Таким образом, в локальном пределе оба интеграла расхо-
расходятся. Интеграл ДМ" который, согласно A7), дает полевой вклад
в массу нуклона, расходится линейно по Л, т. е. обратно про-
пропорционален «размеру» нуклона гЛ. Второй интеграл, согласно
A5), входит в норму «одетого» состояния. На основании A9)
заключаем, что вероятность того, что «одетый» нуклон находится
в голом состоянии в локальном пределе, равна
т. е. стремится к нулю степенным образом. Вероятность состоя-
состояния, содержащего «голый» нуклон плюс один мезон
также стремится к нулю степенным образом и т. д.
Таким образом, в локальном »пределе связи между «голой» и
«одетой» массами, а также между собственными функциями сво-
свободного и полного гамильтонианов становятся сингулярными.

Глава IV. МАТРИЦА РАССЕЯНИЯ
§ 14. Матрица рассеяния
14.1. Теория возмущений. При рассмотрении задачи взаимо-
взаимодействия в квантовой механике исходят из уравнения Шредин-
гера
в которой полный гамильтониан системы Н представляют в виде
суммы гамильтониана свободного движения Но и гамильтониана
взаимодействия Ях:
A)
Поскольку, как правило, получить точное решение уравнения
Шредингера оказывается невозможным, обычно используют метод
теории возмущений. При этом в исходном приближении пренеб-
пренебрегают членом взаимодействия, получая точно решаемую задачу
^W. B)
В теории квантованных полей, как и в нерелятивистской
квантовой механике, точные решения удается получить лишь
в ряде довольно простых моделей. Поэтому здесь также обычно
прибегают к теории возмущений, основанной на исходном при-
приближении невзаимодействующих частиц. При этом приходится
вводить в рассмотрение соответствующие идеализированные сво-
свободные поля и рассматривать взаимодействие как некоторый
дополнительный фактор, мало изменяющий свойства динамиче-
динамической системы, фактор, который может «включаться» и «выклю-
«выключаться». На первый взгляд такая постановка вопроса как будто
не вызывает особых возражений. Действительно, элементарные
частицы интенсивно взаимодействуют лишь при достаточном их
сближении (в процессах столкновений). Поэтому кажется естест-
естественным, что на больших расстояниях взаимодействие между
полями несущественно, и в определенном приближении можно

120 ГЛ. IV. МАТРИЦА РАССЕЯНИЯ
пренебречь им и рассматривать реальные частицы как свободные.
Однако (как, например, хорошо известно из классической элек-
электродинамики) даже свободные частицы взаимодействуют с созда-
создаваемыми ими полями. В квантовом случае это приводит к возму-
возмущению нижнего (вакуумного) состояния —ср., например, задачу
статического источника в § 12.4. Иногда говорят, что частицы
взаимодействуют с вакуумом (свободных полей), как со своего
рода физической средой, в которой эти частицы движутся. Не-
Несмотря на возможную слабость взаимодействия, благодаря малости
размеров частиц эффекты взаимодействия оказываются большими
(в пределе точечных частиц —бесконечными).
Поэтому использование концепции «голых» (т. е. невзаимо-
невзаимодействующих даже с вакуумом) частиц оказывается неудовлет-
неудовлетворительным, и представляется весьма желательным с самого
начала иметь дело с реальными взаимодействующими частицами,
не вводя искусственного представления о фиктивных свободных
полях. Такая программа в известной степени реализуется в так
называемом аксиоматическом построении теории квантованных
полей.
Однако конструктивное проведение ее наталкивается на серь-
серьезные трудности математического характера. Дело заключается
в том. что единственным достаточно разработанным методом изу-
изучения взаимодействующих квантовых полей является сейчас лишь
метод теории возмущений. Этот метод исходит из приближения
невзаимодействующих полей, описываемых линейными уравне-
уравнениями. Все нелинейные вклады (соответственно в лагранжиане —
кубичные, трилинейные и т. д.), в том числе члены, описываю-
описывающие взаимодействия между полями и нелинейные эффекты само-
самодействия (см. §§ 10.2, 19.4), здесь рассматриваются как малые
возмущения. Константы взаимодействий (иначе — константы связи),
содержащиеся в этих членах, считаются малыми параметрами,
по возрастающим степеням которых и строится теория возмуще-
возмущений. Здесь следует подчеркнуть, что обращение к теории возму-
возмущений .молчаливо предполагает возможность использования раз-
разложений в ряд по степеням константы (или констант) взаимодей-
взаимодействия. Такое предположение фактически содержит две гипотезы:
а) Существование предела слабой связи у физически содержа-
содержательных решений уравнений квантовой теории поля. Решения,
обладающие таким пределом, назовем адиабатическими.
б) Аналитичность или достаточно слабую неаналитичность
в окрестности нуля по константе связи у адиабатического решения.
Использование этих гипотез исторически основывается на
квантовой электродинамике, т. е. модели квантовой теории поля,
описывающей взаимодействие электрически заряженных частиц
с электромагнитным полем. В этой модели константой связи
является, электрический заряд е, а параметр разложения теории

§ 14. МАТРИЦА РАССЕЯНИЯ 121
*
возмущений пропорционален постоянной тонкой структуры, кото-
которая в принятой здесь системе единиц имеет вид а = е2/4я.
Фактический параметр разложения имеет порядок 10-3[~а/я —
см., например, C0.5)]. Поэтому высшие члены теории возмуще-
возмущений в квантовой электродинамике являются численно весьма
малыми поправками к основным выражениям, получаемым из
первых неисчезающих порядков теории возмущений.
Такие выражения, вычисленные еще в конце 20-х годов, ока-
оказались очень близкими к экспериментальным значениям, вследст-
Ёие чего возможность использования разложений теории возму-
возмущений в квантовой электродинамике не вызывала сомнений.
Таким образом, гипотеза а) в квантовой злектродинамике
всегда представлялась вполне естественной. Благодаря этому она
фактически принималась справедливой и для других взаимодей-
взаимодействий. Справедливость гипотезы б) в квантовой электродинамике
не подвергалась сомнению по тем же соображениям.
С современной точки зрения правдоподобность гипотез а) и б)
в сильных взаимодействиях не является бесспорной. Эти гипотезы
противоречат некоторым обнаруженным в последние годы решаемым
квантовополевым моделям.
Тем не менее наша дальнейшая программа заключается в том,
чтобы построить аппарат квантовополевой теории возмущений
для вычисления матричных элементов и вероятностей переходов.
Как мы убедимся позднее, этот аппарат прекрасно работает
в квантовой электродинамике (см. ниже § 30)' и, по-видимому,
оправдывает себя в области слабых взаимодействий (§§ 31, 32).
14.2. Представление взаимодействия. При отсутствии взаимо-
взаимодействия система квантовых полей описывается аналогом уравне-
уравнения B) для амплитуды состояния W:
d^ C)
Выполняя формальную квадратуру, получаем
Постоянная амплитуда Ф была введена в § 6. В случае взаимо-
взаимодействия выражение D) уже не будет удовлетворять уравнению
движения
^ У«). E)
Однако мы можем обобщить его, полагая, что Ф зависит от вре-
времени:
Т(/) = е-ш«'Ф(/). F)
Подставляя F) в E), получаем

122 ГЛ. IV. МАТРИЦА РАССЕЯНИЯ
Обсудим смысл полученного уравнения. Плотность <£%" (х) гамиль-
гамильтониана взаимодействия
.Я, = $ «ЯГ (•*)<**,
(в видах экономии места мы опускаем нижний индекс 1 под зна-
знаком интеграла), входящего в правые части E) и G), обычно
является полиномиальной функцией от операторов полей в пред-
представлении Шредингера:
а а
Но, согласно F.20),
е^вЯГ{х)е~ш<* = Пe'W"«(°- *)е~Ш4 = П"«(х),
а а
где иа (х) — операторы поля в гайзенберговском представлении
относительно гамильтониана свободного движения. Поэтому дей-
действие оператора е'^ ...e~i^°t сводится к замене оператор-
операторных функций свободных полей шредингеровского представления
и(х) = и@, х) на операторные функции свободных полей в гай-
гайзенберговском представлении и (t, x) = u{x).
Для новой амплитуды состояния Ф(/), согласно G), имеем
теперь .
*^0. = Я(*)Ф(*). (8)
причем пространственная плотность о%~ {х) оператора
dx (9)
зависит от свободных полей в гайзенберговском представлении.
Такое представление уравнения Шредингера называется представ-
представлением взаимодействия (иногда представлением Дирака).
Приводя к этому представлению среднее от динамического
оператора В
Bt = Ф it) ВЧ (t) = Ф A)еш^Ве-ш«'Ф (t),
видим, что оно может быть записано в виде среднего по ампли-
амплитудам Ф@ представления взаимодействия от выражения
efWBe-t'V = Bm(f), A0)
которое естественно считать представлением взаимодействия для
динамической переменной В. ,
Выполненное ранее преобразование для гамильтониана взаимо-
взаимодействия можно записать в виде
Hn(t) = H(t). A1)

§ 14. МАТРИЦА РАССЕЯНИЯ 123
Поэтому в представлении взаимодействия операторы динамических
величин следует рассматривать как функции от операторов
поля и(х) в представлении Гайзенберга для свободных полей.
14.3. Матрица рассеяния. Заметим, что уже с помощью (8)
мы можем ввести в рассмотрение очень важную характеристику
системы — так называемую матрицу рассеяния, или 5-матрицу.
Пусть мы изучаем процесс, в начале и в конце которого имеются
лишь далеко отстоящие друг от друга частицы, которые можно
считать свободными. Чтобы вычислить амплитуду вероятности для
происходящих в этом процессе рассеяний и взаимных превраще-
превращений частиц, рассмотрим положение, при котором взаимодействие
Н1 it) адиабатически включается в бесконечно удаленном прошлом
и адиабатически выключается в бесконечно удаленном будущем.
Обозначая амплитуду начального состояния через Ф(—со), а ампли-
амплитуду конечного состояния через Ф(со), свяжем их соотношением
Ф(сзо) = 5Ф(— со), . A2)
в котором оператор 5 называется оператором рассеяния. Ясно,
что оператор 5 можно задать совокупностью его матричных эле-
элементов (амплитуд переходов)
где |а) — некоторое начальное состояние, характеризуемое сово-
совокупностью квантовых чисел {а} = а!, а2, ..., представляющих
как дискретные, так и непрерывные наборы значений, а |Р) —
соответствующее конечное состояние. Квадрат модуля |5ра|2 опре-
определяет вероятность перехода из |а) в |Р).
Таким образом, оператор 5 условноможно представить в виде
матрицы бесконечного ранга, составленной из элементов 5ра. Его
обычно называют матрицей рассеяния.
Чтобы получить явное выражение для оператора S, вернемся
к уравнению Шредингера в представлении взаимодействия и
построим его решение в виде разложения по степеням взаимо-
взаимодействия #!, отправляясь от исходного приближения, которое
выберем как функцию Ф(*о) начального состояния в некоторый
«исходный» момент t — t0. Получим
5(*. /0)Ф(д, A3)
причем
5 (t, Q^l- i{ Я (Г) df + (- if \ H {t') df $ Я (t") df + ...
to
...+ (- О" $ я (tx) dtx \ я (g dtt... \ я \ta) dtn+... (И)

124
ГЛ. IV. МАТРИЦА РАССЕЯНИЯ
Члены полученного разложения допускают весьма любопыт-
любопытную перестройку. Продемонстрируем ее на примере третьего
w
¥№')№')
Рис. 14.1. Преобразование области интегрирования при изменении порядка
интегрирования во втором порядке теории возмущений для матрицы рассея-
. ния [см. формулу A4)J,
члена правой части. Меняя обозначения переменных интегриро-
интегрирования t'*-*t" и порядок интегрирования, получаем (рис. 14.1)
t V it
i J H (f) dt' J H (Г) dt" = \df I dt"H {t") H (t%
t0 t0 to f
Представляя затем исходное выражение в виде полусуммы исход-
исходного и преобразованного, находим
t
H (f)dt' J H (t")dt" = ~ J dt' К dt"H (?) H (f) + J dt"H (t")H(t')\.
Выражение, стоящее в фигурных скобках, может быть записано
в более компактной форме
{...} = \dt"T{H(t')H(t")}
to
с помощью нового символа
Я (?) Я i
? > Г,
A5)
— символа хронологического (или упорядоченного по времени) про-
произведения. Общий п-й член правой части в A4) может быть пре-
преобразован к виду
t t
х... J dtnT {H (tj H (/,)... Я (tn)\,
где символ Т {Н (ti).. «Н (tn)} для любого взаимного расположе-
расположения временных аргументов равен произведению гамильтонианов

§ И. МАТРИЦА РАССЕЯНИЯ 125
в порядке невозрастания аргументов слева направо:
т {н (у... я D)} = я (у я (*„)... я (*„) я (д,
*eS**pSs*...Ss*oS**p. A6)
Представляя каждый член правой части A4) с помощью
Г-произведения и вынося символ Т из-под знаков интегрирова-
интегрирования, получаем
A7)
— так называемую хронологическую экспоненту.
14.4. Хронологические произведения. Выражение A7) содержит
хронологические произведения Н (t, х) = Н(х). Такие произведе-
произведения операторных выражений, зависящих от точек 4-мерного про-
пространства-времени, являются непосредственными обобщениями
определений A6). Мы, однако, пойдем по другому пути и отпра-
отправимся от Г-произведения локальных операторных функций поля.
Определим хронологическое произведение п операторов поля
ui(xi)< ыа(*г)> •••> ип(хп) как произведение этих операторов
в порядке, соответствующем неубыванию временных аргументов
слева направо, с учетом общего знака, который может меняться
в случае, если часть операторов квантована по Ферми —Дираку.
Здесь необходимо сделать важное уточнение. Временная последо-
последовательность двух точек xh Xj не является релятивистски инва-
инвариантным понятием в случае их пространственного подобия {xi~Xj).
Поэтому новое определение будет лоренц-инвар иантным лишь для
операторов, (анти) коммутирующих вне светового конуса:
щ (х^ щ (Xj) = щ (xj) щ (х^, Xi~Xj, т] =* ± Г ' A8)
Такие операторы назовем локальными операторами полей.
Очевидно, в частности, что частотные части операторов ы± не
являются локальными. Имеем по определению для локальных
операторов поля ult ... ип:
Т (и, (хг) и, (х2) ... ип(хп)) = ti«ti (*,J ... щп (^J,
xi^xi^...^>xin. (.19)
Здесь символ х~^>у обозначает, что точка х лежит в верхнем
световом конусе точки у или пространственноподобна ей, а т] =
= (—1)р, где р — четность перестановки ферми-операторов при
переходе от порядка A, 2, ... п) к порядку (ix, i%, ... t^).

126
ГЛ IV. МАТРИЦА РАССЕЯНИЯ
Теперь можно ввести хронологическое произведение локаль-
локальных операторных выражений А1(х1) ... Ап(хп)
Т {Аг(xj) ... Ап(хп)) = ц\ (х{%) ... Ain(xin)y
xcl^xi^...^xin. B0)
Операторным локальным выражением А„ (х) относительно поля
и (х) будем называть операторное выражение, зависящее от поле-
полевой операторной функции и(х) и ее производных, взятых в целом
(ы = «++«-) в точке х и (анти) коммутирующее с оператором
поля при пространственноподобном разделении аргументов
\Аи(х), и(у)}± = 0, х~у.
Такие операторы обычно сводятся к нормальным произведе-
произведениям операторных функций и (х). Они обладают свойством взаим-
взаимной локальной (анти) коммутативности:
At (x) Aj (у) = у\А; (у) At (х), х~у, B1)
вследствие чего определение B0) является непротиворечивым.
Здесь, правда, следует сделать одну существенную оговорку.
Дело в том, что (анти) коммутаторы типа B1) обычно имеют син-
сингулярность при х = у. Поэтому хронологические произведения A9),
B0)' оказываются неопределенными при совпадении двух и более
аргументов (xv .... х%). Этой неопределенностью можно распо-
распорядиться по-разному— см. ниже § 16.
В дальнейшем операторы А (х), содержащие четное число опе-
операторов Ферми, будем называть локальными бозе-операторами
или просто локальными, а операторные выражения, содержащие
нечетное число фер ми-операторов, —локальными операторами
Ферми.
Примерами локальных операторных выражений являются лаг-
лагранжиан ^ (х), тензор энергии-импульса, 4-вектор тока.
14.5. Хронологическая экспонента. Возвращаясь к матрице
рассеяния A2), видим, что для получения S из оператора 5(/1( t0)
следует устремить гг к+сх^ a t0 к — со. С учетом того, что для
моделей, не содержащих производных от функций в лагранжиане
взаимодействия, гамильтониан отличается от функции Лагранжа
лишь знаком, т. е.
получаем
S = S (оо, -oo) = Texp(t \dxZ{x)) = TeiM. B2)
Здесь od — часть действия системы, содержащая взаимодействие,
т. е. действие взаимодействия.
Здесь уместно сделать предупреждение. При рассмотрении
выражений, подобных стоящим в правой части B2), может воз-

§ 15. ОБЩИЕ СВОЙСТВА S-МАТРИЦЫ
127
никнуть искушение вынести не зависящий от времени явно фак-
фактор типа <г/£ из-под знака Г-произведения. Нужно помнить, что,
согласно введенным определениям (ср. A7)), всегда следует пред-
представить такой фактор в виде интеграла от локального оператор-
операторного выражения и внести символ Т под знак интеграла. Например,
второй член разложения B2) будет
Т (я**) *$<&$■ dyT {X (х) ,Х(у)). B3)
Отметим ещё, что хотя мы получили Г-экспоненту от лагран-
лагранжиана B2) с помощью уравнения Шредингера и Г-экспоненты
от гамильтониана A7), выражение B2) оказывается справедливым
и тогда, когда лагранжиан взаимодействия содержит производные
от функций поля. В этом случае оказывается, что можно опре-
определить S-матрицув виде B2), исходя из ряда общих требований —
таких, как причинность, унитарность, релятивистская инвариант-
инвариантность и принцип соответствия (см. ниже§ 15). В то же время ввести
оператор гамильтона Я оказывается затруднительным (подробности
см. во Введении, гл. VII). Поэтому в дальнейшем мы будем
использовать выражение B2) без соответствующих оговорок.
§ 15. Общие свойства S-матрицы
15.1. Матрица рассеяния как функционал. Как отмечалось
в § 14, можно, следуя первоначальной идее Гайзенберга,_ ввести
S-матрицу (соответствующую бесконечно большому интервалу
времени /1 = сх>, /0 = — со) непосредственно, не обращаясь к урав-
уравнению Шредингера, гамильтониану и оператору S (tlf t0) для
конечных tt и t0. Вместо этих свойств и понятий для конкрети-
конкретизации формы S-матрицы используются явно сформулированные
физические условия:
а) причинности,
б) унитарности,
в) релятивистской ковариантности,
г) принцип соответствия,
которые принимаются в качестве исходных аксиом. Такой способ
построения S-матрицы, восходящий к работам Штюкельберга и
Боголюбова начала 50-х годов, принято называть аксиоматиче-
аксиоматическим (см. Введение, §§ 20, 52, а также книгу Боголюбова, Логу-
Логунова, Тодорова A969)). В § 16 мы обсудим содержание и форму-
формулировку аксиом и получим выражение для S-матрицы, аналогичное
A4.22) с соответствующими комментариями.
При этом нам окажется необходимым определить S-матрицу
как функционал от некоторых вспомогательных классических
функций. Дело в том, что обычная матрица рассеяния, описывае-
описываемая выражением A4.22) и соответствующая взаимодействию кван-
квантовых волновых полей во всем пространстве-времени, не зависит

128 ГЛ. IV. МАТРИЦА РАССЕЯНИЯ
от каких-либо обычных функций, и потому ее матричные эле-
элементы не содержат никаких функциональных зависимостей.
Введение в лагранжиан взаимодействия какой-либо неквантован-
ной функции превращает S-матрицу и ее матричные элементы
в функционалы. Вычисляя функциональные производные этих
функционалов, можно ввести в рассмотрение пространственно-
временные свойства различных величин, входящих в теорию
(например, условие причинности). При этом «классические поля»
играют роль вспомогательных переменных в промежуточных
рассуждениях и обычно исключаются из окончательных выраже-
выражений соответствующим предельным процессом.-
Подобное вспомогательное классическое поле можно ввести,
например, в виде заданного внешнего поля uext(x) или заданного
внешнего тока каких-либо частиц Jext (х). Так, при изучении
поведения заряженных частиц во внешнем электромагнитном
поле в лагранжиан взаимодействия вводят внешний неквантован-
ный электромагнитный потенциал:
X-* X (ЛехО = е щ (х) yvi|j (*) (Ay (x) + A$xt (x))u A)
Матрица рассеяния оказывается тогда функционалом -
S->S(i4ext).
Менее физически наглядный, но более удобный технически
способ состоит в процедуре введения в лагранжиан взаимодейст-
взаимодействия классического функционального аргумента в виде «функции
области взаимодействия» g(x). Эта функция позволяет формали-
формализовать операции «включения» и «выключения» взаимодействия.
Чтобы математически описать эту операцию, введем функцию
g(x) со значениями в интервале [0, 1], характеризующую интен-
интенсивность включения взаимодействия. В областях, где g(x) = 0,
взаимодействие отсутствует, там где g=l, оно включено пол-
полностью, а при 0<.g<l 1 — лишь частично. Заменяя действитель-
действительный лагранжиан взаимодействия X произведением X(x)g{x),
мы придем к взаимодействию, «включенному с интенсивностью
Пусть теперь g отлична от нуля лишь в некоторой конечной
пространственно-временной области. В этом случае в достаточно
отдаленных прошлом и будущем поля являются свободными, и
потому начальное и конечное состояния динамической системы
можно характеризовать обычными постоянными амплитудами состоя-
состояния, введенными в гл. II. Эти две величины Ф (— оо) и Ф (со) будут
связаны некоторым оператором- S, преобразующим Ф(—оо)
в Ф (оо) и зависящим от поведения функции g. Фиксируя ампли-
амплитуду начального состояния Ф(—оо) = Ф, мы можем рассматри-
рассматривать конечную амплитуду как функционал от g:
B)

§ 15. ОБЩИЕ СВОЙСТВА S-МАТРИЦЫ 129
Согласно этому определению S (g) естественно интерпретиро-
интерпретировать как матрицу рассеяния для случая взаимодействия, вклю-
включенного с интенсивностью g. Реальный случай, когда взаимодей-
взаимодействие включено полностью во всем пространстве-времени, должен
в данной схеме рассматриваться с помощью предельного пере-
перехода, при котором область, где g= 1, неограниченно расширяется
и в пределе охватывает все пространство-время. При этом обыч-
обычная матрица рассеяния S может быть определена в виде
5 = 5A). C)
Нам придется часто пользоваться понятием функциональной
производной, являющимся естественным обобщением понятия
частной производной. Как известно, частная производная неко-
некоторой функции п переменных zlt ..., zn может быть определена
как коэффициент при dzt в сумме
представляющей дифференциал этой функции.
Пусть теперь мы имеем некоторый функционал / (ы), вариация
которого б/ (и), определяемая как главная часть приращения
/ (ы + бы) — / (и), может быть представлена интегралом вида
б/ (и) = $ Я (х, и) бы dx.
в
Здесь R является функционалом ы, зависящим от положения
точки х в области G, подобно тому как в сумме (*) Rt был функ-
функцией zlt ..., zn, зависящей от индекса i. Тогда, по аналогии
с вышеприведенным определением частной производной, введем
понятие функциональной производной функционала / (и) по ы
в точке х, определив ее соотношением
б/ (и) п , .
—-U. = R(x, и).
Таким же образом можно ввести и функциональные производ-
производные высших порядков, причем легко видеть, что функциональные
производные обладают основными свойствами обычных произ-
производных.
15.2. Релятивистская ковариантность и унитарность. Сформу-
Сформулируем теперь ряд основных физических условий, которым должна
удовлетворять матрица S. Важным физическим требованием, как
всегда, является условие релятивистской ковариантности. Для
его явной формулировки рассмотрим преобразование Р из неод-
неоднородной группы Лоренца, т. е. группы Пуанкаре
х-г+х' = Рх. D)
3 Н. Н. Боголюбов, Д, В, Ширков

130 ГЛ. IV. МАТРИЦА РАССЕЯНИЯ
При отсутствии взаимодействия закон преобразования амплитуды
состояния, соответствующий преобразованию D), согласно F.22)
имел вид
Ф' = иРФ. E)
Теперь же, когда <D = <D(g-), необходимо учесть также, что пре-
преобразованию D) подвергается сама функция g (x), которую можно
рассматривать как некоторое «классическое скалярное поле»; так
как область взаимодействия, описываемая функцией g, при пре-
преобразовании D) остается неизменной, то переход в аргументе g
к новым координатам дает
. F)
Поэтому закон преобразования амплитуды Ф (g) имеет вид
G)
Из соображений релятивистской ковариантности нужно потребо-
потребовать, чтобы закон преобразования B) от начальной амплитуды
к конечной не зависел от системы отсчета, т. е. чтобы
Внося сюда E) и G) со сдвинутым (Pg-*-g) аргументом, находим,
с учетом B),
USiP^O
Ввиду произвольности амплитуды начального состояния Ф это
выражение можно записать в операторной форме:
или, сдвигая аргументы на Р, умножая справа на Up1 и учиты-
учитывая унитарность Up:
S (Pg) = UPS (g) Up = UPS (g)UP. (8)
Эта формула и выражает условие ковариантности оператора S (g).
Сформулируем теперь другое общее обязательное требование —
требование сохранения нормы волновых функций. Применительно
к данному случаю мы должны потребовать
откуда, при условии обратимости оператора S, вытекает, что
S(g)S(g) = S(gK(g) = l, (9)
т, е. оператор 5 (g) должен быть унитарным.

§ 15. ОБЩИЕ СВОЙСТВА S МАТРИЦЫ 131
В соответствии со сказанным в § 14 полученное соотношение
можно также записать в виде
25p,^)Sva(g) = /pa, (9')
у
причем символ ^] обозначает суммирование по дискретным и
V
интегрирование по непрерывным квантовым числам, характери-
характеризующим состояние |у), а символ /^ равен произведению соот-
соответствующих символов Кронекера и б-функ-
ций Дирака.
15.3. Условие причинности. Следует обес- _
печить еще выполнение условия причинно- "ч^у kt
сти, т.е. позаботиться о том, чтобы измене- ■ \t-v
ние закона взаимодействия в какой-либо про- —
странственно-временной области могло ока-
оказать влияние на эволюцию системы лишь
в последующие моменты времени. рис 15 , и
Чтобы сформулировать условие причин- ция' взаимного распо-
ности в явном виде, рассмотрим сначала слу- ложения областей вза-
чай, когда область G пространства-времени, имодействия к форму-
в которой функция g отлична от нуля, рас- ле С3)-
падается на две отдельные подобласти G1 и
G2 такие, что все точки одной из них (G^ лежат в прошлом от-
относительно некоторого момента времени / = т, а все точки другой
(G2) —в будущем относительно / = т (рис. 15.1). Функция g при
этом может быть представлена в виде суммы двух функций
g(x) = gl(x) + g2(x), A0)
одна из которых gx отлична от нуля лишь в Glt а вторая g2—
лишь в G2.
В момент времени т можно определить состояние, характе-
характеризующееся амплитудой Фт, которая по соображениям причин-
причинности не должна зависеть от взаимодействия в области G2 и
может быть поэтому представлена в виде
, (П)
где S (g{) —матрица рассеяния для случая, когда взаимодействие
включено с интенсивностью gi. Конечное состояние Ф (g) может
быть получено из Фх с помощью оператора S (g2), описывающего
взаимодействие в области G2:
<D(sr) = S(&)(Dt. A2)
Сравнивая A0) —A2) с B), находим, что
Sfei + &) = S(£2)Stei) при G2>G±. A3)
б*

132
ГЛ. IV. МАТРИЦА РАССЕЯНИЯ
(Неравенство G2'>G1 обозначает, что все точки области G3 рас-
расположены по времени позже всех точек области Gv) Соотноше-
Соотношение A3) является формулировкой принципа причинности для
случая Gi^-Gi.
Отметим здесь, что если, кроме того, Gt ~ G2, т. е. все точки
области Gi пространственноподобны всем точкам области G2
(рис. 15.2), то временной порядок областей может быть изменен
соответствующим преобразованием Лоренца. Поэтому
S(?,)Sfe) = Sfe)Sfe) при GX~G2. A4)
Формулы A3), A4) представляют формулировки условия причин-
причинности, записанные для оператора S(g) в целом. Для теоретиче-
теоретических приложений оказывается более эффективной дифференци-
дифференциальная формулировка условия причинности.
Рис 15.2. Взаимное расположи-
те областей взаимодействия в
случае, соответствующем фор-
формуле A4).
Рис. 15.3. Иллюстрация к выбору дифферен-
дифференциального условия причинности A6).
15.4. Дифференциальное условие причинности. Для того чтобы
получить его рассмотрим два случая, которые отличаются друг
от друга видом взаимодействия в области G2 и описываются
одной и той же функцией в Gx (рис. 15.3), именно
g' (X) = gi (X) +gl (х), g" (х) = gi (X)+gl (x).
Составляя выражение S {g") S (g1), убеждаемся, что оно не зависит
от поведения функций g" и g' в области Gv В самом деле, так
как, согласно A3),
при G2>Glt
то с учетом свойства унитарности матрицы S (gj) получаем
5 ig") S (gr) = S (gi) S (gl) S (gt) S (gS) = S (gS) S (g'l).
+
Таким образом, произведение S (g") S (gr) действительно не зави-
зависит от поведения функции g в области G^ Это происходит

§ 15. ОБЩИЕ СВОЙСТВА S-МАТРИЦЫ 133
потому, что содержащаяся в S (g") зависимость от состояния
системы до момента времени t уничтожается соответствующей
частью оператора S (g). Поэтому и в более общем случае мы
примем следующую формулировку условия причинности:
Если имеются две функции g" (x) и g' (х), совпадающие
при х°, меньшем некоторого t, то произведение S (g") S {g1)
не должно зависеть от одновременного изменения функций
g1 и g" на одну и ту же величину в области х° < t.
Сформулируем теперь условие причинности в дифференциаль-
дифференциальной форме. Если положить g'(y) = g(y) и g"(y)=g(y)-{-&g(y),
где 8g (у) — бесконечно малая вариация функции g, отличная от
нуля лишь при y°>t, то матрица S(g") может быть представ-
представлена в виде
причем
y°>t
Теперь видно, что произведение
S (g")S (g') = S (g)S(g) + 8S (g)S (g)=l +8S (g)S(g)
не зависит от поведения функции g при x°<.t<.y°.
Переходя к вариационной производной, мы можем поэтому
сформулировать условие причинности как условие независимости
выражения
Со/ v л.
A5)
от поведения функции g(x) в точке х при х<1у. По соображе-
соображениям ковариантности отсюда также следует, что оператор A5)
не может зависеть от поведения функции g(x) и при х^у.
Условие причинности, очевидно, можно записать в виде
Мс/„\\ = о при х<.у. A6)
Это соотношение представляет собой формулировку принципа при~
чинности в дифференциальной форме.
Мы имеем, таким образом, условия релятивистской ковариант-
ковариантности, унитарности и причинности, которые в совокупности
представляют достаточное основание для построения S-матрицы,

134 ГЛ. IV. МАТРИЦА РАССЕЯНИЯ
§ 16. Аксиоматическая ^-матрица
16.1. Разложение по степеням взаимодействия. Теперь мы
поставим задачу построения оператора S(g), удовлетворяющего
условиям ковариантности A5.8), унитарности A5.9) и причинности
A5.16). При этом мы полностью отвлечемся от рассуждений § 14
и полученной там на основе уравнения Шредингера формулы A4.22).
Будем искать оператор S (g) в виде формального функциона-
функционального ряда по степеням g:
^Sn(xi,...,xn)g(x1)...g(xn)dx1...dxn, A)
в котором Sn (xv ... , хп) являются операторными выражениями,
зависящими от полных функций поля и(х^), ..., и(хп) и их част-
частных производных в целом, а не от частотных составляющих ы-
по отдельности, причем фермиевские операторы поля входят в Sn
лишь в четных комбинациях.
Операторные выражения такого типа будем называть полило-
полилокальными. Для двух полилокальных операторов A (xv ... , хп),
В (и ...» ут) имеет место следующее свойство:
, ..., хп), В(уг ут)] = 0,
когда все х{ пространственноподобны каждому у].
В нашем случае условие
[Sn(xlt ..., хп), Sm(ylt ..., ут)] = 0 (xt~yj) B)
имеет важный физический смысл. Если две функции g, и g% лока-
локализованы в таких пространственно-временных областях, что любая
точка одной области пространственноподобна всем точкам другой
области, то S (gx) будет коммутировать с S (g^). Этим, в сущности,
выражается тот факт (также являющийся проявлением принципа
причинности), что сигнал не может распространяться со скоро-
скоростью, большей скорости света.
Возвращаясь к выражению A), видим, что без ограничения
общности Sn можно считать симметричными функциями своих
аргументов х,, ... , хп, так как весовые функции gfai), ... , g(xn)
входят симметричным образом.
16.2. Условия на Sn- Для определения конкретного вида функ-
функций Sn следует подставить разложение A) в условия A5.8), A5.9),
A5.16). Условие ковариантности приводит к линейному условию
(xv ..., xn)UP = Sn (Pxv ..., Pxn), C)

§ 16. АКСИОМАТИЧЕСКАЯ S-МАТРИЦА 135
тогда как условие унитарности дает нелинейные соотношения
+
Sn (Х1> ••• > хп) 4" Sn \Xlt • • • > хп) 4"
+ Л1Р(х1, ..., xk\xk+1, ..., xn)Sk(xlt ..., xk)x
ft +
xSn-tfe+1 лл)=0. D)
+
Здесь Sn — эрмитово сопряженный оператор к Sn, а символ
Р(хг xk\xk+l xn) обозначает сумму по всем nl/kl {n~k)\
разбиениям совокупности точек хх, ..., хп на две совокупности k
и n — k точек. При этом перестановки внутри каждой из сово-
совокупностей не учитываются, так как функции Sk симметричны
по своим аргументам. Например,
Р(хъ хг | х3) S2 (*!, A^)S1(jc^=S2(xl, xi)S1(x3) +
+ St(xl, x9)S1(xJ + Si(xi, xJSM.
Результат использования условия причинности имеет вид
Нп(у\ хг xn)=0, 5
если хотя бы для одного xt (/ = 1, ..., п) ~^>
Здесь Нп — коэффициенты разложения оператора A5.15)
Н(у; g)= 2 rf^Hniy; *i, ••-, xjgfa) ... g (xn) dxj.... dxn, F)
связанные с Sn нелинейными соотношениями
Нп (У, х1} ..., xn) = i 2 P(xv ..., xk\ xk+1 xn) x
X Sk+1 (y; xlt ..., xk) Sn_k (xk+1, ..., xn). G)
Условия B) и (З) фиксируют общие свойства локальной ком-
коммутативности и ковариантности операторных функций Sn, а нели-
нелинейные условия D) и E) могут рассматриваться как рекуррентные
соотношения, что позволяет получить схему последовательного
определения функций Sn через «предыдущие» Sk(l ^k^n—l).
Рассмотрим в качестве исходной величину Sx (x). Из условия
унитарности D) получаем, что
Sl(x) = U6(x), (8)
где X — эрмитов оператор. Формула C) при л=1 дает условие
ковариантности для X, а формула B) при л = яг=1 приводит
к условию локальной коммутативности для Х\
\Х(х), Х{у)] = 0 (х~у). (9)
Условие локальной коммутативности является частным слу-
случаем условия B). Оно налагает существенные ограничения на

136 ГЛ. IV. МАТРИЦА РАССЕЯНИЯ
структуру оператора X (х). В аксиоматическом построении этот
оператор играет роль лагранжиана взаимодействия. В силу усло-
условия (9) X (х) должен зависеть от четного числа ферми-полей,
причем каждое из полей должно входить в X (х) в целом; а не
своими отдельными частотными слагаемыми. Подобные оператор-
операторные конструкции, зависящие от полей в точке х, в § 14.3 мы
назвали локальными. Условие локальной коммутативности, таким
образом, приводит к требованию локальности лагранжиана вза-
взаимодействия.
16.3. Определение явного вида S2 и S3. Для определения S2
запишем условие причинности E) при л = 1:
St(x, y)+S1(x)S1(y) = S2(x
Таким образом,
Si(x, у) = -Э5(х)Х(у) при
В силу симметрии S2 имеем также
() при
Области определений двух последних формул перекрываются
при х ~ у. Требование их совместности приводит нас к условию
локальной коммутативности (9). В то же время эти соотношения
определяют S2 всюду, кроме точки х = у. Имеем
Как видно, поведение Sa при совпадающих аргументах не опре-
определяется рекуррентными соотношениями. Поэтому можно написать
52 (х, у) = /2Г (X (х) X {у)) + /Л, (х, у). A0)
Введенный здесь оператор Л^ по определению обладает свойством
Аг(х, у)=0 при хфу A1)
и потому называется квазилокальным. В более общем случае квази-
локальНый оператор, зависящий от п аргументов, определяется
условием
An(xlt ... хп)=0 всюду, за исключением точки
х1-х2 = ... = хп. A2)
Подставляя A0) в условие унитарности A5.9), получаем, что
оператор-/Л2 должен быть антиэрмитов, а Л2 соответственно эрми-
эрмитов +
А.2(х, у) = Аг(х, у).
Таким образом, использованные аксиомы позволяют определить
оператор S2 через оператор первого порядка Sx с точностью
до квазилокального антиэрмитова оператора /Ла.

§ 16. АКСИОМАТИЧЕСКАЯ S-МАТРИЦА 137
Как можно показать (см. Введение, § 21), такая ситуация
оказывается типичной и для высших Sn (л^З). Так, например,
Sa(x, у, z) = isT(X(x)X(y)X(z)) +
+ i*T(X(x)A2(y, z)) + PT(X(y)Ai(x, z)) +
+ PT (X (г) Л2 (х, у)) + /Л, (х, у, г), A3)
где Л8 —эрмитов квазилокальный оператор.
16.4. Общий вид S(g). В общем случае Sn выражается сум-
суммой, состоящей из слагаемых трех различных типов. Это, во-пер-
во-первых, Г-произведение от X(х^), ..., X(хп), затем сумма различных
Г-произведений отX(х}) и квазилокальных операторов Av ..., An_j
и, наконец, «новый» квазилокальный оператор Л„:
5„(Xl xn) = i"T(X(Xl)X(х2) ...X(хп)) +
+ ЦТ{Х, Alt Л2 АП^} + !АП(Х1 хп), A4)
Сравнивая формулы (8), A0), A3), A4) с разложением Г-экспо-
ненты, полученной ранее в § 14, видим, что выражение
Sn(х, xn) = i"T(X(Xl) ...X(xn)),
соответствующее
S(g) = T{exp(i\X(x)g(x)dx)], A5)
и в пределе g->■ 1 — формуле A4.22), в которой оператор X есть
лагранжиан взаимодействия, является допустимым в смысле удов-
удовлетворения всем наложенным на Sn условиям. Оно, однако,
не является самым общим. Для того чтобы получить выражения
для Sv S2,..., Sn, необходимо, кроме локального оператора X(х),
задать цепочку квазилокальных операторов А„(х1, х2),...
Мы пришли к несколько странным на первый взгляд резуль-
результатам, Для полного определения матрицы S (g) задания лагран-
лагранжиана взаимодействия оказывается недостаточным, и необходимо
задать еще бесконечную цепочку квазилокальных операторов Л„.
Однако можно показать, что выражение для S(g) при Л^, ..., Л„,
отличных от нуля, может быть приведено к виду
(x; g)dx)), A6)
в котором «лагранжиан» X (х; g) определяется соотношением
%(х; g) = X(x)g(x) +
()---S(Xv)dx1...dxv. A7)
В силу квазилокального характера функций Av все интеграции
здесь снимаются и X (х; g) фактически зависит от функций поля

138 ГЛ. IV. МАТРИЦА РАССЕЯНИЯ
и(х) в точке х, являясь поэтому локальным оператором. Кроме
операторов поля и выражение X (х; g) зависит также от функций
g(x), которые можно рассматривать как «классическое» поле. Сле-
Следовательно, выражение A6) удовлетворяет всем наложенным на
S (g) условиям и может рассматриваться как выражение для
матрицы рассеяния. Разлагая A6) в ряд по степеням g, мы полу-
получим выражения A4) для Sn {хг, ... , хп), удовлетворяющие всем
необходимым условиям.
Переходя к физическому пределу g = 1, получаем
S = S A) = Г (exp(f $•£(*; l)dx)), A8)
где
%{х, 1) = #(х) +2(-^~ j Лт (х, х1,..., xv)dXl...dxv. A9)
Следовательно, реальная матрица рассеяния S(l) полностью
характеризуется лагранжианом взаимодействия системы %{х\ 1),
который в теории возмущений иногда представляется в виде ряда.
§ 17. Теоремы Вика
17.1. Приведение к нормальной форме. Прежде чем приступить
к вычислению матричных элементов от S-матрицы, следует озна-
ознакомиться с рядом свойств алгебраического характера, которыми
обладают операторные выражения, построенные из квантованных
свободных полей.
Ввиду очевидного удобства нормальной формы представления
операторных выражений для последующего вычисления матрич-
матричных элементов приобретает важность вопрос о соответствующей
методике приведения к нормальной форме.
В первую очередь мы рассмотрим технику приведения для
обычных произведений (первая теорема Вика), а затем для хро-
хронологических произведений (вторая теорема Вика), встречающихся
в матрице рассеяния.
Ясно, что для приведения к нормальной форме операторных
выражений, полиномиально зависящих от полевых операторов,
достаточно уметь приводить произведения типа Ах(Xj) ... Ап(хп),
в которых А (х) будут «линейными операторами», т. е. линейными
комбинациями соответствующих и+(х), и~ (х).
В каждом данном случае непосредственное преобразование
такого произведения не представляет принципиальных затрудне-
затруднений. Для этого совершенно достаточно последовательно переме-
перемещать ы+ налево, а иг направо и при каждой «передвижке»
использовать перестановочные соотношения. Тем не менее ввиду
большого числа получающихся при этом членоз уже при срав-
сравнительно малых п целесообразно иметь рецептуру для возможно

§ 17. ТЕОРЕМЫ ВИКА 139
более автоматического выполнения операции приведения к нор-
нормальной форме.
Такая рецептура вытекает из одной важной теоремы, уста-
установленной Виком, к формулировке которой мы сейчас и перейдем.
17.2. Первая теорема Вика. Пусть мы имеем произведение
двух линейных операторов А(х)В(у). В этом случае для приве-
приведения к нормальной форме, очевидно, достаточно одна передвижка
операторов иг(х), и+(у), и потому в результате получатся члены
с «правильным порядком» следования положительно- и отрица-
отрицательно-частотных частей волновых функций и вклад от переста-
перестановочных функций, уже не включающий операторных выражений.
Таким образом, рассматриваемое произведение может отли-
отличаться от нормального произведения :А(х)В(у): лишь на с-выра-
жение (ср. выкладку в § 8.2), которое будем называть спарива-
спариванием и обозначать с помощью скобок снизу:
А (х)В(у) = :А {х)В(у): + А{х)В(у). A)
Поскольку вакуумное среднее от нормального произведения
всегда равно нулю, мы можем также определить спаривание как
вакуумное среднее от обычного произведения:
= (А(х)В(у)H. B)
Рассмотрим в качестве примера вещественное скалярное поле.
Исходя из перестановочных соотношений для частотных частей
<j>- (х) ф+ (у) - ф+ (у) ф- (х) = — Ю- (х-у),
получим
()() ()() -Ю-(х-у). C)
Таким образом,
ф (х) Ф (у) = <Ф (х) ф (у)H = ф-(*)ф+ (у) = — iD- (х-у),
уЧ*)у-(у)=о. DJ
Аналогично для случая электромагнитного поля найдем
Лу(*)Лц(у) = <А,(х)А„(у)H = ig^Do (х-у). E)
Рассмотрим еще поле фермионов, для которого
у), F)
и потому
()() iS() G)
а также
(8)

140 ГЛ. IV. МАТРИЦА РАССЕЯНИЯ
И
(9)
Для того чтобы сформулировать теорему Вика, нам понадо-
понадобится также понятие нормального произведения со спариванием,
которое мы определим следующим образом:
:А1 (хг) А2fa) ... A, (xj) ... А{(xt) ... Ап(хп): s=
i . i
ssу\А) (xj) At (xi): Aj. fa) ... АмА/+1 ... А^А^ ... Л„:, A0)
где г| = (—1)р, а р~ четность ферми-перестановок при переходе
от порядка 1, ..., / — 1, у, /+ 1, ..., i■ — 1, i, i+\, ..., п к по-
порядку у, /, 1, ..., /— 1, /+1, .... i— I, i+1, .... л. ■
Совершенно аналогично определим и нормальное произведение
с любым числом спариваний. Именно, выражение
:А1 (xt) А2 (х2) А3 (х3) '... Ak{xk) ■. • Ап_г (дг„_,) Ап (хп):
будем считать равным произведению всех имеющихся спариваний
на нормальное произведение операторов, оставшихся неспарен-
ными, и на число г) = (—1)^, т. е. выражению
т)Л1Лд,Л2Лл_1 :Л3 ... Ак-^Аь^ Лл_2 ... Ап:,
где р — четность перестановок, которым подвергаются ферми-
операторы в процессе вынесения спариваний за знак нормального
произведения.
Так, например,
:|а (х) фр (у) % (г) г|>а (/): = — Щ*(х)Ъу (г)
Из этого определения вытекает сразу же, что нормальное
произведение со спариваниями обладает свойством линейности
по отношению к своим сомножителям и что при их перестановке
под знаком такого произведения оно умножается на г) = (—1)р
где р — четность перестановок ферми-операторов.
Мы можем теперь Дать простую формулировку первой теоремы
Вика. Согласно этой теореме
обычное произведение линейных операторов равняется сумме
всех соответствующих нормальных произведений со всевоз-
всевозможными спариваниями, включая нормальное произведение
без спариваний:
Аг ... Ап=:Ах ... Ап: + ^1:А1 ... А, ... А,... Ап: +
1Щ I J
+ 2 -A... Ai...AJ...Ak...Al...An: + ... A1)

§ 17, ТЕОРЕМЫ ВИКА 141
Нетрудно видеть, что эта теорема приложима и к случаю,
когда некоторые из сомножителей входят со знаками нормальных
произведений
.. Ар. ... А/1 ... :Ар ... Ап\.
В этом случае она формулируется точно так же, как и для «чис-
«чистого» произведения Ах ... А„, с тем очевидным отличием, что теперь
не надо принимать во внимание спариваний между множителями,
принадлежащими к одному и тому же нормальному произведению.
Например, не должны учитываться спаривания между Лу+1, ...., А^,
спаривания между Лр, ..., Л„ и т. д.
17.3. Хронологические спаривания. При вычислении матричных
элементов матрицы рассеяния нам придется иметь дело с хроно-
хронологическими произведениями лагранжианов. Для этого нам потре-
потребуется выражать Г-произведения локальных операторных выра-
выражений через нормальные произведения соответствующих операторов
свободных полей.
Рецепт процедуры приведения хронологических произведений
дает теорема Вика для Г-произведений, являющаяся аналогом
теоремы Вика для обычных произведений. Прежде чем приступить
к доказательству этой теоремы, введем важное понятие хроноло-
хронологического спаривания операторов.
Рассмотрим с этой целью формулу A4.19) для случая двух
операторов поля:
Правая часть в соответствии с определением обычного спарива-
спаривания A) может быть преобразована к виду
Uj_ (x) и, (у), х° >у°,
Отсюда видно, что в любом случае Т (иг (х) ы2 (у)) отличается от
:«! {х) ы2 (у)- на с-число, которое мы назовем хронологическим спа-
спариванием операторов иг и ы2, т. е. по определению
Т К (х) щ (у)) = :иг (х) ы2 (у): + и^и, (у) A3)
Отметим прежде всего важную особенность хронологического
спаривания. Под знаком хронологического спаривания можно
изменять порядок сомножителей, точно так же, как и под знаком

142 ГЛ. IV. МАТРИЦА РАССЕЯНИЯ
нормального произведения:
что непосредственно следует из A4).
Определим хронологические спаривания для операторов основ-
основных волновых полей. Заметим для этого, что, вычисляя вакуум-
вакуумное среднее от A3) с учетом основного свойства нормального
произведения и нормированности амплитуды вакуума, мы получим
(T(u1(x)utQ/))H^ii1(x)u,(y). A5)
Таким образом, хронологическое спаривание двух операторов
равно вакуумному среднему от Г-произведения этих операторов.
Имеем в частных случаях:
для скалярного поля .
"Р (*) Ф (У) = i (Ту (х) ф (у))о =
= Q(xo-yo)D-(x-y)-Q(yo-x°)D+(x-y), A6)
для электромагнитного поля
ц (У) =;
x-yy, A7)
для спинорного
* (х) ъ (у) =[ (ТУ* (*) ь (у)\=
б (х° - у°) S«p (х -у)-в (у0 - х°) S+p (х - у) A8)
и т. д. (определение функции б см. (ДУ. 3)).
Как будет установлено ниже в § Г8.2, правые части этих соот-
соотношений являются решениями соответствующих неоднородных
уравнений поля, т. е. представляют собой функции Грина.
Отметим сейчас, что эти правые части соотношений типа A4)
были определены лишь для х°~>у° и х°<.у°. Из установленного
выше свойства ковариантности Г-произведений вытекает теперь,
что они определены всюду, кроме случая х = у. Правила же
интеграции этих выражений в бесконечно малой окрестности
точки х — у можно фиксировать произвольно. Так, например,
можно добавить к правой части каждого из них любую коэффи-
коэффициентную функцию квазилокального оператора Р (дх) 5 (х — у),
где Р (дх) — какой-либо полином по дх = д/дх. Эта необходимость
дополнительного определения спаривания в бесконечно малой
окрестности точки х = у является частным следствием произвола,
содержащегося в Г-произведении. В самом деле, Г-произве-
Г-произведения заданы формальным определением A4.20) и A2) лишь при
несовпадающих значениях своих аргументов.

§ 17. ТЕОРЕМЫ ВИКА 143
17.4. Вторая теорема Вика. Эта теорема для хронологических
произведений состоит в утверждении, что Г-произведение п
линейных операторов равно сумме их
нормальных произведений со всеми возможными хронологи-
хронологическими спариваниями (включая член без спариваний).
Доказательство сводится практически к доказательству теоремы
Вика для обычных произведений. В самом деле, согласно опре-
определению A4.20) Г-произведение всегда равно некоторому обыч-
обычному произведению
Г(А,(хг) ...Ап(хп)) = цАк (хк) ...А/п(х/п).
Применяя к этому произведению первую теорему Вика, видим,
что оно равно сумме нормальных произведений операторов Ак,
..., Ajn со всеми возможными обычными спариваниями. Но так
как порядок следования А< А1п является хронологически
правильным, то обычные спаривания совпадают с хронологиче-
хронологическими, т. е. данное Г-произведение равно умноженной на г|
сумме нормальных произведений операторов Afi Afn со всеми
возможными хронологическими спариваниями.
Как уже отмечалось, под знаком хронологического спаривания,
как и под знаком нормального произведения, операторы можно
переставлять (с учетом изменения знака). Тем самым под знаком
нормальных произведений со всевозможными хронологическими
спариваниями можно восстановить нормальный .порядок сомножи-
сомножителей 1, 2 опустив одновременно множитель ц. Теорема
доказана.
Введем теперь в рассмотрение Г-произведение нескольких
нормальных произведений линейных операторов поля:
Г'(-.А^х) А2(х) ...Ап(х):... :D,{z) ... Dn{z):). A9)
Именно такие Г-произведения встречаются при раскрытии Г-про-
изведений локальных операторов, так как по определению
локальный оператор %{х) представляется линейной комбинацией
членов типа :А1(х)Аг(х) ... Ап(х):.
Для Г-произведений вида A9) формулировка второй теоремы
Вика имеет лишь ту особенность, что не должны учитываться
хронологические спаривания операторов, входящих в одно и то же
нормальное произведение.
17.5. Третья теорема Вика. В приложениях оказывается полез-
полезным предложение, утверждающее, что
вакуумное ожидание от хронологического произведения п + 1
линейных операторов А, Вх, ..., Вп равно сумме п вакуум-
вакуумных ожиданий тех же хронологических произведений со всеми

144 ГЛ. IV. МАТРИЦА РАССЕЯНИЯ
возможными спариваниями одного из этих операторов (напри-
(например, А) со всеми остальными, т. е.
(TAB, ... ВпH = 2 (TAB, ...Bt... BnH. B0)
Это предложение можно назвать теоремой Вика для вакуум-
вакуумных ожиданий или третьей теоремой Вика.
Обратим внимание на то, что в правой части B0), в отличие
от двух первых теорем Вика, не содержится выражений с числом
спариваний, большим единицы.
Тем не менее справедливость B0) непосредственно вытекает
из второй теоремы Вика. Ввиду исчезновения вакуумного ожида-
ожидания нормального произведения любого, отличного от нуля числа
неспаренных операторов, левая часть B0) равна сумме всех воз-
возможных вариантов «полных взаимных спариваний» внутри произ-
произведения операторов
АВх...Вп, B1)
т. е. спариваний, где спарены друг с другом все операторы.
Совершенно аналогично любой из членов суммы в правой части
B0), например первый, может быть представлен в виде
АВ1(ТВгВ3...ВпH
и равен произведению спаривания АВХ на сумму всех возможных
полных спариваний операторов Вг Вп.
Выполняя суммирование по i в правой части B0), получаем
сумму всех возможных полных спариваний операторов B1). Тем
самым третья теорема Вика доказана.

Глава V. ДИАГРАММЫ И ПРАВИЛА ФЕЙНМАНА
§18. Функция Грина свободных полей
В конце предыдущей главы было установлено, что операторные
слагаемые 5-матрицы с помощью второй теоремы Вика сводятся
к нормальным произведениям с хронологическими спариваниями.
Как можно показать, эти последние являются функциями Грина
свободных полей.
18.1. Функция Грина скалярного поля. Покажем прежде всего,
что хронологическое спаривание операторов скалярного поля
выражается через функцию Грина специального вида уравнения
скалярного поля.
Функцию Грина скалярного поля G определим как решение
неоднородного уравнения Клейна — Гордона
(nx-m*)G(x) = -8(x). A)
Здесь и ниже знак перед б-функцией в правой части уравнений
для функций Грина для определенности будем полагать равным
знаку перед массовым членом в левой части.
С помощью фурье-преобразования получаем для G следующее
формальное выражение:
Это выражение является неопределенным, поскольку не заданы
правила обхода полюсов k2 = tn2. Неопределенность отражает тот
факт, что полное решение уравнения A) представляется в виде
суммы частного решения неоднородного уравнения и решений D+
и D' однородного уравнения, взятых с произвольными коэффи-
коэффициентами. Задание правил обхода двух полюсов при &2 = та или
наложение на G граничных условий однозначно определяет эти
коэффициенты.
Покажем это для запаздывающей функции Грина, удовлетво-
удовлетворяющей граничному условию
)=0 при *°<0. C)

146
ГЛ. V. ДИАГРАММЫ И ПРАВИЛА ФЕЙНМАНА
Чтобы представить ее в виде, близком к B), заметим, что при
умножении этой функции на ехр (—гх°), где е>0, в силу C)
она не приобретает каких-либо дополнительных особенностей:
вследствие чего ее можно представить как предел
*)• D)
Согласно определению функция GB удовлетворяет уравнению
{А - (-J- + еJ - mj Ge (x) = - б (х)
и потому в импульсном представлении в пределе е->0 принимает вид
1 1
Таким образом, в соответствии с D) запаздывающая функция
Грина может быть представлена следу-
ющим образом:
Рис. 18.1. Путь интегриро-
интегрирования в комплексной плоско-
плоскости переменной ko для функ-
функции Dret.
Не составляет труда убедиться, что
выражение E) удовлетворяет условию
C). Для этого достаточно выполнить
в явном виде интегрирование по пере-
менной k° с помощью теории вычетов.
Бесконечно малая добавка в знамена-
теле указывает, что оба полюса в комп-
комплексной плоскости переменной k° долж-
должны быть обойдены сверху (рис. 18.1). Поэтому при *0<;0, когда
контур интегрирования может быть замкнут в верхней полупло-
полуплоскости полуокружностью большого радиуса, внутри него не ока-
оказывается полюсов, и мы получаем нуль. При л;°>0 контур инте-
интегрирования замыкается в нижней полуплоскости. Вычисляя вы-
вычеты, находим в этом случае
nret (x\ L_ I
Поэтому
Dr^(x) = Q(x°)D(x). F)
Аналогичным образом можно показать, что опережающая функ-
функция Грина, определяемая условием
= o при

§ 18. ФУНКЦИЯ ГРИНА СВОБОДНЫХ ПОЛЕЙ 147
и удовлетворяющая уравнению A), имеет вид
- - в <- *•> D М- G)
18.2. Причинная функция Грина Dc в квантовой теории поля
играет исключительно важную роль. Она отвечает правой части
A7.16), при х°>у° пропорциональна D~(x — y), а прих°<у0 —
функции D+(x — у).
Не составляет труда убедиться, что эта правая часть может
быть представлена в виде разности
б (х°) D- (х) - б (— х°) D+ (х) = Dret (х) - D+ (х)
решения неоднородного уравнения Dret и однородного уравнения
D+ и, следовательно, удовлетворяет тому же уравнению A), что
и Dret.
Положим поэтому
Dc (*) = 0 (*°) D-(*) — 9(—afi)D*(x). (8)
Чтобы получить для причинной функции Грина Dc выражение
в импульсном представлении, заметим, что разность Dret — D+ мо-
может быть в этом представлении записана следующим образом:
что дает
(здесь & — символ главного значения — см. (ЦУ.б) — (ДУ.8)).
Поскольку перестановочные функции электромагнитного, спи-
норного и векторного полей могут быть получены из функции
Паули — Йордана с помощью дифференциальных соотношений, то
причинные функции этих полей выражаются через Dc {x) теми же
самыми соотношениями:
D(x),
(&v + i^v)D'(*), ( )
причем, например,
S£p (*) = 8 (*°) S" (*) - 8 (-*°) S+(*) =
Bя)* J ma_p2_l-8 e ДР- UU
Теперь мы можем вернуться к вопросу о доопределении хро-
хронологических спариваний в точке х = у. Условимся считать, что

148 ГЛ. V. ДИАГРАММЫ И ПРАВИЛА ФЕЙНМАНА
если при х Фу хронологическое спаривание совпадает с некоторой
причинной функцией Грина, то оно совпадает с этой функцией
и в бесконечно малой окрестности точки х = у. Иными словами:
для скалярного поля
для электромагнитного поля
iv(*) Ai (У) = (TAV (x) Лц (у)H =
—ig Dc (х у) = f — dk A3)
для векторного поля
(у) = (TUv (х) U» (у))о = iDvV (x - у) =
Bnf J m*-№-ie e aR>
для спинорного поля
Bя)* I
18.3. Особенности на световом конусе. Полученные функции
Грина, равно как и перестановочные функции соответствующих
полей, могут быть выражены в явном виде через цилиндрические
функции и сингулярные (обобщенные) функции типа б (л;2), б (х°)
и т. д.
Опуская соответствующие выкладки, приведем выражения для
функций скалярного поля.
Перестановочная функция Паули — Йордана —
Здесь Я = х2 = xl — хг, а е и б —известные разрывные функции.
Из формулы A6) непосредственно вытекает важнейшее свойство
перестановочной функции —она равна нулю вне светового конуса:
D(*) = 0, *2<0. A7)
Частотные части D-функции имеют вид
^xKMV=>). (is)

§ 18. ФУНКЦИЯ ГРИНА СВОБОДНЫХ ПОЛЕЙ 149
Здесь Jx, NL и /Ci — функции Бесселя, Неймана и Ханкеля от
мнимого аргумента. В окрестности нуля они имеют следующие
разложения:
4
— N < ) = — —
К ( \— — 4-
Причинная функция Грина —
причем
V— X + i8 = iVX при Я>0.
Запаздывающая функция Грина —
W> (ТС) B0)
Из приведенных формул следует, что в ^-представлении все
особенности функций D, D±, Dc и Dret сосредоточены только
в окрестности светового конуса. Например:
+ 0(ЯI B1)
М_Л!£
B2)
Полученные выражения имеют особенности четырех типов: полюс
1/Я, 1п|Я|, б (Я) и скачок б (Я). Множители е (л;0) и б (л^) в отдель-
отдельных слагаемых не создают дополнительных особенностей вне све-
светового конуса благодаря тому, что стоят вместе с б (Я) или 8 (Я).
Они проявляются лишь в начале координат.
Имея в виду дальнейшие нужды, отметим, что функции ска-
скалярного и векторного полей обладают структурой
Оскал. вектМ=т^ (т'Я, —у) , B3)
а функции спинорного поля
Р[ ^j B4)

150 ГЛ. V. ДИАГРАММЫ И ПРАВИЛА ФЕЙНМАНА '
В силу этого, например, особенности типа б (Я) и Я-1 в B3)
сопровождаются множителями, не зависящими от массы т, а осо-
особенности In | Я | и б (Я) — содержащими тг.
Таким образом, перестановочные и причинные функции кван-
квантовых полей представляют собой сингулярные функции, содер-
содержащие сильные особенности на световом конусе.
С математической точки зрения такие функции принадлежат
к классу несобственных, или обобщенных функций. В отличие от
обычных функций, обобщенные функции определяются не путем
установления соответствия между значениями функции и значе-
значениями ее аргумента, а заданием правил интеграции произведений
их с достаточно регулярными функциями. Например, б-функция
характеризуется правилом интеграции ее произведения с непре-
непрерывными функциями, производные б-функции — правилами инте-
интеграции их с соответственно дифференцируемыми функциями и т. п.
Иначе говоря, несобственная функция определяется заданием
соответствующего линейного функционала в подходящем «линейном
пространстве» достаточно регулярных функций. Не имея возмож-
возможности вдаваться в сколько-нибудь подробное обсуждение свойств
обобщенных функций (см. с этой целью Введение, гл. III и книгу
Владимирова A976)) отметим лишь проблему умножения обоб-
обобщенных функций друг на друга. Дело в том, что обобщенная
функция задается установлением правил ее интеграции лишь
с достаточно регулярными функциями, а из таких правил рецеп-
рецептура интеграции произведения нескольких обобщенных функций
непосредственно не вытекает.
§ 19. Диаграммы Фейнмана
19.1. Коэффициентные функции. Обсудим математическую при-
природу коэффициентных функций матрицы рассеяния, т. е. функций,
стоящих множителями при нормальных произведениях операторов.
Эти функции очевидным образом входят в матричные элементы
S-матрицы, которые мы рассмотрим в следующем параграфе. Они
могут быть получены с помощью второй теоремы Вика и запи-
записаны в виде
К(хх, ..., хп) = ПD£p (xr-xs), A)
Г, S
где хг и xs пробегают множество значений хи хг,..., хп. (Имеется
в виду коэффициентная функция для Sa(x1 *„).) Как было
установлено в § 18, сомножители правой части A) являются
обобщенными функциями.
Проблема умножения сингулярных причинных функций Грина
является главной трудностью квантовой теории поля. Эта труд-
трудность, именуемая проблемой ультрафиолетовых расходимостей,

§ 19 ДИАГРАММЫ ФЕИНМАНА . 151
на два десятилетия затормозила развитие теории частиц и была
преодолена в конце 40-х годов созданием теории перенормировок.
Мы вернемся к этому вопросу в следующей главе, а пока будем
иметь в виду, что выражения вида A), как правило, определены
чисто формально.
Обратимся теперь к разработке удобной рецептуры получения
отдельных слагаемых в суммах, составляющих операторные выра-
выражения Sn (хх хп). Такие слагаемые представляются произве-
произведением коэффициентной функции вида A) на нормальное произ-
произведение оставшихся неспаренными операторов:
K(Xi хп): ... uk (xk) ...и, (xj) ...:. B)
Построение конкретной функции К, соответствующей данному
порядку спаривания операторов, может быть выполнено с помощью
диаграмм и правил Фейнмана.
19.2. Графическое изображение Sn- В соответствии со второй
теоремой Вика операторные функции Sn (xx хп) представ-
представляются суммой членов, каждый из которых является произведе-
произведением некоторого числа спариваний операторных функций поля
на нормальное произведение оставшихся неспаренными операто-
операторов свободных полей.
Каждому такому члену может быть поставлено в соответствие
графическое изображение, составленное по очень простым прави-
правилам. Это изображение, именуемое диаграммой Фейнмана, содер-
содержит, во-первых, п точек хх, х2 хп — вершин диаграммы, опи-
описывающих аргументы оператора Sn (xx хп). Каждому из спа-
спариваний соответствует линия, соединяющая соответствующие
вершины:
Ut(Xt)Uj(Xj)
Каждому неспаренному оператору ставится в соответствие
линия, выходящая из данной вершины и идущая к краю диа-
диаграммы (линия со свободным концом):
Численные и матричные множители из лагранжиана X (х{) при-
приписываются соответствующей вершине.
Очевидно, что в результате каждая вершина с топологической
точки зрения будет характеризоваться полным набором выходя-
выходящих из (или, если угодно, входящих в) нее линий, каждая из
которых соответствует одному из операторов, стоящих в данном
лагранжиане взаимодействия.

152 ГЛ. V. ДИАГРАММЫ И ПРАВИЛА ФЕЙНМАНА
Так, для лагранжиана взаимодействия спинорно*! электроди-
электродинамики имеем
, • C)
Для того чтобы отличать различные поля, операторам электро-
электромагнитного поля ставится в соответствие волнистая линия, а опе-
операторам поля Дирака —сплошная. При. этом спинору ty(x) отве-
отвечает линия, входящая в точку л:, а сопряженному спинору ар(л:) —
выходящая. Спинорные линии таким образом (в отличие от
электромагнитных) являются направленными.
Графический элемент C) представляет собой как бы нагляд-
наглядное изображение акта испускания (или поглощения) фотона элек-
электроном (или позитроном).
\ У N /
/*
ay f)
<---о-
Рис. 19.1. Диаграммы второго порядка в модели ф4.
Более простой пример дает модель скалярного поля с четвер-
четверным взаимодействием Лф4. Такому лагранжиану взаимодействия
отвечает вершина с четырьмя одинаковыми линиями:
h:p'*(x): оо \я , D)
' / \
В качестве иллюстрации рассмотрим член S2 для этой модели:
S2 (х, у) = ДОГ {:Ф*(х): :ф* (у):} = W :ф4 (дс) Ф4 (г/): +
+ l6i*h\W<p (у) :фз (л;) Фз (у): + 72W[фИУ^ (y)f: ф2 (дс) ф2 (у): +
+ 96.W[Т^Гф (г/)]3: Ф (*) «Р (»): + 24W[фИУ^ (у)]\
Соответствующие диаграммы изображены на рис. 19.1. В более
общем случае га > 2 мы получим набор диаграмм с га вершинами,
содержащих различные комбинации внутренних и внешних линий.

§ 19. ДИАГРАММЫ ФЕЙНМАНА 153
Внешние линии диаграмм имеют простой смысл. Так, диаграмма
рис. 19.1,6 содержит четыре свободные (внешние) линии, что
отвечает как раз четырем неспаренным операторам, стоящим под
знаком нормального произведения. Соответствующие слагаемые
S-матрицы дают вклад в матричный элемент переходов 1«3 и
2<->-2. Поэтому внешние линии можно считать наглядным изо-
изображением движения начальных и конечных частиц.
Внутренние линии соответствуют виртуальным частицам.
19.3. Спинорная электродинамика. Более сложные случаи опи-
описывают взаимодействия различных полей, обладающих матричной
структурой. Обратимся к спинорной электродинамике —см. C).
В этом случае операторное выражение Sn будет иметь следую-
следующий вид:
K...v...(*i, ■.■. *я):...$(**)...4v(*i)...$(*m)...:. E)
Как видно отсюда, S-матрица переводит состояние |а> сдан-
сданным фиксированным набором квантов электромагнитного и спи-
норного полей в состояния с другими наборами. Обращаясь
к формуле (8.21), видим, что если начальное состояние |а) яв-
является физическим, т. е. временные и продольные кванты в нем
либо отсутствуют, либо входят в определенных комбинациях, соот-
соответствующих формуле (8.20), то и конечные состояния | Р) будут
физическими.
Отсюда, в частности, вытекает, что соотношения типа усло-
условия унитарности A5.9') можно писать в виде
7
где суммирование в левой части распространяется на состояния,
содержащие лишь физические составляющие электромагнитного
поля. Напомним, что причина этого свойства, связана с тем, что,
как подчеркивалось в § 4.3, продольная степень свободы % (х) не
связана ни с поперечными Л1г, ни с другими полями (в данном
случае с полем а|э, ар).
Коэффициентная функция K...v...(---X---) из формулы E) яв-
является произведением хронологических спариваний двух типов,
которые условимся изображать различными графическими сим-
символами
, F)
G)

154 ГЛ. V. ДИАГРАММЫ И ПРАВИЛА ФЕИНМАНА
Стрелка в изображении второго спаривания помещена для того,
чтобы различать между собой выражения ty(x)ty(y) и ty(y)ty(x).
Для неспаренных операторов, стоящих под знаком нормаль-
нормального произведения, положим
у. « , (8)
ф(г)
Таким образом, в каждой вершине будут встречаться одна
фотонная линия и две спинорные (причем одна из них «входя-
«входящая», а другая «выходящая»). Здесь следует еще вспомнить о мат-
матрице Дирака, стоящей в каждом из X (х). Условимся эту мат-
матрицу, а также константу связи е ставить в соответствие с вер-
вершиной, подобно тому, как это изображено в C):
r~v_» -ч/ч^л^аТ . (9)
Соотношения F)—(9) образуют полный набор правил соответ-
соответствия для построения диаграмм Феинмана в спинорной электро-
электродинамике. Эти правила установлены так, что диаграмма, соот-
соответствующая одному из слагаемых в Sn, содержит п вершин и
некоторое количество внутренних и внешних фотонных и элек-
электронных линий. При этом в каждый узел входит и выходит одна
электронная линия. Таким образом, электронные линии всей
диаграммы непрерывны в узлах и образуют либо замкнутые фи-
фигуры, либо незамкнутые ломаные линии, начинающиеся и окан-
оканчивающиеся на краях диаграммы. Цепочке аргументов спари-
спариваний
t (х) ЩЦ (у) ЩЦ (г)... ^Щ, (v) y(v)
соответствует последовательность узлов отдельных электронных
линий диаграммы, а парам свободных операторов op (Xf) \|з (л;,-) под
знаком нормального произведения — начало (xi) и конец (xf) от-
отдельных незамкнутых электронных линий.
В качестве примера рассмотрим один из членов второго по-
порядка, входящий в выражение для S2(x, у):
х) А (х) о|> (х) у (у) А
-e2Sp {:S° (у-х) А (х) S° (х-у) Л (у):}. A0)

§ 19. ДИАГРАММЫ ФЕИНМАНА
155
Используя правила соответствия, получаем диаграмму Фейн-
мана — так называемую диаграмму «собственной энергии фотона»,
изображенную на рис. 19.2.
Во втором примере рассмотрим один из членов третьего по-
порядка, входящий в Ss(x, у, г):
{ief :$ (х) i (х) $Щ (у) А (у)
= - <>3D< (х - z) Щ (х) fSc
Щ (г) X (г) ф (г): =
(х - у) A (y)Sc(y- z) уущ (г)-..
A1)
Правила соответствия в этом случае приводит нас к диаграмме,
изображенной на рис. 19.3.
Из рассмотрения этих простейших диаграмм видно, что дви-
движение по направлению электронной линии в точности соответст-
соответствует порядку матричных элемен-
элементов справа налево в надлежащем
члене S-матрицы. Например, в
Рис. 19.2. Диаграмма соб-
собственной энергии фотона
в спинорной электродина-
электродинамике.
X z
Рис. 19.3. Вершинная
диаграмма третьего по-
порядка в спинорной
электродинамике.
случае диаграммы, изображенной на рис. 19.3, получаем тот же
порядок некоммутирующих матричных сомножителей
:$ (х) YVSC (х - у) А (у) S° (у - г) у va|> B):,
что и в A1).
Отметим еще, что в случае наличия ферми-полей необходимо
тщательно следить за знаками. Согласно определению спаривание
ty(x)ty(y) отличается знаком от стандартного спаривания
входящего в правила соответствия:
Эта смена знака существенна в диаграммах, содержащих замкну-
замкнутые электронные циклы. Так, например, по правилам соответст-
соответствия диаграмма рис. 19.2 соответствует выражению
которое отличается знаком от A0). Ясно также, что и в более
общем случае такое отличие в знаке будет иметь место для лю-
любой группы спариваний, соответствующей каждому из замкнутых
Циклов диаграммы, независимо от порядка этих циклов. Отсюда

156 ГЛ. V. ДИАГРАММЫ И ПРАВИЛА ФЕЙНМАНА
вытекает, что выражение, полученное по правилам соответствия,
должно быть дополнительно умножено на
где с — число замкнутых фермионных циклов в данной диаграмме.
Это замечание назовем правилом знаков.
19.4. Поле Янга— Миллса. Большой интерес представляют
квантовополевые модели, содержащие неабелевы калибровочные
поля и описывающие их взаимодействие с полями материи.
Подобно абелеву случаю —электродинамике —такие модели ока-
оказываются весьма экономными с точки зрения структуры членов
взаимодействия и в простейших случаях содержат всего одну
константу связи g. Эта константа входит также в лагранжиан
«чистого» (т. е. невзаимодействующего с другими полями) поля
Янга — Миллса
1{g, В),
который наряду к квадратичной формой Хй содержит кубичные
и четверные члены:
•»i(*. B) = 2gFliv[BlixBv] + g*&BlixBv])*. A2)
(Здесь и ниже для определенности рассматривается калибровоч-
калибровочное поле группы SU B).) По аналогии с рассмотренным выше
примером нелинейного скалярного поля D) возникает стремление
проквантовать поле Янга — Миллса в линейном приближении
(^ym-^-^o). а затем учесть тройные и четверные составляющие
из if, с помощью теории возмущений по степеням константы g.
При этом выражение %Q можно было бы выбрать в виде суммы
«по компонентам»:
^5°) A3)
квадратичных невырожденных форм, аналогичных лагранжиану
электромагнитного поля в форме D.13) или D.19). Однако, как
отмечалось в § 11.1, продольная компонента поля Янга —Миллса,
в отличие от электромагнитного поля, не отщепляются от попе-
поперечных. Вследствие этого матрица рассеяния оказывается неуни-
неунитарной в пространстве физических состояний. Конкретно это
проявляется в следующем. Левая часть условия унитарности
A5.9') содержит суммирование
(SSU = 2 5аДр = Ц S^S-z + 2 SaxSxp A4)
V у %
по промежуточным состояниям \у), среди которых, помимо трех-
мернопоперечных состояний |у), отвечающих безмассовым попе-
поперечным квантам поля Янга —Миллса (эти состояния jy) ниже

§ 19. ДИАГРАММЫ ФЕЙНМАНА 157
именуются физическими), содержатся состояния \%), в которых
присутствует скалярная составляющая %(х). В теории Янга —
Миллса, в отличие от электродинамики, из-за того, что функция
Х(*) удовлетворяет уравнению A1.12) и, таким образом, взаимо-
взаимодействует с поперечными составляющими, матричные элементы
где |а) — физические состояния, оказываются отличными от нуля.
Поэтому, для того чтобы обеспечить унитарность в пространстве
физических состояний, следует модифицировать операторы
так, чтобы они удовлетворяли соотношениям A6.4), в правой
части которых матричное умножение подразумевает свертку лишь
по физическим состояниям |у):
Результативно это сводится к тому, что во всех выкладках, со-
содержащих суммирование по промежуточным состояниям | у) необ-
необходимо вычесть из суммы вклад от состояний, содержащих ска-
скалярные кванты поля Янга—Миллса:
Строгое доказательство описываемой процедуры было полу-
получено в ходе квантования поля Янга — Миллса с помощью пред-
представления функционального интеграла (см., например, гл. III
книги Славнова, Фаддеева A978)).
Мы приведем сейчас элементы диаграммной техники теории
возмущений по степеням константы взаимодействия g для свобод-
свободного поля Янга —Миллса.
В дополнение к элементам, отвечающим полю Янга — Миллса:
внутренним линиям
A6)
внешним линиям

158 ГЛ. V. ДИАГРАММЫ И ПРАВИЛА ФЕЙНМАНА
тройным вершинам
^f A8)
f
и четверным вершинам
следует добавить элементы, соответствующие вычитаемым про-
продольным составляющим. Эти составляющие описываются скаляр-
скалярным безмассовым изовекторным полем |° и на диаграммах Фейн-
мана изображаются в виде внутренних линий поля |:
и тройных вершин, связывающих скалярное поле \ с полем
Янга — Миллса,
Вспомогательное скалярное поле £ часто называют полем
«духов Фаддеева — Попова».
Выписанные элементы удобно отнести к эффективному лаг-
лагранжиану
В этом выражении введены «комплексные» обозначения для
поля духов £->(£, 1). Дело в том, что, как оказывается, замк-
замкнутые циклы духовых линий соответствуют вкладам, содержащим
«дополнительный» множитель (—1). Поэтому формально удобно
считать скалярное поле £ проквантованным по Ферми—Дираку,
что и учитывается введенными обозначениями:
J > B1)
B2)

§ 20. ПРАВИЛА ФЕЙНМАНА В Р-ПРЕДСТАВЛЕНИИ 159
Правила Фейнмана включают теперь еще знаковый фактор
т, = (-1)*, B3)
где g — число замкнутых духовых циклов диаграммы.
Для иллюстрации рассмотрим члены порядка g2 в матрице
рассеяния S2(;t, у), с двумя неспаренными операторами поля
Янга —Миллса, аналогичные выражению A0).
Эти члены, во-первых, возникают из различных спариваний
операторов, стоящих в тройных вершинах:
S2 (х, у) ~ iYWdef :{/^(*)М(*)££(*А (у) к (у) Bfa (у) +
(х) k (x) Bcii(x)FJ<,(y)Be(>(y)Bfo(y) +
k
(х) k (x) k (x) He (У) k (У) к (У)}:, B4)
а во-вторых, из членов, содержащих взаимодействие духового
поля | с полем Янга —Миллса:
S2 (х, У) ~ ig4abczdef :\a (х) dvf (х) В% (х) (d (у) д£е (у) В(,(у):. B5)
С точностью до очевидных модификаций спариваний, стоящих
под знаком производных, как, например,
д f e~ih<x~y> dk-
dxV j _^_,e aR -
эти слагаемые соответствуют двум фейнмановским диаграммам,
изображенным на рис. 19.4.
а) Ю
Рис. 19.4. Диаграммы второго порядка с двумя внешними векторными линиями
для поля Янга — Миллса в пустоте.
Правила Фейнмана для полей Янга —Миллса, взаимодейст-
взаимодействующих с полями материи, читатель найдет в Дополнении VIII.
§ 20. Правила Фейнмана в ^-представлении
20.1. Переход к импульсному представлению. Обратимся теперь
к вычислению матричных элементов матрицы рассеяния, необхо-
необходимых для получения вероятностей переходов. Это вычисление
удобно проводить в импульсном представлении, так как именно
в этом представлении обычно записываются амплитуды состояний
Х(^)Фо- A)

160 ГЛ. V. ДИАГРАММЫ И ПРАВИЛА ФЕЙНМАНА
Для получения матричных элементов переходов между состоя-
состояниями типа A) от слагаемых S-матрицы и-го порядка
Sin) = \ldx1...dxnK(xv ..., xn):...ua(xi)...Ufi(Xj)...: . B)
следует вычислять выражения
Ф...А'... :...«а.--«э---:Ф...А... = Ф/:..-«а..."р...:Ф.-л- C)
При этом операторы рождения и+(х) из нормального произведе-
произведения надо коммутировать с операторами уничтожения аг (р) из
амплитуды Ф^, а операторы уничтожения tr(x) — с операторами
рождения а+(к) из Ф1п до тех пор, пока один из и+ не подейст-
подействует на Фо или один из и- не окажется рядом с Фо, что даст
нуль. Матричный элемент C) может оказаться отличным от нуля,
если для каждого оператора и (х) из нормального произведения
найдется оператор а+ в Фг„ или а- в Ф^ того же поля, который
«погасит» оператор и в результате коммутации с ним. Поэтому
C) будет отличен от нуля тогда, когда сумма числа частиц
каждого поля в начальном состоянии Фг„ и конечном состоянии
Ф/ в точности равна числу операторных функций данного поля
в нормальном произведении. Матричный элемент C) окажется от-
отличным от нуля также в случае, если, кроме операторов, «гася-
«гасящих» нормальное произведение, в Фу и Фг„ содержатся опера-
операторы, гасящие друг друга. При этом полное число частиц в со-
*
стояниях Фу и Ф,-„ превышает число операторов в нормальном
произведении на некоторое четное число. Однако такие матрич-
матричные элементы отличны от нуля лишь тогда, когда импульсы ука-
указанных «лишних» частиц в состояниях Ф( и Ф,„ совпадают, т. е.
«лишние» частицы не испытывают взаимодействия.
Ограничиваясь случаем, когда ни для одной частицы импульс
в начальном состоянии не равен импульсу в конечном состоянии,
приходим к выводу, что матричный элемент C) представляется
в виде произведения результатов коммутации операторов:
с ar(kf).
а
Таким образом, после явного выполнения этих коммутаций
матричный элемент C) сводится к произведению
i

§ 20. ПРАВИЛА ФЕИНМАНА Вр-ПРЕДСТАВЛЕНИИ 161
причем сомножители, входящие в ^[соответствуют частицам на-
чального состояния, а входящие в JJ — конечного.
f
Возвращаясь к исходному матричному элементу S-матрицы
<bfS{n)(£>in= \dx1...dxnK{x1, ...,xn)J\(...x...), E)
можем теперь выполнить интегрирование по переменным хг, ...
..., хп. В силу чисто экспоненциальной зависимости произведе-
произведения Y\ 0T конфигурационных переменных матричный элемент
с точностью до множителей v~(k), v+(k) и степеней числа 2я сво-
сводится к фурье-образу коэффициентной функции К (хг хп).
Поскольку эта функция в свою очередь выражается в виде про-
произведения спариваний, то ее фурье-образ представляется интег-
интегральной сверткой от фурье-образов спариваний.
Подставляя интегральные представления спариваний
4" DU (х-у) = Bя)
в правую часть E), видим, что интеграция по конфигурационным
переменным сводится к интегралам вида
\dxje U >* = Bя)»бB>в). F)
20.2. Правила Фейнмана для матричных элементов. Суммируя
приведенные рассуждения, приходим к диаграммам и правилам
Фейнмана в импульсном представлении.
Для вычисления матричного элемента перехода s->-r (т. е.
процесса, в котором s частиц начального состояния переходят
в г частиц конечного состояния) n-го порядка следует, сначала
нарисовать соответствующую диаграмму по правилам предыдущего
параграфа. На этой диаграмме нужно расставить импульсные
переменные, т. е. каждой внутренней и наружной линии диа-
диаграммы присвоить свой 4-импульс. При этом необходимо провести
различие между внешними линиями, описывающими входящие
частицы (начальное состояние) и выходящие частицы (конечное
состояние), а также учесть все топологически неэквивалентные
возможности.
Вычисление матричного элемента производится затем по сле-
следующим правилам:
1) каждой внешней линии начального состояния с 4-импуль-
сом рш отвечает множитель Bя)-3/г у„ (ры);
2) каждой внешней линии конечного состояния с 4-импуль-
сом kf отвечает множитель Bn)-*/«Wp(ft/);
6 Н, Н, Боголюбов, Д, В, Ширков

162 ГЛ. V. ДИАГРАММЫ И ПРАВИЛА ФЕЙНМАНА
3) каждой вершине отвечает множитель
igQa Bя)* 6
где gOa, — константа связи и матрица из соответствующего лаг-
лагранжиана взаимодействия, в аргументы б-функции входит алгеб-
алгебраическая сумма импульсов всех линий (внутренних и наружных),
встречающихся в данной вершине, а множитель i учитывает фак-
фактор /", стоящий при Sn в выражении для S;
4) каждой внутренней линии с 4-импульсом qj сопоставляется
множитель
причем:
5) по всем аргументам qf проводится интегрирование;
6) в случае наличия ферми-полей необходимо учесть правило
знаков и умножить все выражение на множитель A9.12);
7) полученное таким образом выражение должно быть еще
умножено на числовой множитель — фактор симметрии сп. Мы
обсудим структуру этого фактора ниже —в конце следующего
раздела.
20.3. Иллюстрация для модели <р4. В качестве иллюстрации
рассмотрим вклад в матричный элемент 2-»-2 рассеяния, отве-
отвечающий диаграмме рис. 19.1,6. Обозначим 4-импульсы началь-
начальных частиц символами рг, р2, а импульсы конечных через kv fej.

h
a)
Рис, 20.l. Диаграммы рассеяния второго порядка модели <р4 в импульсном
представлении.
Возможны три топологически неэквивалентных способа при-
присвоения импульсов ph kf внешним линиям. Они изображены на
рис. 20.1, а, б, в Импульсы внутренних линий обозначены сим-
символами qh коротенькие стрелки отвечают алгебраическим знакам
соответствующих импульсов.
Используя сформулированные выше правила с учетом того,
что для скалярного поля

§ 20. ПРАВИЛА ФЕЙНМАНА В Р-ПРЕДСТАВЛЕНИИ 163
получаем для диаграммы 20.1, а
BлL ^._^ х
X \ BлL fl^-ql) W <2")8 б
2-k1-k2) С
Bn)»(\6pl>plk4klI/' J {nfi-q
Соответственно для диаграмм рис. 20.1,6, в
С —
J (m2—с
a —fei —^a) Г
Bл)в
Чтобы получить окончательное выражение для вклада в матрич-
матричный элемент рассеяния d^SO*, необходимо еще учесть фактор
симметрии. Для его определения рассмотрим возможные вари-
варианты коммутаций и спариваний операторов в изучаемом матрич-
матричном элементе
= ^ j dx dy (aja-,T [q>« (x) Ф* (у)] ofoj>0. G)
Диаграмме 20.1, а соответствует следующая схема коммутаций:
Здесь около каждой скобки, обозначающей вид коммутации, стоит
ее комбинаторный вес. Мы начинаем с оператора уничтожения aj.
Он может зацепиться за любой из восьми операторов произведе-
произведения ф£ф£. Поэтому «вес» первого зацепления а^Ф* равен 8. По-
Поскольку топология диаграммы 20.1, а требует, чтобы оператор flg
зацепился за ту же вершину, что и aj. то вес второго зацепле-
зацепления а%(рх равен 3 и т. д.
Следует еще учесть вес хронологических спариваний остав-
оставшихся операторов. Легко видеть, что
(Т :ф*ф*: :Ф^:>0 = 2 (муJ. (8)
Собирая множители, получаем
4) ^ ^
Аналогичные рассуждения для диаграмм 20.1,6, в дают
4 = 4 = 4) = D!J/2.

164 ГЛ. V. ДИАГРАММЫ И ПРАВИЛА ФЕЙНМАНА
Итак, матричный элемент 2-»-2 рассеяния во втором порядке
теории возмущений для модели /ир4 будет
Т C
где
dq
"" я2 J (ma—?* —
is) [m2—(q — ftJ— fe] "
Сформулируем теперь рецепт получения фактора симметрии:
1) В я-м члене разложения S-матрицы содержится множи-
множитель (nl). Этот множитель всегда компенсируется множителем я!,
возникающим за счет перебора вершин хг хп, которые из-за
наличия интегрирования по dxx dxn являются немыми индек-
индексами суммирования.
2) В случае, если лагранжиан взаимодействия содержит k
одинаковых операторных множителей (в рассмотренном случае
k = \), при установлении порядка зацепления и порядка хроно-
хронологического спаривания операторов за счет перебора симметрич-
симметричных возможностей в каждой вершине возникает множитель k\.
3) В случае наличия v топологически эквивалентных вариан-
вариантов спаривания внутренних линий их следует учитывать только
один раз. Это соответствует введению множителя (v!).
20.4. Спинорная электродинамика. Приведем теперь сводку
правил Фейнмана для спинор ной электродинамики (табл. 2).
Эти правила необходимо дополнить правилом знаков и учетом
фактора симметрии.
Как отмечалось, введенные диаграммы фактически одновре-
одновременно описывают несколько различных процессов. Рассмотрим,
например, диаграмму, изображенную на
^\ /**т Рис" ^ • ^ля симметРии все входящие
Х^^^-/ импульсы условно направлены внутрь.
yr^^~\t Если считать, что нулевые составля-
Рг // \ч^2 юш.ие У 4-векторов рг и р2 положительны,
г. пп п тт а у k, и k2 — отрицательны (р?, ра>0:
Рис. 20.2. Диаграмма вто- . ,0 J,o !."«. i v ^ y '
рого порядка спинорной ®* $<°). то диаграмма соответствует
электродинамики с че- однофотонной аннигиляции электрона
тырьмя фермионными ег (р2) и позитрона е* (р^) с последую-
внешними линиями, щим рождением пары е~(К^ = — k2),
e*(Ki = — &i)- Этот процесс изображен
на рис. 20.3, а, где ось времени направлена слева на-
направо.
Если же положить, что pi, £a>0, a pi, £?<0, то мы полу-
получаем процесс рассеяния электрона на электроне с обменом одним
фотоном (мёллеровское рассеяние). В этом случае удобно ввести

§ 20. ПРАВИЛА ФЕЙНМАНА В р -ПРЕДСТАВЛЕНИИ
165
Таблица 2. Правила Фейнмана для матричных элементов в спинорной
электродинамике
№ пп
1
2
3
4
5
6
Частица и ее состояние
Электрон в начальном состоя-
состоянии с импульсом р
-*~Р
Позитрон в начальном состоя-
состоянии с импульсом р
■+-Р
Электрон в конечном состоя-
состоянии с импульсом р
-+-Р
Позитрон в конечном состоя-
состоянии с импульсом р
-+-Р
Фотон в начальном или конеч-
конечном состоянии с поляриза-
поляризацией ev и импульсом к
к
Движение электрона из 1 в 2
(или позитрона из 2 в 1)
1» ч. • °
Фактор в матричном элемент?
Bя) */' os> (р)
Bя)-'/»о5'+0в)
Bя)'Л V2ka
1 Г т+р i
BnLiJ m2—р^—18

166
ГЛ. V. ДИАГРАММЫ И ПРАВИЛА ФЕЙНМАНА
Продолжение табл. 2
Ш iin
7
8
Частица а ее состояние
Движение фотона между вер-
вершинами с индексами сумми-
суммирования (i И V
к
Узел с индексом суммирова-
суммирования v, в который входят
электронная линия р\ и фо-
фотонная линия k и выходит
электронная линия q2
_ й
Фактор в матричном элементе
gUV f. dk
Bя)«; J #S-|-t8
ieyvBnL(p%-Pl-k)
обозначение Ki = — klf Рг = — рг и повернуть диаграмму на 90°
по часовой стрелке. На полученной таким образом диаграмме
20.3, б время течет слева направо.
Случай pi, £?>0, р?, ki<.0 отвечает меллеровскому рассея-
рассеянию электрона на позитроне. Обозначая Рг = — рг и /С2 = — ^
а) й) д) г)
Рис. 20.3. Различные физические процессы, описываемые диаграммой рис 20.2.
получаем диаграмму 20.3, в. Матричный элемент диаграммы в
должен быть добавлен к матричному элементу диаграммы а.
Таким образом, две различные диаграммы 20.3, а и 20.3, в
дают вклад в один и тот же физический процесс
*♦ (Л)+ *-(А)-> «4*i) + s-(Я.) (И)

§ 20. ПРАВИЛА ФЕЙНМАНА В р-ПРЕДСТАВЛЕНИИ
167
(необходимо лишь учесть, что в диаграмме 20.3, в 4-векторы рг
и Кг обозначены через ^ и Pt), полный матричный элемент
которого в рассматриваемом приближении второго порядка тео-
теории возмущений равен сумме двух членов
= *« B0.3, а)
, в),
A2)
соответствующих двум этим диаграммам.
Наконец, случай k\, pl>0; p\, #S<0 отвечает мёллеровскому
рассеянию позитрона на позитроне —см. рис. 20.3, г. Для того
чтобы получить в последнем случае матричный элемент рассея-
рассеяния, необходимо еще учесть антисимметрию физических состояний
относительно перестановок двух тождественных ферми-частиц —
позитронов.
При вычислении величины
$ dx dy (a- (k2) a- (q2) гр (х) А (х) гр (х) гр (у) А (у) гр (у) о+ {kx) o+ (ft))
возникают два варианта «зацепления» ферми-операторов, изобра-
изображенные на рис. 20.4. Матричный элемент процесса
A3)
A4)
представляется теперь разностью
•ЖA3) = *£ B0.4, а) -об B0.4, б)
матричных элементов, соответствующих диаграммам 20.4, что и
обеспечивает упомянутую ан-
антисимметрию и выполнение
принципа Паули.
В заключение отметим,
что в приведенных выше при-
примерах содержатся пропага-
торы скалярного, спинорного
и электромагнитного полей,
не обладающих какой-либо
внутренней симметрией. В
этих примерах отсутствует
также векторное поле с мас-
массой. Для полноты картины приведем поэтому еще выражения
в импульсном представлении для пропагатора поля пи-мезонов:
a)
Рис. 20.4. Прямая и обменная диаграммы
мёллеровского рассеяния позитронов.
A5)
и для пропагатора массивного векторного поля ср. формулу
A8.14)

168 гл. v: диаграммы и правила фейнмана
§ 21. Вероятности переходов
21.1. Общая структура матричных элементов. Как было уста-
установлено в примере § 20.3, матричный элемент перехода содержит
сингулярный множитель в виде б-функции, отвечающей закону
сохранения полного 4-вектора энергии-импульса начальных и
конечных частиц. Нетрудно убедиться, что из правил Фейнмана
для матричных элементов (см. § 20.2, п. 3)) вытекает, что матрич-
матричный элемент перехода s-*-r всегда пропорционален четырехмер-
четырехмерной б-функции
Этот факт является отражением общего свойства трансляционной
инвариантности матрицы рассеяния. Если процесс взаимодействия
происходит во внешних полях, то соответствующая однородность
нарушается и множитель A) частично или полностью исчезает.
Например, при рассеянии во внешнем поле, зависящем от про-
пространственных координат и не зависящем от времени, вместо A)
получим одномерную б-функцию
— закон сохранения энергии.
Возвращаясь к общему случаю взаимодействия в вакууме,
получаем
& {Z'Z)(p'> р), B)
причем для связных диаграмм функция F является гладкой,
т. е. не содержит других б-функций.
Функция F описывается набором фейнмановских диаграмм
с числом внешних линий, равным s-\-r. Введем здесь некоторые
полезные определения.
Мы будем называть диаграмму G связной, если ее нельзя
разбить на части, которые не соединены друг с другом линиями.
Если же диаграмма G распадается на связные «части» Glt G2, ...,
то мы назовем G несвязной, а ее «куски» Gt — компонентами связ-
связности. Связную диаграмму называют слабо связной (или одно-
частично приводимой), если ее можно превратить в несвязную
снятием одной внутренней линии, и сильно связной (одночастично
неприводимой), если это невозможно.
Вклад каждой из компонент связности несвязной диаграммы
в. матричный элемент A) содержит б-функцию. Вклады связных
диаграмм содержат по одной б-функции. Поэтому для связных
диаграмм функция F в правой части B) является гладкой, т. е.
не содержит множителями других б-функций.

§21. ВЕРОЯТНОСТИ ПЕРЕХОДОВ 169
Для определения вероятностей переходов приходится вычислять
квадраты матричных элементов и иметь дело с квадратом б-функ-
ции.
Здесь следует учесть, что, как обычно в квантовой механике,
нас интересуют вероятности переходов, отнесенные к единичному
интервалу времени и единичному пространственному объему.
Принимая еще во внимание, что импульсная 4-мерная б-функция
возникает в результате интегрирования по 4-мерному объему VT
(У->-оо, Г->-оо), находим
[б (р)р = б (р) б @) = б (р) Bя)-* $ dx = б (p) Bя)~* VT,
Имеем поэтому
| (fySOp |« = Bя)-* VT8 Bp-2p')\F(p',p) |2. C)
Аналогичные рассуждения для процесса перехода в статическом
внешнем поле Аех\ дают
| Оу S (ЛехО ФРI2 = Bя)-1 Гб (Ц р0 - Ц p'o) \F(p',p; Aext) |«. D)
Формула D) вполне эквивалентна соответствующим выражениям
для вероятностей переходов нерелятивистской квантовой меха-
механики (см., например, § 84 учебника Блохинцева A976)). Сингу-
Сингулярный множитель Т исчезает при обращении к вероятности
перехода в единицу времени. Наличие другого сингулярного
множителя V в формуле C) является следствием того, что мы
работаем с плоскими волнами. Этот множитель выпадает из выра-
выражения для вероятности перехода, отнесенной к единице объема.
21.2. Нормировка амплитуды состояния. Изучим теперь вопрос
о нормировке амплитуд состояний вида
Поскольку такая амплитуда отвечает частицам со строго фикси-
фиксированными значениями импульсов, она соответствует плоским
волнам, которые не обладают конечной нормой во всем прост-
пространстве. Однако плоская волна, а следовательно, и амплитуда Ф*
могут быть нормированы в единичном объеме.
Для того чтобы аккуратно ввести предельный переход V ->• оо,
рассмотрим одночастичное состояние и введем пакет плоских волн
E)
Норма этого состояния равна
Полагая iV = l, можем считать, что выражение
| Иг (*)!■<**

170 ГЛ. V. ДИАГРАММЫ И ПРАВИЛА ФЕЙНМАНА
дает вероятность того, что частица, характеризуемая внутренним
квантовым числом а, обладает импульсом в интервале dk около
среднего значения k. Сама функция %(k) является, таким обра-
образом, волновой функцией частицы в импульсном представлении.
Поэтому ее фурье-образ
fa(x) = Bn)-'!'\e'**Xo(b)dk F)
есть волновая функция в координатном представлении с нормой,
равной
При N =1 величину
\f(x)\'dx G)
можно интерпретировать как вероятность в конфигурационном
пространстве. Полагая N равным числу частиц, много большему
единицы, находим, что выражение G) есть среднее число частиц
в бесконечно малом элементе объема dx.
Здесь уместно напомнить, что, согласно общей статистической
интерпретации квантовой механики, мы имеем дело с квантовым
ансамблем, т. е. большим числом тождественных систем микро-
микрочастиц или набором тождественных экземпляров одной и той же
системы. В данном конкретном случае этот образ вполне адеква-
адекватен реализуемой на опыте картине. Так, например, пучок частиц
от ускорителя — это разреженный пучок тождественных частиц,
невзаимодействующих друг с другом, которые «по очереди» падают
на мишень одинаковым образом.
Увеличивая теперь неограниченно норму N так, чтобы при
этом Хсг стремилось к выражению BnK/*S(ft — ft0), мы будем полу-
получать волновой пакет со все более фиксированным импульсом.
Из G) находим, что при этом
а потому также
и в пределе на единицу объема будет приходиться одна частица.
Переходя к пределу, получаем выражение для амплитуды
одночастичного состояния, нормированной на единицу объема:
В случае нескольких сортов частиц вместо E) следует рас-
рассмотреть выражение
ф,= П ft Хо, (**)£,, (**) <***}Фд. (8)

§ 21. ВЕРОЯТНОСТИ ПЕРЕХОДОВ 171
где все наборы {ah kt\ различны. Норма такой амплитуды пред-
представится, очевидно, произведением норм s одночастичных состояний
<&,Ф,.= ад...Л,. (9)
Повторяя только что проведенное рассуждение отдельно для
каждого из сомножителей в (8), (9), приходим к выводу, что
амплитуда состояния, нормированная для каждой находящейся
в нем частицы на единицу объема, имеет вид
{,Ц A0)
21.3. Общая формула для вероятности перехода. Поставим
теперь задачу определения вероятности такого процесса, когда
в начальном состоянии имеется s потоков частиц с точно опре-
определенными импульсами fclt ..., ks и внутренними квантовыми
числами alt ..., os, характеризующими массу, заряд и спин, и
требуется найти среднее число частиц, рассеянных с импульсами,
лежащими в бесконечно малых областях dplt ..., dpr, и с внут-
внутренними квантовыми числами plt ..., рг.
В результате взаимодействия система перейдет из состояния
A) в состояние, описываемое амплитудой
где Фк определена согласно B0.1). Поэтому среднее число частиц,
которое окажется в конечном состоянии, описываемом нормируе-
нормируемой амплитудой Фа, согласно общему правилу квантовой меха-
механики равно
Произведенный выбор нормировки отвечает тому, что в началь-
начальном состоянии средние числа частиц на единицу объема равны
единице. Если же эти числа равны соответственно nv п2, ..., пп
то выражение A1) следует умножить на пхпг ... пг.
Нас интересует сейчас число частиц, рассеянных в интервалы
импульсов Арх, ..., Арг около средних значений pv ..., рг.
При этом мы будем полагать, как это было оговорено в § 20.1,
что каждая частица в начальном и конечном состоянии имеет
различные значения импульса. В эксперименте это соответствует
тому, что частицы с неизменившимся импульсом отнесены к основ-
основному первичному пучку, а рассеянными считаются частицы,
изменившие свой импульс.
Амплитуду конечного состояния Фа возьмем в виде

172 ГЛ. V. ДИАГРАММЫ И ПРАВИЛА ФЕЙНМАНА
где область А равна произведению объемов Apf. Поэтому
ФаФа = Bл)*гАр1...Арп
а вместо A1) получаем выражение
равное, по определению области Д,
n!...ns BяK* | 6pSOft |2 Да ... Apr- (l 2)
Структура квадратов матричных элементов типа | Ф ... SO ... |2
была исследована в начале параграфа. Подставляя выражение
C) в A2) и деля на VT, получаем число частиц, рассеянных
в интервал dpv ..., dpr за единицу времени и в единице объема:
Bn)a*-*n1...ns\F(p, £)|абBр —2*LPi ...dpr. A3)
Используя формулу D), находим также соответствующее выра-
выражение при рассеянии стационарным классическим полем в еди-
единицу времени в виде
Bя)«-! п,... л, | F (р, к, ЛехО Р б B Р° - S к0) dpx... dp г. A4)
Таким образом, для определения вероятности перехода следует
вычислить сначала матричный элемент B) и полученную функ-
функцию F подставить в формулу A3) (соответственно в A4)).
Отметим, что в связи с переходом от B0.1) к A0) оказывается
удобным изменить нормировку матричного элемента. Положим
вместо B)
4- у <» + Г>
, к). A5)
Формула A3) принимает вид
п
где
Л{^Ц A7)
— плотность конечных состояний в импульсном пространстве
размерности Зг. Если в конечном состоянии имеются две частицы
(г = 2), оказывается удобным пользоваться плотностью, отнесен-
отнесенной не к 6-мерному, а к 2-мерному фазовому объему (т. е. сняв

§ 21. ВЕРОЯТНОСТИ ПЕРЕХОДОВ 173
четыре интегрирования с помощью б-функций). Она может быть
представлена в виде
где Q=^kh pi=\pi\.
i
В пределе, когда одна частица гораздо тяжелее другой
{т^гпу, рх), имеем
В системе центра масс
21.4. Рассеяние двух частиц. Рассмотрим важный случай рас-
рассеяния двух частиц B->2). Матричный элемент перехода, стоя-
стоящий в левой части A5), может быть отличен от нуля и при
отсутствии взаимодействия, когда S=l, а импульсы и квантовые
числа частиц в начальном состоянии равны импульсам и кван-
квантовым числам в конечном состоянии.
Для того чтобы иметь дело с чистым эффектом взаимодейст-
взаимодействия, «диагональный» матричный элемент вычитают из полного,
т. е. рассматривают выражение
которое не отличается от исходного при р^Ф^. В соответствии
с A5) положим, одновременно несколько изменив нормировку,
(А) ОН (Р2) (S-l)at (ftx) at (ft2) Фо =
Введенная здесь функция / представляет собой амплитуду рас-
рассеяния в релятивистском случае. Нормировка правой части соот-
соответствует случаю рассеяния бесспиновых частиц. Как нетрудно
убедиться, релятивистская амплитуда / является безразмерной
функцией. Можно показать, что она является также релятивист-
релятивистски инвариантной функцией.
Для рассеяния бозона (оператор рождения at (ft)) на фермионе
(оператор рождения b% (q)) амплитуда рассеяния обычно вводится
несколько иным образом:
Ф„ат (*') К (Я1) (S - 1) <Й (*) &v (Я) Фо =
_i8(k'+q'-k-q)f .-, ,. . .
Здесь п, т — изотопические индексы бозонов, a v, ц,—спиновые и
изотопические индексы фермиона. Представление B0) применимо,

174 ГЛ. V. ДИАГРАММЫ И ПРАВИЛА ФЕЙНМАНА
например, для рассеяния света на электронах (комптонов-
ское рассеяние) или для пион-нуклонного рассеяния. Матричная
амплитуда рассеяния /vniM,m имеет размерность [т~1] = см1 и может
быть сделана безразмерной введением соответствующей массы.
Этого, однако, обычно не делают из традиционных соображений
соответствия ее нерелятивистского предела с размерной квантово-
механической амплитудой рассеяния.
Используя нормировку B0), получаем вместо A6)
п1п,Bя)»4^|7|»/?,. B1)
Это выражение равно числу частиц, рассеянных в R2 в единич-
единичном объеме в единицу времени. Его обычно представляют в виде
произведения n^v (к) da, где v (k) — модуль скорости налетающей
частицы в лабораторной системе координат (л. с. к.) (равный
единице для фотона и | k \/k0 для частиц с конечной массой покоя).
Множитель da, имеющий размерность площади см2, пропорцио-
пропорционален элементу телесного угла частицы после рассеяния и назы-
называется дифференциальным эффективным поперечным сечением.
Согласно B1) и A8а) его можно представить в виде
)] ' ' '*
В статическом пределе пион-нуклонного рассеяния
il_|f|2
B3)
Интегрируя дифференциальное сечение по полному телесному
углу, получаем полное эффективное поперечное сечение в лабора-
лабораторной системе координат
a =
4л
Напомним еще, что с помощью так называемой оптической
теоремы (см. Блохинцев A976), § 86; Ландау Лифшиц A974),
§ 125; Давыдов A973); § 107) мнимая часть амплитуды упругого
рассеяния вперед, определенной как предел амплитуды рассея-
рассеяния на малый угол
/(£, 9 = 0) = Нт/(£, 6), B5)
выражается через полное эффективное поперечное сечение
CTtot = tfelast -f CTuneIast B6)
линейным соотношением.

§ 21. ВЕРОЯТНОСТИ ПЕРЕХОДОВ 175
Для введенной в B0) амплитуды пион-нуклонного рассеяния
оптическую теорему обычно записывают следующим образом:
lmUm(k, q; k, ?) = i%i«JSJ, B7)
тогда как для безразмерной амплитуды пион-пионного рассеяния
в нормировке A9) эту теорему удобно выразить через инвариант-
инвариантные переменные: . _______
lmf(k_, k2; k_, kj-t^V-^OtotiS), B8)
21.5. Двухчастичный распад. Допустим теперь, что в началь-
начальном состоянии находится одна частица (s=l) массы М, а в ко-
конечном—две частицы г —2 с массами т1 и т2. Этот случай
соответствует двухчастичному распаду частицы М, который кине-
кинематически возможен при M>ml-\-mi.
Согласно формуле A6) среднее число частиц в конечном
состоянии, попадающих в интервалы dpi, dp2 в единицу времени
и единицу объема, будет
o-J
Переходя в систему покоя начальной частицы, т. е. в систему
центра масс продуктов распада, получаем с помощью A8в) при
Интегрируя это выражение по телесному углу, находим полную
вероятность двухчастичного распада в единицу времени
Q)|». B9)
Величина w имеет размерность массы (в обычной системе
единиц = (г1) и совпадает с энергетической шириной: w = T.
В случае, если существует несколько каналов распада, полная
ширина складывается из суммы выражений вида B9)
2\
i
а время жизни исходной частицы т определяется соотношением
гЧ C0)
Mot/

Г л а в а VI. ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ
И РАСХОДИМОСТИ
§ 22. Техника вычисления интегралов
22.1. Интегралы по виртуальным импульсам. В общем случае
количество вершин диаграммы меньше числа внутренних линий,
вследствие чего матричный элемент представляется выражением,
содержащим интегрирования по виртуальным 4-импульсам:
<Л (... р...) = \ dkx... dkcF (р, k).
Число интегрирований с равно числу «петель» диаграммы, т. е.
числу содержащихся в ней топологически независимых замк-
замкнутых контуров. '
Подынтегральная функция F представляет собой произведение
пропагаторов (свободных функций Грина), имеющих структуру
и соответствующих внутренним линиям, через которые проходит
4-импульс интегрирования, умноженное на произведение множи-
множителей, соответствующих вершинам. Последние состоят из кон-
констант связи, матриц и, возможно, компонент, «проходящих» через
вершину 4-импульсов (в случае, если лагранжиан взаимодействия
содержит производные от функций поля).
Таким образом, наиболее общее выражение для интеграла
по 4-импульсу имеет вид
L
I (р, L) = ± J dk Л {т} - (k + pi)* - Щ -*Р (к, р), A)
где Р — полином по компонентам 4-векторов k,..., р,... с матрич-
матричными коэффициентами.
Наша ближайшая задача — развить технику вычисления инте-
интегралов типа A).

§ 22. ТЕХНИКА ВЫЧИСЛЕНИЯ ИНТЕГРАЛОВ 177
22.2. Альфа-представление и гауссовы квадратуры. Для вычис-
вычисления интеграла A) используем следующий вспомогательный
прием. Представим сомножители знаменателя подынтегрального
выражения в виде интеграла по параметру:
Это преобразование назовем переходом в а-представление. После
такого перехода интегрирование в A) сводится к взятию инте-
интегралов гауссовского вида.
Базовый четырехмерный гауссов интеграл имеет вид
fc =!*-'*•/«. C)
Здесь Ъ — некоторый 4-вектор. Ввиду того, что левая и правая
части покомпонентно факторизуются, вывод формулы C) сводится
к вычислению произведения четырех одномерных гауссовых квад-
квадратур вида
/ (а, р) = \ exp i (— at2 + 2р7) dt.
—оо
Интеграл / для определенности будем считать пределом выра-
выражения
щ, Ь)= $ exp[i(—at2 + 2bt)-r\t2]dt, а>0, tj-
—оо
для вычисления которого произведем замену переменной t->-x:
сводящуюся к сдвигу начала координат на b/а и последующему
повороту контура интегрирования в комплексной плоскости
на 45°. Тогда в пределе т] = 0 получим
x = (n/aiL>exp(+ib2/a), a>0.
Значение аналогичного интеграла при а<0 может быть полу-
получено отсюда операцией комплексного сопряжения
/ (-1 а |, Ь) - / (а, V) = (го/| а |I/» exp (- ib2f\ а |).
Возвращаясь к исходному выражению в левой части C), пред-

178 ГЛ. VI. ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ И РАСХОДИМОСТИ
ставим его в виде произведения
= / (- a, b0) I (а, Ьг) I (a, b2) I (a, b3) = (n2/m2) exp
что и завершает доказательство формулы C).
Обратим внимание на то, что вместо комплексного сопряже-
сопряжения интеграла I (а, Ь) при выполнении интегрирования по Ао
можно было бы перейти к интегрированию по чисто мнимому
аргументу £0 = г&4, что эквивалентно повороту контура интегри-
интегрирования по ko на 90°. Такую операцию, приводящую к 4-мерному
евклидову интегралу
J d*k - J dk° J dF-> i \ dki J dF= i \ (dtk)E,
иногда называют «виковым поворотом».
Остальные необходимые интегралы, содержащие множители k^
в числителе (отвечающие полиному P(k, p) в формуле A)),
могут быть получены из базового гауссова интеграла C) путем
повторного дифференцирования по компонентам Ьч:
Da)
Dб)
J в( + , mdk =,[]. Dв)
Используя формулу B), преобразуем правую часть в A)
к виду
^ ^k, p) exp I (Ak2 + 2Bk-M2 + ieA).
Здесь A = a1 + ... + aL, B=]£alpl, M2 = 2щ(т\-pi). Пред-
ставляя далее Р в виде
P(k, p)~P(p) + №
получаем с помощью C), D)
f da ...da, IB*
f da ...da,

§ 22. ТЕХНИКА ВЫЧИСЛЕНИЯ ИНТЕГРАЛОВ 179
Для выполнения сингулярного интегрирования произведем замену
переменных интегрирования (alt ..., cll)-*-^, •••» *i-i> Л):
A^-K E)
...daL
dx1...dxL_1dA
Принимая во внимание, что
Я2/Л + М2 = Л£> (х, р); D (д:, р) = B адJ + Ц х, (mj -pf), F)
получаем
1
(р; L) = iL С rfЛЛ^- -з f {dxb в*л (-о + w {Qo + j <?! + ..), G)
где
о о о
1 1-*! l-x1—xt l-x1-x2-...-xL_2
= \dx1 \ dx2 \ dx3... \ dxL-lt
о о
Qo (p, x) = P(p)-
Теперь не составляет труда провести сингулярное интегриро-
интегрирование по Л с помощью формул, родственных B):
L>2. (8)
При интегрировании по Л в правой части G) при L<2 и (или)
при наличии спинов у частиц (Р^фО) формула (8) может ока-
оказаться неприменимой, так как индекс k окажется равным нулю
или отрицательным. Такие интегралы содержат неинтегрируемую
особенность при Л=0, связанную с ультрафиолетовыми расхо-
димостями исходных интегралов A), и мы отложим их рассмот-
рассмотрение до § 23.
Изложенная выше процедура вполне достаточна для вычисле-
вычисления фейнмановских интегралов, не содержащих: ультрафиолетовых
расходимостей. В результате выполнения квадратур по А I (р)
представится в виде многократного интеграла по параметрам xt

180 ГЛ. VI. ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ И РАСХОДИМОСТИ
Оставшиеся квадратуры по параметрам хи вообще говоря, не
сингулярны и при /^3 могут быть проведены до конца.
22.3. Фейнмановская параметризация. Приведем еще один,
часто употребляемый способ вычисления интеграла A). Исходным
шагом является формула, использованная в первоначальных
работах Фейнмана:
Полагая (k-\-piJ — mj-\-i8 = alt представим A) в виде инте-
интеграла по параметрам xt
IL(p; L) = {-\)L{L-\)\\{dx}LJL(p, x), A1)
о
где
/ / ч_ ' Г* dkP(k, р)
L{P'X)~tf) [Z(p,k, x)]L'
здесь Z — квадратичная форма по компонентам k:
Z(p, k, х) = JJ*i[(.k+PiY~m* +i&] = k2 + 2bk + b2-D + is.
i
После сдвига переменной интегрирования k-*-k-\-b = q имеем
x)- l CdqP(q-b, p)
где D — форма, введенная ранее формулой F).
Этот интеграл в ряде случаев может быть сведен к более
простому
}b$? 03)
Для того чтобы убедиться в этом, заметим, во-первых, что все
интегралы вида $ qvF (q2) dq, J cfqv-qVF (q2) dq, .... содержащие не-
нечетное число компонент вектора интегрирования qv, по соображе-
соображениям симметрии обращаются в нуль. Из этих же соображений
интегралы с четным числом компонент упрощаются следующим
образом:
J qvq»F (q2) dq = (V4) g» \ q2F (q2) dq,
$. WWF (q2) dq = (Vm) (^v^pa+gvpg»a+gvag»p) J (q2) F (q2) dq.
Поэтому полином P(q — b, p) может быть заменен полиномом по
степеням q2, а следовательно, и по степеням аргумента q2 — D.
Вследствие этого исходный интеграл A2) выразится через линей-

§ 22. ТЕХНИКА ВЫЧИСЛЕНИЯ ИНТЕГРАЛОВ 181
ную комбинацию интегралов
Эти последние в свою очередь операцией интегрирования по D
при /:згЗ сводятся к jg. При /^2 интеграл A4) не существует.
Интеграл A3) может быть вычислен путем комбинирования фор-
формул B), C) и (8). Получаем этим путем
1 f d4°dtl =± f dqod
я2 J (q*0-q*-D + ie)i я* J (-q'-qP-
я2 J (<7| +DK 2D *
Дифференцируя по D, имеем также
Л (р. *) = Г=2~ (L^3). A6)
Подставляя в A1), получаем
— формулу, совпадающую с (9) в простейшем (P(k, p) = \) случае.
Таким образом, оба способа интегрирования приводят к одина-
одинаковым выражениям.
22,4. Ультрафиолетовые расходимости. Как уже неоднократно
отмечалось выше, матричные элементы, формально определенные
правилами Фейнмана в виде интегралов A) по виртуальным
импульсам, могут оказаться не существующими в силу недоста-
недостаточно быстрого убывания подынтегрального выражения в области
больших k.
Расходимости интегралов по виртуальным импульсам в области
больших k называются ультрафиолетовыми. Ультрафиолетовые
расходимости являются типичными для матричных элементов
теории возмущений релятивистской квантовой теории поля. Они
являются не исключением, а правилом.
Простейшая расходимость отвечает однопетлевому интегралу
с двумя бесспиновыми внутренними линиями (рис. 22.1)
~ л5 J
dk
__
(ma—б2—te) [nfi —
который в области больших k расходится логарифмически.
Интеграл / (р) представляет фурье-образ квадрата причинной
функции Грина:
J е'р у*-уI (р) dp ~ {28я6 [Z> (х -у)\\

182 ГЛ. VI. ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ И РАСХОДИМОСТИ
Выражение, стоящее в правой части, является неопределенным
в силу сингулярного характера функции D" на световом конусе.
Оно возникает при раскрытии с помощью теоремы Вика хроно-
хронологического произведения Т {X (х) X (у)), вхо-
„-+Л. дящего в 52 (х, у). В § 14 было установлено,
_^'"' Ny_^. что это выражение неопределено при х—у,
Р ч„ „' Р ав§16 было показано, что оно может быть
Р~к доопределено с помощью квазилокального опе-
Рис. 22.1. Скаляр- ратора А^(х, у).
ная однопетлевая Оказывается возможным выбрать оператор
диаграмма второго Д2 таким образом, чтобы доопределенные выра-
порядка. жения типа A6), A7) оказались конечными.
Подобная программа известна как процедура
устранения ультрафиолетовых расходимостей с помощью метода
перенормировок. Мы рассмотрим ее более подробно ниже в
§§ 27, 28,
Для анализа характера ультрафиолетовых расходимостей и
выбора адекватных А2, Л3, ... оказывается удобным использовать
процедуру вспомогательной промежуточной регуляризации расхо-
расходящихся интегралов. К рассмотрению различных вариантов этой
процедуры мы сейчас перейдем.
§ 23. Вспомогательные регуляризации
23.1. Необходимость регуляризации. Как было установлено
в § 18.3, причинные функции Грина, фигурирующие в правилах
Фейнмана, являются сингулярными функциями, обладающими
особенностями на световом конусе. С математической точки зре-
зрения они представляют собой обобщенные функции. Интегралы по
виртуальным 4-импульсам, введенные в предыдущем параграфе и
отвечающие замкнутым петлям диаграмм, представляют фурье-
образы произведений причинных Ас-функций, аргументы которых
соответствуют элементам этих петель.
Как отмечалось в конце предыдущего параграфа, простейший
интеграл
1 (Ф~5г« J (m»_pa_fe)[ma_(p_ft)»_»e] ' (*)
отвечающий однопетлевой диаграмме с двумя скалярными внут-
внутренними линиями (см. рис. 22.1), является фурье-образом произ-
произведения двух пропагаторов с совпадающими аргументами:
/ (k) = 16лЧ \ eik* [Dc (x)f dx. B)
Такие произведения, согласно формуле A8.22), содержат квад-
квадраты сингулярных обобщенных функций вида б (Я), Я (где Я = ха)
и потому не являются хорошо определенными величинами. Иными

§ 23. ВСПОМОГАТЕЛЬНЫЕ РЕГУЛЯРИЗАЦИИ 183
словами, с математической точки зрения произведения пропага-
торов и их фурье-образы нуждаются в доопределении.
Подчеркнем, что необходимость специального определения
произведений вообще типична для обобщенных функций. Дело
в том, что обобщенная функция задается правилами интегриро-
интегрирования ее произведения с достаточно регулярными функциями,
а из таких правил рецептура интегрирования произведения не-
нескольких обобщенных функций не следует.
Для того чтобы сконструировать необходимые определения,
можно воспользоваться методом несобственного предельного пере-
перехода и попытаться определить соответствующие произведения
Y\ {&c(Xr — xs)\ и их фурье-образы вида B2.1) с помощью после-
довательности регулярных выражений. Здесь возможны два раз-
различных подхода.
Один из них основан на получении регулярных приближений
к самим причинным функциям, т. е. к замене обобщенных сингу-
сингулярных функций
Ac(*)->regAc(x)
на некоторые регуляризованные приближения, являющиеся непре-
непрерывными на световом конусе вместе с необходимым числом своих
производных. При этом произведения регуляризованных пропа-
гаторов J][ {reg Дс (xr — xs)} также оказываются регулярными.
Весьма употребительной процедурой такого рода является регу-
регуляризация Паули — Вилларса.
Второй способ действии оставляет неизменными исходные выра-
выражения для пропагаторов и заключается в построении регулярных
приближений к их произведениям и интегралам по виртуальным
4-импульсам. К этому типу относятся регуляризация обрезанием,
а также размерная регуляризация.
23.2. Регуляризация Паули — Вилларса. Она заключается в за-
замене сингулярных функций Грина свободного поля с массой т
на линейную комбинацию
А (т) -> reg^ А (т) = А (т) + % с, A (Mt) ■ C)
Здесь символом А (т) обозначена функция Грина поля с массой т.
В дальнейшем мы всегда будем подразумевать под символом А
причинную функцию Грина, хотя процедура Паули —Вилларса
формулируется единым образом как для Ас, так и для Aret, Aadv,
А+, Д-. В правой части A (Mi) — вспомогательные величины,
являющиеся функциями Грина фиктивных полей с массами Mit
а с; —некоторые коэффициенты, удовлетворяющие специальным
условиям. Эти условия подбираются таким образом, чтобы регу-
ляризованная функция reg А (х; т), рассматриваемая в коорди-

184 ГЛ. VI. ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ И РАСХОДИМОСТИ
натном представлении, оказалась достаточно регулярной в окрест
ности светового конуса, или, что эквивалентно, функция reg А (р; т)
в импульсном представлении достаточно быстро убывала в области
больших значений |р2|.
Так, для полей с целым спином на основании заключитель-
заключительных формул § 18.3 видим, что наиболее сильные особенности на
световом конусе б (Я) и Я входят в D(x; m) с коэффициентами,
не зависящими от массы т. Поэтому, налагая на с{ условие
1 + 2> = 0, Dа)
i
мы получим для regA(x; m) выражение, не содержащее особен-
особенностей б (Я), Я-1. Его фурье-образ regA(p; m) в области боль-
больших |р2| будет убывать как |р2|~2. Подобным образом условие
m2 4-2c,Mf = 0 D6)
i
обеспечивает отсутствие Bj"egA(x) особенностей вида 6 (Я), In Я и
приводит к тому, что reg А (р) в ультрафиолетовой области убы-
убывает как | р21~6.
Снятие регуляризации Паули — Вилларса осуществляется пере-
переходом к пределу Mi-^oo.
Простейший случай регуляризации Паули — Вилларса сводится
к введению одной вспомогательной массы М с коэффициентом
с = —1, удовлетворяющим условию Dа). В импульсном пред-
представлении
»Лр) = 1~ + тЧмВЛр)=1^-г-Ш^г E)
Проводя регуляризацию E) в подынтегральном выражении пра-
правой части A), получаем
= я5 J dp U2-P2 ~~ M*-p*\ lmt-{p-k)* ~ M^—(p—kfY
Правая часть этого уравнения является конечным выражением и
может быть вычислена с помощью техники § 22. Получаем этим
путем
/ (А) = г2 \ ^^-ek'^+&[
О
CrfrinF
J lxM*-j-(l—x)mf—x A—x) k*' A — x) м*+хт*
-x)k* I
—x A — x) k2}'

§ 23. ВСПОМОГАТЕЛЬНЫЕ РЕГУЛЯРИЗАЦИИ 185
Здесь мы использовали формулы вида
А +«е
(см. Дополнение VI).
Теперь следует приступить к снятию регуляризации. Устрем-
Устремляя М2 к бесконечности, имеем
1
/ (k) а* - In ^ + J dxln [ L_J J + о ^J, F)
и
где ц.2 — произвольный положительный параметр.
Таким образом, снять регуляризацию непосредственно не
удается. Можно лишь в явном виде выделить из I (k) ультра-
ультрафиолетовую бесконечность
regM I(k) = - In ^ + /кон ш (», ц2), G)
где конечная часть /кон может быть вычислена в явном виде
(см. ниже § 24.1).
Приведем еще без выкладок результат вычисления с помощью
регуляризации Паули — Вилларса квадратично расходящегося
интеграла
d
входящего составной частью во вклад диаграммы собственной
энергии фотона (см. ниже § 24.2). В пределе Ма->оо получаем
g/(^)
где конечная часть
Z(x, k2) = m2-x(l-x)k2-ie
может быть проинтегрирована до конца.
Ряд других формул для часто встречающихся расходящихся
интегралов приведен в Дополнении VII.
23.3. Размерная регуляризация. Эта регуляризация состоит
в том, что интеграл по 4-мерному многообразию виртуальных
импульсов заменяют на символ, формально соответствующий

186 ГЛ. VI. ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ И РАСХОДИМОСТИ
интегралу по пространству /г = 4 — 2е измерений. При этом е счи-
считается малой положительной величиной, и кратность регуляри-
зованного интегрирования п оказывается нецелой.
Мы обозначаем здесь, следуя установившемуся обычаю, неце-
нецелую часть размерности с помощью того же самого символа е,
который используется для определения причинной функции.
В этом разделе мы будем использовать его лишь в новом значе-
значении, молчаливо подразумевая, что т? = тг — i8 F-> + 0).
В евклидовом случае операция введения размерной регуляри-
регуляризации выглядит следующим образом:
]{#р)Е= J dQ\p*dp-+\dnpszy,™ J dQjp*-Vdp, A0)
а D) 0 Q (л) 0
причем объем Q (п) единичной сферы в я-мерном пространстве
интерполируется с помощью Г-функции Эйлера:
а зависимость от параметра ц., имеющего размерность массы,
введена из соображений сохранения общей размерности.
Вместо этого можно также непосредственно интерполировать
формулы предыдущего параграфа. Основная гауссова квадратура
принимает вид
я2 J г \ я / аа v/
Основной интеграл в фейнмановской параметризации может
быть теперь вычислен путем комбинирования формул A1) и B2.8).
Он оказывается равным
Вычислим интеграл A) методом размерной регуляризации с по-
помощью перехода в а-представление:
-flg \ {m^
00
= U^f f Лай$№кг-1& + Ыт* f ^
- _ ЛЛ2\Е f
1 oo

§ 23. ВСПОМОГАТЕЛЬНЫЕ РЕГУЛЯРИЗАЦИИ 187
Для вычисления появившегося интеграла воспользуемся квадра-
квадратурой B2.8). Находим
rege/(ft) =-(£)8Г(е) $ [m2_,(f_^,]e. A3)
Теперь необходимо снять регуляризацию, т. е. устремить е
к нулю. Используя соотношение
Г(е)->1-С + О(е) (С = 0,5772...), е->+0,
о
получаем
rege/(fc)->-l/e + /K°« <«>(£), A4)
где
+ In я + С.
Таким образом, в методе размерной регуляризации сингулярная
часть интеграла, логарифмически расходящегося в ультрафиоле-
ультрафиолетовой области, принимает обличие полюса е-1.
Приведем еще без выкладки результат вычисления квадра-
квадратично расходящегося интеграла (8):
где
Z = Z(x, k%) = nP-x(\-x)№.
В пределе малых е имеем
rege y,v (*) = i [&v/»a - g|xvm26+Vv]+ C"(8) (*). A5)
причем
•С"(E) (ft) = ^ [m% ~ t) + T J dx №^Z ~ Wv A - 2xf] In Z. A6)
0
Сравнивая формулы F) и A4), заключаем, что логарифмиче-
логарифмические ультрафиолетовые расходимости в методе размерной регуля-
регуляризации выступают в виде полюсов по е. Сравнение формул (9)
и A5) подтверждает это заключение и свидетельствует также
о том, что и квадратичные ультрафиолетовые расходимости в этом
методе приводят к полюсу е-1.
23.4. Регуляризация обрезанием. Она является наиболее про-
простой с интуитивной точки зрения и состоит в обрезании импульс-
импульсных интегралов на некотором верхнем пределе. После приведения

188 ГЛ. VI. ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ И РАСХОДИМОСТИ
4-импульсного интеграла к евклидову виду эта регуляризация
может быть сформулирована следующим образом:
л
]dp = i]{dip)E^i\dpi\dp->xtgA]dp=] dp=i $ dQ[p*dp.
Ол 0D) О
Не составляет труда убедиться, что для расходящихся
импульсных интегралов в фейнмановской параметризации регуля-
регуляризация обрезанием дает
j gln^ + l, A7,
,^(Л»-2ЯIn £-£>).
При использовании а-представления более удобно ввести плавное
обрезание (фейнмановская регуляризация)
dp->regA{F) j" dp = j" dp-—^, A9)
которого оказывается достаточно для логарифмически расходя-
расходящихся интегралов. В простейших случаях оно сводится к ва-
варианту регуляризации Паули — Вилларса и позволяет, модифи-
модифицировав исходный интеграл, использовать без изменения формулы
предыдущего параграфа. Так, для интеграла A) получаем
_1Л? С
я2 J (m2—
dp
2—Р2 Л2—;
j 1 Г wa—x(\— x)№ 1 . Ла ,
nUm2+(l-A;)A2 —л;A—л;)^]"*" lnjj2 +
|jp^^2]} B0)
§ 24. Однопетлевые диаграммы
Рассмотрим теперь подробнее ряд простейших фейнмановских
интегралов, отвечающих однопетлевым диаграммам и содержащих
одно четырехмерное импульсное интегрирование.
24.1. Скалярная «рыба». Наиболее простая диаграмма второго
порядка с двумя внутренними линиями (см. рис. 22.1) известна

§ 24. ОДНОПЕТЛЕВЫЕ ДИАГРАММЫ 189
под названием «рыба». В случае, когда обе внутренние линии
отвечают скалярному полю с массой т, матричный элемент /
имеет вид интеграла
/<*)-^i(^-p.-fe)[*-(p-ffl-/sl- <23Л)
Этот интеграл логарифмически расходится в области больших
значений р. В предыдущем параграфе он был изучен с помощью
различных регуляризации. Сравнение формул B3.6, 7, 14, 20)
показывает, что расходящееся выражение B3.1) после выделения
сингулярного аддитивного вклада, не зависящего от k, сводится
к конечному выражению
A)
Иными словами, можно записать
/(£) = /синг+/кон(£). B)
Расходящаяся константа /сивг при регуляризации Паули — Вил-
ларса равна 1п(|д,а/Ма), при размерной регуляризации— 1пя +
+ С— 1/е, при регуляризации обрезанием— 1 + 1пц.а/Ла.
Конечная часть /кон содержит зависимость от произвольного
параметра ц.2 и определена с точностью до аддитивной постоян-
постоянной. Выбранное нами в A) определение этой константы совер-
совершенно произвольно. Правую часть A) удобно разбить на два
члена
где интеграл
1 1
J(z)= С dxln[l-4x(l-x)z]+2= Cdjcln 17~Jl(l)rfi?
о о
может быть представлен в виде
оо
J B) = A - г) f -- d° C)
Полученное выражение C) имеет структуру интеграла Коши.
Мы будем называть подобные формулы спектральными представ-
представлениями. Спектральное представление C) определяет функцию
комплексного переменного г, имеющую особенность на разрезе
1тг = 0, Rezi^l. На остальной части действительной оси она

190 ГЛ. VI. ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ И РАСХОДИМОСТИ
действительна:
D)
При я > 1 подынтегральное выражение в C) содержит полюс,
правило обхода которого определяется-'бесконечно малой добав-
добавкой + /е. Используя символическую формулу (ДУ.6), получим
— i) при
E)
Таким образом, в ультрафиолетовой области при \
/кон (Р\ V?) = +■ In (| Рг \№) - Ш (р2) + const=
= —1П (—р2/Ц8)+COIISt. av.V"^!!.
24.2. Собственные энергии фотона и электрона. В спинорной
электродинамике диаграммы, топологически эквивалентные рас-
рассмотренной, могут отличаться типом внешних и внутренних линий
(рис. 24.1, а, б). Когда внешние линии фотонные, а внутренние
Рис. 24.1. Однопетлевые диаграммы второго порядка спинорной электродина-
электродинамики: а) собственная энергия фотона; б) собственная энергия электрона.
электронные, мы имеем диаграмму собственной энергии фотона.
Соответствующий интеграл
будучи умножен на ег/16пг = -^, образует так называемый
поляризационный оператор
П1" (*) = £/■" С*). (8)
Фейнмановский интеграл G) в области больших q расходится
квадратично. Для его регуляризации используем вариант про-
процедуры Паули — Вилларса:

§ 24. ОДНОПЕТЛЕВЫЕ ДИАГРАММЫ 191
Регуляризованное выражение
/voiu\ __J_ f dgSp(...) ,q,
где
+ kvqa) - 4gva (<f + qk),
с помощью стандартных преобразований приводится к виду
1 оо
Я?
= 4i f ^ f
о о
Я? (Л) = 4i f ^ f -^ ехр й.[х A - л:) *г - т* - »в] X
X [ix A-х) Bkvka - g™&) + g™ (-J- + "я1)] •
Для выполнения интеграции по Я члены, содержащие в знаме-
знаменателе X и &г, преобразуем по формулам
о , о
Окончательный результат вычислений в пределе М2-*-оо будет
где
Id (k) =^- W- Wka) I [т^, A1)
причем
I(z) = \dx(l-x)xln[l-4x(l-x)z].
о
Явное интегрирование по х позволяет получить выражение, род-
родственное функции J (г) введенной в E):
О
Спектральное представление для / имеет вид

192 ГЛ. VI. ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ И РАСХОДИМОСТИ
Диаграмме собственной энергии электрона (рис. 24.1, б) соответ-
соответствует линейно расходящееся выражение
которое после регуляризации фотонного пропагатора
t
q
сводится к следующему:
У»(о\ - 2 С ЛеBт-хо)In P'*O-*)-Q-*)"'-^'
В пределе Мг -*• со получаем
2Л1(р)~Dт-рIп^ + 1]кон(Р). A6)'
где
1
$x Bm - хр) (in m,^p, + In -j
24.3. Треугольные вершинные диаграммы. Обратимся теперь
к однопетлевым диаграммам, состоящим из трёх линий. В простей-
Г V
■р рЦ р'~р+к У 7" p'=p'+tt
а) 5)
Рис. 24.2. Однопетлевые вершинные диаграммы третьего порядка: а) в скаляр-
скалярной модели, б) в спинорной электродинамике.
шем случае, когда все эти линии скалярные (рис. 24.2, а), соот-
соответствующий фейнмановский интеграл
г (п Ь\-—
сходится. В результате интегрирования по q он приводится к виду
p'=p+k-

§ 24. ОДНОПЕТЛЕВЫЕ ДИАГРАММЫ . 193
Здесь использовано сокращенное обозначение (ДУ.7), введен-
введенное после формулы B2.7).
Рассмотрим важную с физической точки зрения треугольную
вершинную диаграмму спинорной электродинамики, изображен-
изображенную на рис. 24.2, б. Соответствующий интеграл
B0)
— <72 m — q — p m — q—p
в области больших q расходится логарифмически. Проводя
регуляризацию фотонного пропагатора по формуле A5)
получаем после необходимых преобразований в пределе больших М
regM Г> (р', р, к) = yv In -^ + г:ои, B2)
1
о
где
Z (l 'г г — хгх31гг,
+ W {A - хг) A - х,) 05 - р) + 2т (хг - х3)} +
+ (Pv + P'l {A - х2) A-х3)(Р + р)- 2/пх,} -
р - 2хг A - Xi) р'*р' - 2х3 A - ^з) PVP-
В правой части B3) можно провести некоторые упрощения и
выполнить два интегрирования. Ввиду громоздкости мы не будем
проводить эти выкладки. Отметим лишь, что в важном частном
случае, когда электрон до и после акта взаимодействия находится
на массой поверхности, соответствующая проекция вершинной
функции может быть представлена в виде
б (р') По,и (р) = h W п (/?') Yv« (р) + /, (*а) б(/»') {£±f- - Yv} и (р),
■ B4)
т. е. выражена через два формфактора
1 1
h (Л») = 2 \ {dx}3 In -g- + f {dx}, ^., B5)
о о
<**},-§-, B6)
7 H. H. Боголюбов, Д. В. Ширков

194 ГЛ. VI. ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ И РАСХОДИМОСТИ
причем
- 4*! + xf) - 2k* A -хг) A - x3), N% = 4m*xi (x; - 1).
Интегралы в B5) и B6) можно выразить через элементарные
функции. После замены x2 = t(l—x1) получаем для /а
при
и, в частности,
/,@) = -2. B8)
В то же время подстановка xi = t(l—x1) во втором слагаемом
для формфактора ft выявляет неинтегрируемую особенность при
хг = 1. Эта сингулярность является проявлением инфракрасной
катастрофы и соответствует особенности подынтегрального выра-
выражения в исходном фейнмановском интеграле B0) при малых зна-
значениях, q, т. е. интегрированию по импульсам мягких виртуаль-
виртуальных фотонов. Подобная особенность содержится также в произ-
производной оператора собственной энергии электрона A7), взятой на
массовой поверхности. Мы не будем, однако, обсуждать здесь
проблему инфракрасных расходимостеи квантовой электродинамики
и отсылаем читателя к краткому изложению их физических при-
причин, содержащемуся ниже в § 29.4 и цитированной там литературе.
Отметим лишь, что если приписать виртуальному фотону на
диаграмме рис. 24.2, б малую массу Ко, то. упомянутая сингуляр-
сингулярность может быть выражена через логарифм этой массы
(см. по этому поводу раздел 5 Дополнения VI). В то же время
формфактор /i(£a) может быть «сдвинут на константу»
операцией перенормировки константы связи (т. е. электрического
заряда электрона е) — см. ниже §§ 25 и 28.1, вследствие чего
расходящиеся аддитивные составляющие в B5), не содержащие
импульсных зависимостей, не имеют непосредственного физического
смысла.
Второе слагаемое в B4) с помощью соотношения
2п (р1) [pv + p'v - 2ту] и(р) = п (р') [fk - kyv] u(p); k = р' - р,
C0)

§ 24. ОДНОПЕТЛЕВЫЕ ДИАГРАММЫ
195
вытекающего из уравнений Дирака, преобразуется к виду, удоб-
удобному для вычисления радиационной поправки к магнитному
моменту электрона (см. ниже § 30.2).
24.4. Ультрафиолетовые расходимости в высших порядках.
Разобранные примеры простейших однопетлевых диаграмм
Рис. 24.3. Диаграммы второго порядка комптоновского рассеяния.
позволяют заключить, что ультрафиолетовые расходимости
являются типичным, часто встречающимся явлением («правилом»,
а не «исключением»). При переходе к более сложным диаграм-
диаграммам (высшие порядки теории возмущений, большее количество
петель), картина существенно не меняется.
Для иллюстрации схематически рассмотрим процесс компто-
комптоновского рассеяния. В низшем, втором, порядке теории возмуще-
возмущений процесс описывается двумя диаграммами Фейнмана, изобра-
изображенными на рис 24.3. Эти диаграммы не имеют замкнутых петель,
8) д)
Рис. 24.4. Некоторые диаграммы четвертого порядка для комптоновского рас-
а соотвегствующие матричные элементы не содержат интегриро-
интегрирований по 4-импульсам.
В четвертом порядке процесс описывается восемью одно-
петлевыми диаграммами, характерные представители которых
приведены на рис. 24.4. Две диаграммы содержат поляризацион-
поляризационные вставки во внешние фотонные линии (см. рис. 24.4, а); две
диаграммы — собственно энергетические вставки (поддиаграммы)

196
ГЛ. VI. ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ И РАСХОДИМОСТИ
во внешние электрон-позитронные линии (рис. 24.4, б); одна
диаграмма — собственно энергетическую поддиаграмму во внутрен-
внутренней электрон-позитронной. линии (рис. 24.4, в) и Две диаграммы —
вершинные треугольные поддиаграммы (рис. 24.4, г). Согласно
результатам § 24.3 все эти диаграммы содержат ультрафиолетовые
расходимости. Наконец, последняя диаграмма, изображенная на
рис. 24.4, д, имеет замкнутый цикл с четырьмя вершинами.
Соответствующий импульсный интеграл сходится.
Шестой порядок теории возмущений отвечает двухпетлевым
диаграммам; некоторые из них изображены на рис. 24.5. Здесь
В) г)
Рис. 24.5. Примеры диаграмм, шестого порядка для комптоновского рассеяния.
встречаются диаграммы с двумя независимыми однопетлевыми
поддиаграммами (подобные изображенным на рис. 24.5, а), а также
диаграммы, в которых расходящаяся однопетлевая поддиаграмма
входит в элемент, содержащий второе импульсное интегрирова-
интегрирование. Примеры подобных случаев изображены на рис. 24.5, б, в, г.
При этом, как правило, оба интегрирования содержат ультра-
ультрафиолетовые расходимости, которые, таким образом, накладываются
друг на друга.
Наша ближайшая цель — установить общую структуру расхо-
расходящихся вкладов, в матричные элементы переходов и построить
процедуру их устранения (процедуру перенормировок).
§ 25. Выделение расходимостей
25.1. Структура однопетлевых расходимостей. Как мы убеди-
убедились в предыдущем параграфе, всем расходящимся однопетлевым
интегралам присуще замечательное свойство: ультрафиолетовые
бесконечности могут быть выделены в виде аддитивных составляю-
составляющих (см. формулы B4.2), B4.10), B4.16), B4.22)). Последние

§ 25. ВЫДЕЛЕНИЕ РАСХОДИМОСТЕИ 197
имеют вид полиномов по степеням компонент внешних импульсов
с расходящимися (в пределе снятия регуляризации) коэффициен-
коэффициентами.
Если теперь перейти от импульсного представления к коорди-
координатному, то расходящиеся вклады представятся полиномом по
производным от б-функций. Так, например, формулы B3.1), B3.2)
и B4.2) дают
(р2) dp = ^/««6 (*) + &е (*), A)
где сингулярная константа в регуляризации Паули —Вилларса
равна /Синг = 1п(ц2/Л12), а функция
^ М = Щ¥ $eriP (p2> ^)йр B)
свободна от ультрафиолетовых расходимостей.
Подобным образом
reg [IPV (*)] = — & Sp {f reg Sc (x) yv reg Sc (— *)] =
W, C)
reg [2 (*)] = - feVS« W Vv reg Dj (x) =
reg Гv (x, z; y) = ii reg Dj <x - z) fSc (x - y) yvSc (y - z) Vvl =
= Ж Vv ln 5"б (*- У)б (* - 2) + Tv (*. 2; у), E)
причем функции П, 2, Г являются фурье-образами конечных
выражений B4.11), B4.16) и B4.23).
25.2. Вклад в 5-матрицу. Обратимся к структуре вкладов
в матрицу рассеяния от расходящихся слагаемых из правых
частей формул A), C), D) и E).
Начнем со скалярной «рыбы». В модели <5? = g<p3 член второго
порядка в 5-матрице содержит отвечающее ей слагаемое типа
собственной энергии частицы (рис. 25.1)
St(x, у) = Р?Т(ч?(х)<Г(у)) = 18? :<?(x)[D4x-j/)Y?(!,):+...,
содержащее ультрафиолетовую расходимость. После регуляриза-
регуляризации на основании A) получаем
52 (х, у) = &С :Ф (хN {х-у) у (у): +18Я2 :Ф (х)[& (х- у)} <р (у): +
+ ... = ieV:<?(xN(x-y)<p(y)i+§t(x, у), F)
где С = (9/8я2) 1п(Л12/Ц2)| a S2 свободно от ультрафиолетовых рас-
ходимостей. При вычислении матричных элементов от 5а скаляр-
скалярной «рыбе» соответствует конечное выражение B). . . ■

198 ГЛ. VI. ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ И РАСХОДИМОСТИ
Подставляя выражение F) в разложение для S-матрицы,
находим
к, у)dxdy + ...=
J{х, y)dxdy+..., G)
где
А X (х) = 4р С : ф2 (х):. (8)
Таким образом, выделение из S2 расходящегося квазилокаль-
квазилокального вклада ф (х) б (х — у) ф (у) эквивалентно добавлению в St
локального слагаемого АХ(х). Подобные слагаемые называются
контрчленами.
-^_S~ А-А "ч---:;^-
Рис. 25.1. Диаг- Рис. 25.2. Диаграм- Рис. 25.3. Диаграмма
рамма собственной ма рассеяния вто- «орех», представляю-
энергии второго по- рого порядка в мо- щая собственную энер-
рядка в скалярной дели ф4. гию второго порядка
Ф3 модели. в модели ф4.
Скалярная «рыба» входит также в член второго порядка
в модели <5? = /1ф4:
52 (х, у) = wr (ф4 (х) Ф4 (у)) = 1Ш : Ф2 (х) Щ (х - у) Ф2 (у): -
-i96h*:(i>(x)D'c(x-y)<p(y):+..., (9)
дающий вклад в амплитуду рассеяния 2«->-2 (рис. 25.2).
Второе слагаемое в правой части (9) отвечает диаграмме
«орех», изображенной на рис. 25.3. Соответствующий матричный
элемент расходится квадратично. Вычисления дают
^^ &x), A0)
где при регуляризации Паули — Вилларса
А а\п А
а &1 свободна от ультрафиолетовых расходимостей. Подставляя
(9), A0) и A) в разложение S-матрицы, получаем формулу вида
G), причем Aif состоит из трех контрчленов:
(х) = Ch2 :у* (х): + Ajfi* :у* (х); - А^-.д^у д»у:> (И)

§ 25. ВЫДЕЛЕНИЕ РАСХОДИМОСТЕИ
199
В 5-матрице спинорной электродинамики член второго порядка
содержит расходящиеся слагаемые, отвечающие C) и D):
St(x, y) = — i:
а член третьего порядка включает слагаемые (рис. 25.4), содер-
a)
S)
в)
Рис. 25.4. Расходящиеся вклады третьего порядка в матрицу рассеяния спи-
' норной электродинамики.
жащие множителями как собственные энергии C), D), так и тре-
треугольную вершинную диаграмму E):
S,(x, у, г) й:
2, у;
-ie :ф(х) vMv(x)Sc(х-гJ(г-у)Ъ(у): +
ie :AV (х) П^(x-z)Dcvp (z-
Выделение из 2, П и Г локальных слагаемых
2 (х - у) = (am + ibb) б (х - у) + 2' (х-у),
№v (x-y) = cg^8 (x-y) + d(&»u+ ^v) б (х -
Г^ (х, г; у) = /vv« (л: - г/) б (л: - г) + r'v (x, г; у)
", A2)
приводит к следующей перестройке вклада второго порядка:
\ J 52 (д;, у) dxdy i J ^р (х) (am + /6д) ф (х) dx +
-■» \ \ (х) [cg»v + d(g^a+ №)] Av (x) dx +
A3)

200 ГЛ. VI. ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ И РАСХОДИМОСТИ
и вклада третьего порядка
~ jj S3(x, у, z)dxdydz =
= ie :\ А» {х) [cgw + d fa* Q , + ft dV)] Dpv (x-y)x
X Ф iy) ?р1Ф (У):dx dy — ie \ :гр (x) (am + ibbx) x
X Sc (x - y) VMV (у) гр (у): dx dy + (
- ie j Щ {x) VMV (a;) Sc (x - y) {am + bby) гр (у) :dxdy +
- ief j :f (д:)^v (д:) vvip (x): dx + ~ j 5^ (д:, г/, г) Лсdy dz. A4)
Видно теперь, что два первых слагаемых в правой части A3)
и четвертое слагаемое в правой части A4) могут быть отнесены
в член первого порядка
J Sx (х) dx-+l\ {X (х) + AcSf (x)] dx,
AcSf (*) = — :$ (x) (am + ibb)^{x):-c:Av (x) Av (x): +
-d :А^(х) □ A^ixy.+d-.id^) (dvAv): -ef :$(x)A(x)Mp(x):. A5)
В то же время первые три члена в правой части формулы A4)
могут быть представлены в виде
■f- J Т {X (х) + АХ (х), X (у) + АХ (у)} dxdy-
- ~ jj T(£(x)£(y))dxdy = i* j T(X(х), Aje(y))dxdy+ ....
причем под символом АХ следует понимать правую часть A5)
за вычетом последнего слагаемого.
Таким образом, мы убедились, что выделение из S2 и S3 син-
сингулярных вкладов, отвечающих квазилокальным слагаемым в A2),
эквивалентно добавлению локальных контрчленов A5) в лагран-
лагранжиан взаимодействия X (х).
Эта эквивалентность является основой метода устранения
ультрафиолетовых расходимостей, известного как метод перенор-
перенормировки.
25.3. Контрчлены и перенормировки. Идеология перенормировок
основана на том факте, что контрчлены (9), как правило, имеют
структуру отдельных слагаемых исходного полного лагранжиана.
Рассмотрим модель действительного скалярного поля с четвер-
четверным взаимодействием:
VP д*р - -£ Ф2 (*)■+Aq>* (х).
Сравнение с формулой A1) показывает, что расходящиеся контр-
контрчлены имеют структуру отдельных слагаемых полного лагран-
лагранжиана.

§ 25. ВЫДЕЛЕНИЕ РАСХОДИМОСТЕЙ 201
Для того чтобы установить физический смысл добавления
к лагранжиану кантрчленов такого типа, отвлечемся на время
от расходимостей и рассмотрим контрчлены
АХ (х) = -^ <ЭцФ ^Ф - ^ ф* (х)+ су* (х) . A1')
с конечными коэффициентами а0, а2, с. Складывая =5?полн с A=Sf,
получаем
^^ A6)
где z1=l+a0, г1т'г = п _ _
Обсудим сперва смысл коэффициента zv Два первых члена
в правой части A6) представляют собой умноженный на гх лаг-
лагранжиан свободного скалярного поля с массой т'. Абсолютная
нормировка свободного лагранжиана проявляется лишь при кван-
квантовании поля, т. е. в уравнениях типа G.1). Не составляет труда
убедиться, что, производя замену
ф -> ф' = VT1 ф, A7)
мы приходим к перенормированному полю ф' (х) с нормальными
коммутационными соотношениями (8.4). Подставляя A7) в A6),
преобразуем X' к виду
где
Таким образом, мы видим, что совокупный эффект трех контр-
контрчленов A1), AГ) сводится к перенормировке двух физических
параметров модели: массы т и константы связи h.
В реальном случае коэффициенты при контрчленах (типа С,
Ао, А2 в формулах A1), (8)) сингулярны, т. е. стремятся к бес-
бесконечности при снятии регуляризации. Вследствие этого становятся
сингулярными соотношения типа A9), связывающие исходные
«затравочные» значения т, h с физическими «перенормированными»
значениями т', h'.
Подобные соотношения перенормировок для массы и нормы
операторной волновой функции были нами получены в модели
тяжелого нуклона (в § 13.4). Напомним читателю, что эти соот-
соотношения становились сингулярными при переходе к точечному
нуклону. В релятивистской квантовой теории поля природа ультра-
ультрафиолетовых расходимостей также обусловлена локальным точеч-
точечным характером взаимодействия. Этот факт особенно ясно виден
на разобранных в § 24 примерах диаграмм собственной энергии

202 ГЛ. VI. ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ И РАСХОДИМОСТИ
электрона и вершинной диаграммы. Использованная там регуля-
регуляризация фотонного пропагатора B4.15) равносильна «размазке»
точечного электрона, т. е. переходу к нелокальному взаимодей-
взаимодействию
/ц (х) А» (*) -v /„ (х) j К (х - у) A» (y)dy,
где формфактор
е пределе УИ2-»-оо стремится к б-функции.
В методе перенормировок, который более подробно излагается
ниже (см. §§ 28, 29), сингулярные соотношения перенормировок
типа A9) рассматриваются чисто формально. При этом имеется
в виду то обстоятельство, что затравочные значения констант
типа тик, фигурирующие в исходном лагранжиане и отнесенные
к свободным полям (точнее, к полям с бесконечно слабым взаимо-
взаимодействием), не имеют физического смысла, так как подобные
идеализированные поля в природе не существуют и невозможно
связать затравочные параметры с какими-либо даже мысленными
экспериментами.
В то же время учет радиационных поправок высших порядков
приводит к тому, что не только 5,, но и высшие Sn (n ^2) зависят
лишь от перенормированных масс и констант связи. Поэтому
оказывается возможным связать перенормированные параметры
с измеряемыми на опыте величинами и считать их физическими
массами и зарядами.
Факт зависимости полученных в результате процесса перенор-
перенормировки свободных от расходимостей матричных элементов только
лишь от перенормированных физических масс и констант связи
g' = fg(m, g, Л), m'=fm(m, g, A) B0)
и отсутствие дополнительных зависимостей от затравочных т, g и
сингулярного параметра Л и каких-либо других параметров по
отдельности является важным свойством некоторого класса моде-
моделей, которые называются перенормируемыми.
25.4. Расходимости и обобщенные функции. Возможна еще
одна точка зрения на процесс устранения ультрафиолетовых рас-
расходимостей, который эффективно сводится к вычитанию из расхо-
расходящихся матричных элементов соответствующих полиномов. Обра-
Обратим внимание на то, что расходящимся фейнмановским интегралам
по виртуальным импульсам в координатном представлении всегда
соответствуют произведения некоторого числа пропагаторов Dc (x),
Dl(x), Sc(x), ... Как было установлено в § 18 3, эти. последние
содержат слагаемые типа 6 (#°), б (х2) и с математической точки
зрения являются обобщенными функциями, В отличие от обычных

§ 25. ВЫДЕЛЕНИЕ РАСХОДИМОСТЕИ 203
функций математического анализа, отвечающих отображению
число-»-число, обобщенные функции определяются как ядра линей-
линейных функционалов и задают отображение функция-v число.
Поэтому операция умножения обобщенных функций друг на друга
требует особого определения. Не вдаваясь в подробности этого
довольно сложного вопроса (см. Введение, §§ 18, 19), отметим
здесь, что переход типа
[Dc (x)f -+ reg [Dc (x)f -*- Щ (x)
можно рассматривать как определение произведения D*. Иными
словами, можно положить
De(x)-De(xKa'&e(x), B1)
где правая часть определена согласно B).
При таком способе рассуждений ультрафиолетовые расходи-
расходимости вообще не фигурируют в 5-матрице и нет нужды заниматься
бесконечными перенормировками масс и зарядов. Следует лишь
однозначно фиксировать произвол в конечных величинах, связан-
связанный с параметрами типа ц2 из формулы B4.1).
При этом оказывается, что в перенормируемых моделях кван-
квантовой теории поля матричные элементы выражаются через неко-
некоторые функции параметров лагранжиана т, g и произвольных
констант типа ц
g = <Pg(m, g, \i), m = фт (m, g, ц) B2)
и не зависят от т, g и ц по отдельности. Более подробно эти
вопросы будут рассмотрены в следующей главе.

Глава VII. УСТРАНЕНИЕ РАСХОДИМОСТЕЙ
§ 26. Общая структура расходимостей
26.1. Расходимости высших порядков. В предыдущем пара-
параграфе мы рассмотрели ультрафиолетовые расходимости двух низ-
низших порядков теории возмущений скалярной нелинейной модели
и спинорной электродинамики. Там, во-первых, было установлено,
что для простейших однопетлевых диаграмм Фейнмана ультра-
ультрафиолетовые расходимости могут быть выделены в аддитивные
квазилокальные слагаемые. Во-вторых, было показано, что в силу
квазилокального характера подобные слагаемые дают вклад
в матрицу рассеяния, имеющий структуру членов более низкого
порядка теории возмущений, и благодаря этому в конечном итоге
сводятся к локальным вкладам в лагранжиан, т. е- к контр-
контрчленам.
Сейчас мы проведем аналогичный анализ диаграмм высшего
порядка и покажем, что, хотя в общем случае расходящиеся
вклады и не имеют квазилокальной структуры, тем не менее они
также сводятся к контрчленам. Для простоты ограничимся ска-
скалярной нелинейной моделью с четверным самодействием
A)
Диаграммы второго порядка, изображенные на рис. 25.2 и
25.3 были рассмотрены в § 25.2. В третьем порядке процесс рас-
рассеяния описывается двумя двухпетлевыми диаграммами, изобра-
изображенными на рис. 26.1.
Диаграмма 26.1, а представляет итерацию диаграммы «рыба»,
и соответствующий матричный элемент в координатном представ-
представлении пропорционален выражению
DlU-y)Dl(y-z). B)

§ 26. ОБЩАЯ СТРУКТУРА РАСХОДИМОСТЕИ 205
После регуляризации с помощью B5.1) имеем
Ш
+ Щ(х-у)Ш(у-г). C)
Соответственно этому в импульсном представлении фурье-образ
сводится к квадрату интеграла B3.7), т. е. к выражению
[regA, / @)Т = (in ^-J - 2 In i£ /кон (V) + (/кон (*■))«, D)
где /Кон описывается формулой B4.1).
Структура сингулярных составляющих диаграммы рис. 26.1,6
может быть установлена наиболее просто в импульсном представ-
а)
Рис. 26.1. Двухпетлевые диаграммы рассеяния третьего порядка в модели <р*.
лении. Используя обозначения импульсов, указанные на рис. 26.2,
рассмотрим двухпетлевой феинмановскии интеграл
f X
Как нетрудно убедиться, этот интеграл расходится в области
больших импульсов. Введем «плавное обрезание» по каждой пере-
переменной интегрирования:
- *4). F)
Получаем
В этом сходящемся выражении мы установили определенную
последовательность интегрирований и воспользовались введенным

206 ГЛ. VII. УСТРАНЕНИЕ РАСХОДИМОСТЕИ
ранее обозначением B3.1). Используя формулу B3.7) под знаком
интеграла, находим
regA, (л К = — In ~JJ regAi (л / (А) +
. С idg M* 1
я* Л1«—<
a—<
Структура первого слагаемого ясна из формулы B3.7). Второе
слагаемое также содержит сингулярность в пределе М2->-оо, как
это следует из асимптотической формулы B4.6) для /кон. Не
составляет труда убедиться, что этот сингулярный вклад аддити-
аддитивен.. Вычисления показывают, что он про-
% порциона лен квадрату «большого» логарифма
ln/W2. Опуская соответствующие выкладки,
приведем окончательный результат:
regA, {F) К = (in f J - In £ /ков (*) -
+ ^0H(...^...)- (8)
Здесь первые два члена в правой части соот-
Рис. 26.2. Импульсные ветствуют первому слагаемому правой части
обозначения в интег- формулы G).
рале E). Полученные выражения D) и (8) имеют
общую структуру. В пределе больших М
они имеют вид полиномов по In M. Коэффициенты при (In M)a
являются числами, а при In М — функциями импульсных пере-
переменных.
В случае более высоких порядков диаграммы рассеяния
D-хвостные диаграммы) также расходятся логарифмически. Полное
выражение для каждой из них в пределе больших М представ-
представляется полиномом по степеням \пМ. Старшая степень расходящегося
логарифма равна числу петель I (т. е. числу независимых 4-им-
пульсных интегрирований) диаграммы. Коэффициент при (In М)'
является числом, а коэффициенты при младших степенях 1пМ —
функциями импульсных переменных.
26.2. Связь с контрчленами и перенормировки. Покажем теперь,
что члены с младшими степенями расходящихся логарифмов, не
имеющие квазилокальной структуры в ^-представлении, также
сводятся к контрчленам и перенормировкам.
Введем для этого графическое изображение процесса выделения
расходимостей. Формуле B4.2) сопоставим рисунок

§ 26. ОБЩАЯ СТРУКТУРА РАСХОДИМОСТЕИ
207
на котором заштрихованная «рыба» отвечает конечной функции
/кон» а крестик, обведенный кружком, — расходящемуся логарифму.
Тогда вклад диаграммы «рыба» в матричный элемент рассеяния
второго порядка B5.9) изображается в виде
Вклад диаграммы рис. 26.1, а, согласно формуле D), будет
Для диаграммы рис. 26.2, б соответственно
( '
• A2)
На последнем рисунке крестиком в двойном круге изображен
третий член формулы (8), т. е. расходящаяся часть второго сла-
слагаемого из правой части G). Все остальные обозначения очевидны.
Собирая вклады слагаемых A0), A1), A2) в матрицу рассея-
рассеяния, получаем
A3)
Мы видим, что расходящиеся вклады из многопетлевых
диаграмм высших порядков, имеющие квазилокальную структуру,
дают вклад в член первого порядка Sl3 т. е. в контрчлены
лагранжиана, что в данном примере приводит к перенормировке
константы связи:
..J.

208 ГЛ. VII. УСТРАНЕНИЕ РАСХОДИМОСТЕИ
Сингулярные составляющие второго типа, не имеющие квази-
квазилокального характера и в импульсном представлении зависящие
от импульсов [подобные вторым слагаемым в правых частях фор-
формул D) и (8)], приводятся в нашем примере к структурам,
подобным членам второго порядка матрицы рассеяния, и эффек-
эффективно перенормируют константу связи.в 52:
Рассмотренная иллюстрация является типичной для целого
класса квантовополевых моделей взаимодействующих полей —
класса, включающего самодействие скалярного поля Лф4, а также
такой физически важный случай, как спинорлая электродинамика.
Для моделей этого класса все без исключения расходящиеся
составляющие матричных элементов сколь угодно высокого по-
порядка приводятся к контрчленам, добавленным к лагранжианам
взаимодействия в составляющих 5-матрицы более низших поряд-
порядков, что в свою очередь оказывается эквивалентным перенорми-
перенормировкам физических параметров модели, т. е. масс, констант связи
и волновых функций.
Модели взаимодействующих полей этого типа называются
перенормируемыми.
26.3. Степень расходимости диаграмм. Рассмотрим теперь
более подробно описанное выше свойство перенормируемости и
сформулируем критерий, которому должны удовлетворять пере-
перенормируемые модели квантовой теории поля.
Возьмем типичный фейнмановский интеграл в импульсном
представлении
> A4)
отвечающий связной диаграмме я-го порядка. Здесь в аргументах
б-функций стоят алгебраические суммы импульсов внутренних
линий диаграммы и внешние для данной v-й вершины, импульсы ^.
Пропагаторы представим в виде
^ A5)
где Pi — некоторый полином степени ги характеризуемый спином
соответствующего поля.
Как было установлено, интегралы типа A4) в силу ультра-
ультрафиолетовых расходимостей, вообще говоря, не существуют и тре-
требуют регуляризации. Мы, однако, не будем здесь ее вводить и
рассмотрим свойства подынтегральных выражений в области
больших \pi\ с целью определения характера соответствующих
ультрафиолетовых расходимостей.

§ 26. ОБЩАЯ СТРУКТУРА РАСХОДИМОСТЕЙ 209
В силу связного характера рассматриваемых диаграмм с по-
помощью 6-функций снимется 4 (я— 1) интегрирований (последняя
б-функция выразит закон сохранения полного 4-импульса),
вследствие чего останется 4(L —я-fl) независимых переменных,
где L обозначает полное число внутренних линий.
Подобно тому как при интеграции по трехмерному простран-
пространству в качестве переменной удобно ввести радиус, введем
в 4 (L — п-\- 1)-мерном пространстве соответствующий «радиальный»
импульс Р. Тогда произведение независимых дифференциалов dpi
даст фактор P4(Z-~fl+1>dP/P. Учитывая лишь старшие степени
импульсов в функциях Ас, получаем множитель
Z'i~2L И(';-2)
Р' =Р1
и поэтому в подынтегральном выражении множитель при dP/P
в области больших Р будет вести себя как Ра, где
a>(G) = ]?l(rl + 2)-4(n-l). A6)
Число о назовем индексом диаграммы.
Интеграл по Р окажется сходящимся при 0)(G)<0 и расхо-
расходящимся в противном случае.
Разумеется, из сходимости интеграла по Р еще не следует
сходимость интеграла типа A4) в целом. Здесь может возникнуть
положение, подобное тому, когда при вычислении интеграла
dx \ dy-
oJ
интеграл
A+Р2ЯП2ф)а
по радиальной переменной p = x/cosq) = «//sin ф сходится, но остаю-
остающийся интеграл по <р из-за особенности в точке ср = О оказыва-
оказывается расходящимся.
Примеры такого типа дают интегралы, отвечающие диаграммам,
изображенным на рис. 26.3. Обе диаграммы имеют отрицательный
индекс « = — 2, однако каждая из них имеет поддиаграмму,
которая расходится логарифмически или квадратично.
Таким образом, условие
A7)
является необходимым для сходимости, но недостаточным.
Как видно из примеров расходящихся диаграмм, рассмотрен-
рассмотренных в §§ 24, 25, степень расходимости интеграла, равная о,

210 ГЛ. VII. УСТРАНЕНИЕ РАСХОДИМОСТЕИ
при 0M=0 определяет структуру расходящихся вкладов соответ-
соответствующего регуляризованного интеграла в пределе снятия вспо-
вспомогательной регуляризации.
Интегралу с индексом ю>0 соответствует выражение
причем
reg/ш(р, М)-vа0М* + alPM^ + ... а^р^М + а*рР + С„(р),
где /кон — «конечная часть» интеграла /," не зависящая от пара-
параметра регуляризации, da — коэффициенты, которые могут зави-
зависеть от In M.
■ > О <■
а) - S)
Рис. 26.3. Примеры скалярных диаграмм, имеющих отрицательный индекс, но
содержащих расходящиеся поддиаграммы.
Мы видим, что индекс диаграммы определяет степень полинома
по компонентам импульсных переменных с сингулярными коэф-
коэффициентами, после выделения которого интеграл становится
конечным. Этот полином в координатном представлении является
полиномом по производным от б-функций.
Итак, если рассматриваемая диаграмма G объединяет п вер-
вершин и обладает s внешними линиями, то соответствующий квази-
квазилокальный оператор представится выражением типа
:«! (xt) ...us (xs): Za(д/дх) б(xt-х2) ... б (xn-t-хп),
причем степень полинома Za равна индексу диаграммы <о.
Интегрируя это выражение по всем переменным xt, кроме одной,
получим контрчлен лагранжиана. При выполнении этих тривиаль-
тривиальных интеграции производные с б-функций перейдут на операторы
поля ив и результат представится в виде нормального произве-
произведения некоторого числа операторных функций поля и их произ-
производных. При этом максимальная суммарная степень производных
оказывается равной индексу диаграммы o(G), а степень всего
выражения по операторным функциям — числу внешних линий s.
26.4. Свойство перенормируемости. Поэтому, если какая-либо
теория приводит к сильносвязным диаграммам с неотрицательным
индексом, у которых числа o(G), s оказываются ограниченными,
то для полного исключения всех расходимостей такая теория
требует введения контрчленов конечного числа типов. Под типом
контрчлена здесь подразумевается его операторный тип и степень

§ 26. ОБЩАЯ СТРУКТУРА РАСХОДИМОСТЕЙ 211
производных у каждого оператора поля. В противном случае
число типов контрчленов оказывается бесконечным.
Проанализируем теперь зависимость индексов <о (G) от числа
внешних и внутренних линий диаграммы. Введем для этого поня-
понятие индекса вершины, определив его равенством
2
'lot
причем суммирование производится по всем внутренним линиям,
входящим в г-ю вершину. Нетрудно заметить, что индексы диаг-
диаграммы выражаются через индексы входящих в диаграмму вершин
следующим образом:
поскольку каждая внутренняя линия входит одновременно в две
вершины. Для данного типа вершин индекс «/ принимает макси-
максимальное значение Q/ в том случае, когда все линии, входящие
в вершину, оказываются внутренними.
Максимальный индекс вершины Q,, очевидно, является харак-
характеристикой лагранжиана взаимодействия, точнее его отдельных
слагаемых. Его можно назвать индексом лагранжиана. Если все
О,<0, B0)
то из A9) следует, что o(G)^4. Напротив, если хотя бы для
некоторых типов вершин (некоторых слагаемых лагранжиана
взаимодействия)
О*>0, B1)
то всегда можно построить такую диаграмму G, содержащую
достаточное число вершин этого типа, чтобы о (G) оказалось боль-
большим любого наперед заданного числа. Таким образом, либо
индекс диаграмм не превышает четырех, либо он может быть
сделан сколько угодно большим.
Учитывая, что
'ext
где lext — индексы внешних линий, входящих в данную вершину,
зависимость <о (G) от числа внешних линий можно записать в виде
B2)
причем суммирование в последнем члене производится по всем
внешним линиям данной диаграммы. Поэтому в случае B0) число

212 ГЛ. VII. УСТРАНЕНИЕ РАСХОДИМОСТЕЙ
внешних линий диаграммы с положительным индексом не превы-
превышает четырех. В этом случае обе величины о(G) us ограничены
числом 4, количество типов соответствующих контрчленов оказы-
оказывается конечным и может быть осуществлена их детальная клас-
классификация. В случае же B1) обе суммы в правой части B2)
могут быть сделаны сколь угодно большими при неотрицательном
o)(G). Обе характеристики, «(G) и s, оказываются неограничен-
неограниченными, и для компенсации расходимостей возрастающих порядков
приходится вводить контрчлены с возрастающими степенью
«линейности» и количеством производных. Замкнутого выражения для
полного эффективного лагранжиана при этом получить не удается.
В соответствии с указанным все взаимодействия могут быть
разбиты на два класса:
а) взаимодействия перенормируемого типа (все £2,=^0);
б) взаимодействия неперенормируемого типа (некоторые из
Qi>0).
Квантовополевые модели, содержащие взаимодействия первого
класса, являются перенормируемыми. Здесь, однако, следует
заметить, что условие Q,-^0 является достаточным, но не необ-
необходимым. Это замечание иллюстрируется моделью Вайнберга —
Салама, рассмотренной ниже в § 32.
§ 27. Полные функции Грина
27.1. Пропагаторы физических полей. Для более систематиче-
систематического изучения физического смысла различных контрчленов и свя-
связанных с ними перенормировок нам потребуются так называемые
полные функции Грина и вершинные части, т. е. объекты, учиты-
учитывающие радиационные поправки, возникающие в результате
взаимодействия квантовых полей и потому отвечающие реальным
физическим частицам.
О
Рис. 27.1. Пропагатор скалярной частицы с радиационными поправками низ-
низших порядков в модели <р*.
Начнем с одночастичных B-хвостных) функций Грина, т. е.
с пропагаторов. Радиационные поправки к пропагаторам свободных
полей обусловлены диаграммами собственно энергетического типа.
На рис. 27.1 изображены собственно энергетические вставки
низших порядков в пропагатор скалярной частицы в модели /up4.
Их сумма приводит к полной функции Грина скалярного поля.

§ 27, ПОЛНЫЕ ФУНКЦИИ ГРИНА 213
Из собственно энергетических диаграмм можно выделить класс
сильносвязных или одночастично неприводимых диаграмм (т. е.
диаграмм, которые не могут быть приведены к двум несвязным
путем снятия одной внутренней линии). Сумма таких диаграмм
Рис. 27.2. Сумма сильносвязных диаграмм, представляющих массовый оператор.
изображена на рис. 27.2. Она отвечает так называемому массо-
массовому оператору М (р2).
Полная функция Грина скалярного поля Д (р; g), т. е. пропа-
гатор скалярной частицы, учитывающий виртуальные процессы
рождения и поглощения дополнительных частиц при движении
Рис. 27.3. Представление полной функции Грина через диаграммы, содержа,
щие итерации массового оператора.
первоначальной частицы через вакуум, связан с массовым опера-
оператором М(р2; g) соотношением, отвечающим рис. 27.3;
f SAo^-Ao+... A)
Здесь
а нормировка массового оператора (выделение множителя г) сле-
следует введенным в § 24 простейшим однопетлевым вставкам.
В низшем порядке теории возмущений, отвечающем диаграмме
«орех» (см. рис. 25.3), имеем
М(р2; g) = g*Mi(p*)=-^fi §dkdqA(q)A(k)A(p + q + k). B)
Как легко видеть, правая часть соотношения A) имеет структуру
геометрической прогрессии и может быть представлена в сверну-
свернутом виде. Получаем
Д = До [ 1 - ША0 + (- ШД0)а + ...] = До A + ШД0)-\
т. е.

214
ГЛ. VII. УСТРАНЕНИЕ РАСХОДИМОСТЕИ
Подобным образом можно представить полные функции Грина
частиц со спином, например, электрона и фотона в спинорной
электродинамике. Так, вводя массовый оператор электрона 2,
согласно рис. 27.4 получаем
G(p) =
— i
м—
, a)
D)
Вклад от сильносвязных собственно энергетических диаграмм
фотона образует поляризационный оператор Пй„(&; а) и т. д.
+
Рис. 27.4, Сильносвязные диаграммы, образующие массовый оператор электрона.
В низ1ием порядке теории возмущений эти операторы сводятся
к введенным в § 24 (см. формулы B4.8) и B4.14)) выражениям
2(р;а)=а2(р)+а2...,
г E)
Мы отложим рассмотрение матричной структуры поляризационного
оператора до § 29, где будет введено и использовано условие
градиентной инвариантности.
Рис. 27.5. Сильносвязные диаграммы третьего и пятого порядков, представля-
представляющие электрон-фотонную вершину в спинорной электродинамике.
Аналогичным образом можно ввести суммы многохвостных
диаграмм, в том числе суммы сильносвязных диаграмм с 1^3
внешними линиями, образующие так называемые eepmeiccu, или
верЩинные функции (см., например, рис. 27.5). В дальнейшем

§ 27. ПОЛНЫЕ ФУНКЦИИ ГРИНА 215
мы будем обозначать собирательным термином полные функции
Грина выражения, отвечающие наборам связных диаграмм с дан-
данным числом внешних линий, равным или большим двух. Пропа-
гаторы физических полей в этой терминологии отвечают 2-хвост-
ным полным функциям Грина.
27.2. Высшие функции Грина. Введенные выше понятия опи-
опирались на полуинтуитивные рассуждения, использующие сумми-
суммирование членов, соответствующих определенным типам диаграмм.
Мы дадим сейчас аналитические формулы для полных функций
Грина.
В основу соответствующего формального выражения для
я-хвостной функции положим вакуумное ожидание
F)
содержащее под знаком Г-произведения матрицу рассеяния
S = T (exp io>0), G)
где &£ = \Х (х) dx. С одной стороны, выражения типа F) родст-
родственны матричным элементам S-матрицы для переходов nin-+nf;
«in+ «/ = «• С другой стороны, при я = 2 подобные выражения
являются естественными обобщениями одночастичных функций
Грина свободных полей на случай взаимодействия.
Разлагая Г-экспоненту, получаем из F) при я = 2 ряд
<7Ч (х) и2 (у) S)Q = (Тщ. (х) и, (у)H +1 <7Х (х) и2
+ ■£-(Тиг(х) и2(у) ^2>0 + ~(TUl(х) и2(у)&?аH +..., (8)
последовательные члены которого содержат радиационные поправки
к первому члену (Т|ы1ы2)о> представляющему собой элементарное
(свободное) спаривание.
Здесь уместно сделать одно важное техническое замечание,
относительно выражений, содержащих под знаком операции
(Г(...)H операторные сомножители, не зависящие явно от вре-
времени, подобные показателю экспоненты в G) или, например,
операторам полей в импульсном представлении. Может возникнуть
искушение вынести такой «не зависящий» от времени сомножитель
из-под знака Г-произведения. Однако в результате этой операции
после вычисления вакуумного ожидания мы придем к выражению,
в котором некоторые хронологические спаривания окажутся
заменёнными на обычные, т. е. придем к неверному результату
В выражениях подобного типа всегда следует сначала выполнить
операцию (Т (.. .))„, а затем уже интегрировать по конфигурацион-
конфигурационному пространству, Например, трети) член в правой части (8)
есть по определению
Х (х) и2 (у) а*?2H = I dzx dz2G(x, у; zv z2),

216 ГЛ. VII. УСТРАНЕНИЕ РАСХОДИМОСТЕЙ
где
G (х, у; гг, г2) = (Тиг {х) и2 (у)% (гг) £ (г2)H.
Таким образом, операции <Г...H и ^dx непереставимы и
запись типа (8) является чисто символической.
Слагаемые правой части (8) содержат члены, соответствующие
диаграммам с двумя внешними линиями, выходящими из точек х
и у, подобным изображенным на рис. 27.1. Однако, помимо диа-
диаграмм, приведенных на рис. 27.1, третьему слагаемому правой
части (8) соответствует несвязная
х* 'У lZ" *У диаграмма, изображенная на рис.
О^~~ч 27.6, а, четвертому слагаемому —
Г\7) диаграмма рис. 27.6, б и т. д.
чХ/ Подобные несвязные диаграммы
а) $) имеются во всех высших поряд-
п о-? с и ках. Они отвечают определенному
Рис. 27.6. Несвязные диаграммы -. » v J
второго и третьего порядков, отве- способу спаривании операторов,
чающие слагаемым правой части когда операторы «t (x) и Ы2 (г/)
формулы (8). спарены друг с другом через часть
промежуточных вершин г1( ..., zm.
Операторы из остальных вершин zm+1, .... zn в диаграммах дан-
данного я-го порядка спарены только между собой. Соответствующие
вклады фактор изуются:
(Т {Ulu2 {ieJ)m})?- (Т {Ш)п-тH.
Введенный здесь верхний индекс обозначает связные вклады.
Вершины г1г .... zm могут быть выбраны из п вершин nl/ml (n — т)\
способами. Имеем поэтому
Меняя порядок суммирования, получаем
= (TUlu2S)cQBSQ; SQ = (SH. (9)
Таким образом, вакуумные вклады SQ факторизуются и в полном
выражении
Поэтому полные одночастичные функции Грина определим
следующим образом:

§ 27. ПОЛНЫЕ ФУНКЦИИ ГРИНА
217
Выражение A0) учитывает все радиационные поправки, соответ-
соответствующие связным диаграммам Фейнмана, и в пределе выключе-
выключения взаимодействия переходит в функцию Грина свободных полей.
Проведенное рассуждение, приводящее к факторизации вакуум-
вакуумных вкладов, может быть повторено для вакуумных ожиданий
при k>2. Здесь, однако, после удаления вакуумных вкладов
выражения
So1(Tu1...ukS)o, A1)
вообще говоря, содержат слагаемые, в которых часть операто-
операторов «!,..., Щ входит в одну компоненту связности несвязной
диаграммы, а остальные utn, ..., ик в другую (другие). Такие
члены отвечают произведению диаграмм, входящих в полные
функции Грина с меньшим числом внешних линий.
Ю
ю
Рис. 27.7. Представление 3- и 4-хвостных функций Грина через 2-хвостную
функцию Грина Д и сильносвязные вертексы, отмеченные двойной штрихов-
штриховкой. Квадратом Q обозначен «обратный пропагатор> Д~1.
Поэтому выражения типа A1) при k~>2 не могут быть при-
приравнены полным &-хвостным функциям Грина. Исключение состав-
составляет 3-хвостка
Soi(Tul(x)u2(y)u3(z)S)Q, A2)
представляющая собой сумму связных вкладов.
Для связной 4-хвостки приведем без вывода формулу
G1234 (х, у, г, t) = So1 (Тих (х) и2 (у) и3 (г) ы4 (/) S)o -
- гД12 (х, у) Д34 (г, t) - гД13 (х, г) Д24 (у, t) - г'Д14 (х, t) Д23 (у, г). A3)
27.3. Сильносвязные многохвостки (вертексы). Введенные выше
многохвостные функции Грина содержат все слабосвязные (т. е.
одночастично приводимые) вклады. Этот тезис иллюстрируется
рис. 27.3 и 27.7, на которых сильносвязные составляющие отме-
отмечены двойной штриховкой.

218 ГЛ. VII. УСТРАНЕНИЕ РАСХОДИМОСТЕЙ
Соответствующие формулы, выражающие связные многохвостки
(полные функции Грина) через сильносвязные вертексы, могут быть
получены на основе аппарата производящего функционала с по-
помощью представления полных функций Грина и вертексов через
соответствующие вариационные производные. Отсылая любозна-
любознательного читателя к имеющейся специальной литературе (см.,
например, § 38 Введения), приведем здесь окончательные фор-
формулы, отвечающие рис. 27.7 для скалярного поля:
Ga(x, у, г) =
= \A{x-x')dx'Y3(x', у', z')dy'A(y'-y)dz'A(z'-z), A4)
GAx, У, г, t) =
=lA{x-x')dx'A{y-y')dy'Ti(x',y',z',t')dz'A{z'-z)dt'A{t'-f) +
^(x, у, x)dxA-1(x-x')dx'G3(x', z, t) +
(х, z, x)dxA-1(x-x')dx'G3(x', у, t) +
+ \ G3 (x, t, т) dxД-1 (т - xf) dx'G$ (х\ у, t). A5)
Здесь Д-1 — функция, обратная к Д в смысле интегральной свертки,
т. е. по определению
\-y) = 6{x-y). A6)
Заметим, что в импульсном представлении фурье-образы функ-
функций Д и Д-1 взаимообратны в алгебраическом смысле:
С помощью функции Д не составляет труда записать фор-
формулы, обратные к A4) и A5). Имеем, например,
Гз(*. у, г) =
= \A-Hx-x')dx' A-l(y-y')dy'G3{x',y',z')dz' А-Цг'-г). A7)
Приведем еще формулу типа A4) для спинорной электродинамики:
= J 5е (х- х') dx'DT (z -z') dzTv (*', у', z') dy'S* (у' -у). A8)
В заключение отметим, что процедура перехода от слабосвяз-
слабосвязной треххвостки G3 к сильносвязной Г3 сводится к исключению
радиационных поправок из внешних линий и поэтому иногда
именуется «ампутацией» внешних линий. Для более высоких функ-
функций Грина соответствующий переход, как видно из формулы A5),
не ограничивается ампутацией внешних линий.
27.4. Редукционные формулы. Рассмотренные выше функции
Грина могут быть связаны простыми соотношениями с матричными
элементами матрицы рассеяния.

§ 28. ПРОЦЕДУРА ПЕРЕНОРМИРОВОК 219
Довольно ясно, что матричный элемент перехода т->п
(Ф...U>i, • • •, Рп)SO(д1г ..., qmH, A9)
где + *
...ат(да) Фо,
описывается теми же самыми диаграммами Фейнмана, что и связ-
связная (п + т)-хвостная функция Грина Gn+m.
Отличие состоит в множителях, отвечающих внешним линиям.
В матричном элементе A9) внешним линиям, согласно правилам
Фейнмана из § 20, соответствуют амплитуды начальных и конеч-
конечных частиц f^(k). Например,
f±(k) = ±(l6n3k0)~lf' для бесспинового поля,
f±(p) = Bn)-'/>Vj1(p) для спинорного поля,
f±(q) = ±A6n3q0)-1/i ev(q) для электромагнитного поля,
причем отрицательно-частотные амплитуды /- отвечают частицам
в начальном состоянии, а положительно-частотные /+ —частицам
конечного состояния.
В то же время в функции Грина, взятой в импульсном пред-
представлении
Дм {К kn) = \е12 V7 Д(я) (Xl хя) dxx... dxn B0)
внешним линиям соответствуют свободные пропагаторы полей.
Поэтому, как можно показать,
<Ф (А Рп) 5Ф (qt qm)H = Щ Д W (Л)А*' Ш X
хД(п+т)(р1 рп; -д» •.., -qm) П Ут(яд&11ШЬ B1)
Множитель i в правой части обязан своим происхождением стан-
стандартному определению функций Грина, а т] = ± 1 — знаковый
фактор, учитывающий перемены знаков при перестановках фер-
мионных операторов.
Соотношение B1) является редукционной формулой в импульс-
импульсном представлении.
§ 28. Процедура перенормировок
28.1. Перенормировка вкладов в функции Грина. Наша бли-
ближайшая программа — провести процедуру вычитания расходимо-
стей в полных функциях Грина и получить для них выражения,
не содержащие ультрафиолетовых бесконечностей (т. е выраже-
выражения для так называемых перенормированных функций Грина).

220 ГЛ. VII. УСТРАНЕНИЕ РАСХОДИМОСТЕИ
Такие выражения еще будут нести на себе печать произвола,
связанного с неоднозначностью процедуры вычитания бесконечно-
бесконечностей. Однако зависимость перенормированных функций Грина от
соответствующих неопределенных конечных постоянных для ренор-
мируемых теорий имеет довольно простой и в то же время спе-
специфический характер. Это позволяет отнести произвол в такие
параметры, как массы, константы связи, нормировки операторов
полей и в конечном итоге получить для перенормированных функ-
функций Грина выражения, зависящие от так называемых перенор-
перенормированных масс и констант связи и не содержащие каких-либо
дополнительных неопределенных констант. Перенормированные
массы и константы связи в свою очередь однозначно выражаются
через непосредственно наблюдаемые величины.
Мы начнем згу программу с анализа одночастичных функций
Грина.
Как было установлено в § 27.1, в импульсном представлении
одночастичная функция Грина G (р) выражается через сильносвяз-
сильносвязную 2-хвостную вершину Г2 (р; g), равную массовому оператору,
алгебраическим .соотношением
0r2G0 + ... = (Gtl-r2)-\ A)
В результате вычитания расходимостей функция Г2, формально
определенная правилами Фейнмана через сильносвязные диа-
диаграммы, заменяется выражением Г2 (р), не содержащим расходи-
расходимостей. Структура Г2 (р) существенно зависит от типа рассматри-
рассматриваемой модели квантовой теории поля.
Для перенормируемых моделей взаимодействия, когда макси-
максимальный индекс вершины равен нулю, степень расходимости
диаграмм не зависит от порядка теории возмущений и для диа-
диаграмм с двумя наружными бозонными линиями равна 2, а для
диаграмм с двумя фермионными линиями равна 1.
Поэтому в первом случае Г2 имеет следующую структуру:
$я(р% Bа)
тогда как во втором случае
?2(р)=ар + Ьт + ГГв(р), B6)
т. е. в обоих случаях в силу релятивистской инвариантности Г2
содержит две конечные произвольные константы.
Напротив, в неперенормируемых моделях степень расходимости
зависит от числа вершин и неограниченно возрастает вместе
с порядком теории возмущений. В каждом конечном порядке
функция Г2 содержит конечный полином по степеням р2 или р
с произвольными коэффициентами, степень которого возрастает
вместе с порядком диаграммы. Поэтому полная функция ? v являю-

§ 28. ПРОЦЕДУРА ПЕРЕНОРМИРОВОК 221
щаяся бесконечной суммой вкладов различных порядков теории
возмущений, зависит от бесконечного числа произвольных пара-
параметров (т. е. от произвольной функции).
Для скалярного случая с помощью A) и B) получаем
G (р) = [A - Ь) т*~ A + а) р2 - П°н (р2)]'1. C)
Определим квадрат перенормированной массы скалярной ча-
частицы тг как положение полюса правой части уравнения C) по
переменной р2, т е.
G-i (т2) = A - Ь) т2 - A + a) fh> - Пой (т2) = 0, Dа)
Последнее соотношение можно представить в виде
где
Г«°«(т2)
« ттг- Eа)
— сдвиг квадрата массы, обусловленный квантовыми (радиацион-
(радиационными) поправками. Для фактического определения in? и Am2
следует решать трансцендентное уравнение Dа).
В окрестности полюса р2 = т2 перенормированный пропагатор G
можно представить в виде
где
r ?- ^ . Gа)
Повторяя рассуждения для спинорного пропагатора, находим
= 0, D6)
, Am = — -g±|- m- -\_^ , E6)
и). G6)
Мы видим, что в каждом случае две произвольные постоян-
постоянные в конечном счете входят в перенормировку массы Am и пере-
перенормировку пропагатора Z2 (т. е. в перенормировку функции
поля).
Перейдем теперь к высшим функциям Грина, т. е. к вертек-
вертексам. Для конкретности будем рассматривать параллельно два
объекта: 4-хвостку для скалярных частиц Г4 и 3-хвостную

222 ГЛ. VII. УСТРАНЕНИЕ РАСХОДИМОСТЕИ
бозон-фермионную вершину Г3 для моделей, содержащих частицы
с целым и полуцелым спином (наподобие спинорной электро-
электродинамики).
В моделях с равными нулю максимальными индексами вершин
(перенормируемых моделях) индексы диаграмм, образующих обе
указанные вершины, не зависят от порядка теории возмущений
и равны нулю. Поэтому структура неопределенностей в обоих
случаях одинакова:
K(Pi р4)=<* + ЛГ(...р.-.), (8а)
к(Ри •••> Р3) = с0 + Л3кон(...р...). (86)
Здесь с, d — произвольные конечные константы, О — дираковская
матрица, отвечающая лоренцевой структуре 3-вертекса, а Ап —
суммы радиационных поправок, которые вместе с затравочным
вкладом от первого порядка теории возмущений образуют полные
вертексы Г„. Так, в модели /мр4
(9а)
тогда как в спинорной электродинамике
ГГ = <% + (ЛзКог. Об)
Как видно, первые слагаемые в правых частях формул (8а),
(86) имеют ту же структуру, что и затравочные члены, вследствие
чего эффект постоянных с, d сводится к модификации констант
связи
A0)
(символом g обозначаем здесь константу связи, отвлекаясь от кон-
конкретной модели).
Вертексы с числом внешних линий, большим четырех, мы не
будем обсуждать, поскольку, согласно формуле B6.22), диаграммы
с таким числом внешних линий в перенормируемых моделях
в целом сходятся и им не соответствуют какие-либо новые
константы.
28.2. Теорема о перенормируемости. Проведенные выше рас-
рассуждения носили схематический характер. В них, в частности,
не нашел отражения важный факт наличия расходимостей в под-
поддиаграммах данной диаграммы и не обсуждалась структура соот-
соответствующего произвола.
Для иллюстрации этого факта заметим, например, что при
вычислении вклада пятого порядка в 4-вертекс Г4 в скалярной
модели Лф4 от диаграммы, изображенной на рис. 28.1, а, необхо-
необходимо вычислить квадратично расходящуюся поддиаграмму собст-
собственной энергии (рис. 28.1,6) и логарифмически расходящуюся
поддиаграмму рассеяния (рис 28.1, в). Поэтому второе слагаемое

§ 28. ПРОЦЕДУРА ПЕРЕНОРМИРОВОК 223
в правой части (8а) зависит как от произвольных констант а, Ь,
введенных в B), так и от константы d.
Ограниченный объем изложения не позволяет нам входить
в детали этих важных вопросов. Отсылая интересующегося чита-
читателя за подробностями к более специальной литературе (см., на-
например, гл. V Введения и гл. II, III книги Завьялова A979)),
Ю в)
Рис. 28.1. Логарифмически расходящаяся скалярная диаграмма пятого порядка
(а) и ее расходящиеся поддиаграммы (б) и (в).
мы лишь отметим здесь, что общее утверждение о перенормируе-
перенормируемости теории возмущений составляет сущность фундаментальной
теоремы о перенормировках (теорема Боголюбова —Парасюка),
а удобный практический рецепт однозначного вычитания расхо-
димостей следует из так называемой R-операции Боголюбова.
С практической точки зрения наиболее важный аспект про-
процедуры перенормировки заключается в необходимости соблюдения
некоторых простых правил, обеспечивающих ее внутреннюю само-
самосогласованность. Согласно этим правилам в любой данной расхо-
расходящейся диаграмме вычитание следует производить одним и
тем же способом независимо от того, выступает ли она как само-
самостоятельная диаграмма или как поддиаграмма какой-либо слож-
сложной диаграммы. Например, обе произвольные константы, возни-
возникающие при вычислении конечной части диаграммы второго
порядка «орех» в скалярной модели /ир4 (см. рис. 25.3), должны
определяться одним и тем же способом, как при вычислении
вклада второго порядка в пропагатор, так и при любых вычис-
вычислениях сколь угодно сложных диаграмм, в том числе диаграммы
рис. 28.1, а.
При этих условиях возникающие в процессе устранения бес-
бесконечностей произвольные константы входят в окончательные
выражения для функций Грина и матричных элементов в виде
небольшого числа комбинаций
mt = fi(m, g; а, Ь, ,..), ~gk = ^k(m, g; a, b, ...),
которые могут быть отождествлены с физическими массами и
физическими" константами связи.
Таким образом, оказывается возможным последовательно про-
провести во всех порядках теории возмущений переход от первона-

224 ГЛ. VII. УСТРАНЕНИЕ РАСХОДИМОСТЕИ
чальных параметров (масс и констант связи), входящих в лагран-
лагранжиан и правила Фейнмана, к новым перенормированным
параметрам
Перенормированные вертексы и наблюдаемые матричные элементы
зависят теперь только от перенормированных масс и констант
связи и не зависят от исходных масс, констант связи и произ-
произвольных параметров а, Ь, с, ... по отдельности.
28.3. Рецепт вычитания на массовой поверхности. Приведем
теперь наиболее удобный для практических вычислений способ
определения произвольных параметров, возникающих при вычи-
вычитании расходимостей. Заметим прежде всего, что, согласно фор-
формулам Eа), E6), параметрами а, Ь можно распорядиться таким
образом, чтобы сдвиг массы Am оказался равным нулю. В ска-
скалярном случае для этого следует положить
Подставляя это соотношение в B), получаем
Г, (р) = а (р2 - т2) + ГГ (р2) - IT" (m«).
Если теперь распорядиться постоянной а так, чтобы перенорми-
перенормированная Г имела при р2 = т2 нуль второго порядка
A3)
то, согласно G), мы получим, что константа перенормировки
функции поля Z2 равна единице.
Заметим, что рецепт A2), A3), эквивалентный определению
ГГ (р2) = г;ов'(р') - г;он <У) - (р3 - т2) г;кон (т2), A4)
сводится к вычитанию из конечной части Гков ее первых двух
членов разложения в ряд Тейлора в точке рг — тг, т. е. на мас-
массовой поверхности. Этот рецепт вычитания на массовой поверх-
поверхности одновременно обращает в нуль перенормировку массы и
изменение нормы функции поля:
что является весьма удобным с практической точки зрения.
В спинорном случае соответствующая формула имеет вид
ГГ(р) = ГГ(р)-ГГнИ-(^-т)г;кон(т). A5)
Здесь имеется в виду, что функция Г™", зависящая от матрич-
матричного аргумента р и скалярного аргумента р2, путем отождествле-

§ 28. ПРОЦЕДУРА ПЕРЕНОРМИРОВОК 225
ния р2 = (/J рассматривается как функция одного аргумента р.
Именно в этом смысле понимается производная в последнем
члене правой части: Г'кон = (д/др)Гкои.
Как будет установлено ниже в § 29.4, производная массового
оператора электрона 2' в точке р = т обращается в бесконеч-
бесконечность из-за так называемой инфракрасной расходимости, обуслов-
обусловленной безмассовостью фотонов. Поэтому, вообще говоря, может
статься, что вычитание производной более удобно производить
не на массовой поверхности, а в какой-либо другой точке р = р#
(например, при р = 0). В этом случае формула A5) примет вид
ГГ (р) = ГГ (р) - YT (т) -(р-т) Г'кон (р,). A6)
Такой вариант вычитания соответствует перенормировке спи-
норного поля, равной
£г' = 1+г;кон(т)-Г;кон(Р*). A7)
28.4. Неоднозначность перенормировки вертекса. Перейдем
к перенормировкам вершинных функций. Как показано в Допол-
Дополнении VII, скалярная 4-хвостка Гл(рг, ..., р4) является функ-
функцией шести независимых скалярных переменных. Мы будем,
однако, записывать явно зависимость от семи переменных
Tr^Fipl pi pi pi; s = (Pl + p2)\ t = (Pl-\-p3f,
« = (Рх + р4J). A8)
имея в виду линейную связь между ними (см. (ДУП.7)).
Переход на массовую поверхность фиксирует первые четыре
из них, оставляя три последних связанными соотношением
s + * + « = 4m2. A9)
Точка вычитания 4-хвостки, таким образом, не фиксируется
однозначно при выходе на массовую поверхность. Остающийся
двухпараметрический произвол ограничен лишь условием действи-
действительности. Как было показано в § 26.2, произвольная константа d
из правой части (8) эквивалентна 4-мезонному контрчлену dy*
в лагранжиане и потому должна быть действительна. Поэтому
константа d может быть определена через значение вершины
rtOH(s, и, t) = F{m\ т\ т, т\ s, и, t) B0)
в области значений аргументов s, и, t, ограниченной условиями
s^£4m2, t^4m2, ы«=4т2. B1)
Происхождение этих условий объяснено в Дополнении VII.
Возможной точкой вычитания является точка, отвечающая
порогу реакции в одном из каналов, например точка s = 4m2,
и = t — 0. Значение 4-хвостки и амплитуды рассеяния в этой
8 Н. Н. Боголюбов, Д. В. Ширков

226 ГЛ. VII. УСТРАНЕНИЕ РАСХОДИМОСТЕЙ
точке пропорционально так называемой s-волновой длине рассея-
рассеяния и может быть непосредственно измерено на опыте.
Если положить
ЛГГ (... р...) =ЛГ (s, и, t) - ЛГ Dт2, 0, 0), B2)
то полная вершинная функция согласно (9) будет удовлетворять
соотношению
ГГDт9, 0, 0; g) = g, B3)
которое можно рассматривать как определение перенормированной
константы связи.
Часто используют другую, так называемую симметричную,
точку вычитания s = u = t = 4m2f3. В этом случае
ЛГ(...р...) = ЛГE, и, 0-ЛГDт2/3, 4т9/3, 4т9/3) B4)
; g). B5)
Константы связи B3) и B5) могут быть выражены друг через
друга. Обозначим через IT" вершинную функцию, нормированную
в симметричной точке, т. е. удовлетворяющую соотношению B5).
Соответствующую константу связи обозначим через ^яы, т. е.
^ 1^
i \ 3 ' 3 ' 3 ' */ ^ • ( '
Процедуре вычитания на пороге сопоставим Г4ОР и gnop:
ГГDт2, 0, 0;^пор)=^пор. B7)
Тогда
(^^^) B8)
и, наоборот,
ПимDт9, 0, 0; /им) = /ор. B9)
§ 29. Перенормировки в спинорной электродинамике
29.1. Условие градиентной инвариантности. В квантовой тео-
теории поля, описывающей электромагнитные взаимодействия, важ-
важную роль играет требование градиентной инвариантности. Как
было показано в § 4, градиентное преобразование потенциала
электромагнитного поля
A)
не меняет значений компонент электрического и магнитного полей
и, следовательно, не должно приводить к каким-либо наблюдае-
наблюдаемым эффектам.

§ 29. ПЕРЕНОРМИРОВКИ В СПИНОРНОИ ЭЛЕКТРОДИНАМИКЕ 227
Требование инвариантности матричных элементов 5-матрицы
по отношению к преобразованию A) называется условием гра-
градиентной инвариантности матрицы рассеяния. Для того чтобы
сформулировать его в явном виде, заметим, что при преобразо-
преобразовании A), где f — произвольная бесконечно малая функция, член
я-го порядка матрицы рассеяния
\ Sn (х, ..., х„) dxx.... dxn
получит приращение, главная часть которого имеет вид
Интегрируя это выражение по частям, находим, что оно обра-
обращается в нуль, если тождественно
д dSn(xi. .... xn)_Q
-U B)
Нетрудно убедиться, что полученное условие обеспечивает инва-
инвариантность 5-матрицы и при конечных градиентных преобразо-
преобразованиях.
Условие B) можно рассматривать применительно к формаль-
формальному определению 5-матрицы в виде хронологической экспоненты
от лагранжианов взаимодействия. Можно показать (см., например,
Введение, §§ 28.2 и 33.2, 33.3), что градиентная инвариантность
S-матрицы, представленной произведениями пропагаторов согласно
правилам Феинмана, обусловлена уравнением непрерывности фер-
мионного тока в представлении взаимодействия.
Мы будем рассматривать условие градиентной инвариантности
применительно к матрице рассеяния, не содержащей расходимо-
стей, т. е. подразумевать под коэффициентными функциями Sn
выражения, полученные после вычитания расходимостей.
29.2. Градиентное преобразование фотонного пропагатора. За-
Заметим теперь, что если рассматривать функцию f(x) в правой
части градиентного преобразования A) как оператор, зависящий
от операторных потенциалов Лц, то для хронологического спари-
спаривания электромагнитного поля можно получить более общее
выражение, чем использованное в правилах Феинмана диагональ-
диагональное выражение, которое мы запишем в виде
(Я) = (Г A» (k) Av (q)H = =|£ б (k+q). C)
Рассмотрим градиентное преобразование от потенциалов
удовлетворяющих соотношению C), к потенциалам
8*

228 ГЛ. VII. УСТРАНЕНИЕ РАСХОДИМОСТЕЙ
где af —некоторая с-функция. Определяя хронологическое спа-
спаривание новых операторов А', получаем
Л7(ад (?) = ~ {(&v - Щ + "ж ^ <*■>} б (*.+ Я): D)
причем
Первое слагаемое в правой части D) пропорционально попереч-
поперечному проекционному оператору P^v, второе — продольному про-
проекционному оператору Р^, т. е.
Согласно условию градиентной инвариантности матричные эле-
элементы не должны зависеть от dt (k2).
Полагая d/ = 0, получаем из D) выражение, удовлетворяющее
условию поперечности,
При dt = 1 возвращаемся к обычному диагональному спари-
спариванию C).
29.3. Пропагатор фотона с радиационными поправками. В § 24
были проведены вычисления простейших однопетлевых диаграмм
спинорнои электродинамики. Там было показано, что диаграмме
поляризации вакуума рис. 24.1,6 соответствует квадратично рас-
расходящийся интеграл Ц^ (см. формулы B4.7), B4.8)), представ-
представляющий низшее приближение к поляризационному оператору.
Конечная часть этого интеграла, согласно B4.11), B4.12) может
быть записана в виде
П,^, (k) = ag^ •+ (g^k2 — kpky) \b •+ / (|^aj —, F)
где а и b — произвольные конечные постоянные, а интеграл
1
/ B) = 2\dxхA -х) In [I - 4х A -х) z-is]
о
после элементарных преобразований может быть представлен как
оо _ _
da(l+2/a)
где функция J (г) в явном виде определяется формулами B4.4,5).
В пределе больших \z\

§ 29. ПЕРЕНОРМИРОВКИ В СПИНОРНОЙ ЭЛЕКТРОДИНАМИКЕ 229
Используем теперь условие B) для определения входящих
в n^v неопределенных констант. Заметим для этого, что поляри-
поляризационный оператор входит в 52 (х, у) следующим образом:
Поэтому условие градиентной инвариантности дает
^nV(,(x) = o, kmvll(k)=o. G)
Подставляя правую часть F) во второе из соотношений G), полу-
получаем а = 0. Оператор поляризации вакуума в силу условия гра-
градиентной инвариантности имеет чисто поперечную форму
(k) = (*Vv-*Л) [Ь +1 (£-2)] £.. (8)
Рассмотрим теперь обусловленную П^ радиационную поправку
к пропагатору фотона, который соответственно формуле D) за-
запишем в произвольной калибровке:
где PiT и Р1 — проекционные операторы, введенные в E). Согласно
выводу в § 29.2 коэффициент dt может зависеть от ft2. Однако
здесь и всюду ниже будем считать di = const.
Рис. 29.1. Вклад итераций простейших однопетлевых диаграмм в пропагатор
фотона.
Для вычисления поправки к (9) следует прибавить выражение
PD^o (k) ГРР (k) Z)pV (k). Подставляя в него (8) и (9), находим
где
Учет повторных однопетлевых вставок в фотонный пропагатор
(рис. 29.1)
D - DUD + DUDUD - DUDUDUD +...
снова приводит нас к выражению A0), где теперь d(k2, а) пред-
представлена геометрической прогрессией
а) = 1+£(/ g

230 ГЛ. VII. УСТРАНЕНИЕ РАСХОДИМОСТЕЙ
которая после формального Суммирования дает
где
Здесь уместно сделать неколько замечаний. Видно, во-первых,
что условие градиентной инвариантности приводит к отсутствию
перенормировки массы фотона (а = 0). Однако «параметр второго
вычитания» Ъ, аналогичный параметру а в формуле B8.2), остается
произвольным и дает вклад в перенормировку поперечной части
электромагнитного потенциала. С учетом того, что, согласно B4.13),
/@) = 0, получаем
По аналогии с рассуждениями § 28, константу Ь удобно поло-
положить равной нулю. В этом случае фотонный пропагатор не пере-
перенормируется на массовой поверхности фотона и не дает вклада
в эффективное значение константы связи.
Рис. 29.2. Слагаемые поляризационного оператора.
Заметим, во-вторых, что формула A1) имеет весьма общую
природу. Если под Пцу понимать не диаграмму второго порядка,
а сумму всех сильносвязных поляризационных диаграмм (рис. 29.2),
то мы снова получим формулу A1), в которой теперь
K{k\ a) = -£/+a2/3 + a3/3 + ... A2)
Здесь /„ (k2) — вклад я-петлевых сильносвязных диаграмм, норми-
нормированный, согласно только что сделанному замечанию, в нуле;
/„.@) = 0. На массовой поверхности
d@, a) = l.
Наконец, следует сказать, что изученная в этом разделе
радиационная поправка, представляющая низшее приближение
эффекта поляризации вакуума, становится существенной в ультра-
ультрафиолетовой области при ) k2fm21 ^> 1.
С помощью формулы A0) находим

8 29. ПЕРЕНОРМИРОВКИ В СПИНОРНОЙ ЭЛЕКТРОДИНАМИКЕ 231
и, следовательно,
d(k\ а)-> 1 . A3)
&
29.4. Полный пропагатор электрона. Оператор собственной
энергии электрона 2 во втором порядке теории возмущений фор-
формально определен соотношениями
2 (x)~-fcVSe (*)/#,.(*),■ A4а)
Приведем без выкладок результат вычисления линейно рас-
расходящегося в ультрафиолетовой области интеграла A46):
\, A5)
где
С nfidx /»21
3 ^=^2 = ?1
Если проводить вычитание на массовой поверхности, то, полагая
с2 = 0, получим
2(/п) = 0. A6)
Однако при вычислении производной дЪ/др в точке р2 = т2 мы
встретимся с логарифмической расходимостью функции А (р2).
Эта расходимость связана с поведением подынтегрального выра-
выражения при малых значениях 4-импульсов k (т. е. поведением
в окрестности точки й^ = 0) и потому называется инфракрасной
особенностью. Физически она обусловлена равенством нулю массы
фотона и возможностью излучения заряженной частицей (электро-
(электроном или позитроном) большого числа очень мягких фотонов. Мы
не можем здесь обсуждать этот важный вопрос подробно и ото-
отошлем читателя к более специальной литературе (см., например,
Введение, § 35.4; Бьеркен, Дрелл A978), § 17.10; Ахиезер, Бере-
стецкий A969), §§ 29, 39).
Здесь возможны два различных пути. Первый из них состоит
в том, что фотону формально приписывается малая масса Хд.
Вводя соответствующее слагаемое k2 + ie ->■ k2 — К + 'в в знамена-
знаменатель подынтегрального выражения A46), приходим к выраже-

232 ГЛ. VII. УСТРАНЕНИЕ РАСХОДИМОСТЕЙ
нию A5), в котором произведена замена А (рг) на
(от2_
что дает
Теперь можно вычислить константу ct из условия
?Ш =2'И = 0, A8)
др р=>т К К '
л О /о /4 \ Л (т? 0|2\ ОН /1 Q\
t*-| — л \О — иц ** У.''*- , "О/ — £l*i> V /
В окончательных выражениях для наблюдаемых вероятностей
перехода величина \Х0\ играет роль параметра, описывающего
неопределенность значения импульса заряженной частицы, свя-
связанную с возможностью излучения мягких фотонов, нерегистри-
руемых в данном эксперименте (см цитированную выше лите-
литературу).
г Другой путь заключается в том, что второе вычитание мас-
массового оператора электрона можно делать не на массовой
поверхности.
Полагая с2 = 0, запише'м A5) в виде
где
«(Р) =* (*±*) А 0) + *,[£$! + (| + $) А (Л]. B0)
Видно теперь, что выбор
d-3-rf,, s@) = 0 B1)
приводит к тому, что пропагатор электрона, представленный
с помощью B7.4) в виде
в окрестности массовой поверхности имеет вид
Z?**l+ ^[2C-dt) A (m«, Ц)-3-dt].

§ 29. ПЕРЕНОРМИРОВКИ В СПННОРНОИ ЭЛЕКТРОДИНАМИКЕ 233
29.5. Вершинная часть и тождество Уорда. Вклад третьего
порядка в вершинную часть представляется выражениями
Av(p', p; k = p'-p; Ъ)~ B4)
" d^Df" (р - <7; d,) 7ц5с (q + k) ^S' (q) ya.
Второе из них отвечает расстановке импульсных переменных на
рис. 29.3. Фотонный пропагатор D^ определен формулой (9).
Интеграл B4) расходится логарифмически в ультрафиолетовой
области.
Ввиду громоздкости мы не будем приводить здесь конечную
часть вершинной функции Av в произвольной калибровке электро-
электромагнитного поля. (Соответствующее выражение содержится, на-
например, в § 35.3 Введения.) Для наших целей окажется вполне
достаточным выражения для Av, вычисленного в § 24.3 в диаго-
диагональной калибровке при dt=\.
Положим
ЛГ (Р', р; k; dL=l) = csyv + ГГ (р , Р\ Ь у? = т% B5)
где Tv°H определено в B4.23), а са — произвольная постоянная.
Эта постоянная, однако, не является независимой и может быть
выражена через константу ct из выражения
A5) для массового оператора с помощью
условия градиентной инвариантности B).
Применим это условие к слагаемым третье-
третьего порядка матрицы рассеяния S3 (х, у, z),
которые удобно разбить на две группы.
В первую группу войдут члены, содержа-
содержащие произведение трех операторов А (х), q
А {у), А (г), а во вторую-выражения, ли- Рис 29.3. Выбор им-
нейные по А. В силу различной оператор- пульсных обозначений
ной структуры члены первой и второй групп в интеграле B4).
дают вклады в различные матричные эле-
элементы. Поэтому условия градиентной инвариантности можно ис-
исследовать для них по отдельности. Рассмотрим это условие при-
применительно к диаграммам второй группы. Соответствующий вклад
в S3 может быть записан как сумма трех членов
:Ау{х)Г(х\у, г): + :Ау(у)Г(у\г, x): + :Av(z) P(z\x, у):,
отличающихся перестановкой переменных интегрирования х, у, г.
Условие градиентной инвариантности принимает вид
~Г(х\у, г)=0. B6)

234 ГЛ. VII. УСТРАНЕНИЕ РАСХОДИМОСТЕЙ
Функция Jv содержит четыре слагаемых, отвечающих диаграм-
диаграммам, изображенным на рис. 25.4 и еще четыре слагаемых, отличаю-
отличающихся от первых перестановкой аргументов z и у.
Заметим, во-первых, что дивергенция от слагаемого, отвечаю-
отвечающего диаграмме рис. 25.4, г,
Грт (х - z) D№ (х - у) :ф (у) ?Ч (у):
после устранения расходимостей обращается в нуль вследствие
условия градиентной инвариантности конечной части поляриза-
поляризационного оператора G). Поэтому следует рассмотреть сумму трех
первых диаграмм рис. 25.4. Она может быть представлена в виде
:ф (z) Ау (z, у; х) ф (y): + $(z) 2 (z - </) S° (у -х) yvq (x) +
+ у (х) yyS° (х-г)Ъ(г-у)^ (у).
Применяя к этому выражению операцию id/dxv, получаем после
небольших преобразований с помощью уравнений Дирака для
■ф(х), тр(х) и соответствующих неоднородных уравнений для 5е:
+ S (z - </) 6 (у - *) - 6 (л - г) S (z - у)} у (у).
Таким образом, условие градиентной инвариантности связы-
связывает вклад в вершинную часть Av с вкладом в собственную энер-
энергию электрона 2:
X) -z)-8(y-x)}. B7)
Переходя к импульсному представлению по формулам
Av(z, у; x) = Bny8\eik*+iP!/~ip'*Av(p', p; k) 8(p + k-p')dp'dpdk,
имеем
k*Av(p', p; A) = 2(p')-2(p); P'=p + k. B8)
Эта формула доказана нами для вкладов низшего порядка
в Av и S- Можно показать однако, что аналогичное соотношение
имеет место и в высших порядках, связывая почленно вклады
в вершинную функцию
Г- (р', р; k | а) = у- + 2 аПАМ (Р'> Р'> k)
и вклады в массовый оператор 2(л) с одним и тем же значением
индекса п. При этом соответствующие вклады описываются сильно-
сильносвязными вершинными диаграммами с 2л+ 1 вершинами и сильно-
сильносвязными диаграммами собственной энергии электрона с 2п вер-
вершинами.

§ 29. ПЕРЕНОРМИРОВКИ В СПИНОРНОЙ ЭЛЕКТРОДИНАМИКЕ 235
Суммируя соотношение B8) по всем п, получаем с учетом
B7.4)
kT(', р; k\a) = G-1(p; a)-G^{p'\ a). B9)
Эта формула известна под названием обобщенного тождества
У орда (тождества Уорда — Такахаши).
Тождество Уорда в виде B8) связывает конечные части низших
радиационных поправок B0) и B5) и устанавливает связь между
константами сх и с3:
2 C0)
Мы предоставляем читателю проделать соответствующие выкладки.

Глава VIII. ОПИСАНИЕ РЕАЛЬНЫХ ВЗАИМОДЕЙСТВИЙ
§ 30. Электромагнитные взаимодействия
Изложенная схема описания взаимодействий квантовых полей
с помощью теории возмущений имеет шансы на успех в том слу-
случае, если взаимодействие полей может считаться слабым. Таким
свойством, несомненно, обладает электромагнитное взаимодействие,
которому отвечает безразмерный малый параметр a = е2/4яйс~
<-- 10-2—так называемая постоянная тонкой структуры.
Наиболее простой оказывается модель теории поля, состоящая
из взаимодействующих спинорного и электромагнитного полей.
Такая модель адекватна взаимодействию электронов и позитронов
с фотонами, поскольку в очень широком интервале энергий ока-
оказывается возможным отвлечься от слабых и сильных взаимодей-
взаимодействий даже в виртуальных эффектах. Эту модель —спинорную
электродинамику — мы и рассмотрим в первую очередь.
30.1. Спинорная электродинамика. В собственном смысле слова
она описывает процессы и эффекты, включающие электрон-позит-
электрон-позитроны и гамма-кванты в начальных, конечных и промежуточных
состояниях. К этим процессам относятся такие процессы, как
рассеяние фотонов на электронах (комптоновское рассеяние), рас-
рассеяние электронов на электронах (мёллеровское рассеяние),
а также аналогичные процессы с участием позитронов, образова-
образование и аннигиляция электрон-позитронных пар, взаимодействие
электронов с внешним магнитным полем (аномальный магнитный
момент), тормозное излучение электрона во внешнем электроста-
электростатическом поле (например, поле атомного ядра) и некоторые другие,
в том числе чисто электромагнитные взаимодействия мюонов и
адронов друг с другом и с электронами.
Мы не будем здесь сколько-нибудь подробно рассматривать эти
процессы и эффекты и ограничимся описанием общих закономер-
закономерностей и наиболее яркими иллюстрациями.
Рассматриваемые явления можно условно разбить на два класса.
К первому из них отнесем процессы, которые в главном прибли-
приближении могут быть поняты и рассчитаны путем учета электромаг-

§ 30. ЭЛЕКТРОМАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ 237
нитных эффектов в рамках нерелятивистской квантовой механики,
точнее говоря, в рамках квантовой теории взаимодействия веще-
вещества с излучением. Мы имеем здесь в виду такие задачи, как
движение электрона в кулоновском поле ядра, рассеяние света
на свободных электронах, двухфотонная аннигиляция электрон-
позитронной пары, тормозное излучение электрона в поле ядра
и некоторые другие.
Общим для них является то, что основной вклад в матричные
элементы дают диаграммы Фейнмана, не содержащие замкнутых
петель и интегрирований по виртуальным 4-импульсам (так назы-
называемые древесные диаграммы). Соответствующие расчеты были
выполнены в конце 20-х годов вслед за созданием квантовой
механики. Оказалось, что теоретические результаты находятся
в хорошем согласии с экспериментом.
Примером этому является полученная в 1929 —1930 гг. Клей-
Клейном, Нишиной и Таммом формула для дифференциального сечения
рассеяния фотона с импульсом kx и энергией k1-=\k1\ на покоя-
покоящемся электроне:
da 2 k\
Здесь го = а/т — так называемый классический радиус электрона,
9— угол рассеяния электрона, а &2 —энергия рассеянного фотона,
связанная с^ив фомулой Комптона
2
m-f Ai (I — cos6)"
Формула Клейна — Нишины — Тамма соответствует квадрату суммы
матричных элементов, отвечающих двум диаграммам второго
порядка, изображенным на рис. 24.3.
Вычисление вклада диаграмм четвертого порядка (см. рис. 24.4)
натолкнулось на трудности, связанные с ультрафиолетовыми рас-
ходимостями. Для преодоления этих трудностей потребовалось
около двух десятилетий. Лишь во второй половине 40-х годов
была построена так называемая ковариантная теория возмущений,
в рамках которой была сформулирована процедура перенормиро-
перенормировок.
Создание метода перенормировок в теории возмущений открыло
дорогу для вычисления поправок к формулам древесного при-
приближения. Радиационная поправка к формуле A), отвечающая
диаграммам четвертого порядка, была рассчитана Броуном и
Фейнманом в 1952 г.
Ко второму классу явлений можно отнести явления, которые
самим своим существованием обязаны радиационным эффектам.
Среди них —сверхтонкое расщепление электронных уровней

238 ГЛ. VIII. ОПИСАНИЕ РЕАЛЬНЫХ ВЗАИМОДЕЙСТВИЙ
в атоме водорода, лэмбовский сдвиг уровней, рассеяние фотона
фотоном, аномальный магнитный момент электрона.
30.2. Аномальный магнитный момент электрона. Как хорошо
известно, уравнение Дирака для электрона, взаимодействующего
с внешним электромагнитным полем, содержит член, отвечающий
магнитному взаимодействию (ДП.ЗО). Этот член может быть также
получен из матричного элемента, отвечающего борновскому взаимо-
взаимодействию электрона с электромагнитным полем A&xi магнитного
типа (>4«* = 0, |*| = 0).
В выражении
— еп+-*(р') yvur-Чр) Av(k) =eu+'s(p')уА (*) иг-s(p),
p'=p + k, B)
записанном в представлении взаимодействия перейдем к расщеп-
расщепленному представлению спиноров и матриц (ДП.22), (ДП.23).
и воспользуемся свободными уравнениями движения для двух-
компонентных спиноров ф и %. Исключая малые позитронные
компоненты % с помощью следующих из этих уравнений соотно-
соотношений
представим B) в виде
е [ф (р') а А% (р)+%(р') о-Дф (р)] =
= ^ [Ф iP') М (*)) («V) + W) {аА (к)) ф (рI
Используя затем формулы умножения матриц Паули (ДП.28),
получаем окончательно
2~ Ф (/>') {'о[* х А (*)] + (р +р') А (к)} Ф (р).
Первый член полученного выражения имеет вид чисто магнит-
магнитного взаимодействия
4 *Ф (Р W
где
Н{к) = i[kxA (*)], Мо =
а
— магнетон Бора.

§ 30. ЭЛЕКТРОМАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ 239
Выражению B) отвечает диаграмма фундаментального электро-
электромагнитного взаимодействия, изображенная на рис. 30.1, а. Эффекты
радиационных поправок приводят к тому, что выражение B)
следует заменить на
- еп+-s (/>') Г £ен (р', Р\ к) «-•s (p) AT (к),. B')
где матричный элемент пТи может быть представлен в виде, ана-
аналогичном B4.24):-
п (/>') Пи (р) = h (k\ а) п (/>') yv« (p) +
}{p). D)
Примем теперь во внимание, что, согласно B4.30), второй
член в правой части при & = 0 обращается в нуль, вследствие
чего электрический заряд элект-
электрона определяется первым слагае-
слагаемым. Поэтому в точке & = 0 форм-
фактор Д обычно нормируют на
единицу:
МО, о) = 1. E)
Такая нормировка достигается со- рис Диаграммы маг„иТНого
ответствующим выбором неопре- М0Мента, отвечающие магнетону
деленных конечных параметров, Бора и поправке Швингера.
возникающих при вычитании уль-
ультрафиолетовых расходимостей (например, выбором параметра ц
в формуле B4.23)), и отвечает определению перенормированного
электрического заряда е как величины, описывающей взаимо-
взаимодействие электрона с электромагнитным поле"м исчезающе малой
частоты.
Из условия E) теперь вытекает, что аномальный магнитный
момент целиком определяется вторым слагаемым правой части
формулы D). Вклад этого слагаемого в выражение B') с помощью
формулы B4.30) может быть представлен следующим образом:
= -~h{k\a)u(p')au(p)H{k).
Таким образом, величина е/2 @, а)/2т представляет собой
поправку к магнитному моменту электрона, который может быть
записан в виде
^K0, + ...].

240 ГЛ. VIII. ОПИСАНИЕ РЕАЛЬНЫХ ВЗАИМОДЕЙСТВИЙ
Первая радиационная поправка к боровскому магнетону
соответствует диаграмме рис. 30.1,6 и выкладкам § 24.3 и была
вычисленаЮ. Швингером в 1948 г. (см. упражнение М5). Для вычис-
вычисления следующего вклада потребовался учет пяти двухпетлевых
диаграмм, изображенных на рис. 30.2. Соответствующий результат
а4 = ^- + 5-яЧп2 + !-£C)^0,328479... F)
был получен Петерманом и Зоммерфельдом в конце 50-х годов.
Для определения вклада ав необходимо рассмотреть 40 раз-
различных трехпетлевых диаграмм. Аналитический расчет практи-
практически невозможно произвести вручную из-за непомерно длинных
Рис. 30.2. Двухпетлевые диаграммы, дающие вклад в аномальный магнитный
момент электрона.
выкладок. Первый расчет ав, выполненный в 1971 г., содержал
большую неопределенность: ав = 1,49±0,25, связанную с прибли-
приближенным численным способом вычислений значительной части
интегралов. В течение последующих лет благодаря использованию
электронно-вычислительных машин для выполнения аналитических
вычислений удалось аналитически рассчитать до конца 30 из 40
трехпетлевых диаграмм, что привело к существенному повышению
точности. Современный результат имеет вид*)
ав-1,183±0,011 = 1,183 A1). G)
При достигнутой точности теоретических расчетов в формуле G)
приобретает важность соответствующая точность в определении
постоянной тонкой структуры. Современное значение or1 =
= 137,035987B9) оказывается достаточно аккуратным для этих
целей и вместе с F) и G) дает следующую величину аномального
магнитного момента:
(й/йо)теоР = 1,00115965236 B8). (8)
При этом более половины погрешности результата связано с неоп-
неопределенностью в численном значении постоянной а.
*) Здесь употребляется запись неопределенности численного результата,
введенная в § 1 (см. стр, 11).

§ 30 ЭЛЕКТРОМАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ . 241
Экспериментальное значение, полученное в 1978 г.,
(ц/Ио)»ксп = 1,00115965241 B0) (9)
находится в соответствии с теоретическим значением (8). Достиг-
Достигнутый уровень соответствия между теоретическим и эксперимен-
экспериментальным значениями (< 1 • Ю-10 в относительных величинах)
является рекордным в физике.
30.3. Пределы спинорной электродинамики. Приведенный при-
пример является весьма впечатляющим. Что касается других эффек-
эффектов квантовой электродинамики, то в них либо точность экспе-
эксперимента не столь высока, либо теоретические расчеты указывают
на необходимость учета эффектов, выходящих за рамки чистой
электродинамики.
Так, например, экспериментальное значение величины сверх-
сверхтонкого расщепления уровня ISy, в атоме водорода, обусловлен-
обусловленного взаимодействием электрона с магнитным полем протона,
известно сейчас с рекордной точностью (до 13 порядков)
v^ff = 1420,4057517864 A7) МгГц, A0)
однако теоретические расчеты дают лишь 7 знаков, причем уже
с учетом конечных размеров протона.
Лэмбовский сдвиг, т. е. тонкое расщепление 2S4l и lPVa уров-
уровней в атоме водорода известен с точностью порядка 10~в:
stc°p = 1057,89 B) МгГц,
8эксП = 1057,89B) МгГц, ( )
причем эффекты, выходящие за рамки спинорной электродинамики,
имеют порядок 10~5 и учтены в теоретическом значении.
В целом следует сказать, что вся совокупность эксперимен-
экспериментальных данных по большому числу эффектов находится в согла-
согласии с результатами расчетов теории возмущений спинорной электро-
электродинамики в тех случаях,, когда в этих эффектах сильные взаимо-
взаимодействия оказываются несущественными, либо поддаются учету.
Существует, однако, область, в которой замкнутость электро-
электродинамики нарушается. Здесь имеются две причины.
Во-первых, электромагнитные взаимодействия адронов оказы-
оказывают влияние на электродинамику лептонов (электрон-позитронов
и мюонов) через виртуальные состояния. Так, например, в про-
процессы, идущие через однофотонную аннигиляцию
и реализуемые на ускорителях со встречными пучками, дают
существенный вклад диаграммы Фейнмана, содержащие вставки

242 ГЛ. VIII. ОПИСАНИЕ РЕАЛЬНЫХ ВЗАИМОДЕЙСТВИЙ
в виртуальные фотонные линии, отвечающие адронной поляриза-
поляризации фотона (рис. 30.3, 30.4).
Благодаря резонансному взаимодействию двух пионов (так
называемый р-резонанс) сечение процессов A2) при энергиях
порядка 700—800 МэВ в системе центра масс более чем на поря-
порядок превышает величину, вычисленную по электродинамической
теории возмущений.
Во-вторых как мы видели при вычислении низших электродина-
электродинамических радиационных поправок в §§ 24, 29, эти поправки
V
Рис. 30.3. Влияние «адронной поляризации вакуума> на процессы аннигиля-
аннигиляции и рождения лептонных пар.
•s\rjf \sv
N
Рис. 30.4. Вклад пионных и нуклонных петель в «адронную поляризацию
вакуума».
содержат логарифмически растущие вклады, пропорциональные
ультрафиолетовому логарифму L = \n—2. Анализ высших радиа-
радиационных поправок показывает, что фактическим параметром раз-
разложения теории возмущений становятся произведения aL, либо aL2.
В ряде случаев (в области высоких энергий) члены вида aL2,
aL могут вносить значительные вклады в сечения процессов и
другие наблюдаемые величины. Их приходится рассчитывать и
учитывать вносимые ими поправки при анализе процессов,
измеряемых с достаточно высокой точностью.
Однако в целом проблема учета высших радиационных попра-
поправок имеет пока еще в основном теоретическое значение.
§ 31. Слабые взаимодействия
31.1. Взаимодействия Ферми. Эти четырехфермионные взаимо-
взаимодействия контактного типа являются заметно более слабыми по
сравнению с электромагнитными взаимодействиями. Как отме-
отмечалось в § 10, безразмерный параметр, образованный константой
связи Ферми G и массой протона Мр, оказывается на три порядка
меньше постоянной тонкой структуры а.

§ 31. СЛАБЫЕ ВЗАИМОДЕЙСТВИЯ 243
Простейшие примеры слабых взаимодействий были рассмотрены
в § 10.1. Там было упомянуто, что лагранжиан взаимодействия
Ферми имеет вид произведения ток х ток
•sp=yg-/iiW7ii(«). A)
где /ц — так называемый слабый ток, билинейный по фермион-
ным полям. Выражение такого типа было предложено Ферми
в 1934 г. для описания р-распада нейтрона. Однако потребова-
потребовалось более 30 лет для того, чтобы установить структуру слабого
тока (точнее его лептонной части) во всех деталях.
Слабый ток /v является суммой квадратичных операторных
структур вида
^ B)
(по i нет суммирования!), причем операторы щ и vit вообще
говоря, принадлежат различным полям. Часть слагаемых со-
содержит лишь лептонные поля и образует лептонную составляю-
составляющую слабого тока (короче — лептонный ток) lv. Остальные сла-
слагаемые, включающие адронные поля, образуют адронный ток hv.
Таким образом,
/ ft C)
причем каждая из двух составляющих является суммой структур
вида B). Примеры конструкций подобного рода были приведены
в формуле A0.12).
Произведения двух лептонных токов друг на друга образуют
лептонную часть лагранжиана Ферми. Они ответственны за чисто
лептонные слабые процессы вида
D)
и т. д.
Произведения лептонных составляющих на адронные ftjv отве-
отвечают так называемым полулептонным процессам, в которых участ-
участвуют как лептоны, так и адроны. Примером полулептонных взаи-
взаимодействий являются
n-+p + e- + ve,
Vn + rt^-P + м.-, E)
Л->/з+е- + ?е
и многие другие.
Наконец, в нелептонных слабых взаимодействиях, соответст-
+
вующих произведению h^hv, участвуют лишь адроны. Соответст-

244 ГЛ. VIII. ОПИСАНИЕ РЕАЛЬНЫХ ВЗАИМОДЕЙСТВИЙ
вующие реальные процессы осуществляются путем комбинации
сильных и слабых взаимодействий. Важными примерами таких
процессов являются распады странных адронов
-,
Л + р + я ()
и т. п.
31.2. Структура слабого тока. Структура матриц О, входящих
в составляющие слабого тока, была установлена в середине
50-х годов вслед за открытием несохранения четности в слабых
взаимодействиях. Было обнаружено, что слабый ток представляет
собой сумму вектора У и аксиального вектора А. Взаимные про-
произведения У на А в лагранжиане A) приводят к переходам,
в которых не сохраняется четность.
Такой структуре слабого тока в общем случае отвечает
матрица О следующего вида:
0$ =Ja(l+giVd, G)
где gi — некоторые константы. С учетом эрмитовости у5 константы^
следует полагать действительными.
Опыт показал, что для лептонных слагаемых все константы g-,-
равны единице. Этому важному свойству лептонных. токов
la = ё (X) Уа A +у6) Ve (X) + (I (X) уа A +уь) V»(x) + ... (8)
отвечает свойство двухкомпонентности нейтрино (см. § 9.2).
Таким .образом, лептонная часть взаимодействия Ферми
содержит всего один параметр G. Этот параметр может быть опре-
определен из времени жизни мюона (см.^упражнение Ф4). При этом
оказывается, что
'С^ = ^^= 1.0262A)-1(Н. (9)
Что же касается адроннои составляющей, то она имеет несколько
более сложную структуру. Так, например, в нуклонной компо-
компоненте адронного тока рОап, ответственной за Р-распад нейтрона,
константа gA, определенная через время жизни нейтрона и соот-
соотношение (9), оказалось равной g^—1,25.
Отмеченная выше недиагональность слабого тока приводит
к тому, что слабый ток меняет квантовые числа фермионов: пре-
превращает нейтрино в электрон, нейтрон в протон и т. д. Рассмот-
Рассмотренные выше токи меняют электрический заряд Q. Они называются
заряженными токами. (В этой терминологии обычный электромаг-
электромагнитный ток электрон-позитронов является незаряженным, т. е.
нейтральным.) В адроннои составляющей слабого тока имеются
также компоненты, меняющие странность адронов на единицу.
Для них принято обозначение ha(AS = l). Таким образом, полный

§ 31. СЛАБЫЕ ВЗАИМОДЕЙСТВИЯ 245
адронный ток может быть представлен в виде суммы
При этом для второго слагаемого выполняется правило AS = AQ.
Несколько лет назад было доказано существование нейтраль-
нейтральных слабых токов /&, не меняющих электрического заряда. Про-
Произведение нейтральных токов входит в лагранжиан аддитивно,
т. е. выражение A) следует заменить на
£(x)p.* (х)]. A1)
Нейтральные токи также можно представить в виде суммы /° =
= l°+h0, причем лептонная составляющая имеет относительно
простую структуру:
& (х) = ~% (х) уа A + ys)ve (х) +1 <ь (х) уа A + у6) Г|1 (х) +
+ e(x)ya(gv+gAy5)e(x) + (e*+\i), A2)
где gv, gA~константы, меньшие единицы.
31.3. Неперенормируемость и ультрафиолетовое поведение.
В целом теория слабых взаимодействий находится в положении,
которое можно сравнить с положением квантовой электродина-
электродинамики до появления метода перенормировок.
Лагранжиан взаимодействия известен и содержит небольшое
число констант связи, а матричные элементы, вычисленные в дре-
древесном приближении, находятся в хорошем согласии с большим
количеством экспериментального материала. В тех случаях, когда
удается отвлечься от эффектов сильных взаимодействий, можно
надеяться, что точность согласия лимитируется радиационными
поправками, имеющими электромагнитное (малость а/л~ 1/400)
или слабое (малость GMZ >~~> 1О) происхождение. Однако вычис-
вычислять радиационные поправки по слабому взаимодействию мы не
можем.
Лагранжиан A), B) имеет индекс Q = + 2 и по классификации
§ 26.3 принадлежит к неперенормируемому типу. Отражением
этого свойства является размерность константы связи G и сте-
степенной рост матричных элементов в ультрафиолетовой области.
Так, например, полное сечение упругого рассеяния двух фер-
мионов за счет слабого взаимодействия первого порядка ведет
себя как
a(s)~G2s ($^>m3{), A3)
т. е. неограниченно растет с ростом полной энергии W = ]/1
в системе центра масс. Следует также ожидать, что радиационные
поправки к любым процессам за счет слабых взаимодействий
будут расти подобным образом. Иными словами, эффективная

246 ГЛ. Vlll. ОПИСАНИЕ РЕАЛЬНЫХ ВЗАИМОДЕЙСТВИЙ
безразмерная комбинация, содержащая константу G и представ-
представляющая параметр разложения в теории возмущений, зависит от
энергии и равна
GW2 = G-s. A4)
Из сравнения A4) и (9) видно, что при энергиях порядка
W* ~№*МР^Ж ГэВ A5)
взаимодействие Ферми перестает быть слабым. Энергию W* иногда
называют энергией унитарного предела.
31.4. Гипотеза промежуточного бозона. Структура взаимодей-
взаимодействия Ферми (ток X ток) наводит на мысль, что выражение вида
A) может не быть фундаментальным, а являться производным
й возникать вследствие того, что слабые токи / взаимодействуют
между собой через некоторое промежуточное поле,
Для того чтобы пояснить эту идею, вернемся к спинорной
электродинамике
и мысленно ограничимся на время рассмотрением таких началь-
начальных и конечных состояний, в которых отсутствуют фотоны. Тогда
фотоны остаются лишь в виртуальных состояниях, а на диаграм-
диаграммах Фейнмана —в виде виртуальных линий. Вообразим еще, что
виртуальные фотоны имеют массу М. Тогда (рис. 31.1) можно
Рис. 31.1. Формальное описание внутренних линий с помощью нелокального
эффективного лагранжиана.
формально исключить электромагнитное поле, заменив его нело-
нелокальным эффективным лагранжианом
eVv (х) DZ (х - у) /ц (у) -> ^эфф = eVv (*) \ £>$ (х - у) /ц (у) dy.
При этом в импульсном представлении
Если все интересующие нас импульсы и массы частиц много
меньше массы «тяжелого промежуточного фотона» М, то в пра-
правой части последнего выражения можно пренебречь k2 по сравне-
сравнению с М2 и получить
DW{x-y) + ^b{x-y), Xem(x) + ~Jv(x)J4x). A6)

§ 32. МОДЕЛЬ ВАЙНБЕРГА - САЛЛМА 247
Поэтому образ промежуточного векторного поля с большой мас-
массой М позволяет «естественным» образом объяснить размерность
константы Ферми и порождает надежду на возможность построе-
построения такой новой формулировки слабых взаимодействий, при кото-
которой они окажутся перенормируемыми. Разумеется, для этого
приходится с самого начала допустить, что масса промежуточного
векторного бозона М существенно больше достижимых в настоя-
настоящее время энергий (имеются в виду энергии в системе центра
масс) лептонов, т. е. являются величинами порядка нескольких
десятков, если не сотен ГэВ.
В настоящее время большую популярность приобрела модель
слабых взаимодействий, основанная на идее промежуточных бозо-
бозонов, являющихся квантами неабелева калибровочного поля —
модель Вайнберга — Салама. Эта модель имеет довольно сложную
структуру, однако сложности модели с лихвой окупаются тем,
что, кроме перенормируемой формулировки слабых взаимодей-
взаимодействий, она органически включает и электромагнитные, т. е.
является единой теорией слабых и электромагнитных взаимо-
взаимодействий.
§ 32. Модель Вайнберга — Салама
32.1. Основные свойства. Здесь мы изложим в общих чертах
единую модель слабых и электромагнитных взаимодействий, пред-
предложенную в конце 60-х годов Вайнбергом и Саламом. Эта модель
замечательна в нескольких отношениях.
Во-первых, она содержит основанную на поле Янга — Миллса
модель слабых взаимодействий лептонов, которая в области «доста-
«достаточно низких» энергий (<50 ГэВ в системе центра масс) соответ-
соответствует взаимодействию Ферми. Универсальность константы Ферми
получает естественное объяснение через универсальность калибро-
калибровочной константы взаимодействия.
Во-вторых, модель довольно простым образом объединяет сла-
слабые и электромагнитные взаимодействия лептонов и позволяет
ввести массивные промежуточные бозоны с помощью спонтанного
нарушения симметрии ценой введения лишь одного хиггсова бозона.
В-третьих, она предсказала существование нейтральных слабых
токов, которые были затем обнаружены экспериментально.
Далее, условие перенормируемости «кваркового расширения»
модели, т. е. варианта, содержащего описание слабых взаимодей-
взаимодействий адронов через калибровочное взаимодействие составляющих
их кварков, привело к необходимости существования четвертого
(«очарованного») кварка и нового квантового числа (очарования).
Это предсказание также подтвердилось на опыте.
Наконец, все наиболее существенные численные результаты
модели зависят всего от трех параметров: двух калибровочных

248 ГЛ. VIII. ОПИСАНИЕ РЕАЛЬНЫХ ВЗАИМОДЕЙСТВИЙ
констант связи g и g1 и массы M\V заряженных промежуточных
бозонов W±.
Постоянная электромагнитного взаимодействия е и константа
Ферми G? выражаются через них следующим образом:
(g2+g?)V' ' V2 8Mb ' {1)
Если использовать для е и GF известные экспериментальные
значения, то остается всего одна числовая степень свободы. Она
обычно связывается с арксинусом отношения elg
g
который называется углом Вайнберга.
Через тройку е, G?, bw, как правило, и выражают предска-
предсказания модели. Так, с помощью A) и B) можно получить для
массы заряженного промежуточного мезона формулу и оценку
1 37,7 ГэВ _-7 7 г R .„.
32.2. Структура бозонного сектора. В основе модели лежит
гипотеза о существовании двух калибровочных полей. Одно из
них (Аа, а= 1,2,3) трехкомпонентно и отвечает присоединенному
представлению группы SU B), а второе (В) однокомпонентно и
его калибровочная группа — 0A).
Таким образом, калибровочная группа модели Вайнберга—
Салама —это полупростая группа SU B)х£/ A). Она содержит
два числовых параметра, обозначаемых g и gv Четыре калибро-
калибровочные векторные частицы необходимы для описания трех про-
промежуточных (массивных) мезонов и фотона. Из четырех частиц
две (компоненты Аг, Л2) заряжены и две (А3 и В) нейтральны.
Поскольку поля А3 и В имеют одинаковые квантовые числа,
между ними возможно смешивание. Физические нейтральные век-
векторные частицы — фотон и массивный Z-мезон оказываются супер-
суперпозициями полей А3 и В. Чтобы сделать векторные мезоны мас-
массивными, используют механизм спонтанного нарушения симметрии
(см. § 11.3), для чего вводят вспомогательное двухкомпонентное
комплексное (четыре степени свободы) скалярное поле ср. Три
степени свободы из четырех уходят на то, чтобы с помощью
механизма Хиггса «создать» по лишнему поляризационному состоя-
состоянию у трех векторных компонент, а четвертое приводит к физи-
физическому массивному бозону Хиггса.
Таким образом, бозонный сектор модели Вайнберга —Салама
основывается на лагранжиане
Хв = -1 GMv - j/vAv i-1 ЗД« - x (IФ f - Л2J- D)

§ 32. МОДЕЛЬ ВАЙНБЕРГА — САЛАМА 249
Здесь F — тензор абелева поля
О\ю ~тензор неабелева поля
поле ф — изотопический (калибровочной группы SU B)) дублет
комплексных полей
w
— ковариантные производные:
f^ E)
Спонтанное нарушение симметрии реализуется сдвигом на дей-
действительную константу т] второй компоненты поля ф:
Л-0. F)
В результате сдвига член | D^cp |2 дает следующий вклад в «мас-
«массовую матрицу» (т. е. в члены, билинейные по компонентам Аа, В):
-g1Bvp. G)
Диагрнализация этого вклада выполняется линейным преобразо-
преобразованием
(Av, Bv) —>- (Zv> Av),
где
gjBy л _
>1А ' v"
Вводя обозначения
запишем форму G) в виде
M*wWvWv + (Vt) MiZvZv. A0)
Здесь в целях дальнейшего удобства введены новые взаимно
комплексно-сопряженные поля для промежуточных заряженных
мезонов:
Wi-= л4тМЗ ^ WysaWv, $V = W$. A1)

250 ГЛ. VIII. ОПИСАНИЕ РЕАЛЬНЫХ ВЗАИМОДЕЙСТВИЙ
Если представить компоненты дублета ср в виде
ш (Х) - ф1(*) + 'Фа(*) „, (х) _ о(*ЖФ,(х)
то последний член в D) приводит к выражению
из которого явствует, чю поле а имеет массу
та = Ят), A2)
а компоненты Фо представляют собой голдстоуновские поля. Они
могут быть устранены калибровочным преобразованием, в резуль-
результате которого три компоненты неабелева калибровочного поля
приобретают лишнюю поляризационную компоненту (эффект
Хиггса). В итоге последний член правой части D) сведется к
32.3. Фермионный сектор. Как известно, слабое взаимодей-
взаимодействие не сохраняет четность. Правополяризованное нейтрино на
опыте не наблюдается. Поэтому структура фермионного сектора
лептонов в первую очередь должна учесть эти свойства. С этой
целью левополяризованная компонента электронного спинора е (х)
и электронное нейтрино ve(x) объединяются в «левый» дублет
Le(x), а правополяризованная часть е(х) образует «правый» син-
глет относительно группы SU B):
е (х)
Аналогичные мультиплеты вводятся для мюона и мюонного ней-
нейтрино:
Такая структура мультиплетов удобна тем, что позволяет оста-
оставить в заряженных составляющих слабых токов лишь левые ком-
компоненты лептонов, объединенные в дублеты L.
Считая, что левые дублеты участвуют в калибровочном взаимо-
взаимодействии группы SU B)xU A), а правые связаны лишь с абелевой
подгруппой, приходим к следующим членам в лагранжиане:
(х) = О. (х) Г (<?ц - f тЛц + -f- Вц) L (х) +
A5)

§ 32. МОДЕЛЬ В АЙН БЕРГА- САЛАМА 251
Здесь мы опустили нижние индексы ([г) и (v), подразумевая, что
по ним необходимо произвести независимое суммирование.
Прямое введение массовых членов для лептонов
/n(LR + RL)
нарушает калибровочную инвариантность. Однако если предпо-
предположить, что мультиплеты L и R, подобно калибровочным полям
Ац и Вц, взаимодействуют со скалярным полем ф, введенным
в D), то они приобретут массу в результате спонтанного нару-
нарушения симметрии.
Полагая, что соответствующий член взаимодействия имеет
юкавскую форму
A6)
получаем, что в результате «сдвига» F) поля ф на константу
в лагранжиане появляются массовые лептонные члены
— теё (х) е (х) - т^ (х) [г (х),
причем
ф12 С/2 A7)
Таким образом, полное выражение для лептонной части лагран-
лагранжиана, основанное на слагаемых A5), A6) и записанное в пере-
переменных W, А, ф, будет иметь вид
Ж (х) = Xw (х) + Xw (x) + ^?ер (х), A8)
где
Xw (x) =
■х)А»(х)—±ё[х)е(х)а[х)-\
X [v. (х) у» A + у&) v, (х) - 2ё (х) у» [f + ^=М.) е (х)] Z» (х), A9)
Х^) получается из<5?(г) заменой e(x)-*-\i(x), ve->-Vpi и =ЗДр — сво-
свободный лагранжиан полей е(х), \i(x), ve(x), v)l(x):
%ЪР (х) = i% (x) bve (x) +1% (х) ^ (х) +
+ ё (х) (id - те) г (х) + (I (х) {id - тJ ji (х). B0)
Из формулы A9) вытекает, что константы электромагнитного
взаимодействия е и слабого взаимодействия в форме Ферми Gf
связаны с g, gx и Mw формулами A).
Напомним еще, что масса хиггсова бозона та выражается
через параметры лагранжиана формулой A2).

252 ГЛ. VIII. ОПИСАНИЕ РЕАЛЬНЫХ ВЗАИМОДЕЙСТВИЯ
32.4. Лагранжиан и квантование. Собирая результаты, находим,
что полный классический лагранжиан модели Вайнберга —Салама
имеет вид
^WS=^B + ^fep+i;^@, ■ B1)
(О
где Хв — бозонная часть, определенная соотношением D), X(i) —
лептонные составляющие вида A9), а <5??ер —сумма свободных
лептонных вкладов B0). Первый член Хв, записанный в пере-
переменных Wv, Д,, а, содержит следующие квадратичные слагаемые;
%% (х) = -1 (ЗА - МцJ + \ (ад* - ^- о
B2)
Это выражение вместе со свободным лептонным лагранжианом
<5?1еР, описываемым выражением B0), и представляет полную «сво-
«свободную» (точнее сказать — билинейную) составляющую часть
лагранжиана Вайнберга —Салама, которую необходимо прокван-
товать для построения теории возмущений по константам связи g,
gv G(i) (или их комбинациям). Процедура квантования абелева
сингулярного лагранжиана для электромагнитного поля была
рассмотрена в § 8.5, а для неабелева поля обрисована в § 19.4.
Там было показано, что правила Фейнмана для поля Янга —
Миллса содержат дополнительные элементы, которые могут быть
выражены с помощью вспомогательного фиктивного поля духов
Фаддеева —Попова. Мы не будем излагать здесь процедуру кван-
квантования, отослав читателя, интересующегося правилами Фейнмана
для массивного поля Янга —Миллса, к Дополнению VIII.
Сделаем еще замечание относительно ультрафиолетовых расхо-
димостей. Модель Салама — Вайнберга имеет довольно сложную
структуру и включает массивные векторные поля. Пропагаторы
таких полей (см. A8.14)) содержат в числителе полином второй
степени по компонентам импульса и поэтому, согласно анализу
§ 26, на первый взгляд приводят к неперенормируемым ультра-
ультрафиолетовым расходимостям. В то же время первоначальный
лагранжиан типа D) до сдвига скалярных полей на константу
содержит безмассовые векторные частицы и, как можно показать,
является перенормируемым. Ввиду того, что исходный лагранжиан
и конечный, полученный в результате спонтанного нарушения
симметрии, являются физически эквивалентными (и отличаются
лишь выбором переменных), бозонный сектор модели оказывается
перенормируемым.
Более тщательное исследование показывает (см., например,
гл. IV, V в книге Славнова, Фаддеева A978)), что реальная труд-

§ 32. МОДЕЛЬ ВАЙНБЕРГА-САЛАМА 253
ность для перенормйруемости возникает в фермионном секторе.
Она связана с несохранением четности и проявляется в так
называемых аномальных треугольных диаграммах (рис. 32.1),
в которых все три внутренние линии фермионные, а наружные —
векторные калибровочные и в вершинах которых имеются матри-
матрицы у5 (СР- первую строку в правой части формулы A9)). Расходи-
Расходимости этих диаграмм нельзя перенормировать так, чтобы сохранить
калибровочную инвариантность. Их однако мож-
можно скомпенсировать.
Одна из возможностей компенсации связана
с кварковым расширением модели. Если до-
добавить в описанную лептонную модель Вайн-
берга —Салама слабые взаимодействия аДро-
нов, введя их через калибровочные взаимодей- ^г1" "Ч,
ствия фермионных кварковых полей, то мойно
достичь перенормируемости расширенной моде- j^. ;^„™!^Л"
ли при выполнении условия баланса между диаграмма неабеле-
лептонами и кварками. Четырем лептонам (е, вой калибровочной
f-Ц ve, Vpi) должны соответствовать четыре квар- теории.
ка. Именно эти соображения, дополненные не-
некоторыми качественными физическими доводами, и привели к ги-
гипотезе о четвертом кварке с новым квантовым числом (очарова-
(очарованием), столь эффектно подтвердившейся открытием семейства
1|>частиц в 1975 г. и последующим обнаружением адронов
с отличным от нуля очарованием.
32.5. Физическое содержание и экспериментальный статус.
Дадим теперь краткое описание физического содержания модели
Вайнберга —Салама и его соответствия с данными опытов.
Существенным свойством модели является наличие нейтральных
токов (связанных с нейтральным промежуточным мезоном). Эти
токи были обнаружены в 1973 г. в опытах по взаимодействию
нейтрино с нуклонами. Измеренные количественные характеристики
согласуются с предсказаниями модели при Qwc^30°, sin2^^
~0,23 ±0,02. Подставляя это значение в C) и (9), получаем
приближенные значения для масс промежуточных бозонов: Mw~.
~75 ГэВ, Mz^87 ГэВ. Этим значениям соответствует радиус
действия слабых сил /-сл ~3- Ю-16 см.
Для того чтобы непосредственно обнаружить эффекты, свя-
связанные с существованием столь тяжелых частиц, необходимы
достаточно высокие энергии ускорителей. Так, например, нейт-
нейтральный Z-бозон может быть рожден в установке со встречными
е+е~ или рр пучками, энергия каждого из которых должна быть
не менее 40 — 50 ГэВ. Подобные ускорители могут появиться
в ближайшем десятилетии.
Модель содержит скалярный хиггсов бозон. Его масса т<,
определяется формулой A2), содержащей свободный параметр Я.

254 ГЛ. VIII. ОПИСАНИЕ РЕАЛЬНЫХ ВЗАИМОДЕЙСТВИЯ
Поэтому масса т0 может быть «выбрана» достаточно большой
для того, чтобы отсутствие на опыте тяжелого скалярного ней-
нейтрального бозона еще долгое время не являлось источником
беспокойства.
§ 33. Общая картина
33.1. Сильные взаимодействия. При обсуждении взаимодействий
между полями в § 10 были выписаны лагранжианы юкавского
типа в псевдоскалярном A0.17) и псевдовекторном A0.19) вариан-
вариантах. Как там также отмечалось при введении пион-пионного
взаимодействия A0.22), нет никаких серьезных оснований считать
подобные выражения фундаментальными. Их можно рассматривать
в чисто феноменологическом плане и пытаться определить конк-
конкретный вариант лагранжиана взаимодействия и численное значение
констант связи из сравнения с данными опыта. Такие попытки
неоднократно предпринимались главным образом в течение 50-х
годов. Было установлено, что некоторые выражения этого типа
могут быть положены в основу перенормируемой теории возму-
возмущений. Таковы, например, лагранжианы A0.17) и A0.22). (В то
же время юкавское псевдовекторное взаимодействие A0.19) непе-
ренормируемо.) Однако никаких удовлетворительных количествен-
количественных описаний процессов сильных взаимодействий на этом пути
получить не удалось.
Довольно прозрачная (хотя и не единственная) причина неудач
связана с тем, что константы связи g, h, а следовательно и
параметры разложения теории возмущений, в сильных взаимо-
взаимодействиях не являются малыми по сравнению с единицей. Так,
например, константа связи g юкавского пион-нуклонного псевдо-
псевдоскалярного взаимодействия, оцененная с помощью метода диспер-
дисперсионных соотношений (см. ниже § 33.3), оказалась равной
£3/4л~14,7. A)
В 70-х годах в связи с разработкой составной кварковой мо-
модели адронов выражения типа A0.17), A0.22) постепенно «вышли
из моды», и усилия теоретиков в последнее время сосредоточились
на так называемой глюон-партонной модели, в которой основную
роль играют гипотетические «истинно фундаментальные» состав-
составляющие адронов — кварки. Фермионные и кварковые поля связаны
между собой калибровочным полем, кванты которого — векторные
частицы — называются глюонами.
Благодаря свойству асимптотической свободы калибровочных
полей (см. ниже § 33.3), кварк-глюонное взаимодействие ослабевает
с ростом энергии, вследствие чего в ультрафиолетовом пределе
кварки и глюоны ведут себя как квазисвободные точечные объекты.
На опыте в высокоэнергетических, так называемых глубоконеуп-

§ 33. ОБЩАЯ КАРТИНА 255
ругих процессах адроны проявляют сложную структуру и выглядят
как бы состоящими из точечных составляющих — партонов. Эта
наблюдаемая картина и находит естественное объяснение с помощью
свойства асимптотической свободы. Роль партонов при этом играют
кварки, представление о которых возникло в начале 60-х годов
в связи с феноменологической схемой классификации адронов и
адронных резонансов, основанной на концепции унитарной сим-
симметрии.
Квантовополевая модель, описывающая взаимодействия ферми-
онных кварковых полей с помощью калибровочного глюонного
поля, называется квантовой хромодинамикой.
Мы не имеем здесь возможности вдаваться сколько-нибудь
подробно в физику сильных взаимодействий и детали квантовой
хромодинамики. Отметим лишь, что, согласно современным пред-
представлениям, применение описанного в этой книге метода перенор-
перенормируемой теории возмущений к некоторым физическим ситуациям
оказывается здесь оправданным. Тем не менее основные физические
проблемы кварк-глюонной модели, связанные с отсутствием кварков
и глюонов в свободном состоянии, еще ждут своего решения. Они
не могут быть исследованы с помощью аппарата слабой связи
(т. е. в рамках обычной теории возмущений).
Таким образом, область применения методов перенормируемой
теории возмущений естественным образом ограничивается моделями
квантовой теории поля с численно малыми значениями констант
связи. Существуют и другие ограничения.
33.2. Ограничения метода теории возмущений. Оказывается,
например, что даже при численно малых константах связи имеются
области значений кинематических переменных, в которых после-
последовательные члены разложений теории возмущений могут не убы-
убывать. Как было установлено выше, при вычислении однопетлевых
поправок к пропагаторам в области больших значений импульсов р
(ультрафиолетовая асимптотика) эти поправки возрастают лога-
логарифмически (см., например, формулы B4.6), B9.6)), вследствие
чего их относительный вклад в пропагатор пропорционален про-
произведению g2L — квадрата константы связи g на большой «ультра-
«ультрафиолетовый» логарифм
L = ln(pVA2). B)
Анализ высших радиационных поправок показывает, что в ультра-
ультрафиолетовой области я-петлевые вклады растут как (g2L)n. Анало-
Аналогичная ситуация возникает в области малых импульсов (инфра-
(инфракрасная асимптотика) в некоторых квантовополевых моделях,
содержащих безмассовые поля. Так, например, в спинорной
электродинамике радиационная поправка к пропагатору электрона,
обусловленная испусканием и поглощением безмассового фотона,
содержит (см. формулы B9.17), B9.20)) произведение а/ —пара-

256 ГЛ. VIII. ОПИСАНИЕ РЕАЛЬНЫХ ВЗАИМОДЕЙСТВИЙ
метра разложения а = е2/4зг на «инфракрасный» логарифм
который неограниченно возрастает при приближении импульса
электрона р к массовой поверхности (р2-*-тг). Высшие радиаци-
радиационные поправки содержат произведения (а/)".
Тем самым в ультрафиолетовой и инфракрасной областях
произведения типа g%L и g4 оказываются фактическими парамет-
параметрами разложения теории возмущений. В этих областях происходит
эффективный выход за рамки слабой связи даже при малых чис-
численных значениях констант взаимодействия. Сказанное относится
не только к одночастичным пропагаторам, но и к высшим вер-
вершинным функциям.
Возникает задача определения и суммирования подобных
больших вкладов высших порядков. Эта задача в отдельных слу-
случаях поддается частичному решению с помощью некоторого усо-
усовершенствования техники теории возмущений. Пример дает
формула B9.13) для ультрафиолетовой асимптотики фотонного
пропагатора. Однако в общем случае необходимо привлечение
методов, существенно выходящих за рамки обычной теории воз-
возмущений, или по крайней мере их комбинирование с результатами
теории возмущений (см. ниже § 33.3).
Таким образом поле применения изложенного в гл. IV —VII
этой книги аппарата перенормируемой теории возмущений
оказывается ограниченным с нескольких сторон.
Во-первых, этот аппарат работает лишь в так называемых
перенормируемых взаимодействиях. Он, в частности, не может
быть использован для слабых взаимодействий в форме Ферми
(как об этом было сказано в § 31.3) и для гравитационных взаи-
взаимодействий (ввиду того, что спин гравитона равен 2 и его про-
пагатор сильно растет в ультрафиолетовой области).
Во-вторых, в перенормируемых моделях квантовой теории поля
метод теории возмущений может быть использован лишь в случае
малости констант связи. Этому условию удовлетворяет спинорная
электродинамика и ее «обобщения в сторону слабых взаимодей-
взаимодействий», типа модели Вайнбергй — Салама. Однако в подавляющей
части перенормируемых моделей сильных взаимодействий теория
возмущений не может быть использована из-за большого значения
константы связи (ср. (I)).
Наконец, как только что было показано, даже в перенорми-
перенормируемых моделях с численно малыми константами связи имеются
кинематические ограничения. Для их преодоления используются
различные приемы и методы, позволяющие хотя бы частично выйти
за рамки изложенной в этой книге «стандартной» теории возму-
возмущений.

§ 33. ОБЩАЯ КАРТИНА 257
33.3. Другие методы квантовой теории поля. Ввиду отмеченной
ограниченности возможностей применения теории возмущений
к реальным процессам, особенно к задачам физики адронов,
большое значение приобретают любые успешные теоретические
пути анализа задач теории частиц, не связанные непосредственно
с малостью константы связи и степенными разложениями. Таких
зарекомендовавших себя подходов известно три. Это —метод дис-
дисперсионных соотношений, метод функционального (или контину-
континуального) интегрирования и метод ренормализационной группы.
Метод дисперсионных соотношений основан на аксиоматической
формулировке квантовой теории поля, представление о которой
читатель получил в гл. IV. Сформулированные в § 15 аксиомы
были употреблены в § 16 для построения разложения матрицы
рассеяния по степеням малости взаимодействия, т. е. по степеням
константы (или констант) связи. Полученные результаты оказа-
оказались эквивалентными решению уравнения Шредингера методом
итераций, приведенному в § 14.
Несколько расширенный вариант аксиом § 15 (боголюбовская
аксиоматика) был использован одним из авторов в середине 50-х
годов для обоснования метода дисперсионных соотношений (см.
Введение, гл. X). Решающими элементами строгого математиче-
математического вывода явились формулировка условия причинности в диф-
дифференциальной форме A5.16) и соединение методов теории функций
нескольких комплексных переменных с теорией обобщенных
функций.
Дисперсионные соотношения формально являются следствиями
теоремы Коши из теории функций комплексного переменного,
примененной к амплитуде рассеяния / (Е), аналитически продол-
продолженной в комплексную плоскость переменной энергии E-*-E-+}V.
Обычно они записываются с помощью интегральных соотношений
вида
между вещественной и мнимой частями амплитуды двухчастич-
двухчастичного рассеяния вперед:
каждая из которых может быть выражена алгебраическими соот-
соотношениями (см. формулы § 21.4) через две непосредственно изме-
измеряемые величины — полное эффективное сечение а(Е) и диффе-
дифференциальное сечение рассеяния на нулевой угол hq= ^
Аналитическое продолжение амплитуды рассеяния / (Е) в комп-
9 Н. Н. Боголюбов, Д. В. Ширков

258 ГЛ. VIII. ОПИСАНИЕ РЕАЛЬНЫХ ВЗАИМОДЕЙСТВИИ
лексную плоскость энергии оказывается возможным благодаря
условию причинности.
„ Дисперсионные соотношения представляют собой строгие след-
следствия основных аксиоматических положений локальной квантовой
теории поля, сформулированные в виде интегральных по энергии
соотношений для наблюдаемых величин. Эти соотношения не
образуют системы уравнений, достаточных для теоретического
определения входящих в них функций. Они, однако, могут
непосредственно проверяться на опыте, а также представляют
собой основу для получения строгих качественных и приближен-
приближенных результатов.
В течение последующих десятилетий метод дисперсионных
соотношений получил большое развитие и вплоть до 70-х годов
являлся единственным средством количественного анализа про-
процессов сильных и электромагнитных взаимодействий адронов.
Метод функционального интеграла основан на фейнмановской
формулировке квантовой механики в виде интеграла по путям.
(см. § 138 в учебнике Блохинцева A976)). Амплитуды переходов
и функции Грина выражаются через некоторые формальные
выражения (функциональные интегралы), которые можно пред-
представлять себе как пределы многократных интегралов при стрем-
стремлении числа интегрирований к бесконечности. Оказывается воз-
возможным ввести определенные правила обращения с функциональ-
функциональными интегралами и в ряде случаев способы их явного вычисления.
К настоящему времени метод функционального интеграла заре-
зарекомендовал себя как метод получения общих результатов в кван-
квантовой теории поля. С его помощью были проквантованы неабелевы
калибровочные поля (см. книгу Славнова, Фаддеева A978)),
весьма элегантно выведены формулы калибровочных преобразо-
преобразований полных функций Грина в квантовой электродинамике (см.
гл. VIII Введения), а также получены некоторые другие важные
результаты. В самые последние годы ряд интересных свойств,
относящихся к структуре ряда теории возмущений в целом, был
установлен с помощью приближенного вычисления функциональ-
функционального интеграла методом функционального перевала, являющегося
аналогом метода перевала из теории функций комплексного
переменного. Этим путем удалось показать, что ряды квантово-
полевой теории возмущений являются асимптотическими (и, сле-
следовательно, не имеют области сходимости).
Метод ренормализационной группы основан на групповом
характере конечных перенормировок функций Грина и констант
связи, отвечающих различным способам устранения расходимостеи
(например, различным точкам вычитания ^-операции — см. § 28).
Математическая формулировка групповых свойств (см. гл. IX
Введения) приводит к функциональным соотношениям, связы-
связывающим между собой функции Грина для различных схем пере-

§ 33. ОБЩАЯ КАРТИНА 259
нормировок. Соответствующие групповые дифференциальные урав-
уравнения (уравнения Ли) оказываются весьма удобными для иссле-
исследования ультрафиолетовых и инфракрасных асимптотик функций
Грина, т. е. анализа тех случаев, когда, как было указано
выше в § 33.2, происходит эффективный выход за рамки слабой
связи.
Следует отметить, что, в отличие от основной массы резуль-
результатов, полученных с помощью дисперсионных соотношений и
представления функционального интеграла, основные физические
результаты получаются здесь в итоге своего рода симбиоза
вычислений по теории возмущений и строгих ренормгрупповых
соотношений. К ним относится свойство асимптотической свободы
ряда квантовополевых моделей, содержащих поля Янга — Миллса.
Квинтэссенция явления асимптотической свободы выражается
формулой
/ c>0, |Л» |-^оо D)
для так называемой эффективной (или инвариантной) константы
взаимодействия g, зависящей от квадрата 4-импульса и описываю-
описывающей эффективное изменение интенсивности взаимодействия в обла-
области больших импульсов (т. е. малых расстояний). Формула D)
представляет собой сумму «старших» ультрафиолетовых логариф-
логарифмических вкладов (g2L)n из всех порядков теории возмущений и
отличается от аналогичной формулы спинорной электродинамики
для инвариантного электрического заряда
a(k\a)= iL__, ■ |А»|_^оо E)
алгебраическим знаком логарифмического слагаемого в знамена-
знаменателе. (Выражение E) является непосредственным следствием
формулы B9 13) для фотонного пропагатора и отвечает сумме
ультрафиолетовых асимптотик вкладов итераций простых элек-
трон-позитронных петель—см. рис. 29.1.)
Это отличие приводит к важным физическим следствиям.
Формула E) соответствует «нормальной картине» экранировки
(подобной картине экранировки точечного заряда, внесенного
в поляризуемую среду), когда эффективный заряд а увеличива-
увеличивается вместе с k2, т. е. с уменьшением расстояния (рис. 33.1).
В противоположность этому формула D) приводит к уменьшению
эффективного взаимодействия с ростом импульса, которое в асимп-
асимптотическом ультрафиолетовом пределе стремится к нулю, а поля,
участвующие во взаимодействии,— к свободным (рис. 33.2). Этот
феномен «самовыключения» взаимодействия на малых расстояниях
и называется асимптотической свободой. В свое время он явился
9*

260
ГЛ. VIII. ОПИСАНИЕ РЕАЛЬНЫХ ВЗАИМОДЕЙСТВИИ
решающим аргументом для утверждения калибровочного меха-
механизма взаимодействия полей в качестве единственно возможного
для сильных взаимодействий.
а
Рис. 33.1. Эффект поляриза-
поляризации вакуума в спинорной
электродинамике, приводя-
приводящий к картине «нормальной
экранировки>.
Рис. 33.2. Уменьшение эф-
эффективного взаимодействия
с ростом импульса в неабе-
левой калибровочной тео-
теории.
33.4. Заключение. Изложенный в этой книге метод перенор-
перенормируемой теории возмущений является основным регулярным
рабочим инструментом квантовой теории поля. Он позволяет
получать надежные количественные результаты, описывающие
широкий круг физических явлений микромира. Существенным
элементом метода является процедура устранения ультрафиоле-
ультрафиолетовых расходимостей с помощью перенормировок. Иногда выска-
высказывается мнение, что факт существования этих расходимостей
представляет собой серьезный дефект квантовой теории поля —
дефект, который приходится «прикрывать» математически неудов-
неудовлетворительной операцией перенормировок.
В этой связи следует подчеркнуть два момента. Наличие
ультрафиолетовых расходимостей органически связано с локаль-
локальностью квантовой теории поля. Поэтому расходимости и перенор-
перенормировки неизбежно будут сопровождать любую модификацию
современной формулировки квантовой теории поля при условии
сохранения ее локального характера.
Процедура перенормировок в свою очередь в настоящее время
представляет собой математически строгую операцию, выполняе-
выполняемую по рецепту, в основе которого лежит теория обобщенных
функций. Физический смысл перенормировок состоит в том, что
влияние «малых» расстояний на физику «больших» расстояний
может быть эффективно учтено с помощью ограниченного числа
конечных параметров.

Дополнение I. ИЗОТОПИЧЕСКИЙ ФОРМАЛИЗМ
Формализм изотопического спина был введен Гайзенбергом для того, чтобы
описать независимость ядерных сил от электрического заряда. В этом форма-
формализме нейтрон и протон рассматриваются как два различных (зарядовых)
состояния одной и той же частицы (нуклона).
Нуклонная волновая функция при этом наделяется свойствами двухком-
понентного спинора относительно преобразований вращения в некотором фик-
фиктивном трехмерном пространстве—пространстве изотопического спина (изото-
(изотопическом пространстве). Аналогичные свойства приписываются волновым
функциям других зарядовых мультиплетов. Так, например, пионный триплет
я", я0, я~ описывается тремя функциями, являющимися компонентами вектора
в изотопическом пространстве и т. д.
Инвариантность относительно вращений в изотопическом пространстве
физически соответствует равноправности частиц внутри мультиплетов. Очевидно,
что эта равноправность нарушается электромагнитными взаимодействиями.
Однако если отвлечься от последних, то свойство изотопической инвариант-
инвариантности оказывается справедливым для сильных (ядерных) взаимодействий.
Ниже мы дадим конспективный перечень основных формул изотопического
формализма для нуклонов и пионов. Для более детального ознакомления
читателю может быть рекомендована гл. 3 книги Перкинса A975).
1. Дублет нуклонов. Рассмотрим прежде всего изотопический дублет нукло-
нуклонов. Спинор трехмерного (изотопического) пространства имеет две компоненты,
которые соответствуют протонной i|)p и нейтронной i|)n полевым функциям:
Операторы вращений в изотопическом пространстве строятся из матриц
2-го ранга, которые совпадают с матрицами Паули (ДП.8), но обозначаются
другими символами:
/О 1\ /0 —i\
Ti=(ioj> T*=\i О)' Ts
Матрицы т антикоммутируют друг с другом
V^+T&Ta = 0 (афЬ), xj = l C)
и удовлетворяют соотношениям
т1та = 1'т3 (и циклические перестановки индексов 1, 2, 3). D)

262 ДОПОЛНЕНИЕ I
Операторы изотопических вращений нуклонов связаны с матрицами т соотно-
соотношением
. . /а = то/2. E)
В силу C), D) они удовлетворяют коммутационным соотношениям для опера-
операторов вращения
[Ilt 1ц] = Н3 (и циклические перестановки индексов 1, 2, 3), F)
а также соотношению
вследствие чего .собственное значение полного изотопического момента враще-
вращения /, определяемого из квантовомеханического соотношения
оказывается равным / = Va-
Линейные комбинации матриц тх и т2
G)
"/
переводят нейтронное состояние в протонное и наоборот:
<)-$)■ >ff)-O-
вследствие чего т+ и т_ иногда называют операторами «повышения» и «пони-
«понижения» электрического заряда. Формулы преобразований спинора Ч*1 при вра-
вращении изотопического пространства вокруг оси га на угол ф имеют вид, ана-
аналогичный (ДН.18):
где
Ла(ф)=е аЧ> = е ТаФ =cos -|— £xasin ^-.
Билинейные формы Ч?таУ (а=1, 2, 3) образуют пространственную плот-
плотность вектора изотопического спина
третья компонента которого связана с электрическим зарядом и гиперзарядом:
Q=/,+£±* = /,+-£. (8)
2. Триплет пионов. Тройка псевдоскалярных пионов я", я0, я~ образует
изотопический триплет, который описывается тремя псевдоскалярными поле-
полевыми функциями, образующими изотопический вектор. Обычно используют два
представления этих функций. В первом из них функции поля действительны:
яг={я1, я2, я3Ь ла(х) = ла(х). (9)
Во втором представлении из двух действительных функций nv л2 образуют
Яве комплексные комбинации
Яч — (я» Я14-('я2 ,,п.
Ф1 ~у2' 'Р2"=Ла' ф8= /о

ДОПОЛНЕНИЕ I 263
Преобразование от (9) к представлению
может быть записано в матричном виде
Ф = Оя, 0 = 1 У* у А A2)
V 1/У2~ 1/У2 О/
где О — унитарная матрица
00=1.
Формулы преобразования изотопического вектора (9) при вращениях трехмер-
трехмерного изотопического пространства имеют вид
зх -*•►• зх — Л (ct) зх. 1\ (сс) ^^ б ■ I
где а„ (л=1, 2, 3) —углы вращений, а ш„ —матрицы изотопического спина
в представлении (9):
/О О О\ /00 (\ /0 — t ON
0I= О О -П, ш2= 0 00, ш3= ( 00. A3)
\0 i 0/ \—i 0 0/ \0 О О/
Квадрат матричного вектора «в равен
ш (ш +1) = wf + ш| + а>\ = 2.
Поэтому ш является оператором момента вращения с собственными значениями
1, 0, -1.
Оператор преобразования вращения на угол а вокруг оси 2S может быть
представлен в виде
/cos a — sin а 0\
Л(а) = е~гШзОС= 1 — wl + wjcosa — ia>3 sin a = I sin a cosaON A4)
\ 0 0 1/
Компоненты матриц A3) могут быть выражены через совершенно антисиммет-.
ричный единичный тензор третьего ранга
Матрицы (йа удовлетворяют коммутационным соотношениям
[щ, ша]=10)з (и циклические перестановки индексов 1, 2, 3). A5)
Переход к представлению A1) достигается унитарным преобразованием
Тп = Оа>п6.
Матрицы Гп имеют вид
/0—1 Оч / 0 / 0\ /1 0 0\
1 01 Т10-1)- Гз=00 ° A6)
0 10/ ^2\ 0 ( О/ \0 0 -1/
и удовлетворяют коммутационным соотношениям A5). Существенно, что мат-
матрица Т3 диагональна. Это свойство отражает тот факт, что в представлении A1)
компоненты <pv соответствуют определенным значениям электрического заряда.
На основании (8) следует отождествить
ф,.~л+, фа~я°, фз~я-. A7)

264 ДОПОЛНЕНИЕ II
Дополнение II. МАТРИЦЫ ДИРАКА И УРАВНЕНИЕ ДИРАКА
Это дополнение содержит технический материал по матрицам Дирака,
уравнению Дирака и трансформационным свойствам спинорных функций, яв-
являющийся вводным к § 5, а также полезным для вычисления матричных эле-
элементов. Упражнения к материалу этого дополнения помещены в задании
«Сентябрь».
1. Матрицы Дирака. Свойства четырех гиперкомплексных чисел yv (v=0,
1, 2, 3) определяются основным антикоммутационным соотношением
VM.Vv + WVn=2gnv- A)
Из этого соотношения во-первых вытекает, что 16 величин:
единичная матрица I = gWyVyv (нет суммирования!),
четыре величины yv,
шесть величин avli=(yvyVL—yvy4)/2i (V < (i), B)
одиа величина Yb^
и четыре величины
образуют алгебру над полем комплексных чисел. Иными словами, совокуп-
совокупность элементов, определенная всевозможными линейными комбинациями вели-
величин B) с комплексными коэффициентами, а также всевозможными произведе-
произведениями таких величин и их комбинаций друг с другом, является замкнутой
относительно операций сложения элементов, умножения элементов друг на
друга и на комплексное число.
Отметим, что формы aV(l являются билинейными по у, формы Dv — трой-
тройными, а 7s — единственной формой четвертого порядка. Все остальные формы
четвертого порядка, все формы пятого и высших порядков с помощью фунда-
фундаментального соотношения A) сводятся к одной из величин B).
Используя ряд алгебраических теорем, можно показать, что ранг г непри-
неприводимого матричного представления системы гиперкомплексных чисел связан
с числом п линейно независимых элементов соотношением
которое является совершенно естественным, если гиперкомплексные числа
представляются в виде квадратных матриц
Не составляет труда показать, что шестнадцать матриц B) являются ли-
линейно-независимыми Для этого необходимо, во-первых, рассмотреть шпуры
всех этих матриц и убедиться, что все шпуры, кроме шпура единичной мат-
матрицы Sp/ = /\ равны нулю. Доказательство основано на возможности цикли-
циклической перестановки матриц-сомножителей под знаком шпура. В качестве при-
примера рассмотрим шпур произведения yvYM пРи v ¥= ц Используя последова-
последовательно цикличность и основное соотношение A) получаем
Sp VvYm = SP VnVv = (V2) Sp (VvYu + VnVv) = 0.
На втором этапе следует рассмотреть линейную форму
F = al +
И путем, вычисления шпуров от / и от произведений Fy4, Fa^, FDV. Fy* по-
последовательно убедиться, что предположение о юм, что''F=0, приводи! к це*

ДОПОЛНЕНИЕ II 265
почке соотношений
а = 0, bv=0, сИ*=0, dv = 0, e = 0.
Таким образом, в нашем случае л=16, и из формулы п = г2 теперь следует,
что гиперкомплексные числа у\ определенные соотношением A), могут быть
представлены в виде квадратных матриц четвертого порядка—матриц Дирака.
Из фундаментального соотношения A) вытекает также, что четыре мат-
матрицы Yv могут быть выбраны унитарными, если условия эрмитова сопряжения
наложить в виде
Vv = Vv, G\Э=%а- C)
Замечая еще, что матрица уь антикоммутирует с yv (v=0, I, 2, 3), а ее
квадрат равен + 1, можем записать
УтУп + УпУт = ^тп> <П, /1 = 0, 1, 2, 3, 5, D)
где по определению
£55=1-
При этом
Уь=Уъ = уЬ-
Основные соотношения A) и все полученные из них следствия являются
инвариантными относительно унитарного преобразования
где О — произвольная неособенная (т. е. обладающая обратной) матрица, кото-
которую с учетом C) следует считать унитарной.
Тем самым матрицы Дирака вообще определены с точностью до унитар-
унитарного преобразования. Обычно употребляют представление
I---;::-1
(точками обозначены нули), в котором т° является диагональной. Оно оказы-
оказывается особенно удобным при рассмотрении нерелятивистского предела (см.
ниже). Мы будем называть представление E) стандартным представлением
матриц Дирака.
Это представление матриц у связано с употребляемыми иногда матри-
матрицами а, р, а и р посредством соотношений
а» = 7оУ (л=1.2, 3); р = 7°;
(n=1. 2. 3). ,Л=°23. аа = а31. <^з=^; F)
Pi = — V?. Ра °6 °

266 ДОПОЛНЕНИЕ II
Стандартное представление E) может быть записано в так называемом
«расщепленном» виде
через дву-хрядные матрицы Паули
/О 1\ /О -А /1 0\
ai==(ioJ- a* = (i о]' a3 = (p-ij- •
удовлетворяющие соотношениям
а также единичную и нулевую матрицы второго ранга
/=\0 1/' °\0 oj"
Вернемся к шпурам матриц Дирака и их произведений. Шпур единичной
матрицы равен рангу представления, т. е.
Sp / = Sp i>VYv = 4 (нет суммирования по v!).
Принимая теперь во внимание доказанное выше обращение .в нуль шпу-
шпуров матриц Суд, и £>v, имеем
№. SP
0.
—gvpgMO.
v, ц, p, a = 0, 1, 2, 3.
Как общее правило, получаем, что шпуры произведений нечетного числа
матриц у всегда равны нулю, а шпуры произведений четного числа у с точ-
точностью до множителя 4 выражаются через антисимметризованные произведения
множителей guv, причем знак слагаемого 4g., g „ ...g,. в выражении
для Sp (Vvj^-'-Vvj^) определяется четностью перестановки Pv^^*' '"'у2п-
Приведем еще ряд формул для шпуров от сверток у-матриц с 4-векторами
<2=avYv, вытекающих из A0);
Sp<2£=4(a*), (Па)
Spubccl = 4{(ab)(cd)+(ad)(bc)— (ac)(bd)}, A16)
(V4)Sp f(^i + m1)(^+ms)(^+ms)(l«^-m4)] =
= (XiX2) (X3X4) + (ВД (^2X3) - (XiK.) (/C2X4), A1 в)
где
+
Связь между шпурами, «содержащими массы», и «безмассовыми» шпурами,
аналогичная связи между формулами (Ив) и A16), имеет место и при нали-
наличии большего числа сомножителей.
2. Уравнение Дирака. Это матричное линейное уравнение первого порядка
в частных производных
^^=0. A2)

ДОПОЛНЕНИЕ II 267
Функция поля г|)а четырехкомпонентна (а=1, 2, 3, 4). Действуя на A2)
слева оператором (й + т), получаем с помощью A)
Ф+т) (id — т)г|) = [— дг—т2]\|> = (Q — т2)г|> =0.
Таким образом, каждая из компонент г|>а удовлетворяет уравнению Клейна —
Гордона,
Сопряженное уравнение получается из уравнения Дирака в два этапа.
Беря эрмитово сопряжение от A2), получаем с помощью C)
Это выражение не обладает «правильной» лоренц-симметричной формой. Умно-
Умножая его справа на у>, с учетом того, что
VoVvVo = Vv=Vv. - A3)
получаем
^L =Q A4)
— сопряженное уравнение Дирака. Входящий в него спинор
■$■=■$7° A5)
именуют «сопряженным» относительно г|).
Спиноры г|) и г|) часто представляют в виде четырехкомпоиентных столбца
и строки. При всей своей наглядности такое представление иногда может при-
приводить к некоторым неудобствам, например при введении операции зарядового
сопряжения (см. § 9.3). Практически в случае необходимости достаточно иметь
в виду вторую форму записи уравнения A2)—записи в компонентах.
3. Трансформационные свойства. Отсылая читателя, интересующегося вы-
выводом, к имеющейся обширной литературе, приведем здесь лишь окончатель-
окончательные формулы преобразований спинорных функций поля.
При преобразованиях сдвига, на основании общих соображений из § 1.3,
имеем
i|)(*) = i|>'O'). x'=x+a.
При пространственных поворотах в плоскости хтхп на угол <р
Кг =хт cos Ф — хп sin Ф' х'п = хп cos <f + xm sin Ф
соответствующее преобразование является матричным:
у!е(х)-+у(х') = \т,п)(<?)у!е(х), A6)
где матрица поворота Л имеет вид
Л(т, л, (Ф) = ехр ^— iamn -|J,
а атп — введенная в B) «матрица тензора спина». Таким образом,
г|>' (*') = cos |-г|) (л:) - i sin -|amni|) (л:). A7J

268 ДОПОЛНЕНИЕ II .
При преобразовании лоренцева поворота в плоскости х°хп (п = 1, 2, 3)
— л:п sh <р, х'п=хпс\\ ф — *-6sh ф
соответственно имеем
Л|0„, (ф) = ехр (iam -|-j = ch-|- + iann sh-|-.
Полученные формулы могут быть объединены
Можно показать, что выписанные формулы находятся в соответствии
с: уравнением Дирака/ Для этого, во-первых, следует убедиться в том, что
матрицы A,,jv>, отвечающие преобразованию
x'=Lx, x'v = L^#;
обладают свойством
ч*) = Ч^' Av^A-i-^v,. A9)
Умножая затем уравнение Дирака A2) слева на Л, получаем
A(ivv5v—m)\|)=[[ (AvvA'1)^ —m] Лг|) =
= (iLviVv-m) V (*') = (Гд'-т)у (х')=0.
Здесь было принято во внимание, что в соответствии с A9)
Как известно, уравнение называется ковариантным, если после преобразо»
вания, т. е. записанное через преобразованные функции и переменные, оно имеет
прежнюю форму.
Таким образом, мы убедились, что в силу матричного преобразования A6)
уравнение Дирака оказывается ковариантным относительно преобразований
группы Лоренца.
Аналогичный вывод для сопряженного уравнения Дирака может быть сде-
сделан с помощью формулы преобразования для сопряжениого спинора
ф(*')=^МА-Ч<р), B0)
которая получается из A6) операцией эрмитова сопряжения и умножения
справа на уа с учетом того, что
VoAVo=Vo exp
Из формул пространственного вращения A7) непосредственно вытекает
неоднозначность спинорных функций. Полагая ф = 2я, находим, что полному
пространственному обороту системы координат соответствует матрица преобра-
преобразования ЛBя)=—1, т. е. при таком преобразовании функция поля меняет
знак. Поскольку, однако, поворот на 2я приводит систему координат в перво-
первоначальное положение, т. е. совпадает с тождественным преобразованием, то
отсюда следует, что спинорные волновые функции всегда- определены с точ-
точностью до знака.

ДОПОЛНЕНИЕ II 269
Приведем еще вид матрицы Л для преобразований отражения координат
ных осей. Замечая, что формулы преобразования при отражениях четного
числа различных пространственных осей, сводящихся к поворотам, вытекают
из A7), ограничимся преобразованием отражения всех трех пространственных
осей (Р-преобразование):
*'л=_*л(я = 1, 2, 3), х">=Х°,
ф(х') = г\(Р)Лту(х), A123=Y°- ( '
В силу двузначности спинорного представления фазовый множитель т) подчи-
подчиняется условию тJ(Р)=± 1.
Формулы «лоренцевых преобразований» для матриц у в совокупности с фор-
формулами преобразований для г|) и г|) позволяют получить законы преобразова-
преобразований билинейных форм вида трОф. Действительно, на основании A6) и B0)
получаем ■ ■
гр' (x')Of (x')=ty (х)
С помощью A9) находим теперь:
а) 0=1, ^(*W (*')=$>Ж*).
б) О = w, t' (*') Vvf (*') = i-vu* (*) n
в) 0=<rm iF'a4li|''=ivv'Lnn'^v'n'1l' и т- Д-
Таким образом, рассматриваемые квадратичные формы преобразуются по
тензорным представлениям группы Лоренца. Особо рассмотрим случаи, когда
в О входит множителем матрица уь. Нетрудно проверить, что матрица пово-
поворотов A8) коммутирует с уь:
В то же время матрица B1) отражения нечегного числа пространственных
осей антикоммутирует с уъ:
В результате получаем следующую классификацию билинейных форм:
г|и|) — скаляр, г^вг|5—псевдоскаляр,
■ф-у^ф — 4-вектор, г|) VvVs'i' — псевдовектор,
г^сг^г|)—тензор второго ранга.
4. Нерелятивистский предел. Нерелятивистский предел уравнения Дирака
отвечает случаю \р\<^т. Для перехода к нерелятивистскому пределу удобно
представить 4-компонентный спинор 4-мерного пространства —времени через
два 2-компонентных спинора % и <р.3-мерного евклидова пространства:
B2)
и, фиксировав стандартное представление E), перейти к матрицам а, 0:
e=U-o> Ho-/J- B3)
Вошедшие в а матрицы второго ранга а — матрицы Паули — определены в (8).

270 ДОПОЛНЕНИЕ II
Исходя из уравнения Дирака A2), записанного в импульсном представ-
представлении
о—ру-т1)и(р)=0 B4)
(здесь под и(р) подразумевается отрицательно-частотная часть спинора и~(р)),
получим, умножая его слева на т>о = Р и используя B2) и B3), два уравнения
для двухкомпонентных спиноров ф и-/:
(р°-т)-ф(р)+'(рог)х(р) = 0, B5)
О. B6)
В нерелятивистском приближении, как видно, спинор % много меньше спи-
спинора ф. Действительно, получаем из B6)
<Р>- B7)
Поэтому обычно спинор ф описывает электронные компоненты (ср. формулу
E.12)), а х — позитронные компоненты.
Подставляя B7) в B5), B6), получаем уравнение для ф
Если воспользоваться матричным соотношением
(aa)(ab) = (ab) — i(a[axb]), B8)
то видно, что оператор в правой части оказывается диагональным по спинор-
ным индексам. Переходя в координатное представление и выделяя множитель
exp (imt),
получим для ф (х, t)
— уравнение Шредингера.
Когда имеется внешнее электромагнитное поле, то, по общему правилу
удлинения производных (см. § J0.3), вместо B4) следует записать:
[(р°-еА0)у0-(р-еА)у-т1] и(р) = 0. B9)
Повторяя переход к двухкомпонентному электронному спинору, получаем, пре-
пренебрегая еА0 по сравнению с 2т:
к Нф- C0)
Здесь H=roiA — вектор магнитного поля.
Это уравнение называется уравнением Паули. Оно имеет вид уравнения
Шредингера с гамильтонианом
Н=~(р-еАГ' + еА0-{цН), C1)

ДОПОЛНЕНИЕ III 271
где последний член описывает энергию магнитного диполя
во внешнем магнитном поле Н. Величина ц0 отвечает магнитному моменту
электрона и называется магнетоном Бора.
Дополнение III*). НЕПРЕРЫВНЫЕ ГРУППЫ
В этом дополнении приводятся справочные сведения по теории непрерыв-
непрерывных групп. За подробностями формулировок и доказательствами приводимых
фактов мы отсылаем читателя к имеющимся руководствам по теории групп.
Дадим вначале ряд определений, относящихся к абстрактным группам, т. е.
группам, [на природу элементов и групповых операций которых не наложено
пока никаких ограничений.
1. Общие определения. Группой называется множество G (элементы кото-
которого мы будем, как правило, обозначать gv g2 и т. д.), в котором определена
операция, однозначно сопоставляющая каждой паре элементов группы^ и g2
некоторый элемент g того же множества Групповая операция обычно назы-
называется умножением и записывается в виде
При этом g называют произведением элементов группы g± и g2. Для конкрет-
конкретных групп, элементами которых могут являться числа, отображения, матрицы,
операторы и т. п. групповыми операциями могут быть соответственно сложе-
сложение или умножение чисел, умножение матриц и операторов, композиция отоб-
отображений и т. д. Групповая операция должна обладать следующими свойствами:
1. Для любых трех элементов gu g2, g3 группы имеет место ассоциатив-
ассоциативность, т. е. **). ■
V
2. В группе G существует единственный элемент е, называемый единичным
или просто единицей группы G, обладающий тем свойством, что для любого
элемента g группы G
ge=eg=g.
3. Для любого элемента g группы G существует один и только один эле-
элемент этой группы, называемый обратным к g и обозначаемый g'1, такой, что
Заметим, что перечисленные свойства групповой операции (которую мы
в дальнейшем всюду будем называть умножением) не предполагают ее комму.
*) Написано Н. А Свешниковым, которому авторы выражают свою при-
признательность.
**) В данном дополнении мы будем использовать ряд принятых в матема-
математической литературе сокращений—кванторов: V= «для любых», е= «при-
«принадлежит», 3 = «существует».

272 ДОПОЛНЕНИЕ III
тативности, т. е., вообще говоря, giMi¥=gigi для произвольных элементов
группы G.
Если для дайной группы G произведение коммутативно, т. е.
Vgi. SieG gig2=g*gi,
то группа G называется абелевой или коммутативной. Простейшим примером
абелевой группы является множество действительных чисел, обозначаемое сим-
символом R, где в качестве группового умножения выбрано обычное сложение
чисел. Очевидно, что при этом единицей группы является число «О», а эле-
элементом, обратным к «х», оказывается «—х».
Подгруппой К группы G называется любое подмножество G, замкнутое
относительно групповых операций, т. е.
V&. 8% е К glg2 <= К, Vg e.K г1 е К.
Так, в приведенном выше примере можно указать подгруппу Z группы дей-
действительных чисел, состоящую из всех целых чисел. Любая группа G обла-
обладает двумя так называемыми тривиальными подгруппами, одна из которых
совпадает с самой группой G, а другая состоит из одного, элемента—единицы
е группы.
В теории групп важную роль играют понятия простых и полупростых
групп. Для их определения введем сначала понятие инвариантной подгруппы.
Подгруппа К группы G называется инвариантной подгруппой или, что то же,
нормальным делителем группы G, если для любого элемента g группы G мно-
множество, состоящее из элементов gkg'1, где k пробегает всю подгруппу К, сов-
совпадает с К, т. е.
Группа G называется простой, если она не имеет инвариантных подгрупп.
Группа G называется полупростой, если она не имеет абелевых инвариантных
подгрупп. Отметим, что к этим классам относятся такие важные для теории
элементарных частиц группы, как группа Лоренца и группы унитарной сим-
симметрии.
Исторически первыми группами, возникшими в теоретической физике,были
группы симметрии кристаллов. Примером таких групп является группа вра-
вращений плоскости на углы, кратные 60°. Групповым умножением является
в данном случае композиция вращений. В качестве другого примера конечной
группы, т. е. группы с конечным числом элементов, можно привести совокуп-
совокупность преобразований полевых функций, образованную введенными в § 9 опе-
операциями С, Р и Т, тождественным преобразованием / и всевозможными их
комбинациями. Не составляет труда убедиться в том, что ввиду свойства
и коммутативности преобразований С, Р, Т полное число элементов данной'
группы равно 8.
2. Группы Ли. В квантовой теории наибольший интерес представляют
бесконечные группы, т. е. группы, содержащие бесконечно много элементов.
Бесконечные группы можно разделить на два больших класса—дискретные
и непрерывные группы. Структура бесконечных дискретных групп весьма

ДОПОЛНЕНИЕ III 273
близка структуре конечных групп: они обладают тем свойством, что все их
элементы «заметно» отличаются друг от друга. Примером такой группы может
служить уже упоминавшаяся абелева группа целых чисел. В противополож-
противоположность этому в непрерывной группе существует дополнительная структура
(топология), позволяющая вводить понятия близости элементов группы, не-
непрерывности предела и т. д. Существование такой структуры делает возмож-
возможной непрерывную параметризацию элементов групп точками некоторого топо-
топологического пространства. При этом групповые операции должны быть непре-
непрерывными преобразованиями в пространстве параметров. Говорят, например,
что элементы «]» и м2» группы R близки, если близки соответствующие им
действительные числа х± и х2. Если для данной группы в качестве простран-
пространства параметров может быть локально выбрано конечномерное евклидово про-
пространство, то эта группа называется группой Ли. Более точно, непрерывная
группа G называется л-параметрической группой Ли. (или группой Ли раз-
размерности л), если некоторая окрестность любого ее элемента может быть вза-
взаимно однозначно и взаимно непрерывно отображена в некоторую область л-мер-
ного действительного евклидова пространства R". Практически все непре-
непрерывные группы, возникающие в исследованиях по физике частиц, являются
группами Ли. Этим определяется первостепенное значение теории групп Ли
для квантовой теории.
Простейшим физически интересным примером группы Ли может служить
абелева группа вращений плоскости на произвольные углы <рг£2я — группа
U A). Элементы группы U A) могут быть непрерывно и однозначно параметри-
параметризованы с помощью точек отрезка [0, 2я] действительной прямой с отождест-
отождествленными концами по правилу:
«вращение на угол <р»—► число фэ[0, 2я]. A)
Таким образом, в соответствии с приведенным выше определением группа U A)
является группой Ли размерности 1. Другая параметризация элементов группы
UA) возникает при сопоставлении вращению на угол ф точки единичной
окружности на комплексной плоскости С:
«вращение на угол ф»'—► число г=г!'бС. B)
В физике частиц группа U A) возникает как абелева группа калибровочных
преобразований, связанных с сохранением аддитивных зарядов.
Важным классом групп Ли являются группы невырожденных линейных
преобразований конечномерных векторных пространств, с которыми можно
однозначно связать группы квадратных матриц. Элементами таких групп
являются матрицы с ненулевыми определителями, а в качестве групповой опе-
операции используется умножение матриц. В названии групп матриц принято от-
отражать свойства ее элементов. Так, при отсутствии ограничений на внд невы-
невырожденных матриц—элементов группы — в названии группы ставится буква L
(от английского linear — линейный), унитарность элементов группы отмечается
буквой U (unitary), их ортогональность (для действительных матриц) —буквой О.
Если матрицы — элементы группы —имеют единичный определитель, то этот
факт отмечается буквой S (special) в названии группы. В скобках после назва-

274 ДОПОЛНЕНИЕ III
ния, как правило, указывается размерность (число строк) матриц, составляв
ющих группу. Например,труппа SU (N) состоит из всех унитарных матриц раз-
размерности NxN, определители которых равны 1. По существующей традиции
названия ряда групп матриц таких, как SU (N), SO (N), SL(N) и т. д. пере-
переносятся, на соответствующие им абстрактные группы, т. е. группы Ли, облада-
обладающие теми же групповыми и топологическими свойствами. Так, группа
SL B, О есть группа Ли, между множеством элементов которой всеми и двух-
двухрядными комплексными матрицами с единичным определителем может быть
установлено взаимно однозначное и взаимно непрерывное соответствие таким
образом, что произведению элементов группы соответствует произведение
матриц, взятию обратного элемента — обращение матрицы.
Большую роль в теоретической физике играет группа спина SU B), кото-
которая являет собой простейший пример неабелевой группы Ли. Действительно,
легко проверить, что для двурядиых унитарных матриц А и В соотношение
АВ = ВА, вообще говоря, несправедливо. Комплексная матрица 2x2 пара-
параметризуется, очевидно, восьмью действительными числами. Условие унитарно-
унитарности накладывает на эти числа 4 независимых условия, единичность определи-
определителя — еще одно. Таким образом, произвольный элемент группы SU B) пара-
параметризуется тремя действительными числами, т. е. размерность SU(N) равна 3.
Аналогичным образом можно показать, что размерность SU C) равна 8,
размерность SU (N) равна Na—l. Произвольный элемент g группы SU B)
может быть записан в виде
C)
где Тд —матрицы Паули, а* — действительные числа такие, что a=s(a?+a|-f'
-f-ai)>/'sg я. Заметим, что, как и в случае группы £/A) (см. формулы A), B)),
область изменения параметров в формуле C) замкнута и ограничена в соответ-
соответствующем евклидовом пространстве. Как оказывается, этот факт есть не след-
следствие выбранной параметризации, а отражение общего для групп U A) и Si/B)
свойства, называемого компактностью. Вообще группа Ли G называется ком-
компактной, если множество ее элементов является компактным многообразием,
т. е. если из любой бесконечной последовательности ее элементов может быть
выделена сходящаяся подпоследовательность. Следствием компактности является
возможность непрерывной параметризации группы Ли точками некоторой замкну-
замкнутой и ограниченной (т. е. компактной) области соответствующего евклидова
пространства. Важными примерами компактных групп Ли являются группы
SU (АО и SO (N) при любых N. Теория компактных полупростых групп Ли
есть наиболее разработанный раздел общей теории групп Ли.
В качестве примеров некомпактных групп Ли можно привести группу Т
сдвигов пространства-времени и группу Лоренца L.
Элемент аг группы Т определяется как параллельный перенос точек про-
пространства-времени М на вектор оеМ:

ДОПОЛНЕНИЕ III 275
Очевидно, что произведение элементов ат и bт группы Т дается формулой
где элементу [а-\-Ь)т группы Т соответствует вектор a-f b пространства М.
Элемент, обратный к ат есть (—а)г Ясно, что группа Т является абелевой.
Понятие близости (а следовательно, и понятие сходимости) элементов группы Т
совпадает с понятием близости соответствующих им векторов пространства-
времена Таким образом, некомпактность группы Т есть прямое следствие
неограниченности М.
Произвольный элемент Л группы Лоренца может быть представлен в виде
суперпозиции пространственного вращения R и чисто лоренцева преобразова-
преобразования (называемого часто бустом) В, переводящего систему из состояния покоя
в состояние равномерного прямолинейного движения со скоростью v
Пространственные вращения образуют компактную подгруппу группы Лоренца —
группу SO C). Некомпактность группы связана с тем очевидным фактом, что
величина гиперболического угла эс = arcth (f/c) непрерывно параметризующего
буст В (v), может меняться в бесконечных пределах:
Группа Пуанкаре Р— «главная» группа всей релятивистской физики —
является объединением групп Т и L в том смысле, что любой ее элемент р
может быть представлен в виде
р=ат\,. D)
причем произведение элементов ръ р2 е Р дается формулой
а2 г\) = (^ + ЛЛ) г (
Смысл формулу D) состоит в утверждении, что любое линейное преобразова-
преобразование пространства-времени, сохраняющее интервалы между событиями, может
быть представлено как результат последовательного выполнения преобразова-
преобразования Лоренца Л системы отсчета и сдвига начала координат на вектор а. Ясно,
что тот же результат можно получить, производя сначала сдвиг на вектор Ло'>
а затем лоренцев аоворот на Л. Поэтому преобразование р может быть записано
также в виде
р = ajA = Л (Л a)r.
Легко проверить, что группа сдвигов Т является абелевым нормальным делите-
делителем Р. В силу этого группа Пуанкаре не является ни полупростой, ни тем
более простой.
3. Представления групп Ли. В физических исследованиях нас обычно инте-
интересуют конкретные реализации данной абстрактной группы. Если ограничиться
рассмотрением реализаций групп линейными операторами, то мы придем к поня-
понятию линейного представления группы. Более точно, линейным представлением
группы G называется непрерывное отображение этой группы в группу линей-
линейных операторов в некотором векторном пространстве X, коммутирующее
с групповым умножением. Таким образом, если g e G — произвольный элемент

276 ДОПОЛНЕНИЕ III
группы, A (g) —соответствующий линейный оператор в X, то
Vft.«f2eG A toft) = A
Эти формулы показывают, что групповое умножение и обращение элемента
группы заменяются для операторов представления умножением операторов
в пространстве X и взятием обратного оператора соответственно. Размерность
пространства X называется размерностью представления.
Для представления размерности N можно заменить операторы соответст-
соответствующими им матрицами (в некотором базисе пространства X) и изучать пред-
представление исходной группы как группы матриц NxN. Для любой группы
возможно тривиальное одномерное представление, сопоставляющее каждому
элементу число «1».
Представление А группы О называется точным, если различным элементам
группы #! и g2 соответствуют различные операторы A (gj) и A (g2), т. е. если
между множеством элементов группы и множеством операторов, образующих
ее представление, установлено взаимно однозначное соответствие. Точное пред-
представление полностью воспроизводит структуру группы Ли.
Линейное представление А .группы G в пространстве X называется приво-
приводимым, если в X существует собственное (т. е. отличающееся от {0} и X)
подпространство Хг, которое переводится в себя всеми операторами представ-
представления
В противном случае представление А называется неприводимым, В физике
частиц наибольший интерес представляет изучение унитарных линейных пред-
представлений, т. е. представлений, элементы которых являются унитарными опе-
операторами и сохраняют тем самым нормировку векторов состояния. Можно
показать, что любое приводимое унитарное представление U группы G распа-
распадается на сумму неприводимых представлений, т. е. все матрицы U (g) имеют
в подходящем базисе блочнодиагональный вид
Таким образом, изучение произвольного унитарного представления сводится
к изучению неприводимых представлений.
Приведем ряд примеров. Для любой абелевой группы все неприводимые
представления одномерны. В частности, для группы R неприводимые унитар-
унитарные представления имеют вид
где р — действительное число, фиксирующее выбор представления. Выше мы
упоминали о том, что групповые и топологические свойства ряда групп (SL (к),
SU (N), SO (АО и т. д.) идентичны свойствам соответствующих групп матриц.

ДОПОЛНЕНИЕ III 277
Ясно, что в этом случае группа матриц, название которой совпадает с назва-
названием данной группы, реализует ее точное неприводимое представление. Для
SU B), SU C) и некоторых других1 часто используемых в квантовой теории
групп это представление принято называть фундаментальным.
Большую роль в теории групп Ли играет понятие присоединенного пред-
представления группы. Оказывается, что любая n-параметрическая группа Ли
имеет представление размерности я, вид которого полностью определяется
локальной структурой данной группы. Способ, построения этого представления
будет нами указан после введения понятия алгебры Ли (см. раздел 4 данного
Дополнения). Здесь отметим, что для компактных, простых групп, каковыми,
в частности, являются группы SU (N) и SO (N) при любом значении N, при-
присоединённое представление неприводимо. Таким образом, для группы SU B),
например, присоединенное представление имеет размерность 3. В-заключение
этого раздела заметим, что в теории поля группу SU B) часто ассоциируют
с группой спина (или изоспина), а группу SU C) — с группой унитарной сим-
симметрии. В таком случае векторы пространства <5f, в котором реализовано
неприводимое представление группы SU B), можно отождествить со спиновыми
(изоспиновыми) мультиплетами, группы SV C) — с унитарными мультиплетами.
Существуют спиновые мультиплеты любой размерности. В то же время унитар-
унитарные мультиплеты могут иметь лишь выделенные размерности 1, 3, 8, 10, ...,
т. е. не при любой размерности пространства X в нем может быть построено
неприводимое представление SU C).
4. Генераторы и алгебра Ли. Из самого определения группы Ли следует,
что эта группа локально (т. е. в бесконечно малой окрестности любого эле-
элемента) обладает структурой евклидова пространства. Это дает возможность
ввести на группе такие понятия, как разность бесконечно близких элементов,
производная и т. д. Замечательным результатом теории групп Ли является
утверждение о том, что элемент группы Ли является не только непрерывной,
но и дифференцируемой и даже аналитической функцией параметров. Рассмот-
Рассмотрим малую окрестность единицы группы. Без ограничения общности можно
считать, что единице соответствуют нулевые значения параметров. Тогда про-
произвольный элемент g из рассматриваемой окрестности может быть с точностью
до членов второго порядка малости записан в виде
я
g(altai, ... an) = e + i £ Xkcik, E)
где величины
dak
F)
называются инфинитезимальными генераторами группы Ли или просто генера-
генераторами. Введение мнимой единицы в формулу F) дает то преимущество, что
в физически интересных случаях так определенные генераторы группы оказы-
оказываются эрмитовыми операторами физически важных величин типа импульса,
энергии, спина, заряда и т. д.

278 дополнение ш
Можно показать, что законы группового умножения требуют выполнения
следующих соотношений для генераторов
№• */]=<• 21 c*i,xk, G)
4=1
№■■ [X], Хк]] + [Х/. [Х„, Xi]] + lXk. IXi, Х,]] = 0, (8)
последнее из которых представляет собой тождество Якоби. Здесь [X, Y] =
= XY — YX — коммутатор двух генераторов, С*/ — числа, - называемые струк-
структурными константами группы Ли. Указанные выше свойства генераторов
обычно формулируют в виде утверждения о том, что генераторы груцпы Ли
образуют базис алгебры Ли. Множество А называется алгеброй Ли, если оно
является действительным или комплексным линейным пространством, т. е.
VX, Ye=A и V чисел а, Р
и замкнуто относительно операции коммутирования элементов, т. е. V, XY е А
[X, Y]e=A.
Отметим, что последнее свойство отличает алгебру Ли от обычной алгебры,
замкнутой относительно операции умножения элементов, обладающей свойством
ассоциативности. Можно показать, что набор структурных констант, т. е. чисел
со свойствами
w/
(9)
первое из которых следует из G), а второе может быть выведено из тождества
Якоби, полностью определяет структуру алгебры Ли, т. е. в силу E) локаль-
локальную структуру группы Ли. Наиболее простой вид алгебра Ли имеет для абе-
левой группы. В этом случае все структурные константы равны нулю. В част-
частности, генераторы группы Т образуют 4-вектор импульса Рц, причем
[PA,>v] = 0.
Алгебра Ли группы SU B) задается коммутационными соотношениями между
тремя ее генераторами I/, (это могут быть операторы компонент орбитального
момента, спина, изоспина и т. д.)
з
где 8 —полностью антисимметричный тензор. Такие же коммутационные соот-
соотношения выполняются для генераторов группы SO C), т. е. группы SU B) и
SO C) локально совпадают.
Как и для группы Ли, для алгебр Ли можно ввести понятие линейного
представления, т. е. отображения алгебры Ли в алгебру операторов некоторого
векторного пространства. Представление алгебры Ли связано с соответствующим
представлением группы Ли формулами E), F), в которых нужно только заме-
заменить элементы абстрактной группы и алгебры их конкретными реализациями

ДОПОЛНЕНИЕ IV 279
в виде операторов соответствующего пространства. Заметим, что если представ-
представление группы унитарно, то в силу F) элементы алгебры Ли являются эрмито-
эрмитовыми операторами. В частности, для группы SU B) генераторами фундамен-
фундаментального представления являются матрицы 2x2
генераторами присоединенного представления —матрицы 3x3
Вообще присоединенным представлением алгебры Ли размерности п называется
представление матрицами лХл, генераторы которого составлены из структур-
структурных констант
/уприсЧ/ — {Г1
Легко убедиться, используя свойство (9) структурных констант, что так опре-
определенные генераторы удовлетворяют G) и, следовательно, задают представления
алгебры Ли. Соответствующее этому представлению по формуле E) представ-
представление групп называется присоединенным представлением группы Ли. Заметим,
что относительная простота теории компактных полупростых групп Ли связана
с тем, что любой элемент такой группы (а не только бесконечно близкий
к единичному) может быть представлен в так называемой нормальной форме
\
У] Xkak).
\ 4-1- /
В заключение выпишем коммутационные соотношения, определяющие алгебру
Ли группы Пуанкаре Р. Общее число генераторов группы равно 10, четыре
из них — операторы компонент импульса Рц — связаны с подгруппой Т, осталь-
остальные— компоненты момента /M^v — с группой Лоренца. Можно показать, что
A0)
Дополнение IV. ОПЕРАТОРНЫЕ ПРЕОБРАЗОВАНИЯ
1. Линейные непрерывные преобразования. Пусть задано некоторое непре-
непрерывное линейное преобразование операторов ai, зависящее от параметра ф
аг—a'i = L{/((p)a/, a' = I/ (cp) all (ф)
и обладающее групповым свойством
Тогда явный вид унитарного оператора U, который в силу упомянутого свой-
свойства с необходимостью имеет экспоненциальный вид
может быть найден следующим общим приемом.

280 ДОПОЛНЕНИЕ IV
Рассмотрим инфинитезимальное преобразование (ср->-е<< 1)
Приравнивая
получаем .
A=i[a,V] A)
—основное уравнение для определения явного вида оператора V. Пригедем
ряд важных примеров:
а) Преобразование сдвига на с-число:
* * *
а +
или
а'=а + <р —
t/= ехр ((фи + t'^f )•
Основное уравнение дает
l=f(au — ua), l=f[a, u],
1=[а, о], — 1=[а, к]. .
Видно, что и и о должны быть линейны по бозе-операторам а, а:
[*1 * * г* *1
a, aj=aa—аа = 1, [а, а]=|а, aJ=O,
Получаем
« = i(a— a), v = \a+a),
вследствие чего
i/=exp (аф—аф). B)
Отметим, что соответствующего решения для операторов Ферми не существует.
Операция сдвига в этом случае" требует замены с-числовых объектов ф, ф на
образующие алгебры Грассмана.
б) Преобразование ^поворота» {a=(alt a^)}:
а|[=а1со8ф—аг sin ф, то же для а[;
a^=aiayscp+a1 sin ф, то же для а%.
К таким преобразованиям сводятся, например, преобразования вращения
в изотопическом пространстве.
Основные уравнения дают
ai = i[a2, V], ^a2 = i[alt V], C)
а также эрмитово сопряженные соотношения
£=f{i,.v], -^ = j[S2, V]. C')
В отличие от предыдущего, оператор V должен быть билинейным по ak и а^\
V = сам + da&i+е {а^ + ^ai) + if (^Л — (hfli) ■
Подставляя это наиболее общее эрмитово выражение в C) и C'), находим
1, т. е.
() D)

ДОПОЛНЕНИЕ IV 281
Полученное выражение справедливо как для бозе-, так и для ферми-опе-
ферми-операторов.
в) Преобразование Боголюбова для бозе-операторйв:
&h P6
Основное уравнение дает
lf=i[bi, V], S1 = t[62. V]
и соответствующие эрмитово сопряженные уравнения. Решение имеет вид
т. е.
{/ (Ф) = ехр |.ф (бЛ - Мя)]- F)
г) Преобразование Боголюбова для ферми-операторов:
* * *
аг= % cos9 + a2sin9, ai= ^совф+аавш <р,
* * I')
<zi = —a1 sin cp + a2cos<p, a2 = —% sin
Основное уравнение дает
Ъ =-i fa, Vh a\=i[alt V]
и эрмитово сопряженные соотношения. Решение имеет вид
V = i {а^ — а^) == i l^aias,—a^),
Г /• * М ( >
U (ф) = ехр [ф {а^ — а^аЛ
д) Лорениевы ^повороты» матриц Дирака:
Построим оператор U (ф) преобразования матриц Дирака
где L — матрица лоренцевых 4-поворотов координатного вектора х'=
Для пространственного (евклидова) поворота в плоскости xlt x2
— 7а sin ф, 7a = 7i ™ ф+7гСО8ф, 7о=7о. 7з=
для лоренцева поворота в плоскости х0, х^
Основное уравнение дает
-У2 = 1[Ъ,УхгЬ 7i = t[72. Vn], [7o,
71=1 [То. V-u],- 7o = »[7i. Vu],. [7а.
Решения имеют вид
Полученные результаты могут быть объединены в одну формулу
_ (9)

282 ДОПОЛНЕНИЕ IV
2. «Распутывание» экспонент *) Пусть
где Л и В не коммутируют между собой. Требуется факторизовать зависимости
от операторов А и В. В частном случае, когда А содержит только операторы
рождения, а В —лишь операторы уничтожения, подобная задача возникает
при приведении оператора U к нормальной форме.
В общем случае оператор U можно представить в виде
U=eAQeB,
причем множитель Q, вообще говоря, содержит зависимость от операторов А
и В, а также от их повторных коммутаторов.
Для определения явного вида Q воспользуемся методом бесконечно малых
приращений. Введем для этого вспомогательный параметр т:
{/->1/(т) = ет<л + в>=етЛ3(т, А, В, \А, В], ...)ехВ,
и, продифференцировав по т, запишем для Q дифференциальное операторное
уравнение:
Q' (т) = е-тЛВетЛ£(т) — Q (т) В, Q(т = 0)= 1.
Наиболее прост случай, когда коммутатор операторов А и В
[А, В] = С
является с-числом (см. формулу B)). Тогда
е-тЛВетЛ = В - тС, Q (т) = ехр (— т2С/2),
и мы приходим к так называемой формуле Бэйкера — Хаусдорфа
(С=[Л, В]~с-число!) еА+в = еле-с/2ев. A0)
Для распутывания формул F), (8), возникающих в результате канониче-
канонического преобразования Боголюбова, оказывается важным случай, когда комму-
коммутатор С является оператором, однако операторы А, В, С образуют замкнутую
коммутативную алгебру специального вида
[А, В}=С, [А, С]=-2|Л, [В, С]=2|В. A1)
Этот случай также может быть исследован дифференциальным методом.
Предоставляем читателю самостоятельно убедиться, что искомый результат имеет
вид
причем
а(т) = _J_th(T/|), 7(т, £) = jlnch(T^i). A3)
В случае бозе-операторов
А=ЪХ, В = —6i62, C=l-bX-bX, |=1,
*) Изложение этого раздела следует Приложению Б из книги Киржница
A963), в котором содержится также ряд других полезных формул.

ДОПОЛНЕНИЕ V 283
тогда как для ферми-операторов
A=aia2, В = — аха^, С=1—а^—*1
3. Коммутаторы с оператором плотности числа частиц п (к). Получим еще
ряд полезных формул для коммутаторов с оператором плотности числа частиц:
п (ft) =a (ft) a (ft) =a+ (ft) a~ (ft).
Введем линейную суперпозицию операторов а+ и а~:
A± = \k±(q)a±(q)dq. A4)
+ \±
"Тогда
[л (ft), A±]=±%i.(k)a±(k)
и
\n(k), A]=K(ft)=A.+ (ft)a+(ft)-Mft)a-(ft),
причем коммутатор операторов А и К является с-числом:
[A, /C(ft)]= — 2X.2(ft). X2(ft) = X+(ft)X._(ft).
Поэтому
и, следовательно,
[л(*), е±А]={+К(к)+кЦк)}^А. ' A5)
Дополнение V. СВОДКА СИНГУЛЯРНЫХ ФУНКЦИЙ
1. Вспомогательные сингулярные функции. Четырехмерная б-функция Ди-
Дирака: .
б (х) = б (*>) б (х)=б (х«) б (л;1) б (л:^) б (л3). B)
Разрывные функции б (а) и е(а):
•<•>->!-■?-{ J: :<;■'
5—символ главного значения).
Частотные части б-функции:
(б)

284 ДОПОЛНЕНИЕ V
Некоторые полезные соотиошения:
G)
2. Функции скалярного поля. Перестановочная функция Паули — Йордана D:
jD(,x-y); (8.4)
D (х) = —— f
С
J
dk eikx sin
2
, д:)
дх<>
x°=0
—
2д
'); -(9)
ПО)
A8.16)
В окрестности светового конуса D имеет вид
1
т2
~ 8д" 8
Частотные части функции Паули — Йордана D* и D~:
[ф-W, ф+(й] = {ф{
D±
|ф+(лс),.qr@]—Ld+(x-0) = H>-@ -jc);
g±ix°Vk'+ m'-xk _
= _L 8 (*o) б (X) --^i [e (*•) A (m VI) : W, (m
8д on у X
1
(П)
A2)
™ A8Л7)
В окрестности светового конуса D+ и D~ имеют вид

ДОПОЛНЕНИЕ V 285
Свойства четности и вещественности:
В±(— x)=-D^(x)=-(D±(x))*, £>(*) = —D(—*) = D(x). A5)
Причинная функция Грина Вс:
)>в=1в':(х-у); A8.12)
(Ш.9)
A8.18)
e
Поведение £>с в окрестности светового конуса:
^^ g^^ A8.21)
Причинная функция при массе, равной нулю:
Запаздывающая и опережающая функции Грина Dret и DaAv'
Dret(*) = 0 при ж«><0, Dadv(*) = 0 прн
J ^ль^° w A8-5)> A86)
. 1 (* p-ikx
D <*)=B^ S
°ret w=ii9 (л0) {б (X) ~8 (X) ¥FIУ1 (m
Связи между функциями D, D+, D~, Dc, Dlei, Dadv:
x), A8.8)
:), A8)
Dadv(x) в(— x°)D(x) = Dc(x)-D-(x), A9)
D(*) = Dret(x)-.Dadv(*). B0)
3. Функции электромагнитного, векторного и спинорного полей. Электро-
Электромагнитное поле:
B1)
B2)

286 ДОПОЛНЕНИЕ VI
Функции Do, D^j, Dq и т. д. получаются из функций скалярного поля D, D-,
Dc при т = 0, например:
UB^$!^ B3>
Векторное пом:
[U^x), Uv (</)] = Ю^(х--у), B4)
<l/|iWl/v(y)>e = «jIv(JC-»). B5)
B6)
Функции D v, O^,, O^v и т. д. могут быть получены из соответствующих
функций скалярного поля действием дифферевциального оператора
например
g\iv ——
Спинорное поле:
[**(*). tp@L iSap(x-y), (9.4)
'S-p(^-y), B8)
=-^(»-ll)- ' B9)
Функции S, S±,SC и т. д. могут быть получены из соответствующих функций
скалярного поля действием оператора
например:
S (х) = -^ J е~1кХг №(k + m)b(k*- m*i dk, C0)
C1)
C2)
Дополнение VI. ФОРМУЛЫ ИМПУЛЬСНОГО ИНТЕГРИРОВАНИЯ
1. Альфа-представление. Формула перехода в а-представление:
оо
_J__= i С «*»«"-«'+W da ■ B2.2)
и ее обобщение:
оо
■(D^j8^ --»«■- - —■ *>0- B2;8)

ДОПОЛНЕНИЕ VI 287
Основные гауссовы квадратуры (а — положительное число, Ь — 4-вектор):
■L'[ 4ке1<ак'+2Ьк> = -±-е-""'а^Па, Ь*), B2.3)
-У [ dke1 <■**'+ 2bk) [*»] = [- -£-] / (в, ftt), B2.4a)
^ J dke1 «*2 + 26*> {*'№] = [J*^±i^] / (в, 6*), B2.46)
I J dteИ =[]/(а, *)( B2.4в)
Выделение бесконечного интегрирования:
ОО ОО 1 00
JdOi... J dan = ^ \dx}n ^ daan~\ B)
оо о
где •
„, xv=avla,
. dx2... dxnd(l—xl—x2—...-xn). C)
Типичные интегралы по а:
оо
00
I
E)
^5
F)
В случае, когда В и D содержат большой параметр Л2 E = 6Л2, D = dA2),
получаем из F) в пределе Л2-»-оо:
G)
2. Фейнмановская параметризация. Исходная формула:
1
1
причем символ {d*}n определен в C).
Импульсные квадратуры типа
B2Л0)
,n,_i С ^ _(-l)£+1(I—3I

288 дополнение vi
для практических целей удобно обобщить (сдвинуть переменную интегрирования):
F ID' k\-l '<& Г»- 1 Г dp - 0--3)!
FL(D, k)-JL{k _?>_ — j [p22kp + D]L — {Dk* + ie)L-2
(8)
и т. д.
3. Размерная регуляризация:
= H2e f dQ ?рл-Мр, n = 4 — 2e. B3.10)
£2(л) о
Модификация гауссовых квадратур:
~ Jdte = fi^l)^-e = /e(aj 6)> B3.11)
f|](в,П A2)
^ j ^^^")[^]_^+^]/.te И A3)
(эти три формулы отличаются лишь заменой I (а, б2) -*- /е (а, б2) от формул
B2.3) И B2.4а, 22.46)); /
-L
и т. д.
Заметим, что формула A4) может быть получена либо из B3.11) дифферен-
дифференцированием по параметру а, либо из A3) суммированием по лоренцевым
индексам. В последнем случае необходимо учесть, что
n=4-2e. A6)
С учетом этого свойства при выполнении операций с матрицами Дирака сле-
следует пользоваться обычным соотношением
(И, V=0, 1, 2, 3).

ДОПОЛНЕНИЕ VI 289
Модификация формул фейнмановского интегрирования:
A8)
-Lf 1 r
я2 J [p2_2p^+D]L
я2 J [pt — 2pk+D]L \ 2(L + e— 3) / L
_i_ Г p2dnp _ J 2-е ) e
j_ f" PvP ^"P—^=yfevf^2_j Zll—(D—k2)\FRr (D, k2)., B1)
■ я2 J [p2 —2р^+О]^ I L + e—3
Из приведенных формул с учетом того, что при е-*-О Г (е)-»- 1/е—С (где
консганта Эйлера С=0,5772 ...), в частности, вытекает:
B3)
i Г» Pv
^ J [p2_
,- r pvPlldnp _ gfiV kJb gliV Г (lfl-Руя t J
л2 J [p2_2pjfe + D]3 4e +2(^-D)+ 4 [ ц2 + cJ s
и т. Я.
4. Регуляризация обрезанием:
л
j dp = I \ (d4p)£ -»■ i J dQ J p3 dp = regA \ dp.
£2D) 0 ^
Приведем здесь сводку наиболее употребительных расходящихся интегралов.
Детали соответствующих вычислений можно найти, например, у Ахиезера и
Берестецкого A969) в § 36.
I
ге§л-^Г
2-3D 4 \
J^j B9)
t С pv
H J (p2_
pvpu dp _ guv < A2 | guv
4 шц2+ 4 \j j
C0).
10 H. H. Боголюбов, Д. В. Шириов

290 ДОПОЛНЕНИЕ VI
Сравнение этих формул с формулами B2) — B6) показывает, что конечные
части рассмотренных интегралов совпадают с точностью до конечных констант
для логарифмически расходящихся интегралов и с точностью до конечных
полиномов первой или второй степени —для линейно и квадратично расходя-
расходящихся интегралов.
5. Простейшие однопетлевые квадратуры. Выпишем еще некоторые резуль-
результаты вычислений для однопетлевой диаграммы, состоящей из двух внутренних
скалярных линий с различными массами
±_ Г ■ dk
я2 J (т*—к2—(г) [ц2 — (k + pJ — te] "
C1)
Конечная часть функции / может быть записана следующим образом:
1
»; т2, "
i
хт2 + A-х)ц2
Это выражение действительно при р2<(т + цJ и нормировано в нуле, т. е.
Вычисляя интеграл по я, получаем
д £ \,„ т* _l * (Р) г „ Ъ-Р*-Р*К(р) , п0.
где Е =
Второе слагаемое в C2), содержащее логарифм, обозначает три разных выра-
выражения при различных действительных значениях р2:
К(Р) T*j=—1 ^Li_^-_^i_'_in j±—г ^j^_ при ^ ^v,,._
— 1'я/С(р)прир2:
при (m — f
причем
В случае одинаковых масс (fx=m) получаем
Отметим, что функция J была введена в § 24 и может быть записана в пиде
1 со
J 1—4^A—^) J Ко" (а— 1)(а—г + ie)
о . i

ДОПОЛНЕНИЕ VII 291
Согласно B4.12) через / и ее производную записывается поляризационный
оператор фотона во втором порядке теории возмущений. Если же одна из масс
равна нулю (ц = 0), то
/(р2; m2, 0) = i—!-1пA— г) — 1, г=р2/т2.
Подобные выражения встречаются при вычислении собственной энергии элект-
электрона (см. B4.17)) и вершинной части. Отметим в этой связи, что логарифмиче-
логарифмическая функция возникает из параметрического интеграла
\dxm2 т*—р2
который оказывается сингулярным на массовой поверхности, т. е. при р*=т?.
Эта сингулярность является проявлением так называемой инфракрасной расхо-
расходимости и связана с особенностью подынтегрального выражения исходного
фейнмановского интеграла при малых значениях виртуального импульса k.
Поэтому переход к пределу ц = 0 в некоторых случаях необходимо прово-
проводить более аккуратно. Как нетрудно убедиться, при малых, но конечных ц2
интеграл в левой части следует (см. § 29.4) заменить на
Представление функции / через А
lim / (р2; т2, ц2) = -£—~ А (р2)-1 C3)
оказывается полезным при проведении вычитания массового оператора элект-
электрона 2 (р) на массовой поверхности, а также при вычислении вершинной
функции (см. §§ 24.3, 29.4, 29.5).
Дополнение VII. КИНЕМАТИЧЕСКИЕ СООТНОШЕНИЯ ДЛЯ ВЕРШИН
1. Тройная вершина (рис, fl.VIl.l). Из трех 4-векторов р-ц р%^ рд, сумма
которых равна нулю
можно составить три инвариантных выражения:
Р?. Р! и р! = (р1 + раJ. A)
Эти величины независимы. Однако ие все тройки значений могут быть реали-
реализованы с помощью действительных значений компонент 4-векторов plf pa и ps.
В квантовой электродинамике представляет интерес случай, когда два
квадрата- положительны и равны квадрату массы MeKTpoBat а третий квадрат
равен иулюз '
р| = р| = т2, £2 = 0 (*=р3). B)
10*

292 ДОПОЛНЕНИЕ VII "
При соблюдении условия действительности компонент всех 4-векторов система
соотношений B) приводит к требованию ^ = 0, pj =—р2. Таким образом, все
три конца электрон-фотонной вершины могут находиться на массовой поверх-
поверхности лишь для фотонов исчезающе малой частоты.
Область
pf = p§ = m2, fc2<0, C)
отвечающая испусканию или поглощению электроном пространственно подобного
фотона, равно как и область
р2 = р2=т2, jfe2^4m2, D)
соответствующая аннигиляция пары, является кинематически разрешенной.
В случае мезон-нуклонного З-гертекса, описывающего юкавское взаимо-
взаимодействие (импульс мезона p3=k), невозможно одновременно выйти на массовую
поверхность по всем трем импульсам. Точка
pf=p! = M2, £2 = }l2<M2 E)
не является кинематически разрешенной. Этот факт необходимо принимать во
внимание при формулировании рецепта вычитания расходимостей в соответст-
соответствующих моделях квантовой теории поля.
"h*
Рис. ДУПЛ. Кине- ■ Рис. ДУП.2. Кине-
Кинематические обозна- матические обозна-
обозначения 3-хвостной чения 4-хвостной
вершины: вершины.
2. Четверная вершина. Скалярная 4-хвостная вершина (рис. ДУН.2) в силу
лоренц-инвариантности является функцией скалярных произведений четырех
своих 4-импульсных аргументов Pip/. Из-за закона сохранения полного
4-импульса
только шесть скалярных произведений являются независимыми. Четыре из них
естественно выбрать в виде квадратов внешних 4-импульсов pit а два остальных
обычно представляют выражениями вида (рг + р/J. Всего может быть состав-
составлено три подобных выражения:
S = (Pl + P2J=(P3 + P4J, / = (Р1 + РзJ, « = (/>1 + Р4J, F)
которые в силу закона сохранения полного 4-импульса удовлетворяют соотно-
соотношению
Pi. G)
Для того чтобы понять физический смысл переменных s, t, и, заметим,
что рассматриваемый 4-вёртекс может описывать шесть различных процессов

ДОПОЛНЕНИЕ VII 293
типа 2 частицы — 2 частицы:
1 + 2-3 + 4, 1+3-2 + 4, 1+4-2 + 3,
3+4—1 + 2, 2+4—1+3, 2+3—1 + 4. ()
Здесь цифры означают индексы частиц. Три последних связаны с предыдущими
изменением знака всех 4-импульсов и отвечают тем же самым значениям
квадратичных импульсных переменных. Поэтому для наших целей достаточно
различать три возможности:
I II
1+2—3+4 1+3~2+4
Pi + P2->-(— РзЖ— Pi) Р\+Рз'-*■(— Рг)+(~ Pi)
>-(— Pi) + (— Рч) Рг + Pt-*■(.— Pi) + (— Pa)
III (9)
P1+P4—(—Рз) + (—Рз)
Рг + Рз^-(— Pi) + (— P4).
каждая из которых объединяет некоторую реакцию (прямую) и ей обратную
и, как говорят, отвечает определенному каналу.
В первом канале переменная s = (p1+j?2J играет роль релятивистски
инвариантного квадрата полной энергии, а переменная / = (л + ЛJ—инва-
ЛJ—инвариантного квадрата 4-импульса, переданного от частицы 1 частице 3. Пере-
Переменная u=(Pi+P4J описывает перед.чу 4-импульса от частицы 1 частице 4-
Поэтому в физической области канала I .
и, /<0.
В дальнейшем мы будем предполагать массы всех четырех частиц равными
друг другу. Тогда
sSs4m2, uscO, isgO. A0-1)
Аналогично физические области каналов II и III
A0-III)
При этом, согласно G), на массовой поверхности переменные s, t, и удовлет-
удовлетворяют правилу суммы
s + u + / = 4m2. A1)
Картина может быть представлена на плоскости, причем оси переменных s,
и, t отличаются по направлениям на 120° (рис. ДУП.З).
В физических областях A0) амплитуда рассеяния, пропорциональная
матричному элементу матрицы рассеяния, является комплексной величиной.
Поэтому точку вычитания 4-хвостки нельзя выбирать в этих областях. Исклю-
Исключение составляют точки, отвечающие порогам реакций:
s = 4m2, / = u = 0, A2-I)
/ = 4ma, s=u=0, A2-II)
u=\m\ s=t=O. A2-111)

294
ДОПОЛНЕНИЕ VIII
Вершина оказывается действительной внутри треугольника, ограниченного
прямыми s=4m2, и=4т2, /=4т2, соответствующими двухчастичным порогам
реакций I, II и III. Уже во втором порядке теории возмущений в модели ф4
/ /
—A
\
Рис. ДУП.З. Плоскость кинематических переменных s, и, t 4-хвостной вер-
вершины. Физические области отмечены двойной штриховкой. Центральный тре-
треугольник, определенный условиями s, и, /sg4/n2, отвечает области, в которой
4-вертекс действителен.
в 4-вертекс дают вклады диаграммы «рыба», которые, как показано явным
вычислением в § 24.1, имеют мнимую часть, отличную от нуля выше двух-
двухчастичного порога.
Дополнение VIII. ПРАВИЛА ФЕЙНМАНА ДЛЯ ПОЛЕЙ
ЯНГА —МИЛЛСА
В этом Дополнении приведены правила построения матрицы рассеяния по
теории возмущений для квантовополевых моделей, содержащих неабелевы
калибровочные поля. Ввиду сложности процедуры квантования мы не имеем
возможности обсуждать вывод этих правил. Отметим лишь, что поля Янга —
Миллса удалось проквантовать во второй половине 60-х годов, причем для
этого были использованы такие сложные приемы, как представление матрицы
рассеяния в виде функционального интеграла (см., например, монографию
Славнова, Фаддеева A978)). В то же время модели квантовой теории поля,
основанные на полях Янга—Миллса, в последние годы приобретают все
большее значение как в электромагнитных и слабых (единые модели типа
модели Вайнберга—Салама—см. § 32), так и в сильных взаимодействиях
(партон-глюонные модели).
1. Свободное поле группы SU B). Начнем с наиболее простого случая
свободного поля Янга—Миллса В", отвечающего калибровочной группе SU B).
Классический лагранжиан запишем в виде
%(B)=—±FVLvF~W—^(dB)(dB), A)

ДОПОЛНЕНИЕ VIII ' 295
отличающемся от выражения Хчж, использованного в § 11.1, наличием
второго слагаемого, фиксирующего калибровку поля Bv. Введение подобного
члена в лагранжиан абелева калибровочного поля обсуждалось в § 4.3,
Лагранжиан X удобно разбить на два слагаемых:
В, g), B)
к первому из которых отнесем члены, квадратичные по компонентам В и их
производным _
Х0(В) = -^НуУт^~~(дВ)\ C)
где
а второй содержит члены высших степеней
Напомним (ср. § 4.3), что благодаря наличию второго слагаемого диф-
дифференциальный оператор лагранжиана
E)
оказывается несингулярным, т. е. имеет обратный
g »}. F)
Квадратичный лагранжиан C),. E) часто называют «свободным» лагранжиа-
лагранжианом. В этом случае поля, описываемые лагранжианом вида A1.9) и A), име-
именуют «полями Янга—Миллса в пустоте». Для того чтобы избежать смешения
понятий (и а соответствии с терминологией § 19) мы будем называть поле,
описываемое линейными уравнениями, вытекающими из квадратичных лагран-
лагранжианов уЗ), E), полем линейного приближения или «линейным полем Янга —
Миллса». Поле Янга — Миллса, описываемое лагранжианами A1.9) и A) и
удовлетворяющее нелинейным уравнениям вида A1.11), не содержащим чле-
членов взаимодействия с другими полями (т. е. с полями материи), фигурирует
у нас как «свободное поле Янга—Миллса» в соответствии с физикой дела.
Если теперь считать константу g малой величиной (£<<1), то можно
поставить задачу построения теории возмущений по степеням g, отталкиваясь
от линейного приближения. Такая теория возмущений схематически была
рассмотрена в § 19.4. Диаграммная техника в этом случае содержит безмас-
безмассовый пропагатор в произвольной калибровке
flj; до)

296 ДОПОЛНЕНИЕ VIII
*
где
e-ib*dk
и вершины, соответствующие кубичным и четверным составляющим из D),
Как было объяснено в § 19, она приводит к трудности с унитарностью, кото-
которая может быть преодолена путем введения фиктивного безмассового скаляр-
скалярного поля духов (Фаддеева—Попова) \а (х), преобразующегося по присоединен-
присоединенному представлению калибровочной группы (см. A9.22)):
где
}. A0)
При этом поле духов £ формально следует полагать проквантованным по
Ферми—Дираку, что результативно проявляется в том, что каждому замкну-
замкнутому *духовому циклу ка диаграмме Фейнмана в матричном элементе отвечает
множитель — 1.
Таким образом, диаграммы Фейнмана для свободного поля Янга—Миллса
содержат внешние и внутренние линии поля Янга—Миллса, а также внутрен-
внутренние линии поля духов. Соответствующие правила Фейнмана в конфигурацион-
конфигурационном представлении были сформулированы в § 19.4.
В импульсном представлении правила Фейнмана свободного поля Янга —
Миллса содержат следующие элементы:
а) проп.агатор безмассовых векторных частиц
б) вершину тройного самодействия векторных частиц
— РУ/8щ>\ б (P+k + q) A2)
(v,6)
(на этой диаграмме и ниже на всех вершинных диаграммах все 4-импульсы
для опреде.1енности считаются входящими);

ДОПОЛНЕНИЕ VIII 297
в) вершину четверного взаимодействия
g,^)+(* ~ р)+(^2 *)} б см A3)
(p.a)
(р,С) FJ)
г) пропагатор духов
р " '
д) вершину взаимодействия духов с полем Янга —Миллса
Ц A5)
\ к
(С)
е) знаковый фактор
A6)
где g — число замкнутых петель фиктивного поля £.
2. Взаимодействие калибровочного поля с полями материи. Как отмеча-
отмечалось в § 11.2, взаимодействие калибровочных полей с полями материи вводится
единым образом путем ковариантного удлинения производных.
Поэтому каждому спинорному полю материи \|)° с массой т в правилах
Фейнмана соответствует:
а) спинор ный пропагатор
(а) , F)

298 дополнение vm
б) вершина взаимодействия с калибровочным полем
VWB = ~SVv Ф%ь в (А + А + ?) ■ .A8)
в) знаковый множитель
^-(-1)/, .
где /—число замкнутых фермионных циклов.
Каждому (псевдо) скалярному полю материи иа с массой (х соответствует:
а) скалярный пропагатор
(аУ__ (Ь)
б) тройная вершина взаимодействия с калибровочным полем
VaaB = -S(T%b(k-p)>i8(k + p + q) B0)
W, ,
\
в) четверная вершина взаимодействия с калибровочным полем
■ B1)
У
(b) 6),d)
г) другие возможные вершины самодействия скалярного поля (вида и4)
или его взаимодействия с другими полями материи.
3. Массивное поле Янга—Миллса. Сформулируем теперь правила Фейнмана
для калибровочного поля с массой, возникающей с помощью механизма Хиггса
в результате спонтанного нарушения симметрии вспомогательным скалярным
полем.
В целях соответствия с моделью Вайнберга—Салама будем рассматривать
случай поля Янга —Миллса группы SU B), взаимодействующего с-комплекс-
с-комплексным скалярным полем ф°, преобразующимся по спинорному представлению
(а=1, 2) калибровочной труппы. Поле (р, таким образом, содержит всего

ДОПОЛНЕНИЕ VIII 299
четыре скалярных действительных поля. Этот случай является простейшим
расширением модели спонтанного нарушения калибровочной симметрии, описан-
описанной в § 11.4.
В результате сдвига второй компоненты дублета ф на действительную
константу т] и перехода к четырем новым действительным скалярным полям а,
С (С\ С2, О)
исходный лагранжиан вида A1.20) принимает следующую форму:
+ l-
-f
Здесь использованы следующие обозначения:
B3)
а также
М = Ж, та=цк. B4)
Лагранжиан B3) содержит три массивных векторных поля В" (масса М),
одно скалярное поле Хиггса а с массой та и три безмассовых голдстоуновских
поля С. ,
Из-за наличия недиагонального члена
МВ^дН: ~B5)
голдстоуновское поле С (х) и продольная часть векторного поля не являются
независимыми динамическими переменными. Поэтому подходящим выбором
калибровки можно обратить в нуль либо С, либо дВ. Калибровка С = 0 назы-
называется унитарной. В этой калибровке лагранжиан содержит только физические
поля—триплет массивных векторных мезонов и один массивный хиггсов мезон.
Для вычислений оказывается более удобной так называемая поперечная
калибровка дВ=0, в которой векторный пропагатор принимает следующий вид:
guv —
В этом случае, благодаря условию поперечности поля Янга—Миллеа, член
оказывается неэффективным, так как хронологические

300 ДОПОЛНЕНИЕ VIII
спаривания дивергенции <МЗц становятся равными нулю (иногда говорят, что
«поле дВ не распространяется»).
Кроме поперечного пропагатора векторного поля B6), правила Фейнмана
содержат функции распространения духов Фаддеева — Попова и вершины их
взаимодействия A5) с полем Янга—Миллса, функции распространения голдсто-
уновских частиц
P2»fc^ B7)
и хвггсова бозона
многочисленные вершины взаимодействия полей В, С, а, которые легко восста-
восстановить по третьей и четвертой строкам лагранжиана B3), а также, возможно,
пропагаторы и вершины типа A7) —B1) различных полей материи.
Напомним, что как поля, соответствующие духам Фаддеева — Попова, так
и поля С (*), описывающие голдстоуновские бозоны, встречаются лишь во внут*
ренних линиях феинмановских диаграмм.

ЗАДАНИЕ «СЕНТЯБРЬ» К ГЛАВЕ I
С1. Явным вычислением, исходя из определения B.7) и используя урав-
уравнение движения B.2), показать, что тензор энергии-импульса Т^ удовлетворяет
уравнению непрерывности B.8).
С2. Вывести формулу B.22) для тензора момента векторного поля. С этой
целью, исходя из A.6), получить явное выражение для матрицы А в формуле
B.20), затем определить матрицу V бесконечно малого приращения компонент
функций поля и воспользоваться формулой B.13).
СЗ. Явным вычислением, используя определение B.22), показать, что-тен-
что-тензор момента удовлетворяет уравнению непрерывности.
С4. Показать, что симметрия тензора энергии-импульса Т^у приводит
к сохранению спина. ,
С5. Исходя из лагранжиана C.1), с помощью формул B.2) и B.7) полу-
получить уравнение движения C.2) и тензор энергии-импульса C.3) для веществен-
вещественного скалярного поля.
Сб. Исходя из лагранжиана C.16), с помощью формул B.2), B.22) и B.28)
получить уравнения движения и явные выражения для тензоров энергии-
импульса, спинового момента и вектора тока комплексного векторного поля.
С7. Рассмотреть поле пи-мезонов, преобразующееся по присоединенному
триплетному представлению изотопической группы SU B). В вещественном
представлении я = {яь я2, я3}, па — па изотопические преобразования запи-
записываются следующим образом:
па-*-п'а=А.аЬ(а)пь, Л(а)=ехр(—iatp.^.
Здесь ccj (/ = 1, 2, 3) — числовые параметры (углы) изотопических вращений,
а ш/ — генераторы поворотов, которые в действительном триплетном представле-
представлении могут быть-выбраны в виде
/ 0 0 i\ /0 — i 0\
ш,= 00 0, ш3 = U 00,
\— i 0 О/ ДО О О/
—совершенно антисимметричный тензор третьего

302 ЗАДАНИЕ «СЕНТЯБРЬ»
Найти матрицу О унитарного преобразования 7\=OcfyO~*, приводящего
к представлению, в -котором
/10 0V
Т3= 0 0 0.
\о о - \)
С8. С помощью теоремы Нётер, исходя из лагранжиана
построить соответствующие «изотопические> токи и сохраняющиеся во времени
«изотопические заряды». Проверить, что лагранжиан инвариантен относительно
рассматриваемых в задаче С7 преобразований.
С9. Аналогично предыдущей задаче рассмотреть изотопический дублет
нуклонов
где х—матрицы Паули,
СЮ. Показать, что формулы, обратные к C.8), имеют вид
$± (k) «= УЩ ф± (к) = Bя)~гн \ е+ikx fйоФ (х) + i<p (x)] dx, k0 =
СП. Переходя к импульсному представлению по формулам C.8), показать
явным вычислением, что «вклады с одинаковыми частотами» в энергию и
импульс обращаются в нуль, т. е.
j dx [q>± (х) Ф ±- (х)+«V (*) 'Ф* WJ == Jd*t* W ФГ* W = °-
С12. Подставляя импульсные разложения C.18) в нулевые компоненты
формул C.17) и выполняя интегрирование по конфигурационному пространству,
получить выражения C.19) — C.21) для векторов энергии импульса, спина и
для электрического заряда комплексного векторного поля.
С13 *). Найти решение уравнения Клейна—Гордона —Фока
(Q-/rt2)(p(*)=0,
предполагая ф и ф=дф/д/ заданными на плоскости t = tp. Выразить через
Ф'(/, у) и <p(t, у) и частотные части функции Паули—Йордана
положительно- и отрицательно-частотные части функции поля ф (х).
С14. Убедиться, что для векторного поля лагранжиан C.16) автоматически
приводит к уравнениям Клейна—Гордона и дополнительным условиям Лоренца.
CIS. Исходя из лагранжиана C.11) для векторного поля, получить выра*
жения зля Г^, Pv и обсудить их отличие от C.17а) и C.19).
Курсивом помечены номера задач повышенной трудности.

ЗАДАНИЕ «СЕНТЯБРЬ» 303
С16. Используя переход к локальному реперу C.24), провести диагонали-
зацию квадратичной формы C.23). Получить формулу C.25).
С17. Вводя с помощью C.27) амплитуды Ьп, отвечающие круговым поля-
поляризациям, диагонализовать выражение C.26) для проекции спина векторного
поля на направление движения.
С18. Исходя из лагранжиана D.13) для электромагнитного поля, получить
пространственные плотности вектора энергии-импульса Tov и вектора спина 5.
СГ9. Переходя к импульсным амплитудам по формулам D.22) и используя
разложение D.23) по локальному реперу, с помощью условия Лоренца получить
выражения для векторов энергии-импульса и спина электромагнитного поля.
С20. Исходя из лагранжиана E.5) для спинорного поля, получить тензор
энергии-импульса и вектор тока в форме E.6) и E.7).
С21. Пусть
Показать, что
5 = / (v = 0, 1, 2, 3).
С22. Используя свойства цикличности шпура и закон перестановки матриц
Дирака E.1), доказать, что шпуры всех матриц (Д.П.2), кроме единичной,
равны нулю,
С23. Используя результаты предыдущей задачи, доказать линейную незави-
независимость 16 матриц (Д.П.2)
С24. Показать, что шпур нечетного числа матриц Дирака равен нулю,
а также получить рекуррентную, формулу, выражающую шпур, произведения 2л
матриц через шцуры произведений In — 2 матриц.
С25. Вычислить
Sp [h (Pi+«i) к (Рз+«2)]. Sp [kik2 (Р1 + /П!) (p2+ma)].
C26. Выполнить суммирование по а в произведениях
YoYvYa. Y'YVYa.
C27. Показать, что
где gi*vpo_ совершенно антисимметричный единичный тензор 4:го ранга.
С28. На основе результатов задачи С25 и рассмотрения шпуров от шести
сомножителей типа
Sp [%L (pi+«i) h (p2 + Щ) %3 Срз+«зI. Sp [ktki (pi + /Th) (pa+m2) й3й4]
найти общую формулу связи между
2p3%3--Pm---h] и Sp[k1P1Pik2Piki...Pm..An],
где Pi =
С29. Исходя из формул лоренцевых преобразований для спиноров
(ДП.16, 18, 20), получить явные выражения для генераторов Л^^' и А^ *M'V'
вращений спиноров ф йф в плоскости x>>-xv, введенных в B.20), через матриц-

304 'задание «октябрь»
ный тензор спина a^v, определенный по формуле (ДН.2), и с помощью фор-
формулы B.24) получить выражение E.8) для тензора спина спинорного поля.
СЗО. С помощью формул (ДП.18) преобразования спинора при лоренцевых
поворотах получить из E.12) формулы E.26).
С31. В представлении (ДП.5), (ДП.7) найти нормированные решения
uSl — (ft), s = 1, 2 уравнения Дирака, являющиеся собственными функциями
оператора спиральности
и удовлетворяющие условиям ортонормированности
«'•• + (fc)«s-±(ft)=^6".
С32. Построить оператор проектирования, выделяющий состояния с опре-
определенной спираль ностью.
ЗАДАНИЕ «ОКТЯБРЬ» К ГЛАВЕ II
01. Получить реализацию собственных функций tyn и операторов а и а
для гармонического осциллятора в координатном и импульсном представлениях.
Убедиться в выполнении соотношений
+ + + + +
[а, а]=аа—аа=1, [а, а]=[а, а]=0.
02. Исходя из коммутационных соотношений предыдущей задачи и условия
нормировки нижнего состояния
вычислить норму состояния тл = (аI
03. Вычислить норму одночастичного состояния
фх = ^dq w (q) a (q) Фо, ФоФо = 1»
где оператор a (q) удовлетворяет перестановочным соотношениям F.8), а ш (q) —
с-функция. Рассмотреть предел
w(q)-+8(q-P),
где Р — фиксированный вектор.
04. Исходя из коммутационных соотношений G.4), содержащих оператор
заряда Q, показать, что Для комплексного поля операторы и— понижают заряд,
а операторы и?1— повышают, т. е., например, если Q®q = q®q, то 0ц±Ф9 =
05. Получить аналог уравнения G.4) для изотопических преобразований.
Рассмотреть частные случаи: а) дублет нуклонов (/ = 1/2), б) триплет пионов

ЗАДАНИЕ «ОКТЯБРЬ» 305
06. Доказать соотношения G.14). Получить аналог этих соотношений для
триплета пионов, используя решение задачи 05.
07. Получить оператор момента количества движения для скалярного поля
в координатном и импульсном представлениях. Получить перестановочные
соотношения для его компонент. Показать, что
рИ,^, ф (*)] = I (х^ду,—х^) ф (х).
08. Исходя из условия эрмитова сопряжения операторов
и формулы G.19) и используя свойство положительности метрики в гиль-
гильбертовом пространстве Ф [ А [2 Ф Э= 0, определить тип перестановочных соотно-
соотношений для частиц с целыми и полуцелыми спинами.
09. Предположив, что скалярные поля ф (*) квантуются по Ферми —Дираку,
а спинорные tJj(лг) — по Бозе—Эйнштейну, обсудить поведение антикоммутатора
{ф(*), ф((/)} и коммутатора |/ф (*), ф (у)] при (*—уJ<0.
010. Исходя из коммутаторов G.19), с помощью преобразования переходя
к локальному реперу C.24) получить коммутационные соотношения для вектор-
векторного поля (8:14).
ОН. Полагая fi=v=O в коммутационном соотношении (8.17), доказать,
что коммутатор для временных псевдофотонов противоречит свойству положи-
положительности метрики в гильбертовом пространстве. Указание. Умножить комму-
*
тационное соотношение для а% (q) и а^ (ft) на f (q) f (ft) и проинтегрировать
по q и ft.
012. Используя антикоммутационные соотношения (9.4), вычислить ком-
коммутаторы
Щ (х) 7*ф (*), ф Of) v^ (У)Ъ № [х) у*ф (х), ф (у) 7*ф (у)]
и рассмотреть их поведение вне светового конуса.
013. Определить поведение вне светового конуса (при *~</) коммута-
коммутаторов \Х (х), <3?(jO] при:
б)
014. Вычислить фурье-образы F(q) = \el4xF (x)dx от следующих произ-
произведений D и S функций одинаковой частотности:
а) fi(x) = D-(x)D-(x);
б) F (х) = Sp 1-fS- (x) v5S+ (-х)],
в) F(x) = Sp[y»S-(x)y>iS+(-x)].
015. Вычислить фурье-образ вакуумного ожидания коммутатора свободных
спинорных токов je«P«-m ([J^(x), Jv(y)] )odx при
а) Л{х) = Щх)^(х),
б)

306 ЗАДАНИЕ «НОЯБРЬ»
016. Исходя из двухкомпонентных уравнений Вейля (9.15) для безмас-
безмассового спинорного поля, показать, что средние значения оператора спиральности
P
по состояниям ф_,_ равны ± 1, т. е., что спин нейтрино в состоянии ф+(/>)
направлен по направлению движения, а в состоянии ф_(р)—против направ-
направления движения. -
017. Исходя из формул (9.24), (9,28) и (9.29) и условия унитарности
матрицы Y°t вывести формулу (9.30).
018. С помощью формулы (9.29) получить явный вид матрицы зарядового
сопряжения С в стандартном (ДП.5) и спиральном (9.21) представлениях
матриц Дирака. Прокомментировать одинаковый вид матриц С в этих двух
частных представлениях.
ЗАДАНИЕ «НОЯБРЬ К ГЛАВЕ III
HI. Построить лагранжианы взаимодействий, содержащие минимальные
степени полей и не более одной производной:
а) скалярного поля ф со спинорным полем т]э;
б) псевдоскалярного поля ф со спинорным полем т]э;
в) действительного скалярного поля ф с аксиально-векторным полем Sv;
г) спинорного поля \|) с векторным полем Av.
Н2. Построить изотопически инвариантные лагранжианы взаимодействий,
содержащие минимальные степени полей:
а) дублета спинорных полей с триплетом скалярных;
б) дублета спинорных полей с триплетом псевдоскалярных;
в) дублета спинорных полей с триплетом векторных;
г) дублета спинорных полей с триплетом аксиально-векторных;
д) дублета спинорных полей с триплетом скалярных полей с векторной
связью;
е) дублета спинорных полей с дублетом псевдоскалярных.
НЗ. Построить минимальный локально-калибровочно-инвариантный лаг-
лагранжиан взаимодействующих а) спинорного и электромагнитного полей, б) ска-
скалярного и электромагнитного полей. _
Н4. Исходя из формул A1.3) и определения ковариантной производной
A1.4), показать, что она преобразуется подобно полевой функции, т. е. дока-
доказать формулу A1.6).
Н5. Исходя из определения A1.7) и формул преобразования A1.5) -для
поля Янга-Миллса, найти закон преобразования тензора поля Янга-Миллса f^v.
Нб. Построить калибровочную модель поля -Янга-Миллса группы SU B),
взаимодействующего с триплетом скалярных мезонов ф и дублетом ферми-
онов т]э.
Н7. Найти статические (dq>/dt = O) решения задачи со спонтанным нару-
нарушением симметрии

ЗАДАНИЕ «НОЯБРЬ» 307
удовлетворяющие граничным условиям, jp (z, ±со)=±фо, гдеф(г, /)—функция
поля в двумерном пространстве-времени *=(z, t), № и ф^ —некоторые поло-
положительные константы. Обсудить характер локализации энергии и импульса.
Н8. Линейной подстановкой дйагонализовать лагранжиан
где
Н9. То же для лагранжиана
НЮ. Найти оператор U (а), осуществляющий унитарное преобразование
+
бозе-операторов а, а, которые удовлетворяют соотношениям
[+1 + + с+ +1
а, а\ = аа—аа = 1,' [а, а]=[а, aJ=O,
к новьш операторам
А = U-i (a) all (а)=а+ а,
А — f/-i(«)«С/(а)=вН- а,
где а—действительное с-число.
НИ. Найти явный вид оператора U, осуществляющего унитарное пре-
+ +
образование от бозе-операторов а, а, Ь, Ь, удовлетворяющих соотношениям
[a, a\ = [b, b] = i, [a, 6]-fa, b] = [a, b] = [a, b]=0,
к новым операторам
Л=£/~(ф)а£/(ф) = асозф + &япф, S = f/~1 (ф) bU(q>)=b созф—авшф.
Н12. Провести каноническое квантование лагранжиана задачи Н8, Полу-
Получить одновременные коммутационные соотношения.
Н13. Провести диагоналнзацию гамильтониана
содержащего бозе-операторы а, Ь, которые удовлетворяют соотношениям
[a, a] = [b, £] = 1, [a, b]=,[a, +b] = [a, b] = [a, б]=0.
Построить собственные состояния, выразив их через а) полевые операторы
диагонального представления; б) собственные состояния свободного гамильто-
гамильтониана Яо.
Н14. То же для гамильтониана
k\ [а(к), a(q)] = 6(ft-q).
HIS. Рассмотреть переход к локальному релятивистскому пределу
в выражениях задачи Н14 для сдвига энергии вакуума и нормы собственных
состояний,

308 ЗАДАНИЕ «ДЕКАБРЬ»
Н!6. Доказать, что в однонуклонном секторе решение задачи тяжелого
нуклона сводится к решению уравнения A3.9).
Н17. Проверить прямой подстановкой, что выражение
A3.23)
удовлетворяет уравнению
u #' (ft), A3.22)
причем состояние Ч^' определено соотношением A3.15) и удовлетворяет
уравнению A3.17), а Н — гамильтониан A3.1) — A3.3) задачи тяжелого нуклона.
Н18. Определить общий вид ядер со (ft, q) и J (klt ft2; qlt q2) в операторе
, q)aWa(q)+
+ ^ dftx dk2 dq1 dq2 J (ku k2; qu q^) a (ftx) a (ft2) a (qx) a (q2),
при котором этот оператор может рассматриваться в качестве гамильтониана
системы, в которой! сохраняется число частиц и 3-вектор импульса.
Н19. Определить явный вид функций со и У и правила квантования
операторов а, а в гамильтониане предыдущей задачи таким образом, чтобы
а) гамильтониан Н описывал полную энергию системы одноименно заря-
заряженных тождественных нерелятивистских бозе-частиц с классическим потен-
потенциалом кулоновского взаимодействия
vi , . 1 е2
* 4я | х—у |'
б) гамильтониан Н правильно описывал полную энергию системы тожде-
тождественных релятивистских фермионов (например, нуклонов) с юкавским потен-
потенциалом взаимодействия
ЗАДАНИЕ «ДЕКАБРЬ» К ГЛАВЕ IV
Д1. Решить итерациями уравнение Шредингера для S-матрицы
Провести рассмотрение «-го члена. Решение привести к виду хронологической
экспоненты,
Д2. Рассмотреть следующие лагранжианы взаимодействия (здесь ср (х) —
скалярное поле, ф (х) — псевдоскалярный изотриплет я-мезонов, 1P={i|)p, г|)„} —
изодублет нуклонов, е (х)—поле электронов, ц(х) — поле мюоновг v (*) — поле
нейтрино):
a)£=
б) t5?=
' в) ^=

ЗАДАНИЕ «ФЕВРАЛЬ» 309
г)
полей с
д).
е) =
ж)
з)
и) ■
а
la
лагранжиан
взаимодействия электронного, нуклонного и пионного
: электромагнитным полем:
S?=£Y(*)ty
S? = (//H)>P (х
% = %ta,+
# = <#<») +
#=^/«<*
= \е(х)уаA
W (ж) <р (*);
) xy»YvlF (ж) <3v9 (ж);
:)/'°D где /e = /e+Aef
— Ye) e (*) + vu (JC)Ya A — Ys)M. (x),
Для каждого из этих лагранжианов с помощью второй теоремы Вика записать
в нормальной форме хронологическое произведение Т (j6 {x) j6 (у)).
ДЗ. То же для лагранжиана самодействия калибровочного поля Янга —
Миллса:
где
Здесь /^-структурные константы соответствующей группы Ли. Указание. Выде-
Выделить из «5?уи квадратичные члены и рассматривать в качестве лагранжиана
взаимодействия оставшуюся часть.
Д4. То же для хронологических произведений Т (% (х) X (у) X (г)) из
задач 2а) —2в).
Д5. Для лагранжианов из задач 2 и 3 построить правила фейнмана
в импульсном представлении.
Д6. Пользуясь комбинациями лагранжианов из задачи 2, нарисовать
простейшие диаграммы и выписать "соответствующие им вклады в 5-матрицу
в импульсном представлении для следующих процессов: а) е+е~-*-рр; б) е+е" ->-
->- я+я~; в) рассеяние я+ на протоне; г) я+я~ ->- я+я~, я+я+ ^- я+я+; д) юкав-
ское рассеяние пр -*-пр; е) комптоновское рассеяние ур-*-"ур\ ж) мёллеровское
рассеяние ер-»-ер; з) яo^-2Y; и) взаимодействие нейтронов с фотонами;
к) я—->-n±v; л) я+р-»-я+я°р; м) ц-vevv.
ЗАДАНИЕ «ФЕВРАЛЬ» К ГЛАВЕ V
Ф1. Получить формулу для дифференциального сечения упругого рассе-
рассеяния двух спинорных частиц.
Ф2. Вывести формулы для вероятностей процессов распада одной частицы
на две и на три частицы и времени жизни исходной частицы.
ФЗ. Воспользовавшись результатами задачи Д6, вычислить дифференци-
дифференциальные сечения аннигиляции электрона и позитрона по следующим каналам:
а) е+е"-)-ц+ц-; }
6)e+e--*2v;
в) е+е~-*-я+я-.

310 " ЗАДАНИЕ «ФЕВРАЛЬ»
Ф4. Получить значения времен жизни исходных частиц в следующих
процессах распадов:
a) |i--».e-+ve-|-v,i;
Указание. Воспользоваться результатами задачи Д2 г), д), и). Сравнить полу-
полученные результаты с экспериментальными данными. Последние можно ззять,
например, из книги Перкинса A975).
Ф5. Получить распределение по энергиям вылетающих электронов для
Р-распада
Указание. Воспользоваться лагранжианом взаимодействия, приведенным в зада-
задаче Д2 и). Сравнить полученные результаты с экспериментальными данными,
приведенными в гл. IV книги Перкннса A975).
Ф6. Вывести отношение парциальных ширин распадов
в зависимости от спина ф-мезона.
Характеристики частиц следующие:
ф масса 1019, спин = ?, изоспин 0,
четность = — , G-четность = — ;
/С* масса 494, спин 0, изоспин 1/2,
четность = —, G-четность = -)-;
К", К0 масса 498, спин 0, изоспин 1/2,
четность = —, G-четность = -j-,
Пользуясь данными эксперимента
Г (ф -» К+К~)/Г (ф -*- K°R°) =* 1,5,
высказать соображения в вероятном значении спина ф-мезона.
Ф7. Рассчитать отношение вероятностей распадов я— -мезонов
я1*-»- H^ + Vp, и- л±-\—t-e±ve
и сравнить с отношением экспериментальных значений, равным 1:A,24.±
± 0,03) ■ 10~4, Указание. Использовать механизм распада, изображенный на
диаграмме
N
и слабые лагранжианы из задачи Д2.

ЗАДАНИЕ «МАРТ» 311
ЗАДАНИЕ «МАРТ» К ГЛАВЕ VI
Ml. Вычислить разность фейнмановских интегралов / (k) — / @), где
соответствующую диаграмме второго порядка собственной энергии мезона в тео-
теории с лагранжианом взаимодействия <S?=(g/3): <р3 (х):. Вычисление провести
двумя способами: а) переходом в а-представление, б) использованием фейнма-
фейнмановских параметров.
М2. Теми же двумя методами вычислить диаграмму третьего порядка вер-
вершинной функции мезона в теории j6—g<^
МЗ. Вычислить время жизни я-мезона, обусловленное распадом я°-^2у
через виртуальное состояние NN. По известному экспериментальному значению
времени жизни определить константу пион-нуклонного взаимодействия g. Ука-
Указание. Воспользоваться результатами задачи Ф2 и задач Д2 г), д).
М4. Вычислить вклад в S-матрицу диаграммы второго порядка собственной
энергии электрона в спинорной* электродинамике. Пропагатор фотона взять
в произвольной калибровке
Использовать три метода.регуляризации:
а) регуляризацию Паули—Вилларса
1 1
/П2 — р2 /П2 —р2 М> — р2 '
б) обрезание импульса виртуального фотона при р2 = Л2;
в) размерную регуляризацию .
Изучить поведение полученных выражений при Л2, М2->-со, е->-0. Полу-
Получить аналог формул B4.16), B4.17).
Найти значение di, при котором рассматриваемая диаграмма не содержит
расходимостей.
М5. Вычислить швингеровский вклад в аномальный магнитный момент
электрона, соответствующий вершинной диаграмме порядка рис. 24.2, б. Ука-
Указание. Воспользоваться формулами B4.24)—B4.26) и C0.4).

312
ЗАДАНИЕ «АПРЕЛЬ»
Мб. Вычислить аномальный магнитный момент нейтрона, исходя из лагран-
лагранжиана взаимодействия задачи Д2 г) и д). Указание. Рассмотреть вершинные
диаграммы вида
^ j .. ч. „
п
п
п
ЗАДАНИЕ «АПРЕЛЬ» К ГЛАВЕ VII
А1. Вычислить вклад в 5-матрицу диаграммы второго порядка собственной
энергии мезона в теории с кубичным самодействием
Произвести устранение расходимостей.
А2. Найти максимальный индекс вершины для скалярной теории со степен-
степенным самодействием
в iV-мерном пространстве-времени. Определить возможные значения пар чисел
(М, k) для перенормируемых моделей.
A3. Найти амплитуды яя-рассеяния во втором порядке теории
•Найти пороговые значения (при s = (p1-\-p2J = 4m*t) амплитуд и сечений про-
процессов упругого рассеяния я+я°, я°я°.
А4. Найти сечение процесса «*е~-»-'я+я~ с точностью'до второго порядка
по а и А включительно в теории с лагранжианом взаимодействия
%ъг (х) = еАv (х) {^ (*OуФ (х) + 'ф (^) T3dv<f (х)} + -^- А (<р (ж)ф (ж))',
X N + ,.
А5. Найти вклад поляризации вакуума в поправку к закону Кулона
.... 1
ЛО
"ext

ЗАДАНИЕ «АПРЕЛЬ»
313
А6. Вычислить вклад в 5-матрицу диаграммы третьего порядка «рюмка»
для лагранжиана
42
Сформулировать /?-операцию, устранить расходимости и обсудить структуру
конечного произвола в окончательном выражении.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Эта книга представляет собой пособие к годовому курсу, состоящему из
30 с небольшим лекций и такого же числа семинаров. Каждый параграф при-
примерно соответствует одной полуторачасовой лекции. Упражнения, собранные
в тематические Задания, предназначены для семинарских занятий. Для этой
же цели может быть использован технический материал из Дополнений. Итоги
проработки Заданий целесообразно подводить в форме коллоквиумов по два
раза в семестр.
В оглавлении курсивом отмечены разделы, которые можно опустить при
первоначальном ознакомлении с предметом. Остальной материал образует
«минимум», рекомендуемый при недостаточном знакомстве студентов с разделами
«Основы релятивистской теорию и «Квантовая теория многих частиц» универ-
университетского курса квантовой механики, а также в случае неполной продолжи-
продолжительности учебного года. - " , -
Этот минимум выглядит следующим образом:
1-й семестр: §§ 1—5, 6*. 7, 8*, 9*, 10*, 14, 17* и 18 —всего 13 лекций;
2-й семестр: §§ 19*. 20—22, 23*, 24 — 26, 27*. 28, 30, 31 и 33—всего 13 лекций.
(Звездочка рядом с номером параграфа означает материал за вычетом подпараг-
рафов, отмеченных в оглавлении курсивом.)
К содержанию «минимума», в зависимости от конкретных условий и инте-
интересов преподавателя, можно в различных комбинациях добавлять материал,
отмеченный курсивом. Со своей стороны в качестве «первого резерва» мы реко-
рекомендуем §§ 9.4, 10.3, 12, 23,3 и 29. Из остального материала выделим «наборы»:
а) §§ 8.4, 8.5, 11, 19.4, 32 и Дополнение VIII1, б) §§ 15 и 16, которые целесо-
целесообразно вводить целиком.
Желательный объем знаний для студентов, приступающих к изучению этой
книги, помимо стандартного курса квантовой механики, включающего упомя-
упомянутые выше два раздела, содержит небольшой курс теории непрерывных групп
и их представлений (особенно представлений группы Пуанкаре), а также
элементарные сведения о физике частиц.

ЛИТЕРАТУРА
Введение — Боголюбов Н. Н., [Цирков Д. В., Введение в теорию квантованных
полей, 3-е изд. —М.: Наука, 1976.
Ахиезер А. И., Берестецкий В. Б. 1969, Квантовая электродинамика. —3-е
изд.—М.: Наука.
Блохинцев Д. И. 1976, Основы квантовой механики, —5-е изд. —М.: Наука.
Боголюбов Н. Н. A970), Лекции по квантовой статистике, в т. 2 «Избранных
трудов» в трех томах, Киев:_Наукова думка.
Боголюбов Н. Н. A979), Избранные труды по статистической физике.—М.:
Изд-во МГУ.
Боголюбов Н.Н., Логунов А. А., Тодоров И. Т. 1969, Основы аксиоматического
подхода в квантовой теории поля.—М.: Наука»
Бьеркен Дж., Дрелл С. A978), Релятивистская квантовая теория. Мл Наука.
т. 2.
Вигнер Е. A971), Этюды о симметрии.—М.: Мир.
Владимиров В. С. A976), Уравнения математической физики. 3-е изд. —М.:
Наука.
Давыдов А. С. A973), Квантовая механика. 2-е изд. —М.: Наука.
Дирак П. А. М, A968), Лекции по квантовой механике. — М.: Мир. См. также
Дирак A979), стр. 408—475.
Дирак П. А. М. A979), Принципы квантовой механики. —М.: Наука.
Елютин П. В., Кривченков В. Д. A976), Квантовая механика.—М.: Наука.
Завьялов О. И. A979), Перенормированиые диаграммы Фейнмана.—М.: Наука
Киржниц Д. А. A963), Полевые методы теории многих частиц,—М.: Атомиздат.
Клаудер Дж., Сударшан Э. A970), Основы квантовой оптики,—М/. Мир.
Ландау Л. Д., Лифшиц Е. М. A974), Квантовая механика. —М.; Наука.
Липким.Г. A977), Квантовая механика:—М.: Мир.
Медведев Б. В. A977), Начала теоретической физики. —М.: Наука.
Мессиа А. A978), Квантовая Механика. М.: Наука, т. I.
Перкинс Д. A975), Введение в физику высоких энергий, М.: Мир.
Славное А. А., Фаддеев Л. Д. A978), Введение в квантовую теорию калибро-
калибровочных полей.—М.: Наука.
Фейнман Р. A978), Теория фундаментальных процессов:—М.: Наука.

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Аксиоматическая теория поля 84, 127,
257
Альфа-представление 177
Амплитуда рассеяния 173
— состояния 57
вакуума 60
, нормировка 169
Асимптотика ультрафиолетовая 255
Асимптотическая свобода 259
Боголюбова преобразование ПО, 281
Вайнберга—Салама модель 247
Вайнберга угол 248, 253
Вектор 16
— ковариантный 9
— состояния см. Амплитуда состоя-
состояния
— тока 24
Векторное поле 28
калибровочное 93
комплексное квантование 70
промежуточное 247
Янга—Миллса 94, 97
, квантование 157
Вероятность перехода 171
Вертекс 214, 217
Вершина диаграммы 152, 154, 158
Вершинная функция 192, 212
— — сильносвязная см. Вертекс
Взаимодействия полей 89
— — калибровочные 93, 97
Ферми 87, 242
— частиц 11, 85
нелептонные 243
электромагнитные 85, 236
Взаимопревращаемость частиц 12
Виртуальные частицы 153
Внутренние симметрии 12, 24
Время жизни 11, 175, 309, 310
пиона 12
Вторичное квантование 49
Гамильтониан 49, 55, 103
—, диагонализация 108
Гамильтонов подход 106/
Глюоны 254
Голдстоуна теорема Ю1
Голдстоуновские бозоны 101, 226
Градиентная инвариантность 33, 226
матрицы рассеяния 227
Градиентное преобразование 33
фотонного пропагатора 227
Группа 271
— абелева 272
— калибровочная 94, 97, 248
— Ли 273
, генераторы 277
■ , представления 276
— Лоренца 14
, представления 15
— неабелева 94
— простая 272
— Пуанкаре 14
— ренормировок 258
Действие 17 .
Диаграмма Фейнмана 151
вершинная 192
древесная 237
— —, индекс 209
связная 168
собственной энергии 190
Дирака матрицы 41, 264
— поле 40
— —, квантование 75
— спинор 42
— уравнение 41, 266
— —, нерелятивистский предел 269
Дисперсионные соотношения 257
Духи Фаддеева—Попова 158, 252
Законы сохранения 12
: заряда 24
энергии-импульса 20

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
317
Заряд 23, 24
— электрона 11
Зарядовая симметрия 65
Зарядовое сопряжение 65, 81
операторов 84
— — спинорного поля 81-
Изовектор 90
Изотопическая группа 94, 301
— симметрия 12, 24
Изотопический дублет 94, 261
— мультиплет 94, 100
— спин 262
— триплет 94, 262, 301
— формализм 261
Инвариантность лоренцева 14
— Пуанкаре (релятивистская) 14
Индекс вершины 211
— диаграммы 209
— лагранжиана 211
Индефинитная метрика 75
Инфракрасная особенность 231
— расходимость 225
Калибровка 37, 102
— диагональная 37
— кулонова 38
— поперечная 299
— унитарная 299
Калибровочное взаимодействие 92, 96
Калибровочные поля 93
— преобразования 23, 94
локальные 92, 95
Квантование каноническое 53, 54
— полей 49
—, релятивистская схема 56, 57
Квантовая хромодинамика 255
Ковариантная производная 92, 95
Когерентное состояние 116
Компенсирующие поля 93, 97
Константа связи 87, 89
инвариантная 259
перенормированная 201, 226
Контрчлены 198, 201
Коэффициентные функции 150
Лагранжев формализм 17
Лагранжиан 17
— взаимодействия 89
—, локальность 18, 136
— сингулярный 36
— поперечный 35
Локальная коммутативность 67, 135
Локальное выражение 126
Локальный оператор 125
— репер 31, 39
Лэмбовский сдвиг 241
Магнетон Бора 238, 271
Магнитный момент электрона 238
— — — аномальный 239
Масса протона 11
— промежуточных бозонов 253
— электрона 11
Массовый оператор 213, 214
Матрица рассеяния 123
— —, ковариантность 129
, причинность 131—133
— —, унитарность 130, 157
Матрицы Дирака 41, 264
, спиральное предегевление80
, стандартное представление 265,
266
, унитарность 42
, шпуры произведений 266
— Паули 266
Модель Вайнберга—Салама 247
—статического источника 108
— тяжелого нуклона 112
Нейтральные токи 245
Нейтринное поле 77, 87, 244, 245, 250
Несобственные функции см. Обобщен-
Обобщенные функции
Нормальное произведение 68
— — со спариваниями 140
Обобщенные функции 150
— —, умножение 183, 203
Обращение времени 83
Оператор д'Аламбера 10
— квазилокальный 136, 198
— массовый 213
— поля 56
— — локальный 125
— поляризационный 190, 191,214,228
— проекционный 34
— унитарный 57
Оптическая теорема 174, 175
Осцилляторы поля 14, 52
Паули—Йордана функция 67, 147, 148,
284
Паули матрицы 266
— теорема 66
— уравнение 270
Перенормировка 112, 200
— вертекса 225

318
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Перенормировка константы связи
201, 208, 222, 226
— массы 201, 221, 224
— полевой функции 201, 221
—, теорема 223
— функций Грина. 219, 221
Перенормируемость 202, 208, 212
— модели Вайнберга—Салама 252, 253
Перестановочная функция 64
— — векторного поля 71, 286
скалярного поля 67, 147, 284
— — спинорного поля 76, 286
электромагнитного поля 75, 285
Перестановочные соотношения 50, 53,
55, 61, 62
— — Бозе—Эйнштейна 66, 67, 70, 72
— — одновременные 54, 104, 106
Ферми—Дирака 66, 76
Планка постоянная 11
Поле векторное 28
— калибровочное 93
— нейтринное (Вейля) 77
— скалярное 24
— спинорное (Дирака) 41
— Хиггса 103, 248 •
— электромагнитное (Максвелла) 32
— Ян га—Миллса 94
Поляризация вакуума 242
Постоянная тонкой структуры 88, 240
Правила Фёйнмана 151—154
, импульсное представление 161,
162
поля Янга—Миллса 157—159,
296—300
— —, спинорная электродинамика
153, 154, 165, 166
Правило знаков 156, 162
Представление взаимодействия (Ди-
(Дирака) 122
— Гейзенберга 56, 104
— матриц Дирака — см, Матрицы Ди-
Дирака
— фоковское 61
— чисел заполнения 49
— Шредингера 55, 113
Преобразование Боголюбова ПО, 281
— градиентное 33 -
— зарядового сопряжения 65, 81
— калибровочное 33, 95, 96
— Лоренца 21, 268
— обращения времени 83
— пространственного отражения 16,
269 -
— Пуанкаре 14, 129
— унитарное 57, 58
операторов 56, 57, 59, 84, 109,
110
Преобразование фазовое 23
локальное 92
Причинная функция Грина 147
Промежуточный векторный бозон 90
Пропагатор см. Причинная функция
Грина - -
Радиационные поправки 195, 228, 232,
240, 242
Распад двухчастичный 175
Рассеяние 173
— комптоновское 236, 237
— мёллеровское 166, 167, 236
Расходимости инфракрасные 194, 231
— ультрафиолетовые 181, 197, 202, 204
Регуляризация обрезанием 188, 289
— Паули—Вилларса 183, 190, 192,
193, 198 . ■
— размерная 186, 288
— фейнмановская 188
Редукционные формулы 219
Релятивистская инвариантность 14
— ковариантность S-матрицы 129
Сверхтонкое расщепление 241
Сечение поперечное 174, 257
Сингулярные функции см. Обобщен-
Обобщенные функции
— лагранжианы 36
Скобки Пуассона квантовые 54
— — классические 54
Сопряжение дираковское 42
— зарядовое 81
Спаривание операторов 139
хронологическое 141
-Спектральное представление 189
Спин 22
Спинор 15
Спинорная электродинамика 236
Спинорное поле 40
— безмассовое 77
, законы преобразования 267—
269
, квантование 76, 77
Спиральное представление 80
Спиральность 78
Спонтанное нарушение симметрии 98,
99
Сохранения законы 19, 20
Тензор 15
— Минковского 9
— момента количества" движения 22
— спина 23

предметный указатель
319
Тензор электромагнитного поля 32
— энергии-импульса 19
Теорема Вика 140, 143, 144
— Нётер 20, 103
— о перенормировках 223
— Паули 66
— СРТ 84-
Тождество Уорда 234
— Уорда—Такахаши 235
Ток заряженный 244
— нейтральный 245
Ферми взаимодействие 88, 242
— постоянная 87, 244
Формула Клейна—Нишины 237
— Комптона 237
Формфактор электрона 193, 239
Функции Грина 145, 285, 286
полные 212, 215
причинные 147, 285, 286
Функционал 127
Функциональная производная 129, 133
Функциональный интеграл 258
Угол Вайнберга 248, 253
Узел диаграммы см. Вершина диа-
диаграммы
Унитарный предел 246
Уравнение Вейля 78
— Гайзенберга 56, 104
— д'Аламбера 36, 37
— Дирака 41, 77, 266
— Клейна—Гордона 24
— Паули 270
— Прока 29, 33
— Шредингера 50, 55, 270
Уравнения Максвелла 32
Условие Лоренца 34, 35
— — ослабленное 73, 74
— причинности 131
— — дифференциальное 133
Хиггса бозон 103, 248
— механизм 103, 248, 250
Хронологическая экспонента 126, 137
Хронологическое произведение 124, 125
— спаривание 141
СРГ-преобразование 84
Четность 16
Экранировка заряда 112, 259
Электромагнитное взаимодействие 85,
236
минимальное 93
Эффективное сечение см. Сечение