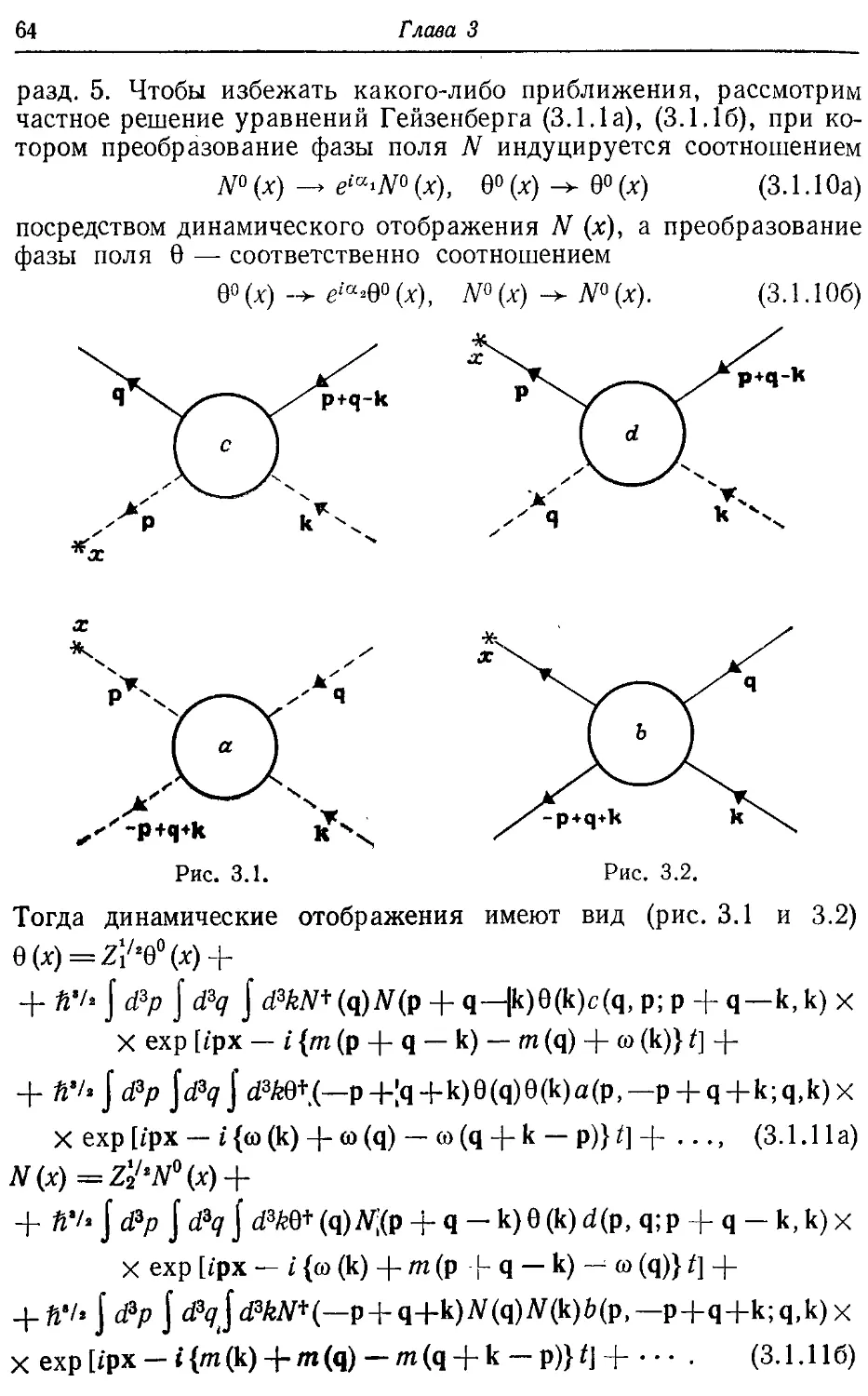
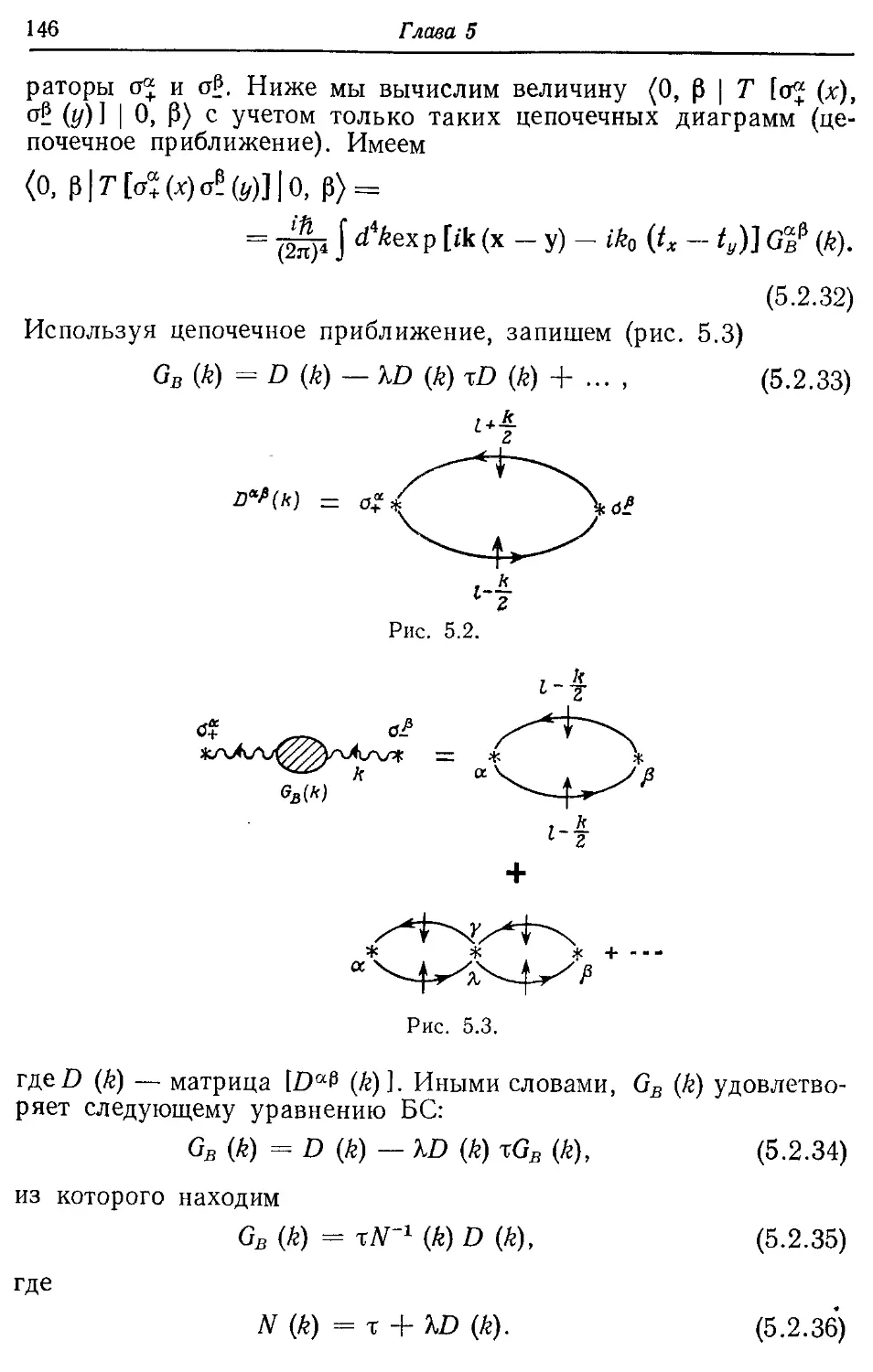
Text
Х.Умэдзава, Х.Мацумото, М.Татики
ТЕРМОПОЛЕВАЯ ДИНАМИКА И КОНДЕНСИРОВАННЫЕ СОСТОЯНИЯ
В этой книге дается формулировка квантовой теории поля при конечных
температурах, позволяющая описывать упорядоченные состояния систем многих
тел, в которых может возникать много протяженных топологических объектов
разного типа, взаимодействующих с квантами. В этом формализме с единой точки
зрения описываются классические, квантовомеханические и квантово-полевые
объекты; это достигается благодаря последовательной схеме описания
макроскопических объектов, сосуществующих с квантами. В настоящее время
системы, в которых сосуществуют микроскопические и макроскопические
объекты, привлекают большое внимание физиков, работающих в различных
областях. Данная книга ставит своей целью дать читателю ясное представление
об этом круге вопросов. Предполагается, что она представит интерес не только
для физиков, занимающихся изучением твердого тела, но и для исследователей в
других областях, таких, например, как физика высоких энергий и космология,
несмотря на то что большинство примеров взято из физики твердого тела. Общая
точка зрения, которая проводится в книге, а также краткий обзор ее содержания
приведены в гл. 1.
ОГЛАВЛЕНИЕ
Предисловие редактора перевода 5
Предисловие 7
Глава 1. Введение 9
1.1. Квантовая теория систем многих тел 9
1.2. План книги 15
1.3. Обозначения 17
Глава 2. Квантовая теория систем многих тел 21
2.1. Представление чисел заполнения; операторы рождения и уничтожения 21
2.2. Унитарно неэквивалентные представления 24
2.3. Пространство Фока 25
2.4. Некоторые примеры унитарно неэквивалентных представлений 31
2.5. Представление физических частиц и динамическое отображение 39
2.6. Свободные поля для физических частиц 47
Литература 61
Глава 3. Представление физических частиц, S-матрица и составные 62
частицы
3.1. (N, 0)-модель 62
3.2. Представление физических частиц и вычисления по теории 83
возмущений
3.3. Представление физических частиц и вариационный принцип 89
3.4. Общий анализ представления физических частиц 90
3.5. Формула редукции и формула Лемана—Симанзика—Циммермана 96
(ЛСЦ)
3.6. Спектральные представления двухточечных функций 100
Литература 104
Глава 4. Квантовая теория поля при конечных температурах 106
4.1. Термополевая динамика 106
4.2. Динамическое отображение при конечных температурах, правило 122
подстановки тильды и соотношение Кубо—Мартина—Швингера
4.3. Спектральное представление двухточечных функций 131
4.4. Уравнение Бете—Солпитера при конечных температурах 136
Литература 137
Глава 5. Некоторые примеры вычислений в рамках термополевой 138
динамики
5.1. Электрон-фононная система 138
5.2. Модель контактного взаимодействия в ферромагнетизме
коллективизированных электронов 142
5.3. Модель Гейзенберга в ферромагнетизме локализованных спинов 148
5.4. Сверхпроводимость 159
5.5. Плазменные колебания в нормальных металлах 186
Литература 191
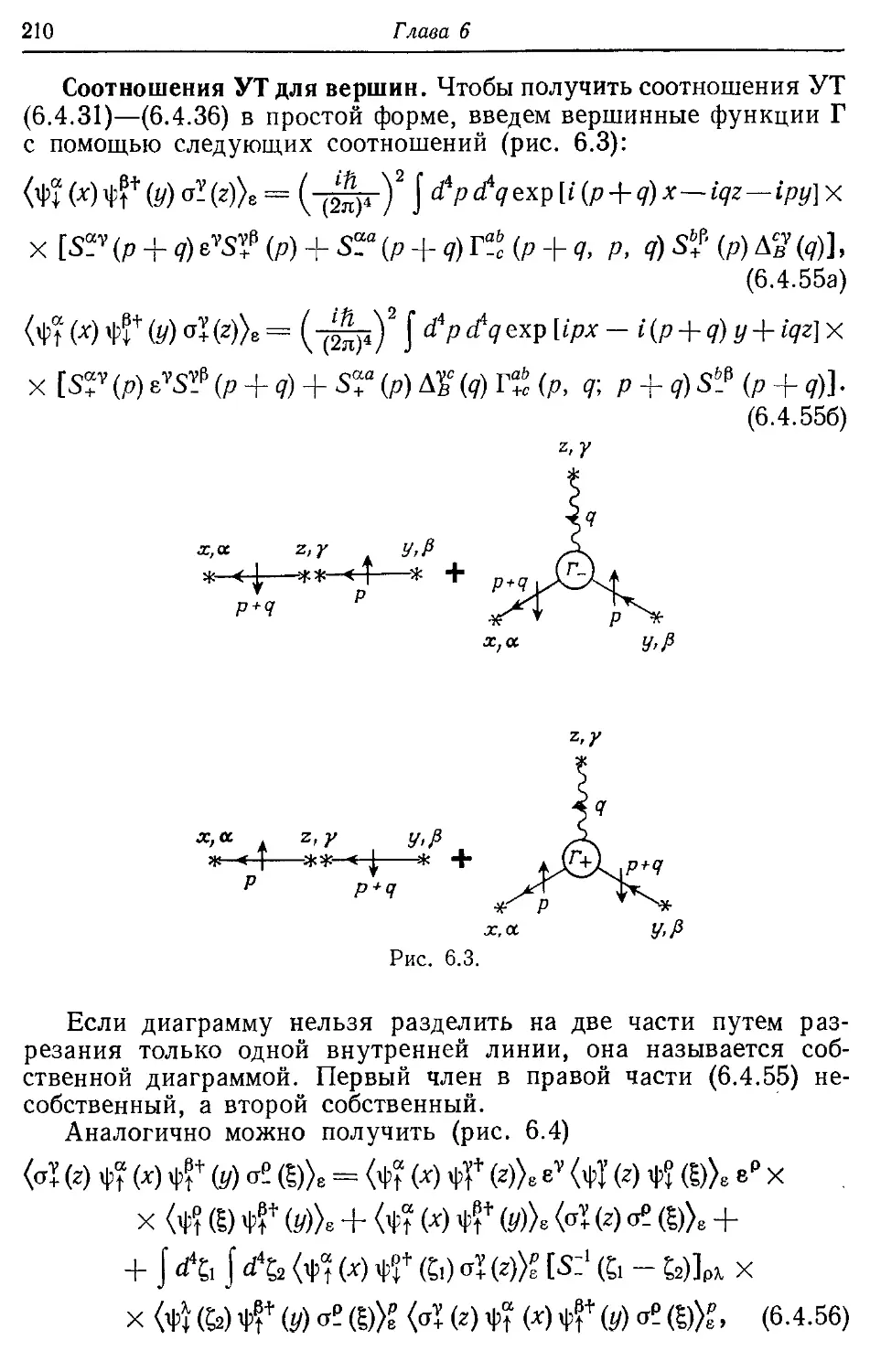
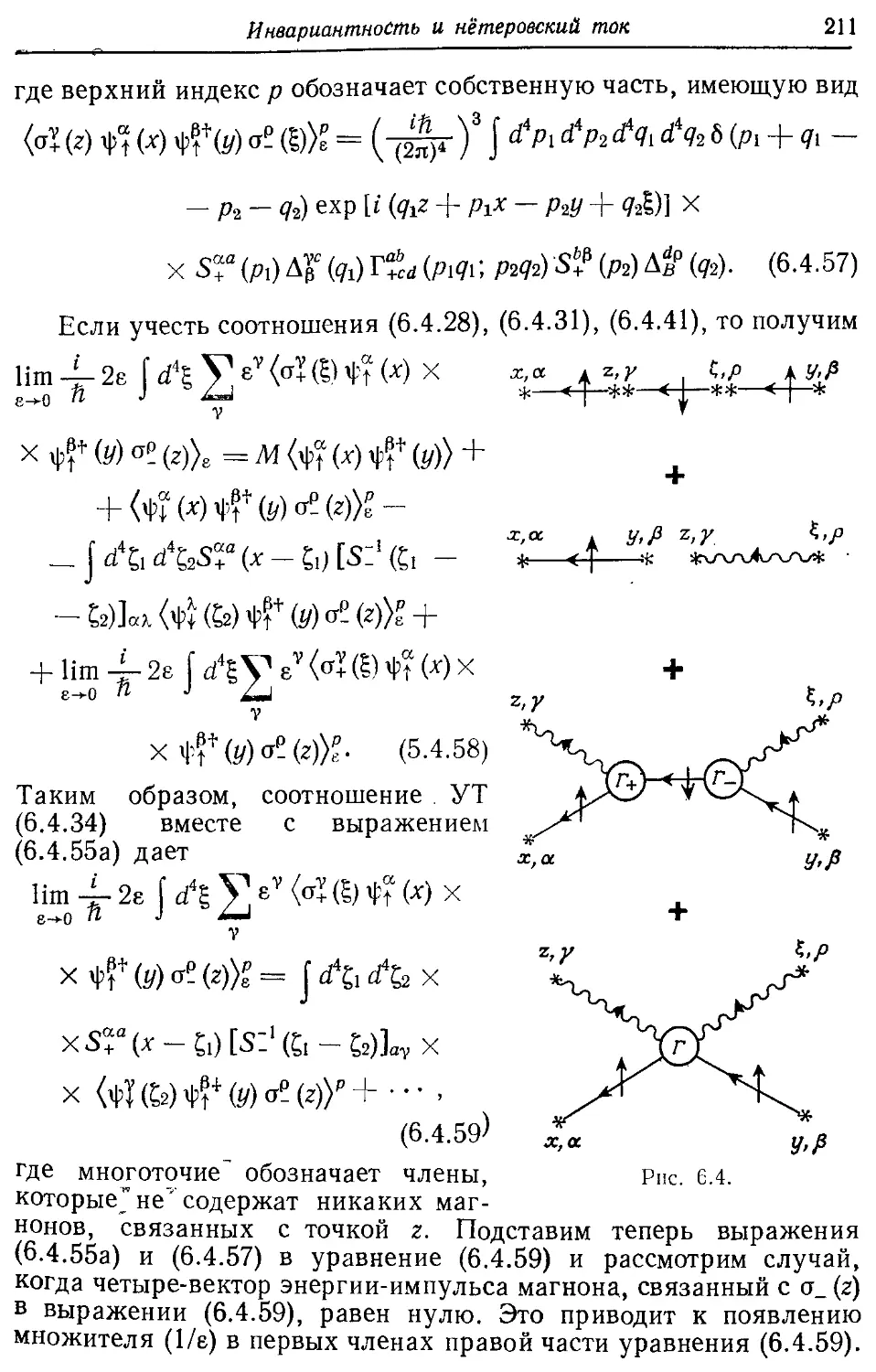
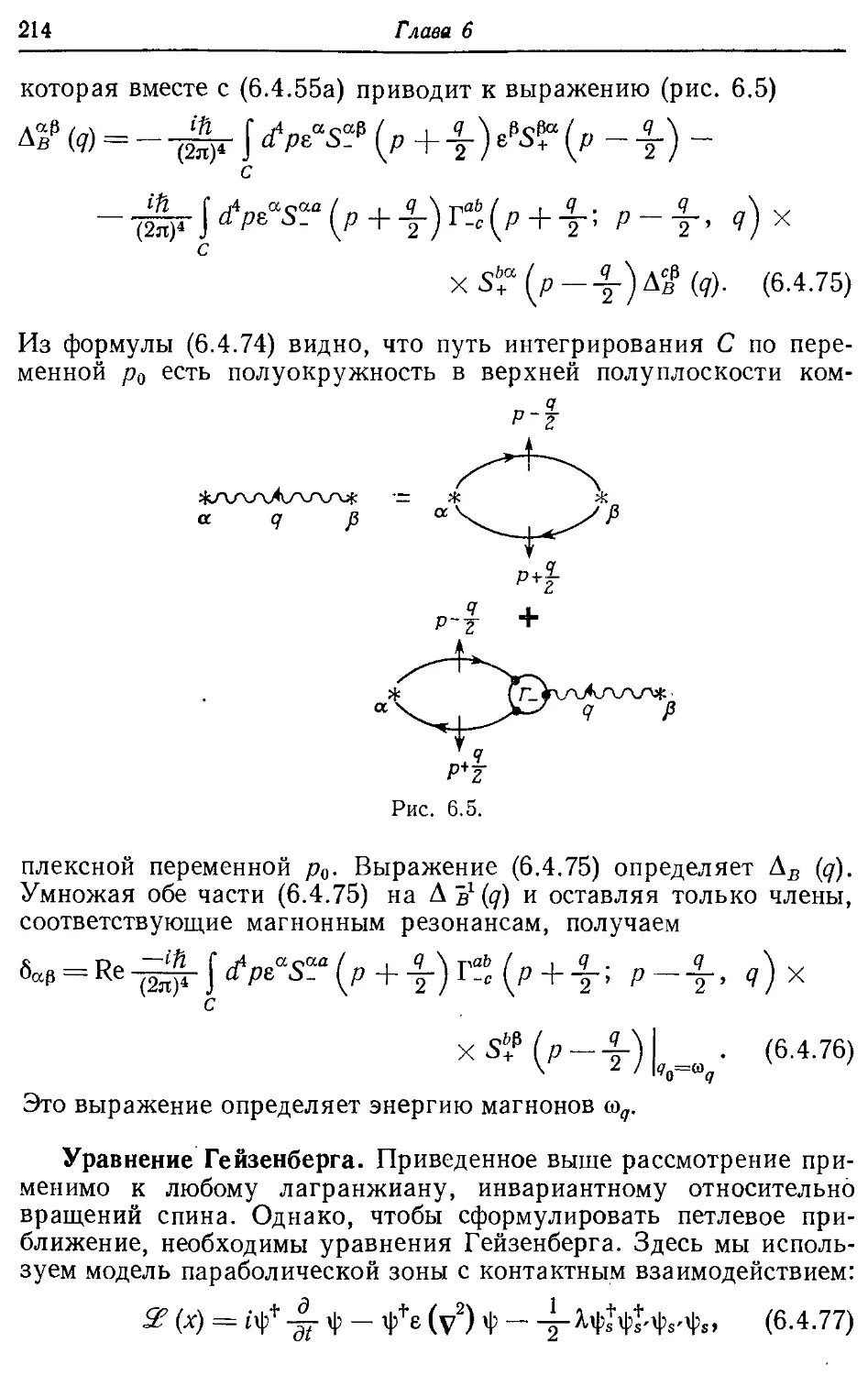
Глава 6. Инвариантность и нётеровский ток 192
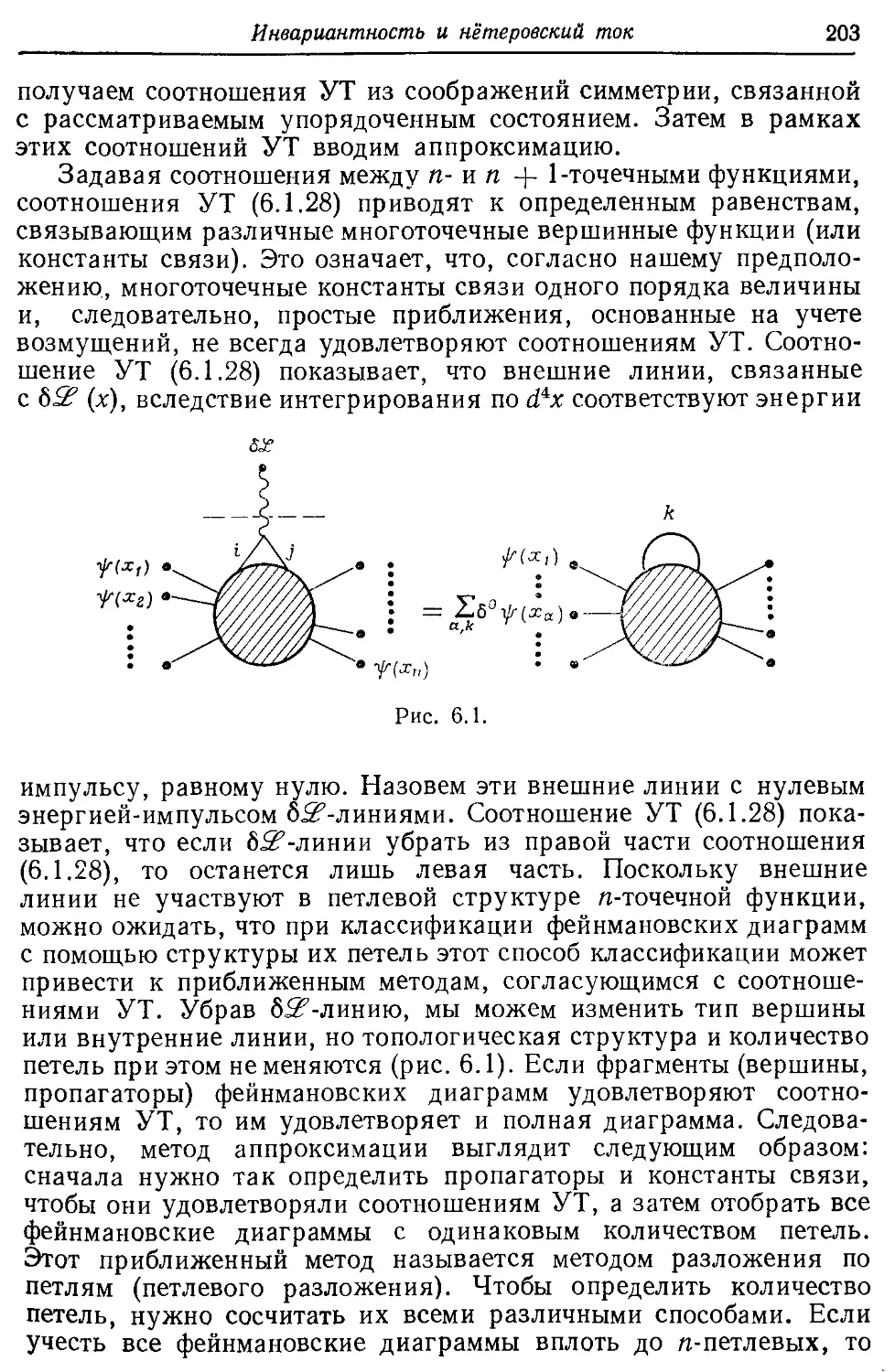
6.1. Нётеровский ток и соотношения У орда—Такахаши 192
6.2. Соотношения Уорда—Такахаши при конечных температурах 198
6.3. Простой пример соотношения Уорда—Такахаши 199
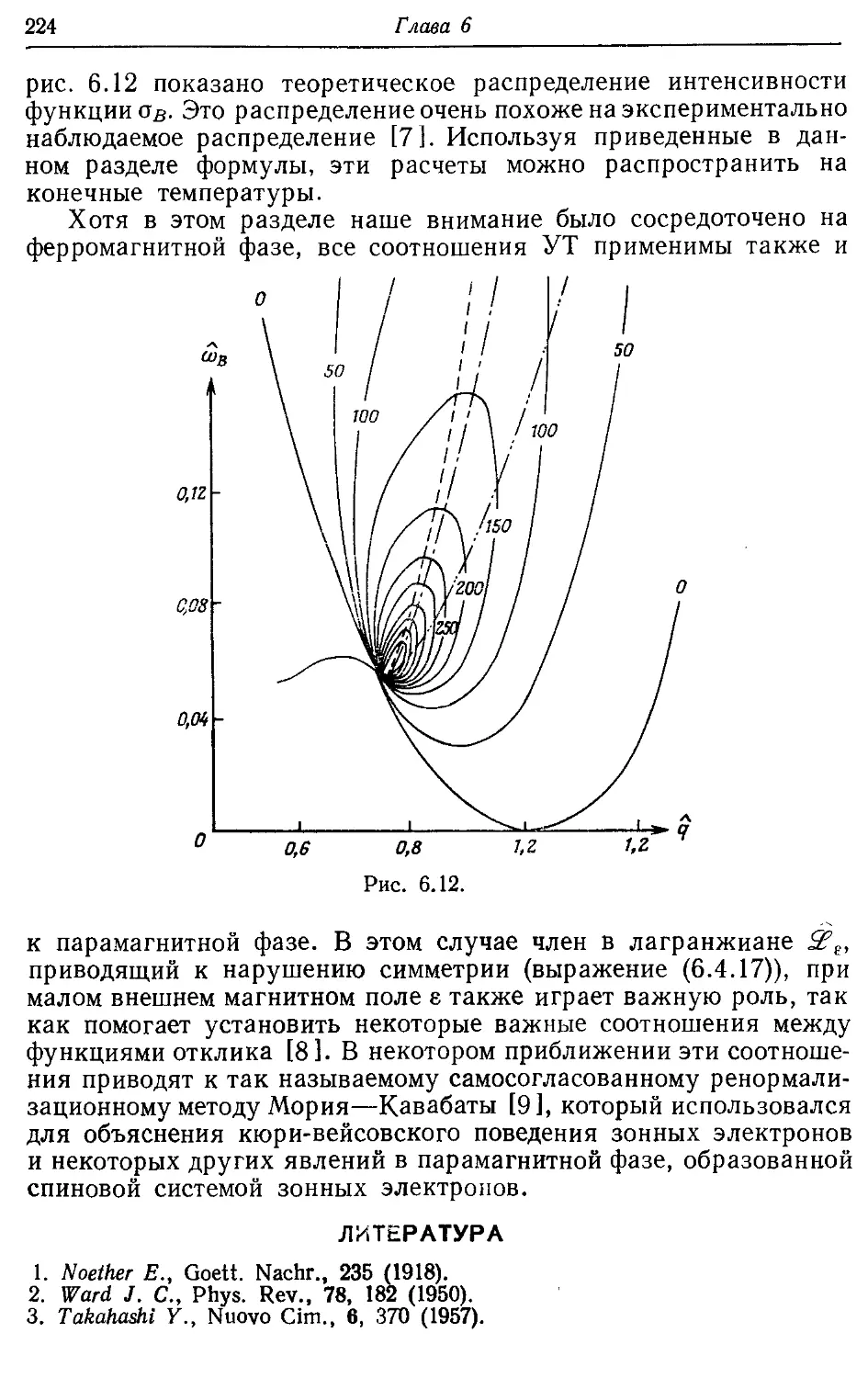
6.4. Пример петлевого разложения; ферромагнетизм зонных электронов 202
Литература 224
Глава 7. Динамическая перестройка симметрии и динамическое 226
отображение
7.1. Общее рассмотрение 226
7.2. Фазовая симметрия 240
7.3. Динамическая перестройка спиновой симметрии 243
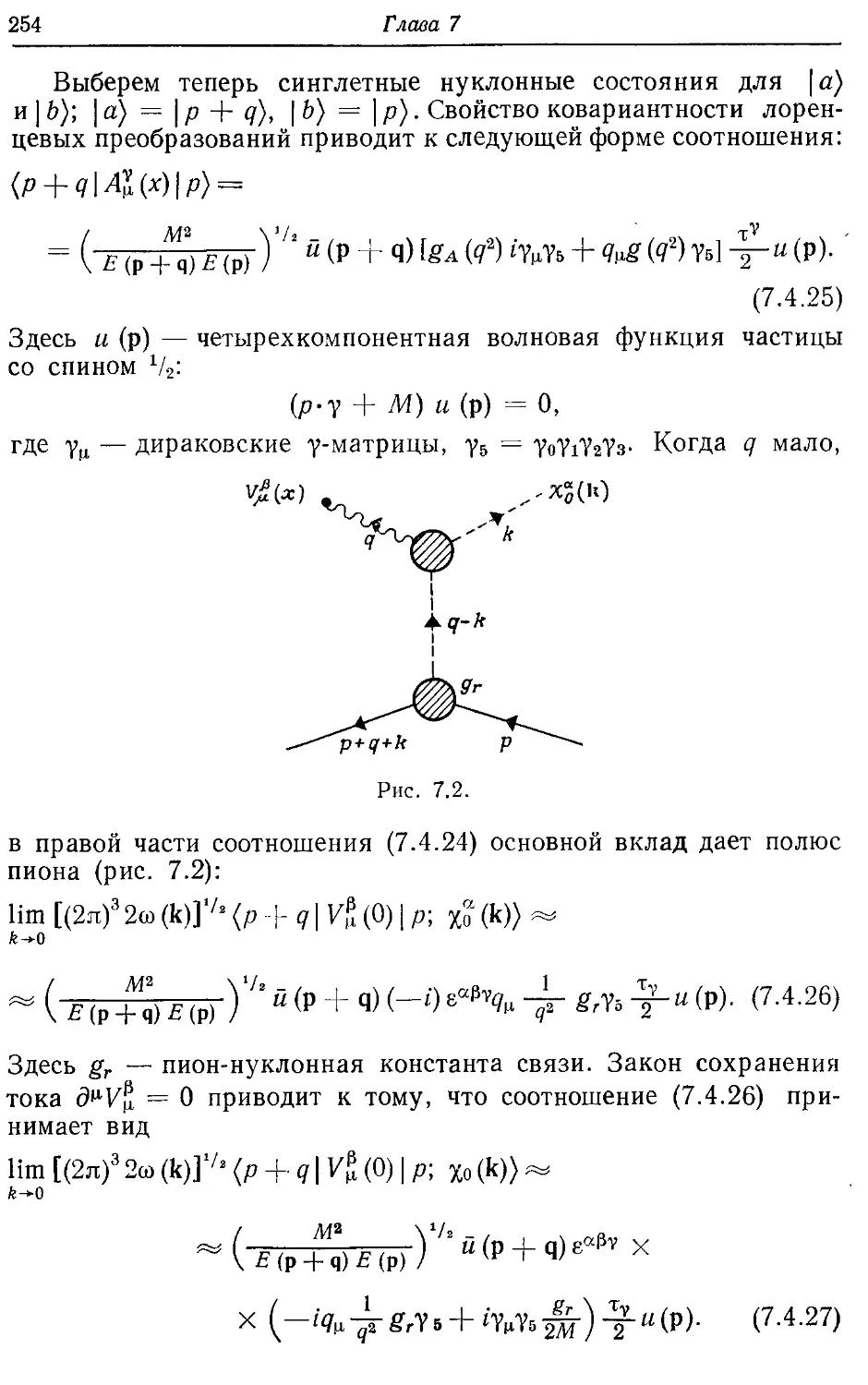
7.4. Перестройка симметрии и теоремы для низких энергий 249
7.5. Перестройка симметрии и сжатие группы 257
7.6. Инфракрасный эффект голдстоуновских бозонов и параметр порядка 262
7.7. Кристаллы 264
Литература 278
Глава 8. Квантовая электродинамика твердых тел. I. Перестройка 288
калибровочной симметрии и динамическое отображение
8.1. Сверхпроводимость 288
8.2. Квантовая электродинамика нормальных металлов 298
Литература 309
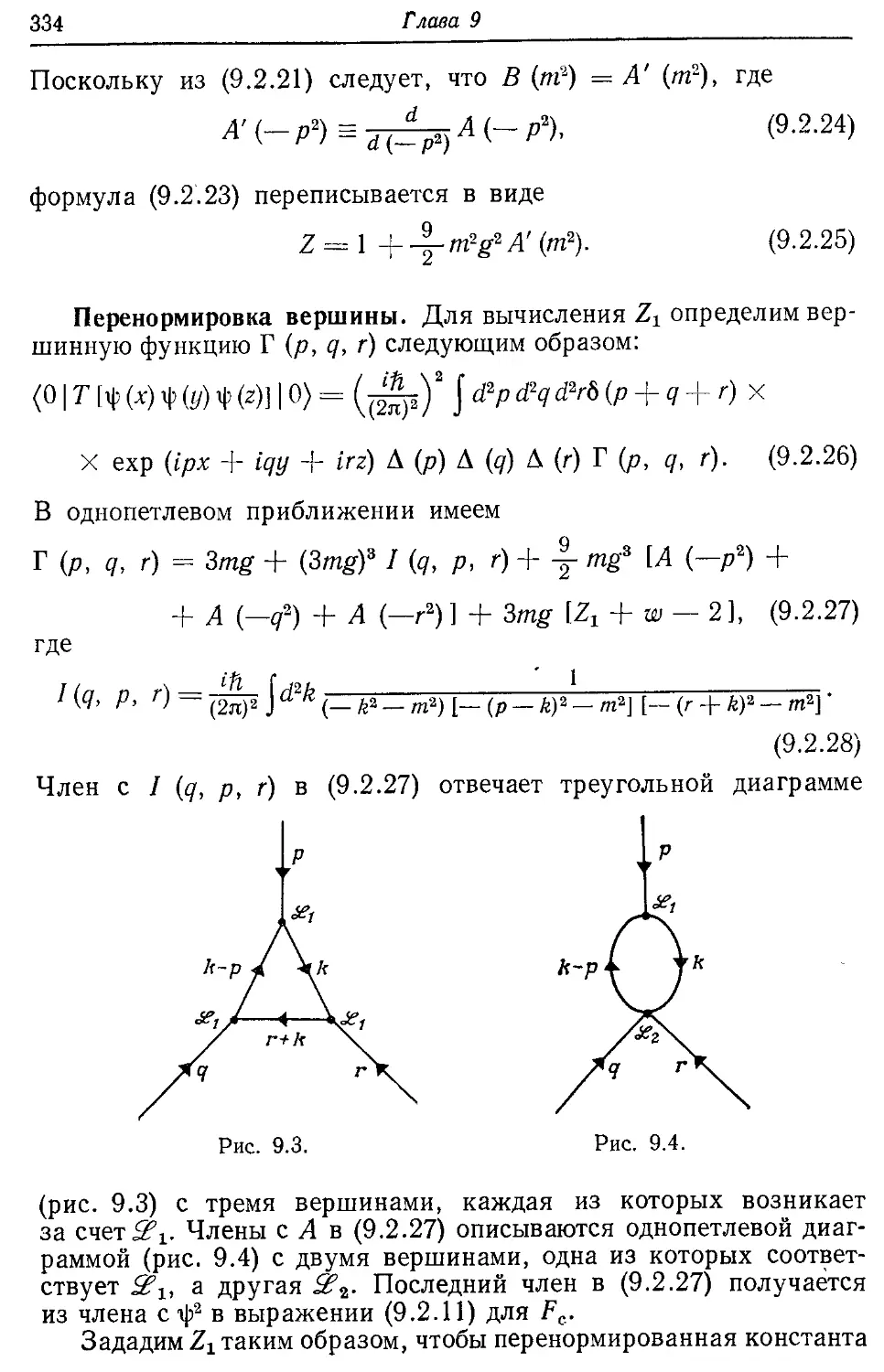
Глава 9. Протяженные объекты квантовой природы 310
9.1. Простое рассмотрение 310
9.2. Простой пример 329
9.3. Общее рассмотрение бозонного преобразования 340
9.4. Асимптотическое условие и асимптотический гамильтониан 348
9.5. (сф-превращение и обобщенная координата 358
Литература 372
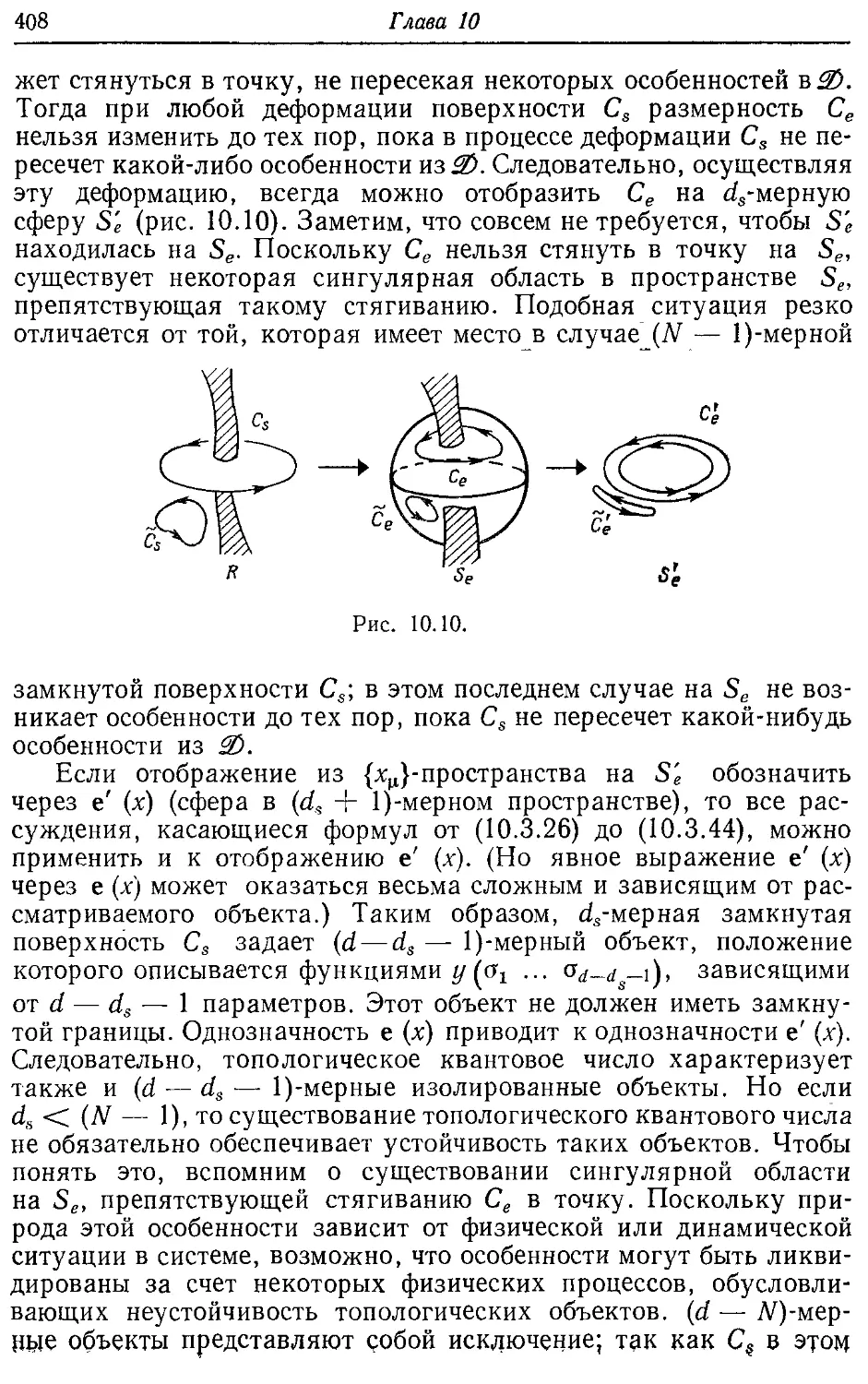
Глава 10. Протяженные объекты с топологическими особенностями 374
10.1. Общие соображения 374
10.2. Протяженные объекты в кристаллах 385
10.3. Топологические особенности, связанные с неабелевыми группами 398
симметрии
Литература 419
Глава 11. Квантовая электродинамика твердых тел. П. 420
Макроскопические явления
11.1. Вывод классического уравнения Максвелла 420
11.2. Проводимость и диэлектрическая проницаемость. 425
11.3. Сверхпроводимость 429
11.4. Магнитные сверхпроводники 457
Литература 470
Глава 12. Явления, связанные с граничной поверхностью 473
12.1. Введение 473
12.2. Звуковые волны на поверхности кристалла 474
12.3. Эффект Джозефсона 479
12.4. Поверхностное магнитное поле в сверхпроводниках 487
Литература 493
Глава 13. Заключительные замечания 494
Предметный указатель 497
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Адиабатический множитель 84 однородное 79
Адлера теорема 249 при конечных температурах
Андерсона — Сула механизм 459 136, 137
Андерсона — Хиггса — Киббла БКШ модель 159
механизм 181 Елоховская стенка в магнитных
Анизотропные сверхпроводники 455 сверхпроводниках 464
Асимптотическое поле 366 Елоховский член в намагниченности
— условие 75, 349 159
Бете — Солпитера амплитуда 78 Боголюбова преобразование для
уравнение 78, 139 бозонов 32, 37, 44
для магнона 145 фермионов 36, 44
(N, 0)-модели 78, 81 с учетом влияния термостата
сверхпроводящего 107, 108, 110, 115, 124
электрона 161 Бозонное поле, сдвиг (трансляция)
составной частицы 80 37, 38, 45, 241, 247, 249, 312,
фазона 165, 171 341
неоднородное 81 — преобразование 312, 342, 420
в квантовой электродинамике
422
для фононов 384, 386
параметры 414
при наличии топологических
особенностей 374, 383, 399, 414,
473
теорема 312, 340, 341 Бозоны
22
— конденсация 38, 239, 310, 329, 343,
376, 386
— характеристическая функция 183,
435
Брауера степень 407
Бриллюэна функция 153, 462
Бъянки тождество 402
Бюргерса вектор 384, 389, 391, 393
Вакансия в решетке 398 Вакуум 25,
28,39
— зависящий от температуры 108
— устойчивость 77, 95
Ван Хова модель 4
Вершинная функция 100
Вигнеровское вращение 360, 365, 370
Вихри в сверхпроводниках 439
взаимодействие 441, 445
инверсия магнитного поля
465
спонтанное образование 466
электроны сердцевины 343,
447
энергия сердцевины 449,
465
Внутреннее произведение векторов
состояния 26
волновых функций 51
Возвратная сверхпроводимость 459
Волновой пакет 21, 28, 88, 247
Входящие поля 9, 76, 93
Выходящие поля 76, 93
Гамильтониан в слабом смысле 354,
355
— для гейзенберговских полей 41, 42
модели Ван Хова 44
Гейзенберга 148, 149, 153
физических частиц 40
— при наличии протяженных
объектов 354, 355
— термостата 107
Гейзенберга модель для
локализованных спинов 148
—уравнение 41, 45
в термополевой динамике 113,
123
для коллективизированных
электронов 142, 143, 215
модели БКШ 160, 161
Гейзенберга 150, 154
Ли 82
(N, 0)-модели 62
электромагнитного поля см.
Гейзенберговские поля 9, 41
Гельмгольца свободная энергия 113
в модели БКШ 185
Гиббса термодинамический
потенциал в магнитных
сверхпроводниках 465
смешанного состояния 450
Гильбертово пространство,
сепарабельное 24, 27
Глубина проникновения 490
лондоновская 181, 435
Голдбергера — Треймана
соотношение 253, 255
Голдстоуна теорема 10, 143, 230, 238
Голдстоуновские бозоны 10, 14, 143,
176, 230, 239, 241, 249, 284, 420
инфракрасные 262
комплексные 261
— квантовые состояния 473
Голдстоуновского типа модель 241
Горькова уравнения 437
Границы зерен 390
плоские 394
соотношение непрерывности
394
типа кручения 393
наклона 393
Дайсона теорема 249
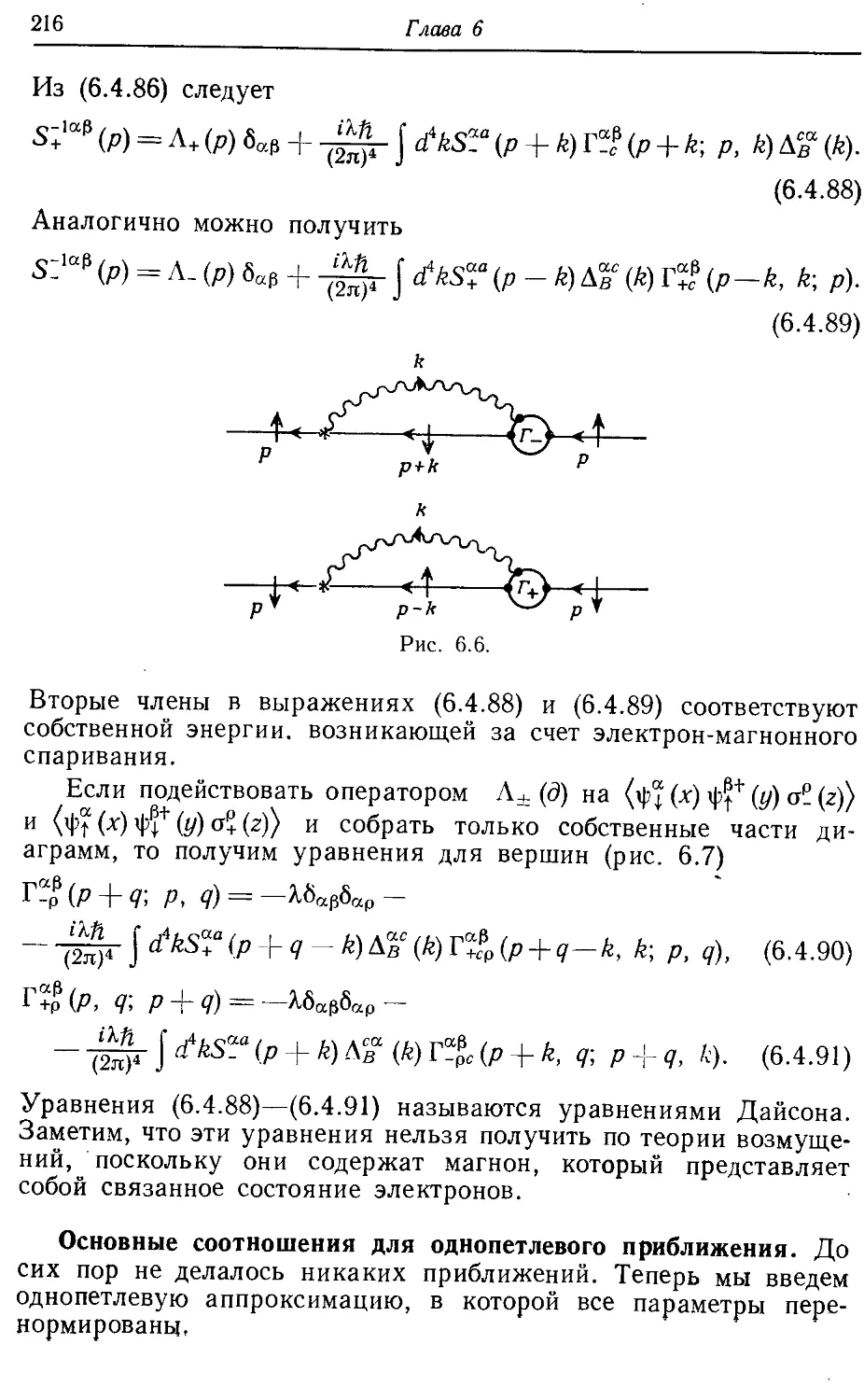
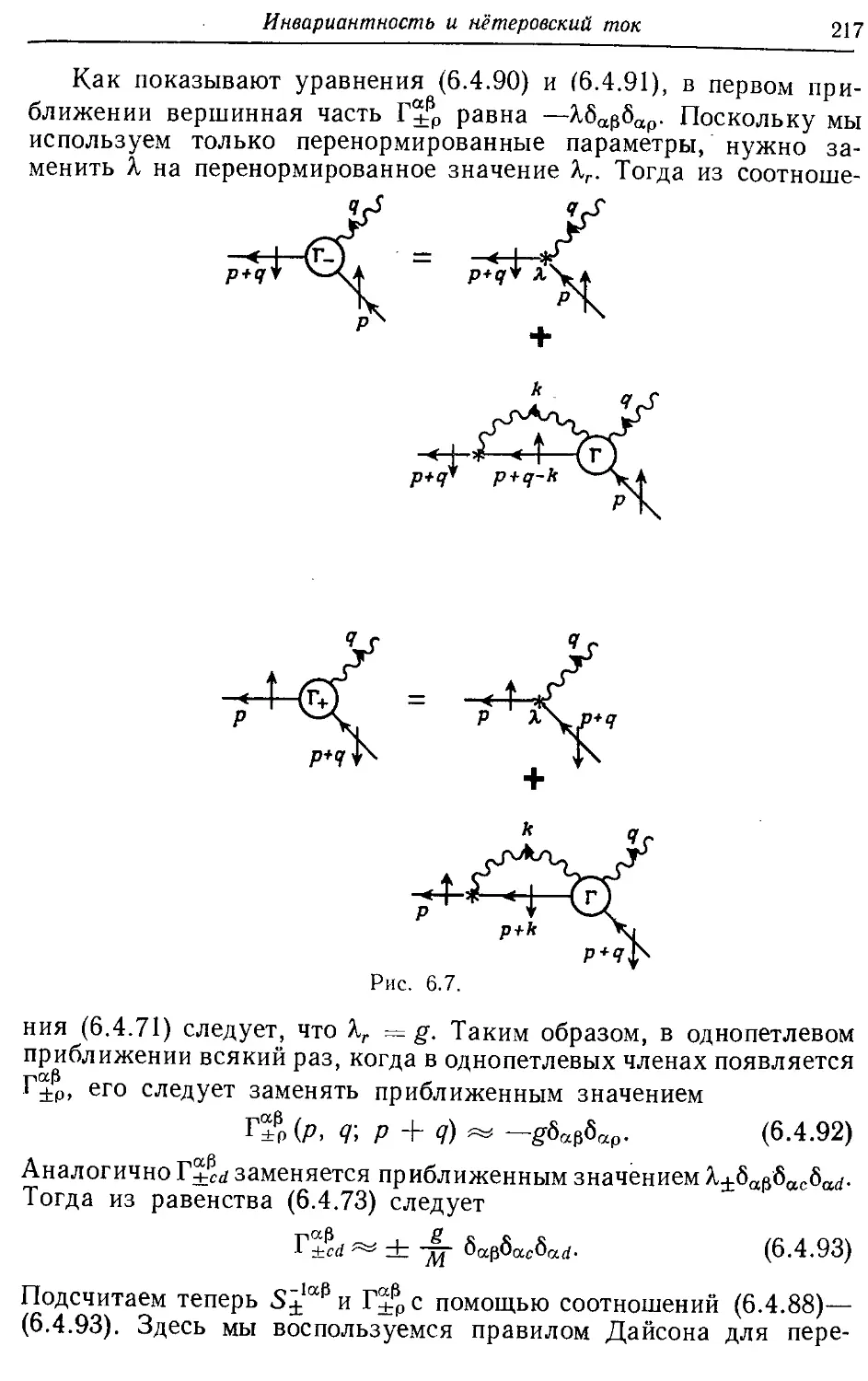
— уравнение 216
Дайсоновский член в
намагниченности 159
Двумерная особенность 381
осциллирующая 474
сферическая 396
Двухточечные функции 100, 144, 187,
201
для магнона 158, 207, 213, 221
плазмона 289
плотности заряда 174, 187
тока 187
фазона210
правила умножения 121
при конечных температурах
114—116, 120, 131, 134
спектральное представление
101,131
Деформация группы 257
Джозефсона эффект 479
периодическая конфигурация в
контакте 282
Дивизор 49, 56
— для плазмонов 289
Динамическая матрица колебаний
решетки 271
— перестройка симметрии 11, 226,
237, 257
в кристаллах 274
калибровочной 292, 302
О(пJ61
спиновой 143,243
SUB) 246, 247
SUB)xSUB) 261
SU(nJ61
трансляционной 324
фазовой 177, 178, 241
Динамическое отображение 9, 46, 90,
227, 338
в кристаллах 274
случае бозонного
преобразования 313
нормального металла 302,
421
сверхпроводника 176,
178, 242, 291, 293
термополевой динамике 124,
130
для модели голдстоуновского
типа 242
(N, 0)-модели 63, 71
спиновых операторов 155
Дисклинация 394
Дислокация 388
— винтовая 389
— краевая 389
Диэлектрическая проницаемость 427,
428
тензор 426
Длина когерентности 183
Древесное приближение 316 «Духи»
282, 300, 420
Звуковые волны на поверхности
кристалла 474
поля смещений 475
Импульса оператор для физических
частиц 41, 47
с учетом влияния
термостата 107
Индефинитная метрика 283
Инстантон 414
— Полякова 418
— т'Хофта 418
Калибровка 399
— кулоновская 438, 479
Калибровочная инвариантность 186
Калибровочное преобразование 182,
197, 280, 298
матрица 400, 418
— условие 286, 299
Калибровочные поля 416
теория 416
Квант потока 440
Квантование потока 383, 424, 440
в джозефсоновских контактах
485
магнитных
сверхпроводниках 465
Квантовая координата 320, 344, 348,
357
Квантовомеханические объекты 329,
366
Киральная SU B)xSU B)-симметрия
253
Классические объекты 329, 366
Когерентное представление 343
— состояние 38, 312
Коллективная мода 10
Константы перенормировки 335
Координатное пространство и
пространство симметрии,
взаимное соответствие 420
Критическая температура
сверхпроводников 164
Критические значения хд 445
Кубо — Мартина — Швингера
соотношение 128
Кулоновская калибровка 438, 479
Кюри закон 463
Кюри-вейсовское поведение зонных
электронов 224
Ламе коэффициент 387
Немана — Симанзика —
Циммермана формула 99
в компактной форме 99
при конечных
температурах 128
Ли модель 82
Лоренцева «поворота» оператор 355,
357
Магнетизм и сверхпроводимость,
взаимность влияние 458
Магнитные примеси в
сверхпроводниках 458
Абрикосова — Горъкова
теория 459
— сверхпроводники 457
антиферромагнитный порядок
460
дипольное взаимодействие 458
обменное взаимодействие 458
экранировка 463
спин-периодическая фаза 464
фазовая диаграмма 467
энергетическая щель 468
Магноны 143, 145, 148, 157, 208, 209
—энергетический спектр 158, 214,
220
Маки параметры 452
Максвелла уравнение, классическое
423, 425, 461
Максвелловского типа уравнение 423
в сверхпроводниках 429,
433, 436, 438, 440, 479
анизотропных 456
магнитных 461
Матрица приведения к эрмитову виду
50
Мацубары формализм для
температурных функций Грина
11
Мейсснеровский ток 425
Мейсснеровское состояние 443
Минимальное взаимодействие 421
Модули упругости 277
Модуль сдвига 387
Монополь 398, 410, 413
Марии — Кавабаты метод 224
Намагниченность в системе
коллективизированных
электронов 144, 220
локализованных спинов 152.
159
приближение среднего
поля 153,462
Намагничивания кривая в магнитных
сверхпроводниках 466
сверхпроводниках П/1 рода
445,451
Нейтронов рассеяние на спиновых
волнах 209
Нётеровский генератор 194, 229
— ток 194, 197
Низких энергий теоремы 249
для магнонов 248, 249, 251
пионов 249, 252
и низкие температуры 256
Нормальное произведение 46
(N, 0)-модель 62
[0]-множество 25
Обобщенные координаты 325, 358,
369
Оптические моды 278
Особенности типа расходимости 347,
374
— топологические 347, 374
Параметр порядка 262, 400
в сверхпроводниках 242, 432
условие однозначности 402
Парастатистика 22
Перенормировка вакуумного
среднего 335
— вершины 334
— волновой функции 333
— константы связи 219
— химического потенциала 142, 143,
159,220
— энергии 141, 160, 162, 332
Перестройка симметрии см.
Динамическая перестройка
симметрии
Петлевое разложение 202
Плазменные колебания 181, 186
уравнения 190, 287, 424
энергия 181, 190
Плазмой 181, 186, 190, 286, 420
Плотное множество 27
Поверхностная сверхпроводимость
468, 492
Поверхностное магнитное поле в
сверхпроводниках 487, 491
Поверхностные волны 15
— фононы 478
Подгруппа устойчивости 244, 259
Подстановка для физических полей
227
Полярон 141
Правило сумм 56, 58
Представление взаимодействия 84
Причинность 58, 59
Пространственный сдвиг 47
Редукции формула 98
РККИ механизм 459
Рождения и уничтожения бозонов
операторы 22
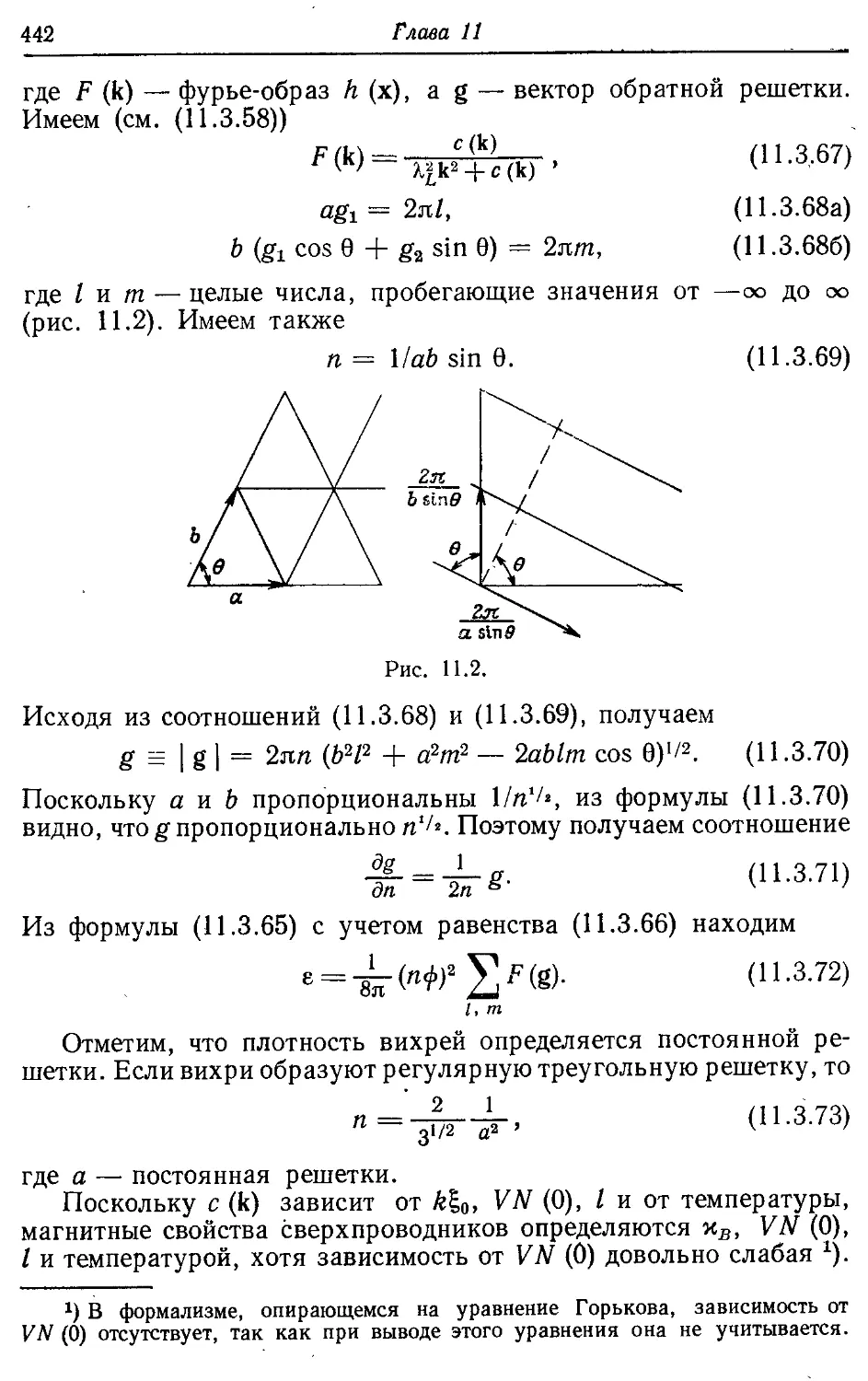
волновых пакетов
операторы 29
операторы, проектирование
60
фермионов операторы 23
физических частиц
операторы 47
Рэлеевская волна 15, 478
Самосогласованные вычисления 43,
63,73
Самосогласованный метод 42
— потенциал 14, 316, 317, 337, 343,
375
вихрей в сверхпроводниках 446
двумерной особенности 478
поверхность кристалла 473
Сверхпроводники 54, 280 см. также
Анизотропные
сверхпроводники, Магнитные
сверхпроводники
— бесконечная проводимость 429
— влияние кулоновского
взаимодействия 179
— I рода 443
— II рода 444
затухание ультразвука 447
—11/1 рода 444
— II/2 рода 444
Свободное движение двух вихрей
372
протяженных объектов 366, 381
Связывающие поля 76, 93, 241
Сжатие группы 247, 257
Синус-Гордона модель 340
Синусоидальное спиновое
упорядочение 347
Слабые соотношения 42 S-матрица
76, 88, 93, 99
Смешанное состояние 443, 464
Собственная энергия 140, 141
коллективизированных
электронов 215
фотона 186, 295, 305, 433
Солитон 15, 337
Составная частица 43, 71, 73, 76, 82
Спектральное представление 100,
169, 207
двухточечных функций 101,
131,201,207,212
неприводимой части
собственной энергии 140
при конечных температурах
131
Спиновая симметрия 204
Спин-периодическая фаза 464, 470
Спиральные спиновые структуры 347
Спонтанное нарушение симметрии
10, 11, 230 см. также
Динамическая перестройка
симметрии
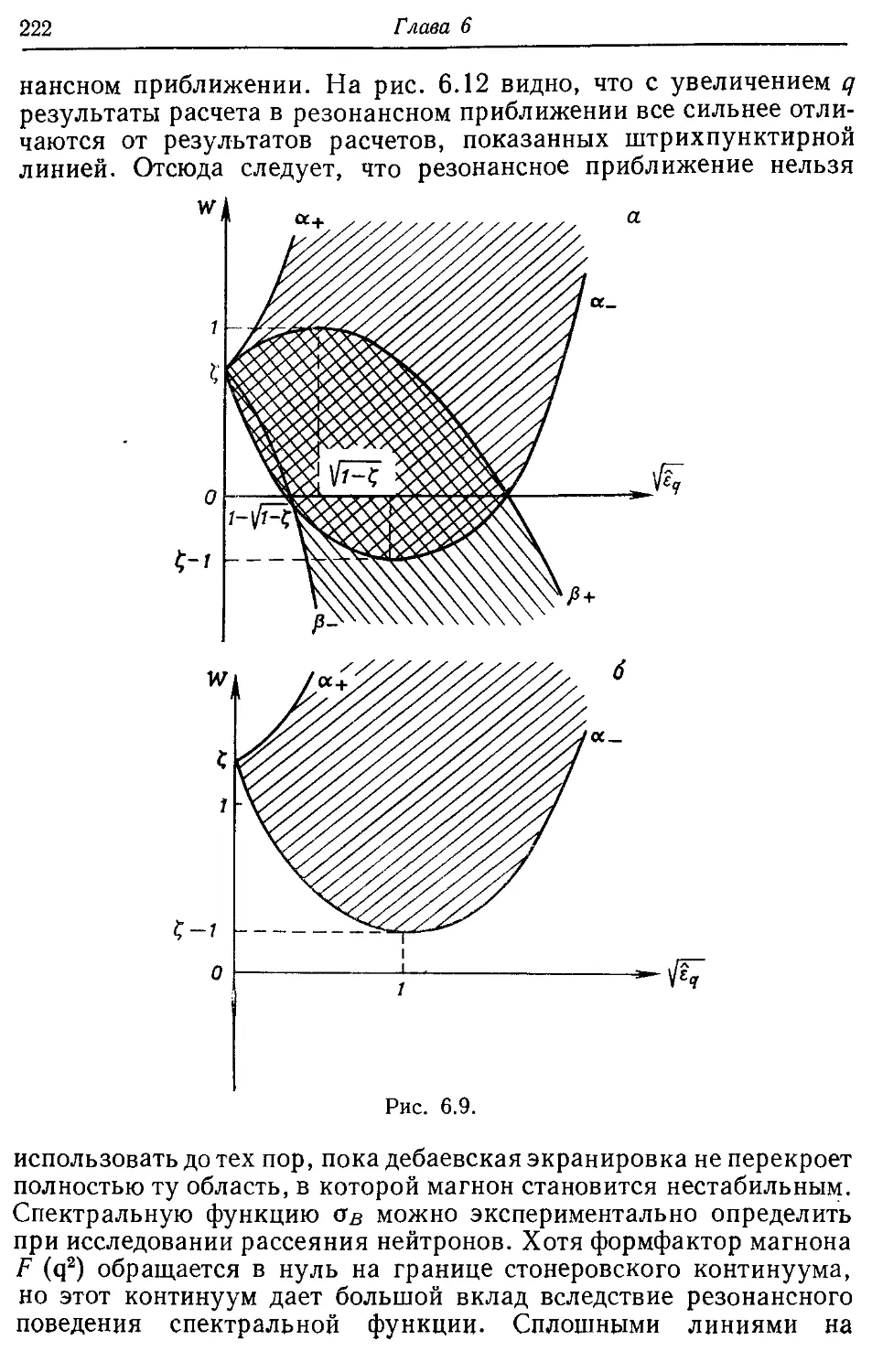
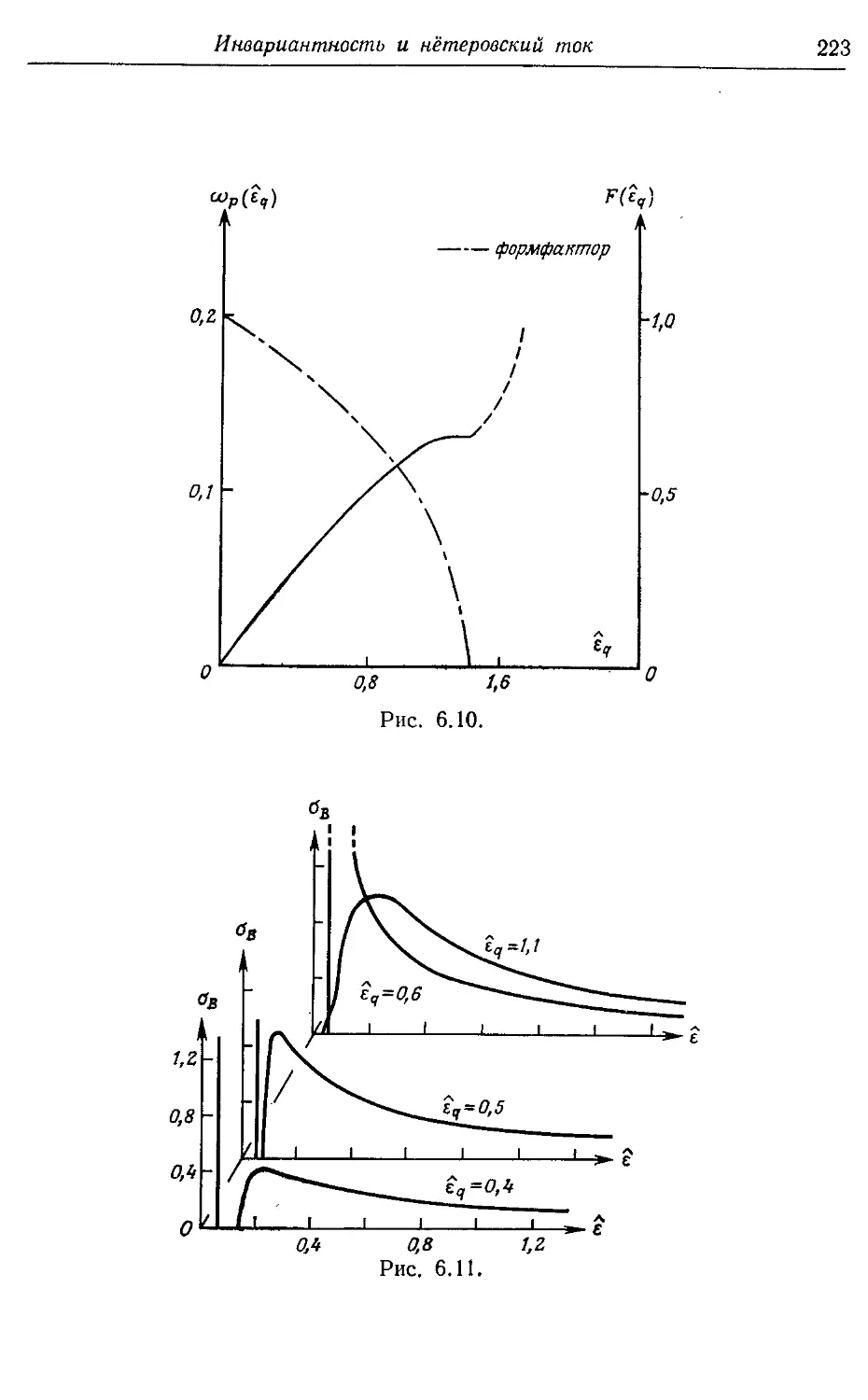
Стонеровский континуум 221, 222
s—f-взаимодействие 463, 470
— в магнитных сверхпроводниках
459
Термополевая динамика 11, 110
Термополевой дублет 115, 120, 123,
124, 139, 144, 145, 150,1160, 205
Термостат 106, 107
Тильда операция ПО
правило подстановки 127, 132
Тонкие пленки, сверхпроводимость
492
Топологические квантовые числа
382, 383, 398, 406, 410, 424
— особенности 13, 347, 374, 375, 377
двумерные 381
кольцевые 380
линейные 378
полное условие 377, 379
Топологический заряд 376, 391
— объект 13
с неабелевой симметрией 398
Точечная группа 268
Точечные дефекты 396
Трансляционная мода 320, 344
Тройные редкоземельные соединения
459
Унитарно неэквивалентные
представления 24, 31, 35, 37, 38
У орда — Такахаши соотношения 43,
192, 195, 198, 228, 232
для спиновой симметрии
205, 206, 212
фазовой симметрии 200
компактная записи 196
обобщение 197
при конечных температурах
198
Упорядочения оператор в
термополевой динамике 154,
160, 187
Упорядоченные состояния 10, 11, 14,
143,163,227,239,310
Упругие постоянные 277
Уравнение для щели в
сверхпроводниках 163
обобщение 173
Уравнения свободного поля для
физических полей 48
и статистика 59
типа 1 48, 53, 58, 59, 104
типа 2 48, 53, 56, 59, 103
Условие свободной поверхности 395
Фазовое преобразование в модели
голдстоуневского типа 241
Ли 82
нормальных металлах 298
(N, 0)-модели 64, 70, 71
сверхпроводниках 242, 280,
284
Фазон 177, 181,241,285
— энергия 182
Фермионы, определение 22
Ферромагнетизм
коллективизированных
электронов 142, 204
Физические кванты 9, 39
— поля 9, 47
— состояния 283, 300
— частицы 9, 39, 45, 47
представления 39, 42, 46, 90,
102
в (N, 0)-модели 74
теории возмущений 83,
85
и вариационный принцип 89
при конечных температурах
109
Фока пространство 27, 63
расширенное 325, 351
Фононы 138, 266, 280
— акустические 268, 278
— оптические 278
— уравнение 268, 270, 276
Франка формула для болынеугловых
границ зерен 393
Фраунгоферова дифракция для
джозефсоновского тока 486
Химический потенциал 113, 149, 220
затравочный 159
перенормировка 142, 143, 159,
220
Цепочечное приближение 146, 161,
166,433,437
(с,я)-превращения 358, 364
Числа заполнения оператор 22, 24,
109
Чисто калибровочная теория 416
Энергетическая щель в
сверхпроводниках 162
магнитных 468
Энергия конденсации 184, 443
— основного состояния в
термополевой динамике 113
— протяженных объектов 344
— сердцевины вихря 448
в магнитных
сверхпроводниках 465
Энтропия 113, 185
Янга — Миллса теория 416
Янга — Фельдмана уравнение 311
ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
«Термополевая динамика и конденсированные состояния» —
не стандартная книга по квантовой теории твердого тела. Если
ее просмотреть, не вникая в содержание, то может показаться,
что главное внимание в ней сосредоточено не на физическом смысле,
а на математическом выводе формул физики конденсированного
состояния. Действительно, формул, уравнений, соотношений не-
привычно много. Однако нестандартность книги не в этом.
Подход авторов резко отличается от того, к которому мы при-
выкли. Понимание атомной структуры вещества и главное то
обстоятельство, что движение структурных единиц материн
(электронов, атомов, молекул) подчиняется законам квантовой
механики, предельным случаем которой является классическая
механика, не ликвидирует определенной эклектичности, обычно
имеющей место при описании твердых тел. Наряду с микроскопи-
ческими степенями свободы (которые требуют квантовомеханиче-
ского описания) феноменологически вводятся макроскопические
объекты, априорно описываемые на языке классической механики.
Переход от микро- к макроописанию, как правило, остается «за
кадром».
Умэдзава, Мацумото и Татики — известные специалисты по
квантовой теории поля — сделали попытку построить после-
довательную теорию, последовательную в том смысле, что по-
строение исходит только из существования квантовых частиц,
а макроскопические объекты (в частности, имеющие топологиче-
ские особенности: вихри в Не-П, в сверхпроводниках, дислокации,
границы кристаллитов и кристалла и т. п.) возникают как ре-
зультат спонтанного нарушения симметрии и конденсации голд-
стоуновских бозонов.
Такой подход требует разработки специальной теоретической
техники. Этому и посвящена большая часть книги. Отметим, что
термин «термополевая динамика» введен авторами (он подробно
разъяснен в гл. 4).
Новое изложение квантовой теории твердого тела, добиваясь
большой логичности, теряет в наглядности. И к этому нужно Сыть
готовым при чтении книги. Более того, изложение специально
формализовано. Главное внимание уделено не вьшоду конкретных
Предисловие редактора перевода
соотношений (составляющих содержание большинства имеющихся
учебников и монографий по квантовой теории твердого тела),
а формальным возможностям, содержащимся в квантовополевом
описании. Ударение сделано не на том, как описать, а на том,
как должно строиться описание: чтобы существовал тот или
другой объект, описывающие его уравнения должны иметь те
или иные свойства. Книга несомненно будет полезна физикам-
теоретикам, интересы которых сосредоточены на решении глу-
боких задач теории многих частиц, в каких бы конкретных усло-
виях эти частицы ни существовали. В этом смысле претензии ав-
торов, выраженные в их предисловии, а также в гл. 1 и 13, не
чрезмерны, хотя всякое обобщение, естественно, требует решения
новых и, возможно, весьма сложных задач.
Строгая — в смысле использования математического аппа-
рата — «Термополевая динамика» написана сравнительно свобод-
ным языком, употребляемымТна*семинарах"и|конференциях. Для
одного и того же понятия авторы часто используют разные тер-
мины, не по всей книге принята одна и та же система единиц.
Стремясь сохранить стиль книги, мы не вносили изменений, на-
деясь, что это не помешает читателю разобраться в содержании
оригинальной и нестандартной монографии.
Перевод выполнили: К. И. Кугель (гл. 9—11), Т. Ю. Ли- ¦
совская (гл. 6—8 и 12, 13) и Ю. Г. Рудой (предисловие
и гл. 1—5).
М. И. Каганов
ПРЕДИСЛОВИЕ
В этой книге дается формулировка квантовой теории поля при
конечных температурах, позволяющая описывать упорядоченные
состояния систем многих тел, в которых может возникать много
протяженных топологических объектов разного типа, взаимодей-
ствующих с квантами. В этом формализме с единой точки зрения
описываются классические, квантовомеханические и квантово-
полевые объекты; это достигается благодаря последовательной
схеме описания макроскопических объектов, сосуществующих
с квантами. В настоящее время системы, в которых сосуществуют
микроскопические и макроскопические объекты, привлекают боль-
шое внимание физиков, работающих в различных областях. Дан-
ная книга ставит своей целью дать читателю ясное представление
об этом круге вопросов. Предполагается, что она представит ин-
терес не только для физиков, занимающихся изучением твердого
тела, но и для исследователей в других областях, таких, например,
как физика высоких энергий и космология, несмотря на то что
большинство примеров взято из физики твердого тела. Общая
точка зрения, которая проводится в книге, а также краткий обзор
ее содержания приведены в гл. 1.
Авторы хотели бы подчеркнуть, что данная книга является
полностью замкнутой в смысле изложения проблем теории мно-
гих тел. Предполагается поэтому, что она окажется подходящей
и для студентов, обладающих лишь первоначальными знаниями
в области квантовой теории поля.
Книга появилась в результате сотрудничества трех авторов.
В течение нескольких последних лет каждое лето в Эдмонтоне
(Канада) проходили небольшие рабочие совещания по некоторым
проблемам физики твердого тела и квантовой теории поля. На
этих совещаниях кроме нас присутствовало много физиков из
разных стран, причем такие совещания оказывали чрезвычайно
стимулирующее влияние и доставляли участникам большое удо-
влетворение; мы надеемся, что так будет и в дальнейшем. Зимой
наше сотрудничество продолжалось с помощью дальних средств
связи. Культурной программой летних совещаний ведала миссис
Тамаэ Умэдзава, чье гостеприимство делало эти совещания чрез-
8 Предисловие
вычайно приятными. Мы хотим поблагодарить ее за приложенные
усилия и посвящаем ей эту книгу.
Финансовую сторону летних совещаний обеспечивали Исследо-
вательский совет по естественным и прикладным наукам Канады,
Институт теоретической физики и факультет естественных наук
Университета провинции Альберта, а также Министерство об-
разования, науки и культуры Японии. Мы благодарны этим орга-
низациям за поддержку.
В ходе подготовки книги мы пользовались помощью и поддер-
жкой ряда своих коллег. В частности, д-р Г. Семенов любезно
прочитал всю рукопись и сделал ценные замечания. Многие части
книги улучшились благодаря нашим дискуссиям с д-ром Ф. Ман-
чини, д-ром Н. Папастоматиу, д-ром И. Такахаси, д-ром М. Умэд-
зава и Дж. Уайтхедом. Мы очень благодарны этим коллегам за
полезные замечания.
Эдмонтон, 1981 X. Мацумото
М. Та/пики
X. Умэдзава
ГЛАВА 1
ВВЕДЕНИЕ
1.1. Квантовая теория систем многих тел
Квантовая теория поля возникла первоначально как аналити-
ческий метод описания в физике элементарных частиц. Но в ходе
ее развития в ней постепенно начали проявляться черты, делающие
се пригодной для анализа квантовых систем многих тел. Начало
этому было положено теорией представления Фока (представления
вторичного квантования); именно оно показало, что квантовая тео-
рия поля предлагает язык, пригодный для описания квантовой си-
стемы, в которой состояния можно классифицировать набором
числовых последовательностей. Очевидно, что квантовая система
многих тел требует для своего описания такого языка.
Двойственный характер описания. Квантовая теория поля
еще больше приблизилась к физике твердого тела, когда ее удалось
сформулировать в терминах свободных (входящих) полей. Было
показано, что, хотя основные соотношения квантовой теории поля
выражаются через так называемые гейзенберговские поля, ее
результаты могут быть описаны с помощью понятия входящих
полей. Тот факт, что входящие поля свободны, напоминает о так
называемых квазичастицах, или квантах, определяющих наблю-
даемые явления в физике твердого тела. В этой книге свободные
поля, через которые выражаются результаты теории, называются
«физическими частицами» или «физическими квантами». Примером
физических квантов могут служить фонолы, магноны, плазмоны
и другие квазичастицы.
Таким образом, язык квантовой теории поля обладает двойст-
венной структурой; основные соотношения теории выражаются
через гейзенберговские поля, тогда как наблюдаемые величины
описываются с помощью «физических полей». Решить задачу
в квантовой теории поля означает найти соответствие между этими
двумя описаниями; такое соответствие называется динамическим
отображением.
Теория упорядоченных состояний. Серьезное продвижение
вперед в квантовой теории поля было достигнуто после того, как
удалось полностью осмыслить в рамках этой теории явление
спонтанного нарушения симметрии. До 1955 г. в квантовой тео-
10 Глава 1
рии поля рассматривались только такие решения, для которых
все инвариантные преобразования унитарно эквивалентны. Но
начиная с 1953 г. появились математические работы, указывающие
на то, что в квантовой теории с бесконечным числом степеней
свободы канонические преобразования не обязательно должны быть
унитарно эквивалентными.
В результате успешного развития теории сверхпроводимости
Бардина—Купера—Шриффера квантовая теория поля естествен-
ным образом подошла к решению проблем, включающих унитарно
неэквивалентные преобразования, поскольку спонтанное наруше-
ние симметрии относится к этой категории явлений. Возникнове-
ние упорядоченных состояний в физике твердого тела — результат
спонтанного нарушения симметрии, поэтому квантовая теория
поля оказалась способной дать теоретическое описание таких
состояний. В основе такого описания лежит знаменитая теорема
Голдстоуна, которая практически сводится к тому, что существо-
вание упорядоченных состояний обеспечивается некоторыми бес-
щелевыми (не имеющими щели в энергетическом спектре) бозо-
нами, называемыми голдстоуновскими бозонами. Это обстоятель-
ство широко известно специалистам по физике твердого тела, так
как оно встречается при изучении различных упорядоченных
состояний (фононы в кристаллах, магноны в ферромагнетиках
и т. п.). Точнее говоря, коллективная мода, которая служит пере-
носчиком в процессе поддержания упорядоченного состояния, —
это голдстоуновская мода. Другими словами, упорядоченное
состояние существует благодаря конденсации голдстоуновских
бозонов. При спонтанном нарушении симметрии преобразования
симметрии упорядоченного состояния регулируют характер кон-
денсации бозонов. Тот факт, что в этом процессе регулирования
участвует огромное число конденсированных бозонов, объясняет,
почему соответствующее'преобразование не является унитарно
эквивалентным. В связи с явлением спонтанного нарушения сим-
метрии возникает интересный вопрос. Решение, соответствующее
нарушенной симметрии, является также решением исходного
уравнения Гейзенберга, которое инвариантно относительно пре-
образований симметрии, связанных с нарушенной симметрией.
Поэтому исходная инвариантность^должна каким-то образом
сохраниться в этом решении. Вопрос состоит в том, каким образом
сохраняется эта инвариантность в процессе нарушения симметрии?
При ответе на этот вопрос очень полезной оказывается двойст-
венность языка квантовой теории поля, о которой упоминалось
выше. Симметрия отражает инвариантность, но характер этого
отражения может изменяться в процессе перехода с одного языка
на другой. Наблюдаемый вид симметрии выражается на языке
физических квантов и может отличаться от соответствующего вы-
ражения на языке гейзенберговских полей. В этом смысле спои-
Введение 11
тайное нарушение симметрии (т. е. возникновение упорядоченных
состояний) понимается как перестройка симметрии при динамиче-
ском отображении. Эту ситуацию можно резюмировать следующим
образом:
создание упорядоченных состояний = спонтанному
нарушению симметрии = динамической перестройке
симметрии.
После создания прекрасного формализма для описания упоря-
доченных состояний квантовая теория поля приобрела еще боль-
шую ценность как мощный метод расчета в физике твердого тела.
Квантовая теория поля при конечных температурах. Очевидно,
что для успешного исследования проблем физики твердого тела
квантовую теорию поля следует переформулировать с учетом теп-
ловых эффектов. Начиная с 1955 г. широкое развитие получили
методы, связанные с функциями Грина при конечных температу-
рах. Но формализм, в котором учитывается как временная, так и
температурная зависимость, не может полностью использовать
преимущества метода причинных функций Грина, который поз-
воляет достичь таких больших результатов в обычной квантовой
теории поля, о чем свидетельствует диаграммная техника Фейн-
мана. С другой стороны, известный формализм Мацубары может
использовать преимущества диаграммной техники Фейнмана,
но с его помощью трудно изучать явления, зависящие от времени.
Кроме того, в методе температурных функций Грина не удается
просто использовать многие типы операторных преобразований.
Поэтому весьма желательно полностью переформулировать всю
структуру квантовой теории поля с учетом тепловых эффектов.
Начиная с 1963 г. благодаря развитию аксиоматической теории
ноля стало ясно, что квантовую теорию свободных полей при ко-
нечных температурах можно последовательно сформулировать,
если удвоить число степеней свободы. Аксиоматический подход
в дальнейшем успешно развивался, и в настоящее время полу-
ченные строгие результаты легли в основу статистической механики
квантовых систем. Но совсем другое дело — формулировка кван-
товой теории поля при конечных температурах в форме, удобной
для практического использования при вычислениях в физике
твердого тела. Теория такого типа сформулирована и носит наз-
вание термополевой динамики. В ней, в частности, показано, что
может быть использован не только формализм причинных функций
Грина, но и все методы обычной квантовой теории поля.
Макроскопические объекты в квантовых системах многих тел.
При использовании квантовой теории поля для описания упоря-
12 Глава 1
доченных состояний сразу возникает новая группа вопросов.
Поскольку первоначально квантовая теория поля формулирова-
лась для описания физики частиц высокой энергии, она была
пригодна лишь для систем микроскопических объектов (квантов).
Однако в других разделах физики редко удается найти чисто кван-
товые упорядоченные состояния без каких-либо протяженных объ-
ектов. Например, трудно найти кристаллы без дислокаций, гра-
ниц зерен или дефектов. В таких кристаллах существует много
различных квантовых возбуждений, таких, как фононы и другие
кванты. Дислокации — это макроскопические объекты с клас-
сическим поведением; они возникают в кристаллах и взаимодейст-
вуют с фононами и другими квантами. Коротко можно сказать,
что кристалл с дислокациями представляет собой пример системы,
в которой микро- и макроскопические объекты сосуществуют и
взаимодействуют друг с другом. В физике твердого тела подобная
ситуация встречается часто: таковы, например, вихри в сверх-
проводниках, магнитные домены в ферромагнетиках и т. п. Обыч-
ные макроскопические токи, наблюдаемые в твердых телах,
также макроскопические объекты. По существу многие из наблю-
даемых в твердых телах явлений отражают макроскопическое по-
ведение квантовых систем многих тел. Таким образом, мы при-
ходим к необходимости описания квантовых систем многих тел,
в которых самосогласованно возникают некоторые макроскопи-
ческие объекты.
Объекты природы принято описывать с помощью структур-
ных, или стратифицированных, понятий. Простейшая классифи-
кация такого типа подразделяет объекты по масштабу на космо-
логические, земные и далее на молекулы, атомы и т. д. Затем
подчеркивается, что земные объекты состоят из молекул, те в свою
очередь из атомов и т. д. При этом явления, принадлежащие раз-
личным «стратам», рассматриваются как правило различными фи-
зическими теориями. Особое различие проводится между уров-
нем земных объектов и уровнем молекул. Объекты, принадлежа-
щие уровню молекул (или еще меньшему), обычно называют мик-
роскопическими, а остальные — макроскопическими. Неодно-
кратно указывалось, что динамика микроскопических объектов
описывается законами квантовой теории, а динамика макро-
скопических объектов — законами классической физики. Это
привело к постановке вопроса о взаимосвязи квантовой и класси-
ческой физики. Поскольку большинство измерительных при-
боров представляют собой макроскопические объекты, обладаю-
щие классическим поведением, указанный вопрос открыл путь
к изучению самого механизма измерения, и этим занималось много
исследователей в течение полувека. Но природа слишком сложна,
чтобы ее можно было описать с помощью упомянутой выше про-
стой «линейной» классификации по «стратам». Это становится очс-
Введение 13
видным при беглом взгляде на многие явления, происходящие
в упорядоченных состояниях, при которых возникает большое
число различных макроскопических объектов, взаимодействующих
с квантами.
Итак, мы приходим к фундаментальному вопросу: каким об-
разом макроскопические объекты возникают из микроскопиче-
ских? В физике твердого тела часто удается проследить эту связь —
примером может служить вычисление электропроводности. Это
макроскопическая величина, так как она определяется отноше-
нием макроскопического тока к макроскопическому электриче-
скому полю. Теория линейного отклика связывает эту макроскопи-
ческую величину с определенными эффектами квантовых флукту-
ации, которые являются микроскопическими (эта связь осущест-
вляется посредством так называемой флуктуационно-диссипаци-
оннойтеоремы). Но перечисление известных примеров из физики
твердого тела не может привести к адекватному ответу на постав-
ленный выше вопрос. Хотелось бы иметь общий математический
формализм, позволяющий получать макроскопические резуль-
таты на основе микроскопической теории. Кроме того, желательно,
чтобы подобный формализм оказался полезным при практическом
анализе квантовых систем многих тел с участием макроскопиче-
ских объектов.
В принципе оказывается возможным обобщить формулировку
квантовой теории поля так, чтобы включить в нее макроскопиче-
ские объекты, возникающие в квантовых системах многих тел.
Эта обобщенная формулировка включает в себя теорию линейного
отклика и содержит систематические методы для анализа кванто-
вых систем многих тел с протяженными объектами. Согласно этой
формулировке, макроскопические объекты в квантовых системах
многих тел возникают в результате конденсации бозонов опре-
деленного вида.
Топологические объекты. Существует много различных видов
макроскопических объектов, обладающих топологическими осо-
бенностями. Например, вихри в сверхпроводниках и дислокации
в кристаллах несут на себе линейные особенности. Как показано
в последующих главах, границы зерен, точечные дефекты в кри-
сталлах, а также джозефсоновские контакты несут поверхностные
топологические особенности. Можно доказать, что макроскопи-
ческие объекты, связанные с топологическими особенностями,
могут возникать только в результате конденсации бесщелевых
бозонов (т. е. бозонов, минимальная энергия которых равна
нулю). Этим объясняется тот факт, что в любом упорядоченном
состоянии можно обнаружить различные виды макроскопических
объектов, обладающих топологическими особенностями; действи-
тельно, как отмечалось выше, упорядоченные состояния поддер-
14 Глаза 1
живаются голдстоуновскими бозонами, не имеющими щели в энер-
гетическом спектре.
Беспорядок в упорядоченных состояниях. Примечательной чер-
той макроскопических объектов, обладающих топологическими
особенностями, является то, что эти объекты проявляют также
определенную разупорядоченность, связанную с тем, что на осо-
бенностях параметры порядка обращаются в нуль. В результате
в упорядоченном состоянии возникают области беспорядка, не-
смотря на то, что создание самих макроскопических объектов
требует наличия определенного порядка. Примером может слу-
жить следующая цепочка объектов: молекулярная система—
кристалл —дислокации в кристалле—аморфный материал.
Взаимодействие между макроскопическими объектами и кван-
тами. Естественно ожидать, что, поскольку макроскопические
объекты возникают в квантовых системах, состояния самих кван-
тов испытывают воздействие со стороны этих объектов. Это воз-
действие макроскопических объектов может быть описано в тер-
минах потенциала, действующего на кванты. Такой потенциал
называют самосогласованным потенциалом. Например, на элект-
роны в окрестности центра вихря в сверхпроводнике воздействует
самосогласованный потенциал, создаваемый этим вихрем, в ре-
зультате чего энергия электронов понижается. В этом состоит
природа так называемой энергии твердой сердцевины вихря.
Другим примером может служить влияние поверхностей на фононы
в кристаллах, в результате чего возникают поверхностные фо-
ноны.
Поверхностные явления. Все реальные физические системы
обладают конечными размерами. Если граничная поверхность
не поддерживается внешними силами, то это происходит самосогла-
сованным образом за счет внутренних взаимодействий. Устойчи-
вость системы означает, что ее граничная поверхность поддер-
живается за счет определенных дальнодействующих корреляций
(или коллективной моды). При различных попытках искусственно
изменить форму границы коллективная мода стремится вернуть
ее к наиболее предпочтительной форме сразу же после прекраще-
ния внешнего воздействия. Иными словами, система выбирает
наиболее предпочтительную форму своей границы из бесконечно
большого числа возможных. Отсюда ясно, что даже при рассмотре-
нии стационарной системы конечного размера эта система обладает
бесконечным числом степеней свободы. Интуитивно ясно, что
граничная поверхность системы в упорядоченном состоянии яв-
ляется макроскопическим объектом (обладающим топологической
особенностью), который возникает в результате конденсации
Введение 15
голдстоуновских бозонов. Некоторые типы колебаний границы
обладают весьма стационарными свойствами и создают своего
рода поверхностную волну. Примером может служить рэлеевская
волна, представляющая собой поверхностную звуковую волну
в кристалле. Аналогично многие типы поверхностных явлений
могут быть связаны с поверхностными особенностями.
Другим примером поверхностного эффекта является эффект
Джозефсона. Обычно этот эффект описывают на основе микроско-
пического туннелирования куперовских пар, но его можно также
рассматривать как макроскопический ток, который естественным
образом индуцируется наличием макроскопической поверхности.
Квантовая теория поля, квантовая механика и классическая
теория. Исторически квантовая теория поля возникла в резуль-
тате квантования классической теории, нов предшествующем изло-
жении использован обратный порядок. А именно, теоретическое
описание мы начали с обычной квантовой теории поля для чисто
квантовых систем и лишь затем, используя математический фор-
мализм конденсации бозонов, перешли к описанию возникновения
в квантовой системе макроскопических объектов. В результате
мы приходим к теории, которая охватывает квантовополевые,
квантовомеханические и классические объекты. Таким образом,
исторический цикл развития теории получает интересное завер-
шение: квантовая механика и классическая физика выводятся
из квантовой теории поля. Это проливает свет на характер взаимо-
связи микроскопических и макроскопических теорий.
Примечательной чертой современной науки является то, что
исследователи в разных областях используют сходные понятия
и методы. Изучение упорядоченности, нарушения симметрии и
макроскопических объектов находится в центре внимания не только
в физике твердого тела, но и в физике частиц высоких энергий,
астрофизике, химии и биохимии. К этой же группе проблем следует
отнести изучение в математике на основе нелинейных уравнений
солитонов и квантовых солитонов. Поэтому имеются веские ос-
нования считать, что квантовая теория поля окажется полезной
для широкого круга научных проблем.
1.2. План книги
В этой книге квантовая теория поля излагается в порядке,
определенном в предыдущем разделе. Изложение общих понятий
сопровождается многочисленными практическими примерами из
физики твердого тела.
В гл. 2 и 3 излагается теория пространства Фока для кванто-
вой системы, состояния которой классифицируются с помощью
числовых последовательностей; здесь же описывается двойствен-
16 Глава 1
ная структура языка квантовой теории поля (гейзенберговские
поля и свободные физические кванты). Обсуждаются также так
называемые унитарно неэквивалентные представления.
Общий формализм квантовой теории поля при конечных тем-
пературах (термополевая динамика) излагается в гл. 4. Согласно
построению этой теории, подробно рассматриваются спектраль-
ные представления причинных двухточечных функций (причинных
корреляционных функций) и их произведений. Эти спектральные
представления и правила их умножения служат ключевыми эле-
ментами систематизации и упрощения многих практических вы-
числений для систем при конечных температурах. В гл. 5 термо-
полевая динамика применяется ко многим задачам физики твер-
дого тела. В этой главе ставится две цели: с одной стороны, она
знакомит с многими типичными примерами из физики твердого
тела, с другой — позволяет проиллюстрировать многие вычисли-
тельные приемы термополевой динамики. Если читатель сочтет
некоторые из этих примеров слишком трудоемкими и громозд-
кими, он может отложить их разбор до тех пор, пока не будет
уяснена основная идея книги.
При исследовании задач для систем многих тел оказывается,
что многие физические свойства определяются некоторыми ин-
вариантными чертами динамики системы. Используя какие-либо
приближения при описании свойств системы, следует соблюдать
особую осторожность, чтобы не нарушить указанную инвариант-
ность. Поэтому полезно иметь определенные математические соот-
ношения, отражающие инвариантные свойства системы. Такие со-
отношения действительно'существуюти носят название соотноше-
ний Уорда—Такахаши (УТ); их описанию для системы при конеч-
ных температурах посвящена гл. 6. На основе использования этих
соотношений в гл. 7 излагаются общие соображения об упорядо-
ченных состояниях, связанных со спонтанным нарушением сим-
метрии, а также обсуждаются теорема Голдстоуна и динамическая
перестройка симметрии. Рассматриваются также некоторые при-
меры упорядоченных состояний.
В гл. 8 развитая квантовая теория поля применяется к особенно
важной проблеме, а именно к квантовой электродинамике в твер-
дых телах, в том числе в нормальных и сверхпроводящих металлах.
Это рассмотрение иллюстрирует метод учета калибровочной ин-
вариантности.
Анализ возникновения макроскопических объектов в кванто-
вых системах многих тел начинается в гл. 9. В этой главе дано опи-
сание общих черт теории квантовых систем многих тел при наличии
макроскопических объектов. Особенно важный случай таких
объектов, содержащих топологические особенности, обсужда-
ется в гл. 10. Изложение в этих главах является естественным про-
должением и развитием квантовой теории поля, изложенной в пред-
Введение 17
шествующих восьми главах, поскольку возникновение макроско-
пических объектов с топологическими особенностями обусловлено
наличием голдстоуновских бозонов, поддерживающих упорядо-
ченное состояние; сами топологические объекты являются резуль-
татом конденсации голдстоуновских бозонов. В гл. 10 изучаются
также конкретные примеры: дислокации, границы зерен и дефекты
в кристаллах.
В гл. 11 формализм, развитый для макроскопических объектов,
применяется к описанию макроскопических явлений, связанных
с квантовой электродинамикой в твердых телах. Рассматрива-
ются такие макроскопические величины, как макроскопический
ток и поле, электропроводность, диэлектрическая проницаемость
и т. п. В качестве одного из результатов получена теория линей-
ного отклика. Подробно рассматривается явление сверхпроводи-
мости и обсуждается его взаимосвязь с магнетизмом.
Глава 12 посвящена описанию явлений, вызванных наличием
топологических поверхностных особенностей. Общее рассмотрение
дополнено следующими тремя примерами: поверхностная звуковая
волна в кристалле, джозефсоновский ток и проникновение внеш-
него магнитного поля в сверхпроводник.
Вследствие недостатка времени и ограниченности объема книги
опущены многие важные и интересные вопросы; некоторые из
них кратко упоминаются в последней главе.
1.3. Обозначения
Ниже приведены обозначения, которые используются в этой
книге; при использовании других обозначений в тексте будут
сделаны соответствующие оговорки.
Для пространственных координат х и времени t мы часто ис-
пользуем четырехмерное обозначение х^ (ц = 0, 1, 2, 3):
xt (ц = i; пространственная координата),
, . . , . A.3.1)
г (ц = 0; временная координата).
Четырехмерный волновой вектор k^ имеет следующий смысл:
k; (и, = i\ волновой вектор),
/ л ч A.3.2)
со (|л = 0; частота). v '
Простое обозначение х соответствует четырехмерному векто-
ру хп, а полужирный символ (например, х) — пространственному
вектору. Таким образом, запись / (л:) обозначает зависимость
от х и t.
Метрические тензоры g]iv и gllv определяются соотношениями
?•<¦ =-?00=1, gn = -goo=h A-3.3)
iV=v, A.3.4)
18 Глава 1
а векторы с верхними индексами — выражениями
X!i = g^xx, k'x = g»vkv. A.3.5)
Везде предполагается суммирование по повторяющимся дважды
индексам. Скалярное произведение трехмерных векторов к и х
обозначается к-х, а четырехмерное скалярное произведение k-x
определяется следующим образом:
k-x = k^x» = &% = k-x — co^. A.3.6)
Оператор дифференцирования д11 определяется как
i (ц = I),
тогда
f д dxt (ц —0>
*..=-^Н-а/а (м = о). A-3'8)
Используется также символ \<:
Vj = а/йл;,-; A.3.9)
тогда V2 имеет смысл
V2=SViV,. A.3.10)
i
Функция от оператора дифференцирования F (д) определяется
своим действием на фурье-образ:
F (д) ехр {ik-x} = F (ik) exp {ik-x}. A.3.11)
Для простоты в дальнейшем множитель i в выражении F {ik)
мы опускаем и записываем ^просто F (k). Таким образом, если
функция g (x) имеет фурье-образ, определяемый выражением
g (х) = J d*xG (k) exp {ik-x}, A.3.12)
то действие на эту функцию оператора F (д)"дается выражением
F (д) § (х) -= J d4F (k) G (k) exp {ik-x}. A.3.13)
Трехмерная дельта-функция обозначается б (х):
б (х) = б (jO б (х2) б (х3), A.3.14)
а четырехмерная — б'1' (х):
б<4' {х) - б (/)б (х). A.3.15)
Введение 19
Фундаментальные постоянные й, с и другие записываются
в явном виде; так, энергия элементарного возбуждения (квази-
частицы) Е выражается через частоту со следующим образом:
Е - /zco. A.3.16)
Полевая переменная ^ (х) и сопряженный ей импульс я (х) удов-
летворяют каноническому перестановочному соотношению
[я (х, t), у (у, /) 1± = -№ (х - у). A.3.17)
Нормировка свободных полей определяется так, чтобы удовлет-
ворялось это соотношение.
Поскольку связь энергии Е и частоты со записывается в виде
Йсо, обратная температура р определяется соотношением
Г) Е = Рсо, A.3.18)
откуда
р = %lkBT. A.3.19)
При рассмотрении электромагнетизма выражения для х0
A.3.1), k0 A.3.2) и д° A.3.7) удобно несколько видоизменить, за-
писав их в виде
, . 1 -JQ 1 3 ,, Л Qpjs
' ° >0 с ' с dt -••/
Такие обозначения используются в гл. 8 и 11; при этом нормировка
всех полей также изменяется благодаря множителю с. Чтобы
убедиться в этом, рассмотрим лагранжиан
д?(х\ = !_5 х<5^х> A.3.21)
g (х) = -L [<г2 (д%,Щ2 - (VxJ|. A.3.22)
Отсюда находим
я (х) = с~1д°% = с d%/dt, A.3.23)
что приводит к выражению
fx (х, 0. ¦% (У' 01 = 'с2Й6(х - У)- A-3.24)
20 Глава 1
Четырехмерный вектор-потенциал Ац (х) определяется соот-
ношениями
А, (х) (и, = i),
w <"=0). <L3'25>
При выводе формул используются рационализованные единицы
Хевисайда—Лоренца (система СИ), которые затем переводятся
в единицы Гаусса (система СГС) для практических приложений.
Тогда ток /д в гл. 8 и 11 определяется так, чтобы удовлетворялось
уравнение Максвелла
-d*F^ = U, [A.3.26)
где
^v = a^v-dv^^. A.3.27)
Следовательно, /„ имеет смысл плотности заряда р, а ток j включает
множитель с по сравнению с обычным определением.
Физические поля обозначаются верхним индексом нуль (па-
пример, х°> Ф° и т. п.).
ГЛАВА 2
КВАНТОВАЯ ТЕОРИЯ СИСТЕМ МНОГИХ ТЕЛ
2.1. Представление чисел заполнения;
операторы рождения и уничтожения
Классификация одночастичных состояний и волновые пакеты.
Рассмотрим систему частиц, для которых одночастичные состояния
классифицируются посредством дискретного индекса i -- 1, 2,
3, .... Для выяснения его физического смысла следует напомнить,
что, согласно волновой механике, состояние одной частицы опи-
сывается волновой функцией г|з (х), которая должна бьпь норми-
руемой:
]>х|ф(.г)|2<«>. B.1.1)
Таким образом, г|з (х) не может быть плоской волной, а является
волновым пакетом. В этой книге термин «волновой пакет» исполь-
зуется для обозначения любой локализованной в пространстве
волновой функции. В частности, волновые функции электронов,
локализованных вблизи узлов решетки в кристалле, также счи-
таются волновыми пакетами.
Любая нормируемая функция г]) (х) может быть разложена сле-
дующим образом:
1> М = S <^г (*). B.1-2)
i
гдефункции gt(x) образуют счетное множество {gi(x);i=l, 2, ...}
ортонормированных функций:
xgt(x)g/(x) = bii. B.1.3)
Хорошо известным примером полного ортонормированного
набора {gt} является система волновых функций гармонического
осциллятора, классифицируемых посредством главного кванто-
вого числа. Коэффициенты разложения с* в B.1.2) могут зависеть
от времени. Если частица обладает спином, необходим еще один
индекс, классифицирующий спиновые состояния. В этом случае
предполагается, что индекс i классифицирует как ортонормирован-
ные волновые функции, так и спиновые состояния. При этом все
одночастичные состояния удается классифицировать дискретным
индексом I.
22 Глава 2
Классификация многочастичных состояний и числовые после-
довательности. Рассмотрим состояние системы многих тел. Число
частиц, занимающих i-e одночастичное состояние, обозначим че-
рез я,. Тогда состояние системы многих тел будет определено,
если задать /г,- для всех значений L Такое состояние обозначается
| tii, /г2, •••); объединяя все такие состояния, образуем множество
{\п1, п2, ...)}. Если числам n-t разрешено принимать любые не-
отрицательные целые значения, то частицы называются бозонами.
Если же числа пг могут принимать лишь значения 0 или 1, то
частицы называются фермионами. Заметим, что частицы указанных
двух типов не являются единственно возможными в рамках кван-
товой теории поля. Принято говорить, что частицы, отличающиеся
от бозонов и фермионов, подчиняются так называемой параста-
тистике. Но в этой книге мы рассматриваем только бозоны и фер-
мионы.
Операторы уничтожения и рождения для бозонов. Рассмотрим
сначала систему бозонов и введем оператор уничтожения аг
и оператор рождения а] с помощью соотношений
а,|/1ь ..., ni, ...) ¦--- п\12\пъ ..., п1— 1, ...), B.1.4)
а? |ль ..., пи ¦¦¦) -= (it + l)Vl|/ii. .... tn+ 1, ...) B.1.5)
соответственно. В пределах множества {| nlt n2, ...)} можно
перейти от любого заданного состояния к любому другому с по-
мощью повторного действия операторов рождения и уничтожения.
Из соотношений B.1.4) и B.1.5) можно получить в качестве
следствия еще одно соотношение
Ni\nu ..., nh ...)--ni\nl, ..., а-,, ...), B.1.6)
где оператор Nt определяется следующим образом:
Nt = а^аг (суммирования по i нет). B.1.7
Этот оператор называется оператором числа заполнения состояния
/; тогда оператор
N ¦= Ц JV; B.1.8)
i
имеет смысл оператора полного числа частиц.
Соотношения B.1.4) и B.1.5) приводят также к следующим
равенствам:
[a,-, a/J|«i, «2, ...) = Ьц\пъ п2, ...), B.1.9)
[а,, a,)\nlt щ, ...) = 0, B.1.10)
[а?, а]\\пъ п2, ...)=0. B.1.11)
Квантовая теория систем многих тел 23
Операторы уничтожения и рождения для фермионов. Рассмо-
трим далее систему фермионов. Операторы уничтожения и рож-
дения для нее вводятся посредством следующих соотношений:
ОС;|И1, ..., Я,-, ...) =
( 0 при 11, ¦--- О,
-= / м 1 \ 1 B.1.12)
{ 1) («ь ..., П1_х)\пъ ..., я; — 1, ...) при яг = 1,
( 0 при я, = 1,
= / м .1\ B.1.13)
[ 11 (Яь ..., n/_i)|nb ..., Я; + 1, ...} ПРИ Я, = 0.
Фазовый множитель ц (пъ ..., п;_х) выбирается в виде
¦п (я1? ..., /ij.j) = (—1)S'<'"'. B.1.14
Такой выбор упрощает операцию [аь aj]+, которая определя-
ется соотношением
[А, В]+ = АВ + ВА. B.1.15)
Действительно, полагая для определенности i j>/, из B.1.12)
и B.1.13) получаем
гъ ..., я/, ..., пь ...) =
-1)м+' | Яь ..., Я; + 1, ..., Hi — 1, ...) При Я/ = 0, Я; = 1,
в остальных случаях,
B.1.16)
а также
a)ai\nx, ..., я/; ..., я,-, ...) =
| (—1)'м|«1. ••¦> '1/ + 1, .-., tit — 1, ...) при я/ — 0, Я/ — 1,
1 0 в остальных случаях,
B.1.17)
где
М ее 2 «/• B.1.18)
Рассмотрев по аналогии случаи i <! / и t =— /, нетрудно получить
[а,-, а^]ь|яь я2, ...} = Ьц\пи я2, ...), B.1.19)
[а„ сзс; ]+ | лх, я2, ...} - 0, B.1.20)
[at, а)]+\пъ пг, ...) = 0 B.1.21)
24 Глава 2
при любых значениях i и /. Оператор
Ni = a\at (суммирования по i нет) B.1.22)
называется оператором числа заполнения состояния i; его дейст-
вие определяется соотношением
Ni\nu ..., пь ...) = ni\nlt ..., tii, ...) B.1.23)
Оператор полного числа частиц определяется равенством
N = S Nt. B.1.24)
i
i
1.1. Унитарно неэквивалентные представления
Несчетность множества {| п1( ...)}. Существенное свойство
множества {| пъ п2, ...)} состоит в его несчетности. Проще всего
убедиться в этом в случае системы фермионов, для которой nt = О
или 1. Используя двоичную систему счисления, рассмотрим
набор чисел {А = О, пъ п2, ..., п,, ...}, в котором п,- = 0 или 1.
Этот набор чисел заполняет интервал @, 1) вещественной оси
и находится во взаимно-однозначном соответствии с множеством
{| пъ «2, ..., щ, ...)}. Отсюда следует, что множество {] пъ п2, ...,
пи •••)} не является счетным. Этот вывод, очевидно, остается
справедливым и для системы бозонов.
Унитарно неэквивалентные представления. Ввиду несчетно-
сти множества {| пъ пг, ...)} оно не может быть использовано
в качестве базиса сепарабельного1) гильбертова пространства.
Для построения сепарабельного гильбертова пространства с по-
мощью элементов множества {| пъ п2, ¦•••)} следует выбрать счет-
ное подмножество и использовать его в качестве базиса гильбер-
това пространства. Но существует бесконечно много способов вы-
бора таких счетных подмножеств. Если какие-либо два различных
подмножества можно использовать в качестве базиса представле-
ний для операторов (ah a]; i = 1, 2, ...), то эти два представ-
ления являются унитарно неэквивалентными по отношению
друг к другу в том смысле, что вектор одного представления не
является суперпозицией базисных векторов другого представле-
ния. В этом состоит причина очень глубокого различия между си-
туациями в обычной квантовой механике и квантовой теории поля.
В квантовой механике, которая является квантовой теорией для
х) Пространство Ж называется сепарабельным, если оно содержит счетный
базис {?п}, такой что любой вектор % в Ж может быть с произвольной точностью
аппроксимирован линейной комбинацией векторов \п (т. е. 2ncn?n). Это озна-
чает, что для любого % из 26 и любого е > 0 существует последовательность
{с„}, такая, что \\—2пс„5п I <е при произвольном е.
Квантовая теория систем многих тел 25
конечного числа канонических переменных, выбор представлений
для этих переменных не вызывает затруднений: все возможные
представления унитарно эквивалентны друг другу [1]. Но в слу-
чае квантовой теории поля ситуация резко меняется1), что, как
показано в последующих разделах, приводит к далеко идущим
следствиям.
2.3. Пространство Фока
[Ol-множество и вакуум. На первый взгляд кажется вероят-
ным, ^что множество {| пъ п2, ...)} излишне велико для описания
реальных физических систем. Ведь в конечном итоге во всех эк-
спериментах возбуждается лишь конечное число квантов, хотя
это число и может быть сколь угодно велико. Поэтому можно пред-
положить, что для описания физических процессов достаточно
следующего подмножества:
, [[О Ьмножество =[{\пъ п2, ...,); 2 ni — конечное число}. B.3.1)
Это множество содержит^состояние, в котором частицы пол-
ностью отсутствуют (п/ = 0|для всех г); это состояние назы-
вается вакуумом и обозначается 10):
|0> =|0, 0, ...). B.3.2)
С другой стороны, [0]-множество не содержит многих состояний,
которые имелись в исходном множестве {\пъ я2, ...)}; например,
в [0 ]-множестве отсутствует, очевидно, состояние с nt = 1 для
всех I.
Счетность [0]-множества. Докажем, что [0]-множество яв-
ляется счетным. Поскольку сумма 2п,- конечна, для любого эле-
мента [0]-множества можно найти целое, число т, такое, что
nt = 0 при i > т, причем пт Ф 0. Кроме того, каждому элементу
[Oj-множества можно поставить в соответствие второе целое число
s, такое, что 2лг = s. Тогда ,для любого значения целого числа ms
имеется конечное число соответствующих элементов [0]-множества,
которые поэтому можно упорядочить. Точнее, общий элемент
[0]-множества можно представить в виде
1а(а= 1, 2, ...), B.3.3)
где при возрастании а значение ms возрастает или остается неиз-
менным. Таким образом, доказана счетность [0]-множества,
которое может быть теперь задано в виде {|а; а = 1, 2, ...}.
х) Проблема унитарно неэквивалентных представлений канонических ком-
мутаторов возникла в модели Ван Хова [2]. Детальный математический анализ
этой проблемы впервые дал Фридрихе [3]; дальнейшие результаты были полу-
чены Уайтманом и др. [4].
% Глава 2
Построение [0 ]-множества на вакууме. Векторы [01-множе-
ства строятся посредством повторного применения операторов
рождения а\ к вакуумному состоянию. В случае системы бозонов
вектор | пъ n2, •••) записывается в виде
\пъ л2, ...} - П(л;!)"'/2(а')'!'|0). B.3.4)
i
а в случае системы фермионов — в виде
\nlt По, ...> =П'4|0>, B.3.5)
i
где П' означает, что индекс i пробегает только те значения, для
которых tit —- 1. Кроме того, операторы aj располагаются слева
направо в соответствии с возрастанием значения i.
Внутренние произведения. Введем теперь сопряженные век-
торы (tii, Щ, ¦¦¦ | и предположим, что определены их внутренние
произведения с исходными векторами. Обозначим эти внутренние
произведения через (п\, ri2, ... j П!, п2, ...). В частности, вектор,
сопряженный вакууму, обозначается @|, и предполагается, что
@|0) = 1. B.3.6)
Операции а] и at определяются так, что аг эрмитово сопря-
жена а). Тогда из соотношений B.1.4) и B.1.5) следует
(ль ..., /и, ...\а[ = n/2(tii, ..., tic — I, ...\, B.3.7)
{tii, .... rii, ...\at = (tit + 1)V. (ль ..., а-, + 1, ...| B.3.8)
для системы бозонов. Тогда имеем
{ni, п2, ...\ = @|П (л,!)"'''2 (а/)"'- B.3.9)
i
Заметим, что в силу соотношений B.1.4) и B.3.7) имеем
а, | 0) = 0,
@|а? = 0.
Кроме того, из соотношений B.1.4) и B.1.5) следует
ПA/л:!)(а1-)"'(а1-)".|0) = |0).
с
Используя соотношения B.3.10)—B.3.12), получаем
(Ль «2, ¦ • • ] «1, П2, . . .) = П Ьп.п'г
B.
B.
B.
B
3.
.3.
.3.
.3.
10)
11)
12)
13)
Квантовая теория систем многих тел 27
откуда следует, что [0 ]-множество ортонормирование». Анало-
гичное свойство может быть доказано и для системы фермионов,
для которой
{пъ 7ia, ...| = <0|П'а,; B.3.14)
i
заметим, что операторы at стоят здесь справа налево в соответствии
с возрастанием значения i .
Используя обозначение ?„ B.3.3), условие ортонормированно-
сти B.3.13) можно записать просто в виде
(?ь-?а) = 6аЬ. B.3.15)
Рассмотрим далее два вектора
S :== ^J ^аёа> 5 == 2-1 СаЪа\
а а
их внутреннее произведение (!•?') определяется выражением
(?¦?')= S 1>с*ас'ьAа-1ъ)= B.3.16)
а Ь
; = ?^Г B.3.17)
а
Норма вектора \ определяется как (?, |)'/« и обозначается ниже
через | \ \.
Пространство Фока. Если определить линейное пространство
соотношением
Ж [а]= 6 = Yi СаЪа, И I са |2 — конечное число , B.3.18)
{ а а )
то такое пространство сепарабельно [5]. Это гильбертово про-
странство называется пространством Фока [6]. Здесь вектор
5 = S?=ica5a определяется как предел (при N -> ехэ) последова-
тельности векторов ?W = Yia=ica%a, которая является последо-
вательностью Коши, сумма 5ja^=i|ca|2 конечна. Иными словами,
I In — In- |2 можно сделать меньше любой сколь угодно малой
величины е при выборе достаточно больших значений N и N'.
Из выражений B.3.4) и B.3.5) следует, что, действуя всеми воз-
можными полиномами по а] на вакуум, получаем множество
D = { XI ca?«; N—конечное целое число}, B.3.19)
которое является плотным *) в Ж [а]. По этой причине процесс,
г) Множество D называют плотным в нормированном векторном пространстве
96, если для каждого вектора \ в Ж и любого е > 0 существует вектор ? в D,
такой, что | ? — ? | < е. Интуитивно ясно, что D «почти заполняет» Ж. Напри-
мер, множество рациональных чисел плотно во всем множестве вещественных
чисел.
28 Глава 2
используемый при построении Ж [а], называют «построением
пространства с помощью циклического действия операторов ро-
ждения на вакуум». Детальное математическое описание построе-
ния гильбертова пространства не входит в задачи этой книги, и
мы адресуем читателя к работам [4, 5].
Вакуум в пространстве Фока. Вакуумное состояние |0), оче-
видно, принадлежит к фоковскому пространству Ж feel и удов-
летворяет условию
<хг|0) = 0 для всех I. B.3.20)
Кроме того, если вектор'\ из Ж [а] удовлетворяет условию аг ? =
= 0 для всех г, то этот'вектор \ связан с вакуумным состоянием
соотношением Е~с|О), где с — некоторое с-число.
Перестановочные соотношения. Соотношения B.1.9)—B.1.11),
а также B.1.19)—B.1.21) приводят к следующим следствиям:
(о |k-, a)]±\b) = bt,{a\b), B.3.21)
{а\\ас, aj]±\b) = (a\{a], a|]±|b)=0, B.3.22)
где | a) и \b) — любые два вектора, принадлежащие плотному
множеству D. Здесь использованы обозначения
[А, В]± = АВ ± ВА; B.3.23)
\А, В]_ и [А, В]+ называются соответственно коммутатором
и антикоммутатором операторов А и В. В соотношениях B.3.21)
и B.3.22) коммутаторы используются в случае системы бозонов,
а антикоммутаторы — в случае системы фермионов. Из этих соот-
ношений следует, что Ж [а ] реализует представление операторов
аг, алгебраические свойства которых определяются соотношениями
[at, a|]± = 6,/, B.3.24)
\ai, aj]±--=[al ajL = 0. B.3.25)
Операторы рождения и уничтожения для частицы, описывае-
мой произвольным волновым пакетом. Напомним, что возмож-
ность классификации состояний посредством дискретного индекса i
обусловлена тем фактом, что в одночастичном состоянии простран-
ственное распределение описывается волновым пакетом, т. е.
квадратично интегрируемой функцией в конфигурационном про-
странстве. Как видно из выражения B.1.2), подобные волновые
пакеты всегда могут быть выражены посредством счетного мно-
жества ортонормированных функций gi (x):
igt, gi) = j (Pxg} (x) g, (x) = б(/. B.3.26)
Квантовая теория систем многих тел 29
Тогда внутреннее произведение таких волновых пакетов имеет
вид
(f,g). \cF:xr(x)g(x), B.3.27)
(/,g)=5jc?d,, B.3.28)
если / (х) и g (x) выражаются формулами
/(х)=5]с.-&(х), B.3.29)
g-(x) = 5j digt (x). B.3.30)
Ввиду того что одночастичное состояние, связанное с волно-
вым пакетом gt (x), представляется в фоковском пространстве
3$ [а] вектором а] | 0), вектор состояния, связанный с волновым
пакетом / (х), должен представляться некоторой суперпозицией
вида 2;Cjat | 0). Оператор рождения одной частицы в состоянии,
описываемом пространственным распределением / (х), обозначим
через а}; тогда
a/ = 2j Ctai • B.3.31)
i
Соответствующий эрмитово сопряженный оператор имеет смысл
оператора уничтожения
a/ = 5j c*at. [B.3.32)
i
Тогда в силу условий B.3.24) и B.3.25) имеем
[а/, «?1± = (Л В), B.3.33)
[а;, ag}± = [a?, ag]± = 0. B.3.34)
Представление Фурье. Ввиду того что функции, описывающие
волновые пакеты, имеют фурье-образы, удается сформулировать
теорию фоковского пространства в терминах представления
Фурье. Как будет показано в последующих главах, такая форму-
лировка чрезвычайно полезна в практических приложениях.
Обозначим фурье-образ функции gi (x) через gt (к):
?i (k) е'к*. B.3.35)
Тогда условие ортонормировки B.3.26) принимает вид
ei (k) Si 00 = в.7- B-3-36)
30 Глава 2
Аналогично, вводя фурье-образы функций / (х) и g (x)
кх, B.3.37)
!кх, B.3.38)
можно записать их внутреннее произведение в виде
г(к), B.3.39)
(!,п)=ЪсЫ1. B.3.40)
С точки зрения фурье-анализа в качестве «базиса» в простран-
стве волновых пакетов удобно использовать плоские волны
exp (t'kx). Но плоские волны не могут описывать пространственное
распределение в одночастичных состояниях, поскольку они не
являются нормируемыми, а также не образуют счетного множе-
ства. Удовлетворить обоим требованиям удается только путем
введения нормировки на б-функцию, которое осуществляется
следующим образом (для простоты мы не рассматриваем спино-
вые степени свободы).
Введем операторы а (к) с помощью соотношений
[а (к), а+A)]± = 6 (к — 1), B.3.41)
[а (к), а A)]± = [а+ (к), а+ A) 1± = 0- B.3.42)
Поскольку б-функция определена только в смысле теории обоб-
щенных функций, приведенные выше соотношения следует по-
нимать в том же смысле, а именно
B.3.43)
и т. д., где / (к) и g A) — соответствующие пробные функции.
Таким образом, мы приходим к необходимости отождествления
J +(к), B.3.44)
откуда
[a.!,r4)± = (f,g), B.3.45)
\а,, ael±=[ctf. aJ]± = 0. B.3.46)
Эти соотношения согласуются с B.3.33) и B.3.34); на этом
основании а; рассматривается как оператор рождения ча-
Квантовая теория систем многих тел 31
стицы с пространственным распределением / (х). Сравнивая вы-
ражение B.3.31) с B.3.44), окончательно получаем
4 = Bя)~3/2 J cfkgi (к) а+ (к). B.3.47)
Это выражение согласуется с исходным определением aj", согла-
сно которому а\ является оператором рождения частицы в со-
стоянии, описываемом пространственным распределением gi(\).
Следует заметить, что операторы a (k) и а+ (к) не определены
на векторах фоковского пространства: при действии на векторы
фоковского пространства они порождают состояния с бесконечной
нормой. Рассмотрим, например, вектор | k) = a+(к) | 0); со-
ответствующая норма для него определяется внутренним произ-
ведением (к | к) = 8<3> @), которое бесконечно велико. В этом и
состоит нормировка на б-функцию, о которой упоминалось выше.
Поэтому операторы a(k) не реализуются в нашем гильбертовом
пространстве; польза от их введения состоит в их связи с фурье-
представлением оператора at, которое дается выражением B.3.47).
Заключительное замечание. В заключение заметим, что фоков-
ское пространство в этом разделе строилось чисто эмпирически;
нам нигде не пришлось говорить о специфике динамического по-
ведения рассматриваемой системы. Последние три раздела можно
рассматривать как формулировку языка квантовой теории, на
котором можно описывать данную систему. Этот «язык», а точнее
фоковское пространство можно, следовательно, использовать
во всех случаях, когда мы имеем дело с квантовыми системами,
состояния которых описываются последовательностями чисел. По-
этому построенная выше общая схема применима в столь различ-
ных областях, как физика твердого тела и физика высоких энергий.
2.4. Некоторые примеры
унитарно неэквивалентных представлений
В предыдущих разделах было показано, что, хотя множество
всех возможных состояний вида \nlt n2, ...) несчетно, в качестве
базиса нашего сепарабельного гильбертова пространства можно
использовать [0]-множество. Гильбертово пространство такого
вида называется пространством Фока, причем это пространство
строилось путем циклического действия оператора а] на вакуум.
Поэтому алгебраические соотношения B.3.24), B.3.25) сами по
себе не могут однозначно определять представления at (даже с точ-
ностью до унитарной эквивалентности); необходимо еще определить
вакуумное состояние. Проблема выбора представления алгебраи-
ческих соотношений B.3.24) и B.3.25) очень сложна.
32 Глава 2 I
Преобразование Боголюбова бозонных операторов. Проиллю-
стрируем унитарно неэквивалентные представления на конкретном
примере, рассмотрев два набора бозонных операторов уничтоже-
ния а (к) и Р (к). Следуя соображениям, изложенным в преды-
дущих трех разделах, построим [01-множество и соответствующее
фоковское пространство, которое обозначим через Ж \а, р].
Вакуумное состояние 10) в нем удовлетворяет соотношениям
а(к)|0) = 0, Р(к)|О) = О. B.4.1)
Алгебраические свойства операторов а (к) и р1 (к) даются со-
отношениями
[а (к), а+AI = 6 (к — 1), B.4.2)
[р(к), Р+AI = 6 (к — 1); B.4.3)
остальные коммутаторы обращаются в нуль.
Введем далее операторы а (к) и b (k) с помощью следующих
соотношений:
а (к) = cha (к) - 4Р+ (-к), B.4.4)
b(k) =Cfep(k)-4«+(-k). B.4.5)
Здесь численные коэффициенты с и d — вещественные функции к2;
они удовлетворяют соотношению
4 —d|=l. B.4.6)
Последнее соотношение гарантирует, что а (к) и b (к) имеют те
же алгебраические свойства, что и а (к) и Р (к), т. е .
[а (к), а+A)] = б(к-1), B.4.7)
U>(k), 6+A)] = 6(к-1), B.4.8)
а все остальные коммутаторы обращаются в нуль. Иными словами,
преобразование, определенное равенствами B.4.4) и B.4.5),
является каноническим; оно носит название преобразования Бо-
голюбова 17].
Следуя соображениям, изложенным в предыдущем разделе,
введем операторы волновых пакетов at и bt:
а] = Bп)~3/2 J d*kgt (k) a+ (k) и т. д. B.4.9)
Действие этих операторов на векторы в Ж [а, р ] определено
соотношениями B.4.4) и B.4.5).
Упростим ситуацию, считая коэффициенты ch положительными.
Тогда в силу B.46) можно положить
cft = ch eA, dh = sh 9ft. B.4.10)
Квантовая теория систем многих тел 33
Введем далее оператор
G (9) = ехр [А (9)], B.4.11)
где
А (9) = J d*kQk la (к) р (-к) - р+ (-к) а+ (к) ], B.4.12)
так что
[а(к), Л (9)] = -9fep+(-k), B.4.13)
[pt(-k), Л F)] = -9fta(k). B.4.14)
Повторно применяя эти соотношения, получаем
G (9) а (к) G (9) = а (к) ch 9ft — р+ (—к) sh 9ft, B.4.15)
откуда, используя B.4.4), имеем
a (k) = G (9) а (к) G (9). B.4.16)
Аналогично можно показать, что
6 (k) = G'1 (9) В (к) G (9). B.4.17)
Последние два соотношения позволяют предположить, что
преобразование Боголюбова (соотношения B.4.4) и B.4.5)) явля-
ется унитарным. Для более тщательного рассмотрения этого во-
проса вычислим матричные элементы G(9), начав с вакуумного
среднего от G'1 (9):
/0 (9) = @.10-46I0). B.4.18)
Для вычисления этой величины заменим параметр 9 (к) на 9 (к) +
+ еб (к — 1) с произвольным 1. Изменение /0 (9) за счет указан-
ного изменения параметра обозначим через б/ (9; 1). Тогда функ-
циональная производная определяется равенством
-^r/0(e) = lim-i-6/(e; 1). B.4.19)
Но, согласно B.4.11), имеем
¦щ- /о (в) = - @ | а A) р (-1) G-i (9) | 0) B.4.20)
или
^ /„ F) = @ | С"* (9) р+ (-1) а+ A) | 0). B.4.21)
ПосколькудО~10 = G (—9), получаем
а (I) р (-1) G'1 (9) = С F) С'1 (-9) а A) р (-1) G (-9) =
= G (9) [а A) ch 9, + р+ (—1) sh 9, ] [р (—1) ch 9, +
+ a+(I)sh8/], B.4.22)
34 Глава 2
где использовано соотношение B.4.15), с заменой 8Й на —Qh.
Тогда из B.4.20) получаем
¦щ- /о (9) = ~«C) @) sh 9; ch 9,/0 (9) - sh* 9, @1G~' (9) р+ (-1) а+A) 10),
B.4.23)
а из B.4.21) находим
-^-/„@) = -6C) @)th9,/0(9). B.4.24)
Здесь
6C) @) = lim б (к). B.4.25)
Поскольку 69^/69^ = б (к — I), решение уравнения B.4.24) с на-
чальным условием /0 @) = 1 имеет вид
/0 (9) = ехр (—б<3) @) J dsk In ch9ft). B.4.26)
Величина А (9) в B.4.12) содержит только пары операторов
(аР и Р+а+), поэтому достаточно ограничиться изучением лишь
следующих матричных элементов:
/„ (9; 1) = <0| [а A) р (-1)]" G-1 (9)|0). B.4.27)
Отсюда находим
±fn (9; 1) = -@1 [а A) р(-1)]» [аA)Р(-1) - р+(-1) аЦ1)]0-Щ \ 0) =
= -/»+! (в; 1) + п2[б<3> @)]Чп-ЛЪ !)• B-4.28)
Решение последнего уравнения имеет вид
/„ (9; 1) = п\ [б(з> @) ]» ехр (—8<3> @) J <Pk In ch 9ft) (th 9,)",
B.4.29)
откуда следует
О)) = G'1 (9)|0) = B.4.30)
= /о (9) ехр (бC) @) j d3to+ (k) p+ (-k) th 9Л) | 0), B.4.31)
где /о (9) определено в B.4.26).
Если учесть теперь тот факт, что величина 6<3> @) бесконечна
(а следовательно, /„ (9) = 0), то из B.4.31) видно, что при раз-
ложении | 0)) по базисным векторам Ж [а, р ] каждый коэффи-
циент разложения обращается в нуль, так что | 0)) не принадлежит
Ж [а, р ]. Иными словами, G (9) не отображает^ [а, р ] на себя.
Заметим, что в силу B.4.16) имеем
а (к) | 0)) = 0, Ъ (к) | 0)) = 0, B.4.32)
Квантовая теория систем многих тел 35
откуда следует, что | 0)) — вакуум в отношении действия опера-
торов а (к) и b (k). Предположим, что строится [0 ]-множество,
причем а] и Ъ\ — операторы рождения, & Ж [а, Ь] — соответ-
ствующее пространство Фока. В этом пространстве Фока имеется
вакуумное состояние | 0)), удовлетворяющее равенству B.4.32).
Приведенные выше соображения показывают, что этот вакуум
10}) не принадлежит Ж [а, р]. Таким образом, Ж [а, Ь] и
Ж [а, Р ] — два унитарно неэквивалентных представления в том
смысле, что в Ж [а, Ь] существует вектор, который нельзя пред-
ставить в виде суперпозиции базисных векторов Ж [а, р]. Фак-
тически в рассматриваемом случае можно показать, что никакой
вектор из Ж [а, Ь] не может быть представлен в виде линейной
суперпозиции базисных векторов из Ж [а, Р]. Эта ситуация обычно
описывается интуитивным утверждением об ортогональности про-
странств Ж [а, Ь] и Ж [а, р].
Причину этого явления можно уяснить, вспомнив формулу
б (к) = Bп)~3 J dsxelk*, B.4.33)
откуда интуитивно ясно, что
8<3) @) = Bя)-3 X (объем системы). B.4.34)
На этом основании можно было бы сделать вывод, что в действи-
тельности упомянутая выше унитарная неэквивалентность может
и не существовать, поскольку каждая система имеет конечные раз-
меры. Но такая точка зрения представляется слишком оптими-
стичной. При изучении стационарной системы конечных размеров
пришлось бы всерьез учитывать влияние ее границ. Как будет
показано в последующих главах, существование этой границы
обеспечивается благодаря наличию в системе некоторых коллек-
тивных мод. Граница ведет себя подобно макроскопическому объе-
кту с поверхностной особенностью, причем такой объект также
обладает бесконечным числом степеней свободы. В этом смысле
стационарная система с естественной (самоподдерживающейся)
границей существенно отличается от системы, искусственно огра-
ниченной «ящиком».
Как указано в разд. 2.2, причина появления многих унитарно
неэквивалентных представлений состоит в том, что множество
{| «1, п2> •••)} является несчетным.
Полученные выше результаты не означают, что мы не можем
определить действие операторов а, и bt на векторы в Ж [а, р].
Действительно, как было показано выше, действие операторов
at и bt на векторы в Ж [а, р ] определяется соотношениями
B.4.4) и B.4.5). То, что мы показали выше, сводится к утвержде-
нию, что каноническое преобразование B.4.4) и B.4.5) не реали-
зуется с выполнением условия унитарности. Если гильбертово
36 Глава 2
пространство ^является пространством Фока Ж [а, |3], то at
и bt не могут быть операторами уничтожения, поскольку в Ж [а, Р(
не существует вакуума, связанного с операторами at и bt.
Преобразование Боголюбова фермионных операторов. Случай
фермионов может быть исследован аналогичным образом. Рас-
смотрим два набора фермионных операторов уничтожения а (к)
и Р (к):
[а (к), а+ A)]+ = б (к —1), B.4.35)
[р(к), р+AI+ - 6 (к — 1), B.4.36)
[а (к), р A))+ = [а (к), р+ AI = 0 и т. д. B.4.37)
Повторяя рассуждения предыдущих разделов, построим простран-
ство Фока Ж [а, |3]. Вакуум в нем удовлетворяет условиям
а (к) | 0) = 0 и р (к)|0) = 0. Введем далее операторы а (к)
и bjjs) с помощью соотношений
а (к) = а (к) cos 0Л — |3+ (—к) sin в,4> B.4.38)
Ъ (к) = р (к) cos 9/t + a+ (—к) sin 8A, B.4.39)
где Qh — функция к2. Это преобразование называется преобразо-
ванием Боголюбова [7]. Легко видеть, что а (к) и b (к) удовлетво-
ряют тем же алгебраическим соотношениям, что и a(k)n^(k):
[а {к), а? A)]+ = б (к —1), B.4.40)
fb(k), 6+0I+ = S(k —1), B.4.41)
[а (к), Ь A)]+ - [а (к), Ь+ AI+ - 0 и т. д. B.4.42)
Можно показать, что
a (k) = G'1 F) а (к) G F), B.4.43)
Ь (к) = G'1 F) р (к) G @), B.4.44)
где GF) = ехр [—Л (в)], B.4.45)
причем
А F) = J d3k 6ft [а (к) C (—к) — C+ (—к) а+ (к) ]. B.4.46)
Вычисление показывает, что
| 0» = G (в) [ 0> = B.4.47)
= /0. F) ехр (б<3> @) j d3k In {1 + а+ (k) p+ (—k) tg 8ft}) | 0).
B.4.48)
Здесь f0 F) = ехр (б<3> @) j d'k In cos 8ft), B.4.49)
причем эта величина обращается в нуль ввиду бесконечности
б<3) @). Отсюда видно, что, в этом случае (как и в случае бозонов)
Квантовая теория систем многих тел 37
представления Ж [а, |3] и Ж\а, Ь] унитарно неэквивалентны
друг другу, если только не выполняется условие Qh = О для всех к.
Несмотря на то что B.4.47) приводит к равенству
a(k)|0)> = b(k)|0», B.4.50)
вектор | 0)) не принадлежит Ж [а, |3]. Поэтому а (к) и Ъ (к) не
могут считаться операторами уничтожения, если в качестве гиль-
бертова пространства выбрано Ж [а, |3 ]. Но действие операторов at
и hi на векторы в Ж [а, |3] определяется соотношениями B.4.38)
и B.4.39).
Сдвиг бозонного поля. В качестве последнего примера рас-
смотрим набор операторов уничтожения бозонов а (к) и введем
операторы а (к) с помощью соотношения
а (к) = а (к) + Cft, B.4.51)
где с-число ch является функцией к. Такое соотношение также
называется преобразованием Боголюбова. Поскольку преобразо-
вание B.4.51) индуцирует сдвиг бозонных операторов на с-число
ch, его часто называют сдвигом поля. Так как ck является с-чис-
ловой функцией, операторы а (к) удовлетворяют бозонным пере-
становочным соотношениям. Таким образом, сдвиг поля является
каноническим преобразованием.
Легко видеть, что
a (k) = G'1 (с) а (к) G (с), B.4.52)
где
G (с) = ехр (- J d*k [da (к) - C/ia+ (к)]). B.4.53)
Используя формулу Бейкера—Хаусдорфа
еЛев = ехр {Л + В -Ь 4" И, 51 ~|- -^ И, [А, В\] | }, B.4.54)
получаем
G (с) = ехр ( i- jd3/e| ck |2) ехр (- j d3fefta+ (k)) X
Xexp (j dAkc*ka(k)y B.4.55)
Это приводит к соотношению
|0» = G-i(c)|0)= B.4.56)
= ехр ( L j cPk | ch |2) exp (- J d*kcha+ (k)) | 0). B.4.57)
Если имеет место равенство
j dsk\ch\2 = с», B.4.58)
38 Глава 2
представления Ж [а] и Ж [а] унитарно неэквивалентны друг
другу. Хотя вектор | 0)) удовлетворяет соотношению а (к)| 0)) =
= 0, он не принадлежит Ж [а]. Поэтому, если мы выбрали
в качестве пространства Фока Ж [а], оператор а (к) не может
быть назван оператором уничтожения. Заметим, что равенство
B.4.58) имеет место, например, при выборе ch — с8 (к).
Конденсация бозонов. Рассмотрим структуру состояния | 0)).
Как видно из B.4.57), это состояние (по крайней мере формально)
соответствует суперпозиции состояний произвольного числа а-
бозонов (это утверждение имеет лишь формальный смысл, если
выполняется условие B.4.58)). Можно интуитивно представлять
себе состояние 10)) как состояние, в котором конденсируются
а-бозоны; подобное явление называется конденсацией бозонов.
Можно сказать, что сдвиг поля B.4.51) индуцирует конденсацию
бозонов, даже если выполняется условие B.4.58). Величина
@|a+(k)a(k)|0) = |cft|2 B.4.59)
называется числом конденсированных бозонов с импульсом к.
Интуитивно можно видеть, почему Ж [а] является унитарно
неэквивалентным Ж [а] при с (к) = сб (к). В этом случае про-
странственное распределение конденсированных бозонов является
однородным (т. е. соответствующим к = 0), а полное число кон-
денсированных бозонов равно
d3k\c(k)\2 = с2б<3) @). B.4.60)
Из B.4.34) видно, что плотность конденсированных бозонов равна
dB = у- j d3k | с (k) |2 = Bjt) с2 (V — объем), B.4.61)
причем эта величина конечна, даже если объем V стремится
к бесконечности. Интуитивно ясно, что для возможности создания
локально наблюдаемых эффектов при конденсации бозонов плот-
ность конденсированных бозонов dB должна быть отлична от
нуля. Если пространственное распределение конденсированных
бозонов однородно, полное число конденсированных бозонов равно
VdB и становится бесконечным, если бесконечно V. Поскольку
векторы в пространстве Фока Ж [а ] практически не содержат
состояний с бесконечным числом a-бозонов, интуитивно понятно,
почему состояние |0)) не может принадлежать Ж [а].
Следует отметить, что действие а (к) на векторы в Ж [а] оп-
ределяется соотношением B.4.51), даже если выполняется ра-
венство B.4.58).
Заметим в заключение, что сдвиг поля вида B.4.51) индуцирует
так называемое когерентное состояние [8].
Квантовая теория систем многих тел 39
2.5. Представление физических частиц
и динамическое отображение
Пространство Фока для физических частиц. Существование
бесконечно большого числа представлений, унитарно не эквива-
лентных друг другу, приводит к вопросу о правильном выборе
одного из них для данного пространства Фока. В квантовой теории
в качестве исходного принимается положение, что гильбертово
пространство содержит все наблюдаемые состояния. На этом
основании мы требуем, чтобы гильбертово пространство было
пространством Фока, связанным с частицами, наблюдаемыми
Рис. 2.1.
в эксперименте. Такие частицы носят название физических частиц
или физических квантов. Таким образом, мы выбираем простран-
ство Фока, построенное путем циклического действия операторов
рождения физических частиц (или физических квантов) на физи-
ческий вакуум, или, короче, мы используем представление физи-
ческих частиц.
Полная энергия и энергия физических частиц. Чтобы выяс-
нить поведение физических частиц, рассмотрим более детально из-
мерение энергий в реакциях между частицами. В любой подобной
реакции имеется некоторое количество сталкивающихся частиц
(например, Л и В) и определенное количество частиц съ ..., cN,
покидающих область столкновения (рис. 2.1). Полная энергия
системы, в которой происходит столкновение, определяется по-
средством измерения энергий падающих частиц А и В до их вхо-
ждения в область столкновения; при этом полная энергия равна
сумме энергий частиц А и В. Если измерить также энергию ча-
стиц сь с2, ..., cN после столкновения, то мы обнаружим, что
сумма энергий этих частиц равна определенной выше полной
энергии. Если мы хотим интерпретировать этот эксперименталь-
ный результат как закон сохранения энергии, то энергию следует
определить как сумму энергий всех физических частиц, имеющихся
в данном состоянии. При таком определении неявно подразуме-
вается, что реакции между частицами происходят без затраты
энергии взаимодействия, что весьма необычно. В гл. 3 будет пока-
зано, каким образом такое предположение становится возможным.
40 Глава 2
В физике твердого тела энергетический спектр физических
квантов может быть в принципе определен с помощью некоторых
внешних воздействий. При этом измеряемая полная энергия ока-
зывается равной сумме энергий возбужденных квантов. Итак,
потребуем, чтобы энергия квантовой системы была равна сумме
энергий всех физических частиц.
Свободный гамильтониан и оператор импульса для физических
частиц* Пусть ftco (k) — энергия одной физической частицы с им-
пульсом ftk. Тогда .сформулированное выше требование означает,
что
[ ] B.5.1)
откуда получаем
[Яо, а+(ki) I a+(ka) ... а+(к„)|0> =
= Ли (кх) а+(kj ...а+(к„)|0). B.5.2)
Здесь #0 — оператор, собственные значения которого являются
значениями энергии системы. Соотношение B.5.2) верно для лю-
бого п, поэтому очевидно, что
[Яо, а+ (к)] = йсо (к) сс+ (к). B.5.3)
Поскольку энергия является вещественной величиной, Яо — эрми-
тов оператор. Следовательно, беря эрмитово сопряжение от
B.5.3), получаем
[Яо, а (к) ] = —йсо (к) а (к). B.5.4)
На основе B.5.3), B.5.4) и B.5.1) находим
Яо = П \ dska (к) cd" (к) а (к). B.5.5)
Оператор Яо называется свободным гамильтонианом физических
частиц.
В терминах операторов рождения волновых пакетов а],
определенных равенством B.3.44), имеем
[Яо, а)] = ft Bп)/г J d3ka (к) / (к) а+ (к). B.5.6)
Действие Яо на состояния волновых пакетов понимается сле-
дующим образом:
Ноа)\ 0) = ft Bя)/2 j Лео (к) / (к) <х+ (к) 10), B.5.7)
Н,а)а\ | 0) = ft Bя) j d3k j d3t [© (к) + © A)] ? (к) / A) а+ (к) а+ A) | 0)
B.5.8)
Квантовая теория систем многих тел 41
и т. д. Из соотношения B.5.8) становится очевидным линейный
характер энергии. Поскольку Яо не содержит членов взаимодей-
ствия, частицы, рождаемые посредством оператора а+ (к), назы-
вают свободными.
С помощью аналогичных рассуждений можно найти оператор
импульса Р:
Р = П \ d3kka* (к) а (к). B.5.9)
Проведенное выше рассмотрение показывает, что, поскольку
все наблюдаемые состояния частиц являются состояниями волно-
вых пакетов, в нашем гильбертовом пространстве отсутствуют
собственные состояния операторов Яо и Р. Наблюдаемая энергия
частицы в состоянии | ag) = а^ | 0} определяется не каким-
либо из собственных значений Яо, а средним (ожидаемым) значе-
нием (ag | #01 cxg). Но это обстоятельство не создает никаких труд-
ностей с применением понятия энергии, так как (по крайней мере
в принципе) среднее значение можно сделать сколь угодно близ-
ким к собственному значению Яо, выбрав волновой пакет, очень
близкий к плоской волне. Аналогичные соображения применимы
к понятию импульса.
Гейзенберговские поля и уравнение Гейзенберга. Несмотря
на то что наблюдаемые значения энергии системы определяются
собственными значениями свободного гамильтониана Яо, тем не
менее если между частицами'происходят какие-то реакции, то Яо
не может быть истинным гамильтонианом системы. Поэтому не-
обходимы некоторые фундаментальные величины, определяющие
динамику системы. Поскольку рассматривается квантовая система,
эти фундаментальные величины являются операторами, действую-
щими в нашем пространственно-временном мире. Обозначим эти
операторы \\> (х); они называются обычно гейзенберговскими
полями. Тогда динамика системы определяется пространственным
и временным изменением гейзенберговских полей.
Изменение полей ¦ф (х) определяется некоторым уравнением,
которое*'называется уравнением Гейзенберга. При рассмотрении
некоторой системы весь теоретический анализ начинается с оп-
ределения гейзенберговских полей и уравнения Гейзенберга.
При этом требуется, чтобы любой оператор, появляющийся при
анализе системы, выражался в виде линейной комбинации произ-
ведений гейзенберговских полей.
Гамильтониан для'уравнения Гейзенберга. Мы требуем, чтобы
все пространственно-временные преобразования генерировались
некоторыми операторами. В частности, отсюда'следует требование
существования гамильтониана, генерирующего сдвиг во времени.
42 Глава 2
Этот гамильтониан обозначается через Я. Тогда каноническое
уравнение вида ih (dty/dt) = [ty, Я] является уравнением Гей-
зенберга. Для вычисления входящего в это уравнение коммута-
тора [ij), Я] необходимо ввести предположение о том, что гейзен-
берговские поля удовлетворяют одновременным каноническим
перестановочным соотношениям.
Представление физических частиц для гейзенберговских полей.
Если приведенные выше соображения объединить с утверждением,
что наше гильбертово пространство является пространством Фока
свободных физических частиц, то уравнение Гейзенберга должно
решаться таким образом, чтобы гейзенберговские поля реализо-
вались в пространстве Фока свободных физических частиц. Иными
словами, уравнение Гейзенберга решается таким образом, чтобы
гейзенберговские поля выражались через состояния некоторых
свободных частиц, т. е. чтобы все матричные элементы (а\\р (х)\Ь)
для векторов \ а) и | Ь), принадлежащих пространству Фока сво-
бодных частиц, были определены. Указанные свободные поля
рассматриваются далее как свободные физические частицы, а про-
странство Фока является тогда представлением физических частиц
для гейзенберговских полей. Таким образом, пространство
Фока 36 [а 1 можно определить, потребовав, чтобы гейзенбер-
говские поля выражались через операторы рождения и уничто-
жения некоторых свободных частиц, которые являются свобод-
ными физическими частицами. В следующей главе будет показано,
что это требование приводит к соотношению
(а\Н\Ь) = {a\H0\b) + W0(a\b), B.5.10)
где Wo — с-число, а \а) и | Ь) — векторы в пространстве Ж [а],
реализующем представление физических частиц. Заметим, что
условие B.5.10) не является столь строгим, как условие Я =
= Яо + Wo, поскольку оно требует, чтобы разбиение II --- Яо --
-|- Wo осуществлялось только тогда, когда Я реализуется в спе-
циальном представлении (а именно в пространстве Фока Ж [а]).
Соотношения между матричными элементами, связанные с кон-
кретным представлением, называются слабыми соотношениями.
Поэтому соотношение B.5.10) является слабым условием, которое
можно использовать в качестве критерия для определения Ж [а].
Самосогласованный метод. После того как задан гамильто-
ниан Я, мы сталкиваемся с дилеммой: хотя вычисление матричных
элементов (а\Н\Ь) требует знания пространства Фока Ж [а],
к которому принадлежат векторы | а) и | Ь), нам ничего не из-
вестно относительно физических частиц (а тем самым относи-
тельно Ж [а]) до тех пор, пока не решена вся задача. Причина
возникновения этой дилеммы состоит в существовании бесконеч-
Квантовая теория систем многих тел 43
ного числа неприводимых представлений, унитарно неэквивалент-
ных друг другу; подобная дилемма не возникает в случае кванто-
вой механики с конечным числом канонических переменных.
Эта дилемма относится к числу проблем, которые обычно разре-
шаются с помощью самосогласованного рассмотрения. В данном
случае мы имеем дело с проблемой самосогласования между
гамильтонианом Я и выбором пространства Фока для физических
частиц.
Самосогласованный подход состоит в следующем. Прежде
всего с помощью различных физических соображений составляют
набор «кандидатов» на роль физических полей, причем эти канди-
даты классифицируются с помощью определенных параметров.
Затем строят пространство Ж [а], а неизвестные параметры опре-
деляют с помощью соотношения B.5.10). Для примера рассмо-
трим гамильтониан для нуклонного гейзенберговского поля.
В качестве начального набора физических частиц выберем изодуб-
летное свободное дираковское поле, которое рассматривается как
физический нуклон. Оставляя массу физического нуклона неоп-
ределенной, пробуем решить уравнение B.5.10), используя одно-
временные канонические перестановочные соотношения. При
этом мы обнаруживаем, что соотношение B.5.10) не удовлетво-
ряется при любом выборе массы физического нуклона. Тогда в на-
бор физических полей вводится новый член, после чего можно убе-
диться в том, что соотношение B.5.10) удовлетворяется. Новый
член набора оказывается физическим дейтроном, представляющим
собой составную частицу. В гл. 3 мы демонстрируем применение
самосогласованного метода во всех деталях на примере одной
разрешимой модели — так называемой Л'б-модели.
В гл. 6 показано, что использование канонических перестано-
вочных соотношений и так называемых соотношений Уорда—Та-
кахаши во многих случаях значительно упрощает самосогласован-
ные вычисления.
Некоторые простые примеры самосогласованных вычислений.
Чтобы получить представление о самосогласованном подходе, рас-
смотрим гамильтониан, обладающий простой структурой. А
именно рассмотрим гамильтониан вида
Я = п\ d3k [ел {at (k) а (к) + Ь+ (к) Ь (к)} +
+ vft {а (к) Ь (-к) + Ь+ (-к) а? (к)} ], B.5.11)
где а (к) и b (к) — гейзенберговские операторы, удовлетворяющие
бозонным перестановочным соотношениям, eh и vh —¦ положи-
тельно определенные функции аргумента к2, причем eh > vh.
Конкретным примером подобной системы могут служить спино-
вые волны в антиферромагнетиках [9].
44 Глаза 2
Поскольку гамильтониан B.5.11) имеет вид, не совпадающий
с видом свободного гамильтониана, а (к) и b (к) не имеют смысла
операторов уничтожения физических частиц.
Применяя преобразование Боголюбова B.4.4) и B.4.5), где
ch = ch Qk, du " sh 0/;, можно записать гамильтониан B.5.11)
в другой форме
Я = #„ + Wo, B.5.12)
где
\ Ркщ [а+ (к) а (к) + р+ (к) р (к) ]; B.5.13)
здесь выбор 0ft произведен в виде
ch20ft= ч , sh28fe^ Vft . B.5.14)
D-v*)/f D-^)/z
Согласно B.5.13), операторы а (к) и р (к) являются операторами
уничтожения физических частиц, и наше гильбертово простран-
ство является пространством Фока Ж [а, |3]. Энергия физической
частицы йсо^ и энергия вакуумного состояния Wo, как легко найти,
имеют вид
<o* = (e|-v|)V., B.5.15)
Wo = Й6<3> @) J d3/fe (щ — ek). B.5.16)
Заметим, что, несмотря на бесконечное значение Wo, плотность
энергии конечна, если конечное значение имеет интеграл в B.5.16);
величина 6<3) @) определена выражением B.4.34).
Если входящие в B.5.11) операторы а (к) и b (к) удовлетворяют
фермионным соотношениям анти коммутации B.4.40)—B.4.42),
то преобразование Боголюбова B.4.38) и B.4.39), где
cos2S'=(?RF' s'n2e*=^«FRF' B5-l7>
приводит Н к виду B.5.12), причем
a* = (e| + vS)'/., B.5.18)
Wo = —Йво> @) J d4 (coft - eh). B.5.19)
Заметим, что в рассматриваемом фермионном случае нет необхо-
димости в условии гк > Vft.
Рассмотрим еще один пример — модель Ван Хова [2]. В этой
модели гамильтониан имеет вид
Н = й\ dsk [е/{а+ (к) а (к) + vk {а (к) + а+ (к)} ], B.5.20)
Квантовая теория систем многих тел ¦ 45
где а (к) — бозонные операторы, а с-числа eh и vh — вещественные
функции к2. Переводящее гамильтониан в форму B.5.12) преобра-
зование Боголюбова есть сдвиг поля B.4.51), а именно а (к) =
г- а (к) -f cft, где ch =¦ —vh/e;,. Тогда имеем
щ = е,„ B.5.21)
Wo = —Й813) @) J d3k (v'i/ek). B.5.22)
В рассмотренных случаях получено сильное соотношение Я —
—¦ Яо ~\- Wft, а не слабое соотношение вида B.5.10), т. е.(а\Н\Ь) =
¦- (а | Яо | Ь) + Wo (а | 6). Это объясняется слишком упрощённым
характером моделей: гамильтониан B.5.11) содержит только
билинейные члены, а гамильтониан B.5.20) — билинейные и
линейные.
Динамическое отображение. Обратимся теперь к временной
зависимости операторов физических частиц и гейзенберговских
операторов. Поскольку Яо, определяемый выражением B.5.5),
— гамильтониан физических частиц, временная зависимость опера-
торов уничтожения физических частиц имеет вид
a (k, t) = eiTio'a (к) е-'"»' = B.5.23)
= а (к) ехр [—ш (к) t]. B.5.24)
Соответственно для эрмитово сопряженного оператора получаем
а+ (к, t) = е''"»'а+ (к) е-'"»' = B.5.25)
= <*+ (к) ехр [ш (к) t) B.5.26)
(здесь Яо = Яо/Й).
С другой стороны, временная зависимость гейзенберговских
операторов а (к, t) определяется уравнением Гейзенберга, или кано-
ническим уравнением движения
ih -^- а (к, I) = [а (к, t), H\, B.5.27)
так что
а (к, t) = eiT"a (k) е~'т, B.5.28)
где Я = Я/ft.
В случае бозонов с гамильтонианом B.5.11) преобразование
Боголюбова B.4.4), B.4.5) определяет временную зависимость
гейзенберговских операторов следующим образом:
а (к, /) = ch 9Ae~"Va (k) - sh е/и"'|3+ (—k), B.5.29)
b (k, t) = ch 9ft<>"'mh'fi (k) ~^ sh 8fte"°"'a+ (—k). B.5.30)
46 Глава 2
В случае фермионов с гамильтонианом B.5.11) находим
а (к, 0 = cosefte""°^a(k)-sine^'ffl^p+(—к), B.5.31)
Ь(к, Q = cosefte~'Vp(k) + sin8;/fflft'a+(_k). B.5.32)
В случае модели Ван Хова B.5.20) имеем
а (к, t) = е-ш!'-'а (к) + ch. B.5.33)
Соотношения B.5.29)—B.5.33) определяют все матричные
элементы гейзенберговских операторов, а именно (а\а(к, t)\b)
и (a\b (k, t)\b) между векторами в пространстве Фока Ж la, CJ
физических частиц. Например, из B.5.33) следует
(а | а (к, /) | Ь) = е-'и"' (а | а (к) | 6) + сА (а | Ь). B.5.34)
Другими словами, соотношения B.5.29)—B.5.33) показывают,
каким образом гейзенберговские операторы реализуются в пред-
ставлении физических частиц. Эти соотношения выражают ре-
шения уравнения Гейзенберга B.5.27) в терминах операторов
физических частиц а (к) и |3 (к). Выражение такого рода называется
динамическим отображением. В рассмотренных выше простых
примерах динамические отображения линейны [с дополнитель-
ными слагаемыми ck (с-числами) в случае B.5.33)] и выражаются
сильными соотношениями B.5.29)—B.5.33). Но в более сложных
случаях динамическое отображение содержит произведения выс-
шего порядка по операторам рождения и уничтожения физиче-
ских частиц и определено только с помощью матричных элементов
(слабые соотношения). Мы вернемся к этим вопросам ниже. В рас-
смотренных выше примерах с помощью решений уравнения Гейзен-
берга, выраженных через операторы свободных полей, удается
естественным образом записать Н в виде Яо + Wo- Это иллюстри-
рует общую ситуацию, в которой решения уравнений Гейзен-
берга удовлетворяют условию B.5.10) для представления физи-
ческих частиц. Заметим, что, вообще говоря, условие Н = Но +
+ Wo выполняется только в слабом смысле, хотя в рассмотренных
выше простых примерах оно выполнялось также и как сильное
соотношение.
Нормальное произведение. При появлении в динамическом
отображении произведений высших порядков по операторам фи-
зических частиц их следует располагать в виде линейных комби-
наций так называемых нормальных произведений. Нормальным
называется произведение операторов рождения и уничтожения
физических частиц а+ (к) и а (к), в котором все операторы рож-
дения располагаются слева от всех операторов уничтожения.
Таким образом, все операторы уничтожения в нормальном произ-
ведении уничтожают частицы в кет-состоянии, тогда как все\опе-
Квантовая теория систем многих тел 47
раторы рождения рождают частицы в бра-состоянии. Иными сло-
вами, при вычислении матричных элементов нормальных произ-
ведений не встречаются спаривания операторов рождения и унич-
тожения. Если нормальное произведение содержит п операторов
рождения и т операторов уничтожения, его матричные элементы
соответствуют переходу из состояния с т частицами в состояние
с п частицами. Это свойство нормальных произведений делает их
всегда удобными при записи динамического отображения.
Резюме. В этом разделе введены следующие понятия: физи-
ческая частица, представление физических частиц, динамическое
отображение гейзенберговских операторов и нормальное произве-
дение операторов физических частиц.
2.6. Свободные поля для физических частиц
Свободные физические поля. В этом разделе вводится опера-
тор, описывающий пространственно-временное поведение физиче-
ских частиц. Этот оператор называется оператором свободного
физического поля.
Пространственно-временная зависимость операторов рождения
и уничтожения. Для построения свободного физического поля
рассмотрим пространственную и временную зависимости опера-
торов рождения и уничтожения физических частиц. Временная
зависимость описывается выражениями B.5.24) и B.5.26):
а (k, t) = ее (к) ехр [—ш (к) t], B.6.1)
а+ (к, t) = а+ (к) ехр [ш (к) П. B.6.2)
Поскольку оператор импульса Р является генератором простран-
ственных сдвигов, пространственная зависимость операторов рож-
дения и уничтожения определяется следующим образом:
а+ (к; х, /) = е-™*а (к, t) eiTx = B.6.3)
= а (к) ехр [i {kx — a(k)t}], B.6.4)
сс+ (к; х, t) = е-'Тха+ (к, t) е'Тх = B.6.5)
= а+ (к) ехр [—t {kx - со (к) /}], B.6.6)
где Т = Р/й. Следует отметить, что оператор уничтожения об-
ладает отрицательной частотой, а оператор рождения — поло-
жительной.
Требования, накладываемые на свободные физические поля.
Потребуем, чтобы свободное физическое поле являлось линейной
комбинацией операторов a (k; x, t) и а+ (к; х, t) с коэффициентами,
48 Глава 2
не зависящими ни от х, ни от t. Потребуем, кроме того, чтобы сво-
бодные физические поля строились таким образом, чтобы существо-
вала процедура проектирования, позволяющая избавиться от
всех операторов рождения или уничтожения. Это требование га-
рантирует, что динамические отображения операторов Гейзен-
берга могут быть выражены через произведения свободных физи-
ческих полей, хотя первоначально динамические отображения
выражаются через операторы рождения и уничтожения. В конце
этого раздела показано, каким образом удовлетворяются эти
требования. Если физическая частица обладает спином или дру-
гими степенями свободы, то имеется несколько операторов уничто-
жения, а именно a<r> (k; x, t), г = 1, 2, .... При наличии одновре-
менно частиц и дырок (или античастиц) можно использовать
а<г) для частиц и рс> для дырок.
Уравнения свободного поля для физических полей. Поскольку
физическое поле ф° является суперпозицией плоских волн B.6.4)
и B.6.6), оно удовлетворяет однородному дифференциальному
уравнению
К (д) ф° (х) = 0, B.6.7)
где х = (х, t). Если физическая частица обладает спином или дру-
гими степенями свободы, ф°(х) представляется вектором-столб-
цом:
B.6.8)
в этом случае % (д) является матрицей п хп- Например, для элек-
трона ф° — спиновый дублет. В столбце B.6.8) объединяются
обычно только поля, имеющие одинаковый энергетический спектр
со (к): в дальнейшем мы будем считать это условие выполненным.
Классификация уравнений свободного поля. Уравнение B.6.7)
называется уравнением свободного поля типа 1, если оно может
быть сведено к уравнению на собственные значения
(id/dt — е (V)) Ф° = 0, B.6.9)
и уравнением типа 2, если соответствующее уравнение на собст-
венные значения имеет вид
(dVdf + со2 (V)) ф° = 0. B.6.10)
Дифференциальные операторы е (V) и со (V) в уравнениях B.6.9)
и B.6.10) определены следующим образом:
е (V) е'к<х = е (к) е'к-" и т. д.; B.6.11)
Квантовая теория систем многих тел 49
указанное определение дифференциальных операторов исполь-
зуется на протяжении всей книги. Заметим, что в случае уравне-
ния типа 1 энергия со (к) дается выражением | е (к) |. Если вели-
чина е (к) неотрицательна, то ф° включает только операторы унич-
тожения. Если е (к) становится отрицательной в некоторой об-
ласти значений к, то ф° содержит также операторы рождения.
Последнее может возникнуть только в том случае, если ф° — фер-
мионное поле. Отрицательные значения е (к) соответствуют дыроч-
ным состояниям фермионов. В случае уравнения типа 2 поле ф°
содержит как операторы уничтожения, так и операторы рожде-
ния, соответствующие каждому значению импульса.
Дивизор. Из уравнений B.6.9) и B.6.10) следует, что должен,
существовать дифференциальный оператор d (д), удовлетворяю-
щий соотношению
d(d)X(d) = i~lr—B(V) B.6.12)
для уравнения типа 1 и соотношению
d {д) К,(д) = —(дЧдР + ©a(V)) B.6.13)
для уравнения типа 2.
Оператор d (д) называется дивизором1) уравнения B.6.7).
Покажем, что с помощью этого оператора можно построить функ-
цию Грина для уравнения B.6.7). Заметим прежде всего, что в силу
B.6.12) и B.6.13) det [d(d)]det [X (д)] Ф 0, поскольку произ-
водные d/dt и V независимы друг от друга. Таким образом, опе-
раторы К (д) и d (д) не являются сингулярными и потому обладают
обратными операторами. Применяя оператор А,-1 (д) к обеим ча-
стям равенства B.6.12) и замечая, что получающаяся в правой
части матрица кратна единичной, находим
А, (<3) d (д) = id/di — г (V) B.6.14)
для уравнения типа 1. Аналогично для уравнения типа 2 полу-
чаем
к (д) d (д) = —(дЧд? + со2 (V)). B.6.15)
Обозначим далее через Ао (х) функцию Грина любого из урав-
нений B.6.12) или B.6.13):
(id/dt — г (V)) Ло (х) = б (х) б (*) (тип 1), B.6.16)
—(d*/df + со2 (V)) AG (х) = б (х) б (t) (тип 2). B.6.17)
х) Дивизор для уравнения свободного поля впервые был введен в реляти-
вистской квантовой теории поля [10]. Здесь это понятие обобщается на нереля-
тивистские случаи.
50 Глава 2
Отсюда получаем важный результат: функция d (д) Аа (х) яв-
ляется функцией Грина для уравнения B.6.7):
к (д) d (д) As (х) = б (х) б (*). B.6.18)
Матрица приведения к эрмитову виду. Определим функцию
к (р) равенством
к (р) exp U (рх — pot)} =к{д) ехр И (рх — pot) ]; B.6.19)
тогда соотношение к (р) и = 0 для вектора и является уравнением
на собственные значения, откуда находим р0 = ±со (р). Поскольку
собственные значения со (р) вещественны, соотношение к (р) и — 0
должно быть эквивалентно уравнению на собственные значения
для некоторой эрмитовой матрицы (с собственными значениями
Ро — ±и (р))- Тем самым предполагается существование несин-
гулярной матрицы т), приводящей r\ k (р) к эрмитову виду
АЛ (р) л+ - i\K (р). B.6.20)
Принимая во внимание условие B.6.19), получаем
Я+ (—д) if = цк(д). B.6.21)
Используя затем выражения B.6.12)—B.6.15), находим
1цк (д) ] [d (д) rf1) = Id (д) ц-1 ] [цк (д) ], B.6.22)
откуда, а также из уравнений B.6.14) или B.6.15) следует, что
d (p) ц-1 также является эрмитовым оператором:
(ЧТ1 d+ (-д) = d (д) л, B.6.23)
поскольку г\К (р) — несингулярная матрица. Матрица г\ назы-
вается матрицей приведения к эрмитову виду [10].
С учетом выражения B.6.21) эрмитово сопряжение уравнения
B.6.7) дает
Ф° (х) к (—д) = 0, ' B.6.24)
где д означает, что производные берутся от величин, стоящих
слева, а ф° определяется следующим образом:
Ф° (х) = Ф°+ (х) i\. B.6.25)
Заметим, что если ф° (х) — вектор-столбец, то ф° должен быть
вектор-строкой.
Лагранжиан для свободных физических полей. Величина
S% = J d4V (x) к (д) ф° (х) B.6.26)
вещественна. Очевидно, что это —¦ лагранжиан для поля ф°,
так как применение к нему вариационного принципа приводит
к уравнению свободного поля B.6.7).
" Квантовая теория систем многих тел 51
Внутреннее произведение волновых функций. Предположим,
что к (д) является полиномом по оператору d/dt не выше второй
степени; тогда к (д) можно записать в виде
X (д) = X<°)(V) + Ш1» (V) (d/dt) + АЯ (V) (d/dtJ. B.6.27)
Введем оператор [10, 11]
"г = № (V) — Ш2> (S/)*dldt, B.6.28)
где использовано обозначение
*d/dt = d/dt — d/df. B.6.29)
Тогда имеем
4- J d3xf (х) Yg(x) = \ (Pxf (x) (-i- + 4") Х(" W^ W -
- t J d3xf (x) [(а/Й)а - (d/dtJ] km (V) я (x) =
= - i J d3xf (x) [X E) - X (—d)] g (x), B.6.30)
где по пространственным переменным проведено интегрирование
по частям. Если / (х) и g (x) удовлетворяют уравнению свободного
поля B.6.7) [а тем самым и уравнению B.6.24)], то выражение
B.6.30) обращается в нуль, а потому величина
*xf (х)Ъ(х) B.6.31)
не зависит от времени. Поэтому указанную величину называют
внутренним npou3eedenueM волновых функций / (х) и g (x), удов-
летворяющих уравнению свободного поля B.6.7). Следует заме-
тить, что внутреннее произведение вида B.6.31) не обязательно
является положительно определенным. По существу это свойство
и не требуется, поскольку внутреннее произведение не имеет пря-
мого отношения к понятию вероятности. Вероятность для физи-
ческих реакций лишь связана с внутренними произведениями
векторов в пространстве Фока.
Полная ортонормированная система решений уравнения сво-
бодного поля B.6.7). Используя приведенное выше определение
внутреннего произведения, построим теперь полную ортонорми-
рованную систему решений уравнения свободного поля B.6.7).
52 Глава 2
Предположим сначала, что уравнение B.6.7) является уравне-
нием типа 2. Тогда оно обладает решениями как с положительной,
так и с отрицательной частотами:
W (к, х) -- иг (к) exp U {кх — со (к) /}], B.6.32)
vr (к, х) = V (к) exp [—i {кх — со (—к) *}]. B.6.33)
Здесь индекс г относится к спиновым или иным степеням свободы.
Используя соотношение B.6.19), имеем
к (k) W (к) = О для k0 - со (к), B.6.34)
I (—k) if (к) --= 0 для fen = со (—к). B.6.35)
Подставляя в выражение B.6.31) иг (к, х) и г/ (I, х) вместо
f (х) и g (x) соответственно, легко видеть, что оно представляет
собой суперпозицию слагаемых вида exp U {со (к) -|- со (—1)} /].
Поскольку выражение B.6.31) не должно зависеть от времени,
отсюда следует, что оно равно нулю. Таким образом, получаем
следующую теорему ортогональности:
J d\Ur (k, x)*Tvs A, х) = 0, B.6.36)
j (PxV (к, х)*Тиг A, х) = 0. B.6.37)
Выберем // (к, х) и vr (к, х) так, чтобы удовлетворить следую-
щему условию ортонормированности:
J <Рхпг (к, х)*Ти* A, х) = йбг5б (к — 1), B.6.38)
J d3xvr (к, x)*Tvs (I, x) = — йрбг8б (к — 1); B.6.39)
смысл знакового множителя р будет пояснен ниже. Индекс г
классифицирует собственные векторы из набора эрмитовых ма-
триц, коммутирующих друг с другом, а также с цХ (k) (и тем са-
мым с т)Г). Таким образом, для всех величин, входящих в B.6.38),
можно выбрать одинаковый знак. Поскольку оператор к (д)
в уравнении B.6.7) определен только с точностью до знака, всегда
можно выбрать его знак (а следовательно, и знак Г) таким обра-
зом, чтобы величина B.6.38) была положительной. Но если
знак к (д) фиксирован требованием положительности B.6.38),
это еще не означает положительности B.6.39). По существу вы-
Квантовая теория систем многих тел S3
ражение B.6.39) может иметь любой знак в зависимости от струк-
туры Г. Именно этим объясняется появление знакового множителя
р - ±1 B.6.40)
в условии B.6.39).
Используя обозначения
Я(П (к) е** - Ж') (V) р'кх и т. д., B.6.41)
введем величину
Г (к, Е) = М» (к) — 2Е№ (к). B.6.42)
Тогда условия ортонормированиости, выражаемые соотношениями
B.6.38) и B.6.39), примут вид
пг (к) Г 1к, со (к) J «s (к) - Bп)~3 SrSft, B.6.43J
vr (к) Г I—к, —со (—к)] Vs (к) = — Bn)~3 pbrSfi. B.6.44)
В случае уравнений типа 1 решениям иг (к, х) сопоставляются
положительные е (к), а решениям vr (к, х) — отрицательные е (к).
Условие ортонормированности выражается соотношениями B.6.43)
и B.6.44).
Структура физического поля. После проведенной подготовки
можно определить свободное физическое поле. Свободное физи-
ческое поле ф° задается выражением
Ф° (х) = J] j d3k [W (k) а! (к) exp (i {к- х — со (к) t}) +
г
+ vr (к) рг+ (к) ехр (—г {к- х — со (—к) t})} B.6.45)
для уравнений типа 2 и выражением
Ф° (х) = j d3k {9 [е (к) ] иг (к) а! (к) +
+ 6 [—е (—к) ] vr (—к) |У+ (—к)} е**-'* (к)' B.6.46)
для уравнений типа 1. Здесь 6 (х) — разрывная функция («сту-
пенька»): 6 (х) — 1 для х > 0 и 6 (х) = 0 для х < 0. Отрицатель-
ные значения е (к) могут появляться только в случае фермионов.
Некоторые примеры уравнений свободного поля. Приведем
некоторые примеры, иллюстрирующие изложенные выше общие
соображения. Простой пример уравнения типа 2 дается операто-
ром вида
X (д) - — дЧд? — со2 (V). B.6.47)
54 Глава 2
В этом случае имеем
11 = 1, d (д) = 1, B.6.48)
"г = i (dldf), B.6.49)
Г (к, Е) = 2Е, B.6.50)
р = 1. B.6.51)
Тогда из B.6.43) и B.6.44) следует
и (к) = v (—к) = Bя)-'/. [2и (к)]-1/^1/,, B.6.52)
откуда
,f,0 (Х) = Bл)--'/»Д'/, f (Pk ( a(k)w e' [kx-co <Ь) П -1-
B.6.53)
Более сложный пример представляет собой уравнение свобод-
ного поля физических электронов в сверхпроводниках [12]:
Md)=(^-T3+/AT2-e(V2). B-6.54)
Это уравнение типа 2, хотя оно включает лишь производную по
времени первого порядка. В уравнении B.6.54) А — постоянная,
а т — матрицы Паули размерности 2 х2:
/0 1\ /0 —i\ /1 0\
d ) ( ) Н )
о)' T«=(f о)' т
так что поле ф° является дублетом.
Легко показать, что -
Л = т3, B.6.56)
d (д) = j -|-Тз + i Ат2 + е (V2), B.6.57)
jg_ + co2(V)), B.6.58)
со (к) = D + А2)'А, B.6.59)
7 = т3, B.6.60)
Г (к, Е) = т3. B.6.61)
Здесь величина eh определяется соотношением гк exp (tkx) =
= е (V2) exp (ikx). Из условий B.6.43) и B.6.44) находим
м+ (к) и (к) = Bл)-3 Й, B.6.62)
о+ (к) о (к) = — BяГ3рй. B.6.63)
Квантовая теория систем многих тел 55
Поскольку величина vfv положительно определена, получаем
р = —1. B.6.64)
Стандартный метод построения волновых функций и (к, х)
и v (к, х) состоит в использовании дивизора согласно соотноше-
ниям
и (к, х) = d (д) ц^т exp {i [kx — со (к) t\), B.6.65)
v (к, х) = d (д) ti© exp {—i [kx — со (—к) t]}. B.6.66)
Здесь www — вектор-столбцы, определяемые условиями B.6.62)
и B.6.63). Из выражения B.6.15) видно, что эти волновые функции
удовлетворяют уравнению А, (д) ц>° = 0. В выражениях B.6.65)
и B.6.66) вместо d (д) использован оператор d (д) тр1, поскольку
последний является эрмитовым [ср. с B.6.23)]. Используя выра-
жения B.6.56) и B.6.57), находим
и (к) = [со — Дтх + е,гт3] w, B.6.67)
v (к) = [—со — Дт! + ekr3] w, B.6.68)
где со ^ со (к) = со (—к).
Очевидно, что
м+ (к) v (к) = о+ (к) и (к) = 0; B.6.69)
из выражений B.6.67) и B.6.68) находим
it (к) и (к) = 2сош+ [со — Дт! + ekx3] w, B.6.70)
о+ (к) v (к) = —2сой)+ [—со — Дтх + ehrs] w. B.6.71)
В дальнейшем можно применить любой выбор w и w при условии
их линейной независимости; поэтому используем простейший
выбор
I . B.6.72)
Тогда из B.6.70) и B.6.71) получим
н+ (к) и (к) = 2сос2 (со + вА), о+ (к) v (к) = 2сое2 (со + ей).
Сравнивая эти соотношения с B.6.62) и B.6.63), находим с =
= с = [BпK2со (со + eh) Yll*ffl2. Поэтому имеем
B.6.73)
/sin 0fe
(coseJ B.6.74)
где
cos 9ft = [(со + eft)/2<D]V., B.6.75)
Sin 6ft = Д/ [2со (со + eft) ]V. = [(to — е,,)/2со ]'/,. B.6.76)
56 Глава 2
Свободное поле дается выражением
Ф° (х) = J d3k [и (к) а (к) е{ <кх-а>о ^ v (к) pt (к) e-i (кх-а>0]. B.6.77)
Приведем простой пример уравнения типа 1:
M<5)=;^4-iv2, B.6.78)
откуда
Л = 1, d(d) = 1, B.6.79)
1г= 1, Г (k, E) = 1. B.6.81)
Тогда условие нормировки принимает вид
м+ (к) и (к) = Bя) ft, B.6.82)
откуда
и (к) = Bя)~3/2 Й1/2, B.6.83)
Здесь е обозначает е(к).
Правило сумм. Вернемся к уравнению для свободного поля
общего вида B.6.7) и введем важное правило сумм. Рассмотрим
сначала уравнения типа 2; полученные результаты нетрудно
будет модифицировать применительно к уравнениям типа 1.
Введем две функции
5_^_exp{±ilkx-(o(±k)/|}, B.6.85)
обладающие следующими интересными свойствами:
д+ (_х) ^ _д- (х), B.6.86)
^ -4-SW6(a B-6.87)
±(x) = 0. B.6.88)
Объединяя последнее свойство с выражением B.6.15), получаем
К (д) d {д) А± (х) = 0, B.6.89)
Квантовая теория систем многих тел
57
Обозначив размерность матрицы X (д) через п, рассмотрим
произвольный постоянный вектор
w=
w2
Тогда векторы
{х — x')
(д) Д± (х — х') w
B.6.90)
B.6.91)
являются решениями уравнения поля X (д) ф* = 0. Разложим
их по ортонормированным решениям иг (к, х) и vr (к, х), которые
даются выражениями B.6.32) и B.6.33). Поскольку поле ср+
(или ф-) содержит только отрицательные (или положительные)
частоты, имеем
d (д) А+ (х - х) w = ^ J d3kct (k, х) и (к, х), B.6.92)
г
d(д)А-(х-х)ю=*%1 (fkc7(к, х)v (к, х). B.6.93)
г
Учитывая условия ортонормированности B.6.38) и B.6.39),
можно определить коэффициенты с? (к, х') следующим образом:
hct (к, х) = j ixu (к, х) 'Tel (д) Д+ (х - х) w, B.6.94)
ЙсГ(к, х') = —
-/)». B.6.95)
Подставляя затем выражения B.6.85) в B.6.94), получаем
Пс1 (к, х) = -Г
{«^ (к, х') Г (к, *„) d (k) w}ka=a (k). B.6.96)
С другой стороны, из выражений B.6.27) и B.6.42) следует
р /I, и \ д а ,,, ,п t; Q7\
1 (К, "о/^^ ~Л(Г—'"{"•)> (Z.O.cm)
откуда, применяя соотношение X (k) d (k) = k\ — со2 (к), полу-
чаем
V (U k \ r! lh\ I 1 tb\ ^ Л ik\ 9k (9 6 QR\
Таким образом, имеем
[п' (к, х) Г (к, Ло) d (/г) Ь0=и (k) = 2ю (к) йг (к, х'), B.6.99)
5S Глава 2
так что из выражения B.6.96) следует
ПсЦк, х) = — Шг (к, х) w. B.6.100)
Аналогично находим
По; (к, х) = ipvr (к, х') w. B.6.101)
Окончательно выражения B.6.92) и B.6.93) приводят к следую-
щему правилу сумм:
2 J d3kur (к, х) пг (к, х) = Ш (д) Л+ (х — х), B.6.102)
Г
2 j <$kvr (к, х) vr (к, х) = —ipHd (д) А' (х — *'). B.6.103)
Для уравнений типа 1 с положительными значениями е (к)
[== ю (к)] можно доказать правило сумм B.6.102) при условии, что
А+ (х) определена следующим образом:
А+ (х) = —i Bя)-3 J d?kel ^-^t). B.6.104)
Из этого определения следует
б (*) А+ (х) = — i& (x) б @, B.6.105)
+(*) = 0. B.6.106)
В случае уравнений типа 1 вместо соотношения B.6.98) полу-
чаем
Г (k, ko) d (k) + K(k)^d (k) = l. B.6.107)
Перестановочные соотношения и статистика. Поскольку ф°
имеет вид B.6.45) для уравнений типа 2 или B.6.46) для уравне-
ний типа 1, правила сумм B.6.102) и B.6.103) приводят к следую-
щим перестановочным соотношениям:
[ф/° (х), Ф2 (У) 1± = Щи (д) 1А+ (х-у) + рр'А- (х -у)].
B.6.108)
Здесь обозначение [ ]+ для коммутатора (антикоммутатора) отно-
сится соответственно к бозонным (фермионным) полям, а
0 для уравнений типа 1 с положительным е (к),
+ 1 для уравнений типа 2 бозонного поля, B.6.109)
—1 для уравнений типа 2 фермионного поля.
Введем теперь требование причинности, согласно которому
операторы Fit соответствующие наблюдаемым величинам, должны
Квантовая теория систем многих тел 59
коммутировать друг с другом, если они относятся к различным точ-
кам пространства в один и тот же момент времени, так что
[Ft (x, t), Fj (у, t)]=0 при хф у. B.6.110)
Поскольку все наблюдаемые, связанные с фермионными полями,
являются функционалами от билинейных комбинаций фермион-
ных полей, требование причинности для них выполняется тогда
и только тогда, когда
[ф/ (*), Ч>% (У) 1± б (tx - ty) = 0 при х Ф у. B.6.111)
Для уравнения типа 1 (р' = 0) из соотношений B.6.108) и
B.6.105) ясно, что требование причинности выполняется автома-
тически.
Для уравнений типа 2 из B.6.85) имеем
А+ (х — у) + Л~ (х — у) = 0 при tx = tv,
B.6.112)
^ге.к.(х-у) при tx==tr
B.6.113)
Тогда из требования причинности следует
рр' = 1, B.6.114)
где учтено соотношение B.6.108).
Если ввести функцию
Л (*-#) = А+ (х - у) + А" (х — у), B.6.115)
то перестановочные соотношения для свободного поля примут
вид
[ср° (*), ф° (у) ]± = iM (д) А(х — у) B.6.116)
для уравнений типа 2 и
[Ф° (*), ф° (у) ]± = «d E) А+ (х - у) B.6.117)
для уравнений типа 1.
Вернемся теперь к условию B.6.114), из которого с учетом
B.6.109) следует вывод
+ 1 для бозонных полей,
, , „ B.6.118)
—1 для фермионных полей.
Таким образом, мы приходим к неожиданному результату: тре-
бование причинности однозначно определяет статистику частиц,
описываемых полевыми уравнениями типа 2. Действительно, в силу
требования причинности р = р', причем уравнение поля опреде-
ляет величину р, тогда как статистика определяется величи-
60 Глава 2
ной р'. В случае релятивистского полевого уравнения соотноше-
ние B.6.118) является условием, которое приводит к хорошо из-
вестным соотношениям между спином и статистикой [13].
Канонически сопряженная величина для ц>°. В случае, описы-
ваемом уравнением B.6.47), т. е.
Я, (д) = — дЧд? — со2 (V), ' B.6.119)
согласно B.6.51), имеем р = 1, и, следовательно, поле ф° должно
быть бозонным полем. В этом случае d (d) = 1 и г} = 1 согласно
B.6.48); следовательно, из соотношения B.6.116) имеем
[q>° (х), Фо+ (у) ] = ША (х — у). B.6.120)
Поскольку B.6.87) принимает вид
6(/)-|-Д(*) = -6(хN(*), B.6.121)
соотношение B.6.120) дает
[<р° (х), ф°+ (у)] = ihb (x — у) при tx - ty, B.6.122)
где ф0+ = (d/dt) ф0'1'. Отсюда видно, что величины ф° и ф0+ кано-
нически сопряжены друг другу. Это утверждение согласуется
со структурой лагранжиана S^ в B.6.26).
Для примера, описываемого соотношением B.6.54), когда
К (д) = i-j-тз + ;Лт2 - е (V2), B.6.123)
имеем р = —1 в соответствии с B.6.64), откуда следует, что
Ф° — фермионное поле. В этом случае из B.6.116) имеем
[ф° (х), Ф° (У) 1+ = ih (« -|-т8 + /Атя + е (V2)) А (* - у),
B.6.124)
где ф° = ф0+т3. Из этого антикоммутационного соотношения
получаем
[<р° (х), Фо+ (у) I = йб (х — у) / при tx = tv, B.6.125)
где / — единичная матрица размерности 2 х2. Таким образом, ф°
и ф0+ образуют пару канонически сопряженных полей, что согла-
суется со структурой лагранжиана 2?%.
Проектирование операторов рождения и уничтожения. Закон-
чим этот раздел тем, что продемонстрируем возможность проекти-
рования операторов уничтожения или рождения, при котором они
полностью исключаются из свободного поля ф°. В начале этого
раздела мы потребовали существования соотношений, связываю-
щих операторы уничтожения и рождения со свободным физиче-
Квантовая теория систем многих тел 61
ским полем ф°. Это требование гарантирует, что динамическое
отображение, выражающееся через операторы уничтожения и
рождения, может быть выражено также через физические поля.
Покажем теперь, каким образом можно связать аг (к) и рг+ (к)
с ф° (х). Если свободное поле ср° задано в виде B.6.45), методом
проектирования можно исключить операторы рождения и уничто-
жения с помощью формул
Ыг (к) = | й3хпг (к, х) Тц>°(х), B.6.126)
щ\ (к) = —р | d3xvr (к, х) Гер0 (х). B.6.127)
Эти формулы непосредственно следуют из B.6.45) при учете соот-
ношений ортонормированности B.6.36)—B.6.39). Обобщение этого
рассуждения на случай уравнения B.6.46) представляется оче-
видным.
ЛИТЕРАТУРА
1. von Neumann J., Math. Ann., 104, 570 A931).
2. van Hove L., Physica, 18, 145 A952).
3. Friedrichs K. 0., Mathematical aspects of the quantum theory of fields, Inter-
science, New York, 1953.
4. Wightman A. S., Schweber S. S., Phys. Rev., 98, 812 A955).
Garding L., Wighlman A. S., Proc. Nat. Acad. Sci. USA, 40, 617; 622 A954).
5. Dunford N., Schwartz J. Т., Linear operators I, II, Interscince, New York,
1963. [Имеется перевод: Данфорд Н., Шварц Дж. Линейные операторы.
Т. I. Общая теория.—М.: Мир, 1962; т. II. Спектральная теория.—М.:
Мир, 1966. J;
von Neumann .!., Mathematische Grundlagen der Quanten-
mechanik, Springer, Berlin, 1932. [Имеется перевод: Нейман Дж. Математи-
ческие основы квантовой механики. —М.: Наука, 1964.]
6. Fock V., Zs. Phys., 75, 622 A932).
7. Боголюбов И. Н., ЖЭТФ, 34, 73 A958).
8. Glauber R. J., Phys. Rev., 131, 2766 A963).
9. Anderson P. W., Phys. Rev., 83, 1260 A951); 86, 694 A952);
Kubo R., Phys. Rev., 87, 568 A952).
10. Takahashi Y., Vmezawa H., Nucl. Phys., 51, 193 A964);
Aurilia A., Vmezawa H., Phys. Rev., 182, 1682 A969).
11. DeFacio В., Hammer С L., J. Math. Phys., 17, 267 A976).
12. Nambu Y., Phys. Rev., 117, 648 A960);
Элиашберг Г. М., ЖЭТФ, 38, 966 A960).
13. Pauli W., Phys. Rev., 58 716 A940).
ГЛАВА 3
ПРЕДСТАВЛЕНИЕ ФИЗИЧЕСКИХ ЧАСТИЦ,
5-МАТРИЦА И СОСТАВНЫЕ ЧАСТИЦЫ
3.1. (N, в)-модель
Введение. В гл. 2 введены некоторые фундаментальные поня-
тия и методы, требуемые для построения квантовополевого фор-
мализма при описании систем многих частиц. В данной главе
такой формализм представлен в наиболее общей форме. В каче-
стве подготовительного материала в этом разделе исследуется
точно решаемая модель, чтобы с ее помощью проиллюстрировать
построение представления физических частиц, S-матрицу и поня-
тие составных частиц.
(N, в)-модель. Эта модель определяется двумя гейзенбергов-
скими полями N (х) и 9 (х), уравнения Гейзенберга для которых
имеют вид
(; ± - e(V2)) N(x) = K \ Фу \ d*za (х-у)а(х- zN+ (у) N(х) 9(г),
C.1.1а)
(» -J- - И (V2)) 6 (х) = К J фу J Фга (х-у) а (у- z) N* (у) N (у) 0 (г).
C.1.16)
Предполагается, что N (х) — фермионное поле, удовлетворяющее
антикоммутационному соотношению
IN (х), т (у) ]+ б D - tv) = Йб<«) {х-у), C.1.2а)
а 0 (х) — бозонное поле, удовлетворяющее коммутационному
соотношению
[9 (х), 9+ (у) ]8(tx — ty) = Йб«) (* — у). C.1.26)
Здесь б<4) (х) обозначает б (tx) б (х); принято также, что
[N (х), 9 (у) ] б (tx - ty) = [N (x), 6+ (г/) ] б (tx - tv) = 0, C.1.2в)
а функция а (х—г/) имеет вид
a(x-y)=a(x-y)8(tx-ty). C.1.3)
Упростим далее модель, предположив, что а (х—у) является
функцией только от | х—у |; функция а играет роль обрезающего
множителя в области больших импульсов.
Представление физических частиц 63
Канонические уравнения
iH^-N(x) = [N(x), H], m^rQ(x) = [Q(x), H\ C.1.4)
выполняются, если гамильтониан имеет вид
Н = j dzx {№ (х) г (V2) N (х) + 6+ (х) ц (V2) 8 (х) +
+ К j d*y J tfza (х-у) а (х- г) #+ (х) N (х) 0+ (у) 0 (г)). C.1.5)
Заметим, что гамильтониан и уравнения Гейзенберга C.1.1а),
C.1.16) инвариантны относительно двух независимых преобразо-
ваний фазы:
преобразования фазы N : N(x)-+eiai N (х), C.1.6а)
преобразования фазы G:Q(x)->-eia'Q(x). C.1.66)
Самосогласованное вычисление. Для проведения самосогла-
сованного вычисления, кратко описанного в разд. 2.5, необхо-
дим начальный набор свободных полей в качестве «кандидатов
в физические поля», с которыми связано построение физического
пространства Фока. Рассмотрим в качестве пробного следующий
набор: свободное фермионное поле № (х) и свободное бозонное
поле 0° (х). Энергии этих полей (остающиеся пока неизвестными)
обозначим т (к) и w (к). Запишем фурье-представления этих по-
лей в виде
No(x) = -^-L \dskN(k)exp[ikx- im(k)t], C.1.7a)
Bя) /2 •>
во (х) = -Z^j- [ d3kQ (к) exp [tkx - ко (к) /]. C.1.76)
Bя) 2 J
Здесь JV (к) и 6 (к) — операторы уничтожения квантов № и 0°
соответственно, так что
[N(k), tf+(l)]+ = 6(k-l), C.1.8a)
[в (к), в+A)] = 6(к-1). " C.1.86)
Эти соотношения приводят к каноническим перестановочным со-
отношениям для свободных полей
[№ (х), N°f (у)}+ б (tx - g = MW (x - у), C.1.9а)
[б" (х), 0°t (у)] б (tx - tv) = П№ (x - у). C.1.96)
Гильбертовым пространством является в данном случае простран-
ство Фока, связанное со свободными полями № и 0°.
Наша задача состоит в вычислении матричных элементов гей-
зенберговских полей. Полученные результаты ариведут к опре-
деленным выражениям для N (х) я Q (х) через нормальные произ-
ведения свободных физических полей. Эти выражения и будут
представлять собой динамическое отображение, введенное в гл. 2,
64
Глава 3
разд. 5. Чтобы избежать какого-либо приближения, рассмотрим
частное решение уравнений Геизенберга C.1.1а), C.1.16), при ко-
тором преобразование фазы поля ./V индуцируется соотношением
№ (х) — eia>№ (х), 0° (х) -»- 6° (х) C.1.1 Оа)
посредством динамического отображения N (х), а преобразование
фазы поля 0 — соответственно соотношением
Во (Х) _*. eia*Q° (х), № (х) -> № (х). C.1.106)
p+q-k
p+q-K
X
^-'-p+q+k
N
Рис. 3.1. Рис. 3.2.
Тогда динамические отображения имеют вид (рис. 3.1 и 3.2)
ft1/. J d?p J dsq J d3k№(q)N(p + q—pc)9(k)c(q, p; p + q—k,k) X
X exp [tpx — t {m(p + q — k) — fn(q) + co(k)}/] -j-
X exp [tpx - i{© (k) + © (q) - w (q + k - p)} f] + ..., C.1.1 la)
+ ft1/. J d3p J d3<7 J d%9+ (q)JVi(p 4- q - k)9(k) d(p, q;p + q - k, k) x
X exp [ipx - i {© (k) 4- m (p h q - k) - со (q)} /] +
4- П'1' j d?p j ^<7]й3^+(-р4-Я4-к)Л/(Ч)Я(к)Ь(р,-р+Ч+к;Ч,к) х
- . C.1.116)
Представление физических частиц 65
Здесь многоточиями обозначены нормальные произведения более
высокого порядка, каждое из которых содержит более двух опе-
раторов уничтожения и более одного оператора рождения. Им-
пульсы в функциях с и d упорядочены согласно правилу с (N, 9;
N, 9) и т. д.
Из выражений C.1.11а), C.1.116) и C.1.7а), C.1.76) находим
е(х)|0) = 0, C.1.12а)
6t (х) | о) = z;/*e°+ (х) | о), C.1.1 за)
N (х)\ 0) = 0, C.1.126)
W+ (х) | 0) = Z\i*N^ (х) | 0), C.1.136)
где | 0) — вакуумное состояние. Из этих выражений с учетом
C.1.9а), C.1.96) следует
@ | [9 (х), 8+ (у) ] | 0) б (tx - /„) = ZJW (jf _ у),
@ | IN (x), № (у) ]+ | 0) 6 (tx - ty) = Z2ft6№ (x-y).
Нормировочные множители Zx и Z2 определяются с помощью
соотношений C.1.2а) и C.1.26) следующим образом:
Zx = Za = 1. C.1.14)
Учитывая соотношения C.1.12а), C.1.126) и C.1.13а), C.1.136),
из уравнений Гейзенберга C.1.1а), C.1.16) находим
= 0, C.1.15а)
(t-|--F(V2))<0| во (*)=(), C.1.156)
что приводит к следующему определению энергий т. (к) и со (к):
m(k) = eAl co(k>==^ft, C.1.16)
где величины eft и \ih определены соотношениями
efte^ = 8 ^ etkK и т_ д C.1.1 7)
Выражения C.1.16) предполагают отсутствие собственных энер-
гий.
Введем обозначения
| 9 (к)) = 9+ (к) | 0), | 9 (к) 9 A)) = 6+ (к) 9+ A) | 0) и т. д. C.1.18)
Вычисляя матричные элементы вида (9(&) I C.1.16) |9(pH(q))
и (N (к) |C.1.1а)| N (р) N(q)), получаем
а (р + q — к, к; р, q) = Ъ (р + q — к, к; р, q) = 0. C.1.19)
66 Глава 3
Вычислим далее (N (q—р) | C.1.16) | N (q—к) 9 (к)) при ?Ф к.
Получаем
[со (р) — со (к) - т (q — к) + т (q - р)] с (q - р, р; q - к, к) =
= - Тгкг аРа* ~ ХПаР f d4a'c (Ч-lh q-k, к), C.1.20)
где ah — фурье-образ функции
k(x-y)]. C.1.21)
Рассмотрим временную зависимость второго слагаемого в пра-
вой части уравнения C.1.11а) и положим с (q, р; р + q — k, к)
равным фурье-образу запаздывающей функции; тогда из C.1.20)
получим
c(q — p,p;q —k,k)=bcp[(o(k)-f/n(q—k)—(o(p)—/ra(q
X
-I, I; q - к, к)) , C.1.22)
где е -> + 0. Отсюда находим
Х a>(k) + m(q-k)-a>(p)-/B(q-p) + /e ' (зл-23)
где
/ (q, к) = ft J сРра* [со (к) + m (q - к) - © (р) - /я (q - р) + /в].
C.1.24)
Аналогичное вычисление для (9 (р) | C.1.1а) | N (q—к) 9 (к))
приводит к равенству
d (q — Р, Pi q — к, к) = с (q — р, р; q — к, к), C.1.25)
что можно усмотреть также из рис. 3.1 и 3.2.
Канонические соотношения. Рассмотрим канонические пере-
становочные соотношения. Для простоты ограничимся лишь со-
стояниями, в^которых имеется не более двух частиц. Рассмотрим
сначала [N (x), Q (у)] 8 (tx—ty). Поскольку выражение C.1.10а)
индуцирует преобразование фазы поля N, а C.1.106) — поля'Д
оператор [N (х), 9 (у) I уничтожает один квант № и один квант 9°.
Следовательно, достаточно вычислить лишь матричный элемент
Представление физических частиц 67
(О | 1М (л:), 9 (у) ] | N, 9). Динамические отображения, определяе-
мые равенствами C.1.11а) и C.1.116), дают
(О | Ш (х), 9 (у)] | N A - к) 9 (к)) б (tx - tv) =
= —Щп- еПу [ dsp exp {ip (х - у)} ехр [ - i {т A - к) + со (к)} tx) x
х [с (р, 1 — р; 1 — к, к) — d (р, 1 — р; 1 — к, к) ] X
X б (tx — ty) = 0, C.1.26)
что согласуется с каноническим соотношением [N (х), 9(г/)]х
Хб (tx-ty) = 0.
Аналогично находим
(N A + к) | [№ (х), 9 (у)] 19 (к)) б (tx - ty) =
^7Г{сA + к, р; 1 + р, к) +
+ d* A + р, к; ! + к, р)} + А A + к, р; 1 + р, к)] х
X ехр {—Их - ip (х - у)} ехр [i {т A + к) - со (к)} tx], C.1.27)
где Л A + к, р; 1 + р, к) = П3 f dsqc A + к, р; 1 + к +
+ р - q, q) d* A + р, к; 1+ к + р - q, q) = C.1.28)
= й3 J d*qc (I + к, р; 1 + к + р - q, q) с* A + р, к;
1+к + р —q, q). C.1.29)
Чтобы упростить запись, введем обозначения
^J^,) , C.1.30)
lq A) = со (q) + m A - q). C.1.31)
Тогда имеем
ЛA + к, p; 1 + p, k) = tepafcj-gra^|f(l + p+k, q) |2 X
-ikO + P + k)-^]-1. C.1.32)
С другой стороны, из C.1.30) следует
F (q, к) - F* (q, к) = -21я | F (q, к) |2 Z (q, к), C.1.33)
где Z (q, к) определено соотношением
a\Z (q, к) = Jd3pap6 [|к (q) - U (q)l- C.1.34)
Поскольку Ip (q) зависит только от ра и (р—qJ, можно записать
ald?p = tf [| q |, cos 9, ?р (q) ] d|p (q) d cos fcty/2n, C.1.35)
68 Глава 3
где 8 — угол между векторами q ир, iV — некоторая функция.
Тогда из C.1.34) следует
atf (q, k) = J d cos QN [| q]\, cos 0, g* (q) ]; C.1.36)
заметим, что, согласно C.1.34), величина Z (q, k) положительна.
Учитывая соотношение C.1.33), можно переписать C.1.32)
в следующем виде:
ЛA + к, р; 1 + р, к) =
A + к 1 + Р, k)J ff). a|Z(l + P + k, q) X
где
sv /1 I L- n- 1 I rt 1r\ aPaft« 1 /Q 1 QQ\
U A H— K, U, I 4— p, КI r—: т. r ;—: , \O,l ,oo
/Я1 gk — Sp + lK
здесь и в дальнейшем используется сокращенное обозначение |q
вместо ?q A + р + к).
Используя формулу
—4-. Ц- = —2ш'6((о) C.1.39)
и учитывая равенства C.1.24), C.1.30) и C.1.34), перепишем
выражение C.1.37) в следующем виде:
ЛA + к, р; 1 + р, к) =
= 2я1 7^3-0A +к, р; 1 + р, к)а^A+р + к, к)-
, p; 1 + р, k)ap2F*0 + P + k. P)
k, q)
х
, q)
Х( 5S + te ii + *e )
х
( |q_^_fe -ip
Представление физических частиц
69
Заметим, что первое и второе слагаемые равны соответственно
[—й2/Bя)'/* ] с(Н-к, р; 1 + Р, к) и [—йа Bя)'М d* A+р, к;
1+ к, р). Таким образом, получаем
Bя)8/»
:, р; 1 + р, k) + d*(l + p, к; 1 + к,
+ Л (I + к, р; 1 + р, к) =
1 к
с d°q I
J BяK V"
X
Z A + р + к, q) 1 - XI A + р + к, q)
X l?q — Ik + Щ'1 Hq — Ip + ie] — компл. сопр.^ C.1.41)
Рис. 3.3.
Это выражение определяет правую часть равенства C.1.27). Вы-
берем ?q в качестве одной из переменных интегрирования, и
пусть i0 является граничным значением, с которого начинается
горизонтальный разрез в этой плоскости. Тогда выражение
C.1.41) приобретает смысл контурного интеграла, контуром для
которого является сх + с2 (сх — обход снизу вещественной полу-
оси от оо до !0, а с2 — обход той же полуоси сверху от |0 до оо).
Поскольку интеграл по бесконечности удаленной части контура cs
равен нулю, контур интегрирования в плоскости | может быть пре-
образован в замкнутый контур сх + сг + с3 (рис. 3.3).
Если функция [1 — XI A + р + k, q) H не имеет особенностей
внутри замкнутого контура с, интеграл в C.1.41) равен нулю,
и равенство C.1.27) становится каноническим перестановочным
соотношением. Но так бывает не всегда. Чтобы убедиться в этом,
70 Глава 3
используем соотношение C.1.24), записанное в виде
/ A + р + к, q) = ft J cPra* [gq — gr + ie], C.1.42)
и примем, что константа связи Я допускает одно значение ?, при
котором
1 = Mz J>ra? [? - |г]-х, ? < |о. C.1.43)
Заметим, что величина ? зависит от полного импульса 1 + к + р,
т. е. ? = ? A -f- к + р). Условие C.1.43) удовлетворяется, на-
пример, если ?г является возрастающей функцией г2, Я, отрица-
тельна и | Я | достаточно велико. Физический смысл двух послед-
них условий состоит в том, что (N, 9)-взаимодействие является
притягивающим и достаточно сильным.
Равенства C.1.42) и C.1.43) приводят к соотношению
1 _ U A _|. р + k) q) = %П (?, - р j cPraj [&, - g, + us]'1 [? - Ir]'1,
C.1.44)
откуда видно, что вклад в интегрирование в C.1.41) дает лишь
полюсная особенность при |q = ?. Тогда можно записать
l-X/d + p + k,,) = BAlt-tk) +r)(l + P + k) q), C.1.45)
где т) A + р -f k, q) не содержит полюсной особенности. Тогда
из C.1.44) находим
(j^j"; C.1.46)
отметим, что величина В A -\- р -(- к) положительна.
Учитывая равенства C.1.35) и C.1.36), из C.1.41) получаем
р;
И
+ А (! + к, р; | + р, к) — ^ -^ +^ . C.L47)
Это соотношение вместе с C.1.27) указывает на нарушение вто-
рого канонического соотношения в C.1.2в).
Составные частицы. Для исправления этой ситуации изменим
первоначальный набор свободных физических полей, введя в него
новое фермионное поле V0 (х). Изменим условия C.1.10а), C.1.106)
следующим образом: преобразование поля N индуцируется со-
отношениями
№{х)-+е'а'№{х), V°(x)-*eia>V°(x), 0»(лг) —-е°(*), C.1.48а)
Представление физических частиц
а преобразование поля 0 — соотношениями
в» (х) -> е'^9° (х), V°(x)-+--eta*V°(x), №(x) ->• №{х). C.1.486)
Такое предположение мотивировано тем, что V0 представляет
собой^«составную^частицу» из N и 9.
В "этом случае динамические отображения C.1.11а), C.1.116)
также изменятся (рис. 3.4) и примут вид
9 (х) = 6° (х) + НУ> J d?p J d3q J d3k№ (q) N (p + q — k) 9 (k) X
X с (q, p; p + q — k, k) exp [tpx — i {m (p + q — k) —
- m (q) + со (k)} t\ + n\d*p\ dHg A, p; p +
+ 1) № A) V (p + 1) exp [tpx — i {M (p + 1) —
— m(l)} Л + .... C.1.49a)
N (x) = N° (x) + ft3/* j d3p J d3^ J d3k№ (q) ^V (p +
+ q — k) 9 (k) d (p, q; p + q — k, k) exp [tpx —
— i{(u(k) + m(p + q—k) —со
+ 1)>хр [tpx — i {M (p + 1) —
— со A)} t] +... . C.1.496)
Здесь многоточиями обозначены нор-
мальные произведения более высокого
порядка, V (к) — оператор уничтоже-
ния кванта V0 с импульсом к и энер-
гией М (к). При написании выражений
C.1.49а), C.1.496) использовался тот
факт, что соотношения C.1.14), C.1.19),
C.1.23) и C.1.25) сохранили прежний
вид, несмотря на наличие поля V0.
Вычисляя матричные элементы (Af AI
C.1.16) | V(p + 1)) и (9 A) | C.1.1а)
I V (р + I)), находим
g0, р; Р +
Рис. 3.4.
-1)-M(p+./-co(p)-m(l)Jd3^g(PH-k,k;P + l),
C.1.50а)
h A, р; р + 1) = g (I, p; p -(- 1). C.1.506)
Вводя далее величину
р (р + 1) = %\d?kak g (p + 1 — к, к; р + I), C.1.51)
72 Глава 3
из C.1.50а) получим
Подставляя последний результат в C.1.50а), получаем
1 = Ш \ d3ka% [М (Р + 1) - ik (Р + 1) Г1, C.1.53)
или в другой форме
1 = Ш \ dsra? Ш (р + 1 + к) — б,]. C.1.54)
Сравнивая C.1.54) с C.1.43), находим, что М (р -f к + 1) — соб-
ственное значение ?, определяемое уравнением C.1.43), т. е.
М(р + 1+к) = ?. C.1.55)
Иными словами, энергия М (р -f- I -f к) кванта V0 совпадает
с величиной полюсной особенности функции [1 —KI A +р +
+ К q)].
Нормировочный множитель Р (р + I) В C.1.52) остается не-
определенным. Наличие частицы V0 изменяет соотношение C.1.27)
следующим образом:
(N A + к) | [т (х), е (у)] | е (к)) б D - g =
J^-fcfl-l-k, p; 1+р, к) +
+ d* A+ р, к; 1 + к, р)} + А A + к, р; 1 + р, к) +
+ Wg A + к, р; 1 + р + к) h* A + р, к; 1 + р +
+ к) j ехр {—Их — tp (x — у)} exp [i {m A +
+ к) —ю(к)}/х]. C.1.56)
Учитывая, что
g A + к, р; 1 + к + р) h* A + р, к; 1 + к + р) =
и принимая во внимание C.1.47), находим
(N A + к) | [N* (х), 9 (у) ] | 9. (к)) б (/х - ty) = 0, C.1.58)
если выбрать р (р + 1 + к) следующим образом:
|1 р + к). C.1.59)
Таким образом, каноническое соотношение [УУ+ (х), 8 (у)] б (tx —
—ty) = 0 восстанавливается благодаря наличию частицы V0.
Представление физических частиц 73
Из определений C.1.59) и C.1.52) следует
Вычисляя матричные элементы других канонических коммута-
торов (или антикоммутаторов), можно показать, что выполняются
все канонические перестановочные соотношения C.1.2а)—C.1.2в).
Указанное вычисление ограничено подпространством гильбер-
това пространства, в которое входят состояния | 0), | 9), | N),
| 9, N), | N, N), | 9, 9), | V) и их линейные комбинации; ниже это
подпространство будет обозначаться &s.
Используя равенства C.1.136) и C.1.49а), можно показать, что
Н О- Р; Р + О ехр [фх - i {М (р + 1) - т{\)} t] =
= (N A) | 9 (дс)| V (р + 1)) =
^-ny(Ql^(y, t)Q(x, t)\V(p + \)). C.1.61)
Отсюда ясно, что динамическое отображение Af (x) 9 (х) имеет
следующий вид:
, p; р + 1O(р + 1)Х
X exp[i(p + l)x-fM(p + l)f]+ ••• • C.1.62)
Здесь многоточие обозначает нормальные произведения более
высокого порядка. Согласно этому соотношению, V (р +1) яв-
ляется одним из слагаемых в линейной суперпозиции при динами-
ческом отображении гейзенберговского оператора N (х) 9 (х).
В этом случае мы заключаем, что У°-квант — составная частица,
состоящая из N и 0. Приведенные выше соображения показывают,
каким образом составная частица вводится в процессе самосогла-
сованного вычисления [1]. Примечательно, что канонические пере-
становочные соотношения играют решающую роль в вопросе о
наличии составных частиц.
Гамильтониан. Используя динамические отображения C.1.49а),
C.1.496), можно вычислить матричные элементы гамильтониана Н,
определяемого выражением C.1.5). Применяя уравнение Гейзен-
берга C.1.16), можно записать Н в виде
Я = J d3* (#t (x) e(V2) N {х) + i9t (x)-J-6(*)) . C.1.63)
74 Глава 3
Из соотношений C.1.49а), C.1.496) и C.1.16) имеем
= Bя)« Й26 (к - 1) j dV {M (к) - т (к - р)} \g (к - р, р; к) |«,
C.1.64)
(У (к) | j d4№ (х) е (V2) N (x)\V A)) =
= BяK Й26 (к - 1) j d3pm (к - р) | g (к - р, р; к) |2, C.1.65)
где учтено также равенство C.1.506). Используя далее C.1.46),
получаем
(V(k)\H\V(l)) =
= ПМ (к) В (к) 6 (к - 1) J d», [Д1(к)_т(р)а1д(к.р)], - CМ^
= ИМ (к) 6 (к - 1). C.1.67)
Таким образом, имеем
(V(k)\H\V(\)) = (V (k)\H0\V (\)), C.1.68)
где Но — свободный гамильтониан физических полей:
Яо = Й j d3yfe [со (к) 9+ (к) 6 (к) + т (к) Л^+ (к) N (к) +
+ М (к) 1/+ (к) V+ (к) V (к) ]. C.1.69)
Из этого вычисления видно, каким образом естественно возни-
кает свободный гамильтониан для составных частиц.
Аналогичное вычисление показывает, что
(а1Н\Ь) = (а\Ц9\Ь). C.1.70)
Используя динамические отображения C.1.49а), C.1.496)., можно
подтвердить равенство C.1.70) для состояний \а) и | Ь), принад-
лежащих подпространству &s. Та же задача для всего простран-
ства становится весьма громоздкой. Но приведенные выше сообра-
жения показывают, каким образом выполняется условие реал.иЗ?<-
цпп представления физических частиц B.5.10)..
Представление физических частиц 75
Асимптотическое условие. Обратимся теперь к анализу асимп-
тотического условия. С этой целью получим из динамических ото-
бражений (З.Ь49а), C.1.496) следующие соотношения:
(а|%(/) | Ь) = -J-^- j d3kg(k) Jd»*exp{-ikx + m(k)t}(a\Q(x)\b) =
= (a| J d^g (k) 0 (k) | ft) + ..., C.1.71a)
(a | ^ @ | b) = Jg?- j cPkg (k) j Л ехр {_Лх +
+ i/n(k)/}(a|tf(x)|6) = (a| j>% (k) JV (k) 16)-f ... . C.1.716)
Здесь g (k) — квадратично-интегрируемая функция, | а), \ b) —
состояния, принадлежащие физическому пространству Фока SF.
При выводе соотношений C.1.71а), C.1.716) учитывались равен-
ства C.1.7а), C.1.76), дающие фурье-разложение свободных по-
лей.
Как видно из C.1.23), слагаемые, представленные многото-
чиями, имеют вид
Функция «размазывания» / (Е) возникает благодаря тому, что
состояния | а) и | Ь) являются волновыми пакетами. При интегри-
ровании в C.1.72) используются следующие формулы:
lim —_! _е( <?-*.)<= О, C.1.73а)
lim -z—I е1 <?-?«» 1=2т8(Е - ?„). C.1.736)
Определим теперь поля 9in (k) и 0out (к):
(а | [ d3kg (к) ein (к) | Ъ) = lim (a | Qg (t) | b), C.1.74а)
(a\{d3kg(k)Q°^(k)\b)= Urn (a\Qg(l)\b). C.1.746)
Тогда из равенства C.1.73а) видно, что 9in (к) дается соотноше-
нием
ein(k) = 6(k), C.1.75)
так что 9in (k) является оператором уничтожения для поля 9°.
Это обусловлено выбором с (q, p; p -j- q — к, к) и других коэф-
фициентов разложения в динамических отображениях в виде за-
паздывающих функций [см. C.1.23)].
76 Глава 3
С другой стороны, из C.1.746) вместе с C.1.736) и C.1.49а)
следует
0out (р) = е (р) — 2Я1 Bя)8/* h J d?q J tPkN* (q) N (p + q —
-kH(k)c(q, p; p + q-k, k)+..., C.1.76)
где
?(q-p, p; q-k, k) = ^ffi !_;J(q, к) X
X б [со (к) + tn (q — к) — со (р) - m (q — p) ]. C.1.77)
Каждое слагаемое, обозначенное многоточием в C.1.76), со-
держит б-функцию, что обусловливает сохранение энергии для
соответствующего матричного элемента. Например, из C.1.76)
и C.1.77) имеем
(N (q - l)|e-t (p)\N(q - k) 0 (k)) = 6 (p - 1) F (p - k) -
- 2ni-^p-F (q, k) б {со (k) + m (q — k) — со (p) — m (q - p)}).
C.1.78)
Входящее поле 0in (x) определяется как свободное поле 0° (х),
а выходящее поле 0out (x) —• как свободное поле
e°ut
= -JLL- [ d3kQ™1 (k) exp {ikx - Ш (k) /}. C.1.79)
Bя) '2 J
Приведенное рассуждение показывает, каким образом с помощью
гейзенберговского поля 0 (х) устанавливается связь между 0in
и 0out.
Вообще говоря, если динамическое отображение гейзенбергов-
ского оператора [например, \р (х) ] содержит только одно линейное
по полю слагаемое (например, ф°), то \|з (х) осуществляет связь
между полями ф'п и фои*. Таким образом, iVin (х) и №ut (x)
получаются с помощью предельных переходов при t -> + оо
поля Ng (t) в C.1.716); иными словами, гейзенберговское поле N (х)
является связующим между iVin (x) и iVout (x). Аналогично из
C.1.62) видно, что гейзенберговский оператор N (х) 0 (х) является
связующим полем между Vin (x) и Voui (x). Тем самым иллюстри-
руется возможность связи входящего и выходящего полей состав-
ной частицы с помощью произведения гейзенберговских полей.
5-матрица. Введем теперь 5-матрицу, определив ее равен-
ствами
(x) =S~lVin(x)S.
C.1.80)
Будем искать матрицу S, предполагая ее унитарной.
Представление физических частиц 77
В соответствии с равенствами C.1.746) и C.1.486) преобразо-
вание фазы 9in ->¦ eia'Qin и Vm -> eia*Vir) индуцирует преобразо-
вание 0°ut _>. ea20out> yout _y. gta^out^ если учеСТЬ, ЧТО N (x) 0 (x)
является связующим полем между Vin и Vout- Аналогично можно
показать, что преобразование фазы iVin ->¦ eia'N'm и l/in-ve'a«l/in
индуцирует iVout -+eia*Nmt, V0ut-->eiaiV0Xlt. Отсюда можно заклю-
чить, что матрица 5 инвариантна относительно преобразования
0in _^ eia*®n, Nin -v eia*Nln, V'm -> eia^a*Vm¦ Это означает, что
если выразить 5 с помощью линейной комбинации нормальных
произведений свободных физических полей (9in, JVin, V'm), то каж-
дый член в E — 1) содержит операторы уничтожения и операторы
рождения парами. Поэтому имеем
S|0) = |0). C.1.81)
Далее из C.1.13а) вместе с C.1.14) следует
G°»t + (х) | 0) = ein + (х) | 0), C.1.82а)
iVout+ (х) | 0) = Nin + (х) | 0). C.1.826)
Трансформационные свойства, определяемые равенствами C.1.48а),
C.1.486), приводят к следующему выводу: каждое слагаемое более
высокого порядка, представленное многоточием в динамическом
отображении N (х) 9 (х) в C.1.62), содержит как операторы унич-
тожения, так и операторы рождения. Таким образом, мы видим,
что при вычислении iV+ (х) 0+ (х) \ 0) дает вклад только первый
член (линейный по V) в правой части C.1.62). Тогда, учитывая,
что V°ut является выходящим асимптотическим пределом произ-
ведения N (х) 9 (х), имеем
1/°и*+(*)|0) = !/'" + (*) |0). C.1.82b)
Из соотношений C.1.82а)—C.1.82в) следует
51 9 (к)) = | 9 (к)), C.1.83а)
51N (к)) = | N (к)), C.1.836)
C.1.83b)
где учтено равенство C.1.80). Из соотношения C.1.81) следует
устойчивость вакуумного состояния, а из соотношений C.1.83а)—
C.1.83в) — устойчивость одночастичных состояний.
Используя равенства C.1.80) и C.1.83), можно с помощью
C.1.78) получить матричный элемент 5-матрицы:
(N (q - р) 0 (l)\S\N (q - k) 0 (k)> = 8 (p -1) (8 (p - k) -
- 2ni -??- F (q, k) 6 [a> (k) + /n (q — k) — a> (p) - m (q — p) ]).
C.1.84)
78 Глава 3
Отсюда имеем
(N (q - р) в A)|S+S|JV (q - к) Э (k)) = 6 (р - I) [6 (р - к) -
X б [со (k) + т (q — к) — со (р) — т (q — р) ], C.1.85)
где использовано равенство C.1.34). Так как соотношения C.1.30)
и C.1.24) дают
(ffF(q, k)--g-F(q, p)N[a>(k)+/n(q-k)-co(p)-m(q-p)]=O,
C.1.86)
то равенства C.1.85) и C.1.33) приводят к соотношению
(N (q - р) в A) | S+S | tf (q - к) в (к)) = 6 (р - I) 6 (р - к).
C.1.87)
Таким способом легко убедиться, что
(a|S+S|&) = (a\b) C.1.88)
для | а) и | Ь), принадлежащих подпространству Ss. Это оправ-
дывает сделанное предположение об унитарности матрицы S.
Для случая, когда | а) и | Ь) принадлежат всему пространству 9,
доказательство свойства C.1.88) весьма громоздко.
Уравнение Бете—Солпитера. Общепринятый подход к изу-
чению составных частиц основан на использовании уравнения
Бете—Солпитера [2]. Амплитуда Бете—Солпитера для частицы V
определяется выражением
G (х, у; к) = @\Т Ш (х), Э (y)]\V (k)) =
= Q (tx - ty) @\ N (х) Q (y)\V (к)) +
+ Э (t, - tx) @\Q(y)N (х) | V (к)}. C.1.89)
В силу уравнения Гейзенберга C.1.1а) имеем для G (х, у; к)
(id/dtx-e<yx))G(x, у; к) =
= I J d4 | d%a (х-1)а(х-\) ф\Т [6+ (?) N (х) 6 «), в (г/)] J У (к)),
C.1.90)
78
Глава 3
Отсюда имеем
(N (q - р) 0 (l)|S+5|iV (q - к) 0 (k)) = б (р - I) [б (р - к) -
X
X б [со (k) + m (q — к) — со (р) — от (q — р) ], C.1.85)
где использовано равенство C.1.34). Так как соотношения C 1.30)
и C.1.24) дают
(j^-F(q, k) — ^-F(q, p)N[co(k)+m(q—k) —co(p)—m(q —p)]=0,
C.1.86)
то равенства C.1.85) и C.1.33) приводят к соотношению
(N (q - р) 0 A) | S+5 | N (q - к) 0 (к)) = б (р - I) б (р - к).
C.1.87)
Таким способом легко убедиться, что
(a|S+S|ft) = (a\b) C.1.88)
для | а) и | Ь), принадлежащих подпространству 9S. Это оправ-
дывает сделанное предположение об унитарности матрицы S.
Для случая, когда | а) и | Ь) принадлежат всему пространству *§,
доказательство свойства C.1.88) весьма громоздко.
Уравнение Бете—Солпитера. Общепринятый подход к изу-
чению составных частиц основан на использовании уравнения
Бете—Солпитера [2]. Амплитуда Бете—Солпитера для частицы V
определяется выражением
G (х, у; к) = ф\Т Ш (х), 0 (y)]\V (k)) =
+ е (t, - tx) @\Q(y)N (x) | V (к)). C.1.89)
В силу уравнения Гейзенберга C.1.1а) имеем для G (х, у; к)
(id/dtx-e<yx))G(x, у; к) =
= I J d4 \ d%a (x-l)a(x~l)@\T [0+ (i) N (x) 6 (Q, в (у)] J V (к)),
C.1.90)
Представление физических частиц
79
где использован тот факт, что lN_(x), Q (у)\ =0 при tx = ty.
Уравнение Гейзенберга C.1.16), где а (х — |) = а (х — 1) б (tx —
— ^l), приводит теперь к уравнению
(idldty - \i (%)) (id/dtx - в (V|)) G (x, у; к) =
= il J ^? j d%a (X-I)a(x- Q @1 [0 (j,), 6+ (?) iV (x) Q (Q] | 7(k)) X
Xb(tx- tu) + W \ d^m'dX'd (X-I)a(x-Qa(jy- ?') X
X а (г/ - О @1Г [0+ a) N (x) 0 (Q, iV+ (Г) iV (g') 6 (?')] I 7 (k)) =
= i^fto(x - г/) j d%a(x-QG(x, t,\ k). C.1.91)
Рис. 3.5.
Здесь использованы свойства @| iV+ = @| 6+ = 0, а также
равенство
@|7 Ш(х), Q (Z)]\V (к)) = @\N (х) Q (Q\V (к)) для /, = tz.
C.1.92)
Уравнение C.1.91) можно записать в интегральной форме:
G (х, у; к) = — an \ d'ld^zS (х — g) А (у — ?) а X
X (g_?)u(g-z)G(g, z; k). C.1.93)
Это так называемое однородное уравнение Бете—Солпитера
(рис. 3.5). Здесь А и 5 — функции Грина:
(t-0-.-р (у2)) А (х) = i№ (x), C.1.94а)
(t -щ- - 8 (V2)) 5 (х) = i8W (x). C.1.946)
В уравнении C.1.93) нет неоднородного члена, так как
@\T[N°(x), Q°(y)]\V(k)) = 0.
Введем теперь функцию
G (х; к) = J d'ya (x - у) G (х, у; к). C.1.95)
Тогда уравнение C.1.93) принимает вид
G (х; к) = J d%Q (x - |) G (|; к), C.1.96)
80 Глава 3
где ядро
Q(x-l) = -UHS (х - 1) J d'ydKa (x-y)A(y-Qa(Z-Q.
C.1.97)
Фурье-образ ядра Q (k), определяющий его разложение Фурье
Q(x)=-&V-\#kQ(k)e"«, C.1.98)
имеет вид
п (к) = -М. f dH l- ^ = C.1.99)
= Xn\d4-, -г, ^r—r-t-^-- C.1.100)
J /fe0— и A) — m (k— 1) + ig v 7
Поскольку функция G (я, к) является матричным элементом
между состояниями | 0) и | V (к)), она имеет вид
G (х; к) =G(k) exp {tkx — Ш (k) /}, C.1.101)
где М (к) — энергия кванта V0. Тогда в силу уравнений C.1.96)
и C.1.100) получаем
Последнее означает, что М (к) является собственным значением
уравнения
1-кП[ cPlxnn л? к—п = °- C.1.103)
J М (к) — со A) — т (к — I) v ;
Тем самым воспроизводится результат, полученный при анализе
уравнения C.1.53), и иллюстрируется возможность определения
энергии связанного состояния с помощью уравнения Бете—Сол-
питера.
Если использовать C.1.95) и C.1.101), то уравнение C.1.93)
при х = у дает
@1N (х) 9 (*) | V (к)) = —1Ш \ &Ч&% ехр \1к\ -
- Ш (к) tt} S(x — l) A(x~ Q~a (I - S)G (к). C.1.104)
С другой стороны, в силу C.1.62) имеем
@ \N(x)Q (х) | V (к)) = ¦ ?'*и exp {ikx - Ш (кH j d3 lg (к - 1, I; к).
C.1.105)
Представление физических частиц , 81
Легко показать, что уравнение C.1.104) переходит в C.1.105)
при использовании C.1.62). Неопределенный нормировочный мно-
житель Р (к) (а следовательно, и G (к)) определяется, как было по-
казано выше, каноническим перестановочным соотношением. Дру-
гой способ определения нормировочного множителя р (к) состоит
в использовании матричного элемента @|Т [N (x) Q (х),
Nf (у) 0+ (у) ] |0>. Поскольку согласно C.1.12а), 9 (х) | 0) =0,
получаем
@|Г [N(x)Q(x), N*(y)Q*(y)}\0) =
= е (tx - tu) (o\N(x) e (x) m (у) е+ (у)\о) =
= 9 it* - tv) J d3? @| iV (*) 0 (*) I 7 (k)> X
X <l/(k)|iV+ (г/) G+ (г/)|0>+ ..., C.1.106)
где многоточия обозначают слагаемые, содержащие все промежу-
точные состояния, отличные от состояний с одной У°-частицей.
Из уравнения C.1.106) находим
<0|7 W(x)Q(x), N*(y)Q*W\0) =
= Q(tx- ty) J d3k exp {ik (x - y) - Ш (k) (tx ~
- g}|<o|iv @) e (o)|v(k))|2 +.... C.1.107)
С другой стороны, вводя функцию
G (х, у; г) = @1 Т Ш (х), 9 (у), 0+ (z) iV+ (г) ] 10) = C.1.108)
= Q(tx- tu) 9 (ty - tz) @\N (x) 9 (у) 9+ (z) № (z)|0) +
+ 9 (fe - 4) 9 (tx - у @| 9 (y) N (x) 9t (г) № (z) |0> +
- 0 (^ - 4) 9 D - 4) @19 (y) G+ (г) ЛГ+ (г) ЛГ (дг) | 0) -
-Q(tx-tx)Q{tx-ty){O\&r(z)W(z)N(x)Q(y)\O)-
-Q(tt-ty)Q(ty-tx)@\Q*(z)N4z)B{y)N(x)\0) C.1.109)
и повторяя выкладки, которые привели к уравнению C.1.93),
получаем неоднородное уравнение Бете—Солпитера (рис. 3.6)
G (х, у; т)) = S {х — ц) А {у — г\) — 1Ш \ d%&% d*zS (x — I) X
X А (у - ?) a (S - S) a (S - г) G (g, z; r]). C.1.110)
Решая это уравнение, находим функцию G (х, у; г), которая при
х = у определяет матричный элемент
@|7 W{x)Q(x), tf+(z)e+(z)]|0).
Сравнивая этот результат с C.1.107), можно найти матричный
элемент @1 jV @) 0 @) j V (k)}. Полученный таким способом ре-
82
Глава 3
зультат не только согласуется с выражением C.1.105) при х = 0,
но и определяет также нормировочный множитель р (к), который
оказывается равным аналогичному множителю в C.1.59).
Составные и элементарные частицы. Закончим этот раздел
замечанием о связи между""составными и элементарными части-
цами. С этой целью"введ ем "модель Ли [3], в которой имеются три
гейзенберговских поля N (х), 9 (х) и V (х). Поля N (х) и V (х)
удовлетворяют каноническим антикоммутационным соотношениям
для фермионов, а Э (х) — каноническим перестановочным соотно-
шениям для бозонного поля. Уравнения Гейзенберга имеют вид
(id/dt - е (V2)) N (х) = g J d*ya (x - у) 6+ (у) V (x), C.1.111a)
(id/dt - fx (V2)) 6 (x) = g J d*ya (x - y) № (y) V (x), C.1.1116)
(id/dt - Mo (V2)) V(x)=gj d*yd (x-y)N (y) Q(y). C.1.111b)
Эти уравнения могут быть решены аналогично тому, как это
делается в (N, 9)-модели. Уравнения Гейзенберга C.1.111а) —
C.1.111b) инвариантны относительно преобразований фазы:
N(x)-+e!a'N(x), Q(x)->eia*Q(x), V (х)-+eia*+ia'V (x). C.1.112)
Предполагая, что существуют три физических поля JV° (х), 0° (х)
и V0 (х), решим уравнения Гейзенберга C.1.111а)—(ЗЛ.Шв)
при условии, что преобразование фазы C.1.112) индуцируется сле-
дующим преобразованием:
№(x)-+eia'N°(x), e°(x)-+eia*Q°(x), V°(x)-reia>+i<*>V°(x).
C.1.113)
Представление физических частиц 83
Тогда динамические отображения для N (х) и Э (х) имеют вид соот-
ветственно C.1.49а) и C.1.496), тогда как динамическое отображе-
ние для V (х) дается выражением
V(x) = Z9(q)V°(x)+.... C.1.114)
В результате вычисления приходим к следующему соотношению
для Z3 (q):
^r \ Ы [@ (k) + m (Д k) _ M (q)].) - 1 • C-1.115)
Введем теперь перенормированную константу связи g-r (q)
с помощью соотношения
ф (q) = Z3 (q) g2. C.1.116)
Тогда из C.1.115) имеем
^ (
(«О = 1 ~ W^ (q) f ** (со (k) + m (q - k) - M („)]¦ •
Предполагая величину gr отличной от нуля, рассмотрим предел
Z3 (q) -v 0. При этом C.1.117) переходит в C.1.46) с перенормиро-
ванной константой связи
1 C.1.118)
BяK ?'V4/ —-ччл
Кроме того, как было показано, S-матрица, выраженная через
перенормированную константу связи, согласуется с 5-матрицей
для (N, 6)-модели, если положить Z3 (q) = 0 и использовать
связь C.1.118). Таким образом, составная частица оказывается
специальным случаем элементарной частицы [4 ]; этот специаль-
ный случай соответствует условию Z3 = 0.
Для выяснения физического смысла этого результата полезно
рассмотреть задачу о нейтроне п, протоне р и дейтроне d. Появ-
ление физического нейтрона, физического протона и физического
дейтрона в эксперименте может стать поводом для введения
гейзенберговских полей n, p и d. Из приведенных выше соотноше-
ний ясно, что если перенормирующий множитель для d обра-
щается в нуль, то дейтрон — действительно составная частица.
При этом можно формулировать теорию с помощью только двух
гейзенберговских полей пир [5].
3.2. Представление физических частиц
и вычисления по теории возмущений
Введение. Точно решаемая модель, рассмотренная в разд. 3.1,
иллюстрирует, как выполняется условие реализации представле-
ния физических частиц. Показано в явном виде, что гамильто-
84 Глава 3
ниан может быть в слабом смысле равен свободному гамильто-
ниану физических частиц даже при наличии реакций между ча-
стицами (т. е. при 5 Ф 1). Сдругой стороны, в соответствии с обыч-
ной формулировкой разложений в ряд по теории возмущений 5-
матрица вычисляется на основе гамильтониана взаимодействия.
Отсюда возникает интересная задача: проанализировать, каким
образом обычная теория возмущений согласуется с условием для
представления физических частиц. Эта задача рассматривается
в данном разделе.
Адиабатический множитель. Вычисления по теории возмуще-
ний обычно проводятся с помощью введения так называемого
представления взаимодействия [6] *). Для его построения необ-
ходимо заменить гамильтониан взаимодействия h (t) на
h (t) exp (—e|*|) (адиабатическое включение взаимодействия).
К этому приходится прибегать, поскольку часто не существует
унитарного преобразования между представлением Гейзенберга
и представлением взаимодействия, если не введен адиабатический
множитель ехр (—е|^|). Величину h (t) exp (—е|^|) мы будем
обозначать через hz (t).
Начнем с краткого изложения теории представления взаимо-
действия. Каждому оператору A (t) в представлении Гейзенберга
соответствует оператор Aint (t) в представлении взаимодействия,
связанный с A (t) унитарным преобразованием
А (х) = и-1 (t) Alni (x) и @, C.2.1)
где t обозначает tx. Унитарный оператор и (t) выбирается так,
чтобы выполнялось соотношение
1П -|-Л,„4 (х) = [Аш (х), Но), C.2.2)
где #0 ¦— свободный гамильтониан физического свободного поля ф°:
tfo=j tfVfe© (k) а+ (к) а (к). C.2.3)
При выполнении условия C.2.2) гамильтониан взаимодействия
hs (t) определяется посредством временной зависимости и (t)
следующим образом:
»Й-|-и@=Ав@и@- C-2.4)
Тогда из определения C.2.1) получаем
it -!La (x) = и'1 @ Uint (х), Но + К @ ] и (t). C.2.5)
*) Подробное описание представления взаимодействия дано в учебниках,
цитированных в работе [6].
Представление физических частиц 85
С другой стороны, если Я — гамильтониан в представлении Гей-
зенберга, то
Ш-^-А (х) = [А (х), Я]. C.2.6)
Уравнение C.2.5) должно переходить в C.2.6) в пределе е -> -\-0;
поэтому получаем
Я = lim {и'1 (t) [Яо + К (t) + Wo] и (t)}, C.2.7)
где Wo — с-число. Поскольку© (к) — энергия физического кванта,
/ге (t) не должно приводить к появлению какого-либо сдвига энер-
гии (т. е. собственной энергии). Иными словами, hb (t) содержит
контрчлен собственной энергии. Согласно C.2.7), h (t) — опера-
тор в представлении взаимодействия. Поэтому его зависимость
от времени определяется уравнением C.2.2). Другими словами,
производная по времени от h (t) появляется за счет действия Яо.
Представление физических частиц. Докажем теперь соотно-
шение
К1 (t) 1Н0 + Wo + h& (t) ] и (О}/=о = Яо + Q + Wo, C.2.8)
справедливое для малых е, где Q — оператор со следующим свой-
ством:
(a|Q|&> = 0(e). C.2.9)
Символом 0 (е) обозначаются величины порядка е. Состояния | а)
и | Ь) являются состояниями волновых пакетов физических ча-
стиц.
Для вывода соотношения C.2.8) вспомним, что физическое поле
Ф° (х) удовлетворяет уравнению
*g-=-L[H0, ер»], C.2.10)
а производная по времени от h (t) определяется действием Но:
j- [Но, К @1 = ехр (-е 111) -^-. C.2.11)
Из C.2.11) получаем соотношение
-—{u-^^Wo, he(t)[u(t)} =
= «-1 @ { —7f 1^0, К @] + -^Г ^ (t) } U (t) -
(t). C.2.12)
86 Глава 3
Поскольку при t -*- —оо имеем и (f) -> 1 и hE (t) -*¦ О, выражение
C.2.12) дает
о
{и'1 (t) [Яо, Ле @1 и (О)<=о = #0 + J Л'" (О Л (О «(Г) -±г е^ =
о
= Яо + е J tfV1 (/') ЛЕ (Г) и (Г) = C.2.13)
о
—оо
dt'K(t')+ .... C.2.14)
При получении C.2.14) из C.2.13) использовано соотношение
t
^'MO"(O, C-2.15)
которое может быть получено из C.2.4). Второе слагаемое в C.2.13)
представляет собой оператор Q из C.2.8). В линейном приближе-
нии теории возмущений Q совпадает со вторым слагаемым
в C.2.14).
Для вычисления этого слагаемого заметим, что при t <C 0
имеет место соотношение
(W | К (t)\W) = е" (W | exp (-L Hot) h @) exp (- -L Hot) | W) =
= (Г | Л @) | W") ee' exp (-^- (№ - W") ^) , C.2.16)
где j W) и | W) — собственные состояния Яо:
H0\W)= W\W) и т. п.
Таким образом,
о
')8w.v, C.2.17)
где использовано соотношение
^w-w'-im=—W8w-w- C-2л8)
Исследуем подробнее соотношение C.2.17), предполагая, что
рассматриваемая система ограничена «ящиком» объема V. Тогда
импульсы физических частиц имеют дискретные значения, а опе-
раторы уничтожения физических частиц нормированы соотно-
шением
^6k>1. C.2.19)
Представление физических частиц 87
Множитель УУBяK обеспечивает стремление правой части C.2.19)
к 6 (к — 1) в пределе V -+ оо. Величина в C.2.17) представляет
собой матричный элемент Q в первом приближении. Для изучения
структуры этой величины рассмотрим, например, член вида
ос+а+аа, входящий в Q:
+(!)а(РЖк + 1-р); C.2.20)
здесь учтено, что каждый оператор а или а+ в ф° (х) содержит
множитель BяK/V, равный объему ячейки в импульсном про-
странстве:
Множитель V в числителе выражения C.2.20) обусловлен инте-
грированием по пространству в гамильтониане. Напомним, что,
поскольку вектор к имеет три компоненты, суммирование в C.2.20)
проводится по девяти переменным (kiy lt, pi, I = 1, 2, 3). Но
только восемь из них независимы друг от друга, поскольку,
согласно C.2.17), величина Q (к, 1, р) обращается в нуль, если
не выполнено условие
со (к) + со A) = ю (р) + со (к + 1 — р). C.2.21)
Учитывая далее, что V = Ls, мы видим, что все матричные
элементы оператора C.2.20) — величины порядка ML при боль-
ших L. Заметим, что при конечных е закон сохранения энергии
C.2.21) нарушается на величину порядка 0 (е). Поэтому матрич-
ные элементы C.2.20) порядка 0 (е) в пределе L -> оо. Используя
те же аргументы, можно доказать, что матричные элементы всех
нормальных произведений, входящих в Q (кроме члена вида а+а
и постоянного численного слагаемого), — величины порядка 0 (е).
Поскольку оператор а+ (к) а (к), очевидно, сохраняет энергию
любого состояния, закон сохранения энергии не накладывает
никаких ограничений на матричные элементы этого оператора.
Отсюда следует, что матричные элементы оператора а+а остаются
конечными при предельных переходах V -*- оо и е -> +0. Но опе-
ратор а+а вносит вклад в собственную энергию, и, поскольку
собственная энергия уже входит в Яо, оператор Q не содержит
члена а+а. Кроме того, оператор Q не содержит также никакой
численной константы, поскольку Wo — полная энергия основного
состояния. Таким образом, доказаны соотношения C.2.8) и C.2.9).
Ситуация не изменится, если рассмотреть также члены более
высокого порядка в разложении по теории возмущений C.2.13),
доскольку каждый матричный элемент более высокого порядка,
88 Глава 3
входящий в Q, содержит такой же множитель 8^, w-, как и член
первого порядка в C.2.17).
Из выражения C.2.7) вместе с C.2.8) и C.2.9) следует, что
гамильтониан Н в слабом смысле совпадает со свободным га-
мильтонианом #0 + Wo; оператор Q не дает вклада ни в один
матричный элемент оператора Я в пределе е ->¦ +0.
Реакции между частицами. Вычислим теперь 5-матрицу, ис-
пользуя оператор Q в качестве взаимодействия. В низшем порядке
теории возмущений имеем
оо
S = 1 + lim — \ dt ехР (~е И) Q- (З-2-22)
Отсюда видно, что (S — 1) не исчезает даже в пределе е —у- +0,
хотя Q порядка е; тем самым становится ясно, почему реакции
между частицами все же возможны, несмотря на то, что гамиль-
тониан Я равен Яо + WQ в слабом смысле. Хотя взаимодействие
между асимптотическими частицами в каждый момент времени
практически пренебрежимо мало, оно действует в течение беско-
нечно долгого времени и приводит, таким образом, к конечному
наблюдаемому эффекту рассеяния.
Приведенные выше соображения показывают, что условия
C.2.8) и C.2.9) для представления физических частиц выполняются
только в пределе У-»- оо. Это можно понять интуитивно следу-
ющим образом. Рассмотрим две частицы, которые взаимодействуют
друг с другом, когда расстояние между ними становится меньше
радиуса взаимодействия. Вероятность нахождения двух частиц
в пределах радиуса взаимодействия становится тем меньше, чем
сильнее возрастают размеры соответствующих этим частицам
волновых пакетов. Взаимодействие полностью исчезает, когда
два волновых пакета приобретают бесконечную протяженность.
Но последнее возможно лишь при условии, что объем V бес-
конечен.
Это рассуждение показывает, что существование представления
физических частиц основано на естественном расплывании вол-
новых пакетов частиц. Как будет показано в гл. 10, систему конеч-
ного объема можно рассматривать, начав с предельного случая
системы, не имеющей границ. Иными словами, мы сначала изучим
систему бесконечного объема с помощью представления физиче-
ских частиц, а затем создадим замкнутую поверхностную осо-
бенность, разделяющую систему на две части, расположенные
внутри и снаружи поверхностной особенности. Подобная осо-
бенность ведет себя как макроскопический поверхностный объект,
который индуцирует самосогласованный потенциал (гл. 9 и 10).
Представление физических частиц 89
Этот потенциал воздействует на волновые функции физических
частиц. Рассматривая лишь область внутри поверхности, можно
изучать систему, приближенно ограниченную областью конеч-
ного размера.
3.3. Представление физических частиц
и вариационный принцип
Рассмотрим набор параметризованных операторов уничтоже-
ния {а (к, 9)}, где 0 — параметр. Связанное с этими операторами
(при определенном значении 9) пространство Фока обозначим
$ (9). Принимая, что гейзенберговское поле \|з (х) реализуется
в пространстве Фока % (9), определим
wo(Q) = (о, е|я|о, в), (з.зл)
где Я — гамильтониан гейзенберговского поля, а | 0, Э) — ва-
куумное состояние в % (9), причем
а (к, 9) | 0, в) = 0,
можно доказать, что представление физических частиц соответ-
ствует минимальному значению Wo (8).
Пусть 90 — значение параметра, соответствующего представ-
лению физических частиц:
Я = J &Ы (k) at (к, в0) а (к, в0) + Wo F0). C.3.2)
Перейдем теперь к близкому пространству Фока % F0 + dQ),
для которого соответствующие операторы уничтожения имеют вид
а (к, 90 + 69) = а (к, в0) + ба (к). C.3.3)
Здесь ба (к) — линейная комбинация нормальных произведений,
состоящих из а (к, 90 + 69) и а+ (к, 90 + 69). Каждый член
с нормальным произведением в ба (к) содержит численный коэф-
фициент порядка 69. Действие a (k, 90) на векторы в пространстве
& (90 + 69) определено выражением C.3.3), поскольку а (к,
90 + 69) — оператор уничтожения в пространстве % (90 + 69).
Так как нас интересуют только члены первого порядка по 69,
а (к, 90 + 69) и а+ (к, 90 +69) в 6а (к) можно заменить просто
на а (к, 90) и а+ (к, 90). Тогда действие оператора а (к, 90 + 69)
на векторы в представлении физических частиц Ф (90) также опре-
деляется выражением C.3.3). Таким образом, C.3.3) хорошо опре-
делено в обоих представлениях 9 (90) и Ф (Qo + 69).
Используя C.3.2) и C.3.3), имеем
Я = f d3k® (k) [a+ (k, 90 + 69) a (k, 90 + 69) —
— a+(k, 90+69Na(k)—6a+(k) a(k, 90 + 69)] +Wo(90)+0F92).
C.3.4)
90 Глава $
Последнее слагаемое 0 (бб2) имеет вид ба+ (к) ба (к) и потому
положительно. Далее, поскольку
(о, е0 + 681 а+ (к, е0 + se> = о, а (к, е„ + бе) [ о, е0 + ав) = о,
из C.3.4) следует
(о, е0 + бе | я [о, е0 + бе) = w0 (в0) + о (бе2), (з.з.б)
а это означает, что Wo (Эо) — минимальное значение.
Этот результат обнаруживает тесную связь между самосо-
гласованным и вариационным методами в квантовой теории поля.
3.4. Общий анализ представления
физических частиц
Динамическое отображение. Рассмотрим гейзенберговское
поле \|) (х), гамильтониан которого Н. Примем, что уравнение
Гейзенберга и одновременные канонические перестановочные со-
отношения приводят к реализации \|) (х) в пространстве Фока $,
связанном со свободным физическим полем ф° (х). Иными словами,
мы считаем, что получено динамическое отображение
$(х) =!>(*; Ф°)- C-4.1)
Это отображение представляется в виде линейной комбинации
нормальных произведений полей ф°:
Ц (х) = х + ^Ф° (x) +
%F (x - \,х - 1) : Ф° (g) ф° (S) :+.... C.4.2)
Здесь % — численная константа, а перенормирующий множитель Z
может содержать пространственные производные. Постоянная %
равна нулю в том случае, если поле \|) фермионное. Соотношение
C.4.2) является слабым в том смысле, что знак равенства означает
равенство матричных элементов между векторами в 9. Поскольку г|)
определяется слабым соотношением C.4.2), уравнение Гейзен-
берга и канонические одновременные перестановочные соотно-
шения также должны рассматриваться в слабом смысле. Для
того чтобы знать «рецепт» прочтения уравнения Гейзенберга,
содержащего некоторые произведения полей \|), необходимо опре-
делить произведения г|) (х; ц>°). Они неявно использовались
в разд. 3.1, а именно правило для произведений гласит, что прежде
всего вычисляются произведения нормальных произведений q>°,
причем они представляются в виде линейных комбинаций нор-
мальных произведений. Интегрирование по пространству и вре-
мени следует выполнять только после надлежащего вычисления
произведений нормальных произведений. При записи разложения
C.4.2) предполагалось, что трансляционная симметрия феномено-
Представление физических частиц 91
логически не нарушена (иными словами, основное состояние 10)
трансляционно инвариантно). В гл. 7 показано, каким образом
можно феноменологически нарушить трансляционную симметрию.
Интегрирования по времени (dti, dtz и т. д.) в C.4.2) рас-
пространяются от —оо до оо. Существенно, что состояния \а)
и | Ь) в (а | i|) (х) | Ь) являются не плоскими волнами, а волно-
выми пакетами. Если бы эти состояния были плоскими волнами,
интегрирование по времени в C.4.2) сводилось бы к интегриро-
ванию монохроматических осциллирующих функций и никогда
не приводило бы к конечным результатам; сходимость обеспе-
чивается только благодаря тому, что используются состояния
волновых пакетов. В этом случае области бесконечно удаленного
прошлого или будущего не вносят вкладов в интеграл, и поэтому
допустимо интегрирование по частям.
Связь между Н и Но. Покажем теперь, что гамильтониан
системы Я в слабом смысле равен свободному гамильтониану Яо
для ф° (с точностью до численного Wo, когда существует динами-
ческое отображение, выражаемое равенством C.4.1)). Для упро-
щения ситуации предположим, что\|) и ф° вещественны. Обобщение
рассмотрения на случай комплексных полей производится непо-
средственно. Свободный гамильтониан для ф° имеет вид
Яо = J d?ke> (k) at (к) а (к). C.4.3)
Соотношение
приводит к следующему равенству:
-j-{a\[H0, i
+ \d%\d%F{x-l, *_^^
C.4.5)
Применяя далее интегрирование по частям, получаем
{а | [Но> 4" (х)] | Ь) = 4- -щ- (а I * WI fe>- <3-4-6>
Сравнивая C.4.6) с соотношением
(а | [Я, ф (х)] | Ъ) = 4- 4~ {а | * (х) | &), C.4.7)
находим
(а | [Яо, ф (*) ] | Ь) = (а | [Я, ф (*) ] | *>>• C-4.8)
92 Глава 3
Это вычисление можно обобщить следующим образом:
(а\ [#о, произведение \р] \b) = (a | [Я, произведение if] |6).
C.4.9)
Пусть $ — неприводимое представление набора операторов,
состоящего из всех произведений \|); тогда равенство C.4.9) озна-
чает, что Я в слабом смысле равен Яо + Wo, где Wo — с-число.
Таким образом, 9 является представлением физических частиц.
Другой способ получения соотношения C.4.6) состоит в вы-
числении фурье-образа матричных элементов в правой части
равенства C.4.2). Имеем, например,
F[-k, co(k); 1, со A)] х
X и* (к) ft (к) и A) f, (I) ехр \ i A - к) х + i [со (к) - со A)] t} C.4.10)
при i Ф /, где | аг) и | а^ — состояния волновых пакетов:
C-4Л1)
а и (к) — волновая функция в выражении
фо (х) = х Г dsjfe /u (k) a (к) ехр [ikx - ico (к) *] +
Bя) /2 J
+ и* (к) a+*(Jfe) ехр [—ikx + "о (к) /]}. C.4.12)
Величина F (к, ?0; 1, /0) в C.4.10)—фурье-образ от F (х — |,
C.4.13)
Зависимость от времени слагаемого в C.4.10) явно указывает на
выполнение равенства C.4.6), поскольку со (к) и со (!) — соб-
ственные значения Яо в бра- и кет-состояниях соответственно.
Асимптотический предел и 5-матрица. Запишем уравнение
свободного поля для ф° в виде B.6.7), а именно
Я (д) Ф° (х) = 0. C.4.14)
Тогда действие оператора Г, определенного выражением B.6.28),
приводит к B.6.126):
a (k) =-L^d3xu (к) ехр [—ikx + ico (к) t] Гср° (*). C.4.15)
Представление физических частиц 93
Если ф° вещественно, то п — и*. Введем оператор
ft
а (к, t) = ~ J d3xu (к) ехр [—/кх + ш (к) /] rz-1/, fy (х) ~
C.4.16а)
и построим
ф, (*) = J d»*g (к) а (к, t), C.4.166)
где g- (к) — квадратично-интегрируемая функция. Определим да-
лее величины ain (k) и aout (к):
lim (a\%(t) \b) = (a\\ d3kg (к) aout (к) | Ь), C.4.17)
t-*-\-<x>
lim (a\$g(t) 16) = (a| J d3kg (k) ain (к) | b). C.4.18)
*->¦—oo
Существование этих пределов основано на использовании состоя-
ний волновых пакетов. Осциллирующие компоненты, входящие
в [¦§ (х) — % ] и не находящиеся в фазе с волновой функцией
свободной частицы, исчезают в пределах t->- ±оо. В результате
входящее и выходящее поля обладают той же энергией, что и
свободное поле ф°.
Оператор р = Z^ (ф — %) называют связывающим полем
для ain и aout.
До сих пор мы принимали, что поле ф° имеет смысл для всех
физических свободных полей {ф?; i = 1, 2, ...}. Если существует
матрица 5, удовлетворяющая соотношению • >.¦ ^г'эШ-Хи!
a?ut(k) = S-1ajn(kM для всех i, C.4.19)
то ее называют 5-матрицей.
Между элементами набора гейзенберговских полей {ч|з} и эле-
ментами набора физических полей {ф0} не обязательно должно
существовать взаимно-однозначное соответствие. Предположим,
что существуют физические поля, которые не могут быть пред-
ставлены в виде линейного слагаемого в динамическом отобра-
жении любого из полей (я);}. Тогда можно утверждать, что эти
физические частицы составные, и искать такое произведение i|),
для которого линейный член в динамическом отображении давал бы
искомое составное физическое поле. Если для образования такого
произведения необходимо по крайней мере п полей г|), то соответ-
ствующая составная частица называется л-частичным связанным
состоянием. Указанное произведение полей ч|> (из которого следует
вычесть его вакуумное среднее значение) действует Как связыва-
ющее поле для составной частицы в том смысле, что входящее
и выходящее поля для составной частицы получаются как асимпто-
94 Глава 3
тические пределы этого произведения. При этом асимптотические
пределы определяются так же, как в выражениях C.4.17) и C.4.18).
Примем теперь, что коэффициенты разложения в динамическом
отображении C.4.2) являются запаздывающими функциями, так
что
F(x — l,x—Q=e(tx — tt) Э (tx - *Е) F (х - I, х — ?); C.4.20)
в этом случае ср'п (х) = ф° (х) [т. е. ain (k) = а (к)].
Поскольку предельный переход (t ->¦ оо) в C.4.17) приводит
к исчезновению всех осцилляции в а (k, t), не совпадающих по
фазе с физическим полем, имеем
a0"* (k) = а"» (к) + ... , C.4.21)
где многоточием обозначены нормальные произведения более
высоких порядков, содержащие как ain, так и ain+. В выражение
C.4.21) не входит численное слагаемое, поскольку, согласно
C.4.16), динамическое отображение a (k, t) не содержит с-числа.
Устойчивость вакуума. Вспомним теперь, что частота, соот-
ветствующая матричному элементу (а (I) | т|з (х) | а (р) a (q)), со-
гласно C.4.6), равна переданной энергии [со (р) + со (q) — со A)].
Поскольку при переходе к пределу (t —>~ со) в C.4.17) остаются
только волны с частотой со (к), очевидно, что
(а @ |a°"t (к) |a (p) a (q)) ~8(l+k-p-q)X
X б [со A) + со (к) — ю (р) — ю (q) ], C.4.22)
так что данный матричный элемент сохраняет энергию и импульс.
Аналогично можно показать, что вообще все матричные элементы
aout (k) сохраняют энергию и импульс.
Таким образом, имеем
(а | aout (k) | 0} = 0 C.4.23)
для любого состояния \а)\ при этом подразумевается, что если
одночастичная энергия со (к) обращается в нуль при некотором
дискретном значении к, то его вклад в состояние волнового пакета
имеет нулевую меру. В этом случае
(a(k)S|0)=0, C.4.24)
где использовано определение C.4.19) с ain (k) = а (к). Поскольку
соотношение C.4.24) выполняется при любом к, очевидно, что
состояние 5 | 0) является вакуумным: S | 0) = с \ 0), \с \ = 1.
Здесь и всюду ниже оператор S предполагается унитарным.
Это предположение означает, что полная вероятность частице
вступить в реакцию равна единице.
Представление физических частиц 95
Без потери общности фазу S можно выбрать так, что с = 1.
Т огда имеем
S|0} = |0). C.4.25)
Это соотношение называется условием устойчивости вакуума.
Устойчивость одночастичных состояний. Рассуждение, ана-
логичное приведшему к C.4.22), указывает, что матричный эле-
мент (а | aout (k) | а (р)) пропорционален б [со (р) — со (к) —... ],
где многоточие обозначает энергии частиц в состоянии \а).
Если энергия одного кванта никогда не превышает порога
многоквантовых энергий, т. е. если
со (кх + ... + кл) < со (кх) + ... + со (к„), п ^ 2, C.4.26)
то, применяя те же рассуждения, которые привели к C.4.23),
получаем
(а | a°u* (k) | a (p)) = 0 для | а) ф | 0). C.4.27)
Здесь существенно заметить, что \а) — состояние волнового па-
кета, так что вклад состояний, удовлетворяющих знаку равенства
в C.4.26), пренебрежимо мал (имеет нулевую меру). Из уравне-
ния C.4.27) следует
= сб (k —
Поскольку в динамическом отображении aout вклад
в @ | aout | а) дает только линейный член, которым является ain,
находим, что с = 1. Поэтому имеем
а (к) 5 | а (р)} = б (к - р) S | 0} = б (к - р) 10),
где использовано определение C.4.19). Получаем далее
где с — с-число; отсюда, используя C.4.25), находим
c = @|S|a(p))-<0|a(p)) = 0.
Окончательно приходим к соотношению
S|a(p)) = |a(p)), C.4.28)
которое указывает на устойчивость одночастичного состояния.
Заметим, что устойчивость основана на выполнении условия
C.4.26).
Комплексные поля. В приведенных выше рассуждениях пред-
полагалось, что \|з и ср° — вещественные поля. Очевидно, однако,
что все полученные результаты остаются в силе, даже если i|5
96 Глава 3
и ф° — комплексные. В этом случае равенства C.4.3) и C.4.12)
заменяются соответственно на
Но = J d3ka> (k) {а+ (к) а (к) + Р+ (к) Р (к)}, C.4.29)
Ф° (х) = -^77 } d?k {и (к) а (к) ехр [«кх - ш (к) t] +
+ и (к) р+ (к) ехр [—/кх + ш (к) *]}. C.4.30)
Здесь р (к) — оператор уничтожения античастицы (или дырки).
Для построения входящего и выходящего полей в дополнение
к tyg (t) из C.4.16) требуется оператор
/. [ф (х) - х*] Го (к) х
хехр [—tkx + i(fl(k)*], C.4.31)
где р = —1, если ср° — фермионное поле и уравнение для него
C.4.14) относится к типу 2; в остальных случаях р = 1. Чтобы
понять, с какой целью вводится % (t) с помощью C.4.31), полезно
напомнить выражение B.6.127), откуда имеем
Р (к) = — -|- J й3х<р° (х) Tv (к) ехр [—tkx + ш (к) Ц. C.4.32)
Входящий оператор Р'п (к) и выходящий оператор Pout (к) полу-
чаются соответственно переходом к пределу (t ->¦ —оо) или (t -*-
->• оо) в матричных элементах tyg (t) — в полной аналогии с полу-
чением а'п и aout.
3.5. Формула редукции и формула
Лемана—Симанзика—Циммермана (ЛСЦ)
Формула редукции. В этом разделе мы введем общее выраже-
ние для динамического отображения вида C.4.2), выбирая опера-
торы входящего поля для свободного физического поля ср°, т. е.
a'n(k)=a(k), P'"(k)=p(k). C.5.1)
Прежде всего получим так называемую формулу редукции [7].
Рассмотрим матричный элемент
(а (к), a\ST [Fj. (xj ... Fn (xn)]\b), C.5.2)
где S — S-матрица, которая предполагается унитарной, а символ
| а (к), а) обозначает
|<х (к), а) = а+ (к) |а> = Saout (к) S'1 \а). C.5.3)
Состояния | а) и | Ь) принадлежат пространству Фока 9, связан-
ному с физическими частицами. Операторы Ft (xt) состоят из
гейзенберговских полей г|).
Представление физических частиц 97
Из C.4.17) имеем
J dskg (к) (a (k), а | ST [Fj. (хг). . . Fn (хп)] \ Ь) =
= J cPkg (к) (а | Sa»-« (к) Т [^ (х,). . . Fn (х„)] 16) =
= 4- Hm f cPkg (к) f d3xu (к, х) Г (а | ST ty (х) F, (xL) ... Fn (xn)] \ Ъ),
C.5.4)
где ^ обозначает tx, ф (х) — связывающее поле для ф'п и фои*:
Ф(х) =Z-v. M,(x)-X], C.5.5)
а п (к, х) = п (к) ехр [—ikx + ico (к) Л. При получении C.5.4)
использовано соотношение
lim Т [ф (х) Fj. (хх) ... ] = Hm ф (х) Т [Ft (Xl) ... ].
Для упрощения обозначений опустим в дальнейшем интегри-
рование по импульсам d3kg(k). Из C.5.4) находим
(а (к), а|S7 [M*0 ...Fn(xn)]\b) =
= 4-(Hm - lim | [ сЕхп (к, х)Г (a\ST^(x)F1\(x1).. .Fn(xn)]jb\)+
+ e(a\ST[F1(xx)...Fn(xv)]a(k)\b), C.5.6)
где e = 4-1 (—1). когда необходимо четное (нечетное) число пере-
становок фермионных полей при переходе от a (k) F± ... Fn
к F1 ... Fna (к).
Используя соотношение B.6.30), т. е.
4- j dV(*) Г^ (х) = -i j Л/ W [^ (д) - ^ (-d) ] g (x), C.5.7)
можно переписать C.5.6) в виде
(а(к), a|ST[i71(x1)...Fn(xn)]6> =
= - -i- jd*x« (к, х) Я (д) (а | S7 ty (x) F, (xj ... Fn (х„)] 16) +
. + е (а | S7- [Fx (xj . .. Fn (х„)] а (к) 16), C.5.8)
где учтено, что п (к, х) Я, (—д) = 0. Второе слагаемое в правой
части C.5.8) описывает реакцию, в которой квант, порождаемый
а (к), вообще не взаимодействует с остальными квантами; иначе
говоря, этот квант не связан с другими. Пусть (а | А | Ь)с обо-
значает матричный элемент А для перехода \а)->¦ \ Ь), явля-
98 Глава 3
ющегося «одночастично связанным» (т. е. нет частиц, не связан-
ных с другими). Тогда из C.5.8) находим
(а (к), a\ST [M*i)--.fn(*n)]|&>e =
= i- J d*xu (к, х) X (д) (a | ST [ф (x) F, (Xl) ...Fn (xn)} \ b)c.
C.5.9)
Это одна из так называемых формул редукции, с помощью которой
квант а (к) исключается из бра-состояния.
Аналогично можно получить следующие формулы редукции:
(a\ST [M*i)---^(*n)]|P(k), b)c =
= —й" Р J di™ (k> *) b(d)(a\ST [Ft (Xl) ... Fn (xn) ф (x)) | b)c,
C.5.10)
<P(k), a\STlF1(x1)...Fn(xn)]\b)c =
*x(a\ST$ (x) F± (Xl) ... Fn (xn) }\b)cl (-0) v (k, x),
C.5.11)
(a|ST [F1(x1)...Fn(xn)]\a(k), b)c =
= -j-\dix(a\ST[F1 (Xl) . . . Fn(xnL> (x) )\b)cX (-д) и (k, x)
C.5.12)
Здесь v (k, x) = v (k) exp [—tk, x + ico (k) t), ф = 0+т), а г] —
матрица приведения к эрмитову виду. При получении последних
соотношений использовалась формула C.4.31).
Формула ЛСЦ. Выберем далее в качестве Fx (хг) ... Fn (xn)
поле г[> (х). Применяя повторно формулы редукции C.5.9) —
C.5.12), можно исключить все частицы в бра- и кет-состояниях.
В результате получим следующее динамическое отображение для
оо оо
2 S (- т)"+т J d"xi ¦ ¦ ¦diXnd% ¦ ¦ •diym х
2 S (
n=0 m=0
X :[f°(
X @|T ЬИ*Ж*!) .--Ф (Хп)Ш ¦ ¦ ¦ Ф(Ут)]\0)е X
X [X(-д\) Ф°Ы] • • • [^(-^)ф°Ы]:- C-5.13)
Представление физических частиц 99
Эта формула носит название формулы Лемана—Симанзика—Цим-
мермана (ЛСЦ). Ее можно записать в компактной форме
C.5.14)
Здесь угловые скобки обозначают взятие вакуумного среднего
значения от Т-произведения гейзенберговских полей г|з, ф и ф>
а символ нормального произведения : ( )с: обозначает нормальное
произведение физических свободных полей ср° и ф°, которые
связаны с /° и /° следующим образом:
7° (х) =1р° (х) К (д), C.5.15)
Р (х) = X (—д) ф° (х); C.5.16)
при этом /° — /otr].
Заметим, что индекс с в C.5.13) можно опустить, после того
как матричные элементы полностью переведены в форму вакуум-
ных средних значений. Но мы сохраняем индекс с для напомина-
ния о том, что в функцию Грина C.5.13) дают вклад только одно-
частично связанные диаграммы. Вклад, содержащий одночастично
несвязанную часть, всегда пропорционален величине
(х) К (дх) @\Т[ф (х) ф (у)] 10} I (-ду) ф° (у),
которая равна нулю.
Заменяя г|> (х) на единицу, получаем динамическое отображе-
ние S-матрицы:
iJ )])- C-5.17)
Если Он (х) — гейзенберговский оператор, состоящий из г|) (х)
и ф (х), то динамическое отображение S0H (x) имеет вид
S0H(x) = : (Т [0н(х) ехр (- j- J d% {Ъ © ф^ + f © J°«)}) ] )с :•
C.5.18)
Можно написать
{0\Т[ф(Х1) . . . ф(хп)ф(У1) . . . ф(ут)}\О)с =
- J йЪ . . . й^йХг . . . d%mG° (хг - go) ... Go (ха - 1п) X
хHh • - • U; Ь ¦ ¦ • UG°&i~yi) - • - C?o(U-<W. C.5,19)
100 Глава 3
где функция G" (х — у) определена с помощью равенства
G° (х- у)=@\Т [Ф° (х) ф° (у) ] 10). C.5.20)
Функция fill-.. In', ?i--- ?m) называется вершинной функцией.
Динамическое отображение S-матрицы выражается через вер-
шины следующим образом:
ОО ОО
S = 2 2 J Л1 ¦ • • d"xnd% ¦ . . d4tfm :Ф°(*1) • • • Ф°(-^) X
n=0 m-=0
Xf(Xl. . . хп; У1. . . г/т)ф«(й) • • • Ф°Ы :• C.5.21)
Структура функции G0 (х — у) рассматривается в следующем
разделе.
3.6. Спектральные представления двухточечных
функций
Многоточечные функции. В предыдущем разделе показано,
что динамическое отображение любого оператора может быть
получено с помощью формулы редукции ЛСЦ, если известны асимп-
тотические поля. Формула ЛСЦ выражается через вакуумные
средние значения Г-произведений гейзенберговских операторов.
Функцию С^в'"с (ххх2 ... хп), определенную соотношением
G?}B-C (Xl ... хп) = @\Т[А (Xl) В (х2) . . . С (хп)} 10), C.6.1)
назовем причинной n-точечной функцией. Задача построения
динамического отображения сводится к вычислению таких функ-
ций. В этом разделе рассматривается общая структура причинной
двухточечной функции; вводятся также запаздывающая и опере-
жающая двухточечные функции.
Причинная, запаздывающая и опережающая двухточечные
функции определяются соответственно выражениями
аЛВ (х-у) = @\Т1А (х), В(у)]\0)= C.6.2)
= Q(tx-ty)@\A(x)B(y)\0)±
±Q(ty-tx){O\B(y)A(x)\O), C.6.3)
GrB (x-y) = Q (tx - ty) @1 [A (x), В (у)]± 10), C.6.4)
G*B (x-y) = -9 (ty - tx) @1 [A (x), В (у)]± 10). C.6.5)
Знак перед ступенчатой функцией 8 (ty — tx) в C.6.3) должен
выбираться так, чтобы знак + соответствовал случаю бозонопо-
добных операторов А и В, а знак — — случаю фермионоподоб-
ных операторов А и В. Здесь под бозоноподобными (фермионо-
подобными) операторами понимаются операторы, предстарля-
Представление физических частиц 101
ющие собой произведения четного (нечетного) числа фермионных
полей и некоторого числа бозонных полей. В выражениях C.6.4)
и C.6.5) коммутаторы выбираются для случая бозоноподобных А
и Б, а антикоммутаторы — для^случаяфермионоподобных А и В.
Спектральные представления двухточечных функций. Фурье-
образ причинной двухточечной функции определяется выражением
GcB (х -у)= -A J d4k exp [ik (х - у)] G?B (k) и т. д. C.6.6)
Применение формулы
6 (tx - ty) = Шпо JL. J [dw-^rft exp [-iw (tx - tv)] C.6.7)
' —oo
приводит к выражению
Q*B (k) =Jdw( f" (\\ - p а"У' ~kfi} ) , C.6.8)
о
где использованы следующие обозначения:
C.6.9)
f+1 для бозоноподобных А и В,
\ —1 для фермионоподобных А и В,
Здесь \п) обозначает элементы из полного набора собственных
векторов энергии и импульса. Соответствующие собственные зна-
чения энергии и импульса обозначаются через Еп и kn. Вводя
обозначение
а (ю, к) = 9 (ш) алв (и,, к) — р0 (—w) oB* (~w, —к), C.6.11)
можно записать C.6.8) в виде
(8.6.18)
Выражения C.6.8) и C.6.12) называют спектральными пред-
ставлениями причинной двухточечной функции [8].
Если в суммировании в выражении C.6.9) принимают участие
определенные одночастичные состояния с энергией <в (к), величина
оАВ принимает вид
олв (Ш| к) = Zab (к) § [ш _ © (к)] + оАВ (w, к). C.6.13)
Здесь ZAB определяется вкладом, обусловленным одночастичными
состояниями, а аАВ — многочастичньши состояниями. В послед-
102 Глава 3
нем слагаемом область изменения w для данного к представляет
собой некоторый континуум, поскольку энергия многочастичных
состояний даже при точном указании импульса к не определена
однозначно. Поэтому слагаемое, содержащее ZAB, дает вклад
в правую часть C.6.8) за счет однополюсных сингулярностей
в плоскости k0, тогда как слагаемое с дАВ создает линию разреза
вдоль вещественной оси k0. Это результат применения представле-
ния физических частиц: если бы причинная двухточечная функ-
ция имела особенности, отличные от простого полюса или линии
разреза вдоль вещественной оси, это означало бы, что гейзен-
берговские операторы не имеют реализации в представлении
физических частиц.
Выражение C.6.9) показывает, что
@1А (х) В (у) 10) = JJL. | d4 \ dm*™ {w> k) exp [ik (x _ у) _
_&&-*„)], C.6.14)
dwa(w, к).
C.6.15)
Здесь коммутатор (антикоммутатор) применяется для бозонопо-
добных (фермионоподобных) полей А и В.
Если В оказывается канонически сопряженным А, то имеем
[А (х), В (у) ]± б (tx - g = Йб<«> (х - у), C.6.16)
что вместе с C.6.15) приводит к правилу сумм
J dwa (w, k) = 1. C.6.17)
ш—оО
С другой стороны, если В = Л+, то C.6.9) приводится к виду
аАВ (а>, к) 5в0, C.6.18)
откуда, учитывая C.6.13), получаем
ZAB (k) ss 0, aAB{w,k)^0. C.6.19)
Если В = Л+, причем А —фермионоподобный оператор, то из
C.6.11) находим
a (w, к) ss 0. - C.6.20)
Таким образом, если Л+ — оператор, канонически сопряженный
фермионоподобному полю Л, то C.6.17) и C.6.20) выполняются
одновременно, так что 1 ^ 2ЛЛ+ (k) ^ 0.
В качестве другого примера предположим, что Af(x) — бо-
3ohhq§ поде, в = (d/dt) Л+ (х) и § канонически сопряжено с Л+,
Представление физических частиц ЮЗ
В этом случае в силу C.6.9) приходим к выводу, что знак вели-
чины оАВ (w, к) совпадает со знаком w. Тогда из выражения
C.6.11) следует C.6.20), откуда получаем 1 ^ ZAB (к) :>= 0.
Обратимся теперь к запаздывающей и опережающей двух-
точечным функциям. Фурье-образ этих функций записывается
так же, как C.6.6) для Gc. Вычисления приводят к следующим
спектральным представлениям:
Возвращаясь к причинной функции, предположим, что имеет
место случай, когда физическое поле ср° можно представить как
линейное слагаемое в динамическом отображении А (х), а линей-
ным слагаемым в динамическом отображении В (х) является
фо = фо+Т].
А (х) = Z* (V) ф° (*)+-.., C.6.23)
В (х) = ZB (V) ф° (х) +. . . . C.6.24)
В этих выражениях многоточия обозначают нормальные произ-
ведения более высоких порядков. Тогда имеем
GoB (x-y) = ZA (V*) ZB (V,) (%(x-y) + ..., C.6.25)
где многоточие обозначает вклады многочастичных состояний,
a G° (х — у) — двухточечная функция физического поля:
GI (х - у) = @1 Т [Ф° (х), ф° (у) ] 10) - C.6.26)
± 6 (ty - tx) @1 ф° (у) Ф° (х) 10). C.6.27)
Причинная двухточечная функция физического поля. Правила
сумм B.6.102) и B.6.103) дают
@1 Ф° (х) ф° (у) 10) = ifid (д) Д+ (х - у), C.6.28)
@1 ф° (у) ф° (х) 10) = -tpftd (д) А" (х-у). C.6.29)
Здесь принято, что ф° (х) удовлетворяет уравнению свободного
поля типа 2. Используя B.6.86), получаем
02 (х - 0) = ifi [в (tx - ty) d (д) А+ (х — у)-
- 6 (tv- Q d (д) Ы(х — у)] = ifid (д) А, (х-у) +
+ tft [0 (tx — У, d (д) ] А (х — у), C.6.30)
104 Глава 3
где использовано соотношение 8 (t) = 1 — 8 (—t). Функция А (х)
определена в B.6.115), а Ас (х) определена выражением
Ас (х) = 0 (t) А+ (х) — 8 (—0 А" (х). C.6.31)
Из выражений B.6.87), B.6.88) и B.6.112) находим
(—д21д? — со2 (V)) Д, (х) = 6<4> (х), C.6.32)
откуда следует, что Ас (х) — причинная функция Грина для
оператора [—(d/dtJ — со2]. Вводя уравнение для ср°
X (д) ф° = 0, C.6.33)
учтем, что причинная функция Грина для него дается, согласно
B.6.18), действием оператора d (д) Ас(х). Если производная по
времени в d (д) первого порядка, выражение C.6.30) принимает вид
Gc (х — у) = Ш (д) Ас {х — у), C.6.34)
где учтено B.6.112). В этом случае G° (x)— причинная функция
Грина.
Для уравнения типа 1 с положительными е(к) выражение
C.6.27) дает
G» (х — у) = iftG (tx — t,j) d (д) А+ (х — у), C.6.35)
где А+ определяется выражением B.6.104). Используя B.6.105)
и B.6.106), получаем
[id/dt — е (V) ] Ас (х) = б<4> (х), C.6.36)
если Ае (х) определено соотношением
Ас (х) = 8 @ А+ (х). C.6.37)
В силу C.6.35) имеем
G°c (x — y) = ikd (д) Ас (х — у) + Ш [8 (tx - tu), d (д) ] А+ (х - у).
C.6.38)
Если d (д) не содержит производной по времени, то
G« (х — у) = ihd (д) Ас (х — у); C.6.39)
согласно B.6.18), это функция Грина для уравнения свободного
поля.
ЛИТЕРАТУРА
\. Rest J., Srinivasen V., Umezawa H., Phys. Rev., D3, 1890 A971).
2. Nambu Y., Progr. Theor. Phys. (Kyoto), 5, 614 A950);
Salpether E. E., Bethe H. S., Phys. Rev., 84, 1232 A951);
Gell-Mann M., Low F. E., Phys. Rev., 84, 350 A951).
3. Lee T. D., Phys. Rev. 95, 1329 A954).
4. Vaughan M. Т., Aaron R., Amado R. D., Phys. Rev., 124, 1258 A961).
Представление физических частиц 105
5. Ezawa H., Kikkawa К., Umezawa H., Nuovo Cim., 23, 751 A962);
Ezawa H., Muta Т., Umezawa #., Progr. Theor. Phys. (Kyoto), 29, 877 A963).
6. Totnonaga S., Progr. Theor. Phys. (Kyoto), 1, 27 A946);
Schwinger J., Phys. Rev., 74, 1439 A948);
Umezawa H., Quantum field theory, North-Holland, Amsterdam and Inter-
science, New York, 1956. [Имеется перевод: Умэдзава X. Квантовая теория
поля. — М.: ИЛ, 1958.];
Боголюбов Н. Н., Ширкав Л. В. Введение в теорию квантованных полей.
Изд. 3-е. — М.: Наука, 1976;
Schweber S. S., An introduction to relativistic quantum field theory, Harper
and Row, London, 1961. [Имеется пзревод: Швгбер С. Введение в релятивист-
скую квантозую теорию поля. —М.: ИЛ, 1933.];
Lurie D., Particles and fields, Interscience, New York, 1969;
Nishijima K-, Fields and particles, W. A. Benjamin, New York, 1969;
Roman P., Introduction to quantum field theory, Wiley, Ne.v York, 1969;
Takahashi Y., An introduction to field quantization, Pergamon, Oxford, 1969.
7. Lehmann H., Symanzik K-, Zimmermann W., Nuovo Cim., 6, 319 A957).
8. Umezawa H., Kamefuchi S., Progr. Theor. Phys. (Kyoto), 6, 543 A951);
Kallen G., Helv. Phys. Acta, 25, 417 A952);
Lehmann H., Nuovo Cim., 11, 342 A954).
ГЛАВА 4
КВАНТОВАЯ ТЕОРИЯ ПОЛЯ
ПРИ КОНЕЧНЫХ ТЕМПЕРАТУРАХ
4.1. Термополевая динамика
Квантовые возбуждения при конечных температурах. До сих
пор рассматривались только изолированные квантовые системы.
В действительности, однако, большинство систем не изолированы,
а погружены в «тепловой резервуар» (термостат). Поскольку
система взаимодействует с термостатом, на процессы возбужде-
ния и релаксации влияет обмен энергией между системой и тер-
мостатом. Для определения абсолютной температуры Т исполь-
зуем символ
где kB — постоянная Больцмана. Если в системе уничтожается
квант энергии со (k, fS), то этот процесс можно рассматривать
как результат действия оператора а (к), удовлетворяющего из-
вестным перестановочным соотношениям
[a(k),a+(l)]± = 6(k~l). D.1.2)
Тогда гамильтониан системы Н равен (в слабом смысле) свобод-
ному гамильтониану (с точностью до численного слагаемого Wo):
(a\H\b) = (a\H0\b) + W0(a\b), D.1.3)
tf0 = ft \ d3k® (к, р) a+ (k) a (к). D.1.4)
До сих пор рассуждения в точности совпадают со случаем
изолированной системы. Однако влияние температуры прояв-
ляется в структуре оператора а (к). Наличие термостата приводит
к существованию некоторого числа возбужденных квантов. По-
этому поглощение энергии системой происходит двумя спосо-
бами: либо за счет возбуждения дополнительного числа квантов,
либо за счет заполнения свободных мест в пространстве частиц —
уничтожения дырок, существующих благодаря термостату. Если
имеет место второй процесс, то говорят, что уничтожается й-квант
(дырка) с отрицательной энергией [—йсо (к) ] и отрицательным
импульсом (—Ш). Возбуждение дополнительного кванта опи-
сывается с помощью некоторого оператора рождения a+ (k, fS),
а уничтожение й-кванта — с помощью оператора a (k, |3)
Квантовая теория поля при конечных температурах
107
(рис. 4.1). Поскольку оператор а. (к) выполняет две независимые
операции, он должен представляться в виде линейной комбинации
операторов а (к, р) и а+ (к, Р):
ос (к) = с (к, Р) а (к, Р) + d (к, р) а+ (к, р), D.1.5)
где с (к, Р) и d (к, Р) — некоторые численные функции к и р.
Поскольку фазовые множители этих функций могут быть вклю-
чены в соответствующие фа-
зовые множители операторов
а, (к, р) и й+ (к, р), функции
с (k, P) и d (к, р) можно счи-
тать вещественными. Вы-
бранное нами гильбертово
пространство является про-
странством Фока, связанным
с операторами уничтожения
{а (к, р), а (к, р)}; это про-
странство обозначим 3 (а (Р),
а (Р)). Ниже мы обсудим
эквивалентность построенной
таким способом квантовой
теории поля и статистиче-
ской теории ансамблей Гиб-
бса.
Гамильтониан и импульс
с учетом влияния термоста- <^1М)-^шн
та. Поскольку оператор
а+ (к, р) рождает квант с
энергией йсо (k, P) и импуль-
сом йк, а оператор й+ (к, р) —
квант с энергией [—йсо (к,
Р)] и импульсом (—йк), га-
мильтониан и импульс пол-
ной системы с учетом влия-
ния термостата должны быть
равны в слабом смысле сле-
дующим величинам:
со
Рис. 4.1.
Н=н\ йР?© (к, р) [а+ (к, р) а (к, р) - а+ (к, р) а (к, р)], D.1.6)
a+(k, р)а(к,р)-а+(к,Р)а(к,РI. D.1.7)
Преобразование Боголюбова. Поскольку операторы {а (к)},
{а (к, Р)} и {а (к, р)} удовлетворяют уже известным перестано-
вочным соотношениям, преобразование D.1.5) должно быть кано-
ническим, а следовательно, оно является преобразованием Бого-
108 Глава 4
любова (гл. 2). Отсюда вытекает требование, чтобы выполнялось
условие с2 (к, р) — pd2 (к, р) = 1 (р = +1 для бозонов, р = —1
для фермионов); удобно ввести оператор а (к), определив его
равенством
а (к) = с (к, Р) а (к, р) + pd (к, р) а+ (к, р). D.1.8)
Преобразования D.1.5) и D.1.8) удобно записать в следующей
форме:
а (к) = ch %а (к, р) + sh 6fea+ (к, р), D.1.9а)
й (к) = ch Gfcfi (к, р) + sh 0fea+ (к, р) D.1.96)
для бозонов и
а (к) = cos Qha (к, р) + sin 9fea+ (к, р), D.1.10а)
й (к) = cos 9Aa (к, р) — sin 6fea+ (к, р) D.1.106)
для фермионов. Здесь параметр Qk является функцией к и р,
которая будет определена ниже. Обратные преобразования имеют
вид
а (к, р) = а (к) ch Qk — a+ (k) sh Qk, D.1.11a)
a (k, p) = a (k) ch Qk — a+ (k) sh Qk D.1.116)
для бозонов и
a (k, p) = a (k) cos Qh — a+ (k) sin 8ft) D.1.12a)
a (k, P) = a (k) cos 6ft + a+ (k) sin Qk D.1.126)
для фермионов. В дальнейшем наборы операторов {a (k, P)}
и {а (к, Р)} сокращенно обозначаются а (Р) и a (P) соответственно.
Заметим, что Но сохраняет вид свободного гамильтониана, даже
если его выразить через операторы ос (к) и a (k):
Яо = Н J d3kw (к, р) [а+ (к) а (к) — а+ (к) а (к) ], D.1.13)
поскольку комбинация [а+ (к, Р) а (к, р) — а+ (к, Р) а (к, Р) ]
инвариантна относительно преобразования Боголюбова. Анало-
гично имеем
Pt = Й J (Pkkt [a+ (к) а (к) — а+ (к) а (к) ]. D.1.14)
Вакуум, зависящий от температуры. Основным состоянием
при конечной температуре является состояние | 0, Р), для кото-
рого имеют место следующие равенства:
а (к, р)|0, Р> = 0, D.1.15)
а (к, р)|0, р> = 0. D.1.16)
Квантовая теория поля при конечных температурах 109
Представление физических частиц *) при температуре Т дается
с помощью 9 [а (Р), б(Р)].
Определение параметров 6Й. Определим теперь параметры 8Й,
вычислив среднее по основному состоянию от оператора числа
частиц. Как указано в начале этого раздела, оператор а+ (к)
описывает возбуждение в системе. Поэтому оператор числа кван-
тов в системе имеет вид
N (к) = а+ (к) а (к). D.1.17)
Следовательно, согласно D.1.9) и D.1.10), среднее значение
плотности числа частиц равно
^,Р)= D.1.18)
= sh2 9ft для бозонов, D.1.19)
n (к) = sin2 Qh для фермионов. D.1.20)
Здесь V = BяK 8C) @) — объем системы (см. в этой связи ра-
венство B.4.34)). Сравнивая этот результат с хорошо известными
формулами для плотности числа частиц в статистической меха-
нике, находим
sh29fe = -p^ для бозонов, D.1.21)
Qk =
для фермионов, D.1.22)
где со обозначает со (к, |3). Эти соотношения представляют собой
аксиому, определяющую температуру системы в состоянии тепло-
вого равновесия. По существу они предполагают, что среднее
значение по вакуумному состоянию от оператора числа частиц
равно среднему значению по каноническому ансамблю от числа
-1) Теоретики, занимающиеся аксиоматической теорией поля [1], полагали,
что для построения квантовой теории поля при конечной температуре понадо-
бится удвоить число степеней свободы. Изложение в настоящей книге направ-
лено на создание формализма для взаимодействующих полей, удобного для прак-
тического использования. В простейшей форме подобный формализм изложен
в последней главе обзора [2]. Более точная формулировка предложена в ра-
боте [3] и названа термополевой динамикой. Детальный анализ аналитических
свойств причинных функций Грина дан в работе [4]. Именно этот анализ дает
возможность полностью использовать преимущества теоретико-полевого под-
хода, основанного на применении причинных функций Грина. Практические
вычисления значительно упрощаются при использовании таких причинных
функций. Взаимосвязь между аксиоматическим подходом и термополевой ди-
намикой анализируется в последней из статей [1].
Формулировка, основанная на так называемых температурных функциях
Грина, получила широкое развитие [5]. Существует много учебников [6], в ко-
торых излагается этот формализм, поэтому мы не описываем его здесь.
110 Глава 4
частиц. Это утверждение можно без труда обобщить на любой
оператор, состоящий из а и а+, например А (а, а+). А именно,
вакуумное среднее значение от такого оператора @, Р | Л (ос,
at) I 0. Р) равно среднему значению по ансамблю от А (а, а+).
Таким образом, статистическая механика квантовой системы
многих частиц становится квантовой теорией поля, реализован-
ной в зависящем от температуры пространстве Фока *3 [ос (Р),
а (р)]. Соответствующий формализм носит название термополевой
динамики.
В дальнейшем используются обозначения
DЛ-24)
Заметим, что преобразования Боголюбова D.1.9) и D.1.10) при-
нимают вид
а (к) = [1 + Ы©)]1/' a (к- Р) + о [/в (©)]•/• 5+ (к, р), D.1.25а)
а (к) = [1 + fB (со)]'/* а (к, р) + a [fB (©)]'/. at (к, р) D.1.256)
для бозонов и
а (к) = [1 - fF (со) ]'/. а (к, р) + a [/, (со) ]''¦ 5+ (к, р), D.1.26а)
а (к) = ll—fF (со) ]'/. б (к, р) — a [fF (со) ]V, a+ (к, р) D.1.266)
для фермионов; при этом сохраняется произвол в выборе значения
a = +1 или a = —1.
Поскольку a (k, Р) | 0, Р) = 0, из выражений D.1.11) и D.1.12)
следует
(th 8fea+ (к) |0, Р) для бозонов,
а (к) 10, р) = , ' 1 '; . D.1.27)
4/1 ll I tg 0Aa+ (к) 10, Р) для фермионов. ч '
Из этих соотношений видно, что добавление кванта a (k) к основ-
ному состоянию |0, Р) эквивалентно исключению кванта а (к);
в этом смысле квант a (k) ведет себя подобно дырке кванта а (к).
Операция тильда. Сформулируем теперь правило, связываю-
щее операторы с тильдой с операторами без тильды. Рассмотрим
сначала свободное поле (см. B.6.45))
Ф° (ж) = J йЧ Ы (к, х) о! (к) + vr (к, х) рл+ (к) ], D.1.28)
удовлетворяющее уравнению типа 2
к (д) ф° (х) = 0. D.1.29)
Квантовая теория поля при конечных температурах Щ
Поскольку «операция тильда» заменяет к и в (к) на —к и —<в (к)
соответственно, определим поле
ф° (х) = | d3k Ы* (к, х) аг (к) + хГ (к, х) Рг+ (к) ], D.1.30)
удовлетворяющее уравнению
Я* C) Ф° (*) = 0. D.1.31)
Операторы иг и vr имеют произвольные фазовые множители,
поэтому выражение D.1.30) приводит к следующему правилу
для операции тильда:
$> = с*фо = (Сфо*)*) D.1.32)
где с — с-число. Сравнивая уравнения D.1.29) и D.1.31), мы ви-
дим, что правило D.1.32) сохраняет силу, даже если с является
дифференциальным оператором с (д):
Цд)р = с* (д) ф° = [с (д) ф°* ]*. D.1.33)
Согласно преобразованиям D.1.25) и D.1.26), получаем правило
a (k) = pj,a (k), a (k, P) = pFa (k, p), D.1.34)
если потребовать, чтобы операция тильда, примененная к а (к, |3),
не зависела от р. Здесь pF — знаковый множитель:
[ +1 для бозонов,
Pf= , л. D.1.35)
[ —1 для фермионов.
Принимая во внимание выражения D.1.33) и D.1.34), общее
правило для операции тильда можно сформулировать следующим
образом:
6а = 61о„ D.1.36)
+ сА = cfOi + с|02, D.1.37)
0 = р^О, D.1.38)
где г
+1 для бозоноподобных операторов,
, , ^ D.1.39)
—1 для формионоподобных операторов.
Оператор называется фермионоподобным (бозоноподобным), если
он представляется в виде линейной комбинации слагаемых,
каждое из которых содержит нечетное (четное) число фермионных
полей.
112 Глава 4
Пусть Яо [ф° ] — свободный гамильтониан для ф°:
#0 [<р°] = п\й3Ы (к) [а+ (к) а (к) + р+ (к) р (к) ]; D.1.40)
здесь и в дальнейшем мы опускаем спиновый индекс г. Операция
тильда дает
#„ = #о [фо*1 = D.1.41)
= Й J d3kw (k) [5+ (к) а (к) + р+ (к) р (к) ], D.1.42)
где последнее соотношение получено путем операции тильда,
примененной к выражению D.1.40).
В силу выражений D.1.28) и D.1.30) имеем
ih ± ф« (х) = [Ф« (х), Яо], D.1.43)
1П^г^(х) = -1^(х),Н0]. D.1.44)
Полученные уравнения являются самосогласованными в том
смысле, что применение операции тильда к обеим частям уравне-
ния D.1.43) приводит к уравнению D.1.44). Согласно D.1.44),
гамильтониан для поля ф° равен (—Яо), так что полный гамильто-
ниан равен
Я0 = Я0-Я0. • D.1.45)
Как показано выше, это выражение можно записать в виде
Яо = ft J d3k(o (k) [а+ (k, p) a (k, р) + р+ (к, р) р (к, р) —
- 5+ (к, р) а (к, Р) - р+ (к, р) р (к, Р)]. D.1.46)
Здесь операторы уничтожения р (к, Р) и р (к, р) связаны с р (к)
и р (к) преобразованием Боголюбова, имеющим вид D.1.25)
и D.1.26). Несмотря на то что энергия кванта зависит от темпе-
ратуры, она здесь и ниже обозначается просто со (к).
В случае уравнения типа 1 все приведенные выше рассуждения
сохраняют силу, если просто игнорировать величины vr, P (к),
Р (к), р (к, Р) и р (к, р).
Операция тильда и уравнение Гейзенберга. Обратимся теперь
к уравнению Гейзенберга. Пусть Я [ф] — гамильтониан системы,
состоящей из взаимодействующего гейзенберговского поля if.
Тогда оператор Я получается из Я посредством операции тильда:
Я = И* [^*]. D.1.47)
Квантовая теория поля при конечных температурах 113
Полный гамильтониан Я дается выражением
Н = Н — Н. D.1.48)
Каноническое уравнение движения
ih-дг\р = [\р, Н] D.1.49)
приводит к уравнению
Л-кг^, = — [if>, Я]; D.1.50)
отсюда следует,, что Я является гамильтонианом полей я|) и я|).
Потребуем, чтобы гамильтониан Я бб^л б слабом смысле равен
Но в D.1.46). Зависимость со (к) от температуры проявляется
через собственную энергию, обусловленную взаимодействиями. Это
иллюстрируется примерами в гл. 5. Заметим, что энергия основного
состояния системы дается не выражением @, р | Я | 0, Р), а вы-
ражением @, Р | Я | 0, Р). Согласно D.1.3), Я в слабом смысле
равен Я0 (с точностью до постоянного численного слагаемого Wo).
Конкретный вывод соотношения D.1.3) дается в следующем раз-
деле.
Если 3? [г|з]—лагранжиан, который с помощью канониче-
ского формализма приводит к гамильтониану Я, то SB =
= SB* [if)* ] — лагранжиан, который приводит к Я. Полный
лагранжиан равен 2Е = SB —¦ 3?.
Если система содержит большое, но определенное число исход-
ных частиц (описываемых гейзенберговским полем ¦»])), той? имеет
вид 21 = 2PS+ \iN, где ц. — химический потенциал, a N — опера-
тор числа исходных частиц. Таким образом, гамильтониан Я
также содержит слагаемое с химическим потенциалом (—\iN),
поэтому наблюдаемая зависящая от температуры энергия со (к)
зависит от химического потенциала.
Свободная энергия Гельмгольца имеет вид
F = @, Р|Я|0, р) -S, D.1.51)
где S — энтропия:
5 = — ft У | щ-AL (со) log /А (со) — [рА + U (со)] X
Xlog [1 + рд/д (©)]}. D.1.52)
114 Глава 4
Здесь V = BлK 8<3> @) — объем системы, ю обозначает ю (к),
а функции /А и рА имеют вид
Г fB для бозонов,
[ fF для фермионов,
f 1 для бозонов,
9а ={ 1 , D.1.54)
г { —1 для фермионов. v '
Примеры свободных полей и двухточечных функций для них.
Рассмотрим некоторые простые примеры свободных полей при
конечных температурах. Пусть свободное поле ф° удовлетворяет
уравнению X (д) ц>° = 0, в котором К (д) имеет вид
Чд) = 1--Ш№- D-1.55)
Имеем тогда
2 = j Лсср°+ (i ~ - ю (V)) ф", D.1.56)
^ = | ^9°+ (— i-^- - со (— V)) Ф°, D.1.57)
где учтено соотношение ю* (V) = со (—V). Соответствующие
гамильтонианы имеют вид
D.1.58)
D.1.59)
а операторы
ф» (X) =
поля
= Bя)-!
Я =
Я =
V.ftV,
J
j
j d'
dh
d3k
а (к)
ш (V) Ф°,
(- V) Ф°,
exp [ikx
ф° (x) = Bл)-3'>П'/* J d*ka (k) exp [—tkx + ш (к) Л. D.1.61)
Тогда из D.1.58) и D.1.59) следует
Н = Н\ d3ka (к) а+ (к) а (к), D.1.62)
Н = П J Лео (к) а+ (к) а (к). D.1.63)
Операторы а (к) и б (к) связаны с а (к, |3) и а (к, р) преобразова-
нием Боголюбова D.1.25), D.1.26). Все приведенные выше соот-
ношения справедливы как для бозонов, так и для фермионов.
Энергия ш (к) для бозонов положительно определена, а для фер-
мионов она может становиться отрицательной при определенных
Квантовая теория поля при конечных температурах 115
значениях к. Но даже в последнем случае выражения D.1.60)
и D.1.61) сохраняют силы, как это видно из следующих сообра-
жений. Поставив в соответствие оператор уничтожения положи-
тельной частоте, а оператор рождения — отрицательной, имеем
Ф° (х) = Bn)-3/2ft*/* J d3k {a (к) 9 [со (к) ] +
+ 6+ (к) 0 [-со (к)]} ехр [—ш (к) t + ik-x]. D.1.64)
Операторы а (к) и bf (к) связаны с а (к, Р) и 6 (к, р) преобразова-
нием Боголюбова
•а+(к, р), D.1.65а)
6+ (к) = {1 - fF [- со (k)]}1/. b+ (k, p) - {/,. [- со (к)]}1/. Б (к, р).
D.1.656)
Заметим, что в D.1.656) использовано значение а — —1, причем
этот выбор играет существенную роль в нижеследующем выводе
выражений D.1.60) и D.1.61). Поскольку fF [со (к) 1 = 1 —
— fF [—со (к)], имеем
а (к) 6 [со (к) ] + № (к) 8 [—со (к) ] =
= {1 - fF [со (к)]}1/, {а (к, р) 8 [со (к)] - Б (к, р) 8 [- со (к)]} +
+ {Мсо(к)]}1/* |а+(к, р) 8 [со (к)]+ 6+(к, р)9[—со (к)]}. D.1.66)
Далее, так как оператор в первой (второй) фигурной скобке со-
держит только операторы уничтожения (рождения), можно опре-
делить а (к, Р) и б+ (к, Р) следующим образом:
а (к, р) = а (к, р) 8 [со (к)] — В (к, р) 9 [—со (к)], ' D.1.67а)
а+ (к, р) = а+ (к, р) 9 [со (к)] + 6+ (к, р) 9 [—со (к)]. D.1.676)
В этом случае выражение D.1.64) принимает вид D.1.60), а при-
меняя к нему операцию тильда, получим D.1.61).
Уточним теперь модель, предположив, что ф° — фермионное
поле. Для упрощения обозначений введем для термополевого
дублета символ
(^) = (фп+)- D-1.68)
Причинная двухточечная функция определена следующим
образом:
Sf (х - у) = @, р | Т [Фа (х) фв+ (у)] | 0, Р) = D.1.69)
- 9 (ty - tx) @, р | ФР+ (у)Ф« (х) 10, р); D.1.70)
116 , Глава 4
импульсное представление для нее имеет вид
Sf (х-у) = -У^\ dtk exp [ik (х - у) - ik0 (tx - ty)\ Sf (k).
D.1.71)
Тогда получаем
ca (со) сР(ш) — с (со) rf (со) 4 с (со) d (со)
^ар ,,о / ^0 — (?> + i6k0 — й> — F' *0 — @ + tfi ' ko — (u—i6
с («Л — I _ с (М) rf (Ц) c(co)riu) <Р (со) с2 (со)
k0 — со + 'б ka — со — гб ' k0 — со + 'б k0 — со — (б
D.1.72)
где со = со (к), б — положительная бесконечно малая величина,
с(ю) = [1—М©)]1/., d(<a)= [M<o)]V.. D.1.73)
Примечательно, что выражение D.1.72) можно записать в сле-
дующей простой форме:
| D.1.74)
= U (со) [^0 - со + /бт] f/+ (со). D.1.75)
Здесь U (со) — унитарная матрица
с (со) d(co)
d (со) с (со)
а матрица т определена выражением
1 0 .
D.1.77)
Возможность записи Sc(k) в простом виде D.1.75) делает эту
причинную функцию очень полезной в практических вычислениях
по методу термополевой динамики.
Запаздывающая двухточечная функция Sr (x — у) и опере-
жающая двухточечная функция 5а (х —¦ у) определяются следу-
ющим образом:
5?3 (х - у) = 0 (tx - ty) @, р | [Фа (х), Фр+ (у)]+10, р), D.1.78)
f (x-y) = ~Q(tB - ts) @, p| [Фа (х), Фв+ (y)]+10, p). D.1.79)
Квантовая теория поля При конечных температурах 117
Фурье-образы этих функций определяются с помощью соотноше-
ний, аналогичных D.1.71), и имеют вид
Рассмотрим теперь бозонное поле ф°, для которого оператор
К (д) задан выражением D.1.55); здесь вновь используется дублет-
ное обозначение D.1.68). Причинная двухточечная функция
имеет вид
,P>= D-1.82)
= 9 (tx - /„) @, p | Фа (x) фЗ+ (у) 10, p) +
+ 6 (/„ — У @, p | cpPt (y) ф« (X) | o, p), D.1.83)
а ее фурье-разложение
Af (x - у) = ^ J d4? exp [tk (x - y) - i*,, (fK - tp)] Af (k).
D.1.84)
Используя выражения D.1.60) и D.1.61) и учитывая преобразо-
вание Боголюбова, определяемое равенствами D.1.25) и D.1.26),
найдем
:в (со) йв (ю) св (со) rfB (со)'
ifr0 — Ш -f F A>0 — @— /6'
CB (CO) dB (@) Сд (@) rffi (@)
fe0 — to -j- гб k0 — to — F ' k0 — со. -f- /6 ^o — ш — 'в/
D.1.85a)
= Uв (со) т [й0 — со + ;8тГх f/B (со), D.1.856)
где со = со (k), a
/св (со) dn (со)\
t/(co) в; ; в; ;
; ; ; ; , D.1.86)
(СО) СВ {(?>)}
причем
св (со) = [1 + fB (со)]1/,, dB (со) = \fB (со)]1/,. D.1.87)
Заметим, что матрица UB не унитарна, но удовлетворяет соот-
ношению
UB%UB = т. D.1.88)
118 Глава 4
Запаздывающая и опережающая двухточечные функции Дг и Аа
определяются равенствами
Л?р {х - у) = 9 (*х - у @, р | [Фа (дг), фр+ (у)] | 0, р>, D.1.89)
ДаР (*-«/) = - в (*„- У @, р | [<ра (х), срр+ (у)] 10, р>, D.1.90)
а их фурье-образы имеют вид
д2р(Л) = -г—^ --. D.1.92)
v ' &„ — со— F v ;
Рассмотрим теперь несколько более сложный случай
К (—д) = — [(а/5/J + со2 (V) ]. D.1.93)
Как указано непосредственно после выражения B.6.119), поле ф°
должно быть бозонным полем. Если предположить, что ф° —
вещественное поле (ф°+ = ф°), то в силу B.6.53), где р (к) = а (к),
имеем
Ф° (дг) = Bп)- '/.й'/. J _^- {а (к) exp [t (kx - cot)] +
+ а+ (к) exp [— t(kx - (of})}, D.1.94)
откуда
ф° (х) - Bя)" §'.ftV. J -?!L- {а (к) exp [- i (kx - со^)] +
+ at(k)exp[/(kx — at)]}. D.1.95)
Операторы a (k) и a (k) связаны с операторами физических ча-
стиц a (k, Р) и а (к, Р) преобразованием Боголюбова D.1.25а),
D.1.256). Причинная, запаздывающая и опережающая двух-
точечные функции определены равенствами D.1.83), D.1.89) и
D.1.90) соответственно. Фурье-образы этих функций имеют вид
Ас (А) = Uв (со) т [k\ + (со - гбтJ] UB (со), D.1.96)
Спектральные представления двухточечных функций для взаи-
модействующих полей приведены в следующем разделе.
Квантовая теория поля при конечных температурах 119
Рассмотрим последний пример, для которого
X (д) = i -|- - 8 (V2) т3 + Дтх. D.1.99)
Поскольку имеет место равенство (см. B.6.54))
К (д) = т3 (i ~ т3 - 8 (V2)
свободное поле ф° определяется выражением B.6.77)
Ф° (х) = J d3k {и (k) at (к) exp U (кх — «О ] +
+ v (к) а\ (к) exp [—t (кх — ш*I}. D.1.100)
Согласно соображениям, иысказанным после формулы B.6.123),
Ф° — фермионное поле. В D.1.100) использованы обозначения
af (к) и a4. (к) вместо а (к) и Р (к) соответственно, так как Р
используется для обозначения отношения filkBT. Указанные
операторы удовлетворяют фермионным антикоммутационным со-
отношениям. Волновые функции и (к) и v (к) приведены в B.6.73)
и B.6.74):
/ cos 9ь\
и (к) =B*0-v'ftv'(_sineft), D.1.101)
sin 6ft \
(iCosGJ» D-1.102)
где
cos 9ft = [(со + eA)/2<o]V., D.1.103)
sin Qk = [(со — e,)/2co]V% D.1.104)
со = со (k) = (el + A2I/,. D.1.105)
Таким образом, имеем
Ф° (х) = j d3k {и (k) at (k) exp [—i (kx — af) ] +
+ v (k) a| (k) exp [i (kx — eof) ]}. D.1.106)
Операторы a^, j (k) и att | (k) связаны с операторами физи-
ческих частиц ati + (k, Р) и ati | (к, C) преобразованием Бого-
любова. А именно
«t. 1 (к) - П -/р (co)]I/2 at. Ф (к, р) ± [/F(co)]1/2 a|. ^ (к, р), D.1.107)
«t.l(k) = [l-/H«)]I/2«t. |(k,P)=H=[/F(co)]'/24,nk, P), D.1.108)
где верхний (нижний) знак соответствует случаю спина вверх
(вниз).
120 Глава 4
Согласно B.6.56) и B.6.57), имеем ц = 1 и
did) = i-§f + * (V2) т3 - Atx. D.1.109)
Таким образом, правила сумм B.6.102) и B.6.103) вместе с вы-
ражением B.6.85) дают
BяK иа (к) иь (к) = ( + X )аЬ, D.1.110)
Bя)" va (к) vb (к) = (М~е2 + ДТ1 )вй' D.1.111)
где а = 1 или 2 и b = 1 или 2.
Используем вновь обозначение термополевого дублета D.1.68):
D.1.112)
Заметим, что это по существу четырехкомпонентный вектор-
столбец, так как q>° — вектор-дублет. В дальнейшем будем обо-
значать ф1 и ф2 через фа, а = 1, 2. Причинная, запаздывающая
и опережающая двухточечные функции определены выражениями
D.1.70), D.1.78) и D.1.79) соответственно. В результате вычисле-
ния находим
ATl [U (со) (*0 - со
l [U (- со) (k0 + со + t6T)-i U* (- со)]вр, D.1.113)
где с7 (со) приведено в D.1.76), со обозначает со (к).
Определение причинной, запаздывающей и опережающей двух-
точечных функций дано в D.1.70), D.1.78) и D.1.79) для фермионов
и в D.1.83), D.1.89) и D.1.90) для бозонов. Применяя эти опреде-
ления к приведенным выше примерам, получаем уравнения для
функций Грина
К (д) S"P (x — y)=* ih№ (x — у) 6*0, D.1.114)
к (д) АаВ (х — у) = ih8W (Х — у) т*3; D.1.115)
здесь S обозначает Sc, ST, Sa, a A — Ас, Аг, Аа.
Канонические коммутаторы также слегка видоизменяются
в обозначениях термополевого дублета и имеют для бозонов и фер-
мионов соответственно следующий вид:
[я« (х), фР (у) ]tx=tu = -Шх«Ч (х - у), D.1.116)
[я« (х), фР (y)Uix=tu = -№в*Рв (х - у); D.1.117)
здесь яа (х) — величина, канонически сопряженная с фа (х).
Квантовая теория поля при конечных температурах 121
Правила умножения для двухточечных функций. При практи-
ческих вычислениях часто встречаются замкнутые петлевые диа-
граммы, соответствующие произведениям двухточечных функций.
Ниже приводятся выражения для подобных величин.
Начнем с произведения' бозонных двухточечных функций,
описываемых выражением D.1.85). Имеем
\^Ь.\и (х ) т (/ -J- -^- — х + И
J 2я [_ \ ° ' 2 + ^
I \ 2 I
¦ \ dxa (х; х+, х_) [UB (х) т {/е0 - х + /бт} Uu (x)]«p, D.1.118)
/в
где
а (х; х+, х_) = б (х — х+ ± х_) [/в (х+) — /в (±х_) ]. D.1.119)
Вывод последней формулы требует вычисления каждого матрич-
ного элемента. Например, компонента A, 1) матрицы о вычисляется
следующим образом:
о i и ъ х
db (x_)
/в—-^ х_ —«
_ / _ Л / СВ (Х+) С?Ъ (X.) ^Д (Х+) СД (X.) \ =
*¦ -1 \ k0 — х+ + х_ + F fe0 — х+ + х_ — (б /
X
/ ев (х) ^Ь (х) \
\ и -j A- if. Ъ -j [б / *
При этом действительно для о (х; х+, х_) получается выражение
D.1.119). Случай нижнего знака в D.1.119) легко получить, если
учесть соотношение с% (х) = —d% (—х).
Формула для произведения фермионных двухточечных функ-
ций имеет вид
X
x; x+, x_) [f/B (x) т {^o - и + (бт} t/B (x)]efJ, D.1.120)
122 Глава 4
где еа = таа и
а (х; х+, х_) = — б (х — х+ + х_) [/, (х+) — fF (x_) ]. D.1.121)
С другой стороны, формула для фермионной двухточечной
функции, состоящей из фермионной и бозонной двухточечных
функций, записывается в виде
X [f/B (x2) т {/0 =F (x2 — tf
= t J dxa (х; хь xa) [U (х) {/г0 - х -1- tfix} W (хIаР, D.1.122)
-оо
где
0(х;х1;х2) = _6(х-х1 + х2) [/B(±x2) + l-/if(x1)]> D.1.123)
если бозонная двухточечная функция имеет вид D.1.85). Если же
бозонная двухточечная функция имеет вид D.1.96), то формула
записывается в виде
J g [U (хх) {й0 - /0 - х, + /8т}-1
X [UB (х2) т {/^ - (х2 - /бтJ} f/B (х2)]аР =
= i J dxo (x; x1; xj) [U (к) {ko-x + /бт}1/+ (x)]eP, D.1.124)
-оо
где
о (х; хь х2) = — ^ [б (х - хх - х2) {/в (х2) + 1 - /F (щ)} -
- б (х - х, + х2) {/в (- х2) + 1 - U (х,)}]. D.1.125)
4.2. Динамическое отображение при конечных
температурах, правило подстановки тильды
и соотношение Кубо —Мартина —Швингера
В гл. 3 введены общее понятие динамического отображения и
представление физических частиц для изолированной системы.
В этом разделе дается обобщение указанных понятий на случай
учета влияния температуры.
Уравнение Гейзенберга при конечных температурах. Согласно
сказанному в разд. 4.1, имеется не только гейзенберговское поле
Квантовая теория поля при конечных температурах 123
ty (x), но и сопряженное ему (в смысле операции тильда) поле
¦ф (х). Уравнения Гейзенберга имеют вид
Л (д) г]) (х) = F [г])], D.2.1)
Л* (д) ф (х) = F* [ip*]. D.2.2)
Заметим, что F* [ф* ] получается из F [г])] посредством операции
тильда. Как показано в примерах разд. 4.1, двухточечные функции
имеют сравнительно простой вид при использовании обозначений
термополевых дублетов. Здесь дается обобщение этих обозначений.
Для любого оператора F определим термополевой дублет
с помощью соотношения
F для а = 1,
Ь для а = 2. <4-2-3>
Если F — функция других операторов, например АВ ... С:
F = аАВ ... С, D.2.4)
где а — численный коэффициент, то Fa, согласно определению
D.2.3), задано выражением
Fa = aPa (АаВгл ... О); D.2.5)
здесь Ра — оператор упорядочения, определенный соотношением
А'-В1 ... С1 для а = 1,
, _ о D-2-6)
Используя дублетные обозначения, уравнение Гейзенберга можно
привести к виду
Л (д) г])* (х) = PaF [г])« (х) ]. D.2.7)
Если г]) описывает электронное поле, то оно является спи-
новым дублетом. Вообще говоря, если исходный оператор Гейзен-
берга г|> (х) выражается с помощью вектор-столбца, термополевой
дублет имеет вид
ib (х) для а = 1,
т+ \ w о D-2.8)
г|з+ (х)( для а = 2. v '
Здесь верхний индекс t обозначает операцию транспонирования
вектора. Если г|з (х) преобразуется под действием преобразования
симметрии согласно
г]) (х) -^ {/г]) (х), D.2.9)
то, как видно из определения D.2.8), ,г|)а (х) преобразуется ана-
логично;
Уа.{х)*+Ща{х), D.2.10)
124 Глава 4
Это свойство, характерное для термополевых мультиплетов,
может упростить вычисления.
Динамическое отображение при конечных температурах.
Пусть ф° и ф° — свободное физическое поле и тильда-сопряженное
поле соответственно. Уравнения для этих полей имеют вид
Х(д)ф° = 0, D.2.11)
%* (д)фо = 0. D.2.12)
Если температура отлична от нуля, многие квантовые моды ста-
новятся неустойчивыми. Во многих случаях эти квантовые моды
рассматриваются приближенно как физические кванты. Неустой-
чивость, обусловленная влиянием температуры, учитывается по-
средством структуры соответствующих двухточечных функций
резонансного типа.
Следуя рассуждениям гл. 3, запишем динамическое отображе-
ние в терминах некоторых свободных полей. Поскольку два урав-
нения D.2.1) и D.2.2) не связаны друг с другом, можно выбрать
Ф° и ф° так, чтобы г]) содержала только^0, а -ф — только ф°. Влия-
ние температуры проявляется лишь в том, что а (к) и а (к) пере-
стают быть операторами уничтожения; они выражаются через
операторы уничтожения а (к, Р) и а (к, C) согласно формулам
D.1.25) и D.1.26):
а (к) = а (к, Р) gV. (к, р) + 0Й+ (к, Р) /V, (к, р), D.2.13)
а (к) = а (к, Р) gV. (к, р) + ара* (к, Р) /V. (к, Р), D.2.14)
где р = 1 для бозонов и р = —1 для фермионов. Функции g (k, P)
и / (к, р) определены следующим образом:
g(k, p) = е^Ч^ь - р), D.2.15)
/(к, Р) = 1г/(е<Ч_р). D.2.16)
Заметим, что coft обозначает со (к), а
g(k, P)//(k, Р)=ерш*. D.2.17)
Хотя поле г]) не содержит поля ф0, a aji — поля ф°, имеем
@, Р|ф+г|>|0, Р)#0, D.2.18)
поскольку
@, P|q>°V|0, P)?=0. D.2.19)
Именно по этой причине многие физические величины, содержащие
энергию ю (к), зависят от температуры.
Квантовая теория поля при конечных температурах 125
Динамическое отображение для г|) можно записать в виде
n, m
X at (kl) ... a+ (kn) a (qi) ... a (qm). D.2.20)
Тогда операция тильда дает
Ф (*)=]>] J dki ••• ^P.^i ••• dqmF* (x; kx ... kn : q± ... qm) X
X a+(k1)...at(kn)a(q1)...a(qm). D.2.21)
Из выражений D.2.20) и D.2.21) следует, что Н и Н равны
в слабом смысле Яо и Но соответственно (см. разд. 3.4). Таким
образом, полный гамильтониан Н = Н — Н равен в слабом
смысле #0 = #о— Но. Операторы а (к) и а (к) связаны с физи-
ческими операторами a (k, Р) и а (к, |3) посредством преобразова-
ния Боголюбова.
Правило подстановки тильды. Обратимся теперь к соотноше-
нию D.1.27), согласно которому
a (k) 10, Р) = а ехр фщ/2) at (k) 10) р>. D.2.22)
При его выводе учтено, что а (к, р) | 0, Р) = 0. Кроме того, со-
отношение а (к, Р) | 0, Р) = 0 приводит к равенству
at (k) 10, р) = стр ехр (—pcofe/2) a (к) 10, р). D.2.23)
Повторное применение D.2.22) и D.2.23) приводит к выражению
г]) (х) 10, р) = е ехр (-|- (Яо - Яо)) & (х) 10, Р), D.2.24)
где
Но = J d3kaka* (k) a (к), D.2.25)
Но = \d*kwka* (к) а (к), D.2.26)
е — знаковый множитель.
Знаковый множитель е определяется следующим образом.
Рассмотрим сначала оператор a+ (kx) ... at (kn) a (qx) ... a (qm),
где а A) — фермионный оператор. Число перестановок ферми-
онных операторов в этом произведении равно
nF = V2 (л + т) {п + т — 1). D.2.27)
Предположим, что среди операторов a+ (kx) ... а+ (кп) имеется
v фермионов с о = —1 и (п —v) фермионов с а = +1, а среди
операторов a (qx) ... a (qm) имеется \i фермионов с 0 = —1 И
126 Глава 4
(т — \i) фермионов с ст = +1. С учетом соотношений D.2.22)
и D.2.23) получаем дополнительный знаковый множитель от опе-
раторов а с ст = —1 и от операторов а+ с ст = +1. Таким обра-
зом, знаковый множитель е принимает вид
е = (— \)"F (~ l)n'v (— If = (— 1)пр+п (— lf""v- D.2.28)
Поскольку
nF + п = -j- (п — т) (п — т + 1) + 2пт,
J_ („ _ т) (п _ т + 1) + (|1 _ V) =
= -J- Ь — m + 2 (ц — v) ] [п — т + 2 (ц — v) + 1 ] —
- 2 (л - m) (|i - v) - 2 (ц - vJ,
имеем
е_ / j\V2 [(n-v) - (m-ц) +M.-V} {(n-v) - (m-ц) +n-v+l}_ ,^ g 29)
Тогда D.2.24) можно записать в виде
D.2.30)
Здесь F — оператор числа фермионов, определенный выражением
F = J d3ka [a+ (k) a (k) — a+ (k) a (k) ]. D.2.31)
Если имеется еще несколько типов фермионных и бозонных полей,
то ст-множители для них можно определить, пользуясь правилом
сохранения полного числа фермионов. Для этого примем, что,
как для обычных фермионов, ст = +1 для частиц и ст = —1 для
дырок. Здесь под частицей (фермионом) понимается квант, свя-
занный с волновой функцией иг (к) в B.6.45) и B.6.46), а под
дыркой — квант, связанный с vr (k). В случае модели свободного
поля D.1.55) фермион с отрицательным значением со (к) является
дыркой, и, следовательно, в D.1.656) использовалось значение
ст = —1. В случае модели D.1.99) выражение D.1.100) показы-
вает, что дыркой является фермион со спином вниз. Поэтому зна-
чение ст = —1 в D.1.107) и D.1.108) приписывается фермиону со
спином вниз. (Если фермиону со спином вниз приписать значение
ст = +1, выражение для причинной двухточечной функции станет
более громоздким; U и f/+ поменяются местами во втором члене
выражения D.1.113), а не в первом. При этом правила умножения
причинных двухточечных функций усложняются.) Что касается
элементарных бозонов, то мы можем всегда использовать значе-
ние a = 4~1. Если рассматриваются также срстаэные частицы
Квантовая теория поля при конечных температурах 127
(бозоны или фермионы), значение 0 определяется формулой
а = (—\)F(F+D.2t
где F — число всех фермионов, входящих в составные частицы.
Пусть nt — число фермионов в i-й частице. Тогда полное число
фермионов дается выражением
F = f &k 2 nt!«' (k) at <k) - "' (k)б' СОЬ D.2.32)
J t
Заметим, что F, Ho и Но коммутируют друг с другом и, кроме
того, F | О, р) = 0.
Соотношение D.2.30) допускает следующее обобщение:
ехр (-|-#о) Он(х)\0, р) = (- l)<™>F/2exp (-Ё-Я0)б?(дг)|О, р),
D.2.33)
где Оя (х) — произвольный оператор Гейзенберга, состоящий из
операторов г]).
Применяя к D.2.33) операцию эрмитова сопряжения, получаем
@, р | Оя (х) ехр (-§-#о) = @, Р10^ (х) ехр D Яо) (- 1)<™> f'2,
D.2.34)
где вместо Он стоит Он. Соотношения D.2.33) и D.2.34) выра-
жают правило подстановки тильды.
Соотношение Кубо—Мартина—Швингера. Рассмотрим два опе-
ратора A (t) и В (t), являющиеся произведениями гейзенбергов-
ских полей в момент времени t. Число фермионов, сопоставляемое
с оператором A (t) или В (t), обозначается пА или пв соответ-
ственно. Поскольку полный гамильтониан Н = Н — Н в слабом
смысле равен гамильтониану Но = Но — Но, при вычислении
матричных элементов A (t) и В (t) можно использовать формулу
A (t) = ехр UH0 (t — Г)] А (Г) ехр [—Шо (t — Г) ] и т. д. D.2.35)
Поскольку число фермионов в А равно (—пА), а также учитывая,
что Я | 0, Р) = 0, имеем
X @ р | Л+ (/ + 4
@, р | Л+ (/ + 4" Ф)В @10, р). D.2.36)
Заметим, что А содержит только ф°, тогда как В (t) — только ср°.
Поэтому перестановка операторов Л+ (t + l/2tp) и В (f) приводит
128 Глава 4
к появлению только знакового множителя (—\)папвш Таким об-
разом, получаем
(О, р | А (О В (/') | О, Р) = (— l)^) "лР (— \)папв х
X @, р | В (О A*(t+±-ф) 0, р). D.2.37)
Использование D.2.33) приводит к соотношению
= (_ 1)(пл-') "л/2 (_ \)пАпв (_ 1)("л+1) пл/2 х
= (о, р | В (f) Л (t + ф) | О, Р) =
= @, P|fi(*'M C + tP)|O, P), D.2.38)
которое обычно называют соотношением Кубо—Мартина—Швин-
гера [7 ]. Выше везде учитывался тот факт, что вакуумное среднее
значение D.2.38) обращается в нуль при пА Ф —пв.
Пусть \п, т) — вектор состояния, который строится посред-
ством n-кратного действия циклической операции а+ (Р) и т-
кратного действия циклической операции а+ (Р) на | 0, Р). Тогда
операция тильда приводит к соотношению
(n, m 11|) (л:) | n', m') = (n, m 11|) (a:) | n', m')* =
= (— \)Пт-Пт'{п, m 1 -ф (лг) | Я', /и')*, D.2.39)
где пт — число фермионов в состоянии \т). При получении
D.2.39) использовано выражение D.1.34) для повторной операции
тильда.
Соотношения D.2.33), D.2.34) и D.2.39) используются ниже
при выводе спектрального представления для двухточечных
функций.
Обобщение формулы ЛСЦ на случай конечных температур.
Обобщим теперь формулы C.5.13) и C.5.14) на случай конечных
температур. Рассмотрим сначала вещественное бозонное поле г]).
В этом случае ф° имеет вид
1 С
Ц) \Х) — з , I CL FC \ЬЬ in у JC) СС (КI —— VL in. лj ОС ("/1* I т: ¦ ^ • тИ_//
Bя) '2 J
где и (к, х) = и (k) exp [tkx — ш (к) t]\ D.2.41)
кроме того, X* (д) = X (д).
Квантовая теория поля при конечных температурах 129
Поскольку
a (k, p) = gV. (к, р) а (к) - а/V. (к, р) а+ (к), D.2.42)
а (к, Р) = ?*'. (к, Р) а (к) - а/V. (к, р) а+ (к), D.2.43)
имеем
i
а (к, р) =-i- J <fx«* (к, Jt)T{gV, (a, р) ф» (х) ~
- а/V. (а, р) ф° (*)}, D.2.44)
а (к, Р) = --L J Ли (к, *)TfeV, (a, p) ф° (х) -
- а/V. (a, P) ф° (х)}, D.2.45)
где g (д, Р) и / (д, Р) определены следующим образом:
Я (,?, р) е'кх = g (к, р)(кх и т. д. D.2.46)
Заметим, что в выражении D.2.45) использовано (—Г) вместо Г,
поскольку полный лагранжиан равен 9? = 2? — 3?.
Из D.2.44) и D.2.45) следует, что величина
г]) (х, р) ее gi/* (а, Р) {г]) (х) - х} - а/'/* E, Р) {t W - х} D-2.47)
является связующим полем для а'п (к, Р) и aout (к, Р), а величина
^ (х, р) - ?1/2 E, Р) {^ (х) - х> - а/'/2 (а, р) {г]) (х) - х} D-2.48)
¦— связующее поле для ain (к, Р) и aout (к, Р); здесь
Х = @, Р|ф|О, Р) = @, Р|^|0, Р).
Заметим, что
J d3x {ф° (х, р) ?aj) (х, Р) - ф° (х, р) "Гф (х, р)} =
= J d3x {ф° (х) F[aJ) (х) - х ] - ф° (х) F [^ (х) - х 1}, D.2.49)
если определить ф° (х, Р) и ф° (х, Р) равенствами
Ф° (х, р) = gi/* E, р) ф° (х) - a/'/2 E, Р) ф° (х), D.2.50)
Ф° (дс, Р) = g!/2 E, Р) Фо (х) - 0/'/2 (а, р) фО (х). D.2.51)
Величина ф° (х, Р) (или ф° (х, Р)) — физическое поле, соответ-
ствующее г]) (х, Р) (или iji (x, P)). При выводе D.2.49) использо-
вано соотношение
g (д, Р) — / (а, р) = 1 для бозонов. D.2.52)
130 Глава 4
Применяя далее соотношение D.2.49) и следуя выводу C.5.14),
получаем динамические отображения
, D.2.53)
([( Щ])^, D.2.54)
где
5= :(т[ехр (- ±-B°> - Щ})'- ¦ D.2.55)
Здесь
o \%\ D.2.56)
\ D.2.57)
где
J° (g) = Ф°Х (д), D.2.58)
7° (g) = фЛ* (д), D.2.59)
^(g) =Z-J/2 Ы)(?)-Х], D-2.60)
?(g) = Z-'/4^(g)-xl. D.2.61)
Если г|з (х) — комплексное поле, то можно получить соотноше-
ния D.2.53), D.2.54) вместе с D.2.55), где 2?j и 3?°j имеют вид
{7°(^© + f ©/(?)), D.2.62)
\ G°(g)?(g) +1 (I) ?E)}. D.2.63)
причем <? = ^>+ti и
7° (х) = ф° (х) X (д), D.2.64)
/о до = ь (_5j фо до, D.2.65)
7° (х) = 5° (х) К* (д), D.2.66)
7° (х) = Я* (—Э) ф° (х), D.2.67)
4> (х) = Z-1/2 [i|) (x) — xl, D.2.68)
? (х) = Z-'/2 [ф (х) — %' ]. D.2.69)
Приведенный результат справедлив независимо от того, опи-
сывает ли г|) бозоны или фермионы. Выше отмечалось, что дина-
мическое отображение \\> можно выразить только через ф°. С дру-
Квантовая теория поля при конечных температурах 131
гой стороны, выражение для 5г|з в D.2.53) содержит наряду с ф°
также и ф°. Это неудивительно, поскольку из D.2.22) и D.2.23)
очевидно наличие связи между ф° и ф°.
Следует отметить, что динамическое отображение при конеч-
ных температурах может быть получено из динамического отобра-
жения для изолированной системы C.5.14) простой заменой
Я?* -*¦ B?j —S°j). Это нетрудно понять, вспомнив, что полный
лагранжиан при конечных температурах имеет вид SB — SB.
Следует также отметить, что хотя физическими полями являются
не ф° (х) и ф° (х), а ф° (х, Р) и ф° (х, Р), тем не менее динамические
отображения D.2.53)—D.2.55) принимают столь же простой вид,
как и для случая нулевой температуры C.5.14), если выразить
их через ф° (х) и ф° (х).
Если Он Ьр, Ф) — оператор, состоящий из \|), \|)f, ф и ф+, то
формулы D.2.53) и D.2.54) получают следующее обобщение:
50я(г|5, $) = :(Т [Он(г|э, ф) exp ( — -^¦(?Bj — 2?Oj))]\ :. D.2.70)
4.3. Спектральное представление
двухточечных функций
Спектральное представление двухточечных функций для изо-
лированной системы обсуждалось в разд. 3.6. В данном разделе
будет получено обобщение этого представления на случай конеч-
ных температур [4].
Рассмотрим двухточечные функции, состоящие из операто-
ров А (х) и В (у). Число фермионов, связанных с оператором
Л (х) (В (х)), будем обозначать FA (FB). Используем векторное
обозначение (см. D.2.3))
*' ш ' D.3.1)
Причинная двухточечная функция определяется следующим обра-
зом (ср. с D.1.70) и D.1.83)):
G?$b (х-у)=@, р | Г [Аа (х), В3 (у)) 10, р) =
= е (tx - ty) (о, р | л- (х) яр (у) | о, р) +
+ р6 (/„ - Q @, р | 5Р (у) Аа (х) | 0, р), D.3.2)
где р = -f-Л или —1 для бозоноподобных или
операторов А и В соответстзенно,
132 Глава 4
Используя формулу
О D - У = Hm -± J dw -^-^ exp {-iw (tx - te)} D.3.3)
и вставляя полный набор 2 \ п, т) (т, п | между операторами А
п, т
и В, находим
Г^ IS 1 А ( °^К Р) ОГ? (W, -р) \
GcAb (р) = с?оу — г^" ~~ Р ——, Гх~ > D.3.4)
-оо
где
afB{w, р) = BяK 2@, Р|Ла@)|л, m)<m, /г|Вр@)|0, р) х
X 6 (р - р„ + рт) б (ш - Еп + ?т). D.3.5)
Функция GcJib (p) в D.3.4) определена как
ОаЛв (х-у) = A- J dV exp {ф (х - у)} G°iB (p). D.3.6)
Величины рп и ?п в D.3.5) — импульс и энергия состояния п,
а (—Рт) и (—Ет) — импульс и энергия состояния т.
Из выражений D.2.33) и D.2.34) имеем
ехр{-р(Яо-Яо)/2}Л(О)|О, р) = (-If ^»/2 Л+ @) | 0, р>, D.3.7)
@, р|Л@)ехр{-.р(Я0-Я0)/2} = <0, Р [Л+ @) (-If C+O/z, D.3.8)
а из D.2.39) получаем
(л, т|Л@)|я', т') = (— 1)Пт""т'(п, т|Л@)|л'; т'>*. D.3.9)
Из этих соотношений находим
@, р|Л+@)|л, m) = (—l)FA(FA-1)/*e-*(B*-Em)P(ot р| Л @)| га, т),
D.3.10)
(п, т|Л@)|0, Р> = (— 1)"™<n, m|А@I0, Р>* =
= (-1)"т<о, р|Л+@)|/и, п) =
= (_1)пт(_1)'лС,|-1)/8в-Р(вт-?п)/8@1 Р|Л@)|т, п), D.3.11)
<п, т|Л+@)|0, p) = (-l)^(^+1)/Vp(?«-?m)/2(rei т|Л@)|0, Р) =
= (_1)^(_ 1)»т@, р(Л@)|/И, Я),
D.3.12)
(л, m|Bf@)|0, p} = (— l)FB(FB+We-HEn-Em)/2(m> л | 5 @)| 0, Р),
D.3.13)
@, Р|5@)|л, m) = (-l)"m(_l)FB(Fs+1)/2e-P(?m-?n)/2x
X (т, Я|В@)|0, р), D.3.14)
@, р|В+@)|л, /й) = (-1)'д(-1)пт(т> л|5@)|0, р). D,3.15)
Квантовая теория поля при конечных температурах 133
Таким образом, имеем
(О, Р|Л«@)|п, т){т, n|fiP(O)|O, Р) = <0, Р|Л(О)|п, in) x
X (т, п\В@) 10, р) х
D.3.16)
(О, р|5В@)|т, п)(п, т\Аа@)\0, Р) = @, р|Л(О)|я, т) х
Х(т, л|5@)|0, р)х
/ е^(Ёп-Ет), (^]fA(FA+1)/2e-HEn-Em)l2 \a*
Х \^\fA(FA+l)/2e-HEn-Em)/2, I J '
D.3.17)
если FA = —.FB. Если же FA =#= —FB, to GcIb обращается
в нуль; поэтому в дальнейшем мы всегда считаем, что FA = —FB.
Тогда D.3.5) принимает вид
о% (w, р) = оАВ (w, р) х
X{{^lfACA-4/2c{w)d{w)i d\W) ) ' ( '
oaBA (—w, —p) = aAB (w, p) x
где
°ab(w, P) = ^
n, m
X(O,P\A@)|n, fh)(m, n\B@I0, P), D.3.20)
c2 (a») = 1 + p/ (a»), d2 (a») = / (a»), D.3.21)
/ (w) = l/(eP" — p). D.3.22)
Напомним снова, что р = 1 для бозонов и р = —1 для фермионов.
Если / (w) становится отрицательным, фазы с (w) и d (w) следует
выбирать так, чтобы с (w) d (w) было вещественным.
Сравнивая выражения D.3.18) и D.3.19) с D.1.72) и D.1.74)
соответственно, находим
+ОО
(р) = J dwoAB (w, p) X
-оо
X (т(V)/V{w)[Pg^w± Iбт]-1 Uf Щ t(fa«)IY D.3.23)
134 Глава 4
для фермионоподобных операторов (р = — 1) и
Gah (р) = J dwoAB (w, p) (xfaI2Vb И т [р0 - w + i 6т]~' х
xUB(w)%FA/2)a^ D.3.24)
для бозоноподобных операторов (р = -fl). гДе U (w) и UB (w)
определены выражениями D.1.76) и D.1.86)
/ c(w) d (w) \
U(w)=[ ,\ \ ,'), D.3.25)
х ; \ —d (w) c{w) J K '
I сB (w) dB (w) \
UB(w)=[?\ \ • D.3.26)
' \dB (w) сB (w) j
Соотношения D.3.23) и D.3.24) дают спектральное представление
причинной двухточечной функции при конечных температурах.
Запаздывающая и опережающая двухточечные функции имеют
вид
- у) = 6 (tx - ty) @, р | [Аа (х), # (у)]± 10, р>, D.3.27)
GaaU (х-у) = -9 {ty - tx) @, р | [Аа (х), Вр (у)]± 10, р) D.3.28)
соответственно, а их фурье-образы определены соотношением
Or, аАв (х-у)= -^|г J <?Р ехр {Ф (^ - »)} G?pfl (p). D.3.29)
Имеем тогда (ср. с D.1.80) и D.1.81), а также D.1.91) и D.1.92))
W-?^, D.3.30)
D.3.31)
для фермионоподобных операторов и
ОЙ. Ю-.,"»/*.??$, D.3.32,
^ D-3-33)
для бдзаноподобных операторов,
Квантовая теория поля при конечных температурах 135
Из D.3.18) очевидно, что
(О, $\А*(х)В»{у)\0, р> =
= ~(§ЯM" J d3f} J *" 6XP [lk (X ~ У) ~ "" ('x ~ *уН °AB (W' P) X
j2_ K)) , D.3.34)
<0'
= -?щг J d3k exp [ik (x - y)] J dwaAB (w, p) (t('+p)/2)»P. D.3.35)
Если В — оператор, канонически сопряженный с А, имеем
[Ла (х), ВР (у))± б (/ж -ty) = n (т<1+р>/2)«Р б<4> (дг - г/), D.3.36)
откуда, учитывая D.3.35), получаем правило сумм
\dwaAB(w,p) = \. D.3.37)
-ОО
Если в суммировании, входящем в D.3.20), участвуют какие-то
одночастичные состояния с энергией со (р), то аАВ имеет вид
oAB{w, р)=2АВ(р)б[ау — ffl(p)] + crAB(ai, p). D.3.38)
Свойства спектральной функции a (w, p), установленные в разд. 3.6,
можно обобщить на случай конечных температур, если заменить
a (w, p) на аАВ (w, p). Заметим, что аАВ (w, p) при конечных
температурах может принимать отличные от нуля значения как
для положительных, так и для отрицательных значений w, по-
скольку знак разности Еп — Ет не определен.
Из D.3.11) и D.3.14) имеем
@, Р|Л@)|п, т){т, n|fi@)|0, P) =
= еЗ(?л-?т)@, р|В(О)|Я, т)(т, й|Л@)|0, р), D.3.39)
откуда
<*ав (w, р) = — рсгвл (—w, р). D.3.40)
Когда теория инвариантна относительно пространственных отра-
жений, имеем
м>, р) = — роВА {—w, —р). D.3.41)
136 Глава 4
Если А—бозоноподобный оператор и В —А, то выражение
D.3.24) можно переписать в виде
оо
Gcab (р) = j dwaAA (w, р) х
о
X (ifa/2Ub (w) т [р\ -(w-i bxfP Uв И /л/2)ар, D.3.42)
где
5аа (w, p) = 2woAA (w, p). D.3.43)
В этом случае запаздывающая и опережающая двухточечные
функции имеют вид соответственно
со
G& (р) = тар J dwaAA (w, р) ф+118)Я_ай , D.3.44)
О
оо
GfAA (р) = хар j dwaAA (w, р) (А)+.еJ_ш2 • D.3.45)
о
4.4. Уравнение Бете —Солпитера
при конечных температурах
Рассмотрим набор гейзенберговских полей \Ьа, удовлетворяю-
щий уравнению Гейзенберга ХаЬ (д) ^ь = Fb [$), которое можно
записать в виде
Х{д)^ = F [ф], D.4.1)
где i|) и Т7 [ijjl — вектор-столбцы с компонентами \|;а и fa соответ-
ственно. Используя D.2.7), получаем
Х{д)^а = Р^ [tya]. D.4.2)
Рассмотрим далее причинную двухточечную функцию
G«P (х, г/) = @, р | Г [Г (х), фР+ (у)] | 0, р) = D.4.3)
+ 9 (^у - У @, р | фМ- (у) Г (х) 10, р), D.4.4)
где верхний знак относится к фермионам, а нижний — к бозонам.
Можно вычислить % (д) GaP с помощью D.4.2), а результат запи-
сать в следующей форме (Fa& (x, у) — некоторая функция):
Я (д) G«P (x, у) = F«P (x, у) + (йбН) (х — у) б«Р D.4.5а)
Квантовая теория поля при конечных температурах 137
для фермионов и
% (д) G«P (х, у) = {xF (х, у)}а$ + MW (х — у) х«Р D.4.56)
для бозонов.
В интегральном виде это уравнение запишется так:
G«f (х, у) = S«P (х - у) - -j- J d4zS«p (х - z) F^ (z, у) D.4.6)
для фермионов и
G«P (*, г/) = Д«Э (* _ у) _ JL J сDгдар ^ _ z) ^Pp (г> ^ D.4.7)
для бозонов. Здесь использованы выражения D.1.114) и D.1.115);
учтен также тот факт, что функция G становится равной S или А,
когда источник F в уравнении D.4.2) обращается в нуль. Вели-
чина FpP (z, у) может содержать многоточечные функции
(О, р|7 W4x)^(y)W(z)...\\Q, p).
Аналогичным образом из уравнения Гейзенберга D.4.1) можно
получить набор интегральных уравнений для многоточечных
функций. Эти интегральные уравнения называют уравнениями
Бете—Солпитера (БС). Обычно они лишь с трудом поддаются
решению. Для этого применяют разнообразные приближения,
использующие метод диаграмм Фейнмана. В следующей главе
приведен ряд подобных примеров.
Могут быть получены также интегральные уравнения для ве-
личин (а | Т [\ра (х), \рР+ (у)] | О, Р), где \а) принадлежит про-
странству Фока [а (Р), а (|3)]. Эти уравнения также называют
уравнениями Бете—Солпитера.
ЛИТЕРАТУРА
1. Ar,aki H., Woods E. J., J. Math. Phys., 4, 637 A963).
Araki H., Wyss W., Helv. Phys. Acta, 37, 136 A964);
Haag R., Hugenholtz N. W., Winnihk M., Comm. Math. Phys., 5, 215 A967);
Ojima I., Ann. Phys., A982).
2. Leplae L., Mancini F., Umezawa H., Phys. Rep., IOC, 151 A974).
3. Takahashi Y., Umezawa H., Collect. Phen., 2, 55 A975).
4. Matsumoto H., Fortschritte der Phys., 25, 1 A977).
5. Matsubara Г., Progr. Theor. Phys., 14, 351 A955);
Зубарев Д. Н., УФН, 71, 71 A960).
6. Абрикосов А. А., Горькое Л. П., Дзялошинский И. Е. Методы квантовой теории
поля в статистической физике. — М.: Физматгиз, 1962;
Киржниц Д. А. Полевые методы теории многих частиц. — М.: Госатомиздат,
1963.
7. Kubo R., J. Phys. Soc. Jap., 12, 570 A957);
Martin P., Schwinger J., Phys. Rev., 115, 1342 A959).
ГЛАВА 5
НЕКОТОРЫЕ ПРИМЕРЫ ВЫЧИСЛЕНИЙ
В РАМКАХ ТЕРМОПОЛЕВОЙ ДИНАМИКИ
5.1. Электрон-фононная система
Модель. Рассмотрим гейзенберговские поля — электронное
\|з (х) и фононное ф (х). Для простоты пренебрежем спином элек-
трона и будем считать \р синглетным фермионным полем. Фонон-
ное поле вещественно: <?+ == ф. Предполагается, что существует
следующий лагранжиан:
. E.1.1)
Дифференциальные операторы е0 (V), а>1 (V) и g (V) определены
с помощью своих фурье-образов
е0(V)<?'кх = е0(к)е'кх и т. д., E.1.2)
а постоянная п должна быть определена самосогласованным обра-
зом с помощью условия
, р). E.1.3)
Предположим, что g (к) — вещественная функция. Величина
g (k)/[2coo (кI1/г, как обычно, описывает электрон-фононное взаи-
модействие. Построим лагранжиан с помощью операции тильда
2 (х) = -^ (« ± + е0 (V)) Ф + т
. E-1-4)
где п определяется в конце вычислений с помощью условия
Я = <0, р | Ф+Ф10, р). E.1.5)
Поскольку п — вещественное число, операция тильда дает
п = п, E.1.6)
что является одним из соотношений, выражающих свойства сим-
метрии этой операции. Полный лагранжиан имеет вид
& = &-&. E.1.7)
Некоторые примеры вычислений 139
Аналогично формуле D.2.3) введем векторные обозначения для
термополевого дублета ip™ и фа
Тогда, учитывая вид лагранжиана .SP, получим уравнения Гей-
зенберга в следующем виде:
(«-J- - е (V)) Г (дг) = Ра [Г (х) g (V) ф« (х) - бе (V) Г (х)], E.1.9)
- 6co2 (V) фа (х)}, E.1.10)
где Pa — оператор упорядочения, введенный в D.2.6). Поскольку
операторы гЬа (х) и <j>a (x) коммутируют, наличие оператора Ра
в E.1.9) несущественно.
Величины бе (V) и бш2 (V) представляют перенормировку
(или сдвиг) энергии:
е (V) = е0 (V) + бе (V), E.1.11)
оJ (V) = cog (V) + бсо2 (V). E.1.12)
Уравнение Бете—Солпитера. Рассмотрим причинную функ-
цию Грина для электронного гейзенберговского поля
G»e (д. _ у) = (о, р | Т [^ (х) ^f (у)] 10, р). E.1.13)
Согласно уравнению Гейзенберга E.1.9), имеем
- 8z(V)Gf (х - у) + /АбD) (.г - г/) 6ар, E.1.14)
где % (д) — U (dldt) — е (V)]. Отсюда получаем следующее урав-
нение Бете—Солпитера:
X @, |31Т [Г (z) g (V) ф* (z) фР+ (у)] 10, р) -
(x~2)S8(v)G"pB~^ EЛЛ5)
Здесь 5™р (л) — причинная функция Грина свободного физиче-
ского электронного поля ф»:
Л (д) Sf (х) = »Йб<4) (х) бар. E.1.16)
140 Глава Ь
Введем далее неприводимую часть собственной энергии
2ар (х — у) с помощью соотношения
@, р | Т W (г) g (V) <f (г) г|,р+ (у)] | 0, р) =
(,_*')<#>(*'-*)• E.1.17)
Тогда, учитывая фурье-представление
Grf (х-у) = -$)Г \d'kexp [ik(x-y)~ika(tx-ty)]Gf (k), E.1.18)
получим уравнение БС в виде
Gf (k) = Sf (k) + S7 (k) Б vp (k) Gf (k) - S? (k) бе (к) Gf (Щ,
E.1.19)
где 2vp (k) — фурье-образ 2vp (*)•
i
дA) к-I ff(l)
Рис. 5.1.
Спектральное представление неприводимой части собственной
энергии. Согласно методу диаграмм Фейнмана, во втором порядке
теории возмущений имеем (рис. 5.1)
IT{k) = l^F Id4g2 {1) Л"Р @ S"P {fe ~ °' E"' -20)
Здесь A^P (Z) — функция Грина свободного физического фонона.
С другой стороны, причинная функция Грина свободного физиче-
ского электрона дается выражением D.1.75), где о (к) следует
заменить на е (к):
Sc (k) = U (e) lk0 — е + Йт]-1 г/+ (в), E.1.21)
где е обозначает е (к). Функция Грина свободного физического
фонона дается выражением D.1.96):
Ас (Щ = Uв (со) т [^о - (<о - t бтJ]'1 г/в (©), E.1.22)
где « обозначает со (к). Используя D.1.124) и D.1.125), получаем
2 (*) = f d*° («. k) ^ (х) 1*о - х + » St]-1 г/+ (х). E.1.23)
Некоторые примеры вычислений 141
Здесь 2 (k) —матрица [2а& (^)Ь причем
_ б (х - е + со) {fB (-со) + 1 - /, (е)}], E.1.24)
где использованы введенные выше обозначения со = со A), е =
= е (к — 1). Выражение E.1.23) дает спектральное представле-
ние для 2 (*)•
Энергия физического электрона. Поскольку гк — энергия фи-
зического электрона, взаимодействие не должно приводить к по-
явлению какой-либо собственной энергии. Иными словами, бе (к)
в E.1.19) должно компенсировать собственную энергию. Подоб-
ная процедура перенормировки энергии становится сложной
в случае конечных температур, поскольку наличие температуры
приводит к неустойчивости многих квантов. Существование ши-
рины энергетического уровня приводит к неоднозначности опре-
деления физической энергии. Если ширина мала, обычный способ
определения физической энергии е (к) состоит в использовании
вещественной части 2|1V- ^ этом случае условие перенормировки
энергии принимает вид
Re 2vp (A) = бе (k) 8vp для k0 = e (k). E.1.25)
Согласно этому условию, физическая энергия определяется как
е (к) = е0 (к) -j- бе (к). Очевидно, е (к) зависит от температуры.
Другой способ определения физической энергии состоит в исполь-
зовании комплексной полюсной особенности в двухточечной
функции гейзенберговских полей. В этом случае физической энер-
гией является вещественная часть этого комплексного полюса,
как будет проиллюстрировано в разд. 5.2.
В металлах перенормировка энергии увеличивает плотность
состояний вблизи уровня Ферми и приводит к росту электронной
теплоемкости (см., например, [1 ]). Даже в диэлектриках элек-
троны могут быть возбуждены в зону проводимости за счет внеш-
них воздействий (например оптических или тепловых возбужде-
ний). Эти электроны также вносят вклад в перенормировку энер-
гии, обусловленный электрон-фононным взаимодействием. Такой
электрон, «одетый» за счет фононов, называется поляроном (см.,
например, [2]). Структура электрон-фононной связи g (/) для ме-
таллов, диэлектриков и полупроводников совершенно раз-
лична.
142 Глава 5
5.2. Модель контактного взаимодействия
в ферромагнетизме коллективизированных
электронов
Модель. Лагранжиан модели имеет вид
1
2 (х) = ф+ (х) A~~г (V2)) ф (х) - Ц\ (х) tf (х) ^ (х) ^ (х) +
1'(*); E.2.1)
здесь ji2 — перенормирующий множитель, с помощью которого
самосогласованным образом подбирается химический потенциал,
а е (V2) определено соотношением
е (V2) eikx = efte'kx, E.2.2)
где
Sft=^-(k2-4)- E.2.3)
Постоянная kF — импульс Ферми. Символ ty обозначает электрон-
ное гейзенберговское поле — спиновый дублет
Заметим, что лагранжиан инвариантен относительно вращения
спинов
41—>-ехр ft (а• G)] ij:> E.2.5)
где 6 — параметр (9Ь 02, 03).
Уравнения Гейзенберга имеют вид
. д
¦ж~г
____ о
Применяя к этим уравнениям операцию эрмитова сопряжения и
операцию тильда, получаем
~эт— е (V )) ф| (х) = Хф| (х) щ (х) ф| (х) — ji ф| (х), E.2.8)
-г:— е (V2) ) ф| (х) = А.ф| (х) ф| (х) ф| (х) — [г2/ф| (х). E.2.9)
Заметим, что
(О, P|^|i);t|0, p) = -i-@, p|^f(l +оз)^|0, Р), E.2.10)
Некоторые примеры вычислений 143
Правые части уравнений E.2.6) и E.2.7) запишем в виде
E.2.12)
— /О RI ibf IО R\l 4-1 — 2
E.2.13)
При получении этих уравнений проведена замена \л2 — ЯA/2)Х
X @, р | ty^ty | О, Р) на Д2 (перенормировка химического потен-
циала). Величина М определена следующим образом:
|0, Р), E.2.14)
причем предполагается, что М Ф 0. Иными словами, предпола-
гается, что основное состояние системы не инвариантно относи-
тельно спиновых вращений. Это означает, что в системе существует
ферромагнитное упорядочение, и симметрия относительно спино-
вых вращений не проявляется при наблюдениях. Можно пред-
положить, что вращательная симметрия, описываемая тремя па-
раметрами (9Ъ 92, 93), заменяется однопараметрической @3) сим-
метрией (цилиндрической симметрией), но в последующих главах
будет показано, что в действительности это не так. Будет пока-
зано, что трехпараметрическая вращательная симметрия заме-
няется другой формой симметрии, также описываемой тремя пара-
метрами (динамическая перестройка симметрии). В этом разделе
мы покажем, каким образом в системе возникают магноны. Появ-
ление магнонов является примером общего утверждения (теоремы
Голдстоуна), что любое упорядоченное состояние поддерживается
с помощью некоторых дальнодействующих корреляций, которые
самосогласованным образом создаются системой. Кванты, сопо-
ставляемые дальнодействующим корреляциям, называются голд-
стоуновскими бозонами. В последующих главах будет показано,
каким образом появление магнонов восстанавливает вращатель-
ную инвариантность.
Используя E.2.12) и E.2.13), можно переписать уравнения
Гейзенберга E.2.6) и E.2.7) в виде
= % [ф| (х) ^ (х) - @, р | ф|Чч|О, Р>] Ь W - »2Ь (х), E.2.15)
))ых)=
(х) ty (х) - @, р | ф|ф| 10, р>] ty (х) - »\ (х), E.2.16)
144 Глава 5
где 8± (V2) = е (V2) =F -5- М. E.2.17)
Если использовать обозначение для термополевого дублета
(ср. с. D.2.3))
ч\ (ь) /УЛ (ь)
то уравнения Гейзенберга примут вид (ср. с D.2.7))
E.2.19)
1>? | о, р>] ^ w д
E.2.20)
Свободные физические электронные поля ф^ | удовлетворяют
уравнениям
(|B))? = 0, E.2.21)
? = 0. E.2.22)
Поэтому причинные функции Грина для этих полей описываются
выражением D.1.75)
S± (k) = f/ (е±) [ft0 - е± + гбт]-1 W (е±), E.2.23)
где е+ обозначает е± (k), a S+ (S_) соответствует направлениям
спина |(|).
Намагниченность. Вычислим теперь М в низшем порядке
теории возмущений. Поскольку
(о, р I ч4 (х) ь м - ф! w чч w I о, р>=
= - lim<0, р | Т [^ (t - е, х) I])} (t + е, х) -
0
е, х)] | 0, р), E.2.24)
Некоторые примеры вычислений 145
можно записать
м = -
где контур интегрирования с в комплексной ^„-плоскости пред-
ставляет собой полуокружность в верхней полуплоскости. Тогда
из E.2.23) имеем
м = -щ» Jd*k У* &> - ^ (е-)> = E-2-26)
Bя)»
E.2.27)
Это уравнение самосогласования, определяющее величину М;
заметим, что величины е± зависят от М.
При низких температурах величина М ведет себя как Г2.
Но этот результат существенно изменяется, если учесть влияние
магнонов, а именно при наличии магнонов в разложении для М
входит слагаемое Т*1* (закон Блоха). Этот вопрос рассматривается
в разд. 6.4.
Уравнение Бете—Солпитера для магнона. Для изучения
свойств магнона введем обозначения термополевого дублета для
операторов рождения и уничтожения спиновых отклонений
где
операторы ст™ и arf взаимно эрмитово сопряжены.
Мы выведем уравнение БС для магнона с помощью диаграм-
много метода Фейнмана, применяемого вместо уравнений Гейзен-
берга E.2.19) и E.2.20).
Рассмотрим петлевую диаграмму, состоящую из двух внутрен-
них электронных линий. Этой петлевой диаграмме соответствует
следующее слагаемое (рис. 5.2):
D^ (k) = - ^§s J dVs!» (Z + A) Sf (/ - 4) ep. E.2.31)
a
0 +
at
(x) =
(x) =
Pa kf
Pa [t|5™
ea =
U
для а =
для a =
= 1,
= 2;
11 (x)
\fcf
w.
w.
E.
E.
E.
2.
2.
2.
28)
29)
30)
Повторение этой петли приводит к появлению многих цепочечных
диаграмм. Петли соединяются друг с другом посредством взаимо-
действия ^Баг|^+г|}™г|)™+\|п, а на обоих концах цепочки стоят one-
146
Глава 5
раторы а% и оР. Ниже мы вычислим величину @, р | Т [о% (х),
°- (уI I О, Р) с учетом только таких цепочечных диаграмм (це-
почечное приближение). Имеем
= (§|з J d*
- У) - 1^о (^ -О] Gf (k).
E.2.32)
Используя цепочечное приближение, запишем (рис. 5.3)
GB (k) =D(k)— ID {k) xD (k) + ... , E.2.33)
Рис. 5.2.
Рис. 5.3.
(^) — матрица LDaP (А)]. Иными словами, GB (k) удовлетво-
ряет следующему уравнению БС:
GB (k) =D(k)— XD (k) %GB (k), E.2.34)
из которого находим
GB (k) = тЛГ1 (k) D (k),
где
N (k) = x + XD (k).
E.2.35)
E.2.36)
Некоторые примеры вычислений 147
Вычисление D(k) и N~l (k). Подставляя E.2.23) в E.2.31)
и используя формулу D.1.120), получаем
D(k) = ] dvn (я, к) Uв (х) т [ко - и + /бт] ?/в (и), E.2.37)
где
оЫ, к) = -^
E.2.38)
Здесь использованы следующие обозначения:
Если ko — вещественная величина, применяем формулу
откуда, а также из E.2.37) и D.1.88) получаем
D*b (k) = R (k) t°3 - ma (k0, k) [UB {hf П, E.2.41)
где
R(k) = P [dna.(K' k) . E.2.42)
Таким образом, имеем
N (k) = [1 + Я/? (А) ] г — iixk (ft0> k) (/| (fto), E.2.43)
_ [1 + ^(й)]т + алст(й0, к)^(й0) E 2 44)
W [1 +XR(k)]2 + lWo*(k(), k) '
где использовано соотношение D.1.88), т. е.
UB(k0)x = xU-Bl{k0). E.2.45)
Окончательно из E.2.35) находим
где R =R (k), о = a (k0, k) и UB = С/в (Ло).
Поскольку е± = e+ при k = 0, из E.2.38) и E.2.27) получаем
а (к, 0) = Мб (к - Ш), E.2.47)
где учтено также, что е_—е+ = КМ (ср. с E.2.17)). Тогда из
E.2.42) имеем
прик = 0. E.2.48)
148 Глава 5
Магнон. Если GB (k) имеет полюсную особенность, полюсный
член ведет себя подобно функции Грина для бозона. Поэтому,
как видно из E.2.46), если существует функция <ав (к), такая, что
[1 + XR (k)] ± iKna (k0, к) = О для k0 = <ав (к), E.2.49)
то существует бозон с энергией сов (к). С другой стороны, как
видно из E.2.47) и E.2.48), значения к0 =0 и к =0 удовлетво-
ряют уравнению E.2.49), откуда следует, что действительно су-
ществует бозон с энергией сов (к), такой, что
шв (к) =0 при к = 0. E.2.50)
Этот бозон называется магноном (или спиновой волной). Заметим,
что существование магнона опирается на условие самосогласова-
ния E.2.25), которое гарантирует, что основное состояние си-
стемы магнитно-упорядочено. Тем самым находит отражение тот
факт, что магнитный порядок поддерживается магноном. Когда
Т Ф 0 и к Ф 0, условие E.2.49) удовлетворяется только при
комплексных значениях сов (к), что обусловливает нестабильность
магнона с отличным от нуля импульсом при конечных темпера-
турах.
Более точные вычисления для модели ферромагнетизма кол-
лективизированных электронов, основанные на использовании так
называемых соотношений Уорда—Такахаши, приведены в гл. 6.
5.3. Модель Гейзенберга в ферромагнетизме
локализованных спинов
В предыдущем разделе рассматривалась модель коллективизи-
рованных электронов, описывающая возникновение магнитно-
упорядоченного состояния. В этом разделе термополевая дина-
мика применяется к системе локализованных спинов.
Модель Гейзенберга. Для описания системы локализованных
спинов широко используется модель Гейзенберга. Обозначим спин,
локализованный в г-м узле спиновой решетки, через S (t); тогда
гамильтониан для модели Гейзенберга примет вид
^-S(i). E.3.1)
i, i i
Здесь Jtj — константа связи обменного взаимодействия (/г/- = 0
при i = /), h — внешнее магнитное поле. Этот гамильтониан
содержит только спиновые степени свободы, связанные с некото-
рыми частицами магнитными ионами.
Локализованные магнитные ионы. Поскольку локализован-,
ный спин связан с магнитным ионом, введем для последнего гей-
Некоторые примеры вычислений 149
зенберговское поле и обозначим его $ (х). Рассмотрим сначала
магнитный ион в изолированном состоянии, обозначив его спин
через /; в этом случае ион обладает 2J -\- \ спиновыми состоя-
ниями. Переходы между этими спиновыми состояниями могут
быть описаны с помощью операторов рождения и уничтожения
(а(т> +, а<т>). Оператор а<т) уничтожает частицу в состоянии
с азимутальным квантовым числом т; это состояние мы будем
называть m-состоянием. Переход от m-состояния к я-состоянию
описывается действием оператора а(п) +а<т>. Ортонормированную
волновую функцию m-состояния обозначим через cp<m> (x). Рас-
смотрим теперь систему, в которой магнитные ионы образуют
решетку и взаимодействуют друг с другом. Тогда гейзенбергов-
ское поле t|5 (x) принимает вид
4>(*) = ftl/lS ? cp<m)(x)a<m>@, E.3.2)
i m=-J
где ф'т> (х) — ортонормированная волновая функция m-состоя-
ния магнитного поля в t-м узле, а а\т) (t) — оператор а(т), отно-
сящийся к иону в i-u узле. Временная зависимость ajm) (t) обус-
ловлена взаимодействием между ионами. Имеются следующие не-
известные коммутационные или антикоммутационные соотношения
(в зависимости от статистики рассматриваемых магнитных ионов):
[a<m> (t), а) (л> (f)]± = ЬптЬц для t = t.
Пусть at (t) обозначает вектор-столбец, компонентами которого
являются операторы ajm) (t) (m = —/, —/ + 1, ..., / — 1, /).
Гамильтониан и операторы спина. Гамильтониан модели Гей-
зенберга для рассматриваемой системы принимает вид
Н = J, yrfat - y2Jo-S WSO") - № ^ hS (t). E.3.3)
.•' a i
Здесь jii — химический потенциал, at обозначает at (t), S (i) обо-
значает оператор S (i; t), определенный следующим образом х):
S (t; t) = ajsfl, (t) = S {s)mnaf} f (t) a\n) (t). E. 3.4)
m, n
J) При изучении модели Гейзенберга часто использовалось представление
Гольштейна—Примакова [3] для спиновых операторов в качестве бозонного
представления для S (i). Но в этой книге в качестве представления для S (i) вы-
брано уравнение E.3.4).
150 Глава 5
Здесь s — спиновая матрица размерности B/ -\- 1) X B/ -f 1),
удовлетворяющая перестановочному соотношению [sit sj] =
— iEUhsh- Применяя операцию тильда для гамильтониана, по-
лучаем
220- E-3-5)
a
Уравнения Гейзенберга. Уравнения Гейзенберга имеют вид
i -gf-di (t) = ца( (t) — 2 JUS (/; f) ¦ sat (t) — gnBh ¦ sat (t),
E.3.6a)
-i -|-at{t) = ц5,@ - 2] ^//S (/; 0• s*o, @ -
E.3.66)
Мы используем следующие обозначения для термополевых дуб-
летов:
l) E-3.7)
/; t) \
V); E-3-8)
в выражениях E.3.7) и E.3.8) верхний индекс t обозначает транс-
понирование матрицы или вектора (ср. с D.2.8)).
Тогда уравнение E.3.6) можно переписать в виде
1Жa'i @ = № if) - Ъ JuPa № (/; 0 • sa? @1 - №Bh• saf @-
E.3.9)
Приближение среднего поля. В приближении Хартри уравне-
ние E.3.9) принимает вид
i -J-a* (*) = Fa? @ - gViB ( 2J V//M (/) + h) • sa? (f),
E.3.10)
Некоторые примеры вычислений 151
где
М @ = g\iB (О, Р | Sa (г, О I О, Р>, E.3.11)
Vti = (gPs)-* Ju- E.3.12)
Заметим, что вектор М (i) параллелен вектору h.
Уравнение E.3.10) показывает, что энергия т состояния
дается выражением
«т @ = И- — g^BtnHM (i), E.3.13)
где Нм (i) — величина вектора
Нм@=2Ь*/М(/) + Ь. E.3.14)
Здесь азимутальное квантовое число т определено по отношению
к направлению вектора h; вектор Нм (i) параллелен h.
Операторы a? (t) и сц (t) выражаются через физические опе-
раторы уничтожения af (p) и af (P) посредством преобразова-
ния Боголюбова:
аГ @ = Wr (Р)gu Ы + аГ+ (Р) fu (со,-)] еш™(i)',
E.3.15а)
S<m> @ = [а}"> (Р) ^1/2 (со, ) + paim) + (Р) /*/2 (со,)] еШт (()'.
E.3.156)
Чтобы оценить средние значения по вакуумному состоянию
от операторов, представляющих собой функции от операторов
квазичастиц а, и а,, нужно обратить особое внимание на сохра-
нение условия хорошо определенных локализованных состояний.
Прежде всего необходимо выполнить требование о независимом
распределении атомов, причем каждый узел решетки должен
быть занят только одним атомом. Такая картина независимого
распределения возникает в пределе \i -*- оо, поскольку вероят-
ность занятия одного узла п частицами пропорциональна е-$п*.
Таким образом, при соответствующей перенормировке состоя-
ние | 0, Р) сводится к вектору состояния в точном представлении
152 Глава 5
чисел заполнения, при котором имеется лишь по одному атому
на узел 1). Тогда намагниченность М (i) = | М (i) | получается
из E.3.11) в следующем виде:
\E.3.16)
где Z (Р) — нормировочный множитель, о котором упоминалось
выше. Поскольку каждый узел занят только одним атомом, то
(о,
'" — p
В пределе ji ¦-*¦ оо имеем
М @ = giiBe~^Z (р) 2 те№вРяЛ1@ т, E.3.18)
= e-^lZ (p) ? ег!Хврял1 «> т. E.3.19)
J) Проиллюстрируем эту ситуацию в случае свободного оператора а'' (?),
для которого энергия дается выражением E.3.13). Состояние | v ), в котором
имеется по одной частице в каждом узле i, имеет вид
а+ (О С") ф) а+ @ | 0),
С1 (Р)
где а+ (/) С('» (Р) а+ («) = ? а(т> + (Г) С#> (Р) о<т>+ («), а С^> (Р) и Zu (P) да-
т
/,-» „ —Вш @/2 т-г / п —Ви @\
ются выражениями С;'' (Р) = е m , Z (Р) = / V е т I ¦
j \ m /
Вакуумное состояние | 0) определяется условием а (?) | 0) = а (i) | 0) = 0.
Вакуумное состояние 10, Р), определенное условием
a (i, Р)|0, р> = й, («, Р)|0, Р) = 0,
формально выражается в виде
1 Ol Р) = Y^ П П (|] ^г [«+ (т) @ с<[> (Р) а+ ^ (О]") I о),
т \ п=о
Если сравнить среднее значение по вакууму вида
(v | [а<т>+ @ а») (/)] • • • fa(m'> + («') а<''> (/')] I ь>
со средним значением по вакууму вида
@, Р | [a""' f @ а(/) (/)] • ¦ • [а(т'» + (/')«<''> (/')] | 0, Р>,
то легко заметить, что состояние | 0) в | 0, Р) не вносит вклада в матричные
элементы. Различие между этими двумя средними значениями состоит, во-пер-
вых, в различных вкладах от многочастичных состояний и, во-вторых, в норми-
ровочных множителях. Если перейти к пределу ц—у оо, оба выражения стано-
вятся тождественными за исключением нормировочных множителей.
Некоторые примеры вычислений 153
Тогда намагниченность М (i) принимает вид
М @ = g]iB ? те^в^м <» '"/? е«М"м «> т = E.3.20)
т I m
= gVBJBj[giiBJ№M(i)}, E.3.21)
где Bj (х) — функция Бриллюэна:
Это хорошо известная формула, получаемая из E.3.1) в прибли-
жении среднего поля.
Спин-волновое возбуждение (магнон). Рассмотрим теперь снин-
волновое возбуждение при наличии спонтанной намагниченности
(h =0). Введем операторы S™ (х) и функцию / (к) с помощью
соотношений
s" («) = w J dV'kx 2e<k J'sa № о. E-3.23)
J"= w Jd3kJ (k) exp [/k (R; ~R/)]- E-3-24)
ов
Символ QB обозначает, что интегрирование по к ограничено пре-
делами первой зоны Бриллюэна. Введем также функции
j d4J (k)exP f'k (x " У)]- E-3-25)
6« (x - y)=w Jd4 exp [/k (x ~ >)'¦ <5-3-26)
qb
Заметим, что функция бд (R; — Ry) пропорциональна 8ц.
Поскольку^0"- (i) удовлетворяет перестановочному соотношению
[Sa(i,t), St(i, *)] = «WT°%S?(t, t), E.3.27)
имеем
[Sa (x), Si (y)]tx=ty = ieabcta% (x - y) Sf (x), E.3.28)
где матрица таР приведена в D.1.77).
Гамильтониан Н из E.3.3) может быть переписан в виде
н=S ^°' ~ 4" Jd3xS{х) J (v) s (x) ~ ^'"^ 1d3xh¦s {x)> E-3-29)
i
где / (V) определен соотношением
j (у) etkx = / (k) e'kx.
154 Глава 5
Имеет место соотношение
J (V) S (х) = J d*yj (х - у) S (у). E-3.30)
Гамильтониан в E.3.29) приводит к следующему уравнению Гей-
зенберга для S (х):
S(x) = ±-{S(x) х /(V)S(x) -/(V)S(x) X S(x)} + gliBS(x) x h.
E.3.31)
Применяя операцию тильда, находим затем уравнение Гейзен-
берга для S (х). Объединяя эти уравнения, получим уравнение
Гейзенберга в виде
~ S» (х) = -L Ра {S* (х) X / (V) S« (х) - J (V) S* (х) X S« (х)} +
+ gVB$a (x) X h. E.3.32)
Здесь Ра — символ оператора упорядочения, определенный
в D.2.6):
f Л1^1 ... С1 при а = 1,
Ра (АаВа...Са) = ~2D2 лъ о E.3.33)
а v ' \ С%В% ... Л2 при а = 2. v '
Поскольку нас интересует случай спонтанной намагничен-
ности, положим h = 0 и
М (Р) = @, р 1S? (х) 10, р) Ф 0, E.3.34)
где М (Р) не зависит от х. Введем далее оператор ра (х) с помощью
соотношения
p*(x) = S«(x)-M$). E.3.35)
Из уравнения E.3.32) следует
i JL- 5? (х) = Is- |S« (x) J (V) [М (р) + Ра (х)] ~
- J (V) S? (л:) [М (р) + Ра (*)]}, E.3.36а)
S- W = - -X" E- (х)J W [
- J (V) S? (а) [М (Р) + Ра W1}, E.3.366)
где
Поскольку
[Sa+ (х), Si (y)]tx=ty = SJ (x) в« (х - у) т0* E.3.37)
tx=ty
Некоторые примеры вычислений 155
имеем
j JL @, р 17 [Sa+ (х) S* (у)] | О, р) = /б* (х - у) б (tx - tu) %а*М (р) +
+ [М (р)/2] (О, р 17 [{/ @) - / (V)} S? (х), S» (у)] | О, р) +
+ -у(О, P|7{JPa[5:(^)/(V)pa(x)-/(VM:(x)pa(x)],S^)}|O)P).
E.3.38)
Если пренебречь последним слагаемым в E.3.38), получим
-Ft 4" М $)[J @) ~ J (Vx)]) (°'V\T [S" W S- № 10, p> =
= tT«P6B (x - у) б (^ - ty) M (P), E.3.39)
откуда следует выражение для энергии спиновой волны
co(k)=-i-M(P)[/@)-/(k)]. E.3.40)
Обозначая через ДрР (k) фурье-образ двухточечной функции
(О, р | 7 [SJ (дг), 5Р (у)] | О, Р), получим из E.3.39) соотношение
. E.3.41)
Полученные результаты для © (к) и ДаР (Л) весьма неточны.
В остальной части этого раздела мы исследуем, как изменяет
последнее слагаемое в E.3.38) энергию спиновой волны и двух-
точечную функцию Д°Р (к).
Вершинная функция и динамическое отображение спиновых
операторов. Чтобы изучить влияние последнего слагаемого
в E.3.38) на полученные результаты, определим вершинную
функцию (рис. 5.4) выражением
@, P
X exp [ikx - iqy +t{q- k)г]. E.3.42)
156 Глава 5
Введем далее соотношение
Г?'р'@, 0; 0) = -Ж'1 (Р) 6a'p'8a-v E.3.43)
с помощью динамического отображения операторов S™ (л:) и 5* (л:).
С этой целью обозначим свободное спин-волновое поле через
Ва (х)\ оно удовлетворяет уравнению
«(x) = 0. E.3.44)
Тогда динамические отображения S? (х) примут вид
Sa до = МЧ, (р) р (V) да+ ДО +. . ., E.3.45)
S? (х) = М''> (р) F (У) Ва(х) + . . ., E.3.46)
где F (к) — некоторая функция. Многоточия обозначают нормаль-
ные произведения более высоких порядков. Согласно D.3.38),
спектральная функция a (до, к) для двухточечной функции
@, р | Т [SJ, SP] 1 0, р) имеет вид
о {w, к) = М (Р) Я (к) б [w — со (к)] + a'Jw'Ji). 1E.3.47)
Здесь d (w, к) описывает вклад слагаемых, обозначенных много-
точиями в E.3.45) и E.3.46). Поскольку результат интегрирова-
ния по всему пространству 5^ (х) не зависит от времени, фурье-
образ S™ (х) при к = 0 имеет нулевую частоту kn = 0. С другой
стороны, состояния ск =0ий0 =0не дают вклада г) в a (w, к),
поскольку вклад в a (w, к) дают лишь многочастичные состояния,
участвующие в суммировании в D.3.20). Таким образом, имеем
a (w, 0) = 0. Далее из E.3.37) получаем
<0 PIIS:W, S*(y)]\0, р),ж=^ = бЛ(х-у)тае. E.3.48)
Последнее выражение имеет тот же вид, что и среднее значение
по вакууму от канонического коммутатора D.3.36), поэтому спек-
тральная функция для него должна удовлетворять соотношению
D.3.37):
+00
^ J dwa(w, k)=l. E.3.49)
—OD
Последнее соотношение при к = 0 дает
F @) = 1, E.3.50)
где учтены выражение E.3.47) и равенство а (до, 0) = 0.
J) Согласно D.3.20), k0 = Еп—Ет, поэтому условие ko= 0 требует совпаде-
ния Еп и Ет. Поскольку энергия многочастичных состояний с данным импуль-
сом покрывает сплошную область, вероятность совпадения Еп и Ет при р^ ф
Ф рт равна нулкр.
Некоторые примеры вычислений 157
Хотя инвариантность основного состояния по отношению
к спиновым вращениям нарушается условием E.3.34), инвариант-
ность относительно спинового вращения вокруг третьей оси
все же сохраняется. Генератор этого вращения S3 имеет вид
53 = J (Px [S3 (х) — 53 (*) ] E.3.51)
и не зависит от времени. Правила коммутации спиновых операто-
ров приводят к равенству
[Sa±(x), S3] = +S±(x). E.3.52)
Из инвариантности основного состояния относительно вращения
вокруг третьей оси следует, что магноны должны принадлежать
к представлению абелевой группы вращений вокруг третьей оси.
Тогда, согласно динамическим отображениям E.3.45), E.3.46),
коммутатор [Br/^ (x), Ва (х)] при вращении вокруг третьей оси
ведет себя так же, как коммутатор [S™ (x), S% (x)]. Поэтому
из E.3.52) получаем соотношение
[В* (х), S,] = —Ва (х), E.3.53)
которое приводит к выражению
S3 = — j d?x: [В+ (x) В (х) - В* (х) В (х)]: =
= — \d3x:'?ieaBa*(x)B{x):, E.3.54)
a
где ea = 1 при a =1 и ea = —1 при a = 2. Здесь нормальное
произведение определено через физические операторы В (х, f>)
и В (х, Р), связанные с В (х) я В (х) преобразованием Боголю-
бова. В выражении E.3.54) мы опустили члены, не содержащие
магнонных операторов, поскольку эти члены не имеют отношения
к дальнейшему рассмотрению.
Согласно E.3.54), динамическое отображение ра (л:) имеет вид
ра (*)= — : 5а+ (х) Ва (х) :+..., E.3.55)
где многоточие обозначает слагаемые с отличным от нуля значе-
нием передаваемого импульса. Подставляя E.3.45), E.3.46) и
E.3.55) в E.3.42), приходим к соотношению E.3.43) 1).
Дисперсионное уравнение для магнона. Используя для Л и Г
в E.3.42) приближенные выражения E.3.41) и E.3.43) соответ-
х) Соотношение E.3.43) не зависит от модели. Действительно, это соотноше-
ние можно получить, пользуясь условием инвариантности теории относительно
спиновых вращений, с помощью так называемых соотношений Уорда—Такахаши,
как показано в гд, 6.
158 Глава 5
ственно, можно вычислить из E.3.38) уточненное выражение
для ЛаР:
?ОД°Р (?) = тарУИ (Р) + ± М (Р) [У @) - У (q)] Лар (?) -
1 i_
2~Bя)
— У (к) Ааа (k) М-1 (Р) бар'Лр'р (?)]. E.3.56)
Контур интегрирования са на комплексной плоскости k0 есть
полуокружность на верхней полуплоскости (обход против часовой
стрелки) при а = 1 и на нижней полуплоскости (обход по часовой
стрелке) при а = 2. Из E.3.56) находим
{?« - 4-М (Р) [У @) - У (q)] - бсо (q)J Аар(?) = тарМ (Р), E.3.57)
где
бсо (q) = 2~ 3 [,
—1
2 BяK
+ -L[y @) - У (q)] -Jjp J d*kfB [со (k)]. E.3.58)
Таким образом, E.3.57) приводит к самосогласованному уравне-
нию для спин-волнового спектра
о> (q) = 4 [J (°) - У (Ч)] (Л* (Р) + -jgjjj J d*kfB [со (k)]) -
~ 2W j d8* [У (q - k) - У (k) - У (q) + У @)] fB [coB (k)]. E.3.59)
Для вычисления со (q) при малых Т с помощью E.3.59) необ-
ходимо знать намагниченность М ф) при низких температурах.
При нулевой температуре В (к) — физический оператор уничто-
жения, поэтому В+ (к) В (к) естественным образом оказывается
нормально упорядоченным произведением. Тогда из E.3.55) и
E.3.35) имеем
S3 = j dsxS3 (x) = М (оо) V — J d3kBf (k) В (k). E.3.60)
Если температура лишь немного выше нуля, то В (к) связан с фи-
зическими операторами В (k, P) и в* (к, Р) посредством преобра-
зования Боголюбова, и можно найти
@, р j Bf (к) В (к) 10, р) = JLfB [со (к)]. E.3.61)
Некоторые примеры вычислений 159
Таким образом, имеем
М (Р) =-- М (оо) - -^ J d*kfB [со (к)] E.3.62)
при низких температурах. Используя далее E.3.59), можно пока-
зать, что температурная зависимость со (q) при низких темпера-
турах обусловлена только вторым слагаемым в правой части
E.3.59), что в свою очередь приводит к закону 7"/* для коэффи-
циента жесткости спиновых волн [4]. Если учесть эту темпера-
турную зависимость со (q), то в разложении М ф) в E.3.62) на-
ряду с обычным членом T'l* (блоховский член) появляется также
член Г4 (дайсоновский член).
5.4. Сверхпроводимость
Лагранжиан. Начнем с лагранжиана для модели БКШ [5]:
Здесь г|;|, j, —электронные гейзенберговские поля, а е (V2) опре-
делено соотношением
s{v2)eikx=ekeikx, E.4.2)
где
e, = ^L(k2-^) E.4.3)
(постоянная kF — импульс Ферми). В выражении E.4.1) затра-
вочный химический потенциал равен ц + (й/2т) k2F. Поскольку
перенормированный химический потенциал должен быть равен
(ft/2m) kp, роль параметра ц, состоит в компенсации сдвига хими-
ческого потенциала вследствие взаимодействия. В выражении
E.4.1) отсутствует электромагнитное взаимодействие; оно будет
рассмотрено в последней части этого раздела.
Введем следующие векторные (дублетные) обозначения:
¦-(*)-$)¦ <ЪЛА)
Тогда антикоммутатор
foa (х), г|N+ (у)]+ = ШаЬЬ (х - у) при tx = ty E.4.5)
с а, Ь = f или | принимает вид
(х), Ф+ Ш+ = й/б (х - у) при tx = ty, E.4.6)
160 Глава 5
где / — матрица размерности 2X2, а \р — дублет, определен-
ный E.4.4).
Уравнение Гейзенберга. Лагранжиан E.4.1) приводит к сле-
дующему уравнению Гейзенберга:
= s (х) + Дт^ (х) — |лт3Ч5 (х); E.4.7)
входящие сюда матрицы it определены в B.6.55):
oj' T2~U о)' Тз
Член, ответственный за взаимодействие, s (x) имеет вид
; E.4.9)
слагаемое Дт^ в обеих частях уравнения E.4.7) обеспечивает
перенормировку энергии.
Введем теперь обозначение для термополевого дублета
J, E.4.10)
где индекс t обозначает транспонирование. Операция тильда и
эрмитово сопряжение переводят оператор s (== s1) в оператор
; E.4.11)
здесь Ра — оператор упорядочения, определенный D.2.6):
при а = 1,
Р_2 E.4.12)
Тогда можно написать
S* = Ра
. E.4.13)
Некоторые примеры вычислений 161
Применяя далее к гейзенберговскому уравнению E.4.7) опе-
рацию тильда и эрмитово сопряжение, получим уравнение Гей-
зенберга для г|Л Объединяя оба уравнения, находим
I (д) г|>а (х) = sa (х) + Ах^а (х) — рт3г|>а (х), E.4.14)
где использовано обозначение
45) = 14- - е (V) т3 + Лтх. E.4.15)
Уравнение БС для @, 0 | 74 Ца, ^] | О, 0). Выведем теперь
уравнение БС для функции
аф (Xl - х2) = (О, Р | Т [фв (хх) г|>р+ (х,)] | 0, р>. E.4.16)
Используя E.4.14), получаем уравнение
* (ад хар (jci - *.) * (-а.) =
= Ж (д±) бD) (^ - х2) бар + 1Й (Дтх — цт8) бD) (^ - х2) бар +
+ t (О, Р | [sa (Xl), ^ (*)]+1 О, Р> б (/! - tt) +
+ @, р | Т [sa (Xl) + (Атх - Ит3) г|)а (^), sP+ (^) +
+ г1)р+(х2)(Ат1-ИТз)]|0, р>. E.4.17)
Для решения этого уравнения используем цепочечное приближе-
ние, в котором учтем лишь цепочечные диаграммы. В этом при-
ближении последнее слагаемое в правой части E.4.17), в которое
входит 7-коммутатор, вообще не дает вклада. Третье слагаемое
можно вычислить с помощью канонических антикоммутаторов:
№ (х), г|>р+ (у)]+ = Йбарб (х - у) при U = tu. E.4.18)
Тогда уравнение E.4.17) в цепочечном приближении приводит
к следующему уравнению БС:
хар (*i - Х2) = sf (Xl - Х2) - -L J d%s7 (х, -1) х
X [At, - Ит3 + ^{v)Ti - XX2V)t3] Sf {I - x3), E.4.19)
где 5™р (л: — у) — причинная двухточечная функция, определяе-
мая выражением D.1.113) и потому удовлетворяющая уравнению
Я E) 5"р (х) = t»6D) (л:) бар, E.4.20)
согласно D.1.114). В уравнении E.4.19) %iv) дается выражениями
Х10) = <0, Р | $ (х) Ь (х) 10, р> = <0, Р | tf (х) f2 (х) 10, р> = E.4.21)
= @, р | ^ (х) ipt (х) 10, Р) = <0, р | ip? (х) г|;| (х) 10, р>, E.4.22)
, 10, р> = <0, Р |tffc10, р>. E.4.23)
162 Глава 5
Заметим, что фазу \j)ti + можно выбрать так, чтобы %iA) было ве-
щественным. Тогда XiA> = xfn. поэтому из E.4.21) и E.4.23)
следует
Х.A) = х!2)- E-4.24)
Это равенство можно назвать соотношением тильда-симметрии.
Перенормировка. Поскольку энергия, входящая в К (д), должна
быть наблюдаемой (т. е. перенормированной), из уравнения E.4.19)
видно, что А + xxiv> = О ДЛЯ v = 1, 2. С учетом E.4.24) полу-
чаем А = — ^xf0 = —^Xi2>, откуда находим А:
А = — К @, р|$\|л|О, P)= E.4.25)
= -А,<0, P|^t|O, P). E.4.26)
Величины xia), входящие в E.4.19), определяются выраже-
ниями
О, Р) = -<0, Mb\0, р>, E.4.27)
0, р>. . E.4.28)
Имеется еще одно соотношение тильда-симметрии
у^ = 1^. E.4.29)
Содержащее т3 слагаемое в уравнении БС E.4.19) исключается
с помощью условия
fi|-Xxf) = O. E.4.30)
Это условие выражает перенормировку химического потенциала.
Таким образом, выбирая (х с помощью условия E.4.30) и опреде-
ляя А с помощью E.4.25), получаем, что электронная двухточеч-
ная функция принимает вид свободной функции:
Хар {хх - х2) = Sf (*, - х2). E.4.31)
Физический электрон и двухточечная функция для него. Поле
физического электрона срОа удовлетворяет уравнению
% (д) Фоа = 0. E.4.32)
Энергия Ek физического электрона дается выражением D.1.105):
Ек = (г1 + А2)'", E.4.33)
откуда ясно, что А имеет смысл энергетической щели.
Некоторые примеры вычислений 163
Фурье-образ причинной двухточечной функции дается выра-
жением D.1.113):
ATl [U (Ek) (k0 -Ek
xi [U (- Eh) (k0 + Ek
E.4.34)
Уравнение для щели. Из выражения E.4.26) видно, что если
д ф 0, то основное состояние не инвариантно относительно изме-
нения фазы электронной волновой функции, поскольку при за-
мене ty -> е'ег|з величина А переходит в е2'еД. Следовательно,
основное состояние является фазово-упорядоченным.
В дальнейшем величину 5С будем обозначать просто через 5.
Согласно E.4.26) и E.4.16), имеем
Д = A, lim [Xi2 (х, /)]х=0 = E.4.35)
= ЛНт [S\\(x, <)]х=о= E.4.36)
^'';(*), E.4.37)
где контур интегрирования с в комплексной &0-плоскости пред-
ставляет собой полуокружность в верхней полуплоскости. Тогда
из^E.4.34) следует
А = - ХНА J ^ ^ [1 _ 2Д, (?„)], E.4.38)
откуда при А Ф 0 получаем
shk11--2'*^1' EA39)
где У = —Ши. Это уравнение называется уравнением для щели,
так как оно определяет энергетическую щель в электронном
спектре. Оно выражает самосогласованное условие возникнове-
ния фазово-упорядоченного состояния: фазово-упорядоченное
(сверхпроводящее) состояние возникает тогда и только тогда,
когда уравнение E.4.39) имеет отличные от нуля решения для
энергетической щели Л (для выполнения E.4.39) X должна быть
отрицательной).
Обозначим энергию Дебая через toD, а плотность состояний
на уровне Ферми — через iV @). Интегрирование в E.4.39) обре-
164 Глава 5
зается на aD, так как взаимодействие БКШ переносится фоно-
нами. Если cud С е,. (где е,. — энергия Ферми), уравнение
E.4.39) можно приближенно записать в виде
(Од
1 = VN @) \ de -L [ 1 - 2fF (E)], E.4.40)
о
где Я = (82 + А2)'/2.
Критическая температура. Критическая температура сверх-
проводящего состояния Тс определяется уравнением E.4.40)
при А = 0:
l = VN@) Jde-J-[1 -2/Р(е)] при Т = Те. E.4.41)
о
Отсюда получаем знаменитое соотношение БКШ для Тс
kBTc = l,13/zcoDexp l—l/N @) V]. E.4.42)
С другой стороны, обозначая А при температуре Т через Д (Т),
находим из E.4.40) А @), полагая р = оо:
(Од
1 = VN @) J йг -L при 7=0. E.4.43)
о
Отсюда находим
А @) = Шд {sh WNV (О)]}'1 « 2сод ехр (— MN @) V), E.4.44)
что вместе с E.4.42) приводит к соотношению
ЙД @) = l,76kBTc. E.4.45)
Для большинства сверхпроводников величина VN @) заключена
в пределах от 0,2 до 0,4 (см., например, [61). Тогда, согласно
E.4.44) и E.4.45), отношение (kBTc/haD) будет порядка 0,01—0,1.
Именно этим объясняется, почему критическая температура боль-
шинства сверхпроводников столь низка.
Операторы тока и плотности заряда. Оператор Гейзенберга
для электрического тока имеет вид
= — -o—г 2j I (V* — Vy) tyt (x) 1$ (y)\x=y E.4.46)
2mi (.
(здесь и ниже мы опускаем тривиальные численные величины).
Некоторые примеры вычислений 165
Применяя к E.4.46) операцию тильда, получаем
i2=ш ? t(v* - v,) ъ (х)# {у)]х=у =
= г^г ? [(v* ~ v"> *'(х) *< <^ *=« • <5-4-47)
Термополевой дублет тока ]а (а = 1, 2) можно записать в сле-
дующем виде:
i" = - еа Ш ? t(v* - v*) *? W ^?+ (У)]*=у E-4-48)
Аналогично оператор плотности заряда имеет вид
Рв = -«Ч2(^Г. E-4.49)
Закон сохранения для плотности тока имеет вид
V-f+ 4-рв=0- E-4.50)
Введем величины
АаР (х - у) = @, р | Г [ра (х) рр (у)] 10, р>, E.4.51)
Da^ (х, у; z) = @, р| Г Й2 W ^Р+ (У) Pv (г)] |0, Р>. E.4.52)
Тогда получим
{х _ 2) = _ JLea7V [тзОаау (^, jc; z)]. E.4.53)
Уравнение БС для ZJ'Pv (дг, у; ^). Уравнение Гейзенберга
E.4.14) приводит к уравнению БС следующего вида:
= - Й2 ^- бD) (^ - 2) бD) (х2 - г) тз
+ /6 & - /2) <0, р | Г [[ {sa (хО + А (т,) фв (хх) -
^ (х2)] + р7 B)] 10, р) +
Дтх - г|;р+ (х2) Ит3}] | 0,
^HO, P) +
T [{sa (Xl) + (ATl - jiT3) yp
(At! - iixs)\ p7 B)] 10, p). E.4.54)
166 Глава 5
В остальной части этого раздела мы используем цепочечное
приближение. Цепочечные диаграммы должны начинаться с точки
ху = x2; поскольку последние три слагаемых не содержат множи-
теля бD> (хх — х2), они не дают вклада в цепочечное приближе-
ние и потому могут быть опущены.
Для более простой записи уравнения БС введем обозначение
D??(Z~z)=D?r(t,l; г), E.4.55)
где суммирование по а не производится. Введем также матрицу
F <6-2) = i us-в, ?«ffeJ- F466)
Тогда уравнение БС E.4.54) в цепочечном приближении при-
мет вид
DaPV Iy ii- у\ е ЯаУ Iy ,1 т QVP /, ,л „V !
LJ \Х, У, Z) — —г- О {X Z) Т3О [Z у) Ь -f-
+ -L J d%Sav (x - |) evFv" (I - z) Svp (? - y). E.4.57)
Решая это уравнение при а = ри х — у, можно найти Day (? — z),
а затем F"/ (| — z); далее с помощью E.4.57) находится и
Da^(x, у; г).
Уравнение для Da$(x—у). Уравнение БС E.4.57) при а — р
и х = у принимает простой вид, если использовать обозначения
E.4.58а)
E.4.586)
E.4.58b)
E.4.59)"
и учесть соотношения
S?! (х) = Szi" (х) = Sfjf (— л-), E.4.60а)
5и (х) = —S22 (—*), E.4.606)
S?/ (х) = S?f (x), E.4.60b)
которые получаются из E.4.34).
Вводя D?p (х) с помощью соотношений
Df(x)=D?i(x), E.4.61а)
D?p (х) = - D%f(x), E.4.616)
Pf (x) = D$ (x) - P°f (x), E.4.61b)
Некоторые примеры вычислений 167
ар
получаем уравнения БС для D, р (х) (рис. 5.5)
X D у
Рис. 5.5.
А (х -У) = — 2t -f Qu(x - у) т + J d% [Qn (x - |) tA(S - У) +
+ Q33 (« - S) tD2 (E - у) - <Э13 (^ - I) тЦ, (| - у)], E.4.62а)
Da (x — y) = —2i -j- Q23 (x — y)x +
+ Q2a (Jt - 6) tD2 (I - у) -
- Q23 (Jt - 1) tD3 (I - y) ], E,4.626)
D3 (x-y) = 2t -J- [Q83 (^ - y) + <3i2 (jc — у) ] т +
4 [-2QM (x - ?) tDj F - if) -
- 2Q23 (x - ?) tD2 (l-y) +
+ {Qn (x-t) + Q33 (x - I)} D3(l-y)}, E.4.62b;
причем
Du (x — y) + D22 (x — y) = 0. E.4.62r)
В уравнениях E.4.62) Dt (x) и Qti (x) — матрицы:
A (x) = W (x)], Qt, (x) = [Qtf (x)] • E.4.63)
Чтобы выразить полученные уравнения БС через фурье-об-
разы, введем фурье-представления
А (х) = J g-4 exp [i (kx - V)] А (Л) (»"=1. 2, 3), E.4.64)
168 Глава 5
Тогда уравнения E.4.62) принимают вид
?>! (ft) = -2е ^ Qu (Л) т + Qu (A) tDx (ft) +
+ Q33 (Л) tD2 (ft) — Qu (ft) xD3 (k), E.4.66a)
D2 (ft) = -2e 4 Q23 (Л) т + Q33 (ft) xDx (ft) +
+ Q22 (ft) tD2 (ft) — Q23 (ft) rD3 (ft), E.4.666)
D3 (ft) = 2e-^ [Q33 (ft) + Q12 (ft) 1 т - 2Q13 (ft) xDx (ft) -
- 2Q23 (ft) xD2 (ft) + {Qla (ft) + Q33 (k)} xD3 (ft). E.4.66b)
Вычисление Qa(k). Чтобы решить уравнения E.4.66), вычис-
лим величины Qu (k). Прежде всего перепишем E.4.34) в виде
(У+ (к)]«р X
(ft) = J dn X + 8fj~ATl W (к) (ft, - к + /
X {6(х- Ek) -b(x + Eh)} = j dxe(>tN(>t2 - E\) x
—00
X (к + еЛ — ДтО [?/ (х) (ft0 — х + 16т)-1 ?/+ (х)]а
E.4.67)
где е (к) — знаковый множитель:
(+1 при к >> О,
8 (Х) = и ^ ' E.4.68)
4 ' 1—1 при х< 0. v '
Вводя величины
Q fflm (х) = i j- S?/ (x) Sft (- x) = E.4.69)
= J $$eexP I' (kx - V)l Qffrm (k) E.4.70)
и используя формулу D.1.120), находим
Q ovrn (ft) = ЙЯеа8р J dxaw,m (x, k) [UB (x) t (ft, - x - /бт) U% (x)]ap.
E.4.71)
Некоторые примеры вычислений 169
где
-|-оо -\-ео
X б (х2_ - Et) 6 (х - к+ + х_) [fr (х+) - fr (х_)] х
X (х+ + е+тз — Дт0*/ (*- + е-тз — ATi)/m. E.4.72)
Здесь &± = е A ± к/2), ?± = ? A + к/2). Выполняя интегри-
рование по к±, находим
щр C~J+jJ- (б (« ~ ?+ - ?-) X
X (Е+ + 8+т3 — Ati)j/ (?_ — е_т3 + ATx)/m —
- б (и + Е+ + Я_) (?„ - 8+т3 + Atj),/ (?. + е_т3 - ATx)/m} -
- 1щ^~ {б (х - Я+ + ^_) (Е+ + е+т3 - A
л /ял I С* ?Г \ / Т7 р -т- I . Л* ) , / /7 р т -4
и I л ¦ L-i i L-i _/ i i-* , о ¦ tз I i_\ «>i / j 7 y-'-' _ ^_ ^3 i
E.4.73)
где f± = fF (E±).
Запишем теперь спектральное представление для Qff (k)
(gf (k) = ftXeV j (Ыи (x, k) [f/B (x) т ik0 — x +
+ t6T]-1?/B(x)Jap. E.4.74)
Тогда из E.4.59) имеем
an (х, к) = а112а (х, к), E.4.75а)
а22 (х, к) = <T22ii (к> к). E.4.756)
a12 (x, к) = сг1Ц1 (х, к), E.4.75b)
а также
а13 (х, к) = а1Ш (к, к), E.4.76а)
а33 (х, к) = а2312 (х, к), E.4.766)
а33 (х, к) = —01212 (и, к). E.4.76b)
Если eF > cod, to в интегрирование в выражении E.4.73)
вносит вклад лишь малая область (ййшд) вблизи энергии Ферми.
Плотность состояний мало меняется в слое энергии толщиной йо)в
вблизи уровня Ферми. Поэтому слагаемыми вида ?+е_ или Е_г+
170 Глава 5
можно пренебречь, так как вблизи поверхности Ферми они ведут
себя как нечетные функции. Опустив эти члены, получим
оп (х, к) = е (х) -— J щ? | (Е+Е^ЕЕ'] (Е+Е- + е+е-) X
X A - /+ - /_) б [х2 - (Е+ + EJ\ - (Е+Е~ЕЕ-] X
V (F F e a \ If f \ f\ Глу2 /Р р \2l| /К И 77\
X \?i+i^_ — ^4- -/ V/+ — /-/ L — \ 4- — -/ J ( • ^O.'i. 1 1J
Аналогично получим
02а (х, к) = сти (х, к), E.4.78)
/ i \ / \ 1 Г d3l / (Е+ + Е ) ,
°ы («, к) = е (х) — j ^pr ( е1е_ X
— /-) б [х2 — {Е+ — E_f ], E.4.79)
ff13 (х, к) = сг33 (х, к) = —хДсгг (х, к), E.4.80)
ст33 (х, к) = ~2Д2аг (х, к), E.4.81)
где функция ат (х, к) определена равенством
(Е I E )
Полезно также ввести функцию
оо
^ар (й) = ftXeV j dxff, (x, k) WB (x) t (fe0 — и +
—oo
1 f/a (x) lop, E.4.83)
так как тогда
<Эзз (k) = -2Д2^ (k), E.4.84)
Qis (k) = Q23 (k) = -^oA^ (Л). E.4.85)
При выводе E.4.85) мы прежде всего, заменили множитель х
(в выражении E.4.80)) на (х — k0) + k0, использовали равенство
Некоторые примеры вычислений 171
(fto — и) (fto — и + гбт)-1 = 1, а также формулу D.1.88) (т. е.
UBxUв = т); кроме того, было учтено соотношение
jdxer(x, k) = 0. E.4.86)
Вспомним далее равенство
М*) =-psTTY = -U+Ы-*)]. E-4.87)
откуда следует
@ 1
Тогда имеем
?/в (х) т (ft0 — к + Йт) ?/в (х) — Uв (—х) т (ft0 +
+ х + tfiT)-1 ?/в (—и) = 2х?/в (к) т [ft2, —
— (и — /бтJ1'1 ?/в (х) при % > 0. E.4.88)
Отсюда с учетом соотношения а (—и, к) = —сг (и, к) находим
оо
р°* (k) = йЯеаее J d?t20 (х) аг (х, к) X
о
X \UB (к) т [>feo - (х - tfTJ]-1 Uв (и)}ар- E.4.89)
Аналогично из E.4.74) имеем
оо
Q?/ (*) = йЯ8а8р J dx29 (x) а и {%, к) X
о
X { Uв (х) т [*§ - (х - ibxf\~x UB (х)}ар, E.4.90)
если только ij не равны 13 или 23. Заметим, что
<Эи (k) = Q22 (Л), E.4.91а)
Qis (k) = Q23 (Л) = -ko^R (k), E.4.916)
Q33 (k) = —2A*R (k). E.4.91b)
Таким образом, найдены все функции Q?j.
Решения уравнений БС E.4.66). Теперь уравнения БС E.4.66)
приводятся к следующему виду:
D+ (k) = _4e 4" Qia (*) т + [Qn (*) +
+ (Эзз (А) ] tD+ (ft) — 2Q13 (ft) tD3 (ft), E.4.92a)
?>, (ft) = 2e -I [Q33 (ft) + Qu (ft) ] т - 2Q13 (ft) tD+ (ft) +
+ {Qi2 (ft) + <Эзз (ft)! tD3 (ft), E.4.926)
D- (ft) = {Qu (ft) - Q33 (ft)} tD_ (ft), E.4.92b)
172 tAaea 5
где
D±(k)=D1(k)±Dt(k). E.4.93)
Из равенства E.4.92в) следует, что D_ (k) = 0, откуда находим
Dx (k) = D2 {k), E.4.94)
так что
D+ (k) = 2Di. (k). E.4.95)
Решая E.4.92), получаем
D3 (k) = 2e i^l [1 - Qu (Л) т - Q33 (*) т] X
X [Q33 (*) + QM (Л) ] t + 4Q13 (Л) tQ13 (*) t}, E.4.96)
где
W (k) = [1 - Qn (А) т - Q33 (A) t] [1 - Qu (k) x - Q33 (k) t] -
- 4Q13 (k) xQ13 (k) x. E.4.97)
Особый интерес представляет функция D3 (k), поскольку суще-
ствует соотношение
Аар {хх - х2) = @, р | Т [ра (xt) Рр W] | О, Р> = E.4.98)
= j ^г ехр [Яс (X! - х2) - /йо (/х - /,)] (-J- tD3 (Л))ар, E-4.99)
следующее из E.4.49), E.4.51) и E.4.61в).
Обобщенное уравнение для щели. Для дальнейшего изучения
D3 (k) заметим, что уравнение для щели E.4.39)
4\k {5-4Л00)
можно обобщить, записав его в виде
E.4.101)
Действительно, правую часть E.4.101) можно переписать в виде
ЖГl W 4 J BлK Е. ^ Z'-;'
она становится равной правой части E.4.100) после замены пере-
менных интегрирования 1 + (к/2) -> 1 в первом слагаемом и
1 — (к/2) -*¦ 1 — во втором. При этом мы пренебрегаем измене-
нием значения импульса обрезания, вызванным этой заменой
переменных, поскольку по предположению к значительно меньше
Некоторые примеры вычислений 173
дебаевского импульса. Уравнение E.4.101) можно записать в виде
матричного уравнения размерности 2 х2:
Т«Р = Mzeaep j dK2Q (к) ае (к, k) {UB (к) т \k\ —
— (х - ;8тJГ1 ?/в (х)}ар, E.4.102)
где а^ (и, k) дается выражением
а,(*,*) = --Lв (х) J^ (i%+?i [^ _ (Е
Ь-) X
-(?+-?_J] (/+-/_)). E.4.103)
Уравнение E.4.102) называется обобщенным уравнением для
щели [7]; при его выводе использовано соотношение
(k2 - Е2) б (и2 - Е2) [Uв (х) а (*§ - ?2 + ibx)~l UB (к)] =
= б (и2 - Е2) т, E.4.104)
которое следует из равенства UBxUв = т.
Вычисление D3 (k). Как видно из E.4.96), для вычисле-
ния D3 (k) необходимо знать величину A — Qnr — Q33T)- Для ее
вычисления используем соотношение
og (я, k) — (Гц (к, к) — сгзз (х, к) =
= — е W 4 1 (§s tkl - (е+ - е_J] X
Определим ш (й) равенством
5» (к) а, (х, к) = - в (х) ^ J (ga (e+ - в.)' ( (Е+Е+Еf -J б [xF -
E.4.106)
174 Глава 5
Сравнивая его с E.4.82), находим
й (к) = 0 при к = 0. E.4.107)
Тогда E.4.105) принимает вид
ай (и, к) — ап (к, к) — ат (к, к) = [Ajj — й2] аг {%, к), E.4.108)
где ш обозначает ш (к). Выражение E.4.108) вместе с E.4.102) дает
1 - Qn (k) т - Q33 (k) x = (k20 - ы2) R (k) т. E.4.109)
Далее из E.4.97) имеем
W (k) = R (k) т [k\ - Г (k)), E.4.110)
где
Г (k) = ш2 + 2А2 (Л§ + ш2) /? (Л)т + (А? - й2) Q,2 (Л) т. E.4.111)
Аналогично можно вычислить числитель в E.4.96); в резуль-
тате приходим к следующему выражению:
D3 (k) = 2е ± [k2_\{k)] [2А2 {k\ + ш2) /? (Л) + (*2 - ш2) Q12 (k)] т,
E.4.112)
или в другом виде
таким образом, вычислена функция D3 (k).
Вычисление двухточечной функции для плотности заряда.
Фурье-образ Аар (k) функции
<0, P\T[pa(x),
определяется следующим образом:
@, $\Т[ра(х), рр^]|0, р> =
^1 Uk (Х ~ У)
E.4.115)
Фурье-образ A (fe) имеет вид
J
Из E.4.111) и спектральных представлений для R и Q12 видно,
что Г может быть записана в следующем виде:
Г (k) = TR (k) — inav (k0> k) xUb (*o). E.4.116)
Некоторые примеры вычислений 175
Здесь
оо
Гл (k) = со2 + АЛ j йЛ (к) [2Д2 (k20 + ш2) аг (к, к) +
о
+ (k20 - ш2) а12 (и, к)] * 2 , E.4.117)
2
х
аг (и, к) = АЛ [2А2 (х2 + со2) ffr (и, к) +
+ (х2-©2) ст1а(х, к)]; E.4.118)
в E.4.117) 5я — главное значение интеграла. Теперь A (k) можно
получить из E.4.115) в следующем виде:
— таг {k\ _ ш2) г/| (/го)]. E.4.119)
Функция Д (k) имеет спектральное представление вида D.3.24)
с FA = 0. Сравнивая мнимую часть выражения E.4.119) с D.3.24)
и учитывая соотношение lim (k0 -> оо) Re A (k) = 0, имеем
Д (Л) = J Лсстд (к, к) ?/в (х) т [/г0 — х + /бтГ1^ (х), E.4.120)
где
... 2е* о (х, к)(х»-т»)
ад(х, к)=-Т—Т^ гт 5 • E.4.121)
Если величина сгр (х. к) равна нулю или пренебрежимо мала,
имеем
ад (к, к) = -g- (х2 - ш2) е (х) б (х2 - ГЛ). E.4.122)
Здесь учтено, что аг (к, к) и сг12 (х, к) (а следовательно, и
(Тд (к, к)) — нечетные функции от х. В E.4.121) и E.4.122)
ГЛ обозначает Г^ (k), куда вместо k0 входит х. Когда
fe2 - Гц (k) = 0 при k0 = сод (k), E.4.123)
A (k) имеет полюсную особенность при k0 = сов (к). Здесь вновь
мы пренебрегли величиной стг (и, к). Используя разложение Тей-
лора для TR (k) вблизи k20 = cos:
Г* (k) = со2в (к) + [h20 - со2в (к)] ГН1 (к) + ¦ • •, E.4.124)
находим
9е2 Юо (к) — ш2 г 9 ,
ад (к, к) = ^- t BJ г^ (к) е (х) б [х2 - (о| (к)] ¦ E.4.125)
176 Глава 5
Обозначим входящий в E.4.125) формфактор через (е2/й) [совт] (k) P;
тогда
Функция т] (к) конечна при к = 0, поскольку отношение й2/соЬ (к),
согласно E.4.107), конечно при к = 0. Из E.4.124) находим
• E-4.127)
Тогда выражение E.4.120) можно переписать в виде
А (*) = ^-©| (к) л2 (к) Uв Ы т [k20 - (сов - ibxf]-lUB (ив) + • • •,
E.4.128)
где первое слагаемое представляет собой вклад от члена с б-функ-
цией (т. е. полюсного) в E.4.125).
Динамическое отображение тока и плотности заряда. Сравним
первое слагаемое в правой части E.4.128) с выражением D.1.96),
дающим представление двухточечной функции свободного бозон-
ного термополевого дублета Ва:
Ва (х) = fth Г —??, —т_ [ва (к) ехр (Лх - mBt) +
+ S+a (к) ехр (— tkx + teat)]- E.4.129)
Можно убедиться, что динамическое отображение гейзенбергов-
ского оператора плотности заряда имеет вид [7]
ра (х) = -^-ц(У)Ва(х)+..., E.4.130)
где В обозначает (d/dt) В, а многоточие — нормальные произве-
дения более высоких порядков от свободных физических полей.
Докажем теперь, что бозон Ва (х) действительно существует.
С этой целью заметим, что E.4.107) и E.4.111) приводят к выра-
жению
T(k)=k20[2A2R (k) + Qi2(k)]x при k = 0. E.4.131)
Таким образом, уравнение E.4.123) допускает решение, для ко-
торого
сов (к) = 0 при к = 0, E.4.132)
откуда следует существование бозона Ва, энергия которого
не имеет щели. Такой бозон с нулевым импульсом устойчив бла-
годаря условию ар @, 0) = 0. Этот (голдстоуновский) бозон под-
Некоторые примеры вычислений 177
держивает упорядоченность фазы, а потому называется фазоном.
Фазон — составная частица, в которую входит электронная пара.
Скорость фазона v (k) удобно определить равенством
сов(к) = и(к)|к|. E.4.133)
Уравнение для фазона имеет вид
[(d/dtf + со| (V)] В" (х) = 0, E.4.134)
где cob (V) = — v- (V) V2.
Из закона сохранения для тока следует
E.4.135)
где многоточие вновь обозначает нормальные произведения более
высоких порядков.
Перестройка фазовой симметрии. Генератор преобразования
фазы tya -у е'ег|за имеет вид EaQa (при а = 1 га = 1, при а = 2
Еа = —1), где Qa — интервал по пространству от плотности за-
ряда:
JJVW- E-4.136)
Вычисление показывает, что вклад в Qa дает лишь первое слага-
емое динамического отображения E.4.130):
Ct = -\] <?Щ (V)Ва (х). E.4.137)
Если оператор exp [iGQaI действует на вектор состояния в про-
странстве 36 lafli), a (P)I, то результирующий вектор не остается
в этом пространстве (разд. 2.4). Поэтому при определении опера-
тора Qa необходима особая осторожность; точнее, Qa может быть
определен только с помощью некоторого предельного значения
нелокального оператора. Чтобы провести этот предельный пере-
ход, введем численную функцию f (x) типа волнового пакета,
удовлетворяющую уравнению для фазона
[(dldff + со! (V) ]/(*)=• 0. E.4.138)
Введем далее оператор Qa (/) с помощью соотношения
EA139>
178 Глава 5
¦«->¦ -<—
где использовано обозначение д0 = д0 — д0. Легко видеть, что
Qa (f) не зависит от времени, Qa (f) = 0. Тогда генератор Qa
определяется с помощью следующего предельного перехода:
(|Q(/)|> E.4.140)
Здесь |а) и \Ь) — векторы в пространстве Фока 36 [а (Р), а ({$)].
Используем далее перестановочное соотношение
[Ва (х), Qp (/)] = -щ (V) / (х) тар, E.4.141)
которое приводит к соотношению
(Г1 (Л Ва (х) G (/) = Ва (х) + г\ (V) / (х), E.4.142)
где G (/) = ехр П % eaQa (f)\ . E.4.143)
Здесь еа = 1 при а = 1 и ек = —1 при а = 2. В пределе f-*¦ Э
величина G (/) индуцирует сдвиг поля Ва (х) -> Ва(х) + Л @) Э.
Поскольку eaQa — генератор преобразования фазы tya (x) ->
-*¦ ехр (/0) -ф06 (я), указанный сдвиг поля индуцирует преобразова-
ние фазы гейзенберговского поля:
гП*; В + т)'@) 0, ф°] = eV(^5 5, ф°); E.4.144)
здесь В обозначает Ва, а ф° обозначает фОа.
Полученный результат формулируется обычно следующим обра-
зом [81: фазовая симметрия гейзенберговского поля перестра-
ивается и приводит к сдвигу фазонного поля. Таким образом, мы
имеем здесь динамическую перестройку фазовой симметрии. Соот-
ношение E.4.144) показывает, каким образом инвариантность
фазы, находит отражение в свойствах фазона. Иными словами,
упорядоченность фазы поддерживается фазоном, что отражает
существование'^ дальнодействующей корреляции* между элек-
тронами.
Учитывая динамическую перестройку симметрии, приходим
к следующему динамическому отображению для ty:
^а (х) = : ехр [щ-1 (V) Ва (х)]^(х; дВ, ц>°) :, E.4.145)
где дВ обозначает действие на В дифференциальных операторов
ненулевого порядка. Последнее выражение показывает, каким
образом могут быть найдены определенные черты динамических
отображений, если известна структура динамической перестройки
симметрии.
Некоторые примеры вычислений 179
Влияние кулоновского взаимодействия. Введем теперь куло-
новское взаимодействие. Тогда гамильтониан примет вид
Не = Н + Нс, E.4.146)
где
Я = J d3x fo+e (у2) ty + tfe (v2) Ь + ^ММЧ ~
ОЙ ^Ш E-4.147)
Гамильтониан Я получается из введенного выше лагранжиана
E.4.1), а #с представляет кулоновское взаимодействие.
Операция тильда дает
Wp2(V-7'0- E-4Л49)
Полный гамильтониан имеет вид
Яе = Не — Не, E.4.150)
где Не = Н + Нс. E.4.151)
Чтобы провести калибровочно инвариантное вычисление вли-
яния кулоновского взаимодействия, используем метод канони-
ческого преобразования. Более полная калибровочно инвариант-
ная формулировка дана в гл. 8.
Используем теперь выражение E.4.137),fкоторое показывает,
что основную роль в динамическом отображении ра (к) при малых
к играет только линейный бозонный член в E.4.130). Поэтому
здесь используется приближение, в котором учтен лишь линейный
бозонный член в ра.
Пусть па обозначает величину, канонически сопряженную Ва.
Поскольку Ва канонически сопряжена с Ва, выражение E.4.130)
можно записать в виде
ра(х)=--1-П(У)яа (х). E.4.152)
Тогда гамильтониан кулоновского взаимодействия принимает вид
Нс = т- (тJ Jd3x Jd3yr] (V) nl (x> ° T^Ti (v) я1 (у> t]>
E.4.153)
причем тильда-сопряженное к нему Нс получается из Яс посред-
ством замены я1 ->• я2.
180 Глава 5
Согласно D.1.3), Н в слабом смысле равен Но (В) + Но (ф°),
где #0 (В) — бозонная часть, а Но (ср°) — квазиэлектронная часть.
Для бозонной части имеем
Яо (Б) = П J dzkaB (k) Blf(k) В1 (к) =
- E.4.154)
В итоге получаем слабое соотношение
4
Нс = Но (ф) + 4 J
+4- (тJ J ^ J d*m (v) л1 (х> ° тгЬгл (v) я1 (У> °- E>4Л55)
Каноническое перестановочное соотношение имеет вид
[Ва (х, t), яр (у, 0] = Ш6 (х - у) тар. E.4.156)
Кулоновское взаимодействие изменяет связь между ла и Ва.
А именно, каноническое уравнение
injrBa = [Ba, He] E.4.157)
приводит к уравнениям
ва (х, о = яа (х, t) +(-^)\ (V) J dV -—tjy л (V) па (у, /),
E.4.158)
яа(х, t) = v2(V)V2Ba(x, f). E.4.159)
Из этих двух уравнений имеем
= 0. E.4.16G)
Заметим, что в последнем слагаемом в E.4.160) не проводится
интегрирование по частям, поскольку 1/| х — у | имеет бесконеч-
ный радиус действия. Применяя операцию V2 к обеим частям
E.4.160), находим
~ ц2 W V2 + 4я (-|-J rf (V) ,2 (V)] V2Ba (х, t) = 0.
E.4.161)
Некоторые примеры вычислений 181
Это означает, что Ва состоит из двух частей: одна из них удовлет-
воряет уравнению
[5г- * (V) V2 + 4я (^-J rf (V) t,2 (V)} В* = О, E.4.162)
а другая — уравнению Лапласа
V2Ba = 0. E.4.163)
Решение уравнения E.4.162) при малых импульсах дает энер-
гию (Opi = (elК) DяI/2т]@)у @). Как будет видно из дальнейших
вычислений, это энергия плазменных колебаний.
Заметим далее, что решения уравнения Лапласа E.4.163)
имеют однородные в пространстве фурье-образы. Поэтому соот-
ветствующие моды не наблюдаются как квантовые возбуждения.
Иными словами, единственные наблюдаемые бозонные возбужде-
ния — это плазменные колебания; бесщелевые возбуждения (фа-
зоны) исключаются из числа наблюдаемых за счет кулоновскоо
взаимодействия. Это явление носит название механизма Андер-
сона — Хиггса — Киббла [9]. С другой стороны, наличие дина-
мической перестройки симметрии E.4.144) указывает на то, что
фазовое преобразование электронного гейзенберговского поля
¦ф-> exp (t0)^ индуцируется с-численным постоянным сдвигом
фазонного поля Ва (х) -v Ва (х) + ц @) 0. Это утверждение
остается в силе даже при учете кулоновского взаимодействия.
Тем самым фазон, удовлетворяющий уравнению Лапласа, сохра-
няет свою роль в качестве переносчика фазовой симметрии, не-
смотря на наличие кулоновского взаимодействия.
В итоге можно утверждать, что учет кулоновского взаимо-
действия приводит к появлению плазмона; фазон, который удо-
влетворяет уравнению Лапласа и не может наблюдаться экспери-
ментально как возбуждение, служит все же переносчиком фазового
преобразования.
Все приведенные выше соображения подтверждаются более
точным и не зависящим от выбора модели рассмотрением в гл. 8.
Если использовать соотношения E.4.152) и E.4.159), локаль-
ный закон сохранения для тока приводит вновь к выражению
E.4.135).
Характеристическая функция бозонов. Для практических вьь
числений удобно переписать E.4.135) в виде
]*(*) = ^с (V) Г' (V) VB* (*) + ..., E.4.164)
где с (V) = v2 (V) tf (V)/o* @) rf @), E.4.165)
@)Tf@). E-4Л66>
182 Глава 5
Заметим, что с (V) нормировано следующим образом:
с@) = 1. E.4.167)
Чтобы учесть поперечный векторный потенциал Аа, напомним,
что ехр [щ-1 (V) Ва (х) ] является фазовым множителем электрон-
ного поля. Калибровочное преобразование переводит Ап в Ап +
+ дц% и индуцирует появление у электронного поля фазового
множителя ехр [i (eltic) К], который приводит к замене г\-хВ на
ц^В + (е/Нс) К. Тогда в динамическом отображении любого ка-
либровочно-инвариантного оператора нужно заменить УВа на
[?Ва—(eltic) г) (V) Аа]. Выражение E.4.164) можно переписать в виде
Г (х) = ^ J d'ye (х - у) (тГ1 (V) VBa (у) ^--^Аа (у)) , E.4.168)
где
J(Wc№e'kx> E-4Л69)
причем, согласно E.4.167),
J dsxc(x) = 1. E.4.170)
Обозначим через XL (T) величину %L при температуре Т. Вы-
числение при Т — 0 показывает [7], что
E.4.172)
где п — электронная плотность. Объединяя E.4.166) и E.4.172),
находим
!'S (i^y\ E.4.173)
что действительно совпадает с энергией плазменного колебания.
В работах [7, 10] показано, что
LH]3= I f 2 \с1гЩР-, E.4.174)
• С)/ о
где сод — энергия Дебая.
При нуле температуры величин сов (к) и г\ (к) вычислены чис-
ленно. Энергия фазона сов (к) ведет себя следующим образом:
©в (к) = 4" о?" [1 — VN @) ] к2 при малых к, E.4.175)
а затем плавно выходит на насыщение, стремясь к значению 2А
при больших к.
Некоторые примеры вычислений 183
Функция с (k), определенная выражением E.4.165), называется
характеристической функцией бозонов. Согласно E.4.164), эта
функция является формфактором тока; при Т = 0 она получена
с помощью численного расчета. При значениях VN @) = 0,2—
— 0,4 она может быть хорошо описана формулой [11]
с (k) = exp {-v №0Г\, E.4.176)
где k = | к |, т] = 2,207 — 0,7857 IW @), v = 0,559 — 0,4257У# @),
1о — длина когерентности при нуле температуры; она определена
выражением
Е0 = Йо,/яА0, E.4.177)
где Ао — значение А при 7 = 0. Формула E.4.176) достаточно
хорошо аппроксимирует численный результат, но при больших к
она приводит к слишком быстрому спаданию. Действительно,
с помощью аналитических расчетов показано [12], что в асимпто-
тической области с (к) ведет себя согласно соотношению
с (k) = (A/klo) exp (—Bklo), E.4.178)
где А и В — некоторые функции VN @). Если при анализе кон-
кретных задач требуется высокая точность, то иногда оказывается,
что отсутствующий в формуле E.4.176) «хвост» играет решающую
роль. В этом случае следует использовать численный результат,
а не интерполирующую формулу; соответствующий пример при-
веден в гл. 11.
Если температура отлична от нуля, вычисление характеристи-
ческой функции бозонов становится сложным вследствие тем-
пературной нестабильности коллективной моды. Первое вычисле-
ние такого типа было выполнено еще до того, как была дана фор-
мулировка спектрального представления двухточечных функций
в термополевой динамике. Поэтому вычисление было приближен-
ным. Численный результат [13], полученный в результате грубого
приближения, описывается интерполирующей формулой
с (k) = exp {—v [kl (t) ]ч}, E.4.179)
где т] = — 0,7857WV@) + 2,207, v = —0,4257VW@) + 0,559.
Температурная зависимость проявляется только через масштаб-
ный фактор |:
l(t)=y(t)lo, E.4.180)
где
у (t) = 1 + а [*»/A — 0™], E.4.181)
а = — 0,0536V4V @) + 0,3719, E.4.182а)
п = 0,3714V4V @) + 3,846, E.4.1826)
m = — 0,041 WN @) + 0,556. E.4.182в)
184 Глава 5
Здесь t обозначает приведенную температуру t = Т/Тс; резуль-
таты получены для 0,2 < VN @) < 0,4. Примечательно, что
показатель г\ практически не зависит от температуры.
Хотя полученная формула для с (k) при отличной от нуля
температуре Т является результатом грубого приближения,
использование E.4.168) с этой функцией с (к) приводит к разум-
ному согласию с экспериментом в различных расчетах явлений
сверхпроводимости. Желательно, однако, вычислять с (к) с по-
мощью новых уточненных формул E.4.121).
Энергия основного состояния. Вычислим теперь энергию кон-
денсации [5, 61 в пренебрежении электромагнитным взаимодей-
ствием. С этой целью рассмотрим среднее значение @, р | Н | 0, р),
где Я — гамильтониан системы E.4.147). Приближение Хартри —
Фока дает следующее выражение для плотности энергии основ-
ного состояния:
, р|Я|0, P) = 1j
E.4.183)
= -^ J dsx lm {-8 (V2) Тг [т35" (дг)]}*-о+ -i- A2 + ft f -^r e*.
E.4.184)
Здесь учтено выражение E.4.26); Vs — объем системы. Послед-
нее слагаемое в E.4.184) возникло благодаря перестановке ij)j
и ^t в первом слагаемом в правой части E.4.183).
Используя уравнение для щели E.4.39), выражение E.4.184)
можно переписать в виде
J #k Тг
-A- J
с
8, -
где контур интегрирования с на комплексной &0-плоскости —
полуокружность в верхней полуплоскости. Согласно E.4.34),
имеем
\^^- 2f,(Ek)] =
1^[l-2f
E.4.186)
Некоторые примеры вычислений 185
тогда получаем
2ft f d3k
- "Г J W\ ,(k)J
бодная энергия Гельмгольца и
E.4.188)
Согласно D.1.51), свободная энергия Гельмгольца имеет вид
F WS
Из D.1.52) находим
E.4.189)
(множитель 2 обусловлен спиновой степенью свободы). Имеем
тогда
E<4Л90)
Свободная энергия Гельмгольца Fn для нормального состояния
совпадает с величиной F при значении А, равном нулю:
EЛ191)
Тогда разность между значениями свободной энергии Гельмгольца
для металла в нормальном и сверхпроводящем состояниях вы-
ражается формулой
F = F»-F. E.4.192)
Принято вводить величину НС(Т), определенную уравнением
Н2с(Т)/8п = Т. E.4.193)
Из E.4.190) и E.4.191) находим при Т = 0
Н2С @)/8я = yAf@) A2. E.4.194)
Поскольку А (Т) имеет бесконечную производную при Т = Тс,
теплоемкость Т (dS/dT) не непрерывна при Т = Тс\ было пока-
зано, что
с*-с" =1,43 при Т = ТС, E.4.195)
где сп и cs — электронные теплоемкости нормального и сверх-
проводящего состояний соответственно.
186 Глава 5
5.5. Плазменные колебания
в нормальных металлах
В разд. 5.4 изучалась система электронов проводимости в сверх-
проводниках. В этом разделе мы рассмотрим электронный газ
в нормальных металлах. Широко известно, что электронный газ
с фоном положительных ионов приводит к появлению коллек-
тивной моды (плазменных колебаний), в результате чего фотоны
в металлах ведут себя подобно массивным квантам, называемым
плазмонами. В этом состоит причина непрозрачности металлов
для света. Квантовомеханическое описание плазменных колебаний
и их влияния на энергию основного состояния было подробно
рассмотрено Бомом и Пайнсом, а также другими авторами [14].
В квантовой электродинамике калибровочная инвариантность
является важным свойством симметрии. Если в ходе вычислений
делается то или иное приближение, особое внимание следует уде-
лять выполнению требования о сохранении калибровочной ин-
вариантности. В последние годы развита полезная и красивая
методика учета калибровочной симметрии [15]. В гл. 8 с помощью
этой методики дана самосогласованная формулировка квантовой
электродинамики в твердых телах. В этом разделе мы вычислим
неприводимую фотонную собственную энергию 2,^ для электро-
магнитного поля в нормальных металлах при конечных темпе-
ратурах на основе следующего лагранжиана:
- епеА° - -1 /^/Vv, E.5.1)
где Ац — (А, Л0) — электромагнитный векторный потенциал,
¦ф — электронное гейзенберговское поле
E-5-2)
(—епе) — положительная плотность заряда ионов. Электромагнит-
ное поле F^ = дцЛ,, — д„Лц, где д° = A/с) (d/dt), а д0 =
= —A/с) (d/dt). В этом разделе используется рационализирован-
ная система единиц Хевисайда — Лоренца.
Операторы тока и плотности заряда. Плотности тока и заряда
даются выражениями
№ЯЪ№ AW »'=1, 2, 3, E.5.3)
= -j-№4-nn.). E.5.4)
Некоторые примеры вычислений 187
Предполагая, что плотность пе постоянна во времени и однородна
по пространству, мы исходим из равномерного распределения
плотности заряда ионов. Тогда полная электронейтральность тре-
бует, чтобы выполнялось условие
(О, р|ч>+(*Ж*)|0, р) =Ппе. E.5.5)
Посредством операции тильда-сопряжения получаем величины ty,
Ац, 3?, j и р. Используя поля — термополевые дублеты -tya и Л^,
имеем
(^ ^ ) E.5.6)
Ра (jr (Г+Г - Ал.)) : E-5.7)
оператор упорядочения Ра определен в D.2.6).
Двухточечные функции для/и р. В однопетлевом приближении
имеем
fif (х - У) = (О, Р | Т [/? (х) /f (у)] | 0, р) =
= - (e/2mf eaepSpa (у - х) *д fdfSa& (x - у), E.5.8а)
= (ie2/2mH) eaEp5pa (у - лг)"а?5ра (х - у), E.5.86)
/?f (х-у) = @,ЩТ[ра (х) рр (у)] | 0, р) =
= - (elhf eaep5pa (у - х) 5ра (х - у). E.5.8в)
Здесь 5 (х — у) — причинная двухточечная функция физического
электрона ф°. Поскольку ср° удовлетворяет уравнению
° = 0, E.5.9)
где e(v) = -^r(v2 + 4), [E.5.10)
фурье-образ функции 5 (х — у) дается выражением D.1.74), так
что
Sc (k) = U (гк) lk0 - гк + t-бт]-1 W (гк), E.5.11)
где Eft = (ft/2m)'(k2 — #).
Обозначим фурье-образы функций /г/- (х — у), Jt0 (x — у)
и /00 (х — у) через /,/ (?), /го (^) и /00 (й) соответственно:
~У) = -ЩГ \ №elk <*-*)/,/ (*), .... E.5.12)
188 Глава 5
Применяя формулу D.1.120), получаем
Ло (*) = в8 J -||r J dxo (х; в+, е_) [UB (х) r{ko-x + i бт} UB (x)],
E.5.13)
где а (х; е+) б.) = — б (к — е+ + е_) [fF (е+) — /> (е_) ]. E.5.14)
Здесь
Существенно отметить, что е± может принимать как положитель-
ные, так и отрицательные значения.
Аналогично можно получить
Jm (k) = ? J -щг h J dw (x; e+> e_) [UB (x) x {k0 - x +
+ iftr}-1f/B(x)]> E.5.16)
x ft/iJ(x)T{^r-x + /6T}-1f/iJ(x)], E.5.17)
откуда видно, что /,•/ (k) = 1ц (k). Можно показать, что имеет
место также равенство Jl0 (k) = /Oj (k). Если учесть, что е+—е_ =
= (й//п) A-к), то получим
2 Г d3l Г
^i/го = <? J -B^K- J dx (e+ - е-) а (*; е+- е-) X
X [UB (х) т {Ло - х + i бт}-1 Uв (х)] =
E.5.18)
отсюда, используя E.5.13), находим
^i-[/i,(e-)-/ir(e+)]T = O> E.5.19а)
где kn = (к, ^0). При выводе соотношения E.5.19а) использовано
соотношение UBrUB = т.
Аналогичным образом можно доказать соотношение
<*) = —1Г J15SF/j l/к (е-) - ^ (е+Iт- E-5- 19б>
Некоторые примеры вычислений 189
Для дальнейших вычислений потребуются формулы
J W-/г V' w - /' &)]=т *'»'• E-5-21>
При выводе формулы E.5.20) проведена замена переменной ин-
тегрирования 1 -у 1 Ч1 (к/2), а в E.5.21) учтено, что из E.5.5)
следует
E-5-22)
Тогда соотношения E.5.19) приводят к выражению
- E-5-23)
д
Поскольку правая часть E.5.13) является функцией к2 и k0
и обращается в нуль при к = 0, можно ввести 2„ (k) с помощью
соотношения
(*К E-5.24)
где 20 (k) — матрица B?Р) размерности 2x2. Тогда можно
получить
т.. iu\ п п Ь2Т I \'И, Т„. (Ь\ (Ъ Ъ 9Ъ\
= п— иек т -4- knjnn (k) == E.5.26)
= - -g- «ek\ - й2ок22о (k) x, E.5.27)
где использованы равенства E.5.19а) и E.5.23).
Из E.5.27) следует, что /г/ имеет вид
т (k) Гц (к) - ?220 (k) ^L x) , E.5.28)
где 2г (&) — матрица BгР) размерности 2 х 2, a Ttj (к) — проек-
ционный оператор поперечной компоненты:
/ (/^) E.5.29)
Из E.5.28) следует
Ег (й)=-г B/ft м+^~Я1гпе+k&°{k)} • E-5-30)
190 N Глава 5
Матрицы Sr и So могут быть вычислены с помощью E.5.24)
и E.5.30). Из E.5.19а) имеем
k,Ji0 (k) = k0J00 (k) = -?0k220 (k) т. E.5.31)
Поперечные и продольные плазмоны. Обозначим физическое
фотонное (плазмонное) поле в нормальных металлах через ?/" (а =
— 1,2):
A%{x) = u%{x)-\ . E.5.32)
Поперечные и продольные плазмоны обозначим через иаТ и uaL
соответственно. В однопетлевом приближении получим следующее
динамическое отображение для фурье-образов ja и ра:
iaT (*)= - 2 s"p (*) -'т- (*)+¦••• <5-5-33)
W (k) -H^i (k) - kokZ%* (k)ul {k))+ ¦¦-, E.5.34)
pa (k) = - 2 [k22o°p (*) «o0 (*) - 2?P (*) йо (k -^-)] f • • • . E.5.35)
P
В выражениях E.5.33)—E.5.35) многоточия обозначают слага-
емые, отличные от линейного плазмонного слагаемого. При вы-
воде E.5.33)—E.5.35) использованы формулы E.5.24), E.5.28),
E.5.31), а также соотношение между /ц (х) и Ап (х) из теории ли-
нейного отклика. Символы \аТ и ]aL обозначают поперечную
и продольную части ]а соответственно.
С другой стороны, из уравнений Максвелла следуют соотно-
шения
= -j-Jr' E.5.36а)
Ao = -^jL, E.5.366)
d0(V-A)-VMo = P, E.5.36b)
а также тильда-сопряженные к ним. Эти соотношения вместе
с динамическими отображениями E.5.33)—E.5.35) приводят к сле-
дующим уравнениям плазменных колебаний [16]:
j ([р2 - (po/cfl бар + ^ *т* (Р)) ирГ (Р) = 0, E.5.37а)
[бар + Е0«Р (р)] и^ И = 0, E.5.376)
[бар + 2?р (/7)] 4 (Р) = 0. E.5.37в)
Из этих уравнений видно, что 2Г (р) и A/^) 2о (р) — неприво-
димые собственно-энергетические части поперечных и продольных
Некоторые примеры вычислений 191
фотонов. Приведенные выше соотношения определяют энергии
плазмонов. При нулевой температуре вычисления дают [14]
к2 ' ' E.5.38а)
E.5.386)
при малых к, где
dJpl =ze2ne/m. E.5.39)
Таким образом, энергии поперечного плазмона ЕТ и продольного
плазмона EL при нулевой температуре даются выражениями
El(k) = ^l + 4r^k2+..-, E.5.40а)
Е\ (k) = со2р/ + ^ + -L -?- ] k^ + • • • E.5.406)
при малых к.
ЛИТЕРАТУРА
1. Schrieffer J. R., Theory of superconductivity, Benjamin, London, 1969.
[Имеется перевод: Шриффер Дж. Теория сверхпроводимости. — М.: Наука,
1970.]
2. Polarons and excitons. Ed. by С. G. Kuper and G. T. Whitefield, Oliver and
Boyd, London, 1962;
Polarons in ionic crystals and polar semiconductors. Ed. by J. Devreese, North-
Holland, Amsterdam, 1972.
3. Holstein Т., Primakoff H., Phys. Rev., 58, 1098 A940).
4. Dyson F. J., Phys. Rev., 102, 1217 A956).
5. Bardeen J,, Cooper L., Schrieffer J., Phys. Rev., 108, 1175 A957).
6. Superconductivity. Ed. by R. D. Parks, Marcel Dekker, New York, 1969.
7. Leplae L., Umezawa H., Mancini F., Phys. Rep., 10C, 151 A974).
8. Umezawa H., Nuovo Cim., 40, 450 A965).
9. Anderson P. W., Phys. Rev., 110, 827; 1900 A958);
Yosida K-, Progr. Theor. Phys., 21, 731 A959);
Higgs P., Phys. Rev., 45, 1156 A960);
Kibble T. W. В., Phys. Rev., 155, 1554 A967).
10. Richayzen G. — in: Superconductivity, ed. by R. D. Parks, Marcel Dekker,
New York, 1969.
11. Leplae L., Shah M. N.. Umezawa H., Physica, 80B, 493 A975).
12. Mancini F., Physica, 81B, 119 A976).
13. Shapira I., Shah M. N., Umezawa #., Physica, 84B, 213 A976).
14. BohmD., PinesD., Phys. Rev., 82, 625 A951); 85, 338 A952); 92, 609 A953);
Gell-Mann M., Brueckner K., Phys. Rev., 106, 364 A957);
Sawada K., Phys. Rev., 106, 372 A957);
Sa.wa.da K-, Brueckner K-, Fukuda N., Brout R., Phys. Rev., 108, 507 A957).
15. Nakanishi N., Progr. Theor. Phys., 35, 1111 A966); 49, 640 A973); 50, 1388
A973);
Lautrup В., Mat. Fys. Medd. Dan. Vid. Selsk., 35, 1 A967).
16. Matsumoto H., Semenoff G., Tachiki M., Umezawa H., Fortschritte der Phys.,
28, 67 A980).
ГЛАВА 6
ИНВАРИАНТНОСТЬ И НЁТЕРОВСКИЙ ТОК
6.1. Нётеровский ток и соотношения
Уорда—Такахаши
При анализе систем многих частиц важную роль играет иногда
инвариантность теории. Именно из-за требований инвариантности
возникают определенные соотношения между матричными элемен-
тами операторов поля, отвечающих некоторым существенным свой-
ствам таких систем. В этой главе дается общий метод рассмотрения
инвариантности в рамках квантовой теории поля. Чтобы про-
демонстрировать применение этого метода, в последнем разделе
обсуждается его применение к ферромагнетизму коллективизи-
рованных электронов.
Нётеровский ток и лагранжиан. Рассмотрим систему, динамика
которой определяется плотностью лагранжиана 3? Щ (х), д$ (х)].
Здесь ty(x) — набор гейзенберговских полей г^ (t = 1, 2, ...).
Непрерывное преобразование
i|> (х) +г|/ (*') = ф (х) + Щ (х), F.1.1)
Хц -+Х1 = % + ббхц, F.1.2)
где 6 — бесконечно малая константа, приводит к следующему
изменению лагранжиана:
&х'2 (г|/ (*') д'^' {х')) - dW (г|) (а:), д^ (х)) = вй*х8& (х).
F.1.3)
Здесь использованы четырехмерные обозначения
X[i ~ \xo> X\, x%, Xg), Хо = г, д^ =
= (dldt, №хъ д/дхг,д/дх3), д^ = g^d\
~goo = Sa = 1. в остальных случаях g^v = 0.
Эта специфическая форма преобразования лагранжиана приводит
к ряду соотношений между многоточечными функциями
@1Т I'vf (х), ... ] 10), которые называются соотношениями Уорда —
Такахаши (УТ). Соотношения УТ играют важную роль при ана-
лизе тех свойств систем, которые основаны на определенной
симметрии динамических уравнений. Как мы увидим, соотношения
УТ основаны на канонических перестановочных соотношениях
для операторов, взятых в один и тот же момент времени. Начнем
Инвариантность и нётеровский ток
со случая, когда 8ty(x) в выражении F.1.1) — линейное преоб-
разование с постоянными численными коэффициентами:
6% (х) = aft, (x).
Определим
0боя|) (х) = Мр' (х) — Мр (х).
Поскольку
Мр' (х') = г|/ (*) + 9бл:м^г|) (х),
справедливо равенство
6°Мр (х) = бф (х) — бд;цаиг|) (х).
Если мы учтем соотношение
д (xixr2X3x'o)/d (х^глгзхо) — 1 + бб^бял,
то из соотношения F.1.3) получим
(
где 5" (х) обозначает SE [а|) (х), д^ (х)]. Поскольку
aw (хг) = д„$ (х) + еад бо|з (х) - eavi|) w д» 6Xv, F.1.
из равенства F.1.9) следует
(x) = ^- бгр (х) + Щ- д^ бг|) (х) - Щ- д^ (х) дп 8xv + &> bx^SB
где использовано уравнение Геизенберга
дЗ'/дМр =
В приведенных выше соотношениях
% = д^.
Используя уравнение F.1.12), получаем
Таким образом, выражение F.1.11) можно переписать в виде
(х) = ад l-Щ- (Ц - д^ 8xv) + Ьх»3?\ ¦ F.1.15)
Учитывая соотношение F.1.7), получаем
frN» = 62? (х),
ГД6 N^j^b^ + bx
194 Глава 6
Из соотношения F.1.16) следует, что изменение лагранжиана
равно дивергенции тока Л^. Этот ток называется нётеровским
током [1].
Нётеровскии ток и генератор. Заметим, что поле, определенное
соотношением
п (х) = д&Щ0, F.1.18)
является канонически сопряженным полю ty (х):
Ы (х), Ц> (у)}± б (** - Q = —»Й6<*> (х - у).
Таким образом, из соотношения F.1.17) следует
ЛГ„ (х) = яг (х) {Cijtyj (х) — \71|3| (л:) бх — фгбл:0} + блс,,^ =
= яг (л;) {с,/ф (*) — уЧ>г (*) 6х} — ^oh (x), F.1.19)
где 'ф = dty/dt, a h (x) — плотность гамильтониана:
/г = ягфг — 2. F.1.20)
Выражение F.1.19) вместе с одновременными каноническими пере-
становочными соотношениями приводят к соотношению
И>, (х), N(t))8(t- tx) = 1ПЬ (t - tx) {cij^i (x) -
— V4j7f (x) бх — 4>г бл:0} = tft6 (/ — у 8% (x), F.1.21)
где N (t) = \ d3xN0[(x). F.1.22)
Приведенное соотношение показывает, что N (t) генерирует пре-
образование вида exp {iQN}i!p ехр {—iQN} = ^ + 6б°я|з + ... .
При выводе соотношения F.1.21) мы использовали каноническое
уравнение
1Щ = Ь|>, Я],
где Н — гамильтониан
H = \<Pxh(x). F.1.23)
Вывод соотношений Уорда—Такахаши. Заметим теперь, что
а=1
...W (t), Ц, (*„)] . .. ф (дся)] 10) + @1 Т [N @, а|5 (^) . . . q (xn)] \ 0).
F.1.24)
Поскольку из соотношения F.1.16) следует
), F.1.25)
Инвариантность и нётеровский ток 195
соотношение F.1.24) можно переписать в виде
J
JL(o\T[N(t),
a=l
.. . 64 (ха) . .. ф (хп)] 10) + J сРх @1Г [62> (х), г|> (*0 • • • Ч> (*„)] 10).
F.1.26)
Выполним в обеих частях соотношения F.1.26) интегрирование
по t (в пределах от —оо до +оо). Если п = (Q\N\0) Ф 0, го N
содержит неоператорный (численный) член. Из-за него при ин-
тегрировании по t в левой части возникает бесконечность. С дру-
гой стороны, замена N -*¦ N—@1N 10) не изменяет соотношения
F.1.21). Следовательно, соотношение F.1.26) не изменится, если
провести следующую замену:
N (t) -+N @ — @1 N~(t)\ 0), F.1.27а)
ЪЗР ^bS — @16540). F.1.276)
Во всех формулах этой книги принято, что такая замена выпол-
нена во всех случаях, когда п Ф 0 (и, следовательно, @1 Ь3? \ 0) ф
ф 0). Даже если эта замена проведена, может оказаться, что,
когда динамическое отображение N содержит линейный по без-
массовому физическому полю член (скажем, %°), при интегрирова-
нии левой части может возникнуть неоднозначность из-за дально-
действующей природы пропагатора безмассового поля. В этом
случае используется следующий прием: к лагранжиану доба-
вляется небольшой член 3?е(х), чтобы у %° появилась собственная
энергия. В конце вычислений переходят к пределу &г (х) -*~ 0.
В разд. 6.3 мы поймем физический смысл члена 2\ (х). С помощью
этого приема интегрирование по времени левой части выражения
F.1.26) дает нуль, и результирующее соотношение имеет вид
in (о | т и> (Xl)... б> (Ха)... ц>:(*„)] | о)
= J
d«* @ | Т Ш (х) y_(Xl) . . . г|) (хп)] | 0). F.1.28)
Это соотношение Уорда — Такахаши (УТ) 1), связанное с преобра-
зованиями F.1.1), F.1.2).
г) Исторически первым было получено соотношение для векторной вершины
электромагнитного взаимодействия при нулевом передаваемом импульсе. Это
соотношение было названо тождеством Уорда [2]. Соотношение при конечном
передаваемом импульсе выведено Такахаши [3]. В более поздних работах назва-
ние «соотношение Уорда—Такахаши» используется в более широком смысле:
любое соотношение, основанное на специфическом поведении лагранжиана при
некотором преобразовании, называется соотношением УТ.
7*
196 Глава 6
Компактная запись соотношений Уорда—Такахаши. Рас-
смотрим сначала случай, когда я|)г (х) — бозонные поля, и введем
WJ = \d*xJ,(x)ipi(x), F.1.29)
где /; (х) (i = 1, 2, ...) — численные функции, разложимые в ряд
Фурье. Преобразование типа F.1.1) и F.1.2) приводит к замене
Wj на
&,¦ = j d'x'Jt (x) # (х) = J d\xJ{ (x) ф; (x) =
= j d*xJt (x) 4>, (x) + e j d*xJt (x) 64* W = &j + 9 j d*xJt (x) 60ifc (x),
F.1.30)
откуда следует
6^y = (i/e)(F}-^,)= F.1.31)
= \dixJt(xN%(x). F.1.32)
Умножая обе части уравнения F.1.28) на / (хх) ... / (хп) и ин-
тегрируя по хг ... хп, получаем
i%n @1Т [bWj(Wj)n-i] 10) = ( d*x @1T \bS (x) (Sjf\ 10), F.1.33)
что приводит к компактной записи соотношения УТ:
= - j d*x @ | Т [-L ЬЗ? (х) exp (JL Wj) ] | 0). F.1.34)
Чтобы увидеть, каким образом из соотношения F.1.34) полу-
чается соотношение УТ, определим функциональную производ-
ную
-l^f = 6tl6«>(x-y). F.1.35)
Подействовав на обе части соотношения F.1.34) оператором
(—ift) б/б/ (xi) и перейдя к пределу при / -->- 0, получим соотно-
шение
@164 (х,) 10) = - J d*x @1Т (-i- bS (x) ф (x,)) | 0), F.1.36)
которое является соотношением УТ F.1.28) для п = 1.
Если на обе стороны F.1.34) подействовать оператором
(—ihJ [б/б/ (дс,) I [б/б/ (дс2) ] и перейти к пределу при / -»• 0,
получим соотношение
@ | П6°г|> (*,), г|) (х2)] | 0) + @ | Т[г|) (хх), б^ (х2)] | 0) =
= - J d*x @ | Т (±-Ь2 (х), г|> (х0, г|» (х2)) |0), F.1.37)
Инвариантность и нётеровский ток 197
которое является соотношением УТ F.1.28) для п = 2. Таким
образом, все соотношения УТ могут быть получены из F.1.34).
Резюмируя, можно сказать, что если учесть преобразования
F.1.1), F.1.2), то сначала следует вычислить б°4> (х) и Ь2', после
чего сразу можно получить соотношение УТ F.1.34) *).
Если операторы ^ (х) — фермионные поля, соотношение УТ
F.1.34) остается справедливым, если Jt (x) можно считать внеш-
ними источниками фермионного типа, т. е. Jt (х) (/=1,2,...)
антикоммутируют (а не коммутируют) друг с другом, а также
с любым фермионным полем. Таким образом, б/б/, (д;) также
антикоммутируют с фермионными полями. Соотношение F.1.35)
справедливо даже в том случае, когда J; (х) — источники фер-
мионного типа.
Обобщение соотношений УТ. Мы можем распространить изло-
женное выше рассмотрение на преобразования вида
&|>« (х) = а, (х) Fj [г|> (*)] + dt (х), F.1.38)
где сц (х) и dt (x) — некоторые числовые функции от хп, а опера-
торы Fj[^(x)] —линейные комбинации произведений ty (x),
для которых
[г|> (х), F, [г|> (у)}}± б (tx - ty) = 0. F.1.39)
Тогда нётеровский ток, описываемый соотношениями F.1.17)
и F.1.19), равен
No (х) = щ (х) {си (х) F, [ф (х)\ + dt (х)~Щ (х) бх} - bxoh (x), F.1.40)
откуда следует соотношение F.1.21), т. е.
[ф, (х), N @16 (/ — Q = ihb (t — tx) б0^ (х). F.1.41)
Следовательно, ни одна из формул F.1.25)—F.1.37) не требует
изменений. В частности, не требует изменений соотношение УТ
F.1.34). Калибровочное преобразование — пример преобразова-
ния, описываемого соотношением F.1.38).
Если ij) комплексно, 3?j и bS?j нужно заменить на
Wj = j d'x D (х) ф,- (х) + i|)t (x) Jt (x)), F.1.42а)
bWj = j <?x [J] (x) 6\ (x) + 6V (x) Jt (x)]. F.1.426)
Важно отметить, что соотношению УТ F.1.34) нельзя доверять,
когда лагранжиан не допускает описания в рамках канонического
х) Читатели, знакомые с функциональным формализмом квантовой теории
поля, могут сразу заметить, что этот метод формально эквивалентен выводу
соотношений УТ в рамках функционального формализма. Действительно, в этом
формализме F.1.34) превращается в соотношение УТ, если заменить выражение
@1 Т-скобка |0) функциональным интегралом [3]. Приведенный здесь вывод
соотношения УТ сходен с выводом в работах [5], где интегрирование по вре-
мени ведется с использованием генератора jV при t = ±oo, а не S"e (*)¦
198 Глава 6
формализма, поскольку при выводе F.1.21) использованы одно-
временные перестановочные соотношения.
Соотношения Уорда—Такахаши для локального тока. Нёте-
ровский ток введен с помощью выражения F.1.17); его диверген-
ция удовлетворяет соотношению F.1.16). Теперь мы покажем,
что и-точечные функции, содержащие Nlt (х), удовлетворяют
некоторому условию, наложенному на их дивергенцию, которое
также называется соотношением УТ.
Используя определение Т-произведения, получаем
=? 6(t -ta
a=l
..ЛВД, 1>(*а)]...1>(*Л
+ @1T [bS (x), ф (Xl) ... 4> (xn)] | 0). F.1.43)
Если рассмотреть выражение F.1.19), то можно убедиться, что
общая форма коммутатора [No (х), ty (у)] имеет вид
х), Ч> (y)]t =t,, = -»Йв (х - у) 64 (х) + in bx0V [F (х) б (х - у)],
у
F.1.44)
где F (л:) — некоторый оператор. Это выражение следует из
соотношения
N (х), h (y)]tx=ty = Ш ^ (х) б (х - у) + V [F (х) б (х - у)}, F.1.45)
являющегося следствием уравнения
[г|> (х), Н] = i/гф (х). F.1.46)
Если бл:0 = 0 или F = 0, что в большинстве случаев справедливо,
условие F.1.43) упрощается и принимает вид
(ха) ... (хя)]|0> + <0|Т[6<?(д), у(Х1)...Ц (хп)]\0). F.1.47)
Это локальная форма соотношений УТ.
6.2. Соотношения Уорда—Такахаши
при конечных температурах
Тильда-сопряжение. Как показано в гл. 5, когда мы рассма-
триваем систему при ненулевой температуре, кроме гейзенбергов-
ского поля \|5 возникает тильда-сопряженное ему поле ф.
Инвариантность и нетеровский ток 199
Соотношения Уорда-Такахаши. В этом случае соотношение УТ
F.1.34) изменяется следующим образом:
(О, P|
= - Jd*x<0, |3|Т [-jLe<?(*)exp (\$j)] 10, P), F.2.1)
где Zj = \<?x[J?(x)tf(x) + yr(x)ft{x)\, F.2.2)
j (x) = \(fx[JT (x) 6V (*) + 6V+ (x) Jf (x)], F.2.3)
). F.2.4)
Здесь мы использовали введенное в гл. 4 обозначение термополе-
вого дублета
1}\ = Ь\ t? = ^- F.2.5)
В выражении F.2.4) 6i? и Ь& — изменения 3? у.3? соответственно.
Эти изменения выражаются формулой F.1.11). Соотношение УТ
F.1.28) легко обобщить на случай конечных температур, если \|з
обозначает г|)а и ^, Ь2! заменено на 83?, а | 0) — на | 0, ft). Тогда
из выражения F.1.28) сразу следует выражение F.2.1).
6.3. Простой пример соотношения
Уорда—Такахаши
В этом разделе мы рассмотрим простой пример соотношения
УТ, чтобы дать общее представление о том, как эти соотношения
можно использовать.
Простая модель описывается лагранжианом S = [3?0 (\р, г|)+) +
-|_ С (\|з -f. \|з+)], где \р — комплексное скалярное поле, С — дей-
ствительная постоянная, а 3?о (яр, i)+) принимается инвариантным
относительно фазового преобразования
г|) ->е!'егр. F.3.1)
Если Э бесконечно мало, то справедливо равенство
9б°гр = Щ. F.3.2)
Предполагается, что введенный выше лагранжиан совместим
с каноническим формализмом.
Изменение лагранжиана за счет фазового преобразования
F.3.1), когда 6 бесконечно мало, равно
Q827 = С9х, F.3.3)
где х = 1-(ф_ tpt). F.3.4а)
200 Глава 6
При вычислениях мы воспользуемся также вещественным полем </>,
определяемым с помощью соотношения
ф = ф + г|>+. F.3.46)
Если мы рассматриваем системы при конечной температуре,
то для описания используем термополевой дублет_г|:а (%а и </>а),
определяемый следующим образом: гр1 = г|з и 42 = ^+- Поскольку
термополевой дублет для лагранжиана S определяется как пара
i?1 = 2', i?2 = i?+ = i?, полный лагранжиан имеет вид
^ = 2 еа^а, F.3.5)
а
где еа = 1 для а -= 1 и га = —1 для а = 2. Тогда можно напи-
сать
^=2еаB;о+СЛ- F-3.6)
а
Так как (е'е)+ = <°'е, фазовое преобразование термополевого
дублета г|а имеет вид
у* -+ е^а, F.3.7)
и бесконечно малым преобразованием его можно привести к виду
= Ща. F.3.8)
Таким образом, изменение полного лагранжиана при этом преоб-
разовании составляет
= е 2 гас%а. F.3.9)
а
Теперь соотношение УТ F.1 28), в котором г|з обозначает г|)а,
а Ь9? обозначает 6S7, дает
/Й@, р|в«Ц)«(дг)|О, p> = Jd*y(O, pITie^fe), rW]|0, P), F.3.10)
tft@, Р|6Ч-«+(дс)|0, p) = J>0(O, р| Г [6^ (у), Г+(*)]|0, Р>.
F.3.11)
Эти соотношения преобразуются к виду
-Й @, Р | Г W 10, Р) = С S j ^ @. РI ^ 1е°Х° (У)- Г W1 I 0. Р).
F.3.12)
Й @, р | Г+ W10, Р> = С 2 J ^ @, р | Т [eV (У), Г+ W] 10, р).
F.3.13)
Инвариантность и нётеровский ток 201
Таким образом, имеем
V^t^-^ctyeVte-x), F.3.14)
где к" = @, Р|</>а|0, Р), F.3.15)
Л«р (х - у) = @, Р|Т [%а (х), х3 (у)] 10, р). F.3.16)
Если использовать фурье-представление
Af (х - у) = -^L- J dtp exp [ip (х - г/)] Аяр (р), F.3.17)
то соотношение УТ F.3.14) принимает вид
va = — -jL 2 еаАда @). F.3.18)
Спектральное представление Дар (/?) выражается равенством
D.3.24), где FA = 0, т. е.
Л (р) = | dwa (w, р) (/в И х[р0 — w + 1'бт]-1 (/в (да); F.3.19)
-оо
здесь а (ш, р) — спектральная функция. Это приводит к выра-
жению
Л@) = - jdwo(w, 0)UB(w)r
= —9> ^dw-^-a(w, 0)т —ш J daya (ay, 0) 8 (ш) [(/в (оу)]2, F.3.20)
-оо ~оо
где использованы формулы
w — (от w
и Uв (до) %U'в (до) = т- Поскольку
V в17 [{/в HlL = gpl~1 *° Для « = 1, 2, F.3.22)
с
получаем
оо
V е-'Л'7'2 @) = —& f day -^- а (до, 0) для а ¦•= 1, 2. F.3.23)
202 Глава 6
Таким образом, соотношение УТ F.3.18) приводит к следующему
правилу сумм:
оо
0*=-?-0» [dw — a(w, 0) для а=1, 2, F.3.24)
— оо
где va не зависит от а; у1 = у2.
Соотношение УТ F.1.28) позволяет получить много других
соотношений для многоточечных функций. Эти соотношения удоб-
нее выразить в терминах вещественных полей хаи ра (= фа — и"'),
чем в терминах tya. Преобразование F.3.8) дает
8Yl = —(vri + pa), F.3.25а)
б>« ---. ха. F.3.256)
Заменяя ij; на %аили ра в соотношении F.1.28), можно, например,
получить
т (о, р | т [б°ха (х), рр (у)] |о, р> + ш(о, р| Tir(x), б^рр (у)] | о, р>-
(г), х» (х), рР (г/)] 10, |3). F.3.26)
Если использовать уравнение F.3.9) и F.3.25), то это соотноше-
ние примет вид
@, р |Т[р« (х), РР (г/)]|0, р) -@, р|Пха W, Хр (У)]|О, Р) =
, р), F.3.27)
откуда получаем соотношение между двухточечными и трехточеч-
ными функциями. Другие соотношения можно получить с по-
мощью аналогичной процедуры.
6.4. Пример петлевого разложения;
ферромагнетизм зонных электронов
Методы аппроксимации и соотношения Уорда—Такахаши.
R конкретных расчетах в физике обычно приходится использовать
некоторые приближения. Затем мы пытаемся улучшить ситуацию,
заменяя некоторые теоретические параметры их эксперименталь-
ными значениями. Например, мы часто заменяем перенормирован-
ные константы связи их экспериментальными значениями. Чтобы
сделать это согласованным образом, нельзя нарушать некоторые
важные соотношения. Поскольку упорядоченные состояния вы-
текают из определенной симметричной структуры лагранжиана,
наши приближенные методы не должны нарушать соотношения
УТ, так как последние являются проявлением этой симметрии.
Таким образом, основной стратегический план таков: сначала
Инвариантность и нётеровский ток 203
получаем соотношения УТ из соображений симметрии, связанной
с рассматриваемым упорядоченным состоянием. Затем в рамках
этих соотношений УТ вводим аппроксимацию.
Задавая соотношения между и-ия + 1-точечными функциями,
соотношения УТ F.1.28) приводят к определенным равенствам,
связывающим различные многоточечные вершинные функции (или
константы связи). Это означает, что, согласно нашему предполо-
жению, многоточечные константы связи одного порядка величины
и, следовательно, простые приближения, основанные на учете
возмущений, не всегда удовлетворяют соотношениям УТ. Соотно-
шение УТ F.1.28) показывает, что внешние линии, связанные
с Ь3? (х), вследствие интегрирования по d4x соответствуют энергии
Рис. 6.1.
импульсу, равному нулю. Назовем эти внешние линии с нулевым
энергией-импульсом б^-линиями. Соотношение УТ F.1.28) пока-
зывает, что если бй'-линии убрать из правой части соотношения
F.1.28), то останется лишь левая часть. Поскольку внешние
линии не участвуют в петлевой структуре n-точечной функции,
можно ожидать, что при классификации фейнмановских диаграмм
с помощью структуры их петель этот способ классификации может
привести к приближенным методам, согласующимся с соотноше-
ниями УТ. Убрав бй'-линию, мы можем изменить тип вершины
или внутренние линии, но топологическая структура и количество
петель при этом не меняются (рис. 6.1). Если фрагменты (вершины,
пропагаторы) фейнмановских диаграмм удовлетворяют соотно-
шениям УТ, то им удовлетворяет и полная диаграмма. Следова-
тельно, метод аппроксимации выглядит следующим образом:
сначала нужно так определить пропагаторы и константы связи,
чтобы они удовлетворяли соотношениям УТ, а затем отобрать все
фейнмановские диаграммы с одинаковым количеством петель.
Этот приближенный метод называется методом разложения по
петлям (петлевого разложения). Чтобы определить количество
петель, нужно сосчитать их всеми различными способами. Если
учесть все фейнмановские диаграммы вплоть до n-петлевых, то
204 Глава 6
в петлевом разложении возникнет член, отвечающий и-петлевому
приближению. Наиболее трудоемкая часть метода состоит в том,
чтобы выработать согласованную процедуру перенормировки;
каждый перенормированный контрчлен должен быть суммой
в петлевом разложении. За исключением этой процедуры перенор-
мировки, метод петлевого разложения является совершенно яс-
ным. Но поскольку метод петлевого разложения основан на фейн-
мановских диаграммах, он не может быть непосредственно при-
менен к ситуациям, когда имеются связанные состояния. Это
ограничение метода довольно существенно, если мы хотим при-
менить его к проблемам физики твердого тела, поскольку коллек-
тивные моды (такие, как фононы, магноны и т. д.) часто оказы-
ваются связанными состояниями. Хотя правило образования
петлевого разложения предполагает, что соответствующим обра-
зом определенные пропагаторы связанных состояний должны
быть включены в качестве внутренних линий диаграммы, сама
структура этих пропагаторов зависит от приближения. Следова-
тельно, и в данном случае требуется самосогласованное рассмо-
трение образования связанного состояния. Мы продемонстрируем
возможности метода петлевого разложения в случае систем со
связанными состояниями на примере ферромагнетизма зонных
электронов.
Спиновая симметрия. Лагранжиан имеет вид 2 Щ (х), ^+ (х)],
где гр (л:) — гейзенберговское поле электрона:
/ гЬ| (х) \
* <*> = и! <*)) ¦ F.4.D
Лагранжиан инвариантен относительно поворота спина:
г|> (х) ->i|/ (х) = ехр {»е-о/2}г|> (х). F.4.2)
Когда в бесконечно мало, 8°4> (х) становится вектором; обозначим
его 6°г|) (х):
Щ (х) = i (<т/2)г|) (х). F.4.3)
Полный лагранжиан равен
§'- = 2-2, F.4.4)
где лагранжиан 2 инвариантен относительно поворота спина,
примененного к полю, тильда-сопряженному по отношению
к F.4.2):
$ (х) -+tp (х) = ехр {—М-о* 12} $ (х), F.4.5)
где ¦=(*!)• FА6)
Инвариантность и нётеровский ток 205
Таким образом, имеем
6°ф (д) = —i (o*/2) tp (дс), F.4.7)
откуда следует
6<У (х) = —iijj< (x) а/2. F.4.8)
Здесь ар' означает транспонирование в пространстве спинов:
1>< = (г|)Ь %). F-4.9)
Следуя обозначениям гл. 4, используем символику термополе-
вых дублетов. Поскольку 3?^ = ?, выражение F.4.4) можно
переписать в виде
& = %га2?п. F.4.10)
ее
Выражения F.4.3) и F.4.8) можно объединить:
ща (х) = j (a/2) ^а (х) F.4.11)
Мы также используем спиновые операторы, определяемые следую-
щим образом:
а± (х) = гр+ (х) ст±г|5 (х), F.4.12)
а8 W = о|з+(дс) (т8ф (дс), F.4.13)
где а± определяется выражением
0± = —@1 ± «ст2). F.4.14)
Их термополевые дублеты имеют вид
а± (*) = Рг, [фа+ (х) а±-ф"х (х)] = 8а4"+ (*) а±г|)а (>;), F.4.15)
<тз (х) = Ра [^+ W о^п (х)] = еаЦ)а+ (х) 03\ра (х). F.4.16)
Чтобы определить направление намагничивания, введем малое
внешнее магнитное поле е, которое добавляет к прежнему лагран-
жиану член
&*(x)=%*a&Z(x), F.4.17)
а
ГДе 2t(A) = eaf(*). F.4.18)
Переход к пределу е -> 0 должен быть выполнен в конце вы-
числений.
Соотношения Уорда—Такахаши для спиновой симметрии.
Изменение лагранжиана вследствие поворота спина получается
из выражения F.4.11) и имеет вид
F.4.19)
a
где f>Sa = 6^ea (x) = 4- «Pa l^" [a3, о] гра1. F.4.20)
206 Глава 6
Таким образом, имеем
a (х) = -L (б, ± »б2) &а (х) = F.4.21)
(*), F.4.22)
a (х) = 0. F.4.23)
Из выражения F.4.19) получаем
Ь±§ (х) = ±ie ? eVi (x). F.4.24)
а
Теперь соотношение УТ F.1.28), в котором \)з обозначает^™
и г|)а+, а б^ обозначает ЬЗБ', можно переписать в виде
@,
= ± \ е J dV J] @, р | Т [eV± (у) г|? (х,) ^f-+ (х2)] | 0, р), F.4.25)
где 8°г|)а1- определяется выражением
6°±^at = 4" (б? ± /6§) ^at = F.4.26)
= — t4pf (a±/2). F.4.27)
Умножая обе части соотношения F.4.25) на ea (aT)S'S и полагая
х1 = х2 = х и a = р, получаем
@, Р | с? (х) | 0, р> = -L 2е j d4«/ J] @, р | Г [eVL (у) аа± (х)] 10, р).
F.4.28)
Аналогично можно получить любое соотношение УТ для много-
точечных функций. В дальнейшем мы используем обозначения
= @, Р|Т[Л]|0, Р), F.4.29)
(A) = lim@, Р|Г[Л]|О, Р). F.4.30)
0
8->-0
Соотношения УТ приводят нас ко многим утверждениям, которые
включают вид энергетического спектра и ряд соотношений между
Инвариантность и нётеровский ток 207
константами связи. Мы приведем некоторые соотношения УТ,
которые в дальнейшем будут использованы:
<1>? (х) № {у)\ - fo? (х) г|>?+ (У)% =
= - -i-2e \й*г^гр(ор+(г)^(хLЧу))г= F-4.31)
р
= - -L 2е J dAz 2 ер (^ (х) г|>?+ (у) ар (z)>e, F.4.32)
р
<^-(дг) Ч>?+ (У) а! (г)>в - (^ (х) ф?+ (у) a3v (г)>е =
= -^-2е |^2еР<а'^)Ф?МФ?+(У)^(г)>в, F.4.33)
р
<^ (х) 4f (У) °У- (г)% + <^" (х) ^ (У) ol (г))Ё =
=т2е Jd^ 2еР <стР+ (Ю *"(х) ^^+ Сг/) ст! (г)>Е> F-4-34)
р
<ф? (х) # (у) а! (г)>8 - D4 (дг) ^?f (у) а| (г)>Ё =
= - -L 2e j dAl J] ер <аТ (г) ф? (х) ^?+ (у) ар. A))г, F.4.35)
р
" (У) «г? (г))8 + (^ (х) ф5+ (у) Л (z)>6 =
= Т 2е J ^ 2 еР <а1& tf W ^+ (У) <* E)>е- F-4.36)
5+ : *
- : *
Рис. 6.2.
Используем фурье-представление двухточечных функций (рис.6.2):
{\$ (х) \^+ (г/)) = J1 .4 [ d4/? exp [ip (x — у)] 5+р (/?), F.4.37)
<Чч (*) фГ (у)) = 72^" Idip exp [t/? (Л: ~ у)] 5-Р (р)> F-4-38)
(а? (х) а? (г/)) = -A- J d4p exp [t> (дг - у)] Af (p). F.4.39)
208 Глава 6
Поскольку последующие вычисления довольно запутанны, полезно
помнить, что 5 и А обозначают фермионные и бозонные двух-
точечные функций соответственно, а индексы «-|-» и «—» при 5
обозначают спин, направленный вверх и вниз соответственно.
Существование магнона. Докажем теперь, что, когда в пределе
е -> 0 намагниченность не исчезает, т. е.
lim Мг ф 0, F.4.40)
из соотношения УТ F.4.28) следует существование магнона. Здесь
Ms е= @, р | <т" (*) 10, Р). F.4.41)
Если учесть выражение F.4.39), то соотношение УТ F.4.28)
принимает вид
Мг = —2е U ерД|а @). F.4.42)
Спектральное представление A% (p) задается соотношением
D.3.24), где FA = 0:
оо
Дв (р) = J dwaB (w, p) UB (w) х[р0 — w + i бт] UB (w). F.4.43)
-оо
Используя D.1.88) и соотношение
ер [Uв И UI (w)]pa = j^~| -* 0, F.4.44)
можем переписать F.4.42) в виде
ME = E^\dw~aB(w, 0). F.4.45)
Здесь использована формула
j I
Рй — w ± i& р0 — w °
Спектральная функция ав (w, p) может быть представлена
в виде
Ов (ЙУ Р) == У (Р) н 0"^ 1^> Р) j ^О.тс.4 / )
где 0в (ш, р) — часть, которая определяется условием
Нт<&(ш, р) - 0. F.4.48)
ш->-0
р-0
Заметим, что, когда х (р) ^ 0, существуют стабильный или неста-
бильный бозоны; стабильная частица отвечает случаю, когда
у (р) = 0, т. е. первый член в F.4.47) равен % (р) б (w — со^ — аг).
Инвариантность и нётеровский ток 209
В выражении F.4.47) аг — сдвиг энергии бозона, обусловленный
внешним :магнитным полем. Подставляя выражение F.4.48)
в F.4.45) и переходя к пределу при е -> 0, получаем
X (Р) Ф 0, У (р) = 0, coJ; = 0 при р = 0, F.4.49)
так как правая часть равенства F.4.45) не обращается в нуль
при переходе к пределу при е ->• 0. Из F.4.49) следует
°в (w, 0) = х @) б (w — аг), F.4.50)
а это вместе с F.4.45) дает
= -?-Х@). F.4.51)
Таким образом, мы делаем вывод, что существует бозон, стабиль-
ный при р = 0, который возникает в ст± (лт)-каналах. Этот бозон
называется магноном. Функция Ав (р) называется двухточечной
функцией магнона. Согласно F.4.49), энергия магнона юр равна
нулю при равном нулю импульсе. Другими словами, энергетиче-
ский спектр магнона не содержит щели. При ненулевом импульсе
энергия магнона имеет конечную ширину, обусловленную темпе-
ратурными флуктуациями. Чтобы найти величину а в выражении
F.4.51), вспомним, что интеграл по пространству от величины
A/й) а3 (х) есть генератор поворотов вокруг третьей оси. По-
скольку этот генератор не зависит от времени, имеем
\d3x[a3 (х), ст.. (у)_] = 2/гст_ (у). F.4.52)
Сравнивая с каноническим уравнением
\Н, а_(у)] = -^-а_(у), F.4.53)
мы видим, что собственная энергетическая функция, обусловлен-
ная дополнительным членом в гамильтониане взаимодействия
—га3 (х), равна 2е. Поскольку сдвиг энергии магнона равен еа,
находим, что а -^ 2. Таким образом, соотношение F.4.51) можно
переписать в виде
X @) = М. F.4.54)
Выписанное соотношение показывает, что интенсивность вызван-
ного спиновыми волнами неупругого рассеяния нейтронов вперед
равна объемной намагниченности.
Заметим, что нет таких соотношений УТ, которые требовали
бы существования бесщелевого бозона в а3-канале.
210
Глава 6
Соотношения УТ для вершин. Чтобы получить соотношения УТ
F.4.31)—F.4.36) в простой форме, введем вершинные функции Г
с помощью следующих соотношений (рис. 6.3):
X [SaJ (p + q) t?Sf (p) + S™ (р + д) Fa.bc (p + д, p, q) S? (р) Д? (q)],
F.4.55а)
X
Г (p) г^} (/
S? (p) Mc (q) Yt (p,q;p^q) Sf (p + q)].
F.4.556)
z,y
z,y
z'y
* +
x, a
Рис. 6.З.
Если диаграмму нельзя разделить на две части путем раз-
резания только одной внутренней линии, она называется соб-
ственной диаграммой. Первый член в правой части F.4.55) не-
собственный, а второй собственный.
Аналогично можно получить (рис. 6.4)
(al (г) \|з™ (х) \|3|+ (у) а. (?))е = (\|з" (х) ^ (г)N е7 (\$ (г) \|)J (|)N ер X
+ [ d*?, f d% (tf (x) ^f (?,) ст?(г))? [5:1 (Si - S2)]Px X
X <^j (?2) ^f+ (У) °- (i))e <°+ (г) ^t W ^t+ (У) °P- (D>e » F.4.56)
Инвариантность и нётеровский ток
211
где верхний индекс р обозначает собственную часть, имеющую вид
(ol (z) itf (х) tf*(y) ap. (l))ps = (-^тK J <*Vi d^2 Ai Л2 6 (Pl + </, -
— />a — <7г)
x ST fa) Af Ы Tfcd (/>,?,; p2<72) 5*3 (p2) Л^р (^). F.4.57)
Если учесть соотношения F.4.28), F.4.31), F.4.41), то получим
X ^?f (У) °Ч (Z)>e = M <tf
х
+ lim
2e
f d% V
J V
X
X^(y)^-iz)% E-4.58)
Таким образом, соотношение УТ
F.4.34) вместе с выражением
F.4.55а) дает
X
F.4.59)
Рис. 6.4.
где многоточие" обозначает члены,
которые^не' содержат никаких маг-
нонов, связанных с точкой г. Подставим теперь выражения
F.4.55а) и F.4.57) в уравнение F.4.59) и рассмотрим случай,
когда четыре-вектор энергии-импульса магнона, связанный с a_(z)
в выражении F.4.59), равен нулю. Это приводит к появлению
множителя A/е) в первых членах правой части уравнения F.4.59).
21? Глава 6
Тогда члены, обозначенные многоточием, можно не учитывать,
и мы получаем
Г$(р; р, 0) = -М Ц T**d(p, 0; р, 0).
С
Аналогично можно определить вершинную часть Г_^:
= (le^T J ^ ^ ^ d^6 0»i + ft - Р2 - Я*) X
X exp W (^z + p-iX — p2y - q.?)] X
X 5!" (Pl) Mc (<?,) \tbcd (pxqx; P2^/2) Slp (/?•>) A^p (<?2). F.4.60)
Наконец, соотношения УТ F.4.33)—F.4.36) в пределе е -> 0
приводят к следующим равенствам:
ТаЛ{р; р, О) = -ЛГ 2 Г&О*. 0; р, 0)= F.4.61)
= МЪЛ{р, 0; /,, 0), F.4.62)
T?d (р, 0; /?) = -М 2 Г^с 0», 0; /?, 0) = F.4.63)
= МЯТ*Цс{р, 0; /7, 0). F.4.64)
с
С другой стороны, переходя к пределу при е ->• 0 в соотноше-
ниях УТ F.4.31) и F.4.32) и учитывая равенства F.4.55) и F.4.42),
находим
s:lap о?) - s;lap (/?) = м 2] r^f (p, o; /?) = F.4.65)
с
= MUr?f(/j; p, 0). F.4.66)
с
Соотношения F.4.61)—F.4.66) являются соотношениями УТ, ко-
торые используются в дальнейшем изложении.
Написанные выше соотношения УТ становятся чрезвычайно
простыми при р — 0. Чтобы показать это, начнем со спектраль-
ного представления D.3.23):
оо
S± (р) = \dws± (алр) U И [р0 — w + tSx]-1 [/+ (а;). F.4.67)
-оо
При р0 = 0 оно принимает вид
|Ро=о = ~9> \ dws± (w, р) -1- бар + /л5± @, р) ( ° 1) ,
F.4.68)
Инвариантность и нётеровский ток 213
откуда получаем
sT* (р) I Ро=о = - -r4st k (dws± &• р) -ir б«р +
ш±@, р)(л 0) , F.4.69)
Г I2
где К(р)=Ь> ^dws±(w, p)-!- + n2[s±@, p)]2. F.4.70)
L _оо -J
Из этого выражения видно, что диагональные элементы S +1 @)
вещественны, а недиагональные — мнимые. Поэтому из соотно-
шений УТ F.4.65) и F.4.66) при р = 0 следует, что вершинные
части могут быть параметризованы следующим образом:
.-, о { —S для а = Р,
?Г«рс@, 0, 0)= 1 , ^„ F.4.71)
с ( —2wb2 для а Ф Р;
кроме того,
: -4- -о- ffAf для а = Р,
- 2 S F.4.72)
' [^1 Z^ &2^] ДЛЯ аФ$-
Параметры |i2, §•, bx и &2 вещественны и определяются значе-
ниями s± (ш, 0).
Из соотношений УТ F.4.61)—F.4.64) и равенства F.4.71)
получаем
__ - ( -л-glM для а = Р,
), 0; 0, 0)= *. , ... , я F.4.73)
7 ' ' г>-"и 1М для а Ф р.
Мнимые части равенств F.4.71)—F.4.73) появились вследствие
конечной температуры. Поэтому можно ожидать, что Ьх и Ь2 при
низких температурах малы.
Двухточечные функции магнонов и энергия магнонов. Обра-
тим теперь внимание на энергию магнонов сор. При рассмотрении
будем использовать формулу
<ст? (х) а? (у)) = lim <еа ^+ (х + б) ^ (х - б) а! (у)), F.4.74)
6-S-+0
214
Глава 6
которая вместе с F.4.55а) приводит к выражению (рис. 6.5)
Л*Р(я) = - |^Р{р + i)е^а("
X
X
ST (р-±.)А<? (q). F.4.75)
Из формулы F.4.74) видно, что путь интегрирования С по пере-
менной р0 есть полуокружность в верхней полуплоскости ком-
Рис. 6.5.
плексной переменной р0. Выражение F.4.75) определяет Дв (q).
Умножая обе части F.4.75) на А Ъ1 (q) и оставляя только члены,
соответствующие магнонным резонансам, получаем
-1П
бар = Re
BяL
\-t p-\, q)
X
X
F-4-76)
Это выражение определяет энергию магнонов
УравнениеТейзенберга. Приведенное выше рассмотрение при-
менимо к любому лагранжиану, инвариантному относительно
вращений спина. Однако, чтобы сформулировать петлевое при-
ближение, необходимы уравнения Гейзенберга. Здесь мы исполь-
зуем модель параболической зоны с контактным взаимодействием:
(х) = t
±
F-4.77)
Инвариантность и нётеровский ток 215
где суммирование ведется по спиновым индексам s и s'. Энергия
е (к2) равна
^Гк2-^2, F-4.78)
где jj,2 — химический потенциал. Уравнения Гейзенберга можно
записать в виде
(« -J- - е (v2)) ^ (x) = Ц*- (х) 4V (х) Ь (х). F.4.79)
Поскольку член Aa^iJv^s в F.4.79) соответствует собственной энер-
гии A,(i[\r\|v)) перепишем уравнение F.4.79) в виде
1~д1-~е (V2) - *л-) ^ (х) = Ц\ (х) ф+ (х) Щ (х) - Xrt-^t (х) и т. д.,
где и_ = (\|з| (л:) 1|з+ (л:)). При этом уравнения Гейзенберга при-
нимают вид
Л+ (д) $ (х) = -КРаа- (х) г|ч (х) - Ы.$ (х), F.4.80а)
Л_ (д) $ (х) = -^ЯРаст^ (х) ^t (x) - Хп+^ (х), F.4.806)
где A±(<5) = i^--e(v2)-X/iTl F.4.81)
п. = <ф1 (х) ^ (х)) = <^J (х) ^ (х)), F.4.82)
«+ = <Ч>| (дг) ^t (дг)> = <*| (дг) *t (х)) F.4.83)
и имеется соотношение
М = я+-п_. F.4.84)
Вывод уравнений Дайсона. Уравнение Гейзенберга F.4.80)
приводит к равенству
(х - у) б«р - К {Раоа: (х) $ (х) tf* (у)) - Хп. {^ (х) р? )</)>•
F.4.85)
Если использовать выражение F.4.55а), то получим (рис. 6.6)
{Р + А) Г
где Л+ (р) определяется выражением
Л+ (р)е'р* = Л+ E) ёР*. ' F.4.87)
216 Глава 6
Из F.4.86) следует
S;lap (р) = Л+ (р) б«э + -$$- J d4kS*a (p + Л) Г?ср (р + к; р, к) А%а (к).
F.4.88)
Аналогично можно получить
SI (р) = Л- (р) б«р + '2j^4 f d4kSi" (p — к) Авс (к) Г+с (р—к, к; р).
F.4.89)
к
Вторые члены в выражениях F.4.88) и F.4.89) соответствуют
собственной энергии, возникающей за счет электрон-магнонного
спаривания.
Если подействовать оператором Л+ (д) на (lp™ (х) щ* (у) a9, (z))
и (ip'f (х) щ+(у) a9-(z)) и собрать только собственные части ди-
аграмм, то получим уравнения для вершин (рис. 6.7)
^ q; p, <7) = -Л6ар8ар~
J d4kST (p + <7 - к) А%с (к) Va+!P (p + q-k, k; p, q), F.4.90)
, q; p + q) = -ЯбаЭбар -
- Jd4/fe5?a (^ + *) ^ <*) г-рс ^ + *• ^; ^ +1' ft>- F-4-91)
Уравнения F.4.88)—F.4.91) называются уравнениями Дайсона.
Заметим, что эти уравнения нельзя получить по теории возмуще-
ний, поскольку они содержат магнон, который представляет
собой связанное состояние электронов.
Основные соотношения для однопетлевого приближения. До
сих пор не делалось никаких приближений. Теперь мы введем
однопетлевую аппроксимацию, в которой все параметры пере-
нормированы,
Инвариантность и нетеровский ток
217
Как показывают уравнения F.4.90) и F.4.91), в первом при-
ближении вершинная часть Г+р равна —Я-барбар. Поскольку мы
используем только перенормированные параметры, нужно за-
менить X на перенормированное значение %г. Тогда из соотноше-
Р+Ч
р+к
Рис. 6.7.
ния F.4.71) следует, что %т = g. Таким образом, в однопетлевом
приближении всякий раз, когда в однопетлевых членах появляется
Г^-р, его следует заменять приближенным значением
Г±р(/?, q\ р + q) «=< — gba$ap-
Аналогично Г+ы заменяется приближенным значением к^
Тогда из равенства F.4.73) следует
±cd ~- _ jh
F.4.92)
F.4.93)
Подсчитаем теперь S±lap и Г+Рр с помощью соотношений F.4.88)—
F.4.93). Здесь мы воспользуемся правилом Дайсона для пере-
218
Глава 6
нормировки перекрывающихся расходимостей, которое требует
замены множителя X перед интегралами F.4.88)—F.4.91) на g,
а также симметризации в случае появления двух вершин, если
константы связи в Г в этих интегралах заменены их перенорми-
рованными значениями (рис. 6.8). Это правило получено из рас-
смотрения структуры фейнмановских диаграмм. Теперь мы полу-
чаем
(k), F.4.94)
Bл)*
= —Ябарбар —
ь я; р
о2
я) =
F.4.95)
-Bя)« м\*к № (Р + Ч-Ъ А^ W 6Рр -
- S^(p + k) Af (k) бар]. F.4.96)
p+q p+q-k
Важно заметить, что равенства"F.4.94)—F.4.96) удовлетворяют
соотношениям УТ F.4.65) и F.4.66), что означает внутреннюю
согласованность расчетов.
Из соотношений F.4.71) и F.4.96) следует
j d'k [ST (-k) AT (k) - 6«a (k) AT (k)], F.4.97)
М
где не проводится суммирование по а. Далее соотношения F.4.72)
и F.4.94) дают
+ Sa.a(k)AaBa(k)}, F.4.98)
Инвариантность и нётеровский ток 219
где также не проводится суммирование по а. Из соотношений
F.4.72), F.4.94) следует также равенство
(k) = J ctkS22 (+k) Af (k), F.4.99)
причем эти величины вещественны. Эти условия могут быть
подтверждены прямыми вычислениями.
Исключая неперенормированные константы [х2 и Я из выражений
F.4.94)—F.4.96) с помощью соотношений F.4.97) и F.4.98),
получаем
(р) = Л± (р) б,р - -Д. g j (
^^\ F.4.100)
>, д; р + д) =-gSafi8ap-
F.4.101)
где Л±(/;)==/;о---!^Р2 + И2±-^М- F.4.102)
Эти соотношения приводят к следующим простым соотношениям
между S+ и Г±:
~2~) °Рр ~ *-*+ ^—Т/ ар~
) F.4.103)
Заметим, что, как и следовало ожидать, они согласуются с соот-
ношением УТ F.4.66).
Воспользовавшись соотношениями F.4.103) и F.4.75), вычис-
лим теперь двухточечную функцию магнонов в однопетлевом
приближении. Подставив F.4.103) в соотношение F.4.75), найдем
D (q) As' (q) =-%¦№ (Я) qo-N (q) т], F.4.104)
220 Глава 6
где D (q) и N (q) — следующие матрицы размерности 2x2:
°а" (?) = W J d^s-" (p +1) ^ ("-+)• <6А105>
F.4.106)
Уравнение F.4.104) определяет Ав:
Ад(?) = Л*т „„^^ • F-4.107)
Энергия магнона a)q определяется уравнением
q0 - D'1 (q) N (д) = 0 для q0 = со,. F.4.108)
Теперь можно определить однопетлевое приближение следующим
образом. Члены однопетлевого разложения получаются интегри-
рованием основных соотношений F.4.97), F.4.100)—F.4.102),
F.4.107) и F.4.108). В этих интегралах мы пользуемся прибли-
женным равенством
F.4.109)
F.4.110)
где учтено, что химический потенциал Д2 равен энергии Ферми
гр = ЬШ2т. В этом приближении найдем Ав (q) с помощью
соотношения F.4.107). Результат получается тот же, что и в при-
ближении случайных фаз, когда все параметры заменены их
перенормированными значениями. Подставляя это приближенное
значение Ав и выражение F.4.110) для S+P (р) в интегралы,
входящие в F.4.100), F.4.101), получим S*P (p) и Г^ в одно-
петлевом приближении. Перенормированная константа связи g
находится из выражения F.4.97).
Намагниченность системы определяется формулой
c?pf[sr{p)-S™{p)\, F.4.111)
с
где суммирование по а не производится. Здесь путь интегрирова-
ния С по переменной р0 есть полуокружность в верхней полу-
плоскости комплексного переменного р0. Если воспользоваться
спектральным представлением F.4.67) для S± (p), то формула
F.4.111) принимает вид
М = -JL_ J cPp J dw [&, (w, p) - s_ (w, p)] /, (w). F.4.112)
Конкретные расчеты значительно упрощаются, если исполь-
зовать спектральное представление для S± и Ав и правила для
произведений, приведенные в гл. 4.
Инвариантность и нётеровский ток 221
Последовательное улучшение петлевого приближения. Теперь
очевидно, как усовершенствовать приближение. Начав с выраже-
ний для S± (р) и Г±р, полученных выше, мы вычисляем по фор-
муле F.4.75) уточненное значение Лв, а затем проводим более
точное вычисление величин S± и Г^Гр по формулам F.4.88) —
F.4.91).
Конкретные вычисления и приложения. Были проведены рас-
четы в однопетлевом приближении при нулевой температуре [6].
Было обнаружено, что функция магнонов имеет вид
где многоточием обозначены члены, в которых нет магнонного
полюса.
При малых q энергия магнона пропорциональна q2. Когда | q|
превышает критическое значение, скажем qc, a)q совпадает с элек-
трон-электронной или электрон-дырочной энергией и магнон
становится нестабильным. Эта область называется стонеровским
континуумом. На рис. 6.9 представлена область, где спектральная
функция а в не равна нулю (рис. 6.9, а для случая ? < 1, рис. 6.9, б
для случая ? > 1). Параметр ? определяется выражением
I = gMl&F. F.4.114)
Поведение энергии магнонов aq представлено на рис. 6.10.
В точке окончания сплошной линии спектр магнонов переходит
в стонеровский континуум. Магнонный полюс сохраняется и после
перехода спектра в область стонеровского континуума, но уже
в виде резонанса. Штриховая линия на рис. 6.10 приблизительно
соответствует положению резонанса. Неустойчивость этого состоя-
ния (и, следовательно, мнимая часть энергии магнонов у (/?))
быстро возрастает при удалении резонанса в глубь стонеровского
континуума.
На рис. 6.11 показана зависимость спектральной функции от
&д = Hq2/2m. Здесь в качестве единицы энергии использована
величина гр: eq = гч/гр. Вклад реального, т. е. стабильного,
магнона показан в виде б-функциональных всплесков, высота кото-
рых определяется величиной формфактора F(q2). На рис. 6.11
заметен острый пик в области стонеровского континуума. Даже
если &q настолько велико, что магнон становится нестабильным,
этот пик сохраняется, что отражает существование магнонного
резонанса. На рис. 6.12 показано положение такого пика спек-
тральной функции бозонов; штрихпунктирная линия и штрихпун-
ктирная линия с двумя точками отмечают положения пика расчет-
ной кривой ов при постоянной энергии и постоянном импульсе
соответственно, а штриховая линия — результат расчета в резо-
222
Глава 6
нансном приближении. На рис. 6.12 видно, что с увеличением q
результаты расчета в резонансном приближении все сильнее отли-
чаются от результатов расчетов, показанных штрихпунктирной
линией. Отсюда следует, что резонансное приближение нельзя
Рис. 6.9.
использовать до тех пор, пока дебаевская экранировка не перекроет
полностью ту область, в которой магнон становится нестабильным.
Спектральную функцию ав можно экспериментально определить
при исследовании рассеяния нейтронов. Хотя формфактор магнона
F (q2) обращается в нуль на границе стонеровского континуума,
но этот континуум дает большой вклад вследствие резонансного
поведения спектральной функции. Сплошными линиями на
Инвариантность и нетеровскии ток
a
0,2
0,1
-
/
)
\
/
f
N
/
f
\
г
1
формфакгпор
1
1
1
1
\
\
\ , «г
0,8 1,6
Рис. 6.10.
¦1,0
¦0,5
*-?
о,8
Рис. 6.11.
224
Глава 6
рис. 6.12 показано теоретическое распределение интенсивности
функции ов. Это распределение очень похоже на экспериментально
наблюдаемое распределение [7]. Используя приведенные в дан-
ном разделе формулы, эти расчеты можно распространить на
конечные температуры.
Хотя в этом разделе наше внимание было сосредоточено на
ферромагнитной фазе, все соотношения УТ применимы также и
0,04 -
к парамагнитной фазе. В этом случае член в лагранжиане ?'е,
приводящий к нарушению симметрии (выражение F.4.17)), при
малом внешнем магнитном поле е также играет важную роль, так
как помогает установить некоторые важные соотношения между
функциями отклика [8]. В некотором приближении эти соотноше-
ния приводят к так называемому самосогласованному ренормали-
зационному методу Мория—Кавабаты [9], который использовался
для объяснения кюри-вейсовского поведения зонных электронов
и некоторых других явлений в парамагнитной фазе, образованной
спиновой системой зонных электронов.
ЛИТЕРАТУРА
1. Noether E., Goett. Nachr., 235 A918).
2. Ward J. С, Phys. Rev., 78, 182 A950).
3. Takahashi Y., Nuovo Cim., 6, 370 A957).
Инвариантность и нётероеский ток 225
4. Matsumoto #., Papastamaiiou N. J., Umezawa #., Nucl. Phys., B68, 236 A974);
B82, 45 A974).
5. Nakanishi N., Prog. Theor. Phys., 51, 1183 A974);
Takahashi Y., Phys. Rev., D15, 1589 A977).
6. Matsumoto H., Seki S., Tachiki M., Umezawa H., Phys. Rev., B17, 2276 A978).
7. Ishikawa Y., Shirane G., Tarvin J. A., Kohgi M., Phys. Rev., B16, 4956 A977);
Ishikawa Y., J. Magn. Mat., 14, 123 A979).
8. Whitehead J., Matsumoto H., Umezawa H., Phys. Rev., В A982).
9. Moriya Т., Kawabata A., 3. Phys. Soc. Jap., 34, 639 A973);
Moriya Т., J. Mag. Magn. Mat., 14, 123 A979).
ГЛАВА 7
ДИНАМИЧЕСКАЯ ПЕРЕСТРОЙКА СИММЕТРИИ
И ДИНАМИЧЕСКОЕ ОТОБРАЖЕНИЕ
7.1. Общее рассмотрение
Перестройка симметрии. В предыдущих разделах мы исполь-
зовали два языка: один основывался на гейзенберговских полях
(например, г|>), в терминах которых записаны основные уравнения,
а другой — на свободных физических полях (например, ср°),
с помощью которых построено пространство Фока. Переход от
одного языка к другому называется динамическим отображением и
обозначается символом г|> (х; <р°). Эта дуальная структура языка
квантовой теории поля приводит к чрезвычайно сложному меха-
низму проявления симметрии.
Предположим теперь, что уравнения Гейзенберга имеют форму,
инвариантную относительно непрерывного преобразования (пре-
образования с непрерывными параметрами):
Ч>-Ч>' = Q №). G.1.1)
Часто оказывается, чтоосновное состояние не имеет такой Q-сим-
метрии. Хорошо известный пример — кристалл, в котором про-
странственно-трансляционная симметрия нарушена за счет обра-
зования решеточной структуры, хотя уравнения Гейзенберга для
взаимодействующих полей молекул трансляционно инвариантны.
Другой классический пример — ферромагнетик, в котором нару-
шена спин-вращательная симметрия. Хотя это и не очевидно из
визуальных наблюдений структуры, сверхпроводимость представ-
ляет собой пример нарушения градиентной инвариантности. Эти
явления называются спонтанным нарушением симметрии [1, 2].
Важнейшей чертой этих явлений является то, что начальная Q-сим-
метрия не просто теряется, а при этом возникают определенные
структуры (упорядоченные состояния), такие, как кристаллические
решетки, системы поляризованных спинов в ферромагнетиках
и т. д. Естественно ожидать, что появление нового порядка есть
проявление исходной инвариантности. Здесь очень важно раз-
личать понятия «симметрия» и «инвариантность». Очевидно, что
инвариантность теории никогда не может исчезнуть. Но, поскольку
симметрия есть проявление инвариантной природы, форма сим-
метрии уравнений Гейзенберга может отличаться от форм симме-
трии наблюдаемых явлений. Это изменение проявления симметрии
называется динамической перестройкой симметрии [3].
Динамическая перестройка симметрии 227
Чтобы пояснить приведенную выше аргументацию, напомним,
что гейзенберговское полег|> (х) выражается через физическое поле
<р° (х) с помощью динамического отображения
у(х) =г(>(*; Ф°)- G-1-2)
Если динамическое отображение G.1.2) известно, линейная комби-
нация произведений г|> (например, F (г[з)) получается с помощью
умножения и дополнительных правил действий над матрицами
(т. е. операционного правила для преобразования произведений
нормальных произведений ср° в сумму нормальных произведений
тех же физических полей).
Зная динамическое отображение G.1.2), мы можем ввести
операцию, называемую подстановкой. Подстановка есть операция,
при которой в динамическом отображении ср° заменяется на функ-
ционалы от ф° (например, Ф (ср0)). Если матричные элементы
(а\^Ф(х)\Ь) = (а\^[х; Ф(Ф°)]|&> G.1.3)
хорошо определены1), то подстановка G.1.3) превращает г|э (х)
в новый оператор-фф (х), который действует на пространстве Фока
для <р°. Поэтому подстановка не изменяет пространство Гильберта.
Если Q-преобразованное гейзенберговское поле г|/ (х)
(=Q [i|>]) представляет собой сумму конечного числа произведе-
ний г|> (х), то г|/ (х) хорошо определено в пространстве Фока для
Ф°: его динамическое отображение имеет вид
У (х) =$' (х; ф°). G.1.4)
Поскольку г|> (х) иг|/ (х) удовлетворяют одному и тому же уравне-
нию Гейзенберга, существуют определенные соотношения, свя-
зывающие матричные элементы г|з с матричными элементами г|/.
Отсюда следует, что, по-видимому, можно сделать подстановку
Ф° ->¦ ф0', которая удовлетворяет условию
г|/ (х; ф°) = i|) (х; Ф0'). G.1.5)
1) Часто для определения г|)ф (х) требуется совершить некоторый предельный
переход. Простым примером является подстановка %° (х) —>%° (х) + 9 (9 — по-
стоянная, а х° — безмассовое физическое поле), примененная к члену вида
д2 (A/д2) : х° М2 '¦ )• Чтобы избежать трудностей, связанных с тем, что про-
цедура применения оператора A/д2) к константе бессмысленна, вспомним, что
| а) и | Ь) в выражении (а I г|>ф I Ь\ — состояния, соответствующие волновым
пакетам. Поскольку каждый оператор %° в нормальном произведении либо уни-
чтожает частицу в состоянии | Ь), либо рождает частицу в состоянии | а) и,
следовательно, эти состояния представляют собой состояния с определенными
волновыми пакетами, каждое поле %° (х) размазано за счет квадратично интегри-
руемой функции (функции волнового пакета), что следует учитывать при расчете
выражений типа (а | г|)ф I by Это приводит нас к следующей простой процедуре
определения указанной выше подстановки: сначала производится подстановка
Х°—*¦ Х° Ч~ 9 / (х), где f (x) пробегает бесконечный ряд квадратично интегрируе-
мых функций, приближаясь к единице, а затем выполняется переход к пределу
с помощью соотношения lim д2 (A/д2) р (х)) = 1.
228
Глава 7
Как будет показано в этом разделе, такая подстановка действи-
тельно существует, когда Q-преобразование непрерывно и имеет
вид F.1.4) или F.1.38). Преобразование ф° в <р0' мы будем называть
(/-преобразованием:
фо -+фо' = ^(фо). G.1.6)
Таким образом, имеем
Q 1^
G.1.7)
Следовательно, мы установили, что Q-симметрия переходит
в ^-симметрию (рис. 7.1).
¦f(X)
Рис. 7.1.
Спонтанное нарушение симметрии не означает потери инва-
риантности, оно лишь приводит к тому, что структура с Q-сим-
метрией отлична от структуры с ^-симметрией. В качестве примера
рассмотрим ферромагнетик. Q-симметрия есть спин-вращательная
симметрия трехпараметрической группы SU B). На первый
взгляд в ферромагнетиках имеется только однопараметрическая
симметрия, связанная с вращением вокруг направления спиновой
поляризации. Но две другие инвариантности не могут просто
исчезнуть. Тщательное изучение показывает, что ^-симметрия
в действительности является трехпараметрической симметрией,
хотя она и не относится к группе SU B). Мы вернемся к этому
вопросу в разд. 7.3.
Соотношение УТ для Q-симметрии. Теперь мы получим соот-
ношение, которое является основным инструментом при исследова-
нии перестройки симметрии. Чтобы это сделать, напомним чита-
телям разд. 6.1, в котором вводятся нётеровский ток и соотношение
УТ. Рассмотрим преобразование, отвечающее изменению ty на
величину б°г|з, определенную соотношением F.1.5). Изменение
лагранжиана ЬЗЁ определяется выражением F.1.9). Предположим,
что лагранжиан SB инвариантен относительно рассматриваемого
Динамическая перестройка симметрии 229
преобразования (т. е. Ь2? = 0). Добавим к нему бесконечно малый
эрмитов член [4]
2?г = гФ(х), G.1.8)
который нарушает инвариантность. В конце вычислений нужно
перейти к пределу при е, —>- 0. Если рассматривается случай
ферромагнетика, физический смысл члена 3?z можно интуитивно
понять. Чтобы в этом случае установилось направление намагни-
чивания, требуется чрезвычайно слабое магнитное поле (в этом
случае е — магнитное поле, а Ф (х) — магнитный момент). В целом
роль S?г (х) состоит в том, чтобы определить направление, в котором
нарушается симметрия. Ф (х) можно рассматривать как элемент,
осуществляющий определенное представление (Фх ... Ф/), группы
Q-симметрии. Для удобства мы выберем Ф = Ф/. В дальнейшем
будем считать, что поле Ф вещественное; если Ф; окажется ком-
плексным, перейдем к вещественным полям Ф = (Фг + Ф}).
Если рассматриваемое преобразование содержит п параметров
0; (i = 1, 2, ..., п), то существует п нётеровских генераторов Nt
(i = 1, 2, ...,п).
Согласно выражению F.1.9), Ь2? (х), полученное в результате
9Гпреобразования, определяется соотношением
вА& (х) = е {Ф' (*') - Ф (х)} + еО* (д%хх) Ф (х) =
= 8,е{6,Ф(х)-Нд*6,хI)Ф(*)Ь G.1.9)
из которого следует
(x) = 9ге j tfx {бгФ (х) - &гххд*Ф (х)\ =
*x6W>(x). G.1.10)
Здесь мы использовали определения 9гб;Ф (х) = Ф' (х1) — Ф (х)
и 9гб?Ф (х) = Ф' (х) —Ф(х) и соотношение F.1.7). Поскольку
QiNt (t) порождает преобразование Ф (х) -> Ф (х) + 0гб°Ф (х), из
соотношения F.1.21) находим
[Ф (х), Nt @] б (t - tx) = 1ПЬ (t - tx) б?Ф (х). G.1.11)
Заменяя г|> (xj в выражении F.1.28)"на б°Ф (х) и пользуясь
соотношением F.1.276), получаем соотношение УТ
in @18?8?Ф (х) | 0} = 8 j d*y @1Т {[б?Ф (у) - а], б^Ф (х)} \ 0), G.1.12)
где d = @1 б?Ф (х) 10). Тогда имеем
[6?Ф (х), N, @] б (/ - tx) = ШЬ (t - tx) ЬЩФ (х), G.1.13)
где использовано соотношение F.1.21).
230 Глава 7
Теорема Голдстоуна. Примем теперь, что для определенного
выбора (t, /) справедливо неравенство
Пт@|6?8?Ф(х)|0)#0. G.1.14)
е-»0
Тогда при интегрировании по d4«/ в соотношении G.1.12) должен
возникнуть член, пропорциональный 1/е, поскольку в спектраль-
ном представлении правой части выражения G.1.12) содержится
полюсная особенность, связанная с теми энергиями, величина
которых при нулевом импульсе порядка е (т. е. при е = 0 энерге-
тический спектр бесщелевой). Это приводит нас к теореме Голд-
стоуна [1, 2, 5], утверждающей, что если выполняется условие
G.1.14), то возникают физические бозоны с бесщелевым энергети-
ческим спектром. Обозначим эти бозоны %? (х) (i = 1, 2, ..., т.).
Эти бозоны называются голдстоуновскими. Без потери общности
мы можем так выбрать эти бозоны, чтобы все они были веществен-
ными. Заметим, что если Л^|0) = 0 для всех i и е = 0, то из
выражения G.1.13) следует, что все элементы @|6?8°Ф|0) обра-
щаются в нуль в пределе е —>- 0. Таким образом, из условия
G.1.14) при е->-0 следует, что для некоторого значения
i Ni(t)\0)^ 0, и, следовательно, основное состояние не инвариан-
тно относительно преобразования типа ехр 17 2 9*^1. Именно по
этой причине неравенство G.1.14) называют условием спонтанного
нарушения симметрии.
Приведенные выше соображения показывают, что динамическое
отображение [6°Ф (х) — с, ] содержит в качестве линейных членов
голдстоуновские бозоны:
б?Ф (х) - ct = ? Сц (д) хН*) + • • • • G-1.15)
/=1
Коэффициент Сц (д) может содержать производные.
Мы можем написать
где Юр = 0 при р = 0. Здесь мы приняли, что уравнение свобод-
ного поля для х? типа 2. Из соотношения G.1.16) следует
lim e I tfy @1Т {[6?Ф (у) -ct], б/°Ф (х)} 10) =
= lim e f <Py @1Т {[б?Ф (у) - с{], [8°,Ф (х) ~ с,]} 10) =
е-«-0 J
G.1.17)
Динамическая перестройка симметрии 231
Когда голдстоуновский бозон х° удовлетворяет уравнению свобод-
ного поля типа 1, поле имеет комплексное значение. В таких
случаях комбинации (%° + xot)/21/2 и i (%° — хо+)/21/2 являются
вещественными полями, причинные двухточечные сЬункции кото-
рых имеют полюсные члены вида
~Т\ po—a + ea+i8 ^ — р0 — а' + еа + /6 /' G.1.18)
где со = со (р) и со' = со (—р). Это опять приводит нас к соотноше-
нию G.1.17).
Поскольку Ф (х) и Nt — вещественные, б°Ф (х) также вещест-
венны. Таким образом, коэффициенты Cih @) вещественны, а ма-
трица, ij-k элемент которой равен 2ft (l/ak) Cih @) Clh @), ве-
щественна и симметрична. Следовательно, эту матрицу можно
диагонализировать с помощью ортогональной матрицы, например
и = («;,). Тогда линейный член в динамическом отображении
2 «,/б/Ф для каждого i содержит не более одного голдстоуновского
бозона. Кроме того, если мы используем для генераторов выраже-
ние 2 utjNj, то эти генераторы вызывают изменения Ф, равные
2 «г/8°Ф. Поэтому мы можем всегда так составить генераторы Nt,
чтобы линейный член динамического отображения б?Ф для каж-
дого i не содержал более одного голдстоуновского бозона:
б?Ф (х) - а = Z\u (д) х? (х) + ... . G.1.19)
В дальнейшем мы будем предполагать, что генераторы Nt по-
строены описанным выше образом. Тогда имеем
Zi = 0 для i = т + 1, . . ., п, G.1.20)
Ni\0)=?0 для i = 1 т, G.1.21)
lirn @1 ЩФ (х) | 0} = Vi&th G.1.22)
Ф 0 для i = 1, ..., т, .
л • , , G.1.23)
= 0 для i = т + 1, ..., п.
При этом соотношение G.1.12) вместе с G.1.23) и G.1.17) приводит
к соотношению
vt = Zt @)/аг для i = 1, .... т. G.1.24)
Условие G.1.21) или G.1.23) определяет число голдстоуновских
бозонов. Тогда уравнение свободного поля для х? записывается
в виде
h (д) X? (х) = 0 для i = 1, ..., т. G.1.25)
232 Глава 7
Поскольку энергетический спектр голдстоуновских бозонов бесще-
левой, имеем
К @) = 0. G.1.26)
Исключение г из соотношений УТ. Поскольку ЬгЗ? (х) =
= еб?Ф (х), из соотношений УТ следует
ih ? @1Т [О, (*,)...8Юа(ха)...] 10} =
а
= в\#у@\Т{[б?Ф(у) - с{], О, (х,). . .} | 0), G.1.27)
где г|> (ха) в F.1.28) заменено символом Оа(ха), обозначающим
любой гейзенберговский оператор. В соотношении G.1.27) б?Ои (х)
определено соотношением
[Оа (х), Nt (t)] б (t - tx) = itti (t - tx) ЬЮа (x). G.1.28)
Чтобы исключить е из соотношения УТ G.1.27), воспользуемся
формулой
lim е [ <?у @1Т \[б?Ф (у) - с(\,. ¦ ¦} 10) =
= -~ j #yh (ду) @ | Т [б?Ф (г/),. . . ] | 0). G.1.29)
Чтобы ее доказать, заметим сначала, что если F (х) — функция,
фурье-амплитуда которой не содержит полюсной особенности,
связанной с бесщелевым энергетческим спектром, то справедливо
равенство J d^yki (ду) F (у) = 0, так как К @) = 0. Поскольку
члены, обозначенные в динамическом преобразовании G.1.19)
многоточием, не порождают полюсной особенности в спектральном
представлении двухточечных функций, состоящих из гейзенбергов-
ских операторов F^Ф — сг), то мы имеем
j (tykt (ду) @1Т |б?Ф (у), [6?Ф (z) - с,]} 10} =
= Zt @) j ityh (ду) @1Т [Х? (у), г) (г)] 10) = ihZt @) 8И, G.1.30)
где использованы соотношения C.6.34) или C.6.39), из которых
следует, что @|Г [%°i%°]\0) — гриновская функция дифферен-
циального оператора kt (д):
h (ду) @1Т [х? (У), X? W] | 0) = Й6<*> (у - г) 6,/.
С другой стороны, выражение G.1.17) с Ctk @) = Z]/2 @) б
ih
Динамическая перестройка симметрии 233
приводит к соотношениям
lim e J d*y (О IТ {[б?Ф (у) - ct], ЩФ B) - с,]} | 0) =
- Inn ZV* @)Z)'* @)e J cty <01T [X? (if) x/ (zI10I = iMtl J- Zt @).
G.1.31)
Соотношения G.1.30) и G.1.31) дают
Hm 8 J tfy @1T {[б?Ф (г/) - ct], [б?Ф (г) - C/]} 10) =
= -1- j tfifo (д„) @1T ЩФ (у), ЩФ (z) - c,\) | 0). G.1.32)
Это частный случай формулы G.1.29). Чтобы получить формулу
G.1.29), нужно воспользоваться также равенством
= j <?г @1Т {[б?Ф (у) - а], [6?Ф B) - а]} 10) q (г) G.1.33)
(суммирование по i не производится), где q (z) — некоторая функ-
ция. Эта формула может быть получена из рассмотрения общей
структуры фейнмановских диаграмм. Используя выражения
G.1.32), G.1.33) и соотношение ^ (д) сг = Я,-@)с* = 0 (ср. с
G.1.26)), получаем формулу G.1.29).
Используя формулу G.1.29) и полагая е = 0, можно переписать
соотношение УТ G.1.27) в виде
xi)...]\0) для i=\,..., m.
G.1.34)
Таким образом, мы исключили е из соотношения УТ G.1.27).
Перестройка симметрии. Пусть <р? (t = 1, 2, ...) — все физи-
ческие поля, кроме голдстоуновских бозонов. Их уравнения запи-
сываются в виде
A<(d)«p? = O. G.1.35)
Затем, поскольку Z-'/2 (д) [б^0)Ф (х) — ct] (i = 1, 2, ..., m) —
связывающее поле для %? (см. равенство G.1.19)), соотношения
C.5.17), C.5.18) дают
SH>W = :<T[i|5(x)exp^])c:, G.1.36;
S = : (Пехр *\)е, G.1.37)
234 Глава 7
где определение скобок под знаком Т-произведения приведено
в абзаце, следующем за формулой C.5.14); кроме того,
=--И
G-1.38)
Здесь <j>i — связывающее поле для ф1/. Для свободных физических
полей мы выберем входящие поля (т. е. %? = %'", ф? = фГ)-
Будем искать такое ^-преобразование
x?(v)->x?W-F0Ax/°W,
Ф?(*)>Ч7°(*Iе-б/ф?(*) ( j
которое пopoждaeт^Q-пpeoбpaзoвaниe гейзенберговского поля
т|) (л;), не меняющее величины S (вследствие инвариантности урав-
нения Гейзенберга). Поскольку Q-преобразование непрерывно,для
нашей цели достаточно рассмотреть только бесконечно малые
преобразования. Тогда соотношения G.1.36) и G.1.37) приводят
к условиям
/ ©) ехр ^1 \ : G.1.40)
и
0 = - -j-: / Т Г J d4^ J] 6,Х? (I) ^ И 271/2б°Ф (I) -1-
1\ G.1.41)
соответственно. Здесь О (х) обозначает гейзенберговский оператор.
Заметим, что соотношение G.1.41) является частным случаем соот-
ношения G.1.40) (при О (х) = 1).
Динамическая перестройка симметрии 235
С другой стороны, из соотношения УТ G.1.34) следует
1П:{Т[8Ю(х)ехрЩс: +
1 %°, (?) К, (д)
= -±- J ЛД; (д): (| Т [б?Ф (у) О (х) ехр Щс:. G.1.42)
Сравнивая G.1.42) и G.1.40), находим
/Г / m "
: ^ Т | О (х) J d4^ 2 [2Г'/2Х/ (?) Л/ E) б?б/0Ф (I) +
Л, (д) Щ,- (I)] -
JL-kt(dNIO® ехр
: = 0 G.1.43)
для t = 1, 2, ..., т. Это определяет ^-преобразование.
Чтобы перейти к дальнейшим выкладкам, вспомним следующую
лемму. Рассмотрим уравнение для свободного поля Я (д) g (х) = 0.
Если двухточечная функция для гейзенберговского оператора
г}> (л;) не содержит особенности типа полюса К'1 (д), то
J tfxg (х) X (д) @1 Т ty(x) . . . ] 10) = 0. G.1.44)
Это можно доказать с помощью интегрирования по частям.
Поскольку Ф (х) — элемент неприводимого представления
группы и поскольку по предположению бесконечно малое преобра-
зование имеет вид
b4<5>k = i(K)km<5>m, G.1.45)
справедливы следующие равенства:
6?Ф=» (*,,),„ Фт> G.1.46)
^ Ы + {Ч */})*» Фт. G.1.47)
236 Глава 7
Так как Kt — матрицы преобразования группы, перестановочные
соотношения для них подчиняются алгебре Ли
ftt, M = 1СтК- G.1.48)
С помощью соотношений G.1.46)—G.1.48) можно параметризовать
7 +-..., G.1.49)
к
где
eiik(d) = -~-lCijh + diik], G.1.50)
a dilk определяется с помощью равенства
{Я,,, М/тФт = «U (^)(тФт + • • • ,
причем
dm = diik. G.1.51)
Члены, обозначенные многоточием в G.1.49) и G.1.50), не со-
держат связывающего поля голдстоуновских бозонов и, следова-
тельно, согласно предыдущей лемме, не дают вклада в левую часть
соотношения G.1.43). Заметим, что эти члены не возникают, если
{К;, Я,;} = idijhlh.
Мы можем выбрать связывающие поля так, что
в?*/ (х) = ? ет (д) фк(х)+..., G.1.52)
k
где многоточие обозначает члены, не содержащие связывающих
полей cp/jj (х) (k = 1, 2, ...). Последние члены не дают вклада в ле-
вую часть G.1.43). Мы видим, что по той же причине вклад в G.1.43)
дают только те eilk (д), для которых х/ и %? имеют одну и ту же
энергию (т. е. %t (д) = Kh (д)). Аналогично в выражение G.1.43)
дают вклад только те ецк (д) из G.1.52), для которых Ak (д) =
= А, (д).
Соотношение G.1.43) приводит теперь к следующему q-npe-
образованию:
Ь°а° (х) = [Z)u @)/аЛ 6„ - ?' (Zi/Zk) в{к, {-д) il (x), G.1.53)
k
x) = - ?' ещ (-д) <р% (х). G.1.54)
k
В соотношениях G.1.53), G.1.54) символ 2' означает, что сумми-
рование проводится только по тем полям, энергии которых равны
энергии поля, входящего в левую часть. Преобразования G.1.53),
G.1.54) являются ^-преобразованиями, которые представляют
собой наблюдаемые проявления Q-преобразования. В следующем
Динамическая перестройка симметрии 237
разделе мы приведем некоторые примеры перестройки симметрии.
Форма перестройки симметрии накладывает ограничения на форму
динамического отображения.
Докажем теперь, что уравнения свободного поля для физи-
ческих полей X/ и ф/ инвариантны относительно q-преобразования.
Первое слагаемое в G.1.53), которое появляется в результате
трансляции поля %°, не нарушает инвариантности уравнений
свободного поля, так как спектр голдстоуновских бозонов не
обладает щелью, т. е. Я,у- @) = 0. Второе слагаемое в G.1.53) не
нарушает инвариантности уравнения свободного поля, так как
в него входят только линейные комбинации голдстоуновских полей
с одной и той же энергией. Аналогично и G.1.54) не нарушает
инвариантности уравнения свободного поля.
Докажем затем, что ^-преобразование оставляет инвариантными
канонические соотношения для физических полей. Когда q-npe-
образование получено в виде
6<Х/ = № @)/аЛ 6„ + i (ti)ik %l G.1.55a)
6i4>? = t (<*)/* Ф&. G.1.556)
каноничность физических полей вытекает из условий
(tt)fk = (ii)k/ = -(tt)k/. G.1.56)
(<т*)*/, G-1.57)
причем вещественность %/ видна из G.1.56). Соотношения G.1.56),
G.1.57) представляют собой условия унитарности для линейной
части G.1.55). Здесь мы докажем только справедливость соотноше-
ния G.1.56), поскольку справедливость равенства G.1.57) может
быть доказана аналогично.
Заметим сначала, что Q-преобразование любого гейзенбергов-
ского оператора можно вывести из ^-преобразований G.1.53),
G.1.54), поскольку формула G.1.43) справедлива для любого
О (х). Если динамические отображения операторов А и В заданы,
динамическое отображение произведения А В получается заменой
произведений нормальных произведений свободных физических
полей на линейные комбинации нормальных произведений тех же
полей:
Л (х°) В (х°) = АВ (к0). G.1.58)
Для простоты мы рассмотрели только случай голдстоуновских
бозонов. Справедливо равенство
АВ (х°) + в' (в?Л5) (х°) = АВ (х° + в V). G-1 -59)
238 Глава 7
где левая часть — результат Q-преобразования, примененного
к АВ, а правая часть — результат ^-преобразования. С другой
стороны, поскольку
[А (/) + в'в!л (х0)] [в (х°) + е'в?в (/)] = ав (х°) + е'в?лв (х°),
G.1.60)
то мы имеем
А (х° + e<6iX°) BJx° + G'-6,x°) = АВ (х° 4- е«бгх°), G.1.61)
откуда следует, что две операции, а именно подстановка G.1.53),
G.1.54) и взятие произведения, коммутируют друг с другом. Если
мы сравним матричные элементы в обеих частях равенства G.1.61),
то обнаружим, что часть полей х°. в которых произведено'спарива-
ние, участвующая в образовании произведения А В (%°), не участ-
вует в ^-преобразованиях правой части равенства.Следовательно,
вклады от них должны обращаться в нуль. В частности, если для
А и В выбраны связывающие поля %t (х) и %,¦ @) соответственно, то
среднее по вакууму от величины, определяемой G.1.61), равно
(о | х? (х), е*б*х? (у) | о) + (о | еЧх? (*). х° (у) I о> + g (*, у) = о,
G.1.62)
где G (х, у) содержит два или более спариваний полей %°. Переходя
к Т-произведениям, получаем
<о | г [х? (х) х? (^)] | о> »-е* (f*)// -h
+ Ю* (ik)tl @ | T [x? (x) tj (y)} | 0) + Gc (x, y) = 0. G.1.63)
Члены, которые содержат в импульсном представлении G.1.63)
полюсы, возникают только из первых двух слагаемых, следова-
тельно, (th)ji = —(tk)a- С другой стороны, поскольку %Ч и бх/
вещественны, из преобразования G.1.55а) видно, что (tt)jk мнимая
величина. Таким образом, мы получаем соотношение G.1.56).
Мы показали, что каждое ^-преобразование есть комбинация
трансляции поля голдстоуновских бозонов [%Ч (х) -> X/ (х) +
+ с-число] и образования линейной комбинации физических полей
с одной и той же энергией [6—8], и эта операция оставляет инва-
риантными уравнения для свободных физических полей и канони-
ческие коммутационные соотношения.
Заметим, что генератор, который смешивает некоторые свобод-
ные поля с одной и той же энергией, имеет вид 2 а^а,-. Следова-
тельно, он разрушает вакуум. Условие Nt\0) Ф 0 для некоторых
значений i приводит к тому, что ^-преобразование должно включать
трансляцию голдстоуновских полей, когда имеется спонтанное
нарушение симметрии. Таким образом, спонтанное нарушение
симметрии требует существования бозонов х° с бесщелевым энерге-
тическим спектром. Это еще одно доказательство теоремы Голд-
Динамическая перестройка симметрии 239
стоуна. Тот факт, чтоуг ф 0G.1.23), служит проявлением порядка,
который возникает при спонтанном нарушении симметрии.!;Не
обращающиеся в нуль параметры vt называют параметрами по-
рядка.
Интуитивно понятно, что в упорядоченном состоянии должна
быть система некоторых квантовых возбуждений, находящихся
в основном состоянии, причем таким образом, что их квантовые
числа «отпечатываются» в этом состоянии, создавая структуру.
Эти квантовые возбуждения должны подчиняться статистике
Бозе, чтобы была возможна их конденсация в основном состоянии.
Другими словами, в процессе динамической перестройки возни-
кает нулевой уровень энергии бозонов, и конденсация бозонов
в этом f состоянии создает структуру основного состояния. Эти
бозоны являются голдстоуновскими бозонами. Когда гейзенбергов-
ского поля бозе-типа нет, при динамической перестройке, естест-
венно, возникают составные частицы, являющиеся голдстоунов-
скими бозонами. Если возникает конденсация, при которой плот-
ность конденсата зависит от времени или положения в простран-
стве, то в результате образуются протяженные во времени или
в пространстве объекты. Эти протяженные объекты мы рассмотрим
в последующих главах.
Обратим наше внимание теперь на физические поля ф°, энерге-
тический спектр которых имеет щель, и получим соотношение для
спаривания типа (%;</>;</>;) в случае, когда ф? и ср? обладают различ-
ными энергетическими спектрами (т. е. Л/ (<Э) Ф Л, (<Э)). Из соот-
ношения УТ G.1.34) вместе с равенством G.1.52) получаем соот-
ношение
Л (^ ет <0 | Т [фк (х) ф\ (у)] | 0) + 2 епк <01Т [ф, (х) фХ (у)] 10)\ =
I
\ k I
= -L. \ d?zh (дг) @1Т [6?Ф (г) ф, (х) ф\ (у)] | 0). G.1.64)
Поскольку представление G.1.52) унитарно, имеем
em = — ehi- G.1.65)
Рассмотрим теперь тот факт, что, поскольку фг — связывающее
поле для ср?, линейный член в динамическом отображении j>t
содержит только ф°. Следовательно, содержащий полюс член
в спектральном представлении (OJT [фк (х) ф] (г/)]|0) обращается
в нуль при k Ф1. Тогда из соотношений G.1.64) и G.1.65) следует
item {@1Т [ф, (х) ф] (у)] 10) - @1Т [ф, (х) ф! (у)} 10)}р =
= -L J d*zX, (дх) @ | Т [б?Ф (х) ф, (х) ф] (у)] | 0)р, G.1.66)
где индекс р относится к вкладу полюсных членов ф° и ф". Предпо-
ложим, что ф? и ф/ имеют один и тот же энергетический спектр.
240 Глава 7
Тогда левая часть обращается в нуль, а правая становится элемен-
том 5-матрицы, соответствующим переходу ср? -*¦ ср? + (%° с нуле-
вой энергией). В этом случае равенство G.1.66) — частный случай
теоремы о низколежащих уровнях энергии S-матрицы, которая
устанавливает, что энергия нулевого состояния %° не дает вклада
в 5-матрицу. С другой стороны, когда энергия ср? меньше, чем ср?
при заданном импульсе, мы оставляем в выражении G.1.66) лишь
члены с полюсом у ср", что приводит к соотношению
Шеш (О1 T[fr (х) $ (у)]\ 0)Р/ = -i-
G.1.67)
Здесь индекс Рг обозначает член с полюсом в ср?. Правая часть
соотношения — внешняя по отношению к энергетической оболочке
часть fj\ она может быть использована для определения (y,ij>$i)-
спаривания. Таким образом, G.1.67) становится соотношением
для константы (%;</>,</>,)-спаривания, если энергетический спектр ср/
отличен от спектра ср?. Такое (%,-^>/</>/)-спаривание может индуци-
ровать процесс ср? -*- ср? + yj и делать ср? нестабильным. Аналогич-
ное рассуждение приводит к выводу о том, что ср? становится не-
стабильным, когда энергия поля ср? больше энергии ср?. Подводя
итог, можно сказать, что в представлении {</>,} g-группы ср? не
могут различаться по энергиям. С другой стороны, нарушение
симметрии стремится снять вырождение по энергии у ср?. Таким
образом, часто оказывается, что многие поля ср? становятся синглет-
ными представлениями ц-группы. Этот процесс порождает большое
количество ср?, не меняющихся при q-преобразованиях; эти поля ср?
«заморожены». Таким образом, спонтанное нарушение симметрии
стремится заморозить «массивные» поля ср?, т. е. поля, энергети-
ческий спектр которых имеет щель.
Конечные температуры. Завершим этот раздел замечанием
о том, что все приведенные выше результаты могут быть распро-
странены на случай систем при конечных температурах, поскольку
структура динамического отображения D.2.53)—D.2.55) и соотно-
шение УТ F.2.1) те же, что и при нулевой температуре, хотя при
не равной нулю температуре возникает тильда-сопряженное поле.
7.2. Фазовая симметрия
Рассмотрим лагранжиан комплексного гейзенберговского поля
яр (х). Будем считать, что лагранжиан S (яр, ар+) инвариантен при
фазовом преобразовании ip ->¦ exp (t'6) ip. Примем, что
V ее @|я|)(*) +Ф(х)\0)ф0. G.2.1)
Динамическая перестройка симметрии 241
Модель такого вида называется моделью голдстоуновского типа
[2, 6]. Мы выберем приводящий к нарушению симметрии лагран-
жиан &ъ в виде S?8 = е (\|з + я|)+), т. е.
Ф(х) =я|) (х) + ф (х). G.2.2)
Таким образом, фазовое преобразование приводит к тому, что
6°Ф (*) = % (х) = i [г|з (х) — г|з+ (*) ]. G.2.3)
Поскольку имеется только один генератор, появляется лишь один
голдстоуновский бозон [6]%° (х), уравнение для которого имеет вид
D (д) х° (*) = 0. G.2.4)
Здесь отсутствие щели в энергетическом спектре %° (х) проявляется
в следующем свойстве:
D @) = 0. G.2.5)
Гейзенберговское поле % (х) является связывающим полем голд-
стоуновского бозона:
% (х) = Z'/. (д) х° (*) + .... G.2.6)
Единственная частица, которая появляется в (г|з +^+)-канале,
обычно нестабильна, так как она может распадаться на голдсто-
уновские бозоны.
Соотношение G.2.3) приводит к равенству
б°б°Ф (*) = — Ф(*). G.2.7)
Поскольку в правой части G.2.7) нет б°Ф и поскольку в Ф (я)-ка-
нале не появляется ни одного бозона %°, соотношения G.1.49) и
G.1.53) приводят к равенствам
бх° (*) = Z1/» @)/а = t»Z-v. @), G.2.8)
так как из G.1.24) следует, что v = Z @)/а. Таким образом,
фазовое преобразование
г|з->-е'егр G.2.9)
индуцировано преобразованием
t (х) -+%° (х) + oZ-v. @) 0, G.2.10)
которое представляет собой сдвиг поля %и (х). Преобразование
G.2.9) определяет Q-преобразование, а G.2.10)—д-преобразова-
ние. Таким образом, мы получили динамическую перестройку
фазовой симметрии [6]. Приведенные выше результаты показы-
вают, как фаза системы определяется конденсацией голдстоунов-
ских бозонов, которые в этом случае называются фазонами.
Этот результат можно также вывести из правила,"" согласно
которому ^-преобразование должно включать сдвиг поля голдсто-
уновского бозона и может также содержать смешивание физиче-
242 Глава 7
ских полей. Поскольку существует только один генератор, сущест-
вует лишь один голдстоуновский бозон. Таким образом, ^пре-
образование есть просто сдвиг поля голдстоуновского бозона.
Поскольку сдвиг поля 1° G.2.10) порождает фазовое преобразо-
вание G.2.9) гейзенберговского поля-ф, динамические отображения
¦ф (х) и S имеют вид
ф (х) = : exp (i-ZV. (д)Х°(х)) F [д%°\:, G.2.11)
S = :S[dx°\:, G.2.12)
где символом д%° обозначены производные от %°.
Рассмотрим теперь фазово-инвариантную модель фермионного
гейзенберговского поля, описывающего спиновый дублет i|?tij (х).
Лагранжиан инвариантен при фазовом преобразовании
г|з+>4. -^exp (t9/2)\|3+,+ (х).
Модель этого типа называется моделью сверхпроводимости. В этом
случае параметр порядка равен
v = @ | Ч>+ (х) г].Ч (х) -\- $ (х) ф| (х) | 0) ф 0, G.2.13}
а приводящий к нарушению симметрии лагранжиан 3?Ё = еФ, где
Ф (х) = ф+ (х) 4>t (х) + t|jJ (х) ф! (х). G.2.14)
В этом случае имеем выражение
X (х) = б°Ф (х) = i [ф+ (х) ф+ (х) - ф| (*) i|;t (л)], G.2.15)
которое определяет связывающее поле %° для голдстоуновского
бозона:
%(х) = ZV. (д) х° (*) + .... G.2.16)
Большая часть аргументов в пользу справедливости голдстоу-
новской модели применима и для модели сверхпроводимости.
Единственное существенное отличие состоит в существовании
квазиэлектрона ф°. Таким образом, мы можем показать, что сдвиг
поля
%° (х) -+%° (х) + fti>Z-'/.@) Э G.2.17)
приводит к фазовому преобразованию
г|?-*-exp (ifte/2) ф. G.2.18)
Динамические отображения^ и S имеют вид, сходный с G.2.11),
G.2.12):
ф (х) = : exp (-L- ZV. (д) f (х)) F [дх°, Ф°]:, G.2.19)
S = :S[dx°, Ф0]:. G.2.20)
Динамическая перестройка симметрии 243
Вспомним теперь, что плотность
р (*) = ^ (х) я|> (*) G.2.21)
удовлетворяет перестановочным соотношениям для операторов,
взятых в один и тот же момент времени:
Ь|з (*), ^ (у) Ц(у)]8 D - ty) = hq (х) 6«> (х - у), G.2.22)
откуда следует, что
N = — j cPxMp* (х) ф (х) G.2.23)
является генератором фазового преобразования. Поскольку N
генерирует фазовое преобразование, генератор N конструируется
при помощи величины, канонически сопряженной величине
BV)'1 Z'/* (д) х°, а именно
N = 2и j d3xZ~'/2 («5)_|_ хо. G.2.24)
Поэтому динамическое отображение р (х) имеет вид
р (х) = -2oZ-V. E) -А. Х° W + • ¦ ¦ • G-2.25)
Вспоминая, что N — нётеровский генератор, мы будем считать,
что р (х) — четвертая компонента нетеровского тока: р (х) = —iV0-
С другой стороны, поскольку энергетический спектр %° не имеет
щели, равенство G.2.4) можно переписать в виде
?>(l (д) дд° = 0. G.2.26)
Таким образом, из закона сохранения тока д^Ыц = 0 следует, что
динамическое отображение N^ имеет вид
N» (х) = -2DZ-'/* (д) DX (х) + .... G.2.27)
7.3. Динамическая перестройка
спиновой симметрии
В этом разделе мы изучаем спонтанное нарушение спин-враща-
тельной симметрии, которое приводит к состоянию с упорядо-
чением спинов (ферромагнитному состоянию).
Пусть S (х) — гейзенберговское поле спина:
[S? (*), S, (у) ] б (tx - ty) = ieUkSk (х) б* (* - у), G.3.1)
где etI-k — полностью антисимметричный тензор, на компоненты
которого наложено условие е123 = 1.
Чтобы уточнить, каким образом нарушается спиновая симме-
трия, введем дополнительный лагранжиан
S& (x) = eS3 (*), G.3.2)
244 Глава 7
который приводит к нарушению спин-вращательной симметрии.
Бесконечно малая константа е имеет смысл слабого внешнего
магнитного поля, которое определяет направление поляризации.
В конце расчета нужно выполнить предельный переход при
8-^0.
Группа вращений спина содержит повороты вокруг третьей оси,
которые составляют абелеву подгруппу. Заметим, что ЗСг в ра-
венстве G.3.2) инвариантно относительно преобразований этой
абелевой подгруппы. Такую ситуацию можно охарактеризовать
утверждением, что эта абелева подгруппа есть подгруппа устой-
чивости.
Поскольку мы принимаем, что вращательная симметрия отно-
сительно третьей оси не нарушается, потребуем выполнения усло-
вия
± 0. G.3.3)
Изменения St (x) и 9?е (x) из-за поворота вокруг /-й оси на беско-
нечно малый угол 9; равны соответственно
вде, (х) = QjSjikSk (x), G.3.4)
Поэтому, например, можно написать
,40 С (Y\ С jY\ (П О С\
UjOg \™) '2. \ /' \ •*-'.*-'J
6°S3 (x) = S, (x), G.3.7)
Ь\2е (х) = —eS2 (*), G.3.8)
Ь\%, (х) = eS, (*), G.3.9)
b\b\Sz (x) = 6°6°S3 (x) = -S3 (*). G.3.10)
Тогда равенство G.1.12) при i = / = 1 и Ф (х) = S3 (х-) приводит
к соотношению УТ
—ihv = ej d4y@|r [S2(y), Ss(*)]|0). G.3.11)
Аналогично равенство G.1.12) при t = / = 2 и Ф (х) = Ss (x)
приводит к соотношению
—iHv = e|d4i/@|T [Si (у), Sx(x)]|0). G.3.12)
Вспоминая соотношение G.1.19) и полагая Ф = S3, можно по-
казать, что здесь имеются два голдстоуновских бозона %? и %°,
в энергетическом спектре которых нет щели, и что S, (t = 1,
2) — связывающие поля этих голдстоуновских бозонов:
S, (х) = 62S3 (х) = ZVz (д) Х2 (х) + ..., G.3.1 За)
52 (х) = —6?S3 (х) = —ZI/2 (d) х? (*)+¦••• G-3.136)
Динамическая перестройка симметрии 245
Здесь нормировочный множитель Z (д) для Si и S2 один и тот же,
поскольку симметрия вращения относительно третьей оси сохра-
няется. Следствием этой вращательной симметрии является также
то, что %° и %°2 удовлетворяют одному и тому же уравнению
Я(д)Х? = О, t = l, 2. G.3.14)
Поскольку в спектре этих бозонов нет щели, имеем
Л@) - 0. G.3.15)
Далее, из соотношения G.1.24) следует
v = Z {0)/а, G.3.16)
где а определяется равенством G.1.18).
Удобно ввести комплексное поле
X^-'MxS-'X?)- G-3.17)
Эрмитово сопряженное поле определяется выражением
XW=2-I/'(xS+«X?)- G-3.18)
Очевидно, что
Мд)Х° = 0. G.3.19)
Поле х0+ порождает квантовое возбуждение, называемое
магноном, а поле %° уничтожает его. Связывающее поле магнона
S_ = 2'2 (Sx — iS2) равно
S_ (x) - Z'/. (д) х0+ (*) + .... G.3.20)
Заметим, что справедливы следующие равенства:
6?62°53 = 6206?S3 = 0, G.3.21)
b%S3=O, G.3.22)
6036?S3 = S1 = 6^3 G.3.23)
e3fe = S2 = -6?S3) G-3.24)
6?б?53 = б°2б205з = ~S3. G.3.25)
Таким образом, соотношение G.1.49) дает
«ей E) = -eMi(a) = 1, G.3.26)
остальные eijh (д) = 0. G.3.27)
з выражения G.1.53) теперь видно, что поворот относительно
первой оси на бесконечно малый угол 9Х вызван преобразованиями
246 Глава 7
xSW-xSW. G-3>28)
а поворот относительно второй оси на бесконечно малый угол 92 —
преобразованиями
Поворот относительно третьей оси на бесконечно малый угол Э3
вызван преобразованиями
Если угол 63 конечен, то вследствие того, что вращательная сим-
метрия относительно третьей оси не нарушается, G.3.30) при-
нимает вид
С другой стороны, повторное применение преобразований G.3.28),
G.3.29) показывает, что эти преобразования остаются справедли-
выми^ при конечных Qx и 92. г?-
Таким образом, мы видим, что преобразования G.3.28), G.3.29)
и G.3.31) являются преобразованиями ^-симметрии, которые
индуцируютя спиновые вращения гейзенберговского оператора.
Поскольку группа ^-симметрии состоит из двух сдвигов поля и
одного поворота, она является двумерной евклидовой группой сим-
метрии (т. е. группой Е B)).
Приведенные выше]результаты можно сформулировать следую-
щим образом: группа симметрии SU B) (группа спиновой симме-
трии) при динамической перестройке переходит в группу Е B),
если подгруппа симметрии U A) (группа вращений вокруг третьей
оси) есть подгруппа устойчивости.
Это замечательный случай в том смысле, что даже структура
группы изменяется при перестройке симметрии. Причина этого
изменения станет очевидной, если мы вспомним, что генераторы
вращения спина получаются при интегрировании S? (х) подпро-
странству:
Si (x) = J d3xSt (x). G.3.32)
Чтобы выразить этот факт в терминах физических полей %° и %2.
мы должны сначала найти динамическое отображение St (x;
X?» Ул) оператора спиновой плотности, вычислив матричные эле-
менты (а| St (х) | Ь), где | а) и | Ь) принадлежат пространству Фока
Динамическая перестройка симметрии ' 247
для магнонов. Поскольку \а) и \Ь) — волновые пакеты, соответ-
ствующие состояниям магнонов, при расчете (а \ St (х) | b) всеми
членами порядка XIV (V — объем) можно пренебречь. Следова-
тельно, динамическое отображение St, определяемое выражением
(a\Sl\b)= J d3x (a | St (x) \ Ь), G.3.33)
удовлетворяет некоторым алгебраическим соотношениям, которые
могут отличаться от соответствующих соотношений для St. Таким
образом, изменение группы симметрии вызвано тем фактом, что
динамическое отображение есть соотношение в слабом смысле, и
расчет динамического отображения включает предельный переход
l/
Как упомянуто в разд. 7.1, ^-преобразование в динамическом
отображении определяется как подстановка. Матричные элементы
оператора л\> [х; q (%°) ] после ^-преобразования получаются с по-
мощью образования произведения и дополнительных правил для
Х°. Поскольку матричные элементы гр (х; %°) связаны с переходами
между состояниями, соответствующими волновым пакетам,
с-числа, возникающие при сдвиге поля %° ->- %° + (с-число), нужно
понимать в смысле предела %° -*¦ %° + (с-число) / (х) при f (х) —>- 1,
где / (х) —• квадратично интегрируемая функция (см. примечание
по поводу выражения G.1.3)). Это то же самое, что и предельный
переход XIV -»- 0.
Из теории групп известно, что сжатие группы SU B), если
U A) — подгруппа устойчивости, дает группу Е B). Мы можем
сформулировать результаты этого раздела следующим образом.
Если вращательная симметрия относительно третьей оси сохраня-
ется, динамическая перестройка группы симметрии SU B) явля-
ется. результатом предельного перехода X/V-+O, который вызы-
вает" сжатие группы SU B) ->¦ Е B), где St/J2)J— группа Q-сим-
метрии, а Е B) — группа ^-симметрии. ,,)
Обратимся теперь к динамическому отображению. Пусть
Он (х) — любой гейзенберговский оператор, который инвариантен
относительно поворота спина. Поскольку поворот спина вокруг
первой и второй осей вызван сдвигом поля голдстоуновского бозона
%°с (i = 1, 2), в динамическом отображении Он (х) должны содер-
жаться производные:
Он (х) = Он [х; д%°, д%<*1 G.3.34а)
Более того, поскольку поворот относительно третьей оси приводит
к фазовому преобразованию х° —» е~т%°, оператор Он (х) должен
оставаться инвариантным при фазовом преобразовании. Поскольку
5-матрица инвариантна относительно вращения спина, имеем
S = 5 1д%°, д%°*], G.3.346)
248 Глава 7
откуда следует, что в 5-матрице нет членов, отвечающих магнонам
с нулевой энергией, поэтому последние не участвуют ни в каких
взаимодействиях. Это утверждение называется теоремой о низко-
энергетических магнонах. Все эти вопросы подробно рассмотрены
в следующем разделе.
Мы завершим этот раздел вычислением констант Z @) и а
в выражении G.3.16). Поскольку F @) = Z @)Ш при М = v, из
выражения E.3^50) немедленно следует результат а = 1. Чтобы
продемонстрировать различные способы вычисления, обратимся
к выражению
J d*x @1 St (x) St (у) 10) \tx=ty - lim J tPx @1T [St (x) St (у)) \ 0) |<я> ty.
*х^гу
Мы можем вычислить эту величину с помощью спектрального пред-
ставления G.1.18). Учитывая соображения, предшествовавшие
написанию равенства E.3.48), мы видим, что вклад от членов, не
содержащих полюса, обращается в нуль при'интегрировании по
пространственным переменным. Таким образом, получаем
\dsx(Q\Si(x)Si(y)\0)\tx-^y=-^Z@) для i=l,2. G.3.35)
Это дает
@\SiSi\0) = 4rZ@)V для/ = 1,2. G.3.36)
С другой стороны, поскольку v — плотность спиновой поляри-
зации, суммарный спин системы равен
\d3x@\S3 (x)\0) = W. G.3.37)
Кроме того, поскольку вращательная симметрия относительно
третьей оси не нарушается, основное состояние |0) есть собствен-
ное состояние S3, т. е.
S3|0) = 1>У|0). G.3.38)
С другой стороны, поскольку спины полностью поляризованы
вдоль третьей оси, справедливо выражение
2l l ), G.3.39)
которое, согласно G.3.36) и G.3.38), равно Z @) V + {vVf. Таким
образом, имеем
Z @) = v, G.3.40)
откуда следует, что Z @) — плотность спинов. Теперь из соотно-
шения G.3.16) следует, что а = 1.
Динамическая перестройка симметрии 249
7.4. Перестройка симметрии и теоремы
для низких энергий
Теоремы о состояниях с низкими энергиями. Конкретная
форма перестройки симметрии приводит к ряду соотношений между
некоторыми матричными элементами. В эти соотношения всегда
входит по крайней мере один матричный элемент, связанный
с состоянием, содержащим голдстоуновский бозон в предельном
состоянии с нулевой энергией. Поэтому упомянутые выше соотно-
шения называют теоремами о состояниях с низкими энергиями
(теоремами для низких энергий). Наиболее общая теорема этого
типа гласит, что голдстоуновские бозоны в предельном состоянии
с нулевой энергией не участвуют ни в каких взаимодействиях. Это
непосредственное следствие того факта, что сдвиг поля (%а -*¦
-*¦ %а + са) голдстоуновского бозона %« порождает инвариантное
преобразование, и, следовательно, в S-матрице %а всегда содер-
жатся некоторые производные. Если эту теорему применить к слу-
чаю ферромагнетизма, мы увидим, что магнон в пределе нулевой
энергии не участвует ни в каких взаимодейстиях. Это согласуется
с результатом Дайсона [9], который установил, что элементы
S-матрицы, связанные смагноном низкой энергии, малы. В физике
высоких энергий эта теорема для низких энергий переходит в тео-
рему Адлера [10], которая определяет положение нулей в ампли-
туде рассеяния пионов, рассматриваемых как голдстоуновские
бозоны.
Проиллюстрируем теперь более сложные теоремы для низких
энергий в случае спонтанного нарушения симметрии SU B)
с группой устойчивости U A) (случай ферромагнетизма). Как
указано в разд. 7.3, наблюдаемая группа симметрии есть группа
Е B). Принято, что преобразованием группы устойчивости U A)
является поворот относительно третьей оси в пространстве пред-
ставлений SU B)-преобразований. Тогда равенства G.3.28) и
G.3.29) показывают, что поворот вокруг первой (второй) оси
вызывается сдвигом поля голдстоуновских бозонов х? Ос")- Обозна-
чим гейзенберговское поле через ty и будем считать, что оно пред-
ставляет собой SU B)-дублет. Рассмотрим оператор G [а|з], кото-
рый состоит из полей-ф и-ф1". Символ т обозначает матрицы Паули
размерности 2 Х2. Если степени свободы дублета ij) являются спи-
новыми степенями свободы, то т — спиновые матрицы ст. Мы
используем символ т при рассмотрении общего случая симметрии
SU B). Напишем динамическое отображение G в виде G [%Ч,
Х°, ...], где многоточие обозначает свободные физические поля,
не являющиеся голдстоуновскими полями. Рассмотрим теперь
поворот вокруг первой оси на бесконечно малый угол 6. Поскольку
250 Глава 7
сдвиг поля %i ->- хЧ + Эу вызывает преобразование г|з ->¦
—>-ехр (i -п- 9тх j г|з, имеем
(a|G [exp(i-^QTl)y]\b) = (a\G[fl + Qv,y>Z,...]\b), G.4.1)
где б обозначает константу, равную"^-'/2 @) (см. G.3.28)). Когда,
состояния \а) и \Ь) не содержат"квантовых возбуждений %°
с нулевым импульсом, справедливо соотношение
Шп Bш,) V. Bя)'/2 (а |; хо (л-) хо до. . . . | Ь. %о {щ = (а\:$(у). . . :\Ь),
G.4.2)
где \Ь; %? 00) — состояние, содержащее \Ь) и голдстоуновский
бозон х? с импульсом к. В G.4.2) мы рассматриваем случай, когда
X? имеет вид
%°. (х) = П11* j d3\/z [2(o (k)]-1/* [a. (k) e»x-'»< + a* (k)
где со обозначает со (к). Тогда получаем
l + Qv, хо,.. .] - G [ху, х2°,.
6(a|Grx0, Х§.- • •] |Ь; X?(Ю)= G.4.3а)
ft-*0
= lira BяK/, [2со (k)/ft]V. б (а; х? (к) | ,G [x?, ll ¦ ¦ ¦ ] I b). G.4.36)
Если учесть определение
61G[^] = Hm-i-{G[exp(f-i-eT1)i|;] -G[i|j]}f G.4.4)
соотношение G.4.3) принимает вид
(а 16,G [ф] | Ь) = Ига Bл)а/, [2со (k)/ft]V. у (a | G Щ \ Ь\ %\ (к)) = G.4.5)
k-+0
= lim Bл)8/, [2со (k)/ft]V. б (а; х? (к) | G [ф] 16). G.4.6)
k-*0
Если выбрать G; в виде G,- = г|з+т^г|з, то
6iGi = U е2 ,-/1|5+Т/1|).
Тогда из G.4.5) и G.4.6) получаем соотношения
(а | ? е, ,д|з+тл|? 16) = v lim BяK/, [2© (к)/Й]'/. (а | ф+т,ф 16; х? (к)) = ¦
G.4.7)
= б lim Bя)§/. [2со (k)/ft]V. (а; ху (к) | ф+т^ 16>.
G.4.8)
Динамическая перестройка симметрии 251
Аналогично вращение вокруг второй оси приводит к соотношениям
= v lira Bя)§/. [2© (к)/Й]'/. (а | ф+т^ 16; %2° (к)), G.4.9)
ft-»-О
= v lim BлK/* [2ш (k)/ft]V* (а; ^о (^ | ^ ^ | ь). G.4.10)
Эти соотношения —результат проявления перестройки симметрии
SU B) -> ? B). Если заменить тг на а,-, соотношения G.4.5) —
G.4.10) становятся соотношениями для магнонов с низкими
энергиями.
Теоремы для низких энергий в случае рассеяния спиновых волн.
Если G — S-матрица, имеем 8tS = 0, так как S-матрица инва-
риантна для группы рассматриваемых преобразований. Тогда из
G.4.5), G.4.6) получаем соотношения
lim [BяK2(о(к)/й]'/2(а\S\b; %°.(к)) = 0, G.4.11)
ft->-0
Пт[BлK2(о(к)/й]1/2(а; %4(k)\S\b) = 0. G.4.12)
Чтобы продемонстрировать, как можно использовать эти
соотношения, применим их к расчету амплитуды рассеяния спино-
вых волн друг на друге (klt k21 S | к3, к4), где кг — импульсы спино-
вых волн. Поскольку волновое уравнение для спиновых волн
принадлежит к типу 1, нормировочный множитель Bu)ky/* нужно
исключить из соотношений G.4.11) и G.4.12) (а также и из после-
дующих соотношений). Множители B<ou)''i сокращаются, поэтому
окончательные результаты справедливы для обоих типов волновых
уравнений голдстоуновских бозонов. Г-матрица находится из
уравнения
={къ к2|к3, к)-in
f
n [Bj[Kf(;)]V8 x
X Т (кх, к2; к3, к4) б [со (кх) -f ю (к2) - © (к3) - со (к4)] х
Хб(к1 + к2-к3-к4). G.4.13)
Тогда соотношения G.4.11), G.4.12) приводят к условию
lim T(kb ка; к3) к4) = 0, G.4.14)
где кг —• любой из четыре-импульсов спиновых волн. Это означает,
что магноны с нулевым импульсом не участвуют во взаимодействии.
Допустим, что пространственно-вращательная симметрия не
нарушена, даже если нарушена симметрия относительно вращений
спина. Тогда Т является функцией кг-к/. Поскольку матрица Т
252 Глава 7
симметрична относительно замены (кх *-* к2) или (к3 *-* к4) вслед-
ствие бозонной природы магнона, Т с малыми к, (i = 1, 2, 3, 4)
имеет вид
Г(кь к2; к3, к4)~а + &(к1.к2) + с(к2+к2!)+..., G.4.15)
где а, Ь, с — некоторые константы. Чтобы получить выражение
G.4.15), мы использовали тот факт, что для малых импульсов
закон сохранения энергии приводит к равенству
k?-;-ki = k§-bk?. G.4.16)
Теперь из условия G.4.14) следует а = с = 0. Следовательно,
при малых импульсах Т ведет себя как
Т(къ к2; к3, к4)-6(к1-ка). G.4.17)
Это следствие теоремы для низких энергий.
Теорема для низких энергий в случае л—л-рассеяния. Ана-
логичное рассмотрение можно провести применительно к физике
высоких энергий, например, рассматривая пионы как голдстоунов-
ские бозоны %°, возникновение которых обусловлено спонтанным
нарушением киральной симметрии SU B) X SU B) с подгруппой
устойчивости SU B). Тогда пион представляет собой SU B)-трип-
лет (%[, %°, %1). Очевидно, что массой пиона следует пренебречь.
Было обнаружено, что в этом случае симметрия SU B) X SU B)
перестраивается в симметрию трехмерной евклидовой группы
Е C) (сдвиг поля и преобразование SU B)). Рассмотрим теперь
амплитуду я—л-рассеяния {kx<Zi, k2a2 \ S \ k3a3, k^a^, где a, (i = 1,
2, 3) — индекс группы SU B). Т-матрица, определяемая уравне-
нием G.4.13), должна быть инвариантной относительно реляти-
вистских преобразований. Поэтому она является функцией s, t
и и, определяемых выражениями
s = —(*! + &2J = —(кх + k2J + (©! + ©2J,
t = _(Й1 _ k3f, G.4.18)
и = -{kl - k,f.
Кроме того, справедливо равенство
*? = k?-a>! = 0, G.4.19)
поскольку масса пиона считается равной нулю. Из бозонной при-
роды пиона следует симметрия относительно замены
G 4 1-0)
, (ksas)} ->{(—k3as), (—kxa^} и т. д.
Динамическая перестройка симметрии 253
Если рассмотреть уравнение G.4.14) с учетом этих симметрийных
соотношений, выражение для Т-матрицы в случае пионов с малыми
энергиями будет иметь вид
Т' (k\CL\, kia2\ k3-X3, ^«4) = a[Sa1a,6a,a1S +Sa,a,S0[,a^ + 6a1a4Sa,a,«].
G.4.21)
В действительности масса пионов не равна нулю. Следовательно,
симметрия, заключенная в G.4.21), в точности не реализуется.
Если допустить, что справедлива гипотеза приближенного сохра-
нения аксиального векторного тока (ПСАВТ) [11 ], то обнаружится,
что в выражении G.4.21) нужно произвести замены
s -*- s — т„, t -> t — /пя, и -> и — т%.
Соотношение Гольдбергера—Треймана. В случаях когда базис-
ная группа симметрии есть SU B) х SU B) или SU C) X SU C),
можно вывести соотношения, аналогичные соотношениям G.4.7)—
G.4.10). Некоторые из них называются соотношениями каллен-
треймановского типа для распада /С-лептонов (например, соотно-
шения между характеристиками распадов /С->/л и /("->-/2я,
где / обозначает лептоны). Ниже мы в качестве примера выведем
соотношение Гольдбергера—Треймана [12].
Преобразования киральной группы симметрии SU B) х SU B)
определяются с помощью следующих изменений векторного и
аксиального токов V^ (х) и А^ (х):
Р (х) = ea&7Vl (x), G.4.22а)
4apv(x), G.4.226)
(x), G.4.23а)
(x). G.4.236)
Здесь (&v + бд) индуцирует киральное SU B) х SU B)-преобра-
зование. Преобразование, связанное с 8А, вызвано сдвигом поля
голдстоуновских бозонов, которые мы считаем «безмассовыми»
пионами. Из соотношений G.4.23а) и G.4.5) следует
e«Pv (a IА у (х) | Ь) = lim [BяK 2© (к)/пу* v (а \ V® (х) | Ь; %0 (к)).
G.4.24)
Из этого соотношения можно вывести некоторые соотношения
между формфакторами аксиального и векторного токов [13].
Поскольку ниже используются релятивистские волновые функции,
читатели, мало знакомые с этой областью, могут эту часть про-
пустить *). В этом подразделе мы положим й = с = 1.
г) Полное рассмотрение релятивистских волновых уравнений уже имеется
в литературе (см., например, [14]).
254 Глава 7
Выберем теперь синглетные нуклонные состояния для \а)
и|Ь); \а) = |/7 + q), \ Ь) = \р). Свойство ковариантности лорен-
цевых преобразований приводит к следующей форме соотношения:
" (Р + 1Г
G.4.25)
Здесь м (р) — четырехкомпонентная волновая функция частицы
со спином 1/2:
(p-Y + M) w(p) =0,
где yw — дираковские у-матрицы, уъ = YoYiY2Y3- Когда q мало,
I
I
p+q+k p
Рис. 7.2.
в правой части соотношения G.4.24) основной вклад дает полюс
пиона (рис. 7.2):
lim [BяK2со (к)]'7' (р [- <7| 7g @) | р; х? (к)) «,
'й(р +q) (-'")8ар7^ -F" ^ ^"(р)- G-4-26)
Здесь gr — пион-нуклонная константа связи. Закон сохранения
тока d^V® = 0 приводит к тому, что соотношение G.4.26) при-
нимает вид
lim [BлK2со (k)]'/2 {p + q\ V* @) | р; ъ(к)) ~
k0
X (-'^^-grTs+iWs^^afP). G-4.27)
Динамическая перестройка симметрии 255
Сравнивая выражения G.4.24) и G.4.27), обнаруживаем, что
" §(cl2)\^o = ~ivgr-^. G.4.28)
С другой стороны, когда | а) = | %% (q)) и | Ь) = | 0), из соотноше-
ния G.4.24) имеем
iv |0) = Hm [BяK 2со (k)]V. v (Xos (q) | 7? | x? (*<)>• G-4.29)
Поскольку
G.4.31)
[BnK2w(q)]'/2[BnK2w(k)]1/2
с учетом того, что
F @) = 1, G.4.32)
из G.4.29) получаем
/я = v. G.4.33)
Тогда, объединяя соотношения G.4.28) и G.4.33), находим
gA @) = /„&/2Л1; G.4.34)
это и есть соотношение Гольдбергера—Треймана. Если ty (х) —
гейзенберговское поле нуклона, то оно преобразуется киральным
SU B) х SU B) -^-преобразованием следующим образом:
8л v|) (х) = i —к-ув^р {х), G.4.35а)
6vi|) (х) = t -^ if» (х). G.4.356)
Тогда из соотношения G.4.5) получаем
(a\i-%- vrvHx) I b) = v lim (a I ifi (x) | ft; x« (k)> 1BяK2со (к)]1/». G.4.36)
Если выбрать состояния следующим образом: \а) = |0), а в ка-
честве \Ь) — основное состояние нуклона \р), то найдем
/.^^^»^ GЛ38)
256 Глава 7
где gr (k) — функция, заданная условием gr @) = gr. Теперь
равенство G.4.36) приводит к соотношению
Из соотношений G.4.39) и G.4.28) получаем
gA@) = l. G.4.40)
Если киральная симметрия существенно нарушается из-за отлич-
ной от нуля массы пиона, этот результат требует пересмотра.
Теоремы для низких энергий и поведение системы при низких
температурах. Грубо говоря, температурное поведение некоторой
физической величины определяется тепловыми возбуждениями,
которые дают вклад в эту величину. При низкой температуре
возбуждаются только низколежащие энергетические уровни, и,
следовательно, поведение системы при низкой температуре опре-
деляется в основном ее поведением в области низких энергий.
Предположим, что динамическое отображение оператора А
получено при нулевой температуре:
Л=2 F(ki...kn; ql...qm)a\...alaq...aq G.4.41)
ft, tJl
Когда температура слегка повышается, ak можно выразить через
физические операторы a (k, fi) и а+ (k, fi) с помощью преобразова-
ний Боголюбова; тогда для бозонных операторов ак справедливо
равенство
@, P|fl+flJO, Р) = /э [ш (к) ] 6 (к — q).
Если среднее по вакууму от А известно, то
@, р|Л|О, Р)=Е F(kx...kn; q,...qm)X
п, т
X @, Р | G+. • • Mtaqi ...aqJ0, P), G.4.42)
причем температурная зависимость появляется в множителе
/в [со (к)], возникающем при спаривании a\t и aq. в выражении
G.4.42). Поскольку низкотемпературное поведение fB [со (к)]
существенно определяется поведением голдстоуновских бозонов
с к я» 0, зависимость от температуры @, f>\A |0, fi) определяется
зависимостью коэффициентов F (ki ... kn; qx ... qm) от малых им-
пульсов. Можно сформулировать следующее утверждение: поведе-
ние системы при низких температурах определяют теоремы для
низких энергий системы голдстоуновских бозонов в упорядоченном
состоянии. Расчеты такого рода приведены в разд. 5.3.
Динамическая перестройка симметрии 257
7.5. Перестройка симметрии и сжатие группы
В разд. 7.4 приведены некоторые примеры перестройки сим-
метрии. Перестройка симметрии есть результат того, что динами-
ческое отображение представляет собой слабое соотношение и для
расчета матричных элементов используется предельный переход
1/V ->¦ О (V — объем) или / (х) ->- 1 (/ (х) — некоторая размытая
функция). При заданной форме динамической перестройки можно
установить ряд соотношений между матричными элементами с по-
мощью процедуры, описанной в разд. 7.4 (теоремы о низколежа-
щих уровнях системы). Поэтому желательно иметь общее правило
для определения характера перестройки симметрии. В общем
случае, когда одна алгебра получается из другой с помощью не-
прерывной деформации, первая называется деформацией послед-
ней алгебры *). В этом смысле перестройка симметрии может всегда
рассматриваться как деформация исходной группы. В частности,
если новая алгебра получается с помощью сингулярного линейного
преобразования исходной алгебры, эта процедура называется сжа-
тием исходной алгебры [17]. Поскольку сингулярное преобразова-
ние есть предельный случай регулярного преобразования, алгебра,
полученная сжатием, есть особый случай деформации. В разд. 7.3
нам встречался пример, в котором перестройка симметрии при-
нимает форму сжатия группы SU B)-> Е B).
Теперь возникает вопрос: при каких условиях динамическая
перестройка неабелевой симметрии принимает форму сжатия
группы? Этот вопрос вызван тем, что получаемая в результате
сжатия группа имеет простую структуру, обеспечивающую про-
стой метод получения теорем для низких энергий.
Начнем с определения сжатия группы [17]. Обозначим эле-
менты алгебры Ли символами {Z-J:
[Lh L,] = iCiihLh. G.5.1)
Здесь Oak — структурные постоянные. Определим новые элементы
алгебры Lt (e), связав их со старыми с помощью линейного пре-
образования
Lt (г) = UijLj + eVijL,-, G.5.2)
где det U = 0, a det (U + eV) Ф О при е Ф 0. Если элементы
Lt (е) при е -*~ 0 имеют предельные значения Lt, то алгебра, обра-
зованная из элементов X,, есть сжатие исходной алгебры. Соответ-
*) Более точное определение см. в работах [15, 16]. В работе [16] рассмотрено
приложение процедуры деформации к перестройке симметрии.
9 УиЗЛЯЯВЯ Y а .-
258
Глава 7
ствующими преобразованиями L; (e) и Lt (e) матрицы U и V
можно привести к виду
1
И
О
V =
1
G.5.3)
Элементы, относящиеся к необращающимся в нуль компонентам
U, отметим верхним индексом A), остальные — индексом B).
Тогда получим соотношения
?» (е) = Lil) + е
(г
A < i, j < г), G.5.4)
a < n). G.5.5)
Вычислим коммутаторы операторов Lt (e) при бесконечно малом е.
Например,
[Li" (e),
(е)]
e) + i ±
G.5.6)
Чтобы алгебра с элементами L,- (е) в пределе при е ->- 0 была
хорошо определена, должно выполняться равенство
С\% = 0. G.5.7)
С помощью аналогичного расчета можно показать, что алгебра
с элементами Lt существует только в том случае, если LJ1' обра-
зуют замкнутую подгруппу, a Za2) — инвариантную абелеву
подгруппу:
G.5.8)
где
A)
ijk
B)
Хорошо известным примером сжатия группы является процедура
перехода от группы Галилея к группе Лоренца (с-*- оо, где с —
скорость света).
Динамическая перестройка симметрии 259
В примере сжатия группы SU B) ->¦ Е B) новая алгебра Е B)
является предельным случаем (е -*- 0) алгебры, образованной
с помощью преобразований
~LX (e) = eLb L2 (e) = eL2, L3 (e) = L3, G.5.10)
где Li—элементы алгебры спинов SU B). Для того чтобы
limE_o Li (e) был хорошо определен в представлении Lt, размер-
ность пространства представлений должна возрастать при умень-
шении е. Если рассматривается /-представление спина для Lt,
легко видеть, что Lt (e) стремится к нетривиальному пределу,
когда е уменьшается, а Ы стремится к константе. В этом смысле
У(объем)тт>-оо(и, следовательно, к бесконечности стремится общий
спин системы) участвует в сжатии группы для спиновой системы.
Как показано в разд. 7.1, когда имеет место перестройка
симметрии, для того, чтобы возникли некоторые преобразования
исходной симметрии, требуются определенные сдвиги поля голд-
стоуновских бозонов. Поскольку эти сдвиги поля образуют абе-
леву группу, часто случается, что перестройка симметрии стано-
вится сжатием группы. Ниже мы исследуем условие, при котором
перестройка симметрии принимает форму сжатия группы.
Рассмотрим динамическую перестройку Q-симметрия -^-сим-
метрия. Примем, что преобразования Q-симметрии формируют
группу Q. Пусть %° — голдстоуновские бозоны. Другие физиче-
ские поля обозначим символами ц>°. Мы рассмотрим те случаи,
когда параметры преобразования 9; не зависят от времени и поло-
жения в пространстве. Эти элементы симметрии называются вну-
тренними. Элементы ^-симметрии, связанные с этим Qt, имеют вид
(см. G.1.53), G.1.54))
%f (х) = li (x) - 8, S' (Z,/Zft)Vi eiki (-д) %l (x) + {Z\u @)/ai) 8,,
G.5.11)
cpf (x) = <p? (x) - 9, ?' etk, (-d) <pl (x). G.5.12)
k
Другими словами, #-преобразования являются суперпозициями
сдвига поля голдстоуновских бозонов и смешивания физических
полей.
Предположим, что Н — подгруппа Q и что Я-симметрия
сохраняется; Н называется подгруппой устойчивости группы Q.
Пусть N1; ..., Nn — генераторы Q-преобразований. Обозначим
символами "Ni соответствующие генераторы #-преобразований.
Выберем^Nm+i,*...,Nn в качестве генераторов Я-преобразований.
Таким образом, т <j'ra. Поскольку1Я'— группа устойчивости,
для i > т должно быть Nt | 0} =0. Пусть Я обозначает группу,
образованную теми ^-преобразованиями, которые индуцируют
9*
260 Глава 7
Я-группу преобразований гейзенберговских полей. Поскольку
группа Я должна оставлять вакуум инвариантным, генераторы Nt
(i >m) группы Я приводят к аннигиляции вакуума:
ATj|0> = 0 (i>m). G.5.13)
Тогда Ni (i >m) представляют собой комбинацию только членов
вида ajay, составленную таким образом, что удовлетворяются
соотношения G.5.11) и G.5.12); следовательно, Я вызывает только
смешивание свободных физических полей.
Предположим теперь, что имеется генератор, скажем Na,
а <: т, который создает только линейную «смесь» физических
полей. Поскольку уравнение свободного поля для физических
полей инвариантно относительно преобразований G.5.11) и G.5.12),
генератор Nt такой «смеси» полей не зависит от времени и пред-
ставляет собой суперпозицию членов вида aja/, откуда следует,
что Na\0) = | 0). При этом смешивании вакуум остается инва-
риантным, так как exp {iQNa} |0) = | 0). Для i >m выполняется
также равенство [Nt, Na] | 0) = 0, поэтому Na принадлежит
группе устойчивости. Следовательно, когда нет группы устой-
чивости, более широкой, чем Я, каждый из генераторов Nlt ..., N-
(которые соответствуют Л^х, ..., Nm) помимо смешивания физи-
ческих полей должен вызывать определенный сдвиг голдстоунов-
ских бозонов. Следовательно, количество голдстоуновских бозонов
1° равно т (/ = 1, ..., т); при ^-преобразованиях нарушение сим-
метрии проявляется в сдвиге голдстоуновских полей.
Поскольку Nlt ..., Nm вызывают сдвиг поля голдстоуновских
бозонов, они кроме вызывающих смешивание физических полей
билинейных членов содержат некоторые линейные %°-члены (члены,
канонически сопряженные yj). Поскольку Я-группа сохраняется,
а х? и Ni при Я-преобразованиях ведут себя одинаково, (Л^х, ..., Nm)
и (%i> •••> %°т) образуют одни и те же m-мерные представления
групп Я и Я соответственно. В общем случае (%[, ..., %%,) распада-
ется на несколько неприводимых представлений Я.
Когда алгебра Nt образуется сжатием Nit она должна, согласно
G.5.8), содержать замкнутую подалгебру {Ni1'} и инвариантную
абелеву подалгебру {Ni2)}. Алгебра, составленная из элементов
{Nt; i > т), есть замкнутая подалгебра, так как при i > m
Nt — генераторы группы устойчивости. Если Nt (i <: т) содержат
только линейные %°-члены, они образуют абелеву подалгебру.
Действительно, можно показать [8 ], что только в том случае, когда
Q-симметрия является компактной симметрией группы Ли, ^-сим-
т
Динамическая перестройка симметрии 261
метрия образуется сжатием Q-симметрии. Кроме того, используя
соотношения G.1.50), G.1.51) и G.1.56), можно показать, что
6j/ft = (—1/2) Cj/ft для i, j, k < т. Отсюда следует, что Nt (i < m)
не содержат билинейных членов тогда и только тогда, когда Сцк
(i, j, k < т) в выражении G.1.50) обращаются в нуль. Следова-
тельно, если Q-симметрия является симметрией относительно
компактной группы Ли, то ^-преобразование является сжатием
тогда и только тогда, когда исходная алгебра Ли удовлетворяет
условиям
[На, Hb] = iCabcHc, G.5.14а)
[На, Nt) = iCaUNj, G.5.146)
lNt, Nj] = iCilaHa, G.5.14в)
где Ha — генераторы группы устойчивости Н (т. е. а, Ь, с >т),
a Nt — дополнительные к ним генераторы (i, j < m). Заметим, что
члены, содержащие Сцк с i, /, k < m, исключаются. В этом случае
q выражается в виде полупрямого произведения Я и Г, т. е.
Н ? Т, где Т состоит из сдвигов голдстоуновских полей.
В частности, если Q — компактная простая группа Ли, усло-
вия G.5.14) устанавливаются просто, поскольку Я есть максималь-
ная подгруппа.
Ниже мы приведем несколько примеров. В последнем разделе
исследуется модель группы SU B) в случае, когда Я есть группа
U A). Возникают два голдстоуновских бозона (или один комплекс-
ный голдстоуновский бозон) xl и %°2. Поскольку U A) — макси-
мальная подгруппа SU B), перестройка симметрии должна иметь
вид сжатия группы [7]: SU B)-»- U A) ? f B) = Е B). В реаль-
ной модели скалярного поля группы SU B) X SU B), если
подгруппа устойчивости есть изоспиновая группа SU B), появля-
ются три голдстоуновских бозона, которые образуют триплетное
представление группы SU B), и при сжатии SU B) X SU B) ->¦
->¦ Е C) идет динамическая перестройка. С другой стороны,
в случае изодублетной скалярной модели симметрии SU B) и
группы устойчивости, состоящей из единичных элементов, было
показано [18], что ^-симметрия не возникает при сжатии Q-сим-
метрии. Это и понятно, поскольку Я не является максимальной
подгруппой. В случае Q = SU (п) и Я = SU (п — 1) X U A)
перестройка происходит при сжатии
SU (п) -+ SU (п — 1) X |/A)оП2(п-1)] = EU (п — 1),
поскольку SU (п — 1) Х{/A) — максимальная подгруппа
SU (п). В случае G = О (п) и Я = О (п — 1) перестройка симме-
трии есть сжатие О (п) ^-О (п — I) D f (п — I) = Е (п — 1).
262 Глава 7
Когда размерность группы велика, максимальная подгруппа
может быть выбрана различными способами. Например, для
G = SU C), если Н выбрать в виде Я = SU B) х U A), про-
исходит сжатие S U C) ->- Е U B), а при другом выборе, т.е.
Н = SU B), генераторы GIH реализуются в пятимерном непри-
водимом представлении SU B). В этом случае динамическая пере-
стройка симметрии связана со сжатием группы SU C) ->
->¦ SU B) ? Т E). Когда сохраняется симметрия только меньшей
группы, из сжатия групп не обязательно вытекает перестройка.
7.6. Инфракрасный эффект голдстоуновских
бозонов и параметр порядка
Как показано в разд. 7.1, сдвиги поля голдстоуновских бозонов
играют жизненно важную роль в восстановлении исходной сим-
метрии. Поскольку сдвиг поля вида %а^-%а + Са меняет %&,
добавляя к нему константу Са, он влияет только на моду, отвечаю-
щую нулевой энергии голдстоуновского бозона. Таким образом,
мы видим, что за перестройку симметрии и поддержание упорядо-
ченного состояния ответственны голдстоуновские бозоны с очень
низкой энергией (инфракрасные бозоны). В этом разделе мы
затронем еще один эффект, возникающий благодаря этим инфра-
красным бозонам, а именно разрушение упорядоченного состоя-
ния, когда влияние этих бозонов становится чересчур сильным.
Особенно часто это происходит в системах низкой размерности
(одномерных или двумерных) х).
Для определенности продемонстрируем наше рассмотрение,
воспользовавшись фазово-инвариантной моделью. Если t|) — гей-
зенберговское поле, мы примем, что лагранжиан фазово-инва-
риантен:
=5Чг|)]. G-6.1)
Рассмотрим фазовый параметр порядка
v = @H>t (*)iM*)|0). G.6.2)
х) Физики, работающие в области твердого тела, хорошо знают, что в одно-
и двумерных системах трудно создать упорядоченные состояния [19]. В ра-
боте [20] для объяснения невозможности существования сверхпроводимости
в одномерном случае приводится соображение об инфракрасных эффектах та-
кого рода у голдстоуновских бозонов. Этот довод был уточнен в работе [21],
где было показано, как влияние инфракрасных голдстоуновских бозонов пре-
пятствует появлению упорядоченного состояния при нуле температуры в одно-
мерном случае и при конечной температуре в одно- и двумерном случаях. Коле-
ман [22] привел доказательство того, что спонтанное нарушение симметрии не-
возможно при размерности пространства-времени 1 -f- 1. Хотя его рассмотрение
не включает калибровочных полей, результат остается справедливым, если даже
они существуют, В этом разделе мы следуем работе [21].
Динамическая перестройка симметрии 263
Здесь мы приняли, что if — спиновый дублет. Тогда появляется
один голдстоуновский бозон х°. и динамическое отображение -ф
имеет вид G.2.19), т. е.
'Чг ( rf\ */0(r\ I Fx i ГЛгО rnOl- П Р. Ч^
' \— / А \ / / т> * 1"л , ку |., I / .и.оI
где ф° обозначает физические поля, не являющиеся голдстоунов-
скими бозонами.
Для исследования влияния инфракрасных голдстоуновских
бозонов выделим в х° инфракрасную часть %^, а все остальное обо-
значим х°: Х° = Хл + Xs- Под инфракрасным вкладом мы подразу-
меваем вклад полей с импульсами меньше определенной беско-
нечно малой пороговой величины (т. е. |к| <т]). Поскольку поле
Х° входит в Ft> ф под знаком производной, вклад %^ в F пре-
небрежимо мал. Собирая выражения exp [(i/2v) Z'/2 (—д) х? (х)]
и Ft, | вместе, мы можем переписать равенство G.6.3) в виде
\. I hi Ф°]- G.6.4)
где Z обозначает Z @), a Ft 4. не содержит %ц. Тогда выражение
G.6.2) дает
X (О | :ехр (irZ'f^ (х)) :: exp (^ Z'/.x« (.,)) : | о). G.6.5)
Это можно записать в компактном виде
) G.6.6)
где ?)„ @) = @1 [Х» WJ210) = G.6.7)
T-r G.6.8)
(Р) v ;
для размерности пространства п. Если температура рассматри-
ваемой системы равна Т, состояние | 0) нужно заменить на
| 0, jj) (p = filkT), и выражение G.6.8) принимает вид
А,<0) = @, P|^W]2|0,P)= G.6.9)
Поскольку в случае спонтанного нарушения фазовой симметрии
264 Глава 7
для малых | р | величина со (р) пропорциональна | р |, из выражения
G.6.10) следует, что при п = 1 или п = 2 Dv@) расходится и
параметр порядка v обращается в нуль (ср. с G.6.6)). Отсюда
следует, что в случае размерности пространства п, равной 1 или 2,
гомогенного состояния с упорядоченной фазой не существует.
Следует заметить, что все рассмотрение в этом разделе бази-
руется на допущении о бесконечности объема системы. Грубо го-
воря, если рассматриваемая одно- или двумерная система имеет
линейный размер L, параметр порядка приближенно пропорцио-
нален ехр (—cL) или ехр (—с In L), где с — положительная кон-
станта. Ситуация может существенно измениться, если элементы
системы приобретут хотя бы небольшую свободу, связанную
с третьим измерением.
Приведенные выше доводы могут быть применены к случаю
ферромагнетизма, если мы изменим определение Dn @) следую-
щим образом:
п-тг [dnpQ(n- Iph-Lp. G.6.11)
2Bя)"
Здесь В (х) — поле магнона. Поскольку со (р) вблизи р = 0 ведет
себя как Dp2, получаем тот же вывод, что и для фазовой модели.
Хотя конечный размер системы меняет приведенные выше сооб-
ражения, мы имеем достаточно оснований считать, что полученный
результат в целом справедлив. Для системы конечного размера
необходимо учесть влияние поверхности. Если рассматривать
очень малый магнетик в трехмерном пространстве, его магнитный
момент будет малым из-за влияния поверхности. Та же ситуация
сохраняется и в случае более низкой размерности: конечность
размера образца не очень выгодна с точки зрения существования
упорядоченного состояния, так как поверхностный эффект стре-
мится разрушить порядок. Но рассмотрение, проведенное в этом
разделе, не исключает появления близкого порядка, связанного
с дискретными элементами симметрии, даже в системах с низкой
размерностью. Состояния Костерлица—Таулеса [23] в двумер-
ных системах и солитоны в </>4-модели— вот некоторые примеры
такого рода. Последний пример связан с дискретными элементами
симметрии; он рассматривается в гл. 9.
7.7. Кристаллы
В предыдущих разделах этой главы мы рассмотрели те случаи,
когда спонтанное нарушение симметрии не нарушает пространст-
венно-временную симметрию. В этом разделе мы исследуем слу-
чай, когда вращательная и трансляционная симметрии спонтанно
Динамическая перестройка симметрии 265
нарушаются. Рассмотрение проводится на примере кристалла
[24—2611) (в работе [26] приведены основные результаты ра-
бот [24, 25]).
Условия периодичности. Отправным пунктом рассмотрения
является лагранжиан 3? (х), который включает молекулярное поле
"ф (х): 3? (х) = & [ч|5 (х) ]. Мы принимаем, что лагранжиан обла-
дает трансляционной и вращательной инвариантностью, т. е.
J <Рх 2 [ф (х)} = j dxx9? [ф {х + а) ] G.7.1)
для любык а [а = (О, а)], а также допускаем, что взаимодейст-
вие таково, что может образоваться кристалл с векторами решетки
a, (i = 1, 2, 3), т. е.
v (х + а,) = а (х), G.7.2)
где v (х) —среднее значение оператора плотности «(%) =
v(x) = @\n(x)\Q). G.7.3)
Введем полный набор ортонормированных вещественных пе-
риодических функций {фх (х); Я, = —1, 0, 1,2, ...} с периодич-
ностью решетки <р^ (х + аг) = ср^ (х). Выберем их следующим
образом:
Ы (х)} = {Ф_! (х) = 1, ф0 (х), Фг (х), ...}; G.7.4)
здесь Ф/ (х) = Ц (V-v,)t/ V,v (x), i = 1, 2, 3, G.7.5)
а ф0 (х) определяется равенством
v (х) = у_! + уофо (х), G.7.6)
где у0 и у_! — две константы. Матрица V размерности 3X3 опре-
деляется из условия
QV4/ = j d*x Vtv (x) VjV (x), G.7.7)
я
где Q — объем элементарной ячейки кристалла.
Соотношение Уорда—Такахаши. Поскольку лагранжиан транс-
ляционно инвариантен, выбираем систему отсчета, добавляя к лаг-
ранжиану 2! (х) небольшой нарушающий симметрию член
х)Ъ(х). G.7.8)
J) При обычном подходе квантуются только смещения ионов в определенных
Узлах решетки, в результате чего возникает ансамбль фононов [27].
266 Глава 7
Сравнивая G.7.8) и G.1.8), видим, что функцияФ (х) должна быть
выбрана в виде
Ф (х) = о(х)ф+ (*Ж*)- G-7.9)
Пространственная трансляция приводит к замене -ф(л:) на
я|/ (х) — -ф (х + G, t). При этом Ф (х) изменяется следующим об-
разом:
Ф' (х) = v (x) n (х + в, *). G.7.10)
Если в — бесконечно малая величина, то
б?Ф (х) = v (x) Vtn (x), i = 1, 2, 3. G.7.11)
Вспомним теперь соотношение Уорда—Такахаши F.1.28) и
используем Ф (хг) вместо "ф (xi). Поскольку 8,,2' = е6?Ф (х), по-
лучим
Ш @1 б«Ф (*) | 0) = е [ d4i/ @1 Т [б?Ф (г/), Ф (х) ] | 0), G.7.12)
что можно записать в виде
ln(x), V,n(?/)]|0)o(y)= G.7.13)
= еу (х) J d4y @1 7 [А (х), Угй ((/) ] | 0) v (у) +
+ е [у (х) Р f d*yv (у) V;y (у). G.7.14)
Здесь
А (х) = п (х) —V (х), G.7.15)
откуда следует @ | й (х) \ 0} = 0. G.7.16)
Последний член в G.7.14), очевидно, обращается в нуль. Интегри-
руя по частям в первом члене G.7.14), получаем соотношение УТ
ihSiV (х) = — е j d*y @ | Т [А (х), А(у)]\0) Wtv (у). G.7.17а)
Используя G.7.5), последнее выражение можно записать в виде
МЫ (х) = -е { d*y @ | Т [А (х), п(у)]\ 0) Ф; (у). G.7.176)
Фононы. Следуя выводу выражения для спектрального пред-
ставления двухточечных функций, проведенному в разд. 3.6, мы
можем получить соотношение
@1ТЩх), п[у)] 10) = -J2L- J dk0 J №* с-„> х
ав
X (У&* (х, у, k)+¦¦•], G.7.18)
Динамическая перестройка симметрии 267
где k (х — у) = к (х — у) — k0 (tx — ty), а Ла (х, у, k) обозна-
чает член, который содержит сингулярность типа полюса:
Д. (Х) у. k) = 2^f.x)^(k,y)
Здесь еСа (к) отвечает сдвигу полюса вследствие влияния 9?е(х).
В выражении G.7.19) функция Fa (k, х) периодична с периодом
решетки:
Fa (к, х + а,) = Fa(k, х). G.7.20)
Многоточие в выражении G.7.18) обозначает члены с обрезан-
ными сингулярностями, a QB — объем первой зоны Бриллюэна.
Для простоты в G.7.19) приведено спектральное представление
при нулевой температуре, хотя выражение G.7.19) легко модифи-
цировать, введя в него температурные эффекты, аналогично тому,
как это сделано в разд. 4.3 и 6.2. Все результаты этого раздела
остаются справедливыми при конечных температурах.
Разлагая периодическую функцию Fa (k, х) в ряд по фх (х):
Fa (К х)=Ет?(к)фл(х), G.7.21)
можно переписать G.7.18) в виде
@1Т [Л (х), А (у)} | 0} = -A. j dk0 f e<* (*-*> J] Фл (х) Au, (k) <&. (у),
QB Л, ?.'
G.7.22)
где
5(к)^>(к) + • • • ¦ G-7.23)
(к) + « ^ V ^
Переходя к пределу при 8->0в G.7.17) и используя соотно-
шения G.7.22), G.7.23), получаем
Фг (х) = lim (-в) I] Фх (х) А„ @), i - 1, 2, 3. G.7.24)
Поскольку члены с обрезанными сингулярностями, которые обо-
значены многоточием в выражении для A u- (k) G.7.23), не порож-
дают никаких сингулярностей типа 1/е, находим
со'а @) = 0, G.7.25)
6// = 2 Т? @) С«' @) yf @), G.7.26)
Т?@) = 0, Я^= 1, 2, 3. G.7.27)
Полнота соотношений G.7.26) требует по крайней мере трех типов
бозонов (а = 1, 2, 3), энергетические спектры которых не имеют
268 Глава 7
щелей (см. G.7.25)). Эти голдстоуновские бозоны являются аку-
стическими фононами. Таким образом, набор физических кванто-
вых состояний состоит из трех фононов %%. и квазимолекулы ф°.
Они удовлетворяют уравнениям свободного поля в виде
К (д) %Ъ (х) = 0, G.7.28)
I (д) ф° (х) = 0, G.7.29)
где, в частности,
Мд)= 5г-м!(У), G.7.30)
а дифференциальные операторы cod (V) (а = 1, 2, 3) определены
• соотношением
coa(V)e =(oa(k)e . G.7.31)
Точечная группа и векторы поляризации. Уравнение для фоно-
нов G.7.28) может быть записано в более привычной форме с по-
мощью векторов поляризации ef (V). Чтобы ввести векторы поля-
ризации, рассмотрим точечную группу кристаллической решетки.
Для простоты ограничимся только теми случаями, когда кристал-
лическая решетка инвариантна при некоторых дискретных пре-
образованиях вида
xt -> (Dx)t = S DtjXj, G.7.32)
/
которые составляют так называемую «точечную группу». Распро-
странение нашего рассмотрения на более общие случаи проводится
непосредственно. Матрицу Di} будем называть координатным
представлением операции D—элемента этой точечной группы.
Действие этого элемента на любой вектор состояния будем также
обозначать символом D. Матрица D унитарна:
D+ = D-K G.7.33)
Инвариантность кристаллической решетки относительно преоб-
разований точечной группы приводит к соотношениям
v (Dx) = v (x), G.7.34)
D | 0} = | 0). G.7.35)
Пусть Ва+ (а = 1, 2, 3) обозначают операторы рождения фо-
нонов. Тогда эти операторы для заданного к образуют представ-
ление D, что означает
«+ (к) D = Ц ВР+ (Dk) 0Pa (к). G.7.36)
Из G.7.36) и соотношения унитарности G.7.33) следует
« (к) D-1 = 2 ^ (Dk) Ща (к). G.7.37)
Динамическая перестройка симметрии 269
Представление 0ра(к), хотя оно, вообще говоря, зависит от к,
может быть записано в терминах ?Юц, которые не зависят от к,
следующим образом:
2>Ь* (к) - 2 еЪ* (Dk) 0tJef (к). G.7.38)
Это соотношение определяет векторы поляризации ef (k), которые
выбраны так, чтобы удовлетворялись соотношения унитарности
2 еТ (к) е\ (к) = 6вЭ, G.7.39)
i
I>e?(k)ef(k) = bi/. G.7.40)
а
Фононное поле. Поскольку D коммутирует с общим гамиль-
тонианом Н, для любого целого п справедливо равенство
= 2 Hn®ba(k)\B* {Dk)), G.7.41)
3
где использованы соотношения G.7.35), G.7.36). Это приводит
к уравнению
[»<* (к)]" 2 0ра (к) | ВР (Dk)) = 2 [сор (Dk)]« 0Ра (к) | ВО (Dk)>.
G.7.42)
Таким образом, имеем
3V (к) К (к)]» = [сор(Dk)]" 0Ра(к). G.7.43)
Если соа (к) не вырождены (нет пересечений между тремя ветвями
фононного спектра), мы всегда можем перенумеровать фононные
моды, расположив их в порядке убывания:
Ml (k) > со2 (к) > со3 (к) (к Ф 0). G.7.44)
Тогда из уравнения G.7.43) следует
соа (к) = соа (Dk). G.7.45)
Если имеется вырождение, может оказаться, чтосоа (k) = cop (Dk).
Даже в этом случае мы можем перенумеровать фононы так, чтобы
равенство G.7.45) оставалось справедливым.
Упростим ситуацию, приняв, что система инвариантна отно-
сительно обращения времени х). Тогда имеем
2>эа(к)=Д>$а(-к), G-7.46)
ef (к) = ef* (—к), G.7.47)
соа(к)==соа(-к). G.7.48)
i х) Случай, когда инвариантность относительно обращения времени нару-
шается, рассмотрен в работе [24].
270 Глава 7
Соотношения G.7.46) и G.7.47) дают
3>1, = Ф„. G.7.49)
Используя соотношения G.7.37), G.7.38), G.7.43) и G.7.49),
можно показать, что
? е« (k) DBa (к) D-1 ехр [—ша (к) t] =
а
= I! Л е? (к) Вр (Як) 0;а (к) ехр [-коа (к) t] =
ее р
= 2 Я» (Dk) ехр [-top (Dk) f] 2 Ж;а (к) ef (к) =
= S ехр [—пйц (Dk) /] В» (Dk) ? е? (Dk) S5/(-. G.7.50)
Р /
Отсюда видно, что фононные поля х? (i = 1, 2, 3), определяемые
выражением
x?(*) =
= П а/ У f d3k —ту- \e* (k) B« (k) exp fikx - tm (к) Л +
образуют представление точечной группы:
Dtf (х) D-1 = 2 xj (Dx) &„. G.7.52)
Здесь Dx обозначает (Dx, t). В выражении G.7.51) е? (V) опреде-
ляется соотношением
e*(S?)eikx=ef(k)eikx.
Вводя матрицу
со?/ (к) = U еЧ (к) со2а (к) ef (к), G.7.53)
а
можно привести фононное уравнение G.7.28) к виду
Мд)Х?(*) = 0, G.7.54)
где
a of/ (V) определяется соотношением
М2. (у) е'К* = со^. (к) е*к«. G.7.56)
Динамическая перестройка симметрии 271
Матрица 'кц(д) называется динамической матрицей колебаний
решетки.
Эквивалентность координатного представления и представле-
ния фононного поля. Докажем, что представление Фи для на-
бора \хЧ (х)\ эквивалентно координатному представлению. Чтобы
это сделать, заметим, что, согласно спектральному представлению
G.7.18), динамическое отображение"п (х) имеет вид
n[x) = v (х) + 2 Fa (V, x)%l(x) + ..., G.7.57)
а
гДе ^а (V, х) определяется соотношением
Fa (V, х) е** = Fa (к, х) е'кх. G.7.58)
Многоточие в выражении G.7.57) обозначает нормальные произве-
дения более высоких порядков. Динамическое отображение
G.7.57) может быть представлено в виде
n(x) = v (х) + 2 Ft (V, х) х? (*) + ••-. G.7.59)
i
где Ft (k, х) ее ? Fa (к, х) еТ (к). G.7.60)
а
Динамическое отображение G.7.59) приводит к соотношению
Dn (x) D-1 = v (х) + 2 Ft (V, х) х? (Dx) 3>/t + ... . G.7.61)
С другой стороны, поскольку гейзенберговское поле "ф (х) преоб-
разуется как
Щ> (х) D'1 = ф (Dx), G.7.62)
имеем
Dn(x)D~1 = n(Dx). G.7.63)
Сравнивая это с соотношением G.7.61), находим
/%• (k, Dx) = 2 Fj (D-Xk, x) &jl, G.7.64)
где принято, что матрица &)ц вещественна и унитарна, т.е. Фт =
= ^)~1. Заменяя D на D в соотношении G.7.64), получаем
Ft (к, D-'x) == 2 ^/ Фк, х) 3>,t. G.7.65)
/
С другой стороны, соотношения G.7.21) и {7Л.27) дают
Ft @, х) = 2 Ф/ (х) Л^/ь G.7.66)
272 Глава 7
где NH = ? У? @) <?Г («)• G.7.67)
Кроме того, поскольку у (?)х) = у (х) и фг = (V-1/2);/ V,-v (х),
справедливо равенство
Ф* (?>-1Х)= Д] Ф/ (х) (У'/.ду-'/,),... G.7.68)
Тогда выражение G.7.66) приводит к соотношению
Ft @, D-'x) = 23 Ф/ (х) (V1/. DV-'l'N)^ G.7.69)
а равенства G.7.65) и G.7.66) дают
Ft @, D"!X) = S Ф/ (х) (М2>)„. G.7.70)
/
Таким образом, имеем
Ф = ц @) Drf1 @), G.7.71)
где матрица т]@) определяется выражением
i\t, @) = (ЛМУ'/.L/. G.7.72)
Ниже мы введем зависящую от к матрицу ц (к), которая совпадает
с г] @) при к = 0. Этим объясняется то, что мы используем обо-
значение т] @) вместо т].
Соотношение G.7.71) показывает, что набор {%?} соответствует
координатному представлению нормировочной матрицы т] @).
Докажем теперь, что
13>, NTN] = 0, G.7.73)'
где NT — транспонированная матрица N. Для этого используем
соотношение G.7.66), которое дает
J d4Fi @, х) F, @, х) = (NTN)lh G.7.74)
Поскольку левая часть инвариантна при преобразовании x->-Z)x,
получаем соотношение G.7.73).
Динамическая перестройка трансляционной симметрии. Иссле-
дуем теперь вопрос о том, какого рода преобразования %° и ф°
вызывают пространственный сдвиг гейзенберговского поля "ф (х).
Чтобы провести детальный вывод этого преобразования, необхо-
димо обобщить формулу G.1.40) для динамического отображения,
а также выражение G.1.41), которое следует из G.1.40), приняв
во внимание периодическую пространственную структуру кри-
сталла. Такой вывод преобразования приведен в работе [24].
Здесь мы выберем более короткий путь. Согласно общим сообра-
жениям, приведенным в конце разд. 7.1, исследуемое преобразо^
Динамическая перестройка симметрии 273
вание принадлежит к числу преобразований, оставляющих урав-
нения свободного поля для х? и ф° инвариантными. Кроме того,
нарушение симметрии возникает только при сдвиге поля х?
(X? ->¦ X? + с-число). Таким образом, в рассматриваемом случае
мы приходим к следующему преобразованию, вызывающему про-
странственную трансляцию гейзенберговского поля г|) (х) —>
-> г|) (х + 9):
X? (х) -* х1 (х + в) + 23 в,с„, G.7.75а)
/
Ф° (х) -» ф° (х + 9). G.7.756)
Здесь 9 обозначает совокупность параметров (в, 0). Чтобы опре-
делить с-числа Сц, вернемся к динамическому отображению
G.7.59), которое можно переписать в виде
n(x) = v (х) + I] ft @, х) х? (*)+•••. G.7.76)
i
где многоточие заменяет не только нормальные произведения бо-
лее высоких порядков, но также линейные по % члены, содержа-
щие дифференциальные операторы в положительных степенях.
Если смещение 0 бесконечно мало, то из выражения G.7.76) сле-
дует
п (х + 0) = v (х) + (G-V) v (х) + Д] F( @, х) х? (х + 6) +
+ JjXHx+Q) (в-V) ft @, х) + • ¦ • = v (x) +
S Ф, (х) {8(V^ + N]t%* (x + 9)} +
+ 5] X? (* + в) (в-V) ft @, x) + . . . , G.7.77)
i
где использованы равенства G.7.5) и G.7.66). Это выражение
можно переписать в виде
п (х + 9) = v (х) + ? Ф/- (х) #/, (х? (* + 9) + 2] Л» @) 9/) +
+ 23 X? (х + 9) (в-V) ft @, х) + . . . . G.7.78)
i
Поскольку преобразование поля х?, примененное к квадратичным
по х° членам в выражении G.7.76), образует линейный по х° член,
третий член в правой части G.7.78) должен возникать из квадра-
тичного члена выражения G.7.76). Поэтому мы фиксируем свое
внимание только на первых двух членах правой части равенства
G.7.78). Тогда мы находим, что константы Сц, появляющиеся при
274 Глава 7
сдвиге поля G.7.75а), должны быть равны г\а @). Подводя итоги,
делаем вывод, что преобразование вида
X? (х) -> х? (* + 9) + Е 4U @) 8/, G.7.79а)
фо (Х) _^ фо (Х + е) G.7.796)
вызывает пространственную трансляцию гейзенберговского поля
-ф (х) ->¦ ijj (л; + 8). Это и есть динамическая перестройка трансля-
ционной симметрии в кристаллах. Вывод остается справедливым
и в случае, когда 9г не бесконечно малы.
Динамическое отображение. Выражение G.7.79) для пере-
стройки пространственной симметрии показывает, что динамиче-
ское отображение любого гейзенберговского оператора (например,
Он (х)) имеет вид
Он (х) = :Ц Фх [х + X" (х) ] О}. (х; дХ°, Ф°) :, G.7.80)
л
где поля фононов XI (i = 1, 2, 3) определяются выражением
A?(x) = Ttf(V)X/°(*)- G-7.81)
Здесь г] (V) — дифференциальный матричный оператор, удовле-
творяющий условию
Чи (к) = ть/ @) для к = 0. G.7.82)
Функции фЛ — элементы полного ортонормированного набора
G.7.4). Символом (ЭХ0 в равенстве G.7.80) обозначена совокупность
X°i, содержащих любое число производных. Оператор О} при пре-
образованиях дХ° (х) -> дХ° (х + 9) и ф° (х) -*¦ ф° (х"+ 0) ме-
няется: ОЛ (х)-> Од (х + 9). Таким образом, О^ (х) обладает
трансляционно-инвариантной формой C.4.2), т. е.
О% (х) = У] j rf4xi.. .dVr^x (л- — Jfi, x — x2..., x — yn)x
П
X :дХ°(Х1)дХ<>(х2)...ч>о(уп):. G.7.83)
Отметим, что область импульсов физических полей Х° и ф° огра-
ничена первой зоной Бриллюэна.
Импульс, тензор напряжений, энергия. В дальнейшем мы
допустим, что лагранжиан поля взаимодействующих молекул
¦ф (х) имеет вид
S{x) =4 (^4г - НИ) ~ Ш*Р1* - V(t, ¦*), G.7.84)
где М — масса молекулы, а V ("ф, "ф+) — функционал, зависящий
от -ф и "ф+ и не содержащий производных. Поскольку лагранжиан
Динамическая перестройка симметрии 275
инвариантен при фазовом преобразовании "ф -*- e'ei|), справедлив
закон сохранения
-|-n(jf) + V.j(x)=O, G.7.85)
где
i (*) = -щ- W W ^ W - v^+ W * WJ- G-7-86)
Это означает, что число молекул сохраняется.
Закон сохранения для канонического тензора энергии-напряже-
ния T^v имеет вид
^]]№ = 0, G.7.87)
/
где
Pt (х) = Toi (х) + А1ц (х), G.7.88)
Тц (х) = -^-(ViP Vyip + V/l>+ ¦ V;40 + fif/S1- G-7.89)
Операторы Р; и Тц называются плотностью импульса и тензором
напряжений.
Рассматривая динамическое отображение п (х) G.7.59) и при-
нимая во внимание равенство G.7.85), мы видим, что линейный
по %° член в динамическом отображении j (и, следовательно, Р).со-
держит производные по времени первого порядка. Чтобы найти
линейный й0-член (%° = d%°/dt) в динамическом отображении
Pt (x), вспомним, что оператор
Ki = — J d3xPi (x) G.7.90)
является генератором пространственной трансляции. Поскольку
это должно привести к преобразованию G.7.79), соответствующее
динамическое отображение должно иметь вид
I ^с/ w- G-7-91)
где учтено, что ц*, @) = г\п @). Здесь /Сг [ф°] — оператор сво-
бодного импульса, который порождает пространственную транс-
ляцию ф°.
Из выражения G.7.91) видно, что Pt (x) содержит линейный
по %° член, формфактор которого для ф_1 (х) (=1) при нулевом
импульсе равен —т^/ @). В этом случае Pt (x) имеет вид
G.7.92)
276 Глава 7
Отсюда определяются г\$/ (V) и, следовательно, г\ц (V), удовле-
творяющее условию G.7.82).
Из эрмитовости Pt (x) следует
t|;((V) = t,/((-V) = t,+ (V). G.7.93)
В терминах Х°, определяемых G.7.81), выражение G.7.92) при-
нимает вид
G.7.94)
где
P,/(V) = ^(V)%/(V). G.7.95)
Фононное уравнение G.7.54) может быть переписано в терминах
XI следующим образом:
Л?у(ад = 0, G.7.96)
Л,/ Н = -Р|/ (V) -Jr - Ф/у (V). G.7.97)
Здесь
Фг7(к) = [т,+ (к)со2(к)т,(к)]г/, G.7.98)
где со2 (к) — матрица, определенная выражением G.7.53).
Используя закон сохранения G.7.87) и фононное уравнение
G.7.96), тензор напряжения Тц можно записать в виде
Тц{х)= Ц d7(V)VmX?(*)+ 2 2 <P;i(x)riA(V)X2 (*)+...,
G.7.99)
где
Е| = Фу(к). G.7.100)
. G.7.101)
Поскольку Р = Л4j, закон сохранения G.7.85) вместе с выраже-
нием G.7.94) приводит к равенству
2j Фь (*) Yw (V) Щ, (V) Л? (л:) + .... G.7.102)
-l t. /
Динамическая перестройка симметрии 277
Здесь матрица уи определена выражением
Yw(V) = — "зй" 2 (V/V/w ^ + 2 «u-YA'^V)), G.7.103)
где
flu- = if- J ^Зхфх (х) Vi4V (*)• G.7.104)
а
Из выражений G.7.76) и G.7.66) следует
yu@) = Nu для i = 1,2,3, G.7.105а)
•ух. @) = 0 в остальных случаях. G.7.1056)
Многоточия в выражениях G.7.94), G.7.99) и G.7.102) обозна-
чают как нормальные произведения %° более высоких порядков,
так и члены, содержащие ср°.
Величины c[f (k) определяются из равенства G.7.99). Обычно
их называют упругими постоянными (или модулями упругости),
хотя они и зависят от к. Эти величины обладают следующими эле-
ментами симметрии:
c/«(k) = cj«(k), G.7.106а)
c™i(k) = c[f(k), G.7.1066)
с#" (к) = с'™ (—к). G.7.106b)
Эти три свойства следуют из симметрии Тц, эрмитовости Ф;/- (к)
и соотношений G.7.47) и G.7.93). Из G.7.106) ясно, что при к = 0
упругие постоянные вещественны и только 21 из них независима.
Полный гамильтониан Я в слабом смысле эквивалентен сво-
бодному гамильтониану с численной константой Wo:
0{a\b). G.7.107)
Здесь Я (х°) и Я (ф°) — свободные гамильтонианы для Х° и <р°.
Таким образом, имеем
Я (Х°) = 4" J dzx № (х) р„ (V) Л? (х) + [V,*? (*)] <# (V) iVmX°- (x)]}.
G.7.108)
Резюмируя, можно сказать, что в процессе вывода уравнений
для упорядоченного состояния кристалла мы обнаружили суще-
ствование трех акустических фононов, являющихся голдстоунов-
скими бозонами. Мы также выяснили структуру динамической
перестройки трансляционной симметрии и получили выражения
для динамического отображения некоторых операторов, напри-
мер оператора плотности молекул п {х), оператора молекулярного
тока j (jc), оператора импульса Р, оператора тензора напряжений и
27S Глава 7 ________________
энергии T/j {x). Следует отметить, что фононное поле низких
энергий (т. е. Х° без производных) входит в динамическое ото-
бражение G.7.80) в комбинации х + Х°, что согласуется с обыч-
ной интерпретацией фононного поля как поля смещений. Со-
гласно фононному уравнению G.7.96), величина, канонически
сопряженная XI, есть рг/ (V) Х°. Тот факт, что рцХ° (х) появ-
ляется как главный член динамического отображения импульса
Р в G.7.94), связан с тем, что оператор импульса канонически
сопряжен векторной координате х + Х° (х).
Следует отметить,^что в общем случае все возбуждения не
исчерпываются акустическими фононами. Структура кристалла
определяет вид представления точечной группы и, следовательно,
число возбуждаемых мод. Последнее равно 3N, где N — число мо-
лекул в элементарной ячейке. Если N >1, возникают 3N — 3
моды, которые не являются акустическими; их называют оптиче-
скими модами. Операторы физического поля оптических мод со-
держатся в членах, обозначенных многоточием в выражениях для
динамических отображений, приведенных в этой главе.
ЛИТЕРАТУРА
1. Nambu Y., Jona-Lasinio G., Phys. Rev., 122, 345; 124, 246 A961).
2. Goldstone J., Nuovo Cim., 19, 154 A961).
3. Umezawa #., Nuovo Cim., 40, 450 A965);
Leplae L., Sen R. N., Umezawa #., Suppl. Prog. Theor. Phys. (commemora-
tion issue for the 30th Anniversary of the Meson Theory by Dr. H. Yukawa),
637 A965);
Leplae L., Umezawa #., Nuovo Cim., 44, 410 A966).
4. Bogoliubov N. N., Phys. Abhandl. Sov., 6, 113; 229 A962);
Wagner H., Zs. Phys., 195, 273 A966);
Matsumoto H., Papastamatiou N. J., Umezawa H-, Nucl. Phys., B68, 236 A974).
5. Goldstone J., Salam A., Weinberg S., Phys. Rev., 127, 965 A962).
6. Matsumoto H., Papastamatiou N. J., UmezawaH., Nucl. Phys., B82, 45 A974).
7. Matsumoto #., Umezawa #., Vitiello G., Wyly J. K., Phys. Rev., D9, 2806
A974).
8. Hongoh M., Matsumoto #., Umezawa #., Prog. Theor. Phys. (Kyoto), 64,
315 A981).
9. Dyson F. J., Phys. Rev., 102, 1217 A956).
10. Adler S. L., Phys. Rev., 137, B1022; 139, B1638 A965);
Weinberq S., Fhys. Rev. Lett., 17, 616 A966).
11. Gell-Mann M., Levy M., Nuovo Cim., 16, 705 A960).
12. Goldberger M. W., Treiman S. В., Phys. Rev., 110, 1178 A958).
13. Fujimoto Y., Papastamatiou N. J., Nuovo Cim., 40, 468 A977).
14. Schweber S. S., An introduction to relativistic quantum field theory, Harper
and Row, New York, 1966. [Имеется перевод: Швебер С. Введение в реляти-
вистскую квантовую теорию поля. — М.: ИЛ, 1963.];
Nishij.ima K-, Fields and particles, W. A. Benjamin, New York, 1969;
Takahashi Y., An introduction to field quantization, Pergamon, Oxford, 1969.
15. Hermann R., Math. Phys., 2, 155; 251; 3, 53; 75 A966); 5, 131; 157 A967).
16. Joos #., Weimar E., Nuovo Cim., 32, 283 A976);
Weimar E., Acta Phys. Austr., 48, 201 A978).
17. Inonu E., Wigner E. P., Proc. NAS, 39, 510 A953).
Динамическая перестройка симметрии 279
18. Matsumoto H., Papastamatiou N. J., Umezawa H., Phys. Rev., D13, 1054
A976).
19. Hohenberg P. С, Phys. Rev., 158, 383 A967);
Mermin N. D., Wagner H., Phys. Rev. Lett., 17, 1133 A966).
20. Leplae L., Mancini F., Umezawa H., Phys. Rep., IOC, 153 A974).
21. Matsumoto H., Papastamatiou N. J., Umezawa #., Phys Rev., B12, 1836 A975).
22. Coleman S., Comm. Math. Phys., 3, 259 A973).
23. Kosterlitz J. M., ThoulessD. J., J. Phys., C16, 1181 A973).
24. Wadati M., Matsumoto H., Takahashi Y., Umezawa H., Fortschr. Phys., 26,
357 A978).
25. Wadati M., Matsumoto H., Umezawa #., Phys. Rev., D18, 4077 A978).
26. Wadati M., Phys. Rep., 50, 87 A979).
27. Born M., Huong K-, Dynamical theory of crystal lattices, Oxford University
Press, Oxford, 1954. [Имеется перевод: Борн М., Хуан Кунь. Динамическая
теория кристаллических решеток. — М.: ИЛ, 1958.];
Ziman J., Electrons and phonons, Oxford University Press, Oxford, 1960.
[Имеется перевод: Займан Дж. Электроны и фононы. —М.: ИЛ, 1962.];
КШе1 С, Quantum theory of solids, Wiley, New York, 1963. [Имеется пе-
ревод: Киттель Ч. Квантовая теория твердых тел. —М.: Наука, 1967.];
Maradudin A. A., Montroll E. W., Weiss G. H., Theory of lattice dynamics
in the harmonic approximation, Solid State Physics Series, Academic Press,
New York, 1963. [Имеется перевод: Марадудин А. А., Монтролл Е. У.,
Вейс Г. Г. Динамическая теория кристаллической решетки в гармоническом
приближении.—М.: Мир, 1965.];
Kallaway J., Quantum Theory of the Solid State, Academic Press, New York,
1976. [Имеется перевод: Каллуэй Дж. Теория энергетической зонной струк-
туры. — М.: Мир, 1969].
ГЛАВА 8
КВАНТОВАЯ ЭЛЕКТРОДИНАМИКА
ТВЕРДЫХ ТЕЛ
I. ПЕРЕСТРОЙКА КАЛИБРОВОЧНОЙ
СИММЕТРИИ
И ДИНАМИЧЕСКОЕ ОТОБРАЖЕНИЕ
8.1. Сверхпроводимость
В этой главе методы, развитые в гл. 7, применяются для иссле-
дования квантовой электродинамики твердых тел. В первом раз-
деле мы исследуем перестройку фазовой и калибровочной симме-
трии в сверхпроводящих металлах. Если известна перестройка
симметрии, то известны и основные характеристики динамических
отображений электромагнитного поля и тока.
Лагранжиан. Поле электрона -ф и электромагнитное поле,
описываемое вектор-потенциалом А^, являются гейзенбергов-
скими полями. Электроны взаимодействуют друг с другом посред-
ством электрон-фононных (и других) столкновений. Лагранжиан
имеет вид
(8.1.1)
где /Vv = 0,А-— 0А- (8-1.2)
Структура Н зависит от динамических свойств системы. Выше мы
использовали рационализированную систему единиц Хевисайда—
Лоренца, в которой е2/4яйс = 1/137. Значение потенциала Лд
отличается от его значения в гауссовых единицах множителем
Dя)-1/«. Дифференциальный оператор д^ определяется как че-
j)
тыре-вектор д„ =
Лагранжиан инвариантен относительно фазового преобразо-
вания -ф -v ехр [—i (е/йс) 8], а также калибровочного преобразо-
вания
()(*). (8-1-3)
Ali(x)-^All(x) + dliK(x), (8.1.4)
где калибровочная функция К (х) должна удовлетворять условию
существования фурье-образа.
Допустим, что положительные ионы образуют фон с зарядом
епе, где пе — число. При этом в лагранжиане возникает дополни-
Квантовая электродинамика твердых тел. 1 281
тельный член — еА0 (х) пе, который при интегрировании по сРх
калибровочно инвариантен, поскольку условия, наложенные на
функцию к (х), требуют обращения ее в нуль при 111 ->- сх>
(а также при | х | -> оо). Так как система в целом электроней-
тральна, имеем
(О | р (х) | 0} = —ел,, (8.1.5)
где р (х) — плотность заряда электронов.
Мы не обращаем много внимания на электрон-фононные (и дру-
гие) столкновения, поскольку получаемые в этой главе резуль-
таты не зависят от природы столкновений.
Как хорошо известно (см., например, [1 ]), в теории Максвелла
лагранжиан (8.1.1) не допускает канонического формализма, так
как Ао не имеет канонически сопряженной величины (т. е.
6.276Л0 = 0). Поэтому мы попытаемся модифицировать лагран-
жиан таким образом, чтобы можно было применять канонический
формализм. Для этого добавим к лагранжиану S член [2 ]
2В (х) = В (х) D» (д) А» (х)-±-В (х) а (д) В (х). (8.1.6)
Здесь В (х) — новое гейзенберговское поле, а дифференциальный
оператор D^ (д) — четыре-вектор вида
Дифференциальные операторы а (д) и vB (д) определяются так,
чтобы теория формулировалась в терминах физических частиц.
Мы связываем величины Vх и V^ с помощью метрического тензора
env'- Уд=й|1УУу. Тензор g^v диагоналей; диагональные элементы
равны
git = —goo = 1- (8-1.8)
Канонические коммутационные соотношения и уравнения
Гейзенберга. Лагранжиан 3? ~f- S?B допускает канонический фор-
мализм, поскольку A/с) В — величина, канонически сопряжен-
ная Ао. Канонические коммутационные соотношения для бозон-
ных полей имеют вид
[Ло (*), В (у)} б (tx - ty) = icMW(x - у), (8.1.9)
1В{х), В(у)]6&-д = 0, (8.1.10)
lA^x), Лч(у)]б(/х-д =0, (8.1.11)
[A, (x), B(y)]b(tx-ty) -0, (8.1.12)
W, (x), Foj (у) ] б (tx - tt) - -ШЩх - у) Ь„, (8.1.13)
[Foi(x), B(y)]8(tx-ty) = 0, (8.1.14)
lAo(x),Foi(y)]b(tx-ty) = 0. (8.1.15)
282 Рлава 8
Здесь i и / пробегают значения 1,2,3. Операторы электронного
поля-ф (х) и-ф+ (х) коммутируют с В (у), Av (у) и Foj (у) при tx = ty.
Уравнения Гейзенберга для электромагнитного поля имеют
вид
= /v-?>v (<?)?• (8.1.16)
^ = a(d)B, (8.1.17)
где /ц — электрический ток:
/ц = 6276 Л*, (8.1.18)
удовлетворяющий закону сохранения
0% = О. (8.1.19)
Голдстоуновский бозон и поля духов. Рассматривая совместно
уравнения (8.1.16) и (8.1.19), приходим к любопытному выводу,
что гейзенберговское поле В (х) свободно:
D(d)B = 0, (8.1.20)
где D(d)=&Dll(d). (8.1.21)
Считая, что vB (д) — vB {—&), получаем D {—д) = D (д).
Это соотношение подтверждает тот факт, что хотя поле В ведет
себя как канонически сопряженное Ло, оно не взаимодействует ни
с каким другим полем. Согласно уравнению (8.1.20), энергия
кванта В дается формулой
*> (Р) = МР) | Р |. (8-1-22)
где vB (p) определяется соотношением
vB {д) е'Р* = vB (p) е'Р*. (8.1.23)
Заметим, что энергетический спектр w (p) не имеет щели.
В дальнейшем мы будем считать, что /w выражается только
через г];, г|з+ и А, а также, возможно, через их производные по коор-
динатам. Тогда имеем
иц(х), /v(y)]6(k-g = 0, (8.1.24)
Ш(х), UWU(tx-tv) = 0. (8.1.25)
Поскольку из соотношения (8.1.16) при v = 0 следует
B = —dtFi0—j0, (8.1.26)
из уравнений (8.1.13)—(8.1.15), (8.1.24) и (8.1.25) получаем
[В(х), B(y)]8(tx-ty) =0, (8.1:27)
[В (х), At (у) ] б (*, - ty) = ichd*8{4)(x - у), (8.1.28)
IB (x), Л0(г/)]бD-д = 0. (8.1.29)
Здесь мы использовали обозначение G = A/с) (д/dt) G.
Квантовая электродинамика твердых тел. 1 283
Вспомним теперь, что уравнение (8.1.20) для В второго порядка
относительно производной по времени. Таким образом, из урав-
нений (8.1.10) и (8.1.27) следует
1В(х), В (у)] -0, (8.1.30)
откуда вытекает, что свободное поле В имеет равную нулю норму
[2]. Поскольку в пространстве Фока нельзя определить одноча-
стичное состояние без нормы, поле В есть суперпозиция двух
бозонов х° и Ь° [3—5]:
В = ZB (д) (Ь° - х°), (8.1.31)
где D (д) %° = 0, D (д) Ь° = 0. (8.1.32)
Чтобы В имело нулевую норму, норма %° должна быть поло-
жительна, а норма Ь° — отрицательна:
[%° (х), %° (у) 1 б (ts - tv) = icH8W(x - у), (8.1.33)
[b° (x), 6° (у) ] б D - ty) = -icH8W(x - у). (8.1.34)
Таким образом мы обнаружили, что пространство Фока есть ли-
нейное пространство с индефинитной метрикой. Поле Ь° назы-
вается полем духов. Заметим, что нормировка %° отличается от нор-
мировки в B.6.122) множителем с2.
Возможность конструирования линейного пространства с ин-
дефинитной метрикой стала известна после того, как Гупта и
Блойлер [6 ] предложили формулировку квантовой электро-
динамики (детальное исследование индефинитной метрики см.
в работе Наканиши, цитированной в [6]). Мы не будем здесь под-
робно показывать, как конструируется пространство с индефи-
нитной метрикой. Кратко можно сказать, что мы должны изменить
определение внутренних произведений: внутренние произведения
состояний определяются следующим образом: (п[ ... | пх ...) =
= П{бл л'. (—1)", где п — полное число Ь°-квантов в состоянии
\пъ п2\..).
Поскольку В (х) не взаимодействует ни с какими полями, мы
можем определить наблюдаемые физические состояния как со-
стояния, которые удовлетворяют условию
l%°(x) — b°(x)Y->\a) = 0. (8.1.35)
Здесь (—) обозначает ту часть оператора, которая отвечает уни-
чтожению, а | а) — любое наблюдаемое состояние.
Условие существования наблюдаемого физического состояния
(8.1.35) гарантирует выполнение уравнений Максвелла, поскольку
соотношение (8.1.16) приводит к тому, что для наблюдаемых со-
стояний \а) и \Ь)
\b) = {a\u\b). (8.1.36)
284 Глава 8
Обратим теперь внимание на фазовую инвариантность. Лаг-
ранжиан 3? -f 3?в инвариантен относительно фазового преобразо-
вания
(^)(x). (8.1.37)
Бесконечно малый член лагранжиана, приводящий к наруше-
нию инвариантности, равен 9?г = еФ, где
Ф (х) = ф; (х) t|,t (х) + г|>| (х) г|>} (*). (8.1.38)
Важнейшее условие возникновения сверхпроводимости состоит
в том, что параметр порядка для фазы не обращается в нуль:
v = @|Ф (х)|0)=^0. (8.1.39)
Определим гейзенберговское поле % с помощью выражений
G.2.15):
Тогда, согласно выражению G.2.16), голдстоуновский бозон (фа-
зон) %°а соответствует линейному члену в динамическом отобра-
жении %:
(8.1.41)
Уравнение свободного поля для %Ъ записывается в виде
ЭДЭЙ(*) = О. (8.1.42)
Поскольку энергетический спектр бозона не имеет щели, Da @) =
= 0.
Примем теперь, что
}0 = -±.(цЦ-Нпе). (8.1.43)
Тогда имеем соотношение
1% (х), /о (у) ] S (tx - ty) = -2ЙФ (х) bW(x - у), (8.1.44)
которое вместе с равенством (8.1.26) дает
[5 (х), %(y)]8(tx- tv) = -21еФ (х) 8Щх - у). (8.1.45)
Мы получаем
()(°\Т['ВW' *ШIо) =
b(xy) + {0\T[B(x)x, (У)]\О), (8.1.46)
откуда следует
D (дх) @\Т[В (х), % (у)] 10) = -^ 6<*> (х-у). (8.1.47)
Квантовая электродинамика твердых тел. 1 285
Совместное рассмотрение этого выражения и соотношений (8.1.31)
и (8.1.41) показывает, что %а должно совпадать с %°:
%(х) = гУ> (д) х° (х) + . . ., (8.1.48)
D(d)%°(x) = 0. (8.1.49)
Таким образом, мы обнаружили, что %° (х) есть голдстоуновский
бозон (фазон).
Вспомним теперь, что дифференциальный оператор D^ (д)
еще точно не определен. Но из уравнения (8.1.49) ясно видно, что
оператор DM (д) должен быть выбран так, чтобы уравнение (8.1.49)
при условии D (д) = Dv- (д) дм было уравнением для голдстоунов-
ского бозона. Таким образом, левая часть калибровочного соот-
ношения (8.1.17) теперь точно определена.
Соотношения (8.1.31), (8.1.47) и (8.1.48) определяют перенор-
мировочный множитель ZB в динамическом отображении В:
B = -^Z-^(d)(b°~%°). (8.1.50)
Определение калибровочного условия. Соотношения (8.1.12)
и (8.1.28) дают
= ind*bw (x - у) + @1 TIB (х), А, (у)] 10), (8.1.51)
а это соотношение вместе с (8.1.20) приводит к уравнению
D (д) @\Т IB (x), Ai (у) ] | 0) = -iW*bw(x - у). (8.1.52)
С другой стороны, имеем
= tftdS6<4) (х-у)+@\Т[В(х), АО(у)] 0), (8.1.53)
где учтены соотношения (8.1.9) и (8.1.29). Совместное рассмотрение
соотношений (8.1.52) и (8.1.53) приводит к уравнению
D (д) @ | Т 1В (х), А» (у)) | 0) = -Ш*6D)(х - У)- (8-1.54)
Из этого уравнения видно, что линейные по %° и Ь° члены при-
сутствуют в динамическом отображении в следующей форме:
ZK° (д)дЬ0(х) + ^ (д)В (х) + ... . (8.1.55)
При выводе учитывалось соотношение (8.1.50). Поскольку урав-
нение свободного поля для В является уравнениемвторого по-
286 Глава 8
рядка относительно производных по времени, мы без потери общ-
ности можем допустить, что Рц (д) не содержит производных по
времени порядка выше первого. Тогда имеем
D» (дх) @ | Т [Л„ (х), % (у)) | 0) = р^ (дх) D» (дх) X
X <0| Г [В(х), %(у)]\0)+ ... , (8.1.56)
где многоточие заменяет вклады от членов, обозначенных много-
точием в выражении для динамического отображения Лд (8.1.55);
эти члены не содержат множителя \ID (д).
С другой стороны, поскольку Аи (х) коммутирует с г|) (у) и
т|)+ (у) при tv = tx, из соотношения (8.1.17) с учетом условия
(8.1.47) получаем
D» (дх) @ | Т [А,х (х), х(у)]\0)=а (дх) @\Т[В (х), %(у)]\0) =
Тогда имеем
^(д) D» (д) = а (д). (8.1.58)
Чтобы определить р^ (д) и а (д), вспомним, что, так какг]) ком-
мутирует с FOi и с Лц, то х, согласно (8.1.40), также коммутирует
с ними. Поскольку
Л, = Г jo OiAq,
находим
lAt(x)x(y)]u(t*-ty) = O. (8.1.59)
Это уравнение вместе с (8.1.48), (8.1.55) дает
М0)=О. (8.1.60)
Поскольку Do (д) = A/с) dldt и так как сс(д) не содержит произ-
водных по времени, из соотношения (8.1.58) теперь следует
а(д) = 0, Р„(а)=О. (8.1.61)
Подводя итог, мы видим, что из условия v Ф 0 следует, что кали-
бровочное условие имеет вид
D» (д) А» (х) = 0, (8.1.62)
а динамическое отображение А^ не содержит линейных по х°
членов:
^ = ^-2;/'(d)a/-b-•• (8.1.63)
Плазмон. Из соотношений (8.1.11) и (8.1.62) следует
D» (д) @ | Т [Л„ (х), А, (у) ] | 0) = 0, (8.1.64)
Квантовая электродинамика твердых тел. 1
где учтено равенство (8.1.7). Этому условию нельзя удовлетво-
рить, если Ь° — единственный линейный член в динамическом
отображении (8.1.63). Поэтому введем векторное поле и?:
А» = -Щ-Z*% W<^° + Z^/2) » «° + ¦ ¦ • > (8.1.65)
где многоточие обозначает нормальные произведения более высо-
ких порядков. Векторное поле н? называется плазмоном.
Чтобы выделить продольную и поперечную части, нужны
проекционные операторы L(lv для продольной части и Tnv для
поперечной:
(8.1.66a)
(8.1-666)
Мы можем написать
ZMV (д) = Zt (д) Т^ + Zi (д) L^, (8.1.67)
где и1 = ТЩ%, uL = Llu%. (8.1.69)
Очевидно, что
Z>(d)«? = O, uT = 0. (8.1.70)
Уравнения для поперечного и продольного плазмонов можно
записать в виде
[д2 - т\ (д)] и-l (х) = 0, (8.1.71а)
1Лх) = 0, (8.1.716)
D* (д) ы? (*) = 0, (8.1.71b)
причем последнее уравнение получено из калибровочного усло-
вия (8.1.62).
Поскольку при нулевом импульсе поперечные и продольные
состояния неразличимы, имеем
Z, @) = Z, @), (8.1.72)
тг@) = т@). (8.1.73)
288 Глава 8
Все три уравнения (8.1.71) можно объединить в одно условие
вида [4]
А^(д)и°(х) = 0, (8.1.74)
Л^ (д) = dVv - ^dv ~ т2 (д) ^v (d) + 8т2 (д) Т*\ (8.1.75)
где Sm2 (д) = т2 (д) - т\ (д) и
/ - [vB (
' (8.1.76)
° ¦<;
Из соотношения (8.1.73) следует
бт2 @) =0. (8.1,77)
Докажем теперь, что из уравнения (8.1.74) вытекают три
уравнения (8.1.71). Для этого заметим, что
= {-д\ + ^ vl (a)v2) Lt + a' (-d°Lov - ^-^ (a) ^'l/v) -
= {D (d) gtp - d'DP (d)} Lpv, (8.1.78)
p - д°др) lpv = v2l°v - aVl/v =
(d)/cf V2 - ^5} L°v -
f d''
- a0 {(ys (d)/cf d'L
iv
= [vB (d)/cr2 [D (d) gOP - dW? (d)} Lpv. (8.1.79)
Эти два соотношения можно записать в виде одного уравнения
[dYP ~ д»др] Lpv = r,w (d) {D (д) gl - d,D° (д)} Lav. (8.1.80)
Таким образом, A^v (д) в (9.1.75) имеет вид
Л^ (а) = [& - т2 (д) — Ьт2 (д)} Т^ +
+ rf р (а) \{D{d) - m2(d)]g^ - дрЕГ(д)) LI. (8.1.81)
Тогда уравнение (8.1.72) немедленно приводится к виду (8.1.71а)
причем
ml (д) = от2 (а) — Ьт2 (д), (8.1.82)
а также к виду
тГ (а) {[D(д) - т* (д)] g°p ~ др& (д)} «? = 0. (8.1.83)
Умножая уравнение (8.1.83) на д^ и используя равенство^
avT,vP = ^pv^ = [Vb (d)/c]-2DP (д), (8.1.84)
Квантовая электродинамика твердых тел. I 289
получаем уравнение
[vB (д)/с]-2т2 (д) D° (д) и'6 = 0.
Из этого уравнения следует (8.1.71 в), которое вместе с урав-
нением (8.1.83) приводит к уравнению (8.1.716). Таким образом,
мы доказали, что уравнение (8.1.74) эквивалентно трем уравне-
ниям (8.1.71), т. е. представляет собой уравнение плазмона.
Двухточечная функция и дивизор для плазмона. Построим
теперь двухточечную функцию плазмона Av-K (x), определенную
следующим образом:
(х). (8.1.85)
Следуя методу, изложенному в разд. 2.6, введем дивизор для про-
дольного плазмона. Докажем, что дивизор dilv (<?) определяется
выражением
dv» (д) = {g* - m-2(д) <у> (<?)} л-1 (д). (8.1.86)
Поскольку
{gp - m-2 (д) dj)? (д)) {[D (д) - /и2 (д) ] gpa - dpDa (д)} =
= {D(d)-m*(d)}glla, (8.1.87)
мы можем доказать следующие соотношения:
Lwd,™ (д) Л„, (а) = {D (д) - т* (д)} L»v, (8.1.88)
LvJT» (д) = dw (д) L". (8.1.89)
Из соотношения (8.1.88) видно, что d^ есть дивизор для продоль-
ного плазмона.
Теперь мы можем записать
A^(x) = T^AT(x) + dpll(d)LpvAL(x), (8.1.90)
где
[д2 — т\ (а)] Аг (jc) = /8D) (х), (8.1.91)
[D (д) — т2 (д)) AL (x) = i6<*) (x). (8.1.92)
Поскольку из (8.1.86) следует
D» (д) d^ (д) = -т~2 (д) {D (д) - т2 (д)} D't^ (д) (8.1.93)
и так как
?> Vv (д) = 1»в (д)/с ]2 ад, (8.1.94)
из выражения (8.1.90) и соотношения D^Tm — 0 следует
D^v (х) = — imr2 (д) lvB {d)lc\2 dv8<4> (x). (8.1.95)
10 Умэдзава X. и др.
290 Глава 8
Используя построение свободных полей, выполненное в разд. 2.6,
и соотношение C.6.30), получаем
@1Т [4 (х), uk (у)] 10) = Ml (д) LpvAL (х) -
- Шс2 [d? @), 0 (tx - tyj\ LPX (x-y) +
+ itic2 [< @), 0 (iy - tx)] LpvA" (x - y), (8.1.96)
где A±(jt) —функции, определенные в B.6.85). Множитель с2 во
втором и третьем членах соотношения (8.1.96) обусловлен различ-
ным выбором нормировки. При выводе этого соотношения ис-
пользовано выражение B.6.86). Теперь из (8.1.86) с учетом B.6.87)
следует
@1Т [4 (х), "v (У)] 10) = К @) LpvAL (х-у)-
- t%06v0m-2 (d) [vB (d)/cf б<«> (х - у). (8.1.97)
Таким образом, из (8.1.90) получаем соотношение
@| Т [ul (х) и% (у)]\ 0) = ЙЛ^ (х-у)-
- inb^om-2 (д) [vB {дIс? б(«> (х - у), (8.1.98)
а оно с учетом выражения (8.1.95) приводит к равенству
?>*@)(О|Г ЦМ, «S (у) 1 I 0) =
= — ifimT2 (д) lvB (д)/с? [д$ — дЖ0] бD) (х — у). (8.1.99)
Пусть Аь — причинная двухточечная функция поля Ь°:
Ай (х) = @ | Т [Ь° (х), Ь°{у)]\ 0). (8.1.100)
Она удовлетворяет условию
D (д) Аь (je) = — №М (х). (8.1.101)
Знак минус — следствие отрицательности нормы Ь°. Отсюда имеем
0?0$Д6(х-у) = @\Т[д^Ь°(х)дф°(у)] 10) - йб^оМ14* (х - у).
(8.1.102)
Таким образом, получаем
?><* <0.| Г [0^°^). dJfi{y)]\O) =
= 1П [dxv — ^6v0] 6W (x — у). (8.1.103)
Предварительное рассмотрение динамических отображений.
Теперь мы готовы к тому, чтобы определить линейный по ы° член
в динамическом отображении Лц. В самом деле, из (8.1.65) следует
<0|7 [А„(х), Av{y)]\0) =
= (Пс/2еиJ Zx (d) @ | Т [д„,Ь° (х), дф° (у) ] | 0) + ~
+ Z™ р @) Z<v'> а (д) @ | Т [и°р (х), и°а (у)] | 0) + . . . , (8.1.104)
Квантовая электродинамика твердых тел. I 291
где многоточием обозначены члены, образованные нормальными
произведениями более высоких порядков. Таким образом, из соот-
ношений (8.1.64), (8.1.99) и (8.1.103) получаем
(Hc/2evJ Zx (д) = т~2 (д) Zo (д) [vB {дIс]\ (8.1.105)
где Z0(d) = Z,(d) + ... . (8.1.106)
Многоточие заменяет вклады от членов, обозначенных многото-
чием в выражении (8.1.104), a Z, определено в (8.1.67). Из соот-
ношения (8.1.105) следует
/п2 (д) = Bеу/ПсJ Zo (д) Z~xl (д) [vB (д)/с]2. (8.1.107)
Это выражение определяет энергию продольного плазмона [4].
В случае нулевого импульса эта энергия равна
/я @) = -|^ Zj'« @) Z~v° @) vB @)/c. (8.1.108)
Резюмируя, запишем выражения для динамических отображений
бозонных полей (ср. с (8.1.48), (8.1.50), (8.1.65))
(8.1.109)
-b\x)), (8.1.110)
+ ... , (8.1.111)
где многоточия обозначают нормальные произведения более вы-
соких порядков. С другой стороны, из результатов разд. 7.2,
а именно из соотношения G.2.19), следует, что динамическое ото-
бражение i|) (jc) имеет вид
[d1°, Ф°, и», 6°]:, (8.1.112)
где ф° — квазиэлектрон. Знак минус в экспоненциальном множи-
теле обусловлен выбором заряда электрона равным (—е). Из вы-
ражения (8.1.109) видно, что связывающее поле для %° есть
%%/г (д) Х- Кроме того, согласно равенствам (8.1.110) и (8.1.111),
связывающие поля для Ь° и и% равны соответственно
b(x)= --grZf (d)B(x) + Z-%i/2(d)%)(x)= (8.1.113a)
= &°(хН ¦ (8.1.1136)
/д (х) ~ Z"(I/2) % (х) + (Hc/2evf Z% (д) Z"(I/2) ЧВ (х) -
W= (8.1.114а)
(8.1.1146)
292 Глава 8
Таким образом, динамическое отображение гейзенберговского
оператора (например, О(х)) имеет вид
SO (х) = :(ТЮ(х) ехр {^}])с:, (8.1.115а)
S = :(Пехр{^}])с:, (8.1.1156)
где учтены соотношения C.5.17), C.5.18). Здесь
+ «° (х) л^ (а) иУ (х) + Фо+ (х) яф (а) ф (х) + ф+ (х) яф (-а) ф° (х) ),
(8.1.116)
где ф (х) — связывающее поле для квазиэлектрона ф° (V*), уравне-
ние для которого имеет вид Яф (д) ц>° (х) = 0.
Динамическая перестройка калибровочной симметрии. Рассмо-
трим теперь вопрос о том, как преобразуются физические поля
при калибровочном преобразовании
г|з (х) ->- ехр [—i (е/Пс) к (х) ] г|з (х), Лц (х) ->- Лд (х) +
+ адХ (х), В (х)-+ В (х).
Здесь к (х) — бесконечно малая неоператорная функция, имеющая
фурье-образ; никаких других условий на X (х) не накладывается.
Тогда изменение SO (x) в результате калибровочного преобра-
зования вызвано изменением гейзенберговских полей внутри
скобок Г-произведения в правой части соотношения (8.1.115).
С другой стороны, поскольку калибровочное преобразование есть
частный случай соотношения F.1.38), можно использовать соот-
ношение УТ F.1.28). Из этого соотношения следует
(g), F]|0) = Hl@\Tlb0F]\0), (8.1.117)
где F — любая комбинация гейзенберговских полей, a &F — ее
изменение при калибровочном преобразовании. Символ ЬЗЕ обо-
значает изменение лагранжиана при калибровочном преобразо-
вании. Из (8.1.115) и соотношения УТ (8.1.117) получаем
б {SO (x)} = -j-:\d4{T Ш (I) О (х) ехр {Щ\)с:, (8.1.118)
где б {SO(x)} — изменение SO(x) при калибровочном преобразо-
вании.
Изменение лагранжиана происходит только из-за изменения
3?в-{-3?в, где SEв определено выражением (8.1.6) при а(а) = 0,
а 2?ъ — еФ, где Ф определено в (8.1.38). Таким образом, имеем
Ь9? (х) = B(x)-D (д) I (х) + 2ег% (х) % (х). (8.1.119)
Квантовая электродинамика твердых тел. I 293
Поскольку % (х) — произвольная функция, @1 Т [%{х) % (х)...] | 0)
не может содержать сомножителя 1/е. Следовательно, при
в -*- 0 вторым членом в выражении (8.1.119) можно пренебречь.
Тогда имеем
. (8.1.120)
С другой стороны, преобразования
%V) + xV) + |r^1/"(-dL*).
(8.1.121)
изменяют s? на величину
ЬбФ = — -J- J <РхЬ (х) D (д) В (х). (8.1.122)
Таким образом, если к (х) бесконечно мало, при этом преобразо-
вании выражение в правой части (8.1.115а) заменяется на
-± : J<ПЯ (I) D (дъ) (TIB AH(х) ехр {^}])с :. (8.1.123)
Это выражение совпадает с выражением для б {SO(x)} (8.1.120).
Таким образом, мы доказали, что преобразование (8.1.121) вызы-
вает калибровочное преобразование гейзенберговских полей (ди-
намическую перестройку калибровочной симметрии [3, 4]). Это
приводит к заключению, что динамическое отображение любого
калибровочно инвариантного оператора содержит %° и Ь° только
в виде комбинации (%° — Ь°).
Поскольку
SB(l) = :(T IB (I) ехр {зФ)])с:, (8.1.124)
из выражения (8.1.120) при О (х) = 1 следует
8S = —i- S J d^k (I) D (%) В (I) = 0, (8.1.125)
где учтено соотношение (8.1.20). Из этого результата видно, что
S-матрица калибровочно инвариантна.
Общая структура динамического отображения. Вводя поле
фазона /° (jc) и линейный векторный потенциал aji с помощью вы-
ражений
L, (8.1.126)
rZ]l2(d)dllb0(X), (8.1.127)
294 Глава 8
а также учитывая соотношения (8.1.109)—(8.1.112), можно запи-
сать динамические отображения г|) (х), А^(х) и В (х)[4] в виде
(8.1.128)
^ (*) = < (х) + : А» (х; а% - Ц- dvf°, д (%° - Ь°), Ф°) :, (8.1.129)
^1/2oo (8.1.130)
Дифференциальный оператор, стоящий при комбинации (%° — Ь°)
в выражениях (8.1.128), (8.1.129), отражает тот факт, что преоб-
разование (%° ->- %° + const) порождает фазовое преобразование
г|з (х) (см. разд. 7.2). Эти динамические отображения имеют чрез-
вычайно простую структуру, что представляет собой результат
проявления калибровочной инвариантности теории.
Резюмируя, можно сказать, что калибровочное преобразова-
ние порождается преобразованиями (8.1.121). Динамические ото-
бражения гейзенберговских полей имеют структуру выражений
(8.1.128)—(8-1.130).
Заметим теперь, что поскольку член сЛ„ в (8.1.129) возникает
в Л^-канале, он должен содержать гриновскую функцию плазмона
Лд\, (д). Кроме того, из калибровочного условия ?>МЦ = 0 сле-
дует, что член с А содержит дифференциальный оператор
[D (д) g^ — a^Dv (д) 1, поскольку
D» (д) Ю (д) g^ - dllDv (д)]=0. (8.1.131)
Таким образом, динамическое отображение Лц (х) имеет вид
Лц (х) = 4 + [D (д) g? - <у)р (д)] X
flS-JjidvA H%°-b°), Ф°). (8.1.132)
Если зависимость Л от пространственных переменных гладкая,
можно положить
[D (д) g^ - ^Dp (д)) Apla (д) « 1, (8.1.133)
поскольку энергия плазмона много больше энергии голдстоунов-
ского бозона. В этом случае разумно применить линейную аппрок-
симацию
Ail(x)^a°il(x). (8.1.134)
Еще одно замечание по поводу динамического отображения
касается структуры F в выражении (8.1.128). Поскольку фазовая
симметрия спонтанно нарушается, связывающее поле <р° нетйожет
быть равно -ф, а является суперпозицией г|з и г|з+. Следовательно,
линейный член в динамическом отображении F является суперпо-
Квантовая электродинамика твердых тел. / 295
зицией ф° и ф+0. Именно по этой причине фазовое преобразование
трЦх) не может быть выведено из фазового преобразования <р° (х).
Собственная энергия фотонов и бесконечная проводимость.
Полученные до сих пор результаты основывались только на ком-
мутационных соотношениях и калибровочной инвариантности.
Попытаемся теперь получить дальнейшие результаты, используя
в явном виде уравнение Гейзенберга [5]. Таким образом, мы воз-
вращаемся к уравнению Гейзенберга (8.1.16), из которого следует
(х), Лv(у)]\0) =
= @1Т [}„ (х), Av (у)] 10) - IHg^W (х-у)-
-Dll(d)@\T[B(x)> Av(y)}\0). (8.1.135)
Учитывая выражение (8.1.54), мы можем переписать это равен-
ство в виде
(-а2^ + д^) @1Т [Ак (х), Лv (у)] 10) =
= @1Т [/„ (х), Лv (у)) 10) - ifig^w (x-y) +
+ 1ПО11(д)дх,-^щ-8{')(х-у). (8.1.136)
Введем обозначения
@1Т [А„ (х), Av (у)]! 0) = -Ж? J dVP ix-y)K, (P), (8.1.137)
<0|Г [/V (х), А, (у)] |0) = -А Jrf*p^(*-^v(p). (8.1.138)
Обозначив символом 2wv(/7) собственно энергетическую функцию
фотонов, можем написать
P)- (8.1.139)
Теперь уравнение (8.1.136) принимает вид
{P2gl~ P^ + ^l(p)}^tv(p)-=~g^ + ~pTDtl(p)pv. (8.1.140)
Здесь использованы обозначения D (д) е'рх = Ш„ (р) eipx,
D (д) е{Р* = —D (р) е1Р*.
С другой стороны, из соотношения (8.1.64) следует
?4p) = 0, (8.1.141)
а закон сохранения 5% = 0 вместе с выражением (8.1.24) при-
водит к уравнению
р»2„(р) = 0. (8.1.142)
Для простоты предположим, что теория обладает инвариантностью
относительно вращений. Поскольку перекрестных вкладов от про-
296 Глава 8
дольных и поперечных членов возникать не может, 2^ (р) можно
записать в виде
V (р) = 2г (Р) Т^ + 20 (р) (р*Ь^ - PllPJ, (8.1.143)
где учтено уравнение (8.1.142). Теперь уравнение (8.1.140) при-
нимает вид
\[Р2 + 2г (р)] Tl -Ь [1 + 20 (/>)] (/4 - W')) A^v (P) =
Чтобы его решить, полезно написать следующие соотношения,
которые легко вывести из определения 1]^:
[vB (р)/с]~2 %v (P) Dv (p) = Pll, (8.1.145)
[vB (p)/c] D» (р) г|^ (р) = pv, (8.1.146)
P2L»v - PuPv = D (p) Llr\vX (p) - [vb (p)/c)'2 D^ (p) Dv (p). (8.1.147)
Если в левой части уравнения (8.1.144) учесть соотношения
(8.1.141) и (8.1.147), то мы получим
XLPV О (р) U (P) Pv\ р» + 2Г (р) ^
р) - (vB (pycf-fl-rptfv] . (8.1.148)
На последнем этапе вывода выражения (8.1.148) использованы со-
отношения (8.1.145), (8.1.146).
Следуя приведенному в разд. 3.6 методу спектрального пред-
ставления, потребуем, чтобы A^v (p) не имело двойного полюса,
т. е. члена типа [\lD(p)]2. Тогда выражение (8.1.148) позволяет
заключить, что [1 + 20 (р)] имеет вид
Jt <8лл49>
где принято, что [1 + ^о(р)^1 должно быть пропорционально
гриновской функции продольного плазмона (т.е. l/[D(p) +
+ пг2 (р)]). Отсюда следует замечательный факт: 20 (р) содержит
особенность типа 1/D (р) и, следовательно, расходится при р = 0.
В одной из последующих глав мы покажем, что электропровод-
ность пропорциональна 20 (р). При этом рассмотрении мы убе-
димся, что проводимость сверхпроводников бесконечна, как это и
следует из названия «сверхпроводник» [5]. Этот результат под-
тверждают также приближенные расчеты 20 (р). Рассмотрим для
примера приближение случайных фаз. Поскольку 20 (р) есть не-
Квантовая электродинамика твердых тел. I 297
приводимая часть собственно-энергетической функции фейн-
мановских диаграмм (т. е. фрагментов диаграмм, которые нельзя
разделить на две, разрезая только по одной линии), в рамках при-
ближения случайных фаз она не может включать электромагнит-
ного взаимодействия. С другой стороны, если пренебречь электро-
магнитным взаимодействием, из результатов предыдущей главы
(а именно из соотношения G.2.27))вытекает, что @ | Т [j^, /v] | 0)
имеет особенность типа 1/D (р). Таким образом, полученный с по-
мощью приближения случайных фаз вывод о том, что 20 (р) имеет
полюс типа 1/D (р), согласуется с приведенными выше общими
соображениями. В приближении случайных фаз электромагнитное
взаимодействие приводит к многократному повторному действию
20, вследствие чего @ | Т [j^, /v] | 0) пропорционально
2
+ 20 (р)] ~ D (p)/[D (p) + п? (р)].
Таким образом, электромагнитное взаимодействие порождает
плазмонные моды.
Получим теперь окончательное выражение для A^v, объединив
(8.1.148) и (8.1.149). Результат имеет вид
(р) Tiiv ~
к()И (8лл50)
где vB обозначает vB (p). Выделяя полюсные члены, получаем
\А ln\— Zt (р) Г Zl (р) L'ip (п\ Г 4
-, (8.1.151)
где пгт, Zt (p), Z, (р) и Zo (p) определены выражениями
2г (Р) =-- п?т (Р) + [Zt1 (Р) - 1] [р2 + т\ (р)| + • • •, (8.1.152)
Z; (р) = Z (р) для D (р) = -т2 (р), (8.1.153)
Z0(p) =Z(p) для D(p) =0. (8.1.154)
Многоточием в выражении (8.1.151) обозначены члены, которые
не содержат особенности типа полюса.
Покажем теперь, что приведенные выше результаты следуют
непосредственно из динамического отображения (8.1.111). Если
298 Глава 8
учесть выражения (8.1.98), (8.1.102), то из динамического отобра-
жения (8.1.111) следует
Zt (p) Т Zl
(8.1.155)
где многоточием обозначены члены, не содержащие особенности
типа полюса. При выводе выражения (8.1.155) использовано соот-
ношение (8.1.107). Вспомним теперь выражение (8.1.86), т. е.
< (р) Lpv = {g? + т-2 (р) PyJ? (р)) г!0 (р) Lav =
- ti^Ip (р) Lpv + m (P) (vB/cf PvJ>4, (8.1.156)
где учтено равенство Dp (p) rjpv (p) = {vBlcf pv. Таким образом,
выражение (8.1.155) преобразуется к виду
Г1р
+ m (p) (yfl/cJ /?^v] + m-2 (p)Z0(p)(yB/cJ -щ^- P^Pv .... (8.1.157)
Это согласуется с (8.1.151). Из этого результата следует, что вве-
денное в выражении (8.1.105) Zo (p) определяется равенством
(8.1.154).
Мы завершаем этот раздел замечанием о температурных эф-
фектах. Когда используются методы термополевой динамики
(ср. гл. 4), возникают операторы, тильда-сопряженные гейзенбер-
говским операторам. В рассмотренном здесь случае кроме всех
приведенных выше соотношений возникают также тильда-сопря-
женные соотношения.
8.2. Квантовая электродинамика
нормальных металлов
Лагранжиан. В этом разделе мы рассмотрим электромагнит-
ные свойства твердых тел в нормальном состоянии [5]. Лагран-
жиан i?(i|5, Л) определяется выражением (8.1.1) и инвариантен
при калибровочном преобразовании г|з->» ехр [—i (e/ftc) X (х)],
Л^-^- Л л + дцА,. Лагранжиан также инвариантен при фазовом
преобразовании г|з ->¦ ехр [—i (е/Пс) В] г|з, Л№ ->- А^.
В этом разделе мы примем, что ^
0. (8.2.1)
Квантовая электродинамики твердых тел. 1
Другими словами, мы допустим, что спонтанного нарушения сим-
метрии не происходит (т. е. система находится не в сверхпроводя-
щем, а в нормальном состоянии).
Следуя методу, развитому в предыдущем разделе, мы введем
величину В (х), канонически сопряженную Ао- Таким образом, мы
добавим к лагранжиану член вида
2В (х) = В (х) № (а) А„ (х) - -L Я» а (д) В (х). (8.2.2)
Дифференциальные операторы D^[(d) и а (д) определим самосогла-
сованным образом. Допустим, что D» (д) имеет вид (8.1.7):
(д) = ((vB (d)lcf V, 4-|-) ¦ (8-2-3)
Чтобы упростить анализ, допустим, что v%(d) = v%{—д). По-
скольку фазовая симметрия не нарушается, нам не нужно вводить
член S?г. Тогда лагранжиан имеет вид
SB (г|з, Л„) - еАопе + В (х) D» (д) А„ (х) i-fi (x) а (д) В (х).
(8.2.4)
Уравнение Гейзенберга, калибровочное условие и условие
физического состояния. Уравнения Гейзенберга для г|з и Ац
возьмем в том же виде, что и в предыдущем разделе, например
-fl^v = /v - Dv (д) В. (8.2.5)
Из уравнения (8.2.5) и равенства dv/v = 0 следует соотношение
(8.1.20):
D (д) В = 0, (8.2.6)
из которого вытекает, что В — свободное поле, энергетический
спектр которого не имеет щели. Калибровочное условие имеет
вид (8.1.17), т. е.
D» (д) Л„ (х) = а (д) В (х). (8.2.7)
Все канонические одновременные перестановочные соотноше-
ния (8.1.9)—(8.1.15), а также соотношения (8.1.24)—(8.1.30)
остаются справедливыми и в этом разделе. Таким образом, мы
видим, что образуются два бозона %° и Ь° с энергетическим спек-
тром, не имеющим щели, через которые можно выразить поле В
в виде (8.1.31)
B = ZB(d)(b°~%0). (8.2.8)
Уравнения для %° и Ь° имеют вид
D (д) %° = 0, D (д) Ь° = 0. (8.2.9)
300 Глава 8
Бозон %° имеет положительную норму, а Ь° — отрицательную
(т.е. Ь° — бозон-дух). Физически наблюдаемые состояния \а)
должны удовлетворять уравнению (8.1.35):
(%° — Ь°у-)\а) = 0. (8.2.10)
Уравнение (8.1.54) может быть выведено и для данного случая:
D (д) @\Т[В (х), Лц (</)] | 0) = — Ш?8D) (х — у). (8.2.11)
Существенная разница между нормальным и сверхпроводя-
щим состояниями проявляется в том, что в случае сверхпроводи-
мости из условия v Ф 0 следовало, что % = i ('Фф'Фф — '^ti't) —
связывающее поле для %°. Отсюда было выведено соотношение
(8.1.61) (т. е. а(д) = 0) и, следовательно, калибровочное соотно-
шение (8.1.62). В данном же случае, поскольку v = 0, % не должно
быть связывающим полем %°, следовательно, а (д) не должно обра-
щаться в нуль и калибровочное соотношение имеет вид (8.2.7).
Приведенные соображения показывают, что равенство (8.1.64)
в данном случае не выполняется, поскольку при его выводе ис-
пользовалось калибровочное условие. В самом деле, если исполь-
зовать выражение (8.2.11), мы получим соотношение
№ (д) @1 Т [А», (х), Av (у)] 10) = а (д) @1 Т [В (х), Av (у)] 10) =
(8.2.12)
= -1Ы (д) д^-щщ-^ (х - у). (8.2.13)
Из выражений (8.2.11) и (8.2.8) следует
Л = Z^2) v (д) i? - Z-J (д) dj>° + pV (д) (*° - X°) + • • ¦ . (8-2.14)
где многоточием обозначены члены более высоких порядков,
а и? — векторное поле, называемое плазмоном. Третий член в
(8.2.14) в случае сверхпроводника не возникает (ср. с (8.1.61)),
так как а (д) обращается в нуль; в данном случае а (д) не обра-
щается в нуль.
Из калибровочного условия (8.2.7) следует
D»(d)Z$/2)v(d)u0v = Q, (8.2.15)
D* (д) р„ (д) = а (д) ZB (д) +a(d)D (д), (8.2.16)
а члены, обозначенные многоточием в (8.2.14), не дают вклада
в Dv-A^. В соотношении (8.2.16) а(д) — некоторый дифферен-
циальный оператор.
Из соотношения (8.2.16) следует
^ (8.2.17)
Квантовая электродинамика твердых тел. I 301
где учтено равенство (8.2.3). Здесь учтен также тот факт, что,
согласно (8.2.14), Р№ (д) не содержит множителя [1/D (д)].
Плазмон. Перенормировочный коэффициент Z^v может быть
представлен в виде (8.1.67), т. е.
ZBV (д) = Zt (д) 7VV + Z, (д) L^, (8.2.18)
где Tnv и L^v — проекционные операторы для поперечной и про-
дольной компонент соответственно. Таким образом, м? = Т^и% и
и^ = Ц,Ц% — поперечный и продольный плазмоны. Из соотно-
шения (8.2.15) следует
ЕР(д)и1 = 0. (8.2.19)
Уравнения для м? и м? можно написать в той же форме, что и
уравнение (8.1.71):
[д2-т2т(д))и1 = 0, (8.2.20а)
[D (д) - т2 (д)] и? = 0. (8.2.206)
Тогда уравнение для плазмона принимает вид (8.1.74):
Al(d)u°v(x) = 0, (8.2.21)
A^v (д) = Pg^ - а„^ - m2 (д) 1\^ (д) + 6m2 (d) TMV. (8.2.22)
Справедливы также выражения (8.1.98), (8.1.99), т. е.
@\Т[и°»(х), u°v(y)]\O) =
= ЙА^ (х-у)- i%o6vom-2 (d) [ов (а)/с]2 6<4> (дс - (/), (8.2.23)
= -ihrn2 (д) [vB (d)/cf [dv - a?6v0] 8D) (x - y), (8.2.24)
а гриновская функция A^v (л:) удовлетворяет соотношению
Л? (д) Avx (х) = ig»x8{i) (x) (8.2.25)
и определяется выражением (8.1.90).
Перестройка калибровочной и фазовой симметрии, динамиче-
ские отображения и перенормированный заряд. Чтобы определить
структуру нормальных произведений более высоких порядков
в динамическом отображении (8.2.14), исследуем перестройку сим-
метрии. В данном случае нужно использовать генератор, а не соот-
ношения УТ.
Если воспользоваться в данном случае соотношением F.1.19),
то генератор Ng для калибровочного преобразования приобретает
вид
Nb @ = - 4" J d*x I^of (*) diX (*) - B W ^ W+/o W *- ML (8-2-26)
302 Глава 8
поскольку —c~lFu (i = 1, 2, 3) —величины, канонически со-
пряженные Л;> а с~хВ (х) — величины, канонически сопряженные
Ло {х). Последний член в (8.2.26) приводит к преобразованию
г|э -v ехр [—i (е/Пс) X]ty. Так как % (х) по предположению — глад-
кая функция, которая достаточно быстро убывает при | х | ->- оо,
в (8.2.26) можно выполнить интегрирование по частям. Тогда
уравнение Гейзенберга (8.2.5) при v = 0 приводит к выражению
Ne @ = —¦7"J d3xld0B (х)Л (х) — В (х) д0К (х)], (8.2.27)
так как" ?>„ (д) = д0 г(= —c~ldldt)."Отсюда гвидно, что N* (t) не
зависит от времени, если % (х) — решение уравнения D (д) К (х) =
= 0. Этот результат согласуется с тем фактом, что при D (д) К (х) =
= 0 даже член ^лагранжиана (8.2.2) инвариантен относительно
калибровочного преобразования. При последующем изложении
мы не будем требовать выполнения условия D(d) Я, (х) = 0. Если
учесть выражение (8.2.8), то легко получить
ехр (•?-#,(/)) Х°(дг)ехр (-JL#,(*)) = %°(х) - ZB (д)Ъ(х),
ехр (-i- Ng (О) № (х) ехр (- -L Ng (t)) = Ь» (дс) - ZB (д) X (х).
Таким образом, мы можем заключить, что калибровочное преобра-
зование г|5 ->- ехр [—i (е/Нс) Я, (х) ], А^~> А^ + д^%, В -> В вы-
зывается преобразованиями
%° (х) -+ %° (х) - ZB (д) I (х),
Ь° (х) -> Ь° (х) — ZB (д) X (х). {o.z.zo)
Это — динамическая перестройка калибровочной симметрии
в квантовой электродинамике нормальных металлов. Сравнивая
(8.2.28) и (8.2.21) и учитывая соотношение (8.1.50), приходим
к любопытному результату: динамическая перестройка калибро-
вочной симметрии в данном случае та же, что и в случае сверх-
проводимости.
Поскольку преобразования (8.2.28) вызывают калибровочные
преобразования, динамические отображения гейзенберговских
полей Ау и г[) имеют вид
Л^ (х) = Z^2'v (д) 4 (лг) - Z11 (д) djP (х) +
(д) [Ь° (х) ~ х° (х)\ + : А„. [х; и%, (№ - х»), Ф«]:, (8.2.29)
~%°), Ф°]1 :•
(8.2.30)
"v,
Квантовая электродинамика твердых тел. I 303
Динамическое отображение В определяется равенством (8.2.8),
т. е.
В (х) = ZB (д) {Ь° (х) - х° (х)}. (8.2.31)
Если символом О (х) обозначить произвольный калибровочно-
инвариантный оператор, структура его динамического отображе-
ния будет иметь вид
О(х) = : б [х; u°v, (b° - х°), Ф°]:. (8.2.32)
Условие наблюдаемости физического состояния (8.2.10) приводит
к тому, что возбуждение квантов b и %° при измерении любой
калибровочно-инвариантной величины становится ненаблюдаемым.
Обратим внимание теперь на фазовое преобразование г|э ->
-> ехр [—i (е/йсN]г[), А^-+Ап, В->В. Генератор его имеет вид
КР = - -^ J d3xj0 (x). (8.2.33)
Поскольку ток/^ сохраняется, Np не зависит от времени. Согласно
общим соображениям, приведенным в разд. 7.1, преобразование
симметрии свободных физических полей есть комбинация линей-
ного смешивания физических полей и трансляций поля бозонов
с бесщелевым энергетическим спектром. Следовательно, динами-
ческое отображение Np содержит линейные и билинейные по фи-
зическим полям члены. Кроме того, линейные члены должны соот-
ветствовать бозонам с бесщелевым спектром. Поскольку Ь° и %°
не имеют заряда, билинейные по этим полям члены в Np не воз-
никают. Поэтому можно написать
= -7Г J d4 (т ф°+ W ф°{Х) + Свд°[№ {Х) ~ %°{Х)]) • (8'2-34)
Константы еТ и св исследуются ниже. Появление во втором члене
оператора д0 обусловлено независимостью от времени генератора
Np.
Генератор Np, определенный выражением (8.2.34), порождает
преобразования
exp (i- eQNp) Ф« (х) ехр (- -j- eBNp) = exp (-t fa б) Ф" (х),
exp (-fteBNp) %°(x)exp (- -^еШр) =Х° (*) - cBQ%° (x), (8.2.35)
exp (± eQNp) b° (x) exp ( —^- eQNp) = b° (x) -
С другой стороны, из выражения (8.2.30) видно, что динами-
ческое отображение г|з (х) содержит множитель exp H (е/Нс) X
х z~?{d) %° (х) ]. Поэтому второе из преобразований (8,2.35) при-
водит к появлению фазового множителя ехр [—i {elbc) cBZ~i @) 0],
304 Глава 8
Поскольку спонтанное нарушение фазового преобразования от-
сутствует, г|з (х) должно быть пропорционально <р°. Таким образом,
полный фазовый множитель, возникший при преобразовании
(8.2.35), есть ехр [—(i/Пс) [er + ecBZ~ii @)] 0], и он должен быть
равен ехр [—i (е/йс) 9]. Поэтому имеем
er + ecBZ'Bl @) = е. (8.2.36)
Пусть | <р°) обозначает состояние с одним физическим электро-
ном. Поскольку оно должно удовлетворять условию наблюдае-
мости физического состояния (8.2.10), имеем
(Ф° | ecNv | ф°) = ет (ф° | ф°). (8.2.37)
Ч
\
—^ - - ecBZ-B'(O)
Рис. 8.1.
Отсюда следует, что ет — перенормированный заряд. Это помо-
гает ответить на вопрос, почему электрический заряд изменяется
от е до ет, даже если общий заряд сохраняется и фазовая симме-
трия не нарушается. Интуитивно понятно, что разность зарядов,
равная е — ег, чтобы стать ненаблюдаемой, должна уйти на беско-
нечность, если не встретится поверхность, препятствующая утечке
(рис. 8.1). Как показало предыдущее рассмотрение, математически
этот процесс состоит в том, что разность зарядов связана с ненаблю-
даемыми квантами %° и Ь° и уходит в ненаблюдаемое подпростран-
ство гильбертова пространства. Если образец имеет конечные
размеры, избыток заряда собирается около поверхности. Это на-,
водит на мысль, что, хотя микроскопическое возбуждение %° или Ь°
становится ненаблюдаемым, скопление ОС ° или Ъ° (т. е. конденса-
ция бозонов) вблизи определенных особых областей (таких, как
поверхностная особенность) вызывает макроскопические и наблю-
даемые явления. Мы вернемся к этому вопросу в гл. 11.
Квантовая электродинамика твердых тел. I 305
Калибровочное условие (8.2.7) вместе с динамическим отобра-
жением (8.2.29) приводит к равенству
D* (а) \ [х; и°, (Ь° - %°), ф°] = 0. (8.2.38)
Теперь аналогично тому, как мы вывели соотношение (8.1.132),
покажем, что динамическое отображение А^ имеет вид
Л„ (х) = -ZBl (д) дфй (х) + ^ (д) [Ь° (х) - Х° (х)] + z?/2) р (д) и°р (х) +
f [D (д) g? - а^р (а)] ЛР1СТ (д) % [х; ul (b° - х°), ф°]. (8.2.39)
нелинейный член очень мал, если А — гладкая функция
пространственных переменных, так как
[D (д) & - д^ (д)] Л-Р1 (д) « 1. (8.2.40)
Другими словами,
А» (х) ~ -гъх (д) dj? (х) + ^ (д) [Ь° (х) - х° (х)] + Z™ р (д) и°р (х).
(8.2.41)
Собственная энергия фотонов. Получим теперь дополнитель-
ную информацию из уравнений Гейзенберга. Следуя изложению
последнего раздела (ср. с (8.1.137) и (8.1.138)), введем
@1Т [А» (х), Лv W10) = -^ } dVp 1х-в)А& (Р), (8.2.42а)
@\Т [/„(х), Лv(у)] 10) = J2L. J tfpe1" {x-y)Jt,(P). (8.2.426)
Обозначая неприводимую часть собственной энергии фотона
2цл> (р)> получаем соотношение (8.1.139), т. е.
J$v(p) = -2p»(p)t&(p)- (8-2.43)
Мы можем взять 2^ (р) в форме (8.1.143):
2,v (р) = 2r (jo) Т^ + So (p) (p^v - ^pv). (8.2.44)
Из уравнения Гейзенберга следует уравнение (8.1.144), т. е.
(|>2 + 2Г (р)] Tl + [1 + SoCo)] (AJl - РПРХ)} Axv (jo) =
= -7VV - д^- {D (p) L^v - ^ (p) pv}. (8.2.45)
Калибровочное условие (8.2.7) приводит к уравнению (8.2.13),
которое можно записать в виде
D^v (p) = -а (р) -^Lj- pv. (8.2.46)
306 Глава 8
Переписав левую часть (8.2.45) с учетом соотношений (8.1.147)
и (8.2.46), мы можем разрешить уравнение (8.2.45) относительно
A^v (Р) = - p2 + 2r(p) ?Vv ~ {i + ^(p)]D(P)Lk^ (Р)
где Q (р) = а (р) - { + ^ (р) [ув (р)/с]«. (8.2.48)
Эта ситуация резко отличается от той, которая возникает в слу-
чае сверхпроводимости, когда а (р) = 0. В данном случае а (р) Ф
Ф 0, и, следовательно, из условия, что A^v (p) не должно содер-
жать члена [1/D (р) ]2, не следует, что 20 (р) должно содержать
член 1/D (/?). Таким образом, нет оснований, чтобы 20 (/?) рас-
ходилось при р = 0. Поэтому объемная проводимость нормаль-
ного металла имеет конечное значение. Представим теперь 1/[1 +
+ 20 (р)] в виде
Это уравнение нужно сравнить с уравнением (8.1.149).
Терерь Q (р) имеет вид
Q (Р) = «(Р) + [fв (Р)/С]2Z (р) - DD{p}
Напишем следующее равенство:
Z (р) = Zo (р) + D (p) Z (р), (8.2.51)
где Z0(p) = Z(p)\D(p)=0. (8.2.52)
Затем, чтобы избавиться от членов типа U/D (р) ]2 в A^v, выберем
а (р) в виде
а (р) = -Zo (p) К/сJ. (8.2.53)
Калибровочное условие (8.2.7) определено с точностью до выбора
vB (Р)-
Из равенств (8.2.53), (8.2.17) следует
(V (а) = й (д) д„ - z0 (д) zB (д) -±г (д№ - аоб^), (8.2.54)
где й (д) еще не определено,
Квантовая электродинамика твердых тел. I 307
Используя соотношения (8.2.47), (8.2.49), (8.2.50), (8.2.53),
получаем следующее выражение для AAV:
\А / ч 1
7|iV + D(p) + m2(p) "оТрГГ1
?)%] (^Ig (8.2.55)
Объединяя члены с полюсами, получаем
ДЛ /Л Zt (p) гр
Auv [Pi — -5—;—.... /_ч l ii.v —
§^[%lp(P)^-pv + m(p)(-^-) PvP-\-
\ , (8.2.56)
где многоточие обозначает члены, которые не содержат особен-
ности типа полюса, а т\, Zt, Z, и Zo определяются выражениями
(8.1.152)—(8.1.154):
2Г (р) = m2r (р) + [Z, (р) - 1] {р2 + т2Т (р)) -| , (8.2.57)
Z;(p) = Z(p) для D(p) = —m2(p), (8.2.58)
для ?> (р) = —т2 (р). (8.2.59)
Сравним теперь выражение (8.2.56) с выражением для A$v
полученным непосредственно из динамического отображения
(8.2.14). Учитывая равенства (8.2.23) и (8.1.88), из соотношения
(8.2.14) получаем
АА (п) — Zt ^ T ___Zi_(p)____ jp /ч г |
A^v ^ — — Р2 + /И2(р) ^ liv — о (р) + т2 (р) Оц (р) Lpv +
+ Zb (Р) -щ^ PuPv - Zb1 (p) {P^ Go) pv + Pv (p) P^} -щд + • • • =
(p) T Zf(p) [,faw
m\ (p) ^V ~ О (P) + «2 (P) l11^ (P) pV
- ^ (P) (-T-JAWv] + [ (Zb2 (P) - 2Й (p) Zi1 (p)}
+ -j?Zo (P) (Pu C°v - Pofivo) + (fli - Роб^о) Pv}] "o^r + • • • • (8.2.60)
Первые два члена — полюсные члены плазмона — соответ-
ствуют аналогичным членам соотношения (8.2.56). Чтобы сравнить
308 Глаза 8
члены, пропорциональные IID (р), нужно заменить р0 в числи-
теле на lvB (р)/с] | р |. Тогда члены Аоо (р), пропорциональные
IID (р) в (8.2.56), становятся равными
а члены в Аоо (р), пропорциональные \ID (p) в соотношении
(8.2.60), равны
Сравнивая два этих выражения, получаем соотношение
ZB (p) - 2а (р)ZB (Р) = ^г- + -^у (^—j - Zo
(8.2.61)
Аналогичный анализ выражений для Аог, Аго и Аи также при-
водит к соотношению (8.2.61).
Если 2цу (р) вычислено, немедленно определяются т\ (р),
m2 (p), Zt (p), Z/ (р) и Zo (p). Из соотношения (8.2.61) затем опре-
деляется й (р) (и, следовательно, C^ (р)) как функция ZB (p)
и vB (p). Поскольку в этих выражениях использованы величины,
обратные ZB и vB, потребуем, чтобы
ZB(p)?=0, t»B(p)#O. (8.2.62)
В остальном эти две функции произвольны. В самом деле, из
условия (8.2.10) для физического состояния с определенностью
следует, что ни одна из величин C^ (р), ZB (p) или vB (p) не наблю-
даема.
Динамическое отображение тока /^ можно получить, исполь-
зуя уравнение Максвелла (8.2.5) и динамические отображения
(8.2.9) и (8.2.31), в виде
Л* (*) = (~d2gl + <^v) Лv (х) + D^fi (л) = - [m2 (d) i\l (д) - У
- k2(d)fj4l/2|4W - 2B(d) [1 +2о(а)]ОЛ&°М-Х0М)] + ... •
(8.2.63)
Здесь использованы соотношения (8.2.9), (8.2.21) и (8.2.54). Теперь
мы видим, что константа св в (8.2.34) определяется выражением
св = ZB(d)ll +Z0(d)) (8.2.64)
и, следовательно,
ег = — eZ0{0). (8.2.65)
Таким образом, мы выявили общую структуру динамических
отображений гейзенберговских операторов и рассчитали все
параметры.
Квантовая электродинамика твердых тел. I 309
Как и в случае сверхпроводимости, при конечных температу-
рах справедливы все соотношения этого раздела, а также соотно-
шения, тильда-сопряженные к ним. Приближенный расчет [5, 7]
собственной энергии фотона рассмотрен в разд. 5.5.
ЛИТЕРАТУРА
1. Wentzel G., Quantum theory of fields, Interscience, New York, 1949.
2. Nakanishi N., Prog. Theor. Phys., 49, 640 A973); 50, 1388 A973);
Lautrup В., Mat. Fys. Medd. Dan. Vid. Salsk., 35, 1 A967).
3. Matsumoto #., Papastamatiou N. J., Umezawa H., Vitiello G., Nucl. Phys.,
B97, 61 A975).
4. Matsumoto H., Umezawa H., F. Phys., 24, 357 A977);
Matsumoto #., Tachiki M., Umezawa #., F. Phys., 25, 273 A977).
5. Matsumoto H., SemenoffG., Tachiki M., Umezawa #., F. Phys., 28, 67 A980).
6. Gupta S. N., Proc. Phys. Soc. (London), A63, 681 A950);
Bleuler K., Helv. Phys. Acta., 23, 567 A950);
Nakanishi N., Suppl. Prog. Theor. Phys. (Kyoto), 51, 1 A972).
7. BohmD., PinesD., Phys. Rev., 82, 625 A951); 85, 338 A952); 92, 609 A953);
Gell-Mann M., Brueckner K., Phys. Rev., 106, 364 A957);
Sawada K., Phys. Rev., 105, 372 A957);
Sawada K-, Brueckner K., Fukuda N., Brout R., Phys. Rev., 108, 507 A957).
ГЛАВА ?
ПРОТЯЖЕННЫЕ ОБЪЕКТЫ КВАНТОВОЙ
ПРИРОДЫ
9.1. Простое рассмотрение
Протяженные объекты в квантовополевых системах. В преды-
дущих главах мы изучали некоторые характерные особенности
упорядоченных квантовых состояний. Однако в реальных ситу-
ациях мы редко можем найти эти упорядоченные системы в чисто
квантовых состояниях. Например, кристаллы, изучавшиеся
в гл. 7, являются совершенными кристаллами, реальные же
кристаллы всегда содержат некоторые протяженные (или макро-
скопические) объекты, такие, как дислокации, границы зерен,
точечные дефекты, ультразвуковые волны и т. д. Эти протяженные
объекты образуются в результате конденсации фононов. Даже
граничные поверхности кристаллов являются не искусственно
созданными, а формирующимися самосогласованным образом мак-
роскопическими объектами. Вихри в сверхпроводниках также
представляют собой протяженные объекты, которые образуются
естественным образом в квантовополевой системе фазово-упоря-
доченного состояния. Кроме того, большинство наблюдаемых
на макроскопическом уровне токов и электромагнитных полей
в обычных веществах также можно рассматривать как макроско-
пические объекты, имеющие квантовую природу. По существу
большинство явлений вокруг нас являются макроскопическими.
Это подводит нас к вопросу о том, как эти макроскопические
объекты образуются из квантовополевых систем [1 ]. Когда мы
подходим к этому вопросу, сразу же осознаем ту интереснур
особенность, что большинство стабильных или стационарных
макроскопических объектов появляются в определенных упорядо-
ченных квантовых состояниях. Это можно понять, если мы вспом-
ним проведенное в гл. 7 рассмотрение, основанное на том, что
порядок в квантовополевых системах поддерживается благодаря
некоторым коллективным бозонным модам (голдстоуновским бо-
зонам), поскольку конденсация бозонов —- простейший путь
к накоплению большого числа квантов, необходимых для макро-
скопического проявления квантовых эффектов. Тот факт, что
энергетический спектр голдстоуновских бозонов не имеет щели,
упрощает возможность конденсации. В этой и последующих гла-
вах мы попытаемся дать подробное описание механизма образо-
вания протяженных объектов квантовой природы.
Протяженные объекты квантовой природы 311
В данной главе проводится элементарное рассмотрение с целью
выделения наиболее важных черт механизма образования про-
тяженных объектов.
Уравнение Гейзенберга. Рассмотрим уравнение Гейзенберга
Л (д) г|>(*) = Яг|> (*)], (9.1.1)
где г[) (х) — гейзенберговское бозонное поле, a F [г|э ] — некоторый
функционал от него. Без потери общности мы можем так выбрать г|э,
чтобы @ | г|з | 0) =0. Упростим ситуацию, приняв, что состав-
ные частицы отсутствуют и можно пользоваться методом разложе-
ния в ряд теории возмущений. Более общие случаи рассматри-
ваются в разд. 9.3. Предположим также, что бозе-поле г|э веще-
ственно (г|э+ =г|з) и величина, канонически сопряженная о|з, есть
(d/df)ty. Из (9.1.1) следует уравнение Янга — Фельдмана
-ф (х) = Z'/2 (V) ф° (*) + Л (а) Лг|з (х)], (9.1.2)
где ф° — свободное бозонное поле, удовлетворяющее уравнению
Л (а) ф° = 0, (9.1.3)
a Z1!' (V) — перенормировочный множитель.
Решая уравнение (9.1.2) методом последовательных прибли-
жений, приходим к обычному ряду теории возмущений. Результат
представляет собой линейную комбинацию нормальных произве-
дений свободного поля ф°:
у(х) = Z'/2 (V) ф° (х) + ... . (9.1.4)
Здесь многоточие обозначает нормальные произведения более
высокого порядка. Оператор Л (а) в уравнении (9.1.3) мы выбираем
так, чтобы ф° представляло собой свободное физическое поле.
Тот факт, что такой же дифференциальный оператор Л (а) по-
является в левой части уравнения (9.1.1), означает, что произ-
ведена перенормировка энергии, иными словами F[ty] содержит
энергетический контрчлен. Обозначая теперь Z-1/» (V) г|з через г|э,
можно сформировать такое г|з, которое является перенормирован-
ным гейзенберговским полем:
-Ф (дг) = ф° (х) + ... . (9.1.5)
Тогда F[ty] в (9~"Л.1) содержит явным образом множитель Z.
Соотношение (9.1.5) представляет собой динамическое отображе-
ние перенормированного гейзенберговского поля г|э. В дальнейшем
мы будем считать, 4toij; в уравнении (9.1.1) уже перенормировано.
Его динамическое отображение обозначается через г|з (х; ф°):
г|з (х) = г|) (х; <р°). (9.1.6)
312 Глаза 9
Бозонное преобразование. Введем теперь функцию f(x), удо-
влетворяющую уравнению
A(d)f(x)=0. (9.1.7)
Мы можем теперь получить обобщение уравнения Янга — Фельд-
мана [2]:
г|> (х) = ф° (х) +f(x) + Л (д) F [г|з (*)], (9.1.8)
где я|), очевидно, удовлетворяет уравнению Гейзенберга (9.1.1).
Решая уравнение (9.1.8) методом последовательных приближений,
получаем новое решение уравнения (9.1.1)
V (х) =Ц(х; ф° + /). (9.1.9)
Отметим, что г|^ равно г|э с заменой ф° на ф° + /. Эта замена
называется бозонным преобразованием х). Тот факт, что г|5 и tyf
удовлетворяют одному и тому же уравнению Гейзенберга, соста-
вляет содержание теоремы о бозонном преобразовании [3, 4]
А(д)ф = Fty]. (9.1.10)
Поскольку бозонное преобразование представляет собой транс-
ляцию поля ф° ->-ф° + /, оно описывает конденсацию бозонов ф°.
Результатом этой конденсации является образование некоторого
протяженного объекта.
Физический смысл гейзенберговского поля г|/, полученного
с помощью бозонного преобразования. Запишем динамическое
отображение 1|э в виде
rc=O
X с (х; аг .. . an) : ф° (аг) ... ф° (ст„) :. (9.1.11)
Отсюда получаем I
f V 1
л=0
где
if/"' (х) = J dffi ... скт„с/ (х; CTi . .. стп) ф° (cti) . . . ф° (оп). (9.1.13)
х) Если / (х) имеет фурье-образ, то бозонное преобразование эквивалентно
преобразованию трансляции для операторов уничтожения а (к)—>- а (к) + с&,
которое определено в B.4.51) и отвечает образованию когерентного состояния.
В данном случае бозонное преобразование приводит к возникновению конкрет-
ного когерентного представления, которое подчиняется условию (9.1.7). Но вы-
полнение требования, чтобы функция / (*). определяющая бозонное преобразо-
вание, имела фурье-образ, не обязательно. Когда / (х) не имеет фурье-образа,
бозонное преобразование не может рассматриваться как трансляция а (к). Осо-
бенности, связанные с / (к), рассматриваются в гл. 10.
Протяженные объекты квантовой природы 313
Здесь коэффициенты Cj определяются выражением
с»
(9.1.14)
Основной член в (9.1.12) представляет собой с-число:
^(л;)=^0) (*) = (9.1.15)
= @|^(х) |0) = (9.1.16)
= cf(x). (9.1.17)
Это с-число описывает классический протяженный объект. От-
метим, что классическое поле <f>f (x) возникает даже при h Ф О
(h —¦ постоянная Планка). Это можно понять следующим обра-
зом. Поскольку конденсируется большое число бозонов, кванто-
вые флуктуации hAn могут стать значительно меньшими, чем
полное число квантов hn:
h An An „ . /Q 1 1 R\
hn n \ • • I
Условие (9.1.18) не зависит от h. Следовательно, объект, облада-
ющий классическим поведением, может возникнуть даже в том
случае, если h Ф 0.
Второй член в динамическом отображении (9.1.12) линеен
по ф°:
•ф}1» (Х) = J doc; (x; а) Ф° (а). (9.1.19)
Матричные элементы этого оператора описывают поведение от-
дельного кванта под действием протяженного объекта. Члены
более высокого порядка в (9.1.12) отвечают реакциям между
квантами в присутствии протяженного объекта. Таким образом,
tyf описывает систему квантов и протяженных объектов.
Компактное выражение для динамического отображения, отве-
чающего г^. Разлагая г|з (х; ф° + /) в ряд Тейлора, можем запи-
сать динамическое отображение г|э' в виде [5 ]
g^Jg7^ (ж): + ... . (9.1.20)
Вводя обозначение
j^ (9'L21)
314 Глава 9
можем представить (9.1.20) в виде
л=0
откуда
^(х) = F{)пф,(х). (9.1.23)
Это приводит к соотношению
}"). (9.1.24)
Самосогласованный потенциал, создаваемый протяженными
объектами. Заменим теперь / (х) на / (х) + eg- (x), где g (x) удо-
влетворяет уравнению для / (х), i. e.
A(d)g(x)=0, (9.1.25)
а е — бесконечно малая константа. Имеем
в#? (х) ^ lim ± [ф1+eg <*) - ^ (*)] = J ctyg (у) ^-. (9.1.26)
Введем обозначение
Jf (х) = @ | F[^ (л:)] | 0). (9.1.27)
Тогда из уравнения Гейзенберга (9.1.1) получим
А (д) р (х) = Jf (х), (9.1.28)
откуда
Л (д) ф1«* = Jf+*'. (9.1.29)
Разность уравнений (9.1.28) и (9.1.29) имеет вид
(9.1.30)
При заданной функции / (х) мы можем вычислить ц>1 и JL
Исключая /, выразим Jf через <j>f:
Jf (x) = J (x; ff). (9.1.31)
Функциональную производную 6Jf/8f в (9.130) можно предста-
вить в виде
J
4 6jf(x)
в/ (У) J &tf (г) б/ (У) '
Поскольку ф° удовлетворяет уравнению (9.1.25), можно исполь-
зовать ф° вместо g. Тогда уравнение (9.1.30) принимает вид
(9.I.32)
Протяженные объекты квантовой природы 315
где учтено (9.1.26). Уравнение (9.1.32) можно представить в виде
Л (a) 6}<ff (х) = 6fJt (x), (9.1.33)
если использовать формулу
Sis* /.л
= (9.1.34)
где G — произвольный функционал от ft.
Повторяя проведенное рассмотрение, получаем
Л(д)F,)»^ (х) = (8,N'W. (9-1.36)
При п = 1 это уравнение совпадает с (9.1.32), которое можно
записать в виде
Л (а) $1) (х) — J d4zVf (х; г) $> (г) = 0, (9.1.37)
где
Vf (х; г) = 6Л (х)/6р (z). (9.1.38)
Действуя на обе части этого уравнения оператором б/ и исполь-
зуя формулу (9.1.35), получаем
\\{z)Vf{x; у, z), (9.1.39)
где
Vf (х; у, z) = —I— -±- Л (х). (9.1.40)
8ф1 (у) оф' (г)
При п = 2 уравнение (9.1.39") совпадает с (9.1.36). Аналогич-
ным образом можно в явном виде представить действие оператора
(8f)n в уравнении (9.1.36), которое является уравнением относи-
тельно^"'. Правая часть (9.1.36) может быть выражена через tyjm)
при т <; п; при п >> 1 уравнение (9.1.36) неоднородно. Уравнение
(9.1.37) для ijjf1' однородно и, следовательно, не определяет пол-
ностью -ф/1'. Мы покажем ниже, чтог^1' определяется уравнением
(9.1.37), а также выражением для одновременного канонического
коммутатора.
Вспомним теперь, что оператор ^У описывает поведение
отдельного кванта под действием протяженного объекта. Уравне-
ние (9.1.37) показывает, что этот квант ведет себя как частица
в потенциале V1 (х, z). Иными словами, на физический квант
влияет потенциал, создаваемый протяженным объектом. Этот
потенциал описывает взаимодействие между квантом и протяжен-
316 Глава 9
ным объектом. Поскольку потенциал создается протяженным
объектом, возникающим самосогласованным образом в квантово-
полевой системе, он называется самосогласованным потенци-
алом [5].
Древесное приближение и уравнение Эйлера. Решение уравне-
ния (9.1.8) методом последовательных приближений приводит
к рассмотрению множества диаграмм типа фейнмановских. Все
петли, появляющиеся в этих диаграммах, обусловлены спарива-
ниями физических полей. Диаграммы, в которых отсутствуют
петли, называются древесными диаграммами, а приближение,
в котором петлевые диаграммы не учитываются, носит название
древесного приближения. При использовании древесного при-
ближения У, 1|з}п) и <j>f обозначаются соответственно как $f, ip(fn)
и <f>f. Отметим, что каждая внутренняя линия содержит в качестве
сомножителя постоянную Планка h.
Поскольку разность между средним по вакууму от произведе-
ния полей i|)f и соответствующим произведением вакуумных сред-
них от i|)f обусловлена спариваниями физических полей, имеем
{0\F№\0) = Fty ] + ..., (9.1.41)
где многоточие обозначает вклад петлевых диаграмм.
Исходя из уравнения Гейзенберга (9.1.1), приходим теперь
к заключению, что ft удовлетворяет уравнению Эйлера
A(d)ft (х) = Flft (*)]. (9.1.42)
Таким образом, мы доказали, что вакуумное среднее от tyf (х)
в древесном приближении удовлетворяет классическому уравнению
Эйлера [2].
Достигнутый в последнее время прогресс в области класси-
ческой нелинейной теории поля вскрыл тот факт, что уравнения,
описывающие классические нелинейные поля, имеют некоторые
решения, отвечающие порциям локализованной энергии. Эти
решения называются солитонами (см., например, обзоры по соли-
тонам [6]). Солитоны представляют собой протяженные объекты
с классическим поведением; они подчиняются классическим урав-
нениям Эйлера, поэтому исследуемые протяженные объекты часто
называют солитонами.
Для продолжения рассмотрения введем величину F<n) Iff (x) ]
посредством соотношений
A) lf]li)-y), (9.1.43а)
и т-д-
(9.1.436)
Протяженные объекты квантовой природы 317
Если размерность пространства-времени есть d, четырехмерная
8-функция должна быть заменена на 8d (x —у). Формально мы
можем написать
Fin) = (ЫЬф')п F. (9.1.44)
Из уравнения (9.1.37) следует1)
{АC) - FA) p (х)]}%A) (х) = 0, (9.1.45)
откуда видно, что F'1' — самосогласованный потенциал в древес-
ном приближении. Исходя из (9.1.39), получаем
\А(д) - FA) [ф1 (х)]} $2> (х) = FB) $ (х)] [$" (х)]2. (9.1.46)
Поскольку
6fFinnV(x)) = Fin+i) $(х)П11) (х), (9.1.47)
действие оператора 8^ на (9.1.46) приводит к соотношению
= 3FB) & (хI $}'> (х) W (х) + F<3> $f (x)] №» (х)]3. (9.1.48)
В древесном приближении порядок действия операторов ф?п
и ^р1 не имеет значения.
Общий вид рекуррентной формулы в древесном приближении
может быть получен непосредственно из уравнения Гейзенберга
(9.1.10), которое записывается в виде
\п=о /
Здесь можно не учитывать в древесном приближении некоммута-
тивность операторов 1|з}п>. Разлагая в ряд Тейлора (вблизи <j>>)
правую часть уравнения (911.49), получаем
тСфРЬп^.Г, (9.1.50)
где
2о, = г, Еа^=л, (9.1.51а)
0 <nx<n2 <... <л. (9.1.516)
Суммирование в (9.1.50) проводится по всем возможным наборам /,
«г, ah удовлетворяющим условиям (9.1.51а) и (9.1.516). Легко
1) Это уравнение называется уравнением устойчивости [7].
318 Глава 9
видеть, что при п = 1, 2, 3 (9.1.50) совпадает с уравнениями
(9.1.45), (9.1.46), (9.1.48) соответственно.
Трансляционные моды и квантовая координата. Однородное
уравнение (9.1.45) требует особой осторожности, поскольку это
уравнение допускает решения, отвечающие не только рассеянным
волнам, но также связанным состояниям; мы сталкиваемся тут
с хорошо известным конфликтом между итерационным методом
и появлением связанных состояний в задаче о потенциальном рас-
сеянии. Чтобы упростить ситуацию, будем считать протяженный
объект статическим, т. е. / (х) = / (х) и j>f (х) = j>f (х). В этом
случае самосогласованный потенциал не зависит от времени. Если
уравнение (9.1.45) записать в виде
$'> (х) = ф°(дг) + Л-1 C)FA) [?'(x)]$'> (х), (9.1.52)
то итерационный метод приводит только к решению, отвечающему
рассеянным волнам. Это решение мы обозначим через Хо (х). Чтобы
показать в явном виде структуру %*, введем собственную функ-
цию и (х, к):
{Л(д, щ) - FA) [j>f (х)]} и (х, к) = 0, (9.1.53)
где
Л(д, со) = A(a)k=_(ffl. (9.1.54)
Тогда Хо (х) записываются в виде \
XS (х) = J d3k _^7- [и (х, к) а (к) e-'-V +
+ u'(x, k)a*(k)e"V]. (9.1.55)
Здесь а (к) — оператор уничтожения для состояний, отвечающих
рассеянным волнам. Но %1 и (д/dt) %s0 не могут удовлетворять
каноническому коммутационному соотношению для \!р (х)
и (д/dt) i|) (x). (Заметим, что в формуле (9.1.12) только ¦ф;1' обеспе-
чивает в древесном приближении появление 8-функции в выра-
жении для коммутатора.) Это обусловлено тем, что уравнение на
собственные значения (9.1.53Удопускает также наличие некоторых
решений с дискретными значениями энергии
Щ {-ЩдТ^д}- Fw $f (x)]}>, (x)> 0. (9.1.56)
Очевидно, что функции ut (x) должны отвечать связанным состо-
яниям_ф°-кванта и протяженного объекта.
Протяженные объекты квантовой природы 319
Мы можем выбрать и (х, к) и щ (х) таким образом, чтобы они
образовывали полный набор ортонормированных функций:
\ePxu* (х, к) и (х, 1) = б (к — 1), (9.1.57)
} cfxu' (x) И/(х) = 6Ф (9.1.58)
\tPxui (х) и(х, к) = 0. (9.1.59)
Получаем правило сумм
J d3ku (х, к) и* (у, к) + 2 «/ (х) "<* (У) = б (х - У). (9.1.60)
Чтобы доказать, что уравнение (9.1.45) всегда допускает не-
которые решения, отвечающие дискретным значениям энергии,
напомним, что если / (л:) удовлетворяет уравнению Л (д) / = 0,
то этому же уравнению удовлетворяет и функция / (х + а), где
а — постоянный вектор. Поскольку <f>f зависит от х только через
/ (х), мы видим, что как <j>f (x), так и <j>f (x + а) удовлетворяют
уравнению Эйлера (9.1.42). Поэтому мы можем подействовать
дифференциальным оператором на обе части уравнения (9.1.42):
AE)V?/(x) = F(I)[?f (x)]V?'(x). (9.1.61)
Отсюда видно, что dt<f>f (x) (i = 1, 2, 3) — решения уравнения
(9.1.56), отвечающие нулевой энергии:
{Л (а, 0) - FA) [ф{ (х)]} S/ff (x) = 0. (9.1.62)
Введем обозначение
V,, = J t?xd$ (x) д,$ (х), (9.1.63)
используя которое, можно записать следующее выражение для
Щ (х):
щ (х) = ? {V~lu)u д$ (х) (i = l, 2, 3), (9.1.64)
так как эти функции удовлетворяют не только уравнению на
собственные значения (9.1.62), но также условиям ортонормиро-
ванности (9.1.58) и (9.1.59). Квантовые моды, описываемые волно-
вой функцией щ (х), называются трансляционными модами. Если
/ (х) зависит только от одной компоненты вектора х (скажем, от хх),
то мы имеем только одну трансляционную моду, поскольку da<j>f =
— d3<j>f — 0. Аналогично если / (х) зависит от двух компонент
вектора х, то возникают две квантовые моды. При дальнейшем
320 Глава 9
рассмотрении мы полагаем, что / (х) зависит от всех компонент
вектора х. Поэтому имеют место три квантовые моды дгф( (i =
= 1,2,3).
Будем пользоваться следующими обозначениями: щ (i — 1,
2, 3) — волновые функции, отвечающие трансляционным модам,
а мг (i >3) — волновые функции других связанных состояний.
Введем определение свободного поля %* (х) для состояний с i > 3
rfw-v *'"
B©|) '•
(9.1.65)
Операторы уничтожения аь отвечают связанным состояниям с
Может возникнуть искушение описывать аналогичным образом
трансляционную моду, воспользовавшись при i < 3 выражением
щ (х) (а, + а?). Но это было бы неправильно, поскольку трансля-
ционные моды отвечают нулевой энергии и, следовательно, не
наблюдаются в качестве возбужденных мод. Определим поле,
связанное с трансляционными модами, через 2 Щ (х) Рь гДе Рг
(i = 1, 2, 3) — некоторые операторы, коммутирующие с at и
а (к). Ниже будет показано, что канонические одновременные
коммутационные соотношения для гейзенберговского поля тре-
буют введения операторов Пг (i = 1, 2, 3), канонически~топря-
женных операторам рг, т. е. [рг, Пу] = ШЬц. Удобнее выразить
2 Щ (х) pj через д$ (i = 1, 2, 3):
Ц Mi(x)P; = — (q-V) ^(x), (9.1.66)
где
Rt = —Jj (V~4t )(/P/. (9.1.67)
Здесь учтено соотношение (9.1.64). Оператор q называют кванто-
вой координатой [5]; он коммутирует с at и а (к). Сопряженный
этой координате импульс дается выражением
Pt = — S П, (Vl'%, (9.1.68)
поскольку при этом
\.Яи Pi] = ^u- (9.1.69)
Ниже символом а обозначаются как ah, так и at при i > 3.
Правило сумм (9.1.60) приводит к следующему соотношению:
[Х° (х) ~ (q-V) ? (х), х° (У) - (P-V) ф' (у)] б (/, - ty) =
— у), (9.1.70)
Протяженные объекты квантовой природы 321
где
ЗС° (*) = ЗСо (*) + ЗСо (*)¦ (9.1.71)
Заметим теперь, что при использовании древесного приближения
вклад в каноническое коммутационное соотношение вносит только
линейный член Щ1}):
[У' (*); 4г^1)
Таким образом, воспользовавшись (9.1.70), а также (9.1.72),
получаем
# (х) =x0W-(q-V)?f(x), (9.1.73)
q = p + ... . (9.1.74)
Выражение (9.1.73) со всей ясностью демонстрирует, что кано-
ническое коммутационное соотношение для tyf требует наличия
квантовой координаты q. Многоточие в (9.1.74) отвечает произ-
ведениям более высокого порядка, составленным из р, и поэтому
в древесном приближении не вносящим вклада в б-функцию,
имеющуюся в выражении (9.1.72) для канонического коммутатора.
Из формулы (9.1.74) видно, что координата q, введенная с по-
мощью соотношения (9.1.66), зависит от времени. В тех случаях,
когда мы хотим подчеркнуть это обстоятельство, она обозначается
как q (t). He зависящий от времени набор канонических пере-
менных (q, p) может быть определен с помощью [q (t), p (t) ] в опре-
деленный момент времени (например, при t = 0): q = q @) и т. д.
Поскольку временная эволюция гейзенберговских операторов
определяется гамильтонианом Н, квантовая координата для
любого гейзенберговского оператора определяется соотношением
Так как Н содержит операторы рождения и уничтожения
частиц (<%+, а), то их содержит и Q (t). Следовательно, Q (t) может
не коммутировать с а и а+, в то время как q (t) коммутирует с а
и а+ по определению. На качественном уровне можно сказать,
что Q включает в себя наряду с обычными квантовомеханическими
флуктуациями q квантовые флуктуации, обусловленные воз-
бужденными состояниями. Но в древесном приближении различие
между q (t) и Q (t) не имеет значения. Поэтому мы используем
в (9.1.73) Q (t) вместо q (t). Поскольку Q (t)-\ff (x) должно удо-
влетворять уравнению (9.1.45) и так как в Л (д) входит вторая
производная по времени, из уравнения (9.1.62) следует
Q = 0, Q(*) = q + Qf. (9.1.75)
V
322 Глава 9
Проявление связанных состояний при бозонном преобразова-
нии может зависеть от способа определения предела для итера-
ционного метода решения уравнения Шредингера (9.1.52). Оно
может зависеть также от способа определения суммы степенного
ряда (9.1.14) при п = 1, т. е.
оо
с, (х; а) = 2 7Г J d% ¦ • • d%c {x> CT?i *' ' ^ f &> •'¦* &>¦
1=0
(9.1.76)
Суммирование должно быть определено так, чтобы выполнялось
каноническое коммутационное соотношение в совпадающие мо-
менты времени. Данная ситуация с итерационным методом ана-
логична той, которая была обнаружена для случая (N, 8)-модели
в разд. 3.1. Там было показано, что итерационный метод не поз-
воляет выявить связанное состояние (N, 8) (называемое У-кван-
том), наличие которого требуется для выполнения канонического
коммутационного соотношения в совпадающие моменты времени.
Поэтому гильбертово пространство строится так, чтобы учесть
существование У-кванта. Аналогично появление трансляционных
мод и других мод с дискретными значениями энергии^-ббусловлен-
ных наличием протяженного объекта, приводит к необходимости
перестройки гильбертова пространства, чтобы учесть эти связан-
ные состояния. Поэтому процесс бозонного преобразования не так
прост, как это кажется на первый взгляд.
Подводя итог, отметим, что протяженный объект приводит
к появлению самосогласованного потенциала, благодаря которому
Ф°-квант либо рассеивается, либо образует связанное состояние
с протяженным объектом. Каноническое коммутационное соотно-
шение, которое можно интерпретировать как условие полноты,
приводит к требованию, чтобы i^11 включало в себя как рассеян-
ные волны, так и связанные состояния. В числе этих связанных
состояний появляются трансляционные моды с равной нулю
энергией, которым отвечает квантовая координата Q. Происхож-
дение трансляционных мод связано с трансляционной инвариант-
ностью теории; как только возникновение протяженного объекта
нарушает трансляционную симметрию, динамика системы
естественным образом приводит к появлению трансляционных
мод, призванных сохранить трансляционную инвариантность
теории. Трансляционные моды обладают нулевой энергией, по-
скольку изменение положения протяженного объекта не влечет
за собой никакого изменения наблюдаемой ситуации.
Квантовая координата и динамическое отображение. Рассмо-
трим теперь i|)/2> и, используя древесное приближение, исследуем
322
Глава 9
Проявление связанных состояний при бозонном преобразова-
нии может зависеть от способа определения предела для итера-
ционного метода решения уравнения Шредингера (9.1.52). Оно
может зависеть также от способа определения суммы степенного
ряда (9.1.14) при п = 1, т. е.
с, (х; а) =
7Г
1=0
(9.1.76)
Суммирование должно быть определено так, чтобы выполнялось
каноническое коммутационное соотношение в совпадающие мо-
менты времени. Данная ситуация с итерационным методом ана-
логична той, которая была обнаружена для случая (N, 8)-модели
в разд. 3.1. Там было показано, что итерационный метод не поз-
воляет выявить связанное состояние (N, 8) (называемое У-кван-
том), наличие которого требуется для выполнения канонического
коммутационного соотношения в совпадающие моменты времени.
Поэтому гильбертово пространство строится так, чтобы учесть
существование У-кванта. Аналогично появление трансляционных
мод и других мод с дискретными значениями энергии<^)бусловлен-
ных наличием протяженного объекта, приводит к необходимости
перестройки гильбертова пространства, чтобы учесть эти связан-
ные состояния. Поэтому процесс бозонного преобразования не так
прост, как это кажется на первый взгляд.
Подводя итог, отметим, что протяженный объект приводит
к появлению самосогласованного потенциала, благодаря которому
Ф°-квант либо рассеивается, либо образует связанное состояние
с протяженным объектом. Каноническое коммутационное соотно-
шение, которое можно интерпретировать как условие полноты,
приводит к требованию, чтобы i^11 включало в себя как рассеян-
ные волны, так и связанные состояния. В числе этих связанных
состояний появляются трансляционные моды с равной нулю
энергией, которым отвечает квантовая координата Q. Происхож-
дение трансляционных мод связано с трансляционной инвариант-
ностью теории; как только возникновение протяженного объекта
нарушает трансляционную симметрию, динамика системы
естественным образом приводит к появлению трансляционных
мод, призванных сохранить трансляционную инвариантность
теории. Трансляционные моды обладают нулевой энергией, по-
скольку изменение положения протяженного объекта не влечет
за собой никакого изменения наблюдаемой ситуации.
Квантовая координата и динамическое отображение. Рассмо-
трим теперь i|jJ> и, используя древесное приближение, исследуем
Протяженные объекты квантовой природы
323
вопрос о том, как в i|)f (л:) появляется Q (t). Действуя на обе части
уравнения (9.1.61) оператором д;, получаем
[А{д) - F{1) [? Ш д&Р (*) =
= FB)[?(x)]a^/(x)ai/ (x). (9.1.77)
Аналогичным образом из уравнения
{Л C) - FA) [ft (x)]}-x° (х) = 0 (9.1.78)
следует
{Л C) - F(I) [?' (х)]) vx° (x) = F{2) [ft (х)] v?f (x). (9.1.79)
Поскольку (9.1.73) приводит к соотношению
(U0J = (х0J -h [(Q @ ¦ v) Ф!Г - 4° Ю @ • vl Ф1, О-1.80)
из (9.1.46) с учетом (9.1.77) и (9.1.79) получаем^
{AC)-F(I)[?f (x)]}bW = FB)[?' (х)][х0(*)]2, (9.1.81)
где
Х2 (х) = ?/B) (х) + 2 [Q @ ¦ V] Х° (х) - [Q @ ¦ V]2 V (X)- (9-1.82)
Таким образом, динамическое отображение (9.1.12) принимает вид
¦•¦ • (9.1-83)
Повторяя аналогичные выкладки, получаем
л=0
(9.1.84)
где
x — Q(t)= [x — Q(t), tx]. (9.1.85)
Из соотношения (9.1.82) видно, что если пренебречь квантовой
координатой, то \}>/2) становится раэным Ха- Обозначим через %п
такое выражение для ^п), в котором не учитывается квантовая
И*
324 Глава 9
координата. Тогда (9.1.50) приводит к рекуррентному соотно-
шению
' с
где
Ъ = 1°- (9.1-87)
Соотношение (9.1.86) при п = 1илия = 2 сводится соответственно
к (9.1.78) или (9.1.81). При п = 3 (9.1.86) получается из уравне-
ния (9.1.48) при замене tyfn) на %п:
{Л (д) = F"> [^ (х)} ь (х) = 3^B> [?' (х)] х° (*) Х2 « +
3. (9.1.88)
Динамическое отображение (9.1.84) приводит к
^ (9.1.89)
Это соответствует утверждению, что х и Q (t) появляются
только в виде комбинации х — Q (t). Соотношение (9.1.84) пока-
зывает справедливость этого утверждения вплоть до п = 2.
В разд. 9.4 мы доказываем его с самых общих позиций. Это озна-
чает, что, как только возникновение протяженного объекта при-
водит к нарушению трансляционной симметрии, появляется
квантовая координата, которая ведет себя как голдстоуновская
мода х). Другими словами, трансляция в пространстве х -*-х + а
индуцируется преобразованием
Q-vQ — a. (9.1.90)
Это представляет собой определенную форму перестройки трансля-
ционной симметрии пространства.
Хотя приведенные выше результаты определяют конкретный
способ появления Q, мы не выяснили еще, каким образом в Vpf
появляется р (или Q). Ниже мы вернемся к этому вопросу.
Гильбертово пространство для системы с протяженными объ-
ектами. Данное гильбертово пространство представляет собой
произведение гильбертова пространства Жч = \\^q)\ для кван-
товой координаты и пространства Фока Ж? = || Wp)} для мод,
отвечающих возбужденным состояниям системы:
(9.1.91)
:) Исследование квантовой координаты, основанное Щ методе интегрирова.'
цщ по траекториям, см. в работе [8].
Протяженные объекты квантовой природы 325
Это гильбертово пространство мы будем называть расширенным
пространством Фока. Мы пользуемся символом 10) для обозна-
чения вакуумного состояния в 36F. Поэтому определение
(9.1.16) классического поля ф1 (х) должно быть модифицировано
следующим образом:
ф1 (х) = <0h>'(*)|0>p=q=0. (9.1.92)
Обобщенные координаты. Исследуем теперь, используя дре-
весное приближение, как Q (и, следовательно, р) появляется
в динамическом отображении i|)f. В древесном приближении поря-
док действия Q (t) и Q не играет роли. Для дальнейшего нам
потребуется формула
где символ dt означает, что оператор дифференцирования по вре-
мени действует не на Q (/), а только на временную компоненту х.
В (9.1.93) учтено, что в соответствии с соотношением (9.1.75)
отсутствует член Q; (d/dQ;L>f- В дальнейшем мы будем исполь-
зовать символ dp = (di; dt). Чтобы конкретизировать ситуацию,
примем
ЛC)=32 — т2. (9.1.94)
Тогда уравнение Гейзенберга (9.1.10) примет вид
= F[V]. (9.1.95)
Для любого вектора V мы можем определить вектор Vj-, по-
перечный по отношению к Q, а также вектор VL, продольный по
отношению к Q:
^V), (9.1.96а)
±sQ(Q), (9.1.966)
где Q2 = (Q-Q). Вводя обозначения
W (9л-97а)
v. (Qx)> (9Л-976)
326 Глава 9
имеем
V2 - (Q. уJ = V2 + Ct{d'tf - 2 (Q v') d't, (9.1.98a)
d2t-2(Qy)dt^(d'tJ + Q2(d'tJ-2(Qv')d't. (9.1.986)
При этом уравнение (9.1.95) принимает вид [9]
[a'2 —m2]^ = F Ь|)П. (9.1.99)
Как было выяснено выше, х следует заменить на xQ = х — Q @.
что приводит к замене х' и f на X и Г соответственно, где
X = xQr+ {1_гф)Чш xQL, (9.1.100а)
T = (l-Q2)V^-^r^T7r(QxQ). (9.1.1006)
Величины X, Т называют обобщенными координатами.
Теперь ясен рецепт нахождения динамического отображения
грь сначала следует решить уравнения для гр" при ipj1' ->-%0, а за"
тем заменить (х, t) на (X, Т), чтобы учесть QnQ(i). Если Л (д)
имеет вид, отличный от (9.1.94), то (9.1.97) и (9.1.100) должны быть
соответствующим образом модифицированы. В одном из последу-
ющих разделов мы рассмотрим обобщенные координаты, не поль-
зуясь древесным приближением.
Квантовые поправки и перенормировка* Покажем теперь, что
полная структура динамического отображения ipf, включающая
квантовые поправки, может быть получена, если известно выра-
жение для ipf в древесном приближении. Заметим сначала, что,
согласно теории перенормировок, F [гр] в уравнении Гейзенберга
(9.1.1) содержит контрчлен Fc [гр]:
F [гр] = FQ [гр] + Fc [гр]. (9.1.101)
Контрчлен Fc [гр] компенсирует разность между перенорми-
рованными и затравочными параметрами. Процедура перенорми-
ровки иллюстрируется в следующем разделе на примере простой
модели. В теории перенормировок древесное приближение при-
меняется для рассмотрения уравнения
что приводит к уравнению Эйлера
A(d)$=F0[$]. (9.1.103)
Если наше рассмотрение начинается с решения этого уравнения,
то <j>f следует выразить через f[. Чтобы выполнить это, еосполь'
Протяженные объекты квантовой природы 327
зуемся уравнениями (9.1.42) и (9.1.103) для получения следующего
соотношения:
А(д) А$ = Fo[fto + А$] - Fo[$] + рЛфо + Ч']> (9.1.104)
где
Ьф! =ф/ _$. (9.1.105)
Используя разложение в ряд Тейлора
^(^)', (9.1.106)
1=0
мы можем, исходя из (9.1.104), получить Л<^, выраженное через
фо- Поскольку выше мы выразили i|)/n) через ф ( = ^о + &у)>
мы можем записать tyjn) и через ф^. Величина Л<^ представляет
собой квантовую поправку, обусловленную эффектом перенорми-
ровки.
Обратим теперь внимание на другие вклады в квантовые по-
правки, которые возникают за счет спариваний свободных полей.
Сначала не будем учитывать квантовые координаты и исследуем
классическое поле
ф'(х) = @W (jc) | O>P=q=o, (9.1.107)
которое включает все квантовые поправки, кроме квантовой коор-
динаты. Имеем
ф* (х) = ф1 (х) -f A^f (х) + ЛУ (х), (9.1.108)
где Аф? — величина, которая находится из динамического отобра-
жения ty при осуществлении всех возможных спариваний физи-
ческих полей:
(9-1.109)
В качестве примера рассмотрим однопетлевую поправку
A^(x)«4-<°IU2)Wl°>- (9.1.110)
Исходя из (9.1.46) и (9.1.73) и пренебрегая квантовой координа-
той, в однопетлевом приближении получаем
(Л (д) - F^ [Й (*)]} ЛУ (х) = 4" Fо'' $ М <° I (Х° WJ1 °>-
(9.1.111)
328 Глава 9
С другой стороны, (9.1.104) в однопетлевом приближении при-
обретает вид
(A(d)-FA) [$(*)]}Д?(*) = Ъ$(*)]• (9.1.112)
Таким образом, имеем
(Л (д) - FA) [ф'о (х))\ (ф'(х) ~ U Ml =
= Fc U>'o (х)) -\- \ Ff [$ (*)] @1 [Х° (х)]210). (9.1.113)
Отсюда определяется (<j>f — <f>Q (а следовательно, и ф<) в одно-
петлевом приближении.
Квантовые эффекты в линейном члене i|^" могут быть рассчи-
таны аналогичным образом. В этом случае мы рассматриваем
г|э}2/+1) и проводим все возможные спаривания 2/ физических
полей. В результате получаем поправки к ¦фр), обусловленные
диаграммами с / линиями. Таким способом мы можем вычислить
квантовые поправки к любому члену динамического отображе-
ния i|)f.
Симметризация квантовых координат. Квантовая координата
(q, Q) в i|)/ учитывается с помощью следующего метода. Сначала
заменяем, согласно (9.1.100), (х, t) на (X, Т); затем, используя
(9.1.75), разлагаем каждую из величин ^п) в ряд по произведе-
ниям q и Q. Наконец, симметризуем порядок действия q и Q,
например
DQ + Qjqt)- (9.1.114)
Симметризация требуется по следующей причине. Динамическое
отображение ^ имеет вид
*' = 2 J dai ¦¦¦ da«g (х>ст' ¦¦¦<*»)'• xti]) (о\) ¦ ¦ ¦ 4>Г Ы :•
(9.1.115)
Поскольку I1»!?/1'(ffi) ... i|)?u (а„): симметрично по ах ... ап, тем же
свойством обладает и g (х; а± ... ап). Каждая из величин ^"'^i)
линейна по q и Q. Поэтому проводится симметризация по q и Q.
Построение tyl. Вычисление of осуществляется следующим об-
разом. Сначала мы пренебрегаем квантовой координатой и нахо-
дим щп) в древесном приближении с помощью соотношения
(9.1.50) при условии Щ1* ->%0. Это позволяет определить дина-
мическое отображение tyf, если задана функция / (х). Затем вы-
числяем величину A<j>f, определяемую эффектом перенормировки,
Протяженные объекты квантовой природы 329
чтобы выразить i|)f через f[. После этого находим квантовые по-
правки, связанные со спариванием физических полей. Наконец,
проводим замену (х, t) ->-(X, 7") и осуществляем симметризацию
по q и Q. В результате получаем динамическое отображение tyf.
Примечательно, что знание / (х) (а следовательно, классического
поля j>[ (л;)) полностью определяет динамическое отображение i|)f.
В рамках обычной процедуры квантования классической меха-
ники часто использовалась симметризация по q и Q. Проведенное
выше рассмотрение обосновывает теперь этот традиционный метод.
Но мы не исследовали упорядочение по Q и (а, а+). Этот вопрос
обсуждается в разд. 5.
Классические и квантовомеханические протяженные объекты.
Приведенное выше рассмотрение показывает, что
(*)|0>, (9.1.116)
где X зависит от квантовой координаты [Q (t), Q]. Если квантовые
флуктуации величин Q (t) и Q пренебрежимо малы, то <f>f (X) л*
я=* <j>f (x) описывает классический протяженный объект, если же
флуктуации Q (t) и Q становятся заметными, то протяженный
объект обладает квантовомеханическим поведением. Следова-
тельно, как классические, так и квантовомеханические объекты
естественным образом возникают в квантовополевых системах
в процессе конденсации бозонов.
Завершим этот раздел следующим замечанием. Оператор унич-
тожения а (к), входящий в выражение (9.1.55) для физического
поля Хо (х)> не совпадает с оператором уничтожения (скажем,
а (к)) для физического поля ср° (л:) в отсутствие протяженных
объектов. Существование протяженных объектов оказывает вли-
яние на физическое поле %*0, и а (к) становится сложным функци-
оналом от a (k), a; (i ^> 3), квантовой координаты (Q, Q) и пара-
метра бозонного преобразования /, т. е. а (к) = а [а (к), аь
Q, Q, /]. Когда производится разложение а (к) в ряд по нормаль-
ным произведениям а (к), а+ (к), а,- и а], коэффициент при каж-
дом члене этого разложения является функционалом от Q, Q и /.
9.2. Простой пример
Модель. Чтобы проиллюстрировать общее рассмотрение, про-
веденное в разд. 9.1, обратимся к простой модели. Эта модель
представляет собой ^A + 1)-мерную модель типа Я,р4:
(д2 + ц2) р (*) = V (х), (9.2.1)
где а2 = —(дЧд?) + (дЧдх2).
330 Глава 9
Прежде всего сформулируем процедуру перенормировки. Для
этого требуются четыре перенормировочных параметра: физи-
ческая масса т, перенормированная константа взаимодействия g,
вакуумное среднее @1 р 10) и перенормировочный множитель Z
для волновой функции, определяемый равенством р = @|р|0) +
+ Z'/«i|). Здесь 1|з — перенормированное гейзенберговское поле,
обладающее свойством @|i|)|0) =0. Эти четыре неизвестных
параметра нужно определить в процессе вычисления квантовых
поправок. Вместо того чтобы воспользоваться четырьмя указан-
ными выше параметрами, мы сформулируем процедуру перенор-
мировки с помощью четырех перенормировочных множителей Z,
Zi, Z2 и w, определяемых следующим образом. Член Хр3 в уравне-
нии (9.2.1) возникает благодаря лагранжиану взаимодействия
(А,/4) р4, который приводит к появлению члена типа i|K, имеющего
вид XZ3/* @ | р | 0) i|>3. Если не учитывать квантовые поправки,
то этот член равен X @ | р | 0) -ф3. Задаем перенормированную
константу взаимодействия g, вводя для указанного члена типа \|?3
обозначение (mg/2) ф3; получаем при этом X @ | р | 0) = mg/2.
Заметим, что член типа г|K приводит к появлению треугольной
вершинной диаграммы с весом 3! (mg/2) = 3mg, поскольку имеются
3! способа выбора внешних трех линий. Беря вакуумное среднее
от обеих частей уравнения (9.2.1) и не учитывая квантовых по-
правок, получаем \i2 = X [@ | р | О}]2, а для линейного по г|з
члена имеем уравнение (д2 + ц,2) -ф = ЗА, [@ | р | 0) ]2 -ф. Послед-
нее уравнение приводит к следующему выражению для физиче-
ской массы т2: т2 = —ц2 -j- ЗХ [@ | р | 0) ]2. Из этих двух
соотношений получаем т2 = 2 ц,2 и 2л, [@ | р | О)]2 = т2. Тогда
соотношение X @ | р | 0) = mg/2 приводит к равенствам g2 = 2Х
и @ | р | 0) = m/g. В результате без учета квантовых поправок
имеем \i2 =тУ2, X = g-/2 и @ | р | 0) = m/g. Квантовые по-
правки изменяют эти соотношения, приводя к появлению некото-
рых перенормировочных множителей. Мы вводим перенормиро-
вочные множители Zx, Z2 и w посредством соотношений X —
= (ff"/2) ZXZ'\ \i2 = (m2/2)Z2Z и @ | р | 0) = Zl^(m/g).w
соответственно. Таким образом, имеем
(9.2.2а)
(9.2.26)
(9.2.2b)
Очевидно, что без учета квантовых поправок Z = Zx = Z3 = w —
= 1.
Протяженные объекты квантовой природы 331
Мы можем переписать уравнение Гейзенберга (9.2.1) в виде
(д- — т2) 1|з = F [г|з], где F [-ф ] содержит g, m, Z, Zb Z2, w и я|з.
Обозначим через Fo [ifi] значение F [ф ] при Z = Zx = Z2 = w —
= 1 и введем «контрчлен» Fc [-ф ], написав F [ф] = Fo [-ф ] +
+ Fc h|>]. Очевидно, что Fc [ф j обращается в нуль при Z = Zx =
= Z2 = ш = 1. Уравнение Гейзенберга (9.2.1) записывается те-
перь в виде
(а2 — /л2) ф (л:) = Fo [ф (л:) ] + Fc [-ф (ж) ], (9.2.3)
где
Ь-^-ёЧя, (9-2.4)
Г 3 7 2 Г7 I ! 7 М I ¦
L * L ^ / J
1) g-2i(K -}- A — Z) (а2 — т2) т)з =
(9.2.5)
= _^!(Za_Z)(-2-a> + i|3>) + -^(Z1-Z)(-^-a»+ ^
1 m2 v ,, ,,
_-_Za»(l -и;2) —
--|-^2A -Z)f +
f(l - Z) (a2 - m2) 1)з. (9.2.6)
Заметим, что
o> = o,
Z = 1 +
Zt = 1 +
Ш == 1 +
o(g-:
o(g-!
2)>
2), i = 1, 2,
2)-
Здесь и ниже символ О {gn) обозначает члены порядка
В однопетлевом приближении можем написать
ZV (Z, — Z) » (Z« — Z), t = 1, 2,
zV(i
A
— Zay) «
2A
:B-
— a;),
- Z — ш)
(9.2.7)
(9.2.8a)
(9.2.86)
(9.2.8b)
gn-
(9.2.9a)
(9.2.96)
(9.2.9b)
332 Глава 9
при произвольных I и п. Таким образом, имеем
— — A -o;)-3m2(l — ау)т)з— -|-gmB — Z — w)^2 —
- 4~ 8* (! ~ z) 4>3 + A - z) (a2 - m2) Ч>, (9.2.10)
откуда получаем
FchM «4~T"tZi - 2Я - 2 A - w)] +
+ m2|^-CZ1-Z2-2Z)-3(l -w)
О i i О ^ О / 1
4 4" ? A Z) ^+A ~Z) ^ - m2) if-
(9.2.11)
Для вычисления констант перенормировки полезно заметить,
что выражение (9.2.4) для Fo получается из лагранжиана i?i
+ 2"а, где 2Х = A/2) ?/т|>3, а ^2 = A/8) /4
Перенормировка энергии. Собственно-энергетическая часть
2 (—р2) в однопетлевом приближении дается выражением
2 (- />2) = -^g2Ao + 4" m^M <- ^ ~ б^2 + С1 - Z) (- Р2 - /?'2)-
(9.2.12)
где
*)ГЧО)= (9.2.13)
(9-2-15)
бц2 = — m2 [4-CZ1-Z8-2Z)-3(l -ш)]. (9.2.16)
Первый член (с Ао) в правой части (9.2.12) описывается петлей
(рис. 9.1), имеющей одну вершину, отвечающую S?^, а второй член
(с А (—р2)) соответствует петле с двумя вершинами, возника-
ющими за счет9?х (рис. 9.2). Член 8ц2 в (9.2.12) появляется благо-
даря второму (линейному по i|>) члену в выражении (9.2.11) для
«контрвзаимодействия» Fc, а последний член в (9.2.12) соответ-
Протяженные объекты квантовой природы 333
ствует вкладу последнего члена из формулы (9.2.11). 2 (—р2)
при р2 = —т2 определяет изменение массы, обусловленное вза-
имодействием. Поскольку значение тг выбрано так, что оно равно
наблюдаемому, указанное изменение т2 должно равняться нулю.
Таким образом, из (9.2.12) получаем
?2 | ?2Д + т'8*А (т*> (92л 7>
Учет (9.2.16) приводит к некоторому соотношению между пере-
нормировочными множителями.
P *z F k'P
Рис. 9.1. Рис. 9.2.
Перенормировка волновой функции. Поскольку двухточечная
причинная функция А (р) получается за счет повторного действия
2 (—р"), используя (9.2.17), находим
д-1 (р) = _у _ tn2 — ? (—Р2) = (9.2.18)
2
— A — Z) (-р2 — т2). (9.2.19)
Если ввести обозначение
А (~р2) — А (т2) = В (—р2) (—р2 — т2), (9.2.20)
то из (9.2.19) получим
П~' _..,,', • (9-2.21)
С другой стороны, А (р) имеет вид
__„,|_т, + ---, (9-2.22)
где многоточие отвечает членам, не имеющим особенности типа
полюса. Заметим, что вычет А (р) в полюсе р"- + т% = 0 равен
единице, поскольку -ф — перенормированная функция. Таким
образом, (9.2.21) приводит к следующей формуле для Z:
Z = 1 + ymVB (m2). (9.2.23)
334
Глава 9
Поскольку из (9.2.21) следует, что В (т2) = Л' (т2), где
формула (9.2.23) переписывается в виде
(9.2.24)
(9.2.25)
Перенормировка вершины. Для вычисления Z± определим вер-
шинную функцию Г (р, q, r) следующим образом:
(О | Т[Ч> (х) х|) (у) х|) B)] | 0) = (^J J (Pp <Fq сРгв (р + q + г) х
X exp (ip* + iqy + irz) A (p) A (q) А (г) Г (р, q, r). (9.2.26)
В однопетлевом приближении имеем
Г (р, q, г) = 3mg + Cmgf I (q, p, r) + -j mg3 IA (—p2) +
+ Л (—q2) + A (—r2) ] + 3mg [Zx + w — 2 ], (9.2.27)
где
/»2 /772 \ Г / *\ />Л 2 /?j21 f (r ., 1.. fe\2 /77^1
(9.2.28)
Член с / (</, p, г) в (9.2.27) отвечает треугольной диаграмме
к-р
Рис. 9.3.
Рис. 9.4.
(рис. 9.3) с тремя вершинами, каждая из которых возникает
за счет^!. Члены с Л в (9.2.27) описываются однопетлевой диаг-
раммой (рис. 9.4) с двумя вершинами, одна из которых соответ-
ствует 9?ъ а другая 3?г. Последний член в (9.2.27) получается
из члена с i|J в выражении (9.2.11) для Fc.
Зададим Zx таким образом, чтобы перенормированная константа
Протяженные объекты квантовой природы 335
взаимодействия g определялась соотношением
Т(р, q, r)p*=q,=rl=_mi = 3mg. (9.2.29)
Тогда из (9.2.27) получаем
2 — Zx — w = 9m2g2I (m2) + -|- g2A (m2), (9.2.30)
где
/ (m2) = / (p, q, r)p2=?2=r2=_m2. (9.2.31)
Это соотношение определяет Zb если известно w.
Перенормировка вакуумного среднего. Вычислим теперь сред-
нее по вакууму от обеих частей уравнения Гейзенберга (9.2.3).
Результат имеет вид
4 gm Д 0 + ±- gin [Z, + w - 2 ] Д 0 + 4" "f-1 Zi - ^2 - 2 A - ш) ] = 0,
где первый член обусловлен вкладом Fo, а остальные возникают
за счет Fc. Поскольку в однопетлевом приближении
A — Zx — о») [Z, — Zx — 2 (а; — 1) ] «
да — [Z2 — Zx — 2 (да— 1)],
получаем
| « 4"Г [Za - 2i - 2 (ш - 1)]. (9.2.32)
Константы перенормировки. Объединяя (9.2.16), (9.2.17),
(9.2.25), (9.2.30) и (9.2.32) в систему уравнений, для констант
перенормировки в однопетлевом приближении мы можем получить
следующие выражения [10]:
= 1 + 3m*g2 [З/ (т2) + -|- А' (яг2)] , (9.2.33а)
11 О о Д ______ л-2 Г А {tYi'2i\ ш2 Л ' (**j2\ i /Q
*J " n L\n '' '"c\" ' id I / \//i ^ »/f /1 l//t M. ( \J.
w
' (9-2-33в)
Z = 1 + \m2g*A' (т2). (9.2.33г)
336 Глава 9
Из соотношений (9.2.14), (9.2.15) и (9.2.31) находим
(*' + «2)Vl]. 0.2.34а)
Л (т2) = {L-j > (9.2.346)
v ' 6C)'«т2
l-T! jM» (9.2.34b)
18C) '• 6я /
/ (т2) = Й/8 C)Vi m4. (9.2.34г)
Статический солитон. Получим теперь с помощью бозонного
преобразования протяженный объект. Метод Янга — Фельдмана
приводит к уравнению (9.1.2), в котором физическое поле ф°
удовлетворяет следующему уравнению:
(д* — т2) ф° = 0. (9.2.35)
Указанное уравнение Янга — Фельдмана обусловливает динами-
ческое отображение г|; (х; ц>°). Получаемое в результате бозонного
преобразования гейзенберговское поле tyf дается соотношением
tyf = ф (х; ф° + /), в котором неоператорная функция / (х) должна
удовлетворять уравнению
(д* — т2) / = 0. (9.2.36)
Получаемое с помощью бозонного преобразования гейзен-
берговское поле i|jf также удовлетворяет уравнению Гейзенберга
(9.2.3)
(д2 - т2) V = Fo [^]+ Fe Wl (9.2.37)
Классическое поле ft определяется соотношением (9.1.16)
ф1 (х) = <0|V (jc) 101>. (9.2.38)
Величина <j>f в древесном приближении обозначается через <j>f0
и удовлетворяет уравнению Эйлера (9.1.103)
(д* - т2)^ = 4-г/п (^J +^ё2 № ¦ (9-2.39)
Рассматривая вакуумное среднее от обеих частей уравнения
Янга — Фельдмана (9.1.8), получаемого в результате бозонного
преобразования, и пренебрегая членом Fc, связанным с учетом
петлевых поправок, получаем
(9.2.40)
Протяженные объекты квантовой природы 337
Это уравнение совпадает с интегральным уравнением, которое
получается из уравнения Эйлера (9.2.39), если использовать
параметр бозонного преобразования / (х) в качестве линейного
члена.
Поскольку мы рассматриваем A + 1)-мерную модель, можно
написать х = (xly t). Выберем следующее статическое решение
уравнения (9.2.36):
/(*х) = Ае-'пхк (9.2.41)
Решая уравнение (9.2.40) методом последовательных прибли-
жений, получаем [2]
[ " )] (9.2.42)
где а находится из условия
А = — 2 — етя.. (9.2.43)
Функция, определяемая формулой (9.2.42), представляет собой
хорошо известное статическое солитонное решение нелинейного
уравнения (9.2.39).
Взаимодействие между отдельным квантом и протяженным
объектом. Согласно уравнению (9.1.45), на квант действует само-
согласованный потенциал FJ,1' [^>П, создаваемый статическим
солитоном. Здесь F^11 определяется соотношением F'^ l\p] =
= 8/у&ф. Таким образом, из выражения (9.2.4) получаем
Уравнения на собственные значения (9.1.53) и (9.1.56) принимают
вид
[а>1 f (d/dxtf - ni - F(ol) [ф1 (дг,)]} и <хи k) = 0, (9.2.45а)
{ш? + (d/dxdJ -tn2- Fbl) [ф1 (xi)]) Щ (Xl) = 0. (9.2.456)
Если использовать переменную ?, определенную выражением
1 = -^Ц (xi) + 1 = th-f-(Xl - a), (9.2.46)
то дифференциальные уравнения (9.2.45) сводятся к дифферен-
циальному уравнению Лежандра
((l-C2)^r-2^ + v(v+l)-r^)«(Q = 0, (9.2.47)
где v =2, ц2 = (т2 — @2)/(т2/4). Решение уравнения (9.2.47),
не имеющее особенностей при % = ±1, представляет собой функ-
338 Глава 9
цию Лежандра Р% (?). Случаи, когда ц = 2ш, отвечают решениям
типа рассеянных волн, а случаи, когда ц = 1, 2 (целое число), —
решениям, описывающим связанные состояния. Таким образом,
полная ортонормированная система собственных функций уравне-
ний (9.2.45) имеет вид
где k = ти, а % = (k2 + т'2I^ = т A + мгI/г,
"i (*i) = C/4)'/. A — ?2) при ©! = 0, (9.2.49)
«2 (jci) = C/2I/. S A — Z2L* при со2 = C/4I/. т. (9.2.50)
Таким образом, возникают два связанных состояния, одно
из которых, а именно иъ представляет собой трансляционную
моду. Отметим, что
«1 = C/4)'/г / J|L )-JL ,?/;. (9.2.51)
Согласно соотношению (9.1.73), имеем
W (х) = X W ~ Q @ -^7" ^° (х')' (9.2.52)
где
I Д и (у \ \г/ (Ь\ ff—i<n2t _J_ r/+ ^^ /9'<i>2^1 /^Q 9 ^Ч^
B(o2) /2
Q @ = C/4)'/. B?/m2) p @. (9.2.54)
Здесь Q (t) — квантовая координата. Мы определили р (t) таким
образом, чтобы выполнялось равенство (см. (9.1.66))
d
Динамическое отображение г|/. Динамическое отображение tf
в древесном приближении имеет вид
iff (X, Т) = фЪ (X) +%°(Х, Т) + ..., (9.2.56)
где
1 ' ~"ЧП (9.2.57а)
1T-n-Q[Xi — Q(t)]. (9.2.576)
Протяженные объекты квантовой природы 339
Здесь мы учли соотношения (9.1.100). Чтобы быть точными,
нам следует симметризовать (9.2.56) по q и Q.
Однопетлевая поправка к классическому полю. Вычислим
теперь (ф! — <j>l) в однопетлевом приближении. Уравнение
(9.1.113) записывается в виде
--^.gmp-Z-w) (ЙJ - -^g°- A - Z) far +
+ A - Z) (a2 - m2) & + -|- ?2 (-J- + &) @1 ft» (x)f | 0), (9.2.58)
где использованы выражения (9.2.10) и
Последняя формула получена из (9.2.44) при учете равенства
F^ [if] = б/7;11/^. Используя (9.2.39) и (9.2.44), мы можем
записать уравнение (9.2.58) в виде
{д2
= ^- [З^2 @1 (х°(х)J10) - т2 (Z2 - Z)] (f
+4-^(zi-z)(T+^K~|m2+jF(I)[^1}'f"A~ffi')- (9-2-60)
Проводя дальнейшие преобразования, получаем
{д2 _ т2 _
4 {3^2 <° I ГХ° Wl210) - т2 (Zs - Z)} (|-
= 4" (|
+4-^2(z1-z)(t+^K- (9-2-61)
При учете (9.2.33) это уравнение приводится к виду
{д2 _ т2 _ Л„ ^f]} ^f _ ^ _ Л.A _ „,)) =
= -|- (ЗёГ2<0[ ГХ° Wl210) - 3?2Д0 + -|- m'S2A (m2)) (-J- + Щ -
~ \т^ (б/ (т2) + 4- ^г^ (т2) + ЗЛ' (т2)) (-f- + &K.
(9.2.62)
340 Глава 9
Из этого уравнения можно определить величину однопетлевой
поправки к j>f.
Согласно формулам (9.2.34), только Ао является расходящейся
величиной, а А (/и2), Л' (т2) и / (т2) имеют конечные 'значения.
Кроме того, конечной является и величина
[(О | (х0J | 0) - А„] = @ | [(х0J - (Ф0J] | 0),
поскольку самосогласованный потенциал не приводит к изменению
рассеянных волн с бесконечным импульсом. Следовательно, мы
получаем, что однопетлевая поправка, входящая в выражение
для фГ, конечна. В C + 1)-мерном случае (т. е. при х = (х, t))
До и А (т2) расходятся, хотя I (т?) и А' (т2) имеют конечные
значения. Вычисления показывают, что даже в этом случае рас-
ходимости в правой части уравнения (9.2.62) сокращаются [10].
Это является примером общего утверждения, согласно которому
в теории, перенормируемой в отсутствие протяженных объектов,
при возникновении любого протяженного объекта перенормиру-
емость не нарушается. Этот вопрос рассматривается в разд. 9.3.
Квантовую координату можно учесть, если заменить <j>f (x)
на <j>f (X). Квантовая координата Q (t), появляющаяся в выраже-
нии для X, превращает солитон в квантовомеханический объект.
В этом разделе мы изучали A + 1)-мерную модель типа Лр4
в рамках метода бозонного преобразованияJ). Аналогичное рассмо-
трение может быть проведено и для модели типа синус-Гордона2).
9.3. Общее рассмотрение
бозонного преобразования
В двух предыдущих разделах мы описали метод бозонного
преобразования на примере простых случаев, когда составные
частицы отсутствуют и поэтому для решения уравнения Янга—
Фельдмана (9.1.2) применим метод последовательных прибли-
жений. Однако на практике часто встречаются случаи, когда, про-
тяженные объекты возникают путем коденсации составных бозо-
нов (например, фононов в кристалле, магнонов и т. д.). В этом раз-
деле мы формулируем метод бозонного преобразования в общем
виде.
Теорема о бозонном преобразовании. Предположим, что урав-
нение Гейзенберга (9.1.1)
Л(<Э)г|) = F Ь|>] (9.3.1)
*) Рассмотрение этой модели с помощью других методов можно найти в ра-
ботах [11].
2) Рассмотрение модели типа синус-Гордона с помощью методов, отличных
от метода бозонного преобразования, можно найти в работе [12].
Протяженные объекты квантовой природы 341
отвечает появлению набора свободных физических полей (cpj,
Ф», ..., ф?, ...)• Здесь ф& (а = 1, ..., п) — бозоны, а осталь-
ные физические поля — фермионы. Уравнения свободного поля
для бозонов имеют вид
%* (д) ф? = о, (9.3.2)
где суммирование по а не производится.
Динамическое отображение обозначим следующим образом:
т|> (х) = : у (х; ф° ...):. (9.3.3)
Чтобы вычислить F [яр] в правой части уравнения Гейзенберга
(9.3.1), вспомним правило умножения, введенное в разд. 3.4;
согласно этому правилу, мы должны сначала вычислить произ-
ведения нормальных произведений физических полей и преобразо-
вать их в линейные комбинации нормальных произведений.
Интегрирование по пространственным и временным координатам
следует производить только после этого.
Осуществим теперь операцию трансляции для рассматривае-
мых полей
ф? (X) -V ф? (*) + /« (X) (9.3.4)
как формальную замену в динамическом отображении. Здесь
fa (х) (а = I, ..., п) — неоператорные функции. В результате
этой замены на основе динамического отображения гейзенбергов-
ского оператора яр(х) получаем определение нового оператора
V (х):
У(х) = :-ф (jc; q>°a + fa, ...):. (9.3.5)
До тех пор пока каждый член в разложении по степеням
(фа + fa) остается хорошо определенным, на fa (x) не наклады-
,вается никаких условий.
Теорема. Если fa (x) удовлетворяет тому же уравнению,
что и (рпа (х):
№ (д) fa (x) = 0, (9.3.6)
то оператор ipf (x) удовлетворяет тому же уравнению Гейзенберга,
что и tj> (x):
x) = FW(x)]. (9.3.7)
Преобразование (9.3.4) при условии (9.3.6) называется бозон-
ным преобразованием, а эта теорема носит название теоремы
о бозонном преобразовании.
Доказательство- Рассмотрим произведение операторов гр (х),
например F [(Ф (х)]. Трансляция полей на неоператорную величину
не оказывает влияния на спаривания полей ф?, которые могут
встретиться, если переписать F [(^(х)] в виде нормальных произ-
342 Глава 9
ведений фа (х). Поэтому если мы записываем все величины, исполь-
зуя разложение в ряд по степеням (фа + /а), то произведение
гейзенберговских полей, подвергнутых бозонному преобразованию,
равно результату действия бозонного преобразования на произ-
ведение гейзенберговских полей. Другими словами, эти две опе-
рации (бозонное преобразование и перемножение операторов)
коммутируют между собой:
F [i|>M = (F ly))f. (9.3.8)
Здесь (F [ty])F означает, что бозонное преобразование действует
на динамическое отображение F [i|)]).
Рассмотрим затем некоторый дифференциальный или интеграль-
ный оператор D (дх; ...), действующий на ф„ (х). Здесь дх в D
отвечает какой-либо операции (дифференцирования или интегри-
рования), совершаемой над ф« (х). Многоточие показывает, что D
может зависеть и от других переменных. Если D (дх; ...) действует
на ц>°х (х), то имеем
D (дх; ...)ц>°а (х) = Д, (дх; .. .) ф& (лг), (9.3.9)
гдеDo — результат некоторых манипуляций. Операторы D (дх; ...)
и Do (дх; ...) связаны между собой соотношением
D(dx; ...) = D0(dx; . . .) + ? а«> (дх; .. .) [Ха (дх)}'. (9.3. Ю)
i
Поскольку /а (х) и фа (х) удовлетворяют одному и тому же урав-
нению (9.3.2) или (9.3.6), имеем
D (дх; ...) [Фа (дг) + fa (х)] = Do (дх; ...)[<$ (дг) + /, (дг)]. (9.3.11)
Это означает, что
D(dx; ...) [ср& (дг)]^ = [Do (дх; . . .) Ф» (х)У = [D (дх; .. .) ц>°а (x)\f.
(9.3.12)
Здесь обозначение [D (дх; ..-) q>a (x)V соответствует тому, что
бозонное преобразование осуществляется после действия опера-
тора D (дх; ...) на ф^ (х). Отсюда следует, что любая операция
дифференцирования (или интегрирования) коммутирует с бозон-
ным преобразованием. Поскольку нахождение решения уравнения
Гейзенберга включает в себя только использование комбинаций
процессов интегрирования и дифференцирования, очевидно, что
= (F Ь|>])' = F Ь|Л. (9.3.13)
Таким образом, мы пришли к теореме о бозонном преобразо-
вании, которая утверждает, что подвергнутое бозонному преобра-
зованию гейзенберговское поле г|з/ также удовлетворяет уравне-
нию Гейзенберга (9.3.1), если обе части уравнения (9.3.1) пред-
Протяженные объекты квантовой природы 343
ставлены в виде разложения по степеням (ф« + /а). Это утвержде-
ние завершает наше доказательство.
Теорема о бозонном преобразовании формулируется с исполь-
зованием степенного ряда по (ф„ + fa). В общем случае бозонное
преобразование не вполне эквивалентно соответствующему пре-
образованию для когерентного представления, так как / (х)
подчиняется условию (9.3.6) и, кроме того, не требуется, чтобы
функция / (л;) имела фурье-образ. Другими словами, когда / (х)
имеет фурье-образ, бозонное преобразование приводит к конкрет-
ному когерентному представлению, подчиняющемуся условию
(9.3.6).
Самосогласованный потенциал. Возможно, что в результате
суммирования степенных рядов по fa выявляются некоторые физи-
ческие состояния с дискретными значениями энергии. Пример
такого рода ситуации в явном виде описан в разд. 9.1. Воспользо-
вавшись интуитивными представлениями, можно сказать, что
бозонное преобразование отвечает конденсации бозонов, которая
приводит к возникновению некоторых протяженных объектов.
Эти протяженные объекты создают самосогласованный потенциал,
оказывающий влияние на квантовые состояния. Этот потенциал
обусловливает появление некоторых новых уравнений с дис-
кретным спектром энергий, причем появляющиеся состояния
представляют собой связанные состояния протяженного объекта
и кванта. До настоящего времени не сформулирована систематиче-
ская процедура расчета самосогласованного потенциала для слу-
чая, когда протяженный объект образуется в результате конден-
сации составных бозонов. Но на практике имеется много примеров
из области физики твердого тела, когда проявляются определенные
эффекты, связанные с наличием самосогласованного потенциала.
Электроны, на которые действует самосогласованный потенциал,
создаваемый вихрями в сверхпроводниках (электроны вблизи
сердцевины вихря), а также фононы в окрестности дислокаций
в кристаллах представляют собой некоторые примеры такого
рода.
Квантовая координата. Среди упомянутых выше связанных
состояний всегда имеются трансляционные моды с нулевой энер-
гией. Как показано в разд. 9.1, происхождение трансляционных
мод связано с трансляционной инвариантностью теории. Рассмот-
рим сначала гейзенберговское поле чр (х, t), над которым не было
проведено бозонное преобразование. Тогда, учитывая трансля-
ционную инвариантность теории, можно видеть, что яр (х + a, t)
с постоянным вектором а также подчиняется уравнению Гейзен-
берга. Кроме того, если fa (x, t) удовлетворяет уравнению для
свободного поля (9.3.6), то ему же удовлетворяет и/а (х + a, t).
344 Глава 9
Поэтому i|)f (x + a, t) удовлетворяет тому же уравнению Гей-
зенберга, что и i|?f (x, t). Операция х -vx + а не приводит к из-
менению теории. Квантовые моды, связанные с этой трансляцией
в пространстве, являются теми же трансляционными модами, ко-
торые мы рассматривали в двух предыдущих разделах. Поскольку
операция х -»- х + а не требует затраты энергии, трансляционные
моды отвечают нулевой энергии. Следовательно, эти моды не на-
блюдаются как возбужденные состояния. Следуя рассуждениям,
приведенным в разд. 9.1, мы будем описывать эти моды, исполь-
зуя квантовую координату q, а не операторы рождения и уничто-
жения. Оператор q является тем оператором, который приводит
к пространственным.трансляциям. Другими словами, q ->-q — a
индуцирует х ->¦ х + а, поскольку х и q появляются в tyf только
в виде комбинации х — q. В разд. 9.4 появление q рассматривается
с общей теоретико-полевой точки зрения.
Квантовая координата и внутренняя симметрия. До сих пор
мы считали, что фа не обладает какими-либо степенями свободы,
кроме тех, которые связаны с пространственными и временными
переменными. Симметрии, никакие связанныес пространствен-
ными и (или) временными переменными, называются внутренними
симметриями. Изоспин и спин — примеры проявления внутрен-
них симметрии. Если ij>° обладает изоспином, то возникновение
протяженных объектов может привести к нарушению изоспиновои
симметрии. Поэтому следует ожидать, что протяженный объект,
описываемый <j>f, может иметь не только обычную квантовую коор-
динату, но и квантовую изоспиновую координату (квантовые
изоспиновые углы), отвечающую нулевой энергии. В следующем
разделе показано, что несферический объект в (I + 3)-мерном про-
странстве обладает квантовыми координатами, отличными от Q.
Энергия протяженных объектов. Попытаемся кратко описать
процедуру вычисления энергии протяженных объектов, возник-
ших за счет бозонного преобразования. Обозначим символом Н
гамильтониан системы
Я=)лИх;1|)], (9.3.14)
где т|) — гейзенберговское поле, a h [х; Щ — оператор плотности
гамильтониана. Гамильтониан W, получаемый в результате бо-
зонного преобразования, дается выражением
Hi = \d?xh [х; ф]. (9.3.15)
Если используется древесное приближение, то, исходя из
тех же соображений, что и при выводе классического уравнения
Протяженные объекты квантовой природы 345
Эйлера (9.1.42), можно доказать, что
@|//'|0)«. \d?xh lx; ф1]. (9.3.16)
Если не использовать древесное приближение, то энергия
протяженных объектов определяется выражением
(О | W\ 0) = J d?x @ | h [x; хрЦ\ 0). (9.3.17)
Здесь важно отметить, что интегрирование по пространственным
переменным должно осуществляться только после вычисления ва-
куумного среднего от плотности гамильтониана, получаемого в ре-
зультате бозонного преобразования.
Как показано в гл. 3, гамильтониан Я в слабом смысле равен
свободному гамильтониану с добавочной константой Wo:
(a\H\b) = (а | #0 [ф°] | b) + Wo (a | Ь). (9.3.18)
Данное соотношение основывается на том факте, что ф° — распро-
страняющаяся волна. Поэтому если / (х) — распространяющийся
волновой пакет, то мы можем обобщить соотношение (9.3.18)
следующим образом:
(а\НЦЬ) = (а\ #0 [ф° + /1 | Ь) + Wo (a \ b). (9.3.19)
Но это соотношение не выполняется, если функция / имеет какую-
либо особенность, приводящую к отсутствию у нее фурье-об-
раза. Когда / не имеет фурье-образа, в выражении (9.3.17) для
энергии появляются члены, содержащие более высокие степени /,
если не имеется каких-нибудь конкретных причин, препятствую-
щих возникновению таких членов. Заметим также, что вели-
чина, определяемая формулой (9.3.17), представляет собой опе-
ратор, включающий квантовомеханическую переменную р.
Перенормируемость и протяженные объекты. Предположим,
что уравнение Гейзенберга (9.3.1) перенормируемо, если не про-
водилось бозонного преобразования. Рассмотрим сначала простой
случай, когда имеется только одно физическое поле ф°, являю-
щееся бозонным полем. Зададим динамическое отображение т|)
в виде
2
rt=0
(9.3.20)
346 Глава 9
Динамическое отображение гейзенберговского поля, полученного
в результате бозонного преобразования, имеет вид
оо
w = 2 тг J dffi • • • da»cf (*;
2
n=0
(9.3.21)
Коэффициенты этого разложения ct (х; ox ...) связаны ее (х; о^ ...)
посредством соотношения (9.1.14)
с, (х; а1 ... о„) = .
(9.3.22)
Поскольку уравнение Гейзенберга, которому удовлетворяет^,
перенормируемо, коэффициенты разложения с (х; аг ...) в фор-
муле (9.3.20) являются ограниченными функциями, если они
выражены через перенормированные значения энергии и перенор-
мированные константы взаимодействия. Тогда выражение (9.3.22)
показывает, что коэффициенты cf (x; аг ...) не содержат расхо-
димостей, если они представлены в виде разложения в ряд по
степеням /. Вспоминая тот факт, что утверждение о перенормиру-
емости всегда связывалось с некоторыми разложениями (напри-
мер, с разложением в ряд теории возмущений, с разложением по
петлевым диаграммам и т. д.), мы можем сформулировать при-
веденный выше результат в виде утверждения, что если коэффи-
циенты с (х; ох ...ап) перенормируемы, то таковыми являются и
Cf (x; аг ... ап). Другими словами, возникновение протяженных
объектов не нарушает перенормируемости. Хотя мы пришли
к этому заключению, рассматривая простой случай, когда един-
ственное физическое поле — бозон ф°, легко распространить
приведенное выше рассмотрение на общий случай. Полученный
выше вывод находится в согласии с тем очевидным фактом, что
протяженный объект не является локальным объектом в микро-
скопическом смысле.
Условия образования статических протяженных объектов.
Статические объекты возникают при бозонном преобразовании
с функцией / (х), не зависящей от времени. Покажем теперь, что
уравнение свободного поля, которому удовлетворяет не зависящая
от времени функция / (х), приводит к появлению некоторого осо-
бого свойства статических объектов.
Протяженные объекты квантовой природы 347
Чтобы избежать ненужных усложнений, опустим индекс а
и обозначим fa просто через /. Функция / (х) удовлетворяет урав-
нению (9.3.6)
I (д) f (х) = 0. (9.3.23)
Обозначим через со (к) энергию бозона ср° с импульсом к. Будем
считать, что со (к) — неотрицательная величина. Пусть со (к) =0
при к = к<а) (а = 1, 2, ...). Другими словами, со (к) отвечает
мягкой моде при к = к<а). Предположив, что функция / (х)
имеет фурье-образ, обозначим его через / (к). Тогда из (9.3.23)
следует соотношение со (к) / (к) =0, где подразумевается, что
/ (х) представляется в виде суммы периодических функций:
/ (*) = ? са exp [tk<a> x]. (9.3.24)
а
Этот статический протяженный объект возникает в результате
конденсации бозонов на уровнях с нулевой энергией. В физике
твердого тела существует много примеров таких периодических
объектов: синусоидальное спиновое упорядочение в хроме, спи-
ральные спиновые структуры в Tb, Dy, Но и т. д.
Все другие статические объекты обладают некоторыми осо-
бенностями, которые приводят к отсутствию фурье-образа
f (x). Эти особенности либо типа расходимости, либо топологи-
ческие. В данном случае термин «особенность типа расходимости»
означает, что / (х) расходится при | х ||= оо по крайней мере вдоль
одного из направлений вектора х. Пример протяженного объекта
с особенностью типа расходимости приведен в разд. 9.2 (формула
(9.2.41)). Наличие топологической особенности означает, что
/ (л;) не является однозначной функцией. Если / (х) имеет особен-
ность, то говорят, что протяженный объект сингулярен.
Если равенство со (к) =0 имеет место только при к = 0,
то формула (9.3.24) приводит к тривиальному выбору /(х),
а именно / (х) = const.
Итак, возникновение несингулярных статических объектов воз-
можно тогда и только тогда, когда при некотором отличном от
нуля значении к имеет место смягчение со (к). И обратно, если
to (к) =5^= 0 для любого отличного от нуля значения к, то статиче-
ские объекты всегда сингулярны.
Этот вывод привлекает наше внимание к изучению протяжен-
ных объектов, обладающих некоторыми особенностями.
Хорошо известным примером протяженного объекта с тополо-
гической особенностью является вихрь в сверхпроводнике. В этом
случае уравнение (9.3.23) превращается в уравнение Лапласа
V2/ = 0, Пусть 0 — угол в цилиндрической системе координат
Эокруг оси х3. Тогда имеем уравнение V29 = 0; 0 представляет
собой многозначное решение уравнения Лапласа, Вихрь в виде
348 Глава 9
прямой линии отвечает выбору / (х) =0. Дислокация в кристалле—
еще один пример протяженного объекта с топологической особен-
ностью. В физике твердого тела мы обнаруживаем множество про-
тяженных объектов с линейными или с поверхностными тополо-
гическими особенностями. В гл. 10 мы проводим систематическое
рассмотрение протяженных объектов с топологическими особен-
ностями.
9.4. Асимптотическое условие
и асимптотический гамильтониан
Введение. В разд. 9.2 вычисление членов низшего порядка
в разложении я|^ показало, что х и q появляются в комбинации
х — q. В данном разделе мы исследуем эту проблему с точки зре-
ния общего подхода к рассмотрению квантовополевой системы
с протяженным объектом. Чтобы осуществить такой подход, по-
лезно вспомнить ситуацию в случае отсутствия протяженных объ-
ектов (см. для сравнения гл. 2 и 3), когда нахождение гейзен-
берговского поля о|з проводилось в рамках самосогласованного
метода, в котором ключевая роль отводилась картине свободных
физических частиц. Эта картина, где физические частицы рассма-
триваются как свободные, отражает асимптотическое условие,
качественная формулировка которого заключается в том, что
частицы становятся свободными в асимптотическом пределе
(t -v ±оо). В этом разделе мы изучим вопрос о том, как нужно
сформулировать асимптотическое условие при наличии протяжен-
ного объекта и каковы следствия этого асимптотического условия.
В дальнейшем мы сосредоточим наше внимание только на случае,
когда протяженный объект является статическим (т.е. f(x)
не зависит от времени).
Квантовая координата. Обозначим через х0 макроскопическое
положение статического протяженного объекта. Тогда макроско-
пическая величина ф = @ [ г|/ | 0) является функцией х — х0.
Поскольку оператор полного импульса Р для гейзенберговского
поля представляет собой генератор трансляций в пространстве,
он должен приводить к сдвигу х0 (х0 -vx0 — а), который выполняет
роль трансляции применительно к х, а именно х — хо->х +
+ а — х0. Поэтому следует ожидать, что х0 имеет смысл величины,
канонически сопряженной Р, хотя х0 и не является оператором.
Это означает, что х0 сопутствует оператору q, появляясь в комби-
нации х0 + q, где q — оператор, канонически сопряженный Р;
трансляция q (q -> q — а) приводит к трансляции х0 (х0 + q -*¦
-> х0 — а + q). Короче говоря, ф есть функция х — х0 — q.
Неопределенность квантового оператора q отражает произвол
Протяженные объекты квантовой природы
349
при выборе координаты х0. Указанный произвол коренится в тран-
сляционной инвариантности теории. Строго говоря, положение
протяженного объекта задается величиной х0 + q, где оператор
q — квантовая координата. Заметим, что q зависит от времени
даже в том случае, когда / (х) не зависит от t.
Асимптотическое условие. Асимптотическое условие заклю-
чается в том, что любое физическое квантовое поле %° становится
свободным полем, если его координатах отвечает точке, настолько
удаленной от того места, где расположен протяженный объект,
что х оказывается вне радиуса действия самосогласованного по-
У "
Рис. 9.5.
тенциала, создаваемого этим объектом. Поскольку положение
протяженного объекта задается величиной х0 + q, асимптотиче-
ское условие сводится к утверждению, что %0 является функцией
х — х0 — q, обладающей свойством
Л(д)хо(*) = О (9.4.1)
при больших значениях | х — х0 — q |. Здесь | х — х0 — q | сле-
дует понимать как среднее квадратичное значение длины вектора
(х — х0 — q) (рис. 9.5).
Комбинация (х—х0—q). Поскольку все наблюдаемые резуль-
таты зависят только от относительного расположения точки, где
производятся измерения, и протяженного объекта, гейзенбергов-
ское поле г|^, получившееся в результате бозонного преобразова-
ния, должно зависеть от х только в комбинации (х — х0 — q). В
этом состоит физический смысл появления комбинации (х —
— х0— q) при выводе соответствующих формул.
Формальное доказательство утверждения о том, что х и q
появляются только в виде комбинации (х — х0 — q), может быть
получено, исходя из следующих соображений [13]. Согласно со-
отношению (9.1.22), зависимость г|з^ от х обусловлена зависимо-
стью от х функции ff. Поскольку х содержится в ft только в виде
350 Глава 9
комбинации (х — х0 —¦ q), в том же виде х входит и в г|з'. Хотя
подобное формальное доказательство и возможно, приведенные вы-
ше физические аргументы позволяют более глубоко разоб-
раться в причинах появления комбинации (х — х0 — q).
Оператор трансляции Р. Хотя асимптотическое условие фор-
мулируется довольно просто, некоторые его следствия оказы-
ваются весьма неожиданными. В частности, оно определяет струк-
туру генератора пространственной трансляции Р. Генератор
Р представляет собой оператор импульса, который находится из
лагранжиана для поля ij>. Поскольку х° содержит х и q только
в виде комбинации х — q, а Р генерирует трансляцию q -*¦ q —
— а, операторы рождения и уничтожения (а+, а) в %° (см. соот-
ношения (9.1 -55)v (9.1.65) и (9.1.71)) не должны никак меняться
при трансляции в пространстве, откуда следует.
[Р, ah] = [P, at] = 0. (9.4.2)
Поэтому, вводя определение
Р = @ | Р | 0) , (9.4.3)
получаем
Р = р. (9.4.4)
Мы видим, что р и q образуют множество канонических опера-
торов, коммутирующих с а и а1". Фактически {q, p; а, а+} —
это те операторы, с помощью которых строится упомянутое выше
гильбертово пространство.
В гл. 2 физическое пространство Фока строится путем цикли-
ческого действия на вакуум 10) операторов рождения волновых
пакетов, отвечающих физическим квантам:
Здесь g (к) — нормированная квадратично-интегрируемая функ-
ция. Теперь мы имеем дополнительные квантовомеханические опе-
раторы (р, q). Поэтому состояние, в котором отсутствуют ча-
стицы, представляет собой произведение 10) и квантовомехани-
ческого состояния, отвечающего операторам (р, q). Указанное
состояние определяется выражением
I 0; g0) = J d*kg0 (k) gk X | 0), (9-4.5)
где |k — собственное состояние оператора р:
plk = ftkgk. (9.4.6)
Нормированная квадратично-интегрируемая функция g0 (k) кон-
кретизирует состояние протяженного объекта, Таким образом,
Протяженные объекты квантовой природы 351
состояния в гильбертовом пространстве строятся путем цикличе-
ского действия операторов рождения волновых пакетов ctg на
состояния { |0; g0)} типа волновых пакетов, соответствующие про-
тяженному объекту:
Ж = { | ?}; | ?} - а+ Ы . . . а+ Ы | 0; g0)}. (9.4.7)
Это гильбертово пространство представляет собой расширенное
пространство Фока. Заметим, что вплоть до предыдущего подраз-
дела мы считали, что квантовые координаты, отличные от q,
отсутствуют. Любой оператор в данной теории может быть выра-
жен через {q, p; а, а+}.
Соотношение (9.4.2) отвечает ситуации, резко контрастирующей
со случаем, когда отсутствуют какие-либо протяженные, объекты;
в этом случае Р представляет собой сумму импульсов отдельных
квантов:
= й j d3kkalak (9.4.8)
и генерирует трансляцию в пространстве х -»-х + а для опера-
тора ah exp (ikx) посредством преобразования ak -vaft exp (tka).
Если же существует статический протяженный объект, то кван-
товая координата q появляется в комбинации х — q, и трансля-
ция в пространстве возникает за счет преобразования q -»-q — a,
так что не требуется, чтобы оператор ah изменялся при трансляции,
поскольку ak связан с волновой функцией и (х — q —¦ х0) к). В
результате имеет место равенство (9.4.4).
Тот факт, что структура оператора Р существенным образом
меняется за счет бозонного преобразования, не вызывает удивле-
ния, если вспомнить ситуацию, имеющую место в квантовой тео-
рии поля без протяженных объектов. Рассматривая этот последний
случай, предположим, что константа взаимодействия g имеет
критическое значение gc в том смысле, что при g > gc возникает
составная частица. Если g меняется от значения, немного меньше
gc, до значения, несколько большего gc, то в операторе Р неожи-
данно появляется новый член, описывающий импульс составной
квантовой частицы. В случае же квантовополевой системы с про-
тяженными объектами возникновение трансляционных мод при-
водит к появлению квантовой координаты q и в то же время
к исключению всех а и сс+ из выражения для оператора Р.
Соотношение (9.4.4) оказывается принципиально важным,
если попытаться построить а^, используя г|з(п), полученные из
решения дифференциального уравнения (9.1.50). Решения этого
уравнения определены с точностью до функции, удовлетворяющей
однородному уравнению вида Л (д) и == 0. Указанная неодно-
значность исключается, если учесть соотношение (9.4.4). Это
352
Глава 9
было показано с помощью непосредственного вычисления в ра-
боте [14].
Оператор углового момента J. Когда размерность простран-
ства больше 1, преобразования группы Пуанкаре включают вра-
щения в пространстве. Пространственное вращение х ->7?х,
где R —матрица вращения, обусловливает преобразование опера-
торов
R'hp (х, /) R = if (Rx, t). (9.4.9)
Здесь мы для простоты полагаем, что гейзенберговское полет)) (х)
скалярное. Генератор вращения R определяется оператором
углового момента J:
#-i = exp( ^-J-в), (9.4.10)
где 0 — параметр преобразования.
В дальнейшем мы будем рассматри-
вать случай, когда {q, р, а, а+} об-
разуют полный набор физических опе-
раторов, действующих в гильбертовом
пространстве. Это возможно, если про-
тяженный объект является сферически-
симметричным в покоящейся относи-
тельно него системе отсчета [13]. По-
скольку квантовая координата q
появляется только в комбинации х — q,
соотношение (9.4.9) выполняется, если
оператор J приводит к вращению q,
удовлетворяющему условию
R'1 (х — q) R = х — If1* = R'1 (Rx — q>. (9.4.11)
В динамическом отображении поля г|з (х) появляются комбина-
ции (х — qJ, р- (х — q) и к (х — q), где к — вектор, отвечаю-
щий оператору уничтожения частиц сск. Отсюда следует, что пре-
образования неоператорных величин х-»-х' = ./?х и к -»-к' =
= Rk обусловлены следующими преобразованиями операторов
(рис. 9.6): _ _
R-*qR = /ГЧ iT'ptf = iT'p, (9.4.12)
R-hxkR = щк, (9.4.13)
где частицы считаются бесспиновыми. Поэтому угловой момент
J представляет собой сумму орбитального момента L, соответствую-
щего квантовой координате, и орбитального момента 1, описыва-
ющего возбужденные частицы:
J = L + 1, (9.4.14)
Рис. 9.6.
Протяженные объекты квантовой природы 353
где
L = q X р, (9.4.15)
U = — \itiH J ikal (к,-щ) ак + эрмит. сопр. (9.4.16)
Отметим, что L и 1 коммутируют между собой. Когда имеются
дискретные уровни с отличной от нуля энергией (j-состояния),
1 должно включать в себя орбитальный момент, соответствующий
этим уровням.
Если в системе отсутствуют частицы, то, чтобы индуцировать
преобразование пространственных координат, отвечающее вра-
щению, достаточно осуществить вращение протяженного объекта.
Но если в систему вносятся частицы, то полная система перестает
быть сферически-симметричной и 1 играет роль внутреннего спина
объекта.
Чтобы естественным образом обобщить проведенное выше
рассмотрение на случай, когда объект не является сферическим (или
круговым), потребуются новые квантовомеханические операторы,
играющие роль внутреннего спина объекта. На классическом
языке это отвечает эффекту, связанному с моментом инерции.
Рассмотрим в A + 2)-мерном мире статический объект, не явля-
ющийся круговым. Несферическая форма приводит на феноменоло-
гическом уровне к нарушению круговой'симметрии, а квантовые
флуктуации 0 проявляются в виде моды с энергией, равной нулю.
Поэтому для выполнения канонического коммутационного соот-
ношения для tyf требуется наличие новой квантовомеханической
координаты Qq (и канонически сопряженной ей величины 0р).
Поскольку неопределенность Qq должна проявляться в неодно-
значности угла 6, 9, и 9 должны образовывать комбинацию
@ — 0?). Имеем три квантовые координаты: <7i> Цъ и %• По
той же причине появляются новые квантовые координаты для не-
сферического объекта в A + 3)-мерном мире. В этом случае алге-
браическая ситуация с этими новыми квантовыми координатами
несколько осложняется тем, что группа вращений не является
абелевой.
Если г|з обладает некоторыми внутренними степенями свободы,
обусловленными соответствующими симметриями (такими, как
спиновая симметрия, изоспиновая симметрия и т. д.), и если на-
личие некоторых протяженных объектов нарушает на феноменоло-
гическом уровне внутреннюю симметрию, то появляются «внутрен-
ние квантовые координаты».
Чтобы избежать усложнений, в дальнейшем мы будем рассма-
тривать сферически-симметричные объекты, для которых един-
ственными квантовомеханическими операторами, появляющи-
мися в теории, являются {р, q}.
354 Глава 9
Гамильтониан в слабом смысле. Мы видели, что, как только
в системе возникает протяженный объект, появляются и необходи-
мые для сохранения трансляционной инвариантности квантово-
механические операторы (р, q), не зависящие от операторов физи-
ческих частиц (а, а+). Оператор q всегда встречается в комбина-
ции (х — q). Но если вспомнить тот факт, что сдвиг во времени
генерируется гамильтонианом Я, мы немедленно обнаружим,
что комбинация (х — q) приобретает более общую форму [х —
— Q(Q]. где
(9.4.17)
Иными словами, гейзенберговское поле i|tf зависит от q только
через комбинацию [х'— Q(t)]. Величина Q (t) описывает кван-
товые флуктуации положения объектов в том случае, когда со-
существуют протяженный объект и некоторое количество кван-
товых частиц.
Вообще говоря, величина Q (t) зависит от {ось а|}, поско-
льку Я включает в себя а и а+. Это можно понять на качествен-
ном уровне, если учесть тот факт, что присутствие некоторых
квантов оказывает влияние на квантовые флуктуации положения
протяженного объекта. И наоборот, если объект флуктуирует,
то из-за этого возникает некоторая неопределенность при иденти-
фикации энергии квантов, приводящая к уширению квантовых
энергетических уровней. Это означает, что гамильтониан, выра-
женный через физические операторы, не является просто суммой
энергий, отвечающих независимым модам. Асимптотическое усло-
вие и пространственно-временная симметрия налагают жесткие
ограничения на корреляцию между квантами и протяженным
объектом [15].
Асимптотическое условие приводит к одному важному след-
ствию, касающемуся энергии. В гл. 3 мы видели, что в случае
отсутствия какого-либо протяженного объекта Я эффективно
или (в слабом смысле) играет роль свободного гамильтониана:
Я = Яо, (9.4.18)
где Яо = Й [ i3kaknk, (9.4.19)
пк = ссдЛ. (9.4.20)
Это отражает тот факт, что измеренная полная энергия представ-
ляет собой сумму результатов измерения энергий для каждого фи-
зического кванта (асимптотически свободной частицы). В случае
когда присутствует статический протяженный объект, солитон об-
ладает полным импульсом р. Кроме того, отдельный квант может
быть идентифицирован только в асимптотической области. Га-
мильтониан Я не зависит от q, поскольку Я получается в ре-
Протяженные объекты квантовой природы 355
зультате интегрирования по пространству плотности гамильто-
ниана, в которую q входит в виде х — q. Таким образом, асимпто-
тическое соотношение (9.4.18) заменяется утверждением, что
Н зависит только от р и гаА:
Я = Я (р, nh). (9.4.21)
Конкретная структура Я (р, nk) зависит от пространственно-
временной симметрии лагранжиана. Ниже мы проиллюстрируем
это обстоятельство. В противоположность ситуации с Яо гамиль-
тониан Я (р, nh) по своей структуре не обязательно является
линейной функцией от nk, что обусловлено взаимной корреляцией
между протяженным объектом и квантами. Формула (9.4.21)
представляет собой модификацию соотношения (9.4.18), обуслов-
ленную наличием статического протяженного объекта, и ее сле-
дует понимать, подобно (9.4.18), как соотношение, справедливое
в слабом смысле.
Из (9.4.21) непосредственно следует
Q (*) = «>»»/* [q, Hit] e-ш//* = дН/др. (9.4.22)
Поэтому Q (t) включает в себя зависимость от р и п,,\
Q @ = Q (*; р, nk). (9.4.23)
Таким образом, мы видим, что Q коммутирует с Я и, следова-
тельно, не зависит от времени:
Q = 0. (9.4.24)
Это отражает тот факт, что трансляционные моды отвечают нуле-
вой энергии. Из (9.4.24) и (9.4.17) следует
Q @ = q + t&. (9.4.25)
Получается следующая сводка коммутаторов для величин Н,
Р, Q и Q:
[Я, р] = [Я, Q] = 0, (9.4.26)
i [Н1П, q] = i [Н1П, Q] = Q = дН/др. (9.4.27)
Пространственно-временная симметрия и гамильтониан в сла-
бом смысле. Зададим теперь вопрос, каким образом симметрия,
отвечающая группе Лоренца, оказывает влияние на вид гамильто-
ниана в слабом смысле. Оператор лоренцева «поворота» К удовлет-
воряет коммутационным соотношениям
i iKt, Pf] = ПНЬи, (9.4.28)
i 1Кг, Я] - hPt, (9.4.29)
i\Ku К,} = b*iihJh, (9.4,30)
12*
356 Глава 9
Здесь J — генератор вращения, определяемый соотношениями
(9.4.14)—(9.4.16).
Оператор К не меняет числа частиц. Запишем этот оператор
в виде
(//q + qA0^$^- + 6K, (9.4.31)
где М построен из операторов nh. Тогда оператор бК. включает
в себя только р и nh, поскольку он коммутирует с р, согласно
(9.4.28). Исходя из (9.4.27), получаем
а- = —Н~ХК- -I- — Я д Н — (р х ^' 4- Н~1ЬК- С9 4 321
Это приводит к соотношению
i [q, Я] = —/ [Я-ХК, Я] = -НрН~\ (9.4.33)
откуда имеем
<Э/дргЯ = ptH-1. (9.4.34)
Отсюда получаем, что Я имеет вид
Я = [р2 + УИ2 (nh) ]'/.. (9.4.35)
Соотношение (9.4.30) выполняется в том случае, если указанная
выше величина М (nh) совпадает сМиз (9.4.31). 6К. коммутирует
с р, Я и К. Из соотношения (9.4.22) находим теперь
^ __. (9.4.36)
Формулы (9.4.35), (9.4.36) приводят к релятивистским выраже-
ниям для энергии и импульса, в которых Q играет роль скорости:
Я = М (nh)/{l — Q2I/*, (9.4.37а)
р = М (nh) Q/(l — Q8I/., (9.4.376)
Q = р/ [p2 + УИ2 (nft) ]'/.. (9.4.37b)
Чтобы найти массовый оператор М (nh), рассмотрим ситуацию,
когда среднее квадратичное значение р пренебрежимо мало.
В этом случае энергия Е системы есть сумма массы покоя солитона
Мо и энергий [со (kj), © (k2) ...] асимптотически свободных кван-
тов:
Е = Мо + © (kx) + © (kj) + . . . . (9.4.38)
Эта энергия должна быть равна собственному значению оператора
/Vf («ft). Следовательно, имеем
М Ю = М9 + Щ, (9.4,39)
Протяженные объекты квантовой природы 357
где
Яо = Й J d3ka (к) лк = ft J d3?co (к) а+ак. (9.4.40)
Когда имеются некоторые связанные состояния протяженного
объекта и квантов, выражение (9.4.40) изменяется следующим
образом. Обозначим энергии возбуждения этих связанных состоя-
ний через йсо;, где связанные состояния нумеруются индексом i.
Полная энергия, отвечающая t-му состоянию, равна Мо + йсог.
Возбуждение i-ro состояния и исчезновение этого возбуждения
описываются с помощью оператора рождения а] и оператора
уничтожения а; соответственно. Если солитон возникает в t-м
состоянии, то УИ0 в (9.4.38) заменяется на Мо + йа>;. При этом
равенство (9.4.39) остается справедливым, если формулу (9.4.40)
модифицировать следующим образом:
Яо = Й j cPka (k) c4ak + ? Паца^оц. (9.4.41)
i
Поскольку М (nh) не зависит от р, равенство (9.4.39) выполня-
ется, даже если среднее квадратичное значение р не мало. С по-
мощью выражений (9.4.35) и (9.4.39) мы определили Я [в слабом
смысле.
Отметим, что член #-1бК в выражении (9.4.32) может быть
исключен выбором соответствующего представления. Рассмотрим
унитарный оператор ехр (—iNItt), где N — функционал от р
и nh. Функционал А^ выбирается таким образом, чтобы выполня-
лось соотношение
eiN/nqe-iN/fi = q _ #-! щг з (9.4.42)
что приводит к условию
^-N = —H'lbKi. (9.4.43)
N коммутирует с Я и поэтому не зависит от времени. Следова-
тельно, если г|з удовлетворяет уравнению Гейзенберга, то этому
уравнению удовлетворяет и преобразованный оператор г|з. В даль-
нейшем, выбирая соответствующее представление, мы будем по-
лагать бК. = 0. При этом выражения (б.4.32) и (9.4.31) примут вид
q = -Я-К +4-РЯ- - F7LXJ_, (9.4.44)
К = - ~ (ЯЧ + ЧЯ) - j^. (9.4.45)
В A + 1)-мерном случае «спин» отсутствует и последний член
В этих выражениях оказывается ненужньщ,
358 Глава 9
9.5. (cq)-превращение и обобщенная координата
(^-превращение есть проявление корреляции между класси-
ческими и квантовыми аспектами поведения протяженного объ-
екта. Его смысл заключается в утверждении, согласно которому
требуется, чтобы любое преобразование неоператорных величин
(с-чисел) было непосредственным образом связано некоторым опе-
раторным преобразованием.
Чтобы проиллюстрировать (^-превращение, обратимся сна-
чала к простейшему случаю, отвечающему пространственной
трансляции. Мы видели, что х и Q появляются в виде комбина-
ции (х — Q), поэтому трансляция неоператорной величины обу-
словлена преобразованием оператора (G-числа): Q^-Q — а. В
этом состоит (^-превращение, связанное с пространственной
трансляцией и выражаемое соотношениями
ехр (—ip-a/Й) (х — Q) ехр (tp-a/Й) = (х' — Q)x-=x+a (9.5.1)
или ехр (—/ра/й) i|)f (х) ехр (tpa/й) = i|)f (л:'). (9.5.2)
В этих соотношениях правая часть представляет собой преобра-
зование с-чисел, а левая — д-чисел.
Обобщенная координата и преобразование Лоренца. Изучим
теперь, к каким следствиям, касающимся лоренцевых «вращений»,
приводят ограничения, связанные с (сд)-превращением. Рассмот-
рим сначала A + 1)-мерный пространственно-временной мир
[13, 15].
Число частиц не меняется в результате преобразования Ло-
ренца. Следовательно, в любой оператор, не вызывающий какого-
либо изменения состояний частиц и поэтому содержащий ah
и а\ в комбинации nh, координата х должна входить только через
обобщенную координату X (х, t), удовлетворяющую условию
(сд)-превращения
е-свк/пх (х, t) е{вк'к = X (х!, Г), (9.5.3)
где х' = х ch 9 + t sh 9,
t' = x sh 9 + / ch 9. (9'5-4)
В частности, гейзенберговское поле выражается следующим об-
разом:
ф (х) = ф [X (х, t)] + ... , (9.5.5)
Где j> (x) определяется выражением
x)\0)p^M, (9,5.6)
Протяженные объекты квантовой природы 359
Многоточие в (9.5.5) не означает, что в опущенные члены х и t
входят только через X (х, f). В дальнейшем мы покажем, что
из (9.5.3) следует соотношение
X(x,()=-L{lx-Q (t) ] A - Q2)-1/* + A - Q2)-'/,[x-Q(од.
(9.5.7)
Выражение (9.4.45) в A + 1)-мерном случае имеет вид
К = XT{qH + Hq}. (9.5.8)
Из (9.4.37в) получаем
[q, Q] = «Й -f- = 'Й A - Q2) Я- (9.5.9)
Таким образом, из соотношений (9.5.8) и (9.4.27) следует
-j-ib, К] --A-Q2), (9.5.10)
1
-j- [Q @. -
Вводя определение
получаем
откуда следует
где Л находится из
Уравнение для q (9),
-iq, K]=-L(qi
к] = —t + -5- f(
Q /0\ __ e—iKe/fiQe
A.Q@) = -[1-
Q (9) = th (Л -
условия
Q = th Л.
определяемого l
2 + Q
3@ <i
-Q2(e;
-в),
*ак
g (9) = е-скв/HqeiKe/n,
получается из соотношений (9.5.11) и
д 1
м q(Q) 2 \
\q (9) th (Л — 9)
[ (9.5.
+ th
q),
1 +
15):
(A-
QQ(t)
— Q)q
].
(9)}
(9.
(9.
(9.
(9.
(9.
(9.
(9.
5.11)
5.12)
5.13)
5.14)
5.15)
5.16)
5.17)
Это уравнение имеет решение
9 (9) = -L{B ch-1 (Л — 9) + ch-1 (Л — 0) В+}, (9.5.18)
где B = qchA. (9.5.19)
360 Глава 9
Поскольку (9.5.16) приводит к выражению ch А = A — Q")'/2 =
= HlM(nh), из (9.5.8) и (9.5.19) следует простое соотношение
K = ~±-M{nh)(B + B*). (9.5.20)
Отсюда видно, что (В + В+) коммутирует с К, а значит, остается
инвариантным при преобразовании Лоренца.
Если использовать формулу (9.4.25), величина XJ^x, t),
задаваемая соотношением (9.5.7), выражается через А и Ъ сле-
дующим образом:
Х(х, t) = х ch A — t sh A ~ (В + fit). (9.5.21)
При этом из (9.5.15) и ($.5.18) получаем
X (х, t; 9) = e-'KWX (x, t) elK-^ =
= х ch (Л — 9) — t sh (Л — 9) i- (В + Д+) =
= .v' ch Л — t' sh Л 1- (В + Б+) = X (x , Г). (9.5.22)
Таким образом, величина X (х, t) удовлетворяет условию
(сд)-превращения (9.5.3); она называется обобщенной простран-
ственной координатой. Заметим, что в древесном приближении со-
отношение (9.5.7) принимает вид (9.1.100а) (или (9.2.57а)).
Обратимся теперь к A + 3)-мерному случаю. В этом случае
мы могли бы соблазниться возможностью обобщить условие (9.5.3)
следующим образом:
ехр (—ЮК/Й) X (х, t) exp (iQK/Л) = X (х\ Г),
где х' и f — значения пространственной и временной коорди-
нат, получающиеся в результате лоренцева «вращения», а 0 =
= (91( 92, 93) — параметры, описывающие «вращения». Можно
показать, что величин X, которые удовлетворяли бы приведенному
выше условию, не существует. В этом нет ничего удивительного
по следующей причине. Хотя наша модель статическая, квантовая
координата тем не менее зависит от t, и, следовательно, объект
движется со скоростью, определяемой квантовым оператором Q.
Поскольку лоренцово «вращение» для движущегося объекта вклю-
чает вращение, называемое вигнеровским, представляется разум-
ным модифицировать приведенное выше условие следующим об-
разом:
ехр (—iQK/ti) Xt (x, /) ехр (ЮК/Й) = Ri} (9) Xj (x', f), (9.5.23)
где Ri/ (9) — ортогональная матрица, элементы которой зависят
от 0 и Q. Если мы рассмотрим сферически-симметричный объект,
Протяженные объекты квантовой природы
361
то @1 г|з (л:) 10) при р =q =0 будет функцией от х2, которую
мы обозначим через <j> (х2). Наличие квантовой координаты при-
водит к тому, что данная функция приобретает [вид <}> (Х*Х)
благодаря замене х2 ->-Х*Х.
Чтобы найти величину X, удовлетворяющую соотношению
(9.5.23), рассмотрим лоренцево «вращение», отвечающее Гскоро-
сти v, и образуем набор взаимно ортогональных векторов .v,
рх и е, где pj.— проекция р на плоскость, перпендикулярную
v, а е—единичный вектор, направленный вдоль vxp (рис. ^9.7):
Px = P-v-^-, (9.5.24)
(9.5.25)
е = ¦
—т- (v X р).
Таким образом, любой вектор А может быть
представлен в виде
А = \AV + рхЛх + еАе. (9.5.26)
При этом для вектора, эрмитово сопряженного
Л, получаем выражение
А+ = Л+v + А\ р , + Л+е. (9.5.27)
v I XrX I e v /
В частности,
Р = vpv + рх-1-
Мы можем записать 0К в виде
6К = (9/o)/(vK) =
где 0 определяется соотношением
th 0 = v = I v I
Рис. 9.7.
(9.5.28)
(9.5.29)
(9.5.30)
Для каждого оператора А можно ввести обозначение
А (9) = exp (—ivQKvfh) A exp (ivQKJti). (9.5.31)
Отсюда видно, что A (G) получается из Л в результате лоренцева
«вращения».
Поскольку Нар образуют 4-вектор, получаем
Я (9) = Я ch 9 — vpv sh 0,
vp0 (9) = vpv ch 9 — Я sh 0,
P±(Q) =Px = 1.
Это приводит к соотношению
dH (9)/d9^= — vPv (9).
(9.5.32a)
(9.5.326)
(9.5.32b)
(9.5.33)
362 Глава 9
Так как Q @) равно р @)/Я@), имеем
Qv @) = Pv (в)/Я @), (9.5.34а)
Qx @) = 1/Я @), (9.5.346)
Qe @) = Qe = 0. (9.5.34b)
Из (9.4.29) следует
^- [Я, К ] = рЯ~2, (9.5.35)
поэтому, исходя из (9.4.30) и (9.4.14), находим
-^-[H'Ki, К}] = Н-*РгК,+ тщ + М) ei/ft[p Х(р X l)]ft + ei/ft-^-.
(9.5.36)
Далее можно вывести формулу
-^-[я-Мр xi)A К/] =
1 М
= Я(Я + М) е'М[Р х (Р х Ok -ег/Л —+ Яр/(Р X 1),. (9.5.37)
Таким образом, получаем простое соотношение
-+-[&, К,) ^Н-т-рй, (9.5.38)
где
| = _Я-1К-^я-(рх1)= (9.5.39)
= 4 ~ лкя + м) (Р х 0 + т Ря" (9-5-40)
Учитывая (9.5.29) и (9.5.31), из (9.5.38) получаем
~l(Q) =-^Я-1@)Р(О)[1@)-у]. (9.5.41)
Используя обозначения (9.5.26), можно записать
е?е. (9.5.42)
При этом соотношение (9.5.41) представляется в виде
lA% (9.5.43а)
в), (9.5.436)
(9.5.43b)
Протяженные объекты квантовой природы
Если учесть (9.5.33), то из соотношения (9.5.43а) находим
?» (в) = ТГ75Г &»¦ (9.5.44)
/7 It/I х '
Тогда (9.5.436) принимает вид
d t. (Q) =v — ? (9 5 454
откуда следует
Sx(e) = Ex + wshe-^gj-gt,. (9.5.46)
Из (9.5.43) получаем
Ь @) = I,- (9.5.47)
Последнее соотношение отражает простое свойство вектора |:
его компонента, перпендикулярная плоскости, образуемой век-
тором скорости v, отвечающей лоренцеву «вращению», и вектором
квантовой скорости Q, не меняется при лоренцевом «вращении».
Квантовая координата q не обладает этим свойством. Кроме того,
имеем следующие соотношения:
[&. рА = [ft, Pi] = №ц, (9.5.48)
- -Y [5, Н] = - -^- [q, Я] = Q. (9.5.49)
Таким образом, оператор
Q§ @ = 5 + Q^ (9.5.50)
удовлетворяет коммутационным соотношениям
[QS (О, Р/] = /Йб.., (9.5.51)
_ _i_[QS(/)( Я] = 0 = 05. (9.5.52)
Благодаря этим простым свойствам 1 обобщенная коорди-
ната, как следует из проводимого ниже рассмотрения, пропор-
циональна (х — 1). Тем не менее мы не называем величину |
квантовой координатой, так как ее компоненты \ъ ?2) ?3 не комму-
тируют между собой в отличие от компонент вектора q.
Поскольку х и / образуют 4-вектор, имеем
x'v = vxv ch 9 + t sh 9, (9.5.53a)
f = t ch 6 + vxv sh 9, (9.5.536)
x'L = xj_, (9.5.53b)
x'e = xe. (9.5.53r)
364 Глава 9
Из формул (9.5.44), (9.5.46), (9.5.47) и (9.5.50) следует
xv — Qv (t, 9) = xv Zv (9) 7ГШ7 == н (9) \ ° ~u я" / ==
=-^вГ ^ - QHOL (9-5.54)
*x - Qi (t, 9) =.vl - gx (G) - -^-г1 -
= *x - Qi (/') + v sh 9 -^ [x; - Q| 0')], (9.5.55)
где мы учли соотношения xv = (x-v)/y2,
Ql (t) = (Qs @ ¦ v)/y2, Q\ @ = A /p!) (p± • Qi (/)) и т. д.
Поскольку хе = х'е и Q\ (t, 9) = Q! @ = Q! (f) (так как Qe =
= H~xpe = 0), приведенные выше результаты могут быть записаны
в виде следующего соотношения:
x-Ql (t, 0) = х' - Q^ (Г) +
) sh е -
Введем теперь величину
В результате лоренцева «вращения» Цц принимает вид
г\ц [Р (9)] = bt, + M[H{q) + M] Pi (9) Pi (9). (9-5.59)
[H{q)
Если определить оператор [16]
Xt = Xt [x - Qs @, Q] = i\t, (p) [*/ - Q) (t)l (9.5.60)
то можно показать, что он удовлетворяет условию (сд)-превраще-
ния (9.5.23):
Xt [х - Q^ (t, 6), Q (t) ] = 7?iy @) X/ [x' - Q? (/'), Q ]• (9-5.61)
Если потребовать затем, чтобы оператор X линейно зависел от х
и при равных нулю р и q сводился бы к х, то X, определенный
формулой (9.5.60), окажется единственным решением, удовлетво-
ряющим условию (с^)-превращения. Ортогональная матрица
Ri/ (9) имеет вид
R (9) = exp Itcp(e-t)], (9.5.62)
Протяженные объекты квантовой природы 365
где tt (i = 1, 2, 3) — спиновые матрицы размерности 3X3:
ltt, tj\ = iB,]hth, (9.5.63)
(tdik = -i*iJh. (9.5.64)
Следовательно, выражение (9.5.62) показывает, что R (9) вызы-
вает поворот вокруг вектора е на угол ф. Угол ф определяется
из соотношений [16]
cos ф == 1 + р (9) p°i A — ch 6), (9.5.65а)
sin ф = —р (9) | рх | \vpv A — ch 0) + (Я + М) sh 0}, (9.5.656)
где Р(9)= ihw + muh + M)- <9-5-66>
Для вычисления каждого матричного элемента мы можем исполь-
зовать соотношение
R (9) = 1 + i (e-t) sin ф + (e-tJ (cos ф — 1), (9.5.67)
которое следует из равенства (e-tK = (e-t).
Таким образом, обобщенная координата X определяется фор-
мулой (9.5.60). В приведенном выше выводе выражения для
обобщенной координаты не используется каких-либо приближе-
ний. Обобщенная координата в древесном приближении дается
выражением (9.1.100а); она имеет вид Xt = г\ц (р) [х,- — Q/ (t)].
Это приближенное выражение для Xt, даваемое формулой
(9.1.100а), отличается от точного (9.5.60) членом (q — |).
Классические и квантовомеханические протяженные объекты.
Мы видели, что протяженный объект описывается не просто
посредством <j>f (х — q), а величиной <f>f [X (x, t)], в которой
обобщенная координата X содержит не только р и q, но еще и
nh (= a?aft), поскольку Q = рН~1. Величина $ (х) определяется
как
р (х) =<0|^(*. /)|О)|р=^о, (9.5.68)
а <j>f (X) получается из <j>f (x) с помощью замены х2^-Х+Х.
Если квантовые флуктуации входящих в X величин q и Q при-
водят к измеримым эффектам, то j>f (X) описывает квантово-
механический объект. Например, ширина линий мессбауэровского
спектра для мелкодисперсных частиц при очень низкой темпера-
туре может выявить флуктуации квантовой координаты. Атомные
ядра больших размеров также могут вести себя подобно кванто-
вомеханическим протяженным объектам. Если же квантовыми
флуктуациями q и Q в X можно пренебречь, то протяженный
объект характеризуется классическим поведением. Таким обра-
зом, на основе квантовой теории поля можно получить как клас-
сические, так и квантовомеханические объекты.
366 Глава 9
Замечательная особенность поля <j>f (X) для статических объ-
ектов состоит в том, что оно описывает не только покоящиеся,
но и движущиеся протяженные объекты; понятие «статический
объект» не означает, что объект покоится, поскольку для ста-
тического объекта <j>f не зависит от времени, если пренебречь
наличием Q и q. Так как состояние, в котором отсутствуют ча-
стицы (вакуумное состояние), характеризуется волновым пакетом
10; gb)> определяемым формулой (9.4.5), вакуумное среднее
@; §о I ф! (X) | 0; go) не обязательно является не зависящим от
времени; <j>f (X) может описывать все виды равномерного класси-
ческого движения, которые обусловлены наличием в X квантового
оператора скорости Q. Однако <j>f (X) не описывает каких-либо
ускоренных движений, поскольку для ускоренного движения
требуется действие внешней силы. Движения, описываемые по-
средством <j>f (х), называются свободными.
Уравнение свободного поля и (с^)-превращение. Построим
асимптотическое поле %0 с помощью метода ЛСЦ, описанного
в разд. 3.5. Для этого сконструируем внутреннее произведение
)г|/ (х) — ф' [X (х, t)]} и каждого из элементов множества орто-
нормированных собственных решений (например, и (х)) уравнения
Шредингера с самосогласованным потенциалом (см. уравнение
(9.1.37)) и рассмотрим каждое внутреннее произведение в пределе
t ->- оо. В результате процесса нахождения предела по временной
переменной изг|)' выделяются только те члены, которые находятся
в резонансе по времени с собственными решениями и (х). Таким
образом, предел каждого внутреннего произведения представляет
собой оператор а с некоторым перенормировочным множителем.
Умножим каждый оператор а (или а+) на и (х) (или на и* (х))
и просуммируем по всем элементам множества собственных ре-
шений. Эта процедура определяет предел
W (х) - ф1 [X (х, /)]} — * Хо (х). (9.5.69)
Следовательно, %0 (х) удовлетворяет уравнению Шредингера с са-
мосогласованным потенциалом (см. выражения (9.1.55), (9.1.65)
и (9.1.71)). Динамическое отображение if>f имеет вид
l>f (*) = ф' [X (х, t) ] + %0 (х, t) + ... , (9.5.70)
где многоточие заменяет нормальные произведения более высоких
порядков, составленные из а и а+. Эти члены не находятся в ре-
зонансе по времени с собственными решениями и (х) и не вносят
вклад в выражение (9.5.69) для предела. Если среднее квадратич-
ное значение величины | х — q | в состоянии типа волнового па-
кета, описывающем протяженный объект, становится столь боль-
Протяженные объекты квантовой природы 367
шим, что х оказывается вне радиуса действия самосогласованного
потенциала, то %0 (х) превращается в свободное поле г|H (л:):
(х, 0]} Т^Г* ^(x), (9.5.71)
Л (д) % (х) = 0. (9.5.72)
Исследуем теперь структуру свободного поля г|;0 (л;), рассма-
тривая асимптотический гамильтониан (9.4.35) с учетом формулы
(9.4.39) и условия (^-превращения. Поле г|H (х, t) представляется
в виде интеграла Фурье:
ifo (x, t) = -L f ak [Ak (p, a, a+) exp {/k (x - q) - mkt\ +
4- компл. сопр.]. (9.5.73)
Здесь учтен тот факт, что пространственная трансляция т|50 (л:)
обусловлена оператором Р = р (см. (9.4.4)). Здесь и далее ин-
декс k обозначает к.
Поскольку сдвиг во времени обусловлен оператором Я, должно
выполняться условие
(9.5.74)
Это приводит к соотношению
ё~ш^Ак (р, а, <х+) = ехр [Ш (р) ЦП] Ak (р, а, а+) ехр X
х [—Ш(р + к) №]. (9.5.75)
Здесь Я (р) совпадает с Я, определяемым формулой (9.4.35).
Если, не особенно задумываясь, положить Ah = ah, то окажется,
что выбранное таким образом Ah не удовлетворяет соотношению
(9.5.75). Поскольку действие Ah сводится к уничтожению одной
частицы, мы можем записать Ah в виде линейной комбинации
операторов а, с коэффициентами, зависящими от р и nh. Пред-
положим, что к в (9.5.75) равно 1 в покоящейся системе отсчета
(р =0). Здесь р = 0 означает, что среднее квадратичное зна-
чение р пренебрежимо мало. Поскольку к связано с 1 посред-
ством функции от р (а также a+a), Ak имеет вид
Ah = J dsl8 (k — К;) F'ah (9.5.76)
где Р и К| — некоторые функции от р и a+a. В результате из
(9.5.75) получаем условие
Йсок, = Я (р + К;, щ + 1) - Я (р, щ). (9.5.77)
368 Глава 9
Из этого соотношения находим
"«* = dW/, & + Q-TJ, (9.5.78)
Здесь использованы обозначения (9.1.96). Поскольку со|-г — К/ =
= [i2, имеем
©? — I8 = \i\ (9.5.80)
где fi — масса, отвечающая свободному полю г|H.- Отсюда
ю, = о», + Р/2УИ, (9.5.81)
(9-5-82)
где М обозначает М (nk). Подставляя (9.5.76) в (9.5.73), получаем
i|>0 (х, 0 = -f^- f dH [fWq exp {tK/ (x - q) - Шк/} а, +
+ эрмит. сопр.]; (9.5.83)
здесь символ 9>q означает, что любое q долн<но быть помещено
справа от всех других операторов, а
/•' = Fi/BaKlY': (9.5.84)
Коэффициент /' определяют с помощью условия («^-превращения
¦фо (х', f) = exp (—tK-O/Й) г|H (х, t) exp (tK-в/Й). (9.5.85)
В A + 1)-'мерном случае коэффициент /', удовлетворяющий
условию (9.5.85), можно найти, если учесть тот факт, что выраже-
ние для К имеет вид
и из (9.5.85) следует условие
[фо @, 0), К] = 0. (9.5.87)
После громоздких вычислений [15] получаем следующее решение:
/ Н+а>к \ V»
Г = 1 я ) 'о' (У.б.ЬЬ)
Функция fl0 представляет собой нормировочный множитель, не
зависящий от р. Поле г|з0, определяемое формулой (9.5.83) с /',
даваемым выражением (9.5.88), удовлетворяет уравнению сво-
бодного поля (9.5.72) и условию (с^)-превращения (9.5.85).
Протяженные объекты квантовой природы 369
Интересно отметить, что если воспользоваться формулами
(9.5.78) и (9.5.79), то ч|э0 (х, t) можно записать также в виде
(/л)
(/л)
-(-эрмит. сопр. (9.5.89)
Здесь X (х, t) я Т (х, t) — обобщенные координаты, определяемые
выражениями
X (х, 0 = L_- [* - Q (/)], (9.5.90)
T(x, i) = A - Q'jv, f - $[x~.Q [^ . (9.5.91)
При наличии оператора 9*ч, упорядочивающего q, операторы
X (х, t), определяемые формулами (9.5.7) и (9.5.90), действуют
одинаковым образом. Отметим, что при выводе соотношений
(9.5.89), (9.5.90) и (9.5.91) не использовалось никаких прибли-
жений.
В A + 3)-мерном случае иметь дело с условием (9.5.85) было бы
весьма утомительно. Поэтому мы рассмотрим этот случай в дре-
весном приближении. Поскольку в древесном приближении не
учитываются коммутаторы со сложной структурой, имеем
К, Я] & hahahM/H. (9.5.92)
В древесном приближении в левой части соотношения (9.5.77)
следует ограничиться линейными членами разложения по йсог
и ЙК,:
(^). (9.5.93)
Согласно (9.5.78) и (9.5.79), полученное приближенное выражение
равно Н [аК[ + (щ — й,) (MlH)\. Поэтому из соотношений
(9.5.77) и^(9.5.80) следует
щ = щ и f2 = J2 (9.5.94)
Обращаясь к формулам (9.5.81) и (9.5.82), видим, что это соответ-
ствует со/УИ <? 1. Поскольку использование формулы (9.4.45)
приводит к выражению
-St/aPita [«ft, Я + М J' (9-5-95)
370 Глава 9
имеем
[ал, 2_(у.
-v[ak, H(qv + -^PvH-2)] -\Px\Q-*)[<*k.-rrhr]- (9-5-96)
С другой стороны, из (9.4.16) с учетом (9.5.64) находим
^— [ай, h] = iei/ofy -щ- ah = /г, (fy/o -^
щ;*к, (9.5.97)
где к' связано с к посредством поворота вокруг i-й оси.
Таким образом, (9.5.96) приводит к следующему соотношению
для оператора ah (9), получающегося из ah при лоренцевом
«вращении»:
-g§- a* @) = i -|f- A/ (e • t)/e -Jt- «^ (9) -
- -i- и [aft (9), H (9) (<7B (9) f -L pv (9) Я^ (9))] -
(9'5-98)
где ф — угол, отвечающий вигнеровскому повороту. При выводе
выражения для первого члена в правой части (9.5.98) использо-
вано соотношение
которое следует из (9.5.65). С другой стороны, если
k'i = Rj}(Q)ki, (9.5.100)
где R (9) — матрица вигнеровского вращения, то имеем
"Ж"ak' = ["Ж" k'i(-е'^1'а~Щ~ак" ^9.5.101)
Сравнивая это соотношение с (9.5.98), мы можем записать
ak (9) = а^е'Л(е), (9.5.102)
где k' дается формулой (9.5.100). При этом из (9.5.98) следует
0) Я (в))] -
(9.5.103)
Протяженные объекты квантовой природы 371
Если воспользоваться соотношением (9.5.92), то (9.5.103) при-
нимает вид
^{)vL' (9-5Л04)
где 1 дается формулой (9.5.40). В результате имеем
м
A(9) = -(Dfcsh0-^rgo. (9.5.105)
Введем теперь величину
= (l-Q*//,f_ ' [Q-x-ОЧО]- (9-5.Ю7)
Вид Г после лоренцева «вращения» (т. е. Т (9)) можно найти, ис-
пользуя соотношения
Я (9) t — p F) х = Hf — р-х\ (9.5.108а)
9.5.1086)
где х и t' — значения х и t, получаемые в результате лоренцева
«вращения». Обозначая через 7" выражение для Т, в котором х
и t заменены на х at', имеем
(9) = щТ' + А (9). (9.5.109)
Принимая во внимание соотношения (9.5.61) и (9.5.102), можно
видеть, что ak exp UkX — iakT] удовлетворяет условию (cq)-
превращения:
ак (9) exp UkX (9) — mhT (9) ] =
= ak. exp Uk'X' — mk.T ]. (9.5.110)
Таким образом, получаем
is1/г (. ^
^° ^X' ^ = /o\v, /o ^V. ^eXP (/kX ~ 1<йкП + ЭРМИТ- «Hip.],
Bя) '2 J Bшй) /2
(9.5.111)
^.,^, (9.5.112)
Где Т — обобщенная временная координата.
Свободные и вынужденные движения протяженных объектов.
Как отмечено в абзаце, непосредственно следующем за формулой
(9.5.68), в статическом случае </>(Х) может описывать всевозмож-
ные равномерные движения, если рассматривать вакуумное сред-
372 t/iaea 9
нее @; go | Ф (X) | 0; g0), которое может зависеть от t через Q (t).
Эти равномерные движения сопутствуют движениям с нулевой
энергией, обусловливающим появление квантовой координаты.
Поэтому указанные движения называют свободными. Если рас-
смотреть объект, не имеющий сферически-симметричной струк-
туры, то кроме квантовой координаты Q (t), связанной с транс-
ляциями, появляется угловая квантовая координата Qq; в этом
случае свободные движения представляют собой комбинации
трансляций и поворотов. Интересным примером такого рода
является случай двухточечного объекта на плоскости. Подобную
систему можно рассматривать как один протяженный объект,
не обладающий круговой симметрией. Поэтому его движение
есть совокупность трансляции и вращения вокруг центра масс.
Практическим приложением такой модели может служить сво-
бодное движение двух параллельных прямолинейных вихрей.
Если рассмотреть плоскость, перпендикулярную этим вихрям,
то их можно спроектировать в две точки на плоскости. Таким
образом, мы видим, что свободное движение этих двух вихрей
есть комбинация трансляций и поворотов одного относительно
другого. Описанное движение двух вихрей наблюдалось в сверх-
текучих жидкостях.
Протяженные объекты с захваченными фермионами. Если
в системе имеются физические фермионы, которые взаимодей-
ствуют с протяженным объектом, то гамильтониан Яо в (9.4.39)
должен включать в себя свободный гамильтониан этих фермионов.
Особенно важен случай протяженных объектов, которые захваты-
вают фермионы, поскольку фермионы должны последовательно
заполнять все состояния, начиная с состояния, отвечающего наи-
низшей энергии. Если фермионы представляют собой нуклоны,
такая картина применима для описания ядер. Если же фермионы —
это кварки, то данная модель приводит к модели мешка. В физике
твердого тела становится очень модным изучение солитонов
в одномерных моделях. Особое внимание привлекли к себе со-
литоны, захватывающие фермионы [17].
ЛИТЕРАТУРА
1. Umerawa H., Matsumoto H. — in: Symmetries in science, eds. В. Gruber and
R. Millman, Plenum, New York, 1980, p. 411.
2. Matsumoto #., Sodano P., Umezawa H., Phys. Rev., D19, 511 A979).
3. Leplae L., Mancini F., Umezawa H., J. Math. Phys., 10, 2038 A969); Phys.
Rev., B2, 3594 A970); Phys. Rep., 10C, 151 A974).
4. Matsumoto H., Papastamatiou N. J., Umezawa H., Nucl. Phys., 82, 45 A975);
B97, 90 A975).
5. Matsumoto H., Oberlechner G., Umezawa M., Umezawa H., J. Math. Phys.,
20, 2088 A979).
Протяженные объекты квинтовой природы 373
6. Scott А. С, Chu F., McLaughlin D., Proc. IEEE, 61, 1443 A973)-
Raiaraman R., Phys. Rep., C21, 227 A975).
7. Jackiw R., Rev. Mod. Phys., 49, 681 A977).
8. Gervais J.-L., Sakita В., Phys. Rev., Dll, 2943 A975);
Gervais J.-L., Jevicki A., Sakita В., Phys. Rev., D12, 1038 A975);
Callan C. G., Jr., Gross D. J., Nucl. Phys., B93, 29 A975).
9. Matsumoto H., Semenoff G., Umezawa #., Umezawa M., J. Math. Phys., 21,
1761 A980).
10. Semenoff G., Matsumoto H., Umezawa #., Prog. Theor. Phys., 63, 1393 A980).
11. Dashen R., Hasslacher В., Neveu A., Phys. Rev., D10, 4114; 4136 A974);
Gervais J.-L., Jevicki A., Sakita В., Phys. Rev., D12, 1038 A975).
12. Корепин В. Е., Фаддеев Л. Д., ТМФ, 25, 147 A975).
13. Matsumo H., Papastamatiou N. J., Umezawa H., Umezawa M. Phys. Rev.,
D22, 1339 A981).
14. Semenoff G., Matsumoto #., Umezawa H., J. Math. Phys., 22, 2208 A981).
15. Matsumoto H., Papastamatiou N. J., Semenoff G., Umezawa H., Phys. Rev.,
D24, 406 A981).
16. Yamanaka #., Matsumoto #., Umezawa #., Phys. Rev., D24, 2607 A981).
17. Su W. P., Schrieffer J. R., Heeger N. J., Phys. Rev., B22, 2099 A980);
Takayama #., Lin-Liu Y. R., Maki K., Phys. Rev., B21, 2388 A980);
Jackiw R., Schrieffer J. R., UCSB preprint A981).
ГЛАВА 10
ПРОТЯЖЕННЫЕ ОБЪЕКТЫ
С ТОПОЛОГИЧЕСКИМИ ОСОБЕННОСТЯМИ
10.1. Общие соображения
Бозонное преобразование при наличии топологических осо-
бенностей. В гл. 9 мы исследовали вопрос, каким образом в кван-
товых системах многих тел могут возникать протяженные объекты.
В частности, в разд. 9.3 показано, что, за исключением тех слу-
чаев, когда энергия бозонов со (к) обращается в нуль при некото-
рых отличных от нуля значениях импульса, уравнение
А, (д) f (х) = О для параметра бозонного преобразования / (х)
не может иметь никакого статического решения, обладающего
фурье-образом. Особенности, препятствующие существованию
фурье-образа, либо типа расходимостей, либо представляют со-
бой топологические особенности. Наличие особенности типа рас-
ходимости означает, что/ (л:) расходится при | х | = оо по крайней
мере для некоторого направления х, а топологическая особенность
связана с неоднозначностью функции / (х). В данной главе мы
дадим систематический подход к описанию топологических осо-
бенностей [1, 2]. Рассмотрению неабелевых симметрии посвящен
разд. 10.3.
Если функция / (л:) обладает некоторой топологической осо-
бенностью, то она не однозначна, и, следовательно, ее значение
в точке х зависит от пути подхода к этой точке. Хорошо известным
примером величины, зависящей от пути, является в цилиндриче-
ской системе координат угол 9 поворота вокруг некоторой пря-
мой (например, вокруг третьей оси). Этот угол представляет собой
решение уравнения Лапласа V29 = 0. Кроме того, имеется хорошо
известная формула V X V9 = 2яб (xj) 6 (х2) е3Ф 0, где е3 — еди-
ничный вектор, направленный вдоль третьей оси. Этот пример
демонстрирует общее свойство топологических особенностей, со-
стоящее в том, что некоторые производные не коммутируют
между собой в области существования особенности.
Ниже мы рассмотрим набор бозе-полей ц>°а (а = 1, 2, ...),
над которыми производится бозонное преобразование ф«—*-ф« +
+ fa- Уравнения для ц>% запишем в виде
Л«(д)фО=О. A0.1.1)
Функции /а удовлетворяют тому же уравнению
^(д)/а = 0. A0.1.2)
Протяженные объекты с топологическими особенностями 375
Введем величину
б$М = [дй, dv]fa(x). A0.1.3)
Если
G™+ (х) Ф 0 для некоторых х, |i, v и а, A0.1.4)
то область переменной х, в которой выполняется это соотношение,
называется областью топологической особенности. Кроме того,
наличие зависящей от пути функции fa (x) приводит к требова-
нию, чтобы величина dja была однозначной:
Kdv]dJa(x)=0. A0.1.5)
Соотношения A0.1.4) и A0.1.5) представляют собой условия
существования топологических особенностей.
В соответствии с рассмотрением, проведенным в гл. 9, про-
тяженные объекты, возникающие в результате бозонного преоб-
разования, приводят к появлению самосогласованного потен-
циала, оказывающего влияние на квантовые состояния системы.
Если функции /а (л:), определяющие бозонное преобразование,
обладают некоторыми топологическими особенностями, то струк-
тура самосогласованного потенциала серьезным образом зависит
от структуры этих особенностей. В разд. 10.2 показано, что так
называемая «энергия сердцевины» вихря в сверхпроводнике свя-
зана с наличием электронов, захваченных самосогласованным
потенциалом вихря, представляющего собой протяженный объект
с линейной топологической особенностью. Имеется много других
примеров такого рода. Но до сих пор отсутствовал систематиче-
ский подход к построению самосогласованного потенциала, вы-
зываемого протяженными объектами, существование которых
связано с топологическими особенностями.
Топологические особенности и голдстоуновские бозоны. Дока-
жем теперь, что функция /а (х) может обладать некоторыми топо-
логическими особенностями тогда и только тогда, когда в энерге-
тическом спектре со™ (к) для бозонов ф^ отсутствует щель [3, 4]:
со« (к) = 0 при к = 0. A0.1.6)
Чтобы доказать это, заметим, что уравнение A0.1.2) всегда
может быть представлено в виде
[Da (д) д„ +1?] /«(х) = 0, A0.1.7)
где ца — некоторые константы, a Da (д) — некоторые дифферен-
циальные операторы. Из соотношений A0.1.3) и A0.1.5) следует
Dl (д) G$ (х) = Da (д) dvfa (х) - dvDa (д) fa (х) = {Da (д) + &} dvfa (х),
A0.1.8)
Ра (д) = Z>? (д) ац; A0.1.9)
376 Глава 10
суммирование по а здесь не проводится. Таким образом, имеем
x). A0.1.10)
Поскольку Gam! имеет фурье-образ, a Gtt = —&$., находим
А* C)/„(*)= 0 (т.е. |хо = 0). A0.1.11)
Так как Da @) = 0 в соответствии с формулой A0.1.9), это озна-
чает, что в энергетическом спектре бозонных полей ц>°а отсутствует
щель.
Отсюда мы заключаем, что протяженные объекты, существо-
вание которых связано с топологическими особенностями, могут
возникать только благодаря конденсации бозонов с бесщелевым
энергетическим спектром. В этом состоит причина того, что
протяженные объекты с топологическими особенностями обычно
появляются в состояниях, определенным образом упорядоченных,
поскольку упорядочение связано с наличием голдстоуновских
бозонов, не имеющих щели в энергетическом спектре (примерами
таких объектов являются дислокации, границы зерен и точечные
дефекты в кристаллах, вихри в сверхпроводниках).
Поскольку данный раздел посвящен исследованию топологи-
ческих особенностей, мы будем полагать, что fa (x) (а следова-
тельно, и фа) удовлетворяет уравнению A0.1.11). Если структура
топологической особенности задается посредством Gj^ в A0.1.3),
то dja определяется соотношением A0.1.10) при (ха =0:
+Ж A0.1.12)
Из этой формулы находится зависящая от пути функция fa (x)
[1, 2].
Топологический заряд. Рассмотрим теперь величину, зада-
ваемую интегралом по контуру
<fe4/a, A0.1.13)
с
где с — замкнутый контур, не проходящий через область тополо-
гической особенности. Обозначая через S поверхность, ограни-
ченную контуром с, мы можем переписать выражение A0.1.13)
в виде
\ A0.1.14)
s s
элемент поверхности. Отсюда видно, что константы N?
не изменяются при замене контура с другим замкнутым контуром,
Протяженные объекты с топологическими особенностями 377
не проходящим через область топологической особенности. Эти
константы Nt называются топологическими зарядами (см., на-
пример, обзор Коулмена [5]).
Полное условие, определяющее топологическую особенность.
Мы видели, что если топологическая особенность задается некото-
рым конкретным выражением G^v. то dja определяется формулой
A0.1.12). Используя это д^а, мы можем затем вычислить G^v =
= [д„, dv]/a, [дц. dv] dPfa и Da(d)fa. Первоначальный выбор
G^v оправдан в том и только в том случае, если это вычисление
приводит к исходному G^v, а также к выполнению соотношений
A0.1.5) и A0.1.11). Действуя таким образом, мы можем найти
полное условие, определяющее топологическую особенность.
Чтобы исследовать это полное условие, удобно ввести вели-
чину G«v, дуально сопряженную Gr$:
4 W = 00.1.15)
где е^р — полностью антисимметричный тензор, у которого
еош _ j j43 A0.1.16) следует уравнение непрерывности
^Ggv = O. A0.1.17)
Отсюда получаем
е^ЧС = 0. A0.1.18)
что приводит к соотношению
d^aft + дР0Ц + difC = 0. A0.1.19)
Используя далее A0.1.12), находим
1
¦ It (д)х (%$ =
что совпадает с соотношением A0.1.3). В проведенном вычислении
использованы равенства G^v = —Gvjt и A0.1.9). Кроме того,
очевидно, что выражение A0.1.12) удовлетворяет условию
A0.1.5), поскольку A0.1.12) показывает, что dnfa обладает фурье-
образом. Из A0.1.1-2) следует также, что Da (д) fa = D? (д) dja =
= 0, так как G% = —Gvjt- Итак, мы доказали, что уравнение
непрерывности A0.1.17) представляет собой полное условие,
определяющее топологическую особенность.
378
Глава 10
Вычисление величины д^а начинают с решения уравнения
непрерывности A0.1.17) с целью выбора подходящего G«v. Далее
из соотношения A0.1.15) находят G^t в виде
х).
A0.1.20)
Тем самым определяется структура топологической особенности.
Затем из A0.1.12) получают выражения для функций д^а.
Линейная топологическая особенность. Примерами протяжен-
ных объектов с линейными топологическими особенностями могут
служить дислокации в кристаллах и вихри в сверхпроводниках.
В общем случае линия особенностей может быть описана с по-
мощью одного пространственного параметра а и временного пара-
метра т. Таким образом, линейная особенность представляет
собой набор линий, каждая из которых определяется величиной
уа\х (т, о) (а = 1,2, ...). Поскольку величины GaV (х) не обращаются
в нуль только в том случае, если х лежит на такой линии, мы
можем записать
6SV (х) -
J ^т J
da
f ff] 6W [х - у" (т., а)], A0.1.21)
где vaa — некоторые константы, а д [уп, yv]/d [т, а] — якобиан
д [Уц, У у] _ дуй dyv дУ)х dyv
д{т, а] — дт да да дт " (lU.l.^J
Из A0.1.21) следует
(х) = 5У J 6, J da (- %¦? + Ж ?
A0.1.23)
Поскольку т — временной параметр, выберем т так, чтобы вы-
полнялось равенство
у"(т, а) = т для всех а. A0.1.24)
Так как граничные значения временного параметра равны ±°°,
первый член в круглых скобках можно заменить на д2у°/додх,
воспользовавшись интегрированием по частям. Проводя дальней-
шее интегрирование по частям относительно переменной о, полу-
чаем
(х) =
v" J Л ^
уа (т,
.1.25)
Протяженные объекты с топологическими особенностями 379
где о? (т) и а° (т) — краевые точки линии уа (т, а) в момент вре-
мени т. Воспользовавшись снова равенством A0.1.24), находим
дЛ" (х) = Л vaa [8 {х - уа [tXl ol (tx))) у* [tx, 0? (tx)] -
а
-6{x-ya[tx, <ja2(tx)]}yav{tx, оа2(Ш, A0.1.26)
где у" (т, 0) = (д/дх) у% (т, 0). Из этого соотношения видно, что
если линия имеет изолированную краевую точку внутри системы,
то уравнение непрерывности A0.1.17) перестает выполняться.
Поэтому совокупность рассматриваемых линий должна образо-
вывать сетку, в которой отсутствуют краевые точки внутри си-
стемы. Если линии из некоторого набора уь (т, о) (Ь = 1,2,...)
соединяются друг с другом в точке у (т) (называемой вершиной
или узлом), то из уравнения непрерывности A0.1.17) и из соот-
ношения A0.1.26) следует
2 (±vab) = 0, A0.1.27)
ь
где знаки «+» и «—» отвечают соответственно первому и второму
членам в правой части соотношения A0.1.26). И обратно, правая
часть соотношения A0.1.25) обращается в нуль при всех ее, если
•равенствоA0.1.27) выполняется в каждой вершине.Следовательно,
A0.1.27) представляет собой полное условие, определяющее ли-
нейную топологическую особенность. Константы vab задают
«силу» особенностей.
Таким образом, полное условие, определяющее линейную
особенность, состоит в том, что линия не должна иметь ни одной
краевой точки. Отметим, что краевые точки на границе системы
не являются краевыми точками особенности, так как сама гранич-
ная поверхность представляет собой двумерную топологическую
особенность. Двумерные особенности мы рассмотрим ниже.
Если рассматривать статические протяженные объекты, то у"
не зависит от т (рис. 10.1):
Уа = Уа (о-). A0.1.28)
При рассмотрении одной линии нам не требуется индекс а, и
соотношение A0.1.21) принимает вид
GSV (х) =va\dx\da ffi; Uaf 6D> [x - у (т, 0)], A0.1.29)
где у0 = т.
Прямолинейная особенность вдоль третьей оси определяется
соотношением
yi(a) = o8id (/ = 1, 2, 3), A0.1.30)
380
Глава 10
Отсюда имеем
Gui (х) = -Ga° (х) = va8 fa) б (х2), A0.1.31)
откуда получаем
G?2+ (x) = -G2a,+ (x) = va6 (хО б (х2). A0.1.32)
Другие компоненты G?v и G^t обращаются в нуль. Из соотношения
A0.1.12) в данном случае следует, что fa (х) зависит только от
х1 и хг:
а,/а (х) = -va -^щ-Dl (д) б (Xi) б (х?), A0.1.33)
<52/а (х) = va
a (д) б (х,) б (х2), A0.1.34)
A0.1.35)
Рис. 10.1. Рис. 10.2.
Кольцо (рис. 10.2) задается выражением
у (а) = (а cos а, a sin а, 0), 0 <: а <: 2я,
где а — радиус кольца. В этом случае получаем
A0.1.36)
A0.1.37)
A0.1.38)
A0.1.39)
G°2 (х) = va6 [x, - (a2 - д|)У«] б (хз),
G°a3 (х) = G'J (x) = 0 (I, /=1,2, 3).
В качестве примера зависящей от времени особенности рас-
смотрим движущуюся прямую линию. Пусть эта линия располо-
жена вдоль третьей оси и движется со скоростью v в направле-
нии хх. В этом случае имеем
у (а, т) = (vx, 0, а), A0.1.40)
Уо(Р,х)=х, A0.1.41)
откуда получаем
Gl3 (х) = — Gl0 (x) = va6 (xi - vt) б (х2), A0.1.42)
Gi3 (x) = — G3J (x) = vau6 (xi - vt) б (хз). A0.1.43)
Другие компоненты G«v обращаются в нуль,
Протяженные объекты с топологическими особенностями 381
Замечательная черта поведения особенностей состоит в том,
что оно определяется только уравнением непрерывности A0.1.17)
и не зависит от вида уравнения для ф&. Например, даже в том
случае, когда уравнения Гейзенберга и уравнения для ср& инва-
риантны относительно преобразований Лоренца, это отнюдь не
вынуждает топологические особенности вести себя в соответ-
ствии с законами специальной теории относительности. Имеется
широкий выбор различных особенностей. Выбор же свободных
движений, определение которых дано в разд. 9.5, сильно огра-
ничен.
Двумерная топологическая особенность. Межзеренные границы
в кристаллах, доменные стенки в ферромагнетиках, джозефсонов-
ские контакты в сверхпроводни-
ках — все это примеры двумерных
топологических особенностей. Су-
ществующие в отсутствие внешних
воздействий граничные поверхности
некоторых упорядоченных состояний
{например, поверхность кристалла)
также являются двумерными топо-
логическими особенностями. ~
Мы видели, что допустимо су- *-¦ - ис' ' '
ществование любой линейной осо-
бенности, если она не имеет краевых точек. Поэтому можно
сделать вывод, что допустима также любая поверхность, образо-
ванная линиями, у которых отсутствуют краевые точки. Если
описывать поверхность двумя пространственными параметрами
(а, 1) и одним временным параметром т, то G?v можно представить
в виде
СГ (х) = J dr J da\ dk d%Xt\ б<4> (Х - У)' <10"l -44>
где уц (т, а, ?) описывает поверхность, а <f>a — некоторые функции
от т, а и i (рис. 10.3). Мы можем выбрать у0 следующим образом:
0о (т, о, 1) =т. A0.1.45).
Если мы рассматриваем статическую двумерную особенность,
у и фа зависят только от а и 1:
у = у@, 1), ф« = ф"(о, 1). A0.1.46)
В этом случае из соотношений A0.1.44) и A0.1.45) получаем
G°* (х) = -G*° (x) = J da J dl д [/^ **] б (x - y). A0.1.47)
Остальные компоненты Gav обращаются в нуль,
382 Глава 10
Если статическая особенность расположена в плоскости A, 2),
то мы имеем
ух (а, 1) = а, у2 (а, 1) = 1, у3 = 0. A0.1.48)
При этом из A0.1.47) находим
G°' (х) = -Gi° (x) = д2фа (хи х2) б (х3), A0.1.49)
G°a (х) = —Ga° (х) = —д{фа (хи х2) б (х3). A0.1.50)
Остальные компоненты обращаются в нуль.
Рели особенность расположена в плоскости A, 2), а временная
зависимость этой особенности возникает только за счет «силы»
фа (t, Хъ х2), то из A0.1.44) получаем
G? (х) = -GL0 (х) = д2фа (t, хи х2) б (х3), A0.1.51)
Ga (о — —G«o (x) = —д{фа (t, хи х2,) б (х3), A0.1.52;
G™ (х) = —Ga (х) = — -|- ^а (t, хи х2) б (х3). (ЮЛ .53)
Остальные компоненты обращаются в нуль.
В качестве примера замкнутой двумерной особенности рас-
смотрим статическую сферическую поверхность радиуса а. Тогда
у (а, 1) = (a sin а cos %, a sin а sin 4, а cos а), A0.1.54)
где 0 <: а < я, 0 <: | %. 2я. A0.1.55)
Величины GaV находятся из соотношения A0.1.44).
Топологическое квантовое число, квантование потока для
вихрей и вектор Бюргерса дислокаций в кристаллах. С помощью
формулы A0.1.13) мы ввели топологические заряды Nt- Часто
случается, что некоторые из этих топологических зарядов могут
принимать определенные дискретные значения. Если это имеет
место, то константы Nj называются топологическими квантовыми
числами.
Чтобы увидеть, как возникают топологические квантовые
числа, обозначим через Он (х; фа, дф«, ...) динамические отобра-
жения гейзенберговских операторов, описывающих наблюдаемые
величины. Здесь многоточие отвечает свободным физическим по-
лям, отличным от бозонов ф& с бесщелевым энергетическим спек-
тром, а дф& обозначает производные от ф„. Предположим, что Он
инвариантно относительно преобразования ф« ->- ф„ -J- паса :
Протяженные объекты с топологическими особенностями 383
Здесь са — некоторые заданные константы, а па — целые числа.
Бозонное преобразование превращает 0н в Он".
0fH = Он (х; Фа + L, ду°а + dfa, . . . ). A0.1.57)
Поскольку 3/а — однозначная функция, сосредоточим внимание
только на fa, не обращая внимание на производные.
Рассмотрим теперь замкнутый контур. В соответствии с соот-
ношением A0.1.56) для однозначности определения наблюдаемых
величин Он требуется, чтобы изменение /а вдоль замкнутого кон-
тура было равно паса. Поэтому из A0.1.13) следует
Nt = п"са, A0.1.58)
а это означает, что ЛГ™ — топологическое квантовое число. Дан-
ное рассмотрение показывает, каким образом топологическое
квантовое число связано со структурой динамического отображе-
ния наблюдаемых, которая жестко контролируется свойствами
инвариантности исходного лагранжиана.
Обратимся для примера к фазово-инвариантной скалярной
модели, рассмотренной в разд. 7.2, или к квантовой электроди-
намике, которой посвящена гл. 8. В этих случаях динамическое
отображение ty (скалярного поля в фазово-инвариантной модели,
описанной в разд. 7.2, или электронного поля в случае квантовой
электродинамики) имеет вид
Ф (х) = : exp [i%° (х)/ц] ф [дх°, ...]:. A0.1.59)
Здесь х° — голдстоуновский бозон, а г) — константа. Рассматри-
вается следующее бозонное преобразование:
Х° (*)-* Х° (*) + Л/(*)• A0.1.60)
Поскольку %%1 представляет собой фазу я|з (х), из однозначности
¦ф (х) следует наличие топологического квантового числа
A0.1.61)
в случае фазово-инвариантной скалярной модели. Здесь п — це-
лое число. В случае сверхпроводимости следует учесть тот факт,
что все гейзенберговские операторы, отвечающие наблюдаемым
величинам, содержат четные степени электронного поля я|з, по-
скольку электронное поле является фермионным. Поэтому одно-
значность наблюдаемых приводит к условию
A0.1.62)
Как показано в гл. 11, магнитный поток, связанный с вихрями
в сверхпроводниках, пропорционален NT. Следовательно, усло-
вие A0.1.62) приводит к квантованию потока.
384 Глава 10
В гл. 8 мы выяснили, что в случае нормальных проводников
фазовое преобразование i|) -> exp (t0) г|з обусловлено комбинацией
двух преобразований
Х° (х) -> х° (*) + У)въ A0.1.63а)
Ф° (*) -> exp [t (9 — в])] ф°. A0.1.636)
Поскольку A0.1.63а) не является единственным источником фа-
зового преобразования, для однозначности наблюдаемых не тре-
буется выполнения равенства A0.1.62). Иными словами, хотя
однозначность наблюдаемых приводит к соотношению NT + 6i =
= пп, величина 9Х может быть подобрана произвольным образом.
Поэтому в нормальных металлах отсутствует закон квантования
потока.
Другой интересный пример топологического квантового числа
дают дислокации в кристаллах. Как видно из соотношения G.7.80),
динамическое отображение Он (х) имеет вид
Он (х) = : S Ф>. [х + Х° (х)\ 6Х (х; ах», ...):. A0.1.64)
Здесь Xе — поле фононов, а функции ц>к (х) являются элементами
полной ортонормированной системы периодических функций:
Фа (х) = Фл (х + а,), A0.1.65)
где a.t (i =1, 2, 3) — базисные векторы кристаллической ре-
шетки. Бозонное преобразование для фононов имеет вид
[Х° (х) -> Х° (*) + f (*). A0.1.66)
Таким образом, из A0.1.64) и A0.1.65) следует, что для одно-
значности Он (х) требуется выполнение условия
A0.1.67)
где п; — целые числа. Отсюда видим, что три компоненты век-
тора Nr представляют собой топологические квантовые числа
[7]. Вектор Nr называется вектором Бюргерса [6].
В общем случае протяженные объекты, обладающие определен-
ными квантовыми числами, термодинамически устойчивы, по-
скольку топологические заряды не могут непрерывным образом
обращаться в нуль. Именно по этой причине в сверхпроводниках
никогда не могут самопроизвольно возникать прямолинейные
вихри; они являются результатом проникновения в систему
через граничную поверхность внешнего магнитного потока. С дру-
гой стороны, в нормальных металлах устойчивых вихрей не
бывает. .
Протяженные объекты с топологическими особенностями 385
10.2. Протяженные объекты в кристаллах
В предыдущем разделе описан общий формализм, применяе-
мый для рассмотрения протяженных объектов с топологическими
особенностями. В данном разделе мы проиллюстрируем этот об-
щий подход на примере кристалла. Мы кратко покажем, каким
образом на основе микроскопической теории может быть построена
теория, описывающая дислокации и другие протяженные объекты
в кристаллах [7].
Уравнение для фононов. В разд. 7.7 мы нашли трехкомпонент-
ное фононное поле Х° = (Х\, Х°, XI), удовлетворяющее уравне-
нию G.7.96):
здесь Atl (д) = -р,7 (V) -У + 2] C'i? W V, Vm, A0.2.2)
причем использовано соотношение G.7.100). Мы можем предста-
вить A0.2.2) в виде
Ац (д) = 2 С^У (V) дцду, A0.2.3)
IX, V
где О}] при (х = 0 или v = 0 определяется следующим образом:
C°/(V) = — p«v(V), A0.2.4a)
С$ (V) = С?/(V) = 0. A0.2.46)
Сингулярное бозонное преобразование. Если функции Д (х)
(t =1, 2, 3), определяющие бозонное преобразование, обладают
некоторой топологической особенностью, то из формулы A0.1.12)
следует
ft, /Л, р
где A,ft (x) — функция Грина, удовлетворяющая условию
? Ai{ (д) Aih (x) = 8ik6w (x). A0.2.6)
Динамическое отображение любого гейзенберговского опера-
тора имеет вид G.7.80)
Он (х) = : Е Фх [х + Х° (х)] 6к (х; дХ, Ф°):. A0.2.7)
к
Протяженные объекты возникают за счет конденсации фононов,
386 Глава 10
описываемой бозонным преобразованием
XI (х) -»»XI (х) + /, (х), i=l, 2, 3, A0.2.8)
в котором неоператорные функции /; (х) должны удовлетворять
уравнению для фононов
S Л,/(д)//(*) = <). A0.2.9)
В результате бозонного преобразования Он (х) заменяется на
(x)]dk(x;dX0 + df, <р°) :. A0.2.10)
В частности, для плотности импульса Р(х), тензора напряжений
Тц (х) и плотности числа молекул п (х) имеем соответственно
Р\ (х) = - ? Pl7 (V) [Х°, (х) + /, (х)] + >
lj (х) = S CfT (V) Vm [X? (х) + /, (х)] +
/, m
+ И И Ф^ (х) Г!/Л (V) [X? (х) + /, (х)] + . . . , A0.2.12)
кФ-i i
f (х) = v (х) - -L 2] V,Pl7 (V) [X? (х) + ff (x)] +
При выводе этих результатов мы использовали соотношения
G.7.92), G.7.99) и G.7.102) соответственно.
Плотность гамильтониана имеет вид
=4- 2
i j
2
i, j
4-[v'(x?+/')]c'-/I(v)[Vm(x?+//)]+- • • • A0-2Л4)
i, i I. m
Как видно из выражения G.7.108), члены более высокого порядка,
обозначенные многоточием в A0.2.14), не вносят вклада в гамиль-
тониан при f = 0. Но, как выяснено в разд. 9.3, вклад этих чле-
нов более высокого порядка не обращается в нуль, если мы осу-
ществляем бозонное преобразование с функцией /, имеющей
особенность.
Изотропное, длинноволновое и линейное приближение. По-
скольку в этом разделе мы хотим дать краткое описание метода
Протяженные объекты с топологическими особенностями 387
рассмотрения протяженных объектов в кристаллах, нами исполь-
зуется линейное и изотропное приближение. Другими словами,
мы полагаем, что рц (V) *« р (V) $ц, и не учитываем члены,
обозначенные многоточием в выражениях A0.2.11)—A0.2.14),
а также члены, содержащие ср^ (х) с К Ф —1. Кроме того, мы
пользуемся длинноволновым (соответствующим малым значе-
ниям импульса) приближением, в рамках которого рц (V) и
С if1 (V) заменяются на рц @) и С1™ @). Поэтому выражение
A0.2.2) принимает вид
At, (д) ^ - роб,/ ^ + 2j С!-/1 @) V/Vm, A0.2.15)
/, m
где p0 = p @). При этом формулы A0.2.11), A0.2.12) и A0.2.13)
записываются в виде
Pft(x)^—po[X°i(x)-\-h(x)], A0.2.16)
Tft, (x) ** Е С{Т @) Vm [X? (х) + /; (х)], A0.2.17)
I, m
^\u(x) + l(x)}. A0.2.18)
В этом приближении плотность гамильтониана № (х) имеет вид
+ 4" Ц 2С^@) [V' W + АИ [Vm(Aj+ /,)]. A0.2.19)
i, i I, m
Если используются соотношения G.7.106), то С1™ @) можно
выразить через два параметра К и jx:
Cif @) = ц F,film + б(тб/7) + Ми8,п. A0.2.20)
Константа р0 называется плотностью, а К и jx — коэффициент
Ламе и модуль сдвига соответственно [6].
Соотношение A0.2.15) принимает теперь вид
АG (Р) = Рйр% - №2б4.. - {К + ц) piPj, (Ю.2.21)
где Ац (р) определяется соотношением Atl (д) exp (ipx) —
= Ац (р) exp (ipx). Мы можем переписать A0.2.21) в виде
388 Глава 10
где
vt = (ЫРоУ/г, A0.2.23а)
Vi = [(К + 2ц)/р0]1/.. A0.2.236)
Из формулы A0.2.22) видно, что энергии поперечного и продоль-
ного фононов равны соответственно щ (р) = v t | p | и о»; (р) =
= v,\p\.
Функция Грина в импульсном пространстве Д,-у- (р) опреде-
ляется выражением
* W J #Ре"" Д'/ ^)« (Ю.2.24)
и равенство A0.2.6) принимает вид
? Аи (р) Ajh (p) = 6/ft. A0.2.25)
Из A0.2.22) находим
A0.2.26)
В статических случаях удобно работать с функцией Грина
в координатном пространстве
A W
ехР <*• х>[А'/ W]p.-o = A0.2.28)
3^ 1 fij _±±Е__1
где г = | х |. Из A0.2.5) получаем
J V + ( | г-г'I
( ) ( ;) ( ^) "+ (/) A0-2i30)
Из этого соотношения определяется f (x) для статических объектов.
Дислокации. Рассмотрим теперь дислокацию, представляю-
щую собой объект, содержащий линейную особенность. Функции
Gfv (х) даются формулой A0.1.29), где а = i, у0 = т, у = у (а):
r^e(x-y). A0.2,31)
Протяженные объекты с топологическими особенностями 389
Остальные компоненты G?v обращаются в нуль. Топологические
заряды (вектор Бюргерса) определяются соотношением A0.1.14):
= 4" 2 J dSklG^ W = A0.2.32)
ft, / S
%\dSkGf(x), A0.2.33)
k s
где dSft = A/2) гм1 dSij. Можно осуществить такую параметри-
зацию пространственных координат х = х (^, ?2> ?з)> чтобы ли-
ния, определяемая равенством ?2 = ?3 = 0, совпадала с кривой
у (о). Тогда имеем
^- в (х - у) = жШг^й б & ~ ^ б ®>6 fe)- A0-2'34)
В этом случае из A0.2.31) следует
Без потери общности в качестве поверхности, по которой произ-
водится интегрирование, можно выбрать плоскость A2, 13):
^ = -Г§Т5гЙ"8*'^^- (Ю.2.36)
Поскольку
1 „ dxh д Iхt> */] д [xlt xt, xa] /10 9 47^
Т^ТБГ71БПЛ""УТЕП5ГИ A0237)
получаем
j-') = v<" f
&) б (?з) = v(°. A0.2.38)
Следовательно, вектор Бюргерса имеет вид v = (vO, v<2), v<3>).
В разд. 10.1 мы видели, что этот вектор обладает дискретным
спектром (существуют топологические квантовые числа).
Обозначим через к] (а) единичный вектор, направленный по
касательной к кривой у (а). Если в некоторой области изменения
параметра а справедливо равенство
vt](a) = 0, A0.2.39)
то в этой области существует краевая дислокация (рис. 10.4),
а равенства
v-ij(ff) = ±|v| A0.2.40)
отвечают соответственно правовинтовой и левовинтовой д
циям (рис 10.5).
390 Глава 10
В качестве примера рассмотрим теперь прямолинейную осо-
бенность, расположенную вдоль третьей оси, г/,- = o8i3. В этом
случае, согласно формуле A0.1.32), имеем
GS1 (х) = -G% (х) = v(/N (*,) б (х2). A0.2.41)
Остальные компоненты обращаются в нуль. Винтовая дислокация
определяется условием v<!> = v<2> = 0. В этом случае выражение
A0.2.30) принимает вид
=--Ег*(8>^Ьга'» A0-2-42a)
^^^в,,, A0.2.426)
x) = O. A0.2.42b)
м ч
Рис. 10.4. Рис. 10.5.
Таким образом, вне особой линии хх = х2 = 0 поля смещений
имеют вид
h (х) = U (х) = 0, /3 (х) = -2^v<3> arctg (x2/xx). A0.2.43)
Несущественные константы интегрирования выбраны здесь так,
чтобы получились простые выражения для /; (х). В случае крае-
вой дислокации (v<2> = v<3> = 0) из выражения A0.2.30) получаем
(f)
) A0.2.446)
/s(x) = 0. A0.2.44b)
Границы зерен. Обратим теперь наше внимание на двумерные
особенности. Обычные материалы представляют собой не моно-
кристаллы, а совокупность малых кристаллических зерен. Гра-
ничная поверхность между двумя монокристаллическими зернами
называется межзеренной границей. Межзеренная граница — это
макроскопический объект (протяженный объект), возникающий
за счет конденсации фононов.
Протяженные объекты с топологическими особенностями 391
Величина Gfv для двумерных особенностей дается выражением
A0.1.44) с заменой а на i. Предположим, что «сила» особенности
постоянна вдоль поверхности. Другими словами, мы предпола-
гаем, что
ФЧУ) = 53 v'^fc(T, a, I). A0.2.45)
Кроме того, ограничим наше рассмотрение статическим случаем
г/о = т, у = у (<r, I), v<° = 0. A0.2.46)
Тогда не обращающиеся в нуль компоненты Gfv имеют вид
Gf (х) = _G?° (x) = Jv" jAr J <g ^^1 6 (x - y). A0.2.47)
i
В каждый момент времени топологическая особенность представ-
ляет собой поверхность у @, ?). Как будет показано ниже, ма-
трица vil связана с поворотами областей, разделенных этой по-
верхностью. Введем такую параметризацию пространственных
координат х = х (|ь ?2, |3), чтобы поверхность, задаваемая ра-
венством |3 = 0, совпадала с поверхностью у (а, ?). Используя
соотношение
6{х-у)=all;tilб(|1 ~а)б(^2-1)б(?з)> A0-2-48)
мы можем переписать формулу A0.2.47) в виде
Из A0.1.13) находим топологические заряды
NtT=\dS]idJt(x) = A0.2.50)
с
= _1 | rfS^Gj? (x) = A0.2.51)
s
= J rfS*G?* (x), A0.2.52)
s
где dSk определяется так же, как в формуле A0.2.33). В качестве
контура с выберем замкнутый контур, проходящий под поверх-
ностью A3 = 0_) от точки Q (Ъ[, %[, 0) к точке Р (?{, Ц, 0), а затем
возвращающийся над поверхностью (|3 = 0+) из Р в Q. Вектор Nr
представляет собой сумму векторов Бюргерса, отвечающих ин-
392
Глава 10
тервалу PQ. Поскольку S — площадь, охватываемая контуром с,
имеем
ft' *А d%1dla + dJ**' *;'| dl^dlX A0.2.53)
Используя соотношения A0.2.49), A0.2.52) и A0.2.53), получаем
A0-2-54)
= S *' J (жdh+жdL) =
/ Q
Рис. 10.6.
гдеУ = (Vi, V2, V3) — вектор, направленный из точки Q в точку Р:
Vt = xt Ш, lL 0) - Xl (l\, U, 0). A0.2.55)
Матрица v'7 определяет взаимную разориентацию граничащих
между собой зерен. Предположим, что зерна А и В повернуты
на <оА = ЭАал и (»в = 6лав соответственно относительно кри-
сталла, принятого за систему отсчета. Здесь а°° (а = А, В) —
единичный вектор, который задает направление оси поворота,
а 6а (а = А, В) — угол поворота вокруг оси а°°. Введем век-
торы V+: вектор V+ направлен из точки Q на поверхности в точку Р+
внутри зерна В, а вектор V_ соединяет Q с точкой Р_ внутри
зерна А (рис. 10.6). Смещение вектора V+, обусловленное поворо-
том юв зерна В, равно \в (V+), а смещение вектора V_ при пово-
роте юА зерна А равно iA (V_). Следовательно, в пределе V+ =
= V_ = V имеем
fA (V) = [ехр A0дал- J) — 1] V, A0.2.56а)
iB (V) = [ехр (;0вав- J) — 1] V, A0.2.566)
Протяженные объекты с топологическими особенностями 393
где Ji — генератор поворотов вокруг оси xt. Если замкнутый
контур с в A0.2.50) есть QP+P_Q> то в результате интегрирования
по нему получаем if (V+) — if (V_). Затем, снова рассматривая
случай V+ = V_ = V, находим
N't = f?(У)-ft (У). A0.2.57)
Используя выражения A0.2.54) и A0.2.56), получаем
v'/ = [exp (;eBas- J) — ехр (Шлал- J) ]tJ. A0.2.58)
Тогда по формуле A0.2.54) для вектора Бюргерса находим
N7 = as (V а8) - аА (V-aA) + [V - as(V-as)] cos 6B -
— [V — a^(V-a^)]cos9A + sines(Vxas) — sin 9Д (V х ал). A0.2.59)
Рассмотрим случай аА = —as = d. В этом случае кристалл,
принимаемый за систему отсчета, всегда можно ориентировать
таким образом, что 9Д = Эв = A/2) 6; поэтому A0.2.59) при-
нимает вид
Nj. = 2(V х d) sin A/2) 9. A0.2.60)
Это формула Франка для большеугловых границ зерен. Если
вектор d лежит в плоскости межзеренной границы, то такая гра-
ница называется границей наклона. Если же вектор d перпенди-
кулярен граничной поверхности, то она называется границей
кручения. В общем случае граница имеет смешанный характер,
и существуют составляющие, отвечающие как наклону, так и
кручению.
Здесь уместно сделать следующие два замечания. Во-первых,
нужно отметить, что при построении матрицы vil, определяющей
взаимную разориентацию зерен, совсем не имеется в виду, что
поля смещений в зернах А и В отличаются только ориентацией.
В общем случае поля смещений f; по обе стороны границы вклю-
чают не только вращение, но и растяжение (или сжатие). Во-вто-
рых, в ходе рассмотрения, начиная с формулы A0.2.56) и кончая
формулой A0.2.60), используется предположение об отсутствии
на граничной поверхности растяжения (или сжатия). Мы подчер-
киваем здесь слова «на граничной поверхности», поскольку допу-
стимо растяжение (или сжатие) внутри каждого из зерен. Мы вер-
немся к этому вопросу ниже, когда будут в явном виде выписаны
выражения для поля смещений в обоих зернах.
Так как мы рассматриваем двумерные особенности, образован-
ные линиями, не имеющими концов, удовлетворяется уравнение
непрерывности d^Gfv = 0. Рассмотрим теперь совокупность меж-
зеренных границ (а = 1, 2, ..., п), описываемую формулой
ОГ (х) = J v? J dx J do J dl д%;*'*] бD) (х - УП- (Ю.2.61)
в, %
394 Глава 10
Ограничимся статическим случаем. Линия, общая для более чем
двух границ зерен, называется линией узлов. Рассмотрим линию
узлов, описываемую функцией у (?). Границы, пересекающиеся
по линии у (?), мы будем обозначать через уь (Ь = 1, 2, ..., т).
Поскольку уравнение непрерывности приводит к условию A0.1.27)
в каждой узловой точке линейной особенности, мы приходим
к условию
И U(±)v^(Q = 0, A0.2.62)
а I
где п (?) = ду (?)/д? — вектор, направленный по касательной
к линии узлов у (?). Соотношение A0.2.62) носит название соот-
ношения непрерывности для границ зерен. Более подробный вы-
вод условия A0.2.62) можно найти в работе [7]. В качестве част-
ного случая рассмотрим ситуацию, когда т = 1, т. е. когда
имеется только одна межзеренная граница. Заметим, что условие
A0.2.62) выполняется, если одна из компонент вектора п (напри-
мер, п3) не обращается в нуль, a v[3 (i = 1, 2, 3) равны нулю.
Таким образом, межзеренная граница может оканчиваться внутри
кристалла. Этот случай представляет собой пример дисклинации
(поворотной дислокации) [6].
Рассмотрим теперь в качестве примера плоскую границу зерен,
определяемую равенствами
г/i (о, I) = а, уг (а, \) = I, у3 (а, I) = 0. A0.2.63)
Согласно A0.2.47), не равные нулю компоненты Gfv имеют вид
G?1 (х) = —Gl° (x) = v'26 (x3), A0.2.64а)
Gf (х) = -G?0 (х) = — vn6 (x3). A0.2.646)
Из A0.2.5) и A0.1.20) получаем
djt (х) = v»/0 (*,), A0.2.65а)
djt (х) = V2/o (x3), A0.2.656)
d3h (х) = (-v316a - v326;2 - j^ (v11 + v22N,3) /0 (x3), A0.2.65b)
где
Обозначим через Оц тензор напряжений; ац представляет
собой /-ю компоненту силы на единицу площади в плоскости,
Протяженные объекты с топологическими особенностями 395
внешняя нормаль к которой параллельна положительному на-
правлению оси xt. Согласно закону Гука A0.2.17), имеем
or,/ = Е СЦ @) dtfh (x) = A0.2.66)
Примечательно, что условие свободной поверхности аш — 0
(i =1, 2, 3) автоматически выполняется благодаря соотношению
A0.2.65). Мы накладываем на интеграл /0 (х3) следующие гранич-
ные условия:
I , 1 @ при х3>0,
/0 (х3) = lira 4~ \ dp3 —Ц- в'"»** = , Л A0.2.68)
0 v зу Е^о+ 2п } ™ p3 + is [ 1 при х3 < 0. v ;
Поэтому поле смещений f (х) вне особой точки х3 = 0 дается соот-
ношениями
f (х) = 0 при х3 >0, A0.2.69а)
f (x) = f/x при х3 <0, A0.2.696)
где матрица ?/ имеет вид
2 ; A0.2.70)
% (VU -|. V22)
Если бы поле смещений f (x) могло быть следующим образом
представлено с помощью ортогональной матрицы TR: f (x) =0
при х3 > 0, f (х) = (TR — /) х при х3 < 0, то зерну в области
х3 < 0 можно было бы придать ту же ориентацию, что и при
х3 > 0, посредством чистого вращения, т. е. зерно, отвечающее
х3 < 0, оказалось бы идеальным кристаллом. Однако можно до-
казать, что (/ + U) не является ортогональной матрицей, за
исключением тривиального случая U = 0. Поэтому всегда наряду
с вращением имеется и растяжение (или сжатие).
Мы можем выбрать \Ч таким образом, чтобы поле смещений
при х3 = 0_ описывалось чистым вращением. Например, при сле-
дующем выборе параметров: v11 = v22 = cos Э — 1, v12 = —v21 =
= sin 8, v31 = v32 =0 получаем
'°\
A0.2.71)
396 Глава 1д
где
/ COS
= I —sin
\ о
e
e
cos
COS
0
e
e
0
0
l
A0.2.72)
Таким образом, Ux при х3 = 0 описывает чистый поворот на
угол 0. Второй член в правой части выражения A0.2.71) показы-
вает, что поворот сопровождается растяжением или сжатием вдоль
третьей оси. Если угол 0 очень мал, то это растяжение (или
сжатие) квадратично по 0.
Теперь полезно вспомнить вывод формулы A0.2.60). В рамках
этого вывода (в частности, когда мы записывали формулу A0.2.56))
неявно предполагается, что сжатия или растяжения структуры,
прилегающей к граничной поверхности, не происходит. Приведен-
ное выше рассмотрение показывает, что это предположение не
всегда справедливо. Кроме того, даже если данное предположение
верно, выражение A0.2.71) показывает, что эффекты, связанные
с растяжением (или сжатием), проявляются в области вдали от по-
верхности. С ростом 0 эта область приближается к межзеренной
границе.
Точечные дефекты. Будем рассматривать точечный дефект
как двумерную сферическую особенность радиуса R:
Уо — т, У = (# sin a cos ?, R sin a sin g, R cosjr). A0.2.73)
Подробное исследование такого объекта при произвольных vil
проведено в работе [7]. Здесь мы рассмотрим только простой
случай
v" = vS,,. A0.2.74)
Проведя соответствующие вычисления, получаем
ЬМ = -ГТ+1;Г*' при 0<r<R, A0.2.75а)
r>R' (Ю-2.756)
где г= |х|. Объемное расширение (вычисленное на сфере),
обусловленное точечным дефектом, дается выражением
= dS-f(x)= A0.2.76)
r>R
(Ю.2.77)
Протяженные объекты с топологическими особенностями 397
Согласно формуле A0.2.67), тензор напряжений о(]- равен
ПРИ 0<r<R' A0
при г > Я. A0.2.786)
Т^-ЩГ8" ПРИ 0<r<R' A0-2-78a)
Определим теперь величину
^^-оц^. A0.2.79)
Тогда из соотношений A0.2.78) следует
ПрИ
7^ при r>jR- (Ю.2.806)
Отметим, что агг непрерывна в точке г = R. Это можно дока-
зать при любом выборе va. Из A0.2.76) и A0.2.80) получаем
orr=—??AV при г>Я. A0.2.81)
Из формулы A0.2.756) видно, что Vf = 0 при г > R. Поэтому
JS.V в A0.2.76) не зависит от выбора поверхности интегрирования,
если только эта поверхность не пересекает особенность при г = R.
Иными словами, AV — топологическая постоянная. Однако эта
топологическая постоянная не является топологическим кванто-
вым числом, поскольку не требуется, чтобы спектр ее значений
был дискретным х).
Плотность энергии деформации w равна @ | hf (x) | 0), где
плотность гамильтониана дается выражением A0.2.19). Таким
образом, получаем
-2 °«-^.
i. / l, к ' l i, j
где использована формула A0.2.66). Отсюда с помощью выраже-
ния A0.2.80) получаем
0<г<Я, A0.2.83а)
г > R. A0.2.836)
х) Хотя для точечных дефектов отсутствует топологическое квантовое число,
гарантирующее их устойчивость, они обычно устойчивы, поскольку их существо-
вание обусловлено наличием либо атомных вакансий, либо примесей замещения;
малая скорость диффузии атомов обеспечивает достаточно большое время жизни.
Мы могли бы сказать, что атомный номер играет роль топологического кванто-
вого числа, хотя он не имеет ничего общего с топологией.
398 Глава 10
Полная энергия деформации W равна
W — [ d3xw (х) — 2v2u2
w - j a xw (X) — zv ц
Разумно предположить, что увеличение объема, обусловленное то-
чечным дефектом, порядка объема, приходящегося на один атом.
Поэтому если мы примем грубое допущение, что R я» а (а — по-
стоянная решетки), то из выражения A0.2.77) получим, что v
порядка единицы. Известно, что типичные значения К и (л, порядка
1012 дин/см2. Тогда полная энергия деформации порядка 1 эВ,
что качественно совпадает с энергией образования вакансии в ре-
шетке.
В гл. 12 мы применяем методы, описанные в этой главе, к за-
даче о поверхностных волнах.
10.3. Топологические особенности, связанные
с неабелевыми группами симметрии
Введение. Как показано в разд. 10.1, термодинамическая
устойчивость топологических объектов (т. е. объектов с топологи-
ческими особенностями) часто обусловлена наличием некоторых
топологических квантовых чисел, характерных для этих объектов.
Появление таких квантовых чисел и условия их существования
жестко связаны с симметрией фундаментальной теории. Если
фундаментальная симметрия имеет неабелеву природу, то тре-
буется дальнейшее развитие того подхода, который использован
в предыдущих разделах. Примером топологического объекта
с неабелевой симметрией является объект типа монополя [8].
Предполагалось, что объект типа монополя может возникать
в жидких кристаллах [9], в случае магнитных доменов [10],
в сверхтекучем 3Не [11 ] и т. д. По-видимому, другие топологиче-
ские объекты с неабелевой симметрией будут еще обнаружены
во многих областях физики твердого тела. Имеются отличные
работы по топологической классификации протяженных объек-
тов [12]. Большинство из них основано на использовании гло-
бальных свойств топологических объектов, причем некоторые
из этих работ предназначены для физиков, занимающихся эле-
ментарными частицами высоких энергий. В физике твердого тела
часто требуется выяснить локальную структуру топологических
объектов, которая не определяется полностью глобальными гра-
ничными условиями. Поэтому желательно описывать топологиче-
скую природу таких объектов на языке пространственно-времен-
ных координат особых точек. Чтобы осуществить это, мы обобщим
рассмотрение, проведенное в разд. 10.1, придав ему форму [13],
удобную для описания топологических объектов с неабелевой
Протяженные объекты с топологическими особенностями 399
симметрией. Такое описание в значительной степени опирается
на использование понятия «калибровка». В рамках рассмотрения,
проведенного в разд. 10.1, локальные свойства топологической
структуры описываются с помощью [6^, dv] f, а следовательно,
и с помощью величины [д^, dv] U (х), где U (х) = exp [if (x)],
поскольку данная величина пропорциональна [дп< dv] f. В случае
неабелевой группы симметрии (например, G) фазовый множитель
exp [if (х)] мы заменяем матрицей U, с помощью которой вво-
дится калибровочная функция.
Матрица калибровочного преобразования. Рассмотрим набор
гейзенберговских операторов {-фа (%); а = 1, 2, ..., N\, который
отвечает гейзенберговским полям, образующим некоторое пред-
ставление n-параметрической группы G. Для простоты будем
считать, что G — компактная группа. Предположим также, что
уравнение Гейзенберга и одновременные канонические коммута-
торы инвариантны относительно преобразований группы G и что
возникает некоторое число (например, т) физических бозонов
[%а (х)> а = 1> ¦¦¦, т\ с бесщелевым энергетическим спектром.
Нас интересуют протяженные объекты, возникающие при бозон-
ном преобразовании %а (х) -> %а (х) + /а (х). Гейзенберговское
поле, трансформированное бозонным преобразованием, обозна-
чается символом^. Мы видели в гл. 9, что неоператорная часть я|>/
'а
A0-зл)
(без учета квантовых координат) однозначно определяет гейзен-
берговское поле г|)д. Сконцентрируем наше внимание на неопера-
торных функциях va (x), которые будем называть параметрами
порядка. Поскольку параметры порядка в древесном приближе-
нии (h ->-0) соответствуют решениям классического уравнения
Эйлера, большая часть проводимого ниже рассмотрения приме-
нима также и к чисто классическим полям.
Будем использовать векторные обозначения ^ {х) и v (x)
для г|)д (х) я va (х) (а =1, ..., N) соответственно. Векторное про-
странство представлений группы обозначим символом Звв,
Поскольку ^ (х) и v (х) — некоторые представления компактной
группы G, выберем эти представления так, чтобы они были уни-
тарными. Определим затем внутреннее произведение двух произ-
вольных векторов v1 и v2 в пространстве Жа следующим образом:
(v1.v2)= 2oj4?. A0.3.2)
а
Если задать в группе G некоторое унитарное преобразование и,
то получим
(uv^wv2) = (vx-v2). A0.3.3)
400 Глава 10
Обозначим через е0 некий фиксированный единичный вектор
в пространстве Жв. Выберем е0 так, чтобы он был инвариантен
относительно всех преобразований группы Н, представляющей
собой подгруппу G. Символом h обозначим размерность группы Н.
Предположим, что параметр порядка v (x) имеет вид
v (х) = U (х) еоу (*), A0.3.4)
где v (х) — неоператорная функция, a U (х) — унитарная ма-
трица с зависящими от х элементами. Это соотношение представ-
ляет собой условие, накладываемое на параметр порядка v (x).
Число независимых переменных в U (х) е0 равно (n — h). Учиты-
вая наличие v (х), получаем, что общее число переменных в пра-
вой части соотношения A0.3.4) составляет (п —h + 1), т. е.
N = n—h+ 1. A0.3.5)
Это накладывает ограничения на выбор представления, отвечаю-
щего параметру порядка. Мы имеем соотношение
v2(x) = [v(*)-v(*)l. A0.3.6)
Матрица U (х) называется матрицей калибровочного преобразо-
вания. Удобно определить вектор
е (х) ~ v (x)/v (х) = U (х) е0, A0.3.7)
поскольку он характеризует топологическую структуру протя-
женных объектов.
Чтобы выразить топологические свойства в дифференциальной
форме, определим матрицу /д (х) посредством соотношения
Д, (х) = -Ш-1 (*) d»U (х), A0.3.8а)
или
д»и (х) = Ш (х) /д (х). A0.3.86)
С другой стороны, поскольку матрица U (х) унитарна, ее можно
представить в виде
U (х) = exp {ita0a (x)}, A0.3.9)
где ta (а = 1, ..., п) — матрицы NXN, представляющие собой
генераторы преобразований группы G, а ва — параметры, зави-
сящие от х. Чтобы вычислить /д (х), исследуем матрицу
U (т, *) = exp {ixtaQa {x)\ A0.3.10)
и введем величину /д (т, х), определяемую выражением
fM (т, *) = -W-1 (т, *) d»U (т, х). A0.3.11)
Протяженные объекты с топологическими особенностями 401
Тогда имеем
+ U-1 (т, х) дд {taQa (х) U (х, х)) = [Г1 (т, *) *вдд9в (х) U (х, х).
A0.3.12)
Поскольку fp (т = 0, х) = 0, отсюда следует формула
/д (*) = А* (т= 1, х) = J dtt/-1 (т, х) WA (*) f/ (т, *). A0.3.13)
о
Матрица U (х) может быть представлена [13] в виде контурного
интеграла от /д (х).
Условие интегрируемости и топологические особенности. Если
требуется, чтобы вектор е (х) был хорошо определен в качестве
многозначной функции, то условие интегрируемости
[дц, dv] е (х) = 0 A0.3.14)
должно выполняться везде, за исключением некоторых особых
точек. Здесь особыми называются те точки, в которых функция
е (х) становится плохо определенной. Такие особенности являются
топологическими. Обозначим символом SD множество этих особых
точек. Определяя величину /„v посредством соотношения
[0Д, dv] U (х) = Ш (х) /д„ (*), A0.3.15)
находим
/mv (*) = djv (x) - ау/д (х) + i % (х), Д, (х) I A0.3.16)
Область 2) задается следующим образом:
Ф 0 при х с: Я),
= 0 в других случаях. (Ю.3.17)
Если 2&и — множество топологических особенностей матрицы
U (х), то оно состоит из точек, где [дй, dv] U Ф 0 (т. е. f^ Ф 0).
Очевидно, что 3) не обязательно совпадает с ?Ои, и имеет место
соотношение SD s S)y. Благодаря такой возможности неабелев
случай существенным образом отличается от абелева.
Поскольку дифференциальный оператор (т. е. U'1 (x) d^U (x))
является локальным по своей природе и по определению не дол-
жен нигде зависеть от траектории, получаем
fdv. дд] h (х) = 0 в любой точке х. A0.3.18)
Если определить дуальный тензор /Jv посредством соотношения
402 Глава 10
то из A0.3.18) следует тождество Бьянки
dufjiv (*) + »[/*• /Jv] = O. A0.3.20)
Оно соответствует формуле A0.1.17) в абелевом случае.
Условие однозначности параметра порядка. Рассмотрим зам-
кнутый контур С, который описывается функциями хц (s), зави-
сящими от вещественного параметра s, причем выполняются соот-
ношения
0 <s« 1, хд@)=*|1A).
A0.3.21)
е(х) е^)
Рис. 10.7. Рис. 10.8.
Поскольку вектор е0 инвариантен относительно любого преобра-
зования (например, Uh) из И, т. е.
Ufa = е0, Uh e H, A0.3.22)
из однозначности е (л:) следует
U [х(\)\ = U 1х@)] Un. A0.3.23)
Это условие более слабое, чем условие U [х A)] -— U [х@)].
Взаимное соответствие между координатным пространством
и пространством симметрии. Посредством вектора е (х) коорди-
натное пространство R отображается на пространство симметрии:
Хц ->¦ е (х) = U (х) е0. A0.3.24)
Таким образом, R отображается на (N — 1)-мерную сферу Se
единичного радиуса (е2 = 1), отвечающую представлению Ж>0
(рис. 10.7).
Топологические особенности. Чтобы проанализировать струк-
туру множества особенностей 2D, исследуем отображения всех
возможных замкнутых поверхностей Cs на сферу Se (рис. 10.8).
Пусть ds — размерность Cs. Тогда для задания Cs требуется ds па-
раметров. Поскольку размерность Se равна Л^ — 1, некоторые
параметры или некоторые их комбинации должны остараться
Протяженные объекты с топологическими особенностями 403
инвариантными для каждого отображения Cs на Se, если ds
больше N — 1. Поэтому при дальнейшем рассмотрении мы будем
полагать, что ds <. N— 1. Если d—-размерность нашего про-
странства-времени, то ds < d.
Начнем рассмотрение со случая ds =N—1, предполагая,
что d 5s N. Тогда Cs и Se имеют одинаковую размерность N — 1.
Если Cs не пересекает никаких особенностей, то Csможно един-
ственным образом отобразить в виде замкнутой поверхности
на Se. Отметим, что данное отображение может быть многознач-
ным. Если же Cs пересекает некоторые особенности из множе-
ства^), то параметры порядка в этих особых точках определяются
только для конкретной траектории, задаваемой Cs (рис. 10.9).
В общем случае мы обозначаем посредством Се ту из траекторий,
которая получается в результате отображения Cs на Se; иными
словами, осуществляется отображение Cs -*-Ce.
Рис. 10.9.
С другой стороны, при рассмотрении части Se (например, s)
площадь поверхности, занятая областью s, дается интегралом
по ориентированной поверхности
», A0.3.25)
где со — внешняя дифференциальная форма, заданная на ориен-
тированном многообразии и определяемая выражением
-'лмф'1Л<Ч Л • • • AdeiN_v A0.3.26)
Полная площадь Q поверхности Se равна
A0.3.27)
В выражении A0.3.26) elt ..., eN — координаты в пространстве,
отвечающем представлению Ж^, a &u,..i — полностью антисим-
метричный тензор N-то ранга. Так как Se — (N — 1)-мерная
404 Глава 10
единичная сфера, она может быть параметризована с помощью
углов @Ь ..., 0jv_i) в полярной системе координат
ех = sin 0Х sin 02 ... sin QN^ cos QN_lf
e2 = sin 0X sin 0a ... sin SN_2 sin QN_!,
A0.3.28)
%-i = sin 9X cos 02,
eN = cos Q±.
В этом случае выражение для со имеет вид
со = ± (sin В^-2 (sin e^^-3 ... (sin 9^_2) d&i... dQN_lt A0.3.29)
где знак «+» или «—» выбирается в соответствии с ориентацией
поверхности. Полная площадь поверхности Q дается формулой
Q = Bя) (я1/2)^-2^ {N12). A0.3.30)
Определим v с помощью интеграла по поверхности A0.3.25),
где s =Се:
= [со. A0.3.31)
Чтобы преобразовать этот интеграл в интеграл по нашему коорди-
натному пространству, представим параметр порядка е (х) [ =ео (х),
а = 1, ..., N] в виде A0.3.28), введя функции Qx (x), ...,
®n-i (х)- Тогда интеграл по поверхности A0.3.31) на Se превра-
щается в следующий интеграл в координатном пространстве:
г..д (х) dx»i Adx^A---A dx^-г, (Ю.3.32)
где
(y\ —L—e(x)E- ¦ d[eh(x)---eiN-l(X)] /inoooN
= (—1)('/2) (^-2) <"+1> [sin 9X (x)]"-2... sin 0w_a (x) x
Протяженные объекты с топологическими особенностями 405
Используя теорему Стокса, находим
...цдг., (*) <Ь? Л ^i Д • • • Л ^^ = (Ю.3.35)
= тгг JG^-^ W ^ Л • • ¦ Л ^- (ю.3.36)
Здесь функция G^...^ (х) определяется следующим образом:
Gtv..»N(x)=Zdlligll2...llN, A0.3.37)
a Sc — область, ограниченная поверхностью Cs. Символ 2а
обозначает суммирование слагаемых, получающихся из выписан-
ных антисимметризацией по индексам. Поскольку выполняется
соотношение
2д а — 1 ( д [eh (*) ¦ • • eJN W] .
а также соотношение
5 [e(i (х) ... в|дг (х)]/а [^i ... х^] = 0, A0.3.39)
которое находится из условия е2 (х) =1, получаем
/М- /ч V^ V /\ л d\ei(x)...ei (х)]
Он...^ (х) = ^ ^Аг...% = 2j efl W е/г..*Л1 "ГГИ^ i^j—•
л л о L* • • • х j
A0.3.40)
Так как это выражение состоит только из членов, включающих
в себя коммутаторы от производных, оно не обращается в нуль
только в точках, отвечающих топологическим особенностям функ-
ций еа (х) (а = 1, ..., N). Из соотношения A0.3.36) видно, что
G'li1...liN(x) — совокупность Af-мерных 6-функций. Таким обра-
зом, эта величина определяет (d —• Л^-мерную область в d-мерном
{Xpj-пространстве. Данная область представляет собой множество
топологических особенностей, которые, согласно A0.3.40), имеются
в Gj ...ц . Это множество обозначим символом 3)d_N- Проводя
интегрирование в A0.3.35), можно видеть, что v остается постоян-
ным при непрерывной деформации поверхности 5С, если только
ее сечение между Cs и 3) не меняется. Таким образом, мы видим,
что v ¦— топологическая постоянная, а также что 2Dd_N не может
быть большей. В результате имеем три типа областей топологи-
406 Глава 10
ческих особенностей. ?DU — область особенностей, связанных
с матрицей калибровочного преобразования (т. е. множество
fixv (х) Ф0), a.2) — область особенностей параметра порядка е (х)
(для которых fuv (х) е0 Ф 0). Топологические особенности, вно-
сящие вклад в формирование топологической постоянной v, обра-
зуют область ?>d__N (где G^ ...^ (х) Ф 0). Вся область 2)и
не наблюдаема, поскольку наблюдаются только особенности, вхо-
дящие в 2D. Такая ситуация резко контрастирует со случаем абе-
левой симметрии, где 2?>и = 3). Задавая множество 2)d_N с по-
мощью величин //д (стх ... od_N), зависящих от (d—N) пара-
метров, находим
(dZ%i fc^ j °l ¦ ¦ ¦ d°d-N x
С помощью дуального тензора
GH.. .,d_N (x) = -^ e^.'.'.iiX- ¦ -дат W (*°-3-42)
соотношение A0.3.37) может быть переписано в виде
^:Xa^-^=g^^n- A0-3-43)
Из A0.3.41) находим
A0.3.44)
В рамках рассмотренного подхода могут быть локально идентифи-
цированы топологические особенности, топологическая постоян-
ная которых представляет собой интеграл по (N — 1)-мерной
замкнутой поверхности, а размерность равна (d — ./V).
В случае абелевой симметрии N ~ 2, поэтому формула A0.3.28)
имеет вид ех = cos 9Ь е2 = sin 9Х. Отсюда, согласно A0.3.34),
g-ц (х) = дц®! (х); при этом A0.3.37) превращается в соотношение
GJv = [д^, dv] Qt (х), совпадающее с A0.1.3) при fa (х) — 9Г (х).
В этом случае выражение A0.3.44) сводится к A0.1.21).
Топологическое квантовое число и устойчивость протяженных
объектов. Если особенность изолирована в том смысле, что ее
можно отделить от других особенностей замкнутой поверх-
ностью Cs, то благодаря однозначности е (х) Се образует замкну-
тую поверхность на Se. В этом случае v в формуле A0.3.31) при-
нимает целое значение (топологическое квантовое число), по-
скольку Се должна оборачивать Se целое число раз. Если сово-
Протяженные объекты с топологическими особенностями 407
купность особенностей образует объект, окруженный поверх-
ностью Cs, то целое значение v приписывается этой совокупности.
Весовой множитель Qv (v — целое число) в выражении A0.3.44)
определяет топологическое квантовое число, относящееся к объ-
екту, положения особенностей которого задаются функциями
Ур (о± ... od_N). Это целое число — индекс, называемый сте-
пенью Брауера (см., например, [14]). Объект с отличным от нуля
топологическим квантовым числом является устойчивым или ча-
стично устойчивым, поскольку он не может исчезнуть до тех пор,
пока ему не встретится объект с квантовым числом противополож-
ного знака. Приведенные выше соображения показывают, что
происхождение топологического квантового числа связано с усло-
вием однозначности е (х), а также с тем условием, что замкнутая
поверхность Cs не пересекает какую-либо часть области существо-
вания особенностей.
Выше выяснено, что вклад в формирование топологического
квантового числа v вносят особенности, образующие множе-
ство Ф d_N. Если множество^) более широкое, чем 3)d_N,TO e (х)
обладает некоторыми топологическими особенностями, не уча-
ствующими в образовании топологического квантового числа.
Поскольку эти последние особенности, по-видимому, неустойчивы,
наиболее важными являются те случаи, когда вклад в формиро-
вание топологических квантовых чисел вносят все особенно-
сти из S).
Полное условие, определяющее топологические особенности
в 2t>d_N~ Отметим, что из соотношения (Ш.3.43) следует равенство
^iGh-^.n = 0' A0.3.45)
являющееся обобщением A0.1.17). Если применить условие
A0.3.45) для анализа выражения A0.3.44), то мы увидим, что
исследуемый объект является (d — Л/)-мерным и не имеет замкну-
тых границ. Это согласуется с тем фактом, что величина v сохра-
няет смысл топологической постоянной до тех пор, пока замкну-
тая поверхность Cs не пересекает рассматриваемый объект. Заме-
тим, что точка (т. е. N = d) рассматривается в качестве 0-мерного
объекта, не имеющего замкнутой границы.
Множества топологических особенностей, имеющие более высо-
кую размерность. Мы рассматривали до сих пор только (N — 1)-
мерную замкнутую поверхность Cs. Обратимся теперь к вопросу
о том, каким образом замкнутые поверхности Cs более низкой
размерности (т. е. ds <. N — 1) в {.^-пространстве позволяют
описывать топологические особенности в области 3). Если по-
верхность Cs отображается на Se, то в результате получается
с!в-мерная поверхность Се. Рассмотрим ситуацию, когда Са не мо-
408 Глава 10
жет стянуться в точку, не пересекая некоторых особенностей
Тогда при любой деформации поверхности Cs размерность Се
нельзя изменить до тех пор, пока в процессе деформации Cs не пе-
ресечет какой-либо особенности из<2>. Следовательно, осуществляя
эту деформацию, всегда можно отобразить Се на с^-мерную
сферу S'e (рис. 10.10). Заметим, что совсем не требуется, чтобы S'e
находилась на Se. Поскольку Се нельзя стянуть в точку на Se,
существует некоторая сингулярная область в пространстве Se,
препятствующая такому стягиванию. Подобная ситуация резко
отличается от той, которая имеет место в случае (# — 1)-мерной
замкнутой поверхности Cs; в этом последнем случае на Se не воз-
никает особенности до тех пор, пока Cs не пересечет какой-нибудь
особенности из 2D.
Если отображение из {^-пространства на S'e обозначить
через е' (х) (сфера в (ef5 + 1)-мерном пространстве), то все рас-
суждения, касающиеся формул от A0.3.26) до A0.3.44), можно
применить и к отображению е' (х). (Но явное выражение е' (х)
через е (х) может оказаться весьма сложным и зависящим от рас-
сматриваемого объекта.) Таким образом, ^-мерная замкнутая
поверхность Cs задает (d — ds — 1)-мерный объект, положение
которого описывается функциями у (в1 ... ad_d {^, зависящими
от d — ds — 1 параметров. Этот объект не должен иметь замкну-
той границы. Однозначность е (х) приводит к однозначности е' (*).
Следовательно, топологическое квантовое число характеризует
также и (d — ds — 1)-мерные изолированные объекты. Но если
ds < (N — 1), то существование топологического квантового числа
не обязательно обеспечивает устойчивость таких объектов. Чтобы
понять это, вспомним о существовании сингулярной области
на Se, препятствующей стягиванию Се в точку. Поскольку при-
рода этой особенности зависит от физической или динамической
ситуации в системе, возможно, что особенности могут быть ликви-
дированы за счет некоторых физических процессов, обусловли-
вающих неустойчивость топологических объектов, (d — Л^)-мер-
объекты представляют добой исключение; так как С? в этом
Протяженные объекты С топологическими особенностями 409
случае имеет размерность (N — 1), на Se отсутствуют особен-
ности, и топологический объект, обладающий топологическим
квантовым числом A0.3.31), становится устойчивым.
Подводя итог, отметим, что замкнутые ^-мерные поверхности
(ds = 1, 2, ..., N — 1) задают топологические особенности в 2D,
представляющие собой совокупность (d — ds — 1)-мерных объек-
тов, не имеющих замкнутых границ и описываемых величиной
Gtll,,.il(l_d , определяемой выражением A0.3.44). Таким обра-
зом, 3) состоит из объектов, которые можно рассматривать как
Рис. 10.11.
дискретную или непрерывную суперпозицию а-мерных объектов
без замкнутых границ, причем а удовлетворяет условию
d — N^.a^.d — 2. A0.3.46)
Если множество^^состоит из объектов размерности а, то оно
будет обозначаться символом 2)а. Наименьшей размерностью об-
ладает множество 3)d-N- Изолированные (d —; Л^-мерные топо-
логические объекты описываются топологическими квантовыми
числами, которые возникают вследствие однозначности е (х) и
обеспечивают устойчивость этих объектов (рис. 10.11).
Модель SU B)-триплета и монополь. Проиллюстрируем про-
веденное выше общее рассмотрение на простом примерех).
Поскольку мы уже видели, как на основе этого рассмотрения;для
случая абелевой симметрии воспроизводятся результаты разд. 10.1,
рассмотрим теперь модель 5[/B)-триплета (т. е. G = SUB) и
Af = 3). Предположим, что е0 в A0.3.24) — единичный вектор,
направленный вдоль третьей оси в векторном пространстве Жа.
Тогда е (х) выразится в виде
е (х) = U (х) е3. A0.3.47)
Инвариантная подгруппа Н — это [/A) (h = 1), которая описы-
вает повороты вокруг вектора е3.
х) В литературе исследовались и некоторые другие примеры. См., в част-
ности, работы [12, 15].
410 Глава 10
Из A0.3.28) получаем
ех = sin 0Х cos 82,
е2 = sin 0! sin 92, A0.3.48)
е3 = cos Qy.
В этом случае из A0.3.33) находим
__ 1 d\ej(x), е„(х)} _d[Q2(x), cosM*)] ,]n,^
ftiv — -Yefitih d(Xll, xv) ~ d(Xll, xv) • К1"-*-™)
С другой стороны, поскольку U (х) — унитарная матрица,
ее можно представить в виде
U (х) = е1^ W ^ес^ <*> Ч><* <*> *\ A0.3.50)
где вх (х), 82 (х) и ф (х) — некоторые функции, at — спиновая
матрица размерности 3x3. Без потери общности можно выбрать
0Х (х) и 02 (х) в A0.3.49) совпадающими с обозначенными теми же
символами функциями в A0.3.50). Будем считать, что {хA}-про-
странство A + 3)-мерно, d = 4.
Топологическая особенность, имеющая наинизшую размер-
ность (т. е. соответствующая 0d_N), описывается формулой
A0.3.44):
GM (x) = 4nv | dx Щ^- б<4> [х - у(т)]. A0.3.51)
Согласно A0.3.45), имеем
дЮ^ (х) = 0. A0.3.52)
Соотношение A0.3.43) записывается в виде
4аЧ?ар(*) = МА (ю.3.53)
что эквивалентно соотношению (см. A0.3.37))
дивы М + д^ё^ (х) + dig^ (x) = 4vx (x), A0.3.54)
где
Glvji(*) = e?v».Gp(x). A0.3.55)
Поскольку особенность представляет собой точку в пространстве,
она может быть полностью окружена замкнутой поверхностью Cs.
Поэтому v принимает только целочисленные значения (т. е. яв-
ляется топологическим квантовым числом) v =0, ±1, ....
Если мы будем рассматривать т как временной параметр, то
в этом случае особенность — точка, перемещающаяся с течением
времени (ее траектория задается функцией у (г). Такой объект
называется монополем.
Попытаемся теперь выразить приведенные выше результаты
с помощью величины /wv. Если воспользоваться выражениями
I Протяженные объекты с топологическими особенностями 411
A0.3.50) и A0.3.8а), то непосредственное вычисление производ-
ной д^О (х) приводит к следующей формуле:
M*) = fn. (*)'*. A0.3.56)
где вектор fM = (/Jl1), f?\ /[?) определяется выражениями
f\l} (х) = sin 9, (х) cos ф (л:) 6^2 (х) - sin ф (х) 0^9, (х), A0.3.57а)
/f (х) = sin 0i (x) sin Ф (х) д^2 (х) + cos ф (х) д^ (х), A0.3.576)
/<?> (х) = cos 0, (х) Зцба (х) + ^ф (х). A0.3.57b)
При этом A0.3.49) принимает вид
g»v = - № (х) Д2) (х) - ff (х)/<!) (х)] = -ез- f»(x) хfv(x). A0.3.58)
Удобно также определить вектор fRV:
/(lv(x) = f,vW't. A0.3.59)
Из A0.3.16) и A0.3.58) находим
/$=/»$(*) +Яду, A0.3.60)
где
IV W = дЛ — ^д- A0.3.61)
Так как
dxKv + d^ + dJi^^O, A0.3.62)
из формул A0.3.54) и A0.3.60) следует
GU (х) = dkf$ + д^ + dv/$ • A0.3.63)
Это и есть Gjvj.! выраженное через Д^. Данная формула в явном
виде демонстрирует тот факт, что Gjvx определяет топологические
особенности этой конкретной комбинации, а не самой вели-
чины f^. Особенности, отвечающие f[lv, образуют область 2Du,
в то время как особенности, связанные с /Mve3 и G^v?., образуют
области Ф и Ф1 (= ^_аг) соответственно. Отметим, что S)x в каж-
дый момент времени состоит только из точек.
Чтобы увидеть взаимосвязь между этими тремя областями,
вычислим теперь f^, используя формулы A0.3.16) и A0.3.57),
В результате получим
fill = sin 9i cos ф [д», dv] 92 — sin ср [д^, dv] 0Ь A0.3.64а)
/^ = sin 9i sin ф [5ц, dv] 02 + cos ф [dv., dv] Qt. A0.3.646)
/JS = cos 9, [d#, av] 02 + [d» dv] Ф. A0.3.64b)
Эти выражения показывают, что f^v (а следовательно, и
имеет линейные особенности, если хотя бы у одной из функций
412 Глава 10
9Х (х), 92 (х), ф (х) имеется топологическая особенность. Согласно
формуле A0.3.63), эти линейные особенности не вносят вклада
в Gjvx. поскольку 3)г в каждый момент времени включает в себя
только отдельные точки. (Указанные линейные особенности пред-
ставляют собой (N—2) (=1)-мерные замкнутые петли, абелевы
по своей природе.) Поскольку из A0.3.50) следует
U (х) е3 = е1^ <*> *>е1в* « <2е3) A0.3.65)
при исследовании области особенностей^, определяемой соотно-
шением [д^, дх] U (х) е3 ф 0, можно выбрать q> = 0. Можно
также выбрать 92 (х) пропорциональной азимутальному углу:
tg (98/p) = х2!хъ A0.3.66)
где р — некоторая константа. Тогда получаем
1д1г д2] 92 = 2яр6 (Xl) б (х2). A0.3.67)
Из выражений A0.3.64) (при ер = 0) находим
№ (х) = 2яР6 (*,) 6 (х2) sin 9, (х),
,(i), , л A0.3.68)
lixv (х) = 0 в остальных случаях,
/$ (*) = [д„, dvVO, (х), A0.3.69)
f\f (x) = 2ярб (х,) 6 (х2) cos 9: (х), ,..57ffi
fix{ (х)~0 в остальных случаях.
Используя эти выражения, получаем
Gf23 (х) = аз/JI* (х) = 2прб (Xl) б (х2) да [cos 0i (*)], .,.._,.
+ (lU.o./l)
x) = 0 в остальных случаях
и
Л»е8 = (f 12 • t) e3 = (—0 /й'ея + tf[V* =
= —2ntp8 (jcj) б (*,) sin Эх (ж) еа + t [3i, dt] вх (ж) elf A0.3.72a)
/nves = i'Idji> 5V] 9 (х) ех в остальных случаях. A0.3.726)
Отсюда видно, что /^е3 (а следовательно, и $5) имеет линейные
особенности, которые возникают за счет 0! (х) и 02 (х).
Если выбрать 9Х (х) следующим образом:
cos 9, (х) = лгз/r (г2 = *2 + ^ + х§), A0.3.73)
то получим
б (лгх) 6 (х2) cos Эх (х) = е (х8) б (xj 6 (х2),
б (xj) 6 (х,) sin 9; (x) = 0 при х, ф Q (,10.
Протяженные объекты с топологическими особенностями 413
И
К' ду\ ei (*) = ° при х ^ 0. A0.3.746)
Значение 0Х в начале координат (хх = х2 — х9 = 0) не является
хорошо определенным. В этом случае из A0.3.72) следует
/MVe3 = 0 при х ф 0. [(Ю.3.75)
В данном конкретном случае область 2D не содержит линий; она
представляет собой точку в начале координат. Поскольку A0.3.71)
и A0.3.74) приводят к соотношению
G\k{x) = 2яР6 (*,) б (х2) б (*3), '(Ю.3.76)
2frx также оказывается точкой, расположенной в начале коорди-
нат: Ф = 3>х. Отсюда видно, что сделанный выше выбор отвечает
существованию статического монополя в начале координат. Одно-
значность е (х) обеспечивает целочисленность р, а это означает,
что в данном случае е'е» <*> '» однозначно.
Обобщим наше рассмотрение на такую ситуацию, когда на
третьей оси расположено несколько монополей. Потребовав, чтобы
G+2a (x) из A0.3.71) представляла собой суперпозицию б-функций,
получим
б (Xl) б (*я) д3 [cos 0! (х)] = у 6 (х,) б (х2) J] vt8 (х, - at), A0.3.77)
с
где ах <a2 <.... Благодаря условию квантования здесь vt —
целые числа. Таким образом, имеем
б (хг) б (.vg) cos 8X (х) = (v0 + -т- 2j vfi (*з — ai)\ б (дгх) б (х2). A0.3.78)
\ < /
Чтобы в качестве топологических особенностей выступали только
монополи, необходимо обращение б (хг) б (х2) sin Bx (х) в нуль
везде, кроме #з = «i> «a> ••• (см- A0.3.72)). Это означает, что
cos Эх = ±1 на каждом из отрезков оси х3 (т. е. при хг — х2 = 0),
на которые ее разбивают точки аг. При этом имеются следующие
возможности выбора параметров:
1) v0 = -1, vx = p, v2 = -р, ..., A0.3.79а)
2) v0 = 1, Vl = —р, v2 = р A0.3.796)
Отсюда следует, что монополи и антимонополи должны чередо-
ваться вдоль третьей оси при данном конкретном типе упорядоче-
ния, отвечающем одноосной симметрии [13, 16].
414 Глава 10
В общем случае топологический заряд зависит от выбора зам-
кнутой поверхности Cs, и мы имеем соотношение
ь
4nv == J dxi dx2 J dxA (x) = 4я -i- [cos 0, @, 0, b) - cos 0i @, 0, a)].
a
A0.3.80)
Замечание об инстантоне. Если заменить время t на it, то
пространство Минковского превратится в четырехмерное евкли-
дово пространство. В этом пространстве (d = 4) квадруплетная
модель (N = 4) неабелевой симметрии приводит к появлению
топологического объекта в некоторой точке пространства-времени
(например, при х№ = 0), поскольку d — ./V =0; эта точка пред-
ставляет собой область 3)d_N. Как показывает общее рассмотре-
ние, проведенное в данной главе, указанный объект обладает то-
пологическим квантовым числом. Этот объект называется инстан-
тоном [17, 18]; он привлек большое внимание физиков, работаю-
щих в области частиц высоких энергий. Lj
Метод бозонного преобразования. Зададим теперь вопрос,
каким образом за счет бозонного преобразования возникают рас-
сматриваемые топологические объекты. До сих пор мы описывали
топологические свойства с помощью функций U {х) и /„v (x).
С другой стороны, рассматриваемые топологические объекты обра-
зуются посредством конденсации некоторых бозонов {%а (х); а =
= 1, ..., т\. Нас интересует теперь, как /MV зависит от пара-
метров бозонного преобразования /" (х). В методе бозонного пре-
образования сначала рассматривают гейзенберговское поле if,
которое реализуется в пространстве Фока физических полей if =
= г|э (х; хй). Гейзенберговское поле, отвечающее той же системе,
но с протяженными объектами, описывается операторами ipf (x) =
= ^ (*; X" + /а)> гДе неоператорные функции fa удовлетворяют
уравнениям свободного поля для %а. Все неоператорные вели-
чины, такие, как матричные элементы матрицы калибровочного
преобразования U (х), компоненты параметра порядка v (x), ве-
личины /^ и т. д., являются некоторыми функционалами от fa (x).
Следовательно, происхождение топологических особенностей
должно быть связано с функцией fa, определяющей бозонное
преобразование. Чтобы выявить этот факт, представим U (х)
в виде
U(x)= 2 \№r[df{x)r\dll...d\lFl{x;ll...\l)df{ll)...df{ll),
A0.3.81)
Протяженные объекты с топологическими особенностями 415
где / обозначает fa, а символ df отвечает некоторым производным
от fa; Ft —• коэффициент разложения, являющийся однозначной
функцией своих аргументов (х, ^ ... ?;). Поскольку dfa — одно-
значные функции и имеет место соотношение
Ц, сМ I/ (*)]" = я I/ (х)Г-1 К, dv] f (x), A0.3.82)
получаем
y?^-ldll, dv]f(x), A0.3.83)
где
X j dlx ... dllFl (x, h... I,) df fo) ...df (I,). A0.3.84)
Таким образом, мы выяснили, что матрица [(/^)ар1 имеет вид
¦/,« W = ? са [/j [ад, av] /»w, (ю.з.85)
а
где
Q/J = U-Wlbfa. A0.3.86)
Это соотношение показывает в явном виде, как топологическая
особенность в /^v появляется за счет топологической особенности
в fa (x). В разд. 10.1 показано, что топологическая особенность
у fa может возникнуть в том и только в том случае, если в энерге-
тическом спектре %а-бозона отсутствует щель. Следовательно, то-
пологические объекты, рассмотренные в этом разделе, могут воз-
никнуть (даже в случае неабелевой симметрии) только путем
конденсации бесщелевых бозонов.
Теория калибровочных полей. Выше мы рассмотрели гейзен-
берговский оператор г|;, отвечающий Af-мерному представлению
компактной группы G, имеющей размерность п, и ввели матрицу
калибровочного преобразования U (х). В общем случае г|) вклю-
чает в себя гейзенберговские поля. Рассмотрим теперь случай,
когда г)? — гейзенберговское поле, и введем п векторных полей Лд
(т. е. Л?, а = 1, ..., п), а затем рассмотрим лагранжиан S (г|), А^),
инвариантный относительно преобразования
1> (*) -*-*' (*) = U (*) 1> (*). A0.3.87а)
Лц (х)-+А* (х) - U (х) (X (х) --!/,»(х)) LH (х), A0.3.876)
416 Глава 10
где /ц определено соотношением A0.3.8). Здесь g— некоторая
константа; Ац (х) в A0.3.876) — матрица Д, (х) = A^-ta. Теория
такого типа называется калибровочной теорией, а А^ (х) — ка-
либровочным полем. Простейшим примером подобной теории
является квантовая электродинамика. Вихрь в сверхтекучей
жидкости представляет собой топологический объект с линейной
особенностью в модели, отвечающей абелевой симметрии (т. е.
фазовой инвариантности), а Д, принимает вид дц1 (х). В данном
случае калибровочное поле отсутствует. Вихрь в сверхпровод-
нике — топологический объект того же типа, но уже в калибро-
вочной теории (т. е. в квантовой электродинамике). Калибровоч-
ная теория, соответствующая неабелевой симметрии, называется
теорией Янга—Миллса [19]. Если U (х) не обладает топологиче-
скими особенностями, то наличие /№ (х) не приводит к наблюдае-
мым эффектам благодаря калибровочной инвариантности теории.
Теория калибровочных полей, в которой отсутствует г|з, назы-
вается чисто калибровочной теорией.
Если мы введем величину
/> (*) = д„Ау (х) - dvAtt (х) + iglA^ (x), Av (x)}, A0.3.88)
то из A0.3.87) получим
/> (х) = <Vi; (*) - дуА» (х) + ig [АЬ (х), А; (х)] =
-Цх), A0.3.89)
где/ду определено в соотношении A0.3.16). Если у U (х) нет топо-
логической особенности, то мы находим, что f^ = 0, и, следо-
вательно,
Flv{x) = U (x) Fnv (x) U-1 (х). A0.3.90)
Таким образом, лагранжиан
2 (Лд) = ~ J #x Tr [F,,v (x) F*" (х)} A0.3.91)
инвариантен относительно калибровочного преобразования, если
у U (х) отсутствуют топологические особенности1). Поэтому мы
будем использовать 3? (А^) в качестве лагранжиана чисто ка-
либровочной теории. Лагранжиан 3S (Аи) приводит к уравнению
для чистого поля Янга—Миллса
-d*F$ (х) + ig К М. ^ (х)] = 0. A0.3.92)
х) Напомним, что в квантовой электродинамике требуется, чтобы калибро-
вочная функция к (х) имела фурье-образ.
Протяженные объекты с топологическими особенностями 417
Вводя величины FuV (=F?V, a = 1 п) и Ац (=Л?, а = 1, ...
.... я):
^iiv (*) = 2№а» A0.3.93а)
а
Л (*) = ?< (*) *а, A0.3.936)
а
можем написать
l^W-^Wl- A0.3.94)
Матрица ?а нормирована так, что Тг[ур] = -5-бар-
В качестве примера рассмотрим теорию Янга—Миллса, отве-
чающую группе SUB), где t — матрица размерности 2x2:
ta = оа/2, а = 1, 2, 3. A0.3.95)
Здесь оа — спиновые матрицы Паули размерности 2x2.
Особое внимание было привлечено к решениям вида
4.W = y*i.vdvpW. A0.3-96)
где {.^-пространство считается евклидовым. Здесь д^ опреде-
ляется соотношениями
a0J = —djo = — —Oj (/ = 1, 2, 3),
A0.3.97)
Из уравнения Янга—Миллса A0.3.92) получается следующее
уравнение для р:
а„ (daPJ - 2^^ (daPJ = о. (ю.з.эв)
В частности, исследуем следующие два решения: решение Поля-
кова [17]
рР = In A + г2), A0.3.99)
и решение т'Хофта [18]
( ^) (Ю.3.100)
Здесь г2=:.х?-|-*2 + *з + -^- Из решения Полякова следует
Определим величину а^ {х) по аналогии с A0.3.96), заменив а^
A0.3.103)
418 Глава 10
а из решения т'Хофта получаем
^ (Ы (Ю.3.102)
на auv:
где
ст0;- = —0/о = — °/> Ojy= — Rijh^h- A0.3.104)
Любопытно, что Яц (х) также удовлетворяет уравнению Янга—
Миллса A0.3.92). С помощью некоторых преобразований можно
показать, что Л^ HaJ связаны друг с другом соотношением
Л? = */(*) (а?+-±-/ц) и~1(х). A0.3.105)
Здесь U (х) — матрица калибровочного преобразования, отвечаю-
щая группе SU{2):
з
U (х) = е0 (х) + Ц е, (х) о,, A0.3.106)
где
бц (х) = xjr, r2 = Ху/Р, A0.3.107)
которая удовлетворяет условию
4+ IJ 4=1- (ю.3.108)
Топологическая особенность матрицы U (х) представляет собой
точку с координатами х^= 0, т. е. особенность типа инстантона.
Заметим, что /„ {х) в выражении A0.3.106) можно представить
в виде
/„ (х) = —it/-1 (л:) ад^/ (*) = — ffBvav In r2, A0.3.109а)
а
/„(jc) = —if/ (л) дд?/-' (х) = — a(lvdv In r2. A0.3.1096)
Решение Полякова Л? на бесконечности стремится к чисто ка-
либровочной функции fn (x), в то время как решение т'Хофта а^
в начале координат стремится к /^ (х):
• Al-y?- -— fv., A0.3.110а)
al *_-L/ A0.3.1106)
Протяженные объекты с топологическими особенностями 419
Кроме того, А.%, — везде регулярная функция, а а? имеет осо-
бенность при г = 0. Поэтому а? можно рассматривать как ре-
шение с источником в начале координат.
ЛИТЕРАТУРА
1. Matsumoto Я., Papastamatiou N. J., Umezawa Я., Nucl. Phys., B97, 90 A975);
Phys. Rev., D14, 3536 A976).
2. Wadati M., Matsumoto #., Umezawa Я., Phys. Rev., D18, 520 A978).
3. Matsumoto #., Sodano P., Umezawa H Phys. Rev., D19, 511 A979).
4. Umezawa H., Matsumoto H., Orders in nature: from quantum to classical.
Symmetries in science, Plenum, New York, 1980, p. 411.
5. Coleman S., Lecture at Erice Summer School, 1976.
6. Friedel J., Dislocations, Pergamon Press, Oxford, London, New York, 1964.
[Имеется перевод: Фридель Ж. Дислокации.—М.: Мир, 1967.];
Hirth J. P., Lothe J., Theory of Dislocations, McGraw-Hill, New York, 1968.
[Имеется перевод: Хирт Дж., Лоте И. Теория дислокаций. —М.: Атом-
издат, 1972.)
7. Wadati M., Matsumoto Я., Umezawa Я., Phys. Rev., B18, 4077 A978).
3. 't Hooft G., Nucl. Phys., B79, 276 A974).
9. Анисимов С. И., Дзялошинский И. Е., ЖЭТФ, 63, 1460 A972);
Toulouse G., J. Phys. Lett., 38, L67 A977).
10. Feldtkeller E., Zs. Angew. Phys., 19, 530 A965);
Slonczewski J. C, J. Appl. Phys., 45, 3129 A974);
Hagedom F. В., J. Appl. Phys., 45, 2705 A974).
11. Maki K-, Physica, 90B, 84 A977).
12. Finkelstein D., J. Math. Phys., 7, 1218 A966);
Arafune J., Freund P. G. 0., Goebel С J., J. Math. Phys., 16, 433 A975);
Patani A., Schlindwein M., Shafi 0., J. Phys., A9, 1513 A976);
Toulouse G., Kleman M., J. Phys. Lett., 37, L149 A976);
Юетап M., Michel L., Toulouse G., J. Phys. Lett., 38, L195 A977);
Воловик Г. Е., Минеев В. П., ЖЭТФ, 72, 2256 A977).
13. Matsumoio H., Umezawa Я., Umezawa M., Fortschr. Phys., 29, 441 A981).
14. Milnor J. W., Topology from the differential view point, University of Virgi-
nia, Charlottesville, 1965. [Имеется перевод переработанного издания: Мил-
нор Дж., Уоллес А. Дифференциальная топология.-—М.: Мир, 1972.]
15. Поляков А., ЖЭТФ, 68, 1975 A975);
Тюпкин Ю. С, Фатеев В. А., Шварц А. С, Письма в ЖЭТФ, 21, 91 A975).
16. Schiff Я., J. Phys., All, 173 A978).
17. Belavin A., PolyakovA., Schwartz A., Tyupkin Y., Phys. Lett., B59, 85 A975).
18. 7 Hooft G., Coral Gable Conf., 1977;
Jackiw R., Nohl C, Rebbi C, Phys. Rev., D15, 1642 A977).
19. Yang С N., Mills R. L., Phys. Rev., 96, 191 A954).
ГЛАВА 11
КВАНТОВАЯ ЭЛЕКТРОДИНАМИКА
ТВЕРДЫХ ТЕЛ
II. МАКРОСКОПИЧЕСКИЕ ЯВЛЕНИЯ
11.1. Вывод классического уравнения Максвелла
Макроскопические явления. Эта глава посвящена исследова-
нию макроскопических электромагнитных явлений в твердых
телах с помощью метода бозонного преобразования, который развит
в двух предыдущих главах. Хотя все явления, изучаемые физикой
твердого тела, имеют микроскопическую природу, многие из них
проявляются на макроскопическом уровне. Например, прово-
димость есть отношение макроскопического тока к макроскопиче-
скому электромагнитному полю. Вихри в сверхпроводниках дают
нам пример макроскопических объектов с топологическими особен-
ностями. В этом разделе мы выведем уравнение типа уравнения
Максвелла, которое определяет макроскопический ток и электро-
магнитное поле. Чтобы проделать это, мы осуществим некоторые
бозонные преобразования в приведенных в гл. 8 динамических
отображениях величин А» и /„.
Динамические отображения. Поле плазмонов «?, голдстоунов-
ские бозоны х° и духи Ь° появляются как в случае сверхпроводни-
ков, так и в случае нормальных проводников. Введем обозначение
P(x)=Zc(dOL°, (П.1.1)
где
Zc[(d)=-^Z]!2(d) A1.1.2а)
в случае сверхпроводников (см. (8.1.126)) и
Zc(d)=^rZ-Bi(d) A1.1.26)
в случае нормальных проводников (см. (8.2.30)). Согласно (8.1.112)
или (8.2.30), динамическое отображение гейзенберговского поля
электронов содержит фазовый множитель ехр (—if). В обоих
случаях, исходя из (8.1.50) или (8.2.31), получаем
B = --jrZ-ci(d){b°-xQ). A1.1.3)
Из лагранжиана (8.1.1) можно видеть, что существует электро-
магнитное взаимодействие двух типов. Одно из них вводится
Квантовая электродинамика твердых тел. II 421
путем замены dH -*-i (е/йс) А^ + дй в свободном лагранжиане
для электронов. Это взаимодействие называется минимальным
взаимодействием. Взаимодействие другого типа зависит от вектор-
потенциала только через F;/. Оно называется взаимодействием
F;;-THna. Обозначим через а? линейные члены в динамическом
отображении Ли:
В случае сверхпроводимости из (8.1.65) видно, что а? представляет
собой линейную комбинацию uJJ и д^Ь°. В случае нормальных
проводников а? кроме wj} и ддЬ0 содержит еще В. Поскольку г|з
имеет фазовый множитель ехр (—if0), определим функцию ф =
= ехр (if0) г|э, которая калибровочно инвариантна. Выражая через
¦ф уравнение Гейзенберга для поля электронов, видим, что в случае
минимального взаимодействия Лд заменяется выражением А^ —
— (tide) dj0, линейный член которого представляет собой комби-
нацию [ajj,— (tide) du/°]. Поэтому в динамическом отображении
любого калибровочно инвариантного оператора величина dj°
появляется только в указанной выше комбинации, в то время как
аЦ может также входить в выражение вида
/?/ = д,а?-д/а?. A1.1.5)
Таким-образом, динамические отображения Л„ и о|з имеют вид
А* (х) = а0» (х) + : А„ (дг; &-&- dxf°, fi{, В, Ф°) :, A1.1.6а)
*(*) = : ехр [-if0 (х)] ф (х; о» - Ц- d%f, /?/, В, <?°) :, A1.1.66)
где ф° — поле квазиэлектронов. Эти соотношения следуют из
(8.1.128) и (8.1.129), а также из (8.2.29) и (8.2.30).
Поскольку ток/ц калибровочно инвариантен, его динамическое
отображение имеет вид
-'-, A1.1.7)
где /° = -S; (д) (a°v - М- д/) . A1.1.8)
Многоточие в формуле A1.1.7) заменяет нормальные произведения
более высоких порядков, составленные из а° — (tide) dkf°, fj/, В
и ф°. Формула A1.1.7) включает динамические отображения /„
(как в случае сверхпроводника, так и в случае нормального ме-
талла), полученные в гл. 8. Из приведенного выше результата
видим, что
14 Умэдзава X. и др.
422 Глава 11
представляет собой неприводимую часть собственной энергии
фотона. Здесь gj[ — метрический тензор.
Динамическое отображение/,? получается из A1.1.8), если мы
исключим из 2^ (д) и 2jlv (д) производные по времени, используя
уравнения свободных полей для «JJ и %° и Ь°. Сделаем теперь очень
важное замечание относительно бозонного преобразования. Когда
/° подвергается бозонному преобразованию/0 + / (х) и неоператор-
ная функция / (х) содержит топологическую особенность,
D (д) dj (х) Ф О, даже если D (д) f (х) == 0. Поэтому, подготав-
ливая формулу, описывающую динамическое отображение, для
осуществления бозонного преобразования, необходимо учитывать
порядок действия производных в тех случаях, когда для исключе-
ния производных по времени используются уравнения свободных
полей. В A1.1.8) сохранены производные по времени.
Выразим уравнения свободных полей, используя не и^,, %"
и Ь°, а а?, /°, В. Соответствующие уравнения имеют вид
?>(д)/° = 0, A1.1.9а)
D (д) В = 0, A1.1.96)
(~d2gl + d»dv)a% = /° - Щ(д) fiS + с»{д)В. A1.1.10)
Бозонное преобразование. Рассмотрим бозонные преобразова-
ния, которые оставляют приведенные выше уравнения неизмен-
ными:
/° (*)->/° (*) + /(*), A1.1.11а)
В(х)-*В(х), A1.1.116)
Поскольку это преобразование должно сохранить инвариантность
уравнений свободного поля A1.1.9), неоператорные функции / (х)
и а^ {х) удовлетворяют соотношениям
(-а2^ + д»ду) о, = Уд - Щ (д) flh A1.1.12)
D(d)f(x) = 0, A1.1.13)
где
J^-K(d)(av-^-dvf), A1.1.14)
U^dtuj-djat. A1.1.15)
Заметим теперь, что условия калибровки (8.1.62) или (8.2.7)
представляют собой составную часть уравнения Гейзенберга. Эти
условия приводят к уравнению
D»(d)aVL = Q. A1.1.16)
Квантоёйя электродинамика твердых тел. It 423
Уравнения A1.1.12), A1.1.13) и A1.1.16) называют уравне-
ниями максвелловского типа. Эти уравнения отвечают за макро-
скопические аспекты электромагнитных свойств твердых тел
[1—3 ]. Заметим, что условие, определяющее физическое состояние
(8.1.35) или (8.2.10), не изменяется в результате преобразования
A1.1.11).
Формулы A1.1.6а) и A1.1.7) показывают, что вещественный
классический вектор-потенциал и ток даются выражениями
йд = @|Лй|0)= A1.1.17)
= а„+..., A1.1.18)
^ = <0|/J0)= A1.1.19)
= ^ - ^ (d) A/+ .... A1.1.20)
Здесь многоточие заменяет произведения более высоких порядков,
составленные из J}, и /гу-.
Беря вакуумное среднее от уравнения Гейзенберга (8.1.16)
или (8.2.5), мы можем получить классическое уравнениеМаксвелла
(-^ + ^vMv = J(l. A1.1.21)
Из этого уравнения видно, что члены высших порядков в разложе-
нии A1.1.20) включают в качестве множителя оператор (—cPgl. -\-
+<wo ¦¦
7» (*) = У „ (х) - Щ[ (д) fti (х) + (-d2gl + ^dv) Fv (x; JK, ft]),
A1.1.22)
где Fv — нелинейные члены разложения, составленные из J^
и ft,-.
Топологические особенности. Рассмотрим теперь важную тео-
рему, согласно которой бозонное преобразование A1.1.11) может
приводить к макроскопическим эффектам только в том случае,
когда / (х) обладает некоторыми топологическими особенностями.
Чтобы доказать это, вспомним уравнение (8.1.143) или (8.2.44),
в которых величина 2Ц„ разделена на продольную и поперечную
части:
2uv (р) = 2Г (р) 7VV + 20 (р) (р*Ь^ - р^). A1.1.23)
Заметим, что, поскольку p^L^ = pv и L^vpv == р№, мы имеем
Anv - PuPv = (p2gl - рУ) Uv = (ИЛ-24)
pVv). A1.1.25)
424 Глава 11
Заметим также, что
П dvf = Т{ dj = -^г (V8,, - didj) d,f = -^-д/ [д,, ds] /, A1.1.26)
(d^v _ дк&) dvf = ^ [dv, 54 /. A1.1.27)
Если / не имеет топологических особенностей, то [д^, dv] / = О
и, следовательно, 2^ (д) dvf = 0. Таким образом, / выпадает из
уравнения максвелловского типа A1.1.12), т. е. любое / без топо-
логических особенностей не приводит к макроскопическим явле-
ниям. Причина этого лежит в калибровочной инвариантности
теории. Поскольку / — фаза электронного поля, при отсутствии
у нее какой-либо топологической особенности ее действие заключа-
ется просто в изменении калибровки и не приводит к наблюдаемому
эффекту. Как видно из уравнения A1.1.1), /"совпадаете голдстоу-
новским полем %° (если исключить множитель Zc). Поскольку /° —
свободное поле, соответствующее голдстоуновскОму кванту, оно
имеет фурье-представление, выражаемое через операторы рожде-
ния и уничтожения. Как показано в разд. 8.1, состояния, отвечаю-
щие этому голдстоуновскому кванту (а также духам), ненаблю-
даемы благодаря накладываемому на физические состояния огра-
ничению (8.1.35) или (8.2.10). Эта ситуация описывается посред-
ством утверждения, что поле/0 (а также поле духов Ь°) устраняется
с помощью выбора соответствующей калибровки; оно не наблю-
даемо. Если неоператорная функция / (х) имеет фурье-образ, то ее
тоже можно исключить посредством выбора калибровки. Но / (х)
с топологическими особенностями может приводить к наблюдаемым
явлениям.
Если / не вносит вклада в J^, то уравнение A1.1.12) принимает
вид
{-d2gl + д^) о, = - 2* (д) av - 2^ (д) fih A1.1.28)
Это уравнение, описывающее классические плазменные колебания.
В разд. 10.1 мы убедились в том, что макроскопические объекты
в нормальных проводниках не обладают топологическими кванто-
выми числами. Следовательно, эти объекты неустойчивы. Поэтому
мы можем пренебречь / (х) в уравнении максвелловского типа
A1.1.12). С другой стороны, макроскопические объекты в сверхпро-
водниках могут иметь топологические квантовые числа (например,
связанные с квантованием магнитного потока вихрей). Таким
образом, / (х) играет существенную роль при описании макроскопи-
ческих явлений в сверхпроводниках.
Любопытно, что классическое уравнение Максвелла имеет
один и тот же вид как в случае сверхпроводников, так и в случае
нормальных проводников. Но поведение 2^ в статическом пределе
различно: для сверхпроводника величина 2^ @) отлична от нуля,
Квантовая электродинамика твердых тел. II 425
в то время как для нормального металла она обращается в нуль.
Благодаря наличию члена 2^av в выражении для тока даже
в статическом пределе возникает мейсснеровскииток и появляется
глубина проникновения в сверхпроводниках, а этот же член при
более высоких частотах приводит к тому, что свет почти полностью
отражается как от сверхпроводников, так и от нормальных метал-
лов (плазменная частота). Другая характерная особенность, кото-
рая отличает сверхпроводники от нормальных проводников и
делает сверхпроводники диамагнитными, заключается в кванто-
вании потока для вихрей в сверхпроводниках. Благодаря этому
прохождение магнитного потока через сверхпроводник затруд-
нено. Существует еще одно свойство, отличающее сверхпровод-
ники, а именно их бесконечная проводимость. Это свойство рас-
сматривается в разд. 11.2.
Линейное приближение. Если отсутствует взаимодействие
F;/-THna, то fa в выражении A1.1.22) обращается в нуль, a F^
представляет собой разложение по степеням только линейного
тока /и, причем каждый член размазан в пространстве. В этом
случае член с F^ может стать пренебрежимо малым, когда / (х)
не испытывает нигде резких изменений, поскольку на Fu в A1.1.22)
действует дифференциальный оператор. Итак, получаем
J^^J», A1.1.29)
а^а», A1.1.30)
и линейное уравнение A1.1.12) превращается в уравнение Макс-
велла A1.1.21). Это приближение называется линейным.
11.2. Проводимость и диэлектрическая
проницаемость
Магнитная индукция и электрическое поле. В этом разделе
мы воспользуемся линейным приближением. Магнитная индукция
В и электрическое поле Е даются выражениями
A1.2.1)
Ei = (-V»Ob + dQat) = fOi. A1.2.2)
Эти две величины связаны между собой соотношением
d0B=VxE. A1.2.3)
Заметим, что
426 Глаза И
Для простоты примем, что взаимодействие ^г/-типа отсутствует.
Постулируем также наличие внешнего тока /^xt, инжектируемого
в металл. Таким образом, уравнение максвелловского типа при-
нимает вид [1 ]
-д%» = -2Ъ(д) (a%-^Ldxf)+iT- (П.2.4)
При учете соотношения A1.1.23) уравнение A1.2.4) выражается
через В и Е следующим образом:
[l+2o(d)]V-E = -J?-2o@)V-[V, do]/ + /oxt, (H.2.5)
[1 + 20 (д)] (V X В - д°Е) = [2Г (д) + <3220 (д)\ -L х
х (vxb +M-Vi\sih v]/)_Jiso(a)^[aXl vi/ + jext. (i 1.2.6)
Рассмотрим явления, обусловленные только внешним (пробным)
током, т. е. при / = 0. Соотношения между пробным током и
электромагнитным полем имеют вид
?gxt = [l + 2o(d)jV.j, A1.2.7)
j«* = V X B-E--Jr[2r(fl)-do2o(d)]VxB-2o(d)E. A1.2.8)
Диэлектрическая проницаемость и проводимость. В электро-
динамике часто используется величина, называемая электрической
индукцией D, которая вводится с помощью соотношения
V-D^/S'V). A1.2.9)
При этом тензор комплексной диэлектрической проницаемости
йц (р) определяется следующим образом:
Dt(p)=bt,(p)E,(p), A1.2.10)
где D (р) и Е (р) — фурье-образы D (х) и Е (х):
D W = W JdipD {p) e'PX и Tl д- (П-2.11)
Имеется некоторая неопределенность в задании электрической
индукции D (х), поскольку соотношение A1.2.9) не определяет ее
однозначным образом.
Обычный метод исключения этой неоднозначности заключается
в использовании поляризации Р, обусловленной локализованными
молекулами или локализованными электронами и ионами; Р
даетфя выражением
O-e-fP, (И.2Л2)
Квантовая электродинамика твердых тел. II 427
где использованы единицы Хевисайда. Поскольку
-V-P = /Jnd(x), A1.2.13)
где у?Л (х) — наведенный ток, определяемый выражением
/!Га(*)==-^м» (*)-/"'(*), A1.2.14)
имеем
V.P = -/ondW = V-jind(x), A1.2.15)
Таким образом, можно отождествить
P = jind(jr). A1.2.16)
Используя A1.2.10), A1.2.12) и A1.2.16), находим
/1nd (Р) = ipo [8ц - hi Ш Е, (р). A1.2.17)
Выражение для наведенного тока A1.2.14) может быть преобразо-
вано с помощью соотношения A1.2.3), связывающего В и Е,
к виду
/1nd (р) = -^ BГ (Р) б,7 - [2г (Р) + Р&о (р)] Ш1-) Е, (р), A1.2.18)
/Jnd(rt = «-2O(P)(P-E). A1.2.19)
Сравнивая A1.2.17) с A1.2.18), имеем
«</ (Р) = б.'/ - -jf Bг [р) 8,7 - [2
= 6i/--l-2i/(/J). A1.2.20)
Поскольку из A1.1.23) следует равенство
ptli/(p) = pl^0(p)Pi, A1.2.21)
получаем соотношение
-E=^xt, A1.2.22)
которое согласуется с определением A1.2.9). Подводя итог, заме-
чаем, что тензор диэлектрической проницаемости &ц может быть
вычислен в соответствии с A1.2.20) [1 ]х). Комплексная диэлектри-
ческая проницаемость е (р), определяемая из соотношения
p.D(p) = e(p)p.E, A1.2.23)
дается формулой
е (р) - 1 + 20 (р). A1.2.24)
г) См. статью Нозьера и Пайнса [1], в которой рассматриваются диэлектри-
ческая проницаемость и проводимость нормальные металлов,
428 Глава 11
Это демонстрирует нам физический смысл перенормировки заряда:
когда в систему вносится пробный заряд, полный заряд с учетом
поляризации равен
er = V-E= е (д) V-D = е/A + 20),
что приводит к формуле ег = —eZ0, где Zo == —1/A + 20) (см.
(8.2.49) и (8.2.65)).
Тензор комплексной проводимости дц (р) определяется соот-
ношением
i?d(p) = dt,(p)E,(p). A1.2.25)
Отсюда, согласно A1.2.17), имеем
ail(p) = ip0[8ij-sij(p)], A1.2.26)
что с учетом A1.2.20) дает
Ъц(р) = 1-^2ц(р). A1.2.27)
В теории линейного отклика проводимость связывается с ослаб-
лением корреляции ток—ток. Поскольку электрическое поле Е
представляет собой сумму внешнего и наведенного полей, эффект
перенормировки фононов включен в Е. Поэтому проводимость
определяется не всей корреляционной функцией ток—ток, а только
ее неприводимой частью (т. е. 2г/). Принимая это во внимание, мы
видим, что соотношение A1.2.27) согласуется с результатом,
следующим из теории линейного отклика [4].
Из A1.1.23) видно, что сумма 2Г (р) + Ро^о (р) Должна обра-
щаться в нуль при р = 0, чтобы функция 2UV (p) была хорошо
определена при р = 0. Использовав еще раз A1.1.23), получим
соотношение
2,7 (Р) = -р&о (р) б,7 при р = 0. A1.2.28)
Таким образом, тензоры ёг;- (р) и бц (р) в пределе р = 0 диаго-
наль ны:
е,7 Со) = [1 + 20 (р)] 6„ при р = 0, A1.2.29а)
frj/ (Р) = —iPo^o (р) «г/ при р = 0. A1.2.296)
Диэлектрическая проницаемость 8 и проводимость <т в статическом
пределе определяются вещественными частями ё и д при р = 0:
e=limRe[l + So(p)]p=o, A1.2.30а)
Ро->
q = lim Im[/>0?0 (p)]P=g. A1.2.306)
Pt-Q
Квантовая электродинамика твердых тел. II 429
В случае нормальных металлов 20 (р) обладает структурой
если учесть влияние примесей и температуры. Но в случае сверх-
проводников из (8.1.149) видно, что 20 (р) имеет полюс типа
MD (р), обусловленный наличием коллективной моды. Даже при
учете влияния примесей и температуры коллективная мода устой-
чива при р = 0. Следовательно, 20 (р) при р = 0 имеет слагаемое
с полюсом типа 1/рц и дает вклад в а типа б (р0), а это означает, что
проводимость сверхпроводников бесконечна.
Наконец, исследуем поперечные составляющие 2Г (р) в одно-
родном и статическом пределе. Соотношения A1.2.28) и A1.2.31)
показывают, что в нормальном металле 2Г (р) обладает струк-
турой
Следовательно, в статическом пределе 2Г (р) — 0, что означает
отсутствие мейсснеровского тока. В сверхпроводниках существо-
вание полюса у 20 (р) предотвращает обращение 2Г (р) в нуль
в статическом пределе, обусловливая мейсснеровский ток. Таким
образом, мейсснеровский ток и проводимость тесно связаны друг
с другом.
11.3. Сверхпроводимость
Уравнение максвелловского типа. В случае сверхпроводимости
могут появиться разнообразные топологические объекты, связан-
ные с наличием топологических особенностей функции / (х).
Поэтому мы оставим эту функцию в уравнении максвелловского х)
типа (см. A1.1.12)). Сначала будем предполагать, что взаимодей-
ствие Fjy-типа отсутствует. При этом имеем 2)
(~d2gl + d»dv) av = -2; (д) (av - Щ- dv/) = 4л/ц, A1.3.1)
D(d)f(x) = 0, A1.3.2)
D» (д) а» (х) = 0. A1.3.3)
x) В этом разделе при описании магнитных свойств сверхпроводников вместо
единиц системы Хевисайда используются единицы гауссовой системы.
2) Заметим, что если мы хотим использорать ковариантное выражение, ток }
иметь множитель 1/е,
430 Глава 11
Уравнение Лапласа. Введем функции
(П.3.4)
AL3-5)
A1.3.6)
В формуле A1.3.5) dSy — элемент поверхности, ограничивающей
систему. Сингулярная область также должна быть заключена
внутрь граничной поверхности. Поскольку [дц, dv] dj = 0
функция ft (х) не имеет особенностей. Таким образом, /s — сингу
лярная часть /. Заметим, что *)
V2/s = 0. A1.3.7)
Поскольку вклад в величину поля /wv и тока J^ вносит только
сингулярная часть, мы можем в A1.3.1) заменить / на/8. При этом
уравнение A1.3.2) заменяется уравнением Лапласа A1.3.7). Из
этого уравнения видно, что V/s — «поперечный вектор», так как
V-V/s =0. Другими словами, мы имеем ^
Tudjft = dtft. A1.3.8)
Вот почему в уравнении максвелловского типа член с dvf, хотя он
по виду и является продольным, может привести к появлению
поперечного тока.
Энергия протяженных объектов. Рассчитаем теперь энергию,
связанную с макроскопическими током и полем, воспользовавшись
линейным приближением. В этом приближении мы учитываем
только билинейные члены в гамильтониане. Поэтому оператором
энергии оказывается гамильтониан для свободных полей и0,
Ь° и %°. Поскольку
A1.3.9)
представляет собой уравнение для ы?, поле плазмонов в операторе
энергии должно описываться членом
A/8л) Ш + A/2) (Ш + фГ (д) al\.
Здесь использована гауссова система единиц. Кроме того, вклад
поля х° обусловливает замену а? на [а$, — (йс/е) dj°]. Таким
1) Подход, основанный на использовании кулоновской калибровки, непо-
средственно приводит к уравнению Лапласа у2/ = 0 (см. рассмотрение, следу-
ющее за формулой A1.3.42)).
Я° = Ж J
Квантовая электродинамика твердых тел. II 431
обравом, оператор электромагнитной энергии в линейном прибли-
жении должен иметь вид
Т
Бозонное преобразование A1.1.11) приводит к возникновению
состояния с энергией Е [f] = @|#?|0), где #? — гамильтониан
#0 после бозонного преобразования. Из A1.3.10) следует
х)] A1.3.11)
Этот результат получен в работах [2, 5 ].
Ниже мы будем рассматривать только статический случай
f (х) = / (х). Так как av и / равны нулю, уравнение A1.3.1) при-
нимает вид
— 2? (д) av. A1.3.12)
С другой стороны, из A1.1.23) следует
2v0(d)av = -~-Z0(d)V2a0. A1.3.13)
Таким образом, имеем
[1 + 20 (d)] V4 = Q, A1.3.14)
откуда получаем У2«о = 0- Поскольку нас интересуют только
такие Оц, которые обусловлены существованием / (т. е. а^ =0
при / = 0), видим, что av = 0 для /, не зависящих от времени,
а следовательно, До = 0. Кроме того, исходя из уравнения A1.3.3),
имеем Va = 0, а это означает, что а имеет только поперечные
компоненты. Теперь A1.3.11) приводит к следующему выражению
для энергии в статическом случае:
= AL3-15)
A1.3.16)
A1.3.17)
A1.3.18)
где Н (х) — локальное магнитное поле:
Н (х) = V X а, A.3.19
а GJv определяет топологическую особенность, согласно A0.1.3),
$ (И.3.20)
432 Глава 11
В A1.3.18) мы использовали Н вместо В. В рассматриваемом
случае В (х) «= Н (х), но выражение A1.3.18) остается верным
даже в том случае, если равенство В = Н нарушается из-за
взаимодействия F^-rana. Из A1.3.18) видно, что энергия опре-
деляется величиной магнитного поля в тех точках, где имеются
особенности.
Параметр порядка. Бозонное преобразование A1.1.11), в ре-
зультате которого г|з заменяется на г|э/, приводит к зависимости
параметра порядка от /:
A1.3.21)
В соответствии с A1.1.66) и A1.1.14) А (х) имеет следующую
структуру:
А (*) = ехр [-2// (*)] F (х; JJ, A1.3.22)
где F = \ А (х)\ — разложение по степеням J^. Другими словами,
F зависит от df через J^, в то время как / без производных появля-
ется в A1.3.22) только в фазовом множителе. Отметим, что как ток,
так и параметр порядка определяются функцией /, отвечающей
бозонному преобразованию; эти две величины связаны между
собой посредством /. Если параметр порядка при J = 0 обозначить
через А, то
F(х) = А + J d4| J d*oF»" (x - I, x - о) /ц (|) J4 (a) + ... . A1.3.23)
В F отсутствует член, линейный по J^. Все коэффициенты разло-
жения не зависят от /, так как зависимость F от / появляется
только благодаря /д (х). Поскольку /„ (х) — всюду гладкая
функция, следует ожидать, что каждый нелинейный член разложе-
ния по степеням </д также будет гладкой функцией. В выражении
для тока /№ (х) нелинейные члены включают в себя дифференциаль-
ный оператор (cPg^ — дцдУ) (см. A1.1.22)). Поэтому вклад от не-
линейных членов в 7и (х) предполагается малым. С другой сто-
роны, нелинейные члены параметра порядка могут быть не столь
малыми, как в выражении для тока. Действительно, F (х) в A1.3.23)
должно обращаться в нуль в точках, где/ имеет особенности, чтобы
параметр порядка А (х) A1.3.22) был хорошо определенной
функцией в этих точках. Поэтому нелинейные члены в | А (х) |
должны вносить столь существенный вклад, чтобы скомпенсировать
А в особых точках. Если рассматриваемая точка далека от особен-
ности, то следует ожидать, что вклад от нелинейных членов, обус-
ловленный интегралами перекрытия, окажется малым и не будет
резко изменяться. Эти интегралы перекрытая начинают постепенно
Квантовая электродинамика твердых тел. // 433
вносить вклад при приближении к особым точкам на расстояниях
меньше эффективного радиуса действия коэффициентов в формуле
A1.3.23) С
На первый взгляд создается впечатление, что уравнение для
параметра порядка, поскольку оно содержит а, вместе с уравне-
нием Максвелла образует единую систему. Однако эти два уравне-
ния расцепляются благодаря наличию члена 5v/b уравнении макс-
велловского типа. Как только задана функция / (х), векторный
потенциал а (х), внутреннее магнитное поле Н (х) и ток J (х)
можно получить из уравнения максвелловского типа A1.3.1).
Воспользовавшись полученной таким образом функцией а (х),
можно попытаться вычислить параметр порядка А (х).
Вычисление неприводимой части собственной энергии фотона.
Чтобы завершить вывод уравнения максвелловского типа A1.3.1),
необходимо вычислить 2^ (д). Мы воспользуемся гамильтониа-
ном БКДП E.4.1) и учтем электромагнитное взаимодействие. Иными
словами, наш лагранжиан включает в себя как электромагнитный
лагранжиан (8.1.1), так и член, описывающий электрон-электрон-
ное взаимодействие типа БКШ Уф+Ф+ф^. Это взаимодействие
мы будем называть V-взаимодействием.
Попытаемся сначала вычислить 2UV в однопетлевом приближе-
нии. К сожалению, при этом не возникает особенности типа полюса
IID (р), обусловленной коллективной модой (т. е. полем /°).
Полюсная особенность в 2^ весьма существенна: как мы видели
в предыдущем разделе, именно с этой особенностью связана
бесконечная проводимость сверхпроводников. Поэтому мы обра-
тимся к цепочечному приближению. Так как 2UV (p) определяется
неприводимыми диаграммами, ее нельзя разделить на две части,
рассекая внутреннюю фотонную линию. Следовательно, все петли
соединяются между собой за счет V-взаимодействия. Если цепочка
состоит более чем из одной петли, то петли на обоих концах имеют
вершины двух типов: векторную вершину, обусловленную током, и
скалярную, возникающую благодаря V-взаимодействию (рис.
11.1). Каждая из этих крайних петель пропорциональна р. По-
этому цепочки, включающие более одной петли, хотя и приводят
к появлению полюса 1/D (р), вносят вклад только в продольную
часть 2^. По существу член с полюсом 1/D (р) представляет собой
434 Глава 11
множитель при проекционном операторе, выделяющем продольную
часть 2j,v.
В результате даже при использовании цепочечного приближе-
ния поперечная составляющая тока определяется однопетлевой
диаграммой, в то время как в продольный ток вносят вклад все
цепочечные диаграммы. Поэтому 2^v, определяемая цепочечными
диаграммами, не удовлетворяет соотношению (8.1.142)
p»\v (p) = 0, A1.3.24)
которое является следствием закона сохранения тока. Другими
словами, в рамках цепочечного приближения нарушается закон
сохранения тока.
Очевидно, что соотношение р^^ (р) = 0 должно автомати-
чески выполняться при учете всех диаграмм. Поскольку цепочеч-
ные диаграммы, включающие более одной петли, вносят вклад
только в продольную часть 2UV) эти диаграммы следует дополнить
другими, чтобы удовлетворить условию /^2^ (р) = 0. Хотя это
равенство нелегко получить с помощью фейнмановских диаграмм,
мы будем им пользоваться, чтобы найти недостающую поперечную
часть 2UV. Поскольку в неприводимой части собственной энергии
отсутствуют мостики, состоящие из одной фотонной линии, она
в цепочечном приближении совпадает с величиной
п
если не учитывать электромагнитное взаимодействие. Данная
величина была вычислена в разд. 5.4; она равна йА (&), где A (k)
дается выражением E.4.128) х)
2оо (Р) = -4л |L г!2 (р) plUB (сов) -—¦ tUb М + .. . , A1.3.25)
где сов в D(p) = —pi -\- с~2сов заменено на сов — ?8т. Многоточие
отвечает членам, не имеющим полюсной особенности. Отметим, что
линейный по /° член в динамическом отображении /„ должен
быть пропорциональным D^ (p), поскольку из соотношения
д^Оц (д) /° —D (д) /° = 0 следует закон сохранения тока д"/ц =
= 0. Поэтому выражение A1.3.25) можно обобщить следующим
образом:
2»v (Р) = -4я ? yf (p) ?>„ (р) UB (coB) jL- XVB (coB) Dv
A1.3.26)
В случае явлений, характеризующихся медленными изменениями
(т. е. малыми р0), 2№V (p) можно с хорошей точностью описать
1) В E.4.128) pi заменено на сш|.
Квантовая электродинамика твердых тел. II 435
полюсным членом, пренебрегая членами, обозначенными много-
точием (полюсное приближение). Если мы будем рассматривать
A1.3.26) как продольную часть Suv, то условие A1.3.24) приводит
к выражению
V (р) = 4я -|гrf (p) UB Ы [(^) V. (р) -
] A1.3.27)
где матрица г\^у определяется формулой (8.1.76):
— (vB/c)~2
О
A1.3.28)
О ' " "
При выводе выражения A1.3.27) использовано соотношение
P-Xv (р) = (vB/c)-* Dv (p). A1.3.29)
Отсюда -находим
v --^-av/)T, (п.з.зо)
где использована формула D.1.88), т. е.
UbtUb=t. A1.3.31)
Наблюдаемый ток определяется матричным элементом тп в
A1.3.30). Обозначая наблюдаемый ток тем же символом /„, имеем
^-^д4), (Н.3.32)
так как ти = 1. Результат A1.3.32) учитывает эффекты, связанные
с коллективной модой (т. е. имеется член типа IID (р)), и находится
в согласии с условием р^^ = 0.
Характеристическая функция бозонов и лондоновская глубина
проникновения. В разд. 5.4 ввели посредством формул E.4.165)
и E.4.166) характеристическую функцию бозонов с (р) и лондонов-
скую глубину проникновения iL соответственно:
с (Р) = v% (р) г]2 (p)/t& @) г!2 @), A1.3.33)
= Dле2/й2с2) v% @) ri2 @). A1.3.34)
436 Глава 11
Используя эти величины, мы можем записать A1.3.32) в виде
_ йс л А /11 q ос\
„ —J--Uvjrj — {II.0.00)
= - -Jp- | d3t/c (х — у) tiH (d) (av (у) - Ц- dvf (y)\ , A1.3.36)
где ty = tx, a
^--3-c(k)e'kx. A1.3.37)
Согласно формуле A1.3.33), имеем
с (к) = 1 при к = 0, A1.3.38)
откуда следует
\d3xc(x) = 1. A1.3.39)
В этом случае уравнение максвелловского типа принимает
вид [2, 3, 5]
(д% - d»dv) av (x) = ~\ d'ye (x - у) г,* (д) (av (у) - -^ dvf (у)) .
A1.3.40)
Функция с (к) и константа KL получены в разд. 5.4. В част-
ности, согласно E.4.171), при Г=0 KL определена соотношением
1 %L). A1.3.41а)
Плотность сверхпроводящих электронов ns определена соотно-
шением
A1.3.416)
где т — масса электрона. Отметим, что плотность ns не обяза-
тельно равна электронной плотности п. Хотя Dяе2п/т) равно
(vplJ, где vpl — плазменная частота, \/К\ в формуле A1.3.41)
не всегда равно (vp/J/ca. В самом деле, в ns (а значит, и в 1/Х/,)
вносят вклад только электроны, находящиеся в окрестности по-
верхности Ферми (т. е. те, которые образуют куперовские пары),
в то время как при вычислении (vp,J учитывается существенно
большее число электронов. Это является отражением упомянутого
выше факта, что A/Я1)с(р) отвечает ^(р) не при ро = юр/,
а при р0 = сов (р; < сор/.
Вычисления показывают, что уравнениеA1.3.40) в случае одного
вихря приводит к появлению линейного тока J^, который равен
нулю в центре вихря, постепенно растет в области г < KL, про-
ходит через максимум и экспоненциально спадает при больших г.
Следовательно, J^ везде является гладкой функцией. Поэтому мы
Квантовая электродинамика твердых тел. II 437
полагаем, что разумно воспользоваться линейным приближением:
?ц ^ /ц и й„ = йц. Гладкость функции /^ обусловлена коллек-
тивной модой, благодаря которой формфактор с (х — у) оказыва-
ется сильно нелокальным. Это можно понять, исходя из того, что
с (х — у) возникает за счет особенности типа \ID (р) в 2UV (/?).
Если для вычисления 2^ использовать цепочечное приближе-
ние, то, как было показано выше, вклад в поперечный линейный
ток (т. е. в поперечную часть J^) вносит только однопетлевая
диаграмма, которая ведет себя как 1/г в окрестности центра
вихря. Такое быстрое увеличение линейного тока вблизи центра
вихря является следствием того факта, что однопетлевая диа-
грамма не обладает особенностью типа полюса, которая обуслов-
лена коллективной модой, отражающей влияние флуктуации купе-
ровских пар. Резкое изменение линейного тока в окрестности
центра вихря приводит к возрастанию нелинейных членов, кото-
рые, как предполагается, стремятся ликвидировать расходимость
типа 1/г в центре вихря. В этом случае ожидается, что ток будет
чрезвычайно быстро расти в малой области около центра, прохо-
дить через максимум, а затем уменьшаться по закону 1/г. При
больших г ток должен обладать асимптотическим поведением,
характерным для линейного тока, т. е. экспоненциально спадать.
Подобное поведение демонстрирует ток, найденный в результате
численного расчета на основе уравнения Горькова [6, 7] г) в пре-
деле низких температур. Мы не будем обсуждать уравнение
Горькова [8], так как оно очень хорошо исследовано и описыва-
ется в любой книге по сверхпроводимости (см., например, [9]).
При выводе уравнения A1.3.40) мы воспользовались приближе-
нием другого типа, при котором в линейном токе учитывается
влияние коллективной моды, и условие р^^у = 0 выполняется
точно. В этом приближении по причине, указанной выше, нели-
нейные члены в 7Й считаются малыми. Но вопрос о том, насколько
малы эти нелинейные члены (т. е. JM—J^), остается открытым.
Важно отметить, что условие калибровки A1.3.3) также явля-
ется следствием уравнения максвелловского типа A1.3.40). Чтобы
показать это, вычислим d^J^ с помощью формулы A1.3.35). Ис-
пользуя соотношения д'1ц^ (д) = (vB/c)'2Dv (д) и D (д) / = 0,
находим, что d^J^ пропорционально D» (<?) ай. Соотношение
d^Jp, = 0, которое следует из уравнения максвелловского типа,
приводит к условию калибровки Du (д) а^ = 0. Таким образом,
условие калибровки A1.3.3) в неявном виде содержится в уравне-
нии максвелловского типа A1.3.40).
1) Линейная часть тока, определяемая из уравнения Горькова, совпадает
с той, которая находится на основе цепочечного приближения. Из уравнения
Горькова можно определить также нелинейную часть тока,
438 Глава 11
Покажем теперь, что зависимость параметра порядка | А (х) |
от пространственных координат учтена в выражении для тока
A1.3.36). Для этого изучим следующий вопрос: каким будет выра-
жение для линейного тока j, если величину | А (лг) j считать по-
стоянной. Для ответа на этот вопрос введем величину <f>f (х) по-
средством соотношения tyf (х) = ехр [—if (x)] <j>f(x). Величина
j>f {х) является функционалом от а и V/. Постоянная | А (х) |
отвечает приближению, в рамках которого пренебрегают всякой
зависимостью <j>f (х) от а и V/. Тогда, поскольку ф* (х) V<?/ —
вектор, не содержащий ни а, ни V/, его среднее по основному
состоянию обращается в нуль, как этого и следует ожидать для
среднего значения вектора по любому однородному основному
состоянию. Поэтому выражение для токапринимает^вид
где п — электронная плотность. Сравнивая его с A1.3.36), мы
видим, что наличие с (х— у) в A1.3.36) частично отражает эф-
фекты, обусловленные зависимостью | А (я) | от пространственных
координат.
Кулоновская калибровка. В разд. 5.4 вычисления проводились
на основе кулоновской калибровки. Чтобы рассмотрение, прово-
димое в этом разделе, сформулировать на языке кулоновской
калибровки [2, 5], необходимо провести калибровочное преобразо-
вание Оц -*-а,5 = ай + 3ЙХ, гдеХ = —A/V2) V-a. Таким образом,
& = &, A1.3.42а)
«co = «o + ^-(V-a). A1.3.426)
где аг — поперечная часть a, aj = Тгуау-. Уравнение максвеллов-
скоготипа A1.3.40) для пространственных компонент (jx = 1,2,3)
принимает вид
д^ (x) = -±-j d?yc (х - у) (а* (у) - Ц-• V/. (У)) , A1.3.43)
где /s дается формулой A1.3.4) и, следовательно, удовлетворяет
уравнению Лапласа A1.3.7).
Чтобы переписать уравнение максвелловского типа для четвер-
той компоненты, рассмотрим соотношение D^ (д) а^ = 0, из
которого при учете формулы A1.3.426) следует
V4 = (vb/c)'2 D(d)ao. A1.3.44)
Отметим также, что
1Р {д) dof = {vBlcf V2 dqf - dlf = (vp/cf [V2, д0] f.
Квантовая электродинамика твердых тел. II 439
Поскольку /s — единственная сингулярная часть /, выполняются
равенства [V2, д0] f = [V2, <?„] /Sj= V2<?o/S- Отсюда находим
D (д) д„/ = {vBlcf VWS- A1 -3.45)
Уравнение максвелловского типа A1.3.40) для четвертой компо-
ненты принимает вид
VVO = kl (vb/c)'2с (д) [а0 - (Пс/е) dof}'
Используя A1.3.44), получаем
A1.3.46)
где использовано и соотношение A1.3.45). Итак, мы получаем
A1.3.47)
где g(y) = [-D(d) + Xl\(d)]-lts. A1.3.48)
Уравнения A1.3.43) и A1.3.47) представляют собой уравнения
максвелловского типа в случае кулоновскои калибровки. Это
согласуется с результатами, полученными в разд. 5.4.
В^дальнейшем мы будем работать не с кулоновскои калибров-
кой, "а с калибровкой D^ (д) а^ = 0.
Вихри. Рассмотрим не зависящую от времени функцию / (х),
имеющую прямолинейные особенности в направлении х3. Функция
/ (х) для отдельного вихря с центром в начале координат строится
с помощью соотношений A0.1.29) и A0.1.30), откуда находим
СЪ (х) = -С2+! (х) = v6 (Xl) б (х2). A1.3.49)
Остальные компоненты Gjv обращаются в нуль. Равенство A1.3.49)
можно представить в виде
(V X V) / = ves6 (Xl) б (*,), A1.3.50)
где е3 — единичный вектор в направлении х3. Уравнение A1.3.2)
для не зависящей от времени функции / (х) превращается в урав-
нение Лапласа
V2/=0. A1.3.51)
Из A1.3.50) и A1.3.51) следует, что / (х) = (v/2n) 6, где 6 — угол
поворота вокруг оси х3 в цилиндрической системе координат.
Условие квантования A0.1.62) для v приводит к появлению топо-
логического кванта v = sn (s — целое число), откуда получаем
/(*) = 4-е. (п.3.52)
440 Глава 11
Итак, мы имеем
Vf(x) = ±-Le(x), A1.3.53)
где х = (xlt хг), г = | х |, а е (х) — единичный вектор в азимуталь-
ном направлении, т. е. е (х) = (—хг1г, xjr). .
Поскольку энергия вихря пропорциональна s2, случай s = 1
обычно отвечает выбору энергетически выгодного состояния.
В дальнейшем, если это специально не оговаривается, мы считаем
s = 1.
В статическом случае уравнение максвелловского типа
A1.3.40) принимает вид
V X Н (х) = - -L J d?yc (х - у) [а (у) - М- V/ (у)] = A1.3.54)
A1.3.55)
где с {д) определяется соотношением с (д) exp (tpx) = с (р) ехр X
X (грх), а Н = V X а. Исходя из A1.3.55), получаем
VW (х) = -ji-с (д) [Н (х) - Щ- V х V/ (х)] . A1.3.56)
В случае отдельного вихря обозначим Н .через h. Тогда из
уравнения A1.3.56) при v = sn находим
V2h (x) = -jj- с (д) [h (x) - s«?e36<2> (x)], A1.3.57)
где ф = nfic/e. Отсюда получаем, что h (x) = h (x) e3, где
dk g(k) cikx П13 58}
Bя)«
Здесь и далее к и х — двумерные векторы, к = (&ъ &2) и т. д. Эта
формула определяет магнитное поле, создаваемое отдельным
вихрем с v = sn и с центром в начале координат. Интегрируя
данное выражение по всей плоскости (хъ хг), находим поток
Ф-= | d*xh (x) = sf A1.3.59)
Именно по этой причине ф называют квантом потока.
Обратимся теперь к случаю многих вихрей, линии которых
параллельны оси х3. Поскольку уравнение A1.3.2) для / (х)
линейно, мы можем получить / (х) в виде суперпозиции соответ-
ствующих функций / для каждого отдельного вихря:
Квантовая электродинамика твердых тел. II 441
где 8 (х — g,) — угол поворота вокруг линии, характеризуемой
координатой ?;. Отсюда находим
(V X V)/(x) = яе3 ? б<2) (х - gf). A1.3.61)
Здесь мы предположили, что s = 1 для каждого из вихрей. При
этом из уравнения A1.3.56) получаем
H(x)=23h(x-g,). A1.3.62)
с
Поток определяется выражением
Ф = \d*x(H-t») = N<j>, A1.3.63)
где ./V — число вихрей.
Энергия электромагнитного поля, создаваемая этими вихрями,
дается формулой A1.3.18):
Это выражение показывает, что (</>/8я) h (g* — %,) — энергия
взаимодействия двух вихрей, характеризуемых координатами ?г
и ?,-. Другими словами, энергия взаимодействия двух вихрей
пропорциональна магнитному полю h (г) отдельного вихря, где
г — вектор, соединяющий центры обоих вихрей. Отрицательная
часть h (r) отвечает притяжению между вихрями. Таким образом,
мы видим, что притяжение обусловлено сменой знаком поля, а это
означает, что некоторая часть тока вращается в обратном направле-
нии. Увеличение энергии за счет изменения электронных состоя-
ний (энергия сердцевины) будет рассмотрено ниже.
Если вихри образуют периодическую решетку с элементарной
ячейкой в виде параллелограмма, то из A1.3.64) можно получить
следующее выражение для плотности энергии:
(?')' (П.3.65)
где п —- плотность вихрей. Макроскопическая магнитная индук-
ция В равна пф.
Обозначим через а и b длины сторон параллелограмма, а через
Э — угол между ними. Можно получить соотношение
g) A1.3.66)
I, т.
442
Глава 11
где F (к) — фурье-образ h (х), a g — вектор обратной решетки.
Имеем (см. A1.3.58))
J(V> <П-3'67>
= 2я/, A1.3.68а)
Ь (gx cos 9 + g2 sin 9) = 2я/п, A1.3.686)
где I я т. — целые числа, пробегающие значения от —оо до оо
(рис. 11.2). Имеем также
п = l/absin 9. A1.3.69)
Рис. 11.2.
Исходя из соотношений A1.3.68) и A1.3.69), получаем
g ~ | g | = 2пп (ЬЧ2 + а2т2 — 2ablm cos 6I/2. A1.3.70)
Поскольку а и Ъ пропорциональны 1/п1/г, из формулы A1.3.70)
видно, что g пропорционально п1/г. Поэтому получаем соотношение
Из формулы A1.3.65) с учетом равенства A1.3.66) находим
I. m
Отметим, что плотность вихрей определяется постоянной ре-
шетки. Если вихри образуют регулярную треугольную решетку, то
л=!&г4-' (И.3.73)
где а — постоянная решетки.
Поскольку с (к) зависит от &?0, VN @), / и от температуры,
магнитные свойства сверхпроводников определяются %в, VN @),
/ и температурой, хотя зависимость от VN @) довольно слабая х).
1) В формализме, опирающемся на уравнение Горькова, зависимость от
VN @) отсутствует, так как при выводе этого уравнения она не учитывается.
Квантовая электродинамика твердых тел. II 443
Здесь |0 — длина когерентности при нулевой температуре. Она
определена формулой E.4.177), согласно которой |0 = fivF/nA0,
где Ао — значение А при 7=0. Константа кв равна
KB^KL@)/l0, A1.3.74)
где %L @) — лондоновская глубина проникновения при нулевой
температуре. Константа / — длина свободного пробега, связанная
с наличием примесей.
Влияние примесей. Влияние немагнитных примесей на урав-
нение максвелловского типа исследовали Манчини и др. [10].
При этом к плотности лагранжиана, рассмотренной в разд. 5.4,
добавляется потенциал примесей, имеющий вид v (х) p (х), где
р = tyttyf + i|)|i|)|. Уравнения Бете—Солпитера, приведенные
в разд. 5.4, изменяются благодаря наличию потенциала примесей.
Влияние примесей усреднялось по их конфигурациям с помощью
метода Абрикосова и Горькова [11 ]. Результат сводится к замене
|0 на |0 @ = у (I) |0, где у (/) — некоторая функция.
Лондоновская глубина проникновения XL (I, T) также рассчи-
тывалась в зависимости от длины свободного пробега /. На прак-
тике удобно обозначать |0 (/) и KL (I, Т) через |0 и XL G1) соответ-
ственно. В дальнейшем мы будем пользоваться такими обозна-
чениями.
Сверхпроводники I, II/1 и Н/2 рода. Сверхпроводящее состоя-
ние, в котором отсутствуют какие-либо протяженные объекты,
называется мейсснеровским, состояние с вихрями — смешанным.
Обозначим через F разность плотностей свободной энергии мейссне-
ровского и нормального состояний. Эта величина, которая носит
название энергии конденсации, вычислена в разд. 5.4. В прибли-
жении Хартри получена формула E.4.192). Поле Нс (см. E.4.193))
обычно определяют выражением
1 = ~Н2С. A1.3.75)
Если проводник остается в мейсснеровском состоянии при
#ext < Не и скачком переходит в нормальное состояние при
#ext = #с, то он называется сверхпроводником I рода [9]. Здесь
#ext — внешнее магнитное поле (которое не следует путать
с внутренним магнитным полем Н (х)). При #ext = Нс происходит
фазовый переход первого рода. На рис. 11.3, а показан типичный
вид кривой намагничивания (зависимости*—inM от #ext) для
сверхпроводника I рода.
Часто бывает, что между мейсснеровским и нормальным со-
стояниями появляется смешанное состояние. В этом случае
мейсснеровское состояние существует при Hext < Яс1, смешанное
444
Глава 11
— при Нс1 < #ext < Яс2 и нормальное — при #ext > Яс2. Если
реализуется такая ситуация, то этот сверхпроводник называют
сверхпроводником II рода. Фазовый переход при #ext = Яс2
является переходом второго рода. Поскольку площадь под кривой
намагничивания равна энергии конденсации, мы видим, что
нс1<не<на.
Существуют два вида сверхпроводников II рода [12]. Если
при #ext = Нс1 имеет место фазовый переход первого рода, то
3
а
НС1 НСг
в
Рис. 11.3.
такой сверхпроводник называют сверхпроводником П/1 рода,
если имеет место переход второго рода, то его называют сверхпро-
водником П/2 рода. На рис. 11.3, б и 11.3, в показан типичный вид
кривых намагничивания для сверхпроводников П/2 и П/1 рода
соответственно.
Фазовый переход первого рода при #ext == Нл в сверхпровод-
никах П/1 рода обусловлен притяжением между вихрями [13];
благодаря притяжению вихри сразу накапливаются таким обра-
зом, что расстояние между ними соответствует притяжению. Это
приводит к скачкообразному возникновению магнитного потока
(или резкому спаду кривой намагничивания) при #ext = Нл.
Значение скачкообразно возникающей при этом магнитной индук-
ции обозначим символом Во. Очевидно, что Во определяется вели-
чиной расстояния dlt на котором проявляется притяжение между
Квантовая электродинамика твердых тел. II
445
вихрями. Если вихри образуют треугольную решетку, то из
формулы A1.3.73) следует
Ж- A1.3.76)
На рис. 11.4 представлено в увеличенном виде типичное
поведение (вблизи #ext = Яс1) теоретической кривой намагничи-
вания для сверхпроводника П/1 рода. Кривая, выгнутая внутрь
Рис. 11.5.
(Ь —> с), демонстрирует влияние притяжения. Если вне области
притяжения имеется значительное отталкивание, то кривая вы-
гибается наружу (а-^b). Поле Нс1 определяется положением
вертикальной линии, при котором разделяемые ею заштрихован-
ные области имеют равную площадь. Мы пользуемся также сим-
волом Я (п), обозначающим значение Hext, соответствующее
В = пф. На рис. 11.4 Я @) — значение Я (и) при п = 0.
На рис. 11.5 представлено поведение магнитного поля h (r)
(г = | х |) отдельного вихря. На этом рисунке область притяже-
ния показана в сильно увеличенном виде. Минимум при г = dx
отвечает наиболее сильному притяжению. Это дает нам точное
определение dx. При этом скачок Во намагниченности при Hext ^
«=! Яс1 дается формулой A1.3.76). На практике притяжение при
г = d-L очень слабое. Например [14], если взять значения пара-
метров VN @) = 0,32, %в = 0,8, то мы получим | h {dx) \/h @) «=*
;=» 10~3. Вычисления [14] показывают, что АЯ = Я @) — Нс1
равно 3|/i (<4)|, а это означает, что отношение АЯ/Яс1 крайне
мало. При заданной температуре Т существуют два критических
значения %в, обозначаемые кв1 (Т) и кВ2 (Т). Они определяются
следующим образом: случай кв < -лш (Г) отвечает сверхпровод-
никам I рода, случай кт (Т) < кв < кв1 (Т) — сверхпроводни-
кам П/1 рода, а случай кв >nBi (^) — сверхпроводникам II/2
446 Глава 11
рода. Значение кв1 (Т) находится из условия Во = 0, что соответ-
ствует D=00.
Любые экспериментальные данные, касающиеся величины Во,
чрезвычайно полезны для проверки применимости уравнения
максвелловского типа A1.3.40), так как <4 (а значит, и Во) опреде-
ляется только с помощью этого уравнения. Если взять VN @) =
= 0,32 и хв = 0,8 (чистый ниобий), то из уравнения максвеллов-
ского типа следует [14], что c!i *=* 6XL при Т = 0. Это значение
близко к получающемуся на эксперименте [12]. Эксперименты
по рассеянию нейтронов [15] позволяют провести очень точные
измерения Во. Экспериментальные результаты для температур-
ной зависимости Во (Т)/Во @) сравнивались с теоретическими ре-
зультатами [16], полученными из уравнения максвелловского
типа. Согласие между экспериментом и теорией оказалось очень
хорошим. Для теоретического определения. хв1 (Т) требуется
знать функцию с с чрезвычайно высокой точностью. Поскольку
подгоночная формула E.4.176), предназначенная для расчетов на
ЭВМ, слишком груба для указанной цели (см. обсуждение, пред-
шествующее формуле E.4.178)), были использованы значения
функции с, полученные в результате численного счета, а не под-
гоночная формула. Значение хвгпри котором притяжение обра-
щается в нуль, определялось из условия равенства dx и d2
(рис. 11.5). В результате теоретического рассмотрения [17] по-
лучено значение хв @) = 1,073. Это близко к эксперименталь-
ным данным. Эксперименты [18] показали, что чистый ниобий
остается сверхпроводником П/1 рода даже при Т1ТС =0,95.
Это также согласуется с предсказаниями теории [16].
Электронные состояния в центре вихря и энергия сердцевины.
В разд. 9.1 показано, что протяженные объекты приводят к по-
явлению самосогласованного потенциала, который оказывает
влияние на квантовые состояния. Следовательно, на электроны
вокруг вихря действует самосогласованный потенциал, создавае-
мый вихрем. Расчет этого самосогласованного потенциала пред-
ставляет собой непростую задачу. Если считать, что V-взаимо-
действие (Угр{*|э]лр+1р+) вносит определяющий вклад в формиро-
вание самосогласованного потенциала, и воспользоваться приб-
лижением Хартри, то для грубой оценки потенциала взаимо-
действия можно применить выражение А (л:) (.ipjipi + гМ'+)* Таким
образом, самосогласованный потенциал оказывается пропорцио-
нальным параметру порядка А (х). Используя эту грубую оценку
для самосогласованного потенциала, получаем, что электронные
состояния в окрестности центра вихря описываются собственными
функциями уравнения Шредингера (см E.4.15) и E.4.32))
[Е — г {д) т3 + Д (х) тх] ф° {х) = 0, A1.3.77)
Квантовая электродинамика твердых тел. /'/' 447
где Е — собственное значение энергии, а ф° (х) — волновая функ-
ция физического электрона. В большинстве подобных исследо-
ваний авторы ограничивались случаем грязных сверхпровод-
ников [19]. К сожалению, вычислить параметр порядка А (х),
вообще говоря, трудно, хотя обычно предполагается, что энер-
гия наиболее низколежащего электронного уровня в окрестности
центра вихря значительно меньше Д, поскольку | А (х) | должно
обращаться в нуль в центре вихря и, следовательно, значительно
меньше А для х вблизи центра вихря. Возбуждение электронов
на низколежащие уровни может приводить к затуханию ультра-
Сверхпроводящий
электрон
Рис. 11.6.
звуковых волн, распространяющихся в сверхпроводниках, ко-
торые находятся в смешанном состоянии. В рамках такого под-
хода было успешно объяснено поведение коэффициента затуха-
ния ультразвука [20 ] при Т <=& Тс или #ext ^ Нс2.
Электроны, находящиеся в связанном состоянии вблизи центра
вихря за счет самосогласованного потенциала, называются элек-
тронами сердцевины (рис. 11.6). Электроны серцевины вносят
вклад в энергию каждого отдельного вихря. Эта энергия назы-
вается энергией сердцевины и обозначается символом Е (п),
так как она зависит от плотности вихрей п. Начнем с рассмотрения
энергии сердцевины одного изолированного вихря и обозначим
ее Ег. На основании теоремы вириала мы можем ожидать, что энер-
гия электронов сердцевины определяется произведением числа
электронов и кинетической энергии одного электрона [3]:
Ег=Шпг>*- (П.3.78)
Здесь г0 — радиус цилиндрической области, внутри которой
заключены электроны сердцевины, kr — среднее значение им-
пульса, a ns — плотность сверхпроводящих электронов (см.
A1.3.416)). Среднее значение импульса kr находится из принципа
неопределенности 2krr0 <=* H. При этом из A1.3.78) для энергии
сердцевины отдельного вихря получается выражение
448 ' Глава 11
Заметим, что в приведенном выше вычислении мы следовали хо-
рошо известному методу оценки энергии основного состояния,
используемому в квантовой механике. Если плотность вихрей
возрастает и плотность тока вокруг находящейся в нормальном
состоянии сердцевины вихря падает, то А (л;) сглаживается и энер-
гия сердцевины Е (п) может уменьшиться. Многовихревые эф-
фекты начинают проявляться, когда становится существенным
взаимодействие между вихрями. Изменение энергии сердцевины,
обусловленное многовихревыми эффектами, можно рассчитать сле-
дующим способом. Обозначим изменение энергии основного со-
стояния электронов, обусловленное вихрями, через ^соге (х).
Здесь уже не учитывается электромагнитная энергия, опреде-
ляемая выражением A1.3.18). Поскольку все наблюдаемые вели-
чины являются некоторыми функционалами от линейного тока
J^ (x), это относится и к самосогласованному потенциалу. Таким
образом, энергия сердцевины зависит от электромагнитного поля,
создаваемого током J^, а ?соге (х) становится функционалом от
магнитного поля Н (л;), определяемого формулой A1.3.62):
?соге (х) = .Есоге (х; Н). Поскольку вихри образуют решетку,
для энергии сердцевины на один вихрь мы можем записать выра-
жение
Е (и) = Jds*?Core(x), . A1.3.80)
где Q — объем элементарной ячейки решетки вихрей. Энергию Е(п)
можно разделить на две части: одна из них определяется вкладом
вихря, находящегося в ячейке Q, а другая — вкладом остальных
вихрей. Запишем Н (х) в виде
Н(х) = h(x— g0) + Eh(x—?/), A1.3.81)
где g0 — координата вихря внутри ячейки Q, и разложим ?core (x)
в ряд по hint (х) (= Ij h (х — gy)\: ^
Есоге (х; Н) = ?соге (х; h0) + J dsyEcore (x; h0; у) hmt'(y) + ... ,
A1.3.82)
где h0 = h (x - g0), hmt (x) = 2] h (x — g/),
F /x. h • v\ — 6?core (x; h0)
tc (X П У) щ-^
core (X, По, У) — щ^
Отметим, что
Ег = [ dsxEcore (х; h0) = lim \ сРхЕсоте (х; h0).
Квантовая электродинамика твердых тел. II 449
Поле h0 (x) вблизи центра вихря описывается хорошо локализо-
ванной функцией, а вдали от вихря спадает по экспоненциальному
закону. Поэтому, если п не слишком велико, ?core(x, h0) для х
из n-й ячейки приближенно пропорционально h0 (?г), а Есоге (х;
h0; у) определяется в основном вкладом области х~у~0 (центра
вихря). Отсюда получаем
J сРг/Есоге (х; h0; у) hlnt (у) «* cohst-hir)t (n),
\d3x— [ сРх\ Ecore (x; h0) «=< const -hm (ft),
Гпр hini-(n\ \ h IT Л (\\ Я RVi
1 ДС И Щ) 0 7 П Ife/Ь \L 1.O.OOJ
/
Штрих у знака суммы показывает, что h (?/) при ?;- = 0 не учи-
тывается. Таким образом, Е (п) — Ег приближенно пропорцио-
нально h'mi (n):
Е (п) & Ех — E2hM (и). A1.3.84)
Параметр Е2 можно считать не зависящим от п, поскольку коэф-
фициенты в разложении A1.3.82) зависят только от Ло. Члены бо-
лее высокого порядка в A1.3.82), в которые hini (n) входят в бо-
лее высокой степени, несущественны до тех пор, пока п не станет
очень большим, поскольку h (?) — экспоненциально спадающая
функция. Полная плотность энергии сердцевины определяется
выражением п Е(п).
Для вычисления термодинамического потенциала Гиббса не-
обходимо учесть член, регулирующий термодинамику локального
потока в состоянии теплового равновесия. Этот член должен быть
пропорционален nhint, так как в случае немагнитного сверх-
проводника магнитное поле совпадает с магнитной индукцией.
Поскольку термодинамический член может быть включен в член
вида nE2hint, входящий в выражение для энергии сердцевины,
при вычислении термодинамического потенциала Гиббса Е2
можно рассматривать в качестве термодинамического параметра;
Е2 определяется из условия, что фазовый переход при Нс2 является
переходом второго рода.
Приведенная выше оценка энергии сердцевины, конечно,
очень груба. Тем не менее она позволила найти Нс1 и Нс2 для
ванадия и ниобия, температурная зависимость которых оказалась
в качественном согласии с экспериментом. Пока не будет полу-
чена более точная формула для энергии сердцевины, выражение
пЕ (п), где Е (п) определено формулой A1.3.84), может использо-
ваться в качестве грубой, но полезной оценки энергии сердце-
вины.
450 Глава 11
Термодинамический потенциал Гиббса. Чтобы получить соот-
ношение, связывающее внешнее магнитное поле #ext с плотностью
вихрей п, необходимо минимизировать термодинамический по-
тенциал Гиббса.
Термодинамический потенциал Гиббса в смешанном состоя-
нии дается выражением
Gs = 8 + пЕ (п) — ~BHext- ST, A1.3.85)
где В = пф, г определяется формулой A1.3.65), Е (п) —энер-
гия сердцевины на один вихрь A1.3.84), a S — плотность энтро-
пии. Поскольку в рамках термополевой динамики энтропия микро-
скопического происхождения уже учтена при вычислении 8,
в S вносит вклад только движение вихрей. Поэтому членом ST
можно пренебречь. Тогда из A1.3.85) получаем
где Я = Jj'hfo). A1.3.87)
Плотность вихрей п определяется из условия
4rG» = °> A1.3.88)
при этом Hext представляется как функция от п: __
H(n)=\h@) + ^-E1+-^(\~E2){\+n-^.)h. A1.3.89)
Если п = 0, то для Я @) («* Яс1) получаем выражение
Я@)=-^Л@) + ^-?1. A1.3.90)
Отсюда находится приближенное значение Нс1. Теперь формула
A1.3.89) записывается в виде
Я(/г) = Я@) + ^A-?2)A+«4-)Я- (П.3.91)
Обозначим через пс плотность вихрей п при Яех1 — Я.2. Поскольку
при Яех1 = Яс2 Яс2 = В, имеем соотношение
Яс2 = пеф, т. е. Я (пс) = псф. A1.3.92)
Отсюда, используя A1.3.91), находим
Квантовая электродинамика твердых тел. //
451
С другой стороны, термодинамический потенциал Гиббса
в нормальном состоянии дается формулой
Gn==-^-(H2c-H2ext). A1.3.94)
Поскольку при #ех, = Яс2 Gs =Gn, из A1.3.94) и A1.3.86) с уче-
том формулы A1.3.90) получаем
Н2С = псф \2Н @) - псф] + псф A - Е2) [Я]п=Пс. A1.3.95)
Два соотношения A1.3.93) и A1.3.95) определяют одновременно пс
и параметр Е2.
Условие Gs = Gn при п = пс означает, что термодинамический
потенциал Гиббса в нормальном и смешанном состояниях имеет
0,05
0,10 0,15
Я/(ф/х1@))
Рис. 11.7.
0,20
0,25
одинаковые значения. Условие же #ext = В (=псф) означает,
что Gs и Gn имеют общую касательную при Яех1 = Hi2. Из этого
условия находится параметр Е2.
Поскольку Ех <^ (</>/2) h@) при больших кв, имеем
-к-h @) при больших кв.
A1.3.96)
Рассмотренный выше метод вычисления функций Я (и), Яс1,
Яс2 и параметра Маки xi = Яс2/21''2ЯС при различных температу-
рах был применен к ниобию. Результаты с разумной точ-
ностью согласуются с экспериментом *). На рис. 11.7 представ-
лены типичные кривые намагничивания для сверхпроводника П/1
рода при различных температурах.
1) В работе [16] использовалось полученное экспериментально, а не теоре-
тически (в рамках приближения Хартри) значение энергии конденсации. Это
осуществлялось путем введения параметра б = [#С2/^с]г=о- ^3 эксперимен-
тов было найдено, что S « 2. В теоретическом анализе [16] использовалось зна-
чение б = 2,25. Если воспользоваться энергией конденсации, найденной в рам-
ках приближения Хартри (формула E.1.192)), то теоретические результаты не-
много изменятся.
4f>2 Глава 11
Параметры Маки. Имеются три параметра, которые часто
используются при рассмотрении магнитных свойств сверхпровод-
ников II рода. Они обозначаются символами хх (t), x2 (t), к3 (t)
и определяются соотношениями [9 ]
HJHC = 2'/% @, A1.3.97)
д
дН
= !
н~не р [2x1@-4 '
1/2
1 3 98)
Нс1[фИ1 (*)] = хз @/21/2 Bя), A1.3.99)
где Я — внешнее магнитное поле, а р1 — константа, зависящая
от структуры решетки вихрей, определение которой дано ниже.
Вычислим эти параметры. Для удобства в этом подразделе
нормируем все величины так, чтобы они измерялись в единицах
tyAHOl. так чт0 °s^ ty/M(*)l2G,, пф^ tytt(f)]n, H^
^,'i @ ] Я и т. д. При этом выражение для термодинамиче-
ского потенциала Гиббса A1.3.85) принимает вид
°«(") = -?-*(")--?-#> (П.3.100)
где Я — внешнее магнитное поле. Величина g (n) может рассма-
триваться как эффективная энергия каждого отдельного вихря
в многовихревой системе. Из условия A1.3.88) находится Н
в зависимости от п (см. A1.3.91)):
+п±)8(п). A1.3.101)
При Н = Яс2 (т. е. при п = пс) Gs(n) =Gn(n) и Яс2 = В = пс,
где Gn (n) — термодинамический потенциал Гиббса для нормаль-
ного состояния, определяемый формулой A1.3.94). В результате
из A1.3.100) и A1.3.101) получаем
Hi = nAg (пс) - пс\, A1.3.102)
nc=±r(\+nc^-)g(nc), A1.3.103)
откуда следует
g(nc)/nc= 1 +(Яс/псJ, A1.3.104)
dg (пс)/дпс = 1 — (Нс/псJ. A1.3.105)
Эти два соотношения определяют пс и параметр Е%. Параметр
их (t) находится из соотношения A1.3.97), которое записывается
в виде
Xl (t) = 2-1/2 (пс/Нс). A1.3.106)
Квантовая электродинамика твердых тел. // 453
Параметр к3 (t) получают, используя выражение для энергии кон-
денсации Щ/8л (см. A1.3.75)), согласно формуле A1.3.99), при-
нимающей вид
х3 (t) = 21/2 Bя) Нс. A1.3.107)
Заметим, что из приведенных выше соотношений следует
«с =^*1 (О МО, A1.3.108)
R @ = 1 - DяЯ?/ле) = A1.3.109)
= -%jtrM)-Mt)l (П.з.по)
Заметим также, что в проведенном рассмотрении структура g (и)
не конкретизируется. Воспользуемся теперь выражением A1.3.86),
которое дает
g(n)= ? h (С/) + 8l - 82Я (п), A1.3.111)
где (см. A1.3.87))
Я(п)= ?'й(С/). A1.3.112)
Согласно формуле A1.3.79), имеем
ех= 1/4я. A1.3.113)
Параметр е2 находится из соотношений A1.3.104) и A1.3.105).
Используя равенство A1.3.66), мы можем вычислить g (n) и опре-
делить е2. В результате получаем
где
2i = ne2]>fe). A1.3.115a)
^F(g); A1.3.1156)
г, m
в случае треугольной решетки g дается формулой (см. A1.3.70))
g^ = 4n2nc-^-(l2^rm2-lm). A1.3.116)
Штрих в A1.3.115) означает, что член, отвечающий g =0 (т. е.
/ = т =0), опускается. Вычисление величины R (t), определяе-
мой формулой A1.3.109), с помощью выражения A1.3.102) при-
водит к результату
Я (9 = IST t8i + Si - **h (°) + ^- (П-3.117)
454
Глава 11
Нас интересует ситуация при значениях Т, близких к Тс
(т. е. при t «=> 1). Не имеет смысла проводить рассмотрение точно
при Т = Тс, поскольку вычислить функцию с при Т = Тс чрез-
вычайно сложно. Это можно понять, если учесть, что мы имеем
дело с рассмотрением коллективной моды в критической области.
Лучшее, что мы можем сделать, — это выбрать значение Т очень
близким к Тс (например, при t = 0,99) и вычислить R (t) с помощью
формулы A1.3.117), используя выражения E.4.179) для функции с
и E.4.193) для энергии конденсации. Мы приняли VN @) = 0,3.
Чтобы упростить расчет, используем равенство пс =A/2я)Хд,
полагая к3 = щ, и посмотрим, воспроизведется или нет условие
Таблица 11.1
0,797
0,0217
0,0033
0,0054
0,0102
10
102
103
104
0,0185
0,0228
0,0229
0,0229
к3 = X! в конечном результате для R. Результаты при t =0,99
приведены в табл. 11.1. Они показывают, что при t « 1 R (t)
практически равно нулю. Из A1.3.110) следует, что этот резуль-
тат действительно согласуется с соотношением
МО = МО при t= 1. A1.3.118)
Это соотношение было предсказано в рамках теории Гинзбурга-
Ландау.
Параметр Гинзбурга—Ландау к определяется как х3 (t) при
t = 1. Если для энергии конденсации воспользоваться прибли-
женным выражением E.4.193), то получим
х = 0,96хв = 0,96 [KL @)/? @)]. A1.3.119)
Обратим теперь внимание на щ. Наклон кривой намагничи-
вания дается формулой
дН
а из A1.3.101) следует
Из этих соотношений с учетом A1.3.106) получаем
д DлМ)
дН
1
Рх @ [2*1@-1] '
A1.3.120)
A1.3.121)
A1.3.122)
Квантовая электродинамика твердых тел. II 455
где
1 + _^
+ 2*? @-1 1-х? @ яс
Выберем р так, чтобы при t = 1 P = Pi- При этом, согласно
A1.3.98), имеем
МО = «2 @ при f = 1. A1.3.124)
Таким образом, получаем
Xl (t) = х2 @ = к3 (t) = х при*=1. A1.3.125)
Из выражения A1.3.123) видно, что Р немного больше единицы.
Значение производной d%g/dn2 при п = пс (а следовательно, Р)
зависит от деталей распределения очень малого по величине тока
при поле Н, близком к Яс2.
Анизотропные сверхпроводники. До сих пор мы рассматривали
изотропные сверхпроводники. Однако, строго говоря, изотроп-
ные сверхпроводники встречаются крайне редко, поскольку почти
все сверхпроводники обладают анизотропией свойств, обуслов-
ленной проявляющейся на микроскопическом уровне анизотро-
пией сверхпроводящей электронной системы [21 ]. Поэтому про-
водилось много экспериментальных и теоретических исследова-
ний анизотропных сверхпроводников. В дихалькогенидах, та-
ких, как NbSe2 и TaS2, плоскости, образованные атомами халько-
генов, упакованы вдоль оси с кристалла, а плоскости, в которых
ионы металла образуют треугольную решетку, вставлены между
халькогенными плоскостями с интервалом в две хальгогенные
плоскости. Следовательно, перенос электронов между ионами
металла в плоскости происходит более интенсивно, чем между
плоскостями. В NbSe2 было обнаружено, что значение верхнего
критического поля сильно зависит от угла между внешним магнит-
ным полем и металлической плоскостью. Соединения типа А-15
V3Si и Nb3Sn известны как высокотемпературные сверхпровод-
ники. В этих кристаллах выше температуры сверхпроводящего
перехода происходит мартенситное превращение из кубической
структуры в тетрагональную. Если, как считают некоторые ав-
торы, основную роль в мартенситном превращении играет зонный
эффект Яна—Теллера, то при мартенситном превращении следует
ожидать существенного изменения электронной структуры в ок-
рестности уровня Ферми. Такое изменение электронной струк-
туры, естественно, оказывает влияние на сверхпроводящее со-
стояние, и в результате появляется анизотропия в уравнении мак-
свелловского типа, а также анизотропия свободной энергии сме-
шанного состояния. Мы привели в качестве примера только не-
456 Глава 11
которые из многих типов анизотропных сверхпроводников. Даже
в случае сверхпроводников с кубической симметрией, таких,
как Nb и РЬ—Т1, наблюдалась очень малая анизотропия пове-
дения магнитных свойств. Эксперименты по рассеянию нейтро-
нов и с применением метода декорирования показали, что имеется
корреляция между решеткой вихрей и кристаллической решеткой.
Обобщим теперь уравнение максвелловского типа, чтобы учесть
наличие анизотропии свойств [3]. Если мы рассматриваем анизо-
тропную систему, то энергия голдстоуновского бозона /° перестает
быть функцией р2. Она имеет вид
со| (р) = (рв (р)/сK V,, (р) PiPi, A1.3.126)
где Уц (р) — не единичная матрица. Отсюда видно, что опера-
тор D (д) в уравнении A1.3.2) для / (х) имеет следующую струк-
туру:
D (д) = до - Ыд)/сJ Vudidf, A1.3.127)
этот оператор может быть представлен в виде D (д) = Da (д) д^,
где
DB (д) = {д0, [vB (д)/с? Vudj). A1.3.128)
При таком определении D^ (д) калибровочное условие
D^ (д) аа = 0 (см. A1.3.3)) остается в силе. Из закона сохране-
ния d'xJu =0 в данном случае видно, что определение величины
t]^v (р) (см. A1.3.28)) должно быть модифицировано следующим
образом:
¦ (vB/c)-
о
A1.3.129)
Итак, уравнение максвелловского типа A1.3.40) остается справед-
ливым даже в случае анизотропных сверхпроводников, если оп-
ределить У]^ (д) посредством формулы A1.3.129). Функция / (х)
удовлетворяет уравнению D (д) f = 0, где D (д) дается формулой
A1.3.127). Уравнение максвелловского типа приводит к условию
калибровки D^ (д) а^ = 0, где Du (д) имеет вид A1.3.128).
Для энергии статических объектов остается справедливой
формула A1.3.18). Поэтому h (r) описывает взаимодействие между
вихрями даже в случае анизотропных сверхпроводников.
Если симметрия кристалла ниже кубической и он обладает
столь сильной анизотропией, что Уц (р) при р = 0 намного отли-
чается от единичной матрицы, то обычно основную часть эффек-
тов, связанных с анизотропией, можно учесть, рассматривая
только матрицу Уц @). При этом всегда можно так нормировать ]/ц,
чтобы det | Уц | = 1. В подобных случаях мы можем использо-
Квантовая электродинамика твердых тел. II 457
вать функцию с, в которой р2 заменено на Уцр,ру, кроме того,
надо определить t^v согласно формуле A1.3.129). Матрица Vtl
находится на основе информации об анизотропной структуре элек-
тронных энергетических зон. Первые расчеты подобного рода
приведены в работах [22], в которых теоретически исследовались
аномалии теплоемкости и коэффициента поглощения ультразвука
[23], наблюдавшиеся у V3Si в смешанном состоянии.
В случае кубических сверхпроводников с анизотропной по-
верхностью Ферми анизотропия исчезает при р = О IVц @) =
— 8ц]. Поэтому анизотропная структура функции с и матрицы
Va (р) при р Ф 0 должна находиться на основе данных о струк-
туре анизотропной поверхности Ферми. Такой расчет проведен
в работе [24]. Оказывается, что уравнение максвелловского типа
A1.3.40) с t^v, даваемым формулой A1.3.129), приводит к анизо-
тропии функции h (r), описывающей взаимодействие между вих-
рями. Поскольку притяжение между вихрями в слабых полях
определяет структуру решетки, образованной вихревыми нитями,
мы можем предсказать структуру этой решетки, исследуя полу-
ченную теоретически функцию h (г). В слабых полях при низких
температурах возникает множество вихревых решеток с различ-
ной структурой, и теоретические результаты, касающиеся пред-
почтительных ориентации вихревых нитей в решетке, хорошо
согласуются с экспериментом [25] для Nb и РЬ—Т1. Это важно,
поскольку теоретические результаты основываются только на
уравнениях максвелловского типа. Изучение анизотропного по-
ведения Нс1 и Яс2 при низкой температуре требует вычисления
термодинамического потенциала Гиббса [26]. Эти результаты на-
ходятся в качественном согласии с экспериментом *).
11.4. Магнитные сверхпроводники
Введение. До сих пор мы рассматривали сверхпроводимость,
предполагая, что электронное взаимодействие проявляется в форме
минимального взаимодействия, т. е. оно вводится путем замены
Если в систему входят элементы, характеризуемые спином S,
то необходимо добавить магнитное взаимодействие вида — В-М,
где М = g\iBS, которое является взаимодействием /^-типа.
Если спины выстраиваются за счет некоторого спин-спинового
взаимодействия, то система находится в магнитоупорядоченном
состоянии, рассмотренном в гл. 5. Мы сталкиваемся здесь со ста-
1) Вычисление термодинамического потенциала в области сильных полей,
основанное на теории Гинзбурга—Ландау, приведено в работе [27].
458 Глава И
рой проблемой сосуществования магнетизма и сверхпроводи-
мости.
Происхождение магнетизма связано со спиновой симметрией,
а сверхпроводимости — с фазовой симметрией. Поскольку эти
симметрии независимы, с симметрийной точки зрения допустимо
состояние, в котором одновременно имеется упорядочение обоих
типов. Однако ситуация не так проста, как это кажется на первый
взгляд, поскольку взаимодействие между спиновой системой, от-
ветственной за магнетизм, и электронами проводимости, ответ-
ственными за сверхпроводимость, может подавлять действие меха-
низмов, обусловливающих возникновение каждого из указанных
упорядоченных состояний.
Эти две системы (электронов проводимости и спиновая) взаимо-
действуют за счет а) спин-спинового взаимодействия, обусловлен-
ного обменом
lpS, A1.4.1)
и б) электромагнитного (дипольного) взаимодействия
НЕМ = — fif|H»B-S - j (я|>, я|>+) А. A1.4.2)
Первое из них модифицирует как эффективное взаимодействие,
обусловленное электрон-электронным рассеянием, так и спин-
спиновое взаимодействие. Второе взаимодействие приводит к
изменению вида уравнения Максвелла, рассмотренного в преды-
дущем разделе, вызывая некоторое взаимное влияние этих двух
систем. В предыдущем разделе мы видели, что мейсснеровский
ток, создаваемый сверхпроводящими электронами, способствует
диамагнетизму, а магнитный ток ]т = \ х М способствует пара-
магнетизму. Поэтому если говорить о магнитных свойствах, то
парамагнетизм спиновой системы и диамагнетизм сверхпроводя-
щей системы конкурируют друг с другом в уравнении Максвелла,
приводя к различным необычным явлениям. В этом разделе мы
сконцентрируем внимание главным образом на электромагнит-
ных свойствах.
Исторические замечания. Ранние исследования в этой области
касались в основном магнитных примесей, поэтому изучалось
влияние взаимодействия типа A1.4.1). Взаимодействие между
примесью и электронами проводимости описывается в общем виде
[28 ] выражением
Hi = J d*x ( 2 ^i (x ~ R*) ^+ (*) Ф (*) + 2 и2 (х - R/) S/i|>+ (х) вц (х)\,
A1.4.3)
где U\ и U2 — потенциалы, создаваемые немагнитной и магнит-
ной примесями соответственно, S/ — спин /-го атома примеси.
Квантовал электродинамика твердых тел. II
а о — спин электрона проводимости. Как выяснено в работе [29],
эффекты, обусловленные магнитными и немагнитными примесями,'
довольно сильно различаются между собой. Первое серьезное
исследование, основанное на методе функций Грина, было про-
ведено Абрикосовым и Горьковым [30]. Они предсказали сущест-
вование области с бесщелевым энергетическим спектром (см. об-
зор по этому вопросу [31 ]). Ими было также показано, что при
достаточно большой концентрации примесей они разрушают
коллективную моду (т. е. куперовские'пары), приводя к подавле-
нию сверхпроводящего состояния. Исследование тех случаев,
когда магнитные ионы образуют периодическую решетку, требует
более тщательного учета спин-спиновых корреляций между маг-
нитными ионами.
Имеется много механизмов возникновения спин-спинового
взаимодействия между магнитными ионами. Оно может быть свя-
зано со спиновым обменом между электронами проводимости и
магнитными ионами (s — /-взаимодействие). Это так называемый
механизм РККИ [32]. Другой механизм имеет электромагнит-
ную природу (магнитное дипольное взаимодействие). Андерсон
и Сул [33 ] показали, что восприимчивости электронов прово-
димости в сверхпроводящем и нормальном состояниях сильно
различаются, и это различие приводит к существенной модифика-
ции взаимодействия РККИ. Принимая, что спин-спиновое
взаимодействие осуществляется с помощью тех же электронов
проводимости, которые ответственны за сверхпроводимость, они
предсказали возможность появления в сверхпроводниках неболь-
ших похожих на домены структур с ферромагнитным порядком.
Сул и Маттиас [34] показали также, что могут сосуществовать
сверхпроводящие доменные стенки и ферромагнитные домены.
Тройные редкоземельные соединения. Начиная примерно
с 1977 г. широко ведутся экспериментальные и теоретические ис-
следования различных магнитных сверхпроводников, представ-
ляющих собой тройные или псевдотройные соединения, содержа-
щие редкоземельные ионы (RE Rh4B4, RE Mo6Se8, RE Rh^. Sny
и др., где RE — редкоземельные ионы). Эти соединения обладают
многими необычными свойствами. В процессе охлаждения соеди-
нения ErRh4B4 [35] и HoMoeS8 [36] становятся нормальными
ферромагнетиками, проходя через сверхпроводящее состояние
(рис. 11.8). Такое явление носит название возвратной сверхпро-
водимости. Вблизи температуры возврата в нормальное состояние
наблюдается сильно выраженный температурный гистерезис.
Эксперименты по рассеянию нейтронов показали наличие длин-
нопер иодической магнитной структуры (спиральной или синусо-
идальной) в узком температурном интервале, ограниченном снизу
температурой возврата [37]. Кроме того, удельное сопротивление
460
Глава 11
этих соединений не возвращается к обычным значениям, характер-
ным для нормального состояния. Такие соединения, как GdMo6S8,
TbMoeS8, DyMoeS8 и т. д., также становятся сверхпроводниками
при некоторой достаточно низкой температуре, а при дальнейшем
"8
I
100
15
50
25
0
-25
300
250
ZOO
150
100
50
j
- /
¦¦''
-
-
-
.
-
.
¦ tij*
Z 3 4 5 6
Температура, К
Рис. 11.8.
10
t i
/--
i
i
i
i /
¦ W
Mg2, измеренное
^ — ^ ^ no сопротивлению
ч
\
^ ^\\
/ :::!A
\ •
i i i i i t \ ?
7
6
5
J -
2 -
012345618 9 10
T, К
Рис. 11.9.
понижении температуры в них возникает антиферромагнитный
порядок. Этот антиферромагнитный порядок сосуществует со
сверхпроводимостью. Сверхпроводящее состояние соединений как
ферромагнитного, так и антиферромагнитного типа характери-
зуется необычной температурной зависимостью верхнего крити-
Квантовая электродинамика твердых тел. II 461
ческого поля Яс2 (рис. 11.9). А именно, Яс2 сильно уменьшается
вблизи температуры магнитного фазового перехода [38] (см.,
например, обзоры экспериментальных результатов Ишикавы и
др. [39]). В этих соединениях при замещении магнитных редко-
земельных ионов на немагнитные изменение Тс обычно мало, что
свидетельствует о слабости обменного взаимодействия между
спинами электронов проводимости и редкоземельных ионов.
Расчеты в рамках зонной теории [40] также показали, что это об-
менное взаимодействие в рассматриваемых тройных соединениях
является крайне слабым. Поэтому следует ожидать, что решаю-
щую роль играет электромагнитное взаимодействие между не-
затухающим током и редкоземельными магнитными ионами.
Точнее говоря, микроскопическая картина такова. Электроны,
ответственные за сверхпроводимость, — это в основном 4с(-элек-
троны Rh и Мо. Притяжение типа БКШ действует между электро-
нами проводимости, а между электронами проводимости и спи-
нами редкоземельных ионов существует крайне слабое s—/-
взаимодействие1). Электромагнитное поле взаимодействует как
с электронами проводимости, так и с магнитными моментами редко-
земельных ионов. Взаимное влияние этих двух систем, обуслов-
ленное электромагнитным взаимодействием, рассматривается в
следующем разделе.
Уравнение максвелловского типа. Описывая сверхпроводящее
состояние, обобщим уравнение максвелловского типа, включив
в него магнитное взаимодействие [41]. Чтобы сократить рассмо-
трение, мы не будем приводить полного микроскопического вы-
вода, а ограничимся лишь кратким изложением. Магнитная ин-
дукция В = V х а определяется суммой магнитного поля Н, соз-
даваемого незатухающим током J, и магнитного момента редко-
земельных ионов т:
В = Н + 4ят, A1.4.4)
VxH-i^-. A1.4.5)
Незатухающий ток J определяется выражением A1.3.36).
Из соотношений A1.4.4) и A1.4.5) следует
№ - Vv) «v (х) = -?г1dV (х - у) тй <д) (ov (у) - Ц- dv/ (у)) -
4Vxm),-, A1.4.6)
х) Тем не менее в реальных соединениях именно оно определяет структуру
и основные характеристики неоднородного состояния. Подробнее см. обзор
[56* ]. — Прим. перев.
462 Глава II
— метрический тензор. Магнитный момент m определяется
выражением
m (х) = йгцв ? Sn6 (х - Rn), A1.4.7)
где Sn — спин, локализованный в узле Rn кристаллической ре-
шетки. В статическом случае уравнение A1.4.6) можно предста-
вить в виде
V2B (х) = -±- J dPyc (х - у) [ В (у) - Ц- V X V/ (у)] + 4дУ2т. A1.4.8)
Здесь и далее т— поперечная составляющая намагниченности.
Энергия дается формулой
Е = ЕЩ- 4- j cPxm (х) Yo (V) m (x) + ECOte, A1.4.9)
где
Е [Я = ж JdSx [-гМч -{ai~4- d'f) 4я/< - 8ят-в]'
A1.4.10)
а ?соге — энергия сердцевины вихря. Приведенное выше выра-
жение для Е [/] отличается от A1.3.11) тем, что в нем добавлен
последний член, описывающий магнитное дипольное взаимодей-
ствие. Второй член в A1.4.9) отвечает взаимодействию между
спинами резкоземельных ионов, обусловленному всеми возмож-
ными механизмами (в том числе и слабым s—/-взаимодействием),
за исключением магнитного дипольного взаимодействия, описы-
ваемого последним членом в выражении A1.4.10) для Е If].
Дифференциальный оператор Yo (V) определяет величину спин-
спинового взаимодействия между редкоземельными ионами.
Используя уравнение A1.4.8), можно вывести формулу
xWf, A1.4.11)
имеющую такой же вид, как и полученное выше соотношение
A1.3.18) для немагнитного случая. Но в данном случае Н не сов-
падает с магнитной индукцией В..Магнитный момент m (x) вычис-
лен в гл. 5 в рамках приближения среднего поля. Он дается фор-
мулой E.3.21):
\m(x)\=giiBJNBjlg\iBjp\Hm(x)\], A1.4.12)
где Нт (х) = В (х) + vo (V) т (х). A1.4.13)
Здесь предполагается, что m и В параллельны друг другу, Af —
число магнитных ионов в единичном объеме, Bj — функция
Бриллюэна, а р = \l(kBT); Hm — молекулярное поле, действую-
Квантовая электродинамика твердых тел. II 463
щее на редкоземельные ионы. В линейном приближении из A1.4.13)
следует закон Кюри
т(х) = -р-Нт(х), A1.4.14)
где С — постоянная Кюри. Объединяя уравнения A1.4.8) и
A1.4.14), можно найти В (х) и т(х).
Для реальных расчетов требуется знание характеристической
функции бозонов с (х). До сих пор в большинстве расчетов исполь-
зовалась приближенная формула E.4.179). Слабое s—/-взаимо-
действие может слегка изменить параметр |0 и спиновое взаимо-
действие у0 (k), поскольку оно влияет на величину А. Мы рассма-
триваем |0, KL и VN @) в качестве параметров теории.
Эффект экранировки и фаза с периодическими упорядоченными
спинами. При решении уравнений A1.4.8) и A1.4.14) удобно
воспользоваться фурье-представлением. Определим величину у0 (р)
посредством соотношения уо(р)ехр [ipx] =Yo(V)exp [ipx]. Если
из A1.4.8) и A1.4.14) исключить В, то получим
[7-Cv(p)]m(p) = 0, A1.4.15)
Y (Р) = Yo (P) + 4я. A1.4.17)
Из уравнения A1.4.15) видно, что эффективное обменное взаимо-
действие описывается величиной у, а не у. Согласно соотношению
A1.4.16), это эффективное взаимодействие экранируется незату-
хающими токами. Этого и следовало ожидать, исходя из того,
что благодаря незатухающим токам сверхпроводник становится
диамагнитным.
Обычно полагают, что уо (р) имеет вид [(Тт/С) ¦—¦ 4я —
— (D/C) р2], откуда следует
-%L__g.p2. A1.4.18)
Если мы рассматриваем ферромагнитный сверхпроводник,
то Тт > 0. В этом случае у (р) имеет максимум при р = 0, что
показано штриховой кривой на рис. 11.10. В сверхпроводящем
состоянии у (р) сильно экранируется в области малых р. Это по-
казано на том же рисунке с помощью сплошной кривой. Следова-
тельно, у имеет максимум при некотором ненулевом значении | р |
(например, Q\ p |). Величина Q порядка DnC/DLlXY*. Исходя
из A1.4.15), можно видеть, что при понижении температуры
(при Т = Су (р), где ] р | = Q) появляется бесконечно малый маг*
464
Глава 11
У(Р)
l
Тр/С
нитный момент m (р) с |р| = Q. Это показывает 1), что в сверх-
проводящем состоянии возникает спиновый порядок с периодом,
определяемым волновым вектором Q [42 ] (в рамках теории Гинз-
бурга—Ландау возможность спирального спинового состояния
описана в работах [43]). Как упомянуто выше, результаты экс-
периментов по дифракции нейтронов показали, что в HoMoeS8
возникает периодическое спиновое упорядочение, а в ErRh4B4
проявляются большие спиновые флуктуации периодического
типа.
Наличие спин-периодической фазы оказывает также влияние
на электромагнитное поле вследствие его связи с магнитным мо-
ментом. Фактически если исклю-
чить m из обоих уравнений A1.4.8)
и A1.4.14), то в получившемся
уравнении для В (р) появляется
множитель [Т—Су(р)] (помимо
обычного множителя, связанного
с плазмонной модой), характе-
ризующий влияние спиновых волн
на электромагнитное поле.
В ферромагнитном образце
^_ обычно имеется множество блохов^
р ских стенок. Структура магнит-
ных моментов в блоховской стенке
напоминает магнитную спираль-
ную структуру. Поэтому прове-
денное выше рассмотрение позволяет предположить, что внутри
блоховской стенки имеется область, которая остается сверхпро-
водящей даже при температуре ниже температуры возврата в нор-
мальное состояние Тм [44]. Это могло бы объяснить, почему
удельное сопротивление ErRh4B4 и HoMo6S8 не возвращается
к значению, характерному для нормального состояния при Т <
< Тм.
Многие тройные соединения являются сверхпроводниками
II рода, если температура близка к температуре сверхпроводя-
щего перехода Тс. Теоретическое рассмотрение смешанного со-
Q
Рис. 11.10.
х) Мы обнаружили спин-периодическую фазу довольно случайным образом.
Когда в конце 1978 г. мы изучали смешанное состояние в ErRh4B4, оказалось,
что наш компьютер не может выполнить до конца всю программу расчета. Затем
выяснилось, что трудности в счете связаны с наличием особенности у корреля-
ционной функции, что свидетельствовало о существовании спин-периодической
фазы [42]. Позднее мы узнали, что примерно в это же время спин-периодическую
фазу обнаружил Сул (см. работу Суда [43]). Сразу же после того как мы закон-
чили наш препринт о спин-периодической фазе, нами был получен от Блаунта
и Вармы препринт [43], из которого следовало, что они независимо от нас по-
лучили тот же результат.
Квантовая электродинамика твердых тел. II 465
стояния этих сверхпроводников включает те же этапы, что и
в немагнитном случае (исследование магнитных свойств магнит-
ных сверхпроводников в рамках теории Гинзбурга—Ландау
см. в работе [45]). При вычислении термодинамического потен-
циала Гиббса мы должны учитывать изменение энтр'опии за счет
локализованных спинов. Энергия сердцевины равна пЕ(п),
где Е (п) дается формулой A1.3.84) Е (п) = Ех — E2hiat. Но
определение /iint (см. A1.3.83)) должно быть модифицировано сле-
дующим образом:
где b (х) — магнитная индукция в точке х при наличии единствен-
ного вихря, расположенного в начале координат. В немагнитном
случае b равно магнитному полю h, создаваемому отдельным вих-
рем, и, следовательно, выражение A1.4.19) согласуется с A1.3.83).
В магнитных сверхпроводниках b (?) экспоненциально спадает,
a h (?) ведет себя по-другому из-за наличия магнитного момента.
Рассмотрение, следующее за формулой A1.3.80), доказывает спра-
ведливость выражения A1.4.19) для /iint.
Особое свойство магнитных сверхпроводников обусловлено
квантованием потока. Рассмотрим один вихрь с единичным по-
током. Поскольку за часть этого потока ответствен магнитный мо-
мент, магнитное поле ослабляется и может даже сменить направ-
ление, если магнитный момент достаточно велик. Эта инверсия
магнитного поля, приводящая к инверсии тока, способствует уси-
лению притяжения между вихрями, поскольку межвихревое
взаимодействие, согласно формуле A1.4.11), определяется маг-
нитным полем. Благодаря этому появляется тенденция к изме-
нению рода сверхпроводника в направлении П/2 -> П/1 -> I
[41, 46].
Влияние экранировки на у и усиление эффекта инверсии маг-
нитного поля представляют собой два существенных механизма,
основываясь на которых можно понять многие необычные явле-
ния. Влияние экранировки на y подтверждено в экспериментах
по затуханию ультразвука [47].
Рассматривая смешанное состояние магнитных сверхпровод-
ников в сильных полях, следует проявлять особую осторожность
при учете эффекта насыщения магнитного момента вихрей. Даже
если магнитный сверхпроводник находится в антиферромагнит-
ном состоянии, спиновое упорядочение может стать ферромаг-
нитным, если внешнее магнитное поле (<#с2) оказывается доста-
точно сильным. Отражением этого изменения спинового порядка
является провал на графике зависимости #с2 от температуры вбли-
зи точки Нееля.
466 Рлава It
Чтобы анализировать магнитные свойства магнитных сверх-
проводников, полезно заметить, что температурная зависимость
магнитной индукции В в них до некоторой степени схожа с той,
которая имеет место в немагнитном случае. Грубо г.оворя, резкие
изменения магнитного поля Н=В — Апт связаны с поведением
магнитного момента. Поэтому обычно полезно строить график не
только зависимости Я от Т, но также и В от Г. Например, график
зависимости Яс2 от Т следует дополнить графиком зависимости Ве
от Т, где Вс — магнитная индукция при Я = Яс2 (т. е. при п =
= «с)-
В некоторых условиях следует ожидать, что вихревое состояние
в ферромагнитном сверхпроводнике окажется устойчивым в отсут-
ствие внешнего поля. Чтобы исследовать механизм, ответственный
за существование спонтанно возни-
кающих вихрей [48], положим тем-
{-knM0)=yH°/us\ пературу равной нулю. Если в обра-
\нт =о\ зец через единичную площадку
проникают п вихрей, то для усред-
ненного молекулярного поля, дейст-
вующего на редкоземельный ион,
можно записать выражение
.„о h°cz ' Нт = пф-4пМ^-уМ. A1.4.20)
н°(=ьпм) Если поле Нт положительно, то об-
рис л л разец намагничен однородно, а зна-
чение намагниченности насыщения
равно Ng\iBJ. Вычисление свободной энергии показывает, что в
ферромагнитном сверхпроводнике 4пМ играет роль внешнего
поля для орбитального движения электронов. Обозначим через
Н°с2 и Я°[ верхнее и нижнее значения критического поля неко-
торого образца, аналогичного данному, но в котором отсутствуют
спины, ответственные за образование магнитоупорядоченного
состояния. Если 4пМ удовлетворяет условию
Н°с1<4пМ<Н%, A1.4.21)
то в образце могут спонтанно возникнуть вихри. Намагничен-
ность стабилизируется магнитным полем, создаваемым током
вихрей, а вихри самосогласованным образом стабилизируются
намагниченностью. Таким образом, для устойчивости спонтан-
ных вихрей необходимо, чтобы одновременно удовлетворялись
два условия, A1.4.21) и Нт >0 (рис. 11.11). Эти условия вы-
полняются, если х и М велики.
На рис. 11.12 показаны типичные графики зависимости на-
магниченности М от внешнего магнитного поля Я при различных
температурах вблизи точки перехода в магнитоупорядоченное со-
стояние. Сплошные линии соответствуют сверхпроводящему со-
Квантовая электродинамика твердых тел. II
467
стоянию, а штриховые — нормальному состоянию. Поскольку
вблизи точки магнитного перехода намагниченность увеличи-
вается, закон квантования потока указывает на появление ин-
версии поля, приводящей к притяжению между вихрями и пре-
вращающей образец в сверхпроводник П/1 рода. Поэтому кривые
намагничивания на рис. 11.12 демонстрируют наличие перехода
первого рода при Н = Нс1.
0,6
0,5
Ofi
0,3
0,2
0,1
0
л *
/
/
/ /
1 '
1 1
•
1 1 t
1 1
//
/ /
/ /
/ /
/
/
/
/
/
1 /
I
Jj
1
1
0,1
6
0,18
/ / '
/
/
/
/
/
f /
о,г
м/
20
0,30
/
/
/
/
/
0,40
/
^0,60
'o,eo
I i ^
0,3 O,if
Рис. 11.12.
Поскольку существует много возможных типов фаз, таких,
как мейсснеровское состояние, спин-периодическое сверхпроводя-
щее состояние, состояние со спонтанными вихрями, нормальное
ферромагнитное состояние и т. д., фазовая диаграмма оказы-
вается весьма сложной. Были проведены соответствующие теоре-
тические расчеты для магнитных сверхпроводников как ферро-
магнитного, так и антиферромагнитного типа [49].
Вычисление параметров хь х2 и хз было обобщено на случай
магнитных сверхпроводников в работе [50].
Было указано также, что в области вблизи поверхности или
в тонкой пленке магнитного сверхпроводника ферромагнитного
468 Глава И
типа ферромагнитное упорядочение может сосуществовать со
сверхпроводимостью при температуре (например, Ts), более вы-
сокой, чем Тм [51 ]. Такая поверхностная сверхпроводимость крат-
ко рассматривается в гл. 12.
Параметр порядка. Мы завершаем этот раздел кратким заме-
чанием, касающимся щели А в электронном энергетическом
спектре. Для простоты рассмотрим предельный случай неупругого
электронного рассеяния, обусловленного спинами (предельный
случай упругого рассеяния рассмотрен в работе [52]). Чтобы оце-
нить А, дополним гамильтониан БКШ следующим членом, опи-
сывающим взаимодействие:
¦L J
(х) о'Ч> (х) х1'- (х - у) ^ (у) оЛ|> (у),
где %!> (х) — восприимчивость локализованных спинов относи-
тельно поля, сопряженного параметру порядка. В приближении
Хартри—Фока получаем следующее уравнение для щели [53]:
(П.4.22)
где A (k) — энергетическая щель, зависящая от к2, % (к) — фурье-
образ % (х):
^X) = WI№^W' . (П.4.23)
Ek = [el + Д2(&)]1/2, а V — константа связи, характеризующая
взаимодействие БКШ.
Выберем % (к) следующим образом:
Это выражение с учетом A1.4.18) можно записать в виде
(k)
В случае немагнитных сверхпроводников мы использовали
приближение (см. E.4.40)), при котором интегрирование по угло-
вым переменным, имеющееся в уравнении для щели, заменялось
на интегрирование по поверхности Ферми. Если воспользоваться
тем же приближением в случае уравнения A1.4.22), то это приво-
дит к появлению инфракрасной расходимости при Т = Т,п, в ре-
зультате чего А обращается в нуль при Т, близких к Тт. По-
скольку инфракрасная расходимость логарифмическая, следует
проверить, приводит или нет более точное вычисление к ослабле-
нию эффекта, обусловленного этой расходимостью. Тщательное
рассмотрение интегрирования в уравнении A1.4.22) показывает,
Квантовая электродинамика твердых тел. II 469
что подобная инфракрасная расходимость не должна существо-
вать (тот же результат был получен в пределе упругого рассея-
ния [52]).
Будем использовать следующее приближение:
1. Область интегрирования заключена в пределах е^ — <oD <
<" е <;,е.р + ©о, гДе f°D — дебаевская энергия; фо <^ е^.
2. Вблизи поверхности Ферми A (k) — гладкая функция
только от k и, следовательно, может быть приближенно заменена
на A (kF).
3. Плотность состояний в рассматриваемом интервале является
гладкой функцией от е: N (е) ^ N @).
Поскольку Тс значительно меньше coD, имеем | Т — Tm [ <^ aD
при Т <: Тс. В этом случае уравнение A1.4.22) принимает вид
i+a(t_tm)
где tD = (?>D/kBTc0 (Tc0 — критическая температура при Р = 0),
А^ = A (kF)/(aD, t = Т/Тс0, А = CP/V) (C/W&), а = TJW®,
b = ©|,/16е|?. Поскольку Ъ Ф 0, А может оставаться конечным
при t = tm. Имея в виду ErRh4B4 и HoMoeS8, выберем в качестве
пробных следующие типичные значения параметров: VN @) = 0,3,
с(=4яС/Гт) =2, 3P/V = 1. В качестве грубого приближения
для Dk2F/Tm имеет смысл воспользоваться выражением BяJ х
X (радиус взаимодействия спинов/постоянная решеткиJ. Этот
параметр может иметь любое значение больше 5, хотя представ-
ляется вероятным, что оно превышает 30. Отметим, что при росте
этого параметра А уменьшается, а А увеличивается. Если мы вы-
берем Dkp/Tm «=« 5 или 10, то параметр порядка заметно умень-
шается вблизи Т = Тго, хотя он нигде не обращается в нуль.
Если же А на порядок меньше (т. е. Dk2FITm на порядок больше),
то уменьшение параметра порядка почти незаметно [54].
В приведенном выше рассмотрении мы использовали восприим-
чивость относительно поля, сопряженного параметру порядка,
описывающую нормальное состояние. Если воспользоваться та-
кой восприимчивостью для мейсснеровского состояния, то вели-
чину у (к), определяемую выражением A1.4.25), следует заменить
на y (к), в которой учтено экранирование флуктуации в системе
локализованных спинов, обусловленное незатухающими токами.
Если параметры выбираются таким образом, что в сверхпроводя-
щем состоянии не появляется спин-периодическая фаза, зависи-
мость А от t оказывается более гладкой, чем та, которая дается
уравнением A1.4.26). Но в том случае, когда возникает спин-пе-
470 Глава It
риодическая фаза (Тр > Тм), знаменатель в выражении для %
обращается в нуль при Т == Тр, и интегрирование в уравнении
A1.4.22) при T<zTp приводит к инфракрасной расходимости,
обусловленной наличием спин-периодической фазы. Не очевидно,
что эта расходимость исчезнет при более точном вычислении пара-
метра порядка. В любом случае следует ожидать появления в си-
стеме некоторой анизотропии, что позволит легко исключить ин-
фракрасную расходимость.
В качестве заключительного замечания укажем, что, согласно
[33, 35], сосуществование спин-периодической фазы со сверхпро-
водимостью возможно также благодаря s—/-взаимодействию.
ЛИТЕРАТУРА
1. Matsumoto Н., Semenoff G., Tachiki М., Umezawa #., Fortschr. Phys.,, 28,
67 A980);
Nozieres P., Pines D., Nuovo Cirn., 10, 470 A958).
2. Matsumoto H., Umezawa H., Fortschr. Phys., 24, 357 A977).
3. Matsumoto H., Tachiki M., Umezawa #., Fortschr. Phys., 25, 273 A977).
4. Kubo R., J. Phys. Soc. Jap., 12, 570 A957).
5. Leplae L., Mancini F.t Umezawa #., Phys. Rep., 10C, 152 A974).
6. Eilenberger G., Zs. Phys , 214, 195 A968).
7. Pesch W., Kramer L., J. Low Temp. Phys., 15, 367 A974).
8. Горькое Л. П., ЖЭТФ, 34, 735 A958); 36, 1918; 37, 1407 A959).
9. Superconductivity, ed. R. G. Parks, Marcel Dekker, New York, 1969. [Имеется
перевод двух обзоров из этого сборника: Коэн М., Глздстоун Г., Иенсен М.,
Шриффер Дж. Сверхпроводимость полупроводников и переходных метал-
лов. — М.: Мир. 1972.]
10. De Lillo S., Mancini F., Physica, 92B, 239 A977);
Mancini F., Marinaro M., Zannetti M., Physica, 93B, 291 A978);
De Lillo S., Mancini F., Umezawa H., Physica, 95B, 53 A978).
11. Абрикосов А. А., Горькое Л. П., ЖЭТФ, 36, 319 A959).
12. Krageloh U., Phys. Stat. Sol., 42, 559 A970);
Essman U., Trauble H., Phys. Lett., A24, 526 A967);
Seeger A., Comm. Sol. St. Phys., 3, 97 A970);
Schelten J., Ullmaier #., Schmatz W., Phys. Stat. Sol. (b), 48, 619 A971);
Finnemore D. K-, Clem J. R., Tromberg Т. К-, Phys. Rev., B6, 1056 (I972)'.
Kumpf V., Phys. Stat. Sol. (b), 44, 829 A971);
Auer J., Ullmaier H., Phys. Rev., B7, 136 A973).
Wollan J. J., Haas K- W., Clem J. R., Finnemore D. K-, Phys. Rev., B10,
1874 A974).
13. Eilenberger G., Buttner #., Zs. Phys., 224, 335 A969);
Leplae L., Mancini F., Umezawa #., Lett. Nuovo Cim., 3, 153 A970);
Dichtel K-, Phys. Lett., 35A, 285 A971);
Brandt E. H., Phys. Lett., 39A, 193 A972);
Hubert A., Phys. Stat. Sol. (b), 53, 147 A972);
Jacobs A. E., J. Low Temp. Phys., 10, 137 A973);
Leplae L., Srinivasan V., Umezawa H., Phys. Lett., 45A, 177 A973);
Mancini F., Phys. Lett., 45A, 179 A973);
De Cesare L., Mancini F., Phys. Stat. Sol. (b), 65, 419 A974);
Leplae L., Srinivasen V., Umezawa H., Lett. Nuovo Cim., 9, 711 A974);
Mancini F., Scarpetta G., Srinivasan V., Umezawa H., Phys. Rev., B9, 130
A974).
14. Leplae L., Shah M. N., Umezawa H., Physica, 80B, 493 A975).
Квантовая электродинамика твердых тел. // 471
15. Christen D. К-, Spooner S., Thorel P., Kerchner H. R., J. Appl. Cryst., 11,
680 A978).
16. Mancini F., Tachiki M., Umezawa H., Physica, 94B, 1 A978).
17. Mancini F., Teshima R., Umezawa H., Sol. St. Commun., 24, 561 A977).
18. Wollan J. J., Haas K- W., Clem J. R., FinnemoreD. K-, Phys. Rev., BIO,
1874 A974).
19. Caroli C, de Gennes P. G., Matricon J., Phys. Lett., 9, 307 A964);
Caroli C, Matricon J., Phys. Kondens. Mat., 3, 380 A965).
20. Maki K-, Phys. Rev., 156, 437 A967);
Kagiwada R., Levy M., Rudnick I., Kagiwada H., Maki K-, Phys. Rev. Lett
18, 74 A967).
21. Anisotropy effects in superconductivity, ed. H. W. Weber, American Elsevier,
New York, 1977.
22. Tachiki M., Koyama Г., Phys. Rev., B15, 3339 A977);
Tachiki M., Umezawa H., Phys, Rev., B15, 3332 A977).
23. Muto Y., Toyota N., Noto K-, Akutsu K-, Isino M., Fukase Г., J. Low Temp.
Phys., 34, 617 A979);
Toyota N., Fukase Т., Tachiki M., Muto Y., Phys. Rev., B21, 1827 A980).
24. Koyama Т., Tachiki M., Matsumoto #., Umezawa H., Phys. Rev., B20, 918
A979).
25. Thorel P., Christen D. K-, J. Appl. Cryst., 11, 654 A978);
Christen D. K., Kerchner H. R., Sekula S. Т., Thorel P., Phys. Rev., B21,
102 A981).
26. Koyama Т., PhD Thesis, Tohoku University, 1979.
27. Takanaka K-, Prog. Theor. Phys., 46, 357; 1301 A971); 49, 64 A973);
Rogers M., Kahn R., Delrieu J. M., Phys. Lett., A50, 291 A974).
28. Herring C, Physica, 24, 1845 A958).
29. Suhl H., Matthias В. Т., Phys. Rev. Lett., 2, 5; Phys. Rev., 114, 977 A959).
30. Абрикосов А. А., Горькое Л. П., ЖЭТФ, 39, 1781 A960).
31. Maki К- in: Superconductivity, ed. R. D. Parks, Marcel Dekker, New York,
1969, p. 1035.
32. Ruderman M. A., KUtel C, Phys. Rev., 96, 99 A954);
Kasuya Т., Prog. Theor. Phys., 16, 45 A956);
Yosida K-, Phys. Rev., 106, 893 A957).
33. Anderson P. №., Suhl H., Phys. Rev., 116, 898 A959).
34. Suhl H., Matthias В. Т., Phys. Rev., Lett., 4, 51 A960).
35. Fertig W. A., Johnston D. C, Delong L. E., McCallum R. W., Maple M. В.,
Matthias В. Т., Phys. Rev. Lett., 38, 987 A977).
36. Ishikawa M., Fisher 0., Sol. St. Commun., 23, 37; 24, 747 A977).
37. Moncton D. E., J. Appl. Phys., 50, 1880 A979);
MonctonD. E., MoWhanD. В., Schmidt P. H., Shirane G., Thomlinson W.,
Maple M. В., МасКау Н. В., Woolf L. D., Fisk Z., Johnston D. C, Phys.
Rev. Lett., 45, 2060 A980);
Lynn J. W., Shirane G., Thomlinson №., Shelton R. N.. Phys. Rev. Lett., 46,
368 A981).
38. OttH. R., Fertig W. A., JohnstonD. C, Maple M. В., Matthias В. Т., J. Low
Temp. Phys., 83, 159 A978).
39. Ishikawa M., Fisher O., Muller J., J. de Phys., C6, 1379 A978);
Maple M. В., J. de Phys., C6, 1374 A978);
Ishikawa M., Maple M. B. — in: Ternary superconductors, eds. Q. K. Shenoy,
B. D. Dunlap and F. Y. Fradin, North-Holland, New York, 1981.
40. Jarlborg J., Freeman A. J., Watson-Yang T. J., Phys. Rev. Lett., 39 1032
A977);
Freeman A. J., Jarlborg Т., Watson-Yang T. J., J. Mag. Magn. Mat., 7, 296
A978);
Freeman A. J., Jarlborg Т., J. Appl. Phys., 50, 1876 A979);
Jarlborg Т., Freeman A. J., Phys. r>-v. Lett., 44, 178 A980).
472 Глава 11
41. Tachiki M., Matsumoto #., Umezawa #., Phys. Rev., B30, 1915 A979).
42. Matsumoto H., Umezawa H., Tachiki M., Sol. St. Commun., 31, 157 A979);
Tachiki M., Kotani A., Matsumoto #., Umezawa H., Sol. St. Commun., 31
927 A979).
43. Suhl H. — in: Felix Bloch Festschrift, 1980;
Blount E. /., Varma С. М., Phys. Rev. Lett., 42, 1079 A979).
44. Matthias В. Т., Suhl H., Phys. Rev. Lett., 4, 51 A960);
Tachiki M., Kotani A., Matsumoto #., Umezawa #., Sol. St. Commun., 32,
599 A979).
45. Krey U., Int. J. Magn., 3, 65 A972); 4, 153 A973).
46. Adrian H., Miller K., Saemann-Ischenko. G., Phys. Rev., B22, 4424 A980).
47. Tachiki M., Koyama Т., Matsumoto H., Umezawa #., Sol. St. Commun., 34,
269 A980);
Schneider S. C, Levy M., Johnston D, G., Matthias В. Т., Phys. Lett., A80,
72 A980);
Toyota N.. Wood S. В., Muio Y., Sol. St. Commun., 37, 547 A981).
48. Tachiki M., Matsumoto H., Koyama Т., Umezawa #., Sol. St. Commun., 34,
19 A980);
Kuper C. G., Revzen M., Ron A., Phys. Rev. Lett., 44, 1545 A980).
49. Matsumoto #., Umezawa H., Teshima R., Tachiki M., University of Alberta
preprint, 1981;
Sakai O., Tachiki M., Koyama Т., Matsumoto H., Umezawa H., Phys. Rev.,
B24, 3830 A981).
50. Matsumoto H., Umezawa H., Tachiki M., University of Alberta preprint, 1981.,
51. Tachiki M., Kotani A., Takahashi S., Koyama Т., Matsumoto H., Umezawa H.
Sol. St. Commun, 37, 113 A981);
Kotani A., Tachiki M., Matsumoto H., Umezawa В., Phys. Rev., B23, 5960
A981);
Kotani A., Takahashi S., Tachiki M., Matsumoto H., Umezawa #., Sol. St.
Commun, 37, 619 A981).
52. Lee Ting-Kuo, Sol. St. Commun., 34, 9 A980).
53. Maekawa S., Tachiki M., Phys. Rev., B18, 4688 A978).
54. Semenoff G., Matsumoto H., Teshima R., Tachiki M., Umezawa H., Univer-
sity of Alberta preprint, 1979.
55. Bulaevskii L. N., Rusinov A. I., Kulic M., Sol. St. Commun., 30, 59 A979);
J. Low Temp., Phys., 39, 255 A980);
Machida K-, Matsubara Т., Sol. St. Commun., 31, 791 A979).
56*. Буздин A. #., Булаевский JI. #., Кулич M. JI., Панюков С. В., УФН, 44,
вып. 4 A984).
ГЛАВА 12
ЯВЛЕНИЯ, СВЯЗАННЫЕ С ГРАНИЧНОЙ
ПОВЕРХНОСТЬЮ
12.1. Введение
В гл. 10 рассматривается общий формализм, применяемый для
изучения макроскопических явлений с топологическими особен-
ностями. Там же показано, как можно подойти к описанию макро-
скопических явлений при наличии двумерных (поверхностных)
особенностей. Этот метод затем применен к границам зерен в кри-
сталлах.
Наиболее интересная область применения этого формализма —
изучение макроскопических явлений, связанных с границами
упорядоченных систем. Явления, связанные с граничной поверх-
ностью, обычно сводят либо к граничной задаче (при этом граница
представляется оболочкой, в которую заключена рассматривае-
мая упорядоченная система), либо просто к двумерной задаче,
ограничиваясь только поверхностью. Обычно считается также,
что с этими поверхностями связаны определенные потенциальные
барьеры. Но существует и иной подход к исследованию этих яв-
лений. Он основан на той точке зрения, что реальные системы
редко находятся в оболочке. Поскольку их граничные поверх-
ности образуются самосогласованным образом самими системами,
эти поверхности попадают в категорию поверхностных особенно-
стей, рассматриваемых в гл. 10. Когда метод, описанный в гл. 10,
применяется к граничным явлениям, нужно знать граничное усло-
вие, с помощью которого устанавливается природа двумерной
особенности.
Изложенная выше точка зрения на естественную границу при-
водит к следующему приближенному методу изучения упорядо-
ченных систем конечного размера. Сначала рассмотрим упоря-
доченную систему бесконечного размера. Затем создадим замкну-
тую двумерную особенность с помощью бозонного преобразова-
ния и изучим эффекты, связанные с этой особенностью. Отметим,
что двумерная особенность, естественно, создает самосогласован-
ный потенциал, обсуждаемый в гл. 9, который влияет на кванто-
вые возбуждения. Мы не рассматриваем систему вне граничной
поверхности, ограничиваясь волновыми функциями внутри зам-
кнутой области. Заметим, что голдстоуновские квантовые состоя-
ния с волновыми функциями внутри ограниченной области, нахо-
дящиеся под действием самосогласованного потенциала, могут
474 Глава 12
иметь энергетическую щель порядка 1/L, где L — линейный раз-
мер внутренней области.
Другим интересным приложением, в котором используются
поверхностные особенности, является расчет макроскопических
токов, текущих через контакт двух систем. Обычно в явлениях та-
кого рода микроскопически рассчитывается туннельный ток.
Но их можно рассматривать также как макроскопические явле-
ния, возникающие благодаря наличию двумерной особенности
(контакта).
В этой главе мы не рассматриваем проблему исследования
систем конечного размера. Вместо этого мы сконцентрируем вни-
мание на некоторых типичных поверхностных явлениях, упомя-
нутых выше. В следующем разделе мы изучим звуковую волну
на поверхности кристалла как пример явления, связанного с су-
ществованием границы. В разд. 12.3 мы рассмотрим в качестве при-
мера контактного явления эффект Джозефсона. В разд. 12.4 будет
рассмотрено поведение поверхностных магнитных полей в сверх-
проводниках.
12.2. Звуковые волны на поверхности кристалла
В разд. 10.2 мы рассмотрели одномерные и двумерные осо-
бенности в кристаллах. Здесь мы применим тот же метод к звуко-
вым волнам на поверхности кристалла.
Осциллирующие двумерные особенности. Волну на поверх-
ности кристалла можно рассматривать как волну, связанную с
с осциллирующей двумерной границей [1]. В разд. 10.2 форма
двумерной особенности описывается функцией у (т, alt а2), где
т — времениподобный, a at и а2 — пространственноподобные
параметры. Рассмотрим поверхность, которая лежит на плоско-
сти (хъ х2), т. е. уз = 0. Когда эта поверхность осциллирует та-
ким образом, что направление распространения совпадает с осью
xlt то уз не равно нулю: у3 = Re (Ле'?) (рис. 12.1), где А — ам-
плитуда, а
l = qai — сот. A2.2.1)
Таким образом, колеблющаяся поверхность определяется соотно-
шениями
Уъ = т, Ух = °ъ Уъ = о„ у3 = Re (Ae*). A2.2.2)
Принимая, что одномерные особенности равномерно распре-
делены по поверхности, мы используем соотношение A0.2.45), т. е.
*'=X!att0i- A2-2.3)
Явления, связанные с граничной поверхностью
475
Подставляя его в уравнение A0.1.44), мы можем вычислить Gfv,
а затем с помощью уравнения A0.1.20) вычислить G\?v. Результат
имеет вид
& (х) = (а
где
. = И ааё^ и
л,
A2.2.4)
Л cost)), A2.2.5)
A2.2.6)
Рис. 12.1.
Из выражения A2.2.5) видно, что G^v (x) Ф 0 только в области
х3 — A cos t], которая содержит осциллирующую двумерную осо-
бенность.
В дальнейшем мы будем считать, что осцилляции малы, и
выражение A2.2.5) можно разложить в ряд по степеням А. Мы
будем учитывать только члены до первого порядка по А. Тогда
из уравнения A2.2.5) получаем
GJX (х) ~ Н^у (х) + AKlv (х),
где
^у (х)
'б(Л'з),
i д
A2.2.7)
A2.2.8)
A2.2.9)
Поля смещений, Поле смещений f (л;) определяется выражением
A0.2.5), т. е.
2 2 Ц lP^ IP) eipx- A2.2.10)
= 2 2 j Цз А^
k, I К, p
Потребовав, чтобы зависимость от времени в характеристиках
рассматриваемых явлений возникала только за счет осцилляции,
476 Глава 12
получаем, что ft = 0, если А = 0. Тогда выражения A2.2.7) и
A2.2.10) дают
а'° = 0. A2.2.11)
При этом выражение A2.2.8) соответствует A0.2.64). Мы уже вы-
числили поле смещений, возникающее благодаря двумерной осо-
бенности, описываемой уравнением A0.2.64). В разд. 10.2 сказано,
что выражение A0.2.67) автоматически удовлетворяет условию
свободной границы ai3 = 0. Это согласуется с представлением,
что рассматриваемая граница самосогласованным образом под-
держивается свободной до тех пор, пока какая-то внешняя сила
не заставит ее двигаться.
Для простоты мы не учитываем влияние поверхностной дефор-
мации. Так, мы потребуем, чтобы при А = 0 выполнялось равен-
ство f = 0, откуда, согласно A0.2.65), следует
а" = а21 = а31 = а32 = а11 = а22 = 0. A2.2.12)
Таким образом, не равны нулю только члены a'3 (i =1, 2, 3).
Обратимся теперь к членам первого порядка по А. В качестве
расчетного приема уберем сначала в выражении A2.2.9) символ
Re и вещественную часть выражения возьмем только в конце вы-
числений. Эта операция оправдывается тем обстоятельством, что
теория линейна по Kjn>. Фурье-компоненты K^v (х) будем обозна-
чать символами Kjtv (/>)• Не равные нулю компоненты имеют вид
«4 (Р) = -Чо (Р) = i BяKа"«)б (Ро ~ «) б (Р1 ~ q) б (р2), A2.2.13а)
К[3{р) = -Щ1(Р) =/Bя)"a»qb(po-a)&(Pl ~q)b(Pi). A2.2.136)
Подставляя эти выражения в A2.2.10) и принимая во внима-
ние соотношение A0.2.27), получаем
) dift (x) = Re -iA 2j 2j C>k'a ~t ~^~- {I'{X) bik + Ji/i (X)}
\ к. I I J
A2.2.14a)
<52/* (jc) = 0, A2.2.146)
d3ft (x) = Re (Л©2 V a»{ix W а„ + J., (x)} + .
^i4{ ). A2.2.14b)
k, i i
-Ш-Ш=Т-ЯГШ- A2-2Л4г)
Явления, связанные с граничной поверхностью 477
Здесь
h (х)=\-%?- 2 ' 22 S (р0 - со) б (Pl - q) б 0i2)e"» =
— шр/"*' A2-2Л5)
= {v, -vt)]-^PiPk {pl_vy){pl^y) e ~
(-w{q8il ~iKAs) {q8hl ~iKt8k3) eKtH ~
l\ A2.2.16)
При интегрировании надо учитывать, что /i (x) -> 0 и Jik (x) -> О
при д:3 ->—оо. В приведенных выше выражениях использованы
следующие обозначения:
К? = <72--^-, A2.2.17а)
Kf = ^__^.> A2.2.176)
где vt я V[ — поперечная и продольная скорости фононов соответ-
ственно.
Теперь мы можем вывести дисперсионное соотношение для
поверхностной волны. Потребуем, чтобы поверхность, заданная
уравнением х3 = 0, была свободной. После некоторых громозд-
ких преобразований выражений A2.2.14) условия на свободной
поверхности
0;з = О (I = 1, 2, 3) при х3 = 0 A2.2.18)
приводят к уравнению
'(<f+K?J-4K,K,<f О О
О о] К? О
О 0 (<7а+К?)-4К<К,<7*
Первая, вторая и третья строки матричного уравнения соответ-
ствуют условиям 013 = 0, 023 = 0 и 0зз =0 соответственно. Из
уравнения A2.2.19) следует
A2.2.20)
а23 = 0. . A2.2.21)
Поверхностная волна возникает тогда и только тогда, когда
выполняются эти условия. Если учесть соотношения A2.2.17),
478 Глава 12
можно получить следующее дисперсионное соотношение для по-
верхностной волны:
со = qvta, A2.2.22)
где а удовлетворяет уравнению
[ -(-^J]=0. A2.2.23)
Заметим, что а зависит только от отношения поперечной и про-
дольной скоростей звука. Соотношение A2.2.22) вместе с уравне-
нием A2.2.23) представляет собой хорошо известный результат
для поверхностных волн, полученный Рэлеем [2].
Из приведенного выше вывода дисперсионного соотношения
следует, что 0 <]а2 <. 1 (ср. с A2.2.17)). Можно доказать, что
уравнение A2.2.23) всегда имеет два вещественных решения (а
и —а), удовлетворяющих условию 0 <а2 <| 1.
В частном случае % = \i уравнение A2.2.23) вместе с условием
О < а2 <¦ 1 дает
со = ± @,9194) qvt. A2.2.24)
Поучительно сравнить приведенный выше вывод уравнения
для поверхностной волны с общепринятым.
1. В приведенном выше выводе функции djt (х) однозначны,
а функции ft (х) — нет. Следовательно, Д (х) нельзя выразить
в виде фурье-образа. В общепринятом же выводе предполагается
однозначность функций ft (х).
2. В общепринятом методе вводится линейная комбинация
продольных и поперечных компонент, чтобы удовлетворить усло-
виям на свободной^ловерхности. Другими словами, соотношения,
возникающие в результате условия существования свободной гра-
ницы, формулируются в терминах поперечных и продольных ком-
понент, и при выводе дисперсионного соотношения необходима
процедура диагонализации. В приведенном здесь выводе диспер-
сионного соотношения поверхностная волна описывается в терми-
нах ais, и матричное уравнение A2.2.19) оказывается диагональ-
ным.
Хотя в этом разделе рассматривались только линейные по-
верхностные волны, можно получить и нелинейные свойства по-
верхностных волн, если воспользоваться полным выражением
для Gft (x) A2.2.5).
Закончим этот раздел двумя замечаниями. Во-первых, двумер-
ная особенность порождает самосогласованный потенциал. Под
влиянием этого потенциала и границы фононы, находящиеся
вблизи поверхности, становятся поверхностными фононами. Этот
метод получения поверхностных фононов до сих пор не разраба-
тывался. Во-вторых, когда приведенное выше рассмотрение по-
Явления, связанные с граничной поверхностью 4?9
верхностных волн применяется к осциллирующей границе зерен,
может возникнуть поверхностная волна, распространяющаяся
вдоль границы зерен. Волны такого вида не рассматривались.
12.3. Эффект Джозефсона
Общий анализ эффекта Джозефсона основан на рассмотрении
микроскопического туннелирования куперовских пар. В этом
разделе мы исследуем эффект Джозефсона как макроскопическое
явление1), вызванное поверхностной особенностью, связанной
с контактом. Оставляя в стороне случай контакта произвольной
формы (см. [4]), мы рассмотрим только случай плоского контакта.
Уравнения максвелловского типа A1.3.40) в кулоновской ка-
либровке сводятся к A1.3.43) и A1.3.47), т. е.
0V (*) = -j^- J &ус(х - у) [а' (у) - Ц- ЧШ], A2.3.1а)
аЪ (х) = - -1- М. J d3yc (x-y)g (у). A2.3.16)
Здесь
g(y)=(-D(d) + -±r-c(d)y1 fs, A2.3.2)
где /, = A/с) dfjdt и
( ^) A2.3.3)
В разд. 11.3 показано, что /s — сингулярная часть /:
К, dv]f. - Id», dv]f. A2.3.4)
Из соотношения Н = V х ас следует
«-T^^W.. A2-3.5)
где т2 определяется равенством т2 (к2) =-^-с(к2). Заметим,
что из соотношения Е = —Va0 + доас следует
, A2.3.6)
*) Предварительное рассмотрение этого вопроса дано в работе [3]. В данном
разделе используется постановка вопроса, приведенная в работе [4]. Прекрас-
ные обзоры по эффекту Джозефсона см. в работах [5].
480 Глава 12
где д0 = — A/с) (d/dt). Поскольку A2.3.3) дает
v \
выражение A2.3.6) принимает вид
„ _ По т* ., _. , . he [1 - (VеJ]
-— е m*-D(d) l0> VJ/ ~ e m*-D(d) т?-д^
A2.3.7)
(здесь использовано выражение A2.3.4)).
Выражения для плотности тока и заряда имеют вид
4яЗ = V X Н + д0Е, A2.3.8а)
4я/0 = V-E. A2.3.86)
Мы рассматриваем только явления, в которых имеется слабая
зависимость от времени, т. е. предполагается, что р\ С гп2- Тогда
из выражений A2.3.5) и A2.3.7) следует
A2.3.96)
где со2 = — (vBlcf V2. ^^
Рассмотрим теперь плоскую особенность, соответствующую
плоскому контакту:
Уй = т, f/i = сть г/2 = 02) г/3 = 0. A2.3.10)
Функция ^> в A0.1.44) зависит от т и ctl :
* = *(т, стх). A2.3.11)
Для простоты будем считать, что толщина контакта много меньше
длины когерентности, так что можно принять, что существует един-
ственная двумерная особенность. Когда толщина контакта недо-
статочно мала, нужно ввести сингулярную область, являющуюся
тонким слоем, определяемым тремя параметрами а1( ст2, ov
Если мы допустим справедливость выражений A2.3.10),
A2.3.11), то С* можно получить из A0.1.44). Необращающиеся
в нуль компоненты G1" и G^v равны G02 = —G20, G21 = —G12,
G?3 = -Gti и G& = -G?,:
G02 (x) - G? (x) = 5,^ (/, xi) б (х3), A2.3.12a)
Gn (x) = GJo W = ^ (*, Jfi) 5 (*»)• A2.3.126)
Явления, связанные с граничной поверхностью 481
Поскольку Gjv = [dp, dv] f, из A2.3.9) получаем
Н1(х) = Н9(х) = 0, A2.3.13а)
^ f д Ь{) A2.3.136)
JfJ mV , A2.3.14а)
Е.г(х) = 0, A2.3.146)
(x)- Пс mi \B6tt х)&(х\\ Пс ll-(v*/cWs,
X /!vJ^(t *iN(*3)]. A2.3.14b)
Тогда из выражения A2.3.86) следует, что плотность заряда равна
% ^а«6^)]- A2.3.15)
Из закона сохранения тока следует, что изменение во времени
величины /0 создает ток
^ ^ A2.3.16а)
У| (х) = У» (jc) = 0. A2.3.166)
Величины Jo и Js существуют в очень узкой области вблизи ха = 0
(т. е. | х31 < (vBlc) XL). Заметим, что (vB/c) XL много меньше, чем
iL (например, для чистого ванадия и ниобия vBlc — 10). По-
скольку ток Js, создаваемый осцилляциями локальной плотно-
сти заряда Js0, локальный, он не дает вклада в джозефсоновский
ток, если размер образца металла в направлении xs много больше
(vB/c) %L. Рассчитывая ток J по формуле A2.3.8а), легко видеть,
что J состоит из двух частей:
J = JC + J«. A2.3.17)
Здесь Je — стационарный ток
V-JC = O. A2.3.18)
Из выражения A2.3.16 а) можно видеть, что ток Js создает только
первый член правой части соотношения A2.3.14в), в то время как
остальные слагаемые Е вместе с магнитным полем Н создают ток
Je, который вызывает объемный джозефсоновский ток.
Согласно выражению A2.3.12), поскольку Gjv имеет фурье-
образ, его имеют и функции dxj> и do<j>. Следовательно, ф имеет вид
ф (t, хх) = 2 Шхх + NQct + фр (t, xx) 1, A2.3.19)
482 Глава 12
где fF ((t, xt) — функция имеющая фурье-образ:
Фр (t, хг) = { dp0 j dpi exp (iptft — ipoct) ф (p0, pj). A2.3.20)
Выражения A0.1.12) и A2.3.12) приводят к соотношению
dj (x) = -6 (х3) ф (t, Xl) б^з + dj (t, хъ x3), A2.3.21)
где
/ (t, хъ х3) = [!) (x3) — 0 (~x3) ] (NXl + Noct) +
Здесь р = (ръ р3) и a (p2) = [vB (p2)/c]2. Первый член правой
части A2.3.21) является единственным, обладающим топологиче-
ской особенностью, поскольку только он дает вклад в G^v —
= [<3Д, dv] f. Роль члена d^f состоит в том, чтобы обеспечить воз-
можность для f удовлетворять волновому уравнению для коллек-
тивной моды D (д) f = 0. Рассчитав Id^, dv] f с помощью выра-
жения A2.3.21), легко воспроизвести соотношения A2.3.12). Из
соотношений A2.3.5) и A2.3.7) видно, что вклад в наблюдаемые
Н и Е дает только топологическая особенность. Таким образом, /
не дает вклада в наблюдаемые эффекты. ^^
Первый член в правой части выражения A2.3.21) указывает
на то, что 2ф (t, Xi) есть разность фаз параметра порядка по обе
стороны контакта. Действительно,
dx3d3f (X) = / (+оо) - / @+) + / @_) - / (-оо),
и граничные условия / (±о°) = 0 приводят к тому, что
ф (t, хЛ) = / (х) |,3=с+ - / (х) |,3=0_. A2.3.23)
Поскольку ф (t, Хг) — интеграл от плотности распределения вих-
рей, отсюда следует, что интеграл от плотности распределения ра-
вен половине разности фаз.
Рассмотрим случай, когда периодическая конфигурация дви-
жется вдоль контакта (рис. 12.2). В этом случае функция ф (t, хг)
периодична по хх и становится функцией от хх — g (t), где g (t) —
функция только t
4>(t, х,) = ф [Xl-g(f)l A2.3.24а)
ф 1х1 + и—цф] = ф 1хг — g @ ] + яп. A2.3.246)
Здесь п — целое число. При выводе выражения A2.3.246) мы учли
тот факт, что 2ф — разность фаз параметра порядка и, следова-
тельно, ехр [21ф] должна быть периодической. Период и мы опре-
Явления, связанные с граничной поверхностью
483
делим ниже. Условие A2.3.24а) вместе с A2.3.19) приводит к тре-
бованию выбора g(t) в виде
ir
A2.3.25)
здесь gF (t) — функция, имеющая фурье-образ; кроме того, функ-
ция фр (t, хх) должна иметь вид
A2.3.26)
Рис. 12.2.
где фр (хх) имеет фурье-образ. Таким образом,
ф (t, хх) = 2 [N [Xl - g (t) ] -{- j dpa {p) exp {ip [xx - g(t) ]}),
A2.3.27)
где a (p) — фурье-амплитуда функции фг (хх).
Периодическое условие A2.3.246) приводит к тому, что
N = яя/2и, A2.3.28а)
A2.3.286)
<*(Р) =*%<*$ (р-¦*?-)-
Здесь / пробегает все целочисленные значения. Кроме того, по-
скольку фр вещественно, a* = a-t. Таким образом, находим
ф (t, Xl) = 2\^-
L
cos
+ б,) ,
J
A2.3.29)
где g(t) —функция вида A2.3.25). Выше использовано обозначе-
ние
A2.3.30)
484 Глава 12
Среднее от доф (t, хх) по оси хх равно
**)= A2.3.31)
^TaT A2.3.32)
Если среднее электрическое поле определить выражением
и
% (xs> t) = ~ J dxiE, (х), A2.3.33)
то из A2.3.14) получим
Е1 (jcs.O = ?2 (*з, t) = 0, A2.3.34а)
A2.3.346)
где учтено соотношение A2.3.32). Заметим, что т2 и со2 — функ-
ции у2. Если мы учтем, что со (р2) = 0 для р2 = 0, то увидим, что
электрическое поле A2.3.34) создает потенциал
V (t) = J dxaE3 (x3, f) = _л -g- -i- g(t), A2.3.35)
— 00
который равен (—tele) ф0 (t). Если внешний потенциал V (t) задан,
уравнение A2.3.35) определяет функцию g(t). В частности, если
V (t) — постоянная величина, равная Vo, из уравнения A2.3.35)
следует
A2.
A2.
A2.3
A2.3
3.36)
3.37)
.38а)
.386)
I_f
Сравнивая это с уравнением A2.3.25), получаем
8f V) = 0.
Магнитное поле находится из соотношения A2.3.13). Это маг-
нитное поле сосредоточено в области | х31 < hL. Из A2.3.29)
следует
и
^ @ ее -L j dxr drf (t, xt) = A2.3.39)
о
= пп/и. A2.3.40)
Явления, связанные с граничной поверхностью 485
Таким образом, из A2.3.136) получаем
и
Я3 (xa, t) = -i- j dxxH2 (x) = A2.3.41)
<12-3-42)
Полный поток, проходящий через слой с границами хх — 0 и
хх — и, равен
оо
и J dx3H2 (x3, t) = пф, A2.3.43)
где ф — единичный поток nficle. Это означает, что поток квантуется.
Эту ситуацию интуитивно можно представить следующим об-
разом: когда к системе приложен внешний электрический потен-
циал V (t), он приводит к появлению зависящей от времени плот-
ности заряда вблизи границы х3 = 0 (см. A2.3.15)), в то же время
он вызывает движение групп вихрей вдоль контакта. Эти вихри
создают объемный джозефсоновский ток, а изменение со временем
локальной плотности заряда создает локальный ток Js. Сравнивая
выражения A2.3.13) и A2.3.14), мы видим, что <30Е много меньше,
чем V X Н при pi <С /га2. Поскольку мы пренебрегаем Js, из соот-
ношения A2.3.8а) следует
4яЛс ^VXH. A2.3.44)
Согласно A2.3.9а), фурье-амплитуда Н содержит множитель
\/[пг*(р") + р'2], где р2 = р\ -f p\. Допустим, что множитель
имеет полюс при /г = —т\, где т\ — положительное число.
Тогда можно записать
" г. A2.3.45)
p2 + m2(p2) p' + ml '
где Z (р-) — некоторая функция. Z (—т'1) обозначим просто через
Z. В работе [4] рассчитаны магнитное поле Н и ток Jc, исходя из
уравнения A2.3.45); они экспоненциально затухают с расстоянием
от поверхности.
Ток в цепи, проходящий через контакт длины L, определяется
выражением
a+L/2
; f Av \i"lv\\ Л2 3 461»
/net— J "-Xi IJ з \Х)}ха—0' ^l^.o."±u;
a-L/2
486
Расчет дает
оо
/net fy 2nl l 1
где
a nil определяется
Г,. / nlL
_""Ч и
h =
Глава
2я/
и
= б, +
Ф
4,
соотношением
12
2nL r
' и ® ^ '
Bя//«) а,
¦ Bnlluf.
,)] , A2.3.47)
A2.3.48)
A2.3.49)
A2.3.50)
Согласно выражению A2.3.43), полный поток, проходящий через
контакт, дается выражением Ф (L) = я фЬ/и. Мы можем выра-
зить /net в терминах Ф (L) вместо Liu следующим образом:
2я/
Ф(Ц
A2.3.51)
Это выражение описывает картину фраунгоферовой дифракции
для Ф, которую предсказал Джозефсон [6] и которая наблюда-
лась в эксперименте Роуэлла [7]; при этом jF (/) считалась фено-
менологической константой. Зависимость б, от а может быть вклю-
чена в g(f), поскольку, согласно A2.3.35), внешний потенциал
V (t) определяет не функцию g(t), а только ее производную по
времени.
Когда внешний потенциал определяется выражением
V @ = Vo + Vx cos vt, A2.3.52)
из выражения A2.3.35) следует
A2.3.53)
что согласуется с соотношением A2.3.25). В этом случае из выра-
жения A2.3.51) следует
х
4-' + 5')' 02.3.54)
Деления, связанные с граничной поверхностью 487
где /s — функция Бесселя. Этот результат показывает, что по-
стоянный ток через контакт возникает тогда и только тогда, когда
2еУ0!Пс = nvs/l, (I2.3.55)
т. е. когда 2eV0/fic является гармоникой или субгармоникой ча-
стоты v.
Статический эффект Джозефсона можно изучать, положив
в приведенных выше выражениях V (t) — 0.
12.4. Поверхностное магнитное поле
в сверхпроводниках
Полубесконечные немагнитные сверхпроводники. В качестве
типичного примера проникновения внешнего воздействия через
поверхность твердого тела рассмотрим проникновение внешнего
статического магнитного поля через граничную поверхность сверх-
проводника.
Рассмотрим сверхпроводник, ограниченный плоскостью х3 = 0
и заполняющий полупространство х3 > 0. Предположим также,
что внешнее статическое поле Н направлено параллельно поверх-
ности. Поскольку плоскость х3 = 0 является поверхностной син-
гулярностью, выберем 1/ц и ф в виде
Ун = (т, 01, 02, 0), A2.4.1)
ф = v^. A2.4.2)
Тогда из выражений A0.1.20) и A0.1.44) видно, что не равные нулю
компоненты G^v равны
G2f3 (х) = —G3f2(х) = — v26 (хз), A2.4.3а)
GU (х) - —GJ, (х) = -v,6 (jf3), A2.4.36)
GfQ3 (х) = —G$o (дг) = vo6 (xa). A2.4.3в)
Поскольку внешнее электрическое поле отсутствует, положим
Ооц = 0. Тогда имеем v0 = 0.
Вспомним теперь уравнение максвелловского типа A1.3.43),
которое в статическом случае имеет вид
V2a
(x) =-J-\d»yc{x - у) (а(у) - Ц-Vffy)) . A2.4.4)
С другой стороны, поскольку Gjtv == [5ц, dv] f, из соотношений
A2.4.3) следует
V/ (х) = -^е1 + v3e2) 9 (*,), A2.4.5)
488
Глава 12
так как это дает
V X V/ (х) = (v2ex - vie2) б (х3). A2.4.6)
Здесь е1 и е2 — единичные векторы в направлениях хг и х2 соот-
ветственно.
Используя соотношения A2.4.4) — A2.4.6), мы можем рас-
считать вектор-потенциал а (х), магнитное поле h (x) =V X а (х)
и ток 4nj (х) = V х V х а (х). В результате имеем
dk с (ft) sin (kx3)
f dk
A2.4.7)
dk c (ft) cos (kx3)
2я Щ k'2 + с (ft)
A2.4.8)
kc (ft) sin (kx3)
Цк- + с (ft)
A2.4.9)
Из этих выражений видно, что h и j перпендикулярны друг другу
и лежат в плоскости, параллельной поверхности х3 = 0; они со-
средоточены в слое, примыкающем
к поверхности. Заметим, также,
что a, h и j зависят только от х3.
В приведенных расчетах выпол-
ол няется интегрирование по всему
пространству (—оо <^х3 <С°°),
»- хотя образец занимает только по-
Хз лупространство х3 > 0. Это соот-
ветствует ситуации, когда ток и
магнитное поле отражаются от по-
верхности; вклад от области х3 <;0
можно заменить вкладом от облас-
ти х3 > 0 с помощью замены пе-
ременной х3 —»- —х3 и тем самым
описать отраженные поле и ток (рис. 12.3). При этом отражении
полярные векторы, такие, как ток, изменяют свое направление, в
то время как аксиальные векторы, такие, как магнитное поле, не
меняют. Изменение условия отражения на границе требует из-
менения особенности.
Согласно выражению A1.3.11), свободная энергия единицы
объема равна
\
'Уз X
\
Рис
F. = Fs0 + -g-jr j d"x (W (x) - -?- a (x)) j (x) -\- JL j db
A2.4.10)
Явления, связанные с граничной поверхностью 489
где V — объем образца, a Fs0 — энергия мейсснеровского состоя-
ния. В действительности всегда имеется поверхность, даже если
нет внешнего магнитного поля. В приведенных выше расчетах a, h
и j влиянием этой поверхности пренебрегали.
Самосогласованный потенциал, обусловленный поверхностной
особенностью, воздействует на электроны и создает энергию серд-
цевин вихрей. Следовательно, мы можем предположить, что внеш-
нее магнитное поле мало влияет на энергию сердцевин. По этой
причине в выражении A2.4.10) энергией сердцевин вихрей пре-
небрегалось.
Из соотношений A2.4.7)—A2.4.9) следует
f rift i-J?* ,.., A2.4.11)
где
v = (v? + xiY'% A2.4.12)
a L — линейный размер образца в направлении х3. Термодинами-
ческий потенциал равен
h A2.4,13)
где Н — внешнее поле, а Б — индукция:
-^-^- A2.4.14)
(h (x3) = | h (x) |). Условие устойчивости
¦|rGs = 0 A2.4.15)
приводит к выражению
^]№ёГ- ('2.4.18)
о
= Л@), A2.4.17)
откуда следует, что индукцированное магнитное поле h (x) на
поверхности х3 = 0 равно приложенному полю [8]. Выражение
A2.4.17) определяет параметр v при заданном Н. Заметим, что
выражение A2.4.17) не вводится как внешнее граничное условие.
Это промежуточный результат наших расчетов, причем он отра-
жает тот факт, что поверхностное состояние самосогласованным
образом контролируется всей системой, которая подстраивает себя
под внешние условия.
490 Глава 12
Определим теперь глубину проникновения выражением
% = Tj6J\dxsh(x). A2.4.18)
о
Тогда из A2.4.8) следует
A2.4.19)
где g (иБ) определяется равенством
A) A2.4.20)
причем при 7=0 ив = X,L/|0. Сравнивая выражения A2.4.16) и
A2.4.19), получаем соотношение между Н и v:
tf = -|?_JL. A2.4.21)
Если учесть соотношения A2.4.8), A2.4.9) и A2.4.21), то магнитное
поле h (х3) = | h (х) | и плотность тока / (х3) = | j (x) | можно за-
писать в виде
оо
2КН f A^ с (k) cos (kx3) A2 4 22)
о
Расчет проделан в работе [8], в которой для бозонной характери-
стической функции с (k) использовано соотношение в форме
E.4.179), а значение VN @) взято равным0,32. Расчет показал, что
глубина проникновения возрастает при уменьшении кв (следова-
тельно, и = 0,95хв) и X/XL -> 1 при Ив-* оо. Было показано также,
что, если ив невелико (например, кв <Сквс), магнитное поле
h (х3) меняет знак на некотором расстоянии от поверхности и ведет
себя как затухающая осциллирующая функция. Эта ситуация,
более явно выраженная при малых иБ, аналогична той, которая
существует в сверхпроводниках П/1 рода. Как было показано
в разд. 11.3, магнитное поле каждого вихря меняет знак на некото-
ром расстоянии от центра вихря, вызывая притяжение между
вихрями. Фактически критическое значение иБС очень близко
к граничному значению иБ, соответствующему переходу от сверх-
проводника П/1 рода к сверхпроводнику П/2 рода. Например,
Иве <=> 1,2 при Т = 0. Расчет / (хя) показывает [8], что ток исче-
зает на границе х3 = 0, возрастает на расстоянии К и затем снова
Явления, связанные с граничной поверхностью 491
убывает до нуля. Мы обнаруживаем, что для образцов с яв <хвС
ток меняет знак и ведет себя как затухающая осциллирующая
функция, так же как и магнитное поле.
С учетом соотношений A2.4.22), A2.4.23), A2.4.17) ток в цепи
рассчитывается по формуле
X оо
= 4" J <**»/ <*»> = "ёг J d* Ц07Щ П - cos (Щ\ = A2.4.24)
Критический ток можно получить, если положить Я = Яс.
^Распределение плотности термодинамического потенциала как
функции x3/XL приведено в работе [8]. При его рассмотрении об-
наруживается замечательный результат: для любого значения Я
всегда существует область вблизи поверхности, в которой термо-
динамический потенциал для сверхпроводящего состояния меньше,
чем для нормального состояния, откуда следует, что сверхпро-
водящее состояние локально выгоднее [8]. Это создает поверх-
ностный барьер, препятствующий проникновению макроскопиче-
ского потока. Наличие поверхностного барьера приводит к мета-
стабильным состояниям и мешает внешнему полю Я проникать
внутрь, до тех пор пока Я не превосходит критическое значение
Hs, которое больше Нс. Поле Я;, интенсивно изучалось Де Женом
и др. [9]. В нескольких работах [8, 10] рассчитана величина Hs
как функция хв.
Полубесконечные магнитные сверхпроводники. Случай особых
магнитных сверхпроводников, таких, как ErRh4B4, HoMo6S8,
рассмотрен в разд. 11.4. Соотношение A1.4.8) является модифи-
цированным уравнением максвелловского типа. Было приведено
также выражение для термодинамического потенциала Гиббса.
Как было подчеркнуто, процессы в этих системах жестко регу-
лируются двумя механизмами: незатухающим током в системе,
экранирующим осцилляции магнитного момента [3], и законом
квантования потока, вследствие которого магнитные моменты ко-
ренным образом меняют магнитное поле. Эти механизмы стремятся
создать обращение магнитного поля (и тока), что приводит к силь-
ному притяжению между вихревыми нитями. Таким образом, эти
механизмы стремятся установить сверхпроводимость Н/1 или
I рода.
С другой стороны, рассмотрение приведенного выше немагнит-
ного случая показало, что внутреннее магнитное поле h (x3)
в сверхпроводниках П/1 рода ведет себя как затухающая осцил-
лирующая функция от х3. Таким образом, мы видим, что такое ос-
циллирующее поведение h (х3) усиливается в рассматриваемых
492 Глава 12
магнитных сверхпроводниках. Детальный анализ этого поведения
приведен в работе [11]. Приведенный там расчет показал, что
вблизи поверхности ферромагнитное состояние сосуществует со
сверхпроводимостью при температуре ниже некоторого критиче-
ского значения Ts; Ts всегда выше Тр — критической темпера-
туры перехода в спин-периодическое сверхпроводящее состояние,
а также выше температуры спонтанного рождения вихревых
нитей. Сосуществование поверхностного ферромагнетизма со
сверхпроводимостью можно понять следующим образом: экрани-
рование спиновых флуктуации незатухающим сверхпроводящим
током ослабляется из-за наличия поверхностной особенности,
следствием чего является усиление магнитного эффекта.
Тонкие пленки. Для изучения сверхпроводников в виде тонких
пленок может быть применен метод, аналогичный описанному вы-
ше. Рассмотрим пленку толщиной 2а, локализованную в слое
—а < х3 < а. Принимая, что слабое внешнее магнитное поле
Н приложено в плоскости поверхности и направлено параллельно
поверхности, введем две поверхностные особенности в плоскостях
х3 = ±о. Тогда уравнение A2.4.6) приводится к виду
V X V/ (*,) = Ке1 — vxe2) [б (х3 + а) + б (*, — а) 1. A2.4.26)
Будем считать, что магнитное поле зеркально продолжено за пло-
скости х = ±а; тогда мы можем выполнить пространственное
интегрирование по всему пространству, предполагая, что поверх-
ностные особенности образуют периодическую структуру с перио-
дом 2а, что позволяет учесть эффекты многократного отражения.
Таким образом, a (xs), h (x3) и / (х3) становятся периодическими
функциями переменной х3 с периодом 2а.
Мы обнаружили, что в случае рассмотренных выше магнитных
сверхпроводников поверхностный эффект усиливается и возможно
сосуществование ферромагнетизма и сверхпроводимости. Это дает
основание ожидать, что в тонких пленках такого рода материалов
можно наблюдать «сверхпроводящий ферромагнетизм». Согласно
расчетам в работе [12], это действительно происходит при а<
< XL. Критическая температура Ts, ниже которой это происхо-
дит, ниже температуры Тт (фиктивной температуры Кюри для
нормального состояния массивного образца, см. разд. 11.4), но
выше, чем ТР. Если а у> %L, то области спонтанного намагничи-
вания, ограниченные размерами XL и расположенные вблизи по-
верхностей, далеко разнесены в пространстве, так что Ts перестает
зависеть от а и совпадает со значением Ts для изученного выше
полубесконечного образца. Если а становится сравнимой с %L,
области намагничивания начинают взаимодействовать друг с дру-
гом, в результате чего Ts приобретает осциллирующую зависи-
мость от а. Если al"kL <C 1, то Т3 существенно возрастает с умень-
Явления, связанные с граничной поверхностью 493
шением а, поскольку влияние экранирования значительно ослаб-
ляется всюду внутри пленки. В пределе a/XL ->• О TS стремится
к Тт.
ЛИТЕРАТУРА
1. Wadati M., Matsumoto Н., Umezawa\H., Phys. Rev., B18, 4077 A978V
Wadati M., Phys. Rep., 50, 87 A979).
2. Rayleigh, Proc. Lond. Math. Soc, 17, 4 A887);
Stroh A. N., J. Math. Phys., 41, 77 A962);
BatnettD. M., Lot he J., Vishioka K-, Asaro R. J., J. Phys., F3, 1083 A973).
3. Leplae L., Umezawa H., Mancini F., Phys. JRep., IOC, 151 A974).
4. Mancini F., Matsumoto H., Wadati M., Umezawa H., Prog. Theor. Phys., 62,
12 A979).
5. Anderson P. W., Progress in low temperature physics, Vol. 5, ed. C. J. Gor-
ter., North-Holland, Amsterdam, 1967, ch. 1;
Josephson B. D. — in: Superconductivity, ed., R. D. Parks., Dekker, New
York, 1969, ch. 9;
Solymar L., Superconductive tunneling and applications, Wiley Interscience,
1972. [Имеется перевод: Солимар Л. Туннельный эффект в сверхпроводни-
ках и его применение.—М.: Мир, 1974.]
6. Josephson В. D., Phys. Lett., I, 251 A962).
7. Rowelt J. M., Phys. Rev. Lett., 11, 200 A963).
8. Mancini F., Umezawa H., Physica, 95B, 45 A978).
9. Groupe de Superconductivite d'Orsay. Quantum fluids, ed. D. F. Brewer, North-
Holland, Amsterdam, 1968.
10. Marticon Т., Saint-James D., Phys. Lett., 24A, 241 A967).
11. Tachiki M., Kotani A., Takahashi S., Koyama Т., Matsumoto H., Umezawa #.,
Sol. St. Comrnun., 37, 113 A981);
Kotani A., Tachiki M., Matsumoto H., Umezawa H., Phys. Rev., B23, 5960
A981).
12. Kotani A., Takahashi S., Tachiki M., Matsumoto H., Umezawa H., Sol. St.
Commun., 37, 619 A981).
ГЛАВА 13
ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
В этой книге мы пытались изложить квантовую теорию поля
в форме, удобной для исследования проблем многих частиц. По-
скольку понятия упорядоченных состояний и протяженных объек-
тов играют ключевую роль во многих областях физики, в том числе
в физике твердого тела, физике высоких энергий и в космологии,
рассмотрению этих понятий мы уделили особое внимание. Чтобы
ограничить объем книги, мы постарались не рассматривать те по-
нятия, которые содержатся в большинстве стандартных учебни-
ков по физике твердого тела и проблемам многих частиц. Несмо-
тря на это, книга оказалась довольно большой. Кроме этих обще-
известных понятий опущено много важных вопросов. Это обуслов-
лено либо соображениями, связанными с объемом книги, либо
тем, что формулировки этих вопросов еще недостаточно устоялись.
Ниже перечислены некоторые из этих вопросов.
Критические явления. Поскольку структура термополевой
динамики в целом сходна со структурой обычной квантовой тео-
рии поля, в которой первоначально возникла формулировка поня-
тия ренорм-группы, мы, очевидно, можем сформулировать метод
ренорм-группы применительно к критическим явлениям с исполь-
зованием термополевой динамики. Однако, поскольку имеется
много прекрасных статей и книг по применению метода ренорм-
группы к критическим явлениям, в данной книге мы этот вопрос не
рассматриваем. При подготовке книги мы планировали сделать
следующее. Используя модель взаимодействующих спинов, мы
хотели в явном виде вычислить амплитуду, а также вещественную
и мнимую части частот коллективных мод вблизи точки фазового
перехода. Для интерпретации поведения коллективных мод (голд-
стоуновских бозонов) можно построить качественную картину
механизма критических явлений: уменьшение скорости коллек-
тивных мод в критической области и нарушение симметрии, воз-
никающие при фазовом переходе второго рода. На основе этих
интуитивных представлений мы хотели распространить метод
ренорм-группы на динамические явления. Но это потребова-
ло бы значительных усилий и времени, что оказалось неприемле-
мым.
Заключительные замечания 495
Эффект Кондо. Эффект Кондо — результат взаимодействия
между электронами, описываемыми с помощью квантовых полей,
и спином примеси, описываемым с помощью квантовомеханиче-
ского оператора. Следовательно, гильбертово пространство яв-
ляется прямым произведением фоковского пространства кванто-
вого поля и пространства спинов, отвечающего спину примеси.
По-видимому, это явление — хороший пример расширенного пред-
ставления (см. гл. 9), включающего квантовомеханические пред-
ставления и представление пространства Фока.
Теория лазера и эффект Рамана. Поскольку преобразование
бозонов тесно связано с когерентным представлением, теория
лазера, по-видимому, согласутеся с задачей данной книги. Факти-
чески рассмотрение этих вопросов входило в первоначальный план
книги.
Приложение теории солитонов. Когда топологические объекты
связывают фермионы (например, нуклоны), мы можем сформули-
ровать теорию тяжелых ядер, включающую как поверхностные
волны и вращательные моды, так и оболочечную структуру. Когда
мы рассматриваем связанные кварки, то приходим к модели меш-
ков в квантовой хромодинамике. В физике твердого тела сущест-
вует множество приложений теории протяженных объектов, свя-
зывающих фермионы. В связи с магнитными и тепловыми свойст-
вами полимеров большое внимание привлекли вопросы о модах
с нулевой энергией у связанных фермионов. Объединение рассмо-
трения, проведенного в гл. 9, с термополевой динамикой, изло-
женной в гл. 4 и 5, может дать хороший аппарат для анализа со-
литонных явлений в физике твердого тела.
Некоторые фундаментальные вопросы. Что касается движения
протяженных объектов, то в этой книге мы обсудили кратко лишь
свободное их движение. В физике твердого тела само по себе^дви-
жение объектов очень важно для понимания физических явлений.
Для расчета сопротивления в смешанном состоянии сверхпровод-
ников требуется знать поток вихрей. Было снято несколько филь-
мов, иллюстрирующих движение дислокаций в кристаллах.
В физике твердого тела так много проблем подобного рода, что мы
здесь даже не пытаемся их перечислить.
Для статических явлений, как мы видели, физически реали-
зуемое состояние протяженного объекта в принципе получается
при минимизации свободной энергии по всем возможным выборам
формы особенностей (хотя в реальных расчетах эта процедура тре-
бует применения метода проб и ошибок). Но мы еще не нашли
эффективного способа описания коллективных движений протя-
женных объектов. Мы можем создать объекты произвольной формы
496 Глава 13
(т. е. особенности) с помощью методов, описанных в этой книге.
Если есть несколько объектов произвольной формы, то вследст-
вие взаимодействия они движутся с изменением формы. Остается
открытым вопрос о том, каким образом законы, управляющие этим
движением, могут быть получены из исходных уравнений поля.
, ~ Если эту проблему решить, то можно задаться вопросом, можно
ли объяснить движение топологических объектов на геометриче-
ском языке, поскольку большую часть классических движений
в классической теории можно описать на этом языке. Мы могли бы
попытаться провести исследование сингулярных объектов (таких,
как черные дыры) и их взаимодействия с квантами в общей теории
относительности, расширив круг идей, изложенных в данной книге.
Если эти вопросы удалось бы решить, концепции этой книги можно
было бы распространить и на космологию, что привело бы к еди-
ному взгляду и подходу в широкой области физики, включающей
физику твердого тела, физику высоких энергий и космологию.
В этой книге мы видели, что системы, в которых сосуществуют
макрообъекты и кванты, можно описывать в рамках квантовой тео-
рии поля. При этом квантовомеханические операторы, связанные
с протяженными объектами, естественным образом включаются
в теорию. Но до сих пор еще не известно, где лежит граница
между макроскопическими и микроскопическими объектами. Ней-
тронная звезда, очевидно, макроскопический объект. Но если
уменьшать по одному количество нуклонов, то мы достигнем в
конце концов однонуклонного состояния, являющегося, очевидно,
микроскопическим. Между ними, например в тяжелых ядрах,
наблюдаются некоторые макроскопические явления типа деформа-
ции ядра или поверхностных колебательных мод, хотя тяжелое
ядро — еще квантовая частица. Квантовая теория поля как
теория, описывающая одновременно и макроскопические и микро-
скопические объекты, находится еще на ранней стадии своего
развития.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Адиабатический множитель 84
Адлера теорема 249
Андерсона — Сула механизм 459
Андерсона — Хиггса — Киббла меха-
низм 181
Анизотропные сверхпроводники 455
Асимптотическое поле 366
— условие 75, 349
Бете — Солпитера амплитуда 7й
уравнение 78, 139
для магнона 145
(N, е)-модели 78, 81
сверхпроводящего элек-
трона 161
• составной частицы 80
фазона 165, 171
¦ неоднородное 81
однородное 79
при конечных температурах
136, 137
БКШ модель 159
Блоховская стенка в магнитных сверх-
проводниках 464
Блоховский член в намагниченности
159
Боголюбова преобразование для бо-
зонов 32, 37, 44
фермионов 36, 44
с учетом влияния термостата
107, 108, ПО, 115, 124
Бозонное поле, сдвиг (трансляция)
37, 38, 45, 241, 247, 249, 312, 341
— преобразование 312, 342, 420
в квантовой электродинамике
422
для фононов 384, 386
параметры 414
при наличии топологических осо-
бенностей 374, 383, 399, 414, 473
теорема 312, 340, 341
Бозоны 22
— конденсация 38, 239, 310, 329,
343, 376, 386
— характеристическая функция 183,
435
Брауера степень 407
Бриллюэна функция 153, 462
Бъянки тождество 402
Бюргерса вектор 384, 389, 391, 393
Вакансия в решетке 398
Вакуум 25, 28, 39
— зависящий от температуры 108
— устойчивость 77, 95
Ван Хова модель 4
Вершинная функция 100
Вигнеровское вращение 360, 365, 370
Вихри в сверхпроводниках 439
взаимодействие 441, 445
¦ — инверсия магнитного поля
465
спонтанное образование 466
электроны сердцевины 343,
447
-> энергия сердцевины 449, 465
Внутреннее произведение векторов
состояния 26
волновых функций 51
Возвратная сверхпроводимость 459
Волновой пакет 21, 28, 88, 247
Входящие поля 9, 76, 93
Выходящие поля 76, 93
Гамильтониан в слабом смысле 354,
355
— для гейзенберговских полей 41, 42
модели Ван Хова 44
Гейзенберга 148, 149, 153
физических частиц 40
— при наличии протяженных объек-
тов 354, 355
— термостата 107
Гейзенберга модель для локализо-
ванных спинов 148
—уравнение 41, 45
в термополевой динамике 113,
123
для коллективизированных элек-
тронов 142, 143, 215
модели БКШ 160, 161
Гейзенберга 150, 154
jju 82
(JV, 6)-модели 62
электромагнитного поля tot
Гейзенберговские поля 9, 41
498
Предметный указатель
Гельмгольца свободная энергия 113
в модели БК.Ш 185
Гиббса термодинамический потен-
циал в магнитных сверхпроводни-
ках 465
смешанного состояния 450
Гильбертово пространство, сепара-
бельное 24, 27
Глубина проникновения 490
лондоновская 181, 435
Голдбергера ¦— Треймана соотноше-
ние 253, 255
Голдстоуна теорема 10, 143, 230, 238
Голдстоуновские бозоны 10, 14,
143, 176, 230, 239, 241, 249, 284,
420
инфракрасные 262
комплексные 261
— квантовые состояния 473
Голдстоуновского типа модель 241
Горькова уравнения 437
Границы зерен 390
плоские 394
соотношение непрерывности 394
типа кручения 393
наклона 393
Дайсона теорема 249
— уравнение 216
Дайсоновский член в намагниченности
159
Двумерная особенность 381
осциллирующая 474
сферическая 396
Двухточечные функции 100, 144, 187,
201
для магнона 158, 207, 213, 221
плазмона 289
— плотности заряда 174, 187
— — тока 187
— — — фазона 210
правила умножения 121
при конечных температурах
114—116, 120, 131, 134
спектральное представление 101,
131
Деформация группы 257
Джозефсона эффект 479
периодическая конфигурация
в контакте 282
Дивизор 49, 56
— для плазмонов 289
Динамическая матрица колебаний
решетки 271
— перестройка симметрии 11, 226,
237, 257
в кристаллах 274
калибровочной 292, 302
О (я) 261
спиновой 143, 243
SU B) 246, 247
SUB)X SUB) 261
SU(n) 261
трансляционной 324
фазовой 177, 178, 241
Динамическое отображение 9, 46,
90, 227, 338
в кристаллах 274
случае бозонного преобра-
зования 313
нормального металла 302,
421
сверхпроводника 176, 178,
242, 291, 293
— термополевой динамике 124,
130
для модели голдстоуновского
типа 242
(М, 6)-модели 63, 71
—• спиновых операторов 155
Дисклинация 394
Дислокация 388
— винтовая 389
— краевая 389
Диэлектрическая проницаемость 427,
428
тензор 426
Длина когерентности 183
Древесное приближение 316
«Духи» 282, 300, 420
Звуковые волны на поверхности кри-
сталла 474
— поля смещений 475
Импульса оператор для физических
частиц 41, 47
— с учетом влияния тер-
мостата 107
Индефинитная метрика 283
Инстантон 414
— Полякова 418
— т'Хофта 418
Калибровка 399
— кулоновская 438, 479
Калибровочная инвариантность 186
Калибровочное преобразование 182,
197, 280, 298
матрица 400, 418
— условие 286, 299
Калибровочные поля 416
теория 416
Квант потока 440
Предметный указатель
499
Квантование потока 383, 424, 440
в джозефсоновских контактах 485
магнитных сверхпроводни-
ках 465
Квантовая координата 320, 344,
348, 357
Квантовомеханические объекты 329,
366
Киральная SU B) X SU ^-симме-
трия 253
Классические объекты 329, 366
Когерентное представление 343
— состояние 38, 312
Коллективная мода 10
Константы перенормировки 335
Координатное пространство и про-
странство симметрии, взаимное
соответствие 420
Критическая температура сверх-
проводников 164
Критические значения %в 445
Кубо — Мартина — Швингера соотно-
шение 128
Кулоновская калибровка 438, 479
Кюри закон 463
Кюри-вейсовское поведение зонных
электронов 224
Ламе коэффициент 387
Лемана — Симанзика — Циммермана
формула 99
в компактной форме 99
при конечных температу-
рах 128
Ли модель 82
Лоренцева «поворота» оператор 355,
357
Магнетизм и сверхпроводимость,
взаимность влияние 458
Магнитные примеси в сверхпроводни-
ках 458
Абрикосова — Горькова тео-
рия 459
— сверхпроводники 457
антиферромагнитный порядок 460
дипольное взаимодействие 458
обменное взаимодействие 458
экранировка 463
спин-периодическая фаза 464
¦ фазовая диаграмма 467
энергетическая щель 468
Магноны 143, 145, 148, 157, 208, 209
—энергетический спектр 158, 214,
220
Маки параметры 452
Максвелла уравнение, классическое
423, 425, 461
Максвелловского типа уравнение 423
в сверхпроводниках 429, 433,
436, 438, 440, 479
анизотропных 456
магнитных 461
Матрица приведения к эрмитову виду
50
Мацубары формализм для темпера-
турных функций Грина 11
Мейсснеровский ток 425
Мейсснеровское состояние 443
Минимальное взаимодействие 421
Модули упругости 277
Модуль сдвига 387
Монополь 398, 410, 413
Мории — Кавабаты метод 224
Намагниченность в системе коллекти-
визированных электронов 144, 220
локализованных спинов 152.
159
приближение среднего
поля 153, 462
Намагничивания кривая в магнитных
сверхпроводниках 466
сверхпроводниках Il/l рода
445, 451
Нейтронов рассеяние на спиновых вол-
нах 209
Нётеровский генератор 194, 229
— ток 194, 197
Низких энергий теоремы 249
— для магнонов 248, 249, 251
пионов 249, 252
и низкие температуры 256
Нормальное произведение 46
(N, 9)-модель 62
[0]-множество 25
Обобщенные координаты 325, 358,
369
Оптические моды 278
Особенности типа расходимости 347,
374
— топологические 347, 374
Параметр порядка 262, 400
в сверхпроводниках 242, 432
условие однозначности 402
Парастатистика 22
Перенормировка вакуумного сред-
него 335
— вершины 334
— волновой функции 333
— константы связи 219
— химического потенциала 142, 143
500
Предметный указатель
159, 220
— энергии 141, 160, 162, 332
Перестройка симметрии см. Динами-
ческая перестройка симметрии
Петлевое разложение 202
Плазменные колебания 181, 186
уравнения 190, 287, 424
энергия 181, 190
Плазмон 181, 186, 190, 286, 420
Плотное множество 27
Поверхностная сверхпроводимость
468, 492
Поверхностное магнитное поле в сверх-
проводниках 487, 491
Поверхностные волны 15
— фононы 478
Подгруппа устойчивости 244, 259
Подстановка для физических полей 227
Полярон 141
Правило сумм 56, 58
Представление взаимодействия 84
Причинность 58, 59
Пространственный сдвиг 47
Редукции формула 98
РККИ механизм 459
Рождения и уничтожения бозонов опе-
раторы 22
волновых пакетов опера-
торы 29
операторы, проектирование
60
фермионов операторы 23
физических частиц опера-
торы 47
Рэлеевская волна 15, 478
Самосогласованные вычисления 43, 63,
73
Самосогласованный метод 42
— потенциал 14, 316, 317, 337, 343, 375
— — вихрей в сверхпроводниках 446
двумерной особенности 478
поверхность кристалла 473
Сверхпроводники 54, 280 см. также
Анизотропные сверхпроводники,
Магнитные сверхпроводники
— бесконечная проводимость 429
— влияние кулоновского взаимо-
действия 179
— I рода 443
— II рода 444
затухание ультразвука 447
— И/1 рода 444
— II/2 рода 444
Свободное движение двух вихрей 372
протяженных объектов 366, 381
Связывающие поля 76, 93, 241
Сжатие группы 247, 257
Синус-Гордона модель 340
Синусоидальное спиновое упорядоче-
ние 347
Слабые соотношения 42
S-матрица 76, 88, 93, 99
Смешанное состояние 443, 464
Собственная энергия 140, 141
коллективизированных элек-
тронов 215
фотона 186, 295, 305, 433
Солитон 15, 337
Составная частица 43, 71, 73, 76, 82
Спектральное представление 100,
169, 207
двухточечных функций 101, 131,
201, 207, 212
неприводимой части собствен-
ной энергии 140
при конечных температурах 131
Спиновая симметрия 204
Спин-периодическая фаза 464, 470
Спиральные спиновые структуры 347
Спонтанное нарушение симметрии 10,
11, 230 см. также Динамическая
перестройка симметрии
Стонеровский континуум 221, 222
s — /-взаимодействие 463, 470
— в магнитных сверхпроводниках 459
Термополевая динамика 11, ПО
Термополевой дублет 115, 120, 123,
124, 139, 144, 145, 150,5.160, 205
Термостат 106, 107
Тильда операция НО
правило подстановки 127, 132
Тонкие пленки, сверхпроводимость
492
Топологические квантовые числа 382,
383, 398, 406, 410, 424
—"особенности 13, 347, 374, 375, 377
двумерные 381
кольцевые 380
• линейные 378
полное условие 377, 379
Топологический заряд 376, 391
— объект 13
с неабелевой симметрией 398
Точечная группа 268
Точечные дефекты 396
Трансляционная мода 320, 344
Тройные редкоземельные соедине-
ния 459
Унитарно неэквивалентные предста-
вления 24, 31, 35, 37, 38
Предметный указатель
501
Уорда — Такахаши соотношения 43,
192, 195, 198, 228, 232
для спиновой симметрии
205, 206, 212
фазовой симметрии 200
компактная записи» ¦ 196
обобщение 197
при конечных температу-
рах 198
Упорядочения оператор в термополе-
вой динамике 154, 160, 187
Упорядоченные состояния 10, 11, 14,
143, 163, 227, 239, 310
Упругие постоянные 277
Уравнение для щели в сверхпроводни-
ках 163
обобщение 173
Уравнения свободного поля для физи-
ческих полей 48
и статистика 59
типа 1 48, 53, 58, 59, 104
типа 2 48, 53, 56, 59, 103
Условие свободной поверхности 395
Фазовое преобразование в модели
голдстоуновского типа 241
Л„ 82
нормальных металлах 298
(дг, 6)-модели 64, 70, 71
сверхпроводниках 242, 280,
284
Фазон 177, 181, 241, 285
— энергия 182
Фермионы, определение 22
ферромагнетизм коллективизирован-
ных электронов 142, 204
Физические кванты 9, 39
— поля 9, 47
— состояния 283, 300
— частицы 9, 39, 45, 47
представления 39, 42, 46, 90,
102
в (N, 6)-модели 74
теории возмущений 83, 85
-и вариационный принцип 89
при конечных температу-
рах 109
Фока пространство 27, 63
— — расширенное 325, 351
Фононы 138, 266, 280
— акустические 268, 278
— оптические 278
— уравнение 268, 270, 276
Франка формула для большеугловых
границ зерен 393
Фраунгоферова дифракция для джо-
зефсоновского тока 486
Химический потенциал 113, 149, 220
затравочный 159
перенормировка 142, 143, 159,
220
Цепочечное приближение 146, 161,
166, 433, 437
(«^-превращения 358, 364
Числа заполнения оператор 22, 24, 109
Чисто калибровочная теория 416
Энергетическая щель в сверхпровод-
никах 162
магнитных 468
Энергия конденсации 184, 443
— основного состояния в термополе-
вой динамике 113
— протяженных объектов 344
— сердцевины вихря 448
в магнитных сверхпроводни-
ках 465
Энтропия 113, 185
Янга — Миллса теория 416
Янга — Фельдмана уравнение 311
ОГЛАВЛЕНИЕ
Предисловие редактора перевода 5
Предисловие 7
Глава 1. Введение 9
1.1. Квантовая теория систем многих тел 9
1.2. План книги 15
1.3. Обозначения 17
Глава 2. Квантовая теория систем многих тел 21
2.1. Представление чисел заполнения; операторы рождения
и уничтожения 21
2.2. Унитарно неэквивалентные представления 24
2.3. Пространство фока 25
2.4. Некоторые примеры унитарно неэквивалентных представ-
лений 31
2.5. Представление физических частиц и динамическое отобра-
жение 39
2.6. Свободные поля для физических частиц 47
Литература 61
Глава 3. Представление физических частиц, S-матрица и составные
частицы 62
3.1. (N, 9)-модель 62
3.2. Представление физических частиц и вычисления по теории
возмущений 83
3.3. Представление физических частиц и вариационный принцип 89
3.4. Общий анализ представления физических частиц.... 90
3.5. Формула редукции и формула Лемана—Симанзика—Цим-
мермана (ЛСЦ) -. 96
3.6. Спектральные представления двухточечных функций . . 100
Литература 104
Глава 4. Квантовая теория поля при конечных температурах 106
4.1. Термополевая динамика 106
4.2. Динамическое отображение при конечных температурах,
правило подстановки тильды и соотношение Кубо—Мар-
тина—Швингера 122
4.3. Спектральное представление двухточечных функций ... 131
4.4. Уравнение Бете—Солпитера при конечных температурах 136
Литература 137
Глава 5. Некоторые примеры вычислений в рамках термополевой ди-
намики 138
5.1. Электрон-фононная система 138
Оглавление
5.2. Модель контактного взаимодействия в ферромагнетизме
коллективизированных электронов
5.3. Модель Гейзенберга в ферромагнетизме локализованных
спинов
5.4. Сверхпроводимость
5.5. Плазменные колебания в нормальных металлах ....
Литература
Глава 6. Инвариантность и нётеровский ток
6.1. Нётеровский ток и соотношения Уорда—Такахаши . . .
6.2. Соотношения Уорда—Такахаши при конечных темпера-
турах
6.3. Простой пример соотношения Уорда—Такахаши ....
6.4. Пример петлевого разложения; ферромагнетизм зонных
электронов
Литература
Глава 7. Динамическая перестройка симметрии и динамическое отобра-
жение
7.1. Общее рассмотрение
7.2. Фазовая симметрия
7.3. Динамическая перестройка спиновой симметрии....
7.4. Перестройка симметрии и теоремы для низких энергий . .
7.5. Перестройка симметрии и сжатие группы
7.6. Инфракрасный эффект голдстоуновских бозонов и пара-
метр порядка 262
7.7. Кристаллы 264
Литература 278
Глава 8. Квантовая электродинамика твердых тел. I. Перестройка ка-
либровочной симметрии и динамическое отображение .... 288
8.1. Сверхпроводимость 288
8.2. Квантовая электродинамика нормальных металлов .... 298
Литература 309
Глава 9. Протяженные объекты квантовой природы 310
9.1. Простое рассмотрение 310
9.2. Простой пример 329
9.3. Общее рассмотрение бозонного преобразования 340
9.4. Асимптотическое условие и асимптотический гамильто-
ниан 348
9.5. (ся)-превращение и обобщенная координата 358
Литература 372
Глава 10. Протяженные объекты с топологическими особенностями . . . 374
10.1. Общие соображения 374
10.2. Протяженные объекты в кристаллах 385
10.3. Топологические особенности, связанные с неабелевыми
группами симметрии ЗЭ8
Литература 419
Глава 11. Квантовая электродинамика твердых тел. II. Макроскопиче-
ские явления
11.1. Вывод классического уравнения Максвелла
11.2. Проводимость и диэлектрическая проницаемость. . .
11.3. Сверхпроводимость
11.4. Магнитные сверхпроводники
Литература
504 Оглавление /
\
Глава 12. Явления, связанные с граничной поверхностью 473
12.1. Введение 473
12.2. Звуковые волны на поверхности кристалла 474
12.3. Эффект Джозефсона 479
12.4. Поверхностное магнитное поле в сверхпроводниках . . . 487
Литература 493
Глава 13. Заключительные замечания 494
Предметный указатель 497
X. Умэдзава, X. Мацумото, М. Татнки
ТЕРМОПОЛЕВАЯ ДИНАМИКА
И КОНДЕНСИРОВАННЫЕ СОСТОЯНИЯ