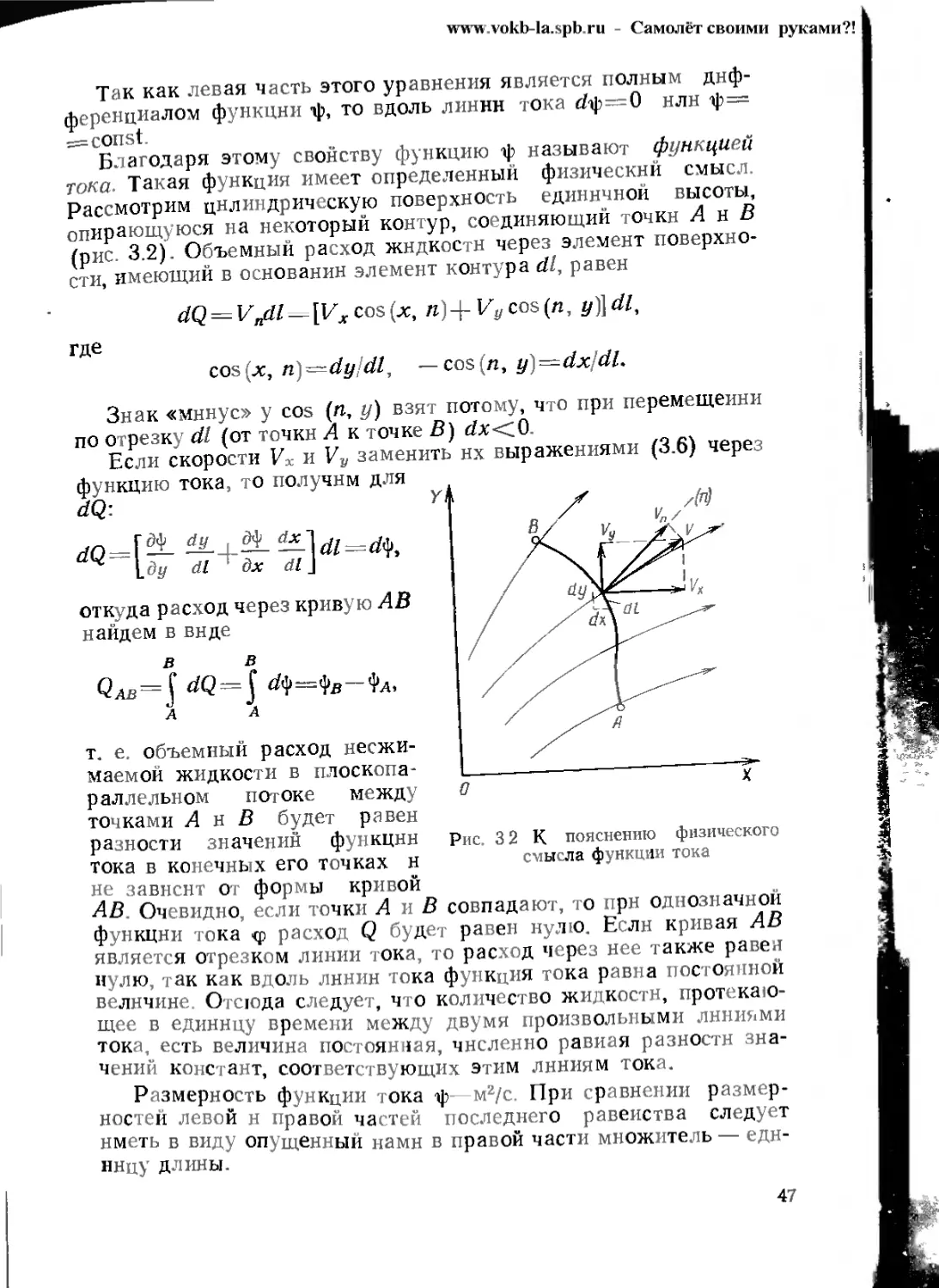
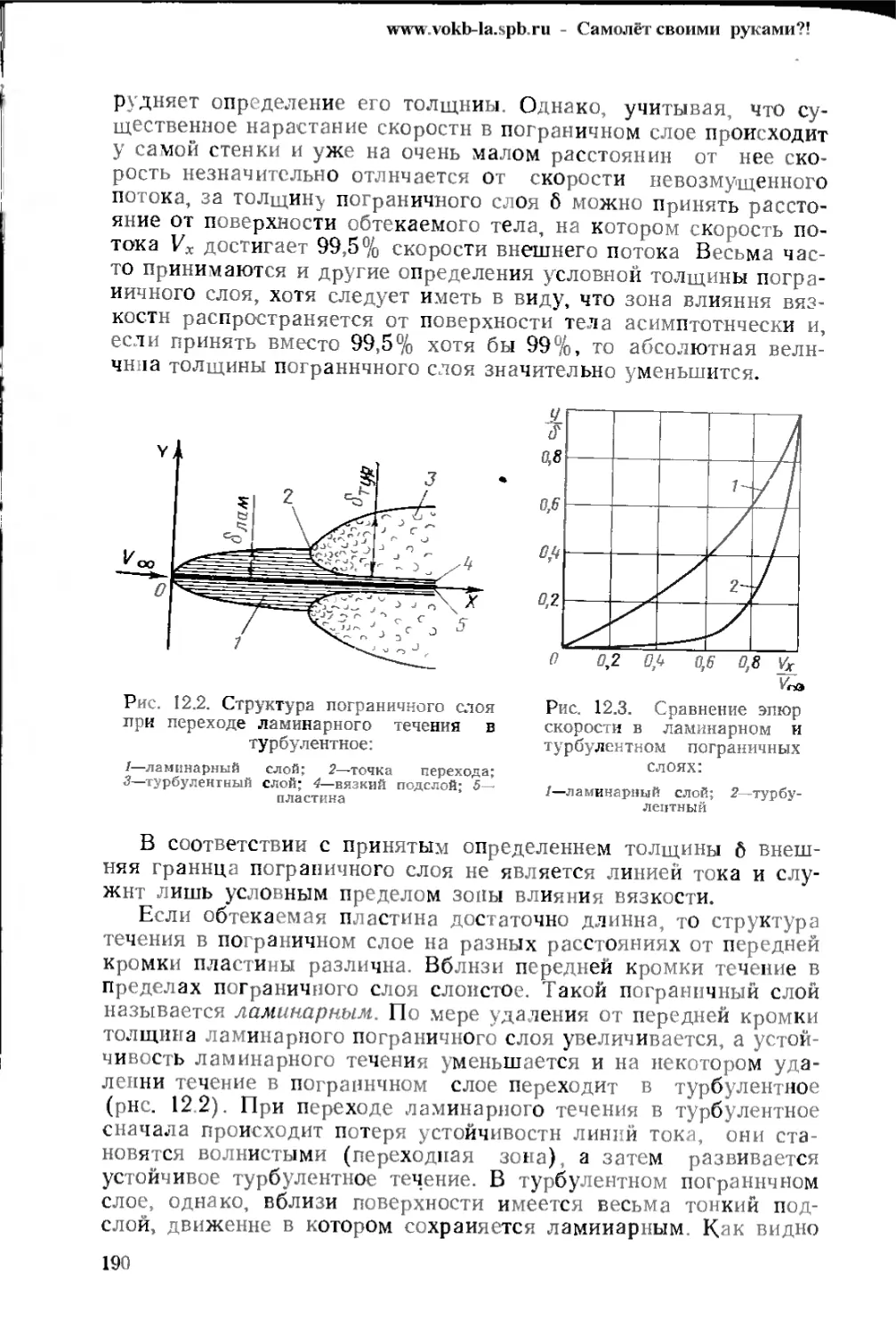
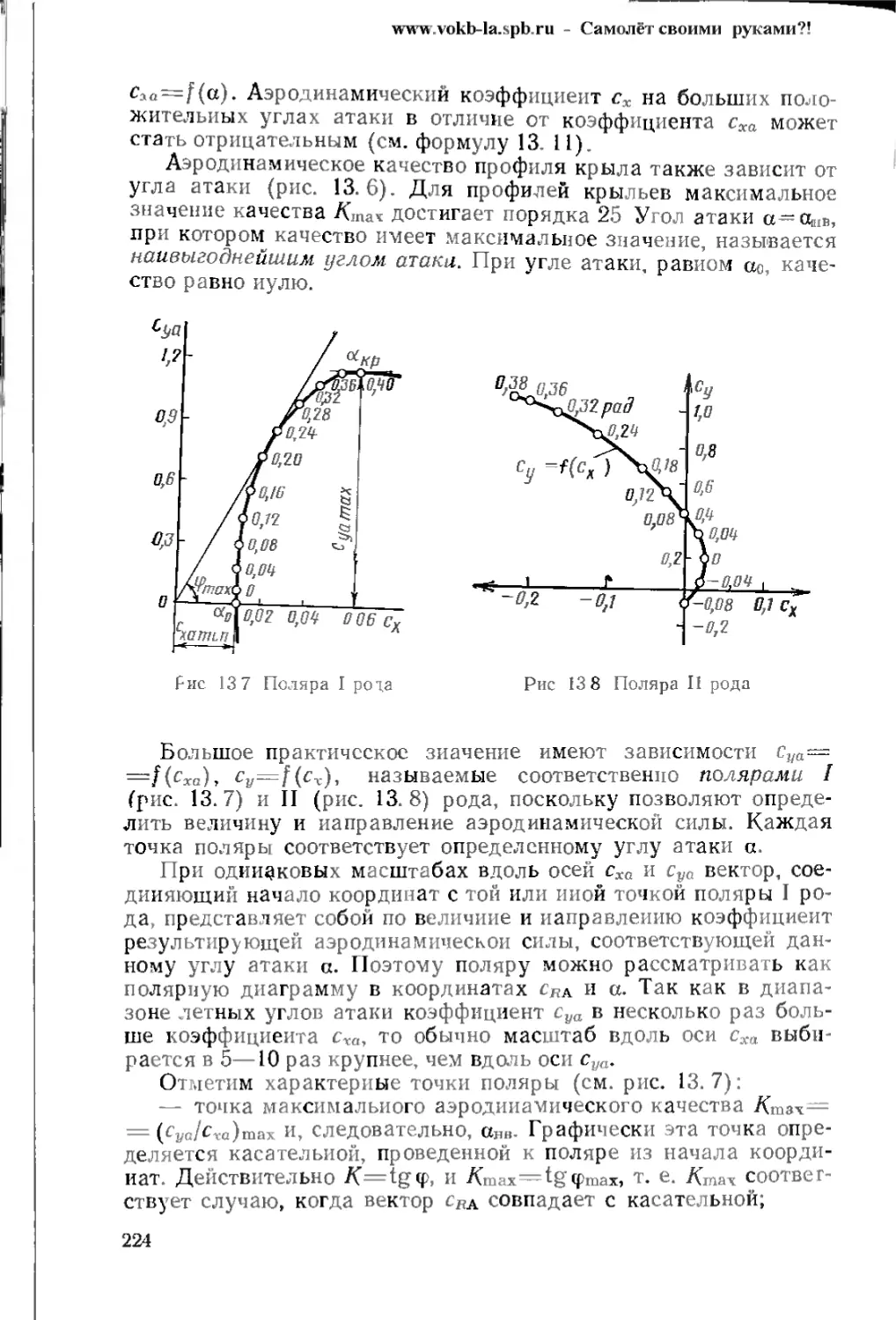
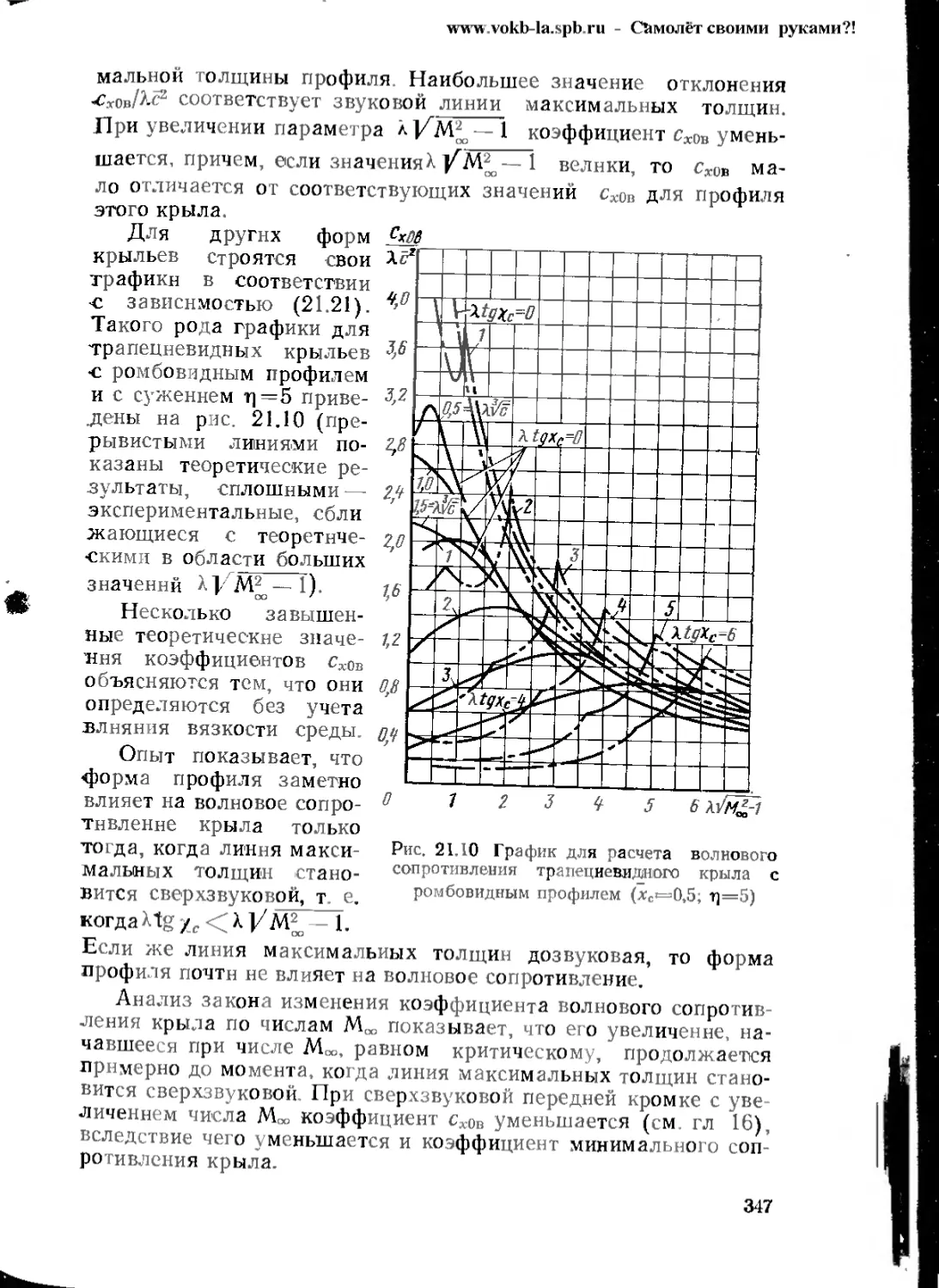
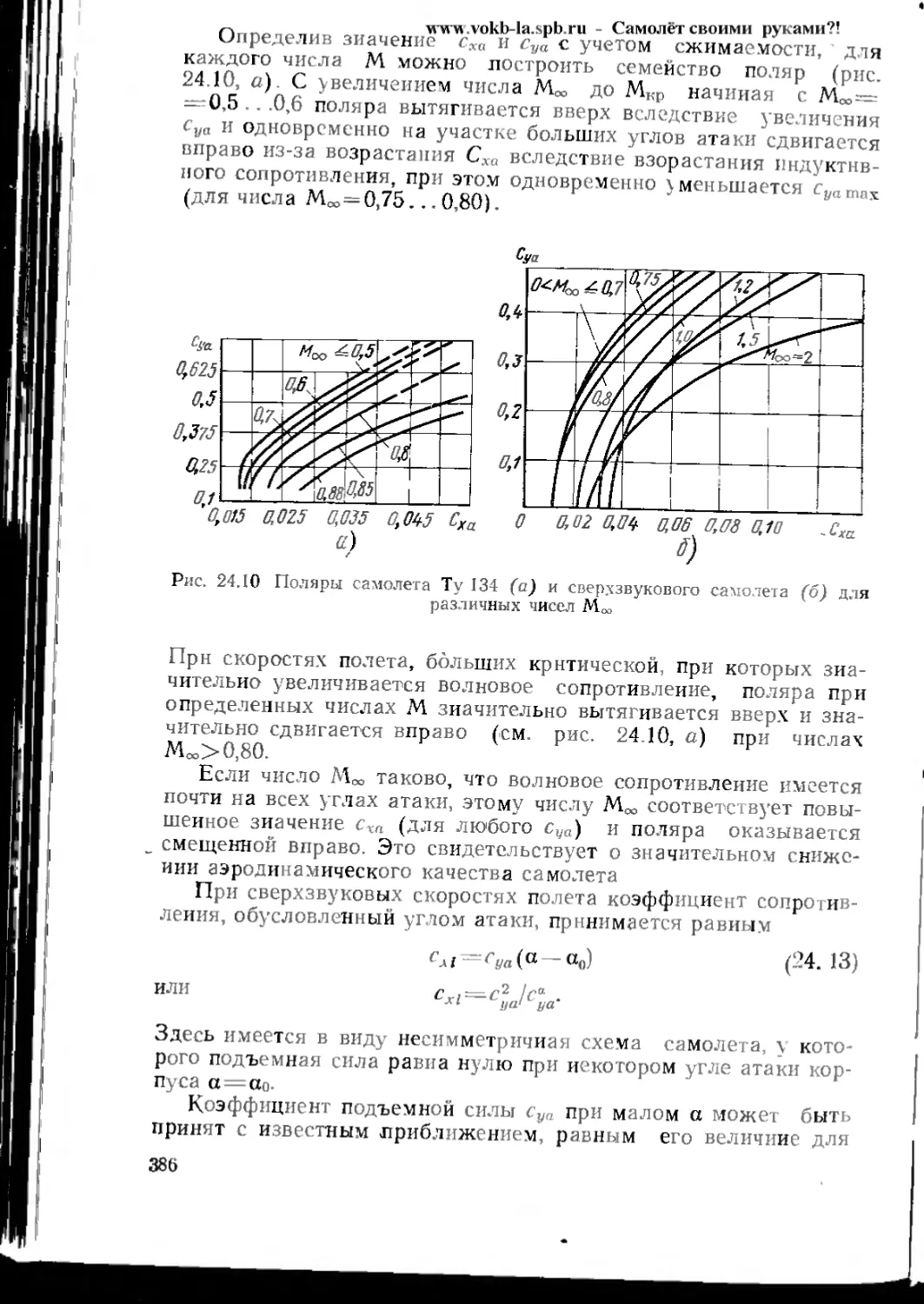
Text
амо.
своими рука
А. М. Мхитаоян
АЭРОДИНАМИКА
ИЗДАНИЕ ВТОРОЕ, ПЕРЕРАБОТАННОЕ И ДОПОЛНЕННОЕ
Допущено
Министерством высшего и среднего
специального образования СССР
в качестве учебника
для студентов авиационных специальностей
высших учебных заведений
Москва
«МАШИНОСТРОЕНИЕ»
1976
www.vokbla.spb.ru С амолет своими руками:;
533(6Т5)
М93
УДК 533.6(075)
Научный редактор д-р техн наук, проф Г. Ф. Бураго
Рецензенты д-р техн, наук, проф. А. П. Мельников, проф. В. И Путята
М93 Мхитарян А. М. Аэродинамика. М, «Машиностроение»,
1976.
448 с. с ил.
В учебнике изложены законы движения газов и погружен-
ных в них тел, законы подобия газовых потоков и теория
скачков уплотнения. Даны основы теории пограничного слоя
и крыла конечного размаха. Рассмотрены аэродинамические
характеристики профилей крыльев, оперений, тел враще-
ния и самолета в целом. Даны основы аэродинамики воздуш-
ных винтов (тянущего и несущего). Во второе издание (1-е
изд. 1970 г.) включена глава о двух режимах движения жид-
кости, а также материалы по расчету сверхзвукового сопла,
расширен раздел задач и примеров. Приведен новый материал
по аэродинамическим характеристикам.
„ 31808-149
М-------------- 149-76
038(01)-76
533(6Т5)
© Издательство «Машиностроение», 1976 г.
Предисловие,
Учебник «Аэродинамика» соответствует программе одноимен-
ного курса по специальности «Эксплуатация самолетов и двига-
телей», который изучают в вузах Министерства гражданской ави-
ации (МГА) и иа факультетах гражданской авиации вузов
Министерства высшего и среднего специального образования
СССР.
Во втором издании материал учебника значительно перера-
ботай. В учебник включена глава о двух режимах течения жид-
кости. Значительно переработаны главы «Аэродинамические
характеристики тел вращения», «Элементы теории подобия»,
«Элементы экспериментальной аэродинамики», «Изэнтропические
течения газа», «Основы теории пограничного слоя», «Аэродина-
мические коэффициенты профиля в дозвуковом потоке», допол-
нены новым материалом главы, в которых рассматриваются
крылья малых удлинений, аэродинамические коэффициенты са-
молета. Исключена глава «Особенности аэродинамики при по-
летах на гиперзвуковых скоростях и больших высотах» В главах
по аэродинамическим профилям крыла самолета в дозвуковом
и трансзвуковом потоках приведены аэродинамические харак-
теристики самолетов Ту-124, Ту-134, Як-40, Ил 18.
При подготовке второго издания были учтены замечания,
отмеченные в рецензии, опубликованной в журнале «Прикладная
механика» (Киев, «Наукова думка», 1970, т VI, вып. 10).
Автор выражает искреннюю благодарность Герою Социалис-
тического Труда академику АН СССР Л. И Седову за ценные
замечания, сделанные им при просмотре рукописи, Заслуженно-
му деятелю науки и техники РСФСР д-ру техн, наук А. П. Мель-
никову и проф. В. И Путяте, взявших на себя труд по рецензи-
3
www.vokbla.spb.ru Самолёт
своими руками?!
роваиию книги, а также д-ру техн, наук, проф. Г. Ф. Бураго за
научное редактирование рукописи.
Автор также выражает признательность за помощь в напи-
сании главы 25 («Воздушные винты») канд. техн, наук П. С. Лаз-
нюку, главы 26 («Особенности аэродинамики несущего винта
вертолета») канд. техн, наук А. Н. Базилевскому и канд. техн,
наук А. Г. Баскаковой за помощь, оказанную ею при подготовке
рукописи к печати.
Автор будет благодарен читателям за замечания по содер-
жанию второго издания книги.
Все замечания следует направлять по адресу: 107885, Москва,
Б-78, 1-й Басманный пер., 3.
www.vokbla.spb.ru Самолёт своими руками
ВВЕДЕНИЕ
B.L ПРЕДМЕТ АЭРОГИДРОМЕХАНИКИ
Аэрогидромеханика (механика жидкости и газа) — наука,
изучающая законы движения и равновесия жидкостей и газов и
их силового взаимодействия с обтекаемыми телами или гранич-
ными поверхностями. Механика жидкого тела называется гидро-
механикой, механика газообразного тела — аэромеханикой.
Законы движения жидкостей и газов при малых скоростях
оказываются во многом одинаковыми *. При сравнительно боль-
ших скоростях течения начинает проявляться сжимаемость га-
зов, которая учитывается при решении многих задач течения
газа с большими скоростями. Сжимаемость капельной жидкости
учитывается только при решении специальных задач (например,
при расчете гидравлического удара или подводного взрыва
Аэромеханика больших скоростей отличается от гидромеханики
как методами исследования, так и результатами.
Развитие воздухоплавания, авиации и ракетостроения вызва-
ло особый интерес к исследованиям силового взаимодействия
воздуха и других газообразных сред с движущимися в иих тела-
ми (крылом самолета, фюзеляжем, винтом, дирижаблем, раке-
тами и др ).
В данном курсе рассматриваются законы движения, общие
для жидкостей и газов, законы, присущие только газу, а также
законы силового взаимодействия газообразной, в частности, воз-
душной среды с движущимися в ией телами. Эта область аэро-
гидромеханики, называемая аэродинамикой, имеет большое зна-
чение для авиации и ракетостроения и своим развитием обязана,
главным образом, этим отраслям техники.
Аэродинамика базируется иа ряде наук и, в первую очередь,
на положениях теоретической механики.
Следует отметить, что, кроме общих законов, существуют законы, свой-
ственные только газу или жидкости
5
www.vokbla.spb.ru Самолёт своими руками?!
При рассмотрении движения газа со скоростями, соизмери-
мыми со скоростью звука, вместо термина «аэродинамика» ис-
пользуется термин «газодинамика». Часто газодинамику выделя-
ют в специальный раздел аэродинамики, в котором изучаются
законы движения газа (воздуха), движущегося с большими до-
звуковыми и сверхзвуковыми скоростями.
Аэродинамика (или газодинамика) совместно с другой нау-
кой— динамикой полета — является теоретической основой ави-
ации и ракетной техники.
Дальнейшее развитие авиации и ракетной техники положило
начало новым направлениям аэродинамики — аэродинамике
очень больших скоростей и аэродинамике разреженного газа,
или, как их принято называть, гипер- и супераэродинамике.
Основы современной аэродинамики созданы трудами гени-
альных русских ученых Н. Е. Жуковского и С. А. Чаплы ина и
зарубежных — Л. Прандтля, Т. Кармана и др. Большой вклад
в развитие аэродинамики внесли советские ученые В. В. Голубев,
А. А. Дородницын, М. В. Келдыш, Н. Е. Кочии, М. А. Лавренть-
ев, Л. И. Седов, В. В. Струминский, С. А. Христиаиович,
Б. Н. Юрьев и др.
Основоположниками науки о механике жидкости, являющей-
ся составной частью аэрогидромеханики, являются члены Рос-
сийской Академии наук Л. Эйлер (1707—1783) и Д. Бернулли
(1700—1782) *.
В.2. ГРАЖДАНСКАЯ АВИАЦИЯ
С рождением Советского государства партия и правительство
уделя. и граж аиской авиации особое внимание. В 1923 г. в
стране был создан Совет по гражданской авиации. На создание
самолетов были направлены лучшие специалисты, выделены зна-
чительные средства, и уже через 12 лет гражданская авиация
перешла па эксплуатацию самолетов только отечественного про-
изводства. С 1935 г. советские воздушные корабли начали успеш-
но конкурировать с лучшими иностранными самолетами.
В эти же годы быстро развивалась сельскохозяйственная
авиация. В 1931 г. в стране было создано Управление сельскохо-
зяйственной авиации, а с 1934 г. сельскохозяйствеииая авиация
и ее научные учреждения перешли в ведение Главного управле-
ния Гражданского воздушного флота (в настоящее время Ми-
нистерство гражданской авиации СССР).
В последующие годы постоянная борьба за скорость и даль-
ность полета привела к созданию современных воздушных лай-
неров с газотурбинными силовыми установками, которые пришли
на смену самолетам с поршневыми двигателями.
* См, например, Механика в СССР за 50 лет (в 4 томах). Том 2. Me
ханика жидкости и газа, под ред. акад. Л И. Седова. М., «Наука», 1970 г.,
880 с.
6
www.vokb-la.spb.ru - Самолёт своими рукам!
Увеличение скорости и дальности полета, с одной стороны,
необходимость сокращения взлетно-посадочных дистанций и
обеспечения безопасности полета, с другой, требовали улучше-
ния аэродинамических характеристик самолета. Эта задача ре-
шалась путем улучшения компоновки основных частей самолета,
усовершенствования авиационных двигателей, выбора оптималь-
ных профилей крыла, применения мощной механизации крыла
и различных методов управления пограничным слоем.
Новый этап развития гражданской авиации начинается с
1956 г., когда на воздушные трассы нашей Родины вышел пер-
вый в мире пассажирский реактивный самолет Ту-104, который
опередил на 2 года американский «Боинг-707» и английскую
«Комету» и на три года французскую «Каравеллу».
За последнее десятилетие темпы развития отечественной ави-
ации достигли невиданных размеров. На смену реактивным и тур-
бовинтовым пассажирским самолетам «первого поколения»
Ту-104, Ил-18, Ан-10 пришли новые совершенные самолеты с
более низкой себестоимостью эксплуатации: Ту-124, Ту-134, Ту-
154, Ил-62, Ан-22, Ан-24, Як-40, Як-42 и сверхзвуковой пасса-
жирский самолет Ту-144. В 10-й пятилетке на воздушные трассы
страны должен выйти аэробус Ил-86.
За рубежом также появились новые высокоэкономичные са-
молеты: «Боинг-747», Виккерс «Супер VC-Ю», «Супер Каравел-
ла», сверхзвуковой пассажирский самолет «Конкорд».
По общей протяженности воздушных линий наша страна за-
нимает первое место в мире. В настоящее время предприятия
аэрофлота обслуживают более 3,5 тысяч населенных пунктов.
Советские лайнеры совершают полеты во многие зарубежные
страны (в данное время их насчитывается 60). С помощью граж-
данского флота ведется разведка природных богатств, осваива-
ются нефтяные и газовые месторождения, строятся нефтепро-
воды и газопроводы, высоковольтные линии электропередач,
проводится борьба с лесными пожарами. Неоценимую помощь
оказывает авиация сельскому хозяйству.
Предполагается в 10-й пятилетке увеличить пассажирообо-
рот воздушного транспорта в 1,3 раза.
Техническое перевооружение гражданской авиации вызвало
необходимость переподготовки летного, инженерно-технического
и обслуживающего персонала.
В.З. ОБРАЩЕНИЕ ДВИЖЕНИЯ
В аэродинамике для упрощения теоретического и экспери-
ментального исследований обычно используется обращение дви-
жения. Возможность рассмотрения обращенного движения при
решении поставленной задачи возникает на основе принципа от-
носительности классической механики, установленного еще в
7
www vokb-la.spb.ru - Самолёт своими руками?!
XVII веке Галилеем, который можно рассматривать как след-
ствие закона инерции Ньютона Согласно этому принципу меха-
ническое взаимодействие нескольких движущихся тел зависит
только от их относительного движения, которое ие изменяется,
если движению всех тел сообщить дополнительное поступатель-
ное движение с постоянной скоростью. Суть обращения движе-
ния заключается в следующем: если в неподвижной воздушной
среде тело (иапример, самолет в воздухе) движется прямоли-
нейно и равномерно со скоростью то при одновременном
сообщении среде и самолету обратной скорости —У*, получается
так называемое обращенное движение, т. е. иа неподвижное тело
избегают воздушный поток (иапрнмер, поток воздуха в аэроди-
намической трубе на неподвижную модель самолета), при этом
скорость иевозмущеиною потока равна —Уте. И в том, и в другом
случае уравнения, описывающие относительное движение само-
лета и воздуха, будут инвариантными. Таким образом, аэроди-
намические силы зависят только от относительного движения
тела и воздуха.
В.4. СВЯЗЬ ТЕОРИИ С ЭКСПЕРИМЕНТОМ
Упрощенные модели явления, положенные в основу аэроди-
намической теории, иногда приводят к результатам, противоре-
чащим практике, например, известный парадокс Даламбера —
Эйлера. Суть этого парадокса состоит в том, что согласно зако-
нам течения идеальной жидкости суммарное сопротивление тела,
равномерно движущегося в жидкой среде, отсутствует, тогда как
в реальной (вязкой) жидкости оно существует.
Опытные данные, собираемые без обобщения и направляю-
щего воздействия теории, также могут приводить к неправиль-
ным выводам. Примером является парадокс Дюбуа Дюбуа
опытным путем пришел к выводу, что сопротивление покоящего-
ся тела, на которое набегает поток водь! в канале, больше, чем
сопротивление тела, движущегося с той же скоростью в непод-
вижной жидкости. Этот результат противоречит принципу отно-
сительности классической механики, согласно которому силы
взаимодействия зависят только от относительного движения
взаимодействующих тел. Впоследствии И. Е. Жуковский объяс-
нил, что причиной этого парадокса является наличие вихрей,
появляющихся в реальных условиях у стенок канала при тече-
нии в ием воды.
После открытия Менделеевым существования двух режимов
течения жидкости (ламинарного и турбулентного), после про-
веденных Рейнольдсом экспериментальных исследований условий
перехода ламинарного течения жидкости в цилиндрических тру-
бах в турбулентное, а также после создания теории подобия ста-
ло ясно, что без теории, обобщающей результаты эксперимента,
не может быть иаучио поставленного эксперимента.
8
www vokb-la.spb ru - Самолёт своими
Для определения аэродинамических характеристик тел (на-
пример, крыла, фюзеляжа и других частей летательного аппа-
рата) обтекаемых воздушным потоком, в настоящее время
используется синтез теоретических и экспериментальных мето-
дов: теоретические расчеты с введением экспериментальных
поправок или экспериментальные исследования с уче- ом теоре-
тических поправок (на влияние вариации критериев по дабия,
граничных условий и т. д.) Ив том, и в другом случаях для рас-
четов и обработки экспериментальных данных широко исполь-
зуются ЭЦВМ После создания летательного аппарата завер-
шающим этапом являются летиые испытания — эксперимент в
натурных условиях Непосредственно измерить аэродинамичес-
кие силы (как, например, в аэродинамических трубах) при лет-
ных испытаниях затруднительно. Аэродинамические характери-
стики определяются путем обработки измеренных во время
испытаний параметров движения летательного аппарата относи-
тельно воздуха. Для получения достаточного количества опыт-
ных данных полеты производятся на различных режимах.
В.5. ПРИМЕНЕНИЕ АЭРОДИНАМИКИ ПРИ ПРОЕКТИРОВАНИИ
САМОЛЕТОВ
Проектирование и расчет самолетов (вертолетов) основыва-
ются на результатах, полученных при аэродинамических иссле-
дованиях. С учетом аэродинамики можно выбрать рациональную
внешнюю форму самолета (принимая во внимание взаимное
влияние его частей) и установить допустим ic отклонения во
внешней форме, размерах и т. д. при производстве.
Для аэродинамического расчета самолета, т. е для определе-
ния возможного диапазона скоростей, высоты и дальности поле-
та, а также для определения таких характеристик, как устойчи-
вость и управляемость самолета, i еобходимо знать силы и мо-
менты, действующие на самолет в полете. Для расчета летатель-
ного аппарата на прочность, надежность и долговечность необ-
ходимо знать величины и распределения аэродин; мических сил
по поверхности летательного аппарата. Ответ на эти вопросы д< -
ет аэродинамика.
Очень важным является определение аэродинамических ха-
рактеристик летательного аппарата и его частей при полете со
сверхзвуковыми скоростями, так как в этом случае возникает
дополнительная задача опреде.) ения температуры на поверхности
обтекаемого тела и теплообмена между телом и средой.
Аэродинамика играет большую роль не только при проекти-
ровании и расчете самолета (вертолета), но и при его летных
испытаниях. С помощью данных аэродинамики и летных испыт; -
ний устанавливают допустимые для самолета величины дефор-
маций, скоростей, а т 1кже режимы полета, при которых имеют
место вибрации, тряска самолета и т. д.
www vokb-la.spb ru - Самолёт своими руками?!
ГЛАВА 1
ОСНОВНЫЕ ФИЗИЧЕСКИЕ СВОЙСТВА
ЖИДКОСТЕЙ И ГАЗОВ. ЗЕМНАЯ АТМОСФЕРА
1.1. ПОНЯТИЕ О ФИЗИЧЕСКОЙ СТРУКТУРЕ
ЖИДКОСТИ И ГАЗА
Жидкость — это физическое тело, обладающее двумя свой-
ствами:
1) она мало изменяет величину своего объема при изменении
давления и температуры, т. е. оказывает значительное сопротив-
ление сжатию. В этом отношении жидкость сходна с твердым
телом;
2) она обладает свойством текучести, способности испыты-
вать большие иеупругие деформации сдвига при действии на нее
малых внешних сил (силы связи между молекулами жидкости
очень малы и она слабо сопротивляется деформации сдвига).
Благодаря этому жидкость не имеет собственной формы и при-
нимает форму того сосуда, в котором находится. Текучесть, обус-
ловленная подвижностью частиц, является одним из основных
механических свойств жидкостей и газов.
Жидкость и газ не оказывают сопротивления медленной и
очень малой деформации сдвига. В то же время силы сопротив-
ления быстрым деформациям могут иметь конечную и иногда
очень большую величину.
Жидкость отличается от газа тем, что она в какой-то мере
оказывает сопротивление растягивающим усилиям, тогда как газ
такого сопротивления практически не оказывает. Будем, однако,
полагать, что и жидкости, и газы ие оказывают сопротивления
растягивающим усилиям
Заметное молекулярное силовое взаимодействие в жидкости,
обусловленное крайне малыми межмолекулярными расстояния-
ми, объясняет два характерных признака жидкого состояния
молекулярное давление и связанное с ним поверхностное натя-
жение на границе жидкости с любой другой средой. Молекулы
поверхностных слоев жидкости находятся в особых условиях,
взаимодействуя как с молекулами данной жидкости, так и с
10
www vokb-la.spb.ru - Самолёт своими руками?!
молекулами соседней среды. Равнодействующая сил взаимодей-
ствия обусловливает поверхностное молекулярное давление, ве-
личина которого весьма значительна: в различных жидкостях
она составляет от 1000 до 10 000 кгс/см2. Именно большой вели-
чиной молекулярного давления объясняется малая сжимаемость
жидкости по сравнению с газом. Опыты показывают, что, напри-
мер сжимаемость воды в 13 900 раз меньше сжимаемости возду-
ха при атмосферном давлении.
Наличием больших межмолекулярных расстояний в газе объ-
ясняется, с одной стороны, стремление газа заполнить любое
замкнутое пространство, в котором он находится, а, с другой сто-
роны, возможность его сжатия под очень большим давлением до
очень малого объема.
Хотя газ и обладает значительной по сравнению с жидкостью
сжимаемостью, однако в случае слабых перепадов давления,
малых скоростей движения, отсутствия значительного нагрева
газ можно с достаточной степенью приближения рассматривать
как несжимаемый. Иначе говоря, степень сжимаемости жидкос-
тей и газов зависит от структуры, а также от динамических и
термодинамических условий течения.
При высокой температуре, близкой к критической (темпера-
тура, при которой разность молекулярных объемов сухого насы-
щенного пара и жидкости становится равной нулю), свойства
жидкости сходны со свойствами газа.
В нашем курсе термин «жидкость» будем употреблять в ши-
роком смысле этого слова, указывая в частных случаях, что рас-
сматривается—газ или жидкость. В дальнейшем везде, где это
специально не оговорено, речь пойдет о газе. Свойства газа ие
всегда будут учитываться во всей полноте, например, иногда не
будут учитываться сжимаемость газа или силы сцепления между
молекулами и т. д., но выбор тех или иных допущений будет за-
висеть от характера исследуемых течений газа.
С точки зрения молекулярной физики газ представляет собой
совокупность хаотически движущихся мельчайших частиц —
молекул, расстояния между которыми значительно превышают
их линейные размеры.
Несмотря на то, что газовая среда является дискретной сре-
дой, при изучении движения газа и особенно его взаимодействия
с обтекаемыми телами газ обычно рассматривается как сплош-
ная материальная среда, в которой отсутствуют межмолекуляр-
ные промежутки. Это предположение, называемое гипотезой не-
прерывности (континуума) или сплошности газовой среды, было
введено в науку Даламбером в 1744 г. и Эйлером в 1753 г. в про-
тивоположность гипотезе Ньютона о том, что газ состоит из
отдельных, равных и не взаимодействующих между собой частиц.
Согласно гипотезе непрерывности считается, что даже в элемен-
тарных объемах, весьма малых по сравнению с обтекаемыми те-
лами, находится достаточно большое количество молекул, раз-
11
www vokb-la.spb.ru - Самолёт своими руками?!
меры и длины свободных пробегов которых, в свою очередь,
очень малы по сравнению с указанными объемами. Гипотеза не-
прерывности позволяет рассматривать кинематические н динами-
ческие характеристики движущегося газа (скорость, давление и
др.) как непрерывные функции координат и времени, что в зна-
чительной степени облегчает применение аппарата математичес-
кого анализа, хорошо разработанного для непрерывных функций
Следует отметить, что применение теоретических выводов, в
основе которых лежит гипотеза непрерывности газовой среды,
ограничено, с одной стороны, размерами частиц, сравнимыми с
молекулярными, с другой — количеством молекул, находящихся
в рассматриваемом объеме. Так, например, гипотеза непрерыв-
ности не прнменнма для сильно разреженных газов.
При строгой математической постановке решение задач аэро-
динамики сводятся к решению сложных систем дифференциаль-
ных уравнений в частных производных. Значительную помощь
прн решении таких задач может оказать применение современ-
ных электронных цифровых или моделирующих машин Для ря-
да теоретических расчетов течения несжимаемой жидкости ока-
зывается полезным использование так называемой электрогндро-
динамической аналогия (ЭГДА): замер скоростных полей в
потоке жидкости заменяется замером разностей электрических
потенциалов на специальной электропроводной бумаге или в
электролитической ванне. При исследовании сверхзвуковых
течений взамен ЭГДА применяется так называемая газогндроди-
намическая аналогия (ГАГА). В этом случае изучение обтекания
тела сверхзвуковым газовым потоком производится путем на-
блюдения волпы, отражающейся на поверхности воды, обтека-
ющей тело той же формы Чаще всего для решения дифферен-
циальных уравнений движения жидкости или газа применяются
различные приближенные методы.
1.2. ПЛОТНОСТЬ И УДЕЛЬНЫЙ ВЕС
Важной характеристикой жидкости или газа является массо-
вая плотность — количество массы в единице объема. По этому
определению согласно гипотезе непрерывности массовая плот-
ность в любой точке пространства, занятого газом, определяется
как предел отношения
р — И m
Am
д¥
где Am — масса газа в объеме АТТ.
В технической системе единиц массовая плотность измеряет-
ся в кгс -с2/м4, в системе СИ—кг/м3. Величина плотности зависит
от природы газа, а также от давления и температуры. Для воз-
духа при нормальном давлении (760 мм рт. ст.) и температуре
12
www vokb-la.spb ru - Самолёт своими руками?!
15ЭС в системе СИ плотность q0= 1,2257 кг/м3, в технической
системе ро=О,125 кгс-с2/м4.
Наряду с плотностью q в аэродинамике используется понятие
весовой плотности (удельного веса)—вес вещества в единице
объема. Весовая плотность в любой точке пространства, занятого
газом, определяется как предел отношения
,. дб
y = lim —
ддр-—0 Д1^’
где AG — вес газа в объеме A W7
В технической системе единиц размерность весовой плотности
кг/м3 в системе СИ — Н/м3. Массовая и весовая плотности свя-
заны довольно простым соотношением y-’QJ/, где g = 9,81 м/с2 —
ускорение силы тяжести.
1.3. ВНУТРЕННЕЕ ТРЕНИЕ И ВЯЗКОСТЬ. ЗАКОН ПЕРЕНОСА
Важнейшим свойством жидкостей и газов является возникно-
вение в них касательных напряжений вследствие вязкости при
относительном перемещении соседних слоев жидкости, т. е. спо-
собность жидкостей и газов к сопротивлению усилиям сдвига.
В состоянии относительного покоя касательные напряжения в
жидкости (газе) отсутствуют, т. е. свойство вязкости проявляет-
ся только при движении.
В жидкости, обладающей даже малой вязкостью (например,
вода, воздух), движущееся твердое тело испытывает заметное
сопротивление из-за наличия трения и завихрений.
Причиной возникновения сил внутреннего трения в газах
является обмен количеством движения между соседними слоями
движущегося газа вследствие диффузии молекул и молярных
объемов. Часть молекул одного слоя за некоторый промежуток
времени проникает в другой. Если молекулы первого слоя обла-
дают большим количеством движения, то, попадая во второй
слой, они ускоряют его движение. В то же время такое же коли-
чество молекул вследствие предполагаемого равновесного рас-
пределения молекул жидкости по всему объему переходит в пер-
вый слой. Так как они обладают меньшим количеством движе-
ния, то замедляют движение первого слоя. Следует отметить,
что диффузия молекул имеет место и в жидкости. Однако в жид-
кости по сравнению с газом более заметную роль в создании
касательных напряжений играют силы межмолекулярного сцеп-
ления (Механизм сил межмолекулярного сцепления весьма сло-
жен. В частности, эти силы существуют и в невязкой жидкости,
-однако касательных напряжений в ней не создают).
Экспериментально установлено, что вязкость оказывает су-
щественное влияние иа движение жидкости вблизи поверхности
разрыва скоростей (например, вблизи поверхности обтекаемых
13
www vokb-la.spb.ru - Самолёт своими руками?!
тел и на поверхности раздела двух жидкостей, движущихся с
различными скоростями).
Скорость течения жидкости вблизи поверхности тела в раз-
ных его точках неодинакова. Прилегающий к твердой плоской
поверхности слой жидкости, имеющий на самой поверхности ско-
рость, равную нулю, благодаря вязкости тормозит лежащий
выше слой, замедляя его движение, последний же, в свою оче-
Рис. 1 1. Изменение скорости тече-
ния вблизи твердой стенки по нор-
мали к ней;
/—пограничный слой; 2—внешнее те-
чение
редь, тормозит слои, лежащий над
ним, н поэтому значение скорости
набегающего потока К» сохраня-
ется на некотором удалении от
поверхности тела. Прилегающий
к обтекаемой поверхности слой
жидкости или газа, *в котором
происходит изменение скорости
течения от нуля на поверхности
до скорости основного потока Ко
(рис. 1.1) называется погранич-
ным слоем.
Таким образом, в вязких сре-
дах происходит явление сдвига
одних слоев по отношению к дру-
гим, соседним слоям, движущим-
ся с меньшими скоростями. На-
пряжение сдвига, возникающее
между слоями, и характеризует
силы внутреннего трения жидкос-
ти. Внутреннее трение, возникаю-
щее при движении вязких жидко-
стей, неизбежно сопровождается
потерей (диссипацией) механической энергии, преобразующейся
в тепловую. Сила трения, возникающая между слоями жидкости,,
характеризуется величиной касательного напряжения, т. е. силой
трения, отнесенной к единице поверхности Если сила давления
направлен а по нормали к поверхности тела, то сила трения на-
правлена по касательной.
Для определения величины касательного напряжения рас-
смотрим два соседних слоя жидкости или газа, параллельных
поверхности тела (см. рис. 1.1). Пусть скорость первого слоя,,
расположенного на расстоянии п от поверхности тела, будет рав-
на V тогда скорость второго слоя, расположенного на расстоя-
нии ri+dn, вследствие увеличения скорости будет равна V+dV.
Относительный сдвиг слоев, происходящий при этом, характери-
зуется градиентом скорости dVIdn. Ньютон предположил, что»
касательные напряжения в жидкостях пропорциональны гради-
енту скорости по нормали к слоям
14
wvnii vokb-la.spb.ru - Самолёт своими руками?!
x=^(dVldn\ (1.1)
где н—коэффициент пропорциональности, называемый динами-
ческим коэффициентом вязкости.
Опыты показывают, что коэффициент вязкости р в значи-
тельной мере зависит от температуры и почти не зависит от дав-
ления и плотности среды. Согласно кинетической теории газов,
динамический коэффициент вязкости пропорционален корню
квадратному из абсолютной температуры Т. Практически эта
зависимость оказывается более сложной.
Для определения динамического коэффициента вязкости воз-
духа может быть использована приближенная степенная фор-
мула р=ц0(71/71о) , где ро — значение коэффициента вязкости
при некоторой температуре То; р — показатель степени (0,5<р<
<1,0)1 обычно принимаемый равным 0,76.
Величина коэффициента вязкости р для жидкостей не зависит
от градиента скорости, но является функцией состояния жидкос-
ти (убывает с увеличением температуры).
Таким образом, коэффициент вязкости является одной из фи-
зических характеристик жидкости при определенном ее состоя-
нии. Чем больше коэффициент вязкости данной жидкости по
сравнению с какой-либо другой, тем большие касательные на-
пряжения будут возникать в ией при прочих равных условиях.
Единицей измерения коэффициента вязкости в системе СИ
является Ньютои-секунда, деленная на квадратный метр
(Н-с/м2).
В аэродинамике обычно используется отношение динамичес-
кого коэффициента вязкости к плотности жидкости, так называ-
емый кинематический коэффициент вязкости (м2/с)
v-p/q. (1.2)
В табл. 1.1 приведены значения динамического и кинемати-
ческого коэффициентов вязкости сухого воздуха для различных
температур при давлении /7=0,981 бар (1 бар = 105 Н/м2).
Таблица 11
Температу- fl. 104 v-104 Темпера ту- М-104 v-104
pa /, °C Н-С/м2 м2/с pa t, °C Н-с/м2 м2/с
0 0,175 0,137 60 0,205 0,196
20 0,186 0,157 80 0,214 0,217
40 0,196 0,176 100 0,222 0,238
Следует отметить, что вследствие физического различия ме-
жду вязкостями газа и жидкости вязкость капельных жидкостей
уменьшается при возрастании температуры (механические связи
между частицами жидкости ослабевают), а вязкость газов уве-
15
www vokb-la.spb.ru - Самолёт своими руками?!
личивается (с увеличением температуры переносимое молекула-
ми нз слоя в слой количество движения увеличивается).
При теоретическом решении многих задач гидро- и аэроди-
намики считают, что жидкости и газы не имеют сил треиия или
вязкости. Такие жидкости и газы называются гидродинамически
идеальными.
В идеальных жидкостях и газах отсутствует ие только вязкость,
ио и перенос тепла и вещества В отличие от идеальных жидкостей,
в реальных жидкостях имеют место процессы теплопереноса и диф-
фузии покоящихся и движущихся жидкостей. Законы переноса
тепла и массы имеют вид, аналогичный закону трения Ньютона.
Перенос тепла определяется законом Фурье q-'k(dTldn), а пе-
ренос вещества—законом Фика W—D(dc[dn), где q и IF — коли-
чество тепла и вещества, переносимое через единицу площади
в единицу времени; Т и с — температура и концентрация ве-
щества в потоке; Z и D — соответственно коэффициенты тепло-
проводности и диффузии.
Таким образом, количество тепла, переносимое через единицу
площади в единицу времени, пропорционально градиенту темпе-
ратуры, а количество вещества — градиенту концентрации этого
вещества в потоке. Теплопроводность связана с вязкостью общ-
ностью молекулярного механизма. Коэффициент теплопроводно-
сти X, как и коэффициент вязкости р, зависит главным образом
от температуры
1.4 ГИДРОСТАТИЧЕСКОЕ ДАВЛЕНИЕ
Рассмотрим какое-либо жидкое тело, находящееся в равно-
весии. Разделим его мысленно иа две произвольные части н одну
из частей удалим. Удаленная жидкость оказывала воздействие
иа остальную часть и поэтому для сохранения равновесия необ-
ходимо к плоскости разреза п приложить силы Р, заменяющие
по величине и направлению воздействие отброшенной части
жидкости. Пусть из упомянутых сил на площадку До действу-
ет сила ДР, тогда средняя величина напряжения в пределах
этой площади
ДР/Д’=/’СР.
Если площадку Да уменьшать вокруг некоторой точки, то
одновременно с приближением До к нулю среднее напряжение
ДР/До будет стремиться к некоторому пределу, характеризую-
щему собой гидростатическое напряжение в данной точке р=
= lim (ДР/Да). Внутри жидкости, находящейся в равновесии,
Да-И)
существуют только сжимающие напряжения, направленные по
внутренним нормалям к элементам поверхности (р=рп), отделя-
16
www vokb-la.spb.ru - Самолёт своими руками
ющим рассматриваемую часть жидкости от остальной жидкости
или твердых границ.
Абсолютная величина этого напряжения в некоторой точке
не зависит от ориентировки в пространстве элемента поверхности
раздела. Скалярная величина р, ие зависящая от орта нормали
л, называется гидростатическим давлением в данной точке.
В системе СИ гидростатическое давление измеряется в Н/м ,
в технической системе единиц — в кгс/м’.
1.5. СИЛЫ, ДЕЙСТВУЮЩИЕ в ДВИЖУЩЕЙСЯ ЖИДКОСТИ
По своей природе или характеру действия силы, приложен-
ные к частицам жидкости или газа, можно разделить на два
класса: массовые силы и поверхностные силы.
Массовые силы пропорциональны массе жидкости выделен-
ного объема.
Поверхностные силы — силы взаимодействия между частица-
ми, расположенными по различные стороны элементарной по-
верхности, пересекающей рассматриваемый объем жидкости или
ограничивающей его. Природа поверхностных сил связана с уп-
ругостью, вязкостью и поверхностным натяжением. Поверхност-
ные силы складываются из поверхностных сил, направленных по
нормали к выделенной площадке, и поверхностных сил, направ-
ленных по касательной к этой площадке.
Все последующие рассуждения имеют место при пренебреже-
нии силами поверхностного натяжения нли при их отсутствии
Так в покоящейся жидкости имеет место только нормальная
составляющая поверхностной силы, в движущейся же жидкос-
ти— нормальная и касательная составляющие. Последняя опре-
деляет силы трения. Поверхностные силы оказывают значитель-
ное влияние на движение жидкости.
Следует заметить, что реально поверхностная сила, действу-
ющая на элемент поверхности внутри жидкости в некоторый мо-
мент времени, представляет собой геометрическую сумму дис-
кретных сосредоточенных сил, действующих на отдельные моле-
кулы. Однако в соответствии с гипотезой сплошности — непре-
рывности мы рассматриваем ее как непрерывно распределенную
по элементу поверхности Ап с напряжением /7 = Нш (дР/Дз). Не-
Дс -»0
прерывное распределение поверхностных сил такая же полезная
абстракция в аэродинамике, как и непрерывное распределение
материи, она неприменима при тех условиях, когда неприменима
гипотеза сплошности среды.
Все силы, действующие на выделенный объем, можно разде-
лить также на две группы;
силы внешние силы, обусловленные взаимодействием час-
тиц, расположенных внутри данного объема, с частицами среды
или другими физическими телами, находящимися вне его,
17
www vokb-la.spb ru - Самолёт своими руками?!
силы внутренние — силы, обусловленные взаимодействием
’частиц, расположенных внутри данного объема, с другими час-
тицами среды или другими физическими телами, находящимися
внутри этого объема.
1.6. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА
Основными параметрами, характеризующими состояние иде-
ального газа, являются давление, температура и плотность. Урав-
нение f (р, q, Т) =0, устанавливающее связь между этими парамет-
рами, называется уравнением состояния. Из этого следует, что
состояние любого газа определяется только двумя параметрами,
например, плотностью и температурой, так как третья величина
является уже ие независимым параметром, а функцией состояния.
Для уравнения состояния существенно понятие температуры,
которое, строго говоря, можно ввести только для термодинами-
чески равновесных процессов. В дальнейшем будут рассматри-
ваться главным образом такие процессы.
Температура Т является количественной характеристикой
интенсивности молекулярного движения в газе. Измеряется тем-
пература либо по температурной шкале Цельсия и обозначается
t, либо по абсолютной температурной шкале Кельвина и обозна-
чается Т,
Для идеальных газов, которые можно рассматривать как
первое приближение к реальным, используется известное из тер-
модинамики уравнение состояния идеального газа — уравнение
Клапейрона —Менделеева:
pv=R7\ (1.3)
где и — объем килограмма массы газа (удельный объем); /? —
газовая постоянная для одного килограмма данного газа.
В технической системе единиц Л измеряется в кгс-м/(кг-
•град), в системе СИ —в Дж/(кг-град) или м2/(с2-град).
Газовая постоянная* R для воздуха при условиях, близких к
нормальным (^=15° и барометрическое давление £?о = 76О мм
рт. ст.), равна 287,14 м2/(с2-град) или 29,27 кгс-м/(кг-град).
При высоких температурах (свыше 2000°) газовая постоянная R
изменяет свое значение. Так, при температуре 7= 10 000 К газо-
вая постоянная R равна 583,6 м2/ (с2 • град), а при 7 =15 000 К га-
зовая постоянная Я = 871,3 м2/(с2-град). С учетом соотношения,
связывающего плотность и удельный объем рп = 1 или р-1/v,
уравнение состояния (1.3) в системе СИ приводится к виду:
P=qRT. (1.4)
Mhoi счисленные эксперименты подтверждают справедливость
уравнения состояния (1.4) для реальных газов при обычных тем-
пературах до давлений порядка 100 кгс/см2 или 101 3 бар. Откло-
нения поведения реальных газов от уравнения (1 4) могут стать
18
www vokb-la.spb.ru - Самолёт своими
заметными, если газ сжат или охлажден до сжижения. При дав-
лении около 200 кгс/см2 (202,6 бар) и температурах Т от 253 до
323 К погрешность этого уравнения для реальных газов состав-
ляет всего несколько процентов.
1.7. НЕКОТОРЫЕ ВОПРОСЫ ТЕРМОДИНАМИКИ
Уравнение (1.4) связывает между собой параметры газа,,
определяющие его состояние. Состояние газа изменяется при
сообщении ему энергии — механической, тепловой или обеих од-
новременно, при отборе от него энергии, а также при переходе
одного вида энергии в другой. Соотношения, описывающие про-
цессы изменения состояния, зависят от условий перехода газа
из одного состояния в другое: прн постоянной температуре, не-
изменных объеме или давлении и т. д. Эти соотношения устанав-
ливаются в термодинамике.
Процесс изменения состояния газа, происходящий прн посто-
янной температуре, называется изотермическим. Для таких про-
цессов
р!ц—RT=с onst. (1.5>
Работа, совершаемая при сжатии газа, увеличивает его тем-
пературу, если только тепло, эквивалентное этой работе, не по-
кидает газ, переходя в окружающую среду. Представляя удель-
ный объем в виде г/=1/р, получим еще одну форму уравнения
состояния для этого случая
рю —const. (1-6)
Процесс изменения состояния газа, происходящий при неиз-
менном давлении, называется изобарическим, а процесс измене-
ния состояния прн постоянном объеме — изохорным. В изобари-
ческом процессе давление
P=qRT—const (1.7)
и в этом случае объем фиксированной массы газа пропорциона-
лен его температуре. Процесс изменения состояния газа, проис-
ходящий при отсутствии теплообмена с окружающей средой, на-
зывается адиабатическим. Адиабатические обратимые процессы,
т. е процессы, протекающие при отсутствии теплообмена и по-
терь (при постоянной энтропии), называются изэнтропическими.
Весьма близкими к адиабатическим являются процессы, проис-
ходящие настолько быстро, что теплообмен с окружающей сре-
дой незначителен. Адиабатические и близкие к ним процессы
имеют место в двигателях внутреннего сгорания, в такте сжатия
Обычно сжатие воздуха в этих двигателях происходит так быст-
ро, что за время процесса сжатия воздух не успевает потерять
сколько-нибудь значительного количества тепла в окружающее
пространство.
wviu vokb-la.spb.ru - Самолёт своими руками?!
В аэродинамике в большинстве случаев приходится иметь
дело именно с такими быстро протекающими процессами в газах,
поэтому законы адиабатических изменений состояния газа для
движения воздуха с большими скоростями представляют осо-
бый интерес.
Для таких процессов
jTOft=const или /?/ofe=const, (1-8)
где k = cP!cZ1 cVi cv — удельные теплоемкости газа соответственно
при постоянном давлении и постоянном объеме
Величина ср всегда больше cv. Это объясняется тем, что ко-
личество тепла, которое идет на увеличение внутренней энергии,
не зависит от типа процесса при изменении состояния — при по-
стоянном объеме или при постоянном давлении. Количество же
тепла, которое превращается в работу расширения, целиком за-
висит от условий, при которых происходит расширение, и при
постоянном объеме газа равно нулю. Значения ср и cv постоянны
только для термодинамически идеального газа. При нормальных
условиях удельная теплоемкость воздуха при постоянном давле-
нии ср=1000 Дж/(кг-град)—в технической системе единиц
ср=0,240 ккал/(кг-град), при постоянном объеме сг=716 Дж/
/(кг-град) или cv—0,171 ккал/(кг-град).
Для идеального газа показатель k — постоянная величина,
а для реальных газов величина k зависит от молекулярной струк-
туры газа: для одноатомных газов k—1,66, для двухатомных (в
том числе и для воздуха) k— 1,4, для многоатомных газов k =
= 1,33.
Так как теплоемкости cv и ср зависят от температуры, то k
тоже зависит от температуры, но изменяется прн изменении тем-
пературы незначительно (табл. 1.2).
Таблица 1.2
Зависимость показателя адиабаты для воздуха от температуры
т к 273 287 373 473
k 1,406 1,405 1,396 1,383
Из этой таблицы видно, что, за исключением высоких темпе-
ратур, величина k близка к постоянной. Прн расчетах для воз-
духа можно принять &=1,4.
Внутренняя энергия газа
Общая энергия данной массы газа может быть представлена
как сумма отдельных видов энергии: £=Ек+ £П+С7, где £к —
кинетическая энергия массы газа в механическом движении;
20
£п— потенциальная энергия массы газа в некотором внешнем
силовом поле (например, в поле земного тяготения); U — внут-
ренняя энергия газа, обусловленная в основном тепловым дви-
жением молекул.
В изохорном процессе (газ не расширяется и не производит
внешней работы) тепло dQ, подведенное к газу, идет только на
увеличение внутренней энергии. dQv=dU=cr>dT, при этом в об-
щем случае cl, = cidp, Г), а в некоторых частных случаях cv =
= СЪ(Т) ИТИ —const.
Если сь —const, то можно записать
4/™|с^Г^сХ (1.9)
о
т. е. изменение внутренней энергии зависит только от темпера-
туры.
В изобарном процессе dU=/=Q, dQp = cpdT.
Внутренняя энергия в данном ст учае, как и в предыдущем,
изменится на величину dU=cvdT.
Первый закон термодинамики
Уравнение так называемого первого закона (или начала)
термодинамики может быть записано следующим образом:
dQ~dU\-pdv, (1-Ю)
где dQ — элементарное количество тепла, подведенное к системе,
dU — изменение внутренней энергии системы; pdv — элементар-
ная внешняя работа, совершаемая системой.
Уравнение (1. 10) после интегрирования принимает вид
<2=(4/2-4/J+J pd-v.
Vi
Первый закон термодинамики является частным случаем об-
щего закона сохранения энергии н выражает эквивалентность
тепловой и механической энергии. В любом так называемом ква-
зистатическом (или почти статическом) процессе изменения со-
стояния газа все подведенное к системе тепло идет на при-
ращение внутренней энергии и на работу расширения газа.
Теплоемкость. Теплосодержание
Подставив в уравнение (1 10) значения dQ и dU для изобар-
ного процесса получим cpdT=cvdT+pdU,
откуда p(dUldT)=cp — c7}. (1-11)
В правую часть этого равенства входят постоянные величины,
поэтому и его левая часть должна быть постоянна. Из уравне-
www.vokb-la.spb.ru - Самолёт своими руками?!
ння состояния (1.3) следует, что при р — const p{dU]dT) = R..
Тогда формула (1.П) примет вид
R=cp-cv. (1.12>
В технической системе единиц —cr), где /=1/Л, А—
тепловой эквивалент механической работы. Следует отметить^
что в технической системе единиц А = 427 кгс-м/ккал, а в систе-
ме СИ /=А—1. Отношение удельных теплоемкостей k=cplcVt,
тогда из уравнения (1. 12) найдем
(L13>
В большинстве задач газовой динамики используется выра-
жение для теплосодержания или энтальпии I в виде
/=срГ, (1.14>
в таком случае приращение теплосодержания di будет представ-
лять собой приращение тепла dQ в процессе р=const.
В аэродинамике часто встречается иное выражение для эн-
тальпии, которое можно получить из приведенной выше формулы
с помощью уравнения состояния (1.4)
i^=cpT—cp{p^R'). (1. 15>
Если учесть, что согласно (1.12) R = cp—cv и что k=cvlcVt то
для I можно получить и другие выражения:
i —или 1=—^—RT. (1. 16>
k— 1 Q k—\
Второй закон термодинамики
Первый закон термодинамики не определяет направления'
реальных процессов изменения состояния замкнутых систем. На
этот практически важный вопрос дает ответ второй закон тер ю-
динамики. Он устанавливает также характерные свойства теп-
лоты (тепловой энергии). Второй закон термодинамики имеет
ряд формулировок. Приведем некоторые из ннх:
1. Теплота не может переходить от холодного тела к теплому
без затраты энергии.
2. Для перевода теплоты в работу необходим температурный
перепад.
3. В замкнутом процессе теплота источника не может быть
полностью превращена в работу.
Энтропия и ее изменение
Правая часть уравнения (1.10), выражающего первый закон
термодинамики, не является полным дифференциалом, поэтому
22
www vokb-la.spb.ru - Самолёт своими руками?!
нельзя получить из него зависимость подведенного к газу тепла
<2 от параметров, характеризующих его состояние. Отсут-
ствие такой зависимости объясняется тем, что величина Q опре-
деляется не только конечным и начальным состоянием газа, но
зависит и от промежуточных состояний протекающего процесса.
Введем некоторую функцию S, характеризующую состояние газа
и называемую энтропией. Понятие энтропии находит широкое
применение в газовой динамике. Обычно говорят об изменении
энтропии, которая зависит только от конечного и начального
состояния газа. Математически его можно представить в виде
dS=dQ/T^O. (1.17)
Согласно первому закону термодинамики (1.10)
dS^dU/T+(p/T)d'v. (1.18)
С увеличением энтропии увеличивается та часть внутренней
энергии, которая не может быть превращена в работу С учетом
уравнения состояния (1.3) и уравнения (1.9) получим уравнение
dS — cv(dT/T) +R(dvlv)t интегрирование которого позволяет по-
лучить выражение для энтропии
5---гда1п7' [A'ln у [ const. (1-1^)
С учетом соотношений R — cp—cv, k = cp/cv выражение (1.19)
можно представить в следующих вариантах:
S-- съ InT(k— 1) In^-j-const;
/ 1 \
S-Ц lnl^-^J+const; (1.20)
S=c.,, In I ) 4- const.
\c J
Учитывая, что произведение pv=\, получим также уравнение
S = cv In (pvh) +Ci, связывающее энтропию с давлением и удель-
ным объемом жидкости. Здесь Ci новая постоянная.
При квазистатнческом адиабатическом процессе, когда S=
=cons , из соотношений (1 20) можно получить
1
const или p/Qk—const. (1-21)
Выражение (1.21), как видим, является уравнением изэнтро-
пического процесса, следовательно, при S = const идеальный ади-
абатический процесс может быть назван также изэнтропическим
процессом, k — показателем изэнтропы.
Таким образом, параметры газа при изэнтропических процес-
сах связаны между собой определенными соотношениями, назы-
ваемыми уравнениями Пуассона, которые для двух его состоя-
ний на основании (1.21) могут быть записаны в виде
1 ft
Р2 _ / 6? ft. 62 / ?2 у—1. _£2_—. /] 22)
Pi \Qi/ ’ 6i \7’i/ * Pi \ Л /
23
www vokb-la.spb ru - Самолёт своими руками?!,
Изэн ропнческне процессы являются частными случаями
адиабатических процессов, когда не только эн альпия газа i, но*
и энтропия S остаются неизменными, изэнтропические течения
называют также «обратимыми» адиабатическими течениями
газа. Необратимые адиаба ические течения называются неизг-
энтропическими
Как известно, второй закон термодинамики форм глнруется
так. прн всех процессах изменения состояния изолированной сис-
темы ее энтр( пня не уменьшается (dSZ^O). Сог таено этому
закону при реальных необратимых пр< цессах, протекающих в
конечной изолированной системе, энтропия как термодинамичес-
кая функция состояния возрастает, а при обратимых процессах
остается неизменной. Следует отметить, что в реальных систе-
мах, в том числе реальных жидкостях и газах, все процессы
необратимы, а обратимые процессы рассматриваются только
как некоторое по Резное приближение.
1.8. СЖИМАЕМОСТЬ ГАЗОВ.
СКОРОСТЬ РАСПРОСТРАНЕНИЯ ЗВУКА В ГАЗЕ
Отличительным свойством газов, как уже отмечалось, явля-
ется сжимаемость. Сжимаемостью называется способность газа
изменять свой объем (а следовательно, и плотность) под внеш-
ним воздействием. Несжимаемая жидкость под действием внеш-
них сил может изменять только свою форму, но не объем
Характеристикой сжимаемости газовой среды может служить,
отношение приращения давления Ар к приращению плотности
Aq, вызванному изменением давления. Предел этого отношения
прн Aq—^0 равен квадрату скорости распространения в среде
малых возмущений или квадрату скорости звука
а’=Нт(^=^
Aq-M) \Д£? / dQ
(1-23)
Следовательно, скорость р спространения звука в среде мо-
жет служить мерой сжимаемости среды под действием малых
давлении.
Поскольку у малосжимаемых жидкостей и газов со значи-
тельными изменениями давления плотность изменяется незначи-
тельно, то скорость распространения звука в такой среде велика;
у сильносжимаемых газ в и при малых изменениях дав тения
изменение плотности велико и скорость звука мала. Например,
в воде, имеющей малую сжимаемость, скорость распространения
звука значите ьно больше (1500 м/с), чем в воздухе (340 м/с на
уровне моря) В абсолютно несжимаемой среде скорость распро-
странения звука бесконечно велика, и малые возмущения распро-
страняются мгиов шно.
wwvt vokb-la.spb ru - Самолёт своими руками?!
При изэнтропическом процессе изменения состояния газа
Р/Ро=(e/t?o)fc и dp[d$(e/Q0)*=kp/Q,
В этом случае
a=}^kp/Q (1.24)
«ли с учетом уравнения состояния (1.4)
(1.25)
При постоянных значениях k и R скорость распространения
звука в газе зависит от его абсолютной температуры Если счи-
тать, что для воздуха А=1,4; /?=287,14 Дж/кг-град, то
а^20]Л7\ (1.26)
В аэродинамике часто скорость звука а используется для
получения безразмерной скорости газа
V/a=M. (1.27)
Это отношение носит название числа Маевского или числа
Маха.
Для абсолютно несжимаемой среды (л=-ос) число М=0
Влияние сжимаемости иа характеристики течения газа начинает
сказываться на скоростях (М<1) при М0.4 ... 0,5 и возрастает
с увеличением числа М, вызывая не только количественные, но
п качественные изменения характеристик течения при звуковых
<(М=1) и сверхзвуковых (AV>1) скоростях.
1.9. АТМОСФЕРА
Атмосферой называется газообразная оболочка, окружающая
земной шар и вращающаяся вместе с ним. Верхняя часть атмос-
феры состоит из ионизированных частиц, захваченных магнит-
ным полем Земли. Атмосфера плавно переходит в космическое
пространство и ее точную высоту установить трудно Условно
высота атмосферы принимается равной 2500 км; иа этой высоте
плотность воздуха близка к плотности космического простран-
ства. Исследование состояния атмосферы представляет большой
интерес для авиации, так как от свойств атмосферы зависят лет-
аю технические характеристики летательных аппаратов Особен-
но большое влияние на летиые качества самолетов оказывают
метеорологические условия.
С увеличением высоты падают давление и плотность воздуха
Параметры атмосферного воздуха зависят от координат места
и изменяются с течением времени в определенных пределах.
Значительное воздействие на состояние атмосферы оказывает
солнечное излучение. Атмосфера находится в непрерывном вза-
имодействии с космосом и землей.
Атмосфера состоит из нескольких слоев; тропосферы, стра-
тосферы, химосферы, ионосферы, мезосферы и экзосферы, каж-
25
www vokb-la.spb ru - Самолёт своими руками?!
дый из которых характеризуется различным изменением темпе-
ратуры в зависимости от высоты.
1. В тропосфере температура уменьшается с высотой в сред-
нем на 6,5° через каждые 1000 м
2. В стратосфере температура остается почти постоянной
3. В химосфере теплый слой воздуха лежит между двумя
холодными слоями, поэтому там существуют два температурных
градиента: внизу в среднем +4° на 1000 м, а вверху — 4,5° на
.1000 м.
4. В ионосфере температура возрастает с высотой в среднем
на 10° через каждые 1000 м.
5. В мезосфере температура уменьшается в средне.! на 3° че-
рез каждые 1000 м.
Все слон отделяются друг от друга зонами толщиной 1—2 км,
называемыми паузами' тропопаузой, стратопаузой, химопаузой,
ионопаузой, мезопаузой.
Наибольший интерес для авиации в настоящее время пред-
ставляют нижние слои атмосферы, в частности, тропосфера в
стратосфера.
Многолетние наблюдения состояния атмосферы в различных
местах земного шара показали, что значения температуры, дав-
ления и плотности воздуха изменяются в зависимости от време-
ни и координат в весьма широких пределах, что не позволяет
точно предсказывать состояние атмосферы в момент полета.
Например, в Сибири температура воздуха зимой на уровне оке-
ана иногда достигает 213 К, а летом 303 К, т. е. в течение года
она изменяется иа 90 К В средних широтах температура изме-
няется примерно на 70 К В изменениях температуры на различ-
ных высотах также наблюдаются значительные колебания.
Значителен диапазон колебаний давления: в средних широ-
тах на уровне океана оно изменяется от 1,04 до 0,93 бар (1 бар —
= 105 Н/м2). Соответственно изменяется и плотность воздуха (в
пределах ±10%).
Отсутствие определенности в состоянии атмосферы у Земли
и в изменении ее состояния с увеличением высоты создает серь-
езные затруднения при аэродинам (ческих расчетах летных ха-
рактеристик самолетов, которые, как уже отмечалось, сущест-
венно зависят от состояния атмосферы. Необходимость
унификации расчетов, связанных с летательными апп ратами.
при решении практических задач, например, единообразное гра-
дуирование различных л ггных приборов (измерители скорости,
махометры и т. п ), пересчет летных характеристик самолетов,
полученных в конкретных атмосферных условиях, на другие при-
вела к созданию условных характеристик атмосферы-—стандар-
тов. Такие характеристики были введены в форме условной
стандартной атмосферы (СА), которая ] меет вид таблицы чис-
ленных значений физических параметров атмосферы для ряда
высот, взятых на основе данных среднегодовых многолетних на-
26
www.vokb-la.spb.ru - Самолёт своими
руками
•блюденнй для географической широты 45°32 40'', т. е. представ-
ляет собой как бы идеализированное состояние атмосферы для
средней широты с осредненными в течение года значениями.
Для определения давления н плотности в пределах тропо-
сферы рассмотрим условие равновесия элементарного объема
воздуха, находящегося в призме единичной площади с высотой
Му н расположенного на высоте у от поверхности земли. Воздух
в призме снизу испытывает давление р, сверху p-\-dp, а разность
этих давлений уравновешивает вес воздуха в призме, поэтому
$gdy=—dp. (1.28)
Это уравнение может быть проинтегрировано в некоторых
случаях. Так при небольших разностях высот (а в случае не-
сжимаемой жидкости для любой разности высот) можно пола-
гать Q = Q0 = const (случай однородной атмосферы). Тогда, пола-
гая при у=Н® р = Ро и интегрируя (1.28) от Но до Н и соответ-
ственно от pQ до р, получим
Н-Н Р±-.Е . (1.29)
еся
Если рассматривать воображаемую атмосферу как однород-
ную по всей высоте, тогда, полагая //о=О и р = 0, найдем соот-
ветствующую высоту Н называемую высотой однородной ат-
мосферы
H*=P<^g=RTdg- (1.30)
Исключив из уравнения (1.28) плотность р с помощью урав-
нения состояния (1.4), получим соотношение
dplp^-dyglRT, (1.31)
-которое может быть проинтегрировано, если известен закон
изменения Т=Т(у). В частности, при постоянной температуре
Т = Т0=Т (И) = const, что характерно для стратосферы, имеем
Мр(р=—dy[H*. Интегрируя это уравнение от ро до р и от Но
до Н, получим
н
Ро
тде е — основание натуральных логарифмов. Так как в случае
постоянства температуры А — q/qo — p/Po, то
Я-Яо
д=—==е И* . (1.33)
ео
В случае линейной зависимости температуры от высоты, что
характерно для тропосферы,
Т=~Т0 — ру, (I-34)
27
www.vokb-la.spb.ru - Самолёт своими руками?!
где Го — значение абсолютной температуры прн у=0, ц— гра-
диент температуры по высоте.
Подставляя соотношение (1.34) в уравнение (1.31) и интегри-
руя это уравнение в пределах от р0 до р н от Но до Н, получим
(i-35>
л \ rj \ н. I '
(i.36>
с» \ т0) \ н,) ' '
В качестве начальных условий для стандартной атмосферы
принимают:
для тропосферы (прн р=0,0065 град/м) Но —О (от условного^
уровня океана), Г--288 К, р(1--10,13 105 Н/м2, go= 1,225 кг/м3;
для стратосферы (при ц=0) Но= 11 000 м, Т= 216 K=const
Используя выведенные зависимости для давления н плотности'
с учетом начальных условий, получим следующие выражения
для расчета стандартной атмосферы:
1. Тропосфера (для высот до 11 км)
р О Н \5.256
—1 — ~^0~^ ) илн барометрическое давление
Н \4,256
44300/
5=760
И ^5,256.
443Э0 / ’
р~ 1,225
Н X 4,256
’ 44300 )
(1.37)
(1.38)
2. Стратосфера (для высот, больших И км)
_ к—И 000 _ я—И 000
5 = 169,4е 6340 ; р=0,0371е 6340 . (1.39)
Обычно нет необходимости проводить вычисления по приве-
денным выше формулам. Для этого используется специальная
«Таблица стандартной атмосферы» (см. приложение).
Вопросы для повторения
1. В чем заключается отличне газов от жидкостей н твердых
тел?
2. Что называется давлением, какова его единица измерения?
3. Дайте определение адиабатического, изотермического,,
изэнтропического процессов.
4. Объясните различие между изэнтропическим н неизэнтро-
пнческимн процессами в газах.
5. Что такое сжимаемость газа и чем она характеризуется?
28
www.vokb-la.spb.ru - Самолёт своими руками?!
6. Объясните природу вязкости газа.
7. Что называется земной атмосферой и как распределяете»
по высоте плотность воздуха?
Задачи
I. Как изменяются температуры и плотность воздуха при
квазистатическом адиабатическом сжатии от давления 0,980 до
19,6 бар, если начальная температура воздуха Л°=30 С
Решение. При квазистатическом адиабатическом процессе-
сжатия
А— 1 I
/ Р2 \ k . Q2 / Р2 k
Ti \pl) ’ 61 \ Pl )
Для воздуха
i
*=1,4и -Й—20 м =8,51;
Qi
О 4
11 = 20^=2,35.
Ti
Ответ: -^-=2,35; -^-=8,51.
Л Q1
2. Найти, иа сколько отличаются максимальные скорости пог-
лета самолета:
1) зимой при температуре —40° С;
2) летом при температуре +40°С, если максимальное число
М, допустимое для этого самолета, равно 0,8
Решение.
Vm„=aMnm=;20 /273+7^-20.0,8 /273-Л,
т. е. зимой
летом
^=161/^33=244,2 м/с (—879,5 км/ч);
l/max=16 J 3I3 283 м/с (— 1018,5 км ч).
О тее т; летом скорость полета выше.
3. Определить число ЛА. самолета при полете со скорости»
V= 1080 км/ч на высотах Н = 1, 10 и 25 км
О тее т: — 0 89; М2= 1 0; М3 — 1,02.
4. Рассчитать зависимость энтальпии i и внутренней энер-
гии U от высоты в пределах тропосферы. Вычислить величины
энтальпии и внутренней энергии на верхней границе тропосферы.
Ответ: 1н-иооо=2,18-105 Дж/кг; /7н-нооо= 1,55-105 Дж/кг_
www.vokb-la.spb.ru - Самолёт своими руками?!
ГЛАВА 2
КИНЕМАТИКА ЖИДКОЙ СРЕДЫ
2.1. МЕТОДЫ ИССЛЕДОВАНИЯ ДВИЖЕНИЯ ЖИДКОСТИ
Движение твердого тела, как известно из теоретической ме-
ханики, в некоторый момент времени можно разложить на по-
ступательное движение вместе с произвольно выбранным полю-
сом и вращательное движение относительно мгновенной осн,
проходящей через этот полюс, что позволяет найти скорость лю-
бой материальной точки, входящей в состав твердого тела, как
геометрическую сумму скоростей ее в каждом из составляющих
движений. В жидкости в отличие от твердого тела отдельные
частицы вследствие текучести обладают почти неограниченной
свободой перемещения—одна относительно другой, при этом
каждая частица имеет свою собственную скорость движения,
только в определенной степени зависящую от скорости других
частиц.
Эйлер разработал два метода исследования движения жидко-
сти — локальный и субстанциальный (индивидуальный).
При анализе движения жидкости Эйлер в большей мере поль-
зовался первым методом. Второй метод в дальнейшем развил
Лаграиж, поэтому в литературе субстанциальный метод называ-
ется методом Лагранжа, а локальный — методом Эйлера.
При исследованиях по методу Лагранжа в жидкости рассмат-
ривается движение отдельных (индивидуальных) частиц. Ско-
рость и другие кинематические параметры определяются в виде
функции времени и некоторых независимых параметров, которые
•однозначно определяют ее начальное положение в пространстве.
Методы Лагранжа и Эйлера отличаются друг от друга тем,
что в первом случае переменные х, у, z являются переменными
координатами движущейся жидкости, во втором случае — это
координаты фиксированных точек пространства, мимо которых в
данный момент времени протекают различные частицы жидкос-
ти. Это различие можно уяснить на примере полета группы са-
молетов. Эйлерово описание полета самолетов соответствует
наблюдениям находящегося на земле зрителя за движением раз-
-30
www.vokb-la.spb.ru - Самолёт своими руками?!
личных самолетов, проходящих через выбранный участок про-
странства. Лагранжево описание, напротив, соответствует наблю-
дениям за движением одного и того же самолета, пилот которого
сообщает о своем полете с борта самолета. Метод Эйлера благо-
даря своей простоте получил большее распространение, чем ме-
тод Лагранжа. Мы будем изучать движение жидкости по методу
Эйлера, в отдельных случаях используя метод Лагранжа. В соот-
ветствии с методами описания Лагранжа и Эйлера могут быть,
получены два вида уравнений для определения скоростей и-
ускорений. С помощью этих уравнений решается вопрос о дви-
жении отдельных частиц жидкого тела в пространстве в зависи-
мости от времени. Существуют методы перехода от переменных
Эйлера к переменным Лагранжа и наоборот.
Заметим, что при неизменных во времени кинематических
параметрах в фиксированных точках пространства с координата-
ми х, у, z движение называется стационарным илн установив-
шимся. В этом случае dVIdt—dQ/dt~dT/dt=G Если же в фик-
сированных точках пространства кинематические параметры со
временем изменяются, то движение называется нестационарным
или неу становившимся. Иначе говоря, при стационарном движе-
нии кинематические параметры являются функциями только,
координат х, у, z, а при нестационарном движении не только ко-
ординат х, у, z, но и времени t.
2.2. ЛИНИЯ ТОКА ТРУБКА ТОКА.
ЭЛЕМЕНТАРНАЯ СТРУЙКА
Выше были описаны два метода исследования движения жид-
кости Каждому из них соответствует свой способ геометричес-
кого изображения потока Если для метода Лагранжа определя-
ющим является понятие о траектории частиц, то для метода,
Эйлера характерным является понятие о так называемых линиях
тока жидкости. Для выяснения этого понятия представим себе
поле скоростей потока жидкости, соответствующее какому-ни-
будь определенному моменту времени.
Пусть в данный момент времени в какой-либо точке 1 прост-
ранства, заполненного жидкостью, вектор скорости равен Е*
(рис. 2.1, а) Возьмем точку 2, бесконечно близкую к точке 1 и
находящуюся на векторе У\. В этот же момент времени t в точке
2 вектор скорости равен Еа. Точно так же в точке 3, бесконечно
близкой к точке 2 н находящейся на векторе Еа, вектор скорости
в тот же момент времени равен Eg и т. д Таким образом для мо-
мента времени t получаем ломаную линию 1,2,3,... В другой
момент времени t' получаем другою ломаную линию (см пунк-
тир на рис. 2 1, а). Если число точек неограниченно увеличивать,
31;
www vokb-la.spb.ru - Самолёт своими руками?!
а расстояние между ними устремлять к нулю, то в пределе по-
лучится кривая, называемая линией тока.
Линия тока, проведенная внутри движущейся жидкости, »
•обладает тем свойством, что каждая частица жидкости, находя-
щаяся на ией в данный момент времени, имеет скорость, совпа-
дающую по направлению с касательной к этой линии.
Жидкая частица при своем движении описывает траекторию.
При установившемся движении линии тока и траектории тож-
дественны. При неустановившемся движении линии тока не сов-
ладают с траекториями. На рис. 2.1, б показано, что жидкая час-
Рис 2 1. Линия тока (а) и траектория движения (б)
тица, проходя в моменты времени t2, is, h через точки А, В, С,
D, переходит с линии тока 1 на линию тока 2, далее иа линии то-
ка 3, 4 и т. д. Следует отметить, что через каждую точку прост-
ранства, заполненного жидкостью, можно в фиксированный мо-
мент времени, провести только одну линию тока
Если траектория частицы фиксирует изменение положения
одной и той же частицы с течением времени, то линия тока ука-
зывает направления скоростей разных частиц в один и тот же
момент времени. Траектории могут пересекаться, а линии тока
не пересекаются, ибо в противном случае в точке пересечения
лектор скорости в данный момент времени имел бы два разных
направления, что физически невозможно. Исключением могут
-быть особые точки потока, например, точка полного торможе-
ния, где скорость частицы равна нулю, или точки, где скорости
теоретически бесконечны.
Для получения дифференциальных уравнений линий тока
воспользуемся тем, что элемент касательной к линии тока dl
направлен вдоль вектора скорости V (рис. 2 2, а).
Обозначим через а, 0, у углы элемента касательной к линии
тока (а следовательно и вектора скорости) с осями координат.
32
www.vokb-la.spb.ru - Самолёт своими руками?!
Проекции вектора dl на оси координат определяются соотноше-
ниями
dx dl cos a, dy = dl cosp, dz—dl cosy,
а проекции вектора скорости на оси координат соотношениями
V\=l/cosa, V\=lZcosfi, l/z = l/cosy.
Разделив первую группу уравнений на вторую получим
dx]V x=dy]V y = dz]V z, (2. 1)
где dx, dy, dz — проекции вектора dl на координатные оси; Vx=-
-V\-(.r, у, z, t); Vy=Vy(x, y, z, t)\ Vz=Vz{x, y, z, t) —проекции
Рис 2 2. Линия (а) и трубка (б) тока
вектора скорости на координатные оси (проекции скорости яв-
ляются функциями координат х, у, z\ время t здесь гараметр)
Совокупность уравнений (2.1) ноент название дифференци-
альных уравнений линий тока.
Таким образом, задача об определении линий тока по задан-
ному полю скоростей приводится к инте рированию системы
дифференциальных уравнений.
Система (2.1) представляет собой совокупность двух незави
енмых дифференциальных уравнений, например
V ydx~V xdy\ Vzdy = V ydz, (2.2)
связывающих попарно проекции скорости с проекциями переме-
щения по линии тока на три координатные оси.
Для введения понятия о трубке тока и об элементарной
струйке построим вокруг точки 1 замкнутый контур С, имеющий
бесконечно малую площадь do (см. рис. 2.2, б). Через каждую
точку этого контура проведем линию тока. Совокупность прове-
2 626
33
www .vokb-la.spb.ru - Самолёт своими руками?!
денных таким образом линий тока образует поверхность, кото-
рая называется трубкой тока. Жидкость, протекающая внутри
трубки тока, принято называть элементарной струйкой. Жид-
кость не может пересекать границы элементарной струйки, по-
скольку скорость течения жидкости внутри трубки тока везде
параллельна боковой поверхности струйки. Если все линии тока,
расположенные внутри трубки и на ее поверхности, нормапьны к
поверхнчсти сечения, то такое сечение называют нормальным
или ортогональным (живым) сечением трубки.
2 3. УРАВНЕНИЕ НЕРАЗРЫВНОСТИ
Уравнение неразрывности, отражающее условие сохранения
массы применительно к движущейся жидкости, принадлежит к
числу основных уравнений аэродинамики.
Для получения уравнения неразрывности выделим в потоке
жидкости замкнутый объем W, ограниченный неподвижной по-
верхностью, сквозь которую свободно проте-
// у кает жидкость (рис. 2 3).
\ Масса жидкости внутри фиксированно-
Г° °бъема в момент времени t
m — J f f &IW (2.3)
При неустановившемся движении эта
масса с течением времени может изменять-
ся, причем изменение массы в единицу вре-
мен и равно
Рис. 2 3. К выводу
уравнения неразрыв- / V VV U 22- dW (2 4)
носги dt dt ( J J J " I .U J dt
Изменение массы происходит из-за того, что количество жид-
кости (расход), втекающей внутрь заданного объема за единицу
времени, может не быть равным количеству жидкости, вытека-
ющей за пределы объема (за счет изменения плотности жидко-
сти в объеме IF).
Обозначим через 5 поверхность, ограничивающую объем IF,
тогда расход жидкости через элементарную площадку AS ори-
ентация которой в пространстве определяется внешней норма-
лью и, составит— gV?iAS. Отрицательный знак здесь вызван
тем, что для жидкости, втекающей внутрь поверхности S, огра-
ничивающей объем IF, составляющая скорости У„ направлена в
сторону, противоположную внешней нормали.
Суммарный расход жидкости через всю поверхность, ограни-
чивающую объем IF, определяется интегралом
(2.5)
34
wwwvokb-la.spb.ru - Самолёт своими руками?!
В случае отсутствия внутри объема источников или стоков на
основании закона сохранения массы интегралы (2.4) и (2 5)
должны быть равны между собой, т. е.
(IF) (S)
Используя далее формулу Гаусса—Остроградского
Hcv„1ys=Jjfdiv(ei7)rfW’,
(S) on
преобразуем предыдущее уравнение к следующему виду:
(IF) (IF)
Fdiv
dt
или
(IT)
dQ
dW-().
г
{-div (gl/)—-0.
(2-6)
Поскольку объем IF выбран произвольно, то последний ин-
теграл будет равен нулю, если
dp
dt
Это и есть уравнение неразрывности в дифференциальной
форме.
Уравнение неразрывности (2 6) может быть записано в раз-
личных формах. Так, заменяя div (pF) ее значением, выражен-
ным через проекции скорости на оси прямоугольной системы
координат, получим
dg
dt
d(QKr) । d(QVg)
dx
или в полной записи
dp
dt/
d (Q^z) Q
dz
(2.7)
dp
dt dx
Это уравнение носит название дифференциального уравнения
неразрывности для сжимаемой жидкости. Если движение сжима-
мой жидкости установившееся, то будем иметь =0 и
d(gFr) j d(pVi/)
dx dy
dp
dy
дх
dp
dz
dVy
дУ
= 0
d(QVz) _0
dz
(2-8)
35
i
www.vokb-la.spb ru - Самолёт своими руками?!
или в векторной форме* div(()V)=O. Заметим, что при о=
=f(x, у, z, О
dQ-^-dx + ^-dy+^-dz + ^dt
дх ду ' дг 1 dt
dt dt 1 дх 1 и ду 1 гдг
Сравнивая последнее соотношение с (2.7'), получим
— + е(— + — + ~ ) = 0 (2.9)
dt 1 к дх ду ' dz } 1 ’
или ^-4-cdiv V=0. (2.10)
Если жидкость несжимаема, т
разрывности для установившегося
е. 2='const, то уравнение
движения примет вид
не-
Рис. 2 4. К выводу уравнения
неразрывности для струйки
div V=0
dVx i dVy । dVz n
или -—Ч-------Ч----~=0.
дх ду dz
(2.11)
(2. 12)
Для решения многих практи-
чески важных задач желательно
иметь уравнение неразрывности в
такой форме, которая позволила
бы установить связь между ско-
ростью и площадью поперечного
сечения струйки или потока. Рассмотрим два ортогональные
(живые) сечения струйки, расположенные на бесконечно близ-
ком расстоянии (рис. 2.4). При известных значениях скорости V,
плотности q и площади До в первом сеченин массовый расход
жидкости через это сечение будет составлять (эЕДсг, а через вто-
рое сечение
С1/Дз+-^Д°) ds.
За счет разности величин массового расхода в первом и вто-
ром сечениях масса жидкости, заключенная в объеме между эти-
ми сечениями, уменьшится за время dt на величину
^^Ldsdi. (а)
ds 1 7
Если в некоторый момент времени масса жидкости в этом
объеме составляет pAcrds, то через отрезок времени dt могут
измениться плотность жидкости и площадь живого сечения
струйки, а следовательно, изменится и масса, которая в этом
случае будет равна
3b
www.vokb-la.spb.ru - Самолёт своими руками?!
В этом случае приращение массы будет равно
<nQM)-dtds. (б)
dt
На основании закона сохранения материи можно утверждать,,
что приращения масс, определяемые выражениями (а) и (б)г
одинаковы по величине, но противоположны по знаку и, следо-
вательно,
д(оДо) I д(дУДо)_q <2 13)
dt ds ' * '
Действительно, когда масса жидкости, вытекающая через
второе сечеиие, меньше, чем втекающая через первое сечение,
происходит накопление массы жидкости между двумя сечени-
ями.
Соотношение (2.13) выражает условие неразрывности для
элементарной струйки в неустановившемся потоке сжимаемой
жидкости. Для установившегося потока все параметры нс зави-
сят от времени и =0. поэтому из (2.13) следует, что
д(рУДа)
—L——откуда
ds
,\G—plzA(T- const (2.14)
для всех живых сечейий струйкн.
Равенство (2.14) выражает условие неразрывности для ус-
тановившегося течения сжимаемой жидкости вдоль элементар-
ной струнки.
Поток конечных размеров можно рассматривать как совокуп-
ность бесконечно большого числа элементарных струек, для каж-
дой из которых выполняется условие (2.14). Если скорость от
струйки к струйке изменяется, то, интегрируя выражение (2.14)
по живому сечению, получим
f pVT/a—const.
Полагая, что плотность в точках живого сечення изменяется
незначительно и вводя среднюю скорость Еср из условия
V%=— Vda,
С *1
(°)
получим
G=qI/cpct=const. (2.15)
Это и есть запись уравнения неразрывности для потока сжи-
маемой жидкости в канале переменного сечения по длине, кото-
рое показывает, что массовый расход жидкости вдоль потока
неизменен.
37
www.vokb-la.spb.ru - Самолёт своими руками?!
Уравнение (2 15) можно получить и при любом законе изме-
нения плотности по живому сечению в виде: (рГ) рсг= const.
Для несжимаемой жидкости (о—const) условия (2 14) и
(2 15) принимают более простой вид:
1/До—const; (2. 16)
Q = l/cpO=const. (2. 17)
•
Уравнение (2 17) выражает условие постоянства объемного
расхода вдоль потока несжимаемой жидкости. Из выражения
(2.17) для двух сечений струйки можно записать
1/1о1=1/2а2 или 1/1/1/2=с2 °i- (2.18)
Таким образом, для двух сечений струйки скорости Vi и V2 и
площади ортогональных (живых) сечений сц и сг2 находятся в
обратно пропорциональной зависимости, т. е. в любом сечении с
увеличением живого сечения струикн скорость течения во сто, ь-
ко же раз уменьшается и наоборот.
Необходимо отметить, что последний вывод справедлив толь-
ко для несжимаемых жидкостей. В случае сжимаемой жидкости
постоянство объемного расхода может и не иметь места. Прн оп-
ределенных условиях расход жидкости через два сечения струй-
ки может отличаться за счет изменения плотности жидкости
между ними и при этом не нарушается закон сохранения массы.
Это явление объясняется увеличением плотности жидкости меж-
ду двумя сечениями за счет сжимаемости. Отметим, что при
больших (сверхзвуковых) скоростях, как мы увидим дальше,
увеличение площади поперечного сечения струйки сопровожда-
ется увеличением скорости течения и наоборот.
2.4. ТЕОРЕМА КОШИ — ГЕЛЬМГОЛЬЦА О РАЗЛОЖЕНИИ
СКОРОСТИ ЖИДКОГО ЭЛЕМЕНТА
Из курса теоретической механики известно, что движение
любой точки твердого тела в каждый момент времени состоит
из поступательного перемещения вместе с точкой, принятой за
полюс, и вращения вокруг мгновенной оси, проходящей через
этот полюс.
Движение жидкой частицы сложнее, так как при перемещении
юна еще и деформируется. Коши и Гельмгольц установили, что
движение любой точки жидкой частицы можно рассматри-
вать как результат сложения поступательного движения по тра-
ектории вместе с некоторой начальной точкой, вра нательного
движения вокруг оси, проходящей через начальную точку, и де-
формационного движения, которое, в свою очередь, состоит из
линейной деформации и деформации скашивания.
38
www vokb-la.spb.ru - Самолёт своими руками?!
Для доказательства этой теоремы рассмотрим движение эле-
мент aj иого жидкого параллелепипеда с ребрами Дх, Az/, Az
(рис 2 5). Обозначим компоненты вектора скорости V в точке
А(х I/ z) через 14, Vy, Vz и компоненты вектора скорости V(C>
через V (С)- Vy(C); Гг(С). Разложив компоненты скорости-
точки Св ряд Тейлора в окрестности точки А и, опустив члены
ряда содержащие бесконечно малые порядка выше первого, по-
лучим
' ! л ' дх
сг(С)=сг+^дх-|
ф^дгН
ду
<^ДН
ду
дУ z
ду
дУ±
dz
дУу_
dz
dz
Дг;
Д-г;
дг.
(2.19)
Затем к правой части первого уравнения (2 19) прибавим и
вычтем двучлен вида
1 [дУу
2 ( дх
дУг
дх
н сгруппируем члены следующим образом:
1/Л(С)=^+^дх4
дх
1 dvx . дУу\ А
— —- Ч------ Дг/
2 \ ду 1 2 дх
1 /дУх . дУг \ А
— ——4-—— дг
2 \ dz дх /
. 1 [дУх дУу X А .1 [дУх дУг X А
Н---——------— A U А---— ------- Дг
2 \ ду дх / 2 \ dz дх /
(2.20)
Аналогичные соотношения для составляющих Vz и Vy могут
быть получены путем циклической перестановки букв и индек-
сов Введя следующие обозначения для полусумм и полуразно
стей частных производных
d ~-L[^ I fi fi 1 (дУу .дУх\
' 2 \ ду ' dz ) » 2 (дг + дх)1 2 [дх +~д^)’
(2.21)
- 1 /дУх дГг\ 1 1дУу дУх\.
2\ду dz)'
(2. 22)
формулу (2 2 ) и аналогичные ей можно записать в виде:
39
www vokb-la.spb.ru - Самолёт своими руками?!
Л Дх -р $zLy “р^Д-^ -р(<о^Д-^ — wz^y >
ох
&у -4-бхД.гД-бгДх1 -Й^Дх— ш^Дг);
. ду J
ДгЦ-б^ДхЦ-б^Д//] -р^Д#—(й^Дх).
дг
(2. 23)
Гис 2 5 К выводу теоремы Коши
Гельмгольца
Выясним физическим смысл отдельных слагаемых, входящих
в систему уравнений (2.23). Члены dVxfdx, dVyfdy, dVJdz опре-
деляют составляющие скорости относительной деформации рас-
тяжения нли сжатия вдоль осей координат.
Действительно, длина гра-
ни параллелепипеда Дх нап-
равленной вдоль оси Ох, вслед-
ствие разности скоростей на ее
концах за секунду изменится
на величину (б14/дх)Дх_ Раз-
делив это выражение на длину
грани Дх, получим скорость от-
носительной продольной де-
формации вдоль оси ОХ. Ана-
логично происходит деформа-
ция вдоль осей ОУ и OZ.
Члены 0Х, 0^, Oz есть вели-
чины, пропорциональные сос-
тавляющим скорости угловых
деформаций двугранных углов
параллелепипеда Действитель-
но, рассмотрим одну грань параллелепипеда в плоскости УОХ
(рис. 2.6).
Вследствие разности скоростей угловых точек грань АВ пря-
моугольника ABFE за время Д/ повернется на угол а (положе-
ние АВ'), грань АЕ — на угол р (положение АЕ'), точка F пере-
местится в точку F'. Таким образом, прямоугольник ABFE де-
формируется н превратится в параллелограмм АВ F'E', при этом
грани АВ и FE повернутся против часовой стрелки с угловой
скоростью dVJdx, а грани BF и АЕ — по часовой стрелке с уг-
ловой скоростью dVjdy.
Сумма dVxIdy+dVyldx характеризует составляющую скоро-
сти угловой деформации относительно оси 0Z Аналогично
можно рассмотреть две другие грани параллелепипеда и опре-
делить две составляющие скорости угловой деформации парал-
лелепипеда относительно осей ОХ н ОУ.
Полусуммы, обозначенные через 0Х, 0У, 0г в уравнении (2.21),
характеризуют скорость относительного сдвига каждой пары па-
раллельных граней параллелепипеда
40
www vokb-la.spb ru - Самолёт своими руками?!
>
Члены Wx, oiy, «г являются составляющими вектора угловой
скорости вращения со. Допустим, что жидкость вращается вок-
пуг оси ОУ с угловой скоррстью соу, а величины Vv, <ох, соу рав-
ны нулю. В этом случае проекции скоростей &VX и &VZ в точке
Д (рис. 2.7), расположенной на малом расстоянии от осей коор-
динат, определяются равенствами: fTZ—' _Av
откуда <о„=—
у 2
6Vx=0)y62 И 6V2 = —СОудХ,
Ъг Ъх I
В предельном случае, когда dx->0, $z->0,
I (dVx dVz \
oju = f----------.
у 2 [ dz дх }
Аналогично можно получить выражения для сох и сог
Рис 2 6. К определению скорости де-
формации
Рис. 2.7. К определению угловой
скорости вращения
Угловую скорость вращения в векторной форме можно запи-
сать в виде
и =—rot V*—— 2. (2.26)
2 2
Модуль вектора угловой скорости ю = 1
Следует отметить, что поступательное, вращательное движе-
ние и деформация элемента жидкости происходят одновремен-
но независимо друг от друга.
Таким образом, в системе уравнений (2 23) слагаемые К,
Vy, Vz являются компонентами поступательной скорости, суммы
в квадратных скобках компонентами скорости деформации, в
круглых скобках — компонентами вращательной скорости.
* rot V — ротор или вихрь скорости В дальнейшем удвоенный вектор
мгновенной угловой скорости вращения будем называть вихрем
41
www.vokb-la.spb.ru - Самолёт своими руками?!
В векторной форме выражение для скорости жидкого элемен-
та имеет вид
^ = ^4-^ + ^. (2.27)
Теорема Коши—Гельмгольца о разложении жидкого элемен-
та является видоизменением известной теоремы Даламбера для
твердого тела, однако она справедлива лишь для бесконечно
малой жидкой частицы, так как разложение (2.19) имеет место
только для частицы в точке С, находящейся на малом расстоя-
нии (Ах, Аг/, Дг) от точки А.
Частный случай движения, когда частицы не вращаются во-
круг мгновенных осей, называется безвихревым или потенциаль-
ным (смысл последнего названия будет пояснен в гл. 3).
Вопросы для повторения
1. В чем отличие методов исследования жидкости Эйлера и
Лагранжа?
2. Дайте определение линии тока и трубки тока. Чем отлича-
ется линия тока от траектории частиц?
3. Объясните физический смысл уравнения неразрывности.
Как математически записывается это уравнение для случаев
сжимаемой и несжимаемой жидкости, установившегося и неус-
тановившегося движений?
4. Объясните физический смысл теоремы Коши—Гельмголь-
ца о разложении жидкого элемента.
Задачи
1. Возможно ли течение жидкости, заданное проекциями
скорости
Уд———Зг/; I/zl=0; 1/л2 = — Зх; VV2= ^z2—0.
Решение:
^1 з дУщ з и дУу] j dVyi дУz] _ з । з q
дх * dty dx dy dz
т. е. такое течение возможно, так как удовлетворяет уравнению
неразрывности движения несжимаемой жидкости. Во втором
случае
дУХ2 г дУУ2 I дУг2 ___з_з ф о
дх ду ' dz
т. е. уравнение неразрывности не соблюдается, что свидетельст-
вует о нарушении сплошности потока.
2 Найти уравнение линии тока по заданному полю скоростей
Ух ау, Уу—ах, У %—0.
Ответ: линия тока представляет собой семейство гипербол
у21С—>х21С~=1, где С — произвольная постоянная.
42
wwvi.vokb-la.spb.ru - Самолёт своими руками?!
ГЛАВА 3
ОСНОВЫ ТЕОРИИ плоских ПОТЕНЦИАЛЬНЫХ
ТЕЧЕНИЙ
3.1. ПОНЯТИЕ О ПОТЕНЦИАЛЬНОМ ТЕЧЕНИИ
Перейдем к изучению частного случая течения идеальной
жидкости, когда частицы жидкости или газа перемещаются без
вращения. Такой вид течения, называемый безвихревым или по-
тенциальным, имеет большое значение в аэродинамике.
Вращение частиц жидкости может быть вызвано силами внут-
рижидкостного трения, которые в реальных жидкостях заметно
проявляются далеко не везде. Поэтому многие задачи аэроди-
намики решаются при предположении, что поток безвихревой, в
частности, для удобообтекаемых тел с достаточной для практи-
ческих расчетов точностью можно полагать, что вращение частиц
жидкости или таза в потоке отсутствует. Такое предположение
справедливо во всем потоке, за исключением тонкого пристен-
ного пограничного слоя. Вне этого слоя основной поток жидко-
сти, обтекающей тело, является безвихревым Поэтому практи-
ческие расчеты, связанные с распределением давлений по по-
верхности тел в газовом потоке, аэродинамических нагрузок, а
также решения ряда других задач выполняются при предполо-
жении потенциальности потока
Методы исследования безвихревых течений жидкости или га-
за значительно проще, чем вихревых.
В настоящей главе рассмотрим чисто кинематические зако-
номерности безвихревого течения. При безвихревом течении, как .
отмечалось выше, мгновенная угловая скорость вращения час-
тицы жидкости везде равна нулю, т. е. (ох=(оу=(ог=0. В этом
случае из равенства (2 22) получим:
dV2/dy = dVy/dz, dVx]dz—dVzdx, дУу/дх dVx]dy. (3.1)
Из этих равенств следует, что можно подобрать такую функцию
ЧР(Х, У у z), которая связана с составляющими скорости Vx, Vy и
Vz соотношениями
Vy—д^^ду, {/Z—Oy'dz. (3.2)
43
www.vokb-la.spb.ru - Самолёт своими руками?!
Если функция, определяемая соотношениями (3.2), существу-
ет, то равенства (3.1) обращаются в тождества. В теории диффе-
ренциальных уравнений доказывается, что равенства (3.1) не
только необходимы, ио и достаточны для существования функ-
ции <р. Таким образом, при безвихревом течении жидкости мож-
но подобрать некоторую скалярную функцию от координат <р=
— <Р(Х> У, которая дает возможность определить составляю-
щие скорости частиц жидкости вдоль координатных осей по фор-
мулам (3.2). Рассмотрим теперь произвольное направление, за-
данное ортом е (элемент дуги вдоль него ds). Как известно, про-
изводная функции <р по направлению е определяется соотноше-
нием:
_Нт +eAs) —у(7) /Д'? Дх Ду Ду । Д»Р =
ds Дх Ду-^ОуАх As Ay As A^ As
— 1Дсоз(с, x)-|- l/ycos(e, у) -f- V^cosfe, z) = 7cos(7, e) =
(3.3)
где через Vs обозначена проекция скорости на направление ор-
та е. В частности, в случае цилиндрических координат (х, г, 0)
имеем ds^~dx\ ds^~dr\ ds^=rdQ и соответственно
v,=Al: (3.4
дх dr ds г дв
где Vr— проекция скорости на радиус-вектор г
Функция <р, вполне характеризующая даииый безвихревой
поток, называется потенциалом скорости, а само безвихревое
течение — потенциальным.
Таким образом, всякое течение жидкости, происходящее без
вращения частиц, определяется своим потенциалом скоростей
и, наоборот, если существует потенциал скоростей, то течение
является безвихревым. Наличие потенциала скорости дает воз-
можность построить сравнительно простую теорию безвихревых
течений.
Потенциальные течеиия наблюдаются в потоках как сжима-
емой, так и несжимаемой жидкости В настоящей главе рассмот-
рены свойства потенциальных течений без учета эффекта сжи-
маемости. Это сделаио, во-первых, потому что такой подход поз-
воляет более просто познакомиться с основными свойствами по-
тенциальных течений, во вторых, в гл. 5 будет показано, что при
числах М<0,5 влиянием сжимаемости можно принебречь.
3 2 СВОЙСТВА ПОТЕНЦИАЛА СКОРОСТИ
Для потенциального движения жидкости уравнение нераз-
рывности можно записать в форме, ие содержащей составляю-
www.vokb-la.spb.ru - Самолёт своими руками?!
щих скорости Vx, Vy и Vz. Действительно, если в уравнение не-
разрывности несжимаемой жидкости (2.12)
dVjdx 4- 0Vy ду 4- dVz]dz — О
подставить зиачения составляющих скорости Тх, Vv и Vz сог-
ласно формулам (3.2), то оно принимает вид
^>/дла4-^?/д^4-^р/д^=0. (3.5)
Это уравнение называется уравнением Лапласа.
Функции, удовлетворяющие уравнению Лапласа, носят наз-
вание гармонических функций.
Таким образом, можно сделать следующий вывод: всякому
безвихревому движению жидкости отвечает некоторая гармони-
ческая функция и, наоборот, любая гармоническая функция оп-
ределяет некоторый безвихревой поток несжимаемой жидкости.
Эту единственную неизвестную функцию, определяющую полно
стыо кинематику безвихревого потока, можно найти из решения
уравнения (3.5). Это уравнение является линейным дифферен-
циальным уравнением в частных производных 2-го порядка и
имеет бесчисленное множество решений. Очевидно, для каждого
конкретного случая необходимы дополнительные условия, напри-
мер, граничные условия при обтекании тела потоком жидкости.
Весьма важное значение при изучении безвихревого движе-
ния жидкости имеют так называемые эквипотенциальные поверх-
ности, во всех точках которых величина функции <р(х, г/, г) сох-
раняется постоянной.
Пусть имеются несколько потенциальных потоков жидкости
с потенциалами скоростей <р1э срг,..., <рп. Тогда функция ср —
=<Р1-г<Р2+. • • <рп в силу линейности уравнения Лапласа будет
являться потенциалом скоростей некоторого «результирующего»
потока жидкости, составляющие скорости которого вдоль коор-
динатных осей определяются выражениями:
vx=ду/дх=д^/дх4-д^2'дх +.. -4-д^п'дх = 14 v"v-4 • • • 4“v w
Vy=^!dy=d^ ду-\-д^2]ду-\~.. .-j-d^Jdy^ Hw4- Vy2-i~..
v г==dyx]dz4-d^dz4-.4-dyjdz = У У+ * • + Vzn,
Из этих равенств видно, что в потоке, представляемом функ-
цией <р, составляющие скорости вдоль координатных осей равны
алгебраическим суммам составляющих скоростей вдоль этих
осей в потоках, представляемых функциями дд, <рг,. . <рп- Таким
образом, в результирующем потенциальном потоке вектор ско-
рости частиц равен геометрической сумме скоростей составляю-
щих потоков.
Этим свойством потенциальных потоков широко пользуются
при решении многих задач аэродинамики. Весьма сложные по-
45
www vokb-la.spb ru - Самолёт своими руками?!
токи жидкости получают путем суммирования более простых
потоков и, наоборот, во многих задачах прибегают к разложе-
нию сложных потоков на составляющие элементар! ые потоки.
3.3. ПЛОСКОПАРАЛЛЕЛЬНОЕ ТЕЧЕНИЕ ЖИДКОСТИ
ФУНКЦИЯ ТОКА
Плоскопараллельным течением жидкости будем называть та-
кое течение, когда частицы жидкости, расположенные на пря-
мой, перпендикулярной к заданной плоскости, движется по оди-
наковым траекториям и с одинаковыми скоростями (рис. 3.1).
В этом случае достаточно знать движение в одной плоскости,
которою обычно называют ос-
новной плоскостью течения.
В случае плоского движе-
ния задача изучения потока
существенно упрощается.
Плоское движение встречается
во многих прикладных задачах
и наиболее изучено теоретиче-
Рис 3 1 Плоское течение
ски.
Если при изучении плоского
движения ось 0Z направим
перпендикулярно основной
плоскости, тогда дЕ /Дг = 0 и
уравнение неразрывности
(2 12) примет вид
&V Х]дх dV у) ду=0.
Нетрудно видеть, что это уравнение удовлетворяется при ус-
ловии существования такой функции ф — ф(х, у), что
dtydy = ]/х, — dfy'dx = Vy.
(3.6)
В этом можно убедиться, подставив в уравнение неразрыв-
ности вместо Vx и Vy их значения (3 6) Можно показать, что
указанное условие является не только достаточным, но и необ-
ходимым.
Таким образом, каждому плоскому течению жидкости соот-
ветствует некоторая функция ф, связанная с компонентами ско-
рости частиц соотношениями (3 6)
Можно показать, что эта ф нкция сохраняет постоянное зна-
чение вдоль линии тока. Действительно, подставив в уравнение
ли ии тока (2 1), имеющее вид dxjVx—dy/Vy или Vydx—Vxdy=
= 0, вместо скоростей и Vy их значения (3 6), получим
(дф/дх) dx-]~(dty/dy)dy—0.
46
www.vokb-la.spb ru - Самолёт своими руками?!
Так как левая часть этого уравнения является полным диф-
ференциалом функции ф, то вдоль линии тока б/ф=О нлн ф=
=const
Благодаря этому свойству функцию ф называют функцией
тока. Такая функция имеет определенный физический смысл.
Рассмотрим цилиндрическую поверхность единичной высоты,
опирающуюся на некоторый контур, соединяющий точки А н В
(рис. 3.2). Объемный расход жидкости через элемент поверхно-
сти, имеющий в основании элемент контура dl, равен
dQ = Vndl — [IZyCospc, /1)+ cos(z2, y]\dl,
где
cospc, ri)~dy!dl, —cos(n, y)=dx]dl.
Знак «минус» у cos (л, у) взят потому, что при перемещении
по отрезку dl (от точки А к точке В) dx<Z®
Если скорости Vx и Vy заменить нх выражениями (3.6) через
функцию тока, то получим для
dQ:
dQ=f^ t!JL+®LaJL\dl=^,
|_й(/ dl ' дх dl J
откуда расход через кривую АВ
найдем в виде
в в
Qab = J dQ ~=^ д?ф==фв~фл,
А А
т. е. объемный расход несжи-
маемой жидкости в плоскопа-
раллельном потоке между
точками А н В будет равен
разности значений функции
тока в конечных его точках н
Рис. 3 2 К пояснению физического
смысла функции тока
не зависит от формы кривой
АВ. Очевидно, если точки А и В совпадают, то прн однозначной
функции тока расход Q будет равен нулю. Если кривая АВ
является отрезком линии тока, то расход через нее также равен
нулю, так как вдоль лннин тока функция тока равна постоянной
величине. Отсюда следует, что количество жидкости, протекаю-
щее в единицу времени между двумя произвольными линиями
тока, есть величина постоянная, численно равная разности зна-
чений констант, соответствующих этим линиям тока.
Размерность функции тока ф—м2/с. При сравнении размер-
ностей левой н правой частей последнего равенства следует
иметь в виду опущенный нами в правой части множитель — еди-
ницу длины.
47
www vokb-la.spb.ru - Самолёт своими руками?!
Отметим, что понятие функции тока имеет место не только
для плоских потоков, но и для осесимметричных потоков. При-
мером осесимметричного потока может служить поток, образую-
щийся при симметричном обтекании тела вращения.
Отметим также, что функция тока существует в плоских по-
токах независимо от того, являются они вихревыми или безвих-
ревыми. Это следует из того, что при определении функции тока
мы исходили только из предположения о непрерывности движе-
ния в сплошной среде.
3 4. ПЛОСКИЕ ПОТЕНЦИАЛЬНЫЕ ТЕЧЕНИЯ ЖИДКОСТИ
Мы установили, что для потенциального плоского течения не-
сжимаемой жидкости характерны две функции: потенциал скоро-
сти <р(х, у) и функция тока ф(х, у). Между этими функциями
можно устаиовить связь, если воспользоваться выражениями
для составляющих скоростей (3 2) и (3 6). Величина скорости
должна быть одна и та же, независимо от того, через какую
функцию она выражается.
Приравнивая правые части соответствующих равенств, полу-
чим
у) __ду(х, у) ty(x,y) д?(х, у) 3 у.
ду дх ’ дх ду
Полученные уравнения иосят названия условий Коши—Ри-
мана.
Для плоского безвихревого движения функция тока н потен-
циал скорости удовлетворяют уравнению Лапласа и, следова-
тельно, являются гармоническими функциями. Действительно,
взяв вторые производные от левых и правых частей соотношений
Коши—Римана, получим
у) dfyfx, у) д2$(х, у) = _ д2у(х, у) .
ду2 дхду ’ дх2 ду дх ’
д2ф (х, у)д2у(х, у)(х, у)<32у(х, у)
ду дх дх2 дх ду ду2
Сложим этн уравнения и заметим, что значение производной
не зависит от порядка дифференцирования по координатам х и
у, в котором она взята.
В результате получим уравнения
Д д2ф(л:, у) q д'У(лз у) д2ч>(х, У)=q
дх2 ду2 ’ дх2 ду2 ’
из которых следует, что функция тока может служить потенци-
алом скорости некоторого другого течения и наоборот.
Чтобы выяснить, какой поток представляет функция тока,
рассматриваемая в качестве потенциала скорости, введем поня-
тие так называемой гидродинамической сетки.
48
www.vokb-la.spb.ru - Самолёт своими руками91
Полный дифференциал потенциала скорости, равный нулю
вдоль эквипотенциальной линии, можно записать в виде
dy = O.
ду
dv=XX
дх
Тогда тангенсы углов а и аь образуемые с осью абсцисс со-
ответственно касательной к эквипотенциальным линиям и каса-
тельной к линии тока, запишутся
, Vu ду/ду , dy д^/дх
tga = ^— Y ; tgal=—=---------—.
Vx ду/дх ь 1 dx
Перемножив эти два выражения, получим
д'? ду
tga«tgol=l, (3.8)
что, как известно, является признаком взаимной перпендикуляр-
ности касательных. Таким образом, семейство линий тока
ip(x, у} — const и семейство линий равного потенциала <р(х, у) =
= const образуют ортогональную сетку.
Такая сетка, образованная двумя взаимоортогональными се-
мействами линий <р = const и ф = const, называется гидродинами-
ческой сеткой.
Если функцию тока ф рассматривать в качестве потенциала
скоростей, то в соответствии с условиями Коши Римана потен-
циал скорости исходного потока станет функцией тока, т е. эк-
випотенциальные линии исходного потока станут линиями тока
в новом потоке
Векторы скоростей частиц в новом потоке можно получить,
повернув I а л/2 в одну сторону векторы скоростей частиц исход-
ного потока
Таким образом, функции (риф можно менять местами. Два
потока, которые описываются этими функциями, называются
сопряженными.
Перейдем к рассмотрению отдельиь х примеров потенциаль-
ных течении жидкости
3.5. ОДНОРОДНЫЙ ПОСТУПАТЕЛЬНЫЙ ПОТОК
Рассмотрим поток жидкости, в котором все частицы движут-
ся параллельно оси ОХ с постоянной скоростью Vo- В этом слу-
ае составляющие скорости имеют следующие значения' Vx=
= V0=const; Vv=0; Vz=0,
Поэтому иа основании равенства (3.2) имеем
о=д^!дх=const или IZO --dxddx,
откуда следует
d^^V^dx или c? = [/ox-j-C. (3.9)
49
www.vokb-la.spb.ru - Самолёт своими руками?!
Последнее уравнение представляет собой уравнение семей-
ства эквипотенциальных плоскостей, перпендикулярных к оси
ОХ.
Для плоского течения полный дифференциал функции тока
dty=(dtydx} dx -р (дф/cty) dy = — Vydx Vxdy*
Для рассматриваемого одномерного потока получим уравне-
ние
d^—Vbdy,
(3. 10)
интегрирование которого позволяет полечить выражение для
функции тока
Ф=И.у + С. (3. 11)
Произвольные постоянные интегрирования С в выражениях для
функции тока чр и потенциала скорости ср можно и опустить, так
как прн решении конкретных задач используется только раз-
ность значений каждой из этих функций в двух выбранных точ-
ках.
Уравнение (3.11) представляет собой на плоскости ХОУ се-
мейство прямых, параллельных оси ОХ.
3.6. источник и сток
Источником называется поток, в котором жидкость вытекает
из некоторого центра с одинаковой по всем направлениям ско-
ростью.
Рис 3.3. Плоские источник (а) и сток (б)
Если центром является точка, источник называется простран-
ственным. Если источник — прямая линия, из каждой точки ко-
торой жидкость вытекает непрерывно и одинаково по направле-
ниям, перпендикулярным к ней, то такой источник называется
плоским (рис. 3.3, а)
Стоком называется отрицательный источник. В этом случае
жидкость притекает к стоку, как пока ано на рис 3 3, б.
50
www .vokb-Ia.spb.ru - Самолёт своими руками ".
Такие течения приближенно соответствуют реальному исте-
чению жидкости из физического источника илн притеканию к
физическому источнику с постоянным расходом. Следует отме-
тить, что прн математическом описании таких течений в самих
источниках и стоках должна иметь место бесконечно большая
скорость (особые точки течения), которая физически не может
быть реализована. Поэтому при решении физических задач при-
ходится тем или иным способом исключать особые точки из об-
ласти, занятой жидкостью. Рассмотрим в качестве примера пло-
ский источник. Пусть секундный расход жидкости, вытекающей
из источника единичной длины, будет Q. Возьмем далее на пло-
скости окружность радиуса г с центром, расположенным в ис-
точнике. Скорость, направленная по радиусу, на расстоянии г
от источника
И —Vr=Q/2jtr. (3. 12)
Выражая скорость Vr через потенциал скорости согласно
(3 4), будем иметь
Vr—dytdr—dyjdr. (3. 13)
Сравнивая, наконец, выражения (3.12) и (3.13), получим
уравнение
d^jdr _ Q/2nr,
интегрируя которое, найдем потенциал скорости
<?(*, */)=^-1пг, (3. 14)
где г = У^^-у2.
Таким о( разом, мы получнлн выражение для потенциала ско-
рости плоского источника (см рис. 3.3, а).
Полный дифференциал функции тока плоского источника
^=(^/<?л) dx-^ (дуду) dy.
Используя же условия Коши—Римана (3 7), запишем полный
дифференциал в виде
(3 |5)
дх ду лг г2 v '
Интегрируя выражение (3 15), получим функцию тока источ-
НИКИ
Ж j)=-2-arctg-2-+ С. (3. 16)
ЯГ X ' '
51
www vokb-la.spb ru - Самолёт своими руками?!
В полярных координатах с учетом равенства tg0 = ///x вы-
ражение для функции тока источника принимает вид
Ф(*. в, (3.17)
/Л
где 0 — полярный угол (см. рис. 3 3). Очевидно, что в данном
случае линии тока — радиальные.
Для плоского стока получим выражения, аналогичные (3.14)
и (3.17), только со знаком минус:
(3'|8)
= (3-19)
Точка г~0 для функции потенциала скорости является осо-
бой, поэтому прн решении практических задач ее исключают из
области течения, заключая в сферу малого радиуса rG~а для
пространственного источника или в цилиндр — для плоского.
Обычно этот прием не противоречит реальным условиям тече-
ния жидкости.
3.7. ПАРА ИСТОЧНИК — СТОК
Рассмотрим пару источник — сток, расположенную на оси ОХ
симметрично относительно оси ОУ и на расстоянии ±а от иее
(рис. 3 4). Возьмем произвольную точку т(х, у) на плоскости
ХОУ. Расстояния от точ-
Рис 3.4 Пара источник — сток
ки т(х, //) до источника
и стока соответственно
будут:
г1=Г^+а)2+Л
г2—]/(х — а)г+«/2.
Потенциал суммарно-
го потока получим, сло-
жив потенциалы стока и
источника одинаковой ин-
тенсивности, определен-
ные по формулам (3 14)
и (3 18):
?(*, Z/)=-^-(inr1 —lnr2)
или <?(*, #) = -^-1п—.
2л Г2
(3.20)
52
www vokb-la.spb ru - Самолёт своими руками?!
Суммарную функцию тока в этом случае на основании фор-
мул (3 17) и (319) можно записать так:
zJI
(3.21)
Рис. 3 5 Сложение источника и стока при
равных расходах
Если источник и сток имеют одинаковые расходы, то все ли-
нии тока, идущие от источника, замкнутся в стоке (рис. 3.5).
3.8. ДИПОЛЬ
Помещенные на бесконечно малом расстоянии дх Друг от
друга, источник и сток с секундными расходами ±Q, когда рас-
стояние дх в пределе стремится к нулю, а расход — к бесконеч-
ности, но произведение Q6x=Af остается постоянной величиной,
называют диполем с моментом М
Для нахождения потенциала диполя в соответствии с форму-
лой (3 20) найдем при указанных выше условиях предел функ-
ции
Q
Cj — г2
Г2
Q 1
Ф— —— 1п
2л Г2 2л
Из рисунка 3 6 следует, что и—r2=dxcos0. Подставив это
значение в формулу потенциала и полагая г2=г, получим
Q 1 / , । Sx cos 6 \
Определим предел правой части формулы при йх—>0
Qdx—>-Af = const:
53
wwvi vokb-la.spb ru - Самолёт своими руками?!
lim 1
2л
3-r COS 6 \ __ 1. J QBx cos 6 M COS 0
r / 2л г 2лг
Учитывая, что cos0=x/r, найдем выражение для потенциала
скорости диполя
Мх М х
О ------ ИЛИ ср =----------
2лг2 Т 2л X2 + '
3. 22)
Из этой формулы следует, что эквипотенциальные линии ди-
поля являются семейством окружностей, касающихся оси ОУ и
имеющих центры на оси ОХ (пунктир на рис. 3 7),
Рис 3 6. Диполь Рис, 3.7 Линии тока и эквипотен-
циальные ЛИНИИ ДИПОЛЯ
Аналогично из уравнения (3 21) определим функцию тока
ф=Нт —— (6 — ^)= 11т
2л
56 j___ М sin 6
2л Вх J 2лг
Учитывая, что sin
получим функцию тока диполя:
Af у
. Af и ,
ф—------------— ИЛИ Ф= —
2л г2 2л х2 + 1/2
(3.23)
Из формулы (3 22) следует, что эквипотенциальные линии
диполя являются семейством окружностей, касающихся оси О¥
и имеющих центры на оси ОУ (см рис. 3.7).
39. НАЛОЖЕНИЕ ОДНОРОДНОГО ПОТОКА НА ДИПОЛЬ
Рассмотрим диполь в однородном потоке (рис. 3.8). Потен-
циал потока получим, сложив потенциал поступательного пото-
ка (3.9) с потенциалом диполя (3.22):
М х
2л г2
(3.24)
54
www.vokb-la.spb.ru - Самолёт своими руками?!
Аналогично получим функцию тока, сложив выражения
(3 11) н (3 23)!
(3. 25)
Приравнивая функцию тока произвольной постоянной величи-
не, получим уравнение для семейства линий тока:
У.У
М у
2л г2
При С~0 получим уравнение для нулевой линнн тока:
Vo!/ 1 —
откуда следует, что у—0 или
Из второго условия имеем
2 М
rL —----- или
2лК0
Это уравнение — уравнение
координат и с радиусом
м >
2яГ0г2 ?
j М
2лУог2
м
2nV0
окружности с центром в
начале
го=
Л1
2лК0
Значит, линия тока состоит из прямой, совпадающей с осью
ОХ, и окружности радиуса г0 с центром в начале координат. По-
ток разделяется на две облаети -
внешнюю и внутреннюю, разде-
ленные непроницаемой для жид-
кости цилиндрической поверхно-
стью. Поверхность непроницаема
для жидкости, поскольку ее попе-
речное сечение есть линия тока, а
скорость течения по определению
всегда касательна к линии тока
Это свойство позволяет рассмат-
ривать течение во внешней н
внутренней областях раздельно
В частности, течение во внешней
области не изменится, если заме-
нить внутреннюю область твер-
дым телом, имеющим форм1 кру-
Рис 3 8 К определению потен-
циала скорости при наложении
поступательного потока на ди-
поль
гового цилиндра. Вообще любую
область, находящуюся внутри замкнутой линии тока, можно за-
менить твердым телом соответствующей формы. Прн такой за-
мене особая точка автоматически исключается из области, за-
нятой жидкостью.
55
www.vokb-la.spb ru - Самолёт своими руками?!
Таким образом, прн наложении поступательного потока на
диполь получим обтекание кругового цилиндра (рис. 3.9). Вели-
чина радиуса г0 этого цилиндра зависит от М и Vo. Прн извест-
ных значениях радиуса г0 н скорости невозмущенного потока из
(3.26) можно определить момент диполя М = 2лУоГо2. Подстав-
Рис 3 9 Наложение поступательного потока
на диполь (обтекание кругового цилиндра)
ляя эту величину в формулы для потенциала скорости (3.24) и
функции тока (3.25), получим
(^2 \ / 2 \
l+4)=v'«( >+4 rcose; (3-27)
(2 ' / 2 \
1--v) = V„( l-^-)rsinO, (3.28)
Г2 / \ Г2 / 7
где
Подставляя в выражение для проекций составляющих ско-
ростей в полярных координатах (3 4) значение потенциала ско-
рости (3 27) и дифференцируя по координатам г и 0, получим
/ г2 \
Vr-lG( 1 —-AlcosS; (3.29
(2 \
i+—)Sine. (3.30)
/ 1
На поверхности цилиндра радиуса г=г0 будем иметь
Уг=0, I/S=-2I/Osin в. (3.31)
Следовательно, скорость частицы жидкости на поверхности
цилиндра направлена по касательной к окружности и равна
2Vosin 0 В точках Л и В разветвления потока около кругового
56
www.vokbla.spb.ru - Самолёт своими руками?!
цилиндра (см. рис. 3 9) скорости потока равны нулю. Точки А и
В называются критическими точками.
Можно решить и обратную задачу, более важную для прак-
тики, когда вместо наложения известных потоков и получения
результирующего потока около тела некоторой формы можно
подобрать потоки, наложение которых дало бы нам поток около
тела заданной формы
Подобный метод наложения элементарных потоков, основан-
ный на линейности уравнения Лапласа, в настоящее время ши-
роко используется в прикладной аэродинамике; для получения
однозначного решения обычно используется дополнительное ус-
ловие Жуковского — Чаплыгина, которое будет рассмотрено
дальше.
Вопросы для повторения
1 Объясните физические свойства потенциального течения.
2 . Что такое функция тока и потенциал скорости? Объясните
их основные свойства.
3 Дайте определение эквипотенциальных поверхностей и опи-
шите их свойства.
4 . Что представляет собой гидродинамическая сетка?
5 Что такое однородный поток, источник, сток и диполь?
Напишите формулы для потенциалов скорости указанных тече-
ний
6 . Объясните физический смысл «наложения» однородного по-
тока на диполь.
Задачи
1. Плоский установившийся поток жидкости задан проекци-
ями скоростей на оси координат:
где r = +
Найти потенциал скорости <р и уравнения эквипотенциальных
линий и линий тока
Ответ: 1 С*2-!-//2)3 эквипотенциальные линии -
о •
семейство окружностей х2+у2—Сц линии тока -— семейство пря-
мых у-С2х.
www vokb-la.spb.ru - Самолёт своими руками?!
ГЛАВА 4
ОСНОВЫ ТЕОРИИ ВИХРЕВОГО ТЕЧЕНИЯ
4.1. ВИХРЕВОЕ ТЕЧЕНИЕ ЖИДКОСТИ.
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
Теории вихревых течений жидкости отводится значительная
роль в аэродинамике вообще и при определении силового взаи-
модействия жидкости и твердого тела в частности.
Вихревые движения могут быть обнаружены, например, при
обтекании воздухом крыла самолета и водой быков моста, при
движении судов в воде и т. п, Часть потока вблизи поверхности
тела всегда является завихренной. Циклоны, антициклоны и
смерчи, рассматриваемые с аэродинамической точки зрения, то-
же представляют собой концентрированные вихревые образова-
ния в атмосфере.
На образование вихрей вблизи движущегося тела и на их
поддержание затрачивается некоторая энергия. Источником
этой энергии является энергия движущегося тела или силовой
установки летательного аппарата, который должен преодоле-
вать сопротивление обтекающего его газа (в частности, возду-
ха). Сопротивление, вызываемое образованием вихрей, называ-
ется вихревым сопротивлением
Согласно теореме Коши—Гельмгольца движение частицы
жидкости можно разложить на три части- поступательное движе-
ние, вращение и деформацию. Вихрь вектор мгновенной угло-
вой скорости—определяет вращение частицы жидкости вокруг
некоторой мгновенной оси вращения.
Если завихрена вся рассматриваемая область жидкости, мож-
но говорить о поле вихря: в каждой точке пространства может
быть построен вектор, изображающим угловую скорость враще-
ния частицы жидкости, находящейся в этой точке в данный мо-
мент времени.
Может оказаться, что только в определенных локализован-
ных областях потока течение вихревое, в то время ка*к в осталь-
ной части потока течение потенциально.
58
www vokb-la.spb ru - Самолёт своими руками?!
Зная распределение скоростей в произвольном вихревом те-
чении жидкости и определив производные скоростей, мы можем
иайти угловые скорости вращения в любой точке потока.
Из теоретической механики известно, что при движении твер-
дого тела вращательная составляющая скорости всех его точек
определяется одним и тем же вектором мгновенной угловой ско-
рости В отличие от твердого тела в жидкости
частицы могут иметь различные мгновенные
угловые скорости, поэтому в общем случае
нельзя говорить о вращении конечной массы
жидкости как единого целого — говорят о
вращении элементарной частицы жидкости
или о мгновенной угловой скорости в данной
точке потока.
Подобно тому, как линии тока дают неко-
торое представление о поле скоростей, вихре-
вые линии дают аналогичное представление о
поле вихрей. Понятие вихревой линии можно
ввести по аналогии с линией тока Отличие
даже соседние
Рис 4.1 Вихревая
линия
заключается в том, что линии тока строятся
по векторам линейной скорости V, а вихревые
линии — по векторам угловой скорости со
'—>
(или по векторам вихря £2).
Следует отметить, что в любом потоке можно мысленно про-
вести линии тока, в то время как вихревую линию можно прове-
сти не всегда и не везде
Например, вихревую линию нельзя провести в потенциаль-
ном потоке.
Вихревой линией называется такая линия в потоке жидкости,
в каждой точке которой (1, 2, 3 .,в данное мгновение вектор
угловой скорости to (или вектор вихря скорости £2) совпадает с
касательной к ней (рис 4 1). С течением времени вихревые ли-
нии могут изменять свою форму и положение в пространстве
Вихревые линии в общем случае не совпадают с линиями тока
и могут пересекаться с ними. Так как вектор угловой скорости в
каждой точке направлен по мгновенной оси вращения частицы
жидкости, то вихревая линия может быть представлена как во-
ображаемая криволинейная ось вращения группы частиц, враща-
ющихся вокруг нее в данный момент времени. Таким образом,
линия тока является огибающей векторов скорости V, а вихревая
линия — огибающей векторов угловой скорости со. Дифференци-
альные уравнения вихревых линий по аналогии с дифференци-
альными уравнениями линии тока (2 1), очевидно, имеют вид
dx^x=dyi<£>y —dz]&z.
(4. 1)
59
www.vokb-la.spb.ru - Самолёт своими руками?!
После подстановки в эти уравнения значений составляющих
угловой скорости согласно (2 22) получим систему независимых
дифференциальных уравнений, интегрирование которых дает
уравнения вихревых линий в конечной форме.
Заметим, что подобно линиям тока, при установившемся дви-
жении вихревые линии со временем не изменяются Если вихре-
вые линии и линии тока совпадают, то векторы линейной и угло-
Рис 4 2 Вихревая трубка
4 2) Через точку 1 проведем
1—2, а на ней вокруг точки I
заключающий в себе площадь
вой скоростей вихря парал-
лельны Такое движение жид-
кости называется винтовым.
Уравнения винтовых линий на-
ходятся из условия параллель-
ности векторов линейной и уг-
ловой скорости:
Иж/«>ж=И^=Иг/«>г. (4.2)
Рассмотрим какую-либо
вихревую линию 1—2 (рис.
плоскость, нормальную линии
- небольшой замкнутый контур,
Совокупность вихревых линий, проходящих через каждую
точку этого замкнутого бесконечно малого контура или контура
конечных размеров, образует поверхность, называемую вихревой
трубкой.
Часть движущейся жидкости, ограниченная вихревой труб-
кой, называется вихревой нитью или вихревым шнуром Вне
вихревой трубки движение жидкости может быть потенциаль-
ным.
4.2. НАПРЯЖЕНИЕ ВИХРЕВОГО ШНУРА
ТЕОРЕМА ГЕЛЬМГОЛЬЦА
Напряжением илн интенсивностью вихревой нити называют
произведение величины внхря скорости в какой-либо точке вих-
ревой нити на площадь поперечного (нормального к вектору
вихря) сечения нити
= (4.3)
Напряжение илн интенсивность вихревой нити может слу-
жить мерой завихрения жидкости, заключенной внутри вихревой
нити. Иногда интенсивность вихревой нити выражают через уг-
ловую скорость в виде dl~2^aon. Интенсивность вихревого
шнура определяется интегралом
/ = j 2с/оп.
(4 4)
* Поскольку имеются расхождения в определении этих понятий, го в
дальнейшем будем называть вихревой нитью вихрь с бесконечно малыми
поперечными размерами, а вихревым шнуром — вихрь конечной толщины
60
www vokb-la.spb ru - Самолёт своими руками?!
Величины Q ио изменяются вдоль данного вихревого шнура,
однако, интенсивность вихревого шнура I на всем его протя-
жении остается постоянной, т. е. во всех его сечениях одинако-
ва. В этом заключается смысл теоремы Гельмгольца. Эта теоре-
ма является чисто кинематической и справедлива для любой
сплошной среды независимо от ее физических свойств прн усло-
вии, что поле скоростей является непрерывной функцией коор-
динат. Докажем эту теорему методом Жуковского Записав част-
ные производные по х, у и z для Q =
— 2со, исходя из уравнений (2 22)
д^х 1 d2Vy \.
дх \ дудх дгдх /
д£у __ J < д^Ух d2Vz у
ду , дгду дхду )
dQz ( д2Уу д2Ух \
дг \ дхдг дудг У
и, сложив их, получим уравнение
dQx 1 dQy । dQz g 45)
Рис 4 3 Возможные формы
вихрей
z
Ьх ' ду 1 dz
аналогичное уравнению неразрывности (2 12), если представить,
что несжимаемая жидкость внутри вихревой трубки движется
со скоростью Q Таким образом, уравнение (4.5) можно считать
уравнением неразрывности для вектора Q, для которого должны
оставаться справедливыми все соотношения, вытекающие из
уравнения (2 12) для вектора V. В частности, аналогично (2 17)
можно записать
Qan= const (4 6)
Из этого равенства следует, что внутри жидкости при непре-
рывности поля скоростей вихри не могут обрываться. Действи-
тельно, предпо. сжим, что у вихревого шнура, напряжение кото-
рого / — в некоторой его точке площадь поперечного сече-
ния ап стала равной нулю, но прн О/,-^0 по теореме Гельмголь-
ца (уравнение 4.6) получим Q-*-oo, что физически невозможно.
Таким образом вихрь никогда не обрывается в жидкости, он мо
жет лишь опираться на ее твердые границы на свободную по-
верхность нли сворачиваться в кольцо (рнс. 4 3).
4.3. ЦИРКУЛЯЦИЯ СКОРОСТИ И ЕЕ СВЯЗЬ С ПОТЕНЦИАЛОМ
СКОРОСТЕЙ
Как следует нз теоремы Гельмгольца, характерной величи-
ной для любой вихревой трубки является произведение Qun, ко
61
www.vokb-la.spb.ru - Самолёт своими руками?!
Рис. 4.4. к определению циркуля-
ции скорости
торое и определяет интенсивность вихря. Интенсивность вихря
тесно связана с понятием циркуляции скорости по замкнутому
контуру. Величина циркуляции, как увидим впоследствии, опре-
деляет очень важные свойства
потока, обтекающего крыло.
Формальное определение цир-
куляции скорости сводится к сле-
дующему. Проведем мысленно
внутри движущейся жидкости не-
который неподвижный замкнутый
контур. В общем случае этот
контур может охватывать твер-
дое тело, находящееся в потоке
(рис. 4.4)
Пусть V — скорость в некото-
рой точке С контура. Рассмотрим
элементарный вектор ds, по вели-
чине равный длине дуги контура
ds и направленный вдоль поло-
жительного направления каса-
тельной к контуру ds—tds, при
этом за положительное направле-
ние касательной будем принимать направление, соответствую-
щее такому движению вдоль контура, при котором ограничивае-
мая им область остается слева. Интеграл от скалярного про-
изведения векторов V и ds, взятый по незамкнутому участку АВ
контура
в в
[ (VWs) = f Vsds,
А А
4 л tz JWh
иосит название линейного интеграла скорости, а взятый по замк-
нутому контуру L — циркуляции скорости *:
Г= С (l/flfs)— { Vsds.
(i) (Ъ
(4.7)
С математической точки зрения эта формула идентична из-
вестной из механики формуле для определения работы, произ-
веденной силой F на пути $, однако физическое их значение раз-
лично. Интеграл (4.7) является криволинейным интегралом.
Выражение для циркуляции скорости по замкнутому конту-
ру можно записать в иной форме, если скалярное произведение
* Часто циркуляцией скорости по некоторому контуру называют интег-
рал от скалярного произведения векторов V и ds, взятый по всему контуру
или по его части.
62
wvnv.vokb-la.spb.ru - Самолёт своими руками?!
векторов V и ds выразить через проекции этих векторов на пря-
моугольные координатные оси:
Г = (Vxdx + Vydy -J- Vzdz\ (4,8)
(i)
В частности, для плоского потока (К=0) или плоского кон
тура (c/z=O) получим
(4- 9)
(А)
На основании этих формул можно доказать, что циркуляция
скорости по замкнутому контуру при безвихревом движении,
описываемом однозначным потенциалом скоростей, равна нулю.
Действительно, подставив значения lzx, Vy и К в соответст-
вии с равенством (3.2) в выражение (4.8), получим
в
г=Ф(17‘/х+^^+^’‘/г)=?1?=1рв“1рд’ (4Л0)
(Z) а
где <рл и фв — значения потенциала скорости в начале и в кон-
це пути интегрирования.
Ясно, что если в безвихревом потоке контур замкнутый и по-
тенциал скорости <р(х, у, z) однозначен в каждой точке потока,
то циркуляция скорости по замкнутому контуру равна нулю
А
Г=х у^(р==<рл_ 94=0, (4.Н)
А
следовательно, если циркуляция скорости по замкнутому кон-
туру не равна нулю, то течение вихревое. Исключение может
составлять только частный случай безвихревого течения с неод-
нозначным потенциалом скоростей.
4.4. СВЯЗЬ ЭЛЕМЕНТАРНОЙ ЦИРКУЛЯЦИИ С НАПРЯЖЕНИЕМ ВИХРЯ-
ТЕОРЕМА СТОКСА
Рассмотрим элементарный контур Oabc (рис. 4.5) в виде
плоского прямоугольника, выбрав оси координат таким обра-
зом, чтобы ось 0Z была направлена по нормали к плоскости
контура в ту сторону, смотря с которой положительный обход
контура представлялся бы направленным против часовой стрел-
ки, а оси ОХ и ОУ, параллельные сторонам контура, составля-
ли бы с осью 0Z правую систему координат.
Обозначая длину сторон прямоугольника через Дх и Ду, по-
лучим выражение для циркуляции скорости элементарного кон-
63
www vokb-la.spb ru - Самолёт своими руками?!
тура ГЭл- В соответствии с (4.9) с точностью до малых величин
высших порядков
Гм=ГвДх Г(гв-|—р- дх) Д» Д«/) Ах-
-v^y+...- Ai-Лк) дхд»+...=е2д3-|-.... (4.12)
У дх ду )
Нетрудно видеть, что эта формула остается справедливой не-
зависимо от выбора осей координат, если ее записать в виде
Гвл = 2„До + ... = и2Да + .... (4.13)
По аналогии с формулой для расхода жидкости (2.16) вели-
чину, стоящую в правой части соотношения (4 13), называют
Рис. 45 К расчету циркуляции
скорости по элементарному
прямоугольнику
Рис. 4 6 К расчету циркуляции скорости
по замкнутому контуру
потоком вектора вихря через элементарную площадку До. Фор-
мула (4 13) выражает теорему Стокса для вихревой нити. Рас-
пространим ее на случай контура конечных размеров. Пусть
L — произвольный односвязный замкнутый контур, ограничива-
ющий часть о некоторой поверхности, полностью находящуюся
в жидкости.
Вспомогательными линиями разделим поверхность о на ко-
нечное число элементарных площадок До (рис. 4.6). Тогда для
ломаного контура, ограничивающего часть о, состоящую из це-
лых прямоугольников, в соответствии с (4.13) будет иметь
Г2ЭЛ — QnДог4 . -.. Суммируя правые и левые части этого соот-
ношения, получим
2r'S,=22"A°i+-- <4-141
1=1 1=1
64
www vokb-la.spb.ru - Самолёт своими руками?!
Однако нетрудно видеть, что при суммировании в левой части
слагаемые, соответствующие внутренним линиям раздела, вза-
имно уничтожаются (каждый элементарный отрезок принадле-
жит одновременно двум соседним площадкам Да, а при вычис-
лении циркуляции каждый из них будет пройден дважды в про-
тивоположных направлениях н, следовательно, даст два слагае-
мых, равных по величине и противоположных по знаку). Таким
образом прн суммировании левой части получим циркуляцию
по указанному выше ломаному контуру
Г,0„=22»д’. + — (4-15)
1-1
В пределе при Даг->0 н п->оо ломаный контур переходит в
заданный контур L и приближенное равенство — в точное:
Г= (4.16)
а а
Аналогично можно показать, что это соотношение остается
справедливым для иеплоских контура L и части поверхности а,
если только контур одно связан и часть поверхности не выходит
за пределы жидкости. Теперь можно окончательно сформулиро-
вать теорему Стокса:
Циркуляция скорости по произвольно му замкнутому одно-
связному контуру равна потоку вектора вихря через поверхность,
опирающуюся на этот контур и не выходящую за пределы жид-
кости, или сумме напряжений (интенсивностей) вихревых нитей,
пересекающих эту поверхность.
Из теоремы Стокса следует: если на поверхности вихревой
трубки провести замкнутый контур, охватывающий вихревую
трубку, то циркуляция скорости по такому замкнутому контуру
будет равна напряжению вихревой трубки; если на поверхности
вихревой трубки провести замкнутый контур Л, не охватываю-
щий трубку, то циркуляция скорости по такому контуру равна
нулю.
4 5. ЦИРКУЛЯЦИОННОЕ НЕВИХРЕВОЕ ДВИЖЕНИЕ
Для плоского источника в соответствии с формулами (3.14)
и (3.17) имеем
<р=~2-1цГ
т 2л ’ т 2л
Поменяем местами в этих формулах выражения для функции
тока 4 и потенциала скорости (р и исследуем плоский поток жид-
кости, в котором потенциал скорости
f=5~-e. (4 17)
^л
функция тока 4=J2_in/-
2л
3 626
65
www vokb-la.spb ru - Самолёт своимирукамТ^
Если величина Q для плоского источника ранее была расхо-
дом, то в последнем случае ее физическая сущность является
иной. Каждому значению функции тока соответствует вполне
определенное значение радиуса
г—е .
Это означает, что линии тока, определяемые уравнением
const, представляют собой семейство концентрических ок-
ружностей, центр которых совпадает с началом координат (рис.
Рис. 4.7. Вихрь на плоскости
4.7). Для радиальной и
циальной составляющих
сти в произвольной точке
лярпыми координатами г
лучнм
у ______
s г дв
Если Q>0,
больше нуля, а
жидкости в точке т дви-
танген-
скоро-
т с no-
li 6 по-
(4. 19)
2лг
то скорость Vs
это значит, что
частица
жется в сторону увеличения угла
9, т. е. против часовой стрелки.
Из выражения (4.19) следует,
что все частицы жидкости движутся по концентрическим окруж-
ностям с постоянной для данной окружности скоростью Вместе
с тем наличие потенциала скорости свидетельствует о том, что
рассматриваемое движение жидкости безвихревое. Таким обра-
зом, двигаясь по окружностям, частицы жидкости должны одно-
временно деформироваться так, чтобы мгновенная угловая ско-
рость вращения со каждой частицы была равна нулю. Такое дви-
жение называется циркуляционным невихревым движением.
Оно может быть физически реализовано везде, за исключением
малой окрестности начала координат, являющегося особой точ-
кой, так как при г-»-0 14->-оо, что физически невозможно.
Этой особенности можно избежать, если считать, что уравнения
(4. 17) — (4 19) имеют место во всей плоскости, за исключени-
ем круга некоторого радиуса а с центром в начале координат.
Если рассматривать уравнения (4 17) и (4 18) как уравнения
плоского движения в трехмерном пространстве, записанные в
цилиндрической системе координат (г, 0, я), и дополнить форму-
лы (4.19) условием
Vz=d<f/dz=0, (4.20)
то вместо особой точки появится особая линия г—0 Легко ви-
деть, что кинематические граничные условия для невязкой жид-
66
www.vokb-la.spb.ru - Самолёт своими руками?!
кости при г=а будут выполняться и в том случае, когда среда,
заполняющая пространство внутри цилиндра радиуса г=а, бу-
дет иметь вращательное движение с произвольной угловой ско-
постью ю вокруг оси z, т. е.
при Vr=0, Vz-=0.
В частности, при to—0 указанная выше
Отметим, что с точки зрения
ния вне цилиндра радиуса г—а
совершенно безразлично, какая
именно сплошная среда запол-
няет пространство внутри ци-
линдра: твердое тело, жид-
кость, газ Однако практически
приходится рассматривать сле-
дующие случаи: если и внутри
и вне цилиндра находится од-
на и та же жидкость (газ), то
говорят, что уравнения (4. 17)
и (4. 18) с дополнительными
условиями (4.21) описывают
безвихревое циркуляционное
течение при наличии изолиро-
ванного вихревого шнура; если
вне цилиндрической поверхно-
кинематики
(4 21)
среда неподвижна
безвихревого тече-
Рис. 4.8. Движение частиц вокруг
вихревого шнура
сти r-zZa находится жидкость или газ, а внутри — твердое тело,
то говорят о чисто циркуляционном обтекании цилиндра.
Отметим далее, что с точки зрения кинематики внешнего тече-
ния не имеет значения величина угловой скорости со среды, нахо-
дящейся внутри цилиндрической поверхности г=а. Однако, ес-
ли при переходе через эту поверхность составляющая Vs скоро-
сти изменяется непрерывно, что имеет место в случае вихревого
шнура, то при г~а должно выполняться соотношение асо=
— Q/ (2.т«), откуда 2 =Q/2jtg2, Таким образом, в этом
случае
Q = jra22 = ZI
(4. 22)
т. е. величина Q представляет собой интенсивность вихревого
шнура
Рассмотрим теперь произвольный контур, охватывающий ци
линдрическую поверхность г~г0 (рис. 4 8) Если внутри этой
п° еР,х^ССти находится вихревой шнур, то в соответствии с тео-
ремой Стокса (4 16)
= (4.23)
ПР° ерить н ^посредственным вычислением цирку-
Ц , ели взять контур в виде окружности r=rQ и воспользо-
67
www.vokb-la.spb.ru - Самолёт своими руками?!
ваться выражением (4.19). Теорема Стокса, однако, не наруша-
ется и в том случае, если рассматривается чисто циркуляцион-
ное безвихревое обтекание твердого цилиндра, так как в этом
случае контур, охватывающий цилиндр, уже ие будет односвяз-
ным, что соответствует многозначности потенциала <р. Действи-
тельно, из (4 17) видно, что при /г-кратном обходе любого кон-
тура, охватывающего начало координат, полярный угол 0 воз-
растает на 2/?л, чему соответствует приращение потенциала при
возвращении в исходную точку на величину &(p=kQ = kr. Если
рассматриваемый контур не охватывает цилиндрическую поверх-
ность г=г0, то циркуляция по этому контуру во всех случаях
равна нулю: в случае изолированного вихревого шнура послед-
ний не охватывается, а в случае обтекания цилиндра контур бу-
дет односвязным н прн его обходе полярный угол не увеличива-
ется на л, а возвращается к исходному значению Эти соображе-
ния приводят к весьма важной идее о принципиальной возмож-
ности замены твердого тела системой особенностей при изуче-
нии его обтекания. Впервые эту идею плодотворно использовал
Жуковский, Он ввел понятие о так называемых присоединенных
вихрях, которыми можно заменить твердое тело, не нарушая
внешнего течения невязкой жидкости Если учесть, что в выра-
жениях (4.17), (4.18) величина Q равна циркуляции скорости Г,
то выражения для потенциала скорости <р и функции тока -ф при-
нимают внд:
а) © = (Г/2 л) 6; б) ф=(Г/2л) In г. (4. 24)
Учитывая, что tgO=y/x (6=arctg у/х), г=> (см.
рис 4.7), в прямоугольной системе координат получим
<P=~arctg—, ф=-^1п
2л х 2л
В последней формуле для потенциала скорости приведено
главное значение аргумента Выражение для полного значения
потенциала скорости можно записать так:
г
<0=---
2л
Arctg —.
X
Поскольку функция Arctg (уlx) многозначна, то и потенциал
многозначен При постоянном значении функции потенциала ско-
рости нз равенства (4.24) имеем ф= (Г/2л)0 = const.
Это означает, что эквипотенциальные линии будут пред-
ставлять собой семейство прямых линий, выходящих из начала
координат н ортогональных к линиям тока — концентрическим
обтекаемому цилиндру (вихревому шнуру) окружностям.
68
www vokb-la.spb.ru - Самолёт своими руками?!
Выражения для радиальной и тангенциальной составляющих
скорости (4.19) с учетом равенства (4 23) принимают вид
l/r = 0, Vs-T/2«r. (4.25)
Таким образом в рассматриваемом потоке все частицы пере-
мещаются вдоль окружностей в сторону увеличения угла 0, не
вращаясь относительно мгновенных осей, при этом по мере при-
ближения к оси вихревого шнура, т. е. с уменьшением радиуса г,
скорость увеличивается по гиперболическому закону, достигая
максимального значения Vo на поверхности вихревого шнура
Внутри вихревого шнура скорость Vs увеличивается пропорци-
онально расстоянию от осн вращения. Распределение скорости
внутри вих] евого шнура и во внешнем окружающем его потоке
показано на рнс. 4.8
4 6 ФОРМУЛА БИО — САВАРА
Предположим, что в жидкости имеется одиночный вихревой
шиур с напряжением /—Г. Такой шнур, как показывают иссле-
дования, индуцирует в окружающем потоке поле скоростей, под-
чиняющееся определенному закону. Скорость dV, индуцируемая
элементом вихря dL в некоторой точке А, определяется форму-
лой
dV — - sin
4лг2
(4. 26)
где г — расстояние от точки А до элемента вихря; 0 — угол, об-
разуемый отрезками г и dL
Эта формула, называемая формулой Био—Савара, устанав-
ливает известную аналогию между аэродинамикой и электроди-
намикой
Если предположить, что вихревой шнур жидкости заменен
электрическим линейным проводником с током, сила которого
то магнитное поле, возникающее вокруг такого проводни-
ка, действует на единицу магнитной массы в точке вне шнура с
силой, величина которой определяется по формуле Био—Савара
(4.26). Формула Био—Савара нашла широкое применение в тео-
рии крыла самолета, лопаток турбин и др. Для вихря длиной L
полная скорость индуцируемая в точке А,
V = f dV.
d)
Ра м трим участок прямолинейного вихря с напряжением
др/ Л °пРеДелнм скорость, индуцируемую им в точке А (рис.
) Предположим, что углы 0t и 02 между осью вихря и отрез-
69
www.vokb-la.spb.ru - Самолёт своими руками?!
ками прямых rt, г2, г0 заданы. Выделим на участке MN вихря
бесконечно малый элемент BD—dL. Этому элементу dL соот-
ветствует угол £?0. Из треугольника АВС, учитывая, что rf0cO,
имеем ВС— —rd®.
Из треугольника BCD также находим
sin в — BC/BD— —rd6/dL
или
dL — —rdtysin 6
Из треугольника О АВ имеем r—ro/sm 0
Подставляя этн значения в формулу (4.26) н интегрируя ее в
пределах от 02 до 01, иаходнм скорость, индуцируемую участком
внхря MN в точке А:
Рис. 4.9. К расчету скорости, инду-
цированной прямолинейным оди-
ночным вихревым шнуром
V ————(cos62— cos б!). (4.27)
4лг0
При 01=л/2, б2=0 имеем бес-
конечно длинный вихревой полу-
шнур от точки О до бесконечно-
сти, В этом случае формула
(4. 27) принимает вид
4лг0
(4.28)
При 61 = л, 02—0 имеем бес-
конечно длинный шнур от минус
бесконечности до плюс бесконеч-
ности. В этом случае
П = Г 2лг0. (4.29)
Как и следовало ожидать, бесконечный вихревой шнур вызы-
вает вдвое большую скорость, чем полубесконечный вихревой
шнур той же интенсивности Следует отметить, что формулу
Био—Савара можно применить и в общем случае как для ко-
нечного количества дискретных вихрей, так и при непрерывном
распределении вихрей, разбивая вихревое поле на отдельные
вихревые нити
4.7. ПОНЯТИЕ О ТЕОРЕМЕ ТОМСОНА
Теорему Томсона можно сформулировать так: если внешние
массовые силы, действующие в баротропной невязкой жидкости,
имеют потенциал то циркуляция скорости по любому замкну-
тому жидкому контуру остается постоянной во времени. Матема-
тически эта теорема выражается следующим образом dT/dt—O
или Г=const т е. производная циркуляции по времени равна
нулю
70
www.vokb-la.spb.ru - Самолёт своими руками?!
Из теоремы Томсона следует, что если в какой-либо части
движущейся или неподвижной идеальной баротропной жидкости
в некоторый момент времени циркуляция скорости по замкнуто-
му контуру равна нулю, то она остается равной нулю и в после-
дующие моменты времени Иначе говоря, если движение жидко-
сти было безвихревым, то и в последующие моменты времени
оно остается безвихревым.
Таким образом, циркуляция скорости не может возникнуть
или исчезнуть в невязкой баротропиой жидкости при условии,
что массовые силы имеют потенциал. Следует, впрочем, отме-
тить, что теорема Томсона и вытекающие из нее следствия не
имеют места для вязкой или небаротропиой жидкости, а также
для жидкости невязкой и баротропной при наличии в ией по-
верхности разрыва скорости.
Вопросы для повторения
1. Дайте определение вихревого движения.
2. Что такое вихревая линия, вихревая трубка, вихревой
шнур? Напишите уравнение вихревой линии.
3. Что такое напряжение вихря?
4. Что такое циркуляция скорости и как оиа связана с нап-
ряжением вихря?
5. Чему равна циркуляция скорости иа контуре L, внутри ко-
торого имеются две вихревые трубки с равными по величине нап-
ряжениями, ио с противоположными направлениями вращения?
6. Объясните физический смысл формулы Био Савара
Задачи
1. Составить уравнение семейства вихревых линий для дви-
жения, в котором Vx=3y--z, Vy=3z+x, Vz=3x-]-y.
Ответ; x=z/ + C1, x=z-,rC2.
2. Вычислить циркуляцию скорости по окружности радиуса
с центром в начале координат и определить полную скорость
в любой точке этой окружности, если потенциал скорости
m arete (у/х).
Ответ: Г=2лт, y—m/R.
(Г
WWW vokb-la.spb ru - Самолёт своими руками?!
ГЛАВА 5
ДИНАМИКА ИДЕАЛЬНОЙ ЖИДКОСТИ
5.1. ОБЩИЕ ПОНЯТИЯ
Основной задачей динамики жидкости является установле-
ние зависимостей между кинематическими и динамическими ха-
рактеристиками течений жидкости и, в частности, изучение ди-
намического взаимодействия между жидкостями и твердыми те-
лами при их относительном движении.
Кинематические характеристики течений были рассмотрены
выше. Динамические характеристики определяются распределе-
нием в потоке и, в частности, на границах между жидкостью и
твердым телом нормальных и касательных напряжений В слу-
чае идеальной жидкости касательные напряжения отсутствуют,
а нормальные, как и в случае равновесия жидкости, определяют-
ся одной скалярной величиной, называемой давлением.
Исследование динамики жидкости основано на том, что в не-
который момент времени воображаемой или частично реальной
замкнутой контрольной поверхностью выделяется некоторая
часть жидкости, при этом действие отбрасываемой среды, внеш-
ней по отношению к контрольной поверхности, заменяется соот-
ветствующими поверхностными силами. Применение к выделен-
ной части жидкости общих законов механики позволяет полу-
чить уравнения динамики жидкости в интегральной форме.
Переходя к пределу (уменьшая объем выделенной части до ну-
ля), полученные соотношения можно переписать в виде диффе-
ренциальных уравнений движения жидкости, которые в отличие
от дифференциальных уравнений движения твердого тела пред-
ставляют собой дифференциальные уравнения в частных произ-
водных. Следует иметь в виду, что упомянутый предельный пе-
реход является правомерным только в том случае, если все па-
раметры течения изменяются непрерывно, что ие всегда имеет
место, в частности, разрывы непрерывности имеют место в не-
которых случаях при течении газов со сверхзвуковыми скоростя-
ми. При наличии разрывов непрерывности дифференциальные
уравнения движения можно использовать только в пределах
72
www.vokb-la.spb.ru - Самолёт своими руками?!
каждой области между поверхностями разрыва, сопрягая меж-
ду собой параметры потока для смежных областей с помощью
определенных соотношений (так называемых соотношений дина-
мической совместности), получаемых из уравнений движения в
интегральной форме. Впрочем, ввиду сложности интегрирования
системы уравнений в частных производных при разработке неко-
торых приближенных методов динамики жидкости (например,
в теории пограничного слоя) используются непосредственно
уравнения движения в интегральной форме.
5.2. УРАВНЕНИЯ ДВИЖЕНИЯ ИДЕАЛЬНОЙ ЖИДКОСТИ
Фиксируем в потоке жидкости замкнутую контрольную по-
верхность S (ограничивающую объем IV), через которую сво-
бодно протекает жидкость (рис 5 1), и рассмотрим материаль-
ную систему, состоящую из частиц жидкости, заполняющих объ-
ем внутри 5 в некоторый момент вре-
мени t. Обозначив массовую силу, дей-
ствующую на единицу массы жидкости
в момент времени t в точке простран-
ства с радиусом — вектором г, через
F, найдем главный вектор массовых
сил, действующих иа указанную систе-
му, в виде:
Рис 5.1. К выводу диф-
ференциального уравне-
ния движения жидкости
Ш
где л (г, t) — плотность жидкости.
В соответствии с третьим законом механики силы взаимо-
действия между частицами внутри объема W уравновешиваются
и лишь силы, действующие на поверхностные частицы, могут
быть иеуравиовешеиы При анализе движения идеальной (не-
вязкой) жидкости из поверхностных сил учитывают только силы
давления.
Как известно, сила давления является функцией координат
и времени и действует по направлению внутренней нормали к
поверхности. Поэтому результирующая сил давления, действую-
щих иа поверхность 5, ограничивающую объем жидкости W7,
равна — fj pndS, где п—орт внешней нормали. Обозначая
(5)
ускорение частицы, находящейся в момент времени t в точке с
радиусом-вектором г, через dVjdt и добавляя на основании прин-
ципа Даламбера к внешним силам, действующим на частицы
системы, силы инерции (с обратным знаком), уравнение движе-
73
www vokb-la.spb.ru - Самолёт своими руками?!
ния для момента времени t можем записать в интегральной
форме:
(Ю (S) (^)
Заметим, что это уравнение справедливо независимо от того,
будут ли параметры движения непрерывными или разрывными
функциями координат. Если параметры движения и их первые
производные непрерывны в области IV и на ее границе S, то
можно использовать преобразование Гаусса — Остроградского
[ f pndS— f f J grad pd IV.
(Ч) (ip)
Тогда полупим — grad p p dW = 0.
(W)
Поскольку объем W был выбран произвольно, то подынтеграль-
ное выражение должно быть равно нулю. Это позволяет полу-
чить дифференциальное уравнение движения идеальной жидко-
сти (уравнение Эйлера) в векторной форме:
F---— grad p=dV}dt.
е
(5.1)
В координатной форме уравнение (5.1) записывается в виде
системы трех уравнений:
у 1 др ____ dVx . у 1 др _____ dVу . у 1 др ______ dVг
Q дх dt ' Q ду dt ' Q dz dt '
(5.2)
где X, Y, Z — ускорения от объемных (массовых) сил по нап-
равлению осей координат.
Перепишем систему уравнении Эйлера в развернутом виде,
учитывая, что производные от координат по времени равны про-
екциям скорости на координатные оси
др ___ дУл- 1 у дУя । । у дУх .
q дх dt х дх ду z дг
L др дУу . у
v dVt/ •
Q dy dt х дх 11 ду z dz
___ др_ дУг . у дУг . у дУг . у dVz
Q dz dt х dx у dy dz
(5- 3)
Уравнения (5.3) в случае несжимаемой жидкости содержат
четыре неизвестные функции Vx, Vy, Vz и р. Добавляя к инм
уравнение неразрывности (2 12), получим замкнутую систему
74
www vokb-la.spb.ru - Самолёт своими руками?!
дифференциальных уравнений движения невязкой несжимаемой
жидкости.
В случае сжимаемой жидкости, как в уравнениях движения»
так и в уравнении неразрывности появляется еще одна неизвест-
ная функция q Добавление к системе уравнений уравнения сос-
тояния (2.7) ие замыкает систему, так как появляется еще одна
неизвестная функция — температ} pa Т. Поэтому для замыкания
системы необходимо составить еще одно (шестое) уравнение —
уравнение переноса энергии (см. например, [62]).
Без этого уравнения можно получить замкнутую систему
уравнений, если известна иепосредствеиио связь между р и р, в
виде е=р(р). Жидкость, к которой применима такая зависи-
мость, носит название баротропной. Заметим, что термодинами-
чески идеальный газ можно рассматривать как баротропиую
жидкость, если известен термодинамический характер изменения
его состояния. Например, при изотермическом состоянии газа
p/Q=C, (5.4)
при адиабатическом
р!^к — С. (5.5)
В этих случаях замкнутая система уравнений состоит из пя-
ти уравнений с пятью неизвестными функциями 14, Vy, Vz, р, о.
Уравнения Эйлера (5 2) или (5 3) нелинейные, и общее реше-
ние их ие найдено. Можно иайти решения только для частных
случаев. При установившемся движении несжимаемой жидкости
из уравнений (5 3) выпадают слагаемые dVxjdt, dVy[dt, dVzjdt.
При 14= 14= 14=0 из уравнения (5.2) получим дифферен-
циальные уравнения гидростатики
X----L^£_ = o; у----—-^- = 0; Z------^- = 0. (5.6)
Q дх Q dy a dz '
Если эти уравнения умножить соответственно иа dx, dt/, dz и
сложить, то после преобразовании получим
^-dx-\-^-dy -\--^-dz~^(XdxA-Ydy-\-Zdz).
дх ду дг
Левая часть этого уравнения представляет собой полный
дифференциал функции р=р(х, у, z) dp=Q(Xdx\-Ydy-\-Zdz}.
Очевидно полученное уравнение может удовлетворяться и,
следовательно, равновесие возможно только в поле массовых
сил, имеющих потенциал. Существует некоторая функция
U(x, У, z)* называемая потенциалом массовых сил, частные про-
изводные которой по переменным х, у, z равны проекциям на
координатные оси ускорений, вызываемых этими силами.
X— —dU/dx, У= —dU/dy, Z= — dU]dz. (5.7)
Тогда dp^—QdU или (5.8)
75
www vokb-la.spb.ru - Самолёт своими руками?!
Последнее уравнение называется гидростатическим уравне-
нием давления. Дифференциальные уравнения движения идеаль-
ной жидкости (5.2), а также дифференциальные уравнения гид-
ростатики (5 6) получены Эйлером в 1755 г. и носят его имя.
Обычно внешней массовой силон, как отмечалось выше, яв-
ляется сила тяжести Но в некоторых случаях, например, при ус-
коренном или криволинейном движении твердого тела (жидко-
сти), если происходящее при этом обтекание тела рассматрива-
ется в связанной с движущимся телом системе координат, к мас-
совым силам добавляются инерционные силы, необходимые для
создания движения жидкости относительно связанных с телом
осей координат.
Потенциал силы тяжести имеет аналитический вид. Если по-
лагать, что координатная ось Оу перпендикулярна поверхности
земли и направлена вверх (положительное направление), уско-
рение силы тяжести вдоль этой оси постоянно и равно У= —g,
а составляющие ускорения вдоль двух других осей равны нулю,
тогда из (5 7)
~dUldx=O, Y=^~dU!dy=~g, Z^~dUfiz=-§.
Из этих уравнений находим— U— —gy+C, поэтому уравнение
(5.8) запишется в виде p=Qgy-$-C
Или
р/у|-у--сопН. (5.9)
Это и есть известное уравнение гидростатики.
53 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ
ИДЕАЛЬНОЙ ЖИДКОСТИ В ФОРМЕ ГРОМЕКИ
Уравнения движения идеальной жидкости в форме Громеки
есть преобразованные уравнения (5.3) Прибавляя и вычитая в
правой части первого уравнения (5 3) величиныПу Vг
после преобразования получим
1 др dVx , (у dVx
Q дх dt \ х дх ^Vy дх 1 u Z Н дх /
_|_у рЕг—(5.10)
1 z \ dz дх J у\дх ду } 4 ’
„ I/ дУг I IZ 1_Т/ zj v
Сумма V- —— -f- V у —— -j- V z —— представляет собой выра-
дх ду дг
д fVt \ dVх dVz dVu dVx
жение —I- , величины —--=- и ——-~ Представ-
dx \ 2 / dz дх дх ду
ляют собой удвоенное зиачеице компонент угловой скорости
76
wwm vokb-la.spb ru - Самолёт своими руками?!
(Ox и (oy. С учетом аналогичных вычислений для двух остальных
уравнений система (5 3) может быть записана в виде
X 1 dp . dVx 4- d (V2 14-2(Vzcoy — ^y^z »
Q dx dt 1 dx \ 2 J
r 1 dp dVy 1 д 1 ' K2 X |4_2(VrJt.io.j.—
Q дУ dt 1 dy \ . 2 J
Z Q dp dz dVz dt T—| dz 1 f V2 ' ( 2 > ^4" 2 (V^yiax —
(5.11)
Это и есть преобразованные уравнения гидродинамики Эйле-
ра в форме Громеки В случае потенциального течения третьи
слагаемые правых частей уравнений системы (5 11) обращаются
в нули.
Подставляя в уравнения системы (5.11) значения проекций
массовых сил X, Y, Z согласно (5 7), после ряда преобразований
получим
дх 1 q 2 / dt 1 k z у
54. ИНТЕГРАЛ БЕРНУЛЛИ — ЧАСТНОЕ РЕШЕНИЕ УРАВНЕНИИ
ЭЙЛЕРА — ГРОМЕКИ
(5. 12)
Для установившегося течения dVy/d/=0, dVjdt=
—О, и уравнения (5.12) в этом случае имеют вид
-£(t/+T-+v)=2 (
дх \ р 2 /
— (и+^+^)=2<Ул~(5- 13)
- — (J4--—+^-1=2(Ил-1/А).
Умножая первое из этих уравнений на dx, второе на dy и
третье на dz и суммируя, после преобразований получим урав-
нение
—Vy^z)dX-\~(yx^z—&у-\-
+ VxPy)dz\,
www.vokb-la.spb.ru - Самолёт своими руками?!
правую часть которого можно представить в виде определителя
-d(l/+^+^)=2
\ е 2 j
dx
o)x
dy dz
(5-14)
При определенных условиях определитель (детерминант) об-
ращается в нуль. В этом случае
fl’t7+v+d(!r)~o- (5‘15)
В частном случае, если изменениями потенциальной энергии
можно пренебречь (например, для газовой среды при малой раз-
ности высот), можно перейти к приближенной формуле
Соотношение (5.15), в частности, выполняется, если прира-
щения координат dx, dy, dz берутся вдоль линии тока (2.1) или
вдоль вихревых линий (4.2). Если при этом жидкость несжима-
ема или баротропиа, то вдоль линии тока или вдоль вихревой ли-
нии после интегрирования соотношения (5.15) полечим
£7-j- const. (5.17)
Соотношение (5.17), устанавливающее связь между параметра-
ми течения вдоль линии тока или вихревой линии при устано-
вившемся течении называется интегралом Бернулли. В случае
несжимаемой жидкости (q=const)
—Н—^-=const. (5.18)
Если из массовых сил действует только сила тяжести, то про-
екции ускорения массовой силы на оси координат X=Z=O,
— g, и с учетом выражений (5.8)
— dU—Ydy——gdy или £7=gT/-|-const. (5. 19)
Подставив это значение U в уравнение (5.18), найдем, что
У + ~+~~= const, (5.20)
Y
где у— Qg.
Для двух точек потока, взятых вдоль одной н той же линии
тока, уравнение Бернулли можно записать в виде
у2 V2
(5.21)
Y 2g Y 2g V 7
78
www.vokb-la.spb.ru - Самолёт своими руками?!
Для некоторых частных случаев установившегося течения со-
отношение (5.15) и все вытекающие из него последующие соот-
ношения справедливы при произвольных dx, dy, dz, что имеет
место при безвихревом течении (сох=соу=со2=0) и при винто-
вом движении, когда в соответствии с (4 2) (Or/l/T=(o1//V'p=(oz/l/z.
В этих случаях интегрирование уравнения (5.15) приводит к
соотношению
dp . V2
—— 4---=const,
Q 2
(5.22)
формально совпадающему с (5 17). Эти два соотношения, одна-
ко, отличаются тем, что постоянная в правой части (5.17) имеет
различное значение для различных линий тока (вихревых ли-
ний), в то время как в выражении (5 22) постоянная одинакова
для всего потока.
Таким образом, соотношение (5.22) представляет собой ин-
теграл уравнений Эйлера и в связи с этим носит название ин-
теграла Бернулли—Эйлера. Следует при этом отметить, что ин-
теграл Бернулли—Эйлера справедлив только для частных слу-
чаев установившегося движения невязкой барогропиой жидко-
сти, в то время как уравнение Бернулли справедливо для любо-
го (в частности, для вихревого) установившегося движения не-
вязкой баротропиой жидкости.
При винтовом движении, когда линия тока одновременно яв-
ляется и вихревой линией, постоянная в уравнении Бернулли
(5 18) одинакова для всего потока.
Члены yi и у2 с геометрической точки зрения представляют
собой высоты центров тяжести сечений ггруйки над горизонталь-
ной плоскостью отсчета. Члены Pi/v и Л ?/V представляют собой
пьезометрические высоты (или пьезометрические напоры), соот-
ветствующие пьезометрическим давлениям в указанных центрах
тяжести сечений. Члены \'\2/2g и V?z/2g представляют собой ско-
ростные высоты (или скоростные напоры) Эти члены по вели-
чине равны высотам, с которых должно падать тело (без учета
сопротивления среды), чтобы к конц\ своего падения развить
скорости, соответственно равные \\ и (/2.
С физической точки зрения цмма у+ply представляет собой
удельную потенциальную энергию, а член Ё2/2^ удельную ки-
нетическую энергию. В самом деле, если вес частицы равен
G=mg, то кинетическая энергия ма<сы жидкости т, движущей-
ся со скоростью V, есть mVz/2 Онсуда кинетическая энергия
mV2 у2
жидкости, отнесенная к единице веса, оудет — - =-.
2mg 2g
Если обозначить удельную кинетическую энергию через
£i<=V2/2g, а удельную потенциальную через Еп—у+р!у, то
7У
полная удельная энергия элементарной струйки £ равна Е=
= £n+EK = const
или Е=у ф- — + ~~ • (5- 23)
Значит для идеальной жидкости прн перемещении частиц из
одного сечения в другое количество энергии остается постоян-
ным, но при этом происходит перераспределение энергии из ки-
нетической в потенциальную и наоборот.
В задачах аэродинамики величинами, выражающими работу
массовых сил (прн небольших разностях высот), можно преие-
Рис. 5.2. Обтекание тела потоком
жидкости
бречь, как малыми величинами
по сравнению с внутренними
силами давления и силами
инерции. В этом случае в ин-
теграл Бернулли (5 17) не вхо-
дит функция U и интеграл Бер-
нулли имеет вид
С _]—Е_ = const. (5.24)
j р 2
В случае несжимаемой
жидкости
£+q-~ = const, (5.25)
где р— статистическое давление; q(V2/2)— динамическое дав-
ление *
Если применить уравнение (5 25) к центральной струйке, раз-
ветвляющейся в точке А и охватывающей обтекаемое тело (рис.
5 2), взяв сечение I /на достаточно большом расстоянии от те-
ла, где поток считается иевозмущенным (V=V’0O, р—р^) а вто-
рое сечение //—II в критической точке, где скорость V—0, а
давление р%—ро, тогда можно записать
V2
(5 26)
£
Сумма статического и динамического давлений дает полное
давление ро, или давление в точке торможения потока (Ео=О)
Запишем уравнение Бернулли при обратимом адиабатическом
изменении состояния баротропного газа (5.5), когда
-Л- const - С
Q
* Поскольку в различных источниках имеются расхождения в определе-
нии понятии скоростного напора и динамического давления, то мы будем на-
зывать величину V /2g — скоростным напором, так как она представляет
собой скоростную высоту и имеет линейную размерность, а величину рГ2/2,
имеющую размерность давления — динамическим давлением Графическая
интерпретация этих понятий показана на рис. 10 16
80
Учитывая, что значение р для газа является переменным, после
дифференцирования уравнения (5 5), получим
dp~CkQk Wp
или — - — Ckok~2dQ.
Q
Интегрируя это выражение, найдем
С——о^1.
j е k— 1
Подставив значение С из выражения (5.5), найдем
г dp k _р__
J q k — I Q
С учетом этого выражения уравнение (5.24) принимает вид
k V2
k— i q * 2 —
const.
(5. 27)
Используя уравнение состояния газа p/q=J^T, уравнение
Бернулли можно записать в виде
—— RT 4- =const (5.28)
k — I 2
или
р I V2 । RT ,
——------------=const, (5. 29
Q 2p ft—i k
p I V2 I RT .
откуда следует ——---------------=const.
Y 2< (k — 1)£
RT
В этом уравнении слагаемое ———— называется тепловым
напором. Таким образом при адиабатическом движении идеаль-
ного газа сумма пьезометрического p/у, скоростного V2/(2g) и
теплового RT/(k—l)g напоров есть величина постоянная вдоль
каждой струйки.
Для двух различных частиц, расположенных на одной и той
же линии тока, уравнения (5.27), (5.29) имеют вид
. у 2 . и2
k Р\ v 1 ___ k Д2 I v2 .
k — 1 Qi 2 k — I Q2 ‘ 2
Д1 4 rt^^p^. RT±
Qi ' 2 k~ 1 q2 ‘ 2 ‘ft — 1’
(5.30)
Из этих уравнений следует, что у различных частиц на одной
и той же линии тока удельная механическая энергия, отнесен-
ная к единице массы жидкости, не одинакова Это означает, что
при адиабатическом движении газа часть механической энергии
превращается в тепловую и наоборот.
81
www vokb-la.spb.ru - Самолёт своими руками?!
Как известно, уравнение Бернулли справедливо не только
для частиц жидкости, расположенных на одной и той же линии
тока, ио и для частиц, лежащих на одной и той же вихревои
линии и на оси винтового течения, а также для любых частиц
потенциального потока.
Используя формулу (1.25), согласно которой a2 = kRT, из
уравнения (5.24) можно получить зависимость между скоростью
таза и скоростью звука в данной точке:
1 ~const, (5. 3
1--------------------------------2
Из этого уравнения следует, что с увеличением скорости
•изэнтропического движения газа скорость распространения зву-
ка в данной точке уменьшается, а с уменьшением скорости дви-
жения газа — увеличивается.
Найдем связь между скоростью движения газа и его тепло-
содержанием (или энтальпией) I. Воспользовавшись соотноше-
нием (1.16), запишем уравнение (5.28) в виде
i -4--^-=const. (5.32)
2
Согласно этому уравнению вдоль линии тока сумма тепло-
содержания и кинетической энергии газа есть величина постоян-
ная. Это уравнение справедливо также и для адиабатических
необратимых процессов. Уравнение (5.32), отнесенное к двум се-
лениям газового потока
тде it и Vi — теплосодержание и скорость газового потока в
первом сечении, a i2 и V2 — во втором.
5 5 ПРЕДЕЛЫ ПРИМЕНИМОСТИ УРАВНЕНИЯ БЕРНУЛЛИ
ДЛЯ НЕСЖИМАЕМОЙ ЖИДКОСТИ К ГАЗУ
Уравнение Бернулли для струйки несжимаемой жидкости
^5 25) проще, чем уравнение Бернулли для струйки газа (5.27).
Определим, при каких условиях можно использовать уравнение
(5 25) для вычисления давления в газе. Для этого сопоставим
значения давлений, полученные при одинаковых скоростях по
уравнениям (5 25) и (5 27).
Рассмотрим обтекание некоторого тела потоком несжимае-
мой жидкости (см. рис. 5 2) Если скорость и давление невоч-
мущенного потока в достаточно удаленном от тела сечении име-
ют значения и то значение постоянной С в уравнении
(5.25)
V2
С = Poo~\-Qoe ——-
«2
www vokb-la.spb.ru - Самолёт своими руками?!
и уравнение (5.25) принимает вид
р<=о j Qoo 2 Q 2 *
В критической точке тела А скорость равна нулю, а давление
Ро имеет максимальное значение
V2
ИЛИ /Л) —(5.33)
что совпадает с выражением (5 26).
Теперь определим давление в точке А с учетом сжимаемос-
ти газа. Предположим, что течение изэнтропическое, т, е.
/7 '(/ . _const—С
или e==Goo
\ Рос /
Первый член уравнения (5.27) с учетом этого равенства при-
нимает вид
k Р_ _ Poo k f р .
л— 1 q k~ i\Poo /
Тогда уравнение (5 27) можно записать так:
Qoo Ц Р«, ,1 2
Определим С из условий на бесконечности, считая давление
и скорость соответственно равными р*, и К»:
Л Рос I ОС
Подставляя значение С в предыдущее равенство, получим
Рос kip V2 _ Л Роо .
бос 1 \ Рос/ 2 k~ 1 ?ос 2
В критической точке А р—Ръ и V=0. Из последнего уравне-
ния находим
Pop I Ро \~fc~_ Роо * ос
k~ 1 Qoo \ Pool ~k~l Q*, 2
(. 1 о V2 \
] L-1 tfap °0 1А-1
* /
wwTft .vokb-la.spb ru - Самолёт своими руками?!
Учитывая, что скорость звука а=У kp/Q и число A'ioo= V^/a^,
ПОЛУЧИМ
fe
Ро1 I 1 м2
I О ос I
Рос < 2 /
Рассмотрим дозвуковое течение газа (Моо<1) Для воздуха
k 1
k—1,4 и, следовательно,----значительно меньше единицы.
2
Это дает нам основание при разложении правой части послед-
него уравнения в биномиальный ряд ограничиться первыми нес-
колькими членами*
1 1 ' <£
Подставляя
ЕЫражение (5.33) запишем в виде
Ро = 1 I k
Рос ^-1
— М2 -4
2 00
. / М2 \ и V2 / м2 \
Df) 1 I £ / 1 I 1иоо I I 1 I # г ОС / 1 I ОС I I
ИЛИ -^- = 1 4-—М2 1 Ц------------к ...1=1 + ——5-1 1 Я-----?- + ••• *
Учитывая, что d^ — kp^jQ^
Ро _ | I k
~р 2
* ОС
V2
Так как то
2
откуда р0—/?ос4-7оо •••
или р0 — рос ОС + ДА
м2
где Др ^оо——+•••• (5.34)
*х
Сравнивая формулы (5.33) н (5.34), видим, что величина Ар
представляет собой погрешность в определении давления при
использовании формулы (5 33). Если величину Др отнести к
динамическому давлению, получим относительную погрешность
'в!
www .vokb-la.spb ru - Самолёт своими
в первом приближении
ер=—=—-р- £р~ер100%.
4 ни
“ оо
Соответственно формулу (5.34) можно записать в виде
/7о=/?<»-И?оо(14"ер (5,35)
В таблице приведены значения относительной погрешности
ер в зависимости от числа М«/
Моо о,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0
Ер 0,25 1,0 2,25 4,06 6,2 9,0 12,8 17,3 21,9 27,5
Из таблицы видно, что при нормальных атмосферных усло-
виях н числах М«, до 0,3 погрешность в определении давления
с помощью уравнения (5 33) мала н сжимаемостью можно пре-
небречь. Следовательно, при малых скоростях движения газа
его сжимаемость можно не учитывать.
Вопросы для повторения
1. Объясните физический смысл отдельных членов уравнения
Эйлера.
2 Напишите уравнения Бернулли для сжимаемого и несжи-
маемого газа.
3, Объясните смысл членов уравнения Бернулли
4. Как зависит относительная погрешность уравнения Бер-
нулли для сжимаемого газа от числа М?
Задачи
I Определить повышение давления в критической точке по-
тока при обтекании тела: а) потоком воздуха со скоростью
120 м/с (пренебрегая сжимаемостью воздуха); б) потоком воды
(р= 1000 кг/м3) со скоростью 20 м/с.
Ответ; Дрв=8820 Н/м2; Лрв0Ды=-2-105 Н/м2.
2. Определить скорость полета, если статическое давление
за бортом самолет! рст= 1,013 бар, а давление в критической
точке равно 1,108 бар.
Ответ; V = 450 км/ч.
3. Определить давление в критической точке носа фюзеляжа
при полете со скоростью V=900 км/ч на высоте Я=8000 м.
Ответ: р = 0,55 бар. ,
www.vokb-la.spb.ru - Самолёт своими руками?!
ГЛАВА 6
ОСНОВЫ ТЕОРИИ ОБТЕКАНИЯ ТЕЛ
ПОТЕНЦИАЛЬНЫМ потоком жидкости
6.1. БЕСЦИРКУЛЯЦИОННОЕ ОБТЕКАНИЕ КРУГОВОГО ЦИЛИНДРА.
ПАРАДОКС ДАЛАМБЕРА — ЭЙЛЕРА
Рассмотрим обтекание кругового бесконечно длинного ци-
линдра радиуса г0 плоскопараллельным потоком жидкости (рис.
6.1). Такое течение мы получили ранее при наложении плоско-
параллельного потока на диполь. Тогда же были получены вы-
ражения для потенциала скорости (3.27), функции тока (3.28)
и проекций скоростей в полярных координатах (3 29) и (3.30):
(6. I)
В точках Л(0=л) и В(0 = 0) (см. рис. 6.1) скорость потока
равна нулю. Эти точки являются точками разветвления потока
и называются критическими. На цилиндре при г=го согласно
(6 1)
V,=0; Vs=—2’/osin0.
(6.2)
Из первого равенства следует, что скорость частицы жидко-
сти на поверхности цилиндра везде направлена по касательной.
В этом случае линией тока является окружность, происходит ее
безотрывное обтекание. Второе равенство определяет изменение
скорости вдоль поверхности цилиндра. С учетом выражения
86
vokb-la.spb ru - Самолёт своими руками?!
(6.1) для Vs можно получить значение циркуляции скорости во-
круг цилиндра согласно формуле (4.7):
2я
о
cos 0
т. е. в данном случае циркуляция скорости вокруг цилиндра
равна н^лю.
Рис. 6 I. Бесциркуляционное
обтекание кругового цилиндра
Рис. 6.2. К определению силового
воздействия потенциального пото-
ка на цилиндр при его обтекании
Рассмотрим силовое воздействие потенциального потока на
бесконечно длинный круговой цилиндр радиуса г0- Сила давле-
ния, действующая по нормали к боковой поверхности цилиндра
на единицу длины, равна pds (рис. 6 2), а проекции этой силы
dX и dY можно записать в виде
dX=—р cos fids; dY=— р sin Qds. (6.3)
Интегрируя выражение (6.3) и учитывая, что элементарная
дуга ds—rodQ, получим
2л 2л
X — — С р cos 0го<70; — Г р sin 0го<76.
о о
(6. 4)
После подстановки значений давления/?
г 1/2
G — Р“ (массовы-
ми силами пренебрегаем, так каких влияние сводится к действию
87
www vokb-la.spb ru - Самолёт своими руками?!
Архимедовой гидростатической силы) и скорости
=—2 Vo sin 0 выражения (6.4) принимают вид
2п
Х = —r0 1/2 sin2 6 cos 6(70,
о
2л
К——r0J С—|-l/2 sin2 6^ sin 6(76.
о
Поскольку
VS=V=-
(6.5}
2л
j sin 9(79=0;
б
2л
j cos 0(79=0;
2л
J sin2 0 cos 9(76 = 0;
2л
J sin39(70=0,
то окончательно получим
X=0, Г = 0 (6.6)
Таким образом при бесциркуляционном обтекании цилиндра
потенциальным потоком жидкости горизонтальная и вертикаль-
ная составляющие сил давления со стороны потока на цилиндр
равны нулю, т. е. в невязкой жидкости сопротивление движению
цилиндра отсутствует. В реальных условиях на цилиндр при об-
текании его жидкостью всегда будет действовать гидродинами-
ческая сила. Противоречие между результатами эксперименталь-
ного и теоретического исследований этой задачи получило назва-
ние парадокса Даламбера — Эйлера.
К тому же выводу можно прийти и непосредственно — рас-
смотрев распределение давления по поверхности цилиндра.
Уравнение Бернулли для двух точек потока жидкости (беско-
нечно удаленной точки, находящейся в невозмущенном потоке,,
и точки, расположенной на поверхности цилиндра) имеет вид:
, vl , из 7
А+е—=р+е^-> (Ь.7)
и2
откуда с учетом выражения (6.2) р—р0=д—-—— (—21/0 sin 6)2
2 2
или/7 — pQ—q——(1 — 4 sin29). (6 8)
2
Отношение разности давлений к скоростному напору невоз-
мущенного потока является безразмерной величиной и называ-
ется коэффициентом давления:
~__ Р~ Ро Р~ Ро
<1
(6-9)
где
к о
88
www.vokb-la.spb.ru - Самолёт своими руками?!
При бесциркуляционном обтекании цилиндра коэффициент
давления с учетом (6.8) равен
^—1-4 sin2 0. (6. 10)
Из этого соотношения следует, что величина р не зависит
ют плотности, давления, скорости иевозмущенного потока, радиу-
са цилиндра и является четной функцией угла 0. Это делает
коэффициент давления единой характеристикой распределения
давления по поверхности рассматриваемого тела для всех случа-
ев обтекания.
Определим пределы изменения коэффициента давления р.
При 0 = л и 0=0, как известно, sin 6 равен нулю и р = 1; при
0 = ±т/2 sin 6 равен единице и р=—3.
Таким образом, величина р достигает максимального значе-
ния в точках А и В (см. рис. 6.1).
В точках С н D коэффициент давления имеет минимальное
значение, т. е. здесь имеет место максимальное разрежение.
При симметричном распределении давления по поверхности
цилиндра результирующая сила давления потока на цилиндр
равна нулю.
Если в потоке идеальной жидкости взамен цилиндра располо-
жить тело произвольной формы, то при безотрывном, бесцирку-
ляционном обтекании результирующая сила давления на тело
также 65 дет равна нулю.
Рассмотренные теоретические выводы являются условными
в силу принятого предположения об идеальности жидкой среды.
В реальном потоке жидкости благодаря наличию вязкости
при движении любое тело испытывает сопротивление. Поэтому
экспериментальные данные по распределению давлений во мно-
гих случаях не совпадают с результатами теоретических рас-
четов.
При обтекании кругового цилиндра потенциальным потоком
идеальной жидкости поле давлений симметрично относительно
осей координат, проведенных через центр окружности, и, следо-
вательно, в этом спучае иа цилиндр не действуют никакие силы
При обтекании кругового цилиндра реальной жидкостью поле
давлений, оставаясь симметричным относительно оси абсцисс,
является несимметричным относительно оси ординат, что вызы-
вает появление проекции силы на направление движения -
силы сопротивления.
Экспериментальная и теоретическая (построенная по форму-
ле (6.10)) кривые изменения коэффициента давления р в зави-
симости от угла 6 показаны иа рис. 6.3. Результаты теоретичес-
ких расчетов (кривая /) и экспериментальные данные (кривые
2 и 3) почти совпадают лишь иа передней стороне цилиндра
вблизи 6=0, на задней же стороне срыв потока приводит к рез-
89
www.vokb-la.spb.ru - Самолёт своими руками?!
Рис 6.3 Сравнение теоретической и
экспериментальной кривых распреде-
ления давления по цилиндру при его
симметричном обтекании:
1—теоретическая кривая; 2—эксперимен-
тальная кривая (Re1.85 • 10е); 3—экспе-
риментальная кривая (Re=6,7- 105)
кому расхождению опытных и те-
оретических данных. В частности,
при углах 0 = 84°, 6 = 120° поток
перестает омывать цилиндр и
срывается с него, образуя за ци-
линдром вихревую область.
Теоретическая (1) и экспери-
ментальная (2) картины распре-
деления давления по сечению
кругового цилиндра при его сим-
метричном обтекании показаны
на рис. 6.4.
Рис 64. Распределение давления
по сечению кругового цилиндра,
помещенного в поступательный
поток:
1—теоретическое распределение давле-
ния; 2—экспериментальное
I
6 2. ЦИРКУЛЯЦИОННОЕ ОБТЕКАНИЕ КРУГОВОГО ЦИЛИНДРА
Рассмотрим циркуляционное обтекание кругового цилиндра,
получаемое при сочетании бесциркуляционного обтекания ци-
линдра и циркуляционного течения, обусловленного «плоским»
вихрем, совпадающим с осью цилиндра. В этом случае потен-
циал скорости равен сумме потенциала скорости симметричного
потока, обтекающего заданный круговой цилиндр (3.27), и по-
тенциала скорости вихря (частицы жидкости движутся по на-
правлению вдоль окружности по часовой стрелке) (4 24а);
(2 \
l+-^lrcos0—J-6. (6.11)
Натожение циркуляционного потока, как видим, нарушает
симметрию линии тока. Функция тока в рассматриваемом случае
90
www.vokb-la.spb.ru - Самолёт своими руками?!
«а основании формул (3.28) и (4.246)
Рис 6.5 Циркуляционное обтека-
ние жидкостью кругового цилинд-
ра при Г<4л1Лсг0
Рис. 6.6. Циркуляционное обтека-
ние жидкостью кругового цилинд-
ра при Г—4л17оГо
Проекции скоростей Vr и Vs в какой-либо точке потока опре-
делим с помощью потенциала скорости (6.11):
л / г2 \
1/г = ^=У0(1---- cos 6; (6. 13)
дг \ г2 /
=_L*t=_v (1+А)
г °\ г2/
sin 6
г
2лг
(6.14)
Из выражений (6 13) и (6.14) найдем значения скоростей
Vr и Vs на поверхности цилиндра (г=г0):
1/ =0; Vs------2V0 sin 6-----— . (6.15)
2лг0
Как видим, по абсолютной величине скорости течения жид-
кости над цилиндром больше, чем под цилиндром. Это объясня-
ется тем, что над цилиндром скорости плоскопараллельного по-
тока и чисто циркуляционного течения складываются, а под ци-
линдром — вычитаются (смена знака ysinO) Следует отметить,
что такое распределение скоростей имеет место при Г>0. Естес-
твенно, что наложение циркуляционного потока нарушает сим-
метрию линий тока относительно оси ОХ (рис. 6.5)
Если при бесциркуляционном обтекании точки с нулевыми
скоростями (А и В) лежали на оси ОХ (см. рис. 6.1), то в рас-
сматриваемом случае они располагаются ниже оси ОХ Положе-
ние этих точек (0 = Окр) найдем из формулы (6.15), полагая в
ней Vs=0:
sm екр=
Г 1
4л Уого
(616)
91
www.vokb-la.spb.ru - Самолёт своими руками?!
Очевидно, что прн Г<4лУоГо существует два критических
угла, расположенных в III н IV квадрантах, определяемых нера-
венствами
3
— л
2
я ®1кр
и -|- л < 02кр <2л.
При Г=4л Wo из формулы (6.16) получим
3
2
sin6..D—— 1 или 0КО
Л.
(6-17)
Это означает, что обе критические точки совмещаются в одну
(рис. 6.6). При Г>4лУоГо из (6 16) получим значение синуса»
Рис. 6.7. Циркуляционное обтекание
жидкостью кругового цилиндра при
Г>4л Wo
Рис. 6.8. Распределение дав-
ления по цилиндру при не-
симметричном обтекании
(Г^О)
большее единицы, что невозможно Это означает, что критичес-
кая точка «сходит» с цилиндра, а течение распадается иа ряд
областей, в одной из которых (7) имеет место движение по
замкнутым, хотя и не круговым, траекториям (рис 6.7)
Характериой особенностью рассматриваемого типа течения
является симметричность поля скоростей относительно осн ОУ
и отсутствие симметрии относительно оси ОХ В связи с этим
главный вектор сил давления жидкости на поверхность цилинд-
ра отличается от нуля и направлен вдоль оси ОУ.
Распределение давления при несимметричном обтекании ци-
линдра, соответствующем значению при Гт^О, показано
на рис. 6.8 Для получения приближенной картины циркуляци-
онного обтекания цилиндра в плоскопараллельном потоке надо
привести цилиндр во вращение вокруг своей оси.
92
www.vokb-la.spb.ru - Самолёт своими руками?!
6.3 ПОДЪЕМНАЯ СИЛА КРУГОВОГО ЦИЛИНДРА
В НЕСИММЕТРИЧНОМ ПЛОСКОПАРАЛЛЕЛЬНОМ ПОТОКЕ
Определим силовое воздействие плоского потока идеальной
жидкости, направленного перпендикулярно к образующим бес-
конечно длинного кругового цилиндра радиуса г0 (см. рис. 6 5)
Поскольку в рассматриваемой задаче цилиндр обтекается пото-
ком идеальной жидкости, то на его поверхность со стороны жид-
кости будут действовать нормальные силы, обусловленные дав-
лением.
Определим проекции равнодействующей сил давления на оси
ОХ н ОУ, обозначив их соответственно через X и Y. Выделим иа
цилиндре участок высотой, равной единице. Проекция элемен-
тарной силы давления pdsA на оси координат ОХ, ОУ в окрест-
ности точки, находящейся на окружности цилиндра, согласно
(6.3) имеют вид
dX =—р cos Bds‘, d¥ ~—р sin Ods.
Подставив в эти уравнения значения давления из интеграла
Бернулли (5.25) и заменив ds выражением г dQ, после интегри-
рования получим формулы для определения силы лобового соп-
ротивления X и подъемной силы Y
2к
Р f 172 \
Х= — I r0 С — q--------j cos 04/0; (6.18)
. J \ 2 J
о
’ V2 \
С — о—। sin 04/0.
2 /
(6. 19)
После подстановки в эти выражения скорости в виде (6.15)
формулы для определения X и Y принимают вид
2it
О
Г2
4л2Г0
2тс
ЛГо
F2
sin 0 j r0 cos 04/0;
(6 20)
Г2 2У0Г
—tvH-----— sm 0
4л2Го лг0
r0 sin 04/0.
О
(6.21)
Поскольку входящие в подынтегральное выражение (6 20)
интегралы
2тс
2it 2it
J sin2 0 cos 04/0; Г sin 0 cos 04/0
о 0
о
равны ну лю, то очевидно, А—О, т. е сила лобового сопротивле-
ния при циркуляционном обтекании кругового цилнидра беско-
93-
www.vokb-la.spb.ru - Самолёт своими руками?!
нечной длины потоком идеальной жидкости равна нулю. Такой
результат, как известно, не соответствует реальным условиям
обтекания, но является вполне логичным в силу принятого пред-
положения об обтекании тела потоком идеальной (невязкой)
жидкости. В подынтегральное выражение (6 21) входят также
(2п 2х \
I* sin Ог/О; J sin30z/0 I равны
о о /
(2к X
J sin2 Ог/О1 равен л.
о J
С учетом этих значений из выражения (6.21) получим, как
увидим далее, основную формулу аэродинамики, называемую
формулой Жуковского
Г-eVoT, (6.22)
из которой следует, что при обтекании бесконечно длинного ци-
линдра поступательно-циркуляционным потенциальным потоком
невязкой жидкости со стороны потока на цилиндр в направле-
нии оси ОУ действует сила, равная произведению плотности
жидкости на скорость набегающего невозмущенного потока и
на циркуляцию скорости по любому замкнутому контуру, охва-
тывающему обтекаемый цилиндр. Направление подъемной силы
можно определить, повернув вектор скорости невозмущенного
потока на прямой угол в сторону, противоположную направ-
лению циркуляции.
Отметим также, что в этом случае в точках, лежащих на од-
ной вертикали, давление на верхней поверхности цилиндра мень-
ше, чем на нижней; скорость течения, наоборот, на верхней по-
верхности больше чем на ннжней.
6.4 ТЕОРЕМА ЖУКОВСКОГО О ПОДЪЕМНОЙ СИЛЕ
ДЛЯ СЛУЧАЯ ОБТЕКАНИЯ ЦИЛИНДРИЧЕСКОГО ТЕЛА
ПРОИЗВОЛЬНОЙ ФОРМЫ
Выше была доказана теорема Жуковского для частного слу-
чая обтекания идеальной жидкостью кругового цилиндра беско-
нечной длины.
Теперь рассмотрим обтекание плоским потоком произвольно-
го тела и докажем, что теорема Жуковского справедлива и для
данного случая.
Если предположить, что вне цилиндра поток является без-
вихревым (потенциальным), то согласно теореме Стокса цирку-
ляция скорости по любому замкнутому конту ру, охватывающему
обтекаемый цилиндр, будет иметь одну и ту же для всех конту-
ров величину, которую мы обозначим через Г. Проведем далее
вокруг цилиндрического тела произвольной формы замкнутый
$4
www vokb-la.spb ru - Самолёт своими руками?!
конт-
ДВ 11-
Рис. 6.9. К доказательству
теоремы Жуковского для
произвольного плоского ксн-
тура
выде-
контур «S (рис. 6 9). Применим к жидкому объему, заключенно-
му между поверхностью тела L и произвольной поверхностью S>
которую мы будем называть
рольной, теорему о количестве
ження.
Поскольку вес жидкости в
ленном объеме уравновешивается из-
менением по высоте сил давления, рас-
пределенных по контрольной поверх-
ности, то мы не учитываем силу веса
и весовое давление, т. е рассматри-
ваем среду как невесомую. Кроме этих
сил, на выделенный объем жидкости
действует реакция со стороны тела и
давления, распределенные по контроль-
ной поверхности, силы трення не учи-
тываем (жидкость идеальная).
Определим количество движения, выносимое нз выделенного
объема за единицу времени, сквозь контрольную поверхность.
Выделим на контрольной поверхности 5 элементарную пло-
щадку ds l и проведем к ней внешнюю нормаль п, которая об-
разует с осями координат углы а и |3 (см. рис 6.9). Если проек-
цию скорости частиц, протекающих через площадку ds-1, иа
нормаль п обозначить через Vn, то, очевидно, что масса жидкос-
ти, протекающей в единицу времени сквозь эту площадку, будет
равна qV„z/s-1. Соответственно количество движения, переноси-
мое этой массой, запишется Количество движения рас-
сматриваемой массы жидкости, переносимое в единицу времени-
сквозь всю контрольную поверхность, выразится интегралом
[ Проекции этого количества движения на координат-
ор)
ные осн соответственно равны
j j QVyVnds.
(S) (S)
Определим теперь действующие на выделенный объем жид-
кости внешние силы и их проекции на координатные оси. Со-
стороны окружающей жидкости на контрольную поверхность
действуют силы давления, направленные перпендикулярно к по-
верхности. Сила, приложенная к площадке ds-l, равна pds,
проекции ее на оси координат соответственно равны — р cos ads.
и —р cos pds. Следовательно,
рх = ~ j Р cos ads и Ру = ~^ poos^ds.
($) (S)
Со стороны внутреннем границы выделенного объема жидко-
сти на тело действуют нормальные силы давления, приложенные
95-
www vokb-la.spb.ru - Самолёт своими руками?!
к поверхности тела L. В таком случае согласно третьему закону
Ньютона со стороны тела и а окружающую жидкость действуют
силы равные им по величине, но имеющие обратное направление.
Если проекции результирующей силы, действующей на тело со
стороны окружающей его жидкости, обозначить через X и Y, то
проекции силы реакции со стороны тела будут равны —X, —Y.
Импульсы этих сил за единицу времени будут —X и —У. Изме-
нение количества движения иа поверхности выделенного объема
жидкости за единицу времени равно по законам механики сум-
ме приложенных к поверхности внешних сил. В проекциях иа
«оси координат эта теорема запишется в виде
qVxVnds^—X— cos ш/s;
(S) (5)
J Q^Vnds=—К — f pcospds.
(S) ($)
(6. 23)
Соответственно силы, действующие иа тело со стороны окру-
жающей его жидкости, определяются следующим образом:
- А'- : — j qV xVnds — у р cos ads\
[S} (6.24)
Y= — QVyVnds — J* p cos $ds.
(S) (S) f
Таким образом, для определения силы лобового сопротивле-
ния тела X и подъемной силы У необходимо знать давление и
скорость в каждой точке контрольной поверхности. Подставив
в интегралы соотношений (6 24) значение давления, определен-
ное по формуле Бернулли (5.25) с учетом равенства cos£ =
— sin а, получим
Г с с qV"2
X —— I QVx]/nds — C \ cos ads—— cos ads; j
(S) (S) (S) I (6.25)
с с c
У:-—\ QVyVnds~C sin adssin ads. |
(S) (S) (S) '
В этих равенствах вторые интегралы равны нулю, так как
cos а —
dy
ds *
dx
sin а =-------,
ds
а при обходе по замкнутому контуру <S переменные х и у возвра-
щаются к своему первоначальному значению. Итак,
cos ads = — \
' J ds
(S) (S)
dy=O;
(S)
96
www.vokb-la.spb.ru - Самолёт своими руками?!
(' С dx С
\ sin ads=—\ ------ds = \ dx-Л).
J J ds J
(S) (S) (S)
Таким образом, равенства (6.25) принимают вид
=Q \ (“^ C°S ° "
(S)
К=q sin а — Vy]/njds,
($)
1
।
(6. 26)
Следует отметить, что формулы (6.26) получены для случая
несжимаемой жидкости. Когда скорость невозмущенного потока
направлена по оси ОХ и равна потенциал скорости можно
записать в виде
(х, у},
(6.27)
где q/(x, у) — потенциал добавочных возмущенных скоростей,
удовлетворяющих уравнению Лапласа. Учитывая выражения
(6.27), для проекций скорости Гх, Vy получим соотношения:
vr=4L=K»+4r-; (6-28)
(6.29)
ду ду
Функции q/(x> У) на бесконечности удовлетворяют условиям
—О, =0. (6.30
\ дХ /со \ ду /со
Выражение для скорости Уп
у dy ду dx । ду dy
dn дх dn ду dn
с учетом (6.28) и (6.29) принимают вид
Vп= ( cos а sin а. (6.31)
Полагая, что контур S настолько велик, что в силу условий
(6.30) величинами (дф'/дх)2 и (дф'/ду)2 можно пренебречь, оп-
ределим произведения V Кх и VnVy:
УгУх — Uсо -L cos а;
У Уу~Усоcos а.
4 626
97
www.vokb-la.spb.ru - Самолёт своими руками?!
С учетом этих выражений равенство (6 26) принимает вид
р ‘ оК2 р
X — \ Vnds-}—cos ads.
(S) (S)
Интеграл j* $Vnds представляет собой расход жидкости
сквозь замкнутый контур. Поскольку внутри контура отсутству-
ют источники или стоки, этот интеграл равен нулю. Кроме то-
го, из геометрических соображений следуетJ cosar/s=0. Таким
(5)
образом X — 0, т. е. сила лобового сопротивления тела, обтекае-
мого плоскопараллельным потоком идеальной жидкости, равна
нулю. Этот результат (парадокс Даламбера — Эйлера) мы уже
получили в частном случае для кругового цилиндра. Перейдя ко
второму равенству (6.26), будем иметь
с
У=~Q—— \ sin ads—оК» \ Vsds,
r 2 J
(5) (S)
где K_—-2-= — sin a 4—— cos a.
ds \ gx J ' dy
Первый член этого равенства равен нулю, а второй согласно
(4.7) представляет собой циркуляцию скорости по замкнутому
контуру, следовательно,
У=-СУсоГ. (6.32)
Результат, выражаемый формулой (6 32), обычио формули-
руется в виде теоремы Жуковского: если поток, имеющий в бес-
конечности скорость Коо, обтекает контур, и циркуляция скорос-
ти по этому контуру равна Г, то равнодействующую сил давле-
ния жидкости на контур получим, если умножим вектор, пред-
ставляющий скорость потока в бесконечности, на циркуляцию
скорости и на плотность жидкости. Таким образом, получена
формула для определения подъемной силы единицы длины ци-
линдрического тела бесконечного размаха. Знак минус, стоящий
в правой части формулы, дает возможность установить направ-
ление действия силы. Если зиаки V» и Г различны, то сила
будет положительна и паправтена вверх, при одинаковых знаках
Коо и Г подъемная сила направлена вниз.
Следует отметить, что при доказательстве теоремы предпо-
лагалось, что поток, обтекающий тело, плоскопараллельный.
Таким можно считать поток, обтекающий цилиндрическое крыло
бесконечиого удлинения.
Из теоремы Жуковского следует: для получения подъемной
силы тела произвольной формы, обтекаемого плоскопаралтель-
98
www.vokb-la.spb.ru - Самолёт своими руками?!
ным потенциальным потоком, необходимо обеспечить такое ско-
ростное поле, при котором циркуляция скорости по замкнутому
контуру вокруг крыла была бы отлична от нуля Для кругового
цилиндра, обтекаемого вязким потоком, этого можно достичь
вращением цилиндра В идеальном невязком потоке в этом не-
обходимости нет — соответствующим подбором формы тела с
заостренной задней кромкой можно добиться его обтекания с
циркуляцией Г=£0. Эта циркуляция будет создаваться не реаль-
ным, а фиктивным вихрем. Жуковский назвал его «присоединен-
ным». Очевидно, что Г — есть циркуляция скорости, обусловлен-
ная наличием вихря.
Таким образом, при определении подъемной силы можно
представить себе крыло замененным одним или несколькими
присоединенными вихрями, которые будучи неподвижно связаны
с крылом, создают в потоке такую же циркуляцию скорости по
любому замкнутому контуру, охватывающему крыло, какую в
действительности создает крыло. На возможность замены тела
эквивалентной системой присоединенных вихрей указал впервые *
Жуковский еще в 1905 году. Эта идея Жуковского оказалась ис-
ключительно плодотворной для решения многих практических
задач не только в авиастроении, но и в турбостроении, корабле-
строении и др.
Теорема Жуковского указывает также путь повышения подъ-
емной силы крыла при данной скорости его движения в потоке
путем увеличения циркуляции скорости по контуру, охватываю-
щему крыло.
Циркуляцию же можно увеличить различными способами,
например, увеличением кривизны крыла, воздействием на погра-
ничный слой, приведением в движение части поверхности крыла
и т д. В общем случае при движении тела в жидкости циркуля-
ция скорости вокруг него будет изменяться с течением времени.
Если циркуляция скорости по произвольному контуру, охваты-
вающему тело, переменна во времени, то такой поток не может
быть везде потенциальным. Он должен содержать отдельные
или непрерывно распределенные вихри.
Теорема Жуковского для случая произвольного движения
крыла в идеальной несжимаемой жидкости была доказана
Л И. Седовым {58].
6 5 ВОЗНИКНОВЕНИЕ ЦИРКУЛЯЦИИ СКОРОСТИ
И ПОДЪЕМНОЙ СИЛЫ НА КРЫЛЕ
постулат Жуковского — чаплыгина
Следует отметить, что вопрос об истинной величине циркуля-
ции скорости, входящей в формулу Жуковского, является в об-
щем случае неопределенным. Строго говоря, с точки зрения тео-
www vokb-la.spb ru - Самолёт своими руками?!
Рис 6 10 К пояснению посту-
лата Чаплыгина — Жуковско-
го:
а—Г.>0, гГ-Г2^О; в—Г3<0; г—Г*<0;
(|Г*1 > |Г8[)
рии идеальной жидкости эта величина может быть произволь-
ной, так что решение задачи об обтекании профиля получается
неоднозначным. Поэтому любому
произвольно выбранному значе-
нию Г соответствует некоторое
конкретное решение. На рис. 6.10
показаны полученные теоретичес-
ким расчетом некоторые потоки
идеальной жидкости, обтекаю-
щие профиль крыла и соответст-
вующие различным значениям
циркуляции. Если воспользовать-
ся теоремой Жуковского о подъ-
емной силе, то в каждом потоке
мы получим для одного и того же
тела различные значения подъ-
емной силы.
Чаплыгин впервые подметил,
что для каждого обтекающего те-
ло потока весьма характерно по-
ложение задней критической точ-
ки, каждому значению циркуля-
ции вокруг контура, охватываю-
щего тело (а значит и подъемной
силы) соответствует вполне опре-
деленное положение задней кри-
тической точки — точки схода
струй с крыла. Вместе с те i
Чаплыгин указал, что в том случае, если профиль крыла имеет
заднюю кромку в виде угловой точки и при этом задняя крити-
ческая точка не совпадает с задней кромкой, то теоретическое
значение скорости у последней стремится к бесконечности. Так
как при реальном обтека: ин бесконечно большие скорости фи-
зически невозможны, то Жуковский н Чап. ыгин приняли допу-
щение (постулат Жуковского — Чаплыгина), согласно которо-
му при обтекании профиля с острой задней кромкой физически
реализуется такое (единственное) значение циркуляции, при
котором задняя крити геская точка совпадает с задней кромкой.
Таким образом, для случая профиля с острой задней кромкой
постулат Ж\ ковского — Чаплыгина, косвенно у читывающий
влияние вязкости и в действительности регулирующий циркуля-
цию, позволяет определить величину циркуляции и, следователь-
но, подъемной си. ы
Для профилей с закр г енной ; адней кромкой постулат Жу-
ковского — Чаплыгина неприменим. Для получения однознач-
ного решения в этом случае необходимо иным обра ом задать
дополнительное условие. Однако эта задача полностью до сих
пор не решена.
100
www.vokb-la.spb.ru - Самолёт своими руками?!
Наблюдения показывают, что в начале движения крыла име-
ют место течения, близкие к изображенному на рис. 6 10, в, ког-
да задняя критическая точка находится на острие задней кромки.
Заметим также, что формирование вихрей за крылом проис-
ходит не только при разгонном движении крыла, т. е. при воз-
никновении циркуляции на крыле, ио и при замедленном движе-
нии, т. е. при исчезновении циркуляции, только в последнем слу-
чае за крылом будет формироваться вихрь противоположного
знака.
Теорема Жуковского о подъемной силе крыла и постулат
Чаплыгина — Жуковского о конечности скорости на задней
кромке крыла, определяющий величину наложенной циркуляции
(или же интенсивность присоединенного вихря), разрешают
проблему теоретического определения подъемной силы и силово-
го воздействия потенциального потока на обтекаемое тело сост-
рой задней кромкой. Их можно считать основой современной '
аэродинамики.
Вопросы для повторения
1 Объясните физический смысл парадокса Даламбера —
Эйлера.
2 Что такое коэффициент давления?
3 Чем отличается бесциркуляционное обтекание цилиндра от
циркуляционного?
4 . Объясните физический смысл теоремы Жуковского о
подъемной силе.
5 . Поясните значение постулата Жуковского — Чаплыгина
для определения подъемной силы на профиле.
Задачи
1. Во сколько раз изменится подъемная сила единицы раз-
маха крыла в соответствии с теоремой Жуковского при том же
угле атаки н той же скорости, если высота полета Н изменится
с 5000 до 15000 м.
О т в е т: Уп- 5оооМ7н—isooo = 3,08.
2. Определить распределение давления по сечению вихря,
если его ядро, вращающееся по закону твердого тела с угловой
скоростью о), имеет радиус /?0- Газ считать несжимаемым
Решение: Составим условие равновесия элементарного
цилиндрического с поя:
kr^drrdti= —prdft -\-d prdti~— prd$-\- \{prdb-\-{dp!dr') • rdrdty],
откуда и При г—/?0, £—C’o имеем p=pQ—
www.vokb-la.spb.ru - Самолёт своими руками?!
ГЛАВА 7
ОСНОВНЫЕ СООТНОШЕНИЯ ГАЗОВОЙ ДИНАМИКИ
7.1. ОСНОВНЫЕ СООТНОШЕНИЯ ДЛЯ ОДНОМЕРНЫХ
ИЗЭНТРОПИЧЕСКИХ УСТАНОВИВШИХСЯ ТЕЧЕНИЙ ГАЗА
При приближенных расчетах течение газа в трубе с перемен-
ным сечением в большинстве случаев можно рассматривать как
Рис 7.1. Одномерное изэнтропическое
течение газа
одномерное. Одномерным ус-
тановившимся течением на-
зывается течение, при котором
все газодинамические и термо-
динамические величины газо-
вого потока являются функци-
ями одной переменной.
Рассмотрим изэнтропичес-
кое течение газа вдоль трубки
тока (рис. 7.1). Обозначим па-
раметры газового потока ТЛ, U
Л, pi, Ci в сечении AtBi и V, I,
Т, р, Q в сечении АВ. Запишем далее уравнение энергии (5.28)
применительно к этим двум сечениям:
ь . V? k .Г2
-Z—R1\-{---*- = -^RT+ — .
k-1 1 2 k-1 2
Если предположить, что во входном сечении сопла скорость
Vt = O (состояние покоя), энтальпия io и температура TG, то при
изэнтропическом процессе течения газа в сопле получим урав-
нение
, (7.1)
£-1 « /,-1 2
откуда "7" * ^7‘2^
Температура TG называется температурой торможения (иа*
пример температура воздуха на передней кромке крыла само-
лета, где скорость V—0).
102
www vokb-la.spb.ru - Самолёт своими руками?!
Прирост температуры при торможении ДГ— Го — Г — * 1 .
Для воздуха А—1,4; Л? = 287,14 м2/с2 град, •
Действительный прирост температуры может быть несколь-
ко меньше, так как в реальных условиях процесс торможения не
является строго изэнтропическим Особенно велик прирост тем-
пературы при полете со сверхзвуковыми скоростями.
Параметры: температура TG, давление ро, плотность q0» теп-
лосодержание i‘o, характеризующие состояние воздуха при ско-
рости, равной нулю, называются параметрами изэнтропического
торможения. При известных скоростях движения или числе М
параметры течения можно выразить через параметры торможе-
ния. Так, разделив обе части уравнения (7.2) на Т, по пучим
выражение для безразмерной температуры заторможенного газа
Zo = 1 I ^-1 V2
Т ' kRT 2
или с учетом (1.25)
= (7.3)
Г 1 2 fl2 1 2 v
Теплосодержание i прямо пропорционально температуре (см.
формулу 1.16), следовательно,
(7.4)
I Т 1 2 k
Для представления давления и плотности через параметры
изэнтропического торможения воспользуемся соотношениями,
вытекающими из уравнения состояния (1.4) и уравнения изэнт-
ропического процесса (1-22):
тр__/ Qo У"1_/ Ро \~Т~
Т \ Q / р )
Подставив в это выражение значение То/Т в соответствии с
(7.3), получим
^_(1-|-^рМ2)~! ; (7.5)
1 а
^=1 1 -Ь-—-М3)*-1. (7.6)
Полученные зависимости показывают, что с увеличением ско-
рости течения давление, плотность, температура и теплосодер-
жание газа уменьшаются.
103
www.vokb-la.spb.ru - Самолёт своими руками?!
Поскольку квадрат скорости звука в воздухе прямо пропор-
ционален температуре, то на основании уравнения (7.1) можно
сделать вывод, что местная скорость звука зависит от скорости
течения. Для установления связи между скоростью течения и
местной скоростью звука в явной форме запишем уравнение
энергии (7.1) в виде:
Ъ V2
—р —
1 ° k- 1 2
Из этого уравнения следует, что скорость распространения
звука в газовой среде наибольшая при У=0: UQ2=kRTQ,
При дозвуковом течении местная скорость звука больше ме-
стной скорости течения, при этом с увеличением скорости тече-
ния она уменьшается. При сверхзвуковом течении местная ско-
рость звука меньше скорости течения. Режим течения газа, при
котором его местная скорость равна местной скорости звука, на-
зывается критическим. В этом случае критическими называются
и такие параметры течения газа, как давление ркр, плотность gKpi
температура Ткр.
Критическую скорость аКр можно определить из равенства
(7.7), полагая в нем a = v = «кр,
<7-8)
Учитывая уравнение состояния (1.4) и формулы (1.25),
(1.16), для критической скорости можно получить еще и следую-
щие соотношения:
-^=—а’=—2/0.
Р к + 1 Qo А- + 1 ° к + 1
Критические параметры определяются соотношениями (7.3),
(7.5), (7.6) , если положить в них М = 1:
. (7> Ю)
^кр 2
; (7.11)
ркр \ 2 /
£o=M+lto . /7.
Окр \ 2 /
Например, для воздуха (&=1,4) найдем Ткр/Т0 == 0,831;
ркр/р0=0,528; е«р/ео=0,636. Число М является параметром, по
которому определяется характер течения (дозв} ковое или сверх-
104
।
।
wwift vokb-la.spb.ru - Самолёт своими руками?!
зв новое) Однако этот параметр не всегда удобен в расчетах
хотя бы потому, что из-за изменения местной скорости звука
местная скорость течения не пропорциональна местному числу
М. Поэтому наряду с числом М, широкое распространение по-
лучил другой параметр, называемый коэффициентом скорости
и равный отношению скорости течения к критической скорости:
Х_— . (7. 13)
акр
При дозвуковой скорости течения М<1 и Л<1, при сверх-
звуковой М>1 и Л>1. При скорости течения, равной критичес-
кой, М —Л = 1. Критический режим единственный, когда числен-
ное значение М равно X. При других скоростях течения их чис-
ленные значения отличаются.
Для установления связи между числами ?. и М возведем в
квадрат обе части равенства (7 13) и, учитывая, что V—М«, вы-
разим местную скорость звука и критическую скорость
местную и критическую температуры
акр 1 кр
Отношение температур TfTvv найдем из соотношении
и (7.3):
Т £4-1
Гкр 2 + (*-1)М2 *
Подставляя это выражение в предыдущую формулу,
чим
2— (* + НМ2____
" 2 + (£ — 1)М2
При изменении скорости течения число М изменяется
рее, чем коэффициент скорости X. При неограниченном возраста-
нии числа М у двуатомных газов (k—1,4) величина X2 стремит-
ся к пределу, равному шести. В расчетах коэффициент скорости
Л может быть использован наравне с числом М Входящий в фор-
Ь_ 1
мулы (7 3), (7.5), (7.6) двучлен 1 —-у— М2 может быть выра
жен через коэффициент 1:
------ -----= I *212 X2
через
(7.10)
(7. К)
полу-
(7. 15)
бы ст-
105
www vokb-la.spb ru - Самолёт своими руками?!
так что формулы связи между параметрами торможения и па-
раметрами потока могут быть преобразованы к следующему
виду:
—= 1-^—(7.16)
Го к + 1 7
(7.17
Qo \ *+1 ) J
k
_А=Л (7.18
ро \ k I }
При Л=1 они примут вид формул (7 10) — (7.12) для пара-
метров газа в критическом режиме течения
Очень часто при анализе течения газа используется такой
параметр как максимальная скорость, равная скорости, при ко-
торой температура газа равна нулю. Следует отметить, что мак-
симальная скорость представляет собой математическую абст-
ракцию или теоретический физический предел, в то время как
критические параметры — вполне реальные физические вели-
чины.’’Из уравнения (7.1) видно, что по мере увеличения скорос-
ти течения температура убывает и при некотором максимальном
значении скорости становится равной нулю. Полагая в уравне-
нии (7 1) Т=0, получим выражение для У= Vmax:
9b
(7-19)
JrC 1
Используя формулы для определения критической скорости
(7.7) и (7.9), из уравнения (7 19) получим
1/2=-----==-А_й2=-------- (7.20)
max k~ 1 кр k— 1 0 k— 1 Qo k— 1
Для воздуха при T0 = 288 К Утах=756 м/с. Максимальная
скорость соответствует переходу всей внутренней эи ‘ргии в энер-
гию кинетическую Скорость, близкая к максимальной, может
быть получена при истечении газов из сопла ракеты, летящей в
космическом пространстве.
Разделив почленно равнение (7 7) на его правую часть, по-
лучим уравнение энергии для струйки газа:
Для каждой струйки газа зависимость между скоростями V и
а графически изображается эллипсом с полуосями Ушах и «о
106
www vokb-la.spb.ru - Самолет своими руками?!
7.2. ЗАВИСИМОСТЬ МЕЖДУ ПЛОЩАДЬЮ ПОПЕРЕЧНОГО
СЕЧЕНИЯ СТРУЙКИ И СКОРОСТЬЮ ГАЗА
Как известно, основные параметры газового потока изменя-
ются при изменении площади поперечного сечения газовой
струйки. При анализе этого явления воспользуемся уравнением
Эйлера для установившегося одномерного движения (предпола-
гая, что ось струи газового потока совпадает с осью ОХ) и урав-
нением неразрывности (2.15):
V—— = —-—— ; gl/a=const.
dx q dx
После дифференцирования последнего уравнения и деления
членов полученного выражения на gVo получим
откуда
d/Q . dV ( da Q
Q V ' а
/ \
dQ dV dV / q \
er q V V I dV j
\ V /
(7. 22)
Используя уравнение Эйлера, предыдущую формулу запишем в
виде
da dV
V
- 1
a
или с учетом того, что для
dQ 1
изэнтропического процесса —— =—
dp а2
в виде
da
dV
(7. 23)
или
da
а
dV х.2
— (М—
а
Уравнение (7 23), называемое уравнением Гюгонио, устанавли-
вает связь между площадью поперечного сечения струйки и ско-
ростью изэнтропического течения идеального газа. На основа-
нии анализа этого уравнения можно сделать следующие вы-
воды:
/ V2 \
1. При V <cl (М<1) {—-—1 <0 и, следовательно, знаки
\ a2 J
do и dV противоположны, т. е. при дозвуковом течении газа, так
же как и в случае несжимаемой жидкости, с возрастанием пло-
щади поперечного сечения вдоль струйки скорость в ней убы-
вает, а давление увеличивается и, наоборот, при уменьшении
площади поперечного сечения скорость возрастает, а давление
убывает.
107
www.vokb-la.spb ru - Самолёт своими руками?!
2. При 1/^>л(М^>1) I-------1} 3> 0 и, следовательно, знаки
\ а2 /
do и dV совпадают, т. е. при сверхзвуковом течении газа с воз-
растанием площади поперечного сечения вдоль струйки ско-
рость в ней возрастает, а давление убывает и, наоборот, при
уменьшении площади поперечного сечения скорость уменьшает-
ся, а давление увеличивается. Это объясняется тем, что, напри-
мер, возрастание скорости при сверхзвуковом течении газа свя-
зано не только с изменением давления, но и с уменьшением
плотности, при этом относительное изменение плотности превос-
ходит по величине относительное изменение скорости.
3. Прн V=&(M=1)----------1 = 0, т е. do=0. Это означает, что
а2
в месте, где скорость движения газа достигает скорости распро-
странения звука в нем, поперечное сечение струйки газа должно
достигать своего максимального нли минимального значения.
В максимальном сечении скорость течения газа не может быть
равной скорости звука, так как максимальному значению попе-
речного сечення струйки предшествует расширяющийся участок,
в котором при дозвуковом течении скорость убывает, а при
сверхзвуковом возрастает. Следовательно, скорость изэнтропи-
ческого течения газа может достигнуть скорости звука только в
минимальном сечении. Минимальное сечение газовой струи,
в котором V=а = акр, называется критическим.
Следует отметить, что одним сужением дозвуковой струи
газа нельзя получить сверхзвуковые скорости течения Обычно
непрерывный переход от дозвуковых скоростей к сверхзвуковым
при изэнтропическом течении газа осуществляется в канале
переменного сечения. В сужающейся части канала скорость те-
чения доводится до критической, а в расширяющейся части реа-
лизуются уже сверхзвуковые скорости. На таком принципе по-
строено сопло Лаваля, используемое для получения сверхзвуко-
вых скоростей истечения газа.
7.3 РАСЧЕТ СВЕРХЗВУКОВОГО СОПЛА
Сопло Лаваля представляет собой насадок, состоящий из ко-
роткой сужающейся части и следующей за ней более длинной
расширяющейся части. Если через сопло Лаваля протекает газ
со скоростью, меньшей скорости распространения звука, то во
входной части сопла скорость нарастает, в наиболее узком сече-
нии достигает максимума и в выходной части убывает (кривая
I на рис. 7.2).
Если через сопло газ протекает со сверхзвуковой скоростью,
то во входной части сопла скорость уменьшается, в наиболее уз-
ком сечении (Л—Л) достигает минимального значения и в вы-
ходной части нарастает (кривая II на рис 7.2). Если в наиболее
узком сеченин V=a, то обе кривые соприкасаются в точке, со-
108
wwre vokb-la.spb.ru - Самолёт своими руками?!
ответствующей этому сечению, при этом поток продолжает ус-
коряться вдоль сопла, и распределение скорости переходит
с кривой типа I на кривую типа II, т. е. в этом случае происхо-
дит плавный переход от дозвуковой скорости к сверхзвуковой.
Рассмотрим изэнтропическое изменение давления вдоль оси
сопла, соответствующее различным случаям течения газа. По
кривой I происходит изменение давления в случае чисто дозву-
кового течения, по кривой II — в случае чисто сверхзвукового
Рис. 7.2. Распределение скорости (а) и давления
(б) газа вдоль сопла Лаваля
течения. И в первом и во втором случаях давление нигде не
достигает критического значения ркр. По кривым III и IV про-
исходит изменение давления при переходе через скорость звука
в наиболее узком сечении сопла (Р=акр), при этом кривая III
характеризует разгон газа от дозвуковых до сверхзвуковых ско-
ростей, а кривая IV — изэнтропическое торможение газа от
сверхзвуковых скоростей до дозвуковых скоростей.
Для сопла Лаваля типичной является кривая III. Следует
отметить, что эти кривые имеют в основном только теоретичес-
кое значение, так как трение и наличие скачков уплотнения при
течении реального газа в соплах нарушают изэнтропический ха-
рактер течения.
Рассмотрим истечение газа через сопло из достаточно большого резер-
вуара, в котором скоростью Vo можно пренебречь, а остальные параметры
(плотность, давление и температура) являются параметрами торможения
Применим уравнение энергии (7 1) для двух сечений, первое из которых—
сечение в резервуаре, второе — на выходе из сопла:
ь k V"2
— ^~ГГТ^ + -, <724>
откуда скорость течения газа в выходном сечении, т. е. скорость истечения,
запишется в виде
(7. 25)
109
wwm vokb-la.spb.ru - Самолёт своими руками?!
Р
Ро
ft [равенство (1.22)], поэтому вираже -
Согласно уравнению состояния газа (1.4) RTo^po/p0t а для изэнтропичес-
у. . k 1
кого течения справедливо-----=
Го
ние (7.25) примет вид
(7. 26)
Очевидно, что при дозвуковом истечении давление р и температура Т в
выходном сечении сопла будут равны соответственно давлению и темпера-
G,kz/c
итах
Сверхзву- \Дозви\.
новые новые \
режимы 'режимы \
О р„„/р„ 1 р/р0
Ркр/ро
туре внешней среды, т. е. р — рБК. Из полу-
ченной формулы видно, что скорость исте-
чения V тем больше, чем выше температура
газа Гц в резервуаре и чем меньше давле-
ние на выходе из сопла р.
При р/р0=1 1А=0, т. е. истечение от-
сутствует.
При p/p<—0 V=Vn,ax, т. е. истечение
происходит с максимальной скоростью:
2* Ро
k— 1 Qo
Рис. 7.3. Изменение расхода G
в зависимости от относительно-
го давления р/ро
что согласуется с формулой (7.19).
Весовой расход газа является одинаковым для всех сечений сопла
случае изэнтропического истечения определяется по формуле
и в
1
G = qc[7 = Qo с И — Qo \
Qo \ Ро!
(7. 27)
После подстановки в последнее соотношение выражения для скорости
истечения (7.26) получим
(7.28)
По мере уменьшения отношения р/ро расход G увеличивается и при
1 2 4 Й
—-----= {--------1 (для воздуха прн /?=1,4 ркр/ро = О,528) достига-
Ро Ро \&+ 1 '
ет максимального значения При дальнейшем уменьшении отношения р/ро
скорость истечения из сопла становится сверхзвуковой, относительное давле-
ние больше не влияет на величину расхода (рис. 7.3) и наступает явление
«запирания» критического сечения.
Постоянство расхода газа при сверхзвуковом истечении из сопла объяс-
няется тем, что изменение внешнего давления на выходе из сопла распро-
страняется как малое возмущение со скоростью звука, а поток является
сверхзвуковым, и внешнее возмущение не может распространяться против
потока внутрь сопла. Только при дозвуковой скорости истечения давление на
выходе из сопла может быть равно давл' нию внешней среды. При сверхзву-
ковом же истечении давление на выходе из сопла не зависит от внешнего
давления. В силу этого формула (7 28) справедлива и для сверхзвукового ис
течения.
Для двух сечений сопла, -выходного и критического (V=aKp), из уело
вия постоянства расхода можно записать G^poV = pKpOi(p«Kp-
110
www.vokb-la.spb.ru - Самолёт своими руками?!
Но в критическом сечении сопла согласно (7.8) скорость
— дКр —
2А р0
k + 1 Q
(7.29)
и ее величина зависит только от состояния газа в резервуаре. Расход газа
в этом случае запишется в виде
„ 6кр / 2 i /
^тах — Qo °крйкр — I , ,1 I/ , , . 6ойО®кр —
УО 1” 1 / у Л + 1
При k = 1,4 и R = 287,14 Дж/кг-град
^тах 0,048сКр __ кг/с, (7.30)
V 7о
т. е. максимальный расход газа зависит от величины критического (мини-
мального) сечения сопла и от параметров торможения (состояния газа в ре-
зервуаре).
На кривой зависимости весового расхода от относите чьи ого давления (см.
рис. 7.3) максимальному расходу соответствует Gmax = Окр«кр°кр-
Для установления связи между давлением и площадью сечения сопла
при сверхзвуковом изэнтропическом истечении воспользуемся уравнением рас-
хода дли двух сечении G = QiViaj = Q2^2°2
02 Q[V\ Q йкр
или — —---------= ---------,
°1 62^2 Q2V2
(?Ойкр
Учитывая соотношение (7.17) для р/ро и обозначая У/дкр<=Л, получим
£2
а1
Л1 I Л1
1
(7.31)
Как видно из этой формулы, отношение площадей поперечного сечения
струи в двух произвольных сечениях сопла зависит от Л2 и природы
газа. Если скорости V и акр, входящие в выражение для коэффициента Z,,
выразить соответственно соотношениями (7.26) и (7 29), то получим
(7. 32)
Если положить далее в формуле (7.31) о2—о, tfi = crKp, ?2=Z, и Ai=l, то вэт м
случае формула будет иметь вид
(7.33)
Ш
www vokb-la.spb ru - Самолёт своими руками?!
Эта формула с учетом (7.32) принимает вид:
или
(7.34)
Таким образом, при известном контуре сопла и заданных внешнем дав-
лении и отношении о7окр относительное давление р/р0, температура T/Го и
плотность р/ро в каждом сечении сопла являются определенными величинами.
Отметим, что формулы (7.33) и (7.34) справедливы как для дозвукового, так
и для сверхзвукового истечения газа через сопло. Учитывая равенство (7 15),
мож io выразить отношение а/окр (7.33) в зависимости от числа М
а
°кр
й-1
-----Др И*"1)
2 /
Для воздуха при й=1,4 эта формула принимает вид:
2____(1 +0,2М2)3
акр ~ 1.73М
(7. 35)
(7.36)
Используя приведенные выше формулы, можно провести элементарный
расчет сопла. При равенстве расчетного давления на срезе сота р и внеш-
него давления режим течения внутри сопла называется расчетным. Во всех
случаях течения газа в сопле, когда внешнее давление не равно расчетному
вя, б льше или меньше), режим течения называется нерасчетным.
В правильно выполненном сопле плавное увеличение скорости до расчет-
ной будет осуществляться только на расчетном режиме работы, при котором
давление на срезе сопла равно давлению окружающей среды Методика про-
филирования сверхзвуковых сопел и анализ их работы на переходных режи-
мах не входят в программу данного курса.
7.4. ПОЛУЧЕНИЕ СВЕРХЗВУКОВОГО ПОТОКА
В ПОРИСТОЙ ЦИЛИНДРИЧЕСКОЙ ТРУБЕ
Кроме сопла Лаваля для получения сверхзвуковых скоростей
истечения газа используются и другие, так называемые негео-
метрические сопла: расходные, тепловые, механические и т. д.
Так в цилиндрической трубе постоянного сечения с пористыми
стенками масса движущегося газа m — qVo является перемен-
112
www vokb-la.spb ru - Самолёт своими руками?!
ной. После дифференцирования уравнения переменной массы по
х и деления на poV получим
1 dQ । 1 dV , 1 da 1 dm
Q dx V dx a dx tn dx
Воспользуемся далее уравнением Эйлера V -----------
а также равенством
dp dp dQ dQ
dx dQ dx dx
и после несложных преобразований получим уравнение
1 \ dV .I
V J dx а
da 1 dm
dx m dx
которое с введением числа M принимает вид
(Ма- 1) —
dx
V da V dm
a dx tn dx
(7.37)
В случае течения в цилиндрической трубе постоянного сече-
ния doldx — Q последнее уравнение принимает вид
(М2 — 1) — =—. (7.38
dx tn dx
Анализируя это уравнение, можно заключить, что подача
газа в трубу увеличивает скорость дозвукового течения (М<1,
dm.ldx>Q, dV/dx>0) и уменьшает скорость сверхзвукового те-
чения (М>1, dmldx<S), dV/dx<0). Удаление .аза из трубы
уменьшает скорость дозвукового течения (М<1, dm}dx<zS}) и
увеличивает скорость сверхзвукового течения (М>1, dmldx<C.Q').
Скорость звука достигается в некотором критическом сечении
в котором изменение массы, движущейся по трубе dmidx, равно
пулю. Используя эту зависимость, можно создать так называе-
мое расходное сопло.
Так, если в цилиндрическую трубу с дозвуковой скоростью
на входе подавать через стенки газ (рис. 7.4, а), то скорость по-
тока растет, достигая в критическом сечении скорости звука.
Если за этим сечением газ отсасывать из трубы, то скорость до-
полнительно возрастет, достигая заданного сверхзвукового зна-
чения.
Следует отметить, что в геометрическом сопле на расчетном
режиме можно получить поток только с одним заданным чис-
лом М. Расходное же сопло путем изменения расхода массы
вдоль сопла позволяет получить различные сверхзвуковые по-
токи.
113
www vokb-la.spb.ru - Самолёт своими руками?!
Принцип работы теплового сопла аналогичен расходному,
оказывают такое же действие, как
отвод и подвод газа в цилиндриче-
ской трубе (см. рис. 7.4, б).
Кроме геометрического, рас-
ходного, теплового и механичес-
кого способов получения сверх-
звуковых скоростей, можно вос-
пользоваться комбинациями ука-
занных сопел.
Переход от сверхзву ковой ско-
рости к дозвуковой теоретически
возможен в канале, который су-
жается в сверхзвуковой зоне при
одновременном уменьшении ско-
рости течений до величины акр, а
затем расширяется в дозвуковой
зоне, причем уменьшение скоро-
сти выполняется плавно. Однако
в природе непрерывным является
только процесс увеличения ско-
рости от дозвуковой до сверхзву-
ковой. Всякое торможение сверх-
звукового потока имеет скачко-
образный характер (сверхзвуко-
вая скорость скачкообразно переходит в дозвуковую). Природа
скачков, причины их появления и закономерности изменения
параметров на скачках уплотнения газа рассмотрены в следую-
щей главе.
так как отвод и подвод тепла
а - —
b -
О
С
с
ZZ)
По ввод газа.
Отвод газа
d
D
d
t / f // Q Utifi/viJ fffUfffr
V
c
Подвод
тепла g Отвод тепла
Ц ..
ТПТГШЛ1Г
d
S)
Рис. 7 4 Геометрическое (а), рас-
ходное (б) и тепловое (в) сопла
Вопросы для повторения
1. Чем объяснить более быстрое возрастание числа М по
сравнению с коэффициентом скорости 1 при увеличении скорос-
ти потока?
2. Какие параметры характеризуют полную энергию потока?
3. Как связаны параметры торможения с критическими пара-
метрами газа?
4. Чем объясняется увеличение скорости сверхзвукового по-
тока в расширяющемся сопле?
5. Каким образом можно получить сверхзвуковое течение в
цилиндрической трубе?
Задачи
1 Определить скорость истечения газа из дозвукового сопла
реактивного двигателя при полете на высоте 8000 м, если тем-
пература торможения То“970 К и давление заторможенно о
114
www vokb-la.spb ru - Самолёт своими руками?!
потока ро~О,552-1О5 Н/м2. Принять значения газовой постоян-
ной /?=287 дж/кг-град, показателя адиабаты £=1,4.
Решение: определим значения коэффициента скорости в
выходном сеченин сопла нз формулы
k
Р___/1__£ 1 }2 'fcZi.
ро \ £ + 1 /
Дя=8000м =0,356- 10s Н/м2, 0,775.
Определяем критическую скорость
|/ Oh(,=570 м/с;
У k + 1
V =ллкр=0,775-570=442 м/с.
2. Определить весовой расход воздуха через аэродинамичес-
кую трубу и разреженность в рабочем участке, если воздух за-
сасывается из состояния покоя с параметрами р0 = 105 Н/м2,
Уо= 1 225 кг/м3. Скорость в рабочей части трубы 200 м/с. Пло-
щадь сечения рабочего участка о = 0,01 м2.
Решение: Определяем критическую скорость и коэффици-
ент скорости в рабочей части трубы
/2k рГ)
k + 1 Qo
2,8 1Q5
2,4 1,225
=308 м/с,
).=200/308=0,65.
Определяем давление н плотность воздуха в рабочем участке:
JL = [ 1 „^_х2^ = 0,83;
до \ £4-1 /
—=( 1 — = 0,774;
Qo \ £ +1 /
А=0 83- 10s Н/м2; е = 0,774 1,225 =0,99 кг/м3;
^p—p~-pQ‘, 0 = 0,95-0,01-200=1,9 кг/с;
Д/?= — 0,17 10Б Н/м2.
3. Определить величину критической скорости потока возду-
ха, если известна температура торможения 75-^310 К.
Ответ: якр=Р=321 м/с.
4. При полете на /7 = 2000 м со скоростью 850 км/ч макси-
мальная скорость на профиле крыла достигла местной скорости
звука. Чему равна скорость течения в этой точке^
Ответ: V= 318 м/с.
итги vokb-la.spb.ru - Самолёт своими руками?!
ГЛАВА 8
МАЛЫЕ ВОЗМУЩЕНИЯ И СКАЧКИ УПЛОТНЕНИЯ
В ГАЗОВОМ ПОТОКЕ
8 I. РАСПРОСТРАНЕНИЕ МАЛЫХ ВОЗМУЩЕНИЙ
Каждая точка поверхности тела, движущегося в газе, явля-
ется источником повышения (или понижения) давления, плот-
ности и других параметров газового потока. Изменение указан-
ных параметров, вызванное движением твердого тела, называет-
ся возмущением. В механике жидкостей и газов рассматривают-
ся малые (слабые) н конечные (сильные) возмущения. Основное
отличие этих двух видов возмущений состоит в поведении пара-
метров потока, определяющих течение. При малых возмущени-
ях все параметры течения являются непрерывными функциями
координат и времени. Скачкообразно изменяются не сами пара-
метры газа (р, е, Г), а только скорости их изменения, т. е. их
производные, или градиенты.
Обычно при малых возмущениях величина приращения како-
го-либо параметра мала по сравнению с его значением до появ-
ления возмущения. Скорость распространения малых возмуще-
ний равна местной скорости звука.
Конечные (сильные) возмущения характеризуются скачко-
образным изменением на некоторых поверхностях в потоке са-
мих параметров на конечную величину, т. е. наблюдается разрыв
непрерывности изменения параметров газа.
В аэродинамике сильные возмущения называются скачками
уплотнения или ударными волнами.
Рассмотрим в сверхзвуковом газовом потоке некоторую не-
подвижную точку О (рис. 8.1), являющуюся источником малых
возмущений. Возмущения от нее распространяются во все сто-
роны с местной скоростью звука а в виде сферических волн уп-
лотнения или разрежения. В неподвижной среде границей воз-
мущенной зоны является расширяющаяся сферическая поверх-
ность с центром в точке О. При равномерном движении среды
сферические волны, возникающие в точке О, сносятся потоком в
направлении скорости течения.
116
www vokb-la.spb.ru - Самолет своими руками?!
За время t радиус сферической волны, исходящей из возму-
щающей точки О, станет равным at, а центр волны будет снесен
потоком’ на расстояние Vt относительно этой же точки О. Волны,
возникающие позднее, имеют меньший радиус и находятся бли-
же к центру.
При сверхзвуковом движении среды (V>a) поверхность, оги-
бающая сферические волны, образует конус возмущений с вер-
шиной в точке 0 Синус угла при вершине такого конуса (угла
слабых возмущений), как видно на рис. 8.1, может быть пред-
Рис. 8.2. Распространение
волн от источника возмуще-
ний, движущегося со скоро-
стью звука (V=fl)
Рис. 8 1. Распространение волн от источни-
ка возмущений, движущегося со скоростью,
большей скорости звука (при V>a образу-
ется конус возмущений)
ставлен в виде sin p,=a//W—a/V= 1/М Кощс, определяемый
этим условием, обычно называется характеристическим конусом,
или конусом Маха. Коническая поверхность с углом раствора 2ц
является границей, в пределах которой распространяются малые
возмущения, идущие нз точки О, и за пределы которой они не
выходят.
Из выражения, определяющего конус Маха, видно, что при
увеличении числа М угол ц уменьшается, тем самым умень-
шается возмущенная зона, и наоборот при уменьшении числа М
угол ц увеличивается, тем самым увеличивается возмущенная
зона.
Когда газовый поток движется со скоростью, равной скорос-
ти распространения возмущений, исходящих из точки О (V—а,
М=1), угол ц —л/2 В этом случае границей возмущения явля-
ется плоскость, нормальная к направлению скорости V (рис 8 2).
При дозвуковой скорости потока (V<a, М<1) возникающие
в точке О сферические волны расширяются быстрее, чем сно-
сятся потоком, вследствие чего возмущенная зона неограниченно
расширяется во все стороны относительно точки О (рис. 8 3)
Таким образом, в дозвуковом потоке возмущения, возникшие в
некоторой точке, распространяются на весь поток, а в сверхзву-
117
www.vokb-la.spb.ru - Самолёт своими руками?!
ковом потоке локализуются внутри конуса с углом раствора
2р^л.
Заметим, что малые возмущения возникают также при обте-
кании тонкого тела с острой передней кромкой (рис. 8 4). При
этом поверхность, огибающая волны возмущений, может быть
цилиндрической (плоское тело) или более сложной формы (тело
вращения и др.)
Крылья современных скоростных самолетов, артиллерийские
снаряды и ракеты с некоторым приближением могут рассмат-
V<c
>
Рис 8.3. Распространение волн
от источника возмущений, дви-
жущегося с дозвуковой скоро-
стью (V<g)
Рис. 8.4. Распространение волн
возмущений при обтекании
тонкого остроконечного тела
сверхзвуковым потоком
риваться как топкие тела. Спектры обтекания заостренного
тонкого профиля под нулевым углом атаки при дозвуковых и
сверхзвуковых скоростях показаны на рис. 8 5. При дозвуковых
скоростях потока граница возмущений находится впереди тела
на бесконечно большом расстоянии (рис. 8.5, а), при сверхзву-
ковых — у самого острия тела (см. рис. 8.5, б), при этом до
границы возмущения тело не оказывает никакого влияния на
поток, т. е. поток не возмущен.
Любая точка потока, в которой скорость отличается от ско-
рости соседних точек, может рассм 1триваться как источник воз-
мущений, и, следовательно, как вершина характеристического
конуса, ограничивающего возмущенную зону. Пересечение боко-
вой поверхности этого копуса с плоскостью течения, проходящей
через источник возмущений, дает след на плоскости течения, на-
зываемый линией возмущения.
Линия возмущения наклонна к направлению вектора скорости
под углом ц —arcsin (tz/V). Линия возмущения прямолинейна при
слабых возмущениях и может быть криволинейной при сильных
возмущениях (обтекание толстого тела сверхзвуковым потоком).
В случае обтекания сверхзвуковым потоком прямолинейной
гладкой стенки, параллельной вектору скорости невозм^щенного
118
www vokb-la.spb ru - Самолёт своими руками?!
потока, течение оказывается невозмущепным. Однако в реальных
условиях трудно создать идеально гладкую стенку. Наличие да-
Рис. 8.5. Спектры обтекания тонкого профиля при дозвуковых (а) п
сверхзвуковых (б) скоростях
же незначительных бугорков шероховатости на прямолинейной
стенке или изменение кривизны твердой стенки приводят к по-
явлению возмущений в потоке.
8.2, ОБТЕКАНИЕ УГЛОВ ПЛОСКОПАРАЛЛЕЛЬНЫМ
сверхзвуковым потоком
Обтекание слабовогнутой (выпуклой) цилиндрической по-
верхности сложной конфигурации плоскопараллельным сверх-
звуковым потоком можно представить как обтекание последова-
тельности внешних или внутренних тупых углов. Ребра двугран-
ного угла являются источниками возмущений, которые, однако,
имеют различный характер в зависимости от того, будет тупой
угол внешним, или внутренним
Обтекание внешнего тупого угла
Предположим, что нсвязкий сверхзвуковой поток газа дви-
жется вдоль горизонтальной стенки АО со скоростью Vi и оги-
бает двугранный угол АОС (рис. 8.6, а)
Источником возмущения параметров течения является от-
клонение стенки ОС на угол 0 относительно начального направ-
ления АО Если величина угла АОС незначительно отличается
от л, то эти возмещения являются весьма малыми, и область
возмущенного потока отделяетсн от области невозм} щепного
линией возмущения ОВ, наклоненной к направлению невозму-
щенного потока под углом m=arcsin Щ/Vi За линией возму-
щения поток движется с иной скоростью V, направленной парал-
лельно стенке ОС и по величине несколько большей, чем Vi, при
этом соответственно несколько уменьшаются давление и плот-
ность. Вниз по течению за линией возмущения ОВ' поток дви-
жется с постоянной по величине и направлению скоростью V
без дальнейших возмущений.
119
www.vokb-la.spb.ru - Самолёт своими руками?!
Если величина угла АОС отличается от л на конечную вели-
чину, то скорость потока вниз по течению изменяет свое направ-
ление и возрастает по величине постепенно, так что возникаю-
щие в точке О возмущения распространяются на область, огра-
ниченную линиями возмущений ОВ, OB'. Линия ОВ направлена
под углом pi = arcsin (aJVi) (^ и Vi — соответственно скорости
Рис. 8.6. Схема обтекания сверхзвуковым потоком внешнего
тупого угла (а); обрывающейся стенки (б); выпуклой лома-
ной поверхности (в)
звука и потока до линии возмущения ОВ), За линией возмуще-
ния поток поворачивается, постепенно расширяясь до линии воз-
мущения 0В\ образующей со стенкой ОС угол p = arc in V)
(а и V — соответственно скорости звука и потока за линией
возмущения ОВ').
Каждому углу поворота соответствует определенное умень-
шение давления Чем больше угол поворота потока, тем больше
разрежение. Наибольшее значе 1ие угла поворота 0тах = 2,21 рад,
соответствующее максимальному разрежению (давление, плот-
ность и температура воздуха равны нулю, М->оо), имеет место
при числе Mi = I (см. рис. 8.6, б).
При числах Mt невозмущениого потока, больших единицы,
максимальный угол поворота 0Шах уменьшается. При Mi = oo
угол поворота 0тах= О
120
www.vokb-la.spb.ru - Самолёт своими руками?!
При обтекании криволинейной стенки образуется непрерыв-
ная возмущенная область, в которой линии возмущения отходят
от каждой точки кривой стенки под местным углом М. ц =
= arcsin Via, образованным с касательной к стенке в данной
точке (8.6, в).
Обтекание внутреннего тупого угла
Рассмотрим обтекание сверхзвуковым потоком внутреннего
тупого угла АОС (рис. 8.7). Здесь, как и в предыдущей задаче,
течение плоское. Поток за точкой
сжатие, скорость V становится
меньше скорости
При величине внутреннего
тупого угла, близкой к л, кар-
тина обтекания внутреннего ту-
пого угла аналогична картине
обтекания внешнего тупого
двугранного угла. Все возму-
щения ограничиваются линией
возмещения ОВ, за которой
скорость V, несколько меньше
скорости Vi, постоянна и па-
раллельна стенке ОС.
Если величина угла АОС
отличается от л на конечную
величину 6, то рассуждения,
ана чогичные предыдущим, при-
водят к заключению, что воз-
мущения потока должны на-
чаться на линии возмущения
OB', составляющей со стенкой
ОС 5 гол р = arcsin a/V. Однако
в этом случае скорость за ли-
нией возмущения V меньше
скорости невозмущенного пото-
ка Vj и cz>czi, а следовательно,
угол ц больше угла щ и тем
более цЧ-0>|Н1. Таким образом,
О сужается, происходит его
Рис. 8 7. Схема обтекания свсрхзв\-
ковым потоком внутреннего тупого
угла.
а— теоре ическая модель. (/—физически
невозможное течение; 2—косой скачок уп-
лотнения); б—реальное течение
предполагая процесс уменьше-
ния скорости при обтекании угла, меньшего л, непрерывным,
приходим к физически невозможному выводу о том, что процесс
этот должен закончиться (на линии OB') раньше, чем ои нач-
нется (на линии ОВ")
Опыт показывает, что в этом случае вместо непрерывного из-
менения скорость и другие газодинамические параметры меня-
ются скачкообразно при прохождении через поверхность скачка
уплотнения, образующегося внутри угла В'О В".
121
www.vokb-la.spb ru - Самолёт своими руками?!
Если угол 0 не превосходит некоторого максимального зна-
чения (см, разд. 8.7), то поверхность скачка представляет собой
плоскость, а ее пересечение с плоскостью течения — прямую ОВ
(см рис. 8.7, б).
Таким образом, обтекание внутреннего тупого угла сопро-
вождается торможением потока и образованием скачка уплот-
нения (и прн обтекании ломаной поверхности — системы скач-
ков).
Предположение о том, что скачок уплотнения представляет
собой геометрическою линию или поверхность, означает, что пе-
реход от параметров невозмущенного потока к параметрам за
скачком совершается в бесконечно тонком слое. В реальном —-
вязком —- газе весьма интенсивное, но все же постепенное из-
менение параметров происходит в некотором переходном слое,
толщина которого, как показывают расчеты, имеет порядок
удвоенной длины свободного пробега молекул и уменьшается
с увеличением интенсивности скачка. В обычных условиях тол-
щина скачка уплотнения настолько мала, что при расчетах
вполне может быть использована схема бесконечно тонкого скач-
ка. Однако использование этой схемы вносит значительные по-
грешности при расчетах скачков в разреженных газах, где длина
свободного пробега молекул и толщина переходной области су-
щественны по величине.
Скачки уплотнения
Итак, прн торможении сверхзвукового потока газа в нем по-
являются скачки уплотнения или система скачков уплотнения,
которые можно представить как поверхности сильного разрыва,
на которых функции газодинамических величин терпят разрыв.
Скачок уплотнения при движевип твердого тела в воздухе со
сверхзвуковой скоростью можно рассматривать также как фронт
стационарной ударной волны, которая не изменяет своего поло-
жения относительно источника возмущения, двш аясь вместе
с ним.
Скачки уплотнения возникают при взр 1вах или в сверхзву-
ковых потоках газа, например, в соплах, при обтекании крыла,
фюзеляжа, корпусов самолетов, снарядов и ракет. Образование
скачков уплотнения является результатом наложения слабых
возм} щений.
Скачки уплотнения подразделяются на прямые и косые.
Прямым, называется скачок, фронт которого составляет прямой
угол с направлением потока (рис. 8 8, с), а косым — скачок,
Фронт которого расположен наклонно к направлению потока
(см. рис. 8.8, б). Косой скачок образуется в том случае, когда,
пересекая фронт скачка, поток должен изменить свое направ- -
ление, например, при сверхзвуковом обтекании газом клиновид-
ного тела (рис. 8.9, а) и конуса (см рис. 8 9, б) При опреде-
122
www.vokb-la.spb.ru - Самолёт своими руками?!
ленных условиях, которые будут рассмотрены позже, иа некото-
ром расстоянии впереди тела образуются скачки уплотнения
с криволинейным фронтом (рнс. 8.10, а, б). В этом случае ска-
рне 8.8. Схемы скачков уплотнения -
прямой, б — косой
чок называется отсоединенным в отличие от присоединенного
скачка, расположенного вплотную у заостренного носка тела
(см рис. 8.9, а, б) В центратьной части отсоединенного скачка
Рис, 8 9 Теневые фотографии косого
скачка уплотнения при сверхзвуке
вом обтекании клина (а) и конуса
(б)
Рис 8 10 Теневая фотография скач-
ка уплотнения при сверхзвуковом об-
текании тела вращения (а) и про-
филя (б)
образуется прямой скачок, который при удалении от оси сим-
метрии переходит в косой скачок, вырождающийся иа больших
расстояниях в слабую волну возмущения.
123
www.vokb-la.spb.ru - Самолёт своими руками?!
При интенсивном подводе илн отводе тепла в газовый поток
на небольшом участке потока возникают также скачкн, называе-
мые тепловыми. Среди существующих различных типов тепло-
вых скачков наибольший интерес представляют широко встре-
чающиеся в практике аэродинамического эксперимента, в соплах
Лаваля, в проточных частях турбомашин скачки конденсации,
связанные с движением двухфазной жидкости (например, влаж-
ный пар — воздух).
Анализ свойств скачков конденсации основывается на ряде
допущений. Основными уравнениями скачка конденсации явля-
ются общие уравнения скачков уплотнения.
8.3. ОСНОВНЫЕ СООТНОШЕНИЯ ДЛЯ ПРЯМОГО СКАЧКА
УПЛОТНЕНИЯ
Рассмотрим аналитически вопрос о связи параметров газа
за прямым скачком уплотнения р, р, Т, V с параметрами газа
до скачка plt Tlr для чего воспользуемся четырьмя урав-
нениями: неразрывности, количества движения, энергии, состоя-
ния.
Параметры газа при его прохождении через скачок уплотне-
ния меняются скачкообразно, однако, наличие поверхностей раз-
рыва- не препятствует применению на скачках уплотнения ос-
новных уравнений механики в интегральной форме, в частности
уравнений количеств движения.
На основании закона сохранения массы уравнение неразрыв-
ности (постоянства расхода) газа в сечениях до и после прямого
скачка при условии постоянства площадей поперечного сечения
можно записать в виде:
Gil/1=eiz. (8. 1)
Прн пренебрежении объемными н поверхностными силами
изменение количества движения газа на скачке равно импульсу
снл давления, действующих по нормали к поверхности скачка,
н уравнение количества движения для прямого скачка можно
записать в виде
Рх — Р^QiVi (V- V\). (8. 2)
Поскольку при прохождении через скачок полная энергия
остается неизменной (го=const), в этом случае, считая процесс
перехода газа через поверхность скачка адиабатическим и учи-
тывая выражение (1-16), можно использовать уравнение энергии
в виде (5 30)
т/"2
—— — --^-4 — RTq. (8.3)
2 k— 1 Qi 2 k — 1 q k— 1 0
Уравнение состояния газа соответственно запишется
pfe-RT. (8.4)
124
www.vokb-la.spb.ru - Самолёт своими руками?!
Уравнения (8 1), (8.2), (8.3), (8.4) являются основными урав-
нениями теории прямых скачков уплотнения и выражают «усло-
вия динамической совместимости» двух течений, разделенных
поверхностью скачка. Таким образом, составлена система
рех уравнений с четырьмя неизвестными
Прежде всего установим связь между скоростями до и
скачка уплотнения. Используя уравнение неразрывности
запишем уравнение количества движения (8.2) в виде
у у=Л----------ЕУ—
1
или, умножая на произведение скоростей УК получим — I/i—
_-£1-У = У1У(У1-У).
01 р уч k — I
Из уравнения энергии (8 3) следует, что—= Л?Т0-----—,
k~\
_---------. Подставив последние выражения в уравне-
Qi 2 k
ние (8.5), после несложных преобразований получим равенство
—RTG = —-—которое с учетом соотношения (7.8)
k + 1 k + 1
приводится к так называемой формуле Прандтля
четы-
после
(81),
8.5)
(8 6)
Из этой довольно простой формулы следует, что при прямом
скачке уплотнения критическая скорость акр является средним
геометрическим между скоростями до и после скачка уплотнения,
т. е в прямом скачке уплотнения всегда осуществляется пере-
ход от сверхзвуковой скорости к дозвуковой.
Если перейти к скоростным коэффициентам с помощью соот-
ношения (7 13), то формула Прандтля принимает еще более
простой вид:
где
ХХ1=1;
X = V /йкр; f у = V j/#Kp.
(8 7}
Таким образом, прн наличии неравенства Vi>V на прямом скач-
ке всегда Е<а1{р<К или Очевидно, что в случае сверх-
звукового течения перед прямым скачком уплотнения после скач-
ка течение будет дозвуковым. Соотношения для плотностей до
и после скачка можно найти, используя уравнение (81):
_e_=H-ZL= VL_
е, v w, а2р -
(8 8)
12»
www vokb-la.spb.ru - Самолёт своими руками?!
или с учетом формулы (7.6):
611 Л 2 + (£— I)Mj
(8.9)
Чтобы получить выражение для соотношения давлений до и
после скачка, приведем уравнение (8.2) к виду
Рис 8 11 Изменение параметров газового потока в скачке
уплотнения (а — давления; б — плотности; в — температуры)
в зависимости от числа Mi
Учитывая, что ai2=kpi/Qt, a Vi = CiMi и заменяя отношение V/Vi
его значением согласно (8.9), получим для отношения давлений
выражение
Р______ 1
pl k + I 1 k + I k + I
M?-1Y
U-i 1 J
(8. 10)
Имея выражение для отношений давлений (8 10) и плотнос-
тей (8.9) до и после скачка, нетрудно получить выражения для
отношения температур:
—= р1W—----------------------------------kl\ (8.11)
Л ле U + V U-1 1 / \ 1 м? )
Зависимости отношений параметров газа до и после скачка
от числа Mi приведены на рис. 8.11
126
www.vokb-la.spb.ru - Самолёт своими руками?!
Определив значение Mi2 из уравнения (8.10) и подставив его
в (8.9), получим уравнение Гюгонио:
р р + I 61 (Р ~Р Об (Р 0 Q1 k 1 Q ?g
р\ (k+ I)Q1 — (k- I)Q fe Л- 1 Q1 _ k — I Q
или k +1? p 1 6 Л — I pi Ql Pl k~ 1 Pl + + I
которое устанавливает связь между отношениями плотностей и
давлений до и после скачка. Подставив значение Mi2 в (8.11)т
Рис. 8.12. Зависимость
плотности газа от давле-
ния при прямом скачке
(1) и изэнтропическом
(2) процессе
Рис. 8.13 Изменение дав-
ления в зависимости от
температуры при изэнт-
ропическом процессе (1)
и прямом скачке (2)
получим связь между отношениями температур и давлений до
и после скачка:
££ р / Р \2
Г _ £ — I pl \pi /
Л +1 Р . .
А— 1 /?!
Зависимость между параметрами состояния газа до и после
скачка существенно отличается от зависимости между ними &
обратимом адиабатическом процессе, характеризующимся соот-
ношениями (1-22).
Из сравнения процессов изменения параметров газа в скачке
с обратимым адиабатическим или изэнтропическим процессом
(рис. 8.12 н 8.13) следует, что при сжатии газа в скачке происхо-
127
www.vokb-la.spb.ru - Самолёт своими руками?!
дит более быстрое увеличение температуры, объяснимое необра-
тимым (переходом части механической энергии в тепловую, вы-
зывающим дополнительный нагрев газа.
Увеличение температуры в скачке уплотнения по сравнению с
изэнтропическим процессом обуславливает более медленное
увеличение плотности газа за скачком при увеличении давления
невозмущенного потока — кривая 1 на рис. 8 12 проходит кру-
че, чем кривая, отражающая обратимый адиабатический про-
цесс. Кривая /, построенная по уравнениям (8.12), называется
адиабатой Гюгонио.
Адиабата Гюгонио имеет вертикальную асимптоту, соответ-
ствующую режиму М 1->оо или, как это следует из соотношения
(8.9), режиму q/qi=(£+1)/(A’ 1). Действительно, когда ско-
рость перед скачком приближается к бесконечности, плотность
за скачком стремится к определенному конечному пределу. Ве-
личину этого предела можно определить из формулы (8.9):
n (k 4- 1) М? ъ 4- I Л ,
lim — = Iim —-----L_L_ _(8.14)
Qi Mi-*« 2 -p (k — 1) M & 1
Для воздуха (£=1,4) этот предел равен шести. Причиной ог-
раниченного увеличения тотности газа за скачком является
сильный разогрев газа при прохождении его через скачок уплот-
нения.
В отличие от адиабаты Гюгонио в обратимом адиабатическом
процессе, описываемом уравнениями (1.22), неограниченному
увеличению давления соответствует неограниченное возрастание
плотности
Отношение скоростей на скачке уплотнения в соответствии
с уравнением неразрывности обратно отношению плотностей, по-
этому скорость V после скачка не уменьшается до нуля при не-
ограниченном увеличении Mj, а уменьшается в воздухе лиш > в
шесть раз.
Звуковую волну можно рассматривать как предельный слу-
чай ударной волны. Из равенства (8 1) следует, что
qLj-q - /8. 15х
е Hi
Исключая из этого выражения разность скоростей с учетом
уравнения (8 2), получим зависимость
l/1 = 1 /Р^-Р t (8.16)
у Qi Qi — Q
которая позволяет определять скорость распространения удар-
ной волны конечной интенсивности в неподвижной среде, на-
пример, скорость распространения взрывной волны.
128
wwm vokb-la.spb ru - Самолёт своими руками ?!
Для прямого скачка малой интенсивности
эту зависимость можно записать в виде
(Р~+Р1 и Q->Q1)
Таким образом, звуковая волна является
бесконечно малой интенсивности.
ударной волной
8.4. ДАВЛЕНИЕ В КРИТИЧЕСКОЙ ТОЧКЕ ЗА ПРЯМЫМ СКАЧКОМ
При обтекании сверхзвуковым потоком тел с закругленной
носовой частью на некотором расстоянии впереди тела образу-
ется отсоединенный скачок уплотнения, который оказывает
влияние на величину давления в критической точке tn (рис.
8.14), где до¥=О, V0=O.
Рис. 8.14. К определению давле-
ния в критической точке за скач-
ком уплотнения
Рис. 8 15. Изменение давле
ния в критической точке в
зависимости от числа Mi
при изэнтропическом про-
цессе и при наличии скачка
уплотнения
Течение до и после прямого скачка является изэнтропичес-
ким. Давление торможения р$ за прямым скачком уплотнения
определяется по формуле (7 18). Если в этой формуле коэффи-
циент скорости К за скачком уплотнения выразить через коэффи-
циент скорости Xj перед скачком, то получим
। 1 1___\ft i
Ро \ й +1 *1 /
Подставив в это соотношение значение Xi согласно (7.15), най-
дем
=_________ [ j_(£ ft—1 / Д|2__ А—1
РО L {k +1)2 U - 1 1 )
м?~г
(8. 17)
5 626
129
www vokb-la.spb ru - Самолёт своими руками?!
Для установления непосредственной зависимости между дав-
лением торможения ро за прямым скачком уплотнения и давле-
нием до скачка pi разделим почленно равенство (8.10) иа ра-
венство (8.17) и запишем
k 2k
Р(1 £ -г 1 2(k — ) j g \
Pi / k '
(2----l)fe~l
\ k— 1 1 )
Полагая здесь fe=l,4, получим для воздуха формулу Релея?
166,7М? 166.7М?
pi (7м; - 1)2>5 /7 _ д__\2*5’
\ Mi /
Кривые, определяющие по этой формуле изменение давления
в точке торможения потока в зависимости от числа Mi, приведе-
ны иа рис. 8.15. Зависимость poi/pi~f(Mj) для случая, когда
скачок уплотнения отсутствует, определяется формулой (7.5)
Р01
Pi
—у—М;У-1. Эта формула при £=1,4 принимает вид
Ж = /14-0,2 М2)3-5.
Pi
(8.20)
Следует заметить, что кривая poilpi физически не реализу-
ется.
При прохождении потока через ударную волну происходит
увеличение энтропии, сопряженное с потерями механической
энергии газа, проходящего через фронт скачка. Эти потери ха-
рактеризуются уменьшением давления торможения (полного на-
пора) ро на ударной волне, т. е. появление скачка уплотнения
впереди тела значительно уменьшает давление в его критической
точке. Давление в критической точке при наличии прямого скач-
ка уплотнения меньше, чем при изэнтропическом торможении на
величину потерь давления в прямом скачке.
Полная энтальпия газа при переходе через скачок уплотне-
ния не изменяется lo = toi, поэтому при неизменных значениях
теплоемкости ср температура торможения остается одной и той
же, т. е. То=7,О1, откуда из уравнения состояния (8 4) получаем
Poi/qm—Po/qo или pofpoi — Qo/Qoi = <y, где о — коэффициент потерь
полного давления в скачке.
Для определения коэффициента ст исключим из формул (8 181
и (7.5) давление pi. Тогда получим
k -4- 1
2 + (й - 1) Mf
*—1
*
-
м;~(й—1)
130
www.vokb-la.spb.ru - Самолёт своими руками?!
Коэффициент ст изменяется от 1 до 0 При коэффициенте 1
число Mi=l, и потери полного давления отсутствуют При уве-
личении числа Mi значение о стремится к нулю. Для двухатом-
ных газов (k= 1,4) формула для коэффициента о имеет вид
_й_=_________166,7М,
Л" /7_—Y’S(l+0,2M|)3-5
1м?/
(8 21)
На рис. 8.16 показан характер изменения коэффициента о
в зависимости от числа Mi.
Рис 8.16. Изменение коэффи-
циента потерь в зависимости
от числа Mi
Рис. 8 17. К расчету косого
скачка уплотнения
8.5. КОСЫЕ СКАЧКИ УПЛОТНЕНИЯ
Образование косых скачков уплотнения можно проследить
на простейшем примере обтекания стенки АОВ, повернутой в
точке О на некоторый конечный угол 6 навстречу иевозмущеи-
ному потоку (рис. 8.17). Поток движется параллельно стенке
ДО со скоростью Vi, затем на косом скачке отклоняется на угол
6 и приобретает новую скорость V, направленную параллельно
стенке ОВ
Предположим, что фронт косого скачка уплотнения образу-
ет угол р с направлением невозмущенного потока Для определе-
ния параметров газа за косым скачком обозначим их до скачка
через pi, Vi, pi, It, а после скачка — через q, V, Т. р Скорости
течения газа до и после скачка представим в виде составляющих,
нормальных к фронту скачка У1П, Vn и касательных Ущ Vp.
Для решения основной задачи о косом скачке воспользуемся
условиями динамической совместимости двух течений, разде-
ленных поверхностью скачка
5*
131
www.vokb-la.spb.ru - Самолёт своими руками?!
1. Уравнение секундного изменения количества движения
газа на единичной площадке скачка в направлении, перпендику-
лярном к его фронту
Р — Рх Vin (У1п ~ KJ.
(8.22)
В проекции на плоскость скачка аналогичное уравнение
e1VJ„(VJU-V,)=O, (8.23)
так как давление вдоль поверхности скачка остается постоян-
ным. Следовательно, касательные составляющие скоростей до и
после скачка равны между собой, т. е.
V„-V„ |8.24)
а разрыв претерпевают только нормальные составляющие ско-
рости.
2. Уравнение сохранения энергии единицы массы газа при
переходе через скачок при отсутствии теплообмена и трения
* IZ^
+TL=rAT/?7’- (8-25>
k—I Q 2 k — I Qi 2 k— I
3. Уравнение неразрывности (уравнение сохранения массы)
ЫЛ„-е1/„. (8.26)
Такой вид уравнения неразрывности объясняется тем, что
массовый расход газа через плоскость скачка определяется не
значением полной скорости Vi (или У), а только ее нормальной
составляющей.
4. Уравнение состояния p=$RT
Для установления связи между нормальными составляющи-
ми скоростей до и после скачка преобразуем уравнение количе-
ства движения (8 22), используя уравнение неразрывности
(8.26):
-2- V„).
е ei
Подставляя в это равенство значения отношений давления к
плотности, полученные из уравнения энергии (8.25)
г/2
Р1 __jyj' _____1 k ~~ I
21 ° 2 k ’
и учитывая, что У* 2=УП2+У/2 и
нение
Р ^2
2 2 k
У12=У1д + УД получим урав-
2Л
k + 1
k— 1
k + 1
(8. 27)
132
www vokb-la.spb.ru - Самолёт своими руками?!
первое слагаемое правой части которого согласно (7.8) равно
квадрату критической скорости. Окончательно
(8.28)
В случае прямого скачка 1^ = 0 и из выражения (8.28) по-
лучается формула (8.6). Равенство (8.28) подтверждает, что на
косом скачке уплотнения разрыв претерпевает только нормаль-
ная составляющая скорости, а касательная составляющая оста-
ется неизменной. Следовательно, после прохождения косого
скачка поток может остаться сверхзвуковым.
Для косого скачка можно записать соотношение (см. рис.
8.17) Vtn = Vi sin р. Заменяя в зависимостях (8.9), (8.10), (8.11)
для прямого скачка уплотнения число Mi числом
= Mj sin р, найденным по нормальной составляющей скорости,
получим соотношение для определения плотности, давления и
температуры за косым скачком:
О И1я (fe+l)A^sin2p
61 п 2 + (£ — 1) sin2 р
(8 29)
8. 30)
(8-31)
Исключив величину Mi sin р из соотношений (8.29) и (8.30),
можно получить адиабату Гюгонио (8.12), т. е. уравнение удар-
ной адиабаты для косого скачка уплотнения точно такое же, как
и для прямого скачка.
8.6. СВЯЗЬ МЕЖДУ ПОЛОЖЕНИЕМ ФРОНТА КОСОГО СКАЧКА
И УГЛОМ ПОВОРОТА СВЕРХЗВУКОВОГО ПОТОКА
Угол наклона скачка уплотнения можно определить графи-
ческим способом, если известны величины и направления ско-
ростей потока до и после косого скачка.
Так как касательные к фронту скачка составляющие скорос-
тей потока перед и за скачком равны между собой 1/и=1/г, то
прямая, соединяющая концы векторов скоростей и V, должна
быть перпендикулярна к плоскости косого скачка уплотнения.
Поэтому, если от точки О (рис. 8.18) провести вектор Vi по оси
OX, а V под углом 0 к то направление косого скачка мож-
но найти, соединив прямой линией концы векторов и опустив на
эту прямую перпендикуляр из точки О Этот перпендикуляр и
133
www vokb-la.spb.ru - Самолёт своими руками?!
будет в плоскости течения следом косого скачка уплотнения под
углом р.
Установим связь между углами 0 и р Из рис. 8.18 следует,
4Totg(B — 0)—— или с учетом (8.28)
Рис. 8 18 Определение направления косого
скачка
Из рис. 8.17 следует, что
Vlrt—Vising V,=V1Cosp.
Тогда tg(f- 0)--------2-----------.
ИI sin р cos р
8.32)
(8. 33)
Разделив знаменатель и числитель на tzi2 и заменив ViM на
Mi, получим
йл 4p/^-(*-l)/(* + l)M?COS2p
tg(p - 6)=----------—-—------------
Ml Sin p COS p
(8. 34)
Используя соотношение (7 8), можно написать
дкр гр
Л) т\
Подставляя в последнее выражение значения отношений темпе-
ратур из формул (7.3) и (7.10), получим
——
*+1^ 2 ')
134
www vokb-Ia.spb.ru - Самолёт своими руками?!
2
tg(p—0)=-l+l
С учетом, этого выражения формулу (8.34) можно записать
в виде
k — 1 k— 1 9
1 + -—--М1)"7~Г Micos Р
М2 sin р cos 3
л 2 +(ft- l)M?sin2p
или, преобразовывая, tg(p — 0) —--------------. (8.35)
(ft + 1) Mj sin p cos p
Воспользовавшись известной из тригонометрии формулой
tg(₽-
1 + tg 6 tg р
и решая после подстановки уравнение относительно tg6, по-
лучим
, , Л M?sin2p—1
tg 0=ctg ₽------5------------.
1 + Я (——2- — sin2pl
(8. 36)
По этой формуле построены кривые зависимости )>=/(())
(рис. 8.19). Угол поворота 0 может быть равен нулю в двух слу-
чаях:
1) M^sin2^—1 = 0,
о «1 1
т. е., когда sinp =——=----- или
V5 Mi
В этом случае скачок вырож-
дается в волну слабых возмуще-
ний. Из соотношения (8 29) сле-
дует, что при MfSinp=l Vin =
= Vn, т. е. величина и направле-
ние скорости не изменяются;
2) ctgp-О или р=л/2. В этом
случае фронт ударной волны пер-
пендикулярен течению, т. е. име-
ет место прямой скачок уплотне-
ния
Анализ графиков, приведен-
ных на рис. 8.19, позволяет сде-
лать следующие два заключения-
1. Для каждого числа Mi су-
ществует максимальное значение
угла 0, на который может повер-
нуться сверхзвуковой поток,
пройдя через фронт косого скач-
ка.
Рис 8.19. Зависимость между уг-
лами 6 и р при различных значе
ниях числа Mi
135
www.vokb-la.spb.ru - Самолёт своими руками?!
. 2. При фиксированных значениях числа Mi и угла поворота
О возможны два положения фронта скачка, характеризуемые
двумя углами р. Однако, как показывают опыты, большие зна-
чения углов р не реализуются на практике при обтекании за-
остренных тел с присоединенным скачком уплотнения в плоско-
параллельном потоке (см. пунктирные участки кривых на рис.
8,19),
8,7. УДАРНАЯ ПОЛЯРА И ЕЕ ПРИМЕНЕНИЕ
К РЕШЕНИЮ ЗАДАЧ
При решении задач аэродинамики часто бывает удобно ис-
пользовать систему координат, по осям которой отложены сос-
тавляющие скорости Ух, Vy Плоскость VxVy называется плос-
костью годографа скорости. Для построения ударной поляры сос-
Рис 8 20 К выводу уравнения ударной поляры
тавим уравнение годографа скорости, т. е. найдем геометричес-
кое место концов векторов скорости за скачком уплотнения при
различных значениях угла поворота потока в скачке.
Разложив вектор скорости V по осям координат ОХ и 0Y,
найдем значения состав тяющих скорости (рис. 8.20):
Vx=Vt cos р + ’/я s*n ft Уу = У( sin 6 — Vn cos p. (8.38)
Из формулы (8.28) имеем
" Vln
<> k — 1
a2-------------
к₽ ь i
Подставив в это выражение значения Vm и Vt из (8,32), полу-
чим
л
1
И] sin р
а2
кр
k—l
k + 1
У2 cos2
136
www.vokb la.spb ru - Самолёт своими руками?!
С учетом этой формулы и равенства (8.32) скорость
но (8 38)
Vx соглас-
л л 1
После простых преобразований имеем
И1СО5г?+-
или
cos2 fi=—-
2
кр
Их акр* '
акр
йГ
(8. 39)
(8.40)
откуда находим ctg2£ =
(2/й + 1)Г) + a^/Vi - Vх
Vx и Vy можно вес-
или рис. 8.20. Из рис.
Далее при установлении связи между
пользоваться вторым соотношением (8.38)
8 20 следует, что
..Vy .. =ctg? (или ctg2₽
И • V х
И2
У
(И1 - Ил.)2
Приравнивая правые части выражений (8.40) и
лучим уравнение годографа скорости *
9
акр
TZ2__/IZ IZ >2 1 _
„2
-VS
И1
(8- 41)
(8.41), по-
(8. 42)
I
21— 1
кр ъ л_ I
и
2
Кривая, описываемая этим уравнением, относится к классу
гипоциссоид или строфоид. Следует заметить, что прямая, сое-
диняющая концы векторов скорости V и Vi (см рис. 8.20), об-
разует С ОСЬЮ Vx угол ф, при этом1£[ф — ——-= ctgp, т е. ф =
— Vx
— У—Таким образом, направление плоскости косого скачка
уплотнения всегда перпендикулярно прямой соединяющей кон-
цы векторов V и Vt-
Приведем уравнение гипоциссоиды к безразмерному виду,
2 -
разделив левую и правую части на и введя следующие обо-
значения: Хл.— Ух/акр, Ху = Уй/акр, Тогда формула
(8 42) примет вид
Ч = (Х1-Ц2- , -----• (8-43)
2 .о _ . .
137
www vokb-la.spb.ru - Самолёт своими руками?!
оси н пересекает ее. прн лх =
Рис. 8.21. Ударная поляра
(гипоциссоида)
Кривая, описываемая уравнением гипоциссоиды в координа-
тах лх, ку, показана на рис. 8 21. Петля этой прямой называется
ударной полярой, так как она построена в полярных координа-
тах л и 6 Радиус-вектор любой точки петли гипоциссоиды дает
величину и направление вектора скорости за косым скачком.
Выделим основные свойства ударной поляры.
1 Ударная поляра симметрична относительно горизонтальной
и Их-(точка С) скачок уп-
лотнения вырождается в слабую
волну возмущения- касательные
к гипоциссоиде в точке С распо-
ложены под углом arcsin (1/Mi).
При ЛхЛ1=1 или (точка
Л) происходит переход косого
скачка уплотнения в прямой.
2 Ударная поляра имеет вер-
тикальную асимптоту, проходя-
, 1 1 2 >
щую через точку~Ai
Л1 k + 1
(точка D).
3 С помощью ударной поляры
можно графически определить
для каждого значения угла пово-
рота сверхзвукового потока ве-
личину скорости за косым скачком уплотнения и угол наклона
плоскости скачка.
Луч, проведенный из начала координат под углом поворота
потока на скачке, пересекает поляру в трех точках 1, 2, 3. Это
означает, что каждому значению угла 6 соответствует три зна-
чения скорости за скачком. Точка 3, расположенная на беско-
нечной ветви, не имеет физического смысла (так как она соот-
ветствует скачку разрежения) и каждому значению угла 6 соот-
ветствуют два возможных значения скорости У за косым скач-
ком
Прн увеличении угла поворота потока 6 наклон скачка уве-
личивается, а скорость уменьшается, но почти всегда остается
сверхзвуковой. Исключение составляет небольшой участок поля-
ры BF, в пределах которого скорость дозвуковая (Х<1) При
некотором угле 0 прямая, проведенная из точки 0, коснется кри-
вой в точке В Угол наклона этой касательной называется кри-
тическим углом отклонения потока 0кр.
Когда угол 0 достаточно мал, скачок «садится» на тело и ис-
ходит из его острия 0 (рис. 8 22, о). Если угол заостренного кли-
на становится больше критического, то скачок «отходит» от ост-
рия клина, т е. будет отсоединенным (см рис. 8 22, б) При по-
мощи ударной поляры, используя участок АВ, можно опреде-
лить угол наклона скачка уплотнения, если известен угол пово-
138
www vokb-la.spb ru - Самолёт своими руками?!
рота потока за криволинейным скачком уплотнения. В свою оче-
редь, угол поворота потока за криволинейным скачком можно
определить, когда известно течение газа в области между по-
верхностью тела и скачком. Подобного рода задачи решаются
численными методами. Таким образом, необходимым условием
отхода скачка уплотнения от острия является превышение угла
клина 0 критического угла поворота потока 0Кр.
Рис. 8.22 Обтекание клина:
«-О<0кр; б-е>в ир
(/—сверхзвуковая область; 2—дозвуковая)
Критическому углу поворота потока соответствуют определен-
ные значения угла наклона скачка уплотнения, а также мини-
мальные значения чисел М, при которых еще существует при-
соединенная волна. Эту зависимость и отражает та линия, кото-
рая разделяет сплошные и пунктирные кривые иа рис. 8.19
При изменении скорости иевозмущеиного потока от У1=акр
Г k 1
до Vi = Vmax или от А1=1до — 1 / ----- ударная поляра прн-
у k — 1
нимает различные формы, от точки до окружности Обычно
строится семейство ударных поляр для разных значений Л. Се-
мейство ударных поляр, которое может быть использовано для
расчета скачков уплотнения при сверхзвуковом обтекании клина,
приведено на рис. 8.23. Например, если к. ии с углом полураст-
вора 6—0,175 рад обтекается потоком со сверхзвуковой скоро-
стью, соответствующей Xj —1,7, то можно найти наклон скачка
и относительную скорость X за скачком следующим образом.
Пользуясь рис. 8.23, а, находим, что Л—1,5. Учитывая далее,
что касательные составляющие скоростей до и за скачком рав-
ны и прямая, проведенная через концы векторов скоростей до
и за скачком, перпендикулярна к скачку, проводим отрезок пря-
мой через концы векторов Xi и Л и восстанавливаем перпенди-
куляр ОВ из начала координат к этому отрезку (рис. 8 23, б).
Угол р между перпендикуляром ОВ и горизонтальной осью X и
139
wwm vokb-la.spb ru - Самолёт своими руками?!
есть 5 гол наклона скачка £ = 066 рад. Если потребуется при
6 = 0,175 рад и 1» —0,7 рад определить скорость до скачка (Xi)
и после скачка (X), то для решения этой задачи накладываем
О
Рис 8 23 Сетка ударных поляр для различных значений
линейку на сетку поляр (см. рис. 8.23) так, чтобы Она проходила
через начало координат под углом р=0,7 рад к горизонтальной
оси. Затем, приложив угольник одним катетом к линейке и пере-
мещая его, ищем поляру, удовлетворяющую условиям задачи.
Находим Л1 = 1,8 и 1=1,5. С помощью поляр можно решать и
другие практические задачи.
8.8. ИЗМЕНЕНИЕ ДАВЛЕНИЯ ПРИ ОТКЛОНЕНИИ
СВЕРХЗВУКОВОГО ПОТОКА НА МАЛЫЕ УГЛЫ
Для решения многих задач газовой динамики необходимо
определить изменение давления при отклонении сверхзвукового
140
'"vw vokb-la.spb.ru - Самолёт своими руками?!
потока на небольшой угол, например, при обтекании внешнего
или внутреннего тупого угла.
Рассмотрим обтекание внутреннего тупого угла (рис. 8 24).
Касательную и нормальную составляющие скорости можно оп-
ределить из геометрических построений:
И,—U\cos₽—V cos(p — 6); I/j sin Р; Vn=V sin (0 — 6).
(8.44)
С учетом этих выражений величину изменения давления на
скачке можно определить из уравнения количества движения
(8 22):
qxI/2 sin 0 sin 0
cos p sin (0 — 0)~
cos (0 — 6)
или
sin 0 sin 0
cos (0 — 0)
(8.45)
Эта формула справедлива для всех случаев, когда поверх-
ность скачка плоская. При малых значениях углов 6 можно поло-
жить sin 0^0 и cos (р—6) «у cos р В этом случае согласно (8 37)
tg0 = 1 Тогда формула для определения изменения
К mJ — 1
давления при отклонении потока на малый угол принимает вид
. 26
Лр=—
----, (8.46)
И mJ — 1
откуда находим коэффициент
давления
(8.47)
26
Р '
И М?-1
При 0, близком к нулю,
ударная волна вырождается в
звуковую, поэтому можно по-
лагать, что зависимость (8 47)
останется справедливой и при
малых отрицательных значени-
ях 0, т. е. при обтекании внеш-
Рис 8 24 К определению измене-
ния давления при отклонении
сверхзвукового потока на малые
углы
него тупого утла.
Таким образом, при повороте потока на малый угол 0 изме-
нение давления пропорционально величине динамического дав-
ления невозмущенного потока, углу поворота потока и обратно
пропорционально ]/MJ— 1. Заметим, что если угол 0>0 (под-
жатие), давление после поворота повышается (Др>0), а если
угол 0<О (расширение), то давление после поворота уменьша-
141
www.vokb-la.spb.ru - Самолёт своими руками?!
ется (Др<0). Выражения (8 46) или (8.47) используются при
определении аэродинамических характеристик профилей в сверх-
звуковом потоке.
Вопросы для повторения
1 Что является причиной возникновения скачка уплотнения
при сверхзвуковом обтекании тела?
2. В каких случаях образуется отсоединенный скачок у плот*
нения?
3 Напишите основные соотношения для прямого и косого
скачков уплотнения.
4. Как связана форма головного скачка уплотнения с формой
головной части тела (качественно)?
5. В чем отличие обычного адиабатического процесса сжатия
ог процесса сжатия на скачке?
6. Изобразите график ударной поляры и для какого-либо слу-
чая укажите скорость, возникающую за косым скачком уплот-
нения.
Задачи
1 Определить скорость иевозмущенного потока, если угол
слабых возмущений равен л/6, а тело движется на высоте Н=
-18 000 м.
Ответ: V’ —590 м/с.
2. Найтн скорость воздуха за прямым скачком уп-
лотнения при полете со скоростью V = 640 м/с на высотах Н=
—2000 и 15 000 м.
Ответ: V//—2ооо— 250 м/с; Ин=15ооо —221 м/с.
3. Самолет летит на высоте 5000 м со скоростью 1500 км/ч
относительно земли. Какова скорость самолета относительно ча-
стиц воздуха, по которым только что прошла прямая ударная
волна, вызванная носовой частью фюзеляжа?
Ответ". V —276 м/с.
www vokb-la.spb ru - Самолёт своими руками?!
ГЛАВА 9
ЭЛЕМЕНТЫ ТЕОРИИ ПОДОБИЯ
91. ПОНЯТИЕ О ПОДОБИИ ПОТОКОВ
В аэродинамике особо важное значение имеет теория подобия
потоков, так как она устанавливает возможность перенесения
экспериментальных данных, полученных иа модели, на натурнь i
объект.
Д,| я получения характеристик тел, обтекаемых воздушным
потоком, используется эксперимент, а при помощи теории подо-
бия результаты переносятся на натурный обьект.
Процесс изучения объекта, или физического явления, при
по тощи модели или другого явления называется моделирова-
нием.
Различают два вида моделирования физическое и матема-
тическое. Если физика явлений в исследуемом объекте и его
модели одинакова и если процессы, протекающие в модели i
объекте, описываются одинаковыми математическими и логичес-
кими зависимостями, то такое моделирование называется фи-
зическим.
Основное достоинство физического моделирования состоит
в том, что оно по: вотяет непосредственно наблюдать характер
протекания физического процесса на модели.
В мировой практике самолетостроения при оптимизации па-
раметров и доводке вновь разрабатываемого самолета на совре-
менном уровне науки и техники согласно опубликованным да1 -
ним изготавлива тся значительное число моделей, превышающее
40 50 шт, а суммарное время испытаний различных моделей
одного и того же самолета доходит до 17 000 ч в аэро, инамичес-
кой трубе. Так, в процессе отработки аэродинамики самолета
«Боинг-737» для выбора его оптимальной конфигурации было
испытано около 50 моделей, отличающихся формами и взаимным
расположением крыла, гондол и питонов.
При создании сверхзв} кового самолета «Конкорд» в Англии
и Франции были проведены испытания моделей, изготовленных
в разных масштабах 1:8, 1:30, 1 : 60. Испытания при сверхзву-
143
www vokb-la.spb.ru - Самолёт своими руками?!
ковых скоростях проводились более чем в десяти аэродинамичес-
ких трубах.
Влияние изменения обводов крыла и фюзеляжа иа обледене-
ние самолета «Коикорд» исследовано иа 55 различных конфигу-
рациях самолета.
Ести объект и его модель имеют различную физическую при-
роду, а описывающие их математические и логические зависи-
мости идентичны, то такое моделирование называется матема-
тическим.
Два явления называются физически подобными, если для иих
можно установить соответственные точки пространства и соот-
ветственные моменты времени так, чтобы в этих точках про-
странства в эти моменты времени все физические параметры,
характерные для данных явлений, были пропорциональны. Физи-
ческое моделирование в аэродинамических исследованиях бази-
руется иа понятии физического (в пашем случае механического)
подобия, под которым понимается комплекс условий, обеспечи-
вающих одновременно геометрическое, кинематическое, динами-
ческое подобие.
Геометрическое подобие — подобие формы (расстояний или
координат). Тела или системы называются геометрически по-
• добиыми, если отношения их сходственных линейных размеров
одинаковы.
Следует отметить, что к числу линейных размеров относятся
и размеры, определяющие положение геометрически подобных
тел в пространстве (например, пропорциональность и коллинеар-
ность радиусов векторов сходственных точек относительно нача-
ла координат модели и натуры).
В геометрически подобных телах и системах соответствую-
щие углы равны.
Кинематическое подобие — подобие движения. Движения
двух систем кинематически подобны, если при соблюдении гео-
метрического подобия во всех сходственных точках этих систем
в схотствепные моменты времени векторы скоростей имеют оди-
наковые направления, а отношения модулей скоростей постоян-
ны. В частности, кинематически подобные потоки жидкости име-
ют линии тока одинаковой формы с подобными граничными
условиями.
Динамическое подобие — подобие сил. Две системы динами-
чески подобны, если при выполнении геометрического подобия
выполняются следующие три условия:
— в сходственных точках этих систем в сходственные момен-
ты времени (для стационарных процессов любые моменты вре-
мени являются сходственными) действуют од поименные силы
(одной и той же природы);
отношения между всеми одноименными силами во всех
сходственных точках систем одинаковы;
144
www.vokb-la.spb.ru - Самолёт своими руками?!
движения систем должны ио,1 чиняться одинаковым диф-
ференциальным уравнениям, а также одинаковым начальным и
подобным граничным условиям.
Таким образом, теория подобия дает возможность правильно
обобщить экспериментальные или расчетные данные и по ре-
зультатам исследования модели сделать заключения о характе-
ристиках натурного объекта.
Подобие называется полным, если во всем пространстве,
окружающем натурный объект и соответствующую модель, по-
добие картин движения соблюдается полностью, т. е. если по-
добны многоугольники скоростей, ускорений, действующих сил,
и все однородные физические величины, определяющие движе-
ние, находятся в определенном постоянном от юшеиии в сходст-
венных точках пространства в сходственные моменты времени.
Если это условие не соблюдается, т. е. если ие все физические
величины, характеризующие движение модели и натурного объ-
екта, находятся в определенном постоянном отношении, то подо-
бие называется неполным или частичным. Полное динамическое
подобие — редко достигаемый предел. Наиболее часто экспери-
мента тьиые исследования приходится проводить лишь в условиях
частичного подобия.
Для обеспечения механического подобия двух явлений, опре-
деляющихся имеющими единственное решение системами диф-
ференциальных, алгебраических и ш функциональных уравнений,
необходима и достаточна тождественность основных уравнений
и тож ествениость безразмерных граничных и начальных усто-
вий.
Механическое подобие предусматривает подобие сил взаимо-
действия потока с обтекаемыми им твердыми телами. Это позво-
ляет путем аэродинамического эксперимента иа модели судить
об аэродинамическом качестве натурного объекта.
В данном курсе мы попытаемся изложить очень сжато эле-
менты теории подобия, совершенно ие рассматривая теории раз-
мерностей. Мы ставили задачу из теории подобия получить
критерии подобия, дать их анализ и определить формулы экспе-
риментальной аэродинамики для дальнейшего их использования.
Однако необходимо иметь в виду, что не всегда имеются уравне-
ния, описывающие исследуемый процесс. В этом случае полез-
ным явл [стся метод анализа размерностей Метод анализа раз-
мерностей позволяет определить критерии подобия и базируется
на так называемой л-теореме, априорном утверждении о сущест-
вовании некоторой функциональной связи между параметрами
процесса и элементами системы. Но на этом мы не останавлива-
емся и отсылаем наших читателей к соответствующим источ-
никам *.
* См Седов Л И Методы подобия и раз арности в механике, М„ «Нау-
ка», 1965, 428 с.; Веников В. А Теория подобия и моделирование примени-
тельно к задачам электроэнергетики. М, «Высшая школа», 1966, 487 с.
145
www.vokb-la.spb.ru - Самолёт своими руками?!
/
9.2. МАСШТАБНЫЕ МНОЖИТЕЛИ
(КОЭФФИЦИЕНТЫ ПОДОБИЯ) И ЗАДАЧИ ТЕОРИИ ПОДОБИЯ
Рассмотрим два механически подобных потока, один из кото-
рых соответствует изучаемому явлению в натуре, например об-
теканию крыла, а другой — модели явления, т. е. обтеканию
уменьшенной модели крыла.
Все параметры натурного потока будем обозначать индекса-
ми «н», модельного — «м».
При наличии механического подобия отношения всех механи-
ческих параметров натурного и модельного движений для любых
пар сходственных (соответственных) точек и любых пар сходст-
венных (соответственных) моментов времени будут одинаковы-
ми. Будем называть эти отношения масштабными множителями
или коэффициентами подобия и обозначать буквой А с соответ-
ствующим индексом. Например, если два потока геометрически
подобны и их линейные размеры отличаются величиной масшта-
ба, то
' или /н —(9. 1)
Для сходственных сечений и и объемов II7 в натурном и мо-
делируемом явлениях при наличии геометрического подобия
^к='4> ^Н/Ш\ = Х? (9.2)
или ан —
Для сходственных скоростей, ускорений и интервалов време-
ни в геометрически и кинематически подобных потоках аналогич-
но можно ввести масштабы скорости Ау, ускорения Ай, време-
ни Af.
—V н/^ м> ^а = ан/ам’ (9.3)
причем каждый из этих масштабов может быть выражен через
любой другой и геометрический масштаб. Так
Ху фн >1 X/
откуда At=Aj/AV Далее (9 4)
<2 л dVK/dtH Х[ (9 3')
а*. dVuJdty,\
Для сходственных значений сил, плотностей, напряжений,
масс и других динамических параметров в механически подоб-
ных потоках введем масштабы сил Ар, птотности А? , напряжения
146
www vokb-la.spb ru - Самолёт своими руками?!
(давления) кинематического коэффициента вязкости М , еди-
ничной массовой силы н т. д.
^Q~Qh/£?m’ ^p~Pw Pw g
^g Sal
Если v^const, то необходимо еще рассматривать темпера-
турное подобие, так как v зависит от температуры.
Следует отметить, что движение жидкости в сходственных
точках механически подобных потоков в соответствии с условия-
ми подобия будет подчиняться одним и тем же уравнениям. Как
и все движения, два подобных движения на модели и натуре
подчиняются закону днпамики Ньютона—сила равна массе,
умноженной на ускорение:
Р=та, (9.6)
где т — масса частицы, а — ускорение се движения.
Выражая массу жидкости через плотность р и объем VF, по-
лучим соответственно для натуры и модели
Р = п л р =QMIVZMOM,
И Н г! » М. М М М 7
откуда
щ (9 7)
Рк м^м
или в масштабных множителях
Xp=Vfr«- (9.8)
Учитывая, что Хр=Хг/X;, из равенства (9.8) получим масштаб
силы в виде
или (9 9)
Аналогично для масштаба давлений получим
——>-4. (9 10)
Завнснмостн (9.8), (9 9) и (9 10), называемые характеристи
ческими уравнениями механического подобия, устанавливают
соотношения между масштабными множителями для геометри-
ческих, кинематических и динамических элементов потоков.
Если движение вызывается несколькими силами различной
природы, то пропорциональность с одинаковым масштабом ХР
должна существовать между всеми силами (массовыми, давле-
ния, трения и т. д.), что усложняет выполнение условий подобия
На практике обычно выделяют одну из снл в качестве глав-
ной для изучаемого явления и так ставят эксперимент, чтобы
147
www vokb-la.spb.ru - Самолёт своими руками?!
исключить влияние остальных сил или чтобы оно было пренебре-
жимо мало. В этом случае говорят о частичном механическом
подобии. Для обеспечения надежности и достоверности заклю-
чений о явлениях в натуре иа основании изучения модели сле-
дует стремиться выбирать такие масштабы, строить и испыты-
вать такие модели, при которых второстепенные силы взаимно
уравновешиваются или ими можно пренебречь.
В экспериментальной аэродинамике исследуют модели (на-
«тример, модель самолета) в лабораторных условиях и пересчи-
тывают результаты лабораторных аэродинамических измерений
иа натурные условия.
При этом нужно иметь в виду, что при проведении экспери-
мента в аэродинамической трубе нарушается подобие граничных
условий, так как модель исследуется в ограниченном стенками
трубы пространстве или в ограниченной струе, в то время как
самолет движется в практически неограниченной или частично
ограниченной среде. В связи с этим приходится вводить соответ-
ствующие поправки на влияние границ потока, разработанные
на основе существующих теорий.
9.3. АЭРОДИНАМИЧЕСКОЕ МОДЕЛИРОВАНИЕ.
ОСНОВНЫЕ ЗАКОНЫ ПОДОБИЯ- КРИТЕРИИ ПОДОБИЯ
Научной базой метода моделирования физических явлений
является теория подобия, которая опирается иа учение о размер-
ности физических величин. Основной задачей теории моделиро-
вания является обеспечение подобия явлений. Сущность модели-
рования заключается в том, что иа модели меньшего (а иногда
-большего) масштаба создается аэродинамическое явление, по-
добное тому, которое должно возникнуть в натуре. Например, в
аэродинамическом эксперименте теория подобия помогает иа
модети изучить процесс взаимодействия твердого тела с жид-
костью.
При этом главное достоинство метода моделирования заклю-
чается в обобщении результатов единичного эксперимента на
целый класс явлений. Здесь же результаты исследовании движ' -
ния воздуха можно обобщить на случай движения воды, масла
и других сред и наоборот.
Метод моделирования, если модель меньше натуры, обеспечи-
вает наиболее рациональную организацию исследовании при
значительном сокращении объема экспериментальных работ,
средств и времени. Основной задачей моделирования, от решения
которой зависит успех исследования, является опре деление на-
иболее важных из действующих в рассматриваемом явлении сил
и выбор соответствующих критериев частичного подобия сил.
В предыдущем параграфе были получены характеристические
уравнения, связывающие между собой масштабы различных фи-
зических величин для механически подобных явлении и, в част-
148
www vokb-la.spb.ru - Самолёт своими руками?!
пости, выражения для масштаба сил (9.8) и (9.9) и масштаба
давлений (9 10).
Обозначая через Дри разность давлений в каких-либо двух
точках исследуемого потока в натуре (одна из них может быть
в невозмущенном потоке, довольно далеко от тела) и через
Арм — разность давлений в двух сходственных точках потока,
воспроизведенного при моделировании, иа основании (9.10) мо-
жно написать
Eu=-^V—idem. (9.11)
Безразмерный параметр Ей, одинаковый для сходственных
пар точек механически подобных потоков, носит название па-
раметра или числа Эйлера.
Исследуя уравнения движения жидкости, можно доказать,
что, если в несжимаемой жидкости действуют только силы дав-
ления, то при наличии геометрического подобия и кинематичес-
кого подобия начальных и граничных условий соотношение (9.11)
выполняется автоматически (свойство автомодельности движе-
ний невесомой и невязкой несжимаемой жидкости).
Аналогично, обозначая через Рп величину главного вектора
сил давления на какую-либо площадку (в том числе и на всю
поверхность тела) в натуре и через Рм соответствующую величи-
ну для модели, можно написать, используя (9.9):
Ne= Р“, — Л»' —idem. (9.12)
«Ж «ЛЧ 1
Этот безразмерный параметр, носящий название числа Нью-
тона, также одинаков для всех механически подобных течений
жидкости; если в жидкости действуют только силы давления, то
число Ne, так же как и Ей, зависит от формы тела, его положе-
ния, начальных и граничных условий.
Если в жидкости наряду с силами давления действуют силы
трения, то, очевидно, что в механически подобных системах силы
трения пропорциональны силам давления или, что то же самое,
касательные напряжения пропорциональны давлению На осно-
вании закона Ньютона (1.1) имеем
___ Ни
‘Т---4 ---
Тм Рм м
Ir
Приравняв этот масштаб к масштабу давления, получим
л I/2 л I/2 1*нЕн . Рм^М
Ch v и 1 Ум 1 м — • — ---
*н
149
www vokb-la.spb.ru - Самолёт своими руками?!
откуда находим критерий частичного подобия, обеспечивающий
при геометрическом и кинематическом подобиях пропорциональ-
ность сил вязкости и сил давления'
Re =£нАА = См^А, iclem (9 13)
или Re——н- —idem. (9. 13')
Параметр Re, одинаковый для двух механически подобных
течений, носит название критерия или числа Рейнольдса.
Величины V и I, входящие в выражение для чис. а Рейнольд-
са, представляют собой произвольно выбранные, характерные
для исследуемого течения скорости и длину. Необходимо, чтобы
при подсчете числа Re для подобного течения были взяты сход-
ственные скорости и длины.
Таким образом, если влиянием других сил, кроме сил давле-
ния и сил внутреннего трения, можно пренебречь, то для обес-
печения механического подобия двух течений необходимо и дос-
таточно обеспечить геометрическое подобие, подобие начальных
и граничных условий и равенства чисел Рейнольдса. Иными сло-
вами, при соблюдении указанных условий и равенстве чисел Re-
два течения вязкой жидкости будут механически подобны и, сле-
довательно, у них будут одинаковыми числа Ей и Ne. Если ра-
венство чисел Re не обеспечивается, то у геометрически и кине-
матически подобных течений числа Ен и Ne нс будут одинаковы.
Таким образом, при исследовании течения несжимаемой
вязкой жидкости числа Еп и Ne нужно считать функциями чис-
ла Re. Тогда формулы (9.11) и (9 12) можно записать в виде
Ей =Д (Re); Ne_-£-- /t(Re),
откуда получаем основные формулы экспериментальной аэроди-
намики;
Ap=/!(Re)eV2; Р /2(RcRZVz.
Прн больших числах Re функции Д и f2 стремятся к постоян-
ным значениям (при больших числах Re имеет место автомо-
дельность течений) ч
Следует отметить, что при необходимости учета влияния сил
тяжести появляется еще один критерий частичного подобия,
обеспечивающий пропорциональность сил давления и сил тя-
жести, а именно, число Фруда:
„ Е2 . .
гг =— =idem,
lg
где g ускорение свободного падения в некоторой характерной
точке потока.
150
vokb-la.spb ru - Самолёт своими руками?!
Для двух подобных течений несжимаемой жидкости масштаб
плотности Хс представляет собой заданную постоянную величи-
ну (равную 1, если в обоих течениях участвует одна н та же жид-
кость) .
Для сжимаемой жидкости плотность является функцией ко-
ординат частиц н времени. Поэтому при рассмотрении подобия
сжимаемой жидкости появляется новый критерий подобия, обес-
печивающий выполнение условия
XG—^=^- = idem, (9. 14)
Qm
где qh и Qm — плотность в сходственных точках в сходственные
моменты времени; Дрн. Aqm -разности плотностей в двух сход-
ственных парах точек в сходственные моменты времени или
приращение плотности в сходственных точках в сходственные
интервалы времени.
Учитывая формулы (1.16) и (9.11), выражение для масштаба
плотности (9 14) можно переписать в виде
>2
ло— 2 * 2 ,2 —idem,
ан ам Лд
откуда получим дополнительное необходимое условие подобия
течений сжимаемой жидкости
М=- ————idem. (9.15)
Параметр М, представляющий собой отношение характерной
скорости течения к характерной скорости звука, как было пока-
зано ранее, называется числом М.
Таким образом, для течений невесомой и невязкой сжимаемой
жидкости можно записать Eu=<p (М), Ne—ср2<М)
или А/?—(M)qV2, Р=ср2(М)р/21/2,
где q — некоторая характерная плотность.
Для неустановившегося движения соотношением
устанавливается зависимость между кинематическими масшта-
бами, откуда можно получить дополнительный критерий подо-
бия— число Струхаля (Strouhal)
Sh-^-^^.-idem, (9. 16)
где /п н - характерные сходственные интервалы или моменты
времени.
Так, папример, при исследовании воздушных винтов за ха-
рактерную скорость V принимают скорость движения самолета,
151
www.vokb-la.spb ru - Самолет своими руками?!
за t — время одного оборота винта, за I — диаметр винта D, тогда
для винтов критерия Струхаля принимает вид Sh— V/nJD, где
пс — число оборотов винта в секунду.
Для установившихся движении условия (9 16) выполняются
автоматически, так как /п и /м выбираются произвольно (пара-
метры движения зависят от /).
Подводя итоги сказанного выше, находим, что в общем слу-
чае числа Эйлера и Ньютона могут зависеть от чисел Re, М, Sh,
а возможно и от других критериев, учитывающих влияние других
факторов (например, степени турбулентности течения, степени
шероховатости поверхности тела и т. д.).
Каждый из указанных критериев является показателем час-
тичного подобия. Как было указано выше, при исследовании раз-
личных течений обычно приходится выделять один или два ос-
новных критерия и изучать их влияние на течение жидкости*
пренебрегая влиянием остальных второстепенных критериев или
стремясь исключить их влияние.
9.4. АНАЛИЗ КРИТЕРИЕВ ПОДОБИЯ
В задачах аэродинамики влиянием силы тяжести обычно мо-
жно пренебречь, поэтому в этом случае основными критериями
подобия являются числа Re и М, а в случае неустаиовившегося
движения и число Sh.
При исследовании движения несжимаемой жидкости газа на
малых скоростях основными критериями подобия являются Re,
Fr, Sh, а для установившихся движений (если при этом можно
пренебречь влиянием силы тяжести) только число Re. Следует
отметить, что даже соблюдение только равенства чисел Re в аэ-
родинамическом эксперименте весьма затруднительно. Натурные
числа Рейнольдса в настоящее время весьма велики. Для пр ше-
ра рассчитаем характерное число Рейнольдса для самолета
Ту-134, который имеет крейсерскую скорость полета 850 км/ч
(приблизительно 235 м/с) на высоте полета 11000 м. Кинемати-
ческий коэффициент вязкости на данной высоте равен
0 375-Ю^4 м2/с. В качестве характерной длины при подсчете чис-
ла Рейнольдса для самолета принимается некоторая средняя по
размаху хорда, так называемая средняя аэродинамическая хор-
да, например, у самолета Ту-134, равная 4,319 м. Таким образом*
получаем
23о м с • 4,319 м , 97
Ке“ 0,375-10 4М2/С"" ’
Испытывая модель самолета при скорости 60 м/с в аэродина-
мической трубе на уровне моря v = 0,I44-10 4 м2/с при масштабе
модели 1/20, будем иметь число Рейнольдса
60 м/с-4.319 м -
20-0,144-10-4 м2/с
т. е. в 30 раз меньше, чем в натуре.
152
www vokb-la.spb ru - Самолёт своими руками?!
В результате возникает техническая задача приближения ус-
ловий эксперимента к натурным условиям полета при модели-
ровании по числу Рейнольдса. Из выражения для числа Рей-
нольдса следует, что это можно осуществить следующими спо-
собами:
— увеличением скорости потока в аэродинамической трубе;
— увеличением линейных размеров модели,
— уменьшением кинематического коэффициента вязкости
среды, в которой проводится эксперимент.
Использование первого способа ограничено по двум при-
чинам:
1) при увеличении скорости свыше 100 м/с начинает сказы-
ваться влияние сжимаемости среды, что приводит к нарушению
подобия по числу М;
2) увеличение скорости воздушного потока в аэродинамичес-
кой трубе приводит к быстрому увеличению затрат мощности,
так как мощность привода аэродинамической трубы пропорцио-
нальна кубу скорости потока.
Наиболее широко в настоящее время используется второй
способ — увеличение линейных размеров модели, что, естествен-
но, приводит к увеличению размеров рабочего участка аэроди-
намических труб.
Чаще используется третий способ — уменьшение кинематичес-
кого коэффициента вязкости. Известно, что v = p/Q, при этом ди-
намический коэффициент вязкости практически не зависит от
давления, тогда как плотность q может изменяться в весьма
широких пределах при изменении давления В результате, не-
смотря на ряд технических трудностей, широкое применение на-
чинают получать трубы с повышенным давлением в контуре или
трубы переменной плотности. При увеличении давления в аэро-
динамической трубе до 25 кгс/см2 при сохранении неизменной
температуры плотность увеличивается почти в 50 раз, что позво-
ляет довести число Рейнольдса для указанной модели до вели-
чины
Re
(р) _60 м/с-4,319 м
м — 20-6-10-6 М2/с
= 2,1-10е.
Еще сложнее удовлетворить условиям подобия при необходи-
мости учета двух критериев. Рассмотрим, например, наиболее
важный для задач аэродинамики случай подобия по критериям
Re и М. Если эксперимент проводится в воздухе при температуре
натуры, то коэффициент теплопередачи ам = ап, = Нн и, следо-
ватель: о, масштаб скорости равен единице (V, —1/н) О сюда
следует /mQm~-^hQh, что указывает на необходимость проведения
эксперимента с малыми моделями при повышенной плотности
воздуха
Qm __1
Qh
(9- 17)
153
www vokb-la.spb.ru - Самолёт своими руками?!
т. е. при одной и той же температуре подобия по числам Re и М
может быть достигнуто только при условии, что скорость потока
равна натурной, а плотность (и, следовательно, давление) в ра-
бочем участке аэродинамической трубы во столько раз больше
атмосферной, во сколько раз размеры модели меньше натурных
размеров моделируемого объекта.
Рассмотрим также, при каких условиях можно одновременно
выполнить два критерия подобия: Re = idem, Sh = idem. Оба этих
критерия имеют важное прикладное значение. В рассматривае-
мом случае
------- -------------- и -----------=
vh vm----------------------ZM
и ZM
м ZH
откуда получаем, что, с одной
стороны, — = —
1 zM
Приравнивая правые части полученных равенств,
стороны,
Zm
• Zh
V,.
— , с другой
vM
получим
Zm Zh Zm ИЛИ /2 vh __ Zm
Zh Zm Zh ZM Zh
При моделировании течений практически не удается изменить
масштаб времени и поэтому ^/^, = 1. В итоге получаем связь
между линейными размерами модели и натурного объекта с вяз-
костью воздушного потока в натуре и в аэродинамической трубе:
. Таким образом, при необходимости одновременного
моделирования по критериям Рейнольдса и Струхаля уменьше-
ние линейных размеров модели в п раз требует уменьшения ко-
эффициента кинематической вязкости в аэродинамической трубе
в п2 раз.
Выполнение этого условия можно осуществить в аэродинами-
ческих трубах переменной плотности, в контуре которых может
в широких пределах изменяться давление воздуха. В трубах
переменной плотности иногда применяют газ с малой вязкостью,
например водород или гелий, что позволяет добиться одновре-
менного моделирования по Re и М при меньшем давлении в ра-
бочем участке.
Если моделируется установившееся течение, то равенство
критериев Струхаля для модели и натуры удовлетворяется авто-
матически, т е. наблюдается автомодельность по числу Струха-
ля. Если же процесс периодический, то моделирование по чис-
лам Re и М осуществляется подбором соответствующего мас-
штаба времени.
154
www.vokb-la.spb.ru - Самолёт своими руками?!
(9.18)
Для определения масштаба времени, используя критерии
подобия вычислим отношение скоростей для натуры и модели:
^мОмНн . Ен
Ем ^hQhHm Ем
Полагая, что числа Рейнольдса и Струхаля для модели и натуры
равны и приравнивая правые части этих равенств, получим
tH _^hQhMm
t i
При равенстве температур воздуха в натурных и эксперимен-
тальных условиях рм = Рн. Переходя к масштабным множителям,
получим соотношение (9.18) в виде:
Если температура ГН=ГМ, то масштабы давления и плотности
будут равны, т. е. XG Тогда с учетом (9.17)
(9.19)
Для основных масштабов моделирования при условии, что
состав и температура воздуха в натурных и экспериментальных
условиях одинаковы, имеем: масштаб линейный Л/—-задается;
масштаб времени Zt—Л/ согласно (9.19); масштаб скорости kv—
масштаб плотности Ле=1/Х; согласно (9.17); мас-
штаб давления Хр—— 1Дг (согласно уравнению состояния):
масштаб вязкости Хр. = 1.
Если масштабы подобия выбраны в соответствии с этими дан-
ными, то критерии Рейнольдса, Маха и Струхаля удовлетворя-
ются одновременно.
9.5. ОСНОВНЫЕ ФОРМУЛЫ ЭКСПЕРИМЕНТАЛЬНОЙ
АЭРОДИНАМИКИ
Величина аэродинамической силы, с которой поток воздейст-
вует на обтекаемое тело, и ее направление определяются по
распределению давления р и касательного напряжения т по по-
верхности обтекаемого тела, которые, в свою очередь, зависят
от характера обтекания, т. е. скорости V, плотности р в различ-
ных точках потока. Последние, в свою очередь, будут зависеть
от размеров и формы тела, от его положения относительно пото-
ка, а также от безразмерных критериев подобия Re, М, Sh, учи-
тывающих влияние сил внутреннего трения сжимаемости и не-
стацнонарности течения на формирование течения.
В ря ,е случаев на величину сопротивления большое влияние
могут оказывать и другие факторы. Известно, например, что в
зависимости от условий могут осуществляться два различных
режима течения жидкости: ламинарный и турбулентный (см.
гл. 1 1).
155
www.vokb-la.spb.ru - Самолёт своими руками?!
В случае турбулентного течения начальные и граничные ус-
ловия уже не определяют однозначно поля скоростей, давлений
и плотностей. Рейнольдс, одиако, показал, что при введении в
уравнения движения дополнительных касательных напряжении
эти уравнения совместно с начальными и граничными условиями
однозначно определяют поля осредиеииых величин скоростей»
давлений н плотностей.
Строгой теории турбулентного течения, позволяющей вычис-
лить точные значения дополнительных касательных напряжений
пока ие существует. Однако опыт показывает, что эти напряже-
ния в основном зависят от степени турбулентности е невозму-
щеиного потока, определяемой как отношение осредненной квад-
рэтичной пульсации к величине осредненной скорости
(Е = Vv,2iV). Из этого следует, что к числу критериев механи-
ческого подобия необходимо добавить критерий е, который явля-
ется условием подобия сил турбулентного трения и сил инерции.
Еще один дополнительный критерий подобия получен в связи
с невозможностью осуществления геометрического подобия мо-
дели и натурного объекта из-за наличия шероховатости на по-
верхностях. Геометрически подобными с достаточной степенью
точности считаются тела, размеры которых пропорциональны, а
степени шероховатости одинаковы. Степень шероховатости k
определяется как отношение средней высоты выступов шерохо-
ватости к характерному размеру тела I: k=kjl. Эта величина
и является дополнительным критерием подобия. На основании
изложенного выше для тела заданной формы при заданном по-
ложении относительно направления движения
Ne=(Re’м- Sh- (9-20)
Аналогично можно получить моментное число Ньютона, опре-
деляющее главный момент М системы сил аэродинамического
взаимодействия (аэродинамический момент) относительно неко-
торой точки:
Ne„=^=/2(Re, М, Sh, е, *). (9.21)
Заменяя в этих формулах квадрат линейного размера на про-
порциональную ему характерную площадь S (например, пло-
щадь крыла) и произведение рГ2 на динамическое давление q —
=qV2I2, получим основные формулы экспериментальной аэро-
динамики:
Чгл=^=Огл(Ве. М, Sh, е, Г); (9.22)
c„ = -^- = c„(Re, М, Sh, е, Л). (9. 23)
156
www.vokb-la.spb.ru - Самолёт своими руками?!
Безразмерные векторные величины cR к и ст соответствен-
но называются коэффициентом полной аэродинамической силы
и коэффициентом аэродинамического момента. Эти коэффициен-
ты определяются из эксперимента: точно — при соблюдении ус-
ловий полного подобия или приближенно — при частичном подо-
бии Если cRX и ст известны, то из (9.22) и (9.23) можно полу-
чить
(где^=^у-); (9.24)
M=cmSql. (9.25}
Векторные величины 7?Л и М можно разложить на составля-
ющие, направленные по осям координат, получив таким образом,
шесть различных величин и шесть соответствующих аэродинами-
ческих коэффициентов, определяющих силовое взаимодействие
тела и среды. В частности, модуль аэродинамической силы
для случая плоского движения
ra=VxI+yI,
где Xa=cxaqS — так называемая сила лобового сопротивления;
Ya — cyaqS — так называемая подъемная сила. Здесь С-ха, Суа
соответственно коэффициенты силы лобового сопротивления и
подъемной силы Подробнее эти коэффициенты будут рассмот-
рены в гл. 13.
Вопросы для повторения
1 Назовите основные критерии подобия и объясните влияние
каких факторов они отображают.
2 Как достигнуть одновременного подобия по числам М и
Re?
3 . Напишите общую формулу, выражающую зависимость си-
лы сопротивления от критериев подобия.
4 . Опишите способы пересчета модельных данных на натуру.
Задачи
1. Определить, какое сопротивление преодолевает тело дли-
ной 3 м, погруженное в воду и движущееся со скоростью 3 м/с,
если при продувках в аэродинамической трубе с регулируемым
давлением его геометрически подобной модели длиной 0,3 м
при скорости потока 48 м/с величина лобового сопротивления со-
ставила 3,85 Н Считать, ЧТО /возд=*воды = 15СС, Цвозд/рводы =
= 0,016
157
www vokb-la.spb ru - Самолёт своими руками?!
Решение. Из условия подобия чисел Рейнольдса определя-
ем требуемую плотность воздуха в аэродинамической тр бе
ReH=ReM, откуда
Здесь Х„=^- = —; Х.=А=А = Ю; xv=K^=2=l.
Ивозд 0,0 б ZM 0,3 Рвозл 48 16
Масштаб плотности ?ч) =-----= 100.
0,016-10
Плотность воздуха 10 кг/м3.
Используя уравнение состояния, определяем давление воздушно-
го потока
^ = 0,1-12-^0,75 Н/м2.
бет 1,33
Масштаб силы = \ — =
Хм
\-_100- 102 — ^39 06
Л. । 7
Определяем искомую силу сопротивления воды
Ли=кхХм=39,06-3,85^ 150 Н.
Ответ: Хн«150 Н
2 Проектируемый самолет имеет скорость 1800 км/ч иа высо-
те // — 12000 м (по стандартной атмосфере). Скорость потока
воздуха в рабочей части сверхзвуковой аэродинамической трубы
450 м/с. Какая должна быть температура в рабочей части трубы
для получения аэродинамического подобия по числу М
Ответ: /=—97° С
www vokb-la.spb.ru - Самолёт своими руками?!
ГЛАВА 10
ОСНОВЫ ЭКСПЕРИМЕНТАЛЬНОЙ АЭРОДИНАМИКИ
10.1. ЗАДАЧИ ЭКСПЕРИМЕНТАЛЬНОЙ АЭРОДИНАМИКИ
И МЕТОДЫ ИХ РЕШЕНИЯ
Основной задачей экспериментальной аэродинамики является
исследование законов воздействия воздуха на движущиеся в нем
тела. При этом под телом понимается чрезвычайно широкий
круг объектов: от простейшей модели крыла или фюзеляжа
самолета до сложнейших комплексов, каким 5 вляется натурный
самолет.
Указанные исследования можно проводить двумя методами:
телу сообщается скорость относительно неподвижного воздуха
(прямая задача); воздуху сообщается скорость относительно
неподвижного тела (обратная задача).
Независимо от того, каким методом мы воспользуемся, сог-
ласно принципу относительности Галилея—Ньютона (см. В 3)
силовое взаимодействие между телом и воздухом будет тожде-
ственным
Прямой метод исследований является основой натурных или
летных испытаний, в процессе которых определяются силовые и
моментные характеристики, оценивается устойчивость и управля-
емость летательного аппарата и другие характеристики. Необхо-
димо, о. нако, отметить, что летные испытания, кроме большой
стоимости, имеют тот недостаток, что при их проведении техни-
чески трудно, а во многих случаях практически невозможно осу-
ществить испытания многочисленных вариантов летательного ап-
парата с целью получения оптимальных характеристик. Поэто-
му летные испытания являются обычно завершающим этапом
создания летательного аппарата. А иа предварительных этапах
проектирования широко используются методы, при которых не-
подвижные модели обтекаются движущимся воздухом (имеет
место обращение движения).
Для этой цели строятся аэродинамические трубы. Аэродина-
мическая труба представляет собой специальный физический
прибор, позволяющий получать в одном из его элементов искус-
15»
www.vokb-la.spb.ru - Самолёт своими руками?!
ственный равномерный прямолинейный установившийся поток
воздуха определенной скорости.
Экспериментальные исследования, осуществляемые в аэроди-
намических трубах, позволяют проводить испытания моделей
многочисленных вариантов летательного аппарата, выявлять
взаимное влияние отдельных его эпемеитов и, что очень важно,
обеспечивать идентичные условия эксперимента при повторных
испытаниях моделей.
Аэродинамические эксперименты в трубах можно условно
подразделить на три группы. Целью первой группы эксперимен-
тов является определение аэродинамических сил и моментов для
расчета прочности конструкции и летных свойств летательных
аппаратов в процессе их проектирования. В этом случае созда-
ются модели летательных аппаратов, по размерам значительно
меньшие натуры, которые исследуются в аэродинамических тру-
бах. Объем таких испытаний достаточно большой. Например,
для создания современного сверхзвукового самолета необходимо
изготовить и испытать в аэродинамических трубах более десяти
моделей.
Целью второй группы экспериментальных исследований явля-
ется разработка новых схем летательных аппаратов и получение
их оптимальных характеристик. К этой группе относятся; иссле-
дования в области управления пограничным слоем на малых ско-
ростях, ламиниризации крыльев на больших скоростях, крыльев
перемеииой стреловидности; поиски новых видов крыльев и т. д.
К третьей группе относятся экспериментальные исследования,
связанные с перспективой дальнейшею развития летательных
аппаратов, например, изучение физических явлений, возникаю-
щих при больших числах М и температурах, экспериментальная
проверка новых теорий и гипотез, гзучеиие распространения
сильных ударных волн, исследование плазмы и т. д. Эти иссле-
дования в большинстве случаев проверятся не в обычных аэро-
динамических трубах, а иа специальных экспериментальных ус-
тановках, таких, например, как, ударняе трубы, баллистические
установки, плазматроны и т. д.
10.2. ПРИНЦИПЫ ПОСТРОЕНИЯ АЭРОДИНАМИЧЕСКИХ ТРУБ
Как отмечалось выше, основное иаз {ачение любой аэродина-
мической трубы заключается в том, чт >бы создать в ее рабочей
части равномерный установившийся по' ок воздуха определенной
•скорости.
Теоретической основой расчета аэро динамических труб явля-
ется уравнение энергии движущегося вс щуха в трубе. В частно-
сти, дтя воздушных потоков небольшие дозвуковых скоростей,
используется уравнение Бернулли (5.26 р0—р = р1/2/2 Из этого
равенства следует, что для получения i эздушпого потока опре-
деленной скорости необходимо обеспеч гь избыток потенциаль-
но
www.vokb-la.spb.ru - Самолёт своими руками?!
ной энергии покоящегося газа, т. е. энергии давления. Это требо-
вание определяет конструктивное решение схемы аэродинамичес-
кой трубы малых скоростей (рис. 10.1), в контуре которой обя-
зательно имеются следующие элементы: конфузор (коллектор)
или сопло, рабочий участок, диффузор, вентиляторная уста-
новка.
Основное назначение сопла — увеличение скорости воздушно-
го потока. Согласно закону сохранения массы, который можно
записать в форме уравнения расхода для несжимаемой жидко-
сти (2.18) У15! = У252 или V2/Vi-Si/S2, для увеличения скорости
« 7
Рис. 10 2. Схема аэродинамической
трубы'
1—лабораторное здание; 2 рабочая
часть, 3—коллектор; 4 форкамера; 5—
шахта охлаждения воздуха; 6—диффу-
зор с большим углом расширения; 7—
вентилятор. 8—силовая установка
Рис. 10 1. Схема аэродинамической
трубы замкнутого типа с открытой
рабочей частью:
1 коллектор; 2—рабочая часть; 3—диф-
фузор; 4—двигатель; 5—вентилятор; 6—об
ратный канал; 7—направляющие лопатки
воздушного потока необходимо уменьшать плошадь его попереч-
ного сечения S Поэтому сопло представляет собой сужающийся
канал со специально спрофилированным обводом (образующей
сопла). Характер поля скоростей в рабочей части трубы и потери
энергии, кроме скорости, определяют форма обвода сопла, его
длина и степень поджатия n=Si/S2. Сопло уменьшает неравно-
мерность поля скоростей при этом неравномерность скорости иа
выходе из сопла в п2 раз меньше неравномерности скорости на
входе, что, в свою очередь, приводит к уменьшению турбулент-
ности воздушного потока в рабочей части аэродинамической
трубы
Непосредственно за сопло 1 располагается рабочая часть (ра-
бочий участок) аэродинамической трубы. В ней формируется
воздушный поток необходимой скорости и располагается иссле-
дуемая модель
Рабочие части в аэродинамических трубах выполняются либо
открытыми, либо закрытыми, в силу чего аэродинамические тру-
бы подразделяются на аэродинамические трубы с открытой ра-
бочей частью (обычно замкнутые, т. е. с обратным каналом) и
на аэродинамические трубы с закрытой рабочей частью (могут
быть замкнутые и незамкнутые). Схемы указанных аэродинами-
ческих труб приведены на рис. 10 1 10 4.
6
626
161
www vokb-la.spb ru - Самолёт своими руками9'
Преимуществом труб с открытой рабочей частью является
свободный доступ к модели и приборам, когда не возникает
трудностей с расположением аэродинамических масс.
К недостаткам труб с открытой рабочей частью относятся:
возникновение резких и опасных для конструкции трубы пульса-
Рис. 10.3. Схема аэродинамической трубы незамкнутого ти-
па с закрытой рабочей частью:
1—коллектор; 2—испытуемый объект; 3—рабочая часть; 4 -диффу-
зор; 5«—вентилятор; 6—электродвигатель
ций воздушного потока, связанных с вихреобразованием на вы-
ходе из сопла и на границах свободной струи, резкое увеличение
требуемой мощности вентиляторной установки с увеличением
скорости потока. Трубы с закрытой рабочей частью более г коно-
мичны, но они имеют свои недостатки, связанные в основном с
доступом к модели и сложностью компоновки рабочего участка.
8 7 6
Рис. 10.4. Схема аэродинамической трубы с обратным диф-
фузором:
/—коллектор; 2—первая спрямляющая решетка; 3—первая рабочая
часть; 4—первый диффузор. 5—подвижная часть; 6—вторая спрям-
ляющая решетка; 7—вторая рабочая часть; 8— бргтный диффузор;
9—вентилятор
За рабочей частью аэродинамической трубы располагается
диффузор — постепенно расширяющийся канал, предназначен-
ный ля превращения кинетической энергии потока рабочей час-
ти в энергию давления (потенц шльную).
162
www.vokb- la.spb ru - Самолёт своими руками?!
На работу диффузора оказывают влияние, главным образом,
величина и распределение скоростей на входе в диффузор и ха-
рактер расширения потока в диффузоре.
Требуемый перепад давления в трубе, необходимый для под-
держания движения воздуха, обеспечивается вентиляторной ус-
тановкой.
10.3. АЭРОДИНАМИЧЕСКИЕ ТРУБЫ МАЛЫХ
ДОЗВУКОВЫХ СКОРОСТЕЙ
Наиболее простыми в конструктивном отношении являются
аэродинамические трубы малых дозвуковых скоростей. Такие
трубы получили очень широкое распространение. Размеры этих
труб изменяются в широких пределах, а потребляемые мощнос-
ти — от нескольких до сотен тысяч киловатт.
Аэродинамические трубы могут быть незамкнутыми и замкну-
тыми. Незамкнутые аэродинамические трубы называются еще
Рис. 10.5. Схема аэродинамической трубы с открытой рабо-
чей частью и герметической камерой
трубами прямого действия (см рис. 10.3). В этих трубах воздух
засасывается нз атмосферы и после вентиляторной установки
опять выбрасывается в атмосферу, вследствие чего неравномер-
ность распределения скорости в трубах прямого действия дости-
гает 3—5%, а скосы потока 2—3%. Степень начальной турбу-
лентности характеризуется величиной е—1 5%.
Влияние стенок аэродинамической трубы с закрытой рабочей
частью на обтекание модели сводится к тому, что при сохранении
постоянного расхода воздуха через рабочую часть трубы имеет
место трансформация линий тока обтекающего модель потока,
увеличение скоростей потока в области расположения модели.
Трансформация линии тока существенно влияет на подъемную
силу и положение центра давления крыла.
Очень удобной для монтажа моделей является труба прямого
действия с открытой рабочей частью, которая окружена специ-
альной герметической камерой, называемой камерой Эйфеля
(рис. 10 5) В этой камере, обычно достаточно просторной и
удобной для размещения экспериментаторов и измерительной
аппаратуры, давление выравнивается до статического давления
потока н всегда меньше атмосферного давления Однако следу-
6*
163
www.vokb-la.spb.ru - Самолёт своими руками?!
ет заметить, что в данном случае также имеются недостатки,
свойственные трубам с открытым рабочим участком. В частно-
сти, потери полного давления в рабочей части на 20% больше,
чем в трубах с закрытой рабочей частью.
В аэродинамических трубах замкнутого типа воздух цирку-
лирует по замкнутому контуру. Поэтому в трубах этого типа по-
являются дополнительные элементы: колена с поворотными ло-
патками, обратный канал н формокамера с выпрямляющими
поток устройствами.
В контуре аэродинамической трубы замкнутого типа имеется
четыре поворотных колена, поскольку воздух, прошедший через
рабочую часть, должен в нее возвратиться через сопло, т, е. по-
вернуться на 360°.
Для устранения срывов и скосов воздушного потока в пово-
ротных коленах устанавливаются направляющие лопатки, часто
используемые и для охлаждения воздуха, циркулирующего в
контуре трубы. Форкамера служит для выравнивания и успо-
коения потока после поворота его в четвертом колене На входе
в форкамеру устанавливается хонейкомб, предназначенный для
выравнивания потока, и сетки, гасящне турбулентные возму-
щения.
Хонейкомб представляет собой сотовую конструкцию, состоя-
щую из ячеек длиной по потоку в 5—10 диаметров ячейки при
толщине стенок порядка 0,5—2 мм.
Устанавливаемые за хонейкомбом сетки устраняют неравно-
мерность распределения скорости поперек сечения форкамеры
и гасят возмущения, вносимые в поток хонейкомбом. Сетки, гася-
щие турбулентные возмущения (с возможно минимальным d
проволоки) устанавливаются в месте наименьшей скорости пото-
ка перед рабочей частью трубы. В этом случае возмущения,
вносимые сетками, слабы и гасятся в конфузоре.
104 АЭРОДИНАМИЧЕСКИЕ ТРУБЫ БОЛЬШИХ СКОРОСТЕЙ
Аэродинамические трубы больших скоростей строятся в боль-
шинстве случаев по типу замкнутой трубы с закрытой рабочей
частью (см. рнс. 10 2) При скоростях потока, соответствующих
числам Мто=0,80.. 0,95, вследствие появления в рабочем участ-
ке местных звуковых н сверхзвуковых скоростей, приводящих
к образованию местных скачков уплотнения, возникает так на-
зываемое «запирание» трубы (рис 10.6) В этом случае дальней-
шее увеличение скорости в трубе невозможно даже при значи-
тельном увеличении мощности агрегата привода. Положение еще
больше осложняется при испытании модели на звуковых скорос-
тях. В настоящее время разработаны меры по устранению ука-
занных дефектов у труб околозвуковых скоростей. Так, напри-
мер, в рабочей части трубы перфорируют до 20% поверхности
164
www.vokb-la.spb.ru - Самолёт своими руками/!
ZZZ//////////////z//////
/U &
^М<1
^00^1
Г
^Спутная
струя
/г?
стенок. Это позволяет проводить эксперименты на околозвуко-
вых режимах, соответствующих числам Моо=0,6... 1,3.
Околозвуковые трубы служат главным образом для опреде-
ления величин аэродинамических коэффициентов модели при
переходе через звуковой барьер и для
исследования кризисных явлений.
Трубы сверхзвуковых скоростей бы-
вают кратковременного и непрерывно-
го действия. Работа трубы происходит
за счет разности давлений на входе и
выходе трубы. При этом могут быть
три варианта: повышенное давление
перед трубой и нормальное на выходе,
нормальное перед трубой — вакуум иа
выходе и, наконец, повышенное перед
трубой и вакуум на выходе.
Схема кратковременно действую-
щей сверхзвуковой трубы дана на
рнс. 10. 7. Воздух, засасываемый нз ат-
мосферы через коллектор 1, проходит
через спрямляющую решетку 2, сопло
Лаваля 3 (где приобретает сверхзву-
ковую скорость), затем через рабочую
часть 4, регулируемый диффузор 5,
диффузор 6, ресивер 8 и выходит в ат-
мосферу. Высокий вакуум в ресивере создается с помощью эк->
сгаустера. Перед ресивером расположен быстродействующий
кран 7, включающий трубу на время, равное долям секунды.
В рабочей части трубы, где устанавливается испытуемая мо-
77777777777^777777777777
Рис 10 6. Схема «запира-
ния» околозвуковой -аэро-
динамической трубы скачка-
ми уплотнения
Рис. 10 7. Схема сверхзвуковой аэродинамической трубы
кратковременного действия.
/—коллектор; 2—спрямляющая решетка. 3—сопло Лаваля: 4-пабо-
чая часть; 5-регулируемый диффузор; 6 диффузор; /-быстродей-
ствующий кран; 8—ресивер; 9—испытуемый объект
дель, за с ет разности давлений между атмосферой и ресивером
в течение небо много промежутка времени создается сверхзвуко-
вое течение
165
www.vokb-la.spb.ru - Самолёт своими руками?!
Схема сверхзвуковой трубы кратковременного действия эжек-
торного типа, изображена на рис. 10.8. Компрессором 9 создает-
ся высокое давление в ресивере 8, при открытии быстродейству-
Рис. 10.8. Схема эжекторной сверхзвуковой
трубы кратковременного действия:
f—осушитель; 2—сопло Лаваля; 3 испытуемый
объект; 4—рабочая часть; 5—эжектор; 6—диффу-
зор; 7—кран, в—ресивер; 9—компрессор
ющего крана 7 воздух из ресивера вытекает в атмосферу через
эжектор 5 и диффузор 6. Эжектируемый воздух засасывается
в трубу через осушитель 1, проходит через сопло Лаваля 2, ра-
бочую часть 4, диффузор 6, где смешивается с эжектирующим
воздухом и выпускается в атмосферу.
Схема сверхзвуковой трубы кратковременного действия бал-
лонного типа приведена на рис. 10.9. Батарея баллонов 3 со сжа-
Рис. 109. Схема баллонно-вакуумной сверхзвуковой трубы
кратковременного действия:
1—электродвигатель; 2—воздушный компрессор; 3—баллон для
сжатого воздуха; 4—пусковой быстродействующий кран; 5—спрям-
ляющая решетка; 6—сопло Лаваля; 7—испытуемый объект; в—диф-
фузор; 9—быстродействующий кран, 10—ресивер
тым воздухом устанавливается перед коллектором, а на выходе
из рабочей части трубы установлен ресивер 10 с очень низким
давлением воздуха внутри.
Трубы кратковременного действия недороги и доступны для
обычных учебных лабораторий, тем более, что они не нуждаются
166
www vokb-la.spb ru - Самолёт своими руками?!
в мощных двигательных установках и в ннх можно создавать
необходимые числа М и Re.
Время действия такой трубы зависит от объема ресивера или
баллонов и давления воздуха в них. При малых объемах и дав-
лениях время действия трубы настолько мало, что трудно полу-
чить правильную количественную аэродинамическую характе-
ристику испытуемой модели.
Схема сверхзвуковой аэродинамической трубы непрерывного
действия приведена на рис 10.10. Сверхзвуковое течение в ра-
Рис. 10.10. Схема сверхзвуковой аэродинамической
трубы непрерывного действия-
1—сопло Лаваля, 2—рабочая часть; 3—испытуемый объект; 4-
диффузор. 5—поворотные лопатки; 6— обратные каналы; 7—
электродвигатель; 8—ко.мпрессор; 9—охладитель
бочей части создается с помощью многоступенчатого осевого
компрессора 8. Для понижения температуры воздуха, нагреваю-
щегося при сжатии в компрессоре, установлен охладитель 9. По-
ток воздуха протекает через сопло Лаваля 1, где приобретает
сверхзвуковую скорость, затем проходит через рабочую часть 2,
диффузор 4 и обратный канал 6 с поворотными лопатками 5. Раз-
ные скорости в рабочей части трубы можно получить путем из-
менения режима работы компрессора илн изменения сечений
сопла Лаваля и диффузора, для чего применяются либо сменные
вставки с разными сечениями, либо гибкие стенки, которые мож-
но закрепить так, чтобы получилась нужная площадь поперечно-
го сечения.
Иногда для повышения чисел Рейнольдса испытуемых моде-
лей идут по пути изменения плотности рабочей среды, применяя
вместо воздуха другой газ, например, фреон, который в четыре
раза плотнее воздуха.
В современных околозвуковых и сверхзвуковых трубах широ-
ко применяются автоматы, выдвижные рабочие части с моделью,
дистанционное управление трубой и ее элементами. Наблюдение
за моделью производится телевизионными способами.
Для исследования моделей в диапазоне гиперзвуковых ско-
ростей, соответствующих числам М порядка 15—25, применяют-
167
www vokb-la.spb ru - Самолёт своими руками?!
ся ударные трубы. На рис. 10 И приведена схема такой трубы.
Один ее конец присоединен к камере высокого давления 2, а дру-
гой— к вакуумной камере 8 с глубоким разрежением.
Во время работы трубы в камере высокого давлен я 2 вос-
пламеняется смесь газов (например, смесь кислорода и водоро-
да) Создаются высокая температура и превышающее тысячу
атмосфер давление, которое разрывает металлическую диафраг-
му 4, расположенную между трубой и камерой. Благодаря воз-
никающим при этом мощным ударным волнам, кроме большой
Рис 10.11. Схема гиперзвуковой аэродинамической трубы
ударного типа:
I—компрессор; 2 камера высокого давления: 3—воспламенитель;
4—диафрагма; 5—датчики: 6—рабочая часть, 7—оптический прибор;
8—вакуумная камера
скорости потока, наблюдается значительное повышение темпе-
ратуры. Установившееся течение в рабочей части трубы сохраня-
ется очень короткий промежуток времени — менее одной милли-
секунды. Скорость движения ударной волны в различных точках
трубы определяется электронной быстродействующей аппарату-
рой, а картина обтекания мо хели исследуется оптическими при-
борами.
В экспериментальной аэродинамике применяются также тру-
бы переменной плотности, имеющие большое преимущество пе-
ред обычными атмосферными трубами, так как позволяют удов-
.гетворить одновременно условия подобия по числам Re и М В
последнее время уделяется большое внимание исследованиям и
разработке конструкций самолетов с вертикальным и укорочен-
ным взлетом н посадкой (ВПП КВП). При испытаниях моделей
в обычных дозвуковых аэродинамических трубах сказывается
эффект неполного моделирования из-за стесненности потока
стенками. Поэтому для исследования моделей самолетов ВПП/
КВП строятся специальны i аэродинамические трубы (см
рис 10 2) в которых, как правило, предусмотрены две рабочие
части (часто с перфорированными стенками), неподвижный
экран, система отсоса пограничного слоя с экрана, широкий ди-
168
www.vokb-la.spb.ru - Самолёт своими руками?!
апазон регулируемых скоростей, подвод сжатого воздуха к мо-
дели, специальная измерительная аппаратура и т. д.
При неподвижной стенке трубы и при испытании моделей со
струйными закрылками сильно отклоненная струя частично рас-
пространяется по пограничному слою против потока, существен-
но искажая течение под моделью. Подвижный экран оказывает
существенное положительное влияние на структуру потока, обте-
кающего крыло с сильно отклоненной струей. Для правильного
моделирования необходимо, чтобы скорости экрана и потока в
трубе были одинаковыми. Для этого же применяется система
отсоса пограничного слоя перед экраном.
Для исследования винтомоторной группы или реактивной
двигательной установки и для изучения динамики полета самоле-
та— свободного полета, штопора, полета в возмущенной атмос-
фере— применяются аэродинамические трубы специальных ти-
пов. Более подробно об аэродинамических трубах можно узнать
в книгах по экспериментальной аэродинамике [13], [20], [40], [56]
и др.
С хедует отметить, что по анало _ии с аэродинамическими тру-
бами выполняются и гидротрубы. В гидротрубах рабочей средой
является вода, которая приводится в движение при помощи греб-
ного винта, расположенного в обратном канале замкнутой трубы.
Так как кинематический коэффициент вязкости воды (при 15° С
v-0,012-101 м2/с) значительно меньше коэффициента вязкости
воздуха (v — 0,1453 • 10 4 м2/с)’, то одно и то же значение числа
Рейнольдса можно получить в воде при меньшей, чем в воздухе,
скорости, поэтому гидротрубы также находят применение.
В аэродинамике используются также экспериментальные ме-
тоды, основанные на аналогии между двумя физическими явле-
ниями. Например, для некоторых сложных задач можно соста-
вить общие уравнения и граничные условия, описывающие дви-
жение жидкости (газа), которые, однако, решить вследствие их
сложности обычными математическими методами не удается.
В таких случаях переходят к дру ой физической системе или
другому физическому явлению, которое описывается уравнения-
ми того же вида с аналогичными граничными условиями. При
этом можно получить решение исходной задачи, проводя сравни-
тельно простые экспериментальные исследования в другой физи-
ческой системе, являющейся аналогом исходной системы.
Наиболее сложные задачи практически всегда решаются с
помощью эксперимента. Однако теория учит, как ставить экспе-
римент, как наиболее точ! о проводить измерения, как применить
результаты отдельных экспериментов к более широким классам
явлении н устанавливать количественные закономерности междх
ними.
Аэродинамические трубы оборудуются большим набором из-
мерительных устройств. При помощи весов определяются аэро-
169
www.vokb-la.spb.ru - Самолёт своими руками?!
динамические силы и моменты, действующие иа испытуемую
модель По числу измеряемых компонентов весы разделяют иа
одно-, двух-, трех-, четырех- и шестикомпонеитные. Одна из
Рис 1012 Схема трехкомпонентных
аэродинамических весов с верхней под-
веской модели
!—весы дчя измерения силы сопротивления,
2—весы для измерения подъемной силы, 3—
рычаг для измерения продольной, момента
(момента тангажа), 4—верхняя стенка аэроди
намической трубы, 5—модель
простейших схем трех-
компонентных аэродина-
мических весов показана
на рис. 10.12. В настоя-
щее время имеются со-
вершенные конструкции
механических весов, дей-
ствующих автоматически,
В современной экспери-
ментальной технике полу-
чил широкое распростра-
нение тензометрический
метод измерения усилий,
основанный на примене-
нии так называемых дат-
чиков-теизометров. Су-
ществуют различные ти-
пы датчиков, действие
которых основано на пре-
образовании деформаций,
пропорциональных усили-
ям или перемещениям исследуемого объекта, в фиксируемые
электроприборами изменения электрического сопротивления
(проволочные датчики), емкости (емкостные датчики), индук-
ции (индукционные датчики).
10.5. АЭРОДИНАМИЧЕСКИЕ СПЕКТРЫ
Для выяснения физической сущности некоторых аэродинами-
ческих процессов иногда важно получить качественную картину
обтекания различных твердых тел жидкой или газообразной
средой — получить аэродинамические спектры таких течений
Поток жидкости или газа можно сделать видимым, применяя
различные методы визуализации течения, среди которых на-
ибольшее распространение для определения спектров в потоке
воздуха получили метод дымовых спектров, метод шелковинок
и оптический метод полос.
Для получения дымового спектра в поток воздуха с помощью
насадков или отверстий, расположенных иа поверхности иссле-
дуемого тела, вводятся струики дыма, образованные в специаль-
ных дымогенераторах при сгорании органических веществ или
химическими способами.
Дымовой метод, получивший наибольшее применение при ма-
лых скоростях течения (до 40— 50 м/с), позволяет исследовать
явления отрыва пограничного слоя (рис. 10.13), потери устойчи-
во
www.vokb -la.spb ru - Самолёт своими руками?!
вости ламинарного течения, перехода ламинарного течения в тур-
булентное и т д.
Наиболее простой метод наблюдения обтекания — метод шел-
ковинок (нитеи). Шелковинки одним концом крепятся к поверх-
Рис 10 13 Дымовые спектры обтекания двух вза-
имно вращающихся цилиндров
иости испытуемой модели или на некотором расстоянии от иее
(на тонких проволоках), другой свободный конец показь!вает
характер течения в пограничном слое Прн безотрывном режиме
течения шелковинки остаются спокойными и изображаются иа
фотографии в виде черточек (рис. 10.14,а). Прн отрыве потока
Рис 10 14 Спектр обтекания поверхности закрылка,
октеенной шелковинками
а- безотрывное течение б -течение с отрывом
возникают интенсивные колебания шелковинок, а затем их на-
правление становится обратным направлению основного потока
(см. рис. 10 14,6).
При исследовании околозвуковых и сверхзвуковых потоков
широкое применение получили оптические методы, сущность ко-
17L
www.vokb-la.spb.ru - Самолёт своими руками?!
торых заключается в фиксации изменений плотности среды, вы-
зываемых эффектом сжимаемости воздуха в потоках, движущих-
ся с большой скоростью.
Наиболее распространенным оптическим методом является
метод полос, предложенный Тепл ером. Существует большое ко-
личество оптических приборов, выполненных по различным схе-
мам, основанным на методе полос. Простейшая схема такого
прибора изображена на рис. 10.15. Пучок света из источника А,
пройдя через двояковыпуклую линзу Ц и расположенное в фо-
кусе линзы отверстие пластинки В, попадает на линзу L2, после
Рис. 10.15. Схема прибора, используемого в методе по-
лос Теплера
которой в виде параллельного пучка проходит через исследуе-
мый поток С с помещенной в нем моделью, а затем попадает на
линзу £3, которая вновь собирает пучок и направляет его в фо-
токамеру с пластинкой К.
При постоянной плотности исследуемого потока газа пучок
света проектируется на пластину А равномерно без искажений.
При изменении плотности в какой-либо области потока плоско-
параллельный пучок света, проходящий между линзами, откло-
нится от своего первоначального направления вследствие изме-
нения коэффициента преломления среды, т. е. пройдет выше или
ниже экрана Д.
Задержанные экраном световые лучи либо не попадут на
пластинку К, либо, пройдя мимо экрана, дополнительно осветят
часть пластинки
В зависимости от того, пропускаются ли отклоненные лучи
или задерживаются экраном Z), на пластинке Д появляются
светлые или темные полосы. Обычно экран D устанавливают та-
ким образом по отношению к световому потоку, что зоны уплот
ненного воздуха (повышенного давления) изображаются темны-
ми полосами, а зоны разрежения— светлыми.
10 6 ИЗМЕРЕНИЕ СКОРОСТИ ВОЗДУШНОГО ПОТОКА
Скорость воздушного потока измеряется двумя методами
анемометрическим и пневмометрическим. Анемометрический ме-
тод дает возможность непосредственно измерять скорость тече-
ния, в то время как пиевмометрический способ измеряет не ско
172
www.vokb-la.spb.ru - Самолёт своими руками?!
рость, а скоростной напор, соответствующий определяемой ско-
рости.
Рабочим элементом анемометров, чашечных н крытьчатых
вертушек являются чашечные н крыльчатые устройства, связан-
ные механической системой со счетным механизмом.
Скорость потока в этом случае выражается через число обо-
ротов п: V~an-\-by где а — постоянная прибора, зависящая от
его конструкции и размеров; Ь — величина, характеризующая
трение в передачах прибора и его инерциальные свойства. По-
средством анемометров определяется средняя скорость потока
в месте расположения крыльчатки прибора.
Для измерения мгновенных значений скорости течения воз-
духа применяются термоанемометры. Принцип действия термо-
анемо аетра основан на зависимости электросопротивления на-
гретой электротоком провоточки от температуры. Нагретая элек-
тротоком проволочка отдает свое тепло частицам движущегося
воздуха, при этом сопротивление проволочки изменяется в зави-
симости от скорости потока. Зависимость изменения сопротивле-
ния проволочки от скорости потока устанавливается путем срав-
нения ’результатов измерений с показаниями эталонных насад-
ков для измерения скорости. Малая тепловая инерционность тер-
моанемометров позволяет использовать их при измерении быст-
ро изменяющихся скоростей турбулентных течений, при исследо-
вании пограничного слоя и т. п. Преимуществом термоанемомет-
ров является их высокая чувствительность и, особенно, повыше-
ние чувствительности с уменьшением скорости потока. Термо-
анемометры позволяют измерять также направление потока.
Наиболее распространенным и простым методом определения
малых дозвуковых скоростей в экспериментальной практике
является пневмометрический метод, основанный на измерении
перепадов давлений воздушного потока. Теоретической основой
этого метода является уравнение Бернулли, которое для несжи-
маемого газа можно записать в виде (5.26): /?0=АоД kVlL/2,
откуда получаем
Поо=1/ . (Ю. 1)
у Q
Следовательно, для определения скорости необходимо изме-
рить разность полного /?о н статического р^> давлений воздушно-
го потока и определить плотность движущегося газа. Для изме-
рения разности давлении испо ьзуется система «приемник воз-
душного давления — измерительный прибор». Приемники воз-
душного давления (ПВД) или пневмометры различны по кон-
струкции, но принцип действия их одинаков.
В качестве приемника воздушного давления (ПВД) наиболь-
шее распространение получил насадок или трубка Пито —
Прандтля. В иен совмещены воедино насадок для измерения
173
www.vokb-la.spb ru - Самолёт своими руками?!
полного давления потока р0 н насадок для измерения статичес-
кого давления р^>.
Конструктивное выполнение ко Минированного насадка мо-
жет быть самым разнообразным, но принципиальная схема его
имеет вид, представленный на рис. 10.16. В точке А насадка
происходит полное изэнтропическое торможение воздушного по-
тока, поэтому давление будет равно р0. Форма головной части
насадка и отношение диаметра приемного отверстия к наружно
му диаметру насадка не влияют на измерение полного давления
Рис, 10.16. Измерение статического, динамического и пол-
ного напоров (схема трубки Пито — Прандтля)
/—приемник статического напора; 2—приемник полного напора
в широком диапазоне скоростей, но при этом ось насадка долж-
на быть направлена параллельно вектору скорости потока. Это
необходимо иметь в виду при проведении эксперимента, так как
при углах скоса е>5° (угол между направлением вектора ско-
рости потока и осью насадка) в измерениях появляются сущест-
венные систематические погрешности (см рис. 10 16).
Статическое давление потока передается внутрь трубки ПВД
через отверстие, которое сверлится перпендикулярно боковой
поверхности головной части в точке В. Точка В выбирается на
боковой поверхности головной части насадка таким образом,
чтобы в ней не сказывались влияния носка и державки и пи что-
бы эти влияния взаимно уничтожались Опыт показал, что при-
емник статического давления должен располагаться на расстоя-
нии Li —Зб/ от носнка и = от державки ПВД, где d диаметр-
насадка. В этой точке имеет место компенсация влияния носика
и державки.
При определении okoj озвуковых н сверхзвуковых скоростей
потока измерение по тного и статического давлений производите®
двумя отдельными приемниками давления.
174
www.vokb-la.spb.ru - Самолёт своими руками?!
Полный напор в околозвуковых потоках измеряется приемни-
ком воздушного давления, имеющим специальный кожух неболь-
шой высоты для выравнивания давления на лобовой поверхности
приемника. Применение специальных приемников давления для
измерения статического давления при околозвуковых и сверх-
звуковых скоростях вызвано необходимостью расположить от-
верстия статического давления вне зоны влияния скачков уплот-
нения.
Вопросы для повторения
1. Нарисуйте схемы дозвуковых и сверхзвуковых аэродина-
мических труб и укажите их основные элементы.
2. Объясните принцип действия трубки Пито — Прандтля.
3. Объясните принцип получения аэродинамического
спектра.
4. Нарисуйте схему прибора Теплера.
5. В чем заключается «запирание» аэродинамической трубы?
Задача
1. К трубке Пито, помещенной в дозвуковой поток воздуха,
присоединены два U-образных ртутных манометра. Разность
уровней в первом манометре Дй1=355 мм, во втором ДЙ2 =
= 446 мм. Неподвижный термометр, омываемый потоком, пока-
зывает 22° С. Найти скорость потока.
Решение: отношение давлений равно
р 760—ДЛ2 760 — 446
—=---------=----------- 0,775,
р0 760 —ДА] 760 — 355
k
с другой стороны, _Ро = / j 4 £ — I М2^-1
fe-i
/ До\ * _
откуда M2=bJ--------------= О,290)°’^86-1 = о,378 н М=0,615.
й 1 0,2
2
Скорость звука
/* kRT0----—-------=
=/1,4-287,14-295-0,93=333 м/с.
V=Ma=0,615-333=205 м/с.
Ответ: V= 205 м/с.
175
www vokb-la.spb.ru - Самолёт своими руками?!
ГЛАВА 11
ДВА РЕЖИМА ТЕЧЕНИЯ ЖИДКОСТИ
11.1. ОПРЕДЕЛЕНИЕ ЛАМИНАРНОГО И ТУРБУЛЕНТНОГО
РЕЖИМОВ ТЕЧЕНИЯ ВЯЗКОЙ жидкости
Из раздела динамики вязкой жидкости рассмотрим только
вопрос о двух режимах течения жидкости.
Как отмечалось выше, t в реальных движущихся жидкостях
вследствие их вязкости проявляется касательное напряжение,
что приводит к возникновению внутреннего трения. Опыты пока-
зывают, что для встречающихся в природе потоков вязкой жид-
кости характерны два качественно отличные друг от друга режи-
ма течения ламинарный (т. е. слоистый, от латинского слова
«lamina» что означает «слой») и турбулентный (т. е. беспорядоч-
ный, от латинского слова «бурный», «возмущенный»). Ламинар-
ный режим характерен для малых скоростей течения, турбулент-
ный— для сравнительно больших. Прн ламинарном режиме те-
чения каждая частица потока жидкости движется вдоль плавно
изменяющейся траектории, при турбулентном—мгновенные зна-
чения скорости и давления испытывают нерегулярные пульсации.
Режим течения, ламинарный или турбулентный, определяется
по величине безразмерного параметра, называемого числом
Рейнольдса (9.13'):
или Re = — , (11-1)
[Л V
где р плотность жидкости; V -— средняя скорость течения жид-
кости; I — характерный размер (при течении в трубе диаметр
трубы, при обтекании крыла — хорда или размах крыла и т. п.);
р и v — динамический и кинематический коэффициенты вязкос-
ти По опытным данным ламинарный режим движения в трубе
существует до чисел Рейнольдса, меиьших 2300
При повышении скорости течения некоторой определенной
для данного опыта величины, так называемой критической ско-
рости, нли прн значении числа Рейнольдса, большем 2300, на-
блюдается турбулентный режим течения. Число Рейнольдса*
176
www vokb-la.spb.ru - Самолёт своими руками?!
соответствующее критической скорости течения, называется кри-
тическим:
Re«P=—• (II-2)
V
Для труб величина ReKp порядка 2300 4000, а для профилей,
обтекаемых потоком жидкости, ReKp»3,8*10 ...4-10’.
В отличие от ламинарного при турбулентном течении жид-
кости, кроме составляющих скорости, параллельных осн потока,
имеются также скорости, перпендикулярные к оси потока. На-
личием последних н объясняется поперечное перемещение частиц
жидкости в турбулентном потоке.
Турбулентное течение не следует отождествлять с вихревым
Вращение частиц жидкости, т е. вихревое движение, имеет место
и в турбулентном, и в ламинарном потоках. Отличие, однако,
состоит в том, что прн ламинарном режиме течения частицы
жидкости вращаются упорядоченно и не перемешиваются друг с
другом, прн турбулентном — частицы и вращаются, и перемеши-
ваются. Как известно, при стационарном ламинарном движении
жидкости линии тока совпадают с траекториями движения от-
дельных частиц, однако при этом угловые скорости вращения
частиц не равны нулю. Вихревые линии в круглой трубе являют-
ся концентрическими окружностями, а вихревые поверхности —
цилиндрическими поверхностями.
При турбулентном режиме течения частицы жидкости, участ-
вуя в общем поступательном движении, имеют дополнительные
по сравнению с ламинарным режимом степени свободы, связан-
ные с продольными и поперечными пульсациями. Наличием
пульсационных скоростей в турбулентном потоке обусловлены
дополнительные нормальные и касательные напряжения. Меха-
низм турбулентного течения очень сложен и еще полностью не
изучен.
Следует отметить, что между ламинарной и турбулентной
частью потока есть переходная область, в пределах которой по-
степенно развивается турбулентное течение и иа верхней грани-
це этой области становится полностью турбулентным.
Обычно в практических задачах турбулентность играет отри-
цательную роль, так как при наличии в потоке беспорядочных—
турбулентных пульсаций скорости происходит механическое пере-
мешивание частиц жидкости, и этот процесс создает дополни-
тельное сопротивление, как если бы обычную вязкость увеличи
ли в тысячу, а иногда и в десятки тысяч раз. Поэтому сопротив-
ление тренню самолетов и ракет при обтекании их турбулентным
потоком во много раз больше по сравнению с ламинарным обте-
канием. Однако в ряде случаев турбулентность может играть и
положительную роль. Например, при ламинарном обтекании
кормовой чащи неудобообтекаемых тел происходит более ранний
177
www.vokb-la.spb.ru - Самолёт своими руками?!
отрыв пограничного слоя с кормовой части по сравнению с тур-
булентным обтеканием и, следовательно, общее сопротивление в
этом случае увеличивается. Поэтому для предотвращения ранне-
го отрыва пограничного слоя и уменьшения общего сопротивле-
ния, поток часто искусственно турбулизируют. Кроме того, бла-
годаря перемешиванию жидких масс в турбулентном потоке
улучшается теплопередача, и это свойство часто используется
в соответствующих системах и установках. Однако следует от-
метить, что турбулентный режим течения крайне невыгоден, если
необходимо уменьшить аэродинамический нагрев, например, при
полете на больших скоростях.
Отметим еще одно обстоятельство, имеющее важное значение
при исследовании течении в диффузорных (расширяющихся) н
конфузорных (сужающихся) участках трубы, в частности, при
входе и выходе из рабочего участка в дозвуковой аэродинами-
ческой трубе.
Наблюдения показывают, что критические числа Рейнольдса
в диффузорах и конфузорах зависят не только от структуры по-
граничного слоя и условий входа потока в трубу, ио и от про-
дольного ускорения частиЦ.
Поскольку в конфузорах давление вдоль потока убывает, а
частицы движутся с ускорением, то их тенденция к поперечному
перемешиванию уменьшается, и критическое число Рейнольдса
Re«p увеличивается. В диффузорах давление вдоль потока воз-
растает, и частицы жидкости движутся замедленно, при этом нх
тенденция к поперечному перемешиванию увеличивается, а кри-
тическое число Рейнольдса ReKp уменьшается. Таким образом,
изменяя продольное ускорение частиц, можно в какой-то степени
управлять, переходом ламинарного движения в турбулентное.
На практике в большинстве случаев имеет место турбулентный
пограничный слои при обтекании различных тел, в частности,
частей летательных аппаратов. Учитывая, что в данном курсе
излагаются вопросы, не связанные непосредственно с исследова-
ниями ламинарного течения, мы ие будем останавливаться иа
рассмотрении этого вопроса *.
11.2. ТУРБУЛЕНТНОЕ ТЕЧЕНИЕ ЖИДКОСТИ
При измерении скорости течения жидкости в установившемся
турбулентном потоке электротермоанемометром или другим мало
инерционным прибором наблю, ается беспорядочное пульсирова
ние действительной скорости около своего среднего значения.
Если ту же скорость измерить в том же потоке пиевмометричес-
ким насадком, то скорость окажется постоянной. Таким образом,
при турбулентно: i режиме течения жидкости в каждой точке по
* См., например, Фабрикант Н Я Аэродинамика, М «Наука», 1964,
816 с. или Аржаников Н. С, Мальцев В Н Аэродинамика М., Оборонгиз,
1956, 484 с.
178
www.vokb-la.spb.ru - Самолёт своими руками?!
гока скорость непрерывно изменяется с течением времени
(рис. 11.1), т. е. течение оказывается неустановившимся, при
этом изменение скорости носит непериодический характер и не
подчиняется каким-либо закономерностям.
Для практических расчетов нет особой необходимости в опре-
делении мгновенной скорости или мгновенного давления. Во
многих случаях можно пользоваться осредиеиными (т. е. сред-
ними во времени) значениями скорости, давления и касательного
напряжения.
Рис. II.I. Осциллограмма изменения скорости в данной точке с
течением времени
Задачи исследования турбулентного квази стационарного тече-
ния жидкости достаточно удовлетворительно решаются с по-
мощью полуэмлирической теории, в частности, теории, разрабо-
танной Праидтлем.
Параметры турбулентного течения жидкости (скорость, дав-
ление и т. д.) можно разложить на осредненные по времени ве-
личины и на пульсации, и искусственно из нестационарного ре-
жима выделить главный — стационарный (или точнее — квази-
стационарный) режим, тем самым значитетьно облегчая решение
задачи.
Истинная скорость V в данной точке пространства и в дан-
ный момент времени может быть представлена в виде геометри-
ческой суммы осредненной V и пульсационной V' скоростей
(рис. 11.2): Р = Р + V'.
Составляющие истинной скорости V определяются следующи-
ми равенствами:
^=^+^1 v2=v2+v-;, (u.3)
где V/, Vy', V/ пульсационные добавки или просто пульсации
скорости по осям координат.
179
www vokb-la.spb.ru - Самолёт своими руками?!
Так же как истинная скорость, может быть представлено и
истинное давление: p=jJ+//. Другими словами можно полагать,
что турбулентный поток состоит из двух наложенных друг иа
друга потоков — «осредненного» и «пульсационного».
Дадим математическое определение составляющих осреднен-
ных скоростей и осредненного давления в данной точке Отложим
для этого на осн ординат ис-
Рис 112 К определению осред-
ненной скорости и пульсационных
добавок
тинную мгновенную скорость
V, а по осн абсцисс — время t
(см. рис. 11.2). Заметим, что
зависимость истинной скорости
от времени для данной точки
будет изображаться зигзагооб-
разной кривой Рассмотрим
некоторый промежуток време-
ни (t, t + Т), где время Т ве-
изменении Т осреднениые скорости
лико по сравнению с продол-
жительностью пульсаций, но
мало по сравнению со всем
временем движения. Если при
не изменяются, то течение
является квазистационарным.
Составляющие осредненной скорости в той же точке можно
определить следующим образом.
/-1-7' /+г t+r
= Vxdt, Vjdi, Vt=-^ ( Vjit. (11.4)
t t 1
Аналогичным образом можно иайти осредненное давление в
точке
/+т
- 1 С
р~~т \ pdt'
t
Заметим, что осреднениые по времени значения пульсацион-
ных величин равны нулю Действительно, интегрируя почленно
по t первое из равенств (11.3) в промежутке времени от t до
t+T, получим
щ-г /ч-г f+T (+Т
v \ \ й^+4- \ v;m=v,+ -L\ V'xdt.
t t t t
Поскольку согласно (11.4)
f-j-T
J- V vxdt = V^
t
t+T
TO — \ Vld/=o,
т j
t
180
www vokb la.spb ru - Самолёт своими руками?!
т е осредненные во времени значения пульсационных скоростей
равны нулю. Осредиенную скорость V можно найти н графичес-
ки Из рис. 11.2 видно, что площадь ABCD (или VT) равновели-
ка площади, ограниченной вместо прямой ВС кривой изменения
скорости повремени.
В литературе принято различать изотропную и анизотропную
турбулентности. Полагают, что кинетическая энергия составляю-
щих пульсационного движения потока пропорциональна осред-
нении м величинам квадратов пульсации скорости V2, VуV 2-
Турбулентность называется изотропной, если в рассматриваемой
точке соблюдаются равенствоVx=Vy2~V2t т. е. кинетическая
энергия, определяемая пульсациями скорости, одинакова по всем
направлениям. Турбулентность называется однородной и изотроп-
ной, если это ус. овне соблюдается во всех точках турбулентного
потока В противном случае говорят об анизотропности потока
Степень турбулентности потока, для которого 1/х— У+К/,
Vy~Vy, 14=1//, обычно оценивается безразмерным коэффици-
ентом
(11.5)
г. е этот коэффициент представляет собой отношение квадрат-
ного корня нз среднеквадратичных значений пульсационных ско-
ростей Vxf к осредиениой скорости потока. Степень турбулент-
ности современных малотурбулеитных аэродинамических труб
составляет около 0 7%.
Рассмотрим установившийся турбулентный поток вдоль оси ОХ
около безграничной твердой стенки. В таком случае все произ-
водные от скорости по координате х будут равны нулю При
рассмотрении турбулентного потока у твердой стенки попагают,
что поток разбит га две зоны: тонкую пристенную область — г е
течение жидкости схо но с ламинарным, называемую вязким
подслоем, и внешнюю область турбулентного течения практичес-
ки I не зависящего от вязкости. Обозначая дополнитечьчое каса-
тельное нг пряжение трения в турбулентном потоке через тт и
обычное ламинарное касательное напряжение через гл — р ,
dy
найдем полное касательное напряжение трения в турбулентном
потоке в виде суммы
Г —гл-/гт = р^£^-гт. (11.6)
dy
Из двух составляющих напряжения в вязком подслое преоб
ладает тл, а в турбулентном ядре тт.
181
www.vokb-la.spb.ru - Самолёт своими руками?!
При одномерном турбулентном течении вдоль оси ОХ вслед-
ствие пульсаций скорости частицы жидкости перемещаются и в
поперечном направлении на некоторое малое расстояние (/) об-
мениваясь импульсами с теми частицами жидкости, которые они
замещают, что равносильно действию некоторой добавочной си-
лы трения между слоями жидкости. Для расчета этой добавоч-
ной силы трения выделим в турбулентном потоке жидкости эле-
Рис. 11.3. Турбулент-
ное плоское течение
жидкости
ментарную площадку As, параллельную
плоскости XOZ (рис. 11.3). Элементарная
масса жидкости, перетекающая в едини-
цу времени из первого слоя во второй
вдоль оси 0Y или обратно сквозь пло-
щадку As за счет поперечной составляю-
щей пульсации V , равна А/п = р
Умножив эту массу на продольную сос-
тавляющую V'x пульсации скорости, по-
лучим приращение количества движения
Ашу;=еу/;д5.
В результате такого изменения коли-
чества движения за единицу времени по-
явится импульс силы вдоль оси ОХ и
равный ДР— —qVx'V/AS Знак «минус»
означает, что импульс АР направлен в
сторону, противоположную течению жидкости.
Разделив импульс силы АР на величину площадки AS, полу-
чим касательное напряжение трення тТ) возникающее в турбу-
лентном потоке вследствие перемешивания частиц
ДР I Z ' I 7 '
тт=— или тт = — р1/х1/у.
До
(11.7)
Исходя из предположения Прандтля о том, что турбулентные
пульсации скоростей Vy н V/ по абсолютной величине в сред-
< d\f%
нем пропорциональны произведению * ---, т. е.
dy
v;=+z-^,
dy dy
где l длина пути перемешивания или средний путь пробега
за счет турбулентных пульсаций, эквивалентный среднему пути
свободного пробега молекул в кинетической теории газа, полу-
чим для напряжения тт соотношение в виде
(11.8)
182
www.vokb-la.spb.ru - Самолёт своими руками?
Эта зависимость характеризует те дополнительные напря-
жения трения, которые возникают в турбулентном квазистацио-
нарном потоке жидкости прн наличии поперечных пульсации
скорости Vy\ Vx'. С учетом (11.8) выражение (11.6) запишется:
2
dV,
dy
(11.9)
dK
Т —dy
Необходимо отметить, что в непосредственной близости у
стенкн тт значительно меньше, чем тл. В удалении же от стенки
величина тл значительно меньше тт и поэтому вне вязкого под-
слоя можно пренебрегать величиной тл и полагать согласно гипо-
тезе Прандтля:
-л
(11.10)
Прандтль дополнительно полагал, что длина I возрастает
пропорционально расстоянию от стенкн
1=ъу, (11-И)
где коэффициент пропорциональности и есть некоторая «универ-
сальная» константа, определяемая опытным путем. Для труб по
опытам Никурадзе величина х порядка 0,38.
На основании предположения о существовании подобия меж-
ду полями пульсационных
Т. Карман получил для пути перемешивания I более сложную
формулу
скоростей турбулентных потоков
дУх!ду
(11.12)
/ = х
Опыты показывают, что формулы (11.11) и (11.12) справед-
ливы лишь на большом расстоянии от стенки.
Подставив значения I согласно (11.11) в формулу (11.10) и
полагая вблизи стенки t^tq—-const, после преобразований по-
лучим
1/—
у е dy
Заметим, что величина ]/ t0/q имеет размерность скорости и
обозначается обычно через V*. Эту величину условно называют
«динамической скоростью» или «скоростью касательного напря-
жения». Интегрируя уравнение (11.13), получим
Йх=К±-1пу+С.
(11.13)
(П.14)
Таким образом, в области турбулентного пограничного стоя
осредненная скорость Vx изменяется в зависимости от координа-
ты у по логарифмическому закону (рис. 11.4).
183
www vokb-la.spb.ru - Самолёт своими руками?!
Постоянная интегрирования С определяется из условий не-
прерывного изменения скорости Vx на границе вязкого подслоя.
При более строгом анализе принято считать, что между вяз-
ким подслоем и турбулентной областью имеется весьма тонкая
переходная область (см. рис. 11.4) в которой напряжение тре-
ния т определяется более сложной зависимостью
г — р. dVx (. Z2 / dVx
dy \ dy t
(11.15)
В случае ламинарного пограничного слоя длина пути переме-
шивания /=0, и последняя формула переходит в формулу Нью-
тона. При больших числах Рейнольдса, т. е. при высокой степени
турбулентности потока, первый член формулы (11.15) будет пре-
Рис 11.4. Структура потока при
турбулентном течении жидкости в
трубе
небрежимо мал по сравне-
нию со вторым
При определении толщи-
ны вязкого подслоя бл обыч-
но предполагают, что между
бл, физическими константа-
ми жидкости pi и q и напря-
жением трения т3 существу-
ет зависимость бл~р,хеутго-
Для превращения этого не-
равенства в равенство пра-
вую часть следует умножить
иа некоторый безразмерный
коэффициент а:
= (11.16)
На основании теории размерностей можно записать:
Af
ЛГ2
Сравнивая показатели степени при М L, Т слева н справа,
получим систему уравнений x+y+z=O, —х—Зу—z=l, —х—
—2г—0, решение которой дает следующие значения неизвестных
х=1, #=—1/2, z——1/2 Подставив эти значения х, у, z в равен-
ство (11 16), получим выражение для толщины бл вязкого под-
слоя: 2т0 2 илн, учитывая, что f / —=V*, p.=(v,
Г е
окончательно найдем
V
8л=“ГГ
(И 17)
Коэффициент пропорциональности а является характерной
константой, определяющей турбулентное течение в трубах. По
184
wwwvokb-la.spb.ru - Самолёт своими руками?!
экспериментальным данным а=11,5. В случае течения в круглой
трубе с радиусом г0 формулу (11.17) можно преобразовать к
виду:
frn_„ “V ^niax а *^тах
1 м* " -- I / ’
Го ^niax^O V* Рт
или J^const , (11.18) Г 0 Рт
где Г> о Rm V •
Из этих формул видно, что при значительных величинах чи-
сел вязкий подслой составляет пренебрежимо малую часть
диаметра круглой трубы. Это позволяет считать, что практичес-
ки профиль скоростей в ламинарном подслое является линейным
В дальнейшем будем пренебрегать вязким подслоем и будем
считать течение в трубе полностью турбулентным, за исключе-
нием отдельных случаев.
11.3. СТЕПЕННОЙ ЗАКОН РАСПРЕДЕЛЕНИЯ СКОРОСТЕЙ
Рассмотрим турбулентное течение жидкости в круглой цилин-
дрической трубе, как наиболее изученное. Результаты этого ис-
следования могут быть применены не только для внутренней за-
дачи, но и для внешней задачи обтекания тела.
Формула потери давления на гидродинамическое сопротив-
ление в турбулентном потоке на участке длиной L записывается
в виде (см. [45] или [62])
2 а
где X — коэффициент гидродинамического сопротивления трения
для турбулентного режима течения, d — диаметр трубы В диа-
пазоне чисел Рейнольдса порядка 2,3 103^Re^l05 для коэф-
фициента сопротивления трубы обычно используется эмпириче-
ская формула Блазиуса
0,3164/Re1/4. (11.19)
С учетом этого выражения для потери давления получим сле-
дующую формулу
0,3164 Q^cp L
Pi-P =--------7Г’
/V л \г/« 2 d
(11.20)
V
т. е при Re^ClO потеря давления на трение при турбулентном
режиме течения пропорциональна средней скорости в степени
185
ww w vokb-la.spb ru - Самолёт своими
руками?!
7/4, в то время как при ламинарном течении потеря давления
пропорциональна первой степени скорости. С другой стороны»
падение давления вдоль трубы на длине L связано с напряжени-
ем трения на стенках трубы то соотношением
= (11.21)
Тогда выражение (11.20) принимает вид
To/e=0s03955lZcV(v/flf)1/4. (11.22)
Если учесть, что ^0/6=V то, решая последнее уравнение
относительно Vcp, получим
8 1
1 V1 d1 ‘
V ср = Q,039554/7 *vV7 6’33V*
откуда находим
V*d УД
V /
Иср
^=6,33
*
V*d \i/7
v /
пли
7СР
— =6,99
11.23)
где г0 — радиус трубы.
Очевидно, можно предположить, что с изменением макси-
мальной скорости Vmax в поперечном сечении трубы изменяются
пропорционально скорости и во всех точках этого сечения. Тогда
отношение скоростей для двух точек поперечного сечения потока,
например, скорости на осн трубы Vmax и скорости в произволь-
ной точке, расположенной на расстоянии у от стенки, можно вы-
разить следующим образом:
V
» max
(11.24)
Поскольку функция f(y/ro) зависит только от у/гъ, то ее мож-
но заменить коэффициентом пропорциональности k. Соотношение
между средней по сечению трубы и максимальной скоростями,
очевидно, можно записать в виде:
(11.25)
или V'cp—^Vmax» где k — постоянный коэффициент, который
может быть найден опытным или теоретическим путем.
Тогда на основании (1123) ——-х—ВгВВ/У*^?77,
V* k \ v ]
186
www vokb-la.spb.ru - Самолёт своими руками?!
Если же в последней формуле Ртах заменить местной ско-
ростью согласно (11 24), то получим
(11.26)
V* к \ v / \ го /
Анализируя этн формулы, можно однозначно прнйтн к вы-
воду, что
\Г0 ) \ го/
и тогда равенство (11.24) примет вид
-Z_=/J/-Y/7. (11.27)
итах к го/
Согласно экспериментальным данным максимальная н сред-
няя по сеченню скорости течения связаны соотношением
Umax=l,235V'c₽,
что соответствует коэффициенту £ = 0,815.
Напряжение трення турбулентного потока в этом случае в со-
ответствии с (11.22) можно записать в виде
t=0,0225qIZ2 (—Y/4_ (11.28)
Wy /
Следует отметить, что эта формула получила широкое рас-
пространение прн решении задач пограничного слоя.
Таким образом, при турбулентном режиме течения жидкости
в цилиндрической трубе и небольших числах Рейнольдса ско-
рости течения изменяются вдоль радиуса трубы по закону одной
седьмой (11.27). Однако опытами установлено, что с увеличени-
ем числа Рейнольдса показатель степени в формуле (11.27)
уменьшается до значений 1/10—1/14.
Вопросы для повторения
1. Опншнте физическую картину течения жидкости прн ла
мннарном н турбулентном режимах течения.
2. В чем суть теории турбулентного квазнстацнонарного тече-
ния, предложенной Прандтлем?
WWW vokb-la.spb ru - Самолёт своими руками?!
ГЛАВА 12
ОСНОВЫ ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ
12.1. ПОНЯТИЕ О ПОГРАНИЧНОМ СЛОЕ
Теория движения идеальной жидкости хорошо разработана
и обычно дает вполне удовлетворительные результаты прн ис-
следовании действительных течений (особенно прн больших чис-
лах Рейнольдса), за исключением областей, расположенных в
непосредственной близости от поверхности обтекаемого тела н
областей отрыва потока в случае неудобообтекаемых тел. В этих
областях на характер течения существенное влияние оказывают
силы внутреннего трення жидкости, обусловленные наличием
вязкости. Расстояние, на котором происходит изменение скорости
от нуля (на поверхности тела) до величины, имеющей место в
идеальной жидкости, характеризует область влияния вязкости.
При внешнем обтекании по мере удаления от передней критичес-
кой точки тела к задней кромке толщина этой области растет.
В рассматриваемом случае весь поток условно можно раз-
бить на две области: пристенную область, весьма малой толщи-
ны, называемую пограничным слоем, где влияние сил вязкости
столь же существенно, как и влияние всех других сил (например,
сил давления, сил трення), и область внешнего потока, где влия-
ние сил вязкости пренебрежимо мало. Таким образом, погранич-
ный слой можно определить как прилегающий к поверхности
твердого тела слон жидкости, в котором сосредоточено основное
воздействие сил вязкости на тело.
От структуры течения в пограничном слое в значительной
мере зависит сопротивление обтекаемого тела, его подъемная
сила, аэродинамический нагрев (прн сверхзвуковых скоростях)
и т. д.
Торможение частиц газа в пограничном слое происходит под
воздействием сил, передающих это торможение на некоторое
расстояние от тела в глубь потока. Касательные напряжения
(силы трення), обусловленные силами вязкости уменьшают
скорости частиц газа в пограничном слое и вызывают их вра-
щение, образуя вихри. Изучение структуры и характера тече-
188
www vokb-la.spb ru - Самолёт своими руками?!
ния жидкости или газа в пограничном слое позволяет объяснить
такие важные аэродинамические явления, как возникновение
срыва потока на обтекаемых телах, образование вихревого сле-
да за телом, а также определить силы трения газа на поверхно-
сти тела. Теоретически анализ движения газа в пограничном
слое сводится к решению системы сложных дифференциальных
уравнений. Решение должно удовлетворять граничным услови-
ям: на бесконечности скорость потока должна совпадать по ве-
личине и направлению со скоростью внешнего потока 1/0(а') , на
поверхности обтекаемого тела скорость должна быть равна
НУЛЮ
Рис. 12 1 Схематическое изображение пограничного
слоя на плоской пластине
Проблемой сопротивления трения в жидкостях и газах зани-
мались многие ученые еще до появления теории пограничного
слоя Среди них Галилей, Кулон, Ньютон, Стокс, Рэнкин, Менде-
леев и др. Понятие о пограничном слое впервые было введено
Жуковским.
Теоретические разработки теории пограничного слоя были
начаты Прандтлем в 1904 г. и развиты Блазиусом, Карманом,
Польгаузеном, Милликеном, Г Шлихтингом и др. Развитию те-
ории пограничного сдоя посвящено большое количество работ
советских ученых Л. С. Лейбензона, Н Е. Кочина, А А Дород-
ницына, В. В Голубева, Л Г Лойцянского, А П Мельникова,
К К Федявского и др. Советские аэродинамики провели ряд
важных теоретических и экспериментальных исследований по-
граничного слоя, разработали рациональные формы крыльев и
фюзеляжей, имеющих малое сопротивление трения и обтекаемых
без срыва потока до больших углов атаки.
Рассмотрим вначале течение вязкой жидкости около плоской
пластины (рис. 12 1) Опыты показывают, что частицы жидкос-
ти, соприкасающиеся с поверхностью пластины, полностью за-
тормаживаются По мере удаления от пластины скорость тече-
ния увеличивается, асимптотически приближаясь к теоретиче-
ской скорости, соответствующей обтеканию невязкой жидко-
стью, а в рассматриваемом случае — к скорости внешнего пото-
ка Это обстоятельство делает неопределенным положе-
ние верхней границы пограничного слоя, а следовательно, зат-
189
www vokb-la.spb.ru - Самолёт своими руками?!
рудняет определение его толщниы. Однако, учитывая, что су-
щественное нарастание скорости в пограничном слое происходит
у самой стенки и уже на очень малом расстоянии от нее ско-
рость незначительно отличается от скорости невозмущенного
потока, за толщину пограничного cj оя 6 можно принять рассто-
яние от поверхности обтекаемого тела, на котором скорость по-
тока достигает 99,5% скорости внешнего потока Весьма час-
то принимаются и другие определения условной толщины погра-
ничного слоя, хотя следует иметь в виду, что зона влияния вяз-
кости распространяется от поверхности те та асимптотически и,
если принять вместо 99,5% хотя бы 99%, то абсолютная велн-
чн ia толщины пограничного слоя значительно уменьшится.
Рис. 12.2. Структура пограничного слоя
при переходе ламинарного течения в
турбулентное:
I—ламинарный слой; 2—точка перехода;
3—турбулентный слой; 4—вязкий подслой; 5—
пластина
Рис. 12.3. Сравнение эпюр
скорости в ламинарном и
турбулентном пограничных
слоях:
/—ламинарный слой; 2—турбу-
леитный
В соответствии с принятым определением толщины 6 внеш-
няя граница пограничного слоя не является линией тока и слу-
жит лишь условным пределом зоны влияния вязкости.
Если обтекаемая пластина достаточно длинна, то структура
течения в пограничном слое на разных расстояниях от передней
кромки пластины различна. Вблизи передней кромки течение в
пределах пограничного слоя слоистое. Такой пограничный слой
называется ламинарным. По мере удаления от передней кромки
толщина ламинарного пограничного слоя увеличивается, а устой-
чивость ламинарного течения уменьшается и на некотором уда-
лении течение в пограничном слое переходит в турбулентное
(рнс. 12 2). При переходе ламинарного течения в турбулентное
сначала происходит потеря устойчивости линий тока, они ста-
новятся волнистыми (переходная зона), а затем развивается
устойчивое турбулентное течение. В турбулентном пограничном
слое, однако, вблизи поверхности имеется весьма тонкий под-
слой, движение в котором сохраняется ламинарным. Как видно
190
wwvi vokb-la.spb ru - Самолёт своими руками?!
из рнс. 12.3, в турбулентном слое по сравнению с ламинарным
наблюдается более резкое уменьшение скорости течения у
стенкн.
Пограничный слой на обтекаемом теле имеет примерно ту же
структуру, что и на пластине. За обтекаемым телом погранич-
ные слон, образовавшиеся на нижней и верхней поверхности те-
ла, смыкаются н перехо-
дят в вихревой след
(рнс. 12 4), который по
мере удаления от тела
«расплывается», скорости
в нем выравниваются и
вдали от тела прибли-
жаются к скорости невоз-
мущенного потока.
Решение задач погра-
ничного слоя сводится
в общей постановке к ин-
тегрированию сложных
дифференциальных урав-
нений (например, уравне-
ний Навье- Стокса). Эти
Рис. 12 4. Схема потока при обтекании тела
вязкой жидкостью:
1—ламинарный слой; 2—турбулентный слои. 3—
вихревой след; 4—переходная зона
уравнения представляют собой нелинейные дифференциальные
уравнения в частных производных н их интегрирование прн за-
данных граничных условиях сопряжено с большими математи-
ческими трудностями не только в случае вязкого сжимаемого
газа, но н в случае несжимаемой жидкости. Поэтому прн реше-
нии задач пограничного слоя приходится прибегать к упроще-
нию уравнений Навье—Стокса [38], [70] Существует ряд спосо-
бов упрощения уравнений Навье—Стокса. Большой практиче-
ский интерес для многих задач аэродинамики представляет, на-
пример, метод Прандтля, в основу которого положено представ-
ление о пограничном слое, прн этом жидкость считается мало-
вязкой, а скорость ее движения большой Метод Прандтля при-
годен для течений с большими числами Рейнольдса
12.2. ИНТЕГРАЛЬНОЕ СООТНОШЕНИЕ ДЛЯ
УСТАНОВИВШЕГОСЯ ТЕЧЕНИЯ В ПОГРАНИЧНОМ СЛОЕ
НЕСЖИМАЕМОЙ ЖИДКОСТИ
Рассмотрим течение жидкости в двумерном плоскопараллель-
ном потоке над криволинейной поверхностью малой кривизны
В этом случае удобно ось координат ОХ считать криволинейной,
расположив ее на обтекаемой поверхности вдоль течения
(рис. 12 5).
Проведем через две точки В н D, находящиеся на контуре
обтекаемого тела и отстоящие на расстоянии dx друг от друга,
нормали к контуру.
191
www.vokb-la.spb.ru - Самолёт своими руками?!
Элементарная площадка ADBC длиной dx является основа-
нием выделенного из жидкости объема шириной, равной едини-
це. Применим к этому жидкому элементарному объему теоре-
му об изменении количества движения (теорему импульсов),
при этом количество движения и импульс действующих сил на
этот этемент запишем только для проекции на ось ОХ. Масса
жидкости, втекающая через сечение АВ за время dt с перемен-
ной по сечению скоростью, и масса жидкости, вытекающая че-
рез сечение CD за это же время, соответственно равны:
в , в в ч
. / р d i \
\ V xdy и dt§ \ V xdy-\-dx— \ Vxdy I,
J I J dx i i
о \o о /
Рис 12 5 К выводу интегрального
соотношения для пограничного слоя
в несжимаемой жидкости
/ 8
откуда находим разность вытекающей и втекающей масс жид-
кости
в
Qdtdx— \ V xdy.
дх j
о
Проекция на ось Ох коли-
чества движения жидкости,
втекающей за время dt через
сечение АВ.
в
м. J v2xdy,
О
а проекция кол: чества движе-
ния жидкости, вытекающей че-
рез сечение СП,
в .
dtQ / Vxdy-\-dx-^- Vxdy j.
*0 о /
Из условия сохранения массы через верхнюю границу погра-
ничного слоя АС внутрь объема ABCD должна втекать масса
жидкости, равная разности масс жидкости, вытекающей через
«сечение CD и втекающей через сечение АВ, т. е.
в
ф (
Qdtdx — \ V xdy.
дх j
о
Количество движения, вносимое этой жидкостью,
8
QVodtdx~ \ Vxdy,
дх j
о
192
www vokb-la.spb.ru - Самолет своими руками?!
где Vo — скорость на верхней границе пограничного слоя. Таким
образом, проекция на ось ОХ приращения количества движения
жидкости, находящейся в момент времени t внутри объема
ABDC за время dt,
г 6 х
kdtdxl - V,A-\. (a)
I dx J Ox J /
\ о о /
Количество движения, вносимое в объем ABDC за время dt,
считаем отрицательным, а уносимое нз этого объема — положи-
тельным.
Теперь вычислим проекцию на координатную ось ОХ суммы
импульсов внешних сил, действующих за время dt на жидкость,
заключенную внутри элементарного объема ABDC. Проекции
на ось ОХ внешних сил (сил давления), действующих на грани
АВ, АС и DC, будут соответственно равны
рЬ dx} ds dT,- — pdZ \ — dxd<p
~(p^~— dx) fS 4“ — dx) — — (p4' — dx) (8 4" dS),
\ ' dx f \ dx / \ dx /
где d&/ds — синус угла между гранью АС и осью ОХ Пренебре-
гая малыми величинами высшего порядка и учитывая, что про-
екция силы давления на жидкость элемента стенки BD на ось
ОХ равна нулю, полечим сумму проекций сил давления на ось
ОХ:
рй4”pd§ — (/?4~ “ dx) (34“d8) — рЪ4~pdB — рВ — pdB —
\ дх /
— 3 — dx — dbdx dx.
дх дх дх
Тогда проекцию импульса сил давления на ОХ можно записать
как
— В — dx dt. (б)
дх 1 '
Импульс силы трения, приложенной к нижней грани BD, пло-
щадь которой dx-1, имеет проекцию на ось ОХ, равную
— xodxdt, (в)
где то — касательное напряжение.
Учитывая, что изменение количества движения равно импуль-
су сил, приравняем сумму (а) к сумме выражений (б) и (в) н
после сокращения на dxdt получим
Б 8
Н2.1)
о о
7
626
193
www vokb-la.spb ru - Самолёт своими руками?!
Это равенство, полученное на основании теоремы механики
о количестве движения, называется уравнением импульсов или
интегральным соотношением Кармана для плоского установив-
шегося течения в пограничном слое несжимаемой жидкости.
С помощью этого соотношения без решения системы дифферен-
циальных уравнений можно определить толщину пограничного
слоя и распределение сил трення по поверхности тела. Кроме
того, интегральное соотношение (12.1) применимо и для лами-
нарного, и для турбулентного пограничных слоев Учитывая, что
в уравнении (12.1) в силу стационарности течения все величины
зависят только от координаты х, частные производные можно
заменить полными:
6 S
е /- \ Г V,dy = -8^— т„. (12. 2)
dx J dx J dx
о о
В этом уравнении известными считаются величины Vo, dpidx
(из уравнения Бернулли d о'у-) , плотность р, а неиз-
вестными— to и 6. Поэтому для решения конкретных задач
необходимо иметь еще два соотношения, например VX=VX (у),
то=то(6)
12.3. ПРИМЕНЕНИЕ ИНТЕГРАЛЬНОГО СООТНОШЕНИЯ
ДЛЯ РАСЧЕТА ХАРАКТЕРИСТИК ЛАМИНАРНОГО
ПОГРАНИЧНОГО СЛОЯ ПЛОСКОЙ ПЛАСТИНЫ
Рассмотрим наиболее простой случай — продольное обтека-
ние плоской пластины, сведения о толщине пограничного слоя
и сопротивлении трения которой могут быть использованы для
приближенного расчета тонкого профиля и некоторых других
крыльевых профилей. Для плоской пластины интегральное соот-
ношение несколько упрощается На верхней границе погранич-
ного слоя в этом случае Vo~ — const. Тогда из уравнения Бер-
V2 .
нулли Ах,при const следует, что dpldx^=Q н ин-
тегральное соотношение принимает вид
s г
е л i V*dy-eV„~ \ Vxdy = —10 (12.3)
dx J dx J
о о
Приближенно закон распределения скорости по поперечному
сечению пограничного слоя можно найти, представив функцию
194
www.vokb-la.spb.ru - Самолёт своими руками9'
Vx=f(y) в виде полинома, например, в виде полинома второй
степени *
Vx=-a^by^-cy\ (12.4)
где а, Ь, с — постоянные коэффициенты, определяемые из гра-
ничных условий.
Для пластины граничные условия будут следующими:
а) на нижней границе пограничного слоя т. е. у стенки при
#=0 К-0;
б) на верхней границе пограничного слоя прн у=Ъ К=К>;
в) на верхней границе пограничного слоя отсутствуют силы
трения (т=0), следовательно, на основании формулы Ньютона
при т = р д гх/ду^О; dV х]ду~®.
Из этих граничных условий находим значения коэффициентов;
а^О; 6=2^, (12.5)
ь ’ Ь2 1 7
Тогда закон распределения скоростей по поперечному сече-
нию пограничного слоя (12.4) запишем в виде
^=г»(г-г-4)- <12-6)
\ О о2 /
Воспользуемся формулой Ньютона для определения напря-
жения трения на стенке
Итак, два дополнительных соотношения (12.6) и (12.7) сов-
местно с интегральным соотношением (12.3) позволяют решить
задачу о ламинарном пограничном слое на плоской пластине.
Определяя значения интегралов, входящих в уравнение
(12 3) с учетом (12.6) и (12.7) будем иметь
8 8 V
е\ vxdy^ \~(Чу~^-\dy=-~
J S \ 8 J о
0 0
1ее Т НЫй закон распределения скорости по поперечному сеченню
о ра чно1о л 'я может быть получен при представлении функции Vx~f(y)
в виде полинома третьей или четвертой степени
7*
195
www.vokb-la.spb.ru - Самолёт своими руками?!
При этих подстановках с учетом формулы (12.7) уравнение
(12.3) преобразуется в дифференциальное уравнение:
— = 2р,—
15 iix га ’
которое после разделения переменных принимает вид
8(78 = 15 -р- dx.
Интегрируя это уравнение, получим
— В2 —С. (12,8)
Полагая при х —О д-0 (в начале пластины толщина погра-
ничного слоя равна нулю), находим, что постоянная С —0. Из
соотношения (12.8) следует, что профиль пограничного слоя на
внешней границе представляет собой параболу, вершина которой
находится в начале координат. Из уравнения (12.8) можно найти
толщину пограничного слоя 6 при -различных значениях коорди-
наты х:
8 = 5,48 (12.9)
_____________________________ yz
или 8=5,48 x/]^Rex, где Rex = ——.
Из этой формулы, в частности, следует, что при / = 0°С, р =
— 760 мм рт. ст., Ко=120 м/с, х=1 м, уВОзд=0,1333 • 10-4 м2/с
толщина пограничного слоя 6 — 1,2 мм.
Из формулы (12.9) видно, что толщина пограничного слоя
прямо пропорциональна корню квадратному из кинематического
коэффициента вязкости у (т. е. зависит от температуры) и дли-
ны пластины х и обратно пропорциональна корню квадратному
из скорости на верхней границе пограничного слоя, которая в
данном случае равна скорости нсвозмущенного потока ]/«,.
Подставив полученное значение 6 в формулу (12.7), найдем
то=0,365 I/ -2^-=.. (12.10)
• х
Точное решение задачи о пограничном слое, полученное Бла-
зиусом в результате интегрирования дифференциальных уравне-
ний движения вязкой жидкости, дает для бит выражения:
т() 0,332
(12.11
Характер изменения толщины пограничного слоя и напряже-
ния трения в зависимости от х показан на рис 12 6.
196
wwn vokb-la.spb.ru - Самолёт своими руками?!
Определим силу сопротивления трення Хтр, действующую на
одну сторону пластины шириной b и длиной I. Если на элемен-
тарной площадке сила трения равна т0 bdx, то, очевидно, полная
сила трения на пластине определяется интегралом:
ь
X грt^dx
о
Подставив в этот интеграл значение т0 согласно (12.11), получим
________________ ё _ J_
Лтр=0,332 Vf X 2 dx.
О
(12. 12)
Умножая числитель и знаменатель на величину V cM-’oe, вво-
дя число Рейнольдса Re=VoJ)/v и учитывая, что S=bl, найдем
У 1,328 q 11 л -J о\
у 2
ИЛИ Xrp = CfSQ~^,
где су=1,328//Й. (12.14)
Величина Cf является коэф
фициентом трения плоской
пластины. Коэффициент лобо-
вого сопротивления пластины,
обусловленный силами трения,
действующими на обе Стороны,
гл=2,656/У№.
Рис 12 6 Изменение напряже-
ния трения и толщины погра-
ничного слоя по длине пласти-
ны
Таким образом, в случае ламинарного пограничного слоя
коэффициент Cf обратно пропорционален корню квадратному
нз числа Рейнольдса; чем больше число Re тем меньше этот ко-
эффициент.
12.4 ПРИМЕНЕНИЕ ИНТЕГРАЛЬНОГО СООТНОШЕНИЯ
ДЛЯ РАСЧЕТА ТУРБУЛЕНТНОГО ПОГРАНИЧНОГО СЛОЯ
И ОПРЕДЕЛЕНИЕ СОПРОТИВЛЕНИЯ ПЛОСКОЙ ПЛАС1ИНЫ
Интегральное соотношение (12.3) применимо и для турбу-
лентного пограничного слоя. Однако соотношения (12.6) и (12 7)
в этом случае непригодны, поскольку в турбулентном погранич-
ном слое изменение трения подчиняется другим, более сложным
закономерностям.
Точная теория турбулентных течений пока не разработана,
однако экспериментально установлено, что в турбулентном погра-
197
www.vokb-la.spb.ru - Самолёт своими руками?!
яичном слое распределение скоростей приближенно может быть
представлено, например, в виде степенного закона*:
(12. 15)
Опыт показывает, что для скоростей невозмущенного потока,
ие превышающих половины скорости звука, можно принять п =
= 7. Тогда получим известный закон изменения скорости по се-
чению турбулентного пограничного слоя на плоской пластине
(12. 16)
где 6 — толщина пограничного слоя. При увеличении скорости
течения величина п возрастает. Для определения напряжения
трения т0 на пластине можно воспользоваться формулой, полу-
ченной по аналогии с течением в трубе (11.28)
r„=0,0225eV2„(l/Res)I/\ (12.17)
где Re®—. Здесь следует иметь в виду, что для напряжения
трения при турбулентном режиме Движения жидкости в круглой
трубе используется экспериментальная зависимость. Расчеты по
формулам (12.16) и (12.17) будут достаточно точными при срав-
нительно малых числах Res. Воспользовавшись условиями
(12.16) и (12.17), вычислим значения двух интегралов:
и подставим их в интегральное соотношение (12.3), которое
после преобразований примет вид
= — £1/2— . (12.18)
Сравнивая это выражение для т0 с (12.7), получим равенство
—е1/2 —
72 °° dx
0,0225qI/2oo
которое после преобразований и разделения переменных запи-
шем следующим образом:
- 0,0225 ~ (—\1/4dx.
1 \ v I
v оо /
* Существуют и другие законы распределения скоростей в турбулент-
ном пограничном слое, например, логарифмический
198
www.vokb-la.spb.ru - Самолёт своими руками?!
После интегрирования этого уравнения и определения посто-
янной интегрирования С (нз условия при х=0 6=0) получим
формулу для определения толщины пограничного слоя на пло-
ской пластине при турбулентном режиме течения
S=0,37(v/Uoox)1/5x или 6=O,37(l/Rej1/5x. (12. 19Г
Сопоставляя формулы (12. 11) и (12. 19) для толщины лами-
нарного и турбулентного пограничных слоев, заметим, что тол-
щина турбулентного пограничного слоя пропорциональна х6/5,
а ламинарного х1/2, г. е. толщина турбулентного пограничного
слоя нарастает более интенсивно по сравнению с толщиной ла-
минарного пограничного слоя.
Используя выражение (12. 19), получим из соотношения
(12. 18) формулу для определения касательного напряжения
т0 = O,O289CV^ 1/Rx,
которой воспользуемся для определения силы одностороннего
сопротивления трения плоской пластины
^Tp=J V^=0,0289qV2oo(v/I/oo)W Г dx/fa=
о б
=0,036 (v/I/OT)W°’Wt,
откуда с учетом S~bl для коэффициента одностороннего сопро-
тивления трения получим
qV2
1TS
- - 0,072
ИЛИ Cf
0,072
~Re0,2 ’
(12. 20)
Коэффициент лобового сопротивления пластины cx — 2cft в
этом случае cx=O,144/Reo>2. При изменении чисел Рейнольдса в
диапазоне Ю6^ Re-С 10э хорошее согласование с опытными дан-
ными дает формула
0,458
(lg Re)1’58
(12.21)
Анализ и сравнение формул для коэффициентов сопротивле-
ния трения в ламинарном (12 14) и турбулентном (12 20) погра-
ничных слоях на плоской пластине удобно проводить, пролога-
рифмировав эти выражения.
lgc;=lg 1,328—i-lgRe, lgcv_lg0,072 -A ig Re.
z / 5
199
www vokb-la.spb ru - Самолёт своими руками?!
Графически они будут изображаться в виде прямых линий
(рис. 12.7). С увеличением числа Рейнольдса коэффициенты
Рис. 2 7 Зависимость коэффициента сопротивления
трения плоской пластины от числа Рейнольдса:
/ -турбулентный пограничный слой (формула 12 28); 2—ла-
минарный пограничный слой (формула 12 22)
трения с/ в обоих случаях убывают^ однако, в турбулентном по-
граничном слое медленнее
12.5. РАСЧЕТ СМЕШАННОГО ПОГРАНИЧНОГО СЛОЯ НА ПЛАСТИНЕ
В реальных условиях некоторая зона, начиная с переднеd
кро 1ки пластины, занята ламинарньм пограничным слоем. За
ламинарной зоной ниже по течению располагается турбулентный
пограничный слой. Если предположить, что переход ламинарно-
го течения в турбулентное происходит мгновенно, то вместо
перехо ной зоны можно говорить о точке перехода. Положение
точки перехода зависит от ряда факторов и, в первую очередь,
от турбулентности набегающего потока и шероховатости по-
верхности Неровности поверхности нарушают устойчивость
ламинарного течения, поэтому, чем больше шероховатость, тем
ближе к передней кромке располагается точка перехода. Повы-
шенная турбулентность набегаюп ею потока также благоприят-
ствует более раннему переходу к турбулентному течению в по-
граничном слое. Кроме этих факторов на положение точки
перехода оказывает влияние и распределение лавлеиия по по-
верхности профи пя, которое, в свою очередь, зависит от юомет-
рических характеристик профиля.
Ламинарное течение сохраняется только при отрицательных
градиентах давления вдоль линий тока Поэтому пограничн ш
слои практически может быть ламинарным на профиле только
впереди точки с максимальным разрежением Ламинарное тече-
ние нарушается также при резких переломах в очертании про-
филя, в местах располож ния щелей, выступов и т. и. Если пло-
ская пластина расположена параллельно вектору скорости
невозмущенного потока, то давление вдоль линии тока н 1д пла-
200
www vokb-la.spb.ru - Самолёт своими руками?!
единой будет постоянно. В этом случае точка перехода ламинар-
ного течения в турбулентное определяется критическим числом
Рейнольдса ReKp, которое в зависимости от шероховатости пла-
стины и степени турбулентности набегающего потока находится
в диапазоне 2-105—5-10’. Если часть поверхности занята лами-
нарным, а часть — турбулентным пограничным слоем, то такой
пограничный слой называется смешанным, а величина коэффи-
циента сопротивления трения такой пластниы при ее безгради-
ентном обтекании определяется по приближенной формуле
^=0-^2(Re-Ri,„T37Re;y)^.
(12. 22)
Заметим, что при ReKP=O эта формула принимает вид фор-
мулы (12.20) для турбулентного пограничного слоя, а при
ReKp—Re — вид формулы (12. 14) для ламинарного пограиичио-
ю слоя.
Коэффициент сопротивления шероховатой пластины С; зави-
сит от числа Рейнольдса и степени шероховатости kfb пластины
(k — высота бугорков шероховатости, b — хорда пластины).
С увеличением относительной шероховатости k/b увеличи-
вается и коэффициент сопротивления; при определенном значе-
нии относительной шероховатости, начиная с некоторого числа
Re, коэффициент сопротивления ие зависит от числа Re. В этом
случае сила сопротивления пропорциональна квадрату скорости,
акое изменение режима сопротивления называют квадратич-
ным.
Коэффициент сопротивления за счет шероховатости увеличи-
вается с увеличением числа Re. Поэтому создание гладкой по-
верхности обшивки особенно важно для скоростных самолетов.
12 6 ВЛИЯНИЕ СЖИМАЕМОСТИ ВОЗДУХА
НА ПОГРАНИЧНЫЙ СЛОЙ
В настоящее время имеется много работ, посвященных исследованию
влияния сжимаемости воздуха на пограничный слой И хотя этот вопрос
исследован достаточно полно, мы приведем только его качественный анализ
ввиду сложности теоретических выкладок
Выражение для толщины пограничного слоя и силы сопротивления пла-
стины в несжимаемом потоке могут быть записаны в виде
—t-Г
V е«Я J
(12. 23)
2
гр.нс ~ kiQVooX
m
(12. 24)
ламинарного и тур-
различный для ла-
где k и ki постоянные коэффициенты, различные для
нтн о пограничных слоев, m — показатель степени,
минарного и турбулентного пограничных слоев.
В сжимаемой жидкости плотность q и коэффициент
я переменными величинами. Особенно заметно изменяет-..
ха, так как при торможении в пограничном слое высокоскоростного потока
вязкости ц являю г-
1'СЯ ПЛОТНОСТЬ возду-
201
www.vokb-la.spb.ru - Самолёт своими руками?!
происходит его нагрев. Давление в пограничном слое пластины неизменно.
Если предположить, что течение газа в пограничном слое происходит без
теплообмена, то при р = const согласно (7.3)
6 „ Zk (j I *__________J. д^2
Q0 Г V 1 2
(12.25)
Изменения коэффициента вязкости ц в зависимости от температуры при
отсутствии теплопередачи можно оценить, используя эмпирическую формулу
Р I Т'о X ₽ / А — 1 ? \₽
=(1+—м")
(12.26)
где для воздуха |3«О,75.
Уменьшение плотности воздуха вблизи
ние коэффициента вязкости с увеличением
толщину пограничного слоя и силу трения, характер которого можно оце-
нить, воспользовавшись некоторыми средними значениями этих величин. Ве-
личину средней температуры в пограничном слое между температурой невоз-
мущенного потока и температурой торможения То можно оценить при-
ближенно с помощью постоянного коэффициента а(0<а<1);
Гср = а + (1 - а) Го/Г или Гср/Гот = а + (1 - а)
Это соотношение с учетом (12.25), (12.26) принимает вид
Т'ср
Т
поверхности пластины и увеличе-
числа М„ оказывают влияние иа
(12. 27)
А ~ 1 „2 \
ОО ' •»
Аналогичным образом введем понятие о средней плотности
вязкости. Полагая, что для средних величин справедливы зависимости
(12 25), (12.26)
(12. 28)
и средней
бсо __
бср ~
Pop
(12.29)
Роо \ 1 ОО /
и, вводя их в формулы для определения толщины пограничного слоя (12.23)
и силы трения (12 24), в случае сжимаемого газа получим
Роо У” / Рср б ср
боо^оо^ / \ Роо бср
бср /
бое \
^сж —
\ т
1 = kl
2
-^тр.сж ~ *1бср^а}
Рср
бср^
Рср \т 2
бс₽Иот/ )
т
или
Роо
, боо^оо^
I Рср V
®сж — ^нс !
\ Р,
бср /
тр.сж -^тр.нс ~
Рср боо У”
Р<» бср /
со бср /
| Рср боо У”
ОО \ Р ОО бср J
С учетом соотношений (12.28) и (12.29) выражения для
драничного слоя и коэффициента трения принимают вид
1т(1+₽)
ТОЛЩИНЫ по-
^сж — ^нс
k — 1
2
(12. 30)
£/сж —
7 k — 1
а + (1 — а) И Ь—~
1- т(1 + ₽) ’
(12.31)
202
www.vokb-la.spb.ru - Самолёт своими руками?!
Так как коэффициенты а, т, 0 изменяются в пределах 0<а<1,
О<т(1 + 0)<1 то, очевидно, что с увеличением числа толщина погра-
ничного слоя увеличивается, а коэффициент трения уменьшается независи-
мо от структуры пограничного слоя.
Для воздуха fe=l,4, 0—0,75. В случае ламинарного течения в погра-
ничном слое т—ОД а а можно принять равным ОД из условия согласования
Рис. 12.8. Изменение толщины
ламинарного (7, 2) и турбу-
лентного (3, 4) пограничных
слоев в зависимости от числа
Re:
1—по формуле 12 40; 2—по теории
пограничного слоя; 3—по формуле
12 42, 4—по теории пограничного
слоя
с точными решениями. Тогда расчетные формулы (12.30) и (12 31) примут
следующий вид.
7
5сж=5ис(1+0,1Му8; (12.32)
С/нс
с / сж ~- ] (12.33)
(1+0,IM^
В случае турбулентного пограничного слоя при небольших числах Рей-
нольдса можно принять
п „ 1 2
тп = 0,2, т(1 + р) = — , а--и тогда
3 3
»c«=4c(l+-^M2Jr; (12.34)
£/нс
“ 2 • (12.35)
Формулы (12 32) — (12 35) были получены профессором Г Ф Бураго.
На основании анализа этих формул можно заключить, что с увеличением
числа Мт толщина пограничного слоя увеличивается более интенсивно в слу-
чае ламинарного течения, а коэффициент трения падает более интенсивно в
случае турбулентного течения Кривые изменения толщины пограничного слоя
в зависимости от числа Мж, построенные по приближенным формулам (12 32)
и (12 34), а также на основании теории пограничного слоя приведены на
рис. 12 8
203-
www vokb-la.spb ru - Самолёт своими руками?!
12.7. ИНТЕГРАЛЬНОЕ СООТНОШЕНИЕ ДЛЯ РАСЧЕТА
ДВУМЕРНОГО ПОГРАНИЧНОГО СЛОЯ
НА КРИВОЛИНЕЙНОЙ ПОВЕРХНОСТИ
Величина давления в пограничном слое определяется давле-
нием жидкости во внешнем потоке
При обтекании плоскопараллельным несжимаемым потоком
криволинейной поверхности давление в пограничном слое вдоль
течения изменяется, т. е. продольный градиент давления dpfdx
не равен нулю. При расчетах течения в пограничном слое на
криволинеинои поверхности необходимо пользоваться полным
интегральным соотношением (12. 2):
к г
е V- \ v^y - е17» 4- \ v ж=-S - то •
dx J л dx i dx
о о
(s х s г
Vo \ V xdy |=GH0-— t VVxdy
J I dx J dx J
о / о о
Кроме того, нз уравнения Бернулли следует:
s
4£-=-ei/.^-=-bv(,V'; или 6^=-evov- \dy.
dx dx v dx J
0
С учетом приведенных выше преобразований интегральное
соотношение (12.2) принимает вид
б 8 8 6
\Г Vjdy-e^\\dy-t,
dx J J dx J J
0 0 0 0
8 8
ИЛИ e-j- \1Д(Ц,-1Д)^ + е1/Д (V„-VI)dy=x<>. (12.36)
dx J J
о 0
Величина Vo, выражающая скорость на внешней границе по-
перечного сечения пограничного слоя, не зависит от у н поэтому
ее можно вынести за знак интеграла. Интегра г, входящий во
второе слагаемое левой части этого уравнения, представляет
собой обустовленное влиянием вязкости уменьшение секундного
расхода жидкости через поперечное сеченне пограничного слоя
высотой 6 и шириной равной единице по сравнению с расходом
идеальном жидкое и Иными словами, этот интеграл представ-
ляет собой разность между расходом жидкости сквозь сечение в
204
www vokb-la.spb.ru - Самолёт своими руками?!
пограничном слое в том случае, если бы скорость была равна
скорости Vo, и действительным расходом через то же сечение.
Приравнивая эту разность к расходу идеальной жидкости через
условный слой толщиной б* при постоянной скорости Vo, полу-
чим J(V0— Vx)dy=b*V9.
о
В результате деления этого интеграла на скорость Vo получим
некоторую величину
(12.37)
называемую толщиной вытеснения (рнс. 12.9).
Величина б* является условной толщиной и характеризует
отклонение действительной линии тока относительно линии тока
в невязкой жидкости, вы-
званное влиянием погра-
ничного слоя.
Интеграл, входящий в
первое слагаемое левой
части уравнения (12.36),
по величине представляет
собой обусловленное
влиянием вязкости изме-
нение количества движе-
ния в пограничном слое.
Приравнивая этот инте-
грал количеству движения идеальной жидкости, протекающей
через некоторый условный слой толщиной б** с постоянной ско-
ростью Vo, получим
Частное от деления этого интеграла на Vo2 дает так называе-
мую толщину потери импульса
(12.38)
Следует отметить, что толщина пограничного слоя больше
толщины вытеснения б*, а последняя, в свою очередь, больше
толщины потери импульса б**, т. е. б>б*>б**. Условные тол-
щины б*, б** находят широкое применение при исследованиях
205
www vokb-la.spb.ru - Самолёт своими руками?!
пограничного слоя. Введением величин б* и б** интегральное со-
отношение (12. 36) преобразуется к виду
e-^-(V?6**)+eV'-v(>6*=r0,
dx \ ах )
или е^^+2е^^-б«4-еГ0Н'б*=г0. (12.39)
dx
Разделив это выражение на рУ02, получим интегральное со-
отношение (12. 36) в безразмерном виде:
Il (23** 4- 8*) = (12. 40)
dx Vo р %
илн окончательно ——f-8**V0-kkС2-\~Н)— х „ , (12,41)
dx dx 0I5
где Н=6*/8**.
Это уравнение с параметрами б*, б** и И известно под на-
званием интегрального соотношения Кармана или уравнения
импульсов н применяется для расчета двумерного пограничного
слоя на криволинейной поверхности. Уравнение (12.41) приме-
нимо для расчетов ламинарного н турбулентного пограничных
слоев, поскольку о конкретном выражении касательного напря-
жения через величины б* и б** не было сделано никаких пред-
положений.
В случае обгекання плоской пластины скорость Vo—const и
тогда уравнение импульсов (12.41) упрощается;
dB** т0
dx е^о
(12.42)
Используя это уравнение, запишем формулу для определе-
ния силы трення плоской пластины с одной стороны
ь
О
(12.43)
где Ъ** — то пцииа потерн импульса, вычисленная у задней
кромки пластины
При приближенном решении задач с помощью уравнения
(12 2) предварительно находят приближенный закон изменения
скорости по поперечному сечению пограничного слоя, а затем,
используя это уравнение, определяют напряжение трення т0 на
обтекаемой поверхности, а также толщину пограничного слоя б,
толщину вытеснения б*, толщину потерн импульса б**. Закон
распределения скоростей поперек пограничного слоя можно за-
давать прнбтнженно в виде функций какого-либо характерного
параметра, связывающего влияние формы обтекаемого крыла с
206
I
www.vokb- la.spb ru - Самолёт своими руками?!
характеристикой пограничного слоя. Законы распределения ско-
ростей, выраженные через соответствующий параметр, называ-
ются параметрическими.
Следует отметить, что пограничный слой и область внешнего
течения оказывают друг на друга взаимное влияние. При безот-
рывном обтекании можно приближенно определить взаимное
влияние этих областей. Однако в зоне срыва потока с поверхно-
сти тела теория пограничного слоя неприменима, и здесь пока
приходится пользоваться только экспериментальными данными.
12.8. ОТРЫВ ТЕЧЕНИЯ В ПОГРАНИЧНОМ СЛОЕ
При обтекании криволинейной поверхности, например по-
верхности крыла, могут возникнуть качественно новые явления,
обусловленные отрывом потока жидкости нли газа. Отрыв пото-
ка происходит под действием положительного градиента давле-
ния на пограничный слой, испытывающий сильное влияние вяз-
кости.
Внутри пограничного слоя влияние вязкости проявляется в
том, что скорость течения, параллельная поверхности стенки,
под действием сил трения значительно изменяется по мере при-
ближения к стенке. Скорость потока у самой стенки равна нулю
и с увеличением расстояния у постепенно возрастает, достигая
на границе пограничного слоя скорости внешнего потока. По
сравнению с основным потоком замедленное течение в погранич-
ном слое под действием положительного градиента давления
подвержено дополнительному большому отрицательному уско-
рению; вследствие этого количество движения жидкости вблизи
стенки мало и ее способность к движению в направлении возра-
стания давления оказывается ограниченной. В итоге замедляю-
щийся пограничный слой вблизи стенки под влиянием положи-
тельного градиента давления приобретает даже возвратное дви-
жение, что приводит к срыву потока с поверхности тела.
Точка, в которой производная —— =0 определяется как
у и-ъ
точка отрыва двумерного пограничного слоя. На стенке напря-
дУх
женне трения ?0=ц---- и, следовательно, в точке отрыва оно
ду
обращается в нуль. В точке отрыва поток начинает отходить от
стенки под небольшим углом. За точкой отрыва под действием
положительного градиента давления возникает возвратное тече-
ние (рис. 12 10).
Там, где профиль скорости имеет точку перегиба,
течение очень неустойиво и имеет тенденцию к турбулизации.
Наличие точки перегиба за точкой отрыва обусловлено связью,
существующей между градиентом давления вдоль стенкн н гра-
диентом скорости по нормали к стенке.
207
www .vokb- la.spb ru - Самолет своими руками?!
Линия, начинающаяся в точке отрыва пограничного слоя и
соединяющая токи с нулевой скоростью внутри вязкого слоя, ото-
шедшего от стенкн, может быть определена как линия, нулевой
скорости (граница сорванного потока). Внутри зоны срыва по-
тока положительный градиент давления снижается поти до ну-
ля, так что в кормовой части тела давление значительно умень-
шается по сравнению с давлением, имеющим место при безот-
рывном обтекании тела невязкой жидкостью, а лобовое сопро-
тивление тела сильно
Рис 2 10 Схема течения в области отрыва
пограничного слоя
увеличивается.
Сила лобового сопро-
тивления тела складыва-
ется из сопротивления,
связанного с трением в
пограничном слое н нз
сопротивления, обуслов-
ленного различием дав-
лений в носовой и кормо-
вой частях обтекаемых
тел. Если жидкость не-
вязкая, то сопротивление
тел равно нулю Но в
этом случае и сопротивление давления, как это показано на
примере поперечного обтекания цилиндра (см гл. 6), тоже мо-
жет быть равным нулю (это возможно при безотрывном обте-
кании, когда в кормовой части давление будет таким же, как
н в передней критической точке).
В вязкой среде всегда имеют место н сопротивление трения,
и сопротивление давления. Соотношение между этими составля-
ющими зависит от формы тела. Если тело имеет большие попе-
речные размеры по сравнению с продольным, то на его поверх-
ности всегда наблюдается отрыв пограничного слоя, приводя-
щий к падению давления в кормовой части тела. Тело при этот:
испытывает большое лобовое сопротивление обусловленное сры
вом потока.
Если тело имеет вытянутую по потоку форму с плавными
очертаниями, то срыв потока если и будет, то только на незна-
чительной части его поверхности, н основную долю сопротивле-
ния составит сопротивление трения. Такие тела называются
удобообтекаемыми в отличие от рассмотренных выше, у которых
преобладает сопротивление давления и которые называю ся
неудобообтекаемыми телами. При одинаковых площадях попе-
речного сечения полное сопротивление удобообтекаемых тел мо-
жет быть во много раз меньше чем сопротивление неудобообте-
каемых тел. Поэтому телам, находящимся в потоке (крылу, фю-
зеляжу и др ), всегда придают удобообтекаемую форму, при
которой отрыв пограничного слоя маловероятен нли зона срыва
потока минимальна Ламинарный пограничный слон более под-
208
vt-ww.vokb-la.spb.ru - Самолёт своими руками.”
вержен срыву потока, чем турбулентный. Кроме того, перемеши-
вание при турбулентном течении значительно интенсивнее, чем
при ламинарном, вследствие чего турбулентное течение способно
распространиться на большее расстояние против возрастающего
давления, чем ламинарное.
Опасность появления отрыва пограничного слоя можно
уменьшить, снижая величину положительного градиента давле-
ния (например, придавая телу вытянутую каплеобразную фор-
му) или влияя на характер течения в пограничном слое посред-
ством его искусственной турбулизации. Обычно отрыв погранич-
ного слоя происходит далеко от носовой части тела, в зоне
положительных градиентов давления, где пограничный слой тур-
булентен. Чем больше степень турбулентности течения в погра-
ничном слое, тем интенсивнее происходит обмен количествами
движения между внешними и пристенными слоями, тем большие
скорости вблизи поверхности и тем меньше опасность отрыва.
Степень турбулентности в пограничном слое увеличивается
по мере возрастания числа Re и, следовательно, увеличение чис-
ла Re уменьшает опасность отрыва пограничного слоя.
Степень турбулентности в пограничном слое увеличивается с
повышением степени турбулентности внешнего потока. К сожа-
лению, степень турбулентности атмосферы не поддается управ-
лению, но пограничный слой можно искусственно турбулнзиро-
вать, располагая на поверхности илн вблизи поверхности тела
специальные турбулизаторы, что приводит к увеличению сопро-
тивления трения, которое, однако, компенсируется уменьшением
сопротивления давления.
Влияние степени турбулентности внешнего потока и турбули-
заторов на сопротивление тел очень велико, поэтому степень тур-
булентности аэродинамических труб часто определяется по вели-
чине коэффициента сопротивления шара, помещенного в рабочий
участок трубы. Чем больше степень турбулентности потока, тем
меньше зона срыва потока в кормовой части неудобообтекаемо-
го тела, а значит тем меньше коэффициент его сопротивления.
На рис. 12. 11 показано влияние степени турбулентности потока
на коэффициент сопротивления шара.
На графике, представляющем зависимость сх от числа Re для
удобообтекаемого тела (рис. 12. ]2), можно выделить три зоны.
Зона малых чисел Рейнольдса I соответствует ламинарному те-
чению в пограничном слое. Зона II соответствует числам Re, при
которых существует и ламинарное и турбулентное течение, при
этом увеличение участка с турбулентным течением (с возраста-
нием числа Re) приводит к увеличению сх. В зоне III при пол-
ностью турбулентном течении коэффициент сопротивления сх с
увеличением Re уменьшается.
Прн числах Re<10 происходит отрыв ламинарного потока,
при этом сопротивление давления достигает примерно половины
полного сопротивления.
209
www.vokb-la.spb.ru - Самолёт своими руками?!
При числах Re ^100 наблюдается нестационарное течение,
обусловленное периодическим образованием и срывом вихрей
около кормовой части тела. Область следа вытягивается, поэто-
му преобчадает сопротивление давления.
В интервале чисел Re=103... 105 отрыв потока происходит
гри ламинарном пограничном слое, хотя след за телом является
Рис. 12.11. Влияние чурб^лентно-
и потока на коэффициент ло-
бового сопротивления шара (ei<
<е2<ез<е4)
Рис 12 12 Зависимость коэффи-
циента лобового сопро явления
от числа Re для удобооб-
текаемого тела
турбулентным. Коэффициент сопротивления создается главным
образом за счет сопротивления давления.
При числах Re>105 течение в пограничном слое становится
турбулентным, и точка отрыва при этом смещается вниз по по-
току. Область следа сокращается по сравнению с областью сле-
да в случае отрыва ламинарного пограничного слоя и соответст- >
венно падает сопротивление давления.
12.9. УПРАВЛЕНИЕ ПОГРАНИЧНЫМ СЛОЕМ
Наличие пограничного слоя на обтекаемых поверхностях яв-
ляется причиной больших энергетических затрат при эксплуа-
тации установок, в той или иной форме использующих движу-
щиеся жидкости или газы. Кроме того, наличие пограничного слоя
на несущих поверхностях летательного аппарата приводит к су-
щественному уменьшению подъемной силы по сравнению с ве-
личиной, полученной в соответ с вин с теорией обтекания тел
потоком идеальной жидкости. В частности, подобная картина
наблюдается на взлетно-посадочных режимах полета самолета,
когда крыло самолета располагается под большим углом атаки
и закрылки отклоняются на значительные углы. Такая транс-
формация профиля крыла приводит к появлению существенных
потожнтельных градиентов давления на его поверхности, вслед-
ствие чего происходит срыв потока с верхней поверхности крыла.
Возникает естественная задача о предотвращении отрыва пото-
210
www.vokb-la.spb.ru - Самолёт своими руками?!
ка над верхней поверхностью крыла, т. е. задача об управлении
пограничным слоем (УПС).
Термин «управление пограничным слоем» подразумевает лю-
бой механизм или процесс, который позволяет видоизменять
характер течения в пограничном слое в области отрыва потока.
В качестве примеров механизмов управления пограничным сло-
ем, получивших широкое распространение на современных само-
летах, можно указать на предкрылки, одно- н многощелевые
закрылки, турбулизаторы и т. д.
Существующие системы УПС можно подразделить па пассив-
ные н активные.
В пассивных системах УПС для устранения срыва потока
используется энергия основного потока, точнее избыток энергии,
имеющейся на нижней поверхности крыла по отношению к верх-
ней, в активных — внешние источники энергии, которыми могут
быть либо двигатели самолета, либо специально установленные
компрессоры.
Пассивные системы УПС доведены в настоящее время до вы-
сокой степени совершенства. Однако применение таких систем
не дает возможности получить значения коэффициента подъем-
ной силы, превышающие теоретические. С другой стороны, по-
добные системы чрезвычайно сложны и дальнейшее развитие их
о раничивается объемом крыла, соответствующим уменьшением
объема для размещения топлива, а также сложностью, стоимо-
стью изготовления.
В связи с этим в последнее время большое внимание уделя-
ется разработке активных способов УПС Эти методы, в свою
очередь, можно подразделить на две категории:
1) управление пограничным слоем с целью уменьшения лобо-
вого сопротивления;
2) управление пограничным слоем с целью увеличения подъ-
емной силы.
Для уменьшения лобового сопротивления осуществляется от-
сос пограничного слоя с поверхности обтекаемого тела. Впервые
идею о возможности искусственного управления пограничным
слоем высказал в 1904 г. Прандтль, который реализовал ее на
цилиндре с односторонним отсасыванием пограничного слоя
внутрь цилиндра через узкую щель в его поверхности Поток
воздуха со стороны отсасывания обтекает цилиндр тучше чем
с противоположной стороны, где отсос отсутствует. Для осу-
ществления идеи отсоса на обтекаемой поверхности реальных
объектов, например вдоль размаха крыла, делают продольные
щели, либо всю поверхность выполняют перфорированной. На
рис 12 13 дана схема течения в высокоградиентном диффузоре
прн отсосе и без него.
Применение отсоса позволяет существенно уменьшить сопро-
тивление несущих поверхностей, но подъемная сила не может
превышать значений, полученных в соответствии с теорией не
211
www vokb la.spb ru - Самолёт своими руками!?!
вязкой жидкости, хотя величина ее увеличивается при наличии
отсоса.
Для увеличения подъемной силы крыла в настоящее время
внедряется система сдува пограничного слоя При сдуве орга-
низуется введение высокоскоростной струи в область отрыва воз-
Рис 12 13 Течение в диффузоре с большим уг-
лом раскрытия
а—без отсоса; б—с отсосом через щель:
ленным отсосом
в—с распреде-
душного потока. Для этого иа верхней поверхности крыла
(рис. 12.14) либо перед лобиком закрылка (см. рис. 12. 14, а),
либо непосредственно на нем (см. рис 12. 14, б) монтируется
сопловой аппарат, из которого с очень большой скоростью выду-
вается тонкая струя, ось которой будет касательной к верхней
поверхности закрылка. Струя «прилипает» к криволинейной
поверхности закрылка (эффект Коанда) и обтекает его до задней
кромки, увлекая за собой основной поток, при этом восстаиавли-
Рис 12 14 Схема установки соплового аппарата для
сдува пограничного слоя
а—перед лобиком закрылка, б—иа лобике закрылка
вается безотрывное обтекание профиля. Увеличение подъемной
силы прн сдуве происходит за счет восстановления безотрывного
обтекания путем увеличения составляющей количества движе-
ния струи, а главное за счет увеличения циркуляции скорости по
сравнению с теоретическим, безотрывным обтеканием профилей
212
I
www.vokb-la.spb.ru - Самолёт своими руками?!
Эффективность сдува определяется в основном коэффициен-
том импульса струи
С m'v>
LV-- , ’
—
2
(12.44)
где — массовый расход выдуваемой струн; V3 — скорость
струи на выходе из сопла; — скоростной напор (динамн-
2^
ческое давление) набегающего по-
тока; S — площадь крыла.
На рис 12.15 представлена за-
висимость коэффициента подъемной
силы профиля в функции коэффи-
циента импульса струи н угла от-
клонения закрыла б3. Как видно из
этого графика, сдув пограничного
слоя позволяет существенно увели-
чить коэффициент подъемной силы,
при этом качественно различаются
две области управления погранич-
ным слоем:
— область непосредственного
управления пограничным слоем до
восстановления безотрывного обте-
кания (малые значения с );
— область безотрывного обтека-
ния, в которой энергия струи расхо-
дуется и на формирование «газового
закрылка», увеличивающего хорду
физического закрылка (большие
Рис 12 15 Изменение коэффи-
циента подъемной силы профи-
ля в зависимости от коэффици-
ента импульса и угла атаки
значения сц>0,1) Это приводит к увеличению циркуляции во-
круг профиля (по теореме Жуковского). Поэтому эта область
называется областью «суперциркуляции».
При сдуве пограничного слоя удается по; учить коэффициен-
ты подъемной силы, существенно превышающие значения, полу-
ченные в соответствии с теорией невязкой жидкости.
Вопросы для повторения
1. Каковы причины образования пограничного слоя у твердых
дел, обтекаемых потоком?
2. Какие факторы влияют на положение места перехода ла-
минарного пограничного слоя в турбулентный?
3 Объясните физический смысл членов уравнения импуль-
£0В, /
213
www.vokb-la.spb.ru - Самолёт своими руками?!
4. Изложите методику расчета характеристик пограничного
слоя с использованием интегрального соотношения Кармана.
5. Опишите схемы методов УПС.
Задачи
1. Определить силу сопротивления и коэффициент трения
гладкой пластины с размерами 2=0,5 м; 6=3 м при а=0. Ско-
рость потока 17=12 м/с. Течение полагать; а) ламинарным,
б) турбулентным. Параметры воздуха соответствуют высоте Н~4
= 1000 м. Определить толщину пограничного слоя на конце пла-
стины.
Ответ: а) 2^=0,00417; Х=0,51 Н; 6=4,65 мм; б) 2су=
= 0,01135; Х= 1,36 Н; 6= 14,1 мм.
2. Поток воздуха, имеющий скорость V=30 м/с, обтекает тон-
кою пластину, расположенную по потоку, при нормальных ат-
мосферных условиях. Длина пластины 7=200 мм. Приняв для
критического числа Re, взятого по длине пограничного слоя,
среднее значение 5-10 , показать, что пограничный слой, образу-
ющийся у пластины, является ламинарным. Найти коэффициент
трения Cf. Коэффициент кинематической вязкости воздуха при
нормальных атмосферных условиях v- -0,145-10~4 м2/с.
Ответ: Cf—0,002.
www vokb-la.spb.ru - Самолёт своими руками?!
ГЛАВА 13
ПРОФИЛИ КРЫЛЬЕВ И ИХ АЭРОДИНАМИЧЕСКИЕ
ХАРАКТЕРИСТИКИ
13.1. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПРОФИЛЯ КРЫЛА
Под крылом понимается часть летательного аппарата, пред-
назначенная для создания аэродинамической подъемной силы.
Крылом называют тело, которое создает в потоке жидкости
подъемную силу, значительно превышающую силу лобового со-
противления. Как правило, крыло самолета имеет форму, симмет-
ричную относительно некоторой плоскости — плоскости симмет-
рии.
Рис 131. Геометрические параметры профиля
Любое сечение крыла плоскостью, параллельной плоскости
симметрии крыла, называется профилем крыла. В разных се-
чениях профиль крыла может быть различным по форме, раз-
меру и ориентации.
Один из возможных профилей крыла изображен и а рис. 13 1.
Точка А передняя кромка профиля, В — задняя кромка про-
филя или точка схода профиля. Линия АВ, соединяющая две
наиболее удаленные точки профиля, т. е. переднюю и заднюю
кромки профиля, называется хордой профиля Ь. Хорда делит
профиль на две части — верхнюю и нижнюю. Угол между хордой
профиля и направлением невозмущеиного потока называется
углом атаки а, если вектор скорости иевозмущеииого потока
215
wvrvi vokb-la.spb ru - Самолёт своими руками9'
параллелен плоскости профиля. В более общем случае угол
атаки измеряется между хордой профиля и проекцией скорости
певозмущенного потока па плоскость профиля.
При изучении геометрических характеристик профиля обыч-
но пользуются системой прямоугольных координат, у которой
начало совпадает с передней кромкой профиля, ось ОХа направ-
лена вдоль хорды по направлению к задней кромке, ось OYa —
вверх.
В этой системе координатных осей уравнения верхнего и ниж-
него контуров профиля соответственно имеют вид ув--=1\(х) и
Ь'н=?2 (х).
Толщина профиля в произвольной точке хорды выражается
как разность ординат точек уп и уи. Наибольшая длина перпен-
дикулярного к хорде отрезка — между верхним и нижним конту-
рами профиля, т. е. (ув—#н)тах, называется максимальной тол-
щиной или просто толщиной профиля и обозначается с (см
рис. 13. 1).
Отношение максимальной толщины профиля с к длцне хорды
b носит название относительной толщины профиля: cjb=c или в
процентах с/6-100=с%
Относительная толщина аэродинамических профилей крыльев
и лопастей винтов обычно находится в пределах от 3 до 25%.
Тонкие профили применяются, например, иа концах лопастей вин-
тов и в крыльях сверхзвуковых самолетов.
Линия, соединяющая середины отрезков ув — уп, построенных
в разных точках хорды, называется средней линией профиля
(пунктирная линия иа рис. 13. 1). В частном случае, когда про-
филь симметричен, средняя линия совпадает с хордой. Наиболь-
шая ордината средней линии называется кривизной профиля f,
а ее отношение к хорде называется относительной "кривизной:
ЦЬ—J или в процентах //6-100=/%.
Относительная кривизна современных профилей крыльев и
лопастей винтов обычно не превышает 2%. Кривизна профилей
самолетов 20 и 30-х годов доходила до 6—8%.
Абсциссы наибольшей толщины профиля и наибольшей кри-
визны соответственно обозначаются хс и Xf (см. рис. 13. 1). От-
ношения этих величин к хорде носят названия относительных
абсцисс соответствеиио толщины и кривизны: xc—xc/b, xf~x}jb.
Значения хс у дозвуковых профилей колеблются в пределах
25—30%, у сверхзвуковых 40 50%.
Радиусы кривизны в «головке» и «хвостовике» профиля
(/гол, гхв) также относятся к хорде, например, относительный ра-
диус f=r]b, и часто выражают в процентах от длины хорды.
Серии профилей можно получить путем деформации какого-
либо исходного профиля по заданному закону с сохранением не-
изменными одного или нескольких перечисленных выше безраз-
мерных параметров.
216
www.vokb-la.spb.ru - Самолёт своими руками?!
Величины Ь, с, хс, яу, /, г являются основными геометрически-
ми параметрами профиля, от которых зависят его аэродинамиче-
ские характеристики.
13.2. АЭРОДИНАМИЧЕСКИЕ СИЛЫ И МОМЕНТ
Взаимодействие между газом (воздухом) и движущимся в
ием крылом приводит к возникновению непрерывно распреде-
ленных по всей поверхности крыла так называемых аэродинами-
ческих сил, которые могут быть охарактеризованы величинами
нормального р и касательного т напряжений в каждой точке
поверхности крыла.
Результирующая сил давления и трения, возникающих при
движении летательного аппарата относительно воздушной среды,
сила Д*а, называется полной аэродинамической силой. Часто
под полной аэродинамической силой /?а понимают только ре-
зультирующую нормальных сил, пренебрегая при этом силами
треиия.
Момент полной аэродинамической силы относительно перед-
ней кромки крыла Mz называется продольным моментом или
аэродинамическим моментом тангажа. Момент Mz считается по-
ложительным, если он стремится повернуть крыло в сторону уве-
личения угла атаки а, и отрицательным — в обратную сторону.
Положительный момент называется кадрирующим, а отрица-
тельный — пикирующим.
При теоретическом и экспериментальном исследованиях си
лового взаимодействия движущегося тела с окружающей его
средой обычно рассматривается не результирующая сила /\л,
а проекции этой силы на оси той или иной системы координат,
которая выбирается в зависимости от условий задачи. В аэроди-
намике чаще используются две системы координат: скоростная
и связанная.
В скоростной системе координат ось 0Ya совпадает с направ-
лением скорости полета, ось 0Ya перпендикулярна к оси 0Ха и
лежит в плоскости симметрии летательного аппарата. Ось 0Za
составляет с осями Оха и 0Ya правую систему координат (на-
правлена вцоль правого крыла).
При аэродинамических расчетах начало координат обычно
совмещают с передней кромкой крыла.
В связанной системе координат ось ОХ направлена вдо. ь
хорды крыла или продольной оси самолета, ось 0Y перпендику-
лярна оси ОХ и лежит в плоскости симметрии летательного ап-
парата, ось 0Z составляет с осями ОХ и 0Y правую систему.
В скоростной системе координат проекции силы обозна-
чаются Ха, Уа, Za, а в связанной — X, Y, Z (рис. 13.2).
217
www vokb-la.spb.ru - Самолёт своими руками?!
При рассмотрении плоских течений аэродинамическая сила
раскладывается на две составляющие Ха, Уа(Х, У):
/?;=/№+Г2 или /?Л=ГЛ2+Г’ (13.1)
В скоростной системе координат проекция силы RA на на-
правление, перпендикулярное к скорости невозмущеиного пото-
ка, называется аэродинамической подъемной силой Уа, а проек-
ция силы Ra иа направление, противоположное движению кры-
ла (самолета), называется лобовым сопротивлением Ха.
Рис 13.2. Составляющие полной аэродинами-
ческой силы в скоростной и связанной систе-
мах координат
В связанной системе координат силы У н X называются
аэродинамической нормальной и продольной силами соответст-
венно.
Составляющие силы в этих двух системах координат связа-
ны между собой следующими зависимостями (см. рис. 13.2):
У =Kecosa-j- Ха sin a; Х~Ха cos а — Уа sin а (13.2)
или —К cos а — X sin а; Ха —X cos а4-У sin а. (13.3)
Рассмотрим силы, действующие на цилиндрическое крыло
бесконечного размаха, обтекаемое потоком жидкости, в связан-
ной системе координат, начало которой находится на расстоянии
Л'с от передней кромки крыла (рис. 13.3). Выделим в качестве
характерной длины отрезок крыла длиной I и характерной пло-
щади — площадь S=lb (b — длина хорды).
Сила давления, действующая на элемент поверхности крыла
IdS равна pldS, а проекции этой силы на оси ОХ и ОУ:
йУ~р cos $ldS = +lpdx\ dX~pl sin $dS—lpdtp
218
www vokb-la.spb.ru - Самолёт своими руками?!
Для определения сил X и У необходимо просуммировать эле-
ментарные составляющие по всему контуру профиля.
Вдоль оси ОХ суммирование производим отдельно для верх-
ней и нижней частей профиля, вдоль оси OY — для передней и
задней. Тогда для нормальной и продольной сил получим
в
(13.4)
А
(13.5)
Ян
где рп, р3, рн, рв — соответственно давление иа передней, задней,
нижней и верхней частях профиля
Рис 13 3. К расчету подъемной силы и лобового
сопротивления
Действительная аэродинамическая продольная сила будег
больше расчетной на величину равнодействующей сил трения иа
поверхности крыла.
По величинам У и X для каждого угла атаки с помощью фор-
мул связи (13 3) можно определить подъемную силу Уа и силу
лобового сопротивления Ха.
По опытным данным продольная сила X и толщина профиля
малы по сравнению с нормальной силой У и хордой профиля,
поэтому моментом от продольной силы ввиду его малости обыч-
но пренебрегают. Зная элементарный момент от нормальной
силы
dMz = — dYx= — (рн — Pb)lxdx,
можно определить и полный момент крыла относительно пе-
редней кромки профиля
J (РК~~Рв)^Х.
(А,В)
(13.6)
219
www.vokb-la.spb ru - Самолёт своими руками?!
13 3. АЭРОДИНАМИЧЕСКИЕ КОЭФФИЦИЕНТЫ
И КАЧЕСТВО ПРОФИЛЯ
В главе 9 были приведены общие формулы для определения
подъемной силы и силы лобового сопротивления крыла
= = (13.7)
где/7—Сео— скоростной напор или динамическое давление
невозмущениого потока; суа — коэффициент подъемной силы;
сха — коэффициент лобового сопротивления; S — несущая пло-
щадь крыла; Voo — скорость потока иа бесконечности.
Соответственно формулы для нормальной и продольной сил
имеют вид
r=frfS; X^qS, (13.8)
где с?/> сх — коэффициенты нормальной и продольной сил.
Если обозначить коэффициент полной аэродинамической си-
лы через cflA, а коэффициент полного момента относительной
передней кромки профиля через ст, то
= „ (13.9)
где b — условное плечо момента (обычно хорда профиля). С уче-
том формул (13.1) и (13.8) получим
= (13.10)
В формулах (13.2) и (13.3) от сил можно перейти к их ко-
эффициентам
Су—сУа c°s а-|-сЛд sin а; сх—сха cos а — суа sin а. (13.11)
и Суа = Су cos а — сх sin а; сха—ех cos а-|-Су sin а. (13.12)
Углы атаки, реализуемые в полете, обычно невелики, поэто-
му можно положить cos а ай 1, Sinaia. Учитывая, что иа прак-
тике коэффициент сопротивления сха обычно на порядок меньше
коэффициента подъемной силы Суа, формулы (13. 11) и (13. 12)
можно привести к более простой и чаще употребляемой форме:
Суа Су, Сха — Сх ~}~ CyG,, (*13.13)
И Су^=Суа, Сх—Сха CyaCL. 13. 14)
Используя выражение (13.4), формулу для определения ко-
эффициента нормальной силы профиля представим в виде
£•„=-----2----= 1 (р„-рв)<Д.
где<й=^, я,-
Ь V2 TZ2
СО СО
®СО О Qco Q
220
www vokb-la.spb.ru - Самолёт своими руками9
Диалогично для коэффициента ст можно записать
1 _ — — _
(Рн“Рв)^-
б
При малых углах атаки коэффициент подъемной силы
1
(рн p^dx. 13.15)
о
Таким образом, по распределению давления на нижней и
верхней сторонах профиля, можно определить его коэффициент
подъемной силы Для практической реализации этого метода
расчета необходимы экспериментальные исследования с дрени-
рованной моделью профиля прн условии обтекания, соответст-
вующем бесконечному размаху крыла (плоское обтекание).
Чаще аэродинамические коэффициенты определяются весо-
вым методом, для чего иа специальных весах измеряются непо-
средственно в потоке аэродинамической трубы силы и моменты,
действующие иа модель крыла, а затем расчетным путем опреде-
ляются коэффициенты
Для оценки аэродинамических свойств профиля вводится по-
нятие о качестве профиля К. Аэродинамическим качеством про-
филя называется отношение подъемной силы к силе лобового
сопротивления; К— Ya/Xa или через аэродинамические коэффи-
циенты К=суа/сха. Эта величина представляет собой тангенс
угла наклона полной аэродинамической силы RA к направлению
невозмущениого потока (см. рис. 13.2), т. е.
Чем меньше лобовое сопротивление при той же подъемной си-
ле, тем больше качество.
Безразмерные величины схп, суа, cmi спА и К являются основ-
ными аэродинамическими коэффициентами профиля крыла.
13.4. ЗАВИСИМОСТЬ АЭРОДИНАМИЧЕСКИХ КОЭФФИЦИЕНТОВ
ОТ УГЛА АТАКИ ПРОФИЛЯ. ПОЛЯРЫ ПРОФИЛЯ
Аэродинамические коэффициенты cXG, суа и ст являются неза-
висимыми друг от друга величинами а сдл и К определяются
через коэффициенты сха и суа по соответствующим формулам
Коэффициент полной аэродинамической силы сЛА, а также
его компоненты сха и суа, коэффициент момента ст и аэродина-
мическое качество К зависят от формы профиля, угла атаки,
критериев подобия Re, М, степени турбулентности потока и др.
Этими коэффициентами удобно пользоваться поскольку для ди-
намически подобных течений они одинаковы, поэтому же резуль-
таты экспериментальных исследований приводятся в виде зави-
симостей для аэродинамических коэффициентов. Для данного
профиля при фиксированных значениях чисел Re и М изменение
221
www vokb la.spb ru - Самолёт своими руками?!
угла атаки а влечет за собри интенсивное изменение аэродина
мических коэффициентов пр'офнля.
Типичные кривые зависимости аэродинамических коэффици-
ентов подъемной силы суп от угла атаки а при малых скоростях
обтекаиня, когда влиянием сжимаемости газа можно пренебречь,
приведены иа рис. 13. 4.
Опыт и теория показывают, что иа углах атаки, при которых
-сохраняется безотрывное обтекание («<0,17... 0,25 рад), эти
Рис 13 4 Изменение аэродинамичес-
кого коэффициента в зависимости от
угла атаки и кривизны профиля
зависимости прямолинейны.
На больших углах атаки,
когда прн увеличении градиен-
та давления вдоль профиля
крыла начинается отрыв пото-
ка, лииейная зависимость
суа—Да) нарушается, коэф-
фициент суа увеличивается
медленнее и после достиже-
ния максимального значения
(Суа max) уменьшается. Для
обычных профилей величина
fyamax колеблется в пределах
0,9 1 4.
Угол атаки, прн котором
величина коэффициента подъ-
емной силы достигает макси-
мального значения, иазывается
критическим углом атаки аьр.
Критический угол атаки совре-
менных самолетов составляет
примерно 0,25—0,35 рад. У крыльев малых удлинений анр зна-
чительно больше.
Величина анр в значительной мере зависит от числа Re: с уве-
личением числа Re величина акр и <nmax возрастают. Углы ата-
ки, большие критического, называются закритическими углами
атаки. Угол атаки, при котором <Q=0, называется углом нулевой
подъемной силы и обозначается «о- Он обычио отрицателен и не-
велик (а0=—0,02 . .. —0 05 рад). У симметричных профилей ао---
~-0 Величина «о зависит от относительной кривизны профиля.
Чем больше кривизна профиля f, тем левее проходит график
суа~Да) (см. рис. 13 4).
Разность между критическим углом атаки и углом нулевой
подъемной силы называется диапазоном летных углов атаки.
Линия, проведенная из задней кромки профиля в направле-
нии, прн движении вдоль которого суа—0, иазывается аэродина-
мической хордой профиля, а углы атаки, отсчитываемые от этого
направления, называются аэродинамическими углами атаки и
обозначаются аа (см. рнс. 13. 1).
222
www.vokb-la.spb.ru - Самолёт своими руками?!
На прямолинейном участке кривой cya=f(a) величину коэф-
фициента подъемной силы определяется уравнением
—(13.16)
где с1а — угловой коэффициент прямолинейного участка графи-
ка cyn=f(a).
Изменение коэффициента нормальной силы су в зависимости
от угла атаки подобно изменению коэффициента суа.
Рис 13 5 Изменение аэродинамичес
кого коэффициента сопротивления
профиля крыла схп в зависимости от
угла атаки а
Рис. 13 6 Изменение аэродина-
мического качества профиля
крыла в зависимости от угла
атаки
Коэффициент момента ст является функцией коэффициента
подъемной силы суа, и на углах атаки, соответствующих безот-
рывному обтеканию профиля, определяется уравнением прямой
(13 17)
где сто—коэффициент момента при суа=0, зависящий от кри-
визны профиля f; т=дст1дсуа — угловой коэффициент линей-
ного участка графика cm=f(cya).
Зависимость коэффициента лобового сопротивления сха от уг-
ла атаки а имеет обычно вид параболы (рис. 13.5): сначала cta
изменяется незначительно (в области летных углов), а затем на-
чиная с углов атаки, несколько меньших аьр, быстро возрастает,
что обусловлено усилением отрыва пограничного слоя.
При некотором значении а коэффициент сха достигает мини-
мального значения сха min У симметричного профиля сгатт дос-
тигается при а=0, а у несимметричного с f <0 — при отрица-
тельном значении угла атаки, близком к углу нулевой подъем-
ной силы
Характер изменения коэффициента сх в зависимости от угла
атаки в значительной мере отличается от характера изменения
223
www.vokb-la.spb.ru - Самолёт своими руками?!
Go—f(a)- Аэродинамический коэффициент сх на больших поло-
жительных углах атаки в отличие от коэффициента сха может
стать отрицательным (см. формулу 13. 11).
Аэродинамическое качество профиля крыла также зависит от
угла атаки (рис. 13.6). Для профилей крыльев максимальное
значение качества А1пах достигает порядка 25 Угол атаки а-=ц11В,
при котором качество имеет максимальное значение, называется
наивыгоднейшим углом атаки. При угле атаки, равном cto, каче-
ство равно нулю.
Рис 13 7 Поляра I рот.а
Рис 13 8 Поляра II рода
Большое практическое значение имеют зависимости суа=
—f(cxa), cv=f(cx), называемые соответственно полярами I
(рис. 13.7) и II (рис. 13.8) рода, поскольку позволяют опреде-
лить величину и направление аэродинамической силы. Каждая
точка поляры соответствует определенному углу атаки а.
При одинаковых масштабах вдоль осей сха и суа вектор, сое-
диняющий начало координат с той или иной точкой поляры I ро-
да, представчяет собой по величине и направлению коэффициент
результирующей аэродинамической силы, соответствующей дан-
ному угл у атаки а. Поэтому поляру можно рассматривать как
полярную диаграмму в координатах сЕА и а. Так как в диапа-
зоне летных углов атаки коэффициент суа в несколько раз боль-
ше коэффициента сха, то обычно масштаб вдоль оси сха выби-
рается в 5—10 раз крупнее, чем вдоль оси суа.
Отметим характерные точки поляры (см. рис. 13.7):
— точка максимального аэродинамического качества Атах—
= (Ga/Ga)max и, следовательно, аНв- Графически эта точка опре-
деляется касательной, проведенной к поляре из начала коорди-
нат. Действительно A=tgip, и Amax=tgepmax, т. е. Ашах соотвег-
ствует случаю, когда вектор cRA совпадает с касательной;
224
www.vokb-la.spb.ru - Самолёт своими руками?
— точка минимального коэффициента сопротивления, обычно
соответствующая режиму максимальной скорости в горизонталь-
ном установившемся прямолинейном полете;
— точка максимального коэффициента подъемной силы при
а=«ьр.
Полярой второго рода удобно пользоваться прн расчетах
устойчивости и прочности.
13.5. ЗАВИСИМОСТЬ АЭРОДИНАМИЧЕСКИХ КОЭФФИЦИЕНТОВ
ОТ ЧИСЛА Re, СТЕПЕНИ ТУРБУЛЕНТНОСТИ ПОТОКА
И ФОРМЫ ПРОФИЛЯ
Для данного профиля при неизменных числах М степени тур-
булентности потока е, угле атаки а коэффициент минимального
лобового сопротивления в значительной степени зависит от чи-
сел Рейнольдса. У профилей средних относительных толщин
(с=10... 15%) с увеличением числа Рейнольдса с^атах увели-
чивается. При небольших значениях чисел Re величина коэффи-
циента суатах обусловлена отрывом ламинарного пограничного
слоя. С увеличением числа Re точка перехода ламинарного по-
граничного слоя в турбулентный обычно смещается вверх по
течению и, следовательно, происходит отрыв уже турбулентного
пограничного слоя. Зона срыва при этом уменьшается и коэф-
фициент Суд max увеличивается.
У топких профилей (с = 5...6%) и профилей с заостренным
носиком коэффициент суятах с изменением числа Re остается
почти постоянным, так как отрыв потока у тонких профилей про-
исходит вблизи передней кромки профиля и при малых углах
атаки.
У очень толстых профилей (с—15... 20%) коэффициент
Фуатах обычно невелик и с увеличением чисел Re уменьшается,
так как в кормовой части таких профилей уже при малых углах
атаки возникают большие гра; иенты давления, приводящие к
более раннему отрыву пограничного слоя.
Коэффициент минимального лобового сопротивления cxl mjn
определяется коэффициентом трения плоской пластины С/, кото-
рый, в свою очередь, зависит от числа Рейнольдса: C/^l/Re",
где п—0,5 для ламинарного и и=0,2 для турбулентного погра-
ничного слоя.
Очевидно, что с увеличением числа Re уменьшается коэффи-
циент минимального лобового сопротивления.
С возрастанием начальной степени турбулентности потока
коэффициент Cjcamin увеличивается, коэффициент Cyamax тонких
и толстых профилей изменяется незначительно; коэффициент
Фуатах У профилей средних толщин увеличивается. Такое влия-
ние начальной турбулентности потока на аэродинамические ха-
рактеристики профиля объясняется изменением положения точ-
8 626 225
www.vokb-la.spb.ru - Самолёт своими руками?!
ки перехода ламинарного пограничного слоя в турбулентный с
увеличением начальной степени турбулентности.
Существенное влияние на аэродинамические коэффициенты
профиля оказывают геометрические параметры профиля. С уве-
Рис. 13.9 Изменение коэффициента
Суа шах В ЗЭВИСИМОСТИ ОТ КрИВИЗНЫ
профиля f и абсциссы xf
личением относительной тол-
щины профиля с происходит
увеличение коэффициента ми-
нимального лобового сопротив-
ления сха mIn. Коэффициент
максимальной подъемной силы
Суа max с возрастанием с в диа-
пазоне 5—12% увеличивается,
а в диапазоне 12—20% —
уменьшается Влияние кривиз-
ны / и абсциссы Xf на коэффи-
циент максимальной подъем-
ной СИЛЫ Суа тах дозвукового
профиля большой относитель-
ной толщины показано на
рис. 13 9
С увеличением относительной кривизны профиля f коэффици-
ент схаmin (у профилей средних толщин), коэффициент ст и угол
нулевой подъемной силы (по абсолютной величине) возрастают.
13 6. ЦЕНТР ДАВЛЕНИЯ. ФОКУС ПРОФИЛЯ
Условимся аэродинамические характеристики цилиндрическо-
го крыла с заданным профилем в условиях плоскопараллельно-
го обтекания кевозмущенным потоком всех его сечений, назы-
вать характеристиками профиля крыла.
Рис 13.10 К определению центра давления и фо-
куса профиля
Точка D, являющаяся точкой пересечения линии действия
полной аэродинамической силы с хордой крыла, называется
центром давления (рис. 13 10) Отношение абсциссы центра дав-
226
wirtirt.vokbla.spb.ru - Самолёт своими руками?!
ления к хорде профиля обозначается через хд=хд/6. Для опре-
деления абсциссы точки приложения аэродинамической силы
нужно зиать момент аэродинамической силы относительно какой-
либо точки на профиле (например, относительно передней кром-
ки профиля).
Момент нормальной силы относительно передней кромки про-
филя можно записать в виде
Л/г=—Гхд=—(Kacosa + -¥flsin а)хд, (13. 18)
откуда находится абсцисса центра давления, отсчитываемая от
передней кромки профиля:
х —с-^-Ь (13.19)
А У сУ 1
Используя же выражения (13.8), (13.9), (13. 17), получим
хд=—-w- = -ф т) . (13.20)
СУ \ СУ /
Опыты показывают, что в значительной степени для тонких
и слабонзогнутых профилей величины r“a, т почти не зависят от
формы профиля, а стоо наоборот в значительной степени зависят
от формы профиля.
Момент силы У относительно произвольной точки F на хорде
профиля (см. рис. 13 10) —У(.Гд — xF) — Mz-\-YxF.
Переходя от размерных величин к коэффициентам и учиты-
вая (13. 7), получим
(13.21)
Очевидно, что при xF—~ т коэффициент момента стЪ = сто
и не зависит от угла атаки. Характерная для профиля точка F,
обладающая тем свойством, что вычисленный относительно нее
главный момент сил давления потока ие зависит от угла атаки,
называется фокусом крыльевого профиля.
Для большинства профилей при малых числах М (т. е. без
учета сжимаемости) коэффициент т=—0,22... —0,25. Это оз-
начает, что xF=—т~0,22... 0,25 илн л>=0,22... 0,256, т. е.
фокус профиля крыла находится примерно на расстоянии
1/4 хорды от передней кромки. Неизменное положение фокуса
на хорде возможно лишь при линейной зависимости cm=f(cya)
Для симметричного профиля кривые cm=f(a) и cya=f(a)
проходят через начало координат. В таком случае в пределах
линейной зависимости из двух треугольников (рис. 13.11) по-
лучим
Ст~cf/a = a1tg?2 (13.22)
ИЛИ const. (13.23) сУа tg ¥2
8*
227
www.vokb-la.spb.ru - Самолёт своими руками?!
Следовательно, для симметричного профиля положение цент-
ра давления по у!лам атаки остается неизменным и совпадает
с фокусом профиля.
Рис 13 II Изменение
аэродинамических коэф-
фициентов Суа и ст в за-
висимости от угла атаки
а в случае симметрич-
ного профиля
Рис 13 12 Изменение коэффиц 1ента
центра давления в зависимости от
аэродинамического угла атаки
Рис 13.13. Распределение аэродина-
мической нагрузки по профилю при
угле нулевой подъемной силы «о
Центр давления несимметричного профиля с изменением уг-
ла атаки перемещается вдоль хорды нли ее продолжения от
минус бесконечности до плюс бесконечности (рис. 13. 12). Гра-
фически зависимость .тд от
аэродинамического угла атаки
cta изображается равнобочной
гиперболой В случае
(сплошная линия) центр дав-
ления с возрастанием угла
атаки 'перемещается к носику
профиля, а в случае ст>0
(пунктирная линия) — к хво-
стику.
При а=ао (что соответствует суа=0) центр давления нахо-
дится на бесконечности, так как при отсутствии подъемной силы
аэродинамическое воздействие на такой профиль приводится к
паре сил (рис. 13. 13).
13.7. РАСПРЕДЕЛЕНИЕ ДАВЛЕНИЯ ПО ПРОФИЛЮ
Для расчета крыла на прочность, кроме величии коэффици-
ентов сха, Cy(t, ст необходимо знать распределение давления по
профилю. Распределение давления по профилю изображается
графически в виде координатной или векторной диаграмм Коор-
228
www vokb-la.spb.ru - Самолёт своими руками?!
углах атаки а
13. 14. Эти эпю-
1
Рис. 13 14 Эпюры
распределения
давления по не-
симметричному
профилю на раз-
личных углах ата-
ки:
1—верхняя поверх-
ность профиля; 2—
нижняя поверхность
профиля
динатная диаграмма строится в системе координат, где по оси
абсцисс откладывают относительные расстояния x~x/b (b —
хорда профиля), а по оси ординат — коэффициент давления р=
=Др /Q <х>, где Др—р роо и —Q<xAz
Эпюры распределения давления (координатные диаграммы)
для несимметричного профиля при различных
а= —0,05; 0,20, 0,25 рад) изображены на рис.
ры получены при малых числах М, т е. без
учета сжимаемости потока жидкости.
В критической точке = 1 (для сжимаемой
жидкости /?>1). При отрицательных углах
атаки эта точка лежит на верхней поверхности
профиля, а при а>0 переходит иа нижнюю
сторону. На верхней и ннжией поверхностях
вблизи носика профиля происходит интенсив-
ное ускорение потока с соответствующим сни-
жением давления, прн этом снижение давле-
ния иа верхней стороне профиля происходит
более интенсивно, чем на нижней. Эти участки
профиля являются конфузорными. За точками
минимума давления поток замедляется, а дав-
ление повышается. Эти участки у профиля яв-
ляются диффузорными. На задней кромке про-
филя, где происходит слияние струй, сбегаю-
щих с верхней и иижней поверхностей про-
филя, полное давление не восстанавливается,
так как в пограничном слое имеют место необ-
ратимые потери давления.
Если местные скорости больше У<», то
рмест<Роо и Др<0. В этом случае понижение
давления называется подсосом. Если Умеет <
<УТО, то /?Мест>роо и Др>0. Это повышение
давления называется подпором. В точках, где
местная скорость достигает скорости невозму-
щеиного потока, коэффициент давления равен
нулю.
На углах атаки, больших 0,05 рад, подсос
обычно распространяется почти на всю верх-
нюю поверхность, а подпор—иа всю нижнюю.
Из приведенных эпюр распределения давления (см. рис.
13 14) можно заключить, что при малых положительных углах
атаки понижение давления на верхней поверхности значительно
больше по абсолютной величине по сравнению с повышением
давления на иижней поверхности, следовательно, в этом случае
аэродинамическая подъемная сила профиля создается главным
о )разом за счет подсоса на верхней поверхности и в меньшей
мере — за счет подпора на нижней.
229
www vokb la.spb.ru - Самолёт своими руками?!
Следует отметить, что для сжимаемой среды это положение
справедливо при малых скоростях движения, при сверхзвуковых
скоростях вклады верхней и иижнеп поверхностей в создание
подъемной силы могут быть одинаковыми. При увеличении уг-
лов атаки до критических картина распределения давлений по
верхней поверхности существенно изменяется, подсос иа верхней
стороне достигает очень больших значений (р = —2... —3),
в то время как подпор на иижией стороне по-прежнему харак-
----------------------—, теризу ется величиной Р^1.
Рис. 13.15 Схема обтекания
профиля на критическом угле
атаки:
1—безотрывное обтекание; 2—обте-
кание при наличии отрыва (т—
точка отрыва пограничного слоя)
В этом случае иа верхней по-
верхности профиля появляются
значительные диффузорные
участки, где возникают боль-
Рис 13 16 Векторные диаграммы
распределения давлении
шие положительные градиенты
давления, которые, как известно,
вызывают отрыв пограничного
слоя.
Схема обтекания профиля и а критическом угле атаки, а так-
же эпюры распределения давлений с отрывом пограничного слоя
для потока несжимаемой жидкости показаны иа рис. 13..15.
Точка минимума давления у дозвуковых профилей с относи-
тельной толщиной с=10 .. 14%, располагается на верхней по-
верхности вблизи передней кромки профиля. Это способствует
раииему переходу ламинарного пограничного слоя в турбулент-
ный, а при больших пред критических углах атаки у профилей с
тонким «носиком» приводит к срыву потока.
На векторной диаграмме распределения давления безразмер-
ный коэффициент давлений р изображается в виде стрелок-век-
торов, направленных по нормали к поверхности профиля
(рис. 13. 16). Область подсоса разрежения обозначается зна-
ком «минус», а область подпора — знаком «плюс», при этом под-
сос указывается стрелками, направленными в сторону внешней
230
www vokb-la.spb.ru - Самолёт своими руками9'
нормали, а подпор — в сторону внутренней. Из рисунка видно,
что при малом угле атаки а^а0 на верхней стороне профиля у
Рнс 13.17 Эпюры распределения давлений по двум профилям
различной толщины
передней кромки имеется подпор, который переходит в подсос.
На нижней стороне наблюдается обратное явление
Эпюры давлений позволяют построить график распределения
нагрузки от сил давления по хорде
профиля.
Если вектор р проектируется на
хорду и проекции откладываются
вдоль ординаты, соответствующей
точке максимальной толщины про-
филя, то полученные таким образом
эпюры нагрузок позволяют опреде-
лить коэффициент сх без учета сил
трения.
картину распределения дав-
ления по профилю значительное
влияние оказывает форма профиля;
относительная толщина (рис. 13.17),
положение точек максимальной тол-
щины н кривизны. При малых углах
атаки со смещением абсциссы хс
сдвигается и точка минимального
давления иа профиле (рис. 13.18).
Гис 13 18 Влияние поло-
жения максимальной тол-
щины Профиля на картину
распределения давления
Вопросы для повторения
1. Дайте определение профиля. Напишите аэродинамические
коэффициенты профиля крыла.
2. Как по поляре профиля определить нанвыгоднейший угол
атаки?
3. Как коэффициент подъемной силы суа зависит от угла ата-
ки для симметричного и несимметричного профилей?
231
wwm vokb-la.spb ru - Самолёт своими руками?!
4. Дайте определение центра давления и фокуса профиля.
5. Какие допущения использованы при доказательстве неиз-
менности положения фокуса?
6. Как изменяется положение центра давления профиля при
изменении угла атаки?
7. Проанализируйте эпюры распределения давления по про-
филю для различных углов атаки.
Задачи
1. Определить величину средней циркуляции скорости по кон-
туру профиля прямоугольного крыла самолета с полетным ве-
сом G=588 000 Н, летящего на высоте /7=8500 м со скоростью
У=828 км/ч Размах крыла 7=32 м.
Ответ: Гер — 158 м2/с.
2 Коэффициент сопротивления сха нового самолета был ра-
вен 0,019. В процессе эксплуатации и после ремонтов обшивки
коэффициент сопротивления увеличился до 0,021 Определить,
насколько увеличилась сила сопротивления при .полете иа высо-
те /7=6000 м со скоростью У=648 км/ч. Площадь крыла само-
лета S = 140 м2.
Ответ: &Ха=3020 II.
3. При полете самолета с углом атаки крыла а=0,07 рад,
коэффициент подъемной силы составил 0,4. Чему равен угол
ну [евой подъемной силы, если с“д=5,3.
Ответ- ао——0 0054 рад.
4. Определить значения коэффициентов нормальной и про-
дольной сил, если ^=1,42; сха=0,125 при угле атаки а=
= 0,1745 рад.
От ее т: сх=—0,123, Су— 1,422.
www.vokb-la.spb ru - Самолёт своими руками?!
ГЛАВА 14
АЭРОДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ
ПРОФИЛЯ В ДОЗВУКОВОМ ПОТОКЕ
14.1, ОСНОВНЫЕ УРАВНЕНИЯ УСТАНОВИВШЕГОСЯ
ДВУМЕРНОГО ДВИЖЕНИЯ ГАЗА И ИХ ЛИНЕАРИЗАЦИЯ
МЕТОДОМ МАЛЫХ ВОЗМУЩЕНИЙ
Для теоретического анализа аэродинамических свойств
крыльевых профилей при дозвуковых скоростях с учетом сжи-
маемости воздуха в установившемся плоскопараллельном пото-
ке используем уравнения Эйлера (5. 3) и уравнение неразрыв-
ности (2 8)
(14.1)
d(QVjr) । d Q 2)
дх ду
Последнее уравнение после дифференцирования принимает
вид
Когда /j=p(q) и, наоборот, q = q(p), входящие в уравнение
(14. 3) частные производные д§!дх и д$/ду с учетом формулы для
скорости звука
dp/d^^z. Удр/dQ будут иметь вид р
дх dp дх а2 дх ,, „
др dy др 1 др
ду dp ду а2 ду
Подставив эти производные в (14. 3), получим уравнение
t f dVx I дУУ [ v* dp — Q
\ dx dy J a2 dx a2 dy
233
www.vokb-la.spb.ru - Самолёт своими руками?!
или с учетом (14. 1)
л dVy \ / V* dVx ,VyVx dVx '
\ dx dy J \ a2 dx a2 dy
__ /V* &Vy r dVy \ q
\ a2 dx a2 dy / ’
которое после преобразования примет вид
г \ Q (14>4)
\ а2 / dx \ а2 ) dy а2 \ dy дх )
Полученное уравнение справедливо и для безвихревого и для
вихревого движений.
При безвихревом движении составляющие скорости можно
выразить через потенциал скорости
vx=-^--, V„=-^;
дх ду
дУу г)2<? . dVy д2<р
дх ~’ дх2 * ду ду2 ’
и в этом случае уравнение (14. 4) принимает вид
(VJ-a2) ^+(V;-a2)^- + 2V,V'B-^=0. (14.5)
Это уравнение является основным уравнением установивше-
гося безвихревого движения сжимаемой жидкости в плоскопа-
раллельном потоке. Оно может быть использовано для различ-
ных теоретических исследований обтекания профилей дозвуко-
вым и сверхзвуковым потоками газа. Уравнение (14. 5) являет-
ся нелинейным дифференциальным уравнением в частных про-
изводных для потенциала скоростей <р(х, у), так как скорость
звука, выраженная через составляющие скорости, зависит ог
производных ду/дх и ду/ду. Отыскивание решений таких урав-
нений сопряжено со значительными математическими трудно
стями, полому большое значение приобретают методы преобра-
зования таких уравнений в линейные дифференциальные урав-
нения.
Точные решения уравнения (14. 5) получены лишь для немно-
гих простых течений. Наиболее удачным является решение Чап-
лыгина, который, перейдя в уравнении (14. 5) к новым перемен-
ным (переменные iодографа скорости), после соответствующих
преобразований получил линейное дифференциальное уравнение.
С помощью уравнений Чаплыгина были получены точные реше-
ния ряда струйных задач.
Перейдем к приближенной линеаризации уравнения (14 5).
При обтекании тонкого профиля под малым углом атаки возму-
234
www.vokb-la.spb.ru - Самолёт своими руками?!
щения параметров газа (скорости, плотности, давления) счита-
ются настолько малыми по сравнению с параметрами невозму-
щенного потока, что в уравнениях движения можно пренебречь
членами, содержащими квадраты и произведения этих величин.
Если направление невозмущенного потока совпадает с осью ОХ,
то соответствующие скорости, полную скорость, давление и плот-
ность газа можно выразить следующими формулами:
I (14.6)
= р = Рсо+р'-, I
где Ko, poo, Qco, Vx, Vy — параметры невозмущенного потока;
V/, V/, р', q' — возмущения в произвольной точке, вызванные
обтекаемым профилем. Пренебрегая членами, содержащими про-
изведения малых величин, найдем
(и,-} с)(Иоо4 14г)^ЬхУоо4ч'оо^4-СПсо.
Подставляя эти значения в уравнение (14.2), получим линеари-
зованное уравнение неразрывности
до' ЗУ' dV'
l/TO^- + Qro—JL + Go*_0. (14.7)
дх дх ду
В случае изэнтропического течения
Разлагая правую часть этого уравнения в ряд по степеням
малой величины q7qco и удерживая при линеаризации лишь чле-
ны с первой степенью малой величины q7qk>, получим
1+-£- = 1+Л-£-+-.
Poo Q о
dp' 1 ^оо др' 1 др'
откуда следует -~------------— —5--.
дх k Роо дх аоо дх
После этой подстановки и деления всех членов уравнения (14. 7)
на плотность Qoo получим линеаризованное уравнение неразрыв-
ности в другом виде
|_^+^о. (14.8
QtxXioo дх дх дУ
Линеаризуем теперь уравнение Бернулли (5. 16):
235
www.vokb-la.spb.ru - Самолёт своими руками?!
Подставив значения q н V согласно (14. 6) в произвольно вы-
бранной точке А тонкого профиля (рис. 14 1), получим
(У + У')2
dp—^W .
Пренебрегая малыми величинами второго порядка, имеем
dp = — VocVoorf а после интегрирования р = —Соо^оЛ
Вдачи от крыла р^р^, V'x—0, поэтому С—р^. Вследствие
этого линеаризованное уравнение Бернулли примет вид
С 4. 9)
(14. 10)
р --Рсо Ооо^оо^д.
или с учетом (14. 6) р'=—QooVooVx'.
Рис. 14 1. Тонкий профиль в потоке газа
Уравнения (14.9) или (Т4. 10) являются линеаризованными
уравнениями Бернулли
Подставив найденное значение рг в (14-8) и учитывая, что
Усю/Осо = Моо, получим линеаризованное уравнение неразрывно-
сти в окончательном виде
Выражая для безвихревого течения скорости Vx' и У/ через
потенциал возмущенных скоростей у' и подставляя их значения
в последнее уравнение, получим линеаризованное уравнение для
потенциала скоростей двумерного возмущенного движения
газа:
(1-М2)-^-^-^- —О (14. 11)
' дх^ ' ду* V
14 2. СВЯЗЬ МЕЖДУ ДОЗВУКОВЫМ ПОТОКОМ ГАЗА
И потоком НЕСЖИМАЕМОЙ жидкости около
ТОНКИХ ПРОФИЛЕЙ
Пусть в дозвуковом потоке газа находится тонкий профиль
(см. рис. 14. 1), форма которого задана уравнением y=f(x).
Допустим, что поток газа безвихревой и определяется потенциа-
лом скорости ф = Уж-{-(р'(х, у), где <р'(х, у) — потенциал возму-
236
www.vokb-la.spb.ru - Самолёт своими
щенных скоростей. Линеаризованное уравнение для потенциала
скоростей (14.11) решается при граничном условии на поверх-
ности профиля (в связанной системе координат)
У ду
df \
dx
(14. 12)
Vcc-
Уравнение (14. 11) совместно с граничным условием (14. 12)
однозначно определяет функцию ф' на профиле В случае дозву-
кового потока уравнение (14.11) может быть преобразовано в
уравнение Лапласа введением новых независимых переменных
Xi и У\, связанных с х и у соотношениями:
Уг=уУ^ — Му;
где Z— произвольная постоянная, выбираемая в дальнейшем из
граничного условия (14.12) в новой системе координат. Произ-
водные от потенциала скоростей в новых переменных выража-
ются следующим образом:
dy' _ ду' __ д2у‘ . ду' _ду' dv\ __ду' —д/рг .
дх dxi дх2 дх( * ду ду\ dy ду\
или
бу2 бух X бу ) Чу дух Хду, * °°Г
ду2 ду2 '
д2®' д2у'
Уравнение (14. 11) после подстановки вместо —— и ------ их
дх2 ду2
значений и сокращения на (1 —М^)примет внд
дду' । д2у'
дх‘| ду*
(14. 13)
Последнее уравнение — это уравнение Лапласа.
Сформулируем граничное условие для уравнения (14. 13) в
преобразованной системе координат. При этом будем полагать,
что профиль крыла, угол атаки и скорость набегающего потока
в новой системе координат остаются неизменными. При перехо-
де к новым координатам правая часть выражения (14 12) оста-
ется неизменной, поэтому граничное условие (14.12) в перемен-
ных (Xi, yi) запишется в виде
- = V'=—=-___- х__jT —
dyi — М2 ду \ dx)
г СО
Из граничного условия стедует 1 — М2 .
237
www vokb-la.spb ru - Самолёт своими руками?!
Так как новая переменная#!—#У1- М^,то можно записать,
что
=?' У^Ж, Ул У
или v^vy^yT^Mt,
откуда следует Vx^=V'xJ/1
14.14)
т. е. в потоке газа продольные составляющие вызванных (воз-
мущенных) скоростей больше, чем в потоке несжимаемой
жидкости.
Выразим давтение в точке А через число Моо, для чего вос-
пользуемся уравнением Бернулли в форме (14.9) р—р^-~-
= е!/»!//.
Коэффициент давления в точке
“ Р-Роо СоЛоЛ о У ПА1г.
р— 5——-------------х— = — 2 . (14 15)
о у2 о V2 V
^OQ ОО LOQ ОО ОО
2 2
Если воспользоваться .этим соотношением, то с учетом
(14. 14) можно записать
14 16)
Эта формула выражает известное правило Прандтля — Гчау-
эрта: местный коэффициент давления для тонкого тела в дозву-
ковом сжимаемом потоке с числом в 1/У1—М^раз больше
соответствующего коэффициента давления для того же тела в
несжимаемом потоке. Полученный вывод не распространяется на
те области потока у тонкого профиля, г е отклонения местной
скорости набегающего потока нельзя считать малыми. Это отно-
сится пр(жде всего к областям в районе критических точек но-
совой и хвостовой (на рис. 14. 1 эти области отмечены пункти-
ром). При достаточно малых Моо в критической точке коэффи-
циенты давления с очностью до малых величин второго поряд-
ка связаны меж у собой зависимостью
Рсж.кр Рнс.^р
4
Существуют и другие упрощенные, но более точные методы
учета влияния сжимаемости основг иные также на предположен
238
www vokb-la.spb ru - Самолёт своими
нии о слабом возмущении потока. Более точной по сравнению с
формулой Прандтля является формула Кармана — Тзяна:
(14. 17)
Влияние сжимаемости сказывается в том, что в области поло-
жительных значений р коэффициенты давления для сжимаемой
Рис 14 2 Влияние сжимаемости на распре
деление коэффициентов дав тени я по про-
филю (М«1>М9е2>М«>о)
жидкости будут выше, а в области отрицательных значений —
ниже, чем для несжимаемой жидкости (рис. 14.2). Таким обра-
зом, благодаря сжимаемости увеличиваются абсолютные значе-
ния коэффициента давления, при этом области минимальных
давлении становятся более крутыми и вытягиваются. Поскольку
с возрастанием числа М™ увеличивается площадь, заключенная
между кривыми давлений для верхней и нижней поверхностей,
подъемная сила в этом случае увеличивается
143 ВЛИЯНИЕ СЖИМАЕМОСТИ НА АЭРОДИНАМИЧЕСКИЕ
ХАРАКТЕРИСТИКИ ПРОФИЛЯ
Воспользуемся ранее полученными выражениями для су и ст
(см. гл. 13):
1
гу= [ (Рн~РвШ; ст=- f (ри — pjxdx.
о о
239
www vokb-la.spb ru - Самолёт своими руками?!
Будем считать, что выражения для су и ст относятся к слу-
чаю обтекания профиля потоком сжимаемой жидкости Тогда,
подставив вместо рн и рв их значения, согласно (14. 16) по тучим
Сусж (14. 18)
тсж = с(Янс/УГ1 (14.19)
Если учесть, что согласно (13 21) положение центра давле-
ния и фокуса профиля определяется формулами
v___ dcm . ~ ~ __ Стсж _ _ нс ^оо
/л ’ . 4- ..- »
Су Сусж Су нс Е 1 —
то иа основании (14. 18) и (14. 19), получаем
^'FCtk------Я-дсж “ Х'днс*
(14. 20)
Таким образом, благодаря сжимае-
мости коэффициенты подъемной силы и
аэродинамического момента профиля уве-
личиваются; на положение фокуса и
центра давления сжимаемость влияния
не оказывает.
Формулы (14.18) и (14.19) позволяют
пересчитать значения коэффициентов су
_____________1_»! и ст, полученные (расчетным и опытным
* путем) при обтекании тонкого профиля
Рис. 14.3. Сравнение экс-
периментальных значений
cv в дозвуковой облас-
ти (1) и рассчитанных по
линейной теории (2)
несжимаемой средой, иа большие дозву-
ковые скорости обтекания газом того же
профиля
Значения су в зависимости от числа
Моо, подсчитанные по формуле (1 1.18
и замеренные экспериментально, приведены иа рис. 14.3.
Приведенные выше формулы Глауэрта и Прандтля справед-
тивы при обтекании тонких профилен под малым углом атаки.
Формулы, полученные С. А Христиановичем, действительны для
определения коэффициентов су и ст любого профиля при любом
угле атаки:
Сусж
СУ нс
Vi -м2
г ОО
k\
dCy \ k
da /нс - мте
г
1 щсж
Стнс^
й- м2~
ОО
/ дст \ / дст \
\ дсу /сж \ дсу /нс
(14 21)
(14. 22)
www.vokb- la.spb ru - Самолёт своими руками?!
Коэффициент k зависит от характера распределения давле-
ния по профилю и от числа AV. При малых числах Моо коэф-
фициент k равен единице.
Следует заметить, что формулы (14. 18, 14. 19, 14.21, 14 22)
непригодны, когда число М.<. близко к единице (прн Моо=1 со-
гласно этим формулам су сж стремится к бесконечности).
Коэффициент сопротивления для тонких профилей опреде-
ляется, главным образом, силами треиия. Поэтому сжимаемость
оказывает значительное влияние
иа его величину в силу своего
влияния иа условия течения газа
в пограничном слое.
Рис. 14 5. Изменение коэффициен
та сопротивления пластины в за
висимости от числа Мм и поло
жения точки перехода ламинар-
ного течения в турбулентное;
/—хт=1; 2—хт<1; 3—хт-0
Рис. 14 4 Зависимость толщи-
ны турбулентного погранично-
го слоя на пластине от числа
Мео
Рассмотрим сначала пограничный слой у пластины, при этом
ограничимся чисто качественной Оценкой сжимаемости. На по-
верхности пластины, где скорость обращается в нуль, темпера-
тура газа достигает температуры торможения То.
Вследствие повышения температуры плотность газа в погра-
ничном слое уменьшается, что приводит к увеличению толщи-
ны пограничного слоя. График зависимости толщины погранич-
ного слоя от числа Моо приведен иа рис. 14 4. С другой сторо-
ны, благодаря повышению температуры в пограничном слое
повышается вязкость газа. Увеличение толщины пограничного
слоя оказывает большее влияние иа коэффициент треиия по
сравнению с повышением вязкости, поэтому как показывает рас-
чет, коэффициент трения пластины, находящейся в потоке газа*
меньше, чем в потоке несжимаемой жидкости.
Влияние числа Ж иа величину сх показано на рис. 14 5
Влияние сжимаемости на коэффициент сопротивления мож-
но оценить по приближенной формуле Г. Ф. Бураго:
241
www.vokb-la.spb.ru - Самолёт своими руками?!
В дозвуковом потоке, когда нагрев невелик, изменение cVCHt
довольно точно оценивается формулой К. К Федяевского:
___нс_____
У1+0,2М^
Кроме сопротивления трения, у толстых профилей возникает
и сопротивление давления. Опыт показывает, что сопротивление
давления с возрастанием довольно быстро увеличивается.
Это происходит благодаря увеличению градиента давления:
d Рсж Рис
dx dx 1 1 __ до2
' со
В конфузорной части, где имеется ламинарный участок по-
граничного слоя, увеличение отрицательных градиентов давле-
ния приводит к уменьшению толщины пограничного слоя.
В диффузорной же части, где пограничный слой, как правило,
турбулентный, благодаря увеличению положительных градиен-
тов толщина пограничного слоя увеличивается. Из этого следу-
ет, что степень влияния сжимаемости иа вязкое сопротивление
профиля зависит от протяженности ламинарного участка погра-
ничного слоя, положения точки перехода ламинарного погранич-
ного слоя в турбулентный хт.
Коэффициент сопротивления профиля зависит от ряда основ-
ных факторов: угла атаки, чисел М«> и Re, относительной тол-
щины профиля с (рис. 14.6). При малой относительной толщи-
не профиля (0<с<0,05) сопротивление давления по сравнению
с общим сопротивлением профиля невелико, поэтому коэффициент
сопротивления уменьшается по мере увеличения числа М<» (см.
рис 14.5); у профилей средней толщины (0,05<с<1,22) сопро-
тивление сначала уменьшается, а затем при Мжл0,4. 0,5 на-
чинает увеличиваться за счет сопротивления давления; наконец,
коэффициент сопротивления толстых профилей увеличивается во
всем дозвуковом диапазоне чисел Моо (см. рис 14 6) за счет
увеличения сил трения иа профиле по сравнению с пластинкой.
На рис. 14.7 приведены графики изменения коэффициента
сопротивления давления схр для симметричных профилен с от-
носительной толщиной с=6, 9, 12% при нулевом угле атаки в
зависимости от числа М™.
При числе Мс>=0,7 начинается повышение коэффициента у
профилей с относительной толщиной с—12%, при числе Ма,~
= 0,78 начинается повышение коэффициента схр у профилей с
относительной толщиной с=9%, а при Мос —0,86— у профилей
с с—6%.
242
www.vokb-la.spb.ru - Самолёт своими руками?!
Коэффициент лобового сопротивления профиля при суа—0
можно вычислять по предложенной А. А. Дородницыным фор-
муле
Сю—£лОт1м,
где c'xQ — коэффициент сопротивления данного профиля в не-
сжимаемом потоке при суа~0; к]ж=}(с, хт, Мм) поправочный
коэффициент иа влияние сжимаемости воздуха, зависящий от от-
носительной толщины про-
Рис. 14.7. Изменение коэффи-
циента сХр симметричного про-
филя в зависимости от числа
М и толщины профиля
Рис. 14 6. Влияние сжимаемости воздуха на
коэффициент сопротивления для ряда про-
филей различной толщины
Вопросы для повторения
1. Какое влияние оказывает увеличение числа Мм иа аэро-
динамические коэффициенты сх и су и иа их зависимости от угла
атаки?
2. Как повлияет на поляру профиля крыла сжимаемость воз-
духа?
3. Зависит ли положение точки отрыва пограничного слоя от
сжимаемости воздуха?
4. Как влияет увеличение числа М«> на картину распределе-
ния давления по контуру профиля?
243
www.vokb-la.spb.ru - Самолёт своими руками?!
Задачи
1. Коэффициент подъемной силы сунс профиля при М„=0
составляет 0,3. Определить коэффициент подъемной силы сусж
при Мм—0,8.
Ответ: сусН!=0,5.
2 На сколько процентов увеличивается значение коэффици-
ента подъемной силы профиля при полете на высоте //—5000 м
со скоростью 17=652 км/ч, если учесть сжимаемость?
Ответ: на 17,8%.
3. Подъемная сила участка крыла бесконечного размаха
площадью S=10 м2 при а=0,0434 рад. и скорости полета V=
= 880 км/ч у земли равна 17760 Н. Для профиля 5суа/да=5,40
Определить угол нулевой подъемной силы ао и коэффициент
подъемной силы суа при скорости полета 17=720 км ч и угле
-атаки а—0,069 рад.
Ответ: do=0,0209 рад; суа=0,228.
4. Используя линеаризованное уравнение Бернулли, опреде-
лить приращение скорости и уменьшение плотности в той точке
крыла, где относительное уменьшение давления составляет 10%.
Число набегающего потока М™=0,6.
Ответ: АЙ=5%; \р = 19,8%.
www vokb-la.spb.ru - Самолёт своими руками?!
ГЛАВА 15
ПРОФИЛЬ КРЫЛА в околозвуковом
(ТРАНСЗВУКОВОМ) ПОТОКЕ
15 1. ПОНЯТИЕ О КРИТИЧЕСКОМ ЧИСЛЕ М.
УДАРНЫЕ ВОЛНЫ
С увеличением скорости набегающего (невозмущенного) по-
тока аэродинамические характеристики профиля претерпевают
изменения, которые начинают проявляться уже при числе Моо=
^0,5. .. 0,6.
Профиль крыла, находящийся в потоке газа, вытесняет сво-
им объемом часть газа и сужает обтекающие его струйкн, прн
этом скорость течения вдоль профиля сначала увеличивается,
достигая максимального значения Ушах в наиболее узком сече-
нии струйки, а затем убывает. Следует заметить, что скорости
потока вдоль профиля могут в значительной степени отличать-
ся от скорости набегающего потока.
При адиабатическом процессе с увеличением скорости тече-
ния газа V уменьшается скорость распространения звука в га-
зе а. В точке профиля, где скорость течения газа максималь-
ная, скорость звука a=amin. Следовательно, там, где сечение
струйки наименьшее, достигается максимальное значение мест-
ного числа М=А1тах (рнс. 15 1). Этой точке соответствует так-
же минимальное давление и минимальное значение коэффици-
ента давления (р = -
При определенном значении для данного профиля скорости
набегающего потока Ум иа поверхности профиля может быть до-
стигнута местная скорость течения газа V, равная местной ско-
рости звука (несмотря на то, что скорость набегающего потока
дозвуковая) н, следовательно, местное число М может стать
равным единице
Число Моо невозмущеииого дозвукового потока, прн котором
на поверхности профиля местная скорость течения становится
равной местной скорости звука (местное число М равно едини-
це), называется критическим и обозначается Мкр. Это число всег-
да меньше, или равно единице, н его величина зависит от формы
245
www.vokb-la.spb ru - Самолёт своими руками?!
профиля и его угла атаки. Число Мж=Мкр является верхней,
границей Моо, при которой справедливы соотношения, получен-
ные для полностью дозвукового потока.
При дальнейшем увеличении скорости 14o(Mkp<Moo< I) у
поверхности профиля образуются области местных сверхзвуко-
вых скоростей в которых изменение параметров газа уже не
подчиняется законам дозвукового течения.
Области местного сверхзвукового течения при числах Мж>
>Мир обычно замыкаются местными скачками уплотнения-.
Рис. 151 Обтекание профиля
крыла дозвуковым потоком
Рис. 15 2. Изменение коэффициента ми-
нимального давления в зависимости от
критического числа М:
1—по методу Христиановича, 2—по методу
Бураго
(ударными волнами). Появление скачков уплотнения вызываег
дополнительные потери механической энергии в обтекающем по-
токе. Это явление принято называть «волновым кризисом».
В момент начала кризиса (М.оо=Мкр) звуковая скорость те-
чения на профиле появляется в той точке его поверхности, в ко-
торой давление минимально. Христиановнчем С. А. быто пока-
зано, что Мкр для любого профиля является функцией только
величины минимального коэффициента давления, определяемо
го по картинам распределения давления вдоль контура в несжи-
маемом потоке (см. рис. 15. I). Зависимости Мкр от ртщ для
воздуха, полученные по методам С. А Христиановича С А н
Г. Ф Бураго, представлены в виде графиков на рис. 15. 2.
Таким образом, при М0о>Мкр на обтекаемой поверхности
имеются дозвуковые и сверхзвуковые зоны течения. Зоны с до-
звуковыми скоростями течения не исчезают сразу же при дости-
жении сверхзвуковой скорости полета. В зависимости от формы
профиля это происходит при числах М ОО-- 1,2--. 1,4 и более.
246
www.vokb-la.spb.ru - Самолёт своими руками?!
Режим обтекания, при котором в потоке около профиля имеют
место дозвуковые и сверхзвуковые зоны, называют околозвуко-
вым (трансзвуковым).
15.2. ВЛИЯНИЕ УГЛА АТАКИ И ФОРМЫ ПРОФИЛЯ
НА Мкр И СТРУКТУРУ ТЕЧЕНИЯ ОКОЛО ПРОФИЛЯ
Теоретические кривые изменения Мкр в зависимости от отно-
сительной толщины и угла атаки для одного семейства профилей
приведены на рис. 15.3 С увеличением угла атаки а сужение
элементарных струек на профиле усиливается, и, следовательно,
Мкр уменьшается. Для про-
дольно обтекаемой (а — 0) бес-
конечно тонкой пластины (с=
Рис 15 3. Изменение критического
числа М в зависимости от угла
атаки и относительной толщины
профиля
~0) Mb-P—1, а для всех поло-
жительных углов атаки Мкр ~ 0.
Это объясняется тем, что
Рис. 15 4. Изменение критичес-
кого числа М в зависимости от
угла атаки и относительной
абсциссы Хс
вблизи передней кромки бесконечно тонкой пластины уже на са-
мых малых углах атаки возникают большие местные скорости
течения и местные числа М> 1.
С увеличением относительной толщины профиля местные
числа М вблизи закругленной и утолщенной передней кромки
сначала уменьшаются, а затем увеличиваются, так как даль-
нейшее увеличение относительной толщины начиная с некото-
рого значения с приводит к сужению струек газа за передней
кромкой профиля. Соответственно Мкр сначала увеличивается,
а затем уменьшается.
У симметричного профиля при а=0 местные максимальные
скорости тем меньше, а значения pminnc тем больше, чем тонь-
ше профиль. Следовательно, с уменьшением относительной тол
щины профиля с число Мир увеличивается.
Судя по опытным данным, на распределение давления, а сле-
довательно, н на величину Мкр оказывает влияние не только от-
носительная толщина профиля с, ио и относительная абсцисса
247
www vokb-la.spb ru - Самолёт своими руками?!
.г< (рис. 15.4). Прн малых углах атаки число Мкр возрастает с
увеличением хс, а при больших углах атаки число Мнр умень-
шается.
У симметричных профилей при а=0 (илн при суа=0) значе-
ние М1(р достигает максимума, при этом наибольшие разрежения
сверху н снизу профиля одинаковы. У несимметричных профи-
лей МКр достигает максимального значения на том же угле ата-
ки а (или при том значении суа), при котором наибольшие раз-
режения сверху и снизу профиля одинаковы. Обычно это проис-
ходит иа небольших отрицательных углах атаки. С увеличением
кривизны профиля увеличивается значение суа, при котором до-
стигается максимальное значение Мкр.
Теперь перейдем к рассмотрению структуры потока около
профиля крыла при Ma»>MHp. Как было показано выше, в этом
случае в некоторой точке поверхности профиля скорость пото-
ка равна местной скорости зЪука н коэффициент давления до-
стигает минимального значения. Прн дальнейшем увеличении
чисел Мое за этой точкой образуется зона сверхзвуковых тече-
ний. Очевидно, что в дозвуковом невозмущениом потоке на не-
котором удалении за телом скорость потока должна быть дозву-
ковой, поэтому зона сверхзвуковых скоростей около профиля
будет ограничена как в нормальном к обтекаемой поверхности
направлении, так и в направлении течения, т. е. при числах
Моо>Мкр зоны сверхзвуковых скоростей около профиля носят
местный характер. В этой зоне вначале происходит ускорение
течения газа, приводящее к его значительному перерасширенню,
а затем торможение, обычно сопровождающееся образованием
скачков уплотнения Образующиеся скачки уплотнения замыка-
ют область сверхзвуковых скоростей. Передняя ее граница
представляет собой так называемую звуковую линию, т. е. ли-
нию, вдоль которой происходит переход от дозвукового к сверх-
звуковому течению. Вне зон, ограниченных звуковой линией,
поток остается дозвуковым На рис. 15.5 пунктирными линиями
показаны примерные границы сверхзвуковых зои при разных
числах Моо в закритическом диапазоне обтекания профилей
(МЬр<М«»<1). Расположение скачка уплотнения и протяжен-
ность зоны местных сверхзвуковых скоростей зависят от чис-
ла Моо.
С увеличением числа Моо скачки уплотнения, образующиеся
первоначально иа верхней поверхности профиля, вместе с гра-
ницей сверхзвуковой зоны скоростей перемещаются к задней
кромке профиля Затем сверхзвуковая зона образуется и иа
иижней поверхности профиля. Развитие сверхзвуковой зоны на
нижией поверхности профиля протекает интенсивнее, чем иа
верхней, поэтому прн некотором числе Моо<1 замыкающий ска-
чок уплотнения иа нижией поверхности обгоняет скачок и а
верхней поверхности прн его продвижении к задней кромке
248
ww w vokb-la.spb ru - Самолёт своими руками?!
профиля. При приближении числа к единице сверхзвуко-
вые зоны захватывают почти всю поверхность профиля
Возникающие в потоке около профиля при числах Моо>Мкр
скачки уплотнения оказывают значительное влияние на течение
Рис 15 5. Сверхзвуковые зоны при разных числах М«> в
закритическом диапазоне обтекания профичеи Распре-
деление давлений по профилю при околозвуковых ско-
ростях
в пограничном слое, в свою очередь, пограничный слой влияет
на скачки уплотнения Это влияние проявляется не только в из-
менении поля скоростей, касательных напряжений и толщины
249
www.vokb-la.spb.ru - Самолёт своими руками?!
ней границе пограничного слоя
слоя, но также и во взаимодействии скачков уплотнения и погра-
ничного слоя.
Как известно, скорость течения в пограничном слое изменя-
ется от нулевого значения на поверхности обтекаемого тела, до
значения, равного скорости набегающего потока. Если на внеш-
скорость сверхзвуковая, то по-
граничный слой можно разде-
лить на две части: нижнюю
дозвуковую н верхнюю сверх-
звуковую (рнс. 15.6). Скачок
уплотнения, пересекая сверх-
звуковую область, обрывается
на границе раздела этих обла-
стей. Дозвуковая область в
турбулентном пограничном
слое относительно тоньше, чем
в ламинарном, с тем же значе-
нием Лк». В этом случае осно-
вание скачка почти опирается
на стенку.
Высокое давление за скач-
ком уплотнения распростра-
няется не только по течению, но и против течения через дозву-
ковую область пограничного слоя. Нарастание давления по по-
току влечет за собой утолщение пограничного слоя, а при доста-
точно большом положительном градиенте давления происходит
отрыв пограничного слоя от поверхности тела.
При ламинарном течении в пограничном слое в месте отрыва
потока возникает Х-образный скачок уп тотнения (см. рис. ]5. 5).
При турбулентном пограничном слое оттеснение линий тока
меньше и образуется лишь прямой скачок.
Рис. 15 6. Деление пограничного слоя
на дозвуковую и сверхзвуковую об-
ласти*
/—сверхзвуковая область пограничного
слоя, 2—дозвуковая область,- 3—область
повышенного давления
15.3 РАСПРЕДЕЛЕНИЕ ДАВЛЕНИЯ ПО ПРОФИЛЮ
ПРИ НАЛИЧИИ МЕСТНЫХ СКАЧКОВ УПЛОТНЕНИЯ
И РАСЧЕТ ВОЛНОВОГО СОПРОТИВЛЕНИЯ ПРОФИЛЯ
Выделим у поверхности крыла тонкую струйку. Вблизи наи-
более выпуклой части профиля (точка С на рис. 15.7) имеет
место наибольшее сужение струики. В таком случае часть струй-
ки до точки С — сужающаяся (конфузорная), а после — рас-
ширяющаяся (диффузорная). При отсутствии трения течение в
струйке можно уподобить течению в сопле Лаваля. Рассмотрим
три характерных случая течения.
1. При М.м<МКр течение вдоль всей струики дозвуковое. До
минимального (критического) сечения sKp скорости увеличива-
ются, а давление уменьшается, за этим сечением, наоборот, ско-
рости уменьшаются, а давление увеличивается.
250
www.vokb-la.spb.ru - Самолёт своими руками?!
2. При Моо=Мкр в критическом сечеиии скорость равна ме-
стной скорости звука, а во всех остальных сечеииях течение до-
звуковое. Критическое давление (см гл. 7) ркр=0,528 р0, где
,ро — давление в передней точке профиля (давление торможе-
ния).
3 При Мся>Л1кр за критическим сечеиием возникает местная
зона со сверхзвуковым течением, которая замыкается прямым
скачком уплотнения АВ. Как известно, в сверхзвуковом течении
скорость в расширяющейся струе
растет, следовательно, давление
за точкой С падает. За скачком
уплотнения происходит резкое
увеличение давления.
Характер’ распределения дав-
ления по симметричному профи-
лю, обтекаемому под нулевым
углом атаки при наличии скачка
уплотнения иа верхней поверхно-
сти, представлен иа рис. 15 8 На
ннжией поверхности профиля по-
казана эпюра давления, соответ-
ствующая картине обтекания иа
верхней поверхности В критиче-
ской точке О давление р0 наи-
большее. Далее по профилю дав-
ление уменьшается, и в точке А
Рис. 15 7 Распределение дав-
ления по профилю при различ-
ных значениях М«»
в которой скорость К=акр, дости-
гает значения ркр. В сверхзвуковой зоие АВ давление продол-
жает уменьшаться и лишь на скачке уплотнения ВС скачкооб-
разно увеличивается. За скачком уплотнения давление продол-
жает возрастать до величины давления торможения иа задней
кромке профиля (кривая GH), при этом скорость течения
уменьшается.
Следует отметить, что если бы торможение сверхзвукового
потока происходило без скачков уплотнения, то при тех же ско-
ростях давление в задней части профиля было бы большим и
изменялось по кривой KG Н'. Таким образом, при наличии скач-
ка уплотнения давлеиие в кормовой части профиля меньше по
сравнению с безударным обтеканием. На характер распределе-
ния давлений по профилю заметиое влияние оказывает место
расположения скачков уплотнения, протяженность зон сверхзву-
ковых скоростей (см. рис. 15.5, зоиа сверхзвуковых скоростей
заштрихована).
На околозвуковых скоростях при числах M0o>iMKp заметно
увеличивается коэффициент сопротивления крыла (рис. 15. 9) и
может в несколько раз повысить значение сха, имеющее место
при МооСМьр, поскольку скачки, образовавшиеся у поверхно-
сти крыла, порождают дополнительное, так называемое волна-
251
www.vokb-la.spb.ru - Самолёт своими руками?!
вое сопротивление (достигающее значительных величин даже у
удобообтекаемых тел). Существует ряд приближенных расчет-
ных методов, с помощью которых можно определить волновое
сопротивление: метод С. А. Христиановича — Я. М. Серебрнй-
ского, метод Г. Ф, Бураго.
Рис 15 8 Распределение давления
по верхней поверхности профиля при
М.кр*СМоо < 1
Рис 15 9 Изменение коэффици-
ента профильного сопротивле-
ния для профиля крыла в диа-
пазоне 1<М«<М,р
Рассмотрим метод расчета волнового сопротивления, пред-
ложенный Г. Ф. Бураго. Предполагая, что около верхней по-
верхности крыла образовалась местная зона сверхзвуковых ско-
ростей и замыкающий ее прямой скачок уплотнения (рис. 15. 10),
выделим в потоке элементарную струйку, проходящую через
Рис 15 10 Расчетная схема об-
текания профиля крыла при на-
личии прямого скачка
скачок уплотнения, а в ней два
сечения (I, II) на большом уда-
лении слева и справа от профиля.
Параметры газа в этих сечениях
обозначим соответственно индек-
сами 1м и 2ос, а параметры газа
непосредственно перед и за скач-
ком — индексами I и 2. Тогда из
условия постоянства массового
расхода газа вдоль элементарной
струйки для двух сечений можно
написать
С1оо1/Г1со^1оо=С2оо1/Л2оо^21». (15. 1)
В таком случае для всего потока (единичной ширины вдоль
оси 2) по теореме об изменении количества движения потучнм
уравнение
4- со 4-оо 4-со
Q2ool/ 2oo^J/2co Clool^loo^f/loo---- У (pioo /?2оо) dp
(15.2)
252
www.vokb-la.spb.ru - Самолёт своими руками?!
или, учитывая равенство (15 1),
-Too -Too
^в= J (ploo — p^dy^ J Ci«,Vloo(l/lco — Vi^dy. (15. 3r>
—co —co
В этом уравнении Хв означает волновое сопротивление ци-
линдрического крыла единичного размаха.
В идеальном газовом потоке при отсутствии сил трения во
всех струйках, не пересекающих скачок уплотнения, имеем
plco=p2oo, V100=y2oo. Эти равенства, однако, не выполняются
для струек, пересекающих скачок уплотнения S (см. рис. 15. 10).
В силу этого формула (15. 3) запишется:
^VB= Г (Ploo — р2оо) 4" f Cloo^lco (Vico — V2(X>) dy, (15.4)
s s
где интегрирование выполняется для всех струек, пересекающих
скачок уплотнения S.
Дальнейший анализ в значительной степени упрощается,
если предположить, что далеко за крылом (при х—>-оо) восста-
навливается первоначальное значение скорости течения, т. с.
Vz2co= Vico. При таком предположении получим
X.=PiA( x^^s.\dy- (15.5}
" \ Аоо /
о
М2„=М,^ ^=Z®=O<11 (15.6>
Асо Рт
где о — коэффициент потерь полного давления на скачке уплот-
нения.
Чтобы полностью связать теперь интеграл (15.5) с поверх-
ностью скачка уплотнения, воспользуемся уравнением расхода
Q11/1dS = pi0Ol/i0Ody. Исключая с помощью этого уравнения нз
формулы (15 5) множитель
dy=
QiVi
@Тоо Доо
dS,
получим формулу для определения величины волнового сопро-
тивления
Х.=р,~ \ Cl^' (l-o)dS,
,J eico^ico
(15. 7}
из которой видно, что с уменьшением о величина Хв возрастает.
Так как на скачке уплотнения о<1, то волновое сопротивление
Хв>0. С уменьшением о и увеличением протяженности скачка
уплотнения S величина Алв будет возрастать.
www vokb-la.spb.ru - Самолёт своими руками?!
Коэффициент волнового сопротивления
В
(15.8)
С
Рис 15 11 Изменение
коэффициента подъем
ной силы в зависимости
от числа в критиче-
ской дозвуковой обла-
сти:
1 -эксперимент; 2—теория
А «5 л
Oloo^foo ,
—«
Для определения в первом приближении коэффициента вол-
нового сопротивления Г. Ф. Бураго рекомендует формулу
схв—Д(Мте-МХ (15.9)
где А — коэффициент, зависящий от типа профиля и распреде-
ления давления. Среднее значение этого коэффициента для до-
звуковых профилей равно примерно 11.
Очевидно, что по мере возрастания
увеличивается схъ, что объясняется уве-
личением интенсивности и протяженнос-
ти скачков уплотнения иа профиле в этом
случае. Для снижения схъ необходимо
увеличить М1;р, что в основном достигает-
ся уменьшением толщины профиля
Приближенный анализ волнового со-
противления, проведенный Я. М Сереб-
рийским и С. А Христиановичем, пока-
зал, что в диапазоне резкого повышения
волнового сопротивления при числах Моо,
ие превышающих .величину Мкр + 0,15,
для определения коэффициента волново-
го сопротивления можно рекомендовать
формулу (15.9).
Все расчетные методы определения
коэффициента волнового сопротивления
при Мто>Мкр являются приближенными.
При увеличении критических чисел М уменьшается влияние
числа Моо на характеристики профиля. Увеличение числа М»
оказывает существенное влияние иа характер изменения коэф-
фициента суа. При числах Мео=0,5 0,6 увеличение коэффи-
циента Суа происходит в соответствии с формулой (14 18), спра-
ведливой при числах МооСМцр. При дальнейшем увеличении
Moo>Mhp в связи с появлением на верхней поверхности профи-
ля разрежения (разрежение становится особенно сильным при
наличии Z-образиого скачка уплотнения), происходит интенсив-
ное возрастание суа вплоть до появления скачков на нижиеи
поверхности профиля (рис. 15.11). Развитие скачков уплотне-
ния иа нижней поверхности способствует увеличению разреже-
ния иа ней и падению коэффициента суа.
При числах Моо, больших критических, сжимаемость оказы-
вает значительное влияние на положение центра давления ха
профиля С увеличением Моо>Мкр центр давления сначала пере-
254
www vokb-la.spb.ru - Самолёт своими руками?!
мещается несколько назад по хорде профиля, а затем резко сме-
щается вперед, выходя за пределы хорды. Далее при Моо>0 0
центр давления начинает перемещаться назад, приближаясь к
положению на полухорде профиля. Для получения необходимой
подъемной силы при малом волновом сопротивлении давление
по поверхности профиля должно быть по возможности равно-
мерно распределенным по хорде и малым по величине.
Для возможности сопоставления экспериментальных и тео-
ретических результатов на околозвуковых режимах обтекания
профилей разработаны правила подобия, основанные на урав-
нениях потенциала скорости при изэнтропическом течении для
афинноподобных профилен. Эти правила сводятся к использова-
нию приведенных параметров профиля и приведенных аэроди-
намических коэффициентов.
йог число М~= - (15.
। t \ 1/3 _
Приведенный коэффициент давления р—----------—р. (15. 11)
с2/3
Приведенный угол атаки
(15. 12)
Приведенные коэффициенты подъемной силы и волнового сопро-
тивления:
- . (t +1)|/3 . - (* + |)1/3
с Уа ‘ схв ^jctr
с-/3 с 7
(15. 13)
Оказывается, что для афинноподобных профилей приведен-
ные величины Моо и р в любой точке профиля зависят только ог
относительной координаты точки, если у набегающего потока
приведенные числа Моо и приведенные углы атаки а одинаковы.
При одинаковом приведенном угле атаки приведенный коэффи-
циент давления р зависит только от приведенного числа Моо>
а коэффициент схъ не зависит от относительной толщины с.
Вопросы для повторения
1. Что такое критическое число М и какие факторы влияют
на величину Мкр?
2 Каковы причины возникновения местных скачков уплотне-
ния на профиле?
3. Какое влияние оказывает увеличение числа М на аэроди-
намические коэффициенты суа и сха профилей?
4. Как изменяется положение фокуса профиля прн Моо>Мкр?
5. Объясните причину возникновения волнового сопротивле-
ния Какие факторы н как влияют на величину волнового сопро-
тивления профиля при околозвуковом режиме обтекания?
255
«лап vokb-la.spb ru - Самолёт своими руками9'
Задачи
1. Определите критическое число М профиля, у которого
^т!пнс = 0,75.
Ответ: МКр=0,6 (прн решении использовать график Кри-
стиановича).
2. Определите величину профиля и соответствующую ему
скорость полета на высоте 8000 м, если максимальная скорость
на поверхности профиля составляет 125% от скорости набегаю-
щего потока.
Ответ: Мкр=0,65; У3ф=--720 км/ч.
3. Определите величину минимального давления на профиле
крыла, критическое число М которого прн температуре воздуха
То,—260 К и давлении невозмущенного потока 6000 Н/м2,
равно Мкр=0,72.
Решение. По графику Христиановича на рис. 15.2 опреде-
ляем величину минимального коэффициента статического давле-
ния: pmIn=- 0,4.
Согласно (6. 9)
— Anin Роа
2
- Q V2
откуда pmi„ — рооЧ- Ртш (а)
Для определения плотности воспользуемся уравнением со
стояния (1.4):
Величину скорости найдем с помощью формул (1.25) и (1.27):
v M=MK|,1-'WZ.
Подставляя значения £«> и К» в равенство (а), получим
ртщ=р~(1 + *м^п11л) 6000(1 — 4-0,723*0,4) = 1643 Н/м3.
Ответ: pmin= 1643 Н/м2.
4 Определить коэффициент волнового сопротивления профиля
при полете со скоростью 920 км/ч на высоте 8000 м, если кри-
тическое число М равно 0,71.
Ответ: схв=0,019.
www.vokb-la.spb.ru - Самолёт своими руками?!
ГЛАВА 16
ПРОФИЛЬ КРЫЛА В СВЕРХЗВУКОВОМ ПОТОКЕ
16.1. ОСОБЕННОСТИ ОБТЕКАНИЯ ТЕЛ СВЕРХЗВУКОВЫМ ПОТОКОМ.
ПЛОСКАЯ ПЛАСТИНА В СВЕРХЗВУКОВОМ ПОТОКЕ
Общая задача обтекания тел с закругленным носнком сверх-
звуковым потоком, в котором вследствие торможения потока
впереди тела образуется криволинейный (отсоединенный) ска-
чок уплотнения, относится к классу «смешанных» задач газоди-
намики, так как в потоке имеются области со сверхзвуковым и
дозвуковым течениями.
Сложность этой задачи со-
стоит в том, что границы
скачков уплотнения нельзя
определить заранее и, кроме
того, сверхзвуковое течение
газа за криволинейным
скачком уплотнения являет-
ся вихревым.
В отличие от смешанной
задачи при обтекании плос-
Рис 16 1 Обтекание плоской пласти-
ны сверхзвуковым потоком
ким сверхзвуковым потоком
профиля с острой передней кромкой, установленного под малым
углом атаки, головной скачок почти касается передней кромки
профиля и распадается на верхний и иижиий косые скачки уп-
лотнения. Для решения задач обтекания таких профилен суще-
свует ряд методов различной точности, позволяющих получить
простые расчетные формулы Мы ограничимся рассмотрением
задачи об обтекании под малым углом атаки профиля с острым
носиком.
Рассмотрим простейший случай: обтекание сверхзвуковым
потоком плоской пластины, установленной под углом атаки
(рис. 16. 1). Поток у передней кромки делится иа две части.
Верхняя часть потока поворачивается на угол а и расширяется
на веере характеристик (или линий слабых возмущении).
У задней кромки поток меняет направление и стремится восста-
9 626
257
www.vokb-la.spb.ru - Самолёт своими руками?!
повить первоначальное положение, поворачиваясь на угол а и
поджимаясь.
Таким образом, верхняя часть потока у задней кромки обте-
кает внутренний тупой угол, и здесь возникает скачок уплотне-
ния. В иижией части потока наблюдается обратная картина.
У передней кромки пластины образуется скачок уплотнения, а у
задней кромки поток расширяется на веере характеристик При
малых углах а расширение (или сжатие) происходит практиче-
ски на одной характеристике.
Если угол а положителен, то на нижнеи поверхности пласти-
ны давление больше, чем давление набегающего потока, т. е.
Рн>Р«>, а на верхней поверхности рв<.Роо.
Аэродинамическая сила RA перпендикулярна к пластине и
при а>0 направлена вверх. Таким образом, результирующая
сила, приходящаяся иа единицу размаха пластины с хордой Ь,
1.
Проекция аэродинамической силы на направление скорости
набегающего потока является силой сопротивления Хв и назы-
вается волновым сопротивлением Хв=(рн—pu) d sin а или,
учитывая малость а, АГВ== {рч — ра) Ьа.
Сила волнового сопротивления обусловлена затратами энер-
гии иа образование в потоке волновых возмущений.
Проекция аэродинамической силы Да на направление, пер-
пендикулярное скорости набегающего потока, является подъем-
ной силой Уа:
Ya = {pn— а,
или, учитывая, что при малых углах атаки cosa~l, получим
1 (Рн Рв) Ь.
Для положительных и малых углов а из формулы (8 46)
можно определить избыточное давление под пластиной
Л-p^^OooVt "— (16.1)
V Mt -1
и разрежение иад пластиной
ра —Роо ^—QooV7!(16.2)
M-i
Тогда перепад давлений между нижией и верхней поверхно-
стями пластины получим в виде
/’„-pa=0=oV~-7==-. (16.3)
258
www.vokb-la.spb.ru - Самолёт своими руками?!
Подъемная сила и волновое сопротивление, приходящиеся на
©дин метр размаха пластины, соответственно равны:
ro=e.V'l-7^=; (16.4)
и 1
X,=emVl-^=-. (16.5)
Из выражений (16.4) и (16.5), учитывая что 3=1 Л мож-
но получить формулы для коэффициентов подъемной силы и си-
лы волнового сопротивления пластины:
4а
суа— ’
V С-1
4а°
Гхъ1 , / ---
KMt-l
Кс-1
или с х „ >—------с
Л о L л
(16.6)
(16.7)
(16.8)
Коэффициент подъемной силы суа прямо пропорционален углу
атаки а и может изменять свой знак в зависимости от знака а;
коэффициент волнового сопротивления cXBi зависит от а (или
суа) по квадратичному закону и всегда положителен. Поскольку
коэффициент волнового сопротивления cxili пропорционален
квадрату коэффициента подъемной силы и равен нулю при суа=
= 0, то его называют коэффициентом индуктивно-волнового со-
противления (см- гл. 17, разд. 17.4). Оба коэффициента суа и
в г обратно пропорциональны [/ - - 1.
Эти теоретические формулы удовлетворительно согласуются
с экспериментальными данными при Мсо> 1,5. В качестве формул
первого приближения они могут быть применимы к тонким про-
филям, обтекаемым под малым углом атаки, когда скачок уп-
лотнения, отходящий вниз от носовой части профиля, является
прямолинейным, присоединенным. Полагают, что при Моо, стре-
мящемся к единице, угол атаки а должен стремиться к нулю.
В пробивном случае полученные зависимости несправедливы.
Следует обратить внимание на принципиальные различия в
обтекании пластины сверхзвуковым н дозвуковым потоками.
В сверхзвуковом потоке носик пластины разделяет поток,
а линии тока параллельны пластине; иа иижией и верхней по-
верхностях пластины избыточное давление и коэффициент дав-
ления постоянны по хорде, равны по величине и различны по
знаку (рис. 16. 2, а). Очевидно, что центр давления (точка D)
и фокус пластины в этом случае находятся на середине хорды.
9*
259
www.vokb-la.spb.ru - Самолёт своими руками?!
Напомним, что в дозвуковом потоке в области носика на
верхней поверхности возникает резкий пик разрежения и боль-
шое поджатие на нижней поверхности. Давление изменяется по
длине пластины, а центр давления D и фокус находятся пример-
но на 1/4 хорды от носнка (см рис. 16. 2, б).
Рис. 16 2 Распределение коэффициента давления по пластине в
сверхзвуковом (а) и дозвуковом (б) потоках
С учетом трения коэффициент лобового сопротивления беско-
нечно длинной по размаху пластины представляется в виде двух
слагаемых:
еха-с^: + 2с)=-г^_- + 2е/, (16.9)
К.-1
где с/ — коэффициент сопротивления трения плоской пластины,
определяемый методами теории пограничного слоя.
Подставив в формулу (16 9) значение сХВг согласно (16.8),
получим уравнение поляры пластины:
1/* М2 — 1
*1
которая представляет собой квадратичную параболу. При зна-
чениях Суа, отличных от нуля, с увеличением числа Мж поляра
сдвигается вправо
16 2. РАСПРЕДЕЛЕНИЕ ДАВЛЕНИЯ ПО ПРОФИЛЮ
Сравним картину распределения давления по симметрично-
му профилю при обтекании его дозвуковым и сверхзвуковым
потоками.
При симметричном обтекании дозвуковым потоком носовой
части симметричного профиля (рис. 16.3, а) струйки у носика
несколько расширяются, что приводит к увеличению давления и
уменьшению скорости, а затем быстро сужаются, вследствие че-
260
www.vokb-la.spb.ru - Самолёт своими руками?!
го давление уменьшается, а скорость увеличивается. В кормо-
вой части профиля струйки вновь расширяются, в результате
чего происходит уменьшение скорости и повышение давления.
При обтекании того же профиля сверхзвуковым потоком кар-
тина распределения давления изменяется: при набегании иа го-
ловную волну сжатия струйки невозмущенного потока скачко-
Рис. 16.3. Сравнение дозвукового (а) и сверхзвукового
(6) обтеканий профиля*
1 идеальная жидкость; 2—вязкая жидкость
образно меняют свое направление, при этом происходит умеиь
шение скорости и увеличение давления (см. рис. 16.3,6). Далее
вдоль поверхности профиля вплоть до миделевого сечения ско-
рость постепенно уменьшается, а давление увеличивается. За
миделевым сечением профиля скорость увеличивается (вплоть
до задней кромки), а давление уменьшается. В хвостовой удар-
ной волне давление скачкообразно возрастает, но это уже не
оказывает влияния иа распределение давления по профилю.
Таким образом, при дозвуковом обтекании в кормовой части
профиля происходит восстановление давления, а при сверхзву-
ковом обтекании давление вплоть до хвостовой ударной волны
не восстанавливается.
261
vokb-la.spb.ru - Самолёт своими руками?!
Линейная теория дает завышенные значения коэффициента
давления в
области разрежения (на верхней стороне профиля)
по мере удаления от передней кромки и занижен-
ные значения (на нижней стороне профиля), осо-
бенно у передней кромки.
Как видно нз эпюры распределения давлений,
при обтекании профиля дозвуковым потоком
идеальной жидкости проекция равнодействую-
щей аэродинамической силы на направление
набегающего потока равна нулю, а при обтека-
нии сверхзвуковым потоком эта проекция дает
Рис. 16.4. Из-
менение силы
лобового соп-
ротивления
профиля в за-
висимости от
числа М«:
1—изменение си-
лы лобового соп-
ротивления без
учета влияния на
коэффициент ло
бового сопротив-
ления числа Мю:
2 — действитель-
ная кривая
так называемую силу волнового сопротивления.
В вязкой жидкости появляется дополнитель-
ная сила сопротивления — сила трения в погра-
ничном слое. Однако и в этом случае волновое
сопротивление является основной частью полно-
го лобового сопротивления профиля, которое мо-
жет быть представлено в виде суммы: ХЯ=ХВ-Р
-гХтр. Примерный характер изменения силы ло-
бового сопротивления авиационного профиля в
зависимости от числа MfO приведен на рис. 16 4.
Разность между ординатами линий 1 и 2 дает
величину силы волнового сопротивления
16.3. ТОНКИЙ ПРОФИЛЬ В СВЕРХЗВУКОВОМ ПОТОКЕ
Рассмотрим обтекание сверхзвуковым потоком под углом ата-
ки а тонкого цилиндрического крыла с профилем произвольной
формы, с хордой b и размахом
(рис. 16.5). Выделим на
нижней стороне профиля эле-
ментарный участок dl, углы
наклона которого к оси ОХ
связанной системы координат
обозначим через ун> а к на-
правлению скорости невозму-
щенного потока через ссн: ан=
Рис. 16.5 Обтекание тонкого профиля
сверхзвуковым потоком
Согласно формуле (16. 1) избыточное давление на элемен-
те dl
^Рн Рн ~ Р<Х> = СооРОО г - ~ •
VM1-1
262
www.vokb-la.spb.ru - Самолёт своими руками
Если проекции элемента dl на координатные оси обозначить
dyH и dxH=dxt то получим, что
Sin ун~tgYH—--—.
cZ Jv
Для тонкого профиля ввиду малости угла ун sin ун~Уш сле-
довательно:
Тв=_^; а,=а —(16.11)
Гн dx dx
Элементарная сила избыточного давления, приложенная нор-
мально к элементу нижней поверхности крыла,
dy»
а —---
VMt-i
а проекции этой силы на оси координат и элементарный момент
относительно носика профиля
4 dY^—Lp^fil cos =
dXa=bpjil sin у„- Дд„у,Дх— --Дд„-^ Jx; <ШН= — dY„x.
Моментом силы dX^ пренебрегаем вследствие его малости по
сравнению с моментом силы d¥n.
Итак суммарные силы и момент для нижней стороны цилин-
дрического крыла единичного размаха следующие:
£ tz2
TZ (' л -V ®со со Р ( &Уп \
Гн=\ кр^х = — ..... - а—т- рх;
J V и» _ 1 J \ dx /
О Г тоо 1 О
Л TZ2
А-.= \ A/wfc=---8<” °° U
о у м^_! И "х i dx
М.= - \ dp„xdx=----8~ ” С( a-xdx.
? /Mt-1 гР dx 1
b
Как следует из рис. 16. 5, величина dy" dx — 0, поэтому
v eJi , Г«~ 1/—5 aZ?; Гм^-1 М„=— Гм^-1 Аналогичные выражения роны профиля. J ах 0 тг2 Хн= /мХ-1 И <1Х ) { ъ \ I _^-^4- ^^xdx ). 1 2 1 J dx / \ 0 / можно получить и для верхней сто-
263
www vokb-la.spb ru - Самолёт своими руками?!
Силы и момент, действующие иа обе стороны крыла единич-
ного размаха в связанной системе координат, следующие:
TZ2 / ° л X
М = Лу{-Л4- г6то 00 -| -aF+^-^xdx^A-^xdx ].
V м2 _ 1 I J dx A dx I
1 - о о /
Здесь сила У нормальна к хорде профиля, однако в силу ма-
лости угла атаки а она практически является и подъемной си-
лой Уа.
у
Коэффициент подъемной силы суа=---.
Учитывая, что S=b-\=b и подставляя значение УГ1«У, полу-
чим
суа
4а
(16. 12)
— 1
ОО Л
Из формулы (16 12) следует, что коэффициент подъемной си-
лы не зависит от формы и толщины профиля, а зависит только
ст угла атаки и при одинаковых условиях равен по величине
коэффициенту подъемной силы плоской пластины (16.6).
Лобовое сопротивление Ха имеет направление скорости
Проектируя поэтому силы У и X на направление скорости не-
возмущенного потока н учитывая, что угол а мал, получим
Ха=Уа 16.13)
где величины У и А определяются приведенным i выше фор-
мулами
2а2о V2 b Q V2 г г/Яг/ \ Ми \21
Поэтому а г‘— у ' —*— \ I j 1 I I j I ’
/м2 1 KmL-1 JLU*/ \^/J
'со r 00 О
откуда находим коэффициент сопротивления профиля
где
16.14)
264
www.vokb-la.spb.ru - Самолёт своими руками?!
Представим далее ординаты профиля в виде
Ук=сул\х\ ук — сув(х),
где У = У1С\
ференцируя
с - максимальная толщина профиля. Тогда, диф-
эти величины по коорднь а те х, получим
dyK с dy„ dyB с dyB
dx b dx ' dx b dx
где x=x[b. В таком случае будем иметь B—Kic2, с=с{Ь,
Функция Ki зависит только от формы профиля. С учетом
выражения для В формулу (16.14) можно записать в виде
...+_(16.15)
/м2ю- 1 М-1
Таким образом коэффициент сопротивления профиля в сверх-
звуковом потоке является суммой двух коэффициентов: коэф-
фициента сопротивления профиля нулевой толщины при задан-
ном угле атаки и коэффициента волнового сопротивления, обу-
словленного толщиной профиля.
Коэффициент сопротивления профиля нулевой толщины
(с=0) называют коэффициентом индуктивно-волнового сопро-
тивления, так как он зависит от коэффициента подъемной силы
профиля:
СХВ1
Гм„-1
Этот коэффициент, как видим, не зависит о г формы и тол-
щины профиля, выражается той же формулой, что и коэффи-
циент волнового сопротивления плоской пластины (16.7).
Коэффициент вотнового сопротивления профиля (при а=0)
I ----(16. 16)
V - 1 (Р IA dx / \dx } V Mt -1
при заданном числе Мю зависит только от формы и относитель-
ной толщины профиля.
265
www.vokb-la.spb.ru - Самолёт своими руками?!
С учетом сил трення выражение для коэффициента лобово-
го сопротивления тонкого профиля при малом угле атаки име-
ет следующий вид:
Ся,—1/4°~ (16. 17)
И М^-1
где Cf — коэффициент сопротивления трения.
Из формул (16. 17) и (16. 12) можно получить уравнение
поляры профиля крыла:
]/м2то-1
Сха~-----4---+ (16- 18)
Коэффициент момента профиля относительно его передней
кромки
=-----—(где S-b-1); (16.19)
o4i /Mi-1
1 _ _
ст0 =— 2с \ (-%- -ь-~Чх<1х. 16. 20)
(^ dx dx !
и
Из формулы (16.20) следует что коэффициент Gno зависит
от формы профиля. Для симметричного профиля сто=О
2а
с —------ -.
Г Mi-i
т. е. коэффициент момента не зависит от формы профиля.
Зная коэффициенты ст и суа, можно определить положение
центра давления и безразмерную абсциссу фокуса профиля:
77 _ ст . 77 __ ХР _ дст дст _ дсУа
*— , ‘— ---—----- » »
Су b дсуа да да
Используя выражения (16. 12) для суа и (16.19) для ст, на-
ходим, что xf— 0,5. Следовательно, фокус тонкого профиля про-
извольной формы в сверхзвуковом потоке, как и у плоской пла-
стины, расположен на середине хорды. Согласно формуле
(13 20) в этой же точке находится и центр давления всех сим-
метричных профилей. Все безразмерные аэродинамические ха-
рактеристики тонкого профиля при чисто сверхзвуковом обтека-
нии уменьшаются с увеличением чисел Мю.
С учетом ранее потученных резуаьтатов для дозвуковых и
закритических чисел Мто на рис. 16. 6 показан характер изме-
нения коэффициента лобового сопротивления по числам Мю.
В сверхзвуковой области (Мто>1) сха убывает, оставаясь все же
больше значения сха при Моо^Мкр.
266
www vokb-la.spb ru - Самолёт своими
Линеаризованная теория дает достаточно удовлетворитель-
ные результаты в дозвуковом докритическом потоке при Мто<
<Мкр и в сверхзвуковом диапазоне изменения чисел М*,:
1 2<М00<5 Линейная теория неприменима в трансзвуковой
о / мс
Рис. 16.6 Изменение коэффициента лобового соп-
ротивления профиля от числа М.м (при ^„ = 0)
области, где MI1T<M«><cl,2, так как в этом диапазоне чисел
Мю даже при обтекании тонких тел одновременно возникают об-
ласти местных дозвуковых и сверхзвуковых скоростей.
16.4. АЭРОДИНАМИЧЕСКИЕ КОЭФФИЦИЕНТЫ ПРОФИЛЕЙ
НЕКОТОРЫХ ХАРАКТЕРНЫХ ФОРМ
Рассмотрим треугольный профиль в сверхзвуковом потоке
(рнс. 16.7, а). Производные, входящие в интегралы (16.16) и
(16.20), численно будут равны тангенсам углов наклона гра-
ней профиля к его хорде:
а) на участке АВ: ~ тогда = dx б) на участке ОА. тогда — dx с) на участке О В: dx 'н_. с X Ь — Хс b dyn 1 с <*х 1 - хс dyn & dx хс * b dyn _ Ь _ \ , с dx хс * хс ---0. 267
www.vokb-la.spb.ru - Самолёт своими руками?!
Разделив область интегрирования на две: 0<х<хс и
zc<x<l и подставив в каждый из интегралов (16 16) и (16.20)
соответствующее значение производной dyjdx, получим
2f2 1 . /1С оь
— --------- — _ ’ (16.21)
Ум2 _ 1 хс (1 — хс)
г со
Рис 16 7 Несимметричные треугольный (а) и ромбовидный (б) про-
фили
Из формулы (16.21) следует, что при заданном значении с
коэффициент ов является минимальным при максимальном зна-
чении произведения J—хс(1 — хс). Значение хс, соответствующее
/max, определяется из условия -4^—^--1 — 2хг--О, откуда —4-.
dxc
Таким образом, из класса треугольных профилей минималь-
ным значением схОв обладает профиль, у которого наибольшая
относительная толщина с находится на середине хорды. Для та-
кого профиля коэффициент волнового сопротивления выражается
формулой
к;2
^=-7" ' - (16-23)
Рассмотрим несимметричный ромбовидный профиль в сверх-
звуковом потоке. Если этот профиль представить в виде двух
треугольных профилей с относительными толщинами ci и сг (см
рис. 16. 7, б), то относительная толщина ромбовидного профиля
с— ci+c2. По аналогии с (16.22) и (16.23) формулы для коэф-
фициентов Сх0 И Сто примут вид:
(16.24)
Наименьшее значение коэффициента сх 0 в соответствует мини-
мальному значению J=ci2 + (с — сд)2, которое определяется из
условия dJfdc^Q Минимальное значение схов соответствует
268
www vokb-la.spb ru - Самолёт своими руками?!
^1 = c2=c/2, t. e симметричному ромбовидному профилю. В этом
случае формулы для коэффициентов имеют вид
И _---- ’
/м^-1
(16. 25)
Из сравнения формул (16. 23) и (16 25) следует, что коэффи-
циент Схов ромбовидного профиля в два раза меньше с\ов наи-
выгоднейшего треугольного профиля. Кроме того, у симметрич-
ного ромбовидного профиля коэффициент момента Ст 0 — 0. Та-
ким образом, при обтекании сверхзвуковым потоком ромбовид-
ный профиль более выгоден, чем треугольный.
Рис 16 8 Линзообразные профили
а—с односторонней выпуклостью, б—с двухсторонней вы-
пуклостью
По аналогии с предыдущими выводами можно получить фор-
мулы для определения коэффициентов стов и сто линзообраз-
ных профилей с односторонней и двусторонней выпуклостью
(рис. 16.8), описываемых дугами парабол у=4с(х—х2). Для
односторонней выпуклой линзы:
Для двусторонней выпуклой линзы
32 С1 + с2__. __ 4 Ci — с2 , ip .
СлОв о I/—2--- ’ 3 1/772 7 * ( )
3 v -1 3 V -1
Анализ формул (16. 27) показывает, что когда С[ = с2 = с/2, ко-
эффициент Слав имеет минимальное значение. Для такого про-
филя:
(16.28)
Коэффициент сопротивления симметрично омбовидного про-
филя на 33% меньше симметричного линзообразного профиля
той же относительной толщины. Очевидно, что наибо. ее рацио-
нальной формой профиля крыла в сверхзвуковом потоке явля-
ется ромбовидная или близкая к ней, поскольку профили с та-
кой формой обладают наименьшим волновы i сопротивлением
269
www vokb-la.spb ru - Самолёт своими руками?!
Однако с учетом различных требований, предъявляемых к про-
филю (например, минимальное общее сопротивление при доста-
точной прочности и допустимом нагреве и др.) более рациональ-
ными могут оказаться и другие формы профилей крыльев. Сле-
дует также учитывать вязкие свойства потока газа — наличие
пограничного слоя, а иногда и отрыв потока у задней кромки.
В отличие от дозвукового потока в сверхзвуковом потоке
подъемная сила и сила лобового сопротивления не пропорцио-
нальны квадрату скорости. В частности, из формулы
2q V2S
^со со
а~ ------
V2 S
а = о а
- 1 1 V2 - а2
9 СО ОО
видно, что при 1/со>асо подъемная сила пропорциональна скоро-
сти в степени от 1 до 2, а при очень больших числах М о, когда
Voo^Ooo и —Уоо, подъемная сила пропорциональна
скорости в первой степени.
Вопросы для повторения
1. Напишите формулы для определения коэффициентов подъ-
емной силы и силы волнового сопротивления пластины, обтекае-
мой сверхзвуковым потоком под углом атаки а.
2. Напишите формулу для определения коэффициента лобо-
вого сопротивления тонкого профиля, обтекаемого сверхзвуковым,
потоком под малым углом атаки.
3. Чем различаются картины распределения давления по по-
верхности профиля в дозвуковом и сверхзвуковом потоках?
4. Какие преимущества имеют симметричные профили при
сверхзвуковых скоростях? Как влияет толщина профиля на ве-
личину волнового сопротивления при сверхзвуковых скоростях^
Задачи
1. Во сколько раз минимальное волновое сопротивление ром-
бовидного профиля, обтекаемого сверхзвуковым потоком, мень-
ше, чем чечевицеобразное той же толщины, составленного из
дуг окружностей?
Ответ: в 1,33 раза.
2. Определите коэффициенты подъемной силы, волнового со-
противления и момента пластины, обтекаемой под углом атак»
а=0,06 рал при числе Моо=2.
Ответ: Суа=0,1385, cXBi = 0,00831; cm=0,0692.
3. Определите коэффициенты суа и г\ов ромбовидного профи-
ля толщиной 10,5%, обтекаемого потоком воздуха под углом
о=0э12 рад при М,х>— 1,53
Ответ: сУа~~ 0,413; сгв=0,038.
www vokb-la.spb ru - Самолёт своими руками?!
ГЛАВА 17
ОСНОВЫ ТЕОРИИ КРЫЛА КОНЕЧНОГО РАЗМАХА
В НЕСЖИМАЕМОМ ПОТОКЕ
171 ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ КРЫЛА
Крыло — одна из основных частей самолета, предназначен-
ная для создания аэродинамической подъемной силы. Течение
воздуха, возникающее вокруг крыла и определяющее его аэро-
динамические характеристики, представляет собой трехмерный
поток, степень отклонения которого от плоскопараллельного
движения зависит от формы и размеров крыла. Крылья совре-
менных самолетов весьма разнообразны по своим геометричес-
ким характеристикам. Плоскость симметрии делит крыло на ле-
вую и правую части. Проекция крыла на базовую плоскость,
содержащую центральную хорду крыла и перпендикулярную
плоскости симметрии крыла в связанной системе координат
XOZ, определяет форму крыла в плане.
Площадь и размах являются основными величинами, опре-
деляющими размер крыла. Под площадью крыла S понимается
его площадь в плане (рис. 17.1). Размахом крыла I называется
расстояние между двумя плоскостями, параллельными плоско-
сти симметрии крыла, лежащими всюду вне крыла и касающи-
мися его поверхности.
Профиля, полученные в результате сечення крыла плоскостя-
ми, параллельными плоскости симметрии крыла, в общем слу-
чае изменяются вдоль размаха по форме, размерам и наклону
хорды. Профиль крыла в плоскости его симметрии называется
корневым.
Крыло называется геометрически плоским если хорды всех
сечепий параллельны плоскости XOZ, Если хорда профиля сос-
тавляет с плоскостью XOY некоторый угол фьр, величина кото-
рого изменяется от 0 у корня до фнрк на концевом сеченин (см.
рис. 17 1), то крыло называется геометрически закрученным, а
угол фкр(г) углом геометрической крутки. Крутка может быть
положительной и отрицательной. Под положительной круткой
понимают такую, когда передняя точка хорды по отношению к
271
www.vokb-la.spb ru - Самолёт своими руками?!
базовой плоскости находится выше задней точки (местный угол
атаки увеличивается по сравнению с углом атаки корневого се-
чения). Обычно в реальных конструкциях используется отрица-
тельная крутка.
Проекция крыла на плоскость, параллельную плоскости YOZ
может иметь излом в корневом сечении. В этом случае говорят,
что крыло имеет поперечное V, которое может быть положитель-
Рис. 17 I Геометрические характеристики кры-
ла
пым или отрицательным Поперечное V характеризуется углом
фкр между направлением оси 0Z и проекцией передней кромки
крыла на плоскость YOZ Крыло может иметь форму, при кото-
рой угол ф будет переменным вдоль размаха.
Отношение площади крыла к размаху называют средней
геометрической хордой:
bCp=S/l.
Важной геометрической характеристикой крыла является
удлинение равное отношению квадрата размаха крыла к пло-
щади крыла k=l2/S
Удлинение л, определяющее степень вытянхтости крыла
вдоль размаха, оказывает значительное влияние на его аэроди-
намические характеристики. У дозвуковых самолетов Л=6 12,
а у сверхзвуковых Х=2 . .3. Например, удлинение крыла са-
молета Ил 18 равно 10, Ту-134 7,3. Характеристиками про-
филя крыла называются характеристики цилиндрического кры-
ла, у которого К—оо.
Степень сужения крыла вдоль размаха определяется отно-
шением хорд корневого (Ьо) и концевого (6К) сечений: т] —
272
www.vokb-la.spb.ru - Самолёт своими руками?!
= Ь /Ьк. В общем случае l^-q^oo. Для прямоугольного кры-
ла т]=1, для треугольного т| —ос. Например, трапециевидное
крыло самолета Ил-18 имеет сужение, равное 3, а стреловидное
крыло самолета Ту-134 — 3,14.
В связи с большим разнообразием форм крыльев современ-
ных летательных аппаратов общее определение геометрических
параметров для всех крыльев дать затруднительно. Так, напри-
мер, для кольцевых крыльев все перечисленные выше парамет-
ры неприемлемы.
17.2. АЭРОДИНАМИЧЕСКАЯ МОДЕЛЬ КРЫЛА КОНЕЧНОГО РАЗМАХА
бесконечно длинным
Рис 17.2
пелены за
Образование вихревой
крылом конечного раз-
маха
Согласно теореме Жуковского подъемная сила крыла беско-
нечного размаха пропорциональна циркуляции скорости по кон-
туру, охватывающему крыло, поэтому в первом приближении по
силовому воздействию на невозмущенный поток крыло можно
заменить
вихревым шнуром с такой же по
величине циркуляцией скорости,
как и крыла. Такой вихревой
шнур называется присоединен-
ным. Таким образом, для крыла
бесконечного размаха простей-
шей аэродинамической моделью
может с тужить прямолинейный
бесконечный вихрь.
Обтекание крыла конечного
размаха носит не плоскопарал-
лельный, а пространственный ха-
рактер, особенно вблизи его кон-
цов. При этом концы крыла ока-
зывают влияние на распределе-
ние давления по всей его поверх-
ности, поэтому аэродинамические
характеристики крыта конечного
размаха оттичаются от аэродина-
мических характеристик профиля.
Рассмотрим крыло конечного размаха в
лете с постоянной скоростью. Если на крыле реализуется подъ-
емная сила, то над крылом имеется зона пониженного, а под
крылом — /повышенного давления. Под влиянием разности дав-
лений прои ходит перетекание воздуха через концевые кромки
крыла из области повышенного давления в об пасть понижен
него. Возникает поток, параллельный размаху, причем под кры-
лом движение направлено к концам крыла, а над крылом — к
его средней части (рис 17.2).
В результате в аимодействия верхнего и нижнего потоков
позади крыла образуется вихревая пелена, представляющая со-
прямолинейном по-
273
www vokb-la.spb ru - Самолёт своими руками?!
бой совокупность вихревых нитей, берущих начало на задней
кромке крыла.
Вихревые нити, составляющие вихревую пелену, называются
свободными вихрями. Можно считать, что каждые два симмет-
рично расположенных свободных вихря, замыкаются на крыле
соответствующим присоединенным вихрем (той же интенсив-
ности). Поэтому вихревую пелену совместно с п исоедииенными
вихрями можно представить как совокупность П-образных вих-
ревых нитей (рис. 17.3). Таким образом, аэродинамической мо-
Рис. 17 3. Вихревая система крыла конечного раз-
маха
делью крыла может служить совокупность П-образных вихрей,
состоящих из присоединенных и свободных вихрей. Циркуляция
Л' вдоль каждой элементарной П-образной вихревой нити пос-
тоянна, однако вдоль размаха циркуляция крыла изменяется.
Теоретический анализ и эксперименты показывают, что вих-
ревая пелена позади крыла неустойчива; на некотором расстоя-
нии от крыла она свертывается в два вихревых шнура (рис
17.4). Такие вихревые шнуры можно наблюдать в лаборатор
«ых условиях, и в полете (например, при полете в тумане или
при распылении химикатов).
В приближенных расчетах вихревая система крыла конечного
размаха может быть представлена двумя свободными вихрями,
сбегающими с концевых кромок крыла и замыкающимися одним
присоединенным вихрем. При такой П-образной аэродинамичес-
кой модели крыла циркуляция постоянна вдоль размаха крыла.
Во многих случаях такая упрощенная аэродинамическая модель
крыла позволяет произвести достаточно точные для практики
расчеты.
Одним из первых вопросами, посвященными теории крыла
конечного размаха, занимался С. А. Чаплыгин. В докладе «Ре-
274
www.vokb-la.spb.ru - Самолёт своими руками?!
зультаты теоретических исследований о движении аэропланов»
(1910 г.) он указал на наличие вихрей, сходящих с крыла ко-
нечного размаха, и пришел к основным представлениям о вихре-
вой системе крыла конечного размаха, а в 1913 г. получил общие
выражения для подъемной силы и индуктивного сопротивления
крыла конечного размаха. В 1912 г. Н. Е. Жуковский начал пуб-
Рис. 17.4. Трансформация вихревой пелены в два вихревых
шнура
ликацню серии статей под единым названием «Вихревая теория
гребного винта», в которых излагались принципиальные основы
вихревой теории гребного винта. В основу своей теории Н. Е. Жу-
ковский положил схему вихревых линий, сходящих с задних
кромок лопастей винта и образующих за винтом систему вихре-
вых пелен, т. е. схему, аналогичную схеме крыла конечного раз-
маха.
В основу дальнейших исследований по теории крыла конеч-
ного размаха была положена теория несущей линии, разрабо-
танная Л. Прандтлем в период 1913—1918 гг.
17.3. ИНДУКТИВНАЯ СКОРОСТЬ. СКОС ПОТОКА У КРЫЛА
ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ КРЫЛА
Характерной особенностью потока, обтекающего крыло конеч-
ного размаха под положительным углом атаки, является нали-
чие около крыла скосов потока: при приближении к крылу по-
ступательный поток отклоняется вниз от своего первоначального
направления. Отклонение потока начинается далеко впереди
крыла и нарастает по мере приближения к крылу. Ойо обуслав-
ливается системой свободных вихрей, сбегающих с крыла н ин-
дуцирующих в соответствии с законом Био — Савара в окру-
жающей массе жидкости некоторое поле скоростей.
Вызванные свободными вихрями скорости Vy в плоскости
крыла направлены вертикально вниз и изменяются по размаху
крыла н по его хорде Результирующая от геометрического сло-
275
wwu vokb-la.spb ru - Самолёт своими руками?!
жжения скорости Vy и скорости набегающего поступательного по-
тока скорость К»' определяет течение, линии тока которого
искривляются в вертикальной плоскости. В некотором сечении
крыла скорость VoY направлена под углом Да к первоначально-
му направлению потока (рис. 17 5). Следовательно, угол Да
является углом скоса потока в этом сечении. Угол скоса изме-
няется по размаху крыла, увеличиваясь к концам.
Обозначим среднюю по размаху скорость Vy через Vy ср
Тогда средний угол скоса Даср определяется из соотношения
ig Даср— 1/00.
Обычно угол скоса потока Да мал и поэтому
tg Да..,. Дагп =
о ср ср
ОО
(17. 1)
Рис 17.5. Треугольники скоростей и
сил у крыла конечного размаха
Истинный угол атаки крыла, измеряемый по отношению к
•фактическому направлению набегающего потока, будет отли-
’чаться от геометрического
угла атаки а на величину
угла скоса потока Даср:
О'иСт ^аср- (l^'^)
Согласно теореме Жу-
ковского сила, с которой
давит на крыло плоскопа-
раллельный поток идеаль-
ной жидкости, обтекающий
крыло, по величине равна
произведению плотности
жидкости на величину ско-
величину циркуляции скоро-
ростн потока в бесконечности и на
ст и вокруг крыла. Направление этой силы определяется поворо-
том вектора скорости в бесконечности на прямой угол против
направления циркуляции.
Сила Уа', определяемая теоремой Жуковского,
перпендикулярно вектору К/. Составляющая силы
дикулярная к направлению иевозмущенного потока
JC = Y„ cos ДаС1) Y.
а а а’
направлена
Ya', перпен-
(17.3)
представляет собой подъемную силу крыла. Составляющая силы
Ya' вдоль потока
Xi — г; sin г. Г„Дц(р
(17.4)
представляет собой силу индуктивного сопротивления.
Таким образом, при обтекании крыла конечного размаха по
током идеальной жидкости благодаря наличию свободных вих-
рей, сбегающих с крыла, возникает сопротивление особого рода,
не связанное с вязкостью, — индуктивное сопротивление.
276
www.vokb-la.spb.ru - Самолёт своими руками?!
17.4. ПРИБЛИЖЕННЫЙ РАСЧЕТ ИНДУКТИВНОГО
СОПРОТИВЛЕНИЯ
Индуктивное сопротивление крыла Xt, как видно из рис. 17.3,
пропорционально среднему углу скоса потока на крыле, величи-
на которого Даср определяется соотношением (17 1).
Для приближенного определения средней скорости скоса
Vycp заменим крыло простейшей вихревой системой, П-образ-
ным вихрем, причем взаимодействие этого П-образного вихря с
набегающим потоком должно вызывать такую же подъемную си-
лу и индуктивное сопротивление, как и у реального крыла (рис.
17.6).
Рис. 17.6. К расчету средней скорости скоса потока
Подъемная сила несущего вихря, выраженная через цирку-
ляцию скорости П-образного вихря Г и расстояние между сво-
бодными вихрями Д согласно теореме Жуковского может быть
записана в виде Уа=рооУтоГ/1 С другой стороны, подъемная си-
ла крыла может быть выражена через коэффициент подъемной
СИЛЫ С
где S — площадь крыла. Приравнивая
последние два выражения для силы Уа, получим так называемое
уравнение связи
Г — с — V
2 ““ I,
(17.5)
которое определяет значение циркуляции П-образного вихря,
т. е среднее значение циркуляции вдоль размаха крыла.
Как показывает более подробный анализ, для выполнения
условия равенства индуктивных сопротивлений П образного вих-
ря и реального крыла необходимо, чтобы расстояние между сво-
бодными вихрями li было несколько больше, чем размах крылаI:
где k>L Величина k зависит от формы крыла в плане,
от относительного удлинения и изменяется в пределах 1,02 1,04
277
www vokb-la.spb ru - Самолёт своими руками?!
Средняя по размаху скорость скоса потока, вызванная сво-
бодными вихрями,
Z/2
Скорость Vy(z),
лежащей на линии
формуле Био
— у Vу z}dz.
-ift
индуцированную в произвольной точке т,
несущего внхря (рис. 17 6), определяем по*
Савара, используя ее поочередно для левого и
правого свободных вихрей Принимая во внимание, что свобод-
ные вихри являются полубесконечными вихрями, для Еу(г)
можно написать
Vy (^~^учр (z) ^Улев (я) —
4Л
1
1____L _
к , ‘ к
--- + Z —
.2-2
Полученная зависимость показывает, что по мере приближения
к правому вихрю величина Vv(z) растет за счет увеличения
V'ynjb при этом Уулсв убывает; при приближении к левому вихрю
(г здесь отрицательно) Vv(z) растет за счет увеличения У3/Лев
(см. рис. 17.6). Подставим теперь значение Vy(z) в выражение
длн Vy Ср1
/ 1/2
V —1 /
*/ус₽~4л/
Z/2
dz । р dz
к ~к
—- + Z J — Z
\-i/2 2 —Z/2 2
Для среднего угла скоса имеем
л ГусР Г 1
Дасо = —----—--------In
₽ 2n/rw lx-1
Если теперь подставить вместо циркуляции Г ее
согласно (17 5), то получим
Да =Лй®-1пЛ±2.
р 4л//! /1 -1
Выразив Л через l\k = lk) и заменив после этого в
ле первого множителя F/S иа Л (удлинение), получим
Д«с——In—
ср 4лХ k k — 1
Если учесть, что k в зависимости от формы крыла изменяется
] £4-1
в пределах 1,02— 1,04 то —In----составляет величину, ие-
k k — 1
сколько большую 4. Тог та
A-ln^±J-=4(l + A),
k k-\ k '
-----In
2л/
I
выражение
знамеиате-
где А зависит от формы крыла.
278
www vokb-la.spb.ru - Самолёт своими руками?!
Формула для определения среднего угла скоса потока при-
нимает внд
Даср=-^-(1 + Д).
(17.6)
Очевидно, что чем больше удлинение X, тем меньше угол
•скоса потока АаСр. В случае крыла бесконечного размаха Л—>-оо,
н, следовательно, Ааср->0
Подставив в (17.4) вместо Даср его значение согласно (17 6)
q V2
и полагая Ya~~ суа ” °°S, получим выражение для индуктивного
сопротивления:
2 2
X, = Го Даср=Де- S (1 + Д),
ЛА 2
откуда находим коэффициент ин-
дуктивного сопротивления крыла
Рис. 17 7 Парабола индуктив-
ного сопротивления (1) и по-
ляра крыла (2)
с2
ьуа
лХ
(17.7)
U + A).
Как видим, приближенный рас-
чет дает значения сх{ и Ааср с точ-
ностью до некоторого множителя
(1 + А), несколько большего еди-
ницы
Анализируя полученные зависи-
мости, можно сделать следующие
ВЫВОДЫ.
1. Величина индуктивного сопротивления тем больше, чем
больше коэффициент суа и изменяется в зависимости от суа по
параболическому закону. Кривая, которая изображает эту за-
висимость, носит название параболы индуктивного сопротивле-
ния (рис. 17 7). В реальном вязком потоке жидкости коэффици-
ент полного лобового сопротивления крыла конечного размаха
можно представить в виде суммы коэффициента индуктивного
сопротивления сх{ и коэффициента профильного сопротивления
£хр, обусловленного вязкостью,
Сха сх1~\~^хр'
Если задана поляра крыла (см. рис 17.7), то с помощью па-
раболы индуктивного сопротивления можно выделить из коэф-
фициента полного сопротивления сха коэффициент профильного
сопротивления схр.
279
www.vokb-la.spb.ru - Самолёт своими руками?!
2. Величина индуктивного сопротивления в значительной сте-
пени зависит от относительного удлинения крыла Z: с увеличе-
нием относительного удлинения схг уменьшается. В связи с э им
для получения крыльев с высокими значениями аэродинамичес-
кого качества K—cyJcxa стремятся по возможности увеличивать
удлинение крыла. Стедует иметь в виду, что все сказанное отно-
сится к крыльям, не имеющим каких-либо конструктивных над-
строек (например, концевые шайбы и др ).
17 5. РАСЧЕТ СИЛ, ДЕЙСТВУЮЩИХ НА КРЫЛО КОНЕЧНОГО РАЗМАХА
С ПЕРЕМЕННОЙ ЦИРКУЛЯЦИЕЙ ПО РАЗМАХУ
Теорию крыла конечного размаха можно рассматривать как
теорию первого приближения. При более точном расчете сил,
действующих па крыло, необходимо учитывать изменение цирку-
ляции и угла скоса потока вдоль размаха
Рис. 17 8 К определе-
нию индуцированной
скорости в произволь-
ном сечении крыла
При выводе расчетных формул для крыла конечного размаха
с переменной циркуляцией по размаху будем полагать, что:
а) течение воздуха вокруг крыла индуцировано системой
вихрей;
б) свободные вихри п эямолинейны и направлены по скорости
невозмущенного потока;
в) каждое сечение крыла обтекается под своим углом атаки
и независимо от других сеченни.
Эти предположения позволяют примени ь теорему' Жуков1-
ского о подъемной силе к каждому из элементов крыла. Рас-
смотрим крыло конечного размаха в обращенном движении (рис
17 8) За таким крылом стелется вихревая пелена с изменяю-
щейся вдоль размаха погонной интенсивностью q—с1Г (z)fdz.
Выдетим иа вихревой пелене узкую полоску на расстоянии
от корневого сечения. Для циркуляции по контуру, охватываю-
, „ rfr(Z;) dZi
щему эту полосу, можно записать dl —--------р
dZ\
280
www.vokb-la.spb.ru - Самолёт своими руками?!
В произвольно взятой на оси 0Za точке В, определяемой ко-
ординатой z, вихревая полоса вызывает скорость
(*i) ,
-------dz.
dVу .
’ 4Я (z. - z)
Полная скорость, индуцированная в точке В всей вихревой
пеленой.
dz.
W dVfz.)
J
—I 2
откуда получаем уравнение для определения угла скоса потока
б сечении z (изменением угла скоса вдоль хорды крыла пренеб-
регаем) :
Да (z) =
f" ‘ ДлГт
_ 1 I dz.
V 4л J Zi — z
oo oo _//2 1
(17.9)
Заметим, что полученный интеграл является несобственным,
однако его главное значение может быть получено из соотно-
шу ия
Vа (z) =— lim
4л е^С
dz.
dz.
7 dz.
I dz.
J z.-z
z + e
Физически эта операция оправдывается тем, что мы отбрасыва-
ем влияние элемента вихря на самого себя.
Поскольку угол скоса изменяется вдоль размаха крыла, то
переменным будет и истинный угол атаки аист = а -Аа(г). Гео-
метрический угол атаки в данном сечении можно представить
в виде суммы геометрического угла атаки корневого сечения ац
(угол атаки центроплана) и угла геометрической крутки <ркр(<г):
а = ац+(рКр(г). Тогда истинный угол атаки в данном сеченнн
можно представить в виде
«исг = «ц + (2) — Да (2). (17. 10)
По величине угла скоса потока в отдельных сечениях крыла
можно определить действующие на крыло силы, как сумму сил,
действующих на элементарные участки крыла
При расчете сил, действующих на элемент крыла, в соответ-
ствии с гипотезой плоских сечений будем считать, что данный
элемент крыла работает как соответствующий элемент ци шнд-
рнческого крыла бесконечного большого размаха и что силы,
действующие на элемент крыла, полностью определяются значе-
нием истинного угла атаки в этом сечении.
Гипотеза плоских сечений дает вполне достаточную точность
для крыльев с 1^4.
281
www vokb-Ia.spb.ru - Самолет своими руками?!
Сила, действующая на элемент крыла, по теореме Жуков-
ского
V'^dz,
где Г(г) — циркуляция скорости по контуру,,
охватывающему крыло в сечении выбранного элемента.
Сила dYa' направлена перпендикулярно направлению вектора
Vo/ (рис. 17.9). Раскладывая dYa' на соответствующие состав-
Рис. 17.9. к расчету сил, девствующих на крыло
ляющие, получим подъемную силу элемента t/Ka=QTOr (2) X
X cos &a(z)dz и силу индуктивного сопротивления
dX t= етоГ (z) sin Да (z) dz.
Поскольку угол Да (г) мал, последние формулы можно написать
так:
^Ka=eror(z) V^dz;
dX(z) l/roAa(z) dz — — (z) Vy(z)dz.
Тогда полная подъемная сила крыла определяется интегралом
i
2
j T(z)dzt (17.11)
i
2
а полное индуктивное сопротивление х
z
2
^=-Q J V (z)Vy(z)dz. (17.12)
1
2
Если подставить в (17.12) вместо Vv(z) его значение соглас-
но (17 8), то можно записать развернутое выражение для индук-
о
282
www.vokb-la.spb.ru - Самолёт своими руками?!
-гибкого сопротивления:
rfr(zt) ,
dz\
Z\ — z
dz.
(17.13)
Полученные выражения для Уа и позволяют вычислить
•силы, действующие на крыло в потоке жидкости с учетом изме-
нения вдоль размаха циркуляции и угла скоса потока.
Точность расчета при этом будет зависеть от того, насколько
близки действительные условия работы крыла к принятым до-
лущениям (возможность применения гипотезы плоских сечений,
малость угла скоса потока, пренебрежение изменением угла ско-
са вдоль хорды крыла).
17.6. ОПРЕДЕЛЕНИЕ РАСПРЕДЕЛЕНИЯ ЦИРКУЛЯЦИИ
ВДОЛЬ РАЗМАХА КРЫЛА
Для определения подъемной силы крыла и силы индуктивно-
го сопротивления по формулам (17.11), (17.13) необходимо
найти закон распределения циркуляции вдоль размаха крыла.
Рассмотрим элемент крыла шириною dz как участок цилинд-
рического крыла бесконечного размаха с данным профилем (см.
рис. 17.9).
Подъемную силу, развиваемую на выделенном элементе ши-
риной dz, можно выразить через циркуляцию скорости на осно-
вании теоремы Жуковского или через коэффициент суа'-
£> V2
dYa—рооГ (z) V^dz', dYa=суа (z) b (z) dz,
где b(z) — хорда крыла в данном сечении.
Приравнивая правые части обоих выражений для dYa, полу-
чаем уравнение связи для сечения крыла:
Г (z) =~ еуа (z) b (z) V(17.14)
которое позволяет по коэффициенту подъемной силы сечеиия,
скорости невозмущенного потока и хорде сечения определить
циркуляцию скорости вокруг данного сечения. Выражение для
£уо(г) в соответствии с (13.16) можно написать так:
G/Дг) — &(z)a'a(z), (17. 15)
Ct dCtlfi
где суа = —^ в диапазоне углов атаки, соответствующих ли-
Lda
нейному участку кривой cya(z) ~---f (а); а/ (г)—истинный
аэродинамический угол атаки в данном сечении.
283
ww w vokb-Ia.spb.ru - Самолёт своими руками?!
Истинный аэродинамический угол атаки определяется зави-
симостью
a^(z) = ae(z)—Да(2г), (17.16)
где aa(z) — аэродинамический угол атаки в данном сечении, из-
меряемый между направлением линии полета и направлением
аэродинамическом хорды для данного сечения; Да (г) — угол
скоса потока в данном сечении
Если теперь в уравнение связи (17.14) подставить cy(,(z) из
формулы (17.15), заменив в ней истинный угол атаки aa'(z) его
значением согласно формуле (17.16) с учетом (17.9), то получим
уравнение:
/ ^Г(г) . \
1 / ! //2 ~---------------- dZ} \
rH=V e^(Z)b(Z) \ ------------U ~
2 - I 4ЛГоо J z\ — z I Ь-
\ -?/2 / —
которое носит название основного интегро-дифференииальногъ
уравнения крыла конечного размаха. Это уравнение связывает
искомую функцию Г (2) с известными величинами и позволяет
найти закон распределения циркуляции по размаху крыла.
В общем случае отыскание точного решения уравнения
(17.17) связано с большими трудностями. Существует ряд приб-
лиженных решений основного уравнения, полученных на основа-
нии введения упрощающих предположений или применения раз-
личного рода искусственных методов (методов Глауэрта —
Трефтца, Мультгоппа, Б. Н Юрьева, В. В Голубева, Г Ф Бу-
раго, С Г. Нужина н др ) Предложен также и эксперименталь-
ный метод решения этого уравнения, основанный на аналогии
гидродинамических н электродинамических явлений.
Большинство методов решения основано на приближенном
представлении функции Г(г), j ибо контура крыла в виде ряда
некоторых функций Например, метод Глауэрта — Трефтца за-
ключается в представлении искомой функции Г (г) в виде три-
гонометрического ряда синусов:
Г (z) —2/’/^ 2 A sin «9, (17 18)
Л--1
где 0 — новая переменная, связанная с переменной z (рис. 17 10)
соотношением z~ (//2) cos 0, Ап постоянные коэффициенты
ряда, подлежащие определению.
Поскольку члены ряда (17.18) быстро убывают, то для вы-
ражения функции Г (z) с удовлетворительной степенью точности
достаточно взять вместо ряда с бесконечным числом членов сум-
му сравнительно небольшого их числа т\
Г (г) 2/V^ A, sin «9. (17. 19)
п =1
284
www.vokbla.spb.ru - Самолет своими руками?!
Для определения т неизвестных коэффициентов, которые
должны быть такими, чтобы функция Г(г) удовлетворяла урав-
нению (17.17), необходимо соста-
вить т алгебраических уравне-
ний. Эти уравнения можно полу-
чить, подставив в уравнение
(17. 17) вместо Г (г) его значение
нз (17.19) последовательно для т
различных сечений крыла. Мож-
но показать, что для крыла
с симметричным распределением
циркуляции по размаху члены
ряда с четными индексами обра-
щаются в нуль, и в этом случае
необходимое число уравнений со-
кращается. Решив такую алгеб-
Рис. 17 10. Геометрическое пред-
ставление связи между перемен-
ными гиб
раическую систему уравнений, можно получить значения коэф-
фициентов ряда Лт,
Таким образом, приближенное выражение для циркуляции
имеет вид
Г^2/Уоо (Ai sin 04" A sin Зб-р.. .-р Ат sin m9).
17 7 КОЭФФИЦИЕНТЫ ПОДЪЕМНОЙ СИЛЫ И ИНДУКТИВНОГО
СОПРОТИВЛЕНИЯ КРЫЛА С УЧЕТОМ РАСПРЕДЕЛЕНИЯ
ЦИРКУЛЯЦИИ ВДОЛЬ РАЗМАХА
Зная распределение циркуляции скорости вдоль размаха,„
можно определить си ты, действующие на крыло. Переходя в
формуле (17.11) от переменной z к переменной ofdz sin 6d8^
и подставляя вместо циркуляции Г (г) ее выражение согласна»
(17 18), получим
Так как
то
Ya QeoV’l/2 2 J S*n
Л=1 о
Т (л .
р — при и— 1;
I sin «9 sin Qd$=|
о I 0 при п ( 1,
г<,-е.г2лг4 А
Тогда коэффициент подъемной силы крыла
4
уа Q У2 S 11
^оо оо _
' • о
2
285
www.vokb-la.spb.ru - Самолёт своими руками?!
Заменив l2/S на К окончательно получим
(17.20)
Это выражение для суа показывает, что полная подъемная
сила, развиваемая крылом конечного размаха, определяется зна-
чением коэффициента при первом члене разложения циркуляции
в ряд синусов. Подставив в формулу для определения индуктив-
ного сопротивления (17.13) вместо циркуляции ее выражение
согласно (17.18) и заменив переменные и г на переменную 6,
после несложных преобразований, получим выражение для Хг\
се
п^1
(17.21)
-откуда находим коэффициент индуктивного сопротивления
или
I
I
Если заменить l2/S на X и выразить Ai через суа согласно
(17.20), то выражение для коэффициента индуктивного сопро-
тивления принимает вид
с2
G/ = v(H8), (17.22)
ПЛ
03 .2
ч пА„
тае 8=2^г
л-2
Выражение (17.22) для cXi по форме совпадает с выражени-
ем для cxi (17.7), полученным без учета изменения циркуляции
и скоса потока вдоль размаха, и позволяет уточнить величину
множителя 1+Д Величина поправочного коэффициента формы
крыла в плане б обычно невелика по сравнению с единицей и в
общем случае зависит от геометрических характеристик крыла.
Выражение для среднего скоса потока имеет вид
Даср=^ (14-г), (17.23)
лл
где величина поправочного коэффициента т зависит от распре-
деления циркуляции вдоль размаха и равна
ОО
т= (17.24)
/^2
286
www.vokb-la.spb ru - Самолёт своими руками?!
— . . 1 h T I + 8 v>
Значения коэффициентов ------ и ---- для крыльев различной
л л
формы в плане приведены в табл. 17.1.
Таблица 17 Г.
Форма крыла в плане 1+т л I-R л
Эллиптическая 0,318 0,318
Трапециевидная (»]—2 ... 3) 0,318 0,318
Прямоугольная (%=5 ... 8) 0,375 0,335
Прямоугольная с закругленными концами 0,365 0,318
17.8. НАИВЫГОДНЕЙШАЯ ФОРМА КРЫЛА В ПЛАНЕ
Под наивыгоднейшим крылом понимают крыло, имеющее
наименьший коэффициент индуктивного сопротивления при дан-
ных значениях коэффициента подъемной силы и удлинения кры-
ла. Из формулы (17.22) видно, что величина коэффициента
индуктивного сопротивления будет минимальной при д = 0, т е.
°° » 2
при —^-=0. Это значит, что все коэффициенты разложения
л=2 *
Г (я) в ряд синусов, за исключением Alt должны быть равны
нулю. В этом случае
Г=27ИООА1 sin 9, (17.25}
откуда при 0 = л/2 (в центральном сечении крыла) Го —2/1/ооА1 —
— Гтах- Тогда формула (17.25) принимает вид Г=Го5Ш0.
Перейдя от координаты 0 к координате z ------- cos ,
получим
Таким образом, наивыгоднейшйм крылом является крыло, у
которого циркуляция вдоль размаха (вдоль оси OZ) изменяет-
ся по эллиптическому закону (рис. 17.11).
28?
www.vokb-la.spb.ru - Самолёт своими руками?!
Рис 17 11 Эллиптический закон
распределения циркуляции вдоль
размаха крыла
У крыла с эллиптическим распределением циркуляции ко-
эффициент индуктивного сопротивления выражается формулой
^2
cxi — — , а угол скоса потока Да=— . Следовательно, схг и
лХ лХ
Да вдоль размаха не изменяются. Если приравнять уравнения
(17.14) и (17.25), определяющие
циркуляцию скорости, то полу-
чим
-------—=1, (17.27)
ьо Z-LV-
\ 2 /
где b0=4lcya(z) А.
Это уравнение эллипса с полу-
осями Ьо и 11%, т. е. наивыгодней-
шим является крыло, имеющее
эллиптическую форму в плаце, но
при этом cya(z) во всех сечениях
крыла должен оставаться постоянным, чего достичь довольно
трудно.
К такому же выводу можно прийти, проанализировав урав-
нение связи
V°°’
из которого следует, что эллиптического распределения цирку-
ляции вдоль размаха можно добиться путем варьирования вели-
чин Суа (£}, ад, b (г). Для получения эллиптического распределе-
ния циркуляции при одинаковых значениях суа для всех про-
фильных сечений крыла вдоль размаха и при неизменном истин-
ном угле атаки а/(2) необходимо, чтобы хорды вдоль размаха
изменялись по эллиптическому закону, т. е. крыло должно иметь
в плане форму эллипса.
Одинаковые значения сауа для всех профильных сечений мо-
гут быть получены за счет применения одних и тех же профилей
вдоль размаха, а неизменное а«' — за счет крутки [см. (17.16)].
У крыла эллиптической формы в плане не обязательно доби-
ваться постоянства вдоль размаха величин ад и — неизмен-
ным может быть их произведение c“a(z) (2), что достигается
сочетанием крутки и подбора профилей вдоль размаха.
У крыла прямоугольной формы в плане (ft —const вдоль раз-
маха) эллиптическое распределение циркуляции может быть по-
лучено только за счет изменения по эллиптическому закону про-
изведения г“д(2)а^г:\ что достигается одновременно круткойи
соответствующим подбором профилей. На современных крыльях
эллиптическое или близкое к нему распределение циркуляции
.288
WWW vokb-la.spb ru - Самолёт своими руками?!
достигается обычно за счет одновременной вариации всех трех
сомножителей: г“Л(г), % (г) и b (z).
Следует отметить, что в тех случаях, когда часть крыла за-
нята фюзеляжем, гондолами двигателей и гондолами шасси, до-
биться оптимального распределения циркуляции вдоль размаха
весьма трудно. В этом случае значение д может быть довольно
большим Отметим также, что у неэллиптических крыльев путем
подбора профилей и крутки добиться эллиптического распреде-
ления циркуляции можно только на определенном угле атаки.
17.9. ПЕРЕСЧЕТ АЭРОДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК
КРЫЛА С ОДНОГО УДЛИНЕНИЯ НА ДРУГОЕ
Известно, что коэффициент лобового сопротивления крыла
Сха ~ С-х г Сх р. Независимость профильного сопротивления от
удлинения и формы крыла в плане позволяет делать пересчет
аэродинамических характеристик, известных для крыла с удли-
нением Xi, на крыло с удлинением Аг, что значительно облегчает
использование результатов продувок серийной модели со стан-
дартным \ (обычно равным 5).
Предположим, что для крыла с удлинением Ai аэродинами-
ческие характеристики известны Необходимо сделать пересчет
аэродинамических характеристик известного крыла с удлинени-
ем Ai для другого крыла, набранного из тех же профилей, но
имеющего другую форму в плане и другое относительное удли-
нение А2. Пересчет основывается на следующем предположении'
если крылья имеют одинаковые профили и работают с оди-
наковыми средними истинными углами атаки аИст! = осистз = аИСт,
то для таких двух крыльев коэффициенты суа одинаковы
Пусть Деи и Да2 — средние углы скоса потока на крыльях,
ТОГДа Оист ~ <1ист1 = 0С1 АСЦ, ОСист = С1ист2 ~ Я—A(12,
откуда а<2 = а(+Даа—Дссь
В соответствии с (17.23) имеем
или
Да,=Л!«-(1+г1)1
ЛА]
4 = ^(1+’,)
П К‘2
— п I ~+~ tg
— -----{ 7— - - —-—
k Л Л j. л2
(17. 28)
Эта формула позволяет пересчитать коэффициенты подъ-
емной силы с одного удлинения на другое
Ю 626 289
www vokb-la.spb.ru - Самолёт своими руками?!
У крыльев с различными удлинениями, но с одинаковой фор-
мой профиля углы нулевой подъемной силы сс0 одинаковы. Это
значит, что графики функций cya=f(a) для различных крыльев
выходят из одной точки на оси абсцисс, но имеют разный на-
клон — чем меньше удлинение, тем кривая на графике стано-
вится более пологой (рис 17.12).
Рис 17.12. К пересчету аэродинамических характеристик
крыла на другое удлинение
Угол наклона или тангенс угла наклона линейной части гра-
фика, равный производной dcyjda, можно найти следующим об-
разом. Уравнения линейных частей для крыла бесконечного раз-
маха (1= оо) и крыла с конечной величиной X можно записать
в виде
— Чи=^а(а“а» + Д“)- (17.29)
где с“а= д Уа- для крыла с конечным удлинением
да
Учитывая, что величина угла скоса Да определяется форму-
лой (17.23) и исключая из второго уравнения (17.29) величину
a ao, получим
cava —____. (17.30)
, с tjaK^oo
1 + “ (I -МО
лл
Поскольку частная производная са является угловым коэф
фициентом линейной части графика суа=/(а), то из соотношения
(17 30) можно сделать вывод, что по мере уменьшения удлине-
ния крыла X линейная часть зависимости cya=f(a) становится
более пологой.
290
www vokb-Ia.spb.ru - Самолёт своими руками?!
Коэффициенты лобового сопротивления имеют следующие
выражения для обоих крыльев: (\а1=сЛР4 ^ха2 ^xp~[~^xi2'
Так как крылья набраны из одних и тех же профилей, то для
них коэффициент схр (т. е. профильная часть коэффициента сха)
одинаков. Тогда находим сХаг—сха2=схи—Cxiz- Здесь в соответст-
вии с (17.22) коэффициенты индуктивного сопротивления опре-
деляются формулами:
г2 с2
^п=^(1+У;
Л Л1 И Z.2
В таком случае будем иметь
__________суа / Ц + ^1_1 +
с ха! схаЪ I ,______,
Л \ Л] К2
или
с1а /1 +S] 1+М
Сгл2 — ^xal , I •
Л \ А] Л2 /
(17.31)
На рис 17.12 приведен график, иллюстрирующии применение
зависимостей (17.28), (17.31) для пересчета аэродинамических
характеристик с удлинения At иа удлинение Х2 (М-САг). Путем
приведенного расчета можно получить и характеристики крыла
бесконечного удлинения (профиля).
Вопросы для повторения
1. Объясните природу индуктивного сопротивления. Как вли-
яет удлинение крыла па величину индуктивного сопротивле-
ния?
2. Объясните, как зависит индуктивное сопротивление от уг-
ла атаки?
3. При каком распределении циркуляции по размаху дости-
гается минимальное индуктивное сопротивление? Какую форму
при этом должно иметь плоское крыло?
4. Какие вы знаете методы приближенного решения интегро-
дифференциального уравнения крыла конечного размаха?
Задачи
1 Построить поляру в диапазоне 0<rytt<l Удлинение крыла
А=10, коэффициент профильного сопротивления cv/;-0 008 и
коэффициент 6=0,03
2 . Для условий предыдущей задачи определить графически
и ai алитически максимальное аэродинамическое качество кры-
ла, наивыгоднейший угол атаки и соотношение между профиль-
ным и индуктивным сопротивлениями в случае, если дсуа/да^5,0,
а угол пулевой подъемной силы ссо=0°.
Ответ: Лшах=30,9, аНв = 5,66 , cxp = cxi
10*
www vokb-la.spb ru - Самолёт своими руками?!
ГЛАВА 18
СТРЕЛОВИДНЫЕ КРЫЛЬЯ В ДОЗВУКОВОМ ПОТОКЕ
18.1. ПОНЯТИЕ О СТРЕЛОВИДНОСТИ КРЫЛА И ЕЕ ЭФФЕКТЕ
Экспериментальные данные, а также данные практики поле-
тов показали, что повысить критическое число М, отдалить аэро-
динамически неблагоприятное влияние сжимаемости воздуха,
проявляющееся в возникновении явле-
ний волнового кризиса, уменьшить
волновое сопротивление и тем самым
улучшить аэродинамические свойства
крыла можно применением стреловид-
ных крыльев.
Стреловидным называется крыло,
у которого линия фокуса, расположен-
ная примерно на расстоянии одной
четверти хорды от передней кромки,
составляет с плоскостью, ортого-
нальной центральной хорде крыла,
угол у, называемый углом стреловид-
ности (рис. 18 1).
Иногда при расчетах угол стрело-
видности измеряется не по линии фо-
кусов (1/4 хорд), а по какой-либо дру-
гой линии, например, по передней или
задней кромке крыла. Для случая с из-
Рис. 18 1. Стреловидное меняемой стреловидностью в п лете
крыло с прямой (а) и об- угол стреловидности крыла опреде-
ратной (б) стреловидно- ляется по п вредней кромке центро-
плана (неподвижной части крыла) и,
кроме того, по передней кр< мке кон-
соли крыла (подвижной части крыла) Для определенности обо-
значения угла стреловидности при букве у ставится индекс, по-
казывающий, относительно какой линии измеряется этот угол.
Например, хо— стреловидность по передней кромк , Хе— по ли-
нии максимальной толщины, ху, —по линии фокусов, Х’Л —п0
сер< дине хорд, Xi — по задней кромке и т д. (см. рис. 18 1)
292
wvrvi vokb-la.spb.ru - Самолёт своими руками?!
Стреловидность крыла, как правило, бывает прямой (см.
рис. 18.1, а) и очень редко — обратной (см. рис. 18 1, б) При
обратной стреловидности концы крыла вынесеиы вперед по на-
правлению полета (угол % при этом считается отрицательным).
Если кромки крыла имеют изломы или криволинейны, то угол
стреловидности меняется вдоль размаха крыла.
Работа стреловидного крыла в потоке воздуха основана на
использовании эффекта скольжения. Предположим, что на пря-
моугольное крыло бесконечного размаха набегает поток воздуха
со скоростью Vi, перпендикулярно к его передней кромке (пис.
Рис. 18 2 К объяснению эффекта скольжения
18 2, а). В этом случае при обтекании крыла имеется определен-
ное распределение давления по хорде, которое оказывает влия-
ние на аэродинамические коэффициенты крыла.
При обтекании бесконечно длинного крыла потоком воздуха
в направлении вдоль размаха (см. рис. 18 2, б) скорость V2 не
оказывает влияния на распределение давления по поверхности
крыла и на другие его характеристики (за исключением некото-
рого воздействия на пограничный слой, которое здесь не учиты-
вается) .
При одновременном воздействии на крыло обоих потоков
(продольного и поперечного) результирующая скорость Т—
= Vi+V2 направлена к плоскости симметрии крыла под некото-
рым углом р (см рис. 18 2, в), называемым углом скольжения.
Картина обтекания не изменится, если результирующая скорость
будет параллельна первоначальной скорости К, а рассматривае-
мое крыло повернуто на угол р (см рис. 18.2, г). В этом случае
наблюдается картина обтекания скользящего крыла с углом
скольжения р. Таким образом, обтекание скользящего крыла
эквивалентно косому обтеканию цилиндрического крыла.
Нормальная и касательная составляющие скорости
’' i=/c°spT У2 = sin 3.
Заметим, что при скольжений обтекание профиля крыла в
норма, ьном к образующей крыла сеченин определяется не пол-
но коростью V, а ее составляющей 1Л, которая меньше скорос-
ти У в cos р раз.
293
www vokb-la.spb ru - Самолёт своими руками?!
При одинаковой скорости набегающего потока скорость, пер-
пендикулярная к передней кромке, в случае скользящего крыла
меньше соответствующей скорости прямого крыла. Величины
коэффициентов давлений на поверхности скользящего коыла
также меньше по сравнению с прямым, поэтому критическое
число М возрастает при переходе от прямого крыла к скользя-
щему MKp.cK=M.KP np/cos р, т. е. волновой кризис ыа скользящем
крыле наступает прн больших скоростях полета На стреловид-
ных крыльях эффект скольжения используется не полностью,
поскольку реальные стреловидные крылья имеют конечный раз-
мах, в местах сопряжения двух половин крыла эффект скольже-
ния нарушается.
На стреловидном крыле достаточно большого удлинения
можно ус ювио выделить три об тасти (рис. 18 3).
В центральной части крыла I (вб изи плоскости симметрии)
вследствие сильного взаимного влияния полукрыльев местный
угол скольжения р уменьшается и на некотором участке стано-
вится равным нулю. Это явление, называемое срединным эффек-
том, несколько снижает эффект скольжения, что сказывается
на аэродинамических характеристиках стреловидного крыла.
Эффект скольжения так же существенно снижается и в конце-
вой части крыла III
Область II с установившимся иа большой части размаха те-
чением со скольжением-при изучении стреловидного крыла мож-
но представить как соответствующую часть бесконечно длинного
цилиндрического крыла, расположенного в потоке под углом
стреловидности %, т. е. как скользящее крыло. Вследствие этого
можно приблизительно оценить увеличение Мкр за счет стрело-
видности, полагая, что в средней части полуразмаха, где крыло
работает как скользящее, число М равно Мто cos %, а в централь-
ном сечении, где оно работает, как прямое, число М.=Моо. Сред-
нее значение эффективного числа М на всем крыле приближен-
но будет
Моо + М№ c°s 1 м /1 + cos уд
2 — 2 /
Величина в скобках меньше единицы, поэтому среднее чис-
ло М набегающего потока меньше того числа М, которое было>
бы у прямого крыла. Таким образом уменьшение числа М набе-
1 + COS у
гающего потока в ------—- раз вызывает увеличение критичес-
кого числа М до значения
М - М _________-___
1 ¥1крХ — *¥1кр.пр , ,
F F 1 + cos у
294
www.vokb-la.spb.ru - Самолёт своими руками?!
Влияние эффекта скольжения иа критическое число М вид
но из рис. 18.4. Сравнивая приведенные кривые, можно заклю
Рис 18.3. Схема потока, обтекаю-
щего стреловидное крыло
Рис. 18.4. Изменение числа
МКр к в зависимости от угла X-
1—скользящее крыло: 2—стреловид-
ное крыло; 3—стреловидное крыло
(эксперимент)
чить, что срединные и концевые явления значительно снижают
эффект скольжения.
18.2. ФИЗИЧЕСКАЯ КАРТИНА ОБТЕКАНИЯ
СТРЕЛОВИДНОГО КРЫЛА
Для выявления физической сущности обтекания стреловид-
ного крыла проанализируем направление линий тока иа его по-
верхности.
Положим, что скорость набегающего иа стреловидное крыло
потока К» параллельна оси симметрии крыла (рис. 18.5). Раз-
ложим ее иа две составляющие: нормальную к передней кром-
ке крыла Vn и тангенциальную Ут, вдоль кромки, т. е.
Тангенциальная составляющая скорости у стреловидного
крыла в соседних сечениях примерно одна и та же Уц— Уоо sin /,
а нормальная составляющая Vn изменяется в зависимости от
формы профиля и угла атаки сечения, поэтому искривление ли-
нии тока в основном зависит от величины нормальной состав-
ляющей скорости.
Скорость течения, как показано на рис. 18.5, по мере прибли-
жения к передней кромке крыла уменьшается и непосредствен-
295
www.vokb-la.spb.ru - Самолёт своими руками?!
ио у передней кромки Уэт=0. Далее вдоль хорд, нормальных к
образующей крыла, скорость возрастает, достигая максимально-
го значения в точке минимума давления С. За точкой С ско-
рость снова уменьшается, проходя через второй минимум у зад-
ней кромки, и затем опять увеличивается до величины скорости
певозмущенного потока в точке Е Соответственно изменениям
вектора результирующей скорости линии тока вблизи крыла так-
А
же меняют направление (ли-
ния A'B'C'D'E' на рис. 18.5).
Своеобразное изменение
скоростей по величине и на-
правлению вдоль линии тока
иа стреловидном крыле обу-
славливает существенное от-
личие закона распределения
давления иа поверхности стре-
ловидного крыла по сравнению
с прямым крылом. Во всех се-
чениях прямого крыла боль-
шого удлинения давление рас-
Рис. 18.6 Распределение давления
в разных сечениях стреловидного
крыла (по потоку):
1 — в концевом сечении. 2 — середина по
луразмаха,- 3—в корневом сечении
Рис. 18.5. Изменение скорости и направ-
ления линии тока вблизи поверхности
стреловидного крыла
пределяется примерно одинаково во всех сечениях, в то время
как у стреловидного крыла характер распределения давления
изменяется от сечеиия к сечению. В центральных сечениях крыла
максимум разрежения смещен к задней кромке (кривая 3), а
в концевых сечениях наибольшее разрежение наблюдается у но-
ска крыла (кривая /), при этом ветичина pmin больше в конце-
вых сечениях, чем в средних и центральных (рис. 18.6) Такое
различие в распределении давления по хорде в различных сече-
ниях стреловидного крыла приводит к иному распределению на-
грузки по размаху по сравнению с нестреловидным крылом.
296
www vokb-la.spb.ru - Самолёт своими руками?!
18.3. УСТАНОВЛЕНИЕ ПРИБЛИЖЕННОЙ СВЯЗИ
МЕЖДУ ПАРАМЕТРАМИ СТРЕЛОВИДНОГО И ПРЯМОГО КРЫЛЬЕВ
Положим, что крыло бесконечного размаха расположено по
отношению к потоку под углом % (рис. 18.7). В этом случае хор-
да и толщина в нормальном к образующей крыла сечении Ьп
Рис. 18 7. Стреловидное крыло бесконечного раз-
маха
вдоль по-
(18. 1)
(18.2)
кривизна
(18.3)
и сп могут быть выражены через хорду b и толщину с
тока:
bn = b cos /;
- с с Ь с
сп-—----------=------.
bn b bn cos у.
В таком же соотношении находятся относительная
нормального сечения н сечения по потоку:
f п •
cos X
Если угол атаки в нормальном сеченин аэт, то
h h sin а
sin ап=——---------------------=------.
bn b cos x c°s X
Для небольших углов атаки прн умеренной стреловидности
можно записать
а
------
cos х
(18.4)
Таким образом, нормальный поток обтекает цилиндрическое
крыло бесконечного размаха с несколько утолщенным и более
искривленным, чем у стреловидного крыла бесконечного разма-
ха (скользящего) профилем под углом атаки ctn.
297
www.vokb-la.spb.ru - Самолёт своими руками?!
Рассмотрим стреловидное крыло бесконечного размаха и не-
которое прямое крыло (рис. 18.8), эквивалентное по форме про-
филя стреловидному (оба крыла имеют одинаковые хорды, про-
Рис. 18.8 Стреловид-
ное крыло бесконечно-
го размаха и эквива-
лентное ему прямое
крыло
фильные сечения и углы атаки вдоль по-
тока). Поперечный поток, набегающий на
стреловидное крыло со скоростью =
= Ко cos у, создает подъемную силу
у боУп <>
I ап — Cyan 2 — СУап ° ’
(18.5)
где
у2 у2
e-2L = e-^ cos2Z) т. е. ^=^crPcos2z.
Если полагать, что подъемная сила стре-
ловидного (?.= ос) и эквивалентного ему
прямого крыла на участке размаха I равны,
т. е
1 астр •* ап->
то тогда на основании (18.5)
будем иметь
(18.6)
С/«стр — ГДОПСО5 у.
Таким образом, коэффициент подъемной силы скользящего
или стреловидного крыла бесконечного размаха меньше, чем
Cyan эквивалентного ему прямого (нескользящего) крыла при
равных значениях ТастР= Yan.
Для этих двух крыльев суа стр = сауа стр астр, суап = суапап.
Заметим, что для данного профиля производная с“а = дсуа]ди
является постоянной величиной по углам атаки. Тогда, учитывая,
что согласно (18.3) и (18.6)
Суа стр ~ Cyan е°52 X, астр ~ ал Х>
получим
Са ~са cosy. (18.7)
уа стр yan Л. V '
Так связаны между собой производные с“д скользящего 'и
нескользящего крыльев бесконечного размаха. Соответственно
этому коэффициент подъемной силы:
для нескользящего крыла бесконечного размаха в общем
случае
ya^^CyaX—tx» Cl ,
для крыла конечного размаха коэффициент суа, очевидно, бу-
дет иметь вид
Cya^c^aiu — а0— Да), (б)
298
www vokb-la.spb.ru - Самолёт своими руками?!
где Да — угол скоса потока от пелены свободных вихрей за
крылом. Если полагать, что левые части соотношений (а и б)
одинаковы, то тогда и правые части должны быть одинако-
выми:
где по вихревой теории
лХ
При этой подстановке предыдущее уравнение запишется так:
с“а(а — а0) = с“йх»<х(а — а0) — суа (1 -ф Т) —
— G/aX-oo(a — «о) ' ^аЛ=оо (1 “h"1-) (а ао)»
откуда находим
е а ч । 1/аХ=оо
^аХ«оо £ уа * I С
ЛА
(НП
или
z.“
уак=оо
^=^(1+г)
(18.8)
Для стреловидного крыла конечного размаха соответствую-
щее соотношение приближенно можно получить, подставляя в
предыдущую формулу вместо производной о величину
€JacTPx-oo=^«x-co cos х согласно равенству (18.7)
~ _ <aX-ooC0SX
1 огда получим суастр~------------------------•
1 + “ (l+TCTp)
ЛА
Так как —— —/1-|~tgax,
cos X
то , (18.9)
"астр ------- Суа^
У 1 + tg2x+ (1 + иСТр)
Лл
где величина гСтР, в среднем равная 0 2, учитывает удлинение,
сужение, стреловидиость и распределение циркуляции вдоль
299
www.vokb-la.spb.ru - Самолёт своими руками?!
размаха крыла. С увеличением удлинения крыла X и уменьше-
нием сужения т] величина т несколько возрастает (приблизи-
тельно до 0,3).
Качественное сравнение кривых зависимости cya=f(a) для
прямого и стреловидного крыльев одинакового удлинения, а так-
Рис. 18.9. Зависимости суа~
= f(ct) для крыла бесконечно-
го размаха (7), прямого (2)
и стреловидного (< ) крыльев
конечного размаха, имеющих
равные удлинения
же для крыла бесконечного размаха
(профиля) (рнс. 18.9) показывает,
что производная с“а стреловидного
крыла существенно меньше, чем
прямого крыла и тем более крыла
бесконечного размаха.
Средний угол скоса потока и
коэффициент индуктивного сопро-
тивления стреловидного крыла мо-
гут быть представлены зависимо-
стями, аналогичными зависимостям
для прямого крыла:
Суа сто
стр=^Г
с2
_ I'j/gCTp
Cjci стр ,
U+TciP);
(1 Т^стр)-
(18.10)
(18.11)
Для профильного сопротивления приближенно будем иметь
о стр == Xon cos X или cxq СТр qS^zzcx(mqnS cos у или Cj-q стр^-'Сгсл cos у.
Таким образом, коэффициент профильного сопротивления
стреловидного крыла меньше коэффициента профильного сопро-
тивления прямоугольного крыла. С увеличением угла стреловид-
ности значения с^остр при М>Мьр уменьшаются.
Следует отметить, что в настоящее время имеются весьма
точные численные методы расчета аэродинамических характе-
ристик стреловидных крыльев, включая и моментные характери-
стики. Одна ко эти методы весьма трудоемки и для своей реали-
зации требуют применения специальных счетных машин.
18.4. КРЫЛЬЯ МАЛЫХ УДЛИНЕНИЙ
Вплоть до 50 годов в самолетостроении применялись крылья
со сравнительно большими удлинениями Даже оперения имели
удлинения 7., превышающие 4 Крылья больших удлинений при-
менялись для уменьшения индуктивного сопротивления. Наи-
большая величина удлинения крыльев ограничивалась, гтавным
образом, требованиями прочности и жесткости крыльев.
После 50 годов скорость самолетов начала резко увеличи-
ваться, и бурпое развитие получила ракетная техника. Теперь
при больших скоростях полета потребовались довольно малые
значения коэффициентов суа и роль индуктивного сопротивления
300
www vokb-la.spb ru - Самолёт своими руками?!
летательного аппарата, зависящего от суа, в общем балансе ло-
бового сопротивления оказалась весьма малой. Для получения
сравнительно высокого аэродинамического качества при малых
значениях коэффициента подъемной силы, что требуется в поле-
те с большими скоростями на большой высоте, начали приме-
няться крылья весьма малых удлинений (?.=0,5 ... 3). Особенно
малых удлинений достигли крылья, применяемые на крылатых
ракетах. Попытки применить к этим крыльям хорошо разрабо-
танную, ставшую классической, теорию крыла большого удли-
нения, оказались безуспешными: теория в ряде случаев не
давала даже качественного совпадения с экспериментом.
Рис. 18.10. Характерные формы крыльев малых удлинений в плане
Действительно, для крыла малого удлинения неприменимы
основные допущения теории крыла большого удлинения: гипо-
теза плоских сечений, замена крыла вихревой несущей линией,
пренебрежение измеиеним угла скоса потока вдоль хорды кры-
ла. У крыла малого удлннння большое значение имеет попереч-
ное обтекание крыла, которое приводит к трехмерности потока
и появлению весьма сложного поля давлении иа поверхности
крыла Исключительно большое влияние на аэродинамические
характеристики крыла малого удлинения оказывает его форма
в плане.
Прн исследовании крыльев малых удлинений имеет большое
значение эксперимент. Предложено также много полуэмпирнчес-
ких методов расчета крыльев малых удлинении Основное от-
личие этих методов состоит в использовании различных вихре-
вых моделей, которыми заменяется крыло. Как правило, эти
методы дают возможность рассчитывать силы и моменты, дейст-
вующие на крыло, при весьма малых углах атаки. На рис. 18 10
приведены наиболее распространенные формы в плане крыльев
малого удлинения.
По результатам многочисленных испытании в дозвуковых и
сверхзвуковых аэродинамических трубах для самолета «Кон-
корд» бы по выбрано трехугольное крыло с коэффициентом за-
острения (отношение корневой хорды к размаху) £3=1,5. Это
крыло имеет синусоидальную форму в плане по передней кром-
301
www.vokb-la.spb.ru - Самолёт своими руками?!
ке, так что угол стреловидности у корня и иа концах больше,
чем в средней части.
Кривая Cya=f(a) у крыльев малых удлинений не имеет за-
метного прямолинейного участка, характерного для крыльев
больших удлинений (рнс. 18.11). Такая форма кривой cya=f (а)
объясняется следующим. При малых а благодаря интенсивному
перетеканию воздуха через торцевые кромки крыла с малым уд-
линением давление на верх-
Рис. 18.11. Изменение коэффициента
подъемной силы крыла самолета «Кон-
корд» в зависимости ог угла атаки при
малых скоростях полета:.
1—с учетом влияния Земли; 2*-с учетом вих-
ревой пелены; 3—fa)
ней и нижней поверхностях
крыла выравнивается, что
приводит к уменьшению суа.
При увеличении а по торцам
начинают срываться мощ-
ные вихри, которые приво-
дят к уменьшению давления
на верхней поверхности, сле-
довательно, к значительному
возрастанию суа при малых
скоростях: так при угле ата-
ки 0,28 рад с учетом влия-
ния вихревой пелены суа
увеличивается на 30% (точ-
ка с на рис. 18.11). Влияние
Земли дает увеличение
подъемной силы до 50% при
сравнительно небольших уг-
лах атаки 0,12—0,14 рад
(точка а на рис. 18.11).
У крыльев малых удлинений акр значительно выше, чем у
крыльев больших удлинений. При этом акр для крыльев с удли-
нением Х<2 сохраняет примерно одно и то же значение, близ-
кое к 0,6 рад. Увеличение аКр для крыльев малых удлинений
объясняется выравниванием давления вдоль хорд крыла над его
верхней поверхностью, которое получается за счет интенсивного
перетекания через торцевые кромки
Снижение коэффициента волнового сопротивления схв н уве-
личение Мкр за счет уменьшения удлинения крыла X довольно
велики, хотя менее значительны, чем за счет увеличения угла
стреловидности %.
Крылья малых удлинений, в особенности треугольные и ожи-
вальные, делаются очень тонкими. Так, например, толщина про
филя крыла самолета «Конкорд» у корня — 2,97%, в средин-
ной части 2,15%- Такне крылья обладают сравнительно
малым лобовым (волновым) сопротивлением (рис. 18.12).
Преимуществом крыльев малых удлинений является также
сравнительно малое перемещение фокуса при переходе от до-
звуковых к сверхзвуковым скоростям полета, приводящее к не-
желательным последствиям (изменению запаса устойчивости,
302
www vokb-la.spb.ru - Самолёт своими руками?!
увеличению пикирующего момента), У треугольных крыльев
величина перемещения фокуса может быть снижена до 0,12—
0,15 средней аэродинами-
ческой хорды (рис.
18.13,а). На рис. 18 13,6
показан характер измене-
ния относительной коор-
динаты xf крыла малого
удлинения по числам М».
Применение крыльев
малых удлинений умень-
шает перегрузки от поры-
вов ветра (примерно в
2 раза по сравнению
с современными дозвуко-
выми самолетами), что
обеспечивает больший
Рис. 18.12. Изменение любого сопротивле-
ния крыльев трех форм в зависимости от
числа
комфорт для пассажиров.
Крылья малых удлинений позволяют без уменьшения дальности
летать с дозвуковой скоростью над населенными районами
во избежание звукового удара ч совершать дозвуковой крей-
серский полет в случае аварии или неисправности двигателей.
Индуктивное сопротивление у крыльев малых удлинений в
большой степени зависит от формы в плане и по своей величине
Рис. 18.13. Смещение аэродинамического фокуса крыльев трех форм
(а) и крыла самолета «Конкорд» (б) в зависимости от числа Мм
больше, чем у крыльев больших удлинений (при одинаковых
значениях суа). Коэффициент схг для крыла малого удлинения
можно также представить зависимостью, аналогичной зависи-
мости (17.22) для крыльев большого удлинения:
где параметр б зависит от формы крыла, угла атаки и опреде-
ляется опытным путем Для стреловидных крыльев малых удли-
нении при значениях с?;(,<0,6 параметр б имеет те же значения,
что и для крыльев больших удлинений: 0,05 0,15. Для треуголь-
ных крыльев (Д-крыльев) параметр б оказывается эначи-
303
wwn vokb-la.spb.ru - Самолёт своими руками?!
Рис. 18.14. Поляра (1)и аэродинами-
ческое качество (2) крыла самолета
«Конкорд» на дозвуковом режиме
полета (точка Л, М=0,92; /С=13)
тельно большим (0,4—1,0), при
этом его значения зависят от
удлинения, формы кромок и
величины суа. На рис. 18.14
приведена поляра и изменение
аэродинамического качества
крыла самолета «Конкорд» на
дозвуковом режиме полета.
При расчете летных характе-
ристик самолетов с крыльями
малых удлинений приходится
пользоваться надежными экс-
периментальными данными,
обращая при этом внимание
на подобие испытанного и рас-
считываемого объектов.
Вопроси для повторения
1. В чем заключается эффект стреловидности крыла?
2. Объясните физическую картину обтекания стреловидного
крыла
3. Напишите формулы связи между параметрами стреловид-
ного н прямого крыльев.
4. Как влияет стреловидность крыла на величину коэффици-
ента подъемной силы суа и на сжатш?
5. В чем заключаются особенности аэродинамических харак-
теристик крыльев малых удлинений?
6 Чем объясняется срединный и концевон эффекты стрело-
видного крыла?
Задачи
1. Определить угол атаки аэродинамически плоского крыла
с неизменным профилем по размаху с удлинением X—8 и углом
стреловидности %—0,6 рад, если коэффициент подъемной силы
Суа=0,6, угол нулевой подъемной силы «о —0 06 рад Кроме того,
известно, чтот=0,12 и 2.
Решение: с помощью формулы (18.8) находим
а
/1 + tg2 X + ^°° (] + т„р)
ЛА
Из уравнения (13 16) имеем а = -^—j- а0—0,106 рад—6 4.
С уа стр
Ответ, «-4)4'.
2. Во сколько раз уменьшится коэффициент подъемной силы
стреловидного крыла с %—45е по сравнению с прямоугольным
крылом, если Х=7; ^ах=со=4,9; М«>^0,6; тСТр=0,25.
Ответ: в 1,34 раза.
www.vokb-la.spb ru - Самолёт своими руками?!
ГЛАВА 19
МАКСИМАЛЬНЫЙ КОЭФФИЦИЕНТ ПОДЪЕМНОЙ СИЛЫ.
МЕХАНИЗАЦИЯ КРЫЛА
19 1. СРЫВ ПОТОКА С ПОВЕРХНОСТИ КРЫЛА
Прн полете на закрнтнческих углах атаки обтекание верхней
поверхности крыла сопровождается срывом потока. Срыв пото-
ка появляется прн сравнительно небольших углах атаки, поряд-
ка 0,121—0 175 рад и сначала имеет местный характер. Посте-
пенно по мере увеличения угла атаки зона срыва расширяется,
распространяясь вперед по хорде н вдоль размаха крыла. Соыв-
ные течения на верхней поверхности крыла являются результа-
том отрыва пограничного слоя, имеющего место прн положи-
тельных градиентах давления.
Срывной режим обтекания оказывает существенное влияние
иа аэродинамические характеристики крыла, особенно на коэф-
фициент подъемной силы. О начале развития срыва потока на
крыле свидетельствует нарушение линейной зависимости коэф-
фициента подъемной силы от угла атаки (участок АВ на рис.
19.1). Коэффициент подъемной силы, соответствующий точке А,
иногда называют суа Тр, поскольку прн появлении срывной зоны
на крыле полет самолета, как правило, сопровождается тряс-
кой.
На критическом угле атаки коэффициент суа достигает мак-
симального значения На закрнтнческих углах атаки срыв по-
тока распространяется на большую часть поверхности крыла,
коэффициент подъемной си ш уменьшается.
При монотонном увеличении угла атаки изменение коэффици-
ента суа на срывных режимах происходит по одной кривой (а
ем. рис. 19 1), а прн уменьшении угла атаки в обратную сторо-
ну по другой (Ь см. рис 19.1) Только прн возвращении
на режимы плавного обтекания (а>сстр) обе ветви кривой сли-
ваются. Это явление носит название гистерезиса кривой суа(а).
Величины суатах и акр в значительной степени зависят от гео-
305
www vokb-la.spb ru - Самолёт своими руками?!
метрических характеристик крыла и от числа Re. Место возник-
новения срыва и дальнейшее развитие срывной зоны зависят от
формы крыла в плане.
Рис. 19 1. Зависимость коэффициента подъемной
силы крыла от угла атаки
Рассмотрим влияние геометрических характеристик крыла на
развитие срывных явлений.
Влияние формы крыла в плане
Для каждого из сечеинй аэродинамически плоского крыла
бесконечного размаха с неизменным профилем коэффициент
подъемной силы ограничен значением сутахсеч. Значение
Фуатах сеч (см. гл. 13) для данного профиля зависит от числа
Re = КхФссчА’. Если определить коэффициенты Суа max сеч =f (z)
для данного крыла, то можно построить кривую, являющуюся
верхним пределом изменения суаСсч- В любой точке по размаху
крыла значение суа сеч не может превысить значения, определя-
емого этой кривой. На рис. 19.2 и 19 3 такие прямые 1 построе-
ны для прямого и трапециевидного крыльев (z=z///2).
Построим эпюру распределения суа сеч по размаху крыла, со-
ответствующую некоторому углу атаки а В соответствии с урав-
нением (17.14) имеем
Суа
2Т(г)
(19. 1)
где Г(г) — значение циркуляции скорости в различных сечениях
крыла при заданном угле атаки
306
www.vokb-la.spb.ru - Самолёт своими руками?!
Расчеты показывают, что циркуляция скорости Г(^) У всех
крыльев изменяется по размаху приблизительно по эллиптичес-
кому закону, т. е.
Г(г)^Г0 У1—z'*. (19.2)
В таком случае коэффициенты подъемной силы сечения
крыльев приближенно будут подчиняться закону
Рис 19 2 Эпюры распределения сеч
по размаху крыла прямоугольной фор-
мы в плане для различных углов атаки
(a^>a2>ai)
Рис 19.3. Эпюры распределе-
ния Суа сеч по размаху трапе-
циевидного крыла для различ-
ных углов атаки (аз>«2>Ц1)
Из этой формулы следует, что у прямоугольного крыла, у кото-
рого хорды b (z) —b—const вдоль размаха, коэффициенты суасеч
приближенно будут изменяться по эллиптическому закону
_ 2Г0
уа сеч.пр у h
ооР
(19.4)
Наоборот, у крыла эллиптической формы в плане, у которого
хорды сечения
b(z)~ Ьь /1 — Л (19.5)
коэффициенты подъемной силы сечения приближенно будут
2Г0 /1 - z2
/1-Z2
2Г0
ОО v
(19-6)
т. е. постоянны по размаху эллиптического крыла.
Аналогично будут изменяться по размаху крыла и коэффи-
циенты подъемной силы суа сеч трапециевидного крыла, близко-
го по форме эллиптическому.
307
www.vokb-la.spb.ru - Самолёт своими руками?!
Рис 19 4 Изменение суа вдочь
размаха крыла
в плане крыла отрыв потока
Особый характер изменения коэффициентов суа имеют тре-
угольные крылья, у которых хорды b(z) изменяются вдбль раз-
маха по закону
b(z)—Ьо(1—z). (19.7)
Для такого крыла по формуле (19.3) приближенно будем
иметь
„ _ . 2Г, 2Г0 , /~1+*
i_7 ~ VJ>^ Р ! i ’ 1И-б>
Из графика этой зависимости (рис 19.4) ясно, что самое ма-
лое значение коэффициент суа Сеч имеет в корневом сечении, а на
конце крыла ои теоретически
стремится к бесконечности Ина-
че говоря, вблизи конца такого
крыла практически на любом
угле атаки будет иметь место
срыв потока,
Прн достижении некоторого
угла атаки отрыв пограничного
слоя начнется в том сеченнн кры-
ла, где ординаты кривой суа сеч
наиболее близки к ординатам
кривой Суа max сеч (НЭ рИС. 19.3 Се-
чение z') У прямое го тьиого
начнется в районе центроплана и
быстро распространится на большую часть размаха. У трапе-
циевидного крыла отрыв начнется вблизи концов вследствие
быстрого уменьшения суатахсеч по направлению к концам
(из-за малых значений Re), а также вследствие описанного
выше характера изменения суа сеч. В тех сечениях, где имеет ме-
сто срыв, при дальнейшем увеличении угла атаки значения
Су сеч не будут возрастать пропорционально а, в результате чего
эпюра распределения суп сеч деформируется.
Эпюры распределения суа сеч по размаху при угле атаки а3,
соответствующем срывным течениям на верхней части крыла,
показаны на рис. 19 2 и 19 3. Пунктиром изображены эпюры, ко-
торые имели бы место при безотрывном обтекании, сплошными
линиями — с учетом отрыва. При угле атаки а3 на участке АВ
(см. рис. 19 3) значения суа еще не достигли значений Суатахсеч,
участок ВВ — область развитого срыва потока, соответствую-
щая закритическим местным углам атаки.
Изменение эпюры распределения Суасеч по размаху стрело-
видного крыла с увеличением угла атаки приведено на рис 19 5.
Для стреловидного крыла характерным является резкое умень-
шение Суа сеч в корневой части, что объясняется уменьшением
истинных углов атаки в этих сечениях за счет местного уве-
308
www vokb-la.spb.ru - Самолёт своими руками?!
Рис 19 5 Эпюры распределения суа се«.
по размаху стречовидного крыла для
различных углов атаки (аз>а2>а1)
личения скоса потока Из рис. 19.5 видно, что у стреловидного
плоского крыла с неизменным профилем коэффициент подъем-
ной силы распределяется вдоль размаха весьма равномерно, до*
стигая наибольших значений в сечениях, расположенных у кон*
цов крыла. Это, как и в случае прямого трапециевидного крыла,,
приводит к появлению
срывных явлении в этих се-
чениях
Кроме того, для стрело-
видного крыла характерным
является увеличение толщин
пограничного слоя у концов
за счет составляющей ско-
рости потока вдоль размаха,
что приводит к преждевре'
менному срыву потока на
конце крыла. Для предот-
вращения преждевременно-
го срыва потока применяют-
ся так называемые гребни —
пластины на верхней по
верхности крыла, препятст-
вующие стеканию погранич-
ного слоя к концам.
Таким образом, можно сделать следующие выводы Форма
крыла в плане оказывает весьма существенное влияние на ме-
сто начала срывных явлений на крыле У крыла прямоугольной"
формы в плане срывные явления начинаются в центральной ча-
сти и быстро распространяются на весь размах. У трапециевид-
ного и стреловидного крыльев срыв потока начинается в близи-
концов крыла Применение аэродинамических гребней позволя-
ет избежать раннего срыва потока у концов стреловидного кры-
ла; в этом случае стреловидное крыло ведет себя примерно так
же, как н прямое.
Влияние формы профилей и крутки крыла
У крыла заданной формы в плане, набранного вдоль разма-
ха нз различных профилей, суатах сеч зависит не только от числа
Re, но н от формы профилей: при одних н тех же значениях Re
коэффициент с?уотах зависит от относительной толщины, кривиз-
ны н положения наибольшей толщины профиля по хорде.
С другой стороны, применение неодинаковых профилей при-
водит к перераспределению циркуляции вдоль размаха и, как
следствие, к изменению кривых суа cen=f(z). Набирая крыло из
различных профилей, можно изменять характер кривых суота\сеч
н суа ссч, тем самым регулируя положение зоны начала срыва
потока на крыле.
309-
ww vokb-la.spb.ru - Самолёт своими руками?!
Так, например, применяя в районе ожидаемого начала срыва
более «несущие» профили, г. е. профили с высоким значением
Фуатах практически можно получить срывные явления по всему
размаху крыла.
Для обеспечения поперечной устойчивости полета на боль-
ших углах атаки обычно требуется, чтобы срывные явления
начинались в концевых сечениях крыла. В связи с этим в кон-
цевых сечениях крыла используются более «несущие» профили,
и в корневых применяются профили с пониженными несущими
-свойствами.
Несущие свойства отдельных участков крыла можно увели-
чить с помощью геометрической крутки, для чего в местах ожи-
даемого срыва потока профильные сечеиия, не меняя их фор-
мы, поворачивают так, чтобы местные углы атаки оказались
меньшими, чем на остальных участках крыла. Если концевой
части трапециевидного или стреловидного крыльев дать отрица-
тельную крутку, то можно сдвинуть отрывную зону ближе к
центроплану.
Одновременное применение крутки и неодинаковых профи-
лей вдоль размаха крыла позволяет получить необходимые не-
сущие качества крыла при больших углах атаки.
Влияние удлинения крыла
При больших удлинениях крыла отрыв потока наступает на
углах атаки, близких к аКр для данного профиля. У крыльев ма-
лых удлинений (Л<3) отрыв потока наступает, как правило, при
.значительно больших углах атаки. Затягивание отрыва потока
у крыльев малых удлинений объясняется уменьшением разреже-
ния на верхней поверхности благодаря перетеканию воздуха че-
рез концевые кромки, а также благодаря влиянию на погранич-
ный слой мощных концевых вихрей, сбегающих с крыла.
19.2. РАСЧЕТ МАКСИМАЛЬНОГО КОЭФФИЦИЕНТА
ПОДЪЕМНОЙ СИЛЫ
Максимальный коэффициент подъемной силы является одной
из наиболее важных аэродинамических характеристик крыла.
В горизонтальном полете вес самолета G уравновешивается
.подъемной силой крыла, т. е.
О=Газд(У2/2)5,
откуда V — -i / --—.
у
Максимальное значение суаТпах определяет минимальную ско-
рость горизонтального полета самолета Чем меньше скорость
горизонтального полета, тем меньшее значение посадочной ско-
310
www vokb-la.spb ru - Самолёт своими руками?!
рости может быть достигнуто. Величина посадочной скорости
должна быть по возможности меиьшен, так как оиа определяет
необходимые размеры взлетно-посадочной полосы и безопас-
ность наиболее ответственного этапа полета самолета — посадки.
Следует отметить, что точное определение величины Сца max
крыла связано с рядом затруднений. Трудно выполнить модель-
ный эксперимент для определения суа max в аэродинамической
трубе, так как не всегда имеется возможность получить в иих
необходимые (большие) значения чисел Re, трудно рассчитать
Суа max, поскольку для крыльев современных самолетов харак-
терны неодинаковые профили по размаху, применение крутки и
сложная форма крыла в плайе (переменные по длине сужение,,
стреловидность и т. д.)
Разработанный в ЦАГИ метод расчета суатах крыла пригоден
для прямых и трапециевидных крыльев сравнительно больших
удлинений, избранных из одних и тех же профилей во всех се-
чениях н не имеющих геометрической крутки и стреловидности.
Этот метод основан на предположении, что угол атаки крыла
становится критическим в тот момент, когда по мере увеличения-
угла атаки хотя бы в одном сечении крыла достигается значе-
ние —Суа max сеч. При этом предполагается, что вплоть до>
этого момента во всех сечениях крыла сохраняется линейная за-
висимость Суа сеч ОТ местного уГЛЭ ЭТЭКИ.
На рис. 19.6 показано пунктиром действительное распределе-
ние суаСеч, а сплошной линией — полученное описываемым ме-
тодом.
Если принять, что суа max крыла соответствует случаю, изо-
браженному на рис. 19.6, то можно показать, что для него спра-
ведлива формула
„ / Суд шах сеч \
С УЛ max кр I J >
\ ^асеЧ /min
где Суасеч — значение СуаЪя при угле атаки, соответствующем
значению сУакр=1-
Для расчета СуЯсеч — f (z) необходимо знать распределение
циркуляции по размаху крыла. В этом случае Суатахкр опреде-
ляется графическим путем (рнс. 19 7)
В справочной литературе приводятся данные по распределе-
нию циркуляции скорости вдоль размаха для крыльев различ-
ной формы в плане.
Для приближенной оценки значения суа max крыльев боль-
ших удлинений (Х>3) можно воспользоваться приближенной
эмпирической формулой'
с — с k 1 + cos Ь
У a max кр ^уа max сеч"'1! о »
311
www.vokb-la.spb.ru - Самолёт своими руками?!
где сУа max сеч — максимальный коэффициент подъемной, силы
профиля крыла с хордой, равной средней хорде крыла и прн
числе Re, соответствующем посадочной скорости; — угол
Рис. 19.6. К расчету суа max крыла:
1—значение суасеч, принятое в расчете из
условия, что в сечении ^^^асеч-
~суотах сеч* 2~действительное значение
на угле атаки, при котором в се-
у IT С- С т.
чении Z Суа wi~C-ya max сеч
_ сУаmaxсеч
Рис. 19 7. Зависимость —-------
суа сеч
= f (*)
стреловидности крыла по линии максимальных толщин; kr—
коэффициент, зависящий от сужения крыла тр
I 0,90 4 0,93
2 0,94 4 0,92
Для треугольных крыльев малых удлинений суа max кр прибли-
женно определяется в зависимости иг удлинения крыла:
X 1 2 4
сУа max кр 1,28 1,2 1,0
19.3. МЕХАНИЗАЦИЯ КРЫЛА
В современной авиации с целью повышения скорости полета
применяются стреловидные крылья сравнительно малой площа-
ди с профилями весьма малой кривизны и относительной тол-
щины Такие крылья не могут обеспечить большой подъемной
силы на посадочных режимах из-за раннего срыва потока. Для
•312
www vokb-la.spb.ru - Самолёт своими руками?!
уменьшения взлетной и посадочной дистанции в настоящее время
чрезвычайно остро стоит вопрос об увеличении несущих свойств
современных крыльев на больших углах атаки. С этой целью
на крыльях устанавливаются специальные конструктивные эле-
менты, которые позволяют повысить величину коэффициента
подъемной силы крыла в области критических углов атаки и
заметно уменьшить критический угол атаки Эти элементы, ра-
ботающие на режимах взлета, посадки и на маневрах, называ-
ются механизацией крыла Механизация крыла состоит из ме-
ханизации передней кромки крыла и механизации задней
Рис. 19.8 Щитки:
а простой, б—со скользящим шарниром (выдвижной)
кромки крыла. Для механизации задней кромки крыла с целью
увеличения суатах крыла наиболее широко используются щитки
простые (отклоняющиеся), скользящие (выдвижные) и закрыл-
ки (простые, однощелевые, двухщелевые, выдвижные щелевые,
трехщелевые, выдвижные многощелевые). Для кратковременно-
го уменьшения подъемной силы крыла (для увеличения крутиз-
ны снижения самолета и повышения эффективности торможения
колес прн пробеге) используются интерцепторы или спойлеры.
С помощью механизации передней кромки крыла: предкрыл-
ки скользящие, предкрылки с профи пированной щелью, носовой
щелью, отклоняемые носкн, турбулизаторы; решаются такие за-
дачи, как предотвращение потери боковой устойчивости н уп-
равляемости на больших углах атаки при использовании меха-
низации, способствующей увеличению Суа щах-
Щитком называется отклоняющаяся у задней кромки на
угол 6Щ часть иижней поверхности крыла. Отклонение может
происходить вокруг неподвижного шарнира (простой щиток, см.
рнс. 19,8, а) и вокруг скользящего шарнира (выдвижной щиток,
см рис. 19.8, б). Наиболее просты по конструкции и выгодны
по весу простые шитки, однако при прочих равных условиях они
значительно меньше увеличивают суат»х, чем скользящие (вы-
движные) Располагаются щитки в центральной части крыла и
занимают от 40 до 60% всего размаха крыла.
Значительное увеличение коэффициента подъемной силы при
отклонении щитка объясняется, во-первых, тем, что отклоненный
щнток увеличивает эффективную кривизну профиля, а, во-вто-
рых, повышает давление на нижней поверхности крыла н обра
зует зону разрежения между щитком н крылом, что приводит к
313
www vokb-la.spb.ru - Самолёт своими руками?!
ютсосу пограничного слоя с верхней поверхности крыла у его
задней кромки и соответственно к увеличению скорости -Вслед-
ствие подсасывающего действия щитка сильно увеличивается
вратах (значение которого в некоторых случаях может удвоить-
ся), в то же время критический угол атаки крыла изменяется
незначительно. С увеличением угла бщ кривая cya=f(a) смеща-
ется влево (рис. 19 9, а), а поляра вправо (см. рис. 19.9, б). Эф-
фект повышается при наличии скользящего щитка, так как в
этом случае увеличивается и площадь крыла.
Рис. 19 9 Влияние угла отклонения простого
щитка на зависимость cva—f(a) (а) и поляру
крыла (б) при л -ч- оо
Эффективность щитка оценивается величиной прироста ко-
эффициента подъемной силы Дсуа или Дебатах- На величины
Дсуа и Дентах оказывают влияние относительная длина щитка
I I, форма крыла в плане, угол отклонения щитка бщ, относи-
тельная хорда Ьщ/Ь. Хорда щитков составляет 15—30% хорды
крыла. При очень больших хордах наблюдается существенное
уменьшение роста эффективности механизации (рис. 19 10).
Увеличение относительной длины щитка соответственно увели-
чивает Дсуа и ДСуотах крыла. Максимальные значения Дсуа, оче-
видно, будут у щитков, расположенных по всему размаху.
Эффективность применения щитков повышается у крыльев с
большим сужением, так как прн неизменном размахе увеличи
вается относительная площадь 5щ/5.
Максимальный угол отклонения порядка л/3. Следует от-
метить, что большие углы отклонения щитка наряду с увеличе-
нием коэффициента подъемной силы приводят и к повышению
коэффициента лобового сопротивления, а это, в свою очередь,
сказывается на величине аэродинамического качества: К=
= Суа1сха крыльев с отклоняющимися щитками меньше, чем без
щитков. Увеличение коэффициента сопротивления играет по о-
жительную роль при посадке самолета, так как уменьшает
314
www.vokb-la.spb.ru - Самолёт своими руками?!
дальность пробега после посадки. Однако при взлете наряду с
увеличением коэффициента подъемной силы необходимо, чтобы
коэффициент сопротивления был как можно меньше. Поэтому
при взлете щитки отклоняются не полностью, а примерно на
0,4—0 5 рад.
Рис 19.10 Зависимость вели-
чины Ac,J(I max от ОТНОСИТСЛЬ-
ной хорды щитка.
1—выдвижной тциток; 2—простой
щиток
Рис 19 11. Изменение коэффи-
циента момента крыла сто в
зависимости от угла отклоне-
ния щитка:
1 -простой щиток; 2— выдвижной
щиток
Прн увеличении увеличивается также коэффициент мо-
мента крыла (на рис. 19.11 6щ/6 —0,3; /1Ц//—1).
Закрылки представляют собой отклоняющуюся хвосто-
вую часть крыта (рис. 19.12). Увеличение коэффициента суат&х
при отклонении закрылка происходит в основном в результате
увеличения эффективной кривизны крыла. Прн отклонении ще-
левого закрылка между крылом и передней частью закрылка
обычно образуется профилированная щель, через которую дви-
Рис. 19.12. Закрылки:
а—простой; б—выдвижной
жется поток воздуха, вь текающий с большой скоростью на верх-
нюю поверхнос ь закрылка. Это стабилизирует безотрывное те-
чение в пограничном слое и позволяет отк опять закрытой на
большие углы с сохранением его эффективности.
Отклонение закрылков приводит примерно к тем же эффек-
там, что и отклонение щитков, однако коэффициент лобового
3 S
www.vokb-la.spb.ru - Самолёт своими руками?!
сопротивления в этом случае меньше. Хорда закрылка обычно
не превышает 20 25% хорды крыла, так как с дальнейшим
увеличением 63/6 эффективность закрылка повышается незначи-
тельно.
Величина Асуатах возрастает с увеличением углов отклоне-
ния закрылка. Наибольшая эффективность закрылка достигает-
ся прн 6 — 0,7 . . 0 8 рад, т. е. при несколько меньшем угле от-
клонения, чем у щитка. На рис. 19.13 представлены графики за-
висимости коэффициента подъемной силы самолета Як-40 от уг-
Рис. 19 13. Изменение коэф-
фициента подъемной силы
самолета Як-40 в зависимос-
ти от угла атаки при раз-
личных углах отклонения
закрылка
Рис. 1914. Изменение коэффи-
циента подъемной силы крыла
в зависимости от коэффициен-
та момента ст при различных
углах отклонения закрылка
ла атаки при различных углах отклонения закрылков для числа
М^0,2. Наряду с увеличением коэффициента подъемной силы
с возрастанием угла отклонения закрылка несколько увеличива-
ется диапазон летных углов атаки
Выпуск закрылков сопровождается также увеличением ко-
эффициентов лобового сопротивления сха и пикирующего момен-
ты крыла ст. Зависимость коэффициента суа от ст для прямого
крыла с различными углами отклонения закрылка при /3//=1
приводится иа рис. 19.14
Выдвижные закрылки дают дополнительное увеличение ко-
эффициента подъемной силы, так как отклонение закрылка со-
провождается увеличением площади крыла за счет сдвига оси
закрылка. Наиболее эффективны выдвижные закрылки при
b3/b=G,4. Так, у расположенного по всему размаху крыла за-
крылка с Ьз!Ь — 0,4 в случае угла отклонения б3=0,7 рад вели-
чина суатах почти вдвое превышает суП1П^х при б3 = 0. Следует
отметить, что отклонения закрылка и отклонения щитка мало
влияют иа положение фокуса крыла.
316
www.vokb-la.spb.ru - Самолёт своими руками?!
Обычно закрылки, как и щитки, занимают около 60% разма-
ха крыта, так как часть крыла отводится под элероны. Поэто-
му эффект закрылков и щитков соответственно уменьшается.
Иногда для увеличения подъемной силы крыла элероны тоже
используются как закрылки и с этой целью оба элерона откло-
няются вниз прн посадке самолета.
Аэродинамические характеристики прямого крыла
Типы механизации сУа max ^Суа max акр, рад
Щиток (6щ—л/3, Ьщ — 0,36) 2,16 0,87 0,24
Закрылок без профилированной ще- ли (6з = л, 53=0,361 1,95 0,66 £ 0,21
Щел вой закрылок (б3—л/4, 63 — -0,256) 1,98 0,69 0,21
Выдвижной закрылок (63 = л/4 6э = 0,46) 2,42 1,13 0,26
Для сравнения эффективности применения щитка и различ-
ных типов закрылков, расположенных по всему размаху (см.
таблицу) приводятся аэродинамические характеристики прямого
крыла (Х=5). Наиболее эф-
фективным является выдвиж-
ной закрылок. Увеличение
угла отклонен! я закрылков
с целью увеличения Acyaniax
ограничивается появлением
срыва с самого закрылка и
с крыла и возникновением тря-
ски закрылков. В связи с этим
на самолетах наряду с одно-
щелевым н закрылками приме-
няются цвухщелевые н трехще-
левые. Установка трехщелево-
го закрыпка задерживает срыв
потока до углов отклонения
закрылка б3 —л/3 н значитель-
но повышает коэффициент
подъемной силы суа (рис.
19.15).
Многощелевые кры-
лья. Теоретическое обоснова-
Рис. 19.15 Сравнение эффективности
применения разных типов закрылков
и системы УПС:
закрылок Фаулера; 2— двухщелевой за
крылок; 3— трсхшелевой закрылок; 4- сис-
тема УПС (сдув)
ние эффективности применения многоще левого крыла было дано
С. А Чаплыгиным Наибольшее распространение получили мно-
гощелевые крылья в виде двух- и трехщелевых закрылков Из-
317
www vokb-la.spb.ru - Самолёт своими руками?!
Рис. 19 16. Сравнение поляр исходного (1)
и многощелевого (2) крыльев
вестно, что на верхней поверхности крыла при больших углах:
атаки образуется подсос (р<0), а на нижней — подпор
Если сделать одну или несколько щелей на крыле, то благодаря
перепаду давлений часть воздуха будет перетекать с нижней по-
верхности крыла на верхнюю. Вытекающие струи приведут
к смещению точки отрыва пограничного слоя вниз по потоку.
Эффект будет тем больше, чем ситьнее струя будет сужаться
в сторону направления
потока.
Многощелевые крылья
увеличивают суа в 2,5—
3 раза и более (рис.
19.16). В многощелевом
крыле повышение суа шах.
сопровождается увеличе-
нием акр. Однако необхо-
димо учитывать, что лобо-
вое сопротивление при пе-
реходе к многощелевому
крылу увеличивается (см.
рис. 19.16).
Струйные за-
крылки. В последнее
время проводятся иссле-
дования так называемых
реактивных закрылков и
предкрылков. В узкую
щель, расположенную
вдоль задней кромки крыла (реактивный закрылок), выдувается
сильная струя, благодаря чему улучшается обтекание крыла
и одновременно создается реактивная сила струи. В результате
значительно возрастает коэффициент Суащах (без увеличения
угла акр), что позволяет осуществлять посадку на сравнительно
малых скоростях и малых углах атаки
Носовые щитки и предкрылки В связи с воз-
растанием скорости потока на верхней поверхности крыла при
отклонении закрылков увеличивается местный угол атаки носо-
вой части крыла, что может вызвать появление срыва. Для
борьбы с этим явлением применяются носовые щитки, пред-
крылки, отклоняемые носки. Носовой щиток с острой передней
кромкой (рис. 19,17), будучи отклонен на больших углах атаки,
предотвращает преждевременный срыв потока с передней ост-
рой кромки профиля и тем самым повышает cyemax.
Предкрылок имеет крылообразную форму и располагается
вдоль передней кромки крыла Предкрылок устанавливается в
определенном фиксированном положении. Начиная с некоторого
достаточно большого угла атаки (а>0,175 рад) под действием
318
www vokb-la.spb ru - Самолёт своими руками?!
возникающих аэродинамических сил (подсасывающей силы)
предкрылок выдвигается в рабочее положение.
Изменение контура профиля с выдвинутым предкрылком соз-
дает такое изменение эпюры давления, которое способствует
сдвигу точки отрыва пограничного слоя назад и увеличению
критического угла атаки (уменьшаются пик разрежения и вели-
чина положительного градиента давления).
Рис. 19 17. Носовой щиток
Благодаря действию предкрылка увеличивается критический
угол атаки крыла и коэффициент гуоП1ах (рис. 19.18). Прирост
коэффициента подъемной силы составляет 0,7—0,8. Увеличение
критического угла атаки не позволяет в полной мере использо-
вать эффект предкрылков, так как это привело бы к увеличе-
нию посадочного угла атаки и осложнению посадки и взлета
самолета. Поэтому на большинстве самолетов чаще всего при-
меняются концевые предкрылки, предназначенные для увеличе-
ния эффективности элеронов на
больших углах атаки.
Такой же эффект, как примене-
ние предкрылка, дает отклонение
вниз передней кромки крыла. При
совместном отклонении закрылков
и предкрылков или передних кро-
мок крыльев можно получить высо-
кие значения коэффициента подъем-
ной силы (см. рис. 19.18) и аэроди-
намического качества
Интерцепторы или пре-
рыватели потока представ
ляют собой узкие плоские или слег-
ка искривленные пластины, распо-
ложенные вдоль размаха и выдви-
гаемые через щели в крыле пример-
но по нормали к его поверхности.
Применяются и отклоняющиеся ин-
терцепторы. Интерцептор вызывает
турбулизацию пограничного слоя или
Рис 19.18 Характер зависимос-
ти Суа max ОТ О ПрИ ПрИМеНС-
нии различных видов механи
зации;
1—крыло без механизации, 2—крыло
с предкрылком 3—крыло со щеле-
вым закрылком, 4—крыло со щеле-
ным закрылком и предкрылком
же срыв потока с поверх'
ности крыла за интерцептором в зависимости от высоты его вы-
движения. Это явление сопровождается перераспределением
давления по профилю При этом давление существенно изме-
319
www.vokb-la.spb.ru - Самолёт своими руками?!
нястся не только на той стороне профиля, где выдвинут интер-
цептор, но н на противоположной Перераспределение давления,
вызванное интерцептором, приводит к изменению коэффициен-
тов сха, Суа, ст: коэффициент подъемной силы уменьшается, если
интерцептор расположен сверху крыла, коэффициент лобового
сопротивления увеличивается, при этом резко падает аэродина-
мическое качество. Величина и знак изменения коэффициентов
давления зависят не только от высоты, но и от места расположе-
ния интерцептора вдоль хорды.
пуска интерцепторов на
характер зависимости
с11а от а
Рис. 19.20. Влияние формы
кры.та в плане на эффектив-
ность механизации
Работа интерцептора оказывает тормозящее действие на по
ток перед ннм: местные скорости перед ним уменьшаются, а
давление увеличивается. За интерцептором происходит лвеличе-
ние разрежения, давление понижается н образуется подсос.
Большое влияние на характер изменения кривом суа=$(и) ока-
зывают интерцепторы прн своем максимальном угле склоне-
ния На посадочных углах атаки уменьшение коэффициента
Суа составляет 0,7—0,75 На рис. 19 19 показано влияние интер-
цепторов на протекание зависимости cya=f(a) для самолета
ТУ-124.
Иногда интерцепторы делают гребенчатыми (прерывистыми)
для сохранения плавности обтекания крыла и уменьшения срыв-
ного сопротивления.
На величину коэффициента суатах механизированного крыла
оказывают влияние такие факторы как тнп н размах механиза-
ции, форма крыла (сужение в плане крыла гр удлинение Z, стре-
ловидность х)> хорда щитка илн закрылка Ь3, тип профиля кры-
320
Рис. 19.21. Влияние угла
стреловидности крыла на
относительную величину
Суа max / (Гуа max) Х=о:
/—простые щитки; 2—выдвиж-
ные щитки
www vokb-la.spb.ru - Самолёт своими руками9'
ла и его относительная толщина с, угол отклонения поверхности |
механизации, величина сдвига выдвижного закрылка, форма
щели между крылом и закрылком.
Влияние формы крыла в плане на эффектив- I
и о с т ь механизации. Отклонение щитка или закрылка
практически не влияет на производные слуа и дст’дсуа в преде- ?
лах линейного изменения коэффициентов cya=f(a) и cm=f(cyn)t
но оказывает существенное влияние на значение угла а при
c1ja=0, величина изменения которого определяется типом и гео-
метрическими параметрами механизации.
У стреловидных крыльев значительно меньше, чем у не-
стреловидных крыльев большого удлинения Чем больше угол
стреловидности крыла, тем меньше отношение суатжКсиа тах'х-о
и тем меньше эффективность механиза-
ции (рис. 19.20). Следует иметь в виду,
что для простых щитков н закрылков
снижение суа1азх вследствие стреловид-
ности гораздо ощутимее, чем для вы-
движных (рис. 19 21).
Эффективность механизации резко
снижается у стреловидных крыльев на
углах атаки, близких к критическому.
Например, при %=л/4, т] = 4, Х=4,5
отклонение щитка на угол б —л/3,
практически не дает прироста суа при
значениях а, близких к акр.
При углах стреловидности у (/4,
больших 0,9 рад, щитки и закрылки на
критических углах атаки почти всегда
ность. Аналогичное влияние на эффективность механизации ока-
зывает удлинение крыла: уменьшение удлинения крыла также
снижает эффективность механизации. Уменьшение толщины
профиля уменьшает прирост cyaniax-
Неблагоприятное влияние большой стреловидности и малого
удлинения на эффективность механизации и подъемную силу
крыла вызывает необходимость применения более сильных спо-
собов механизации, например, выдвижных щитков, выдвижных
закрылков и т. д. Кроме того, прибегают также к увеличению
сужения крыла в этом случае относительная площадь закрылка
увеличивается и в связи с этим увеличивается его эффектив-
ность. Иногда на верхней поверхности стреловидных крыльев иа
участках расположения закрылков устанавливают аэродинами-
ческие перегородки. В этом случае поток приближается к плос-
копараллельному, что и увеличивает эффективность закрылков.
Большой эффект дает применение управления пограничным сло-
ем методами сдува (см. рис 19 15) и отсоса, а также струйных
закрылков.
свою
11 626
321
www.vokb-la.spb.ru - Самолёт своими руками?!
19.4 ВЛИЯНИЕ БЛИЗОСТИ ЗЕМЛИ НА МАКСИМАЛЬНЫЙ
КОЭФФИЦИЕНТ ПОДЪЕМНОЙ СИЛЫ И ПОЛЯРУ К₽ЫЛА
При полете самолета вблизи земли (при взлете и посадке)
физические условия обтекания крыла изменяются, так как по-
верхность земли ограничивает поток снизу. В этом случае скос
потока за крылом не может
развиваться подобно тому, как
это происходит вдали от земли.
Рис. 19.22. Влияние близости земли на
распределение давления:
1- вблизи земли; 2—вдали от земли
1,0 \_____________1 л—ч,
0,2 0,4 0,6 0,8 1,0 1,2 h
Рис 19.23. Влияние близости зем-
ли на коэффициент подъемной
силы
В результате повышения давления под крылом на передней
кромке крыла резко увеличивается скорость, что приводит к пе-
рераспределению давления на профиле (рис. 19 22) Поскольку
увеличивается положительный градиент давления, такое пере-
распределение способствует отрыву пограничного слоя на верх-
ней поверхности крыла. В ре-
зультате перераспределения
давления на верхней и нижней
поверхностях коэффициент
подъемной силы при данном а
возрастает, при этом влияние
земли на подъемную силу су-
Рис 19.24. Влияние близости земли
на зависимость cyn — f(a) (б) и по-
ляру крыла (а):
1 вблизи земли, 2—вдали от земли
подъемной силы вдали от земли
щественио только вблизи зем-
ли, когда отношение расстоя-
ния фокуса крыла от земли (А) *
к полуразмаху крыла (1/2)
меньше единицы. В этом слу-
чае прирост коэффициента
подъемной силы у земли cyah
относительно коэффициента
может достичь 20 %. При
отклоненной вблизи земли механизации разрежение на верхней
поверхности крыла и градиент давления в его кормовой части
еще более увеличиваются, что приводит к более раннему отрыву
пограничного слоя. В этом случае наблюдается возрастание
322
www vokb-la.spb ru - Самолёт своими руками?
коэффициента суа и уменьшение критического угла атаки а и
максимального коэффициента подъемной силы (рис. 19.24, б).
Кроме того при полете вблизи земли сопротивление несколько
уменьшается вследствие уменьшения скоса потока за крылом
(поверхность земли не дает потоку скашиваться вниз).
Первое приводит к уменьшению сопротивления от сил давл
ния, а второе — к уменьшению индуктивного сопротивления
крыла В результате поляра крыла имеет меньший наклон и
смещается влево (рис. 19 24, а). Перераспределение давления
имеет еще более выраженный характер у крыла с отклоненной
механизацией (см рис 19.24) Для улучшения обтекания крыла
вблизи земли может использоваться отклоняемый вниз юсок
крыла Влияние близости земли, приводящее к уменьшению ин-
дуктивного сопротивления крыла, сводится как бы к увеличе-
нию удлинения крыла и оценивается введением фиктивного уд-
линения, определяемого по формуле 2.ф— (Хэф/2,23) (я 4Л + 2),
где h — hjll2\ Аэф — эффективное удлинение — см. формулу
(24.2). При удалении самолета от земли на расстояние, равное
примерно величине САХ, влияние земли исчезает.
Вопросы для повторения
1 Какие факторы ив какой мере влияют на величину мак-
симального коэффициента подъемной силы?
2. В каком месте возникает отрыв пограничного с оя при
больших углах атаки у прямого, трапециевидного и стреловид-
ного крыльев?
3 Какие меры принимают для предотвращения отрыва по-
граничного слоя на концевых участках стреловидного крыла?
4. Изобразите графически зависимость суа от угла атаки для
крыла с предкрылком и для крыла с закрылком. В чем состоит
отличие этих зависимостей?
5. Изобразите поляру крыла без механизации и с отклонен-
ными закрылками Как изменяется подъемная сила, лобовое со-
противление и качество крыла при отклонении закрылков? Как
отклонение закрылков влияет на клитический угол атаки?
Задачи
1. Определить максимальный коэффициент подъемной силы
кры а трапециевидной формы в плане с распределением цирку-
ляции вдоль размаха по закону эллипса, если площадь крыла
--32 м, хдлинение крыла Л—8, сужение т] = 5, максимальный
допустимый коэффициент подъемной силы сечения ^Отзхсеч= 1,72.
Решение. Воспользуемся методикой ЦАГИ, опреде. яя
суашахкр ИЗ СООТНОШенИя С,,„ , =(/’,, //• )
F п max кр V ya max сеч/'£« сеч/ппп* ДЛЯ ОП-
ределения суас^.ч предварительно определим геометрические раз-
меры крыла н распределение циркуляции.
и* 323
www.vokb-la.spb ru - Самолёт своими руками?!
Размах крыла I — У8• 32 = 16м.
п_______ с__г,Ьк + т\Ь к
Площадь крьпа 8=2-----------—
ходим величину концевой хорды
b 2S 2-32
h — I (1 +4) —16(Ц-5)
2
Корневая хорда bQ—т]йк=5-------—
3
Средняя геометрическая хорда йср
По условию задачи закон распределения циркуляции по раз-
маху крыта эллиптический, значит
b(—У—1 или Г2-Р<г2=1,
\ Z/2 ) 1
Г= —
г
Ынах
max
2
I
2
bKl
2 (1 +1!), откуда на-
2 _
3
3,33
S
0,67 м.
м.
32 2 м
— — — .
— Z
Z —— .
Z/2
Подставляя в это уравнение значение циркуляции скорости,
выраженной через осреднениую по размаху циркуляцию, на ос-
новании формулы для площади эллипса Гтах
Ггср^-]Чг2-1.
L 4 1
Используя уравнение связи
Суа сеч Н Суа кр 1, О \ ЧИМ Суа сеч Г<;р
Расчеты сводим в таблицу:
где
л
Гср, получим
(17-14)
^Ср
— , где
и полагая
b (z')=bQV 1 — z.
Отношение величин г 0 0,2 0,4 0,6 0,8 0,85 0,9 0,95 1,0
г/гср 1,27 1.25 1,17 1,02 0,76 0,67 0,55 0,40 0
bjb^ 1,67 1,40 1, з 0,87 0,60 0,53 0,47 0,40 0,33
сУа сеч 0,762 0,891 1,032 1,171 1,273 1,265 1,180 0,994 0
Суа шах сеч/£(,сеч 2,26 1,93 1,66 1,47 1,35 1 36 1,46 1,73 СЮ
Далее графическим путем находим суотахкр = 1,35.
2. Для условий предыдущей задачи построить поляру крыла,
если скорость полета у земли У = 250 км/ч, относительная тол-
щина профиля с —0,14, точка перехода ламинарного погранич-
ного слоя в турбулентный xT = 0,2; <3cjro/da = 4,6; 6=0,06 рад,
угол нулевой подъемной силы ао = —0,026 рад. Построить также
зависимость коэффициента подъемной силы от угла атаки и на-
нести углы атаки и а поляру крыла.
www vokb-la.spb.ru - Самолёт своими руками?!
ГЛАВА 20
АЭРОДИНАМИКА КРЫЛА НА ДОЗВУКОВЫХ
И ОКОЛОЗВУКОВЫХ СКОРОСТЯХ
20.1. ВЛИЯНИЕ СЖИМАЕМОСТИ ВОЗДУХА
НА АЭРОДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ КРЫЛА
КОНЕЧНОГО РАЗМАХА В ДОЗВУКОВОМ ПОТОКЕ
При приближении скорости полета к скорости звука заметнее
становится влияние сжимаемости воздуха. Для оценки влияния
сжимаемости на характеристики крыла конечного размаха поль-
зуются гипотезой плоских сечений, предполагая, что аэродина-
мические свойства отдельных сечений крыла полностью опреде-
ляются условиями обтекания в этих сечениях (скоростями и уг-
лами атаки). Гипотеза плоских сечений, как показывает срав-
нение расчетных и опытных данных, применима для крыльев
сравнительно больших удлинении (Х>3) В первом приближении
аэродинамические характеристики профиля в дозвуковом потоке
связаны с аэродинамическими характеристиками профиля в
несжимаемом потоке соотношениями, полученными на основании
линеаризации уравнения (14.10):
сЧд нс .сеч
И/а сж.сеч ~ /----х-
У i-mL
г ОО
(20 1)
Г
1 т сж.сеч
нс.сеч
(20. 2)
Выражение для коэффициента суа крыла конечного размаха
имеет вид
Суа сеч (^)
I
2
Используя в случае сжимаемой жидкости для гуосеч соотно-
шение (20.1), где Гранссеч — коэффициент подъемной силы сече-
325
www vokb-la.spb ru - Самолёт своими руками?!
ния крыла, имеющего удлиюние V 1—М^>, и стреловид-
ность Хнс> и учитывая, что •
/1-М1, dz=dzx, S= Sm /l-ML,
на основании гипотезы плоских сечеиии, получим
ги .ж - . (20.3)
Аналогичным путем можно получить зависимость для коэф-
фициента момента
20.4)
Vi-Ml
где cmHC — коэффициент момента относительно перед юй кромки
сечения крыла с удлинением Хнс и уг ом стреловидности %пс.
Коэффициент подъемной си ы крыла суа нс в области лииеииой
зависимости cya=f (а) с учетом равенства
суа нс — нс 01 О0),
где с*уа нссогласио (18.9)
уа нс
ЛЯХ—оо
V1 + tg2 Хне -ь
" у а)-. = оо
лАнс
причем х з и Хне связаны с действительным углом стреловидно-
сти соотношениями
tgZm=-7=^==, м2
(20.5)
Переходя от величии Хне. Хне, соответствующих несжимаемому
потоку, к аналогичным величинам для крыла в дозвуковом по-
токе, преобразуем выражение для г“я к виду
с*
уа стрхж
2
Ct
1/лХ=оо
лХ
(20. 6)
На углах атаки, близких к критическому, ежнм емость воз-
духа оказывает влияние иа н сущие способности крыла. С уве-
чичением скорости полета (числа М) измвияетс и распредече-
ние давления по поверхности крыла, вследствие чего при очном
и том же у ле атаки несколько увеличивается значение коэф-
фици 'ита подъемной силы (рис. 20.1). Однако благодаря сжи-
326
www.vokb-la.spb.ru - Самолёт своими руками?!
маемости воздуха увеличиваются также градиент давления на
верхней поверхности крыла и толщина пограничного слоя. Од-
новременный рост градиента давления и толщины пограничного
слоя приводят к преждевременным по сравнению с потоком не-
сжимаемой жидкости отрыву потока сжимаемой жидкости н
тряске, т. е. к уменьшению угла атаки возникновения тряски.
Поэтому величина CyaTp с увеличением числа М уменьшается.
Рис. 20.1. Влияние числа М на
зависимость су„=/(а) для са-
молета Ту-134
1—продувки; 2—летные испытания
Например, для крыла самолета
Ту-134 при М=0,6 угол тряски
аТр = 11 И Суа 1, а при
= 0,82 атр=5 3' и сутр= 0,49. Кри-
тический угол атаки акр и коэф-
фициент Суитах с увеличением
Суа так &кр
Рис. 20.2. Изменение коэффи-
циента Суа так И СХкр В ЗЗВИСИ-
мости от числа Мм для само-
лета Як-40
числа М уменьшаются, так как отрыв пограничного слоя прн
большой скорости происходит при меньшем угле атаки
(рис 20.2).
Выражение для коэффициента лобового сопротивления кры-
ла конечного размаха имеет вид
1 1/2
ха г Cxacz4b (z) dz,
О *)
—Z/2
где
С ха сеч сеч Т сеч-
На изменение лобового сопротивления крыла в полете индук-
тивное сопротивление оказывает более значительное влияние по
ср внеиию с профильным При безотрывном обтекании коэффи-
циент профильного сопротивления крыла не зависит от суа н
равен коэффициенту сопротивления при Суа = 0 схр—сх0. Коэф-
фициент индуктивного сопротивления зависит от коэффициента
327
www.vokb-la.spb ru - Самолёт своими руками?!
подъемной силы, удлинения и сужения крыла и определяется
соотношением ,
exi=-^~ (1+8).
ЯЛ
Уравнение поляры крыла в дозвуковом потоке имеет вид
с2
(1 + 4- (20.7)
ЯЛ
Влияние числа на индуктивное сопротивление учитыва-
ется тем, что в формулу (21.7) входит величина суа, зависящая
от числа Л!™. Влияние числа М» на профильное сопротивление
учитывается дополнительным коэффициентом т]м, который мо-
жет быть определен по графикам.
20.2. КРИТИЧЕСКОЕ ЧИСЛО М КРЫЛА КОНЕЧНОГО РАЗМАХА
Критическим числом М крыла, как и профиля, называют та-
кое число М невозмущенного дозвукового потока, прн котором
на поверхности крыла появляются местные сверхзвуковые зо-
ны скоростей.
Критическое число М отделяет дозвуковой режим обтекания
крыла от смешанного (трансзвукового), когда на поверхности
крыла имеются зоны дозвуковых и сверхзвуковых местных ско-
ростей. Число МКр является весьма важной характеристикой,
так как при его достижении аэродинамические характеристики
крыла претерпевают значительные изменения.
Методы определения Мкрпроф позволяют определить величи-
ну Мкр, приемлемую только для прямого крыла бесконечного
размаха Для реальных крыльев из-за наличия стреловидно-
сти и малого удлинения, приводящих к пространственному
характеру обтекания, величина Мкр отличается от М1(рПроф.
Увеличение стреловидности крыла до 35° повышает число Мкр
на 0,06—0,15 по сравнению с МкрпРоф. Точные методы расчета
Мкр для стреловидного крыла не разработаны вследствие слож-
ности учета влияния срединного и концевого эффектов обтека-
ния крыла на Мкр. Поэтому для практических целей наиболее
надежными являются экспериментальные данные по определе-
нию влияния стреловидности крыла на величину Мкр.
Приращение ДМнрх числа М.кр при изменении угла стреловид-
ности, измеренного по линии максимальных толщин, показано
на рис 20 3. Пользуясь этим графиком, во-первых, можно убе-
диться в весьма заметном влиянии стреловидности, особенно при
сравнительно малых Мкр> во-вторых, в том, что любое увеличение
угла стреловидности крыла конечного размаха ие позволяет по-
лучить значение МКР, превышающее единицу, т. е. число Мкр
всегда меньше единицы. Это вытекает из того, что при Моо—
328
www vokb-la.spb.ru - Самолёт своими руками
всегда вблизи поверхности крыла можно иайти зону, в пределах
которой местная скорость больше скорости иевозмущеииого по-
тока С этой зоны и начнется развитие волнового кризиса, когда
местная скорость сравняется с критической скоростью аьр.
Уменьшение удлинения крыла X меиее эффективно увеличи-
вает Мкр, чем увеличение стреловидности крыла. Для определе-
ния приращения ДМКрк можно вос-
пользоваться графиком иа рис. 20.4,
который показывает, что при удли-
нении, большем двух, эта прибавка
МКр ие достигает одной сотой и мо-
жет ие учитываться.
Рис 203 Изменение ДМкр*
в зависимости от пр(1ф
для различных углов стре-
ловидности по линии макси
мальных толщин
Рис 20.4 Изменение ДМкрк
в зависимости от М|<рПроф
(^0=0) для различных уд-
линений крыла
Поскольку удлинение крыльев современных дозвуковых пас-
сажирских самолетов составляет величину порядка 8—12, то для
них изменение удлинения существенно не влияет иа величину
Мкр Совсем другое наблюдается в сверхзвуковой авиации, где
крылья малых удлинений (Х<2) применяются довольно часто.
Таким образом, в общем случае для Mltp крыла можно за-
писать соотношение:
^^кр.п рОф+АМкрхЦ-ДМкрл. (20 8)
20 3. АЭРОДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ КРЫЛА
ПРИ ОКОЛОЗВУКОВЫХ (ТРАНСЗВУКОВЫХ) СКОРОСТЯХ ПОЛЕТА
Превышение в полете числа Мьр всегда связано с появлени-
ем сверхзвуковых зон, замыкающихся скачками уплотнения По
мере возрастания Мж сверхзвуковые зоны развиваются, распро-
страняясь довольно быстро к задней кромке крыла и сравнитель-
но медленно к передней. При Мж=1 дозвуковая зона сохраня-
ется в основном вблизи передней кромки крыла
При Моо> 1 перед закругленной передней кромкой крыла
возникает прямой скачок уплотнения, фронт которого на удале-
329
wwxt vokb-la.spb.ru - Самолёт своими руками?!
нии от крыла изгибается, переходя в косой скачок. По мере
увеличения числа М™ скачок приближается к передней кромке,
дозвуковая зона сокращается. При числах Мтс порядка 1,3—1.4
для крыльев с острой передней кромкой носовой скачок стаио-
Рис 20 5. Изменение производ-
ной с“а в зависимости от чис-
ла Мео для крыльев различной
стреловидности
вится косым и «садится» иа пе-
реднюю кромку. Начиная с этого
момента, трансзвуковой режим
обтекания переходит в сверхзву-
ковой. Закономерности, справед-
ливые для трансзвуковых тече-
ний, уступят место закономерно-
стям для сверхзвуковых течений,
когда по всей поверхности крыла
скорости станут сверхзвуко-
выми.
Теория околозвуковых режи-
мов обтекания позволяет сделать
в основном лишь качественный
анализ таких течений ввиду ис-
ключительной сложности их ма-
тематического описания.
Коэффициенты подъемной силы крыла при околозвуковом ре-
жиме обтекания определяются с помощью уравнения суа —
~суа (а-~ао), справедливого в пределах линейной части зави-
симости cya=f(ct) В сжимаемой среде коэффициент подъемной
силы и производная i с*а для крыла конечного размаха зави-
сят от угла стреловидности, удлинения и числа Мж. Производ-
ная возрастает с увеличением числа М«,, при этом у стрело-
видных крыльев увеличение с“а с ростом чител М«> происходит
в меньшей степени, чем у прямого крыла (рис. 20.5). Отсутству-
ет у стреловидного крыла участок резкого падения производной
г“а, характерный для прямого крыла В значительной степени
на величины са t и суа влияет удлинение крыла- с уменьшением
X величина г“а уменьшается.
Таким образом, в дозвуковом потоке с возрастанием чисел
Моо подъемная сила крыла увеличивается, однако это увеличе
ние тем меньше, чем больше стреловидность и меньше удлине-
ние крыла. Величину г“а обычно находят по графикам, постро-
енным иа основании экспериментальных данных, дающих зави-
симость
“ f 3 у g X
xtgz.’i.x/T),
где X]/1— Xtgx,r), Ху с— параметры подобия в околозвуко-
вом режиме, устанавливаемые теорией подобия.
330
www vokb-la.spb.ru - Самолёт своими руками?!
На рис. 20.6 для одного семейства крыльев приведен график
зависимости
k/1-M2 , Х1Лс ).
J \ • со’ Г ]
Сплошными линиями показаны результаты эксперимента для
одного семейства крыльев с постоянным сужением и неизменным
углом стреловидности.
Лобовое сопротивление крыла в околозвуковом потоке отли-
чается от сопротивления в дозвуковом потоке иа величину до-
полнительного сопротивления, называемого волновым.
Коэффициент лобового сопротивления крыла определяется
по обычной формуле
С ха ~~ CtO Н- ^хг (20.9)
Первое слагаемое схо не зависит от подъемной силы и скла-
дывается из сопротивления треиия в пограничном слое cf и вол-
нового сопротивления сл-ов-
Коэффициент соп-
ротивления трения с/
определяется с помо-
щью формул и графи-
ков, справедливых для
дозвуковых режимов
обтекания. Коэффици-
ент схов, учитывающий
волновое сопротивле-
ние при су(1=0, опре-
деляется опытным пу-
тем
Второе слагаемое
^xi в формуле (20 9)
представляет собой
сопротивление, зави-
^х0 f “F ^хОв-
(20. 10)
Рис. 20 6 График зависимости
са ___________
-2 = /П1-м^ х’/г)
А
сящее от коэффициен-
та подъемной силы. Поскольку на крыле имеются дозвуковые и
сверхзвуковые зоны течения, то эта составляющая по величине
занимает среднее положение между индуктивными сопротивле-
ниями при дозвуковом и сверхзвуковом режимах обтекания.
Приближенный метод определения индуктивного сопротивле-
ния, разработанный С И. Кузнецовым, заключается в следую-
щем Чем больше коэффициент подъемной силы, тем меньше
соответствующее ему критическое число М и, наоборот если за-
даться значением Мкр, то волновой кризис по мере увеличения
cva возникает при вполне определенном его значении, которое
назовем суакр.
331
www.vokb-la.spb.ru - Самолёт своими руками?!
Связь между Мкр н Суокр для верхней поверхности крыла по-
казана иа рис. 20.7.
Рис. 20 7. Зависимость критического
коэффициента подъемной силы суа кр
от числа Мкр для верхней поверхно-
сти крыла
Рис. 20 8. К расчету ин-
дуктивного сопротнвле*
ния крыла при Мм>М1р
Если С1/а^СуаИр, то индуктивное сопротивление возникает за
счет угла скоса Да и определяется по обычной формуле
с2
гх/=^-(Н-8). (20.1В
ЛА
При суа>Суакр дополнительное увеличение подъемной силы н
сопротивления происходит за счет сверхзвуковых зон. При этом
предполагается, что дополнительная аэродинамическая сила
Д/?А в соответствии с законом сверхзвукового обтекания (см.
гл. 16) будет перпендикулярна к хорде крыла, т. е. будет состав-
лять угол а с нормалью к направлению потока (рис. 20.8).
Проектируя силы /?А и Д/?А иа оси координат в скоростной
системе и полагая ввиду малости угла атаки и угла скоса пото-
ка cos a^cos Aa^'l; sin а^а, получим формулы для подъемной
сизы крыла и индуктивного сопротивления:
^--^кр+д^Л/крН-дЯла
нли, переходя к аэродинамическим коэффициентам.
Суа г//«кр“1“ C-xl СхIкр 4~ > (20. 12)
где сХгКр — коэффициент индуктивного сопротивления, определя-
емый по формуле (20.11) при суа~ суаКр.
Исключив из уравнений (20 12) величину Дсуа и заменив
Сггкр согласно (20.11), получим
с2
^(=— °- 1+») -Mrw-t-WKp) a- (20.13)
ЛА
332
www vokb-la.spb.ru - Самолёт своими руками?!
Предполагая, что на околозвуковых режимах справедлива
зависимость ^й=с“аа, формулу (20 13) можно привести к виду
xi
(i_p5)4
(с'/а — сУ<хкр) сУа
Суа
(20. 14)
Величина суокр для каждого числа М полета определяется по
графику. Расчеты показывают, что данные, получевные по фор-
м лпе (20.14), довольво близки к давным, полученным опытным
путем. Нужно только помнить, что
При Суа •Cyait'p ВОЛВОВОИ КрнЗНС ОТ-
'О®
сутствует и в этом случае следует
пользоваться формулой (20.11).
Ураввевие поляры можно полу-
чить, если в равенство (20.9) под-
ставить значение коэффициента ин
дуктнвиого сопротивления согласно
(20.14):
^ха — Cxq
0<Moo<0J55
Рис. 20 9 Поляры крыла для
различных чисел МК) (?.=7,
с=0,09, /г—0,52 рад)
Суа
Суа-
(20.15
£
J22L (1-{-8)-[-
лА
сУа сУакр
Поляры крыла в координатах cva н сха для различных чисел
Моо, построенные по уравнению (20.15), приведены на рис 20 9
Характер поляр для различных чисел Мтс можно проанали-
зировать с помощью графика, приведенного иа рис. 20 7 Пло-
щадь графика разделим на три зоны. В зоне 1 волновое сопро-
тивление отсутствует во всем диапазоне звачевий суа, и поляры
крыла на этих числах Мте выражаются уравнением поляры для
дозвукового потока. Зова I заканчивается числом М^—0,65.
В зоне //, соответствующей числам 0,650,8 волновой
кризис начинается при достижении значения су«=суакр Таким
образом, при малых значениях суа потяры этого диапазона сов-
падают с полярой в дозвуковом потоке, а вачиная с cva=cvavp
и выше — отклоняются вправо. В зоне III волновое сопротивле-
ние будет даже при суа=0 С дальнейшим увеличением чисел
Мто вачииая с Мкр(суи—0) поляры смещаются вправо и ии при
каких значениях суа ие совпадают с полярой крыла в дозвуко-
вом потоке.
20.4. МОМЕНТНЫЕ ХАРАКТЕРИСТИКИ КРЫЛА
Коэффициент момента крыла относительно оси проходящей
через переднюю кромку эквивалентного прямоугольного крыла,
333
www.vokb-la.spb ru - Самолёт своими руками?!
определяется, как и для дозвуковых режимов, соотношением
Ст=СгпЪ xFcyat (^0. 16)
гдс xF — безразмерная координата фокуса крыла.
Рис. 20 10 Изменение коор-
динаты центра давления
изолированного крыла с
симметричным профилем в
зависимости от параметров
околозвукового подобия-
а—для прямого крыла (Mg х =
—0); б—для стреловидного
(Atg Хс=3,0)
К настоящему времени уже накоплен достаточный экспери-
ментальный материал, позволяющий судить о положении фоку-
са крыла для довольно широкого диапазона условий обтекания.
Опыт показывает, что порученные из линейной теории критер] и
подобия достаточно хорошо позволяют обработать эксперимен-
тальный материал в виде зависимостей
— / г------- ъ/—\
—/(>-/1- Xtgz,Ti5X|/г).
На рис. 20.10 приведены два графика — дня прямого и стре-
ловидного крыльев с симметричным профилем (хр=хд). Кривые,
представленные на обоих графиках, соответствуют значениям
Хус =0,5 [33].Из графиков следует, что для крыльев с малым
сужением -q, и особенно для прямых крыльев, фокус смещается
334
www.vokb-la.spb.ru - Самолёт своими руками?!
вперед при приближении Моо к Мкр. Для большинства крыльев,
однако, характерно, что фокус, находящийся при Моо <Мкр при-
мерно на расстоянии одной четвертой хорды от передней кром-
ки, при больших значениях Моо смещается назад, достигая поч-
ти середины хорды.
Экспериментальные кривые иа рис 20.10 позволяют сделать
вывод, что в околозву ковом диапазоне чисел Мто возможны весь-
ма существенные смещения фокуса вперед и назад Это можно
объяснить более ранним развитием сверхзвуковой зоны сначала
на верхней, а затем на нижией поверхностях крыла. Экспери-
менты показывают, что с увеличением угла атаки в околозвуко-
вом режиме фокус смещается назад, особенно при малых значе-
ниях параметров Zig/ и за-
считан в первом приближении зависимость от а в диапа-
зоне углов атаки 0,1 <«<0,4 рад линейной, можно величину
безразмерной координаты xF в этом диапазоне угол атаки опре-
делить по формуле:
= 4 (а*А-о,4- (20.17)
U 5 О
Величины (л>)0-о,1 и (Дхг а=0,4 определяются с помо-
щью графиков.
Вопросы для повторения
1. Какое влияние оказывает сжимаемость воздуха на несу-
щие способности крыла?
2. Как зависит Мкр крыла от его геометрических параметров?
3. Напишите уравнение поляры крыла иа до- и околозвуко-
вых режимах полета.
4. Проанализируйте моментные характеристики крыла.
Задачи
1. Определить коэффициент с“а для стреловидного крыла,
обтекаемого сжимаемым дозвуковым потоком, при условии, что
в несжимаемом потоке = 5,1; %=0,78 рад; Х=6; тСТр=
= 0,15; Моо-0,83.
Ответ: с° —3,5.
у а стр. сж ’
2. Определить Мкр самолета при следующих условиях;
М1{рПроф=0,85, угол стреловидности крыла %= 1,05 рад, удлине-
ние крыла к—1,2.
Ответ: Мкр=0,97.
WWwvokb-la.spb.ru - Самолёт своими руками?!
ГЛАВА 21
АЭРОДИНАМИКА КРЫЛА
В СВЕРХЗВУКОВОМ ПОТОКЕ
21.1. ВЛИЯНИЕ ФОРМЫ КРЫЛА В ПЛАНЕ НА ХАРАКТЕР
ЕГО ОБТЕКАНИЯ СВЕРХЗВУКОВЫМ ПОТОКОМ
В сверхзвуковом потоке, так же как и в дозвуковом, форма
крыла в плане существенно влияет на характер его обтекания,
что обуславливает отличие аэродинамических характеристик
Рис. 21 I. Влияние концов крыла
при обтекании его сверхзвуковым
потоком
(рис. 21 1). Угол полураствора
из сотношения
крыла конечного размаха от
характеристик профиля в
сверхзвуковом потоке. Однако
влияние концов крыла, стре-
ловидности и величины удли-
нения при сверхзвуковых ско-
ростях иное по сравнению с
влиянием этих факторов на
характер обтекания при дозву-
ковых скоростях.
Как известно, в дозвуковом
потоке влияние концов крыла
ощущается на всей его поверх-
ности. В сверхзвуковом потоке
зона возмущений, генерируе-
мых концами крыла, ограничи-
вается двумя конусами возму-
щения с вершинами в перед-
них точках боковых кромок
)нуса возмущения определяется
или tgp=- - = = ' (21. 1>
Вне конусов возмущения влияние концов крыла ие ощущает-
ся. Если при дозвуковом обтекании влияние концов распростра-
336
www vokb-la.spb.ru - Самолёт своими руками?!
няется на всю поверхность крыла S — bl, то при сверхзвуковом
обтекании нх влияние ощущается лишь на площади S'.
В случае прямого крыла с учетом (21.1) получим
_
н отношение площадей
S' _ I
5 Ы /м2то-1 хКм1-1
Следовательно, оценить влияние концевых эффектов на ве-
личину аэродинамических коэффициентов можно с помощью
Рис. 212. Обтекание сверхзвуковым пото-
ком крыла произвольной формы в плане
произведения ь Чем больше удлинение крыла Л или
число Мео, тем меньше доля возмущенных зои S' в общей пло-
щади крыла S, а значит, н меньше влияние концов иа аэродина-
мические характеристики крыла Таким образом, скашиванием
концов крыла под углами, большими угла ц, устраняется влия-
ние концевых эффектов. Значительно большее влияние иа харак-
тер обтекания крыла конечного размаха оказывает положение
передней кромки относительно вектора скорости набегающего
потока. Рассмотрим обтекание под малым углом атаки тонкого
крыла некоторой произвольной формы в плайе (рис. 21.2), пола-
гая при этом, что любая точка на поверхности крыла, в том чис-
ле н любая точка на передней кромке, является источником ма-
лых возмущений. Эти возмущения от каждой точки распростра-
няются внутри конуса с углом полупаствора ц, определяемым
соотношением (21 1)
На участке BD передняя кромка крыла обтекается иевозму-
Щеииым потоком, поскольку все возмущения не выходят вперед
за пределы передней кромки (см., например, возмущения в точ-
ке С). На этом участке в избегающем потоке вплоть до самой
337
www.vokb-la.spb.ru - Самолёт своими руками?!
передней кромки не чувствуется присутствие крыла. Скорость,
давление, плотность в потоке не изменяются до соприкоснове-
ния его с передней кромкой. Такой характер течения типичен
для сверхзвукового обтекания заостренного профиля. Поэтому
в этом случае передняя кромка иазывается сверхзвуковой.
На участке АВ (точка £) поток еще до встречи с передней
кромкой проходит через зону возмущения. В этом случае пара-
метры потока начинают изменяться еще до того, как поток до-
стигнет передней кромки. Такая картина течения характерна для
дозвукового обтекания и поэтому передняя кромка при таких
условиях иазывается дозвуковой.
Если передняя кромка дозвуковая, то потоки и а верхней и
нижией поверхностях крыла взаимодействуют между собой че-
рез дозвуковую кромку. Можно показать, что у дозвуковой пе-
редней кромки нормальная составляющая скорости потока мень-
ше скорости звука, а у сверхзвуковой — больше. Из условия
обтекания передней кромки в точке Е можно записать зависи-
мость между углами стреловидности и полураствора конуса воз-
мущения р в виде
Х>^-И (21-2)
... - 1
откуда cos^<ysinp—------.
Из этого неравенства следует, что Mojcos х<П или VooCos %<;£?.
Так как К*.cos %— lzn, то окончательно можно записать
1/л<а. (21.3)
Следовательно, для дозвуковой передней кромки в сверхзву-
ковом потоке справедливо соотношение (21.3).
При анализе сверхзвукового обтекания конечного размаха ис-
пользуются безразмерные критерии. Так из неравенства (21 2)
следует
tgX>tg —f^=ctgu — -2—
\ 2 } tgg
или с учетом (21.1) получим
(21.4)
Если умножить обе части этого неравенства иа величину уд-
линения крыла X, то получим условие дозвукового характера
обтекания передней кромки в наиболее часто употребляемом ви-
де:
(21.5)
где х — угол стреловидности по передней кромке крыла. Величи-
на ktgx иногда называется приведенной стреловидностью, а
X У— 1 — приведенным удлинением
338
www.vokb-la.spb.ru - Самолёт своими руками?!
Для сверхзвуковой кромки (точка С на рис. 21 2) угол
у<л/2-—р, поэтому в соответствии с (21.4)
(21.6)
и ^<^<=1. (21.7)
Неравенство (21.6) равносильно утверждению, что нормаль-
ная составляющая скорости невозмущенного потока на сверх-
звуковой кромке всегда больше скорости звука в невозмущен-
ном потоке.
Когда лииин возмущений проходят вдоль передней кромки,
тогда
‘8Х = ^А^1; (21.8)
XtgX=X]/M^l (21.9)
и передняя кромка называется звуковой.
Как это следует из теории крыла в сверхзвуковом потоке вы-
ражения XtgJx и 1 являются критериями сверхзвуко-
вого подобия.
При расчетах иногда приходится говорить о дозвуковой и
сверхзвуковой задних кромках, сверхзвуковой и дозвуковой ли
иии максимальных толщин и т. д. В этом случае в неравенствах
(21.5) и (21.9) угол стреловидности % замеряется относительно
соответствующих линий.
Распределение давления по хорде крыла, а также величины
аэродинамических коэффициентов у крыльев с дозвуковой и
сверхзвуковой кромками существенно различны.
Как уже отмечалось, сверхзвуковой поток, набегающий иа
заостренную сверхзвуковую переднюю кромку крыла, остается
невозмущенным вплоть до соприкосновения с передней кромкой
(рис 21.3, а). Передняя кромка разделяет при этом поток на
верхнюю и нижнюю части, не взаимодействующие одна с дру-
гой
В случае дозвуковой передней кромки (см. рис 21.3, б) на
крыло набегает уже возмущенный поз ок, и поэтому потоки иа
верхней и нижней поверхностях взаимодействуют друг с другом:
при положительном угле атаки наблюдается перетекание потока
с иижией поверхности крыла на верхнюю Критическая точка
смещается вниз относительно передней кромки крыла, при этом,
поскольку кривизна передней кромки очень большая, струи оги-
бают переднюю кромку с большой скоростью: на верхней поверх-
ности крыла вблизи передней кромки возникает сильное разре-
жение, которое создает подсасывающую силу, направленную
339
www vokb-la.spb ru - Самолёт своими руками?!
Г
вперед и уменьшающую индуктивное сопротивление крыла (рис.
21.4):
^под-
Подсасывающая сила возникает только
передней кромки и только на углах атаки,
в случае дозвуковой
КОГДа при
Рис 21 3 Обтекание крыла бесконечного размаха со сверхзву-
ковой (а) и дозвуковой (б) передними кромками
этом ее величина существенно зависит от геометрических харак-
теристик крыла. Для увеличения подсасывающей силы при до-
звуковой передней кромке носок профиля крыла слегка притуп-
ляют (закругленный носок), что позволяет получить при прочих
равных условиях более повышенную подсасывающую силу.
Рйс 21 4. Изменение ко-
эффициента индуктивно
го сопротивления тре
в зависимости от числа
с учетом влияния
подсасывающей силы (2)
и без нее (1)
угольного крыла
Кроме того, критические углы атаки у крыльев с закругленным
носиком оказываются значительно больше, чем у крыльев с за-
остренным носиком, что имеет важное значение для обеспече-
ния малых скоростей взлета и посадки
340
«'«'и vokb-la.spb.ru - Самолёт своими руками?!
Коэффициент подсасывающей силы для треугольного крыла
в сверхзвуковом потоке может быть подсчитан по формуле
1 — Mi, cos2 7
^=”7- ------------• (21. 10)
4л cos х
Из этой формулы следует зависи*
ад ость
ст, [ УС-i \
tgx с|в \ tgx !
которая графически представлена иа
рис. 21.5 При дозвуковой передней
кромке (Moo<l/cosx), СподТ^О. При
звуковой передней кромке (Мсо =
= l/cosx) коэффициент подсасываю-
щей силы равен нулю. Подсасываю-
щая сила не может быть реализована
Рис 21 5 К определению
коэффициента подсасы-
вающей силы
во всех тех случаях, когда в окрестности передней кромки про-
исходит срыв потока Действительная подсасывающая сила по
опытным данным примерно в два раза меньше расчетной. Прак-
тически реализация эффекта подсасывающей силы в вязкой
среде до настоящего времени вызывает затруднения.
21.2. ПОДЪЕМНАЯ СИЛА КРЫЛА В СВЕРХЗВУКОВОМ ПОТОКЕ
Величина подъемной силы, а следовательно, и величина ко-
эффициента подъемной силы крыла конечного размаха из-за
влияния формы крыла в плане отличается от аналогичных вели-
чин профиля иа том же угле атаки а Имеющиеся теоретические
расчеты выполнены только для сравнительно простых форм кры-
льев, и, как правило, для сверхзвуковых передних кромок.
Рассмотрим вначале обтекание невязким газовым потоком
стреловидного цилиндрического крыла бесконечного размаха,
полагая при этом, что обтекание крыла в этом случае характе-
ризуется только нормальной к передней кромке составляющей
скорости Уп=Утесозх, а другая составляющая скорости VT~
= VooSinx, параллельная передней кромке, не вызывает ника-
ких изменений в распределении давления по крылу, что спра-
ведливо для невязкого потока Следовательно, в каждой плоско-
сти, перпендикулярной к передней кромке крыла, поле скоро-
стей будет одним и тем же. Это означает, что коэффициенты
давления, подъемной силы и сопротивления скользящего крыла
можно определить по значениям таких коэффициентов, соответ-
ствующим сечению (профилю) крыла в плоскости, перпендику-
лярной к передней кромке Скорость и число Мто, по которым
следует определить указанные коэффициенты, соответственно
341
www.vokb-la.spb.ru - Самолёт своими руками?!
равны Vn= Ко cos х, Mn=MooCosx- Расчет характеристик сколь-
зящего крыла по формулам, полученным для тонкого профиля в-
сверхзвуковом потоке, можно производить в тех случаях, когда
нормальная составляющая скорости набегающего потока на пе-
реднюю кромку крыла К—VooCos х>аоо, а соответствующее
число Мп — MooCosx> 1.
Угол атаки профиля а?1 связан с заданным углом атаки а
скользящего крыла соотношением sin an—sin а/cos /, а при ма-
лых углах атаки ап = a/cos х-
Тогда, используя формулу для давления на профиле в сверх-
звуковом потоке, получим зависимость для коэффициента давле-
ния на скользящем крыле:
Рп— +2а (cos уcos2 z — 1).
Знак « + » здесь соответствует коэффициенту давления на
нижней поверхности крыла, а знак «—» па верхней поверхно-
сти.
В этой формуле коэффициент давления отнесен к скоростно-
му напору —~— = 0,5йрооМ2.
Чтобы получить коэффициент давления р, отнесенный к ско-
ростному напору набегающего потока следует
воспользоваться формулой p=pncos2%, откуда получим
р= ±2а cos Z/КМ^ cos2 у— 1
или р= + са, где г
2 cos х
У M^cos2 х— 1
Чем больше угол скольжения у, тем больше будет коэффи-
циент с, однако с увеличением числа Мж влияние угла у умень-
шается. Таким образом, наличие угла скольжения приводит к
увеличению коэффициента давления на нижией поверхности
крыла и уменьшению иа верхней
Учитывая, что для плоского крыла суа=(ри pB)cosa, а при
малых углах атаки cosa^l, sin a ~a, для коэффициента подъ-
емной силы скользящего крыла получим
ИЛИ Суа
'уа - 4a cos х V los3 у — 1
4а 4a
(21.11)
MJ———
cos2 x
Из этой формулы следует, что коэффициент подъемной силы
скользящего крыта большого удлинения возрастает с увеличени
342
www vokb-la.spb ru - Самолёт своими руками?!
ем угла скольжения %. Это справедливо при условии, что перед-
няя кромка крыла сверхзвуковая. Увеличение коэффициента
подъемной силы скользящего крыла или стреловидного крыла
очень большого удлинения в сверхзвуковом потоке с возраста-
нием чисел Мое является следствием принципиального различия
между дозвуковым и сверхзвуковым характером обтекания (при
дозвуковом обтекании, как известно из гл. 18, скольжение умень-
шает коэффициент подъемной силы).
Обращаясь к крыльям конечного размаха, заметим, что для
крыла прямоугольной формы в плане, обтекаемого сверхзвуко-
вым потоком без скольжения, теоретически получено выражение
для коэффициента подъемной силы:
1
2Х V'М^ ~ 1
____ 4а
Ст~ /с
при ус; овин, что параметр XV — 1^>2Г линии АА' и ВВ' (см.
рис 21 1) ие пересекаются на крыле. Для треугольного крыла
со сверхзвуковой передней кром-
кой теоретически получено выра-
жение для коэффициента подъем-
ной силы:
(21. 12)
_____ 4а
Суа~
Как видим, коэффициент подъ-
емной силы треугольного крыла
при сверхзвуковой передней
кромке такой же как у профиля
и не зависит от угла стреловид-
ности. Для треугольного крыла
всегда произведение Xtgx0 —4,
в чем легко убедиться путем гео-
метрических построений. Следо
вательно, этот критерий подобия
для всех треугольных крыльев
имеет постоянное значение.
Коэффициент подъемной силы концевых участков крыла пря-
моугольной формы в плане, находящихся внутри конуса возму-
щении, рассчитывается по методу конических сечений и равен
, __ 2а
С',а~
На рис. 21 6 показана зависимость с“й=/(Моо,х), подсчитан-
ная для треугольных крыльев методом конических сечеиий *
си мости от
числа М«, и угла % для
треугольного крыла
(21. 13)
* См. например, Аэродинамика частей самолета при больших скоростях
под ред. А. Ф. Доновэн и Г. Р. Лоуренс, ИЛ, 1959, 702 с.
343
www vokb-la.spb ru - Самолёт своими руками?!
Крайняя правая линия, являющаяся огибающей, соответствует
звуковой передней кромке треугольного крыла. Для других
форм тонких крыльев при определении подъемной силы необхо-
димо учитывать три критерия сверхзвукового подобия:
с“ _______________
Mgzi’i). 21.14).
Обычно для практических целей используются графики, пост-
роенные на основании экспериментальных данных; один из та-
ких графиков приведен на рис 20.6 На этом графике стреловид-
ность крыла определялась по линии максимальных толщин кры-
ла.
21 3. СОПРОТИВЛЕНИЕ ТОНКИХ, АЭРОДИНАМИЧЕСКИ
ПЛОСКИХ КРЫЛЬЕВ КОНЕЧНОГО РАЗМАХА
В СВЕРХЗВУКОВОМ ПОТОКЕ
Сопротивление рассматриваемых крыльев в линеаризован-
ной постановке будет складываться из сопротивления крыла, за-
висящего от подъемной силы и
Рис. 21.7. К определению индук-
тивного сопротивления крыла тон-
кого профиля в сверхзвуковом
потоке
сопротивления крыла при суа —0.
Сопротивление, зависящее
от подъемной силы, мало зави-
сит от формы профиля и его*
практически можно рассматри-
вать как для тонкой, плоской
пластины с такой же формой
в тане, как и заданное крыло-
В этом с 1учае равнодейст-
вующая сил давления RA прак-
тически перпендикулярна пло-
скости хорд крыла (рис. 21.7}
и, стедовательно, в скоростной,
системе координат ее можно разложить на две взаимно перпен-
дикулярные составляющие — подъемн ю силу и инду ктивное
сопротивление:
ya=RAcosa^RAi xi~ RA^ (I - RAu^Yau.
Переходя к коэффициентам имеем
Cjcl Суаа
(21. 15)
или в соответ твии с формулой (16.12) для тонкого крыла бес-
конечного размаха
(21. 16)
344
www.vokb-la.spb.ru - Самолёт своими руками?!
Для стреловидного крыла бесконечного размаха коэффици-
ент индуктивного сопротивления в соответствии с формулами
(21.11) н (21 16), получим в виде
l-tg2X 9
Сг! —-------------------с2
х‘ 4 уа
л
«ли сх1 = - ----- а2. (21.17)
V Mt - 1 - tg2 X
Сравнивая формулу (21 16) для прямого крыла бесконечно-
го размаха с формулой (21 17) для скользящего крыла, получим
1/м2 — i
f ОО _______
КхЛ-о J - 1 — tg2 х
Следовательно, при равных у г*
лах атаки индуктивное сопротивле-
ние скользящего крыла при сверх-
.звуковой передней кромке больше
индуктивного сопротивления прямо-
го крыла, поскольку коэффициент
подъемной силы скользящего крыла
больше, чем прямого (рис. 218)
Правильнее, однако, сравнивать
коэффициент сопротивления при
одинаковых значениях коэффици-
ентов су£7, тогда коэффициент индуктивного сопротивления
скользящего крыла будет меньше прямого.
По теоретическим данным коэффициент индуктивного сопро-
тивления треугольного крыла со сверхзвуковой передней кром-
кой будет таким же, как у прямого крыла бесконечного разма-
ха Это следует из формулы (21.13):
Рис. 21 8 Влияние угла % на
величину коэффициента индук-
тивного сопротивления при
сверхзвуковой передней кром-
ке
4а2
ИЛИ Cxi =
УЛ
(21. 18)
Для прямого крыла конечного размаха коэффициент подъ-
емной силы определяется зависимостью (21.12). Тогда для ко-
эффициента индуктивного сопротивления такого крыла получим
соотношение:
cxi /1 1
Z“2 A V 1 \ 2?. У Mt' 1
(21. 19)
зависящее лишь от о .ного пар 1метра а У Mt— 1.
Если передняя кромка дозвуковая, то через нее при а^О
^происходит перетекание воздуха и на передней кромке возника
345
www.vokb-la.spb.ru - Самолёт своими руками?!
ет подсасывающая сила (о чем уже говорилось ранее). В этом
случае аэродинамическая сила будет наклонена немного впе-
ред относительно нормали к хорде крыла вследствие влияния
подсасывающей силы, уменьшающей индуктивное сопротивление
(см. рис. 21.4)*
(21.20)
21.4. ВОЛНОВОЕ СОПРОТИВЛЕНИЕ КРЫЛА ПРИ сув = 0
Волновое сопротивление возникает практически всегда при
сверхзвуковом обтекании тел газовым потоком. Сопротивление
симметричного крыла при суа=0, часто называемое минималь-
Рис. 21.9. Влияние положения мак-
симальной толщины профиля на
волновое сопротивление с10в-
/—теоретическая кривая (хс—0,5); 2—
теоретическая кривая (хс—0,3), 3—экс-
периментальная кривая (хс— 0,5)
циента сопротивления с,хОв от
ным сопротивлением, склады-
вается из сопротивтения, возни-
кающего за счет вязкого трения
в пограничном слое, и сопротив-
ления, возникающего за счет рас-
сеяния энергии в скачках уплот-
нения.
Коэффициент сопротивления
cxj от сил трения определяется
методами теории пограничного
слоя. Что касается коэффициента
сжОв, то во многих случаях его
можно рассчитать теоретически,
но наиболее надежным являются
экспериментальные данное.
В общем случае результаты
теоретических и эксперименталь-
ных исследований удобно приво-
дить в виде зависимости коэффи-
критериев сверхзвукового подобия:
1, Xtg/, П, формы профиля). (21.21)
Сравнение результатов теоретических и экспериментальных
исследований для треугольного крыла (т] = оо) приведено на
рис 21 9 Теоретические кривые 1 и 2 соответствуют двум зна-
чениям положения линии максимальных толщин. хс=0,5 и хс
0,3 Экспериментальная кривая 3 соответствует хс=0,5.
Наличие точек излома А и В на теоретических кривых объяс-
няется тем, что при соответствующих значениях Мю в этих точ-
ках линия максимальных толщин (хс) и передняя кромка ста-
новятся сверхзвуковыми.
Вид кривой сл0в/лс2—f 1) существенно зависит от
параметра 1 и положения на хорде линии макси-
346
WWW vokb-la.spb ru - Самолёт своими руками?!
мальной толщины профиля Наибольшее значение отклонения
соответствует звуковой линии максимальных толщин.
При увеличении параметра Xj/M^ — 1 коэффициент схОВ умень-
шается, причем, если значениях УМ^—1 велнки, то схОВ ма-
ло отличается от соответствующих значении схОв для профиля
этого крыла
Для других форм
крыльев строятся свои
трафикн в соответствии
с зависимостью (21.21).
Такого рода графики для
-трапециевидных крыльев
•с ромбовидным профилем
и с сужением т] =5 приве-
дены на рис. 21.10 (пре-
рывистыми линиями по-
казаны теоретические ре-
зультаты, сплошными-
экспериментальные, сбли
жающиеся с теоретиче-
скими в области больших
значений хгХ,-о
Несколько завышен-
ные теоретические значе-
ния коэффициентов схов
объясняются тем, что они
определяются без учета
влияния вязкости среды.
Опыт показывает, что
форма профиля заметно
влияет на волновое сопро-
тивление крыла только
тогда, когда линия макси-
мальных толщин стано-
вится сверхзвуковой, т. е.
когда XtgZc<X|/M^ — 1.
Рис. 21.10 График для расчета волнового
сопротивления трапециевидного крыла с
ромбовидным профилем (хс<=0,5; ц=5)
Если же линия максимальных толщин дозвуковая, то форма
профиля почти не влияет на волновое сопротивление.
Анализ закона изменения коэффициента волнового сопротив-
ления крыла по числам М» показывает, что его увеличение, на-
чавшееся при числе Моо, равном критическому, продолжается
примерно до момента, когда линия максимальных толщин стано-
вится сверхзвуковой. При сверхзвуковой передней кромке с уве-
личением числа Моо коэффициент схов уменьшается (см гл 16),
вследствие чего уменьшается и коэффициент минимального соп-
ротивления крыла.
347
www.vokb-la.spb.ru - Самолёт своими руками?!
Увеличение угла атаки приводит к увеличению коэффициен-
та индуктивного сопротивления крыла, а следовательно, и к уве-
личению коэффициента лобового сопротивления:
(21.22}
Поляры крыльев, построен-
ные в соответствии с формулой
(21 22), приведены на рис.
21.11. Форма поляр типична
для около- и сверхзвукового
диапазона чисел Мж.
Рис. 21.11. Поляры крыла дчя
около- и сверхзвукового диапа-
зона чисел Л!»
21.5. МОМЕНТНЫЕ ХАРАКТЕРИСТИКИ КРЫЛА
В СВЕРХЗВУКОВОМ ПОТОКЕ
Крылья сверхзвуковых самолетов обычно лишены закрутки
н имеют симметричные или близкие к ним по форме профили,
поэтому коэффициент продольного момента у них при а=0 ра-
вен нулю и пропорционален углу атаки при сравнительно не-
больших углах а. Дтя определения коэффициента момента тре-
угольного крыла в сверхзвуковом потоке относительно оси,
проходящей через вершину крыла, воспользуемся тем, что центр
давления такого крыла совпадает с центром тяжести треуголь-
ника, т. е. хд=2/з^о-
Тогда продольный момент
2 q V2
Мг = -ГЛ =—°° Sb0.
г х* з у 2 0
С другой стороны, вычисляя продольный момент с помощью
коэффициента момента, имеем
Q V
°° 00 Sb.}
2 т 2
Сравнивая оба выражения для Мг, запишем
Vе» (21.23)
илн, заменив су его значением согласно (21.13), получим
Пользуясь формулами (21.23) и (2124), следует помнить,
что в ннх коэффициент ст отнесен к центральной хорде Ьо тре-
утольного крыла.
348
www.vokb-la.spb.ru - Самолёт своими руками?!
Для крыла прямоугольной формы в плане с приведенным уд-
линением 1 величина коэффициента момента относи-
тельно передней кромки и положение центра давлений опреде-
ляются по линейной теории.
Коэффициент момента относительно осн 0Z
ет —
Q V2
СО СО Q
2 р
Момент Mz от сил давления, распределенных по поверхности
крыла, можно найти как сумму моментов подъемных снл относи-
тельно оси 0Z, действующих на различных участках крыла
(рис. 21.12) 'На треугольных участках крыла точка прнложе
ния подъемной силы совпадает с центром тяжести каждого
участка. Несложные вычисления показывают, что момент
9
О
\ о Z
где
r,-2)=T^rr?“(S--4Sll);
34»
www.vokb-la.spb.ru - Самолёт своими руками?!
Учитывая, чтоЪ^- =---->2 ,
2Хкр/м2то-1
получим ст —---2а — (1--------2 ; (21.
I 3XKP|/M2„-J
- — -У; _ Мг = ст ЗХкр— 1 — 2
Д b Yb су 3(2Хкр)Ум^~1-1
Таким образом, по мере увеличения числа Мто в сверхзвуко-
вом потоке центр давления прямоугольного крыла смещается
назад к середине хорды, Анало-
Рис 21.13 Изменение относи-
тельной координаты центра давле-
ния в зависимости от параметра
М2 — 1
г оо
гичное влияние оказывает увели-
чение удлинения крыла (рис.
21.13). Экспериментально уста-
новлено, что сужение крыла мало
влияет на положение центра дав-
ления на средней аэродинамиче-
ской хорде крыла. Центр давле-
ния прямого крыла бесконечного
размаха для всех малых углов
атаки лежит на середине про-
филя.
В общем случае безразмерная
координата центра давления
аэродинамически плоского крыла относительно передней кромки
САХ определяется зависимостью
1, п).
Для стреловидного и треугольного крыльев положение цент-
ра давления можно найти из графиков, подобных приведенным
на рис. 20.10.
Вопросы для повторения
1. В чем различие между дозвуковой и сверхзвуковой кром-
ками крыла?
2. Объясните, в каких случаях при обтекании кры^ а сверх-
звуковым потоком может возникнуть подсасывающая сила.
3. Как изменяются аэродинамические коэффициенты сха, суа
и ст крыла при увеличении числа М:х?
4 Как изменяется индуктивное сопротивление крыла при пе-
реходе от околозвуковых к сверхзвуковым скоростям?
Задачи
1. Найти угол атаки плоского тонкого крыла самолета, летя-
щего горизонтально на высоте Н—10000 м со скоростью У=
350
www vokb-la.spb ru - Самолёт своими руками?!
=473 м/с, если площадь крыла 5=15 м2 н вес самолета (7=
=4900 Н.
О т в е т: а 0,0225 рад.
2. Угол стреловидности передней кромки крыла самолета ра-
вен 1 рад. Определить скорости полета самолета, при которых
передняя кромка крыла будет дозвуковой, звуковой н сверхзву-
ковой.
Ответ: прн скоростях полета, соответствующих М«><1,85,
передняя кромка крыла будет дозвуковой, а прн МЗО>1,85—
сверхзвуковой.
3. Во сколько раз угол атаки скользящего крыла (х=45°)
меньше угла атаки прямого крыла бесконечного размаха, обте-
каемого сверхзвуковым потоком, при постоянном значении коэф-
фициента суа=0,5 и Мео= 1,8 Определить также угол атаки пря-
мого крыла.
Решение: Проверяем характер обтекания передней кром-
ки крыла
УМ^—1 = |/2,24, следовательно,
VA£=l>tgX.
Передняя кромка — сверхзвуковая. Используя соотношение для
коэффициента подъемной силы прямого крыла бесконечного раз-
маха и скользящего крыла при сверхзвуковой передней кромке»
получим равенство
р , 4аС1( _ апр __ У— 1
Ум^-1 KM2M-l-tg2z’ аск /Mi-l-tgSx
Ум^-1 0,5 ,/отГл _
а11р=^й-----------= —р 2,24=0,187 рад;
4 4
Cf/йУм^- l-tg2X 0,5,гт-07
аск =-------------------=— у 1 • 24=0,139 рад;
—= 1,355.
«СК
Ответ: угол атаки скользящего крыла в 1,355 раза меньше
угла атаки прямого крыла.
www vokb-la.spb ru - Самолёт своими руками?!
ГЛАВА 22
АЭРОДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ
ТЕЛ ВРАЩЕНИЯ
22.1. ГЕОМЕТРИЧЕСКИЕ И АЭРОДИНАМИЧЕСКИЕ
ХАРАКТЕРИСТИКИ ТЕЛ ВРАЩЕНИЯ
Изучение методов определения аэродинамических характери-
стик тел вращения имеет важное значение, поскольку фюзеля-
Рис. 22 1 Типичные формы тел
вращения
жи современных самолетов, наружные топливные баки, гондолы
двигателей, корпусы снарядов и ракет обычно имеют форму тел
вращения или близкую к ней. На рис. 22 1 показаны некоторые
352
WWW.vokb-la.spb ru - Самолёт своими руками?!
формы тел вращения. Тело вращения обычной формы (см. рис.
22.1, 5 г) можно разделить на переднюю (головную, или носо-
вую), среднюю (цилиндрическую) и заднюю (хвостовую, или
кормовую) части.
Каждая из указанных частей характеризуется своими гео-
метрическими параметрами
Носовая часть, как правило, имеет вид конуса, оживального
(образованного вращением дуги окружности некоторого ради-
кса) или параболического тела и характеризуется углом раство-
ра т носка тела и удлинением
^ос^иос/^м, (22. 1)
где /пос — расстояние от иоска тела до его миделя сечеиия;
DM — диаметр миделя.
Под миделем подразумевают сечение, перпендикулярное про-
дольной оси тела и имеющее наибольшую площадь. Максималь-
ная площадь у фюзеляжей дозвуковых самолетов располагается
примерно на первой трети их длины. Если тело имеет цилиндри-
ческую часть, то мидель — площадь поперечного сечения цилин-
дра, а /нос — расстояние от иоска тела до его цилиндрической
части. В общем случае под диаметром миделя £>м подразумева-
ют диаметр крута, эквивалентного по площади миделю. Ци-
линдрическая часть тела вращения также характеризуется уд-
линением
- (22.2)
Геометрическими параметрами кормовой части тела враще-
ния являются удлинение
\орм=Сорм/Ом (22.3)
и сужение (22.4)
где — диаметр дойного среза (см. рис. 22.1,5 г).
При отсутствии у тел вращения дойного среза т]Корм=0-
Удлинение тела вращения равно сумме удлинений отдельных
его частей:
?-=\1)с+\1Ил + \Орм=-~ , (22.5)
где LT — полная длииа тела вращения.
Величина, обратная удлинению, называется относительной
толщиной тела вращения:
^=1/Х. (22.6)
Тело вращения с протоком омывается потоком не только сна-
ружи, ио и изнутри. Примером тела вращения с протоком мо-
жет служить гои дол а двигателя
Как и при изучении аэродинамических характеристик крыла
12 626 353
www.vokb-la.spb.ru - Самолёт своими руками?!
аэродинамические силы, действующие на тело вращения, рас-
сматриваются в скоростной или в связанной системах коорди-
нат. В скоростной системе координат формулы для определе-
ния подъемной силы н силы лобового сопротивления имеют сле-
дующий вид:
а == м > а == ^xaQ^M t 22,7)
где Суа и сха — коэффициенты подъемной силы и лобового соп-
ротивления тела вращения; V2/2— динамическое давле-
ние; — площадь миделя.
Переход к связанной системе координат производится так
же, как и для крыла (см. гл. 13).
22.2. ПОДЪЕМНАЯ СИЛА ТЕЛ ВРАЩЕНИЯ
Подъемную силу тела вращения, обтекаемого потоком под
некоторым углом атаки, можно определить, зная закон распре-
деления давления на поверхности тела. При дозвуковых скоро-
стях распределение давления может быть найдено достаточно
Рис 22 2. Распределение давле-
ния по профилю крыла (1) и
меридиональному сечению те-
ла вращения (2) при малых
числах Ми
надежно только экспериментальным
путем. При этом, как показали
исследования, для удлиненных кор-
пусов различие между дав тениями
в несжимаемом и дозвуковом сжи-
маемом потоках невелико.
Как видно из рис. 22.2, эпюра
распределения давления по мери-
диональному сеченню тела враще-
ния (кривая 2), обтекаемого пото-
ком несжимаемой жидкости, каче-
ственно сходна с эпюрой распреде-
ления давления по профитю крыта
(кривая 1) той же относительной
толщины и формы при том же угле
атаки. Однако разрежение на тело
вращения значительно меньше раз-
режения на крыле, что обусловлено
пространственным характером обтекания тела вращения.
Обтекание тела вращения можно сравнить с обтеканием кры-
ла очень малого удлинения, у которого, как известно, разреже-
ние иа верхней поверхности при прочих равных условиях всегда
меньше, чем у крыла большого удлинения вследствие перетека-
ния воздуха через концевые кромки крыла из области повышен-
ного давления в область пониженного Так же, как для крыльев
малого удлинения, зависимость cyn=f(a) для тела вращения
носит в значительной мере нелинейный характер. Таким обра-
зом, характер изменения подъемной силы и силы лобового соп-
ротивления тела вращения в первом приближении качественно
354
www.vokb-la.spb.ru - Самолёт своими руками?!
весьма близок к характеру изменения Ха и Уа крыла как при
малых, так и при больших значениях числа Мто.
Так как на теле вращения разрежение меньше, чем на кры-
ле ю при одинаковых числах Мю в случае обтекания тела вра-
щения влияние сжимаемости сказывается слабее. Поэтому у тел
вращения число Мир значительно больше, чем у крыла. Напри-
мер, профиль крыла толщиной 15% имеет Мкр—0,78, а тело
вращения той же относительной толщины имеет Мкр=0,95.
Рис 22 3. Возникновение на теле вращения нормальной си-
лы, обусловленной поперечным обтеканием
Отмеченные особенности в обтекании тела вращения, несом-
ненно, сказываются на величинах подъемной силы и лобового
сопротивления тела вращения.
При расчете траекторий движения летательных аппаратов в
основном используется скоростная система координат (рис.
22.3). В этом случае коэффициент подъемной силы тела враще-
ния
Суа~Су cos а— сх sin а. (22.8)
Коэффициент нормальной силы тела вращения в связанной
системе координат су определяется по формуле
СУнос + Г1/цил + ^И+С1/корм, (22. 9)
где пос — коэффициент нормальной силы носовой части тела
вращения; суцнл — коэффициент нормальной силы цилиндриче-
ской части тела вращения; суп — коэффициент нормальной силы
цилиндрической и кормовой частей, обусловленный наличием
отрыва потока при больших углах атаки; сукорм — коэффициент
нормальной силы кормовой части тела вращения.
Экспериментально установлено, что цилиндрическая часть,
прилегающая к носовой части тела вращения, также создает
нормальную силу. Величина этой силы небольшая и отдельно
ее не выделяют, а добавляют к нормальной силе носовой части
В этом случае формула (22 9) принимает вид
су~суНос+ч/п+сукорм. (22. 10)
Формулу для определения коэффициента нормальной силы,
отнесенного к площади миделя, согласно линейной теории мож-
wvrvv.vokb-Ia.spb.ru - Самолёт своими руками?!
но представить и в другом виде:
= 22.11)
где сау=дсу>до..
Как показывают экспериментальные данные, коэффициент
зависит ие только от угла атаки а, но и от формы тела вра-
щения и прежде всего от формы его носовой части, структуры
пограничного слоя, числа Мто, удлинения тела вращения 1 и ря-
да других факторов.
Производную о’в общем случае можно представить в виде
суммы:
^=^нос + г“л+г“корм. (22.12)
где С^нос ~ производная по углу атаки от коэффициента нор-
мальной силы носовой части (с учетом цилиндрической части);
— производная по углу атаки от коэффициента нормаль-
ной силы цилиндрической и кормовой частей; КО)М — произ-
водная по углу атаки от коэффициента нормальной силы кор-
мовой части.
Экспериментально установлено, что производная от коэффи-
циента нормальной силы носовой части тела вращения cJHOC
является функцией удлинения носовой и цилиндрической частей
тела вращения, а также числа Мм. Графики для определения
с“нос тел вращения с конической и оживальной носовыми час-
тями приводятся на рис 22 4 а, б
Коэффициент нормальной силы цилиндрической и кормовой
частей тела вращения, обусловленный наличием срыва потока
при больших углах атаки, выражается эмпирической формулой'
Суп ~0,624X2rjrilHJ sin2a tg a. (22. 13)
Производная цилиндрической и кормовой частей может
быть определена нз соотношения
г’ = 1 872X2r tg2a 1-----— sin2a , (22.14)
где Сгцил — коэффициент сопротивления кругового цилиндра
при его поперечном обтекании; сг1ШЯ=0,35 — при турбулентном
пограничном слое; схцил= 1,2 — при ламинарном пограничном
слое
Производная от коэффициента подьемной силы кормовой
части тела вращения определяется по эмпирической формуле:
са = —2Н1 — т]2 ). (22.15)
Поправочный коэффициент | зависит от чисел Re, М*,, формы
кормовой части и учитывает уменьшение коэффициента нормаль-
ной силы из-за утолщения и отрыва пограничного слоя в сужи-
вающейся кормовой части (В=0,15 ... 0,20).
356
wwvi vokb-la.spb.ru - Самолёт своими руками?!
Для тела с расширяющейся кормовой частью
а
|/корм
(см рис 22.1)
22. 16)
определяется выражением:
сл =0,8 1711 —— cos20.
х/корм [\ D / J 57,3
Рис 22 4 График для определения с®йтела враше
ния с конической (а) и оживальной (б) носовыми
частями
Сумма с“пос, с“п, г“корм согласно формуле (22.12) равна с’.
Подставляя в формулу (22 11) значение с*, получим выраже-
ние для коэффициента подъемной силы тела вращения:
^=[г;™с + 0*624хЧцй,а2--2в(1-т12орм)] а. (22. 17)
Учитывая, что для малых углов атаки а*-Ч) имеем
^=Khoc-25(1-^opm)] а. (22. 18)
357
www.vokb-la.spb.ru - Самолёт своими руками?!
Если поперечное сеченне тела имеет ие круглую, а овальную
форму, то расчет ведется по формуле
(22.19)
где су — определяется по формуле (22 18); В— ширина миде-
ля; \м - площадь м-тделя, к которой отнесен коэффициент суов.
Если в носовой части расположен воздухозаборник, то при
работе двигателя на расчетном режиме возникает дополнитель-
ная сила, коэффициент которой Асу
Д^ = 2а-^_, (22.20)
*^м
где — площадь входа в воздухозаборник
22.3. СОПРОТИВЛЕНИЕ ТЕЛ ВРАЩЕНИЯ
В диапазоне сравнительно небольших углов атаки, представ-
ляющих наибольший практический интерес, коэффициент лобо-
вого сопротивления можно представить в виде
G-a = G-0+W, (22.21)
где сх0 — коэффициент сопротивления тела вращения при нуле-
вом угле атаки; k — постоянный коэффициент.
В наиболее общем случае сопротивление тела вращения мож-
но представить в виде двух составляющих; сопротивления, обус-
ловленного силами давления, действующими по нормали к по-
верхности, и сопротивления, связанного с касательными силами
трения, возникающими на поверхности из-за наличия вязкости.
Особенностью обтекания тела вращения с донным срезом
(т]корм^0)« за которым нет струи от двигателя, является воз-
никновение донного сопротивления.
В этом случае сопротивление, обусловленное силами дав-
ления, разделяется на две составляющие: сопротивление от дав-
ления на боковую поверхность (головное сопротивление), сопро-
тивление от давчения на донный срез (донное сопротивление).
Учитывая это, лобовое сопротивление тела вращения при ну-
левом угле атаки можно представить в виде cj ммы трех слага-
емых:
~~ Xр Ч- f
или, переходя к аэродинамическим коэффициентам, запишем для
коэффициента сопротивления, отнеся к площади
= ~ = 2.22)
где схр коэффициент сопротивления, зависящий от распреде-'
ления сил нормального давления по поверхности тела; cXf —
коэффициент сопротивления трения; сгдон — коэффициент дой-
ного сопротивления, обусловленного наличием разрежения иа
кормовом срезе.
358
www.vokb-ia.spb.ru - Самолёт своими руками?!
Коэффициент профильного сопротивления, обусловленного
силами давления и трения, можно определить по эмпирической
формуле:
^лгпр=——Vx/,
в которой коэффициент формы
kk = 1,86 - 0,175Xft 4- 0,01X2.
Параметр называется приведенным удлинением и опреде-
ляется формулой
При дозвуковых скоростях коэффициент схр пренебрежимо
мал. При околозвуковых и сверхзвуковых скоростях схр быстро
возрастает, главным образом, вследствие возникающих у по-
верхности тела вращения скачков уплотнения, при этом величи-
на схр называется коэффициентом волнового сопротивления.
В этом случае
Сл'О * 1х ов Н- ^х дон ^х f’ (22.23)
Коэффициент волнового сопротивления схов можно предста-
вить в виде суммы коэффициента сопротивления носовой части
тела вращения схОн,,|)С н коэффициента сопротивления кормовой
ЧаСТИ Т Ла СхОвкорм (при Ct — 0 С-^Ов гщл— 0) -
Под сопротивлением носовой (кормовой) части тела враще-
ния понимается равнодействующая сила избыточного давления,
приложенная к поверхности носовой (кормовой) части при а —О
При сверхзвуковых скоростях на поверхности носовой части
всегда устанавливается повышенное давление; при дозвуковых
скоростях на некоторых участках поверхности возникает повы-
шенное давление и может появиться подсасывающая сила, на-
правленная против набегающего потока, т. е. сопротивление но-
совой части может быть и отрицательным
Графики зависимости с,ховнос=^(М00) носовых частей тел
вращения с коническими и параболическими образующими при-
ведены на рис 22 5. Участки кривых в диапазоне Моо<1,4 по-
строены на основании результатов экспериментов, в которых
замерялось распределение давления по поверхности тела, а уча-
стки кривых в Диапазоне Моо>1,1 .. 1,4 — на основании теоре-
тических расчетов.
В отличие от сопротивления носовой части сопротивление
кормовой части всегда положительно, так как и при дозвуковых,
и при сверхзвуковых скоростях на сужающейся кормовой части
тела устанавливается пониженное давление. Графики зависимо-
сти схов корм =/(Моо) для кормовых частей с коническими и па-
ра одическими образующими приведены на рис. 22 6 Участки
кривых при Моо>1,6 представляют собой теоретические значе-
ния с-еоккорм, а при Моо<1,6 — ориентировочные.
359
www.vokb-la.spb.ru - Самолёт своими руками?!
Рис. 22.5. Изменение коэффициента волнового сопротивления
носовой части тела вращения конической формы (а) и с па-
раболической образующей (б) в зависимости от числа Мя для
различных значений Л
Коэффициент сопротивления трения тел вращения опреде-
ляется аналогично коэффициенту сопротивления трения крыла.
При этом, как и для других коэффициентов, коэффициент сопро-
тивления трения относится к миделю
-4й- . (22.24)
где Scm — площадь поверхности тела вращения, омываемая по-
током (так называемая «смоченная» площадь); -qc поправоч-
ный коэффициент, учитывающий переход от плоской пласти-
ны к телу вращения; — коэффициент, учитывающий влияние
сжимаемости воздуха; Cf — коэффициент -сопротивления трения
плоской пластины, определяемый с учетом состояния погранич-
ного слоя при числе Re=VLJv. Ввиду того, что число Re для
фюзеляжей очень велико (из-за больших скоростей полета и
большой протяженности фюзеляжей современных транспорт-
ных и пассажирских самолетов), пограничный слой можно счи-
тать турбулентным
На рис. 22 7 приведен график зависимости Cf=f (Re) при
турбулентном пограничном слое-
Увеличение удлинения фюзеляжа приводит к уменьшению
его относительной толщины, и сопротивление фюзеляжа в этом
случае все меньше отличается от сопротивления плоской плас-
тины т е. коэффициент т]с с ростом удлинения уменьшается,
стремясь к единице (рис. 22 8). Коэффициент т]М зависит от от-
360
www.vokb-la.spb.ru - Самолёт своими руками?!
иосительиого удлинения носовой части тела вращения Z„OI. (рис.
При упрощенных расчетах сопротивления трения фюзеляжей
(корпусов) могут быть использованы зависимости для тонкой
пластинки.
Рис. 22.6. Изменение коэффициента волнового сопротивления кормовой
части с прямолинейными (а) и параболическими (б) обводами в зави-
симости от числа Моо для различных значений т) (Хкорм=2)
Рис. 22.7. Изменение коэффициента трения плоской пла-
стины в зависимости от числа Ре при обтекании ее тур
булентным потоком
Полученные результаты следует считать приближенными,
так как не учитывается в общем случае пространственный ха-
рактер течения и форма обтекаемой поверхности.
В условиях дозвукового обтекания причиной появления дой-
ного сопротивления является понижение давления (возникнове-
ние разрежения) в застойной зоне за донным срезом, незапол-
ненной струей от двигателя, вследствие наличия трения между
361
www.vokb-la.spb.ru - Самолёт своими руками?!
внешним потоком и потоком за донным срезом. Степень пони-
жения давления в значительной мере зависит от структуры и
толщины пограничного слоя. Прн турбулентном пограничном
слое разрежение за срезом больше, чем при ламинарном слое
той же толщины, что обусловлено большей эжектнрующей спо-
собностью турбулентного пограничного слоя по сравнению с ла-
минарным. Следовательно, и донное сопротивление при турбу-
лентном слое будет больше. Однако большая толщина турбу-
лентного пограничного слоя способствует уменьшению эжекции
газа из застойной области, поэтому увеличение толщины слоя
приводит к уменьшению разрежения, а следовательно, н к умень-
шению коэффициента донного сопротивления.
Рис 22.8. Изменение по-
правочного коэффициента ту
в зависимости от удлинения
тела вращения
Рис 22 9 Изменение поправоч-
ного коэффициента Диг в зави-
симости от относительного уд-
линения посовой части фюзе-
ляжа
Коэффициент донного сопротивления сЛДОн определяется
обычно экспериментальным путем; при отнесении этой величины
к площади мнделя можно для корпусов ракет и фюзеляжей са-
молетов получить следующее выражение:
-Кцон Р00 Рюн S-ivu / f/дон ____
‘л дон_____________________________________________,,__ п с_Аден I г. I
со о©
2 2
= Q> —9 (AsslV (22.25)
Это выражение, справедливое для дозвуковых и околозвуковых
режимов обтекания, показывает, что коэффициент сХдоп обратно
пропорционален корню квадратному из коэффициента сопротив-
ления трения cxf (отнесенному к площади миделя тела).
При сверхзвуковом обтекании, так же как н при дозвуковом,
основную роль в создании донного давления играет механизм
формирования пограничного слоя и перемешивания в спутной
струе. В зоне смешения в струе существуют трн границы пото-
ков: граница струи, граничная линия тока и линия раздела.
362
www.vokb-Ia.spb ru - Самолёт своими руками?!
Граница струи отделяет область возмущенного потока от
внешнего изэнтропического течения.
Граничная линия тока отделяет газ, входящий первоначаль-
но в вязкий слон на задней кромке, от газа, входящего в возму-
щенную зону внешнего изэнтропического потока в результате
смешения в струе
Линия раздела ограничивает газ, находящийся в застойной
зоне.
При сверхзвуковом обтекании помимо структуры погранично-
го слоя на величину коэффициента схдон влияют расположение
и форма волн расширения и скачков уплотнения.
При сверхзвуковых скоростях течения коэффициент донного
сопротивления определяется по формулам:
г _____ 0,085/? (2 k) „
СЛД0Н--- .,2 °дин» ^ZZ. ZDJ
1 *оо
— 0.085 „2 оу)
д^2 ‘ дон. ^zz, z/ )
оо
где Хэ=|/^;
-S ’ J 1 / Q ' ДОН Q
Формула (22 26) соответствует значениям
(22 27) — k> 1
Рис 22 10 Изменение коэффи-
циента сх Лои в зависимости от
числа Re для разных тел вра-
щения:
------турбулентный пограничный
слой:
------ламинарный пограничный
слой
Рис 22 11 Изменение ко-
эффициента лобового сопро-
тивления тела вращения в
зависимости от числа
для различных относитель-
ных толщин тел вращения
Гис. 22 12 Изменение сха ра-
кеты в зависимости от числа
при сверхзвуковом обте-
кании
363
www.vokb-la.spb.ru - Самолёт своими руками?!
На рис. 22.10 приведены графики изменения коэффициента
дойного сопротивления в зависимости от числа Re (Моо--1,5)
для различных тел вращения.
Суммирование всех составляющих позволяет получить коэф-
фициент лобового сопротивления тела вращения. При дозвуко-
вых скоростях, но при числах МСс>Мкр коэффициент лобового
сопротивления резко возрастает (рис. 22 11).
При сверхзвуковых скоростях коэффициент сх достигает мак-
симального значения при М= 1,0... 1,3, а затем уменьшается
(рис 22.12).
Рис. 22.13. Измене-
ние коэффициентов
Сус, Сха, К цилинд-
рического с коничес-
кой носовой частью
фюзеляжа в зависи-
мости от угла атаки
На рис. 22.13 приведены графики зависимости коэффициентов
Оуа, £\а и К от утла атаки для цилиндрического фюзеляжа с ко-
нической носовой частью.
Вопросы для повторения
1. Каким образом возникает подъемная сила на теле враще-
ния?
2. Напишите выражения для нормальной силы, коэффициента
нормальной силы и производной тела вращения.
3 Каким образом создается донное сопротивление? Как опре-
делить коэффициент донного сопротивления?
4. От каких факторов зависят сопротивление давления и соп-
ротивление трения тела вращения и как они изменяются при из-
менении скорости полета?
Задачи
1 При полете самолета на высоте // = 5000 м со скоростью
V—900 км/ч угол атаки крыла равен 0 085 рад. Определить нор-
мальную силу фюзеляжа, если известно, что установочный угол
крыла (угол между хордой крыла и продольной осью фюзеля-
жа) равен 0,010 рад и фюзеляж имеет следующие геометриче-
ские характеристики: длина фюзеляжа £ф=30 м; длина носовой
части /нос=9 м; длина цилиндрической части /ЦиЛ=16 м; диа-
метр цилиндрической части дцял=4 м; диаметр донного среза
£?дон=1 м; образующая носовой и кормовой частей—прямая
364
www vokb-la.spb.ru - Самолёт своими руками?!
Решение. Так как угол атаки фюзеляжа
иФ~«кр —гкр = 0,075 рад,
то су фюзеляжа находят по формуле (22.18).
Найдем входящие в формулы (22.18) величины. Полагаем Е=
= 0,18.
Пользуясь соотношением (22 4), имеем
ПкоРм=1М=0,25.
Для определения с“нос находим:
а) на //=5000 м; а = 320,5 м/с;
б) V=^=250 м/с; М„=^=0,78;
3,0 320,0
В) Чос=-^==4-=2,25;
г) ]/ -О~м“ = ]/L-°-782^ 0,275;
Лнос г 2,25
д) 1,775, так как X
Ьнсс 2,2а «и* dvi 4
е) из графика са Аид j „ЯуЛ„„..
‘ т г/нос J I , — I находим
\ Лнос Хнос /
-5е='=0,О36, с- =2 06.
а7,3 #нос
Согласно формуле (22.18) имеем
А = Р,06 --2-018(1 - 0,0628)] 0,075 =0,122.
Л1/2
Тогда =1=0,129-5-4а. °2^25ог=35000 н.
Ответ: 35000 Н.
www.vokb- la.spb ru - Самолет своими руками?!
ГЛАВА 23
АЭРОДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ
ОПЕРЕНИЯ И РУЛЕЙ
23.1 АЭРОДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ОПЕРЕНИЯ
Для обеспечения продольной и путевой устойчивости * ** дви-
жения и управляемости * * полетом летательные аппараты снаб-
жаются специальными несущими поверхностями, называемыми
Рис 23.1. Оперение само-
лета :
1—киль; 2—руль направле
ния, 3—сервокомпенсатор
руля направления; 4—руль
высоты, 5—триммер руля
высоты; 6 стабилизатор
оперением.
Оперение, размещаемое в хвостовой
или носовой части фюзеляжа, включа-
ет обычно неподвижные части — киль
и стабилизатор — и подвижные —
руль высоты, предназначенный для
продольного управления, и р>ль на-
правления, предназначенный для пу-
тевого управления (рис. 23.1). Киль с
рулем направления составляют вер-
тикальное оперение, а стабилизатор с
рулем высоты — горизонтальное опе-
рение. Введение управляемого в поле-
те стабилизатора позволяет уменьшить
площадь рулей высоты.
Горизонтальное опереиие, не рас-
члененное на стабилизатор и руль высоты и представляющее
собой единое целое, облегчает продольную центровку н управ-
ление самолетом при больших значениях числа М.
Типы применяемых оперений разнообразны. Некоторые наи-
более характерные формы горизонтального оперения приведены
* Под устойчивостью самолета понимают способность его без вмеша-
тельства летчика возвращаться к исходному режиму полета после прекра-
щения действия сил, вызвавших отклонение самолета от его режима
** Управляемостью самолета называется его способность отвечать на от-
клонение органов управления соответствующими перемещениями в простран-
стве.
366
www.vokb-la.spb.ru - Самолёт своими руками?!
на рис. 23.2. Стреловидные и треугольные оперения применяются
на скоростных самолетах.
Аэродинамические характеристики стреловидного и треуголь-
ного оперений отличаются от характеристик нестреловидного
оперения так же, как отличаются друг от друга аэродинамиче-
ские характеристики крыльев аналогичных форм
При выборе стреловидности оперения исходят из того, чтобы
величина Мкр для оперения была несколько больше Мкр для
крыла, чтобы явления, связанные со сжимаемостью воздуха,
возникли на оперении позже, чем на крыле, и чтобы хорошая
Рис. 23 2. Характерные формы оперения в плане.
1, 4, S—трапециевидное; 2—эллиптическое. 3—треугольное: 6—стре-
ловидное
управляемость самолетом сохранялась н тогда, когда скорость
полета достигла скорости, соответствующей Мкр для крыла.
Если толщины профилей оперения достаточно большие, то
стреловидность оперения делают несколько большей, чем стрело-
видность крыла. Так, на самолете Ту-104 при угле стреловид-
ности крыла 7.-35° оперение имеет угол стреловидности Хго=
На оперение действуют сравнительно небольшие силы, одна-
ко благодаря большому плечу относительно центра массы само-
лета они создают моменты, способные уравновесить суммарный
момент от всех остальных частей; крыла, фюзеляжа, гондол и
т- Д-
Несущие свойства оперения определяются приростом коэффи-
циента подъемной силы, вызванного изменением угла атаки а
(или угла скольжения р), величиной отклонения органа управ-
ления тангажом (руля высоты) на угол бв или органа управле-
ния рысканием (руля направления) на угол би, поэтому основ-
ными параметрами, определяющими эффективность оперения
являются:
для горизонтального
^аг.0/<?а = с“йго;
()/^зп=с®в ;
if и в ^Г«о’
367
www vokb-la.spb.ru - Самолёт своими руками?!
для вертикального
дсга н.о/ <?₽ = 4 в.о ’ в.<Л = о.
Эффективность оперения повышается с увеличением этих про-
изводных и абсолютного наибольшего Приращения коэффициен-
та Дсуа (Дсга) при максимальных отклонениях руля.
Следует отметить, что при отклонении руля на большие углы
его эффективность уменьшается (при 6 = 0,6 .. .0,7 рад подъем-
ная сила ие увеличивается из-за срыва потока с поверхности
оперения). Рули стреловидного оперения эффективнее при
больших углах отклонения по сравнению с рулями прямого опе-
рения.
Для участков линейного изменения характеристик можно за-
писать
г _____ dCtfar.n । дСуг,о _
тг-' ~ да Г-°'Г Л. “
или ^r.„=-V^(ar.o+«M, (23.1)
где коэффициент эффективности руля
(23.2)
Для стреловидного оперения
С/аг. cos Хр.о (аг.0+л8а cos Хв),
да г. о
где /го — угол стреловидности горизонтального оперения по ли-
нии */4 хорд; Хв — угол стреловидности рулей высоты.
Величины дсуат0/д5в и дсуагс/даг0 у стреловидных оперений
меньше, чем у прямых. Стреловидность оперения и особенно ру-
лей неизбежно вызывает уменьшение их эффективности Поэтому
часто для увеличения Мкр у оперения уменьшают относительную
толщину профилей оперения при меньшем угле стреловидности.
Опыты показывают, что величина производной - ——
даго
пестрел обидного оперения в основном зависит от удлинения
Хг.о, мало зависит от профиля оперения и может быть выражена
следующей приближенной формулой:
дсуаг.о _ 0,085Х
даг.о ~ 1,73 +Л *
Коэффициент эффективности руля п при дозвуковых
стях определяется экспериментально или по формуле
где 5ОП — площадь опереиия; 5Р — площадь руля.
368
(23.3)
скоро-
(23.4)
QI
www.vokb-la.spb.ru - Самолёт своими руками..
Наличие на руле вырезов н средств аэродинамической ком-
пенсации (специальных приспособлений, служащих для умень-
шения усилий на органах управления, способствует уменьшению
коэффициента суп.
При околозвуковых скоростях и наличии местных скачков уп-
лотнения коэффициент п сильно уменьшается. Для увеличения
эффективности рулей на околозвуковых скоростях уменьшают
относительные толщины профилей оперения (с целью увеличе-
ния Мкр) или увеличивают площадь цельноповоротного опере-
ния, которое более эффективно
Прн сверхзвуковых скоростях коэффициент эффективности
руля в диапазоне 5Р/5Г0=0,35.. .0,6 определяется по формуле
я 5p/S0I1. (23. о)
Относительная толщина профиля горизонтального оперения
колеблется в пределах 4—10% (меньшая величина относится к
скоростным самолетам). Следует заметить, что дальнейшее
уменьшение относительной толщины профиля становится неоп-
равданным, так как получаемое прн этом незначительное умень-
шение лобового сопротивления не компенсирует конструктивных
трудностей при размещении осевой компенсации руля, пониже-
ния жесткости конструкции и увеличения ее массы. Профили го-
ризонтального оперения обычно симметричны. Относительная
толщина профилен вертикального оперения составляет 4—8°/о,
при этом профиль также выбирается симметричным
Основные параметры оперений современных самолетов при-
ведены в табл. 23 1 и 23 2.
Таблица 23 1
Параметры горизонтального оперения
.о/^кр ^в/^г.о Гг.о
М Мкр 0,15-0,20 0,35—0,45 8-10%
м>мкр 0,20-0,30 0,30-1,0 4-6%
Таблица 23.2
Параметры вертикального оперения
Мпол ^R.o/^кр ^н/^в. > ^в.о
М Wjjp 0,08—0,12 0,35—0,45 6- 8%
М>МКр 0,15-0,20 0,20—0,30 4—6%
369
www vokb-la.spb.ru - Самолёт своими руками?!
В качестве примера на рис. 23.3 приведены графики измене-
ния коэффициентов подъемной силы и лобового сопротивления
Прсфиль оперения
Рис 23 3 Аэродинамические характе-
ристики изолированного оперения
изолированного оперения, ис-
пытанного в трубах ЦАГИ
(5=8%, Х=3, rj = 2, Sp/Sr0 =
= 0,4), в зависимости от угла
атаки оперения и угла откло-
нения руля.
Величина производной с*гю
сохраняется постоянной до уг-
лов б — 0 35 рад, при больших
углах отклонения произв' д1 ая
уменьшается, а при д=0,6 рад
становится отрицательной, что
связано с возникновением от-
рыва потока на поверхности
оперения.
23.2. АЭРОДИНАМИЧЕСКИЕ
ХАРАКТЕРИСТИКИ ЭЛЕРОНОВ
Элероном называется руле-
вая поверхность, которая пред-
ставляет собой отклоняющую-
ся хвостовую часть крыла и
служит для обеспечения ба-
лансировки и поперечной уп-
равляемости самолета. Эле-
роны различных типов пока-
заны на рис. 23.4. Элероны раз-
мещаются вблизи концов
крыльев, поэтому влияние фюзеляжа на их эффективность не-
велико
Площадь элеронов 5Эл— 0 05.. 008 SKp, хорда элерона
бз:1 = 0,25 . .0,30
Кинематически элероны, расположенные на левом и правом
полу крыльях, связаны так, что при движении ручки поперечного
управления самолетом влево или вправо они отклоняются в раз-
ные стороны. У полукрыла с опущенным элероном подъемная
сила увеличивается, а у крыла с подмятым элероне i — умень-
шается Разность подъемных сил полукрыльев создает аэроди-
намический момент крена Мх относительно оси ОХ, под дейст-
вием которого самолет начинает вращаться в сторону поднято-
го элерона Практика эксплуатации показывает, чт) самолет
обладает хорошей поперечной управляемостью только на малых
у л ах атаки. По мере увеличения угла атаки крыла поперечная
управляемость ухудшается и при некоторых условиях нарушает-
ся. На больших углах атаки лобовое сопротивление крыла с опу-
370
www vokb-la.spb ru - Самолёт своими руками?!
щенным элероном увеличивается на большую величину, чем ло-
бовое сопротивление крыла с поднятым элероном. Помимо кре-
нящего момента при отклонении элеронов вследствие разности
лобовых сопротивлений полукрыльев возникает аэродинамиче-
ский момент рыскания
(путевой момент) Му, ко-
торый разворачивает са-
молет в сторону крыла с
опущенным элероном,
т. е. в сторону, противо-
положную крену.
Для уменьшения мо-
мента применяется диф-
ференциальное управле-
ние элеронами- В этом
случае один элерон от-
клоняется вверх на зна-
чительно больший угол,
чем другой вниз при по-
стоянном соотношении
между углами. Элероны с
дифференциальным уп-
равлением отклоняются
вверх на 20—25°, а вниз—
на 15—20°
Рис 23 4 Элер он bi-
as—обычный, б—подвесной; в—надкрыльный; г—
предкрыльный. д—корневой; е—пластинчатый (ин-
терцептор)
Аэродинамическими
характеристиками моментов Л1х и Му отклоненных элеронов яв-
ляются:
^3.6)
где Л1Х, Л1у — моменты относительно осей ОХ и OY тХ1 ту—
коэффициенты моментов; <7=qV2/2 — динамическое давление;
S — площадь крыла.
Графики зависимостей коэффициентов тх и ту от угла атаки
крыла и угла отклонения элеронов для трапециевидного крыла
с обычным элероном приведены на рис. 23.5 Из графиков видно,
что на летных углах коэффициент тх сохраняет постоянную ве-
личину и резко уменьшается вблизи критического угла атаки,
что вызвано наличием срыва потока с крыла; коэффициент ту
на эксплуатационных углах атаки постепенно увеличивается.
Чем больше угол отклонения элеронов, тем больше коэффици-
ент момента ту. Однако эффективность элеронов с увеличением
числа Мто падает.
371
www.vokb-la.spb.ru - Самолёт своими руками?!
Рис. 23 5 Изменение коэффициентов мо-
мента тх и ту в зависимости от угла
атаки и угла отклонения элерона для
трапециевидного крыла с обычным эле-
роном
Вопросы для повторения
1 Напишите и проанализируйте формулу, выражающую за-
висимость коэффициента подъемной силы от угла атаки и угла
отклонения руля
2 . Напишите формулы для определения коэффициента эффек-
тивности руля при дозвуковых и сверхзвуковых скоростях.
3 Объясните назначение элеронов и напишите формулы для
определения аэродинамических коэффициентов, характеризую-
щих их.
WWW vokb-la.spb ru - Самолёт своими руками?!
ГЛАВА 24
ЛОБОВОЕ СОПРОТИВЛЕНИЕ
И ПОДЪЕМНАЯ СИЛА САМОЛЕТА
24 1 ЛОБОВОЕ СОПРОТИВЛЕНИЕ И ПОДЪЕМНАЯ СИЛА
НА ДОЗВУКОВЫХ СКОРОСТЯХ ПОЛЕТА
До настоящего времени мы рассматривали аэродинамические *
характеристики отдельных частей самолета в зависимости от ус-
ловий их обтекания. Но современный самолет представляет со-
бой сложную комбинацию фюзеляжа, крыльев, оперения и руле-
вых поверхностей. И здесь оказывается, что сумма аэродинами-
ческих характеристик взятых отдельно (изолированных)* кры-
ла, фюзеляжа, оперения и рулей не равна полным аэродинами-
ческим характеристикам композиции.
Установлено, что тела, расположенные близко друг к другу’
в потоке воздуха, оказывают взаимное влияние на характер их
обтекания. В результате этого изменяются картина обтекания и
формы линий тока, вихревого следа и возмущений, вызванных
каждым элементом самолета в отдельности, что приводит к пе-
рераспределению сил давления. В результате взаимного влия-
ния частей самолета отдельно взятые элементы — фюзеляж
крылья, оперение, рули, — соединенные в единую конструкцию
летательного аппарата, теряют частично свои индивидуальные
аэродинамические характеристики и приобретают новые.
Таким образом, при рассмотрении аэродинамики летазе ь-
иого ; ппарата как комбинации его отдельных частей возникает
слож зая проблема учета аэродинамической интерференции меж-
ду отдельными се частями.
Интерференция является положительной в том случае, когда
вследствие взаимодействия отдельных частей самолета умень-
шается его сопротивление и увеличивается аэродинамическое
качество, и отрицательной в том случае, когда имеет место об-
ратное явление.
Увеличение сопротивления крыла на дозвуковых скоростях
обусловлено наличием сопряжений крыла с фюзеляжем, фюзеля-
жа с оперением, с гондолами двигателей и происходит главным
373
www vokb-la.spb.ru - Самолёт своими руками?!.
образом из-за влияния фюзеляжа на величину и распределение
циркуляции по размаху крыла При размещении на крыле гон-
дол двигателей индуктивное сопротивление крыла еще более
возрастает. Рост индуктивного сопротивления крыла учитывает-
ся введением эффективного удлинения крыла ЛЭф вместо геомет-
рического удлинения Л:
+ (24 1)
ЛЛЭф
Рис 24.2. Влияние относительного
расположения крыла и фюзеляжа на
интерференционное сопротивление:
'-ПРИ суа~0 <сха еаМ~сха mln>: Р-ПРИ
Рис. 24.1. Изменение коэффици-
ента индуктивного сопротив-
ления самолета Ту 134 в зави-
симости ОТ Су а
(24. 2)
фюзе-
Эффективное удлинение определяется по формуле
х’ф= «7’
1+т
где S — площадь крыла; So — площадь крыла, занятая
ляжем, гондолами двигателей и гондолами шасси.
Очевидно, чем большая площадь крыла занята фюзеляжем и
гондолами, тем меньше эффективное удлинение крыла и тем
больше коэффициент индуктивного сопротивления. На рис. 24.1
приведен в качестве примера график изменения коэффициента
индуктивного сопротивления самолета Ту-134 в зависимости от
коэффициента подъемной силы.
Кроме того, вследствие сопряжения крыла с фюзеляжем воз-
растает профильное сопротивление крыла. Фюзеляж и крыло
сопрягаются двумя криволинейными поверхностями и образуют
вблизи задней кромки двугранный расширяющийся канал (диф-
фузор), в котором пограничный слой нарастает гораздо быстрее,
чем в случае обтекания изолированного крыла Рост толщины
пограничного слоя и градиента давления приводят к прежде-
временному отрыву потока с верхней поверхности крыла вблизи
фюзеляжа, при этом чем больше угол раскрытия диффузора в
зоне сопряжения, тем больше величина градиента давления и
374
www.vokb-la.spb.ru - Самолёт своими руками?!
Рис. 24 3. Полиры самолетов при различ-
ном расположении крыла по высоте фюзе-
ляжа
О 0,02 0,04 0,06 0,08 0,10 Сха
тем резче отрыв. Это явление ухудшает аэродинамические ха-
рактеристики самолета, так как увеличивает сопротивление и
уменьшает подъемною силу. На рис. 24.2 показано влияние от-
носительного расположения крыла и фюзеляжа на сопротивле-
ние интерференции, которое дано в процентах от общего сопро-
тивления крыла. Наибольшее увеличение сопротивления имеет
комбинация фюзеляжа с
крылом, расположенным
ниже оси фюзеляжа, т. е.
схема низкоплана. Наи-
больший диффузорный
эффект, т. е. наибольшее
торможение потока и 'на-
иболее ранний срыв пото-
ка в указанных двугран-
ных углах, имеет место
при круглом сечеиии фю-
зеляжа самолета- У сред-
неплана диффузорный эф-
фект очень мал.
Чтобы уменьшить от-
рицательную интерферен-
цию крыла и фюзеляжа,
обеспечивают такую фор-
му сопряжения этих час-
тей, при которой поток в
зоне сопряжения имел бы
цилиндр ичес ку ю форму
или форму сужающегося
канала. В этом случае
градиент давления в
струйке будет постоянным
самолетах диффузорность потока в зоне сопряжения может быть
устранена соответствующим деформированием стенок фюзеля-
жа, применением зализов (манжет), использованием систем уп-
равления пограничным слоем и т. д.
Поляры самолетов при различном положении крыла по высо-
те круглого фюзеляжа с зализами и без них приведены на рнс.
24.3.
Аэродинамическое качество' высокоппана на 4—5% больше,
чем у низкоплана. Несмотря на аэродинамические преимущест-
ва среднеплана такая схема применяется редко на современных
дозвуковых самолетах по компоновочным соображениям.
При расчете профильного сопротивления его увеличение
вследствие интерференции обычно определяется по формуле
k -
ЛИНТ с
о
или отрицательным. На реальных
(24.3)
^ХОКр ^хоиз.кр
375
www.vokb-la.spb.ru - Самолёт своими руками?!
где Схоиз кр — коэффициент сопротивления изолированного кры-
ла; So —площадь крыла, занятая фюзеляжем и гондолами дви-
гателя при расположении последних на крыле; ЛИ11Т — коэффи-
циент интерференции
Чем большая часть крыла занята фюзеляжем и гондолами,
тем меньшая поверхность крыла обтекается потоком и, следова-
тельно, полный коэффициент сопротивления уменьшается. Что
же касается отрицательных явлений, связанных со взаимным
влиянием крыла и фюзеляжа, то они учитываются в формуле
(24 3) коэффициентом интерференции, который меньше едини-
цы. Чем меньше коэффициент интерференции, тем больше коэф-
фициент сопротивтения крыла сх0Кр При низком расположении
крыпа Л11НТ_0,25.. 0,6, при среднем — Линт—0,85, прн высо-
ком — коэффициент Линт принимается равным единице (над кры-
лом фюзеляж отсутствует). Аналогично можно учесть влияние
фюзеляжа на коэффициент сопротивления горизонтального и
вертикального оперений
Однако следует отметить, что если при определении аэроди-
намических сил крыла изменением динамического давления
вследствие торможения потока в местах сопряжения крыла с
фюзеляжем пренебрегают, то торможением потока у оперения
пренебрегать нельзя, так как в этом случае скоростной напор
у горизонтального оперения может уменьшиться на 20 и более
процентов С уменьшением удлинения горизонтального оперения
торможение потока увеличивается На вертикальное оперение
его сопряжение с фюзеляжем оказывает такое же влияние Кро-
ме того, крыло оказывает специфическое влияние на аэродина-
мические характеристики горизонтального оперения. При поле-
те самолета скос потока, имеющий место за крылом, достигает
горизонтального оперения и существенно изменяет его действи-
тельный угол атаки. Особенно большое изменение углов атаки
горизонтального оперения происходит при выпуске закрылков
крыла. Правильный учет влияния скоса потока от крыла на углы
атаки горизонтального оперения чрезвычайно важен с точки зре-
ния безопасности полетов самолетов
Угол скоса потока в области горизонтального оперен 1я уве
личивается с ростом угла атаки или коэффициента подъемной
силы Суа и с уменьшением удлинения крыла и уменьшается с
увеличением расстояния от крыла до горизонтального оперения
Кроме того, на угол скоса у горизонтального оперения оказы-
вает влияние расположение горизонтального оперения по высо-
те относительно крыла С увеличением расстояния вдоль оси
OYa угол скоса потока уменьшается
При определении угла скоса потока у горизонтального опе-
рения обычно используют определенную вихревую схем\ крыла.
Точность определения угла скоса потока будет зависеть от
того, насколько правильно установлена вихревая схема крыла с
учетом его формы, угла атаки, механизации, стреловидности и
376
www.vokb-Ia.spb.ru - Самолёт своими руками?!
т п Величина угла скоса потока зависит также от того, явля-
ется ли число М большим критического значения или меньшим,
дозвуковое или сверхзвуковое обтекание. Подробно иа этих воп-
росах мы останавливаться не будем
Аэродинамические силы самолета с учетом интерференции
можно представить в следующем виде:
асам
ai р.из
асам
ав.о.иэ
а М.Г.И31
где ДКа — приращение подъемной силы самолета, обусловлен-
ное взаимодействием различных его элементов, Хскриз, Хаг0113,
^авопз, Хамгпз — силы сопротивления крыла, горнзонтального и
вертикального оперений гондол двигателей с учетом интерферен-
ции
Как отмечалось выше, на дозвуковых скоростях приращением
подъемной силы самолета вследствие взаимовлияния его эле-
ментов без существенной погрешности можно пренебречь Тормо-
жение потока над крылом в местах его сопряжения с фюзеля-
жем приводит к уменьшению подъемной силы Однако наличие
фюзеляжа несколько увеличивает эффективные углы атаки кры-
ла (см. разд. 24 2), н вследствие этого несколько увеличивает-
ся подъемная снла крыла Прнращення подъемной силы в том
и в другом случае примерно равны по величине, но различны по
знак\, поэтому AKas = O.
Коэффициент сопротивления самолета представим через ко-
эффициенты сопротивления его частей:
Г
Осам
qV2 nV2
СО Q __ со
2 — с v окр ~
ИЛИ
л Осам ^лОф
4“ КсОв.о
$в.о В о
oV2
в.о
A'Oil. J 2
К г ^м.г
I слОм.г £
° 2
где 5МГ— площадь миделевого сечения гондолы двигателя;
ф — площадь миделевого сечення фюзеляжа
377
www vokb-la.spb.ru - Самолёт своими руками?!
Обозначая отношение скоростных напоров у горизонтально-
го и вертикального оперений к скоростному напору невозм} щеп-
ного потока через коэффициенты торможения потока
получим
СгОсам ^ лОкр~Г ^д-Оф
*^м.г
Величины коэффициентов торможения потока у горизонтально-
го kro и вертикального йв.о оперений равны единице, если на
оперение набегает невозмущенный поток больше единицы,
если оперение находится в струе воздушного виита самолета или
реактивного двигателя. В обычных условиях, когда поток тор-
мозится расположенным впереди элементом самолета, эти коэф-
фициенты меньше единицы. Значения коэффициентов &во и kro
определяются экспериментальным путем.
24.2. ЛОБОВОЕ СОПРОТИВЛЕНИЕ И ПОДЪЕМНАЯ СИЛА
САМОЛЕТА НА ТРАНСЗВУКОВЫХ И СВЕРХЗВУКОВЫХ
СКОРОСТЯХ ПОЛЕТА
Прежде чем рассматривать взаимовлияние отдельных час-
тей самолета на трансзвуковом и сверхзвуковом режимах обте-
кания, следует отметить, что на указанных режимах рассматри-
ваются силы сопротивления всей компоновки самолета в целом.
На режимах трансзвуковых и сверхзвуковых скоростей по-
лета значительную роль играет дополнительное волновое сопро-
тивление, обусловленное интерференцией. Оно возникает на уча-
стках сопряжения крыла с фюзеляжем или гондолами. Эти уча-
стки должны быть спрофилированы так, чтобы можно было из-
бежать появления скачка уплотнения или же сместить его в зо-
ну, расположенную вне крыла.
Размещение по длине самолета крыла гондол двигателей,
оперения самолета и других элементов, обеспечивающее мини-
мальную силу сопротивления всей компоновки, производится в
этом случае по так называемому правилу площадей, которое
вначале было сформулировано на базе линейной теории сверх-
звуковых течений. Согласно этому правилу рассматривается
лишь сопротивление при нулевой подъемной силе самолета. На-
помним, что сила сопротивления на cva=Q складывается из си-
лы сопротивления трения и силы волнового сопротивления (пос-
ледняя по своей природе является силой сопротивления давле
ния). По правилу площадей волновое сопротивление определя-
378
www vokb-la.spb ru - Самолёт своими руками?!
ется в основном распределением площадей поперечных сечений
самолета по его длине, а не суммой сопротивлений отдельных
элементов конструкции, поскольку распределение площадей ока-
зывает влияние на распределение скоростей и давлений. Для
того чтобы сопротивление самолета было наименьшим, эпюра
площадей поперечных сечений самолета по его длине должна
быть возможно более плавной.
Рве 24 4 Комбинация крыло —• фюзеляж, выполненная без уче-
та правила площадей (t) и с учетом этого правила (2)-
а—комбинация «крыло—фюзеляж»; б—эквивалентное тело вращения; в—
распределение площадей поперечных сечений
Как следует из теоретических и опытных данных, волновое
сопротивление на трансзвуковых скоростях комбинации крыло—
фюзеляж при нулевой подъемной силе оказывается примерно
равным волновому сопротивлению эквивалентного тела враще-
ния с одинаковым распределением площадей поперечных сече-
ний вдоль продольной оси (рис. 24 4, о).
Таким образом, уменьшения отрицательного влияния интер-
ференции на режимах трансзвуковых скоростей полета можно
добиться в том случае, когда закон изменения площади попереч-
ных сечений самолета по его длине соответствует закону измене-
ния площадей поперечных сечений по длине тела вращения наи-
меньшего сопротивления. Поэтому представляет теоретический
и большой практический интерес определение распределения
площадей поперечн: ix сечений тел вращения заданной длины и
объема, обеспечивающих наименьшее волновое сопротивление.
Такими телами согласно теоретическим данным являются ожи-
вало Кармана, тело Сирса—Хаака, контуры которых близки
379
www vokb-la.spb.ru - Самолёт своими руками?!
между собой. Распределение площадей последнего определяется
формулой
S(fl) ——— (sin 9---— sin Зб\ (24.
л/ 3 /
где I — длина тела; 6 — переменная Глауэрта, изменяющаяся в
пределах от 0=0 (кормовая часть) до 6 = л (носовая часть те-
ла вращения).
Следует отметить, что волновое сопротивление мало чувстви-
тельно к небольшим отклонениям от оптимальных форм при ус-
ловии плавного распределения площадей поперечных сеченнй
но длине тела
Расчет коэффициента волнового сопротивления тела в этом
случае можно существенно упростить, сведя его к расчету коэф-
фициента волнового сопротивления эквивалентного тела враще-
ния В качестве эталона принимается тело Сирса—Хаака, коэф-
фициент волнового сопротивления которого определяется по
формуле
128 V
CxQbS^h——- 7—
Л о jyyi
где V—объем тела; Sm — площадь миделя, к которой отнесе-
ны аэродинамические коэффициенты; L — длина тела. Коэффи-
циент волнового сопротивления заданного тела, естественно,
будет несколько отличаться от коэффициента волнового сопро-
тивления тела минимального сопротивления некоторым множи-
телем, поэтому
. , 128 V
ГгОв~—КоСдОв$-~Я —— •
Л
Введя в эту формулу относительные величины
параметров тела, получим
геометрических
СгОв
128 „ „
-----г2/?2
л
b 2
L J ’
где г — V/S3^2 —безразмерный объемный параметр; p — S^/lL;
I — размах крыла.
Значение коэффициента k0 зависит от распределения подъем-
ной силы крыла по размаху. Так как «правило площадей» про- *
является лишь по отношению к волновому сопротивлению, то
наибольший эффект от его применения получают на тех режи-
мах полета, при которых коэффициент подъемной силы мал
Внезапное увеличение объема тела, например, в месте не-
плавкого сопряжения крыла с фюзеляжем, необходимо компен-
сировать уменьшением объема других элементов компоновки в
сечении, плоскость которого совпадает с плоскостью скачка уп-
лотнения. Поэтому применение «правила площадей» приводит к
380
www.vokb-la.spb.ru - Самолёт своими руками?!
характерному «поджатию» фюзеляжа в зоне сопряжения крипа
и фюзеляжа (-см. рис. 24.4).
Эксперименты показывают, что при скорости полета, соот-
ветствующей числу Моо—0,95 .. .1,05, «поджатие» фюзеляжа
снижает увеличение сопротивления на 60—80% (рис. 24.5). При
дальнейшем увеличении скорости полета эффект от применения
«правила площадей» уменьшается и при числе Мж—1,7 .. .2.0 он
исчезает.
Эффективность применения «правила площадей» можно объ-
яснить, рассмотрев изменение силы волнового сопротивления
Рис. 24.5. Эффект применения правила площадей:
1 — изолированнь й фюзеляж; 2 — цилиндрический фюзеляж с кры-
л м; 3—фюзеляж с крылом, выполненный с учетом правила пло-
щадей
компоновки самолета в зависимости от числа Мкр. По мере при-
ближения скорости полета к скорости звука местные скорости
на крыле существенно увеличиваются около утолщенной части
этих тел и в еще большей степени увеличиваются скорости тече-
ния в местах сопряжении, например, крыла с фюзеляжем, крыла
с гондолами, расположенными иа пилонах н т п.
Степень уменьшения величины МКР, характерн ующей нача-
ло резкого увеличения сопротивления самолета при околозвуко-
вых скоростях, в значительной мере зависит от взаимного рас-
положения элементов Так, при обтекании комбинации крыло
гондола местные скорости могут достигать скорости звука и да-
же превышать ее при скоростях полета, существенно "меньшнх
скорости звука. Наибольшие местные скорости возникают на по-
верхностях сопрягающихся элементов при совпадении миниму-
мов давлений элементов. Кроме того, большие градиенты давле-
ния, возникающие на кормовых частях гондолы и крыла, скла-
дываясь, приводят к преждевременному отрыву потока от при-
мыкающих поверхностей. Явление отрыва еще больше проявля-
ется, если возникают скачки уплотнения, так как дополнитель-
381
WWW vokb-la.spb.ru - Самолёт своими руками?!
ный положительный градиент давления за скачком уплотнения
складывается с уже имеющимся положительным градиентом
давления.
Можно избежать преждевременного отрыва потока, скомпо-
новав самолет таким образом, чтобы положительный градиент
давления на крыле компенсировался отрицательным градиен-
том на гондоле. Экспериментальные данные, полученные при
различном расположении гондолы относительно крыла, показы-
Рис 24 6 Влияние размещения гондол на поля-
ру самолета (М» —2,7)
вают, что наибольшее приращение сопротивления от взаимо-
влияния этих элементов достигается именно па околокрнтиче-
ских режимах.
Сопротивление, обусловленное интерференцией, оказывается
наибольшим прн совпадении передних кромок крыла и гондолы
(х/6=0). Резкий сдвиг гондолы назад (х/Ь= +1,0) уменьшает
взаимовлияние элементов, и на режимах больших околозвуко-
вых скоростей интерференция становится даже положительной.
Прн сверхзвуковых скоростях полета интерференция частей
самолета определяется в основном распределением скачков уп-
лотнения и волн расширения, возникающих на поверхности тела
н передающих изменения давления соседним телам.
Зоны возмущения обычно невелики, но в этих узких облас-
тях могут наблюдаться большие изменения давления, которые
могут как увеличивать, так и уменьшать подъемную силу и ло-
бовое сопротивление и смещать центр давления на крыле (рис.
24 6)
382
www vokb-la.spb.ru - Самолёт своими руками?!
Рациональное расположение гондол под крылом позволит
значительно уменьшить величину лобового сопротивления при
крейсерских сверхзвуковых режимах полета.
При проектировании самолета приходится тщательно взве-
шивать преимущества и недостатки отдельных вариантов рас-
положения его элементов.
Рис. 24.7. Изменение волнового сопротивления при
нулевой подъемной силе в зависимости от числа М»
для комбинации крыла с корпусом и оперением:
ООО—эксперимент; —------теория —----—эксперимент
Уменьшение полного сопротивления, полученное путем ис-
пользования «правила площадей», может составлять до 20%, и
теоретические значения сопротивления соответствуют экспери-
ментальным (рис. 24.7)
Исключением является область малых околозвуковых ско-
ростей (Мто<1), для которой линейная теория дает нулевое
волновое сопротивление. «Правило площадей» применимо так-
же к расчетам сопротивления при сопряжении гондол двигате-
лей с крылом, к наружной подвеске топливных баков и др. На-
пример, значительное удаление концевых отсеков крыла от фю-
зеляжа и установка на крыле каплевидных гондол позволили
несколько ослабить интерференцию крыла и фюзеляжа на само-
летах Ту-104 и Ту-124. Использование правила площадей при
проектировании самолета позволяет не только уменьшить вол-
новое сопротивление (на 20-—25%), но и улучшить другие лет-
ные качества самолета, например характеристики устойчивости
и управляемости
383
24 3. ПОД®ЁЖЙЙасЙЛА1
- Самолёт своими руками?!
САМОЛЕТА
Для анализа влияния интерференции крыла и фюзеляжа иа
подъемную силу рассмотрим обтекание фюзеляжа с крылом под
положительным углом атаки (рис 24 8). Поток, избегающий на
Рис 24 8 Схема взаимного
влияния крыла и фюзеляжа
на распределение давления
фюзеляж, отклоняется под иим вниз, а
по бокам фюзеляжа — вверх. Следова-
тельно, фюзеляж вызывает скос пото-
ка, увеличивающий угол атаки крыла
а н его подъемную силу. При этом
увеличивается давление под крылом и
разрежение иад ннм.
Имеется и обратное влияние крыла
иа фюзеляж. Если крыло создает
подъемную силу, то над крылом воз-
никает разрежение, а под ним — дав-
ление, распространяющееся соответст-
венно на верхнюю и ннжнюю поверх-
ности фюзеляжа. Поэтому и на фюзе-
ляже из-за разности давлений в пре-
делах распространения зон возмуще-
ния возникает подъемная сила.
Таким образом, с учетом взаимо-
влияния частей самолета
1 асач~' акр-ф ' аг.о* И4-
Определим сначала подъемную силу комбинации крыло-—фю-
зеляж, взаимное влияние которых проявляется в увеличении
подъемной силы,
* акр—ф * акр J 1 аф~~Г 1-1' акр "Г аф'
Если увеличение подъемной силы крыла ДУпкр и фюзеляжа пол-
ностью отнести к крылу, то можно записать
* акр—ф~’-' акр'*' 'г * аф»
где —коэффициент интерференции, учитывающий подъем-
ные СИЛЫ ДУоьр Н ДУаф.
Принимая во внимание отдельно влияние угла атаки а и уг-
ла установки крыла <р (что можно сделать, если углы а и <р ма-
лы), запишем выражение для подъемной силы комбинации кры-
ло-фюзеляж в виде
Пкр_ф = Гот+Г«.. (24.7)
где Y—подъемная сила комбинации крыло—фюзеляж прн
а—0; Yaa—подъемная сила комбинации крыло—фюзе-
ляж при а#=0; <р=0.
В дальнейшем угол атаки будем отсчитывать не от плоскости
хорд крыла, как это делалось ранее, а от оси фюзеляжа
Of
www.vokb-la.spb.ru - Самолёт своими руками..
Обусловленная углом атаки подъемная сила
Уаа^^УУакрола,
где ka — коэффициент интерференции, учитывающий увеличе-
ние подъемной силы крыла и фюзеляжа при <р=0, а#=0 (рис.
24.9)
При а=0 АУаКр=О и подъемная сила, возникающая на кры-
ле и обусловленная только углом установки ф,
(24-9)
где ky — коэффициент интерференции, учи-
тывающий взаимное влияние фюзеляжа и
крыла при а = 0 и фт^О. Подставив в выра-
окоича-
(24. 8)
жеиие (24.7) значение и Yaj,
тельно получим
(24 10)
самоле-
1 акр—ф —1 акРа^аД- * акр^к?.
Поскольку крылья сверхзвуковых
тов обычно набираются из симметричных
профилей, а фюзеляж близок по форме
к телу вращения, то в этом случае справед-
ливы следующие соотношения:
Рис
ДЛЯ
эффициентов
ференции ka
(гм — радиус
левого сечения
ляжа)
24 9. Графики
определения ко-
интер-
и &<р
мнде-
фюзе-
суа$а.— Оакра—
Используя выражение (24.10), с учетом
этих соотношений получим следующую фор-
мулу для определения коэффициента подь-
емиой силы комбинации крыло—фюзеляж:
а + ^акр(^«+ад
(24. 11)
-несущей части крыла,
не занятой фюзеляжем.
а °м.ф
G/акр—ф — С^аф “
ГО
как
ма-
где SK — площадь
т. е. части крыла,
Методика учета взаимовлияния фюзе-
ляжа и горизонтального оперения аиало
гична изложенной для крыла, с той лишь
разницей, что приращение подъемной силы иа фюзеляже от
ризоитальиого оперения будет меньше, чем от крыла, так
зона возмущения от оперения распространяется только на
лую часть фюзеляжа (оперение устанавливается в хвостовой
части фюзеляжа). С учетом изложенного выше коэффициент
подъемной силы всего самолета можно записать в виде
„ -$м.ф
f — z10 _
1Уасам —£'аф
(24 12)
О
>а
уа кр
S
13
626
385
WWW .vokb-la.spb.ru - Самолёт своими руками?!
Определив значение сха и суа с учетом сжимаемости, для
каждого числа М можно построить семейство поляр (рис.
24.10, а) С увеличением числа Мго до Мкр начиная с Мга=
=0,5 .. .0,6 поляра вытягивается вверх вследствие увеличения
Суа и одновременно на участке больших углов атаки сдвигается
вправо из-за возрастания Сха вследствие взорастания индуктив-
ного сопротивления, при этом одновременно уменьшается сватах
(для числа Мте=0,75... 0,80).
Рис. 24.10 Поляры самолета Ту 134 (а) и сверхзвукового самолета (б) для
различных чисел М,»
Прн скоростях полета, больших критической, при которых зна-
чительно увеличивается волновое сопротивление, поляра при
определенных числах М значительно вытягивается вверх и зна-
чительно сдвигается вправо (см рис. 24 10, а) при числах
М«>0,80.
Если число Моо таково, что волновое сопротивление имеется
почти на всех углах атаки, этому числу Мм соответствует повы-
шенное значение схп (для любого суа) и поляра оказывается
смещенной вправо. Это свидетельствует о значительном сниже-
нии аэродинамического качества самолета
При сверхзвуковых скоростях полета коэффициент сопротив-
ления, обусловленный утлом атаки, принимается равным
сЛ/=Гуа(а—сс0) (^4. 13)
или г ;=с2 /с“
уа' уа
Здесь имеется в виду несимметричная схема самолета, у кото-
рого подъемная сила равна нулю при некотором угле атаки кор-
пуса а=ао-
Коэффициент подъемной силы суа при малом а может быть
принят с известным приближением, равным его величине для
386
QI
WWM.vokb-la.spb.Ill - Самолёт своими руками..
крыла. Однако для повышения точности расчетов коэффициент
Суа лучше вычислять с учетом влияния корпуса и оперения.
Уравнение поляры можно записать в виде
= + (24.14)
Примерный вид поляр скоростного самолета показан иа рис.
24.10, б Применение стреловидных крыльев малого удлинения
позволяет уменьшить сх0. Однако при этом ухудшаются несу-
щие свойства летательного аппарата, т. е снижается с“а и, зна-
чит возрастает общее сопротивление.
Рис. 24.11 Изменение лобового
сопротивления самолета в за-
висимости от числа Мм.
I дозвуковой режим; II—околозву-
ковой режим, III сверхзвуковой ре-
жим
7—дозвуковой самолет; 2—сверхзву-
ковой самолет с закругленным нос-
ком крыла, 3 сверхзвуковой само
лет с заостренным носком крыла
При больших Суа величина схг у самолета со стреловидными
крыльями настолько увеличивается, что их преимущество, свя-
занное с уменьшением сх0, теряется, так как увеличивается сум-
марное сопротивление. Характер изменения коэффициента соп-
ротивления сЛо в зависимости от числа Мто у самолетов различ-
ной формы показан иа рис. 24 11.
Как известно, аэродинамическое качество определяется от-
ношением
суа1с ха.
Подставляя в эту формулу выражение для сха, получим
К =
4' -АСуа
Гйе А =—-—(14-8) при дозвуковых скоростях;
лХэф
Д=1/с*а при сверхзвуковых скоростях.
Изменение аэродинамического качества самолета Ту-134 в
зависимости от коэффициента суа для различных чисел
показано иа рис. 24 12, а.
Максимальное качество и соответствующий иаивыгоднейший
коэффициент подъемной силы при дозвуковых скоростях опре-
деляются соотношениями
rj- I Г ЛХЭф . Г
max ДД I/ ~ ~ » П/н,в= |/ ~ . ,ч •
Г <WI + S) У (I + б)
13*
387
www.vokb-la.spb.ru - Самолёт своими руками?!
При сверхзвуковых скоростях
^Н.в —у С^аСх0‘
Максимальное качество с ростом числа уменьшается
(рис. 24.12, б). Как видно из графиков на рис 24.12, а, для чи-
Рис 2412. Зависимость аэродинамического качества самолета
Ту-134 от коэффициента подъемной силы су для разных чисел
Ми, (а) и изменение в зависимости от числа М« (б)
сел Моо порядка 0 75 максимальное К самолета Ту-134 составля-
ет 15,1 и уменьшается до 10,8 при М^—0 85.
Применение стреловидных крыльев и крыльев малых удли-
нений снижает значение суаПъ, так как с уменьшением удлине-
ния и увеличением угла стреловидности уменьшаются <лс и с * .
Вопросы для повторения
1 В чем заключается суть аэродинамической интерференции
частей самолета и ее влияние иа лобовое сопротивление?
2 Напишите формулу величины угла скоса, вызванного на
крыле фюзеляжем, и проанализируйте ее.
3 Сравните подъемную силу самолета с подъемной силой
крыла и дайте анализ.
388
www vokb-la.spb.ru - Самолёт своими руками?!
Задачи
1. Определить коэффициент полного сопротивления дозвуко-
вого самолета, если
+=8,4; L+L=0j3i8. S=140 м2;
Сгоиэ.кр =9,008; л *^м.ф"9,6 ма;
с„ф= 0,076; см=0,8; 5го=27,8ма;
^г.о=0,0096; +=0.8; 5,.0=17ма;
<Л„ =0,0092; +=0,92; Л
гхог.»=0,041 £цнт=0,5;
Площадь крыла, занятая фюзеляжем, составляет 20% от всей
площади крыла.
Решение. Согласно формуле (20 7)
С ха = СгО Ч~ ^х1‘
Из формулы (24.3), следует, что
СсОкр СгОиз.кр fl ^инт ~ ' 0,008 (1 - 0,5 • 0,2) =0,0072.
\ о /
Тогда по формуле (23.8)
Схо=о аду 0,076-9,6 + 0,0096-27,8 0,8 + 0,0092-17 0,92 + 0,041-1,1
140 в
-О.П079 0.73 + 0,213 + 0,144 + 0,0451 Q д
140
Согласно формуле (23.1)
2
(1Ч- 8) = 0,82(1 + 5) =0,0243.
лЛэф л8,4
Таким образом, коэффициент полного сопротивления
Сха=Сха 4- Cxi -- 0,0153 + 0,0243 = 0,0396.
«лги vokb-la.spb.ru - Самолёт своими руками?!.
ГЛАВА 25
ВОЗДУШНЫЕ ВИНТЫ
25.1. ПРИНЦИП ДЕЙСТВИЯ ВОЗДУШНЫХ винтов,
ИХ ГЕОМЕТРИЧЕСКИЕ И КИНЕМАТИЧЕСКИЕ
ХАРАКТЕРИСТИКИ
Сила тяги самолетов с винтовым движителем, необходимая
для полета, создается отбрасыванием назад массы воздуха с по-
мощью воздушного винта Чем больше скорость и масса отбра-
сываемого назад воздуха, т. е. чем больше количество движе-
ния, сообщаемое воздуху, тем больше тяга винта. Винт является
движителем: он преобразует энергию двигателя в работу, совер-
шаемую при движении самолета
Эффективность винта оценивается с помощью КПД
A1KQ '
Здесь мощность на валу винта (АД — вращающий мо-
мент, Q — угловая скорость), преобразуется в полезную мощ
ность PVoo (Р — сила тяги, У» — скорость полета самолета)
Современные винты имеют высокий КПД, достигающий
при докритических скоростях полета 83—86%. Однако при за-
данной мощности двигателя с увеличением скорости полета
сила тяги P=f]N/Voa уменьшается настолько, что самолеты с
винтовыми движителями уступают в экономичности самолетам
с ТРД, чем объясняется применение винтов на самолетах лишь
сравнительно низких скоростей
Основным рабочим элементом воздушного винта является ло-
пасть Форма лопастей воздушных винтов может быть различ-
ной — от прямоугольной до саблевидной. Профили, из которых
составлена лопасть, измен ются от корня лопасти к ее концу.
Лопасть винта характеризуется рядом геометрических размеров,
которые называются геометрическими характеристиками.
Диаметр винта D (2/?) — диаметр окружности, описываемой
концами лопастей при вращении винта. Величина диаметра вин-
та при прочих равных условиях сильно влияет на КПД и опре-
390
www vokb-la.spb.ru - Самолёт своими руками?!
винта к площади, ометаемои
Рис 25 1 Геометрические и кине-
матические характеристики про-
филя лопасти
подъемная сила. Условия ра-
чем крыла, так как ло-
деляется аэродинамическим расчетом. При выборе диаметра
виита учитываются конструктивные соображения, так как, нап-
ример, размеры винта влияют на высоту шасси;’ они должны
быть учтены при компоновке многомоторных самолетов, чтобы
не ухудшить условия работы соседних винтов.
Коэффициент заполнения о — отношение площади проекций
лопастей на плоскость вращения
лопастями при вращении винта.
Ширина лопасти b — длина
хорды сечения лопасти (рис.
25.1). По длине лопасти хорда
изменяется. Для дозвуковых вин-
тов обычно максимальная шири-
на достигается примерно на по-
ловине длины лопасти.
Толщина лопасти с — наи-
большая толщина профиля лопа-
сти. Толщина лопастн умень-
шается от корня лопасти к ее
концу, достигая на конце 4-7%
хорды Толщина лопасти в сред-
них сечениях составляет 10 —
16%, а в корневых —25—30%.
Угол установки сечения лопа-
сти ф — угол, образованный хон-
дой сечения с плоскостью враще-
ния винта (см. рис. 25.1).
При вращении винта каждое
сечение его лопасти обдувается
потоком воздуха, и как у крыла
самолета, на лопасти возникает
боты лопасти виита? однако, слоз
пасть одновременно совершает поступательное и вращательное
движения Углом атаки а сечения лопастн называется угол
между хордой сечения и направлением полной скорости U7 (см.
рис. 25. 1), в первом приближении равной векторной сумме осе-
вой скорости (скорости полета VTO) и окружной скорости U.
Окружная скорость возрастает с увеличением расстояния от оси
вращения, поэтому вдоль лопасти изменяются условия обтека-
ния ее сечений. С ростом окружной скорости углы атаки сечений
увеличиваются. Поэтому прн постоянной угловой скорости на
лопасти угол атаки сечения буд( т том больше, чем дальше сече-
ние отстоит от оси вращения.
Поскольку угол атаки сечения лопастн зависит от расстоя-
ния до оси вращения, то для того чтобы углы атаки сечений ло-
пасти были примерно одинаковыми на любом расстоянии от оси
вращения необходимо делать лопасть с круткой.
391
www.vokb-la.spb.ru - Самолёт своими руками?!
Крутка лопасти — изменение по длине лопасти угла установ-
ки сечения. Обычно это изменение отсчитывается относительно
угла установки контрольного сечения, расположенного на рас-
стоянии 0,75/? от осн вращения, поэтому крутка лопастн харак-
теризуется разностью ф <ро,75» где ф — угол установки рассмат-
риваемого сечения, расположенного на расстоянии г от оси вра-
щения
Рис. 25 2 Изменение геометрических
характеристик по длине лопасти
В эксплуатационных условиях часто контрольное сечение
располагается не иа 0,75 /?, а на другом расстоянии, вполне оп-
ределенном для каждого типа
винтов. Контрольное сечение
отмечается яркой чертой на
лопасти.
При постоянной угловой
скорости вращения винта угот
атаки сечений будет, очевидно,
зависеть от величины осевой
скорости. С ростом осевой ско-
рости угол атаки любого сече-
ния уменьшается и может
стать даже отрицательным
(см. рнс. 25. 1). Отрицатель’
ный угол атаки может быть
получен и вследствие умень-
шения угла установки лопа-
сти ф.
Для обеспечения наивыгод-
нейших условий работы на
всех режимах полета современные винты снабжены устройст-
вом для поворота лопастей. Такие винты называются винтами
изменяемого шага (ВИШ) в отличие от винтов фиксированного
шага (ВФШ)
Невращающийся виит, как н всякое тело в потоке воздуха,
оказывает лобовое сопротивление, которое будет минимальным
если лопасти установить так, чтобы их хорды стали примерно
параллельными скорости полета. Такое положение винта назы-
вается флюгерным.
Как правило, в аэродинамическом расчете геометрические
характеристики винта применяются не в абсолютном, а в отно-
сительном исчислении, т. е в расчете применяют величины
b — b/D; с—с[Ь\ г —г R- Zr D.
Часто эти величины задаются в процентах. Для каждого вин-
та характеристики сечений лопасти изображаюгся.графически в
зависимости от относительного радиуса г (рис. 25 2).
Шаг винта Н — путь, отсчитываемый в осевом направлении,
который пройдет элемент лопасти, расположенный на 0,75/?, за
S2
www.vokb-la.spb.ru - Самолёт своими руками?!
один оборот, двигаясь в окружающей среде вдоль хорды, как в
твердом теле.
Поступь винта (динамический шаг) На — расстояние, кото-
рое винт фактически проходит в воздухе за одни оборот. Вслед-
ствие податливости воздуха винт проходит за один оборот рас-
стояние, как правило, не равное шагу винта. При работе винта
иа месте поступь виита равна нулю
Относительная поступь X—отношение поступи винта к его
диаметру: 1=На/0
Так как за один оборот виит проходит вдоль своей оси рас-
стояние Ha—V^ln^ где пс— частота вращения в секунду, то
\^VjDnc. (25.1)
Абсолютной скоростью W называют скорость, равную геомет-
рической сумме осевой скорости и окружной скорости U Ок-
ружная скорость для сечения лопасти, расположенного на рас-
стоянии г, может быть найдена по формуле U—2лгп<,
или, вводя безразмерный радиус r=riR=2r}D.t имеем U—nDncr.
Тогда абсолютная скорость для этого сечения
W = У V^-YU^=Dnc ]А24-ла73.
Угол притекания рп — угол между абсолютной скоростью н
плоскостью вращения лопасти (см. рис. 25.1) Из рисунка видно,
что tg рп= Ko/t/.
Используя соотношение (25.1) и выражая окружную скорость
через расстояние до оси вращения и частоту вращения, получим
tgpn = tynr. (25.2)
Для сечения, расположенного на расстоянии 0,75/?
Роль = arctg
Угол атаки сечения определяется как разность а=<р— (Зп.
25.2. ТЕОРИЯ ИДЕАЛЬНОГО ВОЗДУШНОГО ВИНТА
Теория идеального воздушного винта является приближен-
ной, она опирается на общие тёоремы механики и не связана с
конструктивными элементами винта, поэтому ею нельзя вос-
пользоваться для проектирования. Однако эта теория позволя-
ет оценить мощность и тягу, а также выявить влияние скорости
полета на тягу и КПД винта.
Воздух полагается средой невязкой, т е. потерн на треиие от-
сутствуют.
Струя воздуха, протекающая через винт, сужается на всем
протяжении, ио наиболее интенсивно это происходит на учаетке
перед диском виита и непосредственно за ним. Практически
393
www vokb-la.spb.ru - Самолёт своими руками?!
можно считать, что область сужения ограничена расстоянием
±D от плоскости вращения вннта.
Обозначим скорость невозмущенного потока впереди винта
через К», осевую составляющую в плоскости вращения винта
через V'i=Vco + o1, осевую составляющую на большом удалении
за винтом через 1/2=К»+у2 (рис. 25.3). Индуцированные скоро-
сти щ и v2 есть отклонения от скорости невозмущенного потока,
вызванные работой воздушного винта.
Рис 25 3 Схема для расчета идеального винта
Величину силы тяги можно вычислить, применяя теорему об
изменении количества движения в проекции на ось вращения
винта:
Р=т (V2 — mv2, (25.3)
где m —секундный массовый расход воздуха через поверхность,
сметаемую винтом
Вннт увлекает за собой воздух, принуждая его вращаться.
Скорость вращения воздуха далеко впереди винта равна нулю.
Полагаем, и это близко к истине, что внутри струн воздуха, про-
ходящей через винт, воздух вращается в каждом отдельно взя-
том поперечном сечении со своей угловой скоростью ю. Обозна-
чим угловую скорость в плоскости вращения винта через он, а
далеко за винтом — через <й2.
Мощность, т. е. энергию, отдаваемую винтом ежесекундно
окружающей среде, можно подсчитать как изменение кинетиче-
ской энергии воздуха, протекающего внутри тела вращения*
M=V+'/2V-—<25-4)
где /2 — момент инерции струи воздуха, прошедшей через вннт,
на большом удалении от плоскости вращения.
394
www vokb- la.spb ru - Самолёт сеЪими руками?!
Из выражения (25.4) следует, что мощность, отдаваемая вин-
том потоку, расходуется на увеличение кинетической энергии в
поступательном движении, параллельном оси винта, и на созда-
ние кинетической энергии вращения, т. е. мы можем предста-
вить мощность винта как сумму «осевой» мощности Noc и «ок-
ружной» мощности N0Kp.
Величина «осевой» мощности
т Ио + V 1
^c=v('/2-v'9=«(b2- и»)—-
нли с учетом соотношения (25.3)
(25.5)
С другой стороны, величина «осевой» мощности равна произве-
дению тягн винта Р иа осевую скорость воздуха в плоскости
вращения винта:
N,.c~PVv (25.5')
Сравнивая формулы (25.5) и (25.5'), получим
^=(^+1/^/2.
Но i/2=i/oo+^2;
тогда ^=^/2. (25.6)
«Окружная» мощность, затрачиваемая винтом на вращение
воздуха, равна произведению угловой скорости ©j в плоскости
вращения виита на момент Л1к, вращающий винт, т. е.
7V—7l4K(o-i.
Cn.pi IV X
Таким образом, полная мощность, отдаваемая винтом воздуху,
может быть выражена в виде следующей суммы:
TV-Pl/j-t-ALo),.
Мощность, отдаваемая винту двигателем, определяется про-
изведением крутящего момента Л|1: на угловую скорость И вра-
щения винта:
Лт=Л1к2. (25.7)
Значит, 7ИК2 == РУ\ Ц-
откуда —Afh(2 — (ot). (25.8)
Коэффициент полезного действия найдем, поделив полезную
мощность ГК» на затраченную, определяемую формулой (25 7);
PVoo PV{ _ РУj
в~ Л1к2 “ РУг MKQ У1 Л1к2 ’
395
www vokb-la.spb ru - Самолёт своими руками?'
Подставив сюда значение из (25.8), получим
’’“ТТ*?9- (25-9>
Назовем первый множитель в правой части формулы (25 9)
осевым КПД, а второй — окружным КПД.
Исходя из сути величии, входящих в формулу (25.9), можно
сделать некоторые выводы
Во-первых, чем меньше угловая скорость вращения воздуха
со± по сравнению со скоростью вращения винта Q, тем выше ои-
ружной КПД винта. Предотвратить вовлечение воздуха во вра-
щательное движение можно было бы установкой так называемо-
го спрямляющего аппарата, однако для самолета это не
представь яется выгодным, так как одновременно с повышением
окружного КПД уменьшается тяга винта из-за сил трения на по-
верхности лопастей спрямляющего аппарата. Реальное увеличе-
ние окружного КПД достигается в установках с соосными вин-
тами, вращающимися в противоположные стороны. В этом слу-
чае вращение воздуха за первым винтом полезно используется
на втором винте
Во-вторых, КПД винта можно увеличить благодаря умень-
шению скорости Vi в плоскости вращения винта, однако следу-
ет иметь в виду, что уменьшение скорости Vt приводит всегда к
уменьшению тяги винта. Это следует из соотношений (25.3) и
(25 6) Уменьшение осевого КПД приводит к увеличению тяги.
Чем больше скорость v2, тем больше тяга, но тем меньше КПД
винта, ибо винт создает тягу, отбрасывая воздух назад со скоро-
стью, превышающей скорость натекания Осевой КПД можно
повысить, увеличивая диаметр винта прн одновременном умень-
шении индуцированной скорости. Однако конструктивно увели-
чивать диаметр винта можно лишь до известных пределов. Кро-
ме того, увеличение диаметра винта ограничено увеличением
сопротивления лопасти.
Итак, соотношение (25 9) можно переписать в виде
Ч,=ЧЛ«р. (25.9')
где согласно выражениям (25 6) и (25 9)
»1оС=—=------------; Т1ОКР=- —- (25.10)
Vi 14-v2/2Vto оКр 2
Поскольку Т]ос< 1 И '»1окр< 1, то Т]в—ПосПокр< 1.
Для выяснения влияния скорости полета V«, на о евой КПД
Т]ос и тягу винта Р проанализируем влияние скорости полета на
величину скорости v2
396
www.vokb- la.spb ru - Самолёт своими руками?!
Подставляя значение тяги из соотношения (25 3) в формулу
(25.5'), получим
Выразим теперь секундный расход т через плотность р, пло-
щадь F, ометаемую винтом, н скорость в плоскости виита-
т =gPV1,
(25 11)
тогда
Л^ос=cP^2IZ2, откуда
^ос .
0^2 ’
Учитывая, что согласно выражению (25.6)
(25.12)
получим е<»4—?_=1/Г —~ (25.13
J 2 |/ qFv2
Из соотношения (25.13) видно, что при постоянной мощности
Noc вызванная скорость v2 изменяется монотонно прн изменении
14, и стремится к нулю при неограниченном возрастании скоро-
сти полета Теперь, пользуясь формулой (25.10), можно сде-
лать заключение о влиянии скорости полета на осевой К 1Д
При У«,=0 получим i]oc=0, так как в данном случае не со-
вершается полезной работы; при 14>—>-ос> и2—И) и 1]ос->-1, т. е. осе-
вой КПД винта увеличивается с ростом скорости полета, стре-
мясь к единице.
Для анализа влияния скорости полета на тягу подставим в
формулу (25 3) величину массового расхода (25.11) с учетом со-
отношений (25.12) н (25.13):
P^=mv2—qF А/^-1—^2=Уе^2^ос-
\ J
Как уже известно, при 14—>-оо вызванная скорость С'2—>4, по-
этому тяга Р уменьшается до нуля. Таким образом, чем больше
скорость полета, тем меньше тяга идеального винта.
Одной из величин, характеризующих работу винта, является
коэффициент нагрузки В на ометаемую винтом площадь.
В
(25. 14)
с °°
4F —
Через коэффициент нагрузки выражаются все основные ве-
личины, рассмотренные ранее. Так, например, для тяги имеем
V +v2 / И2 \
Р-mv2=QFV^=QF (1/2 - Исо)=Ре -f-).
397
www vokb-la.spb.ru - Самолёт своими руками?!
Вводя это значение тяги Р в формулу (25.14), получим
1/2В = 1/2—И2,
оо 2 ооэ
откУДа V^V^VWb. (25.15)
Теперь можно вычислить скорость в плоскости винта:
^=^±^-=-^(1+1/1+1). (25.16)
Подставив это значение скорости в формулу (25.10), выразим
осевой КПД винта через коэф-
фициент нагрузки на ометае- I
мую винтом площадь: ---------]
Рис 25 4. Зависимости осевого КПД
и КПД идеального и реального вин-
тов от скорости полета
Рис. 25 5 Схема работы лопасти воз
душного винта при наличии окруж
ной составляющей скорости воздуш
ного потока
Формулы (25.15) — (25.17) показывают, что с увеличением на-
грузки В увеличиваются скорости и Vr2 и уменьшается осевой
КПД
Графики, выражающие зависимость осевого КПД т|ос, КПД
идеального виита 7]в=Лос^окр и КПД реального винта г]д от ско-
рости полета, показаны на рис 25.4*.
Наличие окружной составляющей индуцированной скорости
.воздушного потока U\ и увеличение осевой составляющей ско-
рости иа величину Vi несколько изменяет структуру обтекания
сечеиия лопасти виита (рис. 25.5). Так, при постоянном угле ус-
тановки сечеиия лопасти виита истинный угол атаки сечеиия
уменьшается, угол притекания струй увеличивается, равиодей-,
ствующая скорость U'J1CT уменьшается.
* Как видно из рис. 25.4, на больших скоростях полета решающее влия-
ние на КПД оказывает профильное сопротивление, что предопределяет пре-
дел применяемости теории идеального винта.
398
wwm vokb-la.spb. ru - Самолёт своими руками?!
25.3. ТЕОРИЯ ИЗОЛИРОВАННОГО ЭЛЕМЕНТА ЛОПАСТИ ВИНТА
В теории изолированного элемента лопастн последняя рас-
сматривается как крыло, при этом делаются следующие допу-
щения:
1 Каждый элемент лопасти работает изолированно (сосед-
ние элементы ие оказывают влияния на его работу). Это допу-
щение позволяет рассматривать любой элемент как элемент кры-
ла бесконечного размаха, т. е. прене-
брегать индуктивным сопротивлением.
2. Воздействие потока иа элемент
лопастн, движущейся по винтовой ли-
нии, такое же, как иа элемент крыла
бесконечного размаха, движущийся
поступательно с той же абсолютной
скоростью и под тем же углом атаки.
Двумя концентрическими поверхно-
стями с центром на осн вращения вы-
режем элемент лопасти длиной dr на
расстоянии г от оси вращения (рис.
25.6). Абсолютная скорость воздуха
относительно выделенного элемента
лопасти определяется формулой
(2о 2), т. е
U7 = Dnc /х24-л272.
Рис. 25.6. Схема сил, дейст-
вующих на элемент лопасти
Тогда для элементарной подъемной силы, возникающей на эле-
менте лопасти, будет справедливо выражение
dYa=суа bdг = с/)2п2 (л2 4- л2г2) b dг.
Учитывая, что b=bD\ dr~~-dr, получим
dYa — &Рпс (л2?2 4- 'rfbdr
Элементарная подъемная сила dYa перпендикулярна полной
скорости
Аналогично для элементарной силы сопротивления элемента
лопасти имеем
dXa = QEYnl (X2 4- л2/2) bdr.
Очевидно, что сумма проекций dYa и dX(1 иа ось вращения
равна силе тяги dP, создаваемой элементом лопасти-
dP = dYacos Qn — dXa sin
399
www vokb-la.spb.ru - Самолёт своими руками?!
Подставив в правую часть этой формулы значения dYa и dXar
получим
dP (X3 4- л2г2) (суа cos рп — сха sin ₽u) bdr. (25. 18)
Сумма проекции dYa и dXa на плоскость вращения, умножен-
ная на окружную скорость 2ллсг, равна элементарной мощности
dN—(dYa sin {\-\-dXa cos рп) 2лпсг,
или, подставив значения dYa и dXa и учитывая, что r—rD(2t по-
лучим
dNQD5nc (К2 Л2г2) (суа sin pn-j-еха cos ₽п) brdr. (25. 19)
Интегрируя выражения (25.18) н (25.19) в пределах от г0 до
г=1, где г0 — безразмерный радиус втулки винта, и умножая
на число лопастей k, получим окончательные выражения для
определения силы тяги винта Р и мощности N
1
Р=—(>D*re^(X2+nV2)(cMcospn-ejtasin ₽„)М7; (25 20)
го
1
N = ~(^ + Л2г2)(суа cos plf суа siп ₽н)brdi\ (25. 21)
ГО
Теория изолированного элемента лопасти не позволяет до-
статочно точно определять значения Р и N, так как она не учи-
тывает вызванных винтом индуктивных скоростей, а также вли-
яния концевых эффектов, подобных концевым эффектам крыла
самолета. Однако эта теория позволяет получить основные зако-
ны подобия, используемые при испытании воздушных винтов и
подборе винтов к самолету.
Тяга и мощность винта существенно более точно определяют-
ся с помощью вихревой теории, созданной Н, Е. Жуковским.
Согласно этой теории лопасти винта заменяются системой при-
соединенных и свободных вихрей. Этот прием позволяет более
точно определить поле скоростей около винта, а значит, и более
правильно определить все аэродинамические характеристики
виита.
25 4 УСЛОВИЯ АЭРОДИНАМИЧЕСКОГО ПОДОБИЯ
И АЭРОДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ
ВОЗДУШНЫХ ВИНТОВ
Различные теории с той или иной степенью точности позволя-
ют определить основные параметры винта — тягу, мощность,
КПД. Однако окончательное заключение о величине параметров;
400
www.vokb-la.spb.ru - Самолёт своими руками?!
винта делается на основе эксперимента, поскольку прн теорети-
ческих расчетах трудно учесть все факторы, влияющие на рабо-
ту винта в реальных условиях.
Экспериментальные исследования проводятся в аэродинами-
ческих трубах иа моделях, геометрические размеры которых
обычно меньше размеров натурных винтов. Поэтому возникает
необходимость выявления условий, при которых геометрически
подобные винты можно считать аэродинамически подобными.
Необходимо прн этом иметь критерии аэродинамического подо-
бия, чтобы переход от параметров на модели к натурным пара-
метрам был правомерным
Критерии подобия можно получить из анализа расчетных за-
висимостей; полученных, например, с помощью теории изолиро-
ванного элемента лопасти. В формулы для определения тяги и
мощности (25 22), (25.23), полученные с помощью этой теории,
входят величины г и Ъ, одинаковые для геометрически подобных
винтов.
Угол притекания рп входящий в тригонометрические функ-
ции, зависит от относительной поступи винта Л и определяется
согласно (25.1) соотношением:
pu = arctg(X/jtr),
где r=r/R.
При равных углах установки лопасти <р аэродинамические
коэффициенты Суа и Сха элемента лопасти при прочих равных
условиях будут зависеть от угла атаки а, который, если пре-
небречь концевыми эффектами, равен разности углов установки
и притекания, т. е. а=<р—рп Значит, угол атаки, а следователь-
но, и коэффициент подъемкой силы и лобового сопротивления
элемента лопасти зависят от относительной поступи винта X
Таким образом, интегралы в выражениях (25 20) и (25.21),
будучи безразмерными, являются в конечном итоге функциями
относительной поступи винта X и эти функции можно записать в.
виде
Р-Л(Х)Сл2£Н; N
Обозначая fi(X) = a и /г(^)^Р, окончательно получим
Р-щтР/Л (25.22)
. (25.23)
Коэффициенты аир называются соответственно коэффици-
ентом тяги и коэффициентом мощности.
401
рнчески
Рис 25 7 Рабочие характе-
ристики воздушного винта
ври ф—const
www.vokb-la.spb.ru - Самолёт своими руками?!
Для КПД винта можно получить, используя формулу (25.1),
«следующее выражение:
PVco aQn^,D4lncD
N ~ ?Qn3c&
или i] = aX/p. (25.24)
Так как коэффициент тяги а и коэффициент мощности р за-
висят от относительной поступи к, то КПД винта тоже является
функцией относительной поступи.
Следовательно, условием аэродинамического подобия геомет-
i является равенство относительных
поступей к этих винтов. Необходимо
при этом помнить, что аэродинамиче-
ские коэффициенты суа и сха зависят
также от сил трения и упругости воз-
духа. Поэтому равенство чисел Re л
Мж для натурного и моделируемого
винтов тоже является необходимым
условием полного аэродинамического
подобия.
Если число Re велико, то силы тре-
ния могут не зависеть от вязкости воз-
духа и будут пропорциональны квад-
ратам относительных скоростей (авто-
модельный по числам Re режим обте-
кания лопастей). В этом случае не
требуется равенства чисел Re для двух подобных винтов.
Теория и эксперименты показывают, что с ростом скорости
полета при постоянной частоте вращения, а значит с ростом от-
носительной поступи X, тяга воздушного винта уменьшается.
Примерно так же изменяется и мощность, передаваемая вин-
том от двигателя потоку воздуха. Графическая зависимость ко-
эффициентов тяги а и мощности р от относительной поступи к
при фиксированном угле установки лопастей называется рабо-
чей характеристикой винта (рис. 25.7)
На графике рис. 25 7 можно выделить три зоны, соответст-
вующие качественно различным режимам работы воздушного
винта В диапазоне значений X, соответствующем отрезку О А на
-оси абсцисс, тяга положительная. На концах этого отрезка К Д
равен нулю, так как в начале координат нулю равна скорость
движения, а в точке А — тяга, т. е. в обоих случаях винт не со-
вершает полезной работы.
Отрезок АВ оси абсцисс соответствует режимам, на которых
тяга отрицательна, а мощность положительна. Эти режимы на-
зываются режимами отрицательных тяг.
Правее точки В расположены режимы, соответствующие от-
рицательным тягам и мощностям. Здесь винт потребляет энер-
402
www vokb Ia.spb.ru - Самолёт своими руками?!
гию не от двигателя, а раскручивается воздушным потоком.
Такие режимы называются режимами самовращения (авторо-
тации).
Характеристики винта зависят от угла установки лопастей.
Поэтому при испытаниях винтов в лабораториях серия рабочих
характеристик снимается на разных углах установки.
Для удобства использования в расчетной практике зависи-
мость коэффициента мощности р и КПД винта к] от относитель-
ной поступи X при разных углах установки лопастей ф приводят-
ся на общем графике аэродинамических характеристик воздуш-
ного винта р=/(ф, X) (рис 25.8,а). На этом же графике нанесе-
ны линии равных значении КПД винта.
При расчете разбега самолета необходимо знать, как изме-
ияются тяга и мощность винта в зависимости от скорости в про-
цессе разбега, поэтому строятся специальные характеристики
коэффициента тяги при различных условиях работы вин-
та для малых значений относительно поступи 7 (рис. 25.8,6).
25.5 ВЗАИМНОЕ ВЛИЯНИЕ ВОЗДУШНОГО ВИНТА И САМОЛЕТА.
ВЛИЯНИЕ СЖИМАЕМОСТИ ВОЗДУХА НА КПД ВИНТА
Изложенная выше теория относится к работе изолированного
винта в несжимаемом потоке. В реальных условиях винт работа-
ет в непосредственной близости от таких элементов самолета,,
как гондола двигателя, крыло, фюзеляж (у одновинтового са-
молета). Эти элементы могут оказывать существенное влияние
иа условия обтекания лопастей винта. Виит, в свою очередь, мо-
жет существенно влиять на обтекание тех частей самолета, ко-
торые оказываются расположенными в его струе. В общем слу-
чае имеет место весьма сложное взаимодействие винта и само-
лет а
На работу винта оказывает влияние также сжимаемость воз-
духа. При определенных условиях сжимаемость может привести
не только к количественным, но и качественным изменениям ха-
рактеристик винта
Рассмотрим вначале взаимное влияние винта и самолета.
Влияние винта на гондолу (фюзеляж у одновинтового само-
лета) сводится к увеличению лобового сопротивления. Это уве-
личение лобового сопротивления объясняется, с одной стороны,
увеличением скорости обтекания гондолы (рис. 25.9), с дру-
гой,-—вследствие работы винта носовая часть гондолы оказы-
вается в зоне повышенного давления за диском винта. Вслед-
ствие этого получает приращение составляющая лобового соп-
ротивления от нормальных сил
Влияние гондолы на винт определяется тем изменением поля
скоростей в районе диска винта, которое вносит гондола. Поток
перед гондолой подтормаживается, поэтому осевая скорость в
диске винта несколько уменьшается. Это уменьшение осевой
403
www.vokb-la.spb.ru - Самолёт своими руками?!
Рис. 25 8. Аэродинамические (а) и тяговые (б) харак-
теристики воздушного винта при (p<=const
-404
www.vokb-la.spb.ru - Самолёт своими руками?!
скорости зависит от взаимного расположения диска винта и
гондолы, от формы гондолы. Среднюю скорость в диске винта
с учетом присутствия гондолы можно приближенно оценить по
графику, приведенному на рис. 25 10
Вследствие подтормаживающего действия гондолы эффектив-
ная относительная поступь винта несколько уменьшается, что
приводит к определенному увеличению тяги винта. Этот прирост
тягн в определенной мере компенсирует увеличение лобового
сопротивления гондолы от обдувки.
Рис. 25 9. Влияние работы вин-
та на обтекание гондолы дви-
гателя (фюзеляжа)
Рис 25.10. График для опре-
деления истинной осевой ско-
рости и диске винта
Влияние винта на гондолу сводится, в основном, к увеличе-
нию лобового сопротивления. Это увеличение сопротивления
обьясняется увеличением скорости обтекания гондолы (см.
рис 25.9).
При практических расчетах взаимное влияние винта и гондо-
лы обычно учитывается путем введения поправки на коэффици-
ент полезного действия винта. С учетом взаимного влияния вин-
та и гондолы КПД винта
’П=Пй3^ф, (25.25)
где т]Нз — КПД изолированного винта, —множитель, учиты-
вающий взаимное влияние винта и гондолы
Коэффициент k учитывает разницу в условиях работы вин-
та иа самолете и экспериментальной установке, с помощью кото-
рой были определены аэродинамические характеристики виита:
^=0,985^/^, (25.26)
где #ф0 — коэффициент, учитывающий условия работы винта на
экспериментальной установке; — коэффициент, учитывающий
действительные условия работы винта
Оба эти коэффициента могут быть определены по графику,
приведенному на рис. 25 11, в функции от соотношения между
эквивалентным диаметром d9 тела за винтом гондолы (или за
винтом опытной установки) и диаметром винта (модели винта).
405
www.vokb-la.spb.ru - Самолёт своими руками?!
Рассмотрим влияние винта на крыло. Это влияние сводится-
практически к увеличению подъемной силы крыла.
В общем случае некоторая часть крыла («обдуваемая» часть)
находится в весьма сложном по структуре потоке за винтом.
Этот поток упрощенно можно рассматривать как закрученною
струю, из-за которой угол атаки в отдельных сечениях крыла
изменяется: в одной части получает приращение, в другой —
уменьшается. Вследствие этого подъемная сила крыла из-за за-
крученности потока практически не изменяется.
Рис 25 11 График для
определения поправки к
КПД винта вследствие
взаимного влияния вин-
та и фюзеляжа (гондо-
лы)
Рис 25 12 Схема для расчета подъем ной силы
крыла с учетом обдувки винтом
Изменение подъемной силы обдуваемой части крыла имеет
место вследствие увеличения скорости потока и изменения угла
атаки по всему размаху обдуваемой части крыла. Это изменение
угла атаки имеет место из-за несовпадения осн винта (следова-
тельно, скорости обдувки) и направления скорости полета.
Оценим изменение подъемной силы крыла от обдувки приб-
лиженно, введя ряд упрощающих предположений.
Будем пренебрегать закрученностью струйки за винтом
Предположим далее, что угол атаки мал, а ось винта совпадает
с хордой крыла.
Полная скорость V обтекания крыла определяется как сумма
осевой скорости v2, вызванной вращением винта, и скорости по-
лета (рис. 25.12).
>/ = Г/то + ^2. (25.-27)
Угол атаки у обдуваемой части винта уменьшается (см.
рис* 25.12) на некоторый угол скоса от обдувки Ла:
аобч=а~ Да- (25.28)
Таким образом, с одной стороны, вследствие увеличения ско-
рости на обдуваемой части крыла должен иметь место прирост
подъемной силы, а с другой стороны из за уменьшения угла
406
www vokb-la.spb.ru - Самолёт своими руками?!
атаки — будет некоторое ее снижение Эффект от увеличения
скорости оказывается более сильным, вследствие чего иа обду-
ваемой части крыла имеет место прирост подъемной силы. Это
повышение подъемной силы крыла благодаря обдувке его части
оценивается приростом коэффициента cyat
Суаобч==Суа~\-&Суа- (25. 29)
Величину Лс//гг можно определить экспериментально, а также
оценить и приближенно расчетным путем.
Определим вначале угол скоса от обдувки Ла Из теоремы
синусов (см. рис. 25.12) следует
sm Да sm (а — Да)
В силу малости углов получаем абсолютное значение Ла.
Да—а
1 5 U2/VTO '
Если принять V5 (V2 —скорость
та), для Ла можно записать приближенно:
потока позади вии-
Да = а(1-1/то/1/2). (25.30)
Угол атаки в обдуваемой части крыла с учетом выражения
^25.30) может быть представлен как
аобл=а — Да = а(1/0о/1/2). (25.31)
Для коэффициента подъемной силы на обдуваемой части
крыла можно записать
иаобд ^№(бд—Суа (^00/^2)-
(25. 32)
Представив полную подъемную силу крыла с учетом обдувки
в виде суммы Кдобч=^аобд-г где Кйобд —подъемная сила
обдуваемой части крыла; Yо6д — подъемная сила остальной ча-
сти крыла, имеем
qV? qV”
сбт = С4Добч I + сУа ~~ ' ($ — *^обд)- (25. 33)
£ At
Здесь 50бд площадь обдуваемой части крыла.
Можно вычислить коэффициент подъемной силы крыла с уче-
том обд\ вки, принимая во внимание (25.32):
• S
^а^обч.1 if
\ ОФ
(25.34)
г — ц _
б\
^fs
где обозначено £ОбД—*$осдА$ — относительная площадь обдувае-
мой части крыла.
407
www vokb-la.spb ru - Самолёт своими руками?!
Можно определить относительное приращение коэффициента
от обдувки'
- 1). (25.35)
Суа \ v со /
С учетом выражения (25 15) последнее выражение может
быть представлено в бо iee удобном для расчета форме
(25.36)
Зависимость Лсуа в_фуикцнн от коэффициента нагрузки В и
обдуваемой площади 6’0бД изображена на рнс. 25.13.
Сжимаемость воздуха начинает сказываться прн больших,
скоростях полета. У винта наибольшая скорость наблюдается на-
концах лопастн, где полная скорость воздуха относитетьно ло-
пасти
а число Мконц-
fya обд
О М 2,0 В
Рис. 25 [3 Влияние
обдувки винтом кры-
ла на подъемную си-
лу
Известно, что прн дозвуковых режимах обтекания с ростом
скорости (Моо) увеличиваются коэффициенты суа и сха. Скорость
нарастания увеличивается с приближе-
нием числа Mo, к МКр. С появлением на
лопастн местных сверхзвуковых скоро-
стей, а вместе с ними н скачков уплотне-
ния сопротивление резко возрастает^
а КПД винта уменьшается. Звуковые
скорости на концах винта достигаются
уже прн умеренных скоростях полета.
Например, для винта АВ-68И на само-
лете Ил-18 прн К»=630 км/ч, Н- 8000 м,
и—1075 об/мин и £> = 4,5 м имеем ско-
рость полета 175 м/с; линейная скорость
вращения на концах лопастн (абсолют-
ная) 254 м/с; полная скорость концов-
лопасти 310 м/с; число М концов лопа-
сти 1 01.
Заметим, что волновой кризис возможен и только иа конце
лопасти, но и в корневой части, несмот я иа то что ее полная
скорость из-за близости к оси враще шя меньше, Ч( м на конце.
Объясняется это тем, что в корневой части относительная тол-
щина лопасти очень велика ( остнгает 30% и более) и на ней
волновой кризис возникает уже при сравнительно малых чис-
лах М.
408
www.vokb-la.spb.ru - Самолёт своими руками?!
Резкое снижение величины КПД из-за наступления волново-
го кризиса является одной из основных причин неприменения
воздушных винтов на скоростных самолетах.
Винт для каждого типа самолета подбирается в процессе
проектирования. Выбор величины диаметра винта осуществляет-
ся для его наиболее характерного режима работы. В качестве
расчетного может быть принят режим полета на максимальной
скорости, режим полета на максимальную дальность, взлетный
режим и т- д. Для транспортных самолетов чаще всего основным
расчетным режимом является полет на максимальную дальность.
Для выбора типа винта и его диаметра должны быть извест-
ны мощность двигателя и частота вращения винта на расчетном
режиме полета, т. е. на расчетных высоте и скорости полета. В
процессе расчета подбираются тип винта и его диаметр, обеспе-
чивающие КПД винта, близкий к максимальному при полете иа
расчетном режиме. На других режимах полета КПД винта мо-
жет быть меньше.
Приближенно диаметр винта определяется следующим об-
разо к Исключив диаметр D из соотношений (25 1) и (25.23),
имеем
В полученной зависимости все величины, кроме коэффициента
мощности и относительной поступи %, должны быть заданы. На
аэродинамической характеристике винта (см. рис. 25.8,а) зави-
симость между % и р изобразится в виде параболы пятой сте-
пени. На этой параболе находим точку, соответствующую наи-
большему КПД, и, определив для нее величину X, находим диа-
метр винта с помощью формулы (25.1): .
Если парабола проходит далеко от максимальных значений
КПД, то нужно изменить частоту вращения винта или обратить-
ся к винтам другой серии.
Этот метод дает величину диаметра винта в первом прибли-
жении.
Более точные методы, позволяющие учесть влияние сжима-
емости, взаимное влияние вннта и самолета и т. д., приведены
в специальной литературе.
25.6. РАБОТА ВИНТА НА РЕЖИМАХ ОТРИЦАТЕЛЬНЫХ ТЯГ
И АВТОРОТАЦИИ
Режим отрицательных тяг винта образуется при возникио
вепии отрицательных углов атаки лопастей винта, что возмож-
но как при неработающем, так и при работающем двигателе.
Режим отрицательных тяг создается также при пробеге само-
лета во время посадки. При посадке к моменту достижения по-
409
www.vokb-la.spb.ru - Самолёт своими руками?!
садочной скорости сектор газа убирается до положения малого
полетного газа, а угол установки лопастей уменьшается до уг-
лов порядка 0,20—0,30 рад. Если сразу же после приземления
перевести сектор газа на земной малый газ, то угол установки
уменьшится до нуля и создается большая отрицательная тяга
Р (см разд 25.8).
При отказе двигателя и системы флюгнрования в полете сис-
тема регулирования переводит винт на малые углы установки.
Вследствие этого создается большая отрицательная тяга, зна-
Рис 25 14 Схема работы лопасти
воздушного винта на режиме ав-
торотации
чительно превышающая по абсо-
лютной величине положительную
тягу' при нормальной работе дви-
гателя. Винт при этом продол-
жает вращаться под действием
набегающего потока воздуха.
Причины самовращения мож-
но уяснить, проанализировав ха-
рактер сил, действующих на эле-
мент лопасти винта (рис. 25.14).
Угол атаки лопасти отрицателен.
Полная аэродинамическая сила
равная векторной сумме
подъемной силы dYa и силы со-
противления dXa, в проекции на
плоскость вращения дает состав*
ляющую dF, направленную в сто-
рону вращения виита. Сила dF,
умноженная па ее плечо относи-
тельно оси втулки винта, дает
момент, раскручивающий винт
в прежнем направлении.
Следовательно, аэродинамиче-
ские силы не только не тормозят
винт, но, наоборот, начинают его раскручивать. Наступает са-
мовращение винта В режиме самовращения винт отнимает
энергию от кинетической энергии самолета, оказывая сильное
тормозящее действие. Мощность, потребляемая для вращения
винта с выключенными двигателями, очень велика, так как одно-
временно с винтом вращаются компрессор и турбина двигателя.
При углах установки лопастей 0,17—0,26 рад (10—15°) час-
тота вращения и тормозящее действие винта будут максималь-
ными При больших и меньших углах установки лопасти сила
сопротивления dP и вращающая сила dF уменьшаются, что
приводит к уменьшению частоты вращения
Для уменьшения сопротивления воздушных винтов при отка-
зе двигателя на самолетах применяются системы флюгнрования
Они переводят лопасти винта во флюгерное положение, при ко-
410
www vokb-la.spb ru - Самолёт своими руками?!
тором сопротивление винта становится минимальным, и винт не
вращается. Автоматическая система флюгировання включается
при падении мощности двигателя во время его отказа.
25.7. ОСОБЕННОСТИ РАБОТЫ ВИНТОВ
ТУРБОВИНТОВЫХ ДВИГАТЕЛЕЙ (ТВД)
В гражданской авиации еще широко распространены самоле-
ты с турбовинтовыми двигателями. Работа винтов таких двига-
телей на взлете, при наборе высоты и в крейсерском полете не
отличаются от работы винтов, устанавливаемых на самолетах с
поршневыми двигателями.
Однако в ряде случаев работа винтов с турбовинтовыми дви-
гателями существенно отличается от работы винтов с поршневы-
ми двигателями. Эти отличия обусловлены особенностями харак-
теристик регулирования турбовинтовых двигателей.
Одной из особенностей регулирования ТВД является то, что
заданная частота вращения турбины двигателя поддерживается
регулятором оборотов, воздействующим на угол установки ло-
пастей винта. Турбовинтовые двигатели пассажирских самоле-
тов Ан-24, Ил-18 и других по своей схеме одновальные. Это зна-
чит, что один и тот же вал приводит во вращение и компрессор,
и турбину. У одновальных ТВД компрессор и винт непосредст-
венно (через редуктор) связаны между собой, и изменение час-
тоты вращения винта непосредственно влияет на работу
компрессора. При резком изменении частоты вращения винта
работа компрессора легко может стать неустойчивой. Чтобы
этого не случилось, применяют такую систему регулирования
одновальных ТВД, которая обеспечивает постоянную частоту
вращения во всем диапазоне режимов работы двигателя, кроме
режима работы на земле на малом газе, когда частота враще-
ния несколько снижается. Номинальная частота вращения ТВД
составляет 12 000—15 000 об/мин, она обуславливается наиболее
выгодными условиями работы компрессора и турбины. При этом
частоту вращения винта снижают при помощи редуктора при-
мерно в 10 раз Так, частота вращения винта АВ 72, который ус-
тановлен на двигателе самолета Ан-24, составляет 15000/12,1 =
= 1240 об/мин.
Другой особенностью турбовинтовых двигателей является то,
что мощность, затрачиваемая на вращение двигателя с заданной
частотой вращения без подачи топлива в двигатель (так назы-
ваемая мощность холодной крутки), несравненно больше, чем
мощность холодной прокрутки поршневых двигателей.
Поскольку мощность холодной прокрутки ТВД велнка, то
при запуске для обеспечения устойчивой работы двигателя иа
режиме малого газа сопротивление лопастей винта должно быть
минимальным, для чего его лопасти должны быть установлены
ла минимальные углы установки (ф=0) Для винтов поршневых
411
www.vokb-la.spb.ru - Самолёт своими руками?!
двигателей такое требование ие обязательно и угол установки
при сравниваемой мощности может быть равен 0,35—0,5 рад
(20—30°). Это обусловлено тем, что мощность холодной про-
крутки ТВД зависит от частоты вращения примерно в третьей
степени, а поршневого двигателя в первой. Кроме того, в про-
цессе запуска ТВД необходимо его ротор раскрутить до более-
высокой частоты вращения, чем частота вращения вала поршне-
вого двигателя В противном случае ТВД будет работать неус-
тойчиво.
С другой стороны, так как крейсерские скорости самолетов
с ТВД значительны, то это требует, чтобы лопасти винта на
крейсерских режимах устанавливались в полете на большие
углы, поскольку угол притекания струй рп при постоянной час-
тоте вращения и окружной скорости лопастей пропорционален
скорости полета. Таким образом, эксплуатационный диапазон
изменения углов установки лопастей винтов ТВД значительно
больше, чем винтов поршневых двигателей. В связи с указан-
ными особенностями в полете при уменьшенной подаче топлива
в двигатель или при отсутствии подачи топлива при отказах
двигателя на вните ТВД может возникнуть большая отрицатель-
ная тяга, значение которой может превысить даже максималь-
ную положительную тягу винта. Возникновение большой отрица-
тельной тяги может привести к аварийной ситуации и резко
снизить безопасность полета.
Возможность получения отрицательной тягн винтов ТВД>
однако, дает определенные преимущества самолетам на посадоч-
ных режимах, так как отрицательная тяга используется для со-
кращения длины пробега самолета
25.8. МЕХАНИЗМ ВОЗНИКНОВЕНИЯ ОТРИЦАТЕЛЬНЫХ ТЯГ В ТВД
Рассмотрим качественно процесс возникновения отрицатель-
ных тяг в ТВД. С этой целью проследим за работой винта в ТВД
прн малых подачах топлива.
На рис. 25 15 изображена зависимость мощности турбины
JVT от подачи топлива GT. На этом же рисунке нанесена кривая
мощности, потребной для холодной прокрутки Мк. Она практи-
чески не зависит от GT при постоянных оборотах. Разность N?—
Мс составляет мошиость, идущую на винт NB.
Прн расходе топлива, большем GTl) располагаемая мощность
турбины превышает потребную мощность на вращение компрес-
сора, и этот избыток мощности передается на вал вннта, так что
мощность иа валу винта больше нуля При дальнейшем уве н-
чении расхода топлива мощность на валу винта увеличивается
Для того чтобы иа этих режимах работы двигателя не было
раскрутки компрессора виит переводится в положение, при кото-
ром ои поглощает избыточную мощность т. е. вннтсуве-
личением расхода топлива GTy>Gn все более «затяжеляется».
412
www.vokb-la.spb.ru - Самолёт своими руками?!
При расходах топлива GT^>GTi располагаемая мощность турби-
ны меньше мощности, потребной для холодной прокрутки ком-
прессора. Для сохранения режимных оборотов компрессора
необходимо отрицательную разность Мт—Л'к снять с винта. На
этих режимах вннт «облегчается». «Затяжеление» или «облегче-
ние» винта обеспечивается переводом лопастей соответственнс*
на большие илн меньшие углы
установки. С изменением угла ус-
тановки лопасти будет изменять-
ся ее угол атаки, и следовательно,
действующие на нее аэродинами-
ческие силы.
Рис. 25 16. Аэродинамические си-
лы сечения лопасти на пропеллер-
ном режиме
Рис. 25.15. Зависимость
мощности турбины от
подачи топлива
Процесс «загружения» или «облегчения» лопасти, и связан-
ное с этим изменение тяги винта, можно определить путем ана-
лиза проекций подъемной силы и силы лобового сопротивления
на ось винта при различных углах установки (как было сделано
ранее). Однако здесь удобнее проследить качественную сторону
происходящих явлений при изменении угла установки не по со-
ставляющим dYa и dXa, а по равнодействующей dRA (рис. 25 16)
Проанализируем процесс «затяжеления» лопастей при избы-
точной мощности Л'7—A\; и их процесс «облегчения» при отрица-
тельном избытке NT Nk- Для простоты положим, что скорость
полета остается постоянной Влияние скорости будет рассмотре-
но ниже. Начало координат системы XaOYa поместим в центр-
давления выделенного элемента и будем полагать, что центр
давления остается в одной и той же точке. Как было указано,
выше, «затяжеление» или «облегчение» винта осуществляется
переводом лопастей на различные углы установки. При постоян-
ной скорости полета и постоянных оборотах (окружная скорость
41а
www vokb-la.spb.ru - Самолёт своими руками?! ,
U— const) угол притекания струй будет постоянным и угол атаки
элемента определяется разностью
а — ср - - ft,—-р - const,
т. е. насколько изменится угол установки, настолько соответст-
венно изменится угол атаки.
Изменим угол установки лопасти, не вдаваясь в подробности,
как он изменяется прн «затяжелении» нли «облегчении», таким
образом, чтобы угол атаки элемента изменялся от угла нулевой
подъемной силы и перешел в область закритических углов атаки.
Тогда конец вектора dRA опишет кривую — поляру АБ* (см
рис 25.16). Точка А приближенно соответствует положению рав-
нодействующей, когда угол установки характерного сечения
лопастн равен углу притекания струи относительно плоскости
вращения вннта, в точке Б угол установки превышает угол при-
текания струй примерно на угол аж0,35 рад. Рассматривая про-
екции равнодействующей силы dRA на ось вннта dP и на плос-
кость вращения dF, можно прийти к выводу: с увеличением утла
установки элемента лопасти, и соответственно, утла атаки вы
деленного элемента до значения, при котором угол атаки выде-
ленного элемента становится равным критическому, проекция
равнодействующей на ось винта (т. е. тяга винта) растет; при
дальнейшем увеличении угла установки тяга винта уменьшается
Отсюда вытекает, что в эксплуатационных условиях углы уста-
новки должны быть такими, чтобы угол атаки элемента не был
больше критического.
Проекция равнодействующей dRA на плоскость вращения
винта с увеличением угла установки и угла атаки соответствен-
но все время возрастает Возрастание проекции dF увеличивает
момент сопротивления элемента лопасти. Понятно, что для со-
хранения постоянной угловой скорости винта при увеличении
угла установки элемента лопасти необходимо к валу винта под-
водить все большую мощность.
Из приведенного анализа следует, что при увеличении подачи
топлива в двигатель и увеличении мощности турбины регуля-
тор оборотов должен переводить лопасти на больший угол уста-
новки, что определяет рост угла атаки элемента и момента соп
ротивления Возрастание момента сопротивления и определяет
термин «лопасть затяжеляется» Собственно перевод лопасти на
большие а глы атаки предотвращает двигатель от раскрутки
При уменьшении подачи топлива частота вращения двигате-
ля должна упасть, но регулятор оборотов переводит лопасти на
малый угол установки, на малые углы атаки. При этом проекция
dF уменьшается, и лопасть становится «легкой», частота враще-
ния винта сохраняется постоянной.
* Мы называем эту кривую полярой условно, поскольку эта кривая в
отличие от поляры, построена в координатах абсолютных значений сил,
414
www.vokb-la.spb.ru - Самолёт своими руками?!
Рис 25 17 Аэродинамические силы се-
чения лопасти при отрицательных уг-
лах атаки
Следует, заметить, что если угол атаки элемента лопасти
таков, что равнодействующая dRA направлена по оси 0Ха (подъ-
емная сила элемента равна нулю), то проекция на плоскость
вращения dF определяет небольшой момент сопротивления, что
при малом расходе топлива и малой мощности турбины может
вызвать уменьшение частоты вращения двигателя (системы тур-
бина — компрессор — винт). Проекция равнодействующей на
ось винта дает в этом случае отрицательную тягу. Итак, прн ма-
лом расходе топлива возникает задача дальнейшего «облегче-
ния» лопасти винта. Обеспечи-
вается это дальнейшим умень-
шением уг; а установки элемен-
та лопастн: углы атаки прн
этом становятся отрицательны-
ми. При отрицательных углах
атаки равнодействующая будет
направлена в противополож-
ную сторону н при дальнейшем
росте отрицательных углов
атаки опишет такую же по ви-
ду поляру, что н при положи-
тельных углах атаки (рис.
25.17). Рассматривая равно-
действующую прн различных
отрицательных углах атаки
можно заметить следующие
особенности. С увеличением
отрицательного угла атаки
лопасти 65дет достигнуто та-
кое значение равнодействующей силы этой лопастн (см точку
С на рис 25 17)^ когда она даст нулевую проекцию dF на пло-
скость вращения, т. е. в этом случае винт не будет иметь аэро-
динамического сопротивления Этот режим работы винта назы-
, вается режимом авторотации. При дальнейшем росте отрица-
тельного угла атаки проекция равнодействующей на плоскость
вращения обуславливает уже не момент сопротивления, а вра-
щающий момент. На к ком-то отрицательном угле атаки про-
екция силы dF будет иметь максимальное значение (см точк /
Д) и это определит максимальный вращающий момент лопа-
стн. Прн дальнейшем росте отрицательных углов атаки уже в
области | а | > | акр |, равнодействующая еще раз совпадает с
осью винта (см. точку Е), момент сопротивления лопасти опять-
будет равным нулю. Режим работы винта, прн котором равно-
действующая сила FRA обуславливает проекцию на плоскость
вращения, способствующую вращению винта, называется ре-
жимом ветряка. Еще прн большем значении отрицательного
угла атаки появится проекция на плоскость вращения dF, соз-
дающая момент сопротивления винта
415
www vokb-la.spb.ru - Самолет своими руками?!
Из рассмотрения равнодействующей на рис. 25 16 и 25.17 сле-
дует, что всякий раз, когда мощность турбины недостаточна для
вращения компрессора и винта с заданной частотой вращения,
лопасти винта регулятором оборотов автоматически переводятся
на малые углы установки; углы атаки лопастей в этом случае
отрицательны и возникает отрицательная тяга. Отрицательная
тяга увеличивается с увеличением отрицательных углов атаки
Из рассмотренного также следует, что большие отрицатель-
ные тяги будут возникать как при отказе двигателя, так и при
резком уменьшении подачи топлива до нуля. Небольшие отри-
цательные тяги могут возникать и на исправно работающих дви-
гателях, когда при данном режиме мощность холодной про-
крутки окажется больше располагаемой мощности турбины
JVT прн данном расходе топлива.
25.9. ВЛИЯНИЕ СКОРОСТИ ПОЛЕТА НА ВЕЛИЧИНУ
ОТРИЦАТЕЛЬНОЙ ТЯГИ ВИНТА
Рассмотрим сначала изменение тяги винта при отказавшем
двигателе (или при нулевом расходе топлива), когда мощность
турбины равна нулю
В этом случае имеется два диапазона скоростей, в которых
изменение отрицательной тяги по скорости полета имеет качест-
венно противоположный характер. Границей этих двух диапазо-
нов является скорость контроля регулятора Ук.р— минимальная
скорость полета, при которой регулятор оборотов, изменяя углы
установки лопастей винта, может поддерживать частоту враще-
ния системы винт — компрессор постоянной.
При увеличении скорости полета до скорости контроля регу-
лятора отрицательная тяга винта растет, при. дальнейшем уве-
личении скорости полета отрицательная тяга уменьшается.
Для качественной характеристики изменения тяги на малых
и больших скоростях рассмотрим сначала располагаемую мощ-
ность винта, работающего на режиме ветряка при различных
скоростях полета и углах установки Сравним эту мощность с
мощностью холодной прокрутки компрессора при постоянной
частоте вращения.
Изменение мощности винта NB, работающего в режиме вет-
ряка, по углам установки при фиксированной скорости полета
изображено на рис. 25.18
На рис. 25.18 по оси абсцисс отложены углы установки эле-
мента лопасти ф, а ниже отмечены соответствующие им углы
атаки лопасти. Как видно из рис. 25 17, наибольший вращающий
момент, а следовательно, и мощность винта NB, будет на режиме,
отмеченном точкой D. На режимах, отмеченных точками С и К
мощность винта равна нулю. На рис. 25.18 эти режимы отмечены
соответствующими точками на кривой ДГв==^(ф) при V— Vj.
-416
www.vokb-la.spb.ru - Самолёт своими руками?!
С увеличением скорости полета V при тех же углах установки
и углах атаки лопасти равнодействующая dRA увеличится и,
кроме того, поляра наклонится ближе к плоскости вращения,
поскольку растет угол притекания струй (рис. 25.19). Это вы-
зовет увеличение максимальной проекции dF на плоскость вра-
щения и рост максимальной мощности винта (рис. 25.18, кривая
1/=V2). Приуменьшении скорости полета (кривая V’= Vs)
Рис 25 18 Изменение мощ-
ности Njj, работающего в
режиме ветряка, в зависимо-
сти от углов установки при
фиксированной скорости
полета
Рис. 25 19. Аэродинамические силы сечения
лопасти при различных скоростях полета
уменьшаются также равнодействующая скорость 1Уз, равнодей-
ствующая сила dRAW2, ее максимальная проекция и мощность
винта.
На рис. 25.18 нанесена также мощность холодной прокрутки
компрессора Из сравнения кривых мощностей вннта и ком-
прессора можно сделать вывод, что при скорости полета У—Уз
мощность, снимаемая с винта, при любом угле установки недос-
таточна для прокрутки компрессора с режимной частотой вра-
щения; при скоростях полета Vj н У2 в диапазоне 1—2 и 3 4
(см. рис. 25.18) мощность винта превышает мощность холодной
прокрутки компрессора. Можно указать скорость, отмеченную
на рнс. 25.18 штриховой линией, прн которой мощность Мв — Nv
только прн одном угле установки Начиная с этой скорости и
выше регулятор оборотов может поддерживать частоту враще-
ния винта постоянной скорость У4 называется скоростью конт-
роля регулятора.
Отметим одну особенность. Если до отказа двигателя само-
лет летел со скоростью полета, равной скорости контроля регу-
14 626
417
www vokb-la.spb.ru - Самолёт своими руками?!
лятора н углы установки лопастей были больше, чем угол,
прн котором Мв = Мк, то после отказа двигателя регулятор обо-
ротов, переводя лопастн на меньшне углы установки, сможет
обеспечить режимную частоту вращения двигателю прн <р=<рь
Если же в момент отказа угол установки лопасти был меньше
фь то после отказа двигателя регулятор оборотов не сможет
обеспечить режимную частоту вращения двигателю, поскольку
прн «облегчении» лопастей мощность винта будет уменьшаться
Рис 25 20. Изменение тяги вин-
та в зависимости от скорости
полета
То же самое можно сказать н о по-
лете самолета с авторегулнрующнм
винтом при установке лопастей
на постоянных углах установки,
меньших <рь Так, если угол уста-
новки лопастей оставался постоян-
ным и равным ф=10°, то при скоро-
сти полета V= V4 регулятор не обес-
печит режимной частоты вращения
двигателю, поскольку при V=Vd
н 10 мощность винта меньше
мощности холодной прокрутки Мц-
Мощность винта достигает уровня
мощности на вращение компрес-
сора jVk, как это видно из рнс. 25.18,
только прн скорости У5Ж1.
Отметим также, то что прн одной и той же скорости полета
возможны два угла установки лопастей, на которых выполняется
условие Nb — Ne. Однако устойчивая работа вннта возможна на
углах установки, отмеченных точками 4, 2 н т. д., т. е. на боль-
ших углах установки — правый склон кривой Мв—f((p)
Перейдем теперь к частному случаю, когда скорость полета
выше скорости контроля регулятора. (Й>Пкр). При скорости
полета V>VKp характерной деталью является то, что частоты
вращения винта и компрессора поддерживаются постоянными
Так, если отказ двигателя произошел при скорости lz2 (рис.
25 20), то лопасти винта будут переведены регулятором оборотов
в положение, отмеченное точкой 4 (см. рис. 25 18). Для каждой
скорости полета имеются свои углы установки лопастей, при
которых частота вращения двигателя будет постоянной режим-
ной. При различных углах установки (см. рис. 25.18) мощность
холодной прокрутки остается почти неизменной. Следовательно,
прн полете самолета на различных скоростях вращающий мо-
мент вннта должен быть также одинаковым. Это, в свою очередь,
требует постоянства проекции равнодействующей RA на плос-
кость вращения, которая определяется по формуле
М-
г2лп
418
www.vokb-la.spb.ru - Самолёт своими руками?!
На рис. 25.19 показаны условные «поляры» при различных
скоростях полета, а на плоскость вращения винта нанесена по-
требная проекция равнодействующей dF Проектируя ее на по-
ляры, получим отрицательные углы атаки, углы установки и ве-
личины отрицательных тяг. Как видно из рис. 25 19, прн большей
скорости отрицательная тяга уменьшается (см. dPw2<^wi)-
Из рис. 25.21 также следует, что при уменьшении с орости поле-
та и при отклонении поляры ближе к оси винта отрицательная
тяга будет нарастать все с боль-
шим градиентом. При скорости
полета, равной скорости конт-
роля регулятора, штриховая ли-
ния, проведенная от потребной
проекции dF, будет касательной
к поляре и отрицательная тяга
в этом случае будет еще больше
(см рис. 25.20) Еще при мень
шей скорости, сколь угодно мало
отличающейся от скорости конт-
роля регулятора, вращающий
момент от винта будет уже недо-
статочен для вращения компрес-
сора с режимной частотой вра-
щения, угол установки быстро
уменьшится до минимума, зара-
нее заданного конструкцией вин-
та, а отрицательная тяга еще
Рис 25 21 Аэродинамические
силы сечения лопасти при раз-
личных оборотах лопасти
больше вырастает (см. рис. 25.20)
и достигает максимального значения. На этом режиме частота
вращения винта начинает уменьшаться
Если угол установки лопастей может уменьшаться до про-
межуточного упора (угол промежуточного упора выбирается
в пределах фуП~ 10 '... 20°), при включении которого лопасти не
могут перейти на меньший угол, то быстрому переводу лопастей
на малые углы установки соответствует участок Л В на рис. 25 20.
При включенном промежуточном упоре лопасти могут перево-
диться еще на меньший угол установки, уменьшаясь до нулевого
значения при этом отрицательная тяга еще больше возрастает
(участок АВС, рис 25.20). Из рассмотренного следует, что угол
промежуточного упора желательно выбирать таким образом
чтобы в случае отказа двигателя не возникала чрезмерно боль-
шая отрицательная тяга. Однако, следует учитывать, что при
большом угле упора может возникнуть настолько большой мо-
мент сопротивления лопастей, что винт становится «тяжелым»,
и при небольших расходах топлива в условиях захода на посад-
ку нарушается устойчивая работа двигателя. Кроме того, при
большом угле промежуточного упора лопасти винта долго не
«затяжелятся». При нормальной посадк самолета с работающи-
14’
419
.vokb-la.spb.ru - Самолёт своими руками?!.
ми двигателями это опасно, ио при уходе на второй круг при рез-
кой даче газа виит «затяжеляется» медленно.
Участок кривой BD соответствует режиму изменения отрица-
тельной тяги винта при скоростях полета, меньших скорости
контроля регулятора на графике рис 25 20 Уменьшение отрица-
тельной тяги с уменьшением скорости полета можно объяснить
следующим образом. На хчастке кривой BD угол установки ло-
пастей постоянен и равен >глу промежуточного упора Посколь-
ку мощность винта на этих режимах недостаточна для вращения
компрессора с режимной частотой вращения, то с уменьшением
скорости частота вращения продолжает падать. Таким образом,
уменьшаются скорость полета, окружная скорость, максималь-
ная тяга (рис. 25 21, V— Vo, К).
Вопросы для повторения
1. Объясните необходимость применения геометрической
крутки лопасти воздушного винта.
2. Почему КПД воздушного виита даже в невязкой среде
всегда меньше единицы? Каким образом можно увеличить КПД
при этих условиях?
3. При каких условиях можно получить отрицательную тягу,
если направление и скорость вращения сохраняется неизменны-
ми, а угол установки лопасти не отрицателен?
4. Как будет изменяться угол установки и угол атаки лопасти
в процессе разгона самолета прн постоянной скорости вращения
воздушного винта?
5. Объясните процесс возникновения отрицательных тяг в
ТВД.
Задача
1 На аэродинамической характеристике виита (см. рис. 26 8)
покажите совокупность режимов работы ВИИ1 (/V~const, п~
= const) и ВФШ (<р~const), если оба эти винта имеют один из
режимов р = 0,50; Л —2,50. Для какого из этих винтов диапазон
значений относительной поступи при КПД, превышающих 0,8,
будет больше?
Ответ: Режимам работы ВИШ иа рис 25 8 соот етствует
горизонтальная линия р — 0,50.
Режимам работы ВФШ соответствует линия для <р = 0 86 рад.
www vokb-la.spb.ru - Самолёт своими руками?!
ГЛАВА 26
ОСОБЕННОСТИ АЭРОДИНАМИКИ
НЕСУЩЕГО ВИНТА ВЕРТОЛЕТА
26 1. ОСОБЕННОСТИ РАБОТЫ НЕСУЩЕГО ВИНТА
В отличие от винта самолета винт вертолета выполняет не
только функции движителя, преодолевая силу лобового сопро-
тивления, но и уравновешивает в полете вес вертолета (отсюда
термин несущий винт). Кроме того, винт вертолета обеспечивает
устойчивость и управляемость полета, а также безопасность
аварийного снижения.
Столь разнообразные функции могут быть выполнены при
условии, если несущий винт (система несущих винтов) позволяет
в широких пределах изменять вектор тяги как по абсолютной
величине, так и по направлению. В широких пределах и доста-
точно оперативно также должен меняться момент тяги.
Имеется множество конструкций несущих винтов, тем или
ивым способом обеспечивающих возможность изменения векто-
ра тяги. Существенную роль при этом играет аэродинамическая
схема вертолета.
Наибольшее распространение получили винты, у которых
плоскость вращения лопастей может менять положение по от-
ношению к оси вала Последнее достигается за счет шарнирного
крепления лопастей несущего винта к втулке и применения спе-
циального механизма, так называемого автомата перекоса, пред-
ложенного в 1910 г. академиком Б. Н. Юрьевым.
На рис. 26.1 изображена схема шарнирного крепления ло-
пасти несущего винта к втулке. Горизонтальный шарнир 1
позволяет изменять наклон лопасти по отношению к плоскости
вращения. Благодаря вертикальному шарниру 2 лопасть имеет
возможность изменять положение относительно втулки в плос-
кости вращения. Осевой шарнир 3 позволяет изменять угол
установки лопасти.
Горизонтальный и осевой шарниры дают возможность лопас-
ти занимать различные положения по отношению к потоку воз-
421
«ни vokb-la.spb.ru - Самолёт своими руками9'
духа и тем самым изменять развивающиеся на них аэродинами-
ческие силы.
Помимо этого горизонтальный шарнир позволяет свести к
нулю изгибающий момент иа лопасти у ее корня. Действительно,
под действием аэродинамической силы Ya и центробежной силы
Рис 26 1 Крепление лопасти несущего винта’
/—горизонтальный шарнир; 2—вертикальный шарнир;
3—осевой шарнир, 4—втулка. 5—вал, f>—лопасть
Ецг> (рис. 26.2) лопасть автоматически займет равновесное по-
ложение, при котором вектор результирующей силы F проходит
через ось шарнира. В результате изгибающий момент в корне-
вом сечеиии оказывается равным нулю. Такой же результат по-
лучим, прибавив к изображенным иа рисунке силам вес лопас-
ти. Такая разгрузка лопасти от изгибающих моментов позволя-
ет получить конструктивно приемлемые прочие размеры лопасти
несущего винта.
Если рассмотреть силы, действующие на лопасть в п юскости
вращения (силы сопротивления и центробежные силы), анало
гичные рассуждения приводят к выводу, что вертикальный шар-
нир разгружает лопасть от изгибающих моментов в плоскости
вращения. В этом основное назначение вертикального шарнира
Благодаря горизонтальному и вертикальному шарнирам ло-
пасть виита в полете под действием изменяющихся по величине
моментов сил все время совершает колебательные движения.
В конструкции винта имеются упоры, ограничивающие поворот
лопастей, например ограничители лопастей на стоянке.
422
.vokb-la.spb ru - Самолёт своими руками?!
Автомат перекоса управляет углами установки лопастей на
работающем винте в зависимости от их положения, которое ха-
рактеризуется углом азимута гр (рис. 26.3), Если увеличивать
углы установки лопастей при значениях гр, близких к 0, и умень-
шать— при гр, близких к л, то вследствие изменения подъемной
силы плоскость вращения лопастей наклоняется вперед, сила
Рис. 26.3. Азимутальное поло-
жение лопасти
Рис 26 4 Схема сил, действую-
щих на вертолет в полете
тягн винта Т создает горизонтальную составляющую Р и верто-
лет начинает перемещаться вперед (рис. 26 4). Если уменьшить
уплы установки лопастей при значениях гр, близких к Зл/2, и уве-
личивать— при гр, близких к л/2, то вертолет начинает переме-
щаться вправо.
Для получения более равномерной работы несущего винта
число лопастей делают обычно больше двух. Лопастям придают
прямоугольную или трапециевидную форму в плайе со слабым
сужением. Они, как правило, имеют крутку, уменьшающую углы
установки по мере приближения к концам лопастей.
26.2. ВЛИЯНИЕ КОСОЙ ОБДУВКИ НА АЭРОДИНАМИКУ ВИНТА
Плоскость вращения лопастей несущего винта вертолета в
полете составляет некоторый угол с направлением полета Этот
угол называют углом атаки винта. В обычном полете угол атаки
отрицателен (рис. 26.5). При углах атаки а=±л/2, соответству-
ющих вертикальному подъему и снижению вертолета, винт вер-
толета встречает воздух в осевом направлении Прн а, отличном
от -4-л/2, внит работает в режиме так называемой косой обдувки.
Косая обдувка приводит к тому, что условия работы лопасти
винта при изменении угла азимута ф изменяются. Разложим
скорость полета V7:x, на осевую составляющую К» sin а и состав-
ляющую в плоскости вращения И» cos а (см. рис. 26.5)
Косую обдувку винта можно представить как сумму осевой
(со скоростью Voo sin а) и поперечной (со скоростью Роо cos а)
423
wwh vokb-la.spb ru - Самолёт своими руками?!
обдувок. Касательная скорость Ut на некотором элементе ло-
пасти (рис. 26-6) благодаря наличию поперечной обдувки равна
Ut—(>>r-\- cos a sin Ф. (26.1)
Скорость Ut зависит от азимутального положения элемента.
На рис. 26.6 показано изменение Ut вдоль лопасти при ф=л2 и
. ф=3л 2 Из рисунка видно, чго
на участке 001 элементы лопа-
сти встречают воздух своей зад-
ней кромкой. Следовательно, при
косой обдувке винта получается
зона обратного обтекания лопа
сти. Можно показать, то эта
зона представляет собой круг (на
рисунке заштрихован). В зоне
обратного обтекания подъемная
сита на элементах лопастей имеет
Рис. 26 5 Угол атаки несущего направление, противоположное
винта Осевая и поперечная обдув- на равлению подъемной силы
ка винта 1
элементов, расположенных вне
этой зоны, т е. в этой зоне со-
здается отрицательная тяга. Чем ботьше скорость VooCOsct, тем
больше зона обратного обтекания н тем сильнее снижается эф-
фективность винта. Образование зоны обратного обтекания яв-
ляется одним из факторов, ограничивающих скорость полета
вертолетов.
Рис 26 6 Касательны с к рости на лопастях несущего винта
Абсолютная скорость элемен га лопасти
It7' = |Z1/^ sin2 а -|- (tor - V cos а sin 2.
424
www.vokb-la.spb.ru - Самолёт своими руками
Угол притекания струй на элементе лопасти определяется
выражением
V sin а
tg 8 =----------------------------
<ог 4- cos а sin ф
достигает иаиоольшего значении
при ф=Зл/2 Угол притекания струй
Рис 26.7 Изменение угла атаки сечения
лопасти по азимуту из-за махового дви-
жения лопасти
Отсюда следует, что полная абсолютная скорость и угот при-
текания струй для данного элемента лопасти зависят от угла
азимута ф Полная скорость
при ф=л/2 и минимального
при ф=л/2 минимальный,
а при ф —Зл/2 достигает
максимума.
Уменьшение угла прите-
кания струй прн изменении
углов азимута ф от 0 до л/2
вызывает увеличение углов
атаки на элементах лопа-
стей. Поскольку при этом
увеличивается абсолютная
скорость, то при изменении
ф от 0 до л/2 растет и подъ-
емная сила.
Рост подъемной силы,
в свою очередь, приводит
к повороту лопасти относи-
тельно горизонтального шар-
нира вверх (к так называе-
мому движению взмаха). Лопасть совершает взмах вверх в тот
период, когда она движется против поперечного потока. Анало-
гично получается движение взмаха лопасти вниз, когда оиа дви-
жется по направлению поперечного потока.
В результате движения взмаха на элементах лопасти появля-
ются дополнительные осевые составляющие скорости Увзч, по-
этому угол атаки на лопасти а, при значениях ф, близких к л/2,
уменьшается, а при значениях ф, близких к Зл/2, увеличивается
(рис. 26.7). На большой скорости полета увеличение углов атаки
при ф—Зл/2 может стать значительным и произойдет срыв по-
тока. Поток срывается на лопастях в тот момент, когда они за-
нимают азимутальные положения, близкие к ф—Зл/2 (зона А па
рис. 26.6).
Из-за срыва потока, а также благодаря наличию области об-
ратных обтеканий лопасти плоскость вращения винта «завали-
вается» в сторону ф=Зл/2. Появление срыва потока на больших
скоростях также является фактором, ограничивающим скорость
полета вертолетов.
425
www vokb- la.spb ru - Самолёт своими руками?!
26.3. УСЛОВИЯ ДИНАМИЧЕСКОГО ПОДОБИЯ винтов
ПРИ КОСОЙ ОБДУВКЕ
Вопросы моделирования для несущих винтов имеют очень
важноё'дзначение. Косая обдувка, весьма сложное движение
лопасти, при котором на вращательное движение накладываются
еще движение взмаха, осуществляемое вокруг горизонтального
шарнира, движение опережения (или отставания), осуществляе-
мое вокруг вертикального шарнира, циклические изменения угла
установки, задаваемые автоматом перекоса, — все это усложня-
ет не только теоретический расчет несущего винта, но и его экс-
периментальное исследование. Если принять во внимание дефор-
мационные движения лопасти при ее изгибе и скручивании (с
деформацией следует считаться нз-за больших диаметров винта
и сравнительно малой жесткости его лопастей), а также необхо-
димость обеспечения подобия инерционных характеристик лопас-
тей, поскольку нх движение происходит с ускорениями, становит-
ся понятной вся сложность проблемы моделирования несущего
вннта вертолета.
Рассмотрим весьма кратко условия динамического подобия
несущих винтов. Для динамического подобия, как всегда, до. ж-
но быть выполнено, прежде всего, геометрическое подобие вин-
тов. По сравнению с обычными винтами здесь необходимо вы-
полнить ряд дополнительных требований в отношении подобного
расположения осей шарниров лопастей, а также подобия звень-
ев системы автомата перекоса.
Кинематические условия динамического подобия винтов при
косой обдувке можно получить, рассматривая раздельно работу
винта прн чисто осевой обдувке и чисто поперечной обдувке.
В осевом направлении винт работает со скоростью К» sin а,
поэтому для относительной поступи винта имеем
V sin а
—------
nD
На основании выводов разд. 25.4 заключаем, что для аэроди-
намического подобия винтов необходимо соблюсти равенство от-
носительных поступей винтов
Прн чисто поперечной обдувке у динамически подобных вин-
тов очевидно, должны быть геометрически подобны п 1аны ско-
ростей. В частное и, зоны обратного обтекания лопастей должны
быть соразмерны с дисками, что приводит к следующему соотно
шению (см. рис. 26.6):
010
(26. 2)
V (cos а
—~-----= р = const.
R
Величина ц называется характеристикой режима работы несуще-
го вин а. Она показывает, какая часть лопасти работает в усло-
виях обратного обтекания (если ц = 0,2, то это означает, что 20%
26.3)
426
www vokb-la.spb ru - Самолёт своими руками?!
лопасти работает в условиях обратного обтекания). Большие
значения р, приводят к потере качества винта и к вибрациям.
Для динамического подобия винтов, работающих в условиях
косой обдувки, помимо равенства поступей, должно быть соблю-
дено равенство характеристик р.
Характеристика режима работы несущего винта р и относи-
тельная поступь Л связаны с едующей зависимостью:
c°s о = а c°sa ctg а
jtnD nD л sin а л
Из формулы (26.4) следует, что вместо равенства значений
р в качестве дополнительного условия динамического подобия
винтов можно принять равенство углов атаки а
Итак, если для винтов при осевой обдувке условие динами-
ческого подобия заключалось в равенстве относительных посту-
пей А, то при косой обдувке для динамического подобия винтов
необходимо обеспечить равенство X и р или X и а.
Задача моделирования несущего винта в точной постановке
должна решаться с учетом циклического изменения угла уста-
новки лопастн при ее азимутальном движении. Необходимо, во-
обще говоря, обеспечить идентичность цик. ического изменения
шага лопасти. Поскольку изменение шага по азимуту задается
углом отклонения автомата перекоса, то при соблюдении геомет-
рического подобия крепления лопастей и звеньев автомата пере-
коса следует обеспечить равенство углов отклонения автоматов
перекоса. Такое требование затрудняет как само моделирование
винтов, так и пользование полученными данными продувок серии
винтов
Поэтому при практических расчетах обычно используют аэ-
родинамические характеристики винтов, полученные в условиях
косой обдувки при фиксированном шаге лопасти, не изменяю-
щемся во время ее движения по азимуту. Как показывает теория,
винт с постоянным шагом динамически подобен винту с изменяю-
щимся шагом, ес и их углы атаки отличаются на некоторую
величину, определяемую специальным расчетом (этот вопрос
подробно рассматривается в специальных учебниках). Такой
винт с постоянным шагом, но уст шовленный с несколько изме-
ненным углом атаки, называется эквивалентным винтом. Введе-
ние понятия эквивалентного винта позволяет широко пользо-
ваг ся результатами продувок серии несущих винтов.
Для обеспечения динамического подобия несущих винтов не-
обходимо соблюсти равенство чисел Рейнольдса: Re=R2o)/v
У несущих винтов, как и у обычных, существует автомодель-
ный режим по числам Re. В том случае, когда оба винт) нахо-
дятся в автомодельной области, нет надобности соблюдать для
них равенство чисел Re. При больших числах М необходимо
обеспечить равенство чисел М = шД/а.
4 7
ww \i vokb-la.spb ru - Самолёт своими руками?!
Поскольку несущие винты имеют весьма длинные и гибкие
лопасти (изгиб измеряется десятками сантиметров, а закручи-
вание достигает 0,05 0,1 рад), для их динамического подобия
необходимо выполнить условие подобия деформаций. Последнее
удовлетворяется при равенстве чисел Коши С=(Л7'^ Е,
где Е—модуль упругости материала лопасти.
26.4 АЭРОДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ
НЕСУЩЕГО ВИНТА
на виит, можно разложить
Рис 26 8. Проекции равнодей-
ствующей аэродинамических
сил несущего винта на направ-
ления скоростных и связанных
осей
плоскости вращения виита в
Перейдем к анализу аэродинамических характеристик несу-
щего винта. Пусть несущий винт работает под углом атаки а
(рис. 26.8). Полную аэродинамическую силу Ед, действующую
а составляющие в скоростной или
связанной системах координат.
В связанной системе коорди-
нат получим перпендикулярную
к плоскости вращения состав-
ляющую Т— тягу винта и со-
ставляющую в плоскости враще-
ния винта Н — продольную силу
винта.
В скоростной системе коорди-
нат У« — подъемная сила винта
и Ха — пропульсивная сила вин-
та.
Для простоты мы ие рассмат-
риваем боковых составляющих
силы связанных с завалом
сторону значения азимута ф —Зл/2
(см. разд. 26.2). Эти составляющие учитываются при решении
вопросов устойчивости и управляемости полета вертолета. В со-
ответствии с законами аэродинамического подобия для состав-
ляющих силы Да можно написать следующие выражения:
т=ст С (<” Д)2 л Д2; Ya = ci!a — е (шД)2 лД2;
х л
н=сн ~=<\а -4 е (<*>Д)2 яД2-
Л X
Здесь ст, ся, суа и сха — коэффициенты соответствующих
сил — безразмерные величины, зависящие от параметров дина-
мического подобия винтов в условиях косой обдувки
Пользуясь понятием эквивалентного винта, в приближенных
расчетах считают, что аэродинамические коэффициенты виита
определяются помимо основных геометрических параметров
(число лопастей коэффициент заполнения о, относительная
толщина профиля с, угол установки лопастей <р), значением по-
428
www.vokb-la.spb.ru - Самолёт своими руками?!
ст^пи %, углом атаки а, числом Re и числом М. Выражение-для
крутящего момента на валу винта
где к—коэффициент крутящего момента.
Совокупность коэффициентов ст, си и к связанной системы,
или суа, сха и Сшк скоростной системы координат определяют
аэродинамические свойства несущего винта и называются его
аэродинамическими характеристиками.
Аэродинамические характеристики одной и другой систем
связаь ы между собой следующими соотношениями (см. рис.
26.8):
СТ—Суа C0S а~ГГлй sln CH = Cxa COS Ct — Ct.
При расчетах летных характеристик вертолетов часто поль-
зуются безразмерными коэффициентами, получаемыми как част-
ное от деления вышеприведенных коэффициентов на коэффици-
ент заполнения а:
j. с т Т.
о 1
h =- =-----------Д---------;
е»яЛ2 (»й)2
f сУа Уа
У а. — ------j -----,
— eon/?2 (w/?)2
( __ сха __ Ха
ха ’ ’»
С 1
7/ __: Стк —______________________
К С 1
— е°л/?3( /?)2
Коэффициентом заполнения о считают отношение суммарной
площади проекции лопастей на плоскость вращения к площади
диска несущего винта.
429
wwm vokb-la.spb ru - Самолёт своими руками?!
На рис. 26 9 в качестве иллюстрации приведены аэродинами-
ческие характеристики несущего винта, полученные эксперимен-
тально.
txa,
О,02
0,01
О
-0,01
-0,02
-0,03
Рис. 26 9. Аэродинамические характеристики несущего
винта
(ы/? Voo \
=0,13; М= — = 0,65; — = 0,2; а = 0,091)
a ы/? /
Вопросы для повторения
1. Объясните причины трехшарнирного крепления лопастей
несущего винта вертолета.
2. Какие условия работы вертолета учитываются характерис-
тикой режима работы винта р?
3. Какие критерии подобия вертолетных винтов используются
при моделировании?
Задачи
1. Определить в общем виде форму границы и положение
зоны обратной обдувки лопастей вертолета.
Решение. На границе зоны обратной обдувки величина
составляющей скорости Ut, определяемой формулой (26.1), равна
нулю. Тогда
tor-J-IZooCOS a sin ф = 0 («)
Переходя к декартовым координатам (см. рис. 26 6), получим
Г=VЛ2+#2, sin Ф=у]+
430
www vokb-la.spb ru - Самолёт своими руками?!
После подстановки этих значений в уравнение (а) и алгебраи
ческих преобразований имеем
а-2 ---------. —----------V
\ 2ы / \ 2<о )
Уравнение (б) описывает границу зоны обратной обдувки,
представляющей собой круг с диаметром 1/^ cos а/w, центр ко-
торого определяется координатами (0, —cos а/2<о).
2. Определить коэффициент подъемной силы несущего винта
вертолета весом 6=2,5-10s Н, который «завис» на высоте 500 м,
если диаметр винта D — 8 м, а частота вращения п—240 об/мин.
Решение.
В режиме “висения" Ya = сУа^ л/?2—G,
откуда
На высоте 500 м
вращения винта
2G
е (ы/?)2 л/?'-
плотность q = 1,167 кг/м3. Угловая скорость
ю=лд/30—25,13 1/с.
Подставляя найденные величины в выражение для суа, находим
2-2,5-105
уа ---------------------=0,84.
Ja 1,167 (25,13-4)2 л-42
3. Определить угол атаки несущего винта вертолета, если
известны относительная поступь 7.--0 6 и характеристика режи-
ма работы винта ц —0 3.
Ответ: a = arctg —— =^0,57 рад.
Л[л
ft to НЕКОТОРЫЕ ВЕЛИЧИНЫ СТАНДАРТНО! 'Л АТМОСФЕРЫ (ГОСТ 4401—64) ПРИЛОЖЕНИЕ
Геометри- ческая высота Н. м Барометрическое давление рн 10-< Н/м2 Температура Гн, К Плотность р, кг/м3 Относитетьная плотность А Скорость звука <7, м/с Кинематическим коэффициент ВЯЗКОСТИ X, м2/с
0 101,325 288,15 1,2250 1,0000 340,28 1,4607 10~5
1000 89,876 281,65 1,1117 9,0751 10-1 336,43 1,5812 10-5
2000 79,198 275,14 1,0067 8,2171 10-1 332,52 1,7146 10-5
3000 70,125 268,64 9,0941 10-1 7,4237 10-1 328,56 1,8624 10-5
4000 61,656 262,13 8,1942 10 1 6,6891 10 1 324,56 2 0271 10 5
5000 54,045 255,63 7,3654 10-1 6,0125 10 1 320,51 2,2103 10 -5
6000 47,213 249,13 6,6022 10- 1 5,3895 10- 1 316,41 2,4153 10-5
7000 41,098 242,63 5,9011 10-1 4,8171 10-1 312,25 2,6452 1 0-5
8000 35,648 236,14 5,2591 10 1 4,2931 10-1 308,05 2,9030 10-5
9000 30,791 229,64 4,6712 10-1 4,6712 10~‘ 303,78 3,1942 10-5
10000 26,491 223,15 4,1357 10-1 3,3761 10- 1 299,45 3,5232 IO-5
11000 22,690 216,66 3,6485 IO’1 2,9784 10-1 295,0 3,8966 10-5
13000 16,572 216,66 2,6648 10- 1 2,1753 IO-’ 295,07 5,3351 10-s
15000 12,107 216,66 1,9467 10-‘ 1,5891 10-1 295,07 7,3029 10-3
20000 5,5269 216,66 8,8871 10-2 7,2547 10 2 295,07 1,3997 10-4
25000 2,5262 216,66 4,0621 10-2 4,3160 ю-2 297,07 3,4998 10-4
30000 1,1836 230,35 1,7901 10 2 1,4613 10-2 о04,25 8,3565 10-4
35000 0,58024 244,01 8,2842 10 3 6,7626 ИГ3 313,14 1,8929 10-3
40900 | 0,29586 257,66 4,0003 !0-3 3,2656 321,78 4,0956 10 3
wwwvokb-la.spb.ru - Самолёт своими руками?!
www vokb-la.spb ru - Самолёт своими руками?!
В настоящее время Международной организацией по стан-
дартизации (ИСО) разработана Международная стандартная
атмосфера (MCA). После утверждения MCA Советом ИСО она
будет рекомендована всем странам для использования. Табли-
цы MCA составлены в функции геометрической и геопотеици-
алыой высот для диапазона высот от 2000 до 50000 м. В табли-
цах MCA все величины даны в системе единиц СИ
’Систематические наблюдения за состоянием атмосферы по-
казывают, что существуют заметные отклонения параметров
от среднего значения В таблицах СА обычно приводятся допол-
нительные сведения о разбросе значений температур, плотности
и давления. В настоящее время этот разброс можно оценить до
высоты 80 км Для большей высоты достаточного количества
наблюдений еще не получено.
С 1 января 1963 года в СССР рекомендована как предпоч-
тительная во всех областях науки, техники и народного хозяй-
ства Международная система единиц, обозначаемая символом
«СИ» (ГОСТ 9867—61). Согласно этой системе за основные ме-
ханические единицы приняты: единица длины — 1 метр (м),
единица массы — 1 килограмм (кг) и единица времени —
1 секунда (с). Все остальные единицы — производные от ука-
занных трех основных величии. Одиако, учитывая особое поло-
жение, которое занимает в технических расчетах понятие сипа,
в системе СИ предусмотрена дополнительная производная еди-
ница, выполняющая функцию основной — Ньютон (Н) — сила,
сообщающая массе в 1 кг ускорение в 1 м/с2 (кгм/с2).
Напомним, что до введения системы СИ в аэродинамике, как
и в других прикладных науках, применялась техническая си-
стема единиц (МКГСС), в которой за основную единицу вместо
килограмм-массы принималась единица силы (килограмм-сила).
Одним из основных преимуществ системы СИ является чет-
кое разграничение единицы массы (килограмм) н силы (Нью-
тон), чем исключается двузначность понятия килограмм.
СПИСОК ЛИТЕРАТУРЫ
1 . Абрамович Г. Н. Прикладная газовая динамика. М., «Наука», 1969,
824 с
2 Александров В. Л. Воздушные винты. М Оборонгиз, 1951, 475 с
3 . Аржаников Н. С., Мальцев В. Н. Аэродинамика, М., Оборонгиз, 1956,
484 с.
4 Аржаников Н С, Садекова Г. С. Аэродинамика больших скоростей,
М, «Высшая школа», 1965, 560 с.
5 . Бай Ши-и. Введение в теорию течения сжимаемой жидкости, М, ИЛ,
1962, 410 с.
6 . Биркгоф Г. Гидродинамика М, ИЛ, 1963, 244 с.
7 Гаухман Р. Н, Касторский В Е., Логачев Ю Г., Стадник И. В.
Аэродинамика и динамика полета транспортных летательных аппаратов, кн. 1
Рижский институт инженеров гражданской авиации, 1968, 458 с.
8 . Гессоу А., Мейерс Г. Аэродинамика вертолета, М, Оборонгиз, 1954
256 с.
9 Гинзбург И. П Аэрогазодинамика М, «Высшая школа», 1966, 404 с.
10 Гинзбург И. П Теория сопротивления и теплопередачи, Л, ЛГУ 1970,
376 с.
II Голубев В. В Лекции по теории крыла М-Л., ГИТТЛ, 1949, 480 с
12 . Голубев В. В. Труды по аэродинамике. М.-Л., Госгехиздат, 1957,
979 с.
13 Горлин С. М. Экспериментальная аэромеханика, М., «Высшая школа»,
1970, 423 с.
14 Горлин Q М., Слезингер И. И. Аэродинамические измерения М, «На-
ука», 1964, 720 с.
1 Горшенин Д. С, Мартынов А. К. Руководство к практическим заняти-
ям в аэродинамической лаборатории. М, «Машиностроение», 1967, 224 с
16 Гошек И. Аэродинамика больших скоростей. М, ИЛ, 1954, 547 с
17 . Гудерлей К. Г Теория околозвуковых течений. М, ИЛ. 1960 421 с.
18 Жуковский Н Е. Избранные сочинения, т 1, 2, М-Л, ГИТТЛ, 1948,
392 с, 422 с
19 Загордан А. М Элементарная теория вертолета, М, Воениздат, 1960,
384 с
20 Закс Н, А Основы экспериментальной аэродинамики, М , Оборонгиз,
1953, 372 с
21 Зауер Р Течения сжимаемой жидкости. М, ИЛ, 1954, 312 с
22 Изаксон А. М. Советское вертолетостроение, М , «Машиностроение»,
1964, 311 с
23 Карафоли Е Аэродинамика крыла самолета, М изд-во АН СССР,
1956, 480 с.
24 Кочин Н. Е., Кибель И А., Розе Н. В Теоретическая гидромеханика,
ч I, 11, М, Гостехиздат, 1948, 1949, 536 с, 612 с.
25 Краснов Н Ф Аэродинамика, М, «Высшая школа», 1971, 632 с
434
www.vokb-la spb ru - Самолёт своими руками?!
26 Краснов Н. Ф Аэродинамика тел вращения, М, «Машиностроение*
1964, 572 с
27 . Краснов Н. Ф. Прикладная аэродинамика, М, «Высшая школа», 1974,
732 с
28 . Курант Р., Фридрихе К. Сверхзвуковое течение и ударные волны, М.
ИЛ, 1950, 426 с.
29 Лаврентьев М. А., Шабат Б. В. Проблемы гидродинамики и их ма-
тематические модели, М, «Наука», 1973, 416 с.
30 Ламб Г. Гидродинамика, М., Гостехиздат, 194’, 928 с.
31 . Ландау Л. Д., Лифшиц Е. Л. Механика сплошных сред, М, ГИТТЛ,
1954, 796 с
32 Лебедев А А., Стражева И. В., Сахаров Г. И. Аэромеханика само-
лета, М, Оборонгиз, 1955, 472 с
33 Лебедев А. А, Чернобровкин Л С. Динамика полета, М , «Машиност-
роение», 1973, 610 с.
34 Левинсон Я. И Аэродинамика больших скоростей. М, Оборонгиз, 1950,
352 с.
35 . Липман Г. В„ Пакет А. Е. Введение в аэродинамику сжимаемой жид-
кости М , ИЛ, 1949, 329 с
36 . Липман Г. В., Рошко А. А. Элементы газовой динамики М„ ИЛ.
1960, 518 с.
37 . Лойцянский Л. Г. Ламинарный пограничный слой. М, Физматгиз,
1962, 479 с.
38 . Лоицянский Л. Г. Механика жидкости и газа. М, «Наука», 1973,
848 с
39 . Мартынов А. К. Прикладная аэродинамика, М, «Машиностроение»,
1972, 448 с
40 . Мартынов А. К. Экспериментальная аэродинамика, М, Оборонгиз,
1958, 348 с.
41 . Мартынов А. К-, Баскин В. Э, Вильдгрубе Л С., Вождаев Е. С.,
Майкапар Г. И. Теория несущего винта, М, «Машиностроение», 1973, 364 с.
42 Мельников А. П. Аэродинамика больших скоростей М Воениздат,
1961, 424 с.
43 . Милн-Томсон Л. М Теоретическая гидромеханика. М «Мир», 1964,
656 с
4. Миль М Л , Некрасов А В., Браверман А. С., Градко Л. Н , Лейканд
М. А. Вертолеты Расчет и проектирование, ч. 1 М «Машиностроение», 1966
^56 с
45 Мхитарян А. М. Аэромеханика и динамика полета летательных аппа-
ратов, ч 1, II, Киев, Киевский инсти ут инженеров гражданской авиации,
1965, 1968, 240 с , 244 с
46 Мхитарян А. М Аэродинамика, М, «Машиностроение», 1970, 428 с.
47 . Мхитарян А. М., Лазнюк П С., Максимов В. С, Межлумян Р А.,
• Тотиашвилн Л. Г., Фридланд В. Я. Динамика полета, М , «Машиностроение»,
1971, 368 с
48 Некрасов А. И. Теория крыла в нестационарном потоке, М -Л изд-во
АН СССР, 1946, 258 с
49 . Остославский И. В. Аэродинамика самолета, М, Оборонгиз, 1957,
560 с
50 . Остославский И, В., Стражева И В. Динамика полета Траектории
летательных аппаратов, М , Оборонгиз, 1963, 430 с
51 . Патрашев А. Н., Кива ко Л. А, Гожий С. И. Прикладная гидродина-
мика, М , Воениздат, 1970, 684 с
52 Пейн П Р. Динамика и аэродинамика вертолета, М Оборонгиз. 1963
491 с.
53 . Повх И Л. Техническая гидромеханш а Л , «Машиностроение», 1969
524 с.
54 . Прандтль Л Гидроаэромеханика, М , ИЛ, 1951, 575 с
435
www.vokb-la.spb.ru - Самолёт своими руками?!
5о Прицкер Д. М., Сахаров Г. И. Аэродинамика, М, «Машинострое-
ние», 1968, 310 с
56 Путята В. И., Сидляр М. М Гидромеханика, Киевский государствен-
ный университет, 1963, 480 с
57 Пэнкхерст Р., Холдер Д. Техника эксперимента в аэродинамических
трубках, М , ИЛ, 1955, 668 с
58 Седов Л. И. Методы подобия и размерности в механике, М. «Наука»,
1965, 428 с
59 Седов Л. И Механика сплошной среды, т I, П, М, «Паука», 1973,
536 с , 584 с
60 Седов Л И Плоские задачи гидродинамики и аэродинамики, М,
«Наука», 1966. 446 с
61 Слезкин Н. А. Динамика вязкой несжимаемой жидкости, М, ГИТТЛ,
4955, 520 с
62 Фабрикант Н. Я- Аэродинамика, М, «Наука», 1964, 816 с
63 Федяевский К- К-, Войткунский Я. И., Фаддеев Ю. И. Л, Гидроме-
ханика, «Судостроение», 1968, 568 с
64 Ферри А Аэродинамика сверхзвуковых течений, М, ГИТТЛ, 1952,
468 с
65 Фридман А. А Опыт гидромеханики сжимаемой жидкости, М , Гос-
техиздат, 1934, 367 с
66 Хоуарт Л. и др Современное состояние аэродинамики больших ско-
ростей, т 1, М , ИЛ, 1955, 491 с
67 Чаплыгин С. А. Избранные работы по теории крыла, М -Л Гостехиз-
дат. 1949, 274 с
68 Черный Г Г. Течения газа с большой сверхзвуковой скоростью, М,
Физматгиз, 1959, 220 с
69 Чертов А. Г. Международная система единиц измерения, М , Росвуз-
издат, 1963, 166 с
70 Шлихтинг Г. Теория пограничного слоя, М, «Наука», 1969, 744 с
71 Юрьев Б. Н. Аэродинамический расчет вертолетов, М, Оборонгиз,
1956. 559 с
72 Юрьев Б Н Экспериментальная аэродинамика, М -Л, Оборонгиз,
1936 (ч 1), 1938 (ч II), 300 с, 275 с
73 Янунович М. С. Практическая аэродинамика соосного вертолета М ,
«Транспорт», 1965, 220 с.
www vokb-la.spb ru - Самолёт своими руками?!
предметный указатель
А абсцисса наибольшей кривизны про-
филя 221
— -толщины профиля 221
авиация гражданская 6
автомат перекоса 433
автомодельность 154 155
авторотация 425
адиабата Гюгонио изэнтропическая 433
—ударная 133
атмосфера Земли 11, 26
— стандартная 28
аэродинамика больших скоростей 6
— разреженного газа 6
— экспериментальная 160, 1и4
аэромеханика 5
Б баротропцость 78
Бернулли—Эйлера интеграл 82
Бернучлп уравнение 81
---линеаризованное 241
Ецо—Савара формула 72
В весы аэродинамические 175
винт воздушный 400
— несущий 431
— изменяемого шага 402
— фиксированного шага 402
- эквивалентный 437
вцхрь П образный 280
— присоединенный 103, 279
— разгонный 105
— свободный 280
— скорости 43
весы аэродинамические 175
возмущения малые 121
волна звуковая 134
— сферическая (разрежения) 121
— ударная 121. 133
вязкость 11
*
Г газ идеальный 11
— реальный 12
газодинамика 6
Гельмгольца теорема 64
гидромеханика 5
гипотеза непрерывности (сплошности)
12
— плоских сеченцй 228
гипоциссоида (сгрофонда) 142
Гдауэрта Трефтца метод 141
годограф скорости 141
градиент скорости 15
Гюгонио адиабата 133
гистерезис 313
Д давление в критической точке за пря
чым скачко 1 134
— Динамическое 83
гидростатическое 18, 83
— донное 367
— полное 83
Датамбера—Эйлера парадокс 92
движение адиабатическое 84
— винтовое 63
— вихревое 61
— изэнтропическое 20, 24. 107
— неизэнтропическое 25
— ламг парное 160, 181
— одномерное установившееся 107
— плоскопараллельное 49
— потенциальное (безвихревое) 44, 46
— потенциальное (плоское) 46
—циркуляционное (вихревое) 69
— неу становившееся (нестационарное)
33
- турбулентное 160 181
— установившееся (стационарное) 33
диаграмма координатная 234
— векторная 235
Диапазон летных углов атакц 227
диполь 56
Дюбуа парадокс 8
Ж жидкость баротропная 78
— гидродинамически идеальная 17
Жуковского теорема 102
Жуковского—Чап чьи ина постулат 104
3 закон термодинамики второй 23
-------- первый 22
— третий Ньютона 152
законы подобия 153
аакрылок струйный 326
— выдвижной 323
— простой 323
И измерение давления 179
— скорости 177
изэптропа 132
интеграл Бернулли Эйлера 82
интенсивность вихревой нити 63
— вихревого шнура 63
— погонная 286
интерференция аэродинамическая 383
интерцептор (прерыватель потока) 327
испытания летные 164
источник плоский 53
К качество аэродинамическое 226
----самолета при скоростях дозвуковых
397
--------сверхзвуковых 397
конус возмущения 122
— характеристический (Маха) 122
Коши—Гельмгольца теорема 41
Коши—Римана условия 51
коэффициент аэродинамической силы
16]
— аэродинамического момента 161
— волнового сопротивления 259
437
www vokb-la.spb.ru - Самолёт своими руками?!
— аэродинамического профиля 225
-----приведенный 260
— — —пластина тонкого профиля в
сверхзвуковом Потоке 271
---— треугольною профиля в сверх-
звуковом потоке 273
----- несимметричного ромбовидно-
го профи чя в сверхзвуковом потоке
274
-----линзообразного профиля 274
— тето Сирса—Хаака 389
— вязкости динамический 15
---- кинематический 16
— давления 92
--- приведенный 260
— индуктивного сопротивления крыла
285
коэффициент лобового сопротивления
пластины 265
— волнового сопротивления тела Сир-
са—Хаака 390
— лобового сопротивления в сверхзву
новом потоке 353
-----профиля 27J
— индуктивно волнового сопротивления
264
— интерференции 384
— лобового сопротивления крыла 285
— — при нулевой подъемной силе 335
— — тела вращения 168
— — тонкого профиля в сверхзвуко
вом потоке 271
— мощности винта 411
----несимметричного ромбовидного
профиля в сверхзвуковом потоке 274
— подобия 151
— подсасывающей силы 350
— подъемная сила крыла конечного
размаха 292
— — плоской пластины в сверхзвуко-
вом потоке 264
—----профиля 225
— полезного действия винта 405
— поправочный в плане 293
---- на удлинение 293
— профильного сопротивления крыла 285
— скорости 110
— давления 92, 243
— сопротивления самолета 387
----тел вращения 369
— эффективности руля 378
коэффициенты аэродинамические про-
филя 225
кривизна профиля относительная 221
кризис волновой 251
критерии подобия 153
----винтов 156, 411
критерии сверхзвукового подобия 348
кромка передняя дозвуковая 347
— — звукова я 348
— — сверхзвуковая 347
крутка крыла 278
лопасти 402
крыло 220
— конечного размаха 277
наивыгоднейшее 293
стреловидное 299
— эллиптическое 294
крылья малых удлинений 307
— многощелевые 325
Л Лагранжа метод 32
линеаризация 239
линия вихревая 62
— возмущения (Маха) 123
— звуковая 253
— профиля Средняя 221
— тока 34
лопасть вднта 400
М метод Бураго 257
метод Глауэрта—Трефтца 290
— Лагранжа (субстанциальный) 32
— малых возмущений 240
— параметрический в теории погранич-
ного стоя 212
— шелковинок 175
— Эйлера (локальный) 32
механизация крыла 320
моделирование аэродинамическое 153
момент аэродинамической силы про-
филя 222
— ----крыла 342. 357, 268
— кабрирующий 222
— пикирующий 222
— тангажа 222
мощность винта 400, 404, 405
— — осевая 405
— — окружная 405
Н напор динамический 84
пьезометрический 82, 84
— скоростной 83
— статический 179
— тепловой 84
напряжение касательное 15
нить вихревая 63
Ньютона закон трения 17
О обтекание кругового цилиндра 90
------ циркуляционное 94
— тупого угла внешнего 124
------внутреннего 126
объем удельный 19
оперение 376
отрыв пограничного слоя 212
отсос пограничного слоя 216, 217
П парабола индуктивного сопротивления
285
парадокс Даламбера—Эйлера 8, 90
— Дюбуа 8
параметры критические [09, 390
— подобия в околозвуковом режиме 338
— сверхзвуковые 348
— профиля геометрические 220
— торможения 108
пелена вихревая за крылом 279. 281
пересчет аэродинамических характери-
стик 295
переход ламинарного течения в турбу-
лентное 182, 188
Пито—Прандтля трубка 179
плотность 13
подобие механическое потоков 149
— физическое 148, 149
— геометрическое 149
— динамическое 149
---кинематическое 149
математическое 149
подслои вязкий 186, 196
поляра второго рода 229
— кры та 357
— первого рода 229
— ударная 141
пол}Ш1'ур вичревой 73
поступь винта 403
— — относительная 403
— газовая 19
постулат Жуковского—Чаплыгина 104
потенциал скорости 47
поток однородный 52
правило площадей 389
— Прандтля—Глауэрта 213
предкрылок 326
— струйный 326
преобразование Гаусса—Остроградско-
го 37, 77
принцип Даламбера 76
438
www.vokb-la.spb.ru - Самолёт своими руками?!
профиль крыла 220
процесс адиабатический 20
— баротропный 83
— изотермический 20
— изохорный 22
— изэнтропический 24, 107
пульсация параметра 186
путь смешения 188
Р размах крыла 278 291
распределение давления по профилю
234
•-----сечение кругового цилиндра 94
------стреловидного крыла 303
— циркуляции скорости 64
Рейнольдса число 155, 181
— —критическое ]82
режим отрицательных тяг 412, 419
— самовращения (авторотации) 413, 425
<3 серия профилен 221
сетка гидродинамическая 51 52
сечение критическое 113
— мнделево 362
сдув пограничного слоя 217
сжимаемость газа 25
сила аэродинамическая полная 222
сила массовая 18
— нормальная 223
— поверхностная 18
— иодсас явающая 348
— подъемная самолета 223
— сопротивления (лобового) 267
----самолета
— продольная 223
— тя и винта 438
— сопротивление самолета 387
система координат связанная 222
— скоростная 222
скачок уплотнения 127
— — косой 127
— —отсоединенный 128
----прямой 127
— скорость звука 25
индуктивная 281
— контроля регулятора 426
— критическая 109
— максимальная 111
— осредненная 184
— относительной деформации 42
— распространения звука в газе 25
— средняя по размаху 282
— угловой деформации 42
скос потока 281
след аэродинамический 196
слой пограничный 15, 193
соотношение Кармана 199
сопло Лаваля 113
сопротивление
— вихревое 61
— волновое 256 263
— давления 213
— донное 367
— индуктивное в околозвуковом режи
ме 311
— индуктивно волновое 264
— кормовой части тела вращения 368
— носовой части тела вращения 368
спектр аэродинамический 175
— дымовой 175
среда баротропная 78
соотношение динамической совместимо-
сти 76
несжимаемая 12
— сжимаемая 25
срыв потока 313
Степень сужения крыла
— турбулентности 161, 186
— шероховатости 161
сток 53
стреловидность крыла 300
—приведенная 347
строфоида (гипоадссоида) 142
струйка элементарная 36
супераэродинамика 6
суперциркуляция 218
Т тело вращения 362
неудобообтекаемое 213
----удобообтекаемое 213
температура 19
— торможения 107
теорема Гельмгольца 63
Жуковского о подъемной силе 98
— Коши—Гельмгочьца 41
— Стокса об интенсивности вихревой
трубки 68
— Томсона 73
теплосодержание 22
толщина вытеснения 210
— лопасти 401
— пограничного слоя 195
— потери импульса 210
— профиля 221
— максимальная 221
Относительная 221
тела вращения относительная 362
точка критическая задняя 104
— отрыва 212
— торможения 107
—критическая 60
траектория частицы 34
трение внутреннее 14
трубка Пито—Прандтля 178
— тока 36
— вихревая 63
трубы аэродинамические 165
— больших скоростей 169
У угол атаки профиля 220
— — — аэродинамический 227
------ — закрнтический 227
— — истинный 282 287
— критический 227
---наивыгоднеиший 229
---- приведенный 260
---- сечения лопасти винта 401
геометрической крутки 274
нулевой подъемной силы 27
— притекания 403
— раствора 362
— скоса потока 252
----— средний 282
— стреловидности 299
— установки сечения лопасти 401
удлинение крыла 278
---- приведенное 347
---- фиктивное 331
----эффективное 331, 384
— тела вращения 362
управление пограничным слоем 215
Уравнение Бернулли 81
—линеаризованное 241
Громеки Эцлера 80
движения Эйлера 77
— движения сжимаемой жидкости 239
— годографа скорости 142
— Гюгонио 132
— Пуассона 25
— импульсов 211
— интегро дифференциальное крыло
конечного размаха 290
— Лапласа 48
— неразрывности 37
— линеаризованное 240
— поляры пластины 265
— профиля крыла в сверхзвуковом по-
токе 387
439
www.vokb-la.spb.ru - Самолёт своими руками?!
— крыла в дозвуковом потоке 336
— поляры самолета в сверхзвуковом по-
токе 397
— для потенциала скорости возмущен-
ного движения газа линеаризованное
241
— связи 283
— состояния 19
уравнение линий тока 33
— — вихревых 62
— характеристические механического
подобия 152
Ф форма крыла в плане 277
------- нацвыгоднейшая 293
фокус крыла 343
—---кругового профиля 232
формула Био—Савара 72
— Бураго для коэффициента волнового
сопротивления 259
— Бураго для коэффициента лобового
сопротивления 246
— Жуковского 98
Дородницына 248
— Ньютона 19
— Прандтля 130, 187
— Релея 135
— Федяевского 247
функции гармонические 48
функция тока 50
Фурье закон переноса тепла 17
Фика закон переноса вещества 17
X характеристика винта аэродинамическая
410
----рабочая 412
— режима работы несущего винта 433
— крыла аэродинамические 413
— — геометрические 277
— Несущего внцта 433
хорда крыла средняя аэродинамическая
227
— — геометрическая 256
— профиля 220
Ц центр давления 231
циркуляция скорости 65
Ч число Маиевского—Маха 26. 156.
— критическое 336, 250
----скользящего крыла 301
— стреловидного крыла 301
— Рейнольдса 181, 214
— Струхаля 156
— Фруда 155
—Эйлера 154
— Ньютона 154
Ш Шаг винта 402
шнур вихревой 63, 280
----бесконечный 73
— присоединенный 279
Щ щиток простой 321
— выдвижной 321
— носовой 326
Э элероны 380
энергия газа 21
энтропия 24
эффект скольжения 300
эффект срединный 301
эффект Коанда 217
ммм vokb-la.spb ru - Самолёт своими руками?!
ОГЛАВЛЕНИЕ
Стр.
Предисловие..............................................; ; ч 3
Введение............................................................ 5
В.1 Предмет аэрогидромеханики................................... 5
В 2 Гражданская авиация......................................... 6
В.З Обращение движения.......................................... 8
В 4 Связь теории с экспериментом................................ 8
В 5. Применение аэродинамики при проектировании самолетов г 9
JTлава L Основные физические свойства жидкостей и газов. Земная ат-
мосфера , . . . ...............................10
1 1 Понятие о физической структуре жидкости и газа .... 10
12 Плотность н удельный вес.....................................12
1 3. Внутреннее трение и вязкость. Закон переноса...............13
14 Гидростатическое давление ...................................16
1 5. Силы, действующие в движущейся жидкости....................17
1 6. Уравнение состояния идеального газа........................18
1.7. Некоторые вопросы термодинамики............................19
1.8. Сжимаемость газов. Скорость распространения звука в газе . 24
19 Атмосфера ..................................................25
Вопросы для повторения Задачи......................................28
Глава 2 Кинематика жидкой среды . . . ...... 30
2.1 Методы исследования движения жидкости . ... 30
*2 2. Линия тока Трубка тока, Элементарная струйка .... 31
2 3. Уравнение неразрывности ...................................34
2.4 Теорема Коши — Гельмгольца о разложении скорости жидкого
элемента . . . . . .........................38
Вопросы дтя повторения. Задачи . . , ...... 42
Глава 3. Основы теории плоских потенциальных течений .... 43
31 Понятие о потенциальном течении ...................... . 43
3-2 Свойства потенциала скорости................................44
3.3. Плоскопараллельное течение жидкости. Функция тока . . 46
3 4. Плоские потенциальные течения жидкости.....................48
3 5. Однородный поступательный поток.................... . . 49
3 6 Источник и сток.............................................50
441
www.vokb-la.spb.ru - Самолёт своими руками?!
Стр,
3.7 Пара источник — сток........................................52
3.8. Диполь.................................................. 53
3.9. Наложение однородного потока на диполь......................54
Вопросы для повторения. Задачи . . .....................57
Глава 4. Основы теории вихревого течения................... 58
41. Вихревое течение жидкости Основные определения ... 58
4.2. Напряжение вихревого шнура Теорема Гельмгольца ... 60
4 3. Циркуляция скорости и ее связь с потенциалом скоростей . 61
4.4 Связь элементарной циркуляции с напряжением вихря. Теорема
Стокса . . . . ...............................63
4.5. Циркуляционное невихревое движение..........................65
4.6. Формула Био — Савара .......................................69
4.7. Понятие о теореме Томсона................................ 70
Вопросы для повторения. Задачи......................................71
Глава 5. Динамика идеальной жидкости................................72
5.1. Общие понятия...............................................72
5.2. Уравнения движения идеальной жидкости ......................73
5.3. Дифференциальные уравнения движения идеальной жидкости
в форме Громеки . . ...............................76
5.4 Интеграл Бернулли — частное решение уравнений Эйлера —
Громеки . . . ..........................................77
5.5. Пределы применимости уравнения Бернулли для несжимаемой
жидкости к газу..................................................82
Вопросы для повторения. Задачи . . .....................85
Глава 6. Основы теории обтекания тел потенциальным потоком жид-
кости . . . ..............................86
6.1. Бесциркуляционное обтекание кругового цилиндра. Парадокс
Даламбера — Эйлера . . ..........................86
6.2. Циркуляционное обтекание кругового цилиндра . . .90
6.3. Подъемная сила кругового цилиндра в несимметричном плос-
копараллельном потоке . . ..........................92
6.4. Теорема Жуковского о подъемной силе для случая обтекания
цилиндрического тела произвольной формы..........................94
6.5. Возникновение циркуляции скорости и подъемной силы ла кры-
ле. Постулат Жуковского — Чаплыгина......................... . 99
Вопросы для повторения. Задачи.....................................101
Глава 7. Основные соотношения газовой динамики.....................102
7.1. Основные соотношения для одномерных изэнтропических уста-
новившихся течений газа ... . ... 102
7 2. Зависимость между площадью поперечного сечения струйки и
скоростью газа..............................................107
73. Расчет сверхзвукового сопла ................................108
74 Получение сверхзвукового потока в пористой цилиндрической
трубе . . . ..........................................112
Вопросы для повторения.^Задачи . . . ...... 114
Глава 8. Малые возмущения и скачки уплотнения в газовом потоке 116
8.1. Распространение малых возмущений...........................116
442
там vokb-la.spb.ru - Самолёт своими руками?!
Стр.
8.2. Обтекание углов плоскопараллельным сверхзвуковым потоком 119
8.3. Основные соотношения для прямого скачка уплотнения . . 124
8.4. Давление в критической точке за прямым скачком . . . 129
8 5. Косые скачки уплотнения.................................131
8.6. Связь между положением фронта косого скачка и углом по-
ворота ^сверхзвукового потока . .....................133
8 7. Ударная поляра и ее применение к решению задач . 136
8.8. Изменение давления при отклонении сверхзвукового потока на
малые углы . . . ................................ 140
Вопросы для повторения. Задачи.................................... 142
Глава 9. Элементы теории подобия . . .....................143
9.1. Понятие о подобии потоков.................................,143
9.2. Масштабные множители (коэффициенты подобия) и задачи тео-
рии подобия . . , . .........................146
9.3. Аэродинамическое моделирование. Основные законы подобия.
Критерии подобия , „ . ........................148
9.4. Анализ критериев подобия ..................................152
9.5. Основные формулы экспериментальной аэродинамики . . . 1о5
Вопросы для повторения. Задачи . . . ...... 157
Глава 10. Основы экспериментальной аэродинамики.....................159
10.1 Задачи экспериментальной аэродинамики и методы их решения 159
102. Принципы построения аэродинамических труб .... 160
10.3. Аэродинамические трубы малых дозвуковых скоростей . . 163
104. Аэродинамические трубы больших скоростей..................164
10.5. Аэродинамические спектры . .........................10
10.6. Измерение скорости воздушного потока...................., 172
Вопросы для повторения. Задачи . . .....................175
Глава 11. Два режима течения жидкости...............................176
11.1. Определение ламинарного и турбулентного режимов течения
вязкой жидкости . . .........................176
11.2. Турбулентное течение жидкости.............................178
11.3. Степенной закон распределения скоростей...................185
Вопросы для повторения............................................: 187
Глава 12. Основы теории пограничного слоя . ...... 188
12 1. Понятие о пограничном слое................................188
-12 2. Интегральное соотношение для установившегося течения в
пограничном слое несжимаемой жидкости......................191
12.3. Применение интегрального соотношения для расчета харак
теристик ламинарного пограничного слоя плоской пластины . 194
12,4. Применение интегрального соотношнеия для расчета турбу-
лентного пограничного слоя и определение сопротивления плос-
кой пластины . . ..................................197
12.5. Расчет смешанного пограничного слоя на пластине . . . 200
12 6. Влияние сжимаемости воздуха на пограничный слон . . . 201
12 7. Интегральное соотношение для расчета двумерного погранич-
ного слоя Ha1 криволинейной поверхности.........................204
12.8. Отрыв течения в пограничном слое . ....... 207
12.9. Управление пограничным слоем..............................210
443
www vokb-la.spb.ru - Самолёт своими руками?!
Вопросы для повторения Задачи . . .....................213
Глава 13 Профили крыльев и их аэродинамические характеристики . 215
13.1. Геометрические характеристики профиля крыла .... 215
13 2. Аэродинамические силы и момент . .................217
13 3. Аэродинамические коэффициенты и качество профиля . . 220
13 4, Зависимость аэродинамических коэффициентов от угла атаки
профиля. Поляры профиля........................................221
13 5 Зависимость аэродинамических коэффициентов от числа Re,
степени турбулентности потока и формы профиля .... 225
13 6 Центр давления Фокус профиля...............................226
13.7. Распределение давления по профилю.........................223
Вопросы для повторения Задачи . . .....................231
Глава 14. Аэродинамические характеристики профиля в дозвуковом по-
токе ...............................................................233
14.1. Основные уравнения установившегося двумерного движения
газа и их линеаризация методом малых возмущений . . . 233
14 2. Связь между дозвуковым потоком газа и потоком несжимае-
мой жидкости около тонких профилей......................236
14 3. Влияние сжимаемости на аэродинамические характеристики
профиля....................................................... 239
Вопросы для повторения Задачи.......................................243
Глава 15. Профиль крыла в околозвуковом (трансзвуковом) потоке . 245
151 Понятие о критическом числе М Ударные волны . . . 245
15.2. Влияние угла атаки и формы профиля на и структуру
течения около профиля....................... ... 247
15 3. Распределение давления по профилю при наличии местных
скачков уплотнения и расчет волнового сопротивления про-
филя . . . . .......................... 250
Вопросы для повторения Задачи . ..........................255
Глава 16. Профиль крыла в сверхзвуковом потоке......................257
16 1. Особенности обтекания тел сверхзвуковым потоком. Плоская
пластина в сверхзвуковом потоке . ...... 257
16 2. Распределение давления по профилю.........................260
16 3. Тонкий профиль в сверхзвуковом потоке . . 262
16 4. Аэродинамические коэффициенты профилей некоторых харак-
терных форм .................................................. 267
Вопросы для повторения Задачи.....................................276
Глава 17 Основы теории крыла конечного размаха в несжимаемом
потоке ...................................................271
17 1 Геометрические характеристики крыла . 271
17 2. Аэродинамическая модель крыла конечного размаха . . 273
17 3 Индуктивная скорость. Скос потока у крыла. Индуктивное
сопротивление крыла............................... . . 275
17 4. Приближенный расчет индуктивного сопротивления . . 276
17 5 Расчет сил, действующих на крыло конечного размаха с пере-
менной циркуляцией по размаху .... . . 279
17.6. Определение распределения циркуляции вдоль размаха крыла 283
www.vokb-la.spb.ru - Самолёт своими pi
Стр-
17.7. Коэффициенты подъемной силы и индуктивного сопротивления
крыла с учетом распределения циркуляции вдоль размаха . 285
17.8. Наивыгоднейшая форма крыла в плане......................287“
17 9. Пересчет аэродинамических характеристик крыла с одного
удлинения на другое . ........................... 289»
Вопросы для повторения. Задачи.....................................291
Глава 18 Стреловидные крылья в дозвуковом потоке...................292
18 1 Понятие о стреловидности крыла и ее эффекте .... 292
18 2. Физическая картина обтекания стреловидного крыла . . . 295
18.3. Установление приближенной связи между параметрами стре-
ловидного и прямого крыльев . ... .... 297
184. Крылья малых удлинений................................. . 300-
Вопросы для повторения. Задачи...............................304
Глава 19 Максимальный коэффициент подъемной силы. Механизация
крыла . 305
19 1 Срыв потока с поверхности крыла......................305
19 2 Расчет максимального коэффициента подъемной силы . . 310
19 3. Механизация крыла ...... ... 312
19.4. Влияние близости земли на максимальный коэффициент подъ-
емной силы и поляру крыла . ...................322
Вопросы для повторения. Задачи................................... 323-
Глава 20. Аэродинамика крыла на дозвуковых и околозвуковых ско-
ростях ........ ..........
20.1. Влияние сжимаемости воздуха на аэродинамические характе-
ристики крыла конечного размаха в дозвуковом потоке
20.2. Критическое число М крыла конечного размаха . . . .
20.3. Аэродинамические характеристики крыла при околозвуковых
/ (трансзвуковых) скоростях полета . . . .
'-е0 4. Моментные характеристики крыла .......................
Вопросы для пцвторения. Задачи....................................
Глава 21. Аэродинамика крыла в сверхзвуковом потоке .
21 1. Влияние формы Крыла в плане на характер его обтекания
сверхзвуковым потоком . ...........................
21.2. Подъемная сила крыла в сверхзвуковом потоке . . . .
213 Сопротивление тонких, аэродинамически плоскт х крыльев ко-
нечного размаха в сверхзвуковом потоке .......................
21.4 Волновое сопротивление крыла при суа — 0.................
21.5. Моментные характеристики крыла в сверхзвуковом потоке
Вопросы для повторения. Задачи ...................................
Глава 22 Аэродинамические характеристики тел вращения
22.1. Геометрические и аэродинамические характеристики тел вра-
щения ........................................................
22 2. Подъемная сила тел вращ ния ............................
22 3 Сопротивление тел вращения.....................
Вопросы для повторения. Задачи . . .....................
Глава
23. Аэродинамические характеристики
325
325
328
329^
335
335
336
I
335
341
344-
346
348
35(4
352
352
354
358
368
366
оперения и рулей
445
www.vokb-la.spb.ru - Самолёт своими руками?!
Стр.
23.1. Аэродинамические характеристики оперения.................366
23.2. Аэродинамические характеристики элеронов.................370
Вопросы для повторения...........................................: 372
Глава 24. Лобовое сопротивление и подъемная сила самолета . . . 373
24.1. Лобовое сопротивление и подъемная сила на дозвуковых ско-
ростях полета................................................ . 373
24.2. Лобовое сопротивление и подъемная сила самолета на транс-
звуковых и сверхзвуковых скоростях полета . ... 378
24.3. Подъемная сила самолета..................................384
Вопросы для повторения. Задачи....................................388
Глава 25. Воздушные винты................................ . 390
25.1. Принцип действия воздушных винтов, их геометрические и ки-
нематические характеристики . .....................390
25.2. Теория идеального воздушного винта.................. 393
25.3. Теория изолированного элемента лопасти винта .... 399
25.4. Условия аэродинамического подобия и аэродинамические ха-
рактеристики воздушных винтов.................................400
25.5. Взаимное влияние воздушного винта и самолета. Влияние сжи-
маемости воздуха на КПД винта.............................. 403
25.6. Работа винта на режимах отрицательных тяг и авторотации 409
25.7. Особенности работы винтов турбовинтовых двигателей (ТВД) 411
25.8. Механизм возникновения отрицательных тяг в ТВД . . 412
25.9. Влияние скорости полета иа величину отрицательной тяги
винта . . . . ...............................416
Вопросы для повторения. Задачи....................................420
Глава 26. Особенности аэродинамики несущего винта вертолета . . 421
26.1. Особенности работы несущего винта .......................421
26.2. Влияние косой обдувки на аэродинамику винта .... 423
26.3. Условия динамического подобия винтов при косой обдувке . 426
26.4. Аэродинамические характеристики несущего винта . . . 428
Вопросы для повторения. Задачи.....................................430
Список литературы . . 432
Предметный указатель................................................ 435
www vokb-la.spb ru - Самолёт своими руками?!
Замеченные опечатки
С р. Строка Напечатано Должно быть
47 11 снизу ? Ф
48 6 снизу ду2 , д2Ф(*, у) 0 dy*
+ ^£d!l = 0 (38>)
ду2
64 3 сверху Гэл — Vу&х -J- Гэл = vxhx +
65 13 сверху =р/. =р' = '-
84 6 снизу Ро = Рсо + Чео + АР> Ро = Рсо+Чю+Ьр' (5.34)
84 5 снизу М2 Лр — Чсо . 4 (5-34) м! 4
86 12 сверху ¥ = М1- Ф = Уо(1-
123 подпись прямой; а — прямой;
под рис. 8.8
126 1 сверху (7-6) (7.15)
131 на рис. 8.17 V/ — Vu
146 6 снизу Хх=Х/'ХУ Х< = X/ Xv
147 формула (9.10) = ХХ^ — ^P^-V
162 3 сверху масс весов
183 В формулах / dVx V / dVx \2
(11 9) (11.10) \ dy J I dy /
197 3 сверху x{lbdx i^ldx
198 7 сверху пластине пластине (11 27)
200 подписи под 7 — турб..., 2 — лам... 2— турб..., 1 — лам
рис. 12.7
213 19 сверху с
218 1 снизу аХ= dX =
237 10 снизу Лапласа. Лапласа (3 8')
284 5 сверху полета потока
298 13 снизу (18.3) (18 4)
348 11 снизу = -Гхд
350 3 сверху мг Мг
У ъ Yb
354 8 сверху 4^9, V2/2 q = рУ2 2
375 15 снизу или и
385 20 сверху а а — с а, = с“ « уа &аГ = суа кра ’ ~ Суа кр?
Заказ 626/241
www vokb-la.spb ru - Самолёт своими руками?!
В ИЗДАТЕЛЬСТВЕ «МАШИНОСТРОЕНИЕ» В 1976 ГОДУ
ВЫЙДУТ КНИГИ:
Комаров А. А. Надежность гидравлических устройств само-
летов. 13 изд. л. 1 р. 10 к.
Функционирование гидросистем, динамика эксплуатацион-
ных показателей; влияние различных факторов на работу гид-
равлических устройств; изменения параметров устройств в про-
цессе эксплуатации, прогнознрованне этих изменений. Методы
определения надежности гидравлических устройств, способы по-
вышения их надежности.
Серьезное А. Н. Измерения прн испытаниях авиационных
конструкций на прочность. 21 изд. л. 1 р. 35 к.
Методика измерений, особенности измерительной аппарату-
ры и требования к ней. Первичные преобразователи и их монтаж
на испытываемой конструкции. Анализ погрешностей, рекомен-
дации по их устранению.
Тищенко М. Н., Некрасов А. В., Радин А. С. Вертолеты. Вы-
бор параметров при проектировании. 25 изд. л. 1 р. 55 к.
Методы выбора параметров винтокрылых машин, основан-
ные на теории прочности. Зависимости, учитываемые прн проек-
тировании вертолетов. Методы расчета стоимости изготовления
и эксплуатации вертолетов, выбора основных параметров по
•стоимости выполняемых работ.
Шавров В. Б. История конструкций самолетов в СССР
(1938—1950 гг.). 45 изд. л. 2 р. 85 к.
Исторический обзор советских самолетов с 1938 по 1950 г.
(около 700 типов). Основные характеристики, конструктивные
особенности, сравнительная оценка, области применения. Внеш-
ний вид самолетов.