Author: Биргер И.А. Шорр Б.Ф. Иосилевич Г.Б.
Tags: прочность сопротивляемость общее машиностроение машиноведение машиностроение прочность деталей машин
ISBN: 5-217-01304-0
Year: 1993
Text
И А Биргер э.ФШорр . Б. Иосилевич
Расчет на прочность деталей машин
СПРАВОЧНИК
4-е издание, переработанное и дополненное
МОСКВА
(МАШИНОСТРОЕНИЕ) 1993
ББК 34.41я2
Б64
УДК [621.81.001.24:539.4] (035)
Федеральная целевая программа книгоиздания России.
Биргер И. А. и др.
Б64 Расчет на прочность деталей машин: Справочник/ И. А. Биргер, Б. Ф. Шорр, Г. Б. Иосилевич. — 4-е изд., перераб. и доп. — М.: Машиностроение, 1993. — 640 с.: ил.
ISBN 5-217-01304-0
Изложены методы расчета на прочность различных соединений н передач, пружин, валов, подшипников, деталей поршневых двигателей, турбомашин, компрессоров, методы расчета контактных иапряжеиий, расчета деталей на усталость, термопрочность, устойчивость; приведены сведения по определению напряжений и деформаций в элементах конструкций, по оценкам надежности, технической диагностике и автоматизированному проектированию.
Четвертое издание (3-е изд. 1979 г.) частично переработано и дополнено материалами по численному расчету и оценке прочности элементов конструкций.
Для инженеров-конструкторов н расчетчиков машиностроительных заводов, проектно-конструкторских организаций; может быть полезен студентам втузов.
ISBN 5-217-01304-0
© Издательство «Машиностроение», 1979 © Издательство «Машиностроение», 1993, с изменениями
ОГЛАВЛЕНИЕ
Предисловие ...............
ОСНОВЫ РАСЧЕТА НА ПРОЧНОСТЬ
Глава 1. Основные виды напряженно-деформированного состояния . .
Напряжение и деформация Растяжение и сжатие. . . Изгиб...................
Срез и смятие...........
Кручение ...............
Концентрация напряжений Температурные напряжения Напряженно-деформированные состояния...........
Глава 2. Механические харак-'• теристикн конструк-
ционных материалов и оценка прочности деталей ...........
Свойства при статических напряжениях...........
Свойства при высоких и низких температурах. . . Свойства при переменных напряжениях.............
Малоцикловая и термическая прочность .........
Прочность при наличии трещин ..................
Разрушения и изломы. . . Оценка прочности........
Запасы прочности при статических напряжениях Запасы прочности по несущей способности ........
Запасы прочности при переменных напряжениях . . . Запасы длительной прочности при работе на различных режимах ............
9
11
11
13
14
19
20
21
22
23
23
24
28
32
36
37
38
39
40
41
42
42
Запасы выносливости при работе иа различных режимах ...................... 44
РАСЧЕТЫ НА ПРОЧНОСТЬ
Глава 3. Резьбовые соединения 45
Материалы, покрытия и контроль крепежных деталей ...................... 45
Упрощенный расчет соединений .................... 47
Уточненный расчет соединений .................... 51
Расчет напряжений кручения ...................... 56
Выбор предварительной затяжки .................... 58
Распределение нагрузки по виткам резьбы и концентрация напряжений в соединениях ................... 58
Прочность при постоянных нагрузках................. 63
Прочность при переменных нагрузках................. 67
Глава 4. Фланцевые соединения .......................... 73
Типы фланцевых соединений ...................... 73
Упрощенный расчет .... 73
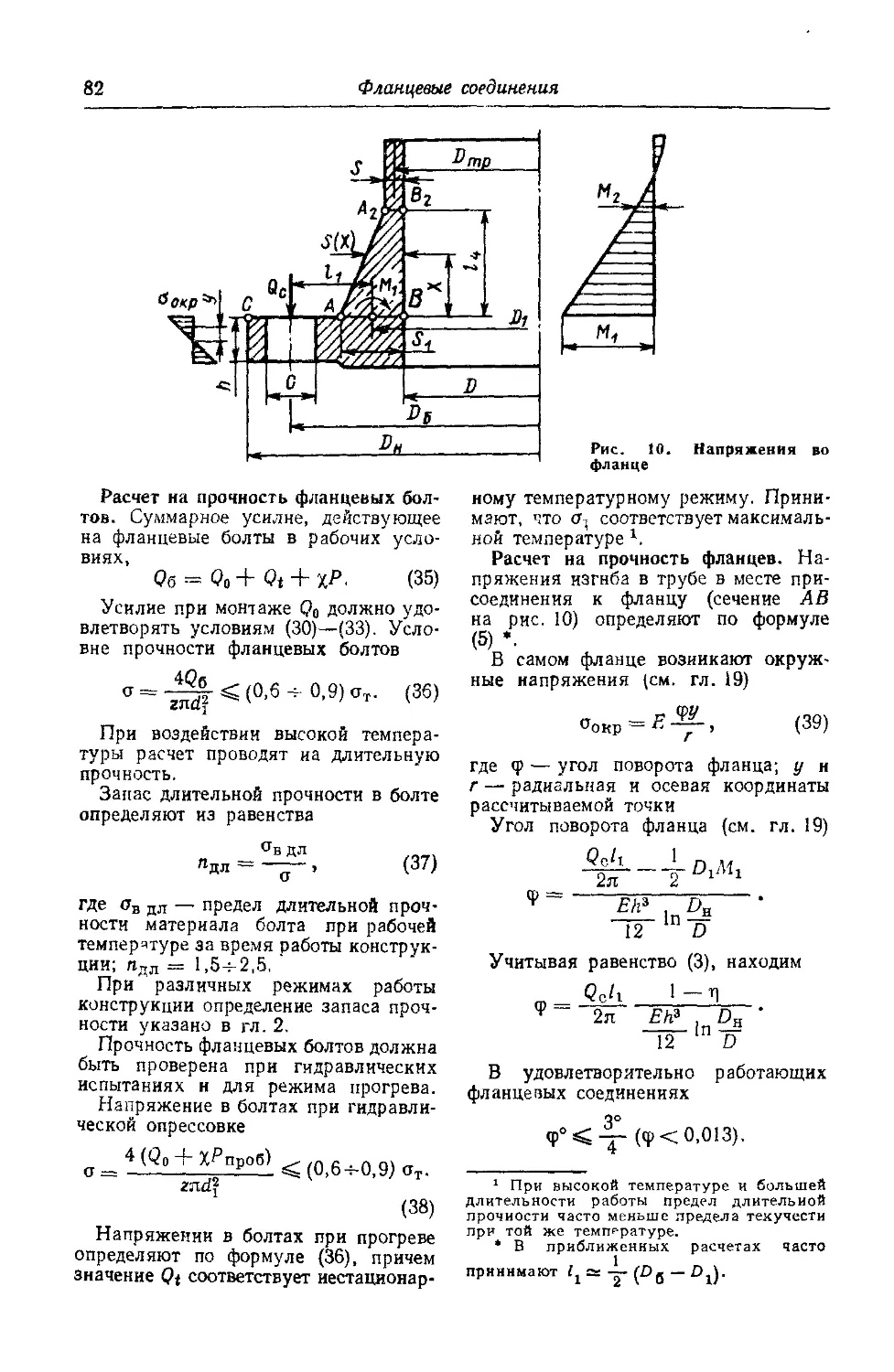
Уточненный расчет соединений с неконтактнрующи-ми фланцами............... 76
Напряженное состояние фланца и трубы............ 83
Глава 5. Шпоночные и шлицевые соединения ... 87
Шпоночные соединения . . 87
Шлицевые соединения ... 90
Расчет шлицевых соединений на прочность.......... 92
Изнашивание соединений 96
4
Оглавление
Глава 6. Соединения деталей с гарантированным натягом........................ 98
Условия неподвижности и контактные давления в соединениях ................. 99
Расчетный и потребный натяги ..................... 103
Прочность при переменных нагрузках................. 105
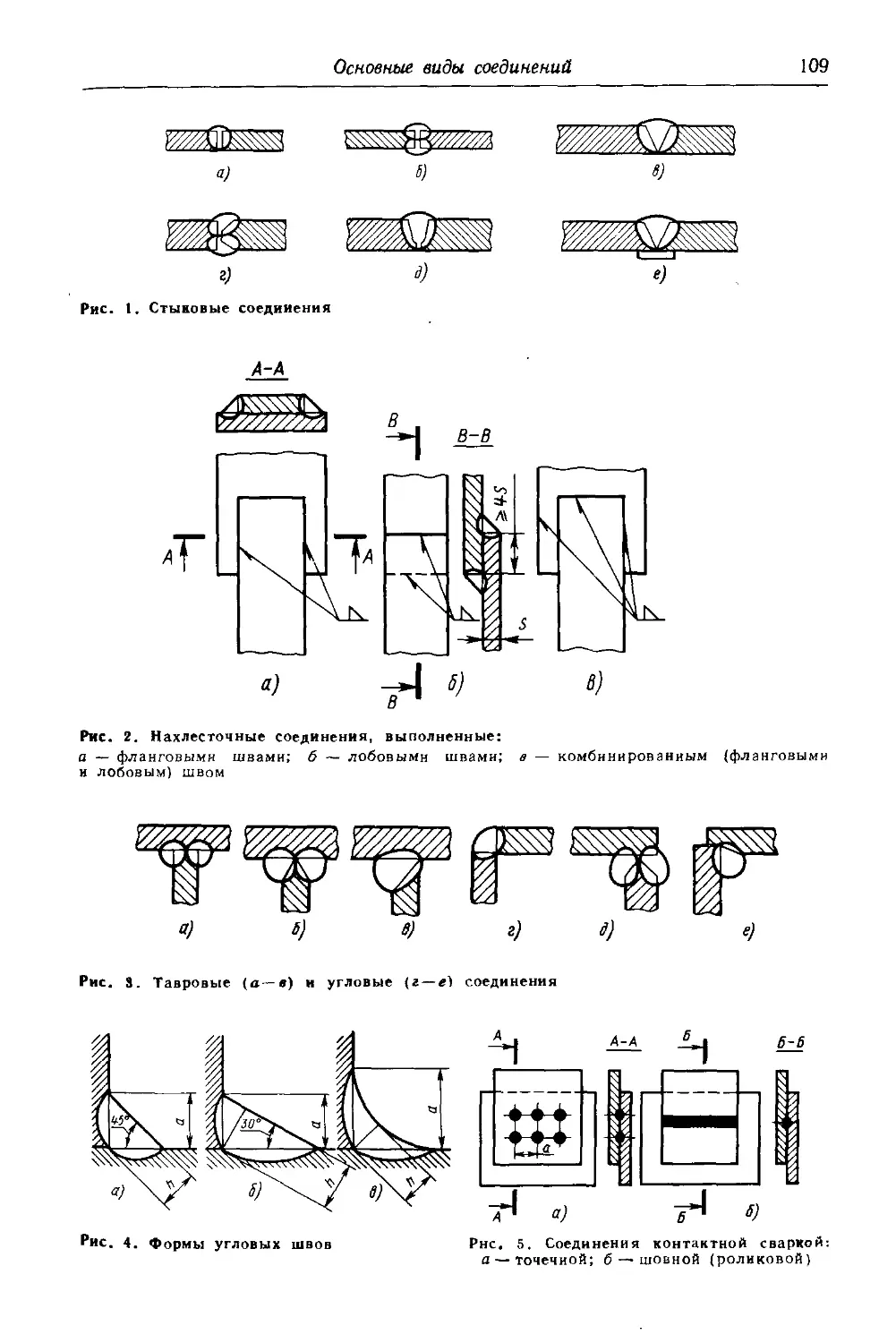
Глава 7. Сварные и паяные соединения.................. 108
Основные виды соединений Контроль качества сварных соединений................ 111
Расчет сварных соединений при постоянных нагрузках 112
Влияние основных конструктивных н технологических факторов на сопротивление усталости........... 114
Расчет на прочность при переменных нагрузках . . . 122
Паяные соединения .... 122
Глава 8. Валы ............... 126
Конструктивные формы и материалы валов........... 126
Основные технические требования .................. 129
Нагрузки на валы и расчетные схемы.............. 130
Расчет статической прочности, жесткости и устойчивости валов.......... 131
Расчет на сопротивление усталости ................ 136
Расчет на колебания . . . 139
Критические частоты вращения валов.......... 140
Глава 9. Подшипники качения 141
Основные конструкции н характеристики ........... 141
Геометрические, кинематические и динамические зависимости в подшипниках качения................... 146
Грузоподъемность и расчет подшипников............... 147
Эквивалентная нагрузка и расчет долговечности Подшипников ................. 150
Смазывание подшипников 156
Некоторые причины прежде-
временного выхода из строя подшипников качения и методы нх предотвращения. . 160
Глава 10. Пружины.......... 162
Общие сведения............ 162
Витые пружины............. 164
Расчет витых цилиндрических пружин............... 165
Расчет на статическую прочность .................... 172
Расчет на сопротивление усталости ................ 173
Расчет на ударную нагрузку 173
Тарельчатые пружины . . , 175
Прорезные пружины.... 175
Кольцевые пружины.... 176
Кольцевые волнистые пружины ..................... 177
Резиновые упругие элементы ....................... 178
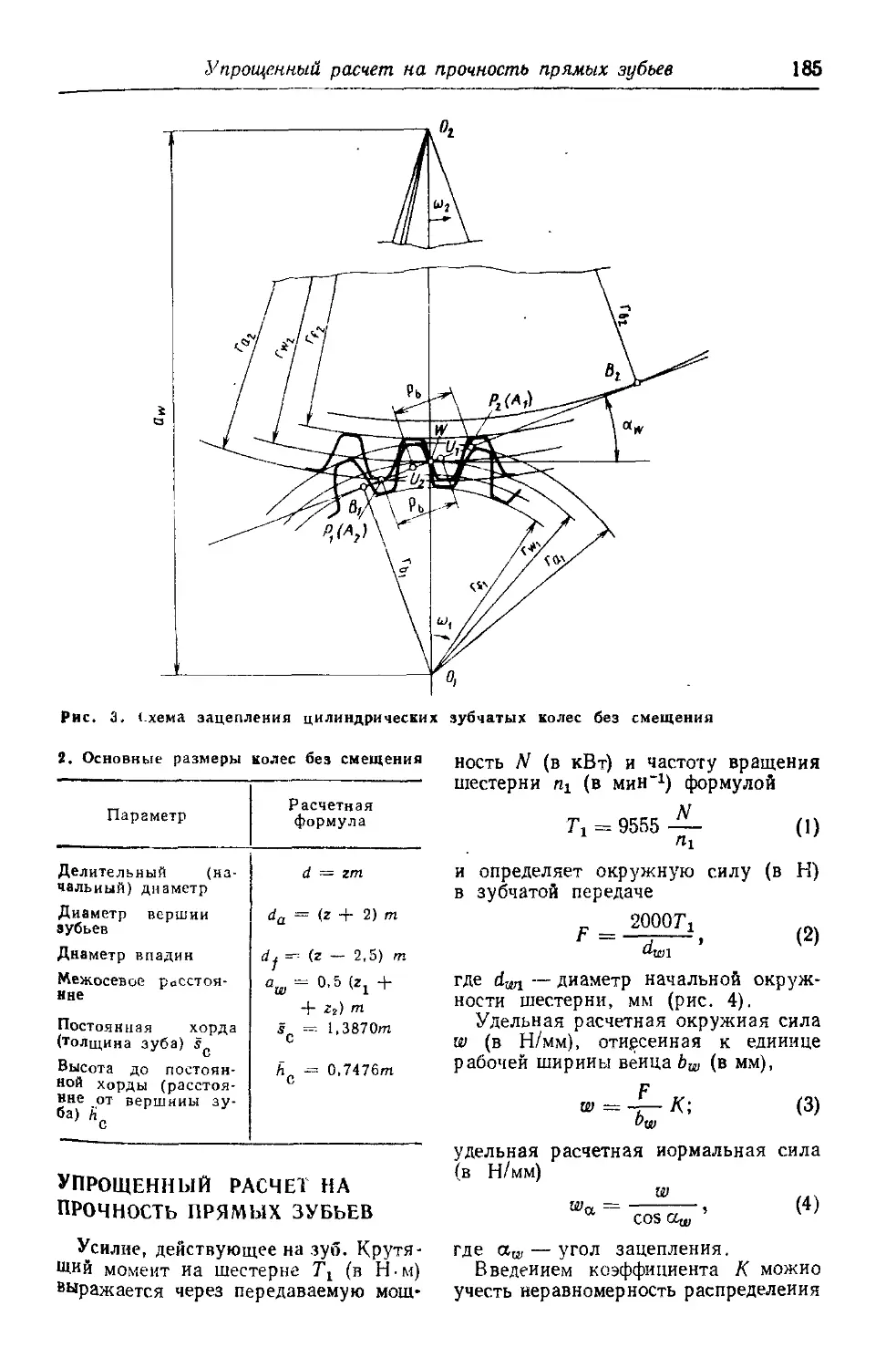
Глава 11. Зубчатые передачи 182
Основные обозначения . . . 183
Упрощенный расчет на прочность прямых зубьев. . . 185
Структура расчетных формул по ГОСТ 21354—87. . 189
Нагрузки, действующие на зуб....................... 190
Неравномерность распределения нагрузки по ширине зуба (коэффициент К$)............... 191
Статическое распределение усилий между зубьями (коэффициент Ка) 198 Динамические усилия на зубьях при крутильных колебаниях (коэффициент КИр) и резонансные режимы.................. 201
Динамические усилия на зубьях при пересопря-женин (коэффициенты Кл и Ко)................... 205
Расчет зубьев на прочность при изгибе................ 211
Расчет на контактную выносливость активных поверхностей зубьев......... 217
Работа передач при различных режимах............ 221
Особенности расчета передач с косыми, шевронными, коническими зубьями и передач М. Л. Новикова. . . 222
Оглавление
5
Косозубые н шевронные
передачи................ 222
Конические передачи . . 223
Передача М. Л. Новикова ...................... 224
Глава 12. Шариковинтовые пе-
редачи ............. 225
Конструкции передач и материалы .................... 226
Расчет передач.............. 227
Глава 13. Ременные передачи 233
Материалы и конструкции приводных клиновых ремней ...................... 233
Механика ременной передачи ..................... 234
Расчет ременных передач 238
Передачи с зубчатыми ремнями ..................... 239
Порядок расчета и проектирования ремеиных передач 243
Глава 14. Цепные передачи . . 244
Конструкции цепей и мате-
риалы ..................... 245
Силы в передаче.......... 247
Выбор основных параметров передачи........ 248
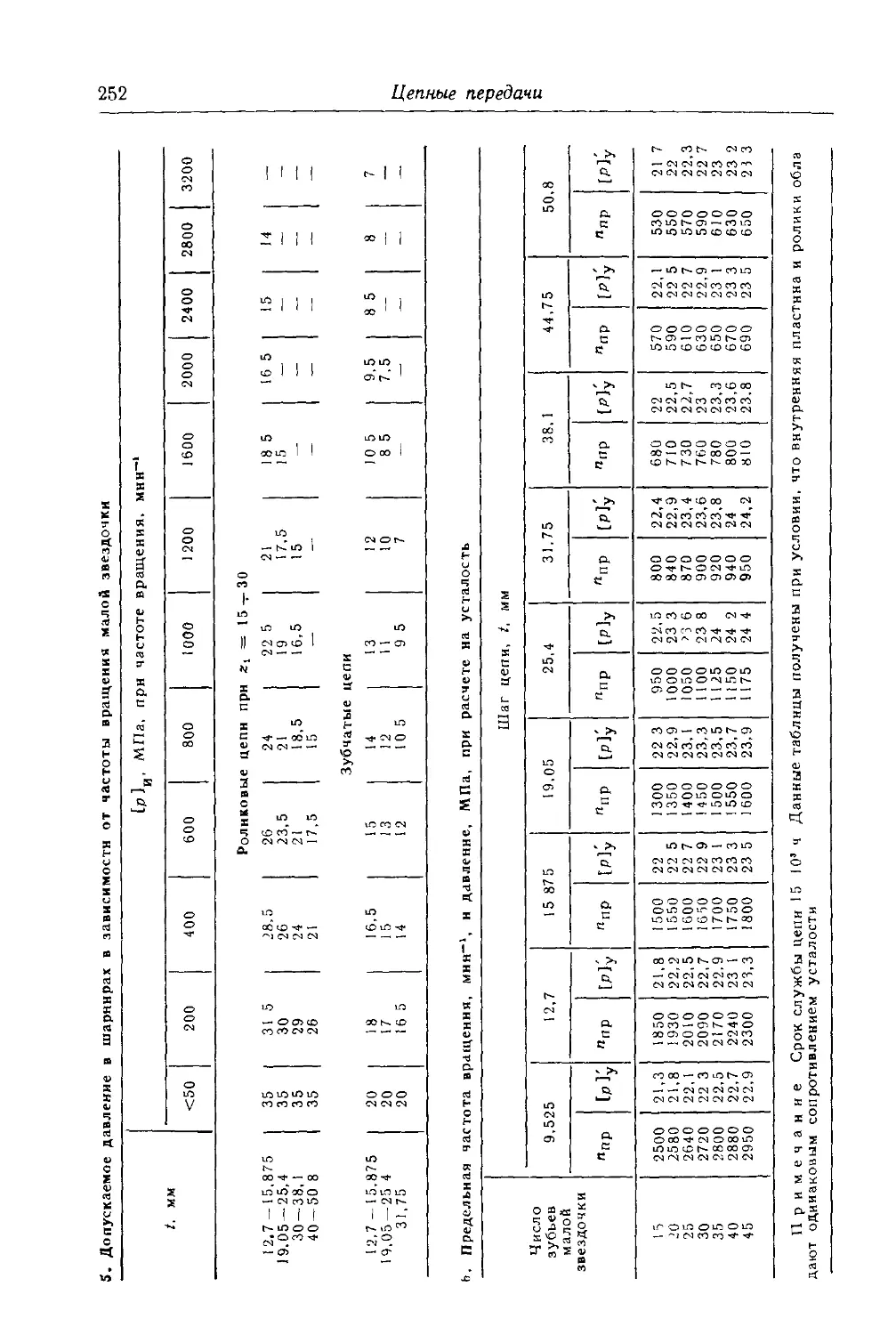
Несущая способность передачи ...................... 250
Особенности проектирования и эксплуатации передач 254
Порядок расчета передачи 255
Глава 15. Расчет деталей пор-
шневых двигателей 256
Расчет коленчатых валов . , 256
Расчет шатунов............. 262
Расчет поршневого пальца 266
Расчет поршневых колец . . 267
Расчет днища поршня . . . 268
Прочность элементов корпуса ...................... 268
Расчет клапанных пружин 269
Глава 16. Расчет деталей тур-
бомашин ..... 270
Расчет лопаток на растяжение от центробежных сил . . 270
Расчет лопаток на изгиб . . 273
Запас прочности профильной части лопатки.......... 281
Равнопрочные лопатки . . . 282
Охлаждаемые лопатки. . . 283
Изгибные колебания лопаток ....................... 285
Закрученные лопатки ... 291
Шарнирные лопатки .... 299
Бандажированные лопатки 302
Расчет замков лопаток . , . 304
Вибрация лопаток....... 308
Расчет дисков. Напряжения на контуре............. 315
Запасы прочности диска . . 317
Профилирование равнопрочных дисков............. 322
Основные уравнения при расчете дисков ..... 323
Напряжения и деформации в диске постоянной тол-
щины ...................... 325
Напряжения и деформации в диске переменной толщины ...................... 327
ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ В ЭЛЕМЕНТАХ КОНСТРУКЦИЙ
Глава 17. Изгиб стержней. . 334
Перерезывающая сила и изгибающий момент......... 334
Напряжения и деформации при изгибе.............. 336
Упругая линия стержня . . 342
Определение прогибов с помощью интеграла Мора . . 346
Прогибы и углы поворота в стержне переменного сечения .................... 350
Изгиб стержня с учетом пластических деформаций 351
Глава 18. Кручение стержней 355
Круглый вал............... 355
Стержень с эллиптическим поперечным сечением. . . 356
Стержни прямоугольного сечения и тонкостенные . . . 357
Распределение касательных напряжений................ 358
Учет пластических деформаций .................... 358
Трубчатые стержни . . . 359
6
Оглавление
Глава 19. Расчет колец. . . . 361
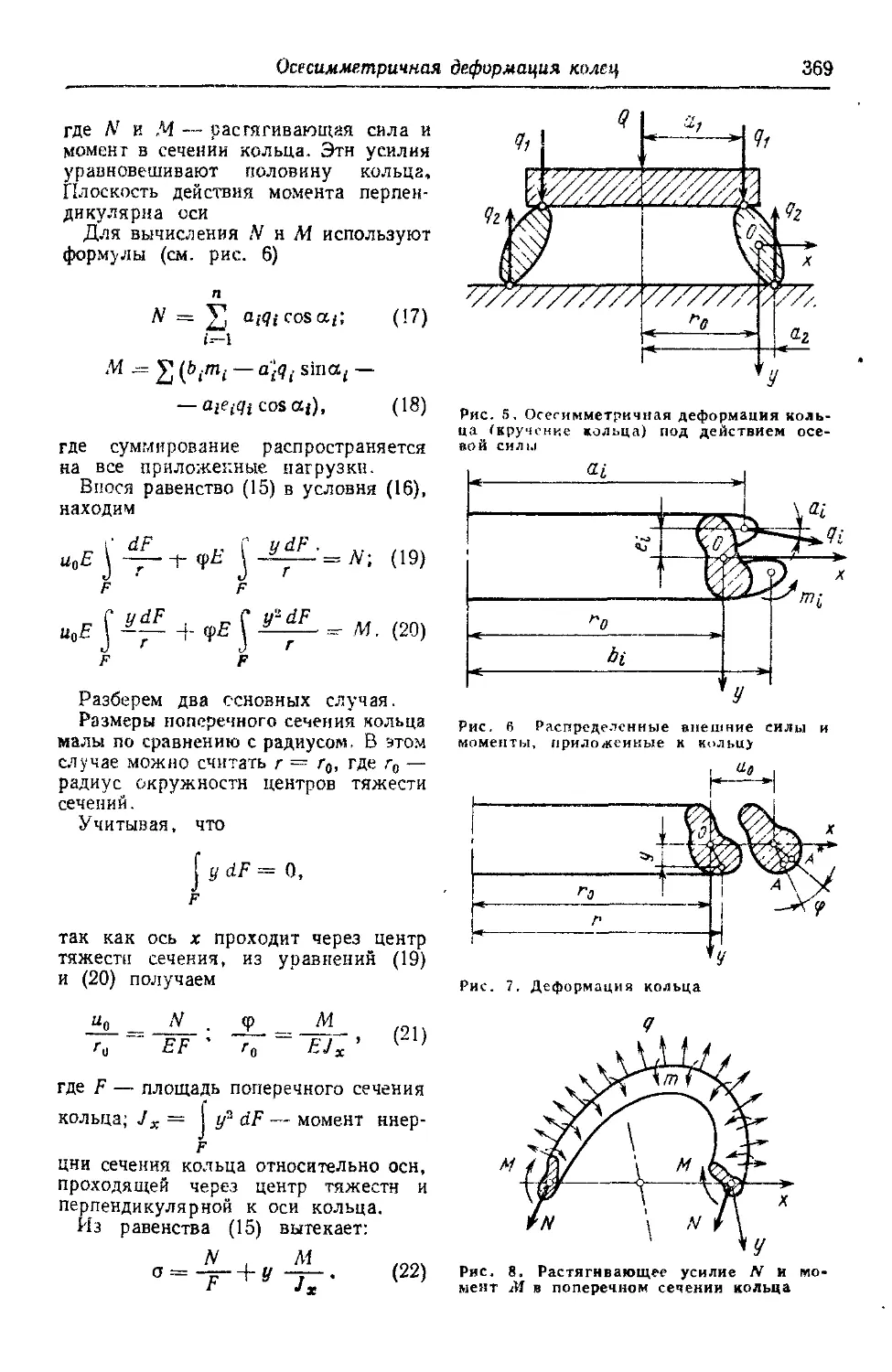
Плоская деформация колец 361 Осесимметричная деформация колец.................. 368
Глава 20. Устойчивость стержней ......................... 373
Формула Эйлера............. 373
Общий случай расчета критической нагрузки .... 375
Таблицы для расчета критической нагрузки.......... 376
Влияние начального прогиба и внецентренного приложения силы на выпучивание стержня.................... 382
Расчет сжатых стержней на прочность и жесткость . . . 383
Потеря устойчивости при упруго-пластических деформациях .................... 385
Выпучивание стержня при упруго-пластических деформациях .................... 386
Динамический анализ устойчивости. Действие следящих нагрузок............. 388
Потеря устойчивости при нагреве ................... 390
Потеря устойчивости плоской формы изгиба .... 390
Потеря устойчивости при скручивании................ 391
Глава 21. Колебания упругих систем....................... 392
Основные понятия......... 392
Метод динамических жесткостей .................... 393
Определение собственных частот системы методом динамических жесткостей . . 394
Крутильные колебания . 396
Изгибиые колебания .... 399
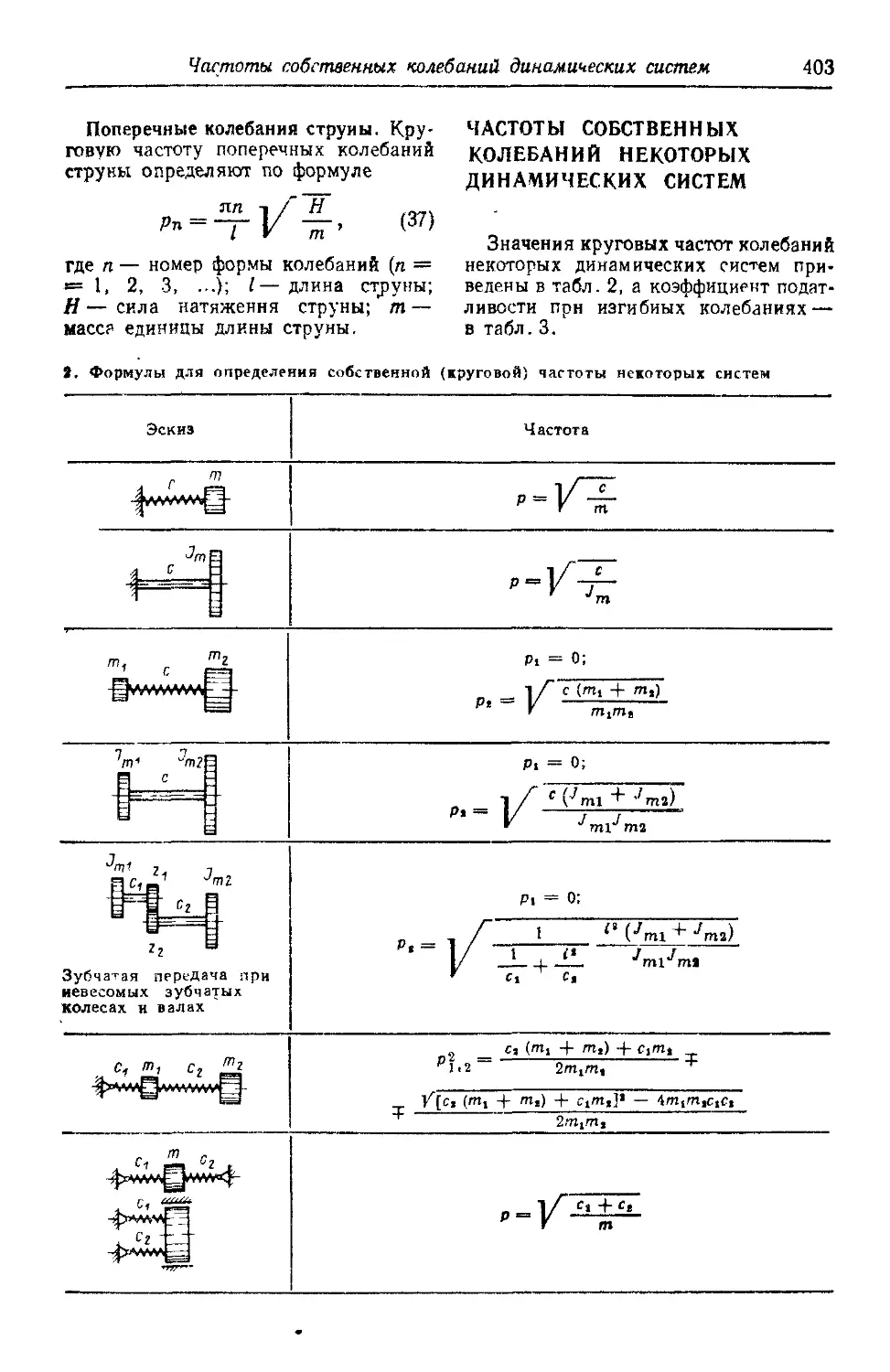
Частоты собственных колебаний некоторых динамических систем................ 403
Глава 22. Критические частоты вращения валов 405
Вал с одним диском .... 405
Вал с несколькими дисками 410
Вал с непрерывно распределенными массами .... 410
Глава 23. Расчет пластинок . . 424
Круглые пластинки .... 424
Прорывные мембраны. . . 440
Прямоугольные пластинки 441
Глава 24. Расчет иа прочность цилиндрических оболочек ....................... 443
Основные зависимости . . . 443
Расчет длинных оболочек 445
Расчет коротких оболочек 447
Температурные напряжения в оболочке............. 458
Глава 25. Устойчивость пластинок, колец и оболочек ............. 459
Устойчивость пластинок . . 460
Устойчивость колец. . . , 463
Устойчивость цилиндрических оболочек.............. 463
Устойчивость конических оболочек................... 472
Устойчивость сферических и эллипсоидальных оболочек ....................... 473
Устойчивость пластинок и оболочек при температурных напряжениях............ 473
Устойчивость анизотропных оболочек............... 474
Устойчивость подкрепленных оболочек............... 475
Глава 26. Численные методы расчета конструкций 477
Вариационные уравнения 477
Вариационно-разностный метод...................... 480
Метод конечных элементов 482
Динамические расчеты. . , 490
Глава 27. Расчет конструкций с учетом пластичности и ползучести . . 495
Уравнения упругости . . . 495
Уравнения пластичности . . 497
Уравнения ползучести . . . 501
Расчет конструкций на прочность с учетом пластичности и ползучести (простое нагружение) ................. 502
Расчет на прочность кон-
Оглавление
7
струкций при сложном нагружении ................ 505
Глава 28. Концентрация напряжений и деформаций в деталях машин ......................... 510
Основные понятия......... 510
Концентрация напряжений около отверстий.......... 511
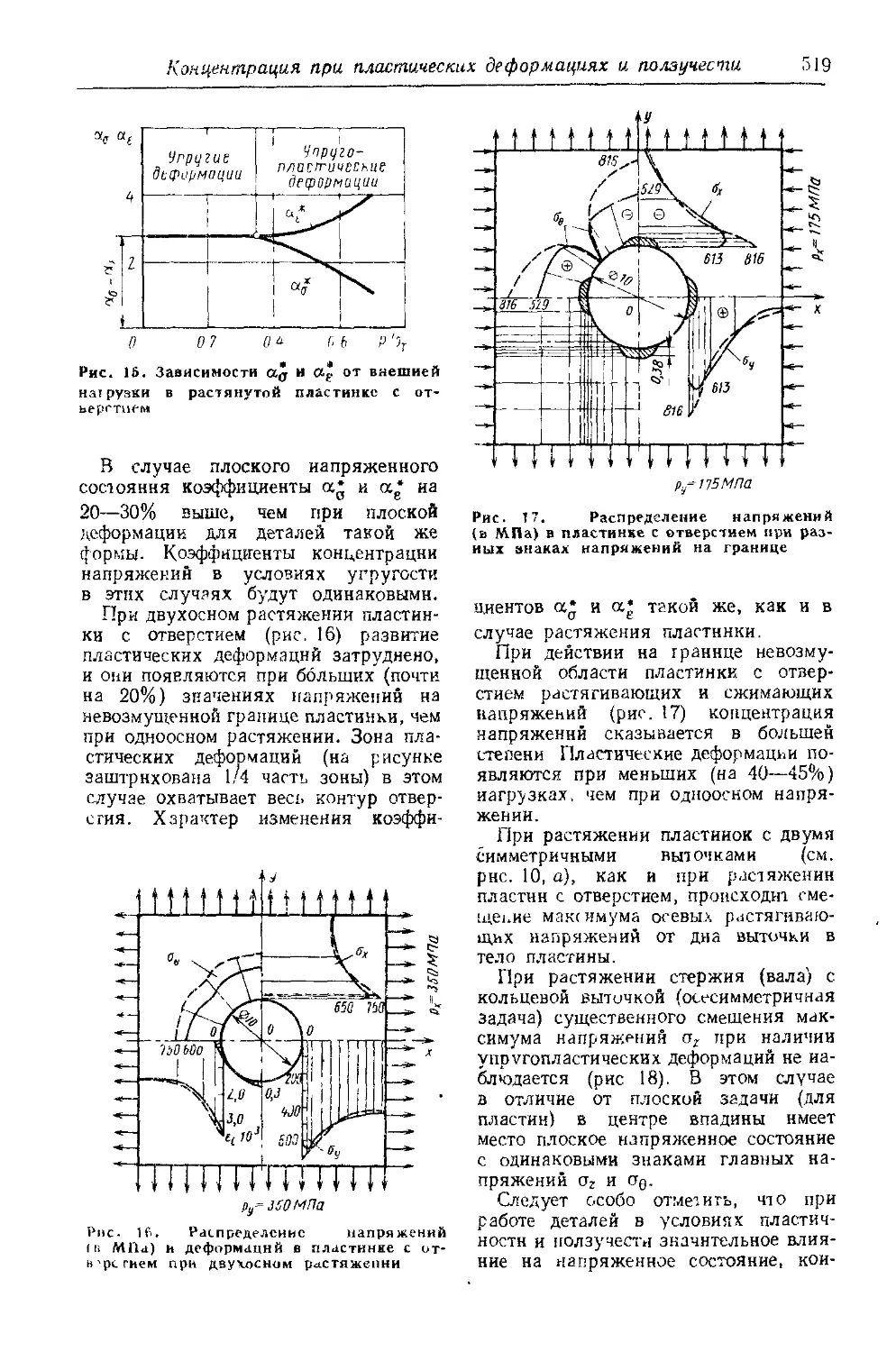
Концентрация напряжений в плоских и осесимметричных выточках и галтелях 516 Концентрация напряжений и деформаций в условиях пластических деформаций и ползучести............. 517
Концентрация напряжений в элементах конструкций 521
Глава 29. Контактные задачи 527
Контакт деталей простой формы.................... 528
Конструкционные контактные задачи............... 535
Общий метод решения конструкционных контактных задач ................... 543
ОЦЕНКА ПРОЧНОСТИ
И НАДЕЖНОСТИ
Глава 30. Расчет на прочность при сложном напряженном состоянии 549
Критерии статической прочности ..................... 549
Критерии длительной и малоцикловой прочности . . . 554
Глава 31. Расчет на усталость 555
Основные закономерности сопротивления усталости 555
Определение пределов выносливости деталей .... 562
Условия сопротивления усталости ................... 564
Определение запасов прочности при усталости .... 566
Статистические модели усталости ..................... 572
Глава 32. Вероятность разру-
шения и запасы прочности......... 573
Вероятность разрушения . . 574
Вероятность разрушения при произвольных законах распределения напряжений и пределов прочности. . . 575
Статистические запасы прочности ...................... 578
Глава 33. Элементы теории надежности ..................... 581
Основные понятия .... 581
Правила надежности . . . 582
Вероятность безотказной работы, плотность распределения и интенсивность отказов ................... 584
Основное уравнение теории надежности ................ 586
Общая закономерность изменения интенсивности отказов по времени наработки 586
Прогнозируемая вероятность безотказной работы Экспоненциальный закон 586
надежности ................ 587
Нормальное распределение времени безотказной работы 588
Распределение Вейбулла для времени безотказной работы..................... 589
Надежность системы последовательных элементов . . 589
Надежность системы параллельных элементов .... 589
Анализ надежности системы с несколькими параллельно работающими элементами 590 Расчет числа изделий, находящихся в эксплуатации 591 Количественные показатели надежности ................ 591
Глава 34. Технологические методы повышения долговечности деталей машин................... 592
Остаточные напряжения . . 592
Упрочнение деталей машин поверхностным пластическим деформированием . . . 595
Термическая и химико-термическая обработка. . . . 600
8
Оглавление
Определение остаточных напряжений................ 601
Глава 35. Основы теории технической диагностики ....................... 605
Постановка задач технической диагностики.......... 605
Вероятностные методы распознавания ............... 606
Методы статистических решений .................... 610
Методы статистических решений при наличии зоны неопределенности ......... 612
Метрические методы распознавания ............... 613
Метод разделения в пространстве признаков.... 615
Логические методы распознавания ................... 617
Глава 36. Основы автоматизированного проектирования ...................... 618
Структура автоматизированного производства. . . 618
Структура математической модели..................... 619
Уровни и классы моделей 620
Общие принципы создания систем автоматизированного проектирования .... 621
Цели и методы оптимизации 623
Список литературы........ 625
Предметный указатель .... 630
ПРЕДИСЛОВИЕ
Вопросы надежности, прочности, долговечности и ресурса являются важнейшими в современной технике.
Вследствие непрерывно возрастающих требований к быстроходности, экономичности, надежности и к снижению массы машин расчеты на прочность становятся все более сложными. Оня должны учитывать различные режимы работы, реальные свойства материалов, условия нагружения, технологические, эксплуатационные и другие факторы.
В расчетах на прочность деталей машин и конструкций все шире используют результаты, полученные в теории стержней, пластин, оболочек, в теории упругости, пластичности и ползучести, в механике разрушений. Все это приводит к тому, что в процессе разработки машины конструктор часто не имеет возможности провести достаточно обоснованные расчеты на прочность, и такие расчеты выполняют расчетные отделы
В книге изложены методы расчета деталей машин на прочность в форме, удобной для использования непосредственно при проектировании машин и конструкций При этом учитывается возможность различной теоретической подготовки конструкторов.
В первом разделе даны основные сведения, необходимые для элементарных расчетов на прочность.
Во втором разделе в большинстве случаев также приведены простейшие расчетные формулы и таблицы, для некоторых типовых элементов конструкций даны уточненные методы расчета Основное внимание уделено выявлению физических основ задачи, простоте, удобству расчета, анализу допустимого уровня напряженности.
В технических расчетах все нужное оказывается простым, а все сложное — ненужным. Основные расчеты приведены в форме, рекомендуемой в ГОСТах и нормативных руководствах, или в форме, используемой в отечественной и зарубежной расчетной практике, что позволяет использовать расчеты для накопления статистических данных по напряженности деталей.
В третьем разделе даны методы определения напряжений в стержнях, пластинах и оболочках, необходимые для расчетов на прочность, жесткость, устойчивость и колебания. В связи с расширяющимся использованием в инженерных расчетах электронных вычислительных машин (ЭВМ) приводятся основные сведения по численным методам расчета конструкций сложной геометрической формы с учетом упругости, пластичности и ползучести конструкционных материалов Расчеты могут проводиться как на универсальных, так и на современных персональных вычислительных электронных машинах
Значительное внимание уделено материалам справочного характера
В четвертом разделе рассмотрены вопросы оценки прочности и надежности деталей машин, а также вопросы автоматизированного проектирования, используемого во многих отраслях современной техники
В четвертом издании в ряд разделов книги внесены уточнения и дополнения.
Главы 4, 17—19, 21, 22, 24, 25, 32, 33, 35 и 36 написаны д-ром техн, наук, проф И. А. Биргером; главы 1, 2, 11, 15, 20 и 23 — д-ром техн наук, проф. Б. Ф. Шорром, главы 6—8, 13 и 14 — д-ром техн, наук, проф.
10
Предисловие
Г. Б. Иосилевичем Главы 3, 5, 10, 12, 27—31 и 34 написаны И А. Биргером и Г Б Иосилевичем, глава 16 — И. А Биргером и Б. Ф Шорром, глава 26 — всеми авторами.
По просьбе авторов глава 9 написана
канд техн, наук А. И. Ерошкиным и инж Б. А. Ерошкиным.
Авторы выражают признательность канд. техн, наук В В. Джамаю за помощь в подготовке части книги к переизданию.
ОСНОВЫ РАСЧЕТА НА ПРОЧНОСТЬ
Глава 1
ОСНОВНЫЕ ВИДЫ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО состояния
НАПРЯЖЕНИЕ И ДЕФОРМАЦИЯ
Во время работы на детали действуют внешние силы (сила тяжести, давление пара, центробежные силы и т. д.), под действием которых они меняют размеры и форму, т. е. деформируются. Для нормальной работы необходимо, чтобы деформации были незначительными
Если подвесить груз Q к стержню (рис. 1), то он удлинится на величину Д/, после чего деформация прекратится. Ей препятствуют внутренние силы, возникающие между частицами тела. Для определения внутренних сил применяют метод сечений. Рассечем мысленно стержень плоскостью П и отбросим верхнюю часть Чтобы нижняя часть стержня осталась в равновесии, в сечении П к ней должны быть приложены внутренние силы Рвн, уравновешивающие груз Q (рис. 2, а) На различные площадки ДЕ будут действовать различные силы ДР Как показывает опыт, отношение
при растяжении стержня во всех точках данного сечения остается постоянным. Величину р называют полным напряжением. Когда напряжения в различных точках сечения неодинаковы, например при изгибе, их определяют из того же соотношения (1), но действующие силы ДР относят к очень малым площадкам В Международной системе единиц (СИ) силу измеряют в ньютонах (Н), а напряжение — в паскалях (1 Па = 1 Н/м2) или в мегапаскалях (1 МПа = = 10е Па) В технике напряжение было принято измерять в кгс/см2 или
кгс/мм2 (1 МПа = 9,81 кгс/см2 яг » 10 кгс/см2 — 0,1 кгс/мм2)
Полное напряжение раскладывают на две составляющие (рис. 2, б) Нормальным напряжением а называют составляющую напряжения, направленную по нормали к площадке. Касательным напряжением т называют составляющую напряжения, действующую в плоскости площадки.
Различать нормальные и касательные напряжения необходимо потому, что материал по-разному сопротивляется их действию.
Нормальное напряжение считают положительным, если оно растягивающее. Знак нормального напряжения важен для расчета на прочность, так как конструктивные материалы сопротивляются растягивающим напряжениям хуже, чем сжимающим Знак касательного напряжения не существенен.
Если через данную точку провести ряд сечений, то в общем случае значения полного напряжения и его составляющих в этих площадках будут различными Когда тело в целом находится в равновесии, то условия равновесия должны удовлетворяться для любого малого его элемента.
Из этих условий следует, что напряжения в разных площадках должны быть связаны определенными соотношениями Зная напряжения, действующие по трем взаимно перпендикулярным площадкам в окрестности точки, можно определить напряжения в любой площадке, проходящей через эту же точку.
Для каждой точки имеются три взаимно перпендикулярные площадки, в которых касательные напряжения равны нулю. Эти площадки называют главными, а действующие в них нор-
12
Основные виды напряженного состояния
Рис. I. Удлинение стержня и перемещение его конца под действием растягивающей нагрузки:
а — положение стержня до деформации; б — р деформированном состоянии
Рис. 2. Внутренние силы в сечениях стержня
мальные напряжения—главными на-пряжениями. Их обозначают at, а2, а3. Главное напряжение Oj является алгебраически наибольшим, иапряже-
ние о3 — алгебраически наименьшим. Наибольшим по величине атах может быть любое из них.
Из условия моментного равновесия элемента объема следует, что касательные напряжения в перпендикулярных площадках равны между собой (см. рис. 2, б). Это свойство называют законом парности касательных напряжений. Наибольшее касательное напряжение ттах = 0,5 | Oj—а3|. Максимальное касательное ттах и нормальное атах напряжения равны между собой только при а3 = —а2, в остальных случаях ттах< атах.
При деформации тела взаимное положение его отдельных точек меняется, точки получают перемещения. Например, под действием груза Q (см. рис. 1) иижиий конец стержня перемещается (опускается) на величину и, в то время как верхний конец остается неподвижным. Различие в перемещениях связано с изменением длины стержня под нагрузкой. Абсолютное удлинение Д / = li — 10 в данном примере равно перемещению и и зависит от длины стержня. Собственно деформация стержня характеризуется относительным удлинением
Д/ 1ь ’
Относительное удлинение — безразмерная величина, иногда выражается в процентах. Например, если стержень, имевший длину l0 = 1 м, удлиняется иа Д< = 1 мм, то
(2)
Е-7000 !00 = °’1%-
Общая деформация элемента тела связана с удлинениями его сторон и сдвигами. Удлинения сторон могут вызывать изменение объема и формы, сдвиги — только изменение формы (рис. 3). Относительное изменение объема 0 = ДУ/У0 выражается через относительные удлинения сторон как
0 « Bj + е2 + е3. (3)
Угол, иа который изменяется первоначально прямой угол элемента, называют сдвигом у = Ут + у2 (рис. 3, г).
В общем случае деформации различны в разных точках детали и по
Растяжение и сжатие
13
Ркс« 3, Разложение общей деформации на относительные удлинения к сденги:
а — общая деформация, б - изменение объема и формы, связанное с удлинениями сторон. в - изменение формы, связанное со сдвигами
разным направлениям для одной и той же точки. При деформации первоначально сплошное тело остается сплошным (до начала разрушения). Из этого условия следует, что деформации по разным направлениям должны быть связаны определенными Воотношениями. Зная деформации в Точке по трем взаимно перпендикулярным направлениям, можно определить деформация по любому направлению.
Для каждой точки имеются три Взаимно перпендикулярных направления, по которым сдвиги равны нулю. Это главные направления деформации.
В реальных материалах напряжения и деформации всегда возникают одновременно Изменение линейных размеров происходит от действия нормальных напряжений, объема — от Среднего напряжения аср = (с^ + *Г а2 + о3)/3, сдвиги — от касатель-йых напряжений.
РАСТЯЖЕНИЕ И СЖАТИЕ
Во многих деталях стержневой формы основная нагрузка действует вдоль оси стержня (штоки прессов, шатуны, рабочие лопатки паровых турбин и пр.), которые в этих условиях растягиваются или сжимаются. Используя метод сечений, можно установить, что в любом сечении растянутого (сжатого) стержня равнодействующая Внутренних сил Рвн равна внешней силе Q, действующей на оставшуюся Часть стержня (см. рис. 2).
Опыт показывает, что в плоских сечениях, удаленных от места приложения внешней силы Q на расстояние большее, чем диаметр стержня, напряжения распределяются по сечению практически равномерно, а сами сечения, перпендикулярные к оси стержня, остаются плоскими и перпендикулярными к осн и после деформации. Это положение носит название гипотезы плоских сечений. Напряжение в поперечном сечении стержня
а = 4’
где F — полная площадь сечения, а напряжения в наклонном сечении, нормаль к которому составляет с осью стержня угол <р (см. рис. 2, б),
аф — a cos’ <р; тф = 0,5а sin 2ф. (5)
Если в стержне имеется ослабление, то в расчет следует вводить минимальную площадь сечения (площадь нетто). В этом случае по формуле (4) определяют номинальное напряжение, не учитывающее концентрацию напряжений
При растяжении продольные волокна стержня получают относительное удлинение е = ДZ/Zo, а поперечные размеры уменьшаются. Величину еп = = (dj — d^ld^ (см. рис. 1) называют относительной поперечной деформацией.
Экспериментально установлено, что до определенных пределов отиоситель-
14
Основные виды напряженного состояния
1. Физические свойства некоторых материалов при Т = 20 °C
Материал Плотность р, г/см8 Модуль Г. X Ю~5, МПа Коэффи-| цнент Пуас-; сона v Коэффициент линейного расширения ах 10е. 1/°С К оэффнцнент теплопроводности X, Вт/(м-°С)
Углеродистые стали (сталь 20, сталь 45 и др ) 7,85 2.0 -2,2 0. 3 1 1 45-70
Легированные стали (30ХГСА. 12ХНЗА) 7,85 2,0-2,2 0.3 11-12 35 — 45
Жаропрочные сплавы ГХН77ТЮР. 12XI8H9T и др ) 8,п- 8 2 2.0 — 2.2 0.3 12—17 12-25
Чугун 6,5 — 7,5 1,0— 1,5 0,25 1 1 35—60
Алюминиевые сплавы (АЛ4, Д1 и др) 2,6 —2.9 0.71—0,78 0,31 20 -25 120— 175
Магниевые сплавы (МА5 и др ) ~1.8 0.4 — 0.45 0,34 27 70—115
Титановые сплавы (ВТЗ и др ) ~4,5 1.1-1,2 0,3 8.5 8—16
Стеклотекстолит 1.6-1,7 0.3 0,29 — —
Ориентированные стеклопласт» к и 9 0.6 -0,7 0.3 — —
Однонаправленный бора лю Минин (20 -60% бора) ~2,5 1.3 -2.8 0.3 10 5 —
Однонаправленные углепластики 1,4 - 1.5 1-2 0.25 1 - 3
ное удлинение пропорционально напряжению (закон Гука)'
Коэффициент Е, зависящий от материала стержня и температуры, называют модулем упругости, он имеет размерность напряжения,
Из формул (2), (4), (6) следует:
д/ = й- (7)
Произведение EF характеризует жесткость сечения стержня при растяжении, величина EF'110 — жесткость при растяжении стержня в целом (она /равна силе, вызывающей удлинение/ равное единице) Чем больше жесткость, тем меньше удлинение.
Эксперименты также показывают, что относительная поперечная деформация
еп = —ve, (8)
где v — коэффициент поперечного сжатия (коэффициент Пуассона), зависящий от материала стержня.
Значения Е и v для некоторых материалов при нормальной температуре приведены в табл. 1.
По формулам (3), (6) н (8)
0 = -^ (l-2v),
откуда следует, что при растяжении объем тел увеличивается (0 > 0), при сжатии — уменьшается (0 < 0).
При деформации сжатия применимы те же формулы, что и при растяжении, однако сжимающее напряжение считают отрицательным. Длина стержня при сжатии уменьшается, поперечное сечение увеличивается. Модули упругости при растяжении и сжатии для большинства металлов и сплавов имеют одинаковые значения, но для свинца, серого чугуна средней прочности, а также для дерева, фанеры, железобетона — различные.
ИЗГИБ
Деформацию изгиба испытывают валы, оси, рельсы, балки, зубья колес, лопатки турбин и компрессоров и многие другие детали. Внешние нагрузки при изгибе направлены перпендикулярно к оси детали и могут иметь вид сосредоточенной силы Р и распределенной по длине нагрузки у; силы — в Н, распределенные иагруз-
Изгиб
15
Рис. 4. Изгиб двухопориого вала с (оисольиым диском:
а — эпюра изгибающих моментов, б — распределение нормальных напряжений в опасном сеченни
ки — в Н/м. Нагрузки могут также вводиться к внешнему изгибающему Моменту М, Н-м.
Для определения внутренних сил при изгибе пользуются методом сечений. Найдя из условий равновесия детали в целом опорные реакции (так, Для двухопорного вала с консольным Диском, рис. 4, они равны РаН и Р (а + проводят мысленно через выбранную точку поперечное сечение, нормальное к оси, отбрасывают одну часть вала и рассматривают условия равновесия оставшейся части. Внутренние силы, действующие в плоскости поперечного сечения сводятся к поперечной силе Q и изгибающему моменту М. При некоторых условиях нагружения в балке может возникнуть только изгибающий момент. Такой изгиб называют чистым.
Проведя линию, параллельную оси балки, и отложив на ней величины Q Н М, действующие в соответствующих сечениях, получим эпюры поперечных сил и изгибающих моментов. Эпюры позволяют весьма просто определить наиболее нагруженные сечеиия. Эпю
ра М. для двухопорного вала с консольным диском приведена на рис. 4, наиболее нагружено сечение вала у правой опоры.
В поперечных сечениях балки действуют нормальные и касательные напряжения. Основное значение для длинных балок (стержней) имеют нормальные напряжения, распределяющиеся в сечении по линейному закону. Это является следствием закона Гука и гипотезы плоских сечений, согласно которой плоское поперечное сечение при деформации изгиба остается плоским и перпендикулярным к деформированной оси балки
Нормальные напряжения связаны с действием изгибающих моментов.
В точках, лежащих на нейтральной оси, которая проходит через центр тяжести сечения, нормальные напряжения отсутствуют. Наибольшей величины напряжения достигают в точках, наиболее удаленных от нейтральной оси, причем
/И
ашах — > (9)
16
Основные виды напряженного состояния
Рис. 5. Изгиб двутавровой балки:
а _ эпюра изгибающих моментов; б — распределение
в опас-
нормальных напряжений
Рис. 6. Изгиб турбинной лопатки силами давления газов:
а — эпюра изгибающих моментов; б — распределение нормальных напряжений в опасном сеченни
где W — момент сопротивления при изгибе, см8;
Ц7 = _2_; (Ю)
Птах
здесь J — момент инерции сечения, см4; ЛГОах — расстояние от оси до наиболее удаленной точки.
Значения J и W для поперечных сечений наиболее распространенных типов приведены в табл. 2.
На рнс. 4—6 приведены примеры определения опасных сечений для некоторых случаев изгиба и показано распределение нормальных напряжений в типичных сечениях.
Касательные напряжения связаны с действием поперечных сил. При чистом изгибе касательные напряжения равны нулю, а в общем случае они обычно малы по сравнению с нормальными напряжениями я в приближен-
Изгиб
17
2. Геометрические характеристики поперечных сечеиий при изгибе
Тип поперечного сечения Момеит инерции сечеиня Момент сопротивления сечеиия
Крут лое сплошное сечение ПР* 64 ЯР* 32
Круглое полое сечение
Прямоугольное сплошное сечение внг 12 ВН' 6
1 1
Прямоугольное полое
сечен не
18
Основные виды напряженного состояния
Продолжение табл 2
Тип поперечного сечения
Момент инерции сечения
Момент сопротивления сечения
Двутавровое сече ние
внг
12
b \
7в~)х
Срез и смятие
19
ных расчетах на изгиб ими часто пренебрегают.
Под действием нагрузок балки прогибаются, особенно сильно на свободном конце при консольном креплении (рис. 6) и в середине пролета между опорами (рнс. 5). При действии сосредоточенной силы Р максимальный прогиб балки определяют по формуле
Р13
l/max - , (И)
где k — коэффициент, зависящий от расположения опор и характера нагрузки.
Для двухопорной балки с силон посредине k = 48, для консольной балки с силой на свободном конце k = 3.
Произведение EJ характеризует жесткость сечения балки на изгиб, величина kEJ/I3 — жесткость на изгиб балки в целом (она равна силе, вызывающей прогиб, равный единице). Обратную величину l3lkEJ называют
податливостью балки на изгиб (она равна прогибу, вызываемому единичной силой). При той же массе наибольшую жесткость на изгиб и наименьшие напряжения имеют балки двутаврового сечения.
СРЕЗ И СМЯТИЕ
В работе заклепок (рис. 7), шпонок (рис. 8), штифтов основное значение имеют деформации среза и смятия. Действительное распределение напряжений в этих случаях сложное, и расчеты ведут по условным напряжениям, которые определяют в предположении равномерного их распределения по площади среза или смятия
Касательное напряжение при срезе
где Рср — сила, вызывающая срез; FCp — площадь среза.
Рис. 7. Схема работы заклепочного соединения: а — схема узла, б — срез заклепок; в — смятие листов
Рис. 8. Схема работы шпоночного соединения:
а — схема узла, б — срез шпоики; в — смятие поверхности шпоночной канавки, г — схема шпоики
20
Основные виды напряженного состояния
Рис. 9. Кручение вала: М5 Р£ГГ
а — эпюра крутящих моментов; 6 — распределение напряжений в опасном сеченнн
Для двух заклепок при двустороннем срезе (рис. 7)
РСр = 0,25Р; Fcp = 0,25л</а.
Для шпоики (рис. 8)
Fcp = (а+ 0,25л6) Ь.
Напряжение смятия
асм = "5^ > (13)
Г см
где Рск — сила, вызывающая смятие; Fск — площадь смятия.
При смятии по цилиндрической поверхности для заклепок (см. рис. 7) считают FCM = dh\ для шпоики (см. рис. 8) Есм ss 0,5са.
КРУЧЕНИЕ
Валы (рис. 9) и ряд других деталей машин испытывают деформацию кручения. Если вал, имеющий частоту вращения п, мни-1, передает мощность У, кВт, то крутящий момент в поперечном сечеиии вала
N
Л4К = 9555-^, н.м
(л*к = 97 400 А
При измерении У
(14)
У
Мк = 7300 —, н.м
у \
Мк — 71 620—, кгс-см ) . (15)
Для определения опасного сечеиия в валах строят эпюры крутящих моментов (рис. 9, а).
При кручении круглого вала в поперечном сечении дей< "вуют касательные напряжения, которые распределяются по радиусу вала по линейному закону. В центре вала напряжение равно нулю, у поверхности достигает максимального значения
Ттах — I (16)
где WK — момент сопротивления сечеиия кручению, см3.
Для полого вала
^ = ^-(1-^). (17)
где d — внешний диаметр вала; а = = d-Jd-, di — внутренний диаметр вала.
При одинаковой прочности полый вал легче сплошного.
Угол закручивания вала в градусах на длине I
МК1 180 Ч’ GJ р л ’
где Jр — полярный момент инерции сечеиия вала, см4;
тг//4
Jp = -^-(l-a4); (19)
G — модуль сдвига, МПа; G — = 0,5£/(1 + V) « 0,38£.
Концентрация напряжений
21
Произведение GJ п характеризует жесткость сечения вала на кручение, величина GJр/1 — жесткость на кручение вала в целом.
КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ
Возле отверстий, галтелей, кольцевых выточек, у шпоночных и шлицевых пазов, у основания резьбы и в других местах, где резко меняется конфигурация детали, а также там, где одна деталь напрессовывается на другую, напряжения распределяются неравномерно, т е. возникает концентрация напряжений.
Отношение наибольшего напряжения в зоне концентрации к номинальному напряжению называют коэффициентом концентрации напряжений:
ао = (20)
ан
или
ат-=^. (21)
тн
Номинальные напряжения рассчитывают по формулам сопротивления материалов, максимальные — методами теории упругости или же определяют экспериментально.
При растяжении пластины с отверстием (рис 10) в качестве номинального напряжения принимают
(22)
где о — напряжение по нагруженным сторонам пластины. Если d Ь, то а0 = 3.
Для пластины с двумя выточками (рис. 11) коэффициент концентрации напряжений зависит главным образом от отношения радиуса закругления р у дна выточки к ширине d, а также от отношения tfd. При р -» 0 величина аа -* оо. Коэффициент концентрации напряжений в основании зуба зубчатого колеса (см. рис. 8, гл. 11) может быть представлен приближенной зависимостью
е
аа = 1 + 0,15 — , (23)
Рис. 10. Концентрация напряжений у отверстия
где S — ширина основания зуба; р — радиус закруглений.
Чем резче меняется форма тела, тем больше коэффициент концентрации. Коэффициенты концентрации аа в правильно сконструированных и в надежно работающих деталях машин обычно не превосходят значений аа = = 2,0-н2,5. В неудачных конструкциях они могут достигать значений аа = 5ч-7 и выше. При конструировании напряженных деталей машин необходимо предусматривать меры по снижению концентрации напряжений (подробнее см. гл. 28). Примеры правильного и неправильного конструи-
Рис. 11. Концентрация напряжений у выточки
22
Основные виды напряженного состояния
Рис 12 Неправильное (а) и правильное (б") выполнение конструктивных элементов
Р"ва11ия некоторых типичных элемен тов показаны на рис 12
Большие местные напряжения воз никают также при передаче усилия с одной детали на другую, прижатую к ней небольшим участком поверхности, например в зонах соприкосно вения зубьев зубчатых колес, в шари ковых и роликовых подшипниках, в замковых соединениях рабочих ло паток турбомашин с диском и т п Такие напряжения называют контактными Так как с увеличением нагрузки размер контактной площадки увеличивается, то контактные напряжения возрастают медленнее, чем на грузка Для обеспечения контактной прочности материалы подвергают поверхностному упрочнению, повышающему их твердость (более подробно см гл 35)
ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ
При нагреве тела равномерно рас ширяются во все стороны, что приводит к относительному изменению объема
0 = ₽ ДТ, (24)
где Р — коэффициент объемного температурного расширения материала,
измеряемый в I °C, АТ — изменение температуры тела
При этом каждая сторона малого элемента тела получает температурную деформацию 8 = 9/3 = а АТ, где а _= [3/3 — коэффициент линейного температурного расширения материала (см табл 1)
Если нагреваемая деталь (стержень, рис 13, а) закреплена в жестком кор пусе, который остается холодным, то длина стержня также должна остаться без изменения и в нем возникнут сжимающие температурные напряже иии
а = —Еа АТ (25)
При охлаждении температурные напряжения будут растягивающими
Температурные напряжения возни кают также и в тех случаях, когда температура в различных точках де тали неодинакова или когда связанные между собой нагретые детали сделаны из материалов с различными коэффициентами линейного расширения
В горячих частях детали и в элементах нагретых конструкций, материал которых имеет больший коэффициент температурного расширения по сравнению с другими элементами, температурные напряжения обычно бывают сжимающими
Температурные напряжения зависят от свойств материалов, от конфигурации детали, от закона распределения температур и могут быть весьма значительными
Рис 13 К ра/чету температурных напряжений 7
Напряженно-деформированные состояния
23
Пример При охлаждении на ЛГ ступенчатого стержня (рис. 13, б) температурные напряжения в узкой части
1 + 2Л-а = ЕаЛТ----------р- .
Если F-i = 0,5Е2 н I = 0,1а, то о = 10,5£а АГ, что для стального стержня уже при АГ = 10 °C дает о = 242 МПа (24,2 кгс/мм2)
Чем выше теплопроводность материала (см табл. 1), тем равномернее прогревается деталь и тем ниже температурные напряжения при прочих равных условиях.
НАПРЯЖЕННО-
ДЕФОРМИРОВАННЫЕ СОСТОЯНИЯ
Различают следующие напряженные состояния:
а) линейное (одноосное) — когда из трех главных напряжений только одно не равно нулю. В одноосном напряженном состоянии находятся детали при растяжении, сжатии, чистом изгибе;
б) плоское (двухосное) — когда из трех главных напряжений два не равны нулю. Практически в двухосном напряженном состоянии находятся вращающие диски, тонкостенные сосуды под внутренним давлением, стержни при чистом кручении и при поперечном изгибе. Свободные от нагрузок участки поверхности деталей любой конфигурации всегда находятся в двухосном напряженном состоянии;
в) объемное (трехосное) — когда все три главных напряжения не равны нулю (толстостенные трубы под внутренним давлением, области контактов различных тел, внутренние области массивных деталей).
Деформации большей частью развиваются по всем направлениям, т. е. соответствуют объемному (трехосному) деформированному состоянию. Состояние, близкое к двухосной деформации, реализуется при нагружении длинных толстостенных труб внутренним давлением.
Характер напряженно-деформированного состояния влияет на условия развития деформаций и разрушения детали.
Глава 2
МЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ КОНСТРУКЦИОННЫХ МАТЕРИАЛОВ И ОЦЕНКА ПРОЧНОСТИ ДЕТАЛЕЙ
Следует различать механические характеристики материала, зависящие от его химического состава, структуры, термообработки, температуры, условий и скорости нагружегия, и механические характеристики изготовленной из этого материала детали, на которые дополнительно влияют ее размеры и форма, а также условия взаимодействия с другими деталями и средой.
К основным механическим свойствам материала относят:
прочность — способность сопротивляться нагрузкам без разрушения;
деформативность — способность изменять размеры и форму без разрушения;
упругость — способность восстанавливать первоначальные размеры и форму после снятия нагрузок;
пластичность — способность получать значительную деформацию, остающуюся по(ле снятия нагрузки; эту деформацию называют остаточной-,
твердость — способность сопротивляться при местных контактных воздействиях пластической деформации или хрупкому разрушению в поверхностном слое;
24
Механические характеристики материалов и оценка прочности
сопротивление усталости — способность сопротивляться усталости, т е. возникновению и развитию трещины под влиянием многократно повторяющихся нагружений.
Материалы, разрушающиеся при значительной остаточной деформации, называют пластичными, при очень малой — хрупкими.
Характеристики прочности, пластичности и твердости определяют при постепенно возрастающих нагрузках; они служат для оценки статической прочности материала. Сопротивление усталости определяют при циклически меняющихся нагрузках, по ней судят о работоспособности материала при переменных напряжениях
По мере увеличения нагрузки или времени ее действия происходит постепенное исчерпание способности материала сопротивляться дальнейшему нагружению; это явление называют повреждаемостью.
Один и тот же материал при различных условиях и скоростях нагружения и при разных температурах может обладать различными механическими свойствами. Количественная оценка механических свойств проводится при испытании стандартных образцов в определенных условиях нагружения.
К основным механическим характеристикам детали наряду с ее прочностью и сопротивлением усталости относят жесткость — способность сопротивляться изменению размеров и формы под действием нагрузок; противоположную характеристику называют податливостью.
Нагрузка, при которой происходит нарушение прочности детали, препятствующее ее дальнейшей работе, может значительно превосходить нагрузку, вызывающую местное разрушение материала в какой-либо точке, вследствие включения в работу ранее менее нагруженных участков детали. Способность детали сопротивляться разрушению при наличии трещин называют трещиностойкостью.
' Большинство используемых конструкционных материалов (стали, алюминиевые и титановые сплавы) имеют одинаковые механические свойства по всем направлениям, т. е. являются
изотропными Наряду с ними встречаются материалы (дерево, многие композиционные материалы, т. е. состоящие из двух или нескольких компонентов), свойства которых по разным направлениям существенно различны. Их называют анизотропными. Механические характеристики деталей из композиционных материалов зависят от способа их изготовления.
Анизотропия может быть специально получена в процессе отливки (детали с направленной кристаллизацией или монокристаллической структурой) для обеспечения повышенной прочности в направлении действия наибольших нагрузок.
СВОЙСТВА ПРИ СТАТИЧЕСКИХ НАПРЯЖЕНИЯХ
Прочность при растяжении. Испытание материалов на растяжение — наиболее простое и распространенное. Чтобы результаты испытаний были сравнимы, применяют геометрически подобные образцы обычно круглого сечения. Образец растягивают на разрывной машине с постоянной скоростью движения захватов и определяют зависимость удлинения расчетной части образца Л/ от нагрузки Р вплоть до разрушения. По этим данным строят диаграмму растяжения (рис. 1), т. е. зависимость относительного удлинения е = AZ/Zn от условного напряжения о = P/Fo, где Fe — площадь поперечного сечения образца до деформации.
В начале нагружения между напряжением и деформацией существует линейная зависимость, что позволяет при расчетах пользоваться законом Гука. Напряжение, при котором отступление от линейной зависимости между напряжением и деформациями впервые достигает некоторой заданной величины, называют пределом пропорциональности аПц (точка 1 на рис. 1). Если в какой-либо момент начать разгружать образец (точка А), то зависимость между напряжением и деформацией при разгрузке изобразится прямой линией АВ, практически параллельной линии нагрузки 01. Деформация в точке А состоит из упругой части вудр, которая устраняется
Свойства при статических напряжениях
25
Рис I Диаграмма растяжения
Рис. 2 Диаграмма растяжения с площадкой текучести
после снятия нагрузки, и остаточной (пластической) части еОст> которая остается после снятия нагрузки Напряжение, при котором остаточные деформации впервые достигают некоторой заданной величины (обычно порядка 0,002—0,005%), называют пределом упругости оу (точка 2) Предел упругости часто считают совпадающим с пределом пропорциональности
При нагружении за пределом упругости остаточные деформации заметно увеличиваются Для низкоуглероди стой стали деформация некоторое время растет без нарастания напряжений, что дает площадку текучести (рис 2) Напряжение, соответствую щее площадке текучести, называют пределом текучести ат.
Многие материалы не имеют площадки текучести Для них определя ется условный предел текучести — напряжение, при котором остаточные деформации достигают некоторой заданной величины (обычно 0,2%), условный предел текучести, соответствующий указанной величине остаточной деформации, обозначают а0,2 (точка 3 на рис 1)
Вначале образец равномерно растягивается по всей длине, при большой деформации происходит потеря устойчивости пластической деформации и образуется местное сужение — шейка, в результате чего нагрузка, воспринимаемая образцом, и условное напряжение уменьшаются, хотя истин иое напряжение, определяемое по действительной минимальной площади по
перечного сечеиия образца, продолжает возрастать, как показано на рис 1 штриховой линией Хрупкие материалы разрушаются без образования заметной шейки
Максимальное условное напряжение, которое выдерживает образец, называют временным сопротивлением, или пределом прочности ав (точка 4) Истинное напряжение в момент окончательного разрушения образца называют истинным пределом прочности — SH
При испытании на растяжение определяют также характеристики пластичности материала относительное удлинение и относительное сужение (уменьшение площади поперечного сечения) при разрыве
Относительное удлинение, численно равное отрезку 0—6 (рис 1), вычисляют по формуле
6= 100%, (1)
‘о
где 1К — суммарная длина разорвавшихся участков расчетной части образца, /0 — Длина расчетной части образца до деформации
Так как после образования шейки образец деформируется по длине неравномерно, то величина б в определенной степени зависит от расчетной длины образца Поэтому удлинение, определенное иа образце, расчетная длина которого в 5 раз превышает диаметр, иногда обозначают б6
26
Механические характеристики материалов и оценка прочности
Рис 3. К определению твердости по Бринеллю
Относительное сужение поперечного сечения
(2)
ф = - "-и---- 100%* с о
где Fo — площадь сечения расчетной части образца до деформации, Fv — конечная площадь сечения по шейке образца после разрушения
Механические свойства сталей и других конструкционных материалов приведены в разделе «Расчеты на прочность»
При пластической деформации объем материала практически ие меняется, поэтому до момента образования шейки Fala FKlK и
6*~-t
(3)
I — ф
После образования шейки формулой (3) определяется местное удлинение в зоне шейки, поэтому значение б* по формуле (3) оказывается большим, чем б по формуле (1) Истинный предел прочности
S ~ о — = —°в - -к ~ в F к 1 - Ф
= ав (1 -I 6*)
При бопыпих пластических деформациях приращение относительной деформации в каждый момент нагрсже ния должно определяться по отношению к текущей длине образна
, dl de = -.
ис-мм
Полное истинное удлинение
е —
К
Г dl , /к 1
— = In к In -т----------------
) / % 1 - Ф
= In (I - б*) (4)
Истинное удлинение меньше условного, однако до значений, типичных для конструкционных материалов, различие между ними невелико Например, при б* = 30% величина е = = 26% В справочниках обычно приводят значения б и ф.
Прочность при сжатии. Стандартных испытаний на сжатие обычно не проводят, так как такие испытания сопряжены с большими трудностями (при некотором эксцентриситете приложения сжимающей силы образцы начинают изгибаться, их форма из-за трения в захватах становится бочкообразной, образцы из пластичных материалов не разрушаются, а сплющиваются) Для большинства конструкционных материалов модуль упругости, предел пропорциональности (упругости) и условный предел текучести при растяжении и сжатии можно считать одинаковыми Предел прочности хрупких материалов (чугуны) при сжатии может быть значительно выше, чем при растяжении
Твердость Обычно чём тверже материал, тем выше его статическая прочность Так как испытание на твердость проводится без разрушения детали, широко применяют приближенную оценку прочности и правильности термообработки по значению твердости
Твердость по Бринеллю (НВ) по ГОСТ 9012—59 определяют вдавливанием в испытуемый материал шарика из закаленной стали диаметром 10 мм под нагрузкой 29,42 кН (3000 кгс) Число НВ равно отношению силы (в кгс;, вдавливающей шарик, к щади поверхности полученного печатка (рис 3)
0,102 2Р
пло-
от-
НВ^-----------.
лО (D-V О2 - d2)
где Р берется в Н
Для оценки твердости иногда пользуют диаметр отпечатка d в
(5)
Свойства при статических напряжениях
27
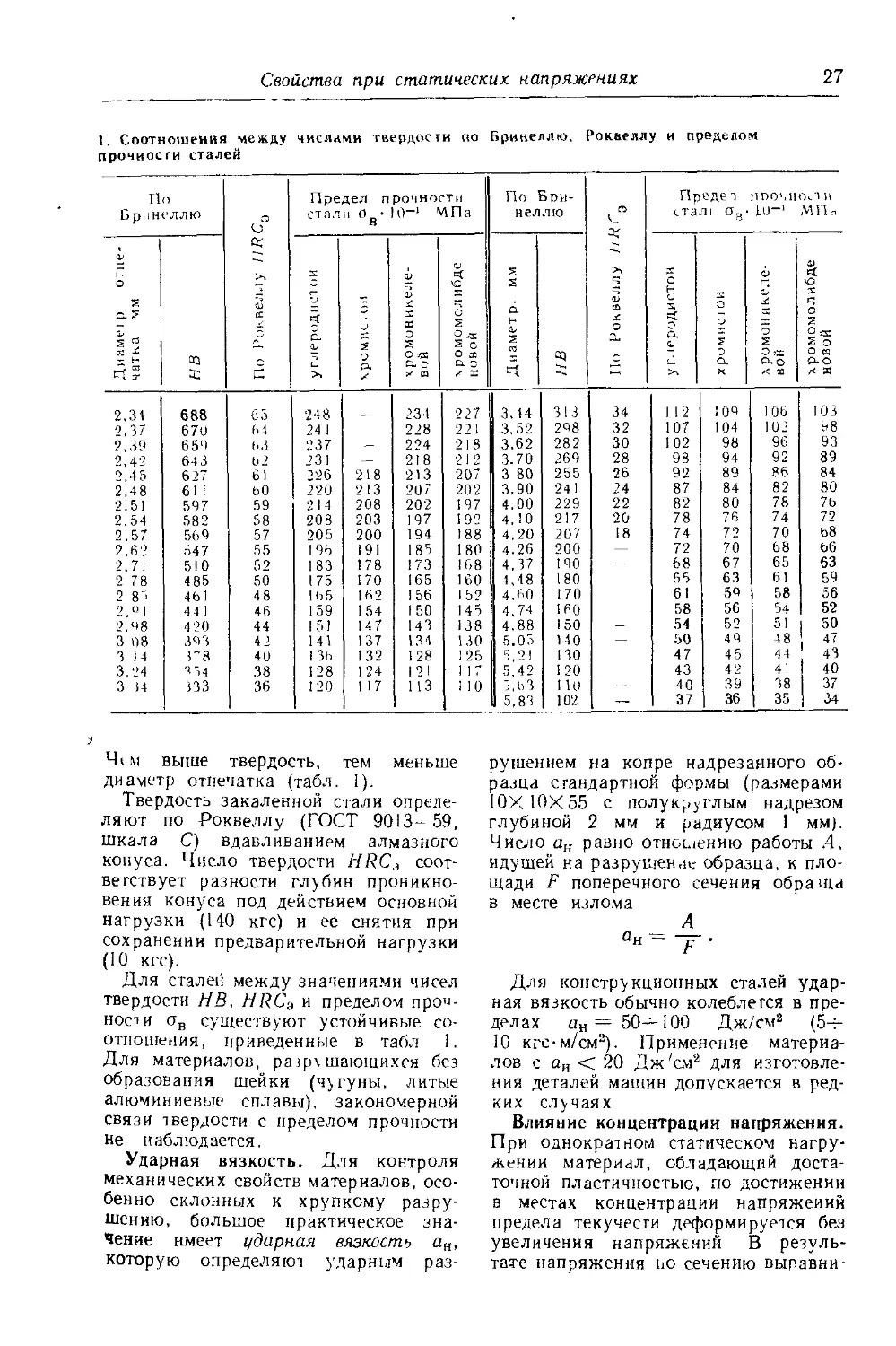
I. Соотношения между числами твердости но Бринеллю, Роквеллу и пределом прочности сталей
По Бринеллю л Предел прочности стали 0 •!0“* МПа
*
ф
ф
о
J-*. ф
2
о. ? X н S X О 2
jj . ' f-j о О
2 2 2 2 о
Дна чать НВ с О О. х ро . ВОЙ о х х г
2.3! 688 63 248 234 227
2.37 670 6 4 24 1 228 221
2.39 659 ЬЗ 237 — 224 218
2,42 643 Ь2 231 — 218 212
2.45 627 61 226 218 213 207
2,48 61 1 ЬО 220 213 207 202
2.51 597 59 214 208 202 197
2.54 582 58 208 203 197 19'2
2.57 569 57 205 200 194 188
2.62 547 55 196 191 185 180
2,71 510 52 1 83 178 173 168
2 78 485 50 175 170 165 160
2 8'’ 46 1 48 165 162 156 152
2, ° 1 44 1 46 159 154 1 50 1 4 5
2.48 4 20 44 151 147 143 138
3 98 393 42 141 137 134 130
3 14 Г8 40 136 132 1 28 1 25
3.24 154 .38 128 1 24 121 1 1 7
3 34 133 36 120 117 113 1 10
По Бри- о Предеч HDO4H L0-1 lei И МПа
нел ЛЮ ста 11
2 2 о. жвеллу hr о X о ф молибде
Ф 2 ? о 2 о 2 о
03 о о о ш Р-О
* X X х ж
ЗЛ4 313 34 1 12 109 106 103
3.52 298 32 107 104 102 98
3.62 282 30 102 98 96 93
3.70 269 28 98 94 92 89
3 80 255 26 92 89 86 84
3.90 24 1 24 87 84 82 80
4.00 229 22 82 80 78 7b
4.10 217 20 78 76 74 72
4.20 207 18 74 72 70 Ь8
4.26 200 — 72 70 68 66
4.37 190 — 68 67 65 63
4,48 180 65 63 61 59
4.60 170 61 59 58 56
4.74 160 58 56 54 52
4.88 150 — 54 52 51 50
5.05 140 — 50 49 48 41
5.21 130 47 45 44 43
5.42 120 43 42 41 40
5.63 1 10 — 40 39 38 37
5.83 102 — 37 36 35 34
Чтм выше твердость, тем меньше диаметр отпечатка (табл. I).
Твердость закаленной стали определяют по Роквеллу (ГОСТ 9013- 59, шкала С) вдавливанием алмазного конуса. Число твердости HRCa соответствует разности глубин проникновения конуса под действием основной нагрузки (140 кгс) и ее снятия при сохранении предварительной нагрузки (10 кгс).
Для сталей между значениями чисел твердости НВ, HRCa и пределом прочности ов существуют устойчивые соотношения, приведенные в табл 1. Для материалов, разрешающихся без образования шейки (чугуны, литые алюминиевые сплавы), закономерной связи твердости с пределом прочности не наблюдается.
Ударная вязкость. Для контроля механических свойств материалов, особенно склонных к хрупкому разрушению, большое практическое значение имеет ударная вязкость ая, которую определяют ударным раз
рушением на копре надрезанного образца стандартной формы (размерами 10X10X55 с полукруглым надрезом глубиной 2 мм и радиусом 1 мм). Число ан равно отношению работы .4, идущей на разрушение образца, к площади F поперечного сечения обра ща в месте излома
А а» - F '
Для конструкционных сталей ударная вязкость обычно колеблется в пределах ан = 50—100 Дж/см2 (5-г 10 кгс-м/см2). Применение материалов с ан < 20 Дж 'см2 для изготовления деталей машин допускается в редких случаях
Влияние концентрации напряжения. При однократном статическом нагружении материал, обладающий достаточной пластичностью, по достижении в местах концентрации напряжений предела текучести деформируется без увеличения напряжений В результате напряжения по сечению выравни-
28
Механические характеристики материалов и оценка прочности
Рис. 4. Кривые длительной прочности при разных постоянных температурах (Tj>
ваются и разрушающая нагрузка практически не изменяется. При повторных нагружениях концентрация напряжений снижает несущую способность детали (см. ниже). В более хрупких материалах неравномерное распределение напряжений сохраняется до момента разрушения и оценивается эффективным коэффициентом концентрации напряжений при постоянной нагрузке, который определяют экспериментально как отношение предела прочности гладкого образца ов к пределу прочности аналогичного образца с концентратором напряжений (обычно с надрезом) авк’
Чувствительность материала к концентрации напряжения оценивают также ударной вязкостью, которую определяют на образцах с надрезом.
СВОЙСТВА ПРИ высоких
И Н ИЗКИ X Т ЕМП ЕРАТУРАХ
С повышением температуры механические свойства материалов изменяются. пределы прочности, пропорциональности и текучести, а также модуль упругости убывают; пластичность обычно увеличивается, но при некоторых температурах она может и понижаться.
Для большинства конструкционных материалов прн нормальной температуре статическая прочность практически не зависят от времени приложения нагрузки. При повышенных тем
пературах, а для некоторых материалов (типа полимеров) даже при нормальной, статическая прочность зависит от длительности нагружения, так как с течением времени могут меняться механические свойства материала, размеры детали и распределение в ней напряжений. Поэтому при высоких температурах определяют не только обычные механические характеристики при кратковременных испытаниях, но и характеристики при продолжительной работе. Прочность материала называют в этом случае длительной прочностью.
Для определения механических свойств образца при продолжительной работе его нагревают в электропечи, установленной на разрывной машние, нагружают и отмечают время до разрушения /р. Чем выше напряжение, тем быстрее разрушается образец.
Напряжение, при котором образец разрушается не ранее заданного времени, называют пределом длительной прочности одл. Обозначение = = 250 МПа указывает, что при напряжении 250 МПа образец разрушается не менее чем через 300 ч. Предел длительной прочности всегда ниже предела прочности при кратковременном испытании.
Зависимость предела длительной прочности Одл от времени при постоянной температуре t называют кривой длительной прочности. В двойных логарифмических координатах эта зависимость в определенных пределах имеет вид прямой линии (рис. 4):
lg *Р2 — Ig *р< =
= tg a (1g Одл1 — 1g Одан).
или
С lZpi = адл2*р2 = С = const' (7)
где т = tg а и С— постоянные для данной температуры испытания. Чем выше температура, тем меньше показатель степени т и тем быстрее убывает по времени предел длительной прочности. Пределы длительной прочности для некоторых материалов приведены в табл 2. По данным таблицы
Свойства при высоких и низких температурах
29
2. Механические свойства (в МПа) некоторых материалов при повышенной температуре
Марка стали или сплава Температура испытания Т, °C Предел прочности пв X1 О*1 Предел текучести w1 °~* Предел длительной прочности 0ДЛ*1О"4 Предел ползучести /
за 100 ч ь 0001 ес о СО rt 7 о о см о о 1 о о см о о
20 72 52 —
300 56 43 .— — — —
400 53 40 — — — —
2X13 450 49 38 40 — —-
500 44 36 — 17 4,8
550 35 28 — — — 3,0
20 65 31
400 44 22 — — —. —
500 43 21 — — —
12Х18Н9Т 600 36 18 25 15 8
700 28 16 13 — — — —
800 18 10 5 — — — —
20 96 68
400 78 49 — — — — —
40Х10С2М 500 68 46 35 — 16,2 20 12,8
550 55 42 24 — 9.5 9 4
600 44 37 — — — 5 2,2
20 84 44 ,
500 69 43 — — — __. —
ХН35ВТ 600 66 42 32 23 —
650 57 41 30 22 15 — 13
700 48 40 — 14 j 6.5 — 8
20 94 60
450 72 50 — —
37Х12Н8Г8МФБ 600 60 45 45 38 35
650 56 43 35 28 30 —
700 50 38 — — 24 —
750 42 33 — — — — -
20 105 70
600 98 63 __
ХН70МЗТЮБ 700 93 60 48 — 18 —-
800 72 55 25 — — —
900 38 28 — — — — —
20 110 70
500 9b 64 — — — — —
ХН77ТЮР 600 87 57 70 56 — 56 —
700 83 56 44 33 — 40 —
800 55 44 22 11 — 17 —
20 1 14 75
600 99 68 __ —
КН70ВМЮТ 700 90 65 50 36 40 —
800 75 58 28 18 — 23 —
900 49 38 12 10 — 10 —
30
Механические характеристики материалов и оценка прочности
Продолжение табл. 2
Марка стали или сплава Температура испытания Г, °C Предел прочности ов X 1 О”1 Предел текучести °0.2- ‘°-' Предел длительной прочности адл» 10”1 Предел ползучести
за 100 ч за 1000 ч У о се t_о ] .001/3 0 о о см о О
20 95 85
800 92 84 52 38 — 38 —
ЖС6К 900 78 52 32 16 — 20 —
1000 54 32 15 6,5 — 6 —
1030 43 26 12 — — — —
900 37 25 —
ЖС6-У 1000 - — 18 11 — — —
1050 — — 1 1 6,5 — —
20 37 22
175 27 20 18,5 — — 18 —
АЛ13 200 26 22 15 — — — —
250 17 10 11,5 — — — —
300 12 7.5 6.5 — — — --
20 45 38
1 50 40 36 29 — 28 —
АК4-1 200 34 29 17 — 16 —
250 28 20 10 — — 8 —
300 17 14 4 — — 3 —
20 50 33
200 38 1 9 — — 16 —
ВД-17 250 24 10 — — 7.5 —
300 18 5,5 — 3,2 —
20 100 95
300 — — — — —
ВТЗ-1 400 76 63 65 55 — — —
500 70 56 36 27 —. 28 —
600 53 25 — — — — —
20 115 103
400 85 72 — — —
ВТ9 500 80 66 65 — 28 —
550 78 62 45 12 — —
600 72 55 23 — — —
20 120/1 1,5»
100 110/1 1
Боралюминий одно- 200 102/10
направленный 300 95/5,5
400 87
500 80
• В числителе приведены пределы прочности в продольном, в знаменателе — в поперечном направлении образцов.
Свойства при высоких и низких температурах
31
С — ат t ° - адл1*р1 •
и формуле (7) можно найти значение постоянных т, С:
'8 7?
771 = ———— , , °ДЛ1 lg ъ— °ДЛ2
Например, для
при Т -= 700 °C
а1ооо 330 мп дл
сплава
а™ = дл
откуда
, 1000
ЯП т=~440- = 8,0;
g 330
С = 440е-100 = 1,4-1023 (МПа)8
ч.
Размеры нагруженных при высокой температуре деталей с течением времени непрерывно меняются, что может нарушить работу машины. Это явление называют ползучестью. При испытании на ползучесть к нагретому образцу прикладывают постоянную нагрузку и через определенные промежутки времени измеряют удлинение образца Зависимость остаточной деформации от времени испытаний при постоянном напряжении и постоянной температуре называют кривой ползучести (рис. 5).
Остаточная деформация вначале быстро нарастает (стадия / — неуста-новившаяся ползучесть), затем в течение основного времени работы скорость ползучести остается примерно постоянной (стадия II — установившаяся ползучесть), наконец, перед разрушением образца скорость ползучести быстро нарастает (/// стадия). Чем выше напряжение и температура, тем быстрее развивается ползучесть.
Наибольшее напряжение, при котором деформация ползучести за определенный период времени не превышает заданного значения, называют пределом ползучести (обозначение ао,2/1оо ~ *50 МПа указывает, что при напряжении 150 МПа ползучесть за 100 ч вызывает относительное остаточное удлинение 0,2%). Пределы ползучести некоторых сплавов приведены в табл. 2.
ХН77ТЮР
440 МПа,
Рис. 5. Кривые ползучести при разных постоянных напряжениях
Когда общая деформация детали по условиям работы остается неизменной (например, вытяжка болта в резьбовом соединении), увеличение с течением времени пластической деформации приводит к уменьшению упругой деформации и падению напряжения (в данном случае к ослаблению резьбового соединения). Это явление называют релаксацией напряжений.
Наконец, при высоких температурах происходит интенсивное окисление ряда материалов. В неравномерно нагретых конструкциях ползучесть приводит с течением времени к перераспределению напряжений: в горячих зонах напряжения уменьшаются, в более холодных — увеличиваются. Это должно учитываться в расчетах на длительную прочность.
Применение обычных конструкционных сталей в условиях значительной напряженности ограничено температурой 300—400 °C. Жаропрочные стали и сплавы на основе никеля и тугоплавких металлов применяют при температурах до 700—800 °C и выше. При еще более высоких температурах применяют металлокерамические и керамические материалы. /
Температурный диапазон применения ряда материалов может быть расширен при использовании защитных жаростойких покрытий. /
При очень низких (или, как их иногда называют, криогенных) температурах механические свойства материалов также меняются повышается прочность и снижается пластичность.
При снижении температуры от нормальной до —200 °C пределы прочности и текучести сталей возрастают
32
Механические характеристики материалов и оценка прочности
в среднем на 20—30%. Относительное удлинение и особенно относительное сужение заметно уменьшаются, т е. материал становится более хрупким. Усиливается чувствительность материала к концентрации напряжений, поэтому прочность надрезанных образцов с понижением температуры обычно падает.
Для каждого материала имеется предельная температура, ниже которой его применение в конструкциях становится недопустимым из-за высокой хрупкости.
СВОЙСТВА ПРИ ПЕРЕМЕННЫХ
НАПРЯЖЕНИЯХ
При переменных напряжениях деталь разрушается от меньших нагрузок, чем при постоянных Усталостное разрушение, как правило, начинается с поверхности в местах высокой концентрации напряжений. Трещина обычно развивается в направлении, перпендикулярном линии действия наибольших нормальных напряжений. Когда прочность оставшейся части становится недостаточной, происходит окончательное разрушение (рис 6)
Переменное напряжение периодически меняется от наименьшего значения omln до наибольшего отах и обратно с размахом Ao = пП1ах — °min (рис 7).
Среднее напряжение
(Птах Д (®)
амплитуда переменных напряжений
° а — 0>5 (Пщах — ®mla)- (9)
Цикл называют симметричным, если наибольшее и наименьшее напряжения равны по величине, но противоположны по знаку. Такой цикл осуществляется при стандартных испытаниях на усталость образцов в виде вращающихся валиков круглого сечения (диаметром 7—10 мм) прн изгибе моментами постоянной величины и направления (рис. 8).
На практике встречаются в основном асимметричные циклы. Коэффициентом асимметрии цикла называют отношение
Г _ ffmln Птах
Для симметричного цикла ат =0, Пта = па = — пшщ, г = — 1. Важным частным случае м асимметричного цикла является огнулевой (пульсационный), когда напряжения меняются от нуля до максимального значения, как. например, при изгибе зубьев зубчатых колес (рис. 9). Для такого цикла Hmln 0> nm — Оа~ О.бОгпах, Г = 0.
Оценку сопротивляемости материала действию переменных напряжений проводят испытаниями на усталость партии из 15—20 однотипных образцов, которые доводят до разрушения при разном уровне амплитуд напряжений. По результатам испытания строят кривые усталости (кривые Велера), по-
Рис. 6. Схема разрушения зуба Рис. 7. Цикл переменного напряжения зубчатого колеса от усталости:
А — точка возникновения усталостной трещины, АВ — линия развития трещины; ВС — область дол ом а
Свойства при переменных напряжениях
33
Рис. 8. Возникновение симметричного цикла переменных напряжений при изгибе вращающегося круглого валика, положения I н II отличаются на половнну оборота вала
Рис. 9. Схема отнулевого (пульсационного) цикла напряжений в зубе зубчаюю колеса
называющие зависимость между числом циклов до разрушения N и максимальным напряжением или амплитудой цикла (рис. 10). По оси абсцисс, а иногда и по оси ординат для удобства откладывают значения lg N и 1g о.
Зависимость разрушающих амплитуд оа от числа циклов до разрушения Л' (в определенных пределах) имеет вид
= С = const, (10)
где т, С — постоянные для данного материала, обычно т— 4—12.
Для большинства сталей прн умеренных температурах кривая усталости, начиная с числа циклов .V га та 10е—107, становится практически горизонтальной, т. е. образцы, выдержавшие указанное число циклов, не разрушаются н при дальнейшем нагружении. Поэтому испытания сталей прекращают при N — (1ч-2)Х X10’ циклов. Наибольшее значение максимального напряжения атах, при ко юром материал может выдержать без разрушения практически неограниченное число циклов, называют пределом выносливости.
Легкие сплавы, а также материалы при высоких температурах и при испытаниях в коррозионных средах имеют кривые усталости в координатах — lg N без горизонтального
2 Заказ 402
участка В этом случае определяют ограниченный предел выносливости, соответствующий определенной базе испытаний (обычно .V = (0,1 — 1) X X 10“ циклов) Для получения надежной оценки предела выносливости число неразрушившился образцов при данном уроьне переменных напряжений должно быть не менее шести.
Предел выносливости симметричного цикла обозначают o.j, так как для такого цикла г——1. Для сталей ориентировочно можно считать
о.! « (0,55 — 0,0001ав) ав,
где ов — в МПа.
Для касательных напряжений т_! та » 0,6О_!.
Рис. 10. Кривая усталости: Q — разру* шившиеся и О-* — неразру шившиеся образцы
34
Механические характеристики материалов и оценка прочности
Рис. II. Диаграмма предельных наиряже» иий
Испытания на усталость при асимметричных циклах проводят на специальных машинах. По результатам испытаний строят диаграммы предель-ных напряжений отах и omln = / (om) (рис. 11) или предельных амплитуд цикла <за = f (om) (рис. 12). Если на диаграмме предельных напряжений провести прямую под углом 45° к горизонтальной оси, ю отрезок АВ даст значение среднего напряжения цикла, а отрезок ВС = BD — значение предельной амплитуды, соответствующей пределу выносливости циклов с коэффициентом асимметрии г, расположенных на луче ОС. Через о0 обозначают предел выносливости отнулевого цикла, для которого t = 0. Всегда Ofl '> 0-1, НО Оа0 O.j.
Постоянные растягивающие напряжения уменьшают сопротивление усталости, поэтому при увеличении среднего напряжения цикла предельная амплитуда оа становится меньше, хотя предел выносливости отах увеличи
вается. Для упрощения расчетов принимают, что на участке диаграмм между симметричным и отнулевым циклом предельные амплитуды изменяются линейно (штриховые линии на рис. 11 и 12):
°а — °-1 — Фа°пи (11)
где ф0 — коэффициент, характеризующий чувствительность материала к асимметрии цикла Аналогичную формулу, но с коэффициентом фт используют для касательных напряжений.
Для циклов с асимметрией до am/a-i = 1/(1 + Фа) (примерно до ат/ов = 0,4н-0,5) значения ф0 и фт для сталей принимают по данным табл. 3. Для титана и легких сплавов ф0 « 0,2н-0,3.
В запас прочности для всех циклов с растягивающими средними напряжениями можно считать ф0 «з о.^Од, что соответствует штрихпунктирным линиям на рис. 11 и 12.
Постоянные сжимающие напряжения до определенных пределов способствуют повышению сопротивления
3. Приближенные значения коэффициентов н фт для сталей прн нормальной температуре
Вид деформации ав- 10“*, МПа
35—52 52 — 72 72 — 100 100—120 120—140
Изгиб и растяжение 0 0,05 0,1 0,2 0,25
Кручение 0 0 0.05 0,1 0,15
Свойства при переменных напряжениях
35
усталости, особенно для малопластичных материалов. В расчетах для сжатия (при ат < 0) обычно принимают фо = 0.
На предел выносливости оказывают существенное влияние следующие факторы.
1. Абсолютные размеры детали. С увеличением размеров детали предел выносливости уменьшается, что оценивается коэффициентом влияния абсолютных размеров поперечного сечения Kd (рис. 13):
= (12)
0-1
Рис. 13. Коэффициент влияния абсолютных размеров:
1 — углеродистые стали, ав = 4004-
500 МПа, 2 — легированные стали, ав = = 1200ч-1400 МПа
где (°-i)d — предел выносливости гладких образцов диаметром d; — то же для стандартных лабораторных образцов диаметром 7—10 мм.
2. Концентрация напряжений. Чем выше концентрация напряжений, тем ниже предел выносливости Влияние концентрации напряжений на сопротивление усталости оценивается эффективным коэффициентом концентрации напряжений при переменной нагрузке Ка, который определяют экспериментально как отношение предела выносливости гладкого образца (a.Jd к пределу выносливости образца того же размера с концентрацией напряжений (например, с надрезом):
к- _ (q-i)d (q-iK)d ’
(13)
Эффективный коэффициент концентрации Ко обычно меньше теоретического коэффициента концентрации при упругом распределении напряжений аа и связан с ним соотношением
1 + <7п («о — 1),
где qa—коэффициент чувствительности материала к концентрации напряжений.
Для конструкционных низкоуглеродистых сталей и жаропрочных деформируемых сплавов q0 = 0,2—0,4; для легированных сталей = 0,6— 0,8; для алюминиевых сплавов q0 — ~ 0,34-0,5. Особенно чувствительны к концентрации напряжений высокопрочные титановые сплавы, для которых qa = 0,84-0,9. С увеличением раз
2*
меров зерна и неоднородности структуры (например, у серого чугуна) коэффициент qa уменьшается до 0,1— 0,2 (см гл. 31).
3 Состояние поверхности. Чем меньше микронеровности поверхности, тем выше предел выносливости детали. Сопротивление усталости повышается после термохимических и механических обработок, которые создают в поверхностном слое остаточные напряжения сжатия и повышают его твердость (цементация, азотирование, поверхностная закалка, наклеп). После шлифования в поверхностном слое могут возникать остаточные напряжения растяжения, которые снижают сопротивление усталости. Важное значение имеет упрочняющая технология (обдувка дробью, обкатка роликом и др), повышающая пределы выносливости деталей (см. гл. 31). Состояние поверхности учитывают при определении Ка или отдельным коэффициентом
(а-1к)д (O-lK)<i
где (о_1к)д — предел выносливости натурной детали.
4 На состояние поверхности существенно влияет окружающая среда. В коррозионных средах (в морской воде и др.) предел выносливости конструкционных сталей, особенно высокопрочных, резко падает. Титановые сплавы малочувствительны к коррозионному воздействию влажного воздуха и морской воды.
36
Механические характеристики материалов и оценка прочности
5. Частота переменных напряжений. С увеличением частоты предел выносливости обычно повышается.
Из формул (12) —(14) следует:
(а-1к)д---°-1-
МАЛОЦИКЛОВАЯ
И ТЕРМИЧЕСКАЯ ПРОЧНОСТЬ
Большинство деталей машин работает определенными циклами пуск, рабочие режимы, остановки. Соответственно этому напряженно-деформированное состояние деталей меняется циклически. За время эксплуатации общее число циклов может меняться от 10—100 для стационарных установок до 104—10s и более для транспортных машин, грузоподъемных устройств и других механизмов.
Хотя в каждом цикле нагружение носит статический характер, но при повторных нагружениях в материале появляются явления, типичные для усталости. Поэтому разрушение деталей при сравнительно небольшом числе циклов (102—106) называют ма-лоцикловой усталостью, а способность материала сопротивляться такому разрушению — малоцикловой прочностью
Закономерности малоцикловой проч ности занимают «промежуточное» положение между закономерностями статической прочности и сопротивления усталости.
При числе циклов N > 104 отчетливо проявляются закономерности усталостного разрушения (влияние концентрации напряжений, качества поверхности и т. д). При малом числе циклов N < Ю3 более типичны особенности статического разрушения.
При малом числе циклов амплитуда напряжений может превосходить предел пропорциональности, и при повторных разгрузках и нагрузках зависимость между напряжениями и деформациями принимает вид петель циклического упругопластического деформирования (петель гистерезиса) с размахом — шириной петли — пластических деформаций Дер (рис. 14). При умеренных нагрузках, допустимых для обеспечения достаточно про-
Рнс. 14. Петли гистерезиса при повторном упругопластическом деформиповании
я
должнтельной работы детали, петли деформирования после нескольких первых «приработочных» циклов обычно стабилизируются, как показано на рис 14.
Для обеспечения высокой малоцикловой прочности материал должен иметь хорошее сочетание прочностных и пластических свойств, а в конструкции детали следует избегать зон с повышенной концентрацией напряжений.
Малоцнкловую прочность материала оценивают по экспериментальным зависимостям амплитуды напряжений а0 или деформаций е0 от числа циклов N до разрушения (рис. 15).
Рнс 15. Типичная кривая малоцикловой усталости углеродистой стали
Прочность при наличии трещин
37
При отсутствии прямых экспериментальных данных для получения сравнительных оценок можно пользоваться эмпирической формулой Мэнсона (или одной из ее модификаций), по которой между размахом полной деформации Де = 2еа и осредненным числом циклов до разрушения N имеется следующая связь:
Ae=(lnT^)0’6yV-0’6 +
д,—0,12 , (15)
£
где ф — относительное сужение поперечного сечения; Е — модуль упругости.
Первое слагаемое описывает изменение пластической деформации, второе — изменение упругой деформации от числа циклов N до разрушения.
Для асимметричных циклов со средним напряжением от в формуле (15) вместо ов принимают ов — от.
Если известны предел выносливости o_i при базовом числе циклов No и показатель кривой усталости т, то формула (15) может быть преобразована к виду
/ 1 \0,6 „ -
Де = ( 1п ) М~°'6 +
\ 1 —ф /
। 2О-! Л _£т\
Е \ N J V ов ) •
В среднем т ~ 8.
При высокой температуре следует считать ф = ф (/), а ов заменить на адл (О-
Разрушение детали может быть вызвано действием температурных напряжений от повторных нагревов и охлаждений, связанных с тепловым процессом машины или внешними условиями. Сопротивление такому виду разрушения называют термической прочностью. При высокой верхней температуре цикла важное значение имеет длительность выдержки при этой температуре. Для повышения термической прочности должны выполняться те же требования, что и для малоцикловой прочности, кроме того, следует принимать меры к снижению температурных напряжений в детали,
уменьшению максимальной температуры и выдержки при ней (например, путем лучшей организации охлаждения). Наиболее полно прочность деталей, узлов и машин в целом оценивается при проведении специальных циклических испытаний по режимам, приближенно соответствующим типичным эксплуатационным циклам.
ПРОЧНОСТЬ ПРИ НАЛИЧИИ ТРЕЩИН
Во всяком реальном материале, даже в ненагруженном состоянии, имеются мелкие микротрещины — несплош-ности и нарушения структуры. Чем точнее метод исследования, тем ^ныие они обнаруживаются. Однако опыт показывает, что наличие микротрещин не препятствует длительной надежной работе машин и конструкций до тех пор, пока связанная с ним повреждаемость не приводит к снижению прочности ниже предельно допустимого уровня.
Допустимую степень повреждаемости устанавливают на основании расчетно-экспериментальных исследований и опыта эксплуатации. До определенных пределов допускаются также некоторые повреждения поверхности в эксплуатации — изнашивание контактных участков, эрозия, забоины, коррозионные точки.
При постоянной нагрузке трешина в некоторых условиях может стабилизироваться, при переменных нагрузках выше определенного уровня длина трещины / постоянно растет. Скорость развития трещины и ее критическая длина /кр, при достижении которой возникает опасность быстрого разрушения конструкции, зависят от коэффициента интенсивности напряжений в вершине трещины Ki — о измеряемого в МПа-мм'^2 или вНХ Хмм~ 3/2 •
При медленно возрастающей нагрузке условием начала разрушения является равенство
= Kic,
где К1г: — характеристика сопротивления материала развитию трещины
38
Механические характеристики материалов и оценка прочности
Рис. 16. Зависимость скорости роста трещины dl/dN от параметра ДК для стали 40ХН2МА с ов = 2000 МПа (21; К1С = 2055 МПа-мм1'2
Рис. 17. Пластичное (а) и хрупкое (ff) разрушение образца
(трещинестойкость), называемая вязкостью разрушения.
Отсюда
Для конструкционных сталей и титановых сплавов Kic = (1-5-3) х X 103 МПа-мм!/2, следовательно, при напряжении о = 500 МПа опасными становятся трещины длиной /кр — — 1,3-5-11 мм, а при о = 1000 МПа — уже /кр = 0,3-1-3,0 мм.
При переменной нагрузке с размахом напряжения До скорость развития трещины по числу циклов dlldN зависит от величины ЛК = (рис. 16). До некоторого «порогового» значения Д/% трещина практически не растет (для сравнительной оценки материалов в качестве Д/% принимают величину Д7С, соответствующую скорости dlldN = 10“7 (мм/цикл). Дальнейшая зависимость dlldN от ДХ носит в логарифмической системе координат до определенных пределов приблизительно линейный характер, т. е.
-^ = СД*т, (17)
где С, т — константы материала.
На этой стадии по мере увеличения длины трещины параметр Д7( увеличи
вается и фактическая скорость разви-. тия трещины dlldN = f (N) постепенно нарастает. При приближении ДХ к критическому значению ДХС, имеющему тот же порядок, что и /(1С, рост трещины принимает лавинообразный характер и происходит усталостное разрушение.
Оценка по скорости развития трещины числа циклов, которое деталь может доработать после обнаружения ее, позволяет в некоторых случаях продлить эксплуатацию дорогостоящей конструкции. Вместе с тем во избежание развития недопустимой повреждаемости состояние ответственных деталей следует периодически контролировать в процессе эксплуатации и при ремонте неразрушающими методами контроля (ультразвуковыми, токовихревыми, люминесцентными и т. п ).
РАЗРУШЕНИЯ И ИЗЛОМЫ
Различают пластическое и хрупкое разрушения (рис. 17). При пластическом разрушении деформация в момент разрушения составляет 10—20%, при хрупком — менее 3% . Характер разрушения определяется в основном свойствами материала, но зависит также от вида напряженного состояния. Низкоуглеродистые стали обычно имеют пластические разрушения, в
Оценка прочности
39
Рис. 18. Излом лопатси компрессора при
переменных напряжениях
литых материалах часто обнаруживаются хрупкие разрушения. В связи с этим конструкционные материалы условно разделяют на пластичные и хрупкие Разделение обычно проводится на основании испытаний на разрыв и на удар:
Пластичные материалы ..........>6 >10 ->50
Хрупкие.............<3 <6 <30
Наиболее опасно хрупкое разрушение, которое происходит внезапно, без заметного предварительного повреждения, начинаясь от зон высокой концентрации напряжений — обычно в конструкциях с большим запасом упругой энергии (резервуары под давлением, вращающиеся роторы). Хрупкому разрушению способствуют-
а) концентрация напряжений, объемное напряженное состояние;
б) работа материала прн низких температурах и в температурном интервале хладноломкости;
в) длительная работа при повышенных температурах,
г) нагружение быстровозрастающими (ударными) усилиями.
Пластичные материалы менее чувствительны к концентрации напряжений, так как в результате пластического течения происходит перераспределение (выравнивание; напряжений.
Для ответственных элементов конструкций необходимо применять материалы с достаточной пластичностью.
Для установления причин разрушения детали важное значение имеет анализ изломов. При статических напряжениях разрушение сталей и сплавов достаточно высокой пластичности
сопровождается значительными пластическими деформациями. Излом имеет неровную волокнистую поверхность.
При переменных напряя ениях разрушение наступает в результате усталости и происходит без заметной пластической деформации, как правило, в зоне концентрации напряжений. Начало разрушений в гладкой части свидетельствует о высоких переменных напряжениях или наличии технологических дефектов.
При усталостном изломе различают (рис. 18). зону 1 — очаг начального разрушения, расположенный, как правило, на поверхности детали; 2 — область развития усталостной трещины с характерными веерообразными усталостными линиями, уступами и притертыми участками, зону 3 — область окончательного кратковременного долома.
При высоком уровне действующих переменных напряжений (оа "> 0,5o_i) часто наблюдаются несколько очагов возникновения усталостных трещин.
При высокой температуре статические изломы идут вдоль границ зерен, усталостные — пересекают зерна и их границы.
ОЦЕНКА ПРОЧНОСТИ
При испытании образцов или натурных деталей устанавливают предельные нагрузки или напряжения, при которых образцы (детали) разрушаются. Для обеспечения нормальной работы максимально допустимые нагрузки и напряжения должны быть меньше предельных.
Отношение предельных напряжений к максимальным напряжениям, возникающим при работе детали, назы
40
Механические характеристики материалов и сценка прочности
вают запасом прочности по напряжениям:
°пред п —-------.
О-пах
Запас прочности должен быть всегда больше единицы, Чем больше запас прочности, тем надежнее деталь в работе. Однако увеличение запаса прочности сверх необходимого значения ведет к увеличению массы и габаритов детали, что невыгодно экономически, а в ряде случаев (например, в авиационных конструкциях) недопустимо Правильный выбор запаса прочности является важнейшим этапом при расчете на прочность.
Запас прочности учитывает разброс механических свойств материала, разброс и неточное знание действующих в эксплуатации нагрузок, приближенность расчетных оценок напряжений и температурного состояния деталей, отступления в геометрии деталей от номинальных размеров, хотя бы в пределах допусков, возможные случайные перегрузки.
При установлении запаса прочности принимают во внимание назначение и ответственность детали, длительность работы, общие требования к конструкции (значение массы, габаритов, стоимости и т, д.) Для наиболее ответственных деталей устанавливают нормы прочности, которые обобщают опыт эксплуатации машин.
Запас прочности используют главным образом как критерий сравнения надежности вновь создаваемой конструкции и подобных конструкций, имеющих положительный опыт эксплуатации.
Если на деталь при работе действуют как статические, так и переменные напряжения, вызванные различными нагрузками, и повышенная температура, а прочностные характеристики материала меняются с течением времени или по числу циклон, следует учитывать возможные отклонения этих параметров от их расчетных значений Расчетные статические напряжения могут возрасти из-за неточного определения максимальных перегрузок, переменные — из-за резонансного усиления колебаний, температура — из-за ухудшения условий охлаждения и
т. д Считая каждое из возможных отклонений независимым, можно установить предельное (разрушающее) значение данного параметра, если остальные останутся неизменными. Отношение предельного значения данного параметра к его расчетному значению называют запасом прочности по данному параметру. Таким образом, запас прочности может оцениваться не толь ко отношением напряжений, но и отношениями HarpyjOK, времени работы, числа циклов и т. д. Для ответственных деталей оценку запасов прочности производят по нескольким параметрам.
ЗАПАСЫ ПРОЧНОСТИ ПРИ СТАТИЧЕСКИХ НАПРЯЖЕНИЯХ
При статических напряжениях в качестве предельного напряжения обычно принимают предел прочности ав и запас прочности определяют по формуле
„ gB ^шах
Обычно пв == 1(3-г2,5.
Иногда запас прочности определяют по пределу текучести, имея в виду недопустимость значительной деформации илн нежелательность нарушения упругих характеристик:
О о-пт =------—
°шах
При кручении
«в
тв
Тщах
Для деталей, работающих при повышенной температуре определяют запас длительной статической прочности за определенное время работы:
(19)
° max а также запас по долговечности
(2°)
где — время до разрушения при расчетных напряжениях и темпера
Запаси прочности по несущей способности
41
туре; t — расчетное время работы. Запас по долговечности должен быть в несколько раз больше, чем по напряжению.
При степенной зависимости предела длительной прочности от времени [см. формулу (7)], когда = С = = const, допустимое время работы детали (расчетная долговечность)
nt п^л
Из рис. 4 следует, «то для условий работы детали, соответствующих точке М, действующее напряжение Отах = Одлг. разоушающее — оЛЛ1, время работы t = tpi, время до разрушения /р2, поэтому
адл1 ^р2 /<7дл1\'п
ПдЛ = ~ > nt ~ f — I Q / >
Одл 2 >pi \Одла/
откуда
П/ = п”п. (21)
Обычно 4<[ m<Z 20.
Для ответственных деталей с высокой рабочей температурой, например для рабочих лопаток газовых турбин, определяют запас по температуре
ДГ = г,, - Ггаах, где Ттах — максимальная рабочая температура детали, Гр —температура, при которой деталь разрушится от исчергания длительной прочности при действующих напряжениях за расчетное время работы.
ЗАПАСЫ ПРОЧНОСТИ
ПО НЕСУЩЕЙ СПОСОБНОСТИ
При растяжении, когда напряжения распределены по сечению равномерно, материал достигает предела текучести сразу по всему сечению, размеры детали резко меняются и она теряет способность выполнять свои функции — теряет несущую способность.
Иначе обстоит дело при изгибе, кручении и других видах деформации, отличающихся неравномерным распределением напряжений по сечению. Пока нагрузка мала (.момент Мх иа рис. 19), деформации упруги Когда напряжения в крайних волокнах достигают предела текучести ст, несущая способность детали сохраняется, так как остальные волокна испытывают напряжения, меньшие ат. Затем область пластических деформаций охватывает все большую часть сечения, пока при моменте М = 44 пред напряжения во всех волокнах (за исключением бесконечно малого центрального ядра) не достигают предела текучести. Если материал неупрочняющий-ся, то дальнейшее увеличение нагрузки невозможно
Нагрузку, при которой несущая способность детали оказывается полностью исчерпанной, называют предельной.
Отношение предельной нагрузки к максимальной нагрузке, действующей прн работе на деталь, называют за
tmax
Рис. 19. Распределение деформаций (а) и напряжений (?) по поперечному се"ению балки при изгибе в зависимости от изгибающего момента; Л( > М„ > Л.'.; М. — и л * з пред
42
Механические характеристики материалов и оценка прочности
пасом прочности по несущей способности (по нагрузке):
n = . (22)
Р max
При изгибе запас по несущей способности
Мцред
П = -г,--•
Мтах
Для балкн прямоугольного сечеиия из пластичного материала максимально допустимый изгибающий момент при оценке прочности по несущей способности оказывается в 1,5 раза больше, чем при оценке по максимальным напряжениям. Однако полностью использовать этот резерв прочности можно только при однократном статическом нагружении, если появление некоторых пластических деформаций не мешает нормальной работе конструкции При сложных нагружениях оценку запаса прочности по несущей способности используют как один из критериев надежной работы детали.
ЗАПАСЫ ПРОЧНОСТИ
ПРИ ПЕРЕМЕННЫХ
НАПРЯЖЕНИЯХ
Если деталь испытывает переменные напряжения симметричного цикла, то предельным напряжением будет предел выносливости с учетом концентрации напряжений, состояния поверхности и коэффициента влияния абсолютных размеров (предел выносливости детали):
(°-1к)д —--те--•
Ао
Запас прочности
(ст-1к)д п„ =-------
где о,! — амплитуда действующих переменных напряжений-.
При расчете по касательным напряжениям запас прочности
(^-1к)д
При совместном действии нормального аа и касательного ха напряжений (изгиб и кручение вала) вводят эквивалентное напряжение
(°а)экв =- /°а + 3< (25)
Тогда запас прочности
(а-1к)д
П = -—г-----—
(аа)экв
где в соответствии с формулой (25) принято
(т-1к)д = Ху=г (О-1к)д
Расчет запасов при асимметричных циклах изложен в гл. 31.
Допустимую величину запаса прочности при переменных напряжениях устанавливают на основе опыта эксплуатации машин. Обычные значения запаса прочности па = 1,54-4,0.
ЗАПАСЫ ДЛИТЕЛЬНОЙ ПРОЧНОСТИ ПРИ РАБОТЕ НА РАЗЛИЧНЫХ РЕЖИМАХ
Детали машин работают, как правило, на нескольких различных режимах, отличающихся напряжениями, длительностью (или числом циклов), а также температурными условиями. В этом случае для оценки работоспособности детали используют представление об эквивалентных режимах и эквивалентных запасах прочности (эквивалентных напряжениях, длительностях, числе циклов).
Эквивалентный запас длительной прочности. Разрушение детали под действием постоянных напряжений за некоторое время (р является результатом постепенного накопления в ма
Запасы длительной прочности при различных режимах
43
тер нале необратимых изменений в виде микротрещин и других повреждений При оценке степени повреждения П условно считают, что для исходного (неповрежденного) материала П = О, для момента разрушения /7=1.
Если время работы на некотором режиме при а: = const равно ti, а разрушение наступает за время /рг-, то в первом приближении степень повреждения П i считают равной относительной продолжительности работы на этом режиме:
/7; = -^- =
*pi
где nti — запас по долговечности на /-м режиме.
При работе на нескольких режимах принимается линейное суммирование повреждений
77 = 771+77» + ••• 4-77)1 =
где k — общее число режимов.
Два режима считают эквивалентными по опасности разрушения, если их степени повреждения одинаковы. Поэтому ту же степень повреждения П можно получить при работе на одном (эквивалентном) режиме, если
77 экв = 77. (29)
Для эквивалентного режима
77экв = 7^- = —, (30)
1 Р Экв nt Экв
Xi- <">
и из (28)—(30) следует формула для эквивалентного запаса по долговечности
k
1
nt экв
1=1
При степенной зависимости предела Длительной прочности от времени °дл<Г,7р = С (Т) запас по долговечности nt, = t-pjti связан с запасом
длительной прочности на том же режиме л, = Одл i/^i соотношением
ti
(32)
Подставив (32) в формулу (31) и учитывая, что для эквивалентного режима п{ зкв = лэкэ”в, получаем
(27)
Обычно в качестве эквивалентного выбирают самый тяжелый режим (1 ~ 1), для которого собственный запас длительной прочности имеет минимальное значение = лт1а. Для жаропрочных сплавов при температурах выше 500—600 °C обычно отэкв 4=8
Эквивалентное время работы. Для сокращения времени испытаний можно привести все режимы к наиболее тяжелому, увеличив время работы на этом режиме с ti До /э„в н использовав соотношение
7р(7’1, 01)
7экв ~ ~
nt экв
(34)
С учетом выражений (31) и (32)
(35)
где zij — запас прочности на наиболее тяжелом режиме.
Величина tjKR всегда меньше суммарного времени работы на всех ре-k
жимах f = £ ti.
1=1
По формулам (34) и (35) можно определить время, необходимое для проведения сокращенных эквивалентных испытаний детали на длительную прочность, обеспечивающих за время 7экв ТУ же повреждаемость по длительной прочности, что и при испытаниях по полной программе за время
44 Механические характеристики материалов и оценка прочности
ЗАПАСЫ ВЫНОСЛИВОСТИ ПРИ
РАБОТЕ НА РАЗЛИЧНЫХ РЕЖИМАХ
Для материалов, не имеющих предела выносливости, а также для режимов ограниченной длительности с напряжениями выше предела выносливости, в том числе при малоцикловой усталости, зависимость разрушающих амплитуд с учетом концентрации напряжений оар от числа циклов N до разрушения имеет в логарифмических координатах вид прямой линии:
аор^ = с = const.
Поэтому для симметричных циклов расчеты эквивалентного запаса предела выносливости, эквивалентных переменных напряжений, эквивалентной циклической долговечности можно проводить по формулам предыдущего пункта, заменив в них действующие напряжения ot на амплитуды время ti — на число циклов Nt, предел длительной прочности оДлг — на ограниченный предел выносливости аар/ и использовав соответствующие значения постоянных т и С (см. гл. 31).
РАСЧЕТЫ НА ПРОЧНОСТЬ
Глава 3
РЕЗЬБОВЫЕ СОЕДИНЕНИЯ
МАТЕРИАЛЫ, ПОКРЫТИЯ И КОНТРОЛЬ КРЕПЕЖНЫХ ДЕТАЛЕЙ
Материалы. Согласно ГОСТ 1759.4—87 механические свойства болтов, винтов, шпилек и гаек, изготовленных из углеродистых и легированных сталей, а также марки сталей должны соответствовать указанным в табл. 1, 2. При жестких требованиях к жаропрочности, коррозийной стойкости, габаритам и массе крепежных соединений для изготовления их используют специальные стали и сплавы.
Покрытия. Для улучшения свинчи-ваемости соединений, устранения заедания в резьбе, а также защиты от коррозии, придания декоративного вида предусмотрены покрытия крепежных деталей (табл 3). Покрытия должны быть более мягкими, чем материал резьбовой детали, и деформироваться без разрушения. Вид покрытия для оп-^еделе.чного материала выбирают по
ОСТ 1759.4—87.
Кроме покрытий, указанных в табл. 3, в ряде отраслей машиностроения для уменьшения коэффициентов трения и их стабилизации наносят свинцовое покрытие и применяют вис-мутироваиие (в растворе, содержащем трилон Б, висмут натрия, сегнетовую соль и едкий натрий).
Висмутирование, цинкование, лужение оловом и особенно кадмирование недопустимы для резьбовых соединений, работающих при температуре свыше 200—300 ®С (см. табл. 3), так как в этом случае наблюдается разрушение затянутых болтов (шпилек) из-за проникновения расплавленного цинка, кадмия и других металлов в металл болта (эффект Ре-биидера). Для нормальной работы
соединений необходимо, чтобы рабочая температура не превышала температуру плавления покрытия.
В процессе гальванического покрытия кадмием, цинком и другими металлами происходит наводороживание поверхностных слоев, которое приводит далее к замедленному хрупкому разрушени1 болтов из высокопрочных сталей (ав > 1100 НПа). Для предотвращения разрушений резьбовых соединений следует проводить разводо-роживание. Повторные гальванические покрытия высокопрочных болтов нежелательны по этой же причине
Для резьбовых соединений, работающих в газовом потоке при высоких температурах, наряду с омеднением применяют химическое никелирование (максимальная рабочая температура до 900°C). В отличие от химического катодное никелирование допускает работу соединений до 800 °C.
Хотя стоимость химического никелирования в 3 раза выше катодного, его целесообразно применять для резьбовых деталей, работающих в агрессивной среде при повышенной температуре взамен многослойных покрытий (никель—хром, медь—никель—хром и др.).
Хорошо предохраняет резьбу от заедания мягкое серебряное покрытие. Высокая стоимость этого покрытия ограничивает область его применения.
Толщина покрытия устанавливается в зависимости от шага резьбы в следующих пределах:
Р, мм .... <0.4 0,4—0.8 >0.8
6, мкм .... 3 — 6 6 — 9 9—12
Контроль. Болты, винты, шпильки и гайки после изготовления подвергают выборочному контролю (см ГОСТ 17769—83):
1. Механические характеристики углеродистых и легированных сталей (при нормальной температуре), применяемых для изготовления болтов винтов, гаек
Болты Г айки "в МПа от МПа 0 0 ан Дж смг
Класс проч ности Марка стали Класс проч ности Марка стали не менее ПО
3 6 СтЗкп СтЗсп 10 1 Окп 4 (тЗкп ( 1Зсп 300 4 00 200 25 Не регламентируется 90 150
4 6 20 10 Юкп 20 400 500 240 >5 5о 1 10 По
4 8 10 Юки 320 14 Не рс гламентнруется
5 6 30 3) 300 >0 г0
5 8 10 ** Юкп ** 20 20кп СтЗсп СтЗкп 6 <.т5 15 15кп 35 500 700 400 10 Не регламент? руется 140 215
6 6 35 45 401 560 н 40
6 8 20, 20кп 8 20 20кп 35 45 600 800 480 8 регламентируется 170 245
f 9 54 0 12
8 8 Зэ ***, 35Х 38ХА, 451 10 ЗэХ, 39ХА 800 1000 640 12 60 225 300
10 9 40Г2 40Х ЗОХГСА, 16ХСН 12 40Х ЗОХГС А 16ХСН 1000 1 >00 900 9 40 280 365
19 9 ЗОХГСА 14 30X1 С 4 1200 14 00 1080 8 40 330 425
14 9 40ХН2М^ 4ОХН7МА 1400 ИОО 1 260 7 30 | 390 и св
Примечания 1 Класс прочности болтов обозначен двумя числами Первое число умноженное на 100, определяет минимальное значение ав МПа второе число умноженное на 10, — отношение or/oD %
2 Наибольшие значения ов н твердости являются справочными
3 Стали обозначенные знаками ** и •** применяют соответственно для d 12 и d < 16 мм
4 Клзсс прочности гаек обозначен числом при умножении которого на 100 получают значение напряжения от испытательной нагрузки, МПа
Резьбовые соединения
Упрощенный расчет соединений
47
2 Механические характеристики коррозийно-стойких, жаропрочных, жаростойких и теплоустойчивых сталей (при нормальной температуре), применяемых для изготовления болтов, винтов, шпилек и гаек
Марка стали ов, МПа ат, МПа б». % а н Дж/см*
Болты Г айки не менее
12Х18Ч10Т 12Х18Н9Т, 10Х17Н13М2Т 520 200 40 40
20X13 20X13 14Х17Н2 700 550 15 60
14Х17Н2 650 12 60
10X1IH2313MP 13X11 Н2В2ЧФ — 900 550 8 30
25Х1МФ Х12Н221 ЗМР 25Х2М1Ф 20Х1М1Ф1ТР 750 10 30
3. Виды покрытий крепежные деталей
Обозначение Покрытие Рабочая температура °C, не более
00 Без покрытия
01 Цинковое с хроматиро ванием 300
02 Кадмиевое с хроматы рованием 200
03 Никелевое, многослойное медь — никель ьоо
04 Многослойное медь — никель — хром 600
05 О «исное 200
06 Фосфатное с промасли ванием 200
07 Оловянное 100
08 Медное 700
09 Цинковое 200
10 Окисное анодизацион ное с хроматированием 200
11 Пассивное 200
12 Серебряное 720
а) форму, размеры, качество резьбы и стержня болта (визуальное выявление поверхностных дефектов),
б) механические характеристики деталей. испытания иа разрыв и ударную вязкость (являются обязательными для болтов классов прочности 8.8—14 9), определение чувствительности к перекосу (испытание на разрыв с косой шайбой), испытания на
длительную прочность (по согласованию с заказчиком), малоцикловую усталость.
Резьбовые детали особо ответственных соединений подвергают 100%-ному контролю формы, размеров, качества резьбы и стержня (визуально и люминесцентным методом), твердости, а также выборочным механическим испытаниям.
УПРОЩЕННЫЙ РАСЧЕТ СОЕДИНЕНИЙ
Основные виды соединений показаны на рис 1. Для предварительного выбора размеров ди алей и для проверки прочности неответственных соединений проводят упрощенный расчет.
Основной расчетный случай. Предварительно затянутое соединение нагружено внешней продольной силой (рис 2). Диаметр болта (шпильки) по заданному внешнему усилию выбирают по формуле
и - 1/ 4УУ
1 I Я [Яр] ’
(1)
где /V — растягивающее усилие от внешних нагрузок, приходящееся на данный болт, [ар] — допускаемое напряжение при растяжении, — внутренний диаметр резьбы болта.
48
Резьбовые соединения
а)
Рчс. 2. Основной расчетный случай
Рис. 1. Основные типы резьбовых соединений:
о ~~ болтом: б — винтом:
<? — шпилькой; г — со вставкой
Допускаемые напряжения в долях от предела текучести указаны в табл. 4, а основные размеры и площади поперечного сечения для метрической резьбы — в табл. 5.
Допускаемые статические нагрузки и моменты затяжки для болтов (шпилек) даны в табл. 6 Момент на ключе при затяжке определен по приближенной формуле
Л4КЛ « 0,1 SQd, (2)
где Q — усилие затяжки болта, d — наружный диаметр резьбы.
Обычно
Л4КЛ = (0,04 ч- 0,07) ст(Р. (3)
Дополнительные расчетные случаи. Соединение нагружено поперечной си-
Рис. 3. Дополнительный расчетный случай
лой. Если болт установлен в отверстие без зазора или с небольшим натягом (рис 3), то диаметр стержня болта определяют из расчета на срез:
где N — поперечная нагрузка на один болт; п — число плоскостей среза; [т] — допускаемое напряжение иа срез, обычно принимают [т] « (0.2-?-0.3) стт.
Если болт поставлен в отверстие с зазором, то поперечная нагрузка должна восприниматься силами трения. Болт рассчитывают на силу за
тяжки
N М
<2о = — = — (5)
где f — коэффициент трения иа стыках деталей.
При расчете принимают следующие значения коэффициентов трения /•
Необработанные стыки со следами окалины.................. 0,3
Обработка стыка:
пескоструйная .............. 0,5
газовой горелкой .... 0,4
методами резания .... 0,10 — 0.15
то же при наличии масляиой
пленки ... . . . 0,06
Окраска стыка алюминиевым порошком . . 0,15
верной антикоррозийной краской . . 0,10
свинцовым суриком .... 0.06
Допускаемое напряжение обычно принимают pip) яа0,6аг.
Момент иа ключе для создания силы затяжки
Л1„л » 0,07атсР.
(6)
Упрощенный расчет соединений
49
4. Отношение [”pj/0T Для резьбовых соединений
Сталь При постоянной нагрузке и диаметре резьбы d, мм При переменной нагрузке от 0 до максимальной н Диаметре резьбы d, мм
6- 16 16 — 30 6-16 16 — 30
Углеродистая 0,20—0,25 0,25-0,40 0,08 — 0,12 0,12
Легированная 0,15 — 0.20 0,20-0 30 0,10 — 0,15 0,15
5. Соотношения наружного диаметра d, шага резьбы Р, внутреннего диаметра н площади поперечного сечения fi для метрической резьбы
d р Ft d Р di F,
ММ мм* мм ММ2
3 0,5 2,386 4,47 1.0 18,773 279
4 0,7 3,141 7,75 1.5 18,160 259
5 0,8 4,018 12,9 20 2,0 17,546 242
1,0 4,773 17,9 2,5 16,932 225
1.0 6,773 36 1.0 20.773 339
1,25 6,466 32,8 22 1.5 20,160 319
2,0 2,5 19,546 300
18,932 281
1.0 8,773 60,4
10 1,25 8,466 56.3
1,5 8,160 52.3 1 0 22,773 407
24 1.5 22,160 386
2,0 21,546 зьь
1.0 10,773 91,1 86 3,0 20.319 324
12 1,25 10,466
1,5 10,160 81
1.75 9,853 76,8 1.0 25,773 522
1,5 25,160 497
27 2,0 24,546 473
1.0 12,773 128 3,0 23,319 427
14 12,160 116
2,0 11.545 105 1,0 28,773 650
1.5 28 160 623
1.0 14,773 171 г,'"' 27,546 596
16 1.5 14,160 157 3,5 25,70s 519
2.0 13.546 144
1 0 16,773 221 1,0 31,773 793
18 1,5 16,160 205 1,5 31,160 763
2,0 15,546 190 эЗ 2,0 30,546 733
2,5 14,932 175 3,5 28,706 647
Диаметр болта по заданной силе Q можно определить также из табл. 6
Если резьбовое соединение должно выдерживать большие растягивающие и срезывающие нагрузки, то применяют специальные пояски, а также
конструктивные элементы в виде шпонок, втулок и других деталей, которые разгружают болты от срезывающих сил (рис. 4).
Методика расчета ответственных резьбовых соединений изложена ниже.
50
Резьбовые соединения
б. Допускаемые статические нагрузки и моменты затяжки для болтов (шпилек)
Резьба Нагрузка, Н . Момент затяжки 10“2, Н« мм Нагрузка, Н Момент за-1 тяжки 10”2> : Н* ММ Нагрузка, Н 1 Момент за-. тяжки 10~8, Н* мм
а р А Б А Б А Б
мм Сталь 45 ЗОХГСА 4UXH2MA
3 0,5 280 840 3,75 370 1100 5,3 450 1350 6.0
4 0.7 580 1500 9,0 760 1960 11.7 950 2450 14,8
5 0,8 1100 2600 19.5 1450 3400 25,2 1800 4250 32,8
6 1.0 1700 3750 34,0 2200 4850 43,2 2700 5950 54,5
1.0 3600 7700 92 4750 10 000 120 5850 12 500 150
8 1.25 3300 7000 64 4300 9150 110 5300 11 300 140
10 1.0 6500 13 400 200 8500 17 500 260 10 500 21 800 320
1.5 5500 11 400 171 7300 15 000 300 9000 18 500 278
1.0 10 500 21 000 300 13 700 27 400 390 17 000 31 000 490
12 1.5 9 300 18 600 270 12 100 24 200 350 15 000 30 000 430
1.75 8 700 17 400 250 11 300 22 600 330 14 100 28 200 410
1,0 15 600 30 400 640 20 400 39 600 820 25 100 48 900 1030
14 1.5 14 100 27 400 570 18 400 35 800 750 22 600 44 000 920
2 12 500 24 400 510 16 500 32 100 670 20 400 40 000 840
1,0 22 000 41 900 1000 28 900 55 000 1320 35 600 67 500 1600
16 1,5 20 000 38 000 920 26 400 50 300 1200 32 400 61 500 1500
2,0 18 600 35 400 850 24 000 45 600 1000 26 900 56 000 1300
1,0 31 200 57 000 1600 41 000 75 000 2000 50 500 92 000 2500
18 1.5 28 800 52 500 1400 38 000 69 500 1900 46 500 85 000 2300
2.0 26 500 48 500 1300 35 000 64 000 1700 43 000 78 000 2100
Примечания 1. Случай А — неконтролируемая затяжка, грубый учет Hafpy зок; случай Б — контролируемая затяжка.
2. ат в МПа сталей стали 45 — 650; ЗОХГСА — 850; 40ХН2МА — 1050.
Рис. 4. Способы разгрузки соединений от сил в плоскости стыка
Уточненный расчет соединений
51
УТОЧНЕННЫЙ РАСЧЕТ СОЕДИНЕНИЙ
При расчете ответственных резьбовых соединений (шатунные болты и др.) необходимо более точно учитывать внешнюю нагрузку, усилие затяжки, дополнительные напряжения от изгиба и кручения, а также влияние температуры деталей, конструктивных и технологических факторов на прочность соединений.
Определение усилий в затянутом соединении при действии внешней осевой нагрузки. В расчетах групповых соединений промежуточные детали заменяют эквивалентными по жесткости (на растяжение-сжатие) втулками, связанными абсолютно жесткой диафрагмой в форме деталей. К диафрагме прикладывают внешние нагрузки.
С помощью такой схематизации осуществляют переход от группового соединения к расчету одиночного (одноболтового) соединения.
Рассмотрим соединение (рис. 5), затянутое с усилием Qo и затем нагруженное внешним растягивающим усилием Л\ приходящимся на данный болт.
Полное усилие, действующее на болт, определяют из диаграммы усилий (рис. 6). На диаграмме приведены кривые деформирования болта (кривая /) и промежуточных деталей (кривая II), выражающие зависимость усилия от удлинения (илн сжатия). При упругих деформациях эта зависимость изображается прямыми линиями.
Углы наклона прямых аа и ад характеризуют соответственно податливость болта и стягиваемых деталей и определяются равенствами
= tga„=J-,
где Xg — коэффициент податливости болта, соответствует его удлинению под действием единичной растягивающей силы; 1д — коэффициент податливости стягиваемых деталей;
а6 = -=4-; (7)
СбГб
здесь ls — расчетная длина болта; “б и Fg — соответственно модуль уп-
Рис. 5. Резьбовое соединение (а) и его расчетная схема (б*)
Рис. 6. Диаграмма усилий в резьбовом соединении
(8)
ругости материала и площадь сечения болта.
Для промежуточных деталей ^д ~ Е F-n
где /д — длина (толщина) промежуточных деталей; Ед — модуль упругости материала деталей; Fa — площадь поперечного сечения деталей *.
Усилие затяжки Qo вызывает удлинение болта на величину бб и сжатие промежуточных деталей на величину бб- Точки Aj и Ао на диаграмме характеризуют усилие и деформации в болте и промежуточных деталях после затяжки.
Внешняя нагрузка У вызывает дополнительное удлинение болта на ве-
• Определение коэффициентов податливости приведено ниже.
52
Резьбовые соединения
Рис. 7. Зависимость полного усилия в болте от внешней нагрузки
личину Л/ и усилие в болте возрастает на величину
„ М
W6 = A/tga6 = — .
Лб
Сила, действующая на промежуточные детали, уменьшится на величину
Это снижение усилия можно найти, проводя через точку Ао прямую //', параллельную прямой //.
Сумма усилий
N6+ Na= N, тогда
‘___।_L. ° 1 Д
2-6 А'Ц
Дополнительное усилие на болт
*6 = X*, (9)
где X — коэффициент основной нагрузки,
Я.Д
<10)
Полное усилие на болт
Q6 = Qo + tf6 = Qo + xAC (Н)
Расчетная зависимость полного усилия, действующего на болт (шпильку), от внешней нагрузки показана на рис. 7.
Если внешняя нагрузка изменяется циклически (от 0 до N), то амплитуда
переменных напряжений в резьбовой части болта
a - (12)
°a~2F1~ 2 Г, (12) и среднее напряжение
Qo+4",V6
Ощ = ------р------- О0 4~ aa, (13)
где о0 — напряжение предварительной затяжки.
Из формулы (9) следует, что в затянутом резьбовом соединении внешняя нагрузка на болт передается лишь частично (% = 0,24-0,3).
Равенство (11) справедливо до начала раскрытия стыка. Усилие на стыке после приложения силы
Qc ~ Qo — д ~ <2о — (1 %) IV,
откуда условие нераскрытая стыка
Qo >(!-%) IV- (14)
Если внешняя нагрузка возрастает до величины
то стык раскроется (точка Ас на рис. 7), н при дальнейшем увеличении внешней нагрузки усилие на болт будет
<2б= <2о + ЛГ*=ЛГ. (15)
где У — внешняя нагрузка, действующая на соединение.
После раскрытия стыка внешняя нагрузка полностью передается на болт, что при переменной нагрузке приводит к появлению дополнительных напряжений ударного характера. Поэтому усилие затяжки следует назначать таким, чтобы при заданной внешней нагрузке У стык оставался плотным.
Для снижения переменных напряжений оа в болте следует уменьшить коэффициент основной нагрузки X, т. е. применять податливые болты (увеличивать 1б) и жесткие фланцы (уменьшать 1д). Преимущества податливых болтов наглядно иллюстрирует рис. 8. Отсюда правило конструирования резьбовых соединений:
Уточненный расчет соединений
53
Рис. 8. Диаграммы усилий для соединений с различной жесткостью болтов при одииа новых условиях работы
жесткие фланцы — податливые болты.
Прн наличии температурной деформации
Af — ссд/д/д (16)
где ад, /д и яб, h — коэффициенты соответственно линейного расширения и температуры промежуточных деталей и болта.
Температурное усилие
Полное усилие на болт в этом случае
С = Со + Ct + = Со + Ct + Х^-
(18)
Определение коэффициентов податливости болта и промежуточных деталей. Для болта постоянного сечення значение Кб определяют по формуле (7). Для болта переменного сечення (рис. 9)
= (19) гб:
гДе hi и F^t — соответственно длина и площадь поперечного сечения t-ro Участка болта.
Для коротких болтов (/< 6d) следует учитывать податливость резьбы ® пределах соединения н головки болта.
Податливость резьбы можно вычис-
лять по формулам:
прн = 6 10
Лр « (0,95 - 0,80) ;
при = 10 4- 20
Лр « (0,80 4- 0,70) ,
(20)
где Р — шаг резьбы.
Если модули упругости болта (шпильки) и гайки (корпуса) различны, то можно принимать
Коэффициент податливости головки болта с высотой Л
. __ 0,15 г“ E6h '
Для коротких болтов коэффициент податливости следует вычислять по формуле п
Лб = 'Ёб S + Ар + Аг (23) 1=1
Коэффициент податливости промежуточных деталей определяют в предположении, что при действии осевой силы деформация, равномериая по
54
Резьбовые соединения
а)
сечению, распространяется в пределах «конуса давления» (рис 10).
На основании теоретических н экспериментальных данных принимают
tg ct = 0,4 4- 0,5, (24)
где а — угол, составленный образующей конуса с осью
Для промежуточных деталей небольшой толщины (/ <Z d0, где d0 — диаметр отверстия под болт) конус давления можно заменить условным полым цилиндром с наружным диаметром (рис. 10, б)
dH = а -Ь 1г tg а,
где a — внешний диаметр опорной поверхности гайки
Коэффициент податливости тонкой промежуточной детали
Д <тт _ *
£ДДГ[(а + /118“) ~4]
(25)
В общем случае для промежуточной детали произвольной толщины (рис. 10, б) коэффициент податливости определяют по формуле
. (а + д!0) (а + 2/t tgct —d0)
8 (a-d0)(a4-2Z1tga + d0)- ' '
Значение X* приведено в табл 7.
Если болт соединяет два фланца (см рнс. 10), то суммарный коэффициент податливости
4,60 д — Endo tg а Х
v Ь (а + ^о) (а + Z tg ct — d0)
Л 8 (a — d0) (a + Z tg а + d0) ’ 1 >
В случае, когда конус давления выходит за пределы промежуточной детали (рис 11), коэффициент податливости определяют по формуле
- 2’3
д End0 tg ct Х
у щ (а + d0) (D — da) ।___4/2
(а—dp)(D-{-do) En(D2 — d%) ’
(29) где
Хд Ed0 Ла’ 1г~1 2tgct (Z? do)’
Уточненный расчет соединений
55
7. Значения безразмерного коэффициента податливости
а 1 Ц при tg а а 1 Xj при tg а
^0 do 0.4 0,5 d. do 0.4 0.5
1,2 1 2 3 1,03 1,31 1.45 0,90 1,11 1,22 1,6 3 5 0.76 0,88 0.65 0,74
5 1 ,ьо 1,32 1 0,35 0,32
1.4 1 2 3 0,64 0,87 0,99 0.57 0,75 0,84 1.8 2 3 5 0,51 0,61 0,72 0.45 0.53 0.61
5 1.13 0.94 I 0,28 0.26
1,6 1 2 0,46 0.65 0.42 0,57 2,0 2 3 5 0,40 0,51 0,61 0.37 0.44 0,52
Подобной формулой можно воспользоваться при часто расположенных болтах (шпильках), когда один конус давления перекрывает другой.
Если для группового соединения li<Z 0,1 I, то при расчете можно учитывать площадь промежуточной детали, приходящуюся на одну шпильку (участком Zj иа рис. 11 пренебрегают).
Расчет усилий в сложных силовых схемах, ьолт соединяет несколько промежуточных деталей (рис. 12;, внешняя нагрузка приложена к произвольным стыкам.
Различают детали системы болта, в которых в результате действия внешней нагрузки абсолютная деформация возрастает (детали 0, 1 на рис. 12), и детали системы корпуса, в которых абсолютная деформация уменьшается (детали 2, 3). Коэффициент основной нагрузки
Сумма коэффициентов податливости деталей системы ______________корпуса__________
Сумма коэффициентов податливости всех деталей
В рассматриваемом случае (см. Рис. 12)
з s 1=1
hi — коэффициент податливости деталей соединения; Хо — то же для болта.
Для уменьшения коэффициента основной нагрузки упругие детали (упругие шайбы и другие детали) следует вводить в систему болта.
Рис. 11. Выход конуса давления за пределы детали
56
Резьбовые соединения
Рис. 12. Сх*ма нагружения силовой шпильки
РАСЧЕТ НАПРЯЖЕНИЙ
КРУЧЕНИЯ
Прн затяжке резьбовых соединений путем завпячиван"я гайки болт (шпилька) скручивается моментом
Mp = Q04-tg(e + P') =
d, nd, Р
— Уо-ч р-
(30)
иля с достаточной точностью
/ р \
/Ир — 0,5Qed3 -р/ру , (31)
где Qo — усилие затяжки; d3 — средний диаметр резьбы; 0 — угол подъ-р ема винтовой линии, tg В — —г;
& nd2 ’ р' — угол трения, соответствующий Коэффициенту трения в резьбе /р,
/р = ----» l,15f, f — коэффи-
C0ST
циент трения материала гайки по материалу болта (шпильки); а — угол профиля резьбы; Р — шаг резьбы.
Момент в резьбе Мр < Л4Кл, так как момент и а ключе должен также преодолевать силы треиия на опорной поверхности гайки, причем
Л1КП — /Ир + Л4Т,
где М т — момент трения на торце гайки.
Для плоского опорного торца гайки
1 а3 — dp
Мт = “о- Со/т —----~2 &
3 a2~d20
(32)
где а — внешний диаметр опорного торца гайки; dn — диаметр отверстия в корпусе под болт; fT — коэффициент трепня на торце гайки.
Значения коэффициентов треиия в резьбе v на торце гайки даны в табл. 8—10
Для приближенных расчетов вместо формул (30) и (31) используют соотношение
УИр ~ kQ^d, (33)
в котором d — наружный диаметр резьбы; k — безразмерный коэффициент, для метрической резьбы приведен в табл. 11.
Напряжения кручения в резьбовой части болта
/ИР
Напряжения кручения в болта (шпильки)
_ ‘^р
Т° ” 0,2d;J
Если ______________
]/ о2 + 3? > 0,8ат>
(34)
стержне
(35)
то болты или шпильки следует предохранять от скручивания при затяжке
Расчет напрялссггай лруч^^л
57
8. Средние значения коэффициентов трения в резьбе соединений при напряжениях затяжки Jq — (0,4-r-U,6) Ст, ТОл£ЦпИа покрытия Ь мкл*
Материал болта и гайки Покрытие, смазочный Материал ПерВал загяя'ка Десятая затяжка
ЗОХГСА Без покрытия То же, масло МК*8 0,18 0,13 0,58
ВТ16 То же, смазка ВНИИНП-232 0.18 0.12
12Х18Н10Т То же, смазка ВНИ11НП-220 То же, смазка ЦИАТИМ-222 0,08 0.11
ЗОХГСА • ВТ16 12Х18Н10Т Кадмиевое 0,25 0,15 0,19 0,16 0,21 0,27 0.3
ЗОХГСА Медное 0.28 0.16 -
ЗОХГСА Цинковое 0,23 -
ВТ16 12Х18Н10Т Серебряное 0,095 О.И 0,18 0,21
* В знаменателе дробя даны значения при смазывании резьбы маслом МК-8.
* • То же со смазкой СТ
Примечание Соединения пз стали ЗОХГСА имели резьбу М12Х 1.5, а остальные М16 X 1,5
9. Средние значения коэффициентов трения на торце гайки /т при напряжениях загяжки а0 — (0,4~-0,6)от
Материал гайки и шайбы Покрытие, смазочный материал Первая затяжка Десятая затяжка
ЗОХГСА В Тб Без покрытия Ти же масло МК-8 Без покрытия То же, смазка ВНИИНП 232 0,16 0,13 0,16 0,06 0,22 О.И 0,17 0,15
ЗОХГСА • ВТ6 Кадмиевое » 0,05 0,06 0.1: 0,14 0.05 0,2
ЗОХГСА •• Цинковое Медяое 0,10 0.12 0,08 0,26 0,18 0.09
*, ** См сноски к табл 8
10. Средние значения приведенного (при / = /т) коэффициента треппя для определения момента на ключе
Резьба
2 к
С 4) Л о
Покрытие m {-сс «о F®
о w « а
О ч
О) О X О £
ю 1 и и 2
Без покрытия 0.2 0,16
Кадмиевое 0,13 0,1
Медное 0,18 0,14
Цинковое 0,22 0, 18
Оксидное 0,24 0.20
Примечание При пов-торныл затяжках приведенный коэффициент трения для Смазочных резьб дол/п^и быть уменьшен на 10 — 30%
58
Резьбовые соединения
Значения f и k для метрической резьбы
Состояние контактных поверхностей гр k
Чисто обработанные поверхности, смазанные Грубо обработанные поверхности 0,1 0,07
смазанные 0 2 0.12
несмазанные 0 3 0 17
Рис. 13. Конструктивные способы разгрузки соединений от скручивания при затяжке
(например, с помощью специального шестигранника, рис. 13, а, или шлицевых втулок, рис. 13, б, в).
ВЫБОР ПРЕДВАРИТЕЛЬНОЙ
ЗАТЯЖКИ
Напряжения затяжки устанавливают из условия плотности стыка — необходимого условия прочности динамически нагруженных резьбовых соединений.
Если напряжение затяжки
°о °вн (1 — X).
то происходит раскрытие стыка. В этом равенстве авн — номинальное напряжение в болте (шпильке) от внешней нагрузки.
Для получения надлежащего запаса плотности стыка напряжения затяжки определяют из условия
do — wBB, (36)
где v — коэффициент затяжки, а напряжение авн — соответствует наибольшему внешнему усилию N.
По условию плотности стыка v = = 1,54-2 для постоянных нагрузок; v = 2,54-4 — для переменных нагрузок.
Допустимое напряжение затяжки а0 < 0,8ат, (37)
где ат — предел текучести материала болта.
Обычно ав ж (0,54-0,7) ат.
Напряжение затяжки для ответственных резьбовых соединений необходимо контролировать. Наиболее распространены на практике методы контроля с помощью измерения:
а) удлинения болта нли шпильки;
б) угла поворота гайки;
в) крутящего момента на ключе.
Последний метод является основным во многих отраслях машиностроения. Он реализуется с помощью специальных динамометрических ключей, тарировку которых осуществляют в лабо раторных условиях.
Для приближенных расчетов можно использовать формулы:
А? к л — fQod,
Мкл = 0,07 <м*>. (38)
РАСПРЕДЕЛЕНИЕ НАГРУЗКИ ПО ВИТКАМ РЕЗЬБЫ
И КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ
В СОЕДИНЕНИЯХ
Разрушения резьбовых соединений, особенно при переменных нагрузках, часто связаны со значительной концентрацией напряжений во впадинах резьбы нз-за неравномерного распределения нагрузки между витками и высокой местной напряженности.
Распределение нагрузки между витками можно охарактеризовать интенсивностью распределения осевых сил по высоте резьбы (рис. 14):
Распределение нагрузки по виткам резьбы
59
где Q (г) — сила, растягивающая стержень болта или сжимающая тело гайки в сечении г:
г
Q (г) = j q(z)dz. (40) о
Записав уравнение совместности перемещения тел болта, гайки н витков резьбы и выразив входящие в это уравнение перемещения через силовые факторы, для стержневой модели соединения получим дифференциальное уравнение
?"(г)--|-?(г) = 0; (41)
здесь Р — коэффициент, характеризующий податливость тел болта и
гайки,. ₽ = „ g- + с. Г , где Eq
Eqcq сгг г
и ЕГ — модули упругости материалов болта и гайки; Fq и Fr — площади поперечных сечений тел болта и гайки; у — коэффициент, характеризующий податливость витков резьбы болта и гайки,
где 1g и 1* — безразмерные коэффициенты, зависящие от геометрических параметров соединения; Р — шаг резьбы, f — проекция боковой поверхности витка на плоскость, перпендикулярную оси г.
Решение уравнения (41) для соединения типа болт—гайка с учетом граничных условий имеет вид
= (42)
где ___
Из соотношения (42) следует, что в болтовом соединении нагрузка на витки возрастает от верхних витков 'К нижним по закону гиперболического Косинуса (рис. 14, б).
Рис. 14. К расчету распределения нагрузки между витками резьбы
Нагрузка на отдельные витки (рис. 15) г+Р
Qp= j q(z)dz. (43) 2
Для соединения типа стяжки
(рис. 16)
_, х Qm Г ch mz , Я ~ ₽shm// L'ftifo'+
причем в зависимости от соотношения жесткости тел болта и гайки максимальное напряжение будет либо в сечении z = 0, либо в сечении г — Н.
При практическом выполнении соединения типа стяжки нецелесообразно стремиться к увеличению площади охватываемой детали, так как зто прн-
Номер витка
Рис. 15. Нагрузка на отдельные витки в % от общей нагрузки (соединение с резьбой М24)
60
Резьбовые соединения
Рис. 16. Схема соединения типа стяжки
ведет к снижению прочности соединения.
Численное решение осесимметричной контактной задачи для резьбового соединения (метод решения дан в гл. 29) подтвердило достоверность приведенного метода расчета распределения нагрузки в соединениях (табл. 12).
Распределение нагрузки по виткам резьбы оказывает влияние иа несущую способность резьбы прн статических нагрузках и особенно существенно влияет иа сопротивление усталости соединений. На основании анализа многочисленных экспериментальных исследований устаиовлеио, что снижение нагрузки на нижнем витке приводит к пропорциональному повышению предела выносливости соединений. Конструктивно улучшить рас-
12. Распределение нагрузок между витками резьбы М!0 (радиус скругления впадии резьбы Р — 0, 108 Р)
Номер витка от опорного торца гайки Нагрузки иа отдельные витки, % от общего усилия, полученные
по формуле (43) из решения контактной задачи
1 36,5 37,35
2 23.75 22,83
3 16 5 16,78
4 12,75 13,40
5 10.50 9 64
пределеиие нагрузки между витками можно путем увеличения податливости витков у и уменьшения податливости тел болта и гайки соответственно при растяжении и сжатии р. Последнее может быть достигнуто введением в соединение резьбовой спиральной вставки (см. рис. 1, г), применением гаек растяжения (рис. 17) и другими методами (рис. 18) *.
Влияние концентрации напряжений иа прочность учитывают теоретическим коэффициентом концентрации напряжений
„ °тах “а ~ а ’ (,ном
где Отах — максимальное растягивающее напряжение в зоне концентрации; оном — номинальное напряжение в сечении по внутреннему диаметру резьбы.
На рис. 19 приведены результаты численного расчета напряжений во впадинах соединения с резьбой М10 при высоте гайки Н = 0,8d и радиусе скругления во впадинах резьбы R = = 0.108Р. Наибольшие напряжения действуют во впадиие под первым рабочим витком, а максимальные напряжения на контуре концентрируются не в центре впадины, а в точке, смещенной к рабочей грани. Последнее связано с тем, что во впадинах имеет место концентрация напряжений от общего потока растягивающих усилий и от изгиба витка Напряжения во впадине под вторым рабочим витком почти в 3 раза ниже, чем под первым витком из-за разгрузки.
Можно использовать следующую приближенную зависимость для вычисления теоретического коэффициента концентрации напряжений в резьбовом соединении типа болт—гайка.
ао= 1 + 1.1 1/4-- (45) * i\
Расчеты показывают, что концентрация напряжений в соединении может быть снижена на 20% простым увеличением радиуса скругления от Pm!n = 0,108? (по ГОСТ 9150—81) ДО #mln = 0,Н4 Р при Ртах = 0,18?
* Подробнее о распределении нагрузки по виткам резьбы см работу [1].
Распределение нагрузки по виткам резьбы
61
4
Рис. 17. Способы улучшения распределения нагрузки между витками резьбы с помощью гаек растяжения
Рнс. 18. Конструкции соединений с улучшенным распределением нагрузки между витками резьбы:
а — сжаго-растянутая гайка, h/d = 1; б — гайка с поднутрением, h/d = 0,47, в — гайка со скошенными витками; г — болт со скошенными витками
0 18
0 10
е~н
Рис. 19, Распределение напряжений во впадинах резь-бы(аном = 1’27 МПа; а ~ * 4.6)
б=1 МПа 0
62
Резьбовые соединения
Рис. 21. Распределение напряжений под головкой болта с двухрадиусиой галтелью.
а — напряжения в стержне б — напряжения на опорном торце, 1 — недеформируемые стягиваемые детали, 2 — деформируемые стягиваемые детали
Распределение напряжений под го-ловкой болта с резьбой М10 показано на рис 20, а; на рис 20, б приведено распределение контактных давлений под головкой при опирании на жесткие стягиваемые детали (кривая /) н стягиваемые детали из одинакового с болтом материала (кривая 2). При увели
чении радиуса скругления под головкой болта концентрация напряжений снижается, однако при этом уменьшается опорная поверхность н возрастают контактные давления Более эффективной оказывается двухрадиусная галтель под головкой болта (рис 21). Причем больший радиус следует прн-
Прочность при постоянных нагрузках
63
менять на участке, прилежащем к цилиндрической части стержня, так как в этой зоне действуют наибольшие контурные напряжения (см. рис. 20). Использование меньшего радиуса на второй части галтелн увеличивает опорную поверхность под головкой болта.
Теоретический коэффициент концентрации напряжений под головкой болта можно вычислить по приближенной формуле ___
«а = 1 + 0,55 ]/ ~ , (46)
где /?е — радиус галтели под головкой; d — диаметр стержня болта.
ПРОЧНОСТЬ ПРИ постоянных НАГРУЗКАХ
Разрушение резьбового соединения при постоянных (статических) нагрузках происходит вследствие обрыва стержня болта (шпильки) илн среза витков резьбы.
Нагрузка, разрушающая стержень болта в его резьбовой части,
Qpaap = -J-Ob» (47)
где og — предел прочности при растяжении стержня с резьбой.
Отношение ав к пределу прочности материала ав по экспериментальным данным приведено в табл. 13.
Если разрушающую нагрузку относить к фактической площади попереч
ного сечения резьбы F, то величина а'в уменьшится. Фактическая площадь поперечного сечення лежит в пределах
^1 _ Р _ nd* “Г<f<T*
Иногда в качестве расчетной используют площадь, отнесенную к условному среднему диаметру (между средним и внутренним диаметрами резьбы):
Предел прочности резьбового стержня в этом случае
. Qpaap ав = -77-
отличается от
Значения отношения приве-
дены в табл. 13. Для болтов из распространенных сгалей (стали 45, 38л А, ЗОХГСА и др.) при расчете по формуле (48) можно принимать
С* = °в-
Стали с пределом прочности ав > > 1600 МПа и с пониженной пластичностью применять для силовых соединений, нагруженных растягивающими нагрузками, не рекомендуется.
<JB <?в
13. Отношения ---- и ----- для сталей различной прочности
% °в
Способ обработки ов, МПа °в Q Q и » •
Нарезанная или накатанная резьба с последующей термообработкой 700-1200 1300-1400 1,35—1,25 1,05—6.9 1,15-1,0 0.9-0.8
Накатанная резьба без последующей термообработки *- — 700—1200 1300 —1400 1,40—1,2 1,2 — 0,95 1.2 — 1.05 1,05-0,85
64
Резьбовые соединения
14. Коэффициент &т для соединений с болтами из сталей и титановых сплавов
°вб °вг Шаг резьбы
Св 1.3 Крупный н первый мелкий Второй и более мелкий 0,7—0.75 0.65-0,7
<1,3 Для всех шагов 0,55 — 0.6
Необходимо иметь в виду, что при наличии после резьбы проточки с диаметром da < d-i прочность стержня определяют в сеченин по проточке или гладкой части стержня, если dc < А.
При наличии проточки разрушающая нагрузка
ndn
Qpaap- с = х<тв > (49)
где х— коэффициент, учитывающий упрочняющий эффект от проточки.
Для проточки в виде полукруглой канавки можно принять х = -у-; для проточки, имеющей цилиндрический участок, х= 1.
Основными конструктивными параметрами, определяющими прочность витков, являются диаметр d и шаг резьбы Р, радиус закругления во впадинах резьбы R, высота гайки Н (длина свинчивания 0, соотношение механических характеристик материалов болта и гайки.
Усилие, вызывающее срез витков: резьбы болта
Qp б ~ ^1^бЯ^тТвб; (^9)
резьбы гайки
Qp. Г = (51)
В этих равенствах и kr — коэффициенты полноты резьбы болта и ганки; для метрической резьбы йд -= kr -- 0,87, для трапецеидальной Лб ~ kv = 0,65, Н —- высота гайки; km — коэффициент, учитывающий неравномерность деформаций витков по высоте гайки при наличии в резьбе
пластических деформаций и особенности разрушения резьбы; теоретически km = 1 лишь для соединений с равномерным распределением нагрузки между витками, разрушение которых происходит в результате чистого среза, на практике такой случай почти не реализуется, и всегда km < 1; TBg и твг — пределы прочности материалов соответственно болта и гайки на срез; можно принимать тв — (0,6-?0,7) ав для сталей и титановых сплавов, тв = = (0,7-? 0,8) а в для алюминиевых и магниевых сплавов.
На основании экспериментальных данных можно рекомендовать для практических расчетов значения коэффициента km из табл. 14.
При расчете несущей способности резьбы соединений стальных шпилек с корпусами из пластмасс, алюминиевых и магниевых сплавов можно принимать km = 0,75—0,85, а для соединений со спиральными вставками km ~ 1-
Для обеспечения равнопрочностн стержня болта и витков резьбы гайки должно быть
Величину Яо, определяемую из условия равнопрочносги стержня и витков резьбы, называют необходимой высотой гайки. Фактическая высота гайки
Я>Я0.
Для резьбовых соединений, воспринимающих значительные статические нагрузки, не следует применять резьбы с отношением диаметра резьбы к шагу d . *0.
При мелкой резьбе < 15^ может наступать явление цепного среза, когда разрушение витков идет одно за другим, и равнопрочное™ гайки и болта нельзя достичь даже при очень большой высоте гайки. Для гаек из пластмасс цепной срез возможен при
Высоту гайки или длину свинчивания, при которой несущая способность
Прочность при постоянных нагрузках
65
{5. Относительная длина завинчивания стальных шпилек в корпус
<jb материала шпильки, МПа H/d для корпусов из материала
дюралюминия силумина чугуна и бронзы
400- 500 900—1 100 0,8 —0,9 1,6 —2.0 1.4-2,0 1.8 —2,0 • 1,2-1,4 2,0 *
* Рекомендуется увеличивать диаметр конца шпильки, ввертываемого в корпус, или применять резьбовую вставку
Примечание. св дюралюминия 360 — 400; силумина 160 — 200; чугуна н бронзы 180 — 250 МПа
резьбы наибольшая, называют предельной. Эта длина свинчивания соответствует максимальному числу витков, несущих нагрузку при наличии в резьбе пластических деформаций, и зависит преимущественно от характера распределения нагрузки по виткам, диаметра и шага резьбы, диаметра (радиальной жесткости) гайки. При диаметре гайки D = 3d предельная относительная высота гайки (длина свинчивания) ~ 1,94-1,95.
При уменьшении диаметра гайки до D = 2d радиальные деформации возрастают и предельная длина свинчн-
/ Н \
вания снижается до —Г = 1,554-
\ d ) п
1,6.
Предельная несущая способность резьбы по разрушающему усилию может быть определена по формулам (50) или (51), для этого необходимо принять в них Н= НП= 1,3d при D = 2d или Нп = 2d при D — 3d.
Длину завинчивания шпилек в корпус можно принимать по табл. 15.
В большинстве конструкций резьбовые соединения подвержены воздействию изгибающих нагрузок от перекоса опорных поверхностей и др.
Болты из высокопрочных сталей с °в > 1300 МПа весьма чувствительны к перекосу опорных поверхностей на 4° и более. Прочность болтов из сталей и титановых сплавов с ов < 1200 МПа при нормальной температуре не снижается даже прн перекосе поверхностей на 8°.
3 Зака; 402
Для силовых резьбовых деталей не следует применять сталь с ударной вязкостью ая < 30 Дж/см2.
Чувствительность стальных болтов к перекосу можно понизить повышением температуры отпуска.
На практике напряжения изгиба снижают прн помощи технологических (введение жестких допусков на перекос поверхности, биение торца гайки и т. п.) и конструктивных мер (рнс. 22).
При проектировании резьбовых соединений, работающих в условиях высокой температуры (/ 350 °C),
необходимо учитывать ползучесть и длительную прочность. Эксперименты показали, что при повышенных температурах чувствительность к концентрации напряжений для большинства жаропрочных сталей и сплавов резко возрастает. На таких болтах целесообразно изготовлять резьбу с увеличенным радиусом во впадинах. Кроме того, следует уменьшать дополнительные напряжения от изгиба и температурных деформаций.
В табл. 16 приведены механические характеристики сталей и сплавов, используемых для изготовления болтов и шпилек, работающих при повышенных температурах.
Для изготовления соединений, работающих длительно при температурах до 1000 °C и кратковременно до 1650 °C, используют молибден. Для повышения жаростойкости болты хромируют или покрывают силицидами.
66
Резьбовые соединения
16. Механические характеристики» МПа, сталей и сплавов, применяемых для изготовления резьбовых соединений, работающих при высоких температурах
Марка материала t, °C °в °100 °200 О 0,2/100 0^ 0,2/1000 Область примене НИЯ (ДО темпера туры. °C)
Стали
20 610 370 — — —
45 400 573 230 300
540 340 150 — — — 65
20 710 350
38 ХА 350 620 — — - —
20 1250 1110 .
I8X2H4BA 400 1080 980 860 — 700 — 400
500 900 830 410 — 200 —
20 9СЮ 750 ..
20ХЗМВФ 500 640 зьо 430 — 350 — 500
600 550 380 330 250 —
20 660 250
12Х18Н9Т 600 400 180 250 230 — 90 600
700 280 160 140 120 — 30
20 1000 700 750 -
4Х12Н8Г8МФБ 600 600 480 — — 350 — 650
700 550 460 310 — 240 —
Сплавы
20 1020 660 — — — —
600 94 0 610 680 660 260 — 750
ХН77ТЮР 700 850 600 420 400 —— 60 *
800 560 460 200 — — —
20 1000 850
ВТЗ-1 400 600 490 600 —— — 450
500 560 4 20 ЗьО — — —
20 1150 1030
ВТ9 400 850 720 — 550
500 800 660 b50 — 280 —
550 780 620 450 — 120 —
°0.2/10000 J°
МПа
Прочность при переменных нагрузках
67
Рис. 22 Конструктивные способы разгрузки резьбы от напряжений изгиба
При расчете прочности определяют запасы прочности по пределу ползучести (пп = 1,4—2,5) и по пределу длительной прочности (пдл = 1,6—4).
При низких температурах часто происходит хрупкое разрушение болтов (без заметной пластической деформации).
Экспериментальные исследования и опыт эксплуатации машин показали, что болты из углеродистых сталей могут работать длительно до температуры —55 °C Болты соединений, работающих при температурах до —70 °C, следует изготовлять из легированных сталей с ав = 1050—1300 МПа При более низких температурах тяжело-нагруженные болты следует изготовлять из коррозионно-стойких статей переходного класса СН-2, СН-2а, ВНС 5
Расчет на прочность резьбовых соединений в условиях понижения температур не отличается от расчета при нормальной температуре.
ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ НАГРУЗКАХ
На рис 23 показана типичная диаграмма предельных напряжений для резьбовых соединений.
3»
На практике переменная внешняя нагрузка изменяется в большинстве случаев по пульсирующему циклу.
Напряжения в резьбовой части болта (шпильки) вычисляют по формулам (12) и (13)
Запас прочности резьбового соединения по переменным напряжениям
«а = ^, (53)
где 0ад — предел выносливости соединения, — амплитуда переменных напряжений от внешней нагрузки.
По формуле (53) можно определить запас прочности, если напряжение предварительной затяжки
0,5о-р,
так как величина оад при этом условии практически не зависит от среднего напряжения ат
При меньших значениях
M, \ ' j _Q £ q г
(54)
где от — среднее напряжение цикла.
68
Резьбовые соединения
Рис. 23. Дна! раммы предельных напряжений для соединений с накатанной (а) и нарезанной (б) резьбой Ml О*
/ — заготовки шпилек термически обрабснаиы, 2 — готовые шпильки термически эбра ботаны
Значения аад можно принимать по табл. 17 нлн вычислять по формуле
0-1
Оад = ~7 Рк упРт. ynKd. (55) Kg
где — предел выносливости гладкого образца при растяжении; kc — эффективный коэффициент концентрации напряжения, ka = 1 + q (аа — 1), где q — коэффициент чувствительности материала болта (шпильки) к концен-
трации напряжений, можно принимать q = 0,5—0,6 — для углеродистых сталей, q = 0,7-?0,8 — для легированных сталей, жаропрочных и титановых сплавов; а0 — теоретический коэффициент концентрации напряжений (см. с. 60); уП — коэффициент конструктивного упрочнения, для соединений стандартным болтом |3К уп = 1, для соединений типа стяжки и со спиральными вставками f)K уп — 1,5-? 1,6; Рт. уп —коэффициент техноло
17. Значения предельной амплитуды аад для соединений типа болт—гайка при °’5 °ад
Болты н гайки ав °-1 аад' МПа, для соединений с резьбой
из стали (сплава) МПа нарезанной накатанной
35 500 — 600 200 45/55 55'65
45 900 — 950 250 50/60 65/75
38ХА 1 100—1200 300 65/70 75/85
ЗОХГСА 1200—1300 300 65/75 75/85
ЗОХГСА 1600—1700 400 90/110
40Х2МА 1600—1700 450 90/100 95/110
13Х11Н2В2МФ 1050—1150 300 50/65 60/70
10Х11Н20ТЗР 1100—1200 300 55/70 60/70
ВТЗ 1 1100—1200 350 45/60 40/60
ВТ9 1150—1250 350 45/60 40/60
ВТ16 1 150—1250 350 45/60 50/70
Примечание В числителе дроби приведены значения пределов выносливости для соединений с болтами, термообоаботаиными после изготовления резьбы, а в знаменателе — то же, термически обработанными до изготовления резьбы^
Прочность при переменных нагрузках
69
гического упрочнения, |3,. уп — 1 — для соединений с нарезанной резьбой, а также для соединений из титановых я бериллиевых сплавов, рт, уп = 1,2-4-1,3 — для соединений нз сталей и сплавов с накатанной резьбой; Кл — коэффициент, учитывающий влияние масштабного эффекта (рис. 24).
Если экспериментальные данные отсутствуют (или для соединений из новых материалов), то
(56) °а Г »в
0-1
где оаа = —т— — предел вынослива
вости соединения при симметричном цикле; — предел выносливости материала болта при симметричном цикле нагружения.
Предел выносливости резьбового соединения возрастает на 10—20% при уменьшении модуля упругости материала гайки благодаря улучшению распределения нагрузки между витками (например, в случае применения гаек из дюралюминия или титановых сплавов). Если модуль упругости материала гайки выше, чем у болта, то предел выносливости соединений понизится (на 20% в случае свинчивания титановых болтов со стальными гайками). Предел выносливости соединений может быть повышен на 20—-50% благодаря применению более совершенных (по распределению нагрузки) гаек (см. рис. 17 и 18).
Увеличение радиуса скругления во впадинах резьбы приводит к наиболее значительному повышению предела выносливости соединений (рис. 25). Особенно эффективно применение увеличенных радиусов в резьбе для соединений из титановых и бериллиевых сплавов.
Для высокопрочных болтов с ав = = 1050-4-1300 МПа можно применять гайки из низкоуглеродистой стали с ав = 700-^900 МПа высотой Н = = (1-4-1,2) d.
Разрушение резьбовых соединений от усталости может происходить и под головкой болта, если радиус закругления под головкой мал или головка получена методами резания.
Рис. 24. Значения для резьбовых соединений при d/P — 8
У болтов со шлицевой головкой нли с головкой, имеющей внутреннее шестигранное отверстие под ключ, усталостные трещины могут распространяться от места перехода до отверстия.
Наряду с разрушениями в первых рабочих витках резьбы и под гс -юбкой нередки усталостные поломки соединений по сбегу резьбы. Для предотвращения таких разрушений необходимо увеличить длину резьбовой части так, чтобы она распространялась под опорную поверхность гайки на 2—3 витка.
Существенное влияние на сопротивление усталости резьбовых соединений оказывает технология изготовления резьбы (в особенности режимы накатывания резьбы). Для повышения сопротивления усталости соединений накатывание резьбы целесообразно выполнять при минимально возможной продолжительности процесса, так как в
Рис. 25. Зависимость а от относитель-Q Д
ного радиуса скругления во впадинах резьбы р/р
70
Резьбовые соединения
Рис, 26. Силовая шпилька транспортного дизеля
этом случае во впадинах резьбы образуется благоприятная система остаточных напряжений. Накатывание резьбы в «замкнутом контуре» (полное заполнение впадин резьбонакатного инструмента) нецелесообразно.
Пример. Рассчитать на прочность силовую шпильку рядного двигателя внутреннего сгорания (рис. 26). Задано давление вспышки р - 8,5 МПа; диаметр цилиндра D — 180 мм.
Определение предварительный расчет. Усилие при вспышке
п Г)2 тт
р - _Д_ 1802-8,5 = 216 кН.
усилий н
Внешняя нагрузка на одну шпильку
No 216
N = "Г = -4- = 54 кН.
Внешнее усилие изменяется по отну-левому циклу.
В качестве материала шпильки выбираем сталь 40ХН2МА(ав = 1150 МПа; ат= 1050 МПа; а_1р = 440 МПа).
Материал гайки — сталь 38ХА.
Диаметр резьбы предварительно выбираем по формуле (1), В соответствии с табл. 4 принимаем
(ст] = 0,15от = 0,15-1050 = = 157 МПа;
„ 54 000 2
Fj > — 344 мм2.
1о, I
По табл. 5 находим, что для предварительного расчета можно принять резьбу d = 24 мм. Выбираем резьбу М24Х2, так как она прочнее резьбы
М24, и отношение = 12 < 15, что рекомендуется для силовых резьб.
Для резьбы М24Х2
F-l = 365 мм2; di — 21,546 мм.
Выбираем диаметр стержня шпильки dc л; di ~ 21 мм; площадь сечення Fc — 346 мм2.
По предварительному чертежу определяем следующие величины:
длина растягиваемой части шпиль-
ки /0. мм ..................... 360
средняя площадь отсека головки блока, приходящаяся на одну шпильку Fi, мм1 . ......... 4600
высота сжимаемой части головки мм ................ . . 70
площадь прокладки, приходящаяся на одну шпильку, F3, мм® . 8500
толщина прокладки /г- мм • 3
средняя площадь рубашки блока, приходящаяся на одну шпильку, Fe, мм’ ....................... 2300
высота блока рубашки 13, мм . . 278
Напряжение затяжкн. Из условия герметичности, в соответствии с формулой (36), выбираем v = — 2,5. Напряжение затяжки при монтаже
о(0) = v 2L 2,5 - 370 МПа.
г 1 ЗЬ5
Усилие затяжки при монтаже Q<,°> = 0oFi = 370-365 = 135 кН.
Прочность при переменных нагрузках
71
Расчетная нагрузка. Принимаем модули упругости, МПа: шпильки Е„ = 2-Ю5; блока и головки блока (алюминиевый сплав) Е2 = Е2 — = 0,72-106 * В *; прокладки £8 = 0,72 X ХЮ6.
Вычисляем коэффициенты податливости, мм/Н:
для шпильки
j_______________________5 2-10-9,
Л» ~ EBF0 ~ 2-106-346 ~5’ ’
для головки блока
, Ji______________70
1 E2Fi 0,72-105-4600
= 0,21-10"’;
для прокладки
, __ ^2____________3_________
2~E2F2~ 0,72-106-8500 ~
= 0,005-10"6;
для блока
Л — —^3 — X3~e3f3-
0,72 -106-2300 - 1>68‘10°-
В рассматриваемом случае к деталям системы болта относятся шпилька и головка блока, к деталям системы корпуса — рубашка блока и прокладка.
Коэффициент основной нагрузки
у _ -^2 + -^3___ __
Л-о + Л1 + Я» + Л3
_________^05 + 1.68 _
5,2-[- 0,21 4- 0,005 4- 1,68 ~ '
Определим усилие, действующее на Шпильку в результате нагрева системы. Принимаем, что в рабочем состоянии все детали нагреваются на 75 °C. Коэффициент линейного расширения для стали а = 11 -10"’ 1/°С, для алюминиевых сплавов а = 22-10"’ 1/°С.
По формуле (17) находим з
У? + ccBtBlB
Qt = -^—3---------------»
S Л/
(22-11) 10"’-360
~ (5,2 4-0,21 +0,005 4- 1,68) 10"’—
= 42 кН.
Усилие затяжки в рабочем состоянии
<?о = <?о0) + Qi = 135 4-42 = 177 кН
Напряжение загяжкн иа работающем двигателе
ао = ао0’ + Go° =
= 370 4- = 485 МПа.
365
Следовательно, напряжение затяжки ниже предельного напряжения, которое будет
0,8от = 0,8-1050 = 840 МПа.
Общее усилие на шпильку
(? = (?» + = 177 + 0,24-54 =
= 190 кН.
Напряжения нии. В резьбовой
р а с т я ж е-части стержня
= 520 МПа.
190-103
365
В стержне шпильки
°с
Q
Ес
190-Ю3
346
= 550 МПа.
Напряжения кручения. Момент, закручивающий шпильку при затяжке, находим по формуле (31), принимая fp = 0,2:
»4-135.10..21,5(3-т^тт +
+ 0,2^ = 332-103 Н-мм.
72
Резьбовые соединения
Касательные напряжения в нарезанной части стержня
Мк 332-103
0,2d3 0,2 (21,5)3
= 166 МПа,
в стержне шпильки
332- Ю3
0,2 (21)3
= 180 МПа.
Проверка стержня болта на скручивание прн затяжке
/(о'°>)2 + 3т2 = = Уз702-|- 3-1662 = = 469 МПа<0,8ат.
Напряжения затяжки также не больше допустимых.
Приведенные напряжения. В резьбовой части шпильки
°1ПР = /"о2 + Зт2 =
= Д/5202 + 3 -1662 = 594 МПа
В стержне шпильки
°с. пр = V°с + Зт* =
= У5502 + 3-1802 = 632 МПа
Запас прочности по пластическим деформациям. В резьбовой части (принимая а' = 1,05от)
°1пр
В стержне от
594 ~ ’,86’
Ю50 , „„
Так как запасы прочности по пластическим деформациям больше 1,3, то нх следует признать допустимыми.
Запас статической
прочности. В резьбовой части
(принимая ап = 1,05ов)
_ в _ 1,05-1150 _
в о1пр 594
В стержне шпильки _________ °в _____ 1150__ „
в ~ Ос. Пр ~ 632 - ’ •
Эти запасы следует признать удовлетворительными.
Необходимая высота гайки. По формуле (44)
но := q 47 х °вб / dc \2 d km Овг \ d /
Имеем овб = И15 МПа; авг = 1050 МПа; х = 1, km = 0,6.
Находим
^_ 0 47-^Н1-5^У d ’ 0,6 1050 24 /
0,7.
Необходимая высота гайки Н = 0,7-24 = 17 мм.
Переменные напряжения в резьбе
X N 0,24 54 000 ,о„_
°а ~ 2 Fx “ 2 365 ~ 8 МПа‘
Запас прочности по переменным напряжен и-я м. Для накатанной резьбы нз стали 40ХН2МА по табл. 14 принимаем аад= = 110 МПа. Учитывая отрицательное влияние больших размеров, уменьшаем аад на 30%, получаем 77 МПа.
Так как напряжение затяжки о0 х х 0,5вт, то запас по переменным напряжениям
_ °ад _ 77
Па ~ оа ~ 18
= 4,25.
Такой запас достаточен. Так как первоначально выбранные размеры обеспечивают необходимые запасы прочности, то расчет резьбового соединения шпильки и гайки на этом заканчиваем.
Упрощенный расчет
73
Глава 4
ФЛАНЦЕВЫЕ СОЕДИНЕНИЯ
ТИПЫ ФЛАНЦЕВЫХ СОЕДИНЕНИЙ
Фланцевые соединения можно подразделить на два основных типа: с иеконтактирующими фланцами (рнс. 1, а) нс контактирующими фланцами (рис. 1, б). Наиболее распространен первый тнп соедниення (трубопроводы, сосуды н аппараты н т. п.). Соединения с контактирующими фланцами часто применяют в конструкциях, не требующих полной герметизации стыка (фланцы корпусов машин, редукторов н т. п.) Получили распространение фланцевые соедниення с контактирующими стыками и с самоуплотняющимися прокладками, обеспечивающие герметичность. Такне соедниення имеют меньшие габариты по сравнению с соединениями первого типа, но более сложны прн нзготовленни н монтаже.
Применяют свободные фланцы (рнс. 2), а также фланцы, изготовленные вместе с трубой (корпусом) илн присоединенные к трубе с помощью
Рис. 1. Типы фланцевых соединений
Рис. 2. Накидные (свободные) фланцы
сварки, резьбы, развальцовки илн заклепок (рис. 3). Некоторые виды фланцевых соединений стандартизованы. Прокладки выполняют в виде плоского листа из паронита, картона, резины, фибры, фторопласта, меди н мягкой стали; применяют асбестометаллические прокладки, металлические гофрированные и зубчатые, металлические линзовые прокладки н др.
Во фланцевых соединениях с контактирующими фланцами используют самоуплотняющиеся прокладки в виде резиновых нли металлических колец.
УПРОЩЕННЫЙ РАСЧЕТ
Расчет выполняют прн предварительном выборе размеров н для проверки прочности неответственных фланцевых соединений.
Расчет соединений с неконтактирующими фланцами. Расчетное усилие, действующее на болты (рнс 4), определяют по формуле
где Dcp. п — средний диаметр прокладки, мм; р — рабочее давление среды, МПа.
Рис. 3. Способы соедниення фланца и трубы
74
Фланцевые соединения
Рис. 4. К расчету фланцевых соединений с неконтактнрующими фланцами
Коэффициент затяжки k:
мягкие прокладки . .
мягкие прокладки в металлических оболочках и металлические фасонные прикладки . . плоские металлические прокладки . ...............
1.5-2,5
2,5 — ЗЛ
3.0 —4,5
Условие прочности фланцевых болтов:
а = -^4-<0,6ат, (2)
где г — число болтов; d1 — внутренний диаметр резьбы болта; ат — предел текучести материала болта с учетом рабочей температуры.
Число болтов для обеспечения более равномерной затяжки стыка часто выбирают кратным четырем (г = 4, 8, 12, 16).
Расстояние между осями болтов (шаг болтов) обычно принимают прн малых давлениях (р С 1 МПа) t -----= (5-i-7) d, прн больших давлениях (р 3 МПа) t — (2,5 — 4) d. Опасным сеченнем прн расчете на прочность фланца обычно является место перехода от фланца к трубе* 1 (сечение АВ на рнс. 4).
Изгибающий мсмечт в этом сечении (на единицу длины)
Qc/i
(3)
1 Предполагается, что Уклон
конического участка приннм ют равным 1/3 (реже 1/4).
где т] 1 — коэффициент, учитывающий, что часть момента воспринимается поворотной деформацией фланца; — расстояние от центра сечения АВ до осн болта; Dx — средний диаметр трубы в сеченнн АВ.
Если коническая втулка (нлн труба) очень жесткая по отношению к фланцу н сеченне АВ не поворачивается, то г] = 1. Значение т| можно определить по приближенной формуле (вывод см. с. 85):
1
,+».82(75-)У^18а
\ ^ср ‘ у Г 1‘Р и
(4)
1
где scp = —• (sj + s) — средняя толщина трубы на коническом участке; гтр — средний раднус трубы; DH и D — соответственно наружный н внутренний диаметры фланца. Значения Т|, вычисленные по формуле (4), приведены в табл. 1.
Напряжения изгиба в опасном сеченнн фланца (сеченне ЛВ)
6Л41 = __6т10Л__ «1 ~ ’Ц£Н-з1)з(
< 0,6ов,
(5)
где ав — предел прочности материала фланца (прн высокой температуре под ав следует понимать предел длительной прочности).
Из формулы (5) следует, что для снижения напряжений во фланцах целесообразно: а) приближать осн болтов к трубе (уменьшать /j); б) увеличивать толщину трубы в месте перехода к фланцу (размер sx). Однако прн большой конусности (1:2) упрочнение получается чисто местным н максимум напряжений сдвигается к более тонкому сечению трубы.
Расчет соединений с неконтактирующими свободными фланцами. Суммарное усилие на болты Qc (рис. 5) определяют нз равенства (1); условие прочности болтов выражается формулой (2).
Прн расчете на прочность фланца принимается, что фланец испытывает поворотную деформацию н в нем возникают окружные напряжения.
Упрощенный расчет
75
Значения коэффициента
со 0.801 0.747 0.674 0.580 0.465 0.336 0.206 0.099
» ci 0.829 0.780 0.713 0.623 0.510 0.377 0.237 0.1 16
о II Я" 2,0 0.865 0.824 0.766 0,686 0,579 0,445 0.291 0.148
0.916 0,889 0.849 0.789 0.702 0.578 0,412 0.229
О 0.961 0.947 0.926 0.893 0.840 0.752 0.609 0.397
3.0 0.890 0.855 0,806 0,734 0.634 0.503 0.34 1 0.180
2^ 0,907 0.876 0.833 0,768 0.676 0.548 0.383 0,208
II V1 X 2.0 ! 0.928 i 0,903 1 0.868 0,814 ! 0.733 0,616 0,451 0,258
ю I 0.956 | 0.942 1 0.918 ! 0.882 0.824 0.733 0.584 0.372
°". 0.980 0.973 0.962 0,943 0.912 0,859 0,757 0.569
о 0,948 ; 0.929 1 0,902 0,860 0.795 0.693 0.536 : 0.329 1
),02 0.956 0.94 1 0.917 1 0.881 0,823 0.730 0,581 0.369
II g.| a о 0,966 0.954 0.936 0.907 0.860 0,782 0.647 0.437
ю 0 980 0.973 0.962 ! 0.943 0,913 0,860 0,758 0.570
04 0,991 0.988 0.982 0.974 0,959 0,931 0,874 0,747
1,0 0.9 0.8 0.7 0.6 0.5 0,4 0,3
Рнс. 5. К расчету фланцевых соединений со свободными фланцами
Условие прочности фланца:
о = 6(?с(Об-Д1) = nDBh2 In -5s.
= 0,83Qc(£>6~ff1' <0,7от, (6) О,4- 1е
где Dg — диаметр окружности осей болтов; Di — средний диаметр кольцевой площадки контакта фланца и трубы; DB — внутренний диаметр фланца толщиной Л; ог — предел текучести материала с учетом температуры фланца.
Расчет соединений с контактирующими фланцами. Расчетное суммарное усилие для фланцевых болтов (рис. 6) определяют из условия
где k — коэффициент затяжки, обычно принимают k — 1,5-4-2,5; Dv — диаметр уплотнения, мм; р — рабочее давление среды, МПа; 1г — расстояние от средней окружности трубы до окружности осей болтов; 1г — расстояние от наружной окружности фланца до окружности осей болтов.
Формула (7) учитывает, что в предельном состоянии раскрытие стыка происходит при повороте относительно точки 0г. Условие прочности фланцевых болтов
а = -^% С (0,6 - 0,8) аг, zndf к
76
Фланцевые соединения
Рис. 6. К расчету фланцевых соединений с контактирующими фланцами
где z—число болтов в соединении; d, — внутренний диаметр резьбы болта
При расчете на прочность фланец рассматривают как стержень, заделанный в сечении АВ (рис, 6) и упругосвязанный с трубой.
Изгибающий момент в сечении АВ
М = (8)
яС>к где Р = —— р — внешнее усилие, действующее на фланцевое соединение; г] — коэффициент уменьшения изгибающего момента (0,5 г; 1) за счет упругой связи фланца и трубы.
Если труба очень жесткая (по отношению к фланцу), то т] = 0,5, для тонкой трубы г] ~ 1. Значения г] вычисляют по приближенной формуле (вывод см. с. 87);
где
Л 2+ Л’
(9)
Л = 0,72 Г—
•1
3 jiDq — ZC л£)Тр
(10)
scp = -g- («! + з) — средняя толщина трубы; с — диаметр отверстия под болт.
В приближенных расчетах можно принимать т| ~ 0,8-? 1- Напряжение изгиба во фланце (в сечении АВ) должно быть
°И= (ЯПб-2С)Р<0’баВ’ (И) где z — число болтов.
Изгибающий момент в сечении LN трубы
Mi = (1 ~у\)Р11 = nDK
= (1-П)-4ЛР/г- (12)
Напряжения изгиба в этом сечении должны удовлетворять условию
аи = -^-т<0,6ов (13)
В формулах (11) и (13) ов — предел прочности материала фланца с учетом рабочей температуры и длительности работы.
УТОЧНЕННЫЙ РАСЧЕТ СОЕДИНЕНИЙ
С НЕКОНТАКТИРУЮЩИМИ ФЛАНЦАМИ
В соединениях этого вида уплотнение создается сжатием прокладки фланцевыми болтами.
Усилие уплотнения, необходимое для герметичности стыка. Это усилие на прокладку должно оставаться на стыке в рабочих условиях для обеспечения герметичности.
Плоские прокладки. Усилие уплотнения определяют по формуле
Руп = (14)
где £>Ср. п — средний диаметр прокладки, мм; Ь — ширина прокладки, мм; q0 — давление на контактных поверхностях прокладки, МПа; обычно принимают q = тр (здесь т — про -кладочный коэффициент1, мм, см.
1 В стандартном американском методе расчета используют приблизительно в 2 раза большие значения т, ио оии соответствуют удвоенному усилию уплотнения
Расчет соединений с неконтактирующими фланцами
77
2. Значения q0 для плоских прокладок
Материал прокладки р, МПа Среда МПа
Резина До 3 Св 3 до 10 — 1,5 + 1,7р 4,5 + 0.7р
Паронит — Нормальной проникающей способности Повышенной проникающей способности (водород, гелий н др ) Ю + р 35
фторопласт 4 До 10 Св 10 до 15 До 15 Жидкая » Г азообразная 1 + р (% mln = 4) 4 + Р 4 + р
Фибра Свинец — -- 40
7
3. Рекомендуемые значения 'толщины Лп и ширины b плоских прокладок и их применение
Материал прокладки hn, мм Ь, мм Применение
р, МПа (не более) Температура, °C
Резина 1-3 Ь > 45п 10 От —30 до +60
Паронит 1—3 12 — 20 15 До 400
Фторопласт-4 0.8 —0,9 10 20 От —73 До +250
Фибра 1-3 8—12 15 До 100
Алюминий Медь Мягкая сталь Сталь типа 12Х18Н9Т 1-2 8—16 50 70 70 100 > 250 >350 > 400 > 600
Примечание Максимальный зазор между уплотнителями поверхности фланцев (без прокладок) не должен превышать 0,15 номинальной толщины прокладки
табл. 4; р—давление среды, МПа).
При увеличении давления среды р Давление уплотнения должно возрастать, при уменьшении — снижаться. Однако давление уплотнения у0 не должно быть меньше некоторого минимального значения ПРИ котором еЩе не нарушается герметичность; значения q0 mln приведены в табл. 4.
Значения qQ для плоских прокладок приведены в табл. 2.
Рекомендуемые значения толщины и ширины плоских прокладок приведены в табл. 3
Фасонные прокладки. Для плоской рифленой прокладки (рис. 7) можно принимать значения т и <70mlrl по табл. 4, уменьшенные на 20%. По данным работы [1], при толщине прокладки hn = 3 мм принимают Ьт = 3 }/г, мм, где г — число гребешков.
78
Фланцевые соединения
4. Приближенные значения прокладочного коэффициента т, минимального давления уплотнения q® t давления обжатия допускаемого давления [д] и модуля
упругости плоских прокладок из различных материалов
Форма н материал прокладки т о mln ^обж ы Еп-‘О"5
МПа
Плоская прокладка, материал прокладки
резиновый лист 2,5 3,5 18 0.4- 10~* X
мягкая резина с тканевой прослойкой 1.2 3,5 5 20 X
или лист из твердой резины твердая резина с тканевой прослойкой 4,5 7 20 \ hn J
пароиит или прессованный асбест 1,6 10 32 ПО 0 03
фторопласт-4 фибра 1.4 4 10 40 0,02
1 4 40 50 80 0,07
асбест, армированный проволочной сет- 1.4 10 30 120 0.03
кой мягкий алюминий 2 50 100 140 0,7
мягкая медь 2.4 70 160 200 1.1
мягкая сталь 2.7 80 250 350 2
сталь типа 15Х5М 3 90 350 550 2
сталь типа 12Х18Н9Т 3.2 100 400 600 2
Гофрированная оболочка с асбестовым на полнителем, материал оболочки
медь или алюминий 1.5 20 42 110 0.04
углеродистая нли коррозионно стойкая 1.6 25 50 130 0,0 5
сталь
Гладкая оболочка с асбестовым наполнителем, материал оболочки
алюминий или медь 1,6 25 50 120 0.05
мягкая сталь монель 1.7 28 55 130 0,06
сталь типа РХ18Н9Т 1,8 30 65 140 0,06
Примечания 1 При уплотнении воздуха илн пара значения т и q® mln должны быть увеличены в 1,8 раза, при уплотнении сред с высокой проникающей способ ностью (водород гелий и т п 1 — в 2 5 раза
2 Обозначения b — ширина и hn — толщина прокладки
Для прокладки круглого сечения между двумя плоскими поверхностями фланцев можно принять в деформированном состоянии b « 2d и расчет усилия проводить по формуле (14) при значениях т и q0 mln, указанных в табл 4.
Для металлических прокладок овального и восьмиугольного сечения, проложенных в кольцевом пазу, при-, 1 о
нимают о = —— d
4
Линзовые прокладки (рис. 8). Их применяют для ответственных фланцевых соединений (обычно при р
100 МПа и f < 900 °C).
Для лучших условий контакта твердость материала линзы должна быть несколько меньше, чем материал трубы. Усилие Муп. действующее на
линзу, и усилие уплотнения Руп
вязаны соотношением
Муп cos (а + р) Рvn — ~ у cos р ’
где р — угол трения (tg р — f; здесь f — коэффициент трения; часто принимают f - 0,15; р = 8°30'). Угол а составляет обычно 20—30°.
Нормальное усилие, необходимое для уплотнения,
N = лОкРуп, (16)
где Руп — нагрузка на единицу длины контактной линии.
Значения руп можно выбирать следующими (давление среды р 75 МПа):
D , мм................. 50, 100, 200
<?у„- Н/мм............ 300, 400. 500
Расчет соединений с неконтактирующими фланцами
79
рж. 7. Сечение рифленой про* кладки
Рис. 8. Фланцевые соединения с линзовыми прокладками: а — конструктивная схема, б — усилие в зоне контакта флаица к ляизы
Величину <?уп можно определить исходя из равенства контактных напряжений пределу текучести материала линзы для создания герметичности. На основании теории контактных деформаций (контакт цилиндра и полуплоскости)
где а- и Е — предел текучести и модуль упругости материала линзы; R — радиус кривизны контактирующей поверхности линзы.
Ширина полоски контакта
Из формулы (17) получаем следующее равенство:
?уп = 5,7—g—. (18)
Например, при ат = 600 МПа; R = = 50 мм; Е = 2-106 МПа
?уп = 5,7-®^==510 Н/мм.
Увеличение <?уп при возрастании R объясняется необходимостью увеличении усилий для создания контактных напряжений, равных ат.
Усилие обжатия и допустимые давления для прокладки. Для обеспечения герметичности стыка прокладка
должна быть предварительно обжата под определенным давлением (для устранения неплотности прилегания).
Необходимое усилие обжатия
^обж — я^ср-п^9обж> (19) где Оср. п — средний диаметр прокладки; Ь — ширина прокладки; ?обж — давление на прокладку для ее обжатия.
Однако при очень больших давлениях на прокладку возможно ее расплющивание, образование трещин н т. п.
Давление на прокладку должно быть меньше допустимого q [<?].
Значения <70бж и (Ч1 Д-1Я плоских прокладок см. табл. 4.
Для плоских рифленых прокладок значения <70бж и [<у] могут быть приняты на 20% меньше указанных в таол. 4.
Для круглых прокладок можно использовать значения табл. 4, если давления относить к ширине прокладки b ~ 2d.
Для линзовых прокладок принимают давление (в МПа) <70б>« st qyn.
Допустимое значение давления (в Н/мм) по формуле (18) при ак = = 0,9ов
Силовая схема фланцевого соединения с иеконтактирующими фланцами.
80
Фланцевые соединения
Рнс. 9. Схема фланцевого соединения с не-контактирующими фланцами:
а — конструктивная схема и усилия, б — силовая схема при действии осевой на* грузки, I — фланец, 2 — труба, 3 — прокладка
Фланцевое соединение рассчитывают по схеме, показанной на рис 9. Изгиб-ной жесткостью болтов пренебрегают. Фланцы относят к системе болта, трубу и прокладку — к системе корпуса На соединение действует внешнее усилие
лС>к
Р ~ Рт-р + Рф ~ —4— Р (20)
В приближенных расчетах диаметр уплотнения обычно принимают
Оц = Вер- п-
Полное усилие, действующее на болты, Q6 = Qo+xP, (21)
где Qa — предварительное усилие на болты до приложения внешней нагрузки (суммарное усилие затяжки); х = = Xi — Хз
Коэффициент осевой нагрузки
Коэффициент осевой нагрузки изменяется в пределах
0<Х!< 1-
В приближенных расчетах можно принимать: прн металлических прокладках Xi = 0,1 -г-0,3; при мягких прокладках (исключая резиновые) Xi — = 0,2 — 0,4; при резиновых Xi — 0,6-И.
Коэффициент внутреннего давления
Л'б Лф Лп ~|- Лтр
где Лф — коэффициент податливости фланца, связанный с радиальной деформацией стенок трубы. Эта деформация вызывает поворот тарелок фланцев и уменьшает нагрузку на фланцевые болты.
В приближенных расчетах можно принимать
о я ScP Х2 = 0,3 —.
Обычно х2 — 0,14-0,3
Приближенная формула для усилия на болты в рабочих условиях
Об = Со- (24)
Определение коэффициентов податливости. Коэффициент податливости болтов
, 1б 4- 0,3d
где Zg — расчетная длина болта; d — диаметр стержня болта; г — число болтов; Eq — модуль упругости материала болта (с учетом температуры).
Увеличением длины на 0,3d приближенно учитывается податливость витков резьбы.
Коэффициент податливости прокладки
1 =
EnjrDCp. nb
где Еп — модуль упругости материала прокладки (см табл 2).
Коэффициент податливости трубы
~
тр ~ EnD^'
Лб + Лф + Лп + ЛТр ’
где 1ц, Хтр, лб, Хф — коэффициенты податливости прокладки, трубы, болтов н фланцев, мм/Н.
Коэффициент податливости фланцев при действии осевой нагрузки опреде-
Расчет соединений с неконтактирующими фланцами
81
ляют с учетом поворотной деформации фланца и изгиба связанной с ним цилиндрической оболочки (трубы).
Если угол поворота фланца под действием усилия Q составляет фф, то коэффициент податливости (для двух фланцев)
9 ФФ*»
АФ = 2 -Q- •
На основании решения, изложенного иа с. 85,
ЛФ= 1,6 Zi (26)
Значения т] приведены в табл. 1. При высокой температуре (/> > 300 °C) следует учитывать уменьшение модуля упругости.
Коэффициент податливости фланцев при действии внутреннего давления на основании решения, изложенного на с. 85 (для двух фланцев),
^-0,8(1
(27)
Усилие на прокладке. После приложения внешней нагрузки усилие на прокладке уменьшается до
/?п = <?о —- (1 — %) А. (28)
Усилие затяжки фланцевых болтов. Усилие затяжки болтов должно обеспечивать герметичность соединения. Исходя из равенства (28), получим
<?о>(1 -XJ/’+J’yn, (29)
где Руп — усилие на прокладку, необходимое для герметичности стыка.
Усилие затяжкн для обеспечения герметичности при рабочих условиях выбирают с некоторым запасом на потерю затяжки *:
Л Г n.D': „
<?•>* pi-х)—с^-р + РуП , ___________ (30)
1 В приближенных расчетах температурное усилие не учитывают, что идет в запас прочности При действии внешнего Изгибающего момента М к величине ^уП Добавляется слагаемое --- .
4 Dcp- и
где р — наибольшее давление среды в рабочих условиях (рабочее давление); k = 1,04-1,4 — коэффициент, большие значения которого принимают для металлических прокладок и для прокладок. подвергающихся действию повторных нагрузок при повышенных температурах. Для резиновых прокладок k = 1.
Для обеспечения условий герметичности при гидравлических испытаниях усилие затяжки болтов
noL „
Qo X1 — X)----ф--- Рпроб + Руп.
(31)
где Рпрос — давление при гидравлических испытаниях (пробное давление).
Величина рПроб устанавливается техническими условиями и составляет обычно (1,1—1,5) р.
Усилие затяжки должно быть больше необходимого усилия обжатия
Qo 5* Робж- (32)
При выборе усилия затяжки рассматривают все три условия (30)—(32) и принимают наибольшее значение Qa. Однако выбранное значение Q должно удовлетворять условию прочности прокладок.
Давление на прокладку
где [<?] — допускаемое давление прокладку (см. табл. 4).
Температурное усилие
__ («ф^ф —<ХбНб
* Л б + Аф + Ап + Атр ’
где аф, /ф и «б, /б — коэффициенты линейного расширения и температуры материала фланца и болтов соответственно.
Коэффициенты податливости в формуле (34) определяют из соотношений (25)—(27).
Разность температур болтов и фланца обычно составляет 10—15 °C при температуре среды 300—400 °C и 15— 20 °C при температуре среды 400— 500 °C.
Разность температур в момент прогрева следует принимать в 3—4 раза большей.
(33)
иа
(34)
82
Фланцевые соединения
Рис. 10. Напряжения во фланце
Расчет на прочность фланцевых болтов. Суммарное усилие, действующее на фланцевые болты в рабочих условиях,
Об = О0 + Qt + %Р. (35)
Усилие при монтаже 0о должно удовлетворять условиям (30)—(33). Условие прочности фланцевых болтов
а=:^'<<0-6 + 0’9)ат- <36)
При воздействии высокой температуры расчет проводят иа длительную прочность.
Запас длительной прочности в болте определяют из равенства
ав дл
"дл = “ ’
где <тв дл — предел длительной прочности материала болта при рабочей температуре за время работы конструкции; лдл = 1,5+2,5,
При различных режимах работы конструкции определение запаса прочности указано в гл. 2.
Прочность фланцевых болтов должна быть проверена при гидравлических испытаниях н для режима прогрева.
Напряжение в болтах при гидравлической опрессовке
о = 4^° + Хрпроб) (0,6+0,9) <гт.
zudj
(38)
Напряжении в болтах при прогреве определяют по формуле (36), причем значение Qt соответствует нестационар
ному температурному режиму. Принимают, что с, соответствует максимальной температуре х.
Расчет на прочность фланцев. Напряжения изгиба в трубе в месте присоединения к фланцу (сечение АВ на рис. 10) определяют по формуле (5) * *
В самом фланце возникают окружные напряжения (см. гл. 19)
аокР = £-^, (39)
где ф — угол поворота фланца; у н г — радиальная и осевая координаты рассчитываемой точки
Угол поворота фланца (см. гл. 19)
Учитывая равенство (3), находим
ф~ 2л Eh? ,„ОН •
12 D
В удовлетворительно работающих фланцевых соединениях
о°
Ф° < (Ф< 0,013).
1 При высокой температуре и большей длительности работы предел длительной прочности часто меньше предела текучести при той же температуре.
* В приближенных расчетах часто принимают = — (Dg — DJ.
Напряженное состояние фланца и трубы
83
В точке В (см. рис. 10) в двух взаимно перпендикулярных площадках действуют сжимающее ои и растягивающее аокр напряжения.
Наибольшее окружное напряжение во фланцах будет в точке В:
оокр^0,83 (40)
Dh‘ 1g
Приведенное напряжение
апр “l- °окр “I" анаокр
< 0,8ов,
(41)
где оп — предел прочности материала с учетом температуры и длительности работы
В равенстве (41) напряжения ои и а0Кп вычисляют по формулам (38) и (40).
Условие (41) обеспечивает запас по напряжениям
п = -^->1,25. (42)
апр
При большой конусности трубы [> 1 : 2 н в трубах больших диаметров может оказаться опасным сечение в месте перехода от цилиндрической части к конической.
Изгибающий момент в сечении х (см. гл 24)
М (х) = Л4ге~cos рх, (43) где коэффициент
Р = (44)
V 5срлтр
здесь координату х см. на рис. 10;
®ср = -у- (Si + з) — средняя толщина конического участка; гтр — средний Радиус трубы
Напряжения изгиба в сеченин А2В2 6М2
= e~PG C°S (45)
где /4 — длина конической части трубы.
Окружное напряжение в этом сечении
°окр = Р —~ • (46)
Прочность оценивают по уравнению (41). Если р/4 > 3,5, то прочность сечения А2В2 обеспечивается, так как изгибающий момент быстро затухает.
Кроме определения запаса прочности по напряжениям целесообразно рассчитывать запас по разрушающей нагрузке.
Разрушающее усилие при кратковременном воздействии внешних нагрузок (см. с. 86).
л (2ов -|- от) Чрээр з х
X [^(Dh-D-2C) + 4 DJ,
(47) причем ав и ит определяют с учетом температуры
Для длительного действия нагрузки
Сразр- дл — Зразр-^. (48) °в
где <тв дт н <тв — пределы длительной кратковременной прочности материала фланца прн рабочей температуре.
Запас прочности фланца по разрушающей нагрузке
Сразр дл яразр = я
где Qc — осевая нагрузка на фланец в рабочих условиях (суммарная нагрузка на болты).
Запас по разрушающей нагрузке в удовлетворительно работающих соединениях Лразр > 2.
НАПРЯЖЕННОЕ СОСТОЯНИЕ
ФЛАНЦА И ТРУБЫ1
Расчетная схема соединения с некон-тактирующимн фланцами. Рассмотрим упрощенную схему фланцевого соеди-
1 Здесь приведено обоснование расчетных зависимостей» используемых при расчете на прочность фланцевых соединений.
84
Фланцевые соединения
Рис. {1 Расчетная схема соединения с не-коитактирующнми фланцами
Угол поворота от действия давления возникает потому, что радиальному перемещению стенок трубы
2
°окргтр РГтп
и — ------- = ----—
Е Es
(51)
препятствует кольцо.
Угол поворота (см гл. 24)
в Ргтр 1,28 Ргтр
Фр Р ,---- ps •
с--> \J Г—s
нении (рис. 11) Трубу заменяем цилиндрической оболочкой постоянной толщины, фланец рассматриваем как кольцо (см гл 19) 1 Такую расчетную схему можно использовать для фланцевых соединений с неконтактнрующнми фланцами Кольцо считаем жестким в радиальном направлении, влиянием перерезывающих усилий в месте соединения фланца и трубы пренебрегаем.
Коэффициент г] Неизвестный (распределенный) момент находят из условия равенства угла поворота фланца и трубы в месте сопряжения (рис. 12)
Используя решения для длинной цилиндрической оболочки (см гл 24), найдем угол поворота оболочки от действии изгибающего момента Mi (при р = 0,3).
Если учесть, что вследствие действия осевых напряжений
РГТр
°х ~ 2s
радиальное перемещение оболочки
»/тр Е
то суммарный угол поворота
1,28 Ргтр фр+Ох = У^~^
= 1,03
Р'тр
Es l/fTps
(52)
Mi Mj
фм1~ 2рО == 1,28 Es3
12-0.91
= 4,25
Mi УттрЗ Es5
(50)
Угол поворота кольца от действия распределенного усилия по окружности болтов (см. гл. 19)
М ^6Г6 ^тр^тр
фч(3 = Eh3 . DB ~ Eh3 , DH ~ ~ПГ1пР "12" ’"О’
1 В гл 19 указаны области применения теории колец вм сто более сложной теории круглых пласт» и
Рис. 12 Условие совместности деформаций фланца и трубы
где /1 = 'а — гТр — (Об ОТр) плечо осевой силы.
Угол поворота кольца от действия распределенного момента
гтр^1 _ .
фм1~ Eh3 . Он ' (
~ПГ1по
Напряженное состояние фланца и трубы
85
Приравнивая углы поворота фланца и трубы
ф?б + Фм? = Фл^ + Фр+ах-
находим
_____________] 03 ргтр
„ Eh3 . £>н fsl/F's
2л —2~ln-£j £SkrTps
Mi -----—=----------------
4,25 + Гтр
Es3 Eh.3 , DH
—ln O'
(55)
Второй член в числителе формулы (55) выражает действие внутреннего давления. Оно уменьшает изгибающий момент Mi, что идет в запас прочности; этим членом можно пренебречь.
Теперь представим равенство (55) в виде
<56>
где
1 Г] = ----------------------------=---------- .
1+0.82(4)’
(57)
Коэффициент податливости фланца при действии осевой нагрузки. На фланец действует суммарное осевое усилие Qc, вызывающее смещение точки Вг относительно Aj иа величину Д (см. рис. 11).
Коэффициент податливости и угол поворота фланца будут
, _ А _ Ф^1 Qc ~ Qc ’
Рис. 13. К определению разрушающей нагрузки
Внося значение ф в равенство (58), получим
д /Hl-Т]) =
^-£Л’-2,30 1g
= 0,83^ (1 (60)
Eh3 lg
Коэффициент податливости фланца при действии внутреннего давления. Из формулы (55) при Qc = 0
М1 = ~р~0,077 (1 - г)).
4 Гтр
(61)
бол-
Уменьшение расстояния по оси тов
д , М1Гтр/1 ф1~ Eh* 1прн 12 D
(62)
Коэффициент податливости, отнесенный к силе Р,
(58)
__ Чбгб Чтргтр ^Гтр _________
£Л3 . Он
-----In ——
12 D
= -^ °-4 (1-11)
Eh3 lg
(63)
Qc/i(l -П) 9тт Е1г3 1п°н 2л ~Т2~ 1п ~D
(59)
Разрушающая нагрузка. При определении разрушающей нагрузки фланец рассматривают как кольцо прямоугольного сечения с учетом ослаблений от отверстий (рис. 13).
86
Фланцевые соединения
Рис. 14. Распределение напряжений во фланце прн разрушающей нагрузке
h
Рис. 15. Расчетная схема фланцевого соединения с контактирующими фланцами
Из равенств (64) и (65) получаем формулу для разрушающего усилия при поворотной деформации фланца:
Предполагается, что в поперечном сечении кольца и в сечении АВ одновременно возникает предельное распределение напряжений (см. гл. 17).
Предельный изгибающий момент в поперечном сечении кольца (рис. 14)
М = I ---------cj х
Г Л2 , , № "I
х LOtT+ (°в-ат) -6~J =
/ D „'k 4i2 (2°в 4“ ат)
~ к 2 CJ~l 3
(64) где с — диаметр отверстия под болт; ав и ат — пределы прочности и текучести материала фланца.
Предельный изгибающий момент в сечении АВ трубы (на единицу длины) 1
441 раэр —
(gB От) S1 6
_ л 2ав + аг
Чраэр — *2 3----- х
х [-^-(Он-О-2С) + 4°1]-
(67)
Расчетная схема для соединения с контактирующими фланцами. В приближенном расчете фланцевого соединения с контактирующими фланцами предполагают, что на окружности болтов имеется заделка фланцев (рис. 15). Фланец следует считать кольцевой пластиной, но при наличии заделки и
D
при 0.5 можно пренебречь влияли
нием кольцевых напряжений и рассматривать фланец как стержень-полоску.
Изгибающий момент. Угол поворота фланца в сечении на расстоянии /г от заделки под действием усилия Р и момента
Pl{ 2пг1^М111
ф = 2£j £V ’
где момент инерции сечения
Из условия равновесия
4гО,.И,»..,. (в6>
1 При более точном выводе следует рассмотреть возможность образования пластическою шарнира в других сечениях конического участка трубы и учесть влияние растягивающего усилия в сеченни
. (лПб — гс) А3
J ~ 12
(69)
В равенствах (68), (69) Р = —р — внешнее осевое усилие, действующее на фланцевое соединение; — изгибающий момент на единицу средней окружности трубы; г — число болтов.
Шпоночные соединения
87
Угол поворота цилиндрической оболочки определяют из формул (50) и
(52): ,___
Л'Ц lArpS л pra ф =- 4,25 ---------h 1 ,03 ——..
т is3 £sy/-Tps
где
1 4- Л
^2-h- <76>
Напряжения изгиба во фланце
(70) Приравнивая выражения (68) и (70), находим
Es ]/ rTVs
Мг ------------. (71)
2?тги гтр$
£2 + 4,25 ~1ПГ
_ Sip’/j
°" (nDs — zc'fh2'
(77)
Разрушающее усилие. Предельное значение изгибающего момента в заделанном сечении фланца
,, , „ , 2ов + о г Л2
Мразр = (л°б — гс) —5-д--L — .
В приближенных расчетах, пренебрегая влиянием внутреннего давления в трубе на изменения угла поворота, получим
<72) JTZ-/-pp Z ~Л
где ________
Л=0,72^(А)3(^б-^).
I \ s / л/jтр
(73)
(78)
Предельное значение изгибающего момента в трубе
^41 разр —
2ов -f- от s2 з Г’
(79)
Напряжения изгиба в стенке трубы
6Л1] °И — s2 •
(74)
Из условия равновесия
^разр ~ 7>разр/1 д7>|р Ifj разр (80)
Учитывая равенства (78) и (79), найдем разрушающее осевое усилие
Изгибающий момент в заделанном сечении фланца
Л1 — Pit — лР1рЛ41 =
-"Ш’Л <га>
I 2а1; -о-, 'разр — ~“ X
X ^(л£>б — zc) ~ + nD rp J .
(81)
Г лава 5
ШПОНОЧНЫЕ И ШЛИЦЕВЫЕ СОЕДИНЕНИЯ
Шпоночные соединения
В машиностроении применяют не-Напряженные соединения (с помощью Призматических и сегментных шпонок, Рис. 1) и напряженные соединения (с помощью клиновых шпонок). Шпонки этих типов стандартизованы, их Размеры выбирают по ГОСТам.
Основной недостаток соединений — отсутствие взаимозаменяемости и, как следствие, необходимость ручной пригонки или подбора.
Наибольшее применение имеют соединения с призматическими шпонками. Такие соединения в сравнении с напряженными более технологичны (легкий монтаж и демонтаж) и обеспе-
88
Шпоночные и шлицевые соединения
Рис, 1, Основные типы шпоночных соединений:
а — с призматической шпоикой, б — с сегментной шпонкой
1. Шпонки призматические обыкновенные (по ГОСТ 23360 — 78), Размеры, мм
Высота
Диаметр вала d шпонкн Ь шпонки h на валу Длина шпонки 1
От 6 до 8 2 2 1,2 От 6 до 20
Св 8 > 10 3 3 1.8 » 6 » 36
» 10 » 12 4 4 2,5 » 8 » 45
Св 12 до 17 5 5 3 От 10 до 56
» 17 » 22 6 6 3,5 » 14 » 70
Св 22 До 30 8 7 4 От 18 До 90
» 30 » 38 10 8 * 22 » 110
> 38 » 44 12 8 5 » 28 » 140
Св 44 до 50 14 9 5,5 От 36 до 160
» 50 » 58 16 10 6 » 45 » 180
» 58 » 65 18 1 ’ 7 » 50 » 200
Св 65 до 75 20 12 7,5 От 56 до 220
» 75 * 85 22 14 » 63 » 250
> 85 » 95 25 14 9 » 70 » 280
» 95 » 110 28 16 10 » 80 » 320
» 110 » 130 32 18 11 » 90 » 360
Св 130 до 150 36 20 12 От 100 до 400
» 150 » 170 40 22 13 » 100 » 400
» 170 » 200 45 25 15 » 110 » 450
чивают лучшее центрирование деталей г. Призматические шпонки имеют прямоугольное сечение с отношением
высоты к ширине от — I (для валов
малых диаметров) до -у = 0,5 (для
1 Во многих случаях посадку деталей на вал осуществляют с натягом
валов больших диаметров, табл. !) Глубина врезания шпонки в вал составляет 7, ж 0,Oh.
Рабочими у призматических шпонок являются боковые узкие грани. В радиальном направлении предусмотрен зазор. В ответственных шпоночных соединениях сопряжения дна паза с боковыми сторонами выполняются по радиусу. Материал шпонок — чисто-
Шпоночные соединения
89
2. Допускаемые напряжения смятия 0ем. МПа, для шпоночных соединений в подъенно-транспортном машиностроении__________________________________________________
Соединение Материал Нагрузка
постоянная реверсивная ударная
Режим
I II III I II Ill I 11 III
Неподвижное Сталь 4yi ун 180 100 165 90 150 80 120 65 110 60 100 54 60 33 55 30 50 27
Подвижное Сталь 60 55 50 50 45 40 36 33 30
Примечания 1 Допускаемые напряжения выбирают по материалу наименее прочной детали (ступнцы. вала, шпонки).
2. Режимы I — легкий, II — средний; III — тяжелый, весьма тяжелый или непрерывный .
тянутая сталь с пределом прочности ав 600 МПа.
Основным для соединений с призматическими шпонками является условный расчет на смятие (упругопластическое сжатие в зоне контакта).
Если принять для упрощения, что нормальные напряжения (давления) в зоне контакта распределены равномерно и плечо главного вектора давлений равно 0,5d (где d—диаметр вала),то
2Л4К , аем~ а]ем’ (1)
где (р — рабочая длина шпонки; t2 = = 0,4Л — глубина врезания шпонки в ступицу; [о]см—допускаемое напряжение на смятие.
По формуле (1) обычно проверяют напряжения в зоне контакта или вычисляют предельный крутящий момент.
При необходимости по формуле (1) можно вычислить длину шпонки, однако обычно ее принимают в соответствии с длиной ступицы.
Проверку прочности шпонок на срез обычно не проводят, так как это условие удовлетворяется при использовании стандартных сечений шпонок и рекомендуемых значений [о]см.
Если условие (1) не выполняется, то в конструкции можно применить две Шпонки, установив их под углом 120 или 180°.
Сегментные шпонки благодаря более Глубокой посадке практически ие имеют
перекоса под нагрузкой; они взаимо" заменяемы. Однако глубокий паз ослабляет вал, и сегментные шпоики используют преимущественно для закрепления деталей на концах валов (или в других малонагруженных участках вала).
Расчет соединений с сегментными шпонками также проводят по формуле (1), принимая /а == h — 1г (см. рнс. 1, б).
Допускаемые напряжения в неподвижных шпоночных соединениях 1<Исм = От/л,
где <гт — предел текучести наиболее слабого материала детали (вала, шпоики или ступицы); п — коэффициент безопасности; при точном учете нагрузок л = 1,25, в остальных случаях л = 1,5-г-2,0.
Если шпонки изготовлены из чистотянутой стали (ГОСТ 8787—68), то принимают [о]см= 804-150 МПа (меньшие значения — для ступиц из чугуна и алюминиевых сплавов).
В редукторостроении для шпонок из стали 45 принимают (см. [2] к гл. 6): [о 1см = 50-4-70 МПа — при непрерывном использовании редукторов с полной нагрузкой;
[о1см= 1304-180 МПа-при среднем режяме использования редукторов;
[а1см = 260 МПа— при предельных статических нагрузках.
В подъемно-транспортном машиностроении [о]см принимают по данным табл. 2.
90
Шпоночные и шлицевые соединения
Для ступиц из текстолита и древесно-слоистых пластиков [о]см — = 20 МПа.
Если шпонки используют в качестве направляющих при осевом перемещении деталей под нагрузкой (подвижные шпоночные соединения), то допускаемые контактные давления в соединении ограничивают во избежание заедания и уменьшения износа. При незакаленных поверхностях и малой скорости перемещения принимают [о]ем= 10-ь-30 МПа.
Применение шпоночных соединений для быстровращающихся, динамически нагруженных валов ответственного назначения не рекомендуется.
ШЛИЦЕВЫЕ СОЕДИНЕНИЯ
Шлицевые соединения имеют преимущества перед шпоночными благодаря более высокой несущей способности при постоянных и переменных нагрузках. Их применяют для неподвижного
и подвижного соединения валов со ступицами деталей. Они имеют меньшие радиальные габариты и обеспечивают хорошее центрирование по сравнению со шпоночными соединениями.
По форме поперечного сечения различают три основных типа соединений.
Соединения с прямобочными зубьями наиболее распространены в машиностроении. Их можно центрировать по боковым граням шлицев, по наружному или внутреннему диаметру вала (рис. 2). Первый способ применяют при числе зубьев г — 10, 16 и наружном диаметре D 90 мм для передачи больших крутящих моментов и при отсутствии высоких требований к точности центрирования деталей.
При высоких требованиях к соосности вала и ступицы детали центрируют по наружному диаметру вала (если зубья в ступице получают протягиванием) или по внутреннему диаметру вала. Нагрузочная способность таких соединений ниже, чем при центрировании по боковым поверхностям зубьев
Рис. 2. Способы центрирования прямобочных соединений:
а — по боковым поверхностям; б — по наружному диаметру; в — по внутреннему дяа метру; г — форма сечення ступицы; д. е — форма сечения вала соответственно для не полнений б и в
Шлицевые соединения
91
3, Основные геометрические параметры прямобочных соединений (по ГОСТ 1139 — 80 и расчетные коэффициенты
Легкая серия
Средняя серия
7 яжелая серия
11
13
16
18
21
23
26
28
26 6 6
30 6 6
32 7 6
0,5 2,21
0.9 2,31
0,94 2,33
14
16
20
22
25
28
32
34
3
3.5
4
5
5
6
6
7
20
23
26
29
32
35
2,5 10 0,94 2,08
3 10 1,46 —
3 10 1,69 2,17
4 10 2.34 —
4 10 2,4 2,09
4 10 3,2 -
32 36
42
46 52
56
62
36
40
46
50
58
62
68
6
7
8
9
10
10
12
2,18
2,23
2,25
2.1
2,16
38
42
48
54
60
65
72
6
7
8
9
10
10
12
40
45
52
56
60
65
72
10 4.3 2,25
10 5,6 2,22
10 7,4 2,31
10 8,2 —
16 10 2,06
16 12,9 —
16 16,2 —
72
82
92
102
112
78
88
98
108
120
5,63
6,4
7, 1
7.9
13
82 12
92 12
102 14
112 16
125 18
2,36
2,42
2,47
2,59
82
92
102
115
125
16
20
20
20
20
18,6
25,9
29,2
45
49
2.29
2.29
2,51
из-за менее благоприятного распределения нагрузки между зубьями.
В зависимости от числа зубьев и их высоты ГОСТ 1139—80 предусмотрены три серии соединений (легкая, средняя и тяжелая, см. табл. 3).
Соединения с эвольвентными зубьями1 (рис 3) более технологичны, нежели соединения с прямобочными шлицами, имеют более высокую прочность (благодаря большому числу зубьев и скруглению впадин) и точность. Они могут центрироваться по боковым граням (наиболее распространенный способ, рис. 3, а) и по наружному Диаметру вала (рис. 3, б). Основные размеры шлицевых соединений даны в табл. 4.
Соединения с прямобочными и эволь-вентными зубьями широко применяют также для направления осевого пере-
' Исходный контур н форма зубьев по ГОСТ 6033-80.
движения деталей, посаженных на вал (например, зубчатых колес в коробках передач). В этом случае твердость поверхности зубьев повышают до НДС 54...60 для уменьшения их изнашивания.
Для неподвижной в осевом направлении посадки на валы дисков турбин, для посадки на валы передвижных косозубых колес используют соединения с винтовыми зубьями, которые уменьшают относительное скольжение диска на валу под нагрузкой и снижают изнашивание.
Соединения с треугольными зубьями (рис. 4) применяют при стесненных радиальных габаритах конструкции.
Для быстроходных передач (авиационные и автомобильные коробки передач) точность центрирования зубчатых соединений недостаточна. Для повышения точности центрирование осуществляют по вспомогательным поверхностям (см. с. 98) либо отказываются
92
Шпоночные и шлицевые соединения
Рис. 3. Эвольвентные соединения
4. Основные геометрические параметры эвольвентных соединений (по ГОСТ 6033 — 80)
Число зубьев z при модуле т
0 8* 1 1.5 2* 2 5
Число зубьев z при модуле т
2*
23
26
30
34
36
38
42
46
48
51
55
50
66
74
18
20
24
26
28
30
34
36
38
40
44
48
54
58
12
14
15
17
1 8
20
22
24
25
26
28
32
35
38
8
9
1 1
12
13
14
16
18
18
20
21
24
26
28
6 65
6 70
8 75
10 80
10 85
1 1 90
12 95
14 100
14 1 10
15 120
16 130
18 140
20 150
22 160
31
34
36
38
41
44
46
48
54
58
64
68
74
20
22
24
25
27
28
30
32
35
38
42
45
48
52
15
12
13
14
15
16
18
18
20
22
24
26
28
30
6
7 7
8
8
9
Ю
1 1
12
13
14
Примечания 1 При выборе наружного (номинального) диаметра и модуля предпочтительны значения, не отмеченные звездочкой
2 Числа зубьев, заключенные в рамки являются предпочтительными
2а0
Рис. 4» Соединение с треугольными зубьями
от применения соединений (колеса изготовляют за одно целое с валом).
РАСЧЕТ ШЛИЦЕВЫХ
СОЕДИНЕНИЙ НА ПРОЧНОСТЬ
Шлицевые соединения подобно резьбовым характеризуются неравномерным распределением нагрузки по длине. В отличие от соединения типа стяжки (см. рис. 16, гл. 3), детали которого работают на растяжение, в соосном зубчатом соединении вал и охватывающая деталь скручиваются. Поэтому закон распределения нагрузки в соединении, когда крутящие моменты прило-
Расчет шлицевых соединений на прочность
93
жены к втулке и валу с разных сторон (рис. 5), будет таким же, как н для соединения типа стяжки. На рис. 6 в качестве примера приведено экспериментальное распределение относительного крутящего момента на валу т* (z) = т (г)/тср (здесь т (z) = = dM (z)/dz, mcp = Mtl) по длине соединения карданной передачи автомобиля.
Соотношение для т (г) имеет структуру, аналогичную формуле для распределения нагрузки между витками резьбы.
Неравномерность распределения нагрузки оказывает существенное влияние на работоспособность соединений и учитывается в расчетах х.
Шлицевые соединения выходят из строя главным образом из-за повреждения рабочих поверхностей (изнашивание, смятие), а также усталостного разрушения зубьев н тонкостенных валов, которому обычно предшествует контактная коррозиция (фреттинг-кор-розия).
Расчет шлицевых соединений включает: 1) расчет шлицевых валов на кручение при действии статических и переменных крутящих моментов (см. гл. 8); 2) расчет зубьев.
В отечественной и зарубежной практике в основу расчета зубьев положено определение напряжений смятия (средних контактных давлений). Напряжения изгиба и среза в основании зуба пропорциональны напряжениям смятия, и последние можно рассматривать как критерий подобия, обобщающий опыт эксплуатации конструкций.
Расчет ведут по формуле
°см “ d^hi^ [а)см’ (2) где dcp — средний диаметр соединений; z — число зубьев; h и I — соответственно высота и длина поверхности контакта зубьев; ф — коэффициент, Учитывающий неравномерность распределения давлений в соединении, обычно ,1’= 0,7—0,8; [а]см—допускаемое напряжение смятия на боковых поверх-
1 Для снижения концентрации напряжений на краях соединения, особенно в условиях перекоса, применяют бочкообразные шлицы
Рис. 5. Схема шлицевого соединения:
1 — втулка, 2 — вал
ностях зубьев. В табл. 5 даны [а]см для соединений подъемно-транспортных устройств. Допускаемые напряжения в станкостроении более низкие: для неподвижных соединений [о]см= = 12-ъ20МПа, для подвижных без нагрузки [а]см = 4ч-7 МПа и для соединений подвижных под нагрузкой [а]см <2 МПа.
Средние напряжения смятия (при ф= 1) для некоторых соединений приведены в табл. 6.
Высота и длина поверхности контакта:
а) для прямобочных зубьев (см. рис. 2)
, D—d , D + d
Л — g ^cp — 2
б) для эвольвентных зубьев (см. рис. 3)
h = Qm; dcp = </д = пи;
здесь 0 = 1 при центрировании по
Рис. 6, Распределение относительного крутящего момента по длине соединения
94
Шпоночные и шлицевые соединения
5. Допускаемые напряжения смятия для шлицевых соединений в изделиях подъемнотранспортного машиностроения (валы и втулки с $в > 500 МПа)
Тип соединения Условия эксплуатации Поверхность зубьев
без термообра ботки с термообработ кой
[о!см. МПа
Обычное (с осевой фиксацией) а б в 35 — 50 60- 100 80—120 40—70 100—140 120—200
Подвижное без нагрузки а б в 15-20 20- 30 25 — 40 20-35 30-00 40 — 70
Примечав t I В таблице. а условия эксплуатации тяжелые (нагрузка знакопеременная с ударами в обоих направлениях значительные угпы перекоса) сма зочкый материал отсутствует б — условия эксплуатации средине (переменная нагрузка не более 10% от посто*нной угол перекоса осей под нагрузкой не более 10', смазка бед ная) в — условия эксплуатации хорошие (статическая нагрузка переменная нагрузка не выше 5% статической угол перекоса осей не более 5 — 7' смазка хорошая)
2 Допускаемые напряжения для подвижных соединений под нагрузкой ниже, чем для неподвижных соединений, в 4 — 5 раз
6. Средние напряжения смятия осм (при ф — 1) в длительно работающих соединениях
Соединение ~ вала Тип соединения HRC втутли асм, МПа
Трансмиссии грузовых и легковых автомобилей
Ведомый диск сцепления — первичный вал коробки передач Вторичный вал коробки передачи — зубчатое колесо 1-й передачи Вторичный вал коробки передач — Прямобочное 45 — 60 До 30 До 65 До 65 48 — 55 До 30 42 — 56 12—18 30 — 60
фланец карданного вала 14—19,4
Подвижные соединения карданных валов До 30
Полуось — почуосевая втулка Зубчатые муфты коробок передач Коробки приво Эвольвеитное а, о в авиационных До 65 50 — 65 50—65 двигателей 35 — 42 110— 160 27 — 70
Валы и зубчатые колеса Эвольвеитное 50—100
Торсионные рессоры 35 — 42 100—150
Примечания 1 Средние напряжения в соединениях трансмиссии тракторов приблизительно такие же как и в автомобилях
2. В подвижном соединении карданного вала автомобиля марки БелАЗ 540 осм = ® 45 МПа
Расчет шлицевых соединений на прочность
95
Рис. 7. Концентрация напряжений при кручении шлицевых валов: д — а = 0е, б — а — 32°; в — а = 30®
боковым поверхностям и 0 = 0,9 при центрировании по наружному диаметру; т — модуль шлицев, da — диаметр делительной окружности;
в) для треугольных зубьев (см. рис. 4)
h = De~da . == tnz.
Предельный момент, передаваемый соединением, р
М8. пр — Йем2*/ Ф = (а1см»
й • (3) где приведенный статический момент dcp
Зсм = ah -g- ф. Значения SCM при ф = 0,75 для примобочных соединений приведены в табл. 3.
При действии переменных нагрузок нередки случаи разрушения деталей со шлицами (в особенности тонкостенных валов) от усталости из-за высокой концентрации напряжений.
В свободной (неконтактирующей) части шлицевого вала имеет место значительная концентрация касательных напряжений. Теоретический коэффициент концентрации касательных напряжений прн кручении шлицевого вала
гДе ттах и тн — соответственно максимальное и номинальное напряжение в зубчатом валу при кручении; для сплошного вала
Мк Мк
~ 0,2<Р’
здесь И7К — момент сопротивления сечения вала кручению; d — внутренний диаметр зубчатого вала.
На рис. 7 показано изменение теоретического коэффициента концентрации напряжений по контуру шлицев прямобочного (рис. 7, а), треугольного (рис 7, б) и эвольвентного (рис. 7, в) профиля с одинаковой высотой h и максимальными радиусами галтелей.
В расчетах на прочность учитывают максимальное значение ах, соответствующее наиболее нагруженной точке на контуре.
В контактирующей части вала касательные напряжения уменьшаются благодаря распределению крутящего момента по длине соединения. Однако в этой части вала появляются нормальные и касательные напряжения от изгиба и сдвига зубьев, наибольшие значения которых также концентрируются в основании шлицев На рис. 8 показано изменение контурных (главных) напряжений в галтелях зубьев при контактном давлении агМ = 10 МПа
Максимальные нормальные напряжения в контактирующей части соединении оказываются обычно ниже касательных напряжений в свободной части шлицевого вала, поэтому разрушение шлицевых валов от усталости происходит, как правило, в неконтактирующей части *.
1 Если разрушение происходит в кои-тактирующей части, то ему предшествует существенный износ шлицев.
96
Шпоночные и шлицевые соединения
Рис. 8. Концентрация напряжений от изгиба зубьев
В приближенных расчетах на сопротивление усталости шлицевых валов учитывают концентрацию напряжений от кручения. Значения теоретических коэффициентов концентрации напряжений при кручении прямо-бочных шлицевых валов приведены в табл. 3.
Для валов с эвольвентными зубьями
при г . .
ах . . при z. . . ат . . . .
11 — 14 .1,55—1,62 . 24—36
1,86-1,92
16—32
1,76—1,82 >38
1,93—1,98
Большие значения ат соответствуют большим г.
ИЗНАШИВАНИЕ СОЕДИНЕНИЙ
Шлицевые соединения выходят из строя в основном вследствие изнашивания боковых (рабочих) поверхностей шлицев (зубьев). Изнашивание наблюдается в шлицевых рессорах, передающих крутящий момент от одного агрегата к другому, в карданных валах, в соединениях валов и зубчатых колес и др.
Изнашивание зубьев связано с практически неизбежными циклическими смещениями деталей соединения поддействием радиальной нагрузки, в результате несовпадения или взаимного наклона осей при действии крутящего момента. Начальный монтажный перекос может возрастать в работе за счет тепловых деформаций, изменения взаимного расположения деталей под нагрузкой и т. д.
Изнашивание шлицевых соединений происходит более интенсивно при развитии иа рабочих гранях контактной коррозии, которая появляется даже в соединениях с высокой твердостью рабочих поверхностей (45—55 НКСЭ) и при сравнительно невысоких средних контактных напряжениях (асм = =- 50 МПа).
Условный расчет на износостойкость можно проводить по допускаемой удельной мощности трения (мощности трения, отнесенной к 1 мм2 контактной поверхности шлицев) х.
Если принять, что ось шлицевого вала в результате монтажа или под нагрузкой получила перекос на угол Д<р (рад) по отношению к оси охватывающей втулки (ступицы колеса), то наибольшее взаимное смещение точек зубьев на одни оборот составит
Д/ = Дф</ср + (5)
где I и dcp — соответственно длина и средний диаметр соединения, мм.
Скорость относительного скольжения, мм/с,
кСн=--6о- V l + ’ ММ
(6) а удельная мощность трения
Л/i = искНасм =
Дф ! Г , , f I \2
~ 60 V l + \.dcp) '
____________ (7)
1 ГОСТ 21425 — 75 рекомендует более сложный метод расчета прямобочных шли-цевых соединений
Изнашивание соединений
97
где и — частота вращения шлицевого вала, мин-1; р — коэффициент трения; (j0M — среднее контактное давление в соединении при ф — 1.
Обычно в удовлетворительно работающих соединениях рессор при твердости поверхностей деталей >50 HRCj, углах перекоса Д<р < ^7'«0,002 рад) и бедной смазке
150 Н-мм/(мм2-с), а при обильной смазке Nx 250 Н-мм/(мм2 с).
Допустимый угол перекоса в шлицевых соединениях по условиям износостойкости
60 [АД]
цасм^ср |/ 1 + !
(8) где [ЛЧ ] — допускаемая мощность трения, Н-мм/(мм2-с). Можно принимать 1 [Nti—SHRCs при бедной смазке (масляный туман и др.) соединений; [Л/i ] - 5 HRC3 для соединений при обильной смазке.
Если затрачиваемая на трение мощность Л\ 1 HRC3 при обильной смазке и Nt 0,6 HRC3 при бедной смазке, то изнашивание в соединениях практически не наблюдается при неограниченно большом числе циклов нагружения.
Из соотношения (8) следует, что допустимый угол перекоса деталей в соединении может быть увеличен за счет снижения контактных давления н коэффициента трения. Для снижения коэффициента трения применяют различные гальванические покрытия (никелевое, медное, серебряное, кадмиевое, окисное и др.). Толщина слоя металлических покрытий 6—15 мкм. Для повышения износостойкости применяют также покрытия из твердых смазок на основе дисульфида молибдена и другие, зазоры заполняют термопластичными полимерами типа эпоксидных и фенольных смол.
Повышение износостойкости наблюдается при использовании твердых и жидких смазок (особенно в случае
1 При неодинаковой твердости поверх-«остей сопрягаемых деталей расчет ведут Для детали с наименьшей твердостью поверхности
4 Заказ 402
непрерывной подачи в зону контакта масла, стабилизирующего тепловой режим).
Эффективным оказывается также применение химико-термической и упрочняющей обработки для повышения износостойкости.
Азотированию подвергают шлицевые валы (рессоры) из сталей 38Х2МЮА, 38ХА, 40ХН2МА. Толщина азотированного слоя 0,1—0,3 мм, твердость азотированной поверхности для стали 38Х2МЮЛ 58—61 HRC3 (в сердцевине 30—37 HRC3); валы из сталей 38ХА и 40ХН2МА имеют твердость поверхности 45 HRC3 и сердцевины 28—35 HRC3.
Валы из сталей 12Х2Н4А, 18Х2Н4МЛ и другие цементируют на глубину 0,2—0,7 мм. Твердость поверхности шлицев HRC-. 55—58, твердость сердцевины 32—41 HRCg.
Валы и рессоры из сталей 12Х2Н4А, 12ХНЗА, 18Х2Н4МА и другие иногда подвергают цианированию на глубину 0,2—0,4 мм. Твердость поверхностного слоя 57—59 HRC3, а твердость сердцевины 32—41 HRC3.
Применяют также закалку поверхности до твердости 45—50 HRC3.
В последние годы для повышения износостойкости широко применяют виброшлифование и дробеструйное упрочнение шлицевых деталей (см. гл. 34). Диаметр шарика обычно <Ап < 0,1г (г—радиус скругления во впадинах шлицев).
Основным методом оценки надежности шлицевых соединений являются ресурсные испытания в стендовых или эксплуатационных условиях. Ускоренные испытания можно проводить с заранее созданным перекосом.
Эффективными средствами повышения износостойкости соединений являются:
а) уменьшение углов перекоса осей сопрягаемых деталей при монтаже и в рабочих условиях (за счет неравномерного нагрева, деформации под нагрузкой и т. п ). Угол перекоса свыше 10' нежелателен для валов (рессор) с dcp — 104-50 мм. Для соединений, допускающих относительное проскальзывание, углы перекоса свыше 40" недопустимы;
98
Соединения деталей с гарантированным, натягом
Рис 9. Способы центрирования деталей в соединениях:
а — по конической н цилиндрической поверхностям, б — по цилиндрическим поверхностям с помощью втулок
б) увеличение твердости контактирующих поверхностей путем азотирования, цементации, обдувки дробью и др.;
в) уменьшение зазоров в шлицевом соединении, применение более
плотных посадок, центрирование по вспомогательным поверхностям и затяжка соединений (рнс. 9).
При проектировании соединений, воспринимающих радиальные нагрузки, зубья желательно располагать симметрично относительно венцов.
Глава 6
СОЕДИНЕНИЯ ДЕТАЛЕЙ С ГАРАНТИРОВАННЫМ
НАТЯГОМ
Соединение деталей машин с натягом осуществляют за счет сил упругости от предварительной деформации деталей.
С помощью натяга — разности посадочных размеров сопрягаемых деталей — можно соединять детали как с цилиндрическими (рис. 1), так и с коническими поверхностями контакта.
Основное применение имеют цилиндрические соединения с натягом, называемые часто поессовыми Эти соединения просты в изготовлении, обеспечивают хорошее центрирование сопрягаемых деталей, могут воспринимать значительные статические и динамические нагрузки (радиальные и осевые).
Основные недостатки соединений: сложность демонтажа, возможность повреждения посадочных поверхностей при разработке, ограниченность несущей способности, особенно при наличии вибраций, возникновение фрет-тинг-коррозии, связанной с взаимными микросмещениями деталей, концентрацией напряжений.
Взаимное смещение деталей в прессовых соединениях предотвращается за счет сил трения на поверхностях контакта, поэтому нагрузочная способность соединений определяется преимущественно натягом, который назначают в соответствии с посадками, установленными ГОСТ 25347—82. Од
Условия неподвижности и контактные давления в соединениях
99
нако возможны случаи, когда посадка не может быть реализована в конструкции по условиям прочности. Поэтому при проектировании соединений должны быть удовлетворены как требования неподвижности соединений, так и условия прочности деталей.
УСЛОВИЯ НЕПОДВИЖНОСТИ и КОНТАКТНЫЕ ДАВЛЕНИЯ В СОЕДИНЕНИЯХ
Для обеспечения неподвижности соединений средние (номинальные) контактные давления qm должны быть такими, чтобы силы трения превышали внешние сдвигающие силы.
При нагружении осевой силой А (рис. 2)
Ak . ...
qm>^dT' (1)
при нагружении крутящим
AfK
2MKk
моментом
(2)
при совместном действии осевой силы и крутящего момента
В формулах (1)—(3) k — коэффициент запаса сцепления, обычно принимают k ~ 1,5-4-2; р — коэффициент
Рис. 2. К расчету соединений с гарантированным натягом
трения; d и I — соответственно диаметр и длина посадочной поверхности.
Значения коэффициентов трения для прессовых соединений даны в табл. 1. При сборке стальных и чугунных деталей гидропрессованием (с подводом масла) принимают р = 0,12.
Для соединений, работающих при переменной внешней нагрузке с частотой f> 10 Гц, значения коэффициентов трения следует понижать на 30—40%.
Из формул (1) и (3) следует, что несущая способность соединений при статических (постоянных) нагрузках определяется номинальными (средними) контактными давлениями. Эти давления зависят от натяга в соединении и условий работы (температурных и др.).
1. Значения коэффициентов трення (сцепления) ц прн посадках с гарантированным натягом (охватываемая деталь из стали)
Способ сборки соединений Материал охватывающей детали
Сталь Чугун Алюминиевые и магниевые сплавы Латунь Пластмассы
Механическая 8апрессовка Тепловая сборка и,06-0 13 * 0 ’4—0, 16 ** 0.07—0,16 0.07 —0.12 0,07 — 0.09 0,02 — 0.06 0.05 — 0,06 0.05 — 0,1 0.05 — 0,14 0.4 —0,5
«• 5оверхности сопрягаемых деталей предварительно смазаны машинным маслом. В знаменателе дроби указаны значения ц при сборке охлаждением охватываемой
4*
too
Соединения деталей с гарантированным натягом
Соединения тонкостенных колец (рис. 3). Контактное давление определяют из условия совместности перемещений колец 1 и 2.
6 ...
«2 — «1 = -у > (4)
где 6 — диаметральный натяг.
Радиальные перемещения колец
«1 — —q^i; «2 = ?^2- (5)
где q — контактное давление; X, — коэффициент радиальной податливости кольца (i = 1, 2 — номер кольца);
<6>
где Rt — радиус срединной поверхности кольца толщиной ht\ Et — модуль упругости материала кольца.
Из соотношения (4) и (5) следует:
6
2 (At + Л2)
(8)
а изменение радиуса кольца после запрессовки
ДД1 = И1 =----Д Л ;
Z (Л1 ф Ла)
= =
2 (Л1 Л2)
Изменение диаметров свободной верхности необходимо учитывать посадке подшипников иа валы,
попри так
как излишний иатяг может не только существенно уменьшить радиальный зазор в подшипниках, но и привести к защемлению тел качения.
Окружное напряжение для тонких колец
°01 8i£ 1 =
£16 Л1 ,
2/?i (Я-i + Яг) *
(9)
£26 Яг
2/? г (Я1 4" *
О0г ~ 82^3 ~
где е1а е3 — относительная деформация 1-го и 2-го колец; е$ — Д/?t/Rt.
Наибольший допустимый натяг в соединении из условия появления допустимых пластических деформаций
6^ = 20,-^^. (Ю)
где <Jtr — наименьшее значение (из двух) предела текучести материала кольца (1=1, 2).
Если соединение будет работать при повышенной температуре, то произойдет расширение колец и натяг в соединении изменится на величину
6Т — 2 (oCiRiTi — (11)
и станет равным
6* = б0 - бт,
(12)
где at и Tt — соответственно коэффициент линейного расширения и изменение температуры кольца;б0 — первоначальный натяг.
В этом случае контактное давление
6*
’ = -T(I7W (13)
Окружные напряжения и наибольший натяг в соединении при повышенной температуре можно вычислить по формулам (9) и (10), подставляя в них значения О(Т и Et, соответствующие рабочей температуре.
Если a2R2T2 > то при Tt = = Т2 = Т найдем температуру, при которой иатяг в соединении исчезает:
Т ------—------. (14)
а2Т?2 — «1/?1
Если кольца вращаются вокруг продольной оси с угловой скоростью
Условия неподвижности и контактные давления в соединениях
101
то радиальные смешения колец от центробежных сил (i = 1,2)
(20)
где pj — плотность материала кольца. Изменение натяга составит
--- 2 (UlQ) ^2to) ------
= 2<о2 (fl? -|i- - Rl -g-) . (16)
Так как отношение р/Е для большинства материалов (сталь, сплавы титана, алюминия и др.) приблизительно одинаково, то
<17)
Из соотношения (17) следует, что во вращающихся соединениях обычно происходит уменьшение натяга.
Угловая скорость (предельная), при которой натяг исчезнет (освобождающая частота вращения),
Соединения дисков и толстостенных цилиндров (рис. 4). После запрессовки дисков (цилиндров) возникнут контактные давления q, которые для деталей одинаковой ширины (длины) можно считать постоянными в зоне контакта.
Условия совместности перемещения дисков описываются соотношением (4), а связь радиальных смещений с давлениями в зоне контакта — зависимостями (5).
Используя решения, приведенные в гл. 16, коэффициенты радиальной податливости дисков 1 и 2 можно записать в виде cxd Л1 = 1Ё7
. __ c.2d
2 ~ 2£3 ’
(19)
гДе ct и са — коэффициенты;
В отношениях (19) и (20) d, dj и d2— диаметры деталей (см. рис. 4); Vj и v2 — коэффициенты Пуассона.
Контактное давление связано с натягом, как и прежде, соотношением (7). С учетом равенств (19) и (20) получим
В табл. 2 приведены значения коэффициентов сг и с2 для стальн х деталей.
Уменьшение внутреннего диаметра охватываемой детали
а увеличение наружного диаметра охватывающей детали
Напряжения в первом диске (цилиндре)
Рис. 4. Соединения дисков (цилиндров]
(24)
1
102
Соединения деталей с гарантированным натягом
2. Значения коэффициентов сх и сг для стальных деталей
dx/d или d/dt djd или d-fd-z Сг
0.0 0.70 • 0,5 1,87 1.97
0.1 0.72 1.32 0.6 1,83 2.43
0.2 0,78 1.38 0.7 2.62 3.22
0,3 0.89 1,49 0.8 4.25 4,85
0.4 1.08 1.68 0.9 9.23 9.83
• Охватываемая деталь имеет сплошное сечение
Напряжения во втором диске (цилии-
где d„ — диаметр сечения, в котором вычисляют напряжения.
Изменение напряжений в деталях соединений с натягом показано на рис. 5. Наибольшие напряжения возникают с внутренней поверхности охватывающей детали (d, = d). Условие отсутствия пластических деформаций
Рис. 5. Напряжения в прессовом соединении дисков
Наибольшие давления в зоне контакта
<7тпах — 0,5от [1 — J
и наибольший расчетный натяг в соединении (по условию возникновения пластических деформаций)
^тах — 0,5(ТтС? ci ' ) X
X [1-1 (28)
Если соединение подвержено действию повышенных температур, то последовательность расчета в этом случае сохраняется такой же, как и для колец.
Для вращающихся относительно продольной оси соединений дисков умень-
Pl Р2 Р
шение натяга при
Ех Е2 Е
и = va = v составит
С, 10
(29) где v — коэффициент Пуассона, v = = 0,3.
Контактное давление в соединении
Угловая скорость, при которой натяг в соединении исчезнет (q — 0), шк = 4 |/^ __ dp (3 v) • (31>
Соединения дисков и валов. Если сопрягаемые детали имеют различную
Расчетный и потребный натяги
103
Рис, 6. Сеточная разметка и распределение контактных напряжений в соединениях
Рис 7 Теоретический коэффициент концентрации напряжений в соединении с гарантированным натягом
упругости Е — 105 МПа) q^^ приблизительно иа 30% ниже, чем для соединений со стальными дисками.
с натягом
длину, то контактные давления распределяются по посадочной поверхности неравномерно.
На рис. 6 показано распределение давлений по длине соединений стальных валов и втулок (дисков) при диаметральном натяге 6 = 50 мкм. полученное из численного решения контактных задач (см. гл. 26 и 29). Наибольшие давления концентрируются вблизи краев втулок, что связано с влиянием выступающих концов вала, затрудняющих его деформацию в пределах соединения.
При уменьшении толщины втулки и, как следствие, увеличении ее радиальной податливости наблюдается снижение теоретического коэффициента концентрации напряжений аа — qmaxiqB (рис 7; <7Н— номинальное контактное давление, вычисляемое по формуле (21)).
С увеличением длины втулки (толщины диска) от 0,5d до 2d значение максимального контактного давления на кромке возрастает иа 30—40% (большие значения соответствуют толстостенным втулкам).
Значения максимальных контактных давлений у торцов ступенчатых втулок практически такие же, как и в соединениях с цилиндрическими втулками соответствующих ТОЛЩИН.
В соединениях стальных валов с дисками (втулками) из чугуна (модуль
РАСЧЕТНЫЙ И ПОТРЕБНЫЙ НАТЯГИ
При проектировании соединений по заданной внешней нагрузке определяют расчетный натяг 6 = — d\,
где йв и d& — измеренные соответственно наружный диаметр вала и внутренний диаметр охватывающей детали. Диаметры измеряют по вершинам микронеровностей, которые затем при сборке частично обминаются, и потребный натяг принимают несколько большим расчетного
6П= б+ 1,2 (/??!-+- Rz2), (32)
и по би выбирают посадку В формуле (32) Rz-i и Rz2 — высоты микронеровностей сопрягаемых деталей (табл. 3).
Посадки следует назначать в системе отверстия. Систему вала можно использовать только в случаях, когда это оправдано конструктивными или экономическими соображениями (например, если необходимо получить разные посадки нескольких деталей с отверстиями на одном гладком валу).
Обоснованно посадку можно выбрать, используя вероятностный расчет. Распределение действительных размеров деталей по полю допуска таково, что предельные сочетания размеров встречаются редко. Можно считать, что работоспособность соединения будет обеспечена, если потребный иатяг будет больше минимального
104
Соединения деталей с гарантированным натягом
3. Классы шероховатости поверхности
Класс шероховатости Разряд Среднее арифметическое отклонение профиля Ra, мкм Высота мик-ронеровно' стей (по 10 точкам) Rz, мкм Класс шероховатости Разряд Среднее арифметическое отклонение профиля Ra, мкм Высота микронеровностей (по 10 точкам) Rz, мкм
2 3 - — 320—160 160—80 80—40 10 а б в 0,160-0,125 0, 125 —0, 100 0 100 — 0.080 as 5Ra
4 5 - - 40 - 20 20- 10
1 1 а б в 0,080 -0.063 0,063- 0.050 0.050-0,040 5Ra
6 а б в 2,5- 2,0 2,0 —1,6 1,6 — 1,25 ~ 4Ra
12 а б в 0.040 — 0,032 0,032-0.025 0,025-0,020 bRa
7 а б в 1,25—1,0 1.0 — 0,80 0.80 — 0.63 « SRa
13 а б в — 0,100 — 0,080 0.080-0.063 0,063 — 0,050
8 а б в 0.63 — 0,50 0.50 — 0.40 0,40 — 0,32 « SRa
9 а б в 0,32 — 0,25 0,25 — 0,20 0.20 —0.16 =» 3Ra 14 а б в 0,050 — 0,040 0,040-0,032 0,032 — 0,025
вероятностного натяга 6р mln при заданном проценте риска.
При нормальном законе распределения размеров
С пип — ^ср
бр шах — бср “Ь (33)
где 6ср — средний натяг, 6ср —- Ав — — Ад (Ав и Ад — средние значения
отклонений стая), Ав =
размеров вала и отвер-es — ei ES — El ~~2~’ Ла =--------2----’
es (ES) и ei (EI) —- верхнее и нижиее отклонение вала (отверстия); Sj =
= + Sg — среднее квадратиче-
ское отклонение табличного натяга, es — ei ES — EI
Ад-—g— , ЛА- g
квантиль нормального распределения. В зависимости от вероятности Р нахождения искомого параметра в расчетных пределах принимают следующие значения t*;
0.5 0,9 0.95 0,97
0 1.28 1,64 1,88
0,99 0,995 0.997 0,999
2.33 2,58 2.75 3.1
Пример. Подобрать посадку зубчатого колеса из стали 45 на вал из стали 40Х, чтобы соединение было способно передавать крутящий момент Л4К = 10® Н-мм.
Размеры соединения: d = 60 мм; I = 80 мм; d2 = 100 мм. Шероховатость посадочных поверхностей вала и отверстия соответствует A?Zi = Rz2 = = 10 мкм. Сборку соединения осуществляем запрессовкой на прессе, сма
зочный материал — трансформаторное масло, и. = 0,08.
По формуле (2) определяем контактное давление в соединении при k = = 1,5:
2Л4КЛ _
Ъп~ рл<Я ~
2-10е-I,5
- 0,08-3,14-60М0
43 МПа.
Прочность при переменных нагрузках
105
4. Вероятностные натяги для различных посадок с натягом
Посадка Вероятностный натяг, мкм Посадка Вероятностный натяг, мкм
min max ^p min ^р max
60H6/s5 42,3 58,7 60Н8(и8 61,8 112 2
60Н7//7 58,6 91,4 60H9/u8 51.0 109,0
60//7/U8 72 И8 60H9/z8 117,2 182,8
60H7/S7 34,6 67,4 60Н9/х8 57,2 122,8
Используя соотношение (21), вычисляем расчетный натяг
6 = qd (-£ + =
\ £1 £2 /
/ 0 7 2 4 \
= 43'60 (-2ЛО^ + -20Ю~40 МКМ-
Потребный натяг (минимальный)
бп min = б + 1,2 (/??! + Ягг) =
= 40+1,2 (10 + Ю) = 64 мкм.
По соотношению (28) вычисляем наибольший расчетный и потребный натяги при от = 470 МПа для колеса из стали 45:
бетах = 0,5oTd (-£- + X \ £1 £я /
_ 0.5.470.60 +
= 141 мкм;
ба шах = 141 + 1,2 (10+ 10) = = 165 мкм.
По формулам (33) при Р 0,95 определяем характеристики рассеяния табличных натягов (табл. 4).
Из сравнения данных расчета с табличными следует, что условию работоспособности соединения будет удовлетворять посадка 60//7/и8.
Более точный выбор посадки можно осуществить, проводя расчет с учетом рассеяния характеристик материала деталей, внешней нагрузки, длины соединения н коэффициента трения.
После выбора посадки вычисляем усилие запрессовки, используя соотношения (1) и (21) при наибольшем вероятностном натяге 6Р тах ~ 118 мкм (см. табл. 4), ас использованием соотношений (2) и (21) при минимальном вероятностном натяге 6р mln = = 72 мкм определяем наименьший крутящий момент, передаваемый соединением.
ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ НАГРУЗКАХ
Предел выносливости соединений с гарантированным натягом в 1,5—3 раза ниже, чем прочность гладких образцов (стандартных). Это объясняется высокой концентрацией напряжений и контактной коррозией, вызываемой местным проскальзыванием деталей при переменных внешних нагрузках (особенно изгибающих).
В табл. 5 приведены значения отношения эффективного коэффициента концентрации напряжений в соединении ka к коэффициенту ео, учитывающему влияние масштабного эффекта, который рекомендуется использовать в расчете валов иа сопротивление усталости.
Значение отношения &т/ет (ПРИ кру-чении валов) можно определить приближенно из соотношения
А. = 1 + 0,6 (— 1 ) . е-r \ ео )
Расчет на сопротивление усталости прессовых соединений приведен в гл. 8.
Одним из распространенных конструктивных способов повышения сопротивления усталости соединений яв-
106
Соединения деталей с гарантированным натягом
5. Значения отношеиия в месте посадки деталей
Диаметр вала, мм Посадка Значения СТ/ CT при ст0. МПа
500 600 700 800 900 1000 1200
Н7/г& 2.5 2,75 3,0 3,25 3.5 3,75 4.25
30 H7/kb 1.9 2.05 2,25 2,45 2.6 2,8 3,2
H7/hC> 1.6 1,8 1,95 2.10 2,3 2.45 2,75
H7/r6 3,05 3.35 3.65 3.95 4.3 4.6 5.2
50 H7'k6 2,3 2.5 2,75 3,0 3,2 3,45 3,9
H7/h& 2,0 2,2 2.4 2,6 2.8 3,0 3,4
/77/56 3.3 3.6 3.95 4,25 4,6 4.9 5.6
100 H7/kC 2.45 2,7 2.95 3.2 3.45 4.0 4.2
и более H7/h& 2.15 2.35 2.55 2.75 3.0 3.2 3.6
Рис. 8. Конструктивные способы повышения сопротивления усталости соединений
ляется утолщение подступичной части вала (обычно диаметр увеличивают на 5—7%) с плавным переходом к утолщению (см. рис. 8, a; J? > 0,2d).
Предел выносливости соединений с утолщением повышается на 20—25% при передаче изгибающего момента через ступицу и на 40—50% при не-нагруженной ступице в сравнении с соединением без утолщения.
Предел выносливости прессовых соединений можно повысить на 30—50% за счет применения накатных разгружающих выточек на . ’,лу (рис. 8, б,
в) или на охватывающей детали (рис. 8, г, д). Обычно диаметр проточки da = (0,92-^0,95) d, а радиус проточки R = (0,14-0,15) dB.
Значительное (на 15—20%) повышение сопротивления усталости соединений можно получить при на-прессовке ступиц конической формы (рис. 8, е).
Сопротивление усталости прессовых соединений со шпонкой (шпоночных соединений на прессовой посадке) такое же, как и для обычных прессовых соединений. Оно определяется кон-
Прочность при переменных нагрузках
107
в. Влияние упрочнения подступнчных частей валов на сопротивление усталости
Образец Материал вала Способ обработки поверхности Предел выносливости при изгибе <j_lt МПа Эффективный коэффициент концентрации напряжений kg
Гладкий d = 50 мкм Ст5 нормализованная Шлифование 230 1
С напрессованной втулкой d=50 мм 100 2,3
Дробеструйная обработка 190 1.2
Гладкий d = 12 мм Сталь 45ХН, ов = — 1250” 1600 МПа Шлифование 483 1
С напрессованной втулкой d = 12 мм 200 2.42
Дробеструйная обработка 575 1.84
Гладкий d=50 мм Сталь 45. ов = = 620 МПа Шлифование 242 1
С напрессованной втулкой d = 50 мм 105 2.3
Обкатка роликом с усилием Р — = 2700 Н 232 1,04
То же. Р = 5400 Н 239 1.01
Гладкий d — 60 мм Сталь 45, ав = ~ 600 МПа Шлифование 215 1
С напрессованным (тепловой сборкой) шарикоподшипником d = 60 мм 100 2,15
Обкатка роликом 170 1,26
центрацией напряжений от посадки.
Для снижения коэффициента концентрации напряжений целесообразно скруглять острые торцовые кромки ступицы радиусом R = Ш6, где /а — протяженность зоны концентрации напряжений, мм; /а = (0,05—0,08) d; 6 — натяг, мм.
Более эффективным средством снижения концентрации напряжений является конусная расточка с торцов отверстия в охватывающей детали с плавным переходом в цилиндрическую поверхность (рис. 9): tg сс2 = 0,016-=-0,020.
Сопротивление усталости прессовых соединений зависит и от материала охватывающей детали. Использование
для изготовления охватывающих де талей более пластичных и менее проч ных материалов, чем для валов, способствует повышению выносливости соединений.
Сопротивление усталости прессовых соединений может быть существенно повышено за счет ряда технологиче-
ских мер.
Рис. 9. Конусная расточка отверстия
108
Сварные и паяные соединения
Рис 10 Конусная расточка отверстия и вала
Во избежание повреждения контактирующих участков вала при сборке рекомендуется изготовлять вал с за-ходиым конусом, а охватывающую деталь — с фаской (рис 10)
Существенное повышение предела выносливости (на 80—100%) можно получить при поверхностном упрочнении подступичной части вала (дробеструйной обработкой, обкаткой роликом, алмазным выглаживанием и
т п ) Такими способами в настоящее время упрочняют валы больших диаметров (до 600 мм) При этом значительно замедляется развитие фрет-тинг-коррозии
Степень повышения сопротивления усталости соединений зависит от режимов упрочнения (табл 6) При дробеструйной обработке мелкой дробью (d =0,5—0,8 мм) подступичных зон валов наблюдается большее повышение прочности (в 2—2,2 раза), чем при обработке крупной дробью
Предел выносливости прессовых соединений может быть повышен в 2— 3 раза за счет химико-термического поверхностного упрочнения (цементацией или азотированием)
При расчете на сопротивление усталости упрочненных валов коэффициент технологического упрочнения можно принимать в пределах Руп = 1,7—2.
Глава 7
СВАРНЫЕ И ПАЯНЫЕ СОЕДИНЕНИЯ
ОСНОВНЫЕ ВИДЫ СОЕДИНЕНИЙ
Различают следующие виды соединений, выполняемых дуговой и газовой сваркой стыковые (рис 1), нахлесточные (рис 2), тавровые и угловые (рис 3)
Для ответственных конструкций применяют стыковые соединения, имеющие прочность, близкую к прочности основного металла В зависимости от толщины деталей сварку выполняют односторонним (рис 1, а) или двусторонним (рис 1, б) швами, а также проводят подготовку кромок [прямолинейный (рис 1, в—г) или криволинейный (рис 1, д) скосы] Если сварку можно производить лишь с одной стороны, то для предотврашения стекания металла с противоположной стороны подкладывают привариваемые стальные или отъемные медные подкладки (рис 1, е)
Нахлесточные, тавровые и угловые соединения выполняют угловыми швами с нормальным сечением — основная форма шва (рис 4, а) и улучшенным сечением (рис 4, б, в)
Нахлесточные соединения тонколистовых конструкций выполняют с помощью контактной сварки — точечной (рис 5, а) и шовной (рис 5, б)
Диаметр сварной точки устанавливают в зависимости от толщины свариваемых деталей d. = 1,2S + 4 мм, этот диаметр не должен превышать d = 1,5S + 5 мм, где S — наименьшая толшина гвариваемых элементов Рекомендуемое расстояние между точками а = 3d при сварке двух элементов и а = 4d при сварке трех элементов
Расстояние от ряда сварных точек до ребер жесткости и кромок уголков должно быть не менее 2d
Электронно-лучевая сварка имеет преимущества перед другими видами сварки благодаря высокой проплавляющей способности луча и возможности регулирования его размеров
1) обеспечивает малые габариты сварных швов и, как следствие, малое коробление деталей в зоне сварных швов,
2) позволяет сваривать металл очень малых и очень больших толщин,
Основные виды соединений
109
Рис. 2. Нахлесточные соединения, выполненные:
а — фланговыми швами; 6 — лобовыми швами; a — комбинированным (фланговыми и лобовым) швом
Рис. 4. Формы угловых швов
Рнс. 5. Соединения контактной сваркой: а—точечной; б — шовной (роликовой)
по
Сварные и паяные соединения
1. Виды соединений, выполняемых электронно-лучевой сваркой
Вид соединения
Толщина свариваемого материала S
Размер кромок
а
1—5 0 — 0.1
Св 5 0-0,2
1 —5 0 — 0,1
Св. 5 0-0,2
0.1 —0.4 0-0.15
Св. 3 0 — 0,1
0.2—1,0
0.5—10 —
0,2-0,8
0.3-10 —
Св. 0,2 0 — 0.1
Св. 1 —
0.3-1,0 0 — 0,15
0 6 — 3.0 0-0,15
п т
0.8—1.5 5 — 8
1,0 —3.0 6 — 10
1,0-2.0 3-4
1.0 —3.0 3 — 6
0.3 —0.8 0.5 —1,0
1,0-10 1,0-1,5
3 — 6
3 — 10
0,6-1.5
— Св. 1
0.5 —2.0 0.1-2,0
0,8 —3,0 6 — 10
1—40
— 2 — 40
Контроль качества сварных соединений
111
Рис. в. Виды паяных соединений
3) допускает сварку через щели наружных стенок;
4) дает возможность сваривать за один : поход несколько деталей, расположенных одна под другой; так как сварку производят в вакууме, окисление металла сварного соединения исключается.
Электронно-лучевая сварка оказывается целесообразной для соединения деталей из тугоплавких металлов, жаропрочных и титановых сплавов.
При использовании электронно-лучевой сварки предъявляются высокие требования к подготовке кромок деталей и точности прилегания.
Отдельные виды соединений, получаемые с помощью электронно-лучевой сварки, показаны в табл. 1.
В паяных конструкциях, помимо соединений встык и внахлестку, распространены следующие: телескопические (рис. 6, а), внахлестку с заклепкой (рис. 6, б) или штифтом (рис. 6, в), внахлестку со шпонкой (рис. 6, г), взамок (рис. 6, д).
КОНТРОЛЬ КАЧЕСТВА СВАРНЫХ СОЕДИНЕНИЙ
Для обеспечения надежности изделий в машиностроении вводят полный или выборочный контроль сварных соединений. Контроль осуществляют визуально, а также с помощью разрушающих и иеразрушающих методов. Выборочный контроль осуществляют обычно путем механических испытаний (статических или усталостных) на прочность или герметичность (вплоть до разрушения).
В турбостроении основным методом контроля сварных швов является ультразвуковая дефектоскопия. Наличие поверхностных трещин, непроваров и шлаковых включений контролируют в этих швах магнитной дефектоскопией, травлением и керосиновой пробой.
Часто применяют рентгеновский контроль.
Для сосудов, работающих под давлением свыше 5 МПа при температуре стенки свыше 200 °C и ниже —70 °C, ультразвуковая дефектоскопия является обязательной для всех швов. При давлении до 1,6 МПа и температуре стеики от —40 до +200 °C контролируют 25% длины швов.
Все места пересечения сварных швов подлежат сплошному контролю. Для ответственных сварных соединений во всех отраслях машиностроения предусмотрены механические испытания образцов-свидетелей, а в исключительных случаях — вырезка контрольных проб из изделия.
Основным видом сдаточного испытания элементов, работающих под давлением, является гидравлическое испытание всех сосудов, трубопроводов и других элементов и узлов после изготовления. По правилам Котлонадзора, при рабочем давлении в сосуде р + + 50 МПа пробное давление должно превышать рабочее давление не менее чем в 1,5 раза (Рпроб+20 МПа). При рабочем давлении р > 50 МПа пробное давление назначают рПроб = = 1,25р, но не менее (р + 30) МПа. Конструкции из литых элементов независимо от рабочего давления подвергают испытаниям при пробном давлении рпроб — 1,5р. но не менее 30 МПа.
Силовой метод контроля повышенным давлением позволяет выявить грубые начальные дефекты.
В тех случаях, когда используют физические неразрушающие методы контроля, пробное давление принимают равным (1,05ч-1,1) р.
В химическом машиностроении для аппаратуры емкостного типа, работающей под давлением, контроль качества сварных швов осуществляют 100%-ным визуальным осмотром и выборочным контролем ультразвуковым и рентгеновским методами. Готовые изделия
112
Сварные и паяные соединения
проходят гидравлические испытания при давлении, увеличенном иа 20— 50% в сравнении с эксплуатационным.
РАСЧЕТ СВАРНЫХ СОЕДИНЕНИЙ ПРИ ПОСТОЯННЫХ НАГРУЗКАХ
Стыковые швы рассчитывают иа прочность по номинальному сечению соединяемых деталей (без учета утолщения швов), как целые детали.
Напряжения растяжения
а = -^-<[а']Р. (1)
где Р — внешняя нагрузка; I и S — соответственно длина шва и толщина соединяемых деталей; [о']р — Допускаемое напряжение сварного шва при растяжении; часто принимают [о']р = (0,94-1,0) [сг]р, где [а]р — допускаемое напряжение при растяжении основного металла (см. табл. 2).
Допускаемая растягивающая или сжимающая нагрузка
Р= [a'JpZS. (2)
Н апряжения в шве при совместном действии внешней силы и изгибающего момента
М
Цщах — --г
zs <[0'Ь:
(3)
здесь М и Р— изгибающий момент и внешняя сила; 1ГС — момент сопротивления сечения шва.
Расчет на прочность угловых фланговых и лобовых швов проводится на срез по сечению, проходящему через биссектрису прямого угла (рис. 7). Площадь расчетного сечения принимают
F = 0,7ApZ, (4)
где k-n — расчетный катет углового шва; I — длина шва.
Наибольшая длина лобового шва не ограничивается, а длину фланцевого шва не следует делать большей
2. Допускаемые напряжения для сварных
швов при статической нагрузке
Допускаемые напряжения для сварных швов
Сварка прн растяжении [o' 1р при сжатии при [ :двиге
Автоматическая, ручная электродами Э42А и Э50А, в среде защитного газа, контактная стыковая [о)р н 0,65 [0]р
Ручная электродами обычного качества 0.9 [о 1 0,6 [<71р
Контактная точечная — 0,5 [Р]р
Примечание, [о ] — допускаемое напряженке при растяжеини основного металла соединяемых элементов.
Расчет сварных соединений при постоянных нагрузках
113
50£р из-за неравномерного распределения нагрузки по длине.
Напряжения среза в расчетном сечении
T=W^[VI’ (5)
где [т' ] — допускаемое напряжение сварного шва на срез.
Если соединение имеет лобовые и фланговые швы, то в формулу (5) вместо I следует подставлять длину всего периметра угловых швов.
Допустимая растягивающая нагрузка
Р - 0,7£р/ [т']. (6)
Швы целесообразно располагать так, чтобы они были нагружены равномерно.
Если фланговые швы размещены несимметрично относительно нагрузки, например, в соединении с уголком (рис. 8), то, полагая, что напряжения равномерно распределены по длине шва, из уравнений равновесия получим соотношения для нагрузок на фланговые швы в виде
__ р.
fli — Па
где ах и а2—расстояния от центра тяжести сечения элемента до центра тяжести сечения швов.
Если задана длина шва
0,7*р [т'] *
то ее целесообразно разместить пропорционально нагрузкам Р, и Рг:
i^i(8) й14-
что эквивалентно условию т, — т2.
Для получения равномерного распределения нагрузки между швами необходимо длину каждого шва принимать обратно пропорциональной расстоянию между центрами тяжести шва и детали.
Расчет комбинированных (фланговых и лобовых) угловых швов под действием момента в плоскости стыка (рис. 9) выполняют, полагая, что швы работают независимо, а фланговые
Рис. 8. Соединение пластины с уголком
швы передают только силы вдоль своей оси.
Из условий равновесия следует:
М = Fc/it+ 1Fct, (9)
0,7£рЛ2
где Fc = 0,7Ар/; «7С = —
откуда
М
(10)
В уточненном расчете можно принять что приваренный элемент стремится повернуться вокруг центра тяжести площади сечений швов. Тогда
М
Trnax = ~f гтгх^[т'], (11) JP
где Jp — полярный момент инерции швов, Jp = Jx + Jу\ Jx и Jу — моменты инерции швов относительно осей х и у, проходящих через центр тяжести площади сечений швов; ггаах— расстояние от центра тяжести до наиболее удаленной точки шва.
Тавровые соединения, выполненные угловыми швами, рассчитывают по формулам (5) и (6), а стыковые — по формулам (1) и (2).
Угловые соединения (см. рис. 3) не используются как силовые, их применяют, как правило, для образо-
Рис. ч К расчету соединений с комбннн-ронанным угловым швом
114
Сварные и паяные соединения
3. Расчетные сопротивления R для ннзкоуглероднстых сталей
Марка стали R. МПа, при
растяжении * сжатии срезе
СгЗ, Ст4 210/180 210 130— 150
10Г2С1, 15ХСНД 290/250 290 170- 200
юхснд 340/290 340 200 — 240
* В числителе дроби приведены значения R. для швов, контролируемых физическими методами, в знаменателе — обычными методами (визуальным и т п )
вания профилей из отдельных элементов.
Прочность стыкового соединения, полученного контактной сваркой, принимают равной прочности основного металла.
Соединение, полученное точечной контактной сваркой, при действии нагрузки в плоскости стыка рассчитывают на срез, принимая равномерное распределение нагрузки между точками
4Р
где Р — усилие, приходящееся на одну точку, i — число плоскостей среза точек.
Швы, получаемые иа роликовых машинах, рассчитывают по формуле
Т = ^Г^[Т'1; (13)
здесь а — ширина шва; I — его длина.
Допускаемые напряжения в сварных швах в долях допускаемых напряжений основного металла приведены в табл. 2. Допускаемые напряжения для основного металла в металлоконструкциях вычисляют по формуле
г , Rm
где R — (0,85-7-0,9) ат — расчетное сопротивление с учетом неоднородности материала (ат — предел текучести материала); т — коэффициент, который принимают в зависимости от типа соединения и условий его работы, обычно т = 0,84-0,9; К — коэффициент перегрузки, обычно К = 14-1,2; для резервуаров с внутренним давле
нием К = 1,2; для подкрановых балок при тяжелом режиме работы К = = 1,34-1,5.
В строительных конструкциях принимают расчетное сопротивление R = = 0,9от. Значения R, принимаемые в ряде отраслей машиностроения, приведены в табл. 3.
ВЛИЯНИЕ ОСНОВНЫХ конструктивных И ТЕХНОЛОГИЧЕСКИХ ФАКТОРОВ НА СОПРОТИВЛЕНИЕ УСТАЛОСТИ
Сопротивление усталости сварных соединений часто оказывается более низким, чем сплошных деталей. Это объясняется следующими факторами: концентрацией напряжений, связанной с геометрией шва, непроварами и т. п.;
неравномерным распределением нагрузки вдоль шва (во фланговых швах и ДР.);
остаточными напряжениями после сварки;
литейной структурой шва и около-шовиой зоны.
Стыковые соединения. Эти соединения по сравнению с соединениями Других типов обладают повышенной прочностью благодаря уменьшению концентрации напряжений. На рис. 10 в качестве примера показано распределение нормальных напряжений в поверхностных слоях образца. Значения эффективных коэффициентов концентрации напряжений в сварных соединениях приведены в табл. 4.
Влияние основных факторов на сопротивление усталости
115
Рис. 10. Напряжения в стыковом соединении
Стыковая сварка является основным видом соединения ответственных элементов конструкции.
На основании экспериментальных исследований и данных практики можно указать следующие основные факторы, существенно влияющие на со
противление усталости стыковых соединений.
Состояние поверхности основного металла в зоне шва. Пределы выносливости деталей из низкоуглеродистых сталей, сваренных без удаления окисных пленок с по-
4. Эффективные коэффициенты концентрации напряжений в сварных соединениях
Элементы соединения н их характеристика Коэффициент kQ для стали
углеродистой низколегированной
Сварные швы Стыковые швы (по оси шва) с полным проваром корня шва
при автоматической н ручной сварке и контроле шва просвечиванием 1,0 1,0
прн ручной сварке без просвечивания Угловые швы поперечные (лобовые) при сварке 1.2 1,4
ручной 2,3 3,2
автоматической 1,7 2,4
продольные (фланговые), работающие иа срез Основной металл У перехода к стыковому шву с усилением 3,5 4,5
без механической обработки шва с механической обработкой абразивным кру- гом или специальной фрезой н стыковании листов1 1,5 1,9
одинаковой ширины и толщины 1 1
разной ширины 1,2 1.4
разной толщины У перехода к лобовому шву при направлении усилия вдоль большого катета и отношении катетов 1-го и 2 го листов 1,3 1,6
kt/k2 = 2 2,3/1,2 • 3,2/1,4 •
k2/k2 =1,5 2,7/1.5 • 3,7/1,9 ♦
У флангового шва У косынок, приваренных встык и втавр 3,5 4,5
без механической обработки 2,7 3.3
с механической обработкой при плавных формах косынок 1,5 1,9
У косынок, приваренных внахлестку 2,7 3,3
У ребер жесткости и диафрагм, приваренных лобовыми швами с плавными переходами 1,5 1.9
* В числителе дроби дано значение kQ для механически не обработанного шва, в знаменателе — для механически обработанного шва
116
Сварные и паяные соединения
Рис. И. Остаточные напряжения в сварном соединении
верхностн, ниже, чем у основного металла, на 40—65% и практически не зависят от режима автоматической сварки и сварочных материалов (электродов, флюса). Для низколегированных и средиеуглеродистых сталей прочность снижается еще в большей мере.
Если окисную пленку удалить методами резания, то предел выносливости соединений повысится на 20— 30%.
Форма и размеры сварного шва. Размеры шва характеризуются высотой усиления шва g, его шириной Ь и углом 0 (см. рис. 10; g = 3 мм; 6=13 мм).
Рекомендуется выполнять швы с усилением при 0= 160ч-170° и отношении 6/g=9=ll; прн этом эффективный коэффициент концентрации напряжений можно принимать по табл. 4. При 0 = 120° и b/g — Зч-5 значения ko из табл. 4 следует увеличивать в 2 раза.
При односторонней сварке, когда невидимая часть шва формируется
на флюсомедной подкладке с водяным охлаждением, можно получить предел выносливости, близкий к пределу выносливости основного металла.
В сварных конструкциях следует избегать пересечения швов, иначе предел выносливости соединений снизится на 17—30%.
Остаточные напряжения от сварки. Если распад аустенита в сталях происходит при высоких температурах (например, в низкоуглеродистых и низколегированных сталях), то после охлаждения шва в околошовных зонах образуются растягивающие остаточные иапряжеиня с высоким градиентом (рис. 11, а). Со временем остаточные напряжения изменяются (см. рис. 11,6), что может привести к появлению трещин в око-лошовиой зоне.
Остаточные растягивающие напряжения иа 30—40% снижают сопротивление усталости стыковых соединений из сталей 22К, 15ГФ и др.
Влияние основных факторов на сопротивление усталости
117
Во многих легированных сталях (например, 20Х2Н4А и др.) распад аустенита происходит при низких температурах. При охлаждении шва в таких материалах в околошовных зонах образуются сжимающие остаточные напряжения.
Для ответственных конструкций после сварки обязательно проводят отжиг (в среде аргона или в вакууме) для снятия остаточных напряжений.
Механическая обработка шва. Зачистка и снятие методами резания усиления шва способствует повышению сопротивления усталости соединений вследствие снижения концентрации напряжений. Эффективным средством повышения сопротивления усталости стыковых соединений из низколегированной стали 15ХСНД и среднелегированных сталей 34ХМ, 40ХН и др. является сочетание механической зачистки шва и термической обработки (снятие остаточных напряжений и улучшение структуры металла околошовной зоны).
Обработка швов и околошовных зон методами поверхностного пластического деформирования (обдувка дробью, чеканка, обкатка роликом и др.) приводит к существенному повышению предела выносливости соединений. Особенно эффективно применение упрочняющей обработки для крупногабаритных деталей. В этом случае можно добиться равнопрочности основного металла и шва даже без обработки усиления шва методами резания. Повышение предела выносливости на таких деталях составляет 50— 100%.
В табл. 5 приведены значения пределов выносливости стыковых соединений при симметричном (c_i) и пульсирующем (о0) циклах нагружений.
Иногда для усиления стыкового соединения лобовыми швами прива-
5. Пределы выносливости стыковых сварных соединений из низколегированных сталей при симметричном и пульсирующем циклах
Сталь Предел выносливо-
сти, МПа
a_i <*0
20Г 89
ЮГ2С1Д 70 150
09Г2С 78 150
10Г2С1 • 68
10Г2С1Д • 68 110
10ХСНД • 80 160
15ХСНД *• 70 98
15Г2СФД 72 —
* Термообработанная Горячекатаная
ривают накладки. В результате этого предел выносливости соединений снижается на 30—40% .
Нахлесточные соединения. В отличие от стыковых нахлесточные соединения имеют более высокую концентрацию напряжений. На рис. 12 показано распределение радиальных аг, окружных од и касательных тгд напряжений в нахлесточных соединениях с лобовыми швами. При уменьшении 0 до 45° концентрация напряжений возрастает, а усталостная прочность снижается на 20% . Применение пологих катетов (р 60°) в сочетании с механической обработкой швов позволяет повысить предел выносливости соединений на 30%.
Значения теоретических коэффициентов концентрации напряжений в соединениях с лобовыми швами даны в табл. 6.
Соединения с фланговыми швами имеют большую концентрацию напряжений, чем соединения с лобовыми швами. Последнее связано с неравно-
₽ис. 12. Напряжения в лобовом шве
118
Сварные и паяные соединения
6. Теоретические коэффициенты концентрации напряжений в нахлесточных соединениях с лобовыми швами
Характеристика углового шва “о
У кромки У корня
= 60° (см. рис. 12) 2.5 2,5
₽ = 45° 3.5 3.5
Р = 45°, шов с непроваром 4.0 4.0
Р = 45°, шов с глубоким 3.0 3.0
непроваром Тангенциальный вогнутый 1.5 3.5
профиль Нетангенциальный вогну- 3.0 4.0
тый профиль Выпуклый профиль 4.0 4.0
мерным распределением нагрузки вдоль шва (рис. 13, а). Поэтому в динамически нагруженных конструкциях нежелательно использовать соединения с фланговыми швами.
В соединении с фланговыми и лобовыми швами последние улучшают распределение нагрузки и повышают предел выносливости соединений на 34—50%. Предел выносливости таких соединений с необработанными швами составляет в ряде случаев 30—45% предела выносливости цельной пластины. Высокий отпуск после сварки нахлесточных соединений не изменяет прочности. Поверхностный наклеп повышает предел выносливости на 25% соединений с фланговыми швами и на 60% — с лобовыми швами.
С увеличением площади поперечного сечения накладки (например, за счет толщины накладки) предел вы
носливости соединений возрастает, так как максимум нагрузки смещается в этом случае в сторону основного листа с площадью поперечного сечения F2 (рис. 13, б).
В нахлесточных соединениях низколегированные высокопрочные стали не имеют преимущества по сравнению с углеродистыми конструкционными сталями.
Сопротивление усталости нахлесточных соединений, полученных контактной сваркой (точечной и шовиой), низкое, что связано с высокой концентрацией напряжений в шве (табл. 7).
Тавровые соединения. Концентрация напряжений в тавровых соединениях существенно выше, чем в стыковых, и зависит от подготовки кромок и степени проплавления (рис. 14).
Цифрами на рис. 14 показаны значения нормальных напряжений в МПа в различных сечениях шва.
Эффективные коэффициенты концентрации напряжений в тавровых соединениях с неподготовленными кромками и без проплавления изменяются от 2 до 4,5, а теоретические — от 3,4 до 5.
Для тавровых соединений с малой глубиной проплавления (рис. 15, а—в) менее прочным является сечение по сварному шву. В соединениях с разделкой кромок элементов при наличии глубокого проплавления (рис. 15, г— е) эффективные коэффициенты концентрации напряжений ko изменяются от 1,1 до 1,7. Меньшие значения ka получают при тщательном выполнении сварки со сквозным проплавлением.
В соединениях толстых листов получение полного провара затруднено и
Рис. 13. Распределение нагрузки по длине нахлесточного соединения
Влияние основных факторов на сопротивление усталости
119
₽йс. 14. Напряжения в «авровом соединении:
fl — детали перед сваркой без скоса кромок, б
детали с двусторонним скосом кромок
рис. 15. Тавровые соединения
120
Сварные и паяные соединения
7. Эффективные коэффициенты концентрации напряжений в соединениях, полученных контактной сваркой
Марка стали илн сплава Толщина листов, мм Состояние материала
10 3- 3 Нормализованная 7,5/5
12Х18Н9Т ЗОХГСА 1,5—1,5 Нагартоваииая Высокий отпуск 12/7,5 12/-
ВТ1 Д16Т В состоянии поставки 10/5 5,5/2,25
Примечание. В числителе дроби указаны значения k для точечной сварки, а в знаменателе — для шовной.
8. Сопротивление усталости соединений с конструктивными элементами
Эскиз соединения Основной металл г °тах' МПа
* / ~ Углеродистая сталь: <JB = 377 МПа; от = 245 МПа 0 200 -220 180 — 210 1,2 (шов обработан) 1.3
190 — 210 160 — 180 1,25 (шов обработан) 1,5
205 175 1.2 (шов обработан) 1.4
185 1,35
_ г ' v“ 80 2.6
оо 1 88 2.6
160 1 6 (шов обработан)
Влияние основных факторов на сопротивление усталости
121
Продолжение табл. 8
Эскиз соединения Основной Металл Г атах, МПа
Углеродистая сталь. ств = 530 МПа; = 360 МПа 0,2 160 — 170 —
СтЗсп: ств ~ 403 МПа; СТТ = 242 МПа; -1.0 55 2,9
70 F-тЙ* 0 116 —
। г >г , I gl СтЗсп' 17в - 430 МПа; оТ = 305 МПа -1,0 96 1,5
9. Максимальные разрушающие напряжения нгаах = + 17 а для сварных соединений
из низкоуглеродистых сталей (N — 107 циклов)
Соединение ’max' МПа- г
— 1 0 + 0.3
Стыковое, выполненное автоматической или ручной 69 130 186
сваркой, при обычном усилении шва Стыковое в случае пересечения его продольным швом 52 106 —
Со вспомогательными элементами (планками, ребрами 40 90 120
нт. д ), лобовыми швами при отношении катетов 1 . 1 Нахлесточное с обваркой по контуру 35 68 —
Нахлесточное с фланговыми швами 23 58 78
удорожает изготовление сварных конструкций. Наиболее рациональным в тавровых соединениях при больших толщинах принято считать применение частичного скоса кромок с сохранением непроверенной щели (см. рис. 15, в), отрицательное влияние которой можно скомпенсировать повышенной прочностью сварных швов. Исследования показали, что при ширине щели До 50% толщины листов несущая способность соединений не снижается.
Соединения с конструктивными элементами, В ряде конструкций к основным силовым элементам приваривают различные конструктивные и связую
щие элементы (косынки, ребра, планки, накладки и др,), образующие обычно тавровые и угловые соединения. В таких конструкциях через сварные швы, как правило, не передается нагрузка на основной элемент. Однако при нагружении основного элемента в зоне присоединения дополнительного элемента создается значительная концентрация напряжений из-за резкого изменения сечения.
Прочность конструкции в результате присоединения элементов может снизиться в несколько раз (табл. 8). Фланговые швы снижают прочность в большей степени, чем лобовые.
122
Сварные и паяные соединения
Для уменьшения концентрации напряжений следует применять косынки с плавным очертанием и механической обработкой места перехода.
Сопоставление пределов выносливости однотипных сварных соединений из низколегированных сталей показывает, что химический состав и механические свойства сталей практически мало влияют на сопротивление усталости соединений в исходном состоянии (без обработки). Сопротивление усталости соединений практически не изменяется даже после термического упрочнения сталей и зависит главным образом от амплитуды переменных напряжений цикла (табл. 9, при коэффициенте асимметрии г = О оа = 1/2ог, при г = — 1 оа — 0Г).
РАСЧЕТ НА ПРОЧНОСТЬ
ПРИ ПЕРЕМЕННЫХ
НАГРУЗКАХ
Если среднее напряжение цикла от и амплитуда оа возрастают пропорционально при нагружении соединения, то запас прочности
Oaka + фа<?т ’
где 0-1 — предел выносливости материала с учетом масштабного фактора; kG — эффективный коэффициент концентрации напряжений (см. табл. 4); ф0 — коэффициент, учитывающий влияние на сопротивление усталости асимметрии цикла; —
0,14-0,2 для стыковых соединений из низкоуглеродистых сталей, ф0 = = 0,24-0,3 — то же для средне- и низкоуглеродистых сталей.
Если прн нагружении соединения возрастает лишь амплитуда переменных напряжений, то запас по переменным напряжениям (например, в случае резонансных колебаний сварных деталей) 0-1 — па =---------------------
Обычно Па >2, Па 2,5.
В крано- и мостостроении расчет сварных конструкций при переменных нагрузках выполняют по допускаемым напряжениям, которые получают
умножением допускаемых значений напряжений при статических нагрузках [а]р на коэффициент у, получаемый опытным путем:
7 ~ (ak0 ± b) — (aka Т &)г ’ '7) где а и b — коэффициенты, характеризующие материал, в краностроении для углеродистой стали принимают а = 0,6; b = 0,2; в мостостроении для низкоуглеродистых сталей а = 0,9; b — = 0,3 и для низколегированных сталей а — 0,95; b = 0,35; kG — эффективный коэффициент концентрации напряжений; г — коэффициент асимметрии цикла.
Верхние знаки в знаменателе дроби формулы (17) соответствуют расчету прн растягивающих отах, нижние — при сжимающих amln. Если конструкция рассчитывается на ограниченный срок службы: Np<Z Nа (где Л'р и А б — соответственно число циклов отработки конструкции за ресурс и базовое число циклов, соответствующее перегибу кривой усталости на уровне предела выносливости), то формула (17) уточняется:
Для предварительной оценки Ар можно пользоваться нормами для кра новых конструкций, установленными Европейской административной федерацией [4]:
Интенсивность использования
Случайное, периодическое Постоянное неинтенсивное . .
» интенсивное .
Непрерывное очень интенсивное .......................
(циклов) 6.3.104 2,0- I05 6.3-105
2,0- )0«
Расчет на сопротивление усталости соединений, полученных контактной сваркой, выполняют аналогично.
ПАЯНЫЕ СОЕДИНЕНИЯ
Паяные конструкции получили широкое распространение в различных отраслях машиностроения и в ряде
Паянные соединения
123
10. Механические характеристики и области применения распространенных припоев
Марка припоя Основа ов. МПа 6». % Назначение
ВПр 1 ВПр 2 ВПр 4 Медь 840—900 330 — 440 690—760 12—18 22 — 46 9-13 Припои теплостойкие для пайки трубопроводов, лопаток газовых турбин и других деталей и узлов из коррозионно-стойкой стали
JI63 (проволока) Медь 450 2 Для пайки стальных изделий неответственного назначения, а также для пайки сталей с нагартовкой при неравномерном нагреве
ПСр 40 ПСр 45 Серебро 380—440 370—510 18 — 37 16-35 Для пайки трубопроводов, патрубков и других деталей и узлов из конструкционных и коррозиоиио стойких сталей Могут работать до температур 350-450 °C
ПОС 90 ПОС 6! ПОС 40 Олово н свинец 43 41 36 25 34 32 Внутренние швы медицинской аппаратуры, детали электротехнической и приборостроительной промышленности
случаев вытесняют сварные соединения.
Пайкой изготовляют не только отдельные детали, но и сложные крупногабаритные узлы.
При конструировании паяных изделий важное значение имеют выбор припоя и способа пайки.
При выборе основного металла следует учитывать паяемость его припоями, обеспечивающими требуемую прочность, чувствительность основного металла к нагреву и склонность его к образованию трещин под действием расплавленных припоев, проникающих между кристаллами по границам зерен.
Например, пайку сталей латунью применяют в ограниченном масштабе, так как медь является основным компонентом, вызывающим охрупчивание соединений. Поэтому в серебряные и никелевые припои для деталей, работающих при повышенной температуре, не вводят медь [2]. Для уменьшения склонности к хрупкому разрушению рекомендуется наносить иа детали никелевое покрытие.
При паянии разнородных металлов необходимо учитывать различие в коэффициентах их термического расширения.
При высокотемпературной пайке ряда разнородных металлов (например, титана с медью и никелем, магния со сталью, алюминия с медью и др.) невозможно получить пластичные и прочные соединения без нанесения иа них барьерных покрытий, предохраняющих разнородные металлы от активного взаимодействия и, как следствие, возникновения в паяном шве хрупких интерметаллидов.
В качестве барьерного покрытия наносят такой металл, который легко паяется и образует прочные связи с основным конструкционным материалом.
Припои должны хорошо смачивать покрытие и другой металл (без покрытия), не образуя с ними иитерме-таллиды.
Например, для пайки стали с титаном иа последний наносят молибденовое покрытие, затем осуществляют пайку медными или серебряными припоями.
В табл. 10 приведены механические характеристики и области применения припоев. Для пайки жаропрочных сталей и сплавов используют припои на основе никеля, марганца и палладия с добавками других элементов (хрома, кобальта, циркония
124
Сварные и паяные соединения
II Зазоры применяемые прн пайке
металлов
Основной металл Основа припоя Зазор, мм
У глеродистые стали Медь Латунь Серебро 0 02 — 0 15 0 05—0 30 0 05 — 0 15
Коррозиоиио стойкие стали Медь Латунь Серебро Никель — хром 0 05 — 0 12 0 05—0 30 0 05—0 12 0 05—0 10
Жаропроч ные стали и сплавы Никель Палладий 0 05 — 0 10 0 05—0 10
Титановые сплавы Серебро Серебро— марганец 0 03-0 10 0 03 — 0 10
Медь н медные сплавы Медь — цинк Медь — фосфор Серебро 0 10-0 30 0 02—0 15 0 03—0 15
Алюминиевые сплавы Алюминий 0 10 — 0 30
12 Прочность прн срезе паяных соединении
Основной металл тв МПа для припоев
ПС 40 ПСр 45
1 2 X 18Н9Т 240—290 180—260
40ХН2МА 330-460
ЗОХГСА 350-460 350-410
Медь 250 250
и др ), а также твердые и газообразные флюсы
Пайку в атмосфере газообразных флюсов (фтористый водород, трехфтористый бор и др ) производят в герметичных контейнерах, нагре ваемых в печах
Пайку корпозионно стойких сталей, жаропрочных и титановых спла вов, керамики и тугоплавких металлов производят часто в вакууме (в вакуумных печах)
На качество соединения существенное влияние оказывает размер паяльного зазора (табл 11) и условия течения припоя в нем Чем лучше припой смачивает поверхность основного металла, тем меньшим можно назначить зазор При активном растворении основного металла расплавленным припоем зазоры устанавливают большими, так как припои повышают температуру плавления и хуже растекаются При увеличении зазоров прочность паяного соединения уменьшается из-за образования пустот, не заполненных припоем, флюсовых включений и т п
Указанные в табл 11 зазоры должны быть выдержаны при нагреве до температуры пайки
Прочность паяных соединений существенно зависит от прочности припоя и активности взаимодействия расплавленного припоя и основного металла При активном растворении припоя в металле прочность соединений на 30—60% выше прочности припоя
Механические характеристики паяных соединений приведены в табл 12— 15 При повышении температуры окружающей среды прочность соединений снижается
Для соединений, работающих при повышенных температурах, целесообразно применять припои, легированные марганцем (ПСр 37,5) и никелем (ПСр 40) Жаропрочные припои на основе меди (табл 14) могут работать до температуры 600 °C С помощью жаропрочных припоев на основе никеля получают соединения с рабочей температурой до 900 °C
Прочность соединений, паяных оло-вянно-свинцовыми припоями, составляет 30—60 МПа (табл 15)
В паяных конструкциях в основном следует применять соединения внахлестку (особенно в герметичных соединениях, рис 16) В соединениях необходимы вентиляционные отверстия для отвода газов, создающих давление при нагреве во время пайки (рис 17)
При пайке фланцев к трубам следует предусматривать посадочный поясок и упор на трубе или фланце (рис. 18), а при пайке конструкции
Паяные соединения
125
13. Прочность при срезе паяных соединений внахлестку при повышенных температурах
Осиовной металл Припой тв, МПа, при температуре, °C
200 300 4 00 600
12Х18Н9Т ПСр 45 160—240 145— 150 30-40
ПСр 37.5 — 310—350 — 110- 180
15Х18Н12С4ТЮ ПСр 40 220 — 320 150—170 50 — 90
14. Прочность при срезе соединений, паянных жаропрочным припоем на основе меди ВПр 1
Основной металл тв МПа, при температуре, °C
-60 20 200 400 500 600
12Х18Н9Т 430 — 580 370—500 300—400 190-220 90- 160
Х15Н9Ю 250—300 210—300 200 -300 190-240 120—200 —
Х17Н5МЗ 190-220 2 10 — 250 190 — 230 210-250 90- 130 —
15. Прочность при срезе соединений, паянных оловянно-свинцовым припоем ПОС 40
Основной металл тв. МПа, при температуре °C
- 196 - 183 — 96 -60 20 85
М3 35 33 34 35 27 16
Л62 29 29 31 27 9 9 14
Сталь 20 60 55 55 51 28 22
12Х18Н9Т 30 34 30 50 32 20
с посадкой деталей с натягом — канавки для лучшего затекания припоя.
При конструировании соединения, пайка которого будет производиться в печах и других установках, следует предусматривать специальные пазы или выемки для укладки на место спая припоя в виде порошка, пасты, проволоки, полос, шайб или нанесения припоев гальваническим способом, с термовакуумным напылением и т. д. (рис 19).
Рис. 16. Паяные соединения внахлестку
В конструкциях, где припой укладывают в виде шайб, фольги или тонкой
Рис. 18. Соединения с и упором
посадочным пояском
126
Валы
Рис. 19. Укладка припоя
полосы, необходимо обеспечить воз-
можность перемещения паяных де-
талей в сторону уменьшения зазора (например, за счет прижимов и т. д.). Паз или выемку для укладки припоя выполняют, как правило, иа детали, имеющей большее сечеиие.
Расчет на прочность паяных соединений проводят так же, как и расчет сварных соединений. Контроль качества паяных соединений аналогичен контролю сварных соединений.
Глава 8
ВАЛЫ
В машиностроении наиболее распространены прямые валы в форме тел вращения, устанавливаемые в подшипниковых опорах.
Валы, передающие только крутящий момент от одной детали к другой, называют торсионными (рессорами).
Часто передача крутящего момента связана с появлением осевых и радиальных сил. Валы обычно подвержены действию крутящего и изгибающего моментов, а также перерезывающих и продольных сил.
Реже встречаются валы, используемые лишь для поддержания вращающихся деталей и не передающие полезного крутящего момента. Такие валы называют осями.
Для обеспечения работоспособности валы и оси должны удовлетворять условиям прочности, жесткости и технологичности.
В специальных конструкциях к валам предъявляют дополнительные требования: износостойкости, устойчивости, минимальной массы и т. п.
КОНСТРУКТИВНЫЕ ФОРМЫ
И МАТЕРИАЛЫ ВАЛОВ
В зависимости от распределения нагрузок вдоль оси вала и условий сборки прямые валы выполняют ступенчатыми (рис. 1, а) или гладкими1 (рис. 1, б).
1 В последние годы гладкие валы благодаря технологичности находят все более широкое применение.
Более распространены валы ступенчатые, близкие по форме к балкам равного сопротивления изгибу. Такие валы удобны при сборке, а уступы используют обычно для упора деталей, насаживаемых на вал, и передачи осевых усилий. При конструировании ступенчатых валов необходимо иметь в виду, что любая насаживаемая неразъемная деталь должна проходить до своего места посадки на валу без натяга (во избежание ослабления посадок из-за повреждения поверхностей) .
Диаметры посадочных поверхностей (под ступицы колес, звездочек и др.) следует выбирать из стандартного ряда посадочных размеров, а диаметры посадочных поверхностей под подшипники качения — из стандартного ряда внутренних диаметров подшипников.
Конструктивная форма зависит от нагрузок на вал и, как следствие, от способа соединения вала с насаживаемыми иа него деталями.
При больших крутящих моментах и повышенных требованиях к центрированию применяют шлицевые соединения (см. гл. 5). Для снижения напряжений на шлицевых участках валов целесообразно увеличивать внутренний диаметр шлицев на 15—20% по сравнению с диаметром вала (рис. 2). Входные кромки шлицев на валу должны иметь фаски для облегчения монтажа и снижения контактных давлений при работе.
Если соединение передает (помимо крутящего момента) осевое усилие, то
Конструктивные формы и материалы валов
127
осуществляют затяжку соединения, фиксируя его в осевом направлении с помощью упорного буртика, который выполняют обычно на гладкой части вала.
При средних значениях крутящего момента и менее высоких требованиях к точности центрирования применяют шпоночные соединения (см. гл. 5). При действии осевых усилий соединяемые детали также фиксируются в осевом направлении затяжкой (рис. 3). Для зубчатых колес 7-й степени точности и выше рекомендуется применять шлицевые соединения независимо от крутящего момента.
Если шпоночное соединение собирается с гарантированным иатягом, то необходимо предусмотреть возможность направления паза ступицы на шпонку до начала участка с натягом (например, за счет удлиненной направляющей фаски и т. д.).
Соединение валов и ступиц (шкивов, колес и др.) часто осуществляют с гарантированным натягом (см. гл. 6). В таких соединениях имеется довольно высокая концентрация напряжений (см. с. ЮЗ). При конструировании валов следует предусмотреть меры по снижению концентрации напряжений вблизи кромок ступиц. Диаметр подступичной части вала для этих же Целей следует увеличивать на 5—10% по отиошению к соседним участкам. Для повышения сопротивления усталости подступичную часть вала желательно упрочнить поверхностным пластическим деформированием.
Для посадки подшипников на валах Делают заплечники или упорные буртики (рис. 4), их высота должна находиться в соответствии с размерами скруглений на кольцах подшипников
и условиями демонтажа подшипников.
Переходные участки валов между соседними ступенями разных диаметров выполняют с полукруглой канавкой для выхода шлифовального круга (рис. 5, а), галтелью постоянного радиуса (рис. 5, 6) и галтелями специальной формы (см. рис. 4).
Сопряжение шейки подшипника с соседним участком вала обычно осуществляют галтелью постоянного радиуса (t/r — 3, rid = 0,2-0,4).
Рнс. 3. Соединение шпонкой
128
Валы
Рис. 4. Сопряжения ступеней вала
Рис. 5. Галтели на валах
Рнс. 6. Шлицевое соединение валов
В ряде конструкций применяют прямые полые валы. Качал уменьшает массу вала, его используют для размещения соосного вала, деталей управления, подати масла и охлаждающего воздуха и т. п.
Часто для подвода масла к подшипникам или других целей вал изготовляют со сквозным поперечным отверстием, создающим высокую концентрацию напряжений. Для повышения прочности валов отверстия подвергаются дорновакию (шариком или дор-иом, см. гл. 34), края отверстий скругляют.
Длинные валы выполняют составными. Соосные валы соединяют с помощью шлицевых соединений (шлицевых муфт, рис. 6), или фланцевых соединений (рис. 7). Для передачи больших крутящих моментов и при ограниченных осевых габаритах используют соединения с торцовыми радиальными шлицами эвольвентного или, реже, треугольного профиля (рис. 8). Протяженность торцовых шлицев иногда сокращают, выполняя их секторами на участках между болтами. Подобным образом осуществ-
ляют соединения валов с дисками компрессоров и турбин.
Для изготовления валов в основном используют углеродистые стали марок 20, 30, 40, 45 н 50, а также легированные стали марок 20Х, 40Х, 40ХН, ЗОХГСА, 40ХН2МА, 18Х2Н4МА и др. (табл. 1).
Рис. 6. Соединение с помощью торцовых шлицев
Рнс. 7 Фланцевое соединена валив
Основшхе технические требования
129
1. Механические характеристики основных материалов валов
Марка сталь Диаметр заготовки, мм. не более Твердость НВ, не менее Св ат <7-1 Т_1 Коэффициенты •
МПа *<, '•’т
Ст5 Не ограничен 190 520 280 220 130 0 0
45 Не ограничен 120 80 200 240 2Z0 560 800 900 280 550 650 250 350 380 150 2 10 230 0 0.1 0,1 0 0 0.05
40Х Не ограничен 200 120 200 240 270 730 800 900 500 650 750 320 360 410 200 210 240 0.1 0,05
40 ХН Не ограничен 200 240 2% 820 920 650 750 360 420 210 250 0, 1 0,05
20 20Х 12ХНЗА 12Х2Н1 А 18ХГТ 00 120 120 120 60. 145 197 260 300 330 400 650 950 1100 1 150 240 400 700 850 950 170 300 420 500 520 100 160 210 250 280 0 0,05 0.1 0,15 0,15 0 0 0,05 0,1 0,1
зохгт Не of раничен 120 60 270 320 415 950 1150 1500 750 950 1200 450 520 650 260 310 330 0.1 0.15 0.2 0,05 0,1 0.1
* См с 138
Выбор материала, термической и химико-термической обработки определяется конструкцией вала (например, валы-шестерни изготовляют из низкоуглеродистых легированных сталей марок 12ХНЗА, 12Х2Н4А и других с последующей цементацией) и опор, требованиями к конструкции н условиями эксплуатации.
Быстроходные валы, вращающиеся в подшипниках скольжения, требуют высокой твердости цапф, поэтому их изготовляют из цементуемых сталей 12Х2Н4А, 20Х, 18ХГТ или азотируемых сталей 38Х2МЮА и др.
ОСНОВНЫЕ ТЕХНИЧЕСКИЕ ТРЕБОВАНИЯ
Технические условия на изготовление валов зависят от требований к конструкции. Обработку валов осуществляют, как правило, в центрах.
5 Заказ 402
Наиболее жесткие требования по точности и шероховатости поверхности предъявляются к шейкам валов, на которые устанавливают подшипники качения.
Отклонения от круглости и цилин-дричностн мест посадки не должны превышать 0,5 допуска на диаметр, а для подшипников классов точности 5, 4 и 2—0,25 допуска на диаметр.
Торцовое биение заплечика для подшипников классов точности 0 и 6 не должно превышать 0,02—0,03 мм, а для подшипников классов точности 5, 4 и 2—0,003—0,018 мм.
Контроль шеек осуществляют индикатором или миниметром.
Параметры шероховатости поверхности шеек под подшипники принимают равными Ra = 0,032 4-1,£5 мкм.
Допуски на относительное радиальное биение шеек валов для посадки зубчатых колес, муфт, шкивов н других подобных деталей в зависимости
130
Валы
от их окружной скорости по внешнему диаметру составляют (0,7—2) 6 (здесь 6 — допуск на диаметр контролируемой шейки вала; меньшее значение соответствует окружной скорости v > > 10 м/с).
Допуски на биение упорных буртиков валов в зависимости от диаметра вала, окружной скорости сопряженных с валом деталей, а также кинематической точности зубчатых колес изменяются от 0,01 до 0,06 мм (большие значения назначаются при диаметрах вала свыше 55 мм).
Допуски , на перекос и несимметричность расположения шпоночных пазов иа валу составляют соответственно 0,56 и 26 (здесь 6 — допуск на ширину шпоночного паза). Если деталь устанавливают на двух шпонках, то допуск на их несимметричность принимают равным 0,56.
Технологический контроль вала включает проверку диаметральных и линейных размеров (скобами и универсальными измерительными средствами) ступеней, взаимного расположения обработанных поверхностей, шероховатости поверхности и твердости.
НАГРУЗКИ НА ВАЛЫ
И РАСЧЕТНЫЕ СХЕМЫ
Для оценки прочности необходимо знать действительное распределение напряжений в сечениях вала от внешних нагрузок (постоянных и переменных).
Внешние нагрузки передаются на валы от сопряженных деталей (зубчатых колес, муфт и др.) и могут быть определены путем расчета (стационарные устройства при установившихся режимах работы: конвейеры с непрерывным питанием, грузоподъемные устройства и т. п.).
Если внешние нагрузки известны, то при расчетном определении внутренних силовых факторов в сечениях вал рассматривают как балку, шарнирно закрепленную в жестких опорах (рис. 9, а) *. Такая модель формы вала
* Введение условных шарнирных опор эквивалентно замене давлений иа валу от подшипиика сосредоточенной силой (силами).
и условий закрепления близка к действительности для валов, вращающихся в опорах качения.
При установке в опоре двух подшипников качения (рис. 9, б) большую часть нагрузки будет воспринимать внутренний подшипник. В этом случае условную опору можно поместить во внутреннем подшипнике либо так, как показано на рис. 9, б. В более точных расчетах вал рассчитывают как многоопорную балку (рис. 9, б) на упругих опорах с осадкой (вертикальным смещением) [1]:
. 4U, 0,74-0.2d
где я — коэффициент, я — "з у ?----
для однорядного радиального шарикоподшипника; k — 0,32+ 0,0026d— для цилиндрического роликоподшипника; k = 0,019+ 0,0015d — для конического роликоподшипника широкой серин; k = 0,022+ 0,0015d — для конического роликоподшипника нормальной серии; Ь — ширина кольца; d- и D — соответственно внутренний и наружный диаметры подшипника, см; Р — радиальная нагрузка, Н. Обычно 6/Р = (5 <-10) 10~5 см/Н.
Условную опору для валов, опирающихся по концам на подшипники сколь жения, располагают на расстоянии (0,25—0,3) I от внутреннего торца (см. рис. 9, в), но не далее 0,5 d от внутренней кромки подшипника [1].
Смещение опоры от центра подшипника в сторону внутреннего торца связано со смещением в эту сторону максимальных контактных давлений вследствие деформации вала и подшипника.
В уточненном расчете следует учесть распределение давлений по длине контакта цапфы н подшипника, рассматривая упругий контакт вала и подшипиика через условный контактный слой (см. гл. 29).
Нагрузки от дисков, шкивов, зубчатых колес и других деталей также передаются на валы через площадки контакта. Распределение давлений (напряжений) в зонах контакта зависит от ряда конструктивных и технологических факторов (см. гл. 29), а рас-
Расчет прочности, жесткости и устойчивости валов 131
Рис. ».
Расчетные схемы опор валов
четное определение этих давлений в соединениях и передачах связано со значительными математическими труд-ностями. В приближенных расчетах валов обычно не учитывают распределение нагрузок по длине зубьев и зубчатых колес и шлицевых соединений, вдоль шпоиок, вкладышей подшипников скольжения и других деталей, и при составлении расчетной схемы вала эти давления обычно заменяют эквивалентными сосредоточенными силами (рис. 9, г), приложенными в середине площадки (площадок) контакта 1.
РАСЧЕТ СТАТИЧЕСКОЙ ПРОЧНОСТИ, ЖЕСТКОСТИ И УСТОЙЧИВОСТИ ВАЛОВ
Основными для валов являются постоянные и переменные нагрузки от деталей передач и рабочих дисков (на
1 Такая схематизация нагрузок справедлив при малой протяженности площадки контакта»
пример, дисков компрессора, турбин и др.).
Переменные напряжения в валах могут вызываться изменяющейся по времени внешней нагрузкой..
Постоянные по величине и направлению силы передач вызывают во вращающихся валах переменные напряжения, изменяющиеся по симметричному циклу. Валы могут быть нагружены и постоянными напряжениями (например, от неуравновешенности вращающихся деталей).
На статическую прочность валы рассчитывают по наибольшей возможной кратковременной нагрузке (с учетом динамических и ударных воздействий), повторяемость которой мала и не может вызвать усталостного разрушения.
Так как валы в основном работают в условиях изгиба и кручения, а напряжения от продольных усилий не велики, то эквивалентное напряжение в точке наружного волокна
= + 0)
5*
132
Валы
2. Моменты сопротивления и площадь сечения сплошных круглых валов
D, мм »и, см- 1ГК, см’ F, см2 D, мм 1ГИ, см’ U7K, см3 F, см2
20 0,785 1.571 3,14 75 41,4 82,8 44,2
21 0,909 1,818 3,46 78 46,6 93,2 47,8
22 1,045 2,090 3.80 80 50,3 100,5 50,3
23 1.194 2,39 4,15 82 54.1 108,3 52,8
24 1,357 2,71 4.52 85 60,3 120,6 56,7
25 1,534 3,07 4.91 88 66.9 133,8 60,8
26 1,726 3,45 5,31 90 71,6 143, I 63.6
28 2,16 4,31 6,16 92 76,5 152,9 66.5
30 2,65 5,30 7.07 95 84,2 16b,з 70,9
32 3,22 6.43 8,04 98 92,4 184,8 75,4
34 3,86 7,72 9.08 100 98,2 196,4 78,5
35 4,21 8,42 9,62 105 1 13,7 227 86,6
36 4,58 9. 16 10,2 ПО 130.7 261 95.0
37 4,97 9.95 10,8 I 15 149,3 299 104
38 5,39 10,77 н.з 120 169,6 339 113
40 6,28 12.57 12,6 125 191.7 383 123
42 7,27 14,55 13,9 130 216 431 133
44 8,36 16.73 15.2 1 35 242 4 83 143
45 8.95 17,89 15,9 140 269 539 154
46 9,56 19,11 16,6 145 299 599 165
47 10,19 20,4 17.3 150 331 663 177
48 10,86 21,7 18,1 155 366 731 189
50 12.27 24,5 19,6 160 402 804 201
52 13,80 27.6 21,2 165 441 882 214
55 16,33 32,7 23.8 170 482 965 227
58 19,16 38,8 26,4 175 526 1053 24 I
60 21.2 42.4 28,3 180 573 1145 254
62 23,4 46.8 30,2 185 622 1243 269
65 27,0 53,9 33,2 190 673 134 7 284
68 30,9 61,7 36,3 195 728 i 156 298
70 72 33.7 36,6 67.3 73,3 38,5 40,; 200 785 1571 1314
где ои — наибольшее напряжение при изгибе моментом Л1И; си = тк — •г и наибольшее напряжение при круче-
нии моментом Л1К, тк и — соответственно лярный моменты сопротивления сечения вала (табл. 2—5),
Ги=—-
_ 2Цк_-
Гк’ и осевой и не-
Запас прочности по пределу текучести
Пг = . (3)
Оэкв
Для залов чения 1ГК =
_ 32 аэКЗ ~ п£)3
где D — диаметр вала.
круглого сплошного се-2№и, в этом случае
/ ЛРН + 0.75Л12., (2)
Обычно принимают п = 1,24-1,8.
Опасное сечение (сечения), в котором следует найти запас прочности, определяется значениями моментов н размерами сечений. Это значение находят после построения эпюр изгибающих и крутящих моментов. Если нагрузки действуют на вал в разных плоскостях, то, проектируя силы на осн координат, вначале строят эпюры моментов в координатных плоскостях. Далее проводят геометрическое суммирование изгибающих моментов.
U7K = 2ГИ -
Расчет прочности, жесткости и устойчивости валов
133
Если угол между плоскостями действия сил не превосходит 30°, то для простоты считают, что все силы действуют в одной плоскости.
Тонкостенные валы могут выходить из строя вследствие потери устойчивости (выпучивания) как от действия крутящих моментов, так и в результате изгиба.
Проверка устойчивости тонкостенных валов является при кручении и изгибе необходимой (см. гл, 25),
Упругие перемещения валов оказывают неблагоприятное влияние иа ра-
боту связанных с ними соединений (шлицевых, прессовых и др,), подшипников, зубчатых колес и других деталей: увеличивают концентрацию контактных напряжений и износ деталей, снижают сопротивление усталости деталей и соединений, понижают точность механизмов и т. п.
Большие перемещения сечений вала от изгиба могут привести к выходу из строг конструкции вследствие заклинивания подшипников. Изгибная и крутильная жесткость валов существенно влияет на частотные характе-
3. Коэффициенты снижения момента сопротивления и площади сечения для валов с центральным каналом
D IF d D IW iF
0 1.000 1,000 0,68 0.787 0,538
0,20 0,998 0,960 0,69 0,773 0,524
0,25 0,996 0,938 0.70 0.760 0 510
0.30 0,992 0,910 0.71 0.747 0.496
0,35 0,985 0.878 0.72 0,731 0,482
0,40 0,974 0,840 0.73 0.718 0.467
0.41 0,972 0,832 0,74 0,701 0,452
0.42 0.969 0.824 0.75 0.684 0,437
0,43 0,966 0,815 0.76 0,666 0,422
0,44 0,963 0,806 0.77 0.C48 0.407
0.45 0.959 0,798 0,78 0,630 0,392
0,46 0,956 0.788 0,79 0 610 0,376
0.47 0 952 0,7’9 0.80 0,59u 0,360
0*48 0.947 0,770 0 51 0 569 0,344
0,49 0,942 0,760 0,82 0.548 0,328
0.50 0.938 0.750 0.83 0,526 0 311
0.51 0,932 0.740 0,84 0,501 0,294
0,52 0.927 0,730 0,85 0,478 0,278
0,53 0,921 0,719 0.86 0,452 0.260
0.54 0,915 0.708 0.87 0,427 0,243
0,55 0,909 0,o98 0,88 0.400 0.226
0.56 0,901 0,686 0 89 0,372 0 208
0,57 0,895 0.675 0.90 0.34 3 0.190 >
0.58 0,888 0,664 0.91 0,314 0,172
0.59 0,879 0.652 0,92 0.284 0.154
0,60 0,870 0,640 0,93 0,252 0.133
0.62 0,862 0.628 0,94 0,219 0,1 16
0,62 0.852 0.616 0,95 0.185 0.098
0,63 0,842 0,603 0,96 0.151 0,078
0,64 0,833 0.590 0,57 0,1 15 0,059
0,65 0,822 0,577 0,98 0,077 0,040
0,66 0.811 0,564 0,99 0,040 0,(P0
0,67 0,800 0.551
Примечание Значения и для валов с наружным диаметром D, ослабленных отверстием диаметрам d, вычисляют умножением приведенных в табл 2 значений W и F соответственно на коэффициенты и Е/7; — U'EW': U7, . ~
F. = Ftf. "° К° ”
134
Валы
4. Моменты сопротивления и площади сечений валов, ослабленных пазом для одной стандартной шпонки
D, мм b x h, мм U7H. CM3 X*-и I F. CM1 О. мм dXA. мм ‘7 3 Й7К. CMa ** и
20 0,655 1.44 2.96 80 44,7 95,0 48,6
21 0,770 1.68 3.28 82 48,4 102.5 51,1
22 6X6 0.897 1.94 3,62 85 24X 14 54,3 114,6 55,1
23 1.038 2,23 3.98 88 60,6 127,5 59,1
24 1,192 2,55 4,34 90 65,1 136,7 61.9
25 1.275 2,81 4,62
26 8X7 1.453 3,18 5,03
28 2,32 4.97 6,79 92 95 67,9 75,3 144,3 159,4 64.2
68,6
32 2.73 5.94 7.64 98 28 X 16 83,1 175,5 73,2
34 10X8 3,333 7.19 8’68 100 88.7 186,9 76,3
35 3.66 7.87 9,22 105 103,7 217 84,4
36 4,01 . 8.59 9.78
4,27 9,24 10,27 110 1 17.4 248 92.2
37 115 32x 18 135,2 285 101,0
38 40 12X8 4,66 5.51 Ю.04 11,79 10,86 12,09 120 154,8 342 110.2
42 6,45 13,72 13,37
125 172.7 364 119,1
44 7.25 15,61 14.58 130 36 X 20 195.8 412 129, !
45 7,80 16,74 15.37 135 221 • 462 139,5
46 14X9 8.38 17.93 15.99 140 248 517 150,3
47 8,98 19,17 16,'г
48 9,62 20,5 17,47
50 10.65 22.9 1 8 84 145 272 .571 160.7
52 16X 10 12,10 25.9 20’4 150 303 634 I 72."
55 14,51 30.8 23,0 1 55 160 40x22 336 372 702 774 184.3 196,7
58 60 62 18X 1 1 16.81 18.76 20.9 36.0 40.0 44.3 25.4 27.3 29.2 165 170 409 4 50 850 932 209 223
65 24.3 5!.2 32.2 175 484 1010 235
180 529 1101 249
68 27.5 58.4 35.1 1 85 45X 25 576 1198 263
70 30,2 63.8 37,3 190 627 1300 278
72 20 X 12 33,0 b9,7 39,5 195 680 1408 293
75 37.6 79.0 43,0 200 736 1521 309
78 42.6 89.2 46.6
Примечание. 1F = .
и 32 I6D
ПО* _ bh~
4
ПР3 Тб““
bh (2D - h)2 \6D
Расчет прочности, жесткости и устойчивости валов
135
136
Валы
ристики системы при возникновении изгибных и крутильных колебаний.
При проектировании валов следует проверять прогибы и углы поворота сечений. Перемещения сечений валов вычисляют, используя интеграл Мора или правило Верещагина (см. гл. 17).
Допустимые величины перемещений (прогибов и углов поворота) сечений вала зависят от требований, предъявляемых к конструкции, от особенностей ее работы. Допустимые величины углов поворота сечения вала в местах расположения деталей (в рад): .
Подшипников шариковых шариковых роликовых скнх . .
качения:
однорядных сферических цилиндрнче-
роликовых конических Подшипников скольжения Зубчатых колес ....
0,005
0.05
0.0025
0.0016
0,001 0,001—0.002
Максимальный прогиб валов, несущих зубчатые колеса, обычно не должен превышать 0,0002—0,0003 от расстояния между опорами, а допустимый прогиб под колесами составляет: 0,01 т — для цилиндрических и 0,005 т — для конических, гипоидных и глобоидных передач (здесь т — модуль зацепления).
Допустимые углы закручивания валов также зависят от требований и условий работы конструкции и лежат в пределах 0,20—1° на 1 м длины вала.
РАСЧЕТ НА СОПРОТИВЛЕНИЕ УСТАЛОСТИ
На практике переменная внешняя нагрузка изменяется либо по симметричному, либо по асимметричному циклу.
Наибольшие напряжения будут действовать в точках наружных волокон вала:
„ А1и )вах .
~ ;ЧИ шт .
и mln - ’
.. (4)
А1к .
тк max — ур ,
.г МК min
1к mln — .у/
Амплитуды и средние напряжения циклов нормальных и касательных напряжений будут:
а _ °тах — qmln .
а 2
_ Ттах — Т т1п .
Та- 2------------’
_ Отах “F ^mla .
Qm~ 2 ’
» Ттах “F Т’пИп
т.т — — .
(5)
Если амплитуды и средние напряжения возрастают при нагружении пропорционально, то запас прочности определяют из соотношения
п = п°пл— ,/„2 , „2
(6)
где па и лт — соответственно запасы прочности по нормальным и касательным напряжениям,
°— k ’
-----kT1---------' (7)
Если известны пределы выносливости реальной детали, то равенства (7) можно переписать в виде
qa -f- фадат
пт =------, (8)
Та + ФтдТт
где фод = 'Фа " ; Фтд = Фт '
В равенствах (7) и (8) o_j и — пределы выносливости стандартного образца и детали при симметричном изгибе; т_х и т_1д — то же при кручении; ka и kx — эффективные коэффициенты концентрации соответственно нормальных и касательных напряжений (табл . 6—8). При отсутствии дай-
Расчет на сопротивление усталости
137
6. Эффективные коэффициенты концентрации напряжений прн изгибе и кручении валов в месте кольцевой канавки (см. рис. 5, а)
Коэффициент ^в- МПа r/d
0,01 0,03 0,05 0,1 0,01 0,02 0,03
, t Три - 0,5 При — = 2
600 1,98 1,82 1,71 1,52 2.43 2,32 2,22
800 2,09 1,92 1,82 1,59 2,56 2.45 2,35
1000 2,20 2,02 1.93 1,66 2.70 2,58 2.47
1200 2,31 2,12 2.04 1,73 2.84 2,71 2,59
При —— = 1 При ™— = 3
600 2,21 2,03 1,91 2,56 2,42
800 2,37 2,14 2,03 _ — 2,73 2,56 —
1000 2,45 2,25 2,15 2,90 2,70 —
1200 2,57 2,36 2,27 — 3,07 2,84 —
600 1,80 1.60 1,46 1,23
k 800 2,00 1,75 1,57 1,28 — — __
1000 2,20 1,90 1.69 1,34 — — —
1200 2,40 2,05 1,81 1,40 — __ —
7. Эффективные коэффициенты концентрации напряжений в ступенчатом переходе с галтелью (см. рис. 5, 6)
Коэффициент rid
МПа 0,01 0,03 0,05 0,1 0,01 0,02 0,05
600 800 1000 1200 1.38 1,41 1.45 1.49 При —— г 1,67 1.76 1.84 1.92 - = 1 1,64 1.73 1,83 1,93 1.50 1,61 1,72 1,83 Пр 1,94 2,03 2,12 2,21 t и —~ 2.02 2,13 2,25 2,37 = 3 2,03 2,16 2 30 2.44
600 800 1000 1200 1,57 1,62 1.67 1,72 При — 1,88 1,99 2,11 2,23 - = 2 1,82 1,95 2,07 2.19 Пр 2.17 2.28 2.39 2.50 t И -у— 2,23 2,38 2,52 2,66 = 5
600 800 1000 1200 1,29 1,30 1,31 1,32 При — 1,42 1,45 1.48 1,52 - = 1 1,44 1.47 1,51 1,54 1,39 1,43 1.46 1,50 Пр 1,59 1,64 1,68 '1,73 t и 1,66 1,72 1,79 1,86 = 3 1,68 1.74 1.81 1,88
ч 600 800 1000 1200 1.40 1.43 1.46 1.47 При — Г 1.57 1,61 1,66 1.71 - = 2 1,57 1,62 1,68 1.74 — Пр 2,24 2,37 2,48 2.6 t >И у— 2,12 2.22 2,31 2.4 1 II 1 1!
138
Валы
8. Эффективные коэффициенты концентрации напряжений при изгибе
и кручении валов со шлицами, шпоночной канавкой, с резьбой и поперечным отверстием
°В, МПа Тип концентратора
Шлицы Шпоночная канавка Метрическая резьба Поперечное отверстие с диаметром а
*а V к0 *т k'T'
600 1.55 2,36/1,46 1,46/1,76 1.54 1,96 1,54 2,05/1,85 1,80
800 1.65 2,55/1,52 1,62/2,01 1,88 2.20 1.71 2,10/1,90 1,95
1000 1.72 2.70/1,58 1.77/2.26 2,22 2,61 2,22 2.20/2,00 1,90
1200 1.75 2.80/1,60 1,92/2,50 2,39 2.90 2,39 2,30/2,10 2.00
В числителе приведены значения
для валов с прямобочнымн шлицами.
в зна-
менателе — для эвольвентиых шлицев.
** В числителе приведены значения для канавок, полученных пальцевой фрезой, в знаменателе — дисковой.
*** В числителе приведены значения для валов с Диаметром отверстия а = (0,05-т-0,1 5) d, в знаменателе — при а = <0.15-?- 0,25) d
9, Значения коэффициентов еа и
Напряженное состояние н материал Значение в прн диаметре вала, мм
15 20 30 40 50 70 100 200
Изгиб для углеродистых сталей Изгиб для высокопрочной легированной стали и кручение Для всех сталей 0,95 0,87 0,92 0,83 0.88 0,77 0.85 0,73 0.61 0,70 0.76 0,65 0.70 0,59 0,61 0,52
ных значения k0 и kx можно вычислить из соотношений
ьа= 1 + ?(а0— 1);
k-t =-- 1 + ?(at — 1);
здесь а0 и ат — теоретические коэффициенты концентрации напряжений прн изгибе и кручении (см. гл. 28); q — коэффициент чувствительности материала к концентрации напряжений, значения q приведены в гл. 31.
Значения эффективных коэффициентов концентрации напряже.ннй для прессовых соединений валов и дисков приведены в гл. 6. еа и ет — коэффициенты, учитывающие масштабный эф-’ фект прн нзгнбе и кручении (табл. 9); Ра и — коэффициенты, учитывающие влияние состояния поверхности (табл. 10); фп и фт — коэффициенты, характеризующие чувствительность материала к асимметрии цикла напряжений.
В приближенных расчетах принимают фо = 0,14-0,2 — для углеродистых сталей при ав < 500 МПа; фо = 0,24-0,3 — для легированных сталей, углеродистых сталей прн ав > 500 МПа, титановых и легких сплавов; фт 0,5фо.
В случае нзгнбных илн крутильных колебаний валов может происходить возрастание переменной составляющей цикла при неизменной постоянной составляющей.
В этом случае необходимо найти запас прочности по переменным напряжениям:
_ __ a-i Фо^т .
поа — т .
a °а еар0
1-1 Фт^т
vt ~ k т Rx та „ о 8трт
(9)
(Ю)
. Расчет на колебания
139
10 Значения коэффициента р гри изгибе и кручении (Ро “ Pt)
Вид обработки поверхности °в сердцевины. МПа Значения 0 для валов
гладких при при а0 = 1,8+ 2.0
Т очение Шлифование • 800—1200 1,1 - 1,2 1 1
Зачалю 1 игровом ТВЧ •• 600- 800 800- ’200 1.5—1,7 1.3 -1.5 1,6-1,7 2.4—2,8
Азотирование 900—1200 1,1- 1 25 1 5—1.7 1 7-2.1
Цементация 700 — 800 1000—1200 1 4- 1.5 1 2 - 1.3 2 __
Дробеструйная обработка 600-1500 1,1-1,25 1,5—1.6 1.7 — 2,1
Обкатка роликом 600 — 1500 1,2-1,3 1,5 - 1,6 1.8 —2,0
* Шлифовочные прижоги снижают сопротивление усталости
•* Для валов больших размеров эффективность закалки снижается
Запас по переменным напряжениям nv определяют по формуле (6).
Для обеспечения надежной работы должно быть п ~ 1,5-г-2,5, п0 > 2,5. Допустимые значения запасов прочности назначаются на основе опыта расчета н эксплуатации подобны» конструкций и т. д.
Для повышения сопротивления усталости валов используют различные методы поверхностного упрочнения пластическим деформированием (см. гл. 3-1)
При нестационарных нагрузках расчет ведут по эквивалентному напряжению
п
>=1
(Ч)
где No — число циклов, соответствующее точке перегиба кривой усталости, обычно принимают NQ = (3—5) 10’ Циклов для валов небольших сечений и JVo — Ю7 циклов — для валов больших сечений, т — показатель степени кривой усталости, т = 6 — для валов
с посадками с натягом, т = 9 — для обычных конструкций стальных валон, -V; — общее число циклов нагружений при напряжении о.; i — номер ступени нагружения.
При известном значении запас прочности находят обычным методом.
РАСЧЕТ НА КОЛЕБАНИЯ
Колебания валов с присоединенными деталями и узлами возникают под действием внешних, постоянно действующих и периодически изменяющихся сил и связаны <_ упругой деформацией валов. Малые колебания около положения равновесия становятся опасными для работоспособности вала и конструкции в целом, когда частота возмущающей силы достигает какой-либо собственной частоты системы (наступает резонанс). Напряжения в вале при этом существенно возрастают и будут определяться в основном не внешней нагрузкой, а силами инерции колеблющихся масс.
На Практике нередко наблюдаются изгибные (поперечные), крутильные
140
Валы
(угловые) и изгибыо-крутильные колебания валов.
Во избежание резонансных колебаний необходимо знать допустимый диапазон (по частоте и оборотам) рабочих режимов, ограничиваемый частотой собственных колебаний системы .
При расчетном определении частоты собственных колебаний вал с присоединенными дисками (зубчатыми колесами и т. п.) принимают в виде стержня (балки) с соредоточенной массой (массами), шарнирно закреплечного в жестких или упругих опорах. В приближенных расчетах массу вала приводят к массе диска (путем суммирования масс с учетом коэффициента приведения массы вала, зависящего от расположения опор и диска, а также вида колебаний).
Методика расчета частот собственных изгибиых и крутильных колебаний систем изложена в гл. 21.
Для предотвращения резонансных колебаний валов и расширения рабочих режимов роторов на практике применяют упругие и деформирующие опоры (см. гл. 22).
Рис. 10. Вертикальный вал пневморапир-ного механизма
КРИТИЧЕСКИЕ ЧАСТОТЫ
ВРАЩЕНИЯ ВАЛОВ
При расчете быстровращающихся валов с дисками необходимо определить их критическую угловую скорость (частоту вращения), см. гл. 22.
Приближение частоты вращения вала к критической проявляется в сильной тряске всей конструкции Амплитуды вынужденных колебаний вала становятся настолько большими, что оказываются опасными не только для прочности вала, но и для опор и всей конструкции.
Для быстровращающихся валов (п > 3000 мин*1) должна быть проведена тщательная балансировка ротора (статическая и динамическая).
Следует также применять раздельную балансировку деталей ротора, для податливых роторов рекомендуется проводить балансировку на эксплуатационной частоте вращения.
Для прохождения через критические частоты вращения необходимы тщательная балансировка ротора; высо
кая демпфирующая способность опор; минимальное время прохождения этих частот.
Пример. Провести поверочный расчет вертикального вала пневморапир-ного механизма ткацкого станка (рнс. 10). Вал изготовлен методами
Рисе 11. Эпюры моментов
Критические частоты вращения валов
141
11. Расчет запасов прочности вала
Параметры Сечение по рис. 10
1 2 3 4
Диаметр вала, мм 32 35 32 40
Момент сопротивления, мм’: И'и 2730 4210 3220 3500
«'к 5940 8420 6430 7000
Изгибающий момент ,М и, Н«мм 7! 000 10! 500 86 600 28 500
Крутящий момент М к. Н-мм 78 000 78 000 78 000 78 000
Напряжения, МПа1 изгиба ои 23.2 23,7 24,! 8,2
кручения тк 13.2 9,2 12.1 1 !,1
Эффективны й коэффициент концентрации напряжений. нормальных !, 75 1,76 1,93 2,0
касательных 1,54 1,3 1,45 1,75
Коэффициент, учитывающий масштабный эффект. при изгибе е0 0,88 0.88 0,88 0,85
при кручении ет 0,77 0.75 0.77 0,73
Коэффициент запаса1 па 5,00 5,25 6 13.75
5,75 9,7 6,6 5,71
Запас прочности п 3,78 4,63 4,44 4,74
резания из стали 45 (ав = 650 МПа; <гт = 470 МПа; a t = 275 МПа; = = 160 МПа).
Крутящий момент на водило механизма передается валом от конического зубчатого колеса. Из кинематического и силового расчетов механизма известно, что крутящий момент, изменяющийся по отнулевому циклу, достигает наибольшего значения Мтах = = 78 000 И-мм, когда центробежная сила Ro mas = 800 Н составляет с осью х угол, равный 37°; усилия на
коническое колесо при этом составляют (см. рис. 10, б): Pj = 2000 Н-Ri = 360 Н; Ai = 1600 Н.
Эпюры изгибающих моментов, действующих на вал, в плоскостях xOz и yOz показаны на рис. 11, а в табл. 11 приведены результаты расчета запаса прочности в четырех наиболее нагруженных сечениях с концентраторами напряжений. Расчет проведен с использованием соотношений (4) — (8) и табл. 1—10.
Глава 9
ПОДШИПНИКИ КАЧЕНИЯ
ОСНОВНЫЕ конструкции И ХАРАКТЕРИСТИКИ
Опоры валов, вращающихся осей и других вращающихся и качающихся деталей наиболее часто выполняют на подшипниках качения. Подшипники качения (рис. 1 и 2) обычно состоят
из наружного 1 и внутреннего 2 колец, тел качения 3 (шариков или роликов), сепаратора 4. На кольцах выполнены дорожки качения, по которым при вращении подшипника движутся тела качения. Сепаратор разделяет тела качения от взаимного соприкосновения.
142
Подшипники качения
В подшипниковых опорах иногда применяют подшипники качения без одного или обоих колец, без сепаратора. В случае использования подшипника без колец дорожки качения выполняют непосредственно на деталях опоры п опирающихся деталях.
Подшипники качения классифицируют по следующим признакам.
1. По форме тел качения подшипники делят на шариковые (рис. 1) и роликовые (рис. 2). Последние, в свою очередь, разделяют по форме роликов на подшипники с короткими (рис. 2, а) и длинными (рис. 2, 5) цилиндрическими роликами, с коническими роликами (рис. 2, г), с бочкообразными роликами (рис. 2, б), с вигыми и игольчатыми роликами (рис. 2, в).
2. По направлению воспринимаемых сил подшипники разделяют на следующие типы:
а) радиальные, воспринимающие преимущественно радиальные нагрузки, действующие перпендикулярно оси вращения подшипника (рис. 1, а, б и 2, а, б, в, б);
б) радиально-упорные, предназначенные для восприятия комбинированных нагрузок, т. е. одновременно дей
ствующих радиальных и осевых нагрузок (рис 1, в, г и 2, г);
в) упорно-радиальные, предназначенные для восприятия осевой нагрузки при одновременном действии незначительной радиальной нагрузки (рис. 1, б);
г) упорные, воспринимающие только осевые нагрузки (рис. 1, е).
3 По способности самоустанавли-ваться подшипники подразделяют на несамоустанавливающиеся и самоуста-навливающиеся (сферические, рис. 1, б и 2, б)
4. По числу рядов тел качения подшипники делят на однорядные (рис. 1, а, в—е и 2, а, в—б), двухрядные (рис. 1, б и 2, б) и четырехрядные.
Подшипники одного и того же диаметра отверстия подразделяют по габаритным размерам (наружного диаметра и ширины) на размерные серии: сверхлегкую, особо легкую, легкую, среднюю, тяжелую, особо узкую, узкую, нормальную, широкую и особо широкую.
Наиболее часто применяют подшипники легкой и средней серий нормальной ширины.
Основные конструкции и характеристики
143
Подшипники различных типов, размеров и серий обладают различной грузоподъемностью и быстроходностью. Подшипники более тяжелых серий ме-иее быстроходны, но обладают более высокой грузоподъемностью. Подшипники шариковые радиальные однорядные и радиально-упорные, а также роликовые с короткими цилиндрическими роликами обладают наибольшей быстроходностью по сравнению с подшипниками других типов.
Для особо высокой частоты вращения и действия легких нагрузок целесообразно использовать подшипники сверхлегкой или особо легкой серий. Для восприятия повышенных и тяжелых нагрузок при высокой частоте вращения обычно используют подшипники легкой серии, а при недостаточной их грузоподъемности размещают в одной опоре два подшипника.
Радиальные шарикоподшипники могут воспринимать как радиальные, так и осевые нагрузки, действующие в обе стороны вдоль осн вращения подшипника, что обеспечивает возможность фиксирования вала в осевом направлении. При использовании этих подшипников предъявляются менее высокие требования к соосности опор и жесткости валов. Они дешевле подшипников других типов, допускают наиболее простои монтаж и демонтаж. Поэтому такие подшипники наиболее распространены в различных машинах и механизмах.
Роликовые подшипники более грузоподъемны, чем шариковые. Однако роликоподшипники с цилиндрическими роликами наиболее распространенных конструкций (с направляющими бортами для роликов на одном из колец подшипника) не могут воспринимать осевых нагрузок, а конические роликоподшипники менее быстроходны.
Широко применяют роликоподшипники как с цилиндрическими, так и с коническими роликами с выпуклой образующей (с бомбиннроваиными роликами). Выпуклость (бомбина) составляет 10 ... 40 мкм в зависимости от диаметра роликов. Такая форма роликов позволяет снизить концентрацию напряжений иа их кромках и
1. Оптимальные углы контакта шарикоподшипников в зависимости от отношения осевой нагрузки F к радиальной Ff
' Q Отношение —-—
Не более 0.35
0.35-0.8
0.8-2,5
Св 2.5
а0
0 (радиальный подшипник) 12 26 36
повысить долговечность подшипников в 2 раза н более.
Раднально-упориые и упорно-радиальные подшипники различают по значению угла контакта а (рис. 1, в, г, д и 2, г). С увеличением угла контакта радиально-упорные подшипники могут воспринимать более тяжелые осевые нагрузки. Однако быстроходность подшипников с увеличением угла контакта снижается. При одновременном действии на радиально-упорный шарикоподшипник радиальной Fг и осевой Fа нагрузок выбор оптимального угла контакта подшипника проводят по отношению осевой нагрузки к радиальной (табл. 1).
Радиальные и радиально-упорные шарикоподшипники могут быть использованы и в случае действия на них только осевой нагрузки, особенно при высокой частоте вращения, прн которой нельзя применять упорные подшипники. Самоустанавливающиеся подшипники применяют в случае повышенной несоосности опор вала (до 2—3°), а также прн повышенной податливости вала.
При действии на опоры значительных осевых нагрузок и работе их с высокими скоростями используют радиально-упорные шарикоподшипники с четырех, трех- или двухточечным контактом. В этих подшипниках внутреннее (рис. 1,г) или наружное кольцо разъемное в плоскости, перпендику-лярно^ оси подшипника. Благодаря такой конструкции колец представляется возможным в подшипнике разместить большее число шариков и повысить таким образом его грузо
144
Подшипники качения
подъемность, применить цельный массивный сепаратор, центрируемый по бортам наружного или внутреннего кольца. Подшипники с многоточечным контактом допускают нагружение осевыми нагрузками в двух направлениях.
Работоспособность подшипников с четырех- и трехточечным контактом значительно снижается, если во время работы возникает одновременно контакт шариков с обеими сторонами арочного желоба. Высокая работоспособность подшипников с многоточечным контактом достигается, когда осевой зазор в подшипнике и осевая нагрузка достаточны для обеспечения во время работы контакта шариков с желобами в двух точках — одной на внутреннем и второй на наружном кольцах.
Для восприятия значительных осевых нагрузок и одновременно сравнительно легких радиальных нагрузок используют упорно-радиальные подшипники (рис. 1, д). Быстроходность таких подшипников невысокая (dmn = (0,25-?0,4) 10е ммХ Хмин"1). Однако эти подшипники обладают высокой осевой грузоподъемностью, особенно упорно-радиальные подшипники со сфероконическими роликами. Последние являются самоуста-навливающимися и могут работать при перёкосе колец или изгибе валов до 3°.
Предельная частота вращения подшипников зависит от их конструкции и точности изготовления, от точности изготовления и монтажа сопряженных с подшипниками деталей, а также от способа смазывания и свойств смазочного материала.
Подшипниковая промышленность изготовляет подшипники качения в соответствии с ГОСТ 520—89 пяти классов точности, которые обозначают следующими цифрами: 0,6, 5, 4 и 2 (обозначения приведены в порядке повышения точности).
Подшипники класса точности 0 обычно используют при отсутствии особых требований к точности вращения, определяемой радиальными и осевыми биениями дорожек качения внутреннего и наружного колец подшипника,
а также при частоте вращения в пределах, указанных в каталоге [4] иа подшипники общего применения.
При использовании подшипников высоких классов точности необходимо посадочные поверхности сопряженных с ними деталей изготовлять с наименьшей точностью, чем точность изготовления подшипников.
Быстроходность подшипников принято оценивать параметром dmn, где drn — диаметр окружности, соединяющей центры тел качения, мм; п — частота вращения подшипника, мин-1.
При применении специальной системы смазывания и эффективного отвода выделяющегося в подшипниках (средних размеров) тепла получено максимальное значение параметра dmn — 3,7- 10е мм-мин-1.
Для шарикоподшипников небольших размеров при смазывании масляным туманом достигают значения параметра dmn — (1,6--1,8) 10е мм-мин-1; при этом частота вращения подшипника равна 90 000—100 000 мин-1, а ресурс подшипников при указанной частоте вращения составляет 2000 ч и более.
Основные характеристики подшипников условно обозначают на кольцах подшипника цифрами и буквами, совокупность которых образует условное обозначение подшипника. Система основных условных обозначений подшипников стандартизована и определена ГОСТ 3'89—89.
Кольца и тела качения подшипников изготовляют в основном из шарикоподшипниковых высокоуглеродистых хромистых сталей ШХ15, ШХ15СГ, а для подшипников, воспринимающих значительные ударные нагрузки, кольца и тела качения изготовляют из цементуемых сталей 18ХГТ, 20Х2Н4А и 20НМ. Для подшипников, работающих при высоких температурах (до 500°C), кольца и тела качения изготовляют из теплостойкой вольфрамо-ванадиевой стали ЭИ347Ш (ТУ 14-1-2244—77) электрошлакового переплава. В условном обозначении правее цифровой части теплостойкие подшипники содержат букву «Р». Подшипники из теплостойкой стали ЭИ347Ш не снижают своей работоспособности до температуры 400 °C.
Основные конструкции и характеристики
145
2. Механические и тепловые свойства керамических материалов, используемых для изготовления подшипников качения
Материал Твердость HRC Плотность, г/см* Модуль упругости Е- IQ-*, МПа Коэффициент Пуассона Теплопроводность, । кал/(см* с-°С). прн 1 •= 21 °C Коэффициент линей ного расширения, а- 10е. !/°С
Нитрид кремния 76 3,11 —3.24 3,16 0,26 6,28 2.9
Карбид кремния 90 3,2 4,15 0.25 29,76 5,0
Окись алюминия 85 3.9 3,58 0,25 6,28 8,5
Примечание, Допустимая максимальная рабочая температура 1094 °C.
Для работы подшипников в агрессивных средах детали подшипников изготовляют из высокоуглеродистой коррозионно-стойкой стали 95X18Ш электрошлакового переплава
(ТУ 14-1-595—73) или из стали 40Х13С1-Ш (ТУ-14-1-377-72). В условном обозначении правее цифровой части эти подшипники содержат букву «Ю».
Подшипники ответственного назначения высокой надежности изготовляют из указанных сталей повышенной чистоты, получаемых электрошла-ковым или вакуумным переплавом.
Для подшипников, работающих с высокой частотой вращения, высокой температурой при отсутствии смазочного материала, в абразивной или агрессивной среде, применяют керамические материалы. Из керамических материалов наибольшее применение получили нитрид кремния Si3N4, карбид кремния SiC, окись алюминия А12О3. Эти материалы теплостойки, обладают высокими пределами прочности и текучести. стойки к окислению, износостойки. Подшипники, изготовленные из этих материалов, могут работать без смазочного материала, несклонны к заеданию и свариванию, могут работать в воде, кислотах, щелочах.
Однако керамические материалы хрупки, склонны к образованию тре-Щйн. Повышенная хрупкость и склонность к растрескиванию нитрида кремния и карбида кремния обусловлена кристаллической структурой, которая
при возникновении напряжений не обеспечивает упругих и пластических деформаций. Поэтому с целью предотвращения растрескивания керамические материалы армируют волокнами.
Долговечность керамических подшипников зависит от пористости материала, однородности структуры и шероховатости поверхности. При увеличении пористости, повышенной неоднородности структуры и грубо обработанных поверхностях качения долговечность керамических подшипников качения значительно снижается. Сопротивление усталости при контакте нитрида кремния выше, чем у стали.
Контактная прочность и вязкость нитрида кремния повышаются при введении в исходный материал связующей присадки из окиси иттрия V2O3 и окиси алюминия А12О3. Детали подшипников из нитрида кремния изготовляют методом изостатиче-ского прессования, что обеспечивает получение материала с требуемой сплошностью. Типичные механические и тепловые свойства керамических материалов, используемых для изготовления подшипников качения, приведены в табл. 2.
Для особо высоких частот вращения или при вращении с повышенными частотами обоих колец подшипника в одну сторону целесообразно использовать гибридные подшипники, в которых тела качения изготовлены из керамического материала, а кольца из стали.
146
Подшипники качения
Сепараторы подшипников разделяют на штампованные (змейковые), центрируемые по телам качения, и массивные, центрируемые по бортам наружного или внутреннего кольца. Штампованные сепараторы изготовляют из низкоуглеродистой стали, латуни, коррозионно-стойкой стали. Массивные сепараторы изготовляют из бронзы БрАЖМц10-3-1,5 (ГОСТ 1208—73); Б рАЖН 10-4-4 (ГОСТ 1208—73); латуни ЛС59-1 (ГОСТ 494—76), алюминиевых сплавов Д1Т (ГОСТ 18475—82) н АК4 (ГОСТ 21488—76), текстолита, низкоуглеродистой стали.
Подшипники с массивным сепаратором наиболее быстроходны. Для ответственных высокоскоростных подшипников бронзовые илн стальные сепараторы имеют антифрикционные покрытия: свинцово-оловяннстое или серебряное толщиной слоя 10 ... 25 мкм.
Для подшипников, работающих в вакууме нли без смазочного материала, сепараторы изготовляют из маслянита В1 н В2 илн фторопласта-4 с порошками никеля и дисульфида молибдена (ФН202).
Основные типы подшипников и их характеристики приведены в каталоге [4].
ГЕОМЕТРИЧЕСКИЕ, КИНЕМАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ ЗАВИСИМОСТИ
В ПОДШИПНИКАХ КАЧЕНИЯ
Диаметры дорожек качения колец раднально-упорных шарикоподшипников определяют по формулам (рис. 3)
Дв = dm Dw cos схв; (1)
Дн = dm -f- Dw cos aH, (2) где dB и DK — диаметры дорожек качения соответственно внутреннего и наружного колец, Dw — диаметр тел качения; ав н ан — номинальные углы контакта тел качения соответственно с внутренним и наружным кольцами.
Диаметры дорожек качения колец радиальных шариковых и роликовых подшипников определяют по форму
лам (1) и (2), приняв ав — ан = 0. Для обычных стандартных подшипников, приведенных в каталогах и используемых в общем машиностроении, диаметр шариков определяют по формуле
Dw = (0,600 4- 0,635) D~~d , (3)
где Dud — соответственно наружный и внутренний диаметры подшипника.
Для ответственных опор повышенной грузоподъемности и долговечности применяют подшипники, в которых диаметр шариков определяют по формуле
Dw = (0,68 4- 0,70) • (4)
Частота вращения сепаратора при “в — “и = а (рис. 4)
nc = 4[nB(l--g-c°sa)±
± п3 1 + coscc^ J , (5)
где лв н лн — частоты вращения соответственно внутреннего и наружного
Рис. 3. Контактные напряжения в подшипнике
Грузоподъемность и расчет подшипников
147
колец подшипника. При вращении колец в разные стороны частота вра-щения наружного кольца в формуле (5) принимается со знаком минус, а при вращении колец в одну сторону — со знаком плюс.
Частота вращения тел качения во-г круг своей осн
пи пв / dm _____
Dw
пи>'---- 2
Dw 3
~г~ cos3 а
“m
(6)
Если вектор нагрузки вращается с частотой пд, то частота вращения кольца подшипника относительно вектора нагрузки будет:
для внутреннего кольца пвЯ =
для наружного кольца пнЯ =
= пн — пн.
Прн вращении тел качения вокруг оси подшипника на каждый из них действует центробежная сила, нагружающая дополнительно дорожку качения наружного кольца:
Рс = ~1Г~
(7)
гдеб, —сила тяжести тела качения, Н; wc — угловая скорость сепаратора.
В расчетах подшипников, вращающихся с высокой частотой, необходимо учитывать центробежные силы тел качения.
Из формулы (5) следует, что при вращении колец подшипника в одну сторону угловая скорость сепаратора зна-4 чительно выше, чем при вращении колец в разные стороны Следовательно, в подшипниках с противоположным вращением колец центробежные силы тел качения будут значительно ниже по сравнению с центробежными силами, возникающими при вращении колец в одну сторону.
Из формулы (6) следует, что при вращении колец подшипника в противоположные стороны высокую частоту вращения вокруг своей оси имеют тела качения В связи с этим при вращении колец роликоподшипников в противоположные стороны ролики должны быть изготовлены и отбалансированы с высокой точностью.
Рис. 4. План скоростей деталей подшип» ника
Если приходящаяся на наиболее нагруженное тело качения внешняя нагрузка меньше центробежной силы тела качения, то в этом случае целесообразно для повышения долговечности подшипника диаметр тела качения уменьшить до оптимального размера [2]. Если приходящаяся на наиболее нагруженное тело качения нагрузка выше его центробежной силы, то диаметр тел качения целесообразно определять по формуле (4).
ГРУЗОПОДЪЕМНОСТЬ И РАСЧЕТ
подшипников
Статическая грузоподъемность подшипников. Подшипники ряда машин периодически подвергаются действию нагрузок при отсутствии вращения.
Статическая грузоподъемность (допустимая нагрузка) невращающегося подшипника назначается из условия, что остаточная деформация тел качения и колец под этой нагрузкой не превысит допустимую [6] = 10“4£>t» (здесь Dw — диаметр тела качения).
Значения статической грузоподъемности для подшипников' различных типов и серий даны в каталогах [4].
Если подшипник нагружен одновременно радиальной н осевой силами, то эквивалентная статическая нагрузка для радиальных и радиально-упорных шариковых и роликовых подшипников принимается большей из расчета по следующим формулам:
P0 = X0Fr+Y0Fa-, P0=Fr, (8)
148
Подшипники качения
3. Значения коэффициентов X, и У,
Подшипники Однорядные подшипники Двухрядные подшипники
Х„ Y, X. Yo
Шариковые радиальные 0,6 0,5 0.6 0.5
Шариковые радиально-упорные при а° 18 20 25 26 30 35 36 40 0,5 0,43 0,42 0,38 0,37 0,33 0,29 0,28 0,26 1 0,86 0,84 0,76 0.74 0,66 0,58 0,56 0.52
Шариковые самоустаиавливающиеся 0.5 0.22 tg а ] 0,44 ctg а
Роликовые самоустаиавливающиеся н конические
где Хо и Уо — коэффициенты радиальной и осевой статических нагрузок (табл. 3).
Выбранный подшипник по статической грузоподъемности должен удовлетворять условию
Ро Со, (9)
где Со — статическая грузоподъемность подшипника. Подшипники, работающие с частотой вращения п > > 1 мин-1 и рассчитанные на сравнительно небольшой ресурс, необходимо также проверять на статическую грузоподъемность, так как допустимая нагрузка, определенная из условия долговечности, для малого ресурса может оказаться больше статической грузоподъемности подшипника.
Для упорных и упорно-радиальных подшипников эквивалентная статическая нагрузка принимается большей из расчета по следующим формулам:
Л>-= Fa + 2,3FrtSa-, (10)
P0 = Fa. (Н)
Выбранный подшипник должен удовлетворять условию
Д0<С0. (12)
Динамическая грузоподъемность подшипников. Усталостное выкрашивание
поверхностей качения является типичным отказом подшипников в работе.
Расчет подшипников основан на известном уравнении кривой усталости
amN = G, . (13)
где а — переменное напряжение цикла; N — число циклов изменения этих напряжений до разрушения детали (образца); т и G — постоянные величины, зависящие от свойств материала и состояния поверхности детали.
Так как контактные напряжения в подшипниках нелинейно связаны с действующей нагрузкой
атет=АР1/й, (И)
то расчет удобнее вести по действующей на подшипник нагрузке,
В этом соотношении А — коэффициент, зависящий от радиуса кривизны соприкасающихся тел, распределения нагрузки между телами качения, коэффициента Пуассона и модуля упругости материала деталей подшипника; b — знаменатель показателя степени (Ь = 3 — для шарикоподшипников; b = 2 — для роликоподшипников).
Г рузоподъемность и расчет подшипников
149
4. Значения коэффициента качества #КаЧ
Класс точности подшипников Материал колец и тел качения
ШХ15. 95Х18Ш ШХ15Ш и ЭИ347Ш (стали элек-трошлакового или вакуумного переплава)
для шарикоподшипников для роликоподшипников с роликами для шарикоподшипников для роликоподшипников с роликами
цилиндрическими бомбини-роваи-ными цилиндрическими бомбиии-роваи иыми
0 ! 1 1,20 1,15 1.15 1,30
6 1,10 1,10 1,25 1,20 1,20 1,35
5 и 4 1,15 1,15 1,30 1,25 1.25 1,40
Так как число циклов нагружения (иеодииаксвое для точек тел качения и дорожек качения) зависит от числа оборотов за время работы подшипника L:
К = BL,
то, подставляя последние соотношения в уравнение (13), получим
т
АВР~ L = G,
где В — коэффициент, зависящий от числа тел качения, среднего диаметра подшипника, диаметра тел качения и угла контакта; L — долговечность, мли. оборотов.
= Ср, найдем
(-^-)Р-^ = б-Ю-»пЛл, (15) где С — динамическая грузоподъемность, Н; р — показатель степени, на основании экспериментальных данных: р = 3 (т = 9) при начальном точечном контакте (для шарикоподшипников); Р = 3,33 (т — 6,66) при начальном линейном контакте (для роликоподшипников); — долговечность, ч; Р — Динамическая эквивалентная нагрузка,, Н; п — частота вращения подшипника, мин-1.
По физическому смыслу динамическая грузоподъемность С эквивалентна радиальной нагрузке, которую под
шипник может выдержать в течение базового числа оборотов 10е.
На основании экспериментальных исследований установлены зависимости для динамической грузоподъемности подшипников, аналогичные по структуре соотношениям для статической гр узоподъемиости.
Значение динамической грузоподъемности для подшипников различных типов и серий нулевого класса точности приведены в каталогах и справочниках по подшипникам [4].
Для подшипников, изготовляемых по более высокому классу точности, чем нулевой, из стали повышенной чистоты с бомбинированиыми роликами, динамическая грузоподъемность принимается по справочнику-каталогу, но с учетом коэффициента качества (табл. 4), т е.
С — Скатывав- (16)
где С — динамическая грузоподъемность используемого подшипника; Скат — динамическая, грузоподъемность подшипника по справочнику-каталогу; /<кач — коэффициент качества.
Если в указанном справочнике-каталоге не приведен используемый подшипник или не приведена его динамическая грузоподъемность, то она определяется по зависимостям, установленным на основании результатов экспериментальных исследований подшипников различных типов [4].
150
Подшипники качения
Если подшипниковый узел содержит несколько одинаковых подшипников, подобранных так, что нагрузка между ними распределяется равномерно, то общую динамическую грузоподъемность подшипникового узла Сд определяют по формуле
Cz = i°’7C, (17)
где i — число одинаковых подшипников в опоре, С — динамическая грузоподъемность подшипника.
Для расчета потребной динамической грузоподъемности необходимо знать эквивалентную нагрузку на подшипник.
ЭКВИВАЛЕНТНАЯ НАГРУЗКА
И РАСЧЕТ ДОЛГОВЕЧНОСТИ ПОДШИПНИКОВ
В большинстве случаев подшипники качения подвергаются совместному действию осевой и радиальной нагрузок. Условия работы (характер действия 'нагрузок, температура и т. д.) подшипников также разнообразны.
Влияние основных эксплуатационных факторов .на работоспособность подшипников учитывают путем введения в расчет эквивалентной нагрузки — критерия подобия, который обобщает накопленный опыт по эксплуатации подшипников в различных конструкциях.
По физическому смыслу эквивалентная нагрузка — механический эквивалент реальных условий нагружения подшипника, равноопасный по степени его повреждаемости с простым нагружением радиальной силой в типичных (лабораторных) условиях.
Эквивалентную нагрузку для радиальных шарикоподшипников и радиально-упорных шариковых и роликовых подшипников находят из соотношения
P = (XVFr+ YFa)K6KT, (18) где X и Y — коэффициенты соответственно радиальной и осевой нагрузок (табл. 5); V — коэффициент вращения, V — 1 при вращении внутреннего кольца; V = 1, 2 при вращении наружного кольца, Fr и Fa — соответ
ственно радиальная и осевая силы, воспринимаемые подшипником; Ха — коэффициент безопасности, учитывающий влияние иа долговечность подшипников характера действия внешних нагрузок (табл, 6); Кт — температурный коэффициент (табл. 7).
Значения коэффициентов X и Y в табл. 5 даны в зависимости от отношения FaIVFT, которое влияет на распределение нагрузки между телами качения. При малых значениях осевой силы Fa (или до некоторого отношения у из-за радиального
зазора в подшипнике возникает повышенная неравномерность распределения нагрузки между телами качения. С ув₽лйчением осевой нагрузки (или
Fa . \ х
при - “ '> е ) происходит выборка
V г г /
зазора, рабочая зона в подшипнике возрастает и улучшается распределение нагрузки.
Р
Поэтому при отношении £ $7 е осевую силу не учитывают (принимают X = 1 и Y = 0) и расчет ведут лишь по радиальной иагр>зке.
Значения е даны в табл. 5 в зависи-р
мости от отношения —(здесь Со — C-Q
статическая радиальная грузоподъемность подшипника).
В ряде отраслей машиностроения (авиа-, вагоностроении и т. д.) при точном определении нагрузок используют более низкие значения подтвержденные опытом эксплуатации (см. табл. 6).
В радиально-упорном шарикоподшипнике от действия радиальной силы возникает дополнительная осевая нагрузка
(19)
S = ер
а в коническом роликоподшипнике
S = 0,83е/>. (20)
Таким образом, если вал установлен иа двух радиально-упорных подшипниках. то осевая нагрузка на одном из них будет состоять из внешней осевой нагрузки и дополнительной осевой силы от другого подшипника.
В. Значения коэффициентов радиальной X н осевой Y нагрузок
Однорядные подшипники
Тнп подшипника Угол контакта а, ° Fa С0 Fg VFr < е >е
X У X У
Шариковые радиальные 0 0,014 0,028 0,056 0,084 0.1 1 0,17 0,28 0,42 0.56 1 0 0,56 2,30 1,99 1,71 1,55 1,45 1,31 1.15 1,04 1.00
Шариковые радиально-упорные 12 0.014 0,029 0.057 0.086 0. 1 1 0, 17 0.29 0.43 0,57 1 0 0,45 1,81 1,62 1,46 1,34 1,22 1.13 1,04 1,01 1,00
18 — 20 24— 26 30 35 — 36 40 - 0,43 0.41 0.39 0,37 0.35 1,00 0,87 0,76 0,66 0,57
Роликовые конические — — 1 0 0,4 0,4 ctg а
Шариковые упорно-радиальные 45 60 75 -- — — 0,66 0,92 1.66 1 1 1
Роликовые упорно-радиальные — — — tg а 1
Двухрядные подшипники е
Ра ра VFr ‘
X У X У
1 0 0.56 2.30 1,99 1.71 1,55 1,45 1,31 IJ5 1,04 1.00 0.19 0.22 0.26 0.28 0.30 0.34 0.38 0,42 0.44
1 2.08 1.84 1.60 1,52 1,39 1,30 1,20 1,16 1.16 1,09 0,92 0.78 0.66 0.55 0.74 2.94 2.63 2,37 2.18 1.98 1.84 1,69 1.64 1.62 1,63 1.44 1.24 1,07 0,93 0.30 0.34 0.37 0,4 1 0,45 0.48 0.52 0,54 0.54 0,57 0,68 0 80 . 0.95 1,14
0.70 0.67 0.63 0,60 0,57
1 0,45 ctg а 0,67 0,67 ctg а 1.5 tg а
1.18 1.90 3.89 0,59 0.54 0.52 0.66 0.92 1.66 1 1 1.25 2.17 4 67
1.5 tg а 0,67 tg а 1 1,5 tg а
Эквивалентная нагрузка и расчет долговечности
152
Подшипники качения
6. Значения коэффициента
Характер нагрузки на подшипник Вибрационные перегрузки рекомендуемые
в авна-ст роенин в общем машиностроении
Спокойная нагрузка без толчков Jg 1.0 1,0 1,0
Легкие толчки, небольшие вибропере- 1 0 < Jg 3.5 1,05—1,10 1,0-1,2
грузки
Умеренные толчки и вибрации 3,5 < J& < 6 1.10-1,15 1,3-1,5
Значительные толчкн и вибрации 6 < Jg < 10 1,15—1,25 1,8 —2.5
Сильные удары и высокие вибропере Jg > 10 1,35—1,60 2,5-3,0
грузки
Эквивалентная нагрузка для подшипников с короткими цилиндрическими роликами
P = FrVK6KT. (21) Эквивалентную нагрузку для упорных подшипников определяют по формуле
Р = РаКбКт- (22)
Для упорно-радиальных подшипников эквивалентная осевая нагрузка определяется по формуле (18) при V =
Если подшипники работают прн изменяющихся со временем нагрузке и частоте вращения, то расчет ведут по эквивалентной нагрузке, равноопасной по сопротивлению усталости переменному режиму нагружения:
^экв =
(23)
7. Значение коэффициента Кт
Твердость НRC Температура
поверхнос тей отпуска к.
колец и тел колеи н тел
качения качения, СС
Не менее 59 255 н ниже 1,0
58—59 250 1,05
57—58 275 1,1 1.25
55—57 300
*
где Plt Р2..... Рп — постоянные
эквивалентные нагрузки, действующие соответственно в течение Lt, Li, , Ln оборотов; L — суммарное число миллионов оборотов за ресурс изделия:
L = Z-i + Li + ...+ Ln.
Число оборотов подшипника (в миллионах) на i-м режиме (i = 1,2,3,
Lt = 6-10~sniLhi, ’ (24)
где nt — частота вращения, мни-1; Lht — время работы подшипника на i-м режиме за ресурс изделия, ч.
Если нагрузка изменяется от Рпцп до Ртах по линейному закону, то
р _____ ^Ш1П + 2^ тпах /Оеч
г экв-----------------------. (20)
При одновременном вращении внутреннего и наружного колец эквивалентную нагрузку определяют с учетом коэффициента вращения по формуле
^экв ~ X
3Ti=n
Х |/ S Р1 («<» ± ^Чн) • (26)
где а/в = ; aiH = ; LIB =
— 6-10 bniBL/lj$ Ltn — 6-10
При вращении колец подшипника в одну сторону в формуле (26) при-
Эквивалентная нагрузка и расчет долговечности
153
иимается знак минус, при вращении колец в противоположные стороны — знак плюс.
Эквивалентные нагрузки определяют с учетом наибольшей допускаемой неуравновешенности вращающихся деталей илн наибольшей неуравновешенности, которую они получают за ресурс, если она изменяется во время эксплуатации изделия. Кратковременные перегрузки прн расчете долговечности могут не учитываться, если они не вызывают снижения долговечности более 3%. Если с изменением режима работы изделия изменяется направление действия осевой силы, то расчетная долговечность определяется для каждой стороны желоба и полученные долговечности сравниваются с требуемыми ресурсами каждой стороны желоба.
Для проектного расчета по эквивалентной нагрузке и требуемому ресурсу определяют потребную (расчетную) динамическую грузоподъемность подшипника по формуле, полученной из (15):
Срас = PL1/₽. (27)
Используя полученное расчетное значение динамической грузоподъемности по справочнику или каталогу с учетом коэффициента качества (Ккач), выбирают подшипник; при этом должно быть удовлетворено условие С > > Срас (С — динамическая грузоподъемность выбранного подшипника).
Если подшипник принят по конструктивным соображениям, то расчетом проверяют его ресурс:
, 10s / С
Lh~ \ Р I '
(28)
В соотношениях (27) и (28) под Р понимают эквивалентную нагрузку при постоянном или при переменном режиме работы; п — частота вращения подшипника, мин'1, определяемая по формуле
ni = П{3 ± ntB илн n-i = niB ± nt3, (29) где niB и riiB — соответственно частоты вращения на i-м режиме внутреннего н наружного колец подшипника; при этом знак плюс принимается
при вращении колец в противоположные стороны, а при вращении колец в одну сторону — знак минус.
При высокой частоте вращения подшипника (dmn>2- 10емм-мин"1) долговечность подшипника может ограничиваться недостаточным сопротивлением усталости при контакте наружного кольца, дополнительно нагруженного центробежными силами тел качения.
Для расчета долговечности высокоскоростных подшипников зависимость (13) удобнее представить в виде
(Иа.'г * (30)
\ °см / ^0
где [а]см — допускаемое напряжение смятия при базе NQ = 107 циклов изменений напряжений; асм — максимальное расчетное напряжение смятия на площадках контакта шарика или ролика с дорожкой качения наружного кольца подшипника, определенное с учетом центробежных сил тел качения. Учитывая (30), долговечность подшипников, ч, можно определить из расчета на контактную прочность по формулам:
для шарикоподшипников
L Ю7 / Мем У° 00лсг \ асм /
для роликоподшипников
L - 107 { У’66
h~ 60ncz \ аом /
(31)
(32)
где лс — частота вращения сепаратора, мин"1; z — число тел качения в подшипнике; (а ]см и [а]с'м — допускаемые напряжения при базе 107 циклов соответственно при точечном и линейном контактах.
Для стали ШХ15Ш и ЭИ347Ш электро шлакового илн вакуумного переплава при HRC^58 допускаемые напряжения [а]см = 3750 МПа, [о]'м = = 3000 МПа. Напряжение смятия определяют по формулам:
для эллиптической площадки контакта (шарикоподшипники)
(33)
154
Подшипники качения
для линейного начального контакта (роликоподшипники)
= (34)
где Ер — суммарная кривизна поверхностей контактирующих тел;
2 Р = Р11 + Ри + Pai + Paa- (35)
Pii- Pia- Pai- Paa — главные кривизны соприкасающихся поверхностен. Первый индекс обозначает контактирующее тело (тело качения, кольцо), второй — определяет плоскость, в которой находится главная кривизна; 1 — ось подшипника расположена в плоскости кривизны; 2 — плоскость кривизны перпендикулярна оси подшипника;
1____!_ 1_________—
т1 i т2
П - , (36)
——и Et (i = 1, 2) —соответственно ту 1 '•
коэффициенты Пуассона и модули упругости материалов контактирующих тел; р. и v — коэффициенты [3]; q — линейная интенсивность распределения нагрузки по длине контакта,
/г — длина площадки контакта; Р2н — суммарная сила, направленная по нормали к площадке контакта тела качения с дорожкой качения наружного кольца,
РГа = Р„ + Р, + —— , (38)
SH а г • cos а ' '
Ра — нормальная составляющая суммарной силы от осевой нагрузки,
° z sin а ’
Fa — осевая сила, действующая на подшипник; а — угол контакта тел качения с дорожкой качения наружного кольца; Рг — нормальная составляющая суммарной силы от радиальной нагрузки:
для шарикоподшипников Р = 5F' •
r z cos а ’
для подшипников с начальным линейным контактом тел качения с кольцом подшипника
4,6F,
z
Р,
(41)
Fr — радиальная сила, действующая на подшипник; Рс — центробежная сила тела качения,
Рс = 0,5mdma>|t (42)
т — масса тела качения;
для цилиндрического ролика
D;
т = ул I; (43)
для шарика
D3
• т = ул ; (44)
у — плотность материала тела качения; I — длина ролика; сос — угловая скорость сепаратора.
При выполнении дополнительного поверочного расчета по напряжениям смятия определение запаса долговечности подшипника проводится по наименьшей расчетной долговечности, полученной при расчете его без учета или с учетом центробежных сил тел качения.
В случае одновременного вращения колец подшипника в одну или разные стороны расчет долговечности проводят с использованием зависимости (30) и с учетом принципа линейного суммирования повреждений, в соответствии с которым в момент разрушения приближенно может быть принято соотношение (101), приведенное в гл. 31:
k
(45}
где Nt — число циклов нагружения, накопленных деталью на i-м режиме за время отработки всех k режимов до разрушения; — число циклов нагружения до разрушения детали при постоянных напряжениях i-ro режима.
Запас долговечности на i-м режиме работы
А/Т
niN = • (46)
Эквивалентная нагрузка и расчет долговечности
155
Запас долговечности при ступенчатом нагружении подшипника, выраженный через отношение числа циклов (115), гл. 31,
Л'*
(47)
/v Б
где N % и Wv — соответственно суммарные числа циклов изменений напряжений за ресурс и до разрушения при ступенчатом нагружении или
(48)
Запас по долговечности и запас по напряжениям связаны равенством
niN = “Та, (49)
вытекающим из уравнения
(50)
Контактные напряжения определяют по формулам Герца (33) и (34), а нагрузку на наиболее нагруженное тело качения определяют по формулам Р =
5ЕГ
= —— для шарикоподшипников и '(41) — для роликоподшипников.
В зависимости от соотношения нагрузок постоянного направления и вращающихся нагрузок, связанных с неуравновешенностью ротора, его прецессионным вращением, рассматривают три случая нагружения подшипника.
1. Вектор суммарной нагрузки отклоняется от направления вектора нагрузки постоянного направления, но не меняет направление на противоположное. В этом случае принимают, что направление нагрузки совпадает с направлением, при котором оиа имеет наибольшее значение. По нагруженной зоне прокатываются ~ шс роликов в секунду (ш0 — угловая скорость вращения сепаратора). Если принять Действующую в контакте нагрузку равной максимальной, то число цик
лов нагружения в секунду дорожки качения внутреннего кольца
77цв = I «>в ыс |, (о!)
где a — угол нагруженной зоны подшипника; <г,в — угловая скорость вращения внутреннего кольца.
При этом в каждом цикле действует суммарная нагрузка
^=^+*0, (52)
где Рй — нагрузка постоянного направления; /?0 — вращающаяся нагрузка.
На дорожку качения, наружного кольца, кроме суммарной нагрузки Р£в> действуют центробежные силы тел качения Рс. Поэтому число циклов нагружения дорожки качения наружного кольца при действии в каждом цикле суммарной максимальной нагрузки
р2н = ро + «о + ^с (53) будет
ctz
^н=^Г |®н-«с|- (54)
Число циклов нагружения в секунду дорожки качения наружного кольца в зоне действия только центробежных сил тел качения Рс
N” = (2jI ~ «) г
ци 4яа
<55)
где сои — угловая скорость вращения наружного кольца.
2. Вектор суммарной нагрузки вращается с угловой скоростью, равной угловой скорости вращения внутреннего кольца подшипника. В этом случае вектор вращающейся нагрузки больше вектора нагрузки постоянного направления. По нагруженной зоне
г прокатываются в секунду |сов—
— <х»с I роликов.
Число циклон нагружения в секунду дорожки качения внутреннего кольца
'Уцв | <ов о>с |. (56)
Прн этом в каждом цикле действует суммарная максимальная нагрузка, определяемая по формуле (52).
156
Подшипники качения
Число циклов нагружения в секунду дорожки качения наружного кольца прн действии в каждом цикле суммарной максимальной нагрузки, определяемой по формуле (53),
|“н + “с-2“в|. (57)
Число циклов нагружения в секунду дорожки качения наружного кольца в зоне действия только центробежных сил тел качения Рс
(58)
3. Вектор суммарной нагрузки вращается с угловой скоростью, равной угловой скорости вращения наружного кольца подшипника. В этом случае вектор вращающейся нагрузки также больше вектора нагрузки постоянного направления.
Число циклов нагружения в секунду дорожки качения внутреннего кольца подшипника прн действии в каждом цикле суммарной максимальной нагрузки, определяемой по формуле (52),
Л/цв = | сов + сос + 2шн I- (59)
Число циклов нагружения в секунду дорожки качения наружного кольца подшипника при действии в каждом цикле суммарной максимальной нагрузки, определяемой по формуле (53),
Лцв — дуд- | <ан — со,. | (60)
СМАЗЫВАНИЕ ПОДШИПНИКОВ
Для смазывания подшипников используют пластичные (консистентные) смазочные материалы, жидкие минеральные или синтетические масла и твердые смазочные материалы. Ниже приведены наиболее часто применяемые смазочные материалы.
Пластичные смазочные материалы обычно используют для подшипников, расположенных в труднодоступных местах, при работе в запыленной среде. При использовании пластичных смазоч
ных материалов параметр dmn < гС (0,4...0,55) 10е мм-мин-1; при этом меньшие значения dmn — для подшипников более тяжелых серий.
Кальциевые смазочные материалы (солидолы) негигроскопичны, не растворяются в воде, .могут использоваться при работе в среде с повышенной влажностью. Их применяют при.длительной работе до температуры подшипника не выше 60 °C, кратковременно до 76 °C. Допустимая окружная скорость вала не выше 10 м/с. Наиболее распространен солидол жировой Ж-
Натриевые смазочные материалы (консталнны) применяют при окружной скорости вала не выше 10 м/с. Эти материалы более тугоплавки, благодаря чему их допустимо использовать при температурах подшипника до 100... 120 °C. Однако консталины гигроскопичны, под действием влаги разлагаются, что вызывает коррозию подшипника. Поэтому консталины целесообразно использовать в подшипниковых узлах, работающих в среде с пониженной влажностью. Для работы при повышенных температурах (до 150 °C) можно использовать смазочный материал НК-50.
Комбинированные натриево-кальцие-вые смазочные материалы (1-13, ЛЗ-ЦНИИ, ЯНЗ-2) используют при окружных скоростях вала до 15 м/с. Смазочный материал 1-13 является материалом общего назначения для подшипников, работающих при температурах от —20 до 100 °C. Смазочный материал ЛЗ-ЦНИИ используют для подшипников букс железнодорожных вагонов.
Литиевые смазочные материалы влагоустойчивы, могут работать при низких и повышенных температурах (от —60 до-} 100 °C). Смазочные материалы ЦИАТИМ-201, ОКБ-122-7, ЦИАТИМ-202 широко используют в подшипниках закрытого типа.
Смазочными материалами многоцелевого назначения являются: ЛИТОЛ-24, ЛИТОЛ-24РК, ФИОЛ-1. В подшипниках автомобилей используют смазочные материалы ЛИТОЛ-24, а также Шрус-4, Ф11ОЛ-2д, ЛЗ-31, № 158.
Для работы при более высоких температурах (от —60 до -f-150cC) и
Смазывание подшипников
157
повышенных окружных скоростях применяют смазочные материалы ЦИАТИМ-221, ВНИИ НП-207 (от—60 до +180 °C), ЦИАТИМ-221 с (от —60 до +200 °C).
Для электрических машин используют смазочные материалы ВНИИ НП-242, Свэм, ФИОЛ-4.
Для летательных аппаратов в последние годы используют смазочные материалы нового поколения: Эра (ВНИИ НП-286М), ВНИИ НП-254, ВНИИ НП-261. Эти материалы термостойки (от —50 до +200°C), обладают высокими противозадирными свойствами, долговечны.
Основным показателем соответствия смазочного материала условиям работы является рабочая температура подшипника, которая должна быть иа 20— 40°C ниже температуры каплепадания принятого смазочного материала.
Корпуса подшипников заполняют консистентной смазкой в объеме 1/3— 1/2 свободного пространства. В зависимости от условий и режима работы через каждые 1—3 года отработавший смазочный материал заменяют свежим.
Твердые смазочные материалы используют в подшипниковых узлах, работающих в вакууме в условиях очень низких температур (ниже —100 °C) или весьма высоких (I > > 300 °C), при работе в агрессивных средах, не допускающих присутствия какого-либо количества масел и даже их паров.
В качестве твердых смазочных материалов для указанных условий работы наиболее часто используют коллоидальный графит, дисульфид молибдена (MoS2), нитрид бора (BNO2) и некоторые другие вещества, обладающие слоистой структурой. Кроме того, в качестве твердых смазочных материалов используют фтористые соединения н некоторые окислы.
Графит обладает адсорбционными свойствами и может использоваться при температурах от —180 до+ 350 °C. При более высоких температурах графит сгорает. Дисульфид молибдена сохраняет свои смазывающие свойства до температуры от —185 до +450 °C при работе в среде воздуха. При более высокой температуре образуется окись молибдена, обладающая абразивными
свойствами. В вакууме н в среде инертных газов дисульфид молибдена сохраняет свои смазочные свойства до температуры 1100—1300 °C.
Для повышения работоспособности и надежности подшипников, работающих в условиях вакуума или в атмосфере, но без подачи смазочного материала, сепараторы подшипников изготовляют из так называемых самосмазывающихся материалов, которые и используют при работе для смазывания рабочих поверхностей подшипника. При этом тела качения, соприкасаясь со стенками гнезд сепаратора, снимают с них тонкую пленку твердого смазочного материала и переносят его на поверхности качения колец подшипника (ротапринтное смазывание).
В качестве жидких масел используют минеральные или синтетические масла. Минеральные масла сохраняют свои свойства до температуры 120 °C при длительной работе и до 150 °C при кратковременной работе. Для более высоких температур используют синтетические масла, некоторые сорта которых стабильны до температуры 250— 300 °C.
В зависимости от условий работы применяют различные способы подачи жидких масел в подшипники. Смазывание посредством погружения тел качения в масляную ванну применяют до значений параметра dmn + 0,6 X X 10е мм-мин'1. При горизонтальном расположении оси подшипников заливку минерального масла в корпус осуществляют до уровня, соответствующего положению центра тела качения, занимающего в подшяпнике нижнее положение.
Подачу смазочного материала в подшипники фитилями или капельное смазывание, отрегулированное на подачу нескольких капель масла в час, применяют для высокооборотных малогабаритных подшипников при значениях параметра dmn С 0,75 X X 10’ мм-мин'1 и произвольном расположении вала. Фитили обычно изготовляют из фетра, который при работе выполняет и роль фильтра.
Для подшипников опор валов редуктора, коробок передач металлорежущих станков, автомобялей часто при/иеняют подачу масла в подшипники разбрыз
158
Подшипники качения
гиванием из общей масляной ванны погруженным в нее на 10—15 мм зубчатым колесом. При этом в корпусе образуется масляный туман, проникающий в подшипники и обеспечивающий их смазывание.
Для лучшего охлаждения и смазывания высокоскоростных легконагружен-ных подшипников (быстроходных элек-трошлифовальных головок, высокочастотных электроприводов небольшой мощности, ультрацентрифуг) весьма эффективно смазывание масляным туманом.
Смазывание масляным туманом применяют при значениях параметра dmn до 1,7-10“ мм-мин'1 и более.
Для охлаждения и смазывания высокоскоростных тяжелонагруженных подшипников (опор валов мощных высокоскоростных редукторов, опор роторов газотурбинных двигателей, мощных электродвигателей) применяют циркуляционное смазывание, при котором подачу масла осуществляют сплошными интенсивными струями из форсунок. Струи масла обычно направляют в зазор между сепаратором и внутренним кольцом подшипника с наклоном к оси подшипника 15—20°.
Общее число струй масла в зависимости от диаметра отверстия подшипника указано ниже.
Диаметр отверстия подшипника, мм . До 40 Св 40 до 70 Св 70 до 100 Св 100 до 150 Св 150
Число струй, выравни-
вающих температуру колец подшипника 1—2 2 — 3
3-4 4-6 6 -10
и более
При значениях параметра dmn^ 2- 10е мм- мин'1 для лучшего охлаждения вращающегося внутреннего кольца необходимо дополнительно подавать масло под это кольцо по пазам, специально выполненным на цапфе или на посадочной поверхности внутреннего кольца подшипника. В этом случае достигается выравнивание температур между кольцами.
Оптимальная прокачка масла (л/мин) в зависимости от значения параметра
dmn и эквивалентной нагрузки может быть определена по формуле
Vo= VP+ l,4-10-’dmn, (61)
где dm—в мм; п — в мин'1, Ур— приращение прокачки, зависящее от эквивалентной динамической >агрузки Рг, определяемой при условии Лг,' = Кт = V — 1. Величина Vp для различных пределов эквивалентной динамической нагрузки приведена ниже.
Динамическая эквивалентная нагрузка, Н До 1 000 Св I 000
до 5 000
Приращение прокачки, л/мин 0,5 1,0
Св 5 000 Св 15 000 Св 25 000
до 15 000 до 25 000
1,5 2,0 2,5
Если к подшипнику дополнительно к теплоте, возникающей от работы трения, подводится теплота от нагретых сопряженных деталей (по валу или корпусу), то для отвода этой теплоты необходимо увеличить прокачку иа величину, определяемую из уравнения теплового баланса-
= c(t } (62)
L 1‘вых 1вх1
где УД — дополнительная прокачка масла для отвода теплоты, поступающего к подшипнику от нагретых дета
лей, л/мин; <?д — количество теплоты, поступающей к подшипнику от нагретых деталей, кДж/мин, с — теплоемкость масла, кДж/(л-°С), 1вши ^вх— температура масла, соответственно выходящего из подшипника и входящего в подшипник, °C.
Общая прокачка масла (л-'мин) для случаев подвода теплоты к подшипнику от нагретых деталей
И=Уо+Уд- (63)
Тепловыделение радиальных роликоподшипников при интенсивном цирку
Смазывание подшипников
159
ляционном смазывании определяют по следующей эмпирической формуле (в кДж/с):
Qp = 4,2КЛ [0W°'5W" +
+ 10~3(0, IF,-)10, — 10—7 dn — 0,04],
где V — прокачка масла, л/мин; е — основание натуральных логарифмов; Хр — параметр, зависящий от прокачки масла,
Хр = (1,96—0,043V) 'О'6;
d — диаметр отверстия подшипника, мм; п — частота вращения подшипника, мин”1; Fr — радиальная нагрузка, Н; О— показатель степени, зависящий от параметра dn,
0 = 0,61 + 10”7dn,
Кр — коэффициент, учитывающий влияние вязкости масла на трение подшипников. Значение коэффициента Кр определяется по следующим уравнениям, аппроксимирующим изменение тепловыделения в подшипниках в зависимости от вязкости смазочного материала прн смазывании маслом с вязкостью, большей или равной вязкости трансформаторного масла при температуре 50 °C, т. е. прн г) >т]тр,
о.оп (-Д------11
Кр = V V ’’тр +
0,011
V
при смазывании маслом с вязкостью, меньшей вязкости трансформаторного масла при температуре 50 °C, т. е.
л"
*r) = LV '
0,015 / т], р
V Т]
гДв т]тр и г) — вязкости соответственно трансформаторного масла при температуре 50 °C и масла, используемого в в действительных условиях работы.
Тепловыделение радиальных и ра-Диальио-упорных шарикоподшипников при интенсивном циркуляционном сма
зывании определяют по следующей эмпирической формуле (кДж/с):
Qm = 4,2Kp [(2,2+ 1,5V) х
X 10 е ш + AQinr + AQmal ’
где Хш—параметр для шариковых подшипников, зависящий от прокачки масла,
Хш~ 10”’(1,93 - 0,58V).
AQuir — слагаемое, учитывающее влияние на тепловыделение подшипников радиальной нагрузки,
AQuir — 4,2-10“3 (0,1Гг)#ш - Сш;
Ош— показатель степени, зависящий от параметра dn,
Ош — 0,61 + 1,2-10-’ dn-,
Сш — тепловыделение подшипника (кДж/с) при радиальной нагрузке FT = = 104Н,
Сш= 4,2-0,03+ l,2-10”7dn;
AQnia — приращение тепловыделения в шарикоподшипниках при действии осевой нагрузки,
AQma = 4,2ft(0,lra)'f,
Fa — действующая на шарикоподшипник осевая нагрузка, Н; h. и ф — параметры, зависящие от значения dn и прокачки V:
А -= 3,2-10~12e°-45V (dn)1’4;
ф = 0,763 — 0,5-10-7 dn — 0,27 X
X 10~3V3’3-
При установившемся тепловом режиме подшипника можно принять, что все тепло, выделяющееся в подшипнике при струйной форсуночной подаче масла, отводится от него маслом, т. е. Qn — Qm-
Количество теплоты (кДж/с), отводимое маслом, определяют по уравнению
Qm go" ('вых ~'• <вх).
где с — теплоемкость масла, кДж/ (л-°C) [для трансформаторного масла с = 1,9 кДж/(л-°С)[; V — прокачка масла, л/мин; р — плотность масла при
160
Подшипники качения
температуре, равной средней арифметической температуре входящего (/вх) в подшипник масла и вытекающего (^вых) нз подшипника масла, кг/л; ^вых— средняя температура вытекающего чз подшипника масла, °C; ?вх — температура масла перед входом в подшипник, °C.
Подставив в уравнение теплового баланса выражение для можно определить среднюю температуру вытекающего из подшипника масла.
, , , 60Qn
'ВЫХ — 'ВХ "I •
НЕКОТОРЫЕ ПРИЧИНЫ ПРЕЖДЕВРЕМЕННОГО ВЫХОДА ИЗ СТРОЯ ПОДШИПНИКОВ КАЧЕНИЯ И МЕТОДЫ ИХ ПРЕДОТВРАЩЕНИЯ
Основные причины преждевременного выхода из строя подшипников связаны с несовершенством конструкции подшипникового узла или самого подшипника, несоответствием выбранного подшипника действительным условиям работы, отступлениями от технических условий на изготовление деталей подшипникового узла или на его сборку, отступлениями от технических условий на эксплуатацию машины, некачественным материалом и изготовлением деталей подшипника. Часто подшипники выходят из строя из-за одновременного влияния на сокращение их работоспособности нескольких из указанных причин.
Усталостное выкрашивание поверхностей качения колец и тел качения может возникать из-за недостаточной работоспособности подшипника для действительных условий эксплуатации, из-за действия на подшипник неучтенных нагрузок. Снижение воспринимаемых подшипником нагрузок, повышение его динамической грузоподъемности, снижение вибрационных нагрузок позволяют повысить надежность подшипника.
При образовании на поверхностях качения даже небольших коррозионных пятен (точек) или раковин существенно снижается долговечность под
шипника из-за усталостного выкрашивания металла в зонах коррозии.
При нарушении режимов окончательных операций обработки поверхностей качения деталей подшипников могут создаваться местные прижоги, в результате которых на поверхности возникают трещины, значительно сокращающие долговечность подшипника из-за усталостного выкрашивания.
Преждевременное усталостное выкрашивание возникает при перекосе колец подшипника. Повышенный перекос колец (осей валов) — одна из распространенных причин преждевременного разрушения подшипников.
Особенно чувствительны к перекосу роликовые подшипники с цилиндрическими и коническими роликами. Для снижения концентрации напряжений ролики выполняют с бомбиной (выпуклыми); при этом разность диаметров роликов в средней части и по их концам в зависимости от размера роликов выполняют в пределах от 0,01 до 0,05 мм.
Усталостное выкрашивание поверхностей качения может возникать из-за металлургических дефектов (повышенное содержание неметаллических включений и карбидов, наличие волосовин трещии, заковов, обезуглероженный поверхностный слой). Металлургические дефекты могут быть выявлены горячим травлением в 20%-ном водном растворе соляной кислоты при температуре 80°С.
Усталостное выкрашивание поверхностей качения может образоваться в зонах механического их повреждения (риски, вмятины), связанного с засорением маслосистемы металлической стружкой. Для предотвращения образования механических повреждений поверхностей качения необходимо в маслоснстеме использовать фильтры с малым размером ячеек (10—15 мкм и менее).
Излом кольца может возникнуть, если оно посажено на вал или в корпус с радиальным зазором.
В подшипниках с повышенным радиальным зазором при действии легких нагрузок и вращении с повышенной частотой может происходить относительное проскальзывание поверхностей качения и, как следствие, изнашивание тел качения и дорожки качения вра
Причины выхода из строя подшипников
161
щающегося кольца подшипника. Меньше изнашивается дорожка качения неподвижного кольца. Изнашивание от проскальзывания повышается с уменьшением воспринимаемой подшипником нагрузки, при увеличении частоты вращения подшипника и радиального зазора, а также при повышении сопротивления вращению комплекта тел качения с сепаратором (повышенная шахматность расположения гнезд сепаратора, трение тел качения о чеканку гнезд сепаратора, наличие в подшипнике пластичного смазочного материала, повышенный перекос колец подшипника).
Проскальзывание чаще возникает в роликоподшипниках. Большое влияние на проскальзывание роликоподшипников оказывает осевой зазор роликов относительно направляющих бортов. При малом или увеличенном осевом зазоре вращение роликов сопровождается их повышенным трением. Оптимальный осевой зазор роликов относительно направляющих бортов равен 0,02. 0,03 мм.
При использовании роликоподшипников с тремя или четырьмя направляющими бортами (типа 12000, 42000 и 92000) необходимо обеспечить в подшипниковом узле расположение буртиков одного кольца строго в одной плоскости с направляющими буртиками другого кольца.
Для уменьшения или предотвращения проскальзывания и изнашивания поверхностен качения целесообразно;
а) повысить нагрузку на подшипник, б) уменьшить радиальный зазор в подшипнике;
в) ограничить допуск на шахматное расположение гнезд сепаратора величиной не более 0,05 мм;
г) не допускать подачу масла в подшипник через отверстия в наружном кольце;
д) не применять смазочные материалы с повышенной вязкостью
Для снижения проскальзывания роликов и их изнашивания целесообразно использовать подшипники с направляющими бортиками на внутреннем кольце и с направлением сепаратора по безбортиковому наружному кольцу. Проскальзывание, может быть устра-6 Заклз 402
нено или существенно снижено путем уменьшения (в 2 раза) числа роликов в подшипнике. Повышенный перекос колец роликоподшипника вызывает изнашивание торцев роликов и направляющих бортиков, при этом на роликах образуется корсетность. Повышенное изнашивание торцев роликов и направляющих бортиков может привести к развороту роликов на 90°.
Изнашивание торцев роликов и направляющих бортиков может происходить из-за неравномерной температуры по ширине колец или повышенной конусности посадочных поверхностей под кольца подшипника, В этом случае также может произойти разворот роликов на 90°. При неуравновешенности роликов (биение фасок, эксцентрическое расположение на их торцах меток) и высокой частоте вращения возникает неравномерное (эксцентричное) изнашивание торцев роликов, что также может привести к развороту их на 90'.
При перекосе колец шарикоподшипников шарики совершают в гнездах сепаратора автоколебания и давят на его поперечные перемычки, создавая переменные растягивающие напряжения в продольных перемычках, что часто вызывает разрыв сепаратора из-за усталости материала. Особенно чувствительны к перекосу колец радиально-упорные шарикоподшипники с четырехточечным контактом и с углом контакта более 26°. Поэтому для повышения работоспособности и надежности радиально-упорных шарикоподшипников целесообразно использовать подшипники с тоех- или двухточечным контактом. С уменьшением угла контакта чувствительность к перекосу радиально-упорных шарикоподшипников снижается. Склонность сепаратора к разрыву увеличивается с повышением осевой нагрузки.
Для повышения надежности сепараторов радиально-упорных шарикоподшипников необходимо их изготовлять из материала с высокими пределами прочности и выносливости. Ряд иностранных фирм (SKF, FAG и др.) сепараторы ответственных шарикоподшипников изготовляют из стали, а для повышения их антифрикционных свойств такие сепараторы покрывают серебром.
162
Пружины
Из-за колебаний и ударов, возникающих при транспортировке машин, на поверхностях качения деталей подшипников могут возникнуть намины и контактная коррозия. Последующая работа подшипника сопровождается усиленным изнашиванием поперечных перемычек сепаратора, тел качения н преждевременным выходом его из строя.
Если во вращающийся с повышенной частотой подшипник не подается масло или подается в недостаточном количестве, то наступает режим работы подшипника в условиях масляного «голодания». В этом случае в связи с недостаточным охлаждением и возрастающим трением значительно повышается температура подшипника, достигая 800... 900 °C и выше; при этом более сильно
разогревается внутреннее кольцо, в результате чего в подшипнике выбирается радиальный зазор. Подшипник подклинивает, и движение качения его деталей переходит в их скольжение, сопровождаемое значительным изнашиванием поверхностей качения. Возникают пластические деформации тел качения и раскатка колец. Поверхности детален подшипника покрываются темной окисной пленкой. Процесс разрушения подшипника при масляном «голодании» проходит сравнительно быстро (за 5...8 мин) в зависимости от частоты вращения и величины действующей на подшипник нагрузки. Кратковременное (до 10... 15 с) прекращение подачи масла в подшипники, вращающиеся с высокой частотой, обычно не приводит к их повреждению.
Глава 10
ПРУЖИНЫ
ОБЩИЕ СВЕДЕНИЯ
В машиностроении распространены витые цилиндрические и специальные пружины.
Основными материалами для пружин являются высокоуглеродистые стали 65, 70, марганцовистая сталь 65Г. кремнистая сталь 60С2А (рабочие температуры для этих сталей от —60 до + 120 °C), хромованадиевая сталь
класс проволоки ......... I
предел прочности. <JB. МПа 1450 — 3150 диаметр проволоки d, мм . . 0.14 — 6
Бдльшие значения ав имеет проволока меньшего диаметра.
Контроль готовых пружин включает внешний осмотр для выявления видимых невооруженным глазом поверхностных дефектов (трещины, заусенцы, риски н т. п.), изменений размеров (наружного и внутреннего диаметров, длины в свободном состоянии и отклонение оси от перпендикуляра к торцовой плоскости) и твердости (обычно 40—48 HRC3). Контроль пружин проводят, как правило, выборочно.
50ХФА (рабочая температура от —180 до +250 °C) и др. (табл. 1).
Пружины, работающие в химически активной среде, изготовляют из цветных сплавов.
Для изготовления пружин в основном применяют стальную углеродистую проволоку диаметром от 0,2 до 5 мм. Эта проволока в соответствии с. ГОСТ 9389—75 выпускается четырех классов:
II
1250 — 2300 0.14 — 8
ПА III
1250 — 2700 1050 — 2350
0.14 — 6 0,14-8
Пружины особо ответственного назначения, помимо сплошного контроля, подвергают технологическим испытаниям пробным грузом для оценки их упругих свойств и др. Клапанные пружины выборочно испытывают на сопротивление усталости. Для защиты поверхности витков от окисления пружины ответственного назначения покрывают лаком или промасливают, а пружины особо ответственного назначения оксидируют, наносят цинковое или кадмиевое покрытие.
Cg I. Механические свойства наиболее распространенных пружинных сталей и сплавов
Сталь (сплав) ратура за- . °C ратура от- Ов °т хт а- ю-‘ б. Применение
£ х 5 4 S х МПа %
5- 2 с не менее
65 840 1000 800 700 500 300 - 350 500 -000 0,83 9 35
70 830 480 1050 850 750 550 Пружины общего на-
55ГС 65Г 820 830 И 50 1000 1000 800 900 700 600 500 300 -380 500 -650 0.83 8 30 значения
55С2 60С2А 820 860 460 1300 1600 120’0 1400 900-1050 1050—1 150 650 — 800 800 — 900 400-450 700 — 750 0.8 6 5 30 20 Пружины подвижного состава ж.-д транспорта, клапанов, регуляторов, рабочая температура от —40 до 4-250 °C
60С2ХА 60С2ХФА 870 850 420 410 1800 1900 1600 1700 1200—1300 1300---1 400 950—1050 1 100 --1200 450 — 500 • 500-550 • 800-850 * 850 — 900 * 0.8 5 20 Крупные пружины и пружины особо от-
50ХГФА 840 300 — 380 500—650 6 35 ветственного назначения. работающие при температуре от —40 до 4-400 QC и в условиях переменных нагрузок
50ХФА 850 520 1300 1200 900—1000 700 — 800 300 — 400 0.8 10 45
50ХВА 350 — 450 550 — 650
БрОЦ4-3 БрКМцЗ-1 100-150 ВОЗ’ дух 1 1 800-900 650 — 750 — 1 1 — — — - а. р } tetn Со 1 — Пружины клапанов и приборов, работающие в магнитном поле, влажной атмосфере, воде н паре при температуре от — 40 до -И 200 °C
* Данные получены яа базе 2* 10* циклов.
Общие сведения
164
Пружины
ВИТЫЕ ПРУЖИНЫ
Основное применение имеют пружины из проволоки круглого сечения, При больших внешних нагрузках применяют пружины с витками квадратного и прямоугольного сечения (пружины, вырезаемые из трубчатых заготовок).
Пружины растяжения (рис. 1, а) обычно навивают без просветов между витками, а в большинстве случаев — с начальным натяжением (давлением) между витками, компенсирующим частично внешнюю нагрузку. Натяжение обычно составляет (0,25—0,3) Р3, где Рг — предельное усилие для пружины, при котором полностью исчерпываются упругие свойства материала. Внешнюю нагрузку такие пружины воспринимают обычно через зацепы в виде отогнутых последних витков (рис. 1, б, г) — для пружин диаметром до 3— 4 мм. Такие зацепы имеют высокую концентрацию напряжений в местах отгиба и пониженное сопротивление усталости. Для ответственных пружин диаметром более 4 мм часто применяют закладные зацепы (рис. 1, д—ж).
Пружины сжатия (рис. 2) навивают с просветом между витками, который должен на 10—20% превышать осевые упругие перемещения каждого витка при наибольшей внешней нагрузке. Для создания опорных плоскостей последние витки пружин сжатия поджимают к соседним и (.ошлифовывают перпендикулярно оси
Соосность пружин с сопрягаемыми деталями достигается установкой опорных витков в специальные тарелки, в расточки корпуса, канавки. Аналогично центрируют и концентрические пружины (рис. 3).
Длинные пружины под нагрузкой теряют устойчивость (выпучиваются). Такие пружины обычно ставят на специальные оправки (рис. 4, а) или в стаканы (рис. 4, б). Концентрические пружины в ряде конструкций также разделяют стаканами (рис. 4, в).
Для повышения несущей способности пружин сжатия в упругой области их подвергают заневоливанию. С этой целью пружины сжимают до соприкосновения витков и выдерживают (от 6 до 48 ч) до получения остаточной осадки.
В результате осадки под нагрузкой в периферийных областях появятся пластические деформации, а в поперечных сечениях проволоки пружины возникнут напряжения, эпюра которых будет совпадать с диаграммой сдвига при первичном нагружении (рис. 5). При разгрузке пружины в ее сечениях возникнут остаточные напряжения, которые далее будут компенсировать (в периферийной наиболее нагруженной области) напряжения от внешней нагрузки, повышая таким образом нагрузочную способность пружины при работе в упругой области.
Пружины, работающие в условиях длительного воздействия переменных нагрузок, повышенных температур
Рис, !. Пружина растяжения к ааиепы
Рис 2. Пружина сжатия
Расчет витых цилиндрических пружин
165
Рис. 3. Концентрические пружины
Рис. 4. Способн предотвращения выпучивания пружин
(150—450 ГС) и коррозионных сред, ие заневоливают, так как сопротивление усталости заневоленных пружин не повышается.
Основные геометрические параметры пружин (см рис. 2):
диаметр проволоки d или размеры сечения,
средний диаметр £>0,
О0
индекс с = а
число рабочих витков п;
длина рабочей части На;
шаг витков i = ——; п
х t угол подъема витков a— arctg.
Последние три параметра рассматривают в ненагружеином и нагруженном состояниях.
Индекс пружины характеризует кривизну витка. Пружины с индексом с < 3 применять не рекомендуется из-за высокой концентрации напряжений в витках.
Обычно индекс пружины выбирают в зависимости от диаметра проволоки в следующих пределах:
4, мм До 2.5 3 — 5 6— !2
С . 5—12 ч- 10 4- 9
РАСЧЕТ ВИТЫХ
ЦИЛИНДРИЧЕСКИХ ПРУЖИН
При центральном приложении силы Р в любом поперечном сечении витка пружины возникают результирующая
внутренняя сита Р, параллельная оси пружины, и момент М=Р плоскость которого совпадает с плоскостью пары сил Р (рис. 6). Нормальное поперечное сечение витка наклонено к плоскости момента под углом а. В этом сечении будут действовать силы и моменты (см. рис. 6)'
Q — Р cos a; N — Р sin а; 1
Л1 ~ Р ”• cosa; Мя — Р ~ sm а. j
(1)
Ввиду малссти угла подъема витков (обычно а < 104-12°) можно считать, чго сечение пружины работает иа кручение.
Максимальное касательное напряжение в сечении пружины
Инах — ~> (2)
где - - момент сопротивления сечения вала кручению
С учетом кривизны витков и равенства (1) соотношение (2) примет вид kPDn
Плах — ~2W— 1т1к> (3)
где k — коэффициент, учитывающий кривизну витков и форму сечения (поправка к формуле для кручения прямого бруса); Р — внешняя нагрузка (растягивающая или сжимающая);
166
Пружины
De — средний диаметр пружины; [т]к — допускаемое касательное напряжение при кручении (табл. 2).
Значение коэффициента k для пружин из круглой проволоки при индексе с 4 можно вычислить по формуле
•з
k = 1 + — , (i)
Рис. в. Силовые факторы в сечении нагруженной пружины
а для пружин прямоугольного сечення
Тщах — ПО рис. /.
Для пружин прямоугольного поперечного сечения
WK — aba2, (5)
2. Допускаемые напряжения для цилиндрических витых пружин растяжения-сжатия
Марка материала Диаметр проволоки, мм Твердость HR С после термообработки [т]к. МПа, для класса пружин
I П ш
60С2А. 65С2ВА, 70СЗА, 50ХФА. 60С2ВА •. 65 • 3—12 14-15 46 — 52 560 480 960 800 1350 1050
Проволока класса 1 0,2-5 — 0,зов 0.5ов 0.6ов
Проволока классов И, На, Ш —
БрОЦ4-3 БрКМцЗ-1 0,3-10 — 0,2оа 0.3ов 0,5ов 0,5ов 0.6ов 0,6св
* Применяют для изготовления пружин классов Н и Ш.
Примечания1 1 Долговечность пружин класса I прн начальной затяжке Pi > 0.2Р3 (Р3 — сила пружииы при максимальной осадке) не менее 5« 1 О6 циклов; пружины класса И при тех же условиях имеют N Ю6 циклов, сюда же относятся все статические пружины, длительно пребывающие под нагрузкой; пружины класса 1Ц — N 2- 10s циклов
2 Значения [т]к даны с учетом кривизны витков.
3. Для сталей, не указанных в таблице, значения [т]к можио ориентировочно принимать для классов пружин I — (0.254-0.3) а • И — (0.454-0.5) о • HI — 0.60 .
Расчет витых цилиндрических пружин
167
Рис. 7. К определению коэффициента k для пружин растяження-сжатня пря нагольного сечения
где Ь — высота, а а — ширина прямоугольника; а — коэффициент, завися-
. b
щий от отношения сторон е = —
(табл. 3).
Если пружина навита из круглой проволоки, то WK совпадает с полярным моментом сопротивления и тогда
Податливость пружины наиболее просто определить из энергетических соотношений.
Потенциальная энергия пружины
Unp —
(* МНЛ1К1
J GJK о
dz,
8kPDa Хп,ах“-^-
8kPc nd2
[т]к-
(6)
Осевое перемещение торцов пружины с углом подъема а < 12°
(8) крутящий момент в от силы Р = 1 Н; сечения витка на
б = ХПР. (7)
где ---
сечении пружины GJ к — жесткость кручение; I « л£>оп — полная длина
рабочей части витков; п — число вит-
3. Значения коэффициентов а и 0
Коэффициент Ь/а
1.0 1.5 1,75 2,0 2,5 3.0 4,0
а 0.208 0.231 0,239 0.246 0,256 0.267 0.282
₽ 5.57 . п7 2.10 1.72 1.26 1.00 0.70
₽. 0,141 0,196 0,214 0,229 0,249 0.267 0.282
168
Пружины
Рис. 4. Характеристика пружины сжатия
Геометрическая жесткость на кручение для прямоугольного сечения
JK = Р^3,
ко >ффициент Pj — по табл. 3.
На рис. 8 показана зависимость между нагрузкой и осадкой пружины сжатия. Если пружина установлена с предварительной затяжкой (осадкой) с усилием Plt то ее установочная длина
= На — = На — nkPv (15)
Длина пружины при действии наибольшей внешней нагрузки Ра
Да = До - 6а = До - гйРа. (16)
При действии нагрузки Р3, соответствующей [т]к, длина пружины будет наименьшей:
Д3 = Д„ — 6а -- Дд — пХРз ==
ков пружины; JK — геометрическая
жесткость на кручение.
Из соотношения (8) следует:
6 = Рп
4GJK ’
Лп —
4GJK
= Лп,
(9)
(Ю)
где X — осевая податливость одного
витка (осадка в мм при действии Р =
= 1 Н), лР% iGJK •
(Н)
Для пружины из круглой проволоки полярный момент инерции сечения
J р — — gg ’ (12)
и тогда формула (11) примет вид
, 8Р* 8с3
Gd* ~ Gd ’
(13)
где G — модуль сдвига, G = = ~2~(1"-|- v) °’384£; Е ~ м°ДУль упругости материала пружины. Для пружин с прямоугольным поперечным сечением
А-В-Д°
А Р Go4
(14)
В соотношениях (15)—(17) До — длина пружины в свободном (иенагру-жениом) состоянии.
Угол наклона прямой Р = f (6) (см. рис. 8) к оси абсцисс
0 = рз = = Р1_ = _!_
68 6а 61 пЛ
(18)
В зависимости от назначения пружины усилие предварительной затяжки ?!= (0,14-0,5) Ра.
Наибольшая допускаемая внешняя нагрузка для пружин растяжения и сжатия
Р3= (1,14-1,3) Ра. (19)
Конечный участок диаграммы пружины от силы Р3 до усилия РПр. сжимающего пружину до соприкосновения витков, может оказаться нелинейным из-за неравномерности шага.
Рабочий ход (осадка) пружины *
Л = Дг — Да = nX (Ра - Pj). (20)
Если ход пружины задан, то необходимое число рабочих витков для обеспечения этого перемещения h п~~ Л(Ра-Р1) •
где а — наименьшая сторона сечеиия (коэффициент р по табл. 3).
• Изменением предварительной затяжки можно регулировать осадку пружины.
Расчет витых цилиндрических пружин
169
Число витков округляют до полувитка п < 20 и до одного витка при л> 20.
Полное число витков
П1 = п+ (1,5+2,0). (22)
Дополнительные 1,5—2,0 витка идут иа поджатие для создания опорных поверхностей у пружины.
Полная длина ненагруженной пружины
Н3 = Н3 + п (t-d), (23)
где Н3—длина пружины, сжатой до соприкосновения соседних рабочих витков *,
Н3 = («1 — 0,5) d; (24)' t — шаг пружины, находящийся в зависимости от наибольшей осадки пружины,
+ , (25)
где наибольшая осадка пружины
6, = лЛР8 = [т]к . (26)
В табл. 4 приведены значения наибольших допускаемых внешних нагрузок Р3 и податливостей витка пружины X в зависимости от индекса с и диаметр а проволоки d.
Длина проволоки, необходимая для изготовления пружины,
L = яРол:
cos а
« 3,2Don,
(27)
где а — угол подъема витков ненагруженной пружины, а = 6+9°.
Для предотвращения выпучивания пружины от потери устойчивости ее гибкость H3/D3 должна быть менее 2,5.
Если по конструктивным соображениям это ограничение не выполняется, то пружину, как указано выше, следует ставить на оправках нли монтировать в гильзах.
Длина пружины растяжения в не-иагруженном состоянии
~ nd + 2hs, (28)
* Полное число витков уменьшено на 015 из-за того, что каждый конец пружины сошлифован иа 0,25л/ для образования плоского опорного торца.
где h3 — высота одного зацепа, h8 — = (O,5+l)Do.
Длина пружины при максимальной внешней нагрузке Рг
Н3 = Яо + nX (Р, - PJ, (29)
где Ру — усилие первоначального сжатия витков при навивке.
Для изготовления пружины из проволоки
L = + 2/, « 3,3Don + 2Z3;
cos а
(30)
здесь 13 — длина проволоки для одного зацепа.
Расчет пружин обычно начинают с определения диаметра проволоки (или размера сечения для некруглой проволоки), задаваясь значением [т]к и индексом пружины с.
Диаметр проволоки находят из условия прочности (7)
kP3c
а = 1’6И-Йг- <31>
Если пружина имеет прямоугольное сечение, то ширина прямоугольника
J5/ kP3D а = 0,795 1/ -н ° - •
Г Pj.e [т]к
Далее по формулам (13), (21)—(27) определяют размеры пружины.
Расчет цилиндрических пружин растяжения — сжатия из проволоки круглого сечения при d = 1,6+7,5 мм; с =3+10 и [т]к-= 400 МПа можно проводить, используя табл. 4.
Пример 1. Заданы: ход пружины h, усилие предварительной затяжки Ру и наибольшая внешняя нагрузка Ра.
Из соотношения (19) находим Р3 и далее по табл. 4 подбираем d, D3 (Do = = cd) и X. Потребное число витков пружины находим из соотношения (21), а размеры пружины — по формулам (22)—(27).
Пример 2. Заданы: наибольшая нагрузка Ра, установочная длина Ну и ход пружины К.
По табл. 4 для заданного значения Ра после вычисления Р3 находим d, D и X. Потребное число витков пружины и ее размеры находим, задаваясь значением Ру IPj = (0,1+0,5) Ра] или hy.
4. Значения максимальной нагрузки при It J =- 400 МПа и податливости одного витка пружины
Индекс пружины Диаметр проволоки d, мм
1.6 2.0 2.2 2,5 2.8 3.0
р, к р, к р, X р, X Р, X Р. X
3 3.5 4 4.5 5 5.5 6 6,5 7 7,5 8 8.5 9 9.5 10 8.95 8.05 7.32 6,71 6,19 5,75 5.37 5.03 4.74 4,47 4,24 4.03 3,83 3,66 3,50 0.0169 0,0268 0.0400 0.0570 0,078! 0.1040 0. 1350 0. 1716 0.2144 0.2637 0,3196 0.3838 0,4556 0,5359 0.6250 13.98 12,58 1 1.44 10.48 9.678 8.981 8.39 7,86 7.40 6.99 6.62 6.29 5.99 5.72 5.47 0,0135 0.0214 0,0320 0.0456 0,0624 0.0831 0. 1080 0.1373 0. 1715 0.21 10 0,2560 0.3070 0,3645 0.4287 0,5000 16.92 15,22 13,84 12.69 1 1,71 10,87 10,15 9.515 8,96 8.46 8,01 7.6! 7.25 6.92 6.62 0.0123 0,0195 0.0291 0,04 14 0.0568 0.0756 0.0982 0. 1248 0, 1559 0.1918 0.2327 0.2791 0,3314 0.3897 0.4545 21.84 19.66 17.87 16,38 15,12 14.04 13.11 12.29 1 1,56 10.92 10.35 9.83 9,36 8.94 8.55 0.0108 0.0171 0.0256 0.0364 0.0500 0.0665 0.0864 0.1098 0.1372 0.1687 0.2048 0.2456 0.2916 0,3429 0.4000 27.40 24.66 22.42 20.55 18.97 17,6) 16,44 15,41 14,51 13,70 12.98 12.33 1 1,74 11.21 10.72 0.0096 0,0153 0,0229 0.0325 0.0446 0.0594 0.077! 0.0981 0. 1225 0. 1507 0. 1829 0.2193 0.2604 0,3062 0.3571 31.40 28.3! 25,74 23.59 21,78 20.22 18.87 17.69 16,65 15.73 14.90 14. 15 13.48 12.86 12.31 0.0090 0.0143 0.0213 0.0304 0.0417 0.0555 0.07 20 0.0915 0.1 143 0. 1406 0. 1707 0,2047 0.2430 0.2858 0.3333
Индекс пружины с Диаметр проволоки d, мм
3,2 3.5 3,8 4,0 4,5 5.0
pt к р. к р, X Р, X Р, X р, X
3 3.5 4 4.5 5 5,5 6 35,79 32.2! 29,28 26,84 24.78 23.0! 21.47 0.0084 0.0134 0.0200 0.0285 0.039! 0.0520 0.0675 42.8! 38.53 35.03 32.1 1 29.64 27,52 25.69 0.0077 0.0122 0.0183 0,0260 0,0357 0,0475 0.0617 50,47 45.42 41.29 37.85 34.94 32.44 30.28 0.0071 0,0113 0.0168 0.0240 0.0329 0.0438 0,0568 55,92 50,33 45.75 41.94 38.71 35.95 33,55 0,0068 0.0107 0.0160 0.0228 0,0312 0,0416 0.0540 70.77 63.70 57.91 53.08 48.00 45,50 42.46 0.0060 0.0095 0,0142 0.0202 0.0278 0.0370 0.0480 87.37 78,64 71.49 65,53 60,49 56.17 52.43 0,0054 0.0086 0.0128 0,0182 0,0250 0,0333 0,0432
Пружины
Продолжение табл 4
Диаметр проволоки d, мм
Индекс пружины с
3 2 3 5 3 8 4 0 4 5 5 0
р, X Р. X Р, 1 Р, X р, X Р. Jl
6 5 7 7 5 8 8 5 9 9 5 10 20 13 18 95 17 89 16 95 16 10 15 34 14 64 14 00 0 0858 0 1072 0 1318 0 1600 0 1919 0 2278 0.2679 0 3125 24 08 22 67 21 40 20,28 19 27 18 34 17 51 16 75 0 0785 0 0980 0 1205 0 1463 0 1755 0 2081 0 2450 0 2857 28 39 26 71 2d 23 23 91 22 71 21 63 20 65 19 7э 0 0723 0 9903 ОШО 0 1347 0 1616 0 1918 0 2256 0 2632 31 45 29 60 27 96 26 49 25 16 23 97 22 88 21 88 0 0687 0 0857 0 Ю55 0 1280 0 1оЗо 0 1822 0 2143 0 2э00 39 81 37 47 35 39 33 ->2 31 85 30 33 28 95 27 69 0.0610 0 0762 0 0937 0 1138 0 1365 0 1620 0 1905 0 2222 49 15 46 26 43 69 41 39 39 32 37 45 35 74 34 19 0 0\>49 0 0686 0 0844 0 1024 0 1228 0 1458 0 1715 0 2000
Индекс пружины с Диаметр проволоки d. мм
5 5 6 0 6 5 7 0 7 5
Р, X р3 X Рз X Р, X Рз X
3 3 5 4 4 5 5 5 5 6 6 5 7 7 5 8 8 5 9 о 5 10 105 72 J5 15 86 оО 79 >9 73 19 67 97 63 43 59 47 55 97 59 86 50 08 4’ 58 4о 31 4 3 25 41 37 0 0049 0 0078 0 0116 0 016о 0 0 27 0 0303 0 0393 0 0499 0 0624 0 0767 0 0931 0 1117 0 1325 0 1559 0 1818 125 82 ИЗ 24 • 102 94 94 37 87 И 80 88 75 49 70 77 66 61 62 91 59 60 56 62 53 92 51 47 49 23 0 0045 0 0071 0 0107 0 01 2 0 0208 0 0277 0 0360 0 0458 0 0572 0 0703 0 08эЗ 0 Ю24 0 1215 0 1429 0 1667 147 66 132 90 120 82 1 10 75 102 22 94 93 88 60 83 06 78 17 73 83 69 95 66 45 63 28 60 41 57 78 0 004 2 0 0066 0 0098 0 0140 0 0192 0 0256 0 0332 0 0422 0 0528 0 0649 0 0788 0 0945 0 1122 0 1319 0 1518 171 25 154 13 140 12 128 44 1 18 56 1 10 09 102 7 о 96 33 90 66 85 63 81 12 77 06 73 39 70 06 67 01 0 0038 0 0061 0 0091 0 0130 0 0179 0 0238 0 0308 0 0392 0 0490 0 0f03 0 0731 0 0877 0 '041 0 1225 0 1429 196 59 176 93 160 85 147 45 136 10 126 38 11/96 1 10 и8 04 08 98 30 93 12 88 47 84 2d 80 42 76 93 0 0036 0 00 >7 0 0085 0 0121 0 0167 0 0222 0 0288 0 0366 0 0457 0 0 ^62 0 0683 0 0819 0 0972 0 1143 0 1333
Ра<чет витых цилиндрических пружин
172
Пружины
Рис. 9. Фасонные пружины
Решение задачи такого типа ие однозначно, на выбор того или иного варианта могут влиять дополнительные конструктивные соображения, связанные, например, с выбором Р, и Рг. Выбор пружин из проволоки диаметром от 0,2 до 50 мм для сталей, при веденных в табл 2 проводят по ГОСТ 13764—86 — ГОСТ 13776—86. Эти стандарты распространяются на винтовые цилиндрические пружины растяжения и сжатия для нагрузок от 1 до IO6 Н с индексами с = 4-4-12 и наружными диаметрами 1—700 мм. В зависимости от долговечности стандартные пружины делятся на классы (см. табл. 2).
При больших нагрузках и ограниченных габаритах используют составные пружины сжатия (см. рнс. 3) — набор из нескольких (чаще двух) концентрически расположенных пружин, одновременно воспринимающих внешнюю нагрузку. Для предотвращения сильного закручивания торцовых опор и перекосов навивку соседних пружин выполняют в противоположных направлениях (левом и правом). Опоры выполняют так, чтобы обеспечивалась взаимная центровка пружин (см. рис. 3, 4).
Обычно составные пружины имеют одинаковые осадки. При их проектировании стремятся к тому, чтобы длины пружин, сжатых то соприкосновения витков, были приблизительно одинаковы, а наибольшие касательные напряжения у всех пружин были равны допускаемому.
Первые Два условия для пружин, навитых из круглой проволоки, эквивалентны равенству их индексов.
При расчете двух концентрических клапанных пружин автотракторных двигателей часто средние диаметры пружин выбирают по конструктивным
соображениям (в зависимости от диаметра горловины клапана) Радиальный . тзор в таких пружинах составляет -2 мм.
Далее, принимая, что наружная пружина воспринимает 50—70% внешней нагрузки, находят диаметр прово-юки (/ — номер пружины)
, л/
аП) - У л [т]к
и определяют длину пружины.
В последние годы получили распространение многожильные пружины, при изготовлении которых вместо одной проволоки используется трос, свитый издв>х — шести проволок малого диаметра (d ~ 0,8—2 мм). По конструктивному решению такие пружины эквивалентны концентрическим пружинам. Благодаря высокой демпфирующей способности (за счет трения между жилами) и податливости многожильные пружины хорошо работают в амортизаторах и других подобных устройствах. При действии переменных нагрузок многожильные пружины довольно быстро выходят из строя от изнашивания жил.
В конструкциях, работающих в условиях вибраций нагрузок, иногда применяют фасонные пружины (рис. 9) с нелинейной зависимостью между внешней силой и упругим перемещением пружины
Расчет фасонных и многожильных пружин дан в работе 16], гл. 27.
РАСЧЕТ НА СТАТИЧЕСКУЮ ПРОЧНОСТЬ
При действии статических нагрузок пружины могут выходить из строя вследствие появления пластических деформаций в витках.
Запас прочности по пластическим деформациям
Лт = —— >1,3, (32)
^тах
где Тщау — наибольшие касательные напряжения в витке пружины, их вычисляют по формуле (7) при Р — ~ Ргпах«
Расчет на ударную нагрузку
173
PAC4FT НА СОПРОТИВЛЕНИЕ
УСТАЛОСТИ
Пружины, работающие длительно при переменных нагрузках (например, клапанные и др.), необходимо рассчитывать на сопротивление усталости.
На рис. 10 показана диаграмма предельных напряжений для пружин, построенная в координатах Тщах итт, где
8Ю о Тщах • niax*
Tmin
~ nd3 m!n’
Tmax 4 tmln . lni — s - ,
Tmax Tmln та — -------------
2
Витые пружины крайне редко работают одновременно на растяжение и сжатие, т. е. симметричный цикл нагружения (предел выносливости Т-J не характерен для пружин. Пульсирующее нагружение, характеризуемое пределом выносливости т0, также встречается редко в динамически нагруженных пружинах. Большинство пружин работает в условиях асимметричного нагружения при тт > т0.
Запас прочности таких пружин находят из соотношения
п =, (33)
~
где ет--коэффициент, учитывающий влияние масштабного эффекта;
фх = ._2Ы.Т_1о„ .
То
Значения т_, и т0 даны в табл. 1. Обычно принимают п -- 1,2-4-2,2.
При определении запаса прочности значение эффективного коэффициента Концентрации напряжений kQ — 1. Концентрацию напряжений учитывают при расчете напряжений (коэффициент k в формулах (31)). Для пружин с Диаметром проволоки d < 10 мм принимают ет = 1.
Для большинства пружинных сталей = 0,1-4-0,2.
Рис. 10. Диаграмма предельных напряжений для пружин
Для клапанных пружин рекомендуется также проверять запас прочности по переменным напряжениям:
= (34)
Та
Должно быть па = 24-3.
Для повышения сопротивления усталости (на 20—50%) пружины упрочняют дробеструйной обработкой, создающей в поверхностных слоях витков снижающие остаточные напряжения. Для обработки пружин используют шарики диаметром 0,5—1 мм. Более эффективной оказывается обработка пружин шариками малых диаметров при высокой скорости полета.
РАСЧЕТ НА УДАРНУЮ
НАГРУЗКУ
В ряде конструкций (амортизаторы и т. п.) пружины работают при ударных нагрузках — нагрузках, прикладываемых почти мгновенно с известной энергией удара. Отдельные витки пружины получают прн этом значительную скорость и могут опасно соударяться.
Расчет реальных систем на ударную нагрузку связан со значительными трудностями (учет контактных, упругих и пластических деформаций, волновых процессов и т. д.), поэтому для инженерного приложения ограничимся энергетическим методом расчета.
Основной задачей расчета на ударную нагрузку является определение динамической осадки (осевого переме-
174
Пружины
Рис, П. Схема нагружения пружинного амортизатора
может быть возвращена при постепенной разгрузке деформированной пружины.
Из уравнения (35) с учетом соотношений (8) и (36) получим
6Д = 6СТ -ф
(37) откуда коэффициент динамического усиления
щения) и статической нагрузки, эквивалентной уд.тоиому воздействию на пружину с известными размерами.
Рассмотрим удар поршня силой тяжести Q по пружинному амортизатору (рис. 11).
Если пренебречь деформацией поршня и принять, что после удара упругие деформации мгновенно охватывают всю пружину, можно записать уравнение баланса энергии
(35)
Первое слагаемое левой части уравнения (35) выражает кинетическую энергию системы после соударения:
V".
2g
Q
Qi
Q
(36)
где с/0 — скорость движения поршня; х — коэффициент приведения массы пружины с силой тяжести Qr к месту соударения.
Если принять, что скорость перемещения витков пружины изменяется
1
линейно по ее длине, то х = о
Второе слагаемое левой части уравнения выражает работу поршня после соударения при динамической осадке пружины на величину 6Д.
Правая часть уравнения (35) — потенциальная энергия деформации пружины (с податливостью Хп), которая
+ 1 + (<? + *<?!> ’ {38}
где 6СТ—осадка пружины при статическом нагружении ее поршнем с силой тяжести Q.
Из формул (37) и (38) следует, что динамическая осадка пружины существенно зависит от скорости движения поршня, а также жесткости пружины и соотношения масс (весов) поршня и пружины.
Если массой пружины можно пренебречь (в сравнении с массой поршня), то вся кинетическая энергия поршня перейдет в потенциальную энергию деформации. Динамическая осадка пружины при этом возрастет и будет б:=чт+1/б2ст+б„-^- (39)
В случае мгновенного приложения нагрузки (и ~ 0)
6д=26ет. (40)
Статическая нагрузка, эквивалентная по эффекту ударному воздействию, может быть вычислена из соотношения
/’эКа=-ф-- <41>
*п
Уточненный расчет пружин можно проводить по схеме волнового метода расчета стержня (с эквивалентной податливостью), подверженного удару жестким грузом (см. гл. 27 [6]).
Прорезные пружины
175
ТАРЕЛЬЧАТЫЕ ПРУЖИНЫ
Тарельчатые пружины (рис. 12, а) относят к классу жестких пружин, их применяют в мощных амортизационных устройствах.
Пружины изготовляют штамповкой из листовой стали (60С2А н др.) толщиной от 1 до 20 мм с наружным диаметром от 28 до 300 мм при отношении диаметров тарелок с = = 2-?3.
Для стандартных пружин угол наклона образующей конуса 0 - 2-?6°. Наибольшая воспринимаемая нагрузка до 52-104 И.
Тарельчатые пружины имеют нелинейную зависимость осадки от действующей нагрузки Р. Для пружин с с <1 2,5
4Е76
(1 -v2) О2 А
х
х[(й-6) + (42)
Наибольшие окружные напряжения на внутренней кромке тарелки (в меридиональном сечении)
4£8
°тах = К£)2 (^° — (43)
где К, Ко, Ki — коэффициенты, принимают по рис. 13.
Для повышения несущей способности тарельчатые пружины заневоливают обжатием до полного спрямления. В этом случае можно допускать отах =
Тарельчатые пружины обычно подбирают по стандартным таблицам.
Для повышения податливости тарелки устанавливают последовательно в виде секций из двух пластин (рис. 12, б). Иногда между тарелками устанавливают шайбы (рис. 12, г) для лучшего гашения колебаний (за счет трения). При больших нагрузках пружины собирают пакетами (рис. 12, в); их несущая способность при этом оказывается пропорциональной числу тарелок.
где Е и v — модуль упругости н коэффициент Пуассона материала тарелки; t — толщина листа; 6 — осадка пружины; А — коэффициент, принимают по рис. 13; h — высота внутреннего усеченного конуса.
Во избежание полного распрямления тарелки расчетная осадка пружины не должна превышать 0,8h.
ПРОРЕЗНЫЕ ПРУЖИНЫ
Прорезные пружины (рис. 14) также являются жесткими. Их применяют в тех случаях, когда радиальные габариты должны быть малыми, а несущая способность — большой. Пружины изготовляют путем фрезерования пазов в трубчатых заготовках.
Рис. 12. Тарельчатые пружины
Рис. 13. К расчету тарель чатых пружин
176
Пружины
Рис. 14. Прорезные пружины
Осадка пружины *
перемычками, Р = 1/2-^-; b — размер сечения в плоскости кольца; х — коэффициент;
2v sin В
X - j •
Р (1 -Ь V) — -g- (1 — v)sin 2Р
(46) Максимальные изгибающий и крутящий моменты действуют в сечениях, граничащих с перемычками;
Л4И шах = 2Л (' X) Р>
мк max — X 2П •
. PR3 .
О = X --5- I,
пВ
(44)
где R — средний радиус кольца шириной b и толщиной h; п — число перемычек на одном из торцов кольца; В — жесткость сечения кольца на изгиб, „ ЬНЯ „ . й
В = —1 — число рабочих колец;
х — безразмерный коэффициент,
х = v (Р — X sin Р); (45)
Q
v — коэффициент, v = -g-, С — жесткость сечения кольца на кручение, (значения v-указаны далее); р — половина угла между
В частном случае при числе прорезей п — 2 кольца квадратного сечения со стороной a (v = 1,54) и при коэффициенте Пуассона ц — 0,3
PR3
6 = 0,972 -4V ‘ Ьа*
(47)
Приведенные максимальные напря-
жения у перемычек
°шах — £ (48)
В расчетах можно принимать при
п=2; р=^-:
h/b ..........................................0.25;
V.............................................0,77;
Е.............................................0.91;
0,5; 0.6b; 1.0; 1.5; 2
0.95; 1.10; 1,54; 2,49; 3.8;
1.0; 1.07; 1,22; 1.33: 1.35;
3 7,42 1,4
КОЛЬЦЕВЫЕ ПРУЖИНЫ
Кольцевые пружины (рис. 15) состоят из внутренних и внешних колец одинаковой толщины, опирающихся друг на друга. С нерабочей стороны кольца несколько вогнуты.
Под действием внешней нагрузки наружные кольца растягиваются, а внутренние сжимаются. Преодолевая силы трения, кольца частично входят
• Пои частом расположении перемычек необходимо учитывать деформации сдвига.
друг в друга, давая пружине осадку
, __ (п — 1) __________/ Он । Од \
~ 2л£ tg р tg (Р + ф) (.Ли FB Г
(49)
где п — число колец (два из инх торцевые, целые или укороченные, работают одной стороной); Р — угол конусности, обычно Р = 14-4-17°; <р — угол трения, tg <р = р (здесь Ц — коэффициент треиия, Ц = 0,1-4-0,15); Он и 7Н — средний диаметр наружного кольца и площадь поперечного сечения; Ов и Гв—то же для внутреннего кольца.
Кольцевые волнистые пружины
177
Рис. 15. Кольцевые пружины
При постепенной разгрузке осадка пружины некоторое время сохраняется до тех пор, пока внутренние силы упругости уравновешиваются силами трения. Затем, преодолевая трение, кольца возвращаются в исходное поло-
жение.
В результате кривые Р = f (6) при нагружении и разгрузке не совпадают, они образуют «петлевидную кривую». Площадь этой петли равна работе трения; она составляет обычно 60— 70% полной работы.
Благодаря высокой амортизирующей способности, связанной с работой сил
трения, кольцевые пружины широко используют в буферных н амортизирующих устройствах.
Напряжение растяжения в наруж-
ном кольце
(50)
напряжение сжатия на внутреннем кольце
= (51)
Энергия, поглощаемая пружиной за один цикл (нагрузка-разгрузка),
Г = 6-^. (52)
где | - 0,64-0,7.
Пружины, работающие в условиях многократных нагружений, следует принудительно охлаждать.
При конструировании пружин необходимо иметь в виду, что угол
всегда должен быть больше угла трения <Г-
На практике обычно используют следующие соотношения между высотой кольца Н, наружным диаметром •пружины £>а н средней толщиной колец i>cp:
/7 1 . 1 />ср । i
Da 5 ‘ 6 ’ Н ~ 3 ‘ 5 ‘
Зазор е между двумя соседними кольцами (наружными или внутренними) при наибольшей внешней нагрузке не должен быть меньше 1 мм.
КОЛЬЦЕВЫЕ ВОЛНИСТЫЕ
ПРУЖИНЫ
Эти пружины (рис 16) являются разновидностью прорезных пружин; их применяют как компенсаторы температурных перемещений, а также в торцевых уплотнениях. Последнее связано с более равномерной передачей нагрузки на уплотняющие кольца, чем прн использовании витых пружин.
При малой осадке грузоподъемность таких пружин высокая, чем обеспечивается компактность конструкции. Их изготовляют штамповкой из тонколистовой стали.
Так как размеры поперечного сечения пружины малы в сравнении с радиусом кривизны, то при определении податливости и прочности можно использовать общепринятые методы расчета стержней малой кривизны (без учета нормальных и перерезывающих сил).
Осадка пружины
PR3
$ = Х-2п/Г’ <53>
где R. — средний радиус пружины; л — число волн пружины: В — жест-
Рис. 16. Кольцевая волнистая пружина
178
Пружины
кость сечения кольца шириной Ь и fell3
высотой h на изгиб; В — —& Е\
х — коэффициент,
х = (а — tga) (1 + 3v) +
+ (1 + v) a tg2 а; (54)
а — половина угла между опорными я
линиями, a — v — коэффициент
(см. формулу (45)).
Наибольшие напряжения изгиба в сечении кольца
атах = £ -^2- > (55)
где
РЕЗИНОВЫЕ УПРУГИЕ
ЭЛЕМЕНТЫ
Резиновые упругие элементы применяют в конструкциях упругих муфт (рис. 17), вибро- и шумоизолирующих опорах (рис. 18) и других устройствах для получения больших перемещений. Такие элементы обычно передают нагрузку через металлические детали (пластины и трубки и т. п.).
Преимущества резиновых упругих элементов: электроизолирующая способность; высокая демпфирующая способность; способность аккумулировать большее количество энергии на единицу массы по сравнению с пружинной сталью (до 10 раз).
В табл. 5 приведены расчетные схемы и формулы для приближенного определения напряжений и перемещений для резиновых упругих элементов.
Материал элементов — техническая резина с пределом прочности <тв )> > 8 МПа; модуль сдвига G — 54-9 МПа.
В последние годы получают распространение пневмоэластичные упругие элементы (рис. 19).
Пример- Рассчитать клапанные пружины (рис. 20) для карбюраторного двигателя, если известно, что при полном открытии клапана (ход клапана h — 11,5 мм) пружины должны воспринимать усилие РШах — 36,2 Н, усилие затяжки Рш1п — 170 Н.
Клапанные пружины являются ответственными деталями. Принимаем в качестве материала пружин сталь 50ХВА (<тв - 1300 МПа, от = = 1100 МПа; t_j = 400 МПа и по табл. 2 для пружин класса I находим [т]к = 480 МПа). В связи с ограниченными габаритами используем в конструкции две концентрические пружины сжатия.
Принимаем, что первая (наружная) . пружина будет воспринимать 63,5% внешней нагрузки, вторая — 36,5%, откуда наибольшие усилия для пружин
Ра) , = 0,635Ргаах = 230 Н;
Р (11 а = 0,365Ртах ~ 132 Н.
Усилия затяжки пружин:
Рdi 1 ~ 0,5Р (1) 2 = 115 Н;
Р (11 1 = Рmm ~ Р(11 I —
= 170-115 = 53 Н.
a) 6) 6)
Рис. 17. Конструкции муфт с резиновыми упругими элементами:
а — втулочно-пальцевая муфта; б — муфта с упругими оболочками: в — муфта с дисковым элементом
Резиновые упругие элементы
179
5. К расчету резиновых упругих элементов
Расчетная схема элемента
Напряжения
Перемещения
Допускаемые напряжения, МПа
X
У g о ± а> 5 х
X 5
ь х
о о Я*
_ Р 2Р Т F ~ n(D+d)h T и
f D-d 0 0,1 0.2 0,3 0,4 0.5
k I 0,93 0.89 0.84 0,81 0,8
Р о — —-
1 G.bGF
300
100
Примечание. Допускаемые напряжения для резиновых элементов упругих муфт [а 1 200 МПа.
180
Пружины
Рис. 18. Резиновый амортизатор
Рис. 19. Пневмоэластич-ный амортизатор
Расчетпервой пружины. Назначаем индекс * пружины с — = 8,7. По формуле (31) вычисляем диаметр проволоки пружины **
, . д 1/’ £<1>Л1> 2^(1) _
d(1) = 1.6 у -
, с 1 / 230-8,7 _ , п
= I.6 |/ ~48о~ « 3,9 мм.
Принимаем dr> ~ 4 мм.
Средний диаметр пружины
^<11 о — ~ 8.7-4 — 34,8 мм
Податливость одного витка
i = 8дто _ 8(34,8)3 Gd^y 0,83-105 (4)"
= 0,016 мм/Н
Необходимое число витков
__ /i(D _
<П ^-<1> (Д(1) а — Р(1) 1)
_________Н.5__________ 0,016 (230 —115)______’ ’
или, округляя до полувитка, получим п<1> ~ 6,5-
Полное число витков
л<1> 1 — л<1> + 1,5 = 6,5 + 1,5 = 8.
* Обычно индекс клапанных пружин с = 74-10
•* Значение [т]к принято с учетом кривизны витков
Длина пружины, сжатой до соприкосновения,
Д<1, з — (л<1) 1 — 0,5) d(1) =
= (8 — 0,5) 4 — 30 мм.
Полная осадка пружины
6(1) а = Л(])Л(1)Р(и 2 =
= 6,5-0,016-230 = 23 мм
Шаг витков
tdi — <i(i> J--’ „ (1) 2 = 4 +
"tn
1 о .93
+ -Чгг~ = 8125 мм-
О, э
Полная длина ненагруженной пружины
Д tn о — Нti) з Ь л<1) (‘<i> ^<11) =
= 30 + 6,5 (8,25 — 4) = 57,6 мм.
Я,,) л 57,6 . сс ,
Так как-у=г-— = ~ i,66 < 2,5,
/-7(1) о 34,6
то опасность выпучивания пружины отсутствует.
Расчет второй пружи-н ы. Принимаем с(а> = с(1> — 8,7 *. По
♦ Можно задаться rf... и из условия
(* >
равенства длин, сжатых до соприкосновения пружин, найти
Резиновые упругие элементы
181
формуле (31) вычисляем диаметр про-
волоки ______________
d(a)=1.6]/ =
г 14к
, r q / 1,16-132-8,7 „ n
= 116 V -------480----~2’9 MM*
Принимаем d(2) = 3 мм.
Средний диаметр пружины
D(2) о — ^(2)^(2) — 8,7-3 — 26,1 мм.
Определяем радиальный зазор между первой и второй пружинами
6г= (-^(1) О — <2> О - ^(1)-^(2)) —
= у (34,8 — 26,1 —4 — 3) = 0,85 мм.
Обычно зазор в клапанных пружинах бг = 1-4-1,5 мм.
Уменьшаем индекс, принимая с(2> = = 8,5 Тогда средний диаметр пружины
О(2) о ^(2)^(2) — 8,5-3 = 25,5 мм, а радиальный зазор 6Г — 1,15 мм.
Податливость одного витка
, 80?,, 0 8 (25,5)=
<2> Gdt2, 0,83-105 (3)4
= 0,0195 мм/Н.
Необходимое число витков при 6(1) = = ^<2)
„ _________6(2)_______=
*2) Л(2) (Р(2) 2 — Р(2) 1)
=___________4,5________
0,0195 (131—55) ’ ’
округляя до полувитка, получим П(2) = 8.
Полное число витков
п<2) 1 — +2) + 1,5 = 8 + 1,5 = 9,5.
Длина пружины, сжатой до соприкосновения,
^(2)з = (п (2> 1 — 0,5) d, 2 > = = (9,5 —0,5) 3 = 27 мм.
Так как Т/(2)<С На>, то втопая пружина не достигнет предельной нагрузки. Полная осадка пружины
6(2) 2 = Л(2)Я(2)Р(2) 2 —
= 8-0,0195-131 = 20,3 мм.
Шаг витков
> Н I 1.26(2)2
‘(2) — “(2) Т--------- —
п(2)
„ , 1,2-20,3
= 3 -------g-----= 6,05 мм.
О
Полная длина неиагруженной пружины
ИW 0 = Д\2) 3 + п(2) (^(2) — d(2>) = = 27 + 8 (6,05 — 3) = 51,4 мм.
Максимальные напряжения в пружине
_ 8W|2) qP(2) 2
42) шах —------------------
8-1,16-25,5-132
“ л (З)3 ~
= 364 МПа < 400 МПа.
Расчет пружин иа прочность. Напряжения в поперечных сечениях пружин:
минимальные:
8+(1)П(1) „Рц) (
т(1) min —-----------------
^(i)
8-1,16-34,8-115 м„ = 166 МПа;
л (4)3
86(2)0(2) <>Р(2) 1
T<2,mln - Mfr, -
8-1,16-26,1-55
= 74 МПа;
л (З)3
максимальные:
8&(i)D(i) 0Р(1) 2 X(i) max —
8-1,16-34,8-230 = 37[ МПа.
л (4)3
Т(2) max — 364 МПа.
Запас прочности по текучести (принимаем тт = 0,6от)
0,6от 0,6-1100 . „
Л(1) т — — — о?"] — *>''•
Т(1) max °' 1
Амплитуды переменных напряжений:
Гц) max +1) mln ______
T(i) а —-----------------------
2
371 — 166 с ------------= 102,5 МПа;
182
Зубчатые передачи
Т<2> max — т<2> mln
т(2) а --------------
2
364 — 74 .АГ_
=------= 145 МПа.
Средние напряжения цикла:
Т<1> max + Т<1> mtn
“(1> т — ---------2 ~
371 + 166 ... . .лгг
—-------2-------- 268,5 МПа;
т(2) piax + Т(2) mln _____
*(2) т —-----------2------------
= .36.4.±7.4- = 219 МПа.
Запасы прочности прн т. = 400 МПа; фт = 0,2; eT = 1:
т(1) а + т
400
____________________________________________9 ЧА-102,5 + 0,2-268,5_____’ '
<2> "£<2) а + Фтт<2> т
_......______________212
~ 145 + 0,2-219 ’
Запасы прочности по переменным напряжениям:
t_i— 'Рт'Чп m
Иц, а ----------------—
Т(1) а
400-0,2-268,5 „ „
=------102+-------= 3’4:
^-1 -- ) ТП
п(2) а “-----z-------------
т(2> а
400 - 0,2-219
=-------145--------= 2’46'
Запасы прочности вполне достаточные.
Глава 11
ЗУБЧАТЫЕ ПЕРЕДАЧИ
Разрушение зубьев при длительной работе можно в основном подразделять на два вида:
1) поломка зуба от изгиба в зоне его перехода в обод, где имеет место высокая концентрация напряжений (рис. 1);
2) повреждение рабочей поверхности зуба, которое обычно начинается с выкрашивания и может привести к обминанию. задирам и поломке зуба (рнс. 2).
У основания недостаточно прочного зуба при повышенной концентрации напряжений (из-за малого радиуса галтели яли наличия грубых следов обработки) на растянутой стороне появляется усталостная трещина, которая, постепенно распространяясь в глубь тела зуба и вдоль его основания, приводит к разрушению. При больших контактных напряжениях микроскопические усталостные трещины появляются на поверхности зубьев (обычно на ножках вблизи полюсной
линии), развиваясь, эти трещины приводят к выкрашиванию мелких частиц металла и образованию пор и ямок, которые затем сливаются, захватывая все большую часть поверхности, вследствие чего передача выходит из строя.
В некоторых случаях зуб может сломаться или получить недопустимую остаточную деформацию в результате большой кратковременной (даже однократной) перегрузки. Такое статическое разрушение представляет опасность для зубьев из относительно хрупких материалов (например, чугуна) или же для зубьев с очень малым радиусом выкружки у корня, когда пластические деформации сильно локализуются.
У длинных зубьев иногда откалываются углы, что связано с концентрацией нагрузки у кромок. Если отколовшиеся частицы не попадут в зацепление, то оставшаяся часть зуба может продолжать некоторое время работать.
Основные обозначения
183
Рис I Поломка 3v6a от изгиба
Рис. 2. Выкрашивание поверхности зуба
Разрешение поверхности зуба может произойти также вследствие заедания, Которое возникает, если из-за большого выделения тепла при трении зубьев и плохом охлаждении значительно повышается температура в зоне контакта При этом вязкость масла уменьшается, и оно выдавливается зубьями
Открьчые передачи подвержены абразивному изнашиванию вследствие попадания между зубьями твердых частиц пыли или грязи. Изнашивание
сопровождается утонением зуба и нарушением его поверхности.
Зубья рассчитывают: а) на выносливость п статическую прочность при изгибе б) на контактную выносливость активных поверхностей (на изнашивание).
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
Схема зацепления прямозубых цилиндрических зубчатых колес без сме-
184
Зубчатые передачи
1. Основные определения н обозначения для прямозубых цилиндрических зубчатых колес
Термин, его определение
Межосевое расстояние — расстояние между осями зубчатых колес передачи по межосевой линии ОХО2
Шестерня — зубчатое колесо передачи с меньшим числом зубьев; относящиеся к нему величины имеют индекс 1
Колесо — зубчатое колесо передачи с большим числом зубьев; относящиеся к нему величины имеют индекс 2
Число зубьев:
шестерни
колеса
Передаточное число — отношение числа зубьев колеса z2 к числу зубьев шестерни г, (и >1)
Делительные диаметры — диаметры делительных окружностей, являющиеся базовыми для определения элементов зубьев и их размеров Начальные диаметры — диаметры начальных окружностей сопряженной пары колес, имеющих общие с зубчатыми колесами оси и катящиеся одиа по другой без скольжения (для колес без смещения начальные окружности совпадают с делительными)
Диаметры основных окружностей — диаметры окружностей, разверткой которых являются эвольвенты зубьев
Диаметры вершин зубьев
Диаметры впадин
Высота зуба h = 0,5 — dy)
Высота головки зуба hQ — 0,5 (dQ — d}
Высота ножки зуба h? — 0,5 (d — d?}
Полюс зацепления — точка касания начальных окружностей
Линия зацепления — общая касательная к основным окружностям, проходящая через полюс зацепления
Активная линия зацепления — часть линии зацепления, по которой происходит взаимодействие зубьев
Угол зацепления — острый угол между линией зацепления и прямой, перпендикулярной к межосевой линии
Диаметры окружности верхних граничных точек однопарного зацепления
Диаметры окружностей нижних точек активных профилей зубьев (в колесах без смещения точки Р2 совпадают соответственно с точками Л2, Лх)
Основной шаг — кратчайшее расстояние по основной окружности между одноименными профилями соседних зубьев
Делительный шаг — то же, но по делительной окружности
Модуль — характеристика масштаба колеса: т — р/л = rft/Zi — d2/zt Коэффиииент перекрытия — отношение угла поворота зубчатого колеса от положения входа зуба в зацепление до выхода его из зацепления к угловому шагу т — 2л/г
Рабочая ширина венца — общая часть ширины венцов зубчатых колес, участвующая в контакте
Толщина зуба (переменная)
Окружная скорость, измеряемая по начальной окружности, м/с
Обозначение по ГОСТ
aw
2* Zj U
dt
dWV
dbr db2 dal’ da2 dfl‘ df2
h
hf W
A,.A,
dur dU2 dPr dP2
Pb
P m eV
s
V
щеиия показана иа рис. 3. В табл. 1 приведены некоторые из основных определений и обозначений по действующим ГОСТ 16530—83 и ГОСТ 16531—83.
Если зубчатое зацепление соответствует стандартному исходному кон
туру, т. е. углу профиля а = 20°, высоте головки зуба ha = т, радиальному зазору с = 0,25m и радиусу закругления у корня зуба р/ = 0,38m, то основные геометрические размеры колес без смещения можно определить с помощью табл. 2.
Упрощенный расчет на прочность прямых зубьев
185
Рис. 3. (хема зацепления цилиндрических зубчатых колес без смещения
2. Основные размеры колес без смещения
Параметр
Расчетная формула
Делительный (начальный) диаметр
Диаметр вершин зубьев
Диаметр впадин
Межосевое расстояние
Постоянная хорда (толщина зуба) $с Высота до постоянной хорды (расстояние от вершины зуба) hc
d = гт
da = (z + 2) т
dj (г — 2,5) т
aw = °'5 +
+ zz) т
—- 1,3870m
hc — 0,7476m
УПРОЩЕННЫЙ РАСЧЕТ НА ПРОЧНОСТЬ ПРЯМЫХ ЗУБЬЕВ
Усилие, действующее на зуб. Крутящий момент иа шестерне Т\ (в Н-м) выражается через передаваемую мощ
ность У (в кВт) и частоту вращения шестерни п1 (в мин"1) формулой
7 = 9555 — (1)
ni
и определяет окружную силу (в Н) в зубчатой передаче
(2)
где dm — диаметр начальной окружности шестерни, мм (рис. 4).
Удельная расчетная окружная сила w (в Н/мм), отирсеиная к единице рабочей ширины веица bw (в мм),
F
w=-^—K; (3)
удельная расчетная нормальная сила (в Н/мм)
где aw — угол зацепления.
Введением коэффициента К можно учесть неравномерность распределения
186
Зубчатые передачи
Из последней формулы
- ттт- •
Подставив 7\ и dw, из равенства (1) и (6) в формулу (5), получим
NK
да = 9,55-10е (и + 1)-^—. (7)
Для передач с внутренним зацеплением (рис. 5, 6)
Пц| ~ 0,5 (d^f^ —dfm) — 0,5^/ц,1 (и — 1), откуда
нагрузки между зубьями и по ширине зуба и дополнительные динамические нагрузки в зацеплении. В предварительных расчетах принимают Д' — = 1,5-ь2,0. Из формул (2)—(3) сле-
дует:
2000?! „
™ = к-
(5)
Для передач с внешним, зацеплением (рис. 5, а) межосевое расстояние
а^ = 0,5 "I- dwi) — 0,5^ (и т- 1),
где dt«i — диаметр начальной окружности шестерни, мм; и = zjz1 — — dwjdwl •— передаточное число.
и формула для определения удельной силы принимает вид
NK да - 9,55-10е (и- 1)—-4- • (8)
Усилие, действующее на единицу ширины зуба, возрастает с увеличением передаваемой мощности и уменьшается с увеличением частоты вращения, межосевого расстояния и рабочей ширины зуба. Усилие вызывает деформацию поверхностного слоя зуба в зонах контакта и общий изгиб зуба.
а)
Рис. 5 . Схема внешнего (а) н внутреннего ((Г) зацеплений
Упрощенный расчет на прочность прямых зубьев
187
Расчет на контактную выносливость. Так как контактная деформация носит местный характер, то для упрощения вместо сжатия зубьев рассматривают сжатие двух цилиндров, радиусы которых р! и р2 соответственно равны радиусам кривизны профилей зубьев шестерни и колеса в зоне контакта (см. рис. 5). При сжатии двух цилиндров па их границе образуется площадка контакта, ширина которой 2а возрастает с увеличением нагрузки (рис. 6, а, б). Поэтому среднее контактное напряжение oHm=wa/2a увеличивается медленнее, чем сила
Фактически напряжения распределяются по ширине контактной площадки неравномерно. Максимальное контактное напряжение (в МПа) для зубьев из одинакового материала
о =0,418 (9)
' Рпр
гдеЕ — модуль упругости, МПа; Рпр — приведенный радиус кривизны зубьев, мм.
Для передачи с внешним зацеплением
о - Р'Рг РПР~ Р2 + Р1 •
(Ю)
Из рис. 5, а следует, что pi sin cCg/'t
р2 ~ 0,5б/щ2 Sill ССщ, — Upi, поэтому
Рпр “ 0,5 - sin
и формула (9) для стальных зубьев с углом зацепления aw = 20° принимает вид
<»-«» 1ЛРФ1. <н>
’ и
где w определяется по формуле (5).
Выразив dm через межосевое расстояние aw по формуле (6), получим
°н — 332 (и + 1) 1/^ ’ С 2)
r UfgfU
где aw — в мм.
Рис. 6. Увеличение ширины контактной площадки с ростом нагрузки (а2 > fit)
Для передач с внутренним, зацеплением (см. рис. 5, б)
или
Рпр 0,5 j— dwL sin и соответственно
о = 469 1/ , (13)
н г dm и
ИЛИ
°я = 332 (“- 1/ l/(>4)
Условие контактной выносливости активной поверхности зуба имеет вид °нр, (1^)
где онр — допускаемое контактное напряжение, которое устанавливают по экспериментальным данным и обычно выражают через твердость поверхности зубьев. В приближенных расчетах можно принимать <знр -- <з°н ।Im; значения в МПа приведены иа с. 220. Для передач с ограниченным числом циклов (М< 107) значения могут быть увеличены на 10— 30%.
Контактные напряжения возрастают с увеличением удельной окружной силы w и убывают с увеличением межосевого расстояния аш. Условием кон-
188
Зубчатые передачи
Рис. 7. К упрощенному расчету зуба иа изгиб
тактной выносливости зубьев опреде
ляется минимально допустимая вели-
чина межосевого расстояния аю, т. е. габариты передачи.
Расчет иа выносливость зубьев при изгибе. Зуб рассчитывают на изгиб как консольную балку переменного
сечения, нагруженную на конце сосредоточенной силой F (рис. 7), которую определяют по формуле (2). Ма-
ксимальное иапряжение в основании
зуба
= а°= si
(16)
где h — высота sy — толщина зуба в опасном сечении; аг; — коэффициент концентрации н .пряжений в переходной части зуба.
Опасное сечение можно приближенно найти, если провести касательную к переходной кривой зуба под углом ~30* к его оси.
Формулу (16) можно представить в виде
т
(17)
где т — модуль, мм, Yp — коэффициент, учитывающий форму зуба (безразмерная величина, численно равная напряжению в МПа для зуба с модулем т = 1 мм под действием нагрузки w = 1 Н/мм). Коэффициент Yp определяется по формуле
Yp =
6/гтаст
(18)
Высота зуба до опасного сечеиия h ~ 2т. Соотношение между толщиной зуба в опасном сечении S] и толщиной зуба на начальной окружности sw 0,5р, где р = пт — шаг зубьев, зависит от числа зубьев и других факторов. Принимая в среднем Sj/So, ~ ~ 1,3 и « 1,3, получим из формулы (18) Yp » 3,7, и формула (17) примет вид
(19)
где w — в Н/мм; т — в мм.
Более точные значения коэффициента Yp приведены ниже.
Условие выносливости при изгибе зуба
(20)
где орр — допускаемое напряжение при изгибе,
здесь Ор11п, — предел выносливости материала зубьев при пульсационном цикле; Sp — коэффициент безопасности (запас прочности). В приближенном расчете принимают Sf = 2,04-2,5
Значения Oplim меняются в пределах от 400 МПа для поверхностно неупрочненных зубьев до 800— 1000 МПа для цементованных и нитро-цементованных зубьев.
Напряжения изгиба в зубе возрастают с увеличением удельной окружной силы w и убывают с увеличением модуля т. Из условия прочности зуба на изгиб определяют модуль т (размер зубьев), а следовательно, и их число г = dim.
Пример. Проверить прочность зубьев при следующих исходных данных: мощность передачи N = 7 кВт, частота вращения шестерни п.г — = 400 мин"1; передаточное число и --= 4, модуль т — 4 мм; межосевое расстояние аж = 180 мм; ширина зуба bw — 80 мм; зацепление внешнее. Материал колес — углеродистая сталь без специальной поверхностной термообработки: твердость НВ 300; °F 11m = 400 МПа-
Структура расчетных формул по ГОСТ 21354—37
189
Приняв К = 1,5, находим по формуле (7) удельную расчетную окружную силу 7-1 5
ю = 9,55.10.(4 4 О ЧооПтаГ = = 87 Н/мм.
По формуле (12) находим расчетное контактное напряжение
«н„332(4+,)/-^ =
= 577 МПа.
Допускаемое контактное напряжение (см. с. 220)
°нр = 2-300-1- 70 =- 670 МПа.
Из сравнения значений ан и очр следует, что условие контактной выносливости удовлетворяется.
По приближенней формуле (19) на ходим напряжение изгиба
3,7-^- = 80,5 МПа.
к 4
Коэффициент безопасности
т. е. величина Sf достаточна.
С целью унификации и сопоставимости результатов расчетов зубчатых передач действует ГОСТ 21354—87, который устанавливает структуру формул расчета зубчатых передач на контактную выносливость активных поверхностей зубьев и на выносливость зубьев пси изгибе. Расчетные формулы по ГОСТу имеют ту же структуру, что рассмотренные выше упрощенные формулы, ьо отличаются рядом поправочных коэффициентов, подробнее учитывающих условия работы зубчатых передач. Для передач с непрямыми зубьями факторы, относящиеся к торцовому сечению или действующие в окружном направлении (силы Ft и Wf), имеют индекс t.
СТРУКТУРА РАСЧЕТНЫХ
ФОРМУЛ ПО ГОС! 21354—87
Расчет на контактную выносливость активных поверхностей зубьев. Проверка контактной выносливости в по-
люсе зацепления проводится по формуле ____
°н — ° но V °7ур, . . (22)
где контактное напряжение при Кн —
== 1 ____________________
л - 7 7 7 т/ и + 1
°НО - V bwdt и ’
(23)
а коэффициент нагрузки
= МнАЛ- (24)
Коэффициенты Z#, Zh, учитывают соответственно механические свойства материалов зубьев, форму сопряженных поверхностей зубьев в полюсе зацепления и суммарную длину контактных линий; Рщ — это исходная окружная сила при расчете на контактную выносливость; коэффициенты Khv, Кнв, Кна учитывают соответственно внешнюю динамическую нагрузку, динамическую нагрузку в зацеплении, неравномерность распределения нагрузки по длине контактных линий и распределение нагрузки между зубьями.
Удельная окружная сила при расчете иа контактную выносливость, Н/мм,
^=4^- (25)
Коэффициент Ze—-в (Н/мм2)" , все остальные коэффициенты — безразмерные.
Допускаемое контактное напряжение
°Н itm^N у ~ у ~ °нр ~ П
где 11п1 — предел контактной выносливости поверхности зубьев при базовом числе циклов напряжений;
S7, — коэффициент запаса прочности; коэффициенты ZK, Zr. Zv, Zx учитывают соответственно влияние числа циклов перемены напряжений, шероховатость сопряженных поверхностей зубьев, окружную скорость, влияние смазки и размер зубчатого колеса.
Расчет зубьев на выносливость при изгибе. Проверка выносливости зубьев проводится по формуле
°F^°FP, W
190
Зубчатые передачи
где ор — расчетное местное напряжение от изгиба в опасном сечении,
<28>
причем Kf — коэффициент нагрузки, Kf - АлАеЛерАесс- (29)
Здесь FfF — исходная окружная сила при расчете зубьев иа выносливость при изгибе, коэффициенты К a- Kfv, Kf$, Kfo. учитывают те же факторы, что и Л'А, Khv. Анр, Кна в формуле (24), ио при изгибе; коэффициенты Уе.ч, Уц, Yt учитывают соответственно форму зуба и связанную с ней концентрацию напряжений, наклон зуба и перекрытие зубьев.
Удельная окружная сила при расчете зубьев на выносливость при изгибе, Н/мм,
(3°)
Все коэффициенты У — безразмерные. Допускаемое напряжение изгиба зубьев
= (31)
где oF ,! m b — предел выносливости зубьев при изгибе при базовом числе циклов напряжений; Sf — коэффициент запаса прочности; коэффициенты Yn, YYR, Ух учитывают соответственно влияние числа циклов переменных напряжений, чувствительность материала к концентрации напряжений, шероховатость поверхности зуба и размер зубчатого колеса.
В приложениях к ГОСТ 21354—87 приведены подробные рекомендации по методике расчета входящих в формулы (22)—(31) параметров и коэффициентов для силовых зубчатых передач внешнего зацепления.
Ниже рассмотрены основные факторы, которые следует учитывать в уточненных расчетах на прочность зубчатых передач (для прямозубых колес индекс t опущен). Условия работы и требования к зубчатым передачам в отдельных классах машин существенно различаются, поэтому уточненный расчет передач проводится обычно для каждого класса машин по
специальным методикам, в которых второстепенные для данного типа передач факторы не учитываются, а превалирующие учитываются точнее.
НАГРУЗКИ, ДЕЙСТВУЮЩИЕ НА ЗУБ
Номинальная удельная окружная сила в данном режиме работы
2000Т,
Расчетная удельная сила в данном режиме отличается от номинальной:
ш = №homA,
где К = 1,3-?-2,0.
Величину К можно представить в виде произведения нескольких коэффициентов, каждый из которых учитывает определенный фактор, влияющий на изменение нагрузки по сравнению с номинальной. Основные факторы, учитывающие нагрузку:
неравномерность распределения нагрузки по длине контактных линии (по ширине зуба), учитываемая коэффициентом Kg;
удар зубьев при входе в зацепление, учитываемый коэффициентом Лф;
динамические нагрузки, связанные с крутильными колебаниями системы, учитываемые коэффициентом АКр-
Одновременный вход в зацепление двух и более пар зубьев (благодаря перекрытию) уменьшает нагрузку, действующую на каждый зуб, что учитывается коэффициентом Ка-
Следовательно,
К = АаАвАцАкр. (33)
При расчете динамических нагрузок, связанных с ударом зубьев при их входе в зацепление, вводят коэффициент
Ад = АаАу, (34) учитывающий одновременно и удар, и перекрытие зубьев, тогда
А = АдАрАкр. (35)
На некоторых режимах передача может вращаться вхолостую, не передавая вращающего момента (и>Ном — 0),
Нагрузки, действующие на зуб
191
однако динамические нагрузки при этом могут действовать. Величину w определяют в этом случае непосредственно из динамического расчета. При расчете на контактную выносливость и на изгиб коэффициенты нагрузки могут иметь разные значения.
При изменении режима (частоты вращения, мощности, направления вращения) меняется как номинальная нагрузка, так и коэффициенты, определяющие расчетную нагрузку. Особенности расчета передачи при работе иа различных режимах изложены ниже (см. с. 221).
Неравномерность распределения нагрузки по ширине зуба (коэффициент К*)
Во время работы зубья могут прирабатываться один к другому, поэтому различают коэффициент начальной неравномерности нагрузки и расчетный коэффициент Кр
Начальная неравномерность зависит от неточности изготовления и монтажа передачи и от упругих деформаций под нагрузкой элементов передачи (валов, опор, корпусов, тел колес и самих зубьев). Полный расчет упругих деформаций системы представляет собой очень трудную задачу, поэтому обычно рассчитывают только деформации изгиба зубьев, кручения ободьев или тел колес н изгиба валов.
Деформация зубьев и кручение ободьев или тел колес (коэффициент КФ). Деформация зуба колеса в сеченни, где действует распределенная нормальная нагрузка w (индекс а опущен)
где с2 — жесткость зуба колеса, которую удобно измерять в Н/мм-мкм (1 мкм = 0,001 мм) (см. ниже).
Чтобы контакт зубьев не нарушился, несмотря на эту деформацию, соответствующее сечение колеса должно повернуться на угол ф3 (рис. 8), причем 62 ~ фй^бз — 0,5фз^и?з cos сбщ.
Аналогичные соотношения справед ливы для шестерни. Деформация пары
Рис. 8. Схема поворота колеса при деформации зуба:
1,2,3 — положения зуба соответственно до деформации, после деформации и после поворота
сопряженных зубьев
6 = 61 62 —
— = 0,5 cos Ощ, X
X (Ф1^ш1 -|- фз^шз), (36)
где 1____________________1_ , 1
С ~ С, с2
Из формулы (36) следует, что нагрузка не изменится по ширине зуба в том случае, если углы поворота шестерни ф1 и колеса ф2 во всех сечениях будут одинаковыми, что возможно лишь при очень малой ширине зуба или при очень жестких колесах. В действительности из-за скручивания тел колес вместе с валом (рис. 9) илн ободьев (рис. 10) углы Ф1 и ф2 меняются, причем особенно резко в тех сечениях, где действуют наибольшие крутящие моменты. В этих сечениях интенсивность нагрузки на зуб возрастает.
Расчетная схема, соответствующая передачам, показанным на рис. 9 и 10, а, б, приведена на рис. 11. Здесь
192
Зубчатые передачи
Рис. 9. Неравномерное распределение нагрузки по ширине зуба из-за закручивания тел сплошных колес вместе с валами; вращающие моменты к валам приложены:
а — с разных сторон, б— одной стороны
Рис. Ю. Неравномерное распределение нагрузки по ширине ободьев колес; вращающие моменты к ободьям приложены: а — с разных сторон; б — с одной стороны; в — к средней
зуба из-за закручивания
части обода
гщ (х) и т2 (х) — распределенные вра-
щающиеся моменты:
связанные с внутренними крутящими моментами Т условиями равновесия элемента вала:
mi (х) = — 0,5и> (х) dwl cos ссш;
т2 (х) = —0,5ш (х) dwi cos «ш, J
(37)
dT1 dx
+ т, - - 0;
^ + m2==0. (38)
Нагрузки, действующие на зуб
193
Из формул (38) и соотношений для относительных углов закрутки
__ Т t . Г2 •
dx — Gi/i ’ dx ~ '
где Gj, G2 — модули сдвига материалов шестерни и колеса; J2 — геометрические жесткости на кручение тел колес с валами (см. рнс. 9) илн ободьев (см. рис. 10), следуют уравнения
d2<p,
~dx*~ '
<Лр2 tn2
dx* G2J2
(39)
Дважды продифференцировав уравнение (36) и учтя выражения (37) и (39). получим дифференциальное уравнение для распределенной нагрузки W(x):
__ = 0, (40)
dx*
где Р’ — параметр (1/мм2), определяемый по формулам:
Р2 = Pi + Ps;
fl2 = 0,25с cos2
₽2 = 0,25с cos2 аш ~
'-'2*' !
(41)
Решение уравнения (40)
w — A sh Рх + В ch Рх, (42)
где постоянные А и В зависят от условий подведения вращающегося момента к телу колеса илн к ободу.
Вращающие моменты Л4; и М2 приложены с разных сторон (см. рис. 9, а и 10, а).
Граничные условия:
при х = 0 7\ (0) = Mt;
<*Ф1 _ Л (0) . Л<рг
dx GjJ; ’ dx
при x—b (bw = b) Tt(b) = Mt\
^Ф1 q. ^ф2 _ T2 (fe)
dx ~ ’ dx ~~ G2/2
(43)
Рис. II Расчетная схема кручения тел сопряженных колес
Так как согласно равенству (36)
.. _ / , d(pt
— -- 0,5 с cos dwi
dx \ dx
-ь dm , (44)
ах '
то условия (43) приводятся к виду: при х = 0 rftt’ п к (°) dwl
—— = - 0,5сcos a.w — 1 =
dx Gvl,
=
при x = b rnS гт... T* W _
dx ' “ G2Ja
= Wmb^22,
где wm — средняя нормальная иая нагрузка, Н/мм. Если Tv
(45)
удель-
Л-в Нм, b, dw — в мм, to
_ 2000Tt (0) 2000Тг (b)
bd^i cos bdw2 cos
Определив из условий (45) постоянные А и В, получим
М Wm Г (fW + Ch & V
X ch fix — (Pii)2 sh PxJ . (46)
Характер изменения нагрузки по ширине зуба ш (х) показан па рис. 9, а и 10, а. Обычно максимальная нагрузка возникает у кромок зуба со стороны приложения вращающегося момента к шестерне (х = 0), так что
3 з к 5 з 4 02
194
Зубчатые передачи
Рис. 12. Зависимости коэффициента неравномерности нагрузки А'^ от отношений 6Ми>1 и и при кручении тел сплошных колес вместе с валами; крутящие моменты приложены: а — с разных сторон [7 — расчет по формуле (47), 2 — по формуле (48)1. 6 — с одной стороны [/ — расчет по формуле (50); 2 — по формуле (51)]; 3 — расчет по формуле (52)
коэффициент неравномерности нагруз-
К “'max - (Рг6)2 + (Pi6)2 Р6 wm Р* sh рб
Для сплошных (см. рис. 9) стальных колес при с = 18 Н/(мм-мкм), G — = 8-КН МПа и =20°, полагая для грубой оценки
32 ’ 32 ’
получим
P^wOJi₽2S»0,7i-— <*ид
(47)
График зависимости (47) показан на рис. 12, а.
Используя приближенные значения функций
sh р* « Р6 + (Р6)3;
ch р& « 1 + -1 (р6)\ получим
(48)
Кривая, построенная по формуле (48), также показана иа рис. 12, а, откуда следует, что при обычных значениях bidm формула (48) обеспечивает достаточную точность.
Вращающие моменты Mi и Л43 приложены с одной стороны (см. рис. 9, б и 10, 6). В этом случае решение уравнения (40) примет вид
<«>
Максимальная нагрузка будет у кромки зуба со стороны приложения
Нагрузки, действующие на зуб
195
вращающих моментов. Коэффициент Лф~ wm = thpft •
Для сплошных стальных колес
(50)
Используя приближенное выражение функции th 0ft 0ft-----5- (fib)3,
О
получим
1 4 0,17
(51)
Графики зависимостей (50) и (51) показаны иа рис. 12, б.
При а 3 неравномерность распределения нагрузки для сплошных колес определяется практически только жесткостью на кручение шестерни, характер приложения вращающего момента уже не оказывает влияния и формулы (47) и (50) или (48) и (51) совпадают.
В рекомендациях к ГОСТ 21354—87 используется формула
|52)
которая дает усредненное значение величины Кф (см. рис. 12).
Дляслучая, показанного иарис. 10, в, вместо полной ширины зуба b следует подставлять в формулы 0,5ft.
Для зубчатых колес с тонкими Ободьями ТОЛЩИНОЙ ft, -С dm и /ц « dws (см. рнс. 10), полагая ~ я» O^Snhjd^, J2~ 0,25л/12</щ2 пРи с ~ = 18 Н/(мм-мкм), G=8-104 МПа и a.w — 20°, найдем
0,25ft "]/Hida#
0,25ft
При этом вместо формулы (50) получим
(53)
Приближенно
Кф = 1+0.02,(;1-)(Д)х
х('+тяг)'
Из формулы (54) следует, что с уменьшением толщины обода неравномерность распределения нагрузки возрастает. Обод колеса следует выполнять достаточно жестким.
Во многих зубчатых передачах применяют колеса с относительно узкими зубьями. Из приведенных формул и кривых следует, что, если b!dm s-4 0,3, то для колес обычной конфигурации Кф ~ 1, т. е. деформацией закручивания в этих случаях можно пренебречь.
Изгибные деформации валов (коэффициент Ку). Силы давления иа зубья, передаваясь на валы, вызывают их изгиб в плоскостях, параллельных плоскости зацепления (рис. 13). Если уБ — суммарный угол перекоса осей колес в этой плоскости, то отклонение от среднего значения нагрузки в точке на расстоянии х от середины зуба Да? = ex tg уБ, где для упрощения принято, что по ширине зуба нагрузка меняется линейно. Учитывая, что у кромок зубьев их жесткость понижается, принимают х —- ayft, где ay = = 0,34-0,4. В этом случае коэффициент неравномерности нагрузки от деформации изгиба валов
= ^т +Ащ = j асЬ2у (55)
где уБ = Ч-х/&тЬ, причем прн малых углах перекоса tg у£ у£. Осредиен-ные значения с == (14-т-18) Н/(мм-мкм).
Угол перекоса уБ следует вычислять дли всей системы валов передачи,
7*
196
Зубчатые передачи
Рис. 13. К расчету концентрации нагрузки по ширине зуба в связи с изгибом валов передачи (колеса условно раздвинуты)
учитывая возможные начальные технологические перекосы, а также податливость опор и корпусов, однако ввиду сложности решения такой за-дачн обычно ограничиваются расчетом деформаций только тех валов, иа которых закреплена данная пара колес. Усилиями, передающимися иа эти валы со стороны других колес, н технологическими перекосами также пренебрегают. В этом случае у2 — угол перекоса осей в сечении, где расположены колеса, от единичной силы, действующей в том же сечении иа валы шестерни н колеса.
Для консольно закреплеииого колеса (рис. 13)
I2
i =~зЁТ(i + !’5й) (56-
где а = а/1.
Для колеса, расположенного между опорами,
V =^-(1-6)6(1-26), (57) or. J
где 6 = ЬП.
В формулу (55) подставляют значение
Vs^lYxi-yJ. (58)
При расположении зубчатых колес по схемам, показанным на рис. 13, а и б, углы перекоса валов складываются, по схеме, показаииой иа рис. 13, в — вычитаются.
В результате перекоса нагрузка возрастает иа участке зуба, ближайшем к опоре. Наибольшие перекосы обычно возникают при одиостороиием консольном расположении колес (рис 13, б).
Общая начальная неравномерность (коэффициентХр). Если при кручении
Нагрузки, действующие на зуб
197
Рнс. 14. Зависимость коэффициента приработки Kw от твердости поверхности зубьев колеса при работе на постоянном режиме; сплошные линии соответствуют расчету на контактную выносливость; штриховые линии — расчету на изгиб
ободьев и изгибе валов нагрузка концентрируется у одного и того же края зуба, то общая начальная неравномерность распределения нагрузки опре-дел яетс я коэффициентом
К&=> + (Кф-') + (К/-1)-
= Кф+К/-1. (59)
Если при кручении и изгибе нагрузка концентрируется у различных краев зуба, то расчет ведется по величине Лр. равной наибольшей из величин или К/.
Неравномерность распределения по длине зуба контактных напряжений ан соответствует неравномерности нагрузки w, поэтому при расчете на контактную выносливость поверхностей зубьев считают !<.%$ = К^. Неравномерность распределения по длине зуба максимальных изгибных напряжений в заделке сглаживается тем сильнее, чем меньше отношение bw/m. Зависимость К'рс, от К°н$ и Ьш/т при btjm 4 может быть приближенно аппроксимирована формулой
X [1 — 0,54е
Концентрация нагрузки у краев зубьев может быть снижена применением продольной коррекции.
Приработка зубьев. Приработка зубьев происходит в результате их истирания или пластической деформации и зависит от твердости поверхностей зубьев, от степени равномерности передаваемой нагрузки, от времени работы, окружной скорости и других факторов.
В расчетах предполагают, что интенсивность приработки пропорциональна местной нагрузке, поэтому наиболее быстрая приработка происходит в первые часы работы передачи, когда нагрузка распределяется по ширине зуба весьма неравномерно. Затем приработка замедляется, а при большой твердости зубьев прекращается.
Расчетный коэффициент неравномерности распределения нагрузки по ширине зуба с учетом приработки определяют по формуле
К₽= (61)
При работе на постоянном режиме коэффициент Ки> зависит от твердости поверхности зубьев колеса, которая обычно меньше или равна твердости поверхности зубьев шестерни. Рассчитанные по формулам ГОСТ 21354—87 кривые для определени значения Kw приведены на рис. 14 С увеличением окружной скорости приработка уменьшается. При работе на переменных режимах условия для приработки также ухудшаются (см. инже).
198
Зубчатые передачи
Зуб может передать всей шириной нагрузку F — wab cos aw или с учетом выражений (31) и (34)
_ wa cos aw b КдКкр
Так как с увеличением ширины зуба коэффициент Кр увеличивается, то при заданном условиями прочности значении давления wa полная нагрузка F достигает при некотором значении Ь° максимума. При определении Кр по формуле (52) и Ки> « 1, К/«1
-- к 2,7^.
у 0,14
С учетом коэффициента К/ получают b4dwx «1-5-3.
Увеличивать ширину зуба сверх 6° нецелесообразно.
Статическое распределение усилий между зубьями (Коэффициент Ка)*
В тихоходных зубчатых передачах с немассивными колесами, где динамические нагрузки невелики, распределение нагрузки между зубьями при наличии перекрытия определяется условиями статики.
Если в контакте одновременно находятся две пары зубьев I и II (рис. 15, а), то сумма нормальных усилий aiai и aiaii должна равняться передаваемой нагрузкеaia0= aio/coscca,, где определяется формулами (30)— (34) при Кд = 1. Опуская индекс «а», имеем
Щ), -j- ц,п Ш)о. (62)
Прн этом основные шаги зубьев в деформированном состоянии должны быть одинаковыми, т. е.
Р'ы = Р'ь2- (63)
Здесь индекс 1 относится к ведущему, индекс 2 — к ведомому колесам.
Шаг в деформированном состоянии р'ь отличается от шага ненагруженных зубьев рь упругими перемещениями
* Решение этой задачи методами теории упругости дано в работах [3 и др. 1.
Рис. 15. К расчету статического распределения усилий между зубьями
(64)
зубьев по линии зацепления (рис. 15, б и в):
P'b\ = Рм _^l l+ 1-
P'b2 ~ Pb2 "+ ^112 2-
Из (64) следует условие совместности деформаций
Д -ф- 6ц — 6i ~ 0, (65)
где Д = рЬг — рЬ1 — ошибка по основному шагу, = 6ц -ф- 612— сближение сопряженных зубьев I вследствие их упругой деформации; 6ц = = 61Ц + 6ц 2 — то же, для зубьев II.
Допуски на основной шаг зубчатых цилиндрических передач fрЬ ~ | Рь — — Рьн | (Рья — номинальная величина шага) определяют по нормам плавности
Нагрузки, действующие на зуб
199
ГОСТ 1643—81 в зависимости от степени точности передачи, модуля и диаметра колес (например, для передачи 3-й степени точности при т = = 3,5 4- 6,3 мм и d2 125 мм f рЬ = ±3 мкм). Максимально возможная ошибка в основном шаге сопряженных зубьев
^тах (Гьг)тах (^bl)mln
~ (Pbl)max ‘ (Рьг)тт f pb 1 + рЬ г-
(66)
В зависимости от соотношений между шагами зубьев рЬ1 и рЬ2 действительные ошибки во время работы передачи могут иметь любые значения в пределах — Дтах < Д -С Атах. т. е. ошибка Д может быть положительной, отрицательной или равной нулю. Однако вероятность сочетания (РЬ2)тах и (₽bi)min ИЛИ1 наоборот, очень невелика. Поэтому в качестве расчетной (вероятной) ошибки До обычно принимают __________
До=]/'^1 + /рЬ2. (67)
вероятность которой имеет тот же порядок, что и вероятность выполнения основных шагов по верхнему или нижнему допуску, и считают Д = ~ ±А0 (если f pbi = f pbzt TO A max = = 2fpb. в то время как До = T/2 f ръ « ~ 1,41( рь)-
Упругая деформация зубьев складывается из изгиба и контактного сжатия. Испытания показывают, что полные упругие перемещения зубьев практически пропорциональны приложенной нагрузке, т. е.
Wj — сЛ;
Шц =Сц6ц,
(68)
где ci и Сц—удельные жесткости зубьев, Н/(мм-мкм).
В простейшей схеме передачи усилия Е = wob (рис. 16, а) общий прогиб сопряженных балок постоянного сечения
У1 + У» —
3 I Е^г
EtJt )
Рис. 16. Простейшая схема деформации зубьев (а) и изменение удельной жесткости двух одинаковых сопряженных балок постоянного сечения (tf) в зависимости от положения точки контакта
и удельная жесткость на единицу дли-ны зуба
3 / П V1
У1 + Уз b \EtJj E2J2/
Удельная жесткость, пропорциональная модулю упругости, имеет максимум при контакте в середине пролета (рис, 16, б) и для геометрически подобных балок имеет одинаковое значение, не зависящее от их абсолютных размеров. Это же справедливо и для зубьев.
По данным различных исследований, для стальных прямых зубьев эволь-вентного профиля нормальной высоты удельная жесткость в полюсе (1Г) сю= (13,54-18) Н'(мм-мкм), в начальной и конечной точках однопарного зацепления (1/г и (/2, см. рис. 3) си = (134-16,5) Н/(мм-мкм), в начальной и конечной точках активного участка линии зацепления и Р2) ср = (9,5—12,5) Н/(мм-мкм). В ГОСТ 21354—87 и в последующих расчетах приняты значения жесткостей, близкие к минимальным.
Решая совместно уравнения (62), (65) и (68), найдем усилия, действующие на каждый зуб при наличии перекрытия зацепления:
“'г -----ГТ" (“'о + си А);
Cl + (69)
Wn = Т-TV- (“'о — Ci А).
Ci -р Сц
200
Зубчатые передачи
Контактные усилия и а'п не могут быть отрицательными. Если ошибка Д > 0 (шаг зубьев ведомого колеса больше шага ведущего), то при Д =- вторая пара зубьев ие будет контактировать (шп - 0, рис. 17); если ошибка Д < 0 (шаг зубьев ведомого колеса меньше шага ведущего), то при абсолютной величине | Л | >K'o/Сц не будет контактировать первая пара (и, = 0).
Полагая Д — ±Л0, получим рис. i7)
и1, > 0 при ;
<’п
ICI! > 0 при Ло < —- . Ст
Эти условия можно объединить ио, т. е.
Точные (До ” 0) упругие зубья встретятся несколько ранее точки Р, (вне линии зацепления), а в тот момент. когда точка контакта пары зубьев I займет положение Ри усилия в зубьях в соответствии с формулами (69) при Ct ~ ср, Сц си и До — 0
(см.
в од-
(70)
где с,Т!ах — наибольшее нз значений Ci и CtI при рассматриваемом положении зубьев.
Если условие (70) не выполняется, то в данном положении зубьев в зацеплении будет находиться только одна пара (фактического перекрытия нет).
Точные, абсолютно жесткие зубья входят в контакт в точке Рг (см. рис. 3). Пока точка контакта вновь вошедшей в зацепление пары зубьев 1 (см. рис. 15) перемещается по линчи зацепления из точки !\ в точку U2, точка контакта предыдущей пары зубьев II перемещается из точки U2 в Р.г. В точке Р2 предыдущая пара размыкается, и в зацеплении на участке UtUr остается одна пара зубьев.
Ср
р, = г , -- “'о ~ °.42№О;
Ср “г I у
WMU, -C-U—Wa == °.58m’o L p г < и
(71)
К моменту перед выходом пары I! из зацепления усилия примут значения (сI - - си, Си= Ср, До - 0):
Е'| и, - с Сг— w0 ~ °’58к,0 ’ Г ср
Ср
-«'о »О,42«'О.
CU i ср
(72)
Характер изменения коэффициента Ка-~ в точных упругих зубьях схематически показан на рис. 18 жирной линией.
В неточных упругих зубьях характер изменения усилий зависит от величины и знака ошибок. Область возможных значений усилий wi и при некоторой ошибке Атах < wjcu на рис. 18 заштрихована. При оценке усилий по величине ошибки До их наибольшие значения в точках Р2 и Р,2 в соответствии с формулами (69)
(^1 P,)mox ~ (te,lj pjmax ~
СУ ср + си
(ш0 4- сиЛ0) «
« 0,42^0 (1 + фк),
(73)
Нагрузки, действующие на зуб
201
где коэффициент
ф = —(74)
®о / “>о \
\ си )
представляет собой отношение ошибки До к упругой деформации зубьев в точках Ui или Ut. Наименьшие значения усилий в точках Рг и Р*
(wl ₽,)min = (“’ll P,)rain
«0,42щв(1 — фк).
Наибольшие значения усилий в точках Ux и Ut
(®| У,)"!'!* ~~ (“’ll У,)тах
Ри<. 18 И >мен'*ние коэффициент сгагн-ческого перекрытия К вдоль рабочего участка линии зацепления прн различных значениях параметра вероятной ошибки 4
= (®о + М>) ~
vu Т" ^р
я* (),58оу0 (1 -Ь ij)c), (75) где
Сп^о /*
Фс = — = Т2- ^И * °'73Фк
«М Ср
(фк =s 1,37фг). (76)
Двухпарное зацепление на всем протяжении участка теоретического перекрытия зубьев Р1Нг и UiP2 будет осуществляться при условии (70), т. е. при
Дд < —или при фк < 1. (77) си
Предельно возможные изменения усилий при фк = 1 показаны на рис, 18 штрихпунктирной линией.
При больших ошибках, когда фк>-> I, но фс< 1. зона двухпарного зацепления будет сужаться, а при
Ло>^- илн при фс > 1 (78)
Ср
в зацеплении будет 1 аходпться фактически только одна пара зубьев, несмотря на наличие теоретического перекрытия зубьев (ev> 1), Условия зацепления см. в табл. 3.
Характер изменения коэффициента Ка = w'lwo при щ' — И)1 и U)' — W11 на активном участке линии зацепления при различных значениях фк и фс показан на рис. 18.
Максимальные статические усилия Щст в характерных точках линии зацепления могут быть представлены
в виде
= “’(Лхр,; WU, == “’О^сгУ/ ww -= “"(Ла^-“у, K’oA\y,: WP, ш0КаР,
(79)
Для точек U2 и Ur (рис. 18) следует считать w' = щ„, т. е. KaUt = KaU1 = = 1. При расположении полюса в зоне однопарного зацепления KnW — 1-Поэтому в расчете на контактную выносливость КНа~ 1
Для точек Pi и Рг при двухпарном зацеплении в соответствии с формулой (73)
^аР, = ^аР, %аР = °-42 (* 4К)-
(80)
Формулой (80) можно пользоваться при фс С 1, т. е. при фк «С 1,37. При больших значениях фк следует считать КаР~ 1-
Для очень тихоходных передач прн расчете усилия w по формулам (31), (34) считают ~ ^a.
Динамические усилия на зубьях при крутильных колебаниях (коэффициент Кир) и резонансные режимы
Зубчатые колеса составляют вместе с валами и другими присоединенными деталями общую упругую систему,
202
Зубчатые передачи
Рис. 19. Схема нагружения колес:
1 — ведущего, 2 — ведомого
динамический расчет которой представляет большую сложность. Однако такая общая система нередко распадается на две части, динамически слабо зависящие одна от другой, так как жесткость зубьев с3 ~ (20 -4-30) Н/(мм-мкм) обычно значительно превышает жесткость валов св як ~ (0,5—2) Н/(мм-мкм). Поэтому при анализе колебаний сопряженных зубчатых колес в связи с упругими деформациями зубьев инерционными нагрузками от других присоединенных деталей пренебрегают и считают, что вращающие моменты постоянны. С другой стороны, при расчете крутильных колебаний зубчатых колес и других деталей в связи с упругими деформациями валов зубья можно считать жесткими.
Частота собственных колебаний сопряженных колес. При контакте зубьев вблизи полюса, когда в зацеплении находится одна пара зубьев, дифференциальные уравнения вращения сопряженных колес имеют вид (рис. 19):
— Л1>! —
* ml — = ' 1 — warbi'y
, (81)
"V
m2 ~dt— ~ wari>2,
где Jmi< J— моменты инерции колес, 7\, — вращающие моменты,
отнесенные к единице ширины зуба.
При равномерном вращении da>-Jdt = = 0, da2/dt — 0, и из равенства (81) следуют соотношения
7\
= ®т = —L rbl
Л, гы
= Ca,6m = const. (82)
Если под воздействием малого случайного возмущения деформация в некоторый момент времени t = 0 увеличилась на Д6О, то возрастает и усилие на зуб, условия равновесия колес при постоянных значениях моментов Л и Tj нарушаются и угловые скорости колес начнут периодически изменяться, что будет сопровождаться изменением усилия и деформации с той же частотой.
Введя в равенства (81) выражения (82) и обозначая Дш = wa — wm, получим
7ml = ~^wrbv
. (83>
причем
Дш=Си)Дб. (84)
Если значение Дб0 достаточно мало, то контакт зубьев при колебаниях не нарушится.
Условие совместного движения зубьев (рис. 20) требует, чтобы ско-
Нагрузки, действующие на зуб
203
Ряс. 20. Схема совместного движения упругих зубьев вдоль линии зацепления: j2 — положения соприкасающихся поверхностей зубьев в момент времени t\ Г, 2' — положения в момент времени t + dt (вся деформация зубьев условно показана в виде деформации смятия)
О,
рость сближения их вдоль линии зацепления равнялась скорости увеличения деформации зубьев
1 Ы
d (AS)
I Г — v —
2 Ь2 ft
(85)
Дифференцируя обе части равенства (85) и подставляя в них значения dajdt и duydt из равенства (83), получим с учетом соотношения (84) дифференциальное уравнение собственных колебаний сопряженных колес
J^+^AS^O. (86)
где /2 2 \
= I -=~ + -=— с№. (87) ' 'mi J ml
Решение ;, ; ;
иых условиях Д6 (0) = А60 и
—о = 0 Д6 = Д6О cos РаЛ
уравнения (86) при началь-
Частота собственных колебаний колес (в Гц) при однопарном зацеплении вблизи полюса
f___Нш
2л
585
V МПр
(88)
где МПр—приведенная масса колес, кг/мм; cw = 13,5 Н/(мм-мкм);
_1_ = гг + Л1пр fcl \ Jmi )
(89)
Для оценки значений Jml и представим колеса в виде дисков с радиусами гЬ1 и rb2, для которых J т\ “ О’5Р1Л^1 > Jm2 ~ ^’^Р2Лгд2» (^0)
где рь р2 — плотности материалов колес.
Выразив rfcl через диаметр начальной окружности ведомого колеса по формуле
^щ/2 COS (Хда
ГЬ1 = 2й
и подставив значения Jт из формулы (90) в формулу (89), получим
8 cos2 Оц, ( — -|- и2 I
\ Ра ’
Для стальных колес прн = 20° d2
Мпр^З.б-Ю-’р^, (92) где dW2 — в мм; МПр — в кг/мм. В общем случае при определении Jml и Jmi должны учитываться полярные
204
Зубчатые передачи
t
Рис. 21. Изменение по времени t силы F, передающейся на колесо со стороны зубьев; Т время одного оборота, с
моменты инерции деталей, жестко связанных с зубчатыми колесами.
С учетом соотношения (92) формула (88) принимает вид
. fw^3,l-10^^±±Li (93)
где dan — в мм; fa, — в Гц.
В периоды двухпарного зацепления частота собственных колебаний сопряженных колес возрастает до
fp = fw 1/~ 1-29/“" <94>
На собственную частоту колебаний сопряженных колес определенное влияние оказывает также податливость обода и тела колес, упругость валов и масляного слоя, податливость опор. Поэтому расчет при использовании формулы (93) дает лишь ориентировочное значение частоты, которое может быть уточнено экспериментально.
Помимо высоких частот колебаний сопряженных колес передачи имеют также ряд значительно более низких частот собственных крутильных колебаний, относящихся к упругой системе, которую образуют колеса вместе с валами и другими вращающимися деталями. При расчете этих частот упругостью зубьев можно пренебрегать. Основы методов расчета крутильных колебаний изложены в гл. 21.
Резонансные и вынужденные колебания. Если частота собственных колебаний колес совпадает с частотой какой-либо переменной силы, действующей в передаче, возникают резонансные колебания, которые могут явиться источником серьезных дефектов.
Основные переменные силы в передаче связаны с периодическим входом зубьев в зацепление, когда за каждый
оборот колесо с г зубьями воспринимает г импульсов, так что изменение по времени t силы F, передающейся на колесо со стороны зубьев, имеет вид, показанный иа рис. 21. Наиболее сильная составляющая такой возбуждающей силы имеет частоту (в Гц)
f 1 пг 100(к' Г95)
fz~ Тг 60 пт ’ (95)
где Тг — период импульсов, с; о — окружная скорость, м/с; m — модуль, мм.
Так как форма импульсов ие синусоидальна, а их характер и период Tz из-за неточностей зацепления ие вполне одинаковы, то наряду с частотой fz могут проявляться возбуждающие силы с кратными ей частотами 2fz, 3fz и т. д., а также с близкими частотами f = п (z ± &)/60, где k ~ 1, 2 и т. д.
При работе на небольших частотах вращения частота fz может резонировать с низкой частотой собственных колебаний системы колес и валов, а при работе с большой частотой вращения — с частотой собственных колебаний сопряженных зубьев.
Изменение усилия, действующего на зуб при низкочастотном резонансе, показано иа рис. 22. Несмотря на ограниченное число циклов, которое зуб успевает испытать за время нахождения в зацеплении, уровень переменных напряжений в зубе может стать значительным, так как резонансное усиление колебаний проявляется весьма интенсивно. Кроме того, возникающие при резонансе колебания колес вызывают дополнительные ударные нагрузки при входе зубьев в зацепление. Работа передачи на резонансных режимах не допускается.
1 В некоторых передачах, например в редукторах поршневых двигателей,
Нагрузки, действующие на зуб
205
крутильные колебания могут иметь вынужденный характер.
Динамические усилия на зубьях, связанные с крутильными колебаниями и учитываемые коэффициентом Ккр. оценивают обычно экспериментально. При проектировании значение Ккр выбирают по опыту работы аналогичных конструкций.
Поломки зубчатых колес могут быть связаны также с резонансными колебаниями ободьев и дисков колес [8].
Оценки возможности резонанса. Для оценки возможности резонанса определяют приведенную массу колес Мпр. собственные частоты колебаний колес при однопарном (/ш) и двухпарном (fp) зацеплении.
Расчетные резонансные окружные
скорости
Урез = ^mfp\ upeJ =
(96)
где при основном резонансе X = ), при резонансе со второй гармоникой к частоте зацепления X = 0,5.
Возбуждение при двухпарном зацеплении обычно бывает более сильным. Из-за жесткости смежных валов частота несколько повышается, а из-за податливости ободов и опор снижается, поэтому для ответственных передач резонансные режимы нужно уточнять экспериментально тенэометрнрованием колес.
При проектировании передач резонансных значений окружной скорости следует избегать.
Динамические усилия на зубьях при пересопряженин (коэффициенты
и Kv)
Пересопряжение зубьев сопровождается колебаниями зубьев, причем полная (динамическая) нагрузка w может существенно отличаться от нагрузки шст, определяемой рассмотренными выше условиями статического нагружения. В большинстве случаев нагрузка и> в характерных точках линии зацепления больше нагрузки шсТ в тех же точках, что позволяет условно считать
w = шст + wB (97)
или
w = ШотКо. (98)
Рнс. 22. Осциллограмма изменения усилия на зубе при резонансе
где we — «сила удара»; Кв > 1 — коэффициент удара.
Однако при большой окружной скорости и отрицательных ошибках (Д < < 0) возможны случаи, когда динамическая нагрузка при однопарном зацеплении реализуется неполностью, так что w на этом участке оказывается меньшим, чем шст, и понятие силы удара лишается смысла.
В общем случае удобнее относить w0 н w к передаваемой нагрузке = — 0’номК'рКкр и считать ц> = ш0Лд, wv = wnKa (Кв — 1), (99) где коэффициент динамической нагрузки
Яд = какв.
Величина /Сд может быть и больше, и меньше единицы.
Для статически ненагруженных зубьев ш,.т = 0, так что
w = wB. (100)
Динамические усилия (удар) испытывает пара зубьев / (рис. 23), входящая в зацепление. Если шаг ведущего колеса с учетом деформации зубьев меньше шага ведомого, то ножка ведущего зуба 1 ударяет по кромке зуба ведомого колеса 2 вне линии зацепления вблизи точки Ру (рнс. 23, а). Такой удар условно называют кромочным. Если шаг ведущего колеса с учетом деформации зубьев превышает шаг ведомого, то пара зубьев / входит в контакт на линии зацепле-
206
Зубчатые передачи
Рнс. 23. Схема возникновения кромочного (а) н срединного (б) ударов зубьев
иия вблизи точки (72 уже после того, как точка контакта зубьев II отойдет от линии зацепления (рис. 23, б). Такой удар условно называют срединным. Если зубья I встречаются ранее точки (72, так что пересопряжение частично происходит еще на линии зацепления, то происходит неполный срединный удар.
Кромочный удар возможен при любых значениях До (табл. 3), в том числе и в точной передаче (при До =- 0), так как при ошибках Д, заключенных в пределах —До =С;Д ^До, всегда возможны случаи, когда шаг ведущего
колеса с учетом деформации зубьев будет меньше шага ведомого. Полный срединный удар возможен только в передачах при фс> 1, когда ошибка До превышает упругую деформацию зубьев.
Неполный срединный удар, возможный при фс^1, имеет несколько ослабленный характер, так как к моменту начала удара входящие в зацепление зубья оказываются уже частично нагруженными.
Характер динамических усилий существенно зависит от соотношений между периодом собственных колеба-ний сопряженных колес
1 1 /" Мпр
Т------2л (101)
и отрезками времени, в течение которых протекают отдельные фазы пере-сопряження зубьев. В формуле (101) принимают f ~ fu, или f = fp в зависимости от участков линии зацепления.
При умеренных окружных скоростях vK= 77ТН < 1 hvc— Т!ТС<. 1, где Тк и Тс — продолжительности начальных периодов кромочного и срединного ударов, когда точка контакта одной из пары зубьев находится вне линии зацепления. При этом за время пересопряжения зубьев успевает произойти несколько колебаний, сопровождающихся перераспределением нагрузки с одного зуба на другой. Реа
3. Влияние параметров неточности зубьев на условия статического зацепления и характер ударов
*к ♦с Условия статического зацепления на участках перекрытия зубьев Характер возможных ударов зубьев прн — До Д До
М>„= о *с “ Двухпарное зацепление Кромочный н неполный срединный
° < ' 0 < *с. « I
> 1 Неполное двухпарное зацепление
М>с > 1 Однопарное зацепление Кромочный и срединный
Нагрузки, действующие на зуб
207
лизуются не только первый, но и последующие максимумы усилия. При срединном ударе зазор между входящими в зацепление зубьями исчезает уже в процессе удара, который полностью реализуется. Благодаря демпфированию в системе колебания от ранее происходящих ударов в значительной мере затухают, что позволяет считать скорость вращения колес к моменту начала нового пересопряжения равн.л-ериой.
С увеличением окружной скорости величины vK и vc становятся больше единицы, и тогда за время пересопряжения зубьев скорость вращения колес практически не успевает измениться. Входящая в зацепление пара зубьев воспринимает иа себя всю дополнительную нагрузку от погрешности в основных шагах, а динамические усилия достигают своих максимальных значений.
При еще более высоких окружных скоростях v3 = 77?’я, где Тя —полное время нахождения в зацеплении пары зубьев, также становится больше единицы. Тогда скорость вращения колес практически не меняется в течение всего времени нахождения пары зубьев в зацеплении. Возникающая при кромочном ударе деформация остается без изменения до выхода зубьев из зацепления, так что реализуется только первый максимум усилия. Срединного удара вообще не происходит, так как зубья отходят от линии зацепления раньше, чем устраняется зазор между ними. Колебаний колес нет, и динамические нагрузки постоянного знака дают дополнительный вращающий момент. Это вызывает изменение среднего взаимного положения колес и требует рассмотрения движения колес в целом.
Полный расчет динамических нагрузок в зубьях — задача очень сложная и полностью не решенная. Ниже приведена приближенная методика расчета, основанная иа теории динамического пересопряжения зубьев и экспериментально проверенная сопоставлением с результатами опытов разных исследователей практически во всем возможном диапазоне измерения параметров относительных ошибок (от Фс 555 0 до фс 50) и достаточно ши
роком диапазоне изменения параметров инерционности передач (vH — — 0,1-4-11 и vc— 0,5 — 10). При экспериментах окружные скорости достигали значений v — 50 м/с, удельная нормальная сила wa — 570 Н/мм, ошибка основного шага До ~ 72 мкм, передаточное число и = 1 -г-2. Расчетные оценки динамических сил вне резонансных режимов соответствуют, как правило, верхним значениям экспериментальных данных. Для расчета динамических сил важное значение имеет правильное определение частоты собственных колебаний передачи и установление действительных наиболее вероятных значений ошибок основных шагов с учетом приработки зуба.
Расчет динамических сил. В табл. 4 приведены формулы для расчета коэффициентов Ка, Л/рПтИ Kv в практически наиболее распространенном диапазоне окружных скоростей, когда v3 = Т/Т3 < 1. Коэффициент динамической нагрузки Л"д = KaKv Относительные ошибки основного шага фс и фк определяются формулами (74) и (76) с учетом (67):
фс = 9,5-~^-; ф„=1,37фс, (102)
wa9
где Ао — в мкм, w,lS) — в Н/мм.
При расчете кромочного удара на заданные значения относительных ошибок фс и фк ‘ 1,37 фс последовательно определяют:
1) отношение радиусов кривизны эвольвент в точке Pj (при входе в зацепление)
Р1Р, _
_________(1 + ц)81П<Хц, _ ( (i+^)2-CoS’a“’
(ЮЗ)
2) время кромочного контакта зубьев вне линии зацепления
Т’; = 6,17-10-4-~ X
/” ^а|) (1 + ( Р‘Р
у Ош sin ' РйР,
208
4. фррмудм. для расчета коуф^виедтр® »»!*»
Удар Точна Ка При .Д'ги. ;;1 , — Диш» 4 '
♦с . »' *с > 1
iKpwew-s ицй ф, <М2 (1 Л %) 1.73 , 1лз+хфе- 1) » + Нт— - *>*Г но ее более _ Xv Ии
у. 0,58 (1 + <Ц>Н) г пр»4в< 1: 1 при > 1 1 + *„ К—~ 1.73 + «с - 1). -ио не менее Д.37
Срединный и, 1 1.42 +- + 0.58*с 1+1/1 + 2.74(*с-1) 1 + «9 Ит - -ov ио не более Ит
. П р и 'м е ч а и и е. Пр» Фс > .1 л кромочном и средимом ударах Кд = 1
Где а*. ** ;в мм; аг» — в Н/мм; о — в м/с; fj — в с;
3) в период собствешиях колебаний сопряженных колес (в с)
т=* (105)
, Лис, г >i
где f&KC — экспериментальное »и ячейке собственной: частоты.
Если оно неизвестно, принимают
, Т« 0,0364'(106)
где приведенную массу Afnj’«лес в кг/мм определяют по формулам (89)— (92);
4) коэффициент
<1071
5) предельно возможный KeVim” фактическийKlvK) коэффициенты удара и коэффициент полной динамической нагрузки /(^к> —• отдельно для точек Pi и Ut (по табл. 4);
6) снлу удара wv и паяную динамическую силу w по формулам (99).
'При расчете срединного удара последовательно определяют:
1) отношение радиусов кривизны эвольвент в точке (прн выходе из зацепления)
₽»» ’’ ’ (1+«)31п а«
• . • -1; (108)
2) характеристическое время срединного удара (в с)
3) коэффициент
- Ti ус = vH -KJ-;
(109)
(ПО)
4) предельно возможный я фактический коэффициенты удара коэффициент полной динамической нагрузки Х'дJ (по табл. 4);
S) симу удара «9 и полную дйиМми-ческую силу • по формулам (99).
Нагрузки, действующие на зуб
209
Более детальные расчеты для быстроходных передач с учетом условий реализации срединного удара и других особенностей могут быть выполнены согласно работам [G, 7 и др |. Из этих расчетов вытекают следующие основные особенности развития динамических нагрузок в прямозубых передачах.
Максимально возможный коэффициент динамической нагрузки в точке Pj при кромочном ударе
11m 11m
Ср
— ~т~ (i +- Фк) да 0,73 (1 -j- фк)
соответствует передачам с большой инерционностью (практически для vK > 1), когда в процессе удара скорость вращения колес и усилие между парой зубьев II не меняются. При меньшей инерционности коэффициент /СдК) определяется формулой
(>Ч)
где коэффициент смягчения удара хк зависит от параметра vK (рис. 24). Эта зависимость хорошо аппроксимируется ломаной линией:
при 0 vK <7 1
хк
сн
еи + СР
I Ср -+ — VK си ,
« 0,58-ф 0,42vK;
при vK > 1 хк = 1, что учтено в табл. 3.
Сила удара w„ = w — шСТдля цельнокованых колес при фс < 1 может быть приближенно оценена по формуле
w0 да 0, lv X
где v — в м/с; aw — в мм; До — в мкм;
Wq и wv — в Н/мм.
При малых окружных скоростях сила удара пропорциональна окружной скорости и увеличивается с ростом ошибки Ао.
Рис. 24 Зависимости коэффициента смягчения кромочного удара х^ от параметра
/ — теоре(ическ 1я [71 2 - расчетная
Максимально возможный коэффициент динамической нагрузки при полном срединном ударе
<С?1т = > +
+ 1/^ 1 + 2 —~ (фс — 1) «а » Ср
да 1 + У 1 +2,74 (фс-1).
Это значение соответствует
передачам с большой инерционностью, когда зазор между зубьями пары I, равный (с учетом деформации зубьев II) До— (и1н/с ), не меняется до полного разжатия этих зубьев. После этого ведущее колесо начинает ускоренно вращаться под действием постоянного вращающего момента, а зубья пары I сближаться, в результате чего происходит удар. При меньшей инерционности удар также смягчается. При неполном ударе динамические нагрузки меньше.
При малой окружной скорости сила срединного удара, как и кромочного, пропорциональна скорости. Для ие-
210
Зубчатые передачи
Рис. 25. Зависимость коэффициента смягчения «ромочного удара статически не нагруженных зубьев х00 от параметра ф
точных передач (при фс> 1) можно считать [7J
wv — 0,32v X СС/
где
Т =
н/мм’ <"2)
1 -Г и \ Р%р, /
/| + -Г+|,37
2,37
Величина Т меняется в пределах от 0,56 до 1. Если принять V 0,6, и2 , ,
считать в среднем утр^РгРз/РаРа)^
1
ж д , ие учитывать снижения жесткости зубьев при кромочном контакте и учесть экспериментальную поправку иа собственную частоту колебаний <Ху = 1,1, то формула (112) примет вид
% = н/мм> (113)
где aw — в мм; До — в мкм; v — в м/с;
£о = /Д^
Выражение (ИЗ), предложенное А. И. Петрусевичем (прн = 0,25), широко применяется для приближенной оценки силы удара зубьев и,
в частности, использовано в ГОСТ 21354—87 (с уменьшенным множителем, который для прямозубых передач без модификации головки принимается
— 0,16).
Сила удара в статически слабо нагруженных передачах. В статически слабо нагруженных передачах (коробки приводов агрегатов и др.) зубья после кромочного удара быстро разжимаются, так что реализуется только первый максимум. Сила удара при этом мало отличается от значения при отсутствии статической нагрузки (шк0 — — 0 или фк-»- оо). Для этого предельного случая сила кромочного удара w — w0 = срЛои“, где коэффициент определяется по графику, приведенному на рис. 25 в зависимости от характеристического угла фкоз, для которого [7]
. - * 1 Т1
Ч» Фкоо VKOO О-т ’
1 Kl
здесь
1 /~ си ~Ь Гр т1= |/---------1.54Т;
Ср
77. =2,24-10"s X Ki у
Др (2и? SIH
(114)
причем dwi', aw— в мм; До — в мкм; v — в м/с; Т (в с) определяют по формулам (105) или (106), а отношение PiPi/PsPj — по формуле (103).
Графиком иа рис. 25 можно пользоваться для оценки силы кромочного удара статически слабо нагруженных зубьев при фс > 1 н vK < 0,5, считая
+ 0,73фкх» (115)
Расчетная динамическая нагрузка.
Расчетную динамическую нагрузку определяют для каждой характерной
Расчет зубьев на прочность при изгибе
211
точки линии зацепления:
- &ок(„к>;
WU, = w0KnU„
(П6)
WP, -=w0KaP,- .
В качестве значений Кяиг и Л’дщ принимают те из коэффициентов и Хдс) для точек U2 и Н7, которые имеют большее значение.
Пример. Найти силу удара wB и динамическую нагрузку ш в передаче с параметрами: aw - 250 мм; и ~ 2; т~ 5 мм; aw = 20°; о -= 15,7 м/с; 7-я степень точности (До --- 28 мкм); w0 — 39,3 Н/мм, Zj — 32; dm — 320 мм.
Последовательно находим для кромочного удара: р1/( /р2/> = 0,223; Фс - 0,677 (фс< 1); фк = 0,928; Т* = = 1,76-10 4 с; Мпр = 7,4 -10-5 кг/мм; Т = 3,11 • 10-4 с; vK = 0,560; в точке Р^ Ха = 0,810;/(„и га= 1,73; Хо = 1,41; Хд = 1,14; а>0 = 131 Н/мм; w = = 448 Н/мм; в точке U2: Ка = 0,975; /Со Um = 1,978; Хо= 1,55; Кя = 1,51; ш0 = 211 Н/мм; w= 595 Н/мм; для срединного удара: р2Р /р1Р — 1,081; Тс‘= 2,05-10-4c;vc=,0,485;Xullm = = 1,81; ХД=Х„= 1,393; w0 = = 154 Н/мм; w = 548 Н/мм.
По расчету согласно рекомендациям к ГОСТ 21354—87 g0 = 5,3; Ко = = 1,468; Кл = 1,19; w0 = 149 Н/мм; ои = 467 Н/мм.
Полный расчет согласно табл. 3 (помимо расчета по ГОСТ 21354—87) целесообразно проводить для вновь проектируемых, особенно быстроходных ответственных передач.
При расчете передач со смещениями параметры ф и v надо определять по фактической геометрии зуба и жесткостям. Уменьшение динамической нагрузки при модификации зубьев можно учесть, принимая в качестве расчетной ошибки
Арасч — Д» — Дао, где Дао — нормальная глубина модификации профиля головки зуба. По
ГОСТ 21354—87 в этом случае принимают 6р — 0,11.
Влияние динамических нагрузок иа контактную выносливость поверхности зубьев обычно проявляется слабее, чем на выносливость при изгибе, особенно в зубьях невысокой твердости. Поэтому Kfo — Ко. а
Хно= 1 + 1) (Ко- 1), (И7) где при твердости НВ > 350 т) = 0,75; при твердости НВ 350 т) = 0,35.
РАСЧЕТ ЗУБЬЕВ
НА ПРОЧНОСТЬ ПРИ ИЗГИБЕ
Напряжения при изгибе. На единицу ширины зуба действует нормальная нагрузка wa, направленная по линии зацепления, и касательная нагрузка от сил тре.шя q = fwa, где при наличии смазочного материала f = 0,05-? 0,08. Силы трения направлены в сторону относительного скольжения зубьев, т. е. на ведущем зубе от полюса, на ведомом — к полюсу (рис. 26). Трение несколько увеличивает изгибающий момент иа зубьях ведущего колеса и уменьшает на зубьях ведомого. Практически при расчете зубьев на изгиб влиянием трения можно пренебрегать.
Под действием нормальной нагрузки wa на растянутой стороне зуба возникают меньшие напряжения, чем иа сжатой. Однако вследствие того, что поверхностные слои материала зуба оказывают меньшую сопротивляемость усталостным растягивающим напряжениям, чем напряжениям сжатия, наиболее опасными являются напряжения, возникающие иа растянутой стороне зуба. Наибольшие напряжения изгиба действуют в плоскости, нормальной к поверхности зуба. Поэтому поломка зуба происходит, как правило, ие по плоскому, а по цилиндрическому или близкому к нему сечению (рис. 27).
Номинальное напряжение изгиба в опасном сечении можно определить по формулам сопротивления материалов. Расчетная схема зуба показана на рис. 28. Действующую по линии зацепления нагрузку wa раскладывают иа две составляющие — из-
212
Зубчатые передачи
Рис. 26. Направление действия сил трения: а — иа ведомом зубе; б — на ведущем
гибающую wa cos ух и сжимающую wa sin уж. Изгибающие напряжения, возникающие в опасном сечении зуба,
Л1И 6що/1яс08уж
°и = "пу----------5----• (Ио)
Ж И S|
напряжения сжатия
aCJK = -^=^^-. (И9)
Рис. 27. Типичная поломка зуба при испытаниях на пульсаторе
Рис. 28. Схема ауба при расчете иа изгиб
где — толщина зуба в опасном сечении; hx — плечо изгиба.
Суммарные номинальные напряжения на растянутой стороне переходной кривой зуба
о0 = ои осж = wa X
х /6йясо81я щпу» у (120)
Формулу (120) можно привести к виду
wv
ао = ^о~. (121)
где удельную расчетную окружную силу wF принято определять по усилию, действующему на делительной окружности, т. е.
^u>i cos а
а>_ = ——- = w---------= wa cos а;
F dt cos Ощ
(122)
здесь а — угол профиля исходного контура.
Безразмерный коэффициент
и sjcosa \ «1 /
(123)
называют коэффициентом, учитывающим форму зуба (коэффициентом формы зуба) при расчете номинальных на
Расчет зубьев на прочность при изгибе
213
пряжений. В ряде прежних работ коэффициентом формы зуба называли обратную величину 1/Kfo. Чем больше коэффициент формы зуба, тем больше напряжения при данных силе и модуле.
Из-за концентрации напряжений иа переходной поверхности местные упругие напряжения ар будут больше номинальных о0, что учитывают введением теоретического коэффициента концентрации напряжений
°F=aoao- <124)
. Местные упругие напряжения, возникающие в зубе при изгибе, могут быть определены как аналитическими методами [3], так и экспериментально, например методом фотоупругости (рис. 29). Наибольшие напряжения соответствуют наибольшей частоте полос и находятся у основания зуба на переходной поверхности.
Максимальные местные напряжения
aF = YFS-^' (!25)
где YFs = aaYFo. (126) Зависимость коэффициента Yrs от
Рис. 29. Интерференционные полосы при статическом изгибе модели зуба нз оптически активного материала
числа зубьев г и коэффициента смещения х для зубьев с исходным реечным контуром по ГОСТ 13755—81 при приложении силы к вершине зуба показана на рис. 30.
рнс. 30. Зависимость коэффициента формы по местным напряжениям: Yps от числа аубьев х и коэффициента коррекции X при приложении нагрузки к вершине зуба при исходном реечном контуре по ГОСТ 13755 — 81
214
Зубчатые передачи
Напряжения изгиба ор пропорциональны нагрузке wp и растут с увеличением ее плеча (но не пропорционально из-за уменьшения в определенных пределах коэффициента концентрации). Так как максимальная динамическая нагрузка действует в первые моменты зацепления, то в худших условиях обычно находится ведомый зуб, для которого опасным может быть приложение нагрузки на кромке зуба (в точке Рх, см. рис. 3) и в точке U2.
Для ведущего зуба опасным также может быть приложение нагрузки на кромке (в точке Р2) или в точке когда проявляется влияние срединного удара и возрастает коэффициент концентрации. Коэффициент формы зуба при приложении нагрузки в точках начала или конца участка однопарного зацепления U:
(127)
Определив из геометрического расчета диаметр окружностей du, па которых расположены точки U, можно найти усредненное значение коэффициента У г в зависимости от параметра
<12»> по формуле
Ye « 1 — 0,35/7. (129)
В развернутом виде для прямозубых передач
Для приближенной оценки теоретических коэффициентов концентрации напряжений можно пользоваться формулой
а0 = 1 + 0,15-^-, (131)
Pzn
где Pzn — средний радиус переходной поверхности; $£ — толщина зуба в опасном сечении.
По мере уменьшения плеча силы от h х (см. рис. 28) до h'x величина аа увеличивается, причем
» аа <132)
пх
Более подробные сведения о коэффициентах формы зуба для передач с другими исходными контурами, а также о коэффициентах ао и Уе приведены в работах [1, 3 и др.].
Пределы выносливости зубьев и запасы прочности. Разрушение от усталости начинается на растянутой стороне. Если зубья испытывают одностороннее нагружение, то цикл нагружения будет отнулевым. Если нагрузки на зуб последовательно прикладываются с разных сторон (например, у промежуточных шестерен) и величины их одинаковы, то цикл получается симметричным. При разных нагрузках по формулам (8) и (9) гл. 2 можно найти среднее ат и амплитудное а а значения нагрузки и номинальные напряжения.
Коэффициент запаса сопротивления усталости зуба определяют как отношение разрушающей нагрузки щразр к действующей w, причем щра3р должна быть приложена в той же точке профиля, что и w:
Sp = ^ (133)
w
Переходя с помощью формулы (121) к номинальным напряжениям, найдем
°о разр
Sf ----------
(134)
где а0 РазР — номинальное напряжение, соответствующее разрушающей нагрузке. Аналогичным способом можно выразить коэффициент запаса прочности через местные напряжения °F и °F разр-
Существуют два метода определения Оразр и запасов прочности.
1-й метод — по данным усталостных испытаний гладких образцов и образцов с надрезом; коэффициент запаса прочности для отнулевого цикла
= X <135)
для симметричного цикла
Sf =
°-1еа С.о0
(136)
Расчет зубьев на прочность при изгибе
215
При разных нагрузках, действующих в ту и другую сторону,
SF = _-----, (137)
~Г~ аоа + Фааот еа
где о_! — предел выносливости материала сердцевины зуба; еа — коэффициент влияния абсолютных размеров; фд — коэффициент влияния асимметрии цикла. При расчете стальных зубьев обычно считают е0 ~ 1, ~
as 0,5ав(, где аве — предел прочности сердцевины зуба.
Эффективный коэффициент концентрации напряжений в зубе устанавливают сопоставлением результатов усталостных испытаний гладких образцов и образцов из того же материала и той же термообработки, но имеющих надрез по форме переходной поверхности зуба и подвергнутых поверхностной механической и химикотермической обработке.
Зависимость между kQ и ао обычно представляют в виде
fco = l+9<J(a0-l), (138)
где qa — коэффициент чувствительности материала к концентрации напряжений, которым условно учитывают также влияние поверхностной обработки.
Для зубьев, подвергшихся нормализации, улучшению и поверхностной или объемной закалке, qa яе 0,8 при твердости HRC3 < 35 и <?о г» 1 при твердости HRC3 > 35.
Если зубья подвергнуты поверхностной химнко-термической обработке, то их напряженное состояние в значительной мере зависит от наведенных напряжений. В этом случае усталостные трещины зарождаются под упрочненным слоем. Эффект концентрации напряжений здесь уменьшается в связи с удалением очага разрушения от геометрического концентратора напряжений (переходной кривой). Для цементованных галтелей принимают <у0 ~ 0,2 или ka устанавливают независимо от значений ая. Для стальных зубьев цементованных, азотированных или цианированных
ka яе 1,2. При грубой оценке прочности можно считать для зубьев из нормализованного и улучшенного материала ka = 1,8, для закаленных зубьев ka = 2,0; для чугунных зубьев ka — 1,2.
2-й метод — по данным усталостных испытаний непосредственно зубьев, как это принято в ГОСТ 21354—87. При таких испытаниях в полной мере учитываются присущие зубчатым колесам технологические особенности изготовления, влияние хнмико-термиче-ской обработки и другие факторы. По имеющимся данным, при базе испытаний 4-10® циклов предел выносливости зубьев цементованных и нитро-цементованных из сталей, содержащих молибден (25ХГМ) или более 1% никеля и не более 1% хрома (20ХН2М, 12ХНЗА и др.), aFIlmb= 950-4-1000 Н/мм2; цементованных и нитро-цементованных из других сталей (20Х, 12Х2Н4А, 20Х2НЧА, 35Х и др.), 700-?800 Н/мм2; азотированных oF llmb = (300+ 18-HRC3) Н/мм2, где 24—40 HRC3 — твердость в сердце-вине зубьев.
При объемной закалке зубьев °+11тЬ~ 500:600 Н/мм2; для зубьев, закаленных npHHarpeBeTB4,aF1Imb= = 700 4-900 Н/мм2 при твердости переходной поверхности 52—62 HRC3 и cfFHmb= 500-4-600 Н/мм2 при 48— 55 HRC3; для зубьев из нормализованной и улучшенной стали при 180— 350 НВ aF !!ш ь = 1,8-НВ.
Шлифование переходной поверхности зубьев снижает указанные значения dp 11т ъ на 20—30%, дробеструйная или электрохимическая обработка повышает их на 10—20%. При симметричном цикле нагружения oF1Imb снижается на 20—30%.
Фактическое число циклов нагружения при работе на постоянном режиме
/VK = 60ал/, (139)
где а — число вхождений в зацепление каждой стороны зуба за один оборот; п — частота вращения, мии-1; t — время работы, ч.
216
Зубчатые передачи
Предел выносливости ар Jlm, соответствующий числу циклов A/H, определяют по формулам
°F нт " aJV.v, (КО)
где ________
’F [ V ,
Гдг = у при Л'т1п -
О'Л (Mi)
чр / t\<
Y*=у —п₽и -v,< Л/°-П42)
При расчете по формулам (135)— (137) Ю7 циклов, oft = а ;
по формулам (140)—(142) Л'F llm = = 4 10е циклов, ой = aFiimb- ^ля зубьев с нешлифованной переходной поверхностью при твердости НВ> > 350 принимают qF — 9, в остальных случаях qF = 6. При твердости сердцевины НВ 350 принимают No == 107 циклов и при твердости НВ > > 350 Л'о--!5-107, Л'т1г1 = 5-10* циклов При меньшем числе циклов проводят расчет на малоцикловую усталость.
При расчетах на выносливость зубчатых колес в общем машиностроении используют следующие значения коэффициента запаса прочности SF:
1,8 — для отливок стальных или чугунных, термически не обработанных;
1,6 — для отливок стальных или чугунных, подвергнутых отжигу, нормализации или улучшению,
1,4 — для поковок стальных, подвергнутых нормализации нлн улучшению;
1,8 — для поковок стальных; зубья подвергнуты объемной закалке (НВ > > 300);
2,2 — для поковок и отливок стальных, термически обработанных; зубья имеют твердую поверхность (НВ > > 350) и вязкую сердцевину.
В передачах, где излом зубьев не допустим по условиям техники безопасности или связан со значительными производственными потерями, коэффициенты безопасности рекомендуется увеличивать на 50% по сравне
нию с приведенными выше. Для авиационных редукторов принимают Sp = = 1,5—3,0. ’
При определении допускаемого напряжения изгиба <т?,р по формуле (31) дополнительные коэффициенты /д, К,-, Yr приближенно равны:
Уй -- 1,08—0,177 1 g т,
Yx-= 1,05 — 1,25- 10~4d,
где т — модуль, мм; d — в мм; при полировании переходной поверхности к — 1,054-1,2.
Более детально рекомендации по выбору пределов выносливости зубьев, коэффициентов безопасности и других коэффициентов приведены в приложениях к ГОС! 21354—87. Особенности расчета при многорежимной работе рассмотрены ниже.
Статическая прочность. Зуб проверяют также на статическую прочность при максимальной кратковремеииой перегр узке.
При твердости сердцевины зубьев НВ < 350 во избежание чрезмерной пластической деформации запас по текучести
<143’ ио
принимают не ниже 1,25.
Для стальных (твердость НВ > > 350) и чугунных колес во избежание хрупкого разрушения запас прочности
принимают 2,0—2,5.
Повысить сопротивление усталости зуба на изгиб можно, увеличивая модуль зацепления, используя усиливающее ножку зуба положительное смещение или применяя более прочный материал. Для снижения динамических нагрузок повышают точность изготовления колес и вводят модификацию поверхности зуба. Для уменьшения концентрации нагрузки у торцов зуб делают бочкообразным. Повышение предела выносливости зубьев обеспечивается: упрочнением поверхности, которое достигается химикотермической обработкой и наклепом впадин; уменьшением шероховатости
Расчет на контактную выносливость
217
поверхности у основания зуба, для чего полезно, в частности, применять направленное полирование впадин (в плоскости, перпендикулярной оси колеса); в ответственных передачах применением стали электрошлакового переплава, в которой отсутствуют неметаллические включения. При нарезании зубьев не следует допускать уменьшения радиусов переходной поверхности. Использование зубьев, не шлифуемых у основания после закалки (с поднутренной конфигурацией ножки), гарантирует отсутствие при-жогов от шлифования, которые снижают предел выносливости.
Следует добиваться возможно большей равнопрочности колеса и шестерни правильным подбором материалов и рациональным распределением смещений между зубьями. При проектировании высоконапряженных зубчатых передач целесообразно использовать специальный исходный производящий контур, возможности проектирования передач значительно расширяются при использовании обобщающих параметров [1].
РАСЧЕТ НА КОНТАКТНУЮ ВЫНОСЛИВОСТЬ АКТИВНЫХ ПОВЕРХНОСТЕЙ ЗУЬЬЕВ
Контактные напряжения. Рассмотрим сжатие двух цилиндрических тел, радиусы которых р2 и Pi равны радиусам кривизны профилей зубьев колеса и шестерни в точке контакта (рис. 31),
Опытами установлено, что деформации каждого цилиндра, как и при обычном испытании на сжатие, про-порционал! на нагрузке и обратно пропорциональна модулю упругости материала Р, т. е.
(145)
где X — некоторый безразмерный коэффициент пропорциональности.
С другой стороны (рис. 31), отрезок
Xj — Pi (I — cos 0j), (146)
где
sin 0! ~. (147)
Рис, 31. К расчету контактных напряжений в зубе: а — наружное зацепление, б - внутреннее
218
Зубчатые передачи
Так как а значительно меньше р,, то
(148)
Pl и
*, ^р,(1-(1-0,50^1^0,5-Д-.
Pi
(149)
Диалогично
х2 яй 0,5 ——. (150)
Ра
Так как ifr -f- Уг = -Ч ± хг» где знак плюс соответствует внешнему зацеплению, знак минус — внутреннему,
Из-за сил трения между зубьями максимальными становятся напряжения на поверхности контактной площадки, они больше на 15% ттах по формуле (157) (при коэффициенте трения f — 0,2). Поэтому в ряде прежних работ в качестве расчетной принимали формулу (157) с коэффициентом 0,145. В рекомендуемом приложении № 1 к ГОСТ 21354—87 в качестве расчетной принята формула максимальных нормальных контактных напряжений
он = -\f WaE™0
V 2л (1 —V2) у Рпр
(151)
откуда
а = 2 /I (152)
* ‘'ПП
« 0,418
^а^пр Рпр
(158)
где приведенный модуль упругости
Е _ z 153>
fcnP~ £, + £,• ( ’
и приведенный радиус кривизны
Для полюса с учетом формул (4), (11) и (13)
оно № 0,591 X
+ 1 2
---------- ЕПр. (159)
и sin 2am р '
л . (154)
Pup — . • Р2 ± Pl
Формулу (159) можно представить в виде ___________
°но = zezh ~ТГ~ ’ (160)
Подставляя выражение (152) в фор-
мулу „ wa Cf — —.... - 2о ’ (155)
где ______
^ = 0,5911///^-; (161) ’ bi -f~ с г
где оНт — среднее напряжение смятия, получим
о =_* 1/^ДД. (i56)
Нт 4/Л Рпр ' ’
Фактически напряжения распределяются по ширине площадки неравномерно и кроме нормальных возникают также касательные напряжения т, причем все напряжения пропорциональны аЯт. Расчеты показывают, что максимальные касательные напряжения возникают на некотором расстоянии от поверхности и определяются по формуле
2 — % __
н /sin 2а®
(162)
причем w — в Н/мм; Е — в МПа;
^(£>1 — в ММ.
Для стальных зубьев Z% --= 190 (МПа)1''2. Для передач, у которых коэффициент суммы смещений xs = Xj 4- х2 — 0, ZH = 2,49.
Так как по мере удаления от полюса приведенный радиус кривизны Рпр уменьшается, при той же нагрузке контактные напряжения возрастают и определяются формулой
~ ано х
Ттах —
0,127
wa^np Рпр
-1/_______“_____Ы
У (1 — ?) (“ ± 5) \ w )
(163)
(157)
Расчет на контактную выносливость
219
rjifi — нагрузка в точке
£=-рз—
-^±1 Р1
(164)
Если точка расположена вблизи основной окружности, то | -*• 1 и о„. оо. В действительности, од-** »
нако, зона контакта имеет конечную ширину, поэтому при больших значениях ан (р) величину £ следует уточнить, определяя ее по среднему значению радиуса кривизны поверхности иа площадке контакта.
Влияние смазки и кинематики передачи на выкрашивание. Масло, проникая в мельчайшие трещинки, возникающие на поверхности зуба в результате усталости, углубляет нх, и частицы материала откалываются. Поверхность зуба становится неровной, что ведет к возрастанию давлений и к дальнейшему разрушению поверхности. С увеличением вязкости масла повышается сопротивляемость поверхностного слоя, так как уменьшается трение, и смазочному материалу труднее проникнуть в микротрещины.
При движении с трением микротрещины, образующиеся в поверхностном слое, наклонены к поверхности (рис. 32). Зубья обкатываются и скользят один по другому. Если направления скоростей качения он и скольжения ос совпадают, то при приближении зоны контакта к микротрещине силы трения сдвигают металл так, что масло выдавливается из трещины, а трещина прикрывается. После того как зона контакта минует микротрещииу, силы трения будут способствовать ее раскрытию, но масло при пониженном давлении проникает внутрь слабо. Если скорости ои направлены в противоположные стороны, силы трения раскрывают микротрещину как раз в области высокого давления, причем устье трещины направлено навстречу масляной волне, что ведет к интенсивному проникновению сжатого высоким давлением масла в глубину поверхностного слоя и откалыванию частиц материала. Направления скоростей vK и vc совпа-
И V,
Рис. 32. Влияние направления качения и скольжения зубьев на проникновение смазочного материала о поверхностные микротрещины
дают в головках зубьев и противоположны в иожках, т. е. условия работы ножек на выкрашивание менее благоприятны, что подтверждается опытом.
Интенсивность выкрашивания возрастает с увеличением сил трения, т. е. с увеличеиием нагрузки и коэффициента трения, который, в частности, зависит от скорости скольжеиия vc. Максимальное значение коэффициента трения соответствует небольшой скорости скольжения ис = 54- 15 м/с, которая бывает в точках, близких к полюсу. Именно в этих точках на ножках зубьев и начинается выкрашивание.
Ухудшение условий работы в полюсе учитывают, условно понижая допускаемые напряжения. Для точек U2 и Р^ допускаемые напряжения повышаются. Опасные расчетные случаи соответствуют положениям, когда наибольшая динамическая нагрузка действует на полюс или ножку ведущего зуба (в точке Pt) Если ведомый зуб имеет менее прочную поверхность, его рассчитывают по нагрузке в полюсе ww. В открытых передачах выкрашивания не наблюдается.
Допускаемые напряжения. После появления первых признаков выкрашивания передача может работать еще довольно длительное время, поэтому коэффициент запаса прочности по контактным напряжениям принимают равным Sh= 1,14-1,2. Условие обеспечения контактной выносливости зубьев имеет вид
ан «S анр, (165)
220
Зубчатые передачи
5. Значения пределов выносливости
Материал зубьев колес
11m* Н/мм*
Сталь; без специальной химико-термической обработки поверхности (твердость НВ < 350) с объемной и поверхностной закалкой (38 — 50 HRCg) цементованная и нятроцементованная (твердость HRC3 >56) азотированная (550 — 750 HV) Чугун (при числе циклов N — 10’) серый ковкий и модифицированный Неметалл (в паре со сталью или чугуиом) текстолит лигнофоль 2- НВ + 70 17- HRC3 4- 200 23- HRC3 1050 1,40- НВ 1,70- НВ 45-55 50 — 80
где допускаемое напряжение оар определяется формулой (26).
Предел выносливости ajy цт при базовом числе циклов Л/ПОст можно принимать в зависимости от средней твердости поверхности зубьев по табл. 5.
В авиационных редукторах допускаются более высокие значения Я/уит (до 26-HRC3) при числе циклов до 107.
Влияние фактического числа циклов нагружения Л/к на предел выносливости учитывается коэффициентом Z.v, который для стальных колес определяется по ГОСТ 21354—87 следующими формулами:
6 / М н \1т
~ I/ -jy При /Vmtn
'С Мн 11m,
(166)
но не более 2,6 (что соответствует Л^пнп = 0,0032Л/н цт) для однородной структуры материала и 1,8 (/VmIn = = 0,029 Л/д ц т) для поверхностного упрочнения;
, 2°/'Л'/П1т
1/ V При
У 'VK
(167) но не менее 0,75.
Базовое число циклов напряжений зависит от твердости
Л/нит = 30 (Янв)2'4. (168)
ио ие более 120- 10е.
Для чугунных колес Nh Um-*- оо, для них:
У ю7
Zn = V При 'VK>'Vmln; (169)
Z1V = 2,6 при Як<Ят1П, (170)
где Mmtn = 3,2-104.
Поправочные коэффициенты в формуле (26) имеют в среднем следующие значения: коэффициент, учитывающий шероховатость поверхностей зубьев, ZR 0,95; коэффициент, учитывающий окружную скорость, Zo ~ 1,1; коэффициент, учитывающий влияние смазки, Zj, = 1; коэффициент, учитывающий размер зубчатого колеса, Zx = 1 при du, Sj 700 мм и ZxH = = 0,9 при da, = 2500 мм.
Для стальных зубьев, подвергаемых чистому шлифованию или шевингованию, анр следует увеличить на 10—15%, а в случае притирки зубьев каждого зубчатого колеса в отдельности с применением специальных приспособлений и паст — на 25% •
Для внеполюсного контакта зубьев допускаемое напряжение повышает в р раз, т. е.
а«/> = ^н/>, (171)
где р = 1,4 в точках U и р = 1,7 в точках Р.
При кратковременных перегрузках поверхность зуба проверяют иа контактную прочность:
°ц шах °НР шах, (>7^)
Работа передач при различных режимах
221
где ад тах определяется по максимальному вращающему моменту Ттах при соответствующем коэффициенте нагрузки Кн шах-
Допускаемое контактное напряжение онр определяется:
для зубьев колес без специальной поверхностной химико-термической обработки — из условия отсутствия пластической деформации адр шах = = 2,8ат, где °т — предел текучести материала колеса;
для зубьев цементованных или поверхностно закаленных — из условия сопротивления хрупкому разрушению аНР шах — 44 #HRCg.
для азотированных зубьев адр шах = = 3 /Zhv-
В передачах, в которых работают обе поверхности, каждую сторону зуба рассчитывают самостоятельно.
Повысить сопротивляемость поверхности зуба выкрашиванию можно увеличением межосевого расстояния, увеличением угла aw, введением смещения, повышением вязкости смазочного материала, уменьшением шероховатости поверхности зуба, применением материалов с повышенной твердостью поверхностного слоя.
Во время работы зубья нагреваются тем сильнее, чем выше давление, скорость скольжения и коэффициент трения. При нагреве вязкость смазочного материала уменьшается, трение усиливается и при определенных условиях может наступить заедание.
Уменьшить опасность заедания можно уменьшением нагрузки в зоне, где велико скольжение (используя, например, модификацию); уменьшением скольжения (применяя зубья с меньшим модулем в пределах, допускаемых прочностью зуба на изгиб); применением противозадирного смазочного материала.
РАБОТА ПЕРЕДАЧ
ПРИ РАЗЛИЧНЫХ РЕЖИМАХ
Многие передачи эксплуатируют на различных режимах, отличающихся передаваемой мощностью, частотой вращения, продолжительностью, иногда направлением движения.
При приведении всех режимов к наиболее напряженному с действующим напряжением а эквивалентное число циклов М2 при степенной зависимости между напряжениями и числом циклов до разрушения согласно формуле (10) гл. 2
где а/, Ni — напряжение и число циклов на i-м режиме; п — общее число режимов работы.
Относя Nt к общему числу циклов п
на всех режимах работы Л'2 = JVf.
i=i получим
2/ a, N.
Н) ж- (174) 1—1 2
При расчете на выносливость при изгибе зубьев с нешлифованной переходной поверхностью с твердостью НВ> 350 величина т = 9; в остальных случаях изгиба зубьев и при расчете на контактную выносливость т = 6.
Эквивалентное число циклов следует определять с учетом полных действующих напряжений на каждом режиме, т. е. с учетом коэффициентов, входящих в формулы (31)—(33), и их изменений по режимам. Так как номинальные напряжения изгиба аро пропорциональны крутящему моменту 7\, а номинальные контактные напряжения адо пропорциональны /7\, формулу (174) можно представить в виде:
при расчете на контактную выносливость
У =N У( УЛ1.
ПНЕ Т1К J N ’
f=l
(175)
при расчете на выносливость при изгибе
1=1
(176)
222
Зубчатые передачи
где, как указано выше, mF равно 6 нли 9.
Так как наибольшему изменению по режимам подвержен коэффициент динамической нагрузки Кд, то
ТliKi ~ _ 7\г- (1 -ф Vi)
Г,К ~ ЛКд - 7.(1 +V) ’ (177) где v = Kv — 1; Kai & Ка-
При постоянных частотах вращения сила удара wv = w^KaV практически не зависит от статической нагрузки, что позволяет считать T^Vj х T\v н использовать в расчетах значение v для очередного режима, считая, как это принято в рекомендациях к ГОСТ 21354—87,
ТnKj ~ 7 ц + vTj 1\К ~7I(l-f-v)'
Режимы, для которых число циклов Ni больше базовых чисел Кит, указанных на с. 216 и 220, прн суммировании по формулам (175) и (176) не учитываются. При суммировании не учитываются также режимы с высокими, но кратковременными нагрузками, так как опыт показывает, что такие нагрузки в сочетании с более низкими, но длительно действующими, не снижают долговечности зубчатых передач, если они удовлетворяют условиям статической прочности. Число циклов на указанных режимах должно быть меньше Ктщ. приведенных выше.
По эквивалентному числу циклов Кие и Кее определяют коэффициенты долговечности 7у и Гу н затем проверяют условия выносливости по формулам (22) и (27). Для режима, наиболее напряженного нз всех режимов «неограниченной» длительности (прн А.^Мнт), необходимо проверить, чтобы коэффициент запаса прочности S был не ниже допустимого.
Характер работы передачи оказывает некоторое влияние на уровень напряжений иа каждом режиме нз-за изменения процесса приработки, что иногда учитывают в расчете. Предполагают, что степень приработки зубьев на i-м режиме пропорциональна номинальной нагрузке се>0( и числу циклов нагружения Д';. Если считать, что при работе на максимальном ре
жиме икотах в течение всего ресурса й/2 коэффициент приработки Kw имеет значение, соответствующее рнс. 14, то относительная приработка на i-м режиме
max^E
относительная приработка за сурс п У WoiNi __ 1=1_________________
^omax^/j
(179)
весь ре-
(180)
Очевидно, что т]2 1.
Коэффициент неравномерности распределения нагрузки на i-м режиме ^i=i + (^°-l)x
х [1 — Hf(l -Kw)]. (181)
При работе на одном постоянном режиме T]i= 1, и формулы (181) н (61) совпадают. Для очень кратковременных режимов т]г = 0 и К$1
* Лр.
ОСОБЕННОСТИ РАСЧЕТА
ПЕРЕДАЧ С КОСЫМИ, ШЕВРОННЫМИ, КОНИЧЕСКИМИ ЗУБЬЯМИ И ПЕРЕДАЧ
М. Л. НОВИКОВА
Для приближенного расчета указанных передач используют те же методы н структурные формулы (24)—(29), что и для прямозубых передач, внося определенные изменения в выражения для снл и коэффициентов К, Z и У.
Косозубые и шевронные передачи
При расчете на контактную выносливость зубьев с углом наклона Р =/= 0 отнесенная к наименьшей суммарной длине контактных линий
<|82>
удельная окружная сила
cos Рь 20007. cos Рь „ “7 = wHt - = -г ——1:2 К, Ке£а bwdanKe.e-a
(183)
Особенности расчета передач
223
где Wfft— расчетная окружная сила, определяемая по формуле (25); Ь,„ = — b — Ьк — рабочая ширина венца (за вычетом ширины канавки между полушевронами); Рь — основной угол наклона зубьев (sin рь = sin Р cos а); Ке — коэффициент среднего уменьшения суммарной длины контактных линий в процессе зацепления, зависящий от коэффициентов осевого ер и торцового еа перекрытий
Приведенный радиус кривизны
_____°^«>1 SHIttfta /10X1
Рпр 2(u+l)cospb’ ( 84)
нормальная сила
иУ/х — ----------:г- . i I и.) 1
cos afal cos Рь
Введя соотношения (183)—(185) в формулу (158), придем к основному выражению (23) для расчетного контактного напряжения ан», в котором
<18й
Ze определяется формулой (161). Коэффициент Ze в ГОСТ 21354—87 рекомендуется рассчитывать по формулам:
Ze^l/4—при ер = 0;
ze = 1/ (4"-^)(1-ч)+~11 ' ' efl ’
при ер < 1;
, 1
Ze — ~ z— при ер > 1.
Vea
Влияние неточности передачи иа неравномерность распределения нагрузки по длине контактных линий Дополнительно учитывается коэффициентом Кна,— 1,05-4-1,1 при степени точности зубьев колес от 6 до 9. При определении коэффициента Кн& учитывают повышенную жесткость косозубой передачи, принимая с =
— 20 Н/(мм-мкм) при 8° < Р < 20° и с ял 15 Н/(мм-мкм) при Р>20°. При расчете силы удара по формуле (113) принимают яг 0,03, а по формуле (117) Т] я» 0,2.
При расчете на выносливость при изгибе коэффициент формы Yfs определяют в зависимости от эквивалентного числа зубьев
z° = —Га ’ (167)
cos3 р '
а
принимают Ye ~ I, Kg « 1 — eg —.
где Р —в градусах (Kg >0,7);
KFa = — 4 ; (188)
еа еа 4
здесь п — степень точности по нормам контакта (при 5 п < 9); при вычислении коэффициента Kfv принимают = 0,06.
Конические передачи
При расчете прямозубых конических передач их заменяют условно эквивалентными прямозубыми цилиндрическими колесами (рис. 33); при этом модуль зацепления
та -= т ( I — 0,5 ; (189)
диаметры колес
J ^iol (2)
“И21Э- cosZ1(2)
х f 1 - 0,5 ;
\ L /
число зубьев
_ _ г‘ <2> !<2)Э COSZ1(2)
передаточное число cos Zj иэ = и------------------ ;
cos Ла
(190)
(191)
(192)
межосевое расстояние
aw — L (1 -0,5 X
X (tg Л, Н-tg Ла); (193) окружная скорость
р, = р (1-0,5-^); (194)
224
Зубчатые передачи
33. К расчету конических зубчатых колес
Рис.
ширина зуба
= (195)
Углы и л2 начальных конусов зависят от передаточного числа и ~-= z2lz1 и угла 6 = /-! + Х2 между осями конических колес:
. sin 6 .
ь 1 + cos б
, и sin б
— ----------г- 196)
ь I -т и cos б
Номинальная удельная нагрузка (в Н/мм)
а»а =
10007', V П- 2u cos б у- и2
7 ь \ *
L 1 — 0,5 —- j bw cos arasin б
(197)
Контактные напряжения для стальных зубьев при а.о — 20° (в МПа)
X T/~l+2ucOs6 + ^ g8)
V usm6 '
где к’а — в Н/мм; L — в мм.
Конические колеса с косыми зубьямн условно заменяют эквивалентными цилиндрическими косозубыми колесами.
Передача М. Л. Новикова
Схема передачи с одной линией зацепления («заполюсной») показана на рис. 34. Рабочая часть профиля ведущего зуба 1 в торцовом или нормальном сечении очерчена по Дуге радиуса р1а с центром в точке La на расстоянии с от осн зуба; ведомый зуб 2 имеет вогнутый профиль с радиусом кривизны р2у > р1О- Обычно принимают р1а « 1,5m и р2/ я» 1, 1р1а. В мягких зубьях после приработки значения радиусов р1а и р2/ сближаются, так что в работе зубья контактируют почти по всей длине дуги ВС. Линия зацепления проходит через точку Л параллельно осям колес, ее
Рис. 34. Схема передачи М. Л. Новикова
Особенности расчета передач
225
рис. 35), максимальные контактные напряжения можно приближенно рассчитать по формуле
аЯ = 0,418 |/
где
-(-Рпр
(200)
L = ВС — 2р1а (aiB,-6), (201)
причем технологический угол 6 = = 54-7°; рабочий угол 2 (at® — 6) = = 30-5-40 .
Приведенный радиус кривизны
Рис. 35. К расчету зубьев кругового профиля
проекция на торцовую поверхность — точка (точечное зацепление), так что для обеспечения непрерывного контакта зубьев их профили равномерно смещаются по длине зуба, образуя винтовую поверхность с углом наклона зубьев к оси Р (рнс. 35). Обычно Р= 10-4-30°.
Применяют также передачи с двумя линиями зацепления («дозаполюсные»), когда ведущий зуб контактирует с ведомым вначале своей вогнутой поверхностью ножки (до полюса), н затем — выпуклой (за полюсом). При этом в зацеплении могут находиться от двух до четырех зубьев.
Действующая на зуб нормальная сила Fa связана с окружной силой Ft соотношением
Fa = 1 + cos2 Р
(199) Контактные напряжения. Считая, что для приработавшихся зубьев контактная площадка имеет форму прямоугольника длиной L н шириной b (см.
_ Га-1Ц V1 + cos2 atw tg2P
Рпр и + 1 sinaltt)sin2 [J
(202)
Произведение АрПр для передачи Новикова в несколько раз больше, чем для аналогичной эвольвентной передачи, чем н объясняется ее повышенная сопротивляемость выкрашиванию.
Расчет на изгиб. Упрощенную формулу для напряжений изгиба можно получить, рассматривая зуб как консольную балку, к которой в точке А (см. рис. 34) приложена сила Fa. Тогда
(203)
где h — плечо силы; sx — ширина опасного сечения; Ьш — ширина рабочей части зубчатого венца; ср — поправочный коэффициент, учитывающий, что напряжения в зубе распределяются неравномерно по всей длине, а концентрируются на участке, непосредственно примыкающем к площадке контакта; ср » 2,0.
Уточненные методы расчета передач с круговыми зубьями изложены в работе [5].
Глава 12
ШАРИКОВИНТОВЫЕ ПЕРЕДАЧИ
В последние годы в машиностроении н приборостроении получили применение шариковинтовые передачи, преобразующие с высоким КПД вращательное движение в поступательное н наоборот.
Основные преимущества передач: высокий КПД (т, « 0,9) *; высокая равномерность движения, малое трение
* В простой передаче винт—гайка Т| =* = 0,2+0,4.
8 Заказ 402
226
Шариковишповые передачи
покоя; возможность полного устранения зазора в резьбе и создания натяга, обеспечивающего высокую осевую жесткость.
КОНСТРУКЦИИ ПЕРЕДАЧ
И МАТЕРИАЛЫ
Типичная конструкция передачи показана на рис. 1. Основные профили резьбы винта и ганки (д нормальном сечении винтовой канавки), применяемые в настоящее время в механизмах, даны на рис. 2.
Наиболее распространен полукруглый профиль (рис. 2, а). Радиус профиля резьбы г2 выполняют несколько большим радиуса шарика ги обычно ~ (0,94-?0,97) гг. При больших значениях г2 снижаются контактные напряжения, ио существенно повышаются потерн на трение из-за различия скоростей на площадках контакта.
Если передачу с полукруглым профилем резьбы винта и гайки изготовить без зазора, то угол контакта ак в не-нагруженной передаче будет равен нулю, а под нагрузкой несколько
Рис. I. Схема шариковинговой передачи:
I — ходовой винт; 2 — гайка, 3 — перепускной
канал: 4 — шарики
Рис. 2. Основные профили винта и гайки (в нормальном сеченнн винтовых канавок):
В, Г — точки контакта шарика; ак — угол контакта
г)
д)
Расчет передач
227
возрастает благодаря контактной деформации. Несущая способность и КПД передач с малым углом контакта невысокие. На практике значительное распространение получили передачи с <хн = 45° благодаря высокой технологичности (возможно изготовление резьбы винта шлифованием без предварительного нарезания).
Применяют также стрельчатый или оживальный профиль резьбы (рис. 2, б, в), который позволяет осуществить передачу без зазора или с натягом за счет применения шариков диаметром, несколько большим номинального. В передаче с полукруглым профилем резьбы для выбора зазора или создания натяга следует применять вторую гайку.
Прямоугольный (рис. 2, г) и трапецеидальный (рис. 2, д) профили наиболее просты в изготовлении. Однако их применение ограничено низкой нагрузочной способностью из-за высоких контактных напряжений. Обычно такие профили применяют в передачах при малой осевой нагрузке и невысоких требованиях к осевой податливости.
Винты изготовляют из сталей ХВГ, 38ХМЮА, 7ХГ2ВМ, 20ХЗВМФ и др., а гайки — из сталей ХВГ, 9ХС, ШХ15, ШХ6 и Др. Рабочие поверхности закаливают до твердости 60 HRC и выше.
Шарики изготовляют из сталей ШХ6 и ШХ15.
Детали шариковиитовых передач обычно изготовляют с высокой точностью и высоким качеством поверхности. Параметр шероховатости резьбы Ra~ 0,324-0,63 мкм; отклонения диаметров, соответствующих точкам касания на винте и в гайке, ие превышают 5—8 мкм на длине 1 м для винта и 3—5 мкм иа длине ганки. Наибольшие накопленные ошибки шага резьбы винта не должны превышать ±3 мкм в пределах одного шага, а наибольшая накопленная ошибка шага резьбы гайки на всей ее Длине — не более 5—8 мкм. Равномерность шариков обычно назначают 1—2 мкм. Меньшие нз указанных допусков применяют для передач с d0 = 204-50 мм, а большие — для передач с d0 = — 60-' 100 мм.
Передачи смазывают пластичной или жидкостной смазкой. Присутствие в смазке графита недопустимо.
РАСЧЕТ ПЕРЕДАЧ
Для расчета грузоподъемности и долговечности шариковинтовой передачи необходимо знать максимальное усилие, действующее на шарик. Это усилие можно найти, рассмотрев распределение нагрузки в передаче. В предварительных приближенных расчетах принимается равномерное распределение нагрузки.
Основные геометрические параметры профиля резьбы даны иа рис. 3.
Общее решение. Уравнение совместности перемещений имеет вид (см. гл. 3)
Д1 + Д2 = [бх (г) + б2 (г) ] —
- I6i(0)+ б2(0)], (1)
где Д2 — удлинение и укорочение участков винта и гайки от 0 до г (рис. 4); бх (г) 4- 62 (z) — сумма прогибов витков винта и гайки, а также контактной деформации в сечении z (в осевом направлении); (0) + + 62 (0) — то же в сечении 0 (индекс 1 соответствует вннту, 2 — гайке).
Перемещения Aj и Д2 определяют по формулам z z
д1= f-^-dz; Д2= f-^-dz, (2)
j £ J £
do
dz
Рис. 3. Основные геометрические параметры резьбы
8*
228
Шариковинтовые передачи
а перемещения 6; (/=1,2) можно
представить в виде
6/ =
X cos 4>t, (3)
где pt — усилие на единицу длины линии контакта боковой поверхности витков; X* и 0,-—безразмерные коэффициенты; — диаметр шарика; Sj-щ — шаг (расстояние между двумя шариками вдоль контактной линии); ф,- — угол подъема винтовой контактной линии (при расчете на прочность можно считать cos ф = 1).
Интенсивность распределения осевых сил по высоте резьбы q (г) и усилия на единицу длины контактных линий связаны соотношением
PtnDlK sin ак созф,- = qS, (4) где S — шаг резьбы; D iK — диаметр цилиндрической поверхности, на которой расположена линия контакта; ак — угол между направлением действия контактного усилия и плоскостью, перпендикулярной к оси резьбы. Принято, что контактное усилие направлено нормально к поверхности контакта. Из условия равновесия шарика вытекает, что направление нормали должно быть общим для точек
контакта иа витках винта и гайки. Учитывая, что
г
= ^4^ = -4- f ? (Zi) dZi, (5)
Ft Ft J
0
где Fi — площадь поперечного сечения винта или гайки, и используя зависимости (1), (3), (4), уравнение совместности деформаций запишем в виде
2 2t
₽ j j <7 (z2) <*z2 dZi = Y? + ТиО273 — c, о о
(6) где
’-£тгк-; <”
i=l
s У' *'
nsinaK DiKEt' i=i
S \2/3 1
л sin ак / dV3
1=1
(9)
Постоянная С = уо (0) + укр2'л в уравнении (6) может быть определена из условия
Н
jq(z)dz = Q, (10) о
где Q — осевое усилие, действующее на соединение; Н — длина свинчивания. Тогда
Н
YQ + Yk j <?2/3 (z) & — о
Н г г1
— Р J J j ? (z2) dz2 dz^dz ООО
(11)
Расчет передач
229
Внося выражение (11) в уравнение (6), запишем последнее в виде интегрального уравнения
¥ (?) = К (?) + <7 СР, (12) где
Ч' (?) = ? + -у- ?2/3; (13)
к (?) = 4
21
j ? (z2) d-Zi dzi — о
Н г г,
— -р- § f § qfz^dz^dz ООО
/-/
<?2/3(z)dz; <14)
о
Q ?ср = • (15)
Разберем случай соединения типа стяжки (рис. 5). В этом случае уравнение (6) принимает вид
2 2i
pj у9(г2)а22аг1__^- = о о
= 7? + Тк?2/3 — С- (16)
Используя условие (10) для определения С, получим уравнение
’F (?) = К (?) + ?0, (17)
в котором
<’о = ‘7ср+ • (18)
Величины Т (д) и К (<?) определяются по (13) и (14). Отметим, что при E.2F2 оо распределение нагрузки в соединениях типа болт—гайка и типа стяжки ие отличаются.
Если Р = 0, то уравнение (12) имеет очевидное элементарное решение
Q
? — ?Ср — уу >
т. е. если болт и гайка ие испытывают деформаций растяжения или сжатия, то нагрузка по виткам распределяется равномерно. В общем случае
Рис. 5. Схема соединения типа стяжки
уравнение (12) может быть решено методом последовательных приближений по схеме
Чг(?/+1) = Х(?1) + ?ср, (19) где qt, qt+l — исходное и последующее приближения Для искомой функции q (г).
Принимаем первое приближение _ Q ^(1) ^ср /у ’
тогда для второго приближения
Т(«га)-ХЦ„)+«.р-
+ ^Чр3+?ср. (20)
Обозначая через f2 правую часть равенства (20), получаем
„ 4.1к 2/3 _ f
Я(2) + у ?(2) - 12-
Это уравнение легко сводится к кубическому, но в практических расчетах его действительный корень более удобно отыскать по методу Ньютона.
Предположим, опуская для простоты индекс 2, что
= ? + у- ?2/3 - f = °-
Разлагая функцию F (q) вблизи некоторой точки q*, близкой к предпо-
230
Шариковинтовые передачи
лягаемому значению корня, и сохраняя только первые члены разложения, найдем
F(q) = F (<?.) + (</.)(<? -9*) = 0,
UI/
откуда
п п -
4 ~Ч* dF , dq
q+^3-f
~q* 1 + 2_A_L ~ 3 у ,2/3
(21)
Величина а в формуле (22) не оказывает влияние на распределение нагрузки. Если выбрать коэффициент таким, что аппроксимирующая прямая становится касательной при q = = ?ср> т0
Дифференцируя уравнение (23) дважды по г, находим
m2q (z) = 0, (24)
Величину q, можно принять в виде
где
Формула (21) обычно дает достаточно точное решение, при необходимости подобным образом уточняют значение корня. Определив значения <7(2) (г), можно найти следующее приближение <7э (г). При вычислении К (<7(2)) по формуле (14) целесообразно использовать численное интегрирование по правилу трапеций. Расчет заканчивается при достаточной близости двух соседних приближений.
В большинстве практических задач достаточно ограничиться вторым приближением. Подобным образом можно решить уравнение (17), заменив <уСр иа ?0-
Приближенное решение. Если величина q ие очень мала, приближенно можно считать
q2'3 = a + bq, (22)
где а и Ь — постоянные коэффициенты.
Уравнение (12) с учетом равенства (22) приведем к виду
Y + Yk* .. , 2 ун
Y+ 3 7^
Из уравнения (24) с учетом известных граничных условий для соединения типа болт—гайка получаем закон распределения нагрузки в обычной резьбе:
, ч Qm ч.
? (Z) = -г—77 СП тг,
' ' ’ sh mH
где т — параметр, зависящий от контактной деформации.
Для расчета необходимо знать упругогеометрические параметры 0, у и ун.
Параметр [} определяется по формуле (7). Выведем соотношения для определения величин А.,* и 6(-, необходимых для вычисления у и ук.
Представим общую податливость витка винта и гайки в виде
б( = б<»+ б<-2) + б<3) + б<к)
(<= 1, 2),
где SP (j — 1, 2, 3) — податливость витка в результате деформаций изгиба, сдвига и радиального смещения основания; 6(К) — контактная податливость. Первые два слагаемых обычно малы и в расчетах ими можно пренебречь.
Податливость витков винта в осевом направлении в результате радиального
Расчет передач
231
смещения основания
б[3) = и{ ctgaK cos ф] -
_ Picos ак CIg ак cos x
2SE, k-^2B
vi ,
податливость витков гайки
623) = u2 ctg ак cos ф2 ==
_ рг cos ак ctg aKda cos фа
2SlTt X
где ui, u2 — радиальные смещения основания витка винта и ганки; vt, v2 — коэффициенты Пуассона материала винта н ганки.
В соответствии с равенством (3)
6<3) = Х; -^-совфь (25)
что позволяет определить значение
Перемещение в результате контактной деформации (в осевом направлении) можно представить в виде
= Ki6 sin aK cos ф X
3 /~7
X]/ (
(26)
где Vp, = J_____L = ^Z^S_
ДГ ГШ Ri Ridw
сумма главных кривизн (приближенно рассматривается контакт шарика и Цилиндрического желоба); Рш = = PiSnii — усилие на шарик; Еа1— модуль упругости материала шарика; Аге — безразмерный коэффициент, зависящий от параметра
4Ri — dw'
(27)
Сопоставляя формулы (3) и (26), находим
0/ = Кц, sin ак X
х'(М).
Максимальное контактное напряжение
шах -- Kia X
(i=l,2), (28)
где Kia — безразмерный коэффициент, зависящий ст параметра
Значения коэффициентов Кц и Kia даны в табл. 1.
Пример. Определим распределение нагрузки по виткам передач типа болт—гайка и типа стяжки. Дано; d0 = ЮО мм; S = 12 мм; ат = 7 мм; R = 3,64 мм; £)1к = 95,05 мм; £)ак = = 104,95 мм; ак = 45°; DB = 70 мм; Dt = 130 мм; И = 72 мм; Q = = 72 000 Н. Материал винта, гайки н шариков сталь ШХ6 (£=2,1Х ХЮ5 МПа; v = 0,3). Твердость контактирующих поверхностен 60 HRC3. Для определения упругогеометриче-скнх параметров передачи предварительно находим внутренние диаметры резьбы винта и ганки (см. рнс. 3):
X cosaH = 92,9 мм;
dt = d„ + 2 р? - (я - J х
X cosaK= 107,1 мм.
Площади поперечных сечений fj = = 29.32 см2; F2 = 42,67 см2. Параметр £1 — = 0,9259. По табл. 1 находим
Я16 = Кг6 = 0,4153; Я10 = Яао =
= 0,2412. Далее вычисляем 6 = = 0,027.10-’ 1/Н; kJ = 9,37; kJ-
232
Шариковинтовые передачи
1. Значения коэффициентов
5 в Ktb & *16 *i0
0,7385 0,5478 0,3070 0.8165 0,5094 0,2873 | 0.9049 0,441 1 0,2537
0.7470 0,5442 0,3051 0.8273 0,5029 0,2841 0.9149 0,4291 0.2477
0,7538 0.54 13 0,3036 1 0,8355 0,4976 0,2814 0.9225 0,4199 0.2434
0,7627 0.5374 0,3016 1 0.8439 0,4919 0.2786 0,9344 0,4039 0,2356
0,7696 0,5341 0,2999 0.8259 0,4859 0,2756 1 0.9425 0.3912 0,2295
0,7767 0.5308 0.2981 0.8617 0.4793 0.2722 0.9510 0,3762 0,2224
0,7862 0.5260 0,2958 0.8679 0,4745 0.2699 0.9602 0,3578 0.2137
0.7936 0,5222 0.2938 1 0.8774 0,4667 0,2660 ! 0.9697 0.3339 0.2024
0,8012 0.5181 0,2918 | 0,8871 0,4582 0,26 18 I 0.9804 0.2997 0,1863
0,8088 0,5139 0,2897 0.8972 0,4483 0.2571 1 0,9924 0,2345 0,1555
Рис 6. Изменение q по длине гвинчивания соединения:
1 — болт--гайка 2 - стяжка
H z z.
— 0,14 J j j <7 (z2) dz2 dZi dz ooo
H
+ 1,74 j ?2/3 (z)dz-f-o
= 17,68; у= 0,687-10-’ см2/Н; 0! = = 0г= 0,55; ук = 8,62-10= см5/3Н~2/3.
Для соединения типа болт—гайка получаем уравнение
<?+ 12,56?2/3 =
= 0,04
j j ? (z«) .0 о
dzt dz2 —
+ 116,96 (3,6 —z)+ 10 000.
На рис 6 показано изменение q по длине свинчивания (кривые построены по решениям последних уравнений).
В результате контактных деформаций распределение нагрузки но виткам в шариковинтовых передачах более равномерное, чем в обычных резьбовых соединениях.
Максимальное усилие, действующее на шарик,
п / , Sdni
max - <7 Wmax nD^ 5Щ cos •
(29)
— 0,14
H z z.
j pOJ 0 0 0
dz2 dz2 dz
н
+ 1,74 j <?2/3 (z)dz+ 10 000 0
Для соединения типа стяжки
q+ \2,56q2l3 =
= 0,04
z z,
j j'7(22)^2^1 —
_0 0
Для соединения типа болт—ганка Phi max “ 651 Н, Ощах — 2087 МПа; для соединения типа стяжки Рш шах — = 456 Н, Птах = 1956 МПа
В длительно работающих передачах (детали из стали ШХ15), воспринимающих осевые усилия (4 4- 70) 104 Н и имеющих параметры Г)г = 99= 166 мм; DB = 50=100 мм, dm — — 7,938 или 10,319 мм с числом витков 2=6 и числом шариков в витке 22=36, контактные напряжения <Тк max = 2100=3500 МПа.
При проектировании шариковинтовых передач, предназначенных для длительной эксплуатации, допускаемые контактные напряжения прн твер-
Материалы и конструкции приводных клиновых ремней
233
дости контактирующих поверхностей деталей 62—64 HRC3 принимают равными [о]к = 30004-3500 МПа, а при 60-62 ВДСЭ [о ]к = 25994-3000 МПа. При кратковременной работе передачи [сг]к= 5000 МПа.
При более низкой твердости (HRCa<_' 60) контактирующих поверх-
HRC ..................... 62 58
кш.......................1.0 0.89
ностей допускаемые напряжения понижают, т. е.
1°1к = 1а1к-
Значения коэффициента Кт зависят от твердости контактирующих поверхностей детали передачи из хромистой стали:
54 49 45 40 35 29
0.79 0.69 0 6 0.5 0.115 0.38
Глава 13
РЕМЕННЫЕ ПЕРЕДАЧИ
РемеНные передачи широко применяют для передачи вращательного движения от электродвигателей (большой и средней мощности) к различным агрегатам, а также для передачи мощности на сравнительно большие расстояния (в строительных и дорожных машинах, текстильных станках н т. п.).
Преимущества ременных передач: простота конструкции и низкая стоимость; высокая гибкость ремня, допускающая различное взаимное расположение осей шкивов; плавность и бесшумность работы.
Недостатки: большие габариты; наличие скольжения ремня; ограниченная мощность и низкая долговечность.
Наиболее широко применяют открытую передачу между параллельными валами (рис. 1), включающую в себя ведущий и ведомый шкивы и гибкую связь — ремень в виде кольца.
а
₽ис. 1. Схема ременной передачи (а) н сечений ремией:
б ~ прямоугольное; в — трапециевидное; г ~ круглое, д — поликлиновое
По форме сечения ремня различают плоско-, кругло- и клиноременные передачи.
В настоящее время в основном применяют клиновые ремни (рис. 1, в).
МАТЕРИАЛЫ И КОНСТРУКЦИИ ПРИВОДНЫХ клиновых РЕМНЕЙ
Ремни изготовляют с кордом из нескольких слоев вискозной или капроновой ткани (кордтканевые ремнн) нлн одного ряда анидных шнуров (кордшнуровыс ремни), намотанных по винтовой линии и заключенных в слой мягкой резины. Кордшнуровые ремни имеют большую гибкость и применяются в нагруженных передачах.
Для работы на шкивах малых диаметров используют клиновые ремни с гофрами на внутренней, а иногда на внутренней и наружной сторонах.
Клиновые ремнн изготовляют бесконечными с углом клина а = 40° и отношением большего основания трапециевидного сечения к высоте WlT « 1,6 (нормальные ремнн) и W/T г» 1,2 (узкие ремни).
Основные размеры клиновых ремней даны в табл. 1. Узкие ремни передают в 1,5—2 раза большие мощности, чем нормальные, и допускают работу при скорости 50 м/с. Это дает возможность уменьшить число ремней в комплекте и ширину шкивов. Четыре сечения этих ремней (см. табл. 1) полностью
234
Ременные передачи
t. Основные размеры и области применения клиновых ремней
Ремень
w'p
UZ
Ус
Лр
F.
смг
U70. кВт. при V, м/с
мм
К-линовой
Клиновой узкий
Z 8.5 10 6 2.1 400-2 500 0,47 63
А 1 ’ 13 8 2,8 560-4 000 0.81 90
В 14 17 10.5 4.0 800 — 6 300 1,38 125
С 19 22 I 3,5 4.8 1 800 - 10 600 2,30 200
D 27 32 19 6.9 3 150 - 15 000 4,76 315
Е 32 38 23,5 8,3 4 500— 18 000 6.92 500
ЕО 42 50 30 1 1.0 6 300-18 000 11,70 800
УО 8.5 10 8 2.0 630 — 3550 0,56 63
УА 11 13 10 2.8 800 — 4500 0,93 90
УБ 1 4 17 13 3,5 1250 — 8000 1,59 140
УВ 19 22 18 4.8 2000 — 8000 2,78 224
2
4
7,5
15
До 5
5—10
4
7.5
15
30
60
120
Св. 10
4
7.5
15
60
200
200
200
Т
С
Е Е
Q 2
Обозначения. UZp — ширина ремня по нейтральному слою; U7 — ширина большего основания трапеции, Т — высота сечення; yQ — расстояние от большого основания до нейтрального слоя, Lp — расчетная длина; F — площадь сечения; ^rnin — минимальный диаметр шкива; — передаваемая мощность; v — скорость ремня.
заменяют семь сечений нормальных ремней.
В последние годы получили распространение поликлиновые ремнн — бесконечные плоские ремни с высокопрочным полиэфирным кордом и рабочими ребрами иа нижней стороне (см. рис. 1,5). Ремень также работает на шкиве с клиновыми канавками. Благодаря высокой гибкости допускается применение шкивов меньших диаметров, чем в клиноременной передаче, большая быстроходность (до 40—50 м'с) и большие передаточные числа. Передача обладает высокой демпфирующей способностью.
Корд и рабочая поверхность расположены по всей ширине ремня, поэтому при одинаковой мощности ширина такого ремня в 1,5—2 раза меньше ширины комплекта нормальных ремней.
Клиновые ремни нормального сечения располагают по ряду предпочтительных чисел /?40 (ГОСТ 8032—84) с предпочтением длин по ряду А?20, а узкие и поликлиновые ремни — по ряд> /?20.
МЕХАНИКА РЕМЕННОЙ ПЕРЕДАЧИ
Сила натяжения ремня. При движении ремень передает энергию с ведущего шкива на ведомый за счет сил сопротивления на поверхностях контакта. Поэтому натяжение ремня, создающее контактные давления между ремнем и шкивом, является необходимым условием работы передачи и эксплуатации.
Если ремень надет на шкивы с натягом, то натяжение его ветвей То будет одинаковым во всех сечениях. Поверхность контакта ремня со шкивами определяется углами обхвата а/ (i = 1, 2; рис. 2).
Под действием движущегося момента Afi в ведущей ветвн передачи натяжение достигает некоторой величины 7\ вследствие появления момента сопротивления Мг, а усилие в ведомой ветви уменьшится до величины Т2. При этом окружное усилие (полезная нагрузка ремня)
P = ^L Di
Т\-Т2 (1)
Механика ременной передачи
235
будет передаваться по всей дуге обхвата.
На первом участке АВ — дуге сцепления — за счет нарастающих тангенциальных сил сцепления (меньших полных сил трения) передается малая часть нагрузки, а сдвиговые деформации ремня приводят к небольшому относительному снижению его скорости .
В точке В силы сцепления становятся равными силам трения, происходит срыв и начинается скольжение ремня по дуге ВС — дуге скольжения. На этой дуге с углом аск за счет нарастающих от точки В к точке С сил трения передается основная часть окружного усилия и имеет место значительное снижение окружной скорости .
Если использовать модель ремня в виде гибкой нити, то усилие (или напряжение) в ведущей ветви передачи можно снизить в ведомой ветви соотношением Эйлера. Условие равновесия (без учета центробежных сил) в радиальном направлении элемента нити, огибающей цилиндр (рис. 3), _(Г + 4Г)-^--Т-^- + ЛУ = 0
и условие равновесия сил в окружном направлении
Т + ц dN — Т — dT = О,
где d\' = q dS — нормальная сила, действующая на элемент ремия от шкива; q — нормальное давление на единицу длины; Т — натяжение ремия; р, — коэффициент треиня.
Из последнего соотношения
ц dN = dT, откуда (с учетом первого условия) dTlT — р. da.
Если скольжение ремня происходит По всей дуге обхвата (граница буксования), то после интегрирования получим формулу Эйлера
_Л_ = е^ск = х. (2) 7 а
Усилия в ветвях нагруженной передачи связаны с усилием начального
Рис. 2. Схема взаимодействия ремня со шкивом
натяжения Та и рабочей окружной силой Р соотношениями
Л = Тв+4; (3)
которые можно получить из условия, что удлинение ведущей ветви ремия равно укорочению ведомой ветви.
Из соотношений (3) следует:
Л + Т2 = 2Т0. (4)
Учитывая, что Т2 — Т2 — Р и = D,
= Р -g- , найдем
Из соотношения (5) следует, что нагрузочная способность передачи будет возрастать при увеличении предварительного натяжения ремня То, угла обхвата а, и связанного с ним угла скольжения агк (в расчетах прини-
Рис. 3. Схема сил, действующих на элемент ремия
236
Ременные передачи
Рнс. 4. Схема сил в сеченнн клинового ремня
мают аск аг 0,7аг) и коэффициента трения между ремнем и шкивами.
Коэффициент трения ц в формулах (2) и (5) соответствует передаче с плоским ремнем. В клиноременной передаче
а smT
Это соотношение несложно получить, положив, что вследствие натяжения ремня его элемент прижат к шкив> усилием dN (рис. 4). Тогда сила трения в окружном направлении
dFт = 2pdR = —L dV = dW sln~F
Если учесть, что для стандартных ремней угол клина а = 40°, то р,, аг аг Зр Отсюда следует, что в клнно-ременной передаче сцепление ремня со шкивом почти в 3 раза выше, чем в передаче с плоским ремнем. Существенно. что при уменьшении угла а можно повысить приведенный коэффициент трения рк. Однако при этом возникает опасность самозаклинива-ния ремня, которое приводит к быстрому его разрушению.
Благодаря высокому сцеплению ремня со шкивом клиноремениые передачи хорошо работают при углах обхвата а, 120° (в некоторых конструкциях допускается а, = 80-=-100°). В передачах с плоским ремнем рекомендуется обеспечивать аг > 150°.
Для увеличения угла обхвата на малом шкиве в передачах с большим передаточным числом применяют натяжные ролики.
Для увеличения тяговой способности передачи необходимо стремиться к использованию более прочных ремней, допускающих высокие начальные напряжения (например, капрон, нейлон и др.). Однако в этом случае возрастают нагрузки на опоры.
Менее эффективным оказывается использование ремней из материалов с высоким коэффициентом трения, что связано с возрастанием потерь на трение и перегревом ремня при упругом скольжении.
Кинематика передачи. Снижение скорости от (для ведущей ветви) до (для ведомой ветви) характеризуется относительным скольжением
£ = (6)
Передаточное число
В расчетах передач принимают следующие значения
Ремень: прорезиненный, текстильный, синтетический 0,01
клиновой кордшнуровой ...............0,01
кордтканевый . . 0,02
Тяговая способность передачи. На практике работу передачи принято оценивать по кривым скольжения, которые строят в координатах: относительное скольжение £ — коэффициент тяги <р == Pl(Tt 4- Г,) = Р/2Т0 (рис. 5).
По мере увеличения относительной нагрузки до некоторого значения ф0 наблюдается линейное нарастание скольжения ремня от упругих деформаций, сопровождаемые ростом КПД передачи из-за уменьшения влияния потерь вспомогательного хода.
Дальнейшее повышение нагрузки приводит к более интенсивному снижению скорости, что связано с увеличением дуги скольжения и ростом потерь скорости при набегании ремня
Механика ременной передачи
13,7
на шкивы. Однако передача устойчиво (без буксования) работает и в этой области, хотя КПД снижается из-за нарастания потерь энергии иа треиие. Лишь при значении <р = <ртах начинается буксование передачи.
Оптимальным считают нагружение, соответствующее наибольшему КПД и некоторому запасу по сцеплению или перегрузке (<р0 = 0,6-4-0,75 — для клиноременных передач, <р0 = 0,4-4-0,5 — для плоскоременных передач), либо нагружение, соответствующее некоторой допустимой величине относительного скольжения.
Быстроходность передачи. Если положить, что ремень является вращающимся со скоростью v кольцом, то окружные растягивающие напряжения в нем от центробежных сил
Оокр ~ рЦ2-
При croup — ао Давление иа всей дуге обхвата будет равно нулю, и передача не сможет передавать нагрузку. Окружная скорость на шкиве при этом ____
а1кр ~ \/~ ~~ > (8)
Г*
где р — плотность материала ремия. Для ремня из капрона можно принять напряжение от начального напряжения о0 == 50 МПа и и1кр = 150 м/с.
С увеличением быстроходности пе-
редачи возрастают потери энергии иа треиие. Расчеты показывают [3], что при окружной скорости на ведущем шкиве
/ V <9)
потери энергии на треиие будут наибольшими. Режимов работы передачи со скоростью plfl следует избегать из-за опасности перегрева ремия.
Нанвыгоднейшая скорость ремней обычно составляет 20—25 м/с, а наибольшая допустимая 30—35 м/с. Узкие клиновые ремни с улучшенным кордом могут работать при скоростях До 40—60 м/с.
Напряжения в ремнях. Изменение напряжений в точке ремня за один пробег показано иа рис. 6.
Рис 5 Кривая скольжения и зависимость КПД от коэффициента тяги ф в клнноре-меиной передаче
При обегании шкива ремнем наибольшие напряжения испытывают наружные волокна:
atnax = । 17 р + Оц + <Ти =
х Р
= jjTry у + С°)
где х = е ск; ср, оц, аи — напряжения соответственно от полезной нагрузки, центробежных сил и от из-
гиба ремня,
Оц = рц2; (' 1)
аи = Е —jy ; (12)
здесь Т и D — толщина ремня н диаметр меньшего шкива. Е — приведенный модуль упругости ремня, для прорезиненных ремней Е — 200— 300 МПа, для капроновых ремней Е = 600 МПа, для клиновых кордтка-невых ремней Е — 250-4-400 МПа, для клиновых кордшнуровых ремней Е = = 500-4-600 МПа.
В передаче с передаточным числом « =/= 1 иа протяжении одного пробега в ремне будут действовать два максимума напряжений разной длительности (см. рис. 6), а в передаче с и = 1 — два одинаковых максимума напряжений
Рнс б. Изменение напряжений в точке ремня за один пробег
238
Ременные передачи
РАСЧЕТ РЕМЕННЫХ ПЕРЕДАЧ
Расчет на усталость. Наиболее часто ременные передачи выходят из строя из-за усталостного повреждения рем-ия Экспериментальные исследования показали что для ремней не удается установить предела неограниченной выносливости, а ресурс * ** ремня М (в циклах) связан с наибольшим переменным напряжением соотношением *’
/ С \т
Л, = Ьг—) • (!3>
\ о max /
Если ввести в рассмотрение число пробегов ремня в секунду v = v/L (у— скорость ремня, м/с, L— длина ремня, м), то при постоянном режиме нагружения и u = 1
= 3600vZuj7',
где гш— число шкивов, Т— срок службы ремня, ч
Отсюда
3600ггш \ аП1ах /
В передачах с а0= 1,2 МПа прн и = 1 принимают для плоских прорезиненных ремней т — 5—6, С — = 60—70 МПа, для клиновых корд-тканевых т = 9—11, С =21 МГ1а, для клиновых кордшнуровых т — = 6-11, С = 30 МПа
Значение атах вычисляют по формуле (10)
На долговечность ремней влияют напряжения от предварительного натяжения Если срок службы ремня при напряжении в ремне от начального натяжения а0 = '>2 МПа принять за 100°о, то при других значениях о0 и прочих равных условиях он в среднем составит (по экспериментальным данным)
0„ МПа 0 4 I 12 15 18
Т % 420 250 100 33 13
Для обеспечения высокой долговечности и работоспособности передач ответственного назначения целесооб
* В передачах с u 1 под N понимают эквивалентное число циклов от действия двух максимальных напряжений
** Получено из известного соотноше иия N — const
разно контролировать а0 и применять автоматические способы натяжения
Значительное влияние на долговечность ремня оказывает диаметр меньшего шкива, от которого зависят напряжения изгиба в ремне. Если срок службы клиновых ремней сечения С при работе на шкивах с D = = 200 мм принять за 100%, то при других значениях D и прочих равных условиях срок службы, по опытным данным, составит:
D мм 160 180 200 225 250 280
Г % 30 56 100 200 370 600
Существенно, что при уменьшении диаметра шкнва температура ремня резко возрастает (из-за увеличения внутренних потерь), что также способствует снижению долговечности
Таким образом, целесообразно стремиться к использованию в конструкциях шкивов больших диаметров. Минимально допустимые диаметры шкивов ограничены (см табл. 1). Для клиновых ремней наименьшие допустимые диаметры шкивов Ош1а можно выбрать по ГОСТ 1284 1—89
Если по конструктивным соображениям приходится использовать шкив малого диаметра, то для обеспечения долговечности ремня следует уменьшить предварительное его натяжение
Повышение скорости и уменьшение межосевого расстояния (длины ремня) сокращает срок службы ремня. Последнее вытекает из соотношения (14) и подтверждается опытными данными. Переменность нагружения ремней учитывают поправками к расчету тяговой способности и введением щраниченнй на частоту пробегов ремня v. Для обеспечения нормальных сроков службы приводных ремней в открытой плоскопеременной передаче назначают [V] «С 3-J-5, в клнноременной передаче [v] sj lO-r-15. Используя эти значения v, можно определить при данной скорости минимальную длину ремня.
Расчет иа тяговую способность кли-иоремениых передач *. Общую мощ-
• Расчет плоскоремениых передач см в работе [5]
Передачи с зубчатыми ремнями
239
ность передачи W (в кВт) и полезную нагрузку Р (в Н) определяют по фор-
мулам
W = W0^~; (15)
Ад
р -'°'"-, <16)
П9К * ' '
где W<, — мощность, передаваемая одним ремнем при угле обхвата а —
180 спокойной работе и гг0 ~ « 1,6 МПа (табл. 2); г— число ремней; Кд — коэффициент динамичности (табл. 3); К = KaKLKz — корректирующий коэффициент; Ка — коэффициент угла обхвата:
а, ° 70 90 НО 130 1 50 180
Ка 0.56 0.68 0.78 0,88 0.92 1
KL = у ----------коэффициент, учи-
тывающий влияние длины ремня на его ресурс; здесь Lp н Lo — соответственно расчетная и условная длины ремня; т— показатель степени уравнения кривой усталости ремня (т = = 6—- 9). Значения Lo для ремней различных сечений;
Сечение . . Z А В С
La, мы ... 1320 1700 2240 3750
Сечение . . D Е ЕО
L,, мм . . — 6000 7100
Кг --- коэффициент, учитывающий неравномерное распределение нагрузки между одновременно работающими ремнями и зависящий от числа ремней г;
»....................2—3 4—6 Св. 6
Кг................. 0.95 0.9 0.85
Значения мощности, приведенные в табл. 2, даны для ремней с тяговым слоем на основе искусственных волокон (вискозы). Для синтетических волокон величины Wa можно повысить иа 10%.
Для обеспечения нормальной работы клиноременных передач непарал-лельпость осей вращения назначают ие более 1 мм на длине 100 мм, а допуск на смещение канавок шкивов — ие более 2 мм на 1000 мм межосевого расстояния и увеличивают ие более
чем на 0,02 мм на каждые 100 мм межцентрового расстояния свыше 1 м.
В «многоручьевой» передаче из-за разной длины ремней и различных упругих свойств нагрузка между ремнями распределяется неравномерно. В связи с этим не рекомендуется в передаче использовать более 8—12 ремней. При точном подборе длин ремней на жестких валах в исключительных случаях устанавливают до 16— 18 ремней.
Тяговую способность узких ремней рассчитывают так же, как и нормальных. Значения Wo и Lo для этих ремней приведены в табл. 4 [4].
В заключение отметим, что передачи с клиновыми ремнями могут вызывать крутильные колебания ведомой системы нз-за неизбежного различия ширины ремня по его длине и, как следствие, изменения передаточного отношения за один пробег ремня.
Передачи с поликлиновыми ремнями ие имеют недостатков, присущих клиноременным передачам. Расчет передач с поликлиновыми ремнямн и основные размеры ремней даны в работе (2].
ПЕРЕДАЧИ С ЗУБЧАТЫМИ РЕМНЯМИ
Зубчатый ремеиь представляет собой по форме бесконечную плоскую ленту с зубцами трапецеидальной формы на внутренней поверхности (рис. 7), входящими в задепление с зубцами на шкивах. Ремни выполняют в основном из армированного металлотросом неопрена или, реже, полиуретана. Спирально навитый по длине ремня трос служит несущим элементом при передаче окружного усилия и обеспечивает неизменяемость шага ремня. Предел прочности троса ав = == 3000 МПа, относительное удлинение б = 44-5%.
Каркас кинематических зубчатых ремней (применяются в контрольной и измерительной аппаратуре) изготовляют из стекловолокна или полиамидного шнура, а ремень— из резины, покрытой для повышения износостойкости тканым нейлоном.
2, Мощность 1У0, кВт, передаваемая одним ремнем
<и « 2 з 2 s Скорость ремня. м/с
Сечечи ремня 5 “ 3 я 2 я х 5 ® к я а. < ж Э 1 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30
Z 63 7! 80 90 и более 0,08 0. 10 0.1 1 0,12 0. 15 0.17 0,20 0.21 0,29 0.32 0,37 0,41 0.42 0.47 0,53 0.58 0,56 0.63 0,69 0.76 0.69 0,78 0.85 0.93 0.82 0.93 1,00 1.11 0,96 1,07 1.15 1.27 1.09 1,22 1.27 1.40 * 1.18 1,30 1,39 1,55 1,26 1,38 1,51 1,67 1.26 1.39 1.55 1.78 1,20 1.32 1.51 1,65 - - -
А 90 100 1 12 125 и более 0.22 0,22 0.22 0.29 0.37 0.37 0.37 0.44 0,66 0.66 0.66 0,74 0,88 0.96 0,96 1.10 1,10 1,18 1,25 1,40 1,33 1.40 1.47 1.69 1.47 1,62 1.69 1.99 1,62 1.84 1.99 2.20 1.77 1.91 2,12 2.33 1.84 1.99 2.29 2,50 1.84 1,99 2,41 2.6 5 1.84 1,99 2.4 1 2.65 1,75 1.91 2.33 2,65 - - -
а 125 140 160 180 и более — 0.59 0.66 0.74 0.81 0,96 1.08 1,18 1,33 1,33 1,40 1.62 1,77 1,69 1,84 1.99 2,20 2.06 2,33 2,50 2,72 2.42 2.65 2.94 3.16 2,70 3.02 3.40 3.60 2,94 3.32 3,76 4,05 2,94 3,54 4.05 4.42 2.94 3,60 4,35 4,71 2,80 3.54 4,35 4,94 2.65 3.40 4,35 4,94 — —
С 200 224 250 280 и более — 1,03 1,10 1,25 1.33 1.77 2.06 2.20 2.36 2,50 2.88 3, 10 3,32 3.10 3,54 3,90 4.20 3.68 4,27 4,64 5.00 4,35 5.00 5,45 5,90 4,94 5.67 6.12 6.70 5,52 6.25 6.63 7,29 6.00 6.78 7, 15 7,58 6.25 7,15 7,50 7.80 6.19 7,15 7.73 8,02 6.05 6.85 7.73 8.10 - — —
D 315 355 400 450 и более — - — 5,45 5.96 6,48 6,94 7.00 7,65 8,24 8,90 8.45 9.20 10,08 10.98 9.70 10.44 1 1.54 12,50 10,70 1 1,54 12,88 13.90 1 1,40 12,50 14. 1 1 15,14 1 1,78 13.30 15,00 16,19 1 1.90 13.72 15.72 17.00 1 1,62 13.82 16.19 17,25 1 1.10 13,60 16.03 17.45 12.92 15.38 17.20 14,70 16.55 14.01 15,72
Е 500 560 630 7 10 и более — — — 8,75 9,87 10,75 1 1.48 11.56 12.60 13.40 14,90 14.00 15.25 16.08 18,00 15,98 17,45 18,70 21,00 17.65 19,20 21.20 22,90 19.00 20,80 23,20 25,20 19,85 22,40 24,80 27,20 20,46 23,60 26,50 29.00 20.46 24.20 27,30 30.20 20,46 24.30 27,50 30,80 20.46' 24.30 27.60 31,40 24,30 27,60 31.80 27,60 31,80
ЕО 800 900 1000 и более — — 13.80 15.45 16.90 17,90 20,20 22,10 21,80 25,20 27,20 25.60 29,10 32,00 29,30 32.90 36,40 32.40 36,00 40. 10 35,00 38,40 42,70 36.80 40.60 44.90 38.20 42,60 47,10 39.80 44.10 48.60 40,00 4 5,60 50.00 40.50 46,30 51,50 40.70 46.30 51,50
240 Ременные передачи
Передачи с зубчатыми ремнями
241
3. Значения коэффициента динамичности
Нагрузка Машины
Спокойная: пусковая нагрузка до 120% нормальной Электрические генераторы, центробежные насосы и компрессоры; станки с непрерывным процессом резания; вентиляторы; ленточиые конвейеры 1
Умеренные колебания нагрузки; пусковая нагрузка до 150% нормальной Поршневые насосы и компрессоры с тремя и более цилиндрами; стаики-автоматы; пластинчатые конвейеры 1,1
Значительные колебания нагрузки; пусковая нагрузка до 200% нормальной Реверсивные приводы1 поршневые насосы и компрессоры с одним и двумя цилиндрами; строгальные и долбежные станки; винтовые н скребковые конвейеры; элеваторы; эксцентриковые и винтовые прессы с тяжелыми маховиками 1.25
Ударная и резконеравномерная иагрузка; пусковая нагрузка до 300% нормальной Молоты, мельницы, ножницы, подъемники, экскаваторы, драги; эксцентриковые и винтовые прессы с легкими маховиками 1,5—1,6
Примечания I. При частых и резких пусках двигателя с большими пусковыми моментами значение следует повышать на 0,15.
2. При двухсменной работе значение Кд необходимо повышать на 0.15, а прн трехсменной работе — на 0.35.
4, Мощность кВт, передаваемая узким (У) клиновым ремием при а = 180° и спокойной нагрузке
Диаметр малого шкива, мм nt, МИИ"1
950 1450 2800
Ремень УО (Lo = 1,6 м)
68 0,78 — 0,88 1.08—1.23 1,74 — 2,02
71 0,99—1,10 1,40— 1,55 2,29 — 2.58
80 1,24—1,33 1,74-1,90 2,90 — 3,19
90 1.50 — 1,60 2,13 — 2,28 3,55 — 3,84
Ремень УА (Lo — 2,5 м)
90 1,70-1.92 2,35—2.69 3,64 — 4,29
100 2,11 — 2,33 2,94 — 3.28 4,64 — 5,28
112 2,60-2,82 3,65 — 3.98 5,79—6,44
125 3,12 — 3,34 4,39 — 4.73 6,99 — 7,65
Ремень УБ (1 -о = 3,55 м)
140 4,29 — 4,75 5,90 — 6,61 8,54-9,86
160 5.47 — 5,93 7,58 — 8,24 10,9—12,3
180 6,62-7,09 9.20 — 9,86 13,0—14,4
200 7,80 — 8.24 10.70 —11.40 14,8—16.1
Ремень УБ ( Lq = 5,6 м)
224 11,3—12,4 14,9—16,7 15,2—18,6
250 13.6 — 14,8 18,0—19,7 16,9 — 20.3
280 16,3-17,4 21,2 — 22,9 17,4 — 20,8
315 19.1-20,3 24,6 — 26,3 —
Примечание. Меньшие значения Wo соответствуют и ~ 1; 2, большие —
242
Ременные передачи
Основной конструктивный пара-t
метр ремня— модуль т= —, где t— шаг ремня.
Значения модуля принимают по табл. 5 с учетом передаваемой мощности и частоты вращения, В зависимости от модуля выбирают ширину ремня:
т, мм Ь. мм
2 .................8 10 12.5 16
3 ................. 12,5 16 20 25
4 ................. 20 25 32 40
5 ................. 25 32 40 50
7, 10 .............. 50 63 80
кроме того, определяют другие параметры: высоту зубьев h = 0,6m, наименьшую толщину S = т, толщину ремня по впадинам Н = т + 1; расчетную длину ремня L = птгр (гр — число зубьев ремня); диаметры делительных окружностей звездочек (рис. 7, б) = mzf, О2 — mz2-, наружные диаметры шкивов зубчатых ремней DH1 — mz1 — 2Д, ~
— тг2 — 2Д, где Д = 0,6 мм прн диаметре троса 0,3—0,4 мм и Д= 1,3 при диаметре троса 0,65—0,8 мм. Шаг зубьев на наружном диаметре
Минимальное число зубьев меньшего шкива принимают равным zmln = 164-
20 при т — 2-1-5 мм и zmln = 20-Т-25 при m = 7-е-10 мм, большие значения назначают при больших скоростях. Число зубьев ремня, находящихся в зацеплении с меньшим шкивом, должно быть не меньше 6. Наибольшая скорость ремия ограничена:
т, мм ................. 2 3 4 — 10
vmax, М//с..................... 30 40
Расчетная удельная (на единицу ширины ремия) окружная сила (в Н/мм) на ремне
Р — [р]о сиснск,
где [ р] о—допустимая удельная окружная сила, зависящая от модуля:
т, мм.................... 2 3 4 5 7 10
[р]0. Н/мм .... 5 10 25 35 45 60
Си — коэффициент передаточного числа, вводится только для ускоряющей
(при u 1 Си = 1):
передачи
и . . 1 — 0,8 0,8—0,6
Си . . . 1 0,95
и ... . 0,4 —0,3
Си . . . 0.85
0,6 —0,4 0,9
<0,3 о;"8
Сн — коэффициент, учитывающий влияние начального натяжения на нагрузочную способность ремня; Сн =' = 0,9 при одном ролике и Сн = 0,8 при двух роликах; Ск— коэффициент, учитывающий неравномерное распределение нагрузки между витками троса и зависящий от ширины ремня:
b, мм.................. * 8 10 12.5
CR.......................... 0,67 0,77 0,83
16 20 25 40 63 100
0,91 0.94 1 1,04 1,09 1.2
Порядок расчета и проектирования передач
243
5. Рекомендуемые значения модуля для передачи с зубчатым ремием
U7, кВт Частота вращения быстроходного вала п, мин”1 U7, кВт Частота вращения быстроходного вала п, мин”1
3500 1750 1200 850 650 3500 1750 1200 850 650
0.05 0,08 0. ] 2 0,18 0.27 0,4 0,8 1,5 2 2 2; 3 2; 3 2. 3 3 2,2 4,0 5.5 7,0 10 13 17 22 30 3, 4 4 4 4 4; 5
3 3 4 4: 5
2, 3 3
5; 7 5; 7 5: 7 5; 7
3; 4
3 7
3; 4
7
3; 4 3; 4 4 5; 7 7
4 7 7, 10 10
Необходимая ширина ремня
Р — <7f2
(18)
где q — масса 1 м ремня шириной 1 см;
т, мм . . . 2 3 4 5 7 10
q- 102, кгЦсм X
Хм). . . 0.32 0,4 0,5 0,75 0,9 1,1
V — скорость ремня, м/с; Р— окружная сила, передаваемая ремнем,
Р =
V
(19)
После определения ширины ремня рекомендуется проверять давление на зубья
Рг = ~ТыГ [p]z> (20)
iCqUiI
где ф — коэффициент неравномерности распределения нагрузки между зубьями ремня и шкива на дуге обхвата, ф — 1,7-=-2,0; г0— число зубьев в зацеплении,
«1
Zo-Zun 36Q ,
Здесь W — передаваемая мощность, Вт; Кд — коэффициент динамичности (см. табл. 3). Окружная сила Р часто ограничивается давлением на зубья в зацеплении с .малым шкивом.
п, мин”1................................200
[р )2, МПа .......................... 2
где аг — угол обхвата на малом шкиве, градусы; [p]z—допускаемое давление на зубья ремня, зависящее от частоты вращения быстроходного вала:
400 1 000 2 000 5 000 10 000
1,5 1 0,75 0.5 0,35
В передаче с зубчатым ремнем не требуется значительное натяжение. Для обеспечения зацепления ремня со шкивом назначают небольшое удельное натяжение S0/b в зависимости от модуля:
т. мм ............. 2 3 4 5 7 10
So/b, Н/см......... 4 6 8 10 14 20
Усилия на валы передачи
Q= (1-1-1,2) Р.
ПОРЯДОК РАСЧЕТА
И ПРОЕКТИРОВАНИЯ РЕМЕННЫХ ПЕРЕДАЧ
Рассмотрим порядок расчета и проектирования на примере клиноременной передачи от электродвигателя мощностью 3 кВт; п = 3000 мин-1; и = 2; работа двухсменная; желательное межосевое расстояние аж « 600 мм. Пусковая нагрузка составляет 150% нормальной.
244
Цепные передачи
1. По табл. 1 принимаем сечение ремня А (возможны варианты сечений Z, В); F = 0,81 см2, Dlmtn = 90 мм, Т — 8 мм.
2. Используя значение желательного межосевого расстояния и рекомендации по выбору межосевого расстояния в клиноременных передачах, принимаем amtn = 0,55 (L>! + О2) + Т; атах = 2 (D, + D2) = 2L>, [ 1 + и (1 -— ё)]. а№ = а,пах и прн 5 = 0,01 для кордшнуровых ремней находим
ат
D1 2[l+u(l-1)]
600
~ 2[1 + 2(1 -0,01)] 100мМ’
3. По формуле (7) вычисляем диаметр второго шкива
£>а = L>,u (1 — |)= 100-2(1-— 0,01) = 198 мм.
4. Определяем наибольшую скорость ремня
nD1n1
3,14-100-3000 ° ~ 60-1000 ~ 60-1000
= 15,7 м/с.
Это значение скорости допустимо для передачи такого типа.
5. Находим длину ремня по формуле
L as л£>ср + а ^2 + J , где
г> / + / . А £>2 — О, ^ср---------5 , а-----------5
т. е.
= 1668 мм.
Полученное значение длины ремня округляем до стандартного L = = 1600 мм.
6. Вычисляем окончательное межосевое расстояние
аяа 1 ~ лРср , 4
+ ~ "|/(£ — лОср)2 — 8Д2 =
1600 - 3,14-149 , 1
~ 4 + 4 Х
X “1/(1600 — 3,14-149)2 — 8 - 49я =
= 564 мм.
7. Определяем угол обхвата на малом шкиве
2А
а = 180 - — 57 = 180-а
2-49-57
567
170°> 120°.
8. По табл. 2 при Dr = 100 мм и о = 15,7 м/с находим мощность, передаваемую одним ремнем, Ц70 = = 1,9 кВт и вычисляем потребное число ремней (КД = 1,1 по табл. 3, К а & as 0,98, Kz « 1, Кь = 0,99):
,.^КЛ 3-1,1 „
WaK 1,9-0,89 ~ ’
Принимаем два ремия.
При необходимости можно оценить долговечность ремня, приняв начальное напряжение натяжения а0 = = 1,2 МПа.
Глава 14
ЦЕПНЫЕ ПЕРЕДАЧИ
Цепная передача, как правило, состоит из ведущей 1 и ведомой 2 звездочек, связанных между собой приводной цепью * (рис. 1). Применяют также
* В машиностроении наряду с приведенными применяют грузовые н тяговые цепи.
передачи с несколькими ведомыми звездочками.
К основным преимуществам передач относят широкий диапазон межосевых расстояний (агаах = 5 м); высокий КПД и отсутствие скольжения (в отличие от ременных передач); возможность передачи движения нескольким ведо-
Конструкции цепей и материалы
245
Z
Рис. 1. Схема цепной передачи
мым звездочкам; меньшая, чем в ременной передаче, нагрузка на валы.
Недостатки передачи: вытягивание цепей (увеличение шага цепей вследствие изнашивания шарниров) и, как следствие, необходимость применения натяжных устройств; необходимость тщательного монтажа (высокая точность установки валов и т. п.) и ухода (смазывание, регулировка); неравномерность хода передачи, шум.
КОНСТРУКЦИИ ЦЕПЕЙ
И МАТЕРИАЛЫ
В качестве приводных применяют роликовые, втулочные и зубчатые цепи.
Роликовая цепь (рис. 2) состоит из последовательно чередующихся внутренних 1 и внешних 2 звеньев, которые шарнирно соединены между собой. Каждое звено выполнено из двух пластин, напрессованных на втулки (внутреннее звено) или оси — валики (наружное звено). Для уменьшения изнашивания' зубьев звездочек перед сборкой звена на втулку надевают ролик 3, свободно вращающийся на ней. Концы цепи соединяют с помощью соединительного звена со шплинтами (рис. 3, а) или штифтами, если цепь имеет четное число шагов. Цепь с нечетным числом шагов соединяется через переходное звено (рис. 3, б). Переходное звено слабее обычного, поэтому стремятся использовать цепи с четным числом шагов.
Основным параметром цепей является шаг t — расстояние между осями Двух смежных роликов наружного или внутреннего звена.
В зависимости от отношения шага Цепи t к диаметру ролика Д (см.
Рис. 2. Роликовая цепь
Рис. 3. Соединительные и переходные звенья цепи
рис. 2) различают цепи легкой (ПРЛ) и нормальной (ПР) серии (при t/dx гС 2) и длиннозвенные (ПРД) цепи (при //<*!> 2).
Приводные роликовые однорядные цепи нормальной серии согласно ГОСТ 13566—75 изготовляют с шагом 8—63,5 мм; разрушающая нагрузка ♦ равна 4600—353 800 Н. Эти цепи широко применяют в различных машинах и механизмах.
Приводные роликовые длиннозвенные цепи (ГОСТ 13568—75) изготовляют с шагом 31,75—76,2 мм; разрушающая нагрузка равна 22700— 100 000 Н. Они отличаются от нормальных цепей меньшей массой и проч-
* Разрушающая нагрузка служит характеристикой прочности цепи и устанавливается заводом-изготовителем экспериментально.
246
Цепные передачи
Рис. 4. Зубчатая цепь
ностью, их применяют в основном в сельскохозяйственных машинах.
При больших нагрузках и скоростях в передачах применяют многорядные роликовые цепи (двухрядные 2ПР, трехрядные ЗПР и четырехрядные 4ПР). Основные размеры и разрушающие нагрузки (пропорциональные числу рядов) для этих цепей регламентированы ГОСТ 13568—75. Многорядные цепи выбирают из тех же элементов, что и однорядные, однако их валики имеют увеличенную длину.
В экскаваторах, кранах и других машинах, эксплуатируемых при тяжелых режимах работы, применяют роликовые цепи с изогнутыми пластинами (ПРИ), подобными переходным звеньям обычных цепей. Благодаря высокой осевой податливости звеньев такие цепи лучше работают при ударных нагрузках, частых реверсивах и т. п. Согласно ГОСТ 13568—75 эти цепи изготовляют с шагом 78,1—140 мм, разрушающая нагрузка равна 360 000—1 200 000 Н.
В машиностроении наряду с роликовыми цепями применяют так называемые втулочные цепи. Выпускаются втулочные однорядные цепи (ПВ) с шагом 9,525 мм и разрушающей нагрузкой 12 000 Н и двухрядные (2ПВ)
с шагом 9,525 мм и разрушающей нагрузкой 18 000 Н.
Зубчатые цепи (рис. 4) обеспечивают плавную работу с меньшим шумом, чем роликовые. Они имеют большую допускаемую скорость и повышенную прочность.
Цепь собирают из рабочих и направляющих пластин, соединяемых между собой сегментными призмами. В рабочей пластине 7 зубообразной формы имеются два фасонных отверстия для призм. Направляющая пластина 2 предохраняет цепь от смещения вдоль оси звездочек во время работы.
Рабочими поверхностями зубьев цепи являются боковые наружные стороны зубчатых выступов пластин, очерченные плоскостями. Этими плоскостями каждое звено садится на два зуба звездочки, имеющих трапециевидную форму.
Основные размеры цепей приведены в табл. 1 и 2.
Пластины роликовых и зубчатых цепей изготовляют из средне углеродистых и легированных сталей 45, 50, 40Х, 40ХН, ЗОХНЗА и затем закаливают до 40—50 HRC. Оси, втулки и призмы изготовляют из сталей 15, 15Х, 20, 20Х, 12ХНЗА, 20ХНЗА, 20ХН4А, ЗОХНЗА, цементуют и под-
Силы в передаче
247
1. Приводные роликовые цепи по ГОСТ 13568 — 75 (размеры в мм, см. рис. 2)
Обозначение цепи t вви, не более d h, ие более F г ОП’ мм* •* Разрушающая нагрузка Н Масса 1 м цепи, кг
ПР-8-460 8,00 3.00 2,31 5,00 7.5 11 4 600 0,20
ПР-9.525-910 9,525 5,72 3,28 6,35 8,5 28 9 100 0,45
ПР-12,7-900-1 12,7 2,40 3,66 7,75 10 18 9 000 0,30
ПР-12,7-900-2 1 2.7 3.30 3,66 7,75 10 21 9 000 0,35
ПР-12.7-1820-1 12.7 5,4 4,45 8,51 11,8 40 18 200 0,65
ПР-12.7-1820-2 12.7 7.75 4,45 8,51 11.8 50 18 200 0,75
ПР-15,875-2270-1 15,875 6,48 5,08 10,16 14,8 55 22 700 0.80
ПР-15,875-2270-2 15.875 9.65 5,08 10,16 14.8 71 22 700 1,00
ПР-19.05-31 80 19.05 12,70 5.96 11,91 18.2 105 31 800 1,9
ПР-25,4-5670 25.4 15,88 7,95 15,88 24,2 180 56 700 2,6
ПР-38.1-12700 38, 1 25,4 11.1 22,23 36.2 395 127 000 5.5
ПР-44,45- 1 7240 44,45 25,4 12.70 25,70 42,4 475 172 400 7,5
ПР-50,8-22680 50,8 31,75 14.29 28.58 48,3 645 226 800 9,7
ПР-63.5-35380 63,5 38,10 19,84 39,68 60.4 1000 353 800 16,0
2. Приводные зубчатые цепи с шарнирами качения по ГОСТ 13552 — 81 (размеры в мм, см. рис. 4)
t ь ft hi s и «ПИ»’1- Н
12,7 22,5 — 52,5 *> 13,4 1,5 4.76 10 000
15,875 30 — 70 •• 16,7 8.7 2 5.95 12 500
19,05 45-93 “ 20.1 10.5 3 7.14 1 5 000
25,4 57— 111*6 26,7 13.35 3 9.52 20 000
31,75 75—129 •’ 33.4 16.7 3 11,91 25 000
*1 На 1 см ширины.
*s Через 6 мм.
•’ Через 8 мм.
•* Через 12 мм.
*6 Через 18 мм.
вергают закалке до 50—65 HRC. Износостойкость цепей можно повысить диффузионным хромированием деталей шарниров.
Технические требования, контроль и испытания роликовых и втулочных Цепей регламентированы ГОСТ 13568—75.
СИЛЫ В ПЕРЕДАЧЕ
Окружная сила в передаче передается за счет давления зубьев ведущей Звездочки иа звенья цепи и давления звеньев ведущей ветви на зубья ведомой звездочки. Усилия между зубьями Звездочек, как и усилия в ветвях, Распределяются иеравиомерио в пределах угла обхвата.
При вспомогательном ходе передачи натяжение в ветвях цепи вызвано ее провисанием от силы тяжести. Если ветвь расположена горизонтально и длина ее приблизительно равна межосевому расстоянию, то иатяжеиие от силы тяжести (в Н)
„ <7<j2 ,
So = g = Iqag,
где q — масса 1 м цепи; g — ускорение свободного падения; а — расстояние между осями звездочек; f — стрела провисания; 6 — — коэффициент.
Наличие провисания обеспечивает более плавную работу передачи, меньшее изнашивание в шарнирах цепи. Минимальное значение стрелы прови-
248
Цепные передачи
сания ведомой ветви в начале работы
новой цепи в горизонтальной передаче принимают /mln = 0,02а. В этом случае £ — 0,25. Если угол наклона ветви к горизонту составляет 40°, то
5 ~ 3. Для вертикальной передачи
1-
В процессе работы передачи под
нагрузкой ведущая ветвь растягивается силой Sj — Р + 30 + Рп + Рд, где Р — полезная сила в передаче;
Р — Ю’ — (здесь кВт; — скорость
W — мощность, цепи, м/с); So —
натяжение в ведомой ветви от силы
тяжести; Рц — натяжение цепи от действия центробежных сил, Рп =. = qv'^; — динамическая нагрузка
в передаче от неравномерности хода цепи [1]. В расчетах цепных передач влияние Рд на работоспособность учитывают с помощью специальных коэффициентов [1].
Ведомая ветвь под нагрузкой растягивается силой
Sa — So + Рц.
На рпс. 5 показана типичная осциллограмма нагрузки па звено цепи за полный оборот вокруг звездочек (участок 1—2 соответствует прохождению звеном ведомой ветви; 2—3 — ведомой звеодочки; 3—4 — ведущей ветви; 4—1 — ведущей звездочки).
При средних скоростях движения цепи (ац < 15 м/с) нагрузка на валы цепей передачи Q — kP. где k — коэф
фициент для горизонтальной и вертикальной передач, соответственно равный 1,15 и 1,05.
ВЫБОР ОСНОВНЫХ ПАРАМЕТРОВ ПЕРЕДАЧИ
Передаточное число передачи (см. рис. 1) г-1 za
U — -~ ,
Ла Zi
где rt! и Zi — частота вращения и число зубьев ведущей звездочки; г,а и z2 — то же Для ведомой звездочки. Для понижающих передач в машинах общего назначения и < 7 (umax = 7). В тихоходных передачах (иц < 2 м/с) при отсутствии толчков и ударов допускается uw„ = 10.
Числа зубьев звездочек и г2 выбирают из условия обеспечения минимальных размеров переда11» и более плавного хода цепи. Для получения наименьших размеров передачи гг должно быть минимальным. Одчако с уменьшением Zj угеличиваются неравномерность хода цепи, динамические нагрузки, шум в передаче и снижается долговечность. На основании экспериментальных исследований и опыта эксплуатации передач во многих странах принято zIm!n = 19 при цц > 2 м/с. В тихоходных передачах (ип < 2 м/с) допускается г, mIn =- 134-15. В передачах, работающих с ударными нагрузками, Zj mln = 23.
Для обеспечения плавности работы, высокой долговечности, ограничения шума в передачах со средними и высокими скоростями рекомендуется принимать z, mln = 29 — 2и > 19.
Излишне большие значения z, вызывают повышенное изнашивание шарниров и увеличение шага цепи (вытяжку цепи). Для роликовых цепей (кроме ПРИ)
200Д’ zi max — >
где К = 2 -----коэффициент высоты
зуба (здесь h — хордальная высота зуба звездочки, ГОСТ 591—69), обычно К = 0,34-0,5; 6/— допускаемое относительное увеличение шага цепи, % •
Выбор основных параметров передачи
249
3. Наибольшие рекомендуемые пНр н предельные пЦр частоты вращения, мин”1, малой звездочки роликовых и зубчатых передач
Шаг цепи, М1л Роликовые ПР, ПРЛ, ПРД Зубчатые Шаг цепи, Роликовые ПР, ПРЛ, ПРД Зубчатые
пнр "пр пнр ппр пнр ппр пнр пьр
8 3000 6000 31,75 630 1000 1320 1500
9,525 2500 5000 — — 38,1 500 900 —
12,7 1250 3100 3300 4000 44,45 400 600 —
15,875 1000 2300 2650 3300 50,8 300 450 — —
19.05 900 1800 2200 2700 63,5 200 300 —
25,4 800 1200 1650 2000 78,1 150 210 — —
Примечания* 1. Прн частоте вращения нДр m<n > 15, а при пп Zj > 20
2 При работе передачи с частотой вращения ппр необходимы повышенная точность изготовления звездочек и монтажа передачи, обильная смазка Цепи ПР применять нецелесообразно
Для более равномерного изнашивания цепи рекомендуется применять малые звездочки с нечетным числом зубьев 11 большие звездочки с четным.
Шаг цепи является основным параметром, от которого зависит несущая способность передачи. С увеличением шага цепи уменьшается быстроходность и несущая способность передачи. Обычно ——
80 25
В табл. 3 приведены рекомендуемые пнр и предельные ппр частоты вращения малой звездочки в зависимости от шага цепи.
Расстояние между осями звездоч.ел а (см. рис. 1) существенно влияет на работоспособность цепи. При малом значении а цепь быстро изнашивается; при большом значении ведомая ветвь сильно провисает, что приводит к ее колебаниям. Нормальная работа передачи обеспечивается при а — (25-е-80) Л Обычно принимают а — (30-=-50)Л Минимальное значение а, мм, определяется углом обхвата цепи (Фтш > 120°);
_ „ £), 4- D,
при и 3 Опии---------------g------
+ (30-5-50);
при н > з аш1п = —
9 + и
10
Потребное число звеньев цепи определяют по предварительно выбранным значениям a, t, гх и г2:
^ +
г1 + г2 2
+
t
а
(1)
В равенстве (1) два первых слагаемых равны потребному числу звеньев при Zj = г2, третье слагаемое учитывает наклон ветви при zx z2. Полученное значение округляют до ближайшего целого числа. При этом рекомендуется принимать w равным четному числу, так как при нечетном числе звеньев приходится использовать соединительные звенья.
Окончательное расстояние между осями звездочек получим из уравнения
Для обеспечения нормального провисания ведомой ветви цепи межосевое расстояние уменьшают на (0,2—0,4)% .
250
Цепные передачи
НЕСУЩАЯ СПОСОБНОСТЬ ПЕРЕДАЧИ
Тяговая способность цепи. Цепные передачи часто испытывают в процессе работы (кратковременно или длительно) значительные статические нагрузки. Для предотвращения чрезмерной вытяжки цепи или ее обрыва полезная окружная сила должна быть
n Qmln - -J- .
где Qmjn — минимальная разрушающая нагрузка (см. табл. 1, 2); А— коэффициент запаса, обычно k = 3-4-5.
Полезная окружная сила в момент пуска машины
_ 2Л4кП rmax — j >
“Д
при движении цепи со скоростью Оц, м/с,
W
Ртах = Ю3 — , чц
где Л}нп — крутящий момент пусковой;
— диаметр делительной окружности ведущей звездочки; W — передаваемая мощность, кВт.
Износостойкость. Основной причиной выхода из строя закрытых и полузакрытых цепных передач общего машиностроения является изнашивание шарниров звеньев цепи, приводящее к увеличению шага цепи (вытяжке цепи), неправильному зацеплению со звездочками и, как следствие, к сползанию цепи со звездочек. Шарнирные соединения работают в условиях граничного трения даже при непрерывном смазывании.
Степень износа передач принято оценивать по относительному увеличению шага цепи 6/ = , %. Норма
предельного износа и связанная с ней продолжительность работы передачи зависят от профиля и числа зубьев большей звездочки, а также требований, предъявляемых к машине по точности перемещений, неравномерности вращения и уровню вибраций и шума.
В приводах полиграфических машин допускается предельная вытяжка ие
свыше (0,5—0,6)% . Предельная вытяжка цепей в машинах общего машиностроения, имеющих, как правило, г2 = = 40—45, ограничена 2—2,5%.
С увеличением нормы износа до 3% часто ослабляются прессовые соединения и снижается прочность изношенных элементов. При невысоком качестве изготовления прессовых соединений возможно проворачивание осей и втулок в пластинах.
В основу расчета работоспособности изнашиваемой цепи положено предположение, что цепь обладает достаточной износостойкостью, если давление р в шарнире ие превышает допускаемого значения [р]и:
РК
Рн — -р—[Р1и- (2)
где Р — полезная окружная нагрузка, передаваемая цепью; = йдйайн X X ^рег^см^реж— коэффициент эксплуатации (здесь йд, ..., йреж—частные коэффициенты, учитывающие условия работы передачи и ее конструкцию, см. табл. 4); Fon— проекция опорной поверхности шарнира (см. табл. 1), Fon = = Bd яз 0,28?а; d — диаметр оси; В — ширина внутреннего звена для втулочных и роликовых цепей (см. рис. 2), В = (1,4-1,75) Ввн.
Если передача работает при нестационарных нагрузках, то в формулу (2) вместо Р следует подставлять значение эквивалентной нагрузки Рэкв.
Из соотношения (2) можно определить предельную полезную нагрузку, Н, передаваемую цепью,
р____ [р]и РопКт
Кэ
и предельную мощность, Вт,
__ [Р1и FопКтУц (4)
где цц = = г2п2/2 — расчетная
скорость движения цепи, м/с; [р]и — допускаемое давление (табл. 5); Кт ~~ коэффициент, учитывающий число рядов цепи т\
2 3 4
I
1
к
ТП
1.7 2,5 3
Несущая способность передачи
251
4. Значения частных коэффициентов
Наименование коэффициента Обозначение Условия работы передачи Значения коэффициента
Коэффициент динамичности нагрузки Спокойная нагрузка Нагрузка с толчками Сильные удары 1 1,2-1,5 1.8
Коэффициент влияния длины цепи (на изнашивание) ^а а = (604- 80) / а = (304- 50) t а < 25/ 0.9 1 1.25
Коэффициент расположения передачи *н Наклон линии центров звездочек к горизонтали. <70° >70° I 1.25
Коэффициент монтажа передачи ь *рег Передвигающиеся опоры Наличие нажимного ролика или оттяжных звездочек (не более двух) Нерегулируемое натяжение I I,! 5 1.25
Коэффициент смазывания ^см Непрерывное смазывание в масляной ванне (Оц = 24- 9 м/с) н циркуляционно-струйное смазывание (Оц > 6 м/с) Регулярное капельное или внутри-шарнирное смазывание Периодическое смазывание 0,8 1 1.5
Коэффициент режима работы ь *реж Односменная Двухсменная Трехсменная 1 1.25 1.4 5
С учетом соотношения (4) определим шаг, мм, роликовой цепиприЁоп= = 0,28/2:
/=бо-1Гт7-\ , (5)
где П] и гх — соответственно частота вращения и число зубьев ведущей звездочки.
Следует принимать цепь с наименьшим шагом, допустимым для заданной нагрузки. Допускаемые давления, установленные на основе многолетнего опыта эксплуатации передач, гарантируют срок службы цепей ~ 15 000 ч при норме предельного износа 6/ = == 3%, если передача эксплуатируется в нормальных условиях (Кэ = 1)-
При расчете зубчатых цепей с шарнирами качения по заданной полезной Нагрузке Р или мощности W, а также
по шагу и скорости определяют ширину цепи (для оц< 10 м/с)
_ 25Р _ 250УЛэ
(6)
Если Од Js 10 м/с, то расчетную силу или мощность в формуле (6) следует умножить на коэффициент, равный , , 0,1<7Оц
1 + —где “7 — масса 1 м цепи.
При расчете передач принимают — = йд, так как информация о значениях других частных коэффициентов, входящих в формулу для определения Кэ, пока не накоплена.
Сопротивление усталости. Высокона-груженные и обильно смазываемые передачи, работающие при низких и средних скоростях (оц< 15 м/с) и переменных нагрузках, часто выходят
5. Допускаемое давление в шарнирах в зависимости от частоты вращения малой звездочки
[р )и, МПа, прн частоте вращения» мнн"1
t, мм <50 200 400 600 800 1000 1200 1600 2000 2400 2800 3200
Роликовые цепи прн Zi — 15-^30
12.7-15,875 35 31 5 28,5 26 24 22 5 21 18 5 16 5 15 14 —.
19.05 — 25,4 35 30 26 23,5 21 19 17,5 15 — — — —
30—38, 1 35 29 24 21 18,5 16,5 15 — — — — —
40 — 50 8 35 26 21 17,5 15 — — — — — — —
Зубчатые цепи
12,7 -15,875 20 18 16,5 15 14 13 1 2 10 5 9,5 8 5 8 7
19,05 — 25 4 20 17 1 5 13 12 1 1 10 8 5 7,5 — —
31,75 20 16 5 14 12 10 5 9 5 7 — — — — —
Ь. Предельная частота вращения, мнн“1, и давление, МПа, при расчете на усталость
Шаг цепи, /, мм
Число зубьев малой звездочки 9,525 12,7 15 87 5 19,05 25,4 31,75 38,1 44.75 50.8
ппр Ыу ппр [р]у rtnp [Р]у rtnp [р]у rtnp [р]у ппр [Р]у ппр [Р]у ппр [Р]у ппр [р]у
1 5 2500 21,3 1850 21,8 1500 22 1300 22 3 950 22.5 800 22,4 680 22 570 22.1 530 21 7
20 2580 21,8 1930 22,2 1 550 22 5 1350 22,9 1000 23 3 840 22,9 710 22,5 590 22 5 550 22
25 2640 22.1 2010 22.5 1600 22 7 1400 23,1 1050 >3 6 870 23,4 730 22,7 610 22 7 570 22,3
30 2720 22 3 2090 22,7 1650 22 9 1450 23,3 1100 23 8 900 23,6 760 23 630 22,9 590 22 7
35 2800 22.5 2170 22,9 1700 23 1 1500 23,5 1125 24 920 23,8 780 23,3 650 23 1 610 23
40 2880 22,7 2240 23 1 1750 23 3 1550 23,7 1150 24 2 940 24 800 23,6 670 23 3 630 23 2
45 2950 22,9 2300 23,3 1800 23 5 1600 23,9 1175 24 4 950 24,2 810 23,8 690 23 5 650 2 5 3
Примечание Срок службы цепи 15 I 0’ ч Данные таблицы получены при условии, что внутренняя пластина и ролики обла дают одинаковым сопротивлением усталости
Цепные передачи
Несущая способность передачи
253
из строя вследствие усталостного разрушения пластин по проушинам, что объясняется высоким коэффициентом концентрации напряжений в этой области и фреттинг-коррозией в прессовых соединениях валиков с пластинами.
При высоких скоростях цепи (уц > > 15 м/с) существенно возрастают ударные нагрузки при входе в зацепление звена с зубом звездочки. В результате даже при небольших нагрузках наблюдаются разрушения звеньев от раскалывания роликов, ослабления прессовых соединений валиков и пластин. Элементы цепи рассчитывают на усталость по общепринятой методике. Запас прочности по переменным напряжениям определяют из соотношения
।
°а —S— + 8<тРа
где O-j — предел выносливости материала при симметричном цикле; еа — коэффициент, учитывающий влияние масштабного эффекта для цепей е0 = 1; Рст — коэффициент, характеризующий состояние поверхности, для пластин с иеупрочиенными отверстиями = 1, для пластин с упрочненными дорнова-нием отверстиями = 1,2-i-1,4; фст — коэффициент, характеризующий чувствительность материала к асимметрии цикла.
В цепных передачах обычно натяжение цепи невелико, от = О,5о0, а фа = 0,14-0,12. В связи с этим запас прочности можно определить, не учитывая влияния среднего напряжения, по формуле
Рис. в. Схема распределения напряжения в пластине
втулки и валики, а также изгиба пластин принимают а0 = 2,84-3.
Амплитуда переменных напряжений
в сеченин пластины по проушинам (см.
рнс. 6)
__ Р max
а ~ 4S(ft —d) ’
(8)
где Ртах — максимальная полезная окружная нагрузка; S — толщина пластины; h — ширина пластины; d — диаметр втулки или валика (см. табл. 1 и рис. 2).
Запас прочности па > 3.
В ряде стран сопротивление усталости цепей оценивают по допускаемому (в условиях переменных нагрузок) давлению в шарнире — критерию подобия, отражающему опыт эксплуатации цепных передач. С учетом соотношения (8) давление в шарнире
Рmax _ 4S (h d)
Ру = -J----= Оа ----тг----
Соп гоп
У
Эффективный коэффициент концентрации напряжений
ka = 1 4- <? (а0 — 1),
где q — коэффициент, характеризующий чувствительность материала к концентрации напряжений, принимают Я = 0,44-0,6; аа — теоретический коэффициент концентрации напряжений. Для пластин с отверстием при d/h = ~ 0,34-0,5 (см. рис. 2) аа = 2,154-2,35 (Рис. 6). С учетом посадки пластин на
Принимая во внимание равенство (7), получим
' = 45 (Л — . (9) У Fon
Сопротивление усталости роликов зависит от контактных давлений между роликами и зубьями звездочек, распределения нагрузки между зубьями звездочки и других факторов. Для обеспечения сопротивления усталости значения допускаемых давлений уточняют с учетом этих факторов. В табл. 6
254
Цепные передачи
приведены значения [р ]'., используемые в расчетах
Для обеспечения прочности динамически нагруженных передач необходимо, чтобы
Ру р к к Ер^у, ( 0) у г опЛцЛт у
где ЛГц — коэффициент качества цепи, для цепей ПР Л Кп = 1, для цепей ПР Кп = 0,85.
При нестационарных нагрузках в выражение (10) вместо Ртах следует подставлять Рэкв.
Для повышения сопротивления усталости пластин отверстия упрочняют дорнованием, путем обжатия в специальных матрицах и т. п.
ОСОБЕННОСТИ ПРОЕКТИРОВАНИЯ И ЭКСПЛУАТАЦИИ ПЕРЕДАЧ
Звездочки к приводным роликовым и втулочным цепям рекомендуется изготовлять в соответствии с ГОСТ 591—69
Звездочки тихоходных передач (цу sj С 2 м'с) можно изготовить из чугуна СЧ 20 с закалкой. В сельскохозяйственном машиностроении используют антифрикционный и высокопрочный чугун с закалкой
В общем машиностроении звездочки или венцы изготовляют из углеродистых и легированных сталей 45, 40Х, 40ХН, 35ХГСА с последующей общей или поверхностной закалкой до 45— 55 HRC, а также из низкоуглеродистых сталей 15, 20Х, 12ХНЗА с последующей цементацией на 1 —1,5 мм и закалкой до 55—60 HRC. Венцы малонагру-женных передач иногда изготовляют из полиамидов
Расположение передач в вертикальной плоскости может быть произвольным Наиболее целесообразным является горизонтальное или наклоненное (под углом 40—45°) расположение линии, соединяющей оси звездочек. Если вертикальное расположение передачи вызвано конструктивными соображениями, то следует обеспечить небольшое взаимное смещение звездочек в горизонтальном направлении для обеспечения некоторого самонатяжеиия цепи.
Ведущей может быть верхняя или нижняя ветвь. Верхняя ветвь должна быть ведущей в горизонтальных передачах с большим межосевым расстоянием (а > 60/) и малыми числами зубьев звездочек во избежание соприкосновения ветвей, а также в передачах с а < 30/ при и < 2 н в вертикальных передачах для предотвращения захвата провисающей верхней ветвью дополнительных зубьев звездочки
Регулирование натяжения цепей является эффективным средством повышения долговечности передачи. Предварительное натяжение устанавливают по стреле провисания f (f ~ 0,02а для горизонтальных и наклонных передач, f = (0,01-=-0,015)а для передач, близких к вертикальным).
Для устранения вредного влияния вытяжки цепей и сохранения предварительного натяжения и провисания в процессе эксплуатации необходимо периодически регулировать натяжение. С этой целью предусматривают либо возможность перемещения опор, либо использование натяжных роликов или звездочек. Натяжные ролики и звездочки рекомендуется устанавливать на ведомой ветви в месте их наибольшего провисания. Для уменьшения вибраций используют ролики оттяжные, которые устанавливают на ведущей ветви с внутренней стороны.
При монтаже передачи необходимо обеспечить параллельность валов, установку и надежное закрепление звездочек в одной плоскости без перекосов (с помощью линейки н уровней) Максимальное отклонение (в мм) звездочек от плоскости принимают равным (0,04—0,08) Уа , а предельный угол смещения (в градусах) примерно равен (2,3—4,6)
—77=-----(а — межосевое расстояние,
У а
мм). После монтажа цепи проверяют правильность хода передачи.
Смазывание можег быть периодическим (с помощью ручной масленки или капельным способом), а также непрерывным (окунанием в масляную ванну, циркуляционной струей от насоса и т. п.). Периодическое смазывание обеспечивает нормальную работу тихоходных передач (скорость цепи иц < 2 м/с). При капельном смазывании и тех же
Порядок расчета передачи
255
условиях допускается скорость цепи Рц < 6 м/с. Масляная ванна обеспечивает хорошую работу передачи при Од = 6-?8 м/с. При скорости > 8 м/с передачи должны работать в условиях циркуляционного смазывания, которое снижает интенсивность развития фреттинг-коррозии и обеспечивает эффективное охлаждение цепи.
ПОРЯДОК РАСЧЕТА ПЕРЕДАЧИ
Пример. Рассчитать горизонтальную цепную передачу при W = = 10 кВт, Hi = 760 мин-1, п2 --= 365 мин-1, 6/ = 3% ; нагрузка спокойная.
1. Выбираем числа зубьев звездочек:
= 29 — 2и = 29 — 2 -2,08 « 25;
z2 = иг-i = 25-2,08 = 52.
2. По табл. 5 принимаем ориентировочно [р]и « 21 МПа. Для однорядной цепи Кт = 1- По табл. 4 принимаем Лд = 1, йд = 1, Ад — 1, йрег 1,25, ЛлМ = 1, £реж = 1. При этих условиях «Аэ = 1,25. Затем определяем шаг цепи
У W Ла
\ - = [р]и
„„ 10-103-1,25 1П ,
- 60 ]/ 21,25.760. ] ^19,1 мм.
3. По табл. 1 выбираем цепь ПР-19,05-3180; t = 19,05 мм; Foa = = 105 мм2; Сддд = 31800 МПа; q = = 1,9 кг.
Для этой цепи по табл. 5 находим 1р]и =. 22 МПа. Так как предварительно принятое значение |.р ]и меньше допускаемого, то выбранная цепь будет Удовлетворять условию износостойкости (5).
4. Определяем скорость цепи
0 __ z^t 25-760-19,05 ц~ 60-Ю3 ~ 60-Ю3 -6м/с.
При этой скорости передача должна работать в условиях циркуляционного смазывания.
5. Определяем полную нагрузку
10-103
1667 Н.
Р = таХ '+
Проверяем статическую грузоподъемность цепи. По табл. 1 находим фт1п = = 31 800 Н. Следовательно, Ртах<
Qmln k
6. Определяем амплитуду переменных напряжений
„_____Р max____
а~ lS(h—d) ~
1667 ,<гл_
4 2,2 (18,2 — 5,96) ~ 16 МПа-
7. Находим запас прочности по переменным напряжениям при ka = 2,8 и о_1 = 200 МПа:
a-i ouka
200
16-2,8
= 4,5 >
8. Определяем давление в шарнире при Кд = 1 и Кт = 1:
Т’тгахК.э 1667-1,25
Ру~ РопКцКт ~ 105-1-1
= 19,8 МПа.
Полученное значение ру< [р]у = = 23,1 МПа (см. табл. 6). Работоспособность цепи обеспечена.
9. Предварительно определяем межосевое расстояние а = 50/ = 50 X X 19,05 = 952,5 мм.
10. Находим потребное число звеньев
.«2-5_+i+i +
+ ( у г‘ У -»»+ \ 2я J а
, 25+ 25 , ( 52— 25 V 1 _
+ 2 + 2л J 50
= 138,87.
Это значение округляем до ближайшего четного числа и принимаем w = 138.
256
Расчет деталей поршневых, двигателей
11. Определяем окончательное расстояние между звездочками
t Г z, ^2 ।
а = т Г—~ +
= £138 - 38,5 +
+ /(138-38,5)._8(^у
= 952 мм.
12. Рассчитываем стрелу предварительного провисания ветви: f — 0,02; а = 0,02 -952 at 19 мм.
Глава 15
РАСЧЕТ ДЕТАЛЕЙ ПОРШНЕВЫХ ДВИГАТЕЛЕЙ
РАСЧЕТ КОЛЕНЧАТЫХ ВАЛОВ
Коленчатые валы разрушаются от усталости в местах наибольшей концентрации напряжений, обычно у выхода отверстия для смазочного материала на коренных и шатунных шейках вала и у галтелей в сопряжениях шеек со щеками.
Рис. 1. Схема сил, действующих на кривошипно-шатунный механизм
Нагрузки. Основными нагрузками являются усилия от давления газа в цилиндре двигателя, передающиеся через поршень и шатун на вал, нагрузки от инерционных сил движущихся деталей кривошипно-шатунного механизма и вибрационные нагрузки, возникающие прн колебаниях вала.
Давление газа в цилиндре рГ для различных углов поворота коленчатого вала а задается индикаторной диаграммой. Сила давления газа на поршень
Рг = (рг Ро) Рп. (1)
где р0 — давление в картере двигателя; Fn — площадь поршня.
Эга сила передается через шатун на шатунную шейку коленчатого вала. Из условия равновесия шатуна следует (рнс. 1):
= Рг tg 3; (2)
<3>
т, = р,. : <’>
COS р
7 __ р (а 4" Р)
Zr~Pr——• (5)
В опорах вала возникает реакция К', которую также можно разложить иа Р', N'r или Т'г, Z'v,
Крутящий момент от окружного усилия Тг
Мк = TrR = РГР Sin^±^).- . (6)
cos р
Расчет коленчатых валов
257
Такой же момент, ио с обратным знаком, который создают силы #г и N', передается на подмоторную раму двигателя,
В движущихся деталях кривошипно-шатунного механизма возникают силы и моменты сил инерции
(7)
где т, J — масса и момент инерции dv
детали; -----линейное ускорение
d<a
центра тяжести; -----угловое уско-
рение.
Массу шатуна тш, совершающего сложное движение, при расчетах условно заменяют двумя эквивалентными массами, расположенными иа осях головок шатуна (рис. 2):
i— > ^ШН = •
(8)
Для автотракторных двигателей ЬЯ1Ь — 0,2-^0,3; для стационарных двигателей LH/L = 0,3-j-0,4.
Это позволяет считать, что к верхней головке шатуна приложена сила инер-
, ЦИИ
?j — (тша + тп) । (9)
t где та, vn — соответственно масса и скорость движения поршня.
Ускорение поршня
^,п « Rto2 ( cos а + -т- cos 2а4) dr \ L )
(Ю)
L Сила Pj вызывает в деталях кривошипно-шатунного механизма усилия Nj, Kj, Тj, Zj и момент М), которые определяют по формулам (2)—(6), если заменить в них Р? на Р].
На шатунную шейку действует центробежная сила инерции
(гПщн 4" гпшш) R(o3t (11)
где тшш — масса шатунной шейки.
Центробежную силу щек
Рщ = тшРшы3 (12)
Рис. 2. К определению эквивалентных масс шатуна
для простоты считают приложенной на радиусе шатунной шейки. Противовесы также вызывают центробежную силу инерции Рпр, плоскость действия которой может не совпадать с плоскостью колена.
Вибрационные нагрузки, связанные с колебаниями вала, определяют экспериментально; они не входят в проектный расчет.
Просуммировав для каждого значения угла поворота коленчатого вала а нагрузки от газовых и инерционных сил. например Z=Zr+Z<— Рт, N = ,Vr + Nj, Т = Tr + Tj и т. д„ строят графики изменения сил за полный цикл двигателя.
При расчете коленчатые валы считают для простоты разрезными, т. е. каждое колено рассматривают как отдельную двухопорную балку, на которую со стороны соседних колен передаются только крутящие моменты, причем
•^к(Г) = Мк ((_!) + TR’, Мк(1) = 0-
(13)
Расчетная схема колена и действующие нагрузки показаны на рис. 3, а типичные эпюры изгибающих и крутящих моментов — на рис. 4—6.
Номинальные напряжения. В коренных шейках изгибающими напряжениями обычно пренебрегают и вычисляют только напряжения кручения.
В шатунных шейках определяют напряжения кручения и напряжения
9 Заказ 402
258
Расчет, деталей поршневых двигателей
Рнс. 4. Эпюра изгибающих моментов в плоскости колена
изгиба. Напряжения изгиба в плоскости колена
— 0.5Za-|-(Pnp — Рщ) b
ииш ’ I1*/
" иш
где а, Ь — см. рнс. 3; — момент
Напряжение изгиба в перпендикулярной плоскости
°иш = 21Гит ’ ('5)
* w иш
Номинальное напряжение у отверстия
аиш = аиш cos v + sin у, (16)
где у — угол между плоскостью колена и плоскостью П, проходящий через масляное отверстие (рис 3).
В щеках наиболее опасными ивлиюг-
ся точки перехода щек в шейки вала (точки 1 и 2 иа рис. 3 и 7). В этих местах действуют напряжения изгиба
(0,5Z 4- Рпр Рщ)
аИЩ 1, 2 - ±
Рис. S. Эпюра нагибающих моментов в плоскостях, перпендикулярных и плоскости колена
ИЩ I 1
(17)
Расчет коленчатых валов
259
Рис. 6. Эпюра крутящих моментов
(плюс относится к точке 2, минус — к точке /) и напряжения растяжения
(сжатия)
0,5Z Рщ арщ - - р-------• (1°)
г пт
Рис. 7. Характер распределения нормальных напряжений в поперечном сечении щеки коленчатого вала
Здесь W'nui 1 — момент сопротивления изгибу сечения щеки в точке <; Рщ — площадь ее сечения.
Разрушение щек реже начинается с угловых точек, где складываются напряжения Орщ4-оИщ 1. г. определяемые по формулам (17) и (18), и напряжения
°ищ з, 4 ~ ±
М* (Ж) '^' ищ 3, 4
(19)
где плюс относится к точке 4, минус — к точке 3. Распределение нормальных напряжений в поперечном сечении щеки показано на рис. 7. Напряжение кручения в щеке обычно будет незначительным.
Подставляя в формулы (14)—(19) наибольшие и наименьшие (с учетом знака) значения силовых факторов в течение цикла, определяют амплитуды оа, та, по которым ведут расчет вала на сопротивление усталости. Влияние средних напряжений обычно невелико.
Коэффициенты неравномерности и концентрации напряжений. Из-за сложной конфигурации коленчатого вала фактическое распределение напряжений в шейках значительно отличается от номинального, что учитывают экспериментальными коэффициентами ₽ [7J. Основную роль играют коэффициенты, значения которых принимают в соответствии о табл. 1 и рис. 8—10.
Величина перекрытия диаметров определяется формулой
А = 0,5 (dH + dm) - R, (20)
Рис. 8. Зависимость коэффициента £hq от отношения длины шейки I к ее диаметру d\
1 — изгиб в плоскости юлена 2 — изгиб в перпендикулярной плоскости
Рис. 9. Зависимость коэффициента . г отношения ширины щеки h ж диаметру шейки d
9*
260
Расчет деталей поршневых двигателей
Рис. 10 Дна1рамма зависимости коэффициента аотн от угла у:
1 — для кручения 2 — для изгиба в плоскости колена, 3 — для изгиба в перпендикулярной плоскости
а коэффициенты $и1, Риа» Риз — приближенно принимают (см. рис. 3):
ри1= 1,0-0,5 А;
В
Риг = 1,9—3 —j-’ '₽из= 1.7-0,4~.
(21)
Непосредственно у масляного отверстия возникает местная концентрация напряжений, которую учитывают эффективными к иффнциентами концентрации:
при изгибе ka = 1,85 + 0,057 X X (ав — 400);
при кручении kx~ 1,70 + + 0,035 (ав - 400),
(22)
где ан — в МПа. Коэффициент влияния абсолютных размеров определяют по рис. 13, гл. 2.
Теоретические коэффициенты концентрации напряжений в галтели сопряжения щеки с шейками (рис. 3) принимают в соответствии с табл. 1
и рис. 11, 12 и относят их при изгибе к номинальным напряжениям изгиба в середине широкой стороны щеки, а при кручении — к номинальным напряжениям в шейке. Коэффициент «иа = 0,6+ 0,25 -А- . (23)
При радиусе галтели г > 3 мм коэффициент чувствительности материала валов обычно достигает значений q — = 0,9—0,95.
Материалы и запасы прочности. Для коленчатых валов применяют стали 35, 45, 40Х, 35ХМ, 18Х2Н4МА и др. Литые валы изготовляют из модифицированных чугунов, а также из стали. Шейки подвергают поверхностной закалке до твердости 50—60 HRC3.
Запасы выносливости для высокооборотных двигателей составляют п — = 1,54-3,0, для средне- и низкооборотных п = 2-4-6.
Пример. В соответствии с расчетной схемой на рис. 3 вал имеет следующие размеры: а = 300 мм; b = 150 мм; В -= = 100 мм; h = 380 мм; dK = dm = — 240 мм; dllt = d1TB = 130 мм; К = ~~ 235 мм; г = 25 мм; у = 0. Материал — сталь 45, частота вращения п = -- 470 мин-1, порядок работы цилиндров 1—4—2—6—8—5—7—3. Центре-
Рис 11 Зависимость коэффициентов czHn и aRl от отно шений толщины щеки В, перекрытия Д, радиуса галтели г и внутреннего диаметра dx к диаметру шейки d
Рис 13 Изменение радиальных Z и окружных Т усилий в зависимости от угла поворота коленчатого вала а
a) ff)
Рнс 12 Зависимость коэффициентов ct, , и <х„, от от-ношений толщины щеки Д ширины щеки h, радиуса галгели г и внутреннего диаметра di к диаметру шейки d
Рис 14 Изменение крутящего момента на шестой коренной шейке вала по углу поворота а
Расчет коленчатых валов
о>
262
Расчет деталей поршневых двигателей
1. Коэффициенты неравномерности напряжений в шейках 0 и концентрации напряжений в галтели а
Изгиб Кручение ,
1"'я ~ ^ло^яг^лз^яз^отн 1'к 1 - ')₽огя
₽ио “ п0 рис 8 ₽Я1 РИ2' ₽из" п0 Формулам (21> 6КО — ПО рис 9
0QTH ~ ПО РИС 10
“и = аио“я1“и2 “к = “ко“к1
аи()— по рис 1 1, а аи1 — по рис 1 1 ’ аи2 ~~ п0 Ф°РмУле (23) — по рис 12, а ак1 — по рис 12. б
2. Расчетные значения напряжений и запаса прочности в сечениях вала
Расчетное сечение Номинальные амплитуды напряжений, МПа Коэффициенты концентра ции с учетом неравномерности Запасы прочности
б-я коренная шейка 6-я шатунная шейка Щека между ними (в точках 1 и 5, см рнс 7) ^4 Сч' Л 11 11 11 11 ’L о ° з а а а н н о о Н о 3,47 3,47 0.90 3,46 2,71 1 .59 Пт = 1,65 п = 1,80 ) , ,, 1 п = 1.76 = 5,55 j ПО1 = !'33 1 1 Щ = 1. 13 2J2 1 п„ = 2.00
бежные силы Щек Рш = 36,25 кН, Рпр = 0.
Кривые изменения усилий Т и Z по углу поворота вала показаны на рис. 13. Расчет показывает, что наибольшая разность Мктах—Л4К mln имеет место на шестой коренной шейке между пятым и шестым коленами (рис. 14). Результаты расчета сведены в табл, 2.
В рассматриваемом примере наиболее нагруженной точкой является середина щеки у галтели, причем расчетный запас прочности незначителен.
РАСЧЕТ ШАТУНОВ
Поршневая головка шатуна. На головку действует переменная по времени сила К = + К] и постоянное давле
Расчет шатунов
263
ние от запрессовки втулки Сила К достигает максимального значения в начале рабочего такта, когда поршень находится у верхней мертвой точки
7^max (Рг шах Ро) Fи
— (гпп 4 ^шв) Л'В2 1 4—/Г/ ' (24)
Минимального (алгебраически) значения Л достигает в начале такта всасывания.
^mln ~ — (тп 4 тшв) /?о>2 1 4" "д’•
(25)
На участке А А (рис. 15) поршневая головка жестко связана со стержнем шатуна, поэтому распределение в ней напряжений носит различный характер в зависимости от направления действия силы Тензометрированне показывает, что когда сила /< сжимает стержень (К>0), нагрузка на нижнюю поло вину головки распределяется примерно по косинусоидальному закону (рис. 16, а), а когда растягивает (К < < 0), то нагрузка на верхнюю поло вину головки распределяется почти равномерно (рис. 16, б). В обоих случаях опасным является сечение вблизи заделки, положение которого определяется углом а; обычно а 90-т-140°.
Рассматривая головку как кривую балку, заделанную в сечении АА и нагруженную, как показано на рис. 16, можно определить изгибающий момент Ма и нормальную силу Na в заделке (рис. 17).
Напряжение в заделке
(26)
где а — ширина; h — толщина стенки головки.
На поршневую головку действует также внутреннее давление со стороны запрессованной в нее втулки
Ег [А 4~ («вт — аг) Trd]
D2 + d2
D2~d2
Pv + ^-d
ВТ
, (27)
где d =
V
Рис. 15. Схема поршневой головки шатуна
Рис. Расчетные схемы нагружения поршневой головки шатуна:
а - при сипе К, сжимиющей шатун, б — при силе К, растягивающей шатун
264
Расчет деталей поршневых двигателей
сечении заделки от угла а при иа-
16, б
Рис. 17. Зависимость гружении поршневой а — по схеме рис
силовых факторов Ма и головки шатуна:
16, а, б — по схеме рнс
где ЕГ; ЕВТ— модули упругости материалов головки и втулки; Л — натяг при посадке втулки в головку (в холодном состоянии); авт, аг— коэффициенты линейного расширения материалов втулки и головки (для бронзы авт « as 18-10-®1/°С, для стали аг as 10 X X 10-я1/°С; Тг — температура нагрева головки при работе двигателя: v — коэффициент Пуассона (v as 0,3). Обозначения диаметров D, d и jBT см. рис. 15.
Постоянное напряжение растяжения от внутреннего давления
«Р ~ -V • (28)
Материал головки нагружается асимметричным циклом с амплитудой
аа = 0,5 (<7t — о2) (29)
и средним напряжением
®тп — “Ь 0,5 (<71 — <7g),
где Ох — напряжение, соответствующее силе /Ст1а, а а2 — то же. силе Кта~Х‘
Рекомендуется иметь запас выносливости не ниже п = 3.
Для повышения прочности поршневой головки следует по возможности уменьшить угол а и не располагать масляные отверстия в области заделки.
Стержень шатуна. Стержень шатуна обычно разрушается от усталости по среднему или по минимальному сечению. При расчете минимального сечения принимают
а = , '(30)
rmln
где FnUn — площадь минимального сечения стержня.
В среднем сечении кроме сжатия происходит изгиб, связанный с эксцентриситетом сжимающей нагрузки и прогибом от центробежных сил, перпендикулярных к оси стержня. На сжатие стержень шатуна рассчитывают по полуэмпирическим формулам [5]
umln — г -X г ср
X + 0,000526 (31)
Расчет шатунов
265
где Fср —- площадь среднего сечения стержня;
- С32)
* ср
Jx — момент инерции сечения относительно оси, перпендикулярной к плоскости движения шатуна, или
_ Лтах °пио — г а.
г ср
X [1 + 0,000132 (4l)2] , (33)
Lx — L — 0,5 (dj + d2), (34)
di и d2 — диаметры отверстий поршневой и кривошипной головки шатуиа;
^ = 4^; <35)
’ сср
Jv — момент инерции сечения относительно оги, лежащей в плоскости движения шатуна.
Растягивающие напряжения
Стах = — ^т1п- . (36)
Гер
Запас прочности определяют по наибольшей абсолютной величине amln. Рекомендуется иметь п= 1,8н-2,0
Кривошипная головка шатуна. Расчет кривошипных головок, которые обычно разрушаются от усталости, носи г сравнительный характер Значения силовых факторов для расчетной схемы, показанной на рис. 18, в среднем (опасном) сечении нижней крышки головки приведены на рис. 19. Здесь Р — сила давления иа крышку в начале такта всасывания:
Р ж (та Шшв) Л’Щ2 1 —— ) -|"
+ тшн7?<о2. (37)
В сравнительных расчетах, приняв а = 130°= const и учитывая, что часть усилий воспринимает вкладыш, считают
а = Р X
0,025с । 0,4
1 _ц _£вкл^ F + Гвкл 38
(38)
Рис. 18. Расчетная схема кривошипной головки шатуиа
где с— расстояние между болтами (с а? 2г); W— момент сопротивления изгибу крышки; F, /''вкл и Л ^вкл— площади н моменты инерции среднего сечеиия соответствеино для крышки и вкладыша головки.
Рис. 19. Зависимость силовых факторов в среднем сечении иижней крышки кривошипной головки шатуна от угла заделки а
266
Расчет деталей поршневых двигателей
Напряжения меняются по пульси-рчющему циклу и при расчете по фор-м\ле (38) достигают amajl = 100-г-300 МПа.
РАСЧЕТ ПОРШНЕВОГО ПАЛЬЦА
Поршневой- палец испытывает сложную деформацию, которую условно расчленяют на изгиб, срез и овализа-цию (рис. 20).
В плавающих пальцах напряжения меняются почти по симметричному циклу. Расчетная нагрузка [6]:
Р = (Рр max Ра) Еп
-mnRtf (1 +- (39)
Расчетные напряжения в пальце определяют согласно рис. 21.
Напряжения при изгибе в продольном направлении
„ Мтах _ Р(/+2&-1,5а) и'~ W 1,2</»(1— а4) ’
(40) где d и dt — соответственно наружный и внутренний диаметры пальца; а = = djd.
Рис. 20. Виды деформаций поршневого пальца:
а - изгиб в продольном направлении; б — срез; в — овалнзацня
Напряжение среза в сечении между бобышкой поршня и головкой шатуна
т = 0,85
(41)
Если напряжения овализации условно считать равномерно распределенными по длине пальца, тс при схеме нагружения по рис. 21,6
X £cos <р + (sirup — <р cos <p) J(
(42)
а напряжения на внутренних волокнах
а<=-7Г
6г — h \
2r — h ) ’
(43)
где h— толщина стенки пальца.
Максимальные напряжения от овализации возникают при <р = 90°.
Действительное распределение нагрузки на палец учитывают экспериментальным поправочным коэффициентом
Л = 1,5—15 (а—0,4)’, (44)
который можно считать действительным при 0,4 sO а -С 0,8.
Тогда расчетная формула для максимальных напряжений овалчзации принимает вид (6];
, Р
max — X
v Г 0.174 (1 + «) (1 — 2д)
L а(1 — а)2
-fS] [1,5— 15 (а — 0,4)3J.
(45)
Рекомендуемые запасы выносливости п > 2.
В транспортных двигателях аи = = 2504-500 МПа; т= 120 -250 МПа; в, max = 120-?200 МПа.
Расчет поршневого пальца
267
Рнс. 21. Расчетные схемы нагружения поршневого пальца:
а — прн расчете на изгиб и срез, б — при расчете иа овалнзацию
Прочность пальца можно повысить химико-термнческой обработкой его поверхностей. Азотирование повышает прочность пальца на 35—45%, цементация на — 15—20%. Недостаточная чистота обработки внутренней поверхности пальца может существенно понизить его прочность.
РАСЧЕТ ПОРШНЕВЫХ КОЛЕЦ
Материалом для поршневых колец обычно служит серый чугун.
Для возможности сборки и большей податливости кольца делают разрезными. Чтобы обеспечить плотное прилегание кольца к цилиндру во время работы, кольцо в свободном состоянии делают большего диаметра, чем цилиндр. Поэтому при вкладывании колец в цилиндр в них возникают напряжения а, величина которых ограничивается условием, чтобы при длительной работе не возникла ползучесть материала, которая может привести к уменьшению давления колец на цилиндр. При надевании кольца на поршень оно упруго разгибается н в нем кратковременно возникают напряжения обратного знака а', которые не должны приводить к значительным остаточным деформациям.
Распределение давлений по кольцу носит сложный характер и зависит от формы кольца в свободном состоянии и от соотношений жесткостей кольца и цилиндра. Специальным выбором
начальной формы кольца можно добиться, чтобы при работе оно прижималось к цилиндру достаточно равномерно по всей поверхности.
Для приближенной оценки напряжений а в кольце можно принять схему нагружения, показанную на рис. 22, в.
Горизонтальное перемещение свободного конца под действием равномерно распределенной нагрузки q, Н/см,
, ЗлО4^ ' = 32EJ ’
Полагая f = 0,5As, где As— разность зазоров кольца в свободном состоянии и после установки в цилиндр, н учитывая, что максимальный изгибающий момент М = 0,5D2q, получим
М 8EJ As
0 = “Г" = Зл£?Г ‘ (47>
Для кольца прямоугольного сечения толщиной h в радиальном направлении имеем
4Eh As ° = ЗлО1
Если цилиндр достаточно жесткий, то
As « л (DK. с — Оц), (49)
где Ок. с — наружный диаметр кольца в свободном состоянии; _ОЦ— внутренний диаметр цилиндра.
По формуле (48) можно также определять напряжения при надевании
268
Расчет деталей поршневых двигателей
Рис. 22 К расчету поршневого кольца: а — копьца вставлены в цилиндр, б — кольцо в свободном состоянии, в — схема нагружения кольца
кольца на поршень а', если считать As к л (Dn— D'K с + 6); Dn— наружный диаметр поршня; D'K с — внутренний диаметр кольца в свободном состоянии; 5— необходимый монтажный зазор.
Напряжения в чугунных кольцах обычно о = 150-4-250 МПа.
Для обеспечения герметичности среднее давление между кольцом и цилин-16EVAs
дром q = —— или (для кольца
прямоугольного сечения) q =
4A/.'As
= —х—хп— не должно быть слишком 9лО4
мало. Обычно q = 50-ь 150 КПа.
РАСЧЕТ ДНИЩА ПОРШНЯ
В приближенных расчетах днище поршня рассматривают как круглую пластин}' постоянной толщины о, заделанную по внешнему радиусу цилиндра
г. Наибольшие напряжения от давления газов рг тах возникают у заделки на внешней (огневой) поверхности
днища Отах = 0,75 Рг max*
Допускают напряжения атах = 50-ь 70 МПа для чугунных и алюминиевых поршней и до 100-4-120 МПа для стальных поршней.
С учетом радиальной и осевой неравномерности температур, вызывающей в поршне дополнительные напряжения, приведенные значения допускаемых напряжений увеличиваются в 2— 2,5 раза.
ПРОЧНОСТЬ ЭЛЕМЕНТОВ
КОРПУСА
По передающимся на корпус нагрузкам /С' и K'j могут быть рассчитаны на прочность его элементы. В ответственных случаях, а также при обнаружении дефектов, проводят тензометрирование. На рис. 23 приведена типичная тензо-грамма напряжений на боковой поверхности крышки опоры коренной шейки вала четырехтактного автомобильного дизеля Период колебаний Т равен времени двух оборотов коленвала, появление двух соседних пиков отражают влияние вспышек в прилегающих к данной коренной шейке цилиндрах Больший пик относится к цилиндру, со стороны которого наклеен тензометр.
Крышка воспринимает усилия только от давления газа, т е. нагружается по отнулевому циклу. В этом случае можно принимать предел выносливости о0 = (1,4—1,6)0-! для стальных и о0 = = (1,24-1,5)а_! для чугунных крышек.
Рнс. 23. Тензограмма напряжений на крышке опоры коленвала
Расчет клапанных пружин
269
РАСЧЕТ КЛАПАННЫХ ПРУЖИН
Клапанные пружины системы распределения поршневых двигателей испытывают прн открытии клапанов повторные ударные нагружения. Так как основной период собственных колебаний пружин вдоль их оси обычно бывает мал по сравнению с отрезком времени между закрытием клапана и последующим его открытием, то при достаточном демпфировании в клапанном механизме каждое открытие клапана можно приближенно считать независимо как единичный удар. В расчетах пружину заменяют эквивалентным по жесткости и массе стержнем постоянного сечения [8] с плотностью рэкв и модулем упругости Еэкв по следующим формулам:
nd2 .
Рэкв — Р Ds ’
где р, G — плотность и модуль сдвига материала пружины; D — средний диаметр; s— шаг; d— диаметр проволоки.
Скорость распространения продольной упругой волны в эквивалентном стержне
. 1/ £экв _ sd 1/ G
ЭКВ У Рэкв Т 2р
период собственных колебаний
2si сэкв
(53)
где I— число витков.
Продольному усилию N соответствуют максимальные касательные напряжения в проволоке
8ND
Ттах----• (54)
Изменение по времени продольных усилий в различных сечениях пружины М (х, I) в процессе удара можно деталь-
Рис. 24, Измеиеиие по времени усилий в клапанной аружнне
но изучить путем расчета по мето^х-прямого математического моделирова-ния (см. гл. 26 н [8]). На рис. 24 приведены результаты расчета усилий в пружине при следующих данных [8] • D = 82 мм; s = 19.2 мм; d — 9 5 мм; р = 7,75 г/см3; G = 7,85- Ю4 МПа; I = = 9,5; максимальный ход кулачка распределительного вала с параболическим профилем h — 38 мм, время открытия клапана = 60 мс. По формуле (53) для периода собственных колебаний Т = 18,8 мс. Сжимающее динамическое усилие относится к сечению, примыкающему к тарелке клапана; N? — к неподвижному сечению у основания пружины.
Для обеспечения безотрывного контакта тарелки пружины с кулачком сила предварительной затяжки должна быть больше максимального растягивающего динамического усилия /Vp max = 151 Н, возникающего прн остаточных колебаниях пружины после закрытия клапана. Ударные напряжения в прово токе ттах — 184 МПа соответствуют максимальному сжимающему усилию Nc щах — 754 Н и являются допустимыми.
В расчетах можно учесть влияние присоединенной массы клапана, а при наличии двух соосных пружин -- их совместную деформацию.
270
Расчет деталей турбомашин
Глава 16
РАСЧЕТ ДЕТАЛЕЙ ТУРБОМАШИН
РАСЧЕТ ЛОПАТОК
НА РАСТЯЖЕНИЕ
ОТ ЦЕНТРОБЕЖНЫХ СИЛ
Напряжения от центробежных сил. Центробежные силы, связанные с вращением колес турбомашин, вызывают растяжение лопаток. При определении растягивающих напряжений лопатку рассматривают как консольный стержень переменного поперечного сечения (рис. 1). На малый элемент лопатки объемом F (r1)dr1 действует центробежная сила
dC = pwVjF (гг)Цгг, (1)
где р— плотность материала лопатки; <о— угловая скорость вращения; F (Г1)— площадь поперечного сечения на расстоянии гг от оси вращения колеса.
Полная сила, растягивающая лопатку в сечеиии на радиусе г,
R
С (г) = pro2 j rtF (ГЦ drlt (2)
где R — наружный радиус лопаточного венца.
В незакрученных (или слабо закрученных) лопатках напряжения распре-
деляются по поперечному сечению равномерно, поэтому
[ ^(О) dr1
(3)
Напряжение растяжения определяется только законом распределения площадей сечений по длине лопатки, но не зависит от абсолютной величины площади сечения.
Лопатка постоянного сечения. В этом случае F (г) = F, и из формулы (2) получаем
С (г) = О.брсо2/7 (/?2 — г2),
а напряжение растяжения
а (г) = 0,5р<о2 (R2— г2). (4)
Распределение напряжений по длине лопатки постоянного сечения показано на рис. 2.
Наибольшее напряжение испытывает корневое сечение лопатки.
Обозначая это напряжение через а0, получаем
°о = 0,5ра>27?2 (1--^-) =
;=0,5рЦд(1 £д), (5)
где ця = <о/?— окружная скорость на конце лопатки; ga = ra/R — относительный радиус втулки.
Рис. 2. Распределение напряжений растяжения в лопатке постоянного сечения
Расчет лопаток на растяжение от центообежных сил
271
1. Значения в зависимости от окружной скорости ur и плотности материала р
Материал Р. г/см1 рм^, МПа, при up, м/с
100 150 200 250 300 350 400 450 500 550
Алюминиевые 2,75 28 62 110 172 248 337 440 557 688 332
сплавы Титановые сплавы 4,5 45 101 180 281 405 551 720 911 1125 1361
Стали 7,85 79 177 314 491 707 96 2 1256 1590 1963 2375
Жаропрочные сплавы 8.15 82 183 326 509 734 998 1304 1650 2038 2465
Значения для разных материалов и окружных скоростей ид приведены в табл. 1.
Равенство (5) иногда применяют в форме, более удобной при проведении газодинамического расчета:
<т0 = 2
Р“ср
А ’
Йде иср = 0,5ш (R + г0) — окружная «'скорость на среднем радиусе; X. — ^Коэффициент длины;
Л = -^Р ; (7)
здесь /?ср = R + г0 — средний диаметр; / = R— г0— длина лопатки.
Из формулы (5) также следует: п - Ч /я\
где S = л (R2 — г§) — площадь проточной части рабочего колеса.
Лопатки постоянного сечеиия проще в изготовлении, чем лопатки переменного сечения. Однако им свойственны
более высокие напряжения растяжения и меньшая вибропрочность из-за нерационального использования материала. Для сильно нагруженных ступеней лопатки постоянного сечения не применяют.
Лопатки с изменением площади поперечного сечения по степенному закону. Площадь поперечного сечения такой лопатки на текущем радиусе
F (г) = F (R) +
(Р — Г \ п
——J ’
или
= d-Х) (1--^!!?, Е(г9) u ’
(9) где F (г0) и F (/?) — площади корневого и концевого сечений лопатки и % = = F (R)/F (г0).
График изменения площади F (л) по длине лопатви для различных значений п при % — 0,25 показан на рис. 3. При п — 1 получается лопатка
1*ис. S. Характер изменения площади поперечных сечений лопатки при различных зна чеииях показатели степени п (для х =“
272
Расчет деталей турбомашин
Рис. 4. Растягивающие напряжения в ло-латке с линейным изменением площади сечений (п = I):
---------= 0.5.--------------~ 0,7
Рис. 5. Растягивающее напряжение в лопатке с изменением площади сечений по параболе (п = 2): ---------to = 0,5;---------So = 0.7
Рис. 6. Растягивающее напряжение в лопатке с изменением площади сечений по кубической параболе (п = 3): --------= 0,5;-------------£0 = 0,7
с линейным изменением площади. Отношение % лежит в пределах 0,2 х Кривые растягивающих напряжений при различных значениях п, отнесенных к напряжению в корневом сечении лопатки постоянного сечения (при одинаковых значениях параметра pufa и относительного радиуса втулки
= ra/R), приведены на рис. 4—6. При резком возрастании площади сечений лопатки у заделки (п > 2) наибольшие растягивающие напряжения находятся не в корневом сечении, а ближе к середине длины лопатки (рис. 6). В приближенных расчетах при X = 0,3-н0,4 можно считать наибольшее напряжение растяжения в лопатке ^tnax = (0,5—0,6) Од.
В табл. 2 приведены отношения объемов V лопатки при данных значениях п и х к объему лопатки постоянного сечения: Vo = F (rn) I.
Если лопаточный венец имеет бандажное кольцо, антивибрационные полки или проволочные связи, следует определить центробежную силу от этих дополнительных масс, приходящуюся на каждую лопатку, и при расчете растягивающих напряжений в сечениих, расположенных на мень-
Расчет лопаток на изгиб
273
2. Относительный объем лопаток переменного сечення V/Vt
п 1 2 3
X 0.2 0,3 0.4 0,2 0,3 0.4 0,2 0,3 0.4
v/v. 0.60 0.65 0.70 0.47 0.53 0,60 0.40 0.47 0,55
ших радиусах, чем соответствующие массы, включить добавочную центробежную силу в выражение для С (г). Обязательно проверяют напряжения в ослабленном из-за отверстия под проволоку сечении.
Вытяжка лопаток. Упругое удлинение лопаток от центробежных сил
Я
гили с учетом формулы (2)
Я Я
Д/у = Р“2 j Е[;Г^- j T1F (rj drt.
(10)
Для лопатки постоянного сечения При модуле упругости Е = const
' Д/у Р“я
"7^ = ^г (’ + 0’5*°)-
(11)
'Лопатка удлиняется также из-за теплового расширения на величину
Я
МТ = j а [Т (г) — TJ dr tv
^а(Тс9-ТЛ)1, (12)
где а — коэффициент температурного линейного расширения материала лопатки; Т (г) — изменение температуры по длине лопатки в рабочих условиях, ’С; ТсР—ее среднее значение; Та = = 20 °C.
Дли турбинных лопаток Д/j- обычно значительно превосходит величину Д/у.
При высокой температуре лопатка удлиняется с течением времени из-за ползучести материала. Если скорость ползучести vp связана с напряжением а степенным законом vp = kon (где
k, п— экспериментальные постоянные материала), то удлинение лопатки за время t под действием постоянных напряжений а составит
Я
Mp = kt j [a(r)]ndr. (13)
Вытяжка приводит к уменьшению радиального зазора между концом лопатки и корпусом и может привести к недопустимому цеплянию лопаток за корпус. Уменьшение зазора может быть вызвано также вытяжкой диска (см. ниже) и уменьшением диаметра корпуса из-за его более быстрого охлаждения, чем диска, при выключении двигателя.
РАСЧЕТ ЛОПАТОК НА ИЗГИБ
Изгибающие моменты от газовых сил. При расчете лопаток на изгиб удобно пользоваться системой координат, показанной на рис. 7. Здесь х, у, г—оси, связанные с вращающимся диском и проходящие через центр тяжести корневого сечения лопатки О. Ось х параллельна оси вращения и направлена по потоку. Ось г направлена вдоль радиуса, ось у лежит в плоскости вращения. Координаты центра тяжести поперечных сечений (выносы) обозначены х (г), у (г). В общем случае линия, соединяющая центры тяжести сечений (ось лопатки), не является прямой, но отношения х/r
1, ylr <С 1. Поэтому можно считать, что поперечные сечения лопатки перпендикулярны оси г.
Через центры тяжести сечений Ох проходят оси хх, ylf соответственно параллельные осям х, у. Главные центральные оси сечений обозначены как g. Т), причем £— ось наименьшей жесткости. Угол а между осями £ и хх определяет установку профилей.
274
Расчет деталей турбомашин
Различают роторы правого и левого вращения. На рис. 7 показан ротор правого вращения,, который вращается по часовой стрелке. е~ли смотреть по направлению потока газа. В этом случае, из соображений газодинамики, угол а > 0.
Газовые силы, Н/м, действующие на единицу длины рабочей лопатки (рис. 8), определяют по формулам
Рх = ——(Р1 — Pi + Plcla (fla — Саа)];
2 л/
Ру PjCia (СХи Сяи)»
(14)
где г— радиус сечеиия, м; z— число лопаток. рх, р3— давление перед и за
Рис. 8. Газовые силы, действующие на лопатку, и треугольники скоростей перед и за рабочим колесом
рабочим колесом, Па; рг— плотность потока на входе в рабочее колесо, кг/м3; с1а, сга — осевые, с!и, csu~ окружные составляющие абсолютной скорости, м/с.
Силы рх, pv и скорости со, си считают положительными, если их направления совпадают с напряжением соответствующих осей, х, у (на рис. 8 са > 0, си< 0, поэтому при | с2и | < | с1£, | сила Ру будет отрицательная).
Фактическое направление газовых сил рх, ру для турбинных и компрессорных лопаток роторов правого и левого вращения показано на рис. 9. У лопаток турбин сила pv всегда совпадает с направлением вращения, у лопаток компрессора— против вращения. Равнодействующая газовых сил = — + Ру во всех случаях направ-
лена в сторону спинки (выпуклой части) профиля.
Для предварительного расчета определяют изгибающие моменты Мх (r0'i и Му (г0) и напряжения в корневом сечении лопатки, причем учитывают только изгиб относительно оси наименьшей жесткости (ось £). Моменты считают положительными, когда они направлены, против часовой стрелкя, если смотреть с положительного на-
Расчет лопаток на изгиб
275
Левое вращение
а-) О
Рис. 9. Положение профилей и действительное направление газовых усилий: а — турбина, б — компрессор
правления соответствующей оси (см. рис. 7 и 8). При рх > 0 момент Му > > 0, при ру > 0 момент Л4х<0-
В приближенном расчете можно считать, что -сила ру вдоль радиуса -постоянна. Изгибающий момент в корневом сечении относительно оси х
Мх (т0) = —0,5руР. (15)
Величину Мх (r0) можно выразить через крутящий момент на валу Л4К, Н-м:
Л4К = 0,5 | Ру | lzDcp = 9555 , (16)
где N— мощность, кВт; п— частота вращения, мин-1.
Исключив из формул (15), (16) силу ру, получим
|/Их(г.)| = ^, (17)
ла
где X = Dcpll.
При определении изгибающего момента относительно оси у обычно можно считать
. 2лг /1 о\
РЙ~(Р1 —Ра) —• (18)
Если величина рх—ps постоянна, то ми (Ло) = 4т (Pi — Ра) X
OZ
х (1--Ео)2(2 4Чо). (19)
где £о =- r0/R.
276
Расчет деталей турбомашин
для лопаток ступеней с постоянной циркуляцией
Для ступеней, спрофилированных по закону постоянной циркуляции (rclu = const), давление рх меняется вдоль радиуса. В этом случае изгибающий момент в корневом сечении (<о) можно определять по кривой иа рис. 10, где р1Ср — давление на входе иа среднем радиусе.
Действительное направление моментов Мх (г0) и Му (г0) определяют по рис. 9.
Момент в корневом сечении относительно оси с наименьшим моментом инерции £
(r0) = Мх (r0) cos а (г0) 4-
+ Mv(r0)sina(r0). (20)
В формулу (20) моменты и угол установки корневого сечения а (г0) подставляют со своими знаками.
В уточненных расчетах находят распределение изгибающих моментов от газовых сил по всей длине лопатки
(для ряда расчетных сечений, обычно от 3 до 10):
Mxi (г) =
R
= — J Ру (Г!) (n — rjdT! = f
R R
= — j j Py(r2)drtdr2-, ' r‘
Myi (г) =
R
= j Px (ri) (ri — r) dr2 = r
R R
= j j px (r2) dr2 dru
где r rx 2?, Я. и моменты
относительно главных осей инерции
каждого расчетного сечения
«5(r) = Mxl (г) cos а (г) 4-
4- MV1 (г) sin а (г);
(r)=— Mxi (г) sin а (г) 4-
4- (г) cos а (г).
(22)
Изгибающие моменты от центробежных сил. Отклонение оси лопатки от радиального направления (выносы центров тяжести сечений) могут быть связаны с технологией изготовления лопатки или специально предусмотрены для разгрузки лопатки от изгиба газовыми силами. Выносы центра тяжести приводят к появлению изгибающих моментов от центробежных сил, которые приближенно (для корневого сечения) могут быть определены по формулам (рис. 11)
Мх (r»)^-p-y(,rcp)C(rty,
• СП
Л4р(го)«-лг(гСр)С(го), (23) где х (гср), У (гср) — выносы оси лопатки на среднем радиусе гср = 0,5Х X (R 4- г0); С (г0) — центробежная сила всей профильной части (пера) лопатки, определяемая по формуле (2)
Расчет лопаток на изгиб
277
при г = г0. Изгибающие моменты от технологических выносов следует учитывать при больших окружных скоростях (ия > 250 м/с), если их отношение к длине лопаткн превышает 1% (при ия = 2504-350 м/с) и 0,3% при ид > 350 м/с.
Для- разгрузки лопатки от изгиба газовыми силами осуществляют наклон оси лопатки по отношению к замку в сторону спинки (рис. 12, а) или смещают ось лопатки вместе с замком в сторону вогнутой части профиля (рис. 12, б).
В уточненных расчетах находят распределение изгибающих моментов от центробежных сил по всей длине лопатки
R
МХ1 (г) = рш2 j rjF (rx) х
Г
(24)
R
= — рш2 f X
* r
X [X (rx) — x (r)] dru )
где r < rx < R.
Моменты относительно главных осей инерции находят по формулам (20) или (22). Изгибающие моменты от газовых и центробежных сил суммируют с учетом их знаков.
Напряжения от изгиба. Для определения напряжений от изгиба необходимо знать положение центра тяжести Oj, главных осей инерции г] и некоторые геометрические характеристики сечении лопатки (рис. 13). Прямую, соединяющую две крайние точки профиля на передней и задней кромках, называют хордой (отрезок АС = Ь). Ось наименьшей жесткости | проходит через центр тяжести сечения Ох практически параллельно хорде.
Напряжении от изгиба определяют в точках профиля, расположенных на передней и задней кромках (точки А и С) и на спинке профиля (точка В). От действия газовых нагрузок на кромках профиля (в точках А и С) возникают напряжения растяжения,
Рис. 12. Конструктивные способы раз-грузки лопатки от изгиба газовыми силами р
Рис. 13. К приближенному определению геометрических характеристик сечения лопатки
а на спинке профиля (в точке В) — напряжения сжатия. Наибольшее растягивающее напряжение обычно получается в точке Ах, близкой к точке А,
Для предварительного расчета определяют только наибольшее растя
278
Расчет деталей турбомашин
гивающее напряжение изгиба от газовых сил в корневом сечении лопатки:
Минимальный момент инерции
» 0,0466’ (1 + ?2), (28)
(Го) Wl min ’
(25)
где /Vfj (г0) находят по формуле (20) без учета знака; U?t mln — минимальный момент сопротивления корневого сечения на изгиб (см. ниже).
При уточненных расчетах находят напряжения изгиба от суммарных изгибающих моментов М> (г), Л'1т> (г) во всех характерных точках профиля М для нескольких расчетных сечений г:
®нМ (г) —
(') Ом (г) Л(Г)
(г)
(26)
где (г), т]м (г) — координаты точек (Л, В, С, 4j) сечения на радиусе г; Ji (г), ^г| (г) — главные моменты инерции этого сечения. В формуле (26)
> 0, Jr, > 0, а моменты и координаты подставляют со своими знаками; если <тиЛ(. > 0, то напряжение изгиба в точке от газовых и центробежных сил растягивающее. Знак координат определяется в соответствии с изогнутостью профиля (см. рис. 9). На рис. 13 |А<0, Т)А < 0; |в>0; т]8>0 и т.д.
В длинных лопагках действительные напряжения изгиба от газовых сил получаются меньше, чем по приведенным формулам, благодаря разгружающему действию центробежных сил на упругих прогибах лопатки.
Расчет геометрических характеристик сечения. При предварительных расчетах, когда чертежа лопатки еще нет, можно пользоваться следующими приближенными формулами.
Координаты центра тяжести сечения (см. рис. 13)
где 5 — максимальная толщина профиля, q = А/6.
Площадь поперечного сечения
F ж 0,766. , (29)
Момент сопротивления
W kb&,
(30)
где k — безразмерный коэффициент, значения которого для точек Alt А, В и С приведены в табл. 3.
Для симметричного профиля (при h = 0) 5Л1 = kB — 0,083, a kA = = kc = °°-
Для точки А можно также пользоваться приближенной формулой, соответствующей значению k да 0,1:
F2 1ГдаО,2^_, о
(31)
Если площадь сечения известна, то, определив коэффициент «полноты» профиля kp = FlЬ8, можно уточнить значение минимального момента инерции по формуле
= 0,0883^56’ (1 + 1,0676q<72). (32)
Значения коэффициентов и kq в зависимости от kp приведены на рис. 14.
Для уточненных расчетов геометрические характеристики определяют непосредственно по данным чертежа лопатки, на котором координаты верхнего ув и нижнего уи контуров профиля задаются в некоторой исходной (конструкторской) системе координат х, у (рис. 15) обычно в виде таблиц ув (хв), ув (хн), причем значения хв и х„ могут не совпадать. Численным интегрированием вдоль верхнего и нижнего контуров находим:
площадь поперечного сечения
т да 0,436; п да 0,76А, (27)
где Ь — длина хорды профиля; Л — подъем средней линии профиля.
F = j yBdxB— j yBdxu- (33)
*A
Расчет лопаток на изгиб
279
3. Значения коэффициента k для определения моментов сопротивления в точках сечения лопатки
Точки на рис. 13 Относительная толщина б — б/л
0,02 0.05 0.10 0,15 0,20
А1 0,094 0,088 0,086 0.084 0,083
А. С 0,02 0,107 0,154 0.276 0,406 0,537
В 0,116 0,082 0.080 0.080 0,080
А1 0.152 0,094 0,039 0,^88 0,087
А. С 0.05 0.155 0.107 0.134 0. 177 0,225
В 0.287 0,116 0,08b 0.08! 0,080
Al 0,278 0,129 0,094 0,089 0,089
А. С 0,10 0,279 0,134 0,107 0, 115 0 133
В 0.675 0,221 0,116 0,093 0.085
Al 0.410 0.176 0,109 0,094 0 091
А. С 0.15 0,410 0.179 0.1 16 0,107 0,111
В 1,000 0,358 0,163 0.1 16 0,098
At 0,542 0,226 0.130 0 104 0.094
А, С 0,20 0.542 0,228 0,134 0.1 11 0. 107
В 1,550 0,5! 1 0,221 0.146 0.1 15
Рис. 14. Значения коэффициентов k для определения геометрических характеристик
лопаточных профилей
статические моменты
*с
SX = °-5 J -
*А
*С
- 0,5 J y2H dxR;
*А
*с
sg = J VA ~
*А
*с
- j
координаты центра тяжести ния 01
ss _ _ _
*01 = —р~ i Уо1 ~ ~p~ i
(34)
сече-
(35)
280
Расчет деталей турбомашин
Рис. 15. Определение геометрических характеристик профиля лопатки по данным чертежа
новые координаты точек верхнего и нижнего контуров
центробежный момент инерции
*1в ~ Хв — х01;
Ухв ~ Ув — Уп> *1н ~ *н — *oi! 51н ~ Ун — Уп>
(36)
Х1С
1 i С ”2 в j
Jxtyt ~ ~2~ J ^1в*1в “х1в
Х1А
осевые центральные моменты инер-
ции
*10
~Т
*1А
(38)
г1С
Xi = ' д' У yiB^lB
*1А
Угол Р между главной осью | и осью Xj определяется по формуле
Х1С
1 С ~з j - .
3” J ^1н dXlH ’
*1А
Х1С
Jy^
Х1А
Лс
- j ^Ih^Ih^Ih;
*1А
2Jx а
tg2E=
J th J *
(39)
(37)
а моменты инерции относительно главных осей
7?= 7jEicos2₽ + + JSt sin2 ₽ — JiiSy sin2p;
Л^хт^З-H-cos2 ₽+ 7^^ sin 2p.
(40)
Запас прочности профильной части лопатки
281
Главные координаты характерных точек профиля М (А, В, С, А,)
(*М *01)COS^ +
Пм = - (*м - г01) sin ₽ +
+ (Ум - У01)cos ₽•
Формулы (33)—(41) удобны для расчета на ЭВМ При ручном счете, особенно для тонких профилей, целесообразно определять минимальный момент инерции по формуле (32).
Осевая сила, действующая на все ло-паткя
Н
Рос = 2л j (р! — ра) г dr (42)
или, если величина рг—р2 постоянна, ^ос = ^2(Р1-Р2)(1-^). (43)
Если давление р, меняется, то Рос можно достаточно точно определить по значению давления р1ср на среднем радиусе.
ЗАПАС ПРОЧНОСТИ
ПРОФИЛЬНОЙ ЧАСТИ ЛОПАТКИ
Для компрессорных (холодных) лопаток запас статической прочности профильной части лопатки
« = V’ (44)
где а — наибольшее суммарное растягивающее напряжение от растяжения и изгиба.
Для турбинных лопаток, а также для компрессорных лопаток последних ступеней определяют запас длительной прочности
Одл л = — . о
(45)
где адл — предел длительной прочности материала с учетом температуры Данного сечения лопатки и длительности работы.
Рис. 16. Распределение температуры и напряжений по длине лопатки газовой турбины
Прн работе на нескольких режимах эквивалентный запас прочности вычисляют по формуле (36) в гл. 2.
Типичное распределение напряжений н температур по длине лопатки газовой турбины показано на рис. 16. Минимальный запас прочности лопаток переменного сечения обычно находится в сечении, расположенном на расстоянии (0,2-4- 0,5) / от корневого сечения (заштрихованная зона). В приближенных расчетах можио определить предел длительной прочности по средней (заторможенной по относительной скорости) температуре газа, а напряжение о вычислять для корневого сечения
Обычно средняя температура лопатки первой ступени турбины на 50—100 °C меньше температуры газа перед турбиной Запас статической прочности в лопатках турбомашнн обычно п = = 1,5-4-2 5
Напряжения растяжения в лопатках газовых турбин в сильной степени зависят от типа и назначения турбины, температуры газа, окружной скорости н других параметров.
Наибольшие напряжения растяжения обычно лежат в пределах 80— 250 МПа, напряжения изгиба только
282
Расчет деталей турбомашин
от газовых сил — в пределах 50—• 150 МПа, суммарные напряжения (с учетом компенсации первоначальными выносами) — 100—300 МПа. Напряжения растяжения в стальных лопатках компрессора составляют 150— 200 МПа для первых ступеней и 80— 120 МПа для последних.
Напряжения изгиба от аэродинамической нагрузки обычно равны 80— 120 МПа для лопаток первых ступеней и 150—200 МПа для лопаток последних ступеней.
Для лопаток из алюминиевых сплавов суммарные напряжения не превосходят 100—120 МПа.
РАВНОПРОЧНЫЕ ЛОПАТКИ
При проектировании рабочих лопаток для высокотемпературных газовых турбин целесообразно исходить из условия, чтобы на большей части длины пера лопатки запас длительной прочности п, определяемый формулой (45). был бы равен минимально допустимому запасу [п]. У конца лопатки, где напряжения малы, а в некоторых случаях и у замковой части, где температура значительно снижается, величина п может быть больше [п]:
п [п].
Если известно изменение температуры Т (г) по длине пера лопатки, то, определив для каждого сечения значение предела длительной прочности
Рис. 17 К расчету напряжений в равно-прочной лопатке
Рис. 18. Условия равновесия элемента лопатки
температуре, найдем допускаемые напряжения
. ^дл (г) = (46)
Действительные напряжения а (г) должны быть равны или меньше допускаемых, что можно обеспечить соответствующим выбором закона распределения площадей поперечных сечений F (г) по длине лопатки (рис. 17). У конца лопатки (участок I) всегда есть область, где а< [а]. Здесь сечение может быть постоянным и равным периферийному сечению F (R). Построив по уравнению (4) кривую ас (г), где ас — напряжения в лопатке постоянного сечения, найдем границу участков I и II (г = гс) как точку пересечения кривых [а] и ас.
На участке II
а (г) = [а (/)].
Чтобы установить, как при этом должна меняться площадь сечения F (г), рассмотрим условие равновесия элемента лопатки (рис. 18):
(а + da) (F + dF) — aF +
+ paPrFdr = 0, откуда
-j-(aF) + paPrF = 0. (47)
ar
Разделив переменные
rfF rfg p&rdr 8)
F ' a ’ a
Охлаждаемые лопатки
283
________-L________________JJl________________| 11_____|
F(r0) a) F(R) F(r0) 6) F(R)
Рис. 19. Различные случаи равнопрочной лопатки:
а — ас < [ст], б — общий случай, в — в
области // ст > [ст ] с
и проинтегрировав в пределах от г до гс с учетом условия а (г) = [а (г)], получим
fw-=F(raiW'
(49)
Температура лопатки у замковой части обычно значительно падает, величина [о] возрастает н площадь, вычисленная по формуле (49), может с некоторого радиуса rd начать уменьшаться, что недопустимо по условиям обеспечения вибрационной прочности лопатки. При г < гц (участок III, см. рис. 17), площадь F следует сохранять постоянной илн несколько увеличивать. Значение точки г = rg определяется условием dFldr = 0 и может быть найдено численно или графически.
Распределение напряжений на участке III (при F = const) определится как
о (г) = о (rd) + 0,5р<о2 (гd — г2);
го < г С rg.
Коэффициент уменьшения площади поперечного сечения
7 . FW F(rc)
Х F (го) F (rd)
_ о (rg) о (’’с)
гс , f г dr
-р“ J TF77H
г А
(50)
В отдельных случаях число участков может быть меньшим (рис. 19).
Полученный теоретический закон распределения площадей сечений по длине пера лопатки может служить исходным материалом для последующей конструкторской проработки.
ОХЛАЖДАЕМЫЕ ЛОПАТКИ
В высокотемпературных газовых турбинах используют рабочие и сопловые лопатки, охлаждаемые изнутри воздухом. В охлаждаемых лопатках температура и напряжения распределяются по поперечным сечениям неравномерно (рис. 20 и 21). Упрощенный расчет на прочность охлаждав-
284
Расчет деталей турбомашин
Рис. 20. Температурное ноле охлаждаемой турбинной лопатки
мых лопаток ведут по характеристикам длительной прочности, соответствующим средней температуре сечений.
При уточненных расчетах учитывают температурные напряжения, которые определяют по формулам, приведенным в гл. 17.
При анализе прочности охлаждаемых лопаток следует иметь в виду, что в центральной, более холодной части сечения возникают растягивающие температурные напряжения, которые, суммируясь с напряжениями от центробежных сил, могут приводить к значительным напряжениям. Однако из-за относительно низкой температуры этой части запас ее длительной статической прочности обычно остается достаточным. На горячих кромках, где температура лопатки может достигать 950 °C и выше, возникают сжимающие температурные напряжения прн сравнительно небольших суммарных напряжениях. Но прн недостаточном охлаждении ограничение по запасу длительной статической прочности горячих частей сечеиия может
стать определяющим. Слишком высокая температура кромок недопустима также из-за снижения антикоррозионных и антиэрозионных свойств материала.
При многочисленных повторных пусках турбин материал лопаток испытывает малоцикловую усталость. Чем сильнее охлаждение, тем больше становится неравномерность температуры по сеченню и тем выше уровень возникающих при каждом нагружении температурных напряжений. Сопротивление жаропрочных сплавов малоцикловой усталости при умеренных температурах может быть не больше, чем при высоких, и в центральной части сечения, где действуют большие растягивающие напряжения, возможно появление трещин от малоцикловой усталости. Это явление усугубляется наличием во внутренних полостях охлаждаемых лопаток значительной концентрации напряжений в местах расположения отверстий, ребер, штырьков и других конструктивных элементов, обеспечивающих необходимое течение охлаждающего воздуха вну
Рис. 21. Распределение напряжений в охлаждаемой турбинной лопатке
Изгибные колебания лопаток
285
три тела лопатки. Поэтому глубина охлаждения лопаток должна выбираться оптимальной с учетом всех определяющих прочность факторов.
ИЗГИБНЫЕ КОЛЕБАНИЯ ЛОПАТОК
Для обеспечения сопротивления усталости лопаток уровень переменных напряжений в них должен быть достаточно низким. Повышенные переменные напряжения возникают в лопатках, в основном на резонансных режимах, когда частота внешних возбуждающих сил совпадает с одной из собственных частот колебаний лопатки. Практическое значение имеют частоты до 10 000—15 000 Гц, а в редких случаях н более высокие.
Для отстройки от резонансов важно уже на стадии проектирования правильно определять собственные частоты колебаний лопаток, особенно первую (низшую) частоту нзгнбных колебаний, связанную с деформацией лопатки относительно оси минимальной жесткости.
Приближенный расчет основной частоты колебаний. Лопатку рассматривают как консольный стержень переменного сечения с непрерывно распределенной массой (рнс. 22), совершающий гармонические колебания в плоскости меньшей жесткости т;0г (см. рнс. 7). В приближенном расчете за-крученностью пренебрегают. Смещение осн лопатки в сечении г = г — г$
т) (г, 0 = Л (z) c°s pt, (51) где г] (z) — амплитуда смещения; р — круговая частота колебаний, рад/с; t — время.
Рис. 22. К расчету нагибных колебаний Лопатки
Частота колебаний, Гц, f = -Р- . ' 2л
Скорость движения лопатки в данном сечении
йг] (z> О , > t
— = — П (z) Р sin pt.
Кинетическая энергия всей лопатки в данный момент времени
о
{
= ~ sin2 pt § F (z) [Г) (z)]2 dz, 0
(52)
где pF (z) — масса единицы длины лопатки.
Внутренняя потенциальная энергия всей лопатки при деформации изгиба в данный момент времени
/7(O = 4“jMS(z’ 0 4(z. t)dz = о
l
Е f
= -|-coS2p;j ;B(z)[<(z)l2rfz, (53)
о
где Afj (z, t) = (z) x? (z, t) —
изгибающий момент относительно оси минимальной жесткости xj (z, t) =
d2n (z, t) , .
= ——- = r] (z) cos pt — упругая
кривизна осн лопатки.
По закону сохранения энергии прн свободных колебаниях полная энергия К (0 + П (t) остается постоянной для любого момента времени, что возможно только при равенстве Ктах --~ ^тах> НЛИ
I
РР2 j f(z) In (z)]2 dz =
o
I
= £ j Ji (z)[r]’ (z)]2dz, о
286
Расчет деталей турбомашин
откуда вытекает формула для частоты собственных колебаний лопаткн (формула Релея)
Если внести в згу формулу приближенные значения Для т) (z), удовлетворяющие условиям закрепления, то при точном вычислении интегралов частота / получается больше действительной.
Из формулы (54) следует.
1. Если амплитудный прогиб увеличивается в k р'аз, частота колебаний не изменяется (величина k войдет и в числитель, и в знаменатель)
2. Для увеличения частоты колебаний следует увеличить жесткость сечения на изгиб в районе заделки, где кривизна упругой линии г)" наибольшая, н уменьшить плошадь сечения у конца лопатки, где наибольшие прогибы Г).
3 Частота зависит от отношения Е/р, которое для большинства конструктивных материалов (стали, алюминия,
Рис. 23 Изменение площади и момента инерции по длине лопатки
титана и др.) изменяется мало и составляет "]/Е/р я; 5,1-10* см/с; поэтому частота изгибных колебаний почти не зависит от материала лопатки.
В качестве приближенного значения для г] (z) можно принять прогиб лопатки постоянного сечения от действия распределенной нагрузки
+ т(тГ-
Примем степенной закон распределения площадей и моментов инерции по длине лопатки (рис. 23):
Е(г) =
= /7(0)[х+(1-х)(Ц1-г)'т!];
/ (г) =
= /(0) +
(56) где
Л F(0) ’ J (0) •
Подставив равенства (55). (56) в формулу (54), получим
f £_ Л/г £ ~\/r J (°) ~
' I* V р г Е(0)~
„SJ-W-A-l/ia, (57)
где X — безразмерный коэффициент (табл. 4). Здесь / — в см; J (0) — в см4; F (0) — в см2; f — в Гц.
При очень большой «конусности» (Х<Е t<l) меньшие, а следовательно. и лучшие значения для X дает функция
Т) (г) =
(58)
что учтено при составлении табл. 4.
Для лопатки постоянного сечения (Х= 1. в= 1) Х= 0,560,
4. Значения коэффициента х
т X п = 1 п — 2 п = 3
е
0 0.2 0,4 0,6 0,8 0 0,2 0,4 0.6 0,8 0 0,2 0,4 0,6 0,8
0 1,152 1,174 1,198 1,221 1,241 1,006 1,106 1 ,149 1,189 1.227 0,872 1,057 1.111 1,163 1,214
0,2 0.856 0,874 0,890 0,907 0,923 0,71 1 0.824 0,855 0,883 0,912 0,616 0.780 0,826 0,864 0,902
1 0,4 0,711 0,726 0,740 0,753 0,767 0,581 0,684 0.710 0,734 0,758 0,503 0,637 0,686 0,718 0,750
0,6 0,616 0,635 0,646 0,660 0.670 0,503 0,595 0.621 0.641 0,662 0,436 0,551 0.600 0,629 0,656
0,8 0,551 0,570 0,581 0,592 0,603 0,450 0,533 0,557 0,576 0,595 0,388 0,493 0, 54 0 0,563 0,589
0 2,024 2,066 2,106 2,145 2.182 1,876 1,950 2,021 2.090 2,155 1,631 1.857 1,954 2,047 2,136
0,2 1,023 1,044 1,063 1,082 1,101 0.842 0,984 1.020 1,055 1,089 0,729 0,923 0,987 1,033 1.077
2 0,4 0,777 0,789 0,804 0,820 0,834 0.627 0,742 0,772 0,797 0,823 0.544 0,688 0.746 0,781 0.816
0,6 0,640 0,660 0,673 0,686 0.699 0,522 0,618 0,646 0.668 0,689 0,452 0,571 0,625 0,656 0,684
0,8 0,559 0,579 0,590 0,602 0.613 0,457 0,540 0,557 0,587 0,605 0,395 0,500 0.547 0,575 0,598
0 3,151 3.215 3,279 3,342 3.390 2,913 3,040 3,151 3,247 3.358 2,658 2,897 3,040 3,183 3.326
0,2 1,087 1,112 1,133 1.154 1.1 75 0,888 1,049 1,087 1.124 1, 162 0,769 0,971 1.052 1,101 1,149
3 0,4 0,785 0.812 0,826 0,842 0,856 0.641 0,759 0,793 0,820 0,845 0,555 0,702 0,767 0,804 0,837
0,6 0,64 6 0,670 0,683 0,694 0,707 0,527 0.624 0,654 0,67b 0,697 0,457 0 578 0 633 0.662 0,691
0.8 0,562 0,583 0,594 0,605 0.616 0,458 0,543 0,570 0.589 0,608 0,396 0,503 0,551 0,578 0 602
Изгибные колебания лопаток
288
Расчет деталей турбомашин
Рис. 24. Отношение момента инерции и площади сечення в середине лопатки к нх значениям в корневом сечении
Для выбора показателей тип можно ориентироваться на отношения Г (0,5/)/Е (0) и J (0), которые соответствуют определенным значениям т и п (рис. 24) Если значения F (0,5/) и J (0,5/) неизвестны, можно в среднем принимать т ж I, и 2.
Пример. Найти основную частоту колебаний для лопатки длиной I = = 20 см с размерами корневого сечения (см рис. 13) b = 8 см, б — 0,6 см, h = 0,8 см н концевого 6=8 см, б --- 0,2 см, h = 0,2 см при линейном изменении толщины и стрелы изогнутости сечений По формулам (28), (29) находим.
F (0) = 0,76 (0) б (0) = 0,7 8-0,6 = = 3,36 см2;
F (!) = 0,7-8-0,2 = 1,12 см2;
F (0,5/) = 0,7-8 0,4 = 2,24 см2;
J (0) = 0,046 (0) б3 (0) {1 +
+ [h (0)/б (О)]2) = 0,04-8-0,63 [1 + + (0.8/0.6)2] = 0,193 см4;
J (1)= 0,04-8-0,23 [1 + (0,2/0,2)2] = = 0,00513 см4;
J (0,5/) = 0,04-8-0,4’ [1 + + (0.5/0.4)2] = 0,0528 см4;
J (0,5/) 0,0528
7(0) ~ 0,193 ~ ’ 4,
По рис. 24 устанавливаем, что т = 1, л « 2. По табл. 4 для этих значений т и л путем линейной интерполяции для х и е находим значение % л? 0,638 По формуле (57)
Уточненный расчет собственных частот. Более точно собственные частоты колебаний лопатки могут быть рассчитаны методом последовательных приближений. Дифференциальное уравнение колебаний лопатки в плоскости меньшей жесткости имеет вид S[£7(z)S]=papf(z)T,(z)’(59? при граничных условиях для жестко заделанной в замке лопаткн.
в заделке
П (°) = -§ (°) = °; (6°)
на свободном конце
£3(/) = ‘
dz*{}
= 4-Г£у (*) згП = °- (б1> dz L dz2Jz=z '
Интегрируя обе части равенства (59) в пределах от z до I, найдем с учетом второго условия (61)
^г£У(г)ед =
dz L ' dz2J
= — р2 j pF (zj т) (Zi) dzu z
Z < ZT < I.
Повторяя интегрирование с учетом первого условия (61), получим
I I
=ь р2 J pF (za) Г) (za) dz2 dzr.
Z г.
Изгибные колебания лопаток
289
Перенося EJ (z) в правую часть равенства и дважды интегрируя в пределах от 0 до z, находим с учетом условий (60)
Z Z,
П (г) = р2 j J EJ X о о
I I
X j J pF (z<) 1] (z4) dZi dz3 dz2 dzv. (62) z, z,
Уравнение (62) решают методом последовательных приближений. Так, для i-го приближения
Т). W P^i-1 (г)' (63)
где под выражением (z) понимают переменный интеграл в правой части уравнения (62), вычисляемый по уже известным значениям Hz-! (z).
В качестве исходной функции т]0 (z) можно принять произвольную функцию, удовлетворяющую условиям закрепления (60), например функцию (58).
После вычисления (z) значе. ние квадрата частот в i-м приближе. нии р~ можно найти из условия наилучшей близости функций Гц и Пг-1-для чего составляем выражение для средней квадратической ошибки <с весом»
I
A; = _rJ (t)i ~ Fdz = о
i
о
и из условия ее минимума ЗД(/ др\ = О находим
I
j F (z) (z) (z) dz
pj = —t-----------------------. (б4)
j F(z) LKtu-i (z)]2t/z 0
Найдя Pj, определяем по уравнению j^3) значение t)/(z). Процесс решения,
10 Заказ 402
как правило, быстро сходится (после двух-трех приближений). В результате расчета определяют ие только первую собственную частоту, но и эпюру относительных прогибов f) (z) = r| (г)/т| (!) при колебаниях по первой форме, что позволяет найти эпюры относительных изгибающих моментов
I I
М (z) = р2 | j pF (z2) fj (z2) dzt dZi * h
(65)
и относительных динамических напряжений
При тензометрировании лопаток тензодатчики наклеивают в сечении, где б максимально.
Методом последовательных приближений с использованием условий ортогональности рассчитывают также более высокие собственные частоты и формы колебаний
Колебания вращающихся лопаток. Центробежные силы, создавая растяжение лопатки, повышают собственную частоту ее колебаний. При колебаниях лопатки в поле центробежных сил эти силы совершают работу Ац, в результате чего потенциальная энергия увеличивается на величину Пц = = —Ад. Если прогиб лопатки в плоскости минимальной жесткости равен г] (z), то на элемент лопатки будут действовать силы dC2 и dCv (рис. 25, а):
dCz г» dC =
= Р<и2 (Го + z) F (z) dz\
dCu « dC = • Г__i_ 9
(66)
рш2у (z) F (г) dz, где у (г) = 1] (z) cos а (г),
ЯП
“ = -зо •
Здесь (О — угловая скорость (рад/с); п — частота вращения ротора, мии“\
290
Расчет деталей турбомаишн
Работа этих сил для всей лопатки
I
Лц = j [te (z) dC (г) -f-o
+ 0,5</ (г) Су (г)] dz. (67)
Множитель 0,5 во втором члене правой части равенства (67) связан с тем, что сила dCu увеличивается пропорционально перемещению у. Перемещение сечения г в радиальном направлении
так как согласно рис. 25, б
— dw = Vdz2 -|- dr]3 —
— dz ж -zr- ] dz.
Из выражений (66)—(68) и (51) следует:
(1)2
ZZц = Лц = cos2 pt X
X
о
г г
0 0
I2 cos2 а (г) F (z) dz .
(68)
о
Закрученные лопатки
291
Добавляя величину /7Ц к выражению потенциальной энергии деформации изгиба (53), получим для слабо закрученной лопатки (при cos а ж ж const) вместо (54) следующую формулу:
f = ]/ /о + Вп1 (69)
где /о — частота невращающейся лопатки, Гц, определяемая формулой (54); В — коэффициент,
В =
I
( (г0 + г) В (z) X %) о
о • )
- I -|-1
j ц3 F (г) dz — cos2 а, _о
(70) лс = <о/2л = п/60 — число оборотов в с.
Коэффициент В можно определить, задавшись приближенно формой прогиба ц (г), например, согласно формуле (58).
Для лопатки постоянного сечения
В •= 0.833Л -I- 0,5 — cos2 а, (71) где X = Dcp/l.
Для лопатки с линейным изменением площади при задании формы прогибов согласно формуле (55)
0,151Л + 0 049 ,
0,206x4-0,051 +
0,091x4- 0,011
+ 0,206х-г 0,051 ~
cos2 а,
(72)
где х = F (R)/F (/„).
При х = 0,5 это дает
В = 0,81 А. 4- 0,37 — cos’ а. (73)
Формулой (73) приближенно можно пользоваться и при других значениях %, а также для расчета лопаток со степенным законом изменения пло-щяпей при т— l-i-3.
При колебаниях в плоскости вращения (а — 0) влияние центробежных сил иа увеличение частоты проявляется 10*
слабее, чем при колебаниях в осевой плоскости (а = 90°).
Для турбинных лопаток учитывают влияние снижения модуля упругости с повышением температуры, что приводит к снижению частоты (см. ниже рис. 45, б). Так как величина В не зависит от упругих свойств лопатки, то собственную частоту вращающейся турбинной лопатки определяют по вытекающей из (69) формуле
f = y/~/204_ + Вл2, (74)
где Ее, ЕТ — модули упругости материала лопатки соответственно при нормальной и рабочей температуре.
ЗАКРУЧЕННЫЕ ЛОПАТКИ
Для обеспечения высоких КПД рабочие лопатки компрессоров и .турбин при D,.d'Z< 10 обычно выполняют закрученными (с переменным углом установки а). Полный угол закрученное™ Да = а (I) — а (0) достигает 45—60°.
Слабо закрученные лопатки. Для слабо закрученных лопаток с относительной толщиной сечений 6/6 >0,2, а также для лопаток, у которых параметр закрученное™
62Да
Т~"~бГ> 11
влияние закрученное™ проявляется только в изменении положения оси наименьшей жесткости £ по длине лопатки. Жесткости на изгиб EJt и на растяжение EF остаются без изменения. Упругая крутизна оси при изгибе в плоскости наименьшей жесткости
xg(e)
ЛД (г)
(г) cos а (г) 4-
+ (z) sin а (г)] (75)
292
Расчет деталей турбомашин
связана с кривизнами оси .ипатки в неподвижной системе координат х, у, г (см. рис. 7) соотношениями
d2y
= cos а;
sta <76)
где х (г), у (г) — прогибы в направлении осей х, у.
Таким образом,
d2x sin а , . . ,
d? = ~ЁД C0S“ +
+ М sta a);
v' ’ (77)
d2u cos a. ...
= ~ж( “cosa +
+ Musina).
Соотношения (77) позволяют рассчитать статические прогибы и провести расчет на колебания слабо закрученных лопаток. Изгибающий момент Л1Х1 вызывает в этом случае прогиб не только в направлении оси у, но и в перпендикулярном направлении вдоль оси х, т. е. лопатка испытывает «косой» изгиб.
Для более сильно закрученных лопаток, особенно с тонкими профилями, закрученность вызывает изменение жесткостей на изгиб и растяжение и приводит к появлению связи между деформациями изгиба, растяжения и
Рнс. 26. Удлинение наклонного волокна закрученной лопатки при повороте сечений
кручения. В этом случае лопатку рас-счиплвают как закрученный стержень.
Основные соотношения теории закрученных стержней. В закрученных лопатках продольные волокна представляют собой винтовые линии. На рис. 26 показано одно из таких волокон, находящееся на расстоянии £ от оси и соединяющее две соответственные точки в сечениях г и г + dr (принято t] < £). Угол наклона волокна
ft tdao ₽о = ^,
где а0 — угол начальной закручен-ности.
При деформациях лопатки закрученность меняется
а = а0 + О и угол наклона волокна становится равным
6-6. + ЛР-Е$...Е(^+^);
при этом длина наклонного волокна d/0 увеличивается на отрезок
dr dr
bdl == —---------~ .
COS ₽ COS po
В лопатках углы р0 и р, как правило, не превышают нескольких градусов, что позволяет считать
sta ₽0 ® tg ₽0 ® ₽0;
cos ₽0 « 1 — 0,5₽£, и аналогично для ₽.
Тогда при Рд « 1
Д dl ъ ± (₽2-₽2) =
~ dr k dr + 2 dr
и дополнительная относительная деформация, связанная с поворотом на-de da0 клониого волокна, при < —г-
r dr dr будет
Де = 61. (78)
d/0 dr dr ъ
Закрученные лопатки
293
Суммируя величину Де с относительным удлинением стержня при плоском изгибе (см. с. 336), для закрученной лопатки получим
/79)
e~e°+ndr + dr dr * ' '79J
где е0 — удлинение волокна, совпадающего с осью лопатки; <р — угол поворота сечеиия относительно осн наименьшей жесткости Поворотом сечений относительно осн г) можно пренебречь
Напряжение в наклонном волокне, практически равное напряжению в поперечном сечении,
о = £в = £ (в, + Ч + + (»)
Из условий равновесия
odF — N; [ or] dF = Л45, (81)
(где N — растягивающая сила; Мj — изгибающий момент в сечении лопатки) следует:
моментом проекций нормальных напряжений в наклонных волокнах на плоскость поперечного сечения аро (рис. 26), так что
dQ Г
Gr-&+ J = (84)
или с учетом формулы (80)
0Т’ £(«•'• +
где
в /drr \* Р
7” = 7’ + -g-(5) (8fi)
F
Подставив в равенство (85) выражения для в,, и ~ из уравнения (82), найдем
= aetN + а0(рЛ45 + авМк, (87)
где аое, ае<р> а$ — коэффициенты подат-
ливости;
dQ dat dr dr
= M5.
Здесь учтено, что оси т| проходят
Через центр тяжести сечения ( x\dF =
Е
= 0), и обозначено
J р J п
(82)
dct.Q J р
da» Jpj а6ф = -я0
(88)
(83)
В закрученных лопатках крутящий момент в сечении Мк уравновешивается не только моментом касательных dQ
напряжений GT (см. гл. 18), ио и
Подставив выражение (87) в равенство (82), получим
во == flgjV OetpMg 4~ ДеоЛ4к;
= ОфеЛ/ 4- 4~
294
Расчет деталей турбомашин
где
ae EF
АЛ2 j2p dr ) F
а<₽ ~
2'И
Oe0 — Opel <2ф0 = а0ф;
da.0\2 JpJpl
Оеф — Офв — а&
лопаток, может быть выполнено по следующим приближенным формулам.
J р » Jp _•= 0,ОвЗЗ^б;
Jpt = 0,02225k pib38h\
Т = О.ЗЗЗЗ^Ьб3;
j t*dF= 0,0125йгЬ66; F
(90)
ТТ « drpn
Для незакрученнои лопатки =
— 0 и соотношения (87) и (89) принимают обычный вид:
d0 Л4К. N _ dy
~dr = ИТ ’ ®° ~ ТГр ’ ~dF = EJi •
(91)
Выражениями (91) можно пользоваться также при расчете слабо закрученных лопаток и лопаток с относительно толстыми сечениями.
Для сечений, симметричных относительно хорды профиля, величины •7рЕ = 0, аф0 = О0ф = 0, аф = l/£7g, т. е. основное соотношение теории изгиба неза крученных стержней
Фр _
dr ~ЁД
остается в этом случае справедливым и для стержней закрученных. Выражениями (91) можно приближенно пользоваться при расчете на изгиб лопаток со слабо изогнутыми сечениями (примерно до +6 Л 0,3, см. рис. 13).
В закрученной лопатке жесткости на изгиб и растяжение убывают, жесткость на кручение возрастает, а все виды деформаций оказываются взаимозаменяемыми.
Геометрические и жесткостные характеристики закрученных лопаток. Определение основных геометрических и жесткостных характеристик, необходимых для расчета закрученных
0,0333( 1-ру)Л>;т2
1 + 1,067/г^2
+ 0,0417 (1 +v) X х kp^GgCTj j
0,0356(1+v)fegO"a0GT
Г'+ l,067AQ+
ae0 = — О.ОвЗЗйеоТбао;
О,267йф0ру ~ афе- 1 + 1,067^ 9’
h b2 da0
W Y = -5-37- (92)
Коэффициенты k находят по данным рис. 14 в зависимости от значения коэффициента kp=F/b8, определяемого по фактической площади сечения. Ориентировочно можно считать kp = 0,704-0,75. Момент инерции Jt определяют по формуле (32).
Раскрутка от центробежных сил. Центробежные силы, действующие на лопатку с прямой осью, приводят к по-
Закрученные лопатки
295
явлению в поперечных сечениях лопатки растягивающей силы
N (г) = С (г) (93)
[см. формулу (2)] и крутящего момента (рис. 27)
R
Мк = pro2 J xydF dr fs г F
R «p(o2jjn^r/r. (94)
Г
Введя формулы (93) и (94) в выражение (87) при = 0 и проинтегрировав его по всей длине лопатки, найдем, что конец лопатки повернется на угол
аее (r) X
I о
К R
X r\F (гг) dr1 + а0 (г) С (гх) х
К
9 (R) — pro2 J
Рис. 27. Возникновение крутящего момента от центробежных сил
dr. (95)
Для равномерно закрученной лопатки постоянного сечения при kF = = 0,7 и v = 0,3
9 (R) = - 0,65 Да (А)3 х £ ‘ + go \ о /
1 + 0,885д2
1 + 0,885t/2 + 0,0364у2 ’ 1 ;
где Да — угол полной закрученности; 7= Да (-§") (“) ’ a а° 0ПРеде' ляется формулой (5).
Из выражения (96) следует, что центробежные силы уменьшают начальную закрученность лопаткн.
С увеличением начальной закрученности угол 9 (R) вначале возрастает, а затем, достигнув максимума, начинает убывать (из-за увеличения крутильной жесткости лопатки). Угол 9 (R) может составлять не
сколько градусов, что необходимо учитывать при газодинамическом расчете. Так как для разных материалов р/Е « яй const, а <70 = р, то угол 9 (R) практически ие зависит от материала лопатки.
Упругое удлинение лопатки. Подставив формулы (93) и (94) в первое выражение (89) при = 0 и проинтегрировав его по всей длине лопатки, найдем, что лопатка удлинится на величину
Д/ = ро>2
riF (гг) dri +
(97)
296
Расчет деталей турбомашин
Для равномерно закрученной лопатки постоянного сечения при kp = = 0,7, v = 0,3
4'-М'+1,’ттгз£х
1 + 0,885<?2
Х 1 -|-0,885<?3-ь 0,0364у2
где Д/у — определяется формулой (11).
С увеличением начальной закрученное™ удлинение Д/ возрастает.
Напряжения от центробежных сил. Пренебрегая влиянием крутящего момента, можно считать
е0 « atN\
~ aWN'<
dQ dr
« a^N,
Рис. 28. Зависимость коэффициента увеличения напряжений в закрученной лопатке kfj от параметров у, g
а распределение напряжений согласно формуле (80) будет определяться выражением
$ “ ffcp £1 + р
Колебания лопаток. При колебаниях закрученной лопатки по основной форме N ~ 0, .Ик «0 и
где среднее напряжение по сечению аср определяется формулой (2).
В закрученной лопатке напряжения от растяжения распределяются по поперечному сечению неравномерно.
В центральной части сечения напряжения выше средних, у кромок — ниже. У оси лопатки (| = т) = 0)
= афМЕ;
dQ °0ф dtp
(101)
о (0) — ^оаср»
где
k0 = EFat, = 1 + Еав .
Для такой же незакручениой лопатки
-^ = аф0МЕ, (102) где
1
йф0 EJi ’
(ЮО)
Зависимость коэффициента k0 от
Ьг da„ параметра Закрученное™ у = — ~
и относительной изогнутости профиля <?= /i/б приведена на рис. 28. Графиком можно пользоваться для приближенной оценки максимальных напряжений от центробежных сил в закрученной лопатке.
Из сравнения выражений (101) и (102) следует, что основную частоту колебаний закрученной лопатки можно приближенно определить теми же методами, что и основную частоту соответствующей незакручениой лопатки (см. с. 285), но с заменой момента инерции сечения Jt эффективной геометрической жесткостью на изгиб J где [
Еа^
Прн растяжении тонких, сильно
2
закрученных лопаток на кромках появляются сжимающие напряжения, что может привести к короблению кромок.
Закрученные лопатки
297
Для равномерно закрученной ло- ч h (0)
патки постоянного сечения при kp = ности, градусы); q (0) — от-
= 0,7 и v = 0,3 носительиая изогнутость корневого се-
/ = /о
0,0316<?:у2
1 (1 4- 0,885<72) (1-|-0,0364у2)
(Ю4)
где /о — частота колебаний соответствующей иезакручеиной лопатки.
Основная частота колебаний убывает с увеличением параметров закру-da.a ,
чеиности у = -=---и относительной
' б dr изогнутости профиля q " hid.
Из формул (101) следует, что изгибные колебания закрученной лопатки сопровождаются поворотом сечений. Относительный угол поворота периферийного сечения лопатки
’'°5’
.где 1] (/?) — перемещение конца лопатки, перпендикулярное хорде.
Для равномерно закрученной лопатки постоянного сечения при kp = = 0,7 угол
0 (^) = °.2 — "j + 0^0364у2 ’ (106)
Таблицы для расчета основной собственной частоты колебаний закрученных лопаток. Первую собственную частоту колебаний консольных закрученных лопаток, Гц, рассчитывают по формуле
/2
где / — длина лопатки, см; б (0) — максимальная толщина корневого сечения, см.
Значения коэффициента 1 приведены _ , Ь2 Да / я \
в табл.5*,где у =
параметр закрученности (6 — хорда - лопатки, см; принята постоянной по ее длине; Да — полный угол закручеи-
* Рзсчеты выполнены В Н. Тюленевым и В. А. Рудавцом по методике работы [3]
чения; 6=6 (/)/б (0), h = h (0), (б (/) — максимальная толщина, h (/) — стрела изогнутости периферийного сечения).
Таблица рассчитана для lib = 1,5, ио при определении А ее можно использовать и при других значениях отношения lib, так как его основное влияние отражено в параметре у.
Пример. Найти первую собственную частоту колебаний для лопатки, данные которой были приведены в примере на с. 288 при угле закрученности Да = 54°.
Определяем
82-54л 0,6-20-180 = 5;
0 8 ?(0) = 0^6 - 1-333:
0 2 0 2
6 = 7^==°,333; л =^ = 0,25.
0,0 0,8
По табл. 5 путем линейной интерполяции находим А = 0,20 и
/= 5,1-106^0,20 =
= 765-0,20 = 153 Гц.
Учет закрученности привел к заметному снижению основной частоты колебаний.
В уточненных расчетах лопатки турбомашии рассматриваются как оболочки переменного сечения с закрученно-изогнутой срединной поверхностью Их статические и динамические численные расчеты проводят на ЭВМ. Используются в основном различные вариационные методы Ритца, конечных элементов.
298
Расчет деталей турбомашин
5. Значения коэффициентов ХДДя
6
h 0,1 0.5 1,0
я (0)
0 0.5 I 0 0.5 I 0 0,5 1
Первая форма X,
0 0 1 0.197 0,217 0,242 0,293 0,159 0,168 0,190 0,218 0,146 0,150 0,171 0,187
1 0 I 0,196 0,218 0,236 0,283 0.159 0,167 0,188 0,214 0,145 0,150 0,169 0,186
2 0 I 0.180 0,193 0,206 0,225 0.264 0,148 0,158 0,165 0,183 0,206 0.136 0,144 0,148 0,166 0,181
5 0 1 0,186 0,192 0,203 0,222 0,153 0,157 0,168 0,181 0.141 0,143 0,155 0.164
10 0 1 0,183 0,185 0.189 0,197 0,150 0,152 0,157 0,162 0,138 0,139 0.144 0.148
Вторая форма х,
0 1 0,404 0,404 0,404 0,449 0,449 0.449 0,480 0,480 0.480
1 0 1 0,440 0,437 0,422 0,435 0.421 0,463 0,463 0,461 0.463 0.461 0,488 0,489 0,488 0.489 0,489
2 0 1 0,517 0,511 0,469 0,507 0,459 0,500 0,500 0,495 0,501 0,493 0,514 0.514 0.514 0.513 0,514
5 0 1 0,588 0,597 0,577 0,622 0,565 0,698 0,697 0,656 0,700 0,641 0,665 0,666 0,661 0.669 0.658
10 0 1 0.574 0,578 0,578 0.590 0.590 0,669 0.675 0,677 0.691 0.697 0,789 0,796 0.797 0.816 0,819
Третья форма
0 0 I 0 593 0,643 0,684 0.984 0.684 0 709 0,748 0,837 0,849 1,082 0,853 0.891 0,944 0,987 1,177
1 0 I 0,592 0,635 0,709 0,710 0,700 0,709 0,745 0,826 0,836 1,034 0.852 0.888 0.939 0.979 1.154
2 0 I 0,592 0,628 0,727 0.693 0,743 0,707 0,738 0,805 0.812 0,980 0,850 0,881 0,926 0,962 1,109
5 0 I 0,810 0,814 0,856 0,825 0,943 0,700 0,716 0,786 0,755 0,906 0.835 0.853 0,883 0.8°8 0,996
10 0 1 1,317 1,339 1.277 1,346 1,200 1,151 1,153 1,161 1,156 1,189 1,040 1,040 1,050 1.0*3 1,082
Шарнирные лопатки
299
ШАРНИРНЫЕ ЛОПАТКИ
В некоторых конструкциях осевых компрессоров применяют лопатки с шарнирным креплением к диску, что накладывает определенные особенности на их расчеты.
Кинематика, Схематическая картина шарнирного замка показана на рис 29, где Рш — ратиус штифта (пальца) шарнира; р2 — радиус отверстия в проушине лопатки Для простоты считаем, что штифт жестко закреплен в диске. Относительный радиальный зазор в шарнирном соединении
Д = Р1..-.Р5-, (ю7)
Обычно Д= 0,054-0,15.
Центробежные силы прижимают лопатку к штифту так, что в исходном положении линия контакта лопатки со штифтом проходит через точку А (рис. 29, а). При отклонении лопатки на угол <р линия контакта перемещается в точку В, определяемую углом ф (рис. 29, б)., При малых отклонениях движение лопатки происходит путем обкатывания без скольжения, т. е. дуги Л2В и АВ между собой равны или
Рш1!’ = Pi (Ф — Ф).
откуда ф = у2ф, (108)
где
Yt = 4-= -----------• (Ю9)
A Pi —Рш
Рис. 29. Схема обкатывания лопатки и шарнирном замке
При движении лопатки как твердого тела перемещение произвольной точки М с координатами у, гш складывается из перемещений от поворота лопатки относительно точки А
v' = — у (1 — cos <р) + + гш sin <р « —0,5у<р2 + гшф;
w' — —у sin ф — гш (1 — cos <р) яг ~ _уф _ 0,5гшФ2
и перемещений самой точки А из-за обкатывания, равных и", w’.
Из рис. 29, б следует:
—о" = pj sin Ф — (Pi — Рш) X
X Sin ф « Р1ф — (Pi — Рш) ф;
—W’ = Pi cos ф — [Рш +
+ (Pi — Рш) cos ф] as
« 0,5 (pj — pra) Ф2 — 0,5р2ф2.
С учетом выражений (108), (109) най
дем, что
у" « 0;
w" аг — 0,5 РшР1— ф2 = Pi — Рш
— — 0,5ршу!ф2.
Суммируя оба вида перемещений, получим
у = -0,5(/ф2-|-гшф; 1
w = —у<р — 0,5 (гш + ршуЦ ф2. J
При малых зазорах, когда у2 велико, радиальное перемещение точек Оси лопатки (у = 0) от обкатывания в шарнирном замке соизмеримо с перемещениями от поворота.
Маятниковые колебания лопатки. При основной форме колебаний шарнирной лопатки ее деформации обычно невелики, что позволяет приближенно считать лопатку твердым телом, совершающим маятниковые колебания с обкатыванием в поле центробежных сил. Кинетическая энергия колебаний лопатки
V
(111)
300
Расчет деталей турбомашин
или с учетом выражения (НО) с точ иостью до квадратичных членов
к = Тр/А(^)2’ (112) где
JA = J (гш + У2) dV = V
= Jk/+^)^- (>13)
L
Здесь интегрирование ведется по всей длине лопатки L. Величины Jxl = — j ya dF обычно малы по сравнению F
с z^F и ими можно пренебрегать.
Потенциальная энергия колебаний жесткой лопатки равна работе центробежных сил с обратным знаком:
П = —= —р<о2 j [уи + (гА +
гш) w + 0.5 (и2 -|- Ki2)] dV, (114)
где гА — радиус точки контакта лопатки со штифтом; лопатка колеблется в плоскости вращения.
Введя в равенство (114) выражения для перемещений (110), получим с точностью до квадратичных членов
П = 0,5р<о2 [rASA +
+ Р?! (SA + rAV)] <р2, (115)
где
sa = ( zmdV = J zmFdz, (116) V L
a V = J F dz — объем лопатки. L
Полагая <p = <p0 sin pt и приравнивая Kmax — Пт№, найдем значение квадрата коэффициента настройки частоты при маятниковой форме колебаний лопатки:
q3- = (-O-Y = м \ <о J
-------------71------— (1!7)
Обкатывание в шарнирном замке увеличивает частоту колебаний лопатки.
Шарнирную лопатку следует проектировать так, чтобы величина qM не равнялась и ие была близка к целому числу (например, выбирать qM в пределах 1,3—1,7 или 2,3—2,7 и т. д.). Этим обеспечивают отстройку лопатки от возбуждения колебаний по маятниковой форме силами, частота которых кратна частоте вращения.
Если штифт посажен в диск с зазором (ра > Рш, где ра — радиус отверстия в диске), то приближенно q* = rS/J, где
rS = rASA(ya-2) + rcScV1 +
+ Рш?Л (5Л + rAV);
J = J a (Ya — 2) + J c Vi >
где Y2= Р2/(Р2-РШ); rc - РадиУс точки контакта штифта с диском; Sc, Jc определяется теми же формулами, что и SA, JA, но с заменой координаты гш на гш—2рш.
Расчет на изгиб. При отклонении шарнирной лопатки иа угол <р центробежные силы дают в текущем сечении лопатки изгибающий момент (рис. 30)
I
Л4Ц = § (и, у------v'jdC = —ра>2<р X
гш
I
X F (ггШ1 r1zm)dznli, (118) гш
где и = <ргш, Oj = <ргш1, a dC определяется согласно формуле (1).
Так как г — гА гш, г1 = гА+
+ Zmi, то
I
Л4Ц = —pco2<prA J F (гш1 - гш) dzml.
гш
Интегрируя последнее выражение по частям, получим
Л4ц = —р<о2<ргА х
l I
X j j Fdzmtdzm. (119)
гш 2Ш1
Шарнирные лопатки
301
Рис. 30. К расчету изгибающего момента от центробежных сил при отклонении шарнирной лопатки
Суммируя момент с моментом от газовых сил МР, получим
Мх1(2ш) = Мг(гш)-РШ>А X
I I
X j* j* F (^шз) ^шз ^2ш1* (120) 2ш гш1
В начале координат (при гш = 0) момент относительно точки А
МХ1 (°) = МА = МГА -Pa^rASA,
(121) где МГА = Мг (0) и
l I
SA = J J F (*шэ) ^2шз =
0 гш1
I
— J ZjnF (2Ш) о
В то же время сила реакции, проходящая при обкатывании через точку контакта В (см. рис. 29) и равная центробежной силе Сл = рш’Рл. где
I
Рп = J rF </гш, о
дает относительно точки А момент
МА = СЛАВ = р<1)2ршУ1<рРл, (122) так как согласно рис. 29 и формуле (108) _
АВ » ршф = РпМф.
Приравнивая выражения (121) и (122), найдем
М
Ф== Р“2 (ГА5А + РшТ/л) ‘ (123)
Таким образом, изгибающий момент в текущем сеченни шарнирной лопатки
Mxi (2ш) = Мг (гш)
l I
М?АГA j j ? (2шз) ^2Ш2 ^гш1
• 9
_________Ш Ш1 ________________
га$а ~Ь Рш^г^л
(124)
Для шарнирной лопатки постоянного сечения F = const, нагруженной на длине пера /п постоянной газовой нагрузкой рг = const (рис. 31), формула (124) принимает вид
^1(^ш) = ^х1(гш)^, (125)
где (2Ш) = 0,5рг (/п — г)г — изгибающий момент в лопатке, жестко заделанной по корневому сечению (0 < г < /п); Мл — коэффициент влияния шарнирного закрепления:
Рис. 31. Изгиб шарнирной лопатки постоянной газовой нагрузкой
302
Расчет деталей турбомашин
Рнс. 32. Типичное распределение изгибающих моментов по длине пера:
1 — жесткой лопатки, 2 — шарнирной лопатки с учетом обкатывания; 3 — шарнир* ной лопатки без учета обкатывания (или при Рш > 0)
'а + РшМ> + 2га) ’
(126)
ками (рнс. 33). Полка создает дополнительную центробежную нагрузку
Сп~раз2Кп^п> (127)
где Vn — объем полки; гп — радиус расположения полкн.
Напряжения в пере бандажирован-ной лопаткн
о (г) = (128)
Полку рассчитывают на изгиб от центробежных сил как консольную балку переменного сечения, заделанную в сечении, примыкающем к перу. Изгибающий момент в сечении х (рнс. 34)
X
М (х) — рш2гп j h (*1) (xi) (х — xi) dxi о
или
М (х) = рш2гп [xV (х) — S (х)], (129)
При обычных значениях РшУх ~ » 1,0 -j-0,5; г А » 1 -1- 3 н 1п л, 0,8 + 0,9 величина Лш « 0,34-0,6, т. е. напряжения в пере шарнирной лопатки значительно ниже, чем напряжения при жесткой заделке.
Смещение точки контакта из-за обкатывания приводит к эффекту упругого защемления, поэтому уменьшение напряжений в реальной шарнирной лопатке оказывается меньшим, чем в идеализированном случае при рш = 0.
Типичное распределение изгибающих моментов по длине пера жестко заделанной и шарнирной лопаток показано на рнс. 32.
Рнс. 33. Лопатки с бандажными полками
БАНДАЖИРОВАННЫЕ ЛОПАТКИ
С целью повышения вибрационной прочности и уменьшения газодинамических потерь лопатки газовых турбин делают иногда с бандажными пол-
Рис. 34. Изгиб бандажной полки центробежными силами
Бандажированные лопатки
303
где х
V (х) = j h (Xj) Ь (Xj) dxj; о
X
S (x) = j Xj/i (xj b (Xj) dxP o
Напряжения изгиба
o(x) =
M (x) F(x) ’
Рис. 35. К расчету натяга по бандажным полкам
где
F (x) = A- b (x) /i2 (x).
Во избежание перегрузки периферийных сечений полку следует хорошо центрировать относительно пера лопатки, а переход полки в перо делать плавным.
Бандажированные лопатки обычно ставят на колесо с некоторым натягом. Если сх — жесткость бандажной полкн на сжатие (включая смятие по контактным поверхностям), а са — жесткость лопаткн на кручение, то нз рнс. 35 следует, что для ступени с бандажнрованнымн лопатками в собранном состоянии должны удовлетворяться следующие соотношения:
ta cos Р = Ь;
ДА = ь — Ьа = ~ ; (130)
С1
то, считая угол упругой закрутки лопаткн прн сборке малой величиной, т. е.
sin Р = sin (Ро + ДР) ~
~ sin Ро + ДР cos Ро;
cos Р = cos (Ро + ДР) ~
~ cos Ро — ДР sin Ро,
получаем нз третьего уравнения (130)
ДР = — -^S- (sin Ро + ДР cos Ро), С2
откуда
ЛВ______(Р<п Sin Ро)/с2
1 + (Р/п cos Рп)/са •
Тогда, подставив в первое уравнение (130) значения b и ро,
получим
tn
Где tn — 2лгп/г — шаг лопаток на радиусе расположения полок; Ьо и b — расстояния между контактными поверхностями соответственно до н после сборки; ₽о н р — угол наклона контактных поверхностей к окружному направлению до и после сборки, Р — сила контактного давления между бандажными полками.
Если задана геометрия полкн в собранном состоянии н выбрана сила Р, то по формулам (130) определяют значения Ьо н Ро для отдельной лопаткн:
*0 = ь + — ; ро = р + -P/n Sin£-.
С1 с2
Если известны размеры н форма полки отдельной лопатки (4>о. Ро),
4- ?-п Ро)/С2
14-(Wn cos р0)/са
=>о-4-, С1
откуда приближенно
*о — tn cos Ро
,—t-------- • 0321
——|- —— (/п — b0 cos Ро) С1 с2
Р
Жесткость полкн на сжатие сг обычно гораздо больше, чем жесткость лопаткн на кручение са, так что первым членом в знаменателе формулы (132) можно пренебрегать.
Значение угла ДР можно найтн как по формуле (131) через Р, так н непо-
304
Расчет деталей турбомашин
средственно по приближенной формуле
до ~ cos ро — cos Р = р ~ sin рп _ _ Ь„ — /п cos Р, ~ tn Sin pn
Величину с2 находят по формулам, для незакрученной лопаткн
(133)
С2=- J gt(z) ; _о
для закрученной лопатки
’ I
^2 = j ав {2)dz _о
• (134)
Мерой натяга по бандажным полкам служит контактное давление
Р аКОНТ — р ‘ КОНТ
характеризуют велн-(п. илн Ь„ — tn cos Pn, достигать значений
где Fkoht — площадь поверхности контакта. Обычноаконт — 20н-40МПа.
Иногда натяг чинами ”-------
cos рп которые могут
~ 1 мм и являются показательными лишь прн сопоставлении однотипных лопаток
В рабочих условиях натяг по бандажным полкам меняется, так как меняются все параметры, влияющие согласно формуле (132) на силу Р.
Шаг /„ увеличивается из-за нагрева диска и лопаток и г'астяження их центробежными силами. Изменение шага Д1П связано с радиальным перемещением диска на наружном радиусе и (Ь) (см. с. 317) н с удлинением пера лопатки Д/ (см. с. 273) формулой
лопатки в поле центробежных сил (см. с. 294) на величину 0 (R).
Жесткости Cj н с2 уменьшаются пропорционально изменению модуля упругости материала лопаткн с повышением температуры.
Увеличение шага и уменьшение жесткостей снижает натяг, увеличение размера полкн и раскрутка пера лопатки прн положении контактных площадок для турбин правого и левого вращения, показанном на рис. 35, ведут к усилению натяга.
РАСЧЕТ ЗАМКОВ ЛОПАТОК
Конструктивные формы лопаток весьма разнообразны. Для лопаток газовых турбин часто применяют замок елочного типа (рис. 36). Идея этой конструкции связана с применением равнопрочной формы Профиль зубцов напоминает профиль упорной резьбы. Применяют от двух до шести пар зубцов. Угол между средними линиями зубцов составляет обычно 25—40°.
Если на зубец действует сила Рг, то напряжения изгиба в основании зубца (рис. 37) определяют по формуле
6Рге
(137)
где bt — толщина обода на радиусе, соответствующем рассматриваемому зубцу (см. рис. 36).
Напряжение среза
bih-i
(138)
Прн расчете принимают, что усилие Pt направлено нормально к контактной поверхности (силы трения не учитывают) Если толщина обода постоянна (b, — const), то величину Р,
2зт
Д/п = — [«(&) + Д/]. (135)
Размер полки Ьо увеличивается из-за ее нагрева на величину
Д&о = а ДТП6„, (136) где ДГП — изменение температуры полки.
Угол Ро увеличивается (по абсолютной величине) из-за раскрутки пера
Расчет замков лопаток
305
Риг. 37. К определению напряжений в зубце замка
определяют из условия, что нагрузка иа все зубцы одинакова:
р. — Сл 1 2п cos а ’
где Сл — центробежная сила, действующая на всю лопатку; п — число пар зубцов в соединении; а — угол между рабочей гранью и направлением, перпендикулярным к оси замка.
При переменной толщине обода {см. рис. 36) предполагают, что контактные напряжения на всех зубцах одинаковы. Тогда нагрузка на i-й зубец будет р. _ ^л_______________h___________
1 2 COS Ot + &2 + * * * “Ь 6ц)
(140)
Напряжения растяжения в хвостовике лопатки определяют в сечениях по впадинам.
В сечении / (рис. 38) растягивающая сила
Qi — Сп + Cj,
где Сп — центробежная сила профиль-ион части лопатки; — центробежная сила ча'сти лопатки между корневым сечением и сечением I (объем этой части Vi; он включает и нижнюю полку лопатки)
Если площадь сечения 1 будет F, = = aj&i, то растягивающее напряжение
В сечении // растягивающая сила Qa = Qn + Ci + Са — 2Р} cos а,
где Pi — сила , приходящаяся иа первый зубец замка.
Растягивающее напряжение
Для сечения 111
Qa~ Сц + Ci + Са + С3 —
— 2 (Pi + Р2) cos а и т. д.
Наиболее важным для оценки прочности хвостовика лопатки является напряжение Oi по первой впадине. Приближенно
• а, = (1,1 - 1,2)-^-, причем центробежная сила профильной части лопатки
Сц = О (r0) F (т0), где а (т0) — растягивающее напряжение в корневом сечении лопатки, площадь которого равна F (г0).
Величину о (г0) определяют по графикам (см. рис. 4—6)
Запас статической прочности хвостовика лопатки определяют по формуле
п
О1
где ОдЛ — предел длительной прочности материала при температуре хвостовика лопатки (обычно температуру
Рис 38. К определению напряжений растяжения в хвостовике лопатки
306
Расчет, деталей турбомашин
в сеченчн принимают на 100—150 °C меньше средней температуры в рабочей части лопатки).
Напряжения растяжения по первой впадине зубцов обычно находятся в пределах 100—180 МПа. Для обеспечения равнопрочности профильной части лопатки н замка прн действии вибрационных нагрузок момент сопротивления замка должен быть
(IT— наименьший момент сопротивления корневого сечения лопаткн). Этим условием учитывается влияние концентрации напряжении в замке. Расчет на прочность замковых выступов диска приведен ниже.
Для лопаток компрессоров часто применяют крепление лопатки замком типа ласточкин хвост (рис. 39).
Применение замка этой конструкции для лопаток турбины ограничивается прочностью перемычек диска, которая прн большом • числе лопаток оказывается недостаточной. Глубина замка /i составляет обычно 6—12% длины лопаткн. Угол а применяют в пределах 15 — 30°. Центробежная сила профильной и замковой частей лопаток уравновешивается усилиями Д', действующими на боковые грани (рис. 40). Пренебрегая силами треиия, получим
N , (141)
2 sin a v '
где Сл — центробежная сила профильной и замковой частей лопатки. Напряжения смятия на боковой
Рис. 39. Замок типа ласточкин хвост
Рис. 40. Усилия в замке типа ласточкин хвост
С л
поверхности замка от действия растягивающей силы
асм = ’ О42)
см F ом 26с sma '
где Ь и с— длина и ширина полоски контакта.
Условно считают, что эти напряжения распределяются равномерно по площади контакта (рнс. 41). Допустив, что контактные напряжения от действия изгибающих нагрузок распределяются по линейному закону, получим, что наибольшее контактное напряжение
п(и) 6 (М + еСд) см ’ ^>С2
(143)
где М — изгибающий момент в корневом сечении лопатки от действия аэродинамической нагрузки н первоначальных выносов; Сп — центробежная сила профильной части лопаткн; е— смещение центра тяжести корневого сечения лопатки от оси замка.
Суммарные напряжения смятия
асм асм Л" асм •
Допустимую величину осм принимают в пределах 50—100 МПа для дюралюминиевых н 200— 350 МПа для стальных лопаток. Усилие Q, отрывающее перемычку замкового выступа диска, определяют нз условия равновесия
Q = 2N sin (а + 0,5(3) + Св,
Расчет вамков лопаток
307
СМЯТИЯ
где Р— угол между осями лопаток (Р = 2зт/г; г—число лопаток); Св — центробежная сила замкового выступа.
Учитывая равенство (141), находим
Q = Сл S'n + св- < 144>
При й0 величина Q—>-со, поэтому применение малых углов а (а < 15°) невыгодно.
Прн большом числе лопаток (г > 50) и угле а > 20° можно считать Q да да Сл 4- Св.
Напряжение, растягивающее перемычку,
^пер
где Fnep— площадь сечения перемычки.
Обычно величина а ие превосходит 300 МПа для стальных дисков.
При широких перемычках может произойти разрушение уголков (рис) 42). Уголки рассчитывают на срез или на изгиб.
Шарнирные замки (рис. 43) рассчитывают на разрыв проушины по сечению А — А.
Рнс. 42. Возможное разрушение широкой перемычки диска
где С — центробежная сила части хвостовика лопатки до сечеиия А — А; Fnn— площадь этого сечения.
Кроме того, эти замки рассчитывают на смятие по поверхности контакта лопатки со штифтом, причем определяют средние напряжения смятия и максимальные контактные напряжения.
Средние напряжения смятия
a™ = -2F7~’ <145)
где Сл — центробежная сила всей лопатки; рш— радиус штифта, /ш — суммарная длина частей штифта, расположенных в лопатке (на рис. 43 величина /ш = /1 + + 1з)-
Максимальные контактные напряжения
Ок = 0,418 1/ 2.Сл (Р1 Т ’
' ^шР1Рш (£1 +-^ш)
(146)
где pj— радиус отверстия в хвостовике лопатки; Elt Ет — модули упругости материала лопатки и штифга.
Рис. 43. Расчетные замка
308
Расчет деталей турбомашин
(147)
Штифт рассчитывают на срез _ Сл + Сш Тш ~ ’
где Сщ — центробежная сила частей штифта, расположенных в лопатках;
1Ш — число поверхностей среза (на рис. 43 их четыре); Гш — площадь поперечного сечения штифта.
Дисковую часть соединения также рассчитывают на срез по сечениям Б — Б (рис. 43), на смятие от центробежных снл лопатки и штифта, а также на разрыв— по сечениям А — А между отверстиями.
Шарнирные замки обладают повышенным демпфированием, почти не зависящим от частоты вращения, благодаря трению по торцевым поверхностям замка. Однако по массе они уступают замкам типа ласточкин хвост.
ВИБРАЦИЯ ЛОПАТОК
Расчетом достаточно точно определяют напряжения в лопатках от действия постоянных газовых нагрузок и центробежных снл, а также соответствующие запасы статической прочности. Эти расчеты служат для выбора исходных размеров лопатки при ее проектировании. Однако большинство дефектов лопаток в эксплуатации бывает связано с действием переменных напряжений, возникающих при вибрациях лопаток.
Оценить уровень переменных напряжений в лопатках можно лишь приближенно, используя статистические данные по выполненным конструкциям. В процессе доводки для обеспечения надежной работы лопаток необходимо определить переменные напряжения экспериментально (тензометрирова-нием) и, если напряжения окажутся значительными, снизить их до допустимого уровня.
Основные виды колебаний. Резонансные колебания вызываются совпадением одной из собственных частот лопатки с частотой переменных газовых сил, действующих на вращающуюся лопатку.
Параметры газового потока (скорость, давление, температура) по ок
ружности газового тракта имеют некоторую неравномерность. Так, непосредственно за направляющими или сопловыми лопатками скорость потока имеет меньшую величину, чем между ними («след» от лопатки). Такой же «след» оставляют разделительные стойки на входе в компрессор. Температура газа обычно имеет несколько пиков, соответствующих числу камер сгорания. К неравномерности параметров газового потока приводит также несимметричность входа в компрессор, наличие окон для отбора или перепуска воздуха, стойки на выходе из турбины, ограниченные размеры испытательного бокса и другие конструктивные особенности установки.
При вращении лопатки, когда оиа последовательно пересекает различные участки газового потока, газовые нагрузки будут также меняться, повторяясь через период Т, равный времени одного оборота ротора:
Т = (148)
«с
где гас— частота вращения, с'1.
Поэтому частота возбуждения от неподвижных источников неравномерности газового потока/возб(в Гц) всегда кратна частоте вращения ротора:
/возб= £яр> (149)
где k~ 1, 2, 3 ... (целые числа).
Величину k называют гармоникой к частоте вращения ротора.
Периодически меняющиеся газовые силы рГ могут быть представлены в виде суммы
Рг (0 = Pep + Pi sin (2лпс^ + <Р1) 4
+ р2 sin [2л (2пс) / + <Р2]+.-- +
+ pAsin[2ji(ftnc)/ + qpft] + .... (150) где рср— средние значения сил на данном режиме, определяемые формулами (14); рг, р2...— амплитуды
сил соответственно первой, второй. ..., й-й гармоник; q>t, <р2> ..., <pfe— нх фазы.
При резко выраженных неравномерностях наибольшее значение имеют амплитуды сил тех гармоник, которые равны илн кратны числу возбудителей
Вибрация лопаток
309
(прн шести стойках на входе наиболее сильно возбуждение шестой гармоникой, но может проявиться и двенадцатая гармоника) Неравномерности, связанные с несимметричностью входа и другими причинами, обычно вызывают целый ряд низших гармоник.
Величина переменных составляющих снл обычно достигает всего нескольких процентов от средней силы, поэтому прн вынужденных колебаниях лопаток напряжения в ннх невелики. Прн совпадении частоты возбуждающей силы /возб с одной нз собственных частот лопаткн fn наступает резонанс н переменные напряжения в лопатке могут сильно возрасти. Условие резонанса
/возб = fn- (151)
С учетом формулы (148) резонансная частота вращения лопаткн, мин"1,
през — —£ , (1°^)
где fn~ в Гц; k = 2, 3... (целые числа).
С первой гармоникой к оборотам (k = 1) рабочие лопаткн, как правило, не резонируют, так как с увеличением частоты вращения изгнбные частоты колебаний увеличиваются, причем частота основного тона ^Л1>пс> а резонанс крутильной .формы колебаний обычно уходит далеко за пределы рабочей частоты вращения.
Для компрессорных лопаток наиболее сильными гармониками являются k = 24-6 (иногда k = 8) н k = zH а, где zH. а— число направляющих лопаток перед н за ступенью.
Для турбинных лопаток наиболее сильными возбудителями являются камеры сгорания и сопловые лопаткн.
Особенно легко возбуждаются колебания по основной нзгнбной форме. Нередко возникают колебания по второй или третьей изгибным, первой нли второй крутильным формам, а также высокочастотные пластиночные формы. В реальных закрученно-изогнутых лопатках колебания носят сложный изгибио-крутильный характер, что ведет к искажению картины узловых лнннй (рнс. 44).
Наиболее наглядно резонансные частоты вращения выявляются с помощью «резонансной диаграммы» (рнс. 45), на которой наносят лучн гармоник к частоте вращения н кривые изменения собственных частот лопатки с учетом влияния центробежных снл н температуры. Точки пересечения кривых собственных частот с лучами гармоник определяют резонансные частоты вращения.
Резонансная диаграмма предварительно может быть построена по результатам расчета собственных частот и данным исследований лопаток на электродинамических вибраторах или с помощью пьезовозбуднтелей, а затем уточнена по данным тензометрировання лопаток на работающей установке. Эффективным способом экспериментального определения собственных частот н форм колебаний лопаток (отдельных нли непосредственно в колесе) является голографическая интерферометрия.
Рис. 44. Схема узловых линий на лопатке при наиболее легко возбудимых формах колебаний:
а, б, в — первая, вторая, третья изгибные формы: г. д — первая и вторая крутильные Формы; е — пластиночная форма
310
Расчет деталей турбомашин
Рнс. 45. Типичные резонансные диаграммы компрессорной (а, <Г) и турбинной (в, г) ступеней:
през — резонансные частоты вращения, г — частота вращения малого газа, пЭр Ср _ частота вращения при резонансе от вращающегося срыва. О — напряжения по первой, Л — по второй форме колебаний
Колебания компрессорных лопаток от вращающегося срыва также являются резонансными. Вращающиеся срывные зоны могут возникать при работе осевого компрессора на некоторых нерасчетных режимах. Срывные зоны вращаются в ту же сторону, что и ротор, ио с меньшей угловой скоростью Псрыв = <йсрывЛс.прнчемйсрЫВМ0,3-7-0,6) Частота возбуждения от вращающегося источника неравномерности газового потока будет кратна разности частот вращения-
/возб = £ (пс — псрыв) ~
~ к (I <йсрыв) пс> (153)
где 6=1, 2, 3, ... (целые числа).
Наиболее сильное возбуждение соответствует k = ?сРыв, где гсрЫв —число срывных зон.
Обозначив k (1 — ©срыв) = Мыв. приведем формулу (153) к выражению (149), но теперь число k' = ксрыв может быть произвольным и, в частности, не целым. В последнем случае величину k' называют «дробной» гармоникой к частоте вращения ротора. На резонансной диаграмме резонансные частоты вращения от вращающегося срыва соответствуют точкам пересечения кривых собственных частот с лучами гармоник k' (на рис. 45, а штриховая линия k' — 2,3).
Срывные колебания возникают в лопатках при работе ступени на нерасчетных режимах. Прн этом переменные
Вибрация лопаток
311
газовые силы не носят четко выраженного периодического характера. Колебания лопаток происходят в основном по первой форме с неустойчивой амплитудой. Сильные срывные колебания обычно возникают в лопатках компрессора на предпомпажных режимах.
Автоколебания лопаток возникают сравнительно редко, но являются очень опасными из-за резкого возрастания напряжений при небольшом изменении режима. Механизм автоколебаний может быть различным. Для лопаток компрессора возможны автоколебания при закритических углах атаки («срыв-ной флаттер»). Если в некоторый момент времени скорость движения лопатки (рис. 46) при колебаниях v = = cos pt, то угол атаки i0 меняется на величину At « vlw^, где — скорость относительного движения потока. Изменение угла атаки ведет к изменению силы, действующей на лопатку, на величину ДР ~ (tg а;) At, где аг — угол наклона кривой зависимости подъемной силы от угла атаки для данного режима (рис. 47). Переменная сила ДР за период колебания Т совершает работу
т
Ат= § bPvdt =
о
т
= — tgat sin2p/d/. (154) о
Если угол атаки на данном режиме t0 меньше критического iKp, то tg а; > О
Рис, 46. Изменение угла атаки Д/ при колебаниях лопатки
Рис. 47. Зависимость подъемной силы Р, действующей на лопатку, от угла атаки 1\ /Кр — критический угол атаки
и работа за период 0, т. е. воздушный поток оказывает сопротивление колебанию лопатки (демпфирует колебания). Если угол атаки i0 больше критического, то tg а; < О и работа за период становится положительной, т. е. воздушный поток снабжает колеблющуюся лопатку дополнительной энергией (поддерживает колебания). Тогда при недостаточной интенсивности демпфирования в материале лопатки и ее замке в результате случайного отклонения могут начаться автоколебания.
В лопаточных венцах возможны также автоколебания лопаток с общей частотой из-за аэродинамического взаимодействия лопаток. Для уменьшения такого взаимодействия вводят разночастотную сборку лопаток, а также повышают их жесткость. Опасность автоколебаний возрастает, если собственные частоты изгибных и крутильных форм колебаний лопаток близки друг к другу. Рекомендуется, чтобы эти частоты отличались не менее чем на 15%.
Особенности вибраций бандажиро-ванных лопаток. В ступенях, где лопатки связаны кольцевой бандажной связью, лопатки колеблются совместно, образуя некоторое число воли перемещений по окружности колеса. При четном числе лопаток z возможны 0,5z разных форм колебаний венца, соответствующих основной форме колебаний изолированной лопатки, при нечетном числе 0,5 (г — 1). С увеличением числа
312
Расчет деталей турбомашин
Рис. 48. Изменение собственных частот колебаний бандажированных лопаток по числу воли перемещений т при разной относительной жесткости бандажной связи EJ
воли т в указанных пределах частота собственных колебаний венца возрастает (рис. 48). В отличие от изолированной лопатки, резонансные колебания
которой могут быть вызваны любой гармоникой к частоте вращения, резонансные колебания лопаточного венца с числом волн т возбуждаются только той же гармоникой k = т к частоте вращения. Поэтому резонансная диаграмма бандажироваиного колеса имеет особый вид (рис. 49), причем резонансные частоты могут меняться по частоте вращения сложным образом. Частота колебаний бандажированных лопаток возрастает с увеличением жесткости бандажной связи и (до определенных пределов) при увеличении радиуса расположения антивибрационных полок или проволоки.
Баидажиые связи увеличивают также механическое демпфирование в системе и способствуют уменьшению переменных напряжений в лопатках.
Тензометрироваиие. Основным методом экспериментального определения переменных напряжений в лопатках турбомашин является тензометрироваиие на работающей машине в условиях, возможно более близких к эксплуатационным. До начала теизометрирова-иия необходимо для правильной ориентировки при проведении испытаний
Рис. 49. Резонансная диаграмма бандажированного колеса
Вибрация лопаток
313
построить расчетную резонансную диаграмму (см. выше). При первых испытаниях проволочные тензодатчики обычно наклеивают вблизи корневого сечения на спинку лопатки. При обнаружении на рабочих режимах резонансов следует возбудить соответствующую форму колебаний лопатки с помощью электродинамического вибратора или пьезовозбудителя и по тензодатчикам установить место расположения максимальных динамических напряжений. Место максимального напряжения может быть установлено также методами голографической интерферометрии. Дальнейшее тензометрирование ведут по датчику, наклеенному непосредственно в зоне максимальных напряжений, или же с использованием коэффициентов пересчета напряжений
k _ gmax аизм
где °тах — максимальное напряжение; оИзм — напряжение в месте измерения.
Не следует пользоваться коэффициентами пересчета k > 3. Надежные значения коэффициентов пересчета могут быть получены только по результатам испытания двух-трех лопаток.
Из-за разброса напряжений на отдельных лопатках тензометрировать необходимо по несколько лопаток на каждой ступени (не менее трех, а обычно по шесть и более). Предварительное тензометрирование на рабочих режимах ведут при медленном изменении частоты вращения.
При обнаружении повышенных напряжений проводят тщательную настройку на резонанс каждой из исследуемых лопаток (из-за разброса значений собственных частот резонансные частоты вращения отдельных лопаток могут несколько различаться). Контроль за показаниями тензометров ведут визуально (по катодным осциллографам) и по записи на пленке или бумаге (с помощью шлейфовых осциллографов). Особое внимание обращают на правильность тарировки аппаратуры.
Если анализ резонансной диаграммы показывает на возможность попадания на основные рабочие режимы высоко
частотных резонансов от сильных возбудителей (например, от сопловых лопаток), целесообразно провести тензометрирование с наклейкой датчика на кромке в верхней части пера лопатки.
Для выявления разброса напряжений между отдельными экземплярами машин проводят тензометрирование по крайней мере двух экземпляров.
При обработке записей определяют значения максимальных переменных напряжений, частоты колебаний и резонансные частоты вращения. По этим данным строят диаграммы переменных напряжений, которые удобно совмещать с частотными диаграммами, как показано на рис. 45.
При ответственных испытаниях показания тензометров записывают на магнитную ленту с последующим спектральным анализом процесса. Спектрограмма переменных напряжений (рис. 50) позволяет установить собственные частоты колебаний лопаток в рабочих условиях fc, относительную величину гармоник возбуждения, наличие других источников возбуждения колебаний лопаток и уровень демпфирования в системе.
Запас выносливости и методы его повышения. Для оценки вибрационной прочности лопаток определяют запас прочности по переменным напряжениям
(155) , иа max
где а_1л — экспериментально определенный предел выносливости лопаток с учетом асимметрии цикла; оа гаах — максимальное переменное напряжение, замеренное при тензометрировании (с учетом коэффициентов пересчета).
При симметричном цикле для лопаток компрессора—стальных о_1л ~ « 400-=-550 МПа, титановых о_1Л ~ « 250-4-450 МПа; для лопаток турбин а-1л ~ 160-300 МПа. Обычно а_1л ~ » (0,5—0,9) о.!, где a_j— предел выносливости образцов.
Запас прочности должен учитывать разброс максимальных напряжений между отдельными экземплярами машин и между отдельными лопатками, неточность определения максимального
314
Расчет деталей турбомашин
Рис, 30. Спектрограмма переменных напряжений в лопатке:
1—10 — гармоники возбуждения
напряжения при тензометрировании, возможность случайного повреждения поверхности лопатки в эксплуатации, эрозию поверхности и ряд других факторов. Поэтому для обеспечения надежной работы турбомашины запас прочности лопатки по переменным напряжениям должен быть достаточно большим (обычно п > 3).
При проектировании лопаток косвенной оценкой надежности могут служить напряжения в лопатке от изгиба статическими газовыми силами (см. с. 277). Однако дальнейшее экспериментальное определение запасов выносливости лопаток является совершенно необходимым.
Если запас прочности по переменным напряжениям оказывается недостаточным, он должен быть увеличен в процессе экспериментальной доводки машины. Основные пути повышения запаса прочности лопаток приведены ниже.
Частотная отстройка является наиболее эффективным средством для машин с узким диапазоном рабочих частот вращения, который может быть полностью освобожден от опасных резонансов. Для машин с широким диапазоном рабочих частот вращения полезно переводить сильные резонансы на малоиспользуемые или проходные обороты. Отстройка большей частью проводится «вверх», т. е. повышением собственной частоты лопатки, хотя в некоторых случаях можно частоту снижать Повышения основной изгиб-ной частоты достигают утолщением
корневого и близких к нему сечений. Необходимое изменение размеров лопатки определяют расчетным путем и уточняют экспериментально. Простым и эффективным средством изменения частот, в том числе высоких форм, является подрезка уголков у периферии пера лопатки. Величину подрезки и ее форму устанавливают экспериментально испытаниями лопатки на вибраторе. При отстройке должен быть обеспечен запас на разброс собственных частот отдельных лопаток за счет технологических допусков. Возможный разброс частот устанавливают по результатам испытаний нескольких (не менее трех) комплектов лопаток серийного изготовления.
Утолщение опасных сечений лопатки, особенно кромок, приводит к перераспределению динамических напряжений и к изменению их уровня. Эффективным оказывается также повышение качества контроля геометрии лопатки и ужесточение допусков.
Изменение режима работы турбомашины, улучшение согласования работы ступеней, различные аэродинамические мероприятия, затягивающие наступления срывов на наиболее напряженных ступенях.
Изменение числа стоек, окон перепуска воздуха и других возбудителей меняет интенсивность отдельных гармоник и соответственно резонансные напряжения. Такой же эффект оказывает изменение формы входного устройства, улучшение аэродинамики стоек и другие мероприитии.
Расчет дисков. Напряжения на контуре
315
Увеличение осевого зазора между направляющими и рабочими лопатками снижает интенсивность возбуждения высокочастотных форм колебаний
Для ликвидации сильного резонансного возбуждения от сопловых лопаток турбины можно применять так называемую разношаговость, т. е. постановку сопловых лопаток с неодинаковым шагом а При этом резко уменьшается интенсивность возбуждения гармоникой k = zc а> но появляется ряд близких гармоник. Аналогично влияет несимметричное расположение стоек, окон перепуска и других возбудителей.
Повышение запаса прочности может быть достигнуто также увеличением предела выносливости лопатки, особенно его минимального значения. Это обеспечивается выбором оптимальных режимов механико-термической обработки и их строжайшим контролем, а также применением специальных методов поверхностного упрочнения лопатки, особенно ее кромок
Следует контролировать уровень остаточных напряжений у поверхности (лучше, если они сжимающие) и предел выносливости лопатки о_1л. Простым и полезным неразрушающим средством контроля является проверка основной частоты колебаний всех лопаток в процессе производства.
РАСЧЕТ ДИСКОВ.
НАПРЯЖЕНИЯ НА КОНТУРЕ
Рассмотрим осесимметричное растяжение дисков от действия центробежных сил и неравномерного нагрева.
В диске возникают напряжения радиальные ог и окружные (тангенциальные) Og (рис 51) Во всех точках цилиндрической поверхности радиуса г (или, короче, на радиусе г) напряжения одинаковы вследствие симметрии
Радиальные напряжения на внешнем контуре огь (рис 52) создаются центробежными силами от лопаток и замковой части диска В центре диска без отверстия ор0 = ог0, что вытекает из условия симметрии Для диска с отверстием радиальное напряжение на внутреннем контуре или равно нулю (ога = О, свободное отверстие), или приравнивается давлению напрессовки на вал
Рис. 51. Направления напряжений в диске
(ога = —р, где р—давление напрессовки в рабочих условиях) При определении радиальных напряжений на ободе предполагается, что они распределяются равномерно по цилиндрической поверхности на радиусе Ь.
Напряжение от центробежных сил профильных частей лопаток
гЬ ~~ 2пЬЬъ ’
(156)
где г— число лопаток, Сп— центробежная сила профильной части лопатки, Нь— толщина диска на радиусе b
Напряжения от замковых частей лопаток и диска выражаются равенством
°"гь = P“%S ’ <157>
,1о
Рис. 52. Граничные условия при расчете дисков
316
Расчет деталей турбомашин
где р— плотность материала; со — угловая скорость диска; г0— радиус корневого сечения профильной части лопатки; 6— радиальная высота замка; hcp— средняя толщина замка диска; hb—толщина диска на внешнем радиусе 6.
При выводе формулы (157) предполагалось, что кольцевой слой между радиусами г0 и Ь целиком заполнен металлом; центробежная сила этого слоя создает напряжения
Радиальные напряжения на внешнем контуре диска
„ г,' I г," I
rb— гй+ rb— 2nbhb +
+ рш2г06—— . (158)
пь
Растягивающее напряжение в опасном сечеиии замкового выступа диска
2л6 ,,,п.
о3. в — огЬ — , (159)
где 2л6/г — шаг лопатки на радиусе Ь; с— ширина перемычки (рис. 53).
В дисках газовых турбин агЬ = = 100ч-180МПа, а значения о3 в 5^ sS 200-ь 250 МПа.
Рис. 53. К определению радиального напряжения на ободе
Запас прочности в замковых выступах дисков газовых турбин
п = > 2,5, (160)
аз. в
где одл — предел длительной прочности материала диска с учетом температуры и длительности работы.
При работе диска на различных режимах запас прочности определяют для каждого режима в отдельности и проводят «суммирование повреждаемости».
Общий запас прочности определяют по формуле (33) в гл. 2.
Формула (158) справедлива и для замков других типов, если центробежные силы замковой части можно учитывать указанными ранее способами.
Для замков типа ласточкин хвост следует принимать во внимание распорное действие клина1 и определять огЬ по формуле
zQ °гЪ ~ 2лЬНъ ~
z(c.sin(a+0,5_P) >
_ \ ______sm а_____ J
2nbhb ’
(161) где Q — сила, отрывающая перемычку замкового выступа диска; Сл = Сп4-+ С3—центробежная сила профильной и замковой частей лопатки; Св — центробежная сила замкового выступа диска [см. формулу (144)].
Если считать
sin (а + 0,5р) sin а
что допустимо, например, при а = 20° и числе лопаток z Js 50, то формулы (158) и (161) совпадают, так как
С3 -f- Св „ £ - „ ~ рш2г0о
2nbhb
ЛСр hb
Величина агь в дисках осевых компрессоров лежит обычно в пределах 20—80 МПа.
1 Если ось замка не параллельна оси вращения, то контактные усилия вызывают скручивание замкового выступа, что в некоторых случаях необходимо учитывать.
Запасы прочности диска
317
Вследствие осевой симметрии точки диска имеют только радиальное перемещение и.
Предполагая деформации Диска упругими, будем иметь перемещение на радиусе г:
и = (о9 — vor) 4- raT, (162)
Р?де Е— модуль упругости материала;
и <тг— окружное и радиальное напряжения; v — коэффициент Пуассона; а — коэффициент линейного расширения; Т— температура диска, °C.
Все величины, входящие в равенство (162), определяют для заданного радиуса.
ЗАПАСЫ ПРОЧНОСТИ ДИСКА
Запас прочности по разрушающей частоте вращения. Одной из основных оценок прочности диска является запас по разрушающим оборотам (частоте вращения)
. лпазр
(163)
Где Цразр — частота вращения, прн которой произойдет разрушение диска (с учетом температуры и длительности работы); п— максимальная (расчетная) рабочая частота вращения диска.
Запас по разрушающей частоте вращения может быть выражен через угловые скорости’
шразр
Запас по меридиональному сечей ию. При приближенном определении разрушающих оборотов исходят из предложения, что в Момеи4 разрушения во всех точках диска
ое О’) = ов W.
IT. е. окружное напряжение равно пре-[Делу прочности материала иа данном Ьаднусе. Разрушение происходит по йгерндиональному сечеиию.
Величина ов в общем случае взметнется по радиусу вследствие неравио-’Мерного распределения температуры.
Значение kB может быть найдено (Из рассмотрения условия равновесия
Рис. 54. К определению запаса прочности по разрушающей частоте вращения половины диска в момент, непосредственно предшествующий разрушению (рис. 54).
В этот момент радиальное напряжение на ободе
где огь — радиальное напряжение иа ободе прн расчетной угловой скорости. Напряжениями иа виутреиием контуре (г = а) можно пренебречь, так как давление иапрессовки, если оио н было в рабочих условиях, к моменту разрушения исчезнет совсем из-за больших радиальных перемещений ступицы диска. Центробежная сила собственно масс диска выражается для половины диска следующим равенством:
С = 2рсо2 J, г разр *
Ь
где J = J r^hdr— момент инерции по-а
ловины меридионального сечення диска относительно осн вращения.
Проектируя все силы иа вертикальное направление, найдем
(О2
2°rb-^bhb+2pu*a3pJ =
ь
— 2 J o3hdr, а
318
Расчет деталей турбомаишн
откуда запас
шразр
*В1 ==
ь
j aBh dr а
orbbhb+pa>2J ’ (164)
Если величина ов одинакова для всех радиусов, то
b Ь
j aBh dr = ов j h dr = aBF, a a
где F— площадь половины меридионального сечения диска.
В этом случае
(165)
Из формулы (165) следует, что для увеличения прочности диска надо увеличивать толщину в области ступицы диска, так как при этом момент инерции возрастает медленнее, чем площадь сечения.
Для дисков, работающих при повышенных температурах, под ав следует понимать предел длительной прочности материала (при заданном ресурсе рабо-ТЫ) — Одл-
Запас по цилиндрическому сечению. Кроме разрыва
по меридиональному сечению возможн разрушение по цилиндрической поверхности и частично в меридиональной плоскости. Такому разрушению способствуют отверстия в полотне диска или местное утонение.
Рассмотрим предельное равновесие при разрушении по цилиндрическом} сечению радиуса г* (рис. 55). Допустим для общности, что на этом радиусе находятся центры отверстий диаметра d.
По всей поверхности разрушения действующие напряжения считаем равными пределу прочности материала
Рассматривая равновесие сил в вертикальном направлении, можно записать
2^-^-^ + 2ро;а3рЛ = b '
= 2 aBhdr +
+ 2ав (г*) 1, (166)
где
b
J* - j hr2 dr. (167)
Из условия равновесия получаю!
*В2 (г*) =
ь
ав (г) h (/) dr + ов (г*) h*r* I 1
Orbbhb 4- P^2J *('*)
(163
Расчет проводят для различных радиусов г* и для оценки прочности принимают минимальное значение kB2.
Если на рассматриваемом радиусе отверстий не имеется, то в формуле (168) полагают d = 0. Формулу (168) применяют при г* > а; при г* — а следует считать
(а) ~ ^в1>
так как цилиндрическая поверхность радиуса а свободна от напряжений. Обычно минимапьный запас по цилиндрическому сечению получается в под-ободной части полотна диска.
Предварительная оценка прочности диска. Такую оценку проводят иа основании определения запаса по разру шающей частоте вращения.
Для уловлетвврительно работающих дисков ’запас по разрушающей частоте вращения (разрушение по мери нальному сечегию) kBi = 1,4-г 1,6.
Минимальное значение запаса по разрушающей частоте вращения при разрушении по цилиндрическому сечению Авя = 1.35-? 1,6.
Прн экспериментальном опреде."г’н"> запасов прочности при условиях, близ
Запасы прочности диска
319
Рис. 55. К определению запаса прочности по разрушающей частоте вращения прн разрушении по цилиндрическому сечению
ких к рабочим, должно быть kB > > 1,2н-1,3.
Частота вращения в момент разрушения должна быть на 20—30% больше максимальной частоты вращения диска в рабочих условиях.
Расчетные значения йв1 и kB2 обычно превышают экспериментальные значения на 5— 10% .
При действии высоких температур под оЕ (г) понимают предел длительной прочности Одд (г, Т, t), соответствующий определенной температуре Т и длительности нагружения t.
При определении запаса по разрушающей частоте вращения температурные напряжения не учитывают. Влияние температуры сказывается на пределе длительной прочности
При работе диска на различных режимах с температурой и длительностью Tj определяют эквивалентный запас по разрушающей частоте вращения (см. гл. 2).
Следует, однако, учесть, что запасы по напряжениям соответствуют квадратам запасов по разрушающей частоте вращения и поэтому эквивалентный запас по разрушающей частоте вращения прн работе на п режимах
______!_____=_______!_____+
Овэкв'Гэкв (*в (1))'"*
(,69)
где «j, ..., шп — показатели в степенных зависимостях длительной прочности при различных режимах.
Если, как обычно, режим 1 соответствует режиму с наименьшим запасом длительной прочности по разрушающей частоте вращения, то принимают тэкв — mi-
По формуле (169) определяют эквивалентные запасы прочности при разрушении по меридиональному £В1экв и по цилиндрическому йЕ2 экв сечениям. Обычно для дисков с центральным отверстием определяющим является запас йВ1, для дисков с тонкой подободной частью — запас йв2.
Для более полной оценки прочности диска вычисляют местные запасы прочности по напряжениям
>, _ аДл (Т, 0 п------т ,
ишах
где Одл — предел длительной прочности, зависящий от температуры и длительности; оп:ях — наибольшее напряжение (радиальное или окружное) на данном радиусе.
Напряжение отах определяют с учетом температурных напряжений н напряжений изгиба.
Запас прочности должен быть km> > 1,5.
При работе на различных режимах определяют эквивалентный запас прочности.
Определение напряжений в дисках рассмотрено далее.
320
Расчет деталей турбомашин
Для дисков транспортных машин или установок с большим числом нагружений следует определять запас по циклической долговечности
ь N*
где Л'* — число циклов нагружения до разрушения; N — число циклов нагружения в процессе эксплуатации.
Для удовлетворительно работающих дисков расчетный запас долговечности
-;> 5.
При экспериментальном определении запаса по долговечности с помощью циклических испытаний в составе изделия или в разгонной камере kN> 3.
Для расчетного определения запаса по долговечности определяют размах деформации в каждом цикле нагружения (от запуска до останова). Максимальная деформация материала диска (с учетом концентрации деформаций) связана с числом циклов до разрушения N* зависимостью
где ф — пластичность материала (поперечное сужение образца при разрушении, обычно ф = 0,2-4-0,4); одл, Е — предел длительной прочности и модуль упругости материала.
При работе материала в упругопластической области
8 — енагр — Вост,
где енагр—деформация при нагружении; еост—остаточная деформация диска после останова.
При числе циклов нагружений N* < < 10® основное значение имеет первый член и приближенно
N* «
1п -----------
1 — ф
Циклическая долговечность диска зависит от пластичности материала
4 F, ’
где F — площадь сечения образца в шейке в момент разрыва, Fo — первоначальная площадь сечения образца
Величина ф при работе материала при высокой температуре уменьшается обычно на 20—50% после наработки нескольких тысяч часов, что следует учитывать при назначении ресурса диска.
Практические рекомендации. При выборе материала диска следует учитывать характеристики прочности и пластичности материала. Параметры прочности материала (пределы прочности, текучести, длительной прочности и ползучести) являются расчетными характеристиками и должны обеспечи вать рекомендуемые значения запасов прочности.
Параметры прочности и пластичности должны контролироваться с помощью образцов, вырезанных из поковок (из ободной и ступичной части) или другими методами контроля (периодической разрезкой и т. п.).
Параметры пластичности (удлинение при разрыве 6, поперечное сужение ф, ударная вязкость ан) должны обеспечивать работоспособность материала при циклических нагружениях в условиях концентрации напряжений (отверстия, галтели, замковые и переходные части и т. п ).
Рекомендуется применять для дисков материалы с величинами 6> 12%. ф > 20%; аЛ > 50 Дж/см2. При S < < 6%, ф < 8%, ан < 20 Дж 'см2 практически трудно обеспечить работоспособность дисков.
Исключение в ряде случаев составляют литые диски малых диаметров (<300 мм), при использовании которых применяют сплошной контроль разгонными испытаниями иа (1,05-4-1,l)nmax.
Диски, предназначенные для больших ресурсов, не должны иметь значительных концентраторов напряжений (резьбы, надрезов и др.), а края отверстий и замковых пазов должны обладать достаточными радиусами закруглений. Качество поверхности должно быть высоким, рекомендуется использование упрочняющей технологии (иаклеп дробью и другие способы обработки).
Пример. Размеры диска даны иа рис. 56. Частота вращения диска п == = 12 300 мин”1 (со = 1290 1/с); мате-
Запасы прочности диска
321
Рис. 56. К примеру определения запаса прочности по разрушающей частоте вращения
риал диска — сплав ХН77ТЮР; плот-ность материала р — 8,1 г/см3 (8,1 X X Ю3 кг/м3).
Расчет начинают с определения радиального напряжения на ободе.
Диск имеет 54 лопатки. Радиус корневого сечения лопатки га = = 19,7 см; площадь корневого сечения F (г0) = 3,54 см2. Радиус концевого сечения лопатки Р= 31,3 см; площадь концевого сечения F (R) = 1,03 см2.
Центробежнаясила профильной части лопатки.
По графику для л = 2 (см. рис. 56) 1,03 noo t 19,7
ПРИ *=334 =0’29’ 5о= ~ЗГГ = = 0,63 определяем а (г0) = О,5ао.
Напряжение
a0 = 0,5p<o2R2(l--jl) =
=0,5-8,1 • 103 -12902-0,313а (I—0,63а) =
= 3,98- Ю3 Н/м2 = 398 МПа.
Таким образом,
о (г о) = 0,5-398 = 133 МПа.
Затем находим
СП= 1,99 • 10е-3,54-10-4 = 7,04 I О4 Н.
По формуле (158) определяем (йсв = = ЛЬ)
= ___54-7,04-104____j. jo3- 12902 X
2л-0,174-0,048 + ’ Х
X 0,197-0,024 = 1,361-103 Н/м2 = = 136 МПа.
Расчет запаса прочности по разрушающей частоте вращения по меридиональному сечению сведен в табл. 6.
В табл. 6 все данные отнесены к сечениям диска на заданных радиусах, которые указаны в первой графе, о1(ю — 100-часовая длительная прочность.
Пользуясь правилом трапеции, вычислим интеграл
b
| стдлй дг ж Дг/ (®юой)i ср-о
Следовательно, необходимо среднее значение а100й на каждом участке умножить на длину соответствующего участка и просуммировать:
b
С „ (6,36- 6,36) Ю5 ,
\ адл/1с(г = 3-1--------------1-
о
, „ (6,36 + 6,36) 105 ,
+ 4 2 +
, с (6,36 + 4,64)10» ,
+ 5 2 +
, с (4,64 + 3,18) 10» ,
+ 5----------2------*
+ m13J3 + 3.34)10-_v2.|0. н
6. Расчет запаса прочности по разрушающей частоте вращения
г- ю2. м ft* 10s. м Г, °C Otoe. МПа Дг* 10я, м С1М Л- 10“’. Н/м г2* 10\ м2 ггН- 10е. ма
0 6.7 300 950 3 6.36 0 0
3 6,7 300 950 2 6,36 9 60
5 6.7 315 950 5 6,36 25 168
10 5.1 380 910 5 4.64 100 510
15 3.7 500 860 2,4 3.18 225 832
17.4 4.8 550 800 3,84 302 1450
1I Заказ 402
322
Расчет деталей турбомашин
Далее переходим к вычислению интеграла
ь
\r2hdrx V дГ1. (гзЛ). ср о ч
Получаем
ь
, f О I 60
J = I r2h dr = / 3--g-----1-
о
, о 60 + 168 , с 168+510 ,
i- 2 ”г о -г
, с 510 + 832 , „ л 832 + 1450 \
+ 5------------L 2,4------g/ х
X 10'8 = 8,12-10‘5 м4.
Вычисление интегралов можно провести в более удобном виде для машинного счета, если ввести столбец значений
0,5 (Аг,- -I-
Запас по разрушающей частоте вращения для длительности работы (100 ч) находим по формуле (164)
^В1
8,73- 10’
1,361-108-0,174-0,048 + + 8,1•103-12902-8,12-IO’6
1/______________
V 1,137+1,095 '
ПРОФИЛИРОВАНИЕ
РАВНОПРОЧНЫХ ДИСКОВ
Профилирование диска состоит в выборе толщины диска h на радиусе г.
Диски турбин и компрессоров часто профилируют так, что напряжения от действия центробежных сил лопаток и самого диска остаются постоянными вдоль радиуса, причем og = csr.
Такой диск называют равнопрочным, что, строго говоря, справедливо только при отсутствии неравномерного нагрева.
Рис. 57. Диск с постоянными напряжениями (полотно диска)
Сечение полотна равнопрочного диска и эпюры напряжений показаны на рис. 57.
Если положить
°0 (г) = Or (г) = О0,
где а0 — допускаемое напряжение в диске, то из условия равновесия (см. с. 324) находим следующее значение толщины диска:
h (г) = hce 2а° , (170)
где hc—толщина диска на радиусе с. Отношение толщины диска в центре Ло к толщине диска на радиусе с
= е 2ст» , (171)
пс
где ис = сое — окружная скорость на радиусе с.
Отношение й0/71с возрастает при увеличении окружной скорости и уменьшается при увеличении допускаемого напряжения в диске.
В реальных конструкциях равнопрочный диск имеет обод (для крепления лопаток). Диск равной прочности с ободом и распределение напряжений в нем показано на рис. 58.
При расчете следует учесть равенство радиальных перемещений при г — с.
Перемещение полотна диска с , , са0 (1 — v)
«с = -g- (ст6 - v<+) = —.
где v — коэффициент Пуассона.
Основные уравнения при расчете дисков
323
Рис. 58. Диск с постоянными напряжениями (диск равной прочности)
Из условия равенства перемещений обода и полотна диска будем иметь
~ — а6 + ры2Ь2 = о0 (1 — v),
(172) где 6 — радиальная толщина обода.
В правой части равенства (172) стоит величина окружного напряжения в ободе.
Из условия (172) получаем
°>ь 4- + Р«2А2 о0 — ——------------,
+'-V ОПЬ
Поскольку же обычно задается величина о0, то
Ь рсо262 6
А,
о0 с
о.
с
(173)
Для ориентировочных расчетов можно считать
~ Аь .
Зависимость (173) служит для определения толщины диска в шейке. Толщину диска в центре определяют из равенства (171).
В реальных конструкциях толщины Диска, определяемые по формуле (170), заменяют толщинами диска более прос-11-
того профиля, у которого возле центра толщина постоянная, а далее (до шейки диска) идет участок конического профиля.
Равнопрочный диск не может иметь отверстия, так как в этом случае нарушается условие og (г) = <зг(г) — а0. Однако при практическом профилировании дисков зависимость (170) часто применяют и для дисков с отверстиями. В этом случае материал центральной части диска в зоне отверстия используют для развития ступицы, так что запас по разрушающей частоте вращения остается таким же, как и для сплошного диска.
Приведем формулы для определения массы равнопрочного диска.
Масса полотна диска
С
М j — 2пр | rh dr = О
= 2лрЛс е 2о° г dr --
О . рш’с1 \ = 2лр/1с-5Ме 2ст” -1Л ры2
где р — плотность материала диска.
Или в другой форме
М± 2лрс2 (Ло — Ас) .
Масса всего диска
М = 2лр Г с2 (й0 — йс) + ААьб1. рш С _J
(174)
При подсчете массы удобно отнести к диску замковые части диска и лопаток, тогда под 6 следует понимать радиальную толщину обода и замковых частей (включая полки лопаток) Для получения массы диска с лопатками добавляют величину гМл, где Мл — масса профильной части лопатки.
ОСНОВНЫЕ УРАВНЕНИЯ
ПРИ РАСЧЕТЕ ДИСКОВ
При определении напряжений и деформаций во вращающемся, неравномерно нагретом диске используют урав-
324
Расчет деталей турбомашин
Рис. 59. Условия равновесия элемента диска
иеиия равновесия, упругости и совместности.
Уравнение равновесия представляет собой условие равновесия элемента диска в поле центробежных сил (рис. 59).
Оно может быть записано в виде
(М) + (°0 — °г) у- + PW2rA = О,
(175) где аг, ав — радиальное и окружное напряжения; р — плотность материала диска; со — угловая скорость вращения; h — толщина диска.
Если к (г) — радиальное перемещение точек диска на радиусе г, то деформации в радиальном и окружном направлениях будут
ее =-2-. (177)
Деформации и напряжения связаны уравнениями упругости
ег =“g'(ar — voe) + aT; (178)
ee =-^-(а0—var) + aT, (179)
где Е, v — модуль упругости и коэффициент Пуассона; а — коэффициент линейного расширения; Т — темпера тура на данном радиусе диска, °C.
Из уравнений (178) и (179) с учетом зависимости (176) и (177) вытекают соотношения
ЕаТ . 1 — v ’
(180) ЕаТ 1 — v '
(181)
Если внесем последние соотношения в уравнение (175), то получим дифференциальное уравнение второго порядка относительно и (г). Решение этого уравнения вместе с граничными условиями позволяет определить напряжения и деформации в диске.
Однако точное решение указанного уравнения возможно только в некоторых частных случаях (диск постоянной толщины, диск гиперболического профиля и др.), и потому для практических расчетов разработано большое число приближенных методов (свыше 40). Два таких метода приведены ниже.
Если за основные неизвестные принимают напряжения, то при решении задачи учитывают уравнение совместности деформаций. Это уравнение основано на соотношении
d / и \ _ du dr \ г Г / ~~ dr ’
ИЛИ
-±(гев) = ег. (182)
С учетом равенств (178) и (179) получим уравнение совместности в напряжениях
w{r [4-^-^)+^] ।= = 4" (стг — VCTe) + “Т1- (183)
Выполнение этого условия означает, что полученная в решении величина радиального перемещения и (г) будет функцией непрерывной, что соответствует физическому смыслу задачи.
Напряжения и деформации в диске постоянной толщины
325
При решении задачи в «напряжениях» исходят из системы двух дифференциальных уравнений первого порядка (175) и (183) относительно двух неизвестных функций аг и од. Преимущество такого способа состоит в более простых граничных условиях, которые задаются обычно «в напряжениях».
НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В ДИСКЕ ПОСТОЯННОЙ толщины
Рассмотрим сначала диск постоянной толщины (рис. 60) с постоянными параметрами упругости. Температура распределяется вдоль радиуса диска по произвольному закону.
Для диска с отверстием при граничных условиях
аг (6) = агЬ, ог (а) = ога, где агь и ага —заданные напряжения, будем иметь
62 /, а2 \
~ °rb Ь2_а2 ( 1 - тг; -
а2 (, Ь*\ ,
-°™~Ьг-а2 (J-72J +
+ " V~ Р“2 (*2 + “2 —
X (184)
ав - °rb b2__a2 ( 1 + 75-) “ а2 / b2 \ ~ ~b2-a2 ( + V / +
+ -Ц^-ра>2 (б2 + а2 + -^--
---'’) + Е Г0 -аз6”- д' X
3 + v / L Ь2 — а2
х (1+-^-)+0(/-)-ат], (185) где
г
0(г) = -1- CraTdr. (186)
Рис. во. Диски постоянной толщины
В формулах (184) и (185) первый член выражает напряжения в диске от нагрузки на внешнем контуре, второй — от нагрузки на внутреннем контуре, следующий член — напряжения от центробежных сил самого диска и последний член — температурные напряжении.
Из этих формул следует, что в равномерно нагретом диске температурные напряжения отсутствуют (это справедливо для дисков любого профиля с отверстиями и без отверстий).
Если температура диска от ступицы к ободу изменяется по степенному закону
T-W-M-(7)’,
где ДТ = Т (Ь) — Т (0) — разность температур между ободом и центром, тогда
Для сплошного диска (без отверстия) при граничных условиях аг(Ь) = агь, аг (0) = 00 (0) получаем
аг = агь + 3 * * ^-V- ро>2 (Ь2 — г2) +
+ £[0(6)-0(г)]; (188)
00 = arb + 3 ^-' Р“2 (b2 —
- TTV '0 + Е [0 {Ь}+0 (И " аТ}'
(189)
326
Расчет деталей турбомашин
где
г
0 (л) = -1- raT dr.
о
Отметим, что
0 (0) = lim 0 (г) = 0,5аТ (0). г-0
Если температура изменяется по степенному закону, то
„ а Л Г / г
Эпюры радиальных и окружных напряжений в диске постоянной толщины при действии контурных нагрузок и центробежных сил показаны на рис. 61 и 62.
Следует отметить, что у внутреннего отверстия напряжения повышаются.
При малом отверстии величина ад при г = а приблизительно в 2 раза больше, чем в сплошном диске. Для дисков с числом нагружений (запусков) более 500 следует избегать неподкреп-ленных отверстий. Распределение температурных напряжений в сплошном диске показано на рис. 63.
На ободе диска окружные напряжения являются сжимающими, если температура возрастает с увеличением радиуса. Такой же вид имеет эпюра температурных напряжений для диска с отверстием, но у отверстия напряжение аг становится равным нулю, а окружное напряжение возрастает.
Радиальное перемещение в диске определяют по формуле
“[' - v +
+ + «’>«, -v) +
a2b2 1 — v2 “I
+-7г-('+«)-'’4тт]+
+ витД^[|-’ +
а2 “I
+ Т2-(> +v)J + 0(r)(l +v)r; (190)
Напряжения и деформации в диске переменной толщины
327
УТ7///7//7/Х
Рассматривая обод как кольцо, получим окружные напряжения в нем
6 с h
°об =• °rb -J — Огс— 4 ры2Ь2,
Рис 63. Температурные напряжения в диске
где агс—радиальное напряжение на радиусе с, hb — толщина диска на внешнем радиусе
Приравнивая радиальное перемещение кольца и диска на радиусе с, найдем
6 | 9L0
°гЬ у - °rc &hb + pw b -
/ с2 4- д2 = аге(-с2—^
на наружном радиусе
/<л агЬ6 /й2 + а2
_ агаЬ 2а2 ра2Ь
Е Ь2 — а2^4ЕЛ
X [i2(l-v) + a2(3 + v)] +
+ Й W ’ <19‘)
+ Iе2 - V) + а1 (3 4- v)l,
откуда
<*гс
6 , Orb -g—|- рО) X
Формулы (190) и (191) справедливы и для сплошного диска, если положить в них а — 0.
Рассмотрим диск постоянного сечения с ободом (рис. 64). Температуру диска будем считать во всех точках одинаковой.
Диски такой конфигурации применяют в тех случаях, когда окружная скорость на ободе невелика (и < < 200 м/с) и нагрузка создается в |всновном центробежными силами лопа-'ток и замков
Рис ь4 Диск постоянного сечення с ободом
Равенство (192) выведено для свободного отверстия (ага — 0) в полотне диска, оно справедливо также и для сплошного диска а — 0 После того как определена величина агс, по формулам (184) и (185) находят напряжения для диска с отверстием, а по формулам (188) и (189) — для сплошного диска.
В указанных формулах величину агЬ заменяют агс, а радиус Ь радиусом с.
В приближенных расчетах толщину полотна диска можно выбрать, задаваясь величиной аге из условия
, _ , агЬ hx,hb . игс
НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В ДИСКЕ ПЕРЕМЕННОЙ
ТОЛЩИНЫ
Метод линейного аппроксимирования. Для решения задачи запишем уравнения равновесия и совместности в интегральной форме.
328
Расчет деталей турбомашин
Интегрируя обе части уравнения (175) в пределах от некоторого начального радиуса а до г, находим
1 Г й , ar = Tj7T(a0-^^-
а
^~ога, (193)
а
где Гх — переменная интегрирования.
Индекс а здесь и в дальнейшем означает, что рассматривается значение параметра прн г ~ а.
В качестве начального радиуса а для дисков с отверстием принимаем радиус отверстия, для сплошного диска — некоторый малый радиус (а ~ at 0,1Ь), в пределах которого с достаточной точностью выполняется условие
а га = Оба- (194)
Запишем уравнение совместности (183) в виде
4[4-(a0_v^)+ar]=
1 + V v
=-----^-(a0-a,).
Интегрируя обе части равенства в пределах от а до г, получим
a0 —ar = —(1 — v)or —
г
— Е С -Цр- (ae — Or) -
J Г1Ь а
— Е (аТ — ааТа) +
Н р~“ (a0a — VaOra) (195)
Обозначая разность окружного и радиального напряжений в диске
ао— от= у (г) (196)
и заменяя величину ог в равенстве (195) значением из уравнения (193), найдем
г
. . 1 — v Г й , . ,
У (г) ---------— J — У (ri) drt —
а г
+ -1 V рю* J гхй drx — Е (аТ —
а £ ааТа) Н р (00a Va^ra) — са
1 — V ------j~ha<jn. (197)
Для диска с отверстием, полагая Ога = 0, запишем уравнение в сокращенной форме:
г г
У = Pi j Я1У&1 + Pi j <ЪУ&1 + а а
+ ^ш + ^г + ава^к, (198) где
1 — V _
Pi =------£—; л = — Е-,
Я1 = у-\ = (199)
Г
fo = 1-^'V рш2 j гхй drx; (200) а
fT = ~E(ccT~aaTa)-, (201)
(202)
са
Это уравнение справедливо и для сплошного диска [условие (194)], но только следует считать
/к = -^-(1-ув)--Ц^-Йо. (203)
Уравнение (197) представляет собой нормальное интегральное уравнение, его решают методом линейного аппроксимирования, использующим правило трапеций для вычисления интеп>алов.
Разобьем диск по радиусу на п участков сечениями я= г0, гх, г,, .... гп = Ь, значения функций в сечении г = rt будем обозначать у (ri) — Уъ Pi (П) =Pii, <7i (r«) = ?ii ит.д.
Напряжения и деформации в диске переменной толщины
329
Длина l-го участка диска
Ai = Н — n.i- (204)
Функции fa и fT в уравнении (198) выражают действие центробежных сил диска и неравномерного нагрева, функция fK связана с нагрузками на краях диска.
Обозначим
/.+/т + Уи=/ (205)
и рассмотрим общий метод решенкя уравнения (198).
Применяя правило трапеций для вычисления интеграле®, можно записать:
в начальном сечеиии г — а
У» — fo<
в первом сечении г= fi
Fi = Ph ~2~ O/ioFt + 9ыУ1) Ai +
+ Pit ~ (<?2О0О + ?21Fl) Д1 + /ь (206)
где Al = fj — г»; fj — значение функции f при г — Г1-
Из равенства (206) получаем
Ри ~2 Я10У0&1 + Р21 ~2 ?юУоА14"/1
1---g- (Pu<hi + РЫЯ21) Ai
Во Втором сечении
Ft = Pi» ^“2" (Я10У0 + QuFi) Д1 + + -у (ftiFi + W2) At] +
+ Рп [-g- О/гоУо + ftift) Ai +
+ + ЯпУ») As] + ft,
«KF*
yt =________________!______________x
1 --0,5 (P12?12 + Pttfe) A2
X [0,5 (P12<710 4~ Рм?2о) А1У0 4-+ 0»5 (Plrfll + P22?21) (Al + Дг)У1 4- /2] •
В общем случае для сечения г = Г( можно записать
У1 =Т=^1 + > <207)
\/=0 /
где
“гг=°.5(р1г<7и+р2г<721)Аг; (208) aij = °’5 (Ми + Ml) (Д/ + Д;+1)-
(209)
В последнем равенстве следует считать До = 0, так как участки начинаются с At = /j — га = Г1 — а. Соотношение (207) позволяет шаг за шагом вычислить значения у (г) во всех сечениях.
В практических расчетах величину у (г) удобно определять от каждого фактора в отдельности в соответствии с равенством (205).
Тогда
У (') = Уа (И 4- УТ (г) 4- а9аУк (г).
(2Ю)
где уш (г), ... получаются прн расчете по формуле (207), если положить соответственно f (г) = fa (г), f (г) = = fT W. f (г) = fK (г).
В равенство (210) входит величина Оба, которая подлежит определению.
Из уравнений (193), (196) и (210) получаем
ar = т j 77 К (г1) + Ут ('1)] +
а
1 Г Л , , А
4- а6а у j — Ук ('’О ^1 -а
— рш2 у- J rxh df\ 4- — ara (211) a
Для диска с отверстием (оГа = 0) иа внешнем контуре из условия
аг (6) = агь, (212)
330
Расчет деталей турбомашин
где огь — заданное напряжение от действия лопаток и замков, находим
Ь
+ Ут (г1)И1 + J а
Ъ
К1 = \ —Ук(г>) dru
Для сплошного диска (сга = О0а) из соотношений (211) и (212) получаем
ь
+ ут (г1)] ^1 + Р“2 J Г1А а
b
Kt = ha + §у-Ук (rtjdr,. а
Зная О0а, из равенств (210) находим у (г) и аг (г) и затем
(214)
(211)
и
°е (') = У'/) + °, (г). (215)
Если в диске произвольного профиля температурная деформация аТ остается постоянной на всех радиусах, то температурные напряжения в таком диске отсутствуют, так как
‘Т Е ~' аа^а) ~ 0-
Пример. Определить напряжения в диске, профиль которого приведен на рис. 56. Материал диска — никелевый жаропрочный сплав ХН77ТЮР, плотность материала р 8,1 г/см*, частота вращения диска л = 12 300 мин-1, напряжение на контуре агь = = 140МПа.
Эпюры радиальных и окружных напряжений в диске,рассчитанные по методу линейного аппроксимирования, показаны на рис. 65. Здесь </ш), а — напряжения соответственно от
(213)
6г,б'в,МПа
Рис. 65. Эпюры радиальных и окружных напряжений в диске
центробежных сил, температурные и суммарные.
Метод последовательных приближений. Расчетные зависимости при этом методе более сложные, чем при методе линейного аппроксимирования, но они позволяют непосредственно вычислить напряжения в диске произвольного профиля.
Радиальное и окружное усилия на единицу длины
Nr (') = (г) h (г)-, (216)
#еМ= ae(r)h(r), (217)
где аг и ад — радиальное и окружное напряжения в диске.
Сплошной диск. В этом случае на малом радиусе а « 0,16 принимают
Nra= N6a. (218)
Здесь и в дальнейшем индекс а указывает, что значение параметра относится к сечению г = а.
Первое приближение для радиального усилия (вывод формул указан в работе [3])
Л/‘” (г) = И + (') + ФТ
(219)
где Nrb = Qrbhb — радиальное усилие иа внешнем радиусе диска.
Напряжения и деформации в диске переменной толщины
331
Функция
Eh dr,
Ф1 (Г) =
ь
f Eh dr,
J r2+v
(220)
Величина Ф] (г) изменяется в пределах 0 Ф1 (г) 1. Усилие от цен-
тробежных сил диска
г
Ф<а (г) = —рш2 j r,/i dr, + а
г
+ Ф1 (г) р<в* J м dr,. (221) а
Тогда, например радиальные напряжения в диске от центробежных сил определяют по формуле
Л'*1’ (г) hh
(227)
Это равенство имеет следующий физический смысл: радиальные напряжения от действия центробежных сил в сплошном диске такие же, как в стержне прямоугольного сечения 1 X Л (рис 66).
Если известно радиальное усилие в диске ,Vr(r). то окружное усилие определяют нз равенства
Eh
(г) = (г) -f- (1 — v2) х
В этом равенстве fj — переменная интегрирования, изменяющаяся в пределах от а до г.
Усилие от неравномерного иагрева
Фт (г) = Гг (г) — Ф1 (г) Гг (6), (222)
X N.dr.+—fT (r) +
J Eh r 1 ги T v ’ a
4- (NQa — vNra). (228)
» Л C, Qfla
С Eh
?т = J г|х j f т (ri) ^11 (223) ' а
В частности, если требуется найти Н1в'’(г), то в это уравнение вносят
(224)
fT (г) = О + v) J aTxdr,— a
— (гаТм. — aaaTa). (225)
Коэффициент Пуассона v предполагается постоянным. В практических расчетах при v = 0,3 можно приближенно считать
Если при расчете ограничиваются определением только первого приближения, то достаточно хороший результат получается в том случае, если положить в предыдущих формулах
Ф1 (г) » 1. (226)
Рис. 66. Радиальные напряжения в сплошном диске от действия центробежных сил (1-е приближение)
332
Расчет деталей турбомашин
ЛГ” ’ (г) и для сплошного диска учитывают равенство (218).
Если при расчете определяют и следующие приближения для <Vr, то формулу (228) используют для последнего приближения [обычно для W*.2’ (г) или N'r3’ (г)].
Второе приближение для радиального усилия
ЛГ<2’(г) = ЛГч» (г)-f-Д‘” (г). (229)
Величина поправки
ДЧ) (г) = (p<*> (г) — ф, (г) <р<*> (Ь), (230) где
Г (г1)
Ф(1) Н = — (1 — v) \ --------------------dri +
Г
а
(231)
В большинстве практических задач достаточно ограничиться вторым приближением (для предварительного выбора конструктивного варианта можно использовать и первое приближение).
Если потребуется вычислить третье
приближение, то его находят из равенства
N™ (г) = ЛГ'В * 1’ (г) + Д(2) (г), (232)
где вторую поправку к первому приближению определяют точно так же, как Д11’ (г), ио исходя из ЛЧ2’ (г).
Окружное усилие в диске определяется из соотношения (228).
Диск с отверстием. Первое приближение для радиального усилия
(г) = Л^Ф, (г) +
+ га I* ®1 (г)] + (г) + Ф? (г)>
(233)
где Nra = orah.a — радиальное усилие на внутреннем контуре.
Если диск напрессован иа вал и в рабочих условиях должно сохраняться давление напрессовки р, то следует положить <тго —р.
Функция
(• Ehdri
J
Ф1 (г) = . (234)
С Eh dri J "71+^ а 1
Для диска с отверстием b
Фш (г) = Ф1 (г) рш2 j Г1Л di\ — а г
— рш2 Jri/idTj; (235) а
Фт(г) = Ет(г)-Ф,.(г)Ет(Ь), (236)
Рис. 67. Схема диска центробежного нагнетателя и диаграмма напряжений;
1— без учета жесткости лопаток; 2 — с учетом жесткости лопаток
Напряжения и деформации в диске переменной толщины
333
где функция Ft (г) определяется равенством (223).
Второе приближение и следующее находят из соотношений (229) и (230). Окружное усилие определяют из формулы (228). Для отыскания окружного усилия на внутреннем радиусе NeQ используют формулу
^еа =-------------------х
а С Eh ,
Eaha J zjx (г,) 1
X —ф (b) -f- Nrb — Nfa X
, . b \
va‘+v 0 EhdrL ] , Eaha J ff+v + a 1 /
b
+ p<oa J rxh. drx — FT (b) . (237) a
Величину <p (b) находят по последнему приближению для Nr [формула (231)]. Для упрощения расчета можно использовать результаты для предыдущего приближения и тогда все члены равенства (237) будут известными.
Общие указания. Для расчета диск разбивают на 5—8 расчетных сечений. При наличии участков с резким изменением толщины число расчетных сечений должно быть увеличено. Все интегралы вычисляют по правилу трапеций.
Для повышения точности расчета следует несколько увеличить число расчетных сечений иа малых радиусах.
Особенности расчета дисков центробежных компрессоров. Лопатки центробежных компрессоров (нагнетателей) расположены на боковых сторонах диска (рис. 67). Обычно при расчете жесткость лопаток на растяжение не учитывают и лопатки рассматривают как присоединенные массы. Тогда диск рассчитывают обычным способом, вводя приведенную плотность материала
Р* = Р (1 +
kzF (г) \ 2nrh ) '
где k — коэффициент, зависящий от расположения лопаток (при одностороннем расположении k = 1, при двустороннем k = 2); z — число лопаток; F (г) — площадь поперечного сечения лопатки.
Учет жесткости лопаток при расчете на растяжение приводит к существенным поправкам (см. рис. 67).
Запас по разрушающей частоте вращения
где
Ь
J* = j pM/idr. а
Для дисков центробежных нагнетателей kB = 1,34-2,2. При наличии покрывающих дисков (закрытые крыльчатки) под h понимают суммарную толщину всех дисков. Запас по разрушающим оборотам должен быть в этом случае увеличен до kB = 2s-2,5.
ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ В ЭЛЕМЕНТАХ КОНСТРУКЦИЙ
Глава 17
ИЗГИБ СТЕРЖНЕЙ
ПЕРЕРЕЗЫВАЮЩАЯ СИЛА И ИЗГИБАЮЩИЙ МОМЕНТ
В общем случае на стержень (балку) могут действовать распределенная нагрузка, интенсивность которой характеризуется силой, приходящейся на единицу длины (? в Н/см); сосредоточенные силы и пары сил (моменты), приложенные к какому-либо сечению балки (рис. 1).
Рассмотрим двухопорный стержень с нагрузкой посередине (рис. 2). В опорах возникают реакции 7?д и
Проведем сечение на расстоянии z от левой опоры, где выбрано начало координат. Тогда, рассматривая равновесие левой (отсеченной) части, приходим к выводу, что в сечении должны действовать перерезывающая сила Q = 0,5Р и изгибающий момент М = 0,5Pz. Такие же по величине силы и момент, только направленные в другую сторону, будут приложены к правой, оставшейся части стержня.
Момент силы для данного сечения вычисляют относительно оси, проходящей через центр тяжести сечения. Эта ось перпендикулярна к плоскости изгиба (плоскости чертежа на рис. 2).
Изгибающий момент в сечении равен алгебраической сумме моментов (относительно рассматриваемого сечения) всех сил, приложенных к отсеченной части стержня (балки). Перерезывающая сила в сечении равна алгебраической сумме всех сил, приложенных к отсеченной части стержня (балки). Изгибающий момент и перерезывающая сила выражают действие отсеченной части стержня на оставшуюся.
Сечение разбивает стержень на две части, из которых каждую можно считать либо отсеченной, либо оставшейся. Удобно в качестве отсеченной рассматривать ту часть стержня, к которой приложено меньшее число внешних силовых факторов.
Соотношение между изгибающим моментом и перерезывающей силой. Рассмотрим элемент стержня длиной dz (рис. 3). В сечении z действуют сила Q и момент М. Так как эти величины изменяются по длине балки, то в сечении z + dz будут действовать сила Q + dQ н момент М + dM. Составим условия равновесия элемента стержня. Проектируя все силы на вертикальное направление, находим
, dQ dQ = q dz или = q.
Взяв сумму моментов относительно оси, лежащей в сечении z+ dz, получим
М + Q dz + 0,5? dz2 — (М + + dM) = 0.
Отбрасывая величину 0,5? dz2 как бесконечно малую второго порядка, будем иметь
Следовательно, производная изгибающего момента равняется перерезывающей силе.
Условия закрепления. Балку считают закрепленной статически определимым способом, если силы (реакции) и моменты (реактивные моменты) в местах закрепления могут быть определены из условия равновесия. Для плоской системы сил имеются три уело-
Перерезывающая сила и изгибающий момент
335
|*ис, 2. Определение изгибающего момента Я перерезывающей силы
Рнс. 5. Примеры закрепления балок
Ряс. 3. Условия равновесия элемента Стержня
«ИС. 4. Опорные
J — шарнионая Шарнирная Целка
закрепления стержня: подвижная опора’ б — неподвижная опора в — за
вия равновесия, поэтому опоры балки при статически определимом ее закреплении не должны создавать более трех неизвестных силовых факторов.
Типичные случаи опорного закрепления стержня (балки) показаны на рис. 4.
Шарнирная подвижная опора может передать вертикальное усилие, шарнирная неподвижная опора — вертикальное и горизонтальное усилия, заделка — вертикальное и горизонтальное усилия, а также момент.
Следовательно, балки, показанные на рис. 5, а, являются статически определимыми, а на рис. 5, б — статически неопределимыми. Как правило, использование статически неопределимого закрепления следует избегать.
Эпюры изгибающих моментов. Эпюры представляют собой графическое изображение распределения изгибающих моментов подлине балки (рис. 6).
Эпюры обладают следующими свойствами:
а) если к балке приложены сосредоточенные силы или моменты, то эпюра состоит только из прямолинейных участков;
б) в сечении, где приложен внешний момент, эпюра изгибающих моментов имеет скачок, равный по величине приложенному моменту.
336
Изгиб стержней
Рнс. в. Эпюры изгибающих моментов
НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ ПРИ ИЗГИБЕ
В основе технической теории изгиба лежит гипотеза плоских сечений', точки поперечного сечения после деформации лежат в одной плоскости. Принятая гипотеза подтверждается экспериментом.
Относительные удлинения волокон при изгибе. Рассмотрим плоский изгиб стержня. Выбранная система координат показана на рис. 7. Ось г направлена вдоль оси стержня, ось у лежит в плоскости изгиба, то«ча О совпадает с центром тяжести сечения.
В силу гипотезы плоских сечений можно считать, что сечение стержня
Рис. 7. Изгиб стержня
получает поворот вокруг оси х на угол <р и осевое смещение ш0 вместе с началом координат (точкой О). Величины <р и ш0 изменяются по длине стержня.
Удлинение волокна стержня, находящегося на расстоянии у от плоскости xz (рис. 8), будет
А*£* - АБ е~ АБ
Длина отрезка АБ равна dz. Отрезок А*Б* = dz w0 + dw0 — у (<р + + d<р) — te»0 + у dtp = dz + dwa — — у d<p. Следовательно,
dw0 dtp dtp
(2)
где e0 — удлинение волокна стержня, совпадающего с осью z.
Для упрощения вывода не рассматривались смещения сечений по оси у (вертикальные прогибы), так как они (в пределах малых деформаций) ие влияют иа удлинение отрезка АБ.
Нормальные напряжения при изгибе. В соответствии с законом упругости
а
(3)
Напряжения и деформации при изгибе
337
Рис. 8. Деформации при изгибе
где а — напряжение в плоскости поперечного сечения стержня (напряжение вдоль волокон); Е — модуль упругости материала.
Напряжениями, действующими на боковые поверхности волокон, пренебрегаем. Из уравнений (2) и (3) следует.
а = £ . (4)
Так как внешняя сила вдоль оси z отсутствует, то из условия равновесия (рис. 9) следует-
J a dF = О, F
где интеграл распространяется на всю площадь поперечного сечения.
Подставляя значение о из равенства (4) и предполагая модуль упругости постоянным, найдем
i/ Лр \
V0 ~У~ЧГ/ dF ~ °' F
Так как |i/d£=O как статиче-F
ский момент относительно прямой, проходящей через центр тяжести, то во = С.
Момент, создаваемый напряжениями а, должен быть равен
j оу dF = —AG-F
Направление момента Мх показано на рис. 9. Подставляя значение из
Рис. 8. Напряжения изгиба
равенства (4) и учитывая, что е0 = О, находим
Е \у2м-мх.
F
Величину
| уг dF = Jx (5) F
называют моментом инерции сечения относительно оси х. Следовательно,
А - <6)
dz £ J х
Внося это значение в равенство (4), получаем основную расчетную формулу
Знак минус в формуле (7) необходим для согласования правила знаков, принятых для момента Мх (положительно направленный момент вызывает сжатие в верхних волокнах), для напряжения а (положительная величина соответствует растяжению) и величины у (положительное направление принято вертикально вверх),
В точках плоскости хг (для этих точек у = 0) напряжение изгиба отсутствует, и эту плоскость называют нейтральной. Ось х, проходящую через центр тяжести сечения и перпендикулярную к плоскости изгиба, называют нейтральной линией.
Распределение напряжений изгиба по поперечному сечению вдоль пря-
338
Изгиб стержней
Рис. 10. Распределение напряжений изгиба по сечению
На основании гипотезы плоских сечеиий аналогично равенству (2)
е = е0 — у
d<P , dz
dz
(9)
мой Л1Л2 показано иа рис. 10. При изгибе часть волокон растягивается, а часть сжимается. В точках, одинаково удаленных от нейтральной линии (оси х), напряжения одинаковы.
Наибольшие напряжения действуют в точках, наиболее удаленных от нейтральной оси (точки Аг и Л2). Напряжения изгиба в этих точках
аА
h •
J X
Мх L.
<8)
Очень часто пользуются понятием момента сопротивления. Если точка сечеиия, иапрнмер точка А, находится на расстоянии у от оси, то момент сопротивления в этой точке W а = — Jxly-
Иногда под моментом сопротивления понимают наименьшее значение W для сечей ин: W — Jx/hrrwt, где Лщах — расстояние наиболее удалеииого волокна от нейтральной линии.
Формулы для }х и W некоторых сечений были приведены в табл. 2 иа с. 17.
Формула (7) справедлива и для стержня переменного сечеиия, если входящие в иее величины относить к рассматриваемому сечеиию.
Нормальные напряжения в общем случае изгиба и растяжения стержня. В общем случае иа стержень могут действовать изгибающие моменты Мх и Му и растягивающее усилие W (рис. 11).
где e0 — деформация, связанная с про» дольным перемещением сечения; (р и ф — углы поворота сечеиия стержня относительно осей х и у соответственно.
Если учесть температурные деформации, то иа основании закона упругости
e = JL+aT, (Ю)
где Т — температура в данной точке сечеиия; а — коэффициент линейного расширения.
Вследствие неравномерного иагрева модуль упругости материала Е может быть различным в разных точках сечения.
Равенство (10) запишем в форме a = Е (е — aТ) =
= Е ^е0 - у-£. + х - ат) .
(П)
Деформацию в стержне характерного Оф зуют три параметра: е0, йг~-Для их определения воспользуемся условиями равновесия:
Напряжения и деформации при изгибе
339
В этих равенствах интегрирование распространяется на всю площадь поперечного сечения F.
В нося в последние зависимости соотношение (11), получим
‘•\EdF-T- №aF+ F F
' dz J F
' — J aTEdF = H; F
(13)
F * 14
— J xaTE dF = My;
F
(14)
-g-F
\ x2E dF dz J
F
e0 J yE dF —
+ ^xEdF-
F
— J yaTEdF — — Mx. (15) F
Для постоянного модуля упругости во всех точках сечения приведенные и главные осн совпадают с обычными главными осями. Способ определения приведенных главных осей сечения описан ниже.
С учетом условий (16) и (17) из уравнений (13), (14) и (15) получим
j аТЕ dF
— + -Ч----------’ <18)
dF EdF
F F
f yaTE dF dtp______Mx f______________.
dz j y2E dF j y2E dF
F F
(19) f xaTE dF
My ! r______________.
x2E dF j x2E dF
(20)
Внося значения e0, —у— и —f— dz dz
Эти уравнения можно упростить соответствующим выбором осей х и у. Выберем положение начала системы координат (точку О) так, чтобы удовлетворялись равенства jxFdF=O; уЕ dF = 0. (16)
F F
В этом случае точку О называют приведенным центром тяжести сечения. Если модуль упругости во всех точках сечения одинаковый, то приведенный центр тяжести совпадает с обычным.
После того как положение начала координат стало определенным, повернем оси х, у в плоскости сечения так, чтобы удовлетворялось равенство
хуЕ dF — 0. (17)
F
Оси координат, удовлетворяющие условиям (16) и (17), называют приведенными главными осями сечения.
в уравнение (11), получим окончательную формулу для напряжений в стерж-
j аТЕdF j yaTEdF
F , F
—7 H У —f
I E dF y2E dF
^xaTEdF \
+ Ц-----------Ctrl. (21)
I x2EdF I
F /
F
340
Изгиб стержней
Первая группа членов в этой формуле выражает напряжения в стержне от внешних сил, вторая — температурные напряжения.
Если модуль упругости во всех точках сечения одинаков, то из равенства (21) вытекает
HaTdF [ уаТ dF
. с I F . F .
+Е у F +у~Тх +
j xaTdF \
+ -----аТ (22)
Jy /
где Jх и Jу — главные моменты инерции сечения.
Если точки сечення стержня имеют одинаковую температуру, то из формул (21) и (22) следует, что температурные напряжения в рассматриваемом сечении отсутствуют. В этом случае напряжения в поперечном сечеиии стержня
о = 4- — У -J*- + * 4^- • (23) Г J Х J у
Из этой формулы вытекает возможность раздельного определения напряжений растяжения (сжатия) я напряжений изгиба (второй и третий член в формуле), которые, в свою оче-
Рис. 12. Определение приведенных главиых осей сечення
редь, можно определять раздельно относительно каждой из главных осей сечения.
Определение приведенных главиых осей сечения. Используем произвольную вспомогательную систему координат (рис. 12).
Координаты приведенного центра тяжести сечения О:
jXlEdF jy^dF
а = А-------; 6 = . (24)
I E dF I E dF
F F
Угол поворота приведенных главных осей х и у
2 j Х1У1Е dF tg 2₽ = -------£------------ . (25)
xjE dF — j y^E dF
F F
Определение приведенных главиых осей и центра тяжести не отличается от обычного способа, если только элементу площади условно приписать «вес» Е. Отсюда следует, что приведенный центр тяжести будет смещаться относительно обычного в сторону, где модуль упругости материала больше.
Пример. Определить температурные напряжения в стержне прямоугольного сечения (рис. 13). Температура распределяется по параболическому закону
Т(х) = 7’тах ’
По толщине стержня температура постоянна. Предполагаем, что модуль упругости Е и коэффициент линейного расширения а постоянны. Из формулы (22) находим
о = ЕаТгаах ].
В центре стержня
о (0) = —д- ЕиТщах.
в крайних точках
2
<т (6) = с (—Ь) --— ЕаТщах-
Напряжения и деформации при изгибе
341
Рис. 13. Температурные напряжения в стержнях прямоугольного сечення
Эта сила изменяется по длине стержня вследствие изменения величины о. Приращение силы Nf должно уравновешиваться касательными напряжениями на горизонтальной площадке dzb. Таким образом,
dN j — —dzbx или
_______1_ dNf_ х~— ь dz
Вследствие парности касательных напряжений такие же напряжения будут действовать в соответствующих точках поперечного сечения. Нормальное напряжение в слое на расстоянии У1 от нейтральной осн
тогда
Для стержня из жаропрочного сплава при Е=2-105 МПа, а = 16Х ХЮ"* 1/°С, Ттах= 200оС находим о (0) = 213 МПа; о (&) = —426 МПа.
Касательные напряжения при изгибе. Если изгиб создается поперечными силами, то в сечении стержня будут действовать касательные напряжения, уравновешивающие перерезывающую силу.
Влияние касательных напряжений на прочность и жесткость существенно только для коротких стержней, высота сечения которых составляет не менее 1/3 его длины.
При определении касательных напряжений считают, что они не влияют на величину нормальных напряжений изгиба. Это позволяет определить касательные напряжения из условия равновесия.
Рассмотрим равновесие части элемента стержня длиной dz (рис. 14).
Нормальная сила, действующая на рассматриваемую (заштрихованную) часть сечения, площадь которой со-ставляет /,
Nf = j a df.
f
MxSf
J X
Величина j yxdf = Sf — статиче-F
ский момент отсеченной части сечения.
Далее находим
dNf dMx St Sf
dz dz J x J x ’
где Q — перерезывающая сила в сечении.
В соответствии с равенством (26) получаем формулу для касательных напряжений в стержне
Wx •
Равнодействующая касательных напряжений равна перерезывающей силе.
Для касательных напряжений в стержне прямоугольного сечения (рис. 15)
о.ьн
Sf — J Ьуг dyY = -1- b (----у2) ;
у
__ ЬН*
12 ’
342
Изгиб стержней
Рис, 14. Равновесие элемента стержня
Рис. 15. Распределение касательных напряжений прн изгибе стержня прямоугольного сечення
чения <р (рис. 16), если пренебречь деформацией сдвига,
В соответствии с равенством (6) dtp _ /И (z) dz EJх (z) ’
где М (z) — изгибающий момент в сечении (рнс. 17, а).
Далее имеем
_ М (?) Г29)
dz2 ~ EJx(z) ' 1 '
Из формулы (28) получаем
т =
ЬИ V 2 И2 /
Распределение напряжений показано на рис. 15. Наибольшее напряжение имеет место при у = 0:
_ 3 Q 3
Ттах - — -Jfj-~ -g- тСр.
Q где тсс = —=----среднее касательное
1 г
напряжение.
УПРУГАЯ ЛИНИЯ СТЕРЖНЯ
Уравнение упругой линии. Ось стержня в изогнутом состоянии называют упругой линией. В пределах малых деформаций угол поворота се-
Выражение (29) представляет собой дифференциальное уравнение упругой линии стержня. Оно справедливо и для стержней переменного сечения. Иногда уравнение упругой линии используют в другой форме — из уравнения (29):
£/х(г) -^-=Af(z),
Рис. 16. Связь между углом поворота сечения н у (г)
343
Упругая линия стержня
дифференцируя по z,
Из энергетических расчетов
d [ ГГ ! \ d у \
-j— ( EJX (г) —tv I =
dz \ dz1 J
F Г s'fdF
(33)
где Q (?) — перерезывающая сила в сечении. Повторив дифференцирование, получаем вторую форму дифференциального уравнения упругой линии:
(30)
где q (z) — нагрузка на единицу длины стержня.
Уравнение упругой линии с учетом влияния перерезывающей силы. Если учесть деформацию сдвига (рис. 17, б), то угол поворота сечения
Т =(3D
где у — деформация сдвига, пропорциональная величине перерезывающей силы в сечении:
7 = k GF (z) ’ (32)
здесь k — безразмерный коэффициент, зависящий от формы поперечного сечения; G — модуль сдвига; F (?) — площадь поперечного сечения.
[см. обозначения к формуле (27)]. Для стержня прямоугольного сечения k — 6/5, для сплошного круглого сечеиия k = 10/9, для тонкостенной трубы k = 2.
Из равенств (31) и (32) находим
dz/ ,
—— = <р — k dz т
Q (г)
GF (г) •
Дифференцируя с учетом зависимости (6) и влияния перерезывающей силы, получаем дифференциальное уравнение упругой линии
&У _ М (?) _ d / Q (г) \ dz2 EJX (г) dz < GF (?) ) '
(34)
Влияние перерезывающей силы на прогибы стержня учитывают в том случае, когда высота сечения соизмерима с его длиной (см. примеры).
Уравнение упругой линии в интегральной форме. Интегрируя обе части равенства (34) от 0 до ?, найдем
M(Z1)
(zi)
d?j —
II!
k GF (z) +*Gf(O)+ dz
344
Изгиб стержней
Повторяя интегрирование, получим
У (г) = f f "Ё7 (?гГ dZ2 dZ1 -
J J CJx{Z2) 0 0
f kQ(O) ,
“J W1 + GF(0) г + 0
+ -^-(O)z + y(O). (36)
В формулах (35) и (36) переменные интегрирования обозначены Zj и z2.
Неизвестные параметры (0) и у (0) определяют из условий закрепления. Если пренебречь влиянием перерезывающей силы на прогиб, положив GF —> со, то
С ( М (Zz) J J ,
J Е}х{гг~ 2 ' + о о
+ + (37>
Уравнение для дополнительного прогиба стержня от сдвига можно получить из формулы (36), положив EJX-+ —»- оо.
Тогда
(• kQ (zj
1/сд (z) = — J Gf’(zj dZ1 +
0
+ -гЯ5Гг + т<0)2+’“<°>-
(38)
Но так как
Рис. 18. Изгиб консольного стержня
(рнс. 18). Изгибающей момент в сечении
М (г) = — Р {1—г).
Перерезывающая сила
Q(z)= Р.
Прогиб от действия изгибающих моментов находим по формуле (37)
ПРИ (0) = 0, у (0) = 0:
f Г Р (/ - z2) . .
У(г) = ~} } Ej d2*dz' = о о
о Р / Zz2 z3 - EJ < 2 6 / ‘
Прогиб на конце консоли
PZ3 __ 4PZ3
У “ 3EJ ~ Ebh3 •
Прогиб от действия перерезывающей силы определяем. с помощью равенства (39). При уС11 (0) =* 0 kP
Усл (2) = др z-
то в окончательном виде
Z
Усл (z) = ~ J др ) dzi + Усл (°)' 0
(39)
Пример. Определить прогибы консоли постоянного сечения под действием сосредоточенной силы Р
Прогиб на конце консоли kP , kPi
Z/ca (О - др ‘ =. gbll ’ Отношение
yCA(Z) _ kE / ft V.
У (I) AG \ I )
*(i+v) '
Упругая линия стержня
Рис. 19. Изгиб стержня на двух шарнирных опорах
так как G = Е/2 (1 + v), где v — коэффициент Пуассона.
При h = I, v — 0,3
Усд (О _ 6(1+ 0,3) _ п 70 //(/) 5-2 ’ '
Пример. Определить прогибы балки постоянного сечеиия под действием распределенной нагрузки (рис. 19).
В опорах балки действуют реактивные усилия
Ra ~ Rb = 0,5ql.
Перерезывающая сила
Q (z) = 0,5ql — qz = q (0,5/ — z).
Изгибающий момент
M (г) = 0,5qlz — 0,5qz2 = — 0,5q (Iz — z2).
Прогиб от действия изгибающего момента по формуле (37)
Z Z,
У = 2?Т f j UZ2 — dZ* dZ' + 0 0
az lb J j \ z d /
0
Из условия у (I) = 0 находим
Таким образом,
„ {,у _ Q ( & г4 \ <?/3
У(г) 2EJ \ 6 12/~24EV Z'
Наибольший прогиб будет при г =
= //2:
у (1/2) =----5--
’ 384 EJ '
Прогиб от действия перерезывающей силы [формула (39) ]
г
Уса (г) =---("Т ~ 9Z1) dZ1 =
о
=-----------— (lz — z2)
GF 2 ( >'
Наибольший прогиб
( I \_ kqP
Уся \ 2 ) 3GF ’
Отношение максимальных прогибов
Уса (//2) _ 384 E J
у (1/2) 40 G F12
48 _£. J
~ 5 G * Fl2 '
Если балка представляет собой тонкостенную трубу с диаметром d и толщиной стеики б, то k = 2; J = = n6d3/8, F = n<5d и при v = 0,3
Усд (</2) У (1/2)
Определение прогибов стержней с помощью непосредственного интегрирования уравнения упругой линии [формулы (37) и (39)1 удобно применять в простейших случаях и для стержней переменного сечения. В последнем случае интегралы целесообразно вычислять приближенно по правилу трапеций. Учет влияния перерезывающих сил на прогиб необходим при учете податливости зубьев зубчатых колес, витков резьбы, шлицев, когда размеры поперечного сечения соизмеримы с длиной.
Для стержней постоянного сечения при действии сосредоточенных сил, моментов, равномерно распределенных
346
Изгиб стержней
нагрузок разработаны специальные методы интегрирования уравнения упругой линии, однако во многих случаях более просто использовать интеграл Мора.
ОПРЕДЕЛЕНИЕ ПРОГИБОВ
С ПОМОЩЬЮ ИНТЕГРАЛА МОРА
Вывод основной формулы. Определение прогибов. Пусть к балке в точке z = а (рис. 20) приложена сила Р, которая равна единице (единичная сила). Если сообщить балке некоторый дополнительный прогиб у, то работа внешней силы у (а) X 1 будет равна работе внутренних сил упругости .
Обозначим изгибающий момент в сечении стержня от действия единичной силы (г). Пусть dq>— относительный поворот двух близких сечений, возникший в результате дополнительного прогиба у балки. Тогда работа внутренних сил (работа деформации, рис. 21)
I
Лвн = j M1(z)d(p =
0
= P1(Z) ^dZ‘ о
Приравнивая работы внешних и внутренних сил, получаем
I
у (а) х 1 = J Mi_ (г) -^-dz. (40)
0
Уравнение (40) должно быть справедливым для произвольного (малого) прогиба стержня.
Предположим теперь, что в качестве у рассматривается прогиб от внешней нагрузки.
Тогда dtp _ М (г) dz ~ EJ х (г) ’
где М (г) — изгибающий момент в сечении от действия внешней нагрузки.
Подставляя отсюда значение dz в соотношение (40), получаем основную расчетную формулу (интеграл Мора)
(4])
0
Следовательно, чтобы найти прогиб в данном сечении стержня, надо приложить единичную силу в этом сечении, определить изгибающий момент A4j (z) от единичной силы и вычислить интеграл (41).
Величина Мг (г) в Н-см/Н, так как в равенстве (41) сокращен множитель 1 Н. Единичный силовой фактор при использовании интеграла Мора еле-
Рнс. 2Ь Работа внутренних силовых факторов
Определение прогибов с помощью интеграла Мора
347
дует считать безразмерной величиной (момент от единичной силы имеет размерность длины).
В большинстве практических задач интеграл Мора определяют с помощью правила Верещагина (см. ниже).
В общем случае интеграл Мора может быть вычислен по правилу трапеций. Равенство (41) справедливо и для упругопластических деформаций, если соответствующим образом опреде-dq> лить —.
dz
Если требуется учесть влияние перерезывающей силы иа прогиб, то уравнение (40) будет иметь вид
I
у (а) = J Mi (z) dz + о
I
+ ^Q1(z)ydz, (42) о
где у = kQ (z)/GF (г) — угол сдвига [см. формулу (32)]; Qi(z) — перерезывающая сила в сечении от действия единичной силы.
Вместо равенства (41) будем иметь
приложения единичной силы на ее направление:
I I
. С МгМ , , , f QjQ , ,
6 = \-irds+k\ ~GF-ds + 0 0
NxN л
—-—• dst
EF 1
(44)
Второй член в этой формуле выражает прогиб от действия перерезывающей силы.
Преимущества определения перемещения с помощью интеграла Мора особенно сказываются для стержней с непрямолинейной осью. Пусть, например, требуется найти проекцию перемещения точки А (рис. 22) на направление I—I, причем следует учесть влияние изгибающих моментов, перерезывающих и нормальных сил.
Повторяя предыдущие рассуждения, Найдем проекцию перемещения точки
где Mt, Qx, Л\ — изгибающий момент, перерезывающая и нормальная силы в сечении стержня от действия единичной силы, М, Q, N — то же в поперечном сечении от действия внешних снл.
Интегрирование распространяется иа всю длину осн стержня, элемент длины обозначается ds.
Определение углов поворота. Формула для определения углов поворота выводится так же, как соотнсшение (44). В сечении, где определяют угол поворота, прикладывают единичный момент (рис. 23). Работа момента будет <р (а) X 1.
В соответствии с этим
I
(а) = j о
Мх (г) М (г)
EJX (z) аг-
(45)
Ф
В этом равенстве Мг (г) — изгибающий момент в сечении стержня от действия единичного момента.
348
Изгиб стержней
Рис. 24. К выводу правила Верещагина
Рис. 23. Работа единичного момента
Вычисление интеграла Мора по правилу Верещагина. Изгибающий момент от внешней нагрузки и изгибающий момент от единичной силы (момента) определяют по одному правилу знаков (например, момент считают положительным, если ои создает сжатие верхнего волокна).
Если при вычислении интеграла (41) или (45) получается отрицательная величина, это означает, что действительный прогиб или угол поворота сечения направлен в сторону, противоположную направлению соответственно единичной силы или единичного момента.
Эпюра изгибающих моментов от единичной силы или единичного момента состоит из отрезков прямых. Рассмотрим участок стержня в пределах от гг до z2 (рис. 24).
Предположим, что изгибающий момент от единичной нагрузки выражается равенством
Mr (z) = Az + В, (46)
где А н В — некоторые числа. Тогда интеграл Мора на рассматриваемом участке
Г Мх (z) М (г)
J EJX (z)
fi
Предположим, что жесткость стержня иа изгиб в пределах участка постоянна, и учтем, что
J М (z) dz = Ft zi
где F — площадь эпюры изгибающих моментов от внешних сил.
Тогда
? dz =
J EJх (z)
= -gj-- A j zM (z) dz + BF .
(47)
Далее следует прииить во внимание, что
Z.
j zM (z) dz = znF, (48)
так как интеграл представляет собой статический момент площади F, а гц — абсцисса центра тяжести площади F.
Формула (48) справедлива в том случае, когда величина F имеет постоянный знак в пределах участка.
Используя соотношение (48), получим из равенства (47)
•Я
{MiWWdz
) EJX (г)
_ F EJX
(Ягц -р В) —.
Е/И1Ц
EJX '
(49)
Определение прогибов с помощью интеграла Мора
349
а.)
Рис. 25. Ограничения для
6)
применения правила Верещагина
где М1Д — момент от единичной нагрузки в сечении гц.
Следовательно, интеграл Мора в пределах участка равен произведению площади эпюры моментов от внешних сил на ординату эпюры от единичной нагрузки в сечении, соответствующем центру тяжести этой площади, деленному на жесткость стержня на изгиб (правило Верещагина).
1. Площадь н положение центра тяжести эпюр
Эпюра Площадь Абсцисса центра тяжести
Ограничения для применения правила Верещагина. 1. Эпюра изгибающего момента от единичной нагрузки должна быть в виде одной прямой линии. На рис. 25, а показан случай, когда это условие не соблюдается. Интеграл необходимо вычислять отдельно для участков / и II.
2. Изгибающий момент от внешней нагрузки в пределах участка должен иметь один знак. На рис. 25, б показан случай, когда правило Верещагина следует применять для каждого из двух участков в отдельности.
Ограничение не распространяется на момент от единичной нагрузки.
3. Жесткость стержня на изгиб в пределах участка должна быть постоянна. На рис. 25, в приведен случай, когда интеграл нужно вычислить отдельно для участков lull. Вспомогательные данные для применения правила Верещагина приведены в табл. 1.
Если эпюра от внешних силовых факторов на данном участке является линейной (например, при действии сосредоточенных сил и моментов), то равенство (46) можно использовать для момента М (г) и тогда, повторяя вывод, найдем
" Л4Х (z) М (г) _ Е1МЦ
(z) EJX ’
где Ej — площадь эпюры моментов от единичной нагрузки; Л4Ц —- ордината эпюры моментов от внешних нагрузок в сечении, соответствующем центру тяжести площади эпюры моментов от
350
Изгиб стержней
единичной нагрузки. Все ограничения, указанные выше для формулы (49), соответствующим образом переносятся на формулу (50).
ПРОГИБЫ И УГЛЫ ПОВОРОТА В СТЕРЖНЕ ПЕРЕМЕННОГО СЕЧЕНИЯ
Если стержень имеет небольшое число участков с различной жесткостью, то при определении прогибов и углов поворота можно применять правило Верещагина.
Пример. Определить прогиб стержня в точке А (рис. 26). Вычисляя интеграл Мора для участков, находим
1 1 РаЬ 2 ab г
У== EJ,. Т 'a~+ba Т а-A-b + r 1 1 РаЬ 2 ab
+ "Ё7Г ~ Т+Ь ° Т а + Ь ~
Ра2Ь2 fa b \
“ ЗЕ (а + 6)2 <“ + ~77 ) ’
Рис. 26. Определение прогиба стержня переменного сечения
ных участков длиной Д = 1,9 см каждый. Составляем расчетную таблицу (табл. 2).
Интеграл Мора по правилу трапеций будет иметь вид
Если жесткости на изгиб участков / и // одинаковы (E/j = EJt = EJ), то
Pa2b2
У = ЗЕ/ (а 4- Ь) ’
I
0
М (г) М (г) л
EJ (г) 2
Табличный метод расчета. При большем числе участков различной жесткости целесообразно применить табличный метод расчета непосредственно по формулам (41) н (45). Интеграл вычисляют приближенным методом по правилу трапеций. Последовательность расчета показана на следующем примере.
Пример. Определить угол поворота вала в сечении А (в месте посадки зубчатого колеса). Размеры вала в мм показаны на рис. 27. Силы Рг = 25 кН, Р2 = 40 кН. Модуль упругости материала Е = 2,1 10s МПа (2,1 • 107 Н/см2).
Реакции определяем нз условия равенства нулю моментов всех снл относительно левой эпюры:
*1 = 25 w + 40-Sr = 25’4KH:
R2 = 39,6 кН.
Для расчета все расстояния между опорными сечениями делим на 10 рав-
г=1
Л4 (zt) Mi(zt) EJ (zt)
( М (0) Мг (0) , \ 2EJ (0) “Г
, М(/)Л4г(/) 2EJ(l)
= 1,9(0 — 0,52 — 0,79— 1,19 —
— 1,15—1,43 4- 1,02 4-0,57 4-
4-0,35 4-0,11 4-0) 10'4 =
= —5,Й-10-4 рад.
Угол поворота сечения
<p = -5,8- IO’4 « —0°2'. т 2л
Знак минус означает, что угол поворота направлен в обратную сторону по отношению к единичному моменту.
Изгиб стержня с учетом пластических деформаций
351
Рнс. 27. Определение угла поворота стержня переменного сечения
2. Расчетная таблица для определения угла поворота сечеиня вала
Значение параметров в сечениях
Параметр 0 1 1 2 3 4 5 6 7 8 9 10
2, см 0 1,9 3,8 5,7 7,6 9,5 1 1,4 13,3 15,2 17,1 19,0
d, см 4,5 4.5 4.8 4,8 5,2 5,2 5,2 5,2 4,8 4 5 4,5
Jх, см4 20,1 20,1 26,1 26, 1 35,9 35 9 35,9 35,9 26,1 20,1 20,1
М • 1 о-4. Н‘ см 22 21,9 21,8 21,7 21,7 21 6 19,2 14 4 9,6 4,8 0
м, 0 -0.1 -0,2 — 0,3 -0.4 -0.5 0.4 0,3 0,2 0,1 0
ММ, ~х 10 •см 0 - 0,52 — 0,79 -1.19 -1.15 -1.43 1.02 0,57 0,35 0,1 1 0
ИЗГИБ СТЕРЖНЯ С УЧЕТОМ ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ
В основе расчета лежит кривая деформирования (рис. 28), представляющая собой зависимость а — f (в), устанавливаемую из опытов на растяжение. Дли конструкционных сталей эта за
висимость имеет такой же вид и при сжатии.
Для расчета обычно используют схематизированную диаграмму деформирования, показанную на рис. 29.
Первая прямая соответствует упругим деформациям (tga = £); вторая прямая проходит через точки, соот-
352
Изгиб стержней
Рис. 28. Диаграмма деформирования
ветствующие пределу текучести и пре* делу прочности tg ~ g-r. Угол
ев ет
наклона аг значительно меньше угла а (tga-j « 0,01 tga), и для расчета вторая прямая иногда представляется горизонтальной линией, как показано на рис. 30 (кривая деформирования без упрочнения).
Наконец, если рассматриваются значительные пластические деформации, то участками кривых, соответствующих упругому деформированию, в практических расчетах можно пренебречь. Тогда схематизированные кривые деформирования имеют вид, показанный на рис. 31
Распределение напряжений изгиба при упругопластических деформациях. Для упрощения задачи рассмотрим стержень прямоугольного сечения и предположим, что кривая деформирования не имеет упрочнения (см. рис. 30).
Рнс. 30. Кривая деформирования без упрочнения
Если изгибающий момент таков, что наибольшее напряжение изгиба a agj aT (рис. 32), то стержень работает в области упругой деформации
_ 6М <-«Ъпах-
При дальнейшем возрастании изгибающего момента в крайних волокнах стержня возникают пластические деформации. Пусть прн данном значении пластическими деформациями охвачена область от 0,5//, до 0,5// (рис. 32). В этой области a=aT. При у <
0,5//, напряжения изменяются по линейному закону a = a
Из условия равновесия момент внутренних сил
, ( Н* И* \ , ЬН1 м М -----------— ) +ar -g-b = М,
откуда
2 1/Т
Яг - -
(51)
Рис. 29. Схематизированная кривая деформирования
Рис. 31. Кривая деформирования при больших пластических деформациях
Изгиб стержня с учетом пластических деформаций
353
"У
Рис. 32. Изгиб стержне прямоугольного сечения в упругопласгичесаой стадии
Если бы материал оставался упругим при любых напряжениях, то наибольшее напряжение
а* =
6М
Тн2
превышало бы предел текучести материала.
Напряжения при идеальной упругости материала показаны на рис. 32. С учетом пластической деформации напряжения, превосходящие предел текучести для идеально упругого тела, снижаются. Если эпюры распределения напряжений для действительного материала я для идеально упругою материала (Сличаются одна от другой (при одних и тех же нагрузках), то
Рнс. 33. Распределение напряжений при действии предельного пластического момента
в теле после снятия внешней нагрузки возникают остаточные напряжения, эпюра которых представляет собой разность эпюр упомянутых напряжений. В местах наибольших напряжений остаточные напряжения противоположны по знаку напряжениям в рабочих условиях.
Предельный пластический момент. Из формулы (51) следует, что при
величина Н, ~ 0, т. е. все сеченне стержня находится в области пластической деформации.
Изгибающий момент, при котором во всех точках сечеиия возникают пластические деформации, называют предельным пластически и моментом. Распределение напряжений изгиба по сечению в этом случае показано иа рис. 33.
В области растяжения а = ат, в области сжатия а — —от. Так как из условия равновесия j a dF — 0, то
F нейтральная линия делит сечение на две равновеликие (по площади) части.
Для прямоугольного сечення предельный пластический момент
Мт = аг 2^1 =CTlJFT. (52)
12 Заказ 402
354
Изгиб стержней
Изгибающий момент, при котором возникает пластическая деформация только в крайних волокнах,
ЬН2
Му = аг ±2- = ат№.
Отношение пластического момента сопротивления Л4Т к обычному (упругому) моменту сопротивления для прямоугольного сечения
ЬН2/4
W bH2/Q
Для двутаврового сечеиия при изгибе в плоскости наибольшей жесткости это отношение составляет 1,15— 1,20; для тонкостенного трубчатого ~1,3; для сплошного круглого сечеиия 1,7.
В общем случае величину Л4Т при изгибе в плоскости симметрии сечеиия можно определить следующим способом (рис. 34); разбить сечение линией аа на две равновеликие (по площади) части. Если расстояние между центрами тяжести этих частей обозначить через е, то
Fg
МТ = aT -g— = arFc, (53)
где F — площадь поперечного сечения; с = 0,5е — расстояние от центра тяжести какой-либо половины сечения до центра тяжести всего сечения (точку О находит на равном расстоянии от точек Oj и 02).
Предельный разрушающий момент. Изгибающий момент, при котором в какой-либо точке сечения возникает
Рис. 34. К определению Л<т
Рнс. 35. Распределение напряжений прн действии разрушающего момента
напряжение, равное пределу прочности материала, называют предельным разрушающим моментом.
Прн определении разрушающего момента будем исходить из кривых деформирования для полностью пластичного материала с упрочнением (см. рис. 31).
Рассмотрим сначала стержень прямоугольного сечения. Распределение изгибающих напряжений показано на рис. 35. В крайних волокнах напряжение равно ов. Напряжение на расстоянии у от оси
2р
a = aT-j-(aB — ат) .
Из условия равновесия разрушающий момент
0,5Н
2J [aT+(oB— aT) ybdy = Л4В,
о
или
атГт+(ов-ат) Г = МВ, (54) где пластический и упругий моменты сопротивления соответственно
ЬН2 . т ЬН2
4’6*
Равенство (54) справедливо для любого поперечного сечения, имеющего две оси симметрии. Приближенно можно считать, что оно справедливо и-для сечеиия с одной осью симметрии.
Круглый вал
355
Это равенство можно записать в другом виде:
М, = А<т[| + (^— |)Х.].
(55)
Глава 18
КРУЧЕНИЕ СТЕРЖНЕЙ
КРУГЛЫЙ ВАЛ
При кручении круглого вала (рнс. 1) образующие цилиндра получают наклон к оси. Поперечные сечення вала остаются плоскими, радиальные направления остаются после деформации прямолинейными; поперечное сечение вала, не деформируясь, поворачивается вокруг оси.
Такая картина деформаций установлена экспериментально.
Если угол поворота концевого сечения <р (/), то угол сдвига на радиусе R
ф(0* у I Величина
(1)
(2)
представляет собой угол закрутки на единицу длины вала. Касательное напряжение в соответствии с законом Гука (рис. 2)
т = Gy = G0r, (3)
где G — модуль сдвига.
Прн кручении круглого вала касательные напряжения распределяются вдоль радиуса по линейному закону.
Из условия равновесия момент касательных напряжений должен быть
Рис. 1. Кручение круглого вала
Например, для стержня прямоугольного сечення прн WlWT = 1/1,5 и ав/ат — 1,5 получаем Л4В « 1,ЗЗЛ1Т. Прн выводе формулы для М в пренебрегали изменением сечения стержня в процессе деформации.
равен внешнему крутящему моменту, т. е.
R
J xr dF= Мк (4) О нли
R
G0 j г2 dF = Мк,
О откуда следует:
GQJp = Мк, (5) где R R
J р = г2 dF = 2л § г3 dr = о о
полярный момент инерции круга диаметром d = 2R.
Из формул (2) и (3) находим
Максимальные касательные напряжв'
ния
Мк „ Мк
Тгаах _ R ~
Мк ~ Мк nd3 ~ 0,2d3 “ИГ
(7)
Угол поворота концевого сечения
Ф(/) = -^-. (8)
Связь между максимальным касательным напряжением и углом закру-
12*
356
Кручение стержней
Рис. 2. Распределение напряжений при
кручении вала сплошного сечения
чивания ф (/) выражается равенством
_ ^рттах^ ^тах 2/
ч(1) =—g7^" = “g“ ~-
(9)
У валов малого диаметра при одном и том же угле закручивания касательные напряжения меньше.
Формулы (6) и (8) остаются справедливыми для полого вала (рис. 3).
Полярный момент инерции полого вала
Jp = ~(di~di)-
Максимальное касательное напряжение
Л4К Л4К
max wp ‘
16 k d* J
Если толщина стенки 5 = 0,5 (d — d^) мала по сравнению со средним радиусом Гер == 0>25 (d + dj), то можно считать, что касательные напряжения постоянны по толщине.
Рис. 3. Распределение напряжений при
кручении круглого вала
В этом случае
2^р6
(Ю)
СТЕРЖЕНЬ С ЭЛЛИПТИЧЕСКИМ ПОПЕРЕЧНЫМ СЕЧЕНИЕМ
При кручении стержня некруглого сечения точки поперечного сечения после деформации не лежат в одной плоскости. Они получают не только поворотные смещения, ио и смещения вдоль оси. Угол закручивания на единицу длины
0 = ф, ('О
где Т — геометрическая жесткость на кручение стержня чения (рис. 4),
л
Составляющие касательного напряжения
эллиптического се-
а3&3 а3 4-д2
(12)
Тгу=..^к х (13)
В точках контура вектор полного касательного напряжения направлен по касательной к контуру. В точках прямой, проходящей через начало координат, векторы полных касательных напряжений параллельны. Наи-
Рис. 4. Кручение стержня еллиптического
сечения
Стержни прямоугольного сечения и тонкостенные
357
Рис. 5. Осевые перемещения при кручении стержня эллиптического сечення
Рнс. 6. Касательные напряжения прн кручении стержня прямоугольного сечения
большее напряжение имеет место в концах малых полуосей:
Тгпах —
Мк
аЬг
(14)
Коэффициент fej с достаточной точностью может быть найден по приближенной формуле
Смещение точек в направлении оси г (депланация сечения) определяется ра-
венством
w =
Мк (а* — &а) 0ла363
ху.
(15)
Распределение w в точках контура показано на рис. 5.
Приведенное решение справедливо для случая чистого кручения стержня концевыми парами при свободных торцах. При стеснении осевых смещений (например, при заделке торца стержня) возникает стесненное кручение.
В зоне стесненного кручения в поперечном сечении возникают нормальные напряжения, распределенные приблизительно по такому же закону, как и величина ш. Максимальные нормальные напряжения в заделке °шах 1>5ттах.
Напряжения стесненного кручения быстро убывают по мере удаления от заделки. Так, например, при z = а величина атах составляет только 0.2тгаах.
СТЕРЖНИ ПРЯМОУГОЛЬНОГО СЕЧЕНИЯ И ТОНКОСТЕННЫЕ
Максимальное касательное напряжение действует на середине большей стороны (а> Ь), как показано на рис. 6:
Мк
(16)
Угол поворота на единицу длины стержня
е = ^Чз-. (17)
Для сечения в виде вытянутого прямоугольника
fej = fea = —— , О
Таким образом,
Л1Н
Тщах — j--------= —b. (18)
4- а*2
Для тонкостенных стержней (открытого профиля)
L
Т = -g- J б3 (s) ds, о
где б (з) — толщина стенки; ds — элемент дуги средней линии, длина которой L.
Наибольшее напряжение
"ЧЛЭХ = -уГ" бщах* (19)
Прн стесненном кручении стержня с сечением в виде вытянутого прямоугольника наибольшее нормальное напряжение в заделке может достигать ^тах 2,5ттах.
358
Кручение стержней
Эти напряжения быстро затухают, т. е. носят местный характер. У тонкостенных стержней (типа швеллера, двутавра) искажение напряженного состояния в районе заделки затухает медленно и при расчете следует учитывать стесненное кручение. Это составляет предмет исследований теории тонкостенных стержней. Если для сечения стержня параметр
k = < 3>
где JmIa — минимальный момент инерции сечения, то можно применять обычную теорию изгиба и кручения стержней.
РАСПРЕДЕЛЕНИЕ КАСАТЕЛЬНЫХ НАПРЯЖЕНИЙ
Согласно гидродинамической аналогии касательное напряжение представляет собой скорость жидкости, вращающейся внутри цилиндрического сосуда, стенка которого совпадает с контуром сечения вала.
Эта аналогия позволяет сделать ряд практически важных выводов (рис. 7).
1. Во всех входящих углах (рис. 7, а) образуется концентрация напряжений. Если радиус закругления вершин входящего угла стремится к нулю, то касательное напряжение стремится к бесконечности.
2. Во внешних выступах (рис. 7, б) касательные напряжения уменьшаются (по гидродинамической аналогии здесь образуются застойные зоны с малой скоростью течения).
По мембранной аналогии касательное напряжение пропорционально уклону резиновой пленки, закрепленной
по контуру сечения и находящейся под действием внутреннего давления.
Объем, образованный пленкой и плоскостью контура, пропорционален жесткости стержня на кручение.
УЧЕТ ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ
При кручении круглого вала картина деформаций остается такой же, как н при упругих деформациях.
Из опытов на кручение тонкостенных труб получена зависимость (рис. 8)
т = Ф (у). (20)
Для приближенного построения можно использовать обычную кривую деформирования (а, е), положив т = = о/уз, у = ]/Зв.
Расчетную зависимость т = Ф (у) ча сто принимают в виде диаграммы, показанной на рис. 9. Допустим, что до радиуса (рис. 10, а) материал вала работает в упругой области. Тогда на участке 7 (область упругости) т = Trr/rj, на участке II (область пластичности) т = тт.
Крутящий момент
С ? f3
Мк = \ тг dF = 2л \ тт — dr +
F 0
R
У 2л J ттг2 dr, ri
или
/ рз ,3 \
Л7к = 2лтт(^------i-). (21)
\ О 1Z /
б)
Рис. 7. Качественные особенности распределения касательных напряжений ври кручении
Трубчатые стержни
359
Рнс. 8. Диаграмма деформирования Рис. 10. Распределение касательных напряжений прн упругопластнческнх деформациях-
Из этого равенства
Г1=-|7 4/?3_ST. (22)
то значение угла сдвига на внешнем радиусе можно определить из соотношения
Предельное значение М„, соответствующее работе стержня целиком в пластической области (г1 = 0):
Л1КТ = ~ л/?3тт. (23)
О
Распределение напряжений в этом случае показано на рис. 10, б. Для угла сдвига справедлива зависимость у = 6г. Для радиуса rL
Т1=-^-=0Н- (24)
В силу соотношения (22)
й- Тт
6 = ~
6МК
(25)
Из формулы (25) следует, что при приближении величины Мк к AfKT деформация вала сильно возрастает. Если исходить из точной кривой деформирования т = Ф (у) (см. рис. 8),
Рнс. 9. Диаграмма деформиро-вания без упрочнения
2«£3f (уд) = Мк, (26) где —
Vh
F (Тв) = -г- \ Ф (у) у2 dy.
У к J о
Функцию F (yR) вычисляют, задаваясь различными значениями yR, и затем строят зависимость = = Л4К (уд) (рис. 11). Искомое значение yR соответствует заданному крутящему моменту.
Расчет следует начинать при уд 5s > тт/6, так как это соответствует началу пластичности в точках внешнего контура.
ТРУБЧАТЫЕ СТЕРЖНИ
При расчете трубчатых тонкостенных стержней на кручение предполагают. что вектор касательного напряжения параллелен касательной к сред-
Рис. 11. Зависимость
П П \ Г\ /
360
Кручение стержней
Рис. 12. Касательные напряжения прн кручении трубчатого стержня
ней линии контура и напряжения распределяются равномерно по тол-щине стенки (рис. 12).
Из условия равновесия элемента стержня, показанного на рис. 13, следует:
~ ^2^3’ или
6 (s) т (s) = const. (27)
Сумма моментов всех касательных напряжений относительно оси, проходящей через произвольную точку сечения (рис. 14), равна J рх (s) 6 (s) ds,
L
где p — длина перпендикуляра, опущенного нз точки О на касательную к контуру. Интеграл берется по всей длине L контура.
Приравнивая этот суммарный момент внешнему крутящему моменту, в соответствии с равенством (27) получим
44к = т (s) 6 (s) j р ds. (28)
L
Так как р ds = 2dFc, где dFc — площадь заштрихованного на рис. 14 сектора, то
j pds — 2FC, L
где Fc — площадь, ограниченная средней линией сечения трубы.
Из равенства (28) вытекает формула Бредта
М
Жесткость стержня при кручении. Потенциальная энергия деформации стержня
0 F
1 С Г Мкб(5) J J
~ 2 J J 4G62(s)F2 dsdz’ о 0
где I— длина стержня; L — длина дуги средней линии (периметр).
Отсюда получаем
&GFI J S(s) о
(30)
Из равенства работ 0,544к<р (/) = U, откуда угол поворота
Ф (0 =
А4К/ GT
Рис. 13. Равновесие элемента стержня
Рис. 14. К определению жесткости стержня иа кручение
Рис. 15. Стержень коробчатого сечеиия
Плоская деформация колец
361
/£
Г ds
где Т= 4F* М -----------геометриче-
I о ская жесткость сечения стержни при
кручении.
Дли трубы с постоинной толщиной стенки
4Я6 Т = ~Г
Например, для круглой трубы радиусом г с толщиной стенки 6
4л2г4б 2пг
= 2№6;
Т =
дли трубы коробчатого профили постоянной толщины (рис. 15)
4а4б 4а
= а36.
Т =
Глава 19
РАСЧЕТ КОЛЕЦ
ПЛОСКАЯ ДЕФОРМАЦИЯ КОЛЕЦ
Предполагается, что одна из главных осей сечении лежит в плоскости кольца. В этой же плоскости действуют внешние нагрузки. Замкнутое кольцо при действии прямоугольной нагрузки ивлиетси 3 раза статически неопределимым.
При расчете на прочность тонкого кольца можно считать справедливыми зависимости, установленные в теории прямолинейных стержней. Основную (статически определимую) систему получим, разрезая кольцо в некотором сечении 0=0 (рис. 1). Неизвестные силовые факторы в сечении обозначим: Xi — растигивающая (сжимающая) сила; Х2 — перерезывающая сила; Х3 —
изгибающий момент. Пренебрегая влиинием нормальных и перерезывающих сил на деформацию, можно записать с помощью интеграла Мора обобщенное перемещение
S_y«*ds. (|)
I
где Мр — изгибающий момент в сечении кольца (в основной системе) от действия внешних нагрузок; Мг — изгибающий момент в сечении кольца от единичной нагрузки; EJ — жесткость сечении на изгиб.
Для решения задачи в соответствии с равенством (1) следует определить изгибающие моменты от единичных
Рис. 1. Статически определимая система и эпюры изгибающих моментов от внешних нагрузок и единичных силовых факторов
362
Расчет колец
силовых факторов, приложенных в направлении х1( х2, х3.
Из условия равенства нулю относительных перемещений получаем систему (канонических) уравнений:
+ 612Х2 + 613Х3 + 61Р = 0; (2) ^21-^1 + 622Х2 + 633X3 + 62Р = 0; (3) 63Л + 632Х 2 + 633 Х3 + 6зР = 0. (4) Коэффициенты, входящие в последние уравнения, называют коэффициентами влияния. Каждый из этих коэффициентов получается в результате умножения эпюр, указанных индексами коэффициентов.
Используя свойства симметричности и кососимметричности эпюр, легко установить, что
612 ~ ^21 = 0» ^2.3 = 632 ~ 0.
Из уравнения (3) находим
Х2 = --^, (5)
022
а из уравнений
6цХ1 + б13Х3 + 61Р = 0;
+ 633X3 + 63р = 0
следует:
У _ б3р613 — 6ip633 . „.
611633 — 613631 ’
V______6ip63i -- 63р6ц
3~ 611633-613631 ' ( >
Перейдем к вычислению коэффициентов влияния. Изгибающий момент в эпюре «/» Л?1 (1) (0) = 1 • R (1 — cos 0).
Момент считают положительным, если он уменьшает кривизну стержня (см. рис. i).
Изгибающие моменты в эпюрах «2» и «5»
Л11,2)(0) = 1-1? sin 0; М1(3)(0) = 1.
Для кольца постоянного сечения:
2л
= £j Mid)Rd0 = о
2л
R3 С/, мм
~ EJ J ( COS0) EJ ’ о
2л
®13 = J ^1 (1)^1 (3)^ =
О
2л
_ R2 С .. 2л/?2 .
£7 J ( cos 9) <70 - EJ , о
2я
б22 = 77- f M2mRdQ = О
2л
/?3 С . 20 л/?3
= £Г J о 2л
®зз = EJ J <3>^ ~ о 2л
- R Г 70 2л7?
- J dQ-^T' о
Далее имеем
2л
= £j J Л/рМ, ц)7? 70 = о
2л
/?2 С
= -7-7- Л4р(1 — cos 0)70;
0
2Л
= EJ У (2)^ d® =
о
2л
R2 С
= ~£j~ i Alp sin 0 70;
о
2л
^зр = ~ЁТ § ^р^1 (3)^ d® =
о
2л
~-Ег1 О
здесь Мр— изгибающий момент в сечении 0 в эпюре Р, т. е. момент ог внешних сил в разрезанном кольце.
Плоская деформация колец
363
Рис. 2. Симметричная (а, б) и кососимметричная (в) нагрузки на кольцо
Теперь подставляй эти значении в равенства (5)—(7), получаем
2л
X1 = i i MP(0)cos0d0; (8)
О 2л
Ха =-----( Мр (0) sin 0 d0; (9)
Л-Л J О 2л
*3 = - ~ j Мр (0) dQ -
О 2 л
— — j (0) cos 0 d0. (10)
о
Изгибающий момент в сечеиии 0
М (0) = МР (0) + (1 —
— cos 0) + Х2Р sin 0 + Х3 или с учетом равенств (8)—(10)
2л
М (0) = Мр (0) - j мР (0) </0-о
2л
cos 0 О
-------— J Мр (0) cos 0 dQ —
о
2л
sin 0 Г
-------— J Мр (0) sin 0 dQ. (11) о
Для вычислении изгибающего момента в сечении кольца следует определить изгибающий момент в разрезан
ном кольце Мр (0) и вычислить интегралы, входящие в равенство (11) *.
При вычислении интегралов можно пользоваться приближенными методами, например правилом трапеций.
Угол 0 отсчитывают от произвольного сечеиия разреза (0 = 0).
Если внешние нагрузки имеют ось симметрии, то разрез целесообразно делать по этой оси (рис. 2, а, б).
Для симметрично нагруженного кольца
М (0) = МР(0) —
2 cos 0 (*
—------- J Мр (0) cos 0 dQ -
о
л
“ Т- У МР (0)dQ- <12) о
При кососимметричной нагрузке (рис. 2, в)
М (0) = Мр (0) -
л
2 sin 0 С
-------— j МР (0) sin 0 dQ. (13) о
Пример. Кольцо нагружено двуми сосредоточенными силами (рис. 3).
Разрез проводим по оси симметрии, разделяя нагрузку поровну по краям разреза, в результате получим
Мр (0) =-----sin 0.
* Момент в сеченин кольца равен моменту в разрезанном кольце за вычетом трех первых членов разложения этого момента в ряд Фурье.
364
Расчет колец
Рис. 3. Кольцо под действием двух сосредоточенных сил
Находим л
J Мр(9)М = о я
PR с
=-----g— \ sin 0 d0 = — PR-,
о
я
j Мр (0) cos 0 d0 = 0. о
Из равенства (12) следует:
М (0) = PR (j-------L sin 0) .
При 0=0 имеем
М (0) = — PR = 0.318РР. л
При 0 = я/2
= —0.182РР.
Пример. Кольцо нагружено двумя сосредоточенными моментами (рис. 4).
В этом случае (рис. 4, а) Мр (0) = 0 при 0 <. 0 С а;
Мр (0) = —М при а 0 я.
Вычисляем
л л
[ MP(0)d0 = — j Md9 =
6 о
= — М (я —а);
л
j Мр (0) cos 0 d0 =
о
л
= —М j cos 0 d9 = М sin а. о
Пользуясь равенством (12), находим
М (0) = МР(0) + — (л —а) —
2 cos 0 .. . ----------М sin а.
л
При 0 < а
М (0) = М 1 —-------sinacosa).
При 0 > а
М (0) = — М х
/ а , 2 \
X------------sin a cos а .
\ я я /
Расчетные формулы для некоторых случаев нагрузки колец даны в табл. 1. Эпюра изгибающих моментов приведена иа рис. 4, б.
Плоская деформация колец
365
1. Формулы для расчета колец
Обозначения: М (0) — изгибающий момент в сечении кольца; положительное направление момента принято, квк указано иа рисунке; 0 — текущий угол (а, Р — фиксированные углы, определяющие положение действующей ивгрузки); бх, бу — изменения диаметре кольца в направлениях х и у; J — момент инерции сечеиия; Е — модуль упругости.
Эпюры изгибающих моментов двиы для значений а, указанных ив эскизах
Эпюры изгибающих моментов
Расчетные формулы
Прн 0 < 0 < а
Кольцо под действием сосредоточенных одинаковых радиальных сил, приложенных с одинаковым шв-гом по окружности 1
N (0) = -
где а -------рвд (п — число сосредоточенных снл).
п
Перемещение точки приложения силы относительно центра кольца
1
2 sin* -у-
При мвлых углвх (а < 20°) Рг» а» Рг 1
£/ 720 EF а
0 < 0 Са a C 0 С я
М (0) = Рг (sin а — M (0) = Pr [-1- (sin a —
— а cos а + а cos 0 — — a cos a + a cos 0) —
— sin а cos а cos 0) — — sin a cos a cos 0^|
— cos 0 + coa а J
Кольцо под действием двух горизонтальных сил
Рг* Г 2 1
б г = — (sin а — а cos а) + -т- (sin а cos а —а)
* EJ Л 2
Л Рг* Г 2 . . . . . sin3 а
би = -=г-г — (sin а — а cos а) -f- cos а Н----------------т-------1
» С, J 1 Л л
1 В этом случве учитывают влияние нормального усилия N (0), которое при п > 8 оказывается существенным. Влиянием перерезывающих снл можно пренебречь.
366
Расчет колец
Продолжение табл. 1
Эпюры изгибающих моментов
Расчетные формулы
0 < 0 < a a < 0 < л
M (0) = MO |-i- (a + M (0) = .M, Г— (a J-I л
4- 2 cos 0 sin a) — Ij 4- 2 cos 0 sin a) j
Кольцо под действием двух сосредоточенных моментов
Кольцо под действием двух вертикальных сил
А /2 , \
= —F7— “77" а — Sin а ;
А EJ I я }
= “ + cos“ -* 1)
О < 0 =6: а
М (0) — Pr (Р sin ₽ + cos ₽ — а sin а —
— cos а — cos 0 sin* a -j- cos 0 sin* P) — sin P 4- sin a
а < 0 < P
M (0) = Pr sin ₽ + cos P — а sin а —
— cos а — cos 0 sin* а 4- cos 0 sin* P) — sin p 4- sin 0
P < 0 < л
M (0) = pr Г— (P sin P + cos p — a sin a —
L "
— cos a — cos 0 sin* a + cos 0 sin* P)
Pr* г t 2
a, = Ц- (sin* a + sin* p) + —- (P Sin p + Cf J I 2 Я
4- cos p — a sin а — cos a) 4- 1 — 2 sin p j;
Pr3 Г I
6y = —-r- (sin P cos p + P — sin a cos a — a) + & c. J I 2
n
4—— (p sin p 4" cos p — a sin a — cos a) 4-
4- sin a — sin p
Плоская деформация колец
367
Продолжение табл. 1.
Эпюры изгибающих моментов Расчетные формулы
^0,216ргг /щур Я\/\а=ЙО0 А:*:' -vJS&'-ltf о 0,1 р_ \f /' / Pr2 \ i Zprsina '0,312 pp 2 0 = 0 . г 1 , sin* а , i / . a sin1 а М (0) = рг‘ — Н + —— 1 Sin а sin’ а 3 sin ос cos а а \ 1 3 .4 4 JJ' 0 < 0 < а М (0) = М (0) — ргг ^sin а cos а — S1^a (i — cos 0)] а < 0 < л м (0) = М (0) +рг‘ (! _ cos 0) _ — -1— (sin® а + sin* 0)]
Кольцо под действием распределенной нагрузки и уравновешивающей вертикальной силы _ 2рг‘ Г i sin а sin' a sin" а °® EJ [ 4 2 + 2 12 i ( a , 3 , , a sin' а \ 1 „ 1 4 + 4 sinacos“+ 2 S'nal , _ 2pr* Г I sin' a sin' a cos a EJ | 12 + 4 12 a sin a cos a i ( a sin* a 4 6 Л 2 + , 3 . , a , \ 1 H—•?— sin о cos a. 4— sin a 4 4 /
/РРОЛОТрп2- ffll HjijP Руо_Т^у\а =30 ° -0,1 /0 0,1 Н_ J Ргг k/q Ti3\z ШШННр Кольцо под действием двух ' 0 = 0 M (0) = pr’ (-y- a Sin* a 3 II H—— sin a cos a) sin* a • 0 < 0 <a M (0) = M (0) —^-sIn’ e- 0 < 0 < л M (0) = M (0) — pr’ ^sin a sin 0 sin’ a j
. pr* Г , sin' a , EJ [ Sin“ 3 + H—— (a + 3 sin a cos a + 2a sin* a) T, " J
368
Расчет колец
Продолжение табл, i
Эпюры изгибающих моментов
Расчетные формулы
. рг* Г . _ sin’ а
— -=г-г sin’ а — а sin а--------------s— cos а —
* с j i <5
2 , 2
„ _ cos а + +
л sin а
2
X (2а sin1 а + 3 sin а cos а 4- а)
0,ч68рг2
Кольцо под действием вертикальной распределенией на! рузки постоянной интенсивности н двух уравновешивающих вертикальных сил
0 = 0
М (0) — pr‘ j—Ь cos а + а sin а — п sin а 4- sin' а
N (0) = рг (sin1 а - 0 < 9 < а
М (6) = М (0) — N (0) г (1 — cos 0) +
4- рг' (0 sin 0 + cos 0 — 1). а < 0 < л
М (0) = М (0) — Л' (0) г (I — cos 0) + 4- рг* (0 sin 0 4- cos 0 — i — л sin 0 4- л sin а)
t>x ----(i 4- sin* а) 4- 2 (а sin а 4- cos а)
йу = ~'^г [^ — 2,467 4- (sin a cos а 4-
4- а — 2 sin а) 4- 2 (а sin а 4- cos а)
ОСЕСИММЕТРИЧНАЯ
ДЕФОРМАЦИЯ КОЛЕЦ
Под действием осевой силы (рис. 5) кольце испытывает осесимметричную деформацию — сечение кольца поворачивается на некоторый угол. В общем случае на кольцо могут действовать равномерно распределенные силы и моменты (рис. 6, сила qt в Н/см распределена по окружности радиусом at, момент mt в Н-см/см — по окружности радиуса bi) н сечение кольца получит радиальное перемещение и0 н поворот на угол <р против часовой стрелки (рис. 7). Рассмотрим приближенное решение, основанное на допущении, что деформации в плоскости сечения кольца отсутствуют (физическая модель такой расчетной схемы — кольцо из жестких шайб, связанных
кольцевыми упругими нитями). Начало координат помещено в центре тяжести сечения. Относительное удлинение в окружном направлении
e=±2_ + yJL. (14)
По закону упругости напряжение в окружном направлении
а = £е = £ + (15)
где Е — модуль упругости материала.
Неизвестные величины Uq и ср, входящие в это равенство, определяют из условий равновесия половины кольца (рис. 8):
^odF = N; ^oydF=M, (16)
F F
Осесимметричная деформация колец
369
где N и М — растягивающая сила и момент в сечении кольца. Этн усилия уравновешивают половину кольца. Плоскость действия момента перпендикулярна оси
Для вычисления «V н М используют формулы (см. рис. 6)
N = S atqi cosaf, (17) i--l
М = 5 (bimi — a'i4i since, —
Рис. 5, Осесимметричная деформация кольца (кручение кольца) под действием осевой силы
-WM cosai), (18)
где суммирование распространяется на все приложенные нагрузки.
Внося равенство (15) в условия (16), находим
dF С уdF. .. /1Л.
uofj—-f-<p£ j ~— = Л; (19)
иеЕ j J =r М. (20)
F F
Разберем два основных случая.
Размеры поперечного сечения кольца малы по сравнению с радиусом. В этом случае можно считать г = г0, где г0 — радиус окружности центров тяжести сечений.
Учитывая, что
j у dF = 0, F
так как ось х проходит через центр тяжести сечения, из уравнений (19) и (20) получаем
Рис. 6 Распределенные внешние силы и моменты, приложенные к кольцу
Рис. 7, Деформация кольца
и„ __ N Ф _ М
EF с о EJ х
где F — площадь поперечного сечения кольца; Jх = j у2 dF — момент ннер-
F цни сечения кольца относительно осн, проходящей через центр тяжести и перпендикулярной к оси кольца.
Из равенства (15) вытекает:
N , м
a = ~r + !f-J^' <22)
Я
Рис. 8, Растягивающее усилие N и момент Л1 в поперечном сечении кольца
370
Расчет колец
Рис, 9. Кольцо прямоугольного сечеиия под действием осевой силы
Кольцо под действием осевой силы. В этом случае (см. рис. 5) общая осевая сила
Q — 2ла1д1 = 2па2<?2.
Из формул (17) и (18) л л
= «2 = —г;
N = 0; М = —ofo 4- alq.2 = с,
где с = а2 — Oj — разность радиусов опорных окружностей.
Угол поворота кольца
_ _ го (агЯг а\Ях) __
ф EJX ~ EJX
= г^с
2лЕ/ х
Осадка кольца (вертикальное перемещение точки приложения силы)
rBQc2 2лЕ.]х
б = <рс =
Напряжения в поперечном сечении
кольца
Для кольца прямоугольного сечения
(рис. 9)
ф= 6r°Qc_-
т nEbh3 ’
Qc 2л7 х
<* = У
6Qc nbh3
Наибольшие напряжения 3Qc amax = ± .
Растягивающие напряжения действуют при у = 0,5h, сжимающие — при у — —0,5h.
Кольцо по, радиальной этом случае (рис. = at7; М = ateq.
Далее находим
Up = МФо r0 Ehbr0
Напряжение в кольце
017 bh.
I действием нагрузки. В
10) «! =0; У1 =
12ata?
Ebh3 •
12ote7 bh3
a
+ У
Температурные напряжения. Рассмотрим неравномерно нагретое кольцо при действии внешних нагрузок. Вследствие влияния температуры модуль упругости в различных точках сечения может иметь различные значения.
Деформация кольца
j EaT dF
= + 4; (23)
r° I Е dF I EdF
F F
| EaTydF
ф = M F________
r° j Ey2 dF ’ f Ey2 dF
F F
(24)
Начало координат осей x, у помещено в приведенный центр тяжести сечения, так что
Рнс. 10. Кольцо прямоугольного сечения под действием радиальной нагрузки
Осесимметричная деформация колец
371
Рис. 11. Общий случай расчета осесимметричной деформации кольца, когда размеры поперечного сечення соизмеримы с радиусом
Расстояния yt и с можно отсчитывать от произвольной оси, в данном случае вспомогательная ось проходит через верхнюю точку сечения.
Ось у направлена параллельно оси кольца и проходит через центр тяжести сечения.
Из уравнений (19) и (20) при условии (7) находим
гзг-; <281 £1 —
F
При его определении единице площади поперечного сечения приписывают «вес» Е.
Напряжение в кольце
(29)
j ЕаТ dF
F
F
Напряжения в поперечном
сечении
кольца
J EaTydF \
+ У —f-----------aT . (25)
J Ey2 dF I
F /
Вторая группа членов в этой формуле выражает температурные напряжения.
Размеры поперечного сечения кольца соизмеримы с радиусом. В этом случае равенство г ~ г0 ие используют, а положение оси (размер с, рис. 11) определяют из условия у JL^L.= С = {26)
F F
что дает
F
Кольцо прямоугольного сечения под действием осевых сил. На кольцо действуют распределенные силы и </2 и распределенный момент т (рис. 12).
Силовые факторы определяем по формулам (17) и (18)
N = 0; М = —mat — (Tq, 4- а%д2-
Рис. 12. Кольцо прямоугольного сечеиия под действием распределенных усилий и момента
372
Расчет колец
Равенство (26) будет удовлетворено, если ось х проходит через центр тяжести сечення.
Далее вычислим
Угол поворота кольца по формуле (29)
<р == 12(д2<72 — д1<71— д1т) . (3!)
Eh3 In
Напряжения в кольце
Ряс. 13. Коническое кольцо под действием распределенных осевых сил
а = Л 12(д1<72 —д?91 —д1^) . (32)
Г h3 In
Г1
Если г» н Г; близки между собой, то In (Г2/Г!) « r2 — rr = b; г = г0 и формулы (31) и (32) совпадают (при т = 0) с полученным ранее решением для кольца, размеры поперечного сечения которого малы по сравнению с радиусом.
Коническое кольцо. Тонкостенное кольцо (6 <С г) находится под действием осевых распределенных снл q1 и q2 (рис. 13).
Введем вспомогательные координаты £ и г], тогда
у-i = £ sin а + т] cos а;
г = rj + £ cos а — т] sin а.
С достаточной точностью можно положить г = + £ cos а.
Для определения с по равенству (27) вычисляем
£ sin а 4- п cos а ,, ,
и находим
6 tg ГХ cos а
Далее определяем у. = J
F
tg2« cos а
в
d£ dr] г + £ cos а
=-----------1п
cos а
X (4 — '?) ~ 2^1 (G — 'Л-
+г?1птг] + -тгС08а1п
Формула Эйлера
373
Напряжения в кольце
а = У_ Ягаг — 91«1 г J*
Осадка кольца (сближение точек приложения сил ?! и ?2)
б = <р (а2 — аО =
= (??аг — 91Д1) (Д2—«i)
EJ*
Пределы применимости приближенного решения. Приведенное решение основано на допущении, что сечение кольца не деформируется. Следовательно, для случая, показанного на рис. 14, а, изложенное решение не пригодно, тогда как для случая, изображенного на рис. 14, б, изложенное решение можно использовать.
Если г21г\<. 1,4, то целесообразно применять решение, основанное на формулах (21) н (22), прн r2//i> 1,4 — более сложное решение [формулы (28)— (30)].
Глава 20
УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
ФОРМУЛА ЭЙЛЕРА
Если тонкий прямой стержень сжимать вдоль оси, постепенно увеличивая силу Р, то вначале он будет оставаться прямым, но затем при некоторой нагрузке Ркр, называемой критической, стержень начнет резко изгибаться. Это явление называют потерей устойчивости (рнс. 1). При потере устойчивости напряжения быстро возрастают, что может привести к разрушению детали. Для нормальной работы большинства конструкций потеря устойчивости недопустима. Обычно допускаемая нагрузка не превышает (0,5-0,7) Ркр.
Чтобы найти критическую силу Ркр, рассмотрим условия, при которых сжатый стержень может находиться в изогнутом состоянии в условиях равновесия (рис. 2). Прн малых прогибах справедливо обычное уравнение изгиба
EJ = М. = —Ру
a) f)
Рнс. 14. Области применения приближенного решения для осесимметричной деформации колец:
а — кольцо заделано в массивное тело — решение ие пригодно; б — кольцо оперто и имеет возможность поворота — решение может быть использовано
Для тонких пластин (Д/(г2—/Д < <0,2) прн г2//'1>2 приближенное решение часто дает большие погрешности и приходится использовать теорию пластин (см. гл. 23).
или
^- + ^=0, (1)
где
(2)
Общее решение уравнении (1) у = A sin kx + В cos kx
для опертого по концам стержня должно удовлетворять граничным условиям у (0) = 0, у (/) = 0, что возможно, если В = 0, A sin kl = 0. Стержень может прогнуться (А ф 0) только прн условии sin kl = 0. Пока сжимающая сила Р мала, так что величина k = ~\/РIEJ < п/l, значение sin kl
0 и стержень остается примолинейным. Прн k = nil или
Г ~ 'кр — р
(3)
стержень может принять помимо прямолинейной формы, которая становится
374
Устойчивость стержней
Рис. I. Потеря устойчивости стержня при сжатии
Рис. 2. Осевое сжатие двухопорного стержня
неустойчивой, новую форму равновесия с изогнутой осью. Для определения величины прогиба при Р Ркр необходимо использовать в уравнении изгиба точное выражение кривизны стержня (см. рис. 2)
EJ = -Ру ds я
и учесть изменение расстояния Л/ между концами стержня в результате изгиба. При малых прогибах это приводит к выражению
При Р/Ркр = 1 прогиб отсутствует, но при дальнейшем увеличении силы Р прогиб очень быстро растет. Так, если сжимающая сила превысит крити
ческую всего на 1,5%, то стержень длиной 1 м прогнется на 11 см.
Критическую силу определяют по минимальному моменту инерции сечения. Величина Ркр зависит от условий закрепления, характера нагружения и конфигурации сечений стержня.
Из сравнения форм прогибов двухопорного стержня, консольного (рис. 3, а) и с двумя заделанными концами (рис. 3, б) следует, что условия потери устойчивости будут у них одинаковыми, если заменить длину стержня I «приведенной» длиной /пр = — vZ; для двухопорного стержня v = 1, для консольного v = 2, а для стержня с заделанными концами v = 0,5.
В общем случае формулу Эйлера (3) можно представить в виде
^кр — Л -р~» (5)
где
(6)
Общий случай расчета критической нагрузки
375
Рис. 3. Формы прогибов при потере устойчивости стержней
Рнс. 4. К общему случаю расчета критической нагрузки
Критической нагрузке соответствует напряжение сжатия
Рнр лгЕ °кр=— = ^2-’
(7)
где коэффициент X характеризует приведенную гибкость стержня с учетом условий его опирания и нагружения:
, 1ор I П I
Л = —— =v— = —--г . (8)
1 1 Vn 1
Здесь । — радиус инерции поперечного сечения,
С учетом выражения (7) формулу (5) можно записать в виде
, rfEF
кр- Л2
(9)
ОБЩИЙ СЛУЧАЙ РАСЧЕТА
КРИТИЧЕСКОЙ НАГРУЗКИ
Дифференциальное уравнение изгиба (1) можно записать в углах поворота 0 = ^ как
dx
откуда
««-Мттйг1 в"=-в<0)' о
(11)
При действии на стержень в сечениях X; нескольких продольных сжимающих сил и распределенной продольной нагрузки q (х) (рис. 4)
51
0 при
М(х) = У (*)) 4-
t=i
I
+ J ? (*1) [у(*1)— У (*)] dxi, (12) X
где
Xi.
(13)
В частном случае, при защемлении стержня в сечении х = О, когда у (0) = 0, 0 (0) = 0.
у(х) = j 0 (Xjjdxn 0О = 0, (14) 0
376
Устойчивость стержней
В безразмерном виде
£ ——• 7 —— ₽<=. — •
I ’ J “ Л ’ 1 РКР'
q~ <7о ’ Q->kp’ Л Ph ’
(15)
где — значение J при х = 0; Ркр — критическое значение одной из нагрузок или их суммы; q0— значение q в некоторой выбранной точке, Q =
I 1
= f q (х) dx = qBl/c; с-1 = J q (E) dg; 0 0
Pl, Q— заданные отношения нагрузок при потере устойчивости.
Тогда из (11) — (15)
0(E) = nK [0(E)], (16)
И
e<m> (£) - т]<т>к<т> (£).
В качестве исходного приближения 0<О) (Е) выбирают функцию, удовлетворяющую кинематическим граничным условиям (для защемленного стержня е (0) = о).
Пример. Найти коэффициент г] для консольного стержня постоянного сечения, сжимаемого силой на конце (J = = 1, Q = 0, Pi = 1, Е< = О- Принимая 0(О) = Е. находим
6 1
к(1) (Е)= J J E2dE2d£i = о 61
где К [0 (£)] — интегральный оператор;
5
К [6 (Е)1 = \ — X
J J (Бх)
о
Уравнение (16) решают методом последовательных приближений- по функции 6(,л—*1 (Е) находят =
— К [0(т—*> (£)] и из условия минимума среднего квадратического отклонения [1] — значение
J (E)K<m>(E)dE
Ч,'”, = -£—,-------------------
j [№m,(E)]2dE
(18)
что мало отличается от точного решения т] — л2/4 « 2,467.
В общем случае интегралы находят численно. При других граничных условиях меняется только вид оператора (17).
ТАБЛИЦЫ ДЛЯ РАСЧЕТА КРИТИЧЕСКОЙ НАГРУЗКИ
Значения коэффициента т] для различных расчетных случаев, полученные методом последовательных приближений, приведены в табл. 1*. Чем больше величина т], тем лучше сопротивляется стержень потере устойчивости. При нагружении несколькими
* Расчеты выполнены Н. А Малин-киной.
Таблицы для расчета критической нагрузки
377
К(блица для расчета
Схема и расчетная
формула п 0 01 0 10
При Pi •> О (PI 4- Pi)Kp - Л
При Рг < О n FJ*
р1кр = ’I —р—
100 00 8 80 9 84
10 00 1 09 6 82
5 00 0 59 4 45
2 00 0 30 2 39
1 00 0 20 1 62
0 50 0 15 1 22
0 20 0 12 0 98
0 Ю 0 1 1 0 90
0 00 0 10 0 82
— 0 10 0 10 0 82
— 0 20 0 10 0 83
— 0 50 0 J0 0 83
— 1 00 0 10 0 83
— 2 00 0 10 0 84
— 5 00 0 10 0 87
10 00 0 10 0 89
Схема и расчетная формула к Схемам 4 — 8
А, 0 00 0 10 1
0 01 47 1 62
0 05 1 54 1 69
0 10 1 62 1 76
0 20 1 75 1 88
0 30 J 87 1 97
0 40 1 97 2 06
0 50 2 06 2 14
0 60 2 15 2 22
0 80 2 32 2 3 5
1 00 2 47 2 47
2 00 3 12 2 94
5 00 4 63 3 86
Продолжение табл 1
к
0 20 0 50 0 80 1 00 1 50 2 00 5 00 10 00
9 80 9 76 9 75 9 75 9 74 9 74 9 73 9 73
7 74 8 20 8 28 8 30 8 33 8 34 8 35 8 35
5 97 6 85 7 06 7 12 7 20 7 93 7 29 7 30
3 64 4 84 5 16 5 28 5 42 5 49 5 6 I 5 65
2 57 3 67 4 01 4 13 4 30 4 38 4 53 4 58
1 97 2 93 3 26 3 38 3 55 3 СЗ i 79 3 84
1 60 2 43 2 74 2 86 3 01 3 Ю 3 25 3 30
1 47 2 26 2 56 2 67 2 82 9 90 3 05 3 10
1 35 2 08 2 36 2 47 2 62 2 69 2 84 2 89
1 35 2 11 2 40 2 51 2 67 2 76 9 91 2 97
1 36 2 13 2 44 2 56 2 73 9 82 2 99 3 05
1 38 2 21 2 57 2 71 2 91 3 0° 3 23 3 31
1 41 2 34 2 78 2 96 3 24 3 40 3 71 3 83
1 44 2 54 3 16 3 45 3 94 4 24 4 96 5 96
1 56 3 15 — — — —
m
0 20 0 30 0 40 0 50 0 60 0 70 0 80 0 90 1 00
1 78 1 94 2 ’0 2 24 2 34 2 41 2 45 2 47
1 84 1 99 2 14 2 26 2 26 2 42 2 45 2 47
1 90 2 04 2 17 2 28 2 37 2 43 2 45 2 47
2 00 2 12 2 23 2 32 2 39 2 43 2 46 2 47
2 08 2 18 2 27 2 35 2 40 2 44 2 46 2 47
2 15 2 24 2 31 2 37 2 42 2 45 2 46 2 47
2 22 2 29 2 35 2 39 2 43 2 45 2 46 2 47 2,47
2 28 2 33 2 38 2 4 2 44 2 45 2 46 2 47
2 38 2 40 2'4 3 9 44 2 45 2 46 2 47 2 47
2 47 2 47 2 47 2 47 2 47 2 47 2 47 2 47
2 80 2 70 2 6 1 2 55 2 51 2 49 2 47 2 4’’
3 37 3 04 2 89 2 67 2 57 2 51 2 48 2 47
Устойчивость стержней
Таблицы для расчета критической нагрузки
379
Продолжение табл.
380
Устойчивость стержней
Продолжение табл
Таблицы для расчета критической нагрузки
381
Продолжение табл.
О о 9,87 О о ос оо ао оо оо ао со оо со со о со — ь- * . . ст? ст? ст? ст? ст? ст? ст? о?" ст? ст? о с-^ ст? ст? ' *
о ст> о еч^ль-стч^софсч^остючо» <0OO03(*)M*iAiA<0<0<0<0<0<0<O C4S®0>0>C>0!CJ>0>CJ>OC7IC7l0> ст> о 11,95 11,77 1 1,60 11,24 10,88 10.53 10,32 10,20 10.05 9,87 10,74 11,76 12,99 16,37 25,9 37,0
о 00 о 0.64 2.82 4,74 6,74 7,62 8,07 8.35 8,52 8.75 8.88 9.05 9.13 9,28 9.33 1 8,Q 1 14.24 13.83 13.45 12.63 11.86 11,14 10.72 10.48 10.19 9,87 10.55 11.33 12,21 14.39 19.08 23.2
0.70 0,28 1,32 2.42 4,07 5,17 5,93 6,47 6,86 7,39 7.73 8.20 8,44 8,87 9,02 о 16,55 15,82' 15,16 13,81 12,62 11,58 11,00 10,67 10,29 9,87 10,44 11.07 1 1,78 13,45 16,78 19,64
0.60 | 0,16 0,76 1,43 2,58 3,49 4,22 4,81 5.28 6,00 6,51 7.29 7.73 8,59 1 8,90 1 9'° 1 18,20 17.15 16.24 14,48 13,01 11,78 11,13 10,75 10.33 9,87 10,40 10.98 11,62 13,13 16,14 18,82
0.50 | 0,10 0.49 0к94 1.76 2,47 3,08 3.61 4,08 4,84 5,44 6,45 7,09 8,49 9.04 Е in о 18,67 I 17,50 16,51 14,63 13,09 11,82 11,15 10,76 10,34 9,87 10,39 10.96 11,60 13,09 16.10 18,82
| око 0.07 0,34 0,67 1.28 1.83 2.33 2.79 3.21 3,94 4.55 5.72 6.52 8.59 9.51 о 18,67 17,52 16.54 14,67 13,13 11.85 11,17 10.78 10,35 9,87 10,38 10,94 11,56 13,01 15,86 18.34 31,3
0.30 0.05 0,25 0.50 0.97 1,41 1,85 2,21 2,58 3.25 3.85 5,08 6,03 8,91 10.46 с*э 6 19,49 18.28 17.22 15.16 13,45 12,03 11.28 10.86 10.39 9,87 10.34 10.84 11.39 12,62 14,88 16,65 24,3
О С4 о 0,04 0,19 0,38 0.76 1.11 1.46 1,79 2,11 2.72 3,28 4.54 5,60 9,50 12.18 С4 о 22.9 21,2 19.73 16,75 14.39 12,53 11.58 11.06 10,49 9,87 10.23 10.61 11.00 11.86 13,28 14,30 18,79
о о 0,03 0.15 0.31 0.61 0,90 1.19 1.48 1.76 2,31 2,83 4.08 5,22 10.44 15.44 о 36,4 31,6 27,5 20.7 16,37 13,46 12.11 1 1,40 10.65 9.87 10.07 10.26 10.47 10,88 11,53 1 1.97 13,99
0.01 0,05 0.10 0.20 0.30 0.40 0.50 0.60 0.80 1.00 1,50 2.00 5.00 10.00 е ОООООЛМС4 — О — С-1 сО СО О О о©1йсч —ooooooooo'o—'im* 2“ 1 1 1 1 1 1 1
Схема и расчетная 1 формула | СТ» У *|" н « II о. ь п = ~: р, При Рг > 0 (Pi + P.Ikp = П При Рг < 0 г, EJ ₽1кр — Ч
382
Устойчивость стержней
сжимающими силами коэффициентом т) определяется сумма этих сил:
п
i=i
при нагружении сжимающей Рг и растягивающими (Р < 0) силами
^кр — 'кр! — т| р •
ВЛИЯНИЕ НАЧАЛЬНОГО
ПРОГИБА И ВНЕЦЕНТРЕННОГО ПРИЛОЖЕНИЯ СИЛЫ
НА ВЫПУЧИВАНИЕ СТЕРЖНЯ
Если в ненагруженном состоянии стержень имеет не вполне прямую ось и сжимающая сила приложена с эксцентриситетом, так что с самого начала нагружения возникает изгибающий момент Ма = —Ру0 (рис. 5), то уравнение изгиба для деформированного со-
(у У о) max
L
0,25
0,20
0,15
0,10
0,05
0
Рис. 6. Зависимость упругого прогиба эксцентрично сжатого стержня от сжима* ющей силы и эксцентриситета
стояния принимает вид
^У~У^ =.-Ру (19)
при граничных условиях для двухопорного стержня у (0) = е, у (I) = е.
Положив, например,
, ЛХ
y0 = « + asin —, (20)
откуда с учетом указанных граничных условий
соз^0,5й/ (1 — cos 0,5kl
получим из (19) d!u ^+k2y-
(21)
Максимальный упругий прогиб при х/1 = 0,5
(У — Уо)тах —
Рис. 5. Сжатие стержня с начальным прогибом и эксцентриситетом приложения силы
Расчет сжатых стержней на прочность и жесткость
383
Р
Р.,
'-Л гнр
(23)
где Ркр определяют по формуле (5). Зависимость —------Уо^а- = f ( ,
* V “нр
€ \
— \ при а=0 показана иа рис 6.
В отличие от идеально прямого центрально нагружаемого стержня изгибине деформации (выпучивание) появляются с самого начала действия сжимающей силы При приближении силы Р к ее критическому значению Рнр прогибы резко возрастают
РАСЧЕТ СЖАТЫХ СТЕРЖНЕЙ НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ
В реальных конструкциях неизбежны некоторые отклонения оси стержня от прямолинейного направления и эксцентричное приложение сжимающих сил. Поэтому уже при нагрузках меньше критических начинается боковое выпучивание стержня и напряжения в его поперечных сечениях распределяются неравиомерио. Максимальное напряжение в сжато-изогнутом стержне при начальном прогибе а (см. рис. 5)
Отаах — О 1 Утах^ > (24)
Р
где о = —; W — момент сопротивления сечеиия при изгибе;
а
Утах = --------— (25)
акр
С учетом формул (7) — (9) получим
Отах = О Л +-----^3—V (26)
\ 1 ~
где
(27)
Когда максимальные напряжения °тах достигнут предела текучести при
Рис. 7. Зависимость предельного напряжения пПред от гибкости X для стали СтЗ: а — критическое напряжение для упругого состояния, б — с учетом пластических деформаций
сжатии ат, среднее сжимающее напряжение а = апред- Обозначив
^пред ,
<р =-------- С 1
т От
(28)
и подставив в (26) соответствующие
значения отах = от и о = апред, получим уравнение
= 1
<₽
АХ
Х2от ’ ~<₽’л2£г
(29)
связывающее коэффициент <р с гибкостью Л, свойствами материала оТ/Е и геометрическим параметром N.
На основании статистических данных можно считать, что влияние начального прогиба и эксцентриситета достаточно надежно учитываются, если принять
-у « (1 4- 2,5) 10-з.
Величина УFJ/W = I для двутаврового, УЗ = 1,73 — для прямоугольного и 2 — для круглого сечеиий. Считая в среднем Ая*Уз-10~’^= = const, можно из уравнения (29) иайти для данного материала зависимость <р (X), определяющую величину апред, *ак показано иа рис. 7. При
384
Устойчивость стержней
2. Значения коэффициента ф
Г иб-кость
X
О 10 20 30 40 50 60 70 80 90 100 1 10
Стали Чугуны Дерево Гибкость X Стали Дерево
Ст2. СтЗ. Ст4 S-45 15ГФ. 10Г2С1. 15ХСНД 10ХСНД СЧ15. СЧ18, СЧ20 СЧ25, СЧЗО Ст2, СтЗ, Ст4 1Л О 15ГФ. 10Г2С1, 15ХСНД юхенд
1.00 1,00 1,00 1.00 1.00 1,00 1.00 1 120 0,45 0.37 0,33 0,3! 0,22
0.99 0.98 0,93 0,98 0,97 0,95 0,99 130 0.40 0,32 0,2е» 0,27 0 18
0,96 0.96 0.95 0.95 0.91 0.87 0,97 1 140 0.36 0,28 0.25 0.23 0,16
0.94 0.93 0.92 0.92 0,81 0.75 0,93 150 0.32 0.25 0.23 0,20 0,14
0.92 0.89 0.89 0.88 0.69 0,60 0.87 1 160 0.29 0.23 0,21 0.18 0,12
0.89 0,85 0.84 0,82 0.57 0.43 0.80 I 170 0.26 0,21 0,19 0,16 0.11
0,86 0.80 0.78 0.77 0.44 0.32, 0 71 180 0,23 0.19 0.17 0.14 0 10
0 81 0,74 0.71 0.68 0.34 0 23 0.61 190 0.21 0,17 0,15 0.12 0.09
0,75 0 67 0.63 0,59 0.26 0.18 0.48 | 200 0,19 0.15 0.13 0.11 0.08
0.69 0 59 0.54 0.50 0 20 о.н 0.38 210 0,17 0,14 0,12 0 10 —
0.60 0.52 0.50 0.43 0.46 0,39 0.43 0,36 0.16 0,17 0.31 0.26 220 0,16 о.!з 0.11 0.09
А- -* 0 величина ср —> 1, т. е. опред — — ст ; при 1 -♦ оо величина <р -*
—► л2/:'Л^сгг, г. е огПред ^кр*
Значения qp (X) для некоторых материалов приведены в табл. 2.
С учетом необходимого коэффициента запаса прочности п (для стали обычно п - 1,6} допускаемые максимальные напряжения при сжатии
(а] , (зо)
а допускаемое среднее по сечению напряжение
[°]ср ф 1°1- (31)
Поэтому условие прочности сжатых стержневых элементов конструкций с учетом возможности их бокового выпучивания принимает вид
о = < ф М (32)
или, в часто употребляемой записи..
°та': ~ ’срЁ”
(33)
В формулы (32) и (33) подставляют площадь брутто (всю площадь сечения без учета местных ослаблении). При наличии значительных местных ослаблений производят дополнительную
проверку на прочность по площади нетто Fu, учитывающей эти ослабления. по формуле
(34) сн
В общем случае нагружения гибкость 1 определяют по формуле (8) с учетом значений коэффициента т| по данным табл. 1.
В ряде случаев работоспособность конструкции может ограничиваться допустимыми значениями прогибов при боковом выпучивании сжатых стержневых элементов. Если нет специальных ограничений, то вводят допустимые предельные гибкости [л]. Для основных строительных конструкций принимают [Л] — 120, для остальных допускают [1] = 1504-200 [3].
Пример. Подобрать размеры двутаврового сечения для шарнирно опертого стержня длиной 2 м, сжатого силой 200 кН. Материал—СтЗ с [oj = =_ 160 МПа.
Задаемся произвольным значением коэффициента 0 < <р < 1, например <р = 0,5; переводим силу в Н, напряжения в Н/м2 и определяем
Р 2-103
~ <р[а] ~ 0,5-1,6-Ю8 “
= 2,5-IO"8 м= =--25 см’.
По сортаменту подбираем дву-тавр №16 (F = 26,1 см2; i = 1,89 см).
Потеря устойчивости п.ри упругопластических, деформациях
385
Определяем гибкость
2
1,89-10~2 ~
105,8.
Х = 4
По табл. 2 с помощью линейной интерполяции находим <р = 0,554, что достаточно близко к принятому выше значению. Величина
Р 2-Ю4
°гаах — (pF ~ 0,554-2,61-10-8 “
= 1,383-108 Н/м2 = 138,3 МПа.
Так как 138,3 < 160, то условие прочности с учетом бокового выпучивания удовлетворено
ПОТЕРЯ УСТОЙЧИВОСТИ
ПРИ УПРУГОПЛАСТИЧЕСКИХ
ДЕФОРМАЦИЯХ
Формула (7) справедлива, пока напряжение <тКр не превышает предела пропорциональности материала сг^ц, т. е. для стержней достаточно большой гибкости А > Апред, где
, АПред = л 1/ — .
' °пц
В качестве значений АпреД обычно принимают: для стали 90—105, дюралюминия 50—60, чугуна 55—80, дерева 110.
На практике многие элементы конструкций имеют гибкость меньше предельной А < Апред. Потеря устойчивости таких стержней зависит от вида кривой деформирования материала Стержни из материалов с выраженной площадкой текучести (низкоуглеродис-тая сталь) теряют устойчивость, как только сжимающие напряжения достигнут предела текучести, так как при акр = ат дальнейшее повышение напряжений невозможно, и возникающий при случайном малом отклонении стержня изгибающий момент остается неуравновешенным.
При определении критической силы стержней из упрочняющихся материалов, диаграмма деформирования которых приведена иа рис. 8, учитывают, что если при постоянном значении * сжимающей силы Р произойдет искривление оси стержня, то волокна у
13 Закал 41)2
Рнс. 8. Диаграмма деформирования линейно упрочняющегося материала
вогнутой (сжатой) стороны догрузятся по закону Д(Тд = £КЛ8Д, где Ек = = tgaj — касательный модуль, зависящий от положения точки на кривой деформирования, а волокна у выпуклой стороны упруго разгрузятся по закону Дс(р = FAeF. В этих условиях жесткость сечения стержня на изгиб определяют с помощью приведенного модуля £пр (модуля Кармана) из соотношения
E^pJ — j" Ejt/% dF — F
= Е j y'jdF-\-EK J yjdF, FP '
где Fp и Fa — площади частей сечеиия, испытывающих соответственно разгрузку и догрузку. Граница между этими частями (положение нейтральной линии, от которой отсчитывают координату ух) определяется условием
j E1yidF = F
= Е j Ух dF -f- EK j dF = 0.
F F
P Д
Для прямоугольного сечеиия
= 4EE«
Пр (|/F + VEK)a
(35)
для двутаврового сечения с тонкой стенкой
2ЕЕ
= <36)
386
Устойчивость стержней
Напряжение, соответствующее критической силе,
Р кр п2£пр
°кр = ~г=
(37)
Так как ЕПр — f (акр), то АЛЯ расчетов по формуле (37) вначале строят обратную зависимость
(о'кр) — п
£пр (Окр) акр
Приведенный модуль ЕПр всегда меньше модуля упругости Е, поэтому критическая сила с учетом упругопластических деформаций всегда меньше кри тической силы по формуле Эйлера.
ВЫПУЧИВАНИЕ СТЕРЖНЯ ПРИ УПРУГОПЛАСТИЧЕСКИХ ДЕФОРМАЦИЯХ
Критическая нагрузка Ркр определяет момент, когда малое случайное отклонение оси стержня при постоянном значении сжимающей силы приводит к внезапному интенсивному росту прогибов (теоретически, в линейной постановке — до бесконечности). Пока нагрузка меньше критической и напряжения ниже предела текучести, стержень сохраняет устойчивую прямолинейную форму и при постепенном возрастании сжимающей силы. Однако в упругопластической стадии нагружения, начиная с некоторого значения нагрузки Ркр < Ркр, прямолинейная форма равновесия при возрастающей нагрузке становится неустойчивой, что ведет к выпучиванию стержня, резко увеличивающемуся при приближении силы Р к ее критическому значению Ркр, т. е. стержень ведет себя так же, как при внецентреииом приложении силы.
Рассмотрим это явление на примере сжимаемой жесткой стойки, опирающейся иг два упругопластических стержня из линейно упрочняющегося материала, каждый площадью F (рис. 9). Пусть при некоторой нагрузке Р и отклонении оси стойки иа малый угол ф оиа находилась в положении
Рнс. 9. Сжимаемая жесткая стойка на упругопластнческих стержнях
равновесия. Если при увеличении нагрузки иа dP равновесие сохраняется, то должны удовлетворяться соотношения:
а) совместности деформаций
de,2 — <&1 = dip; (38)
б) равновесия *
dP
dciy do % — ~р~ »
2/
do3 — da, = -т-р- (P dip ф dP)\ (39) or
в) физические соотношения
d8a = -^-, (40)
hi £2
где Ex, E2 зависят от положения точки иа диаграмме деформирования о — = f (е) и знаков d<r1( doa>
• Положительные приращения do здесь соответствуют сжатию
Выпучивание стержня при упругопластических деформациях
387
Исключив из выражений (38)—(40) приращения деформаций, получим
где
Р*
tPF р . 21а Е1’
b2F п . 21а Е*’
р„ = 2Р'Р’ = b*F 2Е'Е*
Р] 4- Р; 2la Et + Еа ’
(42) и дифференциальное уравнение для функции ф (Р)
dq _ 1 / b Ег — Е2\
dP P**. — P\y+2lEi + Ei)"
(43)
Решение уравнения (43) для участков, на которых Et = const, Ea = = const, с начальным условием ф = ф0 при Р - Ра дает закон изменения углов ф (Р) для равновесных состояний
, , Р*' — Ро
'Р = -piPTZT +
, t> (Ег - Еа) Р-Ро 2l(Et + E2) Р** — Р •
Предположим вначале, что в исходном состоянии стойка была строго прямолинейна, т. е. ф0 = 0 при Ро — 0.
Пока напряжения в стержнях at == = о2 = P,'2F остаются меньше предела текучести от, модули Et, Е2 при малых случайных отклонениях стойки сохраняют исходное значение Ег = = Еа = Е, тогда
' <®>
где Р’— критическая эйлерова нагрузка при упругой деформации даи-вой системы.
13*
Из (44) следует, что если Р’р С Рт = 2ЕаТ, то вплоть до значения Р =Ркр упругая система остается прямолинейной (ф = 0).
Если стержни достигнут предела текучести при нагрузке Рт<Р’р, то при дальнейшем увеличении нагрузки возможны два случая деформирования.
1. Оба стержня продолжают догружаться (dat> 0, da2> 0), модули Е1Л Е2 принимают значение касательного модуля Ек, тогда
р* — р* р** р' ° г р - Р2 - Р - Ркр - 2а[ Ек.
(46)
При этом прямолинейная форма равновесия остается устойчивой, но только до нагрузки Р — Ркр, определяемой касательным модулем Ек.
2. Стержень 2 догружается (da2 > 0), стержень 1 упоуго разгружается (da, < 0). Величины Et и Е2 становятся различными (Ех = Е, Ё2 = Ек), так что
^ = ^кр. ^ = ^Р.
Р** _ Р — £
F -''кр- ^la пр’
где приведенный модуль ЕПр определяется формулой (36)
Из первой формулы (41) следует, что разгрузка первого стержня начинается именно в точке Р = Ркр, где угол наклона (производная) кривой ф (Р) скачком меняется от 0 до конечной величины
йф Ркр b Е — Ек
dP ~ (р — р' \2 21 ЕфЕк’ V кр кр )
После этого стойка начнет постепенно отклоняться от прямолинейного направления в соответствии с вытекающим из (44) уравнением
й(Е —Ен) Р
21 (Е + Ек) Ркр - Р ’
как показано иа рис. 10 (кривая 1). Если искусственно задержать стойку в прямолинейном положении до неко-
388
Устойчивость стержней
Рис. 10. Характер
отклонения стойки ири
упруго пластических деформациях
торого значения Р02> Ркр, дальнейшее отклонение пойдет по линии 2.
Когда в исходном состоянии при Ра — 0 стойка наклонена нг угол ф0, отклонение в упругой области будет изменяться, как это следует из (44), по закону
Ф= Фо
Р3 кр
р3 — р
кр '
После достижения стержнем 2 предела текучести темп отклонения стойка возрастает, причем стержень 1 будет догрчжа1ься до величины Р = -- (1 — 2Д75', после чего он начнет
ра31р\?Л41ТЬСЯ, d HdpdCTdriHe OiK^iOHC' Hji/i пойдет ускоренно п0 кривой 3. Эта кривая на разных участках имеет разные асимптоты как показано на рис. 10 штриховыми линиями. Линди bl Р \
ф' -= — I 1------г- соответствует на-
4<wiу упругой разгрузки стержня 1 (при Р<О-
Линия Рг характеризует начало пластических деформаций прн слабом упрочнении величина Ркр может оказаться меньше Рт и тогда боковое выпучивание при возрастающей нагрузке начинается сразу, как только сжимающая сила достигает величины Рт Если же и станет меньше РТ, то при Р = Нт наступит потеря устойчивости.
ДИНАМИЧЕСКИЙ АНАЛИЗ УСТОЙЧИВОСТИ. ДЕЙСТВИЕ СЛЕДЯЩИХ НАГРУЗОК
В некоторых случаях нагружения стержней оценка потери устойчивости по условию Возможности появления формы статического равновесия в изогнутом состоянии (подход Эйлера) оказывается недостаточной. Более общим является динамический анализ устойчивости, показывающий, как будет двигаться система после некоторого начального малого отклонения. В динамически устойчивом состоянии отклоненный стержень начнет колебаться (без учета сил трении) с постоянной амплитудой, в динамически неустойчивом состоянии прогибы будут неограниченно возрастать со временем. В динамическом анализе имеет значение не только распределение жесткостей, но и распределение масс стержня и ил величина.
Для рассмотренных выше задач прн постоянном направления сжимающие сил динамический анализ приводит к тем же результатам, что и статический. Для следящих нагрузок, направление которых меняется в зависимости от деформации стержня (например, реактивная сила струи, электромагнитные силы в деформируемых проводив ках и т. п.) критическую нагрузку можно иаи,н только динамическим анализом.
Найдем критическое значение следящей касательной силы Ркр в случае консольного стержня с сосредоточенной
Динамический анализ успюйчииисти. Следящие нагрузки
389
Рис. 11. Действие следящей нагрузки а — общий случай, 6 — при р -► оо
массой т. иа конце, Момент инерции которой равен р2т, где р — радиус ииериии Для простоты заменим стержень системой из двух жестких стержней 1 и 2, свяснпы. двумя упругими шарнирами с коэффициентами жесткости с (рис 11, а).
При малом отклонении стержней перемещение у и угол поворота ф массы соответственно
У = a f2vi + ф4); ф •= фу + ф2 и уравнения вращательного движения стержней принимают вид
, й2ф , d2y , p2m_X + m_* п + ^а =
= <n[(2a2 + p2)^ +
Htf2 ! =
m ~dp аЛ~с (lhl ~ '12) + Pa^ =
r. т/2Ф1 , а2ф2 \ ,
4- сфу -t- (№ — с) Фа = 0.
(47)
Если ф10, ф20 — начальные отклоие-dWy . йф2 .
вин и —-г-- (0) = 0, —J— (0> -= 0, ти dt ' dtK
устойчивому состоянию стержня будут соответствовать гармонические колебания
V1 = Фто соь и>(, фа — фао СОо и>1.
при которых из (47) получим однородную систему уравнений
(2a2 -Г о2) Си2ф1Л -+-
+ j^(a2 + Р2) 0/2 —“1 'Фао — 01
^2а2(в2 — ф10 +
.Гоа Ра “ С "I , -I + [_“^2------------J Фго = 0
(48)
Система (48) им. ет ненулевые решения, если ее определитель равен нулю, т. е.
чу1 — 2рш2 + q = 0, (49)
где
р = •> « • [(5a2 2р2) с —
р 2а2р*тц г г /
-k2u»^p2)Pa]; (50)
/ С \2 ~ ( арт ) Корни уравнения (50) определяются формулой
<и2 =.- р ± Ур2 — q (5!)
В отсутствие сжимающей нагрузки рг — q > 0 и система имеет две различные сосютвеиные частоты колебаний:
0)4 - = т— X
1 • 2а*т
1 — 0,1р2±У1 ( 0,61р2 4 Мбр1
Х р2
(52)
где р .= р'д
По мере увеличения сжимающей нагрузки Р коэффициент р уменьшается И Прн
5с I -0,4р^0.4р2
= дг ryw-" (5о) выражение р* — q обращается в нуль, а обе частоты колебаний системы принимают одинаковое значение
При увеличении силы Р сверх критического значения система становится
390
Устойчивость стержней
динамически неустойчивой и ее движение после малого начального отклонения будет представлять собой колебания с неограниченно возрастающими амплитудами. Потеря устойчивости происходит в общем случае при значении <окр У= 0, поэтому отклоненной статической формы равновесия система ие имеет. Но пря очень большом моменте инерции концевой массы, когда р -«• оо, значение и>кр -*0, и в этом случае динамическая величина Ркр = = 2с/а совпадает со статическим значением Ркр для соответствующей системы с неповорачивающимся стержнем 2 (рис. 11,6).
Для упругого консольного стержня с сосредоточенной массой на конце коэффициент г] критической величины следящей силы в формуле (5) равен г] = 20,19 при р -< 0 и л = л2 — == 9,87 при р -* оо. Для свободного стержня, к одному концу которого приложена следящая толкающая сила, q я= НО.
ПОТЕРЯ УСТОЙЧИВОСТИ
ПРИ НАГРЕВЕ
Стержень, зажатый между неподвижными плоскостями, прн нагреве до критической температуры 7’кр выпучивается. Свободный стержень при нагреве до Ткр удлинился бы на величину а/Ткр, где а — коэффициент линейного расширения. Сила, возвращающая его в прежнее положение,
Р — EFaTKp. (55)
Приравнивая силу Р ее критическому значению гКр = —, получим для стержня с шарнирно опертым концом
„ Л2 , ,
ГкР = 5Т2- (j0)
При дальнейшем нагреве стержень получит прогиб
f/max« 2/1/^--1. (57)
* < KD
Пример. Балка двутаврового сечения № 24а длиной 1 = 6 м, жестко заделанная по концам, равномерно нагревается по всей длине. Определить
По сортаменту для двутавровых профилей находим i = 2,42 см. Для Двусторонней заделки v = 0,5, поэтому
vl 0,5-600 ,„,
= =124
_____________________7° Г
~ 11,5-10-*-124» '
ПОТЕРЯ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА
При изгибе прямолинейных стержней (балок) двусимметрнчного поперечного сечення (прямоугольного, двутаврового) нагрузки, действующие в плоскостях главных осей, вызывают прогибы только в тех же плоскостях. Однако, если моменты инерции сечений значительно различаются, io при действии нагрузок в плоскости большей жесткости плоская форма изгиба является устойчивой лишь до определенного предела. При достижении изгибающим моментом некоторого критического значения Л4кр, помимо изгиба в плоскости большей жесткости, стержень начинает резко прогибаться в плоскости меньшей жесткости и закручиваться относительно продольной оси Это явление называют потерей устойчивости плоской формы изгиба. Оно сопровождается значительным повышением напряжении и может привести к разрушению конструкции.
На рис. 12 схематически показаны исходная (а) и Деформированные формы стержня вытянутого прямоугольного сечения при изгибе в плоскости большей жесткости моментами М на концах: б) при М < Л4кр; в) при М > Л4кр. Если ториевые сечения закреплены так, что они ие могут поворачиваться относительно продоль-
Потеря устойчивости при скручивании
391
формы изгиба
ной оси, то критический изгибающий момент определяется формулой
дд ____•rt ~l//£G^min7'
мкр — - —
ложенная к концу консольного стержня, имеет критическое значение
<59>
где Jmln — минимальный момент инерции; Т — геометрическая жесткость на кручение сечения.
Для стержня вытянутого прямоугольного сечения со сторонами b, h при (b/h}* Cl и v — 0,3
b^h Мир = 0,325/; .
Критическое значение нагрузок, вызывающее потерю устойчивости плоской формы изгиба, зависит от их распределения по длине стержня, условий его закрепления, а также от поведения нагрузок в процессе деформации (являются они следящими или нет). Так, изгибающий момент постоянного направления, приложенный иа конце консольного стержня, не вызывает потери его устойчивости, а изгибающий момент, следящий за положением плоскости большей жесткости — вызывает; при этом Л4кр равен 0,5 величины Л4кр, определяемой формулой (58).
Сила постоянного направления, при-
ПОТЕРЯ УСТОЙЧИВОСТИ
ПРИ СКРУЧИВАНИИ
Тонкие длинные стержни под дейст-вием крутящих моментов могут терять устойчивость прямолинейной формы оси, завиваясь в некоторую пространственную кривую. Для стержня длиной I круглого поперечного сечения дна-метра d, скручиваемого действующими по концам моментами, направление которых «следит» за направлением касательной к оси, критическое значение момента
г<‘Г>“ <®>
, nd*
где /Р - 32 •
При совместном действии сжимающей продольной силы Р и крутящего момента М потеря устойчивости происходит при удовлетворении условию
р . = 1
Ркр'Г UkJ
(61)
где Рнр и Л4кр определяются соответственно формулами (3) и (60).
392
Колебания упругих систем
Глава 21 КОЛЕБАНИЯ УПРУГИХ СИСТЕМ
ОСНОВНЫЕ понятия
Простейшая динамическая система, состоящая из массы, закрепленной на пружине, показана на рис. 1.
Если в начальный момент отклонить массу на величину а и предоставить систему самой себе, то возникнут колебания, причем смещение центра массы в момент t будет
у = a cos pt, (1)
где р — круговая частота колебания,
здесь с — коэффициент жесткости пружины, Н/см (усилие при осадке пружины на 1 см); т — масса груза.
Амплитуда колебаний, т. е. максимальное отклонение центра массы от положения равновесия, в данном случае равна а.
Наименьшее время между двумя совершенно одинаковыми положениями колеблющейся системы называют периодом колебания.
Если обозначить период колебания (в с) через Т, то из равенства (1) вытекает
cos pt = cos р (t + Т), откуда
т 2л Р
Частота колебания f = 1/Т — число полных колебаний в единицу времени
Рис. I. Колебания одномассовой системы
(секунду). Частоту колебаний измеряют в Гц (герц — одно колебание в секунду).
Колебания системы без воздействия внешних сил называют свободными.
Так как в системе всегда имеются силы трения, то свободные колебания со временем затухают.
Если к системе приложена внешняя периодическая сила
Q = Qo cos <ot,
то возникают вынужденные колебания с частотой этой внешней силы
Отклонение
у = а0-----а cos tot, (3)
1~^5"
Qo
где а0 = -у----осадка пружины при
статическом действии амплитуды внешней силы; с — коэффициент жесткости пружины.
При совпадении частоты возбуждающей силы с частотой свободных колебаний амплитуда колебаний стремится к бесконечности. Этот случай называют резонансом.
В действительных условиях при наличии трения амплитуды при резонансе остаются конечными, ио достигают значительной величины.
Резонанс представляет собой большую опасность для конструкции, и его следует избегать.
Одна из основных задач расчета конструкции на вибрацию состоит в определении собственных частот колебаний и выявлении опасных (резонансных) частот.
Резонансы устраняют обычно изменением собственной частоты системы; в ряде случаев оказывается возможным изменить частоту возбуждающей силы.
Для определения частот собственных колебаний системы весьма эффективным оказывается метод динамических жесткостей.
Метод динамических жесткостей
393
МЕТОД ДИНАМИЧЕСКИХ ЖЕСТКОСТЕЙ
Этот метод позволяет провести частотный анализ сложной механической системы прн известных динамических жесткостях отдельных ее частей.
Рассмотрим вынужденные колебания одномассовой системы (рис. 2).
Частное решение уравнения движения
m-~ + cy = Q0cos<of, (4)
соответствующее вынужденным колебаниям, будем искать в внде
у == a cos <о/. (5)
Подставляя зависимость (5) в равенство (4), находим
Отношение амплитудного значения силы к амплитудному значению смещения называют динамической жесткостью. Из равенства (6) следует, что динамическая жесткость
ЛА = -^- = -«ш» + с; (7)
здесь т — масса груза.
Зависимость Ка от и показана на рнс. 2 (Ка — в Н/см).
Динамическая жесткость определяется для заданной точки системы. Главной особенностью динамической жесткости является ее зависимость от частоты приложенной силы.
Если частота внешней силы равна нулю (статическая сила), то динамическая жесткость совпадает со статической, т. е. Ка — с- Эт° равенство спра-
ведлнво и для любых значений <о, если система не обладает массой.
Динамическая жесткость свободной от закреплений массы будет
Кт ~ —т<о*.
Статическая жесткость свободной массы равна нулю, но при действии периодической нагрузки масса оказывает сопротивление смещению подобно обычной пружине (силами инерции).
Равенство (7) можно представить в внде
КА = Кб - т&, (8)
где Кб = с — динамическая жесткость системы в точке Б.
Это равенство оказывается справедливым для любой цепной системы. Еслн известна дннамнческая жесткость в точке Б, то дннамнческая жесткость после «перехода» через массу (Ка) получается добавлением (—тша). Определим теперь дннамнческую жесткость в точке А системы, показанной на рнс. 3. Уравнение движения массы
С?и,
~ Qo cos
где у1 — смещение центра массы от начального положения Q1( откуда
О„
Ух = — cos <of.
mco*
Так как разность перемещений концов пружины равна (у — у^), то
с (У — !/1) = Qo cos со/,
что вместе с предыдущим соотношением дает
Q~Qocos
Рис. 2. Вынужденные колебания одномассовой системы
= a cos cof.
Дннамнческая жесткость
С М(02
Это равенство представим в виде
1 J___________1 _ I 1
КА ~ < mafl Кб -г с
394
Колебания упругих систем
Рнс. 3. Определение динамической жесткости
ИЛИ
Къс
Кб + с ’
(Ю)
где Кб — —т®*— динамическая жесткость в точке 5; с— статическая жесткость, равная динамической жесткости пружины
Равенство (10) справедливо для любой системы. Если известна динамическая жесткость в точке 5, то по этому равенству определяют динамическую жесткость в точке А после «перехода» через участок, обладающий только жесткостью.
Выясним зависимость величины Кд от частоты внешней силы. Запишем формулу (9) в виде
КА = —т<о3------L-2-, (11)
1-----г-
PZ
где р, = 1/ —-----частота колебаний
г т
системы при закреплении в точке А.
Зависимость Ка от ш показана на рис 3. При очень большой частоте масса становится «точкой опоры», К а-с.
ОПРЕДЕЛЕНИЕ СОБСТВЕННЫХ ЧАСТОТ СИСТЕМЫ МЕТОДОМ ДИНАМИЧЕСКИХ ЖЕСТКОСТЕЙ
Пусть система, показанная на рис. 4, совершает собственные колебания с частотой р Если разрезать систему в какой-либо точке А, то на каждую ветвь системы будет действовать перио
дическая сила X, неизвестная по величине. Допустим, что положительное амплитудное смещение точки А, равное а, направлено вверх. Тогда динамическая жесткость в точке А для верхней ветви Кдв = Х/а и соответственно для нижней ветви Кав — —Х/а.
Из этих равенств следует основное соотношение
' *АВ + *АН = О. (12)
Так как динамические жесткости зависят от частоты р, то равенство (12) представляет собой алгебраическое уравнение для определения р (характеристическое уравнение системы). Корни уравнения (12) являются частотами собственных колебаний.
Для многомассовых систем уравнение (12) решают графическим или численным методом: строят функции / (р) = = Каи и <р(р)=— Кав< абсциссы точек пересечения которых дают значения собственных частот.
Уравнение (12) получено для сечеиия системы по внутренней точке.
Если сечение проходит через опору, то
Ка=~, ОЗ)
так как перемещение этой точки равно нулю.
В крайней точке системы
Ка = 0, (14)
если эта точка свободна от закрепления.
Рассмотрим в качестве примера систему, показанную на рис. 5.
Определение собственных частот системы
395
Рис. 5. Определение «та-стоты собственных колебаний одно МАССОВОЙ системы
Рис. 4. Сечение '’истемы по методу динамических жесткостей
Динамическую жесткость в тачке А найдем с помощью «Мрмул перехода'».
В точке 8
Кв = 0.
Переходя чепез участок с массой, бучам иметь в силу равенства (Я)
Кб — Кв — тп3 — — тр3.
Далее, пепеходя через участок с жесткостью, получим в соответствии С равенством (10)
К - _ '”Г’‘е
д Ав -+- г с —
Так как сечения проходит через опор}, то
Кд = оо
И, следовательно,
в— тр3 — 0,
откуда получаем частоту
Далее находим
Кв = Кб — тр3 — с— тр3 = 0, что дает полученное ранее значение р.
Для двухмасеовой системы / выберем сечение в точке возле массы тх (рис. 6).
Для верхней ветви найдем последовательно
Кб = °; Кдв = Кб — = — "ЧР*.
Для нижней ветви
Кг = 0, Кв — Кр — т2рг — тЛр3;
ь- ___ КрС m „9 С
*Ав~ Хв + с“ ’ гР с-т,р3 •
Из уравнения (12) следует:
—«зР’-----£--- „ (!5j
с — т2р3 ’
что дает
о = «-.
Графическое решение уравнения (15) представлено иа рис. 6.
Дннамическяч жесткость /Ц при
значениях р = ~ pt имеет
вертикальную асимптоту.
Определим частоты собственных ко-делений системы II (рнс. 7) для иижчей RA-pP и ’
Кв = 0; КБ = —т2р3 ;
„ _ _ тгр3с .
Ан ~~ с2 — тгр3 ’
для верхней ветви’
Knci
Кд.-=ж> Кр= -V-’ = св
Лд + ч
Кдв = Cj — mtp3.
V т
В этом же примере можно найти частоту из условия Кв — 0, переходя от точки А к точке В.
В точке А
К,\ = со.
Пепеходя к точке Б, будем иметь
^ = тЙ- = г.
Рис. 6. Определение частоты собственных колебаний двухмассовой системы 2
396
Колебания упругих систем.
Рис. 7 Определение частоты собственных колебаний двухмасеовой системы II
Из уравнения (12) следует:
4- с, - т1Р* = 0, (16)
С2 - Flip* '
что дает два значения собственной частоты
Графическое решение уравнения (16)
даьо иа рнс. 7. Величина
р.-]/
с
КРУТИЛЬНЫЕ КОЛЕБАНИЯ
В валах поршневых машин (в двигателях внутреннего сгорания, поршневых компрессорах и т. п.) нередко возникают хрутильчые /солебачич, связанные с неравномерностью (по времени) вращающегося момента или момента сопротивления. Такие колебания могут возникать и в валах других машин, если крутящий момент, передаваемый валом, не является постоянным
Расчет крутильных колебаний строят так же, как расчет односвязной ценной системы, изложенный ранее. Одной из основных задач расчета является определение собственных частот системы для выявления резонансных оборотов.
Одномассовая система. Пусть имеется вал постоинчого сеченчч с закрепленным на нем диском (рис 8).
Рассмотрим уравнение движения (вращения) диска при отклонении его от положения равновесия иа угол 9:
, d29
Jm - М, (17)
где Jm — момент инерции массы диска, кг. см2; 9— угол поворота, рад, М — момент, действующий на диск, Н-см
Знак минус в правой части равенства показывает, что момент создается силами упругости, препятствующими отклонению. Если жесткость вала обозначить через с, примем эта величина представляет собой момент в Н см, необходимый для закрутки вала на 1 рад, то
.И = с9. (18)
Из равенства (17) получаем d29
Общий интеграл этого уравнения имеет вид
9 = A cos pt + В sin pt.
где р— круговая частота колебания:
P=V Т~- <!9>
г >'т
Произвольные постоянные А и В определяют из начальных условий.
dQ
Если в момент t — 0, б — а. -тг = 0, , di
' то
0 (Л = a cos pt\ (20)
здесь а— амплитудное значение угла поворота при колебаниях
Уравнение (20) полностью аналогично уравнению (1> причем вместо линейного смещения имеем угол поворота, вместо массы— момент инерци». Соответственным образом переносится и понятие динамической жесткости.
Крутильные колебания
397
Л=4<7
Л = /
К=1,2
Рис. 9. Сечения валоэ
(2!)
Жесткость вала на кручение. Для прямолинейного вала иМеем
С/р С~~Г~
f ~ Е
Где С — -йтг-:—ч----модуль упруго-
Z (1 -f- V)
Сти материала на сдвиг, для сталей [G = (0.78---0.83) 106 /МПа; Jp — полярный момент инерции сечения;
для сплошного вала _ nd4 _ Jp ~ 32"’
Для вала с отверстием _ л(<г4 — d4) .
J Р--------89 ’
здесь d — наружный диаметр; dj — диаметр отверстия.
Если сечеиие вала ослаблено шпоночными канавками или шлицами (рис. 9), го в формуле (21) следует принимать
_ л (d — '’Л)4 /р---------32 ’
где h — глубина канавки.
Значения коэффициента k приведены
На рис. 9. Для полого вала со шлицами
Рис. 10. Переходный участок вала
Если вал имеет ступенчатый переход (рис. 10), то участок с большим диаметром не сразу включается в работу.
В равенстве (2!) длину с меньшим диаметром увеличивают иа М — kd, причем при радиусе закругления г — = 0, Id можно принимать Ъ = 0,055, если < 1,85, и k — 0,125, если d
Если имеются часто повторяющиеся кольцевые выступы типа лабиринтных уплотнений, то ппи определении жесткости их не учитывают
Прн совместно*4 работе на кручение двух деталей, например при шлицевом соединении (рис. 11) или прч прессовой посадке, принимают, что внутренний вал закручивается с каждой стороны на длине tL -s- 0,25d. При подсчете жесткости средней чести учитывают жесткость втулки
Момент инернии Момеитом инепции массы относительно оси называют Сум-
Рнс. 11. Совместное кручение вала и втулки
398
Колебания упругих систем
Рис. 12. К определению момента инерции диска
му ir2Am, распространенную на все частицы тела (здесь г — расстояние до оси вращения):
Jm = jrtpdV, v
где р—плотность материала; V— объем тела.
Для диска (рис. 12) будем иметь
R
Jm = 2лр У r3h dr ~ рл/?4Л =
О
= -2- MR*, (22)
где М — масса диска, кг; момент инерции массы в кг-м2.
Для деталей сложной формы момент инерции определяют экспериментально. Один из методов состоит в том, что на тонком валу (проволоке) подвешивают деталь, момент инерции которой требуется определить. Отклоняя деталь от положения равновесия, вызывают
Рис. 13. Двухмассовая крутильная система
крутильные колебания с периодом Т. Затем к той же проволоке подвешивают диск, момент инерции которого Zml известен. Если период колебания этого диска равен Т\, то
Т»
* m ~ Jmi 2 ’
(23)
Частота крутильных колебаний. Для определения частот будем использовать метод динамических жесткостей.
Для двухмассовой системы (рис. 13) частоту можно определить из условия равенства нулю динамической жесткости в крайнем сечении.
Последовательно находим
Лд — 0; Л'Б — J miP2;
v JmiP*0 .
КГ = Кв - /таР3 =
__ JmiP2e C — J miP3
J тар3 — О-
(24)
Рис. 14. Миогомассовая крутильная система
Изгибные колебания
399
Из равенства (24) получаем
р = 1/ - + Zma). (25)
' J miS m2
Эта система обладает еще и нулевой частотой, которая не представляет интереса при анализе колебаний.
Рассмотрим систему со многими массами (рис. 14) и в соответствии с методом динамических жесткостей разделим эту систему в сечении Г.
Так как амплитудный угол поворота в сечении Г для левых и правых частей одинаков, а направление крутящих моментов различно, то сумма динамических жесткостей левых (Кгл) и правых (Кгп) частей
кгл + Ягп = 0. (26)
Переходя от участка к участку, находим
КА = 0; КБ==-/т1рг;
If __ JmiP*ci
далее
Кгл — Кв — J паР* =
__ 1 ту? тзР* С1 (^mi ~Ь ma) Р2 С1 J mip*
Подобным способом получаем Кз^О; = Кз - Jmip*;
К __ ~~JmtP*c3 .
KE~'c3-Jm^ ’
v J mtP*c3 * о
*Д = —-J™P =
_ тз^тиР4 — сз (^тз + гм) Р* .
С3 J miP* ’
Г° *Д + С2
__сг m3" miPi сз (^тз ~Н Jmi) Р2] .
Jmd miP* — кз Утз + та) + + CtJ mJ Р2 + с2сз
Затем строят графики Кгл и ^гп и находят точки их пересечения (резонансные частоты)
Предварительно определяют значения р;ф, при которых знаменатели
обращаются в нуль (вертикальные асимптоты), и значения pi, при которых числители обращаются в нуль.
Если представить динамические жесткости в виде отношения
Кг - • К (р)
л Фх(Р) ’ Гп ф8(Р) ’
то отыскиваются, следовательно, нули функций <pt (р) и <р2 (р) и функций fi (Р) и /2 (р).
В практических задачах при большом числе масс нули функций находят построением графиков функций. В рассматриваемом случае указанные значения можно получить из аналитических формул
На рис. 14 показано решение уравнения, дающее собственные частоты колебаний.
Рассматриваемая система имеет четыре частоты, если считать также нулевую частоту.
В более сложных случаях частоту определяют с помощью специальных методов, из которых наиболее эффективным является метод Толле (метод остатка).
ИЗГИБНЫЕ КОЛЕБАНИЯ
Колебания этого вида связаны с изгибной деформацией стержней (например, колебания грчза на несущих балках, колебания лопаток турбин и осевых компрессоров и т. д.).
Одномассовая система. Рассмотрим колебания груза на невесомом стержне (рис. 15).
Уравнение движения массы
m^ = ~F’ (27>
где сила упругости
F=—y, (28)
а
В этом равенстве а — прогиб балки (в месте приложения груза) под действием единичной силы (коэффициент податливости).
Из уравнения (27) получаем
'"-ЗИ' + тЬ-0' <29>
400
Колебания упругих систем
Круговую частоту изгибных колебаний определяют по формуле
1 р = — yam
Это равенство справедливо для любой одно массовой системы; груз может быть расположен между опорами или консольно, различие только в величине а.
Решение уравнения (29) прн произвольных начальных условиях будет таким-
У = Уп cos (pt 4- <р), где — амплитуда колебаний; <р — сдвиг фазы, зависящий от начальных условий.
Если подставить это соотношение в уравнение (29), то получим
2 1
Р ^У» = — У о-
Последнее равенство можно истолковать следующим образом; сила упру-
1
гости — у0 равна инерционному усилию р2 *туа, иными словами — амплитудный прогиб у0 вызывается силой р2ту0. Статическая аналогия состоит в том, что вместо колебаний рассматривают амплитудные колебания системы, вызванные амплитудными величинами инерционных сил 1р2туа представляет собой инерционную силу в крайнем положении системы).
Двухмассовая система. Пусть балка несет две массы тг и т2 (рис. 16).
Амплитудный прогиб создается усилиями рЬп^! и ptmty1, поэтому
У1 = ссцР2т1У1 + а^тгуу, )
Уг = ^аР + 'WW J где коэффициенты податливости означают: Иц — прогиб в сеченни /— 1 от единичной силы, приложенной в том же сечении; а1г— прогиб в сечении J—1 от единичной силы, приложенной в сечении 2—2; а21 — прогиб в сечении 2—2 от единичной силы, приложенной в сечении 1—Г, а22— прогиб в сеченич 2—2 от единичной силы, приложенной в том же сечении.
Коэффициенты податливости могут быть определены с помощью интеграла Мора.
Из условия взаимности для упругих систем следует;
«13 = «31-
Уравнения (30) можно записать в виде (р2апШ1 — 1) У! + p2cci2m2j/a = °'. I P2«3i«il/i + (psaMma— 1) у3 == 0. /
(31) Отсюда находим
У1 = ___ Р^тц .
Уг 0^,1^!—!
_ рга22т2— 1
у2 ~ P2a-2iHii
Приравнивая эти отношения, получаем условие для определения собственной частоты ’ (характеристическое уравнение):
р4т1т1 (апа22 — а(?) —
— р2 (а-ит1 — а22т2) 4-1=0.
1 Б более общем случае характеристическое уравнение получается после приравнивания нулю детерминанта системы однородных уравнений.
21
“ Ргтг Уz
Р^У,
Рис. 16. Изгибные колебания двухмассовой системы
Изгибные колебания
401
Из последнего уравнения получены два значения частоты рг и р3:
Pt =
— ']/(апт] + а22т2)2 — 4ш1т2 (апа22 — а|2)
2т1т2 (а, ,а.,, — а}.2)
anmt + а22т2 + V(аиИ1 + а22/п2)2 — 4ш1т2 — а?2) „
(32)
2/п,т2 (апа22 — а^)
Низшей частоте (р2) соответствует форма колебания, когда обе массы двигаются в одну сторону; частоте р2 соответствует движение масс в разные стороны. Если система имеет ч сосредоточенных масс, то опа обладает таким же числом частот и форм колебаний причем каждой частоте соответствует своя форма колебаний (распределение амплитудных отклонений по массам).
Изгибные колебания стержней постоянного сечения. Задача имеет точное решение Частоты колебаний определяют по формуле
<34>
где Хп— безразмерный коэффициент, зависит от формы колебаний (наименьшая частота соответствует первой форме колебаний п = 1) и от условий закрепления. Значения Хп приведены в табл. 1; п— номер формы колебаний (п — 1, 2, 3, ...): I— длина стержня; Е — модуль упругости материала; J — момент инерции сечения стержня; т — масса единицы длины стержня
Если стержень не имеет равномерно распределенных присоединенных масс, то
m = pF,
где р— плотность материала стержня; F— площадь поперечного сечения.
Частота колебаний, Гц,
Гп~ 2л •
Изгибные колебания колец. Рассмотрим изгибные колебания кольца постоянного сечения с равномерно распределенными массами.
1 Теоретически возможен случай, когда двум разным формам колебаний соответствует одинаковое значение частоты, ио такой случай кратных частот ие имеет практического значения.
Плоские колебания кольца с двумя узловыми диаметрами показаны на рис. 17, а.
Круговую частоту колебаний определяют по формуле
РП ' V«a + 1 г3 т ’
где п — число узловых диаметров (номер формы колебаний1), п— 1, 2, 3, ...; г—радиус кольца, EJ2— жесткость сечения на изгиб в плоскости кольца, т—масса единицы длины.
Для колебаний, перпендикулярных к плоскости кольца (рис 17, б), будем иметь
р^-^.^.1
(36)
где GT — жесткость сечения кольца на кручение; Е.1г— жесткость сессии" на изгиб относительно главной оси, лежащей в плоскости кольца. Остальные обозначения те же, что и в формуле (35).
1 Колебанию с одним узловым диаметром (п •= 1) соответствует нулевая частота
Рис. >7. Колебания колец с равномерно распределенными присоединенными мае-сами
1. Значения коэффициента К в формуле (34)
Эскиз
Форма tzrt гтаА о ту ттв
Значение
Колебания упругих систем
Частоты собственных колебаний динамических систем
403
Поперечные колебания струны. Круговую частоту поперечных колебаний струны определяют по формуле
<37>
где п — номер формы колебаний (п = = 1, 2, 3, ...); I— длина струны; Н — сила натяжения струны; т — масс? единицы длины струны.
ЧАСТОТЫ СОБСТВЕННЫХ КОЛЕБАНИЙ НЕКОТОРЫХ ДИНАМИЧЕСКИХ СИСТЕМ
Значения круговых частот колебаний некоторых динамических систем приведены в табл. 2, а коэффициент податливости прн изгибиых колебаниях — в табл.3.
2. Формулы для определения собственной (круговой) частоты некоторых систем
Эскиз Частота
р= И
Ll l.li.1! Ill
невесомых зубчатых колесах и валах
404
Колебания упругих систем
Эскиз
Частота
Продолжение табл. 2
'т1 -a.? f
V А, , 7mi+Jm3+7m3
---j--j — j—~ -----
Стержень с распределенной массой (крутильные колебания)
п -= 1, 2, 3 ...
Обозначения: т — масса груза; Jm — момент инерции массы. кг«смя; Jр — полярный момент инерции; с — жесткость; GT — жесткость сечения стержня иа кручение; pjp — полярный момент инерции единицы длины; i = — передаточное
число.
3. Коэффициенты податливости а при изгибных колебаниях
Эскиз а Эскиз > a
§[ EJ 1 —У р 3EJ £J^ £JZ b T a4>* 3EJJ* + a*b* + 3EJ,P
! I
^/?j. 4 Р 48EJ~ £.7, ^rn ab* , ba 3EJ, + 3EJ
4 44 l. ХЛ-
Обозначения: т — масса груза; EJ — жесткость стержня на изгиб.
Вал с одним диском
405
Г пава 22
КРИТИЧЕСКИЕ ЧАСТОТЫ
ВРАЩЕНИЯ ВАЛОВ
ВАЛ С ОДНИМ ДИСКОМ
Понятие критической частоты вращения. Рассмотрим вал на дв^х опорах с диском посредине (рис. 1), вращающийся с угловой скоростью со.
Для того чтобы выяснить, является ли вращение вала с прямолинейной осью устойчивым, предположим, что вал получил некоторое отклонение и центр тяжести диска стал двигаться по Окружности радиусом у. Тогда на диск действуют центробежная сила и вила упругости:
С — согту; F — — у,
1где т — масса диска, а — прогиб среднего сечения вала от действия единичной силы для вала постоянного сече-
ния,
_ Р
“ ~ 48EJ *
Если С< F, то после отклонения вал снова вернется в первоначагьное Положение, т. е. прямолинейное поло-кение оси является устойчивым.
В момент равновесия, т. е. в момент дачала потери устойчивости, когда Е = F, прогибы мог> г безгранично Возрастать. В этом случае центробежные силы В отклоненном положении равны силам упругости, стремящимся Вернуть пал в исходное состояние. Насте™ вращения, при которых наступает равенство центробежных сил и сил упругости, называют критическими.
Рис. 1. Вал на двух опорах с диском посредине
При критическом значении ш величина С — F, отсюда
Критическая частота вращения, мин’1.
Равенство центробежных сил и сил упругости имеет место при любом прогибе, так как в пределах применимости линейной теории обе указанные силы пропорциональны прогибам.
Можно представить, что при критической частоте вращения вал совершенно теряет жесткость на изгиб; даже малая сила может вызвать значительные прогибы.
Из равенства (1) следует, что критическая угловая скорость совпадает с круговой частотой поперечных (нагибных) колебаний вала. Этот вывод справедлив и в общем случае, если детали, закрепленные на валу, рассматривают как точечные массы.
Учет начального эксцентриситета центра тяжести диска. В практических задачах центр тяжести диска имеет некоторое смещение относительно своей геометрической оси и, следовательно, оси вала.
Для уменьшения этого эксцентриситета быстровращающиеся валы подвергаются балансировке, которая, однако, имеет ограниченную точность. Например, детали массой 100—300 кг балансируют обычно с точностью порядка 50—100 г-см Кроме того, следует учесть, что в рабочих условиях вследствие нагрева, остаточных деформаций и других причин дисбаланс возрастает.
При наличии эксцентриситета вал получает прогибы даже при малой угловой скорости, так как к нему приложена неуравновешенная сила.
406
Критические частоты, вращения валов
Обозначим абсолютную величину эксцентриситета диска е (величине е соответствует дисбаланс Ge, где G — сила тяжести диска).
На диск действует сила инерции С и сила упругости F (рис. 2).
Предполагая величины у и е положительными, получим
С = <о2т (г/4-е); F = -i- у. (2)
Из условия равновесия следует С — F. Подставляя в это равенство зависимости (2), находим
У = =—X—. (3)
— — <О2Щ “к .
Если угловая скорость вращения m мень'пе критической угловой скорости <ок, то решение соответствует положительной величине у (направления прогиба и эксцентриситета совпадают, см. рис. 2).
При <о > <ои (закрнтнческий режим) величина у < 0 (направления эксцентриситета и прогиба противоположны).В закритической области центр тяжести диска расположен ближе коси вращения, чем точка крепления диска к валу.
Из уравнения (3) следует, что при очень больших угловых скоростях (<о оо) у = —е, т. е. центр тяжести диска оказывается на оси вращения.
Такое явление называют самоуста-новлением вала в закритической области.
Рассмотрим теперь критический режим, когда <о = <ок.
Из уравнения (3) следует, что при совпадении угловой скорости с крити
ческой угловой скоростью прогибы вала неограниченно возрастают.
Зависимость прогиба вала от <о показана на рис 3 Подобным образом возрастает и реакция на опоры.
В действительности прогибы при <о = <пк остаются конечными, тек как всегда существуют ограничения (защемление в подшипниках, трение и т. п.) и, кроме того, при больших деформациях нарушается линейная зависимость между силой и перемещением.
Однако приближение угловой скорости к критической может оказаться опасным, и поэтому зону частот вращения от 0,7пк до 1,3пь. не рекомендуется использовать для рабочих режимов.
Во всех случаях желательно работать с жесткими роторами (валами), для которых <в< 9,7ш„.
Работа вала с одним диском при ю шн возможна, но прн этом часто требуются специальные демпфирующие опоры для прохождения через критические частоты и для успокоения вибрации в закритической области.
Если вал имеет несколько дисков и соответственно несколько критических угловых скоростей Wj, w2..... <оп, то
критическое состояние наступает при совпадении игловой скорости с любой из критических скоростей.
Для устойчивой работы вала диапазон частот вращения
0,7й( < <о< 1,3<о(- (i = 1, 2, .... п) рекомендуется исключить из рабочих режимов.
Для вала с несколькими дисками условия для устойчивой работы в закритической области (<в > ci>i) более благоприятны, чем для вала с одним диском.
Вал с одним диском
407
Рис. 4. Вал на пругнх опорах
Учет упругости опор. В действительных условиях опоры вовлекаются в колебания. Если пренебречь массой опоры, то в простейшем случае ее можно схематизировать в виде пружины (рис. 4).
Предположим для простоты, что опоры обладают одинаковой жесткостью. Для определения критических частот вращения следует рассмотреть равновесие системы при изогнутой оси вала. Центр тяжести диска будет перемещаться по окружности радиусом у, центры опор— по окружности радиусом у0.
Если а0 — коэффициент податливости опоры в см/Н, то
Уо = OqR.
Далее следует учесть равенства
С = <£?кту; (4)
с = — Уо), (5)
где а — коэффициент податливости вала.
Так как R = 0,5С, то из уравнения (5) следует:
г 1 1
С = -------;-------у.
1 I ао ^2 а
Приравнивая соотношения (4) находим
(6)
и (6),
<7)
где
°кж = "7— (8)
является критической угловой скоростью вала на жестких опорах.
Из формулы (7) следует, что поправка, связанная с учетом податливости опор, зависит от податливости вала.
Одни и те же опоры можно рассматривать как жесткие или как податливые в зависимости от жесткости вала. В практических конструкциях податливость опор составляет обычно а0 = = (5-н20)10~7 см/Н, причем податливость подшипников качения для вала диаметром 60— 80 мм приблизительно равна (1—3)10~7см/Н.
При критических частотах вращения в вале возникают постоянные по времени напряжения, тогда как в опорах напряжения будут изменяться по времени, что способствует увеличению сил демпфирования.
В технике применяют конструкции, в которых относительно жесткий ротор закреплен на податливых опорах. В силу этого критическая частота может лежать в рабочем диапазоне (<ок< <о), но, как показала практика, это не нарушает нормальной работы.
Прогибы ротора при критических частотах вращения всей системы оказываются малыми, если критическая частота вращения ротора на жестких опорах превышает максимальную
Учет гироскопического эффекта дисков. Рассмотрим центробежные силы, действующие на диск (рис. 5). Ось х является осью вращении, ось х1 направлена по оси диска. Пусть элемент массы dm находится в точке А. К нему приложена центробежная сила dC, действующая в плоскости вращения, причем
dC — dmafir,
где г— длина отрезка ОА.
Центробежная сила dC может быть разложена на две составляющие dCv и dCz, но усилия dCz вследствие симметрии образуют взаимную уравновешенную систему сил и для дальнейшего не существенны.
408
Критические частоты вращения валов
Рис. S. Гироскопический эффект диска
Усилие
dCy = <o’dm (у + ух cos <р), (9)
так как отрезок = у + ух cos ф представляет собой проекцию отрезка ОА на плоскость ху.
Приведем все нагрузки, действующие на диск, к силе С и паре сил М, приложенным в центре тяжести диска.
Сила
С — Су ~ J dCy — v
= (О2 j (у + Ух cos <р) dm, V
интеграл распространяется на весь объем диска.
Величины у (смещение центра тяжести) и <Р (угол поворота плоскости диска) одинаковы для всех точек диска и могут быть вынесены из-под знака интеграла.
Тогда
С ~ и>гу j dm -j- <о2 cos ф j Ух dm.
V V
Учитывая, что
j Ух dm = 0
V
как статический момент относительно прямой, проходящей через центр тяжести, получим
С — <Лпу, (10)
где т — масса всего диска.
Но центробежные силы создают еще и момент, который для рассматривае
мого вида движения 1 (диск неподвижен относительно плоскости, содержащей изогнутую ось вала) может быть легко определен.
Этот момент называют гироскопическим'.
М = j dCyyx sin <p dm v
или с учетом соотношения (9)
М = <о2 j {у + Ух cos ф) Ух sin ф dm.
V
Последний интеграл разбивается иа два:
М — со2 у sin ф j Ух dm + V
+ <о2 cos ф sin ф j yj dm, V
из которых первый равен нучю. Таким образом,
М = ы2 cos ф sin <fJm,
где J т = J Ух dm — осевой момент V
инерции, кгсм2.
Для тонких дисков Jm = 0,5/р.
1 Это движение называют прямой синхронной прецессией Возможны и другие, более сложные движения вала, напоминающие движение гибкого валика во вращающейся трубчатой обойме. Такого рода движения на практике встречаются редко, преимущественно в системах с соосными роторами, имеющими различные частота вращения.
Вал с одним диском
409
Рнс. 6. Влияние гироскопического эффекта
на критическую частоту вращения аала
Так как рассматриваются малые Отклонения вала от прямолинейной |юрмы, то cos ф « 1, 8;П ф AS ф.
Момент, создаваемый диском,
М = ша/тф. (11)
Цри малых углах поворота
Существенно, что этот момент препятствует прогибу. Следовательно, с учетом гироскопического момента дисков критические числа оборотов повышаются.
Перейдем к определению критических частот вращения вала с одним (Деком с учетом гироскопического мо-
у = сЛхту — <и^Утф;
ф = ®2уту — ш’Р/щф или
у (й’ат — 1) — фйау/т = 0; (13)
у<Рут — ф (w!₽/m + 1) = 0. (14)
Приравнивая отношение у к ф из равенств (13) и (14), находим
мУт = саУ т + 1
(Лт — 1 идут или
(и* (ар — у2) mJm +
+ <о! (ат — (Vm) — 1—0.
Из последнего уравнения получаем величину критической угловой скорости
.-----. ( 15)
1/ у (am — pjm) + |/ у (ат — т)2 + mJm (ар — уг)
йента (рис. 6).
Под действием силы С и момента М йал в месте крепления диска прогибается на величину у и поворачивается ра угол ф:
у=аС — SM; ф = уС—₽М, (12) (ГДе а а у — прогиб и угол поворота От действия единичной силы, 6 и Р — 'прогиб и угол поворота от действия единичного момента.
Направление единичных силовых факторов показано на рис. 6 По условию взаимности упругих систем величины у и 5 численно равны.
Подставляя равенства (10) и (11) в уравнение (-12), получим
Если Jm = 0, то получим известный результат
1 “к — - с— .
у ат
Влияние гироскопического момента особенно существенно для дисков, расположенных вблизи опор.
Если вал имеет концевые опоры и несет несколько дисков, то повышение критических частот вращения вследствие влияния гироскопического эффекта дисков невелико.
Учет массы вала. В приближенных расчетах массу вала учитывают уве
410
Критические частоты вращения валов
личением массы диска. Обычно к массе диска добавляют половину массы вала. Приближенный расчет допустим, если масса вала составляет не более 30% массы диска.
ВАЛ С НЕСКОЛЬКИМИ ДИСКАМИ
Определим критические частоты вращения вала с двумя дисками (рис. 7). Гироскопическими моментами дисков пренебрегаем. Прогибы вала создаются двумя силами:
Cj = С2 = <огт2у2. (16)
Введем обозначения- — прогиб в сечении 1—J от единичной силы в том же сечении; а12 = а2] — прогиб в сечении 1—1 от единичной силы в сечении 2—2; а22 — прогиб в сечении 2—2 от единичной силы в том же сечении.
Запишем
Vi = ацС1 + а12С2;
Уг = a21Cj + <^22^2-
Подставляя равенства (16), находим
(сЛхцШ! — 1) yt + иаа1атау2 = 0;
<oaa!i'”i4'i + (<o1 2a22zn2 — 1) у2 = 0.
Приравнивая отношения z/t/z/2 из последних уравнений, получаем
<O2/7lj/n2 (С&ц^22 ^г?) (^11^1 +
+ a22m2) +1=0.
Отсюда находим две критические угловые скорости о»! и <о2:
“J- ^22^2 ——
/(au™i +а22т2)2-
-4m1/n2(a11re22-af2).
(0|------------------------у ----- ,
2т^т2 (а^а^ — а,2)
’ (17)
«11^1 + ®22/л2 +
/(ац^ + а^т )2-= — 4/ntm2 (аца22 -- af2)
2 2m1m2(aI1a22 —af2)
(18)
Рис. 8. Форма прогибов вала с двумя дисками при критических .угловых скоростях
Сравнивая эти равенства с равенствами (32) и (33) гл. 21, можно ви деть, что критические угловые скорости совпадают с круговыми частотами поперечных колебанийх. Этот вывод справедлив при произвольном числе масс. Вал, несущий п дисков, имеет такое же число критических скоростей.
Каждой критической скорости соответствует своя форма прогибов. Для вала с двумя дисками формы прогибов при первой и второй критических скоростях показаны на рис. 8.
ВАЛ С НЕПРЕРЫВНО РАСПРЕДЕЛЕННЫМИ МАССАМИ
Рассмотрим вал с непрерывно распределенными массами с концевыми шарнирными опорами (рис. 9).
Пусть т (х) — масса единицы длины вала в сечении х.
Величина т (х) должна учитывать как массу диска, так и массу вала.
1 Критические скорости рассматриваются без ччета влияния гироскопических
моментов.
Вал с непрерывно распределенными массами
411
Рис. 9. Вал с распределенными массами
Если, например, на участке вала длиной Д/ = 10 см расположен диск массой 20 кг, а масса самого вала в пределах участка 2 кг, то т (х) = = 2,2 кг/см.
Величину т (х) принимаем постоянной на всем участке.
В изогнутом положении вала на него действует распределенная нагрузка
q (х) = (оат («) у (х). (19)
Перерезывающая сила в сечении
х
Q (х) = Ri + j q(x1)dx], 0
где величина хг представляет собой
переменную интегрирования (0 sgl х). Так как изгибающий момент в сечении х и усилие Q (х) связаны равенством
QW=^-,
ТО
X
М (х) = J Q (Xi) dxi =
0
X xt
= RiX + j j q (Xi) dxt dxv (20)
0 0
Из условия равенства нулю изгибающего момента в сечении х = I получаем
I х _
Al (Z) = /?!/+ j j q (х2) dx2 axi = 0,
откуда
I X
Ri =----j- j ^qlxjdxbdxt.
1 0 0
Внося значение в формулу (20), находим
X Xi
M(x)=^q (х.) dx2 dxi — о о
I X
—Т У Уq dXi dX1' (21)
о о
Полученное равенство выражает изгибающий момент в шарнирно опертой по концам балке при произвольной эпюре q (х).
Для рассматриваемого случая q (х) выражается равенством (19) и потому
М (х) = ш2
fx xt
J J m (xa) у (x2) —
'0 0
I X
[ У m (xa) у (xa) dxa dxx 6 b
(22)
Последнее соотношение запишем в более краткой форме:
М (х) = uA4y (х), (23)
где
* *!
АУ (*) = J J т (Хг) У (ха) dx2 dxt — о о
*1
—т У Ут у dXi dX1' о о
Далее следует учесть основное уравнение изгиба вала
d2y М (х)
dx2 ~ EJ (х) ’
(25)
где EJ (х) — жесткость сечения вала На изгиб.
412
Критические частоты вращения валов
Проинтегрировав обе части равенства в пределах от 0 до х, найдем
dy(x) С М (xt)
^Г~ J T7W 1 + у ( О
повторяв операцию, получим
у(х)==Й Tn^dXidX1 +
о о
+ г/'(О)х + г/(О). (26)
В рассматриваемом случае у (0) = 0, а из условия у (/) = 0 следует:
f f Tn^dx*dX1^y' (0)Z^°
J J nJ (Xa) 0 0
или
0 0
Подставив это равенство в уравнение (25), будем иметь
У W = ( (dx*dx^ -
J J \X2) 0 0
~ T J j EJ Va) dXi dX1' (27)
0 0
Это уравнение выражает прогибы вала при произвольном распределении изгибающего момента.
Если учесть соотношение (23), то уравнение (27) можно представить в следующей форме:
у = <огКу,
(28)
где Ку — сокращенная запись интегральных операций (интегральный оператор):
f Г А» (*2) , •
*У~ J J EJ (х,) о о
х (* f Ay (ха) ,
~ I J J EJ (*з) dX1' о о
Уравнение (28) представляет собой интегральное уравнение для определения критических угловых скоростей. Его решают методом последовательных приближений, причем в практических расче:ах больше двух приближений не требуется (второе приближение— для контроля).
Исходное приближение у,^ можно выбрать в виде плавной кривой, удовлетворяющей условиям у (0) = 0 и у (I) = 0, напрнмер
j/,0) (х) = sin —, (30)
ИЛИ
<31>
Окончательный результат не завн сит от выбора исходного приближения Следующее приближение для прогибов j/(]) определяем в соответствии с равенством
^(1) = Ш(1) ^У(О) > (32)
КУ(0) означает, что величина у ((J) должна быть внесена в соотношение (24), и затем после вычисления Ау (х) следует определить интегралы, входящие в равенство (29).
Интегралы определяем приближенно по правилу трапеций.
Первое приближение для определения критической угловой скорости находим нз условия равенства исходного и последующего приближений
5*(1) = У(0)- (33)
Это равенство (в приближенном расчете) не может быть справедливым для всех сечений, поэтому ограничиваются удовлетворением его лишь в сечении, где прогибы наибольшие.
В рассматриваемом случае можно принять в качестве такого сечення х = Z/2 (середину пролета).
Тогда по соотношениям (32) н (33)
Для контроля можно привести еш<-одно приближение.
Вал с непрерывно распределенными массами
413
2050
2592_______________J
Г__________________2699_________________J
*__________________2968,5___________________
____________________3/85___________________J
I ______________________5429,5_____________________J I
3681_________________________J
П___________________________3845___________________________
*___________________________9021___________________________J
Г___________________________9190___________________________
* 9300 J
______________________5340_____________________________________
Оассгрояние между осями подшичнилоВ
Рис, 10. Схема аала компрессора
Величину i/(i, вычисляем из соотношения (32), так как и Ку известны. Величину Ку^ определяем так же, как KyfQ}, но функцию j/(0) заменяем 511(.
1. К расчету критических частот вращения ротора
к, см т (х), КГ/vM EJ (X) 10-Н-сыг V
0 4.0 45 0 0
30 V.8 251 0,260 0.221
во 29,3 283 0,60b 0,ь55
110 27,9 313 0,761 0 723
150 26.0 2% 0.908 0,891
180 24,1 293 0,973 0 968
215 24.8 305 1 000 1.000
255 23 9 313 0,9о5 0,958
285 23,9 зоб 0,894 0.875
310 25,2 297 0.805 0,775
335 22,4 278 0,688 0,650
360 22.4 264 0,545 0,502
380 8,8 204 0,411 0,370
394 7.4 147 0,307 0,272
406 6.6 116 0,211 0,183
430 4.0 45 0 0
Значение то2 находим из равенства
ш2 _ Лш.
<2’ ~ Ку,.
(35)
£ 2
Так определяют первую (наименьшую) критическую угловую скорость.
Расчетные сечення нужно выбирать так, чтобы были отражены резкие изменения в распределении масс и жесткостей системы (см. рис. 9).
Пример. Определить первую критическую частоту вращения ротора центробежного компрессора, эскиз которого приведен на рнс. 10. Частота вращения вала п ЗОиО мин*1.
В табл. 1 приведены расстояния расчетных сечений х до левой опоры, значения т (х), EJ (х), исходное приближение для прогибов j/l0) (х), полученное по равенству (31) и прогибы первого приближения (х). Первое приближение для критической угловой скорости ю(1) = 184,6 рад/с. Второе
414
Критические частоты вращения валов
Рис. 11. Общий случай расчета критиче* ских частот вращения двухопорного вала приближение, определенное по функции прогибов первого приближения р(1), будет со(2) = 187,1 рад/с (пк = = 1788 .мин-1).
Общий случай определении критической угловой скорости. Рассмотрим вал (ротор) переменного сечения (рис. 11) на двух шарнирных опорах, загруженный произвольно распределенными массами и моментами инерции.
Массу, приходящуюся на единицу длины вала, обозначим т (х), момент инерции на единицу длины вала Jm (х).
В соответствии с формулами (10) и (11) на участок dx вала будет действовать внешняя сила
dC = s>2m (х) у (х) dx
и момент
dM = (х) у' (х) dx.
Перерезывающая сила в сечении х
X
Q W = и2 j яг (х4) у (xj) dx^ + о
-|- S (х, dj К1 S (х, d2) Р,, (36)
где
S (х, aj = 0 при х< аг;
S (х, dj = I при х dt;
S (х, а2) = 0 при х d2;
S (х, da) = I при х >• аа.
Введение единичных разрывных функций S (х, dj и S (х, d2) значительно упрощает схему расчета, так как позволяет записать в единой для всего вала аналитической форме выражения для перерезывающей силы и изгибающего момента.
Изгибающий момент в сечении
М (х) — со2
т (-«а) У (*а) dxa dxi +
h j Jm (*i) У' (*i) dxJ + о
+ S (x, /?i (x — ar) -|-
+ S (x, d2)J?2 (x — d2). (37)
Равенства (36) и (37) запишем в более краткой форме:
Q (х) = <Л41г/ (х) + S (х, dj +
+ S (х. a,) R2; (38)
M (x) = шгЛ2!/ (x) + S (x, di) X X Ri (x — dj + S (x, dj) R2 (x — d2), (39) где
X
Aiv (x) = j m (xt) у (Xi) dxii (40) 0
X Xi
Aty (x) = j j m (x2) у (x2) dx2 dxx +
. 0 о
X
' + j Jm ^)y' (xv)dx^ (41) 0
Из краевых условий
Q (/) = 0 и Af (/) = 0 получаем с помощью равенств (38) и (39)
1
— со2 — —- |\1 d2) AYg {!)
а2~ Oi
-Aaw(i)l;
— “1 L
-(/-аОАц, (/)].
(42)
Теперь, учитывая равенства (42), запишем соотношение (39) в виде
М (х) = (х). (43)
Вал с непрерывно распределенными массами
415
причем
Av (х) = Л2„ (х) 4- S (х, ях) ДДг х
X [(/ — Яг) Aiy (0 — А2у (/)] -f-
+ S (х, аг) —----[А2у (i) —
\ —(I — ai) А1у (/) ]. (44)
Уравнения (25) и (26) сохраняют силу. Используя зависимости (26) и (43), получаем
у (х) со2 С С £7777 dxi +
J J tj (x2) о о
+ У (О)х + г/ (0). (45)
Из условий
у (Я1) = 0; у (а,) = 0 (46)
получаем систему двух уравнений для нахождения у' (0) и у (0):
<h х, . .
о б
+ У (0) + У (0) = 0; (47)
?? Ау(х$ о о
. + У (0) Я2 +г/ (0) = 0. (48)
a,^ —
Ay (x3)
EJ (x2)
f p Ay (x2)
01 J .! EJ (xs) dXi dX1 о о
dx2 dXi —
(50)
Для расчета требуется значение у' (х). Его вычисляем по формуле
у' = &К’у, (51)
где
d С Ау(Л)
dT= К'У = J Ё777У +
о
L0 0
а у (Х2)
EJ (х2)
1
Я 2 Ях
Ay (x2) ~EJ {xt)
dx2 dxi —
dx2 dxi
(52)
Определяя из этих уравнений у' (0) и у (0) и внося их в формулу (45), получаем основное расчетное уравнение
у = аЧСу, (49)
где
о о
Уравнение (49) решаем методом последовательных приближений. В качестве исходного приближения можно выбрать
У= С (х — flj (х — я,). (53)
Постоянная С несущественна для расчета. Для однообразия вычислений ее можно определить из условия
У(0) шах = 1 ’
Если, например, наибольшее значение У(0) max ПРИ х = //2- то
В окончательной форме
„ (Х\ - (х-«1)(х-я2)
{/(0) <*)- // \ / I \ ’
I- -а>д-г-а0
(54)
а2 — ау
а» *1
Ay (хг) , , yi .—г- uXg dX]
416
Критические частоты вращения валов
Величины yQ (х) и у0 (х) должны быть подставлены в соотношения (40), (41) и далее в (44) и (50). В результате находим КУ(0)> после чего величину 2
(£>*[) определяем из равенства
2 _ УЮ)
'т
где хт — абсцисса сечения, в котором величина Kf/(0) имеет наибольшее значение; часто это сечение является одним из концевых сечений вала хт = = 0; хт = I или серединой пролета Хт = -Y (“1+ аа)-
Если требуется определить второе приближение, то вычисляют величину
^(1) = “(1)^(0)-
И далее с помощью равенства (52) 5''(1) = “(1)^(0)- (55)
Никаких новых вычислений для определения у(1), в сущности, ие требуется, так как все входящие в равенство (52) величины были рассчитаны ранее.
Определение второй и более высоких критических угловых скоростей. Рассмотрим сначала случай, когда гироскопическим моментом можно пренебречь. Для определения второй критической скорости вместо уравнения
у = &Ку
следует решить уравнение
у = м2К2у, (56)
где
I
j yiKymdx
Кду = Ку - У1 -Ц---------. (57)
j mtfidx о
В этом равенстве Ку определяют прежним способом, а уг (х) представляет собой форму прогибов прн первой критической скорости.
В качестве yt принимают последнее приближение при определении fflj (обычно принимают уг = у(1)).
Исходное приближение при определении второй критической скорости можно выбирать произвольным, ио целесообразно задать такую форму, которая, кроме опорных точек, содержала бы один узел.
Например, предполагая, что узел
I расположен в сечении х = , можно
принять
j/(0) = С (х - а,) (х - а2) (х - -g-)
(58)
и выбрать С таким, чтобы у(0) гаах = 1.
Последнее условие не является обязательным, но оно обеспечивает некоторую однотипность вычислений
Величину получаем дифференцированием равенства (58):
{/(]) = С Зх2 — 2 (a, -f- а2 -|-
Н--X + а1а2 +
+ ai “g—I” а* ~ ' (59)
Равенство (57) можно представить в виде
ТСу = Ку — PiJ/i, (60)
где коэффициент
j my^Kydx
j my\dx 0
(61)
Такая структура формулы (60) объясняется тем, что форма прогибов, соответствующая второй критической скорости, должна удовлетворять условию ортогональности
I
j У1 (*) Уг (*) rn (х) dx = 0. (62) О
Вал с непрерывно распределенными массами
417
Слагаемое в формуле (60) «очищаете оператор Ку от составляющей по первой форме.
При определении третьей критической угловой скорости приходится обеспечить условие ортогональности не только по отношению к первой форме, но и ко второй.
Рассчитывают прогибы по уравнению
у = а*К3у, (63)
где
К3у ~ Ку — PiУ, — ₽2</2> (64)
причем значение Pi находят из равенства (61), а
I
j ту2Ку dx
₽2 -= -Ц---------• (65)
j my^dx о
Исходное приближение целесообразно выбрать так, чтобы оно, кроме точек закрепления, содержало два узла.
Подобным способом можно определить более высокие критические скорости Однако для определения третьей критической скорости необходима повышенная точность расчета, а расчет четвертой н пятой скоростей практически затруднителен. В большинстве конструкций определение этих критических скоростей не требуется, так как они лежат за пределами рабочих частот вращения.
Перейдем к определению высоких критических угловых скоростей с учетом влияния гироскопических моментов дисков.
При определении второй критической скорости следует принять во внимание условие ортогональности в таком виде:
1 .1
j [щ (X) J/J (х) У(2) (X) - Д._ о
— Jm(x)y'i (х)у'ъ (-*=)] dx = 0, (66)
где уг (я) и у2 (х) — формы прогибов при первой и второй критических скорости?.
14 Заказ 402
Расчет ведем по уравнению (56) с учетом равенства (60) для Кгу и принимаем
I
j (mj/jKj/ — Jmy\Ky) dx ₽1==0_-----------------------. (67)
J (^)2]dx о
В этом равенстве К'у = (Ку),
которое находят по формуле (52). Третью критическую скорость рассчитывают по уравнению (63), причем значение берут по формуле (67), а
—4— I
j (ту2Ку — Jту'2К у) dx
. (68)
J [«{/г - (У2)2] dx
о
При очень сильном влиянии гироскопического момента дисков (например, при расположении дисков вблизи опор) может случиться, что при решении уравнения (49) расчет сводится к первой форме yt (х), но соответствующая ей угловая скорость оказывается мнимой (Wj< О). В этом случае нужно перейти к расчету второй критической скорости, используя, как обычно, условие ортогональности по отношению к полученной форме прогибов yt (х).
Вторая расчетная критическая скорость будет для такой системы первой действительной критической скоростью, с которой только и нужно считаться в дальнейшем.
Пример. Определить вторую критическую частоту вращения ротора цен-с тробежного компрессора (по данным j примера на с. 413).
J Определив по формуле (58) исходное приближение у0 (х), найдем коэффициент по формуле (61): Pi = = —6.73-Ю-7. Первое приближение для второй критической скорости со(1) = 758 рад/с, второе приближение со(2) = 766 рад/с (пк(2)=7120 мин-1).
418
Критические частоты вращения валов
Рис. 12. Конструктивные схемы упругих опор:
а — упругое кольцо с чередующимися выступами, б — пакет тонких колец; в — упругое кольцо с прорезями
Расчет критических частот вращения с учетом упругости опор. Во многих практических задачах при расчете критических частот вращения роторов приходится учитывать упругость опор. Для роторов быстроходных машин с успехом применяют специальные упругие опоры, которые дают возможность перевести критические скорости в зону малых частот вращения, не используемых при рабочих режимах. Упругие опоры позволяют изолировать корпус от вибраций ротора и снизить нагрузки на подшипник Ч
1 Полное устранение радиальной нагрузки на опору нежелательно, так как при этом в подшипниках качения режим качения может сменяться режимом скольжения, приводящим к интенсивному изнашиванию.
Применение упругих опор целесообразно сочетать с введением дополнительного демпфирования в систему за счет вытеснения масляного слоя при колебаниях и других видов трения (упругодемпфирующие опоры).
Конструктивные схемы упругодемп-фнрующих опор показаны на рнс. 12. Конструкция упругого кольца приведена на рис. 13, а основные размеры даны в табл. 2.
Силы демпфирования оказывают значительное влияние на частотные характеристики системы, и при определении критических частот вращения ими можно пренебречь.
Схема ротора на двух упругих опорах показана на рис. 14.
Рис. 13. Упругое кольцо
Рис. 14. Ротор иа двух упругих опорах
Вал с непрерывно распределенными массами
419
2. Размеры (мм) упругого кольца (см. рис. 13)
D, D, Число выступов п ^тах 6. я о. 0. Число выступов п ®тах Ь, к
55 58 4 6 0.165 0.152 5 10 125 128 10 12 0,305 0,194 6 15
58 61 4 6 0,120 0.170 129 132 10 12 0,330 0,210
60 63 4 6 0.130 0,180 134 137 10 12 0,370 0,230
65 68 4 6 0.100 0 220
144 147 10 12 0,400 0.273 8 20
71 74 6 8 0,270 0, 138
149 152 12 14 0,299 0,204
75 78 6 8 0.313 0. 155 6 15
154 157 12 14 0,325 0.220
78 81 6 8 0,338 0,168
164 167 12 14 0 386 0,256
83 86 6 8 0,325 0. '94
169 172 12 14 0,430 0,275
88 91 6 8 0.300 0,223
174 178 12 14 0,285 0,200
93 96 6 8 0,240 0 148
’74 183 12 14 0,304 0,210
103 106 8 10 0.334 0,190
184 188 12 14 0,325 0.228
113 116 8 10 0.295 0.236
123 126 8 10 0,294 0.185 199 203 12 14 0.270 0,200
Примечания 1 Материал кольца — стали 60С2А (44- 48 HRC3), 40ХН2МА (30-36 HRCa)
2. Значения бгаах определены иэ условия, что напряжение omsx < 500 МПа.
3. Размер &* назначается конструктором.
14*
420
Критические частоты вращения валов
Прогибы (смещения) в опорах и силы реакции связаны соотношениями
У (01) = — ; (69)
Лд1
У (о2) = - 44, (70)
ЛД2
где ЛД1 и К^г — динамические жесткости опор, Н/см.
Знак минус в этих равенствах согласовывает положительные направления усилий и смещений (см. рис. 14).
Если в опорах не учитывают присоединенные массы, то динамические жесткости опоры равны соответствующим статическим жесткостям:
1 . „ 1 ~ С1 ~ ~ ’
(71) где а, и а2 — коэффициенты упругой податливости (при выводе формулы (7) принимали at = a2 == a0).
Для общих случаев, когда рассматривают сложную динамическую систему, коэффициенты динамической жесткости определяют, как указано в гл. 21.
При выводе расчетного уравнения зависимости (36)—(45) справедливы но вместо условий (46) и (47) будем иметь
о о
+ У' (0) а, + у (0) = - А ; t?2) Лд1
2?С „ I
и J J +
0 о
+ У(0)ц3 4-у(0) = -^-, (73)
Лд2
где и R.2 определяют из отношений (42).
Из равенства (72) и (73) находим величины у' (0) и у (0) и получаем основное расчетное уравнение для ротора иа упругих опорах
у = ш2 [Ку+ к»и]. (74)
где Ку определяется формулой (50), а величина Л,у, учитывающая податливость опор,
1 ( а2 — х
К,гУ ~ (а3-ах)2{ ДЛ1 'Лг}Х
X А1У (/) — А^у (/)] -j-
Н—Цт— [ А2у (/) — Лд2
-(1-а^А^у (/)]!. (75)
Необходимое для расчета значение у' (х) вычисляем из уравнения
у = и2 [К у + Tf'g]; (76)
значение К'у находим из равенства (52), а
I Ки= ,--------рг X
’ (а2—01)-
X — [(/ — Аху (/) — Л2у (/)] — 1ЛД1
— ~ 1А^у (() — (I - at) Ary (/)]l.
ЛД2 )
(77)
Расчет по уравнению (74) ведут методом последовательных приближений.
Если учитывают обычную упругость опор [формулы (71)], то такой расчет не содержит существенных отличий от рассмотренного ранее.
Выбор первого приближения не влияет на окончательные результаты.
В качестве первого приближения можно выбрать
J/oW=l. (78)
При учете присоединенных масс величина К*у зависит от <о2, так как в иее входят динамические жесткости опор. В этом случае условие (33) приводит к алгебраическому уравнению относительно и2.
Пример Определить первую критическую частоту вращения ротора тур-бомашины, эскиз которого показан на рис. 15, иа жестких и упругих опорах. В соответствии с экспернмен-
Вал с непрерывно распределенными массами
421
В равенстве (79)
тальными данными жесткости опор приняты
КЯ1 = 2,5 10е Н/см;
3,3-10’ Н/см.
При расчете методом последовательных приближений получено по уравнению (491 для жестких опор пк = 40 400 мин 1, по уравнению (74) для упругих опор пк = 33 200 мин"1
Вал с равномерно распределенной массой. Рассмотрим чаешь й случай (рис. 16), имеющий практическое значение вал постоянного сечения, несущий большое число одинаковых дисков.
Эта задача имеет .-очное решение.
Если т и jm — масс5 1» момент инерции, приходящиеся на единицу длины вала, то критическая скорость порядка i выражается равенством
(81)
где и0; — критическая угловая скорость вала без учета гироскопического момента ди.ков.
Следовательно,
<i>i = ш01- ---------------. (82)
Из последнего равенства следует, что влияние гироскопического момента для высших критических угло-Boix скоростей увеличивается.
Наименьшая критическая угловая скорость вала в соответствии с равенством i"9) будет
(( = 1, 2, 3, 4, ...).
Форма прогибов, соответствующая критической угловой скорости, будет
inx
у(1)--с sin —— . (80)
Рис. 16. Вал с дисками
422
Критические частоты вращения валов
Для вала постоянного сечения без
присоединенных масс имеем
m = pF = p ,
1 __ nd1 . _ nd*
- — J P -P -gr ’ J “ 64 ’
и тогда
n2d2 I/" E 1
1 4/2 r p Г я2 уз
V “Тб ~Ё
(84)
Если отношение dll значительно меньше единицы, то влиянием гироскопического эффекта можно пренебречь и считать
n2d -1/ Е
“1 = _4р" V V (85)
Влияние начального дисбаланса для ротора с распределенными массами. Уравновешивание по собственным формам. Рассмотрим для простоты системы, для которых можно пренебречь влиянием гироскопических моментов дисков.
При определении критических угловых скоростей использовали интегральное уравнение
у — а2Ку. (86)
Физический смысл этого уравнения таков: прогибы вала у (х) вызываются распределенными центробежными силами ®2т (х) у (х), в свою очередь, зависящими от прогиба.
Очевидно, что уравнение (86) имеет решение у = 0, которое соответствует прямолинейной форме равновесия (начальный дисбаланс считали отсутствующим).
Однако При ИеКОТОрЫХ Значениях О), называемых критическими, уравнение (86) обладает отличными от нули решениями: yt (х), у2(х)... .
Эти решения (с точностью до множителя) и представляют собой формы прогибов при критических скоростях вращения (собственные формы или собственные функции).
Следовательно, собственные формы удовлетворяют уравнениям
У, = ш\Кур 1/2 = ч>1Кур,..., (87) где и»!, ы3 — критические скорости ротора.
Собственные формы ух, у2, у3, ... удовлетворяют условию ортогональности
I
j т-УлУь. dx = 0 (88)
О
Прогиб yt вызывает распределенные силы а прогиб yk — силы
^Ун-
Так как ш; =#= иА, то отсюда следует условие (88).
Рассмотрим теперь вал, имеющий начальный эксцентриситет расположенных на валу масс е(х). Тогда прогиб вала у (х) будет вызывать силы
а>2т (х) [у (х) + е (х)];
у (х) = и2 К (у + е) = (89)
= <Р2Ку + to^e.
Обозначим f (х) прогиб вала от распределенных усилий (Лп(х)е(х):
f = to2tfe. (90)
Тогда уравнение (89) примет вид
у = и>гКу + /• (91)
Это уравнение выражает прогиб вала при любой угловой скорости ш. Прогиб f (х) можно представить в виде ряда
/ = “Ь азУз “Ь (92)
Для того чтобы определить коэффициент ах, умножаем обе части уравнения на тух и интегрируем но всей длине вала:
I I
j" щ/ у, их = и._ j" myl dx 4-
0 о
I I
+ a-з j rny^idx + a3 j" my^dx-i--------
0 0
СиГЛаСНО УСЛОВИЮ ОрТОГОНиЛЬНОС-ТИ все интегралы, содержащие разные
Вал с непрерывно распределенными массами
423
собственные формы, обращаются в нуль, но
I
j mfy-idx
| myl dx о
Точно так же найдем
I
j mfyt <&
а, = . (93) myjdx
о ,.J
Коэффициенты а,- в равенстве (92) называют коэффициентами разложения (прогиба от дисбаланса по собственным формам).
Предположим теперь, что общий прогиб вала у также может быть представлен в виде
У = Mi + btyt + Ms + ' • (94) и требуется определить коэффициенты ^2» ^3’ ••• •
Внося значения (94) и (92) в уравнение (91), получим
bdJi + Ms + • • • = <о’К (Mi + + Ma + • ) + а1У1 +
+ + • • • (95)
Так как величина Ку содержит обычные интегральные операции с функцией у (х), то
К (Mi + Ms + • ) = = b-tKy-L + ЬгКуъ + • • . Учитывая, что из соотношений (87) м. = -^-у>...................
и подставляя эти зависимости в равенство (95), получим
ЕЧ'—?r)-flib +
+1?2 ~ "5г) ~ ЧУг+=°-
Последнее равенство возможно (для всех х) только в том случае, если
‘Ч1—
11 (' ~ тт) “
откуда
“1
“i
Внося эти значения в ряд (94), получаем выражение для прогиба вала в рабочих условиях от начального дисбаланса
У =---------У1 (х) +
1 й)|
Ч Уз (х) + • • • • (96)
1 - А-
(05
Из этой формулы следует:
прогибы могут неограниченно возрастать при совпадении угловой скорости вала с одной из критических угловых скоростей;
для устранения прогибов, связанных с данной критической угловой скоростью <0;, необходимо сделать равным нулю at — коэффициент разложения прогиба от дисбаланса по данной форме.
Расположение уравновешивающих грузов для устранения вибраций, связанных с первой критической угловой скоростью, показано на рис. 17. ’
Рис. 17. Расположение уравновешивающих грузов для устранения вибраций, связанных с первой критической угловой скоростью
424
Расчет пластинок
3. Критические угловые скорости некоторых роторов
Система Формулы Коэффициент влияния
Вал с одним диском
(15)
1 аа6г , 1 a*b*
3EJ, 1‘ 3EJ2
₽ ‘ °’ + 1 b*
3EJ, 1‘ 1 3EJa
V 1 аЬя 1 asb
3EJ, I1 ЗЕ J, l1
(15)
3£J, аЬ‘ + ЗЕ.!, Ь’;
Р = 3EJ, а + EJ, Ь'
Вал с несколькими дисками (без учета гироскопического эффекта)
Примечание. J„ J г — моменты инерции сечения вала; <ок — первая критическая скорость ротора; о>1.ti>n —
то же при наличии t-го диска.
Формулы (90) и (93) позволяют рассчитывать расположение начальных эксцентриситетов е (х) для выполнения условия
at = 0. (97)
Для гибких роторов (т. е. роторов, работающих при и > Mi) обычные методы уравновешивания часто не
дают положительных результатов из-за упругих прогибов роторов при рабочих условиях.
Более эффективным оказывается уравновешивание по собственным формам, сущность которого состоит в выполнении условия (97) для нескольких первых критических скоростей. Критические угловые скорости для некоторых роторов приведены в табл. 3.
Глава 23
РАСЧЕТ ПЛАСТИНОК
(И,
КРУГЛЫЕ ПЛАСТИНКИ
Расчетные формулы. Многие детали (например, диски) рассчитывают на из1иб как круглые пластинки постоянной или переменной толшины h, симметрично нагруженные давлением q (г) в Н/см2, или отнесенными к еди
нице длины нагрузками Qt в Н/см и моментами М< в Н-см/см (см. рис. 1). В центре сплошной пластинки (а = 0) может быть приложена сосредоточенная сила Р в Н.
В сечениях пластинки действуют поперечная сила Q и изгибающие моменты Мг и Mq (рис. 2). Нормаль-
Круглые пластинки
425
Рнс. 1. На1ружение круглой пластинки
Рис. 2. Поперечная сила Q и изгибающие моменты М?, в круглой пластинке
ные напряжения ог и меняются по толщине пластинки по линейному закону; их максимальные значения у поверхности
6М
"й2"
оа == ±
6Л4е й2
(I)
где плюс относится к иижией стороне пластинки.
Из условий равновесия элемента пластинки (рис. 2)
~ЗГ (гМТ) -Me = Qr
(2)
и соотношений упругости
получают дифференциальное уравнение
Eh3
Где D ~2(1"—v2) ; V КОЭФФИЦИ' еит Пуассона; и> — прогибы пластинки (вверх).
Последовательным интегрированием уравнения (4) в пределах от г — а до г находят:
P(r) = P(a)+ б.Р^фП г=1
44г (г) = ф21Р (ц) 4* фааЛ4г (а) 4“ {
... т ।
+ фа< (а) 4- / , 6/фл iPi 4-1=1
4 л
+ ®/Фг2/^/ 4- ф5;
/=1
Мв (г) = ф31Р (а) 4- ф83Л4г (а) 4-т dw
+ Ф34-^Г (°) + 2j +
n
+ ^Мзг/М^Фз;
i l=l
(r) = Ф41-Р (a) 4- Ф4а^г(а) 4~
m f
, dw / ч , V
~Ь / i 1
n
+ S6/<p42/M/H-'P4;
w (r) = w (a) 4- ф51р (a) 4- ф62Л4r (a) 4-m
dw , s Vl
4- Ф&4 (a) 4- / , бгф61/Р/ 4-
<=i
n
+ 2б/'₽52/'М/4-ф?,.
/=!
где P = 2nrQ;
( 0 при r <zrf, i
Si = , . ;
( 1 при r ^ri, ;
426
Расчет пластинок
Г 0 при г <г;; [
I 1 При T^Tj. j
(5)
Нагрузки Р{ и Mj могут быть приложены на любом радиусе в пределах а< ri < b или а < г;-< Ь. Начальные параметры Р (а), Мг (а), (а)
н w (а) определяются граничными условиями на краях.
Например, для края г = а:
свободный край Р = Ра\ Мг = = мга-
шарнирная опора Мг = Mra\ w = 0;
скользящая опора Р = Ра-, = 0;
dw
заделка —j— =0; и» = 0, аг
где Ра, Мга — контурные нагрузки.
Аналогично записываются условия при г = Ь.
Функции влияния <р (г) определяются следующими выражениями:
пластинка с отверстием, а Ф 0:
ф21 “О । 2(1 + v) ,п"7 +
Фаз = ~2~ + VH-(1 —v) J ] ,
(1 — v2) D Г, fa \2*1
Фэ1 = if2(1 + v),n т ~
<P32=41+v-(1 “ЧтО
(1 — v2) D Г , fa \2-| »'=1тг- Ю) 1
<р« = £(1 +v) ~ (1 ~v) у];
+1 - (т) }’ “
ф,, = -J- | 2 (1 + *>ln-J +
пластинка без отверстия, а = 0;
dw dr
(а) = 0:
<Pal = ^[l + (l + v)ln^---444];
<p»i=4[v+(i+v)in т+ + (т) фи = 1;
4)42 = (1 + v)D ’
*4-1-0’};
г2 фи ~ 2(1 + v)D ’
(7) где е — радиус центральной площадки, на которую действует сила Р (0), г «4.
Функции влияния фа1;.ф5а; Опре-
деляются соответствующими формула ми (6) при замене радиуса а на ра
Круглые плпстинки
427
дчусы rt ИЛИ Г). Функции ф* (г) для произвольной нагрузки q (г) имеют вид
Г
фГ = 2л j <7(ri)ri drx\ ср? = Фх J- Ф2; а
Фз’ = ©I - Ф?; ф; = -р- (-[-pv ~
г
- TTv) : <г'* = J ‘Р* (fi) dri'
а
(8) где
Г
Ф1(г) = -^^- J -7^—ф? (Г,) а г
ф2 (г) = 17^ j Г1'Р’ dr'- (0)
а
Для ря°номериой нагрузки а, приложенной к участку пластинки от г — с до r= b (см. рис. 1):
ФГ 0 = л<7бс(г2 —с’);
1 4- v ©t (И = -Ц— «?8е X О
V 1Г -£-) ;
= У=,-< (г’-г’Г;
Ф* (И = -glp- <7«с [(г2 — с’) х
х (гг -|_ М) _
- 4С2 (2г2 4- с’) In ~ ,
(Ю) где
{0 пои г < с
. ________
1 при Г Г.
Формулы (5)—(10) появопчют рассчитывать круглые пластинки при Любых условиях Закрепления и нагрузки.
Пример 1. Рассчитать пластинку, заделанную по внутреннему контуру и нагруженную изгибающим моментом МгЬ по внешнему контуру. Пола-
гая в формулах (5) Р (а) = =
= w (о) = Pt = Mj = ф* = 0 и находя Мг (а} из условия
Л1Г (ft) = фг2 (ft) Мг (а) = Л4гЬ,
полупим
Л1г(г) =
Ф22 (Г) фз2 (^)
1 + V+ (1 — V) )
1 +v+(l -v)
МгЬ;
1 + v — (1 — v) l+v+(l-T)(-2-)2
w,'r) =-^Ц?ГМгЬ =
ф22 (°)
Пример 2. Рассчитать пластинку без отверстия, опертую по наружному контуру и нагруженную распределенной нагрузкой, меняющейся по линейному закону (рис. 3), q (г) = q0 (1 — — r/b). По формулам (8)—(9) находим
ФГ (г) = 2.П7о J ( 1 - -у-) fi dri = О
= л?,/2 (1
Рис. 3. Пластинка под распределенной нагрузкой, меняющейся по линейному закону
428
Расчет пластинок
г
ф‘ j ri (1 - dri“
о
_ (1 - у),7(/г /, _ 4г \ .
8 V 9* > '
„ I — у f , I , 2гА
(л) - 4г2 Яи | Г1 1 — 2Ь / dr' ~ О
_ (! — v) ?Z ( , _ 8л \ .
~ 16 V 15* ) ’
т» /г\ - / 1 64г
44 640 ( 225* /
Полагая в формулах (5) Р (0) = = (0) = Р i = Mj = 0 и находя
Мг (0) из условия
Мг (*) = <р22 (*) Мг (0) + ф2‘ (*) = О,
где ф22 (*) — 1,
получим
М, (г) •= Ф2 (Z) — <₽2 <й) =
4 -L v / г3 \ "I.
45 U “*2 /_Г ме (Л) = Фз* (г) — Ф2* =
= -9о*2 [-^0-
1 4 Зу г2 \ _
3 --j- v *2 /
4 4- v 1 -j- lv г3 \ -|
~~45~ к 4+V 1^/J ’
а-’(г)
(*'" — г2) фг» (*)
2(1 + у) D
-т Фз (г) —
4 ’ ' ’ D L 1440 (1 + у)
+-2H‘~4)J-
Пример 3. Рассчитать пластинку без отверстия, заделанную по наружному
контуру и нагруженную в центре сосредоточенной силой Р. Полагая
в формулах (5) Р (0) = Р, (0) =
= Pt -- Mj = ф* = 0 и находя Мг (0) из условия
(*) -= Ф41(*)^ + Ф42 (*) Mr(0) -= 0, получим с учетом выражений (7) при е -» 0
ЛМО= . '
== [ф21 (И - Ф22 (Г) Р =
D+(i+v) 1пт];
Л18 (г)
= [фз1(г)-Фз2р)^-]р^
р Г Г 1
= -4-- [_v+(i+v) mTJ;
ш (г) = | ф61 (г) — ф51 (*) —
, . - , , , ф41 (*) I „
~ [фб2 (Г) - ф52 (*J] | Р =
Р [ г \
= птт-тт - Р1 + 2г2 In — 1 .
16лО \ b j
В точке приложения сосредоточенной силы Р расчетные моменты и напряжения стремятся к бесконечности. Поэтому сосредоточенную силу надо прикладывать к пластинке через жесткий центр, относительный радиус которого а0 — а0/Ь определяют из условия отзх [а], вследствие чего
(*о) , (11)
где для пластинки с шарнирной опорой по нагруженному контуру
¥ (а0) =
2(1-|-v)lna0 —(1 — v)(l — а§) 4л [ 1 + у + (1 — v) а’] ’
(12) с заделкой по наружному контуру у (а0) =------ а° + 1 . (ГЗ)
( 4л (1 — а„) '
Круглые пластинки
429
При ccg <g 1 и v = 0,3 получаем из формул (12) и (13) соответственно <z0>exp (-1,05 0,2?)
И
а0>ехр (- 1,05 ----0,50^ .
(14)
Расчеты с помощью таблиц. Для удобства расчетов в табл. 1 приведены значения функций ф (г), определенные по формулам (6)—(7) и ф* (г) — по формулам (8)—(10) при v = 0,3 в зависимости от параметра х, соответственно равного отношениям а/r или dr. Если в качестве х принять отношения г ,1г или г/г, получим значения функций фг- (г) или Ф; (г).
Пример 4. Для пластинки без отверстия, заделанной по наружному контуру и нагруженной на радиусе r!b = — 0,2 распределенной нагрузкой Q, найти прогиб на радиусе rib ~ 0,5. Положим в формулах (5) Р (0) =
= ~ (°) = М, = ф* = 0, I = 1, ?! -- 2rsQ, r-Jb -= 0,2.
Из условия
(Ь) == ®/2 (ft) Мг (0) +
+ Ф41, 1 (Ь) — 0,
где согласно табл. 1 при х = alb = 0 ф42 (b) = 0,76923i''D и при xt — rdb = = 0,2 ф41>1 (Ь) = 0,08988ft/P, находим Мг (0) == —0,1168?!.
Далее, из условия
w (b) == w (0) + ф62 (6) МГ (0) +
Ф.52Л GO ~ 0,
где ф52 (Ь) =- 0,38462ft2/D и ф51,1 (6) = = 0,02840 ft2/1, находим w (0) — = 0.01652P16s/D и, полагая для rib = = 0,5 величину х1 = г Jr ~ 0,4, определяем
w (0,5Z>) = w (0) + ф62 (0,5ft) Л4Г (0) +
+ Ф51.1 (0,5ft) = (0,01652 —
— 0,38462-0,53-0,1168 +
+- 0,00887-0,52)
р /)2
_ = 0,00751
Для наиболее важных случаев нагружения в табл. 2 при v — 0,3 приведены значения безразмерных коэффициентов максимальных напряжений Ка, К’„, прогибов кш, K'w И углов поворота Ку, KJ • Если на пластинку действует давление q,
__ „ qb2 .
^max — Л—-j~2~ i ^max
то
_ к дь4 .
w Eh3 '
qb-
* Eh3 ‘
(15)
Если действует сосредоточенная в центре сила ?, то
к" р -к- р'°г
^тах д2 > ^гпах '-w >
dw \
dr ) max
Pt
Eh3 '
(16)
Для распределенной по окружности П нагрузки Q; — Ptl2ftri в формулах (16) надо заменить ? на ?,.
Если приложен распределенный по окружности rj момент Mj, надо в формулах (16) заменить ? на Mj. Знак при Ка или К'о соответствует нижней стороне пластинки. В точках заделки ^ae = V^or: ^ae=v/<ar- На Ра’ диусе приложения момента Мj коэффициенты напряжений претерпевают скачки ДКОГ = 6 и ЛКов == 1,8.
Комбинируя данные табл. 2, можно получать решения для более сложных схем нагружения и опирания.
Пример 5. Для схемы нагружения на рис. 4, а найти прогиб в центре пластинки. Разобьем пластинку на две части (рис. 4, б): 1 — нагружение соответствует схеме 15 при [5=0 н схеме 17 при Р = 1 и II — нагружение по схемам 1 и 5 при f} = a.. Суммируя деформации от силы ? и неизвестного момента Л4” (6J == = —Af’(ftj)= М, найдем отношение М/Р из условия равенства углов поворота обеих частей при г = bi, для чего в схемах 15 и 17 надо принять
1. Функции влияния для круглых пластинок
Функции X
влияния 0 . 0.1 0,2 0.3 0.4 0.5 0.6 0.7 0.8 0,9 1.0
Ф,1 0.26578 0.19324 0.14990 0,11819 0,09260 0.07067 0.05110 0.03311 0,01619 0
Фм 1 0.65350 0.66400 0,68150 0,70600 0,73750 0,77600 0.82150 0,87400 0,93350 1
Ф„ (r/D) — 4,50450 2.18400 1,38017 0.95550 0.68250 0,48533 0.33150 0.20475 0.09606 0
ф»| — 0,21063 0,13976 0.09921 0.07140 0.05082 0,03502 0.02269 0,01306 0.00561 0
Фл1 1 0.64650 0.63600 0.61850 0.59400 0,56250 0.52400 0.47850 0,42600 0.36650 0.30000
Фи 07D) — 4.59550 2.36600 1.65317 1.31950 1,13750 1,03133 0.96850 0.93275 0.91506 0.91000
Ф.1 (D/r) — 0. 14384 0.08988 0.05960 0.03949 0,02332 0,01518 0,00809 0.00343 0.00082 0
Ф., (D/r) 0.76923 0,49500 0.48000 0,45500 0.42000 0,37500 0.32000 0.25500 0,18000 0,09500 0
Фм — 3,56500 1.88000 1,36167 1.13500 1,02500 0,97333 0,95500 0,95750 0,97389 1
Фи (D/r*) — 0,05314 0.02840 0.01601 0.00887 0.00463 0.00218 0.00085 0,00024 0,00003 0
Фи (D/r*) 0,38462 0.23599 0.20781 0,17332 0.13670 0.10086 0.06805 0,04011 0,01859 0,00483 0
Фм (1/г) - 1.88217 1,04923 0,76561 0,60574 0.48777 0.38589 0.28979 0,19478 0.09858 0
ф* (1/?г2) 3,14159 3.11017 3.01593 2.85885 2.63894 2.35619 2.01062 1.60221 1.13097 0.59690 0
Ф£ (1/«г2) 0.20625 0,19627 0.17540 0.14889 0.11972 0.09017 0.06215 0.03745 0.01776 0.00472 0
Ф£ (l/flT-2) 0.11875 0,11051 0,09476 0,07643 0.05798 0,04095 0.02631 0.01470 0.00642 0,00156 0
Ф« [D/qr^) 0.06250 0.05674 0.04631 0,03490 0.02425 0.01527 0,00843 0.00380 0,00120 0,00016 0
Ф* (D/qrl) X 10 0.15625 0.13350 0.09792 0.06463 0.03833 0,01999 0.00875 0.00293 0.00061 0.00004 0
430 Расчет пластинок
Круглые пластинки
431
2. Коэффициенты напряжений прогибов и углов поворота для круглых пластинок
Кае- <• = О С-г — а Кф. г = а к'у г = Ь К'аг. г = а kw, г = а
0.1 — 3,221 0,632 — 0.644 -0.726 — 2,440 0,4677
0.2 -2,342 0.572 — 0.468 — 0.689 — 1.774 0.4518
0,4 — 1,432 0.442 - 0.287 — 0,590 — 1,085 0.3692
0.1 0,6 -0,857 0,299 -0.171 — 0,445 — 0.649 0,2549
0.8 -0,401 0.148 -0,080 — 0,249 — 0.304 0,1280
0,9 — 0,196 0.074 — 0.039 -0.131 -0,149 0,0635
0,2 -2,411 0,704 — 0,966 — 0.835 -1,746 0,3503
0.3 — 1,874 0.612 — 0.749 — 0.758 — 1,354 0,3375
0,2 0.4 — 1,477 0,523 -0.59! — 0,680 — 1,068 0,3071
0.6 — 0,883 0,347 —0,353 -0,498 — 0,639 0,2178
0,8 — 0,414 0.171 — 0,166 — 0,274 — 0.299 0,1106
0,4 — 1,688 0,721 — 1,351 — 1.102 — 1,004 0,1530
0,5 — 1,323 0.590 — 1,058 — 0,925 — 0,787 0,1452
0,4 0,6 -1.010 0,465 — 0,808 — 0.751 — 0,601 0.1256
0,8 -0.473 0,227 -0.378 — 0.392 — 0,281 0,0674
0.6 — 1,325 0,590 — 1.59f — 1.382 — 0,546 0,0439
0,6 0.7 —0,958 0.434 — 1,150 -1,031 — 0,395 0.0396
0,8 — 0,621 0,285 — 0,745 —0,688 — 0,256 0,0291
0,8 0,8 -1,104 0,341 — 1,7 66 — 1,653 -0,227 0,0051
0,9 — 0.540 0,168 — 0.864 -0,818 -0,111 0.0035
0,9 0.9 — 1,023 0,181 — 1,841 — 1.784 — 0,104 0,0006
432
Расчет пластинок
Продолжение табл 2
3 4
, р, 4 -—
'32z£
, 1
. 2а 2а 4
1 2Ъ
3 н 2Ь ?b
а = -2-; ₽ = — а — Т}
Ь р Ь b ' p b
^о9' ^ог’
г = а г = b г — а г = а г — b r = a
0,1 — 2,203 0,504 0,2490 — 1,744 0,455 0.1685
0.2 — 1,377 0,478 0,2080 — 1,089 0,447 0,1578
0,4 — 0,605 0,410 0.1308 — 0,479 0,396 0.1088
0,1
0,6 — 0.233 0,309 0,0638 — 0,184 0,304 0.0553
0,8 — 0.053 0,173 0.0172 — 0,042 0,171 0,0153
0,9 -0,013 0,091 0,0044 — 0,010 0,091 0,0040
0,2 — 1,305 0,533 0,2376 -1,123 0,413 0, 1148
0,3 -0.865 0,484 0,1814 — 0,745 0,405 0,1070
0,2 0,4 - 0,574 0,434 0,1438 --0,494 0,381 0,0899
0,6 - 0,221 0,318 0,0688 -0,190 0,298 0,0480
0.8 — 0,050 0,175 0,0183 — 0,043 0.170 0.0136
0.4 — 0,475 0,510 0,1333 — 0,564 0,31 1 0,0435
0,5 — 0,304 0,428 0,0969 — 0,362 0,300 0,0394
0,4
0, ь — 0,183 0,347 0,0647 -0,217 0,271 0,0302
0,8 -0,041 0.181 0,0174 — 0,049 0,164 0,0096
0.6 — 0,142 0,379 0,0420 — 0,285 0,203 0.0115
0,6 0,7 — 0,076 0.282 0,0257 — 0.152 0.189 0,0095
0,8 -0.032 0.188 0,0123 -0,064 0,149 0,0054
0 8 — 0,021 0,194 0,0050 -0,114 0 099 0.0013
0 8
0,9 - 0,006 0,096 0,0015 — 0,027 0,073 0,0006
0.9 0.9 -0,005 0,097 0,0006 — 0,052 0,048 0.0002
Круглые пластинки
433
Продолжение табл 2
5.
а 3 , гд , ° а 'j ; ₽ = ~Г
2Л
/<09, г = а г = а к'^, г = а К^. г = b
0,1 — 6,12 0,40 -1,58 —0,24
0,2 — 8,05 0.76 — 1,61 —0,50
0,! 0,4 -8,56 1.73 -1,71 -1,52
0,6 — 9,41 2,80 —1,88 —3,21
0,8 — 10,59 3,78 —2,12 —5.59
1,0 — 12,12 4,56 —2,42 —8,64
0,2 — 6,50 1,2! —3,32 —1,00
0,4 — 8,82 2.2! —3,53 —2,05
0,2 0,6 — 9,70 3,33 —3,88 —3,80
0.8 — 10,92 4,38 —4.37 —6,25
1,0 — 12.50 5,25 —5,00 —9.40
0,4 — 8,28 3,39 —8,07 —4,57
0,6 — 11,09 4.63 —8,87 —6,57
0,4
6,8 — 12,49 5,85 —9,99 —9,37
1,0 — 14,29 6,92 —11,43 —12.97
0,6 — 12,75 5,99 —17,46 —13,50
0,6 0.8 — 16.39 7.39 — 19,66 —17,18
1.0 — 18.75 8,68 —22.50 —21,90 4.;
0,8 — 27,33 8.88 —46,61 —42,67
0,8
1,0 — 33.33 10,39 —53,33 —51.07
0,9 — 57,16 10.4! —106,12 — 102,32
0,9
1.0 — 63,16 11,2! —113,68 —110,72
434
Расчет пластинок
Продолжение табл. 2
6 Mj г
17,--- с йу/лу. а zzz^
1— 2а У Г
2rj'\
₽ 2Ь j; ~ 2Ь
“ = ₽ = -Г V 0 ч_ ~b
Ков- Ка к'ш. Kor' Kw,
г — а г — Ъ г — а г — а г = Ь г — а
0,1 — 5,78 0.17 0.277 — 6,00 0 0
0.2 — 7,35 0,34 0.498 — 5.82 0.18 0,230
0,1 0,4 —6,43 1,05 0.929 — 5,09 0,91 0.694
0.6 — 4.90 2.23 1,102 — 3,88 2,12 0.922
0,8 — 2,76 3,88 0,835 — 2,18 3.82 0,734
0,9 — 1.45 4.88 0,495 — 1.15 4,85 0,442
0,2 — 5,17 0.64 0.656 — 6,00 0 0
0,3 — 6,61 0.92 0.880 — 5,68 0.3! 0.258
0 2 0.4 — 6,10 1,31 1,067 — 5,25 0,75 0,493
0.6 — 4.65 2.43 1,207 —4,00 2,00 0.770
0,8 — 2,6! 3,99 0.894 — 2.25 3,75 0,648
0,4 — 3.25 2,1! 0.955 — 6,00 0 0
0,5 — 4,51 2,53 1.084 — 5,35 0.64 0.23!
0.4
0,6 — 3.85 3.04 1.122 — 4,57 1.43 0,394
0,8 — 2.16 4.33 0.846 — 2,57 3.43 0,437
0,6 —1.19 3.70 0.642 — 6.00 0 0
0.6 0.7 — 2.38 4,17 0.666 — 4,78 1,22 0.154
0,8 — 1.68 4.7! 0,576 — 3,38 2,62 0,215
0,8 + 0.52 5.01 0,197 — 6,00 0 0
0.8
0.9 — 0,68 5,48 0,158 — 3,17 2,83 0.054
0,9 0.9 + 1,21 5,54 0.052 -6,00 0 0 .
Круглые пластинки
435
Продолжение табл. 2
8. 7 9 Ч 10_ х
V-' f а а —, а ’--ь
Кае-г — а kw. г — а Каг-г — а Kw. г — ft Каг г = а г = а
0.1 — 2,379 0.750 5,787 0,8266 — 1.802 0,6282
0,2 — 2.126 0,693 5,749 0,8260 — 1.610 0,5847
0.1 0,4 0,6 — 1,45! -0,753 0,504 0,274 5,340 4.336 0.804! 0.7049 X 1 сл о — цэ 0.4302 0,2355
0,8 — 0.215 0.080 2,597 0,4596 — 0,163 0,0694
0,9 -0.057 0.02! 1,413 0,2606 -0,043 0,0186
0.2 -2.192 0.813 3.681 0,5638 -1.585 0,4925
0.3 -1.861 0,711 3.646 0,563! -1.345 0,4383
0.2 0.4 — 1,497 0.586 3,526 0,5570 — 1.082 0.3673
0,6 -0.777 0,317 2,949 0,5014 — 0,562 0.2029
0.8 — 0,222 0,092 1,814 0,3361 — 0,160 0,0600
0,4 -1,710 0,787 1,633 0,1926 — 1.018 0,2113
0,4 0,5 0.6 — 1,288 — 0,888 0,602 0.42! 1,600 1.491 0,19! 8 0.1858 — 0.766 — 0,528 0.1688 0.1219
0,8 -0,254 0.122 0,985 0,1362 -0,151 0,0369
0.6 -1,165 0.530 0,618 0.0383 -0,481 0,0500
0,6 0,7 — 0,702 0.322 0,586 0,0377 -0,290 0.0327
0,8 — 0.333 0.154 0,481 0,0333 -0.137 0,0!63
0.8 0,8 0,9 -0.592 -0,157 0,184 0-049 0.135 0.103 0,0023 0,0020 1 1 О © S кэ 0.0035 0,0010
0.9 0.9 —0,298 0,053 0.032 0,0001 -0,030 * 0.0002
436
Расчет пластинок
Продолжение табл. 2
И. 12.
7 ч
Ж ' НН ж.
г Ли -„г
—Н 2а j J ' 1 га Л 2С
а ₽ 2Ь ' к гь •
а С а а с
а = р = Ъ “ “ — 0 7 ~
^сб- Лат. кш. K(jf<
г = а г = b г ~ а г — а г = b г -- а
0.1 — 0,869 0,747 0,1813 — 0,688 0.728 0,1496
0.2 -0,709 0.701 0.1600 — 0,561 0,686 0,1341
0.4 -0.371 0,534 0,0979 — 0,294 0,526 0,0844
0,!
0,6 — 0,129 0,309 0,0390 — 0,102 0.306 0,0343
0,8 — 0.018 0,098 0,0062 — 0.014 о у97 0,0056
0.9 — 0,002 0,027 0,0009 — 0,002 0,027 0,0008
0,2 -0,672 0.730 0.1753 — 0,579 0.668 0.1120
0,3 — 0.507 0,650 0,1422 —0,436 0,604 0.0944
0,2 0.4 -0.352 0,549 0,1059 — 0.303 0,517 0.0728
0,6 —0,122 0.314 0.0418 -0,105 0.303 0.0303
0,8 — 0,017 0.098 0,0066 — 0,015 0,097 0,0050
0,4 — 0,292 0,596 0,0995 — 0.346 0.474 0.0443
0,6 -0,184 0,464 0,0672 — 0,218 0.387 0.0324
0.4
0.6 — 0.101 0-.330 0,0396 — 0,120 0,288 0,0204
0.8 — 0.014 0,100 0.0063 — 0.017 0,094 0.0036
0,6 — 0.079 0,348 0,0269 — 0.158 0.250 0.0ИЮ
0.6 0.7 — 0.036 0,213 0,0132 — 0.07! 0.169 0,0056
0,8 -0.011 0,103 0,0045 — 0,022 0,089 0.0021
0,8 — 0.008 0.105 0,0020 — 0.040 0.072 0.0007
0,8
0,9 — 0,00! 0,028 0,0003 — 0,005 0.024 0,0001
0.9 0.9 — 0,001 0.028 0,0001 — 0.010 0,019 0,0000
Круглые пластинки
437
Продолжение табл. 2
а ₽ 13 - 1 2а 2г, 2Ь PL 14. “О Л/ г± ь
ь
а
К'аг. г = а K'W' r =ь г ~ а Kw. г = b
0,1 0.2 0,4 0.6 0,8 0.9 1.0 0,666 1.355 1,791 2,136 2,292 2,440 0.0159 0,0985 0.2128 0,3398 0,4042 0.4677 —6.09 — 6.48 — 7,12 — 8.02 -8.57 — 9.18 - 0,349 — 1.291 — 2,317 — 3,243 — 3,628 -3,943
0,2 0.4 0,6 0.8 0.9 1,0 0,678 1.108 1,447 1,600 1,746 0,0432 0,1325 0,2397 0,2952 0,3503 — 6.38 — 7 01 — 7.90 — 8,44 -9,04 — 0,920 — 1.909 — 2,784 — 3,138 — 3,418
0,4 0.6 0.8 0,9 1,0 0,404 0.723 0,867 1.004 0.0274 0.0856 0,1 191 0,1530 — 6.59 — 7,43 -7,93 — 8.50 со ю — -*г О '*’ сч — СО СО СП — <- о —’ с7 ; 1 i 1
0,8 0.290 0.0148 —е,7ь — 0.634
0,6 0.9 0,421 0.0287 — 7.22 — 9,841
1,0 0.546 0,9439 -7,73 — 0,958
0,9 9.1 16 0.0016 — 6,4 1 — 0.165
0.8
1,0 0.227 0.0051 — 6.86 — 0.232
0,9 1.0 0.104 0,0006 — 6.43 — 0,056
438
Расчет пластинок
Продолжение тзбл 2
— ^оО’ г ~ 0 г - 0 к;. г = b г = 0 Ко,, г = * к«,-г = 0
0 0.1 0,2 0.4 0,6 0,8 0,9 ОО — 1,595 -1,159 — 0,709 — 0,424 -0.199 - 0.097 0,552 0,536 0,501 0,400 0,273 0,136 0,068 — 0,669 -0.662 — 0,642 — 0,562 — 0,428 -0.241 — 0,127 оо -1,122 -0.701 — 0,308 -0,118 — 0,027 — 0,006 0,478 0.473 0,458 0,401 0,306 0,172 0,091 0,217 0.205 0.181 0,119 0,059 0,016 0,004
0 17 । ч* t i >-4- 18 1 4- 'J
- чн |„ 2i 2Ь
К or ~ Kafr г =~- 0 г = 0 к;, г = ъ Kfjr — г = Л г — b *«',• Г = 0
0.1 0.2 0.4 0,6 0,8 0.9 1.0 — 3.92 — 3,93 — 4,24 — 4,66 -5,24 -5,60 -6,00 0,17 0.52 1.47 2,52 3,47 3,87 4.20 — 0,08 — 0.34 — 1,34 — 3.02 — 5,38 — 6,80 — 8,40 — 3,86 -3,74 — 3,28 — 2,50 — 1,40 -0,74 0 0,06 0.24 0.96 2.16 3,84 4.86 6,00 0.126 0,352 0,800 ],лл4 0,780 0,467 0
е 19. к »-4- 20. ₽ = -Г
М^ччр 2b L ^--.1 2Ь
Ког ~ КО0. г = 0 кш. г = 0 Кф. Г = b K<jr ~ г = 0 г = b Кш. г = 0
0 0,1 0,2 0.4 0,6 0,8 — 1,238 — 1. 178 — 1,052 -0,718 -0,373 -0.107 0,696 0,679 0,630 0.461 0,251 0,074 — 1.050 — 1.029 — 0.968 — 0,741 -0,430 — 0.136 —0,488 — 0,443 - 0,361 — 0,189 -0.066 -0.010 0,750 0.735 0,691 0,529 0,307 0.097 0,1706 0,1640 0,1459 0,0905 0,0364 0,0059
Круглые пластинки
439
Температурные напряжения. Если температура меняется по толщине и вдоль радиуса пластинки Т = / (г, г), где z — расстояние от срединной плоскости (—0,56 + г + 0,56), то в основных соотношениях (5) появляются дополнительные члены фг (г):
пластинка с отверстием, а + 0:
ФТ1 = 0; фГ2 (л) =
1 —v (*
—2— I ггМт (Г1) dr с,
Фгз (г) = (1 — v) Л4Г (г) - <рГ2 (г);
ФТ4 (г) = ~
ФГ6 (^)
то
Dr
ФГ4 (r!)drj;
= (V+V)
г = Ь = 61, а в схемах 1 н 5 г — а — = Ь^, Ь = 6а и а = bjbt = Ь. Так как
dw1 , <_>
-^ = 6) =
= (W-^nM)^3- =
dw11 . ,
= ___{r = a) =
Ьг t ,
м _ K'^-K'^ -
m~ p +
где 5 = bjbt, h = hjhi, а цифры в индексе при К'^ указывают номер соо ветствующей схемы в табл.
Прогиб при г = 0
w (0) — w1 (0) + а/п (а) =
= [(^15-^17)^3 +
РЛ2 + К' < 4- тК'd —— .
Например, для 6 = 0,4 и h — 0,4 в схемах 1 и 5 следует положить а = =• Р = 6 = 0,4; тогда
-0,669-0,4* + 1,351 п 1ЙО
- —0,162,
2.
m= — 8,4-0,4‘ — 8,07 ш(0) = [(0,552 + 0,162-4,4)-0,46 + + 0,721-0,162-3,39] X
РМ РЫ
X -^- = 0,184 4^-.
Ehl Ehj
(17) отверстия, а — 0:
пластинка
Фт1 = 0’ ФТ2 ('•) = (! -V) X ~ г
A- j riMr^dTi— -^Мт(0) ;
о
Фтз (') = (1 ~v) х
X [Мт- (г) — Мт (0)] — фГ2 (Г);
он
-О’ с
здесь
без
Фт4 (f) = - ~D X
о
1 — v
w+4Mr(0) ;
фТ6(г) = j Фт4(г1И1; о
+0,5/1
ад-44 j
—0,5/1
(18)
г) г dz.
(19)
440
Расчет пластинок
При г -* 0 в формулах (18) г
1 Г
yr j ^Мт 01) dt\ -> 0,5Мт (0), по-о
этому <рг (0) — 0.
Для температурного поля, симметричного относительно срединной плоскости пластинки, Л4г^0. При линейном законе
Т (г, г) = ТСР (г) + ДТ (г) г/Л,
где ДТ — разность температур
по-
верхностей;
Мт (г) =
Е№х ДТ (г) 12(1 — v)
Прнмер 6. Найти температурные напряжения и деформации в пластинке без отверстия для постоянной по радиусу разности температур ДТ = const при свободном и заделанном наружном контуре. Если Мт = const, то по формулам (18) фТ2 = фТз = 0;
, , гМт
Фт4(г)- D(i4-V)’
, х г2Мт
ЧТ5(Г)~- 2£(1+v) •
Для свободного контура Mr (ft) = = Мг (0) = 0, т. е. Мг (г) = Мд (г) = = 0 и напряжений в пластинке нет,
<Ри> Мт
а ее кривизна^- = - по-
стоянна. При заделанном наружном dw b
контуре ^-(ft) = —Мг(0) -ЬМТ
— д'(1 + V) = °- откуда м г (0) = М т, т.е. МГ (г) = Мд (г) = Мт, но и> (г) = 0 (пластинка остается плоской). Максимальные температурные напряжения в пластинке будут
ЕаЛТ
max — 00 max — -g p"_. (20)
Выражение (20) справедливо для пластинки, защемленной по любому контуру.
ПРОРЫВНЫЕ МЕМБРАНЫ
В технике находят применение прорывные мембраны, которые разрушаются при заданном давлеини <?раар-
Рис. S. К расчету прорывной мембраны
Так как такие мембраны обычно изготовляют из высокопластичных материалов, то к моменту разрушения первоначально плоская пластинка толщиной h и радиусом ft сильно прогибается, приближаясь к участку сферы радиусом R = ft/sin (р (рис. 5), толщина ее уменьшается от h до hlt а распределение напряжений по толщине становится почти постоянным (кроме узкой области, примыкающей к заделке). Для участка сферической оболочки нз условий равновесия
„ <?РазрЯ
аразр — стг — а0-----2/^---‘
При больших пластических деформациях сжимаемостью материала можно пренебречь. Первоначальный объем пластинки V = nlPh, объем мембраны в деформированном состоянии — = S-Ji^ где ее поверхность =
= 2jiR2 (1 — cos ф). Из условия Vi = = V слецует.
. . ь*
1 2R2 U — cos ф)
= h sln2 Ф /92)
2(1 — cos ф) ‘ '
В момент разрушения относительная линейная деформация
Ra> , ф .
еразр-ег-ее- т -1 - —;-----------1.
(23)
В качестве условий разрушения при больших пластических деформациях мембраны, находящейся в двухосном напряженном состоянии, примем:
а) интенсивность напряжений а/ должна достичь истнииого предела прочности SR;
Прямоугольные пластинки
Рис. в. Зависимость разрушающего давления Vpd3p и угла ф от относительного удлинения материала при разрыве б
б) интенсивность деформаций е; должна достичь относительного удлинения материала при разрыве б.
Так как для двухосного напряженного состояния при v — 0,5
ct = у0| — 0^2+ о^,
е/ тт?" "V ®i + eie2 + е2’ р о
то при о, - 02 — Оразр и Bi = е2 = = f';n-p имеем Of “ Оразр, &i — 2бразр< откуда условия разрушения
Оразр = 8разр = 0,56. (24)
Из (21)—(24) следует:
_ Suh sin3 <р
?Газр j — cos >
6=-2
Ф sintp
1). (25)
Задаваясь рядом значений угла ф, находим величину <р*, соответствующую заданному значению 6, и по определяем разрушающую нагрузку ?разр.
Приближенно тогда
SK « ов (I 6),
?разрб _ Sin3 <р овЛ 1 — cos «р
(1+6).
(26)
Расчетная зависимость <?разр — f (6) по формуле (26) приведена на рис. 6, где также показана кривая ф(6). Разрушающее давление увеличивается с ростом пластичности материала, так как при этом к моменту разрушения кривизна мембраны становится большей. Однако начиная с 6 ® 40% давление 9радр меняется слабо.
ПРЯМОУГОЛЬНЫЕ ПЛАСТИНКИ
В прямоугольных пластинках (рис. 7) в сечениях, параллельных внешним сторонам пластинки, возникают изгибающие моменты Мх и Му, крутящие моменты Мху = —Мух и поперечные силы Qx, Qy. Из условий равновесия элемента пластинки и соотношений упругости
dlw , „ <3% , d*w q
1К + 2 ~дх-ду2' ' НуГ ~~ ТУ 1
(27)
Решение этого уравнения обычно ищут в форме двойных бесконечных рядов.
Пример 1. Свободно опертая пластинка с размерами сторон а и 6 нагружена давлением, распределенным по закону ях яу
Я = sm -------sin -г- •
а о
Граничные условия: w — О, Мх — О при х = 0 и х = а; ш = О, Му = О при у ~ 0 и у — Ь.
Легко проверить, что в этом случае уравнению (2) и всем граничным условиям удовлетворяет решение
, ях
X sin-----sin
а
яу Ь
3. Коэффициенты прогибов н напряжений для прямоугольных пластинок ___________________________________________
—----------------------- " oJL л — ««nnci " Сосредоточенная сила в центре Р *
Равномерная нагрузка q — const р м „ ___
Отиоше-ние сторон сч0ооднь е <поры — q^LOHst Заде /za? \' JR упоре сделка
b н
- ——— В середине
В середине В центре В центре стороны b
Б центре В центре ~КОХ В центре стороны Ь Ках K'w Ki Ках
1.0 0,0443 0.2874 0,0138 0.308 0.1265 0.0611 0.754
1,1 0,0530 0,3324 0.0164 0,349 0.1391 0.0668 0.845
1,2 0,0616 0,3762 0,0188 0.383 0.1478 0.0706 0.894
1.3 0.0697 0.4164 0.0209 0.412 0,1554 0 0737 0.935
1.4 0.0770 0,4530 0.0226 0.436 0,1621 0,0755 0.962
1.5 0.0843 0,4872 0.0240 0,454 0,1670 0.0768 0.98*
1.6 0.0906 0.5172 0.0251 0.468 0.1714 0,0777 0.991
1,7 0,0963 0,5448 0.0260 0.480 0,1743 0.0783 0.997
1.8 0.Ю17 0,5688 0.0267 0.487 0,1768 0.0786 1.000
1/9 0,1063 0,5910 0.0272 0.493 0,1783 0.0787 1,003
2,0 0.1106 0,6102 0.0277 0.497 0.1803 0.0788 1.004
3.0 0.1335 0,7134 0,0283 0.500 0,1843 0,0790 1.007
4.0 0,1400 0.7410 0,0284 0.500 0.1850 0.0791 1.008
5,0 0,1416 0.7476 0,0284 0,500 0,1851 0.0791 1,008
ао 0,1422 0,7500 0.0284 0.500 0,1851 0.0791 1.008
• В центре К'а = —« £ " >. ->
Расчет пластинок
Основные зависимости
443
Рис. 7. Поперечные силы 0х, 0у, внутренние изгибающие моменты Л1Х, Му и крутящие мо-менты Мху и Мух в пря-моугольной пластинке
Максимальные изгибающие моменты и максимальный прогиб в центре пластинки
2(1 — va) д3а*
4' +(НТ №'
В общем случае формулы для максимальных напряжений И МакСимаЛЬ
ного прогиба прямоугольной пластинки можно записать в виде
„ „ qa2 qa*
°max ~ , t^max — A® ’ >
(28) причем коэффициенты Ка и A’fll зависят от отношения сторон пластинки bl а и от коэффициента v.
Прн действии сосредоточенной силы - Л" Р - К' Ра*
ашах Аст да » ^max £ДЗ *
(29)
Значения коэффициентов Л,, (Л^) и Л'щ (Кш) для некоторых расчетных случаев при v ~ 0,3 приведены в табл. 3.
Глава 24
РАСЧЕТ НА ПРОЧНОСТЬ ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК
ОСНОВНЫЕ ЗАВИСИМОСТИ
Рассмотрим цилиндрическую оболочку постоянной толщины под действием осесимметричных нагрузок и нагрева (рнс. 1). Этот случай имеет основное практическое значение.
Уравнение радиального прогиба оболочки. Если w (х) — радиальное перемещение точек срединной поверхности (положительному значению соответствует перемещение точек на окруж-ноств большего радиуса), то будем
иметь следующее дифференциальное уравнение:
dlw , Eh Eh r
D -r-Y- H----— UI -= q 4 --aT„ —
dx* a2 ' a 0
, r , d2 / KT \ ,,
-O(l+v)-^r (И
Eh?
12 (1 — v2)
цилиидриче-E — модуль
где
ская
D =
жесткость, Нем;
упругости материала; h—толщина оболочки, см; а — радиус срединной
поверхности, см; д — распределенная
444
Расчет на прочность цилиндрических оболочек
Рис. 1. Силовые факторы в сечениях ци* линдрическсй оболочки
растягивающая сила
NQ=--Eh (^-а.Ть'у (4)
изгибающий момент
ms = d[,^. + (1+v)C^L].
(5)
При отсутствии нагрева Mr, = vA4x.
Напряжение изгиба в поперечном сечении распределяется по толщине стенки лииейно
нагрузка, приложенная к срединной поверхности оболочки, Н/см2 (например, внутреннее давление); а — коэффициент линейного расширения, 1/°С; Те — температура срединной поверхности оболочки, °C; ДТ — разность температур наружной и внутренней поверхности оболочки, °C; v — коэффициент Пуассона.
Распределение температур по толщине стенки предполагается линейным .
В поперечном сечении оболочки [сечении, перпендикулярном к осн (рис. 2)] на единицу длины действуют: перерезывающая сила, Н/см,
где z — расстояние от точки до срединной поверхности оболочки.
Касательное напряжение в поперечном сеченни
Q ( 3 6z2 \
Т~ Л (. 2 Л2 /
(7)
В продольном сечении возникают нормальные напряжения растяжения
и изгиба
ай
0Р
7/8 Л
(8)
Q^D
аа
0и
12/Ив
Л3 г-
(9)
(2)
изгибающий момент, Н-см/см,
Г cPw ,. а ДТ ~1
^ = DL^+(1+v) ~7~J-
(3)
В продольном сечении (сечении, проходящем через ось) на единицу длины приходятся:
Нормальное напряжение в продольном сечеиии ;V0 12Л40
0в = —--------z.
В формулах (6), (7), (9) и (10) для 1 .
ружного слоя оболочки Z = -g- п,
1 , внутреннего г —-----
а)
Рис. 2. Напряжения в сечеинях оболочки; а — в поперечном; б — в продольном
6ви 6ер
(Ю) иа-для
Расчет, длинных оболочек
445
Рнс, 3. Длинная и короткая цилиндрические оболочки
Длинные и короткие оболочки. При расчете следует различать длинные и короткие цилиндрические оболочки (рис. 3) Основное отличие длинных оболочек состоит в том, что можно пренебречь влиянием нагрузок, приложенных к одному краю, на напряженное состояние возле другого края.
Более детальное исследование этого вопроса показывает, что оболочку можно считать длинной, если параметр оболочки
Р/ >3,
где
/3(1 -Vj "/ой
(Н)
Принимая v — 0,3, находим
_ 1.285
К =------ е
]/ой
(12)
Для длинной оболочки I > 2.4 1/ah-Если ввести относительную толщину h ~ hla, то получим — 2,4 Д/й"-
Например, при Я ~ находим — it) Q
0,76, прн й — -тхтг- lla 0,24,
РАСЧЕТ ДЛИННЫХ ОБОЛОЧЕК
Общее решение. Рассмотрим сначала случай, когда температурные напряжения отсутствуют (То — 0, ДТ — 0).
Общий интеграл однородного уравнения (1)
W = е~₽* (Cj cos fix +
+ С'а sin Рх), (13)
где величина Р определяется равенством (11). Произвольные постоянные Cj и С2 находят нз граничных условий. Для полного решения к величине w0 (х) следует добавить частное решение неоднородного уравнения (1). Например, при постоянном по длине внутреннем давлении q это частное решение имеет вид
«ч (х) = “дГ
Основные случаи расчета длинных цилиндрических оболочек:
1-й случай (рис. 4. а).
х= 0;
d2w
——— == о-
dx*
<Pw Q . d?' ~ ~D ’
— e—₽x cos ^Л.
w 2P3D ’
a:' (x) = — x
X (cos Px + sin Px);
w (0) = - jjp3!?- ’
= -$- e-^ sin Px; Mx (0) = 0.
P
446
Расчет на прочность цилиндрических оболочек
Рис. 4. Расчетные случаи для длинной
цилиндрической оболочки
2-й случай (рис. 4, б).
„ du> „ d3w Q х=°; -^- = 0; =
w W = T^D е”₽Х Х
X (cos fix -|- sin px);
®(0) = ”4p3D ’ W' (x) = ~ 2P2£> X X sin px; w' (0) = 0;
Mx W = -Я- e“px (sin px — cos Px);
zp
З-й с л
х = 0;
МИО) = ~|.
у ч а й (рис. 4, в).
d2w _ M . cPw _____
~dx^ = ~D~’’ ~d^~ = U;
e~px (cos px — sin Px);
W 2₽2£>
W' (х) :=
,„4 M
W (0) 2p2D ’
e~Px cos Px;
Mx (x) = Me (sin Px + cos Px);
Mx (0) = M.
4-й случай (рис. 4, e).
„ „ d2w M
x = 0; ш — 0; —5-5- — -=r-;
dx2 D ’
® w = — "2^- e~®x sin ₽*;w (°) = °;
Al ____ax
w (X)== 2p“e X
X (cos px — sin px);
, M
W (°)- 2pD ’
Mx (x) — cos fix\ Mx (0) --= M. 5-й случай (рис. 4, д).
x — 0; w = 0; w' — 0;
w (x) = -^r- [1 — e®x(cospx 4- sin px)]; w (0) = 0;
w' (x) = 2p e—|3x sin px; w' (0) = 0;
Mx (x) = -Лг e-Pj! (cos P* ~ sin zp
(0) ~ 2^2 *
Расчет коротких оболочек
447
6-й случай (рис. 4, е).
d2w
х = 0; w = 0; -7-5- = 0; dx2
w (x) = — e~e*cos
w (0) = 0;
»' (*) = Pe_₽* (cos Px + sin Px);
7-й с л у
x = 0:
(0) = ₽ -Й-; E.IX
Ms (x) = — e~B* sin px;
Mx (0) = 0.
чай (рис. 4, ж).
d2w dsw
“dF = 0: ~d^=0'
aa2
ш (x) = 0;
Mx (x) = 0.
w
РАСЧЕТ КОРОТКИХ ОБОЛОЧЕК
Общее решение. Если параметр оболочки Р/ < 3, то следует учитывать условия закрепления по обоим краям оболочки.
Решение уравнения (1) для короткой оболочки может быть представлено В следующей форме:
w (х) = w (0) Ко (рх)
+ Т +
1 d2w
+ ”^2--(0) ^2 (РХ) +
1 d?w
+ “F У-(0)Кз(М +
+- -pjp- J Кз [р (х — Xi)] f (Xi) dxj, o
(14)
ГДе К» (Px), Ki (Px), Кз (Px), K3 (Px) -функции A. H. Крылова, определяемые равенствами:
Кз (Рх) = ch Рх cos Рх;
КЦрх) = -i- (ch Pxsin Px-|-shpxcosPx);
Ks (Px) — sh Px sin Px; _
*S (Px) = -^ (ch px sin Px —
— sh Px cos px).
Значения этих функций приведены в табл. 1.
Функция / (х), входящая в формулу (14), представляет собой правую часть уравнения (1).
Основные случаи расчета коротких цилиндрических оболочек. В приведенных ниже формулах значения функции Крылова при х = I обозначены соответственно через Ко, К1г Кз и К3.
Параметр
1/3(1-у*)..1,285
Р - V a2h? ~ YTh '
Здесь v = 0,3 — коэффициент Пуассона; а — радиус оболочки; h — толщина оболочки.
Цилиндрическая жесткость
1-й с л у ч а й (рнс. 5, о).
Сечение х = 0 свободное, сечение х = I — жесткая заделка:
,пч Q КхКз - К3К0 w <0) - «Рх орз ’ ф! - + 4К,Кз ’
W' (0) = -фх ;
K0K2 + 4Ki .
1 ' Ко + 4К,К3 ’
W (х) =- [<Р1Ко (Рх) — IpjKl (Рх) +
+ К3 (Рх)];
М-х (х) = [—ityiKi (₽х) +
4- 4ф1Кз (Рх) 4* Ki (Рх)].
2-й с л у ч а й (рис. 5, б).
448
Расчет на прочность цилиндрических оболочек
1 Функции А Н Крылова
Рх к, (рх) Л, (Рх) К, (рх) К,(Рх)
0 1 0 0 0
0 002 1 0000 0 0020 0 00000 0 00000
0,004 1 0000 0 0040 0 00001 0 00000
0,006 1 0000 0 0060 0 00002 0 00000
0,008 1 0000 0 0080 0 00003 0 00000
0 010 1 0000 0 0100 0 00005 0 00000
0 012 I 0000 0 0/20 0 00007 0 00000
0 014 1 0000 0 0140 0 00010 0 00000
0 016 1 0000 0 0160 0 000'3 0 00000
0 018 1 0000 0 0180 0 00016 0 00000
0 020 1 0000 0 0200 0 0002 0 00000
0,040 1 0000 0 0400 0 0008 0 00001
0 060 1 0000 0 0600 0 0018 0 00005
0,080 1 0000 0 0800 0 0032 0 00010
0 10 1 0000 0 1000 0 0050 0 00015
0 12 1 0000 0 1200 0 0072 0 00030
0 14 0 9999 0 1400 0 0098 0 00045
0 16 0 9999 0 1600 0 0128 0 00070
0 18 0 9998 0 1799 0 0162 0 00097
0 20 0 0997 0 2000 0 0200 0 0013а
0 22 0 9996 0 2139 0 0242 0 01 177
0 24 0 9995 0 2400 0 0288 0 00230
0,26 0 9992 0 2599 0 0388 0 00292
0 28 0 9990 0 2799 0 0392 0 00367
0 30 0 9987 0 2999 0 0450 0 00450
0 32 0 9983 0 3199 0 0512 0 00545
0 34 0 9978 0 3398 0 0578 0 006э7
0 36 0 9972 0 3548 0 0648 0 00775
0 38 U 9965 0 3797 0 0722 О 00915
0 40 0 9957 0 3996 0 0800 0 0107
0 42 0 9948 0 4196 0 0881 0 0123
0 44 0 9938 0 4394 0 0967 0 0142
0 46 0 9925 0 4593 0 1057 0 0162
0 48 0 991 1 0 4791 0 1151 0 0184
0 50 0 9895 0 4989 0 1249 0 0208
0 52 0 9878 0 5187 0 1351 0 0234
0 54 0 9858 0 5384 0 1456 0 3262
0 56 0 9836 0 5э82 0 1566 0 0292
0 58 0 9811 0 5778 0 1680 0 0325
0 60 0 9784 0 5974 0 1797 0 озьо
0 62 0 9754 0 6169 0 1919 0 0397
0 64 0 9721 0 6364 0 2044 0 0436
0 66 0 9684 0 6558 0 2'73 0 0*79
0 68 0 9644 0 6751 0 2306 0 0524
0 70 0 9600 0 6944 0 2443 0 0574
0 72 0 9552 0 7135 0 2584 0 0621
0,74 0 9501 0 ”326 0 2729 0 0674
0 76 0 9444 0 751 5 1 2877 0 0730
0 78 0 J381 0 7704 0 3029 о 0789
0 80 0 9318 0 7891 0 3185 0 0851
0 82 0 9247 0 8077 0 3345 0 0917
0 84 0 9171 0 8261 0 3508 0 0985
0 86 0 9090 0 8443 0 3675 0 1057
0 88 0 9002 0 8624 0 3846 0 1 132
0 90 0 8931 0 8803 0 4020 0 1211
0 92 0 8808 0 8980 0 4 198 0 1293
0 94 0 8701 0 9155 0 4379 0 1379
0,96 0 8587 0 °328 0 4564 0 1468
0 98 0 84бо 0 9499 0 4753 0 1562
1 00 0 8387 0 9667 0 4944 0 1658
1 02 0 8201 0 9832 0 5139 0 1759
I 04 0 80э6 0 9995 0 5337 0 1364
1,06 0 7902 1 0154 0 5530 0 1973
1,08 0 7740 1 031 1 0 5744 0 2086
1,10 0 "„68 1 0464 0 5951 0 2202
1,12 0 7387 1 0613 0 6162 0 2323
1,14 0 7196 1 0759 0 6376 0 2449
1 16 0 6995 1 0901 0,6593 0 2579
Расчет коротких оболочек
449
Продолжение табл. 1
₽х Ко (Рх) К, (Рх) К, (рх) К, (Рх)
1,18 0,6784 1,1039 0.6812 0.2713
1.20 0,6561 1,1173 0.7034 0,2851
1,22 0,6330 1,1306 0,7259 0,2996
1,24 0,6082 1,1426 0,7486 0,3142
1,26 0,5824 1,1545 0,7716 0.3294
1,28 0,5555 1,1659 0.7940 0,3450
1.30 0,5272 1,1767 0,8182 0.3612
1,32 0,4977 1,1870 0,8419 0,3778
1,34 0,4668 1,1966 0,8657 0,3940
1,36 0,4345 1,2056 0,8897 0,1124
1,38 0,4008 1,2139 0,9139 0,4304
1,40 0,3656 1,2216 0,9383 0,4489
1,42 0,3289 1,2286 0,9628 0,4680
1,44 0,2907 1,2333 0,9764 0,4882
1,46 0.2509 1.2402 1,0122 0,5075
1,48 0.2095 1,2448 1,0370 0,5280
1,50 0.1664 1,2485 1,0619 0.5489
1.52 0,1216 1,2514 1,0870 0,5704
1.54 0,0746 1,2534 1,1120 0,5924
1,56 0,0268 1,2544 1.1371 0.6149
2 0,0000 1,2546 1.1506 0,6273
1,58 0.0233 1,2545 1,1622 0,6379
1,60 — 0,0753 1,2535 1,1872 0,6614
1,62 -0,129! 1.2514 1,2123 0.6854
1,64 — 0,1819 1,2483 1,2373 0,7099
1.66 — 0,2427 1,2440 1,2622 0,7349
1,68 — 0,3026 1,2386 1,2971 0,7604
1.70 — 0.3644 1,2321 1,3118 0,7862
1,72 --0.4284 1,2240 1,3363 0,8129
1.74 — 0,4945 1,2148 1,3607 0,8398
1 76 — 0,5628 1,2042 1,3849 0,8673
1,78 -0,6333 1,1923 1,4089 0.8952
1,80 — 0,7060 1,1788 1,4326 0,9236
1,82 — 0,781 1 1,1640 1,4560 0 9525
1,84 — 0.8584 1,1476 1,4791 0,9819
1,86 — 0,9383 1,1296 1,5019 1 0117
1.88 -1,0203 1,1100 1,5243 1,0419
1,90 — 1,1049 1.0888 1,5463 1,0727
1.92 - 1.1920 1.0658 1,5679 1,1038
1,94 — 1,2815 1,0411 1,5889 1,1354
1,96 — 1,3736 1,0145 1,6095 1,1673
1,98 —1.4683 1,9861 1,6295 1, 1997
2,00 — 1,5656 0.9557 1,6489 1,2325
2,02 — 1,6656 0.9235 1,6677 1,2657
2,04 — 1,7682 0.8891 1,6859 1,2992
2,06 — 1.8734 0.8528 1,7033 1,3331
2,08 — 1.9815 0,8142 1 7199 1,3674
2,10 - 2.0923 0,7735 1,7358 1,4019
2,12 -2,2058 0,7305 1,7509 1,4368
2.14 — 2,3221 0.6852 1,7650 1,4719
2.16 — 2,4413 0,6376 1,7783 1,5074
2,18 — 2,5633 0,5876 1,7905 1.5431
2,20 — 2,6882 0,5351 1,8018 1.5790
2.22 -2,8160 0.4800 1.8119 1.6151
2.24 -2.9466 0,4224 1,8209 1,6515
2,26 — 3,0802 0,3621 1,8288 1,6880
2,28 — 3,2167 0,2992 1,8354 1.7246
2.30 — 3,3562 0,2334 1,8407 1,7614
2.32 — 3,4986 0,1648 1,8447 1,7983
2.34 — 3,6439 0.0935 1,8473 1,8352
2,36 — 3,7922 0,0196 1,8484 1,872.1
2.38 — 3,9435 — 0,0582 1,8480 1.9091
2,40 -4,0976 --0,1386 1.8461 1,9460
2,42 -4,2548 -0,2221 1,8425 1,9829
2,44 — 4,4150 — 0,3088 1.8372 2,0198
2,46 — 4,5780 — 0,3987 1,8301 2,0564
'5 Заказ 402
450
Расчет на прочность цилиндрических оболочек
Продолжение табл. I
вх (Рх) К.(Рх) К,(0х) К, (&х)
2,48 — 4,7439 — 0.4920 1,8212 2,0929
2,50 — 4.9128 — 0.5885 1,8104 2,1292
2,52 — 5,0846 -0.6885 1,7976 2,1653
2,54 — 5,2593 -0,7919 1,7829 2,2012
2,56 -5,4368 — 0,8989 1,7660 2,2366
2,58 — 5.6172 — 1,0094 1.7469 2. ?718
2.60 — 5,8003 -1.1236 1,7255 2.3065
2,62 — 5.9862 -1,2415 1,7019 2,3408
2,64 —6,1748 - 1,3630 1,6759 2,3746
2,66 -6.3661 -1,4881 1,6473 2,4078
2,68 — 6,6580 -1,6477 1,6163 2.4404
2,70 — 6,7565 - 1,7509 1,5826 2,4724
2,72 — 6,9556 — 1,8880 1,5462 2,5037
2,74 — 7,1571 — 2,0291 1,5071 2,5343
2,76 — 7.361 1 — 2,1743 1,4650 2,5640
2,78 — 7,5673 — 2,3236 1,4201 2,5928
2,80 — 7.7759 -2,4770 1,3721 2.6208
2.82 -7.9866 — 2,6346 1,3210 2,6477
2,84 — 8,1995 — 2,7965 1.2667 2,6736
2,86 — 8.4144 — 2,9626 1,2091 2,6984
2.88 — 8,6312 — 3.1331 1, 1481 2,7219
2,90 — 8,8471 — 3,3079 1,0837 2,7443
2,92 — 9,0708 -3,4871 1.0158 2,7653
2,94 — 9.2923 — 3,6707 1,9442 2,7849
2,96 — 9,5158 -3,8588 0,8689 2.8030
2.98 — 9,7404 — 4,0513 0,7898 2,8196
3.00 -9,9669 — 4,2484 0,7068 2.8346
3,02 — 10,1943 — 4,4500 0,6198 2,8479
3,04 — 10.4225 — 4.6557 0,5288 2,8593
3,06 — 10.6516 — 4,8669 0,4336 2,8690
3,08 -10,8815 — 5,0823 0,3341 2,8766
3.10 — 11,1119 — 5,3022 0.2303 2,8823
3,12 — 11,3427 -5,5268 0,1220 2,8858
3. 14 — 1 1,5919 -5,7559 0,0091 2.8872
п -11.5919 -5,7743 0,0000 2,8872
3,16 — 1 1,8045 -5.9897 — 0.1083 2,8862
3,18 — 12.0353 — 6,2281 — 0.2304 2,8828
3,20 - 12,2656 -6,4710 — 0,3574 2,8769
3,22 — 12.4956 — 6,7187 — 0,4893 2,8685
3,24 — 12,7373 — 6,9709 — 0,6262 2,8573
3.26 — 12,9527 — 7,2277 — 0,7681 2,8434
3,28 — 13,1795 — 7,4890 — 0,9153 2,8266
3,30 — 13,4048 — 7.7549 — 1,0678 2.8067
3,32 -13,6286 -8,0252 — 1,2255 2,7838
3,34 — 13,8501 — 8,8000 — 1,3888 2,7577
3,36 — 14,0695 - 8,5792 — 1,5576 2,7282
3,38 — 14.2866 — 8,8627 — 1,7320 2.6953
3.40 — 14,5008 — 9,1506 -1,9121 2,6589
3,42 — 14,71 18 — 9,4427 — 2,0980 2.6188
3,44 — 14,9197 — 9.7391 — 2,2899 2.5750
3,46 -15,1238 — 10.0395 -2.4876 2,5272
3,48 — 15,3238 — 10,3440 — 2.6916 2.4754
3,50 — 15,5198 — 10.6524 — 2.9014 2,4195
3,52 — 15,7108 — 10,9647 — 3.1176 2.3593
3,54 — 15,8971 - 1 1,2808 — 3,3400 2.2948
3.56 - 16.0780 — 11,6007 — 3,5689 2,2281
3,58 - 16,2531 — 1 1,9240 — 3,8041 2,1519
3.60 -16,<218 — 12,2507 — 4,0458 2.0735
Рис. 5. Расчетные случаи для короткой цилиндрической оболочки
Расчет, коротких оболочек
452
Расчет на прочность цилиндрических оболочек
Сечение х = 0 свободное; сечеиие КЧ-К0Кз .
х = 1 — шарнирная опора: 4(К1-КгК3) ’
Q w (0) = <₽а дрз J ^ (*) = 2^5 [<Р«К0 (Рх) —
Ki + 4/q . —' Ф4К1 (рх) + Кз (рх)];
фа ~ 4 (КХК2 - КоКз) ’ О W' (0) = —ф2 ^5; Ко*! + 4К2К3 . Л4Х (х) = [—4<р4К2 (Рх) + + 41р4Кз (рх) 4- К1 (рх)]. 5-й случай (рис. 5, д).
Ъ " 4 (КХЯ2 - КоКз) ’ w (х> = Щ5 [<₽2К° ^х) ~ - ф2Хх (Рх) + Кз (рх)]; Мх (х) = (—4ф2К2 (рх) + Сечение х -- 0 — скользящая заделка; сечение х = 1 — жесткая заделка: ^ (°) = <рз щз; m Ki - кхк3 .
фо КЛКг + 4КзКз ’
+ 4тр2К3 (рх) -|- Кг (Рх)]• 3-й случай (рис. 5, в). Сечение х --- 0 свободное; сечение Ф как, + 4К1 .
х = 1 — скользящая заделка: ъ КоК1 + 4К2К3 ’
^(0) = <₽3-^; w (х) = 1фбК° ^х) ~
Ка + 4К? — ФзКг (рх) + Кз (рх)];
Фз 4(К1Ко + 4К2К3) ’ w‘ = КгКг - кок3 . Мх (х) = [-4<р6К2 (рх) - — ф6К0 (Рх) + Кг (Рх)]. 6-й случай (рис. 5, е).
4d /GKo + 4/СЛз ’ W = Щз [фзКо (?х) -— фзКх (Рх) + Кз (Рх)]; Мх (X) = -jj- [ <рзКз (Рх) + 44’зКз (Рх) + Кг (Рх)]. 4-й случай (рис. 5, г). Сечение х = 0 свободное; сечение х — 1 свободное: Сечение х = 0 — скользящая заделка; сечение х = 1 — шарнирная опора: ® (°) = Фе -^5 ; m _КгК;-К0К3. <₽«- К1 + 4К1 ’ мх(&) , Q D (°) = -ф» др ’ КоК1 4 4К2Кз .
К^ + 4К1 ’
а’(0) = ф^; КгКз — КдКз , W (Х) = 1<РвКо ^Х) — — Ф«К2 (Рх) + Кз (Рх)];
44 4(К1-КгК3) ’ w' (0)=-^; мх (х) = [—4фвКз (Рх) — -фЛо (рх) + Кг (Рх)].
Расчет коротких оболочек
453
7-й случай (рнс. 5, ж).
Сеченне х = 0 — скользящая заделка; сечение х = I — скользящая заделка:
w (0) 4,7 ^з ’
4,7 4 (Kf + Ki) ’
Мх (0) „ /n. Q
-^2 = ^(0) = -^^-;
. *1*2-^».
w = ^3 14,7X0 ~
— (Рх) + Кз (Рх)];
мх = "jr t—44,7X2 —
— "фтКо (Рх) + (Рх)]•
8-й случай (рис. 5, а).
Сеченне х = 0 — скользящая заделка; сеченне х = I свободное:
О
(0) = 4,8 Ор 1
___ ~Ь 4К1К3 .
ф8 ~ 4 (КоК, + 4/ВД ’
К1~К^
4’" ^Л-1 + 4К2/(3’
» (Х) = "Щз 14,8X0 (Рх) ~
— ф8^2 (Рх) + Кз (Рх)];
Мх (X) = А [—4ф8К2 (Рх) -
— фвЛ’о (Рх) 4- Л\ (рх)].
9-й случай (рнс. 5, и).
Сеченне х — 0 свободное; сечение х = I — жесткая заделка:
,п. м . Kl — KBK2 “Ч ) ф» рр2> фз- к% + 4КК3’
ю' (0) = -Ф9-~;
. _М\ + 4Л'2Кз.
4,9 Ц + 4К.К3 ’ м
W (х) = ’Dp214,9X0 ^х) ~
— (Рх) + А2 (Рх)];
(х) = М [—4<p9/(2 (Рх) +
+ 4ф9Кэ (Рх) + Ко (рх)].
10-й случай (рнс. 5, к).
Сеченне х = 0 свободное; сечеиие х = I — шарнирная опора;
Л1
w (°) = <pw -дрз;
= К<Л1 + 4К2К3 .
ф1<> 4(^а-^3)’
,П1 м
ш' (0) = -ф10 ;
.______+ 4Л1 .
4,10 4 (КЛ2 - К0К3) ’
М
(X) = -Щ2 lq)10X0 (РХ) —
— (рх) -Ь /(2 (рх)];
Мх (х) = М [—4ф10Ка (Рх) +
+ 4фюЛ4 (Рх) + Ко (Рх)].
11-й случай (рис. 5, л).
Сеченне х — 0 свободное; сечение х = I — скользящая заделка:
М
да(°)^фиЖ2’
__ ^1^2 ~~ КдКз ,
4,11 4 4Л'2/(3 ’
м
w (0) = —Фп -щ-;
. 4 4^_____.
4,11 K0Ki + 4KaKs ’
М
№ = ’Dp214,11X0 —
- + К2(рх)];
МХ (х) = м [—4фцКг (Рх) +
+ 4фцК8 (Рх) + Ко (Рх)].
12-й случай (рнс. 5, л).
454
Расчет на прочность цилиндрических оболочек
Сечение х — 0 свободное; сечение х = I свободное.
м
w (0) = 4,12 Тр2 ’
К0/С + 4/<5 .
ф1а ~ 4(^-К,К3) ’
М
w (0) = —Ф12-рр;
КоК1 + 4К2К3 .
ф’2 4 (К1 _ КгКз) -
м
w = "Dp f’P12^» ~
— (Р*) + ^2 (рх)];
Мх (х) ~ М [—4<pj2K2 (Рх) +
+ 4^12^3 (Рх) + Ко (Рх)].
13-й случай (рнс. 5, н).
Сечение х = 0 — шарнирная опора; сечение х — I — жесткая заделка:
М w' (0) —<р13 ;
Ф13' К^-КоК3'
। _ К\ КаК% .
4)13 K^-KoKY м
w = Тор5 <₽13^’ “
— 4’|з^"з (Рх) + К2 (Рх)];
Мх (х) = м [4<р,3Л3 (рх) — — 4’13^1 (Рх) -|- Ко (Рх)].
14-й случай (рис 5, о).
Сечение х — 0 — шарнирная опора; сечение х = /— шарнирная опора
w (0)--ФиЖ;
__ К1&2 '— .
ф14 ~ Ki + 4Ал ’
Ф14 = “
Ki 4 4Кз
М
W “Dp* [—<₽14^1 (Рх) —
— (Рх) 4- Кз (Рх)];
Мх (х) = М [4<риК3 (Рх) — — 4'1Л (Рх) + Ко (Рх)].
15-й случай (рис. 5, п).
Сечение х — 0 — шарнирная опора; сечение х -= I — скользящая заделка:
М
w' (0) = —<р16 -рр ;
KoKr + iKiKi .
ф15 - Ki + 4К1 ’
Q (°) ~ foi - ib •
—д— = W (О) == —ф15 —g— , . 4 (KiK2 - КоКз).
ф15 ---^-4^—, м
w = Тор5 ~
— Фхз^з (рх) + Ki (Рх)];
Мх (х) = М [4<р16К3 (Рх) — --- (Pz) 4" Ко (Рх)].
16-й случай (рис. 5, р).
Сечение х = 0 — шарнирная опора; сечение х = I свободное.
„ М w' (0) = —<р13 -рр-;
_ _Къ^ЛК_Кз__. ф1в ~ ЧК,Ki~ КоК3у
K0Ki + 4K^ .
ф1в K.Ki-KoKo'
w(x) - [—<р1вК! (Рх) —
— фю^з (Рх) + Ко (Рх)];
Л1Я (х) = М [4<р1вК3 (рх) -— IpieKl (Рх) + Ко (рх)].
17-й случай (рис. 5, с).
Сечение х = 0 свободное; сечение х = I — жесткая заделка:
од3
ю (0) = Фи;
Расчет коротких оболочек
455
ф1’ ^ + 4^^’
W' (0) = . _ ф" Ki + 4К,К3 ’ оа2
w ~ ~Eh ' 1 —
-ФиК1(₽*)-Ко (рх)];
Мх (х) = -^-1 — Ф17К2 (Р*) + + Ф17К3 (Рх) + Ка (Рх)]-18-й случай (рис. 5, т).
Сечение х — 0 свободное, сечение х — I — шарнирная опора.
да2 w (0) = <р18 ;
m Кз .
ф18“ + KJ^-KoKt'
W (0) = —ф18 ;
ф18 КгКо - К„К3 ’ оа2
W lZ) = -£у 1 1 + Ф18Ко (Р*) — — ipieKi (Рх) — Ко (Рх)];
Мх (X) = фхзКг (Рх) + + ’РхеКз (Рх) -)- 7(4 (Рх)]. 19-й случай (рис. 5, у).
Сечение х — 0 — скользящая заделка, х = I — жесткая заделка:
да2 w (0) = <Р19 ;
_ 4КаК3 — (I ---- Ко) .
Ф” “ Kotfi + 4К2К3
4Кз ф1в ^К1+4ад3 ’
W (х) = Th [ ’ ~ Ф”Л'0 —
— i|)i9Ka (Рх) — Ко (Рх)];
Мх (х) = — [— <p197(2 (рх) —
------4~ ’I’loKo (Рх) + ^2 (Рх)]. 20-й случай (рис. 5, ф).
Сечение х = 0 — скользящая заделка, сечение х = I — шарнирная опора: да2 (0) = Фао ;
m - i___Ко .
ф2° Ki - ’
М = ^(0) = _ф2о-^;
, 4^ .
ф20 ~ + 4^i ’
о а2
W (Z) = Th ! 1 + ф2<,Ко — — ЧзоКа (рх) — Ко (Рх)], Мх W = -р [- фмКз (Рх) — -------’I’ooKo (Рх) 4- ^2 (РХ)] . 21-й случай (рис. 5, х) Сечение х — 0 — шарнирная опора; сечение х = I — жесткая заделка
и>' (0) = (Pai ;
4Kj-K2e~Ko) .
ф21 - KoKs '
^^(o) = -^; ,ь iKrKo-Ko^-Ko) . ф21 ^1^2 - КоКо
w (ж) = Th [ 1 + ф21К1 ~
— '1’21^3 (Рх) — Ко (Рх)];
Мх (X) = ф21Лз (Рх) —
- 4" ф2‘К1 (Р*) + Ко (Рх)] .
456
Расчет на прочность цилиндрических оболочек
22-й случай (рис. 5, ч).
Сечение х = 0 — шарнирная опора; сечение х = I — шарнирная опора:
W (0) = <р22 ;
4*2Ка — *2 (1 — *0) .
<р22 —
*? + 4*^
Q(°) ?«2Р3.
— (0) --Ф22—,
4[*1*а-*з(1-*о)].
Y22 —----------------
*?+4*^
W ~ ~Eh '' + *Р22^] (Рх) — — ф22*3 (Рх) — *0 (Рх)1‘>
Мх (Х) = -^2 Ч>22*3 (0*) —
----------4" Ч’за*! (РХ) + *2 (P*)J • 23-й случай (рис. 5, ш). Сечение х = 0 — жесткая заделка; сечение х = I — жесткая заделка:
Л1х(°) . m qa^.
-----= w (0) = <р2а -gj- , 4*?,-K, (I -*о)
D
ф23 К1 - *, К3
,h ?а2Р3.
~D~ ( —фаз "Eh'
,к _ 4*2*3-Ml -Ко) .
ФгЭ —------------------
*1 - *,*з
W ~ ^Eh 11 <P23^2 (Pz) —
— '1’23*3 (PA') — *0 (P*)]>
Mx (X) = -^2 фзз*о (Px) ------
----•фаз*£ (P*) + *2 (Px) J .
24-й случай (рис. 5, щ).
Сечение х = 0 свободное либо скользящая заделка; сечение х = I свободное либо скользящая заделка:
од2
= ~Eh ’ W> (0) = 0;
W (Х) = ’ Мх (х) = °’
Графики значений функций <pt- и ф; для различных расчетных случаев, соответствующих рис. 5, а—щ, показаны на рис. 6—11.
Приближенный метод расчета очень коротких цилиндрических оболочек. Если длина оболочки мала по сравнению с радиусом, или, точнее, параметр р/ •< 0,4, то могут быть использованы приближенные решения. Они получаются из точных решений, если
Рис. 6. Значения функции ф для 1 —8-го случаев
Рис. 7. Значения функции ф для 1 —8-го случаев
Расчет коротких, оболочек
457
Рис. 11. Значения функции ф для 17 — 23-го случаев
при разложении функций Крылова оставить лишь первые члены.
Для двух крайних случаев можно указать простое истолкование результатов.
Если одно из сечеиий очень короткой оболочки заделано, то основными напряжениями будут напряжения ах, создаваемые изгибающими моментами Мх. Эти моменты (и напряжения) могут быть определены, если представить себе, что оболочка разрезана
вдоль образующих на стержни единичной ширины. Так, например, для оболочки, показанной на рис. 12, будем иметь
М (/) = QI,
где Q — усилие на единицу длины окружности оболочки.
458
Расчет на прочность цилиндрических оболочек
Рис. 12. Очень короткая цилиндрическая
с заделанным сечением
оболочка
I
Рис. 13. Очень короткая цилиндрическая оболочка, свободная от закрепления
Наибольшие напряжения изгиба 6.41 (/) 6QI
Для рассматриваемых случаев окружные напряжения значительно меньше напряжений в поперечном сечении.
Другой крайний случай получается для оболочки, свободной от закрепления (рис. 13). Теперь основными напряжениями будут окружные напряжения 00, а напряжениями аж можно пренебречь. В этом случае можно считать, что образующие оболочки остаются прямолинейными и очень короткую цилиндрическую оболочку можно считать кольцом (см. гл! 19).
ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ В ОБОЛОЧКЕ
Оболочка, свободная от закрепления. Рассмотрим сначала оболочку, свободную от закреплений (рис. 14).
Пусть оболочка нагрета до температуры tB (х), причем по толщине оболочки температура постоянна. Допустим, что величина tB (х) может быть выражена полиномом первой степени
(*) бр bi (х),
где bB, bi — произвольные коэффициенты.
Тогда решение уравнения (1) будет w = аа (Ьв-+ Ьгх).
Из равенств (2) и (4) устанавливаем.
что перемещение w вызывает усилия А 6 и других силовых факторов.
В свободной оболочке нагрев с температурой, распределенной по линейному закону, не вызывает температурных напряжений.
Оболочка с закрепленными краями. Если края оболочки закреплены, то любой нагрев вызывает температурные напряжения.
Пусть, например, оболочка с шарнирно опертыми краями (рис. 15) нагрета до температуры tB, постоянной по длине оболочки. Радиальное перемещение свободной от закрепления оболочки
o>t = aatB.
Предположим, что оболочка принадлежит к классу длинных. Задачу решаем в следующем порядке.
Рис, 14. Оболочка, свободная от закрепле-НИя, при действии ижрева
Устойчивость пластинок, колец и оболочек
459
Рнс. 15. Температурные напряжения в оболочке
Рис, 10. Температурные напряжения при изменении температуры по толщине оболочки
Для определения температурных напряжений прикладываем внешнее усилие Q к краю х = 0 с таким расчетом, чтобы упругое смещение оболочки
w (0) = —ааЛ0.
Пользуясь решением для случая, показанного на рис. 4, а, находим усилие
Q = —^Datga
и напряжения, вызываемые этой силой.
Для края х = I получаем значение температурной реакции, используя решение по рис. 4, б.
Температурные напряжения возникают только вблизи краев оболочки.
Рассмотрим случай, когда существует градиент температур по толщине
оболочки (рис. 16). Величина Д по длине оболочки не изменяется, края оболочки заделаны. В оболочке возникают температурные напряжения, одинаковые по ее длине.
Для точек наружной поверхности
ЕаAt ох-^ав = — 2(1 —V) ’
Для точек внутренней поверхности Еа At
°х ~ °9 ~ 2(1 -v) •
Более подробно вопрос о температурных напряжениях при осесимметричном нагреве цилиндрических оболочек рассмотрен в работе [2J.
Глава 25
УСТОЙЧИВОСТЬ ПЛАСТИНОК, КОЛЕЦ И ОБОЛОЧЕК
Потеря несущей способности тонкостенных конструкций может происходить в результате внезапного роста прогибов и деформаций, когда внешние нагрузки достигают критических значений. Такое явление называют потерей устойчивости, оно связано с возникновением новых форм равновесия конструкции при значительных отклонениях от первоначального положения.
Потеря устойчивости может возникнуть, когда в пластинках и оболочках образуются зоны действия сжимающих напряжений. При наличии в рабочих условиях напряжений сжатия даже
в каком-либо одном направлении пластинки и оболочки должны подвергаться расчету на устойчивость. Обычный расчет состоит в определении запаса устойчивости
Пу
Р КР
Pina\
(О
где Ркр — значение силового фактора (усилия, давления, момента), при котором возникает потеря устойчивости конструкции, Ртах — максимальное расчетное значение силового фактора в рабочих условиях.
460
Устойчивость пластинок, колец и оболочек
В зависимости от назначения конструкции, ее ответственности, последствий потери устойчивости и других факторов принимают
лу= 1,54-5, (2)
причем большие значения используют при наличии первоначальных отклонений от правильной геометрической формы и т. п.
Расчет на устойчивость сводится к определению критических нагрузок или напряжений, приводящих к потере устойчивости.
Предполагают, что при расчетных критических напряжениях материал в упругом состоянии, т. е. интенсивность напряжений
кр —
a2 _i_ q2 — х кр ~ у кр
_ । л 2
°X Кр°у Ир “Г йхху Кр
(3)
От— предел текучести материала.
Если это условие не соблюдается, то в расчетных зависимостях следует заменить модуль упругости Е иа касательный модуль упругости
который значительно меньше Е [ЕИ = = (0,01-т-0,1) Е). В приближенных расчетах можно принять, что пластическая неустойчивость наступает при работе материала конструкции в пластической области, т. е. при условии
^IKP^ «И- (°)
УСТОЙЧИВОСТЬ ПЛАСТИНОК
Прямоугольные пластинки. Пластинка, сжатая в одном направлении (ах Ф 0; os 0; Хху— 0). Критическое напряжение (рис. 1)
V п D &Х кр - aKP — К > (6)
где D = -т^-т---------цилиндриче-
1Z (1 V I
ская жесткость; Е и v — модуль упругости и коэффициент Пуассона;
Рис. 1. К расчету устойчивости пластинки
h — толщина пластинки. Значения К при различных условиях закрепления пластинки даны на рис. 2.
Прогиб шарнирно опертой по всем сторонам пластинки при потере устойчивости
„ . тлх . плу
w = С sm------sm . (7)
а Ь
Минимальные значения критического напряжения (они указаны на рис. 2) получаются при n = 1 (одна полуволна в поперечном направлении) из условия л2О / b , а \2 а«р - + ’ (8)
минимум соответствует ближайшим целым числам mi и т2, заключающим _ а
ттт >
т2.
а
Расчет проводят по формуле (8) для т = тг и т — т2 и выбирают меньшее значение К- При шарнирном опирании по всем сторонам
К min = 4
а и соответствует целым значениям —
(1, 2, 3, 4, ...).
Пластинка, сжатая в двух направлениях, при шарнирном опирании всех четырех сторон. При заданном отношении сжимающих напряжений
кр У =----
КР
О)
Устойчивость пластинок
461
Рис. 2. Коэффициенты К при различных условиях закрепления пластинки, сжатой в одном направлении
лениях
величина ах кр определяется по формуле (6), значения Л' находят по рис. 3. Решение принимают в форме (7), причем минимальное критическое напряжение находят из условия
° у кр — Уах кр- (11)
В равенстве (10) т, п — целые числа (1, 2, 3, ...). Для квадратной пластинки т = п = 1.
Рис. 3. Коэффициент К для шарнирио опертой пластинки, сжатой в двух направ-
Если одно из напряжений (ах или оу} является растягивающим, го в формулах (8) и (9) величина у < 0. Растягивающее напряжение (до определенного значения) повышает устойчивость пластинки.
При наличии значительного растягивающего напряжения в одном нз направлений пластинка практически теряет устойчивость, если интенсивность напряжений [условие (3)]
ai кр —
— 1/ а2 4- о2 — а о = от.
у их кр I у кр х кр у кр т
Растягивающие напряжения при расчете на устойчивость считают отрицательными.
Пластинка под действием касательных напряжений, шарнирно опертая по четырем сторонам (рис. 4). Критиче-
462
Устойчивость пластинок, колец и оболочек
Рис. 4. Пластинка под действием паса-тельных напряжений
ское касательное напряжение находят по приближенной формуле
кр = 62/1" > ,121
где
Ь2
Кх « 5,35 + 4 (Ь<а). (13)
Для пластинки с жестко заделанными сторонами
Кх ~ 8,98 + 5,6— (Ьса) (14)
Ограничение критического напряжения по возникновению пластической неустойчивости
^НР^у-
(15)
Пластинка при совместном действии нормальных и касательных напряжений. Края пластинки шарнирно
оперты, вдоль оси «действует нормальное напряжение ох, по всем краям касательное напряжение ъху.
Условие устойчивости:
ах кр
ах кр
(16)
где а® кр, т°у кр — критические напряжения при раздельном действии нагрузок ^формулы (6) и (12)].
Растягивающее напряжение (ах Кр< < 0) повышает устойчивость пластинки при сдвиге. Ограничение по возникновению пласт нческой неустойчивости
кр "Ь ^Хху кр °Т (17)
Круглые пластинки. Сплошная пластинка постоянной толщины. Под действием контурной нагрузки (рис. 5, а) пластинка теряет устойчивость при
°кр = К , (18)
где D = —2'у _/~2j цилиндрическая жесткость; b и h — радиус и толщина пластинки.
Для пластинки без центрального отверстия, шарнирно опертой но внешнему контуру (рис. 5, б),
К = 4,20.
Рис. 5. Круглая пластинка под действием контурной нагрузки
Устойчивость цилиндрических оболочек
463
Рис. 6. Круглая кольцевая пластинка под действием контурной нагрузки
где Jj — момент инерции кольца (при изгибе в плоскости кольца); R — радиус оси центров тяжести сечений.
Распределенное усилие ?кр предполагают направленным по нормали к поверхности (силы давления среды).
Если усилия действуют всегда радиально (кольцо, загруженное радиальными нитями или мембраной),
9 Е/j
?нр — “тг “рз" • (20'
При возможности неплоской (пространственной) деформации кольца в равенстве (19) под следует понимать минимальный момент инерции сечения
Рис. 7. Коэффициент К для кольцевой пластинки (т - число узловых диаметров):
1 — скользящая заделка по обоим краям;
2 — шарнирное опираиие по обоим краям;
3 — скользящая заделка по наружному краю; 4 ~ шарнирное опирание по наружному краю; в случаях 3 и 4 --- по внутреннему краю прогиб без углов поворота
кольца.
Для радиально направленных внешних усилий при неплоской форме дефор-
мации
?нр —
При скользящей заделке внешнего края коэффициент К возрастает (рис. 5, в):
К = 14,68.
Кольцевая пластинка при одинаковом сжимающем напряжении иа внешнем и внутреннем контурах (рис. 6). Расчет ведут по формуле (18), значения К принимают по рис. 7.
УСТОЙЧИВОСТЬ КОЛЕЦ
Критическое распределенное усилие (рис. 8) определяют по формуле
(19)
12Е72
G7 к
(21)
где £./2 — жесткость при изгибе в перпендикулярной плоскости; GJк — жесткость на кручение.
Приведенные зависимости не учитывают поддерживающее влияние присоединенных элементов конструкций (оболочек) и потому дают заниженное значение критического распределенного усилия.
УСТОЙЧИВОСТЬ
ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК
Устойчивость при внешнем давлении. При потере устойчивости (рис. 9) возникает одна полуволна прогиба
464
Устойчивость пластинок, колец и оболочек
ближенных формул. Вне указанных пределов они могут давать неверные результаты Следует также учитывать ограничения по пластической неустойчивости
°i кр — °0 кр —
?крг
~h~
С °т-
Для длинных оболочек [ —>3 X
X
h /
Eh9
ha 4(1-:^ = °’27£-ЙГ» (24)
что совпадает с окр для кольца единичной ширины [см равенство (19)].
Для коротких оболочек <3х
Рис. 9. Оболочка, потерявшая устойчивость при внешнем давлении
вдоль образующей и несколько волн по окружности.
Критическое внешнее давление шарнирно опертой по краям оболочки (рис. 10) определяют по приближенной формуле П Ф Папковича
2л__________1 Eh9
<7иР'“ зуёТ 4/(1 -v2)3 х
X 1Л— •= 0.92 , (22)
V Г 1г V г ’ ' '
где Е — модуль упругости, h, I, г — толщина, дпина, радиус оболочки. Расчет по формуле (22) проводят для оболочек средней длины
Здесь и в дальнейшем следует строго соблюдать условия применимости при-
Рис. 10. Устойчивость оболочки при внешнем давлении
„ ^Eh3 EhS
9кр 3(1—v2)/-/2 ,b гР ’
(25)
что соответствует критическому усилию сжатия (в окружном направлении) для шарнирно опертой прямоугольной пластинки [см равенство (6)]
кр = а0 кг/1 = ?крг- (26)
Формула (25) дает заниженное значение </Кр, так как сжимающее напряжение в окружном направлении вследствие поддерживающего влияния опор
|Оо1<<?кр-у •
Для приближенного расчета определяют среднее значение окружного напряжения (по длине оболочки) бе и вводят поправочный коэффициент в формулу (25)
г а -=-----,
ав1К
где ад, — среднее окружное напряже ние при давлении q = I.
Влияние краевых условий на критическое давление В каждой точке срединной поверхности оболочки появляются три составляющие упругого смещения- и — вдрлъ образующей, v — вдоль касательной к окружности поперечного
Устойчивость цилиндрических оболочек
465
сечения; w — по нормали к поверхности.
В поперечном сечении действует усилие Nx и изгибающий момент Мх (на единицу длины) (см. гл. 24). Формула (22) установлена при следующих краевых условиях: при х = 0 и х = I w= 0; Мх = 0; Nx= 0; и = 0.
При выводе не учитывалось влияние моментного напряженного состояния возле опорных сечений; принималось, что окружные напряжения по всей длине оболочки
«0 = от-
— < о у —------использовать решение
для критического усилия при свободном • продольном крае пластинки.
Поправочные коэффициенты на начальные неправильности. Для сварных оболочек расчетные значения <уКр рекомендуется уменьшать на 15%, для точеных оболочек расчетные и экспериментальные данные практически совпадают.
Устойчивость прн сил. Формы потери казаны на рис. 12.
Для короткой
действии осевых устойчивости по-
точные значения <7нр- т при различных краевых условиях с учетом момент-,Ного напряженного состояния /(рис. И, а) и без учета его (рис. 11,6) “были получены с помощью численного решения [4].
Результаты на рис. 11 даны в виде поправки к формуле (22) в зависимости от безразмерной длины оболочки. Существенное влияние оказывает только устранение деформаций вдоль о^си оболочки (и — 0), повышающее критическое давление в 1,5 раза. При отсутствии закрепления одного из краев Оболочки критическое давление при j „ г~г
^>3у можно определить по равенству (24), для коротких оболочек
сжатия
критическое напряжение
. ( 1 оболочки —
\ Г
Т’нр а«Р = ~2nrh
(27)
определяется равенством
л2£7г2 пос. Л2 °нр- 12(1-v2)Z2 ~°’9£ Z2 ’
(28)
что соответствует шарнирно закрепленной полоске единичной ширины с площадью сечения h X 1 и длиной /. Короткая оболочка работает на устойчивость при действии осевых сил как пластинка с высотой I и основанием 2лг.
₽нс 11. Поправка к формуле (22) прн различных краевых условиях:
1 - to == о, to' — 0, и — 0, V — 0; 2 — to — 0, to' --= 0, Nx — 0, v — 0; 3 — to = 0!
to’ = 0, и = 0, S = 0, 4 — to = 0, to’ = 0, Nx = 0, S = 0; 5 — w = 0, Mx = 0, и =
= 0, о = 0; 6 — to = 0, Mx = 0, Nx — 0, v = 0; 7 — to = 0, Mx = 0, и = 0, S = 0;
8—to = 0, = 0, N x = 0, S = 0 (S — сдвигающее усилие на единицу длины обо
л очки)
466
Устойчивость пластинок, колец и оболочек
Рис. 12. Четыре формы потери устойчивости цилиндрической оболочки при действии осевой сжимающей силы:
а — короткая оболочка; б, в — оболочка средней длины; г — длинная оболочка
Для оболочки средней длины (1.2 7<3 J/4-у) крити-
ческое напряжение осевого сжатия
h aKP==7W^= 0’605£T-(29)
Критическое осевое усилие, действующее на оболочку, 2л£/1г
ДКР = -т -=~= 3,855». (30) Р У3(1- V)2
Одним и тем же значениям минимального критического усилия [равенства (29) и (30) ] могут соответствовать две различные формы потери устойчивости (симметричная — рис. 12, б и несимметричная — рис. 12, в).
Для длинной оболочки критическое усилие выражает потерю устойчивости оболочки как стержня (рис. 12, г):
n2Er»h Er2h • "кр —----р — 81 р~ ,
______ ?tfp п2 р г2 аир = 1лг/Г = ~ ь ~р =
Г2
= 4,935 4-.
I2
(31)
(32)
Влияние условий закрепления оболочки при действии осевых сжимающих снл сказывается существенным образом на акр коротких оболочек. Например, если оба торца короткой оболочки
заделаны в жесткие кольца (фланцы), то критическое напряжение
h2 аир = 3,6£-yj-. (33)
При других условиях закрепления короткой оболочки используют соответствующее решение для стержней-полосок.
Поправочные коэффициенты иа начальные неправильности. Как показали экспериментальные исследования, влияние отклонений от строгой цилиндрической формы при осевом сжатии весьма значительно.
Практический расчет устойчивости проводят по формуле
С7кр= ас-0,6055
где значения поправочного коэффициента ас следующие: .
e/h ... 250 500 750 1000 1500
ас ... 0.3 0.23 0.2 0.165 0,15
Если начальные отклонения могут быть порядка толщины стенки, то указанные значения ас уменьшаются в 2 раза. Следует учитывать ограничения по пластической неустойчивости
Пнр
Устойчивость прн кручении. По концам оболочки действует крутящий
Устойчивость цилиндрических оболочек
467
Рис. 13. Устойчивость оболочки при Кр}’ чении
момент (рис. 13), создающий в стеньгах касательные напряжения
т
ТкР~ 2№Л ’
(34)
где гн h. — радиус и толщина оболочки.
Для короткой оболочки I — •<
критическое касательное
напряжение определяют как для пластинки высотой I и основанием 2пг (шарнирное опирание краев):
ткр — %х
—А£^_==4 83 -^_ 12(1—v2)Z2 ' Р •
(35)
Для оболочки средней длины
0,7iEh * f hr
Ткр ~ 7(Т_ v2)57T V ~Е~ =
= 0,78£-А)/-А. (36)
Для длинной
оболочки
>9
= 0.25Е А . {37)
Приведенными формулами следует пользоваться, соблюдая указанные ограничения на длину оболочек.
Краевые условия наиболее существенно влияют на ткр коротких оболочек. Если оба края оболочки заделаны в жесткие кольца, то вместо (35) принимают
Eh2
ткр — 8> 11 —р—. (38)
Влияние начальных отклонений учитывают понижением расчетных значений тКр с помощью коэффициента ак: r/h ... 250 500 750 1000 1500
а ... 0.8. 0,7 0,63 0.58 0,5
Для сварных оболочек следует уменьшать указанные значения на 20%. Следует учитывать ограничение по пластической неустойчивости
р 0,58а,,
Устойчивость при изгибе моментами. Изгибающие моменты Л1и, приложенные по торцам (рис. 14), создают в стенках оболочки нормальные напряжения
М
<1И = cos 0. (39)
Критические напряжения (их максимальные значения в сжатой зоне)
т - V2 Е h КР 6(l_v2)3/4£r
Рис. 14. Устойчивость оболочки при дей* ствии изгибающего момента
468
Устойчивость пластинок, колец и оболочек
соответствуют критическим напряжениям при осевом сжатии.
Для короткой оболочки <
^•kp = -^ = 0-9£7^ <40’
Для оболочки средней длины (‘•2]/т<т<3/т)
a“-«p = -^- = 01605£7-- (41)
Значение поправочных коэффициентов на начальные отклонения принимают на 15—20% больше указанных для осевого сжатия, аи — (1,15-М,2) ас.
Устойчивость при изгибе поперечной силой. Поперечная сила (рис. 15) создает в стенках оболочки нормальные и касательные напряжения (без-моментное напряженное состояние)
Qx „ Q . п
= —st-cos 0; ти=—4-sin0. nr2h и nrh
(42)
Опасными для потери устойчивостя будут зоны максимальных нормальных напряжений изгиба (зона /) и максимальных касательных напряжений (зона 2).
Приравнивая критические напряжения изгиба в первой зоне к критическим напряжениям при осевом сжатии, получим:
, / 1 для коротких оболочек /— <
(43)
Qkp = 2.83Е -^- ;
для оболочек средней длины
Q"’/ h .
аи- Rp — nr2h ~ г >
Q^=l,9E — . (44)
Критические усилия при потере устойчивости во второй зоне находят приравниванием касательных напряжений изгиба критическим касатель-
ным напряжениям прн кручении:
для коротких оболочек ^— < 3 X
т Q*p - 4 83 Eh' •
Ти‘Rp — "яг/T — 4,83 Р ’
Рис. 15. Устойчивость оболочки при дей-ствкн поперечной силы
Q^p’ = i5.2£ —;
для оболочек средней длины
ѫР_П7ЯР h l/Z-
~Q,7&E г V Е ’
= 2.45ДЛ’
В качестве расчетного значения кри" тического усилия применяют минимальное значение QKp с учетом поправочных коэффициентов:
<2ир = min
МЗДУ;
“ЛУ-
Устойчивость цилиндрических оболочек
469
Рис. 16. Устойчивость оболочки при действии осевой силы, внешнего или внутреннего давления
Устойчивость при совместном действии нагрузок на цилиндрическую оболочку. Осевое усилие, внешнее или внутреннее давление. Различные случаи действия осевого усилия и давления показаны на рис. 16.
Сжимающее усилие Р и внешнее давление q считают положительными. В оболочке возникают напряжения
Р . qr
°х 2wh ’ °0 h ‘
Условия устойчивости при действии сжимающего осевого усилия и внешнего давления (рис. 16, а):
где ах Кр, ад кр — напряжения в оболочке в момент потери устойчивости (критические напряжения при совместном действии нагрузок): о“ кр — критическое напряжение при действии одной сжимающей осевой нагрузки; а6кр — критическое напряжение при Действии одного внешнего давления. Значения о“кр, aJ(Kp принимаются с учетом поправочных коэффициентов иа начальные отклонения.
Если ах, ад — напряжения в рабочих условиях, то
°х кр = nyaxi °0 кр = Луа0> (46) Где Пу — запас устойчивости (при пропорциональном возрастании нагрузок).
В общем случае, когда возрастает только одна из внешних нагрузок, например осевая нагрузка, то
ах кр = ni/iax’ ав кр = °е- (47)
Внося значения ах кр и ае Кр из соотношений (46) или (47) в условие (45), получаем формулу для запаса устойчивости. При пропорциональном возрастании нагрузок
пу =
ах I , j ge I
гтО ' (10
ихкр I I иекр I
(48)
Подобным образом находят запас устойчивости в других случаях совместного действия нагрузок.
Условия устойчивости при действии сжимающего осевого усилия и внутреннего давления (<7 < 0, рис. 16, б). Расчет проводят по приближенной формуле
<Jx кр “1«р
1 + 0,21 к, \ п >
1+зТ«1£. с. п, (49)
Для оболочки средней длины
а» =ас-°.605дА . (50)
Внутреннее давление (до определенных пределов) повышает устойчивость оболочки при действии осевой сжимающей силы. При большом внутреннем давлении может наступить пластическая неустойчивость, если
Vax кр + а0 кр + ах кра6 кр > ат-
(51)
В последнем соотношении учтено, что напряжения аж кр и 00 кр имеют разные знаки (ох<0, ае>0).
470
Устойчивость пластинок, колец и оболочек
Запас устойчивости по условию (51) и соотношениям (46)
«у = ----- . (52)
У ai + ае + °А
Запас устойчивости практически совпадает с запасом по пределу текучести От (одно из действующих напряжений является сжимающим).
Условия устойчивости прн действии растягивающего осевого усилия и внешнего давления (рис. 16, в, ах > 0, ар<0). Расчет проводят по приближенной формуле
усилие. В стенке оболочки создаются (рис. 17) касательные напряжения
т -
к 2лг2Л ’
осевое и окружное напряжения:
Р qr
Пх " 2nrh ’ “ /г
Крутящий момент и внешнее давление (Оо<0).
Условие устойчивости
а0 кр
о°
°0 кр
(54)
°0 кр F ах кр I
(53) где аекр и ах кр ~~ критические напряжения при действии соответственно только внешнего давления или только сжимающей силы (с учетом начальных отклонений).
Растягивающее усилие (до определенных пределов) повышает критическое внешнее давление. При большом растягивающем усилии следует учитывать возможность пластической неустойчивости, возникающей при условии (51).
Крутящий момент, вн еш-иее или внутреннее давление, сжимающее или растягивающее осевое
где т”р — критическое касательное напряжение при крутящем моменте с учетом начальных отклонений.
Крутящий момент и внутреннее давление (ае > 0). Расчет проводят по приближенной формуле
- + 0,78
\ ткр /
°9 кр
°0 кр
(55)
_ ^0 кр Л
При значениях —> 8 следует °0 Кр
пользоваться зависимостью
, TKD > 2
=°’907 \ ткр /
^0 кр °0кр
(56)
Рис. 17. Устойчивость оболочки прн действии крутящего момента, давления и осевой силы
Внутреннее давление (до определенных пределов) повышает устойчивость оболочки при кручении. При большом внутреннем давлении проверяют условие пластической устойчивости
/Чкр+ЗЧрС<\. (57)
Крутящий момент и
сжимающее осевое усилие (ох < 0). Условие устойчивости:
ткр \2
(Jx кр
СТхкр
(58)
где значения т°кр, ах кр принимают с поправочными коэффициентами, учитывающими начальные отклонения.
Крутящий момент и растягивающее осевое
Устойчивость цилиндрических оболочек
471
усилие (о_г '> 0). Условие устой-
чивости
(59)
при
ах кр
о® х кр
(60)
Растягивающее осевое усилие (до определенных пределов) повышает устойчивость при кручении. При большом растягивающем осевом усилии следует проверить условие пластической устойчивости
Рис. 18. Общий случай устойчивости оболочки при совместном действии нагрузок
У'Ч кр + Зткр < ат-
(61)
Крутящий момент, ви еш-иее давление и сжимающее осевое усилие. Внешнее давление и сжимающее осевое усилие понижают устойчивость оболочки при кручении.
Условие устойчивости
гружения). В общем случае (рис. 18) в оболочке возникают напряжения (х = /):
Р .
°х 2wh ____________ nr-h
cos 0 — пгт
cos 0;
(63)
ае ир
а8 кр
ах кр а2кр
(64)
= 1,
(62)
т = -а—sin 0.
2nrm nrh
(65)
причем критические напряжения т°р, ае кр> ах кр принимают с учетом ас (см. с. 466).
Некоторые случаи трехкомпонеитно-го нагружения. Внутреннее давление или растягивающее осевое усилие повышает устойчивость оболочки при кручении, если соблюдается условие (3). В запас прочности можно считать повышение устойчивости только от одного (основного) стабилизирующего фактора, используя указанные ранее зависимости для двухкомпоиент-ного нагружения [формулы (49), (53), (55) и (56)).
Изгибающий и крутящий моменты, поперечная сила, давление и осевая сила (общий случай на-
Положительные направления силовых факторов показаны на рис. 18, растягивающие напряжения аж и ае считают положительными. Условия устойчивости (62) при сжимающих нормальных напряжениях (ах < 0; ар < 0) записываются в виде
1 / 34к. кр QKpSin0\2
(т°р)2 \ 2лг2Л nrh )
h
^кр
2nrh
Ми. кр
cos
Qnpt iu2h
cos 0=1,
(66)
472
Устойчивость пластинок, колец и оболочек
где значения т°р, og кр, о£ кр принимают для кручения, внешнего давления, осевой сжимающей силы с учетом поправочных коэффициентов, Л4К. кр, Ми. кр- <2кр- ^кр- <?кр — критические значения силовых факторов при совместном нх действия.
Условие (66) применяют для угла О, прн котором левая часть равенства (66) принимает наибольшее значение.
Обычно наиболее опасными являются зоны 1 по концам вертикального диаметра (0 =0; 0 = п) или зоны 2 по концам горизонтального диаметра (Л И Л ЗДТ \ ~
0 = — ; 0 = . В общем случае
расчет проводят для различных значений 0.
При растягивающих нормальных напряжениях устойчивость оболочки повышается, что может быть приближенно учтено по схеме двухкомпонентного нагружения, как это было указано ранее.
УСТОЙЧИВОСТЬ
КОНИЧЕСКИХ ОБОЛОЧЕК
Устойчивость под действием сжимающей силы (рис. 19, а). В сечениях оболочки действует сжимающее напряжение
их =----г——. (67)
х 2яг (х,1 h sin а
Критическое напряжение совпадает со значением, получаемым для цилиндрической оболочки (средней длины):
окр = 0,605В , (68)
где г0 — радиус кривизны конической оболочки.
Наименьшее значение окр соответствует наибольшему радиусу, однако для всех сечений осевое критическое усилие оказывается одинаковым и равным
Ркр = 0,605£Л22л sin2 а = =3,8£й2 sin2 а. (69)
Для практических расчетов следует учесть влияние начальных отклонений, приняв
Ркр= ac.3,8£h2sin2a, (70)
где значение ас приведено на с. 466. Устойчивость под действием внешнего давления (рнс. 19, б). Для оболочек, близких к цилиндрическим (80° < а. < 90°), можно использовать формулу (22)
= 0,92-^-}/’А, (71) I» о г * о
где га — наибольший радиус кривизны конической оболочки.
Для конической оболочки (20° гС а 80°) критическое внешнее давление определяют по формуле
= (72)
^0 r IQ
где I — длина оболочки; го — наибольший радиус кривизны.
Значения К принимают следующими:
/„// ... 0 0.2 0.4 0,6 0.8 К ... 3.00 2,62 2,12 1,63 1,32
Поправки на влияние краевых условий приближенно такие же, как для цилиндрической оболочки.
Рис. 19. Устойчивость конической оболочки
Устойчивость пластинок и оболочек при температурных напряжениях 473
Рнс. 20. Устойчивость сферической оболочки и эллипсоидальной оболочки
УСТОЙЧИВОСТЬ СФЕРИЧЕСКИХ И ЭЛЛИПСОИДАЛЬНЫХ
ОБОЛОЧЕК
Сферическая оболочка под действием внешнего давления (рис. 20, а). В стенках оболочки возникают сжимающие напряжения
«h=a» = —(73)
где г, h — радиус и толщина оболочки.
Критическое напряжение оказывается таким же, как прн сжатии цилиндрической оболочки осевым усилием:
I п
Р V3(l-V«) '
= 0,605£ А . (74)
Критическое внешнее давление
A А3
“?кр ~ 2°кр ~ = 1.212? -yj- . (75)
Практический расчет проводят по формуле
h2
?кр = ас.1,2!£-1_, (76)
где значения ас указаны на с. 466.
Эллипсоидальная оболочка, оболочка вращения под внешним давлением. Критическое давление (рис. 20, б) определяют по формуле
h2
9кр=1,21£^—^5-. (77)
вращения
Прн потере устойчивости вмятины образуются в зоне экватора. Для оболочки, у которой b С а (рис. 20, в), критическое давление
л2А3
?кр= 1,21£-у-. (78)
Потеря устойчивости возникает возле полюсов, где радиус кривизны
а*
Г
В практических расчетах в формулах (77) и (78) вводится поправочный коэффициент ай (с. 466).
УСТОЙЧИВОСТЬ ПЛАСТИНОК
И ОБОЛОЧЕК
ПРИ ТЕМПЕРАТУРНЫХ
НАПРЯЖЕНИЯХ
Если температурные воздействия создают поле напряжений, совпадающее с напряжениями от критической нагрузки, и условия закрепления одинаковы, то потеря устойчивости произойдет при значениях температурных напряжений или усилий, совпадающих с критическими,
РТ = ^кр, °т = а.:Р- (79)
При нагреве пластинки (рис. 21, а), не имеющей возможности радиального удлинения, возникают температурные напряжения
£<ZT ,Оп.
аг = ое = - , (80)
474
Устойчивость пластинок, колец и оболочек
Рис. 21.
Устойчивость пластинки
и оболочки при действии температурных напряжений
где аТ — температурная деформация; Е и v — модуль упругости и коэффициент Пуассона.
Потеря устойчивости произойдет [см. формулу (18)1 при
Е (аТ)кр d ___________ — 4 9-----
1 — V
(81)
При нагреве цилиндрической оболочки, не имеющей возможности осевого удлинения (рис. 21, б), возникает температурное напряжение
УСТОЙЧИВОСТЬ
АНИЗОТРОПНЫХ ОБОЛОЧЕК
Деформации в слое оболочки и действующие напряжения связаны соотношениями упругости (рис. 22):
. — „ °9 •
Ех Ve Е0 ’
, °0 „ °Х .
8e___vx_t
ах = —ЕаТ.
Критическое значение температурной деформации в соответствии с равенствами (79) и (34)
(аГ)кр = аг-0,605 А . (82)
Тхд = тхе/бх0. (83)
Критическое значение температурной деформации (при потере устойчивости пластинок и оболочек от действия температур) не зависит от модуля упругости материала.
При аТ .> (а7)кр начинается быстрый рост прогибов, так как деформация удлинения компенсируется теперь деформацией изгиба.
Если нагреваемая оболочка (рис. 21, в) не имеет возможности радиального удлинения, то в’ней возникнут сжимающие окружные напряжения
ое = —ЕаТ, однако потери устойчивости при равенстве (79) не произойдет, так как условия закрепления отличны от случая внешнего давления.
где EXt vx, vq — модули упругости и коэффициенты Пуассона, Gxq — мо-
Рнс. 22. Связь напряжений и деформаций в слое оболочки
Устойчивость подкрепленных оболочек
475
Параметры упругости ортотропрого материала связаны зависимостью
vx _ v0 Ех ~ Ев •
(84)
Устойчивость при внешнем давлении. Для цилиндрических оболочек
• I п Л r''l
средней длины I — < 3 у ~hr За” крепленных по краям, 2л 1
<7кр = T/T 7(1Х
X <85>
Если Eq = Ех = Е, vx — Ve = v = = 0,3, то зависимость (85) совпадает с формулой (22).
Для длинных оболочек (— >
Eeh3 <7кр‘ 4(1— vxve) ‘
(86)
Для устойчивости оболочки при внешнем давлении модуль упругости в окружном направлении более важен, чем в продольном.
Устойчивость при действии осевых сил. Критическое напряжение при осевом сжатии для оболочки средней Длины | < 3 1/ ~~
\ г У h
(87)
При Ев = Ех = Е; vx = v0 = v = = 0.3 равенства (87) и (29) совпадают, t, Критическое напряжение оказывается одинаковым для симметричной и Несимметричной формы потери устойчивости. Для длинных оболочек следует проверить общую потерю устойчивости как стержня.
Критическое напряжение в этом Случае
= (88)
УСТОЙЧИВОСТЬ
ПОДКРЕПЛЕННЫХ ОБОЛОЧЕК
Для повышения устойчивости оболочки целесообразно не увеличивать толщину оболочки, а применять кольцевые и продольные подкрепления (рнс. 23).
Кольцевые ребра (кольца) часто называют шпангоутами, а продольные ребра — стрингерами.
Внешнее давление. Критическое давление для оболочки средней длины (— < 3 1/ — )
у 27 Ir V г
A3xfiDl/4
= 5,38 —-—£г- , (89)
/гУг
где Ах — жесткость на растяжение в продольном направлении; De — жесткость на нзгнб в окружном направлении,
Лх =-7-^4- + -^-; (90) 1 — Vя /с
Л — I ш /о п
W^)+~7ZT’ (91)
где Е, ft, v —модуле упругости, толщина обшивки, коэф ицнент Пуассона; Ес, Fa, 1а — модуль упругости, площадь поперечного сеченнч, шаг по окружности продольных ребер (стрингеров),
_ 2лг с
(92)
где 7VC — общее число продольных ребер; Ет, Jnl, 1Ш — модуль упругости, моменты инерции, шаг по длине кольцевого подкрепления (шпангоута);
Рис. 23. Оболочка, подкрепленная продольными и кольцевыми ребрами
476
Устойчивость пластинок, колец и оболочек
1т ~ U(Nm + 1): Л'ш — число шпангоутов.
Моменты инерции сечений шпангоутов вычисляют (в запас устойчивости) относительно осей, проходящих через их центры тяжести.
Из равенства (89) следует, что при действии внешнего давления целесообразно применять кольцевые подкрепления (шпангоуты), продольные ребра неэффективны.
Если оболочка подкреплена только кольцами (шпангоутами), то
„ „о Eh2 j Г Т ?кр — 0,92 I? |/ — X
X [1 4 (Л'ш-Ь 1)]3/4; (93)
Л3/
/°б = 12 (1 — v2) ’
70б — момент инерции продольного сечения оболочки; v — коэффициент Пуассона (v яз 0,3).
<vm .................. 2 з 4 5
•'щ/'об ............''° ‘•34 >-51 !,<
Устойчивость п.
ствии осевых сил. Критическое значение общей осевой силы при несимметричной потере устойчивости
для оболочек средней длины
р и д е й-
^кр.н = 4лУ(1 -v2) AxDe, (98) где Ах и Dg — см. формулы (90) и (91).
При симметричной форме потери устойчивости
Ркр.с = 4лУ(1-V2) ЛеРх, (99) где Ад — жесткость на растяжение в окружном направлении; Dx — жесткость на изгиб в продольном направлении,
Л ГЛ
ЕН»
12 (1 -v2) " 7,
(100) ‘Ш
(101)
где Еа1, Fш и /га — модуль упругости, площадь сечения н шаг кольцевых
Следует проверить устойчивость пролета оболочки между двумя шпангоутами по формуле
<?кр- пр = 0,92 (.VUI 1) х
<95>
Наименьшая масса оболочки получается прн равенстве
?кр = ?кр. пр> (96)
что приводит к моменту инерции шпангоута
= 7об + l)1^3----------_|_ । •
(97)
С уменьшением длины пролета (увеличением <Vm) оптимальная площадь шпангоутов возрастает, что обеспечивает общую устойчивость не ниже устойчивости каждого пролета в отдельности.
Значения Ущ/Усд в соответствии с равенством (97) будут такими:
6 8 10 12 14 16 20 26
, 1.77 1,97 2,13 2.27 2,4 2.51 2.71 2.96
подкреплений (шпангоутов); £с, Jc, Zc — модуль упругости, момент инерции и шаг продольных подкреплений (стрингеров).
В качестве расчетного критического усилия принимают наименьшее из двух указанных значений [формулы (98) и (99)].
При рациональном подкреплении должно выполняться условие
Рцр. н = Ркр. с — ?кр (102) или
AxDg — AgDx. (103)
Для повышения устойчивости оболочки при действии сжимающих осевых сил целесообразно подкреплять ее одинаковым образом в продольном и окружном направлениях. Условие (103) будет выполнено, если
ECFс______ш . E^Jс EmJт .
1С /ш ’
(104)
При наличии подкреплений следует проверить устойчивость панели между
Вариационные уравнения
477
двумя стрингерами и шпангоутами.
Критическое осевое усилие, воспринимаемое пологой панелью.
потеря устойчивости отдельных панелей.
Наименьшая масса конструкции будет при
^кр — Ркр- п>
что приводит к условию
n n*Eh3 , Ehl2
Пкр-п- 3(1 _v2)/c + 4П2Г2 • (Ю5)
2яг / n3Eh3 ,
~ \ 3 (1 - v2) /с +
EhQ \
Тлм) Х
Предполагая, что общее осевое усилие распределяется равномерно по площади обшивки (оболочки) и стрингеров (продольных подкреплений), получим
Pi кр. п —
^кр. п
. I сЕс
Ehlc / 1С
, (Ю6)
где Ркр. п — общее осевое усилие иа оболочку, при котором происходит
= 4n"|/(l —V2) AeDx =
= 4лУ(1 -V2) AxDe . (107)
Последнее соотношение вместе с равенством (104) служит для выбора оптимального значения шага продольных подкреплений и других параметров подкрепления.
Глава 26
ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА КОНСТРУКЦИЙ
Появление и развитие ЭВМ изменило математические методы решения инженерных задач. Предпочтение отдается численным методам, поддающимся большей алгоритмизации и удобным для реализации иа современных быстродействующих ЭВМ.
В основе численных методов лежит замена континуальной расчетной модели с непрерывным распределением параметров и бесконечным числом степеней свободы дискретной моделью, имеющей конечное число неизвестных, которое может быть и очень большим (в зависимости от требований, предъявляемых к расчету, и возможностей ЭВМ).
Большое распространение среди численных методов получил метод конечных элементов, который наиболее удобен для реализации на ЭВМ благодаря четкой формализации отдельных этапов решения задачи и матричной форме расчета.
Наряду с этим широко применяются и другие численные методы расчета (вариационные, разностные, интегральные и др.). В основе многих из этих методов лежат вариационные уравнения.
ВАРИАЦИОННЫЕ УРАВНЕНИЯ
Из начала возможных перемещений следует, что действительному напряженному состоянию упругого тела соответствует минимум полной энергии деформации Ф, т. е. ее вариация:
6Ф = 6 (Фе — Фр)
Фе1ар —
j j (Xvu + Yvv -f- Z^w) dS —
V
478
Численные методы расчета конструкций
- j jj (Xu-]-Yv-]-Zw)dV\ =0, (1)
J V I
где Фе — потенциальная энергия деформации тела; Фр — потенциальная энергия внешних сил; V — объем тела; .S — поверхность тела; Фе] — потенциальная функция деформации. Для равномерно нагретого тела Фе1 — потенциальная энергия деформации на единицу объема тела, Х„, Yv, Zv и X, Y, Z — компоненты поверхностной и объем ой нагрузки; и, v и w — компоненты спругого смещения, удовлетворяюще кинематическим граничным условиям.
Соотношение теории упругости в матричной форме имеет вид
{е) = [а] (а] + {аГ} + {е°), (2)
где векторы-столбцы деформаций {е}. напряжений {о}, температурных {а.Т} и дополнительных {е°} деформаций:
1 v
Т ~ТГ
v 1
Е Е
[а] =
0 0
0 0
Вариация потенциальной функции деформации
бФ81 = (б{е)>т{о) = (б (а})т X хМНг}-(б(*})тМН®Л-
-(6{е))т[Л] (в0}, (5)
где (Л ] = [а]-1 — симметричная матрица, обратная матрице упругости; {аГ} — вектор температурных деформаций; {} —вектор дополнительных деформаций; верхний индекс «т» — операция транспонирования; [о°1 = - IA ] (e°j.
®Х Ох
°V
{е} = Sz Уху ; (с) = ^ху
Ууг Taz
Ухх Tzx
|аТ) =--
^УТ
[а] —симметричная матрица упругих коэффициентов размерности 6Х 6. Для изотропного упругого тела матрица упругости
— 0 0 0
Е
- ~ о о о
Е
4 о о о
1 • (4>
° (Г ° °
0 0-1-0
и
О 0 0-1-
и
Дополнительные деформации могут возникнуть в результате фнзико-хими-ческих процессов, происходящих в среде. В некоторых задачах оказывается удобным с помощью введения дополнительных деформаций описать пластичность и ползучесть среды.
Для изотропного тела с параметрами упругости Е и v из уравнения (5) получим
Фе: =(° + 4) (8х + е2 + егН
+ А (ехеи -ф еиег + е2йх) +
Вариационные уравнения
479
С Е
+ —(v^+^z+vlx)- где G= модуль сдвига;
„ Л = ~7Г~т—m----кгг — постоянная
Е , ч _ (1 +v) (1 -2v)
। a~ 8* 8 У + 8z — Ляме.
Для ортотропного тела, матрица
,„0. . ,-о ,, \ /йч упругих деформаций которого имеет
\ахех "Г '' • "Г ^гх'гх), вид
1 Ех VxB vxz 0 0 0
Еу Ег
vi/x 1 Туг 0 0 0
Ех Еу Ег
vzx Ъу 1 0 0 0
[а] = Ех Еу Ег > (7)
0 0 0 1 0 0
&ху
0 о о о 1 о
Gyz
0 0 0 0 0 1
Gzx _
получим следующее выражение потенциальной функции деформации [1J:
Фе1 “= ~2~ (Л118х + Л22®у + Л33®г) +
+ + Азз^убх + Л31егех -f-
+ Т (А4<Уху + Л55^г + Л6бУ«) -
PlT^x PjT Ъу — PgT 8z —
-(aS®x+ •••+^VM), (8)
где элементы матрицы коэффициентов жесткости:
Лп =Е;(1- v^v,y); Л12= Л2> = ^(^ + ^ги). л22 = £;(1-*х^), л13 = лз1 = Е* (v„ + v^), Л23 = Л32 = Е’у (Ууг + Wxz),
Л33 = Ег (1 ~W^)1 л«з ~ GXy', Л66 = Gvt; Аее — GXI,
(9)
причем
о»)
/Я — 1 %Vxyvyzvzx vxzvzx
-- vzyvyz— Vxyvyx'> (11)
коэффициенты
Рг = Лг1ах Al3sav + Л(3аг («= 1, 2, 3). (12)
Уравнение (1), учитывая связь деформаций и перемещений, можно записать в виде
/ ди ди, \
<5Ф ( и, о, w, -z—, . . . , = 0.
\ дх дг
(13)
Вариационное уравнение (13) эквивалентно полной системе дифференциальных уравнений теории упругости и граничным условиям задачи.
Вариационные методы, применяемые для приближенного решения, основаны иа том, что уравнение (13) решается
480
Численные методы расчета конструкций
для некоторого класса функций в предположении
п1
U = 2 Aifi (х> У’ i=l
п,
V = у; (х, у, г);
1=1
п.
» = S СЛ (*> у-*)•
(14)
где фр ф;— заранее выбранные функции, удовлетворяющие кинематическим граничным условиям.
Неизвестные параметры A,, Bi, Ci определяются из системы линейных уравнений (i = 1, 2, п)
дФ дФ дФ
w = o: 1Й7 = О: -ас- = 0 (15)
Для тел сложной конфигурации основная трудность состоит в выборе аппроксимирующих функций. Поэтому тело разбивают на малые, связанные между собой области, в пределах которых подбираются простые аппроксимирующие функции. По такому принципу строятся вариацнонио-раэ-иостные методы и метод конечных элементов.
ВАРИАЦИОННО-РАЗНОСТНЫЙ
МЕТОД
Сущность метода поисиим на примере плоской задачи теории упругости при отсутствии температурных и дополнительных деформаций.
Учитывая уравнение (6) и связь между деформациями и перемещениями и и о (соответственно в направлении осей х и у), можно записать
Фе — Фв1 dS =
S
S
где для плоского иапряжеииого состояния коэффициенты
1 —v2 ’
а
Е Ev
А~-оп-----SV'» В = П<17)
2 (1 —v2) 1 —v2 '
для плоской деформации
Е
л____________________
2(1 +v) (1 — 2v) ’
Ev
В (1 +v)(l — 2v) ‘
В равенстве (16) S—область тела (единичной толщины) в плоскости х, у;
r Е
2(l+v)’
Вариационное уравнение (1) при отсутствии массовых сил
6Ф = б (Фе — ФР) =
ди \2 I ди \21
= 6
до \2 дх /
— j (Xvu -j- Evti) dL I 0, (18) £ )
где Xv и Yv — проекции иа оси x и у компонентов внешней нагрузки на границе области с контуром L.
Для получения приближенного решения уравнения (18) удобно контур области аппроксимировать конечным числом прямолинейных отрезков. Исследуемая область покрывается нерегулярной (или регулярной) сеткой, состоящей из линий х = const и у = = const. Точки пересечения прямоугольной сетки должны совпадать на границах области с точками иа отрезках, аппроксимирующих контур (рис. 1, а).
Кроме того, иа область наносят дополнительную сетку *, линии которой проходят посередине линий основной сетки. Точки пересечения линий
* Наносятся штриховыми линиями лишь для получения разностных уравнений.
Вариационно-разностный метод
481
Рнс. 1. Сеточная размегка
основной сетки называют узлами. Подобласти, границы которых образованы контурными отрезками (линиями основной сетки) н линиями дополнительной сетки, называют ячейками. При этом каждая ячейка (заштрихована на рис. 1, б) содержит одну узловую точку и может быть прямоугольником либо треугольником.
В качестве основных неизвестных принимаем смещения в узловых точках um и vm> где т — номер узла.
Потенциальную энергию деформации каждой ячейки можно найти в предположении, что смещения точек между узлами изменяются линейно и их производные остаются постоянными в каждой ячейке.
Используем конечно-разностные соотношения для первых производных в точке т (см. рис. 1):
ди = Ui,h+i — ut,k .
дх ’
ди ui+1, k — ut, fe
ду > • • • >
где i и k — соответственно номера горизонтали и вертикали; и — шаги сетки (знаки <+» и «—» указывают, что соответствующие шаги приняты в направлении увеличения или уменьшения координаты).
С учетом равенства (16) получим приближенное выражение для потенциальной энергии элементарной ячейки 16 Заказ 402
1 с центральным узлом т (i, k), см. рис. 1, б:
Фе (t) = Фе (i, ft) —
А
Г j Uj, k+i — ut, k \1 2 lA h+x /
( Ui+l,h—V>,k \21
\ / J
T L\ h+x
, i Ui+r, k — Ui,k V ,
д—% Л
\ /
v ( fe ul, h \ >
X I h+ П"
\ У /
+ Д x
\ /
—(19)
где q;— «вес» ячейки (qj= 1 — для /-й ячейки, целиком лежащей внутри области; = 0,5— то же для ячейки, примыкающей к косой границе (треугольной ячейки); <?; = 0— то же для ячейки вне области *; / = 1,2.р —
номер центрального узла.
1 Законтурные ячейки используются для единообразного формирования систе-
мы уравнений иа криволинейной границе области
482
Численные методы расчета конструкций
Влияние температуры учитывается введением в выражение (19) дополнительного слагаемого:
1 — 2v \ ‘
, Vl+l,h — Vl,k \
+ hl Г
Так как аппроксимации для каждой ячейки имеют вид (19), то, суммируя потенциальную энергию деформации (19) по всем ячейкам сеточной области, получим соотношение для полной потенциальной энергии деформации
р
Фе=£Фе(/), С20)
/=1
где р— число узлов на области.
Вариация потенциальной энергии деформации
бфе = ^ЛбЦт + _^6г,т. (21)
Потенциальная функция внешних сил
Фр = У (Хьиъ Д(ь + Уьиь Д^ь), (22) Ь=1
где Хь и У;,— компоненты внешних сил, относящиеся к внешнему граничному узлу ft; ft = 1,2, ...; г— номер граничного узла; Д)ь—длина элемента границы возле узла Ь.
Вариация потенциальной функции внешних сил
= + <23)
Так как вариации Ьит и бот произвольны, то из условия (18) следует: -^-=0, -^-=0 дит dvm
(т=1, 2,.-., р). (24)
Величины ит и vm входят в соотношения (19) лишь для двенадцати (из шестнадцати) ячеек, окружающих узел т.
Поэтому, записав соотношения типа (19) для каждой из 12 ячеек, прилежащих к узлу т, продифференциро
вав их отдельно по ит и vm и просуммировав полученные выражения согласно равенствам (21), с учетом равенств (22) и (23) получим два разрешающих уравнения, связывающих смещения ит и vm в узле т с неизвестными смещениями в восьми соседних узлах (см. рис. 1, б) и действующими в них компонентами внешней нагрузки.
Записывая разрешающие уравнения для всех узлов сеточной области, получим (р + г) линейных алгебраических уравнений; здесь р и г — число неизвестных смещений соответственно “т и t>m*, которые можно представить в матричной форме
[В] {Я}, (25)
где [В] — симметричная, положительно определенная матрица коэффициентов: {(/}—вектор-столбец с компонентами смещений ит и vm; {/?} — известный вектор-столбец, характеризующий внешние нагрузки.
Система линейных алгебраических уравнений относительно смещений решается достаточно просто одним из известных методов. Для получения единственного решения система дополняется граиичиыми условиями в перемещениях.
В результате расчета при заданных нагрузках на контуре находят смещения во всех узлах сеточной области. Далее можно найти деформации и напряжения в каждом узле.
Примеры расчета напряженного состояния в элементах конструкции вариационно-разностным методом приведены в гл. 28 и 29.
Вывод разрешающих уравнений для пространственной задачи аналогичен приведенному.
МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
В последние годы широкое распространение получил метод конечных элементов, который имеет те же принципиальные основы, что и вариациои-
* Число неизвестных смещений ит н vm в общем случае может быть различным (например, если на одной нэ осей симметрии илн в заделке ит — 0).
Метод конечных элементов
483
где ф(л), ..., Ф,(л) — квадратные матрицы (3x3); Ut, ..., Um—векторы -------- -----.... ---- тетраэдра i,
смещения j, I, tn:
Ui =
четырех узлов
Ui
Щ
W{
ит '
vm . .
(29)
форме равенство
Um
Рис. 2. Конечные элементы
но-разностный метод, но более прост при реализации на ЭВМ [3]. Для расчета область расчленяют на конечное число малых элементов, обычно в виде треугольников для плоской задачи и многогранников для пространственной задачи (рнс. 2). В пределах элемента перемещения представляют с помощью суммы аппроксимирующих функций. Например,
и (х, у, г) = У, arfr (х, у, г).
(26)
где fr (х, у, г) — заранее выбранные функции; аГ — неизвестный параметр. Число параметров v выбирается равным числу узлов элемента, что дает возможность выразить смещения как линейные функции узловых смещений этого же элемента.
Для элемента в виде тетраэдра (см. рис. 2) принимают, что смещение ставляет линейную функцию дин ат
и (х, у, г) ~ at -f- а2х + + ОзУ + “4Z-
Обозначая и (х,, yi, ?i) ~ щ;
Уь Zi) = Of, w (Xi, yi, Zi) = u>i.
пред-коор-
В более краткой
(28) можно записать с помощью матриц и векторов, содержащих блоки:
3X1 3X3 3X1
{«п} = [Фп] {Un}.
1X1 1X4 4X1
Здесь и в некоторых случаях в дальнейшем указаны числа строк и столбцов в блоке матрицы (верхние цифры) и числа строк и столбцов в самой матрице (нижние цифры). Если одна из пар цифр состоит из единиц (IX 1), то верхние и нижние цифры можно переставлять. При умножении матриц «внутренние» (обязательно попарно одинаковые) числа «поглощаются».
После того как сформирована матрица аппроксимирующих функций [цп], вектор деформаций (3) записать с помощью матрицы ренцирования
1X1 1X3 3X3
U) = [О] [Фп] 6X1 .......
6X1 1X4
3X1 1X3
UM = [5П] 4X1
6X4
где
(30)
можно диффе-
3X1 UM. 4X1
(31)
(27) v (х>, где “ь V,, и>/ — компоненты смещения узла i элемента п, находим нз (27) вектор смещения для этого узла в виде
’ и (х, у, г)'
{un} v (х, у, г) ,: w (х, у, г)
Ui
U} Ui Um
, (28)
д дх
0
О
О
д ду
О
1X3 [£)] = 6X1
О
О
д дг
д ду
о
д дх
д дг
о
д
_ дг 1X3 3X3 [О] [Фп] = [5п]. 6X1 1X4 6X4
о
д ду д дх _ 1X3
(32)
16‘
484
Численные методы расчета конструкций
В соответствии с законом упругости вектор напряжений [см. уравнения (2) и (5)]
6X1 6X6
1X1 1X1
{оп) = [Л]
1X1 1X1 \
{аТ} - {е«} . 6X1 6X1 /
(33)
Для получения разрешающей системы уравнений используют начало возможных перемещений (для всего тела), что обеспечивает выполнение условий равновесия
JJJ {Мт М dV -
V
- JJJ {6uy{P}dV-J v
-- j [ {<?} dS = 0, (341
где
(35)
— векторы внешних нагрузок (объемной и поверхностной).
Проинтегрировав по всем элементам, будем иметь (А/э — число элементов)
У I f [ [ {&„}’ {on} dV -
АИЯЙ 1 J J J
- jJJ {Р} dV ~
— [j {б^Г = 0. (36)
SnfcS /
Последний интеграл распространяется на поверхности элемента, принадлежащие внешней поверхности тела; для всех внутренних элементов он обращается в нуль.
Учитывая равенства (30), (31) и (33), находим
"э
£ [ jjj (15n) {6Un}f Х и=! ( Vn
X {Un}dV - j [J ([Bn] {6i/n})Tx
X [Л] ({<XT) + {e«J)dV-- J [J ([Фп] {6t/n})T {P}dV~
- j J ([Ф«1 {6t/n})T {(?) dS 1 _ 0 sn€s )
(37) или
3X1 1X1 1X3 .
[S„]T [Д] [Bn] dV\ X 4X6 6X6 6X1 I
3X1 (’(’(’ 3X1 , 1X1
X {Un} - \ \ [Bn]T M] 4X1 ddJ 4X6 6X6 v n
/ txt 1X1 \
X {aT} + {e°} dV -
\ 6X1 6X1/
ШЗХЗ 3X1 [ФПГ {P}dv~ 4X1 1X1
v n
f (’ 3X3 3X1
[Фп]т WJ dS 4X1 1X1
dnt4
= 0.
(38)
Вследствие независимости произвольных вариаций {бУп} соотношение (38) эквивалентно системе ЗМэ линейных алгебраических уравнений
j j 1«П]Т[Л]Х ’'п
X ({аГ}-]- [е°)) dv~
Метод конечных элементов
485
- jjj (ФпГ {P}dV —
- J J [ФпГ {Q} dS | - 0. (39) sn£s )i
Запись n £ i означает, что в уравнение входят только элементы, примыкающие к i-му узлу. Индекс i показывает, что в сумму входят составляющие, связанные с узлом i (в четырехблочном векторе для тетра-идального элемента п сохраняется блок узла i).
Матрица разрешающей системы (39) является редко заполненной (имеет небольшой процент ненулевых коэффициентов) и при надлежащем порядке нумерации узлов имеет ленточную структуру.
Часто используют механическую трактовку уравнения (39), при которой отдельные слагаемые рассматривают как обобщенные усилия, а величину
Ш 3X3
[SnlTM] (Sn]rfV = [£nJ (40) 4X4
v п
как матрицу жесткости элемента л.
Тогда если через {Qn} обозначить узловые нагрузки, которые статически эквивалентны граничным напряжениям
jj [ФпГ
snes
то уравнение (39) для одного элемента (без учета температурных и дополнительных деформаций) имеет вид
[*n] {Un} — {Qn}- (41)
Матрица жесткости элемента п имеет блочную структуру, связанную с блочной структурой векторов {ип} и (Qn):
ka kjj kji k ini
kji kjj kji kjm
kit kij ku kim ’
Pint km] kml kmm
(42)
где ku, квадратные подма.
трицы (блоки) размерности (3X3),
kij- JJJ [В(]т [Л] (43)
где согласно (32) Гб,1 ~ [О] ГФ|п)Т,
Подматрица k)j показывает реакцию (обобщенное усилие) в узле i тетраэдра (элемента п) от единичного смещения его /-го узла при неподвижных узлах i, т, I.
Так как вся конструкция состоит из совокупности элементов, то матрицы жесткости отдельных элементов объединяются в матрицу системы.
В одном узле сетки обычно сходятся несколько элементов и каждый из
иих вносит вклад в матрицу жесткости, и t-я строка суммарной матрицы жесткости будет содержать соответствую
щие компоненты матриц жесткости
элементов, примыкающих к i-му узлу.
С учетом (39) матрица жесткости конструкции [Д'], содержащей N уз-
лов,
[KJ-
*24
*12 ...
К22 ...
...
kiN -
*2N
Knn _
(44)
Обозначая векторы внешних сосредоточенных в узлах сетки усилий и перемещений узлов сетки соответствен-
относительно узловых смещений {(?} -[/<] {U}. (46)
По физическому смыслу уравнение (46) представляет собой уравнение равновесия сное.мы (в смещениях). Для получения единственного решения система должна быть дополнена граничными условиями в перемещениях.
486
Численные методы расчета конструкций
Рис. 3. К расчету пластинки
Благодаря тому, что система уравнений (46) соответствует минимуму квадратичного функционала полной потенциальной энергии исследуемого тела, матрица этой системы симметрична и положительно определена. Эти ее свойства, а также ленточную структуру и «редкозаполнеиность> используют при решении системы точными методами (метод блочного исключения Гаусса, метод квадратного корня и т. п.).
Определив из уравнения (46) узловые перемещения, можно по формулам (33) найти напряжения.
Описанный вариант метода конечного элемента является простейшим. Можно повысить порядок аппроксимации функций перемещения в элементе, вводя, например, дополнительные узлы на ребрах тетраэдра или используя элементы другой формы (прямоугольную призму и т.д.). При этом точность расчета повышается быстрее, чем при измельчении сетки простых элементов.
Метод конечного элемента может быть эффективно реализован при наличии полностью автоматизированной программы, реализующей все этапы расчета конструкции (идеализация конструкции, формирование системы (39) или (46), решение этой системы, подсчет напряжений и других величин). Программа должна быть универсальной, пригодной для широкого круга практических задач.
Весьма эффективны программы, имеющие блок автоматического разбиения области на элементы, сокращающие процесс составления и кон
троля обширной исходной информации. Целесообразно применять графический контроль (вывод на графопостроитель или экран дисплея) данных о геометрии области и характере ее разбиения, а также выходной информации.
Примеры расчета элементов конструкции методом конечных элементов приведены в гл. 28.
Ниже приведен пример решения простейшей задачи, иллюстрирующей основные особенности реализации метода конечных элементов.
Пример. Определить перемещения в квадратной пластинке толщиной 1 мм от заданной нагрузки Р, Н/мм (рис. 3, а).
Для большей наглядности разобьем пластинку всего на два треугольных элемента (рис. 3, б).
Для получения разрешающей системы уравнений сформируем предварительные матрицы [Л] и [Sn] (см. соотношение (40)].
С учетом равенства (9) матрица коэффициентов жесткости [Л] для плоского напряженного состояния имеет вид
1 v 0
Р v 1 0
(47) Рассмотрим элемент /. Соотношения (27) для него будут такими:
и = «1 + а2х + а3у;
v =а4 + Щх + аву. (48)
Метод конечных элементов
487
Коэффициенты <34..а, определяют
через перемещения узлов из следующих систем уравнений (принято — = Ui, Ut — U). U9 = Um):
ai + a2xt + a3yt = uf, “i + Vj 4- а3у) = uf, ai + azxm + VJm = un>
(49)
и
a« + аьХ( + atyt = vt;
«4 + <Wj + Vj = v,\
a4 4" аьхт T а»Ут = vm>
(50)
где xi, tji', xj, y}; xm, ym— координаты узлов.
Определяя alt ..., a, из уравнений (49) и (50) и внося их в соотношения (48), получаем уравнения (28):
и = ~2д- [(a* + btx + сцу) ut 4- (а} 4- bjx 4- суу) Uj 4- (am 4- bmx 4- cmy) umJ;
V — 2Д- Kai "I- Vl + bjx С>У'> v! “I" ^am + bmx H" стУ) uml>
(51)
где коэффициенты a;, bi... выражаются
1 xi У) 1.
at = Ут , aj =
bi - 'Л 1 ; bj =
Ут 1 1 xi
Cf = 1 хт
через определители:
хт xi Ут Х/ yi I xi У1
У1 » =
Ут У1 1 1 1 хт । » — У1 1 У) 1 1 xi I
1 xi ’ ст ~ 1 xi 1
(52)
1 1 xi Vi
д = т 1 xi У) — коэффициент,
1 хт Ут
численно равный площади элемента.
В данном случае (плоская задача) матрицы Ф,......Фт имеют вид
ф‘ = [о ?]
л-, Г 1 0~| / ат 4" Ьтх 4- стУ \
Фт ~ L0 1J \ 2Л J ’
(53)
Для плоской задачи матрица дифференцирования принимает вид
Применяя соотношение (32), находим
(54)
(55)
[О] = 0 дх 0 “Т- ду д д — ду дх —
Так как в рассчитываемом примере
деформации постоянны в пределах
488
Численные методы расчета конструкций
каждого элемента, то матрицы [Sn] ие зависят от х и у.
В этом случае соотношения (40) и (43) примут вид
[£n] = [Sn]T [Л] [5П] Д;
= [Sf]T СЛ] [S;] Д. (57)
Перейдем к расчету пластинки, рассмотрим элемент 1. По формулам (52)
находим:
аТ = 0; а3 = 0; а3 — —а2;
bj = а; Ь2 — —а; Ь3 ~ 0;
<4 = —а; с2 =0; с3 = а.
к- а*
Д 2 ’
Из соотношений (53) получим функ-
ции, стоящие множителями у единичных матриц:
0]
О
I 3“ 2Д
а
О
В
Используя эти зависимости, по формуле (57) находим блоки матрицы
жесткости
р
*и = [^Т MH^A=w_vi)-x
Ф3^, а2
далее с учетом равенства (54) получаем матрицы
Q 0 ‘
0 —а .
—а а
' —а 0"
3 —V 1 + v “1
2 2
1 v 3 — v
—~ ~2
Проводя аналогичные вычисления, получаем остальные блоки для матрицы жесткости 1-го элемента, которая в рассматриваемом примере будет иметь вид
[М =
&21
- &31
^12
&22 ^32
&13
&23
k33 -
2(1— V2)
3 — v 1 4- v — 1 V 1 — V 1 — V 2 1 — V 2 V —1
2 1 4- v 1-^ “ 1 м
2 2 2
— 1 V 1 0 0 —V
1 — V 1 — V 0 1 —V 1 — V 0
2 2 2 2
1 — V 1 — V 0 1 -V 1 —V 0
2 2 2 2
V — 1 —V 0 0 1
Метод конечных элементов
489
Матрица жесткости для 2-го элемента формируется аиалогичио:
1 1 ~v 3 — v 1 v
2 2 2
1 —V 1 -j- v 3 —v
2 2 2
Матрицу жесткости пластинки в представить в виде (верхние индексы
соответствии с равенством при k показывают номер
(39) можно элемента)
[*1 = —- 1 1 ** аг о >5 о " ' со Ю г- Www г- Н* Н*
4V о -(^Ч^2)) (*ЙЧ*Й’)
ь(2) *42 Ь(2) *43 ь(2) *44
*12 *13 0 1
*22 *23 *24 Е
*32 *33 *34 2(1- V2) Х
*42 *43 *44 J
— 1 v
1—V 1—V
~2~ 2~
1—V 1—V
V —1
1 —v 1 —v
2~ ~2~
v —1
О О
О О
° -Ч _!+? о 3—V 1 — ° '| 1 п 3—v j 1—v 1—v ° 2 | 2 2
1—V 2 V 1? - 1—v | 3—v 14-v 2 1 2 2 1—v 1 14-v 3—v V 2'2 2 _
490
Численные методы расчета конструкций
Принимая во внимание краевые условия (Ui —0, U3 = 0), запишем матрицы смещений и внешних сил
известны. Однако благодаря исполь-
зованию краевых условий для перемещений (/j и (73 число уравнений уменьшается на 2, и единственное решение задачи получается путем «вычеркивания» 1-й и 3-й строк и таких же столбцов.
Таким образом, для определения неизвестных смещений используем уравнения
И*1 {[/*} = {Q.}>
где
[К 22 К 24 1
* к
Л 42 Л 44 J
Е
2(1 —V2) Х
При v = 0,3 получим систему уравнений
1 ,35u2 -f- 0 t?2— 0,35u«+ + 0,35о4 = 0;
0 • u2 + 1,35у2 +
+ 0,3u4— 1-р4 = —1,82 —
—0,35ц2 + 0,Зц2 +
~г 1 ,35ц4 — 0,65п4 = 0;
0,35и2— 1-:>2— 0,65и4+ + 1,35п4 = 0,
откуда
1'2 = —3,385 и4 = —2,91
Е Е
ц2 = 0,63-^~; ц4 = — 0,49 ~ .
Е Е
Для определения неизвестных реакций Qlx, Qly и Q3X, Q3j, следует ис-
1 — v 1 — v
—Г"
v —1
3 — v 1 + v
—2 2
1 -j- v 3 — v
2~ 2~~
пользовать соответственно 1-е и 3-е матричные уравнения. Для данного примера разрешающую систему уравнений можно получить значительно проще, путем подстановки функции и и v соотношения (51) в уравнение (18) и удовлетворения условий (24). Однако для сложной задачи (с большим числом элементов) указанный алгоритм метода конечных элементов оказывается наиболее простым и универсальным.
ДИНАМИЧЕСКИЕ РАСЧЕТЫ
Численные методы широко используются при расчетах собственных частот и форм колебаний элементов конструкций, напряжений при установившихся вынужденных колебаниях, при исследованиях границ динамической устойчивости и при решении ряда других сложных проблем динамики. Многие из таких методов, относящихся главным образом к стационарным динамическим процессам, широко освещены в технической литературе [2 и др.].
Динамические расчеты
491
6)
Рис. 4. Разбиение стержня на элементы (а) и напряженно-инерционное состояние элементов в моменты времени t (6) и t + ti (в)
Более сложными и менее разработанными являются методы расчета нестационарных задач для деформируемых конструкций, в особенности при меняющихся граничных условиях (ударное и виброударное нагружения, переходы через резонансные состояния, динамика систем с зазорами и переменными точками контакта, воздействие движущихся нагрузок и пр.). К наиболее математически простым, а вместе с тем физически корректным методам численного анализа нестационарных явлений в континуальных одномерных системах относится разработанный в последние годы метод прямого математического моделирования (ПММ) на ЭВМ процессов распространения волн механических возмущений (напряжений, деформаций, скоростей и т.п.) [ 5].
Его сущность изложим на примере расчета продольных волновых процессов в упругом стержне длиной I постоянного поперечного сечения площадью F, боковая поверхность которого свободна от нагрузок.
Разобьем стержень на п равных элементов длиной Дх — Ип\ номера
элементов /= 1,2, ..., п, номера сечений j — 1,2, .... п + 1 (рис. 4, а). Пусть в момент времени t каждый элемент имеет постоянные в его пределах продольную скорость Vj0, напряжение о;-0 и деформацию е^0, причем Oj0 = = EejQ, где Е — модуль упругости материала (рис. 4, б). На границах смежных элементов эти параметры могут отличаться на произвольную величину (иметь «сильные» разрывы), которые, однако, в тот же момент времени t должны распасться, в результате чего напряжение на правой границе /-го элемента о+ станет равным напряжению на левой границе (/+ 1)-го элемента оу-рр то же относится к границе /-го и (/ — 1)-го элементов и к скоростям:
О; = О7+1, nt = PT+1;
оу==а;_,, рт = с,+_1. (58)
Зоны «возмущения» с параметрами (58) будут распространяться в глубь соответствующих элементов в соответствии с законами механики упругого тела со скоростью с, так что глу
492
Численные методы расчета конструкций
бина их проникновения за время t, будет х, = с/, (рис. 4, в). Так, для правой границы /-го элемента получим следующие соотношения.
Закон сохранения импульса. Изменение количества движения pFx* (v+ - - и/0) массы pfx# должно быть равно импульсу постоянных сил (at — о;0) Ft*, действующих на границах этой массы в течение времени t„, откуда
ot - о/0 .-= рс (и) - р/0). (59)
Условие сплошности тела. Разность перемещений (ut— — vj0) I* границ зоны возмущения за время t, должна быть равна ее абсолютному удлинению (et—е^х#, откуда
ot-v/0 = е(Е/ -е/0). (60)
Закон упругости. Изменение напряжений at — связано с изменением деформаций et — e^0 соотношением
o}-o/0 = £(et-e.0). (61)
Выражения (59)—(61) удовлетворяются совместно только при
(62)
что соответствует известной формуле распространения упругих волн в стержне.
Аналогично для левой границы (/ + 4- 1)-го элемента
а/-н — °/+1. о ” 9е (и/+1 ~ £7+i, о)
(63) и т. д.
Решив уравнения (59)—(63) совместно при учете первых двух условий (58), найдем значения напряжений и скоростей, распространяющихся в глубь /-го элемента от его границы с (j + 1)-м элементом:
о/==0’5[а/+1,0+о/'0 +
+ Рс (v/+l. 0 — р/о)1;
yt = 0,5 [ц/+1 0-ф tb0
+ (°/+1, 0 “ °/о)/Рс],
т. е. напряжение и скорость изменятся на at - a/0 и ut — vj0.
Аналогично для левой границы /-го элемента
ay=O,5[a/_lo4-a/o —
— рс (р/-1,о —р/о)];
(65) р/ = 0,5 +
- («/_,. о — °/о)/Рс1-
Изменение параметров составит °7 - °/о и "7 - vio-
По принципу суперпозиции линейных деформаций волны (64) и (65) распространяются независимо, поэтому эти соотношения будут справедливы в течение времени Д/ = Дх/с до встречи с противоположными границами элемента. В момент времени t Д/ во всем /-м элементе установятся новые напряжения
О/ (< + ДО = а/о + (а+-а/о) +
+ (а7“°/о) = 0/ +а7-°/о (66) и скорости
V/ (t + до = vl0 + (v; - vl0) +
+ (v7 — v/o) = vt + V1 — vi0- (67)
Формулы (64)—(67) образуют систему рекуррентных (повторяющихся) соотношений, позволяющих по известным в момент t значениям напряжений и скоростей в /-м и в двух соседних (j + 1)-м и (/— 1)-м элементах найти новые значения напряжений и скоростей в /-м элементе для момента времени t -+- At. Добавляя условия на внешних границах стержня (заданные напряжения, скорости, перемещения) и последовательно решая эти системы для всех элементов с шагом по времени Д/ = &х/с, получим точную и исчерпывающую картину динамического процесса в стержне при самых произвольных условиях нагружения.
В более общих постановках задачи произвольно меняющиеся по времени нагрузки аппроксимируются ступенчатыми функциями с постоянными в пределах Д/ значениями. Распределенные по длине стержня нагрузки
Динамические расчеты
493
считаются приложенными на границах элементов всечениях/^Р^ /±1). В число внешних сил могут включаться силы трения, неизвестные силы реакции и прочие. Стержни переменного сечения представляются ступенчатыми с постоянными в пределах элементов площадями Fj. Если £ и р меняются по длине стержня, он разбивается на элементы разной длины так, чтобы их длины Дх^ удовлетворяли условию где с} == У£/р> при &t, одинаковом для всего стержня. При этом в пределах /-го элемента принимается = const, Qj= const. При уменьшении отрезков времени &t, а следовательно, и Дх7 принятые условия позволяют воспроизводить переменные характеристики с необходимой точностью.
Так как при принятых допущениях соотношения (64)— (67) являются точными, то процесс расчета абсолютно устойчив при любом числе элементов и временных этапов.
Для общего случая зависимости типа (64), (65) можно объединить, записав их для упругого стержня в виде
Рнс 5. К расчету соударения двух стерж-ней
„± х P/±lC/±lW/±>.o + P/C/V/±(^±l.O-'V/o) + ‘P/./±1 /fiR>
где Nj0— af0Ff, ^/±i.a/±i. o£/±i-
Напряжения определяются затем по формулам (59) или (61) Условия равновесия на границах элементов
^ = */±>±^/±1- <69)
Если — перемещение границы /-го элемента в начале этапа, то в конце его
У* Т Д/) =-- у±0 -j- vjt Д£ (70)
Пример. Упругий стержень длиной 21 и площадью поперечного сечения F ударяет со скоростью о0 но упругому стержню длиной I и площадью 2F из того же материала, имеющему такую же встречную скорость —-ц0 (рис. 5, а). Определим скорость отскока пОгск ПРИ упругом ударе и изучим динамическую картину соударения.
Так как массы и скорости стержней равны, то по элементарной теории соударения упругих тел они разлетятся с той же скоростью Oq-icki” = —v0, ОО1СК2 = Г'о- Однако действительная картина удара из-за разной конфигурации стержней будет иной.
Представим 1-й стержень в виде двух элементов, 2-й — в виде одного элемента длиной Дх, = Лх2 - Лх3 = — I. Начальные условия (в момент начала контакта). о10 — о20 = о30 — — 0; t>l0 = ~ v9; = — о0. Гра-
ничные условия: ор = 0; Oj = 0. При контакте стержней <rj — <rj 0, после отскока 17+ - о: -- 0. Первый шаг по времени t = 1, tt = kt = Дх/с = = Ис\ с = \/Е!р.
Первый элемент левая граница, формула (63):
Р1 = 010 — (°Г °ю)/Рс ~ vo> ai —
494
Численные методы расчета конструкций
правая граница, вторая формула (64)
= 0,5 [ц20 + ц1() + (о20 — о,(,)/рс] =
= vu, of — 0
Новые значения
ai + ДО = + аГ 0,0 = 0>
v} (t + ДО = of + vf — «10 = и10
Второй элемент
левая граница, uj = vj = vtl, о* — = of = 0.
правая граница, формула (68) при f2 = F, F3 = 2F, Р218 = О
+___F3v30 + F2ц20 (FggjQ — F20го)/рс
2 - G 4 F з
—2+1 1
— 3 v0 - — 3 у„;
4
of = аго+ PC (f? — Уго) = — у Р™о<
< 0 есть контакт
Новые значения
а2 (I -р At) -= at -f- а2 — о20 = 4
=------з~ рсс’о.
+ (t + Д/) =. V* Т- — vM =- --у v0
Третий элемент, левая граница-
+ 1
+ — vt--------у +>
2
о? = о30 — рс (с; — о20) -= — -у pcv0 (05 = 0,5af, но ,V; = Nt)-,
правая граница
aj = О, 0+ = Uf0 + (a+ - a3o)/pc= —v0 Новые значения
о, (t )- At) = a+ + 0~ - a,0 = 2
= —-у-рст0, v3(t + At) =
= + + V3 — V30 =-------y- vo.
Затем проводится аналогичный расчет для момента времени t2 = О + + At (, = 2) и далее в том же порядке
На рис 5, б приведены результаты расчета в виде зависимостей Vj и о;-от номера шага t В момент t — 4At, когда упругая волна, отраженная от левой свободной границы первого элемента, возвращается к плоскости контакта, происходит отскок стержней В этот момент второй стержень не на-
7 пряжен и имеет скорость v3 — -у v0, которую он и сохраняет в дальнейшем Элементы первого стержня при этом имеют такую же скорость = о2 =
7
=---у с0, но они испытывают на-
пряжение растяжения = a2 = g
= — рсу0 (В£ всех точках, кроме внешних границ, что является источником последующих колебаний) В дальнейшем первый стержень будет двигаться с той же средней скоростью 7
»СР = °-5 (°! + ^а) = — у уо- но в нем будут происходить незатухающие (в отсутствии сил внутреннего трения) колебательные процессы в виде волн напряжений и скоростей, как показано иа рис 5, б
Полная энергия системы стержней после отскока сохраняется постоянной и равной (например, при определении ее в моменты , = 5, 7 и т д)
3I=Kl + K1+K,-^-l>Fl^x
х['4+1.(Я++Я1=
= 2рР/о§,
что в точности равно начальной кинетической энергии стержней и подтверждает упругий характер удара.
Потеря скорости из-за упругих колебаний стержней в данном случае составляет ~12%
Из приведенного примера следует, что расчет чрезвычайно легко алгоритмизируется.
Уравнения упругости
495
Методом прямого математического моделирования решены задачи кручения и изгиба стержней, деформации струн, плоских и сферических волн, деформации упруговязких и упругопластичных материалов. Им успешно
решаются многие технические задачи, связанные с проблемами анализа нестационарных процессов в деформируемых элементах машин и конструкций , с динамикой поездов и пр. [4, 5, 6]
Глава 27
РАСЧЕТ КОНСТРУКЦИЙ С УЧЕТОМ ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ
Во многих конструкциях возникают деформации пластичности и ползучести (в деталях паровых и газовых турбин, авиационных и других транспортных двигателей). Нагружение часто осуществляется при переменной температуре, когда механические характеристики материала существенно зависят от температуры.
В отличие от технологических задач теории пластичности и ползучести (обработка давлением и т. п.) деформации пластичности и ползучести в работающих конструкциях невелики, однако их учет оказывается совершенно необходимым для расчета на прочность, оценки надежности и долговечности их работы.
В последние годы расчет на прочность элементов конструкций интенсивно совершенствуется за счет широкого использования электронных вычислительных машин (ЭВМ). Открываются возможности более полного описания элементов конструкций с учетом реальных свойств материалов, характера нагружения и условий разрушения.
Ниже рассмотрены основные модели материала и методы расчета напряжений и деформаций в конструкциях при простом и сложном нагружении с учетом упругости, пластичности и ползучести.
УРАВНЕНИЯ УПРУГОСТИ
Уравнения упругости для анизотропного тела с учетом температурных и дополнительных деформаций имеют вид
{е}'=[а]г{а} + {аП + (е0}, (1)
где векторы-столбцы деформаций, напряжений, температурных и дополнительных деформаций
ех
е» ег
1
2 Ухч
1
1
— Yzx
(«П =.
Ох
°?
тху Tyz Tzx
(2)
496
Расчет конструкций с учетом пластичности и ползучести
[а]'—симметричная квадратная матрица упругих коэффициентов размерности 6X6. Верхний индекс е соответствует упругим деформациям.
Введение дополнительных деформаций в равенство (1) связано с последующим использованием модели упругого тела для описания пластичности и ползучести материала. В некоторых задачах дополнительные деформации позволяют учесть структурные и фазовые превращения в материале.
Известно, что напряжения и деформации в точке образуют тензоры. Представление напряженного и деформированного состояния шестимерными векторами, составленными из компонентов тензоров, более удобно для записи уравнений пластичности и ползучести в матричной форме (см. обозначения в гл. 26).
В соотношениях (2) *
ди , ди .
где и, и, w— упругие смещения соответственно по осям координат х, у, г. Значения уХу в технической теории упругости равно удвоенной величине соответствующего компонента тензора деформаций.
Для ортотропного тела матрица упругих коэффициентов имеет вид
* Здесь и в дальнейшем символы (х, у, г) означают, что недостающие соотношения выписываются по правилу круговой перестановки индексов.
— 1 Уху Vxt 0 0 0 —
Ех Еу Ег
Уух 1 Vyz о о о
Ех Еу Ег
v2X vzy 1 о 0 0
[а]‘ = Ех 0 Еу 0 Ez 0 1 0 0 ; (3)
0 0 о о 1 о
2Gy2
0 0 о 0 0 1
2G„
для обычного изотропного тела
- _1_ Е V ~~~Ё V ~"ТГ 0 0 0
V 1 Е V ~ тг 0 0 0
[а]е V ~~Ё 0 V 0 1 Е 0 0 1 2G 0 0 0 0 > (4)
0 0 0 0 1 2G 0
0 0 0 0 0 1 2G
Уравнения пластичности
497
где Е, G — соответственно модули упругости и сдвига; v— коэффициент Пуассона.
Отметим, что в формуле (1) коэффициенты линейного температурного расширения представляют собой средние значения в температурном интервале от 0 до Т.
Например, линейная температурная деформация в направлении оси х
т
ех = ахТ = j а* (0) dQ, (5) О
где а*— истинный коэффициент температурного расширения; 0—текущая температура.
Из последнего равенства вытекает-
«; = -£г (6)
Считая коэффициенты упругости зависящими от температуры, из уравнения (1) получаем
(de}‘= [ц]е {<to}+
+ [а]0 +
+ pT’+f&o}. (7)
Для изотропного тела соотношения (7) в развернутом виде будут такими:
УРАВНЕНИЯ ПЛАСТИЧНОСТИ
Деформационная теория пластичности [3, 4] предполагает наличие однозначной зависимости между суммарными деформациями в упруюпласти-ческом теле и напряжениями. Для изотропного тела основные соотношения деформационной теории имеют вид
1 -4- v
ех —б = —g—ф(аж —а),...;
1 1 -|- v
-2-?хУ = —фтху>... (х, у, г),
(8)
где Е, v— соответственно модуль упругости и коэффициент Пуассона. Средние деформации и напряжение связаны соотношением упругости
е = Azp'’ а + аТ. (9)
здесь е и а— соответственно средняя деформация и среднее напряжение:
в — “о- (ех + £у + Вг);
(10)
V - -у Мд
В равенствах (8) величина ф представляет собой параметр пластичности:
3 г.
* = Т(Г4-^ТН^’ (И)
где аг и ег — соответственно интенсивности напряжений и деформаций,
[°Х — v (Оу + о2)] dT —
~ 1/2 Х
1 dv
~ + °z) ~dT~ +
+ ^~dT + d^...-, d^ = 7Td\y-
х/(ах-°у)1 2 + --- + б(т^+...);
(12)
= —— X
3 х
x/(ex-s)2 + - + у(^у+-);
а* — интенсивность напряжений в упругом теле, соответствующая интенсивности деформаций ег.
В расчетах принимается, что интенсивности напряжений о/ и деформаций
498
Расчет конструкций с учетом пластичности и ползучести
е(- связаны одиозиачиой зависимостью (рис. 1)
Of = Ф (®i)- (13)
Эта зависимость (обобщенная кривая деформирования) предполагается одинаковой для любого напряженного состояния.
При растяжении стержня
ох = <Jq', Оу — 0; — 0; тху = 0;
Tyz — 0; Tzx — 0> вх = во» Ву ” —v*B©» ez = —v*e0; Уху = 0; yyz = 0; yzx 0 и из (12) получим
аг = о»;
_ 2(1+v*)
ei — j Bo> (1*1
где v* — коэффициент Пуассона в области упругопластических деформаций (v v* 0,5). Часто в практических расчетах принимают v* = 0,5, и тогда уравнение (13) представляет собой зависимость а0— е0 при растяжении стержня. При упругих деформациях параметр пластичности ф = 1 и уравнения (8) совпадают с уравнениями упругости
1 е 1 + v
~Ё—^ху’--- (х’ У’ *)•
(15)
Верхний индекс е, как и раньше, означает, что рассматривается упру-
гая часть деформации. Вычитая из соотношений (8) равенства (15), получим выражения для пластической деформации:
j «у
ех “ ~£ (Ф ~ О (°х ~ °).....
(16)
4 =-Цр 1 > тхУ ’ • • • (*- У'z) •
где верхний индекс р соответствует деформациям пластичности.
При выводе последних соотношений учитывали, что для пластических деформаций
°₽=4(е’+1+*п=°
и поэтому в — ее.
Равенства (8) можно записать в векторной форме:
{г}=4рФ{5}’ (17)
где {е} — вектор-девиатор деформаций; {S}—вектор-девиатор напряжений
{а} =
ех — е еу — е ez — е
1
тУху
1
тУуг
1
2
их — а
—а
uz — и
T'ZX
; («} =
(18)
Соотношения (16) можно представить в виде
{е)₽ = -Цр- (ф - П (S).
Вектор пластической деформации коллинеарен вектору-девиатору напряжений. Приведем еще несколько соотношений деформационной теории пластичности. Если каждое из уравнений (8) возвести в квадрат, сложить все
Уравнения пластичности
499
шесть полученных равенств и извлечь квадратный корень, то получим
2(l-f-v) „
ег =— зд фоь
что соответствует зависимости (11).
Подобным образом можно найти интенсивность пластических деформаций из уравнений (16):
Из последних соотношений вытекает:
е — ер -4- 2 (1 + а — еР и
ei — ei П 3£ — Ч I еа
(19)
т. е. интенсивность деформации равна сумме интенсивностей пластических и упругих деформаций.
Для случая растяжения получим
°i = %; = eg-
Так как пластическая протекает без изменения
деформация объема, то
рр — рр — ____ рр-------
2 е0'
Из уравнения (19)
п 4 U Т *
ei = е0 н 3£ °о = ео ~
2(1 Ч-v) о о
Е
ЗЕ
или
1 — 2v
е/ = 8о------------
Е
де-
В качестве обобщенной кривой формирования можно рассматривать обычную кривую деформирования при растяжении а0— е0.
Для приведения кривой деформирования, соответствующей сложному напряженному состоянию, к эквивалентной кривой при простом растяжении, следует положить
ео — е.» +
1 — 2v а,- .
3 Е ’
— ai-
(20)
Экспериментальные исследования показали, что основные зависимости деформационной теории пластичности справедливы по крайней мере при монотонном возрастании и в случае простого нагружения *.
Если (о)0— обобщенный вектор напряжения, соответствующий внешним воздействиям в момент времени t0, то при простом нагружении в момент времени t
{а} = {а}</ (Г), (21)
где f (/)— произвольная, неубывающая функция времени.
Из равенства (21) следует, что в процессе простого нагружения все компоненты вектора напряжения увеличиваются в одинаковое число раз. Следовательно, при одноосном напряженном состоянии нагружение всегда будет простым.
Деформационная теория пластичности нашла широкое применение в практических расчетах. Однако при сложном нагружении, особенно когда на некоторых этапах происходит разгрузка, применение деформационной теории может привести к погрешностям. Основной недостаток этой теории — отрицание роли «истории нагружения».
Во многих случаях более оправданным является применение теории пластического течения [7]
В соответствии с теорией пластического течения приращения пластической деформации в процессе нагружения
T}do.+
+ Гг(аг, 7)d7] (ох-а),...; (22)
4-Ег(ог, T)dT} (х, у, z), где о,- — интенсивность напряжений [см. (12)]; Т—температура.
Применяя равенства (22) для случая простого растяжения при Т —
* Нагружение называют простым, если соотношение между компонентами напряжения остается неизменным в процессе нагружения.
500
Расчет конструкций с учетом пластичности и ползучести
Рис. 2. Кривые деформирования при растяжении с постоянной температурой (а) и с постоянным напряжением (б)
= const, находим функцию напряженного состояния
Fo(<3i, Г) =
3 / ‘___________________
2о,- k Ек (аь Т) Е (Т) ) ’
(23) где Е (Т) — модуль упругости материала при температуре Т', Ек (оа, Т) — касательный модуль, определяемый по обычным кривым демпфирования при о0 — о,, Т — const (рис. 2, и).
Термомеханическая функция
Fr(Oi, Т) -..
= 3 Гв , °t dE (Л "I
2oi LP+ Е'2 (Т) dT J’ где Р = f (в}, Т) — коэффициент температурной податливости, зависящий от напряжения и температуры. В упругой области
о _ о; dE
р £2 dT ‘
Коэффициент р (о,-, Т) определяют по экспериментальным кривым растяжения при о0 = oi = const и непрерывно повышающейся температуре (рис. 2, б), этот коэффициент представляет собой приращение деформаций при oj == const за счет увеличении податливости материала при возрастании температуры на 1 °C.
Термомеханическую функцию можно представить в виде
Ft (Of. Т) =
до (Г, О
= -Fa (аь Т) , (24)
где as (Т, ef.) — мгновенный предел текучести, соответствующий температуре Т и накопленной пластической деформации ef (рис. 3). Величина ef равна сумме интенсивности приращений пластической деформации на всем пути нагружения:
с I* dep.
C = ,25)
о где __
, n V 2 def. = —g— X
X ]/\dep — dep)2+ ... +
+ |[(d^)2 + .••] • (26)
Равенства (22) описывают приращение пластической деформации при выполнении условия активного нагружения « > 0)
ai = a,Hdai>^-dT. (27)
01
Уравнения ползучести
501
Рис. 3. Поверхность деформирования
Если справедливо хотя бы одно из условий
или dot dT, (28) 01
то следует считать, что приращения пластической деформации нет. В этом случае имеет место либо разгрузка, либо упругое нагружение. Равенства (22) можно представить в векторной форме
{de}p = [Fa (оь T)dOi +
+ Рг(ог, T)dT]{S}. (29)
Вектор приращения пластической деформации коллинеарен вектору-девиатору напряжений.
Изложенный вариант теории пластического течения предполагает изотропное упрочнение по мере увеличения и не описывает эффект Баушин-гера. Однако его можно использовать как первое приближение при расчете конструкций в условиях сложного нагружения.
УРАВНЕНИЯ ПОЛЗУЧЕСТИ
Ползучесть материала (возрастание деформаций с течением времени при постоянном уровне напряжений) проявляется в теплонапряженных конструкциях. В современных моделях ползучести приращение деформаций ползучести принимается равным
de'=<I>dt (a% —а),.
= ®dtTxy,... (х, у, г), (30)
где t — время; Ф — функция ползучести, зависящая от инвариантов напряженного и деформированного со
стояния. Верхний индекс «с» соответствует деформациям ползучести.
В векторной форме равенство (30) запишется в виде
{S}. (31)
Вектор приращения деформации ползучести коллинеарен вектору-девиатору напряжений.
Теории ползучести различаются определяющими параметрами. В теории течения [5, 7] принимают
Ф = Ф (а,. Т, t); (32)
в теории упрочнения [5, 7 ]
ф = ф(ар Т, efj, (33)
где 8j — накопленная деформация ползучести.
Величина е,ф определяется соотношениями (25), (26), в которые входят приращения деформаций ползучести * *.
Пусть известна кривая ползучести (рис. 4) и определена скорость деформации ползучести
6 dt ’
где — деформация ползучести при одноосном растяжении.
Применяя теорию течения при ползучести для случая простого растяжения, из уравнений (30) получим
Ф = ^-5(«’йЛ/). (34)
Скорость ползучести определяется по времени нагружения. Потеории упрочнения скорость ползучести зависит от накопленной деформации ползучести и
Ф=1^(а<’л О (35)
где а,- = а0, = eg.
В зависимости (34) историю нагружения отражает время t, в уравнении (35) — накопленная деформация ползучести е.‘ . В расчетах используют
. ,, с
* Соотношения для получаются из равенств (25) и (26) заменой в них верхнего индекса р на с.
502
Расчет конструкций с учетом пластичности и ползучести
Рис. 4. Кривая ползучести
также теорию старения, которая основана на изохронных кривых ползучести
eS=^(ao).
аналогичных кривым деформирования материала. Эти кривые получают перестроением кривых ползучести при Т — const, t — const. Расчет по теории старения аналогичен упругопла-стическому расчету. Основной недостаток теории старения — ограниченные возможности описания сложного нагружения.
РАСЧЕТ КОНСТРУКЦИЙ
НА ПРОЧНОСТЬ С УЧЕТОМ ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ (ПРОСТОЕ НАГРУЖЕНИЕ)
Часто используют модель простого нагружения, при котором в каждой точке тела соотношения между компонентами напряжений в процессе нагружения остаются неизменными.
Использование такой модели не приводит к существенным погрешностям и в тех случаях, когда нагружение является монотонно возрастающим и главные направления тензора напряжений (или направления главных напряжений) остаются неизменными в процессе нагружения.
Определение напряжений и деформаций в элементах конструкций с учетом пластичности и ползучести связано с большими трудностями, так как расчетные соотношения оказываются нелинейными. Для линеаризации задачи можно использовать метод переменных параметров упругости и метод дополнительных деформаций.
Метод переменных параметров упругости основан на предоставлении зависимостей для упругопластического тела в форме уравнений упругости, в которых параметры упругости зависят от напряженного состояния и поэтому переменны в различных точках тела.
Соотношения деформационной теории пластичности (8) и (9) представим в обычном виде закона Гука
ех = [ох —+ о?] + а7’,...;
(36)
2(1+?*)
Тху— р Тку--- (*< У> г),
3
(37)
где переменные параметры упругости зависят от напряженного состояния, т. е.
Е = Е_______________________
* 2(1 +v)4|>+ 1 — 2v ’
ф (I + v) — (I — 2v)
2г|з (I + v) 4- I — 2v ’
здесь ф — параметр пластичности, определяемый
Учитывая
(38)
по формуле (II). уравнения (20), найдем
3
2(1+*)
I - 2v 3
Е Ес
Ф =
о
с °0 •
где Ес = —----секущий модуль кри-
во
вой деформирования (при растяжении).
Внося (39) в соотношения (37) и (38), получим простые равенства
Е* — Ес\
= [1-^(1-2v)J. (40)
Обычно влияние коэффициента Пуассона на напряженное и деформированное состояния невелико и во многих практических задачах можно положить
** = -у- (v + -у) = 0,5v + 0,25 или считать в упругой области v, = v, а при наличии пластических деформаций v. — 0,5. Так как параметр ф (или секущий модуль Ес) заранее
Расчет на прочность при простом нагружении
503
Рис. 5. Схема расчета по методу переменных параметров упругости
неизвестны, то при расчете используют процесс последовательных приближений. В первом приближении, считая материал упругим, при Е, (1) = = Е и — v (где Е и v — модуль упругости и коэффициент Пуассона материала, зависящие от температуры) решают упругую задачу, из которой находят а*( (1) (рис. 5) в каждой расчетной точке. В плоскости а0 — е0 состояние первого приближения изображается точкой 1, лежащей на пересечении линии а*(1) и луча, угол наклона которого равен arctg Е. Этому состоянию соответствует эквивалентная деформация
е - °*(1)
Е0 ( 1 ) - £
и секущий модуль
Е
с (1) —
qHD е0(1)
Во втором приближении полагают 1 Г Е £«(2) = £c(1);v»(2) = ур-----
X (1 —2v)] и, решая ту же задачу при Е, (2) и v, (2) , находят новое состояние 2 и т. д. Расчет заканчивается при достаточной близости двух соседних приближений.
При расчете с учетом деформации ползучести наиболее простая расчетная схема получается для теории старения. В этом случае также используют метод переменных параметров упругости, но для кривой деформирования, соответствующей времени t.
Обычную кривую деформирования применяют для начального момента времени (t = 0).
Учет ползучести по теории течения или упрочнения проводят по этапам времени. На начальном этапе выполняют расчет по уравнению (36). Для нового этапа после времени А/ расчетные уравнения имеют вид
Ех1 — — Iaxi — у» (ayi 4~ azi)l +
+ аТ -)- е£0,..(41)
2(1 + УД Е,
Хху 1 +
Уху i —
+ ^0’”- О- У< г')>
где е£0...усху0 — деформации ползу-
чести, соответствующие напряженному состоянию в начале этапа нагружения.
Из уравнений (30) получим
8л = фо(<’хо-°о)^Р"-; 02)
у^о = фотх4,од/р--- (*• У' г>-где функции Фо находят из уравнений (34) или (35) при значениях определяющих параметров, соответствующих началу этапа нагружения (а;0, То, 0, ecit0= 0). Величины ox0i ...,тжг,0 представляют собой напряжения в упругом материале при отсутствии деформаций ползучести.
Для следующего этапа нагружения уравнения упругости имеют вид
ех2 = [Ях2 — v. (ау2 + °г2)] + х-ф
+ ОТ + > • • • >
Уху2 =
- тхУ2 + ^р--- (X.У-г),
где е^р ..., у* , — деформации ползучести, накопленные к началу этапа нагружения,
ех1 ~ ех0 + Ф1 (°х1 ~ а1) д<2’- • •;
2 ^ху 1 2 ^хуО "0
4~ ф1^ху 1 А^2,• • • (а У. г).
504
Расчет конструкций с учетом пластичности и ползучести
Подобным образом рассчитывают остальные этапы нагружения. Длительность этапов выбирают настолько малой, что изменение напряженного состояния в результате ползучести незначительно.
Наиболее просто изложенный метод расчета можно применять в случае, когда пластические деформации отсутствуют, а деформации ползучести развиваются в упругом теле. Тогда во всех приближениях принимают Е* = Е, v* = v. Если уже иа первом этапе нагружения (t = 0) возникают пластические деформации (напряжения превосходят предел текучести материала), то для расчета используют метод переменных параметров упругости. Этот метод применяют и для второго этапа нагружения, причем расчет считается достоверным, если в точках, в которых имелась пластическая деформация в конце первого этапа нагружения, интенсивность напряжений увеличивается (точнее, пластическая деформация возрастает). Если это условие не выполняется, то расчет проводят снова, причем в точках разгрузки принимают Е„ = Е, = v. Аналогично осуществляется расчет последующих этапов нагружения.
Метод дополнительных деформаций. В этом методе, в отличие от метода переменных параметров упругости, деформация пластичности рассматривается как дополнительная, имеющая характер анизотропной температурной деформации. Основной в этом случае является обычная задача теории упругости с постоянными параметрами упругости, что существенно упрощает «упругое» решение. Однако структура процесса последовательных приближений оказывается несколько сложнее, чем в методе переменных параметров упругости.
Для деформационной теории пластичности основные уравнения имеют вид
«x = -^-lax-v(ay + °z')] +
Ч-аТ + еР,...; (43)
Уху^-^ху + ^х!,’--- (*> У’ г>-
где дополнительная пластическая деформация
(44)
Уху = 2"'j~V) (Ф~1)Тху,... (Х,у,2).
Учитывая соотношения (8), равенства (44) можно записать в виде, часто более удобном для решения задач:
(45)
Y^==(l-v)1’«’--- (х’гЬ
Здесь, как и ранее, под дополнительными деформациями понимается разность между действительными упруго-пластическимн деформациями еж, ... и их упругой частью ех, ... .
В первом приближении, которое совпадает с первым приближением в методе переменных параметров упругости, решается упругая задача при отсутствии дополнительных деформаций. Определяются значения компонентов напряжений a’p ..., т* (1), ... и деформаций ех (1), .... уху(1), .... интенсивности напряжений о( (1). В плоскости а0 — ео состоянию первого приближения соответствует точка 1 (рис. 6).
Значению а* (1) соответствует эквивалентная деформация е0 (1) и определяемая по кривой деформирования величина а,- (1). Тогда параметр пластичности
ф1 = -^. (46)
(1)
Далее находим дополнительные деформации
е*(1) = (' ) (Е*(1)~
(47)
^(i) = 2 (' —
Расчет конструкций при сложном нагружении
505
Рис. 6. Схема расчета по методу дополни» тельных деформаций
Эквивалентная деформация при простом растяжении
е0 (1) = (’ —) ео (1)
показана на рис. 6.
Во втором приближении рассматривается та же упругая задача, но при наличии дополнительных деформаций ех(1). •••> VxhD’ -:
ех (2) =Т^(2)-Ч%(2) + ^(2))]+
+ аТ + еР(1),...; (48)
W) = Q-^1/(2) +--(х,у,г).
В результате второго приближения находят новое состояние, характеризуемое компонентами напряжения ах(2у •••’ тху(2)’ и деформаций ех(2)> ....Этому состоянию
в плоскости а0 — е0 соответствует на рис. 6 точка 2, которая лежит на пересечении горизонтальной линии с*,21 и наклонной линии О22, параллельной линии упругого нагружения 01 и сдвинутой на величину ОО2 =
Далее определяют
е0(2) = g-^" + E0(i)> (49)
а по кривой деформирования — а^2). Последующий порядок расчета аналогичен расчету первого приближения.
Подобным образом строят третье и последующие приближения, причем для всех приближений параметры упругости Е, v остаются неизменными.
Расчет заканчивают при достаточной близости двух соседних приближений. При необходимости учета деформаций ползучести используют изложенный выше метод. Для каждого этапа нагружения (по времени) в уравнения (48) добавляют деформации ползучести, накопленные к началу этапа. Эти деформации остаются неизменными в процессе последовательных приближений, используемых для нахождения деформаций пластичности на данном этапе.
РАСЧЕТ НА ПРОЧНОСТЬ КОНСТРУКЦИЙ
ПРИ СЛОЖНОМ НАГРУЖЕНИИ
Для расчета напряженного и деформированного состояния элемента конструкции нагружение разбивается на ряд этапов. В большинстве случаев оказывается целесообразным проводить расчленение по этапам действительной истории нагружения во времени. На каждом этапе нагружения должны удовлетворяться уравнения равновесия
д Адох . Адтху д AfeTXz . дх ' ду + дх +
, . ,, дг &ъи
+ Р ЬцХ = Р —(X, у, г).
(50)
где AfeOx, ••• — приращение напряжений на k-м этапе нагружения; AftX — приращение массовой силы; р — плотность материала; А^ц — приращения смещения по координате х.
Приращения напряжений должны удовлетворять граничным условиям
AfcOxZ + АдТхуЩ + AhTxZn =
= Дй?х---- U- У. г). (51)
где I, m, n — направляющие косинусы нормали к элементу поверхности; Ад?х — приращение составляющей по
506
Расчет конструкций с учетом пластичности и ползучести
Упругость
Пластичность
Ползучесть
Рис. 7. Модель материала
Р
оси х поверхностей нагрузки на k-м этапе нагружения.
Используя модель материала в виде последовательного соединения моделей упругости, пластичности и ползучести (рис. 7), для приращений деформаций получим
{de} = {de*j 4-{de₽j + (52)
где вектор приращения деформаций
dex dgj, de г
{de) = 1 J “J" dyXj, V d?j,z 4 dytx (53)
Учитывая соотношения для приращений деформаций упругости, пластичности и ползучести, найдем
{de} = [а]е {da) + Fa (at, Т) {£} daf+ + {<Pr) dT + {<Pc} dt (54) где вектор температурных деформаций
X {a} +FT(Oi, Т) {S) (55)
и вектор скоростей деформации ползучести
{<pe)=<D{S}. (56)
В равенстве (54) первое слагаемое выражает приращение деформации упругости в связи с ростом напряжений, второе — подобное приращение деформации пластичности, третье — увеличение деформаций, вызванное повышением температуры, последнее — приращение деформаций ползучести. Век
тор температурных деформаций состоит из трех векторов. Первый учитывает обычную температурную деформацию, второй и третий — влияние температуры иа упругие и пластические свойства материала.
Функции Fa (at, Т) и FT (аг, Г) в случае разгрузки принимают равными нулю.
Для расчета можно использовать метод переменных параметров упругости или метод дополнительных деформаций.
В методе переменных параметров упругости уравнение (54) записывают в форме
{de} = [a] {da} {<pr) dT +
+ {<Pc) df, (57)
где [a] = [a]e+ [a]p. (58)
Для этого надо представить второе слагаемое в равенстве (54) в виде
Fa (аг, Т) (S) dat- = [а]р {rfa). (59)
Учитывая, что
, doi , dGi = d°x + • •' +
+ -|^-dTXj,+ ... (60)
ИЛИ
, 3 ax — a ,
dai=T -3—dax+...+
-|--dxxv + ... (61)
и сопоставляя однородные члены в равенстве (59), найдем элементы симметричной матрицы [а]р размерности 6X6:
3F
an = — °)2.. a2j = а12;
а22 = -2БГ^-а)2;"-;
Расчет конструкций при сложном нагружении
507
(62)
3F
а81 — 2Qt~ (°® Тху’ ' ' '
3F
н,в ~ “2с7” 2Тгж (ах — а)1'
3F агв 2tzx (<3у о),.
2.V j 3f<7 0 а3в — 2ог ^Xzxxxy-
Уравнения (57) соответствуют анизотропному упругому телу с дополнительными деформациями, параметры упругости зависят от напряженного состояния. Интегрируя соотношение (57) по времени для этапа нагружения, получим
{Afe&} = <[а]> {Afta}-H{<pT}>A7’ +
+ ((фЖ (63)
где угловые скобки означают среднее значение.
При расчете используют процесс последовательных приближений. В первом приближении полагают
<[а]> - = [аЦ..! + [а]^, (64)
т. е. принимают параметры упругости, соответствующие напряженному и деформированному состоянию в конце предшествующего этапа нагр\жения. Принимают сначала, что характер нагружения (нагрузка или разгрузка) остается таким же, как и на предшествующем этапе. Аналогичное предположение принимают для векторов
<{фт}> = {фт}й-ь <{фс})= {фс}Л-1-
(65)
Далее проводят расчет £-го этапа нагружения анизотропного упругого тела с заданными дополнительными деформациями. После расчета проверяют условия возникновения пластической деформации:
(бб)
Ад®/ > АдТ1. (67)
где —интенсивность напряжений в конце fe-ro этапа нагружения; ат (Гд’ e'Pi, (*)) —предел текучести, со
ответствующий температуре 7\ и накопленной интенсивности Пластической деформации в конце £-го этапа нагружения; = Т(k} - Т приращение температуры на £-м участке нагружения; Aftof = а(. (Д) — — Qi (k~ 1; — приращение интенсивности напряжений.
Если характер нагружения на £-м этапе остается таким же, как в предыдущем (k — 1)-м, то корректировка значения ие требуется. Если
на k-м этапе предполагали нагружение, но после расчета условия (66) и (67) оказались не выполненными, то расчет этапа следует провести заново, положив
[«lfe-1 = [«]»_!• (68)
Если на k-м этапе предполагали разгрузку [использовали соотношение (68) J, но в действительности было нагружение, то расчет следует провести заново, принимая по равен-
ству (64).
В результате рассмотренной процедуры в первом приближении устанавливают приращение напряжений и деформаций на k-м этапе и значение [п]д.
Если принятые вначале величины [а]?,-! и полученные после расчета значения [а]^ дост точно близки, то расчет этапа зака' чивают и приступают к следующему шагу. Если расхождение параметров упругости велико, полагают
<[а]> =ф~ (№-i+№) (69) и проводят расчет второго приближения.
Расчет k-ro этапа заканчивают при достаточной близости двух соседних приближений, после чего приступают к расчету следующего (k — 1)-го этапа. При проведении расчетов подобным образом уточняют значения {фу-} и {Фс}-
В методе дополнительных деформаций соотношения (54) представляют в форме
{de} -- [а]е {do} [de)p +
+ ({фтГ + {фт}₽)^ + (Фс) dt, (70>
508
Расчет конструкций с учетом пластичности и ползучести
где вектор дополнительной деформации {<И Fa (аь Т) {S} dot. (71) Вектор температурной деформации в упругом материале
+ {а!- (72)
Вектор температурной деформации, связанный с пластическими деформациями,
{Фт! =/г(аь Л {S}. (73)
Интегрируя соотношение (70) по времени для k-ro этапа нагружения, получим
{Аде} = ([а]') (Айа) +
+ <ЛЛ<Д. 7’){S))Afeai +
+ «{фт)е) + <{фг)р»А7’ +
+ ({фс))А<. (74)
Основная трудность расчета состоит в том, что приращение пластической деформации (второе слагаемое правой части) заранее неизвестно и находится в процессе последовательных приближений.
Процесс деформирования будем рассматривать в координатах а0, е0 (рис.8), причем накопленная интенсивность деформации
е1« = < + • (75)
Обобщенная кривая деформирования представляет собой обычную кривую деформирования при растяжении образцов, так как для этого случая
ot = о0;
Ef. = ео + = во- (7б!
Для расчета необходимо иметь сетку кривых деформирования прн различных температурах (термомеханическую поверхность деформирования). В первом приближении проводят расчет напряжений и деформаций, предполагая материал упругим, а дополнительные деформации отсутствующими Далее считают, что из расчета предшествующего этапа известны величины ef.
и, следовательно, положение изображающей точки на
кривой деформирования при Т = Tfe-i-Если точка А^ находится внутри отрезка Oft , например A’k_x, то первое приближение завершает расчет. Рассмотрим поэтому случай, когда точка расположена на кривой деформирования и at (k_^ = (см. рис. 8).
При расчете первого приближения значения [а]е, (фг}е, <фс} принимают соответствующими точке
После проведения расчета проверяют выполнение условия нагружения (67). Если имеет место нагружение, то
Расчет конструкций при сложном нагружении
509
определяют величину Д^1— интенсивность приращений деформаций, полученных из уравнения (74).
Полагая
4'>o( = £к (4—1) 4'4*, где £к (a_d — касательный модуль в точке Ла_1> проводят расчет второго приближения, в котором дополнительную пластическую деформацию считают равной
<1М°р 7W)>4%.
В расчете принимают среднее значение функции Fa [pi, Т) по ее значениям для точек и
При наличии пластической деформации учитывают также дополнительную температурную деформацию
Подобным образом проводят расчет следующего приближения. Расчет заканчивают при достаточной близости двух соседних приближений. В результате расчета находят приращение напряжений и деформаций на 4-м этапе нагружения, векторы напряжений и деформаций в конце этапа нагружения, значения Для начала
расчета следующего (4 -f- 1)-го этапа точку Ak (при заданных значениях
T'k) переносят на кривую деформирования, соответствующую температуре 7\. Расчет (k + 1)-го этапа проводят по указанной выше процедуре.
Пример. Рассмотрим задачу об упругопластическом изгибе стержня прямоугольного сечення при Л4В = 1,6Х X 104Н-см. Стержень (рнс. 9) изготовлен из стали ЗОХГСА, кривая деформирования приведена на рис. 10.
Расчет по методу переменных параметров упругости выполним по схеме, описанной выше.
Напряжения изгиба в стержне а = £у *1-----------• (77)
j Ey2dF F
В первом приближении материал принимаем упругим, и при Е — const
а*,,
= (79)
Деформации е(1) в каждой точке стержня соответствует по кривой деформирования напряжение <т(1) (рис. 10) и модуль упругости
Ее <1> = ’ <8°)
®<1>
Во втором приближении
М
°(*2) = Ес (1 )У Qjh ’ (81 >
26 j Ec<l)y2dy о
е(!) =-£&-. (82)
£С (1)
Далее найдем о(а) и Ес (2) и перейдем к следующему приближению. На рнс. 11 показано распределение напря-
510
Расчет конструкций с учетом пластичности и ползучести
Рис. 11. Распределение напряжений в поперечном сечении стержня при изгибе
жений по сечению стержня в первом и третьем приближении При расчете принимали, что кривые деформирования при растяжении и сжатии одинаковы.
Расчет по методу дополнительных деформаций также выполним по схеме, описанной выше.
Напряжения изгиба в стержне при введении в расчет дополнительных деформаций вычислим по соотношению
а = Е
F
j Еуе.р dF
4 У—(-----------ер
I Еу2 dF
Учитывая, что в рассматриваемом методе основной является упругая задача, при Е — const запишем
j ерУ dF
= + Еу -Г—------------Еер.
J X J X
(84)
В первом приближении принимаем, что ер = 0 и
Деформации е(1) соответствует по кривой деформирования напряжение а(1) и упругая часть деформации
е())~ —g • (85)
Дополнительная деформация в каждой точке сечения
₽р — ₽ _ ₽е — а*'> _ _£<Д_
Е(1)~Е(1) Е(1) ~ Е Е '
(86)
Во втором приближении
, 2ЕЬу
0*2. = 0?i) + -7-2- X
“X
0,5Л
X j efi)W УЛУ~ 'Es^ry); (87) о
е?2)=^. (88)
Далее найдем а(?), е(2) = е‘21 4- ерп, в(2)~ЬЕ?2> и перейдем к третьему приближению. Расчет закончим при малой разности между a(*Z) и a(i).
Существенное преимущество этого метода состоит в том, что упругая задача решается лишь один раз, что позволяет значительно сократить длительность расчета при численном решении задач упругости, пластичности и ползучести. Оба метода расчета приводят практически к одинаковым результатам.
Глава 28
КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ В ДЕТАЛЯХ МАШИН
ОСНОВНЫЕ понятия
При проектировании и оценке прочности деталей, работающих при переменных нагрузках и температурах,
необходимо особое внимание уделять зонам концентрации напряжений и деформаций — источникам образования трещин, приводящим к преждевременному разрушению деталей.
Концентрация напряжений около отверстий
511
Концентрацией напряжений (деформаций) принято называть резкое местное изменение поля напряжений (деформаций), вызываемое:
а) конструктивными факторами — изменением размеров сечений и формы деталей (выточки, галтели, отверстия, пазы, канавки и т. п.);
б) условиями внешних воздействий (силовых, например контактных и т. п., а также температурных);
в) технологическими факторами (трещинами технологического происхождения от лнтья, сварки н т. п.).
Существенная особенность явления концентрации напряжений состоит в том, что в зоне концентратора часто образуется сложное напряженное состояние (даже при одноосном напряженном состоянии на невозмущенной границе области), Зона возмущения поля напряжений обычно невелика, однако, как показывает практика, концентрация напряжений снижает прочность деталей, работающих при переменных нагрузках и в условиях повышенных температур. Детали нз хрупких материалов (например, нз высокопрочных сталей) могут разрушаться преждевременно и при статических нагрузках. Ниже рассмотрена концентрация напряжений в элементах конструкций, обусловленная конструктивными факторами.
Концентрацию напряжений принято оценивать теоретическим * коэффициентом концентрации напряжений а, равным отношению напряжения прн наличии концентратора к напряжению в той же точке при отсутствии концентратора.
Если деталь работает напряженном состоянии невозмущенной области,
при простом на границе то
Тгпах ,,,
; , , НОМ тном
где Отах, ттах — соответственно максимальные местные нормальные и касательные напряжения, вычисленные методами теории упругости или опреде-
* Кроме теоретического коэффициента часто используют эффективный, характеризующий прочность конкретного материала в условиях концентрации напряжений (см. гл. 31),
(2)
(3)
ленные экспериментально; аном, сном— номинальные нормальные и касательные напряжения, найденные без учета возмущений (обычно по формулам сопротивления материалов).
Для деталей, работающих в условиях сложного напряженного состояния (на границах невозмущенной области),
„ max
аа = —------,
°4 ном
где о, max, о, ном — интенсивность максимального местного и номинального напряжения в точке тела.
Для оценки прочности, особенно прн циклических нагружениях, важное значение имеет теоретический коэффициент концентрации деформаций
„ 84 max
=--------
8; ном
В ряде случаев для оценки сопротивления разрушению помимо коэффициентов концентрации напряжений (деформаций) используют градиент напряжений (деформаций) — быстроту затухания напряжений (деформаций) по мере удаления от концентратора. Градиент напряжений (деформаций) находят как отношение приращения напряжений (деформаций) в двух соседних точках к расстоянию между ними.
Расчет концентрации напряжений проводят часто методами теории упругости (с использованием теории аналитических функций и аппарата конформного отображения). В последние годы получили развитие н широкое применение численные методы теории упругости *, позволяющие эффективно решать задачи расчета концентрации напряжений и деформаций в элементах конструкций в условиях упругости, пластичности и ползучести.
КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ
ОКОЛО ОТВЕРСТИЙ
Многие элементы конструкций имеют отверстия конструктивного или технологического назначения.
Прн одноосном (в одном направлении) растяжении пластинки большой ши-
• См. гл. 26.
512
Концентрация напряжений и деформаций
в)
Рис. 1. Распределение напряжений в пластинках с отверстиями различной формы
рины (ф 5d) с круглым отверстием (рис. I, а) в точках на контуре отверстия возникают нормальные напряжения
<Т0 = (1 — 2 cos 20) р, (4)
где угол 0 отсчитывается от оси х к оси у; р — напряжение растяжения на стороне пластинки.
В некоторой точке С, удаленной от центра отверстия на расстояние г (см. рис. 1,а), при р = dllr
я, = 1(1 — Р2) +
+ (1 - 4р2 4- 3p4)cos20]
17 е = [(1 + р2) — (1 + Зр4) cos 20] ;
(5)
тгв = [(I 2р3 — Зр4) sin 20] .
Наибольшие растягивающие н сжимающие напряжения возникают соответственно в точках пересечения контура отверстия с осью у (<ттах = Зр) и с осью х (о = —р), а коэффициент концентрации напряжений
= —^=3. (6)
Если пластинка большой ширины имеет эллиптическое отверстие (рис. 1, б) и растягивается в направлении оси х, то
аа — 1 + 2 — • (?)
Эллиптические отверстия выгодно располагать так, чтобы большая ось эллипса была параллельна действующему усилию.
В пластинках с треугольным (рис. 1,в) и квадратным (рис. 1, г) отверстиями высокая концентрация на-
Концентрация напряжений около отверстий
513
1. Значения для пластины с прямоугольным отверстием
с/а Гц/с
0,04 0.06 0.08 0.10 0,12 0,15 0,20 0.30 0,40 0,50
1,0 4,8 4.2 3.8 3,5 3,4 3,1 2,9 2,9 2,9 3,0
1.5 4,6 4.1 3,7 3,4 3,3 3.0 2,8 2.7 2,6 2,5
2,0 4,5 4,0 3,6 3,4 3,2 2,9 2.7 2,5 2,4 2.3
2,5 4,4 3,9 3,5 3.3 3,1 2,9 2,6 2,4 2.3 2.2
3,0 4,3 3,8 3,4 3,2 3,0 2,8 2,6 2,3 2.2 2,1
3.5 — 3,8 3.4 3.2 3,0 2,7 2.5 2,3 2,2 2.1
4,0 — 3.7 3,5 3,1 2.9 2,7 2.5 2.3 2,1 2,1
5,0 — 3,7 3,3 3,1 2,9 2,7 2,4 2.2 2.1 2,0
Примечание, а, с — стороны прямоугольного отверстия; га — радиус скругления вершин
пряжений имеет место вблизи углов отверстий.
В табл. 1 приведены значения теоретических коэффициентов концентрации напряжений в углах прямоугольного отверстия со сторонами а и с при различных относительных радиусах скругления в углах rQ/a (отверстие расположено в центре пластинки, растягиваемой в направлении большей стороны прямоугольника с).
Прн двухосном растяжеинн пластинки больших размеров (&> 5d), ослабленной отверстием диаметром d, концентрация напряжений снижается и зависит от соотношения рг и р2 на иевозмущенной границе области (рис. 2). При pi = р2 = р (рг — р2 = = 1) теоретический коэффициент концентрации напряжений аа = 2 и нор-• мальные напряжения на контуре будут ^одинаковыми во всех точках. Такая 'Концентрация напряжений типична для дисков компрессоров, где часто в полотне имеются отверстия для стяжных болтов, пропускания охлаждающего воздуха и т. д.
Большой практический интерес пред ставляет случай действия иа границе ; иевозмущенной области пластинки с 'отверстием растягивающих и сжимающих напряжений (см, рнс. 2). Концентрация напряжений в этом случае также зависит от соотношения pt и р2. Такая зависимость встречается в дисках газовых и паровых турбни. где при большом градиенте температур окружные напряжения могут быть сжимающими, хотя радиальные напряжения 17 Заказ № 402 ,
растягивающие. Аналогичное напряженное состояние, лишь с равными нагрузками в невозмущенной области (р, = —р2), имеет место при кручении полых валов трансмиссии двигателей. Теоретический коэффициент концентрации напряжений в этом случае имеет наибольшее значение аа = 4,0 (см. рнс. 2).
На рис. 3 приведены зависимости теоретического коэффициента концентрации напряжений от отношений Ь/а при различных случаях нагружения пластинки больших размеров с двумя одинаковыми отверстиями.
Изменение теоретичес кого коэффициента концентрации напряжений в пластинках, ослабленных рядом отверстий, прн различных условиях нагружения показано на рис. 4.
Прн растяжении полосы конечной ширины теоретический коэффициент концентрации напряжений снижается (рис. 5) прн увеличении диаметра от-
Рис, 2. Зависимость от отношения напряжений на границе невозмущенной области пластинки с круглым отверстием
511
Концентрация напряжений и деформаций
верстия (или уменьшении ширины пластинки), что связано с увеличением номинальных напряжений в наиболее нагруженном сечении:
стном — й Q~ • (8)
Приведенные значения коэффициентов концентрации можно использовать прн расчете перфорированных колец (например, сепараторов шарикоподшипников и др.).
Зависимости теоретического коэффициента концентрации напряжении от отношения основных размеров полосы,
Рнс 4 Зависимости от отношения b/а для при различиях схемах нагружения
Рис 3. Зависимости а от отношения Ыа для растянутых пластинок, ослабленных двумя отверстиями, при различных схемах нагружения
ослабленной смещенным от оси симметрии отверстием, даны на рис. 6. .
Для снижения концентрации напряжений в пластинках на практике иногда подкрепляют отверстия жесткими * впаиваемыми втулками нлч кольцами, а также втулками из основного материала, но большей толщины. На рнс. 7 приведены зависимости коэффициента концентрации напряжений в пластинке от толщины Н н диаметра D подкрепляющего кольца.
Кривые на рис 7 можно использовать дли приближенных расчетов в
* Из материала с бдльшим модулем упругости, чем основной материал пла с-’ инки
пластинок, ослабленных рядом отверстий
Концентрация напряжений около отверстий
515
Рис. 5. Зависимости (7 от отношения п/Д для пластинок конечной ширины с отверг стием
тех случаях, когда -г- <6 и Ен = п
И
= Ео vK = v0, где Ек и vK — соответственно модуль упругости и коэффициент Пуассона для материала подкрепляющего кольца
На практике встречаются случаи цилиндрического изгиба пластинок большой ширины (Ь > 5d) с отверстием. Значения теоретического коэффициента концентрации напряжений в этом случае можно определить по рис. 8, а; в случае изгиба вала с отверстием — по рис. 8, б.
Рис. 6. Зависимости от отношения г/с для пластинок с эксцентрическим отверстием
Рис. 7 Зависимости от отношения H/h для пластинок с подкрепленным отверстием
Рис. 8. Зависимости от отношения а/Лдля пластинки (а) к отношения aid для вала (<Т) с поперечным отверстием 17*
516
Концентрация напряжений и деформаций
Более подробно концентрация напряжений около отверстий рассмотрена в работах (1, 2, 4J.
КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ В ПЛОСКИХ И ОСЕСИММЕТРИЧНЫХ ВЫТОЧКАХ И ГАЛТЕЛЯХ
На рис. 9 приведены эпюры нормальных напряжений (осевых <yz, окружных <т0 и радиальных стг) в наиболее нагруженном сечении растянутого стержня с кольцевой выточкой. Для плоского образца такой же формы наибольшие напряжения в сечении выточки на 20—30% выше, чем для осесимметричного (из-за отсутствия кольцевых напряжений).
На рис 10—13 показаны зависимости теоретического коэффициента
Рис. 9. Распределение напряжений в стержне с кольцевой выточюй
концентрации напряжений при растяжении и изгибе пластин и осесимметричных стержней с выгонками и галтелями от основных размеров. Из графиков следует, что с увеличением радиуса скругления выточки (галтели) концентрация напряжений снижается.
Рис. 10. Зависимости от основных размеров для пластинок (а) и стержней (<Я при растяжении
Концентрация при пластических деформациях и ползучести
517
Рис. II. Зависимости от основных размеров для пластинок при растяжении (а) н изгибе (ff) и ди» стержней при растяжении (в)
Рис. 12. Зависимости прн изгибе симметричной ступенчатой пластинки с выточками (а) и ступенчатого вала с канавкой (6) от основных размеров
КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ В УСЛОВИЯХ ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ
И ПОЛЗУЧЕСТИ
Прн больших нагрузках в зонах концентрации напряжений появляются пластические деформации. На рис. 14 пок1зано распределение напряжений Оу и интенсивности деформаций е; в Нсиболее нагруженном сеченни растя
гиваемой пластинки с отверстием в условиях плоского напряженного состояния, а также изменение нормальных напряжений <те и интенсивности деформаций е!0 на контуре отверстия (материал пластинки — сталь 45, <гт = = 650 МПа). Расчет напряжений и деформаций проведен вариационно-разностным методом. Из рисунка следует, что при наличии упругопласти-ческнх деформаций (зоны пластичности заштрихованы) максимум напряжений
518
Концентрация напряжений и деформаций
Рис. 13. Зависимости при кручении вала е канавкой (а) и ступенчатого вала с галтелью (<Т) от основных размеров
сдвигается от контура отверстия вглубь. Последнее связано с возникновением в глубине зон плоского напряженного состояния с одинаковыми знаками главных напряжений, что затрудняет пластическое течение и делает соответствующие кольцевые слон более жесткими.
Если пластинка работает прн повышенной температуре, то в тех зонах около отверстия развиваются деформации ползучести. Характер напряженного состояния в пластянке не меняется, лишь деформации ползучести появляются прн более низких напряжениях на границе невозмущенной области.
Реальные возможности работы детали в условиях пластичности и ползучести, особенно при циклических нагружениях, целесообразно оценивать не только по коэффициенту концентрации напряжений а*, значения которого уменьшаются в неупругой области, но и по коэффициенту концентрации деформаций а’, значения которого увеличиваются по мере развития не-упругнх деформаций (рис. 15).
Коэффициенты концентрации напряжений а.* и деформаций а,* в области упругопластнческнх деформаций связаны с коэффициентом концентрации
напряжений в идеально упругом материале следующим приближенным соотношением:
0,8 ч- 0,9.
(9)
'а е
«Г
Г1 I I Н I I11 I Ц I Г
р ЧЮМПр
Рнс. 14. Распределение напряжений (в МПа) и деформаций при растяжении пластинки с отверстием в условиях ynpv-гости (штриховые линии) и пластичности (сплошные линии)
Концентрация при пластических деформациях и ползучести
519
Рис. 16. Зависимости сщ и а£ от внешней натрузки в растянутой пластинке с отверстием
В случае плоского напряженного состояния коэффициенты а* и а* на 20—30% выше, чем при плоской реформации для деталей такой же формы. Коэффициенты концентрации напряжений в условиях упругости в этих случаях будут одинаковыми.
При двухосном растяжении пластинки с отверстием (рис. 16) развитие пластических деформаций затруднено, и они появляются при больших (почти на 20%) значениях напряжений на невозмущенной границе пластинки, чем при одноосном растяжении. Зона пластических деформаций (на рисунке заштрихована 1/4 часть зоны) в этом случае охватывает весь контур отверстия. Характер изменения коэффи-
Рис- 16. Распределение напряжений in МПа) н деформаций в пластннае с от* в'рсгнем при двухосном растяжении
У
ру^175МПа
Рис. 17. Распределение напряжений (в NlHa) в пластинке с отверстием при разных знаках напряжений на границе
циентов а* и а* такой же, как и в случае растяжения пластинки.
При действии на границе невозмущенной области пластинки с отверстием растягивающих и сжимающих напряжений (рис. 17) концентрация напряжений сказывается в большей степени Пластические деформации появляются при меньших (на 40—45%) нагрузках, чем при одноосном напряжении.
При растяжении пластинок с двумя симметричными выточками (см. рнс. 10, а), как и при растяжении пластин с отверстием, происходит смещение мак<имума осевых растягивающих напряжений от дна выточки в тело пластины.
При растяжении стержня (вала) с кольцевой выточкой (осесимметричная задача) существенного смещения максимума напряжений при наличии упругопластических деформаций не наблюдается (рис 18). В этом случае в отличие от плоской задачи (для пластин) в центре впадины имеет место плоское напряженное состояние с одинаковыми знаками главных напряжений о2 и ае.
Следует особо отметить, что при работе деталей в условиях пластичности и ползучести значительное влияние на напряженное состояние, кои-
520
Концентрация напряжений и деформаций
10 z
IIHtlfHHIH
во=300МПа
Рис. 18. Распределение напряжений (в МПа) в стержне с кольцевой выточкой при растяжении (штриховые линии соответствуют упругому состоянию, сплошные — упругопластическому состоянию, вертикальные и горизонтальные тонкие линии показывают сеточную разметку области)
центрацию напряжений и деформаций оказывают условия нагружения (последовательность нагружения и т. п.).
На рнс. 19 сравниваются напряженные состояния двух тонких пластинок*. нз сплава ХН77ТЮР (а, = = 560 МПа). В первой пластинке при двухосном растяжении рх = ру =. == 300 МПа пластические деформации отсутствовали (эпюры напряжений на рис. 19 построены сплошными линия, ми).
Вторую пластинку вначале растягивали вдоль оси у (ру = 300 МПа), а затем — вдоль оси х (рх 300 МПа). При первом нагружении в центральной части пластинки (вблизи отверстия справа и слева) образовались две зоны пластичности (одна из них на рисунке заштрихована), в которых а* = 1,97 и а’ = 3. В результате второго нагружения глубина проникновения пластических деформаций несколько уменьшилась вследствие разгрузки и коэффициент концентрации напряжений в
* Плоское напряженное состояние, расчет выполнен методом конечных элементов.
Рис. 19. Распределение напряжений (в МПа) в пластинке с отверстием при простом и сложном нагружении
Концентрация напряжений в элементах конструкций
521
точке А стал равным а* 1,04. Наибольшие напряжения возникли в точке В на контуре отверстия, где а* = 1,86 (эпюры напряжений на рис. 19 после второго нагружения показаны штриховыми линиями).
На рис. 20, а сравниваются напряженные состояния двух пластинок, одна из которых была растянута лишь вдоль оси у (ру — 300 МПа, эпюры показаны сплошными линиями). При этом в центральной части пластинки вблизи отверстия образовались две зоны пластичности (возле точек А и В). Вторую пластинку вначале нагружали в направлении оси х (рх = 300 МПа), в результате чего появились две зоны пластичности возле точек С и D (одна из иих заштрихована), а затем полностью разгружали. В результате разгрузки в точках пластинки возникали остаточные напряжения. На рис. 20, б показано изменение нормальных напряжений в сечениях АА' и DD'. После разгрузки пластинку нагружали вдоль оси у (ру = 300 МПа). Эпюры нормальных напряжений иа контуре отверстия Од, а также напряжений аж и Оу в сечениях Оу и Ох, вычислен
ные с учетом остаточных напряжений от первого этапа нагружения, показаны штриховыми линиями.
В результате второго этапа нагружения зоны пластичности возникли вблизи точек А и В. Глубина проникновения этих зон оказалась меньшей, чем при простом нагружении.
Предварительное нагружение до появления упругопластических деформаций н последующая разгрузка увеличивают упругий диапазон нагружения деталей и снижают коэффициент концентрации напряжений. Этот эффект лежит в основе одного из способов упрочнения деталей машин (например, предварительное растяжение болтов).
КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ В ЭЛЕМЕНТАХ КОНСТРУКЦИЙ
Примозубые цилиндрические передачи. При расчете на изгиб зубьев цилиндрических эвольвентных передач вместо теоретического коэффициента концентрации напряжений используют коэффициент Yf, учитывающий форму зуба и равный значению максимальных контурных напряжений Од от окруж-
522
Концентрация напряжений и деформаций
Рис. 21. Распределение контурных напря* жений (в МПа) в зубе зубчатого колеса (г - 40, т — 1» а =« 20J), нарезанного долбяком — 10, д?0 ~ 0,042)
ным методом и изменение контурных напряжений вдоль сжатой и растянутой сторон показаны на рис. 21. Контурные напряжения достигают наибольшего значения в некотором (опасном) сечеиви зуба в областв переходной крввой.
Графики (рве. 22—25) для определения значений Yp и дополняют матервал гл. 11.
При нареэанив зубьев долбяком значения Yp зависят от чиста зубьев колеса г (рис. 22), а также от числа зубьев долбя ка г0 * и в большей степени от коэффициента смещения дол-бяка х0, характеризующего степень его износа. Наиболее существенное влияние иа велвчину Yp оказывает смещение инструмента х (рнс. 23).
ной силы 1 Н/м, приложенной к вершине зуба с модулем т = 1 (см. гл. 11). Типичная сеточная разметка области зуба прн расчете вариацнонно-разност
• При увеличении числа зубьев долбя-ка уменьшается радиус переходной кривой
Рнс 24 Распределение напряжений (в МПа) в зубьях колес (z = 40, т = I), нарезанных долбяком при различных смещениях: а — х = —1,0; б ~ х — —0,5, в — х = 0, г — х = 0,6, д - х = 1,0, е — х = 1,5
Рис 22 Зависимости Yp от г для зубьев колес, нарезанных новым (кривая 1, = 10, л0 = 0,042),
предельно изношенным (кривая 3, х9 — -0,3) долбчгамн н фрезой (кривая 2)
Рис. 23. Зависимости Yp от X для зубьев колес, нарезанных новым (кривая /, z9 = 10, х9 = 0,042), предельно изношенным (кривая 3, д?о = -0,3) долбяками и фрезой (кривая 2)
Концентрация напряжений в элементах конструкций
523
Рис. 25. Распределение напряжений (в МПа) в зубьях без поднутрения (а) и с поднутрением (<Г)
Рнс. 26. Распределение напряжений (в МПа) в зубе храпового колеса
Последнее связано с изменением ширины зуба в наиболее нагруженном сечении, радиуса переходной кривой и угла давления б (рис. 24).
При производстве высоконапряжен-иых зубчатых передач со шлифуемыми зубьями широкое применение получили колеса с поднутренной ножкой зуба. При этом переходную поверхность зуба не шлифуют и, следовательно, исключают прижоги, растягивающие остаточные напряжения и другие неблагоприятные последствия от шлифования. Глубина поднутрения Ло (рис. 25, б) влияет на наибольшие контурные напряжения. На практике необходимо стремиться к меньшему поднутрению.
Зубья храповых колес. На рис 26 показаны профиль зуба храпового колеса и эпюры контурных напряжений (цифры на эпюрах показывают значения напряжений в МПа), полученные методом фотоупругости при силе Р = — 22,4 Н, приложенной к вершине зуба. Размеры модели из эпоксидной смолы шаг зубьев t = 45 мм; теоретическая высота профиля /т ~ 23,4 мм; притупление зуба с0 = 4 мм; передний угол профиля зуба cq = 10°; половина угла профиля зуба а = 26°; радиус тал гели р —- 2 мм; толщина Ь = 3,6 мм. Наибольшие напряжения действуют вблизи точки сопряжения радиуса участка галтели с прямолинейной рабочей гранью.
Теоретический коэффициент концентрации напряжений в зубьях храповых колес ____
«о = 1 + 2? ]/" -у-,
где у = л —— коэффициент влияния угла профиля; I = /т — с0 — глу-tg а/2
бин а выреза; д ~ ----коэффи-
циент.
Номинальные напряжения в зубьях вычисляют по известной формуле для изгиба бруса постоянной ширины
Оном -
Замковые соединения лопаток. Для закрепления рабочих лопаток в дисках осевых компрессоров, паровых и газовых турбин используют замки различных конструкций (елочный замок, типа ласточкин хвост и т. п.).
Замки в турбинах работают в сложных силовых и температурных условиях. Центробежные силы и изгибающие моменты от центробежных и газовых сил вызывают достаточно высокие осевые номинальные напряжения во впадине первого зубца (100— 150 МПа). При этих напряжениях и достаточно высоких температурах (до 700 °C) уже в начальный момент времени в зонах концентрации напряже-
524
Концентрация напряжений и деформаций
У
ff0 IIО MV а
12,6
Рис. 27. Распределение напряжений (в МПа) и ползучести т
в елочном замке в
условиях пластичности
ний появляются упругопластические, а затем и деформации ползучести материалов дисков и лопаток. Разрушение соединений происходит в зонах концентрации напряжений и деформаций.
На рис. 27 показано распределение напряжений во впадинах елочного хвостовика лопатки при температуре 700 °C, штриховые линии соответствуют /' = 0 ч и сплошные линии — t = = 100 ч (расчет выполнен методом конечных элементов). Материал лопатки — сплав ХН70ВМТЮ. В качестве расчетной принята нагрузка в корне
лопатки от центробежных сил, которая равномерно распределена между зубцами и вдоль зубцов.
Из рис. 27 следует, что наибольшие контурные напряжения действуют вблизи перехода от радиусного участка впадины к прямолинейной рабочей грани первого зуба.
При нагреве хвостовика до 700 °C в начальный момент времени (/ 0 ч)
возникают небольшие упругопластические деформации, хотя номинальные напряжения растяжения в сечении впадины первого зуба составляют ан = = 145 МПа и соответствуют типичному
Концентрация напряжений в элементах конструкций
525
Рис. 28. Зависимость от г для елочного замка
Рис. 29. Распределение напряжений (в МПа) в соединении типа ласточкин хвост
уровню средних напряжений для мно-гих турбинных лопаток Со временем происходит развитие деформаций ползучести (зона этих деформаций через 100 ч рабош заштрихована на рис. 27, цифры указывают наибольшую глубину распространения деформаций ползучести)
Наибольшие напряжения во впадине при этом существенно снижаются и смещаются в глубь тела. Теоретический коэффициент концентрации напряжений также снижается от а’ 0 = 3,5 (при / — 0 ч) до а.* 100 = 3, а коэффициент концентрации деформаций возрастает на 10% и достигает а* 100 = — 3,8, это значение соответствует наибольшей глубине неупругой зоны, равной 0,05 мм. При увеличении нагрузки до ан = 290 МПа происходит существенное развитие зон пластичности (на
* Индексы 0 и 100 соответствуют t — 0 и 100 ч; расчет выполнен по теооии старения с использованием изохронных кривых ползучести, значения ctg вычислены по отношению к о»
глубину 0,27 мм при t = 0 ч) и ползучести (на глубину 0,31 мм через 100 ч работы).
Существенно, что значительное увеличение a* t наблюдается лишь в первые часы работы турбины. В дальнейшем изменения а* t незначительны, и длительная прочность замкового соединения лопаток и дисков турбин при t — 50 ч будет в большей степени зависеть от характеристик длительной прочности материала, чем от концентрации деформаций.
Существенное снижение коэффициентов концентрации напряжений и деформаций в елочных Замках можно получить за счет увеличения радиусов скругления впадин зубцов (рис. 28'1. Однако при увеличении радиусов скругления сокращается перекрытие зубцов лопатки и диска и возрастают контактные давления. Последнее может ускорить развитие деформаций ползучести в зубцах.
В соединениях лопаток и дисков осевых компрессоров распространены
526
Концентрация напряжений и деформаций
«я
/7
15
13
11
9
1
5
3
1
в)
Рис. 30. Зависимости от основных параметров для Т-образного хвостовика: а - p/D = 0,05, б - p/D = 0,075; в — p/D = 0,1. г - p/D = 0.2
замкн типа ласточкин хвост (рис. 29) *. Наиболее нагруженными оказываются перемычки в дисках (между соседними пазами). При угле раствора паза 459 контактные давления и коэффициент .концентрации напряжений снижаются. Однако в этом случае уменьшается перемычка между пазами и меньшее число лопаток может быть размещено на ободе диска.
В ряде конструкций для соединения или взаимного направления деталей используют Т-образные хвостовики, в которых также наблюдается высокая концентрация напряжений. Значения теоретических коэффициентов концентрации напряжений <ха при расчете
* Расчет напряжений выполнен вариационно-разностным методом с использованием сетки, показанной на рисунке
таких хвостовиков (или деталей) можно определить по рис. 30.
В заключение отметим, что для исследования концентрации напряжений в элементах конструкций иа практике широко используют теоретические и экспериментальные методы. Среди теоретических методов наиболее распространены численные методы решения на ЭВМ задач теории упругости, пластичности и ползучести (среди них вариационно-разностный метод и метод конечных элементов, см. гл. 26). Они позволяют достаточно точно исследовать концентрацию напряжений в телах произвольной формы (плоских, осесимметричных и пространственных) при простом и сложном нагружении.
Экспериментальные методы исследования напряжений разнообразны. В
Контактные задачи
527
основном применяют тенэометрирова-ние с использованием датчиков сопротивления, методы фотоупругости и фотопластичности, голографические и
рентгеновские методы, методы муаровых полос, лаковых и гальванических покрытий.
Глава 29
КОНТАКТНЫЕ ЗАДАЧИ
<J о возникает необходимость рассчитывать напряжения и деформации в зонах контакта элементов машин. На рис. ! приведены типичные контактные задачи для элементов простой формы (классические контактные задачи). К ним относятся задачи о контакте шаров, цилиндров и давлении штампа. Результаты решения подобных задач широко используют при расчете подшипников качения, зубчатых передач и др. Обычно при решении классических контактных задач ограничиваются анализом напряжений и деформаций в зонах контакта.
Вторую группу образуют конструкционные контактные задачи (рис. 2). Они характеризуются совместным учетом контактных и общих деформаций сопрягаемых элементов машин. Во многих случаях в конструкционных контактных задачах приходится рассматривать несколько зон контакта (рнс. 2, а).
Основные особенности контактных задач состоят в следующем. В большинстве контактных задач, даже при работе материала в упругой зоне,
зависимость между внешней силой и вызванным ею перемещением оказывается нелинейной. Эго объясняется изменением (увеличением) площадки контакта по мере возрастания силы. Последнее всегда имеет место, если первоначальный контакт деталей осуществлялся в точке (контакт шаров) или по линии (контакт цилиндров). В том случае, когда площадь контакта остается в процессе нагружения неизменной (давление штампа на полуплоскость), зависимость между силой и перемещением (для упругого материала) линейная
Вторая особенность контактных задач состоит в появлении значительных напряжений в зоне контакта, особенно в случаях, когда площадь первоначального контакта равна нулю (контакт в точке или по линии). Однако для зон контакта характерно возникновение всесторонних сжимающих напряжений, что позволяет материалу выдерживать без разрушения высокие поверхностные напряжения.
Контактирующие поверхности деталей должны иметь высокую поверх-
а)
Рис. I. Контактные а — контакт шаров;
6) «)
задачи для элементов простой формы:
б — контакт цилиндров; в — давление штампа на полуплоскость
528
Контактные задачи
Рис 2. Конструкционные контактные задачи для:
а — зубчатого соединения, 6 —г цилиндров конечной длины; в — прессового соединения
постную прочность, что характеризуется одновременно высокой поверх-ностной твердостью. Последнее достигается термической и химико-термической обработкой деталей и т. п.
КОНТАКТ ДЕТАЛЕЙ ПРОСТОЙ
ФОРМЫ
Задачи об упругом контакте деталей простой формы (цилиндры, шары и т. п ) имеют решения в замкнутой форме.
Рассмотрим контакт цилиндров (рис. 3, задача Герца). На расстоянии | от плоское ти, проходящей через оси
цилйндров, возьмем две точки At и А2. Если первоначальный контакт цилиндров (без нагрузки) происходил по линии, параллельной их осям и проходящей через точку В, то расстояние между этими точками вдоль оси у (см. рис. 1)
J2 Е2 Е2
1,1 + 112 ~ Тр? + адГ = ~R ’ (1)
где и R2 — радиусы первого и второго цилиндров; R — «средний! радиус кривизны,
Контакт деталей простой формы
529
Под воздействием нагрузки р произойдет деформация цилиндров в зоне контакта, а их оси переместятся к этой зоне на величины и Л2 Общее кинематическое перемещение (сближение) осей координат, связанных с цилиндрами, Л == А, 4- Л2. Точки Аг и А2 займут при этом новое положение А; и А'г.
Давление в зоне контакта деформирует близлежащие неконтактнрующие поверхности цилиндров, и точки А; и А;, получив перемещения, равные U] и ц>, займут положение А* и AJ.
Если в зоне контакта полуширина полоски контакта а >5, то точки AJ и А.} совместятся, поэтому
А] — «1 + ^2 — V2~ & — U] — c2 =
= T)l + Т)2 = • (3)
Соотношение (3) представляет собой условие совместности перемещений контактирующих точек цилиндров. Оно показывает, что кинематические перемещения цилиндров под нагрузкой компенсируются их смещениями в результате деформации
Предположим, что между сжимаемыми цилиндрами тренне отсутствует. Тогда в точках контакта будут действовать лишь нормальные давления q (х) и условие равновесия примет вид
Если ширина полоски контакта мала по сравнению с радиусами цилиндров, то каждый из них можно приближенно рассматривать как упругую полуплоскость под действием давления <7 (*)•
Смещение точки А с координатой х = £ (рис. 4) можно вычислить, используя известное решение задачи Фламана о действии силы иа полуплоскость:
Vi ~ ~~лЕ
а
J ? (*) I 5 — X I dx + —а
+ ( 2(1 —vf)
In Ri I р
(5)
где Ei и V; — модуль упругости и коэффициент Пуассона материала i-ro цилиндра.
Подставив соотношение (5) в условие
(3) и учитывая равенство (4), получим
а
(0Г+ 0?) j Я(х) )n|g — x]dx =
—а
с2
= -^-+с, (6)
где
С = (9* + 0*) X
dx = р.
(4)
Для решения задачи необходимо выразить смещение в уравнении (3) через контактные давления.
Рис. 4, К расчету перемещений точек полуплоскости
<7>
4 2
Если продифференцируем уравнение (6) по g, то получим
а
(0.Г + 0Г) j = (8)
Задача сводится к нахождению функции q (х), удовлетворяющей условию (4) и уравнению (8) при всех значениях — а $5 $5 а.
530
Контактные задачи
Можно показать, что этим требованиям будет удовлетворить выражение
q (х) == ”[/аа - х< (9)
В соотношении (9)
ч'гпах — > ('0)
а = ~1М (6Г + 0?). (П)
Подставляя в равенство (10) и (11) значения входящих в них величин, получим
Ртах — 0,798
Ri ~r R? р 2R1R1
©1 + 02
(12)
а = 0,798 ]/ р £R^ (0i+ 02),
где
0,
Ле* - 1 ~vi •
2 1 £1 ’
6, = 4-0; =
2
£а
Если цилиндры изготовлены из материалов, у которых
Е1 = Еа и vt =Vj = 0,3, то
9max = 0,42 1/ рЕ R^~R* ; г «1Л 3
а = 1,52
1/ Р ^1^2
У Е R^Rt
НЗ)
Общее кинематическое смещение (сближение осей цилиндров)
нением величины а в процессе нагружения: полуширина а возрастает по мере увеличения р и относительная податливость контактной зоны уменьшается .
Соотношения (13)—(14) применяют в расчетах на контактную прочность деталей машин (фрикционных и зубчатых передач и др ) конечной длины. Использование решения задачи о контакте бесконечных цилиндров в расчетах передач обосновывается тем, что ширина площадки контакта мала по сравнению с высотой зубьев колес и краевые эффекты (возрастание контактных давлений на концах зубьев) распространяются на небольшие участки контактных линий.
В заключение отметям, что определение контактных перемещений при контакте двух цилиндров имеет существенную особенность: общие перемещения возрастают с увеличением размеров поперечного сечения [см. (14)]. В этом случае, как и в аналогичной задаче Фламана, перемещения определяют относительно достаточно удаленной от места контакта точки. В формуле (14) в качестве таких точек взяты центры кривизны 01 и О2 (см. рис. 1). Таким образом, считают, что перемещения центров кривизны определяются только общими деформациями цилиндров (или присоединенных к ним деталей) и не связаны с контактной деформацией.
Другие случаи контакта цилиндров, а также задачи о контакте шаров решаются аналогично.
В табл. 1 и 3 показаны распространенные случаи контакта тел простой формы и даны основные соотношения.
Давление штампа. Для штампа прямоугольного сечения (рис. 5) ширина
2. Значения коэффициентов а, ₽, X
4_^_щ2рЛ„!«Л^о.8,5).
л£ а2 /
(14)
В соотношениях (12)—(14) 7?i н /?2 — радиусы первого и второго цилиндров. Так как полуширина контактной площадки а зависит от р, то смещение А является нелинейной функцией от р, хотя материал цилиндров предполагается упругим. Это объясняется изме-
а Р X
I 0,908 1 2,080
1.5 1,045 0,765 2,060
2 1,158 0.632 2.025
з ' 1,350 0,482 1,950
4 1,506 0,400 1,875
6 1,762 0,308 1,770
10 2,175 0,221 1,613
1. Основные соотношения для задач о жонтажте цилиндров
СХ о с о Е Схема контакта Максимальное давление (напряжение) в зоне контакта ?тах Полуширина площадки контакта а Сближение осей контактирующих тел Д Максимальные касательные напряжения ттах Г лубнна залегания ттах
1 ^7^ ' к °-™ V 2« (0' + 02) 0.798 /2pR (0, + 02) 2р4-(0.41 + 1п^)
2 р р кХ /~ Я.+Я, °-798 V е.2+е.’ 0.798 ]/"2р-5а|1-(01+01) Г Л 1*1“ Al 2₽4х X (о,815 4- 1П ^1^1) \ о* / °'304’тах 0,786а
3 0,798 V ~(Г+9‘ 0,798 ]/" 2р-^1ф-(0.+0,) г Л 1 — A j —
4 'X/R, 1,5Р nab Эллипс с полуосями: а = а х X3/ 2р/йг (0>+а*Ь т *х I'i- К j b = ра ,3/ рг R,+K, V (0>+О,)! — —
Примечания 1 В случае контакта цилиндра и полупространства дано сближение центра цилиндра с поверхностью полупространства (уменьшение радиуса цилиндра).
1 — V/ 1 —у»
2. Коэффициенты 9; = --------; 6 =* — .
1 Е Е
3 Формулы для определения сближения всех цилиндров для случаев 1 — 2 получены при £\ = Et = Е и у, — vt ~ у 4 Значения Ттах и глубины их залегания получены при Et = Ei = 2* 108 МПа н vt = vt = 0.3.
5. Значения коэффициентов а, 3 и X для случая контакта 4 даны в табл. 2
Контакт деталей простой формы
3. Основные соотношения для задач о контакте тел сферической формы
1 № по пор. 1 Эскиз контактирующих тел Максимальное давление (напряжение) в зоне контакта ^тах Радиус площадки контакта а Сближение осей контактирующих тел Д
1 'SC# V ' А 0,918 V «*(6,4-9,)’ 0.72! у2РЛ (9, + 9,) 3 / pl 1,55 V 2E>R
2 3 Г ( А’ + А» у 0,918 V р (е2,^)* 3 Г р р 0,721 1/ 2Р -7, (0. + 0,) г «1 +
3 р X 3 / ( а. -а. у 0,918 у Р (/At)* 3 /~ р р 0,721 у 2Р _д;-(е, + е,) -
4 1 =? (jjy у \г « / 2 Эллипс с полуосями: . л г з „ е, + е, а ~ '> 2 Р х = h = аЧ/^а 1 3 г g — р’х <0* + е’>’
Примечания: I. Соотношения для коэффициентов 6* см. в табл. 1.
1I 1/7?
2. Значения коэффициентов £ н в зависимости от отношения Q ==--------------— даны в табл. 4 (х = l//?t -f- 2/7?t -f-
~F l/7?a — сумма главных кривизн соприкасающихся тел).
3. Зависимости для определения сближения осей контактирующих тел получены при = £2 — Е и vt = va ~ 0,3
4. Максимальные касательные напряжения ттах = 0»31<7тах, глубина их залегания 0,48а.
5. В случаях 1—3 площадка контакта — круг радиуса а, в случае 4 — эллипс с большей полуосью а н меиьшей полуосью b
Контактные задачи
Контакт деталей простой формы
533
4, Значения коэффициентов £а, £ и
О Еб
0,01923 1,013 0,9873 0,9999 0,9999
0.03949 1,027 0.9742 0,9997 0,9997
0,06087 1,042 0,9606 0,9992 0.9992
0,08350 1,058 0,9465 0.9985 0,9985
0.1075 1,076 0,9318 0.9974 0,9974
0,1330 1,095 0.9165 0,9960 0,9960
0,1894 1,141 0,8837 0,9919 0,9919
0.2545 1.198 0,8472 0.9853 0,9852
0.3314 1,274 0,8056 0 9746 0.9744
0,4245 1,381 0.756$ 0,9571 0,9566
0,4914 1,473 0,7216 0.9409 0,9400
0.5161 1,51 1 0.7086 0,9340 0.9329
0.5423 1,554 0.6949 0,9262 0,9248
0,5702 1,603 0,6801 0,9172 0.9155
0,5999 1,660 0,6642 0,9067 0.9045
0,6317 1,729 0,6468 0,8944 0,8916
.0,6662 1,812 0.6276 0,8766 0.8759
0.7037 1,916 0,6059 0,8614 0,8566
0,7449 2.053 0,5808 0,8396 0,8320
0,791 1 2,248 0,5505 0,8082 0,7990
0,8300 2,463 0.5224 0,7774 0,7650
0,8587 2.669 0,4993 0,7504 0,7349
0,8904 2.975 0.4704 0.7144 0,6943
0,9113 ' 3,253 0,4484 0,6856 0.6613
0,9187 3.373 0.4398 0,6740 0,6481
0.9264 3,514 0,4304 0.6612 0.6333
0,9342 3,683 0,4199 0.6467 0,6164
0,9425 3,890 0,4080 0,6300 0,5970
0,9511 4,156 0.3942 0.6104 0,5741
0,9601 4,515 0.3777 0,5864 0,5460
0,9698 5.046 0,3*68 0,5555 0,5096
0,9803 5,976 0.3273 0,51 12 0,4574
0,9923 8,609 0,2722 0,4267 0,3579
площадки контакта равна ширине штампа, а контактное давление
где сжимающая сила
а
Р = j q (х) dx.
—а
Несложно заметить, что вблизи краев штампа (х-* а или —а) напряжения резко возрастают. Для снижения концентрации напряжений следует скруглять края штампа. '
Для круглого цилиндрического штампа контактное давление
р
q —------______ , (] 6)
2ла ^/а2 — г2
Осадка штампа
Л Р(1-У2)
2аЕ
оказывается линейной функцией от нагрузки, так как размер поверхности контакта при нагружении не изменяется . В этом случае также для снижения концентрации напряжений необходимо скруглять края штампа. *
* Под штампом понимают абсолютно твердое тело.
Рис. 5. Схема давления штампа на полуплоскость
534
Контактные задачи
Рис. 6. Изменение нормальных (а), наибольших касательных напряжений и интенсивности напряжений (tf) в контактирующих цилиндрах
Для штампа в виде цилиндра с осью, параллельной полупространству, или шара соотношения для <?т;>х и а получаются, если в соответствующих формулах в табл. 1 и 3 принять Е2~>- °о.
Анализ напряженного состояния. Напряженное состояние контактирующих цилиндров является сложным. Однако в плоскости х = 0, проходящей через оси цилиндров, касательные напряжения тх!/ = =0, а нор-
мальные главные напряжения*
ах — ?шах X
При у — 0, т. е. для всех точек средней линии полоски контакта, ах = ~ ~ ?tnax; <3z = —2v9max-
Для материала с v = 0,5 в этих точках будет всестороннее равномерное сжатие.
На рис. 6 показано изменение главных напряжений от отношения yia при v = 0,3.
На прочность деталей машин существенное влияние оказывают наибольшие касательные напряжения в площадках, нормальных к главным. Расчеты показывают, что наибольшего значения касательное напряжение достигает в точке, лежащей на нормали, восстановленной в середине площадки контакта на глубине у яа 0,786 а:
Су сх
Ттах =-----к---- — 0,ЗО^тах- (18)
— ?max2v X
* Начало координат перенесено в центр полоски контакта, а ось 2 направлена вдоль этой полоски
Это напряжение действует по двум взаимно перпендикулярным площадкам, нормальным к плоскости ху и образующим с осью у углы, равные
Конструкционные контактньи задачи
535
В расчетах на прочность важное значение имеет интенсивность напряжений
a,;=Wx
X V(сх — Оу)2 + (Оу — <h)2 4-'
* ’ ” + (о2-аху + 6 (т^ + т2г + t2J).
(19)
Изменение интенсивности напряжений показано на рис. 6, б. Из графика следует, что максимальное значение (на глубине у — 0,7 а)
ai max = -0,5579гаах.
При контакте шаров для произвольной точки оси z* все площадки, параллельные этой оси, и площадка, перпендикулярная к ней, являются главными. Это следует и из симметрии напряженного состояния относительно оси г. Нормальные напряжения в окрестности произвольной точки оси z
о г = -Qmax ’ (20)
— ®у ~ ?niax X
х [n + v)~T+W"”
— (1 + v)arctg-^-l. U £ J
Из соотношений (20) следует, что при г = 0 напряжение ог = —<7тах (в центре площадки контакта), а при г-*- оо az-> 0.
Напряжения ах и ау в отличие от ог зависят и от упругих свойств материала (коэффициента Пуассона). Для точки 2=0
1 + 2v
ах — ау — Qmax---2 ’
прн v = 0,3 ov = — 0,8qmax, а при у = 0,5 ау = —?тах-
В площадках, нормальных к плоскости гу и наклоненных на 45° к оси 2, действуют максимальные касательные напряжения
. Tmax = ~2 I (<Д ау) |>
• Ось г проходит через центр площадки контакта и перпендикулярна к ней.
которые достигают наибольшего значения при г = 0,48а (при v — 0,3): ’тахб> = °-31<7тах
Интенсивность напряжений максимальна на глубине ’ = 0,48а:
max ~ 0,62ymax.
Точки поверхности контакта, лежащие на пересечении контура круговой площадки с осью х, находятси в состоянии чистого сдвига при напряжениях
1 — 2v
ах — з-------?тах!
_ 1 — 2г
° у — з---Утах-
(21)
КОНСТРУКЦИОННЫЕ
КОНТАКТНЫЕ ЗАДАЧИ
Классические задачи охватывают случаи контакта тел простой формы (цилиндр, шар и т. д.), в них рассматривают только местные напряжения и деформации в зоне контакта.
Многие реальные конструкции имеют более сложную форму и передают нагрузку через несколько площадок контакта (например, в зубчатых передачах, подшипниках качения, резьбовых и зубчатых соединениях и т. п.). При расчете таких конструкций требуется учесть не только местные, ио и общие деформации тел (изгиб, сдвиг и др ) в связи с их действительной формой, особенностями закрепления, с действием других силовых факторов и т. п.
Наиболее простой способ такого учета — разделение контактных и общих деформаций. Для расчета вводят представление об условном контактном слое, в котором сосредоточивается контактная деформация. Во многих случаях такой слой может иметь реальный смысл, если в задачах рассматривать деформацию микронеровностей поверхности деталей.
Упругий контакт стержней. Рассмотрим контакт двух стержней под действием сосредоточенной нагрузки (рис. 7). Будем считать, что контактные давления q направлены вдоль общей нормали к контактирующим поверхностям (силами трения пренебрегаем), а стержень
536
Контактные задачи
Р
Рис. 7. Схема контакта стержней
имеет постоянное сечение вдоль оси х; ось у направлена вдоль общей нормали.
На рис. 8 показаны сечения стержней после деформации. Принято, что О* и О? — центры жесткости сечений, а оси t,t и г]i—главные оси сечения (i — номер стержня, i = 1,2).
Кинематическое условие контакта в точке А имеет вид
V1 + И 01 — (v2 + г20а) =
= -(«г + 62 - е), (22)
где Vi — составляющая поступательного смещения сечения по оси у в результате деформации изгиба и сдвига;
— угол поворота сечения; — контактная деформация; е — зазор между контактирующими точками до деформации.
Предположим, что между стержнями имеется условный нелинейно-упругий
Рис. 8. Сечения стержней после деформации
контактный слой и контактная деформация определяется контактным давлением в этом же сечении:
61 + 62=W- (23)
Это соответствует обычному в технических задачах допущению, что контактная деформация в данном сечении такая же, как и при постоянном по длине стыка давлении *.
Соотношение (23) позволяет приближенно учесть контактные деформации.
Введя компоненты смещения по главным осям, запишем условие контакта в следующей форме:
Cl sin OCJ + Г]! COS + гД —
— $2 sin а2 — Т]2 COS а2 — г202 —
= — (Ф(?)— е]. (24)
Последовательное четырехкратное дифференцирование этого равенства с учетом уравнений деформации и равновесия приводит к дифференциальному уравнению
= (25)
dx4 1 dx2 1 '
ki^ sin2 a-i cos2 (Xf G^Ft
2
VI / sin2 a; cos2 щ \ . Eijti )’
i=l
2
____, V / basing;
~ dxi Zi 1 ’ k ff/in
i—1
, Qin COS (Xf \ .
+ EiJ it ) ’
здесь GiTt, GiFi, Eг-л, E,Jt-; — жесткости стержня соответственно на кручение, сдвиг и изгиб относительно
* Для сложных контактных слоев контактная деформация зависит также от распределения давлений по всей поверхности контакта.
Конструкционные контактные задачи
537
главных осей; ft;;, — безразмерные
коэффициенты при учете деформации сдвига, q,^— составляющие внешней распределенной нагрузки по глав-
ным осям сечения.
При выводе уравнения (25) использовали следующие уравнения деформа- _ ций (i = 1, 2);
^inQin
dx GtF t ’
I kiZQiZ
dx GiFi ’
dOj Mtn dx GiT( '
(27)
Рис. 9. Схема действия моментов и сил иа стержень
и вытекающие из них соотношения
dx2 Е tJ d2'Q Miv ~dx2' ~
kit) dQi^ GtFi dx ’ ______ kit EiJin GiFt dx ’
(28) в которых ф(, фг, 0г —углы поворота сечений; Л4(г, Л1гт), MtK— моменты, Q,j, Qin — перерезывающие силы (рис. 9).
Силовые факторы связаны условиями равновесия (см. рис. 9)
^Qin i
= —?in+ (—>) ?c°s af;
dx
^Qij r
-7—=—9i:+(—1) 9 sina.; (29) ил * *
dM>n dMir
-dT-^ -dT--~^
dAf ;K . . г
где mt — распределенный крутящий момент, постоянный по длине.
Во многих случаях вполне оправдан метод линеаризации контактного слоя.
Если представить равенство (23) в виде
ф (?) = 61 4- 63 = X (g) q (30)
и положить
% (<7) = const = X (<7ср) = х, (31)
то уравнение (25) можно записать в виде
d*q d2q
~dx^ ^'a‘°~dx2~ = ^°’ (32)
где
а» = у; ₽« = -у: to — -j- • (33)
Величину податливости слояХ можно выбрать в процессе решения с помощью последовательных приближений.
Решение уравнения (32) целесообразно представить с помощью нормальных фундаментальных функций в виде
<7 (х) = q (0) Го (х) 4 q' (0) Ej (х) 4-
4-<r (0) У2 (х) + <Г(0) Уз (х)4-
X
4~ j Уз (х — s)fQ(s)ds, (34) о
где q (0), q' (0), q" (0), q" (0) — произвольные постоянные, определяемые из граничных условий в сечении х = 0; У, — нормальные фундаментальные функции:
Уо (х) = "2“~ [2тп ch mx cos пх —
— (т2 — n2) sh mx sin пх];
Pi (х) = s--т-4——тг- [т (Зп2 —
' 2тп (т2 4- п2) v
— т2) ch /пх sin пх — }
538
Контактные задачи
— п (п1 — 3m2) sh mx cos nx], t
i !
У, (x) = -=--sh mx sin nx;
' 2mn f
K3 (x) - r--—4—:—5- [m ch mx X
3 v ' 2mn (m1 4 n2)
X sin nx — n sh mx cos nx]
(35)
В формулах (35)
Если упругие постоянные материалов цилиндров одинаковы, то при v = 0,3
ф (<?) =
0,386 , 0,579
—+ ~х
X 1П £1,725 («1 + Т?2) -yjp; (39)
<*0 = 0,418 j/qE —|- • (40)
Рассмотрим в качестве примера упругий контакт цилиндрических стержней при действии сосредоточенной нагрузки (рис. 10, а).
- Контактная деформация связана с контактными давлениями известным соотношением А, Н. Диниика
61 + 62 = ф (?) = Л (?) ? =
Пренебрегая деформацией сдвига в цилиндрических стержнях (а = 0), получим
^- + Р„? = 0. (41)
Граничные условия при х — I (рис, 10, б)
?" (/) = 0; ?" (/) = 0 (42)
связаны с отсутствием изгибающего момента и перерезывающей силы в этом сечении.
При х— 0
?'(0) = 0; ?" (0) = Л ₽0Р. (43)
С учетом граничных условий
где полуширина полоски
контакта
(37)
(38)
а0 — наибольшее контактное иапря
жение.
+ И.-, у2(х) + а(х) ,
г2ка ч- каК1 у
(44)
Рис. 10. Контакт цилиндрических стержней
Конструкционные контактные задачи
539
где Y i (х) (/=0, 3) — функция
А. Н. Крылова *; Yj — значения этих функций при х = I-
Протяженность половины зоны контакта может быть найдена из условия
q (0 = 0 (45)
или
I
§ q (х) dx = -у Р. (46) о
Условие (45) выполняется для достаточно длинных стержней: L > I. Если I > L, то следует принять I = L и задача значительно упрощается, ее решение выражается уравнением (44) при I = L.
Рассмотрим случай, когда зона контакта занимает часть длины стержня. Для определения I используем условие (45), тогда получим
(47)
ИЛИ
(?ср) С E2J2 )
(48)
Так как
_ Р
Яср —
то соотношение (48) позволяет найти I и затем X. С учетом равенства (47) решение уравнения (44) можно представить в виде
. , Рт Г лх , л (I — х)
, , ИХ . Л (/ — х) 1 . ...
+ sin -у- sh —> 2-- J . (49)
Относительное распределение контактного усилия по длине зоны контакта не зависит от нагрузки. Последняя, как и упругие характеристики
• Соотношения для функций А Н Крылова можно получить из формул (35) и (36), если принять а© = 0
контактного слоя и стержней, влияет только на длину зоны контакта.
Подобным образом может быть решена задача и при учете деформации сдвига стержней. Условие для определения длины зоны контакта в этом случае запишем в виде
th ml tg nl , (50)
где значения тип вычисляют из соотношений (36). При а0 = 0 условия (47) и (50) совпадают.
В общем случае один из наиболее эффективных методов решения состоит в применении интегральных уравнений и использовании алгоритма последовательных приближений. Интегрируя последовательно уравнение (25) и учитывая граничные условия
I _ < \ dq
dx3 |х=/ V С,/,. G2F2 J dx ( h
_^L| = o-
dx2 ’
i
= a j <?(X|)dX|; o
rflfl I dx |*=o
(51)
Ф |x=0 = °’
получим I I
Ф (?) = —a j J Я (*г) dxt dxi + X Xi
I xx I I
+ ₽jj J j q (x4) dxidxadxtdxi. (52) x» 0 x, x,
Вводя безразмерную координату £ = = xU и учитывая равенство
I =-------j-^--------, (53)
2 j q (£) dl о
запишем уравнение (52) в виде нелинейного интегрального уравнения:
540
Контактные задачи
I I
+ ₽ —у- f у J У я (ы х
)б| J q (5) dij * 0 bi.
\o /
ХМ.'Мг. (54)
или в сокращенной форме
q = Kq. (55)
Для решения используем метод «подобной итерации», принимая для ft + -4- 1)-го приближения
?,-+1 = К (М,)- (56)
Определив коэффициент подобия ct из условия
Ям <°> = Mt (°)’ (57)
получим следующее уравнение для вычисления а:
(°) = х
5 1 1
х У У У У Mwm • 0 0 bi.
(58)
В качестве исходного приближения можно принять линейное распределение
<7о (&) = <7о (0) (» — &)» (59)
причем ?о(О)--7^-, (60)
»<0)
где /(е) — исходное приближение для протяженности половины зоны контакта.
Пример. Примем Ri= R2~ 50 мм; £t = Eg = 2-105 МПа; vt = v2 = 0,3; k = 10/9; сила P = 10’ H.
Принимаем для исходного приближения l0 = 2,5 R = 125 мм. В соответствии с равенством (39) м?)=4-[о-з86+
4- 0,579 1п (з,45/? •
Уравнение (58) для определения с0 принимает вид сооо пето. 1,926 . 3,353 5,232 — 0,579 In с0 = —--------?— ,
° с‘1 ‘ С< '
откуда с0 = 1,003.
В процессе последовательных приближений получим
4-= 2,5; 2,82; 2,69; 2,67; R
в(0)-10~4, — = 8; 8,03; 8,50; 8,57. см
На рис. 11 показано распределение q, полученное по уравнению (54) (кривая 3, X = var) и на основании приближенных решений при X = const с учетом сдвига (кривая 2) и без учета сдвига (кривая 1).
Рис. 11. Распределение давлений на стыке двух стержней
Конструкционные контактные задачи
541
Упругий контакт пластинок. Прн осесимметричной контактной задаче для двух круглых пластинок (рис. 12) имеем следующее дифференциальное уравнение:
d4|> (q) 2 d3ty lg)_____1 (q)
dr1 ’’’ r dr3 r2 dr2
4-+ P<? = A (61)
в котором 1
2
(S2)
1=1
здесь
Di =
Eihl 12(1 -v;’)
— цилиндри-
ческая жесткость пластинкИ (h; — тол-
щина пластинки), i — номер пластинки («= I, 2).
Для линейно-упругого контактного слоя уравнение (61) можно переписать в виде
d*q , 2 d3q 1 d?q ,
dtf + dB3 V dtf +
где
a = VPo. Ро = Р/я; = (64)
При выводе уравнения (63) независимая переменная г (г — радиус пластинки) заменена другой В. связанной с ней соотношением £ = аг.
Обозначая
получим
Лг<7 + Я = -jr • (66)
Решение уравнения (66) можно, как и для стержней, представить в виде
<7 (В) = <7 (Вс) К, (5с, 5) +
+ ?'(Вс) Г, (Вс. В) 4-<7* (Вс) Y* (5с, 5) +
+ <7 (&с) К* (5с. £). (67)
где q (Вс), /(Вс). <7* (Вс). <7 ’ (Вс) — произвольные постоянные, Yt (Вс. В) — нормальные фундаментальные функции при Вс от В
Yt (Вс. B) = ^Bc(-u0 (Вс) Йо (В) -
-о’ (Вс) МВ) 4 Г (Вс) Vo (В) +
+ £0(М “о
Yt (Вс. В) = -|- Вс (-«о (Вс) go (В) -
— Vo (Вс) /о (В) 4~ fo (Вс) Vo (В) +
4- go (Вс) «о (В)].
-°
— vo (Вс) go (В) — fo (Вс) “о № 4
4- g'o (Вс) ро (В)],
Yt (Вс. В) = -5- Вс [Uo (Вс) /о (В) -
— Vo (Вс) go (В) — fo (Вс) «О (В) 4-
+ go (Вс) Vo (В))- (68>
В соотношениях (68) Uo, v0, fo. go. «0. v„, fo. go — функции и их производные, определяемые с помощью функций
542
Контактные задачи
Кельвина I и 11 родов нулевого порядка:
где
„ ,£)_у •
0 6 24*k2*)!j2 ’
.. _ У (-!)Ч4*+2 .
* Й 24*+21(2А+ 1)!J2 ’
2 \
In ио (S) +
(69)
где с = 0,577 — постоянная Эйлера.
При больших значениях аргумента можно пользоваться следующими приближенными асимптотическими зависимостями:
1/2
Граничные условия в рассматриваемой задаче:
прн S = Sc <?' (Sc) = 0; <?"' (Sc) =
= A. aQ: (71)
прн S = Soi Qri = 0; Mrt = 0, (72) где Qr и Мг — соответственно перерезывающая сила н радиальный изгибающий момент.
Из уравнений (67) с учетом этих условий найдем
i
Я (Sc) = 4- Qailo (Sc. Sol);
(73)
я" (Sc) = -j Qaiii (Sc. Soi).
где
По (Sc. Soi) =
У 2 [УiSoi + 0 V) У3 1
= - УI l^.So: + (1 - V) yj] . ,74. yn>/Sot + (i-v) Уз)- ’ ’
~У( №t + (’-v)^J
Л1 (Sc Soi)-----------y~. >
здесь Y, и Y[ — значения нормальных фундаментальных функций и нх производных прн Sc от S — Soi (см. рис. 12).
Подставляя значения произвольных постоянных из равенств (71)—(73) в уравнение (67), получим
Я (S) = 4oQ 1Т)“ (Sc’ K1(gc’ £) +
+ Hi (So Soi) Уз (Sc S) + У* (Sc. S)l-(75)
Значение Soi прн условии, что Я (Soi) = 0. находят из уравнении (75) с помощью известных методов решения трансцендентных уравнений. Аналогично определяют и значение Sos-
Решение задачи существенно упрощается, если Soi < Sb и Soz > S2 (см-рис. 12). В этом случае следует принять Soi = Sb и S02 = S2-
На рис. 13 показано изменение давлений на стыке одинаковых пластинок
Общий метод решения конструкционных контактных задач
54j
Рис. 13. Распределение давлений в сты-че двух пластинок
Рис. 14. Схема контакта двух тел произвольной формы
толщиной h^—hz— 18 мм. Податливость слоя определялась из соотношения
л /1+^2
Решение задачи об упругом контакте пластинок можно весьма эффективно использовать при расчете беспрокла-дочных фланцевых соединений [3].
ОБЩИЙ МЕТОД РЕШЕНИЯ КОНСТРУКЦИОННЫХ КОНТАКТНЫХ ЗАДАЧ
Основные уравнения задачи. Рассмотрим для простоты два плоских тела (/ = 1, 2) произвольной формы в декартовой системе координат хОу (рис. 14).
В некоторых двух точках тел О/, удаленных от зоны контакта, поместим системы координат xtOty,, жестко связанные с телами.
Под действием внешних сил произойдет кинематическое перемещение тел относительно общей системы координат хОу на величины Д,, компенсируемые перемещениями в зоне контакта.
В зоне контакта возникнут контактные давления q (х, у).
Уравнения равновесия в рассматриваемой задаче имеют вид (силы трения ие учитываются):
п Vib
Pimx = e f Qdy;
На
n xib
Pimy = e j У ^Х',
a xib
У <p im) =e J 't/xdx 4-
m“1 1 Ha
Hb
+ e j qydy, Ha
где Pimx и Ptmy — проекции на оси x и у внешних сил Ц и т —- соответственно номер тела и силы), q — контактные давления; хщ и x;j — координаты начала площадки контакта в системе xfityi', xtb и ytb то же для конца зоны контакта; е — ширина тела (размер по оси г).
В результате кинематическою перемещения некоторые сопряженные точки At тел (i = 1, 2) займут новое положение А\ (см. рис. 14) с координатами
4/(Д;) = у(А() + д^- 77
х(Д;) = х(А,) + Д[Х,
где Дгх и A;v — проекции перемещений Д; соответственно на оси х и у, &iy = A; cos аг; Д;-х — Д; sin аг; аг — угол поворота осей х» относительно оси Xj в результате кинематического перемещения тел.
544
Контактные задачи
В зоне первоначального контакта деформируются близлежащие участки тел. В результате точки А'- переместятся относительно местных осей на величины 6; и займут положение А’ (рнс. 14):
у1(л;)=уг(л;.)-1>1.;
МЛ7) = МЛ;)-“ь
где О[ и ut — компоненты смещений 6; соответственно вдоль осей у, и Xj.
Принимая во внимание, что условия касания точек имеют вид
у ИГ) = у И?); (79.
х(Д1’) = х(Д.;),
и учитывая связь между системами координат, получим условие совместности перемещений для контактирующих точек тел:
У ИО — У (Д2) = Д1г/ - —
2
— У, (—1)‘ (fj cos a, -j- Ui sin а;); i=l
х (Д i) х Иг) — &1х
2
— У (— 1/(—Iosina/ + utcosa(), i=l
(80)
где у (Л0 и х (Д,) — координаты точек тел в ненагруженном состоянии.
Из уравнения (80) следует, что кинематические перемещения тел под нагрузкой компенсируются их смещениями в результате деформации. Уравнения (80) в точной постановке задачи должны удовлетворяться для всех сопряженных контактирующих точек тел на всех площадках контакта. Решая совместно системы уравнения (70) и (80) с учетом граничных условий, можно найти контактные давления и размеры площадки (площадок) контакта.
Связь между силовыми факторами и перемещениями в зоне контакта. В большинстве контактных задач граничные условия задают в напряжениях на свободных поверхностях (вне зоны контакта), и решение задач выполняют в напряжениях. '
Поэтому для решения систем уравнений (76) и (80) необходимо выразить смещения в уравнениях (80) через силовые факторы (контактные давления и внешние нагрузки).
В классических контактных задачах связь смещений и давлений принимали такой же, как и при действии сил на полуплоскость (из задачи Фламана). Такой подход позволяет учесть лишь деформации н напряжения в зоне контакта.
Если известна система снл, действующих на тело (см. рис. 14), то перемещение некоторой точки С на его поверхности можно определить с помощью функций влияния (функций Грина):
Vi (С) = j К^ (С, 5) q (5) dl + Sa
п
+ S КТ{С< xP)Pim, m=4 (8 1)
u,.(C) = [ K<U)(C. l)q(l)dl + la n
+ 2 УР)Р<т, m=sl
где K^ (С, g) — функция влияния давления q на перемещение точки С, показывающая перемещение точки С в направлении оси yi под действием единичной силы, приложенной в точке 5; (С, £) — то же, что для пере-
мещения точки С в направлении оси х при действии единичной силы в точке Кр* и К(р* — функции влияния сил Pim, показывающие перемещение точки С соответственно в направлении осей yt и Xi от единичной силы, приложенной в той же точке.
Подставив соотношения (81) в условия (80), получим систему интегральных уравнений. С помощью этой системы н уравнений равновесия можно найти неизвестные давления в зонах контакта, размеры этих зон и кинематические перемещения тел.
Общий метод решения конструкционных контактных задач
545
Рис. 15. Распределение давлений в зоне контакта
Эта система уравнений решается достаточно просто, если принять допущение о наличии дискретного контакта в /-х точках каждой зоны (/ — = 1, 2, k), а неизвестную функцию
распределения контактных давлений аппроксимировать ступенчатым законом с постоянными давлениями в зоне /-Й точки контакта (рис. 15). В этом случае уравнения равновесия примут вид (i = 1, 2)
п k
У| Pimx ~ У?
m=I /=1
п k
Pimy = Я)
m=l /=i (82,'
n
m=\ k
= S ^tyn + x/Aljx). /=i
Соотношения (81) можно переписать в виде (/ = 1,2, ..., k)
k п
^/=2 *№,1^ + S K^pPim, 1=1 m=l
„ (83)
k n
E KW>pim, m=\
18 Заказ № *02
где и — функции влияния, показывающие перемещения соответственно в направлении осей х(- и yt точки тела i в сечении / от единичной силы, приложенной в сечении I.
Если вместо нормальных давлений в расчет ввести проекции давлений qx и qy, то в соотношениях (81) появятся дополнительные слагаемые, учитывающие изменение перемещений и и v соответственно от проекций давлений qu и qx.
Таким ббразом, записывая уравнения (80) для всех k точек контакта и заменяя входящие в них смещения соотношениями (83), с учетом уравнений равновесия (82) получим систему линейных алгебраических уравнений для определения неизвестных давлений, кинематических перемещений и размеров зоны контакта. Эта система с учетом граничных условий задачи решается по методу последовательных приближений (для определения размеров действительной площадки контакта).
Определение функций влияния. Дискретность контакта существенно упрощает определение функций влияния. Функции влияния в простых случаях (для стержней, оболочек и пластин) можно вычислить, используя известные соотношения между перемещениями и действующими силами (например, с помощью интеграла Мора для стержней). Для тел сложной формы эти функции достаточно просто вычисляют с помощью одного из численных методов (методом конечных элементов и др.).
Функции влияния в этом случае вычисляют по обычной методике численного расчета напряженного состояния в телах при заданных граничных условиях. При этом учитывают реальную форму тела и его общие деформации (см. гл. 26).
В более сложных задачах функции влияния можно определить экспериментально, измеряя перемещения в различных точках тела под действием сосредоточенных сил.
При определении функций влияния возникает вопрос об уравновешивании свободных (не имеющих точек закрепления) тел прн действии единич-
546
Контактные задачи
Рис. 16. Схема уравновешивания свободного тела
ной силы. Следует уравновешивать единичную силу в начале координат тела (рис. 16, а), удовлетворяя условиям равновесия (рис. 16, б).
Пример 1. Определить контактные давления под головкой болта (осесимметричная задача).
Рассмотрим контакт головки болта и стягиваемой детали из стали (Е = — 2-106 МПа, v = 0,3). Эскиз деталей показан на рис. 17, а.
Граничные условия задачи для головки болта (i = 1) при = 0 и Oj = 1 МПа
Гу =0, Uj = 0; (84)
для стягиваемой детали (втулки, i — 2); при Уч, = 0; хг = 0
f2 = 0; щ. = 0. (85)
Уравнение равновесия
5
а/с = 2 S У/Дг/, (86)
где гс = 5 мм — радиус стержня болта; Лгу — ширина /-й ступени с постоянными давлениями qj в сечении радиусом г = /] под головкой; / — номер ступени (/ = 1,2....5) *.
Учитывая, что при нагружении соединения поворота местных осей координат не происходит (а = 0), из уравнений (80) получим следующие усло
* Неизвестный закон распределения контактных давлений аппроксимирован пятистолбчатой функцией
вия совместности перемещений (/' = = 1,2, ..., 5):
У Hj;) ~ У (Ац) = bu — (f 1/ — tty),
(87) где Ьу = blu + 62JZ — кинематическое перемещение тел (равно расстоянию между точками Ох и О2 при действии внешней нагрузки).
В расчете принимали, что опорные поверхности деталей параллельны, в этом случае у (Л^) — у (A2j) ~ 0 при Oj — 0; трение в стыке отсутствует.
Смещения уравнений (87) и контактные давления связаны соотношением 5
/=1
где K-L]i—функция влияния, показывающая перемещение в точке / болта (i = 1) под действием распределенной по окружности радиусом г = г< единичной силы, Kill — то же для втулки (1=2).
Записывая [с учетом равенства (88) 1 уравнение (87) для пяти сечений радиусов rj, получим систему нз пяти уравнений с шестью неизвестными (пятью контактными давлениями q2, q2, .... qb и кинематическим перемещением Sy).
Решая эту систему совместно с уравнением равновесия (86), найдем неизвестные контактные давления и кинематическое перемещение.
Для вычисления функций влияния в рассматриваемой задаче использовали вариационно-разностный метод (см. гл. 26).
Общий метод решения конструкционных контактных задан
547
Рис. 17. Распределение напряжений иод головкой болта
На рнс. 17, б (кривая /) показано изменение по радиусу контактных давлений под головкой. При опнра-вни головки на жесткое основание (не-деформируемые стягиваемые детали, ъ2 = 0) контактные давления под головкой распределяются существенно неравномерно (кривая 2 на рис. 17, б). Для снижения контактных давлений на кромке отверстия выполняют фаску. . Из графиков на рис. 17, б следует, |что для а — I МПа раскрытия стыка под головкой не происходит (условие раскрытия стыка q (fj) = 0 в одной из точек контакта).
После определения контактных давлений произведем расчет напряженного состояния тела болта. На рис. 17, а показана сеточная разметка тел болта и втулки для вычисления функций влияния и расчета напряженного состояния. На этом же рисунке показано изменение нормальных напряжений на контуре головкн, цифрами обозначены напряжения в отдельных точках (в МПа) прн контакте головки с деформируемой втулкой. При опирании головки на недеформируемую втулку наибольшие напряжения в галтели незначительно снижаются.
I81*
Пример 2. Определение контактных давлений при взаимодействии абсолютно жесткого диска (1 = 1) с упругой полуплоскостью (1 = 2, плоское напряженное состояние).
На рнс 18, а показана сеточная разметка области.
Граничные условия задачи: при у — = —100 мм и х = 0
о=0; и = 0. (89)
Уравнение равновесия 5
У q} fa] = ~ Р, (90) 1=1
где Ах; — ширина ;-й ступени (/ = 5) контактных давлений <?;. Множитель 1/2 в правой части уравнения (90) связан с рассмотрением одной половины полуплоскости (по условию симметрии задачи).
Уравнение совместности перемещений, как и в предыдущей задаче, имеет вид (87), а смещения связаны с контактными давлениями (1=1 2) соотношением
5
v2j = Е Ktjiqi Axt Г-Н) /=1
548
Контактные задачи
Порядок решения задачи ие отличается от изложенного выше. Однако рассматриваемый пример имеет следующие две особенности:
1) разность координат точек в не-нагруженаом состоянии (см. уравнение (&v)j раьна нулю лишв при х = О, а в остальных точках контакта равна зазору между диском и полуплоскостью,
2) размер (полуширина) площадки контакта заранее неизвестен и зависит от внешней на-рузки (по аналогии с задачей о контакте цилиндров). Поэтому задачу целесообразно решать методом последователе пых .риближе-ний. В нулевом приближении полуширину площадки контакта можно принять такой же, как и для контактирующих цилиндров (илн в общем случае произвольно). Далее площадку разбивают на / ступеней (постоянной или переменной ширины), вычисляют функции влияния, по описанной выше методике определяют контактные давления и проверяют выполнение граничных условий: при х = a q(a) = 0.
Если в результате расчета окажется, что принятая в нулевом приближении
полуширина площадки ап больше действительной а* (ал(0)> то в первом приближении принимают новое значение аЛ(1, (например, из условия q (aft = 0, где о; — координата ступени, в которой давления равны нулю) и повторяют расчет вновь (разбивают новую площадку на ступени и т. д.).
Расчет заканчивается, если
(/+1)
где е — принятая погрешность расчета.
На рис. 18, б показано распределение контак.ных давлений при р = — 10 Н/мм (кривая 1 соответствует приближенному численному решении задачи, кривая ? — точному).
Точность решения задачи зависит также от числа разбиений площадки контакта. Ь общем случае для оценки точности решения целесообразно увеличивать число первоначально принятых ступеней (в 1,5—2 раза).
* В результате расчета появляются растягивающие контактные давления.
ОЦЕНКА ПРОЧНОСТИ И НАДЕЖНОСТИ
Глава 30
РАСЧЕТ НА ПРОЧНОСТЬ
ПРИ СЛОЖНОМ НАПРЯЖЕННОМ состоянии
КРИТЕРИИ СТАТИЧЕСКОЙ ПРОЧНОСТИ
Для оценки статической прочности при слоаном напряженном состоянии используют критерии прочности или разрушения, зависящие от напряженного и деформированного состояния, а также механических свойств материала. Эти критерии позволяют перенести результаты опытов по разрушению образцов при простых напряженных состояниях на случай сложных напряженных состояний. В курсах сопротивления материалов нх называют теориями или гипотезами прочности.
Условие статической прочности или разрушения удобно представить в виде
стькв — f (CTi> °j. °s;
Xq, Xj, ...) = ав, (1)
где оэкв — эквивалентное иапряже ние; Oj, <т2 и а3 — главные напряжения, причем Oi о2 > а3; л0, Xt — параметры, зависящие от механических свойств материала; аа — предел прочности материала при одноосном растяжении.
Эквивалентное напряжение устанавливает соответствие между сложным напряженным состоянием и одноосным растяжением.
Если в наиболее напряженной точке детали
то условие прочности считают выполненным. При
(3)
наступает разрушение в опасной точке. Условие (3; является граничным для состояния прочности и разрушения. Условие прочности или разрушений можно представить через деформации
— ф (ei> е2' «з:
^0» ^1’ •••/ “ ьв*
(4)
где е1( е2> е9 — главные деформации (&! > е2 > egj, (о0, — параметры,
Зависящие от меланических свсйсть материала, гв — удлинение в момент разрушения при одноосном растяжении.
Критерии оагичесиой прочности для платинных материалов. Для пластичных материалов условия прочности при растяжении и сжатии совпадают. Разрушение таких материалов определяется преимущественно касательными напряжениями. Основными критериями разрешения являются критерий интенсивности i алряжеьий, выражающий «среднее» касательное напряжение в точке, и критерий максимального касательного напряжения.
Критерий интенсив и о-с т и н а п р я ж е и и й (критерий Г убера—Мизеса).
Для этого критерия условие прочности
СТЙКВ < <Ъ>.
(2)
«зкв = -I < °з>
(5)
550
Расчет на прочность при сложном напряженном состоянии
Рис. 2. Напряжения при кручении образца
где интенсивность напряжений
стэкв = ст^2~Н°к —
V ’* а2)2 + (сг — аж)2 + ” *
^’ + 6(^ + Чг + г1х); (6)
ах. а2, тху, т^г, т2х — нормальные и касательные напряжения в трех взаимно перпендикулярных площадках, нормали к которым обозначены х, у, г.
Для плоского напряженного состояния, когда отличны от нуля компоненты ar, av и тху,
°«В=А+Я/^х'’9 + 3\9- (7) Если оси х. у, г совпадают с главными осями напряженного состояния L Т). С. то
°экв = VF х
XУ(^ — an)2 4- (°п—ст£)2 + (°: —ст5’2
(8) Последнее соотношение не зависит от обозначения главных осей. Если, например, aj = a,, an = a2, aj = a3, TO
I °экв —
XУ(°1-оа)2Д (c2-a3)2 + (as-a1)2.
(9)
В частном случае плоского напряженного состояния
°эьв = /ai~Vn + an =
= Vaf- a,a2 + a22. (10)
Критерий интенсивности напряжений (6) для плоского случая выражается эллипсом (рис. 1).
Если точка а^, находится внутри эллипса, условие прочности соблюдается, при переходе за пределы области наступает разрушение.
Для случая кручения главные напряжения
ап=т, (11)
где т — касательное напряжение в поперечном сечении (рнс 2, площадки главных напряжений направлены под углом 45° к оси вала). Отсюда, с учетом условий (5) и (10), следует связь предела прочности при кручении и растяжении:
TB = S7Fa® ^°’57ов- (12)
V
Это соотношение соответствует экспериментальным данным для пластичных материалов.
Критерий максимальных касательных напряжений. В соответствии с этим критерием условие прочности
^jkb “ — п3 < ав, (1о)
Критерии статической прочности
551
где Oj и аэ — соответственно наибольшее (в алгебраическом смысле) и наименьшее напряжение.
Если главные напряжения а£, и а; не упорядочены по величине, то критерий прочности имеет вид
°экв —
а5 —ап оп-а£ а£— а£
max
(И)
Для плоского напряженного состояния критерий максимальных касательных напряжений выражается шестиугольником, вписанным в эллипс. Как следует из рнс. 1, оба критерия близки между собой.
Для случая кручения получаем
тв — 0,5ав. (15)
Критерии пластичности. Критерии возникноьсния пластической деформации при сложном напряженном состоянии, как показали экспериментальные исследования, часто имеют такую же структуру, как и критерии разрушения, но величина ов заменяется на предел текучести от.
Например, критерий пластичности Губера—Мизеса имеет вид
Of =
xV(o5—an)2 + (an-o£)2 + (a£ -о£)2 =
= от.
(16)
Развитие пластических деформаций, вплоть до разрушения путем среза, определяется в основном действием касательных напряжений. Перед разрушением могут возникнуть существенные изменения первоначальной формы детали, что следует учитывать при составлении условий разрушения.
В тех случаях, когда деформации стеснены и возникает объемное напряженное состояние, создаются условия, благоприятные для хрупкого разрушения. Для оценки прочности подобных состояний приведенные критерии малопригодны.
Например, при равномерном всестороннем растяжении (аг = a2 = a3) критерии (6) и (13) прогнозируют бесконечную прочность, что не соответствует физическому смыслу задачи.
В связи с указанным условия прочности
°экв < °в (17)
по уравнениям (6) и (13) должны быть дополнены ограничением на величину наибольших растягивающих напряжений
01 =
°C
<ов-max
(18)
Тогда общее условие прочности пластичных материалов получит вид
<4 < ав Д а! < ав, (19) где Д — знак конъюнкции (знак логического умножения, т е. одновременного осуществления двух событий).
Общее условие разрушения
Oi V О; > «в. (20)
где V — знак дизъюнкции (знак логического суммирования, осуществление одного нз событий или обоих событий вместе).
Критерии статической прочности для хрупких (малопластичных) материалов. Одно из важных свойств хрупких материалов — прочность при сжатии выше, чем при растяжении. Ответственными за разрушения являются преимущественно нормальные напряжения.
Критерий максимального нормального напряжения. В соответствии с этим критерием условие прочности имеет вид °экв = oj < ав. (21)
Возможность разрушения в области сжимающих напряжений отрицается.
Для случая действия касательных напряжений (кручения)
тк < ав, (22)
где тк — разрушающее касательное напряжение.
Критерий максимальной деформации растяжения. По этому критерию условие прочности принимают в виде
Cj < ев, (23)
где ej — наибольшая деформация растяжения, ев — деформация в момент
552
Расчет на прочность при сложном напряженном состоянии
разрушения при растяжении образцов.
Для хрупких материалов принимают
ев « пв/£, (24)
где Е — модуль упругости материала Далее предполагают, что в момент разрушения
81 ~ ----g- (а2 + а,)] . (25)
Критерий прочности по максимальной деформации растяжения, выраженный в напряжениях, с учетом соотношений (24) и (25) будет
Оэкв = <Д — 0,5 (а2 + а8) < ав. (26)
Область прочности по этому критерию также простирается в бесконечность при сжимающих напряжениях.
Критерий прочности Мора. В соответствии с этим критерием условие разрушения зависит как от касательных, так и от нормальных напряжений в опасной площадке
Эквивалентное напряжение может быть записано в виде
^экв = (27)
где и Хэ — постоянные материала.
Применим выражение (27) к условию разрушения аэкв = ав для случая растяжения и сжатия. Так как при растяжении at = <jB, a3 = 0, при сжатии О1 = 0, <73= —ед», где °сж — абсолютная величина предела прочности материала при сжатии, то получим соответственно
аэкв — ^1ав> аэкв — ^3ac>K — Ов-
Из последних соотношений определяем постоянные материала
Xi= 1, К3 = -
исж
Условие прочности Мора приобретает вид
аэкв = а1 — ~~ Оз < ав (28) °C Ж
или
^экв = Of — %Рз < ав> (29) где % = ав/асж.
Величина х характеризует пластичность материалов, для очень хрупких
материалов X0. Если х = 1, то условие Мора совпадает с условием максимальных касательных напряжений.
На рис. 3 граница области прочности для критерия прочности Мора составляет неправильный шестиугольник AP^CBDPz.
Для случая кручения, когда = = —аэ = т, из условия (29) предел прочности при срезе
или
-£2-=1+х. (31)
Тк
Критерий прочности Писаренко — Лебедева. Рассматриваемый критерий может быть получен, если представить
Оэкв ” V* + (32)
где и Xj — постоянные материала; ai и Oj — соответственно интенсивность напряжений и наибольшее напряжение.
Применяя условие разрушения
®экв = «в для случая растяжения и сжатия, найдем
^-оав ^1ав = ав> ^оас>« = ав-
Из последних соотношений получаем
К = = х; *1= i-х, (33)
исж
и критерий прочности Писаренко—Лебедева приобретает вид
аэкв = Xat + (1 — Х)а1<ав- (34)
При х = 0,5 этот критерий совпадает с критерием Сдобырева.
Для случая кручения при о, -— У 3 т, at = т
_ ________gB__________ qB_______
к~ 1 + (уз -1)х ~ 1 + 0.73Х
(35)
Граница области прочности по Крите рию Писаренко—Лебедева представляет собой неправильный эллипс, опи-
Критерии статической прочности
553
санный относительно шестиугольника Мора (см. рис. 3).
Критерий Нада и. Эквивалентное напряжение представляется в виде
°экв = 4—у (ai аз)‘ (36)
Применяя критерий для растяжения и сжатия, найдем
7-оав 4—у ^1ав — ав>
Т-о^сж ~ — ®в-
Из последних соотношений получаем условие прочности
аэкв - ~2~ (' 4" X) °i + ~2~ —X) X
X (aI J- а2 -L о3) < ав
(37)
где % = ав/ас>к; а; — интенсивность напряжения, olt а2, а3 — главные напряжения. Для прочности при кручении (срезе) из условия (37) находим
------• (38)
+Х)
Наиболее общими условиями прочности являются условия Мора и Писаренко—Лебедева, которые при х = 1 (пластичный материал) переходят соответственно в критерий максимальных касательных напряжений или интенсивности напряжений. При X = О (очень хрупкий материал) критерий Мора и Писаренко—Лебедева совпадают с критерием наибольших нормальных напряжений.
Однако при использовании критериев Мора или Писаренко—Лебедева
554 Расчет на прочность при сложном напряженном состоянии
требуется знание двух пределов прочности материала при растяжении и сжатии. Если величина асж не известна, но имеются результаты опытов на кручение (среза), то по теории Мора
практически применяемые критерии прочности.
В общем случае параметры материала определяют нэ базовых опытов на разрушение:
рв qB
/К хк
(39)
по критерию Писаренко—Лебедева
(40)
при растяжении а, — ад, - ад; а2 -= 0. а3 = 0;
при сжатии at = ас1к; crj = 0; i а2 — 0; а3 -- —Осж!
при кручении at = ]/3 тк, Од = = тк ; а2 = 0, а3 = —тк. > (47)
КРИТЕРИИ ДЛИТЕЛЬНОЙ
И МАЛОЦИКЛОВОЙ ПРОЧНОСТИ
Критерии длительной прочности. Для расчета длительной прочности могут быть использованы критерии прочности для хрупких материалов.
Условие длительной прочности аэкв < адл (Л Т), (41)
где Одл (/, Т) — предел длительной прочности на растяжение при времени t и температуре Т.
Критерий Мора для длительной прочности
аакв — ai Х°з < адл (Л Д)> (42)
Ядл. сн-. (t, Т) — предел длительной прочности на сжатие.
На основании экспериментальных данных следует считать
X С 0,5. (44)
Если величина адл с;!( (/, 7’) неизвестна, то можно принять
X = 0,5. (45)
Обобщенный критерий прочности для пластичных и хрупких материалов. Условие прочности
аэкв ~ т
+ ^-заз < ав- (46)
При надлежащем выборе параметров материала /.0. ... условие (46)
содержит как частные случаи многие
Если пренебречь влиянием «промежуточного» главного напряжения а2 на прочность и положить Х2 = 0, то из условия (46) и (47) найдем
=(2 +УЗ)(1+-^-
\ °C Ж Т1
= (2 -Г V з ) ( 1 - уз -
h =- (2 4- Уз) X
хГ1 + (Уз-1)-^---^’1.
L асж тк J
(48)
На рис. 3 показаны области прочности для различных значений ав/тк при <!в1аСП( — 0,5.
В более общем случае можно использовать опыты на разрушение трубчатых образцов под действием гидравлического давления. Обозначая разрушающее (окружное) напряжение аг, получим
Дв
? = 2 - 1 4-
Яг «сж
- (49)
При этом критерием прочности (46) и равенствами (48) можно воспользоваться, если известны значения ав, °сж и Тк-
Если какая-либо из трех экспериментальных характеристик неизвестна, то следует применять двухпараметрические критерии прочности (например, критерии Мора).
Основные закономерности сопротивления усталости
555
Критерии малоцикловой усталости. Критерий малоцнкловой усталости при одноосном напряженном состоянии — предельный размах полных деформаций Дво [см. гл. 2, формула (16)] обобщается на случай сложного напряженного состояния с помощью размаха интенсивности деформаций Де,, вычисляемого по разности главных деформаций Fj, е2, е3-
* *
Арэкв — Af i — 2 '
X 1/[A(Fi — е2)]2 + [A(f2 — е3)]2 +
+ [Д (е3 - 81)]2 . (50)
Если в наиболее деформируемой точке детали Деякв = Аеа, то наступает разрушение.
Вопросы прочности при малопикло-вых нагрузках рассмотрены в работе [5]. Критерии сопротивления усталости при сложном напряженном состоянии приведены в гл. 31.
Глава 31
РАСЧЕТ НА УСТАЛОСТЬ*
ОСНОВНЫЕ ЗАКОНОМЕРНОСТИ СОПРОТИВЛЕНИЯ УСТАЛОСТИ
Усталостные поломки составляют основной вид разрушения деталей машин и непелко приводят к тяжелым последствиям, так как возникают внезапно.
Связь разрушающего напряжения и числа циклов. Экспериментальные исследования показали, что характер разрушения конструкционных материалов (черных и цветных металлов, жаропрочных СП "’ВОВ и др Л зависит ОТ ЧИСЛЯ ПИКЛОВ нагружений.
При малом числе циклов в образце из пластичных материалов образуется шейка и разрыв происходит по минимальному сечению — статическое разрушение (рис. 1). При числе циклов 162—104 появляются сетка трещин и заметные пластические деформации — наступает разрушение от малоцикловой усталости. Разрушение имеет смешанный характер в изломе видны отдельные участки усталостных разрушений. Наконец, при числе циклов N > 105 наблюдается типичное усталостное разрушение без заметных следов пластических деформаций. При уменьшении знакопеременного (разрушающего) напряжения о число циклов нагружений N возрастает. Число циклов до разрушения имеет статистический разброс и обычно под У пони
• Пепвоначальные сведения см гл 2
маю* средне#* число циклов до разрушения.
На рис. 2 показаны типичные зависимости о = <р (У).
В логарифмических координатах чти зависимости характеризуются полигональной кривой (отрезками прямых линий). Кривая первого типа (рис. 2, а), типичная для деталей из углеродистых сталей, имеет при симметричном цикле нагружения предел выносливости a~i, при напряжениях а < о_, усталостное разрушение не-влчмлжнп. Кривые второго типа (рис. 2, б, высоколегированные стали и титановые сплавы) после точки перелома имеют наклон (tg as 0,1 tg Pj).
Для третьего типа кривых (рис. 2, в, легкие цветные металлы, жаропрочные сплавы в определенном интервале температур) наклон прямой сохраняется вплоть до очень малого уровня напряжений.
Рис. 1. Типы разрушений в зависимости от числа циклов
556
Расчет на усталость
Рис. ?. Три вида зависимости а = $ (N)
В общем случае пределом'выносливости называют наибольшее напряжение цикла, которое может выдержать деталь (образец) без разрушения при базе испытаний База испытаний Л/д может быть больше или меньше Nt.
Точка перелома кривых усталости (в логарифмических координатах) обычно соответствует числу циклов
Ло = 10’4-10’.
При числе циклов N <' N\ (N1 ~ ~ 10s4-104) кривые усталости имеют еще один перелом, связанный с переходом в область малоцикловой усталости, где возрастает роль пластического деформирования.
Разделение кривых усталости на три типа явтяется условным. На практике способность материала сопротивляться переменным напряжениям характеризуется величиной переменного разрушающего напряжения при определенном числе циклов ЛЛ Обычно принимают = 2- Э”ч-5. 'О7 циклов.
Уравнение кривой усталости. Простая и достаточно точная зависимость между а и N может быть принята в виде
amN = С (Л^ < Л’ < No), (1) где т и С — -достоянные, зависящие от свойств материала, температуры испытания, окружающей среды.
В логарифмических координатах уравнение (1) ссответствует прямой линии
1g а = — —L. ig дг ig с. (2)
Тангенс угла наклона Pt по абсолютной величине
itgpii=4"- (3)
При увеличении m наклон уменьшается, а при т -+- оо прямая становится горизонтальной. Обычно значения m лежат в пределах m = 44-10, а для деталей с концентрацией напряжений m — 44-6.
Точка перелома Ао (рис. 3) принадлежит прямой AjA0 и потому
С = a”N0. (4)
Зависимость (1) иногда удобно представить в виде
<5>
Если продолжить прямую Л1Л0 до пересечения с осью координат, то получим предельное сопротивление Of, не совпадающее с пределом прочности ип.
Из соотношения (5) при У = 1 следует:
= Ро 'Vn'o- (6)
Если предел выносливости принять равным разрушающему напряжению в точках перелома a_j = <70 ч No = = 10’ циклов, то
Ст( =0.1.10*'"', (7)
обычно a< ~ (34-10) O-i*
При числе циклов N > No также справедлива линейная зависимость (в логарифмических координатах)
am°N = Со, (8)
Основные закономерности сопротивления усталости
557
Рнс. 3. Зависимость «напряжение— число циклов до разрушения» (в обозначениях опущен знак логарифма)
причем т0 значительно больше т (гщ rv 10m). Так как точка Ао одновременно принадлежит прямым (1) и (8), то постоянные С и Со связаны соотношением
<_С0 = Со„‘°~т- (9)
В области малоцикловой усталости удовлетворительное описание можно получить также с помощью прямолинейной зависимости
am'N = (10)
Если прямая проходит через точку А г, то
С1=а^. (И)
Приближенно для точки /ij можно принять at as ат.
Число циклов iVp соответствующее переходу в малоцикловую область
Nl
\ От /
Обычно Nf составляет 10s—104 циклов.
Влияние постоянных напряжений. Зависимость предельного значения амплитуды переменных напряжений (предела выносливости по амплитуде при асимметричном цикле) аап от среднего (статического) напряжения ат, действующего в той же точке сечения, показана на рис. 4.
Если постоянное напряжение отсутствует, то ааП = a.p При действии постоянных напряжений, равных пределу прочности ат = ав, наступает разрушение уже при ааП = 0.
Исследования показывают, что при сжимающих постоянных напряжениях
предел выносливости повышается (затрудняется зарождение и развитие усталостной трещины). В этом состоит одна из главных причин возрастания сопротивления усталости в результате создания сжимающих остаточных напряжений з поверхностных слоях от упрочняющей обработки.
Для расчетов используют аналогичные зависимости оаП ~ f (см. рис. 4). Наибольшее практическое применение получила линейная зависимость (рис. 5, а)
аап ~ а-1 Фоат> (13)
где коэффициент ф0 принимают по данным табл. 3 гл. 2.
В области сжимающих постоянных напряжений as 0.
В тех случаях, когда известен предел выносливости при отнулевом цикле а0 (напряжения возрастают от нуля до а0) предельную прямую можно принять проходящей через точку отнуле-вого цикла. Тогда в равенстве (13)
Рис. 4. Влияние постоянного (статиче-скоро) напряжения иа предел выносливости (кривая предельны* амплитуд)
558
Расчет на усталость
Рис. 5. Кусочио-лииейные кривые предельных амплитуд
При использовании последнего равенства следует ввести ограничение по статической прочности, приняв (рис. 5, 6}
^ап — Ов Пщ (1S)
При
От > Отв = АВ ~ У~' • ( 5) I ' “фа
Кроме линейных можно использовать зависимости более сложного .вида
£ап,\“= j __ / Ст \5
0-1 / \ Ов /
(17)
где а и р — постоянные материала.
Для углеродистых и легированных сталей удовлетворительные результаты дает зависимость (17) при а = 2, ₽= 1;
Для титановых, алюминиевых и жаропрочных сплавов можно принять а = Р — 1.
Влияние концентрации напряжений. При действии переменных нагрузок концентрация напряжений представляет большую опасность, Значительное число усталостных разрушений связано с недостаточными радиусами закруглений, наличием рисок, отверстий и других источников повышенных напряжений. Усталостные разрушения имеют резко выраженный локальный характер, что и объясняет существенное в зияние местного увеличения напряжений, точечных дефектов материала и т. п.
Концентрация напряжений характеризуется теоретическим коэффициентом концентрации напряжений
а0 = -^, (19)
°н
где Отах — максимальное напряжение в зоне повышенных напряжений; ан — номинальное напряжение в 'этой зоне. Номинальное напряжение определяется по простейшим расчетным формулам, однако всегда должен быть указан конкретный способ их определения. Значения теоретических коэффициентов концентрации напряжений для различных источников концентрации приведены в гл. 28.
Экспериментальные исследования сопротивления усталости показали, что усталостные разрушения начинаются в местах концентрации напряжений при условии
Отах эф = (O-i)d> (20)
где (O-Jd — предел выносливости, определяемый при испытании ' гладких образцов. Величина соответ-
ствует номинальному напряжению при усталостном разрушении. Испытания показали, что эффективное максимальное напряжение аШах эф всегда меньше максимального напряжения, опреде леииого (расчетом или экспериментально) для идеально упругого материала:
Отах эф Г^тах • (21)
Для расчета удобно ввести понятие эффективного коэффициента концентрации напряжений
Ko = f?^. (22)
ан
Основные закономерности сопротивления усталости
559
Условие (21) означает
Ка < <z0, (23)
причем равенство возможно для деталей больших размеров и для материалов с повышенной чувствительностью к концентрации напряжений.
Учитывая условие усталостного разрушения (20), можно записать
где (a_!K)d — предел выносливости детали (образца) с концентрацией напряжений; (a_i)d — предел выносливости гладкого образца (детали) того же размера.
Зависимость между аа и Ко обычно выражается следующим соотношением:
Ка = 1 + q (а0 - 1). (25)
где q — коэффициент чувствительности материала к концентрации напряжений, значения которого для различных материалов приведены ниже:
Литые материалы и .материалы с внутренними источниками концентрации и дефектами (серый чугун и др )............
Литые жаропрочные сплавы, стальное и алюминиевое литье, модифицированные чугуны . . Низкоуглеродистые стали, жаропрочные деформируемые сплавы, аустенитные коррозионно-стойкие стали, алюминиевые деформируемые сплавы . , Среднеуглеродистые стали, низколегированные стали . .
Конструкционные легированные стали ................
Высоколегированные стали (типа коррозионно-стойких сталей мартенситного класса), титановые сплавы ....
0,1—0,2
0,1 —0,4
0,3 —0,5
0,4 —0.6
0,6—0.7
0,7 —0.9
Величина q возрастает прн увеличения абсолютных размеров, при очень сильных источниках концентрации (а0 > 10) наступает своеобразное «насыщение» и величина q уменьшается.
Для учета «насыщения» при увеличении концентрации напряжений величину q в равенстве (25) можно принять в виде
’ = Тм&^тГ’ (26)
где <?0 и а — постоянные материала. Приближенно
ft * (1,1 4- 1,2) ?табл;
а=0,14-0,3, (27)
где <7табл принимают равным значениям q, приведенным выше.
Из равенств (25) и (26) следует, что максимально возможное значение эффективного коэффициента концентрации напряжений при а0 -+ °°
Ка max = 1 Н—~ • (28)
Влияние абсолютных размеров детали (масштабного фактора). Экспериментально установлено, что с увеличением абсолютных размеров деталей их сопротивление усталости снижается (масштабный эффект). Это объясняется статистической теорией разрушения, в соответствии с которой при увеличении абсолютных размеров возрастает вероятность попадания дефектных зерен материала в зону повышенных напряжений.
Существуют и другие причины, способствующие проявлению масштабного эффекта: меньшая однородность материала в деталях больших размеров (например, в валах диаметром >200 h/м), трудность обеспечения стабильности технологического процесса, условий контроля и т. п.
Масштабный эффект оценивают с помощью коэффициента влияния абсолютных размеров поперечного сечения
Kd = (<7~г-^- , (29)
a-i
где (®-i)d — предел выносливости гладкого образца (детали) диаметром d; <г_1 — предел выносливости материала, определяемый на стандартных гладких образцах, обычно диаметром d0 = 74-10 мм.
Масштабный эффект зависит главным образом от поперечных размеров (диаметра) изделия и в меньшей степени — от его длины. В литых материалах, в деталях и материалах, имеющих рассеянные микро- и макродефекты (неметаллические включения, поры и т. п.), крупнозернистое строение, масштабный эффект сказывается
560
Расчет на усталость
сильнее. Легированные стали более чувствительны к неметаллическим включениям и другим дефектам, и для них влияние абсолютных размеров проявляется в большей степени, чем для углеродистых сталей.
При увеличении абсолютных размеров (характерный диаметр детали d) коэффициент Кл стремится к определенному пределу К <х1. Для оценки масштабного эффекта можно использовать зависимость
е-’< (30)
В приближенных расчетах можно принимать: /<00=0,5 — для деформируемых материалов (сталей, титановых и алюминиевых сплавов и т. д.); Коо ~ ОД — для литых материалов. Величину А в первом приближении можно принять равной 0,0!—0,03 1/мм.
Влияние состояния поверхности и упрочнения. Состояние поверхности детали, как показали экспериментальные исследования, существенным образом влияет на сопротивление усталости.
Влияние состояния поверхности на выносливость характеризуется коэффициентом
о(к) __ (q-iK)dn _ (а-1)д * ,□ 11
Р° ” (О-1к)й (q-iK)d ’ ( } где (о_1)д—предел выносливости детали диаметром d с определенным состоянием поверхности; (сг_1к)г; — предел выносливости образца (или аналогичной детали) диаметром d, имеющей такую же концентрацию напряжений, что и деталь, но с состоянием поверхности, соответствующим стандартному образцу.
Таким образом, значения (а_])д и (а-1к)</ могут различаться только из-за состояния поверхностного слоя.
Если влияние состояния поверхности устанавливается для детали, не имеющей концентрации напряжений, то коэффициент состояния поверхности
<32>
Коэффициенты состояния поверхности при наличии и отсутствии кон
центрации напряжений различаются между собой. Это объясняется тем, что взаимное влияние различных источников концентрации напряжений подчиняется статистическим закономерностям.
Коэффициент зависит от трех основных факторов:
шероховатости поверхности и механических свойств поверхностного слоя;
наличия коррозионных повреждений (фреттинг-коррозия, воздействие морской воды и т. д.);
упрочняющей поверхностной обработки (обдувка дробью н т. д.).
В связи с этим коэффициент состояния поверхности можно представить в виде произведения:
Р'к) = К^КккорК°, (33)
₽'0) = 40)СХ> (34)
где индексы «к» и «0» означают соответственно наличие или отсутствие концентрации напряжений в деталях (образцах).
Коэффициент Kf (рис. 6) отражает влияние шероховатости поверхности. Предполагается, что остаточные напряжения и механические свойства в поверхностном слое при различном состоянии поверхности не отличаются существенно между собой.
Легированные стали целесообразно использовать для изготовления деталей, если технологические процессы обеспечивают хорошее качество по-
Рис. 6. Зависимость Кр от предела прочности материала (углеродистая и легированная стали):
/ _ полирование, 2 — шлифование; 3 — тонкое точение; 4 — грубое точение; 5 — наличие окалины
Основные закономерности сопротивления усталости
561
Рис. 7. Зависимость ККОр от предела прочности материала детали:
/ — пресная вода (образец с концентра* иней напряжений); 2 — то же, образец без концентрации напряжений, а также образец с концентрацией напряжений в морской воде, 3 — морская вода (образец без концентрации напряжений)
верхности (шероховатость поверхности, прочность, пластическая деформация поверхностных слоев и остаточные напряжения в них).
Можно считать, что влияние качества поверхности находится в прямой зависимости от коэффициента чувствительности к концентрации напряжений. Влияние наклепа и остаточных напряжений рассматривается в дальнейшем.
Значение коэффициентов /С{-к) и К/?1 определяется как отношение пределов выносливости деталей, изготовленных по действующей технологии, к пределу выносливости аналогичного образца (или детали), выполненного по «стандартной технологии».
Практически установлено существенное влияние коррозии на сопротивление усталости. С увеличением времени наработки в коррозионной среде и числа циклов сопротивление усталости непрерывно падает. Это объясняется возникновением и развитием коррозионных микротрещин, которые становятся дополнительными источниками концентрации напряжений. Обычно коррозия возникает при работе в пресной или морской воде, при работе в агрессивных средах
Снижение пределов выносливости в результате коррозионного повреждения поверхностного слоя характеризуется коэффициентами Ккор — для образцов с концентрацией напряжений и /С^р — для гладких деталей или
образцов (рис. 7). Особенно велико влияние коррозии на стали с высокими пределами выносливости.
Одним из эффективных способов увеличения пределов выносливости при коррозии является создание сжимающих напряжений в поверхностных слоях (обдувка дробью обкатка и др.). С применением титана вместо стали часто резко повышается сопротивление усталости благодаря антикоррозионным свойствам титана. Применяют различные покрытия (хромирование, Полимерные покрытия) для ослабления коррозионного воздействия.
В прессовых, фланцевых, замковых и других соединениях, осуществляемых с помощью посадок с натягом при воздействии переменных напряжений, возникают микросмещения (порядка 0,0025 мм), приводящие к разрушению поверхностного слоя. В зоне контакта протекают не только процессы механического изнашивания, но и физико-химические процессы (окисления и др ). Усталостные разрушения образуются при низких переменных напряжениях (20—80 МПа), что свидетельствует о значительном влиянии фреттинг-коррозии (коррозии трения). При наличии фреттинг-коррозии /Скор = = 0,44-0,6— для прессовых соединений деталей из среднеуглеродистых легированных сталей.
Для уменьшения влияния фреттинг-коррозии увеличивают твердость контактирующих поверхностей, применяют поверхностный наклеп, а также мягкие покрытия (омеднение, серебрение, полимерные пленки).
Коэффициенты /С„к) и равны отношениям пределов выносливости деталей при упрочняющей технологии и деталей, изготовленных без ее применения.
Основные методы упрочнения: пластическое деформирование (наклеп) с помощью обдувки дробью, обкатки роликами и т. п. (рис. 8, 1,Зч-2,2; = 1,14-1,4).
химико-термическая обработка (цементация, азотирование, цианирование и т. д.). Обычно = 1,34-2,5;
К'01 = 1,1 ч- 1,3;
562
Расчет на усталость
Рис. 8. Изменение коэффициента
от KQ в галтелях образцов из стали 45ХН (ов = 1150 МПа), подвергнутых дробеструйной обработке:
/ — расход дроби Q = 10 кг/мин прн частоте вращения ротора машины Пр = = 3500 мнн-1, 2 — при Q — 20 кг/мин, Пр = 2100 мни""1
специальная термическая обработка (нагрев до умеренных температур и быстрое охлаждение поверхности для создания сжимающих остаточных напряжений); обычно
/f<K> = 1,6 4-2,5, K{v0) = 1,2 =1,5.
Эффект пластического деформирования сказывается в большей степени иа деталях из материалов повышенной прочности (твердости) и при наличии концентрации напряжений. При химико-термической обработке создается высокая твердость поверхностного < слоя, что повышает его износостойкость. В результате физико-химчче-ских процессов в поверхностных слоях создаются также остаточные напряжения сжатия.
Закалка токами высокой частоты увеличивает прочность поверхностных слоев благодаря остаточным напряжениям, возникающим в детали после быстрого ее охлаждения.
Значения коэффициентов Kv в значительной степени зависят от режимов обработки деталей.
Более подробно влияние технологии на прочность см. гл. 34.
ОПРЕДЕЛЕНИЕ ПРЕДЕЛОВ ВЫНОСЛИВОСТИ ДЕТАЛЕЙ
Экспериментальное определение.
Наиболее точным способом определения предела выносливости детали является экспериментальное исследование в условиях, наиболее полно имитирующих реальные условия работы. Испытания проводят с помощью универсальных или специальных машии для испытания на усталость.
Среди универсальных машин большое распространение получили электродинамические возбудители вибраций, позволяющие создать переменные напряжения с частотой от 50 до 10 000 Гц. Для определения предела выносливости испытывают 6—20 образцов. При необходимости получения статистических оценок число испытуемых деталей увеличивают до нескольких десятков. Методика экспериментальных исследований сопротивления усталости изложена в работах [2, 4].
Однако экспериментальное исследование натурных элементов (крупногабаритные детали и другие изделия, изготовляемые в небольшом количестве) не всегда возможно и целесообразно.
В таких случаях проводят испытания образцов, имитирующих напряженное состояние в опасных зонах детали с наибольшим приближением по источникам концентрации напряжений, абсолютным размерам, технологии, покрытиям, температуре, среде и т. п.
Расчетио-эксперимеитальное оп ределение. Расчет пределов выносливости основывается на системе экспериментальных данных, полученных с помощью испытания образцов.
Предел выносливости материала определяют испытаниями стандартных гладких образцов диаметром dB (обычно d0 = 74-10 мм). Образец изготовляют по определенной технологии, включающей термообработку, и с определенным качеством поверхности, которое принимают как базовое в дальнейшей системе оценок. Образец подвергают испытаниям на выносливость при определенном напряженном состоянии (например, при переменном изгибе или кручении). Последующие эксперимеи-
Определение пределов выносливости деталей
563
ты проводят при том же виде напряженного состояния.
Предел выносливости детали (О-1К)д с характерным размером (диаметром) d и концентрацией напряжений можно определить с помощью оценки влияния каждого фактора в отдельности. Это можно сделать двумя способами:
К™
= (35)
Add
ИЛИ
(°-iK)d = 0-1 X
0-1
где
^(0) _ , коэффициент влияния
абсолютных размеров поперечного сечения гладких образцов; (37)
---------------эффективный коэф-фициент концентраций напряжений для образцов диаметром d\ (38) д-(к) _ £0-1к)с(-коэффициент влия-
а (0-1к)йо
ния абсолютных размеров поперечного сечения образцов с концентрацией напряжений; (39)
= 7 ° t------эффективный коэф-
(O-lK/rfO
фициеит концентрации напряжений для стандартных образцов диаметром d0. (40)
В первом способе масштабный эффект учитывают по гладким образцам, а эффективный коэффициент концентрации определяют при основной размерности детали. Во втором случае величину устанавливают иа образцах малого (стандартного) диаметра, а масштабный фактор — на образцах с концентрацией напряжений.
Можно сразу учесть концентрацию напряжений и масштабный эффект:
(a-i«)d = OU = —1-, (41)
°-’ где
эффективный коэффициент концентрации (относительно стандартного, гладкого образца).
Сопоставляя равенства (41), (35), (36), находим
_ Xgrf_________2о_
cS К1^ ~ K(dK)
(43)
Выбор расчетной формулы (35) или (35) зависит от имеющихся значений коэффициентов Хо и K.d. При расчетном определении предела выносливости следует также учесть влияние поверхностного слоя.
Предел выносливости детали а_1д с помощью оценки влияния отдельных факторов можно определить также различными способами. Если влияние концентрации напряжений и масштабного эффекта известно, то
О-1д — 0-1
0-1К (°-1к)<<
О-i а-!к
__ „ Л (О-1к)<*п tfW (o_1K)d
а-1 — >
(44) где
р1к) = £лк)ап (45) v'-IkJc*
коэффициент состояния поверхности для образца с концентрацией напряжений размером d. Если ввести общий эффективный коэффициент концентрации напряжений, учитывающий сразу концентрацию напряжений, масштабный эффект и состояние поверхности,
К -= °-1
°д ' - а_1д ’
то
°-1д =
0-1
(46)
564
Расчет на усталость
Величина /ССд определяется при натурных испытаниях. При расчетноэкспериментальном определении предела выносливости основной зависимостью является следующая:
Взаимосвязанное определение коэффициентов /Со, K,i. Ра указывалось ранее;
Ра = ^F^Kop^o-
УСЛОВИЯ СОПРОТИВЛЕНИЯ
УСТАЛОСТИ
Простое (одиокомпонентное) напряженное состояние. Рассмотрим изгиб гладкого вала при действии переменных и постоянных нормальных напряжений. Пусть в опасной точке наиболее нагруженного поперечного сечения действуют переменное аа и постоянное ат напряжения. Принимая линейную зависимость (13), представим условие сопротивления в виде о,а + 'фа°т =а-и (48) где фд — коэффициент чувствительности к асимметрии цикла напряжений, характеризующий влияние постоянных нормальных напряжений.
Если ввести понятие эквивалентного переменного напряжения
°экв = °а Фа°т> (49) то условие сопротивления усталости будет
°ЭКВ = °-1- (50)
При наличии концентрации напряжений и при учете масштабного и поверхностного факторов их действие, как показали экспериментальные исследования, следует отнести только к переменной составляющей цикла. Тогда условие сопротивления приобретает вид
°° = °-1- (51)
Эквивалентное переменное напряжение при наличии концентрации напряжений
^вкв в & a И Фа^т. (52)
Часто условие сопротивления усталости детали удобно записать в другой форме:
оа + ФадОт = °-1д, (53)
где Фап = Фа ----------коэффициент
А Да
влияния постоянных напряжений для
KdPa
детали; а_1д = a_j —--------предел
Да выносливости детали.
В равенстве (53) величины aa и от представляют собой номинальные напряжения в опасной точке детали.
Для условия (53) эквивалентное напряжение
°экв = ’Гд “Ь Фод°т. (54)
Пря действии касательных напряжений условие сопротивления усталости имеет вид
та 4- фттт = г.р (55) где t_j — предел выносливости при кручении; фт — коэффициент чувствительности к асимметрии цикла касательных напряжений.
Для деталей с учетом концентрации напряжений, состояния поверхности и масштабного фактора
та + ФтТт = T_i (56)
или
Та + ФтдТт = Т_1д (57)
Сложное (многокомпонентное) напряженное .состояние. Рассмотрим сначала действие переменных напряжений, изменяющихся по симметричному циклу (постоянное напряжение отсутствует).
На основании экспериментальных исследований для обычных конструкционных материалов можно принять следующее условие сопротивления усталости:
°экв = а1а = "V (аха оуа)3 +
(°уа oza)3 + (°za—Оха)2 +
“Ь 5 (Тзда + Трго + ^1ха) ~ °—1,
(58)
Условия сопротивления усталости
565
где a ia — интенсивность переменных напряжений.
Для случая переменного изгиба н
кручения вала
®уа —
Tyza ~ О»
°za — О»
Тгха ~ О
(59)
только нормальных напряжений, находим
Oja = О-ll °la = °-il ke kj = 1.
(65)
Для случая переменного кручения aia = Уз Т-п Oia = т_х;
<Jxa = °а;
^хуа = т<й
и условие (58) будет иметь вид
У °а 4~ Зт£ =а_,. (60)
k0 УЗ ki = . (66)
T-i
Из уравнений (65) и (66) следует:
рЫ—,);
1/3 _ I \ т_, 7
Поэтому можно записать следующую зависимость пределов выносливости прн кручении и растяжении-сжатии (изгибе):
т_1 = -^=- а_! = О,570_!. (61)
Это значение хорошо подтверждается экспериментально для многих пластичных материалов. Если величина т_х отличается от указанного значения, то можно ввести корректированные двухпараметрнческне условия сопротивление усталости в виде
1/°2 + (т±)Та = 0-Ь <62)
В более общей форме условие (62) будет
-/^- У(°ха °уа)2+ (°Ка (Tza)2+
/ п , \ 2
+ (°za — °ха)2 + 2 ( —-------j X
\ т-1 /
^’"(^уа + ^га + ^а) = °-Ь (63)
Для малопластнчных и хрупких материалов дополнительное влияние ча прочность оказывают переменные главные (нормальные) напряжения. Условие сопротивления усталости в этом случае можно представить в виде
К>а1а + M°ia = a-i> (64) где ко, кх — подлежащие определению параметры материала, а1а — наибольшее переменное главное напряжение.
Применяя условие (50) для испытания иа выносливость прн действии
Внося значения ко и kj в условие (64), находим
_1 / 0-1
УЗ — 1 \ т-i
) °ta +
0-1
Т-1
Oia = O-i-
(67)
Последнее условие сопротивления усталости является более общим, чем условие (63). Прн условии (61) соотношения (58) н (67) совпадают. Для хрупких материалов прн T-i = o_j согласно условию (67) получим
Оэкв = °1а = 0-1 (68)
Для деталей каждый нз компонентов переменного напряженного состояния должен быть соответствующим образом увеличен с учетом концентрации напряжений, масштабного эффекта и состояния поверхности. В результате условие сопротивления усталости (58) для детали будет
Oia = О-1Д. (69)
где а_1д — предел выносливости детали. Подобным образом преобразуются н другие условия прочности (величины а_! н T-х заменяются на а_1д и т_1д). В общем случае каждый компонент напряженного состояния имеет переменную и постоянную составляющие: Оха» Охт» Оуа» Оут
Условие сопротивления усталости можно получить путем обобщения со
566
Расчет на усталость
отношения (48), вводя в него эквивалентные напряжения
°экв а 4" ФоОэкв т — °-1> ('0)
где оэкв а и оэкв m — эквивалентные переменные и постоянные напряжения. Для переменных напряжений в качестве эквивалентного целесообразно выбрать интенсивность напряжений — условие (58) или корректированную интенсивность напряжений — условие (63).
Для постоянных напряжений можно использовать наибольшее нормальное напряжение
°экь т ~ (71)
Другой способ учета асимметрии цикла при сложном напряженном состоянии заключается в приведении его к симметричному циклу путем линейного преобразования, тогда
°х (п) = ° ха “1“ Фо^хт! ау (п) — вуа
<*z (п) — ®za 4“
тху (п) — ^хуа 4" 1₽т'гхут» Tyz (п) = tyza 4" Фт1'!/гт> Tzx (n) = ^zxa 4“ Фт^гхт-
(72)
(73)
Условие сопротивления усталости для интенсивности приведенных напряжений:
(П1 = /— Л/(Ох(п)—°»(п))а4‘
4"(°у (П) °Z (П))2 4- (°Z (П > ~~
(74)
Переменные напряжения цикла увеличивают соответствующим образом при наличии концентрации напряжений с учетом масштабного эффекта и состояния поверхности Можно и более просто учесть указанные факторы с помощью замены значений о_, и Т_1 в равенстве (74) на пределы вы
носливости детали о_1ц и т_1д, коэффициентов фо и фт в равенствах (72)— (73) на фОд и фТд.
ОПРЕДЕЛЕНИЕ ЗАПАСОВ ПРОЧНОСТИ ПРИ УСТАЛОСТИ
Запас прочности характеризует надежность детали при случайном возрастании переменных напряжений, при уменьшении прочности материала и т. п. Запасы прочности — это критерии сравнения вновь создаваемой конструкции и аналогичных эксплуатируемых. Их необходимые значения устанавливаются путем сравнительного и сопоставимого расчета подобных или сходных деталей машин. Обозначим оха, охт, (т^а, Пут ... напряжения, действующие S детали в рабочих условиях, и <з*а, в*хт--- — напряжения в момент усталостного разрушения. Очевидно, что для надежной работы детали действующие напряжения должны быть меньше предельных. Условие усталостного разрушения при действии переменного и постоянного напряжений будет
+ = (75)
где о*, <J*m— предельные значения напряжеиий, соответствующих началу усталостного разрушения.
Для детали с концентрацией напряжения условие разрушения имеет вид
<7б)
При определении запасов прочности при усталости следует учесть возможный характер возрастания переменных и постоянных напряжений. Если переменное и постоянное напряжения возрастают пропорционально от точки М на рис. 9 до точки Л/, например, в зубьях колес, то предельные напряжения
а* = по • о* == ла (77) а а* т т* ' 7
где п — запас прочности по подобному циклу.
Внося эти значения в условие прочности (76), получаем часто применяе-
Определение запасов прочности при усталости
567
Рис. 9. К определению запасов прочности:
- М*Р. Nf>N
Па М„М ’ П М„М
мую формулу для запаса прочности по подобному циклу:
П =-------. (78)
°а „ а-----к Фа°тп
Л dPa
Последнее равенство можно записать и в другой форме, если учесть, что
a —a
O-i г: — °-1Д> Ла
(79)
где а_1д — предел выносливости детали, который может быть определен при натурных испытаниях.
Тогда
п =-----------=_Z±a_. (80)
°a 4- фад°т °экв
Во многих случаях усталостное разрушение может происходить при возрастании переменной составляющей цикла от точки М на рис. 9 до точки Р, тогда как его постоянная составляющая остается неизменной (крутильные колебания коленчатых валов, резонансные колебания лопаток и т. п ). Тогда в момент усталостного разрушения oS = /1a°a; = (8»
где па — запас прочности по переменным напряжениям.
Внося эти значения в равенство (76), находим запас прочности по переменным напряжениям:
„ °-1 — Фа°т
«а = ------*----
а -а К<фа или в другой, эквивалентной форме
Аналогичным образом определяют запас прочности при действии касательных напряжений. Например, запас прочности по переменным касательным напряжениям
Т-1д Фтптт п„ —---------=— .
Полученные значения запасов прочности следует сопоставлять с их допустимыми значениями:
In], па < [nJ.
(84)
(85)
Величины п и [na] определяют из расчета подобных изделий, норм прочности и т. п. Как следует из рис. 9 и расчетных зависимостей, запас по переменным напряжениям (83) всегда больше запаса по подобному циклу (80), па > п.
Однако их не следует сравнивать формально, так как они отражают различные процессы с различными характеристиками рассеяния. Обычно [na] > [п]. Например, для удовлетворительно работающих резьбовых соединений [na ] = 2,5; [п] = 1,5. Поэтому резьбовое соединение с па = = 2,2; п == 1,8 следует признать ненадежным.
Запасы прочности при усталости для сложного напряженного состояния. Рассмотрим сначала определение запаса прочности при совместном изгибе и кручении вала прн действии переменных напряжений, изменяющихся по симметричному циклу. Запас прочности по подобному циклу из условия (62), внося в него мости (77):
найдем завнси-
• (86)
Последнее соотношение можно представить как
-4- = -V + -Д- . (87)
п2 п2 п2 '
О_1 Т_1
где na = —- ; пх = —L — частные
запасы прочности соответственно по нормальным и касательным напряжениям.
568
Расчет на усталость
Равенство (87) часто применяют в виде
л =------№* . (88)
При наличии концентрации напри' жен ий
Рассмотрим определение запасов прочности при совместном действии переменных и постоянных напряжений.
Используя формулу (74), при наличии концентрации напряжений получаем условие прочности
*"’х(т; + ФХд^)2 = °-1д, (9°)
где а*, а^, т*. —значения номи-
нальных напряжений в опасной точке детали.
Запас по подобному циклу, т. е. при условии о*а= паа, а*т = пат>
= пТа’ бУДет
л =--- °~1д
/(^+^д°т)2+(^)2Х
"" Х (та + фХдтт)2
(91)
Последнее равенство можно представить в форме (88), считая частные запасы
п — q-m
° ° а + 'ФадО'т ’
Запас прочности по переменным напряжениям определяется условиями
аа =
Ч = «Л; Vn = *т. (93)
Внося эти значения в равенство (90), находим
]/ (паоа + фадат)2 + ( У X
" X (пата Н- фгдТт) = а-1 д. (94)
Из последнего соотношения получаем квадратное уравнение для определения па. Подобным образом можно определить запасы прочности при возрастании только нормальных или только касательных переменных напряжений. Каждый из рассмотренных запасов отражает особенности нагружения конструкции. Если, например, сравниваются два вала в связи с опасностью крутильных или изгибных колебаний, то реальное соотношение надежности валов лучше отразит запас по переменным напряжениям, учитывающий возможность возрастания «опасных! напряжений. Запасы прочности при наличии нескольких компонентов напряженного состояния определяют подобным образом.
Определение запасов прочности при усталости для нестационарного нагружения. Детали машин в условиях эксплуатации часто нагружаются переменными напряжениями, амплитуда которых изменяется в процессе нагружения (нестационарное нагружение). При многоступенчатом нагружении (рис. 10, а) деталь работает иа нескольких уровнях нагружения. Непрерывное нагружение (рис. 10, б) характеризуется непрерывным изменением амплитуды действующих напряжений. При блочном иагружеиии (рис. 10, в) в каждом отдельном блоке осуществляется работа на разных режимах. Блочное нагружение типично для машин периодического действия.
Расчет иа усталость при нестационарном нагружении основан на принципе линейного суммирования повреждений. Допустим, что повреждение характеризуется положительной величиной П (мерой повреждения). В начальный момент /7=0, в момент разрушения /7=1. По мере увеличения числа циклов N в процессе нагружения величина П монотонно возрастает:
Определение запасов прочности при усталости
569
Рис. 10. Три типа нагружения деталей
дП dN
(95)
Скорость повреждения считают зависящей от действующих напряжений и температуры:
= F[oa(N),om(N),T(N)], (96)
где ао (N), ат (N) н Т (N) -— переменное н постоянное напряжения н температура в момент нагружения N. Время t, соответствующее числу циклов нагружеиня N, зависит от частоты нагружения f:
Пусть ' прн стацноиариом нагружении, происходящем прн постоянных значениях оа, ат и Т, число циклов до разрушения равно N*. Тогда из условия (96)
N*
П (N*) = J F (оа, am, T)dN = о
= F(oa, от, Т) N* = 1. (97)
Из последнего соотношения
F К, am, Т) = -±- .
Величина Л'* также зависит от Oa, °т, Т. Внося значение F в равенство (97), находим в момент разрушения прн нестационарном нагружении
/7(^) =
Л 2
С dN
J W*[oa(N), om(N), T(N)]-1’
где — общее число циклов до разрушения.
Равенство
NS
Г____________™____________=1
J N*[oa(N), om(N), Т (N)]
(98) выражает принцип линейного суммирования повреждений.
При сопоставлении теоретической зависимости (98) с экспернмеитальиымн результатами выяснилось, что лучшее соответствие получается с помощью введения параметра материала а:
Г dN
J N* [aa (N), am (N), T (M)J ~ 0
(99)
В приближенных расчетах можно принимать а= 1.
Число циклов до разрушения N* при постоянных напряжениях и температуре имеет существенное рассеяние (в 2—5 раз), связанное со статистической природой усталости. В равенстве (99) под JV* следует понимать среднее число циклов до разрушения.
Многоступенчатое и а-гружеине, эквивалентный запас прочности. Пусть деталь работает при k различных режимах, причем число циклов иа i-м режиме равно Ni. Суммарное число циклов
k
Nz = S Nt- (10°) i=l
570
Расчет на усталость
Рис. 11. Зависимости а = ф (Л')
Условие разрушения по принципу линейного суммирования повреждений следует из соотношения (98)
<",1)
Кривая усталости для i-ro режима нагружения показана на рис. 11, а. Частный запас прочности на i-м режиме
п( = , (102)
где а* и at — переменные разрушающее и действующее напряжения иа i-м режиме. Циклы нагружения предполагаются симметричными (ami = 0).
Рассмотрим сначала уравнение кривой усталости, одинаковое для любого уровня напряжений,
а’^Л^о^ЛГ;. (ЮЗ)
Условие разрушения можно записать теперь в таком виде:
k k
-
прочности при усталости для многоступенчатого нагружения
пэкв —
(Ю6)
Например, при двухступенчатом на-
гружении
пэкв —
(107)
Многоступенчатому нагружению поставим в соответствие стацяоиарный эквивалентный режим нагружения. Для эквивалентного режима условие (Ю4)
-4- = а. (105) Св
Значение т велико, и потому основным при определении эквивалентного запаса является режим минимального запаса прочности.
Другой способ определения эквивалентного запаса прочности основан иа предположении, что в момент разрушения все амплитуды переменных напряжений а< увеличиваются в пэкв раз. Тогда из условия разрушения (104) находим
* „т
s-f— "’8)
нлн
ЛЭКВ —
(109)
Приравнивая выражения (104) и (105), находим формулу для запаса
Если "У~а » 1, то равенства (107) и (109) дают близкие результаты.
Определение запасов прочности при усталости
571
В некоторых случаях требуется определить эквивалентный запас по долговечности (по числу циклов). Для i-ro режима запас по долговечности
Если нестационарный режим при вести к стандартному режиму, имеющему базу испытаний Ne, то
п1л = “jyy • 10)
°экв
яэкв
(116)
Учитывая равенство (106), находим
Из условия (102) вытекает
(111)
Запас по долговечности значительно больше запаса по напряжениям, так как т >> 1
Равенство (110) представим в виде
Так кай
При работе на одном эквивалентном режиме (k — 1)
a-i^o ~ a*mN£j
то получим формулу для эквивалентного напряжения
т / к
».--И wrS’"*'- <"s>
^ЭЬВ
ЛМ экв
---------= а. (113)
Если исходить из равенства (109), то получим выражение, близкое (118),
Из последних соотношений вытекает
Эквивалентный запас по долговечности можно рассматривать как отношение
п
(115)
где N2 и Л/£—соответственно суммарное число ПИКЛОВ и число циклов до разрушения при ступенчатом нагружении.
Предыдущие формулы распростра-няютсн и на случай, когда для различных режимов кривые усталости различны, например, вследствие изменения температуры.
Эквивалентное напряжение. Понятие эквивалентного напряжения позволяет привести неста ционарныи режим нагружения к эквивалентному стационарному.
Равенство (117) можно записать в виде
т Г к
(120)
Часто оказывается целесообразным привести многоступенчатое нагружение к одному, наиболее тяжелому режиму (режиму с наименьшим запасом прочности). Обозначив этот режим индексом 1, получим
пэкв
°экв
Учитывая равенство (106), найдем
Так как п жение оэия от 01.
> и т > 6, то напря-обычво мало отличается
572
Расчет на усталость
Многоступенчатое нагружение, кривая усталости содержит два участка. Рассмотренные ранее зависимости относились к единой кривой усталости. Такие кривые свойственны некоторым материалам (титановым и бериллиевым сплавам), усталости при высокой температуре и коррозионной среде.
В большинстве случаев более точное описание 'кривой усталости можно получить с помощью кусочно-линейной кривой (в двойных логарифмических координатах, рис. 11, б). Принцип линейного суммирования повреждений остается справедливым и в рассматриваемом случае:
k
Ётг"»- <|22>
Однако связь между долговечностями и напряжениями будет зависеть от уровня напряжений i-ro цикла (в момент разрушения).
При
0*тМ, = о"’М*. (123)
При 3, < O_j
0*т|Д’(=0^*, (124)
Обычно величина ш0 т-
Величина Si — действующее переменное напряжение в i-м режиме в момент усталостного разрушения при нестационарном нагружении.
Следует считать
«И = Пэкв°Ь
(125)
Условимся теперь присваивать номера (индексы) режимов нагружения в порядке убывания действующих переменных напряжений. Пусть для первых s режимов гаэкво1 > o_j. Тогда условие (104) можно представить так:
/ «экв<4 \т +
k
(126)
Если naKBCi < о.!, то все режимы относятся ко второму участку и тогда
(127)
Так как
где —частный запас прочности на i-м режиме, то для определении пэкв будем иметь:
1. Если пэкв ej > о_1( для первых s режимов
пт V _L.
ПЭКВ / I т ' “ П1 1 = 1 »
k
+ “"Л £ <128>
i=s+l {
2. При ПэквО^ О.!
к
<129^ ’ЛИ
i=l i
Уравнение (128) решают относительно пэкв с помощью метода Ньютона или подбором. При ш0оо (второй участок кривой усталости принимают горизонтальным) расчет на долговеч-_ °-i
ность при о; < --------- не проводят.
Пэкв
СТАТИСТИЧЕСКИЕ МОДЕЛИ УСТАЛОСТИ
Экспериментальные исследования показали, что усталость деталей машин имеет статистическую природу, т. е. зависит от целого ряда факторов, значение которых предварительно учесть практически невозможно (состояние поверхности, наличие внутренних дефектов структуры и т. п.). В связи с этим наблюдается значительное рассеяние результатов испытаний, особенно по усталостной долговечности. Детали, изготовленные по одинаковой технической документации, обнаруживают при испытаниях
Вероятность разрушения и запасы прочности
573
на одном уровне нагружения числа циклов до разрушения, отличающиеся в несколько раз.
Для описания долговечности детали при переменных нагрузках наиболее употребительным является логарифмически нормальный закон (нормальный закон для логарифма случайной величины). Плотность распределения логарифма числа циклов до усталостного разрушения при работе на постоянном уровне переменных напряжений о
/ (lg N) =
=________!_____e 2Sfg w
Six а' 1/2л
где IgA' и Sig.v— соответственно среднее значение и среднее квадратическое отклонение логарифма числа циклов до разрушения.
Параметры распределения зависят от действующих переменных напряжений:
lg?7=F1(o), SigN= Ft (о).
При малом уровне действующих напряжений наблюдается отклонение от логарифмически нормального закона е области малых долговечностей.
Удовлетворительное статистическое описание можно получить с помощью введения порогового значения для числа циклов Wn. Предполагается, что разрушение возможно при .V > > Nn. Тогда плотность распределения выражается равенством
/ (lg (N - Nn)) = -!---------7== X
6lg(W-W;iS
X с 2Slg (N~Nn)
Такое распределение содержит три параметра:
й Nn-
Рассеяние пределов выносливости при фиксированном числе циклов значительно меньше, чем рассеяние долговечностей. Приближенно можно считать
51g о ~~г ^Ig N-т
Более полные сведения о статистических моделях усталости содержатся в работе [2J.
Глива 32
ВЕРОЯТНОСТЬ РАЗРУШЕНИЯ И ЗАПАСЫ ПРОЧНОСТИ
Оценка прочностной надежности проводится с помощью допускаемых напряжений, запасов прочности и вероятности разрушения. При использовании допускаемых напряжений условие прочности
°tuax 1° L (1)
где <тк1ах — наибольшее напряжение в детали, [oj—допускаемое напряжение.
Такая оценка весьма удобна, если на практике для однотипных конструктивных элементов, стабильных условий нагружения, устоявшейся технологии, производства разработана система допускаемых напряжений.
Однако оценке прочностной надежности с помощью допускаемых напряжений присущи и существенные недостатки. Величина (о] не дает в явном виде представления о степени надежности, так как в формуле (1) не показано соотношение действующих и предельных напряжений. Величина допускаемого напряжения носит условный характер, так как не отражает характера предполагаемого разрушения (статического, усталостного и т. п.), режима нагружения и других факторов, влияющих на надежность. Допускаемое напряжение, особенно при действии переменных нагрузок, в значительной степени зависит от геометрии детали (концентрации напряже
574
Вероятность разрушения и запасы прочности
ний), материала и технологии изготовления, что затрудняет ее применение в качестве нормативной характеристики.
В современных инженерных расчетах допускаемые напряжения используют главным образом для приближенных, предварительных расчетов. Наибольшее распространение получил расчет по запасам прочности.
Условие прочностной надежности в простых случаях записывают в виде
п=^азр>[пЬ (2) ° max
где п— запас прочности; <Упаэр— разрушающее напряжение; [п ]—допустимый запас прочности.
Под Ораз^ при действии переменных напряжении понимают предел выносливости, гри действии постоянных напряжений — предел прочности или предел длительной прочности.
В более сложных случаях (нестационарные режимы нагружения) при определении запасов прочности используют условия суммирования повреждений.
Условия прочности по допускаемым напряжениям и запасам прочности связаны соотношением
[о] = _£Pgg.P- . (3)'
Величина необходимого запаса прочности имеет довольно стабильное значение, тогда как аразр отражает условия нагружения, геометрию и технологию детали.
При действии статических нагрузок используют также запас по несущей способности
п = 2W, (4)
где Рразр и Р — значения силового фактора (нагрузки) в момент разрушения и в рабочих условиях
Запас по несущей способности отражает перераспределение напряжений, возникающее в пластических материалах при нагрузках, близких к разрушающим.
В ряде областей машиностроения созданы нормы прочности, регламен
тирующие допускаемые запасы прочности и условия их определения.
Недостатком системы допускаемых напряжений и запасов прочности является детерминированный характер условий прочности. Они не учитывают должным образом неизбежное рассеяние разрушающих и максимальных напряжений. Этот недостаток частично устраняется статистическими запасами прочности, которые рассмотрены в дальнейшем.
Другой путь построения статистических моделей надежности — определение вероятности разрушения.
ВЕРОЯТНОСТЬ РАЗРУШЕНИЯ
Рассмотрим оценку вероятности разрушения на примере лопаток компрессора.
Переменные напряжения в лопатке компрессора, возникающие при резонансных колебаниях, обозначим аа. Их определяют с помощью тензоме-трирования в рабочих условиях в местах наибольших напряжений. Величинам оа свойственно значительное рассеяние, связанное с неравномерностью газового потока, условиями демпфирования и т. п. Величину оа сопоставляют с пределом выносливости лопатки о_1л, который также имеет , разброс вследствие отклонений в технологии изготовления и рассеяния механических свойств материала. Предел выносливости соответствует определенному числу нагружений (обычно 107 циклов). Если в данной лопатке переменное напряжение больше предела выносливости
°а 5* О-1Л, (5)
то наступает разрушение.
Рассматриваем оа и о_1л как случайные величины На рис. 1 показаны кривые плотности распределения переменных напряжений и пределов выносливости. Их строят на основании экспериментальных данных по гистограмме распределения.
Допустим, что величины оо и о_зл> которые для краткости обозначим соответственно т) и 5, имеют нормальное
Вероятность разрушения
575
Рис. 1. Кривые плотности распределения переменных напряжений aQ и пределов выносливости d_i
распределение. Тогда и разность этих величин (функция неразрушения)
С = a-гл — «а = П — 5 (6)
распределена нормально, причем параметры распределения — среднее значение и среднее квадратическое отклонение соответственно’
t — 6-1Л — Й — t* 'J
J (7)
Вероятность разрушения равна вероятности условия £< О (рис. 2).
Входящий в последнее равенство корреляционный "момент для независимых случайных величин обращается в нуль. Так как предел выносливости и действующее в лопатке переменное напряжение практически независимы, то
«С = / (8)
f’paap =Р (£< 0) = F (0), (9)
где F (£) — функция распределения случайной величины £,
f©=4~+Ф(~Цр~)’ ^1о)
X
где Ф (х) = j е-0.5«* йи_функ.
Рис. 2. Распределение функции неразру-шення
Из равенства (9) вытекает формула для вероятности разрушения
pw>₽--5- + ®(--^-)-
-4-ф(4-) <">
ИЛИ
Рразр = ~-Ф (~-)> (12)
где vj — коэффициент вариации функции неразрушения,
,е Л. _ . (13)
£ Т) — t
Если воспользоваться приближенным представлением функции Лапласа
_ 1
n Vl о М V
Рразр~~Же х
X(l—v| + 3v£----). (14)
то погрешность оказывается не выше последнего использованного при вычислениях члена ряда.
ВЕРОЯТНОСТЬ РАЗРУШЕНИЯ
ПРИ ПРОИЗВОЛЬНЫХ ЗАКОНАХ РАСПРЕДЕЛЕНИЯ НАПРЯЖЕНИЙ И ПРЕДЕЛОВ ПРОЧНОСТИ
В этом случае вероятность разрушения может быть определена из следующих соображений.
Пусть имеется переменное напряжение оа = £. Вероятность того, что предел выносливости o_in = Л ока' жется меньше данной величины £ (наступит разрушение), будет
Р (П < 5) = Fn Й), (15)
576
Вероятность разрушения и запасы прочности
где (Е.) — функция распределения случайной величины т],
5
J MnW
—со
Для нахождения вероятности разрушения следует учесть все возможные значения £ (все несовместимые пути реализации события) н по формуле полной вероятности
оо
Рразр — f (16)
— ОС
Подобным образом находим равнозначное условие
со
Рразр — j /п ,Т]Ц1 — t1!)) =
—со
со
= 1— I /и (>)) P'i (W<ln- (17)
—со
Нахождение вероятности разрушения теперь сведено к вычислению
интеграла (16) нлн (17).
В общем случае запас прочности
может быть представлен в виде
п = Ора?р , (18)
°экв
где °экв — эквивалентное напряжение.
Например, прн одновременном действии нормальных о и касательных т напряжений
«экв - + Зт2- (19)
Для длительной прочности при нестационарном режиме нагружения функция неразрушения зависит от общего времени работы t
С (0 = Одл W - °зкв (0- (20)
Для длительной статической прочности или сопротивления усталости справедлив степенной закон связи одл н времени (числа циклов) до разрушения
о”(П^ = С, (21)
где т н С — постоянные материала, зависящие от температуры.
Если действующее напряжение в момент времени
о (/*) = о0/ (/•), (22)
где о0 — случайная величина, f (/*) — детерминированная функция времени, то при линейном законе суммирования повреждений
стэкв (Н — °о X
X
« )_L
4~ J m =о0ф(0-
о '
(23)
Для сопротивления усталости при нестационарном нагружении функция неразрушения от общего числа циклов нагружения
W = - оэкв (N). (24)
В каждый момент нагружения действующее напряжение
о (/V) = Oof (А7). (25)
Учитывая завнснмости типа (21)
получим
°акв — uo X
X
.) о
mdN
1 m
= °о,1’(ЛГе)- <26)
Равенства (23) н (26) справедливы при постоянной температуре.
Для расчета должны быть известны среднее значение и среднее квадратическое отклонение пределов прочности н эквивалентного напряжения, причем
Сакв (0 = М (0;
sa (/) = sa ф (0.
иэкв О
При нормальном распределении указанных величин используют соотношение (11). Вероятность разрушения зависит в рассматриваемом случае от времени работы.
Доверительные пределы для вероятности разрушения. При расчете вероятности разрушения по формуле (11)
Вероятность разрушения
577
предполагают, что статистические характеристики пределов выносливости fj, Sn и действующих напряжений Sj относятся к генеральной совокупности (выборке бесконечно больших размеров).
В действительности указанные величины определяют по выборке (объему испытаний), содержащей конечное число образцов.
Если при определении действующих напряжений использованы результаты испытаний, то
I , '=' Г ч = |^ S щ-М*
:=1
(27) Соответственно для пределов прочности (п2 — число испытаний)
(28)
Оценим приближенно наибольшее значение вероятности разрушения.
Очевидно, что оно реализуется при минимальной разности средних значений и максимальном значении Sj.
Будем использовать с доверительной вероятностью Ря следующие односторонние оценки *:
'Чпах^'Чпах^1’ Pn)S5n,;
tmax = (я1- ^д) '-р/~ 1
-9_ S (Л2’ Р„) $п
’'max фтах ' 1 ’In, ___________ (29)
• Значения коэффициентов Стьюден-та i и коэффициентов К е указаны max
во многих работах (см. например, 11 J).
Тогда из равенства (11) получим приближенную оценку
Рразр max — “j
Для расчета может быть использовано и равенство (14). Доверительную вероятность оценки (30) можно приближенно принять равной Рд.
Пример. Определить вероятность разрушения лопаток, если известно, что среднее значение переменных напряжений £ - 100 МПа и среднее квадратическое отклонение Sj = — 20 МПа (по данным тензометриро-вания); среднее значение предела выносливости т) = 200 МПа и среднее квадратическое отклонение З'п = ~ 30 МПа (по данным испытаний на выносливость).
Решение. Находим по формулам (7)_ и (8)
С = П — I = 200 — 100 = 100 МПа;
= У'302 + 202 « 36 МПа.
Вероятность разрушения по формуле (II)
“4"-ф (У)--4—ф(тг)--г-ф<2'78>-
По таблице значений функции Лапласа
Ф (2,78) = 0,49728;
Рраэр - у — 0,49728 =- 0,272- 10~2.
По приближенной формуле (14)
2,78* е 2 X
= 0,277- 10~2.
19 Заказ № 402
578
Вероятность разрушения и запасы прочности
Значения вероятности разрушения, вычисленные по средним значениям и с учетом рассеяния экспериментальных данных, существенно расходятся между собой. В практических расчетах следует указывать, прн каких условиях получено расчетное значение вероятности разрушения.
Вероятность разрушения как характеристика прочностной надежности правильно отражает качественные особенности задачи: она возрастает прн уменьшении запаса прочности и увеличении рассеяния нагрузок и механических свойств материалов. Однако ее использование как нормативной характеристики для определения отказов ответственных конструкций (разрушений с тяжелыми последствиями) ограничено:
а) значение вероятности разрушения зависит от «хвостов» распределений, которые даже по выборкам большого объема (л > 100) определяются весьма неточно (погрешность может составлять несколько порядков). В связи с этим расчетная вероятность разрушения носит условный характер. Реальный смысл имеет только сравнение элементов выполненных и вновь проектируемых конструкции, проводимое в сопоставимых условиях;
б) при расчете допускается возможность аварии (катастрофы), это создает затруднения психологического характера.
Рассмотренная статистическая модель пригодна для отказов с ограниченными последствиями, для которых допустимо использование вероятностей разрушения Рразр > 1 • 10"’.
Более обоснованно использование в качестве нормативных характеристик, особенно для прочностных отказов с тяжелыми последствиями, статистических запасов прочности.
СТАТИСТИЧЕСКИЕ ЗАПАСЫ ПРОЧНОСТИ
Предельное (разрушающее) и действующие напряжения в опасной точке детали можно рассматривать как случайные величины.
Тогда запас прочности конкретной детали представляет величину случайную:
Если F (п) — функция распределения запасов прочности, то величина запаса прочности, соответствующая уровню значимости q, удовлетворяет условию
F [«(?)] = Вер [п < п (01 = q. (32)
В большинстве практических задач параметры функции распределения «восстанавливаются» по выборкам ограниченного объема с определенной доверительной вероятностью. В связи с этим н запас прочности зависит от принятого значения доверительной вероятности
п = n(q, Рл). (33)
Например, запись
л (<?• Рд) = (0.01; 0,95) = 2 означает, что только у 1 % всех изделий запас прочности может оказаться меньше 2, причем это утверждение справедливо по крайней мере для 95% случаев испытаний. С математической точки зрения равенство (33) имеет следующий смысл:
Вер [Вер (п < п (q, Рд)) = = Рд.
(34)
Приближенный метод определения статистического запаса прочности. В практических расчетах запас прочности
п __ (°разр(щ|п __ r(min (°max)max Вшах
Используют нижние значения для пределов прочности и пределов выносливости по справочным данным нли механическим испытаниям.
Прн определении максимального напряжения в опасной точке детали отах учитывают наиболее неблагоприятные условия нагружения и другие факторы, приводящие к возрастанию напряжений. Одиако достоверность оценки Оразр и Отах не указывается, что затрудняет сопоставление надежности по запасу прочности.
Наиболее простой и практически пригодный метод определения стати-
Статистические запасы прочности
579
стических запасов прочности состоит в следующем. Минимальные характе-ристики прочности и максимальные значения напряжений устанавливают в соответствии с нормированным уровнем значимости и доверительной вероятности:
п (?, Ра) =
’Imin Рдч)
Imax (<?£> Рд*}
(36)
где q^, q^, Рт и Рдх — уровни значимости и доверительные вероятности, с которыми определяют (экспериментально) разрушающее напряжение и максимальное действующее напряжение. В практических расчетах можно принять приближенные соотношения:
Я ~ ?п — Я^ (37)
Рц — Рдп — Р д5- (38)
Статистические запасы прочности, как и обычные запасы прочности, имеют условное значение. Они служат критериями сравнения надежности вновь создаваемых изделий с изделиями, удовлетворительно работающими в эксплуатации.
Основное преимущество статистического запаса прочности по сравнению с обычными (детерминистскими) запасами состоит в том. что сопоставление приводится к одинаковым условиям (по объему используемой информации) по рассеянию механических свойств материала и действующих напряжений.
Если разрушающее и действующее напряжения распределены по нормальному закону, то можно принять
n (q, Ря) -=
= рд) S^. s (39)
+ К* (п2, q, Рд)
где ij —среднее значение оразр; «1 — число испытаний (объем выборки), на основании которого определено значение S — среднее квадратическое отклонение для выборки объема +, и — среднее значение
и среднее квадратическое отклонение, полученное для действующею напряжения в опасной точке при п2 испытаниях [см. формулы (27) и (28)]; Кп
19*
(пр q, Ра) и Ki (п2, q, Рд) — односторонние толерантные коэффициенты
Экспериментальное исследование действующих напряжений путем тен-зометрирования часто применяют при определении переменных напряжений (валы, лопатки и т. п.). В других случаях изучают экспериментально условия нагружения (усилия, температуры и др.), оценивают вероятность появления максимальных нагрузок и т. п.
Пример. Требуется определить (при уровне значимости q = 0,01 и доверительной вероятности Ра = 0,99) запас прочности лопатки компрессора, для которой среднее значение предела выносливости, полученное в шести испытаниях (nj = 6), составило a_j = = =-- 420 МПа, а среднее квадра-
тическое отклонение S = 20 МПа. Среднее значение переменных напряжений при тензометрир_рвании 10 лопаток (п2 = 10) оа~ = 60 МПа, а среднее квадратическое отклонение = 15 МПа.
Решение. Минимальное значение предела выносливости
’’min V ^n(nl’ У’
При nj = 6, q — 0,01 и Рд= 0,99 по таблице значений толерантных коэффициентов [1] находим
Кп (6; 0,01; 0,99) = 5,00 и тогда
Пшш = 420 — 5-20 = 320 МПа.
Максимальное значение переменных напряжений
= In, + (п2' Я> Рд) Sgn,.
При л2 = 10, <?= 0,01. Рд = 0,99 по таблице значений толерантных коэффициентов находим
Kj (10; 0,01; 0,99) = 4,06 и
Лтах ~ 60+ 4,06'15 = 121 МПа.
Запас прочности
490
л (0,01; 0,99) = ~ = 2,64.
Нормальный закон распределения повышает опасность больших откло-
580
Вероятность разрушения и запасы прочности
I. Значения вероятности разрушения ^ра3р в зависимости от запаса прочности по средним
п 0.05 при равном % - 0.10
2 3 1
I 1.25 1,5 1,75 2.0 2.5 3.0 4.0 0,5 0,905- 10-’ 0,143- 10“’ 0,5121- IO"1’ 0,18987- 10-’" 0,4036- 10—а® 0,5629- 10-” 0.2934- 10-4’ 0,5 0,17- IO"1 0,3167- I0-4 0.85- 10-“ 0.7787- 10-'* 0,35986- 10-’“ 0.707- 10~” 0.33216- 10-" 0.5 0,6178- 10-1 0,1441- 10-* 0,7802- I0-" 0.143- 10“’ 0,7964- 1 0“14 0,21333- 10-" 0,17886- 10-3’ 0.5 0.5938- 10-‘ 0,2803- 10~« 0,996- I0-4 0,3911- 10-“ 0,127- 10-’ 0,12961- 10-“ 0.17505- Ю”1’
нений и часто более целесообразно использовать усеченные распределения.
Учитывая, что вероятностные расчеты носят сравнительный характер, рекомендуется для единообразия использовать приближенные толерантные коэффициенты.
Рассмотрим теперь случай, когда статистические характернстнкн араар н Отах считают известными. Это означает, что величины f), £ и и Sj признают достоверными на основании предыдущего опыта нлн большого числа исследований. Тогда статистический запас будет зависеть только от уровня значимости.
Прн нормальном распределении будем иметь
Значения uj.g для некоторых значений уровня значимости будут сле-
дующими:
<7 ............. 0.10 0.05 0.01 0.0014
и, „............1.29 1.64 2.33 3.00
l_q
Связь запасов прочности и вероятности разрушения- Вероятность разрушения определяют по формуле
(43)
где oj — коэффициент варнацнн функ-
ции неразрушения,
л (q) = =
t + Mi-gSj
п — I
(44)
I —
1 + “l-qVt ’
(40)
Разделив числитель и знаменатель последнего соотношения на получим
где — односторонний квантиль доверительной вероятности
п — 1
(45)
Рд= 1 -q.
Величина
(41)
представляет собой запас по средним значениям.
Коэффициенты вариации
ST. St
= -X., (42)
П 6
где Oj = Sj/| н уч -= Srj/f) — коэффициенты вариации действующих и разрушающих напряжений; л — запас по средним значениям. Теперь равенство (43) можно записать так:
Рразр----j
(46)
Основные понятия
581
напряжениям
при равном = 0,15 при *’£/€'т)- равном
2 3 1 2 3
0,5 0,1446 0,2275-10“' 0,2401 • 10"’ 0 2001•!0"» 0, 1366- 10"» 0,143- 10"’ 0, 10071- 10"1 *° 0.5 0.2206 0,6811- 10“‘ 0,1539- 10“‘ 0.2803- 10"’ 0.6152- 10“4 0,1239- 10“* О.Ь 10-’ 0,5 0.1492 0,3216 10“* 0.6 569- 10"’ 0.1441-0.996- 10—* 0,1222- 10“4 0,6173- 10"“ 0,5 0.2389 0,9176- Ю“1 0.3005- Ю"‘ 0.914-10"’ 0.9043-10"“ 0.1078’ 10—’ 0,3911- 10“4 0.5 0.305 0,161 1 0.7483- Ю“1 0.3144-10"» 0.5234-10“’ 0,8447-10“’ 0,3167- 10“*
Из этого соотношения следует, что вероятность разрушения определяется запасом прочности по средним значениям разрушающих и действующих напряжений и коэффициентами их вариаций.
Связь вероятности разрушения и запасов прочности показана в табл. 1.
Запасы по средним значениям больше практически применяемых запасов прочности, при определении которых используют наименьшие значения разрушающих напряжений и наибольшие значения действующих напряжений.
Глава 33
ЭЛЕМЕНТЫ ТЕОРИИ НАДЕЖНОСТИ
ОСНОВНЫЕ понятия1
Надежностью называют свойство объекта сохранять во времени в установленных пределах значения всех параметров, характеризующих способность выполнять требуемые функции в заданных режимах и условиях применения, технического обслуживания, хранения и транспортирования.
Отказом называется событие, заключающееся в нарушении работоспособного состояния объекта.
Отказы следует отличать от неисправных состояний, при которых изделие не соответствует хотя бы одному’ из требований технических условий, но сохраняет свою работоспособность.
Катастрофические отказы — разрушение конструкции, взрывы и т. п., создающие опасность для жизни людей или влекущие большой материальный ущерб, должны быть исключены с помощью специальных испытаний.
1 Термины и определения по надежно-
сти указаны в ГОСТ 27.002 —89.
Они не входят в систему количественных оценок теории надежности.
Долговечностью называют свойство объекта сохранять работоспособность до наступления предельного состояния при установленной системе технического обслуживания и ремонта.
Ресурсом называется суммарная наработка объекта от начала его эксплуатации или ее возобновления после ремонта до перехода в предельное состояние. Назначенным ресурсом называется суммарная наработка, при достижении которой эксплуатация объекта должна быть прекращена независимо от его технического состояния.
Прекращение эксплуатации связано с требованиями безопасности или экономической целесообразности.
В пределах назначенного (общетехнического) ресурса обычно предусматривается один или несколько ремонтов.
Ремонтопригодностью называется свойство объекта, заключающееся в приспособленности к поддержанию и восстановлению работоспособного со
582
Элементы теории надежности
стояния путем технического обслуживания и ремонта.
Контролеспособностью называется свойство изделия допускать контроль его состояния в процессе эксплуатации. Контроль осуществляется при помощи датчиков оборотов, температур, вибраций и т. д., а также путем визуальных осмотров с применением оптических и других приборов.
ПРАВИЛА НАДЕЖНОСТИ
Инженерный опыт создания сложных технических систем позволяет сформулировать основные правила надежности, которых надо придерживаться на различных этапах создания изделия.
Проектирование. 1. Система должна содержать максимально возможное число элементов, проверенных на практике. Число «новых событий» в системе должно быть ограниченным Ч
2. Рекомендуется применение «модульного принципа» конструирования (система создается из отдельных автономных узлов), широкое использование стандартных и унифицированных деталей и узлов.
3. Система должна содержать защитные устройства, предусматривающие устранение возможности возникновения катастрофических отказов (ограничение возрастания оборотов, температуры, давления, крутящего момента и т. п.); сигнальные устройства, предупреждающие о нарушении нормальной работы (световые сигналы и т. п.).
4. Система должна обладать высокой контролеспособностью (оснащена контрольной аппаратурой для оценки вибраций, температур; должна быть обеспечена возможность визуальных осмотров, контроля фильтров, зазоров и т. п.).
5. Система должна быть удобной для ремонта, допускать простую замену быстро изнашивающихся деталей, отдельных элементов и узлов без разработки и переналадки всего изделия.
1 К числу «новых событий» относят принципиально новые конструктивные решения, материалы, условия работы и т. п.
6. Нагруженные элементы системы должны подвергаться тщательному расчету на статическую и динамическую прочность. При таком расчете должны быть учтены максимальные нагрузки, наиболее неблагоприятные рабочие условия (температура, воздействие среды и т. п.), минимальная прочность материала и др.
7. Для данного типа систем (изделий) должны быть установлены нормы прочности, регламентирующие допустимые запасы прочности и необходимый объем экспериментальных исследований. Запасы прочности должны учитывать рассеяние механических свойств материала, вероятности рабочих нагрузок различной величины и продолжительности, число циклов нагружений и т. п.
Опытное производство и испытания. 1. Опытные экземпляры изделий должны быть предназначены для всесторонних исследований и испытаний в лабораторных, стендовых и эксплуатационных условиях. При исследовании измеряют параметры рабочего процесса (давление, температуру), тен-зометрированием определяют действующие переменные напряжения и т. д.
Целесообразно проводить опережающие исследования и испытания отдельных элементов (узлов) системы для скорейшего выявления и устранения дефектов.
2. Должны проводиться определения конструкционной прочности, ИЗНОСОСТОЙКОСТИ, коррозионной и эрозионной прочности отдельных элементов системы.
Исследования осуществляют на образцах-имитаторах и натурных деталях. Во многих случаях оказывается необходимым создание специальных испытательных стендов для исследования надежности элементов и узлов.
3. Опытные экземпляры испытывают на надежность в условиях, имитирующих эксплуатационные. Для более быстрого выявления «слабых мест» и потенциальных возможностей изделия проводят ускоренные эквивалентные и форсированные испытания.
4 Следует проводить специальные испоггания, выясняющие работоспособность системы при особых условиях эксплуатации, транспортирования,
Правила надежности
583
хранения и т. п. (климатические испытания, испытания иа перегрузки, на непробиваемость корпуса и т. п.).
При использовании материала нового типа, ранее не применявшегося в подобных изделиях, при использовании принципиально новых конструктивных решеннй, схем, условий работы необходимо увеличивать объем испытаний.
5. Для более полного выявления или подтверждения достаточной надежности систем проводят испытания опытной партии в условиях эксплуатации (для изделий, рассчитанных на серийное изготовление).
6. В процессе опытного производства в конструкцию и технологию должны вноситься изменения, направленные на устранение выявленных отказов и неисправностей. Стадия опытного производства завершается официальными испытаниями и утверждением эталона для серийною производства.
Серийное производство. 1. Технологические процессы серийного производства должны обеспечивать качество изделий (конструкционную прочность и др ) не ниже качества изделий опытного производства.
2. При изготовлении деталей, особенно ответственных, нельзя допускать концентрацию напряжений (недостаточные радиусы закруглений, отсутствие фасок и т. д.).
3 Технологические процессы не должны создавать значительные остаточные напряжения, понижающие прочность изделий. Следует устранять причины, порождающие возможность технологических повреждений (при-жогов, перегревов, трещин и др.).
4. Для ответственных деталей необходимо применять упрочняющую технологию (виброгалтовку, обдувку дробью, поверхностный наклеп), должны использоваться защитные покрытия, предохраняющие деталь от коррозии и других вредных воздействий,
5. Следует установить систему входного контроля (для материалов, поступающих в серийное производство, комплектующих деталей, узлов, агрегатов). Для контроля в процессе производства детали н узлы разбивают на различные группы контроля в зависимости от назначения и ответствен
ности. Условия контроля указывают в чертеже детали. Для ответственных деталей следует применять контроль геометрии, механических свойств, твердости, структуры материала, химического состава и др. Для выявления дефектов (трещин, рыхлот, засорений и т. п.), особенно в литых деталях, сварных швах, поковках, необходимо применять дефектоскопию (цветную, люминесцентную и др-), рентгеноскопический анализ, ультразвуковой контроль. Рекомендуется применять разрезку одной детали из партии для проведения более полного исследования; использовать микрообразцы, вырезаемые из деталей для проверки механических свойств. В отдельных случаях целесообразно применять образцы-свидетели, проходящие вместе с основной деталью определенную технологическую операцию (например термообработку, литье, сварку и т. п.).
Для новых материалов или при изменении поставщиков входной контроль должен быть усилен дополнительными исследованиями (для подтверждения уровня рассеяния свойств, для выявления чувствительности материала к трещинам, перегрузкам и т п.).
6. Условия контроля должны быть более жесткими в начальной стадии производства. При достижении необходимого уровня качества производства и его стабильности обычно имеется возможность упростить контроль (после соответствующего согласования). Должны быть предусмотрены испытания, подтверждающие стабильность технологического процесса, допустимый уровень рассеяния количественных показателей, физических и других свойств, влияющих на надежность (периодическое определение остаточных напряжений, пределов выносливости и т. п.).
7. Изменения, вносимые в технологию изготовления и сборки ответственных деталей, в том числе в размеры заготовок, поковок, изменения припусков посадок и допусков и т. п., должны быть согласованы с конструктором и в большинстве случаев про верены при лабораторных, стендовых или других испытаниях.
584
Элементы теории надежности
Особо тщательная экспериментальная проверка должна быть при внесении изменений в конструкцию деталей и узлов. Часто подобные изменения, «усовершенствования», «очевидные улучшения», введенные без надлежащей проверки, являются причиной появления отказов и разрушений.
Эксплуатация и ремонт. I. Эксплуатация сложных технических систем должна соответствовать техническим условиям и специальным руководствам. При необходимости должны быть указаны допустимые условия по температуре, влажности, загрязненности окружающей среды, продолжительности тяжелых режимов, регламентации переходных процессов и др.
2. Для сложных ответственных изделий должна быть разработана система технической диагностики, осуществляющая сбор, хранение и анализ информации о состоянии изделия. Информация должна непрерывно поступать от датчиков, регистрирующих частоту вращения, температуру, давление, вибрации и т. п. Система технической диагностики должна включать сигнализаторы состояния узлов, наличия стружки в масле, опасного уровня температур и вибраций и т. п. Система должна включать тесты для поиска и локализации неисправностей.
3. Система обслуживания должна содержать регламентные работы, профилактические осмотры и ремонты.
Техническое обслуживание может включать принудительную замену отдельных деталей и узлов после определенной наработки или календарного времени.
4. В пределах общего срока службы изделия могут быть предусмотрены промежуточные ремонты, сроки которых определяются соображениями надежности и экономической целесообразности.
Надежность отремонтированных изделий должна подтверждаться специальными испытаниями.
5. Должны проводиться исследования конструкционной прочности деталей и узлов с эксплуатационными повреждениями (коррозия, эрозия, забоины, изнашивание и др.).
На основании таких исследований и опыта эксплуатации устанавливаются нормы и эталоны на допустимые повреждения.
ВЕРОЯТНОСТЬ БЕЗОТКАЗНОЙ
РАБОТЫ, ПЛОТНОСТЬ
РАСПРЕДЕЛЕНИЯ
И ИНТЕНСИВНОСТЬ ОТКАЗОВ
Время появления отказа t* рассматривают как случайную величину.
Вероятность безотказной работы за время t
Р (/) = Вер (/* >t). (1)
Символ Вер означает вероятность.
Пусть в начальный момент времени работает изделий. Если к моменту времени наработки Ч исправными оказались N„ (Ч) а неисправными V* (ti) изделий, то статистическая оценка вероятности безотказной работы
р di) _ . N* (ti)
(2)
Для простоты допустим, что число изделий настолько велико, что статистическая оценка близка к истинной вероятности . Пусть за время работы
&И -- Н+1 - ti (3)
число отказавших изделий увеличилось на
AV? = v(/t-+1)-V(rz). (4)
Вероятность отказа изделия за время АН
Вер (ti <t* < ti+i)
_ _ &N*(ti)
No Vo ’
Если отнести вероятность отказа в промежутке ДИ к самому промежутку, то получим плотность распределения отказов
Более точно плотность распределения в момент t
&N* (t) I dN*
Z(O=J™o Vo dt •
(6)
Вероятность безотказной работы, интенсивность отказов
585
Плотность (частота) отказов (плотность вероятности отказов) представляет собой число отказов в единицу времени (скорость выбывания), отнесенное к первоначальному числу изделий.’ Если F (0 — функция распределения случайной величины t*, то F (/) - Вер (/*</) = 1 - Р (I). (7)
Функция распределения связана с плотностью вероятности отказов
t t
F (t) — f f(fidt = f f(t)dt, (8) — oo 0
так как время до появления отказа— величина положительная. Из последнего соотношения следует:
Интенсивность отказов X (/) представляет собой число отказов в единицу времени, отнесенное не к первоначальному числу изделий, а к числу изделий, находящихся в эксплуатации в данный момент:
1 /in)
ATT"- (10)
Если учесть, что
— суммарная наработка всех изделий за время Л/; ,то интенсивность отказов равна числу отказов в данном интервале времени, отнесенному к общей наработке изделий в этом же промежутке времени:
оо
Более точно интенсивность отказов в момент времени t
1 dN*
^-WW-dT- <12’
Интенсивность отказов характеризует плотность вероятности отказов в ближайший промежуток времени, если до его начала отказ еще не произошел.
Интенсивность отказов и плотность вероятности отказов связаны соотношением
= (13)
Равенство (13) следует из (12), если записать его в виде
' NB(t) Nodt
и учесть формулу (6).
Пример. В эксплуатацию с ресурсом 300 ч выпущена партия из 500 объектов. Число снятых объектов после различной выработки характеризуется следующими данными:
Время на-
работки, ч. . . 50 100 150 200 250 300
Общее число снятых
объектов ... 20 24 30 34 40 50
Определить плотность вероятности и интенсивность отказов в период времени от 0 до 50 ч и от 200 до 250 ч и вероятность безотказной работы за ресурс.
Решение. За первый период снято 20 объектов и плотность вероятности отказов (для середины интервала — 25 ч).
20
/<»>~-аЯГИГ~<МО-10-’ >/«
интенсивность отказов (среднее число работающих объектов 490)
20
Х<25)- 1903^ = °’82’10’3
За период от 200 до 250 ч снято 6 объектов.
Плотность вероятности отказов
,(225>- МТ»-0'241"”1''4-
Среднее число работавших обьектов 500— 1/2 (34 + 40) = 463.
Интенсивность отказов
Ч225>- «T»=0'26 ltr,|/4'
Вероятность безотказной работы за ресурс
50
Р (300) = 1 - 300 = 0,9.
Среднее время безотказной работы. Если / (/) — плотность вероятности от
586
Элементы теории надежности
казов, то среднее время безотказной работы
СО
7’ср = ?= (14)
о
Интегрированием по частям находим и другую эквивалентную формулу
СО
Tcp=jp(/)dt (15) о
ОСНОВНОЕ УРАВНЕНИЕ ТЕОРИИ НАДЕЖНОСТИ
Это уравнение связывает вероятность безотказной работы с интенсивностью отказов.
Из уравнений (9) и (13) получаем или
dP
~P~(i7 = -X (/) dt.
Интегрируя обе части равенства от О до t, находим
t
In Р (/) j = In Р (t) — In Р (0) = о
t
= — |х(Г)Л. (16)
о
Предполагая, что в начальный момент времени t — 0 изделие находится в исправном состоянии
Р(0)= 1, получаем из равенства (16) t
Р (t) = е ° =
Уравнение (17) является основным уравнением теории надежности, так как позволяет по протеканию интенсивности отказов определять вероятность безотказной работы.
ОБЩАЯ ЗАКОНОМЕРНОСТЬ ИЗМЕНЕНИЯ ИНТЕНСИВНОСТИ ОТКАЗОВ ПО ВРЕМЕНИ НАРАБОТКИ
Практически установлено, что изменение интенсивности отказов по времени для большинства сложных систем (машин, узлов) носит характер кривой, показанной на рис. 1. Период приработки / характеризуется повышенным значением интенсивности отказов; при нормальной эксплуатации (//) интенсивность отказов уменьшается и изменяется сравнительно мало, отказы носят внезапный, случайный характер. В периоде усиленного изнашивания III интенсивность отказов снова резко возрастает. Поэтому перед эксплуатацией сложной системы целесообразно проводить кратковременные сдаточные испытания, отсеивающие дефекты приработки. Система, удовлетворительно прошедшая начальный период, более надежна, чем система, находящаяся в начальном периоде. Замена старых узлов (деталей) новыми целесообразна только в период /// . При профилактической замене деталей на новые в периоде // надежность конструкции не возрастает, а уменьшается. Ресурс изделия следует назначать в начале третьего периода (периода изнашивания и старения).
Рис. I. Зависимость интенсивности отказов от времени наработки
ПРОГНОЗИРУЕМАЯ
ВЕРОЯТНОСТЬ БЕЗОТКАЗНОЙ
РАБОТЫ
Пусть известно, что система проработала без отказа время t. Какова вероятность безотказной работы в следующий период продолжительности т?
Экспоненциальный закон надежности
587
Если случайная величина — время работы до отказа /*, то
Р (т, t) = Вер (t* — t > т) =
Р (< + т)
P(Z)
Р (/) можно рассматривать как начальную (априорную) прогнозируемую вероятность непрерывной работы системы, которая была нсправна в начальный момент времени t ~ 0.
ЭКСПОНЕНЦИАЛЬНЫЙ ЗАКОН
НАДЕЖНОСТИ
Основной период эксплуатации обычно характеризуется почти постоянной интенсивностью отказов. В этом периоде отказы происходят от случайных факторов (попадание посторонних предметов, неблагоприятное сочетание внешних факторов, усталостные разрушения и др ) и носят внезапный ха’рактер. Время появления отказа не связано с предыдущей наработкой изделия.
При экспоненциальном законе надежности предполагается, что интенсивность отказов является величиной постоянной (рис. 2):
X (Г) = X. (19)
Вероятность безотказной работы по уравнению (17)
Р (t) = е~и. (20)
Плотность распределения отказов dP
= = (21)
Среднее время безотказной работы
оо оо
тср = j P(t)dt = j о о
(22)
Вероятность безотказной работы можно теперь записать в такой форме:
_ t
P(t)=e . (23)
Экспоненциальный закон распреде-ле ння справедлив для описания потока отказов с постоянной интенсивностью.
Рис. 2. Экспоненциальное распределение времени безотказной работы
Понятие потока отказов вводится для восстанавливаемых в процессе эксплуатации изделий.
Для потока отказов величина Тср представляет собой среднюю наработку на один отказ.
Важным свойством экспоненциального закона надежности является то, что он относится к «нестареющим» системам. Для такого закона (и только для него!) прогнозируемая вероятность безотказной работы не зависит от предыдущей наработки
р (т t) = Р + ___________
1 ' ' P(t)
_ ,<+Т) _ е-Хт
- е-х/ -
(24)
Пример 1. Изделие имеет ресурс 1000 ч и интенсивность отказов X = = 0,1-10-31/ч (среднее время наработки на отказ Тср -= 10 000 ч).
Определить вероятность безотказной работы первые 10 ч и за весь ресурс, считая справедливым экспоненциальный закон надежности.
Решение. Вероятность безотказной работы за первые 10 ч работы
Р (Ю) = е-0'Ь1°--10 « 0,999;
за весь ресурс
Р (1000) = е-0>|-|0“'10’ = 0,90, ио если известно, что изделие отработало исправно 990 ч. то вероятность отсутствия отказов за последние 10 ч снова будет 0,999.
Рассмотрим определение интенсив-иостн отказов (или средней наработки на отказ) при экспоненциальном распределении. Если известно, что для п
588
Элементы теории надежности
Рнс. 3. Нормальное распределение времени безотказной работы
Однако на практике информация о работоспособности изделий относится к определенному времени эксплуатации, в течение которого часть изделий получила отказы, а остальные отработали его исправно Тогда следует принять для данного времени испытаний
Суммарная наработка всех изделий Общее число отказов
(26)
Пример 2. Определить средн юю наработку до отказа для экспоненциаль ного закона надежности, если за время эксплуатации имеются следующие данные- 30 изделий отработали исправно 3000 ч, 10 изделий по 1000 ч, 7 изделий по 1500 ч; сняты три изделия после наработки соответственно 500, 2000 и 2500 ч.
Решение. Суммарное время наработки
^-30-3000! 10-1000 + 7-1500 +
+ 500 + 2000 + 2 500 = 115,5 X
X 10» ч.
Средняя наработка на отказ
„ <2 115,5-10»
К ~ 3
= 38,5-10» ч.
НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
ВРЕМЕНИ БЕЗОТКАЗНОЙ
РАБОТЫ
Нормальное распределение применяют в теории надежности для описания отказов, вызванных изнашиванием детали. Плотность распределения вре
мени безотказной работы при нормальном законе распределения (рис. 3)
20?
f(t) =
I ot ]/2л
(27)
где параметры распределения t и Of — среднее значение времени и среднее квадратическое отклонение.
При нормальном распределении время t может быть отрицательным, что противоречит физическому смыслу. Однако если среднее время I значительно превышает (7 > отрицательная часть распределения не имеет практического значения.
Функция распределения
i
F (t) — § =-1-
, ... ft — 7
+ Ф /--------
\
(28)
где Ф — функция Лапласа.
Вероятность безотказной работы при нормальном законе распределения
Р(0- 1-Г(П-4-ф(-~^).
(29)
Приведем еще значение интенсивности отказов
х (п =
' ° р (0
(<-0‘ 2о? е '
(30)
Надежность системы параллельных элементов
589
При больших t (I > ? + 2at) величина
(31)
При t > оо
f (t) -* О, X (f) -* оо.
РАСПРЕДЕЛЕНИЕ ВЕЙБУЛЛА ДЛЯ ВРЕМЕНИ БЕЗОТКАЗНОЙ РАБОТЫ
Это распределение используют для статистических моделей надежности в первый период эксплуатации («при-работочные» отказы). Функцию распределения принимают в виде (t > 0)
F (/)=!-— е“мт- (32)
Закон Вейбулла имеет два положительных параметра: Хит. Экспоненциальное распределение является частным случаем распределения Вейбулла при т = 1.
Особенно просто по закону Вейбулла выражается вероятность безотказной работы (рис. 4):
P(t) •= 1 — F(t) = e~wm- (33)
Плотность распределения dF . т-Л um f (/) = е ' (34)
Интенсивность распределения
Х(0 = -^- = Хт(?п"1. (35)
Если 0 < т < 1, то интенсивность отказов со временем убывает.
Рис. 4. Распределение Вейбулла времени безотказной работы (-я < I)
НАДЕЖНОСТЬ СИСТЕМЫ
ПОСЛЕДОВАТЕЛЕН ЫХ ЭЛЕМЕНТОВ
Если система включает несколько элементов, причем отказ одного из них приводит к отказу всей системы в целом, то такое соединение элементов называют последовательным (рнс. 5).
Например, узлы двигателя — компрессор и турбину — можно считать соединенными последовательно, так как отказ одного из этих узлов приводит к отказу всего двигателя.
z
Рнс® 5. Система с последовательными элементами
Предполагая отказы отдельных элементов независимыми, получим вероятность безотказной работы системы из последовательных элементов
P(t)^ (36)
Прн последовательном включении элементов вероятность безотказной работы уменьшается. Например, если для одного элемента Pj = 0,99, то для 10 последовательно соединенных подобных элементов
Р = Р? = O.9910 = 0,90.
Важное свойство системы с последовательными элементами состоит в следующем, Если Xj (t) — интенсивность отказов i-го элемента, то для всей системы
/
- j >-2 W dt
p(t)-=t 0 , (37)
где
п
х2(() = 2 Х.(0. (38)
г=1
Прн последовательном соединении элементов интенсивности отказов суммируются.
НАДЕЖНОСТЬ СИСТЕМЫ
ПАРАЛЛЕЛЬНЫХ ЭЛЕМЕНТОВ
В этом случае (рис. 6) отказ системы наступает только тогда, когда отказали все без исключения элементы.
590
Элементы теории надежности
Рис. 6. Система с параллельными элементами
Вероятность отказа
Г (/)=!-₽(/). (39)
Если Ft (t) — вероятность отказа его элемента, то
F (t)= Fl(t)Ft(t)...Fn(f). (40)
Вероятность безотказной работы системы
Р(0 = !-(!-₽! (0)(1 —
- Ps(Z)k..(l- ?„(*))- (41)
Если вероятность безотказной работы элементов одинакова и равна Pl (0. то
Р (/) = 1 _ (1 _ Р1 (/))". (42)
Из этого равенства можно получить ?1 ((), если задано ? (/):
Pi (0=1- 1 - Р (0 • (43)
Пример. Определить необходимую вероятность безотказной работы элемента, если система из трех параллельных элементов должна иметь вероятность безотказной работы (за время t) Р (/) = 0,999.
Решение. Из уравнения (43) находим
?! (/)=]— рТ— 0,999 = 0,90.
Из равенства (42) и (43) можно сделать вывод, что надежность системы с параллельными элементами значительно выше надежности отдельного элемента.
Параллельное соединение — метод создания надежной системы из «ненадежных» элементов.
Систему, содержащую параллельно работающие элементы, называют системой с резервированием.
Применяют три метода резервирования:
1) система с нагруженным («горячим») резервом;
2) система с облегченным резервом;
3) система с ненагруженным («холодным») резервом.
В первом случае резервный элемент работает в одинаковых условиях с основным (например, многодвигательный самолет).
Во втором случае резервный элемент работает в облегченных условиях, в третьем случае он включается в работу только после отказа основного элемента.
Целесообразность применения различных схем резервирования зависит от особенностей системы, назначения элементов н других факторов. Например, если для включения элемента на заданную мощность требуется значительное время, то возможности использования голодного резерва становятся ограниченными.
АНАЛИЗ НАДЕЖНОСТИ СИСТЕМЫ С НЕСКОЛЬКИМИ ПАРАЛЛЕЛЬНО РАБОТАЮЩИМИ ЭЛЕМЕНТАМИ
Пусть система содержит несколько одновременно работающих объектов (турбины, электростанции, двигатели самолета и т. п.). При этом возможен отказ одного объекта при работе остальных и т. д. Какова вероятность, что будут одновременно работать все объекты или только определенная их часть.
Рассмотрим вопрос на примере системы с одинаковыми элементами. Силовая установка самолета содержит четыре двигателя, причем вероятность безотказной работы двигателя
?! (0 = е~Ч
Вероятность отказа
Л(0= 1-РИП-
Для анализа следует рассмотреть вероятности всех возможных ситуаций (первый двигатель работает, остальные отказали, второй работает и т. д.). Оказывается, что такой анализ выпол
Количественные показатели надежности
591
нить весьма просто, если использовать характеристический полином
[Р, (О + (Ш4 = (0 +
+ 4Р? (/) F, (П + 6Р? (0 Fl (t) +
+ 4?! (о F? а) + п (п = 1.
Первый член PJ (/) выражает вероятность работы всех двигателей, второй — вероятность работы трех двигателей и отказ одного и т. д. Сумма
Р1 Ц) + 4PJ (/) Flt означает вероятность отказа не более одного двигателя (отсутствие отказа или отказ одного двигателя).
Пример. Определить вероятность отказов двигателей за полет длительностью 10 ч на четырехдвигательном самолете при интенсивности отказов X = 1/104 1/ч.
Решение. Вероятность безотказной работы двигателя
_ 10 Р1 = е 101 = 0,999.
Вероятность отказа
F(f) = 0,001.
Вычислим члены полинома:
Р4 = 0,996; 4Р?/7! = 3,988-10~3;
6Р?Р? = 5,988-10-';
4Р1Р3 = 3,966-IO"4;
F4 = МО-42.
Вероятность безотказной работы всех четырех двигателей
Ро = р* = 0,996.
Вероятность отсутствия отказов или отказа одного из двигателей
Р С 1 = Р| + 4РЗР[ = 0,999988.
Вероятность безотказн ой работы не менее двух двигателей (отсутствие отказов, отказ одного или двух двигателей)
Р 2 = Р4 + 4РЗ/4 4-
4- 6P|Pj2 = 0,999999996.
Т ак как самолет может продолжать полет с двумя двигателями, то из примера видна высокая надежность системы в связи с отказом двигателей.
РАСЧЕТ ЧИСЛА ИЗДЕЛИЙ, НАХОДЯЩИХСЯ
В ЭКСПЛУАТАЦИИ
Для расчета используют экспоненциальный закон надежности. Если Тдг— средняя наработка до выбывания изделия нз эксплуатации (в ремонт или на списание), то в момент времени t число изделий в эксплуатации
_ *
N„ (П = Аое ГДс . (44)
Число «убывших» изделий
/V* (t) = No \1 — е Дс ) (45)
В последних формулах No— число изделий, поступивших в эксплуатацию в начальный момент времени i = 0
Рис. 7. < Кривая убыли» изделий из эксплуатации
На рис 7 дана «кривая убыли» — зависимость относительного числа выбывших изделий от времени наработки. При t = Тдс
N*
= 1 — е‘1 = 0,63
No *
Это означает, что 63% изделий будут сняты с эксплуатации и направлены в ремонт.
КОЛИЧЕСТВЕННЫЕ ПОКАЗАТЕЛИ НАДЕЖНОСТИ
Существуют различные показатели надежности, многие из которых включаются в стандарты н технические условия.
592
Технологические методы повышения долговечности
Выбор нормируемых показателей надежности и их регламентация связаны с назначением изделия, режимом его использования, последствиями отказов и другими факторами.
В качестве основных показателей надежности обычно используют следующие: вероятность безотказной работы Р (0 и наработку на отказ Т.
Для ремонтируемых (восстанавливаемых) изделий величина Т представляет среднюю наработку между отказами. Она определяется в рассматриваемом интервале времени
N
т = , (46)
У 1=1
где N— число изделий в статистической совокупности (выборке); tj и тг — наработка и число отказов о го изделия в рассматриваемом интервале времени.
Для отказов, не устраняемых в эксплуатации, в качестве показателя надежности используют среднюю нара
ботку до первого отказа 'Гср. Среднюю наработку до отказа определяют раздельно для отказов различных типов. Например, для пассажирских авиационных двигателей средняя наработка до отказа в полете составляет обычно
То. п « (2-8) 104 1/ч, тогда как средняя наработка на один досрочно снятый двигатель
Г,с.д= (14-6) 103 1/ч.
Указанные характеристики отражают различные характеристики эксплуатации; величина Тдс.д является, в сущности, экономическим показателем.
Практика эксплуатации технических систем показывает, что их надежность по мере увеличения общей наработки парка изделий в эксплуатации возрастает. Это происходит в результате внесения конструктивных и технологических изменений в производство изделий, направленных на устранение отказов. При очень большой наработке (или времени эксплуатации) наступает «старение» парка изделий и наблюдается стабилизация, а затем и понижение уровня надежности.
Глава 34
ТЕХНОЛОГИЧЕСКИЕ МЕТОДЫ
ПОВЫШЕНИЯ ДОЛГОВЕЧНОСТИ ДЕТАЛЕЙ МАШИН
Прочность деталей машин (особенно при переменной внешней нагрузке) зависит от концентрации напряжений, а также от физико-механического состояния поверхностного слоя (остаточных напряжений и других факторов).
ОСТАТОЧНЫЕ НАПРЯЖЕНИЯ
Остаточными называют напряжения, возникающие в деталях в результате обработки (литья, обработки давлением, резанием, термической обработки и т. nj при отсутствии внешних воздействий (силовых и температурных).
Образование остаточных напряжений при различных технологических процессах происходит различным обра
зом. В основе их возникновения лежат необратимые объемные изменения в материале.
Наиболее часто остаточные напряжения возникают в результате неравномерной (или неоднородной) предварительной пластической деформации (при механическом нагружении, а также при нагреве и охлаждении тела).
При равномерной (однородной) предварительной упругопластической деформации, когда распределение напряжений одинаково, остаточные напряжения не образуются. Например, после растяжения гладкого стержня с напряжениями <4 > ат и последующей разгрузки он получит остаточную деформацию (остаточное
Остаточные напряжения
593
Рнс. 1. Кривая деформирования образца из конструкционного материала при на* личии разгрузки
относительное удлинение, рис. 1)
еост = Е1~Е|У,>
где е(у) — упругая деформация стержня (тела) при разгрузке *,
здесь Е— модуль упругости материала, Е = tg а.
При повторном нагружении процесс пойдет по кривой ВАС и новые пластические деформации возникнут при а > Oj. Если внешние растягивающие напряжения при повторном нагружении а Oj, то образец работает в упругой области с новым значением предела текучести ат{1) =0] (в результате первого нагружения увеличивается упругая область работы образца). Если в процессе упругопластического нагружения тела в нем создается неоднородное напряжение или деформированное состояние (например, прн растяжении стержня с выточкой, изгибе или кручении гладкого стержня), то при разгрузке в нем возникают остаточные напряжения.
Остаточные напряжения равны разности между истинными напряжениями в упругопластическом теле и напряже
• Процесс разгрузки можно предста-вить как приложение напряжения с обратным знаком
ниями, которые создавались бы в ием, если бы его материал был идеально упругим. Поясним это на примере чистого изгиба стержня (рис. 2). Для расчета примем схематизированную кривую деформирования без упрочнения (рис. 3), одинаковую для растяжения и сжатия. Если в результате изгиба стержня наибольшие напряжения в крайних (верхних и нижних, рис. 4, а, б) волокнах о sj ат, то стержень работает в области упругой деформации:
6М
°тах — ^2 От-
При М > Oq bh?IB в крайних волокнах возникают пластические деформации.
Предположим, что при дачном значении М область пластических деформаций распространяется от 0,5ft до O.Sftj (рис. 4) и напряжения в ней о = ат. При у < O.Sftj напряжения изменяются по линейному закону
Рис. 3. Схематизированная кривая деформирования без упрочнения
594
Технологические методы повышения долговечности
Рис. 4. Эпюры остаточных напряжений
после пластического изгиба
Из условия равновесия
0,5Л
М = ( abydy = (k2 — ft?)+
—0.5Л
4—g- Oybh2
находим, что
. 2 Уз' 1 /П ~ ~
Л1 = 1/ -Г ОтЬ1г2 — М .
VoTb г 4
Напряжения в продольных сечениях стержня определяются следующими равенствами (рис. 4, б):
а =
2z/ Il 1 , ат~т—; ly|<-n-fti; ill *•
1 , . . 1 , ат; -уЛ1<|^| < -g-ft-
Если бы материал стержня был идеально упругим, то распределение напряжений соответствовало бы линейному закону
После разгрузки (после снятия момента М) остаточные напряжения в стержне аост = а— а*.
СТ 1 С
Например, при У=~^г « аост = ат— 6Л4 . 1 ,
^2 ’ ПРИ У — ~2~ °ОСТ — ®Т 6М hj,
bh2 h
Эпюра остаточных напряжений (рнс. 4, в) здесь, как и во всех других случаях, оказывается самоуравнове-шенной (равнодействующие усилия и моменты равны нулю).
В зоне наибольшей напряженности знак остаточных напряжений обычно противоположен знаку деформации, их вызывающей.
После снятия момента ось стержня будет иметь остаточный прогиб, который также можно определить следующим образом. Прн действии момента М деформация слоя на расстоянии Л,/2 от осн стержня в = h-jlR = ат/Е, где R— радиус кривизны слоя.
Наибольший прогиб осн стержня
, _ L2 1 oTL2
' ~~8R ~~ ~EhT •
а наибольшее напряжение при у — = ±0,5Л
• - 6М атах — Ьнг •
При идеально упругом материале
/?* =
Eh 2gmax
Упрочнение поверхностным пластическим деформированием
595
Рис. 5. Кривая деформирования при изменении направления нагрузки
а наибольший прогиб
,ф amaJ'2 з МР
Г 4Е1г 2 Ebh3 '
Остаточный прогиб /ост — f f* =
1 L2 / От °тах
“ V ~1Г \ ht V'
направлен в сторону прогиба стержня при действии момента М, так как />/*
На процесс образования остаточных напряжений существенно влияет поведение материала прн последовательном изменении направления нагружения (рис. 5).
Кривая ОАС представляет собой обычную кривую деформирования. В точке А начинается разгрузка (участок АВ), а затем проводится нагружение в противоположном направлении (сжатие, участок ВС^)- Кривая ВС\ расположена несколько выше кривой BAtC*, повторяющей ветвь ВАС, что объясняется эффектом Баушингера. Условия появления остаточных напряжений, связанные с неоднородностью предварительной пластической деформации, лежат в основе метода упрочнения детален машин путем их преднамеренного поверхностного пластического деформирования, а также термической обработки.
УПРОЧНЕНИЕ ДЕТАЛЕЙ МАШИН ПОВЕРХНОСТНЫМ
ПЛАСТИЧЕСКИМ
ДЕФОРМИРОВАНИЕМ
Для повышения конструкционной прочности деталей машин широко применяют поверхностное пластическое деформирование (статическое и динамическое), реализуемое различными способами. Такое упрочнение оказывается наиболее эффективным для деталей сложной формы или изготовленных из твердых материалов, а также при наличии концентраторов напряжений.
Эти способы упрочнения основаны иа получении поверхностных сжимающих напряжений за счет неоднородной упругопластической деформации (растяжения поверхностных слоев детали) в зоне контакта детали и цилиндрического или сферического инструмента (ролика, шарика, дорна и т. п.) или рабочего тела (например дроби). Деформирование поверхностных слоев облегчается при скольжении или качении прижатого инструмента по поверхности детали, так как за счет сил трения увеличивается интенсивность напряжений в зоне контакта. Для повышения стойкости инструмента его изготовляют из более прочного материала, чем обрабатываемая деталь. Эффективным оказывается использование материалов с высоким модулем упругости. Дробь изготовляют и из менее прочного материала (чугун, стекло, неметаллы и др.), так как в момент соударения она работает в условиях сжатия.
Упрочнение деталей машин дробью широко распространено во многих отраслях машиностроения. Этому в значительной мере способствовали высокая производительность, небольшие затраты на специальное оборудование и возможность эффективного упрочнения разнообразных деталей из различных материалов, особенно деталей сложной конструкции, когда применение других видов обработки затруднено.
Остаточные напряжения в поверхностных слоях деталей возникают в результате неоднородной упругопластической деформации поверхностных слоев от ударов дроби.
596
Технологические методы повышения долговечности
Рис. в. Зависимость прогибов в контроль-ных образцах после п невмодробеструйной обработки от длительности наклепа при различных давлениях воздуха:
1 - Рв = 300 КПа: 2 - Рв = 400 КПа;
3 — Р* = 500 КПа
В зависимости от способа передачи кинетической энергии дроби различают несколько методов упрочнения дробью.
Пневмодробеструйное упрочнение деталей осуществляется на универсальных установках, в которых кинетическая энергия струи сжатого воздуха передается дроби. Интенсивность наклепа и размеры ядра распыла дроби зависят от диаметра форсунки и насадки сопла.
Для обработки применяют литую стальную дробь ДСЛ диаметром 0,5— 1,4 мм. Если обрабатываемая деталь имеет галтели, то диаметр дроби с! < (1,24-1,6) 7?шШ, где #т1п — минимальный радиус упрочняемой галтели.
Упрочнение деталей из сталей и сплавов осуществляют при давлении воздуха рв = 3004-400 КПа в течение 1—3 мин. Время обработки устанавливают экспериментально на контрольных образцах из того же материала. Продолжительность обработки, после которой прогиб контрольного образца не изменяется, определяет время наклепа [2]. На рис. 6 показана зависимость прогибов контрольных образцов из стали 12Х2НВФА от длительности наклепа т при односторонней обработке. В данном примере при т = = 3 мин достигается оптимальная степень наклепа и сплошность обработки.
Пневмодробеструйной обработке подвергают сварные соединения (швы и околошовные зоны), зубчатые колеса из закаленных цементованных сталей, корпусные и другие детали машин.
При упрочнении плоских сварных образцов из сплава ХН68ВМТЮК дробью ДСЛ диаметром 0,5—1 мм при р = 380 КПа и т = 3 мин создаются
сжимающие напряжения (рис. 7) и ликвидируются растягивающие остаточные напряжения от сварки. Эпюры осевых сжимающих напряжений, построенные для трех образцов, имеют подповерхностный максимум, характерный для деталей, прошедших упрочняющую обработку поверхностным пластическим деформированием. Сопротивление усталости в результате такой обработки повысилось в 2 раза [3].
Пневмодинамическое упрочнение является разновидностью пневмодробе-струйного упрочнения. В отличие от последнего ппевмодинамический способ обработки позволяет проводить местное упрочнение больших деталей или полное поверхностное упрочнение небольших деталей, помещенных в замкнутую камеру (рис. 8). В нижней части камеры размещаются шарики диаметром 1,3— 1,6 мм из стали ШХ15.
При подаче сжатого воздуха (рв — — 3004-700 КПа) к соплам (или щелевидному соплу) образуются многочисленные струи, которые подхватывают стальные шарики и направляют их на упрочняемую поверхность. Отраженные от детали шарики попадают либо сразу в днище, либо устремляются к экрану и от него к днищу.
Зона эффективного упрочнения в камере расположена на расстоянии 60—80 мм вверх от сопла.
Массу шариков для камеры и продолжительность обработки устанавливают экспериментально по контрольным образцам. Обычно т = 15-4-20 мин.
Такой способ обработки часто применяют для упрочнения сварных соеди-
Рис. 7, Зависимость осевых остаточных напряжений в образцах от глубины стравленного слоя
Упрочнение поверхностным пластическим деформированием
597
хвостовиков валов
Воздух д коллектор
нений, шлицевых
и т. д.
Г ид род робестр у иное упрочнение. Особенность этого вида упрочнения состоит в снижении параметров шероховатости поверхности, что важно для зубчатых колес, лопаток компрессора, трубопроводов и др. Обработка деталей осуществляется струей трансформаторного масла при давлении рв = 300-4-500 КПа и стальными шариками. Благодаря применению масла (и других смазы-вающе-охлаждающих жидкостей) понижается температура в зоне контакта шариков с поверхностью и исключается трение без смазочного материала. Образующаяся пленка защищает впадины на поверхности детали, выступы (гребешки) деформируются.
На рис. 9 приведены графики изменения тангенциальных остаточных напряжений по глубине цементованного слоя при различной обработке выкружки зубьев (табл. 1) колес из стали 20ХЗМВФ (число зубьев z — 50, модуль т — 3 мм, коэффициент смещения х = 0, угол профиля исходного контура а = 25°, ширина зуба Ь — = 8 мм).
Зубья нарезали червячной фрезой с протуберанцем, создающим искусственное поднутрение зубьев, которое позволяет осуществлять шлифование эвольвентного участка зубьев со сво-
Воздух
из сети
Рис. 8. Схема камеры для пиевмодииа-мической обработки деталей
бодным выходом круга в зоне переходной поверхности.
Анализ результатов наглядно иллюстрирует эффективность дробеструйной обработки. При шлифовании уменьшаются остаточные напряжения в поверхностных слоях. Наибольшие сжк-
мающие напряжения действуют в нешлифованных переходных поверхностях; сопротивление усталости зубьев оказывается наибольшим. Увеличение давления масла (> 550 КПа) не влияет на сопротивление усталости зубьев. Следует отметить стабильное снижение параметров шероховатости от Ra — = 0,63“ 1,25 мкм до /?а=0,16-г 0,32 мкм.
Рис. 9. Графики изменения кольцевых остаточных напряжений во впадинах зубьев по глубине цементованного слоя
598
Технологические методы повышения долговечности
1. Результаты влияния технологии обработки переходной поверхности зубьев колес на остаточные напряжения и выносливость зубчатых передач
Номер кривой на рис. 9 Характер обработки °G max’ МПа Предельная нагрузка Н/'см
/ Цементация на глубину 0,7 —1,2 мм. закалка, обработка холодом и низкий отпуск при 250 °C; твердость поверхности зубьев Н₽СЭ > 58, твердость сердцевины 32 — 42 НКСЭ — 750 7 600
2 То же, шлифование — 630 7 050
3 То же, шлифование, обработка дробью диаметром 1,6 мм из стали ШХ15 при рм = 530 КПа — 950 10 000
4 То же, рм — 550 КПа — 1260 12 600
5 То же, рм — 650 КПа — 1260 12 150
6 То же, рм = 800 КПа — 1300 12 500
Примечания: 1. Переходные поверхности зубьев колес (см. кривые 4 — 8) не шлифовали.
2. Во всех случаях х — 3 мин на один зуб.
3. Сопротивление усталости оценивали по предельной нагрузке в вершине зуба, отнесенной к ширине венца; нагрузка изменялась от 0 до Р .
Биброгалтовка (вибрационная обработка) является разновидностью гидро-дробеструйнон обработки. Она проводится в контейнере, жестко закрепленном иа столе трехкоординатной виброустановки, стальными шариками диаметром 2,5—5 мм и растворителем. Частота колебаний стола 20—40 Гц, амплитуда 3—6 мм.
Таким образом осуществляют упрочнение сепараторов подшипников, лопаток турбин и др. После виброобработки уменьшается шероховатость поверхности и повышается выносливость деталей за счет абразивного и упрочняющего действия рабочих тел смеси (3].
Внброгалтовку рекомендуется проводить после гидродробеструйной обработки для доупрочнения и зачистки кромок деталей. Такая технология упрочнения позволяет на 50% повысить предел выносливости компрессорных лопаток из сплава ВТ9 [3].
Часто на виброустановках проводят виброшлифование деталей рабочей смесью из стальных шариков диаметром 1,6—2,5 мм, абразивных гранул, паст и растворителя.
Иногда применяют стеклянные и кварцевые шарики диаметром 0,05— 0,2 мм.
Время шлифования деталей составляет 90—150 мин.
В результате виброшлифования уменьшается шероховатость, в поверхностных слоях возникают сжимающие остаточные напряжения, снижается трудоемкость слесарной обработки и т. д.
По данным работ [2, 3], виброшлифование повышает сопротивление усталости компрессорных лопаток на 25— 32% .
Упрочнение микрошариками. Для . обработки тонкостенных деталей, а также деталей с малыми радиусами переходов и галтелей используют микрошарики (стеклянные, фарфоровые и др.) диаметром 0.02—0,2 мм. В результате такой обработки достигают параметров шероховатости поверхности деталей, равных 0,16—0.63 мкм.
Благодаря высокой проникающей способности микрошариков такая обработка оказывается исключительно эффективной для упрочнения резьбовых деталей, елочных хвостовиков лопаток и пазов дисков, а также других деталей сложной конфигурации.
Кинетическая энергия микрошариками сообщается с помощью центробежных дробеметов, позволяющих лег-
Упрочнение поверхностным пластическим деформированием
599
Рис. 10. Графики остаточных напряжений в образцах после различных видов обработки поверхности
ко регулировать скорость полета и размеры ядра распыла дроби.
Уменьшение диаметра дроби н увеличение скорости ее полета приводит к возрастанию остаточных напряжений в поверхностных слоях и уменьшению глубины наклепа.
Возрастанию остаточных напряжений в поверхностных слоях и смещению максимума остаточных напряжений к наружной поверхности способствует смещение максимума интенсивности напряжений аг прн контакте с деталью дроби малого диаметра вследствие уменьшения размеров площадки контакта (см. гл. 29), а также увеличение сопротивления пластическому деформированию при увеличении скорости полета дроби и уменьшение деформированного объема.
Типичные графики остаточных напряжений (рнс 10) после обработки микрошариками (кривая 3), гидродро-беструйиого упрочнения (кривая 2) и точения (кривая У) образцов из титанового сплава ВТ9 подтверждают одно из главных преимуществ такого способа обработки.
Другое важное преимущество упрочнения микрошариками состоит в существенном сокращении длительности обработки дот- 15-45 с при скорости полета микрошариков v = 60-? 70 м/с. Меньшие значения т соответствуют меньшим диаметрам шариков.
Микрошарикамн целесообразно упрочнять сепараторы и кольца подшипников, диски, зубчатые колеса, резьбовые детали и др. В результате обработки шпилек с накатанной резь
бой можно на 40—50% повысить выносливость резьбовых соединений из титановых сплавов.
Обработка микрошариками обеспечивает повышение сопротивления усталости замковых соединений турбин на 20% [3].
Алмазное выглаживание в качестве отделочно-упрочняющей обработки получило широкое распространение. Упрочнение достигается пластическим деформированием обрабатываемой поверхности скользящим индентором из монокристалла синтетического алмаза (корунда, карбида кремния, карбида бора и т. п.), закрепленного в упругой (подпружиненной державке). Алмазный наконечник (индентор) выполняют в виде сферы, цилиндра и, реже, тора.
Благодаря высокой твердости алмаза и других синтетических корундов и карборундов, низкому коэффициенту трения по металлу (особенно при наличии смазывающе-охлаждающих жидкостей), низким параметрам шероховатости и хорошей теплопроводности удается обрабатывать почти все пластически деформируемые металлы (даже при 60—65 HRC3), получая при этом высокие эксплуатационные свойства (износостойкость, коррозионную стойкость, сопротивление усталости и др.).
Алмазное выглаживание деталей осуществляют, как правило, на токарных станках прн закреплении державки в резцедержателе. Радиус сферы индентора 1,5—3,0 мм. Продольная подача назначается такой, чтобы обеспечивалось перекрытие поверхностью индентора линий контакта (0,03—0,08 мм/об). Скорость выглаживания в пределах 35— 45 м/мин обеспечивает минимальное изнашивание алмаза и плавное смятие микронеровностей. Радиальные усилия (150—300 Н) меньше, чем при других подобных методах обработки (обкатка роликом, шариком и т. п.) вследствие малой площади контакта.
Алмазное выглаживание формирует в поверхностных слоях высокие сжимающие напряжения (рис. 11), имеющие подповерхностный максимум [4].
Обычно алмазному выглаживанию подвергают плунжеры насосов, валы и оси. Сопротивление усталости упрочненных деталей на 30—35% выше, чем иеупрочненных.
600
Технологические методы повышения долговечности
Рис. 11. Графики остаточных напряжений после алмазного выглаживания поверх» иости образца
Наряду с алмазным выглаживанием получает распространение виброалмаз-ное выглаживание, позволяющее формировать сложный (узорчатый) рельеф поверхности деталей, что важно для плунжерных пар, маслоуплотнительных колец и др.
Обкатка роликом и шариком. Процесс обкатки осуществляется перемещением прижатого к обрабатываемой детали ролика или шарика, закрепленного в специальной державке (рис. 12). Приспособления могут быть двух-, трех- и многороликовыми (многошариковыми) с механическим, пневматическим и гидравлическим приводом.
В зависимости от усилия на ролик (шарик) различают сглаживающе-упрочняющую и упрочняющую обкатку. В первом случае наряду с небольшим упрочнением при относительно небольших радиальных усилиях достигают снижения параметров шероховатости, что в ряде случаев позволяет исключить шлифование.
При упрочняющей обкатке за счет высоких давлений в поверхностных слоях деталей возникают высокие сжимающие напряжения, параметры шероховатости при этом повышаются.
Упрочняющей обкатке обычно подвергают поверхности валов и осей, впадины зубчатых колес и резьбовых деталей.
Диаметр ролика для обкатки валов и осей диаметром d 20 мм принимают в пределах 0,5 < Dv!d< 5. С уменьшением диаметра ролика и ра-
Рис. 12. Инструмент для обкатки деталей
диуса его профиля R при прочих равных условиях увеличиваются остаточные напряжения в поверхностных слоях и повышаются параметры шероховатости.
При упрочнении (обычно фасонными роликами) галтелей валов зона обкатки должна выходить за галтели на длину не менее 0,05d. Посадочные места валов упрочняются с выходом за зону посадки на длину (0,4—0,5) d.
Режимы обкатки (усилие на ролик, скорость обкатки, подача) устанавливают экспериментально. В результате упрочняющей обкатки сопротивление усталости валов повышается на 25— 40%.
В ряде отраслей машиностроения применяют виброударную обкатку (чеканку) галтелей валов.
Отверстия в деталях упрочняют раскатыванием роликовыми или шариковыми раскатниками, а также протягиванием и продавливанием шарика (для отверстий диаметром <30 мм). В результате такого упрочнения сопротивление усталости детали с отверстием удается повысить на 30—50%.
ТЕРМИЧЕСКАЯ И ХИМИКОТЕРМИЧЕСКАЯ обработка
При термической обработке в поверхностных слоях детали возникают остаточные напряжения. Сжимающие остаточные напряжения могут быть созданы путем быстрого охлаждения после нагрева до температуры ниже критической (например, при нагреве деталей из конструкционных сталей до 600 °C и охлаждения в воде).
Экспериментальные исследования показали, что сжимающие остаточные
Определение остаточных напряжений
601
напряжения .после термической обработки повышают сопротивление усталости деталей без концентраторов напряжений на 10—30% и на 50—80% деталей с концентраторами напряжений.
При поверхностной закалке токами высокой частоты в поверхностных слоях обычно создаются сжимающие остаточные напряжения, повышающие сопротивление усталости деталей с концентрацией напряжений (на 70—200% при наличии посадки с натягом).
В зонах обрыва закаленного слоя, например в галтелях валов, возникают остаточные напряжения растяжения, сопротивление усталости валов в этих местах снижается на 20—30%. Эти зоны после поверхностной закалки необходимо упрочнять (роликом или дробью).
Сжимающие остаточные наприжения в поверхностных слоях деталей образуются при цементации, азотировании и цианировании. Если при шлифовании поверхностей после химико-термической обработки не возникают остаточные напряжения (обычно растягивающие), то сопротивление усталости деталей возрастает.
Обработка дробью поверхностей,подвергнутых химико-термической обработке и последующему шлифованию, оказывает благоприятное влияние на несущую способность деталей при переменных нагрузках, так как стабилизирует свойства поверхностных слоев деталей (устраняет некоторые дефекты и растягивающие напряжения от шлифования).
Остаточные напряжения в поверхностных слоях образуются н прн нанесении гальванических покрытий. При никелировании возникают растягивающие остаточные напряжения, снижающие пределы выносливости деталей на 10—30% (большие значения относятся к сталям повышенной прочности). Несколько меньшее снижение прочности наблюдается в случае хромирования и меднения. При нанесении цинкового, кадмиевого и серебряного покрытий сопротивление усталости деталей не изменяется.
При назначении покрытий необходимо учитывать условия работы деталей (особенно рабочую температуру).
Эффективность упрочняющей обработки может быть оценена экспериментально путем измерения остаточных напряжений или при проведении натурных механических испытаний деталей в эксплуатационных условиях.
ОПРЕДЕЛЕНИЕ ОСТАТОЧНЫХ НАПРЯЖЕНИЙ
Большинство деталей машин после упрочнения оказывается в условиях сложного напряженного состояния. Наибольший практический интерес представляют напряжения в поверхностных слоях. Эти напряжения имеют, как правило, наибольшие значения и оказывают существенное влияние на работоспособность деталей. Обычно определяют остаточные напряжения в направлении главных осей. Если деталь является осесимметричной, то в поверхностных слоях в общем случае имеется двухосное напряженное состояние (рис. 13): Од—тангенциальное напряжение; <7Z—осевое напряжение. Радиальное напряжение аг на поверхности детали равно нулю. В слоях, близких к поверхности, значение о, невелико, н этой составляющей обычно пренебрегают.
Осевые и тангенциальные напряжения в поверхностных слоях деталей определяют механическими методами, в основном путем последовательного
Рис. 13. Схема напряженного состояния цилиндрического элемента
602
Технологические методы повышения долговечности
Рис. 14. Сечение для выявления остаточных напряжений
стравливания поверхностных слоев с призматических стержней и колец толщиной 5—6 мм, вырезаемых из детали электроискровым или другим методом.
Для оценки эффективности режимов упрочнения деталей часто ограничиваются сравнительными исследованиями осевых остаточных напряжений, оказывающих в большинстве случаев наиболее существенное влияние на работоспособность деталей.
Рассмотрим определение осевых остаточных напряжений в призматическом стержне. Предположим, что, за исключением небольших областей у концов стержня, остаточные напряжения постоянны по его длине.
Для определения остаточных напряжений будем последовательно удалять слои материала ABCD (рис. 14), находящиеся в зоне постоянных (по длине) напряжений. Концевые сечения при этом не удаляются, они размещаются в захватах прибора.
Неизвестные напряжения считаем положительными (растягивающими). Они действуют по граням АВ и CD, поэтому удаление области эквивалентно приложению к этим граням равных, но противоположно направленных напряжений. Предполагаем, что остаточные напряжения действуют в площадках, перпендикулярных к оси стержня. Поэтому поверхность ВС не должна быть загружена остаточными напряжениями.
Определим остаточные напряжения а (а), действующие в стержне на расстоянии а от верхней грани стержня
Рис. 15. К расчету остаточных напряжений
(рис. 15). В результате удаления слоя материала толщиной а оставшаяся часть стержня деформируется под действием напряжений по плоскостям АВ и DC.
На расстоянии £ от верхней грани действуют напряжения о (Ej). Изгибающий момент от напряжений на грань АВ относительно середины высоты стержня (точки О)
а
м = [±(ft + a)_g] bdl,
о
где Ь— ширина стержня.
Если стержень изгибается сосредоточенными моментами М на конце, то прогиб
где I—длина стержня; J— момент инерции поперечного сечения,
Влиянием осевых сил на изгиб пренебрегаем, что не вносит существенной погрешности. Учитывая равенства (1) и (2), найдем
З/2
f (£Z) = ~2.Е (h — tf3 Х а
X р(£)[4(Л + а)--ф^- (3) о
Перенося величину (h— а)3 в левую часть равенства и продифференцировав интеграл по верхнему пределу а, получим
(А - а)2 (а) — 3 (Л — а)2 / (а) =
_ _3D
~ 2Е
а
о
Определение остаточных напряжений
603
+ о (a) (h — а) .
(4)
Из уравнения (4) при а = 0 получим формулу для определения остаточных напряжений в наружном слое
а(0) =
4ЕЛ2 З/2
После дифференцирования по а равенства (4) имеем
Проинтегрировав обе части этого равенства, получим
(Л — о)2 (а) — 4 (й — a) f (а) 4-
+ 2 (0) =
О
Q/2
= ~£-[а(а) -о(О)].
С учетом соотношения (5) найдем, что остаточные напряжения на расстоянии а от верхней грани
(Л_й)2^.(а)_
° & = ж
а
— 4 (Л —а)/(а) Ч- 2 j о
Из соотношения (6) следует, что для определения остаточных напряжений необходимо знать не только прогиб в данный момент, но и проследить за изменением прогиба по мере увеличения толщины снятого слоя. Если тол-шина стравливаемого слоя мала в сравнении с толщиной образца (Л/а< < 15), то в соотношении (6) можно пренебречь последним членом и определять остаточные напряжения по равенству
° (а) =3^-[(Л —а)2 X
Х-^-(а)-4(Л-а)На)]. (7)
При h/a > 50 можно сохранить только первый член:
4F df
а(а) = 31Г(Л-а)21С (а). (8)
Формулы (7) и (8) часто используют при расчетах остаточных напряжений (обычно Л = 4-: 6 мм, а = 0,1 —0,3мм).
При вычислениях по формулам (6)— (8) необходимо учитывать правило знаков. Если значение о (а) оказывается положительным, то в слое действуют растягивающие остаточные напряжения. Прогиб f считают положительным, если он направлен в сторону снятого слоя (рис. 16).
На практике ост точные напряжения определяют с помощью специальных приборов. На рис. 17 показана схема прибора, который позволяет индукционным преобразователем и самописцем 2 типа БВ-662 непрерывно записывать прогиб f от времени прн стравливании поверхностных слоев образна 3.
Рис. 16. Схема прогиба стержня при снятии верхнего слоя: а — растягивающие напряжения; б — сжимающие напряжения
604
Технологические методы повышения долговечности
Рис. 17. Схема установки для определения остаточных напряжений
Поверхности, ие подвергающиеся травлению, покрывают воском. Образец закрепляют в держателе 4 с помощью тонких (упругих) пластинок 7, которые не препятствуют повороту его концевых сечений. Прогиб образца через наконечник ' и рычаг 6 передается на преобра;' .атель 1.
Для обеспечен’-! 7 равномерного травления электроду"" перемешивают. Скорость травлешг- образца определяют с помощью взвешивания образца до и после окончания травления. Обычно скорости травления составляют 1— 5 мкм/мин.
В зависимости от состава электролита напряжение на электродах колеблется в пределах 20—30 В, плотность тока 10—13А/дм2. Температура элек тролита 20—60 °C.
Электролит для тпавления образцов из углеродисты t сталей включает 80% фосфорной кислоты (Н3РО4), 15% серной кислоты (HjSOj) и 5% хромового ангидрида.
Для жаропрочных сплавов на никелевой основе используют электролит, содержащий 45% Н3РО4, 45% H2SO4 и 10% воды. Для титановых сплавов
используют электролит, включающий 50% азотной кислоты (HNO3), 10% плавиковой кислоты (HF) и 40% воды.
Особое внимание необходимо уделять вырезанию образца, чтобы избежать наведения дополнительных остаточных напряжений. Для этого часто применяют электроискровой метод, а также резку узким шлифовальным кругом с малой подачей и обильным охлаждением эмульсией.
Отметим некоторые особенности обработки результатов. Во многих практических задачах остаточные напряжения значительно изменяются в пределах поверхностных слоев (при толщине до 0,3 мм). В этом случае для получения надлежащей точности требуется последовательное удаление очень тонких слоев (травление с малой скоростью). Важным является достаточно точное вычисление величин, входящих в формулы (6)—(8).
Непосредственно из эксперимента получают графическую зависимость f (г), которая в условиях равномерного травления эквивалентна зависимости f (а). Требуется определить значения производной этой функции и интервала в расчетных течениях. С математической точки зрения это известная задача теории приближенных вычислений.
Для более точного вычисления производной кривую заменяют параболой, проходящей через три Заданные точки (рис. 18) с координатами аг_, ft-i", at, h’ai+i’fi+i Уравнение параболы вэтом случае имеет вид
f- (а-аг) (а-аг+1)
, « (а —аг-i) (J —a1+i) г (а; — a<-i) (а; — аг+О
, г (а —Qg-i) (a —at) !1'1 (а;+1 —аг-? (аг+1 — аг) ‘
Уравнение производной
df (а) , 2a — ai—ai+l
- }1~х +
(а( — о,_!) (at — ai+l)
। f. 2а ai-i — а,
Постановка задач технической диагностики
605
Рис. 19. График приближенного вычисления производной в начале координат
Рис. 18. График приближенного вычисле-вия производной
Если в соотношении (9) положим i=l, = а(! = 0, /ui = f0 = 0, то получим формулу для вычисления производной в начале координат (рис. 19)
df = /1 (2а — аг) , /2 (2а — gj da ' а, (а, — а2) а2 (а2 — at)
Соотношение для определения напряжения в поверхностном слое можно
получить из равенства (6) прн а = 0:
а(0)
-^LJL(0). 3? da 1 '
Для повышения точности измерения остаточных напряжений рекомендуется применять большие значения l!h (обычно Uh > 10).
Более подробно вопрос об определении остаточных напряжений в элементах конструкций рассмотрен в монографии [3J.
Глава 35
ОСНОВЫ ТЕОРИИ ТЕХНИЧЕСКОЙ ДИАГНОСТИКИ
Основная задача технической диагностики — распознавание состояния системы в условиях ограниченной информации. Информация поступает в виде показаний датчиков вибраций, температур, давлений, путем визуальных осмотров и т. д.
Для сложных технических систем запись параметров ведется дискретно или непрерывно.
Кроме того, в технической диагнос ике рассматриваются поиск и автоматический контроль неисправностей. Это связано с разработкой методов и средств контроля, разработкой диагностических тестов, сценкой контролеспособ-иости технических систем.
Техническая диагностика стала одним из важнейших методов повышения надежности систем в эксплуатационных условиях.
Она допускает эксплуатацию ответственных изделий и их техническое
обслуживание «по состоянию», что дает значительный экономический эффект.
Одной из важных особенностей технической диагностики является распознавание состояния в условиях ограниченной информации, когда требуется руководствоваться определенными приемами и правилами для принятия решения.
Ниже излагаются основы теории технической диагностики.
ПОСТАНОВКА ЗАДАЧ
ТЕХНИЧЕСКОЙ ДИАГНОСТИКИ
Состояние системы описывается совокупностью (множеством) определяющих ее параметров (признаков). Множество определяющих параметров (признаков) может быть различным для разных задач распозиаваиия.
606
Основы теории технической диагностики
Состояние системы часто описывается с помощью комплекса признаков
/С=(/Сх, /Са.... Kj....Kv), (1)
где признак Kj имеет И; разрядов.
Простой признак имеет два разряда (mi = 2), которые можно обозначать Kj и Kj (наличие или отсутствие признака) или любым двоичным символом: да, нет; двоичным числом и т. д. Например, признак «повышение температуры больше 20 °C» является двухразрядным.
Если признак имеет несколько диагностических интервалов, то его называют многоразрядным. Так, признак Kj может иметь три разряда (з зависимости от уровня повышения температуры):
\Т .... <10° 10“ —20° >20“
*.......... «Л «/2 Kj3
Во многих случаях систему удобно характеризовать совокупностью параметров — многомерным вектором
х — (xj, х2, .... Xj, .... xv). (2)
В большинстве случаев параметры Xj имеют непрерывное распределение. Например, параметром Xj можно считать «повышение температуры»
Xj — АТ.
Во многих методах диагностики должно быть известно распределение контрольного параметра для данного состояния системы. Описание системы с помощью дискретных величин (признаков) и непрерывных (параметров) зависит в первую очередь от объема располагаемой информации.
Распознавание состояния системы. Распознавание — процесс установления диагноза — состоит в отнесении предъявленной совокупности признаков к одному из типичных состояний. Число таких состояний зависит от особенностей задачи и целей распознавания. Часто требуется провести выбор одного из двух возможных состояний, например «исправное состояние» и «неисправное состояние». В других случаях необходимо конкретизировать неисправные состояния: «разрушение подшипника», «разрушение шлицевого соединения» и т. п.
Теория распозиаваиия тесио связана с проблемой распознавания образов, изучаемой в кибернетике.
Постановка задачи технической диагностики состоит в следующем.
Имеется техническая система, которая может находиться в одном из таких состояний (диагнозов). Известна совокупность признаков (параметров), характеризующих каждое состояние системы. Требуется построить решающее правило, с помощью которого предъявленный для распознавания объект (набор признаков) был бы отнесен к одному из диагнозов.
Имеются несколько основных методов решения задач распознавания: вероятностные; метрические; логические; методы разделения в пространстве признаков.
Ниже кратко изложены основы указанных методов. Более подробные сведения см. в работе [1].
ВЕРОЯТНОСТНЫЕ МЕТОДЫ РАСПОЗНАВАНИЯ
Метод Байеса. Метод, основанный на обобщенной формуле Байеса, является весьма эффективным, так как позволяет достаточно просто одновременно учитывать признаки различной физической природы — дискретные и непрерывные. Это достигается благодаря использованию единообразных и безразмерных характеристик признаков — частот встречаемости (вероятностей) признаков при различных состояниях.
Если имеется диагноз Dt и простой признак Kj, то вероятность совместного появления событий (наличие у объекта состояния О; и признака Kj)
Р (DjKj) = Р (D{) Р (Kj/Dt) —
- P(Kj)P(Di/Kj). (3)
Из последнего соотношения получим
Р (Dt/Kj) = Р (Dt) , (4)
где в последнем равенстве Р (Di/Kj) — вероятность диагноза Di после того, как стало известно наличие у рассматриваемого объекта признака Kj (апостериорная вероятность диагноза);
Вероятностные методы распознавания
607
Р (Di) — вероятность диагноза D{, определяемая по статистическим данным (априорная вероятность диагноза). Если обследовано К объектов и состояние Dt наблюдается в К,- изделиях, то /’(oi)«4L; (5)
P(Kj!Di)— вероятность появления Kj у объектов с состоянием D;. Если среди Ni объектов с диагнозом Di у появился признак К}, то
P(K;/O,-) = 4~: (6)
Р (Kj) — вероятность появления признака К; во всех объектах независимо от состояния (диагноза) объекта. Пусть из общего числа N признак Kj обнаружен у Nj объектов (с различным диагнозом!). Тогда
P(K>)=4L- (7)
Как будет ясно из дальнейшего, специальное вычисление не требуется.
Пусть проводится обследование ряда признаков К (Ki.... Ку) по v много-
разрядным признакам и К* означает определенную реализацию комплекса признаков. При этом в каждом из признаков Kj появляется один из разрядов, иапример в признаке Kj разряд р:
Kj = KjP.
Обобщенная формула Байеса (для комплекса многоразрядных признаков)
Р (Di/K*) = Р (Dt)
(i=l, 2, п). (8)
Здесь Р (Di/K*) — вероятность диагноза D{, если комплекс признаков К получил реализацию К*-
Формула (8) относится к любому из га состояний. Предполагается, что система находится в одном (и только в одном) из указанных состояний и потому
^P(DS) = 1. (9)
5=1
Вероятность появления комплекса признаков по формуле полной вероят
ности (комплекс признаков проявляется обязательно с одним из диагнозов)
Р (К*) = Р (Dt) Р (К*/Ог) + • • + + Р (Dn) Р (K*/Dn) = = £ Р (°s) Р (K*/Ds). (10)
5=1
Теперь формула Байеса может быть представлена в окончательном виде P(Di/K<)== ^i)P^/Di)_
£ Р (Dg) Р (K*/Dg) 5=1
(Н)
Если комплекс признаков содержит v признаков, то
P(K-/Di) = P(K*l/Di)P(K^/K-iDi)...
...P(K*vlK'iK'2...K'v^Dl)^ (12)
где K'j = К/p — разряд признака Kj, выявившийся после обследования.
Для независимых признаков
Р (K'/D/) = Р X
xP(K2-/oz)...P(K;/nz). (13)
Если при данном диагнозе О; некоторые признаки, например Ki и Кг, оказываются зависимыми, то
Р (К]K'2/Di) Ф Р (K*/Dt) Р (К*2/Di).
(14)
Тогда в равенство (13) вместо произведения двух первых членов следует внести
PW/D^P (Kl/DM) = Р (K\K*2/Di).
(15)
В большинстве практических задач, особенно при большом числе признаков, можно принимать условие независимости признаков даже при наличии существенных корреляционных связей.
Диагностическая матрица. Для определения вероятности диагноза (состояния) следует составить диагностическую матрицу (таблицу).
608
Основы теории технической диагностики
Диагностическая матрица для многоразрядных признаков
D . Dj К1 К, Ку = Ху
сГ сГ еч о. о“ со й. сГ й а. сГ «ч й. сГ со й. о* а «4 й. и? •Ч» оГ й.
0,8 0.2 0 0.1 0.1 0.6 0,2 0,15
D, 0.1 0.7 0,2 0 0 0,3 0." 0,12
Г>п •у -.л
В ней помещаются условные вероятности признаков и априорные вероятности диагнозов.
Рассмотрим применение метода Байеса прн наличии диагностических пара-метровху, распределенных непрерывно. Тогда для каждого из диагнозов D; должна быть известна плотность распределения f (XjtDi). Если для данного объекта получили значение х*, то вероятность появления xj в интервале Л, содержащем точку х*, будет равна / д.
Величина Д будет в числителе и знаменателе выражения (11) и не повлияет на результат. Для учета непрерывного признака в диагностической матрице должны содержаться плотности вероятности. В практических задачах часто используют нормальное распределение, для которого плотность вероятности задается двумя параметрами — средним значением и средним квадратическим отклонением.
В диагностической матрице для признака K.j указаны параметры соответствующего нормального распределения. Тогда при использовании формулы Байеса следует принять
P(K./D0 = f(X/.A) =
1 25*
-----. (16) Si |/2л
Таким образом, метод Байеса можно применять и в том случае, когда часть из параметров задана с помощью непрерывного распределения.
В некоторых случаях оказывается удобным провести замену непрерывного распределения многоразрядным признаком, что не изменяет общего метода расчета.
Решающее правило. Предъявленный для распознавания объект, обладающий комплексом признаков К*, считают принадлежащим диагнозу Dt, если
Р (Dt/K*) = max, (17)
т. е. вероятность диагноза Di оказалась наибольшей.
Сумма вероятностей всех диагнозов
£ P(DS/K*)=1. 5=1
Однако если вероятность Р не слишком велика (например, меньше 0,4—0,5), то следует отказаться от постановки диагноза. Поэтому решающее правило можно сформулировать следующим образом:
К* € Di, если Р (D{/K*) = max, Р (Dt/К*) > Pi,
где Pt — пороговое значение для диагноза Dt (обычно принимают Pi 0,9).
Вероятностные методы распознавания
609
Пример. Пусть при наблюдении за газотурбинным двигателем проверяют два признака: К,— повышение температуры газа за турбиной более чем на 50 °C и К2— увеличение времени выхода на максимальную частоту вращения более чем на 5 с.
Предположим, что для данного типа двигателей появление этих признаков связано либо с неисправностью топливного регулятора (состояние Dj), либо с увеличением радиального зазора в турбине (состояние D2). При нормальном состоянии двигателя (состояние £)3) признак Ki не наблюдается, а признак Кг наблюдается в 5% случаев. На основании статистических данных известно, что 80% двигателей вырабатывают ресурс в нормальном состоянии, 5% двигателей имеют состояние D3 и 15% — состояние О2. Известно также, что признак Кг встречается при состоянии Dj в 20%, а при состоянии О2 — в 40% случаев; признак Кг при состоянии Dr встречается в 30% , а при состоянии О2— в 50% случаев. Сведем все эти данные в таблицу:
Dt P (Kt/Dt) P(Kt/Di) P(Di)
Dt 0,2 0.3 0,05
Dt 0,4 0,5 0,15
Da 0 0.05 0,80
Найдем сначала вероятность состояний двигателя, когда обнаружены оба признака: Ki и К2- Для этого, считая признаки Ki и K2 независимыми, примем формулы (11), (13):
Р (Dr/КгКг) =
_ 0,05-0,2.0,3
0,05.0,2.0,3+ - 0.09;
+ 0,15-0,4-0,5+0,8-0-0,05 аналогично получим
Р (D2/KiK2) = 0,91;
Р ЦУКгКг) = 0.
Определим вероятность состояний двигателя, если обследование показало, что при отсутствии признака Ki признак Кг наблюдается. Отсутствие признака Кг есть признак наличия
20 Заказ № 402
Ki (противоположное событие), причем P(KilDi) = l-P(Ki/Di).
Для расчета применяют также формулу (11), но значения P^K*/D^ заменяют иа Р (KjDi). Получим
Р (Dr/КгКг) =
- 0,05-0,8-0,3
0,05-0,8-0,3 +
+ 0,15-0,6-0,5 + 0,8-1-0,05 и аналогично
Р (D2/KiK2) = 0,47;
P(D3/KiK2) = 0,41.
Вычислим вероятности состояний в том случае, когда оба признака отсутствуют:
Р (Dr/КгКг) =
0,05-0,8-0,7 _
0,05-0,8-0,7+ °' ’
+ 0,15-0,6-0,5 + 0,8-1-0,95
Р (D2/K3K2) = 0,05;
Р (Ог/К^Кг) = 0,92.
Вероятности состояний Dr и D2 отличны от нуля, так как рассматриваемые признаки не являются детерминирующими.
Из приведенных расчетов можно установить, что при наличии Ki и Кг в двигателе с вероятностью 0,91 имеется состояние D2> т. е. увеличение радиального зазора. При отсутствии обоих признаков наиболее вероятно нормальное состояние (вероятность 0,92). При отсутствии признака Ki и наличии признака К2 вероятности состояний D2 и D3 примерно одинаковы (0,47 и 0,41) И для уточнения состояния двигателя требуется проведение дополнительных обследований.
Преимущества и недостатки метода Байеса. Некоторые преимущества метода Байеса указывались ранее. Главное из них — возможность оценки вероятности всех состояний системы на основании использования широкого набора признаков различной природы.
Основной недостаток метода Байеса — необходимость получения боль
610
Основы теории технической диагностики
шой предварительной информаций (составление диагностической матрицы).
Применению метода Байеса должна предшествовать статистическая обработка данных эксплуатации и в некоторых случаях специальные исследования, имитирующие неисправности (например, изменение вибраций двигателя, собранного с дефектной лопаткой и т. п.).
Другой недостаток метода Байеса — «угнетение» редких диагнозов.
Так как решение зависит от Р (D;) — априорной вероятности диагноза, то прн малых значениях Р (Dt) должна быть очень большая вероятность данной реализации комплекса признаков.
Это объясняется тем, что в основной расчетной формуле (11) в качестве множителя стоит Р (Di), и потому данная реализация комплекса признаков для редкого диагноза должна иметь очень высокую вероятность Р (K*/Dt) и малую — при других диагнозах, чтобы величина Р (D ilK*) оказалась наибольшей.
Для компенсации этого недостатка проводят расчет, предполагая все априорные вероятности диагнозов одинаковыми:
Р (DJ = ...=Р (Dn) = -1-.
Это позволяет выяснить, для какого состояния наиболее характерна рассматриваемая реализация комплекса признаков.
МЕТОДЫ СТАТИСТИЧЕСКИХ РЕШЕНИЙ
Метод минимального риска. Этот метод был развит в связи с задачами радиолокации, но может вполне успешно использоваться в задачах технической диагностики.
Пусть проводится измерение параметра х (например, уровня вибраций изделия) и на основании данных измерений требуется сделать вывод о возможности продолжения эксплуатации (диагноз Dr — исправное состояние) или о направлении изделия в ремонт (диагноз D2 — неисправное состояние).
На рис. 1 даны значения плотности
вероятности диагностического параметра х для двух состояний.
Пусть установлена контрольная норма для уровня вибраций хв.
В соответствии с этой нормой принимают:
x<zx0 x£Di — исправное состояние; ] х>х0 xPD?—неисправное состояние. / (18) Знак £ означает, что объект с уровнем вибраций х относят к данному состоянию.
Из рис. 1 следует, что любой выбор величины х0 связан с определенным риском, так как кривые и пересекаются.
Существуют два вида риска: риск «ложной тревоги», когда исправное изделие признают неисправным, и риск «пропуска цели», когда неисправное изделие считают годным.
В теории статистического контроля их называют риском поставщика и риском прнемщнка или ошибками первого и второго рода.
При данном х0 вероятность ложной тревоги со
а — J Л (x)dx (19)
и вероятность пропуска цели
Хо
р = j /2 (*)dx. (20)
Задача теории статистических решений состоит в выборе оптимального значения х0.
По способу минимального риска рассматривается общая стоимость риска
00
R = ^21? (£*1) J fl (х) dx 4-
Х0
+ С12Р (D2) | /2 (х) dxt (21)
—сю
где C2i — «цена» ложной тревоги; С12 — «цена» пропуска цели; Р (Di) и Р (D2) — априорные вероятности диагнозов (состояний), определяемые по предвари-
Методы статистических решений
611
Рис.
1. Плотность вероятности диагностического признака
тельным статистическим данным. Величина R представляет собой «среднее значение» потери при ошибочном решении.
Из необходимого условия минимума
" — —C2iP (Pt) f 1 (Хо)
+ CiP (Р2) /г (хо) = 0 (22)
получаем
/1 (хо) _ СцР (Р2)
М*о) ~
Можно показать, что для одномодальных распределений условие (23) всегда обеспечивает минимум величины R. Если стоимость ошибочных решений одинакова, то
/1 (*о) _ Р Рз) /2(Хо) ~ Р (Pi) •
(24)
Последнее соотношение минимизирует общее число ошибочных решений. Оно вытекает также из метода Байеса.
Метод Неймана—Пирсона. В этом методе исходят из условия минимума вероятности пропуска дефекта при допустимом уровне вероятности ложной тревоги.
Таким образом, вероятность ложной тревоги
ОО j fi(x)dx^a, *0
(25)
где а — допустимый уровень ложной тревоги.
20»
В рассматриваемых однопараметрических задачах минимум вероятности пропуска цели достигается при
СО
j ft (х) dx = а. (26)
Последнее условие и определяет граничное значение параметра (значение Хо).
При назначении величины а учитывают следующее:
1) число снимаемых с эксплуатации изделий должно превышать ожидаемое число дефектных изделий в силу неизбежных погрешностей метода оценки состояния;
2) принимаемое значение ложной тревоги не должно, без крайней необходимости, нарушать нормальную эксплуатацию или приводить к большим экономическим потерям.
В практических задачах можно принимать
a = kP(D2), (2 7)
где k — коэффициент избыточности.
При дефектах с ограняченными последствиями принимают
k = 14-3.
При опасных дефектах
k = 34-10.
Можно использовать другой подход — определять х0 исходя из выбранного уровня пропуска дефекта. Тогда
х
J /2 (х) dx — Ь, (28) —оо
612
Основы теории технической диагностики
причем можно принимать
*Ь
(DO j fi(*)d*4-
kN ’
где k — коэффициент избыточности (k == 1-4-10); N — общее число изделий, находящихся в эксплуатации. Во всех случаях b < 0,05, чтобы вероятность пропуска дефекта была пренебрежимо малой.
МЕТОДЫ СТАТИСТИЧЕСКИХ РЕШЕНИЙ ПРИ НАЛИЧИИ
ЗОНЫ НЕОПРЕДЕЛЕННОСТИ
Правило решения. В тех случаях, когда стоимость ошибок пропуска цели и ложной тревоги очень высока, можно уменьшить риск с помощью введения зоны неопределенности.
Правило решения будет теперь таким (рис. 2):
х ха x^D^, | х > хь xgD2, /
*а < х < хь — отказ от распознавания (зона неопределенности).
Разумеется, отказ от распознавания может иметь нежелательные последствия. Он означает, что для принятия решения необходима дополнительная информация (осмотр, измерения и т. п.).
Метод минимального риска. Общая стоимость риска выражав! ся равенст-
вом
хь
+ Р (D2) j /2 (X) dx
(30)
где Со — цена отказа от распознавания. Необходимые условия минимума:
— = Cl2P (D2) f2 (ха) —
- Со [Р (D0 Л (хо) -Ь Р (D2)f2 (ха)] = 0; дхь ~= —С21Р (О1)/1(хь)4-С0[Р(О1) X X f 1 (хь) -I- Р (О2) f2 (Xi)] ~ 0.
Из последних уравнений следует:
f 1 (Xg)_____(Ci2_-^Co)jP_(D2)_ .
/2 (ха) CaP (Di)
fl (xfe)______C0P (P2) /0 ,,
/2 (хь) ~ (C21 - Co) P (DO • ' >
Если стоимость отказа or распознавания Co = 0, то
ха -> 00, хь оо
и зона отказа занимает всю область.
Система распознавания в этом случае выключается из работы, что минимизирует риск (потери за отказ от распозна-
/? = С21р (DO j Л (х) dx + хь
Рнс. 2. Принятие решений прн наличии зоны неопределенности
Метрические методы распознавания
613
МЕТРИЧЕСКИЕ МЕТОДЫ РАСПОЗНАВАНИЯ
Пространство признаков. Метрические методы связаны с измерением расстояний в пространстве признаков.
Будем характеризовать состояние системы (изделия) вектором параметров
х = (хь х2, хт). (32)
Компоненты вектора х могут быть непрерывными или дискретными величинами. В последнем случае х,- представляет собой многоразрядный диагностический признак.
Каждое состояние изделия в соответствии с равенством (32) может быть представлено точкой в пространстве признаков, а вектор х соединяет эту точку с началом координат. Предполагается, что точки с одним и тем же состоянием (диагнозом) группируются в компактной области пространства признаков («гипотеза компактности»).
Метод эталонов. Допустим, что имеется п, образцов с диагнозом D-(рис. 3). Они образуют обучающую последовательность. Точки, входящие в области диагнозов, обычно располагаются более плотно в центральной части области.
Примем в качестве «типичного» изделия с данным диагнозом «среднюю точку», которую назовем эталоном.
Координаты эталона i-го диагноза
ni
а.. = 1 V а (/=1,2,,.., /п),
1 ГН ——
S 1
(33) где aijs — значение параметра х?- для образца S, принадлежащего диагнозу
Пусть предъявлено для распознавания изделие, характеризующееся вектором х в пространстве признаков.
Решение вопроса об отнесении изделия к диагнозу Dj связано с намерением расстояния до эталонов.
Решающее правило. Принимается по минимальному расстоянию до эталона:
h= ^mln> х £ Di, (34)
Рис. 3. Область диагнозов (состояний) в пространстве признаков
т. е. если точка х ближе всего к эталону диагноза £>;, то вывод делается в пользу диагноза Е>е.
Расстояния до i-го эталона
( т ") Т
= • (35)
Предыдущие равенства определяют обычное евклидово расстояние.
В задачах диагностики часто оказывается целесообразным использовать обобщенные расстояния порядка v
1
( т Л —
'« = { Е 1-и-“оГ [ • (36) (/=1 )
При v = 1 получается расстояние по Хемингу, при v = 2 — обычное расстояние.
При возрастании v увеличивается роль наибольшего отклонения по какой-либо координате.
Расстояние (35) и (36) можно использовать для однородного, изотропного пространства признаков. Таким пространством будет пространство простых (двухразрядных) признаков, кодируемых двоичными числами (0,1).
Однако в задачах технической диагностики часто приходится использовать признаки различной физической природы (например, уровень вибрационных перегрузок и повышение температуры), имеющих различную размерность.
Для учета указанного обстоятельства целесообразно ввести безразмерные расстояния. Например, по координате (направлению) xj для точек х и а!
614
Основы теории технической диагностики
безразмерное расстояние можно принять в виде
*J — аИ аИ
(37)
где Qij — среднее квадратическое отклонение признака Xj для диагноза Dt.
Условие (37) содержит предположение, что для диагностики отклонение следует относить к «характерному масштабу» — среднему квадратическому отклонению. Далее следует учесть различную диагностическую ценность признаков. Для этого введем безразмерные диагностические коэффициенты Cij, и тогда с помощью равенства (36) получим
Последние соотношения дают формулы для расстояний в неоднородном, неизотропном пространстве.
Определение коэффициентов Cij вызывает известные трудности. В первом приближении для признака Xj, имеющего mj диагностических интервалов, можно принять, что величина Cij совпадает с диагностической ценностью признака:
т
= £ Р (Xjs/Di) х $=1
Р (xi4/D.)
X 10g^-4-7^T-> (39)
Г \XjS)
где Р (Xjg/D.) — вероятность интервала S признака Xj для диагноза (состояния) D;; Р (xJS) — вероятность этого интервала для всех состояний.
В тех случаях, когда отсутствуют статистические сведения, величины Cij можно назначать с помощью экспертных оценок или подбирать по опыту диагностики.
Метод минимального расстояния до множества. В этом методе учитывается минимальное расстояние до образцов, входящих в обучающую последовательность.
На рис. 4 показаны расстояния ll mm и h-
Рис. 4. Метод минимального расстояния до множества
Решающее правило имеет вид
Ц min = min *€ Di• (4°)
—>
т. e. если точка x ближе всего к одной из точек обучающей последовательности диагноза Di, то оиа относится к этому диагнозу.
Метод минимального расстояния до множества представляет собой диагностику «по прецеденту», т. е. образцу (изделию), наиболее близко напоминающему объект, предъявленный для распознавания.
Дополнение к решающему правилу в метрических методах. Метрические методы распознавания в отличие от вероятностных основаны на детерминистском подходе. Решающее правило устанавливает диагноз, считая его достоверным.
Обучающая последовательность, как уже указывалось ранее, составляется из образцов (изделий), для которых достоверно известен диагноз.
Смысл задачи распознавания: если минимальное расстояние до эталона диагноза Di мало отличается от других расстояний, то достоверность диагноза Dj вызывает сомнения.
Введем условные «вероятности» диагнозов
1
Рг=-—^--------, (41)
*=1
где I), — расстояние до эталона диагноза Dfe.
Решение в пользу диагноза £>г принимается в случае, если
Pi = Pio,
Метод разделения в пространстве признаков
615
где Pio — уровень принятия решения для ;-го диагноза (обычно Рю > 0,8).
Такой способ сближает вероятностные и детерминистские методы распознавания. Применение метрических методов возможно и в том случае, когда области диагнозов пересекаются.
МЕТОД РАЗДЕЛЕНИЯ
В ПРОСТРАНСТВЕ ПРИЗНАКОВ
Разделяющая функция и решающее правило. Как и в метрических методах распознавания, состояние изделия характеризуется точкой в пространстве признаков.
Предполагается, что области диагнозов не пересекаются и поэтому возможно построить разделяющую поверхность.
Рассмотрим распознавание двух состояний Dj и £>2 (дифференциальная диагностика или дихотомия).
При наличии нескольких диагнозов распознавание может быть сведено к последовательному применению рассматриваемой процедуры.
В основе методов разделения лежит построение скалярной функции параметров (признаков)
}(хъ х2, .... хт)=/(х), (42)
принимающей различные знаки в двух областях диагноза.
Такую функцию называют разделяющей, и тогда
/ (х) > 0 при xEDi; 1
/ (х) < 0 при xgD2. J
Таким образом, разделяющая функция имеет положительное значение для всех изделий, имеющих состояние Di, и отрицательное значение — в противоположном случае.
Условие (43) образует решающее правило для разделения в пространстве признаков.
Если для предъявленного для распознавания объекта, характеризующегося вектором х, значение / (х) положительно, объект считают принадлежащим состоянию Dlt при отрицательном значении f (х) — состоянию
Рнс. 5. Линия, разделяющая функции для двух диагнозов
Уравнение
f (х) = 0 (44)
будет составлять уравнение разделяющей поверхности (поверхности, разделяющей области диагнозов).
Наиболее простой вид имеет линейная разделяющая функция
f (*) == 4” + • • • +
4“ ^тхт 4“ ^m+h' 05)
где т — число признаков (размерность пространства); Хь Х2, ..., Хт— «весовые» коэффициенты.
Разделяющая поверхность будет гиперплоскостью («плоскостью» в многомерном пространстве)
f (х) = 4~ Х2х2 4~ • • • 4~
4- ^-тхт 4~ ^т+1 — 0- (46)
Для случая двух признаков (параметров) разделяющая плоскость будет разделяющей прямой (рис. 5).
Для удобства геометрической интерпретации введем формально еще один параметр
xm+i = 1 07)
Разделяющая функция может быть теперь представлена в виде скалярного произведения
f (х) — ^ixi +- 4- Xvxv +
4- 7-v+ixv+i — Хх, (48)
где X — «весовой» вектор,
X = (X,, Х2, ...» Хт+1). (49)
616
Основы теории технической диагностики
Решающее правило будет таким:
если Хх > О, то x£Di, если Хх < О, то x£D2.
(50)
Уравнение разделяющей гиперплоскости
f(7) = xZ=0. (51)
Из последнего равенства следует, что разделяющая гиперповерхность перпендикулярна к «весовому» вектору и проходит через начало координат (в дополненном пространстве признаков размерности т + 1).
Чтобы осуществить диагностику с помощью линейной разделяющей функции, достаточно знать компоненты весового вектора.
Приближенный способ определения весового вектора. Для построения весового вектора (нахождения коэффициентов X;) используют объекты (изделия) с установленными состояниями и £>2 (обучающие последовательности).
Средние (эталонные) образцы харак-
теризуются векторами и а2, причем компоненты векторов
аов;
a2iS.
(52)
где aij, a2j — значения признака (параметра) xi для образцов, имеющих состояния и D2, /ij и h2 — число образцов, входящих в обучающие последовательности для диагнозов Dv и D2, S — индекс образцов.
Примем, что разделяющая плоскость проходит через точку, находящуюся на середине прямой, соединяющей точки эталонов (точку А, рис. 6), перпендикулярно к этой прямой.
Так как точка А характеризуется вектором 1/2 (at + a2), то уравнение разделяющей плоскости будет
/ (*) = [* 0,5 (<Zj -|- а2)] (а^ — а2) ~ 0.
(53)
Рис. 6. Приближенный способ построения разделяющей гиперплоскости
Скалярное произведение вектора, лежащего в разделяющей плоскости, и вектора, нормального к ней, обращается в нуль.
Развертывая уравнение (53), находим
fx = (all — a21) *1 + '' • + (alm —
- a2m) xm + °’5 (al - aD = °’ (54) где и al — квадраты длины векторов ar и a2.
Сопоставляя равенства (54) и (46), находим составляющие весового вектора:
Л1 = аи — a2i» ~ ai8 — а22>
= aim а.2т\
M>=Ma?-a2)- (55)
Последние соотношения устанавливают приближенные значения компонентов весового вектора.
Определение весового вектора методом последовательных приближений. Предполагают, что имеется обучающая последовательность, в которой содержатся сведения об образцах с диагнозами состояний и D2.
Принимают первое приближение для весового вектора Х<п, например, с помощью равенств (52) или каким-либо другим (произвольным) образом.
Выбирают произвольно образец из обучающей последовательности, которому приписывают условно первый номер х(1); он может иметь состояние Dt или D2. Величину Х<1; «испытывают» по отношению к х<1), т. е. определяют
Логические методы распознавания
617
Если распознавание х<1; произошло с ошибкой, то значение X<i; корректируют.
Принимают следующее приближение:
Х^^Х^-фх^’,
если x(1,€Di, ио Х(1,х(1) <0;
(56)
Х<2> =Х<!> — х'1’,
если х<1; ио Х<1,х<1)>0.
При неправильных ответах к Хл1’ прибавляется или вычитается вектор точки, относительно которой совершена ошибка. Если с помощью XX1’ распознавание вектора х(1) было правильным:
при x<‘»GOi Х<1,х<1’>0;
при х<1,СО2 Х‘1,х<1,<0,
то сохраняется прежнее значение
Х<2> = Х<‘>
и предъявляется следующий образец х<2>.
Если линейное разделение возможно, то указанный процесс приводит к нахождению вектора X за конечное число шагов.
Однако разделение областей диагноза гиперплоскостью не всегда возможно. На рис. 7 приведен такой случай. Если области диагнозов являются выпуклыми (т. е. отрезок, соединяющий любые две точки области, лежит внутри нее) и иепересекающи-мися, то линейное разделение осуществимо.
Рис. 7. Случай, когда невозможно разделение областей диагнозов с помощью гиперплоскости
Приведенное условие образует достаточный признак линейной разделимости. Область диагноза £)2 иа рис. 7 не принадлежит к выпуклым, и достаточное условие не удовлетворяется. Однако признак не является необходимым, так как если «раздвинуть» области диагнозов иа рис. 7, то окажется возможным разделение гиперплоскостью. Укажем теперь необходимый и достаточный признак линейной разделимости. Она возможна, если существует хотя бы одно направление, на котором проекции областей диагнозов не пересекаются.
Линейные методы разделения не могут быть использованы, если области диагнозов имеют сложные и близко расположенные границы (рис. 7).
Более эффективными, но и более сложными являются методы потенциальных функций и методы стохастической аппроксимации, в которых разделяющую функцию принимают в более общем виде
f (*) = Х1ф1 (х) -|- Х2ф2 (х) + ..., где ф! (х), ф2 (х) — функции параметров (признаков).
В более сложных случаях приходится использовать преобразования признаков, указанные в связи с рассмотрением метрических методов распознавания.
ЛОГИЧЕСКИЕ МЕТОДЫ РАСПОЗНАВАНИЯ
Эти методы основаны на установлении логических связей между признаками и состоянием объектов.
В связи с этим рассматривают только простые (двоичные) признаки, для которых возможно только два значения (0 или 1, «да» — «нет» и т. п.).
Точно так же и сами состояния изделия (диагнозы) могут либо быть, либо отсутствовать, т. е. иметь только два значения. Это типично для детерминистского подхода, когда вероятности состояния не рассматриваются.
Вместе с тем использование двоичных переменных для описания признаков и состояний изделия позволяет применить логические переменные и булев
618
Основы автоматизированного проектирования
ские функции, методы математической логики.
Естественно, что детерминистское описание с помощью двоичных переменных является приближенной моделью диагностики. Одиако они могут
быть использованы для начальных этапов распознавания и особенно перспективны для второго направления технической диагностики — поиска и локализации неисправностей.
Глава 36
ОСНОВЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ
Широкое внедрение электронных вычислительных машин (ЭВМ), быстрое совершенствование их параметров оказывает все возрастающее влияние иа современную науку и технику. Существенно расширились возможности решения задач вычислительного характера (сложных задач математической физики, построения математических моделей процессов и т. д.). Коренные изменения произошли в прикладной математике и других областях знаний, возникли новые эффективные методы численных решений (метод конечных элементов и др.). Современные ЭВМ позволяют решать логические задачи (оптимального управления, распознавания образов, постановки диагноза и т. п.). Широкое распространение получили станки с программным управлением, существенно увеличивающие производительность труда; автоматические устройства, роботы и др. Будущее развитие техники связано с автоматизированным производством, основанным на широком использовании ЭВМ.
СТРУКТУРА АВТОМАТИЗИРОВАННОГО ПРОИЗВОДСТВА
Автоматизированным (машинным) производством будем называть производство с помощью электронных вычислительных машин. При этом главные решения все же остаются за коллективом специалистов, руководящим автоматизированной системой.
Производство современных машии разбивается на четыре последовательных, взаимосвязанных этапа: проектирование, коиструироваиие, изготовление и испытание. Если иа каждом из
этапов предусматривается широкое внедрение ЭВМ, то следует говорить об автоматизированном проектировании, автоматизированной технологии и т. д. Общая схема автоматизированного производства показана на рис. 1.
Автоматизированное проектирование представляет собой оптимальное проектирование путем синтеза математических моделей. Оптимальное проектирование подразумевает отыскание иаилучшего, в определенном смысле, варианта проекта. В результате автоматизированного проектирования создается эскизный проект изделия, содержащий его основные параметры, характеристики, скелетную схему конструкции, и математическая модель изделия.
Автоматизированное конструирование осуществляет оптимальный синтез конструктивных элементов с помощью ЭВМ. При конструировании за основу принимают скелетную схему конструкции, полученную на этапе автоматизированного проектирования. Схему дополняют конструктивной и технологической разработкой отдельных элементов (соединительных и переходных элементов, уплотнений), определяют размеры, допуски, посадки и т. п.
В результате автоматизированного конструирования выпускается техническая документация, необходимая дли технологической подготовки производства. Техническая документация содержит чертежи, получаемые на чертежных автоматах по разработанным программам, и технические условия (условия сборки, контроля и т. п.). В производство передается «машинный образ» конструкции в виде пакета программ, содержащий необходимую информацию для изготовления изделия.
Структура математической модели
619
Рис *. Общая схема автоматизированного производства
Автоматизированная технология представляет собой оптимальную технологию, осуществляемую с помощью ЭВМ. На этом этапе разрабатывают оптимальный технологический процесс (выбирают оборудование, инструмент, оснастку, режимы обработки и т. п.). Создают программы для станков, информационных и управляющих систем производства и т. д.
Автоматизированные испытания состоят в экспериментальном подтверждении параметров математической модели. На этом этапе разрабатывают оптимальный план доводочных испытаний, способы идентификации (определения) параметров моделей по данным опыта.
Особенностью автоматизированных испытаний является не только проведение эксперимента с реальным изделием, но и с его математической моделью. Во втором случае оказывается возможным оценить поведение элемента, узла и всей машины в целом при различных внешних условиях, нагрузках и т. п. Это позволяет более полно определить надежность системы, выбрать систему диагностики и т. д.
Ограничимся рассмотрением проблем автоматизированного (машинного) проектирования.
СТРУКТУРА МАТЕМАТИЧЕСКОЙ МОДЕЛИ
Математической моделью условимся называть совокупность уравнений, условий и ограничений, описывающих функционирование элемента, узла или всей машины в целом.
Общая модель должна отражать следующие основные факторы:
1) работоспособность (взаимодействие с внешней средой и другими элементами);
2) энергетический баланс, коэффициенты полезного действия;
3) надежность (запасы прочности, долговечность и др.);
4) экономическую эффективность (стоимость производства и эксплуатации, технологичность и др.).
Общая модель обычно содержит частные подмодели, отражающие отдельные факторы функционирования системы. Структурная схема математической модели (в системе автоматизированного проектирования) показана на рис. 2.
Модель осуществляет преобразование входных параметров, отражающих условия нагружения, среды и т. д., в параметры выхода, характеризующие процессы и состояние самой системы.
Например, при расчете лопатки газовой турбины в качестве входных параметров используют частоту вращения ротора, давление, скорость, температуру и расход газа на входе в турбину, радиусы корневого и концевого сечения и др. Параметры выхода включают показатели, характеризующие состояние газа на выходе из турбины, напряжения и температуру в лопатке, геометрию профилей сечения лопатки на различных радиусах и т. д.
Блоки преобразования содержат блоки и модули, каждый из которых осуществляет физически определенную часть преобразования (например, расчет напряжений в лопатке и т. п.).
Входные параметры подразделяют иа заданные (приходящие из модели более общей системы) и управляющие. Именно управляющие или внутренние параметры позволяют осуществить процесс оптимизации. Последний реализуется с помощью блока внутренней оптимизации. В этом блоке содержатся наиболее простые и универсальные условия оптимизации (минимум массы, максимум коэффициента полезного дей-
620
Основы автоматизированного проектирования
Рис 2. Структура математической модели
ствия), позволяющие достичь локального оптимума. Важную роль играет блок ограничений, устанавливающий область возможных значений управляющих и выходных параметров.
Модель содержит банк данных, хранящий необходимую для работы информацию, и блок управления. Последний позволяет воздействовать на упрочняющие параметры, осуществлять переключение вариантов и др, В модели предусмотрен блок визуализации, с помощью которого формируются изображения и графическая информация. Все блоки модели связаны между собой, сама модель может являться частью более сложной модели.
Работа модели осуществляется по принципу последовательных приближений. Сначала принимают начальные значения управляющих параметров Они вместе с заданными поступают в блок преобразований, где формируются параметры выхода. Выходные параметры направляются в блоки оптимизации и ограничений, в которых вырабатываются указания об изменении исходных значений управляющих параметров. Далее переходят к следующему приближению, причем циклы продолжаются до завершения процесса оптимизации.
Окончательные результаты поступают в банк данных и на вход следующих моделей системы.
УРОВНИ И КЛАССЫ МОДЕЛЕЙ
В процессе автоматизированного проектирования создается большое число математических моделей отдельных процессов, элементов, узлов и т. п. Будем различать уровни и классы моделей.
Уровень модели характеризует ее «качество» — степень глубины и полноты отображения связей, существующих между параметрами входа и выхода.
Различают модели нулевого, первого, второго и более высоких уровней. Разделение на уровни является условным и зависит от назначения, структуры модели, требований точности и других факторов. Часто используют модели следующих уровней: нулевого — модели, основанные на статистической обработке параметров предшествующих или аналогичных изделий; первого — модели, использующие простейшие одномерные теории при ряде упрощающих предположений; второго — модели, включающие все инженерные расчеты, проводимые для рас
Создание систем автоматизированного проектирования
621
сматриваемого элемента, узла и т. п.; третьего — сложные модели, использующие двухмерные и трехмерные теории, специальные численные методы типа метода конечных элементов и т. п.
В системе автоматизированного проектирования целесообразно использовать модели нескольких уровней: более простые модели для предварительного отбора вариантов, более сложные — для формирования окончательной математической модели.
А пасс модели — определяется ее «объемом», т. е. числом элементов, узлов и т. д., функционирование которых описывает модель. Часто оказывается удобным разбиение на три класса моделей: А — изделия; Б — узла; В — элемента.
Например, если класс А представляет собой модель всего двигателя, то модели класса Б — модели компрессора, турбины и т, д., класса В — модели лопаток и т. д. При необходимости могут быть введены подклассы для автономного описания отдельных частей системы.
ОБЩИЕ ПРИНЦИПЫ СОЗДАНИЯ СИСТЕМ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ
При создании систем автоматизированного проектирования целесообразно использовать следующие общие принципы: 1) блочно-модульный; 2) иерархии; 3) адаптации и развития; 4) информационного единства; 5) итерации.
Блочно-модульный принцип построения основан на том, что система создается из отдельных самостоятельных частей блоков и модулей.
Блоком системы автоматизированного проектирования называют часть системы, имеющую функциональную определенность (например, блок ограничений, блок газодинамического расчета и т. п.).
Модули — это наименьшие структурные элементы блока (для определения растягивающих напряжений, расчета крутящего момента и т. п.). Каждый из блоков системы выполняет определенные задачи, имеет свою входную и выходную информацию, составляется и доводится отдельно и только после
этого включается в систему автоматизированного проектирования. Среди блоков системы следует выделить стандартные (например, блок решения систем уравнений, блок плоской задачи теории упругости). Стандартные блоки инвариантны по отношению к элементам и узлам изделия и включаются в математические модели как стандартные элементы. При формировании стандартных блоков широко используют библиотеку , стандартных программ. Применение блочно-модульного принципа необходимо, так как попытки создания системы всей «сразу» всегда заканчивались неудачей.
Принцип иерархии моделей состоит в том, что каждая математическая модель включается как составная часть в модель более высокого класса. Например, математическая модель элемента входит в модель узла, которая, в свою очередь, включается в модель изделия.
Принцип иерархии отражает соотношения «старшинства» в любой сложной системе.
По принципу адаптации и развития система автоматизированного проектирования должна быть согласована со сложившейся практикой проектирования. Методы расчета и проектирования, их программное обеспечение должны стать основой при разработке моделей нулевого, первого и второго уровней.
Целесообразно, чтобы создаваемые модели и их блоки могли использоваться независимо при проведении инженерных расчетов. Это ускорит и облегчит синтез сложных систем, разработку систем автоматизированного проектирования.
Создаваемая система должна предусматривать возможность включения новых моделей и более широкого взаимодействия с другими системами.
По принципу информационного единства все потоки информации в системе должны быть совместимыми. Программирование должно осуществляться на одном из универсальных языков (например, иа языках PL или Фортран). Термины, условные обозначения, размерности физических величин должны быть одинаковыми для всей системы. Целесообразно с самого начала создания системы выработать единые требо-
622
Основы, автоматизированного проектирования
Рис. 3 I хема процесса функционирования системы автоматизированного проектирования
вания к программам, реализующим модели и блоки системы (аннотации, инструкции, описание, графы алгоритмов, тестовые примеры и т.д.).
При большом числе действующих программ оказывается необходимым иметь управляющие программы. Для формирования таких программ и работы с ними удобно использовать специально приспособленные для системы автоматизированного проектирования языки, которые можно построить двумя способами — с помощью дискрипторов (ключевых слов) и командных процедур или путем добавления специальных процедур в универсальные алгоритмические языки.
По принципу итерации система автоматизированного проектирования решается методом последовательных приближений, результаты постепенно уточняются и конкретизируются.
Общая схема функционирования системы показана на рис. 3. Сначала, исходя из потребностей старшей системы и предварительной оптимизации, формулируются технические предложения для основных параметров изделия. Эти параметры поступают в линию анализа, где прорабатываются более детально технические характеристики различных типов изделий и их конструктивных вариантов. Технические условия для всего изделия позволяют
указать требуемые параметры узлов и элементов, что дает возможность выбрать их конструктивные схемы, определить размеры, массу, габариты, провести их локальную оптимизацию.
После того как выяснен «облик» отдельных элементов, начинается синтез. По техническим характеристикам элементов уточняются параметры узлов и всего изделия, и эти параметры поступают в блок оптимизации старшей системы. В блоке оптимизации вырабатываются указания по изменению параметров и характеристик изделия, и их новые значения поступают в линию анализа для второй итерации (второго цикла), и процесс итерации продолжается.
Важно отметить следующую особенность итерационного процесса автоматизированного проектирования. Первые циклы осуществляются только для моделей класса А и лишь частично для моделей класса Б. В них проводится разработка проекта на стадиях технического задания и технического предложения.
Полный цикл для всех классов моделей осуществляется только после того, как выбран основной конструктивный вариант изделия.
Если первые циклы проводятся на моделях нулевого и первого уровня, то на стадии эскизного проекта используются модели второго и более высокого уровней.
Принцип итерации используется ие только для расчета всей системы в целом, но и отдельных моделей.
ЦЕЛИ И МЕТОДЫ ОПТИМИЗАЦИИ
Одно из главных преимуществ систем автоматизированного проектирования — возможность выбора оптимального варианта решения.
Автоматизированное проектирование есть одновременно и оптимальное проектирование.
Понятие оптимального решения подразумевает выбор наилучшего, в некотором смысле, варианта среди множества возможных. Оценка «качества» варианта является сложной, не всегда формализуемой процедурой.
Цели и методы оптимизации
623
Следует учитывать основной принцип оптимизации: оценка «качества» системы данного класса определяется эффективностью ее функционирования в системе более высокого класса. Например, качество ступени компрессора следует оценивать по ее влиянию на работу всего компрессора. В свою очередь, эффективность компрессора должна оцениваться в системе более высокого класса (например, газотурбинного двигателя ит. д.). Естественно, что по мере расширения класса цели оптимизации становятся более общими. Однако в практических расчетах в большинстве случаев можно использовать локальную или внутреннюю оптимизацию элементов, узлов и всего изделия, которая, как правило, оказывается полезной и Для глобальной оптимизации. К целям локальной оптимизации относятся максимум экономичности (максимум коэффициента полезного действия), минимум массы, минимум трудоемкости изготовления и др.
Допустим, что выбрана система обобщенных характеристик или параметров, характеризующих качество системы: gl’ gz> ••• gr-
Условие оптимальности варианта можно записать в виде условия минимума некоторой целевой функции:
w (gr....gr) = min. (1)
В простейшем случае качество системы характеризуется одним параметром gT. Тогда можно принять
w = gr. (2)
если условию оптимальности соответствует минимум параметра gr (например, gi — стоимость, масса и т.д.). Если оптимальность достигается при максимуме gr (например, gr — коэффициент полезного действия), тогда следует принять
w = —gr. (3)
Весьма сложно образовать целевую функцию для нескольких параметров качества, так как для этого надо знать сопоставимую «ценность» различных свойств изделия. Поэтому рассматривают условный минимум целевой функции по одному из параметров, полагая
другие параметры качества лежащими в «допустимой» области:
™---gh. a^gt^b
(I = 1. »¥=*)• (4)
Например, если gr — удельный расход топлива, g2 — удельная масса (масса конструкции на единицу мощности), то имеется оптимальный вариант, обеспечивающий минимум удельного расхода,
о» = gi
при заданной удельной массе
gi В2.
После того как образована целевая функция, возникает задача определения ее минимума.
Параметры качества glt .... gr зависят от параметров системы. Последние однозначно определяют условия функционирования системы: скорости, ускорения, напряжения, деформации, усилия, температуры и т. п. Параметры системы связаны условиями взаимодействия и условиями, отражающими закономерности рабочих процессов.
Однако число связей, как правило, меньше числа параметров, и поэтому часть из них можно выбирать независимо.
Такие параметры называют управляющими и обозначают через иг, и2..
ит. С помощью параметров управления проводится процесс оптимизации.
Остальные параметры системы (их обозначают через Уг, у2..Уп) усло-
вимся называть параметрами состояния. Разделение параметров на две группы условно и определяется постановкой задачи оптимизации, особенностями работы элемента, узла и др.
Пусть имеется т управляющих параметров и;. Так как параметры качества зависят от управляющих параметров, то задача оптимизации в конечном итоге состоит в нахождении минимума целевой функции
w = L [иг.....ит] = min. (5)
Целевая функция w может сложным образом зависеть от управляющих параметров и2..... ит, причем эта
зависимость может включать интегральные и дифференциальные опера
624
Основы автоматизированного проектирования
ции. Параметры состояния и управления связаны условиями связи
Li » Уп* м1» • • •» ит) ~ О
(1 = 1, п), (6)
выражающими уравнения равновесия, сохранения энергии и т. п.
Как указывалось, параметры системы должны удовлетворять определенным ограничениям:
Cj^u^D.. (7)
Разработаны многочисленные методы решения задач оптимизации при различных видах целевой функции, уравнениях связи и типах ограничений (градиентные, случайного поиска, динамического программирования, принцип максимума Понтрягина и Др.), позволяющие решать достаточно общие задачи оптимизации и оптимального управления.
Указанные методы описаны в специальной литературе.
СПИСОК ЛИТЕРАТУРЫ
Главы 1, 2
1. Биргер И. А., Мавлютов Р. Р. Сопротивление материалов. М.: Наука, 1986. 560 с.
2. Конструкционная прочность материалов н деталей газотурбинных двигателей/Под ред. И. А. Биргера и Б. Ф. Балашова. М.: Машиностроение, 1981. 222 с.
3. Конструкционные материалы. В 3-х т./Под ред. А. Т. Туманова. М.: Советская энциклопедия, 1966. Т. 1. 416 с.; Т. 2. 407 с.; Т. 3. 528 с.
4. Композиционные материалы: Справочник/Под ред. Д. М. Карпино-са. Киев: Наукова думка, 1985. 592 с.
5. Мэнсон С. Температурные напряжения и малоцикловая усталость. М.: Машиностроение, 1974. 340 с.
6. Фридман Я. Б. Механические свойства металлов. В 2-х ч. 3-е изд. М.: Машиностроение, 1974. Ч. 1. 470 с.; Ч. 2. 360 с.
7. Шнейдерович Р. М. Прочность при статическом и повтОрио-статиче-ском нагружениях. М.: Машиностроение, 1968. 343 с.
Главы 3, 4
1. Биргер И. А., Иосилевич Г. Б. Резьбовые и фланцевые соединения. М.: Машиностроение, 1990. 365 с.
2. Иосилевич Г. Б., Строганов Г. Б., Шарловский Ю, В. Затяжка и стопорение резьбовых соединений: Справочник. М.: Машиностроение, 1985. 224 с.
3. Сопротивление усталости элементов конструкций/А. 3. Воробьев, Б. И. Олькин, В. Н. Стебеиев и др. М.: Машиностроение, 1990, 240 с.
Глава 5
1. Глухарев Е. Г., Зубарев Н. И. Зубчатые соединения. Л.: Машиностроение, 1976. 198 с.
2. Иосилевич Г. Б. Детали машин. М.: Машиностроение, 1988. 368 с.
3. Иосилевич Г. Б. Концентрация напряжений и деформаций в деталях машин. М.: Машиностроение. 1981, 223 с.
4. Иосилевич Г. Б., Куликов В. С. Распределение нагрузки подлине шлицевых соединений оболочекУУПрочность элементов авиационных конструкций. Вып. 78. Уфа, УАИ, 1974. С. 107—118.
5. Левина 3. М., Решетов Д. Н. Циклическое скольжение в прямобоч-ных зубчатых (шлицевых) соединениях и условный расчет их на износостой-кость/УВестник машиностроения. 1974. № 7. С. 11—17.
Глава б
1. ГречищевЕ. С., Ильяшеико А. А. Соединения с натягом. М.: Машиностроение, 1981. 240 с.
2. Дунаев П. Ф., Леликов О. П. Вероятностный расчет соединений с на-тягомУУВестник машиностроения. 1974. № 9. С. 31—33.
3. Решетов Д. Н. Детали машин. М.: Машиностроение, 1989. 496 с.
4. Решетов Д. Н., Иванов А. С., Фадеев В. 3. Надежность машин. М.: Высшая школа, 1988. 238 с.
Глава 7
1. Кудрявцев В. Н., Наумеи-ков Н. Е. Усталость сварных конструкций. М.: Машиностроение, 1976. 212 с.
2. Николаев Г. А., Куркин С. А., Винокуров В. А. Сварные конструкции. В 2-х ч. М.: Машиностроение. 1982—1983. Ч. 1. Прочность, деформации. 272 с.; Ч. 2. Технология, автоматизация, проектирование. 344 с.
3. Проектирование сварных конструкций в машиностроеиииУПод ред. С. А. Куркина. М.: Машиностроение, 1975. 376 с.
626
Список литературы
4. Сервисен С. В., Когаев В. П., Шнейдерович Р. М. Несущая способность и расчет детален машин иа прочность. М.: Машиностроение, 1975. 480 с.
5. Хряпни В. Е. Справочник паяльщика. М.: Машиностроение, 1981, 348 с.
Гласа 8
1. Валы и оси/С. В. Сервисен, М. Б. Громан, В. П. Когаев, Р. М. Шнейдерович. М.: Машиностроение, 1970. 319 с.
2. Когаев В. П., Махутов Н. А., Гусеиков А. П. Расчеты детален машин и конструкций на прочность и долговечность. М.: Машиностроение, 1985. 224 с.
Глава 9
1. Биргер И. А., Шорр Б. Ф., Иосилевич Г. Б. Расчет на прочность деталей машин. М.: Машиностроение, 1979. 704 с.
2. Ерошкин Б. А. Влияние центробежных сил тел качения на долговечность подшипников при высокой частоте вращения. Проблемы прочности и динамики в авиадвигателестроении// Тр. № 1237, ЦИАМ, 1989. Вып. 4.
3. Перель Л. Я- Подшипники качения. Расчет, проектирование и обслуживание: Справочник. М.: Машиностроение, 1983. 344 с.
4. Подшипники качения: Справоч-иик-каталог/Под ред. В. Н. Нарышкина и Р. В. Коросташевского. М.: Машиностроение, 1984. 280 с.
Глава 10
1. Биргер И. А. Расчет кольцевых изгибных пружии//Расчеты на прочность. М.: Машгиз, 1961. Вып. 7. С. 110—121.
2. Жуков В. Б. К расчету осадки прорезной пружины//Вестиик машиностроения. 1968. № 8. С. 16—18.
3. Иосилевич Г. Б. Детали машин. М.: Машиностроение, 1988. 368 с.
4. Пономарев С. Д., Андреева Л. Е. Расчет упругих элементов машин и приборов. М.: Машиностроение, 1980. 325 с.
Глава 11
1. Авиационные зубчатые передачи и редукторы: Справочиик/Под ред.
Э. Б. Булгакова. М.: Машиностроение, 1981. 374 с.
2. Динамические процессы в механизмах с зубчатыми передачами. М.: Наука, 1976.
3. Иосилевич Г. Б. Детали машин. М.: Машиностроение, 1988. 368 с.
4. Кудрявцев В. Н. Детали машин. Л.: Машиностроение, Лениигр. отд-ние, 1980 . 464 с.
5. Павленко А. Б., Федякии Р. В., Чесноков В. А. Зубчатые передачи с зацеплением Новикова. Киев: Тех-И1ка, 1978. 144 с.
6. Петрусевич А. И., Генкин М. Д., Гринкевич В. К- Динамические нагрузки в зубчатых передачах с прямыми колесами. М.: Изд-во АН СССР, 1956. 134 с.
7. Шорр Б. Ф. К расчету динамических нагрузок иа зубья прямозубых цилиндрических колес//Прочность и динамика авиационных двигателей. М.: Машиностроение, 1969. Вып. 5. С. 127—162.
8. Шорр Б. Ф., Егоров В. А. Применение пьезоэлектрических устройств и голографической ннтероферометрии к исследованию спектров колебаний зубчатых колес//Вестник машиностроения. 1977. № 12. С. 13—15.
Глава 12
1. Биргер И. А., Иосилевич Г. Б. Резьбовые и фланцевые соединения. М.: Машиностроение, 1990. 365 с.
2. Проектирование механических передач: Учебно-справочное пособие для втузов/С. А. Чернавский, Г. А. Снеса-рев, Б. С. Козинцев и др. М.: Машиностроение, 1984. 560 с.
Глава 13
1. Воробьев И. И. Ременные пере- ( дачи. М.: Машиностроение, 1979. 163 с.
2. Пронин Б. А., Ревков Г. А. Бесступенчатые клиноремеииые и фрикционные передачи. М.: Машиностроение, 1980. 320 с.
3. Пронин Б. А., Овчинникова В. Д. Расчет клиноремениых передач//Вест-иик машиностроения. 1982. № 3. С. 23—26.
4. Решетов Д. Н. Детали машин. М.: Машиностроение, 1989. 496 с.
5. Светлицкий В. А. Передачи гибкой связью. М.: Машиностроение, 1967. 155 с.
Список литературы
627
Глава 14
1. Воробьев Н. В. Цепные передачи. М.: Машиностроение, 1968. 251 с.
2. Готовцев А. А., Котенок И. П. Проектирование цепных передач. М.: Машиностроение, 1982. 336 с.
Глава 15
1. Авиационные поршневые двигатели. Кинематика, динамика и расчет на прочность. М.: Оборонгиз, 1950.
2. Ваншейдт В. А. Конструирование и расчеты прочности судовых дизелей. Л.: Судостроение, 1969. 640 с.
3. Двигатели внутреннего сгорания. Конструирование и расчет иа прочность поршневых и комбинированных двигателей/Под ред. А. С. Орлина и М. С. Круглова. М.: Машиностроение. 1983. 384 с.
4. Истомин П. А., Григорьев Е. А. История и перспективы развития расчетных методов исследований динамики и прочности ДВС//Двигателестрое-иие, 1985, № 10. С. 5—9.
5. Кинасошвилн Р. С. Расчет прочности шатунов авиационных двигате-лей//Тр. ЦИАМ. 1945. № 66
6. Кинасошвилн Р. С. Расчет поршневого пальца авиационного двигате-ля//Тр. ЦИАМ. 1947. № 119.
7. Лейкин А. С. Напряженность и выносливость деталей сложной конфигурации. М.: Машиностроение, 1968. 371 с.
8. Шорр Б. Ф., Мельникова Г. В. Расчет конструкций методом прямого математического моделирования. М.: Машиностроение, 1988. 160 с.
Глава 16
1. Биргер И. А. Вариационные методы в строительной механике турбомашин. М : Оборонгиз, 1959. 28 с.
2. Воробьев Ю. С., Шорр Б. Ф. Теория закрученных стержней. Киев: Наукова думка, 1983. 188 с.
3. Динамика авиационных газотурбинных двигателей/Под ред. И. А. Биргера и Б. Ф. Шорра. М.: Машиностроение, 1981. 232 с.
4. Иванов В. П. Колебания рабочих колес турбомашин. М.: Машиностроение, 1983. 224 с.
5. Конструкционная прочность материалов и деталей газотурбинных двигателей/Под ред. И. А. Биргера и
Б. Ф. Балашова. М.: Машиностроение 1981. 222 с.
6. Расчет на прочность авиационных газотурбинных двигателей/Под ред. И. А. Биргера и Н. И. Котерова. М.: Машиностроение, 1984. 208 с.
7. Хроиин Д. В. Колебания в двигателях летательных аппаратов. 2-е изд. М.: Машиностроение, 1980. 296 с.
8. Шорр Б. Ф-, Локштанов Е. А., Халатов Ю. М. Об одном возможном подходе к вероятностной оценке вибрационной прочности деталей турбома-шин//Проблемы прочности. 1972. № Ц. С. 11—14.
Главы П—19
1. Бндермаи В. Л. Механика тонкостенных конструкций. М.: Машиностроение, 1977.
2. Биргер И. А., Мавлютов Р. Р. Сопротивление материалов. М.: Наука, 1986. 560 с.
3. Бояршинова С. В. Основы строительной механики машин. М.: Машиностроение, 1973. 455 с.
4. Прочность. Устойчивость. Колебания- Справочник. В 3-х т./Под ред. И. А. Биргера и Я. Г. Пановко. М.: Машиностроение, 1968. Т. 1. 831 с., Т. 2. 463 с.; Т. 3. 567 с.
Глава 20
1. Биргер И. А. Некоторые математические методы решения инженерных задач. М.: Оборонгиз, 1956. 150 с.
2. Вольмир А. С. Устойчивость деформируемых систем. 2-е изд. М.: Наука, 1967. 984 с.
3. Лейтес С. Д. Справочник по определению свободных длин элементов стальных конструкций. М.: Проект-стальконструкция, 1963. 160 с.
4. Паиовко Я. Г., Губанова И. И. Устойчивость и колебания упругих систем, 2-е изд. М.: Наука, 1967. 420 с.
Главы 21, 22
1. Бндермаи В. Л. Прикладная теория механических колебаний. М.: Высшая школа, 1972. 400 с.
2. Биргер И. А. Некоторые математические методы решения инженерных задач. М.: Оборонгиз, 1956. 150 с.
628
Список литературы
3. Пановко Я. Г. Основы прикладной теории упругих колебаний. М.: Машиностроение, 1967. 314 с.
4. Светлицкий В. А. Случайные колебания механических систем. М.: Машиностроение, 1976. 215 с.
Главы 23, 24
1. Биргер И. А. Круглые пластинки и оболочки вращения. М.: Машиностроение, 1959. 368 с.
2. Валишвили Н. В. Методы расчета оболочек на ЭЦВМ. М.: Машиностроение, 1976. 227 с.
3. Тимошенко С. П. Устойчивость упругих систем. М.: Гостехиздат, 1955.
4. Тимошенко С. П., Войновский-Кригер С. Пластинки и оболочки. М.: Наука, 1966. 635 с.
Глава 25
1. Алфутов Н. А. Основы расчета иа устойчивость упругих систем. М.: Машиностроение, 1978. 309 с.
2. Биргер И. А. Круглые пластинки и оболочки вращения. М.: Оборонгиз, 1961. 368 с.
3. Вольмир А. С. Устойчивость деформируемых систем. М.: Наука, 1967. 984 с.
4. Кармишин А. В., Мяченков В. И., Фролов А. Н. Статика и динамика тонкостенных оболочечных конструкций. М.: Машиностроение, 1976. 376 с.
5. Основы строительной механики ракет/Л. И. Балабух, К- С. Колесников и др. М.: Высшая школа, 1969. 490 с.
6. Прочность. Устойчивость. Колебания: Справочник. В 3-х т./Под ред. И. А. Биргера и Я. Г. Пановко. М.: Машиностроение, 1968, Т. 1. 831 с.; Т. 2. 463 с.; Т. 3. 567 с.
Глава 26
1. Биргер И. А. Общие алгоритмы решения задач теории упругости, пластичности и ползучести//Механика деформируемых сред. М.: Наука, 1976. С. 51—73.
2. Вибрация в технике: Справочник: В 6-ти т. М.: Машиностроение. 1978. Т. 1. 352 с.; Т. 2. 351 с.; Т. 4. 509 с.
3. Зенкевич О. Метод конечных элементов в технике. М.: Мир, 1975. 539 с.
4. Каплунова О. Б. Исследование нестационарных динамических процессов в одномерной дискретно-континуальной системе методом прямого математического моделирования//Механика деформируемых сред. Саратов: Изд-во СГУ. 1990. С. 47—53.
5. Шорр Б. Ф. Математическое моделирование волновых процессов в упруговязкопластических телах//Изв АН СССР. МТТ. 1984. № 4. С. 144—.51.
6. Шорр Б. Ф., Мельникова Г. В. Расчет конструкций методом прямого математического моделирования. М.: Машиностроение, 1988. 160 с.
Глава 27
1. Гохфельд Д. А. Несущая способность конструкций в условиях тепло-смел. М • Машиностроение, 1970. 260 с.
2. Качанов Л. М. Основы механики разрушения. М.- Наука, 1974. 311 с.
3. Малинин Н. Н. Прикладная теория пластичности и ползучести. М.: Машиностроение, 1975. 399 с.
4. Работнов Ю. Н. Ползучесть элементов конструкций. М.: Наука, 1966. 752 с.
5. Термопрочность деталей машин/ И. А. Биргер, Б. Ф. Шорр, И. В. Демь-янушко и др. М.: Машиностроение, 1975. 455 с.
Глава 28
1. Александров А. Я-, Ахметзянов М. X. Поляризационные оптические методы механики твердого тела. М.: Наука, 1973.
2. Вайнберг Д. В. Концентрация напряжений в пластинах около отверстий и выкружек. Киев: Техника, 1969. 220 с.
3. Иосилевич Г. Б. Концентрация напряжений и деформаций в деталях машин. М.: Машиностроение, 1981. 223 с.
4. Петерсон Р. Коэффициенты концентрации напряжений: Пер. с англ. М.: Мир, 1977. 301 с.
Глава 29
1. Биргер И. А. Упругий контакт стержней//Расчеты на прочность. М.: Машиностроение. 1969. Вып. 14. С. 127—136.
2. Биргер И. А. Контактные задачи теории стержней, пластинок и оболо
Список литературы
629
чек//Теория оболочек и пластин. Тр. IX Всесоюзной конференции по теории оболочек и пластин. Л.: Судостроение, 1975. С. 23—25.
3. Иосилевич Г. Б., Мавлютов Р. Р., Ковган С. Т. Расчет соединений с круглыми контактирующими фланцами при действии растягивающих нагрузок// Вестник машиностроения. 1974. № 6. С. 24—26.
4. Расчеты на прочность в машино-строении/С. Д. Пономарев, В. Л. Би-дерман, В. М. Макушин и др. М.: Машгиз, 1956. Т. 1. 884 с.; 1958. Т. 2. 974 с.; 1959. Т. 3. 1118 с.
Главы 30, 31
1. Биргер И. А. Об одном критерии разрушения и пластичности//Механика твердого тела. 1977. № 4. С. 17—19.
2. Когаев В. П. Расчеты иа прочность при напряжениях, переменных во времени. М.: Машиностроение, 1977. 232 с.
3. Писаренко Г. С., Лебедев А. А. Сопротивление материалов деформированию и разрушению при сложном напряженном состоянии. Киев: Наукова думка, 1969. 209 с.
4. Сервисен С. В., Когаев В. П., Шнейдерович Р. М. Несущая способность и расчеты деталей машин на прочность. М.: Машиностроение, 1975. 480 с.
Главы 32, 33
1. Биргер И. А., Шорр Б. Ф., Шией-дерович Р. М. Расчет на прочность деталей машин. М.: Машиностроение, 1966. С. 590—609.
2. Болотин В. В. Статистические методы в строительной механике. М.: Стройиздат, 1965. 279 с.
Глава 34
1. Биргер И. А. Остаточные напряжения. М.: Машгиз, 1963. 239 с.
2. Гринченко И. Г. Упрочнение деталей из жаропрочных и титановых сплавов. М.: Машиностроение, 1971 120 с.
3. Кузнецов Н. Д., Цейтлин В. И. Эквивалентные испытания газотурбинных двигателей. М.: Машиностроение 1976. 120 с.
4. Хворостухии Л. И., ВолковА. Ф. Влияние алмазного выглаживания на усталостную прочность нержавеющих сталей при повышенных температу-рах//Вестник машиностроения. 1975. № 7. С. 42—45.
Глава 35
Биргер И. А. Техническая диагностика. М.: Машиностроение, 1978. 234 с.
Глава 36
1. Биргер И. А. Основы автоматизированного проектирования//Изв. вузов. Машиностроение. 1977. № 8. С. 32—35.
2. Керимов 3. Г., Багиров С- А. Автоматизированное проектирование конструкций. М.: Машиностроение, 1985. 218 с.
3. Принс М. Д. Машинная графика и автоматизация проектирования: Пер. с англ. М.: Советское радио, 1975. 232 с.
4. Хроиин Д. В. и др. Основы автоматизированного проектирования. М.: Машиностроение, 1984. 182 с.
ПРЕДМЕТНЫЙ указатель
Автоколебания лопаток 311
Амортизатор пневмоэластнчный 170
— резиновый 170
Амплитуда колебаний — Понятие 392
— переменных напряжений — Понятие 557
— предельная — Кривая 557, 558
Аналогия гидродинамическая 358 — мембранная 358
Балки — Изгиб — см. Иагиб стержней Байеса метод распознавания 606, 610 Бандажироваиие лопаток 302 — 304, 31 1 — 312
Болты — Диаграммы усилий 51 — Допускаемые статические нагрузки 50 — Момент затяжки 50 — Напряжения кручения в стержне 56 — Полное усилие в болте 52 — фланцевые — Расчет на прочность 82 -- Усилие затяжки 81, 82
Бр^дта формула 360
Валы — Галтелн и выточки на валах 128 — Жесткость 133 ,
— Конструктивные формы 126 — 129 — Критические частоты вращения 140, 141, 405 — 424
— Материалы 128, 129
— Моменты сопротивления сечения и площадь сечения 132 — 135
— Нагрузки на валы 130 — 131
— Основные технические требования 129, 130
— Расчет на колебания 140
— Расчет на сопротивление усталости 131—136
— Расчетные схемы опор 130, 131
— Сечения 397
— Сопряжения ступеней 127
— Устойчивость 133
— Фланцевое соединение валов 128
— Шлицевое соединение валов 128
— Явление самоустановлення 406
Валы гладкие 126
— жесткие 406
— коленчатые — Запасы прочности 260, 262 — Материалы 260 — Определение нагрузок 256, 257 — Определение номинальных напряжений 257 — 259 — Расчет 256 — 262 — Эпюры изгибающих и крутящих моментов 258, 259
— круглые — Кручение 355, 356
— с непрерывно распределенными массами — Определение критических частот вращения 41 0
— с несколькими ^дисками — Расчет критических частот вращения 410
— с одним диском — Критические частоты вращения 405—410
— ступенчатые 126 —128
— торсионные 126
Велера кривые 32
Вероятность безотказной работы — Пример определения для экспоненциального закона 587 — Формулы 584 — прогнозируемая 586
Вероятность разрушения 574, 575 — Значения в зависимости от запаса прочности по средним напряжениям 580,
— при произвольных законах распределения напряжений и пределов прочности 575—577 — Пример определения 577, 578
Виброгалтовка 598
Вибро шлифование 598
Время работы безотказной среднее 585
— эквивалентное 43
Выпучивание стержня — Влияние начального прогиба и внецеитрениого приложения силы 382
— прн упругопластнческих деформациях 386- 388
Вязкость ударная 27
Гайки — Предельная высота 65 — Расчет высоты 64
— растяжение 60, 61
Галтелн иа валах 128
Гармоники частоты вращения 308
Гибкость стержня — Величины 397—381, 384
— предельная — Значения 384
— приведенная 375
Гипотеза плоских сечений 13, 336
Градиент деформаций 511
— напряжений 511
Грузоподъемность подшипников качения динамическая 148 — 150
— статическая 147, 148
Губера —Мизеса критерий 549 — 551
Гука закон 14
Давления контактные в соединениях с гарантированным натягом — Соединения дисков и валов 102, 103
— Соединения дисков и толстостенных цилиндров 101, 103
— Соединения тонкостенных колец 100, 101
Детали крепежные — Виды покрытий 47 — Контроль 45, 47 — Материалы 45—47 — Покрытия 45
Деформация кольца осесимметричная от неравномерного нагревания 370, 371 — под действием осевой силы 370 — под действием радиальной силы 370 Деформация линейная температурная 495 — остаточная 182, 692 — относительная поперечная 13, 14
Предметный указатель
631
— ползучести 495
— упругая 506
— элемента тела — Разложение 13
Деформирование поверхностное пластическое 595
— упругопластическое — Петли гистерезиса 36
Диагностика техническая — Понятие
605 — Постановка задачи 605, 606
Диаграмма деформирования 359
— деформирования линейно упрочняющегося материала 385
— предельных амплитуд 34
— предельных напряжений 34
— растяжения 25
— растяжения с площадкой текучести 25 — сдвига 166
Диски — Граничные условия 315
— Запас по циклической долговечности 320
— Запас прочности 316, 317—322
— Местные запасы прочности 319
— Основное уравнение для расчета 323 — 325
— Предварительная оценка прочности диска 318—320
— Пример расчета 320 — 322
— Расчет напряжений от действия центробежных сил 315 — 317
— Рекомендации для выбора материала 320
— Уравнения равновесия элемента 323, 324
— Уравнения совместности в напряжениях 324
— Уравнения упругости 324
Диски переменной толщины — Определение напряжений и деформаций 327 — 333 — Расчет методом линейного аппроксимирования 327—330 — Расчет методом последовательных приближений 330 — 333
— постоянной толщины — Напряжения и деформации 325—327 — Температурные напряжения 326, 327
— постоянной толщины с ободом — Рас* чет 327
— равнопрочные — Профилирование 322, 323
— центробежных компрессоров — Запас по разрушающим оборотам 333 — Расчет 333
Долговечность — Понятие 581
— расчетная — Формула 41
Жесткость вала иа кручение — Расчет 397 — динамическая — Определение 393 —
Понятие и формула 393
— сечения балки на изгиб — Понятие 19 — сечеиия вала на кручение — Понятие 21 — сечения стержня при растяжении — Понятие 14
— стержня при кручении 360, 361
— цилиндрическая 443
Задачи контактные — Анализ напряженного состояния 534, 535 — Давление штампа 530, 533, 534 — Контакт цилиндров 528 —530, 531
— Основные особенности 527, 528 — Упругий контакт пластинок 541—543 — Упругий контакт стержней 535—540
— конструкционные 527 — Определение функций влияния 545 — Основные уравнения 543, 544 — Связь между силовыми факторами и перемещения-
ми 544, 545
Закон надежности экспоненциальный 587
588 *
Замок елочного типа — Запас прочности статиче$кнй хвостовика 305
— Момент сопротивления 306
— Нагрузки на зуб 305
— Напряжения в хвостовике 305
— Напряжения изгиба в основании sv6a 304 У
— Напряжения среза 304
Замок типа ласточкин хвост — Расчет на-
пряжений смятия 306
— Расчет перемычки 307
— Расчет усилий 306
Замок шарнирный — Расчет на прочность 307, 308 — Схема обкатывания лопатки 299
Заневоливание пружин 164
Запас прочности — Выбор 40 — Формула 40
— вала по касательным напряжениям 136
— вала по нормальным напряжениям 136
— вала по переменным напряжениям 138
— дисков 316, 317, 318, 333
— длительной на различных режимах 42, 43
— длительной статической 40
— длительной эквивалентный 42, 43
— коленчатых валов 260
— лопаток по переменным напряжениям 313
— лопаток профильной части 281, 282
— по несущей способности 42, 574
— при кручении 40
Запас прочности при переменных напряжениях 42
— при статических напряжениях 40, 41
— резьбового соединения по переменным напряжениям 67 — 69
— статический — Приближенный метод определения 578, 581 — Пример определения 579, 580
— при усталости — Определение 566, 567
— при усталости для нестационарного нагружения — Определение 568—572 — при усталости для сложного напряженного состояния — Определение 567
— эквивалентный при многоступенчатом нагружении — Определение 569, 570
Запас устойчивости 459
Затяжка предварительная резьбовых соединений — Выбор величины 58
Зубчатые передачи — Влияние параметров неточности зубьев 206
— Влияние смазки и кинематики передачи иа выкрашивание 219
— Выкрашивание 182, 183, 219, 220, 221
-- Деформация зубьев 191, 198, 199
— Деформация изгибная валов 195, 196
— Допуски иа величину основного шага зубчатых передач 198, 199
— Жесткость удельная 199
— Заедание 221
— Коэффициент запаса сопротивления усталости зуба 214, 215, 216
— Колебания вынужденные 204
— Колебания резонансные 204
— Коэффициент запаса прочности. 216, 219
— Коэффициент динамической нагрузки 205, 207, 208
— Коэффициент концентрации напряжений теоретический 214
— Коэффициент концентрации напряжений эффективный 215
632
Предметный указатель
I I I I I I I I III I I I I I I I I I I I I
— Коэффициент неравномерности распределения нагрузки 191, 194, 195, 197, 222
— Коэффициент приработки 222
— Коэффициент смягчения 209
— Коэффициент статического перекрытия 201
— Коэффициент, учитывающий форму зуба 188. 212. 213, 214
— Кручение ободьев или тел колес 191 — 1 95
Микротрещины 219
Модуль упругости приведенный 218
Момент крутящий в шестерне 185 Нагрузка динамическая 210, 211 Напряжения допускаемые 219—221 Напряжения при изгибе 211—214 Напряжения касательные 218
Напряжения контактные 187, 188,
217, 218, 219
Напряжения местные 213
Напряжения смятия 218
Неравномерность начальная общая 196, 197
Область зацепления зубьев 200
Определения и обозначения 184
Оценка возможности резонанса 205
Пересопряжеиие зубьев 205
Поломка зуба 211, 212
Предел выносливости 214, 215, 220
Приработка зубьев 1 97, 222
Прочность статическая 216, 217
Радиус кривизны приведенный 218
Размеры основные без смещения 185
Разрушение зубьев 182
Распределение нагрузки по ширине зуба 192
— Распределение усилий статическое между зубьями 198
— Расстояние межосевое 186
— Расчет быстроходных передач 209
— Расчет динамических нагрузок в зубьях 207
— Расчет иа выносливость в зубьях при изгибе 188, 189
— Расчет иа контактную выносливость 187. 188
— Расчет иа прочность упрощенный прямых зубьев 185 — 189
— Расчет при кратковременных перегрузках 220
— Сила нормальная удельная 188, 185
— Сила окружная 185
— Сила окружная удельная 185, 190, 212
— Сила ударная 208, 209, 210
— Схема зацепления 185, 186
— Схема зуба при расчете иа изгиб 212
— Схема кручения тел сопряженных колес 193
— Схема поворота колеса при деформировании зуба 191
— Схема совместного движения упругих зубьев 203
— Угол перекоса осей 195, 196
— УдаР кромочный 205, 206, 207
— Удар срединный 206, 207, 208
— Усилие, действующее иа зуб 185, 186
— Усилия динамические 201
— Усилия контактные 199, 200
— Усилия статические максимальные 201 — Условие обеспечения контактной выносливости зубьев 219
— Условие совместного движения зубьев 202, 203
— Условия статического ваЦеплеиия зубьев 206
— Частота возбуждающей силы 204
— Частота собственных колебаний сопряженных колес 202—204
— Число циклов нагружения фактическое 215
— Число циклов нагружения эквивалентное 221
— Шаги зубьев 198
Зубчатые передачи конические — Диаметры колес 223 — Модуль зацепления 233 — Нагрузка удельная 224 — Напряжения контактные 224 — Расстояние межосевое 223 — Скорость окружная 223 — Число зубьев 223 — Число передаточное 223 — Ширина зуба 224
— косозубые и шевронные — Длина контактных линий 222 — Радиус кривизны приведенный 223 — Сила нормальная 223 — Сила окружная удельная 222 — Число зубьев эквивалентное 223 — Новикова М. Л. — Напряжения контактные 225 — Радиус кривизны приведенный 225 — Расчет иа изгиб — Сила нормальная 225— Схема передачи 224
— с внешним зацеплением 186, 187
— с внутренним зацеплением 186, 187
Изгиб — Момент сопротивления 16, 17, 18 — Примеры определения опасных сечений 16, 15
— чистый — Понятие 15
— шарнирных лопаток — Расчет 300—302 Изгиб стержней — Вычисление интеграла
Мора по правилу Верещагина 348, 349
— Зависимость между изгибающим моментом и перерезывающей силой 334
— Максимальные напряжения 593, 594
— Момент инерции сечения 337
— Момент разрушающий предельный 354, 355
— Момент сопротивления сечения 338
— Напряжения в продольных сечениях 594
— Нормальные напряжения 336 — 338
— Определение касательных напряжений 341, 342
— Определение прогибов с помощью интеграла Мора 346, 347
— Определение углов поворота сечений с помощью интеграла Мора 346, 347
— Относительное удлинение волокон 336 — Предельный пластический момент 353, 354
— Примеры определения прогибов 344 — 346
— Схема 593
— Уравнения упругой линии 342 — 344
*-• Условия закрепления 334, 335
— Эпюры изгибающих моментов 336
Изгиб стержней переменного сечения — Определение прогибов и углов поворота 350, 351
— с учетом пластической деформации 351 —355
Изломы 38, 39
Индекс пружины 165
Интенсивность отказов 584, 585 — Общая закономерность изменения по времени наработки 586
Кармана Модуль 385
Колебания валов 139, 140
— динамических систем — Формулы для определения круговых частот 403, 404
Предметный указатель
633
— нзгнбные — Расчет двухмассовой системы 400, 401 — Расчет одномассовой системы 399, 400
— изгибные кольца 401
— изгибные стержней постоянного сече-иня — Определение 401, 402
— крутильные 396 — Расчет жесткости вала на кручение 397 — Расчет одномассовой системы 396 — Частота 398, 399
— маятниковые шарнирных лопаток 299 — 302
— одномассовой системы 392
— одномассовой системы вынужденные 393
— поперечные струны 403
— резонансные лопаток 308
— системы свободные 392
Кольца — Осесимметричная деформация 361 —368
— Плоская деформация 361 —368
— Расчетные формулы 365—368
— Устойчивость 463
— Эпюры изгибающих моментов 361, 365 — 368
Кольца конические тонкостенные — Деформация осесимметричная 372, 373
— поршневые — Расчет иа прочность 267, 268
— Прямоугольного сечения — Деформация осесимметричная под действием осевой силы 371, 372
— упругие 418, 419
Конструирование автоматизированное — Понятие 618
Коитролеспособность — Понятие 582
Концентрация напряжений 21, 22, 510, 513 — Влияние на свойства материалов 27, 28 — Влияние на усталостную прочность 558, 559
— в замковых соединениях лопаток 523 — 527
— в зубьях храповых колес 523
— в прямозубых цилиндрических передачах 521 —523
— в резьбовых соединениях 60—63
— при кручении 358
Коэффициент безопасности, учитывающий влияние на долговечность подшипников характера внешних нагрузок—значение 152
— влияния абсолютных размеров 35, 36
— влияния шарнирного закрепления лопаток 301, 302
— внутреннего давления прн расчете фланцев 80
— концентрации деформаций 518
— концентрации деформаций теоретический 511
Коэффициент концентрации напряжений 21. 518
— для коленчатых валов 260, 262
— теоретический 60, 63, 511, 513, 517, 558
— теоретический в соединениях с гарантированным натягом 103
— эффективный 35, 68, 558, 559
— эффективный в сварных соединениях 115, 120
— эффективный для валов 137, 138 Коэффициент масштабный при кручении и изгибе валов 138
— на начальные неправильности цилиндрических оболочек 466
— напряжений для круглых пластин 431 — 438
— напряжений для прямоугольных пластинок 442
— настройки частоты прн маятниковой форме колебаний лопаток 300
— неравномерности напряжений для коленчатых валов 259, 260
— осевой нагрузки для подшипников качения 151
— осевой нагрузки фланцевого соединения 80
— осевой статической нагрузки для под-' шипииков качеиня 148
Коэффициент податливости 399
— болтов 53, 80
— закрученных лопаток 293
— прокладки во фланцевом соединении 80
— промежуточных деталей в резьбовом соединении 54
— стержня при изгибиых колебаниях 404
— трубы 80
— фланцев 81, 85
— фланцев при действии осевой нагрузки 80, 81, 85
Коэффициент прогибов для круглых пластин 431 —438
— прогибов для прямоугольных пластинок 442
— прокладочный 78
— Пуассона 14
— радиальной нагрузки для подшипников качения 151
— радиальной статической нагрузки для подшипников качения 148
— состояния поверхности 35
— температурный для подшипников качения 152
— трення в резьбе 57
— трения приведенный 57, 58
— трення при посадках с гарантированным натягом 99
— углов поворота для круглых пластин 431—438
— учитывающий влияние масла на трение подшипников 159
— учитывающий влияние масштабного эффекта для резьбовых соединений 69
— учитывающий влияние состояния поверхности при изгибе и кручении валов 139
— чувствительности материала болта (шпильки) к концентрации напряжений 68
Кривые Велера 32, 33
— деформирования 498—500, 509. 593, 595
— длительной прочности 28
— плотности распределения переменных напряжений и пределов выносливости 575
— ползучести 31, 502
— предельных амплитуд 557
— убыли изделий из эксплуатации 591
— усталости 33, 558, 557
Критерий длительной малоцикловой прочности 554
— интенсивности напряжений 549, 550
— максимальной деформации растяжения * 551
— максимального нормального напряжения 551
— максимальных касательных напряжений 550
— Надан 553
— пластичности 551
— прочности Мора 552
— прочности обобщенный для пластичных и хрупких материалов 554
— прочности Писаренко—Лебедева 552,
634
Предметный указатель
553
— статической прочности для пластичных материалов 549 — 551
— статической прочности для хрупких (малопластичных) материалов 551 — 554
Кручение 20
— вала н втулки совместное 597
— вала круглого 355
Кручение стержней 355—361 — Распределение касательных напряжений 358
— круглых 355, 356
— прямоугольного сечення 357, 358
— с учетом пластических деформаций 358, 359
— с эллиптическим поперечным сечением 356, 357
— тонкостенных 357, 358
— трубчатых 359, 360
Крылова функции 448 — 450
Лапласа функция 575, 588
Лопатки -- Автоколебания 311
— Вандажнрованне 311, 312
— Газовые силы, действующие на лопатку 274, 275
— Замки шарнирные 307, 308
— Замок елочного типа 304—305
— Замок типа ласточкин хвост 306
— Запас прочности 281, 282
— Запас прочности по переменным напряжениям 313
— Конструктивные способы разгрузки от изгиба газовыми силами 277
— Определение геометрических характеристик по данным чертежа 280
— Определение напряжений от изгиба 277
— Осевая сила, действующая на лопатки 281
— Основные виды колебаний 308—311
— Положение профилей н действительное направление газовых усилий 275
— Приближенный расчет основной частоты колебаний 285 — 288
Лопатки — Пути повышения запаса прочности 313—315
— Распределение изгибающих моментов по длине пера 302
— Расчет вытяжки 273
— Расчет геометрических характеристик сечення 278—281
— Расчет замков 304—308
— Расчет изгибающих моментов от газовых снл 273 — 276
— Расчет изгибающих моментов от центробежных снл 276, 277
— Расчет нзгнбных колебаний 285 — 291
— Расчет работы центробежных снл при колебаниях лопатки 290, 291
— Резонансная частота вращения 308, 309
— Резонансные диаграммы 310, 312
— Резонансные колебания 308—310
— Спектрограмма переменных напряжений 314
— Срывные колебания 310, 311
— Узловые лннни 309
— Уточненный расчет собственных частот 288, 289
— Частота возбуждения 309
Лопатки бандажироваиные 302—304
— Изгиб бандажной полки 302
— Расчет натяга по бандажным полкам 303, 304
Лопатки закрученные 291, 298
— Геометрические и жесткостные характеристики (приближенные формулы) 294 — Колебания 296, 297
— Параметр закрученности 297
— Пример расчета собственной частоты колебаний 297
— Раскрутка от центробежных сил 294. 295
— Расчет напряжений от центробежных снл 296
— Таблица для расчета собственной частоты колебаний 298
- - Упругое удлинение 295, 296
Лопатки охлаждаемые — Распределение
напряжений в лопатке 284— Распределение напряжений в лопатке 284 — Температурное поле 284
— постоянного сечення — Определение напряжений 270, 271
— равнопрочные — Варианты 283 — Расчет напряжений 282, 283 — Условия равновесия элемента лопаткн 282, 283 — с изменением площади поперечного сечення по степенному закону 271 — 273 — График изменения площади по длине лопаткн 271 — Кривые растягивающих напряжений в лопатке 272
— слабо закрученные 291, 292
— шарнирные — Кинематика 299 — Коэффициент влияния шарнирного закрепления 301, 302 — Маятнико-
вые колебания 299, 300 — Расчет на нзгнб 300—302 — Схема обкатывания в шарнирном замке 299
Ляме постоянная 479
Материалы конструкционные — Механические свойства прн повышенной температуре 29, 30 — Физические свойства 14
Матрица диагностическая 607, 608 Мембраны прорывные 440, 441
Метод вариационно-разностный расчета конструкций 480 — 482
— динамических жесткостей 393, 394,
398 — Определение собственных частот системы 394—396
— конечных элементов расчета конструкций 482—486 — примеры расчета 485 — 490
— минимального риска 610—612
— разделения в пространстве признаков 615—617
— распознавания логический 617, 618
Модели статические усталостной прочности 572, 573
Модель математическая — Основные факторы 617
— Понятие 617
— Структурная схема 618
Модель упругости 14
— приведенный 385
Момент гироскопический 408
— изгибающий в сеченнн 334
— инеринн диска 397, 398
— ннерцни полярный 355, 356
— инерции сечения лопаток турбомашни 294
— ннерции сечения прн изгибе 337
— крутящий 20
— пластический предельный прн изгибе 353, 354
— разрушающий предельный при изгибе 354, 355
— сопротивления кручению 20
— сопротивления при изгибе 338
Предметный указатель
635
Моменты сопротивления сечення валов, ослабленных пазом для одной стандартной шпонки 134
— сплошных (круглых) валов 132
— с центральным каналом 133
— шлицевых 135
Мора интеграл 346
Мора шестиугольник 552, 553
Муфты с резиновыми упругими элементами — Конструкции 178
Мэнсона формула 37
Нагрузка критическая 373. 374 — Общий случай расчета 375, 376 — Таблицы для расчета 376—382
— предельная 41
— следящая 388
Надан критерий 553
Надежность — количественные показатели 591, 592 —- Основное уравнение теории надежности 586 — Понятие 581, 582 — Правила 682—684
Напряжения — концентрация 21
— во фланце 82
— главные 11
— изгиба прн упругопластических деформациях 351 —353
— касательные при изгибе 341, 342
— касательные при кручении 355 — Распределение 358
— касательные при кручении стержня прямоугольного сечення 357, 358
— касательные при кручении стержня с эллиптическим поперечным сече ином 366, 367
— касательные прн кручении трубчатых стержней 359, 360
— контактные 460
— критические 460
— кручения в стержне болта 56
— нормальные при изгибе 336—338
Нкпряження остаточные — влияние термической н химико-термической обработки 600, 601 — Влияние технологии обработки 598 — Влияние на усталостную прочность 601 — Графики после различных видов обработки поверхности и алмазного выглаживания 599, 600 — Образование 592, 593 — Определение 602, 603 — Понятие 592 — Процесс образования 595 — Эпюры распределения 549 Напряжения переменные — Свойства материалов при переменных напряжениях 32—36 — Цикл 32 — при кручении вала 355, 356 — статические — Свойства материалов при статических напряжениях 24 — 28 — температурные — Расчет 22, 23 — температурные в стержне прямоугольного сечения 340, 341
Напряженное состояние линейное (одноосное) 23
— объемное (трехосное) 23
— плоское (двухосное) 23
Наработка до отказа средняя — Пример определения для экспоненциального закона надежности 588
— на отказ — Формулы 592
Натяг потребный 103 — Пример расчета 104, 105
— расчетный 103 — Пример расчета 104, 105
Неймана—Пирсона метод 611, 612
Обкатка роликом и шариком — Инструмент 600
— внброударная (чеканка) 600
— сглаживающе-упрочняющая 600
— упрочняющая 600
Оболочки анизотропные — Устойчивость при внешнем давлении 475 — Устойчивость при действии осевых сил 475 — конические — Устойчивость под действием внешнего давления 472 — Устойчивость под действием сжимающей силы 472
— подкрепленные — устойчивость под действием внешнего давления 475, 476 — Устойчивость при действии осевых сил 476, 477
— сферическое — Устойчивость под действием внешнего давления 473
— эллипсоидальные — Устойчивость под действием внешнего давления 473
Оболочки цилиндрические 443 — Напряжения в сечении 444
— Расчет температурных напряжений 458, 459
— Условие устойчивости при совместном действии нагрузок (общий случай) 469 -471
— Устойчивость при внешнем давлении 463 — 465
— Устойчивость при действии осевых сил 465, 466
— Устойчивость при изгибе 467, 468
— Устойчивость при кручеиин 475
— Формы потери устойчивости 466
Оболочки цилиндрические длинные — Общее решение и основные случаи расчета 445 — 447 — Понятие 445 — Устойчивость при действии осевых сил 465, 466 — Устойчивость прн изгибе 467, 468 — Устойчивость прн кручении 466, 467
— очень короткие — Приближенный метод расчета 456 — 458
Обработка деталей пневмодииамическая — схема 497
— упрочняющая — Эффективность 602
Опоры жесткие 407
— упругодемпфирующие 418
Оптимизация локальная — Цели 621
Осм сечення главные приведенные 340 Отказ 581 — катастрофический 581
Палец поршневой — Виды деформаций 266 — расчет иа прочность 266, 267 — Расчетные схемы нагружения 267 Параметр закручениости лопаток 297 Параметры входные заданные 617 — состояние 621 — управляющие 617, 621
Паяные соединения — Виды 111 — Зазоры, применяемые при пайке 124 — Механические характеристики припоев 123 — Прочность прн срезе 124, 125 Передача — см. Зубчатая передача. Ременная передача и т. д.
Перемещения точек тела при деформации тела 12
Период колебания системы 392
Пластинки кольцевые — Устойчивость 463 Пластинки круглые — Устойчивость 462, 463
— Примеры расчета пластинок 427—429 — Примеры расчета температурных напряжений 440
— Расчеты по таблицам 429—439
636
Предметный указатель
— Расчет температурных напряжений 439, 440
— Расчетные формулы 424—427
Пластинки прямоугольные — Расчет на устойчивость 460—462 — Расчетные формулы 424 —427
— под действием касательных напряже-ний — Устойчивость 461, 462
— сжатые в двух направлениях — Устойчивость 460, 461
— сжатые в одном направлении — Устойчивость 460
Пластинки с отверстиями — Распределение деформаций 518, 519 — Распределение напряжений 512, 518 — 521
Пластичность — Понятие 23
Плотность материала приведения 333
— распределения отказов 584
Поверхность деформирования 501
Подшипники качения - Быстроходность 144
— Выбор 153
— Динамическая грузоподьемность 148 — 150
— Контактные напряжения в подшипнике 146
— Материалы 144, 145
— Основные характеристики 141—146
— План скоростей в подшипнике 147
— Причины преждевременного выхода нз строя 160 — 162
— Смазка 156 —160
— Статическая грузоподъемность 147. 148
— Условное обозначение 144
— Частота вращения сепаратора 146
— Частота вращения шарика 147
Ползучесть 31, 501
Полки бандажные — Расчет на изгиб 302, 303
Поршень — Расчет днища 268
Правило Верещагина 349 — Выполнение интеграла Мора 348, 349 — Ограничение для применения 349
— решающее 613
Предел выносливости — Понятие 33
— детали 42 — Расчетно-экспериментальное определение 562
— материала — Ълиянне различных факторов 35, 36
— ограниченный — Понятие 33
Предел длительной прочности 28
— доверительный для вероятности разру шения 576, 577
— ползучести 31
— пропорциональности 24
— прочности 25
— прочности истинный 25, 26
— текучести 25
— упругости 25
Прессовые соединения — см. Соединения с гарантированным натягом
Принцип итерации 620
— оптимизации основной 621
Прогиб начальный — Влияние иа выпучивание стержня 382, 383
Прогиб оси стержня — Расчет 594, 595
— наибольший 595
— остаточный 595
Проектирование автоматизированное 618, 620
Производство автоматизированное — Понятие 618— Схема 619
Прокладки линзовые — допустимое давление 79 — Усилие уплотнения 78
— плоские — Допустимое давление 79 — Рекомендуемые значения толщины и ширины 77 — Усилие уплощения 76
— фасонные — Допустимое давление 79 — Усилие уплотнения 77, 78
Профилирование равнопрочных дисков 322. 323
Прочность длительная 28
— малоцнкловая 36, 37
— материалов прн растяжении 24 — 26
— материалов при сжатии 26
— резьбовых соединений прн переменных нагрузках 67 — 70 — Пример расчета 70 — 72
— резьбовых соединений при статических нагрузках 63—67
— соединений с гарантированным натягом 105 — 108 — Конструктивные
— способы повышения 106 — 108
— термическая 37
Сопротивление усталости — Влияние абсолютных размеров детали (масштабного фактора) 559, 560
— Влияние концентрации напряжений 558, 559
— Влияние постоянных напряжений 557. 558
— Влияние состояния поверхности и упрочнения 560—562
— Основные закономерности 555—562
— Статистические модели 572
— Условия 564—566
Сопротивление усталости сварных соединений — Влияние конструктивных и технологических факторов 114 — 122 — нахлесточные 117, 118 — с конструктивными элементами 121, 122
— стыковых 114 — 117 — Механическая обработка шва 117 — Напряжения в стыковом соединении 115 — Остаточ ные напряжения от сварки 116 — Состояние поверхности основного металла в зоне шва 115, 116 — Форма и размеры шва 116
— тавровых 118, 121
Прочность фланцев 82, 83
— фланцевых болтов 82
— шлицевых соединений 92—96
Пружины — Диаграмма предельных напряжений 173
— Заневоливание 164
— Материалы 162, 163
— Пример расчета 178, 182
— Расчет на статическую прочность 172
— Расчет иа ударную нагрузку 173, 174 — Расчет на сопротивление усталости 173
— Резиновые упругие элементы 178 — 182 Пружины витые — способы предотвращения выпучиваний 165
— концентрические 165
— растяжения 164, 165
— сжатия 164, 165
Пружины витые цилиндрические— График зависимости между нагрузкой н осадкой пружииы сжатия 168
— Допускаемые напряжения 166
— Значения максимальной нагрузки и податливости одного витка пружины 170, 171
— Касательное напряжение в сеченни 165
— Осевая податливость 168
— Расчет 165 —172
— Силовые факторы в сеченни нагруженной пружины 166
Пружины кольцевые 176, 177
— кольцевые волнистые 177, 178
— многожильные 172
— прорезные 175, 176
— тарельчатые 175
Предметный указатель
637
— фасонные 172
Пуассона коэффициент 14
Разрушение в зависимости от числа циклов — Типы 555 — пластическое 555 — хрупкое 38
Распределение времени безотказной работы
ВеЙбула 589
— нормальное 588, 589
Растяжение — Прочность материалов 24 — 26
— стержня 13
Расчет витых цилиндрических пружин 165-172
— числа изделий, находящихся в эксплуатации 591
Расчет на прочность конструкций с учетом Пластичности и ползучести — Метод дополнительных деформаций, 504, 505. 507—509
— Метод переменных параметров упругости 502 — 504. 506, 507
Расчет соединений с фланцами контактирующими 73, 74
— иеконтактирующими 73, 74
— иеконтактирующими свободными 74, 75
— иеконтактирующими уточненный 76 — 78
Резоианс — Понятие 392
Резьбовые соединения — Диаграмма предельных напряжений 68
— Диаграмма усилий 51
— Дополнительные расчетные случаи 48 — 50
— Конструктивные способы разгрузки от скручивания при аатяжке 58
— Механические свойства материалов 66 — Определение коэффициентов податливости болта и промежуточных детелей 53—55
— Определение усилий в затянутом соединении при действии внешней осевой нагрузки 51 —53
— Основной расчетный случай 47, 48
— Прочность при переменных нагрузках 67-72
— Распределение нагрузки по виткам резьбы 58—63
— Расчет напряжений кручения 56 — 58
— Расчет усилий в сложных силовых схемах 55, 56
— Расчетная схема 51
— Способы разгрузки от напряжений нагиба 65, 67
— Способы разгрузки от снл в плоскости стыка 50
— Способы улучшения распределения нагрузки по виткам 61
— Типы 48
— Условие цепного среза 64
— Уточненный расчет 51—56
Релаксация напряжений — Понятие 31
Релея формула 286
Ременная передача — Быстроходность 237 — Дуга скольжения 235 — Дуга сцепления 235 — Кинематика 236 — Коэффициент динамичности 239, 241 — Коэффициент треиня 235
— Коэффициент угла обхвата 239
— Коэффициент, учитывающий влияние длины ремия иа ресурс 239
— Коэффициент, учитывающий неравномерное распределение нагрузки 239
— Кривая скольжения 236, 237
— Материал ремней 233, 234
— Мощность общая 238, 239
— Мощность, передаваемая одним ремнем 239, 240
— Нагрузка полезная 239
— Нагрузочная способность 235
— Напряжения в ремнях 237
— Недостатки 233
— Порядок расчета 243, 244
— Преимущества 233
— Применение 233
— Размеры клиновых ремней 234
— Расчеты на усталость 238
— Расчет на тяговую способность 238, 239
— Ресурс 238
— Самозаклинивание ремня 236
— Сила натяжения ремия 234 — 236
— Скольжение относительное 236
- Срок службы 238
— Схема 233
— Схема взаимодействия ремня со шки вом 235
— Схема сил, действующих иа элемент ремия 235
— Тяговая способность передачи 236, 237
— Увеличение угла обхвата 236
— Форма сечеиия ремня 233
— Формула Эйлера 235
— Число передаточное 236
Ременная передача с зубчатыми ремнями — Давления удельные иа зубья 243 — Материал ремня 239 — Модуль 242 — Мощность, передаваемая клиновым ремнем 241
— Основной конструктивный параметр 242
— Скорость ремия наибольшая 242
— Схема 242
— Усилие окружное расчетное 242
— Шаг на наружном диаметре 242
— Ширина ремия 242
Ремни клиновые 233 — Основные размеры н области применения 234 — поликлииовые 233
Ремонтопригодность — Понятие 581
Роликоподшипники — Типы 142, 143 —
Характеристика 142, 143
Роторы жесткие 406
Самоустаиовление вала 406
Сварные соединения — Влияние основных конструктивных и технологических факторов иа усталостную прочность 114 — 122
— Допускаемые напряжения для сварных швов при статической нагрузке 112
— контроль качества 111, 112
— Основные виды 109- 111
— Расчет иа прочность при переменных нагрузках Р2
— Расчет на прочность при постоянных нагрузках 122
Сдвиг — Понятие 12
Сжатие — Прочность материалов 26 — стержня 13
Сила перерезывающая — Определение 334
Система двухмассовая — Расчет изгибиых колебаний 400, 401 — Определение частоты собственных колебаний 395 — двухмассовая крутильная — Определение частот» колебаний 398
— миогомассовая крутильная — Опреде-левие частоты колебаний 398, 399
638
Предметный указатель
— одномассовая — Расчет изгибных колебаний 399, 400 — Расчет крутильных колебаний 396 — Определение частоты собственных колебаний 394
— параллельных элементов — Анализ надежности 590, 591 — Надежность 589, 590
— последовательных элементов 589
Скорость угловая критическая — Общий случай определения 414
— некоторых роторов 424
Смазывание подшипников 156 — 160
Соединение деталей с гарантированным натягом — контактные давления 99-ЮЗ
— Прочность прн переменных нагрузках 105- ’08
— Услов я неподвижности 99
Соединен» — см Резьбовые соединения, сворны соединения н т. д.
Срез — касательное напряжение при срезе 19
— заклепок 19, 20
— цепной в резьбовых соединениях 64
— шпонкн 19, 20
Стержни — Влияние начального прогиба и виецентренного приложения силы иа выпучивание 382, 383
— Выпучивание прн упругопластнческих деформациях 386 — 388
— Жесткость сечения на изгиб 385
— Изгиб — см. Изгиб стержней
— Кручение —см. Кручение стержней
— Потеря устойчивости 385, 386
Стержни закрученные — Основные соотношения теории 292—294
— постоянного сечения — Определение изгнбных колебаний 401, 402
— сжатые — График зависимости предельного напряжения от гибкости 383 — Расчет на прочность и жесткость 383—385 — Условие прочности 384
— сжатые эксцентрично — График зависимости упругого прогиба от величины сжимающей силы н эксцентриситета 383
— с кольцевой выточкой — Распределение напряжений 520
Твердость — Понятие 23
- материалов 26, 27
Тензометрированне лопаток 312, 313 Теория пластичности деформационная 497-499
— пластического течения 499 — 501
— попзучести 501
Технология автоматизированная — Понятие 617
Трещина усталостная 182
Угол закрутки единицы длины вала 355
— закрутки стержня с эллиптическим сечением 356
— поворота сечения лопатки от действия центробежных сил 295
Удлинение относительное 12, 25
— полное истинное 26
Упрочнение — Влияние иа усталостную прочность 560 — 562
— деталей — Методы 595
— микрошарикамн 598, 599
— отверстий 600
Упрочнение деталей машин дробью гидро-дробеструйное 597
— пиевмодииамическое 596, 597 — пиевмодробеструйиое 596 Упругая длина стержня 342—344 Уравиовешнванне валов 423, 433 Усилие затяжкн фланцевых болтов 81 — обжатия прокладки 79 — уплотнения, необходимое для герметичности стыка во фланцевых соединениях 76 —78
Условия усталостной прочности. — Простое (однокомпонентное) напряженное состояние 564 — Сложное (многокомпонентное) напряженное состояние 564—566
Усталость малоцикловая 36, 37
Устойчивость — Динамический анализ 388 — 390 — Понятие 459 — Потеря при нагреве 390
— колец 463
— пластинок 460 — 463
— пластинок при температурных напряжениях 473, 474
Устойчивость оболочек анизотропных 474, 475 — конических 472 — подкрепленных 475 — 477
— прн температурных напряжениях 473, 474
— сферических 473
— цилиндрических 463—472
— эллипсоидальных 473
Устойчивость стержней — Потеря 373 — Потеря при упругопластических деформациях 385, 386 — Формы прогибов 375
Фактор масштабный — Влияние на усталостную прочность 559, 560
Фланцевые соединения — Напряженное состояние фланца и трубы 83—87
— Разрушающая нагрузка 85, 86
— Расчетная схема соединения с контактирующими фланцами 86, 87
— Расчетная схема соединения с неконтактирующими фланцами 83—86
— Типы 73, 79
— Упрочненный расчет 73—76
— Уточненный расчет соединений с не-коитактирующими фланцами 76 — 83
Фланцы — Расчет иа прочность
Хрупкость — Понятие 24
Центр тяжести сечения приведенный 339 Цепная передача — Износостойкость 250, 251
— Конструкции 245
— Коэффициент концентрации напряжений эффективный 253
— Недостатки 245
— Основные параметры 245, 246, 248, 249
— Основные размеры 247
— Особенности проектирования 254, 255
— Порядок расчета 255, 256
— Преимущества 244, 245
— Расстояние между осями звездочек 249
— Силы в передаче 247
— Сопротивление усталости 251, 253, 254
— Тяговая способность 250
— Число зубьев звездочек 248, 249
— Число передаточное 248
— Шаг 249
— Эксплуатация 254, 255
Цепь втулочная 246
— зубчатая 246
— роликовая 245
Предметный указатель
639
Цикл переменных напряжений асиммет ричиый 32
— пульсационный 32
— симметричный 32
Частота вращения вала критическая 139, 140
— Влияние гироскопического эффекта 409 — Общий случай определения 414—416 — Определение второй и более высоких критических угловых скоростей 416, 417
— Примеры расчета ротора компрессора 413, 414
— Примеры расчета ротора турбомашииы иа упругих опорах 420, 421
— Расчет с учетом упругости опор 418 — 420
— Учет начального эксцентриситета центра тяжести диска 405, 406
— Учет упругости опор 407
Частота вращения критическая вала с непрерывно распределенными массами 410 — 413
— с несколькими дисками 410
— с одним диском 405 — 410
— с равномерно распределенной массой 421, 422
Частота колебаний 392
— крутильных 398, 399
Частота переменных напряжений 36
Частота системы собственная — Определение методом динамических жестко стей 394—396
Шариковинтовые передачи — конструкция 226
— Материал винтов и шариков 227
— Напряжение контактное максимальное 231
— Основные достоинства 225, 226
— Основные профили виита н гайки 226
— Податливость витка винта и гайки 230, 231
— Расчет 227 — 233
— Схема соединения типа болт —гайка 228
— Схема соединения типа стяжки 229
— Уравнение совместности деформаций 228
— Уравнение совместности перемещений 228
Шарикоподшипники — Оптимальные углы контакта 143 — Типы и характери стика 142
Шатуиы — Определение напряжений 264 — Расчет кривошипной головки 265, 266 — Расчет иа прочность стержня 264, 265 — Расчетные схемы нагружения поршне вой головки 263
Шероховатость поверхности — Влияние иа усталостную прочность 560
Шлицевые соединения — Изнашивание 96, 97
— Концентрация напряжений 96
— Расчет иа прочность 92 — 96
— Способы центрирования 90, 98
— Схема 93
— Фактические средине напряжения смя тия для различных изделий 94
Шлицевые соединения прямобочиые 90 — с винтовыми зубьями 91 — соосные 128 — торцевые 128 — треугольные 91, 92 — эвольвеитиые 91, 92
Ш пнльки — Допускаемые статические иа грузки 50 — Момент затяжки 50 — Схема нагружения 56
Шпонкн призматические обыкновенные 87, 88 — сегментные 88
Шпоночные соединения — основные типы 88 — Расчет 88, 89
СПРАВОЧНОЕ ИЗДАНИЕ
Биргер Исаак Аронович, Шорр Борис Федорович, Иосилевич Геннадий Борисович
РАСЧЕТ НА ПРОЧНОСТЬ
ДЕТАЛЕЙ МАШИН
Редактор Т. С. Грачева
Художественный редактор С. Н. Голубев Технические редакторы: Л. А. Макарова, И. В. Малыгина
Корректоры: (X Е, Мишина, Л.А, Ягупьева
ИВ № 6676
Сдано в набор 17.12.91. Подписано в печать 16.07.92. Формат 60x90/16. Бумага офсе7иая Гарнитура литературная. Печать офсетная. Усл. печ. л.50,89. Усл. кр-отг. 40 Уч.-изд. л 40.
Тираж 10 000 экз. Заказ 402.
Ордена Трудового Красного Знамени издательство «Машиностроение», 107076, Москва, Стромынский пер., 4
Санкт-Петербургская типография № 6 Министерства печати и информации Российской Федерации. 193144, Санкт-Петербург, ул. Моисеенко, 10