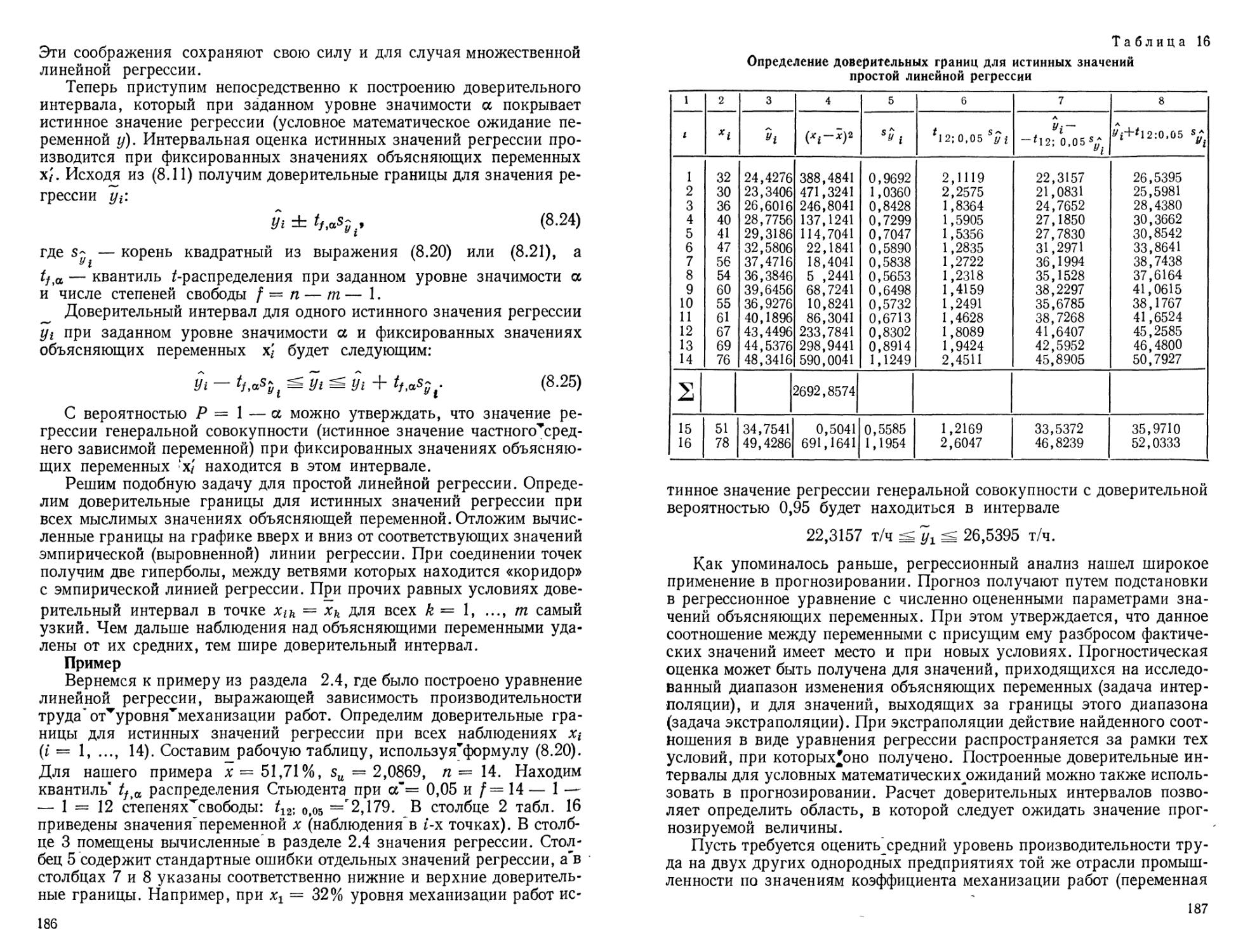
Tags: регрессионный анализ
Text
METHODEN
DER KORRELATIONS-
UND REGRESSIONSANALYSE
Ein Leitfaden fiir Okonomen
Professor Dr. sc. Erhard Forster Dr. sc. Bernd Ronz
Verlag Die Wirtschaft Berlin 1979
Э. ФЁРСТЕР, Б. РЁНЦ
МЕТОДЫ КОРРЕЛЯЦИОННОГО И РЕГРЕССИОННОГО АНАЛИЗА
РУКОВОДСТВО для экономистов
Перевод с немецкого и предисловие В. М. Ивановой
Москва «Финансы и статистика» 1983
frfrK 22.47£
Ф43
библиотечка иностранных книг для экономистов и статистиков
Издательство «Финансы и статистика» выпускает на русском языке серию книг иностранных авторов, рассчитанных на специалистов, нуждающихся в пополнении своих математических и статистических знаний. Задача серии — познакомить советского читателя с методами, применяемыми за рубежом в экономическом анализе и различных хозяйственных расчетах. В серию включаются также работы по общим вопросам статистики.
Вышли из печати книги:
1. М. Броуди. О статистическом рассуждении. 1968.
2. А. Б е р н с т е й и. Справочник статистических решений. 1968.
3. У. Дж. Р е й х м а н. Применение статистики. 1969.
4. X. К р ы н ь с к и й. Математика для экономистов. 1970.
5. С. Д а й м е н д. Мир вероятностей. 1970.
6. А. X ь ю т с о н. Дисперсионный анализ. 1971.
7. С. Л и з е р. Эконометрические методы и задачи. 1971.
8. Эм. Борел ь, Р. Дельтейль, Р. Юрон. Вероятности, ошибки. 1972.
9. Статистические методы исследования корреляций в экономике. 1972.
1'0 . Л. Стол ерю. Равновесие и экономический рост. 1974.
11. Я. Окунь. Факторный анализ. 1974.
12. С. С и р л, У. Г о с м а н. Матричная алгебра в экономике. 1974.
13. Е. Г р е н ь. Статистические игры и их применение. 1975.
14. Д. Тёрнер. Вероятность, статистика и исследование операций. 1976.
15. Э. Кейн. Экономическая статистика и эконометрия. Вып. 1. 1977.
16. Э. Кейн. Экономическая статистика и эконометрия. Вып. 2. 1977.
17. Э. Ко лк от. Проверка значимости. 1978.
18. Г. Дэвид. Метод парных сравнений. 1978.
19. М. Г. Кенуй. Быстрые статистические вычисления. 1979.
20. Дж. Вайнберг, Дж. Ш у м е к е р. Статистика. 1979.
21. Н. Хастингс, Дж. Пикок. Справочник по статистическим распределениям. 1980.
22. А. Гильберт. Как работать с матрицами. 1981.
23. М. Кен дэл. Временные ряды. 1981.
24. Ю. К юн. Описательная и индуктивная статистика. 1981.
25. А. Эренберг. Анализ и интерпретация статистических данных. 1981.
26. П. Мюллер, П. Нойман, Р. Шторм. Таблицы по математической статистике. 1982.
27. Г. Кимбл. Как правильно пользоваться статистикой. 1982.
Подготавливается к изданию:
М. Холлендер, Д. Вулф. Непараметрические методы статистики.
РЕДКОЛЛЕГИЯ СЕРИИ
В. М. ИВАНОВА, В. А. КОЛЕМАЕВ, Г. Г. ПИРОГОВ, А. А. РЫБКИН, Е. М. ЧЕТЫРКИН, Р. М. ЭНТОВ.
1702060000—027
Ф 010(01)—83 33—83
© Verlag Die Wirtschaft, Berlin, 1979 © Перевод на русский язык, предисловие к русскому изданию, «Финансы и статистика», 1983
ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
В наши дни математико-статистические исследования становятся необходимым инструментом для получения более глубоких и полно-ценных^знаний о механизме изучаемых явлений. Предлагаемый вниманию советского читателя перевод книги Э. Фёрстера и Б. Ренца «Методы корреляционного и регрессионного анализа» посвящен методам, широко применяемым для построения математических многофакторных моделей. Как при планировании, так и при проведении экспериментов исследователь чаще всего ставит задачу, сводящуюся к составлению уравнений регрессии и оценке их параметров. Овладение приемами статистической обработки наблюдений и методами составления уравнений, дающих адекватное описание изучаемого явления, — непременное условие получения корректных выводов.
Для понимания методов, обсуждаемых в книге, от читателя требуется математическая подготовка в рамках технического или экономического высшего учебного заведения и знание основных понятий рии вероятностей и математической статистики.
В нашей стране уже издан целый ряд отечественных и переводных работ по математико-статистическим методам исследования взаимосвязей. Выбор именно этой книги для перевода объясняется тем, что в ней содержится систематизированное изложение идей и методов, лежащих в основе корреляционного и регрессионного анализа. Особое внимание авторы обращают на основные предположения при статистическом оценивании, о которых часто забывают при решении конкретных задач, что влечет за собой искажение выводов.
Отличительная особенность книги Э. Фёрстера и Б. Рёнца — ее прикладной характер. Авторы приводят экономические примеры, некоторые из них являются «сквозными». Эти примеры позволяют наглядно продемонстрировать результаты исключения и введения переменных в уравнение регрессии, различные способы обработки данных, достоинства и недостатки показателей связи. При этом следует отметить, ито примеры будут понятны не только экономистам и статистикам, но и другим специалистам различных отраслей народного хозяйства.
Авторы не только дают описание стандартной техники регрессионного и корреляционного анализа. Большое внимание уделяется содержательной интерпретации параметров регрессии и показателей связи.
5
Удачна и структура работы, позволяющая исследователю быстро ориентироваться в ее содержании и находить методы и алгоритмы критериев для решения своих задач. В книге приводятся необходимые сведения как по линейной, так и по нелинейной регрессии. В отдельную главу выделены важные вопросы корреляционного и регрессионного анализа — критерии значимости оценок параметров регрессии, коэффициентов корреляции и детерминации, а также построение доверительных интервалов для них и уравнений регрессии.
Отдельная глава посвящена проблеме мультиколлинеарности. Вскрывая причины мультиколлинеарности в экономических явлениях и ее влияние на свойства оценок, авторы используют различные подходы к определению ее присутствия в результатах анализа.
Для исключения или уменьшения мультиколлинеарности переменных предлагается набор методов с краткой их характеристикой. Имеется также обзор проблем, связанных с корреляцией и регрессией временных рядов. Э. Фёрстер и Б. Рёнц вводят читателя в круг вопросов, возникающих при анализе временных рядов. Наиболее обстоятельно при этом обсуждается автокорреляция переменных и возмущений. Здесь же приведен алгоритм критерия Дарбина—Уотсона для проверки гипотезы об отсутствии автокорреляции, широко используемый в практических расчетах.
В книге затрагиваются также проблемы оценивания структурных параметров эконометрических моделей, состоящих из нескольких уравнений регрессии с взаимозависимыми переменными. После краткого обсуждения наиболее важных вопросов, связанных с идентификацией и предпосылками построения эконометрических моделей, авторы рассматривают ряд методов оценивания систем одновременных уравнений — обычный метод наименьших квадратов, двухшаговый и косвенный методы наименьших квадратов. При этом дается не только общее описание методики: технические приемы иллюстрируются конкретными примерами. В работе содержится также обзор основных показателей связи признаков с качественной вариацией, подробно обсуждается ранговая корреляция.
По форме и стилю изложения, по виду и сложности затрагиваемых вопросов книгу Э. Фёрстера и Б. Рёнца следует рассматривать как введение в круг вопросов многомерного статистического анализа, что и позволяет рекомендовать перевод книги Э. Фёрстера и Б. Рёнца широкому кругу специалистов*, встречающихся в своей работе с исследованием взаимосвязей явлений.
В. М., Иванова
*Читатсли, желающие углубить свои знания об анализе связей явлений, могут обратиться к более полным и фундаментальным работам, ссылки на которые приведены в примечаниях и в библиографии, а также к таким книгам, как: Айвазян С. А., Бежаева 3. И., Староверов О. В. Классификация многомерных наблюдений. М., 1974; Демиденко Е. 3. Линейная и нелинейная регрессии. М., 1981; Б а р д Я. Нелинейное оценивание параметров. М., 1979; В а п н и к В. Н. Восстановление зависимостей по эмпирическим данным. М., 1979; Ч е т ы р к и н Е. М. Статистические методы прогнозирования. 2-е изд. М., 1977; Болч Б., Хуань К. Дж. Многомерные статистические методы для экономики. М., 1979; Себер Дж. Линейный регрессионный анализ. М., 1980.
6
ПРЕДИСЛОВИЕ
Исследование зависимостей и взаимосвязей между объективно существующими явлениями и процессами играет в науке, особенно в экономике, большую роль. Оно дает возможность глубже понять сложный механизм причинно-следственных отношений между явлениями. В настоящее время объективно существующие зависимости и взаимосвязи между экономическими явлениями большей частью описаны только вербально. Значительно важнее количественно измерить тесноту причинно-следственных связей и выявить форму влияний. Для исследования интенсивности, вида и формы причинных влияний широко применяется корреляционный и регрессионный анализ. В приложении к экономическим процессам он может стать тем инструментом, который вскроет сложные комплексы причин и следствий. Выявление количественных соотношений в виде регрессии и сравнение действительных (наблюдаемых) величин с величинами, полученными путем подстановки в уравнения регрессии значений объясняющих переменных, дают возможность лучше понять природу исследуемого явления. А это в свою очередь позволяет воздействовать на выявленные факторы, вмешиваться в соответствующий экономический процесс с целью получения нужных результатов.
Регрессионный и корреляционный анализ находит широкое применение при прогнозировании, при решении задач народнохозяйственного и внутризаводского планирования. Практика показала, что регрессионные уравнения — хорошие измерители связей между экономическими явлениями. Поэтому все больше экономистов в ходе своих исследований обращаются к этому разделу математической статистики, основанному на логике массовых явлений.
Одна из основных задач, которая стояла перед авторами настоящей работы, — дать в руки специалистов, прежде всего экономистов, систематизированное руководство по корреляционному и регрессионному анализу. При изложении материала авторы ориентировались прежде всего на практиков. В качестве примеров приводятся результаты успешно проведенных исследований в различных отраслях народного хозяйства, например результаты анализа себестоимости продукции, изучения спроса населения, показателей национального дохода. Кроме того, указываются задачи, при решении которых корреляционный и регрессионный анализ, по мнению авторов, является необходимым ме
7
тодическим приемом. Особенно это касается задач прогнозирования и планирования.
В основе данной работы лежит книга: Фёрстер Э., Эгер-майер Ф. Корреляционный и регрессионный анализ. Руководство для экономистов (Берлин, Экономика, 1966). Однако они существенно различаются как по структуре, так и по введенным обозначениям связей.
У читателя предполагается наличие статистических знаний лишь в небольшом объеме. В некоторых случаях авторы для формальных математических выводов используют матричную форму изложения. Читателю, малознакомому с матричным исчислением, мы рекомендуем при первом прочтении книги пропустить непонятные ему места и вернуться к ним после пополнения знаний в этой области.
При подборе примеров авторы стремились обеспечить наглядность результатов оценки взаимосвязей и содержательную интерпретацию полученных числовых характеристик. Но если пример относится к области экономики, то это вовсе не означает, что специалисты, занимающиеся другой деятельностью, например техникой, не получат из книги необходимых знаний для изучения и измерения стохастических взаимосвязей и зависимостей.
Мы пользуемся случаем выразить признательность всем, кто помогал нам советами в период осуществления наших замыслов и тем самым содействовал появлению этой книги. Особенно благодарны мы профессору доктору К. Дж. Рихтеру и профессору доктору М. Вёльфлин-гу, которые внесли ряд полезных предложений и сделали ценные замечания во время работы над рукописью. Мы весьма обязаны издательству «Экономика», взявшему на себя труд подготовки к печати и выпуску в свет данной книги, а также Рольфу Баумгарту, который с большой готовностью шел навстречу нашим пожеланиям. Мы будем также признательны всем, кто своими замечаниями будет способствовать дальнейшему совершенствованию книги.
Берлин, 1977 г.
Э. Фёрстер, Б. Ренц
ОСНОВНЫЕ ПОНЯТИЯ И ТЕОРЕТИК©—
, ВЕРОЯТНОСТНЫЕ ОСНОВЫ
I РЕГРЕССИОННОГО
И КОРРЕЛЯЦИОННОГО АНАЛИЗА
1.1. ПРИЧИННАЯ СВЯЗЬ
Явления и процессы в природе и обществе находятся в постоянной взаимной всеохватывающей объективной связи. Мир представляет собой единое нераздельное целое. В особенности это относится к общественным явлениям и процессам. Если мы хотим глубоко и основательно проникнуть в суть явления или процесса, необходимо исследовать и раскрыть его связь с другими явлениями и процессами. Для достоверного отражения объективных общественных явлений и процессов в ходе статистического анализа следует количественно описать самые существенные взаимосвязи. Это — непременное условие научного планирования и управления социалистическим народным хозяйством и объединениями народных предприятий. Без решения этих задач управление и планирование не могут полностью выполнить свои функции. Обсуждаемый принцип приобретает особое значение в условиях народнохозяйственного планирования, поскольку необходимо учитывать как можно большее число связей и зависимостей между явлениями. Статистические методы широко применяются также для управления и прогнозирования общественного производства, для познания объективно существующих явлений общественной жизни и принятия решений. При этом на первое место здесь следует поставить причинное объяснение связей между явлениями и процессами. Под причинной связью мы понимаем такое соединение явлений и процессов реальной действительности, когда изменение одного из них — следствие изменения Другого. Обычно одно и то же явление материального мира, с одной стороны, выступает как результат, следствие, эффект одной или нескольких причин, а с другой стороны, оно служит причиной наступле-ния других явлений или процессов. Такая причинная связь имеет все
9
общий характер и существует объективно. Раскрытие причинных зависимостей приводит исследователя к источнику зарождения отдельных явлений и процессов.
При изучении причинных связей мы задаемся вопросами: «почему?», «каким образом?». Признание факта множественности причин и множественности следствий в реальной действительности нашло свое отражение и при исследовании закономерностей в экономике. Так, на величину себестоимости единицы продукции влияют объем производства, используемая технология, уровень производительности труда. Производительность труда, которая служит причиной формирования величины себестоимости, в свою очередь — следствие различных причин, таких, как уровень развития техники, производственные навыки рабочих, уровень использования парка оборудования, научная организация труда и т. д. Заработная плата рабочего причинно обусловлена нормами, производительностью рабочих, их квалификацией и другими факторами. Урожайность сельскохозяйственной культуры зависит от строения почвы, состава и количества внесенных удобрений, метеорологических условий и других не менее важных причин.
В приведенных примерах речь идет о причинных связях между отдельными явлениями. Но причина и следствие представляют собой лишь звенья цепи в развитии явлений. Имеется множество параллельно существующих явлений, которые вызываются общей для них причиной. Однако необходимо различать связь между явлениями, которая может быть беспричинной, и причинную зависимость. Следовательно, причинная зависимость не целиком охватывает всестороннюю связь материального мира. «Но как раз этот факт доказывает, что мы правильно понимаем причинность, считая ее одной стороной, фрагментом бесконечного сплетения связей и взаимодействий» [15]. Итак, для обнаружения причинной связи между явлениями мы должны отобрать отдельные явления из общей цепи взаимодействий и исследовать их связи обособленно. Познать непосредственно всю картину связей и взаимодействий невозможно.
«Чтобы познавать эти частности, мы вынуждены вырывать их из их естественной или исторической связи и исследовать каждую в отдельности по ее свойствам, по ее особым причинам и следствиям и т. д.»* В. И. Ленин писал об исследовании причинной связи: «... человеческое понятие причины и следствия всегда несколько упрощает объективную связь явлений природы, лишь приблизительно отражая ее, искусственно изолируя те или иные стороны одного единого мирового процесса»**.
Если мы отдельные явления с целью их исследования искусственно вырываем из общего сцепления связей и взаимодействий, то это вовсе не означает, что имеются реально прерывающиеся или подверженные разрыву связи. Явления соединены и продолжают оставаться соединенными объективно существующей общей взаимосвязью, и причинность есть лишь частичка этой связи. Вследствие сложности и мно
*М арке К., Энгельс Ф. Соч., т. 20, с. 20.
**Л е н и н В. И. Поле. собр. соч., т. 18, с. 160.
10
гоГранности реально существующей объективной связи невозможно с помощью системы причинно-следственных отношений охватить всю развертывающуюся перед нами картину бесконечного движения материального мира. Лишь для раскрытия причинных связей с целью анализа отдельные явления рассматриваются изолированно.
Следует иметь в виду, что причинная связь между отдельными яВлениями может возникнуть не всегда, а лишь при определенном комплексе условий. Эти условия должны реализовываться одновременно с действием причин, если между рассматриваемыми явлениями существуют причинно-следственные отношения. Изменения в условиях могут привести к изменениям причинных влияний, к изменениям следствия. Если, например, заработная плата рабочего должна зависеть (наряду с другим) от его квалификации, то это заранее предусматривается в системе оплаты труда. Прибыль предприятия зависит от качества изготавливаемой продукции, если при разработке норм прибыли были заложены такие условия, что нормы прибыли варьируют в соответствии с уровнем квалифицированности труда и, следовательно, в соответствии с качеством изделий. В зависимости от степени реализации заложенных предпосылок усиливается или ослабляется влияние качества работы на прибыль предприятия.
Один из важных признаков причинной связи — соблюдение временной последовательности причины и следствия: причина всегда предшествует следствию. Но не следует идентифицировать отношения действующей причины с отношением предшествующего и последующего, т. е. не каждое предшествующее событие можно считать причиной появления последующего. Так, например, существует сменяемость дня и ночи, но нельзя представить ночь причиной дня, а день — причиной ночи.
В этой связи не меньшую опасность для правильного понимания причинно-следственных отношений представляют факты совпадений и одновременно развивающиеся явления. Например, увеличение числа онкологических заболеваний за последние 20 лет не является причиной роста промышленной продукции за тот же промежуток времени. Далее мы обстоятельно займемся исследованием связей между временными рядами. Другой важный признак причинной связи заключается в ее необходимости, т. е. в данных условиях причина при повторении с необходимостью порождает то же самое следствие. Следует обратить внимание также на условие повторяемости явления, так как только повторяемость обеспечивает практическую возможность раскрытия связи. Перечисленные характерные черты причинной связи позволяют нам развивать методы, с помощью которых можно глубже исследовать причинно-следственный механизм. Некоторые из этих методов будут обсуждаться в последующих разделах.
Причинная связь имеет объективный характер. Она не является мысленно воображаемой связью, но существует независимо от сознания людей и независимо от познания этой связи. Объективный характер причинной связи не означает неизменности комплекса причин и Условий для отдельного явления. Причины и условия многих явлений и процессов в природе и обществе относительно устойчивы. Но с тече
11
нием времени всякое явление претерпевает непрерывные изменения, и мы никогда не найдем точного его повторения. В точности не повторяются ни причины, ни следствия. Изменение причинно-следственного комплекса осложняет познание явления. Учет изменяющихся условий при исследовании причинных связей в обществе играет особую роль.
Большинство экономических явлений представляет собой результат многих одновременно и совокупно действующих причин. При раскрытии связей между ними главные причины, которые обязательно приводят к данному следствию, необходимо отличать от второстепенных. Последние осложняют действие существенных в данном аспекте причин. Кроме того, причинному действию и определяемому им следствию присуща в той или иной степени случайность. Каждый процесс при повторении его причинного комплекса реализуется с отклонением от закона, лежащего в его основе, за счет случайностей. Это нужно учитывать при познании причинно-следственного комплекса и в общественных явлениях. Элемент случайности присущ также социально-экономическим отношениям при социализме. «Случайность как форма проявления необходимости характерна также для социалистической системы ведения хозяйства, она оказывает определенное влияние на развитие социалистического общества. Планирование народного хозяйства, выполненное на самом высоком научном уровне, не может избежать случайных помех» [74]. Случайность признана неизменным атрибутом любого явления. Необходимые и случайные связи существуют в объективной реальности и, следовательно, независимы от сознания человека. Необходимость и случайность образуют диалектическое единство. К действию основной причины присоединяются влияния дополнительных причин. При этом направления этих влияний могут не совпадать. Кроме того, на причинно-следственный комплекс накладываются случайные помехи. Все это видоизменяет действие основной причины и приводит не к такому следствию, каким оно было бы при действии лишь одной основной причины. К сожалению, в силу недостаточности познавательных средств мы часто не в состоянии описать весь сложный комплекс причин. Описание его в общей форме недостаточно для проникновения в суть явления. Поэтому обычно начинают исследование с установления существенных в данных условиях причин и выражения основных причинных отношений в количественной форме. Второстепенные причины, а также вариация" причинных связей, вызванная изменением условий, в которых протекает явление, рассматриваются в одном' комплексе. Этот комплекс, как правило, содержит влияние известных существенных причин, случайные помехи, влияние непод-дающихся количественному измерению'или еще не раскрытых причин. Наличие комплекса влияний затрудняет исследование в экономике и делает невозможным полный охват причинно-следственных отношений. Но опыт науки'показывает, что многое из того, что не могли познать ранее, постепенно, ^развитием методов’познания’и усовершенствованием технических’средств познается. Поэтому' при анализе случайные влияния, а'также влияния еще непознанных причин не отбрасываются.
Упрощено основные типы причинных связей можно представить следующим образом:
.12
а) причинные связи между двумя явлениями у и х, из которых явление х — причина, а у — следствие. Итак, х -> у. Примером такой связи может служить зависимость между наличием основных фондов (х) и амортизацией (у);
б) причинные связи между двумя явлениями, между которыми существует взаимодействие. Итак, у х. Такая связь существует, например, между заработной платой (х) и производительностью труда («/);
в) явление х влечет за собой- несколько других явлений ух, у2 и т. д., т. е.
^2
Так, например, размер заработной платы и наличие оборотных средств зависят от производительности труда;
г) несколько явлений хъ х2, ха и т. д. являются причинами одного явления у. Это можно представить таким образом:
хг~*у х3^
Уровень производительности труда, например, зависит от ряда факторов, таких, как технический уровень производства, производственные навыки рабочих, природно-экономические условия производственного процесса, возраст рабочих и т. д.;
д) явления у, хъ х2, х3 представляют собой причинно-следственный комплекс с последовательным соединением причин. Например,
I | х3~
Так, уровень механизации в промышленности причинно связан с производительностью труда. Производительность труда в свою очередь оказывает влияние на себестоимость, а себестоимость — на выпуск продукции. Кроме того, на себестоимость непосредственное влияние оказывает уровень механизации;
е) исследуемые явления у, х1г х2 и т. д. находятся между собой в сложной взаимосвязи:
f----1
Х^ у
На себестоимость оказывает влияние производительность труда. Себе* стоимость воздействует на оборотные средства, а оборотные средства имеют причинную связь с производительностью труда.
В пунктах а—е перечислены принципиальные схемы причинно-следственных отношений, которые лежат в основе различных видов корреляций и регрессий, обсуждаемых в последующих разделах книги.
13
1.2. ПОНЯТИЕ РЕГРЕССИИ
Различают два вида зависимостей между экономическими явлениями и процессами: а) функциональная и б) стохастическая. В случае функциональной зависимости имеется однозначное отображение множества А в множестве В. Множество Л называют областью определения функции, а В — множеством значений функции. Если — отображение Xi, причем t/i — элемент множества В, a Xi — элемент множества А, то это записывается в виде равенства у = f (х), yt называется значением функции в точке Xi. Приведенное равенство указывает правило соответствия независимой переменной х зависимой переменной у. Для каждого допустимого значения х можно указать вполне определённое значение у. Примером такой однозначной математической функции является у = 2х. Если, положим, х = 3, то соответственно У = 6.
Примеры функциональной зависимости можно привести из области физических явлений. Например, в физике известен закон свободного падения. В условиях безвоздушного пространства скорость падения является произведением ускорения свободного падения на время падения. Закон Ома указывает функциональную связь между электрическим сопротивлением, силой тока и напряжением. Для законов классической механики характерного, что они справедливы для каждой отдельно взятой единицы совокупности и не содержат никаких элементов случайности. В экономике примером функциональной связи может слу-. жить зависимость производительности труда от объема произведенной продукции и затрат рабочего времени.
Совсем по-другому обстоит дело в закономерностях, проявляющихся только в массовом процессе, только при большом числе единиц совокупности. Такие закономерности называются стохастическими (вероятностными). При стохастической закономерности для заданных значений зависимой переменной можно указать ряд значений объясняющей переменной, случайно рассеянных в интервале. Каждому фиксированному значению аргумента соответствует определенное статистическое распределение значений функции. Это обусловливается тем, что зависимая переменная, кроме выделенной переменной, подвержена влиянию ряда неконтролируемых или неучтенных факторов, а также тем, что измерение переменных неизбежно сопровождается некоторыми случайными ошибками. Поскольку значения зависимой переменной подвержены случайному разбросу, они не могут быть предсказаны с достаточной точностью, а только указаны с определенной вероятностью. Появляющиеся значения зависимой переменной являются реализациями случайной величины. Под случайной величиной следует понимать функцию, отображающую пространство элементарных событий в множество действительных чисел. В экономике приходится иметь дело со многими явлениями, имеющими вероятностный характер. В качестве примеров таких случайных величин можно назвать следующие: число бракованных изделий, получающихся’в’процессе изготовления за определенные промежутки времени; количество простоев оборудования за смену; стоимость продукции предприятий; полная себестоимость товарной продукции.
14
Обратимся теперь к понятию регрессии. Регрессия—это односторонняя стохастическая зависимость. Она устанавливает соответствие между случайными переменными. Например, при изучении потребления энергии (у) в зависимости от объема производства (х) речь идет об определении односторонней связи, следовательно, о регрессии. Обе переменный являются случайными. Каждому значению х соответствует множество значений у и, наоборот, каждому значению у соответствует множество значений х. Таким образом, мы имеем дело со статистическими распределениями значений х и значений у. Исходя из этих распределений мы и должны находить стохастическую зависимость между X и у.
Односторонняя стохастическая зависимость выражается с помощью функции, которая, для отличия ее от строгой математической функции, называется функцией регрессии или просто регрессией. Далее мы более подробно остановимся на этом понятии. Здесь мы хотим лишь подчеркнуть характер функции регрессии, показав тем самым разницу между функциональной зависимостью и регрессией. При функциональной зависимости факторный признак х полностью определяет результативный признак у. Кроме того, при функциональной зависимости функция обратима. Так, функция х = у является обратной по отношению к функции у = 2х. Задаваясь значением х = 3, получим у — 6. Задаваясь для обратной функции значением у = 6, получим х — 3. Функция регрессии этим свойством не обладает. Только в предельном случае, когда стохастическая зависимость переходит в функциональную, переход из одного уравнения регрессии в другое становится возможным, т. е. начинает проявляться свойство обратимости.
Разумеется, функция регрессии будет обратима, если за стохастической связью скрывается подлинная функциональная зависимость. Например, это будет иметь место при определении эмпирическим путем суммы углов Многоугольников в зависимости от числа их сторон. Итак, если между явлениями отсутствует функциональная связь, а существует только стохастическая, то функция регрессии необратима. Это обусловлено, во-первых, самой структурой явления, определяющей направление связи; во-вторых, постановкой задачи исследования, когда преследуется вполне определенная цель: как по значениям одной переменной, выбранной в качестве аргумента, предсказать соответствующие значения другой (функции); в-третьих, способом измерения отклонений эмпирических точек. Вследствие этого, если исследуют стохастическую зависимость переменной у от х, то устанавливают регрессию У на х. Если же изучают стохастическую зависимость х от у, то определяют регрессию х на у. Конкретный практический смысл приводит к одной из двух видов регрессий. Например, при исследовании потребления энергии (у) в зависимости от объема производства (х) разыскивают регрессию у на х. Если же, наоборот, изучается механизм влияния объема производства на величину потребления энергии, что может представлять интерес при планировании народного хозяйства, то определяют регрессию х на у. В исследованиях связи между стоимостью товара и спросом при капиталистической форме ведения хозяйства практичес
15
кое содержание, имеют две постановки задачи: зависимость стоимости товара от спроса, а также обратная зависимость —спрос от стоимости товара, так как изменение цен на товары отражается на спросе населения. Хотя в данном случае исходя из логически-профессиональных соображений зависимость обратима, функция регрессии, подлежащая определению, не обладает свойством, обратимости.
Нередко между двумя и более переменными возникают связи, для которых логическое истолкование возможно только в одном направлении, а следовательно, имеет смысл находить только одну функцию регрессии, Так, вполне очевидно, что существует зависимость урожайности сельскохозяйственных культур (у) от количества осадков (хх) и количества внесенных удобрений (х2). Следовательно, нужно устанавливать регрессию у на jq и х2. Другое направление зависимости не представляет практического интереса в силу того, что, например, на количество выпавших осадков не влияет урожайность и количество внесенных удобрений. Итак, в некоторых случаях проблема обратимости регрессии может и не возникнуть.
Проблема обратимости теряет свою остроту также в случае взаимодействия причины и следствия, зависимой и объясняющей переменной, на чем мы более подробно остановимся в главе 12.
Функция регрессии формально устанавливает соответствие между переменными, хотя они могут не состоять в причинно-следственных отношениях. Однако задача научного исследования заключается в определении причинных зависимостей. Только понимание истинных причин явлений придает нашему знанию действенный характер, позволяет предвидеть явления, учитывать или надлежащим образом изменять их, чтобы вызвать новые, желаемые следствия в исследуемой области. В противном случае легко могут возникнуть так называемые нонсенс-регрессии (ложные, абсурдные), которые не имеют практического смысла. Так, например, число преподавателей вузов не зависит от числа онкологических заболеваний. К проблеме выбора причинно обусловленных влияющих величин мы вернемся в следующих разделах. А сейчас рассмотрим различные виды регрессии.
а) Относительно числа явлений (переменных), учитываемых в регрессии, различают:
аа) простую регрессию. Она представляет собой регрессию между двумя переменными. Например, между затратами на производство (зависимая, результативная переменная, или переменная, подлежащая объяснению) и объемом продукции, произведенной промышленным предприятием (объясняющая, независимая, или предсказывающая переменная). В качестве другого примера можно назвать зависимость прибыли предприятия (зависимая переменная) от производительности труда (объясняющая переменная);
аб) множественную или частную регрессию. Это регрессия между зависимой переменной у и несколькими причинно обусловленными объясняющими (независимыми, или предсказывающими) х2,..., хт. Так, имеется множественная регрессия между производительностью труда (зависимая переменная) и уровнем механизации производственных процессов, фондом рабочего времени, материалоемкостью и ква
16
лификацией рабочих (объясняющие переменные). При экономических исследованиях может быть охвачен весь причинно-следственный комплекс явлении.
б) Относительно формы зависимости различают:
ба) линейную регрессию, выражаемую линейной функцией. При этой форме зависимости между исследуемыми переменными объективно существуют линейные соотношения;
бб) нелинейную регрессию, выражаемую нелинейной функцией. В этом случае между исследуемыми экономическими явлениями объективно существуют нелинейные соотношения.
в) В зависимости от характера регрессии различают:
ва) положительную регрессию. Она имеет место, если с увеличением или уменьшением значений объясняющей переменной значения зависимой переменной также соответственно увеличиваются или уменьшаются. Например, регрессия между прибылью и объемом произведенной продукции; z
вб) отрицательную регрессию. В этом случае с увеличением или уменьшением значений объясняющей переменной значения зависимой переменной соответственно уменьшаются или увеличиваются. Например, регрессия между размером прибыли на единицу продукции и затратами на производство.
Положительная и отрицательная регрессии являются понятиями регрессионного анализа. Из названия этих регрессий вовсе не следует делать вывод о том, что положительная регрессия желательна, а отрицательная нежелательна.
Следует заметить, что понятия положительной и отрицательной регрессии, в общем, приобретают смысл только для простой регрессии, где четко определена причинная связь между явлениями. В случае же множественной регрессии предполагается существование множества одновременно развивающихся не зависимых друг от друга цепей причинно-следственных связей, среди которых часть может соответствовать прямой зависимости, а часть — обратной. Зависимая переменная находится под соединенным действием нескольких причин (объясняющих переменных), и мы не можем, как правило, четко отделить одни явления от других.
г) Относительно типа соединения явлений различают:
га) непосредственную регрессию. В этом случае явления соединены непосредственно между собой. Причина оказывает прямое воздействие на следствие, т. е. зависимая и объясняющая переменные связаны непосредственно друг с другом;
гб) косвенную регрессию. Косвенная регрессия имеет место, если объясняющая и зависимая переменные не состоят непосредственно в причинно-следственных отношениях, а детерминируются общей для них причиной, т. е. объясняющая переменная действует через какую-то третью или ряд других переменных на результативную переменную;
гв) нонсенс-регрессию (ложная или абсурдная регрессия). Она возникает при формальном подходе к исследуемым явлениям, без уяснения того, какие причины обусловливают данную связь. В результате Мо>кно прийти к установлению ложных и даже бессмысленных зависи-
17
мостей, которые не будут иметь практического значения, так как с их помощью нельзя предвидеть явления или влиять на их ход развития. Пример такой ложной зависимости уже приводился, а именно зависимость числа преподавателей вузов от числа онкологических заболеваний.
Приведенная классификация служит доказательством разнообразия и многочисленности видов регрессии. Однако на практике все виды регрессии чаще всего встречаются комбинированно. Так, существует простая линейная и простая нелинейная регрессия, множественная линейная регрессия и т. д.
Далее мы увидим, что корреляция и регрессия тесно связаны между собой. Это привело к тому, что иногда регрессию рассматривают как частный случай корреляции, считая тем самым корреляцию более широким понятием. Однако мы придерживаемся того мнения, что ход рас-суждений и постановка задач в регрессионном и корреляционном анализе различны. Это дает нам право обсуждать проблемы регрессии и корреляции раздельно.
1.3. ПОНЯТИЕ КОРРЕЛЯЦИИ
Корреляция в широком смысле слова означает связь, соотношение между объективно существующими явлениями'и процессами. Однако для раскрытия и исследования причинных связей в силу их многообразия недостаточно этого общего определения. Мало установить только наличие связи между двумя или несколькими явлениями. Кроме качественного экономического анализа, большое методологическое значение имеет правильный выбор вида и формы связи. Связи между явлениями и процессами могут быть различны по силе. При измерении степени интенсивности, тесноты, прямолинейности, четкости, строгости связи проблема корреляции рассматривается в узком смысле. Исходя из этого можно сделать следующее определение: если случайные переменные причинно обусловлены и можно в вероятностном смысле высказываться об их связи, то имеется корреляционная (стохастическая) связь, или корреляция.
Понятия регрессии и корреляции непосредственно связаны между собой. В то время как в корреляционном анализе оценивается сила стохастической связи, в регрессионном анализе исследуется ее форма. С помощью оценки значимости решают вопрос о реально объективном существовании связи. В корреляционном и регрессионном анализе много общих вычислительных процедур. Оба вида анализа служат для установления причинных соотношений между явлениями и для определения наличия или отсутствия связи. Итак, соотношение между регрессией и корреляцией условно можно представить в виде
корреляция (в широком смысле)
корреляция
(в узком смысле)
регрессия
функциональная и корреляционная связь — два основных типа вязи, определяющих соотношение между явлениями и процессами, при этом следует подчеркнуть, что любое причинное влияние может выражаться либо функциональной, либо корреляционной связью. Но не каждая функция или каждая корреляция соответствует причинной зависимости между явлениями. Приведем несколько примеров корреляционной связи в области экономики. Так, очевидно, что себестоимость продукции зависит от объема производства. Известно, что промышленные предприятия с одинаковым объемом производства имеют различную себестоимость продукции. Более того, наблюдается рассеяние величины себестоимости при фиксированных значениях объема производства. Это обусловлено тем, что в экономике действует сложный комплекс многочисленных взаимно переплетающихся причин. Так, на себестоимость наряду с объемом производства влияют еще другие факторы, такие, как потери от брака, ассортимент продукции, технология производства, используемое сырье, структура цен и т. д. Кроме того,* на себестоимость оказывают влияние случайные факторы. В общем, существует такая тенденция: чем больше объем производства, тем больше полная себестоимость. Но эта тенденция проявляется только в большой совокупности предприятий. В единичном случае вполне может оказаться, что предприятие А с более высоким объемом производства по сравнению с предприятием В имеет более низкую полную себестоимость продукции. При рассмотрении единичных случаев наблюдается пестрая картина отдельных связей.
Между доходом и потреблением товаров на душу населения также существует корреляционная связь. Относительное потребление продовольственных товаров снижается с увеличением дохода. Но опять мы можем говорить только об общей тенденции. Различные привычки потребителей, неодинаковый ассортимент продовольственных товаров и т. д. могут привести к тому, что в отдельных случаях (т. е. у отдельных индивидов) с увеличением дохода будет повышаться относительное потребление продовольственных товаров.
Между производительностью труда и техническим уровнем производства существует корреляция. Однако технический уровень производства представляет собой только один из многих факторов, оказывающих влияние на производительность труда. Производительность труда, как и многие явления в экономике, — следствие совокупного действия комплекса причин. Причем взаимодействие отдельных компонентов различно. Факторы-причины имеют разное направление и характер влияния. Одна причина может усиливать или ослаблять действие других. Кроме того, причины имеют разную силу или степень воздействия. Если рассматривать только парную корреляцию между приведенными признаками-факторами, то причинно-следственный комплекс будет сильно упрощен. Чем шире охватывается причинно-следственный комплекс, тем глубже вскрываются связи. Это дает возможность всесторонне изучать причинные отношения между явлениями, устанавливая существенные в данных условиях причины и второстепенные.
Для эффективного изучения связей необходимо использовать совокупности, однородные в отношении тех признаков, связь которых изу*
19
1&
чается. Если определяют время, затраченное работником на выработку единицы изделия на предприятиях, различающихся между собой только техническим уровнем производства, то следует ожидать, что в этом случае будет очень тесная связь между этими признаками. Чем теснее связь между явлениями, тем, следовательно, больше исключается действие второстепенных причин и тем меньше сказываются случайные влияния. В результате корреляционная связь приближается к функциональной. Поэтому функциональная связь может рассматриваться как предельный случай корреляции. Между экономическими явлениями преимущественно действуют объективно существующие корреляционные связи. Однако и в экономике необходимо четко различать корреляционную и функциональную связь.
Корреляция между двумя переменными может перейти в функциональную связь, если несколько переменных, соединенных определенным образом, рассматривать одновременно.
Известно, что стоимость товара (W) однозначно определяется средними общественно необходимыми затратами труда. Общеизвестно, что необходимые затраты труда включают количество вложенного овеществленного труда (X) и количество вложенного живого труда (У). Итак, W связано как с X, так и с У. Если мы исследуем связь между W и X или W и У, то W принимает определенные значения при заданных значениях X или У. В этом случае W можно рассматривать как случайную переменную в статистическом смысле. Между W и X, а также между W и У существует корреляция. Однако если мы рассматриваем одновременно X и У, то W теряет свойства случайной переменной, и корреляционные зависимости в совокупности переходят в функциональную зависимость в форме W — X + У. Величина W является функцией от двух переменных X и У и однозначно определяется ими.
Следует отметить, что иногда истинную функциональную связь трудно обнаружить из-за накладывающихся погрешностей измерения изменения условий реализации, ошибочного или формального рассмот рения причинных отношений. Неслучайные переменные, находящиеся в функциональной зависимости, преображаются в случайные, а связь начинает приобретать стохастический характер. Например, закон сво бодного падения выполняется точно только в безвоздушном простран стве. При отклонениях от этого условия закон проявляется в виде кор реляции.
В качестве другого примера приведем теорему Евклида. Предполо жим, мы ее забыли и хотим экспериментальным путем установить, в ка кой зависимости находится сумма углов многоугольника от числа сто рон. С этой целью произведем сначала измерение углов в треугольни ках. Их суммы отнюдь не будут представляться постоянными величи нами. Значения отдельных сумм будут колебаться вокруг 180°. Ана логично измерим и просуммируем углы в четырехугольниках, пяти угольниках и т. д. В результате погрешностей измерения, появляю щихся при неточной установке измерительных средств, вследствие оши бок при считывании показаний, а также из-за субъективных качеств экспериментатора и т. д. функциональная связь между суммой углов многоугольников и числом их сторон будет проявляться в виде корре
ляции. Однако вполне очевидно, что сумма углов в многоугольниках одного вида не является случайной переменной. Она только кажется таковой вследствие накладывающихся погрешностей измерения. В действительности же между числом сторон многоугольника п и суммой его углов (S) существует детерминированная связь, описываемая с помощью функции S — (п — 2) 180.
Мы уже упоминали, что причинное влияние может быть выражено в виде функциональной или корреляционной связи. Но отсюда вовсе не вытекает обратное утверждение, что за любой корреляционной или функциональной связью скрывается причинная зависимость. Во-первых, это связано с многообразием форм причинно-следственных отношений; во-вторых, уже из определения функциональной и корреляционной связи видно, что речь идет об отражении количественной связи между явлениями или об оценке этой связи по числовым данным. Задача же научного исследования состоит в разыскании причинных зависимостей. Только знание истинных причин явлений позволяет правильно истолковывать наблюдаемые закономерности. Однако корреляция как формально-статистическое понятие сама по себе не вскрывает причинного характера связи. С помощью корреляционного анализа нельзя указать, какое явление принимать в качестве причины, а какое — в качестве следствия. Корреляция лишь дает оценку силы, или тесноты, связи.
Вопрос о наличии причинных отношений между явлениями в каждом конкретном случае решается исследователем исходя из логическй-профессиональных рассуждений, которые должны по возможности предшествовать корреляционному анализу. Однако, по нашему мнению, последнее требование не должно быть обязательным условием, так как иногда объяснение причины и следствия можно получить только после эмпирического описания связи. Не приходится сомневаться, что в любом случае этот метод математической статистики служит весьма полезным инструментом для вскрытия связей между явлениями.
Во многих ситуациях относительно легко исходя из логически-профессиональных соображений объяснить, какие переменные представляют собой причину, а что является следствием. Так, существует корреляция между ростом производительности труда и повышением заработной платы. В общем случае рост производительности труда можно считать причиной повышения заработной платы. Но, с другой стороны, повышение заработной платы может быть материальным стимулом роста производительности труда. Между количеством осадков, количеством удобрений и урожайностью сельскохозяйственных культур также существует отчетливая корреляция. Здесь не возникает сомнений, какие переменные принять в качестве причины, а какую переменную считать следствием. Однако иногда трудно выяснить взаимоотношения между переменными. Так, Берксон * утверждает, что, хотя между рос
*В е г k s о n J. The Statistical Study of Association between Smoking and Lung Cancer. — In : Proceedings of the Staff Meetings of the Mayo Clinic, Vol.30 (1955), S. .323.
20
21
том и весом людей существует отчетливая корреляция, нельзя делать заключение о биологической необходимости этой связи, так как неизвестно, сохранится ли корреляция между указанными переменными при осознанно измененной форме питания. Аналогичный вопрос встает при исследовании зависимости заболевания раком легких от курения. Хотя курение в вероятностном смысле оказывает влияние на образование рака легких, нельзя, однако, утверждать, что курение является причиной заболевания. Итак, установление корреляции не означает наличия причинной связи. Особенно это ярко видно на примерах с ложной корреляцией, о которой речь еще впереди.
Рассмотрим теперь различные виды корреляции.
а) Относительно характера корреляции различают:
аа) положительную корреляцию. Она имеет место, если с увеличением или уменьшением значений одной переменной значения другой соответственно увеличиваются или уменьшаются. Положительная корреляция существует, например, между производительностью труда и заработной платой, между ростом и весом, между техническим уровнем производства и производительностью труда, между выполнением производственного плана и затратами рабочего времени, между объемом продукции и объемом импорта и т. д. Положительная корреляция называется также равнонаправленной (или прямой) корреляцией;
аб) отрицательную корреляцию. При этом виде корреляции с увеличением или уменьшением значений одной переменной значения дру гой соответственно уменьшаются или увеличиваются. Отрицательная корреляция существует, например, между производительностью труда и стоимостью изделия, между объемом продукции и затратами на единицу изделия и т. д. Отрицательная корреляция называется также обратной.
б) Относительно числа переменных различают:
аб) простую, или парную, корреляцию. Это корреляция между двумя переменными. Например, между доходом и потреблением, между прибылью и себестоимостью и т.д.;
бб) множественную корреляцию. Это корреляция между более чем двумя переменными. Например, между производительностью труда уровнем механизации производства, квалификацией рабочих, уровнем использования машинного времени; между расходом энергии, объемом производства и температурой внешней среды. С помощью множест венной корреляции мы пытаемся охватить весь причинно-следствен ный комплекс. Особенно это важно в экономике, где отдельные явления как правило, представляют собой следствие не одной, а нескольких причин. Множественная корреляция служит отражением этих объективно существующих множественных связей. Установление этих связей, сопровождаемое их конкретным объяснением, раскрывает механизм яв лений;
бв) частную корреляцию. Это корреляция между двумя перемен ными при «фиксированном» влиянии остальных переменных, включен ных в анализ. С помощью частной корреляции наиболее полно исследуется причинно-следственный комплекс и вскрывается внутренняя структура соотношений. Важность использования частной корреляции
вытекает из того факта, что, как правило, одновременно взаимодействуют несколько причин и оказывают совместное влияние на исследуемый признак. Если определять корреляцию между зависимой переменной (следствие) и каждой объясняющей переменной (причиной) по отдельности, то влияние остальных переменных будет сказываться на степени связности выделенных переменных. Это может привести к ошибочным заключениям. Так, при исследовании зависимости расхода пара от объема производства на одном из предприятий, изготавливающем сборные бетонные конструкции под открытым небом, была установлена отрицательная корреляция, т. е. с увеличением объема производства расход пара снижался. Но это явно парадоксальный вывод. Тщательный анализ показал, что другой фактор оказывает существенное влияние на потребление пара, а именно температура воздуха. При этом отрицательная корреляция между этими переменными настолько сильная, что вывод о наличии связи между расходом пара и объемом производства вполне может оказаться несостоятельным. Следовательно, прежде чем определять корреляцию между расходом пара и объемом производства, следует исключить влияние температуры воздуха на потребление пара. При определении корреляции между температурой воздуха и потреблением пара также следует исключить влияние объема производства на расход пара. В результате будем иметь две частные корреляции, каждая из которых указывает «чистую» стохастическую связь между двумя переменными при элиминировании влияния третьей.
в) Относительно формы связи различают:
ва) линейную корреляцию. При этом виде корреляции между исследуемыми переменными существуют линейные соотношения;
вб) нелинейную корреляцию. При этом виде корреляции между исследуемыми переменными существуют нелинейные соотношения.
г) Относительно типа соединения явлений различают:
га) непосредственную корреляцию. В этом случае исследуемые явления соединены между собой непосредственно. Объясняющая переменная оказывает прямое влияние на зависимую переменную. Непосредственная корреляция существует, например, между производительностью труда, техническим уровнем производства и производственными навыками рабочего; между производительностью труда и себестоимостью изделия; между наличием и оборачиваемостью оборотных средств; между потерями рабочего времени и объемом производства и т- Д. В капиталистическом хозяйстве существует непосредственная корреляция между уровнем цен и соотношением спроса и предложения. Итак, непосредственная корреляция существует, если из одного явления логически вытекает другое, и для объяснения этой корреляции не нужно привлекать другие явления;
гб) косвенную корреляцию. О косвенной корреляции говорят, когда изучаемые переменные не имеют непосредственной причинно-следственной связи, а детерминируются общей для них причиной. Логически такую связь можно объяснить лишь с помощью других явлений. При косвенной корреляции существует опасность перехода на формальный путь исследования, что может привести к ложной корреляции. Так,
22
23
было установлено, что при принятии родов врачами доля мертворожденных детей в среднем больше, чем при принятии родов акушерками, работающими самостоятельно без помощи врача. Если исходя из этого сделали бы вывод, что врачи не должны привлекаться к родам, то, очевидно, это не способствовало бы снижению доли мертворожденных. Между долей мертворожденных и врачебной помощью существует только косвенная связь постольку, поскольку врачи большей частью лишь подключаются при тяжелых родах или осложнениях. Так логический анализ явлений помог объяснить корреляцию.
Существует тесная положительная корреляция между возрастом вступающих в брак мужчин и женщин. Никому не придет в голову идея считать возраст вступления в брак у женщин причиной возраста вступления в брак у мужчин и наоборот. Причина здесь кроется в исторически укоренившихся нормах поведения, в биологических процессах и т. д.
Очень наглядный пример косвенной корреляции дает статистика дореволюционной России. Была установлена тесная корреляция между числом пожаров в стране и размером урожая. В неурожайные годы число пожаров было довольно высоким. Очевидно, плохие урожаи никак нельзя считать причиной пожаров в зданиях, и, кроме того, невозможно бороться с пожарами с помощью агротехнических мероприятий. В действительности же здесь между приведенными переменными существует только косвенная связь. Как размеры урожая, так и число пожаров существенно зависят от третьего явления — метеорологических условий. Сильная засуха, естественно, приводит к плохому урожаю. Она же благоприятствует возникновению пожаров. Только поэтому проявляется связь между урожайностью в сельском хозяйстве и числом пожаров. Этот пример еще раз показывает, что содержательное объяснение исследуемых явлений необходимо для правильного истолкования корреляции.
Не каждую корреляцию можно отождествлять с причинной связью. Высказывание А.А Чупрова о важности логически-профессионально-го истолкования связей имеет большое значение и для экономических исследований. «Мы видим, таким образом, насколько задача изучения взаимной зависимости между явлениями сложнее в действительности, нежели представляется тем, кто исходит из допущения, что либо X должен быть связан неразрывно с У, либо между X и Y не может быть никакой связи. Задача исследования не исчерпывается решением вопроса, есть ли связь. Должен быть установлен ее «закон», далеко не всегда сводящийся, как мы видели, к прямой пропорциональности, а могущий принимать форму функциональной зависимости любого вида. Должна быть так или иначе охарактеризована степень тесноты связи. И наконец, должен быть освещен характер связи: должен быть учтен вес тех «беспричинных встреч», которые способны порождать видимость связи между X и У, перестающей сковывать их, как только мы выходим за пределы первоначального поля наблюдения. Задача истолкования подмеченной связи представляется нередко и наиважнейшей, и наитруднейшей. Обрабатывая сходным образом эмпирические данные, которые имеют совершенно одинаковый вид, исследователь
24
приходит в разных случаях к выводам, глубоко различным по их внутреннему смыслу... Правильное истолкование подмечаемой связи представляется особенно существенным, когда статистическое знание привлекается к обоснованию жизненно важных решений и практических мероприятий. Тут знание связей, остающихся без истолкования или неверно истолковываемых, часто хуже полного незнания. Недостаточное внимание к этому обстоятельству является одним из злейших статистических преступлений. Здесь и корень наиопаснейших для статистики нападок на нее» [126, с. 25—26];
гв) ложную корреляцию. Под ложной корреляцией (нонсенс-кор-реляцией) понимается чисто формальная связь между явлениями, не находящая никакого логического объяснения и основанная лишь на количественном соотношении между ними. Часто ложная корреляция возникает при изучении динамических рядов. Особенно это характерно для экономических явлений. При расположении материала по годам или месяцам легко обнаружить эволюторную компоненту, показывающую основную тенденцию ряда. При сопоставлении рядов такого типа необходимо (прежде чем устанавливать корреляцию между обоими рядами) исключить из них закономерные изменения уровня. Совпадение или противонаправленность эволюторных тенденций, не имеющих общего объяснения и не связанных общностью развития, может послужить причиной искусственной связи, лишенной смысла. Подобная связь ничего не дает для исследования причин, управляющих явлениями. Келлерер приводит пример такой связи: имеется тесная положительная корреляция между количеством импортируемых апельсинов и числом смертных случаев от онкологических заболеваний за последние 50 лет [71].
В связи с этим следует подчеркнуть, что при разыскании причинных связей необходимо учитывать продолжительность исследуемого периода. За время развития явления могут появиться новые факты, способствующие раскрытию причинных связей. Наилучшей иллюстрацией этого утверждения могло бы послужить изучение онкологических заболеваний. С каждым годом все более совершенствуется диагностика рака, используются новые лекарства и новое медицинское оборудование, что нельзя оставить без внимания при рассмотрении числа заболеваний раком во временной последовательности, к*
I Напомним известный в статистической литературе пример ложной корреляции*между числом аистов, свивших гнезда в южных районах Швеции, и рождаемостью в эти же годы в Швеции. Вычисления, выполненные ради шутки, показали положительную корреляцию между этими явлениями. Приведенный пример еще раз*подтверждает, что причинная зависимость*не может быть выведена ни из*какого наблюдаемого совместного изменения явлений.
Проблема ложной корреляции возникает при использовании индексов, процентных чисел, а также когда к обеим сопоставляемым величинам добавляется или из каждой вычитается одна и та же величина. Ложная корреляция может возникнуть и в том случае, когда одна переменная входит в состав другой и тем самым формально обусловливает соответствие обеих переменных друг другу. Например, со-
25
поставление живого и овеществленного труда в расходах совокупного труда показало бы тесную связь. Но было бы ошибкой считать уменьшение доли живого труда в затратах совокупного труда причиной повышения доли овеществленного труда. В действительности же соотношение между затратами живого и овеществленного труда определяется уровнем производительности труда.
Цель приведенного описания типов корреляции — показать разнообразие взаимосвязей между явлениями. Но эти типы корреляции для лучшего их понимания были представлены изолированно. На практике чаще всего они встречаются комбинированно. Так, например, существует положительная линейная простая корреляция, положительная нелинейная множественная корреляция, отрицательная линейная частная корреляция и т. д. Если же речь идет о непосредственной или косвенной корреляции, то в каждом конкретном случае это следует пояснять особо. Ряд других понятий, связанных с корреляционным анализом, мы обсудим в последующих разделах.
1.4. ЗАДАЧИ КОРРЕЛЯЦИОННОГО
И РЕГРЕССИОННОГО АНАЛИЗА
Для планирования и управления социалистическим хозяйством, а также для экономико-аналитических исследований недостаточно установить лишь факт наличия корреляции или функциональной связи между явлениями или факт существования односторонней стохастической зависимости. Чтобы иметь возможность влиять на ход явлений и использовать обнаруженные связи и зависимости для прогнозирования, необходимо их исследовать более обстоятельно. Исследование корреляционных связей мы называем корреляционным анализом, а исследование односторонних стохастических зависимостей — регрессионным анализом. В корреляционном и регрессионном анализе используется ряд элементарных статистических приемов и математико-статистических методов, на которых далее мы остановимся подробно. Но уже здесь нам хотелось бы отметить, что эти приемы и методы — неотъемлемая часть корреляционного и регрессионного анализа. Без них невозможно проводить исследование корреляции и регрессии. При этом корреляционный и регрессионный анализ опирается прежде всего на измерение количественных соотношений между явлениями, что в конечном итоге позволяет найти объяснение следствия одной или несколькими причинами. Это вполне возможно, так как изменение в причине с необходимостью вызывает изменение следствия. По характеру этих изменений мы обнаруживаем свойства причины. «Всякое изменение причины отражается в следствии с необходимостью, определяемой характером связи между ними. Интенсификация или ослабление действия причины усиливает или уменьшает результат ее действия — следствие в целом или определенную сторону следствия, его признак. Не учитываемые в исследовании причины, выступающие как случайные, осложняют действие существенных причин» Г14].
В основе корреляционного и регрессионного анализа лежит логика массовых явлений, объясняющая массовую множественность следствий, отягощенных элементами случайностей. Средствами этой логики разработаны упомянутые выше представления и понятия, ставшие неотъемлемой частью корреляционного и регрессионного анализа. Экономические явления и процессы причинно обусловлены и объективно существуют. С помощью средств математической статистики мы их можем более или менее хорошо отражать, описывая количественные соотношения между ними на основании эмпирических данных. Задача исследования заключается в разыскании закономерностей, скрывающихся за погрешностью измерения, ошибками наблюдателя-регистратора, случайными возмущениями, а также в том, чтобы сделать эти закономерности как можно более очевидными и четкими, абстрагировавшись от всего второстепенного, незначительного и сконцентрировавшись на самом важном, существенном.
Задачи корреляционного анализа:
а) Измерение степени связности (тесноты, силы, строгости, интенсивности) двух и более явлений. Общие знания об объективно существующих причинных связях должны дополняться научно обоснованными знаниями о мере зависимости между явлениями. Для этого производятся соответствующие статистические вычисления. Здесь речь идет в основном о верификации уже известных связей. Но корреляционный анализ может служить также инструментом для обнаружения еще неизвестных связей.
б) Отбор факторов, оказывающих наиболее существенное влияние на результативный признак, на основании измерения степени связности между явлениями. Отобранные факторы используют для дальнейшего анализа. Самые важные факторы в рамках корреляционного и регрессионного анализа те, которые коррелируют сильнее всего с явлениями, подлежащими исследованию. Осознанно изменяя влияющие факторы, можно достигнуть желаемого эффекта в результативном признаке-следствии. Кроме того, на основе полученных связей можно с достаточной точностью значительно быстрее и проще вычислять некоторые экономические показатели. Существенные в данном аспекте факторы используют далее в регрессионном анализе.
в) Обнаружение неизвестных причинных связей. При решении этой задачи необходимо учитывать своеобразие взаимоотношений в причинно-следственном комплексе и особенности научно-методологических правил статистического исследования, опирающегося на количественные связи между явлениями. Корреляция непосредственно не выявляет причинных связей между явлениями, но устанавливает степень необходимости этих связей и достоверность суждения об их Наличии. Причинный характер связей выясняется с помощью логи-чески-профессиональных рассуждений, раскрывающих механизм связей. При выводах следует обращать внимание на возможность появления ложной корреляции.
Задачи регрессионного анализа:
а) Установление формы зависимости. Как уже упоминалось относительно характера и формы зависимости между явлениями, различа
26
27
ют положительную линейную и нелинейную и отрицательную линейную и нелинейную регрессию. На рис. 1 представлены основные формы зависимостей.
Положительная линейная регрессия (рис. 1,л) выражает равномерный рост функции. Положительную линейную регрессию мы наблюдаем, рассматривая зависимость общего расхода материальных' средств от объема производства при постоянных нормах расхода сырья и материалов или изучая зависимость потребления энергии от объема производства.
Положительная регрессия
Отрицательная регрессия
е
д
г
Рис. 1. Основные формы регрессии
Положительная равноускоренно возрастающая регрессия (рис. 1, б) существует, например, между подоходным налогом и заработной платой.
Положительная равнозамедленно возрастающая регрессия (рис. 1, в) возникает при описании зависимости уровня производительности труда от стажа работы.
Отрицательная линейная регрессия (рис. 1, г) выражает равномерное падение функции, например зависимость плотности населения от доли лиц, занятых в сельском хозяйстве; эта доля вычисляется относительно общей численности работающих.
Отрицательная равноускоренно убывающая регрессия (рис. 1, д) в определенных границах наблюдается при изучении зависимости числа посетителей кинотеатров от количества телевизоров, находящихся в употреблении.
Отрицательная равнозамедленно убывающая регрессия (рис. I, е) — например, регрессия себестоимости единицы продукции на объем про дукции. При капиталистической форме ведения хозяйства этот вид зависимости наблюдается при изучении зависимости спроса населения
от стоимости товара. С ростом цен на потребительские товары спрос на них уменьшается и наоборот. Если бы исследовалась зависимость в обратном направлении, т. е. зависимость стоимости товаров от спроса на них, то следовало бы ожидать в результате такого [ обращения положительную равнозамедленно возрастающую регрессию. Согласно этой зависимости с ростом спроса на товары, в общем, увеличивается цена на них, и чем ниже цена на потребительские товары, тем выше спрос на них. Из этого примера, видно, что простое обращение регрессии при исследовании экономических явлений недопустимо, так как получающаяся при этом зависимость часто не соответствует логике.
Рис. 2. Комбинированные формы регрессии
Понятия положительной равноускоренно возрастающей и равнозамедленно возрастающей регрессии, а также отрицательной равноускоренно убывающей и равнозамедленно убывающей регрессии заимствованы нами из [17, с. 347—348]. Эти формы зависимости довольно часто встречаются при исследовании экономических явлений.
В соответствии с основными типами регрессии разработаны критерии, с помощью которых можно оценить корреляцию. При линейной регрессии говорят о линейной корреляции. В случае нелинейной регрессии говорят о нелинейной корреляции. Чаще всего разобранные нами разновидности регрессии встречаются не в чистом виде, а в сочетании друг с другом, как показано на рис. 2. Регрессии такого типа называют комбинированными формами регрессии.
б) Определение функции регрессии.
Как видно из рисунков и приведенных определений, корреляционные связи характеризуются тем, что каждому значению объясняющей переменной соответствует распределение значений зависимой переменной. Разыскивая связь, мы исходим из этих распределений. Важно не только указать общую тенденцию изменения зависимой переменной, но и выяснить, каково было бы действие на зависимую переменную главных факторов-причин, если бы прочие (второстепенные, побочные) факторы не изменялись (находились бы на одном и том же среднем Уровне) и если были бы исключены случайные элементы. Для этого °пределяют функцию регрессии в виде математического уравнения того Или иного типа. Процесс нахождения функции регрессии называют иьтравниванием отдельных значений зависимой переменной. Построение регрессии и установление влияния объясняющих переменных На зависимую переменную — вторая задача регрессионного анализа.
28
29
в) Оценка неизвестных значений зависимой переменной.
С помощью функции регрессии можно воспроизвести значения зависимой переменной внутри интервала заданных значений объясняющих переменных (т. е. решить задачу интерполяции) или оценить течение процесса вне заданного интервала (т. е. решить задачу экстраполяции). Эти задачи решаются путем подстановки в соответствующие уравнения регрессии с найденными оценками параметров значений объясняющих переменных. Результат представляет собой оценку значения зависимой переменной. Таким образом, регрессионный анализ может оказаться полезным инструментом при планировании народного хозяйства и прогнозировании изменений экономических показателей.
Следует отметить своеобразие исследования корреляционных связей между экономическими явлениями. В естественных науках и технике для исследования связей часто применяют эксперимент, где можно добиться в определенных границах элиминирования побочных факторов и поддержания условий проведения эксперимента на неизменном уровне. «Физик или наблюдает процессы природы там, где они проявляются в наиболее отчетливой форме и наименее затемняются нарушающими их влияниями, или же, если это возможно, производит эксперимент при условиях, обеспечивающих ход процесса в чистом виде»*. В экономике едва ли возможно прибегать к экспериментам при исследовании связей в том же самом смысле.«... При анализе экономических форм нельзя пользоваться ни микроскопом, ни химическими реактивами. То и другое должна заменить сила абстракции»**.
Связи между экономическими явлениями весьма разнообразны. Одно и то же следствие может быть порождено разными причинами. Исследуемое явление обычно представляет собой результат совместного и одновременного действия нескольких причин, которые могут усиливать влияние друг друга или ослаблять его в зависимости от своей направленности. Поэтому в экономике определение причинной зависимости очень затруднено. Причинная обусловленность явлений едва ли может быть обнаружена при одной реализации причинного комплек са. Для раскрытия формы, характера и степени корреляционной свя зи необходимо массовое исследование в силу массовости причинного действия и множественности различающихся следствий, сопровож даемых элементами случайности. В экономике массовое исследование носит апостериорный характер, а в естественных науках — априор ный характер. В естественных науках в заранее спланированных экс периментах некоторые факторы-причины, влияния которых в настоя щий момент не должны подтверждаться, можно поддерживать на по стоянном уровне, а те причины, воздействие которых исследуется, дер жать в вариабельном состоянии. Результаты наблюдений далее обра батывают с применением методов корреляционного и регрессионного
*М арке К., Энгельс. Ф. Соч., т. 23, с. 6.
**Там же.
анализа. После краткого изложения некоторых статистических приемов и основных статистических характеристик мы перейдем к описанию этого важнейшего раздела математической статистики. Правильная оценка результатов наблюдений и успешное использование выводов в практике ведения социалистического хозяйства возможны только при осмысленном применении математического аппарата корреляционного и регрессионного анализа. Внедрение в практику быстродействующих ЭВМ и создание стандартных программ корреляционного и регрессионного анализа значительно облегчили обработку обширного статистического материала и предоставили возможность быстро строить многофакторные модели. Но при небольшом объеме наблюдений и на начальных стадиях исследования необходимые вычислительные работы выполняются на КВМ.
1.5. ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ, ВЫБОРКА, СРЕДНЕЕ, ВЫБОРОЧНАЯ ДИСПЕРСИЯ, КОВАРИАЦИЯ. СВОЙСТВА ОЦЕНОК
Перед тем как непосредственно перейти к корреляционному и регрессионному анализу, рассмотрим некоторые основные статистические понятия (см. также [18]).
Объектом статистического изучения служит совокупность единиц, обладающих некоторыми общими свойствами. Исследователь должен четко определить объект наблюдения, а также признаки, носителем которых он является. Так, при переписи населения единицы совокупности — это люди, при изучении рабочей силы — тоже люди, при изучении поголовья скота — отдельные животные и т. д. Недостаточно точное определение единицы наблюдения неизбежно влечет за собой погрешности, искажающие результаты анализа. Исследованию может подвергаться несколько признаков единицы совокупности. Так, при изучении рабочей силы представляет интерес не только общая характеристика численности работников, но и их состав по полу, возрасту, профессии, стажу работы, уровню образования и т. д. При изучении поголовья скота интересуются его породой, возрастом и т. д. Пол, возраст, профессия, стаж работы, уровень образования являются признаками рабочей силы. Размер предприятия и форма собственности — признаки предприятия. Корреляция и регрессия могут существовать как на основе признаков, так и на основе единиц.
Признак может быть выражен в различных формах. Так, например, пол — мужской, женский; возраст рабочего выражается годами; стаж работы — тоже годами; оплата труда — повременная, сдельная. Изменчивость величины признака у единиц, входящих в состав совокуп-ности, называется вариацией. Если вариация признака выражается количественно, то говорят об отдельном значении признака или просто 0 значении признака (варианте). Отдельное значение признака отражает уровень явления. Например, месячная заработная плата 680, 685, НО марок более низкая, чем заработная плата 830, 860, 890 марок.
Вся подлежащая изучению совокупность однородных единиц называется генеральной совокупностью. Число единиц в генеральной
31
30
совокупности называется ее объемом. «Генеральная совокупность (популяция) состоит из всех мыслимых наблюдений над явлением, рассматриваемым под определенным углом зрения» [130]. Другими словами, генеральная совокупность есть множество всех возможных реализаций случайной переменной. Понятие случайной переменной было введено в разделе 1.2. Генеральная совокупность может состоять из конечного и бесконечного множества единиц. При изучении распределения населения по роду занятий имеют дело с конечно большой генеральной совокупностью. При определении среднего возраста лиц женского пола среди населения страны рассматривают также конечно большую генеральную совокупность из лиц женского пола. Хотя обе эти совокупности конечно большие, объем их различен.
Множество всех возможных подбрасываний монеты, а также множество всех возможных вытягиваний шара из урны по схеме возвра щенных шаров (с возвращением вытянутых шаров в урну) образуют бесконечную генеральную совокупность. Предметом изучения в промышленной статистике может служить множество, образованное значениями показателей объема продукции, произведенной всеми промышленными предприятиями за определенный отчетный период; в статистике торговли — множество значений дневного оборота всех торговых предприятий страны за год. При изучении качества продукции рассматривается совокупность значений процента допущенного брака за смену на предприятиях какой-либо отрасли промышленности в течение года. Из приведенных примеров видно, что совокупность мо-жеть состоять не только из множества индивидов и предметов, но и из всех возможных наблюдений над явлением, рассматриваемым поД определенным углом зрения.
В зависимости от степени полноты охвата наблюдением изучаемой совокупности различают сплошное и выборочное наблюдение1. При сплошном наблюдении обследованию подвергают все без исключения! единицы генеральной совокупности.
Если обследованию подлежит только часть или несколько частей статистической совокупности, то такое наблюдение называют выбо рочным. Часть элементов совокупности, отобранных по какому-либо заранее сформулированному правилу, образуют выборку. Задача иа следования состоит в правильной организации и проведении выборов ного наблюдения, которое позволяло бы сделать достаточно достовер ные выводы о характере изучаемой генеральной совокупности. В та ких случаях говорят о репрезентативности выборки.
Переход от сплошного наблюдения к выборочному вызывается ра личными причинами. Не всегда имеется возможность обследовать каж дую единицу изучаемой совокупности, так как обычно это связано с большими затратами труда и времени (например, при наблюдении естественного роста лесонасаждений в масштабах страны), а иногда и с порчей или уничтожением продукции (например, при исследовании
Статистическое наблюдение обычно подразделяют на сплошное и несплош ное. Выборочное наблюдение является одним из видов несплошного наблю дения, к которому относятся также монографическое обследование и метод основного массива. — Примеч. пер.
32
продолжительности горения электрических лампочек, при определении предела прочности посредством разрыва металлических изделий, при определении калорийности топлива и т. д.). Выборочный метод обеспечивает быстроту проведения наблюдений, позволяет лучше и целенаправленнее организовать наблюдение, исключает или доводит до минимума ошибки регистрации, приводит к экономии средств и времени, энергии и сил участников наблюдения.
Отбор единиц в выборку может производиться либо направленно, либо случайно. При случайном отборе все единицы генеральной совокупности имеют одинаковую вероятность быть отобранными. Выборка, организованная по принципу, при котором ни одна единица не обладает преимуществом попасть в отбираемую совокупность по сравнению с другими единицами, называется случайной. Дальше речь пойдет только о случайных выборках. Поэтому для простоты слово «случайная» будет опускаться.
По результатам выборочных наблюдений вычисляются статистические характеристики, например средние, показатели рассеяния и т. д., которые еще будут обсуждаться. По величине этих характеристик делают вывод о соответствующих параметрах генеральной совокупности. В этой связи возникают две статистические проблемы: оценивание параметров генеральной совокупности и проверка гипотез относительно оценок этих параметров. При проверке статистических гипотез используются критерии значимости, однозначно устанавливающие условия, при которых гипотезу либо следует отвергнуть, либо считать непротиворечащей данным наблюдений. Выборочные характеристики представляют собой случайные величины. В этом можно убедиться, отобрав из одной и той же генеральной совокупности несколько выборок. Вычисленные по их результатам характеристики будут варьировать случайным образом от одной выборки к другой около среднего уровня, соответствующего характеристике генеральной совокупности. Так, средние различных выборок случайно рассеиваются вокруг среднего генеральной совокупности; выборочные коэффициенты корреляции — вокруг коэффициента корреляции генеральной совокупности и т. д. Каждая выборочная характеристика (статистика), определяемая как некоторая функция выборочных значений, имеет соответствующий закон распределения. Выборочные распределения статистик, наряду с необходимыми для этого понятиями теории вероятностей, будут рассмотрены в следующем разделе.
Статистические совокупности состоят обычно из большого числа единиц и поэтому трудно обозримы. Для получения информации о поведении изучаемого признака, для сравнения совокупностей удобнее пользоваться некоторыми обобщающими характеристиками, выражающими в сжатой форме наиболее существенные особенности распределения совокупности. Для характеристики уровней признака, свойственных единицам совокупности, используют различные виды средних, чаще всего среднее арифметическое1. Если отдельные значе-
^Далее в тексте речь будет идти о среднем арифметическом, называемом Росто средним. — Примеч. пер.
о
Зак. 1ЦЗ 3.3
ния, принадлежащие совокупности, обозначить через хъ х2, .... хп, то среднее х вычисляется следующим образом:
п
S Xi
Jc = = LzzJL—
n n
(1.1)
где S (читается: сигма) — знак суммирования, символизирующий правило вычисления. Этот знак означает, что все величины, стоящие за ним, суммируются; п — число отдельных значений. Среднее, вычисляемое по списку результатов отдельных наблюдений, называется простым. Ему соответствует формула (1.1). Если по наблюдениям построен вариационный ряд, т. е. значения варьирующего признака приведены с указанием соответствующих им численностей, то вычисляют взвешенное среднее. Обозначим через z19 г2, ..., zm отдельные значения вариационного ряда, а частоты, показывающие, сколько раз встречаются данные значения в ряде наблюдения, выразим через /гъ й2, •••, ^тп-Тогда формула, по которой вычисляется взвешенное среднее, имеет вид
т
2k hfc
2i ~Ьг2 —1____ . (12)
^1+^2 + - • •
т
Можно убедиться, что ^hk = п. По существу, простое среднее — лишь k=\
частный случай взвешенного среднего, когда частоты равны единице.
Среднее обладает рядом математических свойств, из которых мы обсудим одно. Сумма отклонений отдельных значений от их среднего всегда равна нулю:
П „
£(хг-х) = 0. (1.3)
i ®= 1
Это свойство легко доказывается:
п _ п _ п п .2 xi
у (X}—х)= У Xt—nx= У xt----------——=0. (1.4)
i=i i=i i=i п
Среднее характеризует всю совокупность. Оно обобщает индивидуальные особенности единиц совокупности, в нем уравниваются отдельные значения признака. С другими свойствами среднего и способом его вычисления по сгруппированному ряду можно познакомиться в учебниках по статистике.
При сравнении нескольких совокупностей их средние по величине могут совпасть, хотя отдельные значения в различных совокупностях могут существенно отличаться друг от друга как по величине, так и по структуре. Отдельные значения (варианты) могут быть тесно сгруппи
34
рованы вокруг своего среднего, либо, наоборот, сильно удалены от него. Среднее не отражает вариацию, т. е. изменчивость признака. Для характеристики степени рассеяния отдельных значений вокруг среднего используются различные меры. Мы ограничимся рассмотрением тех мер рассеяния, которые будут применяться далее.
Простейшим показателем вариации является вариационный размах V, равный разности между наибольшим и наименьшим значениями признака, т. е.
V == Хщах ^min* (1-5)
Вариационный размах легко вычисляется, но является весьма приближенным показателем, так как он почти не зависит от степени изменчивости вариантов. Кроме того, крайние значения, которые используются для его вычисления, как правило, ненадежны. Если мы хотим при характеристике степени рассеяния (вариабельности) учитывать все значения признака, то можно воспользоваться средним линейным отклонением d. Если обозначить отклонение отдельного значения от среднего через —х|, то
2 |Xi—х| 2
d = '—-------= ----- (1.6)
и п
Если варианты указаны с частотами, то вычисляют взвешенное среднее линейное отклонение:
2 >гь~г|Лл
d = —------------ (1.7)
т
S hk
В корреляционном и регрессионном анализе в качестве меры вариабельности отдельных значений часто используется дисперсия s* или стандартное отклонение sx. Различают простую дисперсию,
и взвешенную,
U—~z)2hh т
si—°- •_-------;n = 2 hk. (1.9)
В (1.8) и (1.9) знаменатель п — 1 есть число степеней свободы. Под Числом степеней свободы понимают количество вариантов совокупности, функционально не связанных друг с другом. До вычисления сред-
2* 35
него мы располагаем п вариантами, не зависящими друг от друга. Согласно определяющему свойству среднего сумма наблюдений должна остаться неизменной, если каждое из них заменить средним, т. е.
п _
= пх. После вычисления среднего для соблюдения этого условия
Z=1
мы имеем в своем распоряжении только п— 1 отдельных значений, не зависящих друг от друга. Аналогичные рассуждения можно привести для суммы отклонений всех отдельных значений от среднего. Поэтому число степеней свободы для дисперсии равно п — 1.
Для выборок большого объема в знаменателе вместо п — 1 можно использовать п. Возникающая из-за этого погрешность в оценке незначительна и ею можно пренебречь.
Арифметическое значение корня квадратного из дисперсии называется стандартным отклонением:
s« = /s*. (1.10)
После соответствующих преобразований и использования (1.1) формула (1.8) принимает вид п
п
s2 = _______—-----------
х п — 1 п—1 п — 1
п \
• (1.11)
1 Z=1 J
Вычисление дисперсии целесообразнее производить не по (1.8), а по (1.11). Как уже было упомянуто, для совокупности большого объема (и > 100) вместо п — 1 в знаменателе можно использовать п:
п
п
s2 « —-п
— —2
1^2— = х2—х , п
(1.12)
— -2
где х2 — среднее квадратов отдельных значений xi9 ах — квадрат среднего. Аналогично можно преобразовать формулу (1.9).
Важную роль в корреляционном и регрессионном анализе играет понятие ковариации. Если у единиц одной и той же совокупности рассматривают два признака х и у с точки зрения их взаимосвязи и вариабельности, то вычисляют меру — ковариацию, обозначаемую cov ху или, по аналогии со стандартным отклонением, sxy, по следующей формуле:
п _ _
Sxy~~ п-1
(1.13)
где Xi и yt — отдельные значения признаков х и у (реализации случайных переменных X и У), i = 1, ..., п. Формулу (1.13) можно после соот-
ветствующих преобразований представить также в виде
п п п пп
2 Xi 2 Xi 2 I п 2 Xi 2# А
= ----=—4- s ,= 1 (1.14)
П — 1 n(n~~ 1) n — 1 \. J П J
Для совокупностей большого объема снова вместо п — 1 в знаменателе можно использовать п:
2 (*i~Х)(У1~ У) ---------------------------------------------------------------------- (1.15) или п----------------------------------------------------------п п
2 xi у* 2 xi 2
Sxy * —---------z==1 z==-- =Ty-xy. (1.16)
tl tin
Ковариация может быть положительной, отрицательной или равной нулю. Если большим (малым) значениям признака х соответствуют большие (малые) значения признака у, то sxy > 0. В этом случае мы имеем дело с положительной (прямой) корреляцией. Если же, напротив, большим (малым) значениям признака х соответствуют малые (большие) значения признака у, то sxy < 0. В этом случае говорят об отрицательной (обратной) корреляции. При sxy = 0 между признаками х и у корреляция отсутствует. Таким образом, в ходе наших рассуждений мы выяснили связь ковариации с корреляцией.
В задачи корреляционного и регрессионного анализа входят выбор функции регрессии, оценка ее параметров, оценка коэффициента корреляции и т. д. Как известно из математической статистики, оценки должны обладать определенными свойствами. Мы рассмотрим самые важные из них, а именно несмещенность и состоятельность.
Пусть из одной и той же генеральной совокупности повторно извлекаются выборки объема п и по каждой выборке вычисляется оценка какого-либо параметра этой совокупности. Если среднее всех q оценок равно параметру генеральной совокупности, то оценку называют несмещенной. Можно дать следующее определение этого свойства: ес-
£ — параметр генеральной совокупности, а сь i = 1, 2, ..., q, — оценки этого параметра, полученные по результатам выборок, то оценку называют несмещенной при Е Е — обозначение матема-
тического ожидания, о котором речь пойдет в следующем разделе.
Оценка называется состоятельной или асимптотически состоятельной, если с увеличением объема выборки (п -> оо) оценка сходится по Вероятности к оцениваемому параметру, т. е. plim с = Другими
П-+оо
Иовами, вероятность того, что оценка с увеличением объема выборки Стремится к параметру g, приближается к единице.
36
37
(1-17)
Для каждой функции выборок, являющейся оценкой параметра, следует доказывать свойства несмещенности и состоятельности. Характер изложения в данной книге не позволяет приводить эти доказательства. Поэтому далее будет лишь указываться, являются ли рассматриваемые оценки несмещенными и состоятельными.
1.6. РАСПРЕДЕЛЕНИЕ СЛУЧАЙНЫХ ВЕЛИЧИН.
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ И ДИСПЕРСИЯ*
Статистическая вероятность идентична понятию относительной частоты, с которой отдельные значения случайной величины появляются при большом числе независимых испытаний, производимых в одинаковых условиях. При этом подразумевается неограниченно большое число испытаний. Допустим, что при п испытаниях значение хг случайной величины X появилось пх раз, тогда Р (хх) будет статистической вероятностью появления значения хх:
Р(Х=х1) = -^=р1. п
Случайные величины могут быть дискретными и непрерывными. Дискретной называется такая случайная величина, которая принимает конечное или бесконечное счетное множество значений, например численность работников промышленных предприятий. Непрерывной называется такая случайная величина, которая может принимать любые значения из некоторого конечного или бесконечного интервала. Очевидно, число возможных значений непрерывной случайной величины бесконечно. Примером непрерывной случайной величины может служить рабочее время в человеко-часах. Совокупность всех возможных значений случайной величины и соответствующих им вероятностей составляет распределение случайной величины, которое может быть задано в виде ряда распределения, функции распределения и плотности распределения вероятностей. Если обозначить вероятности появления отдельных значений хг- случайной величины X через pi, т. е.
Р (X = Х}) = pi при i = 1, 2, ..., m, (ГПа)
то вероятности pt с соответствующими х*ъ составят ряд распределения дискретной случайной величины. Легко можно убедиться, что
т = (1-18)
Z=1
При графическом изображении ряда распределения в прямоугольной системе координат получается фигура, называемая многоугольником распределения. График по виду напоминает полигон частот.
*Для более глубокого усвоения материала данного раздела советуем обра* титься к [104]. Читатель, желающий познакомиться с корреляционным и р£' грессионным анализом лишь в общих чертах, может перейти к главе 2.
Наиболее общей формой задания распределения случайной величины является функция распределения. Она используется как для дискретных, так и для непрерывных случайных величин. Функция распределения F (х) определяет вероятность того, что случайная величина X примет значение, которое меньше фиксированного действительного числа х, т. е.
F(x) = P(X<x). (1.19)
Для дискретной случайной величины
Г(х) = 2 Pi. (1.20)
xi<x
График функции распределения дискретной случайной величины есть разрывная ступенчатая ломаная линия. Функция распределения имеет скачок в тех точках, в которых случайная величина принимает конкретные значения. Величина скачка определяется накопленными вероятностями: F (хх) = рг\ F (х2) = рг + р2; F (х3) = Pi + р2 + + р3; ••• Поэтому данная функция иногда называется кумулятивной функцией распределения. В интервалах между значениями случайной величины функция F (х) постоянна. Непрерывной случайной величине соответствует непрерывная функция распределения, которая на графике в большинстве случаев изображается в виде S-образной кривой.
Распределение непрерывной случайной величины можно, кроме того, задать с помощью плотности распределения f (х). Вероятность попадания случайной величины на элементарный участок х X < < х + dx определится как
(1.21)
Аналогично выражению (1.18) можно доказать, что
"jf (x)dx = 1. (1.22)
— оо
Геометрически это означает, что площадь, ограниченная кривой распределения у = f (х) и осью абсцисс, равна единице. Вероятность того, что непрерывная случайная величина примет любое значение между —оо и +оо, равна единице. Следовательно, это событие достоверно.
Плотность распределения f (х) называется также функцией плотности. Вероятность попадания непрерывной случайной величины X в интервал (а, Ь) равна определенному интегралу от функции плотности, взятому в пределах от а до Ь:
ъ
л <. z?) = J / (x)dx. (1.23)
а
Функция распределения может быть выражена через плотность Распределения следующим образом:
Р (х) = Р (-00 X < х) = J
(1-24)
38
39
Геометрически функция распределения соответствует площади между кривой распределения, осью абсцисс и перпендикуляром, восстановленным из точки Xi. Эта геометрическая интерпретация делает очевидным следующее свойство функции распределения: F (—оо) = О, F(+°o) = 1. Если функция F (%) непрерывна и дифференцируема при всех значениях аргумента, то ее первая производная является плотностью распределения:
d-^-=f(x}. ах
При любых а и & имеет место равенство ь
J f (x)dx = F (b) — F (а). а
(1.25)
(1.26)
Распределение вероятностей в виде ряда распределения, функции распределения или плотности полностью характеризует случайную величину с вероятностной точки зрения. Однако практически часто удобнее пользоваться некоторыми количественными показателями, которые давали бы в сжатой форме достаточную информацию о случайной величине. Такие показатели называются числовыми характеристиками случайной величины. Основными из них являются математическое ожидание [х, или Е (X), или среднее случайной величины, и дисперсия о2.
Если дискретная случайная величина задана рядом распределения, то ее математическое ожидание будет т
р. = Е(Х) = 2 XiPi.
/=1
Для непрерывной случайной величины, возможные значения которой располагаются по всей оси абсцисс, математическое ожидание равно:
4-00
р, = Е (X) = У xf (x)dx. (1.28)
(1.27)
Дисперсия дискретной случайной величины определяется как о2 = 2 - lx)2?,. (1.29)
i
Для непрерывной случайной величины, распределение которой задано в виде плотности вероятностей f (х), дисперсия выражается так:
(1.30)
о2 = f (х — |л)7 (x)dx. — 00
Аналогами математического ожидания и дисперсии случайной величины являются соответственно среднее х и выборочная дисперсия s2 вычисляемые по эмпирическим данным (см. раздел 1.5).
1.7. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ, ^.распределение, /-РАСПРЕДЕЛЕНИЕ, р-РАСПРЕДЕЛЕНИЕ
Нормальное распределение, называемое также распределением Гаусса—Лапласа, — наиболее часто встречающийся вид распределений. Многие распределения могут быть также аппроксимированы нормальным. Оно используется при построении доверительных интервалов и проверке статистических гипотез.
Непрерывная случайная величина распределена нормально, если --'УГППГ'Тк РО пппггплтта™гг..~ -
вид
Рис. 3. Стандартная нормальная кривая
плотность ее распределения имеет
(*—ю2 т=-е 2ff’. (1-31) а у2л
где р — математическое ожидание; о2 — дисперсия случайной величины; е — основание натурального логарифма; л = 3,14. Функция плотности f (х) нормального распределения определена на всей числовой оси х от —оо до 4~оо, т. е. каждому значению х соответствует вполне определенное значение функции. Математическое ожидание [х и дисперсия о2 являются параметрами нормального распределения.
Для табулирования функции плотности целесообразно преобразовать случайную величину. Положим, что
Х = (1.32)
а
Тогда из (1.31) получим выражение нормированной (стандартной) плотности нормального распределения
v !\\ 1 2 ф(Х) = _—е Т/2л
где (х — 0 и о = 1.
На рис. 3 представлен график стандартного нормального распределения, симметричного относительно оси, проходящей через точку = 0. Функция плотности в точке Z = 0 достигает максимума, равного <р (% = 0) = 0,3989. Кривая распределения имеет две точки перегиба при X = ±о. Касательные в точках перегиба пересекают ось абсцисс в точках X = ±2о. Функция плотности стандартного нормального распределения быстро убывает по обе стороны от X = 0, и ветви
(1.33)
40
41
кривой асимптотически приближаются к оси к. Значения нормировал* ной плотности ф (X) для различных % приведены в табл. 1 приложения.
Аналогично (1.24) можно утверждать, что
х
F (X) = f Ф (z)dz. (1.34)
— оо
Функция F (X) — называется функцией нормального распределения. Эта функция указывает вероятность, с которой случайная величина не превысит значение X. Значения F (X) приведены в табл. 2 приложения.
На рис. 4 представ-
Рис. 4. Интегральная кривая стандартного нор мального распределения
лена интегральная кривая стандартного нормального распределения.
С помощью функции распределения можно указать, с какой вероятностью нормальная случайная величина примет значение, принадлежащее интервалу [—X; +Х]:
4-А,
Ф (%) = f ф (z)dz. (1.35) —
На рис. 5 заштрихованные площади соответствуют Ф (X) и F (X). Вследствие симметрии нормальной кривой распределения между F (X) и Ф (X) существуют следующие соотношения (см. рис. 5):
F (X > 0) - 0,5 + 0,5Ф (X),
F (X < 0) - 0,5 — 0,5Ф (X),
(1.36) (1-37) (1.38)
С помощью табл. 2 приложения и соотношений (1.36)—(1.38) мож-указать, с какой вероятностью нормированное значение нормальной ------------------- —т>
но;
случайной величины попадет в заранее выбранный интервал. Например,
Рис. 5. Соотношение между Ф(Х) и Г (X)
\Л 2 3 Л
1-7 0 1
L 2 л
-3 -2 -Л
Интервал
Вероятность
К
1
2
3
±2сг ±3а
0,86268, или 86,3% I 0,95450, или 95,5% 0,99730, или 99,73%
Из приведенных результатов видно, что рассеяние нормальной слу* чайной величины практически укладывается на участке ц = ±3(Т. Этим выводом воспользуемся при проверке результа тов выборки. Например,
пусть принята гипотеза, что имеющиеся эмпирические данные удовлетворяют нормальному распределению. Проверке подлежит значение, попадающее за За-границы нормального распределения. Тогда с вероятностью 0,9973 мы можем утверждать, что проверяемое значение не принадлежит данной генеральной совокупности.
Кроме нормального, при проверке гипотез используются другие виды распределений. Рассмотрим теперь %2-распределение. Случайная величина, представляющая собой сумму квадратов / независимых случайных величин, каждая из которых имеет стандартное нормальное распределение, называется случайной величиной с распределением %2 и f степенями свободы. Сумма квадратов реализации этих случайных величин обозначается через %2:
£Xi = 4 + Xl +.. • + Х% = %2.
Плотность ^-распределения выражается так:
f-2 х2
< С2 *
(%2) е
(1.39)
(1.40)
ф(Х2) = —-—-
Из определения (1.39) следует, что кривая распределения может лежать только в I квадранте (рис. 6). Кривая ^-распределения одно-ЧННЯЯ дгтлл/тлтп'ттттт
Wi
0,5
0,3
0,2
0,1
Область принятая
гипотезы
f=8 область отклонения гипотезы
&
6 8 10 12 16
Рис. 6. %2-распределение
вершинная, асимметричная и асимптотически приближается к оси %2. С ростом f вершина кривой сдвигается вправо от начала координат и Х2-распределение стремится к нормальному, ^-распределением мы будем пользоваться при проверке значимости коэффициентов корреляции (раздел 8.5), коэффициентов ассоциации и сопряженности (глава 13). Задаваясь доверительным уровнем, с помощью таблицы %2-рас-пределения по числу степеней свободы f устанавливают критическое значение %2, с которым сравнивают расчетное значение. Если вычисленное значение %2 меньше табличного, т. е. оно попадает в область принятия гипотезы Яо, то рассматриваемая гипотеза не находится в явном противоречии с данными наблюдений. Если вычисленное значение %2 превосходит табличное или равно ему, т. е. оно попадает в
0
43
42
область отклонения гипотезы Но, то рассматриваемая гипотеза отвергается.
Распределение Стьюдента, или /-распределение, с f степенями свободы широко используется в корреляционном и регрессионном анализе при построении различных доверительных интервалов и проверке значимости коэффициентов регрессии и корреляции. Распределение Стьюдента определяется следующим образом. Если случайная величина х имеет стандартное нормальное распределение, а величина v — распределение %2 с f степенями свободы, причем х и v независимы, то при этих условиях плотность вероятности величины t = име-
V»
ет вид
ф(0
(1.41)
Кривая распределения симметрична относительно оси, проходящей через t = 0; ее ветви асимптотически приближаются к оси t. При малых значениях f кри-(f(t) вая /-распределения бо-
Нормальное t-распределение: f=5 —-
распределение ---- /=/-------------------------
Рис. 7. /-распределение при f=l и f==5 и стандартное нормальное распределение
лее плоская, чем кривая стандартного нормального распределения. Так же, как и %2-распреде-ление, /-распределение с ростом числа степеней свободы приближается к. нормальному (рис. 7). Распределение Стьюден-, та позволяет исследовать распределение выборочного среднего л? нормальной генеральной совокупности при неизвестной дисперсии о2.
При проверке значимости коэффициента детерминации использует-ся F-распределение (см. раздел 8.6). Это отношение двух выборочных дисперсий, построенных по независимым выборкам из одной и той же нормальной генеральной совокупности, впервые было исследовано Р. А. Фишером. Подобно /-распределению F-распределение не зависит от дисперсии о2 нормальной генеральной совокупности, а его параметрами являются /1 — число степеней свободы числителя и /2 — число степеней свободы знаменателя. Плотность вероятности F-распределе-
44
ния выражается следующим образом:
ft-2 f, f2
(1.42)
Поскольку F — это отношение двух квадратов отклонений, F может принимать значения только от 0 до +оо (рис. 8). Кривые F-pacnpe-деления асимметричны и одновершинны. При возрастании и /2 F-pac-пределение приближается к нормальному.
Для проверки гипотез относительно параметров генеральных совокупностей, кроме приведенных, используется ряд других распределений. Например, биномиальное, пуассоновское, логарифмическое, распределение Неймана, усеченное нормальное распределение. Но их описание выходит за рамки данной книги.
1.8. ИСТОРИЯ РАЗВИТИЯ КОРРЕЛЯЦИОННОГО
И РЕГРЕССИОННОГО АНАЛИЗА
Понятие корреляции в принятом нами значении появилось почти в середине XIX века благодаря работам сэра Фрэнсиса Гальтона1 (двоюродного брата Чарльза Дарвина) и Карла Пирсона. Ф. Гальтон
*С разносторонней деятельностью выдающегося ученого Ф. Гальтона и использованием им статистических приемов при изучении наследственности можно познакомиться по книгам: Филипченко Ю. А. Гальтон и Мендель. М., 1925; Канаев И. И. Фрэнсис Гальтон. Л., Наука, 1972. — Примеч.
45
применил для корреляции следующую форму записи: co-relation, откуда становится понятным значение этого выражения — связь, соотношение. Сначала исследования корреляции проводились в области естественных наук, прежде всего в биологии. Лишь позднее применение методов корреляционного анализа распространилось на экономику, где они привели к весьма полезным результатам.
Понятие регрессии также восходит к Ф. Гальтону. После знакомства с книгой Чарльза Дарвина «Происхождение видов» в 1859 г. Ф. Галь-тона стала занимать мысль о том, почему люди из поколения в поко-«ление не сильно различаются по внешнему виду и природным способностям. Это привело его к изучению наследственности. В частности, он занялся выяснением зависимости роста детей от роста родителей. По логике дети должны быть каждый раз очень похожи на своих родителей. Высокие родители должны иметь высоких детей, а низкорослые родители — детей низкого роста. При таком положении вещей через несколько поколений мы имели бы, с одной стороны, род великанов, а с другой — род карликов. Но вскоре в результате обширных статистических исследований и опытов над животными Ф. Гальтон убедился, что такой тенденции нет, а, скорее, напротив, дети очень высоких или очень низких родителей в среднем имеют менее высокий или соответственно менее низкий рост. Кроме того, уклонение роста детей не так велико, как уклонение роста их родителей от среднего роста исследованных лиц. Это движение назад в направлении к среднему Ф. Гальтон назвал регрессией (to regress — двигаться в обратном направлении).
В 1885 г. была издана известная работа Ф. Гальтона «Регрессия в направлении к общему среднему размеру при наследовании роста», где он приходит к выводу, что, в общем, признаки родителей не полностью наследуются детьми, и чем отдаленнее предок, тем в меньшей мере сказывается его свойства на потомке1. «Закон регрессии веско свидетельствует против полного наследования какого-либо признака. Из большого числа детей только немногие будут уклоняться от среднего уровня по сравнению с уклонением одного из родителей, отличающегося своими природными качествами. Чем ярче талант одного из родителей, тем реже родители имеют счастье видеть, что природа также щедро одарила их сына, и еще реже бывает, чтобы одаренность передавалась в последующие поколения. Закон беспристрастен и объективен. Он равномерно распределяет наследование хороших и плохих признаков. Он разрушает чрезмерные иллюзии одного одаренного родителя, лелеющего мечту, что его дети унаследуют все его способности. Закон устраняет также преувеличенные опасения относительно того, что детям передадутся все слабости, недостатки и болезни родителей. Разумеется, эти утверждения не находятся в противоречии с общей теорией, согласно которой дети талантливых родителей имеют
ХВ течение 1885—1886 гг. Ф. Гальтон опубликовал несколько статей, по" священных исследование индивидуальных различий между людьми и наследо* вания роста. В 1889 г. вышла его книга «Природная наследственность» [49], в которую вошли основные результаты этих статей. — Примеч. пер.
46
большую вероятность обладать какими-либо дарованиями, чем дети родителей со средними способностями. Наши рассуждения выражают только тот факт, что самый одаренный из всех детей немногих высокоодаренных родительских пар не так будет талантлив, как самый одаренный из всех детей очень многих родительских пар со средними способностями»*. Понятие регрессии, применяемое вначале только для процессов с тенденцией сдвигаться в направлении к среднему, с течением времени все более обобщалось и сегодня служит для характеристики односторонней стохастической зависимости.
В развитии методов корреляционного и регрессионного анализа особо следует отметить заслуги таких ученых, как К. Пирсон, X. Спир-мэн, А. Бравэ, Г. У. Юл, А. А. Чупров, С. М. Бартлет, М. Г. Кендэл, С. Коллер, М. Езекиэл и многих других.
*Цит. по [129].
0 ЛИНЕЙНАЯ
Z РЕГРЕССИЯ
При исследовании зависимостей сравниваются явления и процессы, связанные между собой. Для сравнения явлений и хода их развития применяются метод соответствия, метод конечных разностей и сравнительные ряды. С этими методами можно познакомиться в соответствующей литературе (см., например, [45]).
Как уже отмечалось, под регрессией мы понимаем одностороннюю стохастическую зависимость одной случайной переменной от другой или нескольких других случайных переменных. В этом смысле регрессия используется для исследования и оценки зависимостей между экономическими явлениями, порожденных, как правило, совокупным действием комплекса причин. Рассматривая причинно-следственные связи, мы хотим из смешанного сочетания причин выявить действие существенных, освободившись от элементов случайности и действия второстепенных причин. При этом следует руководствоваться учени ем диалектического материализма об объективности связи между при чиной и следствием и тем, что каждое изменение в причине находит свое отражение в соответствующем изменении следствия. Математи ческое решение сводится к получению функции регрессии. С помощью методов математической статистики можно исследовать зависимость между такими экономическими показателями, как национальный до ход, капитальные вложения и трудовые ресурсы. Явления, подлежа щие исследованию, должны быть количественно варьирующими вели чинами. Тогда они считаются переменными в статистическом смысле
Прежде чем применять математико-статистический аппарат, явле ние должно быть проинтерпретировано с содержательной точки зре ния. На основе логического анализа исследователь решает, какую из переменных рассматривать как зависимую (следствие), или переменную подлежащую объяснению с помощью функции регрессии, и какие пе ременные в ходе анализа считать объясняющими (причины), незави симыми, или предсказывающими. Причины и следствие должны быть объясненье экономической теорией. Наибольший эффект от корреля ционного и регрессионного анализа достигается при тесном сотрудни честве статистиков и специалистов (экономистов). Такой подход позво ляет предотвратить формализм при вычислениях и интерпретации ре зультатов.
Далее будем обозначать зависимую переменную через у, а объясняющие переменные через xk (k = 1, ..., т). Переменная у таким образом является функцией от переменной xk(k == 1, ..., m). Задача измерения связи решается на эмпирическом материале, содержащем случайности и влияние второстепенных причин, которые своей изменчивостью затушевывают и искажают интересующую нас зависимость. В силу того что случайности и второстепенные факторы не могут быть исключены из опытных данных, зависимость приобретает стохастический характер, за которым может быть скрыта однозначная функциональная связь. С помощью функции регрессии
У ~ f (х^, Х2> •••, -^тп) (2«1)
количественно оценивается усредненная зависимость между исследуемыми переменными. Понятие регрессии всегда связано с определенными средними условиями. Наблюдая за интересующей нас зависимостью при сложном взаимодействии факторов-причин и случайностей, исследователь с помощью регрессии отвечает на вопрос: какова была бы зависимость между следствием и выделенными существенными причинами, если бы прочие факторы не изменялись и тем самым не осложняли и не затушевывали ---------
Случайная переменная
основную зависимость? и,
У — у = и,
J2.2) характеризует отклонение переменной у от средней величины у, вычисленной по функции регрессии (2.1). Случайная переменная и называется возмущающей или, кратко, возмущением. Она включает влияние неучтенных факторов-переменных, случайных помех и ошибок наблюдений. Ее трудно исследовать, поскольку она меняется для каждого наблюдения у. Если бы мы изучали зависимость национального дохода от капитальных вложений, то случайная возмущающая переменная и содержала бы в себе влияние на национальный доход таких факторов, как численность работников в сфере производства, производительность труда, использование основных фондов и т. д., а также различные случайные помехи.
Таким образом, переменную у можно представить в виде
У = У + а, (2.3)
или, с учетом (2.1),
У = f (*i, х2, ..., хт) + и. (2.4)
позволяет интерпретировать случайную перемен-и как учитывающую неправильную спецификацию функции регрессии, т. е. неправильный выбор формы уравнения, описывающего завис 'пт
Этот вид записи ную Г
ЗАВИСИМОСТЬ.
Благодаря введению случайной переменной и переменная у также СТановится случайной, поскольку при заданных значениях объясняющих переменных xlf х2, ...» хт переменной у нельзя приписать или по-таиить в соответствие только одно определенное значение. Если, на-Ример, мы изучаем зависимость себестоимости от объема продукции,
43
49
ТО, задаваясь значением объема продукции, можно указать диапазон, в котором могут находиться соответствующие значения себестоимости.
Объясняющие переменные х19 х2, хт могут быть экономическими и техническими показателями, а также факторами, характеризующими общественные явления, или природными факторами
Статистические зависимости могут быть обнаружены лишь при многократном повторении следствий. Поэтому в дальнейшем мы будем исходить из того, что для tn + 1 переменных имеется п совместных наблюдений, например п предприятий или п отраслей народного хозяйства. Результаты наблюдений можно представить в виде следующей
таблицы или схемы:
Номера наблюдений Переменные
у 1 1 х‘ | • • • 1 хь 1 • . . | xm
1 У1 Хи Хтк . .. xlm
2 У2 Х21 . . . х2н , f. X2m
i У1 хц . . . Xjji ... X[rn
п Уп Хп1 ... xnh • • • Xnm
(2.5)
Каждый столбец схемы (2.5) представляет ряд наблюдений над од ной переменной, например введенных в действие основных фондов или объемы производства на 52 предприятиях. Индекс столбцов k ~ = 1,...,/п указывает соответствующую объясняющую переменную а индекс строки i = 1, ..., п— порядковый номер совместных наблю дений над т + 1 переменными. Таким образом, xik— результат /-го наблюдения над k-Й переменной. Значения и Xik являются эмпири ческими (опытными) данными, полученными в результате наблюдения над переменными у и xk. Желательно погрешности измерения, а также ошибки наблюдателя-регистратора свести к минимуму, так как зави симость между исследуемыми переменными может искажаться в силу Ются величиньГ^ нанесенных на нее точек явля-
ошибок наблюдений над значениями переменных.' г0 из 52 промышлеинн^п^пп^3 И основных Фондов (х) каждо-
В то время как исследователь располагает значениями зависимо f]0 скоплению т предприятии.
и объясняющих переменных в результате совместных наблюдений на основных фондов (х\Ч&К НЭ диагРамме Рис- 9 видно, что с увеличением этими переменными, значения возмущающей переменной и непосред производства (и) ^имеется ясно выраженная тенденция роста объема ственно получить нельзя, поскольку она представляет собой конгл голяпа __а 55^д®”дия_™еет явно линейный характер, бла-
мерат многих, трудно учитываемых и случайных влияний. По этой пр чине и называется также латентной переменной. Лишь после колич ственной оценки зависимости в виде функции регрессии можно пол чить значения возмущающей переменной и по (2.2). Вычисленн оценки значений переменной и далее обозначаются й и называются татками.
Как уже упоминалось, основной задачей регрессионного анализа является установление формы связи, т. е. подбор такой функции, которая как можно лучше характеризовала бы осредненное массовое течение явления. Избранная функция должна отображать экономическую закономерность. Поэтому на этапе, предшествующем построению функции регрессии, необходим обстоятельный качественный экономический анализ исследуемой зависимости. На основе этого анализа формулируется гипотеза о типе функции, правдоподобие которой затем статистически проверяется по эмпирическим данным.
Далее мы рассмотрим линейную регрессию. Линейные и приводимые к линейным формы связи получили на практике большое распространение. Из-за сравнительной простоты вычислительной процедуры, используемой для оценок параметров, исследователи предпочитают линейную связь часто в ущерб более глубокому изучению сущности экономического явления.
2.1. ДИАГРАММА РАССЕЯНИЯ
При анализе зависимости между двумя переменными применяют диаграмму рассеяния, которая является наглядной формой представления информации1. Для ее построения используют прямоугольную систему координат. По оси абсцисс отмечают значения независимой переменной, а по оси ординат— значения зависимой переменной. Результат каждого наблюдения схемы (2.5) отображается точкой на плоскости. Совокупность этих точек образует скопление, или облако. Скопление точек определяет картину зависимости двух переменных. Диаграмма рассеяния является геометрической формой систематизации опытного материала.
По ширине разброса точек можно сделать вывод о степени тесноты связи. Если точки расположены близко друг к другу в виде узкой полоски, то можно утверждать о наличии относительно тесной связи. Если точки разбросаны широко по диаграмме, то имеется слабая связь.
В виде примера рассмотрим изучение зависимости уровня объема производства от основных фондов по п = 52 предприятиям одной отрасли народного хозяйства.
На рис. 9 представлена диаграмма рассеяния, соответствующая результатам наблюдений. Координатами нанесенных на нее точек явля-1ГУГГ»~ — __ _______J и иигл уиПДиП {Л} каждо-
го из 52 промышленных предприятий.
-----------хг//.---nmvvi /1DHU ЛИНСИНЫИ ЛИрИКТер, 0ЛЗ" ГоДаря чему можно попытаться аппроксимировать рассматриваемую зависимость линейной функцией регрессии. Конечно, эта тенденция существует лишь в среднем, она нарушается отклонениями отдельных г°чек. Отклонения от прямой объясняются влиянием прочих неучтен-. 1В советской литературе употребляют также термины «поле корреляции», °ле рассеяния». — Примеч. пер.
50
51
ных или случайных факторов. В результате действия побочных факторов каждому фиксированному значению основных фондов соответствует ряд значений объемов производства.
Диаграмма рассеяния позволяет произвести визуальный анализ эмпирических данных. Но, к сожалению, если изображение зависимости трех переменных еще возможно, хотя и затруднительно, то при большом числе переменных геомет-у. * рическое представление неосущест-
- о вимо.
По диаграмме рассеяния мож-о ° о но графическим путем определить
°о° функцию линейной регрессии. Для
250 _ о°/%о° этого на диаграмме натягиваем во-
ображаемую нить таким образом, °0d0o°° ° чтобы по обе стороны от нее оказа-
лось приблизительно одинаковое о число точек. Нить должна обяза-
" ° тельно проходить через точку с ко^
ординатами х и у (центр рассеяния) > , t 1 , , и по возможности хорошо отра-
То яд зд Ц) 50 жать характер скопления точек.
Положение нити отмечаем прямой Рис. 9. Диаграмма рассеяния на диаграмме рассеяния. Прямую называют прямой регрессии или регрессионной прямой. Прямая регрессии, полученная графическим путем, может иметь следы субъективного подхода. Поэтому она является приближенной и не совсем точно отражает характер изменения эмпирических данных.
2.2. МЕТОД ЧАСТНЫХ СРЕДНИХ
Среднее, связанное с определенными предположениями или вычисленное при определенных условиях, называется частным, условным или групповым средним. Частные средние переменных х и у вычисляются по формулам
nj
/1Xii
Xt = —-----; для j = 1, 2,.., q, (2.6)
ni
np
- £yip
yP =--------; для p = 1,2,..., s, (2.7)
Ир
где Xj — частное среднее переменной х для /-й группы значений переменной у\ ур — частное среднее переменной у для р-й группы значений переменной х; /г7- и пр — число отдельных значений в группе / и группе р; ^п} = = «•
I р
52
В табл. 1 указаны частные средние переменной у, вычисленные для групп предприятий с одинаковыми по величине основными фондами. Следовательно, эти частные средние обусловлены уровнем основных фондов.
Таблица 1
Сведения о стоимости основных фондов и объеме производства за квартал по 52 предприятиям
Частные средние значения объема производства вычислены для каждой группы предприятий с одинаковыми по величине основными фондами.
Предприятия расположены по уровням основных фондов
Порядковый номер Основные фонды, 10* марок Объем производства, 1000 марок Частные средние значения объема производства, 1000 марок Порядковый номер Основные фонды, 106 марок Объем производства, 1000 марок Частные средние значения объема производства, 1000 марок
i xi УР i х. У1 УР
1 12 208 208 27 31 245
2 16 214 216,5 28 31 247 247,7
3 16 219 29 31 251
4 18 222 222 30 32 245 9ztQ
5 21 222 222 31 32 253
6 23 227 32 33 236
7 23 232 232,7 33 33 247 94Я К
8 23 239 34 33 253 Z4:O , О
9 24 231 9Q1 35 33 258
Ю 25 232 9о7 36 34 245
11 25 242 ZJ/ 37 34 251 251,3
12 26 236 38 34 258
13 26 242 241,7 39 36 251
14 26 247 40 36 255
15 28 236 41 36 259 257,5
16 28 240 42 36 265
17 28 242 243,4 43 37 253
18 28 247 44 37 259 zoo
19 28 252 45 38 272 272
20 29 240 242 46 39 265 265
21 29 244 47 41 275 275
22 30 240 48 44 272 275,5
23 30 242 49 44 279
24 30 245 246,2 ' 50 47 283 283
25 30 249 51 48 287 287
26 30 255 52 54 296 296
Если одному значению основных фондов соответствует только одно значение объема производства, то последнее является также частным средним. Если одному значению основных фондов соответствует несколько значений объема производства, то частное среднее вычисляется по этому ряду значений. Итак, частные средние выравнивают различные значения объема производства, соответствующие одному значению основных фондов, показывают средний уровень значения признака. Аналогично получают частные средние переменной х в табл. 2 — частные средние значений основных фондов, соответствующие определенным значениям объема производства.
53
Таблица 2
Сведения о стоимости основных фондов и объеме производства за квартал по 52 предприятиям
Частные средние значения основных фондов вычислены по каждой группе предприятий с одинаковым по величине объемом производства. Предприятия расположены по уровням основных фондов
Порядковый номер Объем производства, 1000 марок Основные фонды, 10б марок Частные средние значения основных ' фондов, 1 О5 марок Порядковый номер Объем производства, 1000 марок Основные фонды, 10б марок Частные средние значения основных фондов, 10б марок
i xi Xj i Уг xi xj
1 208 12 12 27 247 28
2 214 16 16 28 247 31 29,5
3 219 16 16 29 247 33
4 222 18 ЮК 30 249 30 30
5 222 21 1у ,0 31 251 31
6 227 23 23 32 251 34 33,7
7 231 24 24 33 251 36
8 232 23 34 252 28 28
9 232 25 24 35 253 32
Ю 236 26 36 253 33 34
11 236 28 29 37 253 37
12 236 33 38 255 30 оо
13 239 23 23 39 255 36 О о
14 240 28 40 258 33 33,5
15 240 29 29 41 258 34
16 240 30 42 259 36 ОС
17 242 25 43 259 37 □О, 0
18 242 26 97 О 44 265 36
19 242 28 45 265 39 Ol ,o
20 242 30 46 272 38
21 244 29 29 47 272 44
22 245 30 48 275 41 41
23 245 31 о 1 о 49 279 44 44
24 245 32 о! ,о 50 283 47 47
25 245 34 51 287 48 48
26 247 26 52 296 54 54
Вычисленные частные средние переменной у сопоставляются со значениями переменной х (см. табл. 1). Одно из преимуществ применения метода частных средних заключается в том, что сравнение производится не по 52 парам наблюдений, а только по 24. Более наглядная картина получается при графическом представлении частных средних. Для этой цели из точек, соответствующих значениям х, мысленно восстанавливаем ординаты, пропорциональные значениям ур. Вершины ординат последовательносоединяемпрямолинейнымиотрезками. Полученная ломаная линия называется также эмпирической линией регрессии у на х. Линия регрессии показывает, как смещаются ряды распределения у с увеличением х или как в среднем изменяется у с увеличением х.
54
На график рис. 10 нанесены частные средние ур и График отрй жает отчетливую тенденцию к росту частных средних ур с увеличением значений %. Увеличение значений у также вызывает рост частных средних Xj. Поступательный ход обеих эмпирических линий регрессий несколько нарушается зигзагами, которые имеют случайный характер.
Эмпирическая линия у на х, представленная на рис. 10, не совпадает с эмпирической линией х на у. По этой причине необходимо раз
личать направление зависимости Если исходить из того, что х является объясняющей уд переменной, то для каждого значения х получим соответствующие частные средние значений зависимой переменной у. И, напротив, если у рассматри- 250 -вается как объясняющая переменная, то вычисляем частные средние значений переменной х для фиксированных значений у (см. табл. 2). Особенно важным является вопрос о выборе зависимой и объясняющей J переменной при логически и_ необратимых регрессиях. Например, при изучении зависимости урожайности рис-сельскохо зяйственных
между изучаемыми переменными.
----1------1_____1______।_____1______
Ю 20 30 40 50 Л
10. Эмпирическая (ломаная) линия регрессии
культур от метеорологических условий вполне очевидно, что зависимой переменной может быть только урожайность, а объясняющей — метеорологические условия. Поменять местами эти переменные невозможно: это противоречит здравому смыслу.
Как уже указывалось, эмпирическая линия регрессии изменяется зигзагообразно. Величина зигзага зависит в значительной степени от вариабельности отдельных значений и от числа наблюдений, по которым вычисляется соответствующее частное среднее. Поэтому желательно каждое частное среднее сопровождать указанием вариационного размаха или непосредственно максимальным или минимальным значениями из того ряда наблюдений, по которым оно вычисляется. Эмпирическую линию регрессии полезно рассматривать на диаграмме рассеяния на фоне скопления индивидуальных точек, которые она осредня-ет. Зигзаги линии регрессии больше на тех участках, где наблюдений мало, и они уменьшаются в тех частях графика, которые проходят среди значительного числа точек. Эмпирическая линия регрессии называется также регрессией первого рода [43].
55
2.3. ПРОСТАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ
Мы познакомились с двумя простыми приемами предварительного анализа зависимости между двумя переменными — диаграммой рассеяния и методом частных средних. Теперь перейдем к описанию простой линейной регрессии и выясним смысл отдельных составляющих функции регрессии.
Под простой регрессией мы понимаем одностороннюю стохастическую зависимость результативной переменной только от одной объясняющей переменной:
Э = f (*)• (2.8)
Если исходя из соображений профессионально-теоретического характера в сочетании с исследованием расположения точек на диаграмме рассеяния предполагается линейный характер зависимости усредненных значений результативной переменной, то эту зависимость выражают с помощью функции линейной регрессии. Формула (2.8) принимает в этом случае вид
У = Ьо + Ьгх. (2.9)
Это общее уравнение для простой линейной регрессии, гдех—объясняющая переменная. Имеется п наблюдений xt над этой переменной (i =
= 1, 2, ..., п). Неизвестные параметры регрессии Ьо и Ь± подлежат оценке по определенной процедуре. Далее, не вводя дополнительных обозначений, мы будем называть их оценками параметров.
bQ — постоянная регрессии. Ее можно представить в виде коэффициента при фиктивной переменной, принимающей для всех i = 1, ...,/г значение I1. Постоянная 60 определяет точку пересечения прямой регрессии с осью ординат (рис. 11). Так как в соответствии с общим истолкованием уравнения регрессии Ьо является средним значением у в точке х = 0, то отсюда видно, что экономическая интерпретация Ьо часто очень затруднительна или вообще невозможна. Например, если на основе опытных данных получено уравнение регрессии
7 = —84,56 + 2,47х,
определяющее зависимость объема производства от основных фондов (размерность обеих величин в 1000 марок), то интерпретация bQ приведет к парадоксальному результату. А именно, при неиспользовании основных фондов (х = 0) объем производства составит у = —84,56 X X 1000 марок. Теоретически Ьо должно быть в этом случае равным нулю или больше него. Но практически информация, содержащаяся в опытных данных, недостаточна, чтобы предотвратить такой парадоксальный вывод. Постоянная bQ выполняет в уравнении регрессий функцию выравнивания. При этом следует подчеркнуть, что благодаря постоянной &о функция регрессии неошибочна. Уравнение регрессии интерпретируемо только в области скопления точек, а следова-
1Фиктивная переменная обычно не записывается, но иногда с математической точки зрения ее удобно включать в уравнение. — Примеч. пер.
тельно, только между наименьшим и наибольшим наблюдаемыми значениями переменной х. Для большинства практических исследований
величинами, представляющими интерес, являются Ьг и у, а не 60-
Коэффициент Ьг называют коэффициентом регрессии. Он характеризует наклон прямой к оси 0Х. Если через у обозначить угол, который прямая регрессии образует с осью абсцисс, то = tg у (см. рис. 11). Коэффициент регрессии является мерой зависимости переменной у от переменной х или мерой влияния, оказываемого изменением переменной х на переменную у. Согласно уравнению (2.9) Ь± указывает среднюю величину изменения щей переменной х на одну единицу. Знак &х определяет направление этого из
переменной у при изменении объясняю-
менения. При положительном коэффициенте регрессии мы располагаем положительной линейной регрессией, означающей пос-ступательный характер изменения зависимой переменной при увеличении значений объясняющей переменной х. При отрицательном коэффициенте регрессии речь идет об отри-
У
У
11. Регрессионная прямая и ее параметры
цательной регрессии, при рис которой с увеличением значений х значения переменной у убывают. Парамет-
ры регрессии — не безразмерные величины. Постоянная уравнения регрессии bQ имеет размерность переменной у. Размерность коэффициента регрессии Ьг представляет собой отношение размерности зависимой переменной к размерности объясняющей переменной. Здесь же отметим общий принцип, которого будем далее придерживаться. Функции, с помощью которых описывается зависимость между исследуемыми переменными, должны быть линейными относительно оцениваемых параметров. После получения численных оценок параметров может быть вычислено по уравнению регрессии для каждого значения
независимой переменной xt (i = 1, ..., п) значение yt.
Значения функции регрессии yt (Z = 1, ..., п) называются предсказанными или расчетными значениями переменной у для фиксированных xt- При линейной функции совокупность предсказанных значений образует прямую регрессии. Как уже упоминалось, из-за искажающего влияния посторонних факторов-причин для каждого значения xt может наблюдаться несколько эмпирических значений уь т. е. каждому значению xz- соответствует в статистическом смысле распределение вероятностей значений переменной у. Значения функции регрессии yt
57
56
являются таким образом оценками средних значений переменной у для каждого фиксированного значения переменной х.
Отсюда становится очевидной экономическая интерпретация
Значения регрессии yt указывают среднее значение зависимой переменной у при заданном xt объясняющей переменной х в предположении, что единственной причиной изменения переменной у является переменная х, а случайная возмущающая переменная и приняла значение, равное нулю. Разброс наблюдаемых значений переменной у вокруг yt обусловлен влиянием множества не поддающихся строгому учету и контролю причин. Разность между эмпирическим значением yt и расчетным значением уь называемая также остатком, дает численную оценку значения возмущающей переменной и (см. рис. 11).
Таким образом, мы подошли к проблеме оценивания неизвестных параметров регрессии Ьо и Ьх. Различным значениям bQ и Ьг будут соответствовать различные линии. Из бесчисленного множества прямых, которые можно провести на плоскости, следует выбрать одну, наилучшим образом соответствующую опытным данным. Существует процедура расчета оценок параметров, основанная на некоторых предположениях. Изложением этой процедуры мы и займемся.
2.4. ПОСТРОЕНИЕ РЕГРЕССИОННОЙ ПРЯМОЙ
С ПОМОЩЬЮ МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ (по несгруппированным данным)
Исходя из соображений профессионально-теоретического характера, исследователь рассматривает возможность описания зависимости изучаемых явлений линейной функцией. При этом следует учитывать характер скопления точек на диаграмме рассеяния. После экономического анализа можно приступать к выравниванию опытных данных, заключающемуся в построении гипотетической линии. Естественным требованием является сведение к минимуму ошибок при спецификации формы связи между переменными. Но эти ошибки обнаруживаются через отклонения эмпирических данных уг от значений рег-рессии т. е. они формируют значения возмущающей переменной и:
yt—*У1 = ut (I = 1,п). (2.2)
Из графика на рис. 11 видно, что — отклонение опытной точки от оцениваемой линии, измеренное по вертикали. Это отклонение может быть положительным или отрицательным в зависимости от того, по какую сторону от линии лежит конкретная точка.
При подборе прямой можно было бы выдвинуть требование, чтобы сумма отклонений всех точек от линии регрессии была равна нулю, т. е.
п П
= (2.10)
i — 1 i = 1
58
Рис. 12. Регрессионные прямые, удовлетворяющие критерию (2.10)
Другими словами, это условие можно было бы сформулировать таким образом: сумма положительных отклонений должна быть равна сумме отрицательных отклонений. Но соблюдение этого условия не дает возможности однозначно определить положение этой прямой на плоскости. Практически бесконечно много прямых будут удовлетворять условию (2.10), а именно: это будут веете прямые, которые проходят через точку с координатами х и у (рис. 12).
Для нахождения однозначного решения используют одну из естественных характеристик точности подбора прямой. Если все отклонения возвести в квадрат и сложить, то результат будет непосредственно зависеть от разброса точек около искомой линии. Из всех возможных прямых должна быть выбрана такая, для которой мера рассеяния опытных точек (хь будет минимальна. Соображения, по которым минимизируется сумма квадратов отклонений, а не сумма, например, абсолютных величин отклонений, аналогичны тем, по которым стандартное отклонение предпочитается среднему линейному отклонению (см. раздел 1.5).
В соответствии с приведенными рассуждениями вычисляем
выборочную дисперсию, характеризующую меру разброса опытных данных (xf, yt) вокруг значений регрессии, т. е. дисперсию остатков п п
~S (yt— У1)й 2 и1
2_ 1=1 ' = 1
. .................
и—2 и—2
Выражение, стоящее в знаменателе, указывает число степеней свободы. Оно определяется как разность между объемом выборки и числом параметров регрессии, подлежащих оценке. Так как в простой линейной
п п ~ •—1
*Так как 2 = 0, то и = —— = 0. Отсюда дисперсия остатков опре-
деляется как
п — п п
2(UZ-U)2 -°)* 2 2
§2 = - Z==1 ...
и п—2 п—2 п—2
59
регрессии одна объясняющая переменная (m — 1), то число степеней свободы равно:
/г— 1 — 1 = м — 2. (2.12)
Корень квадратный из выражения (2.11) называется стандартной ошибкой оценки регрессии (см. раздел 3.6).
На основе выдвинутого нами требования стандартная ошибка должна быть минимальна, что может быть записано также в виде
2 (у.—7o2^min> f = l
(2.13)
т. е. сумма квадратов отклонений эмпирических значений переменной у от значений, вычисленных по уравнению прямой, должна быть ми--------- -----л-----ооттптты nnuR UTTPT об отклонениях.
нимальна. При
данной
У
У
Рис. 13. Иллюстрация метода наименьших квадратов
постановке задачи речь идет об отклонениях, измеренных по вертикальной оси (рис. 13). Метод, основанный на требовании минимизации суммы квадратов отклонений, называется методом наименьших квадратов. С его помощью отыскиваются такие оценки параметров урав
нения регрессии, которые сводят к минимуму выбранную меру разброса Su. При этом происходит
чае линейной связи между переменными эта
выравнивание эмпирических значений в одну линию регрессии. В слу-линия является прямой,
прямой регрессии1.
Заменим в (2.13) yt через &0 + Ь^ (правая часть формулы (2.9)) и обозначим все выражение символом 3 (&0, Ь±):
S(b0, b^= 2 a/i-6o-Mi)2->min. (2.14)
Z=1
В (2.14) yt и — известные эмпирические значения, a bQ и Ьг — неизвестные параметры. При данных xt и yt величина суммы квадратов отклонений в (2.14) обусловлена этими параметрами. В зависимости от выбора значений параметров и Ьг эта сумма будет увеличиваться или уменьшаться. В соответствии с этим сумма квадратов отклонений 3
Построенная таким образом прямая далее будет называться выровненной линией регрессии, или эмпирической регрессионной прямой, в отличие от истинной (теоретической или гипотетической) линии регрессии, существующей в генеральной совокупности, а также ломаной, полученной по частным средним
(см. раздел 2.2). — Примеч. пер.
является функцией от искомых параметров и blt т. е. функцией от двух переменных: 3 = f (bQt Ьг) = 3 (&0, Ьг). Таким образом, проблема определения прямой регрессии при сформулированном выше требовании сводится к минимизации функции от двух переменных. Из математического анализа известно, что необходимым условием для этого служит обращение в нуль первых частных производных этой функции по каждому из параметров Ьо и blt а вторые частные производные по bQ и Ь± должны быть положительными.
Приравняем первые частные производные функции (2.14) по bQ и Ь± к нулю:
£ (^-^о-= о, (2.15)
дЬ° /=1
а5(Д°’^=-2 £ (yi-b0-b1Xi)x^Q. (2.16)
дЬ'
Из выражений вторых частных производных по параметрам Ьо и Ьг делаем вывод, что они положительны:
?WoA)9 дЪ*
(2.17)
(2.18)
Поскольку речь идет о функции от двух переменных, для существования минимума этой функции требуется также выполнение достаточного условия:
dWo, bbl
dbf ( dbvdbt )
Как видим, это условие также выполняется в силу того, что объясняющая переменная принимает различные значения. Поэтому ее дисперсия положительна, т. е. s| > 0. В противном случае невозможно было бы однозначно определить параметры Ьо и Ьх.
Итак, функция S (b0, bj в (2.14) достигает минимума, если Ьо и Ьх определяются из (2.15) и (2.16). Произведя соответствующие выкладки, получаем из (2.15) и (2.16) следующие уравнения:
п п
nbQ-^-b1 2 xt = Si У” z = i i=l
(2.20)
n n n
bo 2 xi +bi 2 xf = 2 Xi yt. (2.21)
Z=1 Z=1 Z = 1
Мы пришли к системе двух уравнений первой степени относительно Неизвестных параметров Ьо и Ь^ соотношения (2.20) и (2.21) образуют сИстему нормальных уравнений, составленных с учетом требования ^етода наименьших квадратов. На решении этих уравнений базиру
60
61
ется определение прямой регрессии, так как параметры bQ и Ь± минимизируют функцию S (&0, Ьх) тогда и только тогда, когда они удовлетворяют нормальным уравнениям.
В нормальных уравнениях (2.20) и (2.21) не известны только параметры Ьо и Ь±. Их можно определить с помощью детерминантов (правило п
Крамера). Введя для простоты обозначение суммы без индексов, У =
1 = 1
= 2, получим выражения для &0 и
у Sx$ 2хгг/г Sxf 2i/i Sx? —2хг Sx; yt (2.22)
Ьо — п 2хг 2xj 2x? n^xf—^Xi 2хг
L n Zyt 2x; 2xj у % 1 fiSx$ yi SXf Sr/f (2.23)
Ь1 n 2xj 2xj Sx? nSx?—Sxj Sxj
Определив bQ и Ь19 можно по (2.9) вычислить значения регрессии для заданной области значений объясняющей переменной х. Эти значения регрессии представляют собой наилучшее в смысле метода наименьших квадратов линейное приближение (аппроксимацию) к эмпирическим значениям yit так как выбранная мера разброса su сводится при этом к минимуму.
Можно получить значения bQ и bt несколько иным способом. Разделим нормальное уравнение (2.20) на п:
п п
Ьо + ЬхХ = у}
Ьо — у—ЪхХ. (2.24)
После подстановки (2.24) в (2.9) и некоторых преобразований будем иметь:
У = У + by (х — х). (2.25)
Если Ьх найдено, то Ьо легко вычислить по (2.24). Формула (2.25) показывает, что искомая линия проходит через точку средних значений (х, У) —центр тяжести скопления точек на диаграмме рассеяния.
Коэффициент регрессии может быть представлен также следующим образом:
(2.26)
Разделив в формуле (2.26) числитель и знаменатель на (п — 1), полу чим в числителе ковариацию между переменными х и у, а в знаменате ле — дисперсию переменной х (см.раздел 1.5). Итак, коэффициент per
рессии можно представить в виде отношения ковариации sxy к дисперсии sx.
(2.27) sx
Как уже упоминалось, Ь± — это мера, которая в среднем указывает влияние изменения объясняющей переменной х на зависимую переменную у-Часто при экономических исследованиях интересуются не столько самой прямой регрессии, сколько влиянием, которое оказывает одно экономическое явление на другое. В этом случае речь идет прежде всего об определении коэффициентов регрессии.
Рассмотрим теперь пример простой линейной регрессии. Пусть исследуется зависимость производительности труда (у) от уровня механизации работ (х) по данным 14 промышленных предприятий (см. табл. 3). Исходя из экономических соображений уровень механизации работ выбран в качестве объясняющей переменной.
Таблица 3
Рабочая таблица вычисления оценок параметров уравнения регрессии при изучении зависимости производительности труда от уровня механизации работ
Предприятие Производительность труда, т/ч Коэффициент механизации работ, % Промежуточные результаты
i У1 xt xtyt 1 4 1 «1
1 n 20 32 640 1024 400
2 24 30 720 900 576
3 28 36 1008 1296 784
4 r* 30 40 1200 1600 900
5 31 41 1271 1681 961
6 33 47 1551 2209 1089
7 34 56 1904 3136 1156
8 37 54 1998 2916 1369
9 38 60 2280 3600 1444
10 11 40 55 2200 3025 1600
11 41 61 2501 3721 1681
12 43 67 2881 4489 1849
13 45 69 3105 4761 2025
14 48 76 3648 5776 2304
Сумма 492 724 26 907 40 134 18 138
Расположение точек на диаграмме рассеяния (см. рис. 14) позволяет предположить линейную связь между переменными. Поэтому име-ет смысл искать зависимость в виде функции (2.9). Для этого по статистическим данным следует найти оценки параметров Ьо и Ьг. Вначале вставим рабочую таблицу, которая содержит все исходные данные и пРомежуточные результаты, необходимые для вычисления оценок !*араметров.
Таблице приведены значения yt, которые не нужны непосредственно вычисления &0 и Ьг. Но эти значения потребуются нам дальше. По
62
63
таблице находим средние значения обеих переменных:
— — 51,71 %,
14
492 ,
I/= = 35,14 т/ч.
По формулам (2.24) и (2.23) вычисляем Ьо и Ьг:
. 14.26907-724-492 20490 л елос
bi =----------------=-------= 0,5435,
14-40134—724-724 37700
Ьо = 35,14 — 0,5435 • 57,71 = 7,0356.
Оцениваемое соотношение можно записать в виде
'у = 7,0356 + 0,5435х.
Подставляя в полученное уравнение значения х, из табл. 3, вычислим значения регрессии z/;:
Уг = 7,0356 + 0,5435 • 32 = 7,0356 + 17,392 = 24,4276 уг = 7,0356 + 0,5435 • 30 = 7,0356 + 16,305 = 23,3406 Уз = 7,0356 + 0,5435 • 36 = 7,0356 + 19,566 = 26,6016 Уз = 7,0356 + 0,5435 • 40 = 7,0356 + 21,740 = 28,7756 Уз = 7,0356 + 0,5435 • 41 = 7,0356 + 22,283 = 29,3186 Уз = 7,0356 + 0,5435 • 47 = 7,0356 + 25,545 = 32,5806 у, = 7,0356 + 0,5435 • 56 = 7,0356 + 30,436 = 37,4716 Уз = 7,0356 + 0,5435 • 54 = 7,0356 + 29,349 = 36,3846 Уз = 7,0356 + 0,5435 • 60 = 7,0356 + 32,610 = 39,6456 = 7,0356 + 0,5435 • 55 = 7,0356 + 29,892 = 36,9276
Уп = 7,0356 + 0,5435 • 61 = 7,0356 + 33,154 = 40,1896 z/12 = 7,0356 + 0,5435 • 67 = 7,0356 + 36,414 = 43,4496 у13 = 7,0356 + 0,5435 • 69 = 7,0356 + 37,502 = 44,5376 t/u = 7,0356 + 0,5435 • 76 = 7,0356 + 41,306 = 48,3416 Совокупность расчетных значений, называемых также предсказанными, образует прямую регрессии (рис. 14), отражающую зависимость производительности труда от уровня механизации работ, при условии, что остальные неучтенные факторы и случайности не оказывают влияния на производительность труда.
Чтобы провести прямую на графике, достаточно определить значения регрессии для двух значений переменной х, удаленных друг от друга на некоторое расстояние. Через две точки, нанесенные на график, проводится прямая регрессии.
Прямая регрессии пересекает ось ординат в точке Ьо = 7,0356. Тангенс угла наклона прямой к оси абсцисс Ьг = 0,5435. В данном пример6 коэффициент регрессии показывает, что производительность труда а 64
среднем возрастает на 0,5435 т/ч, если коэффициент механизации работ увеличивается на один процент. Итак, коэффициент регрессии является показателем влияния изменения уровня механизации работ на производительность труда в предположении, что влияние прочих факторов отсутствует.
После определения оценок параметров регрессии Ьо и Ъъ а также значений yt можно по формуле (2.2) вычислить остатки щ:
«1 = 20 — 24,4276 = — 4,4276 из = 24 — 23,3406 = 0,6594 и3 = 28 — 26,6016 = 1,3984 ut = 30 — 28,7756 = 1,2244 п8 = 31 — 29,3186 = 1,6814 ил = 33 — 32,5806 = 0,4194 и, = 34 _ 37,4716 = — 3,4716 и8 = 37 — 36,3846 = 0,6154 и9 = 38 — 39,6456 = — 1,6456 «го = 40 — 36,9276 = 3,0724 «и = 41 — 40,1896 = 0,8104 «и = 43 — 43,4496 = — 0,4496 «is = 45 — 44,5376 = 0,4624 «к = 48 — 48,3416 = — 0,3416
Остатки используются в качестве характеристики точности оценки регрессии или степени согласованности расчетных значений регрессии И иябтпптгяожжгTV ,
и наблюдаемых значений пе-
50 к
ременной у (см. главу 3)J
Рассматривая остатки * как отклонения г-х наблюдений от значений, которые следует ожидать в среднем, можно сделать ряд практических выводов. Так, для данного примера можно ответить на вопрос, появятся ли в среднем предприятия с экстремально большими отклонениями в изучаемом показателе.
У=7,0356+0,5435X
40
30
20
Ю
О Ю 20 30 40 50 60 70 60 х
Рис. 14. Диаграмма рассеяния и регрессионная прямая, отражающая зависимость производительности труда от уровня механизации работ
Проведя анализ хозяйственной деятельности предприятий, на которых
3 Зак. 1113
65
были выявлены как положительные, так и отрицательные отклонения от ожидаемого среднего уровня экономического показателя, можно наметить основные задачи по организации социалистического соревнования. С этой точки зрения мы должны были бы прежде всего проанализировать деятельность предприятий 1, 7 и 10, показатели производительности труда на которых отличаются большими отклонениями от предсказанных значений в ту и другую сторону. По остаткам также замечаем, что большинство предприятий имеют положительные отклонения данного экономического показателя, которые уравновешиваются отрицательными отклонениями аналогичных показателей небольшого числа предприятий. Из этого следует вывод о существенной •доли влияния последних на исследуемый признак в общей совокупности 14 предприятий. На предприятиях, обнаруживших отрицательные отклонения фактических значений показателя производительности труда от расчетных, следовало бы уделить особое внимание экономической и идеологической работе*.
Применение метода наименьших квадратов для нахождения оценок параметров регрессии требует выполнения ряда предпосылок относительно возмущающей переменной и. Эти предпосылки мы обсудим для общего случая множественной регрессии в разделе 2.9.
2.5. СОПРЯЖЕННЫЕ РЕГРЕССИОННЫЕ ПРЯМЫЕ
До сих пор обсуждалась регрессия у на х:
У = ьо 4- Ъ\Х, (2.9)
т. е у рассматривалась как зависимая переменная, ах — как объяс-няющая. На практике часто встречаются экономические явления, между которыми существует взаимодействие, т. е. переменная у зависит от переменной х и, наоборот, переменная х зависит от у. В таких случаях говорят о логически обратимых регрессиях. При переходе от одной постановки задачи к другой нельзя просто из уравнения (2.9) выразить х через у. Это связано с тем, что эмпирические точки лежат не на прямой, а подвержены рассеянию (см. диаграмму рассеяния в разделе 2.1). Фиксированному значению х может соответствовать несколько значений у, а данному значению у — несколько значений переменной х. Чем больше разброс точек на диаграмме рассеяния, тем больше будут отличаться друг от друга регрессионные прямые, соответствующие различному направлению зависимости. Уравнения регрессии не выводимы друг из друга. Так как объектом изучения являются стохастические связи между переменными, при исследовании зависимостей между двумя переменными теоретически всегда существуют две различные регрессионные прямые, которые называются сопряженными* 1.
*0 практическом использовании линейной регрессии при анализе хозяйственной деятельности предприятий см. разделы 2.7, 2.10 и главу 10*
1Используется также термин «альтернативные регрессионные прямые» или «функция регрессии первого и второго рода». — Примем, пер.
66
Все рассуждения относительно регрессии у на х, приведенные в разделах 2.3 и 2.4, верны для регрессии х на у.
В предположении линейной зависимости в качестве функции регрессии примем уравнение прямой
Ы + tty. (2.28)
По сравнению с регрессией у на х переменные в (2.28) поменяли свои места. Зависимой переменной, или переменной, подлежащей объяснению, в данном случае является х, а независимой, или объясняющей, переменной — у. Коэффициенты Ь% — параметры регрессии*.
Параметр Ьо снова представляет собой аддитивную постоянную, соответствующую точке пересечения прямой регрессии (2.28) с осью абсцисс. Параметр Ь* называется коэффициентом регрессии х на у. Этот параметр показывает, на сколько единиц в среднем изменится значение переменной х, если значение переменной у изменится на одну единицу. Расчетные значения регрессии х интерпретируются так же, как у в случае регрессии у на х.
Из-за разброса эмпирических точек вокруг прямой регрессии снова можно рассматривать отклонения наблюдаемых значений пере-менной х от расчетных значений регрессии х, которые мы обозначим через Vt.
хг — Xt = (2.29)
Значения являются реализациями случайной возмущающей переменной v. Эти значения — результат влияний на х не учтенных в функции регрессии (2.28) переменных-факторов, включая случайные флуктуации. Возмущающая переменная v в статистическом смысле интерпретируется как ошибка спецификации регрессии (2.28). Переменную х можно тогда выразить как
х = х + v. (2.30)
Из сказанного выше следует, что интерпретация регрессионной прямой, параметров регрессии, расчетных значений функции регрессии х на у аналогична смысловому истолкованию тех же понятий при рассмотрении регрессии у на х. Должно быть принято во внимание только обратное направление зависимости, а также то, что отклонения Vi опытных точек от линии регрессии измеряют по горизонтальной оси (рис. 15). Прямая регрессии х на у строится из условия минимизации суммы квадратов отклонений, измеренных по горизонтали:
п п
У (Xi—Xi)2= 2 (2.31)
i=l i = 1
*Из спецификации формы связи, выбранной в виде (2.9) или (2.28), видно направление зависимости переменных. Поэтому мы отказались от использования индексов (ух) и (ху) при параметрах регрессии. Их различие отмечено звездочкой. В дальнейшем рассматривается только регрессия вида (2.9).
3* 67
После нахождения частных производных по неизвестным параметрам и приравнивая их нулю получаем так же, как в разделе 2.4, систему нормальных уравнений, решение которых дает нам искомые па-
раметры: , (2.32) nSy? —2i/i f nSx, у, St/; Sxf #2 ^3) 1 nSy?— SytSyt
Сравнивая формулы (2.32) и (2.33) с (2.22) и (2.23), видим, что они по своей сущности одинаковы. Только х заменено на у, а у — на х.
Такая же взаимообразная перестановка величин х и у происходит и в других формулах. В соответствии с этим (2.24) в случае регрессии х на у принимает вид
Ь* = х — Ь* у. (2.34)
Пример
Продолжим рассмотрение примера из раздела 2.1, где речь шла об изучении зависимости между объемом производства и показателем использования основных фондов на 52 промышленных предприятиях одной отрасли хозяйства. Исходные дан-
Рис. 15. Сопряженные регрессионные ные приведены в табл. 1.
прямые Вначале построим уравнение
регрессии в виде (2.9), отражающее зависимость объема производства (у) от основных фондов (х). Для этого по (2.23) и (2.24) определим величины bQ и &/:
У = 52-408Ю4—1616-12905 = 2 Qgg
1— 52-53588-1616-1616 ’
Ьо = 248,2 — 2,095 • 31,1 = 183,05.
Оцениваемая регрессия у на х будет иметь такой вид:
7 = 183,06 + 2,095х.
Прямая регрессии пересекает ось ординат в точке Ьо = 183,06, тангенс угла ее наклона к оси абсцисс составляет Ь1 — 2,095 (см-рис. 15). Коэффициент регрессии показывает, что объем производства в среднем увеличивается на 2095 марок, если стоимость основных фон
’Рекомендуем читателю для построения регрессии у на х и х на у составить рабочую таблицу и самостоятельно выполнить все расчеты.
68
Рис. 16. Сопряженные регрессионные прямые в случае отсутствия связи между переменными
дов повышается на 100 000 марок. Итак, коэффициент регрессии Ьг отражает влияние изменения основных фондов на уровень объема производства.
Для планирующих органов иногда представляет интерес вопрос, какой величины должны достигнуть основные фонды предприятия при определенном объеме производства? Ответ на этот вопрос можно получить, определив регрессию х на у в виде функции (2.28). По формулам (2.33) и (2.34) определяем значения b*i и ЬЪ:
1* 52.408104 — 12905-1616 Л ло-
Ь\ —------------------------- 0,435,
52-3218897 — 12905-12905
Ьо = 31,1 — 0,435 • 248,2 = —76,86.
Оцениваемое соотношение можно записать в виде
? = —76,86 + 0,435у.
Коэффициент Ь| показывает, что стоимость основных фондов в среднем возрастет на 43 500 марок, если показатель объема производства увеличится на 1000 марок. Мы ограничимся построением уравнений регрессий.
На рис. 15 представлены обе прямые регрессии. Они образуют «ножницы». Из графика видно, что при стохастической зависимости соотношение b± = 1 : Ь* не имеет места. Лишь в случае чисто функциональной связи обе прямые регрессии сливаются в одну и тогда выполняется указанное соотношение между Ьх и Ь\. По величине раствора ножниц можно судить приблизительно о степени зависимости обеих переменных. Чем более раскрыты ножницы, тем слабее связь.
Если обе прямые регрессии пересекаются под прямым углом, то эмпирические данные не позволяют подтвердить гипотезу о существовании зависимости между переменными. В этом случае отдельные точки случайно разбросаны по всей диаграмме рассеяния, и отсутствует всякая тенденция к ориентации точек в определенном направлении (рис. 16).
Если отсутствует регрессия у на х, то не существует также регрессии х на у и наоборот. При Ьх = 0 обязательно Ь* = 0 и обратно. Если прямая регрессии у на х проходит параллельно оси абсцисс, то это неизбежно влечет за собой вытягивание прямой регрессии х на у вдоль оси ординат. Эта взаимная обусловленность становится очевидной при рассмотрении следующих формул:
* с2 с2
sx sy
Как уже упоминалось в разделе 2.4 (см. пояснение к формуле (2.19)), Необходимой предпосылкой применения регрессионного анализа является выполнение условий: s® > 0 и sj > 0. Следовательно, оба угло-
69
ёё1Х коэффициента регрессии равны нулю, если ковариация sxy == §уХ9 которая в обоих формулах содержится в числителе, равна нулю.
Как видно из рис. 15 и 16, обе сопряженные прямые регрессии пере^ секаются в точке с координатами (х, у). Так бывает всегда, и это можно показать с помощью формул
у ==~у + Ь1(х — х) и х = х + Ь* (у — у).
При х = х имеем у = у, а при у = у получаем также х — х. Так как у = у и х = х — значения регрессии, принадлежащие обеим прямым, обе прямые должны пересекаться в точке (х, у).
Не всегда требуется находить обе сопряженные прямые регрессии. Чаще всего представляет практический интерес зависимость только в одном направлении. А иногда постановка задачи оказывается содержательной только при рассмотрении односторонней зависимости. По этой причине мы не продолжили пример из раздела 2.4, так как, на наш взгляд, в этом примере регрессия х относительно у экономически бессмысленна.
Мы хотели бы подчеркнуть еще одну существенную особенность, вытекающую из наличия двух разных регрессионных прямых, описывающих связь между исследуемыми переменными при различном толковании их роли. Если существует взаимодействие между переменными у и х, то переменная х также зависит от возмущающей переменной и. Но тем самым нарушается важная предпосылка применения метода наименьших квадратов (см. раздел 2.9). Если же, несмотря на это, мы применим метод наименьших квадратов для оценки по опытным данным неизвестных параметров уравнений регрессии у на х и х на у, то допустим ошибку. Более обстоятельно случай взаимодействия переменных будет рассмотрен в главе 12.
2.6. ПОСТРОЕНИЕ РЕГРЕССИОННОЙ ПРЯМОЙ
ПО СГРУППИРОВАННЫМ ДАННЫМ
При большом числе наблюдений рекомендуется производить группировку данных по одной или нескольким переменным. Чаще всего при исследовании зависимостей применяется комбинированная группировка1. Подсчитывая число попаданий отдельных значений в принятую систему интервалов группировок для зависимой и объясняющей переменных, получаем так называемую корреляционную таблицу (см. табл. 4).
Корреляционная таблица систематизирует результаты наблюдений над элементами статистической совокупности по двум сопряженным
1Более подробно с методом группировок можно познакомиться по учебнику: Кильдишев Г. С.,Овсиенко В. Е., Рабинович П. М., Ря* б у ш к и н Т. В. Общая теория статистики. М., Статистика, 1980, а также по кн.: Кильдишев Г. С., Аболенцев Ю. И. Многомерные группировки. М., Статистика, 1978. — Примеч, пер,
70
Таблица 4
Общая форма корреляционной таблицы
Середины интервалов Ук *1 х2 Середины интервалов х< х} xt Сумма частот
У1 Ри Р12 р1} Pit hi
У2 Р21 Р22 Р2] P2t ^2
Ук Pki Pk2 Pkj Pkt hk
Уз Psi Рз2 • • • Ps j • • • Pst hs
Сумма частот gi gj gt " 1
Обозначения:
Xj — середина /-го интервала значений объясняющей переменной, / = 1, 2, ..., Уь— середина k-ro интервала значений зависимой переменной, k — \, 2, s; hk—частота k-vo интервала значений зависимой переменной у\ gj— частота /-го интервала значений объясняющей переменной х; pkj— частота k-ro интервала значений зависимой переменной и /-го интервала значений объясняющей переменной. Частота pkj показывает количество сочетаний различных значений переменных х и у. Ее также называют условной частотой и размещают по отдельным клеткам корреляционной таблицы.
признакам-переменным Л 1Уинтервал включаются’данные, которые больше нижней границы интервала или равны ей и меньше верхней границы. Для исследования зависимостей желательно использовать равные по ширине интервалы группировок. Неравные интервалы могут привести к искажению регрессии и ошибочным выводам. Практика показывает, что наиболее целесообразно при большом объеме изучаемой совокупности образовывать 9—10 интервалов, достаточно заполненных частотами. При небольших объемах совокупности не имеет смысла производить группировку данных. В этом случае метод наименьших квадратов применяется непосредственно к результатам наблюдений.
Каждый столбец и каждая строка корреляционной таблицы (за исключением итоговых) представляют собой условное распределение частот. Частоты в отдельных клетках таблицы связаны с определенными условиями, а именно частота в клетке показывает, у скольких единиц совокупности значение признака х попадает в j-й интервал, а значение признака у — в &-й интервал. Поэтому ее называют условной частотой. Частоты hk, полученные путем суммирования условных частот по строкам, вместе с интервалами переменной у образуют безусловное распределение частот переменной у. Аналогично частоты полученные путем суммирования условных частот по столбцам, вместе с интервалами переменной х образуют безусловное распределение частот переменной х. Эти распределения называются также граничными распределениями или распределениями составляющих переменных. Корреляционную таблицу называют еще таблицей сопряженной вариации двух переменных,
71
По корреляционной таблице можно найти оценки параметров регрессии и тем самым решить задачу отыскания регрессионной прямой. Конечно, результаты, полученные по несгруппированному ряду наблюдений, являются более точными. Но потеря точности есть своего рода уступка за упрощение в расчетах. Принцип вычисления остается тем же. Отличие состоит в том, что при сгруппированном материале исходят из середин интервалов и соответствующих частот. При замене интервального ряда дискретным частоты условно относятся к серединам интервалов.
Для корреляционной таблицы имеют место следующие соотношения:
^Ph}-hk, (2.35)
/
(2-36) k
= = (2.37)
kj k i
Средние x и у вычисляются как средние взвешенные по серединам
интервалов: 2^^ ^Xjgj х = -i = -i- , (2.38) ^gj п i hykhk liVkhk y = -H- = . (2.39) 2** n k
Путем замены в (2.22) и (2.23) отдельных значений хг и серединами интервалов, взвешенных по соответствующим частотам, получим формулы для вычисления оценок параметров по сгруппированным дан-
ным: 5 Ун hk 2 gj — 2 x}g} 2. x} yk pk} Ьо=л _l2 i L2 , П 2 xf gj—2 X} gj 2 xj gj (2.40)
«2 Xjykph}—^1Xjg}yiyhhh £ __ k, / I k ' (2.41)
Пример «3 xf gj—^Xjgj^Xjgj i i /
Пусть исследуется зависимость объема производства от основных фондов по сгруппированному статистическому материалу, собранному на 52 предприятиях. По исходным данным, представленным в табл. 1 и 2 в разделе 2.5, уже была произведена оценка функции регрессии. Для сравнения процедуры расчета и сопоставления полученных результатов воспользуемся теми же данными, построив по ним корреляционную таблицу (см. табл. 5).
12
Таблица S
Зависимость объема производства от основных фондов по данным 52 предприятий за квартал
Объем производства, 1000 марок, Ук
Основные фонды, 100 000 марок, Ху
10—15 15 — 20 20 — 25 25 — 30 30 — 35 35 — 40 40 — 45 45-50 50-55 Итого
200—210 210—220
220-230 230-240 240—250 250—260
260—270 270-280 280—290 290—300
1
1
2
3
7
17
13
2
4
2
1
2
1
2
3
3
8
1
1
9
7
5
2
1
3
2
1
Итого gj
12 17
1 52
3
5
8
3
2
В верхнем и боковом заголовке корреляционной таблицы (сказуемом и подлежащем таблицы) указаны интервалы группировки по х и у. Внутренние клетки таблицы содержат условные частоты — количество предприятий, оказавшихся в соответствующих интервалах по х и у. Подведены горизонтальные и вертикальные итоги частот и указан общий итог — 52. При «чтении» корреляционной таблицы производится предварительный анализ характера зависимости. Так, мы видим, что условные распределения предприятий по объему производства закономерно изменяют свое положение, а именно ряды распределения во внутренних столбцах таблицы закономерно смещаются сверху вниз при рассмотрении таблицы слева направо в сторону больших значений х. Таким образом, по корреляционной таблице мы обнаруживаем прямую зависимость между исследуемыми переменными, т. е. рост стоимости основных фондов сопровождается увеличением объема производства. По степени заполненности клеток таблицы условными частотами можно судить о тесноте связи. Если клетки заполнены только вокруг диагонали таблицы, то имеется относительно тесная связь между переменными. Если условные частоты содержатся почти во всех Клетках таблицы, то это свидетельствует о большом рассеянии значений переменных и, следовательно, зависимость между ними проявляется очень слабо. Таким образом, чтение корреляционной таблицы аналогично рассмотрению диаграммы рассеяния. Для вычислений параметров регрессии снова составим рабочую таблицу (см. табл. 6).
По формулам (2.38) и (2.39) вычислим средние:
х = 2^- = 31,4; у = -в!- = 248,7.
52 7 52 ’
73
Таблица б
Рабочая таблица
Порядковый номер Середина интервала Частота Середина интервала Частота Промежуточные результаты
ы Ук hk xj Vh hk 1 xJg]
1 205 1 12,5 1 205 12,5
2 215 2 17,5 3 430 52,5
3 225 3 22,5 5 675 112,5
4 235 7 27,5 12 1645 330,0
5 245 17 32,5 17 4165 552,5
6 255 13 37,5 8 3315 300,0
7 265 2 42,5 3 530 127,5
8 275 4 47,5 2 1100 95,0
9 285 2 52,5 1 570 52,5
10 295 1 295
Сумма 52 52 12930 1635,0
Продолжение табл. 6
Порядковый номер Промежуточные результаты
х2 i x!?gi xjykPkj
1 156,25 156,25 12,5-205-1 =2562,5
2 306,25 918,75 17,5-215-2 = 7525,0
3 506,25 2531,25 17,5-225-1=3937,5
4 756,25 9075,00 22,5-225-2 = 10125,0
5 1056,25 17956,25 22,5-235-3=15862,5
6 1406,25 11250,00 27,5-235-3 = 19387,5
7 1806,25 5418,75 27,5-245-8 = 53900,0
8 2256,25 4512,50 27,5-255-1=7012,5
9 2756,25 2756,25 32,5-235-1=7637,5
10 32,5-245-9 = 71662,5
11 32,5-255-7 = 58012,5
12 37,5-255-5 = 47812,5
13 37,5-265-2=19875,0
14 37,5-275-1 = 10312,5
15 42,5-275-3 = 35062,5
16 47,5-285-2 = 27075,0
17 52,5-295-1 = 15487,5
Сумма 54575,00 413250,0
Оценки параметров регрессии согласно формулам (2.40) и (2.41) рав
ны: ь 12930-54575— 1635-413250 jg2 0 52-54575 — 1635-1635 ~ ’ , 52-413250—1635-12930 O11C b = = 2,11 o. 52-54575—1635-1635
74
В разделе 2.5 по тем же исходным данным, но несгруппированным в интервалы, мы получили такие числовые значения: Ьо= 183,06; Ьх = == 2,095. Сравнивая их с результатами, полученными по сгруппированным данным, замечаем, что различие между ними несущественное. Причина отклонения оценок, вычисленных по сгруппированному материалу, от оценок, полученных непосредственно по исходным данным, кроется в переходе при расчетах к серединам интервалов и условно принятому равномерному распределению частот по ширине этих интервалов. Но неточности в результатах за счет группировки вполне искупаются упрощением процедуры вычисления.
2.7. ЛИНЕЙНАЯ МНОЖЕСТВЕННАЯ РЕГРЕССИЯ
В действительности каждое явление определяется действием не одной причины, а нескольких, даже комплексом причин. Их совместное действие может по-разному сказываться на следствии. «Следствие порождается совокупным действием множества причин. Сложное сочетание причин приводит к различным результатам. Действуя на следствие в одном и том же направлении, они усиливают влияние друг друга. Если часть причин имеет обратное направление в отношении объекта действия, то их совместное действие на следствие ослабляется или даже сводится на нет. Может возникнуть даже такая ситуация, когда вполне определенная, реально действующая причина не имеет явного следствия. Это означает, что наряду с этой причиной действует другая, поглощающая действие первой» [14]. Итак, необходимо исследовать воздействие различных причин, т. е. исследовать зависимость одного явления от ряда других явлений, вызывающих первое.
Совершенно очевидно, что не все причины и факторы, в какой-то степени оказывающие влияние на изучаемое явление, могут быть исследованы. Мы вынуждены ограничиться только существенными причинами.
Экономическое явление детерминируется множеством одновременно и совокупно действующих причин. Поэтому перед нами стоит задача исследования зависимости одной зависимой переменной от нескольких объясняющих переменных xlt х2, ..., хт в условиях конкретного места и конкретного времени. Эту задачу можно решить с помощью множественного, или многофакторного, регрессионного анализа. При этом снова ограничимся рассмотрением линейного соотношения между зависимой переменной у и объясняющими переменными хъ х2, •••> хт-Мы обсудим также применение регрессионного анализа при нелинейном соотношении между переменными, но только для случая, когда возможна линейная аппроксимация.
Итак, при существовании линейного соотношения между переменными общее выражение уравнения множественной регрессии (2.1) записывается в виде
у &1Х1 Ь2х2 ~|“ ... -|“ Ьтхт. (2.42)
Объясняющие переменные ..., хт оказывают совместное одновременное влияние на зависимую переменную у.
75
Как было сказано, мы не можем охватить весь комплекс причин и учесть случайность, присущую в той или иной степени причинному действию и определяемому им следствию. Поэтому, ограничиваясь наиболее важными объясняющими переменными, в выражение функции регрессии вводим аддитивную составляющую—возмущающую переменную и, дающую суммарный эффект от воздействия всех неучтенных факторов и случайностей. Эмпирические значения у можно вследствие этого представить таким образом:
у = у + и. (2.3)
Итак, возмущающая переменная и интерпретируется так же, как и при простой линейной регрессии.
В выражении функции (2.42) уг (i = 1, ..., п) — расчетные значения регрессии. Они указывают средние значения переменной у в точке i при фиксированных значениях xik объясняющих переменных xk (fe = 1, ..., m) в предположении, что только эти т переменных являются причиной изменения переменной у. Значения у представляют собой оценки средних значений у для фиксированных значений переменных xh в точке i.
Коэффициенты bk (k = 0, ..., т) — параметры регрессии (2.42). Постоянная регрессия &0 снова выполняет в уравнении регрессии функцию выравнивания. Она определяет точку пересечения гиперповерхности регрессии с осью ординат.
Значения Ь13 ..., Ьт представляют собой оценки коэффициентов регрессии. Индекс при коэффициенте соответствует индексу объясняющей переменной. Так, Ъг указывает среднюю величину изменения у при изменении хг на одну единицу при условии, что другие переменные остаются без изменения; Ь2 показывает, на сколько единиц в среднем изменится у. если бы переменная х2 изменилась на единицу при условии, что переменные xh (k Ф 2) остались бы без изменения, и т. д. В то время как регрессия (2.42) охватывает совокупное одновременное влияние объясняющих переменных, коэффициенты регрессии b^ (k = = 1, ..., т) указывают соответствующие усредненные частные влияния переменных xk (k = 1, ..., т) в предположении, что остальные объясняющие переменные сохраняются на постоянном уровне. С точки зрения статистической методологии, таким образом, нет различия между множественной и частной регрессией. (На этом мы еще остановимся подробнее в следующем разделе.) По этой причине в литературе параметры bk (k = 1, ..., tri) называются как коэффициентами множественной, так и частной регрессии.
Такая содержательная интерпретация коэффициентов регрессии могла бы привести к ошибочному заключению, что достаточно определить несколько простых линейных регрессий переменной у по отдельным переменным xk. Но, как мы уже упоминали ранее и в чем мы еще убедимся на примере, множественная регрессия хотя и охватывает одновременное действие т объясняющих переменных, коэффициент регрессии bh исключает влияние остальных объясняющих переменных.
76
в случае простой линейной регрессии дело обстоит иначе. При простой линейной регрессии влияние прочих объясняющих переменных частично отражается в коэффициенте регрессии, что можно объяснить часто существующей двусторонней зависимостью объясняющих переменных. Итак, если располагают достаточной информацией и эмпирическим числовым материалом по нескольким причинам-факторам для переменной у, то целесообразнее и теоретически обоснованнее строить множественную регрессию. В разделе 2.5 мы уже указывали, что из-за рассеяния значений отдельных переменных функция регрессии необратима даже тогда, когда это оправдано логически и обосновано профессиональными соображениями. Необратимость характерна также для множественной регрессии. Если интересуются не только зависимостью переменной у от xlt хт, но также зависимостью переменной %! от у и х2, ..., хт, то следует определить другую функцию (регрессию на у и х2, ...» хт). Теоретически существует т + 1 сопряженных, или альтернативных, регрессий. Уже здесь мы обращаем внимание на то, что многосторонняя зависимость между переменными у и хй (А = 1, ..., /п) нарушает существенные предпосылки применения метода наименьших квадратов. Подробно речь об этом пойдем в главе 12.
Процедуру построения множественной регрессии рассмотрим на примере регрессии с двумя объясняющими переменными. Функция линейной множественной регрессии в этом случае записывается в виде
У = b0 + biXj + й2х2. (2.43)
Задача состоит в оценке параметров регрессии по результатам выборочных наблюдений над переменными, включенными в анализ. Для этой цели снова применяем метод наименьших квадратов. Поставим условие, согласно которому регрессия должна по возможности хорошо согласовываться с эмпирическими данными. Поэтому по тем же соображениям, что и в разделе 2.4, выдвинем требование, по которому сумма квадратов отклонений всех наблюдаемых значений зависимой переменной от значений, вычисленных по уравнению регрессии (т. е. сумма квадратов остатков), должна быть минимальна. Итак, должно выполняться требование
п п
s (ь0, ьъ ь2) = 2 (yt —yt)* = £ min- (2-44)
Подставляя вместо у, выражение (2.43), получим
п
s (Ьо, Ь1, ьг) = Ъ(У> — Ьо — Ь^п — 62хг2)2 -+ min (2.45) z=i
Так же, как в разделе 2.4, S является функцией от неизвестных параметров регрессии. Необходимым условием выполнения (2.45) служит обращение в нулшчастных производных функции S (b0, blt Ьг) по каждому из параметров bQ, Ьх и &8. После соответствующих алгебраичес-
77
ких выкладок получаем следующую систему нормальных уравнений: nbQ + + b2^xi2 = Sz/f, (2.46)
Ь^ЕаХц “Н Ь2^ХцХ12 ^ХцУ/9 (2.47)
^oSx/2 “1“ Ь-^ЕхцХ^ “f" b2^jXi2 == ^Xi2yi» (2.48)
Если мы сравним эти уравнения с нормальными уравнениями простой линейной регрессии, то увидим большое сходство. Они отличаются лишь слагаемым, учитывающим новую переменную х2. Следовательно, включение в анализ новых переменных не представляет больших трудностей.
Разделив обе части уравнения (2.46) на п, получим следующее выражение для постоянной регрессии bQ\
bQ = y — b.x, — b2x2. (2.49)
Подставляя (2.49) в (2.43), после некоторых простых преобразований получим выражение, аналогичное (2.25):
У = У + (*i — *i) + Ь2 (х2 — х2),
или __ _ _ ' _ (2.50)
У — У = &1 (Xi — Xi) + Ь2 (х2 — х2).
Решая систему нормальных уравнений относительно неизвестных параметров, получим
(и Sxjj yi Yyt Sxjj) SXj2)
- У1 ^Уг ^Xj2) (n^Xj-L xi2 ^xi2 g | \
1 ~ (пЕхД — Sxfl) (nSxJ2 — Sx£2 Sxf2)— ’
— (nSXft Xf2—2хг*а) (nSXfi Xf2 — f^xi2 Sxfl)
(nSx?! — Ехц S*h) (nSxi2 yt—^yt ^xi2)—
I) _ (n^xil ^*11 ^xiz) (^xii yt ^>У1 ^*£1) (2 52)
2 (пЗхД — Sxfi Sx^) (nSx?2 — S*i2) —
— -Sxfi Sxf2) (nSxfi xi2 —Sxfa 2*и)
По аналогии с формулой (2.27) для простой регрессии можно коэффициенты множественной или частной регрессии представить через дисперсии и ковариации.
Разделив вначале обе части нормального уравнения (2.46) на п и умножив их на Sxn, вычтем их соответственно из левой и правой частей уравнения (2.47). В результате получим
2 хи Уг — у 2 хч = bi 15 Х‘1 —-*12 +ь2 (2 хи xiz—xt 2
i i \ i i / \ i i)
Затем умножим обе части нормального уравнения (2.46) на Ехг-2, предварительно поделенные на п, и вычтем их соответственно из левой и правой частей уравнения (2.48). В результате получим
2 х1ч Vi—у 2 =ь i( 2 хп хц —~xi 2 х 12^)+ь2 (2 х?3—2 Y
' t \ t t J \ i < }
78
Оба равенства мЫ мо^кём представить следующим образом!
У (xu—£) ilJi—у) = 612*1)2 + 62 2 tai—*1) ta2—£)’ (2.53) i i i
2ta2—^)ta—i')=6i2tai—^)taa-^)+62 sta2-ta)2- (2-54) z i i
Разделив обе части равенств (2.53) и (2.54) на п — 1, найдем, с учетом определений дисперсии и ковариации, выражения коэффициентов регрессии:
к = sigs2— s2ysu_ (2.55)
1 с2 с2_с2 ’
*2 2
, __ sfSjy—s^Siy (2.56)
2 с2 о2_92
г>1 о2 о12
Используя данные примера из раздела 2.4, дополним их результатами наблюдений над второй объясняющей переменной хг — средним возрастом работников. Переменную х, использованную в примере раздела 2.4, обозначим теперь В табл. 7 приведены значения, которые принимает переменная х2, а также промежуточные результаты вычислений, необходимые для нахождения оценок коэффициентов регрессии*.
Таблица 7
Средний возраст работников, средний процент выполнения нормы на 14 предприятиях и промежуточные результаты, необходимые для нахождения оценок параметров регрессии
Предприятие Средний возраст работников Средний процент выполнения нормы Промежуточные результаты
х2 xi2
i xi2 xi3
1 33 127 1089 660 1056
2 31 120 961 744 930
3 41 116 1681 1148 1476
4 39 117 1521 1170 1560
5 46 106 2116 1426 1886
6 43 128 1849 1419 2021
7 34 109 1156 1156 1904
8 38 114 1444 1406 2052
9 42 115 1764 1596 2520
10 35 121 1225 1400 1925
И 39 110 1521 1599 2379
12 44 111 1936 1892 2948
13 40 108 1600 1800 2760
14 41 113 1681 1968 3116
Сумма 546 1615 21 544 19 384 28 533
*В таблице указаны также значения переменной х3, которые будут использоваться для построения другой множественной регрессии.
79
Среднее значение переменной х2:
хг = — 39,0 года.
14
Используя промежуточные результаты из табл. 3 и 7, по формулам (2.51) и (2.52) вычисляем коэффициенты регрессии:
(14- 26907— 492-724) (14 • 21544 —546 •546)—
ь = -(14-19384— 492-546) (14-28533 — 546-724) = 60305448 = g 525g
1 (14-40134 — 724-724) (14-21544 — 546-546)— “ 114661046 ’
-(14- 28533—724 • 546) (14 • 28533— 546 • 724)
(14-40134 — 724-724) (14-19384 -492-546) —
= -(14-28533 —724-546) (14-26907 — 492-724) 18251380 = q j591
2“ (14-40134— 724-724) (14-21544 — 546-546)— “ 114661046
-(14-28533—724 -546) (14 • 28533 —546• 724)
Постоянную регрессии получаем по формуле (2.49):
Ьо = 35,14 — 0,5259 • 51,71 — 0,1591 • 39 = 1,7408.
Итак, в соответствии с формулой функции регрессии (2.43) уравнение регрессии можно записать в виде
7 = 1,7408 + 0,5259*! + 0,1591ха.
Если рассматривать зависимость производительности одновременно от уровня механизации работ и от среднего возраста работников, то производительность труда в среднем изменится на 0,5259 т/ч при условии, что уровень механизации работ изменится на один процент при исключении влияния среднего возраста работников. Если исключить влияние уровня механизации работ, то производительность труда в среднем изменится на 0,1591 т/ч при изменении среднего возраста работников на один год.
По сравнению с коэффициентом регрессии в уравнении с одной объясняющей переменной частный коэффициент регрессии Ьх несколько уменьшился. Это объясняется тем, что переменная х2 коррелирует с х1( в чем мы еще убедимся с помощью количественного показателя. По этой причине переменная хг влияет на переменную у через х2, вследствие чего ослабевает сила зависимости у от хг. Наличие зависимости среди объясняющих переменных нарушает одно из основных предположений линейной модели регрессионного анализа, что влечет за собой особые проблемы. Более подробно эти проблемы мы обсудим в главе 9.
Подставляя последовательно значения переменных *х и х2 в полученное уравнение, найдем расчетные значения регрессии. Вычитая их из наблюдаемых значений переменной у, получим остатки:
У! - 23,8199 ui = —3,8199
у2 ~ 22,4499 «2 = 1,5501
= 27,1963 «3 = 0,8037
80
У4 = 28,9817 у ь = 30,6213 Уь = 33,2994 У1 — 36,6006 у8 = 36,1852 у* = 39,9770
Ую 36,2338 r/ц = 40,0256 у12 — 43,9765 z/13 = 44,3919
Уи = 48,2323
ut = 1,0183 иь = 0,3787 #з = —0,2994
Uf = —2,6006 ив = 0,8148 и» = —1,9770 #10 3,7662
ин = 0,9744 w12 — —0,9765 #13 — 0,6081 #1* = —0,2323
По величине этих остатков можно сделать вывод, аналогичный выводу, сделанному в разделе 2.4 для простой линейной регрессии.
Сравнивая формулы (2.51) и (2.52) с (2.22) и (2.23), а также процедуры расчета, убеждаемся, что включение в регрессию новых объясняющих переменных усложняет аналитические выражения формул, а вместе с этим и вычисления. Обобщение модели множественной регрессии на т объясняющих переменных требует использования матричных обозначений и владения техникой матричной алгебры. Кроме того, это необходимо для компактности изложения и применения некоторых стандартных вычислительных процедур, значительно облегчающих и ускоряющих проведение анализа (31].
Итак, будем исходить из выражения множественной регрессии (2.42). Как упоминалось в разделе 2.3, для постоянной Ьо в уравнении регрессии можно ввести фиктивную переменную х0, принимающую значение, равное 1, для всех i = 1, ..., п:
xl0 sb 1 для всех I. (2.57)
С учетом (2.57), (2.3) и (2.42) линейную модель зависимости можно представить в виде
У = ЬоХо + + ... -|- bmxm Н- и. (2.58)
Результаты наблюдений уъ ..., уп записываем в форме вектор-столбца размерности лХ1. Значения объясняющих переменных х0, xi> •••» хт записываем в виде матрицы X размерности п X (т + 1), а остатки функции регрессии — в виде вектор-столбца размерности п X 1. Параметры регрессии Ьо, Ьъ ..., Ьт образуют вектор-столбец b размерности (т + 1) X 1. Итак, имеем
81
Функций регрессии (2.42) может быть представлена Компактно в матричной форме
Xb, (2.59)
а функция (2.58) — соответственно
у = Xb + и. (2.60>
Для оценки неизвестных параметров b в (2.59) мы снова применяем метод наименьших квадратов. Лежащее в основе этого метода требование о том, что сумма квадратов отклонений эмпирических значений от расчетных значений регрессии должна быть минимальна, в матричной записи имеет вид
5 (Ь) = (у — у)' (у — у) = u'u min, (2.61)
ь
или, подставляя вместо у его выражение,
S (b) = u'u = (у — Xb)' (у — Xb) -> min, ъ
s (Ь) = у 'у — 2b' Х'у + b' X' Xb -> min. (2.62)
ъ
Продифференцировав (2.62) по элементам вектора Ь, приравняем полученное выражение к нулю:
dS(b) = — 2Х' у + 2Х' ХЬ = 0.
db
Отсюда получаем нормальные уравнения, которым должен удовлетворять вектор в при соблюдении требования (2.61):
Х'ХЬ = Х'у. (2.63)
Если матрица Х'Х обратима, то мы получим в качестве решения системы нормальных уравнений вектор-столбец искомых параметров регрессии:
b = (Х'Х)-хХ'у. (2.64)
Матрица Х'Х и вектор Х'у с учетом (2.57) имеют следующий вид:
Х'Х = п 2хг1 • • %im ; X'y=
Хц . Hi —
Вернемся к нашему примеру. Но теперь будем рассматривать зависимость производительности труда одновременно от уровня механи-82
зации работ, среднего возраста работников, а также от среднего процента выполнения нормы. Значения переменных у, хг, х2 и х3 приведены в табл. 7. Построим вектор у и матрицу X:
~20~ ~1 32 33 127“
24 1 30 31 120
28 1 36 41 116
30 1 40 39 117
31 1 41 46 106
33 1 47 43 128
34 1 56 34 109
У = 37 ; х = 1 54 38 114
38 1 60 42 115
40 1 55 35 121
41 1 61 39 НО
43 1 67 44 111
45 1 69 40 108
_48_ _1 76 41 113_
Для Х'Х и Х'у получаем:
г 14 724 546 1615" " 492"
724 40134 28533 82884 26907
Х'Х = 546 28533 21544 62840 ; х'у = 19384
-1615 82884 62840 186891, .56389,
Выполняя действия, предписываемые (2.64), получим вектор оценок параметров регрессии*:
" 52,88929 —0,06869 —0,26929 —0,33603
—0,06869 0,00052 —0,00034 0,00048
—0,26929 —0,00034 0,00489 0,00083
_—0,33603 0,00048 0,00083 0,00242
" 492" 26907 19384 56389_
5,05729"
0,52123
0,15092
—0,02389.
♦Элементы обратной матрицы (Х'Х)-1 указаны с округлением.
83
По формуле (2.59) получим вектор значений регрессии:
“23,6829" 22,5058
27,2379
28,9971
30,8376
32,9866
36,7733
36,2151
39,9222
36,1163
40,1101
43,9682
44,4786
_48,1587
Выполнив операцию вычитания, найдем вектор остатков, или вектор возмущающих воздействий:
У-У = и,
“20" “23,6829" “—3,6829'
24 22,5058 1,4942
28 27,2379 0,7621
30 28,9971 1,0029
31 30,8376 0,1624
33 32,9866 0,0134
34 36,7733 —2,7733
37 36,2151 — 0,7849
38 39,9222 —1,9222
40 36,1163 3,8837
41 40,1101 0,8899
. 43 43,9682 —0,9682
45 44,4786 0,5214
_48_ _48,1587_ _—0,1587.
Таким образом, уравнение регрессии, выражающее зависимость про' изводительности труда от уровня механизации работ, среднего воз' раста работников и среднего процента выполнения нормы, имеет следующий вид:
у = 5,05729 + 0,52123^ + 0,15092х2 — 0,02389х3.
Коэффициенты частной регрессии отражают зависимость производительности труда от соответствующей переменной при исключении влияния на зависимую переменную двух других объясняющих переменных. В то время как в нашем примере коэффициенты частной рег
84
рессии bx и b2 имеют экономический смысл, Ь3 принимает такое значение, которое трудно поддается объяснению с экономической точки (т/ч\
Ь3 = —0,02389 -%- I. Это значение указывает на слабую отрицательную регрессию, т. е. с ростом среднего процента выполнения нормы производительность труда уменьшается. С точки зрения экономиста, это парадоксально. Почему же получился такой результат? На основе данных количественных соотношений между значениями переменных, включенных в анализ, можно еще раз убедиться, что ошибка в результатах вычислений отсутствует. Очевидно, причина кроется в малом числе наблюдений. Рассматриваемые 14 предприятий представляют собой элементы выборки. Если мы увеличим объем выборки, включив в нее большее число предприятий, то получим другие значения коэффициентов регрессии. Поэтому возникает необходимость проверки значимости коэффициента регрессии и указания интервала, в котором могут находиться оценки коэффициента регрессии под влиянием случайностей, присущих выборочным наблюдениям. При проверке значимости оценок коэффициентов регрессии устанавливается, достаточна ли величина оценки для статистически обоснованного вывода о наличии зависимости. Проверку значимости и последствия этой проверки мы обстоятельно обсудим в разделе 8.7.
В случае множественной регрессии более чем с двумя объясняющими переменными рекомендуется преобразовывать переменные. Из всех возможных способов преобразования мы хотим здесь остановиться на одном, который позволяет упростить расчеты определения оценок неизвестных параметров, а также облегчает исследование некоторых вопросов. Выполним следующее преобразование переменных у и xki которое называется стандартизацией (нормированием):
у' = JLzlL- 4 = (k= 1....т), (2.65)
sy sh
где sy и sk — стандартные отклонения переменных у и xh. Все переменные и соотношения между ними будут выражаться в стандартизованном масштабе. В этом масштабе за начало отсчета для каждой переменной принимается значение среднего, а за единицу измерения — величина стандартного отклонения. В стандартизованном масштабе упрощаются линейные соотношения между переменными. Легко увидеть, что при стандартизации фиктивная переменная х0, а вместе с ней и постоянная регрессии Ьо исключаются, что способствует облегчению расчетов. Уравнение множественной линейной регрессии в стандартизованном масштабе приобретает вид
У1 = Ь{х{ + Ь2Х2 4- ... + Ь'тХт, (2.66)
где у', x'k (k = 1, ..., т) — стандартизованные переменные, a bk(k = = 1.....т)— стандартизованные коэффициенты регрессии.
Оценки стандартизованных коэффициентов множественной регрессии находят с помощью метода наименьших квадратов. В результате получаем формулы, аналогичные формулам обычных коэффициентов регрессии (выраженных в натуральном масштабе), но с учетом того, что отсутствуют х0 и Ьо, и происходит замена переменных у на у',
85
a xih на хм- По этой причине мы отказываемся от воспроизведения этих формул. Значительно важнее сейчас указать соотношение между обычными и стандартизованными коэффициентами регрессии bk и bk (см. также раздел 4.3):
bk = — bk или bk = Ы (2.67)
sy sk
Стандартизованные коэффициенты регрессии bk можно вычислить по коэффициентам регрессии bki выраженным в натуральном масштабе, и наоборот. Особенно удобны для сравнения стандартизованные коэффициенты регрессии. Как мы уже неоднократно отмечали, коэффициенты регрессии bk являются размерными величинами. При этом их размерность связана с размерностью исходных данных. В нашем т/ч 1 т/ч примере коэффициент регрессии Ьг имеет размерность -%-, Ь2 — — и т. д. В общем, размерность коэффициента регрессии bh выражается в единицах измерения переменной у на единицу измерения переменной Хь> Любое изменение единицы измерения переменной сказывается на коэффициенте регрессии. Стандартизованные переменные у' и Xk, а также стандартизованные коэффициенты регрессии b'k безразмерны. Благодаря этому становится возможным сравнение.
Сравнение происходит прежде всего при оценке интенсивности влияния объясняющих переменных на зависимую переменную. Из-за различной размерности переменных и коэффициентов регрессии, а также из-за различных средних значений т + I переменных мы не можем для этой цели воспользоваться коэффициентами регрессии bk в натуральном масштабе. Несмотря на небольшое по величине значение коэффициента регрессии, соответствующая переменная может оказывать значительное влияние. Это прежде всего объясняется различным рассеянием (вариацией) значений переменных xk. При стандартизации переменные выражаются в единицах стандартных отклонений, благодаря чему стандартные отклонения преобразованных переменных становятся равными единице. Стандартизованные коэффициенты множественной регрессии характеризуют скорость изменения среднего значения зависимой переменной по каждой из объясняющих переменных при постоянных значениях остальных переменных, включенных в анализ.
Для нашего примера мы получили следующие значения коэффициентов регрессии и стандартные отклонения в натуральном масштабе:
bi = 0,52123-^-,
b2 = 0,15092
ГОД bs=— 0,02389-^-, sy = 8,0752 т/ч, = 14,3925%, s2 = 4,3853 года, s3 = 6,7323%.
86
По формуле перевода (2.67) вычисляем стандартизованные коэффициёй-ты регрессии:
£)( = 0,52123- •4’-39?6 = 0,92899,
8,0752
b'2 = 0,15092 • 4-’3-3- = 0,08196, 8,0752
Ьз = — 0,02389- --7323- = —0,01992.
8,0752
Уравнение множественной регрессии в стандартизованном масштабе примет вид:
р = 0,92899x1 + 0,08196x2 — 0,01992хз.
В отличие от обычных коэффициентов регрессии, выраженных в натуральном масштабе, стандартизованные коэффициенты можно непосредственно сравнивать друг с другом. По ним судят об интенсивности влияния изменений отдельных объясняющих переменных xk на изменение зависимой переменной у. Стандартизованные коэффициенты множественной регрессии показывают, на какую часть стандартного отклонения изменилось бы среднее значение зависимой переменной» если бы значение соответствующей объясняющей переменной увеличилось на стандартное отклонение, а прочие переменные остались без изменения. Благодаря тому, что все переменные выражены в сравнимых единицах измерения, стандартизованные коэффициенты регрессии показывают сравнительную силу влияния каждой объясняющей переменной на изменение зависимой переменной. В нашем примере с данными, собранными на 14 обследованных предприятиях, значения стандартизованных коэффициентов регрессии подтверждают наше мнение о необходимости проверки существенности влияния переменных х2 и х3 на производительность труда. Наибольшее влияние на производительность труда оказывает изменение уровня механизации работ, а затем уже следуют средний возраст работников и процент выполнения нормы. С увеличением показателя механизации работ на величину стандартного отклонения при постоянных значениях переменных х2 и х3 производительность труда в среднем увеличивается примерно на 0,929 единицы стандартного отклонения. Аналогично интерпретируются стандартизованные коэффициенты регрессии &2 и Ьз-
Разобранный пример является иллюстрацией возможного применения множественного регрессионного анализа в практике народного хозяйства ГДР*.
*Примеры применения регрессионного анализа можно найти в следующих работах: W о 1 f f U. Vorrausschatzungen von Valutapreisen fur neue Erzeugnisse mit Hilfe der Korrelations- und Regressionsanalyse. — Statistische Praxis, 22 (1967), 10, S. 592—595; F о r b r i g G., Wolff U. Anwendung der Regressionsanalyse zur Bestimmung von Preisindizes fur Erzeugnisgruppen. — Statistische Praxis, 23 (1968), 10, S. 567—569; Crop er t К., К б n i g E. Zur Anwendung der linearen Regressionsschatzung in der Statistik der Wirtschaftsrech-nungen. — Statistische Praxis, 23(1968), 5, S. 277—284; Meier R. Zum Problem der Anwendung der Korrelations- und Regressionsanalyse in der Agrarokonomie.—
87
2.8. ЛИНЕЙНАЯ ЧАСТНАЯ РЕГРЕССИЯ
При рассмотрении множественной] регрессии исследуется одновременное влияние нескольких объясняющих переменных на зависимую переменную. При интерпретации коэффициента множественной регрессии bk указывалось, что он выражает частное влияние переменной xk при постоянных значениях других объясняющих переменных. Таким образом, с точки зрения статистической методологии между множественной и частной регрессией разницы не существует. Мы хотим теперь это показать.
Если рассматривается регрессия трех связанных между собой переменных у, хг и x2i то нас интересует вопрос, как переменная у зависит от переменной jq при исключении влияния переменной х2 и как переменная у зависит от переменной х2 при постоянных значениях переменной На этот вопрос можно ответить с помощью частного регрессионного анализа. Предполагаем, что между переменными у, хг и х2 существуют линейные соотношения. Для ответа на наш вопрос достаточно представить частную регрессию у на при исключении х2. Вначале найдем простую регрессию у на х2 и регрессию хг на х2. Эти регрессии выражаются с помощью следующих уравнений:
У = Ьо + Ь2х2,
= У + Ь2(х2— х2);
(2.68)
X = &2 %29
«^1 “I- ^2 (*^2
По аналогии с формулой (2.24) из раздела 2.4 запишем:
&о = У — Ь2х2,
(2.69) bo = Xl— b+2 x2.
Исследуя зависимость у от х± при постоянных значениях переменной х2, можно представить себе, что переменная х2 изъята из анализа,
Statistische Praxis, 23 (1968), 1, S. 51—55; Е 1 s t п е г Н., Leimbach М. Oberbetriebliche Gemeinkostennormierung durch Korrelations- und Regressions-analyse — Probleme ihrer praktischen Anwendung. — Statistische Praxis, 26 (1971), 1,S. 33—37; К 6 n i g E. Aufbau eines statistischen Einkommens- und Verbrauchsmodells im Perspektivzeitraum 1971—1975. — Statistische Praxis, 26 (1971), 3, S. 133—138; Becker F., Schleusener H. Mathematisch-sta-tistische Analysen helfen bei Entscheidungen in der Grundfonds- und Arbeitsoko-nomie einer VVB. — Statistische Praxis, 30, (1975), 12, S. 481; Engels W. Analyse der Einfliisse, die auf die unvollendete Production einwirken, untersucht am Beispiel einer DruckgiePerei. — Fertigungstechnik und Betrieb, 17 (1967), 3, S. 148—152; В a n s e G. Zwischenbetrieblicher Vergleich der Arbeitsproduktivitat von Betrieben des Erzeugnisgruppenverbandes Baureparaturen. — Statistische Praxis, 32 (1977), 1, S. 30—32.
88
тогда регрессия у на Хх определяется по данным, из которых исключено влияние х2:
У* = У1 — У( = У1 — b0— b2xi2,
(2.70)
Хц =: Х^—— Xjx == %Ц~— Ьо Z?2 %12'
Используя (2.68)—(2.70), легко показать, что обе средние у* и х{ равны нулю:
у* = х* = 0.
Тогда в соответствии с формулой (2.25) из раздела 2.4 функция регрессии по данным, из которых устранено влияние х2, выразится следующим образом:
?* = МТ- (2.71)
Регрессия переменных с исключением влияния х2, таким образом, полностью определяется коэффициентом Ь1г который мы назовем коэффициентом частной регрессии. Применяя метод наименьших квадратов к (2.71) для нахождения оценки неизвестного параметра blt получим:
2 хпУ*
------• (2.72)
2
Z= 1
Подставляя в (2.72) выражения (2.70) и (2.68) и выполняя ряд алгебраических выкладок, приходим к следующему, удобному для расчетов выражению, по форме аналогичному (2.27):
(п£хи yi SXf2)—
(nSxpj — Sx/2 ^^1*2) —
(rtSXjj Xj2 —2x^2
Сравнивая полученное выражение с формулой (2.51) из раздела 2.7, видим, что они полностью совпадают.
Мы показали, что частная регрессия не приводит к новым результатам при исследовании зависимостей. Следовательно, при изучении регрессии нет необходимости различать частную и множественную регрессию. Поэтому далее мы будем обсуждать только коэффициенты частной регрессии, так как это понятие имеет, как мы показали, четкую содержательную интерпретацию. И, напротив, при изучении корреляции имеется существенная разница между частной и множественной корреляцией»
§9
2.9. ИСХОДНЫЕ ПРЕДПОСЫЛКИ
РЕГРЕССИОННОГО АНАЛИЗА И СВОЙСТВА ОЦЕНОК
При применении метода наименьших квадратов в разделах 2.4 и 2.7 для нахождения оценок параметров простой и множественной регрессии было ясно, что должны выполняться некоторые предпосылки. Они касаются прежде всего случайной переменной и, которая по формуле (2.60) является аддитивной составляющей, учитывающей ошибки измерения и ошибки спецификации. Эти предпосылки имеют общий характер, т. е. они не определяются объемом выборки и числом включенных в анализ переменных. Отметим наиболее существенные из них.
Предпосылка 1. Интерпретация значений регрессии yt показала, что мы с помощью метода наименьших квадратов должны найти такие значения переменной у, которые можно было бы ожидать в среднем для заданных значений переменных xh (k = 1, ..., т). Из этого следует, что при нахождении оценок переменной у (значений регрессии) предполагается существование зависимости переменной у только от тех объясняющих переменных xh (k = 1, .... т), которые включены в регрессию. Таким образом предполагается, что при заданных значениях переменных xh (k = 1, .... m) на переменную у не оказывают влияния никакие другие систематически действующие факторы и случайности. Влияние этих прочих факторов и случайностей учитывается случайной возмущающей переменной и. При этом полагаем, что для фиксированных значений переменных xh (k= 1, ..., т) среднее значение возмущающей переменной и равно нулю:
Е (ut) = 0 или
Е (и) = 0. (2.73)
Следствием этого предположения является такая интерпретация: средний уровень значений переменной у определяется только функцией (2.59) и возмущающая переменная и не коррелирует со значениями П
регрессии (2 = 0 или у'и = 0).
/=1
Из этой предпосылки вытекает, что среднее значение переменной у при фиксированных значениях переменных xh (k = 1, ..., т) (условное математическое ожидание) равно значению регрессии
Е (y/xlt .... хт) = у, ИЛИ
Е (у/Х) = ХЬ = у. (2.74)
Далее, согласно этой предпосылке имеем
2 Уг = 2 «Л! (2-75)
i= 1 i — 1
П А П А П П А
2 = 2 -^) = 2 - 2 ^ = °- <2-76)
1= 1 i=l i = 1 » = 1
90
Как мы уже убедились при применении Метода наименьших квадратов, требование (2.76) удовлетворяется.
Предпосылка 2, Дисперсия случайной переменной и должна быть для всех Ui одинакова и постоянна:
Е (и?) = о*.
(2.77)
Это свойство возмущающей переменной и называется гомоскедастич-ностью. Оно связано с интерпретацией и как переменной, отражающей чистый суммарный эффект от воздействия на зависимую переменную неучтенных факторов-причин и имеющей вероятностный характер. При этом при переходе от одного объекта наблюдения к другому (в примере из раздела 2.4— от одного промышленного предприятия к другому), а при рассмотрении временных рядов—в различные периоды времени эти неучтенные факторы оказывают одинаковое влияние.
Предпосылка 3. Значения случайной переменной и попарно не-коррелированы или, что является еще более сильной предпосылкой, они попарно независимы в вероятностном смысле:
Е (UiUt-s) = 0 (для s #= 0).
(2.78)
Эта предпосылка приобретает большое значение прежде всего в том случае, когда исходные данные представляют собой временные ряды. Тогда говорят об отсутствии автокорреляции возмущающей переменной и. К этому вопросу мы вернемся в разделе 11.3.
Предпосылки 2 и 3 можно обобщить, применяя матричную форму записи:
Е (mi') = cl I,
(2.79)
где I — единичная матрица порядка п. Произведение uu' есть симметрическая матрица порядка п. Поскольку операция нахождения математического ожидания должна быть отнесена к каждому элементу матрицы, имеем
Е (uu') = 2uu' =
Е (uf) Е (их Иг) ... Е (щ. ип)
Е(и.2 и,) Е (и%) ... E(UiUn)
(2.80)
Е (un «J Е (tin ... Е (Ип)
Элементы, стоящие на главной диагонали матрицы (2.80), являются дисперсиями, а элементы вне главной диагонали — ковариациями. Учитывая предпосылки 2 и 3, получим
Е (uu') =2uu' =
~о2и 0 ... 0 '
0 о* ... 0
(2-81)
0 0 ... <
Предпосылка 4. Применяя метод наименьших квадратов, мы уже отмечали, что система нормальных уравнений имеет решение только
91
тогда, когда существует обратная матрица (Х'Х)-1. Поэтому мы Должны предположить, что Х'Х— невырожденная матрица или, что то же самое,
Ранг X = т + 1. (2.82)
Последнее означает, что число наблюдений должно превышать число параметров, иначе невозможна оценка этих параметров (п > т). Таким образом,
det (Х'Х) =И= 0, (2.83)
что является необходимым и достаточным условием существования обратной матрицы (Х'Х)-1.
Обсуждаемая предпосылка касается соотношений между объясняющими переменными, в том числе фиктивной переменной, значение которой всегда равно единице. Согласно этой предпосылке между объясняющими переменными не должно существовать строгой линейной зависимости. Наличие линейной связи между объясняющими переменными называется мультиколлинеарностью, этот вопрос мы обсудим в главе 9.
В случае простой линейной регрессии (т— 1) в силу того, что объясняющая переменная х при i — 1, ..., п принимает различные значения, предпосылка сводится к условию
s5>0.
Это совпадает с достаточным условием (2.19), которое рассматривалось в разделе 2.4 при обосновании метода наименьших квадратов.
Предпосылка 5. Объясняющие переменные не должны коррелировать с возмущающей переменной и, т. е.
Е (Xih-U-i) ” О ИЛИ
Е (Хи) = 0. (2.84)
Эта предпосылка находит свое выражение в том, что переменные xk (k — 1....tn) объясняют переменную у, но мы не можем утверждать
обратное, т. е. переменная у не объясняет переменные xk(k= 1.т).
Итак, предполагается односторонняя зависимость переменной у от переменных xk (k = 1, ..., т) и отсутствие взаимосвязи. Этой проблемой, которую мы уже обсуждали в связи с сопряженными прямыми регрессии (см. раздел 2.5), мы займемся в главе 12.
Нередко еще исходят из предпосылки о законе распределения возмущающей переменной.
Предпосылка 6. Возмущающая переменная распределена нормально. Предполагается, что она не оказывает существенного влияния на переменную у и представляет собой суммарный эффект от большого числа незначительных некоррелированных влияющих факторов. Эта предпосылка одновременно означает, что зависимая переменная у или переменные у и xk (k — 1....т) распределены нормально.
Как мы видели, переменная у формируется частично за счет объясняющих переменных хк (6=1, .... т), а частично за счет возмущения 92
и. Обычно исходя из соображений профессионально-теоретического характера устанавливают общий вид искомой функциональной зависимости. Затем с помощью определенного метода (например, метода наименьших квадратов) оцениваются неизвестные параметры регрессии bk (k = 0, ...» т).
Оценки параметров регрессии зависят от наблюдаемых значений переменных. Большей частью регрессионный анализ производится по результатам выборочных обследований, т. е. по данным, представляющим собой случайную выборку из совокупности всех мыслимых наблюдений над переменными (понятие генеральной совокупности см. в разделе 1.5). Для примера из раздела 2.7 14 предприятий, по которым приведены значения переменных — производительность труда, уровень механизации работ, средний возраст работников и средний процент выполнения нормы, можно рассматривать как элементы выборки из совокупности всех возможных предприятий какой-либо одной отрасли народного хозяйства ГДР. Если бы мы в выборку включили другие предприятия этой отрасли и рассматривали значения указанных экономических показателей за тот же период времени на этих предприятиях, то получили бы другие ряды наблюдений над переменными. Таким образом, значения переменных изменяются от выборки к выборке. Кроме того, мы можем изменять объем выборки (например, отобрать 20 предприятий). При тех же предположениях о виде функции регрессии и том же способе оценивания (метод наименьших квадратов) по результатам новой выборки могут получиться другие численные значения параметров регрессии. Оценки параметров регрессии являются функциями от наблюдаемых значений.
Оценки параметров регрессии зависят также от применяемых способов оценивания. Метод наименьших квадратов— один из наиболее распространенных способов оценивания неизвестных параметров регрессии по эмпирическим данным. Наряду с методом наименьших квадратов для этой цели существуют и другие способы. На них мы остановимся более подробно в главе 12. Здесь же только отметим, что по одним и тем же статистическим данным и при одних и тех же предположениях о виде функции регрессии различные способы оценивания приведут к различным оценкам параметров регрессии. Отсюда следует, что оценки параметров регрессии могут принимать множество различных значений. Исходя из того, что любая статистика, а следовательно, и статистическая оценка в отличие от оцениваемых теоретических (истинных) значений параметров является случайной величиной, мы можем оценку параметров регрессии рассматривать как случайную переменную с определенным распределением вероятностей. Распределение этой случайной величины в большой степени зависит от закона распределения возмущающей переменной и.
В распределении выборочной характеристики величина р является параметром регрессии генеральной совокупности, который указывает действительно существующую зависимость переменной у от переменной х в генеральной совокупности. Параметры регрессии р неизвестны. Если бы они были известны, регрессионный анализ был бы не нужен.
93
Задача регрессионного анализа состоит в нахождении истинных значений параметров, т. е. в определении соотношения между у и х в генеральной совокупности
У = Ро “Ь Р1Л1 ••• 4~ Ртп^т и
или
у = хр + U.
(2.85)
С помощью регрессионного анализа при указанных выше предпосылках находят оценки параметров регрессии, наиболее хорошо согласующиеся с опытными данными. Используя определенный способ
Рис. 17. Распределение вероятностей двух несмещенных оценок параметра регрессии при данном объеме выборки
оценивания, получают возможные реализации случайных величин-оценок параметров регрессии, которые обозначают через bk (k = 1, т). Эти реализации bk более или менее удалены от значения параметра pft (рис. 17). Разность между Ьъ и возникающая за счет оценива-
ния на основе имеющихся в распоряжении данных, называется ошибкой оценки. При выборе
процедуры оценивания регрессии стараются
процедуры оценивания регрессии стараются сделать эту ошибку как можно меньше, т. е. пытаются найти такие оценки параметров регрессии относительно которых с достаточно большой вероятностью можно утверждать что они незначительно отличаются от истинного значения параметра р. В этом смысле оценки параметров регрессии, удовлетворяющие упомянутому требованию, называются хорошими. Методы оценивания называются также хорошими, если их результатами являются оценки с желательными свойствами. Некоторые из этих свойств (без доказательств) мы сейчас рассмотрим (см. также раздел 1.5).
Несмещенность оценок параметров регрессии. Решение нормальных уравнений может быть записано в виде
Ь= (Х'Х)"1 Х'у. (2.64)
Вектор b есть оценка вектора параметров регрессии р. Соотношение, существующее в генеральной совокупности, между переменной у и объясняющими переменными xk (k — 1, ..., т) записывается в виде матричного уравнения
у = ХР + и. (2.85)
Подставляем теперь (2.85) в (2.64):
Ь = (Х'ХНХ' (Хр + и),
(2.86)
b = р + (Х'Х^Х'и.
94
Находим математическое ожидание выражения (2.86), полагая, что значения объясняющих переменных фиксированы:
Е (b) = Е (₽) + Е [(X'X)-iX'uJ,
(2.87) Е (Ь) = р + (Х'Х)-ХХ' Е (и).
Оценки параметров регрессии называют несмещенными, если их математические ожидания равны значениям параметров регрессии р:
Е (Ь|Х) = Е (Ь) = р (2.88)
или для одного параметра регрессии:
Е (Ь |Х) = £(&) = р. (2.89)
Средняя ошибок оценок, вычисленная по всем возможным оценкам Ь, равна нулю. Как следует из (2.87), оценки параметров регрессии являются несмещенными, если выполняется предпосылка 1 (2.73): Е (и) = 0. В противном случае оценки имеют систематическое смещение. Величина смещения определяется вторым слагаемым в правой части матричного уравнения (2.87). Так как в приведенных преобразованиях мы существенно опирались на предположение о постоянстве значений х, величина смещения обусловлена возмущающей переменной и. Оценки, полученные методом наименьших квадратов, обладают свойством несмещенности.
Состоятельность оценок параметров регрессии. Как мы видели, существует разница между оценкой параметра регрессии b и истинным значением параметра р, если регрессионный анализ проводится не по всей генеральной совокупности, а по выборке из нее. Другое желательное свойство оценки — ее состоятельность. Оно состоит в том, что с ростом объема выборки оценка параметра регрессии сходится по вероятности к теоретическому значению параметра р, т. е. ошибка оценки стремится к нулю:
р lim b = р. (2.90)
П->оо
Условие оо означает, что выборка так велика, что она идентична бесконечной генеральной совокупности. Итак, с увеличением числа наблюдений вероятность появления большой ошибки оценки становится меньше.
Состоятельность — важнейшее и минимально необходимое требование, которое должно предъявляться к качеству оценок с тем, чтобы эти оценки были в определенном смысле «хорошими» и «надежными».
Эффективность оценок параметров регрессии. В силу того что оценка параметров регрессии, как всякая статистическая оценка, представляет собой случайную величину, ее можно охарактеризовать дисперсией и математическим ожиданием р. Обозначим выборочную дисперсию оценки параметра регрессии bk через s&k, а стандартное отклонение— через Sbk (способ вычисления см. в разделе 3.6). Величина дисперсии может быть различна. На рис. 17 изображено распределение вероятностей двух несмещенных оценок параметра регрессии. Математическое ожидание распределений обеих оценок совпадает фарамет-
95
ром генеральной совокупности 0. Различные распределения могут возникнуть, например, из-за применения двух различных способов оценивания. При этом оценка b обладает меньшей дисперсией, чем оценка Ь*. В таких случаях говорят, что оценка & эффективнее оценки Ь*. Эффективные оценки параметров регрессии являются несмещенными и обладают наименьшей дисперсией по сравнению со всеми остальными несмещенными оценками:
Е (Ь — р)2 Е (Ь* — Р)2. (2.91)
В этом смысле эффективные несмещенные оценки наилучшие.
Нормальное распределение оценок параметров регрессии. Оценки параметров регрессии при фиксированных значениях объясняющих переменных в силу постулирования нормального закона распределения возмущения и (предпосылка 6) также распределены нормально. Если же возмущающие переменные не следуют нормальному распределению, то при соблюдении других довольно общих предпосылок относительно объясняющих переменных оценки параметров регрессии распределены асимптотически нормально, т. е. с ростом объема выборки их распределение стремится к нормальному. Асимптотически нормально распределенные оценки состоятельны.
Асимптотически несмещенные оценки параметров регрессии. Оценки параметров регрессии являются асимптотически несмещенными, если их математическое ожидание с увеличением объема выборки сходится по вероятности к теоретическому значению оцениваемого параметра:
lim Е (&) = р. (2.92)
П->оо
Это одновременно означает, что ошибка оценки с ростом объема выборки становится меньше. Состоятельные оценки — также’асимптотически несмещенные.
Асимптотические эффективные оценки параметров регрессии. Оценки параметров регрессии называются асимптотически эффективными, если они распределены асимптотически нормально, являются асимптотически несмещенными и обладают асимптотически минимальной дисперсией по сравнению со всеми другими состоятельными оценками.
Асимптотические свойства оценок параметров регрессии имеют большое значение, так как они не относятся к точно фиксированному объему выборки. Какими же свойствами обладают оценки параметров линейной функции регрессии, полученные методом наименьших квадратов (МНК-оценки)?
Если выполняются шесть перечисленных в этом разделе предпосылок, особенно предпосылки 1, 5 и 6, то МНК-оценки параметров регрессии — состоятельные, несмещенные и эффективные. В классе всех линейных несмещенных процедур оценивания МНК-оценки обладают наименьшей дисперсией. В этом смысле они представляют собой наилучшие линейные несмещенные оценки параметров 0.
Те случаи, когда не выполняется одна или несколько предпосылок, не будут здесь обсуждаться. Ответы на эти вопросы можно найти в специальной литературе.
96
2.10. ПОСЛЕДОВАТЕЛЬНОСТЬ ПРОВЕДЕНИЯ
РЕГРЕССИОННОГО АНАЛИЗА
И ЕГО ПРИМЕНЕНИЕ В ЭКОНОМИКЕ
Если читатель усвоил материал, посвященный регрессионному анализу, то можно рекомендовать следующую общую процедуру проведения исследования*.
Формулировка экономической проблемы. В соответствии с целью исследования на основе знаний политической экономии и экономики определенной отрасли хозяйства конкретизируются явления и процессы, зависимость между которыми подлежит оценке. Под этим подразумевается прежде всего четкое определение экономических явлений, установление объектов и периода исследования.
На этом этапе исследования должны быть сформулированы экономически осмысленные и приемлемые гипотезы о зависимости экономических явлений. Затем причинно обусловленная зависимость количественно оценивается с помощью методов регрессионного анализа. Преимущество регрессионного анализа состоит в том, что на его основе делают не только общий вывод о причинно-следственном механизме, а получают конкретные сведения о том, какую форму и какой вид имеет данная зависимость.
Идентифицирование переменных. Для определения наиболее разумного числа переменных в регрессионной модели прежде всего ориентируются на соображения профессионально-теоретического характера. Исходя из физического смысла явления производят классификацию переменных на зависимую и объясняющие переменные.
Сбор статистических данных. В зависимости от цели и задач исследования устанавливают принцип отбора, а именно пользуются либо одновременными перекрестными данными, либо временными рядами. Далее принимают решение о проведении исследования по всей генеральной совокупности или по выборке из нее. После этого приступают к сбору данных по каждой из переменных, включенных в анализ. Если для каких-либо экономических явлений не может быть обеспечено необходимое количество статистических данных, то следует вернуться к первому этапу исследования.
Спецификация функции регрессии. На этом этапе исследования происходит конкретная формулировка гипотезы о форме связи. Содержательные соображения должны подсказать конкретную функциональную форму соотношения между переменными: линейная или нелинейная, простая или множественная регрессия. Существенную помощь в этом может оказать диаграмма рассеяния. К задачам спецификации-относится также проверка предпосылок регрессионного анализа и прежде всего выполнимость предпосылок 4 и 5. Большей частью тип функции регрессии в процессе исследования определяется поэтапно путем исключения переменных, не оказывающих существенного влияния на зависимую переменную, и включения в анализ новых переменных с
*W б 1 f 1 i п g М. Ein Algorithmic fur den Aufbau dynamischer und statis-tischer Regressionsmodelle. — Statistische Praxis, 26 (1971), 3, S. 149—153.
4 Зак. 1113
97
использованием критериев проверки состоятельности гипотетического вида зависимости. Эти процедуры рекомендуется выполнять на ЭВМ.
Оценка функции регрессии. На этом этапе исследования определяются численные значения параметров регрессии. Кроме того, вычисляется ряд статистических показателей, характеризующих точность регрессионного анализа (см. главу 3). Целесообразно также использовать ЭВМ. На любом ВЦ имеются стандартные программы по регрессионному анализу.
Оценка точности регрессионного анализа. Различные вопросы, связанные со статистической оценкой точности регрессионного анализа, подробно обсуждаются в главе 3. Здесь мы хотели бы только подчеркнуть, что этому этапу исследования необходимо уделять особое внимание, поскольку на данной стадии должны быть сделаны выводы о точности результатов.
Экономическая интерпретация. Результаты регрессионного анализа сравниваются с гипотезами, сформулированными на первом этапе исследования, и оценивается их правдоподобие с экономической точки зрения.
Предсказание неизвестных значений зависимой переменной*. Построенное уравнение регрессии находит практическое применение в прогностическом анализе. Прогноз получают путем подстановки в регрессионное уравнение с численно оцененными параметрами значений объясняющих переменных. Прогнозирование результатов по регрессии лучше поддается содержательной интерпретации, чем простая экстраполяция тенденции, так как можно полнее учитывать природу исследуемого явления. Благодаря этому регрессионный анализ находит широкое применение при решении задач перспективного планирования в народном хозяйстве.
Если определена функция регрессии и она экономически обоснована, а точность статистических оценок параметров соответствует предъявляемым требованиям, то прогнозируемые значения обладают достаточной надежностью. По своему характеру они являются средними значениями, которые следует ожидать с большой вероятностью. В силу многообразия явлений и многогранности их выражений отдельные эмпирические значения рассеиваются вокруг средних значений (см. раздел 2.9). Поэтому естественно, что фактические значения зависимой переменной не будут совпадать с расчетными (прогнозами) и мы вынуждены считаться с этими отклонениями. Рассеяние наблюдений вокруг линии регрессии определяет надежность получаемых по уравнению регрессии прогностических оценок.
Итак, с помощью регрессии мы производим оценки значений зависимой переменной при усредненных условиях, что должно быть учтено в практических прогностических исследованиях. Но это обстоятельство не является недостатком регрессионного анализа, а, наоборот, наводит на мысль о необходимости установления допусков, а также о
*Предсказание неизвестных значений зависимой переменной далее кратко называется прогнозом. При этом мы отдаем себе отчет в том, что это понятие не* точно при одновременных обследованиях.
98
Применений системы допусков при планировании и прогнозирований. Ни один инженер не будет требовать изготовления деталей с высокой точностью, например в 1 микрон, если это не связано с техническими требованиями или не обеспечивается точностными характеристиками имеющихся в распоряжении станков, а также если достижение этой точности вызывает недопустимо большие затраты труда. Использование допусков позволит относительно быстро и легко вводить необходимые изменения в планируемые показатели.
Между моментом сбора данных и получением прогностических оценок часто проходит большой промежуток времени. Если за этот срок не произошло существенных изменений в условиях эксперимента, то считается, что регрессия более или менее достоверно отражает действительно существующую тенденцию. Можно полагать, что в этом случае регрессия окажется практически полезным инструментом прогнозирования. Точность прогноза определяется не только точностью полученных оценок параметров регрессии, но и тем, насколько надежно оценены будущие значения объясняющих переменных на основе дополнительной информации. Источником такой дополнительной информации могут быть более обстоятельные исследования, а также профессионально-теоретические соображения в соответствии с экономической и социальной политикой государства.
Каждое прогнозируемое значение должно сопровождаться указанием доверительных границ (см. раздел 8.4).
Статистические методы прогнозирования находят широкое применение в народном хозяйстве. Найденные прогностические оценки после их критического осмысливания могут быть положены в основу плановых показателей. При этом необходимо учитывать возможные изменения в самой тенденции развития экономического явления. Процесс построения статистической модели должен сопровождаться корректировкой оценок параметров регрессии и статистических характеристик в соответствии с ожидаемым изменением обстоятельств их формирования. В ГДР и других социалистических странах регрессионный анализ с успехом применяется при прогнозировании научно-технического прогресса, что нашло отражение в публикациях, помещенных в таких изданиях, как научно-технические журналы университетов и высших школ ГДР, «Вестник статистики» (Москва), «Przeglad Sta-tystyczny» (Варшава), «Revue Statistika» (Прага).
4*
ОЦЕНКА ТОЧНОСТИ
3 РЕГРЕССИОННОГО АНАЛИЗА
3.1. ОБЩИЕ СООБРАЖЕНИЯ
До сих пор в наших рассуждениях мы исходили из того, что под? бор функции линейной регрессии осуществлялся на основе соображений профессионально-теоретического характера, а вычисленные оценки параметров, входящие в уравнения регрессии, наиболее хорошо согласовывались с опытными данными. Критерий соответствия регрессии опытным данным заложен в требовании наименьших квадратов:
i (t/i-^)2= 1 (2.13)
z=i / = i
Результаты различных выборок имеют различное рассеяние. Поэтому может случиться, что построение регрессионной зависимости одного и того же экономического смысла по данным двух выборок из одной и той же генеральной совокупности приведет к различным уравнениям. Степень соответствия этих уравнений опытным данным, несмотря на одинаковый тип зависимости, может быть различна. Однако критерий (2.13) имеет недостаток: хотя его нижняя граница равна нулю, верхняя граница не может быть указана. Поэтому для оценки степени соответствия регрессии имеющимся эмпирическим данным он не используется. Желательно иметь в распоряжении показатель, отражающий, в какой мере функция регрессии определяется объясняющими переменными, содержащимися в ней. В качестве такого показателя можно выбрать коэффициент детерминации.
Прежде чем давать определение коэффициента детерминации, изложим некоторые соображения относительно его статистического обоснования. Выборочная дисперсия, характеризующая разброс наблюдаемых значений переменной у около ее среднего, равна:
п
:--• (3.1)
п— 1
100
Дисперсия Sy называется общей. Она должна как можно больше обусловливаться изменениями объясняющих переменных. Исходя из этого производим разложение дисперсии. Отклонение z-ro результата наблюдения от общего среднего у можно представить в таком виде:
Уг — У = (Di — Уг) + (yt — ~У)- (3.2)
Возведя в квадрат обе части тождества (3.2) и просуммировав по i, получим равенство
2 (У1—у? = 2 (yt~yi)2+2 2 (уг-У1)(У1—у) + 2 (^—#• i= 1 /=р /= /= 1
(3.3)
Учитывая (2.75) и то, что S ytUi = 0, можно показать, что
2 2 (f/«—yt)(yt~У) — ®-1= 1
Тогда (3.3) запишется в виде
2 (^-^)2= 2 (^-£)а+ 2 (yt-у)2- (3-4)
i= 1 1= 1 /= 1
Разделив (3.4) на п— 1, получим
2 (yt—y)2 2 (у1—у№ 2 & —у)9 2 “z
>= 1 __________+______________ = i= 1 1
п—1 п — 1 п — 1 п — 1
п
2 (yt -уУ
। <= 1
say=--sua + s£ (3.5)
Равенство (3.5) дает нам разложение общей дисперсии на две составляющие.
Как указывалось в главе 2, возмущающая переменная трактуется как результат ошибки измерения и ошибки уравнения. Поэтому дисперсия s’u* представляет собой ту часть общей дисперсии Sy, которая не объясняется функцией регрессии. Отсюда она получила название «необъясненная», или остаточная, дисперсия. Она измеряет ту часть рассеяния у, которая возникает из-за случайностей и изменчивости прочих неучтенных факторов. По (3.5) видно, что чем больше s’u приближается к нулю, тем меньше эмпирические значения yt отклоняются от значений регрессии yt. Вторая составляющая общей дисперсии— второе слагаемое в правой части тождества (3.5) — есть дисперсия значений регрессии yt, так как у = у (см. (2.75)). Однако рассеяние значений регрессии происходит только вследствие наклона прямой рег-
101
рессии, который определяется величиной коэффициента регрессии. Таким образом, дисперсия s'~ представляет ту часть рассеяния переменной у, которая в основном обусловлена влиянием переменных xh (k = 1, m). В связи с этим s~2 называют «объясненной» дисперси-
ей или дисперсией, обусловленной регрессией.
3.2. КОЭФФИЦИЕНТ ДЕТЕРМИНАЦИИ
ДЛЯ ПРОСТОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
Рассмотрим вначале коэффициент детерминации для простой линейной регрессии, называемый также коэффициентом парной детерминации.
На основе соображений, изложенных в разделе 3.1, теперь относительно легко найти меру точности оценки регрессии. Мы показали, что общую дисперсию sy можно разложить на две составляющие — на «необъясненную» дисперсию $„2и дисперсию s'-2, обусловленную регрессией. Чем больше s'£ по сравнению с s'M2, тем больше общая дисперсия формируется за счет влияния объясняющей переменной х и, следовательно, связь между двумя переменными у и х более интенсивная. Очевидно, удобно в качестве показателя интенсивности связи, или оценки доли влияния переменной х на у, использовать отношение
1 V? * - П А
— S(m-f)2 s?
Вух -------(3.6)
/г п _ §2
Это отношение указывает, какая часть общего (полного) рассеяния значений у обусловлена изменчивостью переменной х. Чем большую долю в общей дисперсии составляет s~2, тем лучше выбранная функция регрессии соответствует эмпирическим данным. Чем меньше эмпирические значения зависимой переменной отклоняются от прямой регрессии, тем лучше определена функция регрессии. Отсюда происходит и название отношения (3.6) — коэффициент детерминации Вух. Индекс при коэффициенте указывает на переменные, связь между которыми изучается. При этом вначале в индексе стоит обозначение зависимой переменной, а затем объясняющей.
Из определения коэффициента детерминации как относительной доли очевидно, что он всегда заключен в пределах от 0 до 1:
OgB,xsl. (3.7)
Если Вух— 1, то все эмпирические значения yt (все точки поля корреляции) лежат на регрессионной прямой. Это означает, что yt = = yi для i=l, ..., п, т. е. s'u — 0. В этом случае говорят о строгом линейном соотношении (линейной функции) между переменными у и х. Если Вух = 0, дисперсия, обусловленная регрессией, равна нулю, а 102
«необъясненная» дисперсия равна общей дисперсии. В этом случае у. = у. Линия регрессии тогда параллельна оси абсцисс. Ни о какой численной линейной зависимости переменной у от х в статистическом ее понимании не может быть и речи. Коэффициент регрессии при этом незначимо отличается от нуля.
Итак, чем больше Вух приближается к единице, тем лучше определена регрессия.
Коэффициент детерминации есть величина безразмерная и поэтому он не зависит от изменения единиц измерения переменных у и х (в отличие от параметров регрессии). Коэффициент Вух не реагирует на преобразование переменных.
Приведем некоторые модификации формулы (3.6), которые, с одной стороны, будут способствовать пониманию сущности коэффициента детерминации, а с другой стороны, окажутся полезными для практичес-ких вычислений. Подставляя выражение для yt (2.25) в (3.6) и принимая во внимание (1.8) и (3.1), получим:
г. SXbl
ВУх = -±±. (3.8)
sy
Эта формула еще раз подтверждает, что «объясненная» дисперсия, стоящая в числителе (3.6), пропорциональна дисперсии переменной х, так как Ьг является оценкой параметра регрессии.
Подставив вместо Ь\ его выражение (2.26) и учитывая определения дисперсий s| и Sy, а также средних х и у, получим формулу коэффициента детерминации, удобную для вычисления:
~х) 2
В,,х =--------------------.
2^-у)22(хг-х)2 i I
ИЛИ
in 2 xi Уг 2 xi 2 Ui\
вух = —-------------------------------------. (3.9)
/п 2%/ 2х* 2 Xi) fл 2 у1 2 у* 2 у А
\ i i i )\ i i i )
Из (3.9) следует, что всегда Вух = Вху. С помощью (3.9) можно относительно легко определить коэффициент детерминации. В этой формуле содержатся только те величины, которые используются для вычисления оценок параметров регрессии и, следовательно, имеются в рабочей таблице. Формула (3.9) обладает тем преимуществом, что вычисление коэффициента детерминации по ней производится непосредственно по эмпирическим данным. Не нужно заранее находить оценки параметров и значения регрессии. Это обстоятельство играет немаловажную роль для последующих исследований, так как перед проведением регрессионного анализа мы можем проверить, в какой степени определена исследуемая регрессия включенными в нее объяс
103
няющими переменными. Если коэффициент детерминации слишком мал, то нужно искать другие факторы-переменные, причинно обусловливающие зависимую переменную. Следует отметить, что коэффициент детерминации удовлетворительно отвечает своему назначению при достаточно большом числе наблюдений. Но в любом случае необходимо проверить значимость коэффициента детерминации. Эта проблема будет обсуждаться в разделе 8.6.
Вернемся к рассмотрению «необъясненной» дисперсии, возникающей за счет изменчивости прочих факторов-переменных, не зависящих от х, а также за счет случайностей. Чем больше ее доля в общей дисперсии, тем меньше, неопределеннее проявляется соотношение между у и х, тем больше затушевывается связь между ними. Исходя из этих соображений мы можем использовать «необъясненную» дисперсию для характеристики неопределенности или неточности регрессии. Следующее соотношение служит мерой неопределенности регрессии:
1
s,.
uvx =—(3-Ю)
Легко убедиться в том, что
Вух Uyx = 1 £< • у Л*
И
Byx=l — Uyx. (3.11)
Отсюда очевидно, что не нужно отдельно вычислять меру неопределенности, а ее оценку легко получить из (3.11).
Теперь вернемся к нашим примерам и определим коэффициенты детерминации для полученных уравнений регрессий.
Пример 1
Вычислим коэффициент детерминации по данным примера из раздела 2.4 (зависимость производительности труда от уровня механизации работ). Используем для этого формулу (3.9), а промежуточные результаты вычислений заимствуем из табл. 3:
в =_________(14.26907-724-492)8___= Q 93g
УХ (14-40134— 724-724) (14-18138 — 492-492)
Отсюда заключаем, что в случае простой регрессии 93,8% общей дисперсии производительности труда на рассматриваемых предприятиях обусловлено вариацией показателя механизации работ. Таким образом, изменчивость переменной х почти полностью объясняет вариацию переменной у.
Для этого примера коэффициент неопределенности Uyx = 0,062, т. е. только 6,2% общей дисперсии нельзя объяснить зависимостью производительности труда от уровня механизации работ.
Пример 2
Вычислим коэффициент детерминации по данным примера из раздела 2.5 (зависимость объема производства от основных фондов). Необ
104
ходимые промежуточные результаты вычислений приведены в разделе 2.5 при определении оценок коэффициентов регрессии:
в =_____________(52-408104—1616-12905)2______= 0911
vx (52-53588—1616-1616) (52-3218897—12905-12905) ’
Таким образом, 91,1% общей дисперсии объема производства исследуемых предприятий обусловлено изменчивостью значений основных фондов на этих предприятиях. Данная регрессия почти полностью исчерпывается включенной в нее объясняющей переменной. Коэффициент неопределенности составляет 0,089, или 8,9%.
Следует отметить, что приведенные в данном разделе формулы предназначены для вычисления по результатам выборки большого объема коэффициента детерминации в случае простой регрессии. Но чаще всего приходится довольствоваться выборкой небольшого объема (п <. 20). В этом случае вычисляют исправленный коэффициент детерминации В*ух, учитывая соответствующее число степеней свободы. Формула исправленного коэффициента детерминации для общего случая т объясняющих переменных будет приведена в следующем разделе. Из нее легко получить формулу исправленного коэффициента детерминации в случае простой регрессии (/п=1).
3.3. КОЭФФИЦИЕНТ МНОЖЕСТВЕННОЙ ДЕТЕРМИНАЦИИ
Если изучаемое явление зависит не от одного, а от нескольких явлений, то зависимость между ними описывается с помощью множественной регрессии, а для установления доли дисперсии, обусловленной воздействием изменений объясняющих переменных, вычисляется коэффициент множественной детерминации.
Выражение коэффициента множественной детерминации можно получить путем обобщения формулы (3.6) с учетом соображений, изложенных в разделах 3.1 и 3.2:
2 (£-1С2
[Ву. 12.../П = —п-----(3.12)
2 (Уг-i=l
Индекс при В указывает на то, что у является зависимой переменной и вариабельность всех объясняющих переменных х1У ..., хт рассматривается одновременно в изучаемой регрессии.
Интерпретация аналогична интерпретации коэффициента
детерминации для простой линейной регрессии. Коэффициент ВуЛ...т указывает, как велика доля объясненной дисперсии в общей дисперсии, какая часть общей дисперсии может быть объяснена зависимостью переменной у от переменных ..., хт. Величина коэффициента множественной детерминации заключена в интервале
0 Вул ... т 2= 1.
105
Коэффициент детерминации равен 1, если yt = уt. В этом случае говорят о линейной функциональной зависимости. Коэффициент детерминации равен 0, если yt = у. В этом случае говорят об отсутствии линейной зависимости в смысле представлений регрессионного анализа.
Приведем теперь формулу коэффициента детерминации к виду, удобному для вычислений. При этом ограничимся вначале регрессией с двумя объясняющими переменными. Уравнение множественной линейной регрессии можно представить в таком виде:
y't = у + (хц — хг) + b2 (xi2 — х2), или
yi—~y=bi(xtl—x1) + b2(xt2—x2). (3.13)
Возведя в квадрат обе части равенства (3.13) и просуммировав все отклонения, раскроем скобки. С учетом формул (2.53) и (2.54) из раздела 2.7 получим следующее выражение:
2 (^—?)2 2 (*и—*i) (#;—?)+ b2{xl2— Т2) (yi—'y). (3.14)
i i i
Подставим этот результат в (3.12):
или
ВуЛЪ —
bi[n ^у^х^уЛ +ЬЛп%Хь У1— 2 Xi^yt
\ i__i_ i /_V i_i_i
-^У^
i i i
(3.16)
С помощью формулы (3.16) сравнительно легко можно найти коэффициент множественной детерминации для двух объясняющих переменных.
Пример
Определим долю дисперсии производительности труда, обусловленную линейной зависимостью от уровня механизации работ и среднего возраста работников, по данным из раздела 2.7. По формуле (3.16) получим
р _ 0,5259.(14.26 907—724-492)+0,1591-(14-19 384—546-492)
у 14-18138—492-492
Найденная величина коэффициента множественной регрессии означает, что на основе полученной оценки функции регрессии 94,47% общей дисперсии объясняется зависимостью производительности труда от уровня механизации работ и среднего возраста работников. Это свидетельствует о том, что данная регрессия хорошо соответствует эмпи
106
рическим данным. Лишь 5,53% общей дисперсии приходится на влияние прочих, не учтенных в регрессии факторов-переменных.
Формулу (3.15) обобщим для регрессии с т объясняющими переменными:
У (^ii —%i) (.У1 у) 4~ • • • 4~^m S хт) (У1 У)
ВУ1 т=-—---------------------------------------------- . (3.17)
у 2(уг-?)2
i
Разделив числитель и знаменатель формулы (3.17) на . получим: о _ *1 «1»+--+*т smy
Вул...т---------~------- • (o.lo)
sy
Введем вектор
Sxy --
Sly
-smy _
(3.19)
элементами которого являются shy = —Ц- 2 (xik — xh) (yt — y), n i i
k = 1, ..., tn.
Вектор sxy — это вектор ковариаций m объясняющих переменных с зависимой переменной у. Далее, пусть
~ bi'
,Ьщ _
Ь<1) ==
(3.20)
— вектор коэффициентов регрессии. Он получается путем вычеркивания первой компоненты (постоянной регрессии) из вектора параметров регрессии b. С учетом этого условия формула (3.18) принимает вид
b(i)Sx»
°УЛ...т------~i (0.21)
SV
b('i) —транспонированный вектор bv
Пример
Определим с помощью формулы (3.21) по данным из раздела 2.7 долю дисперсии производительности труда, обусловленную зависимостью от уровня механизации работ, среднего возраста работников и среднего процента выполнения нормы. Вектор Ьг получается из вектора b параметров регрессии путем вычеркивания постоянной регрессии Ьо. Вектор sxy ковариаций объясняющих переменных с зависимой переменной строим в виде (3.19). Таким образом, можем записать
Г 0,521231
Ь(1)= 0,15092
—0,02389
sxy
112,5824
15,0769
—28,2088
5^ = 65,2088.
107
В результате получаем значение коэффициента детерминации:
^у.123
[0,52123 0,15092—0,02389]
65,2088
112,5824
15,0769
—28,2088
61,6306
65,2088
0,9451.
Итак, 94,51% общей дисперсии обусловливается зависимостью производительности труда от перечисленных выше объясняющих переменных. И только 5,49% общей дисперсии не может быть объяснено этой зависимостью на основе полученной оценки функции регрессии. Таким образом, предполагая, что уравнение регрессии статистически значимо, его подбор выполнен очень хорошо.
Так же, как коэффициент парной детерминации, коэффициент множественной детерминации не изменится, если изменится размерность переменных или они подвергнутся линейным преобразованиям. Отсюда следует важный вывод: при применении стандартизованных переменных (2.66) остается таким же процентное отношение к общей вариации той ее части, которая определена влиянием объясняющих переменных на зависимую, выраженных в натуральном масштабе. Если для стандартизованных переменных Sy> = 1, то (частный случай)
By.L.'.m — 1 Uy.l.'.m
=i—$;2,
т. е. коэффициент детерминации равен «объясненной» дисперсии, а коэффициент неопределенности равен «необъясненной» дисперсии.
Часто, особенно при небольшом объеме выборки и, пользуются исправленным коэффициентом детерминации В*уЛ..,т, так как число объясняющих переменных существенно уменьшает число степеней свободы. Итак, введение поправки на число степеней свободы дает нам исправленный, несмещенный коэффициент детерминации. Число степеней свободы общей дисперсии разлагается также на две составляющие:
п — 1 = (п — т — 1) + т. (3.23)
Соотношение между двумя коэффициентами — с поправкой и без нее — может быть после соответствующих выкладок представлено в виде
о* _____1 Su ____1 jj п 1 __
(3.24)
п—т—1
(3.22)
При этом Su определяется ло формуле (3.32) (см. раздел 3.6). Коэффициент детерминации без поправки на число степеней свободы никогда не уменьшается с добавлением к регрессии новой объясняющей переменной (возможно даже некоторое незначительное его увеличение), 108
в то время как для исправленного коэффициента это оказывается возможным. Следует учитывать, что всегда
В* < В. (3.25)
Пример
Вычислим по данным из раздела 2.7 исправленные коэффициенты множественной детерминации для регрессии с двумя и тремя объясняющими переменными:
В* = 1 —0,0553 -4~‘ = 0,9346,
*-’2 14—2 — 1
В*. = 1 —0,0549 -14"1 = 0,92863. гл'23 14—3—1
Значения коэффициентов детерминации подтверждают приведенные выше утверждения. Введение новой переменной х3 не привело к существенному дополнению в объяснении переменной у, а точнее, в объяснении ее вариации. Поэтому при двух одинаково приемлемых с профессионально-теоретической точки зрения функциях регрессии рекомендуется отдавать предпочтение той, для которой исправленный коэффициент детерминации оказался больше.
3.4. КОЭФФИЦИЕНТ ЧАСТНОЙ ДЕТЕРМИНАЦИИ
В множественном регрессионном анализе часто полезно определять долю тех изменений, которые в данном явлении зависят от одного фак-тора-переменного при исключении влияния остальных рассматриваемых в регрессии переменных. Для этого используется коэффициент частной детерминации. Ограничимся обсуждением коэффициента частной детерминации для случая двух объясняющих переменных.
Для оценки доли вариации у, объясняемой линейной зависимостью у от хг при исключении влияния х2, вычисляется коэффициент частной детерминации индекс которого указывает на эту зависимость. В разделе 2.8, где рассматривалась частная линейная регрессия, было показано, как устранить влияние переменной х2 на переменные у и х±. При этом получаем значения переменных с исключением эффекта от влияния х2:
У* = У i — У i и
Хц— Xii Xfi, (2.70)
причем
yt = b0 + b2xi2 и
хг1 = Ы + b*2xi2, (2.68)
Воспользуемся методикой определения коэффициента детерминации для простой линейной регрессии применительно к значениям (2.68) и (2.70). Используя формулу (3.9) из раздела 3.2, после некоторых преобразований с учетом того, что у* = х* = 0, получим выражение ко-
Ю9
эффициента частной детерминации:
(3.26)
После дополнительных преобразований
D ___ Byi % V&у1 Ву2 ^12 ^12
У1’2 (1—(1—в12)
(3.27)
Таким образом, коэффициент частной детерминации определяется по коэффициентам парной детерминации. С помощью формулы (3.26) или (3.27) устанавливается доля вариации, обусловленная зависимостью переменной у от при исключении влияния х2. Отсюда становится очевидным отличие коэффициента частной детерминации от коэффициента множественной детерминации. Они имеют различное содержание и не заменяют друг друга.
Формулу (3.26) путем соответствующих преобразований можно привести к такому виду, который позволяет находить коэффициент частной детерминации непосредственно по эмпирическим данным. Вообще целесообразнее вычислять коэффициент частной детерминации по соответствующим коэффициентам частной корреляции, о которых речь пойдет в разделе 4.5.
3.5. КОЭФФИЦИЕНТ ДЕТЕРМИНАЦИИ МЕЖДУ ОБЪЯСНЯЮЩИМИ ПЕРЕМЕННЫМИ
Как указывалось в разделе 2.9 (см. предпосылку 4), для решения системы нормальных уравнений очень важно знать соотношения между объясняющими переменными xk- Используя понятие коэффициента детерминации, введем меру зависимости этих переменных между собой. Обозначим через Bfe.i...(fe_i)(h+i)...7n коэффициент детерминации, характеризующий степень обусловленности /г-й объясняющей переменной остальными объясняющими переменными, входящими в данную регрессию.
Укажем формулу для вычисления коэффициента детерминации между объясняющими переменными. Для ее вывода исходят из матрицы дисперсий и ковариаций объясняющих переменных Sxx:
S
5и
521
$ml
512
S22
Sm2
$1т
S2m
$тт —
(3.28)
где skk = У, (xik — xk)2— дисперсия объясняющей переменной п 1 I
%k> a $ki = 2 (xtk — xk) (хи — Xj) при k I — ковариация
п 1 I
объясняющих переменных xk и xt. Умножив каждый элемент (3.28) на
ПО
п— 1, получим матрицу S*x сумм квадратов отклонений и произведений отклонений:
S11 S12 S^m
S’ = XX ♦ ♦ S21 $22 $2m > (3.29)
-$тЛ $m2 s* mm ___
Хк)\ a i — Xh) (Xu — X[). Матрицу,
i обратную к SJX, обозначим через i V • ’ XX*
~ Ou 012 Olm
(S’ )-‘=Vxx = \ XX) xx On 022 O2nt
Коэффициент детерминации между объясняющими переменными вычисляется по формуле
Вал- (л-i) (ft+i)-m = 1 - (3,31)
где Vkk и s*kk — элементы £-й строки и А-го столбца матриц Vxx и S*x соответственно.
Пример.
Вернемся к примеру с тремя объясняющими переменными из раздела 2.7. Построим следующие матрицы:
Г 207,1429
Sxx = 22,8462
— 48,8132
ls;
' ^2692,8574
297
634,5716
V =
• XX
0,000522
0,000343
0,000477
22,8462 —48,8132 ~
19,2308 —11,1538 !
— 11,1538 45,3242 _
297 —634,5716 '
250 —145 ;
-145 589,2155
—0,000343 0,000477'
0,004891 0,000834
0,000834 0,002417
(Элементы матрицы Vxx указаны с округлением.) По (3.31) получим:
В1.23
-1---= 1---------------!------------ 0,2882;
uu 0,000522-2692,8574
^2.13 — 1
Вз.12 — 1
---1--=1 —
^22 ^2
—!— = i — узз ^3
==0,1822;
0,004891-250
------!---------- 0,2977.
0,002417-589,2144
111
В силу того что величина коэффициента детерминации между переменными также заключена в пределах от 0 до 1, результаты вычислений отражают небольшую зависимость между объясняющими переменными. Проверка значимости коэффициентов детерминации обсуждается в разделе 8.6. Коэффициенты детерминации между переменными будут использованы также при рассмотрении мультиколлинеарности в главе 9.
Различные коэффициенты детерминации не могут быть единственным критерием оценки регрессии. Неосторожное их использование может привести к ошибочным заключениям. Например, если эмпирические данные представляют собой временной ряд или между переменными существуют не только непосредственные, но и многообразные косвенные связи (см. главы 9 и 12), то применение коэффициента детерминации становится весьма проблематично. Поэтому далее мы еще будем обсуждать способы оценки точности подбора функции регрессии.
3.6. СТАНДАРТНЫЕ ОШИБКИ ОЦЕНОК
Качество подбора функции регрессии можно оценить с помощью стандартных ошибок или дисперсий остатков и оценок параметров регрессии.
Стандартная ошибка или дисперсия остатков. Стандартная ошибка остатков называется также стандартной ошибкой оценки регрессии в связи с интерпретацией возмущающей переменной и как результата ошибки спецификации функции регрессии (см. главу 2). О дисперсии остатков шла речь ранее в разделах 2.4, 2.9, 3.1 и 3.3. Возмущающая переменная и является случайной с определенным распределением вероятностей. Математическое ожидание этой переменной равно нулю (предпосылка 1), а дисперсия — (предпосылка 2, см. раздел 2.9). Таким образом, о?— это дисперсия возмущения в генеральной совокупности. Нам неизвестны значения возмущающей переменной. Можно судить о ней только по остаткам и. Вычисленная по этим остаткам дисперсия s« является оценкой дисперсии возмущающей переменной. Несмещенной оценкой дисперсии возмущающего воздействия Оц будет следующее выражение*
£4 > ~ ~
sg = ——-------=------!----u'u. (3.32)
П—(/П-f-l) V n — (tn + 1 )f
В знаменателе формулы (3.32) стоит число степеней свободы п — (т + 1), где п — объем выборки, а т — число объясняющих переменных. Такое выражение числа степеней свободы связано с тем, что остатки должны удовлетворять т + 1 условиям. Эти условия непосредственно вытекают из предпосылок 1 и 5 (см. раздел 2.9). Кратко
*Мы не приводим доказательства несмещенности этой оценки, ограничиваясь лишь ее указанием.
112
поясним это утверждение. Параметры множественной регрессии
у=ХЫ-и (2.60)
вычисляют путем решения системы нормальных уравнений, в матричной форме записи имеющих вид
Х'ХЬ = Х'у. (2.63)
Подставим (2.60) в (2.63):
Х'ХЬ = X' (ХЬ + и).
Раскрыв скобки и сделав соответствующие выкладки, получим
X4t = 0.] (3.33)
Матричное уравнение (3.33) содержит т + 1 условий (уравнений), которые накладываются на остатки, и это приводит к уменьшению числа степеней свободы. При k = 0 в силу того, что х0 = 1 для всех i,
2^ = 0, (2.76)
/=1
что является следствием предпосылки 1 (математическое ожидание возмущающей переменной равно нулю). Из (3.33) при k — 1, ..., т также получим
2 Щ ~ 0, (3.34)
что вытекает из предпосылки 5 (переменные xk (k =1, ..., tri) не коррелируют со значениями возмущения, т. е. xk (k = 1, ..., т) являются действительно объясняющими, а не подлежащими объяснению переменными). Следовательно, в регрессионном анализе могут обсуждаться только односторонне направленные зависимости. Поскольку термин «степень свободы» используется для обозначения независимой информации, в данном случае число связей, налагаемых на п независимых случайных наблюдений, можно интерпретировать как т + 1 параметров (й0, Ь19 ...» bm), которыми определяется функция регрессии.
В связи с тем что вычисление числителя в формуле (3.32) довольно затруднительно, мы хотим, опустив вывод, привести более простой способ его определения:
2 «/’=2 yt—b0 2 yi—bi 2 хпУ1—-^ — Ьт 2 ximyi (3.35) z=i z=t z=i z=i 1=1
или в матричной форме записи:
u'u = у'у— Ь'Х'у.
Выражения сумм в правой части (3.35) содержатся в рабочей таблице для построения регрессии, а оценки параметров уже получены. Если снова обратиться к понятию коэффициента детерминации, введенному в разделах 3.1 и 3.2, то станет ясным физический смысл дисперсии
113
(или стандартного отклонения) остатков — это та доля общей дисперсии Sy, которая не может быть объяснена зависимостью переменной у от переменных xh (k = 1, ..., m).
Стандартные ошибки или дисперсии оценок параметров регрессии. При описании этих показателей будем исходить из заданных значений объясняющих переменных.
Как указывалось в разделе 2.9, оценки параметров регрессии являются случайными величинами, имеющими определенное распределение вероятностей. Возможные значения оценок рассеиваются вокруг истинного значения параметра р. Определим меру рассеяния оценки параметра. Обозначим через 2ЬЬ матрицу дисперсий и ковариаций оценок параметров регрессии:
^bobo dbabt " °b'bm
— °blba Obibi •• °b'bm (3.36)
abmb' * ’’ bm -
Симметрическая матрица (3.36) на главной диагонали содержит дисперсии оценок параметров регрессии k = 0, 1, ..., т
abkbk = E{bk-^ (3.37)
а вне главной диагонали — их ковариации
obkbl — E(bh — pft) (b, - ₽<) (3.38)
для k Ф l и k = 0, 1, m\ I = 0,1, ..., m.
Краткая форма записи матрицы (3.36):
S6b= £[(b-₽) (b -₽)']. (3.39)
Подставив в (3.39) формулу (2.86) из раздела 2.9
b=₽ + (X'X)-1X'u, (2.86)
получим Sb6 = Е [ (X'X)-1X'uu'X (X'X)"1], или
S66 = (Х'Х)-ХХ'£ (uu')X (Х'Х)-1. (3.40)
Далее, в силу того, что
Е (uif) = ои21, (2.79)
имеем
Sb6 = а* (Х'Х)-1. (3.41)
Так как неизвестно, используем его оценку sS. В результате получаем оценку матрицы (3.41),
Sbb=sWX)-\ (3.42)
элементами главной диагонали которой являются искомые оценки дисперсий. Матрицу S66 легко определить, поскольку матрица (Х'Х)"1 известна (см. вычисление оценок параметров в разделе 2.7), a $3 вычисляется по (3.32).
114
Если мы обозначим через x{kk>> элемент главной диагонали матрицы (Х'Х)*”1, то оценка дисперсии параметра регрессии bk будет определяться выражением
sbkbk=Sbk=s2 *ux<kk\ (3.43)
т. е. она равна произведению дисперсии остатков на k-й элемент главной диагонали обратной матрицы (Х'Х)"1. Таким образом, стандартная ошибка оценки параметра регрессии bk определяется как
sbk~Su ~]/x^kkK
(3.44)
Найдем дисперсию и стандартную ошибку оценок параметров 60 и 6Х простой линейной регрессии. В случае простой линейной рег
рессии имеем
(Х'Х) =
а также
(X'X)-i =
— 2
X
2(*<—Л')2
X
S(Xj — X)2 S(xf-x)2
Согласно формуле (3.42) получим
г- 1 “2 -
1 х__________X______
Q п S(Xf-x)2 2(xf-x)2
--su _ X 1
2(Х|-Х)2 S(Xi-X)2
Умножая Su на первый элемент главной диагонали матрицы (Х'Х)-1, получим оценку дисперсии постоянной уравнения регрессии Ьо:
ь° и[ п‘ п _ ’ (3.45)
\ 2 %)2 j
а также ее стандартную ошибку:
/ 1 . х2
Г 2
1
Умножив si на второй элемент главной диагонали матрицы (Х'Х)-1, получим оценку дисперсии коэффициента регрессии bt:
s$, = s%----------
п _
2 (xi~ х)2
(=1
(3-47)
115
а также стандартную ошибку этого коэффициента:
Sb, = su
(3.48)
Рассмотрим более обстоятельно стандартную ошибку коэффициента Ьг простой линейной регрессии. Для этого сумму квадратов отклонений в (3.48) заменим на выражение, полученное путем преобразования формулы (1.8):
2 (хг —х)2=(п—1)«;.
i = 1
Формула (3.48) приобретет вид
sb,=-----------(3.49)
Sx Vtt —1
Итак, стандартная ошибка коэффициента регрессии зависит:
от рассеяния остатков. Чем больше доля вариации значений переменной у, необъясненной ее зависимостью от х, найденной методом наименьших квадратов, тем больше стандартная ошибка коэффициента регрессии. Следовательно, чем сильнее наблюдаемые значения переменной у отклоняются от расчетных значений регрессии, тем менее точной является полученная оценка параметра регрессии;
от рассеяния значений объясняющей переменной х. Чем сильнее это рассеяние, тем меньше стандартная ошибка коэффициента регрессии. Отсюда следует, что при вытянутом облаке точек на диаграмме рассеяния получаем более надежную оценку функции регрессии, чем при небольшом скоплении точек, близко расположенных друг к другу;
от объема выборки. Чем больше объем выборки, тем меньше стандартная ошибка коэффициента регрессии. Здесь существует непосредственная связь с таким свойством оценки параметра регрессии, как асимптотическая несмещенность (см. раздел 2.9).
Стандартная ошибка оценки параметра регрессии используется для оценки качества подбора функции регрессии. Для этого вычисляется относительный показатель рассеяния, обычно выражаемый в процентах:
Чем больше относительная стандартная ошибка оценки параметра, тем более оцененные величины отличаются от наблюдаемых значений зависимой переменной и тем менее надежны оценки прогноза, основанные на данной функции регрессии.
116
(Х'Х) =
14 724"
724 40134
и (Х'Х)-1 =
Пример
Вычислим сначала стандартную ошибку для простой линейной регрессии из раздела 2.4, которой описывалась зависимость производительности труда от уровня механизации работ. Итак, имеем
1,06456 —0,01920“
— 0,01920 0,00037 J ’
а также
S^= 52=4,3553 и su — 2,0869.
Используя формулы (3.43) и (3.44), получим следующие значения дисперсий и стандартных ошибок оценок параметров регрессии:
st, = 4,3553 • 1,06456 = 4,6364 и sba = 2,1532;
= 4,3553 • 0,00037 = 0,00162 и sbt = 0,0402.
По (3.50) относительные стандартные ошибки равны:
, = 2,1532 =0 3060 или 30,60%;
6» 7,0356 °
. = 0,0£02 = 0 07399 или 7 3990/ bl 0,5435 0
Далее по данным из раздела 2.7 вычислим дисперсии и стандартные ошибки оценок параметров множественной регрессии для зависимости производительности труда от уровня механизации работ, среднего возраста работников и среднего процента выполнения нормы. Обратная матрица (Х'Х)"1 для этой множественной регрессии найдена в разделе 2.7. По (3.32) вычислим
st = 4,6521 и su = 2,1568.
Применяя (3.43), (3.44) и (3.50), получим следующие результаты:
s2bo = 4,6521 • 52.88929 = 246,046; sbo = 15,6858; s'bo = 3,1016;
sbl = 4,6521 • 0,00052 = 0,00242; sbl = 0,04918; sbl = 0,09436;
s2b2 = 4,6521 • 0,00489 = 0,02275; sb2 = 0,1508; sb2 = 0,9994;
s2b3 = 4,6521 • 0,00242 = 0,01124; sb3 = 0,1060; sb3 = 4,4384.
В то время как для простой линейной регрессии величины стандартных ошибок оценок параметров были приемлемы, для множественной регрессии такой вывод можно сделать только относительно стандартной ошибки коэффициента регрессии Ь±. Оценка функции множественной регрессии, несмотря на большой коэффициент детерминации (см. раздел 3.3) не очень надежна. Отсюда очевидно, что стандартные ошибки оценок параметров служат источником дополнительной информации о качестве подбора функции регрессии. Более обстоятельно с выводами, вытекающими из результатов данного примера, мы познакомимся в разделе 8.7.
117
Элементы матрицы Sbb, стоящие вне главной диагонали и, как было отмечено выше, являющиеся ковариациями, также могут быть использованы для оценки качества подбора функции регрессии. Они характеризуют связь между отклонениями оценок двух параметров регрессии от их истинных значений. Ковариация положительна, когда знаки отклонений bk от и bz от |3Z совпадают. Если оба отклонения положительные, то оценки являются завышенными, если отрицательные— заниженными. Ковариация отрицательна, если положительному отклонению bk от (3fe (завышенная оценка) соответствует отрицательное отклонение bt от (3Z (заниженная оценка) и наоборот.
Пример
Вычислим для простой регрессии ковариацию между постоянной Ьо и коэффициентом регрессии Ь±:
sbobl = 4,3553 • (—0,01920) = —0,08364.
Отсюда следует, что завышение (или занижение) оценки истинного значения параметра рг сопровождается занижением (или соответственно завышением) (30.
Запишем полностью матрицу ковариаций и дисперсий оценок параметров регрессии, так как далее нам придется еще к ней обращаться:
s Г 4,6364 —0,08364 ~
[--0,08364 0,00162
Вычислим ковариации между оценками параметров для множественной регрессии:
sbobi = 4,6521 (—0,06869) = —0,31954, sbob2 = 4,6521 (—0,26929) = —1,2527, sbob3 = 4,6521 (—0,33603) = —1,5632, sbib2 = 4,6521 (—0,00034) = —0,001581, sblb3=- 4,6521 • 0,00048 = 0,00223, sb2b3 = 4,6521 • 0,00083 = 0,00386.
На основе этих ковариаций можно так же, как в случае простой регрессии, оценить связи между отдельными параметрами регрессии. Но мы не будем здесь на этом останавливаться.
Запишем теперь полностью матрицу ковариаций и дисперсий оценок параметров множественной регрессии:
~ 246,046 — 0,31954 — 1,2527) — 1,5632 ~
— 0,31954 0,00242 — 0,001581 0,00223
bb — 1,2527 —0,001581 0,02275 0,00386
_ —1,5632 0,00223 0,00386 0,01124 _
Эта матрица будет применяться для специальных критериев в главах 8 и 11.
118
л ЛИНЕЙНАЯ
4 КОРРЕЛЯЦИЯ
Как отмечалось в разделах, посвященных линейной регр.ессии и коэффициентам детерминации, при стохастических связях изменения в величинах зависимой переменной не полностью определяются влиянием изменений рассматриваемых объясняющих переменных. На изменения зависимых переменных оказывают влияние также другие, не учитываемые нами или скрытые от нас факторы и случайности. Чем больше изменения зависимых переменных обусловлены изменениями рассматриваемых объясняющих переменных, тем теснее, интенсивнее исследуемая связь между явлениями. Измерением степени, интенсивности, тесноты наблюдаемой связи мы хотим заняться и в последующих разделах. При этом мы снова будем основываться на количественных соотношениях, которые существуют между исследуемыми явлениями.
4.1. ПРОСТАЯ ЛИНЕЙНАЯ КОРРЕЛЯЦИЯ ПРИ НЕСГРУППИРОВАННЫХ ДАННЫХ
Если между двумя явлениями у и х существует линейное стохастическое соотношение (корреляционная связь), линейная регрессия, то мы можем степень, интенсивность связи между обоими явлениями измерить с помощью коэффициента корреляции гух. Для вывода формулы коэффициента корреляции воспользуемся методом, предложенным Бравэ и Пирсоном.
Пусть заданы значения переменных у и х, между которыми существует линейное соотношение. Вычислим по ним средние значения у и х, а также отклонения (yt — у) и (хг- — х). Для получения безразмерной характеристики связи и исключения влияния рассеяния случайных переменных нормируем указанные отклонения, разделив их на стандартные отклонения sy и sx. Затем суммируем произведения полученных относительных отклонений:
£ (хг—х) (yt —'у) 4
Z=1 Sx Sy
Эта сумма будет тем больше, чем больше синхронности в смещении рядов наблюдений над переменными в одном или противоположных
119
направлениях. В обоих случаях большим отклонениям значений переменной у соответствуют большие отклонения значений переменной х. Если это соответствие отсутствует, то связь между исследуемыми переменными менее интенсивна. Кроме того, сумма произведений (4.1) зависит от числа пар наблюдений. Чтобы сделать показатель связи не зависящим от числа пар наблюдений, разделим выражение (4.1) на п — 1. В результате получим показатель, который называется простым линейным коэффициентом корреляции, коэффициентом парной корреляции, или кратко, коэффициентом корреляции:
п __ _
2 (xi—x) (yt —у)
Учитывая (1.13) из раздела 1.5, запишем формулу (4.2) в таком виде:
Из (4.3) видно, что коэффициент корреляции представляет собой отношение ковариации к произведению стандартных отклонений обеих переменных у и х, т. е. является стандартизованной ковариацией. В соответствии с определениями ковариации и соответствующих стандартных отклонений
п __
(-«г—*)*(</«—</)
гух =------~ --------• (4.4)
+ V 2 (xt-x)2 SGi-y)2
r Z=1
Раскрыв в (4.4) скобки и выполнив некоторые простые преобразования, получим
п п п
п s XI У1 — 2 Xt 2 У1 1=1 /=1 Z=l
(4.5)
п \ / п п п
Xi^ Xi в 2 у?— 5 yi 2
i==l / \ i=l /=1
Формула (4.5) удобна для практических вычислений. В ней содержатся только исходные данные и промежуточные результаты, которые можно заимствовать из рабочей таблицы, построенной для вычисления оценок параметров регрессии (см. раздел 2.4). Так же, как при проведении регрессионного анализа, при большом объеме наблюдений для вычисления коэффициента корреляции желательно применять КВМ.
Коэффициент корреляции принимает значения в интервале
-IsS/y^ + l. (4.6)
120
Значения + 1 коэффициент корреляции достигает, если между соответствующими отклонениями (xf — х) и — у) существует прямая связь, а значения — 1 — если между ними существует обратная связь. Чем больше связь между этими величинами отклоняется от прямой или обратной, тем больше сумма 2 (xi — х) (yi — У) приближается к нулю. При положительном коэффициенте корреляции говорят о положительной корреляции, при отрицательном — об отрицательной корреляции. Чем ближе коэффициент корреляции к ± 1, тем теснее, интенсивнее связь. При линейно-возрастающей функциональной зависимости между переменными у и х гух =4-1, при линейно-убывающей гух = — 1. Чем ближе коэффициент корреляции приближается к нулю, тем слабее исследуемая связь. Но если между переменными существует нелинейное соотношение, то гух — 0. Если при практических исследованиях в результате вычислений получено гух=0, то не надо торопиться с выводом об отсутствии связи между переменными. Мы можем лишь утверждать, что гипотеза о линейной связи на основе данного числового материала не подтверждается. Коэффициент корреляции не дает возможности ответить на вопрос, имеется ли нелинейная корреляция между переменными. Значение гух — 0 свидетельствует об отсутствии линейной связи, но вполне возможно, что при этом-существует тесная нелинейная связь, даже нелинейная функциональная. Коэффициент корреляции позволяет делать вывод об интенсивности стохастической связи только при наличии линейных соотноше, ний между переменными. Как видно из структуры формул (4.3) и (4.4). при вычислении коэффициента корреляции безразлично, какая из пе ременных зависимая, а какая— объясняющая. Если мы поменяем местами у и х, то формула (4.4) не изменится. Следовательно, гух — гху. Итак, в случае линейной связи между двумя переменными имеется только один коэффициент корреляции. Отсюда непосредственно следует, что линейный коэффициент корреляции выражает взаимозависимость между переменными. Направление зависимости не отражается на его величине, т. е. он является симметричной функцией относительно х и у. С помощью формулы (4.3) можно показать, что коэффициент корреляции не изменится, если переменные у и х подвергнуть преобразованию или изменить их единицы измерения.
Пример 1
Вычислим по формуле (4.5) коэффициент корреляции для примера из раздела 2.4 (связь между производительностью труда и уровнем механизации работ), необходимые промежуточные результаты заимствуем из табл. 3 (см. раздел 2.4):
ГУх = .—^907-724.492 __ _=0.9687.
+ У (14-40 134 - 724-724) (14-18 138- 492-492)
Пример 2
По той же формуле вычислим коэффициент корреляции для примера из раздела 2.5 (связь между объемом производства и основными
121
фондами):
________________52-408 104 —1616-12 905____________ + 1/(52-53 588 —1616-1616) (52-3 218 897 —12 905-12 905)
= 0,9546.
В обоих примерах мы получили очень высокий коэффициент корреляции. Это свидетельствует о том, что связь между производительностью труда и уровнем механизации работ, а также,между объемом производства и основными фондами очень тесная, хотя и не функциональная. Очевидно, что к действию переменных примешивается влияние побочных факторов. Чем меньше это влияние и ограниченнее воздействие случайностей, тем больше приближается значение коэффициента корреляции к + 1 или — 1. Отсюда видна связь между величиной коэффициента корреляции и регрессией. Функция линейной регрессии отражает линейное соотношение между переменными тем лучше, чем больше коэффициент корреляции приближается к + 1 или — 1. В этом смысле коэффициент корреляции часто служит критерием при выборе вида регрессии. С его помощью устанавливают, действительно ли переменная у зависит от х и в какой степени. Далее мы покажем, что коэффициент корреляции непосредственно связан с коэффициентом регрессии.
В заключение нам хотелось бы привести еще одну формулу коэффициента корреляции, которая часто встречается в литературе. Для этой цели перепишем (4.2) в следующем виде:
гух
=1 у (Xj—x) п~1 /=1 s“
(У: —у) sy
(4.7)
Подставив в (4.7) формулу (2.65) для стандартизованных переменных из раздела 2.7, получи л
= S xi <4-8>
1=1
Коэффициент корреляции, представленный в виде разделенной на п — 1 суммы произведений стандартизованных значений переменных у и х, называется корреляционным моментом Пирсона. Эта форма записи коэффициента корреляции представляет прежде всего теоретический интерес, но она мало пригодна для практических вычислений. Если коэффициент корреляции вычисляется при малом числе наблюдений, то необходимо проверять его значимость (об этом пойдет речь в разделе 8.5).
Корреляционный анализ применяется для решения и других задач, например для отбора факторов, оказывающих существенное влияние на экономический процесс. Дальнейшим развитием корреляционного исчисления следует считать факторный анализ, который исходит из корреляционной матрицы. Его основные задачи — выявление структуры взаимосвязи между переменными, выделение факторов, объяс-122
няющих наблюдаемые связи переменных и снижение размерности исходного набора переменных. К сожалению, у нас нет возможности в рамках данной книги более обстоятельно осветить эти вопросы, поэтому отсылаем читателя к соответствующей литературе [67]*.
4.2. ПРОСТАЯ ЛИНЕЙНАЯ КОРРЕЛЯЦИЯ
ПРИ СГРУППИРОВАННЫХ ДАННЫХ
.Теперь покажем вычисление коэффициента корреляции по данным, представленным в виде корреляционной таблицы. Для этого снова обратимся к табл. 4 (см. раздел 2.6).
Для вывода соответствующей формулы исходим из (4.4) (см. раздел 4.1). Вместо отдельных значений и yt используем середины интервалов Xj и yk. Отклонения (х; — х) взвешиваем по частотам gj /-го интервала значений объясняющей переменной х, отклонения (yk — у) — по частотам hh k-vQ интервала значений зависимой переменной у, а произведения отклонений (х7- — х) (yh — у) — по условным частотам pkj. Формула (4.4) приобретает следующий вид:
2 (Ук—~У) Pkj
гух =------...........- ......- (4-9)
+рЛ 2 sj 2 (^ -~^2 hk
По аналогии с (4.5) из формулы (4.9) получим
п 2 уъ pkj 2 xj gj 2 у^ ^k
r __________________kj _________/______k__________________
гУх ““ —— _—............__ ..— --------- .
+ 1/ {nljrfgj— 2 w2 xj^Vn2^1 hk—^yk hh^ykhk\
V \ i I i J\ k k k )
(4.Ю)
Формула (4.10) очень удобна для практических вычислений при сгруппированном числовом материале. Определим коэффициент корреляции по корреляционной табл. 5 (см. раздел 2.6). Необходимые промежуточные результаты заимствуем из табл. 6 и дополнительно найдем
hk- Тогда по формуле (4.10) получим k
______________52-413 250 —1635-12 930______— 0 9412
УХ У(52-54 575-1635-1635) (52-3231 100— 12930-12930)
*W е b е г Е. Einfiihrung in die Faktorenanalyse, VEB Gustav Fischer Verlag, Jena, 1974; Liberia K. Faktorenanalyse. Springer-Verlag, Gottingen, Heidelberg, Berlin (West), 1974. Русский перевод: И б e p л а К. Факторный анализ. М., Статистика, 1980; ThurstoneL. L. Multiple Factor Analysis. Verlag University of Chicago Press, Chicago, 1947; Harman H. H. Modern Factor Analysis. Verlag University of Chicago Press, Chicago, 1962. Русский перевод издания 1968 г.: X арман Г. Современный факторный анализ. М., Статистика, 1972.
123
Коэффициент корреляции, вычисленный по корреляционной таблице, в нашем примере немного меньше коэффициента корреляции, вычисленного по несгруппированным данным (зависимость между объемом производства и основными фондами). Коэффициент корреляции, вычисленный по несгруппированным данным, точнее, поскольку он свободен от погрешности, вносимой группировкой данных. В общем случае нельзя указать величину погрешности, искажающей коэффициент корреляции. Коэффициент корреляции для сгруппированного материала в одном случае может быть больше, а в другом — меньше соответствующего коэффициента корреляции, вычисленного по простому ряду наблюдений. Но при большом числе наблюдений удобнее и проще определять коэффициент корреляции по корреляционной таблице. Небольшая потеря точности не имеет практического значения.
4.3. СВЯЗЬ МЕЖДУ КОЭФФИЦИЕНТАМИ КОРРЕЛЯЦИИ, РЕГРЕССИИ И ДЕТЕРМИНАЦИИ
Далее мы покажем, какими соотношениями связаны между собой коэффициенты корреляции, регрессии и детерминации при простой линейной регрессии. При этом ограничимся важнейшими из них. С помощью этих соотношений по известным уже коэффициентам можно определить другие, не обращаясь снова к исходным данным.
В разделах 3.2 и 2.4 были выведены формулы
<?2 ь2
= (3-8)
sy
(2.27) sx
Подставляя (2.27) в (3.8), получим
.2
(4Л,) sx sy
Извлечем корень квадратный из (4.11) и с учетом (4.3) получим
-^- = rvx = VB^x. (4.12)
Sx Sy
Таким образом, коэффициент корреляции равен корню квадратному из коэффициента детерминации. Отсюда
Г ух — Вух- (4.13)
Коэффициент регрессии Ь* уравнения регрессии х на у по аналогии с формулой (2.27) можно выразить следующим образом:
Ь{ = ^. (4.14)
sy
Тогда формулу (4.11) можно записать в виде
(4.15)
124
Учитывая (4.13), получим
= М,
(4.16) Итак, коэффициент корреляции равен корню квадратному из произведения двух сопряженных коэффициентов регрессии. Отсюда снова очевидно, что гух = гху, т. е. коэффициент корреляции является симметричной функцией относительно х и у.
.Умножим числитель и знаменатель правой части формулы (2.27) на sy\
(4.17) sxSy sx
Учитывая (4.12), получим
bi = ryx^~. (4.18)
SX
Аналогично если мы умножим числитель и знаменатель правой части формулы (4.14) на sx, то получим равенство
b:=ryx^. (4.19)
sy
Таким образом, если коэффициент корреляции уже вычислен, то с помощью стандартных отклонений можно легко определить требуемый коэффициент регрессии.
Из (4.18) и (4.19) легко вывести следующие соотношения:
гух = Ь^ sv
В соответствии с этим если известен один из коэффициентов регрессии, то можно по нему определить коэффициент корреляции и наоборот.
Теперь перейдем к графической иллюстрации коэффициента корреляции гух, который можно рассматривать как меру угла наклона линии регрессии. Для этой цели воспользуемся уравнением (2.25), переписав его в таком виде:
у — у = (х — х). (4.21)
Подставив в (4.21) вместо Ь± его выражение (4.17), получим
У—У = гух^-(х—х). (4.22)
sx
Разделим это равенство на sv'.
У—У _ _ (х—х) — Гух Sy sx
Введем стандартизованные переменные х и у', которые являются результатами преобразования переменных х и у (см. (2.65) из раздела
(4.23)
125
2.7). Это позволит записать формулу (4.23) следующим образом:
(4.24)
У' = гухх’.
Соответственно при регрессии х на у получим х—х ?у—у
'ух
SX Sy
и
% — ГухУ*
(4.25)
Рис. 18. Стандартизованные регрессионные прямые
Итак, формулы (4.24) и (4.25) представляют собой аналитические выражения двух сопряженных регрессионных прямых для стандартизованных переменных. Коэффициент парной корреляции определяет наклон этих прямых к осям координат, а именно линии регрессии у на х, к оси х', а линии регрессии х на у к оси у'. Отсюда следует, что парный коэффициент корреляции равен коэффициенту регрессии при стандартизованных переменных.
Как показано на рис. 18, стандартизация переменных графически означает перенос начала координат в точку с координатами %, у. Вследствие этого получаем систему координат с осями х' и у'. Обозначим через р угол, образованный обеими линиями регрессии. Углы наклона регрессионных прямых у' = гухх' и х' = гуху' соответственно к осям х' и у' обозначим через а. Учитывая, что tg у = tg (90 — а) == = сtg а = == , получим
1 . . г ух 1 г2
tg Р = tg (у- а) = tg v~tgoc- = (4.26)
1+tgatgy 1 2Гух
1 ~iryx Гух
Если ryx — 1 или ryx = — 1, то tg Р = 0 и р = 0, т. е. обе прямые регрессии сливаются в одну. В данном случае мы располагаем линейной функциональной связью. При гух =0 tg р = оо и угол Р = 90°, т. е. две прямые оказываются взаимно перпендикулярными. Это означает отсутствие линейной связи. Во всех остальных случаях сопряженные прямые регрессии образуют угол между 0° и 90°. Чем меньше этот угол, тем сильнее линейная связь.
Теперь покажем, какие соотношения существуют между коэффициентом Ь'9 коэффициентом частной регрессии и коэффициентом парной корреляции. Этими соотношениями нам придется воспользоваться
126
в следующих разделах. Обсудим эти соотношения для трех переменных (у, хх и х2).
В качестве исходных возьмем равенства (2.53) и (2.54) из раздела 2.7. Разделим обе части их на п — 1. Учитывая определения дисперсии и ковариации, получим
sry = + b2s12i
S2y == &1$12 + b2s%. ( '
Подставим в (4.27) соответствующие выражения ковариаций и дисперсий из (4.3):
fyiSy = V1A +
rУ?.5 У ~ ^2r22S2-
Как упоминалось выше, rhl = rlk. Кроме того, всегда rkk = 1, поскольку в этом случае речь идет о корреляции переменной самой с собой. Из системы равенств (4.28) получаем
1 (ГУ1 Sy)(r12 Sa) 1 lfylr12 I == ' (rу2 sy) 22 __ Sy -72 * । _ 1 (r 11 S1) (r 12 5г) 1 si 1 1 r 12 I (Л 12 Sl) (r22 S2) 1 1 Г12 1 Sy ГУ1 ГУ2Г12 (4 29) S1 1 f?2
I (r 11 si) (ryi sy) I 1 il ГУ1 1 £ 1 (f12 Sl) (fyz Sy) 1 __ Sy 1 Г12 Гу2 1 _ 1 (Г11 $1) (/*12 S2) 1 $2 1 1 Г12 I 1 (r 12 Sl) (f22 S2) 1 1 r12 1 1 = Sy fy2~"ryifi2 ^4 зо) S2 1 ri2
Учитывая (2.67) из раздела 2.7, i дующих коэффициентов b': 1 ryl r12 А» _ 1ГУ2 1 иожем записать выражения для сле- — ГУ1~~ГУ2 г12 /4 411
h' — - Г11 Г12 1 Г12 ^22 1 Г11 ГУ1 Г12 ГУ2 1-Г?2 ’ | ; 1 ГУ2 ГУ1 г12 /д опх
° 2 Сопоставляя формулы (4.2! После деления обеих частей Шем с помощью (4.33) и (4.3- J Sy « Г11 ^12 Г12 ^22 ))-(4. bi = Ь2 = i Урав 4) еле; ^+b'l У 12* 1 Г1 2 32), получим b:t, (4.33) S1 Ь'2. (4.34) s2 нения регрессии (2.43) на sy запи-|;ующее выражение: + • (4.35) S1 s3
127
Исходя из (4.35) b' можно рассматривать как коэффициенты уравнения регрессии для переменных, пронормированных по стандартным отклонениям. Коэффициенты как уже упоминалось, сами по себе являются стандартизованными коэффициентами регрессии. Если мы введем выражения коэффициентов Ь' из (4.33) и (4.34) в равенства (4.28), то после деления обеих частей этих равенств на sy и соответствующих сокращений получим:
ГУ1 = bi + b’2r12, rV2 = ЬУ12 + Ь'2.
(4.36)
В зависимости от того, какие из величин нам известны, мы можем, решая систему этих уравнений, найти либо коэффициенты Ь', либо коэффициенты корреляции.
Из равенств (4.31), (4.32) и (4.36) можно увидеть, что Ь{ = гуГ, ^2 = если ri2 = 0. Итак, при отсутствии взаимозависимости между переменными и х2 коэффициенты Ь' равны соответствующим коэффициентам корреляции.
Соотношения (4.36) для трех переменных можно легко обобщить на большее число переменных, используя матричную форму записи. Введем следующие векторы и матрицу:
(Ь') — вектор стандартизованных коэффициентов регрессии; R — матрица коэффициентов корреляции между объясняющими переменными, причем rkk = I, a rkl = rlh\ г — вектор коэффициентов корреляции между зависимой и объясняющими переменными. С помощью (4.37) теперь можно обобщить (4.36):
(b')'R = г, (4.38)
откуда
J(b')' = R-ir. (4.39)
4.4. ЛИНЕЙНАЯ МНОЖЕСТВЕННАЯ КОРРЕЛЯЦИЯ
Как многократно подчеркивалось, в практике социально-экономических исследований чаще всего встречаются сложные взаимосвязи между явлениями. Отсюда возникает задача определения интенсивности, или тесноты, связи между более чем двумя явлениями (переменными). Для этой цели используется коэффициент множественной корреляции, или совокупный коэффициент корреляции, который характеризует тесноту связи одной из переменных с совокупностью других
Рассмотрим вначале корреляцию между тремя переменными. Пс аналогии с формой записи коэффициента множественной детермина ции”обозначим коэффициент множественной корреляции через гу,12 Он показывает интенсивность связи при условии, что переменная t
128
™S°°EHXnv”C„"T„"сре”и,нь,х * » В предположении линей-ои связи между переменными мы можем исходя из коэгМшптлаи-то детерминации (3.12) с учетом (4.13) записать: К0ЭФФиЦиента
2 (yt — У)2 - 2 i = 1
ГуЛ2 =------------.
У (yi—y)2 — 1
Далее обратимся к (2.50):
У = bi (хг Xj) + b2 (х2 — х2).
Подставим (2.50) в (4.40):
Г2 12_(Хг1~Х1)2+2^^^^и-Г1)(^-2-72)+^(Хга_-)3
£1(У1-У)2
(4.40)
(2.50)
(4.41)
Разделив числитель и знаменатель (4.41) на Д_ „ учитывая выражении дисперсий s! и й, а также ковариации получим
сХа™нийФО„РоаУу“„(4'33)' (4'34> ' соответствующих
гД12 = 61'2 + &22 + 2&1'^Г12.
Умножим первое из уравнений (4.36) на Ц, а второе сложим правые и левые части этих уравнений:
(4.43) на &2- Затем
ryib1+ry2b'2~b'l2 -\-b22 +2Z>; b'2 г12. (4.44)
Правые части равенств (4.43) и (4.44) равны. Отсюда
или ^>2=^1^;+^^; (445)
ГУЛ2
- (4.46)
,и±ИТЫВаЯ отеперь (4-31) и <4’32)> получим формулу коэффициента ХшХйГкорреляции в виде’очень удобном для nXSLa
корреляции в виде, очень удобном для практических
Из (4.47) видно, в пределах
ПМ2-+]/ !^+Г^^У1ГУ2Г12 . (4 47)
что коэффициент множественной корреляции заключен
v = ' Z/.12 = 1 •
лать ™ХЩЬЮ К0ЭФФициента множественной корреляции нельзя сде-ХльнойДк°оппРаКТере взаимосвязи- е- о положительной или отри -льнои корреляции между переменными. Только если все коэффи-
Зак. Н13
129
циенты парной корреляции имеют одинаковый знак, то можно этот знак отнести также к коэффициенту множественной корреляции и утверждать о соответствующем характере множественной связи. Чем больше значение коэффициента приближается к единице, тем взаимосвязь сильнее. Легко увидеть, что (4.47) для случая г12= 0 принимает вид
412 = 4 + г>2. (4.48)
Итак, если объясняющие переменные и х2 не коррелированы, т. е. связь между ними отсутствует, то квадрат коэффициента множественной корреляции равен сумме квадратов коэффициентов парных корреляций. Другими словами, он равен сумме интенсивности взаимосвязи между у и х19 а также между у и х2. Следовательно, при некоррелированности объясняющих переменных анализ взаимосвязи облегчается.
Коэффициент множественной корреляции используется, кроме того, как показатель точности оценки функции регрессии, по нему можно судить, достаточно ли выбранные объясняющие переменные обусловливают количественную вариацию зависимой переменной. Если коэффициент множественной корреляции, который, как мы покажем далее, тесно связан с коэффициентом множественной детерминации, принимает значения, близкие к 1, то вариация зависимой переменной почти полностью определяется изменениями объясняющих переменных. Включенные в анализ объясняющие переменные оказывают сильное влияние на зависимую переменную.
Коэффициент множественной корреляции не меньше, чем абсолютная величина любого коэффициента парной и частной корреляции с таким же первичным индексом. Это справедливо независимо от того, существует между объясняющими переменными причинная связь или нет. Мы не будем останавливаться на доказательстве этого утверждения.
Выражение коэффициента множественной корреляции для любого числа объясняющих переменных можно получить путем обобщения (4.46):
Гу.\2...т — + l^yi + ГУ2 Ь'2 + ... + Гут Ь’т. (4.49)
Используя матричную форму записи (4.37) и обобщая формулу (4.47), получим
4i2...m = r'R-1r. (4.50)
Пример
Вычислим с помощью формулы (4.47) по данным из раздела 4.7 коэффициент множественной корреляции между производительностью труда, уровнем механизации работ и средним возрастом работников. Парные коэффициенты корреляции можно определить по (4.5):
гу1 = 0,9687; гу2 = 0,4257; г12 = 0,3620.
Итак, по (4.47) получаем
__ . т /* (0,9687)2 + (0,4257)2—2.0,9687.0,4257• 0,3620 А П„ОА
.12---Г I /--------------------------------~
У V 1—0,3620^
130
Вычислим по Тем же данным коэффициент множественной корреляций гуЛ2 с помощью^формулы (4.50), выполнив последовательно следующие операции:
. г ГО,96871
’ [0,4257] ’
^.12 = 10,9687 0,4257] Г 1,1508 —0,41661 [0,96871 n q44o
[—0,4166 1,1508] [0,4257] ’ !
rv .и = 4- Кб?9448 = 0,9720.
Г1 0,3620 . гр-i __ [1,1508 —0,4166 [0,3620 1 ]’ [0,4166 1,1508
Если ввести еще одну переменную —средний процент выполнения нормы, то коэффициент множественной корреляции Гу,123 примет следующее значение:
1
0,3620
0,5038
0,3620 —0,5038
1 —0,3778
—0,3778 1
1,4049
К-1= —0,2813
0,6015
—0,2813 0,6015
1,2228 0,3203
0,3203 1,4240
0,9687
0,4257
—0,5189
Гу. 123 = [0,9687-0,4257—
[ 1,4049 —0,2813 0,6015
—0,2813 1,2228 0,3203
0,6015 1,3203 ,1,4240
0,9687
0,4257
—0,5189
= 0,9451,
^.123= + V0,9451 = 0,9722.
В обоих случаях коэффициенты множественной корреляции принимают достаточно высокие значения, близкие к единице, что свидетельствует о тесной связи между соответствующими переменными. В то же время, сравнивая оба значения, убеждаемся, что включение переменной х3 (средний процент выполнения нормы) привело лишь к незначительному усилению связи. Более обстоятельной оценкой полученных результатов мы займемся в главе 8.
4.5. ЧАСТНАЯ КОРРЕЛЯЦИЯ
Как неоднократно подчеркивалось, экономические явления чаще всего приходится описывать многофакторными^моделями. В связи с этим возникают две задачи:
1) определение тесноты связи одной из переменных с совокупностью остальных ^переменных, включенных jb анализ; это является задачей изучения множественной корреляции;
5*
131
2) определение тесноты связи между двумя переменными при фиксировании или исключении влияния остальных. Интенсивность такой связи оценивается с помощью коэффициентов частной корреляции.
Если переменные коррелируют друг с другом, то на величине коэффициента парной корреляции частично сказывается влияние других переменных. Если, например, между и х2 существует тесная связь, и, кроме того, у зависит от хъ то у будет также коррелировать с х2. Вполне возможно, что корреляция между у и х2 не прямая, а косвенная, возникающая вследствие воздействия jq. Поэтому необходимо исследовать частную корреляцию между у и х2 при исключении влияния хг на у. Исключаемые переменные могут закрепляться как на средних, так и на других уровнях, выбранных в соответствии с интересующими нас участками изменения переменных, между которыми определяется связь в «чистой» форме. Здесь следует учитывать профессионально-теоретические соображения об изучаемом явлении.
Если имеется достаточно большое число наблюдений, то для сопоставимости данных можно произвести группировку по переменной х2 и внутри групп исследовать связь между переменными у и xt. В каждой группе тогда в значительной степени исключается вариабельность переменной х2. Сравнивая коэффициенты корреляции, вычисленные по отдельным группам, можно узнать, оказывают ли изменения х2 существенное влияние на связь между у и ^.Однако в практике экономических исследований построение таких группировок сопряжено с большими трудностями в основном за счет ограниченного числа наблюдений.
Применение метода частной корреляции освобождает от образования группировок. Измерение частного воздействия отдельных переменных выполняется на основе частной регрессии и частной корреляции. Следуя форме записи коэффициента частной детерминации, обозначим через гу1.2 коэффициент частной корреляции, с помощью которого оценивается интенсивность связи между переменными у и х± при исключении влияния х2. В соответствии с данным определением, например, г12.г/ также будет коэффициентом частной корреляции, измеряющим тесноту связи между переменными хг и х2 при исключении влияния у.
В разделах 2.7 и 2.8 было показано, что постановка задачи и цели множественного регрессионного анализа совпадают с задачами и целями изучения частной регрессии. Но в корреляции постановка вопросов иная. В то время как при рассмотрении множественной корреляции используется мера зависимости одной из переменных с совокупностью других, при изучении частной корреляции определяется частное воздействие каждой отдельной переменной при предположении ее связи с остальными переменными.
Рассмотрим задачи исследования частной корреляции на примере взаимосвязи трех переменных. Проанализируем коэффициент частной корреляции между переменными у и хг при исключении влияния х2. В разделе 2.8 было получено выражение регрессии (2.71) по данным, из которых устранено влияние х2 (2.70). Основываясь на этих данных, построим коэффициент детерминации по аналогии с (3.6) из раздела 3.2 и потребуем в соответствии с (4.13) из раздела 4.3, что
132
бы этот коэффициент детерминации был равен квадрату коэффициента частной корреляции. Это требование вполне оправдано, так как коэффициент детерминации должен вычисляться по данным, из которых исключено влияние переменной х2. Итак, получаем
1 "
Гь— 1 ;_1
'«’l.»”—"Г---------- (4.51)
г 2! W-?)1 i=l
Учитывая, что z/* == 0, (4.51) можно привести к виду
Формула (4.52) мало пригодна для практических вычислений. Для получения более удобного выражения выполним некоторые преобразования. Подставим (2.71) из раздела 2.8 в (4.52). Учитывая далее (2.70), а также то, что коэффициенты частной регрессии равны коэффициентам множественной регрессии, получим
1 п
I Ьу\ .2 2 ^0(12) ^12
Ту\. 2 =--------. (4.53)
~ Г 2 Ь0(у2)—Ьу2хаУг
1 = 1
Введем следующие обозначения. Пусть ЬуЪ2 = — коэффициент ча-
стной регрессии у на хх и х2; /?0(12) — постоянная, a Z?12 — коэффициент регрессии на х2; 60(г/2) — постоянная, а Ьу2 — коэффициент регрессии у на х2.
В соответствии с su2 в (3.5) из раздела 3.1 получим выражение
si%= " 2 (-^zi ^0(12) bi2xi2)2, (4.54)
п i = l
которое будет необъясненной дисперсией для регрессии хх на х2. Отсюда делаем заключение, что знаменатель в (4.53) представляет собой необъясненную дисперсию для регрессии у на х2. Исходя из этих соображений (4.53) записываем в виде
1/1.^ 2 \
Sy.2
В разделе 3.1 мы показали, что общую дисперсию можно разложить на две составляющие — объясненную и необъясненную дисперсии. Используем это обстоятельство в дальнейших наших рассуждениях. Разделим обе части тождества (3.5) из раздела 3.1 на Sy и, учи
133
тывая (4.13) из раздела 4.3, после некоторых простых преобразований получим
s'u2 = s‘(l-r2yx). (4.56)
По аналогии можно записать
si’2 = s2(1—гиг), (457)
s^.2 = sy (1 г^г).
Подставим (4.57) в (4.55)
(4.58)
40-^2)
Теперь подставим (4.29) из раздела 4.3 в (4.58) и выполним некоторые преобразования:
гг, (ГУ1 ~Г!/2Г12)2 ,л КОЧ
ИЛИ
Гг/Х 2 = -£У1-^Г12.. (4.60)
+Г(1“^2) О-'М
Таким образом, мы получили формулу коэффициента частной корреляции, удобную для практических вычислений. По аналогии с (4.60) можно легко записать выражения для других коэффициентов частной корреляции.
Вычисление коэффициентов частной корреляции сводится к нахождению коэффициентов парной корреляции. Благодаря выведенным формулам легко установить соотношения между этими коэффициентами. Так, если гу2 = г12 — 0, то гу1,2 = гу1. Если г12 = 0 (т.е. переменные и х2 не коррелированы), то jrn. 2| > Ir^l и Ir^.il > Итак, с уменьшением взаимодействия между хх и х2 следует ожидать увеличения коэффициента частной корреляции по сравнению с соответствую щим коэффициентом парной корреляции. Это увеличение тем силь нее, чем больше Ir^l или |гу2|. Далее, \rylt 2| > l^il, если гу2 = 0, и lrz/2.il > lrz/2l, если rz/i =0- В обоих случаях неравенства тем больше, чем сильнее взаимодействие между хг и х2, а следовательно, чем больше г12. Если коэффициенты корреляции гу2 и г12 имеют противоположные знаки, то всегда |rj,i.2| >
Обобщим теперь выражение коэффициента частной корреляции на любое число объясняющих переменных. Воспользуемся для этого формулой (4.58).После извлечения корня квадратного из обеих частей равенства получим
^.2 = ^.2-^X=b-. (4.61)
Sy V1— ^2
По аналогии запишем
riy.2= ^iy.2— 1у2 . (4.62)
«1 |/1 —^2
134
(4.66)
Так как r1Vf2 = гу1.2, то, перемножая соответственно правые и левые части (4.61) и (4.62), получим
Г2у\.2 — ^1У.2> (4.63)
или
^у1.2 V ^yl.2 ^1у.2 •
В соответствии с (4.33) и (4.34) из раздела 4.3
^1.2 = ^1.2 Ь\у,2, или
fyi.Z “ V%1 .2 Ъ\у, 2 . (4.64)
Обобщая, можно записать
ГУ1.2 ... т &У1.2 ... т Ь1у.2.,.т, ИЛИ
^у1,2 ... т — V Ьу\. 2. ..т Ь\у,2..,т • (4.65)
Формула (4.65) позволяет нам вычислять коэффициент частной кор-реляции по коэффициентам частной регрессии.
По аналогии с (4.60), обобщая на любое число объясняющих переменных, получим
г у! .3. . .771 Г 1/2.3...7П Г12.3...ТИ
"|/(l ”r^2.3...m) 0— r12.3.../n)
Как видно из (4.66), вычисление коэффициента частной корреляции порядка т сводится к определению коэффициентов частной корреляции порядка т— I. При использовании (4.66) сначала необходимо знать коэффициенты парной корреляции, а затем приступать к вычислению коэффициентов корреляции более высокого порядка. При более чем четырех переменных вычисление частных коэффициентов корреляции желательно производить на КВМ.
Пример
Вычислим некоторые коэффициенты частной корреляции для сформулированной ранее задачи изучения зависимости производительности труда от уровня механизации работ и среднего возраста работников. Воспользуемся для этой цели формулой (4.60). Значения коэффициентов парных корреляций заимствуем из корреляционной матрицы, приведенной в разделе 4.4:
Г ______________________________0,9687—0,4257-0,3620______q 9657*
!/1-2 - + у(1_Г22) (l-r»g) _ +1/(1-0,42572) (1—0,3620®) “ ’
__ Гуъ—Гу1 Г12 0,4257—0,9687-0,3620 __q ^^42
Гу2Л ~ +1/(1-г»,)(1-/-Ь)= +1/(1 -0,9687®)(1 —о7»Г“ ’
При включении в анализ четвертой переменной — среднего процента выполнения нормы — необходимо вычислять коэффициенты частной корреляции третьего порядка. Для этого нам потребуются также сле-
135
дующие коэффициенты частной корреляции:
гу1.з = 0,9578; гуз,3 = 0,2902; гуз 2 = — 0,5101;
г12.з — 0,2146; г31.2 = — 0,4253
(эти значения получены по формуле (4.60)). По (4.66) вычисляем коэффициенты частной корреляции третьего порядка:
f — гг/1-з rs2.3ri2.3 _ 0,9578— 0,2902-0,2146 __ q ggg।.
+'|/(l-^2.3)(l-rf2T) +V(1-0,29022) (1 -0,21462)
__________гУ2.з—ryi-3r 12.3 r> _ 0,2902—0,9578‘0,2146_____q 3015’ У2ЛЗ- +y(1_"r2[ 3)(1-rf2’ 3) +V(1-0,95782) (1-0,21462) ~ ’
___ ^3,2~^z/i»2r3i.2___—0,5101 —0,9657 (—0,4253) __
/уз.12- +y(1 _r^ 2)(1 ~ri—} ~ +y(i _o,96572)(l-(-0,4253)3) ~
= —0,4229.
Из полученных результатов видим, что коэффициенты частной корреляции третьего порядка меньше коэффициентов второго порядка, а те в свою очередь меньше коэффициентов парной корреляции. Уменьшение коэффициентов частной корреляции означает, что взаимозависимость возникает частично вследствие воздействия фиксированных переменных.
4.6. СООТНОШЕНИЯ МЕЖДУ КОЭФФИЦИЕНТАМИ МНОЖЕСТВЕННОЙ И ЧАСТНОЙ КОРРЕЛЯЦИИ, РЕГРЕССИИ И ДЕТЕРМИНАЦИИ
Далее мы покажем, что между коэффициентами множественной и частной корреляции, регрессии и детерминации существуют соотношения, позволяющие производить вычисления одних коэффициентов по известным другим. Ограничимся наиболее важными соотношениями.
Разделим числитель и знаменатель правой части формулы (3.26) п
из раздела 3.4 на (xii — x*i)2- Путем простого преобразова-
нии
ния с учетом (2.72) из раздела 2.8, а также (4.53) и (4.54) получим следующее соотношение:
= <4.67>
Sy.2
Сравнивая (4.67) с (4.55), можно сделать вывод, что
Byi.z ~ или (4.68)
ГУ1.2 ~ 'V'
Таким образом, мы получили такое же соотношение между коэффициентами частной корреляции и частной детерминации, как и в случае простой регрессии (см. раздел 4.3).Пользуясь этим соотношением 13§
И не прибегая к дополнительным вычислениям по исходным данном, по коэффициенту частной детерминации мы можем сделать вывод о коэффициенте частной корреляции и наоборот. Аналогичное соотношение существует между коэффициентами множественной корреляции и детерминации. Сравнивая (3.12) и (4.40), легко увидеть следующее соотношение:
В у.12... ?п = ry. 1 2 ..tn
ИЛИ ______
гу,12...т~ У^Ву.12...тп* (4.69)
В разделе 4.4 было показано, что при некоррелированности объясняющих переменных имеется равенство
г>.12 = + гЬ. (4.48)
С учетом (4.69) и (4.13) его можно записать в виде
Вулъ ~ Вуг 4" Ву2
или, обобщая на произвольное число переменных,
т
= + 2 Ву*- (4.70)
k=l
Итак, коэффициент множественной детерминации равен сумме коэффициентов парной детерминации, если объясняющие переменные попарно не коррелированы.
Приведем теперь соотношения между частными корреляциями и регрессиями различных порядков. Некоторые из них были получены в предыдущих разделах, например (4.46) и (4.63). Из (4.63) и (4.68) получим
Ву1.2 ~ ^У1.2^1У^2' (4.71)
Связь между коэффициентами частной и множественной корреляции можно представить в таком виде:
или
1—г^.12 = (1—г^1)(1—г>2.1). (4.72)
Соотношения (4.72) легко доказать. Для этого преобразуем (4.36) из раздела 4.3:
Ьу2Л = Гу2 Ьу \ ,2 г12.
Это равенство подставим в (4.43) из раздела 4.5. После соответствующих выкладок получим
Гу. 12 = Гу2 + Ьу\,2 (1 —Г12).
Вычтем левую и правую часть этого равенства из 1:
В соответствии с (4.33) из раздела 4.3 получим
Ьу\,2 ~ byit2 —.
sy
137
Подставим выражение b‘yi.2 в предыдущее равенство:
о 2
У
Преобразуем (4.58) из раздела 4.5:
rtf21.2(l-^2) = ^1.2^-(l-ri12).
У
Подставляя это выражение в предыдущее равенство, в итоге получим
1—Г>,12 = (1 — Г^2) (1—Г^1.2),
что и требовалось доказать. Обобщим это соотношение на т объясняющих переменных:
1 = (1 — Г®1)(1 -Г*2Л) (1 -Г^З.12) ... (1 -Г*ут. 12...т-1). (4.73)
С помощью (4.73) можно вычислить коэффициент множественной корреляции по коэффициентам парной и частной корреляции. Коэффициент rji указывает долю влияния на у, а г^л — прпю влияния х2 на у при фиксировании хг и т. д. Из (4.72) получаем следующее соотношение:
i-rfi _ l~~ryi.2 (4.74)
1 ry2 1 Гу2Л
Это равенство можно использовать для контроля Вычислений коэффициентов корреляции.
4.7. ВЛИЯНИЕ НЕУЧТЕННЫХ ФАКТОРОВ
НА КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ
Далее мы обсудим некоторые важные"факторы, которые могут при известных обстоятельствах оказывать влияние на величину коэффициента корреляции, снижая точность его оценки. В конечном итоге это может привести к ошибочным выводам, особенно при сравнении результатов нескольких обследований.
Один из таких факторов — географический. Например, при изучении зависимости урожайности от показателей качества почвы необходимо учитывать, производились ли исследования в масштабах округа или района. Коэффициент корреляции, вычисленный по результатам наблюдений в районе, в общем, больше коэффициента корреляции, вычисленного по результатам исследования в округе, так как некоторые факторы при этом либо отсутствуют, либо они не так сильно варьируют. Как правило, при сравнительном анализе могут сопоставляться только такие коэффициенты корреляции, которые относятся к однородным единицам обследования, например к округам или районам.
С осторожностью нужно подходить и к обобщению результатов обследования, выполненного в рамках небольшой области. Не всегда правомерно распространять вывод на более крупные территориальные единицы. Например, коэффициент корреляции между доходом и рас
138
ходами на определенные потребительские товары в расчете на душу населения будет сильно варьировать от ^географического признака.
Величина коэффициента корреляции зависит также от фактора времени. Так, при изучении связи между прибылью и себестоимостью следует учитывать, за какой период вычисляется по экономическим показателям коэффициент корреляции — за месяц, квартал или год.
Коэффициент корреляции только тогда является достоверным показателем связи, когда исследуемые единицы однородны в отношении этой связи. Одно из условий однородности — близость значений количественного признака. Так, при изучении зависимости себестоимости от объема продукции сначала необходимо произвести группировку предприятий, например на крупные, средние и мелкие, а затем по группам вычислять коэффициенты корреляции. В связи с этим возникают задачи формирования однородных многомерных комплексов. Исследователь должен располагать теоретически обоснованным критерием определения статистической однородности, чтобы отбрасывать или относить к другой группе те значения, которые не типичны для данной связи. Построение критерия группировки социально-экономических явлений по комплексу признаков — дело достаточно сложное.
Далее мы покажем, что из факта линейной корреляционной связи между абсолютными величинами, по которым вычислены относительные показатели, вовсе не вытекает с необходимостью корреляционная связь между этими относительными показателями. В таких случаях часто возникает нонсенс-корреляция, или псевдокорреляция (ложная корреляция).
Особенно сильное влияние на величину коэффициента корреляции оказывает неоднородность исходного материала, например производственные предприятия, на которых производится исследование связи между производительностью труда и уровнем механизации работ, могут очень сильно различаться между собой. При одном и том же уровне механизации работ одно предприятие может быть оснащено современным оборудованием, а другое — устаревшим. Благодаря этому обстоятельству отдельные значения экономических показателей могут более или менее сильно рассеиваться. Связь между явлениями, в общем, интенсивнее, если исследования производятся на большом числе предприятий. Выводы, основанные на большом числе наблюдений, значительно достовернее. Чем меньше объем наблюдений, тем сильнее подвержена колебаниям интенсивность связи от исследования к исследованию. Иногда коэффициенты корреляции, вычисленные по различным частям одной и той же совокупности, различаются даже по своему знаку. В [72] приведены рекомендации по вычислению коэффициента корреляции, свободного от случайных воздействий.
5
НЕЛИНЕЙНАЯ РЕГРЕССИЯ
Между социально-экономическими явлениями и процессами не всегда существуют линейные соотношения, и часто эти соотношения нельзя упрощенно выразить линейными функциями из-за неоправданно больших ошибок, возникающих при этом. В таких случаях для описания зависимостей используют нелинейную корреляцию и регрессию. Как уже упоминалось, в зависимости от характера связи различают положительную равноускоренно и равнозамедленно возрастающую регрессию, отрицательную равноускоренно и равнозамедленно убывающую регрессию либо их комбинированные формы. Для оценки параметров регрессии будем применять метод наименьших квадратов, а для оценки интенсивности связи между явлениями — соответствующие показатели*.
5.1. ПРОСТАЯ НЕЛИНЕЙНАЯ РЕГРЕССИЯ
ПРИ НЕСГРУППИРОВАННЫХ ДАННЫХ
Для выбора и обоснования типа кривой регрессии нет универсального метода. Односторонняя стохастическая зависимость между явлениями может быть описана, например, с помощью полиномиальной регрессии:
У = &о + + Ь2х2 + Ь3х3 + ..., (5.1)
либо с помощью гиперболической регрессии:
? = + —• (5-2)
X
*С практическим применением нелинейной регрессии можно познакомиться в следующих работах: W е 1 f е W. Uber die Anwendung der Regressionsanaly" se in der Nachfrageforschung. Statistische Praxis, 21 (1966), 3, 4; W a s c h k a u H. Uber die Bedeutung partieller Elastizitatsfunktionen ftir die Regressionstheorie# Statistische Praxis, 23 (1968), 5, S. 269—274; S c h i n k e 1 K. Regressions-und Korrelationsanalyse des Zusammenhangs von Arbeitsproduktivitat und Lohn. Statistische Praxis, 23 (1968), 9, S. 514—516; Fenske A., KuhnL. Erfahrun-gen uber die Anwendung der kombinierten Potenz-Exponential-Funktion bei der Modellierung der individuell bezahlten" Konsumtion. Wirtschaftswissen-schaft, 1969, 2, S. 219.
140
Применяются также степенная, показательная, логарифмическая и тригонометрическая функции. Подбор функции регрессии должен производиться с применением теории той конкретной науки, на базе которой возникает задача измерения связи между явлениями. Чаще всего используются семейства кривых, уравнения которых выражаются многочленами целых положительных степеней (полиномы вида (5.1)). Полином первой степени (прямая линия) не имеет изгибов. С помощью полинома второй степени можно передать одну точку поворота функции. Полином третьей степени отражает две точки поворота функции. О характере зависимости между экономическими явлениями часто судят по внешнему виду эмпирического графика регрессии. Однако при малом числе наблюдений этот путь приводит к неудовлетворительным результатам, так как резкие зигзаги эмпирической (ломаной) линии регрессии затрудняют выявление закономерности. В каждом случае следует проверять возможность применения линейной регрессии хотя бы на ограниченном участке изменения переменных. Далее мы будем более подробно обсуждать проблему проверки линейности, а также степени соответствия выбранной функции регрессии эмпирическим данным. И наконец, необходимо обращать внимание на то, чтобы оценки регрессии производились с достаточной степенью надежности. Информацию об этом дает нам коэффициент детерминации.
Мы различаем два класса нелинейных регрессий. К первому классу относятся регрессии, нелинейные относительно включенных в анализ объясняющих переменных но линейные по неизвестным, подлежащим оценке параметрам регрессии bk, k = 1, 2, ..., р. Поэтому образующие этот класс нелинейные регрессии называют также квазилинейными регрессиями. Их преимущество состоит в том, что для них возможно непосредственное применение метода наименьших квадратов, а следовательно, остаются в силе все исходные предпосылки линейного регрессионного анализа и свойства МНК-оценок параметров регрессии (несмещенность, состоятельность, гомоскедастичность и т. д.). Используются те же самые критерии значимости, аналогично строятся доверительные интервалы и доверительные зоны.
Второй класс регрессий характеризуется нелинейностью по оцениваемым параметрам1. Этот класс регрессий встречается довольно часто при исследовании экономических явлений. Однако он обладает существенным недостатком — не допускает применения обычного метода наименьших квадратов. Для решения получающейся при этом системы нелинейных уравнений привлекают итерационные методы либо прибегают к аппроксимации параметров искомой зависимости. Широко используется также линейное преобразование функции регрессии, которое позволяет применять к преобразованным параметрам статистические критерии линейной регрессии. Строгой теории нелинейной регрессии пока нет. Далее мы еще вернемся к этому вопросу.
1Нелинейные регрессии первого и второго класса называют также соответственно существенно линейными и существенно нелинейными регрессиями.— Примеч. пер.
141
Рассмотрим вначале простую квазилинейную регрессию. Пусть зависимость между двумя явлениями (у и х) представлена в виде параболы второго порядка (целой рациональной функции второй степени)
у = Ьо + Ь±х + Ь2х2. (5.3)
Здесь Ьо — выравнивающая постоянная, которая соответствует точке пересечения, кривой регрессии с осью у\ Ь± и Ь2 — параметры регрессии, характеризующие зависимость переменной у от переменной х. Функция регрессии (5.3) линейна относительно параметров и нелинейна относительно объясняющих переменных х (квадратный трехчлен). Следовательно, мы имеем типичную функцию квазилинейной регрессии.
Для оценки параметров (5.3) методом наименьших квадратов нужно исходить из соотношения
yt = Ьо + b^i + b2xf + i = 1, 2, ..., /г, (5.4)
где u— возмущающая переменная. Приравняв нулю частные произ* водные от суммы ^uf по каждому из параметров Ьо, Ьх и Ь2 (см. раз-i
дел 2.4), получим после некоторых преобразований следующие нор
мальные уравнения:
X yi = nba + h S Xi + b2 2хД (5.5)
i i i
X Х1У1 = b0 2 Xi 4- b-i 2 xf + b2 2 xzs, (5.6)
i i i i
2 xf У1 = Ь0^ xf + 2 xf 4- b2 2 xf. (5.7)
i i i i
Как и в случае простой линейной регрессии (см. раздел 2.4), можно определить Ьо, разделив обе части уравнения (5.5) на п:
Ьо — У — bvx — Ь2х2. (5.8)
Подставив (5.8) в (5.3), после простого преобразования получим
у'= у + (х — х) 4- Ь2 (х2 — х2). (5.9)
Выражения для параметров регрессии Ьх и Ьа найдем путем решения системы нормальных уравнений (5.5)—(5.7):
{^iXiyi—(Х*/—х2Хх*)
— (X xf yt—y 2 хИ (2 xf —х22 Xi)
= —L?----__J—>Л1—_—!—L, (5.1 о;
(X xf —х 2 xt j xf —X2 2 xf j
142
Подставляя в (5.3) вычисленные значения Ьо, Ьг и Ь2, мы тем самым найдем оценку функции регрессии. После проверки значимости оценок параметров регрессии (см. раздел 8.7) при приемлемой величине коэффициента детерминации можно определить расчетные значения регрессии для анализа зависимости между экономическими явлениями.
Пусть исходя из логических рассуждений для описания зависимости используется гиперболическая форма связи
> = + ?
X
(5.12)
Применяя метод наименьших квадратов к (5.12), снова получим систему нормальных уравнений. Решая ее, находим Ьо и Ь*:
По формулам (5.13) и (5.14) мы вычисляем оценки параметров гиперболического уравнения регрессии.
Рассмотрим теперь в общем виде квазилинейную регрессию, т. е. функцию, нелинейную по объясняющим переменным, но линейную по оцениваемым параметрам:
У = b0 + ЬгРг (х) + b2F2 (х) + ... + bpFp (х),
(5.15)
где Fx (х), F2 (х), ... — функции от объясняющих переменных х. Они не содержат других параметров. Так, например, это могут быть функции вида Fx (х) = log х или F2 (х) — у, но не такие, как Fx (х) = = log (х — k) или F2 (х) = .
143
Таблица 8
Квазилинейные функции
Функции Нормальные уравнения
1- = х4"^2 х* 2. у = &о 4~^i х4* bi х2 -j-&3 Xs 3. log у = Ьй+ЬхХ 4. log у = Ь0-1-Ь1х+Ь2х2 5. log у = b0-^~ bi x-j-bi x2~l~ Ьз х3 6. 'y = b0+bilogx 7. log y = b0+b1 log x 8. log^ = 60+61 logx + +Mlogx)2 9. log z/ = b0+b1logx + + &2(logx)2+Z>3(logx)3 Sz/j = &0 n 4-6j Sxj +&2 Sxf, S(/j Xj = b0 Sxj Sx^4~ b2 Sxf, — bo ^xi + bt 4~ bi Sx?. ^yi —— ^0 ti 4-bj ^i4* bi Sxf 4~ ь^ Шх^, Si/j Xi — b0 Sx{ +&! Sx? -j-bi Sx? + 4~ bi Sx*, Sy( xj = Ь„ Sxf +&x Sxt3+ Ь2 Sx?4-+63 Sx3, Sz/j x3 = bi Sx? 4*^1 “l“^2 2x3 4“ 4~ bi Sx3. S logi/i = &0n4-&1Sxil Sxf log У1 b0 SX| 4-&! Sxf . 2 log у 1 = bi n 4-&1 Sxj 4"bi ^xf, S xi log yi = b0 SX| 4-bj Sxf 4- bi ^xf, ^xi log yi = b0 Sx? 4- bl Sx? 4- bi . Такие же, как для функции 2 при замене i/i = logz/i. S(/i = b0 zi4*^i S log xj, Sr/i log Xf = b0 S log хг 4-bx S (log хг)2. 2 log z/j = b„ n 4-&1 S logXj, S (log Xj log yt) = b0SlogXj4- 4-b1S(logXj)3. Такие же, как для функции 1 при замене %i = logXf, х? = (logXf)2, Z/i = logr/i. Такие же, как для функции 2 при замене x^ = logx/, х? = = (10gXj)2, X3 = (logXj)2, У1 = log у 1
144
Продолжение табл. 8
Функции
10. y = b0-i-b1 -|-
— 1 1
11. у — /?о+ ь± % ~рь2
Нормальные уравнения
х I
лг лг лг
Такие же, как для функции 1
1 при замене х$ =—,
Применяя метод наименьших квадратов к (5.15), получим систему нормальных уравнений:
(х) + (х) + ... (5.16)
W = Ьо2Л(х) + (х) + (х) F2 (х) + ... (5.17)
^y.F2 (х) = b02F2 (х) + b^F. (х) F2 (х) + b2ZFl (x) + ... (5.18) i : :
Из (5.16)—(5.18) можно вывести правило составления нормальных уравнений. Учитывая, что отдельные значения суммируются, уравнение (5.16) строится аналогично регрессии (5.15). Нормальные уравнения (5.17), (5.18) и т. д. получаются, если функцию регрессии (5.15) умножить соответственно на F\ (х) и F2 (х), а затем просуммировать. Это правило можно сформулировать, рассматривая также нормальные уравнения для простой и множественной регрессии в разделах 2.4 и 2.7, а также систему (5.5)—(5.7).
Прежде чем перейти к примеру, составим сводку квазилинейных функций, применяемых в экономике (см. табл. 8).
Решая систему нормальных уравнений, мы находим параметры регрессии. Укажем еще один способ представления квазилинейных функций в виде линейной множественной регрессии. В этом случае часто говорят о функциональной регрессии. Так, например, сделав в полиноме второй степени
у~ = Ь*о + Ь*х + Ьгх* (5.19)
следующую замену:
х — х,; х2 = х2;
Ь*о = Ьй- Ь*х = &х; Ь*2 = Ь2, (5.20)
можно записать его в виде:
У = bQ + Ьгхг + Ь2х2. (5.21)
145
Мы получили ту форму записиЗлинейной множественной регрессйй, которая была приведена в разделе 2.4. Следовательно, формулы из раздела 2.4 для определения коэффициентов множественной регрессии Z?x и Ь2 пригодны также с учетом (5.20) для нахождения параметров нелинейной простой регрессии.
Пример.
Пусть исследуется зависимость себестоимости единицы продукции от объема произведенной продукции по данным 15 предприятий (см. табл. 9).
Таблица 9
У 8
Рис. 19. Зависимость между себестоимостью и объемом продукции
Себестоимость единицы продукции одного и того же вида и объем продукции на 15 предприятиях
Предприятие Выпуск в 1000 шт. Себестоимость 1 шт. в марках
i XI У1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 2 3 4 4 5 6 6 6 7 8 9 10 12 13 14 8 10 7 6 5 5 4 3 4 5 3 2 1 1 2
Сумма 109 66
Из рис. 19 видно, что между себестоимостью и объемом произведенной продукции существует нелинейная связь. Выразим вначале зависимость между этими переменными уравнением параболы второго порядка, а затем гиперболическим уравнением, используя следующие значения:
% = 7,2667; х* = 65,4; у = 4,4;
=363; £х/ =981; £х? = 10 189;
i li
£*/ = 115 893;
2^--15.622S;
у-1 = 0,6862. г2 i xi
146
Найдем оценки параметров полинома второй степени по (5.10), (5.11) и (5.8):
(363—4,4 • 109) (115893—65,4 • 981) —
ь _ —(2 551 — 4,4 981) (10 189—65,4 • 109) = _ } .
(981-7,2667-109) (115 893— 65,4-981)— ~
— (10 189-7,2667-981) (10189 -65,4-109)
(981-7,2667-109) (2 551—4,4-981)—
b = — (Ю 189—7,2667-981) (363 —4,4-109) = 0 0571
2 (981—7,2667-109) (115 893— 65,4-981)—
—(10 189 -7,2667-981) (10 189 -65,4-109)
Ьо = 4,4+ 1,541 -7,2667—0,0571 -65,4 = 11,87.
Уравнение регрессии примет вид
7 = Н.87 — 1,541х + 0,0571х2.
Подставляя в это уравнение значения х из табл. 9, получим расчетные значения регрессии, по которым построим кривую регрессии на рис. 19: 7 = 9,02; #^= 7,76; = 6,62; 7^= 5,59; 76,Л, 8 = 4,68; у. = 3,88;
У1о ~ 3,18; Уц = 2,63; у и = 2,17; yiS = 1,60; Уи = 1,49; у^ = 1,49. Кривая регрессии пересекает ось у в точке с ординатой 11,87. Если воспользоваться данной кривой для прогноза, то можно увидеть, что уже при величине выпуска, равной 15 000 штукам, затраты в расчете на единицу продукции снова увеличатся. С экономической точки зрения это так же трудно объяснить, как и величину себестоимости в 11,87 марки при отсутствии выпуска продукции. Поэтому следует попытаться подобрать другую функцию регрессии, которая бы соответствовала эмпирическим данным и в то же время была экономически обоснована. Если выбрать для описания зависимости гиперболическую функцию
то по формулам (5.13) и (5.14) получим следующие оценки параметров:
Ь*о - 0,8701; Ы = 19,286.
Уравнение регрессии в этом случае будет иметь вид:
7* = 0,8701 + 19,286 у .
Расчетные значения регрессии, полученные после подстановки в это уравнение значений х, равны:
#* =10,51; 7* = 7,30;
#8,7,8 = 4,09; #8 = 3,63;
#*2 — 2,80;’ РТз = 2,48;
#3,4 = 5,69; #8 = 4,73;
#*o = 3,28;j t/*i=3,01;
#*4 = 2,35; #*5 = 2,25;
147
Соответствующая кривая регрессии изображена на рис. 19. С увеличением х величина себестоимости единицы продукции приближается к 0,87 марки. С уменьшением х себестоимость единицы продукции возрастает. Для выражения зависимости себестоимости единицы продукции от объема продукции гиперболическая функция более пригодна, чем регрессия (5.1). Однако на некоторых участках переменной х функция (5.1) больше соответствует эмпирическим данным.
В нашем примере мы располагали относительно небольшим числом наблюдений. Поэтому оценки параметров регрессии могут иметь значительные отклонения случайного характера. Отсюда возникает необходимость проверки значимости уравнения регрессии, что будет обсуждаться в главе 8. Себестоимость является относительной величиной в статистическом смысле. В регрессионном анализе такие относительные величины создают особые проблемы, на которых мы более подробно остановимся в разделе 7.7.
В экономике довольно часто встречаются регрессионные зависимости, нелинейные относительно оцениваемых параметров. Использование этого класса регрессий связано с вычислительными трудностями, так как указанные регрессии не допускают непосредственного применения обычного метода наименьших квадратов. Для того чтобы сделать это возможным, исходные данные подвергают преобразованиям, главное назначение которых в линеаризации рассматриваемых зависимостей по оцениваемым параметрам. Так, например, путем логарифмического преобразования можно перейти от зависимости показательного типа к линейной:
7 = abx, (5.22)
log у = log а + х log b. (5.23)
Произведя в (5.23) замену log у = Z, log а = А и log b — В, получим
Z = А + Вх. (5.23а)
К уравнению (5.23а) применяем метод наименьших квадратов. При этом требованиеМНК будет сводиться к условию (?г- — Zf)2->- min, i
а не к условию S (Уг — Следовательно, для (5.23а) не
z
является обязательным равенство
i I
Для определения зависимости вида (5.22) нужно выполнить логарифмическое преобразование переменной у, т. е. прологарифмировать эмпирические значения yh = log yt. Аналогичному преобразованию подвергают исходные данные при изучении зависимости вида у == aVxb. После возведения в квадрат обеих частей уравнения перейдем к логарифмам. Введем следующие обозначения: 2 log у = Z, 2 log а = Л, b = В. В итоге получим: Z = А + В log х. Оценки параметров А и В можно найти снова с помощью метода наименьших квадратов.
148
Таблица 10
Нелинейные функции второго класса
Название функции Аналитическое выражение функции Преобразование функции
1. Степенная 2. Показательная 3. Показательностепенная 4. Экологическая 5. Логистическая 6. Частный случай логистической функции 7. Функция Гомпер-ца 8. Иррациональная 9. Гиперболическая 10. Функция, обратная квадратному трехчлену 11. Дробно-рациональная функция 12. Функция Джонсона 13. Модифицированная экспоненциальная 14. Функция Торн-квиста 1-го типа 15. Функция Торн-квиста 2-го типа 16. Функция Торн-квиста 3-го типа у = ахь y = abx у — ахь сх у = ае~ь^х~~с^ а У~1+Ье~сх а а Jog у = log a-{-bcx у = У a-}- bx-f-cx2 1 V а-|- Ьх 1 а + Ьх+сх2 X У а-\-Ьх~[-сх2 а ь+х+с у = аеЬх ах У~ Ь+х а (x—by у- х ах (х—Ь) у- х+с log = log a-}- blog X log г/= log a+x log b log у = log a-у b log x-j- x log c log у = log a— b2 c2 log e + + 2b2 c (log e) x—b2(log e) x2 / a \ log!— — 1 =logb—ex loge \ У J [ a \ log — —1 = b log e—ex log e \ У / / a \ log — —1 log b—c logx \ У J log (log a—log y) = log (—b) + +x logc y2 = a-\-bX-y-ex2 1 — = a-\-bx У 1 — == a~ybx-\-cx2 У x — = a-y bx-^cx2 У 1 b 1 = — — X (\ogy)—c a a logy=\oga-{-bx loge _1 b_ 1 1 у a x a x — b 1 c = x-f-у a a x~b 1 । c 1 у a a x
149
Итак, некоторые функции с помощью преобразования переменных поддаются линеаризации относительно своих параметров. Параметры регрессии исходных функций находят путем обратных преобразований. Например, если исходная функция является показательной или степенной с дробным показателем, то оценки параметров этих регрессий находят путем потенцирования параметров линеаризованных зависимостей. Линеаризация связей дает возможность применять для нахождения оценок параметров метод наименьших квадратов. Но полученные оценки параметров исходных функций могут не обладать свойствами МНК-оценок. Разработаны способы уточнения этих оценок. Но мы не будем подробно это обсуждать и отсылаем заинтересованного читателя к специальной литературе.
Для наглядности наиболее часто встречающиеся в экономике нелинейные функции второго класса представлены в табл. 10. Особенно значительную роль они играют при изучении спроса. Из приведенных в таблице функций наибольшее затруднение при их определении вызывают оценки параметра а логистической функции и функции Гомпер-ца, параметра с функции Джонсона и параметра b функции Торнквиста 2-го и 3-го типов. Так как параметр а указывает уровень насыщения, то обычно он заранее устанавливается исходя из логико-экономических соображений. Имеются также численные методы, с помощью которых можно вычислить это значение [125]. Другой способ заключается в определении уровня насыщения с помощью функции Торнквиста 1-го типа и подстановки этого значения в логистическую функцию. Но в любом случае мы должны исходить из экономического анализа явления.
5.2. ПРОСТАЯ НЕЛИНЕЙНАЯ РЕГРЕССИЯ
ПРИ СГРУППИРОВАННЫХ ДАННЫХ
Если исследователь располагает большим числом наблюдений, то путем рациональной группировки эмпирических данных можно облегчить вычислительную процедуру. Чаще всего данные группируются по объясняющей переменной. В образованных группах вычисляются частные средние у}. Процедура нахождения оценок параметров аналогична описанной в разделе 2.6. Ограничимся квазилинейными функциями. Для регрессии (5.3) при сгруппированных данных получим следующие нормальные уравнения:
2 Уз gj = nb0 + b1'S1x]gJ + b2^t xj g}, (5.24)
SУз xj gj = b0^Xjgj + br5xj gj + b25x? gj, (5.25)
/ / / /
2У1 xf gj = b0^xj gj + bi^x] gj + &2 2xj gj. (5.26)
При этом yj — частная средняя; х} — середина /-го интервала значений объясняющей переменной; gj — частота /-го интервала; y\gj = п
150
(см. раздел 2.6). Решая систему нормальных уравнений, находят оЦёй* ки параметров регрессии (5.3).
Рассмотрим зависимость логарифмического типа
у = b0 + bx log х. (5.27)
В соответствии с правилом, приведенным в разделе 5.1, получим нормальные уравнения для сгруппированных данных:
3yjg/ = «&o + bi2^1ogx;. (5.28)
_ / ~ /
2 У1 gj logXj = b0 2 gj logXj + b\ 2 gjlog2 Xj. (5.29)
/ / /
В качестве примера исследуем зависимость товарной продукции (у) от введенных в действие основных фондов (х) на 663 предприятиях по исходным данным из табл. 11. Выразим эту зависимость с помощью регрессий (5.3) и (5.27). Решая системы нормальных уравнений (5.24)— (5.26) и (5.28)—(5.29), найдем оценки параметров этих регрессий. Подобранные модели имеют вид:
7= 13 + 1,214х — 0,002384х2,
у = — 204 + 158 1g х.
Т а б л и ца 11
По расчетным значениям per- Товарная продукция и основные фонды
рессии в табл. 11 видно, что на 663 предприятиях
функция (5.3) для нашего
OnttARltM А
примера при Ху = 255 дости- Х-* V Л V DrllJlC фонды, 10* Товарная Расчетные
гает своего максимума, в то марок (середины интер- продукция, 105 марок 5 значения регрессии
время как функция (5.27) не- валов) tf с к
прерывно возрастает. Какая XJ т. 1 ^7*
из двух функций регрессий J 1 7
75 81,3 15 92,2 90,6
лучше всего отражает зави-
симость товарной продукции 85 103,5 13 100,8 99,0
от основных фондов, сразу решить трудно. Если бы мы вычислили коэффициент детер- 95 105 115 125 114,0 115,2 114,8 128,4 25 35 55 69 108,5 115,3 121,6 127,3 106,8 114,2 121,1 127,6
минации для обеих регрес- 135 134,3 84 132,5 133,5
сий, то тогда смогли бы убе- 145 139,7 70 137,4 138,9
диться, что функция (5.3) 155 165 146,7 144,6 63 55 142,0 146,3 143,9 148,4
больше соответствует эмпи- 175 156,1 31 150,4 152,4
рическим данным, чем функ- 185 158,4 34 154,2 156,0
ция (5.27). Таким образом, 195 155,9 21 157,8 159,0
если бы возникла необходи- 205 215 156,0 158,9 28 19 161,3 164,5 161,7 163,8
мость прогноза товарной про- 225 188,8 9 167,6 165,5
дукции по основным фондам, 235 135,3 12 170,6 166,7
; то на указанном диапазоне 245 180,6 2 173,5 167,3
; Изменения переменных сле- 255 265 203,4 159,0 5 5 176,3 178,8 167,6 167,3
1 дует воспользоваться регрес- 275 177,2 10 181,4 166,5
сией (5.3). Однако нужно еще 285 155,3 3 183,9 165,4
проверить, поддается ли со-
151
держательной интерпретации Максимальное значение товарной продукции при данных основных фондах. Только после выяснения этого вопроса можно окончательно решить, какой из функций регрессии отдать предпочтение.
Оценки параметров нелинейных регрессий можно найти также при группировке наблюдений по обеим переменным, т. е. по корреляционной таблице. Процедура вычислений аналогична описанной в разделе 2.6 для простой линейной регрессии. При построении нормальных уравнений следует обращать внимание на то, что середины интервалов ук умножаются на частоты gki середины интервалов xj — на частоты gj, а произведения ykXj — на условные частоты pkj.
5.3. МНОЖЕСТВЕННАЯ НЕЛИНЕЙНАЯ РЕГРЕССИЯ
Несколько явлений могут быть соединены между собой нелиней ныМи соотношениями. В этом случае для описания зависимостей следует воспользоваться множественной нелинейной регрессией. Здесь также различают множественную нелинейную регрессию первого и второго классов. Все рассуждения, приведенные в разделе 5.1, относительно этой проблематики имеют силу и для данной регрессии.
Исходя из логических соображений процедура построения уравнения множественной нелинейной регрессии должна быть аналогична процедуре определения простой нелинейной регрессии. Рассмотрим следующий пример квазилинейной регрессии, ограничившись двумя объясняющими переменными:
у = а + F± (xj + F2 (х2). (5.30)
Если профессионально-теоретический анализ экономического явления позволяет функции от объясняющих переменных представить в виде
Fi (хх) = Ь±х± + c^f + dxxl (5.31)
и
F2 (*2) = b2x2 + c2xl + d2x%, (5.32)
то зависимость (5.30) выражается так:
у = а + + c^i + djxf + b2x2 + с2х$ + d2x*. (5.33)
Применяя метод наименьших квадратов, находят параметры a, blt clt ..., d2. Но в этом случае уравнение (5.33) можно относительно просто свести к линейному виду, обозначив xf = х3; xf = х4; х* = х5 и х2 ~ х6. Ограничившись только этим указанием, мы не будем записывать уравнение в линейной форме.
Из функций множественной нелинейной регрессии второго класса, которые допускают линеаризацию, представляют большой экономический интерес производственные функции. Понятие производственной функции трудно описать вербально. Производственные функции вначале использовались для исследования причинно-следственных отношений в производственной сфере. Затем они стали очень популярным средством анализа экономических явлений, что объясняется как про*
152
стотой вида этих функций, так и широкими возможностями их применения в самых разных ситуациях.
Исторически первой производственной функцией явилась степенная функция Кобба—Дугласа*
7 = ... х*”», (5.34)
где у обозначает выпуск продукции, национальный доход и т. д.; хь ..., хт — влияющие факторы; — нормировочный множитель; bi, ..., bm — коэффициенты эластичности. Если ограничиться рассмотрением товарной продукции (у), затратами труда (хх) и основными фондами (х2), то (5.34) примет вид:
у = (5.35)
Логарифмируя обе части равенства, получим
log у = log b0 + bi log х1 + b2 log х2. (5.36)
Из (5.36) легко найти оценки параметров. Если вводится требование bi + b2 = 1 (линейная гомотетичность), т. е. br = 1 — Ь2, то уравнение (5.35) приобретает вид:
7=VV-M4‘. (5.37)
Путем простого преобразования можно получить
= (5.38)
Записывая (5.38) в логарифмическом виде и применяя формулы из раздела 2.4, находят Ьо и Ь2.
Далее был разработан класс линейно-гомотетичных функций: CES (Constant Elasticity of Substitution) — функция с постоянной эластичностью замены и VES (Variable Elasticity of Substitution) — функция с изменяющейся во времени эластичностью замены**. Этот класс функций дает возможность моделировать изменение эластичности, замены факторов производства с изменением уровня выпуска:
__i_
у = 60(^2хгр + (1—Ь2)*ГР) ” , (5.39)
__1_
7=Ьо(Мгр + (1-Ш[—rs(1+₽>*rp') Р' (5.40)
*D о u g 1 a s Р. Н., Cobb С. W. A theory of production. American Economic Review, vol. 18, 1928, p. 139.
**A rrowK. J.,Chenery H. B., Minhas B. S., SolowR. M. Capital-labour substitution and economic efficiency. The Review of Economic and Statistics, 8, 1961; W о 1 f 1 i n g M. Ein Algorithmus fiir den Aufbau dynamischer ynd ^tatistischer Regressionsmodelle. Statistische Praxis, 26, 1971, S. 342--345.
153
Исходя из дифференциальных уравнений этих функций можно определить р, q и s. Но часто они устанавливаются в соответствии с экономическими требованиями, так что из уравнений (5.39) и (5.40), так же как из (5.38), находят только параметры регрессии Ьо и &2.
Наконец, укажем еще одну производственную функцию для описания научно-технического прогресса:
у = bQх^1 хь<* еь» (5.41)
В этом соотношении научно-технический прогресс рассматривается как экспоненциальная функция от времени, показатель &3 характеризует темп научно-технического прогресса. Насколько эта функция имеет экономическое содержание и соответствует эмпирическим данным, должно быть проверено обширными исследованиями. Вообще нужно отметить, что множественная нелинейная регрессия лучше отражает многообразие связей в экономике. Применение ЭВМ снимает все вычислительные проблемы, которые раньше были препятствием для создания нелинейных многофакторных моделей.
6
НЕЛИНЕЙНАЯ
КОРРЕЛЯЦИЯ
Если между исследуемыми явлениями существуют нелинейные соотношения, то, так же как в случае линейной связи, интересуются теснотой зависимости, ее силой. В главе 4 была введена мера интенсивности связи — коэффициент корреляции, но среди прочих условий предполагалось, что исследуемые явления при этом имеют линейные соотношения. Если эти соотношения отличаются^от линейных, то коэффициент корреляции в его принятой для линейной связи форме не сможет отражать интенсивность связи. Так, если вычислить коэффициент корреляции для двух формальных статистических рядов:
1 2 3 4 5 6 7 8 9 10 11 12 13
11234575 4 3 2 1 1,
то он окажется равным нулю (г = 0), хотя очевидно, что между обоими рядами существует тесная связь. Но из этого вовсе не следует, что линейный коэффициент корреляции в некоторых случаях не приводит к нужным результатам при нелинейной связи рядов наблюдений. Наряду с этим все-таки существует необходимость в достоверном показателе интенсивности связи при нелинейных соотношениях. Таким показателем связи может служить индекс корреляции.
6.1. ПРОСТАЯ НЕЛИНЕЙНАЯ КОРРЕЛЯЦИЯ
ПРИ НЕСГРУППИРОВАННЫХ ДАННЫХ
Рассмотрим вначале измерение интенсивности нелинейной связи между двумя явлениями, объективно существующая зависимость между которыми выражается с помощью квазилинейной функции. Индекс корреляции, используемый для характеристики интенсивности связи, обозначим через Ryx. С помощью соотношения (4.12) из раздела 4.3, которое имеет место также для нелинейных связей, получим
Ryx--h VRyx--Ь
^(У1~У)2 i
(6.1)
SG/i-*/)2
155
Выведем из (6.1) путем некоторых преобразований удобные для ЁЫ-числений формулы индекса корреляции. Разделим числитель и знаменатель в подкоренном выражении (6.1) на п— 1:
(6-2)
Выражение (6.1) мы можем представить также в таком виде:
/ ^(У1~У1? Г
Ryx=Vl-Uvx=l/ 1--------------= 1/ 1—(6.3)
J/ ^(yt-y)* F y
Раскрыв в (6.3) скобки, получим
/2 iy^yi+ny2
--------l------ (6.4)
^У1~У^У1 i I
Так как при квазилинейной регрессии остается в силе равенство = Sy,, при дальнейших упрощениях получим
2Vf—72^
------— (6.5)
2 у! —у ^У1 i i
ИЛИ
Индекс корреляции принимает значения в интервале
Q^Ryx^ 1. (6.7)
Если дисперсия , обусловленная зависимостью переменной у от х, равна общей дисперсии s^, то Ryx == 1. В этом случае уг = yt для всех /, т. е. мы располагаем функциональной связью между наблюдаемыми переменными.
Если необъясненная дисперсия остатков su2 равна общей дисперсии s£, т. е. Su = sy, то Ryx — 0. В этом случае уг = у (см. (6.3)). Линия регрессии параллельна оси абсцисс, из чего можно заключить, что связь в том смысле, как она понимается в корреляционном анализе, отсутствует. Чем больше значение индекса корреляции приближается к 1, тем сильнее наблюдаемая связь. Индекс корреляции связан с коэффициентом детерминации соотношением (6.1). Чем ближе индекс
156
корреляции к 1, тем больше коэффициент детерминации и тем больше определена регрессия включенными в анализ объясняющими переменными.
Пример
Оценим интенсивность связи между себестоимостью единицы изделия и объемом продукции (см. раздел 5.1). При описании зависимости многочленом второй степени получим следующее значение индекса корреляции по (6.6):
п = 15; 2= 369,9749; 2 = 384; i I
U V 15-384—662
Если регрессию представить в виде гиперболической функции, для которой = 358,6303, то
i
^=1/15-358,6303^бГ = ух у 15.384—662
Связь между наблюдаемыми значениями в нашем примере очевидно сильнее, если мы для описания зависимости используем целую рациональную функцию второй степени. На данном интервале изменения переменных более пригодна для прогнозирования эта функция регрессии, чем гиперболическая. На это указывает также коэффициент детерминации 87,6% (и 73% для гиперболической). Как уже обсуждалось в разделе 5.1, гиперболическую функцию следует предпочитать только в соответствии с общими теоретико-экономическими соображениями.
Индекс корреляции не дает возможности судить о характере корреляции (положительная или отрицательная). Об этом можно сделать заключение, лишь рассматривая график кривой регрессии. В данном примере имеем отрицательную нелинейную связь.
Как было показано ранее, линейный коэффициент парной корреляции является симметричной функцией относительно х и у, т. е. гух = ?ху Особо следует подчеркнуть, что этим свойством не обладает индекс корреляции, т. е. Ryx^ RXy
.В разделе 2.5 мы подробно описывали, что в случае простой линейной регрессии имеются две сопряженные прямые регрессии, т. е. функция регрессии не обладает свойством обратимости. Это справедливо также для простой нелинейной регрессии и корреляции. При вычислении индекса корреляции, как известно, исходят из нелинейной регрессии. Естественно поэтому, что мы придем к различным результатам, если вначале будем основываться на функции у = / (х), а затем — на х = g (у). Аналогично тому как при простой линейной регрессии имеем две сопряженные прямые регрессии, так при нелинейной корреляции получаем различные сопряженные индексы корреляции. Это связано с тем, какая из переменных выбрана в качестве подлежащей объяснению. При простой линейной корреляции указывается только один коэффициент парной корреляции. В случае нелинейной связи
157
между Явлениями коэффициент детерминации так же, как индекс корреляции, не является симметричной функцией относительно переменных, т. е. Вух =# Вху. Формулы для Вху и Rxy при нелинейной корреляции легко получить из (6.1)—(6.6) путем замены в них на t/t на xt и у на х.
По аналогии с нелинейной регрессией второго класса мы можем рассматривать нелинейную корреляцию второго класса. В этом случае для измерения тесноты связи можно пользоваться также формулой (6.1). Величина индекса корреляции при этом заключена в границах: О Ryx 1. Индекс корреляции измеряет интенсивность нелинейной связи между явлениями, если параметры нелинейной регрессии второго класса определяются с помощью аппроксимации или с привлечением некоторого итерационного метода. Если же производят линейное преобразование нелинейной функции второго класса с целью подгонки к эмпирическим данным, то индекс корреляции не может служить источником достоверной информации об интенсивности связи между исходными переменными. Он представляет собой тогда вместе с коэффициентом детерминации показатель степени близости кривой регрессии к эмпирическим данным.
6.2. ПРОСТАЯ НЕЛИНЕЙНАЯ КОРРЕЛЯЦИЯ
ПРИ СГРУППИРОВАННЫХ ДАННЫХ
Как уже указывалось, при достаточно большом объеме наблюдений производится группировка данных. Статистический материал при этом становится более наглядным. Но в результате группировки происходит небольшая потеря информации, что сказывается на величине коэффициента корреляции и индекса корреляции. Формулу индекса корреляции для сгруппированных данных можно записать исходя из (6.2):
-------- <6-8»
Одним из достоинств группировки является удобство и сокращение вычислительных операций. Но точность полученных показателей меньше, чем при вычислении по несгруппированному материалу. Чем шире интервалы группировок, тем больше погрешность в вычислениях.
Индекс корреляции можно вычислить также при группировке данных по обеим переменным, т. е. по корреляционной таблице. Отклонения середин интервалов yk зависимой переменной следует при этом взвешивать по частотам hk. Следующая формула индекса корреляции удобна для вычисления по корреляционной таблице:
ъ*=1/ -—— ’ <6-9*
f ^(yh—y^hk ' k
158
где yj — значение регрессии, вычисленное для середины интервала х7-, / = 1, 2, ..., s; yk — середина &-го интервала значений зависимой переменной у, k = 1, 2, /; gj— частота /-го интервала значений
объясняющей переменной; hk — частота k-ro интервала значений зависимой переменной; у — общее среднее зависимой переменной у (см. раздел 2.6).
Для квазилинейной корреляции выражение (6.6) при сгруппированном материале можно записать следующим образом:
(6.10)
По аналогии с этим формула (6.3) для сгруппированных данных примет вид:
/--------------—------
/ yj)*Pkj
^х=1/ 1-----------—-------=------ ‘ (6.11)
У 2 (уц—у)2 hk
’ k
В (6.11) подставляются отклонения значений регрессии z/7- от середины интервалов yk для каждой клетки корреляционной таблицы, взвешенные по соответствующим условным частотам Следует иметь в виду, что, как и для несгруппированного материала, Ryx Ф-¥=Rxy (см. раздел 6.1).
6.3. МНОЖЕСТВЕННАЯ НЕЛИНЕЙНАЯ КОРРЕЛЯЦИЯ
При нелинейных соотношениях между более чем двумя социально-экономическими явлениями, выражаемых с помощью нелинейной регрессии первого класса, индекс корреляции, например, для трех переменных записывается следующим образом:
^у.12 —
По форме он совпадает с (6.1). Различие состоит лишь в том, что уг-здесь — значения регрессии, вычисленные по двум объясняющим переменным. Показатель Ry,12 измеряет тесноту нелинейной зависимости переменной у одновременно от двух переменных х± и х2 и позволяет оценить соответствие множественной нелинейной регрессии первого класса эмпирическим данным. Относительно индекса корреляции, вычисляемого для множественной нелинейной регрессии второго клас
са, можно утверждать все то же самое, что приведено в конце раздела
6.1 при обсуждении простой нелинейной корреляции второго класса.
159
ЧАСТНЫЕ ВОПРОСЫ КОРРЕЛЯЦИОННОГО И РЕГРЕССИОННОГО АНАЛИЗА
7.1. КОЭФФИЦИЕНТ РАНГОВОЙ КОРРЕЛЯЦИИ СПИРМЭНА
Наряду с рассмотренными линейными и нелинейными коэффициентами корреляции существует еще ряд показателей тесноты связи, широко применяемых в экономике в тех случаях, когда признакам наблюдаемого явления не удается однозначно приписать те или иные абсолютные значения. К ним относится коэффициент ранговой корреляции Спирмэна. Его применение, в отличие от приведенных выше коэффициентов корреляции, не связано с предпосылкой нормальности распределения исходных данных.
При применении методов ранговой корреляции исходят не из точных количественных оценок значений признаков-переменных, а из рангов. Для этого элементы совокупности располагаются в определенном порядке в соответствии с некоторым признаком, присущим им в неодинаковой мере. Полученный ряд элементов называют упорядоченным. Сам процесс упорядочения называется ранжированием, а каждому члену ряда присваивается ранг, или ранговое число (порядковый номер). Например, элементу с наименьшим значением признака присваивается ранг 1, следующему за ним элементу— ранг 2 и т. д. Элементы можно располагать также в порядке убывания значений их признака. Таким образом, происходит сравнение каждого элемента со всеми остальными элементами совокупности. Если элемент обладает не одним, а двумя признаками х и у, то для исследования их влияния друг на друга каждому элементу приписывается два порядковых номера’в соответствии с установленным правилом ранжирования. Далее переходим от корреляции признаков-переменных х и у к изучению связи между ранговыми числами путем определения соответствия между двумя^последовательностями порядковых оценок. Другими словами, измеряется теснота ранговой корреляции, Поскольку изучается
связь между двумя переменными, используемый при этом коэффициент ранговой корреляции Спирмэна является парным.
Обозначим ранги, соответствующие значениям переменной у, через v, а ранги, соответствующие значениям переменной х, — через w (см. табл. 12). Коэффициент ранговой корреляции Спирмэна вычисляется по формуле
6 S (^“^)2 Г = I______________
' П(П2_ 1)
где п — объем выборки. Из (7.1) видно, что для вычисления коэффициента необходимо определить только квадраты отклонений рангов. На практике приходится сталкиваться со случаями, когда два или более элемента совокупности имеют одинаковые значения одного и того же признака и исследователь не способен найти существенные различия между ними. Элементы, обладающие этим свойством — отсутствием предпочтений, — называются связанными, а образованная из них группа — связкой. Метод, который применяется для приписывания порядкового номера связанным элементам, называется методом средних рангов. Он заключается в усреднении рангов, которые имели бы элементы, если бы они были различимы. Сумма рангов при этом остается точно такой, как и при ранжировании без связей. Так, например, если у переменной у четвертое, пятое и шестое значения одинаковы по величине, то каждому приписывается ранг у (4 + 5 + 6) = 5. Следующему по величине значению приписывается ранг 7. При наличии связанных рангов в коэффициент ранговой корреляции Спирмэна вводится поправка:
П(П2_1)
—-------S
rSt = (7.2)
|/ (1^1) _2л)^-2) „2Д)
Здесь А и В — поправочные коэффициенты для связок соответственно в последовательностях рангов v и w:
Л = —1(Л?-Л7.), / = 1,2,..., г, (7.3а)
5 =-^-2 (5*—Bk), k=l,2,..., р, (7.36)
12 k
j — порядковые номера связок среди рангов v\ если имеется одна связка, то j = 1, если две, то j = 1, 2 и т. д.; Л; — число одинаковых значений ряда v, принадлежащих одной связке; если второй связке принадлежат пять одинаковых значений, то это обозначают так: Л2 = 5. Аналогично можно дать определения для k и Bh.
160
6 Зак. 1113
161
Коэффициент ранговой корреляции может принимать значения внутри интервала — 1 С г3 + 1. Если vt = то rs = 1. В этом случае имеется полная согласованность между элементами двух последовательностей. Каждый элемент занимает одно и то же место в обоих рядах, что означает полную положительную корреляцию рангов. Если rs = — 1, то элементы двух последовательностей расположены в обратном порядке и между ними полная рассогласованность. Это означает полную отрицательную корреляцию рангов. И наконец, если rs = 0, то это свидетельствует об отсутствии корреляции между рангами.
Пример
Определим тесноту связи между производительностью труда и уровнем механизации работ на 10 промышленных предприятиях. Данные приведены в табл. 12.
Таблица 12
Производительность труда и уровень механизации работ на 10 предприятиях
Предприятие Средняя выработка продукции в единицу рабочего времени, изд./ч Коэффициент механизации работ, % Ранги значений переменных Разнести рангов
1 Vi xi wi vi
1 127 43 1 4 +3 9
2 120 51 2 1 —1 1
3 125 55 3 2 —1 1
4 126 57 4 3 —1 1
5 133 60 5 7 +2 4
6 129 62 6 5 — 1 1
7 132 65 7 6 —1 1
8 135 68 8 8,5 +0,5 0,25
9 135 70 9 8,5 —0,5 0,25
10 140 74 Ю Ю 0 0
Сумма 1 302 605 55 55 0 18,5
Например, ранг v5 = 7 означает, что предприятие 5 по уровню механизации работ стоит на седьмом месте при расположении предприятий в порядке возрастания соответствующего показателя. По данным табл. 12 вычисляем коэффициент ранговой корреляции:
гS = 1-----6-18,5 =0,888.
• 10(102—1)
В последовательности рангов vt имеется одна связанная пара. Вычислим поправочный коэффициент по (7.2). В нашем случае введение поправки не приведет к существенному изменению величины коэффи
162
циента ранговой корреляции, так как число связок и количество рангов в связке невелико. Итак, имеем (/ = 1):
4(2s —2) = 0,5, В = 0,
10(102 — 1)
---------------------18,50-0,5 г81 =--------------— — -6-- = 0,889.
( 10"°‘~'> -2 0)
Величина rs свидетельствует о тесной положительной связи между производительностью труда и уровнем механизации работ. Коэффициент парной корреляции, вычисленный непосредственно по исходным данным, равен: гух — 0,833. Сравнивая rs и гух, убеждаемся, что они мало отличаются друг от друга. Коэффициент ранговой корреляции в общем служит довольно хорошей характеристикой степени связи исследуемых переменных. Его достоинство заключается в том, что он не связан с предпосылкой нормальности распределения исходных данных. Но не следует упускать из вида, что при переходе от первоначальных значений к рангам происходит определенная потеря информации. Коэффициент ранговой корреляции тем больше приближается к коэффициенту парной корреляции, чем меньше корреляционная связь между изучаемыми переменными отлична от линейной и чем сильнее эта связь. Для нормально распределенной генеральной совокупности и при достаточно большом объеме выборки (п 30) между обоими коэффициентами существует следующее асимптотическое соотношение:
= 2 sin (-у г,). (7.4)
Метод ранговой корреляции не требует линейной корреляции между переменными. Но, однако, необходимо, чтобы функция регрессии, отражающая эту связь, была монотонной.
Особенно полезной оказывается ранговая корреляция при исследовании связей между явлениями, не^поддающимися количественной оценке. В таких случаях исследователь на основе своего опыта, или производя сравнение с каким-либо эталоном, приписывает элементам выборки ранги по каждому из изучаемых качественных признаков. Например, ранговую корреляцию можно использовать при исследовании зависимости между сортностью продукции, ее сроком службы и производственными затратами. При изучении качества изделий их часто классифицируют по следующим уровням: «отличное, очень хорошее, хорошее, среднее, плохое». Аналогично можно прошкалировать и другие признаки.
Ранговую корреляцию широко используют также в социологических исследованиях. Например, при анкетировании и опросах населения, при обработке результатов психологических и педагогических тестов. Словом, ранговая корреляция оказывается полезной всегда
6*
163
для изучения связей там, где свойства явлений не поддаются точному количественному измерению, но позволяют производить сравнительную оценку, благодаря которой устанавливаются последовательности рангов.
7.2. КОЭФФИЦИЕНТ РАНГОВОЙ КОРРЕЛЯЦИИ КЕНДЭЛА
Другой коэффициент ранговой корреляции т, не связанный с предпосылкой нормальности генеральной совокупности, был предложен Кендэлом. Он вычисляется по рангам и wit При этом элементы выборки располагают так, чтобы последовательность рангов одной из переменных представляла собой натуральный ряд 1,2, ...,/г. Для каждого r-го члена последовательности рангов второй переменной устанавливаем числа pi и qif отражающие соответственно прямой и обратный порядок расположения последующих рангов1. Затем подсчитываем суммы этих чисел Р = и а также разность полученных
i i
сумм S = Р — Q. Коэффициент ранговой корреляции т представляет собой отношение этой разности к наибольшему возможному значению Р и Q, т. е. к наибольшей возможной сумме pt Такая величина может быть достигнута лишь тогда, когда порядок рангов в обеих последовательностях полностью совпадает. Она равна:
Sroax—”0*"") • (7.5)
коэффициент ранговой корреляции Кендэла можно вычислять по одной из эквивалентных формул:
^тах п (п — 1)
т = 1-----= ——-------------1. (7.7)
п(п — 1) п(п— 1)
Из (7.7) видно, что для определения т достаточно располагать либо величиной Р, либо Q. Чаще всего в формулу подставляют ту величину, которая имеет наименьшее значение.
Величина т лежит в пределах — 1 т + 1. По данным табл. 13 получаем
По величине этого коэффициента можно сделать вывод о тесной связи между производительностью труда и уровнем механизации работ.
Рассмотрим подробнее процедуру нахождения pt и qt по табл. 13. Для этого используется только последовательность рангов За первым членом этой последовательности vt = 4 находится 6 рангов, ко
1Прямым порядком будем называть порядок натурального ряда 1, ..., 10. — Примеч. пер.
164
торые больше 4, и 3 ранга, которые меньше 4. За вторым членом у2 = 1 следуют 8 рангов, которые больше 1, и О рангов, которые меньше 1. Пятое место в последовательности занимает ранг v5 = 7, за которым следуют 3 больших ранга и 2 меньших ранга. Число возможных положений f-го ранга в последовательности равно: (pt + qi) = = п — i. Например, для первого члена последовательности (pi + ^1) = 10 — 1 = 9, для второго (р2 + 9г) Ю — — 2 = 8. Этим можно воспользоваться для контроля. Нельзя дать рекомендаций, какой из коэффициентов ран-
Таблица 13
Производительность труда и уровень механизации работ на 10 предприятиях
Предприятие Ранги Число рангов, расположенных в прямом порядке Число рангов, расположенных в обратном порядке
i vi 1 wi Pi Ь
1 4 1 6 3
2 1 2 8 .0
3 2 3 7 0
4 3 4 6 0
5 7 5 3 2
6 5 6 4 0
7 6 7 3 0
8 8,5 8 2 0
9 8,5 9 1 0
10 10 10 0 0
Сумма 55 55 Р = 40 <2 = 5
говой корреляции предпочтительнее на практике. Коэффициенты
rs и т построены по-разному. При вычислении rs и т по одной и той же последовательности чисел обычно rs > т. Но сравнение этих коэффициентов по величине само по себе не дает никакой дополнительной ин-
формации об интенсивности связи.
7.3. ИНДЕКС ФЕХНЕРА
Другим простым показателем степени взаимосвязи между двумя статистическими рядами является индекс Фехнера. Для его определения вначале по каждому ряду вычисляют средние (х, у) и определяют знаки отклонений — хи yt — у. Каждая пара наблюдений (хь yt) будет характеризоваться совпадающими или несовпадающими знаками (++;-----; +—; —+). Обозначим через v количество совпадений,
а через w— количество несовпадений знаков разностей. Индекс Фехнера i определяется по формуле
. V — W
I------------
v-^w
(7.8)
Половину отклонений, равных нулю, относят к v, половину — к w. Легко убедиться, что + 1 i — 1. При i> 0 имеем положительную корреляцию, при i < 0 — отрицательную, а при i = 0 связь отсутствует.
Для данных, представленных в табл. 1 (см. раздел 2.1):
х = 31,1;
9 = 248,2;
. _44—8 __ 36 “44+8 ~ 52
v = 44;
= 0,69.
w = 8;
165
Если нулевое значение I интерпретируется как свидетельство независимости, то по значению i = 0,69 можно сделать вывод об относительно тесной положительной связи.
Несомненное преимущество индекса Фехнера — простота вычисления. Но его большой недостаток состоит в том, что он учитывает только количество совпадений и несовпадений знаков отклонений. Поэтому он рекомендуется лишь для приблизительной оценки связи.
7.4. КОРРЕЛЯЦИОННОЕ ОТНОШЕНИЕ
Для измерения тесноты связи между двумя явлениями используется корреляционное отношение т), предложенное Пирсоном. Его определяют по данным, сгруппированным по объясняющей переменной либо по корреляционной таблице. В обоих случаях вычисляют частные, или условные, средние yj зависимой переменной по каждой /-й группе значений объясняющей переменной.
Процедуры вычислений корреляционного отношения и индекса корреляции очень схожи. Различие заключается лишь в том, что при вычислении корреляционного отношения исходят из частных средних, а не из соответствующих значений регрессии. Следовательно, оно не связано с определенной функцией регрессии. Чтобы связать эти два понятия, можно корреляционное отношение интерпретировать следующим образом. При его определении предполагаем, что мы исходим из такой функции регрессии, которой соответствует кривая, проходящая через все точки частных средних зависимой переменной. Введем обозначения (см. раздел 2.6): gj — частота /-й группы (интервала) значений объясняющей переменной х, / = 1, 2, ..., yj — частное среднее переменной у для /*-й группы (интервала) значений объясняющей переменной х; ykj — k-e значение зависимой переменной у в /-й группе (интервале) значений объясняющей переменной х, k = 1, 2, ..., s.
По аналогии с индексом корреляции определим теперь корреляционное отношение:
(7.9)
Используя разложение дисперсии на составляющие, представим корреляционное отношение по аналогии с коэффициентом парной детерминации следующим образом:
(7.Ю)
или
<7-“>
166
Здесь s^- — межгрупповая дисперсия, характеризующая рассеяние частных средних yj относительно общего среднего у\ s'2 — среднее из частных дисперсий, служащее для характеристики среднего рассеяния значений переменной внутри групп. Из формул (7.9)—(7.11) видно, что корреляционное отношение вычисляется только по сгруппированному числовому материалу. При использовании любой из этих формул должна быть известна общая дисперсия s£. Если в распоряжении имеются результаты группировок по объясняющей переменной с указанием только частных средних и нет доступа к исходному числовому материалу, то корреляционное отношение вычислить невозможно.
; Если числовой материал представлен в’виде~корреляционной таблицы, то удобно для практических расчетов пользоваться формулами, полученными из (7.9) по аналогии с (6.10):
(7.12)
(7.13)
Здесь yk — середина k-ro интервала значений переменной у\ hk — частота этого интервала, k = 1, 2, ..., s; pkj — условная частота &-го интервала значений переменной у и /-го интервала значений переменной х (частота, указанная в клетке корреляционной таблицы). Возможные значения корреляционного отношения заключены в интервале
1. (7.14)
Если Ук]~Уь т-е- частные средние yj совпадают со значениями переменной у, то t]j/X = 1. Если yj = у, т. е. все частные средние уд- лежат на одной прямой, проведенной параллельно оси абсцисс на расстоянии у от нее, то = 0. В последнем случае говорят об отсутствии связи между переменными в том^смысле, как ее понимают’в’корреляционном анализе.
На величину корреляционного отношения оказывает влияние произведенная группировка статистического материала. Чем больше выделено групп по объясняющей переменной, тем меньше значений зависимой переменной попадает в каждую группу, тем большему рассеянию подвержены частные средние относительно общего среднего, т. е. тем больше сказывается влияние неучтенных второстепенных факторов и случайностей. Следовательно, межгрупповая дисперсия^частных средних yj с ростом числа групп, как правило, увеличивается, а общая дисперсия остается без изменения. В основном наблюдается такая тенденция: с ростом числа групп по объясняющей переменной корреляционное
167
л sr S ч \о cd
Н
Рабочая таблица
52,5 1 ! । 295 295 ч 87 025 87 025
о о CM О О
{Ч^ LO
ю ю cn Tf
CM
CM CO
CO t-H
to to co to to
СМ см CM
СЧ 00 00 co 00
о CO
00 CM
co CM
Ю о to о 00 о о
Г- СО 4 00 о о
см ю см о 00
fs» ^—4 см co о
ео CM
CO to
Ю Ю tO to to 00
СО О 00 см 1—4 CM со"
1Л см см ь- см co СО
сч СМ »ч ’•ф о to о о
ео 00 ю о о Л о
t4'"» ^—4 о
▼—1 СО »ч
О СО
см
гч СО
to О to о CM о со^ II II
О СО ю см r—4 67"^ СО" II II
4 СП СМ СО АЙ АЙ
(ч. г—4 см co ю
(N CM to о АЙ СЧ А» см to
00
О to ю to to ю
to о to CM о
14 ^—4 о 00
со г—4 со
сч CO СО
CO СМ
1—4
О ю ю co to со
ю со см to CM 00
м< см СО о о
ч CH CM со
^^4
00
to
ю
to ю СП
ю CM см см
*> to ю о о см
сч 20 о см CM 42 СС 1 )
СЧ
Ай
СЧ СЧ сх
•Ou Ай So
S A?
tOlOtOlOLOLOtOtOtOtO Ci. С*. Гк"1
*4^ О’—|СМСО'ФЮСО!400СП -at Ai а2 Ьл
_ай смсмсмсмсмсмсмсмсмсм
ь
' '
168
отношение увеличивается. При фиксированном количестве групп по объясняющей переменной корреляционное отношение зависит также от группировки значений зависимой переменной. Чаще всего корреляционное отношение тем больше, чем дифференцированнее группировка по зависимой переменной. Все это надо иметь в виду при использовании корреляционного отношения в качестве показателя тесноты связи.
Как уже отмечалось, при вычислении корреляционного отношения не ориентируются ни на какой вид функции регрессии. Поэтому по нему нельзя сделать никакого вывода о надежности оценки регрессии.Поскольку при вычислении корреляционного отношения исходят из частных средних, вполне очевидно, что л*/х ¥= Лх?/- Поэтому для измерения интенсивности зависимости переменной х от переменной у вычисляют корреляционное отношение, Лх*/> по формуле, которую легко получить из (7.12) или (7.13) подстановкой в них другой переменной.
Вычислим корреляционное отношение для зависимости объема производства от основных фондов (см. табл. 5 из раздела 2.6). В табл. 14 (2 yhPhjY
произведено вычисление выражения k —---, используемого далее
в (7.13). В результате имеем:
/52.3229558,4 + 12 9302 п п-.
52-3 231 100 —12 9302
Полученное значение г]т/х свидетельствует о тесной связи между объемом производства и основными фондами. Коэффициент корреляции Пирсона, вычисленный по тем же исходным данным, равен гух = 0,941 (см. раздел 4.2). Для нашего примера оба показателя незначительно отличаются друг от друга. Соотношения, существующие между обоими показателями, мы рассмотрим в следующем разделе.
7.5. СООТНОШЕНИЕ МЕЖДУ ЛИНЕЙНЫМ
КОЭФФИЦИЕНТОМ КОРРЕЛЯЦИИ, ИНДЕКСОМ
КОРРЕЛЯЦИИ И КОРРЕЛЯЦИОННЫМ ОТНОШЕНИЕМ
Линейный коэффициент корреляции является частным случаем индекса корреляции, когда связь между переменными х и у линейна. В этом можно легко убедиться, подставив в (6.1) или (6.3) вместо yt его выражение для случая линейной зависимости (2.25). Выполнив затем соответствующие преобразования, получим формулу линейного коэффициента корреляции. Для линейной зависимости между переменными имеем Ryx = Rxy = ryx = rxy.
.В связи с тем что корреляционное отношение можно вычислить только по сгруппированному числовому материалу, мы можем обсуждать вопрос о соотношении между ним и коэффициентом корреляции только при наличии сгруппированных исходных данных. Как известно, сумма квадратов отклонений отдельных значений переменной от среднего меньше, чем сумма квадратов отклонений от любого другого чис-
169
ла, т. е.
п _
2 Q/i—Z/)2->min. (7.15)
Х=1
Для частных средних yjt вычисленных по каждой /-й группе значений объясняющей переменной, это свойство можно записать следующим образом:
2 (уи-уУ^ 2 (yu-tiT- (7.16)
i=i i=i
Путем некоторых преобразований (7.16) с использованием разложения дисперсии s* на две составляющие (см. раздел 3.1, формула (3.5)) можно показать, что
Hz/х = Ryx- (7*17)
Оба показателя тесноты связи только тогда равны, когда значения регрессии у; совпадают с частными средними у^ т. е. линия регрессии проходит через частные средние.
При линейной корреляции частные средние приблизительно лежат на одной прямой. В этом случае коэффициент корреляции и корреляционное отношение принимают примерно одинаковые значения (см. пример в разделе 4.7). Следовательно, при линейной корреляции и ЛХу приближенно равны. Чем больше различаются между собой Лг/х и лxj/ и чем больше они отличаются от линейного коэффициента корреляции, характеризующего степень связи между теми же переменными, тем больше регрессионная зависимость отклоняется от линейного вида. Это позволяет величину разности между корреляционным отношением и линейным коэффициентом корреляции использовать в качестве меры линейности корреляции и регрессии. Поскольку корреляционное отношение не может быть меньше индекса корреляции, разность между обоими показателями при нелинейной связи используется так же, как мера соответствия выбранной функции регрессии действительной зависимости. Если разность между обоими показателями велика, то следует попытаться подобрать другую кривую регрессии, которая ближе подходит к ломаной линии регрессии. Однако указанные разности между корреляционным отношением и коэффициентом корреляции, а такжде между корреляционным отношением и индексом корреляции являются только вспомогательными характеристиками оценки подбора функции регрессии. Решающая роль при выборе «наилучшей» из всех возможных функций регрессии принадлежит логически-профессиональному анализу объективно существующей зависимости между явлениями.
7.6. УПРОЩЕННЫЕ СПОСОБЫ ОЦЕНИВАНИЯ ПАРАМЕТРОВ РЕГРЕССИИ И КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ
На практике часто прибегают к различным упрощенным и грубым методам оценивания. В частности, получил распространение метод, известный под названием метода построения регрессии по точкам или метода сумм. На наш взгляд, принципиальные основы этого метода 170
заложены в работах М. С. Бартлета, А. Вальда, В. М. Гибсона и Г. X. Джоветта, 3. Хельвига и других.
Существуют различные варианты этого метода. Один из них — метод двух точек. При его применении достаточно двух различающихся между собой парных наблюдений (уь и (//,-, лу-), которые подставляют в уравнения с двумя неизвестными:
Hi = b0 +
Уз = Ьо + Ь^. (7.18)
Решая эту систему уравнений относительно Ьо и находят приближенные оценки параметров регрессии.
При использовании другого варианта этого метода все пары наблюдений (хь yt) разбиваются на две группы. К первой группе — нижней — относят все те пары наблюдений, которые меньше среднего. Ко второй группе — верхней — относят те пары наблюдений, которые больше среднего. В качестве разделительного элемента, кроме среднего, может быть взято также любое другое значение в интервале между xmIn и хтах или ут1п и угпах. Но чаще всего прибегают к среднему.
Для достижения однозначности в вопросе отнесения пары наблюдений к соответствующей группе в качестве разделительного элемента при определении Ьо и Ь± используют среднее значение объясняющей переменной. К нижней группе приписывают все те пары наблюдений
Уг), Для которых Xt х. Эти наблюдения обозначают xin и yiH. Остальные пары наблюдений (xit для которых хг- > %, относят к верхней группе. Значения этой группы наблюдений обозначают xiB и у^.
При определении оценок параметров сопряженного уравнения регрессии Ьо и Ь* в качестве разделительного элемента используют среднее зависимой переменной. Те пары наблюдений, для которых yt у. приписывают к нижней группе, а для которых yt> у — к верхней группе. В соответствии с этим вводят обозначения наблюдений — и хКи или yt.B и xf.B. Через хн, Рн, *в> Ув,х.н, у.п, х.в и у.в обозначают средние в соответствующих группах наблюдений, а через ин, пв, п,а и П'В — количество пар наблюдений втгруппах. При этом ин + пв = — п,н +. п,в = п. Можно легко убедиться, что точки (хн, Уи)> {х, у) и (хв> Ув) приблизительно лежат на одной прямой в предположении линейной регрессии. Аналогично точки (х.н, //.„), (х, у) и (х.в, у.в) приближенно лежат на сопряженной прямой. Исходя из этих соображений приблизительные оценки коэффициентов соответствующих уравнений регрессий находят с помощью следующих формул:
= У в, (7.19)
Ы = , (7.20)
У.в—Ун
171
Оценки b0 и bo определяют по (2.24), а коэффициент корреляции — по (4.16). При применении этого метода коэффициент корреляции может получиться больше единицы. Кроме того, при определенных условиях у коэффициентов регрессии могут оказаться различные знаки. В этих случаях считают, что гух=0, и не исключено, что имеется нелинейная связь.
Если среднее всей выборки и средние значения групп приблизительно лежат на одной прямой, то формулы (7.19) и (7.20) можно упростить. В этом случае
b^-L-У» (7.21)
X — Хв — X
Вместо средних применяют также соответствующие суммы. Подставив в формулы (7.19)—(7.21) вместо средних их выражения, после некоторых преобразований получим:
2 Угв Лв 2 ^н2^ Л 2 П2^^ "в2^
&х =----------------=---------------= —------------— • (7.22)
«н2х*в—«в2х*н «и2х;~"2х» «2хгв — «в2х<
i i i i i i
Аналогично получают выражение для b*. При линейных соотношениях между переменными метод сумм позволяет определить коэффициенты регрессии и корреляции с достаточной точностью.
7.7. КОРРЕЛЯЦИЯ И РЕГРЕССИЯ ОТНОСИТЕЛЬНЫХ ВЕЛИЧИН 1
В практике экономических исследований часто приходится изучать соотношения между явлениями, признаки которых представляют собой относительные величины. Из-за этого при применении методов корреляционного и регрессионного анализа возникают особые проблемы.
Обозначим через у и х переменные в их исходной форме. Например, у — общие затраты, а х — количество произведенной продукции. Требуется исследовать связь между себестоимостью и количеством произведенной продукции, т. е. определить соотношение между величинами у — их.
X
Можно исследовать также связь между величинами у и у. Например, между производительностью труда y и объемом продукции (у), здесь х—затраты времени. В этих случаях интересуются соотношениями не между исходными переменными, а между признаками, производными от них.
Рассмотрим более подробно зависимость себестоимости от количе-
Шроблемы, затрагиваемые в этом разделе, рассматриваются в статье: Четвериков Н. С. О ложной корреляции. — В кн.: Применение методов корреляции и регрессии в экономических исследованиях. М., Наука, 1979. — Примеч. пер.
172
ства произведенной продукции. Предположим, что уравнение у = = &0 + Ьгх определяет зависимость общих затрат от объема продукции в штуках. Исходя из логически-профессиональных соображений считаем, что зависимость себестоимости от объема продукции выражается
квазилинейной функцией регрессии \ — | = — + Ь2- Эту регрессию \ X ) X
можно построить различными способами: во-первых, основываясь на требовании
„ , .2
L (—-----—-----min,
i \ Х[ Xi /
и, во-вторых, непосредственно по функции регрессии у = b0 + Ьгх путем деления обеих частей этого уравнения на х после оценки его параметров на основе требования 2 (У*— min. В ре-
i
зультате получим + Ь±. Вполне очевидно, что в общем случае
Ьо ¥= и Ь± =7^= Ь2, т. е. оба метода приводят к различным результатам. Это вызвано различными требованиями при оценке параметров. Не-
сомненно, для данного примера функция регрессии [ —] = — + Ь2 на-\Х J X
дежнее, так как
xt)2
. \ xi Xi } i Xi
Это соотношение получается непосредственно из условия
VI у; а2 1 \2
I & ь_____‘l_и 1 m 1 п
i \ xi Xi ]
Изложенные выше соображения справедливы для корреляционных связей линейного вида, за исключением тех случаев, когда частные средние зависимой переменной лежат точно на прямой.
Кроме этих зависимостей между относительными величинами, у на практике встречаются также соотношения, когда переменная -у зависит от переменной г. Сюда относится, например, зависимость производительности труда от основных фондов, т. е. строится регрессия
вида [ —] = F (г). Соотношения между относительными величинами \ х)
могут быть выражены также с помощью функции регрессии типа /у\ I v\
I — I = В таких случаях, например, по связи между исходными переменными у и х мы не можем непосредственно сделать вывод о связи между переменными ~ и х, и наоборот. При переходе к относительным величинам абсолютные различия, существующие между исходными данными, претерпевают изменения. Поэтому между относительными величинами возникают совсем иные соотношения.
173
Другая проблема связана с вычислением средних из относительных величин. Если между двумя переменными, значения которых являются относительными величинами, существует связь, выражаемая
уравнением регрессии
, то, применяя метод наимень-
ших квадратов, получим следующие нормальные уравнения:
i xi i xi
Разделив обе части этих уравнений на и, перейдем к уравнениям, содержащим средние из относительных величин. Эти средние—невзвешенные (простые). На практике же вычисляются взвешенные средние, которые мы не можем привлечь к построению данной регрессии. Простые средние из относительных величин в нормальных уравнениях являются только приблизительными оценками действительных взвешенных средних. Это вызывает затруднения при нахождении оценок параметров регрессии.
Проблемы, возникающие при изучении корреляции и регрессии относительных величин, еще мало изучены. Предположим, мы хотим рассмотреть зависимость оборачиваемости денег, во-первых, от нормы потребления и, во-вторых, от нормы накопления. В этом случае мы должны учитывать, что как норма потребления, так и норма накопления являются долями по отношению к национальному доходу. При повышении одной из норм другая снижается. Если эту закономерность учитывают в регрессии, то нередко приходят к экономически’неинтерпрети-руемым результатам. Другая сложность заключается в том, что доля G может принимать значения’ только в интервале 0 G 1 или О G% 100. Следовательно, значения результативного признака (зависимой переменной) не должны выходить за эти пределы. Одно из условий регрессионного анализа заключается в том, чтобы дисперсия остатков была по возможности постоянна (гомоскедастичность). Но это условие при применении долей в общем не соблюдается. Оно не нарушается лишь в случае, когда зависимая переменная выражается также в долях. Следовательно, исходный материал, представленный в виде долей, следует подвергнуть такой обработке, чтобы к нему можно было применить’модели регрессионного анализа. Это достигается путем преобразования переменных. Затронутые здесь вопросы более подробно рассмотрены в [40], [82], [132]*.
*См. также:" В l i s s СЛI/ Thecalculation of the dorsage-mortality curve. Appendix by R. A.’Fisher. Annals”of’Applied Biology, 1935,Tvol. 22, p. 134; В 1 i s s С. I. The determination of ^the^dorsage-mortality curve from small numbers. Quarterly ^Journal of Pharmacy and Pharmacology, 1938, vol. 11, p. 192; F i s h e r'R.’A.TOn the dominance ratio. Proceedings of the Royal Society of Edinburgh, 1922, vol. 42, p.r321; Math e’r’K. The analysis of the extinction time date in bioassay/Biometrics, 1949, vol. 5, ’p. 127; Stevens W. L. The truncated normal distribution. Annals of Applied Biology, 1937, vol. 24, p. 847.
174
7.8. КОЭФФИЦИЕНТ КОНКОРДАЦИИ
В экономике существует большое число причинно обусловленных явлений, признаки которых не поддаются точной количественной оценке. Это так называемые атрибутивные признаки. Например, профессия, форма собственности, качество изделия, технологические операции и т. д. Специалист или эксперт ранжирует элементы изучаемой совокупности, приписывая каждому из них порядковый номер, соответствующий итогам сравнения по данному признаку с остальными элементами. Если количество признаков-переменных больше двух, то в результате ранжировок п элементов (предприятий или учреждений) имеют дело с т последовательностями рангов. Для проверки, хорошо ли согласуются эти т ранжировок друг с другом, используется коэффициент согласованности W, называемый также коэффициентом конкор-дации Кендэла:
12 2 DJ
W----------1----
т2 («’—п)
(7.23)
При наличии связанных рангвв коэффициент кенкордации 1F вычисляется по формуле
W -----------------. (7.24)
/и2 (п3—п)—тВ v
т
где Dj — 2 Ku — ------> i I, 2, ..., n\ j = 1, 2, ..., m — сумма
/=i n
рангов, приписанных всеми экспертами /-му элементу выборки, минус среднее значение этих сумм рангов; т — число экспертов или признаков, связь между которыми оценивается; п — объем выборки (число предприятий или учреждений), другими словами, это количество чле-л
нов последовательности рангов; В У, (В* — Bk), где Bk — число й=1
связанных рангов, k=l, ... z. Например, если связываютя элементы от восьмого до одиннадцатого включительно, то Bk = 4. Коэффициент W принимает значения в интервале 0 W 1.
Пример
Пусть группа, состоящая из трех экспертов, оценивает качество однотипных изделий, изготовленных на 6 предприятиях. Каждый эксперт упорядочил изделия по степени предпочтения. Результаты приведены в^столбцах 2, 3, 4 табл. 15.
Сумма рангов для каждого Z-го предприятия указана в столбце 5. Для определения D необходимо вначале вычислить среднее значение по суммам рангов:
з 6
----=-61 = 10,5.
6 6
175
Заключения экспертов о качестве изделий, изготовленных на 6 предприятиях
Таблица 15 Полученное среднее значение вычитаем затем из каждой r-й суммы рангов и разность записываем в столбец 6. Сумму квадратов разностей подставляем в числитель формулы (7.24). В знаменателе этой формулы содержится величина В. Для нашего примера В = - (23 —2) + (З3 — 3)=30. Число предприятий п = 6, число экспертов т = 3. Итак,
________12-133___ ___ ~ З2 (63—6) —3-30 ~
-0,8867.
По величине коэффициента W делаем вывод, что при оценке качества изделий мнения экспертов хорошо согласуются. Если вместо экспертов рассматривать признаки явлений, то вполне очевидно, что коэффициент 117 будет единой выборочной мерой связи между этими признаками. Таким образом, коэффициент конкордации можно рассматривать как показатель тесноты связи в случае множественной регрессии. Оценка значимости коэффициента конкордации приведена в главе 8.
ДОВЕРИТЕЛЬНЫЕ
_ ИНТЕРВАЛЫ
8 И ПРОВЕРКА
ЗНАЧИМОСТИ
В предыдущих главах неоднократно указывалось на необходимость оценки значимости коэффициентов регрессии и корреляции. В данной главе мы вплотную займемся этой проблемой. При этом мы ограничимся рассмотрением соответствующих критериев и методов проверки значимости с процедурой расчетов, не касаясь выводов формул. При применении обсуждаемых здесь методов предполагается выполнение исходных предпосылок линейного регрессионного анализа (см. раздел 2.9). Эти методы предназначены только для линейных, квазилинейных или приводимых к линейному виду функций регрессий.
8.1. РАСПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ
РЕГРЕССИИ И КОРРЕЛЯЦИИ
В разделе 2.9 мы упоминали, что оценки параметров регрессии являются случайными величинами с определенными распределениями вероятностей. В силу того что качество оценки определяется ее распределением, рассмотрим более подробно выборочные распределения некоторых статистик. Пусть выполняются следующие предпосылки: соотношение между переменными в генеральной совокупности выражается линейной регрессией;
возмущающая переменная и имеет нормальное распределение (предпосылка 6 из раздела 2.9) с математическим ожиданием Е (ut) = О (предпосылка 1) и дисперсией а» (предпосылка 2);
значения зависимой переменной при фиксированных значениях объясняющих переменных xh (k = 1, т) распределены нормально или приблизительно нормально. Тогда оценки параметров регрессии bk (k = 1, ..., т) распределены нормально с математическим ожиданием и дисперсией о^. Отсюда следует, что величина
имеет стандартное нормальное распределение (см. раздел 1.7).
177
Поскольку дисперсия возмущающей переменной о*, а также дисперсии оценок параметров регрессии ofk неизвестны, вместо них используем выборочные дисперсии s% и sfk. Формула (8. ^приобретает вид:
, (8.2)
Sbk
Статистика (8.2) имеет /-распределение с п—т— 1 степенями свободы. Это следует учитывать особенно при малом объеме выборки (см. раздел 1.7).
Рис. 20. Нормальная корреляция:
а — поверхность нормального распределения; б — эллипсы рассеяния
Коэффициент корреляции вычисляется по результатам выборки. Поэтому его часто называют выборочным коэффициентом корреляции. (Для простоты слово «выборочный» мы будем часто опускать.) Итак, коэффициент корреляции является функцией от выборки. Его значения, вычисленные по результатам различных выборок, отличаются друг от друга. Следовательно, выборочный коэффициент корреляции представляет собой случайную величину с определенным распределением вероятностей. Распределение коэффициента парной корреляции можно считать приближенно нормальным при выполнении следующих условий:
1) случайные переменные у и х имеют совместное нормальное или приближенно нормальное распределение;
2) корреляционная связь между переменными не очень тесная, т. е. коэффициент корреляции не слишком близок ± 1;
3) объем выборки достаточно велик.
Первое условие приводит к так называемой нормальной корреляции, при которой переменные соединены линейным соотношением. Плотность двумерного нормального распределения изображается в системе координат поверхностью, называемой поверхностью нормального распределения (см. рис. 20, а). На рис. 20, а и 20, б параметры 178
генеральной совокупности обозначены греческими буквами. В сечении нормальной поверхности распределения плоскостями, параллельными координатной плоскости xOz, получаются кривые распределения случайной переменной х, соответствующие определенным значениям у. Аналогично в сечении нормальной поверхности распределения плоскостями, параллельными координатной плоскости yOz, получаются кривые распределения переменной у, соответствующие определенным значениям х. Кривые распределения отличаются друг от друга лишь своей крутизной. Они являются графическими изображениями условных распределений соответственно переменных х и у при фиксированных значениях у и х. Если спроецировать на плоскость хбу средние значения условных распределений переменной х и соединить линией полученные точки, то образованная таким образом линия будет называться линией регрессии х на у. Сопряженная с ней линия регрессии у на х является множеством точек, соответствующим средним значениям условных распределений переменной у.
Пересекая поверхность распределения плоскостями, параллельными координатной плоскости xOz/, в проекции на этой плоскости получаем семейство концентрических эллипсов различных размеров с одинаковой ориентацией главных осей и с общим центром в точке с координатами р,х и рс^.Их называют эллипсами рассеяния. Точка пересечения линий регрессии у на х и х на у совпадает с центром эллипсов рассеяния. Вследствие симметричности нормального распределения линии регрессии делят площадь эллипсов пополам (см. рис. 20, б).
Точное распределение выборочного коэффициента частной корреляции гу12,т такое же, как и обычного коэффициента парной корреляции, вычисленного по выборке объема п— k, где k— число исключенных переменных. При перечисленных выше условиях его можно также аппроксимировать нормальным. Распределения коэффициента множественной корреляции, корреляционного отношения и индекса корреляции, напротив, даже при выборках сравнительно большого объема сильно отличаются от нормального.
По второму условию с увеличением интенсивности корреляционной связи сходимость распределения выборочного коэффициента корреляции к нормальному уменьшается. Распределение выборочного коэффициента корреляции становится все более асимметричным. Р. Фишер указал нормализующее преобразование случайной величины г, благодаря которому распределение г может быть приближенно приведено к нормальному:
z = 0,5 In —-±—= 1,1513 lg ——-t—, (8.3)
1 —г 1 —г
где In—(натуральный) логарифм с основанием е (е = 2,71828...); 1g — десятичный логарифм (логарифм с основанием 10). При г = ± 1 соответственно z — ± оо. При г == 0 получаем z = 0.
Р. Фишер показал, что распределение величины z, отдельные реализации которой определяются соотношением (8.3), при оо асим-
17
птотич^ески нормально с параметрами
и «0,51п-Н± +------2---,
‘ 1—Р 2(п —1)
1
(8.4)
(8-5)
Рис. 21. Распределение выборочного коэффициента корреляции при р=0,6
Даже при небольших п приближение достаточно хорошее. Как видно из (8.5), стандартное отклонение crz зависит не от величины параметра р (коэффициента корреляции генеральной совокупности), а только от объема выборки п. С увеличением объема выборки oz становится меньше. Значения ^-преобразования Фишера могут быть определены с помощью таблицы логарифмов. Обратный пересчет z в г проводят с помощью соотношения
г = tanh г, (8.6) где tanh z — гиперболический тангенс от аргумента г, его можно определить по таблице логарифмов либо с помощью соотношения
г = tanh z = —
— z
—z
(8.7)
При невыполнении третьего условия, т. е.
когда объем выборки п мал, распределение выборочного коэффициента корреляции сильно отличается от нормального, что видно из рис. 21. Если р 0, то с уменьшением объема выборки увеличивается асимметричность распределения г. Это осложняет проверку надежности выборочного коэффициента корреляции.
Если коэффициент корреляции р двумерного нормального распределения равен нулю (р = 0), то в этом случае статистика / = —-----------------------------У^2
V1—г2 имеет /-распределение с /г — 2 степенями свободы.
(8.8)
8.2. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ ДЛЯ ПАРАМЕТРОВ РЕГРЕССИИ И ГЕНЕРАЛЬНОГО КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ
В предыдущих главах обсуждались точечные оценки параметров регрессии и коэффициента корреляции генеральной совокупности. Знание точных или асимптотических распределений оценок параметров регрессии и выборочного коэффициента корреляции позволяет произ-180
вести оценку значимости перечисленных статистических характеристик и построить интервальные оценки. Точечная оценка определяется одним числом, интервальная — двумя числами: концами интервала, или его границами.
Надежность оценки определяется вероятностью, с которой утверждается, что построенный по результатам выборки доверительный интервал содержит неизвестный параметр генеральной совокупности. Вероятность интервальной оценки параметра называют доверительной и обозначают Р. Доверительную вероятность обычно выбирают близкой к единице: Р = 0,95; 0,99; 0,9975 и т. д. Тогда можно ожидать, что при серии наблюдений параметр генеральной совокупности будет правильно оценен (т. е. доверительный интервал покроет истинное значение этого параметра) приблизительно в Р-100% случаев и лишь в (100—Р) % случаев оценка будет ошибочной. Если Р близка к единице, то риск ошибки ничтожен. Риск ошибки определяется уровнем значимости а, называемым также доверительным уровнем, соответствующим данному интервалу: а = 1 — Р. В экономических исследованиях чаще всего доверительная вероятность выбирается равной 0,95, или 95%. Тогда риск ошибки составляет 5% (а = 0,05). При этом также говорят о 95 % -ном доверительном интервале.
Обозначим параметр генеральной совокупности через 6, а его оценку — через d. Приведенное определение доверительного интервала записывается в виде следующей формулы:
р (d — kod 6 d + kod) = 1 — а, (8.9)
где k — так называемый доверительный множитель. Он указывает долю стандартного отклонения, которая должна быть учтена, чтобы с заранее заданной вероятностью Р доверительный интервал d ± kad покрывал параметр генеральной совокупности. Как видно из (8.9), значение k зависит от доверительной вероятности Р или от уровня значимости а. Кроме того, k зависит от объема выборки. Обычно значения k табулированы. Если при построении доверительного интервала используется статистика, имеющая нормальное распределение, то k = X— квантиль нормального распределения (см. раздел 1.7). Так, при Р = 1 — а = 0,95 по табл. 2 приложения находим значение k = K= 1,96.
Если используется статистика, имеющая /-распределение, то k = = t — квантиль распределения Стьюдента с соответствующим числом степеней свободы, f. Так, при Р = 1 — а = 0,95 и f = 1; 2; ...; оо по табл. 3 приложения находим k = t = 12,7; 4,3; ...; 1,96.
Доверительный интервал для 6 мы можем указывать в виде
[d—kGd\ d + kod] (8.10)
или
d±kodi (8.11)
где kad называется точностью оценки. Чем «лучше» оценка выбрана для параметра генеральной совокупности при прочих равных условиях, тем меньше ширина доверительного интервала.
181
Теперь перейдем от общих рассуждений к построению доверительных интервалов для параметров линейной регрессии. Заменим в (8.11) d оценкой параметра регрессии bk (k = 0, 1, ...t т). Согласно формуле (8.2) доверительный множитель k будет квантилем /-распределения, определяемым заданным уровнем значимости а и числом степеней свободы f = п — т — 1. И наконец, вместо стандартного отклонения od подставим его оценку sbfe(cM. раздел 3.6). В результате получим доверительные границы, внутри которых на заданном уровне значимости а или при доверительной вероятности Р = 1 — а содержится неизвестный параметр регрессии генеральной совокупности:
bk zfc /r—m-i; а Й — О, 1, ..., Ш, (8.12)
или доверительный интервал:
[bk ^п-т—Г, bk + tn-m—1; а (8.13)
Из (8.13) видно, что при заданном уровне значимости а ширина доверительного интервала для параметра регрессии зависит:
от числа степеней свободы и тем самым от объема выборки п. Чем больше объем выборки (или число степеней свободы), тем меньше при прочих равных условиях значение t и, следовательно, уже доверительный интервал;
от величины стандартной ошибки оценки параметра регрессии sbk. Чем меньше sbk, тем меньше при прочих равных условиях ширина доверительного интервала. В разделе 3.6 было показано, что sbh зависит От стандартной ошибки остатков su и стандартного отклонения объясняющей переменной xh (k = 1, ..., m). Отсюда мы можем сделать вывод: чем меньше su и чем больше sXk (k = 1, ..., m), тем меньше при прочих равных условиях sbh и уже доверительный интервал для параметра регрессии.
Пример
Определим доверительные границы для параметров регрессии генеральной совокупности по данным примера из раздела 2.4 (зависимость производительности труда от уровня механизации работ). Точечные оценки параметров: Ьо = 7,0356; Ь± = 0,5435. В разделе 3.6 были вычислены стандартные ошибки оценок параметров регрессии: sbo = 2,1532 и sbl = 0,0402. Зададимся уровнем значимости a = 0,05. Число степеней свободы для нашего примера f = 14 — 1 — — 1 = 12. По табл. 3 приложения находим, что /12;о,о5 “ 2,179. В соответствии с формулой (8.12) получаем следующие доверительные границы для р0:
7,0356 ± 2,179-2,1532, или
7,0356 ± 4,6918
и доверительные границы для 0Х:
0,5435 ± 2,179-0,0402, или
0,5435;± 0,0876.
182
Итак, с вероятностью 0,95 можно утверждать, что неизвестное значение параметра регрессии ро содержится в интервале
2;3438<р0< 11,7274,
а соответствующий доверительный интервал для другого параметра регрессии Pi имеет вид:
0,4559 0,6311.
Таким же образом могут быть построены доверительные интервалы для параметров частной регрессии по данным примера из раздела 2.7.
При построении доверительного интервала для коэффициента корреляции генеральной совокупности р прибегают к преобразованию Фишера (см. раздел 8.1). Подставляя выборочный коэффициент корреляции г в (8.3), получим значение z\ вычисляем по (8.5). Доверительный множитель в этом случае является квантилем стандартного нормального распределения Za. Доверительные границы для величины г на заданном уровне значимости а определяются как
2 ± (8*14)
а доверительный интервал — по формуле
[z — Xao2; z + XaoJ. (8.15)
Доверительные границы для коэффициента корреляции р находят путем обратного пересчета величины z по (8.6).
Пример
В разделе 4.1 был вычислен коэффициент корреляции между производительностью труда и уровнем механизации работ гух == 0,9687. По (8.3) найдем значение г, соответствующее данному коэффициенту корреляции:
2=1,1513 lg -l+-°-^8Z- = 2.07077.
1—0,9687
По (8.5) вычислим az:
az = —1-----= 0,3015.
V14—3
При уровне значимости a = 0,05 квантиль нормального распределения 1005 = 1,96. Доверительные границы для величины z при Р = 0,95 будут ’ следующими:
2,07077 ± 1,96-0,3015 или
2,07077 ± 0,5909, и доверительный интервал
[1,47987: 2,66167].
183
С помощью (8.6) производим обратный пересчет z в г: tanh 1,47987 - 0,9014, tanh 2,66167 = 0,9903.
Итак, с вероятностью 0,95 можно утверждать, что коэффициент корреляции генеральной совокупности содержится в интервале
0,9014 0,9903.
8.3. ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ ДЛЯ УСЛОВНОГО МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ
Как отмечалось ранее, значения регрессии являются по своему характеру усредненными величинами, подсчитанными на основании полученной эмпирической регрессионной связи при каждом фиксиро-
Рис. 22. Теоретическая и эмпирическая регрессионные прямые
ванном значении объясняющей переменной (см. раздел 2.3). Как все средние, каждое значение регрессии—случайная величина. Выборочные средние подвержены рассеянию вокруг среднего генеральной совокупности, ко-торое в данном случае является истинным значением частного среднего исследуемой зависимой переменной (условное математическое ожидание). Воспользуемся формулой (2.74):
7 £(у/Х) = ХР = у\ (8.16)
В математической статистике под регрессией случайной пере-
менной у на переменные xh понимают условное математическое ожидание £ (у/X). Истинное значение регрессии генеральной совокупно-
сти в точке i равно:
Уг Ро + Р1Лг1 + ••• + X/fJ, i 1, ..., М, (8.17)
где x'i — i-я вектор-строка матрицы X.
По (2.42) получаем:
Hi = b0 + + ... + bmxim = х'Д I = 1, ..., п, (2.42)
где yt — оценка значения регрессии в точке I, полученная по методу наименьших квадратов при фиксированных значениях объясняющих переменных xh (£ == 1, ..., m).
Рассмотрим простую линейную регрессию. На диаграмме рассеяния, приведенной на рис. 22, изображена истинная (теоретическая) регрессионная прямая генеральной совокупности и эмпирическая регрессионная прямая, полученная в результате МНК-оценки функции
184
регрессии. В силу того что оценивание параметров осуществляется по результатам выборки, оценки Ьо и Ьг содержат некоторую погрешность. Погрешность в значении Ьо приводит к параллельному смещению линии регрессии, а колеблемость оценки Ь± — к вращению линии регрессии вокруг точки с координатами (yt xk).
Как видно из рис. 22, между истинным значением регрессии yt и его оценкой yi существует разность
Разделим эту разность регрессии г/г: Уг — Уь . (8.18) на оценку стандартного отклонения значения У\/г- (8.19) yi
Эта величина имеет /-распределение с числом степеней свободы f = = п — т — 1. При построении доверительного интервала для yt используется стандартное отклонение s- (см. формулу (8.11)). Оценка дисперсии значений простой линейной регрессии будет следующей:
(8.20)
Обобщая это выражение для множественной регрессии, запишем оценку дисперсии в матричной форме:
s^s^xHX'X)-1^. (8.21)
Извлекая из (8.20) и (8.21) корень квадратный, получим искомое стан-
дартное отклонение значения регрессии у^
Из формулы (8.20) видно, что s~ зависит от фиксированного зна-у i
чения Х{ объясняющей переменной х. Поэтому для каждого значения регрессии si различны. При прочих равных условиях (одинаковые УI —
п и 2 (хг — х)2) значение s}- тем меньше, чем больше хг приближа-I _ Ji
ется к среднему х, и, наоборот, s~ тем больше, чем дальше удалено _ _ У i
Xi от х. При Xi = х получаем
si =s2 —. (8.22) Уъ п
В этой точке достигает минимума. При xt = 0 с учетом (3.45)
имеем _2 si = s^- + * --^4 (8.23) У1 1 П 1
185
Эти соображения сохраняют свою силу и для случая множественной л и ней ной регресси и.
Теперь приступим непосредственно к построению доверительного интервала, который при заданном уровне значимости а покрывает истинное значение регрессии (условное математическое ожидание переменной у). Интервальная оценка истинных значений регрессии производится при фиксированных значениях объясняющих переменных X/. Исходя из (8.11) получим доверительные границы для значения регрессии yt:
Vt ± (8.24)
где s- — корень квадратный из выражения (8.20) или (8.21), а tfta — квантиль /-распределения при заданном уровне значимости а и числе степеней свободы f = п — т — 1.
Доверительный интервал для одного истинного значения регрессии yi при заданном уровне значимости а и фиксированных значениях объясняющих переменных хг' будет следующим:
Уъ tfivSyi = У г = Уг 4" i (8.25)
С вероятностью Р = 1 — а можно утверждать, что значение регрессии генеральной совокупности (истинное значение частнопГсред-него зависимой переменной) при фиксированных значениях объясняющих переменных >х! находится в этом интервале.
Решим подобную задачу для простой линейной регрессии. Определим доверительные границы для истинных значений регрессии при всех мыслимых значениях объясняющей переменной. Отложим вычисленные границы на графике вверх и вниз от соответствующих значений эмпирической (выровненной) линии регрессии. При соединении точек получим две гиперболы, между ветвями которых находится «коридор» с эмпирической линией регрессии. При прочих равных условиях доверительный интервал в точке xih = xk для всех k = 1, ..., т самый узкий. Чем дальше наблюдения над объясняющими переменными удалены от их средних, тем шире доверительный интервал.
Пример
Вернемся к примеру из раздела 2.4, где было построено уравнение линейной регрессии, выражающей зависимость производительности труда’от^уровня^механизации работ. Определим доверительные границы для истинных значений регрессии при всех наблюдениях Xi (i = 1, ..., 14). Составим рабочую таблицу, используя^формулу (8.20). Для нашего примера х = 51,71%, su = 2,0869, п = 14. Находим квантиль’ //>а распределения Стьюдента при а’= 0,05 и f= 14— 1 — — 1 = 12 степенях^свободы: /12; 0,05 ='2,179. В столбце 2 табл. 16 приведены значения’переменной х (наблюдения м f-х точках). В столбце 3 помещены вычисленные’в разделе 2.4 значения регрессии. Столбец 5 содержит стандартные ошибки отдельных значений регрессии, а”в столбцах 7 и 8 указаны соответственно нижние и верхние доверительные границы. Например, при х±= 32% уровня механизации работ ис-
186
Таблица 16
Определение доверительных границ для истинных значений простой линейной регрессии
1 2 3 4 5 6 7 8
1 xi s«i *1 2; 0,05 Syi У— “*12; 0,05 ^i+*12:0,05
1 32 24,4276 388,4841 0,9692 2,1119 22,3157 26,5395
2 30 23,3406 471,3241 1,0360 2,2575 21,0831 25,5981
3 36 26,6016 246,8041 0,8428 1,8364 24,7652 28,4380
4 40 28,7756 137,1241 0,7299 1,5905 27,1850 30,3662
5 41 29,3186 114,7041 0,7047 1,5356 27,7830 30,8542
6 47 32,5806 22,1841 0,5890 1,2835 31,2971 33,8641
7 56 37,4716 18,4041 0,5838 1,2722 36,1994 38,7438
8 54 36,3846 5 ,2441 0,5653 1,2318 35,1528 37,6164
9 60 39,6456 68,7241 0,6498 1,4159 38,2297 41,0615
10 55 36,9276 10,8241 0,5732 1,2491 35,6785 38,1767
11 61 40,1896 86,3041 0,6713 1,4628 38,7268 41,6524
12 67 43,4496 233,7841 0,8302 1,8089 41,6407 45,2585
13 69 44,5376 298,9441 0,8914 1,9424 42,5952 46,4800
14 76 48,3416 590,0041 1,1249 2,4511 45,8905 50,7927
2 2692,8574
15 51 34,7541 0,5041 0,5585 1,2169 33,5372 35,9710
16 78 49,4286 691,1641 1,1954 2,6047 46,8239 52,0333
тинное значение регрессии генеральной совокупности с доверительной вероятностью 0,95 будет находиться в интервале
22,3157 т/ч 26,5395 т/ч.
Как упоминалось раньше, регрессионный анализ нашел широкое применение в прогнозировании. Прогноз получают путем подстановки в регрессионное уравнение с численно оцененными параметрами значений объясняющих переменных. При этом утверждается, что данное соотношение между переменными с присущим ему разбросом фактических значений имеет место и при новых условиях. Прогностическая оценка может быть получена для значений, приходящихся на исследованный диапазон изменения объясняющих переменных (задача интерполяции), и для значений, выходящих за границы этого диапазона (задача экстраполяции). При экстраполяции действие найденного соотношения в виде уравнения регрессии распространяется за рамки тех условий, при которых*оно получено. Построенные доверительные интервалы для условных математических^ожиданий можно также использовать в прогнозировании. Расчет доверительных интервалов позволяет определить область, в которой следует ожидать значение прогнозируемой величины.
Пусть требуется оценить^средний уровень производительности труда на двух других однородных предприятиях той же отрасли промышленности по значениям коэффициента механизации работ (переменная
187
х) на основе регрессионного уравнения, построенного для 14 предприятий. Значения переменной х для этих двух предприятий приведены в табл. 16 в строках 15 и 16. Для х15 получаем прогностическое значение в результате интерполяции, а для х16 — в результате экстраполяции.
На этом примере можно еще раз убедиться в том, что доверительный интервал при прочих равных условиях тем уже, чем ближе расположено к %, и, наоборот, доверительный интервал тем шире, чем 1 наблюдение xt дальше удалено от х. Вычисленные доверительные границы для значений регрессий нанесены на график, приведенный в разделе 8.4 (см. рис. 23).
8.4. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ ДЛЯ ОТДЕЛЬНЫХ
ЗНАЧЕНИЙ ЗАВИСИМОЙ ПЕРЕМЕННОЙ у
Часто для исследователя представляет интерес доверительный интервал не для средних, а для индивидуальных значений зависимой переменной. В данном разделе речь пойдет об установлении доверительных границ, внутри которых с некоторой степенью достоверности, обусловленной заданным уровнем значимости а, будет расположено отдельное значение зависимой переменной, соответствующее значениям переменных хг. Доверительные интервалы для отдельных значений зависимой переменной широко используются в прогнозировании. Поэтому в литературе их часто называют доверительными интервалами для прогнозов индивидуальных значений
Пусть имеются совместные наблюдения над переменными xh (k = = 1, ..., tri) в точке i, которые записываются в виде элементов вектора х/. Для гипотетического значения некоторого показателя (значения зависимой переменной), которое может реализоваться в будущем при некоторых заранее оговоренных условиях, имеющих наибольшую вероятность, используется термин «прогноз». Из сказанного следует, что прогноз связан с условным утверждением в том смысле, что он обусловлен значениями переменных X/.
Рассмотрим вначале приближенный способ построения доверительных границ для z/j. Определив отклонения отдельных значений |аД = ~ 1У/ — Уг1, вычислим по ним среднее:
2 Ь/-т\
а = . (8.26)
п
Формула (8.26) по своей структуре напоминает среднее линейное отклонение (см. раздел 1.5). При нанесении на график tji ± а или Уг ± 2а для всех i получим прямые, параллельные регрессионной прямой. Они представляют собой доверительные границы для всех наблюдений i переменной у. Преимущество этого способа заключается в простоте вычислений. Но он обладает существенным недостатком: мы не можем указать степень достоверности соблюдения этих границ.
188
При другом способе построения доверительных границ для отдельного результата наблюдения yt учитывается стандартное отклонение остатков (стандартная ошибка остатков) su. Предполагая нормальное распределение остатков, получим следующие доверительные границы:
//z±^asu> (8.27)
и доверительный интервал для прогнозов индивидуальных значений yt:
ЦН ^asu’i Уг 4" (8.28)
где — квантиль нормального распределения при заданном уровне значимости а. Например, с вероятностью 0,95 можно ожидать, что фактическое значение yt при данных наблюдениях объясняющих переменных будет находиться внутри границ yt ± 1,96 su. Возможна и такая интерпретация: если отдельное значение переменной у окажется вне этих границ, то с вероятностью 0,95 можно предположить, что это значение не принадлежит исследуемой совокупности, т. е. оно не типично для изучаемой связи.
Так как значения регрессии yt и su являются оценками, то по (8.27) мы получаем только приближенные выражения доверительных границ. При третьем способе построения доверительных границ для отдельного наблюдения уг исходят из оценки регрессии. Этот способ наиболее точный и математически корректный. Прогностическое значение yi переменной у можно представить в виде
yi =~У1 + Щ. (8.29)
Мы располагаем лишь его оценкой (значением регрессии) на основе построенной регрессии. Допущенная при этом ошибка определяется как разность:
ei = yi~yi- (8-30)
Эта ошибка часто называется ошибкой прогноза, и для ее отличия от других типов ошибок мы вводим новое обозначение — е. С учетом (8.29) имеем
et = yt + tit — yi (8.31)
или
Si = Qi — yi) + Hi. (8.32)
Выражение в скобках в правой части равенства (8.32) представляет собой разность между истинным значением регрессии и его оценкой г/j, с которой мы познакомились в разделе 8.3. Второе слагаемое в правой части (8.32) — остаток оценки регрессии в точке i. Возведя в квадрат обе части равенства и определив математическое ожидание полученных выражений, найдем
se2. = s*+s*, (8.33)
1 «i
189
где s* — оценка дисперсии ошибки прогноза в точке xf; s~ — оцен-I 9 1
ка дисперсии значения регрессии в точке и Su — дисперсия остатков. Вместо s- подставим в (8.33) формулу (8.20) или (8.21) из раздела
8.3. В итоге при простой линейной регрессии получим следующее выражение для оценки дисперсии ошибки прогноза:
или
Для множественной линейной регрессии имеем
$?. = s3x; (X'X)-i X, +s* или
si. - S* (1 +x; (X'X)-ixf). (8.35)
Теперь можно приступить к построению доверительных границ для отдельного наблюдения yt. Поскольку величина
Уг —Уг set
имеет /-распределение c,f~n — т — 1 степенями свободы, то по аналогии с (8.11) запишем выражение доверительных границ для отдельного результата наблюдения yt\
Уг dz /у, а •%, (8.36)
где se. — стандартное отклонение ошибки прогноза (корень квадратный из (8.34) или (8.35)), а /у>а — квантиль /-распределения при f = = п — т — 1 степенях свободы и уровнё значимости а. Доверительный интервал для прогностической оценки yt будет следующим:
а^’, yi + /у,а^|1* (8.37)
Относительно этого интервала с вероятностью Р = 1 — а можно утверждать, что он содержит фактическое значение зависимой переменной уj, соответствующее совместным наблюдениям над объясняющими переменными х/, или в среднем (1 — а) 100% всех возможных значений у/, соответствующих xz:, попадут в этот интервал.
При данном уровне значимости а ширина интервала прогноза снова зависит от объема выборки п, стандартной ошибки остатков su, стандартного отклонения объясняющей переменной sXk (k == 1, ..., т) и (это особенно следует здесь подчеркнуть) от совместных наблюдений над объясняющими переменными в точке i (х,-). Таким образом, наш вывод относительно ширины интервала совпадает с рассуждениями в разделах 8.2 и 8.3.
190
Если нанести на график доверительные границы для прогнозов индивидуальных значений yt для всех Z, то они расположатся выше и ниже линии регрессии в виде ветвей гипербол, ограничивая доверительную зону для yt. Можно снова убедиться в том, что при Xtk = xk для всех k = 1, ..., т доверительный интервал для yi самый узкий. Чем дальше наблюдения объясняющих переменных удалены от своих средних, тем Гшире соответствующий интервал.
30 40 50 60 70 80 X
Рис. 23. Доверительные границы для истинных значений регрессии и для отдельных значений переменной у при простой линейной регрессии
На рис. 23 видно, что доверительный интервал для прогнозов индивидуальных значений уг- включает доверительный интервал для истинных значений регрессии.
Пример
Продолжим рассмотрение примера из раздела 8.3. Определим для зависимости производительности труда от уровня механизации работ доверительные границы^для отдельных значений у^
Таблица 17
Определение доверительных границ для прогнозов индивидуальных значений у t в случае простой линейной регрессии
1 2 3 4 5
1 ч- О2;0,05 *1 2;0,05 « 4^+h2;0,05 set
1 2,3010 5,0139 19,4137 29,4415
2 2,3299 5,0768 18,2636 28,4174
3 2,2507 4,9042 21,6974 31,5058
4 2,2109 4,8176 23,9580 33,5932
5 2,2027 4,7997 24,5189 34,1183
6 2,1685 4,7251 27,8555 37,3057
7 2,1671 4,7220 32,7496 42,1936
8 2,1621 4,7113 31,6733 41,0959
9 2,1858 4,7628 34,8828 44,4084
10 2,1642 4,7159 32,2117 41,6435
11 2,1923 4,7769 35,4127 44,9665
12 2,2460 4,8940 38,5556 48,3436
13 2,2693 4,9449 39,5927 49,4825
14 2,3708 5,1659 43,1757 53,5075
15 2,1604 4,7075 30,0466 39,4616
,6 2,4050 5,2406 44,1880 54,6692
191
В столбце 2 табл. 17 указаны стандартные отклонения ошибок прогноза для результатов наблюдений над переменной х, приведенных в столбце 2 табл. 16. Столбцы 4 и 5 табл. 17 содержат нижние и верхние доверительные границы для наблюдений Например, с вероятностью 0,95 можно ожидать, что фактическое значение уг зависимой переменной у для наблюдения х± = 32% будет находиться в интервале [19, 4137 т/ч; 29,4415 т/ч]. Другими словами, при заданной величине коэффициента механизации работ хг = 32% в среднем 95% значений переменной у следует ожидать в этом интервале. Если мы будем рассматривать другие предприятия этой отрасли промышленности, имеющие коэффициент механизации работ 32%, то с вероятностью 0,95 можно предполагать, что уровень производительности труда на этих предприятиях будет находиться в пределах между 19,41 т/ч и 29,44 т/ч.
В табл. 17 указаны также доверительные границы для значения переменной у в точках i = 15 и i = 16, полученные путем интерполяции и экстраполяции значения объясняющей переменной х. Таким образом, можно оценить или предсказать уровень производительности труда на любом предприятии, однородном с исследованными, если известно значение показателя механизации работ на нем.
8.5. ПРОВЕРКА ЗНАЧИМОСТИ
КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ
Как неоднократно отмечалось, для статистического вывода о наличии или отсутствии корреляционной связи между исследуемыми переменными необходимо произвести проверку значимости выборочного коэффициента корреляции. В связи с тем что надежность статистических характеристик, в том числе и коэффициента корреляции, зависит от объема выборки, может сложиться такая ситуация, когда величина коэффициента корреляции будет целиком обусловлена случайными колебаниями в выборке, на основании которой он вычислен. При существенной связи между переменными коэффициент корреляции должен значимо отличаться от нуля. Если корреляционная связь между исследуемыми переменными отсутствует, то коэффициент корреляции генеральной совокупности р равен нулю. При практических исследованиях, как правило, основываются на выборочных наблюдениях. Как всякая статистическая характеристика, выборочный коэффициент корреляции является случайной величиной, т. е. его значения случайно рассеиваются вокруг одноименного параметра генеральной совокупности (истинного значения коэффициента корреляции). При отсутствии корреляционной связи между переменными у и х коэффициент корреляции в генеральной совокупности равен нулю. Но из-за случайного характера рассеяния принципиально возможны ситуации, когда некоторые коэффициенты корреляции, вычисленные по выборкам из этой совокупности, будут отличны от нуля.
Могут ли обнаруженные различия быть приписаны случайным колебаниям в выборке или они отражают существенное изменение условий формирования отношений между переменными? Если значения выборочного коэффициента корреляции попадают в зону рассеяния, 192
обусловленную случайным характером самого показателя, то это не является доказательством отсутствия связи. Самое большее, что при этом можно утверждать, сводится к тому, что данные наблюдений не отрицают отсутствия связи между переменными. Но если значение выборочного коэффициента корреляции будет лежать вне упомянутой зоны рассеяния, то делают вывод, что он значимо отличается от нуля, и можно считать, что между переменными у и х существует статистически значимая связь. Используемый для решения этой задачи критерий, основанный на распределении различных статистик, называется критерием значимости.
Процедура проверки значимости начинается с формулировки нулевой гипотезы Hq. В общем виде она заключается в том, что между параметром выборки и параметром генеральной совокупности нет каких-либо существенных различий. Альтернативная гипотеза Н1 состоит в том, что между этими параметрами имеются существенные различия. Например, при проверке наличия корреляции в генеральной совокупности нулевая гипотеза заключается в том, что истинный коэффициент корреляции равен нулю (Яо : р = 0). Если в результате проверки окажется, что нулевая гипотеза не приемлема, то выборочный коэффициент корреляции гух значимо отличается от нуля (нулевая гипотеза отвергается и принимается альтернативная Нг). Другими словами, предположение о некоррелированности случайных переменных в генеральной совокупности следует признать необоснованным. И наоборот, если на основе критерия значимости нулевая гипотеза принимается, т. е. гух лежит в допустимой зоне случайного рассеяния, то нет оснований считать сомнительным предположение о некоррелированности переменных в генеральной совокупности.
При проверке значимости исследователь устанавливает уровень значимости а, который дает определенную практическую уверенность в том, что ошибочные заключения будут сделаны только в очень редких случаях. Уровень значимости выражает вероятность того, что нулевая гипотеза HQ отвергается в то время, когда она в действительности верна. Ясно, что имеет смысл выбирать эту вероятность как можно меньшей.
Пусть известно распределение выборочной характеристики, являющейся несмещенной оценкой параметра генеральной совокупности. Выбранному уровню значимости а соответствуют под кривой этого распределения заштрихованные площади (см. рис. 24). Незаштрихо-ванная площадь под кривой распределения определяет вероятность Р = 1 — а. Границы отрезков на оси абсцисс под заштрихованными площадями называют критическими значениями, а сами отрезки образуют критическую область, или область отклонения гипотезы.
При процедуре проверки гипотезы выборочную характеристику, вычисленную по результатам наблюдений, сравнивают с соответствующим критическим значением. При этом следует различать одностороннюю и двустороннюю критические области. Форма задания критической области зависит от постановки задачи при статистическом исследовании. Двусторонняя критическая область необходима в том случае, когда при сравнении параметра выборки и параметра генеральной со-7 Зак. пц 193
вокупности требуется оценить абсолютную величину расхождения между ними, т. е. представляют интерес как положительные, так и отрицательные разности между изучаемыми величинами. Когда же надо убедиться в том, что одна величина в среднем строго больше или меньше другой, используется односторонняя критическая область (право-или левосторонняя). Вполне очевидно, что для одного и того же критического значения уровень значимости при использовании односторонней критической области меньше, чем при использовании двусторонней. Если распределение выборочной характеристики симметрич-
Рис. 24. Проверка нулевой гипотезы Но
но, то уровень значимости двусторонней критической области равен а, а односторонней — у (см. рис. 24). Ограничимся лишь общей постановкой проблемы. Более подробно с теоретическим обоснованием проверки статистических гипотез можно познакомиться в специальной литературе. Далее мы лишь укажем критерии значимости для различных процедур, не останавливаясь на их построении.
Проверяя значимость коэффициента парной корреляции, устанавливают наличие или отсутствие корреляционной связи между исследуемыми явлениями. При отсутствии связи коэффициент корреляции генеральной совокупности равен нулю (р = 0). Процедура проверки начинается с формулировки нулевой и альтернативной гипотез:
Но : различие между выборочным коэффициентом корреляции г и р = 0 незначимо,
Н± : различие между г и р = 0 значимо, и следовательно, между переменными у и х имеется существенная связь. Из альтернативной гипотезы следует, что нужно воспользоваться двусторонней критической областью.
В разделе 8.1 уже упоминалось, что выборочный коэффициент корреляции при определенных предпосылках связан со случайной величиной tf подчиняющейся распределению Стьюдента с f = п — 2 степенями свободы. Вычисленная по результатам выборки статистика
— г ~2
(8.38)
~|/1
сравнивается с критическим значением, определяемым по таблице распределения Стьюдента при заданном уровне значимости а и f = п — 2 степенях свободы. Правило применения критерия заключается в следующем: если |/| > //>а, то нулевая гипотеза на уровне значимости а отвергается, т. е. связь между переменными значима; если |/| /Ла, то нулевая гипотеза на уровне значимости а принимается. Отклонение значения г от р — 0 можно приписать случайной вариации. Данные выборки характеризуют рассматриваемую гипотезу как весьма возможную и правдоподобную, т. е. гипотеза об отсутствии связи не вызывает возражений.
Процедура проверки гипотезы значительно упрощается, если вместо статистики t воспользоваться критическими значениями коэффициента корреляции, которые могут быть определены через квантили распределения Стьюдента путем подстановки в (8.38) t = /^ а и г = рд а:
Pf,g~ r_ tha— (8.39)
Существуют подробные таблицы критических значений, выдержка из которых приведена в приложении к данной книге (см. табл. 6). Правило проверки гипотезы в этом случае сводится к следующему: если г > ру,а, то можем утверждать, что связь между переменными существенная. Если г^ру,а, то результаты наблюдений считаем непротиворечащими гипотезе об отсутствии связи.
Пример
Проверим гипотезу о независимости производительности труда от уровня механизации работ при а = 0,05 по данным, приведенным в разделе 4.1. Ранее было вычислено, что гух = 0,9687. По (8.38) получаем
t =..^УЕ1. = 1з>52.
"|/1 — 0,96872
По таблице распределения Стьюдента для а = 0,05 и f = 12 находим критическое значение этой статистики: /12; 0>05 = 2,179. Поскольку / > /12; о,о5» нулевую гипотезу отвергаем, допуская ошибку лишь в 5% случаев.
Мы получим тот же результат, если будем сравнивать гух — 0,9687 с критическим значением коэффициента корреляции р12; о,о5 = 0,5324, найденным по соответствующей таблице при а = 0,05 и f = 12.
Если нельзя предположить, что р = 0, то не рекомендуется применять формулы (8.38) и (8.39), так как распределение г асимметрично (см. раздел 8.1). В этом случае применяют ^-преобразование Фишера. Учитывая (8.3) и (8.5), получаем статистику
t=^S- = \, 151311g 2±£-1б2±Р-|-|6ГТз, (8.40)
az I г 1—р |
которая имеет /-распределение с f = п — 2 степенями свободы. Далее процедура проверки значимости г проводится аналогично предыдущей с помощью /-критерия.
7* 195
Пример
Исходя из экономического анализа явлений предполагаем в генеральной совокупности сильную связь между производительностью труда и уровнем механизации работ. Пусть, например, р = 0,8. В качестве альтернативной в этом случае можем выдвинуть гипотезу Нг : р > 0,8, так как выборочный коэффициент корреляции гух = 0,9687. Таким образом, мы должны воспользоваться односторонней критической областью. Из (8.40) следует, что
/= 1,1513 1g
1 +0,9687 1—0,9687
lg-1+М 1—0,8
V14 —3 = 3,22.
Полученное значение t сравниваем с критическим значением /12; 0,05 ~ = 1,782. Имеем t >* /12; 0,05- Таким образом, на уровне значимости 5% можно предполагать наличие очень тесной связи между изучаемыми признаками, т. е. исходные данные позволяют считать правдоподобным, что р = 0,8.
Значимость коэффициентов частной корреляции проверяется аналогичным путем. Изменяется только число степеней свободы, которое становится равным f = п — т — 1, где т — количество объясняющих переменных. Значение статистики, вычисленное по формуле
У1-Г2
сравнивается с критическим значением tf, а, найденным по таблице /-распределения при уровне значимости а и числе степеней свободы f = п — т — 1. Принятие или отклонение гипотезы о значимости коэффициента частной корреляции производится по тому же правилу, что было описано выше. Проверку значимости можно осуществить также с помощью критических значений коэффициента корреляции по (8.39), а также используя ^-преобразование Фишера (8.40).
Пример
Проверим статистическую надежность коэффициентов частной корреляции, вычисленных в разделе 4.5, на уровне значимости а = 0,05. Ниже, наряду с коэффициентами частной корреляции, приведены соответствующие им расчетные и критические значения статистики /:
= 0,9657, /=12,33 /11; 0,05 = 2,201,
^2.1=0,3242, / = 1,14, /11; 0,05 = 2,201,
г z/i.23 ~ 0,9581, /=10,58, /10; 0,05 = 2,228,
Г2/2.13 ~ 0,3015, / = 0,99, /10; 0,05 — 2,228,
г уз-12 — —0,4229, / = —1,475 /10; 0,05 — 2,228.
В связи с тем что при а = 5% принимается гипотеза о значимости коэффициентов гу1в2 и ryl23f делаем вывод: уровень механизации работ оказывает существенное влияние на производительность труда при исключении влияния среднего возраста работников (и среднего процента выполнения норм). Отличие от нуля остальных коэффициентов
196
частной корреляции может быть отнесено’за счет случайных колебаний в выборке, и поэтому по ним мы не можем сказать ничего определенного о частных влияниях соответствующих переменных.
О значимости коэффициента множественной корреляции судят по результату осуществления процедуры проверки значимости коэффициента множественной детерминации. Более подробно мы обсудим это в следующем разделе.
Часто представляет интерес вопрос: значимо ли отличаются друг от друга два коэффициента корреляции? При проверке этой гипотезы предполагается, что
рассматриваются одни и те же признаки однородных совокупностей; данные представляют собой результаты независимых испытаний; применяются коэффициенты корреляции одного типа, т. е. либо коэффициенты парной корреляции, либо коэффициенты частной корреляции при исключении одинакового количества переменных.
Объемы двух выборок, по которым вычисляются коэффициенты корреляции, могут быть различны. Нулевая гипотеза: Но : р*1) = р<2\ т. е. коэффициенты корреляции двух рассматриваемых совокупностей равны. Альтернативная гипотеза: Нг : р(1> р(2). Из альтернативной
гипотезы следует, что должна быть использована двусторонняя критическая область. Другими словами, следует проверить, значимо ли отличается от нуля разность А1) — г<2\ Воспользуемся статистикой, имеющей приближенно нормальное распределение:
х ------=====, (8.42)
j/" —3 П2 — 3
где Zj и г2 — результаты z-преобразований коэффициентов корреляции r(i) и г<2); ил2 — объемы выборок. Правило проверки: если X > Ха, то гипотеза HQ отвергается; если то гипотеза Но принимается.
В случае принятия Но величина
2— Z1 ---3)+?2 (П2-3) /g 4g)
«i + «2—6
после обратного пересчета в г с помощью (8.6) служит сводной оценкой коэффициента корреляции р<4 = р<2> = р. Далее может быть проверена гипотеза Но : р = 0 с помощью статистики
+ — 6 , (8.44)
имеющей нормальное распределение.
Пример
Пусть требуется установить при а = 0,05, различна ли теснота связи между производительностью труда и уровнем механизации работ на предприятиях одной отрасли промышленности, расположенных в различных районах страны. Сравним предприятия, находящиеся в двух районах. Пусть для одного из них коэффициент корреляции rfy = = 0,9687 вычислен по выборке объема — 14 (см. раздел 4.1). Для Другого района г$ = 0,885 вычислен по выборке объема = 20.
197
После перевода обоих коэффициентов корреляций в z-величины вычислим по (8.42) значение статистики X:
. 2,0708—1,3984 , „„„
Л =------ ' -....... — = 1.7377.
1Л —-— +—-—
I/ 14—3 20—3
Критическое значение статистики при а = 0,05 составляет Хо 05 = = 1,96. Таким образом, гипотеза принимается, т. е. на основе имеющихся выборок мы не можем установить значимого различия между коэффициентами корреляции. При этом оба коэффициента корреляции значимы.
Используя (8.43) и (8.6), получим сводную оценку коэффициента корреляции для двух районов:
* = 2,0708 (14-3) + 1,3984 (20—3) = } бб25
144-20—6 г = tanh 1,6625 = 0,9305.
Наконец, проверим гипотезу, значимо ли отличается от нуля сводная оценка коэффициента корреляции с помощью статистики (8.44):
Л. = 1,66251/14 4- 20 — 6 = 8,80.
Так как Л0>05 = 1,96, при а — 5% можем утверждать, что в генеральной совокупности имеется существенная связь между производительностью труда и уровнем механизации работ.
Критерий X может быть использован в различных аспектах. Так, вместо районов могут рассматриваться различные отрасли промышленности, например когда требуется определить, значимы ли различия по силе исследуемых связей между экономическими показателями предприятий, принадлежащих двум различным отраслям.
Пример
Пусть на основе двух выборок объема и п2 вычислены коэффициенты корреляции Гух = 0,9687 и г$ = 0,9953, характеризующие тесноту связи между производительностью труда и уровнем механизации работ на предприятиях, принадлежащих двум отраслям промышленности (двум генеральным совокупностям). По (8.42) получим
. I 2,0708—3,0255 |
Л............
____________ -2,4673.
1/ —-—+—-— У 14—3 20 — 3
Так как Х0>05 = 1,96, при а = 0,05 нулевую гипотезу отвергаем. Следовательно’ можно утверждать, что имеются значимые различия в тесноте связи между производительностью труда и уровнем механизации работ на предприятиях, относящихся к различным отраслям промышленности. Этот пример продолжим в разделе 8.7, где будет произведено сравнение регрессионных прямых, построенных для двух совокупностей.
Анализируя приведенные примеры, убеждаемся, что рассмотрение только абсолютной разницы сравниваемых коэффициентов корреляций
198
(объемы выборок пх и п2 в обоих случаях одинаковы) без проверки значимости этой разницы приведет к ошибочным заключениям. Это подтверждает необходимость пользоваться статистическими критериями при сравнении коэффициентов корреляции.
Процедуру сравнения двух коэффициентов корреляции можно обобщить на большее число коэффициентов при соблюдении указанных выше предпосылок. Гипотеза равенства s коэффициентов корреляции между переменными у и х выражается следующим образом: Яо • Р(1) = Р(2) = ... = P(s) = Р- Она проверяется на основе коэффициентов корреляции г(1>, г(2>, ..., вычисленных по выборкам объема п19 п2, ..., ns из s генеральных совокупностей. По(8.3) производится пересчет коэффициентов корреляций в г-величины: zx, г2, ..., zs. Так как р в общем случае неизвестен, находим его оценку через z по формуле, являющейся обобщением (8.43):
2 3)
+. (8.45)
2 з) /-1
Далее для проверки однородности выборочных коэффициентов корреляции используется статистика
Х2 = 1 (г7-~г)3(п~3), (8.46)
i=l
имеющая х2-распределение с f = s — 1 степенями свободы. Вычислен ное значение статистики сравнивается с критическим х2, а, найденным по таблице х2-распределения. Если Х2>Хр, а, на уровне значимости а гипотеза HQ отвергается. Если х2 = Хл«, гипотеза Но принимается.
В последнем случае можно сделать пересчет г, полученного по (8.45), в значение г по (8.6). Определенное таким образом г представляет собой сводную оценку коэффициента корреляции для всех s генеральных совокупностей.
Пример
В условиях примера, приведенного на с. 197, дополнительно рассмотрим коэффициенты корреляции, вычисленные для групп предприятий, расположенных в третьем и четвертом районах. Пусть Гур = 0,92;
0,85; п3 = 18; = 16. В соответствии с (8.45) и (8.46) полу-
чаем
- _ 2,0708-И + 1,3984-17+ 1,589-15+ 1,2562-13 = } 54g5. ~ 11 + 17+15+13
X2 = 0,2728-11 + 0,0225-17 + 0,0016-15 + 0,0854-13 - 4,5175.
По табл. 5 приложения находим Хз; o.os = 7,815. Так как х2 < Хз; о,об> нулевая гипотеза принимается. Данные выборок по четырем районам не позволяют признать существенными различия в тесноте связей между исследуемыми переменными. Поскольку нулевая гипотеза об однородности выборочных коэффициентов корреляции принята, можно най
199
ти сводную оценку коэффициента корреляции для четырех районов.
Для этого сделаем пересчет z-значения в г по (8.6):
г = tanh 1,5485 = 0,914.
Далее можно произвести проверку гипотезы, значимо ли отличается полученная сводная оценка коэффициента корреляции от нуля. Но по причине экономии места мы отказываемся от описания этой процедуры.
Кроме того, сводные оценки коэффициентов корреляции, вычисленные для нескольких районов, можно сравнить по различным отраслям промышленности. Критерий однородности коэффициентов корреляции позволяет произвести глубокий экономический анализ исследуемых явлений.
Рассмотрим теперь критерий для проверки значимости коэффициента ранговой корреляции rs Спирмэна. Нулевая гипотеза заключается в следующем: ZZ0 : ps = 0. Если в генеральной совокупности рз = 0, то можно показать, что распределение выборочного коэффициента ранговой корреляции rs при объеме выборки п 10 связано с /-распределением. А именно статистика
'=г-1/1|г (««)
имеет /-распределение с f = п — 2 степенями свободы. Если t > /у>а, то гипотеза HQ отвергается. Если /§/у>а, то гипотеза Но не противоречит результатам наблюдений. Таким’образом, процедура проверки значимости коэффициента ранговой корреляции Спирмэна аналогична той же процедуре с обычным коэффициентом парной корреляции.
Значимость коэффициента ранговой корреляции т Кендэла при объеме выборок п 10 проверяется с помощью статистики
X =----- т , (8.48)
которая имеет асимптотически нормальное распределение. Если X > %а, то на заданном уровне значимости нулевая гипотеза отвергается. Если то нулевая гипотеза принимается. Для нашего примера из раздела 7.2 по (8.48) имеем
Х =----- °’778 = 3.131.
/~ 2(2-10 + 5) |/ 9-10(10—1)
По табл. 2 приложения для а = 0,05 находим %0>05 = 1,96. Сравнивая расчетное значение с критическим (3.131 >’1,96), убеждаемся в том, что нулевую гипотезу следует отвергнуть. Итак, по десяти ранговым значениям можно сделать вывод о наличии существенной связи между производительностью труда и уровнем механизации работ. 200
200
Для проверки значимости коэффициента конкордации W Фридман* предложил использовать статистику
%2 = т (п— 1) W =-------, (8.49)
тп (п + 1) —--— В
п—1
которая имеет распределение %2 с f = п — 1 степенями свободы. Для примера, приведенного в разделе 7.8, имеем
X2 = 3 (6 — 1) 0,8867 - 13,3.
По табл. 5 приложения для уровня значимости сс=0,05 и f = 5 степеням свободы находим критическое значение %5; o,os = 11,07. Так как %2 = 13,3 > 0,05 = 11,07, нулевая гипотеза отвергается. Та-
ким образом, оценка качества изделия тремя экспертами на уровне значимости а = 0,05 согласована.
8.6. ПРОВЕРКА ЗНАЧИМОСТИ
КОЭФФИЦИЕНТА ДЕТЕРМИНАЦИИ
При выполнении процедуры проверки значимости коэффициента детерминации выдвигается нулевая гипотеза Но против альтернативной Н19 которые заключаются в следующем.
Но: существенного различия между выборочным коэффициентом детерминации и коэффициентом детерминации генеральной совокупности В(г) = 0 нет.
Эта гипотеза равносильна гипотезе Но : = р2 = ... = рт = 0,
т. е. ни одна из объясняющих переменных, включенных в регрессию, не оказывает существенного влияния на зависимую переменную.
Нг: выборочный коэффициент детерминации существенно больше коэффициента детерминации генеральной совокупности 5(г) — 0.
Из постановки задачи ясно, что следует использовать одностороннюю критическую область. Принятие гипотезы Н± означает, что по крайней мере одна из т объясняющих переменных, включенных в регрессию, оказывает существенное влияние на переменную у.
Для оценки значимости парного коэффициента детерминации используется статистика
(8.50)
имеющая ^-распределение Фишера с = т = 1 и f2 = n — 2 степенями свободы. Значение статистики, вычисленное по (8.50), сравнивается с критическим значением этой статистики, найденным по табл. 4 приложения при заданном уровне значимости а и соответствующем числе степеней свободы. Если F > F^. f2- а, то вычисленный коэффициент детерминации значимо отличается от нуля. Этот вывод обеспечивается с вероятностью 1 — а.
*Friedma n М. The use of Ranks ... . Journal of American Statistical Association, 1973, vol. 32, p. 675.
201
Пример
В разделе 3.2 был вычислен поп = 14 предприятиям коэффициент детерминации для регрессии, отражающей зависимость производительности труда от уровня механизации работ, Вух = 0,938. По (8.50) получим
f = _0,938(14--2)_ 1—0,938
Зададимся уровнем значимости а = 0,05. Числа степеней свободы соответственно следующие: Д = 1 и /2 = 12. По табл. 4 приложения находим критическое значение = 4,747. Вследствие того что
Г1;12;о,об, Делаем вывод, что Вух существенно отличается от нуля, и, следовательно, включенные в регрессию переменные достаточно объясняют зависимую переменную.
Можно показать, что при = 1 всегда F = Z2. Тогда (8.50) можно записать в виде
~Г~Й2)- (8-51)
Эта величина имеет /-распределение с f — п — 2 степенями свободы. Если мы теперь учтем, что В = г2, (см. (4.13)), то отсюда следует, что с помощью критерия (8.51) можно проверить также значимость коэффициента корреляции.
Оценка значимости коэффициента множественной детерминации производится с помощью статистики
р _ В (п—т— 1)
“ т(1—В) ’
(8.52)
которая имеет /’-распределение с = т и f2 = п — т — 1 степенями свободы. Здесь т — количество учитываемых объясняющих переменных. Значение статистики (8.52), вычисленное по эмпирическим данным, сравнивается с табличным значением F^ f2-f а. Критическое значение определяется по табл. 4 приложения по заданному а и степеням свободы /у и /2. Правило проверки аналогично процедуре оценки значимости коэффициента парной детерминации.
Пример
В разделе 3.3 были вычислены два коэффициента множественной детерминации, ВуЛ2 = 0,9447 и ВуЛ23 = 0,9541, по п = 14 наблюдениям соответственно для т = 2 и т = 3 объясняющих переменных Имеем:
г, 0,9447 (14—2—1) qq qp q oqo
F = — --------------- = 93,96, г2; и; о,о5 = 3,982,
2(1 — 0,9447) ’ ’ ’
г? 0,9451 (14 — 3—1) qq п о voo
F = — -------------- = 57,38, г3; ю; о,о5= 3,708.
3(1-0,9451)
Итак, в обоих случаях F > f2- а. Коэффициенты множественной
детерминации существенно отличны от нуля, и, следовательно, рассматриваемые регрессии достаточно определены включенными переменными.
202
(8.53)
Для оценки значимости коэффициента частной детерминации используется статистика
р — р — 1)
т(1—В)
которая имеет /^-распределение с = т и f2= п — т — р — 1 степенями свободы. Здесь р — число переменных, исключенных при вычислении коэффициентов частной детерминации. Процедура проверки значимости аналогична описанным выше.
8.7. ПРОВЕРКА ЗНАЧИМОСТИ ОЦЕНОК
ПАРАМЕТРОВ РЕГРЕССИИ
В предыдущем разделе мы познакомились с критерием, оценивающим существенность вклада в общую дисперсию включенных в регрессию переменных. При оценке значимости коэффициента детерминации устанавливалось, существенно ли вариация т объясняющих переменных в целом определяет вариацию зависимой переменной у. Таким образом, приведенный в разделе 8.6 критерий значимости коэффициента детерминации косвенно указывает также значимость статистических оценок параметров, входящих в уравнение регрессии.
Теперь рассмотрим критерии значимости отдельно для оценки каждого параметра регрессии. Выдвинем следующие гипотезы:
HQ : bk = т. е. нет существенного различия между оценкой параметра регрессии, полученной по результатам выборки, и истинным значением параметра |3fe (параметра регрессии генеральной совокупности);
Нг : bk =7^= т. е. имеется значимая разница между оценкой параметра регрессии и соответствующим параметром генеральной совокупности.
При данной альтернативной гипотезе используется двусторонняя критическая область. Альтернативная гипотеза может быть сформулирована также следующим образом: Нг : bk > pfe или bk < pfe, т. е. оценка параметра существенно больше или существенно меньше параметра генеральной совокупности. В этом случае используется односторонняя критическая область.
В разделе 8.1 обсуждались предпосылки, при которых оценки параметров имеют /-распределение. При соблюдении этих предпосылок для проверки значимости оценок параметров, входящих в уравнение регрессии, применяется /-критерий:
t = , (8.54)
Sbk
где sbk — стандартное отклонение оценки параметра регрессии bk (см. формулу (3.44) в разделе 3.6). Число степеней свободы статистики (8.54) следующее: f = п— т— 1, где т— количество объясняющих переменных, включенных в регрессию. Значение /, вычисленное по (8.54), сравнивают с критическим значением //>а, найденным
203
по табл. 3 приложения при заданном уровне значимости а и числе степеней свободы f с учетом того, используется двусторонняя или односторонняя критическая область. Если t > то bh значимо отличается от Рь, т. е. нельзя предположить, что выборка отобрана из генеральной совокупности с параметром регрессии
Если нулевую гипотезу нельзя сформулировать в виде 77О: bh = т. е. нельзя указать заранее числовое значение параметра регрессии Рй генеральной совокупности, то часто при экономических исследованиях выдвигают другое предположение, а именно:
Но : bk = 0, т. е. переменная xk не оказывает существенного влияния на зависимую переменную у\
H-l : bh =/= 0, т. е. переменная xk оказывает существенное влияние на у.
При данной альтернативной гипотезе используется двусторонняя критическая область. Альтернативная гипотеза может быть также сформулирована следующим образом: Н± : bk > 0 или bk < 0, т. е. имеется значимая положительная (прямая) или отрицательная (обратная) зависимость переменной у от переменной xk- В этом случае используется односторонняя критическая область.
В то время как при двусторонней критической области не требуется никакой информации о направлении зависимости у от при применении односторонней критической области на основе экономических соображений должен быть априори известен знак параметра регрессии.
При проверке гипотезы Но : bk = О используется статистика
s^h
(8.55)
имеющая /-распределение с f = п — т— 1 степенями свободы. В частном случае для простой линейной регрессии при проверке гипотезы относительно Ьг (Яо • = 0) используется статистика
(8.56)
выражение которой получается подстановкой в (8.55) вместо Sbi формулы (3.48). При проверке гипотезы относительно Ьо (Но: Ьо = 0) используется статистика
(8.57)
Выражение (8.57) также получается из (8.55) путем подстановки вместо Sb, формулы (3.46).
Проверка гипотезы Но : р0 = 0 имеет второстепенное значение, так как постоянная регрессии чаще всего лишена экономического смысла.
204
Пример
В разделе 2.4 мы вычислили оценку коэффициента регрессии для зависимости производительности труда от уровня механизации работ по п = 14 промышленным предприятиям. Проверим теперь гипотезу Но ; Ьг = 0 против Нг: Ьг> 0, так как исходя из экономического анализа изучаемого явления коэффициент регрессии Ъг должен быть положительным. В разделе 3.6 была вычислена стандартная ошибка коэффициента регрессии by. = 0,0402. По (8.55) имеем
f = 0,5435 — 13,52.
0,0402
При односторонней критической области для а = 0,05 и f = 12 находим по таблице /-распределения критическое значение статистики /12;о,о5 == Ь78. Так как t> /i2;o,o5> bi существенно больше нуля. Коэффициент регрессии Ьг отражает существенную положительную зависимость. Таким образом, обсуждаемый критерий значимости коэффициента регрессии приводит к такому же результату, что и критерий значимости коэффициента корреляции (см. раздел 8.5). То же самое можно сказать о критериях значимости коэффициентов частной корреляции и регрессии.
Пример
Оценим значимость коэффициентов частной регрессии, рассматривая зависимость производительности труда от уровня механизации работ, от среднего возраста работников и среднего процента выполнения нормы. Объем выборки п = 14. Воспользуемся теперь двусторонней критической областью.
В разделах 2.7 и 3.6 были вычислены оценки коэффициентов частной регрессии и их стандартные ошибки:
&! = 0,52123, sbl = 0,04918,
&2 = 0,15092, Sz,2 = 0,1508,
Ь3 = — 0,02389, sb3= 0,106.
По (8.55) получим следующие значения t:
tr = 10,60, /2 = 1,00, /3 = — 0,23.
По таблице /-распределения для а = 0,05 и f = 10 при двусторонней критической области находим критическое значение /1О;о,о5 == 2,228. Поскольку bi существенно отлично от нуля и отражает,
таким образом, значимое частное влияние уровня механизации работ на производительность труда. Напротив, /2 < ^о;о,о5 и t3 < ^ю;о,о5-Поэтому мы не можем утверждать, что Ь2 и Ь3 существенно отличны от нуля. Оба коэффициента частной регрессии статистически не надежны. На основе данной выборки нельзя окончательно решить, значимо ли частное влияние среднего возраста работников и среднего процента выполнения нормы. В данном случае вместо переменных х2 и х3 в исследуемую регрессию могут быть включены другие, экономически обоснованные переменные, такие, как уровень вооруженности труда основными фондами, коэффициент сменности рабочей силы, средняя заработ
205
ная плата, использование рабочего времени, показатель текучести рабочей силы.
Дополнительное статистическое исследование может показать, что не все перечисленные переменные имеют одинаковое значение в исследуемой регрессии. Прежде чем вынести решение об исключении переменных из анализа в силу их незначимого влияния на зависимую переменную, производят исследование с помощью коэффициента детерминации. Если коэффициент детерминации регрессии с тремя объясняющими переменными несущественно изменится по сравнению с коэффициентом детерминации регрессии с одной объясняющей переменной, то это свидетельствует о том, что включение второй и третьей переменных не улучшает соответствия регрессии исходной системе случайных переменных. Так, для нашего примера применение критерия (8.55) показало, что переменные х2 и х3 (средний возраст работников и средний процент выполнения нормы) не оказывают значимого влияния на переменную у. Однако вместе они вносят существенный вклад в объяснение переменной у. Для проверки этого предположения можно применить критерий, который оценивает систематическое влияние дополнительно включенных объясняющих переменных. При этом исходим из двух функций:
у — bQ + t^Xi + ... + + ь mi+l^mi+1 + ... + ЬтХт
(8.58) и
У ~ ^0 4" Ь-jX} + ... + (8.59)
В первой регрессии (8.58) содержится т объясняющих переменных, во второй — только часть из них, а именно т1 объясняющих переменных. При этом /72 = /71! + т2, т. е. в регрессии (8.58) по сравнению с (8.59) содержится дополнительно т2 объясняющих переменных. Теперь следует проверить, вносят ли совместно эти т2 переменных существенную долю в объяснение вариации переменной у. Сформулируем гипотезы:
Я о * bk = 0 для k = т1 + 1, ..., т, : bk 0 для k = т1 + 1, ..., т.
Необходимо иметь в виду, что влияние первых из тг объясняющих переменных здесь не оценивается. При справедливости альтернативной гипотезы принимают регрессию (8.58). При справедливости нулевой гипотезы принимают регрессию (8.59). При проверке гипотез используется статистика
(m-mja-Bm)
которая имеет /•’-распределение с Д = т — ту = m2 и /2 = п — т —1 степенями свободы. Здесь Вт означает коэффициент детерминации регрессии с т объясняющими переменными, а Вт1 — коэффициент детерминации регрессии с тг объясняющими переменными. Разность (Вт— Bmt) в числителе формулы (8.60) является мерой дополнительного
206
объяснения вариации переменной у за счет включения т2 переменных. Поэтому число степеней свободы числителя равно = m2. В критерии базой сравнения служит неопределенность функции регрессии с т объясняющими переменными. Поэтому число степеней свободы знаменателя равно: f2 = n — tn — 1. Чем больше разность (Вт — Вт1), тем реже отвергается нулевая гипотеза. Критическое значение Ffl- f2- а находят по таблице ^-распределения (см. приложение) при заданном уровне значимости а и и /2 степенях свободы. Если F S Ff1} f2; а, то результаты выборки не противоречат нулевой гипотезе Яо. Включенные дополнительно т2 объясняющих переменных совместно не оказывают значимого влияния на переменную у. Если F > Ffl-,f2, а , то гипотеза Но на уровне значимости а отвергается. В этом случае т2 объясняющих переменных совместно оказывают существенное влияние на вариацию переменной у.
Пример
С помощью критерия (8.60) ответим на поставленный выше вопрос: существенно ли совместное влияние на производительность труда (у) среднего возраста работников (х2) и среднего процента выполнения нормы (х3)? При этом Вт = Ву. 123 = 0,9451 — коэффициент детерминации регрессии, выражающей зависимость производительности труда от уровня механизации работ, среднего возраста работников и среднего процента выполнения нормы. Соответственно Вт1 = Ву1 = 0,938— коэффициент детерминации регрессии, выражающей зависимость производительности труда от уровня механизации работ. С помощью (8.60) получаем
F = (0,9451—0,938) (14—3—1) ___0617 (3—1) (1—0,9451)
По таблице ^-распределения для а = 0,05, Л = 2 и f2 = 10 находим критическое значение = 4,103. Так как F < Т^кко.ой, У нас
нет оснований отвергнуть гипотезу //0. После того как мы установили, что для исследованных 14 предприятий каждая из переменных в от-, дельности — средний возраст работников и средний процент выполнения нормы — не оказывает существенного влияния на производительность труда, можно сделать вывод о незначимости их совместного влияния. Критерий (8.60) может быть применен и при нелинейной регрессии, например для полиномиальной модели.
Другой важной проблемой является сравнение оценок параметров регрессии. При этом различают:
сравнение коэффициентов частной регрессии bj и bk одной и той же функции;
сравнение оценок параметров регрессии двух функций.
В первом случае нулевая гипотеза записывается в виде HQ: Р7- = = Pfe, т. е. проверяется равенство коэффициентов частной регрессии в генеральной совокупности. Альтернативная гипотеза исходит из значимого различия обоих коэффициентов частной регрессии в генеральной совокупности — Н}. р7- =^=pfe (двусторонняя критическая область), или Н± : Ру > Рь или Ярр; < pft (односторонняя критическая об
207
ласть). При проверке нулевой гипотезы может быть использован критерий
. b‘~th— V >1, -2s»)»s + si,
с f = п — т — 1 степенями свободы. Так как оба коэффициента частной регрессии оцениваются по результатам одной и той же выборки, они не независимы друг от друга. Поэтому в знаменателе формулы (8.61) должна быть учтена ковариация между bj и bk. В связи с тем что slj = si , s%h = si и = si № (см. раздел 3.6), формулу (8.61) можно записать в виде
t ----- bi~bk ----------, (8.62)
su "
где %W), x(ik} и x<W — элементы матрицы (Х'Х)"1. Решение о принятии или отклонении гипотезы производится путем сравнения расчетного значения t с критическим tft а, заимствованным из таблицы t-распределения.
Пример
Проверим гипотезу о равенстве коэффициентов частной регрессии Ь± и Ь2 зависимости производительности труда от уровня механизации работ, среднего возраста работников и среднего процента выполнения норм *, т. е. #0 : = |32 против Н± : > |32. В разделе 2.7 были вы-
числены коэффициенты частной регрессии Ьг = 0,5212 и Ь2 = 0,1509, а в разделе 3.6 — дисперсии и ковариации обоих коэффициентов: sbl = 0,00242, sbz = 0,02275 и sb{b2 = — 0,001581. С помощью формулы (8.61) получим значение статистики I:
t =0,5212-0,1509- 2 199.
Уб,00242—2 (— 0,001581) +0,02275
По таблице /-распределения для / = 14—3—1 = 10 и а=0,05 (односторонняя критическая область) находим критическое значение /ю;о,о5“ = 1,81. Так как /> /10;0>05, МЬ1 с риском 5% отвергаем гипотезу Яо, т. е. коэффициенты регрессии Ьг и Ь2 значимо отличны друг от друга (&i больше &2). Этот критерий можно обобщить для проверки гипотезы о равенстве нескольких параметров регрессии для одной и той же функции. Заинтересованный читатель может обратиться к специальной литературе, например [57], [117].
На примере простой линейной регрессии продемонстрируем сравнение оценок параметров регрессии двух функций. Используемый при этом критерий можно обобщить на коэффициенты частной регрессии и более чем на две функции. При этом исходим из следующих предположений:
в обеих генеральных совокупностях исследуется содержательно одинаковая зависимость переменной у от переменной х;
*Для описания процедуры проверки гипотезы с помощью критерия (8.61) мы возвращаемся к этому примеру для того, чтобы не вводить новый, хотя по причине ранее установленной незначимости Ь2 и Ь3 их сравнение не имеет смысла.
208
пары наблюдений (уь xt) и (у^, xr), i = 1, ...» nlf V = 1, П2,
являются результатами двух независимых выборок объема пг и п2 из генеральных совокупностей;
по результатам каждой выборки строится простая линейная регрессия и находится дисперсия остатков:
= 1 +&1, 1 = st
УV Ьо, 2 + ^1, 2 Ъ' , sl = sl.
Второй индекс в обозначениях оценок параметров регрессии указывает номер выборки, по данным которой они вычислены. Нулевая гипотеза Но :|3Ь1 = |3Ь2 (k = 0,1) заключается в том, что обе выборки произведены из генеральных совокупностей в среднем с одинаковой зависимостью переменной у от переменной х. Альтернативная гипотеза Н^. : Pk,i¥= Рь,2 (k = 0,1) констатирует различие в этих зависимостях.
Процедура проверки гипотезы разбивается на несколько этапов.
1. Вначале следует проверить, равны ли дисперсии остатков в обеих генеральных совокупностях. Для этого выдвигается гипотеза Но : : of = 02 против Н±: of Проверка осуществляется с помощью статистики
F = (8.63)
имеющей ^-распределение с = пг — 2 и f2 — п2 — 2 степенями свободы. При этом в числителе стоит большая дисперсия. Если F^
^/1; f2; а, то гипотеза Но принимается, а при F> а отклоняется на уровне значимости а. В случае принятия нулевой гипотезы (дисперсии остатков обеих генеральных совокупностей равны) вычисляется сводная оценка дисперсии остатков для обеих регрессий Оц\
С 2__ (П1 2) S1 ~КП2-2) $| /м\
2. Ко второму этапу приступаем в предположении равенства дисперсий остатков. Теперь проверяем равенство коэффициентов регрессии, характеризующих угол наклона регрессионных прямых к оси абсцисс. Выдвигается гипотеза Яо: р1?1 = р1>2 против Н± : Ф 01|2. При проверке нулевой гипотезы используется статистика
/ =----(8.б5)
V S41 + S®1,2
имеющая /-распределение с f = + п2 — 4 степенями свободы. Под-
ставим в (8.65) вместо дисперсий Sbt>t и sgl s их выражения — формулу (3.47). Используя вместо s2 оценкупо формуле (8.64) и учитывая, что 2 (хг — х)2 = (га — 1) Sx, представим (8.65) в виде
/ =...................... Ь'''~Ь'-2..................... (8.66)
/ (nt-2) s?+(n2-2) s* / 1 t 1 \
V rax+«2-4 («1-1)^
209
Сравнивая расчётное значение i с критическим //>а, заимствованным из таблицы /-распределения, принимаем одно из следующих решений: а) если t //>а, то гипотеза Яо принимается. Оба коэффициента регрессии несущественно отличаются друг от друга, т.е. регрессионные прямые параллельны друг другу. Уравнения регрессии могут отличаться друг от друга не угловыми коэффициентами, а своими постоянными;
б) если />/у>а, то гипотеза Яо отвергается. На уровне значимости а можно утверждать, что наклон регрессионных прямых значимо различен и поэтому они не параллельны друг другу.
При принятии гипотезы Яо, т.е. считая, что выполняется равенство Pi 1 = Р1>2 = р1? вычисляем сводную оценку коэффициента регрессии как взвешенное среднее:
ь~ = bl.2 (8 б7)
1 («!-’) *£ +("2 -О®*, ' (
3. В предположении равенства дисперсий остатков и коэффициентов регрессий приступаем к третьему этапу. На этом этапе оценивается расхождение свободных членов в двух сравниваемых уравнениях регрессии. Выдвигаем гипотезу Яо: |301 = ро>2 против Н^. P0,i =# =/= Ро,2- Для проверки нулевой гипотезы Яо используется статистика
/ = (8.68)
S*
имеющая /-распределение с f = п1 + п2 — 4 степенями свободы. Здесь Ь± — сводная оценка коэффициента регрессии по (8.67), Ь1 — другая, независимая от br оценка углового коэффициента для двух уравнений регрессии, полученная в предположении равенства как коэффициентов регрессии, так и свободных членов (постоянных регрессии). Оценка Ь± находится по формуле
у1~у2 , (8.69)
Х±—х2
где индекс в обозначениях средних соответствует номеру выборки.
Далее в формуле (8.68) s* — стандартное отклонение разности (Ьх —
-КУ
—V (8.70)
. п1 /
(«i-D ^ + («2 -О + (7х-Г2)2
где su определяется по (8.64).
Расчетное значение (8.68) сравнивается с критическим tf а. Если t > /у, а, то постоянные регрессии существенно отличаются друг от друга на уровне значимости а. Хотя обе регрессионные прямые параллельны Друг другу, они не идентичны, так как имеется статистически значимое расхождение постоянных.
Если / /у,а, то обе регрессионные прямые считаются идентичными;
имеющиеся различия между этими прямыми можно объяснить лишь 210
случайными колебаниями выборочных данных. Полученная форма усредненной зависимости может быть принята для обеих генеральных совокупностей. Но при этом на всех трех этапах должна быть принята нулевая гипотеза.
Если дисперсии остатков sf и s* различаются значимо, то для сравнения регрессионных прямых точных статистических критериев нет. Для этого случая разработаны рекомендации, основанные на приближенных формулах, точность которых возрастает по мере роста объемов выборок из обеих совокупностей [10].
Пример
Воспользуемся результатами, полученными в разделах 2.4 и 3.6, при построении простой линейной регрессии зависимости производительности труда от уровня механизации работ. Оценки параметров этой регрессии и необходимые нам статистические характеристики будем считать результатами первой выборки. Используя новые обозначения, запишем:
fe0,i = 7,0356, й1Д = 0,5435, пх = 14,
Si - 4,3553, s1 2 *Xi = 207,1429, хг = 51,71, у[ = 35,14.
Для другой отрасли промышленности (вторая генеральная совокупность) была исследована зависимость между такими же переменными на основе выборки объема п2 = 20:
&о,2 = 17,8521, blt2 = 0,6155, п2 = 20,
si = 2,0504, s22 = 547, 5157, х2 = 76,6, у2 = 65.
Выполним поэтапно процедуру сравнения двух регрессионных прямых.
1. Проверим, значимо ли статистически расхождение между дисперсиями остатков s2 = 4,3553 и s$ = 2,0504. По (8.63) получаем
Р = _4 ’3553 = 2 1 241
2,0504
Так как F12,i8- о,об = 2,34, у нас нет оснований отвергать гипотезу Яо об однородности двух дисперсий. По (8.64) находим сводную оценку дисперсии остатков, общую для обеих регрессий:
р _ 12»4,3553 + 18-2,0504 = % д724 14+20—4 ~ ’
2. Так как обе дисперсии остатков не различаются значимо, мы можем проверить гипотезу о равенстве коэффициентов регрессии и и blt2 с помощью критерия (8.66):
, 0,5435—0,6155 . О£;1
4 — ... — п 1 jOUl •
1 / 2 9724 (--------- | ------!---|
V ’ ^12-207,1429 ^18.547,5157/
По таблице /-распределения находим /Зо;о,об = 2,042. Так как
|/| < ^зо;о,об» мы принимаем нулевую гипотезу, т. е. считаем, что оценки обоих коэффициентов регрессии расходятся несущественно. Обе теоретические регрессионные прямые параллельны друг другу
211
в силу того, что постоянные этих регрессий могут отличаться друг от друга. Вычислим сводную оценку углового коэффициента наклона по (8.67):
р = 12-207,1429-0,5435 + 18-547,5157-0,6155 _ q gQj 12-207,1429 + 18-547,5157 ~ ’
3. Поскольку на первых двух этапах нулевые гипотезы были приняты, установим тождественность свободных членов в уравнениях и удостоверимся в идентичности регрессий. По (8.69) и (8.70) получаем
^ = -3-,14~6— = i 1997
51,75—76,6
8* = 1,7241 1/ --------------2--------------(--------!------( — + —'j =
У 12-207,1429 + 18-547,5157 (51,57—76,6)2 \ 14 20/
= 0,0286.
Подставим найденные значения в (8.68):
(= M01-IJ9W ___ 0,0286
Так как |/| > tзо;о,о5> на уровне значимости 5% нулевая гипотеза отвергается.
Теперь подытожим результаты нашего исследования. Для обеих отраслей промышленности (генеральных совокупностей) может быть принята одинаковая усредненная зависимость производительности труда от уровня механизации работ. Но уравнения регрессии для обеих отраслей промышленности не идентичны в силу установленного статистического различия в свободных членах этих уравнений. По одной и той же регрессии нельзя оценить средний уровень производительности труда в обеих отраслях промышленности при заданных значениях коэффициента механизации работ. Кроме того, в разделе 8.5 было установлено, что теснота связи между исследуемыми переменными для обеих отраслей промышленности была различна.
Аналогичная процедура может быть использована для определения структурных изменений во временных рядах. С этой целью исследуемый промежуток времени делят на два периода, для каждого из которых строят регрессионную зависимость. Затем с помощью приведенных выше критериев проверяется их идентичность. Если в результате проверки статистических гипотез подтверждается идентичность регрессий для обоих периодов, то приходят к выводу, что за исследуемый промежуток времени не произошло никаких нарушений, которые могли бы привести к структурным изменениям. Полученные уравнения регрессии принимаются характерными для исследуемого явления.
8.8. ПРОВЕРКА ЛИНЕЙНОСТИ РЕГРЕССИИ
В экономике причинно-следственные отношения между явлениями часто описываются с помощью линейных или линеаризуемых зависимостей. Разработаны статистические критерии, позволяющие либо подтвердить факт непротиворечивости линейной формы зависимости
212
опытным данным, либо отвергнуть предложенный вид зависимости как не соответствующий этим данным. Для проверки линейности регрессии применяется следующий метод. Пусть каждому значению объясняющей переменной соответствует несколько значений зависимой переменной, по которым вычисляют частные средние уъ у2 и т.д. Обозначим через yj частное среднее, соответствующее j-му значению объясняющей переменной:
nj
2 уи
yj = —------= (8.71)
nJ
р
где rtj — число значений у, относящихся кхд (fe = 1, ..., m); S ni~ = n. Найдем теперь средний квадрат отклонений значений yt$ от их частных средних:
р nj
12 2 (уи~ у У
qt = . (8.72)
п—р
Показатель (8.72) является мерой рассеяния опытных данных около своих частных средних, т. е. мерой, не зависящей от выбранного вида регрессии. В качестве меры рассеяния опытных данных вокруг эмпирической регрессионной прямой выбирается средний квадрат отклонений:
. (8.73)
р—т—1
Оба показателя q\ и q* представляют собой независимые статистические оценки одной и той же дисперсии в у. Если q% несущественно больше ql, то в качестве гипотетической зависимости может быть принята линейная.
Если в генеральной совокупности существует линейная регрессия и условные распределения переменной у хотя бы приблизительно нормальны, то отношение средних квадратов отклонений (8.72) и (8.73)
F = — (8.74)
<7i
имеет ^-распределение cj\ = p — т — \ и f2 = п — р степенями свободы. Значение F, подсчитанное по формуле (8.74), сравнивается с критическим Т’/ц/аю, найденным по табл. 4 приложения при заданном уровне значимости а и f19 f2 степенях свободы. Если F F^. у2;а, то разница между обоими средними квадратами отклонений статистически незначима и выбранная нами линейная регрессионная зависимость может быть принята как правдоподобная, не противоречащая опытным данным. Если Ffl-f2; а, то различие между обоими средними квадратами отклонений существенно, неслучайно, и гипотеза о линейной зависимости между переменными несостоятельна. Разработаны также другие критерии проверки гипотезы о линейности регрессии. Заинтересованный читатель может найти их в соответствующей литературе [122], [76].
213
9 МУЛЬТИКОЛЛИНЕАРНОСТЬ
При изучении множественной линейной регрессии часто сталкиваются с наличием линейной связи между всеми или некоторыми объясняющими переменными. Это явление называется мультиколлинеарностью \ На наш взгляд, впервые на проблему мультиколлинеарности обратил внимание Р. Фриш. Мультиколлинеарность между объясняющими переменными вызывает технические трудности, связанные с уменьшением точности оценивания или даже с невозможностью оценки влияния тех или иных переменных. Причина заключается в том, что вариации в исходных данных перестают быть независимыми и поэтому невозможно выделить воздействие каждой объясняющей переменной в отдельности на зависимую переменную. Продемонстрируем это на простом примере.
Пусть исследуется зависимость себестоимости от объема производства и введенных в действие основных фондов. Следует ожидать, что объем производства зависит также от основных фондов. Если мы обе переменные выберем в качестве объясняющих, то, очевидно, коэффициенты регрессии не будут точно отражать зависимость себестоимости от обоих факторов, так как основные фонды оказывают дополнительное влияние на себестоимость через объем производства.
Каковы последствия мультиколлинеарности в регрессионном и корреляционном анализе? Прежде чем ответить на этот вопрос, рассмотрим формы ее возникновения. Мультиколлинеарность может проявляться в функциональной (явной) и стохастической (скрытой) форме. Функциональная форма мультиколлинеарности возникает, когда по крайней мере одна из объясняющих переменных связана с другими объясняющими переменными линейным функциональным соотношением. Линейный коэффициент корреляции между этими двумя переменными в таком случае равен + 1 или —1.
Пусть следует построить уравнение регрессии в виде у = bQ + + Ь2х2. При этом известно, что переменные и jq связаны линейным соотношением х2 = a0Jra1x1. В этом случае можно показать, что определитель матрицы (X' X) равен нулю, т.е. ранг матрицы X меньше т-\~1, и матрица (Х'Х) вырожденная. Это приводит к нарушению предпосылки 4 (см. раздел 2.9) и к тому, что система нормальных уравнений не имеет
1В частном случае при рассмотрении двух объясняющих переменных употребляется обычно термин «коллинеарность». — Примеч. пер.
214
однозначного решения, если по крайней мере одна из объясняющих переменных может быть представлена в виде линейной комбинации остальных.
Однако на практике функциональная форма мультиколлинеарности встречается довольно редко. Значительно чаще мультиколлинеарность проявляется в стохастической форме. Она имеет место, когда по крайней мере между двумя объясняющими переменными существует более или менее сильная корреляция. Система нормальных уравнений тогда хотя и имеет решение (так как определитель матрицы Х'Х отличен от нуля и матрица Х'Х невырожденная), но обнаруживаются необычайно большие стандартные ошибки. Под стохастической формой мультиколлинеарности может скрываться функциональная из-за накладывающихся на нее ошибок наблюдения, измерения или спецификации модели, когда нелинейная регрессия рассматривается как линейная или учитываются не все переменные. Чем сильнее корреляция между объясняющими переменными, тем меньше определитель матрицы Х'Х. Это приводит к серьезному понижению точности оценки параметров регрессии, искажению оценок дисперсии остатков, дисперсии коэффициентов регрессии и ковариации между ними. В этом случае говорят, что стандартная ошибка «взрывается». Следствием падения точности является ненадежность коэффициентов регрессии и отчасти неприемлемость их использования для интерпретации как меры воздействия соответствующей объясняющей переменной на зависимую переменную. Оценки коэффициентов становятся очень чувствительны к выборочным наблюдениям. Небольшое увеличение объема выборки может привести к очень сильным сдвигам в значениях оценок. Кроме того, стандартные ошибки входят в формулы критериев значимости. Поэтому применение самих критериев становится также ненадежным. Из сказанного ясно, что исследователь должен пытаться установить стохастическую мультиколлинеарность и по возможности устранить ее.
Причина возникновения мультиколлинеарности в экономических явлениях — многообразие объективно существующих соотношений между объясняющими переменными. Это касается регрессии, построенной как на результатах одновременных обследований, так и по данным, полученным из временных рядов. В общем случае во временных рядах имеют дело с трендом, который, во-первых, не требует обязательной для регрессии независимости отдельных наблюдений, а во-вторых, в определенной степени автоматически приводит к регрессии с другими объясняющими переменными, если они обладают такой же тенденцией. Кроме того, следует отметить, что для тех переменных, которые находятся в объективной связи, ошибка прогноза при мультиколлинеарности объясняющих переменных в общем относительно мала, если на время упреждения не изменяются все прочие условия.
Теперь перейдем к вопросам установления функциональной и стохастической мультиколлинеарности. Функциональную мультиколлинеарность установить легко, так как получающаяся система нормальных уравнений не имеет однозначного решения. Стохастическую форму мультиколлинеарности мы можем обнаружить с помощью следующих показателей.
21
1. Для измерения стохастической мульТиКоллинеарности можнб использовать коэффициент множественной детерминации. В разделе 4.6 мы показали, что при отсутствии корреляции между объясняющими переменными, т. е. при отсутствии мультиколлинеарности, коэффициент множественной детерминации равен сумме соответствующих коэффициентов парной детерминации:
т
ВуЛЪ...тп ~ 2 &УЪ' (9*1)
k=\
где у — зависимая переменная, a хк — объясняющая, k = 1, .., т. При наличии мультиколлинеарности соотношение (9.1) не соблюдается. Поэтому в качестве меры мультиколлинеарности можно предложить разность М}.
т
= Вул&...т—2 Byk* (9-2)
£=1
Чем меньше эта разность, тем меньше мультиколлинеарность.
2. Другой показатель разработан А. Е. Хорлом *, он основан на использовании для измерения мультиколлинеарности числителя формулы коэффициента множественной детерминации. В предположении множественной регрессии числитель коэффициента детерминации можно представить следующим образом:
S (yi—Xfe) /=1 k i j, k i
(9.3) для/, k — 1,2, ..., tn; i = 1,2,...tin j Ф k. Выражение
2 Xj) Л'й) (9.4)
i
является числителем формулы коэффициента парной корреляции между переменными Xj и xk. При отсутствии коллинеарности между этими переменными он равен нулю. Поэтому в качестве общего показателя мультиколлинеарности можно использовать разность Л12:
= У) -2 2 (xitt-xk)2. (9.5) I k i
Если значение УИ2 мало, то считаем, что мультиколлинеарность тоже незначительна.
3. В качестве показателя мультиколлинеарности можно также воспользоваться выражением (9.2), разделив его на Ву.12...т:
т
2
Af3=l----. (9.6)
Чем больше А43, тем интенсивнее мультиколлинеарность.
*Н о е г 1 А. Е. Application of ridge analysis to regression problems. Chem. Eng. Progr., vol. 58, N 3, March 1962.
216
4. Известен также показатель мультиколлинеарности, являющийся производным от (9.5). Разделив правую и левую части выражения (9.5) на 2 (]Ji — У)2, получим
М4 = 1--------------------. (9.7)
2 —у)2
i
Величина М4 заключена в границах 0 Л44 1. Чем больше Л14
приближается к 1, тем сильнее мультиколлинеарность. Показатели Mlt М2, М3 и Л14 являются весьма приближенными. Их недостаток заключается в том, что неизвестны их распределения и поэтому нельзя установить их критические значения. Кроме того, с помощью этих показателей нельзя определить, какие из переменных «ответственны» за мультиколлинеарность. Теперь рассмотрим методы исключения или уменьшения мультиколлинеарности. Часто довольно трудно решить, какие из набора линейно связанных объясняющих переменных исключить, а какие наиболее полно раскрывают природу и физическую сущность явления и поэтому должны быть учтены в корреляционном и регрессионном анализе. В области экономики эти вопросы должны решаться прежде всего исходя из логически-профессиональных соображений. Итак, разработаны следующие методы уменьшения мультиколлинеарности:
а) Исключение переменных. Этот метод заключается в том, что высоко коррелированные объясняющие переменные устраняются из регрессии, и она заново оценивается. Отбор переменных, подлежащих исключению, производится с помощью коэффициентов корреляции. Для этого производится оценка значимости коэффициентов парной корреляции rjk между объясняющими переменными Xj и xk (j, k = 1,2,..., m; / =0= k). Опыт показывает, что если \rjk \ > 0,8, то одну из переменных можно исключить. Но какую переменную удалить из анализа, решают исходя из экономических соображений. Из-за отсутствия теоретического обоснования этот подход весьма приближенный.
Другой способ исключения переменных был предложен Фарраром и Глаубером*. Процедура отбора переменных, подлежащих исключению, состоит из трех этапов. При этом предполагается нормальное распределение остатков.
На первом этапе мультиколлинеарность выявляется лишь в общем виде. Для этого строится матрица R коэффициентов парной корреляции между объясняющими переменными (см. раздел 4.3, формула (4.37)) и вычисляется ее определитель:
1 г12 ... г1т
^21 1 ••• ^2т
Г ml ^т2 ••• 1
(9.8)
*F а г г а г D. Е., G 1 a u b е г R. R. Multicollinearity in Regression Analysis: The Problem Revisited. —In: Review of Economics and Statistics, vol.49/1967.
217
Далее для проверки наличия мультиколлинеарности вообще среди объясняющих переменных применяется критерий %2. Выдвигается нулевая гипотеза HQ: между объясняющими переменными мультиколлинеарность отсутствует. Альтернативная гипотеза Нр между объясняющими переменными имеется мультиколлинеарность. В качестве критерия используется величина
Х2 = _ (П _ 1 _ (2/п + 5)) In D, (9.9)
имеющая %2-распределение с f = (т — 1) степенями свободы. Если %2 f (см. табл. 5 приложения), то нулевая гипотеза принимается. Считаем, что мультиколлинеарность между объясняющими переменными отсутствует. Если %2 > %&, f, то гипотеза о наличии мультиколлинеарности не противоречит исходным данным. Между какими переменными она возникает, решается на втором и третьем этапах процедуры.
На втором этапе используются коэффициенты детерминации между объясняющими переменными Bk, 12... k-i, ь+1,...т (см. раздел 3.5). Оценка мультиколлинеарности основана на том, что величина
р (п~т) Bfe.l2...fe-1, fe+l....т ,g
(m —1) (1 — Bk..A2...k — 1, k4-1, ... , m)
имеет ^-распределение tf1 = m — 1 и f2 = n — т степенями свободы. Если F > Fa\ (см. табл. 4 приложения), то переменной xh в наибольшей степени присуща мультиколлинеарность. По Фаррару и Глауберу изучение т значений Г-статистик должно показать, какие из объясняющих переменных в большей мере подвержены мультиколлинеарности.
На третьем этапе исследуется, какая объясняющая переменная порождает мультиколлинеарность, и решается вопрос об ее исключении из анализа. Для этой цели привлекаются коэффициенты частной корреляции (/, k = 1,2,..., т\ j k) между объясняющими пере-
менными. Переменная у во внимание не принимается. В качестве критерия используется величина
, _ (rjfe-12...m) ~\/п т
4h~ 1 /-----------
|/ 1 r]k. 1 2...m
имеющая /-распределение с f = п — т степенями свободы. Если /7-, fe>/a,y, то между переменными существует коллинеарность и одна из переменных должна быть исключена. При исключении переменной исследователь должен опираться как на собственную интуицию, так и на содержательную теорию явления. Если tj,h /а>у, то данные не подтверждают наличие коллинеарности между переменными Xj и xk.
б) Линейное преобразование переменных. Другой способ уменьшения или устранения мультиколлинеарности заключается в переходе к регрессии приведенной формы путем замены переменных, которым присуща коллинеарность, их линейной комбинацией. Например, следует построить уравнение регрессии в виде у = Ьо + + Ь2х2.
218
Установлено, что переменные х± и х2 высоко корродированы. Анализ явления и результаты наблюдений позволяют постулировать дополнительное уравнение связи между объясняющими переменными хг и х2, фигурирующими в исходной гипотезе, а именно х% = х± — х2. Переменную Х2 подставляем в уравнение регрессии и получаем: у = Ы + + + &2 * *2- В общем случае переменные х± и х*2 не сильно корре-
лируют. Таким образом, достигается снижение или даже полное устранение мультиколлинеарности.
в) Исключение тренда. При построении регрессии по данным, полученным из временных рядов, рекомендуется исключить тренд или компенсировать изменение последовательных значений переменных (прирост). Этим достигается соблюдение предпосылок регрессионного анализа — независимость наблюдений и уменьшение мультиколлинеарности.
г) Использование предварительной информации. Обычно на основе ранее проведенного регрессионного анализа или в результате экономических исследований уже имеется более или менее точное представление о величине или соотношении двух или нескольких коэффициентов регрессии. Эта предварительная или вневыборочная информация может быть использована исследователем при построении регрессии. В связи с тем что часть оценок, полученных на основе вневыборочных данных, уже имеет достаточно четкую интерпретацию, это облегчает путь обнаружения взаимных влияний изменений различных переменных.
д) Пошаговая регрессия. Процедура применения пошаговой регрессии начинается с построения простой регрессии. В анализ последовательно включают по одной объясняющей переменной. На каждом шаге проверяется значимость коэффициентов регрессии и оценивается мультиколлинеарность переменных. Если оценка коэффициента получается незначимой, то переменная исключается и рассматривают другую объясняющую переменную. Если оценка коэффициента регрессии значима, а мультиколлинеарность отсутствует, то в анализ включают следующую переменную. Таким образом, постепенно определяются все составляющие регрессии без нарушения предположения об отсутствии мультиколлинеарности (см. также [105]).
е) Метод главных компонент г. Метод главных компонент давно применяется для исключения или уменьшения мультиколлинеарности объясняющих переменных регрессии. Этот метод выходит за рамки данной книги и поэтому мы его опишем лишь в общих чертах*.
^Описание этого метода можно найти в следующих работах: Дубров А. М. Обработка статистических данных методом главных компонент. М., Статистика, 1978; [69]; И б е р л а К. Факторный анализ. М., Статистика, 1980. — Примеч. пер.
*Теоретическое обоснование метода главных компонент имеется в кн.: Weber Е. Einfiihrung in die Faktorenanalyse. VEB Gustav Fischer Verlag, Jena, 1974, S. 93. Примеры практического применения метода главных компонент при построении эконометрической модели ГДР содержатся в работе: Wolf-ling М. Ein okonometrisches Modell der Volkswirtschaft der DDR, Forschungs-berichte des Zentralinstituts fiir Wirtschaftswissenschaften. Bd 21, Academie-Verlag, Berlin. 1977.
219
Основная идея заключается в сокращении Числа объясняющих пере* менных до наиболее существенно влияющих факторов. Это достигается путем линейного преобразования всех объясняющих переменных xk (k = 1, т) в новые переменные, так называемые главные компоненты. При этом требуется, чтобы выделению первой главной компоненты соответствовал максимум общей дисперсии всех объясняющих переменных xk (k = 1, ..., m), второй компоненте — максимум оставшейся дисперсии, после того как влияние первой главной компоненты исключается, ит.д. Таким образом, выполненное преобразование содействует уменьшению мультиколлинеарности новых выделенных переменных по сравнению с мультиколлинеарностью набора исходных переменных xh (k = 1, ..., m).
Процедура вычислений по методу главных компонент состоит из следующих шагов.
Строится матрица, элементами которой являются отклонения результатов наблюдений над т переменными от соответствующих средних (xik — xh), i = 1, ..., и, k = 1, ..., m.:
Хц Xj Xj2 %2 • • • %lm
X2j Xi X22 X2 ... %2m %m
(9.12)
_Xni Xj Xn2 %2 ••• %пт
Определяется матрица дисперсий и ковариаций объясняющих переменных
Sxx = —Ц-Х*'Х*. (9.13)
п— 1
Матрица Sxx имеет размерность tn X m, она совпадает с (3.28).
Главные компоненты z7 (/ = 1, ..., т) являются линейными комбинациями объясняющих переменных х£(& = 1, ..., tri) и могут быть записаны в общем виде как
z7- = Х*'а7, / = 1, ..., т. (9.14)
Они должны удовлетворять упомянутому выше требованию: каждый раз выделенная главная компонента должна воспроизводить максимум дисперсии. На неизвестные векторы коэффициентов а7 в (9.14) накладываются дополнительные ограничения:
а}а7 = 1 для j = 1, ..., т (9.15)
(т. е. они должны быть нормированы) и
а)аЛ = 0 для j =f=. h и j = 1, ..., m; h = 1, ..., tn (9.16)
(т. e. они должны быть некоррелированы).
Дисперия главной компоненты z7
~ ay (9.17)
должна принимать наибольшее значение при соблюдении условий (9.15) и (9.16). Для решения проблемы максимизации функции, свя
220
занной дополнительными ограничениями, пользуются методом МНо жителей Лагранжа. В конечном итоге задача сводится к определению собственных значений матрицы Sxx и соответствующих собственных векторов 3Lj [31].
Собственные значения матрицы Sxx определяются из уравнений, которые в общем виде записываются как
|SXX-U| = 0, (9.18)
где X — множитель Лагранжа, а I — единичная матрица. Подставляя последовательно собственные значения, начиная с наибольшего, в уравнение
(S^x - М) а/= 0, (9.19)
получим собственные векторы матрицы Sxx, соответствующие этим собственным значениям. Собственные векторы затем используются для построения искомых векторов коэффициентов в (9.14).
Так как собственные векторы известны, по (9.14) можно определить главные компоненты. При этом обычно довольствуются меньшим, чем т, числом главных компонент, но достаточным, чтобы воспроизвести большую часть дисперсии. По мере выделения главных компонент доля общей дисперсии становится все меньше и меньше. Процедуру вычисления главных компонент прекращают в тот момент, когда собственные значения, соответствующие каждый раз (по возможности) наибольшим дисперсиям, становятся пренебрежимо малыми. Количество выделенных главных компонент г в общем случае значительно меньше числа объясняющих переменных т. По г главным компонентам строится матрица Z.
С помощью главных компонент по аналогии с (2.64) оцениваются параметры регрессии
b = (Z'Z)-1 Z' у. (9.20)
В соответствии с (2.59) вычисляются значения регрессии
у - Zb. (9.21)
При всех своих преимуществах (уменьшение высокой мультиколлинеарности объясняющих переменных) метод главных компонент обладает и недостатками. Во-первых, главным компонентам, как правило, трудно подобрать экономические аналоги. Поэтому вызывает затруднение экономическая интерпретация оценок параметров регрессии, полученных по (9.20). Во-вторых, оценки параметров регрессии получают не по исходным объясняющим переменным, а по главным компонентам. В итоге можно сказать, что метод главных компонент применяется в основном для оценки значений регрессии и для определения прогнозных значений зависимой переменной, что также является целью регрессионного анализа.
Кроме этих методов существует еще ряд способов измерения мультиколлинеарности. Так, в конфлюэнтном анализе, разработанном Р. Фришем, проблему мультиколлинеарности пытаются решить графически [46]. Известен также метод собственных значений, который, по
221
нашему мнению, принадлежит Г. Тинтнеру [ 125]. С помощью этого метода устанавливается число линейно-независимых соотношений между объясняющими переменными в предположении, что дисперсия ошибок наблюдения известна. Но эта предпосылка в условиях экономических исследований трудно выполнима. Далее, мультиколлинеарность может быть исследована с помощью гребневого анализа*. Проблема мультиколлинеарности на сегодня еще окончательно не решена. Однако, используя различные подходы, мы пытаемся определить наличие мультиколлинеарности, чтобы затем по возможности с помощью того или иного метода ее уменьшить. Если же это не удается, то к оценкам коэффициентов регрессии и значениям регрессии надо относиться с большой осторожностью **.
*Н о е г 1 А. Е. Application of ridge analysis to regression problems, in: Chem. Eng. Progress 58, N 3, 1962.
**Проблема мультиколлинеарности обсуждается также в работах: Kelch J., Muller Н., Waschkau Н. Die Multikollinearitat bei regressions-theore-tischen Untersuchungen in der Land-und Nahrungsgiiterwirtschaft. Statistische Praxis, 25 (1970), 1, S. 41—46, 2, S. 87—89; Linke C. Einschrankung der Multikollinearitat fiber EDVA. Statistische Praxis, 32 (1977), 1, S. 32—33.
10 ТИПИЧНЫЙ ПРИМЕР
В этой главе мы хотим продемонстрировать на типичном примере применение методов регрессионного и корреляционного анализа для исследования зависимости экономических явлений.
На одном объединении народных предприятий ГДР изучалась зависимость объема производства (у) от капитальных вложений (xj и выполнения нормы выработки (х2). Для построения модели были собраны данные по исследуемым переменным на 12 предприятиях этого объединения (см. табл. 18). Исходя из экономических соображений предполагаем, что зависимость между переменной у и переменными и х2 имеет линейный характер.
Таблица 18
Объем производства, капиталовложения и выполнение нормы выработки на 12 предприятиях объединения народных предприятий ГДР
Предприятие Капиталовложения, 1000 марок Средний процент выполнения нормы Объем производства, 104 марок
i Xii Xi2 У1
1 16,3 99,5 52,8
2 16,8 98,9 48,4
3 18,5 99,2 54,2
4 16,3 99,3 50,0
5 17,9 99,8 54,9
6 17,4 99,6 53,9
7 16,1 99,8 53,1
8 16,2 99,7 52,4
9 17,0 99,8 53,0
10 16,7 99,9 52,9
11 17,5 100,0 53,1
12 19,1 100,2 60,1
Сумма 205,8 1195,7 638,8
Среднее х1=17,15 х2 = 99,64 у = 53,23
Дисперсия 8^ = 0,9245 «2 =0,1336 х2 8^ = 7,8369
Стандартное отклонение sX1 = 0,9615 SX2 =0,3655 Sy = 2,7995
223
Сначала определим простые линейные регрессии *.
а) Построим уравнение регрессии у = f (%), характеризующее зависимость объема производства от капиталовложений. Используя информацию табл. 18, получим
У = ”52,8 ” 48,4 54,2 50,0 54,9 53,9 53,1 52,4 53,0 52,9 53,1 _60,1 _ X ” 1 16,3” , Х'Х = 12 205,8 ‘ . 205,8 3539,64 .
1 1 1 1 1 1 1 1 1 1 _ 1 16,8; 18,5 16,3 17,9 17,4’ 16,1 16,2 17,0 16,7 17,5 19,1
(X L' X)-» : ' 29,004 — 1,686' , X': ' 638,8 '
. —1,686 0,098. .10977,41
'16,1509' 2,1622
Su = 3,8659
по (2.64),
по (3.32),
112,126 —6,519 '
—6,519 0,3801,
по (3.42).
Построенное уравнение имеет вид: 7= 16,154-2,1622%!,
su = 1,9662,
(0,6165) В,Л = 0,5515,
(3,507) г91 = 0,7426,
F = 12,29, t = 3,506.
В первых скобках под коэффициентом регрессии стоит его стандартная ошибка, а во вторых скобках — значение t, полученное по (8.55). Коэффициент детерминации вычислен по (4.13), значение F — по (8.50), коэффициент корреляции — по (4.20), значение t для оценки его значимости—по (8.38). Далее, Z10;0 05 = 2,228 и Fv,w„0t9b = 4,965.
Сравнивая расчетные значения статистик с критическими, приходим к выводу о значимости полученных оценок при а = 5%. Коэффициент регрессии показывает, что в среднем объем производства увеличивается на 2,1622-104 марок, если капиталовложения возрастают на 1000 марок.
б) Построим уравнение регрессии у = f (х2), характеризующее зависимость объема производства от выполнения нормы выработки. Используя информацию, приведенную в табл. 18, получим
“"Промежуточные результаты вычислений указаны с^округлением, 224
"52,8 " " 1 99,5
48,4 1 98,9
54,2 1 99,2
50,0 1 99,3
54,9 1 99,8
V = 53,9 , х = 1 99,6 „,„_[ 12 1195>7 1 » Zv Л. I 1 ,
53,1 1 .99,8 [1195,7 119143,01 J
52,4 1 99,7
53,0 1 99,8
52,9 1 99,9
53,1 1 100,0
_60,1_ _ 1 100,2_
[6757,92 —67,82 1 [ 638,8 1
, X у = .
—67,82 0,681 J [63659,25
—499,741
5,549
S3 = 4,0958,
27679,7 —277,79
—277,79 2,788
Построенное уравнение имеет вид: 7= —499,74 4- 5,549х2, su = 2,0238,
(1,669) Ву2 = 0,5249,
(3,324) Гу2 = 0,7245.
F= 11,05, / = 3,32.
В этом случае также приходим к выводу о значимости полученных оценок при а = 5%. Коэффициент регрессии показывает, что в среднем объем производства увеличивается на 5,549-104 марок с ростом выполнения нормы выработки на 1 %.
Коэффициенты детерминации обеих линейных регрессий сравнительно малы. Изменения объема производства недостаточно полно объясняются изменениями капиталовложений и выполнения нормы выработки. Поэтому теперь поставим задачу определить множественную регрессию, включив в анализ все три переменные. Итак,
"52,8 " ” 1 16,3 99,5"
48,4 1 16,8 98,9
54,2 1 18,5 99,2
50,0 1 16,3 99,3
54,9 1 17,9 99,8
Гу — 53,9 , х = 1 17,4 99,6
53,1 1 16,1 99,8
52,4 1 16,2 99,7
53,0 1 17,0 99,8
52,9 1 16,7 99,9
53,1 1 17,5 100,0
_60,1 _ _ 1 19,1 100,2_
8 Зак. 1113
225
Г 12
Х'Х =
Г7056.02
(X' X)-1 =
Ь =
—71,78
"—408,458 ' 1,721 4,337 _
205,8
1195,7
205,8 1195,7 "
3539,64 20507,29
20507,29 119143,01
5,62 —71,78
0,106 —0,075
—0,075 0,733
S3 =1,445, Sbb =
’ 638,8 ’ Х'у = 10977,41
^63659,25 _
"10193,41
8,117 _—103,696
8,117 —103,696"
0,153 —0,108
—0,108 1,059
Построенное уравнение множественной регрессии имеет вид:
—408,458+ 1,721хх +4,337х2,
(0,391) (1,029)
(4,399) (4,214)
(0,591) (0,566)
$„=1,2019,
5^.12 = 0,849, F = 25,3, ^.12 = 0,921,
^1.2 = 0,8261, t = 4,398, = 0,8146, t - 4,213.
В третьих скобках под коэффициентами регрессии указаны стандартизованные коэффициенты регрессии, вычисленные по (2.67). Коэффициент детерминации вычислен по (4.69), значение F для оценки его значимости—по (8.52), коэффициент множественной корреляции — по (4.47), коэффициенты частной корреляции — по (4.60), а значения t для оценки их значимости— по (8.41). По таблицам приложения находим критические значения /9;0,05 = 2,262 и /72;9;0>05 == 4,256. Сравнивая расчетные значения статистик с критическими’, приходим к выводу о значимости полученных оценок при а = 5%. Переменные Xi и х2 как в отдельности (значимость коэффициентов регрессий), так и совместно (значимость коэффициента детерминации) оказывают существенное влияние на изменение переменной у. Коэффициент множественной детерминации ВуЛ2 = 0,849 указывает на то, что изменения объема производства в сильной степени определяются вариацией капиталовложений и выполнения нормы выработки. Включение в анализ переменных хг и х2 существенно увеличивает долю объясненной дисперсии. Полученное уравнение множественной регрессии объясняет общий разброс на 84, 9%. В улучшении соответствия регрессии исходным данным можно убедиться также, применяя критерий (8.60). При сопоставлении ВуЛ2 с ВУ1 получим расчетное значение F = 17,73, а при сопоставлении Ву Л2 с Ву2— расчетное значение F = 19,32 при критическом значении = 5,117.
Коэффициент частной регрессии Ьг = 1,721 показывает, что объем производства в среднем возрастает на 1,721 -104 марок с увеличением капиталовложений на 1000 марок при постоянном показателе выполнения нормы выработки. Коэффициент частной регрессии Ь2 = 4,337 свидетельствует о том, что при одних и тех же капиталовложениях и при изменении выполнения нормы выработки на 1 % объем производст
226
ва в среднем изменяется на 4,337-104 марок. Как известно, стандартизованные коэффициенты регрессии показывают сравнительную силу влияния изменения каждой объясняющей переменной на изменение зависимой переменной. Следуя этой интерпретации, видим, что обе переменные оказывают практически одинаковое влияние на изменение объема производства (соответствующие стандартизованные коэффициенты регрессии равны bi = 0,591 и Ь'2 = 0,566). Этот вывод можно подтвердить, рассмотрев коэффициенты парных и частных корреляций (гп, Гу2, гу1Л и Гугл)- Кроме того, с помощью критерия (8.61) можно показать, что различие между коэффициентами частной регрессии Ь1 и Ь2 статистически незначимо. (Расчетное значение статистики составляет \t\ = 2,189 при критическом ее значении /9.0 05 = 2,262).
Для нашего примера коэффициенты частной регрессии меньше соответствующих коэффициентов простой регрессии. Причина заключается в том, что при вычислении коэффициентов частной регрессии каждый раз исключается влияние другой переменной. Очевидно, (или х2) не оказывают непосредственного влияния на переменную у, а воздействуют на нее через х2 (или хх). В связи с этим возникает вопрос о существовании коллинеарности между хг и х2. Ответить на этот вопрос можно с помощью простого коэффициента корреляции, характеризующего тесноту связи между капиталовложениями и выполнением нормы выработки (первая отправная точка установления мультиколлинеарности).
Имеем:
г12 = 0,2678, t = 0,879, /10;0,05 = 2,228.
Критерий не подтверждает значимой корреляции между переменными хг и х2. Осуществим проверку существования мультиколлинеарности дополнительно с помощью критерия Фаррара — Глаубера, который является более надежным общим показателем линейной связи между объясняющими переменными. По (9.9) получим расчетное значение статистики %2 = 0,7067. Так как критическое значение составляет 0,05 = = 3,841, приходим к выводу, что мультиколлинеарность незначима.
Проверка статистической надежности простых и множественной регрессий дает нам удовлетворительные результаты. Однако, как показывает коэффициент детерминации, рассмотрение только простой регрессии недостаточно. Кроме того, расчетные значения статистик при проверке значимости коэффициентов частной регрессии, корреляции и детерминации значительно больше, чем расчетные значения статистик соответствующих парных коэффициентов. Множественная регрессия дает более адекватное отражение экономического явления.
Укажем доверительные границы для множественной регрессии и ее параметров. В соответствии с (8.14) доверительные границы для коэффициентов частной регрессии будут следующими:
0,836 Pi 2,605,
2,009 Р2 6,664.
При построении доверительных границ для коэффициента множественной корреляции по (8.16) и (8.6) вместо квантиля нормального распре
8*
227
деления воспользуемся из-за малого объема выборки п « 12 квантилем /-распределения /э;0,05.*
0,687 p^,12 0,982.
Доверительные границы для значений регрессии, вычисленные по (8.24), приведены во втором и третьем столбцах табл. 19, а доверительные границы для отдельных наблюдений переменной у, вычисленные по (8.36), — в четвертому пятом столбцах.}
Таблица 19
Зависимость объема производства от капиталовложений и выполнения нормы выработки. Доверительные границы для значений регрессии и отдельных наблюдений переменной у
Значения регрессии Доверительные границы для значений регрессии Доверительные границы для отдельных наблюдений переменной у
У t — ts^ 1 «1
51,16 50,08 52,23 48,23 54,08
49,41 47,57 51,26 46,13 52,70
53,64 51,70 55,58 50,30 56,98
50,29 49,07 51,51 47,31 53,27
55,21 54,18 56,24 52,30 58,12
53,48 52,72 54,25 50,66 56,31
52,11 50,77 53,45 49,08 55,14
51,85 50,67 53,03 48,89 54,82
53,66 52,77 54,55 50,80 56,53
53,58 52,46 54,70 50,64 56,52
55,39 54,26 56,52 52,45 58,33
59,01 56,99 61,03 55,62 62,39
РЕГРЕССИЯ
II И КОРРЕЛЯЦИЯ ВРЕМЕННЫХ РЯДОВ
11.1. МОДЕЛЬ РЕГРЕССИИ ВРЕМЕННОГО РЯДА
Взаимосвязанные явления могут рассматриваться в двух различных аспектах. Комплекс явлений может подвергаться изучению в один и тот же момент времени или за один и тот же промежуток времени в различных точках пространства. При построении статистических рядов для анализа явлений в этом случае не имеет значения, в какой последовательности возникли те или иные значения признака. До сих пор мы занимались изучением регрессии по результатам таких одновременных исследований. Примерами таких регрессий служат зависимость себестоимости от объема производства на нескольких предприятиях, зависимость производительности труда от уровня механизации работ и среднего возраста работников в различных цехах одного предприятия, зависимость товарной продукции от основных фондов за определенный промежуток времени в различных отраслях промышленности.
При изучении же развития комплекса явлений во времени последовательность возникновения значений признака приобретает существенное значение. По результатам наблюдений строятся хронологические ряды, называемые также рядами динамики или временными рядами1. Для таких рядов разработаны особые приемы статистической обработки. По многомерным временным рядам строят регрессии. В качестве примера можно привести зависимость месячных производственных расходов от объема производства в течение двух лет для одного и того же предприятия. Методы, применяемые для анализа временных рядов, могут быть обобщены на случай исследования пространственных явлений, когда имеется более одного измерения, подобного времени.
Чисто формально регрессию временных рядов можно обсуждать в тех же терминах, что и регрессию статистических рядов, построенных по результатам одновременных наблюдений.
временной ряд состоит из двух элементов: моментов, или периодов времени наблюдений, к которым относятся статистические данные, и самих данных, называемых уровнями ряда. Оба элемента — время и уровень — называются членами ряда. — Примеч. nep.jj
229
Линейная регрессия временных рядов может иметь, например, такое выражение:
Vt = b0 + Ь±хп + ...+ bmxtm. (11.1)
Зависимая переменная у в определенный момент времени или за определенный промежуток времени t принимает значение
yt= s bth xtk-\-ut, (11.2)
/2=0
где yt — значение зависимой переменной в определенный момент времени /; Ьп— параметр регрессии объясняющей переменной^, он имеет такое же истолкование, что и обсуждавшиеся ранее параметры регрессии (см. разделы 2.3,2.4 и 2.7); xth — значение объясняющей переменной Xh в момент времени Z; yt — значение регрессии в определенный момент времени t\ ut — значение возмущающей переменной (остаток) в момент времени £; t = 1,2,..., Г;?1—число моментов наблюдений за исследуемый промежуток времени; А =0,1, 2,..., т—число объясняющих переменных; xto = 1 для всех t.
Уравнение регрессии строится с помощью метода наименьших квадратов (см. раздел 2.4), применение которого требует выполнения ряда предпосылок (см. раздел 2.9). В связи с этим при определении регрессии по временным рядам возникают некоторые затруднения.
Одной из проблем, в частности, является несовпадение во времени причины и следствия. При наличии некоторых сопутствующих переменных причинные переменные могут опережать, т. е. предшествовать следствию. Этот феномен довольно часто встречается во многих экономических ситуациях. Значения признаков экономических явлений, наблюдаемых в данный промежуток времени, представляют собой результаты причин, действующих не только в этот же промежуток времени, но и в предшествующий период. Интересующая нас переменная систематически связана с другими опережающими ее переменными, благодаря чему образуется круговая цепь причинности. Сдвиги в явлениях могут возникнуть из-за разного рода нарушений, имеющих субъективный характер, например из-за ошибок в наблюдениях, из-за вводимой корректировки статистической отчетности для получения сопоставимых промышленных показателей. Так, для сопоставимости выпуска продукции за календарные месяцы проводят корректировку путем приведения их к стандартному месяцу из 30 дней. Подобные сдвиги возникают при рассмотрении коротких промежутков времени (декада, месяц, квартал). Отставание значений одного статистического ряда относительно значений другого статистического ряда — независимо от того, по каким причинам это происходит, — называется лагом. Причинно обусловленные статистические ряды можно соотносить друг с другом и строить по ним регрессию с учетом поправки на величину лага. Если известно, что эффект от фактора возникает лишь через два последовательных промежутка времени наблюдений, то при построении регрессии значения одного из рядов сдвигаются на эти два промежутка.
230
Этот подход нужно использовать, например, при изучении зависимости между числом вступивших в брак и числом первенцев. Этот пример наглядно показывает, что значения обоих статистических рядов было бы бессмысленно рассматривать в один и тот же момент времени.
При построении регрессионных моделей часто приходится прибегать к включению в правую часть уравнений лаговых значений объясняющих переменных. Уравнение регрессии с учетом лаговых (запаздывающих) переменных записывается в виде
yt = bo i,i 4” b2xt-1,2 (11*3)
или, если обозначить лаг через т = 0,1,2,..., s,
yt — bo + ^l^t-T,l + b2xt^x,2 + ••• (U-4)
Объясняющие переменные могут иметь различный лаг. Кроме того, в некоторых случаях к лаговым значениям объясняющих переменных добавляются одно или несколько лаговых значений зависимой переменной. Например, если зависимая переменная в момент t объясняется своими собственными значениями в предшествующий период, то модель может быть представлена в виде (см. главу 12):
yt = ьо + Mt-1 + b2xt2. (11.5)
При исследовании зависимостей между экономическими явлениями временные сдвиги взаимосвязанных значений статистических рядов большей частью неизвестны. Но если при построении регрессии не учитывать лаг, то вполне возможно, что вычисленные коэффициенты корреляции и регрессии будут содержать большие погрешности. Это в свою очередь приводит к ошибочным выводам. Разработаны различные процедуры определения длины лага, позволяющие при некоторых априорных предпосылках улучшить качество оценок параметров регрессии и повысить адекватность уравнения.
Другая проблема, возникающая при построении регрессии по временным рядам, связана с объемом наблюдений. При редких наблюдениях можно пропустить существенные особенности изучаемой тенденции. Увеличение же точек наблюдения обычно влечет за собой дополнительные расходы. Часто возможность выбора объема наблюдений вообще отсутствует. Особенно приходится с этим сталкиваться при исследовании временных рядов в экономике. Так, для многих отраслей народного хозяйства в ГДР мы располагаем данными для построения рядов динамики только начиная с 1950 или даже с 1960 г. Чем меньше объем наблюдений, тем менее надежны оценки параметров модели.
При изучении временных рядов исследователя подстерегает опасность столкнуться с ложной регрессией. По коэффициенту регрессии между временными рядами нельзя сразу делать вывод о причинно-следственных отношениях, так как явления развиваются во времени параллельно друг другу в одном и том же или в противоположных направлениях. Соответствие в изменениях может быть результатом простого сопутствия в развитии отражаемых в рядах явлений. Колеблемость чисел, составляющих динамический ряд, испытывает на себе
231
влияние фактора времени, а также фактора места, которые, внося скрывающийся за ними сложный комплекс причин, затемняют закономерный ход явления и его связи с другими явлениями. Так, имеется положительная регрессия между динамическими рядами количества онкологических заболеваний в год и числа выпускников школ за последние 30 лет. Тенденции развития обоих явлений связаны с непрерывным ростом численности населения. Логические рассуждения не дают нам оснований предполагать каких-либо причинных отношений между этими явлениями.
Как упоминалось ранее, одна из предпосылок применения методов корреляционного и регрессионного анализа — стохастическая независимость результатов наблюдений. В динамических рядах вследствие влияния фактора времени эта предпосылка часто не выполняется. Фактор времени, вмещая в себя многие другие факторы развития, вызывает направленные изменения социально-экономических и других явлений. Преобладающая тенденция изменения членов ряда, характеризующего данное явление, называется трендом. Следовательно, члены одного и того же ряда связаны между собой: предыдущие члены влияют на последующие. Этот факт называется автокорреляцией. Прежде чем находить количественную оценку связи между временными рядами, нужно проверить существование автокорреляции.
Тот факт, что мы особо подчеркиваем роль автокорреляции во временных рядах, вовсе не означает отсутствия автокорреляции в данных, полученных при одновременных обследованиях. Эта проблема характерна для любых ситуаций. Во временных рядах автокорреляция создает более серьезные трудности для применения обычного метода наименьших квадратов. Прежде чем перейти к более детальному изложению проблемы автокорреляции, уточним некоторые понятия. Так, при обсуждении регрессии и корреляции временных рядов будем различать связь между исходными переменными и связь между остатками (временные ряды исходных переменных и временной ряд возмущений). Вследствие этого будем рассматривать отдельно:
а) автокорреляцию переменных у и измерению автокорреляции переменных посвящен раздел 11.2;
б) автокорреляцию возмущений; этот вид автокорреляции создает дополнительные трудности при ее измерении, автокорреляция возмущений обсуждается в разделе 11.3.
Опыт показывает, что временной ряд удобно представлять в виде суммы нескольких компонентов. Наиболее важные из них — тренд и сезонная компонента. Ограничимся обсуждением влияния тренда на регрессию между двумя временными рядами. При этом будем предполагать, что явления, характеризующиеся временными рядами, причинно обусловлены. Тем самым мы исключаем из рассмотрения ложную регрессию. Но надо иметь в виду, что на практике эта проблема вызывает серьезные затруднения.
Относительно принципов построения регрессии между временными рядами пока еще не сложилось единого мнения. Одни ученые считают, что регрессия непосредственно между временными рядами с трендом возможна, если между ними существуют причинные отношения. Но в 232
этом случае неясно, почему из рядов динамики, а тем самым из регрессии, должен исключаться тренд. Разумеется, в противном случае нарушается предпосылка независимости значений. С этим нарушением, однако, приходится не считаться, если регрессия на основе тренда достаточно определена и по ней получают хорошие прогнозные значения. Другие считают, что регрессию между временными рядами следует находить после устранения тренда. Во-первых, этим достигается независимость наблюдений, во-вторых, уменьшаются или совсем исключаются возмущения. Если тренд не устраняется, то можно показать, что функция регрессии временных рядов может быть заменена функцией тренда. Тем самым учитывается только долгосрочное движение, обусловленное однообразно действующими приблизительно в одном и том же направлении силами. А сезонная и другие компоненты, вызывающие более или менее регулярные колебания относительно тренда, практически не принимаются во внимание. Очевидно, что оба мнения вполне обоснованы. Если задачей исследования является получение по возможности хороших прогнозных значений (это прежде всего необходимо при планировании), то при построении регрессии тренд не исключается. Если же хотят установить лишь общую закономерность между зависимой и объясняющими переменными, то тренд исключается.
Для устранения из временных рядов систематических элементов используются следующие подходы:
определение прироста переменных 1:
Az/г = &о + Ах/i + b2kxt2 + •••; (11-6)
установление влияния лага т = 1 на зависимую переменную:
&Уг = bQ + + b2&xt-li2 + • (Н.7)
Лаги переменных должны быть обоснованы причинно-следственными отношениями между экономическими явлениями. Далее можно зависимую переменную с лагом рассматривать как причинный фактор;
использование значений x*,k, освобожденных от тренда:
У* = Ьо + Ь^*,! + Ь2х*,2 + •••! (11-8)
учет функции тренда F (/) при построении регрессии между временными рядами:
yt = bo + + b2Xti2 + ... + ^ (/)• (11.9)
Возможны также другие подходы, позволяющие уменьшить действие автокорреляции временных рядов на регрессию и остатки. Это касается как квазилинейных, так и нелинейных регрессий. Более подробное изложение этих вопросов не допускает объем данной книги.
11.2. АВТОКОРРЕЛЯЦИЯ ПЕРЕМЕННЫХ
Временные ряды, а при особых обстоятельствах и данные одновременных исследований, необходимо проверить на автокорреляцию, чтобы установить, выполняется ли требование стохастической независимо-
Шриростами ряда называются разности между последующими уровнями ряда и предыдущими. — Примеч. пер.
233
сТи результатов наблюдений. Члены одного и того же ряда взаимосвязаны друг с другом, т. е. ряд автокоррелирован, если существует корреляция между последовательными уровнями ряда. При этом следует рассматривать также корреляцию между значениями, смещенными на лаг т в одном и том же ряду. Итак, корреляция между последовательными или смещенными на лаг т значениями одного и того же ряда наблюдений называется автокорреляцией переменных. Ее следует отличать от автокорреляции возмущений, о которой речь пойдет в разделе 11.3.
Автокорреляция переменных вызывает серьезные затруднения при вычислении коэффициентов корреляции и регрессии между временными рядами, а при их интерпретации, безусловно, необходимо проявлять осторожность. В каждом случае следует удостовериться, применимы ли рассмотренные нами ранее методы корреляционного и регрессионного анализа и приведут ли они к правильным результатам.
Величина автокорреляции статистических рядов может быть измерена с помощью коэффициента автокорреляции. Для этой цели определяют корреляцию между значениями ряда, смещенными на лаг т, т. е. между последовательностями х19 х2,..., хт—% и Xi-j-?, %т.
В данном случае речь идет о нециклической автокорреляции, так как предполагается, что ряд затухает на значении хт. Таким образом, нециклическая автокорреляция*—это корреляция между исходным рядом и тем же самым рядом, смещенным на лаг т.
Если временной ряд имеет циклический характер, т. е. предполагается, что после значения хт общий характер изменений членов ряда повторяется (о чем можно судить по сезонной компоненте и другим более или менее регулярным колебаниям), то автокорреляцию измеряют с помощью коэффициента циклической автокорреляции, введенного Андерсоном Р. Л. В этом случае определяется корреляция между последовательностями Х1? Х2,..., Хт ИХг+1, ^т+2, одного и того
же ряда. Во второй последовательности после Хт располагаются члены х19 х2, ..., хт первой последовательности.
Далее речь будет идти только о коэффициенте автокорреляции первого порядка, который применяется для измерения связи между последовательными значениями уровней ряда при лаге 1. Члены ряда смещаются при этом на одну единицу времени.
Коэффициент нециклической автокорреляции первого порядка /Сх измеряет автокорреляцию между последовательностями х19 х2,..., Хт~! и х2, х3, ..., Хт. По аналогии с (4.5) из раздела 4.1 получим
Г —1 Т-1
т-1 2 xt 2
(11.10)
234
Коэффициент циклической автокорреляции первого порядка отражает интенсивность связи между последовательностями х19 х2, ..., хт и х2, х3, Хт, По аналогии с (4.5) из раздела 4.1 получим после некоторых преобразований
Г-1 _
Х1 ХТ У1 —?х
К; =-------------------------(11.11)
2 х?-Тх2 /=1
Хотя К\ вычислить проще, чем /Сх, при исследовании экономических явлений отдают предпочтение коэффициенту нециклической автокорреляции К19 так как не всегда можно предположить, что временной ряд имеет циклический характер с периодом Т. Но недостатком коэффициента Ki является то, что неизвестно его распределение для малых выборок из нормально распределенных генеральных совокупностей, в которых отсутствует автокорреляция. В экономических же исследованиях приходится иметь дело как раз с выборками небольшого объема. И напротив, распределение К\ известно. Можно показать, что для больших объемов выборок и почти совпадают и что если Т -> оо, то Ki -* Кл- В соответствии с этим критерий для проверки значимости коэффициента циклической автокорреляции, предложенный Р. Л. Андерсоном, пригоден также при больших объемах выборок для проверки значимости Если в генеральной совокупности, из которой отобрана выборка, отсутствует автокорреляция, то дисперсия коэффициента Ki при выборке объема Т составит sj^ = у—у. Для выборок большого объема величина
(11.12)
имеет /-распределение с f = Т — 1 степенями свободы. Р. Л. Андерсон построил таблицу критических значений коэффициента циклической автокорреляции, которая пригодна также при больших объемах выборок для проверки значимости коэффициента нециклической автокорреляции. Выдержка из этой таблицы приведена в приложении (см. табл. 7). Если /Q > /G табл, то эмпирический коэффициент автокорреляции первого порядка указывает на наличие автокорреляции при уровне значимости а. Для выборок небольшого объема такой вывод будет ненадежным. В этом случае привлекают непараметрический критерий, построенный на основе неравенства Бьеномэ — Чебышева. В соответствии с этим критерием вероятность, Р, того, что наблюдаемое значение лежит в интервале
К — hvK К + haK, равна
Р=1------- (11.13)
Л2
или _____
235
К — коэффициент автокорреляции и — стандартное отклонение этого коэффициента в генеральной совокупности. Если мы, например, производим проверку значимости коэффициента нециклической автокорреляции с вероятностью 0,95, или 95%, то по (11.14) получим Лтеор = s= 4,472. Если теперь при выборках малого объема значение t, вычисленное по (11.12), окажется больше, чем 4,472, то можно с вероятностью 0,95 утверждать, что в данном ряду присутствует автокорреляция. Если вычисленное значение t будет меньше 4,472, то данная выборка не позволяет нам сделать вывод о существовании автокорреляции (гипотеза Но принимается). Однако следует подчеркнуть, что непараметрические критерии имеют меньшую эффективность, чем соответствующие параметрические. Но непараметрические критерии не требуют никакого предположения о виде распределения.
Для исследования автокорреляции применяют также другие методы. Среди них прежде всего следует назвать метод Р. Фриша и Ф. В. Воу, метод разностей, разработанный в основном О. Андерсоном и В. С. Госсетом (псевдоним— Стьюдент), а также метод X. Волда и Дж. X. Оркатта. Объем книги не позволяет нам более подробно обсудить эти методы, и заинтересованного читателя мы отсылаем к специальной литературе.
Как отмечалось в разделе 4.1, по коэффициенту корреляции, равному или близкому к нулю, при вычислении его по парам наблюдений хг-, Уг, i = 1,2, ..., п, не может быть сделан вывод об отсутствии связи между изучаемыми явлениями вообще. Это касается также корреляции временных рядов. Наличие временной последовательности причины и следствия иногда не является достаточным основанием, чтобы определять корреляцию по парам наблюдений с тем же самым порядковым номером, т. е. xt, yt.
Необходимо также проверить, существует ли корреляция между парами значений, смещенными относительно друг друга на величину лага. Так, при лаге т = 1 исследуют корреляцию по парам наблюдений xt, yt+1, при лаге т — — 1 — по парам наблюдений xt, yt_1. Эта процедура иногда необходима, чтобы вскрыть объективно существующие взаимосвязи. Ярким примером, иллюстрирующим это положение, служит связь между числом вступивших в брак и числом первенцев. При изучении связей между экономическими явлениями также требуется учитывать соответствующие лаги, например при установлении связи между капиталовложениями и объемом производства, между расходом сырья и материалов и объемом выпускаемой продукции (особенно при индивидуальном производстве). Сроки реализаций капиталовложений и сроки прироста продукции, вытекающие из этого факта, а также время произведенных расходов сырья и материалов и сроки выпуска продукции могут более или менее сильно различаться. Это отставание по времени причинно обусловленных явлений в основном зависит от характера производственного процесса (индивидуальное, серийное, массовое и т. д.), от продолжительности процесса изготовления и периода исследования (декада, месяц, квартал и т. д.). Чем длиннее производственный цикл и чем короче период исследования, тем больше вероятность возникновения лага. Корреляция, определенная
236
по парам значений с единичным запаздыванием, т. е. по значениям, смещенным на лаг 1, называется сериальной (по-английски — serial correlation). Понятие сериальной корреляции чаще всего применяется к автокорреляции временных рядов. Чтобы избежать недоразумений при использовании этого понятия, рекомендуем рассматривать его в узком смысле, предложенном нами. Аналогично вводят понятие сериальной корреляции с запаздыванием (или лагом т), т. е. корреляции между членами временных рядов, отстоящими друг от друга на т единиц. В качестве меры связи используется коэффициент сериальной корреляции. Ограниченные рамками данной книги, мы, к сожалению, не можем более подробно остановиться на проблемах сериальной корреляции *.
11.3. АВТОКОРРЕЛЯЦИЯ ВОЗМУЩЕНИЙ
Будем исходить из того, что найдены МНК-оценки параметров линейной регрессии и вычислены остатки.
При применении метода наименьших квадратов предполагается равенство нулю ковариаций возмущающих членов (см. предпосылку 3 в разделе 2.9). Эта предпосылка особенно важна при построении регрессии по временным рядам. Равенство нулю ковариаций для модели с нормально распределенными возмущениями означает их попарную независимость. Если же возмущающие переменные содержат тренд или циклические колебания, то последовательные возмущения, действующие в различные моменты времени, коррелированы. Такой вид корреляции называется автокорреляцией возмущений, или остатков. Далее будут рассмотрены последствия, вызываемые автокорреляцией возмущений, и критерии, позволяющие установить ее существование. При этом мы заранее отказываемся от доказательств обсуждаемых утверждений.
Зависимость между последовательными возмущениями может быть установлена и оценена с помощью регрессии. Покажем это на простом примере с авторегрессией первого порядка, т. е. в случае линейной зависимости между последовательными возмущениями:
ut = puz_! + et для t = 2 , ..., Т, (11.15)
где р— коэффициент автокорреляции **, для которого выполняется условие р < 1. Переменная et в (11.15) должна удовлетворять требованиям:
Е (et) = 0; Е (ef) = of] E(etet-X) = 0 для т > 0; (11.16)
Е (etUt-x) = 0 для т > 0.
*См. также: Anderson R. L. Distribution of the serial Correlation coefficient. Ann. math. Statistics, 13, 1 (1942).
**Так как согласно предпосылке 3 математическое ожидание возмущающей переменной щ равно нулю, речь пойдет о простой регрессии стандартизованных переменных, при которой коэффициенты регрессии и корреляции совпадают (см. раздел 4.3).
237
Так как значения возмущающих переменных и коэффициента автокорреляции неизвестны, заменим их соответствующими оценками:
ut = put-i+et. (11.17)
Оценка параметра р может быть найдена с помощью метода наименьших квадратов. В соответствии с (2.26) и учитывая (2.73), имеем
т
2 ut-i ut
Р=Ч^:---------• (Н-18)
2 «-1
t — 2
Если р положительно, то мы располагаем положительной автокорреляцией остатков. Она возникает, если возмущения характеризуются трендом или циклическими колебаниями, что часто встречается при экономических исследованиях. Если р отрицательно, то мы имеем отрицательную автокорреляцию остатков. Отрицательная автокорреляция остатков наблюдается, если остатки попеременно принимают, то положительные, то отрицательные значения.
Перечислим последствия, вызываемые автокорреляцией остатков:
1. Матрица дисперсий и ковариаций возмущений (см. формулу (2.80)) не будет более диагональной. При наличии автокорреляции в случае справедливости гипотезы о гомоскедастичности дисперсия возмущающей переменной ut равна:
а£ = т-^—Ог, (11.19)
1 — р2
а ковариация между щ и выражается как
= № = (11.20)
Матрица дисперсий и ковариаций принимает вид:
- 1 р Р2 • РГ-‘П
р 1 Р рг-2 = OuQ.
_рг-‘ рТ-2 рт-3 ., 1
(П-21)
Несмещенная оценка дисперсии возмущающей переменной следующая:
s2 =----!---/и' Q-i щ (11.22)
T-On + l) ’
Итак, при автокоррелированных возмущениях применение известной формулы (3.32) приводит к недооценке дисперсии возмущающей переменной.
2. Результатом автокорреляции возмущений является также недооценка истинной выборочной дисперсии параметра регрессии 0 в слу-238
чае применения формулы (3.41). Определив Е (u'u) при наличии автокорреляции остатков с помощью (11.21) и воспользовавшись (3.40), получим
Sb& = (X'X)-1X'Stttt X (Х'Х)"1. (11.23)
Недооценка дисперсий — препятствие к корректному применению обычного метода наименьших квадратов к модели с автокоррелирован-ными возмущениями, даже если вводятся соответствующие поправки в оценки выборочных дисперсий. Кроме того, возникают затруднения при использовании критериев значимости (см. главу 8), так как распределения вычисляемых статистик отличаются от /- и F-распреде-лений.
Исходя из изложенного ясно, что чрезвычайно важно иметь критерии, позволяющие устанавливать наличие автокорреляции. Здесь мы рассмотрим один из самых распространенных критериев, получивший название критерия Дарбина — Уотсона.
При применении этого критерия формулируется нулевая гипотеза юб отсутствии автокорреляции — Яо: р = 0. Альтернативная гипотеза сможет быть построена на основе использования односторонней критической области — Нг: р > 0, т. е. существует положительная автокорреляция, либо Нг : р < 0, т. е. существует отрицательная автокорреляция, или на основе использования двусторонней критической области — Н±; р =/= 0. При этом применяется статистика d:
2 (ut— Ut-1)2
d = -----------. (11.24)
/=1
Между статистикой d (статистика Дарбина — Уотсона) и коэффициентом автокорреляции р существует приближенное соотношение:
d = 2 (1 — р). (11.25)
Возможные значения статистики лежат в интервале 0 d 4. Если возмущения не содержат автокорреляцию, т. е. р = 0, то значения статистики располагаются вблизи числа 2. При сильной положительной корреляции остатков величина d близка к нулю. Сильная отрицательная корреляция остатков приводит к тому, что величина d приближается к 4.
Статистика d принимает небольшие значения, если последовательные величины ut~i и доказываются очень близки друг к другу. Это может свидетельствовать о наличии тренда или о циклических колебаниях. Если остатки принимают последовательно то положительные, то отрицательные значения, сумма квадратов их разностей становится большой по величине. В результате статистика d также принимает большие значения.
Выборочное распределение статистики d, необходимое для проверки гипотезы о некоррелированности остатков, имеет сложный вид. Чтобы не обращаться непосредственно к этому распределению, можно восполь
239
зоваться методом Дарбина и Уотсона, которые установили верхний dB и нижний dB пределы значимости статистики d. Эти критические значения зависят от уровня значимости а, объема выборки Т и числа объясняющих переменных т. В табл. 8 приложения приведены значения dH и dB для 5%-ного, 2,5%-ного и 1%-ного уровней значимости при Т от 15 до 100 и числе объясняющих переменных, /и, от 1 до 5.
Критерий Дарбина — Уотсона обладает двумя недостатками. Первый из них заключается в том, что критические границы принятия нулевой гипотезы и непринятия альтернативной гипотезы не совпадают. Как показано на рис. 25, критические значения образуют пять областей различных статистических решений. При этом появляются области неопределенности, в которых с помощью данного критерия нельзя
Отвергаем Z/o; принимаем Н\ о существовании положительной автокорреляции остатков ? Принимаем HQ об отсутствии автокорреляции остатков ? Отвегаем Но; принимаем Н\ о существовании отрицательной автокорреляции остатков
0 dB 2 4~~dB 4
Рис. 25. Применение критерия Дарбина — Уотсона
прийти ни к какому решению (нулевая гипотеза не принимается и не отвергается). Второй недостаток заключается в том, что при объеме выборки меньше 15 для d не существует критических значений dH и dB.
Вычисленное по (11.24) значение d сравнивается с dH и dBt найденными по табл. 8 приложения. При этом руководствуются правилами: 1. dB d 4 — dB — принимается гипотеза Н0:р = 0 (автокорреляция остатков отсутствует).
2. 0 d dH — принимается гипотеза Н± : р > 0 (существует положительная автокорреляция остатков).
3. dH d dB и — при выбранном уровне значимости нельзя
4— dB d 4 — dH прийти к определенному выводу (необходимо
дальнейшее исследование).
4. 4 — dH d 4 — принимается гипотеза : р < 0 (существует
отрицательная автокорреляция остатков).
Часто автокорреляция остатков — следствие ошибки спецификации регрессии. Причины возникновения автокорреляции остатков: в регрессии не учтена какая-либо объясняющая переменная, играющая существенную роль в исследуемом явлении;
выбранный тип функции регрессии неадекватно отражает объективную связь (в этом смысле критерий Дарбина — Уотсона может быть использован в качестве критерия линейности);
применяемый критерий не может служить объективным показателем автокорреляции;
числовой материал содержит большие ошибки наблюдений.
Если с помощью критерия установлена значимая автокорреляция остатков, томы должны попытаться исследовать возможные причины ее возникновения и построить такую модель регрессии, где меньше будет угроза возникновения автокорреляции возмущений.
240
12
ОДНОВРЕМЕННЫЕ
УРАВНЕНИЯ
В РЕГРЕССИОННОМ АНАЛИЗЕ
12.1. ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
До сих пор при изучении регрессии рассматривались односторонние стохастические причинные отношения между экономическими явлениями и процессами и нас интересовали методы оценивания одного уравнения:
У f CVlv,
(2.1)
При этом мы исходили из того, что переменная у объяснялась переменными хт и что объясняющие переменные в правой части уравнения (2.1) не находятся под влиянием переменной у. Это предположение нашло свое отражение в предпосылке 5 (см. раздел 2.9).
Однако в экономике редко можно встретить подобные односторонние стохастические причинные отношения. Чаще всего приходится иметь дело с описанием системы соотношений, так как она более адекватно отражает многосторонние реальные взаимоотношения между явлениями. Система уравнений, отражающих наличие одновременных экономических связей, называется системой одновременных уравнений*.
Благодаря возникновению одновременных связей между экономическими явлениями выбор зависимой переменной в регрессии и тем самым направление минимизации возмущающей переменной (см. разделы 2.4, 2.5 и 2.7) до определенной степени произвольны. Это подтверждает необходимость наряду с исходным уравнением (2.1) указывать другие экономические соотношения в форме функции регрессии, чтобы вскрыть многосторонние связи между переменными, их взаимозависимость. В связи с этим возникает задача спецификации и оценивания не
*В этой книге мы не можем обсудить все проблемы, возникающие при изучении одновременных уравнений. Нашей задачей является лишь дать краткий обзор и выяснить, как одновременные экономические связи влияют на выбор известных из прошлых разделов про ^цур.
241
одного уравнения регрессии, а целой системы. Такую систему уравнений регрессии мы будем называть эконометрической моделью. В литературе встречается также термин «регрессионная модель». В дальнейших наших рассуждениях мы будем предполагать, что между переменными эконометрической модели существуют линейные соотношения, т. е. будем рассматривать линейную регрессионную модель.
Обратимся вначале к простой модели, состоящей из двух уравнений 4
В = f (UG, NGE),
UG = f(B,S). (12Л)
Первое уравнение отражает зависимость денежного обращения (В) от оборачиваемости денег (UG) и денежных доходов населения (NGE), Во втором уравнении оборачиваемость денег UG определяется в виде функции от денежного обращения В и размера вклада в сберегательную кассу (S). Между обеими зависимыми переменными — денежным обращением и оборачиваемостью денег — существуют одновременные соотношения, так как каждая из них в одном уравнении выступает как зависимая, а в другом уравнении — как объясняющая величина.
Введем следующие обозначения:
уг — денежное обращение;
z/2 — оборачиваемость денег;
%! — фиктивная переменная х1 при постоянной регрессии;
х2 — денежные доходы населения;
х3 — размер вклада в сберегательную кассу. Так как мы договорились ограничиться рассмотрением линейных связей, получим регрессионные соотношения в общей форме:
У1 ~ а12У2 + Ьц.%1 + L'12^2 4“ ^1, .
Уъ = — а21У1 + Wi + &2 3*3 + и2, '
Линейная эконометрическая модель состоит, таким образом, из определенного числа стохастических уравнений (уравнений регрессии). Они могут быть записаны так:
г/1 = — а12у2—...—аиу1 — ...—algyg + bux1 + ...+blmxm + «i
yt = —апУ1—•••—ai, i-lVi-l — ai, —•••—+
+ ••• + bim Xm + Ui (12.3)
Ув ^glVl ^giVl ••• ^g< g~l yg-l+bgl "1“ •••~^~bgm %m ~i~4g.
Первый индекс при параметре указывает номер уравнения, в которое он входит. Второй индекс параметра соответствует переменной, к кото
Юбозначения переменных в системе уравнений (12.1), а также (12.20) и (12.22) — начальные буквы соответствующих терминов на немецком языке.— Примеч, пер.
242
рой он относится. Можно легко убедиться, что каждое уравнение (12.3) представляет собой обобщение выражения (2.4). Причем через уъ (i =1, ..., g) обозначены те переменные, которые должны быть объяснены с помощью модели. В общем в этих уравнениях причинно обусловленные соотношения между переменными больше не односторонние. Переменные хк как раз являются теми переменными, которые характеризуются односторонней причинной связью, т. е. они объясняют переменные z/i, ..., yg, но сами не объясняются ими. Ради простоты мы особо не выделяем искусственную (фиктивную) переменную, относя ее к классу объясняющих.
Эконометрическая модель в общем случае строится на основе временных рядов. Поэтому результаты наблюдений для переменных yt = 1,..., g) и xk (k = 1,..., rri) указываются через определенные интервалы времени (периоды t = 1, ..., Т).
Запишем систему (12.3), состоящую из g уравнений для текущего периода времени /, причем все переменные yt перенесем в левую часть уравнений:
^пУи + ... + а-цУи + ... + algygt =
— ЬцХи + ... + blkxkt + ... + blmxmt + ult,
^21Уи + ••• + a2iy it + ... + a2gygt = (12.4)
= + ... + b2kXkt + ... + b 2m^mt +
аё1Уи + ••• + agiya + •••+ Ugg ygt =
= bg]Xit ~F ... ~F bghxkt + ... + bgmxmt -F ^gt*
Переходя к матричной форме записи системы уравнений (12.4), получим
Ауг = Bxf + uz; t = 1,..., Т. (12.5)
Здесь уь хь uf — вектор-столбцы, содержащие соответственно g, m и g элементов:
Уи ии
У« = У21 x2t , х,= * ; и,= »2t
-Vgt- ^Xmt_ -Ugt -
а А и В — матрицы порядка g и т, состоящие из коэффициентов при текущих значениях переменных:
all a12 • • • aig &n b12 ... blm
A = ^21 ^22 • • • &2g , в = ^21 b22 ... b2]n
~agl ag2 ... agg- -bgi bg2 ... bgm_
243
Если мы объединим вектор-столбцы по всем периодам £, то получим следующие матрицы значений переменных:
Уп
У21
У12 . . . У\Т
У22 ... У2Т
= 1У1. Уг> •••» Уг],
-Уgi
%21
Уё2 ... ygT_
#12 ••• Т
Х22 ••• ^2 Т
= [хХ) х2, Хт],
_Хт1
-*тп2 • • • ХтТ_
Y =
Х =
и11 . . . U12 ... U\T
и =
^12 . . . И22 ’ * * ^2Т
= [U1,U2......М-
Kgl . . . ^g2 ... UgT_
В итоге (12.5) для всех периодов времени t можно записать в виде
AY - ВХ + U. (12.6)
Если эти рассуждения мы перенесем на наш пример (12.2), то получим
УU + а\.2У21 ~ Ь-цХн + bl2^2t4"^lt> ^21Уи У 2t ~ b2iXlt-\-b23X3f-\~U2f
Вектор-столбцы значений переменных и матрицы коэффициентов при переменных примут вид:
(12.7)
Уи .Уи .
хи
B-
Г1 х =
Ьц _ ^21
1
ult
u2tA
1 а12
. °21 1 .
У11 У12 ••• У1Т _У21 У22 ••• У2Т _
^11 ^12 ••• ^1T
’ Xt - %2t
_X3t „
&12 О
О ^23j ... 1 ’
Х21 Х22 ... Х2Т » U =
_Хз1 Х32 ... <^ЗТ_
Из приведенного примера видно, что не все переменные входят сразу во все уравнения. Для описания функционирования модели вводят обычно априорные ограничения на параметры. Это прежде всего так называемые нулевые ограничения, вызванные тем, что некоторые переменные не входят в определенные уравнения системы. Кроме того, на параметры модели накладываются общие линейные ограничения. Исключая некоторые переменные из определенных уравнений, мы добиваемся необходимой спецификации модели, так как в противном случае нельзя получить оценку модели и достичь ее адекватности изучаемому явлению.
^21 ^22 ••• ^2T-
, A =
244
Выражения (12.5) и (12.6) представляют собой систему одновременных уравнений, записанную в матричной форме. Одновременный характер модели очевиден: зависимая переменная одного уравнения выступает как объясняющая переменная в других уравнениях или объясняющие переменные в одном или нескольких уравнениях включены в другое уравнение системы как подлежащие объяснению, т. е. как зависимые. Отдельные уравнения модели не могут более рассматриваться изолированно друг от друга. К ним должны быть применены и особые приемы оценивания. В силу сказанного принятое нами ранее в регрессионном анализе разделение переменных на зависимую и объясняющие теряет смысл. В последующих разделах мы будем придерживаться другого разделения переменных, которое соответствует требованиям эконометрической модели.
12.2. ПЕРЕМЕННЫЕ В ЭКОНОМЕТРИЧЕСКОЙ МОДЕЛИ
Как уже указывалось в разделе 12.1, при построении эконометрических моделей недостаточно принятого ранее разделения переменных на объясняющие и зависимую, поскольку одна и та же переменная может входить в одно из уравнений как зависимая, а в другое — как объясняющая. Необходима новая классификация переменных, которая более соответствовала бы их сущности в эконометрической модели, отражала бы их роль и характер. Такое разделение переменных относится к проблеме спецификации модели, и ее надо решать только исходя из экономических логико-теоретических соображений. Новая классификация переменных должна отражать объективно существующие отношения между изучаемыми экономическими явлениями, вскрывая их природу и характер, чтобы было ясно, какие из явлений взаимозависимые, а для каких существует только односторонняя зависимость.
Итак, в эконометрической модели будем различать следующие переменные:
1. Эндогенные переменные. Эндогенными переменными являются экономические величины, которые объясняются эконометрической моделью. Значения эндогенных переменных формируются в результате одновременного взаимодействия переменных, образующих модель. Эндогенные переменные зависят от экзогенных и возмущающих переменных. В примере из раздела 12.1 денежное обращение и оборачиваемость денег — эндогенные переменные модели (12.7).
2. Экзогенные переменные. Значения экзогенных переменных в каждый период времени / определяются вне модели. Экзогенные переменные являются внешними наперед заданными экономическими величинами. Они, следовательно, объясняются не моделью, а экономическими факторами и закономерностями, лежащими за границами этой модели.
Экзогенные переменные определяют эндогенные переменные, но сами не находятся под их влиянием. Таким образом, между эндогенными и экзогенными переменными существуют только односторонние стохастические причинные отношения.
245
Экзогенными переменными модели (12.7) являются денежные доходы населения и размер вклада в сберегательную кассу. При практических исследованиях трудно решить, какие из переменных имеют экзогенный характер. Здесь окончательное слово принадлежит экономистам и статистикам. Они несут полную ответственность за спецификацию модели. Вопрос, какие переменные следует рассматривать как экзогенные, решается прежде всего на основе детального анализа экономического явления. Экзогенными переменными могут быть природные, технические, демографические и некоторые социальные факторы.
В связи с тем, что регрессионной моделью нельзя охватить весь причинно-следственный комплекс явлений в экономике, исследователь вынужден выделять только определенную часть связей, отдавая предпочтение наиболее существенным. Неучтенными остаются некоторые влияющие величины, которые не объясняются моделью, или сила их взаимосвязей так мала, что ими пренебрегают. Такие переменные можно также отнести к экзогенным. Решение, какие из переменных, включенных в модель, отнести к экзогенным, а какие — к эндогенным, принимается исходя из положений политической экономии социализма и конкретной экономической науки. При каждой спецификации модели следует заново обстоятельно обсудить проблему разделения переменных, чтобы определить, является переменная экзогенной или эндогенной. Деление переменных на экзогенные и эндогенные относительно. Оно зависит от природы изучаемого явления, а также от цели, с которой эта модель строится.
3. Предопределенные переменные. Эндогенные и экзогенные переменные могут быть также лаговыми. Под лаговой мы понимаем переменную, значения которой отстают на один или несколько периодов. Если x2t — значения обычной переменной х2» то x2,t-i — ее лаговые значения, смещенные на один период. При наличии в модели лаговых эндогенных и экзогенных переменных значение эндогенной переменной в период времени t зависит как от своих собственных значений в предшествующие периоды, так и от значений экзогенных переменных в те же периоды. Каждая из лаговых экзогенных и эндогенных переменных при этом рассматривается как самостоятельная переменная.
Поскольку лаговые переменные в период времени t также не объясняются эконометрической моделью, мы можем отнести их к заранее заданным экзогенным. В связи с этим к классу предопределенных переменных мы относим:
обычные экзогенные переменные; они заранее предопределены, так как объясняются не эконометрической моделью, а факторами, лежащими вне этой модели;
лаговые экзогенные переменные; они заранее предопределены, так как их значения принадлежат предшествующим периодам и объясняются вне модели;
лаговые эндогенные переменные; их предопределенность следует из предшествующего объяснения в эконометрической модели.
Предопределенные переменные обозначим через xh независимо от того, являются они эндогенными или экзогенными. Предположим, что модель содержит т предопределенных переменных, среди которых на-
246
ходится также фиктивная переменная, введенная для постоянной уравнения регрессии. Для обычных переменных мы располагаем наблюдениями в периоды времени t = 1, 71, а для лаговых эндоген-
ных и экзогенных переменных — наблюдениями в моменты времени t — т = 1 — т, Т — т. Через т = 1, ..., s обозначена величина лага.
Элементами матрицы X в (12.6) являются результаты наблюдений над пг предопределенными переменными. При этом мы не будем вводить отдельных обозначений для лаговых переменных. Вектор-строки Хь ..., хт содержат наблюдения над каждой из т переменных, а век-тор-столбцы хь..., Хт указывают совместные наблюдения в момент времени t (i — 1, ..., Т).
Матрица В представляет собой матрицу коэффициентов при предопределенных переменных. Вектор-строки Ь{, ..., bg содержат т коэффициентов при предопределенных переменных в отдельных уравнениях модели. В вектор-столбцах Ьь ..., bm указывают коэффициенты при отдельных предопределенных переменных по всем g уравнениям. В связи с тем, что не все предопределенные переменные содержатся во всех уравнениях модели, некоторые элементы матрицы В оказываются равными нулю (см. пример в разделе 12.1).
В модели (12.2) денежные доходы населения и размер вклада в сберегательную кассу — предопределенные переменные. В этом примере они совпадают с экзогенными переменными. Лаговые переменные, как эндогенные, так и экзогенные, отсутствуют.
4. Совместно зависимые переменные. Совместно зависимыми переменными называются обычные эндогенные переменные, которые объясняются эконометрической моделью в момент времени t. Они совместно зависимы потому, что между ними существуют многосторонние связи, и определяются не одним уравнением, а одновременными уравнениями модели. В связи с этим эконометрическую модель можно рассматривать как способ определения совместно зависимых переменных через предопределенные переменные и возмущения.
Обозначим совместно зависимые переменные через уь а их число в эконометрической модели примем равным g (i = 1,..., g). Элементами матрицы Y в (12.6) являются результаты наблюдений над§ совместно зависимыми переменными за весь период исследования. По аналогии с матрицей X в вектор-строках у {, ..., yg матрицы Y располагаются результаты наблюдений над каждой совместно зависимой переменной, а в вектор-столбцах уь ..., ут — результаты совместных наблюдений над этими переменными в каждый момент времени t = 1, ..., Т.
Матрица А содержит коэффициенты при совместно зависимых переменных. Элементами вектор-строк а{, ..., а^ являются коэффициенты при всех совместно зависимых переменных в отдельных уравнениях, а элементами вектор-столбцов ах,..., а^— коэффициенты при одной переменной по всем уравнениям. Так как не каждая совместно зависимая переменная входит в любое уравнение, не все элементы матрицы коэффициентов А отличны от нуля. Кроме того, в каждом уравнении содержится коэффициент а, равный единице. Это связано с тем, что, несмотря на одновременное определение совместно зависимых пере
247
менных, задача каждого уравнения заключается в объяснений одной из этих переменных, что вытекает из характера самого уравнения регрессии. В результате соответствующего размещения переменных может быть достигнута такая ситуация, при которой коэффициенты, равные единице, окажутся на главной диагонали матрицы А.
В модели (12.2) эндогенные переменные — денежное обращение и оборачиваемость денег — представляют собой совместно зависимые переменные, так как между ними существуют одновременные соотношения.
5. Возмущающие, или латентные, переменные. Возмущения — это экономические величины, которые не входят в уравнения эконометрических моделей, но оказывают влияния на совместно зависимые переменные. Они также формируются за счет случайных влияний и ошибок, допущенных, например, при использовании типа функции, неадекватно отражающей изучаемое явление, или неправильном выборе способа оценивания. Возмущения являются стохастическими переменными. В противоположность совместно зависимым и предопределенным переменным эмпирические значения возмущающих переменных неизвестны. Их значения находят как остатки по отдельным уравнениям после оценки неизвестных параметров модели. Из сказанного очевидно, что содержательная интерпретация возмущающих переменных в эконометрической модели та же, что и в случае одного уравнения регрессии, с которой мы познакомились раньше.
Обозначим возмущающие переменные через и, а их реализации (остатки) — через и. Таким образом, элементами матрицы LJ будут остатки отдельных уравнений для всех моментов периода наблюдений. Вектор-строки iif ,•••» Ug содержат остатки одного уравнения для всех моментов времени, а вектор-столбцы иь..., иТ — остатки для всех g уравнений в один момент времени. Так как возмущения являются случайными величинами, эмпирические значения которых неизвестны, мы должны на этапе спецификации модели принять ряд предпосылок, которые позволят произвести оценивание модели. Эти предпосылки мы обстоятельно обсудим в разделе 12.5.
12.3. ВИДЫ ЭКОНОМЕТРИЧЕСКИХ МОДЕЛЕЙ
В зависимости от постановки экономической проблемы и цели исследований эконометрическая модель может быть представлена в различных видах. Далее мы дадим краткий обзор моделей.
I. Структурная форма эконометрической модели. Модель, представленная в виде
Ayf = Bxf + uf для t = 1, ..., Т, (12.5)
называется структурной. В соответствии с этим отдельные уравнения, образующие модель (12.5), и их параметры называются структурными. Про уравнения говорят, что они описывают структурную форму модели. Структурная форма эконометрической модели описывает одно- и многосторонние стохастические причинные отношения между эконо
248
мическими величинами в их непосредственном виде. Она содержит всю существенную информацию о зависимостях между экономическими явлениями и процессами.
Каждое структурное уравнение модели описывает в отдельности экономическое явление с учетом экономических, технологических, демографических, социологических и прочих факторов. Оно отражает также отдельные воздействия изменения переменных, содержащихся в нем. В структурном уравнении содержится одна или несколько совместно зависимых переменных. Оно включает неизвестные, подлежащие оценке, структурные параметры, а также возмущающую переменную. Характерной особенностью структурных уравнений является определенная автономность их по отношению к предопределенным переменным, так как изменение этих переменных и их параметров в одном структурном уравнении не обязательно приводит к изменениям в других структурных уравнениях.
Наряду со структурными ’’уравнениями эконометрическая модель может содержать так называемые определяющие уравнения — тождества. Они необходимы для адекватного отражения реальной действительности и полного охвата переменных одновременными соотношениями. Тождества не содержат возмущающих переменных, и их параметры известны (в общем случае равны единице). Следовательно, они не подлежат оценке, и при проведении процедуры оценивания параметров модели могут быть заранее исключены.
II. Полная эконометрическая модель. Эконометрическая модель называется полной, если:
а) она охватывает те переменные, которые оказывают существенное влияние на совместно зависимые переменные, а возмущающие переменные имеют случайный характер;
б) она содержит столько уравнений, сколько в ней имеется совместно зависимых переменных, так что каждая совместно зависимая переменная может быть объяснена с помощью соответствующего уравнения (в системе уравнений (12.4) и (12.5) число совместно зависимых переменных равно числу уравнений g)\ i
в) система уравнений и меет однозначное решение относительно совместно зависимых переменных. Следовательно, матрица А невырожденная, т. е.
det А =И=0. (12.8)
Модель должна быть полной в случаях, когда необходимо количественно описать экономическое явление или когда она применяется для прогнозирования.
III. Приведенная форма эконометрической модели. Если эконометрическая модель является полной, то существует обратная матрица А“х. Благодаря этому можно решить систему уравнений относительно совместно зависимых переменных, умножая (12.5) и (12.6) слева на А-1:
Nt = А^Вх, + А“Ч; t = 1,..., Т, (12.9)
или
Y = А~хВХ + A“XUJ (12.10)
249
Форма эконометрической модели, задаваемой в виде (12.9) или (12.10), называется приведенной. Если мы в (12.9) и (12.10) воспользуемся обозначением^
А^В-С, (12.11)
а также
А~хиГ= vf и A-4J - V? (12.12)
то приведенную форму модели можно записать более просто:
yt - Cxt + v, t = 1, ..., T, (12.13)
или
Y = СХ + V? (12.14)
Представим матричное уравнение (12.13) подробно в виде отдельных уравнений
Ун ~ +^12-^2
У21 “ • • • • (12.15)
У gt & glXlt4"^g2^'2i-b’ • • “I" Cg mxmt + Vgt-
Из (12.15) видно, что совместно зависимые переменные являются линейными функциями от предопределенных и возмущающих переменных. В равенстве (12.11) находит отражение тот факт, что коэффициенты уравнений модели в приведенной форме представляют собой конгломерат структурных параметров. Это можно продемонстрировать на примере из раздела 12.1. Запишем уравнения модели (12.7) в приведенной форме. Для этого построим следующие матрицы:
_____}_______—#12
д_1 1 #12 #21 1 #12 #21
--#21 1
__ 1—#12 #21 1—#12 #21
^11—#12 ^21 ^12 —#12 ^23
1—#12 #21 1—#12 #21 1—#12 #21
#21 ^11 Ч~^21 -#21 ^12^23
#12 #21 1 #12 #21 1 #12 #21
Уравнения модели в приведенной форме примут вид:
„ ___ ^11 #12^21 v ( ^12 v । -#12^23 I #11--- #12#2f
Ун----: xit ~r ~ x2t i ~4-------------------:--------
1 #12 #21 *-#12 #21 1-#12 #21 1--#12 #21
n __ ““#21 ЬП +&21 v 1 —#21^12 v, । ^23 v I
У21------: xit ------------x2t i~—-----------%3t ~r
1 #12 #21 1 #12 #21 1 — #12 #21
| --#21 #11 + #21 . ц 2
1 —#12 #21
250
Из (12.16) видно, что коэффициенты уравнений в приведенной форме являются комбинациями всех элементов матрицы А (всех структурных коэффициентов совместно зависимых переменных) и элементов столбцов матрицы В (структурных коэффициентов соответствующих предопределенных переменных во всех структурных уравнениях). Например, коэффициент сп модели в приведенной форме при переменной Xi в первом уравнении составлен из всех элементов матрицы А и структурных коэффициентов &п и Ь21 переменной хг в обоих структурных уравнениях (12.7) — элементов первого столбца матрицы В.
Уравнения в приведенной форме из-за сложности представления коэффициентов теряют по отношению к предопределенным переменным свою автономность, которая характерна для структурных уравнений Если, например, из-за изменения коэффициента Ьп изменится си, то неизбежно изменится и с21, так как &п содержится в нем. Но, с другой стороны, каждое уравнение в приведенной форме характеризуется определенной автономностью относительно совместно зависимых переменных, так как каждое из этих уравнений содержит текущее значение только одной эндогенной переменной, которое выражается как функция всех предопределенных переменных. Итак, очевидно, что взаимосвязи совместно зависимых переменных при переходе от структурной формы к приведенной распространяются на предопределенные переменные, а также на возмущения. Если мы сравним, например, первые уравнения (12.2) и (12.16), то ylt в модели приведенной формы (12.16) объясняется всеми предопределенными переменными модели, т. е. х2, х3, а также остатками обоих структурных уравнений в (12.2) ult и u2t. Но y2t в первое уравнение модели (12.16) не входит.
На основе высказанных соображений становится очевидной интерпретация уравнений в приведенной форме. Коэффициенты этих уравнений отражают непосредственное и косвенное влияние предопределенных переменных на совместно зависимые переменные (общий эффект), в то время как структурные параметры выражают только непосредственное влияние предопределенных переменных (частичный эффект). В этом смысле экономическая интерпретация коэффициентов уравнений в приведенной форме реалистичнее, чем интерпретация структурных параметров. Модель в приведенной форме построена как бы с учетом предпосылки, что «другие объясняющие переменные не изменяются» (см. интерпретацию коэффициентов частной регрессии в разделе 2.7), так как в этой модели каждая совместно зависимая переменная yt объясняется только предопределенными переменными.
Каждое уравнение в приведенной форме представляет собой множественную регрессию (см. раздел 2.7). К уравнениям непосредственно применим метод наименьших квадратов для оценивания неизвестных коэффициентов приведенной формы. Модель в приведенной форме используется для прогнозирования. Если оценки коэффициентов приведенной формы и значения предопределенных переменных приходятся на период времени прогноза, то по модели находят прогнозные значения совместно зависимых переменных. И напротив, структурная форма для прогноза непригодна, так как в каждом структурном уравнении содержится несколько совместно зависимых переменных, для 251
которых не могут быть указаны значения на прогнозируемый период времени, поскольку они еще только подлежат оценке. Однако приведенная форма модели имеет и существенный недостаток. От количественно оцененной модели в приведенной форме не во всех случаях можно перейти к модели в структурной форме, в то время как по заданной в численном виде структурной форме может быть всегда определена приведенная форма (см. раздел 12.4).
Итак, мы убедились, что как структурная, так и приведенная формы выполняют свои специфические функции, позволяют решать определенные задачи и имеют свои достоинства и недостатки. Поэтому регрессионную модель обычно представляют в обеих формах, а затем их интерпретируют.
При построении других форм регрессионной модели исходят из структурной формы (12.4) и исследуют вид матрицы А.
IV. Модель из взаимозависимых переменных. Модель из взаимозависимых переменных представляется в виде системы структурных уравнений, в которых переменные одновременно удовлетворяют нескольким равенствам. Следовательно, переменные являются многосторонне зависимыми. Матрица А структурных параметров совместно зависимых переменных может быть любого вида. Матрица дисперсий и ковариаций возмущающих переменных также может иметь любой вид:
2$ = Е (utuj).
V. Рекурсивная модель. Рекурсивная модель может быть представлена таким образом:
Ун = хи + • • • + хт1 + и1Ь
а21УиЛ‘У(и ~ ^21 ••• + b2m + (12.17)
аб1Уи + аёъУ21 + ••• A~ygt — bglxlt +... bgm xmt Ugt.
Она обладает следующими свойствами:
1. Соответствующим расположением эндогенных переменных и структурных уравнений можно добиться того, что в первом структурном уравнении будет только одна эндогенная переменная, а в последующих уравнениях будут каждый раз добавляться другие эндогенные переменные. Так, в (12.17) в первом уравнении содержится только уъ во втором уравнении к у± добавляется другая эндогенная переменная у2, в третьем уравнении — у3 и т. д. Таким расположением переменных добиваются в каждом структурном уравнении только односторонне направленных зависимостей между переменными. Так, в (12.17), например, у2 зависит от у19 но у2 не оказывает влияния на у19 так как переменная у2 не включена в первое уравнение. Хотя в модели содержится несколько эндогенных переменных, мы не можем больше говорить о совместно зависимых переменных, так как они не являются теперь многосторонне зависимыми. Более того, они образуют одну причинную цепь.
252
В рекурсивной модели матрица А треугольная, на главной диагонали которой элементы равны единице:
(12.18)
ag* ••• 1-
2. Матрица дисперсий и ковариаций возмущающих переменных является диагональной:
О “
О
3^ = £(utu/)
(12.19)
О О
Возмущающие переменные различных уравнений в момент времени t стохастически независимы друг от друга (некоррелированы).
3. Возмущающие переменные первого уравнения не автокоррели-рованы, т. е. Е (uit uit_x)= 0 для всех i = 1,..., g ит^=0.
Следующая система уравнений может быть использована в качестве иллюстрации рекурсивной модели *:
NGE = f (NEP),
KI = f(NGE, KI-ъ BV, (12.20)
Д = Д/ + KG*
Эта модель состоит из двух стохастических уравнений и одного тождества. Она служит для объяснения потребления. В первом уравнении денежные доходы населения (NGE = у±) определяются в зависимости от произведенного национального дохода (NEP = х2). Денежные доходы во втором уравнении выступают как существенная определяющая величина личного потребления (Д7 = у2). Другими существенными объясняющими переменными во втором уравнении являются личное потребление за предыдущий год (Д7-1 = х3), численность населения (BV = х4) и сбережения на конец предыдущего года (S_x = хб). Тождество служит для нахождения потребления (К = Уз) по личному потреблению и общественным фондам потребления (KG = х6). Переменные NGE, Д7 и Д' представляют собой эндогенные переменные модели. Экзогенные переменные NEP, BV и KG вместе с лаговой эндогенной переменной Д/.i и лаговой экзогенной переменной обра
*Эта модель составлена на основе уравнений, полученных в работах: W б 1 f 1 i n g М. Ein mehrsektorales okonometrisches Modell volkswirtschaftlicher Grundproportionen. Berlin, 1973; W б 1 f 1 i n g M. Ein okonometrisches Modell der Volkswirtschaft der DDR. Forschungsbericht. Zentralinstitut fiir Wirtrschafts-wissenschaften der Academie der Wissenschaften der DDR. Bd. 21. Akademie-Verlag. Berlin, 1977. Другие эконометрические модели народного хозяйства ГДР можно найти в работе: В i 1 о w W. u. a. Erfahrungen und Probleme bei der Nutzung mathematisch-statistischer Methoden fiir die mittel- und langfristige Planung. Wirtschaftswissenschaft, 1974, 1, S. 58—75.
253
зуют класс предопределенных переменных модели. Представим модель (12.20) в общем виде, причем хг = 1:
У It = ^ll^lt + ^12
а21Уи^Уи = ^21 Xlt + &23 X3t + ^24 Хц 4- &25X6f 4" U2t > (12.21)
— Уы Л~Уы — x6t-
Матрица А имеет вид:
Г1 A= а21 1
_0 —1 1_
и четко отражает причинную цепь между эндогенными переменными.
VI . Система независимых уравнений. Система независимых уравнений регрессии — частный случай рекурсивной модели, когда матрица А является единичной, А = I. В этом случае в каждом уравнении содержится только одна эндогенная переменная в качестве подлежащей объяснению, которая не зависит от эндогенных переменных других уравнений, и они не оказывают на нее влияния. Таким образом, каждое уравнение независимо от других. Структурная и приведенная формы такой модели совпадают.
Для иллюстрации модели этого вида приведем простой пример*:
~ f (BR, 7?А_2) — ЬцХц + b^2x2t 4" Ь±3х3} 4~ иц,
LS — f (К_1? LS-i/B-i) yzt—bz-pCit 4“ b2^x^i 4- b25 x5t 4~ u2^ (12.22)
TV A — f (LG) у st = b31xlt 4~ b36x6t 4~ ^з/*
В первом уравнении оценивается численность работников пенсионного возраста (RA = уг) по численности населения пенсионного возраста тех же лет (BR = х2) и по той же лаговой переменной (RA^ = х3). Второе уравнение определяет число учащихся (LS = у2) в зависимости от уровня производительности труда за предыдущий год (У_х = х4) и доли учащихся относительно всего населения за предыдущий год (LS-t/B-t = х5). Наконец, третье уравнение указывает число неработающих в трудоспособном возрасте (NA ~ у3) в качестве функции от числа живорожденных (LG = х6), так как речь идет прежде всего о женщинах. Эти три уравнения независимы друг от друга, поскольку в каждом из них мы имеем дело только с одной эндогенной переменной»
12.4. ПРОБЛЕМА ИДЕНТИФИКАЦИИ
Если эконометрическая модель (12.5) предполагается заданной, то возникает вопрос, могут ли быть определены ее структурные параметры на основе данных наблюдений над совместно зависимыми и предопределенными переменными. Эта проблема известна как проблема идентификации. Причина ее возникновения кроется во взаимосвязях экономических явлений и, следовательно, во взаимозависимостях пере
*См. примечание на с. 253.
254
менных. Эконометрическая модель идентифицируется, если идентифицируются структурные уравнения. Таким образом, каждое структурное уравнение должно быть проверено на идентифицируемость. При этом следует учитывать, что идентификация отдельного уравнения зависит не столько от этого уравнения, сколько от вида всех структурных уравнений модели. Идентифицируемость структурных уравнений означает, что путем линейной комбинации некоторых или всех уравнений модели невозможно получить ни одного уравнения, которое бы противоречило модели и параметры которого отличались бы от параметров структурных уравнений, подлежащих проверке.
Если модель полная (см. раздел 12.3) и если параметры структурных уравнений можно однозначно определить по параметрам приведенной формы, то структурные уравнения идентифицируемы. Это означает, что каждой структурной форме модели соответствует только одна приведенная форма, и наоборот.
Приведенная форма модели при условии нормальности распределения возмущающих переменных и их независимости от экзогенных переменных, а также при отсутствии автокорреляции возмущающих переменных и отсутствии функциональной мультиколлинеарности всегда идентифицируема, так как ей не присуща взаимосвязь между совместно зависимыми переменными в отдельных уравнениях. Если регрессионная модель не идентифицируема, то нельзя оценить параметры модели (структурные параметры и матрицу дисперсий и ковариаций возмущающих переменных). В подобных случаях следует начинать не с нового сбора исходных данных, а с новой формулировки всей модели или отдельных ее соотношений.
Для полной линейной регрессионной модели разработаны несколько критериев идентифицируемости. Мы укажем только два из них, не останавливаясь на их выводах. Эти критерии применимы к любому структурному уравнению.
1. Необходимым, но недостаточным условием идентифицируемости модели является следующее требование-критерий: число предопределенных переменных, которые содержатся в модели, но исключены из рассматриваемого структурного уравнения, по крайней мере должно быть равно числу совместно зависимых переменных в рассматриваемом структурном уравнении минус единица.
Обозначим через g число совместно зависимых переменных в модели, gt — число совместно зависимых переменных, которые содержатся в i-м структурном уравнении, т— число предопределенных переменных модели, mt — число предопределенных переменных, исключенных из £-го структурного уравнения.
Тогда сформулированный выше критерий может быть записан в виде
(12.23)
С помощью данного критерия исследуется, достаточно ли введено ограничений (например, нулевых) на параметры модели в отдельных структурных уравнениях, чтобы их можно было идентифицировать. Это означает: при mt = gt — 1 число ограничений достаточно, чтобы однозначно определять параметры структурных уравнений по их при
255
веденной форме (прямая идентификация); при mt > gt—1 структурное уравнение идентифицируется, в этом случае имеется больше ограничений, чем это необходимо для идентификации; при mt <gt— 1 структурное уравнение не идентифицируется, поскольку число ограничений недостаточно и, таким образом, соответствующее уравнение статистически не отличается от другого уравнения.
В первом случае метод наименьших квадратов можно применить к приведенной форме, если выполняются предпосылки относительно возмущений. Во втором случае следует воспользоваться другими мето дами оценивания, например многошаговым методом наименьших квадратов или методом максимального правдоподобия (см. раздел 12.6). В третьем случае оценка параметров структурных уравнений невозможна.
Продемонстрируем применение счетного правила на примере из раздела 12.1. В модели (12.7) содержится g= 2 совместно зависимых и т = 3 предопределенных переменных. Проверим идентифицируемость первого структурного уравнения (12.7). Имеем gr— 1 = 1 и mt = 1. Следовательно, первое уравнение точно идентифицировано. Такой же вывод можно сделать относительно второго структурного уравнения из (12.7), так как g2 — 1 = 1 и mt = 1.
2. Необходимое и достаточное условие идентифицируемости отражено в правиле порядка. Оно позволяет точно установить наличие или отсутствие идентифицируемости. При применении этого правила рассматриваются переменные, исключенные из исследуемого уравнения. По коэффициентам при этих переменных в других уравнениях модели строится матрица. Ранг этой матрицы должен быть не меньше g— 1.
В первом уравнении модели (12.7) отсутствует только переменная х3. Коэффициентом при ней во втором уравнении является &23. Таким образом, матрица состоит только из одного элемента — коэффициента &23. Исходя из экономических соображений можно предположить, что й23 отличен от нуля. Следовательно, ранг этой матрицы равен 1. Так как g— 1=1, структурное уравнение идентифицировано. Такой же вывод можно сделать относительно второго структурного уравнения, так как в нем не содержится только х2.
Недостаток правила порядка заключается в том, что параметры модели должны быть известными. При небольшом числе уравнений можно на основе логически-профессиональных рассуждений предположить, что параметры отличны от нуля. При большом же числе уравнений и переменных такое предположение не всегда оправдано.
На практике при проверке идентифицируемости модели чаще всего пользуются счетным правилом. Оно дает вполне приемлемые результаты. Следует также подчеркнуть, что идентификация структурных уравнений предполагает, что возмущения распределены независимо друг от друга. Но независимость возмущений — одно из требований рекурсивной модели. Таким образом, проблема идентификации рекурсивных моделей не возникает, так как они всегда идентифицированы. Как уже подчеркивалось, с проблемой идентификации приходится иметь дело при изучении систем одновременных уравнений, с помощью которых описываются взаимосвязи между экономическими явлениями.
256
12.5. ПРЕДПОСЫЛКИ ПОСТРОЕНИЯ
ЭКОНОМЕТРИЧЕСКИХ МОДЕЛЕЙ
Для оценивания эконометрических моделей требуется выполнение ряда предположений относительно ненаблюдаемых случайных возмущающих переменных и закона их распределения. Выполнение предположений о вероятностных свойствах возмущений обеспечивает полную спецификацию модели. Эти предположения основаны на предпосылках, введенных нами при оценивании регрессии. Поскольку в разделе2.9 они уже было подробно обсуждены, здесь мы ограничимся лишь небольшими пояснениями.
Предпосылка 1. Возмущающие переменные распределены нормально. В общем случае невозможно априорно определить совместное распределение возмущающих переменных. Постановка же специальных экспериментов вызывает затруднения. Поэтому чаще всего приходится ограничиваться гипотезой относительно вида распределения возмущений. Предполагается, что совместный закон распределения—многомерный нормальный, поскольку такое распределение теоретически легко обосновать, а кроме того, оно характеризуется двумя параметрами (математическим ожиданием и дисперсией) и делает возможным использование классических критериев.
Предпосылка 2. Математическое ожидание возмущающих переменных равно нулю:
Е (uit) = 0 для i = 1, ..., g и t = 1, Т. (12.24)
Предпосылка 3. Матрица дисперсий и ковариаций возмущающих воздействий для любого момента времени /,
= Е (utu;), (12.25)
невырожденная. Практически эта предпосылка означает, что все тождества модели исключаются с помощью специальных преобразований и существует обратная матрица от
Часто пользуются также следующими дополнительными предпосылками.
Предпосылка 4. Возмущающие переменные различных уравнений для каждого момента времени t независимы друг от друга. Предпосылка сводится к требованию, чтобы матрица 2^ была диагональной (см. формулу (12.19)). Эта предпосылка отражает тот факт, что возмущающие переменные действительно носят случайный характер и что все существенно влияющие переменные содержатся в отдельных структурных уравнениях. Ковариации, отличные от нуля, указывают на ошибку спецификации структурных уравнений. Данная предпосылка поэтому играет большую роль при идентификации структурных уравнений эконометрических моделей. Далее эта предпосылка будет одним из условий рекурсивной модели.
Предпосылка 5. Распределение возмущающих переменных инвариантно относительно времени. Эта предпосылка означает неизмен-
9 Зак. 1113
257
ность дисперсии и ковариации для любого периода времени:
= для / = 1,..., Т. (12.26)
Данное условие представляет собой обобщение требования гомоскедас-тичности для линейной регрессии (см. (2.77)).
Предпосылка. 6. Возмущающие переменные в различных структурных уравнениях характеризуются отсутствием автокорреляции:
Е (UitUit^r) = 0 для т^О и всех i и I. (12.27) Если
2Й = Е (ufuj) (12.28)
представляет собой матрицу дисперсий и ковариаций i-ro структурного уравнения для возмущающих переменных всех периодов, то эта матрица при соблюдении предпосылки 6 является диагональной:
ии 0 ... ;о и
^ии — 0 °22 0
.0 0 ’ ’(О Отт
(12.29)
Предпосылка 7. Текущие значения возмущений стохастически независимы от предопределенных переменных. Эта предпосылка имеет место для фиксированного момента времени Л В силу данного предположения лаговые значения эндогенных переменных не коррелируют с возмущающими воздействиями.
Для класса экзогенных переменных среди предопределенных переменных должны выполняться еще более строгие предположения.
Предпосылка 8. Возмущения стохастически независимы от экзогенных переменных для любого момента времени.
Предпосылку 8 следует указывать при определении экзогенных переменных, а предпосылки 7 и 8 должны быть введены в определение предопределенных переменных (см. раздел 12.2).
И последняя предпосылка касается экзогенных переменных.
Предпосылка 9, Экзогенные переменные не коррелируют между собой. Следовательно, предполагается отсутствие мультиколлинеарности.
12.6. МЕТОДЫ ОЦЕНИВАНИЯ
ЭКОНОМЕТРИЧЕСКИХ МОДЕЛЕЙ
После того как мы кратко обсудили наиболее важные проблемы, связанные с идентификацией и предпосылками построения эконометрических моделей, можно заняться вопросами оценивания параметров этих моделей. Разработан ряд методов оценивания. Их выбор определяется в основном видом модели и возможностями идентификации. Далее мы рассмотрим различные методы оценивания, не вдаваясь в особые подробности и не приводя доказательств, а делая основной упор на возможности их применения.
258
I. Метод наименьших квадратов.
1. Применение к модели из взаимозависимых переменных. Для множественной регрессии, о которой говорилось в разделе2.7, предполагалась независимость между объясняющими переменными и возмущениями (см. предпосылку 5 в разделе2.9). Эта предпосылка означала также отсутствие многосторонней связи (как функциональной, так и стохастической) между зависимой и объясняющими переменными.
В различных уравнениях эконометрической модели со взаимозависимыми переменными (см. формулу (12.3)) у объясняется предопределенными и совместно зависимыми переменными. Но совместно зависимые переменные коррелируют с возмущениями того же уравнения. В примере-модели (12.2) совместно зависимая переменная у2—одна из объясняющих величин для уг в первом уравнении. Однако у2 стохастически независима от возмущающей переменной первого уравнения иг. Это можно показать с помощью приведенной формы модели (12.16). Во втором уравнении (12.16) иг содержится в последнем слагаемом правой части. Корреляция между у2 и У\ вызвана одновременными соотношениями между уг и у2.
Если метод наименьших квадратов применяется к первому уравнению (12.2), то оценка его параметров производится так же, как в случае множественной регрессии (см. раздел 2.7). При этом минимизируется в направлении к уг, т. е. предполагается, что иг коррелирует только с уг. Одновременная корреляция между иг и у2 и, следовательно, одновременное соотношение между у± и у2 с помощью метода наименьших квадратов не учитываются. Совместно зависимая переменная у2 в правой части первого уравнения при применении метода наименьших квадратов рассматривается как предопределенная переменная. Аналогичные рассуждения и при применении метода наименьших квадратов ко второму уравнению (12.2). Итак, МНК-оценки параметров эконометрической модели со взаимозависимыми переменными более не состоятельны. Таким образом, существование одновременных соотношений между совместно зависимыми переменными в отдельных уравнениях эконометрической модели и предпосылка метода наименьших квадратов (отсутствие многосторонних связей между переменными) не согласуются.
Несмотря на это противоречие, практика показывает, что при оценивании эконометрической модели со взаимозависимыми переменными методом наименьших квадратов во многих случаях достигается удовлетворительная точность. Кроме того, метод обладает рядом свойств (робастность относительно мультиколлинеарности и ошибок спецификации, простота вычислительной процедуры, возможность обработки небольшого числа наблюдений), которые оказываются полезными при оценивании эконометрической модели.
Продемонстрируем применение метода наименьших квадратов к модели со взаимозависимыми переменными на формальном числовом примере *. Будем исходить из модели (12.1) или (12.7). Денежное обраще-
♦Числовой пример в измененном виде заимствован из [117].
9*
259
ние Q/x), оборачиваемость денег (у2), денежные доходы населения (х2) и размер вклада в сберегательную кассу (х3) представлены в виде отклонений от соответствующих средних (см. табл. 20). Благодаря этому в обоих уравнениях системы (12.7) исчезают постоянные регрессии и й21. Применим метод наименьших квадратов вначале к первому уравнению системы (12.7), которое мы запишем в виде множественной регрессии:
У It ~ ^12^2t + и it* (12.30
Таблица 20
Отклонения значений переменных модели (12.7) от их средних
t y\t i/2t x2t x3t
1 —10 4 —5 11
2 —7 5 —2 8
3 —6 3 —3 2
4 —4 1 —1 5
5 0 2 0 2
6 3 0 0 —2
7 5 —2 2 —5
8 4 —4 2 —3
9 7 —5 3 —8
10 8 —4 4 —10
Оценки параметров регрессии получим в соответствии с (2.64):
Ь = (Х'Х)-1Х'у;
(2.64)
#12
&12
X = (у2 х2) и у = ух.
Произведем следующие операции:
^ylt X2t =
^X2t Уи
X'yx = Г2^(г/и _ ^X2t У It _
[X' X]-x=——
1 463
Х'Х =
116 —83’
—83 72 J’
Г —190] 157J’ 83'
116
"72
83
Ь =
Подставив в (2.64) эти промежуточные результаты, получим МНК-оцен-ку уравнения (12.30):
У it = — 0,444 y2t + 1,669 x2t.
Аналогично представим второе уравнение (12.7) в виде множественной регрессии:
y2t = &21Уи “F" &23X3t 4" ^2t' (12.31)
260
Выполнив соответствующие вычисления, получим МНК-оценку уравнения (12.31):
z/2f = — 0,374 ylt + 0,143 x3f.
Оценки параметров указывают воздействия объясняющих переменных на уг и у2 (см. раздел 2.7). Причем существующие одновременные соотношения между переменными у± и у2 не учитываются. Из уравнения ничего нельзя узнать о характере связи между совместно зависимыми переменными у± и у2, хотя из анализа явления ясно, что с ускорением оборачиваемости денег сокращается денежное обращение, и наоборот (более обстоятельная экономическая интерпретация невозможна из-за формальной конструкции примера и из-за условных данных). Воздействие предопределенных переменных в обоих случаях рав-йонаправленно, т. е. рост денежных доходов населения приводит к ускорению денежного обращения (первое уравнение) и увеличение размера вклада в сберегательную кассу приводит к ускорению оборачиваемости денег (второе уравнение). Но количественная мера этих воздействий оказывается искаженной, так как при применении обычного метода Наименьших квадратов не учитываются одновременные соотношения между денежным обращением и оборачиваемостью денег. Мы продолжим рассмотрение этого примера при оценивании модели косвенным методом наименьших квадратов.
2. Применение к рекурсивным моделям. Будем исходить из рекурсивной модели вида (12.17). Применение метода наименьших квадратов дает состоятельные оценки, если соблюдается определенная последовательность вычислительной процедуры. Вначале следует оценить первое уравнение, в правой части которого содержатся только предопределенные переменные. Если установлены параметры первого урав-ния, то из значений переменной z/lf вычитаются остатки ult, т. е. вычисляются значения регрессии уи. Расчетные значения регрессии подставляются во второе уравнение в виде значений переменной ylt, благодаря чему эта переменная принимает характер предопределенной переменной Затем оцениваются параметры второго уравнения. Так же вычисляются значения регрессии y2t, которые вместе со значениями регрессии ylt подставляются в третье уравнение и т. д.
Если псочередность в оценивании параметров рекурсивной модели не соблюдается, то обычный метод наименьших квадратов дает несостоятельные оценки. Таким образом, если для оценки произвольно отбирается любое уравнение, то это приводит к тем же результатам, что И при модели со взаимозависимыми переменными.
3. Применение к системе независимых уравнений. Поскольку в Этих моделях не возникают многосторонние зависимости между эндогенными переменными, каждое уравнение можно отдельно оценивать с Помощью метода наименьших квадратов, как в случае множественной регрессии. Если соблюдаются предпосылки, введенные в разделе 2.9, то оценки параметров будут обладать свойствами, указанными там же.
261
II. Косвенный метод наименьших квадратов.
Метод наименьших квадратов может применяться к системе одновременных уравнений, которые полностью или только точно идентифицируемы. Конечно, этот метод не может непосредственно применяться при оценивании параметров структурных уравнений, так как они не учитывают одновременных соотношений между совместно зависимыми переменными. Модель вначале представляется в приведенной форме. Это возможно при предположении, что модель полная. Применяя метод наименьших квадратов к каждому полученному уравнению, оценивают все параметры системы в приведенной форме. Так как по предположению все структурные уравнения точно идентифицируемы, на следующем этапе однозначно определяются структурные параметры по параметрам приведенной формы. Итак, структурные параметры оцениваются косвенно через параметры приведенной формы. Поэтому мы говорим о косвенном методе наименьших квадратов. Если соблюдаются предпосылки из раздела 2.9, то оценки, полученные с помощью косвенного метода наименьших квадратов, состоятельны. Метод неприменим, если модель состоит из сверхидентифицированных структурных уравнений, так как тогда структурные параметры не могут быть вычислены однозначно по параметрам приведенной формы. Это большой недостаток косвенного метода наименьших квадратов, так как практически во всех эконометрических моделях содержатся сверх-идентифицированные структурные уравнения.
Мы покажем применение косвенного метода наименьших квадратов, используя данные табл. 20. Так как значения переменных приведены в виде отклонений от их средних, структурная форма модели (12.7) упрощается:
(12.32)
(12.33)
Уи + 0x2^2* = b12x2t + Uu, а21Уи “b y%t = ^2 3-^3t “b ^2t* Приведенная форма этой модели имеет вид:
У It = C12^2f + £13*3f “Ь У 2t = ^22-^2t “Ь ^23-^3t + ^2i*
Каждое уравнение приведенной формы (12.33) необходимо оценить отдельно по методу наименьших квадратов в соответствии с (2.64). Выполним следующие операции с матрицами и векторами:
72 —162"
— 162 420 ’
X —(х2х3), Х'Х =
(Х'Х)-1 1
У = У1. Х'ух =
У = Уг. Х'у2 =
"420 162' 3996 [162 72 J 2^21 l/lt _
У it _
Ун _ _ у21 _
’ 157"
—377J’
'—831
201
262
В итоге получим оценки уравнений в приведенной форме (12.33): у it = 1,218 x2t — 0,428 x3t,
У-zt = — 0,575 x2t + 0,257 x3t.
Так как оба структурных уравнения точно идентифицируемы (см. раздел 12.4), параметры структурной формы однозначно определяются по параметрам приведенной формы на основе системы уравнений (см. (12.Н)):
В = АС
__ 1 #12 £12 £13 __ С12 + £22 £12 £13 4“ £23 £12
^12 О
О ъ.
'23 _
^21 1 _ , ^22 ^23. _ ^-22 “Ь ^12 ^21 ^23 Н- С13 ^21.
В результате получим оценки:
а12 = —= 1,667; а21 = — = 0,472,
С23 С12
Z?12 = С12 “4"" ^22^12 == 0,259, ^23 = ^23 4~ ^13^21 0,055.
Таким образом, структурные уравнения (12.32) имеют вид:
'уи + 1,667 y2t = 0,259 x2t, или ylt = — 1,667 y2t + 0,259 x2t,
0,472 ylt + y2t — 0,055 x3t, или y2t = —0,472 ylt + 0,055 x3f.
По этим уравнениям мы можем сделать следующие выводы:
1. Параметры приведенной формы (12.33) отражают общее воздействие предопределенных переменных на совместно зависимые переменные уг и у2 (см. раздел 12.3).
а) Параметр с12 = 1,218 указывает на непосредственное и косвенное воздействие денежных доходов населения на денежное обращение: В(У1)*-\ —непосредственное воздействие,
if NGE(x^----------косвенное воздействие, возникающее на основе
[jQ^y^ одновременных соотношений между yt и у2.
Параметр с23 указывает на непосредственное и косвенное воздействие размера вклада в сберегательную кассу на оборачиваемость денег:
5(х3) и<3(у2)Л
б) Благодаря существующим одновременным соотношениям между уг и у2 направление воздействия размера вклада в себерегательную кассу (х3) противоположно воздействию оборачиваемости денег (z/2) на денежное обращение (z/J:
В (У1)
i s(x3)
UG (у2) Ч—I
263
Воздействие денежных доходов населения (х2) также противоположно воздействию денежного обращения (уг) на оборачиваемость денег (у2):
5(Ух) ч—।
I NGE (х2)
(7G (у2)
Эти воздействия нельзя обнаружить по структурной форме модели (12.32).
2. Параметры структурной формы (12.32) отражают непосредственное воздействие переменных (см. раздел 12.3). При сравнении Ь12 = = 0,259 с с12 = 1,218 или Ь23 = 0,055 с с23 = 0,257 становится очевидным различие между непосредственным и общим воздействием предопределенной переменной х2 или соответственно х3. Кроме того, взаимные воздействия между денежным обращением и оборачиваемостью денег можно определить по параметрам а12 и а21.
3. При сравнении результатов применения обычного и косвенного методов наименьших квадратов к структурным уравнениям (12.30) и (12.31) обнаруживается четкое различие по всем параметрам:
Параметры Обычный метод наименьших квадратов Косвенный метод наименьших квадратов
Я12 —0,444 — 1,667
&21 —0,374 —0,472
&12 1,669 0,259
^23 0,143 0,055
III. Двухшаговый метод наименьших квадратов.
В связи с тем что обычный метод наименьших квадратов не всегда дает удовлетворительные оценки моделей из систем одновременных уравнений, были разработаны методы оценивания, которые учитывают многосторонние связи совместно зависимых переменных. Мы остановимся лишь на наиболее часто применяемом двухшаговом методе наименьших квадратов.
Двухшаговый метод наименьших квадратов является обобщением метода наименьших квадратов. Он представляет собой обычный метод наименьших квадратов для оценивания параметров структурного уравнения в два этапа. Вначале мы изложим основную идею метода, а затем проиллюстрируем применение этого метода на примере. Отправной точкой является структурное уравнение модели (12.4), которое запишем в следующем виде:
у, = + ХЛ + (12.34)
где yz — вектор наблюдений над совместно зависимой переменной, подлежащей определению с помощью f-го структурного уравнения; Yf — матрица наблюдений над совместно зависимыми переменными, содер
264
жащимися, кроме того, в r-м структурном уравнении; аг- — вектор оценок параметров зависимых переменных, содержащихся в матрице Yf, X/ — матрица наблюдений над предопределенными переменными, которые содержатся в f-м структурном уравнении; — вектор оце-нок параметров этих предопределенных переменных; — вектор остатков f-го структурного уравнения для всех периодов наблюдений. Пусть по счетному правилу это уравнение идентифицируемое. Совместно зависимые переменные, содержащиеся в матрице Yf, не являются стохастически независимыми относительно остатков f-ro структурного урав-нения uf. Поэтому непосредственное применение метода наименьших квадратов приведет к несостоятельным оценкам. Основная идея двухшагового метода наименьших квадратов состоит в замене матрицы Y/ в правой части (12.34) матрицей оценок (матрицей значений регрессий). Благодаря этому содержащиеся в матрице переменные приобретают характер предопределенных переменных, и применение метода наименьших квадратов даст удовлетворительные результаты.
Итак, первый этап применения двухшагового метода наименьших квадратов заключается в определении матрицы значений регрессий Yf. Для этой цели строится приведенная форма совместно зависимых переменных матрицы Yf:
Yf = XCf + Vf. (12.35)
Однако для построения приведенной формы (12.35) должны быть заданы все предопределенные переменные модели (см. раздел 12.3).
Матрица значений регрессий Yf получается из (12.35) путем известного преобразования:
Yf = Yf-Vf = XCf. (12.36)
Значения регрессий матрицы Yf независимы от возмущающих переменных приведенной и структурной форм, так как они являются линейными функциями только от предопределенных переменных. Таким образом, отдельные уравнения (12.36) представляют собой множественную регрессию, для которой выполняется предпосылка 5 из раздела 2.9.
Метод наименьших квадратов может применяться для оценивания параметров матрицы Cf. В соответствии с (2.64) имеем*:
Cf = (Х'Х)"1 X'Yf. |(12.37)
Подставляя (12.37) в (12.36), получим матрицу значений регрессий:
Yf = Х(Х'Х)-1 X'YZ. (12.38)
Таким образом, задача, поставленная на первом этапе применения метода, выполнена.
*3десь следует учитывать, что оцениванию подлежит несколько множественных регрессий.
265
На втором этапе матрицу Yz в (12.34) заменяют матрицей Yz.
При этом следует учитывать, что по (12.36) Yz = Yz + Vz. Итак,
У* = (Yz + Vz) az + ХД- + £ = Yzaz + Xzbz + uz + Vzaz,
или, учитывая, что
= uz + Vzaz, yz = Yzaz + Xzbz + wz.
(12.39)
(12.40)
В полученном уравнении в правой части находятся только предопреде ленные переменные, так как матрица Xz содержит только предопреде ленные переменные, а элементы матрицы Yz «предопределены» через (12.38). При этом значения регрессий Yz больше не коррелируют с остатками wz. Таким образом, выражение (12.40) представляет собой уравнение множественной регрессии, для которого выполняется предпосылка 5 из раздела 2.9. Неизвестные параметры регрессии az и bz могут быть оценены с помощью метода наименьших квадратов. При этом следует учитывать, что остатки (12.40) не являются больше остатками Z-го структурного уравнения (см. (12.39)).
Двукратное (в два этапа) применение метода наименьших квадратов можно представить в виде одной формулы. Для этого образуем систему нормальных уравнений для уравнения регрессии (12.40). Если мы
положим, что
Zz=(YzXz)ndz=
то (12.40) можно представить в виде:
У; = Z;dz + Wi.
(12.41)
(12.42)
Тогда в соответствии с (2.63) из раздела 2.7 мы получим систему нормальных уравнений:
z'M = z;yz. (12.43)
Подставив (12.41) в (12.43), приходим к выражению:
LX/ Уг
у/ хг'
X/XiJLDd
ai
Ь
Y/У.-Х/уг
(12.44)
Используя (12.38) для Yz, можно записать уравнения для вычисления оценок двухшагового метода наименьших квадратов:
"Y/Х(Х'Х)”1Х'Yz Y/ xq-1 [Y; X (X' X)-1 X' у,1
_X/YZ X/xJ
аг
Ьг
[Х/уг
(12.45)
k ^Формула (12.45) представляет собой результат применения двухшагового метода наименьших квадратов к f-му структурному уравнению. Легко видеть, что матрица значений регрессий Yz, полученная на пер-
266
вом этапе применения метода, не содержится в (12.45) в явном виде. В нее входят только матрицы и векторы наблюдений. Преимущество двухшагового метода заключается, во-первых, в том, что он применим к сверхидентифицированным уравнениям, и, во-вторых, в том, что нерассмотренные нами структурные уравнения модели не должны быть точно специфицированы. Разумеется, должны быть известны все предопределенные переменные модели и указаны результаты наблюдений над ними. Недостаток метода состоит в том, что в оценках содержатся не остатки Z-го структурного уравнения — иь а остатки уравнения, полученного на втором этапе, — uz -J- = wf.
Пример
Воспользуемся снова примером-моделью (12.32) и оценим первое уравнение (Z = 1) с помощью двухшагового метода наименьших квадратов. Конкретизируем вначале уравнение (12.34). Переменная уг определяется с помощью первого уравнения модели (12.32). Следовательно, равна уь вектору наблюдений над переменной уг. В первое уравнение включена также другая совместно зависимая переменная у2. Из этого следует, что матрица состоит только из вектора наблюдений над переменной у2. Поэтому полагаем, что = (у2). Благодаря этому содержит только параметр а12. В первом уравнении содержится предопределенная переменная х2, так что в матрице X/ имеется только вектор наблюдений над переменной х2: Xf = (х2). В соответствии с этим
состоит только из параметра Ь12. Вектор становится вектором остатков первого структурного уравнения: uf = ule Уравнение (12.34) принимает следующую конкретную форму:
У1 = «12У2 + ^12*2 + и1- (12.46)
Для оценок параметров а12 и Ь12 в (12.46) воспользуемся формулой (12.45):
По данным табл. 20 получим промежуточные результаты:
(Х'Х)~1 =——
' 3996
’420 162
162 72
х'у2-
—83 v, , X У! =
201
157'
—377
угх2 = х2у2 = (—83), х$х2 = (72), х2у! = (157), у£Х (Х'Х)-1Х'у2 = 99,339, у2Х (Х'Х)"1 Х'ух = — 187,0841.
Подставив в (12.47) эти промежуточные результаты, найдем численные значения искомых параметров:
й12
&12
99,339 —83]"1
—83 72
—187,08411 Г—1,6666'
157 J [ 0,2593
267
Таким образом, оценка первого уравнения (12.32) по двухшаговому методу наименьших квадратов имеет вид:
У1 = — 1,667 у2 + 0,259 х2 + wv
Сравнивая последнее выражение с уравнением, полученным косвенным методом наименьших квадратов (см. с. 263), замечаем, что они совпадают. Это объясняется тем, что первое уравнение модели (12.32) точно идентифицируемо. В случае точно идентифицируемых уравнений модели оценки косвенного и двухшагового методов наименьших квадратов совпадают.
Аналогичным способом можно оценить второе уравнение модели (12.32). Получим результат, идентичный оценке уравнения по косвенному методу наименьших квадратов, так как второе уравнение модели также точно идентифицируемо.
Разработан также ряд других методов оценивания систем одновременных уравнений, среди которых прежде всего следует назвать трехшаговый метод наименьших квадратов, метод максимального правдоподобия с ограниченной и с полной информацией, метод оценок класса k, итеративный метод инструментальных переменных и метод главных компонент. Заинтересованный читатель может познакомиться с этими методами в специальной литературе \
1Более обстоятельно вопросы, затронутые в данной главе, изложены в следующих книгах: Кейн Э. Экономическая статистика и эконометрия. Вып. 1 и 2. М., Статистика, 1977, 1977; Фишер Ф. Проблема идентификации в эконометрии. М., Статистика, 1978 . а также в [69], [89], [123], [124], [125]. — Примеч. пер.
АССОЦИАЦИЯ И КОНТИНГЕНЦИЯ
Признаки явлений не всегда могут быть выражены в количественной форме. Существуют признаки с качественной вариацией, такие, как семейное и социальное положение, пол, профессия, форма собственности, административное подчинение предприятий и т.д. Связи между качественно варьирующими признаками играют большую роль (например, в социологии).
При наличии соотношения между качественно варьирующими признаками говорят об их ассоциации, взаимосвязанности. Возможно также употребление термина «корреляция». (Для обозначения связи количественно варьирующих признаков явлений наряду с термином «корреляция» применяют понятие «ассоциация»). Мы будем использовать понятие «ассоциация» только для объективно существующих соотношений между двумя качественными признаками. Так, с помощью ассоциации мы можем исследовать, существует ли связь между разработкой подземным и открытым способами в горнодобывающей промышленности и медицинскими заключениями «болен» и «здоров». Удовлетворенность характером работы можно исследовать, классифицируя ответы с помощью понятий «доволен», «не доволен». Итак, ассоциация признаков изучается с помощью взаимоисключающих ответов типа «да — нет», «хорошо — плохо», «согласен — не согласен» и т. д. Если качественные признаки принимают более двух значений, то связь между ними называется контингенцией. При исследовании связи между такими признаками числовой материал располагают в виде таблицы. Наблюдаемые значения являются теперь частотами, характеризующими появление отдельных признаков. Ориентировочную оценку существующих соотношений получают путем сравнения табличных значений. Эта процедура заключается в сопоставлении наблюдаемых частот в клетках таблицы с суммами частот по столбцам и строкам *. Далее мы рассмотрим некоторые методы, позволяющие численно оценить связь между качественными признаками.
*Allgemeine Statistik. Lehrbuch. Verlag Die Wirtschaft. Berlin, 1 964, S. 385.
269
13.1. КОЭФФИЦИЕНТ АССОЦИАЦИИ
Если признак обладает альтернативной вариацией, то результаты наблюдений можно представить в виде таблицы ассоциации, называемой также 2x2 -таблицей, или четырехклеточной таблицей. В качестве примера исследуем, существует ли связь между заболеваемостью профессиональной болезнью и способом разработки—подземным или открытым— на одном из предприятий горнодобывающей промышленности. Числовые данные содержатся в табл. 21.
Таблица 21
Число заболеваний при подземном и открытом способах разработки
Число работников
занятых на подземных работах общее обозначение занятых на открытых работах общее обозначение сумма общее обозначение
Больные 137 411 72 *712 209 41
Здоровые 152 421 149 422 301 42
Сумма 289 <31 221 0% 510
Для измерения связи можно воспользоваться коэффициентом ассоциации Ф (произносится: фи), предложенным К. Пирсоном:
ф ±= У11 ^12 ^12 ^21 (13 1)
"1^41 Qz Qi 0.2
По своей конструкции коэффициент Ф соответствует коэффициенту корреляции, примененному к частотам появления отдельных значений признака. Коэффициент Ф принимает значения в интервале — 1 Ф
+ 1. Если = г/22 — 0, то Ф = — 1. При <712 == q21 = 0 коэффициент Ф = 1. Случай qir = q12 = 0 или g21 = q22 = 0 не представляет интереса, так как при таких значениях q нельзя построить четырехклеточную таблицу.
Для нашего примера
У209-301-289-221
По величине Ф можно предположить, что, вероятно, между числом заболеваний и числом работников, занятых на подземных и открытых разработках, существует лишь очень слабая связь. Для проверки этого вывода применим критерий %2. В специальной литературе показано, что ф = ’[// ~Х2- (13.2)
Отсюда следует, что
^2 = Лф2 П (<711 *?22 Q12 <?21)2 (13.3)
414ъ Qi Фг
270
где п — сумма всех частот. Величина %2 для четырехклеточной таблицы имеет одну степень свободы. С помощью критерия %2 можно непосредственно оценить, существует ли вообще связь между изучаемыми явлениями. Но критерий не позволяет сделать вывод о силе связи. Для нашего примера %2 = 11,32. Если мы выберем уровень значимости а == = 0,05, то по табл. 5 приложения найдем для числа степеней свободы» равного 1, критическое значение %о,о5; i = 3,841. Так как %2 > %§,05; i> то делаем общий вывод, что между данными явлениями имеется статистически значимая связь, но коэффициент Ф = 0,149 показывает, что связь очень слабая.
Формулу (13.1) можно вывести, используя ход рассуждений, который будет приведен в разделе 13.2.
Мы представили меру связи дихотомических признаков. Коэффициент ассоциации может быть вычислен только при альтернативной группировке числового материала («да», «нет»; «хорошо», «плохо» и т. д.). При этом ожидаемая частота признака должна быть больше 5» а объем выборки — не меньше 40. Вполне возможно, что эти предпосылки могут не соблюдаться в силу того, что частоты определяются эмпирическим путем. В этом случае для большего соответствия ^-распределению вводят так называемую поправку на непрерывность, или коэффициент Йейтса. Смысл поправки заключается в том, что наблюдаемые частоты, которые больше ожидаемых, увеличивают на 0,5, а наблюдаемые частоты, которые меньше ожидаемых, уменьшают на эту же величину. В результате получаем формулу:
( п П И11 <?22 ^12^21 !
%2 = -3-----------------------£_
91 92 Qi Q2
(13.4)
Другим показателем ассоциации является тетрахорический коэф< фициент гтет. Он также вычисляется при альтернативной (дихотомий ческой) группировке числового материала. Предпосылкой его применения является нормальное распределение генеральной совокупности. Тетрахорический коэффициент вычисляется по формуле
/ 180°
Гтет — COS /------------
911 922
912 921
_______180° ~1/q12 g2i
"0711 922 + "0712 921
(13.5)
(13.6)
Коэффициент гте1 может принимать значения в границах —1 ггет
1. Если распределение частот по границам четырехклеточной таблицы сильно’неравномерно, то гтет становится ненадежным показателем связи.
Известны также другие показатели связи, вычисляемые по четырехклеточной таблице. Из них прежде всего следует упомянуть коэффи-
271
циент ассоциации Q, предложенный Г. У. Юлом в 1900 г.:
Q 711722 712*721 (13 7)
711 722+ 712 721
Коэффициент Q принимает значения в интервале — 1 Q + 1. Если = 0 и q22 = 0, то Q = — 1. Если q12 = 0 или q21 = 0, то <2= + I.
13.2. КОЭФФИЦИЕНТ КОНТИНГЕНЦИИ (СОПРЯЖЕННОСТИ)
Если вариацию качественного признака изучаемого явления можно разбить не на две группы (как в случае дихотомического признака), а на несколько групп, то соответствующий числовой материал располагают в виде таблицы с несколькими строками и столбцами. Такая таблица называется таблицей контингенции, или т х п-таблицей.
Связь между признаками по такой таблице исследуется с помощью критерия %2. Покажем применение критерия на примере. Пусть требуется исследовать, оказывает ли влияние консервирующее средство на сохраняемость продуктов питания. Было заготовлено 1000 упаковок данного вида продуктов питания, из которых 300 упаковок были без добавки, 500 упаковок— с незначительной добавкой, а 200— с большой добавкой консерванта. Продукты питания затем, по степени их сохраняемость, были разбиты на группы: плохая, средняя, хорошая и очень хорошая сохраняемость *. Результаты исследования приведены в табл. 22.
Таблица 22
Связь между консервирующим средством и сохраняемостью продуктов питания
Консервирующее средство Сохраняемость
плохая средняя хорошая очень хорошая сумма
Без добавки 51 <7п 29,4911 175 912 129,6912 74 91з 115,89{з — 714 25,2 9(4 300 71 300
Незначительная добавка 45 7г1 49 7з1 210 722 216 7г2 191 72з г 193 7зз 54 7г4 42 7г4 500 500 92
Большая добавка 2 7з1 19,6 7з1 47 7з2 86,4 732 121 9зз 77,2 9з'3 30 9з1 16,8 9^4 200 200 7з
Сумма 98 Qi 432 Qa 386 Q3 84 Q4 1 000
*В иг khar d t F. Vorlesungen uber angewandte Statistik, gehalten an der Humboldt-Universitat zu Berlin, Berlin, 1957.
Если бы существовала однозначная связь между добавкой консервирующего средства и сохраняемостью продуктов питания, то были бы заполнены клетки только по диагонали таблицы контингенции. Но наш пример не может служить иллюстрацией этого случая. Простое сравнение чисел в заполненных клетках таблицы не даст нам ответа на вопрос, существует ли связь между изучаемыми признаками. Но критерий %2 позволит сделать статистически обоснованный вывод о связи. Для этой цели по имеющимся данным построим таблицу с таким распределением статистической совокупности по ее клеткам, которое соответствовало бы отсутствию связи между обоими признаками. Путем сравнения фактических и теоретически ожидаемых значений можно установить, существует связь или нет. В первом случае наблюдаются значительные отклонения между эмпирическими и теоретическими значениями, а во втором случае эмпирические и теоретические значения почти совпадают.
Итак,
Pi= —, i=l, 2, ..., v, (13.8)
п
— относительная частота (вероятность) появления значения в г-й строке. Далее,
(13.9)
— относительная частота (вероятность) появления значения в /-м столбце. Через п обозначено общее число единиц данной статистической совокупности. В нашем примере п = 1000.
Относительная частота (вероятность) появления значения в ьй строке и /-м столбце (в I, j-й клетке таблицы) выразится следующим образом:
Р» = Pt Pj = (13.10)
Учитывая распределение сумм частот по строкам и столбцам (qt и Qj), получим теоретически ожидаемое значение q'tf.
qii = npi} = -?j^L. (13.11)
п
Так как при вычислении относительных частот предполагалась независимость признаков, то q\^ q{<2, ..., q%\, q22, • •• являются теоретически ожидаемыми значениями в отдельных клетках таблицы. Эти значения имели бы место при отсутствии связи между признаками. Они указаны в каждой клетке табл. 22 под эмпирическими частотами.
Для проверки гипотезы о связи между признаками применяется критерий %2. Величина
W V „Г
(?г/~~^/)2
7= 11= 1 Уи
(13.12)
272
Ю Зак. 1113
273
имеет %2-распределение с f = (и— 1) (w— 1) степенями свободы. Расчетное значение (13.12) сравниваем с теоретическим значением %2, найденным по табл. 5 приложения при заданном уровне значимости а и соответствующем числе степеней свободы. Если %2 > /, то с веро-
ятностью 1 — а можно принять гипотезу о наличии связи между рассматриваемыми признаками.
Вид и силу связи изучают затем с помощью дополнительных исследований, привлекая к этому, например, коэффициент контингенции, который можно вычислить по формуле:
или
(13.13)
(13.14)
Здесь d — наименьшее из двух чисел v и w, т. е. либо число строк, либо число столбцов. Значения С и К лежат в границах между 0 и 1. Если мы применим формулы (13.8) — (13.12) к таблице ассоциации из раздела 13.1, то выведем приведенные там соотношения.
Обратимся к нашему примеру. По (13.11) получим
, 300-98
911 ~ 1000
, 200-84
6/34 ~ 1000
29,4,
16,8.
, 300-432
<712=-----------129,6,...
7 1000
По (13.12) имеем
_ (51—29,4)2 , (175-129,6)2 (30-16,8)2 _ ж д9?
Л 29,4 129,6 16,8
Если бы связь между добавкой консервирующего средства и сохраняемостью продуктов отсутствовала, то %2 несущественно бы отличалось от 0. Для нашего примера число степеней свободы f = (3— 1) X Х(4 — 1) = 6. При уровне значимости а — 0,05, или 5%, находим по табл. 5 приложения критическое значение %о,о5; 6 = 12,592. Так как %2 > Хо,о5; 6, то делаем вывод—консервирующее средство оказывает влияние на сохраняемость продуктов питания. Этот вывод подтверждается также при выборе уровня значимости а = 0,001, или 0,1 %. В этом случае критическое значение Xo.ooi; 6 = 22,457.
Для определения силы связи вычислим коэффициенты контингенции:
С-1/ Ш’997— -0,356,
|/ 144,997 + 1000
/<--=] f.2i4’"Z_. =0,269.
у 1 000(3—1)
Оба коэффициента указывают на существование связи средней силы между добавкой консервирующего средства и сохраняемостью продук-274
Тов. В связи с тем что величина С зависит от числа столбцов и строк таблицы, обычно вычисляют исправленный коэффициент континген-ции с поправкой Стах. Значение Стах с увеличением числа строк и столбцов таблицы приближается к + 1. Для квадратной таблицы кон-тингенции
(13.15)
где через w обозначено число столбцов или строк. Для т х /г-таб-лицы приблизительное значение Сгаах вычисляется как среднее из максимальных значений С соответствующих квадратных таблиц кон-тингенции. Так, для 3 X 4-таблицы имеем С3 = 0,826, С4 = 0,866, п 0,816 0,866 р. ОЛ1
из чего следует, что Стах = ~—— = 0,841.
Исправленное значение коэффициента находим по формуле
сИСПр = #-. (13.16)
шах
Для нашего примера получаем следующий результат:
Сиспр = -^1 = 0,423. испр 0,841
Особенно важно вводить поправку в коэффициент контингенции при малом числе строк и столбцов таблицы.
133. ДВУХСТРОЧЕЧНАЯ КОРРЕЛЯЦИЯ
При экономических, а также социологических исследованиях часто возникает ситуация, когда значения одного признака (х) метрически шкалированы по нескольким ступеням, в то время как другой признак (у) обладает только альтернативной вариацией, представленной в форме «да—нет», «правильно—ошибочно», «согласен—не согласен». Связь между подобными явлениями называется двухстрочечной, или бисериальной корреляцией. Если признак у в действительности принимает различные значения, которые лишь условно разбиваются на две альтернативные группы, то связь между х и у называют непрерывной двухстрочечной корреляцией. Если же, напротив, признак у дихотомический, т. е. природа изучаемого явления такова, что его признак может принимать только два взаимоисключающих значения (например, пол), то говорят о дискретной двухстрочечной корреляции. Этот тип корреляции называют иногда также точечно-бисериальной корреляцией.
При изучении обоих типов корреляции предполагается, что переменная х имеет нормальное распределение. Если о распределении переменной у ничего неизвестно, то вычисляют коэффициент точечно-бисериальной корреляции гт.-бис. Если можно предположить, что переменная у тоже распределена нормально, то вычисляют коэффициент бисериальной корреляции гбис.
10*
275
Таблица 23
Уровни заработной платы и удовлетворенность рабочих ее размером
Уровни заработной платы X Ответы рабочих об удовлетворен-[ ности размером заработной платы
нет | | Да | всего
3 2 2
4 5 2 7
5 8 6 14
6 6 10 16
7 1 7 8
8 — 3 3
Сумма 22 28 50
Продемонстрируем вычисление коэффициентов двухстрочечной корреляции на примере. Пусть исследуется связь между уровнями заработной платы, выраженными в условных единицах, и удовлетворенностью рабочих размером получаемой заработной платы. Результаты опроса 50 рабочих представлены в табл. 23.
Коэффициент бисери-альной корреляции вычисляется по формуле
__ По х0—х 'бис
п Sx<P(M
(13.17)
где и0 — объем наблюдений в столбце с наименьшим числом элементов; и—общий объем наблюдений; х0—среднее значение признака х, вычисленное по данным столбца с наименьшим числом элементов; х— среднее значение признака х, вычисленное по всей совокупности; sx — стандартное отклонение значений признака х относительно х; <р(Х) — значение плотности нормального распределения в точке с абсциссой X, для которой имеет место соотношение F (X) = 1 — .
Для нашего примера п = 50; /г0 = 22; х0 = 4,95; х = 5,6; sx = = 1,2; п0: п — 0,44; F (X) = 1 — 0,44 = 0,56. По табл. 2а приложения при F (1) = 0,56 находим абсциссу ср = 0,15, которой соответствует ф (X) = 0,3945 (см. табл. 1 приложения). В итоге получаем
22 4,95—5,60 псП/|
=-------------------- = — 0,604.
бис 50 1,2-0,3945
Коэффициент гбис принимает значения в интервале 1 ^гбис^ + 1. По данным примера можно сделать вывод: между уровнями заработной платы и удовлетворенностью рабочих размером заработной платы существует относительно сильная связь. Для условий нашего примера мы можем считать, что удовлетворенность размером заработной платы является непрерывным признаком, так как между ответами «да» и «нет» имеется еще целая шкала степени удовлетворенности, которая для упрощения представлена здесь в виде альтернативных ответов.
Если же переменная у обладает альтернативной вариацией, то корреляция будет точечно-бисериальной. В этом случае интенсивность связи между признаками измеряется с помощью следующего коэффициента:
Гт-бис^-^^-У^Т > (13.18)
nsx
276
или
т-бис
х0 — х
sx
(13.19)
где хх — среднее значение признака х, вычисленное по данным столбца с наибольшим числом элементов; — объем наблюдений в столбце с наибольшим числом элементов.
Если считать, что в нашем примере переменная у является дихотомической, то в качестве показателя связи между х и у вычислим коэффициент точечно-бисериальной корреляции:
4,95—5,60 /“22“ А ,А
Гт-бис =---—------1 / — = — 0,4°.
2о
1,2
Так как мы не предполагали нормального распределения, связь между уровнями заработной платы и удовлетворенностью размером ее оказалась немного слабее, чем при бисериальной корреляции. Проверка значимости коэффициентов двухстрочечной корреляции производится таким же образом, что и проверка значимости линейных коэффициентов корреляции (см. раздел 8.5).
При изучении ассоциации и контингенции возникает ряд проблем, на которых здесь мы не будем подробно останавливаться. Наша задача заключалась лишь в том, чтобы показать принципиальную возможность измерения взаимосвязи при различных видах вариации.
Таблица I
to оо
ПРИЛОЖЕНИЕ
Ординаты стандартной нормальной кривой для 0^Х^З,9
% 0,0 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09
0,0 0,39894 0,39892 0,39886 0,39876 0,39862 0,39844 0,39822 0,39797 0,39767 0,39733
0,1 ,39695 ,39654 ,39608 ,39559 ,39505 ,39448 ,39387 ,39322 ,39253 ,39181
0,2 ,39104 ,39024 ,38940 ,38853 ,38762 ,38667 ,38568 ,38466 ,38361 ,38251
0,3 ,38139 ,38023 ,37903 ,37780 ,37654 ,37524 ,37391 ,37255 ,37115 ,36973
0,4 ,36827 ,36678 ,36526 ,36371 ,36213 ,36053 ,35889 ,35723 ,35553 ,35381
0,5 ,35207 ,35029 ,34849 .34667 ,34482 ,34294 ,34105 ,33912 ,33718 ,33521
0,6 ,33322 ,33121 ,32918 ,32713 ,32506 ,32297 ,32086 ,31874 ,31659 ,31443
0,7 ,31225 ,31006 ,30785 ,30563 ,30339 ,30114 ,29887 ,29659 ,29431 ,29200
0,8 ,28969 ,28737 ,28504 ,28269 ,28034 ,27798 ,27562 ,27324 ,27086 ,26848
0,9 ,26609 ,26369 ,26129 ,25888 ,25647 ,25406 ,25164 ,24923 ,24681 ,24439
1,0 ,24197 ,23955 ,23713 ,23471 ,23230 ,22988 ,22747 ,22506 ,22265 ,22025
1,1 ,21785 ,21546 ,21307 ,21069 ,20831 ,20594 ,20357 ,20121 ,19886 ,19652
1,2 ,19419 ,19186 ,18954 ,18724 ,18494 ,18265 ,18037 ,17810 ,17585 ,17360
1,3 ,17137 ,16915 ,16694 ,16474 ,16256 ,16038 ,15822 ,15608 ,15395 ,15183
1,4 ,14937 ,14764 ,14556 ,14350 ,14146 ,13943 ,13742 ,13542 ,13344 ,13147
Продолжение табл. 1
к 0,00 0,01 0,02 0,03 0,04 0, 05 0,06 0,07 0, 08 0,09
1,5 ,12952 ,12758 ,12566 ,12376 ,12188 ,12051 ,11816 ,11632 ,11450 ,11270
1,6 ,11092 ,10915 ,10741 ,10567 ,10396 ,10226 ,10059 ,09893 ,09728 ,09566
1,7 ,09405 ,09246 ,09089 ,08933 ,08780 ,08628 ,08478 ,08329 ,08183 ,08038
1,8 ,07895 ,07754 ,07614 ,07477 ,07341 ,07206 ,07074 ,06943 ,06814 ,06687
1,9 ,06562 ,06438 ,06316 ,06195 ,06077 ,05959 ,05844 ,05730 ,05618 ,05508
2,0 ,05399 ,05292 ,05186 ,05082 ,04980 ,04879 ,04780 ,04682 ,04586 ,04491
2,1 ,04398 ,04307 ,04217 ,04128 ,04041 ,03955 ,03871 ,03788 ,03706 ,03626
2,2 ,03547 ,03470 ,03394 ,03319 ,03246 ,03174 ,03103 ,03034 ,02965 ,02898
2,3 ,02833 ,02768 ,02705 ,02643 ,02582 ,02522 ,02463 ,02406 ,02349 ,02294
2,4 ,02239 ,02186 ,02134 ,02083 ,02033 ,01984 ,01936 ,01889 ,01842 ,01797
2,5 ,01753 ,01709 ,01667 ,01625 ,01585 ,01545 ,01506 ,01468 ,01431 ,01394
2,6 ,01358 ,01323 ,01289 ,01256 ,01223 ,01191 ,01160 ,01130 ,01000 ,01071
2,7 ,01042 ,01014 ,00987 ,00961 ,00935 ,00909 ,00885 ,00861 ,00837 ,00814
2,8 ,00792 ,00770 ,00748 ,00727 ,00707 ,00687 ,00668 ,00649 ,00631 ,00613
2,9 ,00595 ,00578 ,00562 ,00545 ,00530 ,00514 ,00499 ,00485 ,00471 ,00457
0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9
3,0 ,00443 ,00327 ,00238 ,00172 ,00123 ,00087 ,00061 ,00042 ,00029 ,00020
Таблица 2
Площади под стандартной нормальной кривой F (%)— J ср (г) dz для 3,9<%<0
—оо
X 0,00 — 0,01 — 0,02 — 0,03 — 0,04 — 0,05 — 0,06 -0,07 — 0,08 — 0,09
0,0 0,500000 0,496011 0,492022 0,488034 0,484047 0,480062 0,476078 0,472097 0,468119 0,464144
—0,1 ,460172 ,456205 ,452242 ,448283 ,444330 ,440382 ,436440 ,432505 ,428576 ,424655
—0,2 ,420740 ,416834 ,412936 ,409046 ,405165 ,401294 ,397432 ,393580 ,389739 ,385908
—0,3 ,382089 ,378280 ,374384 ,370700 ,366928 ,363169 ,359424 ,355691 ,351973 ,348268
—0,4 ,344578 ,340903 ,337243 ,333598 ,329969 ,326969 ,322758 ,319178 ,315614 ,312067
-0,5 ,308538 ,305026 ,301532 ,297056 ,294598 ,291160 ,287740 ,284339 ,280957 ,277595
—0,6 ,274253 ,270931 ,267629 ,364347 ,261086 ,257846 ,254627 ,251429 ,248252 ,245097
i —0,7 ,241964 ,238852 ,235762 ,232695 ,229650 ,226627 ,223627 ,220650 ,217695 ,214764
—0,8 ,211855 ,208970 ,206108 ,203269 ,200454 ,197662 ,194894 ,192150 ,189430 ,186733
—0,9 ,184060 ,181411 ,178786 ,176186 ,173609 ,171056 ,168528 ,166023 ,163543 ,161087
—1,0 ,158655 ,156248 ,153864 ,151505 ,149170 ,146859 ,144572 ,142310 ,140071 ,137857
—1,1 ,135666 ,133500 ,131357 ,129238 ,127143 ,125072 ,123024 ,121000 ,119000 ,117023
—1,2 ,115070 ,113139 ,111232 ,109349 ,107488 ,105650 ,103835 ,102042 ,100273 ,098525
—1,3 ,096800 ,095098 ,093418 ,091759 ,090123 ,088508 ,086915 ,085344 ,083793 ,082264
-1,4 ,080757 ,079270 ,077804 ,076358 ,074934 ,073529 ,072145 ,070781 ,069437 ,068111
Продолжение табл. 2
•х 0,00 — 0,01 — 0,02 -0,03 — 0,04 — 0,05 — 0,06 — 0,07 — 0,08 — 0,09
—1,5 ,066807 ,065522 ,064256 ,063008 ,061780 ,060571 ,059380 ,058208 ,057053 ,055917
-1,6 ,054799 ,053699 ,052616 ,051551 ,050503 ,049472 ,048457 ,047460 ,046479 ,045514
—1,7 ,044566 ,043633 ,042716 ,041815 ,040930 ,040059 ,039204 ,038364 ,037538 ,036727
—1,8 ,035930 ,035148 ,034380 ,033625 ,032884 ,032157 ,031443 ,030742 ,030054 ,029379
—1,9 ,028717 ,028067 ,027429 ,026803 ,026190 ,025588 ,024998 ,024419 ,023862 ,023296
-2,0 ,022750 ,022216 ,021692 ,021178 ,020675 ,020182 ,019699 ,019226 ,018763 ,018309
—2,1 ,017864 ,017429 ,017003 ,016586 ,016177 ,015778 ,015386 ,015003 ,014629 ,014262
—2,2 ,013903 ,013553 ,013209 ,012874 ,012546 ,012224 ,011911 ,011604 ,011304 ,011011
—2,3 ,010724 ,010444 ,010170 ,009903 ,009642 ,009387 ,009138 ,008894 ,008656 ,008424
—2,4 ,008198 ,007976 ,007760 ,007549 ,007344 ,007143 ,006947 ,006756 ,006569 ,006387
—2,5 ,006210 ,006037 ,005868 ,005703 ,005543 ,005386 ,005234 ,005085 ,004940 ,004799 '
-2,6 ,004661 ,004527 ,004396 ,004269 ,004145 ,004025 ,003907 ,003793 ,003681 ,003573
-2,7 ,003467 ,003364 ,003264 ,003167 ,003078 ,002980 ,002890 ,002803 ,002718 ,002635 i
—2,8 ,002555 ,002477 ,002401 ,002327 ,002256 ,002186 ,002118 ,002052 ,001988 ,001926
—2,9 ,001866 ,001807 ,031750 ,001695 ,001641 ,001589 ,001538 ,001489 ,001441 ,001395 j
0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 | 0,8 0,9 ;
-3,0 ,001350 ,000968 ,000687 ,000483 ,000337 ,000243 ,000159 ,000108 ,000072 ,000048 ;
Таблица 2а
282
Площади под стандартной нормальной кривой F (А) = J ср (z) dz для 0<Х<3,9
—оо
X 1 0.00 1 0,01 0,02 | 0,03 0,04 | 0,05 I 0,06 | 0,07 1 0,08 0,09 ;
0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 3,0 0,500000 ,539828 ,579260 ,617911 ,655422 ,691462 ,725747 ,758036 ,788145 ,815940 ,841345 ,864334 ,884930 ,903200 ,919243 ,933193 ,945201 ,955434 ,964070 ,971283 ,977250 ,982136 ,986097 ,989276 ,991802 ,993790 ,995339 ,996533 ,997445 ,998134 0,0 0,998650 | 0,503989 ,543795 ,583166 ,621720 ,659097 ,694974 ,729069 ,761148 ,791030 ,818589 ,843752 ,866500 ,886861 ,904902 ,920730 ,934478 ,946301 ,956367 ,964852 ,971933 ,977784 ,982571 ,986447 ,989556 ,992024 ,993963 ,995473 ,996636 ,997523 ,998193 0,1 0,999032 | °,507978 ,547758 ,587064 ,625616 ,662757 ,698468 ,732371 ,764238 ,793892 ,821214 ,846136 ,868643 ,888768 ,906582 ,922196 ,935744 ,947384 ,957284 ,965620 ,972571 ,978308 ,982997 ,986791 ,989830 ,992240 ,994132 ,995604 ,996736 ,997599 ,998250 0,2 0,999313 0,511966 ,551717 ,590954 ,629300 ,666402 ,702944 ,735653 ,767305 ,796731 ,823814 ,848495 ,870762 ,890651 ,908241 ,923642 ,936922 ,948449 ,958185 ,966375 ,973197 ,978822 ,983414 ,987126 ,990097 ,992451 ,994297 ,995731 ,996833 ,997673 ,998305 0,3 | 0,999517 0,515953 ,555670 ,594835 ,633072 ,670031 ,705402 ,738914 ,770350 ,799546 ,826391 ,850830 ,872857 ,892512 ,909877 ,925060 ,938220 ,949497 ,959070 ,967116 ,973810 ,979325 ,983823 ,987454 ,990358 ,992656 ,994457 ,995855 ,996928 ,997744 ,998359 0,4 | 0,999663 0,519938 ,559618 ,598706 ,636831 ,673645 ,708840 ,742154 ,773373 ,802338 ,828944 ,853141 ,874928 ,894350 ,911492 ,926471 ,939429 ,950528 ,959941 ,967843 ,974412 ,979818 ,984222 ,987776 ,990613 ,992857 ,994614 ,995975 ,997020 ,997814 ,998411 0,5 | 0,999767 0,523922 ,563560 ,602568 ,640576 ,677242 ,712260 ,745373 ,776373 ,805106 ,831472 ,855428 ,867976 ,896165 ,913085 ,927855 ,940620 ,951543 ,960796 ,968557 ,975002 ,980301 ,984614 ,988089. ,990862 ,993053 ,994766 ,996093 ,997110 ,997882 ,998462 0,6 | 0,999841 | 0,527903 ,567495 ,606420 ,644309 ,680822 ,715661 ,748571 ,779350 ,807850 ,833977 ,857690 ,879000 ,897958 ,914656 ,929219 ,941792 ,952540 ,961636 ,969258 ,975581 ,980774 ,984997 ,988396 ,991106 ,993244 ,994915 ,996207 ,997197 ,997948 ,998511 0,7 0,999892 0,531881 ,571424 ,610261 ,648027 ,684386 ,719043 ,751748 ,782305 ,810570 ,836457 ,859929 ,881000 ,899727 ,916207 ,930563 ,942947 ,953521 ,962462 ,969946 ,976138 ,981237 ,985371 ,988690 ,991344 ,993431 ,995060 ,996319 ,997282 ,998012 ,998559 0,8 0,999928 | 0,535856 ; ,575345 S ,614092 ; ,651732 ,687933 ,722405 ,754903 ,785236 ,813267 ,838913 ,862143 ,88?977 ,901475 ,917736 ,931889 ,944083 ,954486 ,963273 ,970621 ,976704 ,981691 ,985738 ,988989 ,991576 ,993613 ,995201 ,996427 ,997365 ,998074 ,998605 0,9 0,999952
О - — — — — — — — — — о о о •—* о — —
25 а % Односторонняя критическая область о о сп о о о о о о о о о о о о о о о о о. о о о 4 4 4 4 4 4 4 4 ао -444Эосоооооооооооооссоосоооооооооффффффооо — - юфо—о а% 50
12,5 7-1— — — — — — —^ — — — — — — — — — — — — — — — — — — — — — ЬО Г" ОГ XT — — — — — — — — — — — ю Ю Ю Ю к) Ю Ю Ю Ю ^57 4^ С ОПООЧЧЧЧОООООООССООООООО^ФСОФООО - — to ст
СП — — — — — — — — — — — — — — — — — — — — — — — — — — — tOtOtOtOOi 4^0*4000000 — — — — Ь0Ь0С0С0С04^СлСПО400О — W С Ф 4^ - СО СП ЬО — Двуст< 10
2,5 оооооооооооооооо — — •— >— — — — Ю ЮЮ о к 4^ Ь1 к - СО 4 О00ОЬ04^СПСПСлООО*4*400ООО*— ЬОС04^-ООООСоО — О СЛ *4 00 СО О * эронняя К 5
— СО СС Ф W 4^ 4^ Ф 4^ 4^ 4^ 4^ 4^ СЛ СЛ СЛ СЛ Ci СЛ СЛ С1 С: О О С: 4 4 ОО ф О — и <1 СЛ Ф СС ФФФЮФФ4400ФФО — ФФ4^ 014 000Ю010оЮС:Ю004^4014^4Ф ритическая 2
0,5 ФЮЮ(ОФФ10ЮЮЮФЬЭФЮЮФЮЮЮЮЮСОФФФФФФФ^^01ФФ СП О О *4 4 *4 *4 *4 *4 4 00 00 00 00 00 00 00 О О О О О О — ЬО Со СП ~4 О О 00 О *4 00 ЮФООЗфФ 400фО'-ЮО:ОЗСЗ. ООффОзОО'— 03 — 4010 0 — Ф О 4^ Ю О область 1
о,1 СО — to — ^СО СО ^СО СО СО СО СО СО СО СО СО СО СО СО СО СО СО СО СО СО СО СО СО 4^ 4^ 4^ 4^ 4^ СП СП *4 О ЬО 00 О ^ ЬО Ф Ф £ 4^ ф Ф Ф U1 О ф Ф 4 4 СХ) Ф О W СП 4 Ю ОО ~ IO ф ф О4Ф— ФО — ФФСЛ4Ф — О0СЛО0 — СЛФФФСЛФОо^ООФ — Ф4ЮФ — 0,2
0,05 05 СО со СО Со со СО СО СО СО СО СО СО СО СО СО ФФФ4^4^4^4^4^Ф^Ф.СЛСЛСЛО 00 ЬО — 4 ЮСС^.СлОООО4444400СС0СФфОО — ФФФСЛ40Ф.ФСООФОО Ф4ОСЛФО4Ф-Ю^4ФФСлаЮО-4^ЮЮ^фф^ООО- о
Процентные точки /'-распределения.
fi—число степеней свободы
ft 1 2 3 4 5 6 7 8 9 10 и 12
1 161 4052 200 4999 216 5403 225 5625 230 .5764 234 5859 237 5928 239 5981 241 6022 242 6056 243 6082 244 6106
2 18,51 98,49 19,00 99,00 19,16 99,17 19,25 99,25 19,30 99,30 19,33 99,33 19,36 99,34 19,37 99,36 19,38 99,38 19,39 99,40 19,40 99,41 19,41: 99,42
3 10,13 34,12 9,55 30,82 9,28 29,46 9,12 28,71 9,01 28,24 8,94 27,91 8,88 27,67 8,84 27,49 8,81 27,34 8,78 27,23 8,76 27,13 8,74 27,05
4 7,71 21,20 6,94 18,00 6,59 16,69 6,39 15,98 6,26 15,52 6,16 15,21 6,09 14,98 6,04 14,80 6,00 14,66 5,96 14,54 5,93 14,45 5,91 14,37
5 6,61 16,26 5,79 13,27 5,41 12,06 5,19 11,39 5,05 10,97 4,95 10,67 4,88 10,45 4,82 10,27 4,78 10,15 4,74 10,05 4,70 9,96 4,68 9,89
6 5,99 13,74 5,14 10,92 4,76 9,78 4,53 9,15 4,39 8,75 4,28 8,47 4,21 8,2о 4,15 8,10 4,10 7,98 4,06 7,87 4,03 7,79 4,00 7,72
7 5,59 12,25 4,74 9,55 4,35 8,45 4,12 7,85 3,97 7,46 3,87 7,19 3,79 7,00 3,73 6,84 3,68 6,71 3,63 6,62 3,60 6,54 3,57 6,47
8 5,32 11,26 4,46 8,65 4,07 7,59 3,84 7,01 3,69 6,63 3,58 6,37 3,50 6,19 3,44 6,03 3,39 5,91 3,34 5,82 3,31 5,74 8,28 5,67
9 5,12 10,56 4,26 8,02 3,86 6,99 3,63 6,42 3,48 6,06 3,37 5,80 3,29 5,62 3,23 5,47 3,18 5,35 3,13 5,26 3,10 5,18 3,07 5,11
10 4,96 10,04 4,10 7,56 3,71 6,55 3,48 5,99 3,33 5,64 3,22 5,39 3,14 5,21 3,07 5,06 3,02 4,95 2,97 4,85 2,94 4,78 2,91 4,71
11 4,84 9,65 3,98 7,20 3,59 6,22 3,36 5,67 3,20 5,32 3,09 5,07 3,01 4,88 2,95 4,74 2,90 4,63 2,86 4,54 2,82 4,46 2,79 4,40
12 4,75 9,33 3,88 6,93 3,49 5,95 3,26 5,41 3,11 5,06 3,00 4,82 2,92 4,65 2,85 4,50 2,86 4,39 2,76 4,30 2,72 4,22 2,69 4,16
13 4,67 9,07 3,80 6,70 3,41 5,74 3,18 5,20 3,02 4,86 2,92 4,62 2,84 4,44 2,77 4,30 2,72 4,19 2,67 4,10 2,63 4,02 2,60 3,96
14 4,60 8,86 3,74 6,51 3,34 5,56 3,11 5,03 2,96 4,69 2,85 4,46 2,77 4,28 2,70 4,14 2,65 4,03 2,60 3,94 2,56 3,86 2,53 3,80
15 4,54 8,68 3,68 6,36 3,29 5,42 3,06 4,89 2,90 4,56 2,79 4,32 2,70 4,14 2,64 4,00 3,59 3,89 2,55 3,80 2,51 3,73 2,48 3,67
16 4,49 8,53 3,63 6,23 3,24 5,29 3,01 4,77 2,86 4,44 2,74 4,20 2,66 4,03 2,59 3,89 2,54 3,78 2,49 3,69 2,45 3,61 2,42 3,55
17 4,45 8,40 3,59 6,11 3,20 5,18 2,96 4,67 2,81 4,34 2,70 4,10 2,62 3,93 2,55 3,79 2,50 3,68 2,45 3,59 2,41 3,52 2,38 3,45
18 4,41 8,28 3,55 6,01 3,16 5,09 2,93 4,58 2,77 4,25 2,66 4,01 2,58 3,85 2,51 3,71 2,46 3,60 2,41 3,51 2,37 3,44 2,34 3,37
19 4,38 8,18 3,52 5,93 3,13 5,01 2,90 4,50 2,74 4,77 2,63 3,94 2,55 3,77 2,48 3,63 2,43 3,52 2,38 3,43 2,34 3,36 2,31 3,30
20 4,35 8,10 3,49 5,85 3,10 4,94 2,87 4,43 2,71 4,10 2,60 3,87 2,52 3,71 2,45 3,56 2,40 3,45 2,35 3,37 2,31 3,30 2,28 3,23
21 4,32 8,02 3,47 5,78 3,07 4,87 2,84 4,37 2,68 4,04 2,57 3,81 2,49 3,65 2,42 3,51 2,37 3,40 2,32 3,31 2,28 3,24 2,25 3,17
22 4,30 7,94 3,44 5,72 3,05 4,82 2,82 4,31 2,66 3,99 2,55 3,76 2,47 3,59 2,40 3,45 2,35 3,35 2,30 3,26 2,26 3,18 2,23 3,12
23 4,28 7,88 3,42 5,66 3,03 4,76 2,80 4,26 2,64 3,94 2,53 3,71 2,45 3,54 2,38 3,41 2,32 3,30 2,28 3,21 2,24 3,14 2,20 3,07
24 4,26 7,82 3,40 5,61 3,01 4,72 2,78 4,22 2,62 3 90 2,51 3,67 2,43 3,50 2,36 3,36 2,30 3,25 2,26 3,17 2,22 3,09 2,18 3,03
25 4,24 7,77 3,38 5,57 2,99 4,68 2,76 4,18 2,60 3,86 2,49 3,63 2,41 3,46 2,34 3,32 2,28 3,21 2,24 3,13 2,20 3,05 2,16 2,99
284
Таблица 4
а=5% и 1% (напечатано курсивом)
для большей дисперсии
14 16 20 24 30 40 50 75 100 200 500 со
245 246 248 249 250 251 252 253 253 254 254 254 1
6142 6169 6208 6234 6258 6286 6302 6323 6334 6352 6361 6366
19,42 19,43 19,44 19,45 19,46 19,47 19,47 19,48 19,49 19,49 19,50 19,50 2
99,43 99,44 99,45 99,46 99,47 99,48 99,48 99,49 99,49 99,49 99,50 99,50
8,71 8,69 8,66 8,64 8,62 8,60 8,58 8,57 8,56 8,54 8,54 8,53 3
26,92 26,83 26,69 26,60 26,50 26,41 26,35 26,27 26,23 26,18 26,14 26,12
5,87 5,84 5,80 5,77 5,74 5,71 5,70 5,68 5,66 5,65 5,64 5,63 4
]4,24 14,15 14,02 13,93 13,83 13,74 13,69 13,61 13,57 13,52 13,48 13,46
4,64 4,60 4,56 4,53 4,50 4,46 4,44 4,42 4,40 4,38 4,37 4,36 5
9,77 9,68 9,55 9,47 9,38 9,29 9,24 9,17 9,13 9,07 9,04 9,02
3,96 3,92 3,87 3,84 3,81 3,77 3,75 3,72 3,71 3,69 3,68 3,67 6
7,60 7,52 7,39 7,31 7,23 7,14 7,09 7,02 6,99 6,94 6,90 6,88
3,52 3,49 3,44 3,41 3,38 3,34 3,32 3,29 3,28 3,25 3,24 3,23 7
6,35 6,27 6,15 6,07 5,98 5,90 5,85 5,78 5,75 5,70 5,67 5,65
3,23 3,20 3,15 3,12 3,08 3,05 3,03 3,00 2,98 2,96 2,94 2,93 8
5,56 5,48 5,36 5,28 5,20 5,11 5,06 5,00 4,96 4,91 4,88 4,86
3,02 2,98 2,93 2,90 2,86 2,82 2,80 2,77 2,76 2,73 2,72 2,71 9
5,00 4,92 4,80 4,73 4,64 4,56 4,51 4,45 4,41 4,36 4,33 4,31
2 86 2 82 2,77 2,74 2,70 2,67 2,64 2,61 2,59 2,56 2,55 2,54 10
4 60 4,62 4,41 4,33 4,25 4,/7 4,12 4,05 4,01 3,96 3,93 3,91
2J4 2,’70 2,65 2,61 2,57 2,53 2,50 2,47 2,45 2,42 2,41 2,40 11
4,29 4,21 4,10 4,02 3,94 3,86 3,80 3,74 3,70 3,66 3,62 3,60
2,64 2,60 2,54 2,50 2,46 2,42 2,40 2,36 2,35 2,32 2,31 2,30 12
4,05 3,98 3,86 3,78 3,70 3,61 3,56 3,49 3,46 3,41 3,38 3,36
2,55 3,85 2,51 3,78 2,46 3,67 2,42 3,59 2,38 3,51 2,34 3,42 2,32 3,37 2,28 3,30 2,26 3,27 2,24 3,21 2,22 3,18 2,21 3,16 13
2,48 2,44 2,39 2,35 2,31 2,Т1 2,24 2,21 2,19 2,16 2,14 2,13 14
3,70 3,62 3,51 3,43 3,34 3,26 3,21 3,14 3,11 3,06 3,02 3,00
2,43 2,39 2,33 2,29 2,25 2,21 2,18 2,15 2,12 2,10 2,08 2,07 15
3,56 3,48 3,36 3,29 3,20 3,12 3,07 3,00 2,97 2,92 2,89 2,87
2,37 2,33 2,28 2,24 2,20 2,16 2,13 2,09 2,07 2,04 2,02 2,01 16
3,45 3,37 3,25 3,18 3,10 3,01 2,96 2,89 2,86 2,80 2,77 2,75
2,33 2,29 2,23 2,19 2,15 2,11 2,(18 2,04 2,02 1,99 1,97 1,96 17
3,35 3,27 3,16 3,08 3,00 2,92 2,86 2,79 2,76 2,70 2,67 2,65
2,29 2,25 2,19 2,15 2.П 2,07 2,04 2,00 1,98 1,95 1,93 1,92 18
3,27 3,19 3,07 3,00 2,91 2,83 2,78 2,71 2,68 2,62 2,59 2,57
2,26 2,21 2,15 2,П 2,07 2,02 2,00 1,96 1,94 1,91 1,90 1,88 19
3,19 3,12 3,00 2,92 2,84 2,76 2,70 2,63 2,60 2,54 2,51 2,49
2,23 2,18 2,12 2,08 2,04 1,99 1,96 1,92 1,90 1,87 1,85 1,84 20
3,13 3,05 2,94 2,86 2,77 2,69 2,63 2,56 2,53 2,47 2,44 2,42 21
2,20 2,15 2,09 2,05 2,00 1,96 1,93 1,89 1,87 1,84 1,82 1,81
3,07 2,99 2,88 2,80 2,72 2,63 2,58 2,51 2,47 2,42 2,38 2,36
2,18 2,13 2,07 2,03 1,98 1,93 1,91 1,87 1,84 1,81 1,80 1,78 22
3,02 2,94 2,83 2,75 2,67 2,58 2,53 2,46 2,42 2,37 2,33 2,31
2,14 2,10 2,05 2,00 1,96 1,91 1,88 1,84 1,82 1,79 1,77 1.76 23
2,97 2,89 2,78 2,70 2,62 2,53 2,48 2,41 2,37 2,32 2,28 2,26 24
2,13 2,09 2,02 1,98 1,94 1,89 1,86 1,82 1,80 1,76 1,74 1,73
2,93 2,85 2,74 2,66 2,58 2,49 2,44 2,36 2,33 2,27 2,23 2,21
2,11 2,06 2,00 1,96 1,92 1,87 1,84 1,80 1,77 1,74 1,72 1,71 25
2,89 2,81 2,70 2,62 2,54 2,45 2,40 2,32 2,29 2,23 2,19 2,17
285
Продолжение табл. 4
—число степеней свободы для большей дисперсии f 2
/г 1 * 3 4 5 6 | 7 8 9 10 11 12 14 | 16 20 24 30 40 | 50 75 | 1 100 1 200 500 о°
26 27 28 29 30 32 34 36 38 40 42 44 46 48 50 55 60 65 70 80 100 125 150 200 400 1000 00 4,22 7,72 4,21 7,65 4,20 7,64 4,18 7,60 4,17 7,56 4,15 7,50 4,13 7,44 4,11 7,39 4,10 7,35 4,08 7,31 4,07 7,27 4,06 7,24 4,05 7,21 4,04 7,19 4,03 7,17 4,02 7,12 4,00 7,08 3,99 7,04 3,98 7,01 3,96 6,96 3,94 6,90 3,92 6,84 3,91 6,81 3,89 6,76 3,86 6,70 3,85 6,66 3,84 6,64 3,37 5,53 3,35 5,49 3,34 5,45 3,33 5,42 3,32 5,39 3,30 5,34 3,28 5,29 3,26 5,25 3,25 5,21 3,23 5,18 3,22 5,15 3,21 5,12 3,20 5,10 3,19 5,08 3,18 5,06 3,17 5,01 3,15 4,98 3,14 4,95 3,13 4,92 3,11 4,88 3,09 4,82 3,07 4,78 3,06 4,75 3,04 4,71 3,02 4,66 3,00 4,62 2,99 4,60 2,98 4,64 2,96 4,60 2,95 4,57 2,93 4,54 2,92 4,51 2,90 4,46 2,88 4,42 2,86 4,38 2,85 4,34 2,84 4,31 2,83 4,29 2,82 4,26 2,81 4,24 2,80 4,22 2,79 4,20 2,78 4,16 2,76 4,13 2,75 4,10 2,74 4,08 2,72 4,04 2,70 3,98 2,68 3,94 2,67 3,91 2,65 3,88 2,62 3,83 2,61 3,80 2,60 3,78 2,74 4,14 2,73 4,11 2,71 4,07 2,70 4,04 2,69 4,02 2,67 3,97 2,65 3,93 2,63 3,89 2,62 3,86 2,61 3,83 2,59 3,80 2,58 3,78 2,57 3.76 2,56 3,74 2,56 3,72 2,54 3,68 2,52 3,65 2,51 3,62 2,50 3,60 2,48 3,56 2,46 3,51 2,44 3,47 2,43 3,44 2,41 3,41 2,39 3,36 2,38 3,34 2,37 3,32 2,59 3,82 2,57 3,79 2,56 3,76 2,54 3,73 2,53 3,70 2,51 3,66 2,49 3,61 2,48 3,58 2,46 3,54 2,45 3,51 2,44 3,49 2,43 3,46 2,42 3,44 2,41 3,42 2,40 3,41 2,38 3,37 2,37 3,34 2,36 3,31 2,35 3,29, 2,33 3,25 2,30 3,20 2,29 3,77 2,27 3,14 2,26 з,и 2,23 3,06 2,22 3,04 2,21 3,02 2,47 3,59 2,46 3,56 2,44 3,53 2,43 3,50 2,42 3,47 2,40 3,42 2,38 3,38 2,36 3,35 2,35 3,32 2,34 3,29 2,32 3,26 2,31 3,24 2,30 3,22 2,30 3,20 2,29 3,18 2,27 3,15 2,25 3,12 2,24 3,09 2,23 3,07 2,21 3,04 2,19 2,99 2,17 2,95 2,16 2,92 2,14 2,90 2,12 2,85 2,10 2,82 2,09 2,80 2,39 3,42 2,37 3,39 2,36 3,36 2,35 3,33 2,34 3,30 2,32 3,25 2,30 3,21 2,28 3,18 2,26 3,15 2,25 3,12 2,24 3,10 2,23 3,07 2,22 3,05 2,21 3,04 2,20 3,02 2,18 2,98 2,17 2,95 2,15 2,93 2,14 2,91 2,12 2,87 2,10 2,82 2,08 2,79 2,07 2,76 2,05 2,73 2,03 2,69 2,02 2,66 2,01 2,64 2,32 3,29 2,30 3,26 2,29 3,23 2,28 3,20 2,27 3,17 2,25 3,12 2,23 3,08 2,21 3,04 2,19 3,02 2,18 2,99 2,17 2,96 2,16 2,94 2,14 2,92 2,14 2,90 2,13 2,88 2,11 2,85 2,10 2,82 2,08 2,79 2,07 2,77 2,05 2,74 2,03 2,69 2,01 2 65 2 00 2,62 1,98 2,60 1,96 2,55 1,95 2,53 1,94 2,51 2,27 3,17 2,25 3,14 2,24 3, п 2,22 3,08 2,21 3,06 2,19 3,01 2,17 2,97 2,15 2,94 2,14 2,91 2,12 2,88 2,11 2,86 2,10 2,84 2,09 2,82 2,08 2,80 2,07 2,78 2,05 2,75 2,04 2,72 2,02 2,70 2,01 2,67 1,99 2,64 1,97 2,59 1,95 2,56 1,94 2,53 1,92 2,50 1,90 2,46 1,89 2,43 1,88 2,41 2,22 3,09 2,20 3,06 2,19 3,03 2,18 3,00 2,16 2,98 2,14 2,94 2,12 2,89 2,10 2,86 2,09 2,82 2,07 2,80 2,06 2,77 2,05 2,75 2,04 2,73 2,03 2,71 2,02 2,70 2,00 2,66 1,99 2,63 1,98 2,61 1,97 2,59 1,95 2,55 1,92 2,51 1,90 2 47 1,89 2,44 1,87 2,41 1,85 2,37 1,84 2,34 1,83 2,32 2,18 3,02 2,16 2,98 2,15 2,95 2,14 2,92 2,12 2,90 2,10 2,86 2,08 2,82 2,06 2,78 2,05 2,75 2,04 2,73 2,02 2,70 2,01 2t68 2,00 2 66 1’99 2,64 1,98 2,62 1,97 2,59 1,95 2,56 1,94 2,54 1,93 2,51 1,91 2,48 1,88 2,43 1,86 2,40 1,85 2,37 1,83 2,34 1,81 2,29 1,80 2,26 1,79 2,24 2,15 2,96 2,13 2,93 2,12 2,90 2,10 2,87 2,00 2,84 2,07 2,80 2,05 2,76 2,03 2,72 2,02 2,69 2,00 2,66 1,99 2,64 1,98 2,62 1,97 2,60 1,96 2,58 1,95 2,56 1,93 2,53 1,92 2,50 1,90 2,47 1,89 2,45 1,88 2,41 1,85 2,36 1,83 2,33 1,82 2,30 1,80 2,28 1,78 2,23 1,76 2,20 1,75 2,18 2,10 2,86 2,08 2,83 2,06 2,80 2,05 2,77 2,04 2,74 2,02 2,70 2,00 2,66 1,98 2,62 1,96 2,59 1,95 2,56 1,94 2,54 1,92 2,52 1,91 2,50 1,90 2,48 1,90 2,46 1,88 2,43 1,86 2,40 1,85 2,37 1,84 2,35 1,82 2,32 1,79 2,26 1,77 2,23 1,76 2,20 1,74 2,17 1,72 2,12 1,70 2,09 1,69 2,07 2,05 2,77 2,03 2,74 2,02 2,71 2,00 2,68 1,99 2,66 1,97 2,62 1,95 2,58 1,93 2,54 1,92 2,51 1,90 2,49 1,89 2,46 1,88 2,44 1,87 2,42 1,86 2,40 1,85 2,39 1,83 2,35 1,81 2,32 1,80 2,30 1,79 2,28 1,77 2,24 1,75 2,19 1,72 2,15 1,71 2,12 1,69 2,09 1,67 2,04 1,65 2,01 1,64 1,99 1,99 2,66 1,97 2,63 1,96 2,60 1,94 2,57 1,93 2,55 1,91 2,51 1,89 2,47 1,87 2,43 1,85 2,40 1,84 2,37 1,82 2,35 1,81 2,32 1,80 2,30 1,79 2,28 1,78 2,26 1,76 2,23 1,75 2,20 1,73 2,18 1,72 2,15 1,70 2,11 1,68 2,06 1,65 2,03 1,64 2,00 1,62 1,97 1,60 1,92 1,58 1,89 1,57 1,87 1,95 2,58 1,93 2,55 1,91 2,52 1,90 2,49 1,89 2,47 1,86 2,42 1,84 2,38 1,82 2,35 1,80 2,32 1,79 2,29 1,78 2,26 1,76 2,24 1,75 2,22 1,74 2,20 1,74 2,18 1,72 2 15 1,70 2,12 1,68 2,09 1,67 2,07 1,65 2,03 1,63 1,98 1,60 1,94 1,59 1,57 1,88 1,54 1,84 1,53 7,3/ 1,52 1,79 1,90 2,50 1,88 2,47 1,87 2,44 1,85 2,41 1,84 2,38 1,82 2,34 1,80 2,30 1,78 2,26 1,76 2,22 1,74 2,20 1,73 2,17 1,72 2,15 1,71 2,13 1,70 2, И 1,69 2,10 1,67 2,06 1,65 2,03 1,63 2,00 1,62 1,98 1,60 1,94 0,57 1,89 1,55 1,85 1,54 1,83 1,52 1,79 1,49 /,74 1,47 /,7/ 1,46 1,69 1,85 2,41 1,84 2,38 1,81 2,35 1,80 2,32 1,79 2,29 1,76 2,25 1,74 2,21 1,72 2,17 1,71 2,14 1,69 9,11 1,68 2,08 1,66 2,06 1,65 2,04 1,64 2,02 1,63 2,00 1,61 1,96 1,59 1,93 1,57 1,90 1,56 1,88 1,54 1,84 1,51 1,79 1,49 1,75 1,47 1,72 1,45 1,69 1,42 1,64 1,41 7,(5/ 1,40 1,59 1,82 2,36 1,80 2,33 1,78 2,30 1,77 2,27 1,76 2,24 1,74 2,20 1,71 2,15 1,69 2,12 1,67 2,08 1,66 2,05 1,64 2,02 1,63 2,00 1,62 1,98 1,61 1,96 1,60 1,94 1,58 1,90 1,56 1,87 1,54 Д34 1,53 1,82 1,51 1,78 1,48 1,73 1,45 1,68 1,44 1,66 1,42 1,62 1,38 1,57 1,36 1,54 1,35 1,52 1,78 2,28 1,76 2,25 1,75 2,22 1,73 2,19 1,72 2,16 1,69 2,12 1,67 2,08 1,65 2,04 1,63 2,00 1,61 1,97 1,60 1,94 1,58 1,92 1,57 1,90 1,56 1,88 1,55 1,86 1,52 1,82 1,50 1,79 1,49 7,76 1,47 7,74 1,45 1,70 1,42 1,64 1,39 1,59 1,37 1,56 1,35 7,53 1,32 7,47 1,30 7,44 1,28 7,47 1,76 2,25 1,74 2,21 1,72 2,18 1,71 2,15 1,69 2,73 1,67 2,08 1,64 2,04 1,62 2,00 1,60 1,97 1,59 1,94 1,57 1,91 1,56 7,88 1,54 1,86 1,53 7,84 1,52 7,82 1,50 1,78 1,48 7,74 1,46 7,77 1,45 1,69 1,42 7,65 1,39 1,59 1,36 7,54 1,34 7,57 1,32 7,48 1,28 7,42 1,26 7,38 1,24 7,36 1,72 2,19 1,71 2,76 1,69 2,73 1,68 2,10 1,66 2,07 1,64 2,02 1,61 1,98 1,59 1,94 1,57 1,90 1,55 7,88 1,54 7,85 1,52 7,82 1,51 1,80 1,50 7,78 1,48 1,76 1,46 1,71 1,44 7,68 1,42 7,64 1,40 7,62 1,38 7,57 1,34 7,5/ !,31 7 46 1 29 7’43 1 26 1,39 1 22 /’32 !,19 7,28 !,17 7,25 1,70 2,15 1,68 2,12 1,67 2,09 1,65 2,06 1,64 2,03 1,61 1,98 1,59 1,94 1,56 1,90 1,54 1,86 1,53 1,84 1,51 1,80 1,50 1,78 1,48 1,76 1,47 1,73 1,46 7,7/ 1,43 1,66 1,41 1,63 1,39 1,60 1,37 1,56 1,35 1,52 1,30 1 46 1,27 1,40 1,25 1,37 1,22 1,33 1,16 1,24 1,13 /,/9 1,И /,Л5 1,69 2,13 1,67 2,10 1,65 2,06 1,64 2,03 1,62 2,01 1,59 1,96 1,57 1,91 1,55 1,87 1,53 1,84 1,51 1,81 1,49 1,78 1,48 Д75 1,46 1,72 1,45 1,70 1,44 1,68 1,41 1,64 1,39 1,60 1,37 1,56 1,35 1,53 1,32 1,49 1,28 1,43 1,25 1,37 1,22 1,33 1,19 1,28 1,13 Д/9 1,08 1,00 1,00 26 27 28 29 30 32 34 36 38 40 42 44 46 48 50 55 60 65 70 80 100 125 150 200 400 1000 оо
286
287
Таблица 5
Квантили ^-распределения
f а=0,10 а=0,05 а=0,01 а=0,001 f
1 2,71 3,841 6,635 10,827 1
2 4,61 5,991 9,210 13,815 2
3 6,25 7,815 11,345 16,268 3
4 7,78 9,488 13,277 18,465 4
5 9,24 11,070 15,086 20.517 5
6 10,6 12,592 16,812 22,457 6
7 12,0 14,067 18,475 24,322 7
8 13,4 15,507 20,090 26,125 8
9 14,7 16,919 21,666 27,877 9
10 16,0 18,307 23,209 29,588 10
11 17,3 19,675 24,725 31,264 11
12 18,5 21,026 26,217 32,909 12
13 19,8 22,362 27,688 34,528 13
14 21,1 23,685 29,141 36,123 14
15 22,3 24,996 30,578 37,697 15
16 23,5 26,296 32,000 39,252 16
17 24,8 27,587 33,409 40,790 17
18 26,0 28,869 34,805 42,312 18
19 27,2 30,144 36,191 43,820 19
20 28,4 31,410 37,566 45,315 20
21 29,6 32,671 38,932 46,797 21
22 30,8 33,924 40,289 48,268 22
23 32,0 35,172 41,638 49,728 23
24 33,2 36,415 42,980 51,179 24
25 34,4 37,652 44,314 52,620 25
26 35,6 38,885 45,642 54,052 26
27 36,7 40,113 46,963 55,476 27
28 37,9 41,337 48,278 56,893 28
29 39,1 42,557 49,588 58,302 29
30 40,3 43,773 50,892 59,703 30
40 51,8 55,8 63,7 73,4 40
50 63,2 67,5 76,2 86,7 50
60 74,4 79,1 88,4 99,6 60
70 85,5 90,5 100,4 112,3 70
80 96,6 101,9 112,3 124,8 80
90 107,6 113,1 124,1 137,2 90
100 118,5 124,3 135,8 149,4 100
Таблица 6
Критические значения коэффициента корреляции г
Число степеней свободы Уровни значимости а
5% 1%
1 1,00 1,00
2 0,95 0,99
3 0,88 0,96
4 0,81 0,92
5 0,75 0,87
10 0,58 0,71
15 0,48 0,61
20 0,42 0,53
25 0,38 0,49
30 0,35 0,45
35 0,32 0,42
40 0,30 0,39
50 0,27 0,35
60 0,25 0,33
70 0,23 0,30
80 0,22 0,28
90 0,21 0,26
100 0,19 0,25
120 0,18 0,23
150 0,16 0,21
200 0,14 0,18
300 0,11 0,15
400 0,10 0,13
500 0,09 0,11
700 0,07 0,10
900 0,06 0,09
1 000 <0,06 <0,09
и больше
Таблица 7
Критические значения коэффициента циклической автокорреляции при лаге 1
f Положительные значения Отрицательные значения
5% 1% 5% 1%
5 0,253 0,297 —0,753 -0,798
6 0,345 0,447 0,708 0,863
7 0,370 0,510 0,674 0,799
8 0,371 0,531 0,625 0,764
9 0,366 0,533 0,593 0,737
10 0,360 0,525 0,564 0,705
11 0,353 0,515 0,539 0,679
12 0,348 0,505 0,516 0,655
13 0,341 0,495 0,497 0,634
14 0,335 0,485 0,479 0,615
15 0,328 0,475 0,462 0,597
20 0,299 0,432 0,399 0,524
25 0,276 0,398 0,356 0,473
30 0,257 0,370 0,325 0,433
35 0,242 0,347 0,300 0,401
40 0,229 0,329 0,279 0,376
45 0,218 0,314 0,262 0,356
50 0,208 0,301 0,248 0,339
55 0,199 0,289 0,236 0,324
60 0,191 0,278 0,225 0,310
65 0,184 0,268 0,216 0,298
70 0,178 0,259 0,207 0,287
75 0,173 0,250 —0,199 —0,276
289
288
Таблица 8
Критические значения статистики Дарбина — Уотсона при 5 %-ном уровне значимости
m
т 1 2 з 4 5
И d„ dB и н dn dB da dB dn dB
15 1,08 1,36 0,95 1,54 0,82 1,75 0,69 1,97 0,56 2,21
16 1,10 1,37 0,98 1,54 0,86 1,73 0,74 1,93 0,62 2,15
17 1,13 1,38 1,02 1,54 0,90 1,71 0,78 1,90 0,67 2,10
18 1,16 1,39 1,05 1,53 0,93 1,69 0,82 1,87 0,71 2,06
19 1,18 1,40 1,08 1,53 0,97 1,68 0,86 1,85 0,75 2,02
20 1,20 1,41 1,10 1,54 1,00 1,68 0,90 1,83 0,79 1,99
21 1,22 1,42 1,13 1,54 1,03 1,67 0,93 1,81 0,83 1,96
22 1,24 1,43 1,15 1,54 1,05 1,66 0,96 1,80 0,86 1,94
23 1,26 1,44 1,17 1,54 1,08 1,66 0,99 1,79 0,90 1,92
24 1,27 1,45 1,19 1,55 1,10 1,66 1,01 1,78 0,93 1,90
25 1,29 1,45 1,21 1,55 1,12 1,66 1,04 1,77 0,95 1,89
26 1,30 1,46 1,22 1,55 1,14 1,65 1,06 1,76 0,98 1,88
27 1,32 1,47 1,24 1,56 1,16 1,65 1,08 1,76 1,01 1,86
28 1,33 1,48 1,26 1,56 1,18 1,65 1,10 1,75 1,03 1,85
29 1,34 1,48 1,27 1,56 1,20 1,65 1,12 1,74 1,05 1,84
30 1,35 1,49 1,28 1,57 1,21 1,65 1,14 1,74 1,07 1,83
31 1,36 1,50 1,30 1,57 1,23 1,65 1,16 1,74 1,09 1,83
32 1,37 1,50 1,31 1,57 1,24 1,65 1,18 1,73 1,11 1,82
33 1,38 1,51 1,32 1,58 1,26 1,65 1,19 1,73 1,13 1,81
34 1,39 1,51 1,33 1,58 1,27 1,65 1,21 1,73 1,15 1,81
35 1,40 1,52 1,34 1,58 1,28 1,65 1,22 1,73 1,16 1,80
36 1,41 1,52 1,35 1,59 1,29 1,65 1,24 1,73 1,18 1,80
37 1,42 1,53 1,36 1,59 1,31 1,66 1,25 1,72 1,19 1,80
38 1,43 1,54 1,37 1,59 1,32 1,66 1,26 1,72 1,21 1,79
39 1,43 1,54 1,38 1,60 1,33 1,66 1,27 1,72 1,22 1,79
40 1,44 1,54 1,39 1,60 1,34 1,66 1,29 1,72 1,23 1,79
45 1,48 1,57 1,43 1,62 1,38 1,67 1,34 1,72 1,29 1,78
50 1,50 1,59 1,46 1,63 1,42 1,67 1,38 1,72 1,34 1,77
55 1,53 1,60 1,49 1,64 1,45 1,68 1,41 1,72 1,38 1,77
60 1,55 1,62 1,51 1,65 1,48 1,69 1,44 1,73 1,41 1,77
65 1,57 1,63 1,54 1,66 1,50 1,70 1,47 1,73 1,44 1,77
70 1,58 1,64 1,55 1,67 1,52 1,70 1,49 1,74 1,46 1,77
75 1,60 1,65 1,57 1,68 1,54 1,71 1,51 1,74 1,49 1,77
80 1,61 1,66 1,59 1,69 1,56 1,72 1,53 1,74 1,51 1,77
85 1,62 1,67 1,60 1,70 1,57 1,72 1,55 1,75 1,52 1,77
90 1,63 1,68 1,61 1,70 1,59 1,73 1,57 1,75 1,54 1,78
95 1,64 1,69 1,62 1,71 1,60 1,73 1,58 1,75 1,56 1,78
100 1,65 1,69 1,63 1,72 1,61 1,74 1,59 1,76 1,57 1,78
Таблица 8а
Критические значения статистики Дарбина — Уотсона при 2,5 %-ном уровне значимости
m
T 1 2 3 4 5
dB dB dn “в dB dn dB dn dB
15 0,95 1,23 0,83 1,40 0,71 1,61 0,59 1,84 0,48 2,09
16 0,98 1,24 0,86 1,40 0,75 1,59 0,64 1,80 0,53 2,03
17 1,01 1,25 0,90 1,40 0,79 1,58 0,68 1,77 0,57 1,98
18 1,03 1,26 0,93 1,40 0,82 1,56 0,72 1,74 0,62 1,93
19 1,06 1,28 0,96 1,41 0,86 1,55 0,76 1,72 0,66 1,90
20 1,08 1,28 0,99 1,41 0,89 1,55 0,79 1,70 0,70 1,87
21 1,10 1,30 1,01 1,41 0,92 1,54 0,83 1,69 0,73 1,84
22 1,12 1,31 1,04 1,42 0,95 1,54 0,86 1,68 0,77 1,82
23 1,14 1,32 1,06 1,42 0,97 1,54 0,89 1,67 0,80 1,80
24 1,16 1,33 1,08 1,43 1,00 1,54 0,91 1,66 0,83 1,79
25 1,18 1,34 1,10 1,43 1,02 1,54 0,94 1,65 0,86 1.77
26 1,19 1,35 1,12 1,44 1,04 1,54 0,96 1,65 0,88 1,76
27 1,21 1,36 1,13 1,44 1,06 1,54 0,99 1,64 0,91 1.75
28 1,22 1,37 1,15 1,45 1,08 1,54 1,01 1,64 0,93 1,74
29 1,24 1,38 1,17 1,45 1,10 1,54 1,03 1,63 0,96 1,73
30 1,25 1,38 1,18 1,46 1,12 1,54 1,05 1,63 0,98 1,73
31 1,26 1,39 1,20 1,47 1,13 1,55 1,07 1,63 1,00 1,72
32 1,27 1,40 1,21 1,47 1,15 1,55 1,08 1,63 1,02 1,71
33 1,28 1,41 1,22 1,48 1,16 1,55 1,10 1,63 1,04 1,71
34 1,29 1,41 1,24 1,48 1,17 1,55 1,12 1,63 1,06 1,70
35 1,30 1,42 1,25 1,48 1,19 1,55 1,13 1,63 1,07 1,70
36 1,31 1,43 1,26 1,49 1,20 1,56 1,15 1,63 1,09 1,70
37 1,32 1,43 1,27 1,49 1,21 1,56 1,16 1,62 1,10 1,70
38 1,33 1,44 1,28 1,50 1,23 1,56 1,17 1,62 1,12 1,70
39 1,34 1,44 1,29 1,50 1,24 1,56 1,19 1,63 1,13 1,69
40 1,35 1,45 1,30 1,51 1,25 1,57 1,20 1,63 1,15 1,69
45 1,39 1,48 1,34 1,53 1,30 1,58 1,25 1,63 1,21 1,69
50 1,42 1,50 1,38 1,54 1,34 1,59 1,30 1,64 1,26 1,69
55 1,45 1,52 1,41 1,56 1,37 1,60 1,33 1,64 1,30 1,69
60 1,47 1,54 1,44 1,57 1,40 1,61 1,37 1,65 1,33 1,69
65 1,49 1,55 1,46 1,59 1,43 1,62 1,40 1,66 1,36 1,69
70 1,51 1,57 1,48 1,60 1,45 1,63 1,42 1,66 1,39 1,70
75 1,53 1,58 1,50 1,61 1,47 1,64 1,45 1,67 1,42 1,70
80 1,54 1,59 1,52 1,62 1,49 1,65 1,47 1,67 1,44 1,70
85 1,56 1,60 1,53 1,63 1,51 1,65 1,49 1,68 1,46 1,71
90 1,57 1,61 1,55 1,64 1,53 1,66 1,50 1,69 1,48 1,71
95 1,58 1,62 1,56 1,65 1,54 1,67 1,52 1,69 1,50 1,71
100 1,59 1,63 1,-57 1,65 1,55 1,67 1,53 1,70 1,51 1,72
291
290
Таблица 86
Критические значения статистики Дарбина — Уотсона при 1%-ном уровне значимости
т m
1 2 3 4 5
dH dB dH dB dH dB dB
15 0,81 1,07 0,70 1,25 0,59 1,46 0,49 1,70 0,39 1,96
16 0,84 1,09 0,74 1,25 0,63 1,44 0,53 1,66 0,44 1,90
17 0,87 1,10 0,77 1,25 0,67 1,43 0,57 1,63 0,48 1,85
18 0,90 1,12 0,80 1,26 0,71 1,42 0,61 1,60 0,52 1,80
19 0,93 1,13 0,83 1,26 0,74 1,41 0,65 1,58 0,56 1,77
20 0,95 1,15 0,86 1,27 0,77 1,41 0,68 1,57 0,60 1,74
21 0,97 1,16 0,89 1,27 0,80 1,41 0,72 1,55 0,63 1.71
22 1,00 1,17 0,91 1,28 0,83 1,40 0,75 1,54 0,66 1,69
23 1,02 1,19 0,94 1,29 0,86 1,40 0,77 1,53 0,70 1,67
24 1,04 1,20 0,96 1,30 0,88 1,41 0,80 1,53 0,72 1,66
25 1,05 1,21 0,98 1,30 0,90 1,41 0,83 1,52 0,75 1,65
26 1,07 1,22 1,00 1,31 0,93 1,41 0,85 1,52 0,78 1,64
27 1,09 1,23 1,02 1,32 0,95 1,41 0,88 1,51 0,81 1,63
28 1,10 1,24 1,04 1,32 0,97 1,41 0,90 1,51 0,83 1,62
29 1,12 1,25 1,05 1,33 0,99 1,42 0,92 1,51 0,85 1,61
30 1,13 1,26 . 1,07 1,34 1,01 1,42 0,94 1,51 0,88 1,61
31 1,15 1,27 1,08 1,34 1,02 1,42 0,96 1,51 0,90 1,60
32 1,16 1,28 1,10 1,35 1,04 1,43 0,98 1,51 0,92 1,60
: зз 1,17 1,29 1,11 1,36 1,05 1,43 1,00 1,51 0,94 1,59
; 34 1,18 1,30 1,13 1,36 1,07 1,43 1,01 1,51 0,95 1,59
! 35 1,19 1,31 1,14 1,37 1,08 1,44 1,03 1,51 0,97 1,59
: 36 1,21 1,32 1,15 1,38 1,10 1,44 1,04 1,51 0,99 1,59
37 1,22 1,32 1,16 1,38 1,11 1,45 1,06 1,51 1,00 1,59
38 1,23 1,33 1,18 1,39 1,12 1,45 1,07 1,52 l>02 1,58
39 1,24 1,34 1,19 1,39 1,14 1,45 1,09 1,52 1,03 1,58
40 1,25 1,34 1,20 1,40 1,15 1,46 1,10 1,52 1,05 1,58
45 1,29 1,38 1,24 1,42 1,20 1,48 1,16 1,53 1,11 1,58
50 1,32 1,40 1,28 1,45 1,24 1,49 1,20 1,54 1,16 1,59
55 1,36 1,43 1,32 1,47 1,28 1,51 1,25 1,55 1,21 1,59
60 1,38 1,45 1,35 1,48 1,32 1,52 1,28 1,56 1,25 1,60
i 65 1,41 1,47 1,38 1,50 1,35 1,53 1,31 1,57 1,28 1,61
I 70 1,43 1,49 1,40 1,52 1,37 1,55 1,34 1,58 1,31 1,61
' 75 1,45 1,50 1,42 1,53 1,39 1,56 1,37 1,59 1,34 1,62
; 80 1,47 1,52 1,44 1,54 1,42 1,57 1,39 1,60 1,36 1,62
1 85 1,48 1,53 1,46 1,55 1,43 1,58 1,41 1,60 1,39 1,63
। 90 . 1,50 1,54 1,47 1,56 1,45 1,59 1,43 1,61 1,41 1,64
: 95 1,51: 1,55 1,49 1,57 1,47 1,60 1,45 1,62 1,42 1,64
100 1,52 1,56 1,50 1,58 1,48 1,60 1,46 1,63 1,44 1,65
292.
ЛИТЕРАТУРА
1, Ackermann W. Einfiihrung in die Wahrscheinlichkeitsrechnung. S. Hir-zel — Verlag. Leipzig, 1955.
2. Ac t о n F. S. Analysis of Straight-Line Date. J. Wiley and Sons. New York, 1959.
3. A d a m J. Einfiihrung in die medizinische Statistik. VEB Verlag Volk und Gesundheit. Berlin, 1963.
4. A i t к e n A. C. Statistical Mathematics, 8. ed. Oliver and Boyd, Edinburgh, London, 1957.
5. A 1 1 e n R. G. D. Statistics for Economists, 8 ed. Hutchinson University Library, London, 1957.
6; An d’erson R. L., В а и с г о f t T. A. Statistical Theory in Research. McGraw-Hill. New York, London, 1952.
7. Anderson O. Die Korrelationsrechnung in der Konjunkturforschung. Schroeder-Verlag.. Bonn, 1929.
$. Anderson O. Probleme der statistischen Methodenlehre in den Sozialwis-senschaftep, 2. Aufl., Physica-Verlag. Wurzburg, 1954
9. Anderson O. Ausgewahlte Schriften, Band I, II, J. С. B. Mohr (Paul Siebeck). Tubingen, 1963
10. Autorenkollektiv. Methoden der Regressionsrechnung im Verkehrs-wesen. Transpress Verlag, Berlin, 1976.
11. Autorenkollektiv. Rechnen mit Kosten in der Industrie. Verlag Die Wirtschaft. Berlin, 1975.
12. Autorenkollektiv. Quantitative Methoden in der Soziologie. Verlag Die Wirtschaft. Berlin, 1970.
13. Autorenkollektiv. Grundlagen der marxistischen Philosophic. Dietz Verlag, Berlin, 1964.
14. Autorenkollektiv. Kategorien der materialistischen Dialektik. Dietz Verlag. Berlin, 1959.
15. Autorenkollektiv. Einfiihrung in den dialektischen und histori-schen Materialismus. Dietz Verlag, Berlin, 1974.
16. Autorenkollektiv. Mathematik fur die Praxis, Band 1-411, VEB Deutscher Verlag der Wissenschaften, Berlin, 1964.
293
17. Autorenko ilektiv. Allgemeine Statistik (Lehrbuch), 3., iiberar-beitete Auflage. Verlag Die Wirtschaft, Berlin, 1967.
18. Autorenkollektiv. Statistik-Lehrbuch. 2. Aufl. Verlag Die Wirtschaft. Berlin, 1976.
19. В a d e r H., Frohlich S. Mathematik fur Okonomen. Verlag Die Wirtschaft, Berlin, 1964.
20. В a r a n о w L. V. Grundbegriffe moderner statistischer Methodik, Teil I, II, Hirzel-Verlag, Stuttgart, 1950.
21. В a u r F. Korrelationsrechnung. Teubner-Verlag, Leipzig, 1928.
22. Behr J., Briinecke K- Messmethoden der volkswirtschaftlichen Pro-duktionsentwicklung mit Hilfe aggregierter Produktionsfunktionen. Akade-mie-Verlag, Berlin, 1965.
23. В г у a n t E. C. Statistical Analysis. McGraw-Hill, New York, 1960.
24. Бызов Л. А. Графические методы в планировании, статистике и учете. 2-е изд., М., Госстатиздат, 1952.
25. X а й к и н В. П., Найденов В. С., Г а л у з а С. Г. Корреляция и статистическое моделирование в экономических расчетах. М., Экономика, 1964.
26. X о т и м с к и й В. И. Выравнивание статистических рядов по методу наименьших квадратов (способ Чебышева) и таблицы для нахождения уравнений параболических кривых. 2-е изд. М., Госстатиздат, 1959.
27. С h г i s t С. F. Econometric models and methods. John Wiley and Sons. New York, 1966.
28. С 1 a u P G., Ebner H. Grundlagen der Statistik fur Psychologen, Pada-gogen und Soziologen. Volk und Wissen Verlag. Berlin, 1974.
29. Cramer H. Mathematical Methods of Statistics. Almquist-Verlag. Uppsala, 1949. Русский перевод: Крамер Г. Математические методы статистики. М., Мир, 1975.
30. С г о х t о n F. Е., С о w d е и D. Y. Applied General Statistics. 14. ed. Prentice-Hall. New York, 1947.
31. Dietrich G. , S t a h 1 H. Matrizen und Determinanten und ihre Anwen-dung in Technik und Okonomie. Fachbuchverlag. Leipzig, 1968.
32. Д л и н A. M. Математическая статистика в технике. 3-е изд. М., Советская наука, 1958.
33. D г а р е г N., S m i t h H. Applied Regression Analysis. John Wiley and Sons. New York, 1966. Русский перевод: Дрейпер H., Смит Г. Прикладной регрессионный анализ. М., Статистика, 1973.
34. Д р у ж и н и н Н. К. Математическая статистика в экономике. М., Статистика, 1971.
35. Egerm ay е г F., Novak I. Regresni a korelacni analyza pro ekonomy. SNTL-SVTL. Praha, 1964.
36. E 1 d e r t о n W. P. Frequency Curves and correlation, 4. ed. University Press, Cambridge. 1953.
37. Э н г e л ь с Ф. Анти-Дюринг. — Маркс K-, Энгельс Ф. Соч. 2-е изд., т. 20.
38. Е х n е г F. М. Uber die Korrelationsmethode. Gustav Fischer-Verlag. Jena, 1913.
39. E z e k i e 1 M., F о x К. A. Methods of Correlation and Regression Analysis, Linear and Curvilinear. J. Wiley and Sons. New York, 1959. Русский
294
перевод: Езекиэл М., Фокс К. А. Методы анализа корреляции и регрессий, линейных и криволинейных. М., Статистика, 1966.
40. F i п и е у D. J. Probitanalysis. 2 ed. University Press. Cambridge, 1952.
41. Fischer P., Richter K. J., Schneider H. Statistische Methoden fur Verkehrsuntersuchungen, 2. Aufl. Transpress Verlag. Berlin, 197 L
42. Fisher R. A. Statistische Methoden fiir die Wissenschaft. 12. erw. und neu bearb. Aufl. Oliver and Boyd, Edinburgh, London, 1956. Русский перевод: Фишер P. А. Статистические методы для] исследователей. М., Госстатиздат, 1958.
43. F i s z М. Wahrscheinlichkeitsrechnung und mathematische Statistik. VEB Deutscher Verlag der Wissenschaften. Berlin, 1966.
44. F 1 a s k a m p e r P. Allgemeine Statistik, 2. durchges. u. erg. Aufl. Verlag von Richard Meiner. Hamburg, 1956.
45. Forster E., Egermayer F. Korrelations- und Regressionsanalyse. Verlag Die Wirtschaft. Berlin, 1966.
46. Frisch R. Statistical Confluence Analysis by Means of Complete Regression Systems. University. Oslo, 1934.
47. F r i s c h R. Correlation and Scatter in Statistical Variables. University. Oslo, 1951.
48. F г 6 h 1 i c h W. D. Forschungsstatistik. H. Bouvier und Co., Bonn, 1959.
49. G a 1 t о n F. Natural inheritance. Macmillan and Co., London, New York, 1889.
50. Гарецкий С. А., Туковский А. Б. и др. Статистико-математический анализ эффективности производства промышленности строительных материалов. М., Стройиздат, 1972.
51. G е г f i n Н. Langfristige Wirtschaftsprognose. J. С. B. Mohr Tubingen, Polygraphischer Verlag. Ziirich, 1964.
52. G i b s о n W. M., J о w e t t G. H. Three-group Regression Analysis, Applied Statistics, 1957.
53. Г н e д e н к о Б. В. Курс теории вероятностей. 5-е изд., М., Наука, 1969.
54. Гнеденко Б. В., X и н ч и н А. Я. Элементарное введение в теорию вероятностей. 8-е изд. М., Наука, 1976.
55. G о 1 d b е г g е г A. S. Econometric Theory. J. Wiley and Sons, Inc., New York, 1964.
56. Гончарук С. И., Виноградов В. Г. Законы общества и научное предвидение. М., Политиздат, 1972.
57. G г u b е г J. Okonometrische Modelle des Cowles-Commission-Typs: Bau und Interpretation. Paul Parey-Verlag. Hamburg, Berlin (West), 1968.
58. Haavelmo F., Staehle H. The Elements of Frisch’s Confluence Analysis. University. Oslo, 1951.
59. H a u s t e i n K.-D. Prognoseverfahren in der sozialistischen Wirtschaft. Verlag Die Wirtschaft. Berlin, 1970.
60. H e 1 1 w i g Z. Regresja liniowa i jej zastosowanie w ekonomii. Polskie wy-dawnictwa gospodarcze. Warszawa, 1960.
61. H e 1 1 w i g Z. Linear regression and its application to economics. Oxford, 1963.
62. Henrysson St., Haseloff O. W., Hoffmann H. J» Kleines Lehrbuch der Statistik. Walter der Gruyter and Co., Berlin (West), 1960.
295
63. Н о е 1 Р. G. Introduction to Mathematical Statistics. 3. ed., J. Wiley and Sons. New York, 1958.
64, Hofer E. Angewandte Statistik. Verlag Volk und Gesundheit. Berlin, 1974.
65. Hof st at ter P. R., Wendt D. Quantitative Methoden der Psychologic. 3. Aufl. Joh. Ambrosius Barth. Munchen, 1967.
66. Hugershoff R. Ausgleichsrechnung, Kollektivmasslehre und Korrela-tionsrechnung im Dienste von Technik Wissenschaft und Wirtschaft. 2. Aufl. Wichmann-Verlag. Berlin (West), 1948.
67. J a h n W., V a h 1 e H. Die Faktorenanalyse. Verlag Die Wirtschaft. Berlin, 1970.
68. Ястремский Б. С. Некоторые вопросы математической статистики. М., Госстатиздат, 1961.
69. J о h n s t о и J. Econometric Methods. McGraw-Hill Book Company, Inc., New York, San Francisco, Toronto, London, 1963. Русский- перевод: Джон-стон Дж. Эконометрические методы. М., Статистика, 1980.
70. Каминский Л. С. Измерение связи (корреляция). Л., Изд-во Ленингр. университета, 1962.
71. Keller er Н. Statistik im modernen Wirtschafts- und Sozialleben. Ro-wohlt-Verlag. Hamburg, 1960.
72. К e n d a 1 1 M. G., Stuart A. The advanced Theory of Statistics. Ch. Griffin and Co., London, 1951. Русский перевод: Кендалл M., Стьюарт А. Многомерный статистический анализ и временные ряды. М., Наука, 1976.
73. Kendall М. G. Rank Correlation Methods. 2 ed. rev. and enl., Griffin and Co., London, 1955. Русский перевод: К e н д э л М. Ранговые корреляции. М., Статистика, 1975.
74. Klaus G., К о s i и g L. R., R e d 1 о w G. Wissenschaftliche Weltanschauung. Teil I, Dialektischer Materialismus. Dietz Verlag. Berlin, 1959.
75. К I e i n A. Einfiihrung in die Okonometrie. Dusseldorf, 1969.
76. Klezl-Norberg F. Allgemeine Methodenlehre der Statistik, 2. erg. Aufl. Springer-Verlag. Wien, 1946.
77. К о 1 1 e r S. Graphische Tafeln zur Beurteilung statistischer Zahlen, 3. erg. Aufl. Verlag von Dr. D. Steinkopff. Darmstadt, 1953.
78. К г e у s z i g E. Statistische Methoden und ihre Anwendungen. Vandenhoeck and Ruprecht, Gottingen, 1967.
79. Lange O. Einfiihrung in die Okonometrie. Akademie-Verlag, Berlin, PWN. Warszawa, 1968. Русский перевод: Ланге О. Введение в эконометрику. М., Прогресс, 1964.
80. L а и е „М. Ober einige spezielle Probleme der linearen Regressionsanalyse. OFI, Okonomisches Forschungsinstitut der Staatlichen Plankomission, Berlin, 1976, № 6.
81. Ленин В. И. Материализм и эмпириокритицизм. Поли. собр. соч., т. 18.
82. Linder A. Statistische Methoden fiir Naturwissenschaftler, Mediziner und Ingenieure. 3. umgearb. u. stark erw. Aufl. Birkhauser Verlag, Basel. Stuttgart, 1960.
83. Л и н н и к Ю. В. Метод наименьших квадратов и основы математикостатистической теории обработки наблюдений. 2-е изд. М., Физматгиз, 1962.
84. Lorenz С. Forschungslehre der Sozialstatistik. Bd. 1. Duncker and Humblot. Berlin (West), 1951.
296
85. Lorenz P. Anschauungsunterricht in mathematischer Statistik, Bd I—III. S. Hirzel Verlag, Leipzig, 1955, 1959, 1961.
86. L u d e к e D. Schatzprobleme in der Okonometrie. Physica-Verlag, Wurzburg. Wien, 1964.
87. Лукомский Я. И. Теория корреляции и ее применение к анализу производства. 2-е изд. М., Госстатиздат, 1961.
88. L у 1 е Р. Regression Analysis of Production Costs and Factory Operations. Oliver and Body, Edinburgh. London, 1957.
89. M a 1 i n v a u d E. Statistical Methods of Econometrics. North-Holland Publ. Comp. Amsterdam, 1966. Русский перевод: Маленво Э. Статистические методы эконометрии. Вып. 1, 2. М., Статистика, 1975, 1976.
90. М а р к с К. Капитал. Т. 1—3. —Маркс К., Энгельс Ф. Соч. 2-е изд., т. 23—25.
91. Meier R., V a h 1 е Н. Mathematisch-statistische Methoden in der Land-wirtschaft und Nahrungsguterwirtschaft. VEB Deutscher Landwirtschafts-verlag. Berlin, 1974.
92. M e n g e s G. Grundriss der Statistik. Westdeutscher Verlag, Koln und Opladen, 1968.
93. M e n g e s G. Okonometrie. Betriebswirtschaftlicher Verlag Gabler. Wiesbaden, 1961.
94. M i 1 1 s F. C. Statistical Methods. 3. ed. Columbia University. New York, 1955. Русский перевод: Миллс Ф. Статистические методы. М., Госстатиздат, 1958.
95. М i s е s R. Wahrscheinlichkeit, Statistik und Wahrheit. Springer-Verlag. Wien, 1951. Русский перевод: M и з e с P. Вероятность и статистика. М.—Л., Гос. изд-во тип. «Красный пролетарий», 1930.
96. Muller Р. Н.,Neumann Р.,Storm R. Tafeln der mathematischen Statistik. Fachbuchverlag. Leipzig, 1973. Русский перевод: Мюллер П., Нойман П., Шторм Р. Таблицы по математической статистике. М., Финансы и статистика, 1982.
97. Niklas Н., М i 1 1 е г М. Korrelationsrechnung und ihre Anwendung auf Statistik, Versuchswesen, Vererbungslehre, Wirtschaft und Technik. Heling-sche Verlagsanstalt. Leipzig, 1940.
98. N e u r a t h P. Statistik fur Sozialwissenschaftler. Ferdinand Enke Verlag. Stuttgart, 1966.
99. N о 1 1 a u V. Statistische Analysen. Fachbuchverlag. Leipzig, 1975.
100. Pawlowski Z. Einfiihrung in die matherriatische Statistik. Verlag Die Wirtschaft. Berlin, 1971. Русский перевод: Павловский 3. Введение в математическую статистику. М., Статистика, 1967.
101. Pflanzagl J. Allgemeine Methodenlehre der Statistik. Bd I, II, Samm-lung Goschen, Bd 747, 747a, de Gruyter and Co., Berlin (West), 1962.
102. Пугачев В. С. Статистические методы в технической кибернетике. М., Сов. радио, 1971.
103. R а о С. R. Lineare statistische Methoden und ihre Anwendungen. Akademie-Verlag. Berlin, 1973. Русский перевод: Рао С. P. Линейные статистические методы и их применение. М., Наука, 1968.
104. Rasch D. Elementare Einfiihrung in die mathematische Statistik. VEB Deutscher Verlag der Wissenschaften, Berlin, 1968.
105. Rasch D., Enderlein G., Herren dorf er G. Biometrie. VEB Deutscher Landwirtschaftsverlag, Berlin, 1973,
297
106. Reiersol О. A Note in the Signs of Cross Correlation Coefficients. University. Oslo, 1956.
107. R en у i A. Wahrscheinlichkeitsrechnung mit einem Anhang fiber Informa-tionstheorie. VEB Deutscher Verlag der Wissenschaften. Berlin, 1962.
108. Richter K. J. Kybernetische Analyse verkehrsokonomischer Systeme — Verkersokonometrie. 2. Aufl. Transpress Verlag, Berlin. 1971.
109. R i c h t er K. J. Transportokonometrie. Transpress Verlag. Berlin, 1966.
110. Richter-Altschaffer H. Einfiihrung in die Korrelationsrech-nung. Institut fur landwirtschaftliche Marktforschung. Berlin, 1931.
111. Richter-Altschaffer H. Theorie und Technik der Korrelations-analyse. Institut fur landwirtschaftliche Marktforschung. Berlin, 1932.
112. S a c h s L. Angewandte Statistik, 4 Aufl. Springer-Verlag. Berlin (West), Heidelberg, New York, 1974.
113. S a 1 v e m i n i T. Regressione e Correlazione. Edizioni Scientifiche Eina-udi. Torino, 1959.
114. Schelling H. Die wirtschaftlichen Zeitreihen als Problem der Korrela-tionsrechnung. K. Schroeder Verlag. Bonn, 1931.
115. Schmetterer P. E. Einfiihrung in die mathematische Statistik. Springer-Verlag. Wien, 1956. Русский перевод: Шметтерер П. Введение в математическую статистику. М., Наука, 1976.
116. Schmutzler О., Кг i е g е г Н., D а 1 i с h о w К. Statistische Me thoden in der Markt- und Bedarfsforschung. Verlag Die Wirtschaft. Berlin 1975.
117. Schneeweiss H. Okonometrie. Physica-Verlag, Wurzburg. Wien, 1971.
118. S c h 6 n f e 1 d P. Methoden der Okonometrie, Bd. 1, 2. Verlag Franz Vahlen GmbH. Berlin (West), Frankfurt/Main, 196е*.
119. Смирнов H. В., Дунин-Барковский И. В. Курс теории вероятностей и математической статистики для технических приложений. 2-е изд. М., Наука, 1965.
120. Struck R. Kurzfristige statistische Vorausberechnung. Verlag Die Wirtschaft. Berlin, 1973.
121. С т p у м и л и н С. Г. и др. Вопросы статистического измерения связей между явлениями (корреляционный анализ)/Под ред. акад. С. Г. Струмили-на М., Госпланиздат, 1950.
122. Т h е i 1 Н. Principles of Econometrics. Amsterdam. London, 1971. North Holland Publishing Co.
123. T h e i 1 H. Applied Economic Forecasting. North-Holland Publishing Co., Amsterdam, 1966. Русский перевод: T e й л Г. Прикладное экономическое прогнозирование. М., Прогресс, 1970.
124. Т h е i 1 Н. Economic Forecasts and Policy. North-Holland Publishing Co., Amsterdam, 1961. Русский перевод: Тей л Г. Экономические прогнозы и принятие решений. М., Статистика, 1971.
125. Т i n t и е г G. Handbuch der Okonometrie. Springer-Verlag, Berlin (West), Gottingen. Heidelberg, 1960. Русский перевод: Тинтнер Г. Введение в эконометрию. М., Статистика, 1965.
126. Чупров А. А. Основные проблемы теории корреляции. М., Госстатиздат, 1960.
127. Урланис Б. Ц. Статистические методы изучения зависимости явлений. М., Госстатиздат, 1956»
298
128. Van der Waerden B. L. Mathematische Statistik. Springer-Verlag Berlin (West), 1957. Русский перевод: Ван дер Варден Б. Л. Математическая статистика. М., ИЛ, 1960.
129. Walker Н. М. Statistische Methoden filr Psychologen und Padagogen. Verlag Julius Beltz, Wienheim. Berlin (West), 1954.
130. Wallis W. A.,Roberts H. V. Methoden der Statistik. Rudolf Haufe Verlag, Freiburg i. Br., 1960.
131. Waschkau H. Statistische Elastizitatsfunktionen. Verlag Die Wirtschaft. Berlin, 1974.
132. Weber E. Grundriss der biologischen Statistik, 7. Aufl. VEB Gustav Fischer Verlag. Jena, 1972.
133. Williams E. J. Regression Analysis. J. Wiley and Sons. New York, 1959.
134. Winkler W. Grundriss der Statistik, 2. umgearb. Aufl, Verlag Manz. Wien, 1947.
135. Winkler W. Grundfragen der Okonometrie. Springer-Verlag. Wien, 1951.
136. Wold H. Econometric Model Building. North-Holland Publishing Co., Amsterdam, 1964.
137. Wold H., J ureen L. Demand Analysis. Almquist. Stockholm, 1952.
138. Yule G. U., К e n d a 1 1 M. G. An Introduction to the Theory of Statistics. 14 ed. Griffin. London, 1958. Русский перевод: Юл Дж. Э., Кен-дэл М. Дж. Теория статистики. М., Госстатиздат, 1960.
139. Zur Technik und Methodologie einiger quantifizierender Methoden der so-ziologischen Forschung. Dietz Verlag. Berlin, 1966.
СОДЕРЖАНИЕ
Предисловие к русскому изданию 5
Предисловие 7
1. Основные понятия и теоретико-вероятностные основы регрессионного и корреляционного анализа 9
1.1. Причинная связь ........................ 9
1.2. Понятие регрессии ........................14
1.3. Понятие корреляции ........................18
1.4. Задачи корреляционного и регрессионного анализа..........26
1.5. Генеральная совокупность, выборка, среднее, выборочная дисперсия, ковариация. Свойства оценок..........................31
1.6. Распределение случайных величин. Математическое ожидание и дисперсия 38
1.7. Нормальное распределение, ^-распределение, /-распределение, F-распределение. ............................41
1.8. История развития корреляционного и регрессионного анализа . . 45
2. Линейная регрессия ...............................48
2.1. Диаграмма рассеяния 51
2.2. Метод частных средних 52
2.3. Простая линейная регрессия ..............................56
2.4. Построение регрессионной прямой с помощью метода наименьших квадратов (по несгруппированным данным)..............58
2.5. Сопряженные регрессионные прямые .............66
2.6. Построение регрессионной прямой по сгруппированным данным . 70
2.7. Линейная множественная регрессия .............75
2.8. Линейная частная регрессия „.......................88
2.9. Исходные предпосылки регрессионного анализа и свойства оценок .........................................................90
2.10. Последовательность проведения регрессионного анализа и его применение в экономике ........................................97
300
3. Оценка точности регрессионного анализа ..........................100
3.1. Общие соображения .............................100
3.2. Коэффициент детерминации для простой линейной регрессии 102
3.3. Коэффициент множественной детерминации ......................105
3.4. Коэффициент частной детерминации 109
3.5. Коэффициент детерминации между объясняющими переменными НО
3.6. Стандартные ошибки оценок ...................................112
4. Линейная корреляция 119
4.1. Простая линейная корреляция при несгруппированных данных . .119
4.2. Простая линейная корреляция при сгруппированных данных . . . 123
4.3. Связь между коэффициентами корреляции, регрессии и детерминации ........................................................124
4.4. Линейная множественная корреляция ...........................128
4.5. Частная корреляция 131
4.6. Соотношения между коэффициентами множественной и частной корреляции, регрессии и детерминации..........................136
4.7. Влияние неучтенных факторов на коэффициент корреляции . . . 138
5. Нелинейная регрессия.............................................140
5.1. Простая нелинейная регрессия при несгруппированных данных 140
5.2. Простая нелинейная регрессия при сгруппированных данных 150
5.3. Множественная нелинейная регрессия...........................152
6. Нелинейная корреляция............................................155
6.1. Простая нелинейная корреляция при несгруппированных данных 155
6.2. Простая нелинейная корреляция при сгруппированных данных 158
6.3. Множественная нелинейная корреляция..........................159
7. Частные вопросы корреляционного и регрессионного анализа.........160
7.1. Коэффициент ранговой корреляции Спирмэна.....................160
7.2. Коэффициент ранговой корреляции Кендэла .....................164
7.3. Индекс Фехнера...............................................165
7.4. Корреляционное отношение.....................................166
7.5. Соотношение между линейным коэффициентом корреляции, индексом корреляции и корреляционным отношением...................169
7.6. Упрощенные способы оценивания параметров регрессии и коэффициента корреляции ...........................................170
7.7. Корреляция и регрессия относительных величин.................172
7.8. Коэффициент конкордации......................................175
8. Доверительные интервалы и проверка значимости ...................177
8.1. Распределение коэффициентов регрессии и корреляции...........177
8.2. Доверительные интервалы для параметров регрессии и генерального коэффициента корреляции..................................180
8.3. Доверительный интервал для условного математического ожидания ..........................................................184
301
8.4. Доверительные интервалы для отдельных значений зависимой пе-
ременной у . . ..........................................188
8.5. Проверка значимости коэффициента корреляции...............192
8.6. Проверка значимости коэффициента детерминации.............201
8.7. Проверка значимости оценок параметров регрессии...........203
8.8. Проверка линейности регрессии......................г . . - 212
9. Мультиколлинеарность ...................................214
10. Типичный пример..............................................223
11. Регрессия и корреляция временных рядов.......................229
11.1. Модель регрессии временного ряда .......................229
11.2. Автокорреляция переменных..............................'. 233
11.3. Автокорреляция возмущений................................237
12. Одновременные уравнения в регрессионном анализе...............241
12.1. Предварительные замечания................................241
12.2. Переменные в эконометрической модели.....................245
12.3. Виды эконометрических моделей............................248
12.4. Проблема идентификации...................................254
12.5. Предпосылки построения эконометрических моделей..........257
12.6. Методы оценивания эконометрических моделей...............258
13. Ассоциация и контингенция ...................................269
13.1. Коэффициент ассоциации ..................................270
13.2. Коэффициент контингенции (сопряженности).................272
13.3. Двустрочечная корреляции................................275
Приложение.......................................................278
Литература.................................................... • 293
Э. Фёрстер, Б, Ренц
МЕТОДЫ КОРРЕЛЯЦИОННОГО И РЕГРЕССИОННОГО АНАЛИЗА
Книга одобрена на заседании редколлегии серии «Библиотечка иностранных книг для экономистов и статистиков» 30.10.80
Зав. редакцией А. В. Павлюков
Редактор Е. В. Крестьянинова
Мл. редактор О. А. Ермилина
Техн, редакторы К. К. Букалова, Л. Г. Челышева
Корректоры Г. В. Хлопцева, Т. М. Васильева, Л. Г. Захарко и А. Т. Сидорова Худож. редактор О. Н. Поленова
ИБ № 1233
Сдано в набор 30.08.82. Подписано в печать 04.01.83.
Формат 60X90716. Бум. тип. № 2. Гарнитура «Литературная». Печать высокая. П. л. 19,0- Усл. п. л. 19,0- Усл кр.-отт. 19,31. Уч.-изд. л. 19,96. Тираж 7000 экз. Заказ 1113. Цена 2 р. 50 к.
Издательство «Финансы и статистика, Москва, ул. Чернышевского, 7
Московская типография № 4 Союзполиграфпрома
при Государственном комитете СССР
по делам издательств, полиграфии и книжной торговли
129041, Москва, Б. Переяславская ул., д. 46.