Author: G. Xudayberganov A.K. Vorisov X.T. Mansurov B.A. Shoimqulov
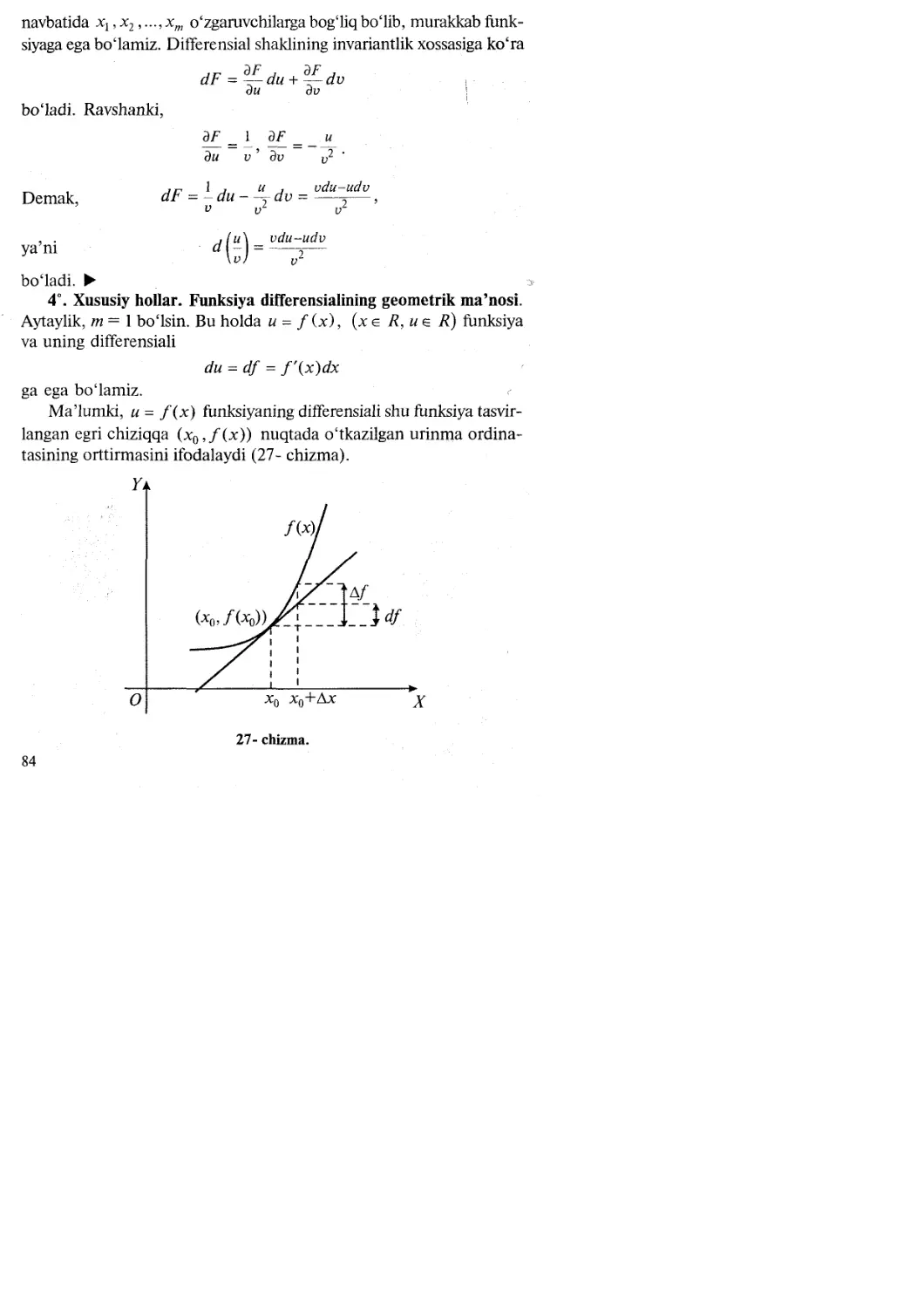
Tags: matematika matematik tahlil oliy matematika toshkent nashriyoti o‘zbek tilida
ISBN: 978-9943-375-31-4
Year: 2010
Text
/И'З/.
O‘ZBEKISTON RESPUBLIKASI OLIY VA
O‘RTA MAXSUS TA’LIM VAZIRLIGI
G. Xudayberganov, A.K. Vorisov,
X.T. Mansurov, B.A. Shoimqulov
M АГЕМЛТ1К ANALIZDAN
MA’RUZALAR
II
5460100—«Matematika», 5440200—«Mexanika» bakalavr
yo ‘nalishidagi talabalar uchun о ‘quv qo ‘llanma
«Voris-nashriyot»
Toshkent—2010
22.1
М31
И
Taqrizchilar:
fizika-matematika fanlari doktori, professor
R.R. Ashurov,
fizika-matematika fanlari doktori, professor
R.N. G‘anixo‘jayev.
Qo‘lingizdagi o‘quv qo‘llanma «Matematik analizdan ma’ruzalar»
(1 - qism) kitobning davomi bo‘lib, dastur materiallari 6 bob, 39 ta ma’ruzaga
ajratib bayon qilingan. Bu ikkinchi qism ko‘p o'zgaruvchili funksiya, uning
limiti, uzluksizligi, differensial va integral hisobi, funksional ketma-ketlik,
funksional qatorlar mavzularini o‘z ichiga oladi.
Mazkur o‘quv qo'llanma matematika va mexanika bakalavr yo‘na-
lishlarida ta’lim olayotgan talabalarga mo‘ljallangan bo‘lsa-da, undan
shuningdek, matematika kengroq o‘qitiladigan oliy ta’lim muassasalari
talabalari ham foydalanishlari mumkin.
ISBN 978-9943-375-31-4
© «Voris-hasfiriyot» MChJ, 2010.
SO‘ZBOSHI
Ushbu o‘quv qo‘llanma «Matematik analizdan ma’ruzalar» (1- qism)
kitobining davomi bo‘lib, dastur materiallari 6 bob, 39 ta ma’ruzaga
ajratib bayon qilingan. Bu ikkinchi qism ko‘p o'zgaruvchili funksiya,
uning limiti, uzluksizligi, differensial va integral hisobi, funksional
ketma-ketlik, funksional qatorlar mavzularini o‘z ichiga oladi.
Qo‘llanmani yozishdagi asosiy tamoyillar 1-qismda yozilgan
so‘zboshida keltirilgan bo‘lib, 2- qismni tayyorlashda ham shu
tamoyillarga amal qilindi.
Mazkur o‘quv qollanma matematika va mexanika bakalavr yo‘na-
lishlarida ta’lim olayotgan talabalarga mo‘ljallangan bo‘Isa-da, undan
matematika kengroq o‘qitiladigan oliy ta’lim muassasalari talabalari
ham foydalanishlari mumkin.
Qo'llanmani tayyorlashda mualliflar Mirzo Ulug'bek nomidagi
O‘zbekiston Milliy universiteti mexanika-matematika fakultetida
matematik analiz fanining o‘qitilish jarayonida yig‘ilgan tajribalaridan
imkon darajasida foydalanishga harakat qildilar.
Kitob qo‘lyozmasini sinchiklab o‘qib chiqib, uning ilmiy va
metodik jihatdan yaxshilanishiga o‘z hissalarini qo‘shganliklari uchun
professor R.R. Ashurov, R.N. G‘anixo‘jayevlarga mualliflar minnat-
dprchilik bildiradilar.
Qo‘llanmaning sifatini yaxshilashga qaratilgan fikr-mulohazalarini .
bildirgan hamkasblarga ham awaldan o‘z minnatdorchiligimizni
bildiramiz.
Mualliflar.
3
11-в о в
SONLI QATORLAR (davomi)
53- ma’ruza
Ixtiyoriy hadli qatorlarda yaqinlashish alomatlari
1°. Leybnits alomati. Ushbu
= q -c2 +c3-c4 + ... + (-l)"~1c„ +... (1)
Л7-1
qatorni qaraymiz, bunda c„ >0, (n = 1,2,3,...).
Odatda, bunday qator hadlarining ishoralari navbat bilan о ‘zgarib
keladigan qator deyiladi.
Ravshanki, (1) qator ixtiyoriy hadli qatorning bitta holidir.
Masalan, ushbu
qator hadlarining ishoralari navbat bilan o‘zgarib keladigan qator
bo'ladi.
1- teorema. (Leybnits alomati.) Agar hadlarining ishoralari navbat
bilan o‘zgarib keladigan (1) qatorda:
1) cn+\ <c„,(n = 1,2,3,...);
2) lim c„ = 0 bo‘lsa, u holda (1) qator yaqinlashuvchi bo‘ladi.
◄ (1) qatorning dastlabki 2m ta (me N) hadidan iborat qismiy
yig‘indisi
*-*2m ~ ~ C2 + C2 — C4 + ... + Cjm-l — ^2m
ni olaylik. Unda ^(m+i) uchun
^2(т+1) — ^2m (^2m+l — ^2m+2 )
bo'lib, c2m+2 <c2m+1 bo‘lganligi sababli (bunda c2m+l~c2m+2 >0
bo‘ladi)
^2(m+i) > 52m, (m = 1,2,3,...)
bo'ladi. Demak, {52m} ketma-ketliko‘suvchi.
4
Endi S2m yig‘indini quyidagicha yozamiz:
^2m = C1 ~ (c2 ~ c3 ) ~ (c4 - c5 ) “ ••• “ (c2m-2 ~ C2m-1 ) “ c2m
Bu tenglikning о‘ng tomonidagi ifodada qatnashgan qavs ichidagi
ayirmalarning, shuningdek, c2m ning musbat bo‘lishini e’tiborga olib,
$2m < C1
bo‘lishini topamiz. Demak, {A2m} ketma-ketlikyuqoridanchegaralangan.
Monoton ketma-ketlikning limiti haqidagi teoremaga ko‘ra
lim S2m = S, (S — chekli son) (2)
mavjud.
Endi (1) qatorning dastlabki 2m — 1 ta (m e У) sondagi hadidan
iborat ushbu
^2m-l ~ C1 ~ C2 + C3 ~ C4 + •" + C2m-1
qismiy yig‘indisini olaylik. Ravshanki,
^2m-I = $2m + C2m
Teoremaning n —> °° da cn 0 bo‘lishi sharti hamda (2) muno-
sabatdan foydalanib topamiz:
lim S2m-i = lim + c2m) = 5.
Shunday qilib, berilgan (1) qatorning qismiy yig'indilaridan iborat
ketma-ketlik chekli limitga ega ekani ko'rsatildi. Demak, (1) qator
yaqinlashuvchi. ►
Masalan, i_l + l_£ + ... + k^2— + ... (3)
2 3 4 и
qator hadlari keltirilgan teoremaning barcha shartlarini qanoatlan-
tiradi. Teoremaga ko‘ra (3) qator yaqinlashuvchi bo‘ladi ((3) qatorning
yaqinlashuvchanligi va yig‘indisi ln2 ga teng bo‘lishi ko‘rsatilgan edi).
2°. Dirixle—Abel alomati. Faraz qilaylik,
a1; a2, a3, a„,
/>!, b2, by, bn, ...
ixtiyoriy haqiqiy sonlar ketma-ketliklari bo‘lib,
S„ = a, + a2 + ... + an
bo‘lsin. U holda V«e N, Уте N uchun
5
n+m n+m-1
ак^к ~ §к (&к ~ ^к-1 ) ^п+т ' ^n+m ~ ^п-Фп 0)
к=п к=п
munosabat o'rinli bo‘ladi.
Odatda, (4) munosabat Abel ayniyati deyiladi.
◄ Ravshanki, ak = Sk - Sk_} bo‘ladi. U holda У, akbk yig‘indiushbu
k=n
n+m n+m n+m
= <5>
k~n k=n k~n
ko‘rinishga keladi. Bu tenglikning o‘ng tomonidagi birinchi qo'shiluv-
chini quyidagicha:
n+m n+m-1
к & к ~~ к & к Sn+m bn+m
k=n k~n
shaklda, ikkinchi qo‘shiluvchini esa quyidagicha
n+m n+m-l n+m-1
^k-1^ к ~ 2, §к^ k+l~ ^п-Фп "* У, $кЬ k+l
k=n k=n-\ k=n
shaklda yozib olamiz. Natijada (5) tenglik quyidagicha:
n+m n+m-1 n+m-1
^k^ к ~~ §к^ к "I" $п+т^п+т ~ , ^k^ k+1 ~^n-l^n ~
k=n k=n k=n
n+m-1
~ Sk (^bk ~ b k+i) — Sn+mbn+ni — Sn_^bn
k=n
bo‘ladi. ► x .
2- teorema. (Dirixe—Abel alomati.) Aytaylik,
^akbk +a2b2 +... + akbk +... (6)
k=l
qator berilgan bo‘lsin. Agar:
1) {bk} ketma-ketlik kamayuvchi va u cheksiz kichik miqdor,
2) ak qatoming qismiy yighndilari ketma-ketligi chegaralangan
k=l
bo'lsa, (6) qator yaqinlashuvchi bo‘ladi.
6
◄ Agar J, ak qatorning qismiy yig‘indisini
k=\
S„ = a, + a2 +... + an
desak, unda teoremaning shartiga ko‘ra, shunday M > 0 son topiladiki,
barcha ne N uchun
|5„|<M (7)
bo‘ladi.
Shartga ko‘ra {bk\ ketma-ketlik kamayuvchi va u cheksiz kichik
miqdor. Unda Ve > 0 ga ko‘ra shunday n0 e N topiladiki, V» > и0 da
n+m
bo'ladi. Endi У akbk yig‘indiga Abel ayniyatini qo‘llaymiz:
k=n
n+m я+zn-l
У, ak^k ~ j §k (bk Ь k+l ) + ~ $n-}bn .
k=n k-n
Natijada
и+m
^akbk
k=n
п+т-Л
- X \$k(bk ~ ^*+l)| + |^+лД+т| + =
k=n
n+m-\
= X \$k\ (bk - bk+i) + |5„+m|+ |S„_i| • b„
k-n
bo'ladi.
(7) tengsizlikdan foydalanib topamiz:
n+m
Yakbk
k=n
и+m-l
— , (bk ьк+1) + bn+m
+ M-bn.
k=n
Agar
и+m-l
У - bk+i) + bn+m = (bn - bn+i) + (6„+1 - b„+2) +... + (b^i - bn+m) + b„+m = bn
k~n
bo‘lishini e’tiborga olsak, unda
n+m
^akbk
k=n
<2M bn
7
bo'lib, (8) munosabatga ko'ra
n+m
^akbk
k=n
< £
bo'ladi. Bundan Koshi teoremasiga ko‘ra
yaqinlashuvchanligi kclib chiqadi. ►
n~m
^akbk <e qatorning
k=n
... , ,, v1 coskx cosx cos2x , cosbc ,
Misol. Ushbu > —-— + ... qator
к 1 2 к 4
.7=1
yaqinlashuvchanlikka tekshirilsin, bunda x — tayinlangan haqiqiy son.
•< Agar x = 2л bo‘lsa, berilgan
cosbc _ y’ cos2it £ 1
к
k=\ k=l k=l
qator garmonik qator bo‘lib, u uzoqlashuvchi bo'ladi.
Aytaylik, x ф 2л bo'lsin. Berilgan qatorda
i к 1
ak = cos kx, bk = —
К
belgilashlami bajaramiz.
Ravshanki, [bk } = ketma-ketlik kamayuvchi va cheksiz kichik
miqdor bo'ladi (£ -> <*> da ~ 0).
Endi У ak
k=l
= У cos kx qatorning qismiy yig‘indisi Sn ni topamiz:
£=1
n
Sn = У cos kx =
k=i
’ ” ' X
X2 sin cos kx -
2
2 Sin k=l
2
i " г
-Uz
2 sin- k=i L
2
X - sin
X
. , 1. . ‘x
sin(n + -)x-sm—
2 2
x
2 sin—
2
8
Keying! munosabatdan, 2л ga karrali bo‘lmagan x lar uchun
bo‘lishi kelib chiqadi. Demak, {£„} ketma-ketlik chegaralangan. Unda
berilgan qator 2- teoremaga ko‘ra yaqinlashuvchi bo‘ladi. ►
Mashqlar
l .Quyidagi munosabatda 2n xatolik topilsin:
. n 1 1 1 1 /.111 \ п/1 1
ln2 = 1= ^1 +- + - + - +...j - 2^-+-
= (1 + 1 + 1 + ;L + ...'I _(i + l + l+ *+ ...'I = o.
\ 2 3 4 ) \ 2 3 4 )
rm
COS—- , I
2 . Ushbu У -p—- 11 + - I qator yaqinlashuvchanlikka tek-
и=1 п(.и+ )
shirilsin.
54-ma’ruza
Cheksiz ko‘paytmalar
1°. Cheksiz ko‘paytma tushunchasi. Faraz qilaylik, biror
{<?„}’ Cl ,c2 ,c3
haqiqiy sonlar ketma-ketligi berilgan bo‘lsin. Ular yordamida ushbu
q -c2 -c3 (1)
ifodani tuzamiz.
(1) ifoda cheksiz ко ‘paytma deyiladi va u ]~[ c„ kabi belgilanadi:
n=l
ПС« =C1 C2 C3 - Cn-,
n=l
bunda c1,c2,...,c„... sonlar cheksiz ko‘paytmaning hadlari, c„ esa
ko‘paytmaning umumiy yoki n- hadi deyiladi.
‘9(
Quyidagi Pn = q c2 ...c„, (n = 1,2,3,...)
ko‘paytma (1) cheksiz ko‘paytmaning n- qismiy ko‘paytmasi deyiladi.
Demak, (1) cheksiz ko‘paytma berilganda har doim uning qismiy
ko‘paytmalaridan iborat ushbu {Pn};
Px,P2,P3,...,Pn,...
ketma-ketlikni hosil qilish mumkin. Masalan,
* Y.fl- * L, (л-2,3,...)
( 22 Д 32 ) ( n2 J
cheksiz ko'paytmaning n- qismiy ko‘paytmasi
_ 1 3 2 4 п-1 «+1 _ 1 a+1
2 2 3 3 ”’ n n 2 n ’
i.
bo‘lib, ulardan tuzilgan {P„} ketma-ketlik
(n = 2,3,4,...)
3 2 5 3 1/7+1
4 ’ 3 ’ 8 ’ 5 ’ 2 ' n~’ ’”
bo'ladi.
1- ta’rif. Agar n da {Pn} ketma-ketlik noldan farqli chekli
P songa intilsa (yaqinlashsa), (1) cheksiz ko'paytma yaqinlashuvchi
deyiladi, P esa uning qiymati deyiladi:
lim7>„=P, / =
► /7=1
Agar {Pn} ketma-ketlik limitga ega bo‘lmasa (yoki uning limiti 0
bo‘lsa), (1) cheksiz ko'paytma uzoqlashuvchi deyiladi.
Masalan, yuqorida keltirilgan ГТ11 - | cheksiz ko‘paytma uchun
A , I tv I
n=2 v /
r n 1-1 Й+1
lim Pn = lim -------
>oo 2 и
J.
2
bo'ladi. Demak, J"J[ 1 - 2- j cheksiz ko‘paytma yaqinlashuvchi va
n=2 V n J
uning qiymati 8a teng.
10
M Yaqinlashuvchi cheksiz ko‘paytmaning xossalari. Aytaylik, biror
ПС« =cl c2 C3 — C„ —
n=l
(1)
cheksiz ko'paytma berilgan bo'lsin.
Ushbu
J Cn Cm+1 • Cm+2 • ••• (2)
n=m+\
cheksiz ko‘paytma (bunda m — tayinlangan natural son) (1) cheksiz
ko‘paytmaning qoldig‘i deyiladi.
1) Agar (1) cheksiz ko‘paytma yaqinlashuvchi bo‘lsa, (2) cheksiz
ko‘paytma ham yaqinlashuvchi bo'ladi va aksincha.
◄ (1) cheksiz ko'paytmaning qismiy ko'paytmasi
= q c2...cn,
(2) cheksiz ko'paytmaning qismiy ko'paytmasi
*-k — m+l ^m+2 ''rr+k
lar uchun Pn = Pm • ,
(bunda n - m + к ) bo'ladi. Bu munosabatdan, n da Pn ning
chekli limitga ega bo'lishidan к <=° da Qkn> ning ham chekli limitga
ega bo'lishi; shuningdek, к -> °° da Qkm} ning chekli limitga ega
bo'lishidan, и -> oo da Pn ning ham chekli limitga ega bo'lishi kelib
chiqadi. ►
2) Agar (1) cheksiz ko'paytma yaqinlashuvchi bo'lsa, u holda
lim(cOT+1 cw+2 •...•cm+A...) = l
m—
bo'ladi.
◄ Aytaylik, (1) cheksiz ko'paytma yaqinlashuvchi bo'lib, uning
qiymati P bo'lsin. Unda ’
P . C • C . . — P
* m Ъл+l ^m+2 ••• ^m+k 1
bo'lib, undan ш da
_ P P
^m+l ' ^m+2 ' ' ^m+k"‘ p p ~ *
rm *
bo'lishi kelib chiqadi. ►
11
3) Agar (1) cheksiz ko‘paytma yaqinlashuvchi bo‘lsa, u holda
lim c„ = 1
bo‘ladi.
◄ Aytaylik, (1) cheksiz ko'paytma yaqinlashuvchi bo‘lib, uning
qiymati Pbo‘lsin:
lim Pn = lim(ct • c2 •... cn) = P.
n—>°°
U holda P„ = Pn_x cn, ya’ni c„ = ф— bo‘lib,
lim c„ = lim -5^- = £ = 1
bo‘ladi. ►
Yuqorida keltirilgan xossalardan quyidagi xulosalami chiqarish
mumkin.
Cheksiz ko'paytmalaming yaqinlashishida, ulaming dastlabki chekli
sondagi hadlarining ta’siri bo‘lmaydi.
Agar cheksiz ko‘paytma yaqinlashuvchi bo'lsa, unda w da
cn -> 1 bo‘lganligi sababli, uning biror hadidan boshlab keyingi had-
larini musbat deb olish mumkin bo‘ladi.
Bu xossalar yaqinlashuvchi cheksiz ko‘paytmalarda ularning
hadlarini musbat deb olish imkonini beradi.
3°. Cheksiz ko‘paytmalar bilan qatorlar orasidagi bogianish. Faraz
qilaylik,
П>„ =q c2 - сл -> (c„>0, n -1,2,...)
n=l
cheksiz ko'paytma berilgan bo'lsin. Bu cheksiz ko'paytma hadlarining
logarifmlaridan ushbu
£lnc„ = Inq + lnc2 +... + lnc„ +... (3)
n=l
qatorni hosil qilamiz.
1-teorema. (1) cheksiz ko‘paytmaning yaqinlashuvchi bo‘lishi
uchun (3) qatorning yaqinlashuvchi bo'lishi zarur va yetarli.
◄ Zarurligj, Aytaylik, (1) cheksiz ko‘paytma yaqinlashuvchi bo‘lsin:
lim Pn = lim(q • c2 •... • c„) = P, (P — chekli son).
12
U holda (3) qatorning qismiy yig‘indisi uchun
n
Sn = In ck - Inq + In c2 +... + Inc„ - ln(q • c2 ...cn)
k=l
bo‘lib,
lim S„ - lim ln(q • c2 •... • cn) = In P
n—>°° n—>°°
bo‘ladi. Demak, (3) qator yaqinlashuvchi.
Yetarliligi. Aytaylik, (3) qator yaqinlashuvchi bo‘lsin:
n
lim Sn - lim V Inck = lim ln(q c2 cn) = S .
Л=1
U holda (1) cheksiz ko‘paytmaning qismiy ko‘paytmasi uchun
= q q •• c„ = е^ с2
bo‘lib, lim Pn = lim eln(q Q -Cn} = es
n—^oo tl—>^
bo‘ladi. Demak, (1) cheksiz ko'paytma yaqinlashuvchi. ►
Ko‘pincha, Pl c« cheksiz ko‘paytmani o‘rganishda, uning umu-
«=i
miy hadi cn ni quyidagicha
cn = 1 + a„
ifodalash qulay bo‘ladi. U holda (1) cheksiz ko‘paytma
n-\
ko‘rinishga, cheksiz qator esa
£ln(l + u„)
n-\
ko‘rinishga ega bo‘ladi.
Faraz qilaylik, n ning (ne N) yetarlicha katta qiymatlarida
an > 0 (yoki an < 0)
bo‘lsin.
13;
2-teorema. Ushbu ]Д(1 + «„)
/7—1
cheksiz ko‘paytmaning yaqinlashuvchi bo‘lishi uchun
n=l
qatorning yaqinlashuvchi bo‘lishi zarur va yetarli.
◄ Ravshanki, ГТ (1 + an) cheksiz ko‘paytma va X qatorning
n=i «=1
yaqinlashuvchi bo‘lishi uchun awalo
lim an = 0
bo‘lishi kerak. Shu munosabat bajarilsin.
Keltirilgan teoremaning isboti
iim = i
an
munosabat hamda 1- teoremaning qo‘llanishidan kelib chiqadi. ►
Masalan, bu teoremadan foydalanib, ushbu
n ) у
cheksiz ko‘paytmaning a > 1 bo'lganda yaqinlashuvchi bo‘lishini
(chunki У —, (a > 1) — yaqinlashuvchi),
П(1 + 1-) = (1 + 1)(1 + |)(1 + {)...(1 + -)...
-1 1 \ nI \ 2) \ 3/ \ n)
cheksiz ko'paytmaning esa uzoqlashuvchi bofilishini (chunki V - ~
“72
n=L
uzoqlashuvchi) topamiz.
14
Mashqlar
A 1. Ushbu П (1 + x2"), (Ixl < 1)
л=1
cheksiz ko'paytmaning yaqinlashuvchiligi ko'rsatilsin va
topilsin.
qiymati
2. Ushbu П“Т ” e
n=l 1+-
П
tenglik isbotlansin, bunda
n 1
c = lim V -
к
k=l
-Inn
(Eyler o'zgarmasi).
15 i
12- В О В
КОТ O‘ZGARUVCHILI FUNKSIYALAR,
ULARNING LIMITI, UZLUKSIZLIGI
55- ma’ruza
Rm fazo. R”1 fazoda ochiq va yopiq to‘p]amlar
1°. Rm fazo tushimchasi. Haqiqiy sonlar to‘plami R yordamida
ushbu
7?x/?x ••• xR = {(x1.x1....,x!l,'):xie R. x2 e R, , xm e R} (1)
m ta
to‘plamni (R ning dekart ko‘paytmalaridan tuzilgan to‘plamni) hosil
qilaylik. Ravshanki, (1) to'plamning har bir elementi m ta x{, x2, xm
haqiqiy sonlardan tashkil topgan tartiblangan m lik
(xb x2, xm)
dan iborat bo'ladi. Uni (1) to‘plamning nuqtasi deyilib, bitta harf
bilan belgilanadi:
X = <Xb X^ xm).
Bunda xb x2, xm sonlar x nuqtaning mos rayishda birinchi,
ikkinchi, m- koordinatalari deyiladi.
Agar x = (xb x2, xm), у = (yv, y2, ym) nuqtalar uchun
Xj = yb x2 = y2, xm = ym bolsa, x= y deyiladi.
Faraz qilaylik,
X = (xb X2, хи), у = (y{, y2, ym)
lar (1) to'plamning ixtiyoriy ikki nuqtasi bolsin. Ushbu
Ж(л-^)2
V £=1
miqdor x va у nuqtalar orasidagi masofa deyiladi va p(x,y) kabi belgilanadi:
Гт "
р(х’У) = , ~xk) (2)
V k^l
Endi masofaning xossalarini keltiramiz:
16
1) Наг doim р(х,у) > 0 va р(х,у) - 0 <=> х = у boladi.
◄ (2) munosabatga ko‘ra, har doim p(x,y)>0 bo‘ladi. Agar
p(x,y) = 0 bo‘lsa, u holda
(.h -*1)2 + (У2 -x2)2 +... + (ym -xm)2 =0
bo‘lib, natijada x} — y{, x2 = y2, xm=ym, ya’ni x — у bo'lishi kelib
chiqadi. Aksincha, agar x^.^, x2 = y2, ..., xm = ym bo‘lsa, unda (2)
munosabatdan foydalanib p(x,y) = 0 bo‘lishini topamiz. ►
2) p(x,y) masofa x va у ularga nisbatan simmetrik bo‘ladi:
p(x,y)= p(y,x).
◄ Bu xossanig isboti (2) munosabatdan kelib chiqadi:
p(*,?) = ~xkf = pM>
V k=\ V k=\
3) (1) to'plamning ixtiyoriy
X = (x1,X2,...,Xm), у = (У1,у2,...,ут) , Z = (Z],Z2,-,Zm)
nuqtalari uchun
p(x,z) < p(x,y) + p(y,z)
tengsizlik o‘rinli bo‘ladi.
◄ Ma’lumki, ixtiyoriy ax, a2,..., am va ,..., bm haqiqiy sonlar
uchun
w m m
^{ak+bk} < £a2k
(3)
bo‘ladi (qaralsin, [1], 12-bob, l-§; odatda, bu tengsizlikni Koshi—
Bunyakovskiy tengsizligi deyiladi). (3) tengsizlikda
^k=zk-yk, {k = 1,2,g)
deb topamiz:
/ tn I tn tn
\~^)2 - ~x^
17
Bu esa
p(x,z) < p(x,y) + p(y,z)
bo‘lishini bildiriladi. ►
• Shunday qilib, (1) to‘plamda (to‘plam elementlari orasida) masofa
tushunchasining kiritilishini hamda masofa uchta xossaga ega bo‘lishini
ko'rdik.
Odatda, (1) to‘plam Rm fazo deyiladi. Demak,
: %! e R, x2 e R,...,xm e R}.
Endi R" fazodagi ba’zi bir to‘plamlarni keltiramiz.
Aytaylik, biror a = (й], a2,am) e R"1 nuqta va r > 0 son berilgan
bo‘lsin.
Ushbu
Br (a) = {(Xj,x2,..,xffl) e Г : 7(*i ~«i)2 +-- + (xm -«„,)2 < r}
yoki qisqacha,
Br(a} ={xe Rm : р(х,й) < r}
to'plam markazi a nuqta, radiusi r bo'lgan shar (m o‘lchovli shar)
deyiladi.
Quyidagi
Br (a) = {x e Rw : p(x, a) < r}
to‘plam Rm fazoda yopiq shar,
B, (a) = {xe Rm : p(x,a) = r}
to‘plam esa Rm fazoda sfera (m o‘lchovli sfera) deyiladi.
Ravshanki,
Br(a) = Br(a)uB°r(a) , i.p.
bo‘ladi.
Ushbu
]^[(01,...,йт;/>1Д,...,6т) =
= {(x1,x2,...,xOT)e Rm : ax < x, < l\, < x2 <b2,...,am < xm < bm]
to‘plam Rm fazoda parallelepiped deyiladi, bunda
b2,-..,bm — haqiqiy sonlar.
18
2°. Rm fazoda nuqtaning atrofi. Biror x° = (x’.x®,...,x® )e Rm
nuqta hamda £ > 0 son berilgan bo'lsin.
1- ta’rif Markazi x° nuqtada, radiusi £ bo‘lgan Rm fazodagi shar
x°e Rm nuqtaning sferik atrofi deyiladi va £7e(x°) kabi belgilanadi:
t/E (x°) = {x e Rm : p(x, x° ) < e} .
2- ta’rif. Ushbu
J7(8i,82...,8m)={(x1,x2,...,xm)e :
: xf -5i < xt < x? +51; x2° -82 <x2 <x2 + S2,...,x“ -8m <xm< x°m +8m}
parallelepiped x° nuqtaning parallelepipedial atrofi deyiladi va
^8i,52,...,8ffl (x°) kabi belgilanadi, bunda 3j > 0, 82 > 0,5m > 0 .
Rn fazodagi nuqtaning bu atroflari orasidagi munosabatni quyidagi
lemma ifodalaydi.
Lemma. x° e Rm nuqtaning har qanday C/e(x°) sferik atrofi olin-
ganda ham har doim x° nuqtaning shunday (x°) paralle-
lepipedial atrofi topiladiki, bunda
bo'ladi.
Shuningdek, x° nuqtaning har qanday (x°) parallele-
pepidial atrofi olinganda ham har doim x° nuqtaning shunday Ufpfi)
sferik atrofi topiladiki, bunda
(7e (X° ) C (/g]62 gw (X° )
bo'ladi.
◄ x() e Rm nuqtaning sferik atrofi
Uz (x°) = {x e Rm : p(x, x°) < e}
berilgan bo'lsin. Demak, e > 0 son berilgan. Unga ko'ra 8 < -~
dm
tengsizlikni qanoatlantiruvchi 8 sonni olib, x° nuqtaning ushbu
f76(x()) = t76o 6(x°) = {(x),x2,...,xm)e Rm :
: xf - 5 < X] < X!0 + 8, x2 - 5 < x2 < x2 + 8,..., x® - 8 < xm < x° + 8}
19
I
parallelepipedial atrofmi tuzamiz. Natijada x° nuqtaning
UJx°) va Us (x°)
atroflariga ega bo‘lamiz.
Aytaylik, Vx e tZs(x°) bo‘lsin. U holda i
|xA - x® | < 5, (A = 1,2,..., m)
bo‘lib,
Jm / tn
~Xk^ = 8 ^
k=\ V k=l
bo‘ladi. Yuqoridagi 3 < ~^= tengsizlikni e’tiborga olib topamiz:
Ж<Хк-4)2 <E.
V k=l
Demak, p(x,x0)<e bo‘lib, xef/E(x°) bo'ladi. Bundan
t7s(x°) c lZE(x°)
bo‘lishi kelib chiqadi.
x° e Rm nuqtaning parallelepipedial atrofi
^8]82-8m (X° ) = {(Xl ’ ^2 >Xm ) G '•
: xi°-8j <%j <x1°+SI,x20-S<x2 < x2°+63...., x^,-8m < xm < x"+5m
berilgan bo‘lsin. Berilgan 8j ,32 musbat sonlar yordamida
e = min
sonini topib, x° nuqtaning ushbu
U£ (x°) - {x e Rm : p(x, x°) < e}
sferik atrofmi tuzamiz. Natijada x° nuqtaning
t/E(x°) va f7S152...5m (x°)
atroflariga ega bo'lamiz.
20
Aytaylik, Vxg U£(x°) bo‘lsin. U holda
m
p(x,x°) = -x^)2 <£< 8fc, (k = 1,2,...,m)
V A=1
bo‘lib,
k-^°l<8^ (k = l,2,...,m)
bo'ladi. Bundan esa x e USlS &m (x°) bo‘lishi kelib chiqadi. Demak,
Bu lemma Rm fazo nuqtasining bir atrofidan ikkinchi atrofiga
o‘tish imkonini beradi.
3°. R"' fazoda ochiq va yopiq to‘plamlar. Aytaylik, Rm fazoda
biror G to‘plam (Gc Rm) berilgan bo‘lib, x° g G bo‘lsin.
Agar x° nuqta G to'plamga tegishli bo‘lgan t/E(x°) atrofga ega
bo‘lsa, (t/e(x°) c G) x0 nuqta G to‘plamning ichki nuqtasi deyiladi.
3- ta’rif. G to‘plamning har bir nuqtasi uning ichki nuqtasi bo‘lsa,
u ochiq to ‘plant deyiladi.
1- misol. R" fazodagi ushbu
Br (a) = {x g Rm : p(x, a) < r}
shaming ochiq to'plam ekanligi ko‘rsatilsin.
◄ Vx° g Br (a) nuqtani olamiz. Unda
r -p(x° ,a)
miqdor musbat bo‘ladi. Uni 5 deylik:
3 = r - p(x°, a) (22-chizma).
Endi x° nuqtaning ushbu
U8(x°) ={xg Rm :p(x,x°)<8}
atrofini qaraymiz.
Bunda и5(х°) c Br(a) bo'ladi. Haqi-
qatan ham,
22- chizma.
Vx g t/s (x°) => p(x, x°) < 8
21
bo'lib, masofaning 3- xossasiga ko'ra
p(x, a) < p(x, x°) + p(x°, a) < 8 + p(x°, a) = r
bo'ladi. Demak,
Vx e U& (x°) => x e Br (x°) •
Bundan t/5(x°) c 2?r(x°) bo'lishi kelib chiqadi.
Demak, Br(a) to'plamning har bir nuqtasi uning ichki nuqtasi
bo'ladi. Binobarin, Br(a) — ochiq to'plam. ►
Aytaylik, FcRm to'plam hamda x° g Rm nuqta berilgan bo'l-
sin. Agar x° nuqtaning ixtiyoriy t/e(x°) atrofida (Ve > 0) Fto'plamning
x° dan farqli kamida bitta nuqtasi bo'lsa, x° nuqta F to'plamning
limit nuqtasi deyiladi.
Masalan, ushbu
Br (a) = {x g Rm : p(x, a) < r}
to'plamning har bir nuqtasi uning limit nuqtasi bo'ladi. Ayni paytda,
B® = {xg Rm : p(x, a) = r}
to'plamning barcha nuqtalari ham shu Br(a) to'plamning limit nuqtasi
bo'ladi. Biroq, bu limit nuqtalar Br (a) to'plamga tegishli bo'lmaydi.
4- ta’rif. Agar F c Rm to'plamning barcha limit nuqtalari shu
to'plamga tegishli bo'lsa, F yopiq to ‘plant deyiladi.
Masalan,
Br (a) = {x g Rm : p(x, a) < r}
to'plam (7Г fazodagi yopiq shar) yopiq to'plam bo'ladi
Biror M c Rm to'plam hamda x° g Rm nuqtani qaraylik.
Agar x° nuqtaning ixtiyoriy Ц(х°) atrofida ham M to'plamning,
ham Rm\M to'plamning nuqtalari bo'lsa, x° nuqta M to'plamning
chegaraviy nuqtasi deyiladi. Mto'plamning barcha chegaraviy nuqtalari
uning chegarasini tashkil etadi. M to'plamning chegarasi Э(Л/) kabi
belgilanadi. Masalan,
B? («) = {x g Rm : p(x, a) = r}
to'plam
Br (a) ~{xe Rm : p(x, a) < r}
22
to‘plamning chegarasi bo‘ladi:
Э(/?») = 5°(й).
Agar FcRm to'plamning chegarasi d(M) shu to‘plamga tegishli
bo'lsa, Fyopiq to‘plam bo‘ladi. Masalan,
Br (o) = {x e Rm : p(x, a) < r}
yopiq to'plam bo‘ladi, chunki
Э(Я(«)) = 5°(Й)СЯ(«)-
4°. R m fazoda to‘g‘ri chiziq va kesma. Faraz qilaylik, Rm fazoda
a = (al,a2,...,am), b = (b^,...^)
nuqtalar berilgan bo‘lsin. Bu nuqtalar koordinatalari yordamida quyidagi
X] = axt + b{ (1 -1),
x2 = a2t + (1 - t),
..................................... (4)
xm = amt + bm(l- /)
ni tuzib, (bunda fe R) t o‘zgaruvchiga bog‘liq bolgan Rm fazoning
x = (x1,x2,...,xm)
huqtalarini hosil qilamiz. Bunday nuqtalar to‘plami
{x = (x1 ,x2 ,...,хт) 6 Rm : X] = art + fy (1 -1),
x2 = a2t + fy (1 - t) ,...,xm - amt + fy„ (1 - /), t e 7?}
Rm fazoda a = ^al,a2,...,am) va = (fy,fy,...,fy;) nuqtalar orqali
o‘tuvchi to‘g‘ri chiziq deyiladi.
Endi yuqoridagi a va b nuqtalarning koordinatalari yordamida
tuzilgan (4) munosabatda 0 < t < 1 bo‘lsin. Rm fazoning bunday nuq-
talari to‘plami
{x - (xj ,x2 ,...,xm) e Rm : xt - axt + fy (1 -1), x2 = a2t + fy (1 -1),
...,xn, =amt + bm(X-t), 0 < t < 1}
Л7" fazoda a va b nuqtalarni birlashtiruvchi to^'ri chiziq kesmasi
deyiladi.
23
Rm fazoda chekli sondagi nuqtalar berilgan bo‘lsin. Bu nuqtalarni
birin-ketin to‘g‘ri chiziq kesmalari bilan birlashtirishdan tashkil topgan
chiziq siniq chiziq deyiladi.
Agar M c Rm to'plamning ixtiyoriy ikki nuqtasini birlashitruvchi
shunday siniq chiziq topilsaki, u ushbu M to'plamga tegishli bo'lsa,
M bog'lamli to'plam deyiladi.
5- ta’rif. Agar M cz Rm to'plam ochiq hamda bog'lamli to'plam
bo'lsa, u soha deyiladi. Masalan,
Br(a) = {xe Rm :p(x, <?)</•}
to'plam soha bo'ladi.
5°. Xususiy hollar, m = 1 bo'lganda Rm = R bo'lib, u barcha
haqiqiy sonlardan iborat to'plam bo'ladi. Bu to'plamning har bir
element! to'g'ri chiziq nuqtasini, to'plamning o'zi esa to'g'ri chiziqni
ifodalaydi.
Ikki x e R, у e R nuqtalar orasidagi masofa
p(x,y) = \x-y\,
xoe R nuqtaning atrofi
IZE (x0) = {x e R : p(x, x0) < e} = (x0 - e, x0 + e)
bo'ladi.
m = 2 bo'lganda Rm = R2 bo'lib, u barcha tekislik nuqtalaridan
iborat to'plam bo'ladi. Bu to'plamning ikki x = (x1; x2), у — (y1; y2)
nuqtalari orasidagi masofa
р(х,у) = у/(У1-х1)2 + (y2 -x2)2 ,
x° = (*o, У о) nuqtaning sferik atrofi
C/e(x°) ={(x,y)e R2 : p((x,y), (х0,у0))<е} =
= {(x,y) e R2 : ^(x ~ x(> f +(y-y0)2 < e}
bo'ladi.
R2 fazoda ushbu
{(x, y) 6 R2 : p ((x, y), (x0, y0)) < r}
to'plam ochiq, quyidagi
24
Y
23- chizma.
{(x, y) e R2 : x > 0, у > 0, x + у < 1}
to'plam esa yopiq to'plam bo‘ladi. Ular 23- chizmada tavsirlangan.
Mashqlar
1. Agar G{ c Rm, G2 c Rm ochiq to‘plamlar bo‘lsa,
Gj u Rm, G2 rx Rm
to‘plamlarning ochiq to‘plam bo‘lishi ko‘rsatilsin.
2. Agar Ft c Rm, F2 c Rm yopiq to‘plamlar bo‘lsa,
Fx u Rm, F2 n Rm
to‘plamlaming yopiq to‘plam bo‘lishi ko‘rsatilsin.
56- ma’ruza
Rm fazoda ketma-ketlik va uning limiti
Г. Rm fazoda ketma-ketlik va lining limiti tushunchalari. Aytaylik,
biror qoidaga ko‘ra har bir natural son n ga Rm fazoning bitta
(/7 = 1,2,...)
nuqtasi mos qo‘yilgan bo‘lsin. Bu moslik natijasida Rm fazo nuqtala-
ridan tashkil topgan ushbu
/ (1) (1) (1) \ /v-(2) v-(2)
25
yoki qisqacha,
(1) (2) Y(«)
to‘plam hosil bo‘ladi. Uni Я"1 fazoda ketma-ketlik deyilib, {x*"’} kabi
belgilanadi. Demak, {x0^} ketma-ketlikning hadlari A'"fazo nuqtalari-
dan iborat bo'lib, bu nuqtalaming koordinatalari tn ta ;
W"’}. H”’}. U"’}, =
sonlar ketma-ketliklarini yuzaga keltiradi.
Faraz qilaylik, Rm fazoda {x(n)}:
x(I),x(2), (1)
ketma-ketlik hamda
a = (л, ,O2,...,am) g Rm
nuqta berilgan bo'lsin.
1- ta’rif. Agar Ve > 0 olinganda ham shunday n0 e N son topilsaki,
barcha n > n0 uchun
p(x("\fl) < £ ,
ya’ni
Ve > 0, g N, Vn>n0: p(x("\fl)<£
bo‘lsa, a nuqta {x(n)} ketma-ketlikning limiti deyiladi va
lim xw = a yoki n -> °° da х(л) -> a
kabi belgilanadi.
V« > л0 da
p(x("\ fl) < s
tengsizlikning bajarilishi, (1) ketma-ketlikning n0 dan katta nomerli
hadlari a nuqtaning Ц(а) atrofiga tegishli bo'lishini bildiradi. Bu hoi
(1) ketma-ketlikning limitini quyidagicha ta’riflash imkonini beradi.
2- ta’rif. Agar ae Rm nuqtaning ixtiyoriy Ufa) atrofi olinganda
ham, {x<n)} ketma-ketlikning biror hadidan keyingi barcha hadlari shu
atrofga tegishli bo‘lsa, a nuqta {x(H)} ketma-ketlikning limiti deyiladi.
1- misol. Rm fazoda ushbu {x(,,)} = I-, -,..., -1 ketma-ketlik-
n nj
ning limiti a = (0, 0, ..., 0) bo‘lishi ko'rsatilsin.
26
◄ Ve > 0 sonini olib, unga ко‘га =
+1 ni topamiz.
U holda V« > n0 uchun
p(x(n),«) = p[-, ...., (0,0,...,0))= =
\n n n] n -Jm
bo‘ladi. Demak, lim x(n) = a. ►
2°. Ketma-ketlik limitining mavjudligi. Faraz qilaylik, Rm fazoda
{хЯ} ketma-ketlik va a e Rm nuqta berilgan bo'lsin.
1- teorema. Agar Rm fazoda
x(n> =(x[n\x^,...,x^), (« = 1,2,...)
ketma-ketlik a =
limitga ega bo‘lsa: lim x(n) = a ,
u holda lim X](n) = <2], lim x^n) = a2, lim x(mn) = am
bo‘ladi.
4 Aytaylik lim x*n> = a bo‘lsin. Limit ta’rifiga binoan \/n > n0 e N
uchun
x(n)e UE (a) = {x 6 Rm : p(x, a) < e}, ( Ve > 0)
bo'ladi. Ravshanki,
UE (a) a Ut (a),
bunda
27
Uz(a) ={(xl,x2,...,xm)e Rm :
ц - e < Xj < й] + £, a2 - e < x2 < a2 + e, am - г <xm <am + e}.
Keying! munosabatlardan, Vn > n0 uchun
й] - e < x{n) < ц + E,
a2 - г < x2n) < a2 + s,
am - e < 4n) < am +
ya’ni jx^* — £?j | < e ,
|Х2И) “ «2 | < e ,
|4w)-om|<£
bo‘lishini topamiz. Bundan esa
lim x.(,!) = «],
A7->oo
lim x^ = a2,
bo'lishi kelib chiqadi. ►
2- teorema. Agar Rm fazodagi
{х"} = {(х1(л), x*n), x^)}, (n = l,2.„)
ketma-ketlik va a - (a^, a2,am) nuqta uchun
lim x.(n) = ax,
lim x^n) = a2,
lim x£n) = am
28
bo‘lsa, u holda {x<")} ketma-ketlik limitga ega bo‘lib,
lim x(n) = a
bo'ladi.
< Teoremaning sharti hamda limit ta’rifidan foydalanib topamiz:
lim x.(n) - ax => Ve > О, e N, Vn> : |x^") - ц I < -4= ,
। ' yjm 9
lim x^ = a2 => Ve > 0, 3/^2) e N, \fn> л£2) : - a21 < ~,
n->o° I I dm
limx^”) = am => Ve > 0, e N, X/n> : Ix^ ~ am\< ~
i 1 dm
bo‘ladi.
Agar
«0 = max^'1' , «o2\ , «om)}
deyilsa, u holda V« > nQ da bir yo‘la
|xl”) - ak I < d=, {k = \,2,...,ni)
1 ' dfn
tengsizliklar bajariladi. U holda
Jm I m , \2
W>-^<k + = = ,
ya’ni
p(x(n),a) < e
bo‘ladi. Demak,
lim = a. ►
Bu teoremalardan quyidagi tasdiq kelib chiqadi.
Rm fazoda {x(w)} = {(x1("), x(2n), x^0)} ketma-ketlik
a = (oj, a2,am) limit:
lim x(") - a
29
ga ega bo'lishi uchun bir yo'la
limx,(") =o1;
lim x2n) = a2,
lim 4й) = am
bo'lishi zarur va yetarli.
Bu muhim tasdiq bo'lib, u Rm fazodagi ketma-ketliklar limitlarini
o'rganishni sonlar ketma-ketliklar limitlarini o'rganishga olib keladi.
Sonlar ketma-ketliklarining limiti esa 6—8- ma’ruzalarda batafsil bayon
etilgan.
Agar (1) ketma-ketlik limitga ega bo'lsa, u yaqinlashuvchi ketma-
ketlik deyiladi.
Yuqorida keltirilgan tasdiqdan foydalanib, isbotlanadigan muhim
teoremani keltiramiz. Awalo Rm fazoda ketma-ketlikning fundamen-
talligini ta’riflaymiz.
3- ta’rif. Rm fazoda {Y"*} ketma-ketlik berilgan bo'lsin. Agar Ve > 0
olinganda ham shunday nQ e N topilsaki, V«> n0, VP> nQ lar uchun
p(x("\ x(P))<e
tengsizlik bajarilsa, {Yn)} fundamental ketma-ketlik deyiladi.
3- teorema. (Koshi teoremasi) {x^} ketma-ketlikning yaqinlashuv-
chi bo'lishi uchun uning fundamental bo'lishi zarur va yetarli.
Bu teorema 9- ma’ruzada keltirilgan 3- teorema kabi isbotlanadi.
3°. Ichma-ich joylashgan yopiq sharlar prinsipi. R" fazoda mar-
kazlari
=(й}п),^л),...,4п)), (и =1,2,...)
nuqtalarda, radiuslari rn > 0 (n = 1,2,...) bo'lgan ushbu
Bt = Br, (a(l)) = [re Rm : p(x, },
B2 = ВГг (a(2)) = {% e Rm : p(x, a(V>) < r2},
Bn = Brn (aw ) = p(x, },
30
yopiq sharlar ketma-ketligini qaraylik. Agar bu yopiq sharlar ketma-
ketligining hadlari uchun quyidagi
Bx => B2 z> ... з Bn =>...
munosabat o‘rinli bo‘lsa, {Bn} ichma-ich joylashgan yopiq sharlar
ketma-ketligi deyiladi.
Aytaylik, {Bn} Rm fazoda ichma-ich joylashgan yopiq sharlar
ketma-ketligi bo‘lsin.
4- teorema. Agar n -» °° da shar radiuslari rn nolga intilsa, ya’ni
lim rn = 0
И—
bo‘lsa, u holda barcha yopiq sharlarga tegishli bo‘lgan a nuqta (a e Rm)
mavjud va u yagona bo‘ladi.
◄ Shar markazlaridan tuzilgan
{a(n)}, (a(n) e Rm, и = 1,2,..)
ketma-ketlikni qaraylik. Uning fundamental ketma-ketlik bo‘lishini
ko‘rsatamiz.
Shartga ko‘ra lim rn = 0. U holda
Ve > 0, 3/Tq e N, n > n() : rn < e
bo‘ladi. Ayni paytda, yopiq sharlar ichma-ich joylashganligidan ixtiyoriy
P > n > л0
uchun Brf (a(P) п ВГп(а(п)))
bo‘lib, p (a("), ) < rp < £ bo‘ladi.
Demak, {<7<и)} — fundamental ketma-ketlik. U holda Koshi teo-
remasiga ko‘ra u yaqinlashuvchi bo‘ladi:
lima(n)=a, (ae Rm).
Bu о nuqta ВГп(ам) to‘plamning limit nuqtasi va ВГп(ам) yopiq
bo‘lganligi uchun as ВГп (a^) , (л=1,2,...) bo‘ladi. Demak, a — bar-
cha sharlarga tegishli bo‘lgan nuqta. Faraz qilaylik, a nuqtadan farqli
barcha sharlarga tegishli bo‘lgan b nuqta (Ac 7?"') mavjud bo‘lsin:
ВГп (a1”1), b ф a. Masofaning 3-xossasidan foydalanib topamiz:
31
p(a, b) < р(а, а(п}) + р(<7(/,) , Ь) < 2г„.
Agar п -» оо da -> 0 bo'lishini e’tiborga olsak, keyingi muno-
sabatdan p(a,b) — 0, ya’ni a = b bo'lishi kelib chiqadi. ►
Odatda, bu teorema ichma-ich joylashgan yopiq sharlar prinsipi
deyiladi.
4°. Qismiy ketma-ketliklar. Bolsano—Veyershtrass teoremasi.
Rm fazoda {x00}:
x(1),x<2),...,xw,...
ketma-ketlik berilgan bo'lsin. Ushbu ketma-ketlik
X<«1) %(«2) x(nk)
bunda nx < n2 < ... < nk < ...; кк g V, k = 1,2,...,
berilgan {Xм} ketma-ketlikning qismiy ketma-ketligi deyiladi va u
{%(^)} kabi belgilanadi. Ravshanki, bitta ketma-ketlikning turlicha
qismiy ketma-ketliklari bo'ladi.
Agar {Xм} ketma-ketlik yaqinlashuvchi bo'lib,
lim = a
2?—» co
bo'lsa, bu ketma-ketlikning har qanday qismiy ketma-ketligi {x(nt)}
ham yaqinlashuvchi bo'lib,
lim x{nk = c.
k—>°°
bo'ladi. Bu tasdiqning isboti ketma-ketlik limiti ta’rifidan bevosita
kelib chiqadi.
Aytaylik, Rm fazoda biror M to'plam berilgan bo'lsin: Me Rm.
Agar Rm fazoda markazi (0,0,...,0) e Rm. radiusi r > 0 bo'lgan shar
U° ={(x15x2,..., xm)e : р^ХрХг,..., xffl), (0, 0,.... 0)) < r}
topilsaki, bunda
Me U°
bo'lsa, M chegaralangan to‘plam deyiladi.
Endi Bolsano-Veyershtrass teoremasini isbotsiz keltiramiz.
5- teorema. (Bolsano-Veyershtrass teoremasi.) Rm fazoda har
qanday chegaralangan ketma-ketlikdan yaqinlashuvchi qismiy ketma-
ketlik ajratish mumkin.
32
5°. Xususiy hollar, m = 1 bo‘lganda Rm = R bo‘lib, undagi
ketma-ketlik sonlar ketma-ketligi bo‘ladi. Ma’lumki, sonlar ketma-
ketligi va uning limiti 6—8- ma’ruzalarda batafsil o‘rganilgan.
m = 2 bo‘lganda Rm = R2 bo‘lib, undagi ketma-ketlik tekislik
nuqtalaridan iborat
(Wi), (x2.,y2(x„, y„),..., (xneR, y„eR, n = 1,2,...)
ketma-ketlik bo‘ladi. Bu ketma-ketlikning limiti {x„} va {y„} sonlar
ketma-ketliklarining limitlari orqali o'rganiladi.
Masalan, ushbu
{(-1"), (-1)"}: (-1,-1), (1,1), (-1,-1), ..., ((-1)", (-1)"), ...
ketma-ketlik limitga ega bo‘lmaydi, chunki
x„=(-l)", y„ = (-!)", (« = 1,2,...)
ketma-ketliklar limitga ega emas.
Mashqlar
1. Agar x° g Rm nuqta Me Rm to'plamning limit nuqtasi bo‘lsa,
M to‘plam elementlaridan tashkil topgan va x° nuqtaga yaqinlasha-
digan
{x^}, (x(n) G №, хм*х0, « = 1,2,...)
ketma-ketlikning mavjudligi ko‘rsatilsin.
2. Agar
limxW=<7, (x(';)GT?m, a e Rm, « = 1,2,...)
bo‘lsa, {х(л)} ketma-ketlikning chegaralanganligi ko‘rsatilsin.
57-ma’ruza
Ko‘p o‘zgaruvchili funksiya va uning limiti
1°. Ko‘p o‘zgaruvchili funksiya tushunchasi. Faraz qilaylik, Rm
fazoda E to‘plam berilgan bo‘lsin: E c RE.
1- ta’rif. Agar E to‘plamdagi har bir x = (Xi, x2,...xm) nuqtaga
biror f qoidaga ko‘ra bitta haqiqiy и son mos qo‘yilgan bo‘lsa, E to‘p-
33
lamda ko‘p o‘zgaravchili (mta o‘zgaruvchili) funksiya berilgan (aniq-
langan) deyiladi. Uni
f : x = (x},x2,...,xm) -> и yoki и = f(x) = f(xi,x2,...,xm)
(x = (x1;x2,...,xm)e Rm, u<= R)
kabi belgilanadi. Bunda E — funksiyaning berilish (aniqlanish) to‘p-
lami, x15 x2, xm (erkli o‘zgaruchilar) — funksiya argumentlari,
и esa Xj, x2, ..., xm laming funksiyasi deyiladi.
Masalan, f— har bir
x = (X| ,x2 ,...xm) e M,
M = {x^ Rm : p(x,0)<l}
nuqtaga ushbu
(Xi, x2,..., x„,) -» 71 - *12 - x2 -...
qoida bilan bitta haqiqiy и sonini mos qo‘ysin. Bu holda M cz Rm
to‘plamda aniqlangan
funksiya hosil bo‘ladi.
Aytaylik, u = f(xx ,x2 ,...,xm) funksiya (ko‘p hollarda bu funk-
siyani и ~ /(x) kabi yozamiz) Ec Rm to‘plamda berilgan bo‘lsin.
x° - (xf, x2,..., x® ) e E nuqtaga mos keluvchi w0 son и = /(x)
funksiyaning x° nuqtadagi xususiy qiymati deyiladi: .
Berilgan funksiyaning barcha xususiy qiymatlaridan iborat ushbu
{и = /(x): хе E} (I)
sonlar to‘plami и = f(x) funksiya qiymatlari to‘plami deyiladi. Agar
(1) to‘plam chegaralangan bo‘lsa, и - /(x) = f(.x}, x2,..., xm) funk-
siya E to‘plamda chegaralangan deyiladi.
7?m+1 fazodagi ushbu
{(x,/(x)) : X = (x!,x2,...xm)e Rm, /(x) e R}
to‘plam ko‘p o‘zgaruvchili u- f(xl,x2,...,xm) funksiyaning grafigi
deyiladi.
34
Faraz qilaylik, yuqorida qaralayotgan f(x{, x2,..., xm) funksiyada
X] = ф1 (?) =
X2 = <p2(t) = Ф2('1Л>-Л),
=<pm(0 = фт(М2>-Л)
bo‘lsin, bunda tp,(r) funksiya (i = T c Rk to'plamda
aniqlangan bo'lib, t = (tx,t2,—,tk) e T bo'lganda unga mos
x = (xl,x2, ...xm) e E bo'lsin. Natijada
/(x(0) = ?J,q>2(?i,..., tk),.... tkf) = F(f,t2,...,tf)
funksiya hosil bo'ladi. Uni murakkab funksiya deyiladi.
2°. Ko‘p o'zgaruvchili fiinksiya limiti (karrali limiti) ta’riflari.
Faraz qilaylik, f (x) funksiya (x e Rm) E c Rm to'plamda berilgan,
x° e Rm nuqta E ning limit nuqtasi bo'lsin. U holda Rm fazoda
shunday {x00}:
r(l) y(2) „(»)
л. ? ; ... 7 Л j...
ketma-ketlik topiladiki, bunda
1) N da xw e E, х(и) * x° ;
2) n -» oo da x(n) x°
bo'ladi (bunday ketma-ketliklar istalgancha bo'ladi).
2- ta’rif. (Geyne ta’riif.) Agar
1) e N da x(fl) e E, x(n) Ф x°;
2) w -> oo da х(и) -» x°
shartlarni qanoatlantiruvchi ixtiyoriy {х(л)} ketma-ketlik uchun
и-» oo da /(х(л)) -^A P
bo'lsa, rison fix)- /(x!,x2,....,xm) funksiyaning x° =(xi,x2,x®)
nuqtadagi limiti (karrali limiti) deyiladi. Uni lim f (x) = A yoki
35
lamda ko‘p o‘zgaruvchili (mta o‘zgaruvchili) funksiya berilgan (aniq-
langan) deyiladi. Uni
f : x = (x1,x2,...,xm) -> и yoki и = /(x) = /(^ ,x2
(x = (x1,x2,...,xm)e Rm, ue R)
kabi belgilanadi. Bunda E — funksiyaning berilish (aniqlanish) to‘p-
lami, Xj, x2, ..., xm (erkli o'zgaruchilar) — funksiya argumentlari,
и esa хь x2, ..., xm laming funksiyasi deyiladi.
Masalan,/— har bir
x = (X],x2,...xffl)g M,
M = {xe Rm : p(x,0)<l}
nuqtaga ushbu
(Xi ,x2,...,xm) -> 7^- Xi - x2 -TZxJ"
qoida bilan bitta haqiqiy и sonini mos qo'ysin. Bu holda Mc Rm
to‘plamda aniqlangan
и = Jl - x2 - x2 -... - x2,
funksiya hosil bo‘ladi.
Aytaylik, u = /(xj ,x2 ,...,xm) funksiya (ko‘p hollarda bu funk-
siyani и = /(x) kabi yozamiz) Ec Rm to‘plamda berilgan bo‘lsin.
x° - (Xj0, x2,..., x° ) g E nuqtaga mos keluvchi u0 son и = /(x)
funksiyaning x° nuqtadagi xususiy qiymati deyiladi: .
Berilgan funksiyaning barcha xususiy qiymatlaridan iborat ushbu
[u = /(x): xg E} (1)
sonlar to‘plami « = /(x) funksiya qiymatlari to‘plami deyiladi. Agar
(1) to‘plam chegaralangan bo‘lsa, u- f(x) = /(X] ,x2 ,...,xm) funk-
siya E to‘plamda chegaralangan deyiladi.
Rm+X fazodagi ushbu
{(x,/(x)) : x = (xt,x2,...xm)G Rm, /(x)g 7?}
to‘plam ko‘p o‘zgaruvchili и - f(x1,x2,...,x>„) funksiyaning grafigi
deyiladi.
34
Faraz qilaylik, yuqorida qaralayotgan f(x}, x2,..., xm) funksiyada
*1 = ф1(/) =
x2 = <p2 (Z) = <p2 (Zj, Z2,
=фт(0 = фт(М2>-Л)
bo'lsin, bunda <p, (t) funksiya (z = 1,2,..., m) T c Rk to'plamda
aniqlangan bo‘lib, Z = (f ,t2,...,iA) e T bo‘lganda unga mos
x = (xj ,x2 ,...xm) e E bo‘lsin. Natijada
/(x(Z)) = /(<p1(Z1,...,Zj,<p2(Z1,...,Zj,....,(pm(i1,...,Z)t)) = F(tx,t2,...,tk)
funksiya hosil bo‘ladi. Uni murakkab funksiya deyiladi.
2°. Ko‘p o‘zgaruvchili funksiya limiti (karrali limiti) ta’riflari.
Faraz qilaylik, fix) funksiya (x e Rm) E c Rm to‘plamda berilgan,
x° 6 Rm nuqta E ning limit nuqtasi bo'lsin. U holda Rm fazoda
shunday {х<и)}:
Y(l) y(2) Y(n)
Л' j -A- j *" * ? 3 * * *
ketma-ketlik topiladiki, bunda
1) Vn e N da x(w) e E, x(n) * x° ;
2) n -> oo da x(n) x°
bo‘ladi (bunday ketma-ketliklar istalgancha bo'ladi).
2- ta’rif. (Geyne ta’riif.) Agar
1) e N da х(и) e E, x(ri) Ф x°;
2) n —> oo da х(п) -и» x°
shartlarni qanoatlantiruvchi ixtiyoriy {х(и)} ketma-ketlik uchun
noo da /(x"” )-^ri
bo‘lsa, A son /(x) = f <X[, x2xm) funksiyaning x° = (x°, x2,x°)
nuqtadagi limiti (karrali limiti) deyiladi. Uni lim /(x) = A yoki
V___v-Q
35
lirn/(x1,x2,...,xm) = И
%! -> x?
x2 -» x2°
Xm Xm
kabi belgilanadi.
E s I a t m a. Agar
{x(,?)}, (х(п) е E, Xм x°, л = 1,2,...),
{/"’}, (?w) G E, y(n) *x°, л = 1,2,...)
ketma-ketliklar uchun и « da
x(n) xf /«) _> x°
bo‘lib,
fix(n))—>A, A* В
bo‘lsa, fix) funksiya x° nuqtada limitga ega bo‘lmaydi.
3- ta’rif. (Koshi ta’rifi.) Agar Ve> 0 son olinganda ham shunday
8 = 8(e) > 0 topilsaki, 0 < p(x, x°) < £ tengsizlikni qanoatlantiruv-
chi Vxg E (E cRf da
\f(x) - Л| < £
tengsizlik bajarilsa, A son f (x) funksiyaning x° nuqtadagi limiti (karrali
limiti) deyiladi.
Bu ta’rifni qisqacha qilib quyidagicha ham aytsa bo'ladi. Agar
Ve > 0, 38 > 0, Vx e E n (t/8(x°) \ {x0}): /(x) /1<s
bo‘lsa, A son fix) funksiyaning x° nuqtadagi limiti deyiladi.
3°. Funksiya limitining mavjudligi. Faraz qilaylik, /(x) =
= f ixl,x2,--.-,xm) funksiya E e Rm to‘plamda berilgan bo‘lib,
x° = (X]°, x2,..., x°) nuqta E to‘plamning limit nuqtasi bo‘lsin.
1- teorema. (Koshi teoremasi.) fix) funksiya x° nuqtada limitga
ega bo‘lishi uchun Ve > 0 son olinganda ham shunday 8 > 0 son
topilib,
36
\/х' g Е n (f/5 (x°) \ {x°}), \/x" e E n (t/g (x°) \ {x°})
nuqtalarda
1/(0-/(O|<£
tengsizlikning bajarilishi zarur va yetarli.
◄ Zarurligi. Aytaylik, /(x) funksiya x° nuqtada A limitga ega bo‘lsm:
lim /(x) = A
x—>x
Limit ta’rifiga ko‘ra,
Ve > 0, 38 > 0, Vxe £ n (£s(x°) \ {x0}) :
|/(x) -A\ < |
bo‘ladi. Jumladan,
x'g £n(£s(x°)\ {x°}), x"g £ n (t/g(x°) \ {x°}):
nuqtalar uchun
)/(x')-Aj<|, !/(О-Л|<|
bo‘ladi.
Keyingi tengsizliklardan
|/(O - /(x') j < | f{x ) - A | + |/(x") - A\ < e
bo‘lishi kelib chiqadi.
Yetarliligi. Aytaylik, Ve > 0 son olinganda ham shunday 8 > 0 son
topiladiki, bunda
Vx'g £ n (£g(x°) \ {x0}), Vx"g £ n (£g(x°) \ {x0})
nuqtalar uchun
tengsizlik bajariladi.
x° nuqtaga intiluvchi ikkita [x1’"' }, {y(n)} ketma-ketliklami ola-
miz: л -> oo da
x<"'^x°, (x(n)e£, w = l,2,...),
yw^x°, (y(n) g £, y("Ox°, и = 1,2,...).
37
Bu ketma-ketliklar hadlaridan foydalanib, ushbu
x(1>, y(1), x(2), ym, ..., Xм, y(n\ ...
ketma-ketlikni hosil qilamiz. Uni {^n)} ketma-ketlik deylik. Ravshanki,
bu ketma-ketlikning ham limiti x° bo'ladi: n —> °° da
z(n)-+x°, z(n)*x°, w-1,2,...),
Limit ta’rifiga binoan yuqoridagi 8 > 0 songa ko‘ra shunday n0 e N
topiladiki, > n°, Vm > n° da
Z^eE^U6(x°)\{x°}),
e £n(C7s(x0)\{*0})
boladi.
Teoremaning shartidan
|/(z("))-/(?"'))!<e
tengsizlikning bajarilishi kelib chiqadi. Demak, sonlar ketma-
ketligi fundamental ketma-ketlik bo'ladi. Binobarin, u yaqinlashuvchi:
n -> oo da f{z^} -> A.
U holda n —> co da
f(x^)^A, f(yM)~>A
bo‘lib, funksiya limitining Geyne ta’rifiga ko‘ra
lim f(x) = A
bo‘ladi. ►
4°. Takroriy limitlar. Faraz qilaylik, /(%) = f(x},x2,....,xm) funk-
siya E g Rm to‘plamda berilgan bo‘lib, x° = (x®, x2,..., x°) g Rm
shu E to‘plamning limit nuqtasi bo‘lsin.
m ta Xp x2, xm o‘zgaruvchilarga bogliq bo‘lgan f(x} ,-.,xm)
funksiyada x2, x3, xm o‘zgaruvchilar tayinlansa, ravshanki, u bitta
хл o‘zgaruvchining funksiyasiga aylanadi. Aytaylik, bu funksiya
X! -» x® da limitga ega bo‘lsin:
lim /(х1,х2,...,хт) = ф1(л^,х3,...,лт).
38
Endi ip1(x2,x3,...,xm) funksiyada x3, x4, xm o'zgaruvchilar
tayinlanib, so'ngra x2 x2 limitga o‘tilsa,
lim (pi (x2 ,x3,xm) = (p2 (*з > * > •••> )
bo‘lib, berilgan funksiyaning
Um lim f(xl,x2,...,xm)
x2-^x2 %!-«]
limiti hosil bo'ladi.
Xuddi shunga o‘xshash f(x}, x2,xm) funksiyaning
\ \ , > \
o‘zgaruvchilari mos ravishda x“, x° ,x? larga intilgandagi limiti
limo ... limo /(x^,...^)
Xik ~’X,k \
ni ham qarash mumkin.
Odatda, bu limitlar f(xx, x2,..., xm) funksiyaning takroriy Umitlari
deyiladi. f(xl,x2,—,xm') funksiya argumentlari x15 x2, xm lar
mos ravishda х°, x2,..., x“ sonlarga turli tartibda intilganda funk-
siyaning turli takroriy limitlari hosil bo‘ladi.
Ko‘p o'zgaruvchili funksiyaning limiti (karrali limiti) hamda uning
takroriy limitlari turlicha munosabatda bo‘ladi. Ular haqida xususiy
holda, keyingi bandda bayon etamiz.
5°. Xususiy hollar, m = 1 bo'lganda bitta o'zgaruvchiga bog'liq
bo‘lgan R fazodagi biror to‘plamda aniqlangan и = /(x) funksiyaga
ega bo‘lamiz. Bu funksiya va uning limiti 11- va 12-ma’ruzalarda
o‘rganilgan va to‘liq ma’lumotlar keltirilgan.
m = 2bo‘lganda R2 fazodagi (tekislikdagi) biror to‘plamda aniq-
langan ikki o‘zgaruvchiga bog‘liq bo‘lgan u = f(x,y) funksiyaga
ega bo‘lamiz. Masalan,
u = fnQ^+y2-1)
^4-x2-y2
39 i
24- chizma.
Bu funksiyaning aniqlanish to‘plami tekislikning ushbu
x2 + y2 -1 > 0,
4 - x2 — y2 >0
sistemani qanoatlantiradigan nuqtalar to'plami 24- chizmada tasvir-
langan halqani ifodalaydi:
Ikki o'zgaruvchiga bog'liq bo'lgan и = f(x,y) funksiyaning grafigi
umuman R3 fazoda (biz yashab turgan fazoda) sirtni ifodalaydi. Masa-
lan, ushbu
2 2
U - x 4- у
funksiyaning grafigi R3 fazoda 25- chizmada tasvirlangan aylanma
paraboloid bo'ladi.
Aytaylik, f{x, y) funksiya E a R2 to'plamda berilgan bo'lib,
(x0,y0) e R2 nuqta E ning limit nuqtasi bo'lsin. Bu ikki o'zgaruvchili
funksiya limiti ta’riflari quyidagicha bo'ladi:
Agar: 1) Vn e Ada (x„, y„)e E, (x„, y„) * (x0,y0)>
2) n -> oo da (x„, y„) (x0, y0)
shartni qanoatlantiruvchi ixtiyoriy {(x„,y„)} nuqtalar ketma-ketligi uchun
л —> °o da /(x„, y„)-> A
bo'lsa, A son funksiyaning (x0, y0) nuqtadagi limiti (karrali limiti)
deyiladi va
lim f(x,y) = A yoki lim f (x, y) = A
(x,y)-»(x0 Xo)
У~»У0
kabi belgilanadi.
40
Agar Ve > 0 olinganda ham shunday 5 > 0 topilsaki,
0 < p((x,y),(xo,yo)) < $ tengsizlikni qanoatlantiruvchi V(x,yXe E da
|/(х,у)-Л| <E
tengsizlik bajarilsa, A son f (x, y) funksiyaning (x0,y0) nuqtadagi limiti
(karrali limiti) deyiladi.
Berilgan funksiyaning ikkita takroriy limitlari:
lim lim f(x,yY lim lim f(x, y)
X-^XQ y->ya y-,yn
bo'lishi mumkin.
1- misol. Ushbu
f(x,y) =
xy
agar
0 , agar
x2 + y2 ^0 bo‘lsa,
x2 + y2 =0 bo‘lsa
funksiyaning (x, y) -> (0, 0) dagi limiti 0 bo'lishi ko'rsatilsin.
< Koshi ta’rifidan foydalanib topamiz:
Ve > 0 son uchun 8 = 2e deyilsa,
0 < p((x,y),(0, 0))<8
tengsizlikni qanoatlantiruvchi V(x,y)e R2 da
xy
7x2+y2
|/(х,У)-0| =
< |a/x2 +y2 = lp((x,y),(0, 0))< j8 = e
bo‘ladi. Demak,
lim/(x,y) = 0. ►
/(x,y)=
2- misol. Ushbu
x2y2 +(x-y)2
funksiyaning (0, 0) nuqtada limiti mavjud emasligi ko‘rsatilsin.
◄ Ravshanki, bu funksiya
л:\{(0,0)}
to‘plamda aniqlangan va (0, 0) nuqta shu to‘plamning limit nuqtasi.
41
(0,0) nuqtaga intiluvchi 0-ketma-ketliklarni
l\n n}\ I\n n)\
olaylik:
(1, U (0,0), (1,-Д-»(0,0)
\n n) \n n)
(-L 1.) hamda ) nuqtalarda («=1, 2, 3) berilgan funksiya-
\n П/ \n n)
ning qiymatlari
bo‘lib,
bo'ladi. Funksiya lirnitining Geyne ta’rifidan foydalanib, berilgan funk-
siyaning (x, y) -> (0, 0) da limitga ega emasligini topamiz. ►
3- misol. Ushbu
f(x,y) = -
xy
^x2+y2
agar x2 + y2 0 bo'lsa,
0 , agar x2 + y2 =0 bo'lsa
funksiyaning (0,0) da takroriy limitlari topilsin.
◄ Berilgan funksiyaning takroriy limitlarini topamiz:
lim f (x,y) = lim-^—— - 0, limlim/(x,y) - 0,
x->0 x-,0 lx2 +y2
lim f(x,y) = lim = 0, lim lim f(x,y) = 0.
y-»0 y->0 lx2 +y2 x-,0 y-,0
Demak, berilgan funksiyaning (0, 0) nuqtadagi takroriy limitlari bir-
biriga teng bo'lib, ular 0 ga teng. ►
2* y , agar x + 3y ^0 bo'lsa,
4-misol. Ushbu f(x,y) = ^x+3y
0 , agar x + 3y = 0 bo'lsa
funksiyaning (0,0) nuqtadagi takroriy limitlari topilsin.
42
◄ Berilgan funksiyaning takroriy limitlari quyidagicha bo'ladi:
1
3 ’
lim lim 1AA - _ 1;
x-»0 x+3y 3
lim = 2,
x+3y
= 2.
Ayni paytda, berilgan funksiya (x,y) -> (0,0) da limitga (karrali li-
mitga) ega bo‘lmaydi, chunki
(1,1) ->(0,0), (-, l)->(0,0)
\n n] \n n) 4 '
ketma-ketliklar uchun
/1 Ц-1 1
\n ’ nJ 4 4 ’
bo‘lib, ular bir-biriga teng emas.
5-misol. Ushbu
5 4\_ 6
n’ nJ 17
£
17
1x + у sin 1, agar x Ф 0 bo‘lsa,
x
0 , agar x = 0 bo‘lsa
funksiyaning (0,0) nuqtadagi takroriy limitlari topilsin.
◄ Bu funksiya uchun
lim/(x,y) = x, limlim/(x,y) - 0
x->0 y->0
bo‘lib,
lim lim/(x,y)
v-^0 x—>0
esa mavjud bo‘lmaydi.
Ayni paytda, (x, y) -» (0,0) da berilgan funksiyaning limiti (kar-
rali limiti) mavjud bo’ladi, chunki
\f (x, y) - Oj = x + у sin 1
< |x| + |y|, (x Ф 0)
bo‘lib,
lim/(x,y) = 0
bo‘ladi. ►
43
Faraz qilaylik, f (x,y) funksiya R2 fazodagi
E = {(x, y) e A2: |x - x01 < a, |y - y01 < b}
to‘plamda berilgan bo‘lsin.
2- teorema. Agar
1) (x,y) -> (x0,y0) da f(x,y) funksiyaning limiti (karrali limiti)
mavjud va
lim f(x,y) = A;
x-^xr,
У->У0
2) har bir tayinlangan x da
lim f(x,y) = <p(x) (2)
mavjud bo‘lsa, u holda
lim lim f(x,y)
x->xo
takroriy limit mavjud va
lim lim f(x.y)-A
X^Xq y^ya
bo‘ladi.
◄ Aytaylik, lim f(x,y) = A
X->Xq
У-^Уа
bo‘lsin. Limit ta’rifiga binoan, X7e > 0 olinganda ham shunday 8 > 0
topiladiki, ushbu
{(х,у)еЛ2: jx-x0|<8, \y-y0| < 8} с E
to‘plamning barcha (x, y) nuqtalari uchun
|/(х,у)-Л| <£
tengsizlik bajariladi. Keyingi tengsizlikdan, у -» y0 da limitga o‘tib topamiz:
|<p(x) - Л| < E.
Demak, lim q>(x) = A . (3)
(2) va (3) munosabatlardan
lim lim /(x,y) = A
X^XQ y^y0
bo‘lishi kelib chiqadi. ►
44
Xuddi shunga o‘xshash quyidagi teorema isbotlanadi.
3- teorema. Agar:
1) (x,y) -> (x0,y0) da/(x, y) funksiyaning limiti (karrali limiti)
mavjud va
lim f(x,y) = A;
У~»У0
2) har bir tayinlangan у da
lim f(x,y) = ф(у)
У-'>Уп
mavjud bo‘Isa, u holda
lim lim f(x,y)
x-^x0 y-,y»
takroriy limit mavjud va
lim lim f(x,y) = A
X->XQ y->y0
bo‘ladi.
Natija. Agar f(x,y) funksiya uchun bir vaqtda yuqoridagi 2- va
3- teoremalaming shartlari bajarilsa, u holda
lim f(x,y)= lim lim /(x, y) - lim lim f(x, y)
X^XQ y-tya y^ytj x-,xn
У->Уп
bo‘ladi.
Mashqlar
1. Funksiya limiti Geyne va Koshi ta’riflarining ekvivalentligi
ko‘rsatilsin.
2. Limitga ega bo‘lgan funksiyalarning xossalari keltirilsin.
3. Ushbu
lim/(x,y) = A
y->oo
limit ta’riflansin.
4. Ushbu
lim (x2 .y2
X—»+oo
y->+oo
limit hisoblansin.
45
58- ma’ruza
Ko‘p o‘zgaruvchili funksiyaning uzluksizligi.
Tekis uzluksizlik. Kantor teoremasi
1°. Ko‘p o‘zgaruvchili funksiya uzluksizligi tushunchasi. Faraz qi-
laylik, /(x) = /(x15 x2, • ••> funksiya /?'" fazodagi E to'plamda
berilgan bo‘Iib, x° e E nuqta E to'plamning limit nuqtasi bo'lsin.
1- ta’rif. Agar
lim/(x) = /(x°) (1)
bo'lsa,/(x) funksiya x° nuqtada uzluksiz deyiladi.
2- ta’rif. (Geyne ta’rifi.) Agar:
1) Vn g N da xW g E,
2) n -> °° da x(") -» x°
shartlarni qanoatlantiruvchi ixtiyoriy {x00} ketma-ketlik uchun
n -> oo da f (xw) -> f (x°)
bo'lsa,/(x) funksiya x° nuqtada uzluksiz deyiladi.
3- ta’rif (Koshi ta’rifi.). Agar
Ve > 0, 35 > 0, Vx g E П U5(x°), |/(x) -/(x°)| < e
bo'lsa,/(x) funksiya x° nuqtada uzluksiz deyiladi.
Umuman, и = /(x) funksiyaning x° g E nuqtadagi uzluksizligi
quyidagini anglatadi:
Ve > 0, 35 > 0, Vxg £Tl t/8(x°), /(x) g t/e(/(x0)) •
Odatda, ushbu
AU = /(x)-/(X°), (X = (X1,X2,..., Xm), X° =(X]°, ..., x£))
ayirma и =f (x) funksiyaning x° nuqtadagi orttirmasi (to'liq orttirmasi)
deyiladi.
Agar
AXj = X! -xf, Ax2 = x2 -x2°, ..., Axm - xm -x®
deyilsa, u holda
Au = /(X]° + AXi, x2°+Ax2, ..., x® +AxOT)-/(Xi°, x2°,..., x°)
bo'ladi. Yuqoridagi (1) munosabatdan foydalanib quyidagi tasdiqni
ayta olamiz:
46
f (x) funksiya x° nuqtada uzluksiz bo'lishi uchun
lim Ди = 0, ya’ni lim Ди = 0
Axj ->0
Д%2 —>0
Дхт->0
bo‘lishi zarur va yetarli.
Yuqoridagi ta’riflar ekvivalent ta’riflar bo‘ladi.
Agar (1) munosabat bajarilmasa, f (x) funksiya x° nuqtada uzilishga
ega deyiladi.
4-ta'rif. Agar f(x) funksiya E to‘plamning har bir nuqtasida
uzluksiz bo‘lsa, funksiya shu E to‘plamda uzluksiz deyiladi.
Ko‘p o'zgaruvchili funksiyalarda funksiyaning nuqtadagi to‘liq
orttirmasi tushunchasi bilan bir qatorda uning xususiy orttirmalari
tushunchalari ham kiritiladi.
Ushbu
AY| u = /(xf + AXj, xf, x3°,..., x£) - /(x?, xf,..., %),
=/(*1°,х2° +Д^,Лз°,...,х“)- /(xf,xf4),
ayirmalar mos ravishda f (x) funksiyaning x° nuqtadagi Xj, x2,xm
o‘zgaruvchilar bo‘yicha xususiy orttirmalari deyiladi. Ravshanki,
lim Д„, и - 0,
Дг, ->о 1
lim Ди = 0 => to2 ->0
lim Дг, и - 0,
\хг ->0 2
lim Д„ и = 0
Хт
bo‘ladi. Biroq, Д -> 0 da Д^и-»0 (Л = 1,2,...,т) bo‘lishidan
lim Ди = 0
bo‘lishi har doim kelib chiqavermaydi (bunga misol keyingi bandda
keltiriladi).
47
2°. Uzluksiz funksiyalarning sodda xossalari. Faraz qilaylik,/(x)
va #(х) funksiyalar EcR" to‘plamda berilgan bo‘lib, x° e E nuqtada
uzluksiz bo‘lsin. U holda
c /U), /(x)±g(x), /(x)g(x), (g(x°)*0)
funksiyalar ham x° nuqtada uzluksiz bo‘ladi, bunda c = const.
Bu tasdiqning isboti 15- ma’ruzadagi mos tasdiqning isboti kabidir.
Aytaylik,
л-2 =
............................................ (2)
funksiyalarning har biri Me Rk to‘plamda aniqlangan bo'lsin. Bu (2)
munosabat natijasida M to‘plamning har bir t = (/] ,/2 ,...,ZA.) nuq-
tasiga mos keluvchi Rm fazoning x = (xj, x2,xm) nuqtasi hosil bo‘-
ladi. Bunday nuqtalar to‘plamini jEdeylik. Ravshanki, Ec 7?mbo‘ladi.
Faraz qilaylik, E to‘plamda
и = /(x) = f(xl,x2,...,xm)
•funksiya aniqlangan bo‘lsin. Natijada
t <= M —>xeE—>ueR,
ya’ni (tj ,t2 ,--,tk) e M (xi ,x2 ,...,xOT) e E -» и e R bo‘lib,
« = /(x(0) = /(ф1(?1,...,/а),ф2(Г1,...,/а),...,ф„,(/1,...^а))-
= ф(О = ф(г1,/2,...,/а.)
murakkab funksiya hosil bo‘ladi.
1- teorema. Agar
Xi=(pi(t), x2 = <р2(Г),xm = (t =
funksiyalar t° - (tf,..., t°k ) e M cRk nuqtada uzluksiz, и = /(x)
funksiya хй = (x^,.x2 & E a Rm nuqtada (xf = <pj (t°),
x2° = <p2 (t°x° =(pm(t0)) uzluksiz bo‘lsa, u holda /(x(z))=
= /(ф1, ф2,q>m) murakkab funksiya t° nuqtada uzluksiz bo‘ladi.
48
◄ Shartga ko‘ra f(x) funksiya x° nuqtada uzluksiz. U holda ta’-
rifga binoan
Ve > 0, 38 > 0, Vxe £nt/6(x°): \f(x) -/(x°)| < e (3)
bo‘ladi. Ravshanki.
Vx 6 E r\ Us(x°) =$ \x, - xz°| < 8, (i = l,2,...,m) (4)
bo'ladi. Shartga ko‘ra <p.(t) (г = l,2,...,m) funksiyalar t° nuqtada
uzluksiz. Ta’rifga binoan 8 > 0 uchun shunday 8, > 0 topiladiki, bunda
Vie M n Us. (t°): |<pz (i) - ф,- (t° )l < 8
bo'ladi, i = 1,2,...,/и.
Endi min{8], 82,...,8m} = 3 deb olamiz. U holda V/ e M oUs(t°)
va barcha i - 1,2,..., m lar uchun
|ф;(/)-ф,(/°){ < 8 , ya’ni jx,-x,°| < 8
bo'ladi. (3) va (4) munosabatlardan Vi e M n t/s(t°) uchun
|/(x(t))-/(x(Z0)| < e
bo'lishi kelib chiqadi. Demak, murakkab /(x(t)) funksiya t° nuqtada
uzluksiz.
3°; To'plamda uzluksiz bo'lgan funksiyalarning xossalari. Endi
to'plamda uzluksiz bo'lgan funksiyalarning xossalarini keltiramiz.
2- teorema. Agar /(x) funksiya chegaralangan yopiq E a. Rm
to'plamda uzluksiz bo'lsa, funksiya E da chegaralangan bo'ladi.
◄ Aytaylik, funksiya shu E to'plamda chegaralanmagan bo'lsin.
U holda
Voe N, 3xf"’ e E : |/(х<и))1 > n, (n -1,2,...)
bo'ladi. Ravshanki, {x*"’} ketma-ketlik chegaralangan. Bolsano—Veyer-
shtrass teoremasiga ko'ra yaqinlashuvchi
{x(n*’}, (х(Пк)<=Е, к =1,2,...)
qismiy ketma-ketlik mavjud:
к -> °° da x{nk ’ -7 x° va x° e E.
49>!
Ayni paytda, f (x) funksiyaning E da uzluksizligidan
Ada /(^>)4/(x°)
bo‘lishi kelib chiqadi. Bu esa
к -> “° da } )| > nk -> +oo 5
deyilishiga zid. Ziddiyat f (x) funksiyaning E da chegaralanmagan de-
yilishidan kelib chiqdi. Demak, f (x) funksiya E da chegaralangan. ►
3- teorema. Agar/(x) funksiya chegaralangan yopiqEcR"' to‘p-
lamda uzluksiz bo‘lsa, funksiya shu to‘plamda o‘zining aniq yuqori
hamda aniq quyi chegaralariga erishadi, ya’ni
3x(*) e E, sup{/(x)} = /(x(*}),
xeE
e E, inf {/(x)} = /(Xе*’)
xeE
bo‘ladi.
◄ Yuqoridagi teoremaga ko‘ra/(x) funksiya E to‘plamda chega-
ralangan bo‘ladi. U holda bu funksiya aniq chegaralarga ega:
sup {/(x)} = a, inf {/(x)} = b.
xeE x<=^
Aniq yuqori chegara ta’rifiga ko‘ra
Xfne N, Hx(n) e E : a - - < /(х(и)) < a, (n = 1,2,...)
n
bo'ladi. Ravshanki, {x00} chegaralangan ketma-ketlik bo‘lib, undan
{x(n*)} qismiy ketma-ketlik ajratish mumkinki,
к -> oo da x(nk} x(t) va xr) e E (5)
bo‘ladi. Berilgan funksiyaning uzluksizligidan foydalanib topamiz:
da /(х(и^)-^/(x(,)).
Ayni paytda,
Vhe ;V da «- -- < f (x("k)) < a
nk
bo‘lib, undan к —> сю da
f(xink',)—>a (6)
bo‘lishi kelib chiqadi. (5) va (6) munosabatlardan
50
/(хГ)) = fl = sup{/(x)}, (x* g E)
bo'lishini topamiz.
Xuddi shunga o‘xshash
/(Xе*’) = b = inf{/(x)}, (xe‘) e E)
bo‘lishi isbotlanadi. ►
4- teoreraa. Faraz qilaylik, f (x) = f(xx, x2,..., xm) funksiya bog‘-
lainli £c Rm to‘plamda berilgan bo‘lsin.
Agar:
1) /(x) funksiya E da uzluksiz,
2) a = (flj ,a2 g E, b = (Z^ ,b2,...,bm) g E
nuqtalarda turli ishorali qiymatlarga ega:
(/(a) > 0, /(/>) < 0 yoki /(a) < 0, /(£) > 0)
bo‘lsa, u holda shunday c = (cj ,c2,...,cm) g E nuqta topiladiki,
/(c) = 0
bo'ladi.
◄ Aytaylik, /(x) funksiya bog‘lamli EcRm to‘plarnda uzluksiz
bo‘lib,
/(a) < 0, f(b) > 0
bo‘lsin.
E— bog'lamli to'plam. Binobarin, a va b nuqtalami birlashtiruvchi
va shu to‘plamga tegishli siniq chiziq topiladi. Agar bu siniq chiziq
uchlarini ifodalovchi nuqtalarning birida / (x) funksiya nolga aylansa,
teorema isbotlanadi.
Agar siniq chiziq uchlarida /(x) funksiya nolga aylanmasa, u
holda siniq chiziqning shunday kesmasi topiladiki, uning bir uchi
a = da /(o') < 0 , ikkinchi uchi b' = {Ь[,Ь^ ,--,b'm')
da /(//)> 0 bo‘ladi.
Endi /(x) = /(x'j ,x2, ...,xm) ni shu kesma
k = {(%i > xi ’ xm)e Rm ; = a\ + “ й1'),
x2 = a2+г(б2'-а2),..., xm = a;+ t(&;- «;)}
(0 < t < 1) da qaraymiz. U holda
51
f(a{ +t(Jf -af), a2 +t(% -af), a'm + t(b'm - a'm)) = F(f)
bo‘lib, bitta t o‘zgaruvchiga bog‘liq funksiya hosil bo‘ladi. Bu funksiya
[0, 1] segmentda uzluksiz va
F(0) = f(a} < 0, F(l) = f(b') > 0
bo‘ladi. U holda 16- ma’ruzada keltirilgan teoremaga ko‘ra shunday
t0 g (0,1) nuqta topiladiki, bunda
F(to) = 0,
ya’ni
f(a{ + /0(^' -a{), a2+f(lf-a2f a'm + ta{b'm -a'm)) = 0
bo'ladi. Agar
c = a[+t0(b[ - o{), c2 = «2 + to Oh - ch), cm = am + q (b’m - a'm)
deyilsa, u holda c - (q, c2, , cm) e E nuqtada
/(c) = 0
bo‘ladi. ►
5-teorema. Faraz qilaylik, /(x) funksiya bog‘lamli E cz Rm
to'plamda berilgan bo‘lsin. Agar:
1) /(x) funksiya E da uzluksiz,
2) a g E, be E nuqtalarda /(a) = A, f(b) = В
qiymatlarga ega va А * В bo‘Isa, u holda A bilan В orasida har
qanday C son olinsa ham, shunday се E nuqta topiladiki, bunda
/(с) = C
bo‘ladi.
◄ Bu teorema yuqoridagi 4- teorema kabi isbotlanadi. ►
4°. Funksiyaning tekis uzluksizligi. Kantor teoremasi. Aytaylik,
/(x) funksiya Eei Rm to‘plamda berilgan bo‘lsin.
5- ta’rif. Agar Ve > 0 son olinganda ham shunday 5 = 8(e) > 0
son topilsaki,
p(x',x") < 8
tengsizlikni qanoatlantiruvchi ixtiyoriy x'e E, x’ g E uchun
|/(^)-/(^')| <e
tengsizlik bajarilsa, /(x) funksiya E to ‘plamda tekis uzluksiz deyiladi.
52
Agar f(x) funksiya E to‘plamda tekis uzluksiz bo'lsa, u shu
to'plamda uzluksiz bo'ladi.
◄ Haqiqatan ham, yuqoridagi ta’rifda x" nuqta sifatida x° g E
olinsa, funksiyaning x° nuqtada uzluksizligi, binobarin, E to'plamda
uzluksizligi kelib chiqadi. ►
f(x) funksiyaning Ec Rm to'plamda tekis uzluksiz emasligi quyi-
dagicha:
3e0 >0, V5 > 0, Эх' g E, Эх' e E, p(x', x") < 3: |/(x') - /(x')|
ko'rinishda bo'ladi.
6- teorema. (Kantor teoremasi.) Agar f (x) funksiya chegaralangan
yopiq E c Rm to'plamda uzluksiz bo'lsa, funksiya shu to'plamda
tekis uzluksiz bo'ladi.
◄ Faraz qilaylik, /(x) funksiya chegaralangan yopiq Ec Rm
to'plamda uzluksiz bo'lib, u shu to'plamda tekis uzluksiz bo'lmasin.
U holda biror e0 > 0 son va e A uchun E to'plamda
p(x(n),y(ra))<-, (n = 1,2,3,....)
n
tengsizlikni qanoatlantiruvchi shunday
x(n) G E, yw G E
nuqtalar topiladiki, bunda
|/(x(”))-/(/”))|>£o
bo'ladi. Ravshanki,
{x(n)}, (x(n) G E, n = 1,2,3,...)
ketma-ketlik chegaralangan. Undan yaqinlashuvchi qismiy ketma-
ketlik ajratish mumkin:
к -> oo da x(nk) -> x° va x° g E.
Masofa xossasidan foydalanib topamiz:
p(y("t),x0)<p(y("i),x("t)) + p(x("*),x0)< —+ p(x("*),x°).
nk
Keyingi munosabatdan, к -> °° da limitga o'tish bilan
y(nk) -+x°
bo'lishini topamiz. /(x) funksiya E to'plamda, jumladan, x°g£'
nuqtada uzluksiz. U holda к —> °° da
53
/(x<"‘>)-»/(x°), -*/(x°)
bo‘lib, undan
/(x("A >) ->)-> 0
bo‘lishi kelib chiqadi. Bu esa
deb qilingan farazga ziddir. Demak, f (x) funksiya E to‘plamda tekis
uzluksiz. ►
Aytaylik, Rm fazoda biror E to'plam berilgan bo'lsin: Ec Rm.
Ushbu
a- sup p(x', x")
xe£,x'e£
miqdor E to ‘plamning diametri deyiladi.
6- ta’rif. f (x) funksiya £cz Rn to‘plamda aniqlangan bo‘lsin. U holda
»(/,£)= sup {|/(x') -/(x")|}
x'eE,x”eE
son f(x) funksiyaning E to ‘plamdagi tebranishi deyiladi.
Natija. f (x) funksiya chegaralangan yopiq E c Rm to‘plamda
uzluksiz bo'lsa, u holda Ve > 0 son uchun shunday 8 > 0 son topiladiki,
bunda E to‘plamni diametri 8 dan kichik bo‘lgan Ek to‘plamlarga
ajratish mumkin:
u Ek = E, Ekn Ef = 0, (k* i)
к
va har bir Ek da
w(/; Ek) < e
bo‘ladi.
◄ Natijaning shartidan /(x) funksiyaning £to‘plamda tekis uz-
luksizligi kelib chiqadi. U holda ta’rifga binoan Ve > 0 uchun shunday
8 > 0 topiladiki, bunda p(x',x") < 8 tengsizlikni qanoatlantiruvchi
ixtiyoriy x'e E,x" e E nuqtalarda
|/(x") - /(x')| < e
bo‘ladi.
Ravshanki, Vx' e Ek, Vx" e Ek nuqtalar uchun
p(x',x") < 8
54
tengsizlik bajariladi. Demak,
|/(^')-/(x')| <8.
Keyingi tengsizlikdan
sup {|/(x') - /(O|} ,
x'eEi ,x'^Ek
ya’ni
aif;Ek)<E
bo‘lishi kelib chiqadi. ►
5°. Xususiy hollar, m = 1 bo‘lganda Rm = R vabundagi to‘plamda
berilgan funksiyaning uzluksizligi bir o‘zgaruvchili и —fix) funksiya-
ning (x e R, и < R) uzluksizligi bo‘lib, uning xossalari 15—17-ma’-
ruzalarda o‘rganilgan. m = 2 bo‘lganda Rm = R2 va undan M to‘p-
lamda berilgan funksiyaning uzluksizligi, ikki o‘zgaruvchili и — fix,у)
funksiyaning ((x,y) e E cz R2 ,u <= R) uzluksizligi bo‘lib, uning
(x0 , Уо) e E nuqtadagi uzluksizligi quyidagicha bo‘ladi. Agar:
lim f(x,y) = fixQ,yQ)
У~>Уо
/ f
bo‘Isa yoki Ve > 0, 38 > 0, V(x, у) e E c\ Us((x0,y0)): A
\f(x,y)~ f(x0,y0)\< 8
bo‘lsa, yoki V«e N da ixn,yn)e E bo‘lgan va я —> °o da
(x„, y„) (x0, y0) bo‘ladigan ixtiyoriy {(xn, yn)} ketma-ketlik uchun
= /(хо>Уо) bo‘lsa, yoki
lim f(x, y) = lim [fix^ + Ex, y0 + Ay) - /(, Jb )] = 0
Дх-аО Дх->0
Ду-»0 Ду->0
bo‘lsa, fix,у) funksiya (x0, y0) nuqtada uzluksiz bo‘ladi.
1- misol. Ushbu
fix,y) = x + y
funksiyaning R2 da uzluksiz bo‘lishi ko‘rsatilsin.
◄ Ve > 0 sonini olamiz. Unga ko‘ra 8 > 0 soni 8 = | deyilsa, u
holda
p((x,у), (x0,y0)) = 7(х^х0)2 +(У -^o)2 < S
55
tengsizlikni qanoatlantiruvchi V(x,y)e R2 nuqtalarda
\f(x,y) = f(x0,y0)\ = \x + y-(x0+y0)\<
<\x-x0\ + \y-y0\<2^x-x())2 < 23 = e >
bo‘ladi. Bu esa ta’rifga ko‘ra berilgan funksiyaning V(x0,y0)e R2
nuqtada uzluksiz bo‘lishini bildiradi. ►
Aytaylik, f(x,y) funksiya E cz R2 to‘plamda berilgan bo‘lib,
(x0,y0) e E bo‘lsin. Ma’lumki, bu funksiyaning to'liq orttirmasi
A/(*o,y0) = f(xo + Ax, Уо + ДУ) - f(xo >Уо) >
xususiy orttirmalari
Ax/(x0 > Уо ) = f(xQ + Ax, y0) - /(xq , y0),
Aj,/(x0,y0) = /(x0, y0 + Ay) - /(x0, y0)
bo'ladi ((xq + Ax, y0 + Ду) e E, (xq + Ax, y0) e E, (xo, y0 + Ay) g E).
Agar lim A¥/(x0, y0) = 0, I lim A /(x^, y0) = 0
Дх—>0 ^Ду-М)
bo‘lsa, f (x,y) funksiya (x0, y0) nuqtada x o'zgaruvchi bo‘yicha (y o'z-
garuvchi bo‘yicha) uzluksiz deyiladi. Ravshanki, f(x,y) funksiya (x^, y0)
nuqtada uzluksiz bo‘lsa, funksiya shu nuqtada har bir o'zgaruvchisi
bo‘yicha uzluksiz bo'ladi.
Biroq, f(x,y) funksiyaning (x^, y0) nuqtada har bir o'zgaruvchisi
bo'yicha uzluksiz bo'lishidan uning shu nuqtada uzluksiz bo'lishi
har doim ham kelib chiqavermaydi.
2-misol. Ushbu
[-4^-, agar x2+y2^0 bo'lsa,
/(X,y)= X2+y2
[ 0 , agar x2 +y2 =0 bo'lsa
funksiya (0, 0) nuqtada uzluksizlikka tekshirilsin.
◄ Berilgan funksiyaning (0, 0) nuqtadagi xususiy orttirmalari
Ax/(0,0) = /(0 + Ax, 0) - /(0,0) = 0,
A,/(0,0) = /(0,0 + Ay) - /(0,0) = 0
bo'lib,
56
lim A /(0,0) = 0., lim A /(0,0) =0
Ax—>0 Ay—>0 y
bo‘ladi. Demak, f(x,y) funksiya (0, 0) nuqtada har bir o‘zgaruvchisi
bo‘yicha uzluksiz.
Qaralayotgan funksiyaning (0,0) nuqtadagi to‘liq orttirmasi
А/(0, 0) = /(0 + Ax, 0 + Ay) -/(0,0) =
Ax +Ay
bo'ladi. Ushbu
lim Af(0,0)
Дх-»0
Ду-»0
limit mavjud bo'lmaydi, chunki
Ax = - -» 0
n
2
Ay = — —> 0
n
2.1.1
z 44
da Af(0,0) = T-U = l^l
Ax = 1 —> 0
n
Ay = 1 -> 0
n
da A/(0, 0) = = 1 -> 1.
Demak, berilgan funksiya (0, 0) nuqtada uzluksiz bo'lmaydi. ►
3- misol. Ushbu
f(x,y) = ~--------
sin лх+snr ny
funksiyaning uzilish nuqtalari topilsin.
◄ Bu funksiya R2 to‘plamning
sin 7LX = 0,
sin ny = 0
sistemasini qanoatlantiruvchi (x, y) nuqtalarida uzilishga ega. Ravshan-
ki, sistemaning yechimi
{(x,y)el?2; x = neZ, y = meZ}
57
to‘plam nuqtalaridan iborat. Demak, berilgan funksiyaning uzilish nuq-
talari cheksiz ko‘p bo‘lib, ular
{(и,/и)е7?2; «gZ, m g Z}
to'plamni tashkil etadi. ►
Mashqlar
1. Agar biror Ec Rm to‘plam va xc Rm uchun
p(x,£) = infp(x,y)
y<=E
bo‘Isa, ushbu
/(x) = p(x,£)
funksiyaning Rm da uzluksiz bo‘lishi isbotlansin.
2. Ushbu
{2x2V 2 2 n 1
~, agar x + у >0 bo Isa,
0 , agar x = у = 0 bo‘lsa
funksiya uzluksizlikka tekshirilsin.
58
13- в о в
КОТ O‘ZGARUVCHILI FUNKSIYANING HOSILA
VA DIFFERENSIALLARI
59-ma’ruza
Ko‘p o‘zgaruvchili funksiyaning xususiy hosilalari.
Funksiyaning differensiallanuvchanligi
1°.. Funksiyaning xususiy hosilalari tushunchasi. Faraz qilaylik,
/(x) = f(xl,x2,...,xm') funksiy Ec Rmto‘plamda berilgan bo'lib,
x° = (X]0,x2°,...,x° )g E, (X]° + A*1, x2°,..., x° )e E, (Axj |0)
bo'lsin. Bu funksiyaning x° nuqtadagi xt o'zgaruvchi bo'yicha xususiy
orttirmasi
f(*°) = f(xl + Дх,, x^,4) - /(xf, x$,£)
Axj ga bog'liq bo'ladi.
AX1/(x°)
1- ta’rif. Ushbu lim —1----------------
A q ->0 AXj
limit mavjud bo'lsa, bu limit /(x) - /(xj ,x2 ,...,xm) funksiyaning
x° = (xf, x2,..., x° ) nuqtadagi Xj o'zgaruvchisi bo'yicha xususiy
hosilasi deyiladi. Uni
kabi belgilanadi:
Э/(х°) =f = Um AX1/(x°) _
0X] %1 AXj^O AXj AX]->0 AXj
Berilgan funksiyaning bu xususiy hosilasini quyidagicha
f tx°1- lim
Jх,\л ) — Ш11---------------------о
deb ta’riflasa ham bo'ladi.
59
f(xx,x2,...,xm) funksiyaning boshqa x2,x3,..., xm o‘zgaruvchilari
bo'yicha xususiy hosilalari ham xuddi shunga o‘xshash ta’riflanadi:
У(х°) = lim aX2/(x°) = /(л?,^+дх2,лв,...,4)-7(лв,
3^2 -»0 ^2 AXj
y<x°) = lim ч/(х°) = lim /Ь0^0>->4-р4+д^)-/(^, ^,...,4)
Эхт Дхя, —>0 ~
(Дх^О, k = 2,3,—, w).
Yuqorida keltirilgan ta’riflardan ko‘p o'zgaruvchili funksiyaning
xususiy hosilalari bir o‘zgaruvchili funksiyaning hosilasi kabi ekanligi
ko‘rinadi. Demak, ko‘p o‘zgaruvchili funksiyaning xususiy hosilalarini
topishda ma’lum jadval va qoidalardan foydalanish mumkin. Jum-
ladan, agar
/(x) - /(Xi,X2,...,Xm), g(x) = g(Xi,X2,...,Xm)
funksiyalar £cz Rm to‘plamda berilgan bo‘lib, хе E nuqtada xususiy
hosilalarga ega bo‘lsa, u holda:
w d 3(c/(x)) Э/(х)
1) Ve e R : - -- = с ;
2) _ У(х) + dg(x).
' dxk dxk dxk '
3) ^№>lWl = ^g(x) + /(x)^;
3x^ 3x^ 3Xj^
d|---- | z ч
(g(x) * 0), к -
bo'ladi.
2°. Ko‘p o‘zgaruvchili funksiyaning differensiailanuvchanligi.
Zaruriy shart. Aytaylik, /(x)= /(xj,x2,...,xm) funksiya Ec Rm
to‘plamda berilgan bo‘lib,
60
х° = (х», х2°,..., х“ )е Е, (Х1° + Axj, х2° + Ах2, ...,х° + Axm)e Е
bo‘lsin. Ma’lumki, berilgan funksiyaning x° nuqtadagi to‘la orttirmasi
Д/(x°) = /(x° + A^, x2° + Дх2,..., x° + Axm) - /(xi°, x2°,..., x° )
bo‘lib, u Дх15 Ax2 ,Axm larga bog‘liq bo‘ladi.
2- ta’rif. Agar Axj, Дх2,Axm orttirmalarga bog'liq bo‘lmagan
shunday At, A2, Am sonlar topilib, funksiyaning x° nuqtadagi to‘liq
orttirmasi ushbu
Д/(х°) = Л1Ах1 + Л2Дх2 + ... + Am/Xxm +
+ Q| Axj + a2Ax2 + ... + amAxm (1)
ko'rinishda ifodalansa, /(x) funksiya x° nuqtada differensiallanuvchi
deyiladi, bunda cq, a2,..., am lar Axj, Ax2,..., Лхт larga bog‘liq va
Axj -> 0, Дх2 -> 0,..., Axm -> 0 da cheksiz kichik miqdorlar.
Agar (х{*, x2,x° ) hamda (%,° + Aq , x2 + Ax2,..., x® + Axm)
nuqtalar orasidagi masofa
p = tJaxj2 + Axj + ... + z\x2
uchun Axj -> 0, Ax2 -> 0,..., Axm -» 0 da
cqAX] + a2 Ax2 + ... + amAxm = 0(p)
bo'lishini e’tiborga olsak, (1) munosabat ushbu
= Л1ДХ1 +Л2Ах2 +... + ЛотДхт +0(p) (2)
ko‘rinishga keladi.
Odatda, (1) va (2) munosabatlar /(x) funksiyaning x° nuqtada
differensiallanuvchanlik shard deyiladi.
l-misol. Ushbu
/(x) = /(Xj, x2,..., xm) = X]2 + xl + ... + x2m
funksiyaning V(Xi°, xj ,..., x° ) g Rm nuqtada differensiallanuvchi
bo‘lishi ko'rsatilsin.
◄ Berilgan funksiyaning x° = (x®, x2 ,x“ ) nuqtadagi to‘liq
orttirmasini topamiz:
61
А/(х°) = (х? + Ах, )2 + (х2° + Дх2 )2 +... + (х° + Дх„,)2 -
-(xf2 + х22 +... + х£ ) = 2х1°Дх1 + 2х2 Дх2 +... +
+2х° Дхт + Дх2 + Дх2 + •
Agar
А. = 2х°, А2 -2х2,...,Ат = 2х°т,
ОС] - ДХ;, а2 = Дх2,..., ат = Дхт
deyilsa, u holda
Д/(х°) = ДДХ] + Л2Дх2 +... + ЛтДхт + oqAXj + а2Дх2 +... + атДхт
bo'ladi. Demak, berilgan funksiya Vx° e Rm nuqtada differensial-
lanuvchi. ►
Agar /(x) funksiya £c Rm to'plamning har bir nuqtasida diffe-
rehsiallanuvchi bo‘lsa, funksiya E to'plamda differensiallanuvchi de-
yiladi.
1- teorema. Agar/(x) funksiya x° e Ec Rm nuqtada differensial-
lanuvchi bo'lsa, и holda funksiya shu nuqtada uzluksiz bo'ladi.
◄ Shartga ko'ra /(x) funksiya x° nuqtada differensiallanuvchi.
Demak, funksiyaning shu nuqtadagi to'liq orttirmasi
Д/(х°) = А1Лх1 + Л2Дх2 +... + 4„Дхт + оцДХ] + а2Дх2 + ... + атДхт
bo'ladi. Ви tenglikdan
lim Д/(х°) = 0
ЛХ1 -->0
Лл'2 ~»0
Дхт-»0
bo'lishini topamiz. Demak, f (x) funksiya x° nuqtada uzluksiz. ►
2- teorema. Agar f (x) funksiya x° nuqtada differensiallanuvchi
bo'lsa, и holda funksiya shu nuqtada barcha xususiy hosilalarga ega va
/;](х°) = 4, Д(х°) = л2,..., a;(x°) = 4
bo'ladi.
•4 Shartga ko'ra /(x) funksiya x° nuqtada differensiallanuvchi.
Binobarin, (1) shart bajariladi. U holda
Дх! 0, z\x2 = Дх3 - ... = Axm = 0
62
deb olinsa, quyidagi
AX[/(x°) = 4 Ax, + cqAxj
tenglik hosil bo‘ladi. Bu tenglikdan topamiz:
Av. f (x°)
lim —!-------= lim (4 + оц ) = 4 •
Axj ->0 AX] Axj
Demak, A' (x°) = 4.
Xuddi shunga o‘xshash f(x) funksiyaning x° nuqtada Д' (x°),
jf' (x°),f 'm (x°) xususiy hosilalarining mavjudligi hamda
4(х°) = Л2, /x'(x°) = Л3,f'm(x°) = Am
bo‘lishi ko‘rsatiladi. ►
Bu teoremadan x° nuqtada differensiallanuvchi f (x) funksiyaning
orttirmasi uchun c
¥U°) = fx, (-^’Ж + Д'(x°)A^ +- + fxm (x°)Axw +0(p)
bo'lishi kelib chiqadi.
Eslat ma. f(x) funksiyaning biror x° nuqtada barcha xususiy
hosilalari
ning mavjud bo‘lishidan, uning shu nuqtada differensiallanuvchi bo‘-
lishi har doim kelib chiqavermaydi (bunga misol keyingi bandda
keltiriladi).
Yuqorida keltirilgan teorema va eslatmadan f (x) funksiyaning x°
nuqtada barcha xususiy hosilalarga ega bo‘lishi funksiyaning shu nuqtada
differensiallanuvchi bo‘lishining zaruriy sharti ekanligi kelib chiqadi.
3°. Funksiya differensiallanuvchanligining yetarli sharti. Faraz
qilaylik, /(x) funksiya Ec. Rm to‘plamda berilgan bo‘lib, 1/§(х°) с E
bo‘lsin (8 > 0).
3- teorema. Agar/(x) funksiya da barcha xususiy hosilalarga
ega bo‘lib, bu xususiy hosilalar x° nuqtada uzluksiz bo‘lsa, f (x) funk-
siya x° nuqtada differensiallanuvchi bo‘ladi.
◄ Ushbu
(xf + Axj, x2° + Ax2,x° + Axm) 6 Us (x°)
63
nuqtani olib, berilgan funksiyaning x° = (x®, x2,x° ) nuqtadagi
to‘liq orttirmasini qaraymiz:
V(*°) = /(4 + ДХр x° + Ax2, x° + Дхт) —/(xp, x2,x°).
Bu orttirmani quyidagicha yozib olamiz:
Д/(*°) = [/(4 +ДХ], x2° + Дх2,x°m + Axm)~ >
~f (4 , 4 + Д*2 , 4 + )] +
+ [/ (X]°, x2 +Ax2, x°m + Axm)~ (3)
-/ (xj°, xt, x° + Дх3,x°m + Axm)] +
+•••+[/(4, 4, •••• 4-i , 4 + д*™) - /(4 , 4 , -, 4)]-
Lagranj teoremasidan foydalanib topamiz:
/(4 + Axj,4 + дх2,4 + д^)- /(4, $ +д^,-> 4 + д^) =
= Л1 (4 +0] • д^, 4 + д^ > -> 4 + д^») • д^ >
/(4,4 + дх,,...,4 + длте)-/(4, 4,4+дз>-> 4+длл) =
= А'2 (4,4 + 02 • д*2> 4 + Дхз, 4 + Д4,)• д^;
/(4,4,-» 4-м4+д^)-/(4> 4,-, 4)= (4)
= fxm (-^1 » ^2 , •••, 4-1 » 4 + 0тД-^т) ’ ДЛи,
(О < вк < 1, к = 1, 2,т)
Shartga ко‘га Д, f*m xususiy hosilalar x° = (x{*, x2,4)
nuqtada uzluksiz. U holda
4 (4 + 0iдх,, 4 + д*2 > 4 + дл„) = 4 )+ ai ’
/х2 (4,4 +02Дх2,4 +Дх3,.„, 4 + Д^)= 42 (лс) + а2,
......................................... (5)
fxm (4,4, -, 4-1,4+ 0тД^) = £„ (^°) +
64
bo‘ladi. Bunda
AXj -> 0, Ax2 -h> 0, Axm -> 0 da a, -> 0, a2 -> 0,am -> 0.
Yuqoridagi (3), (4) va (5) munosabatlardan
¥(*°) = fx} (*0Ж + /x2 (x°)Ax2 + ... + (х°)Ал^ +
4-cC]AjC] + «2Ax2 + ... + amAxm
bo'lishi kelib chiqadi. Demak,/(x) funksiya x° nuqtada differensial-
lanuvchi. ►
Bu teorema f(x) funksiyaning x° nuqtada differensiallanuvchi
bo'lishining yetarli shartini ifodalaydi.
4°. Murakkab funksiyaning differensiallanuvchanligi. Murakkab
funksiyaning hosilasi. Aytaylik, ushbu
= Ф1 (0 = Ф1 Gi > h > •••> 4) >
X2 =ф2(0 = ф2 (hM2>- r
~ Фт(0 ~~ Фт (h ’ ^2 ’ ^k )
funksiyalarning har bir Me Rk to'plamda,
и = /(хь x2,..., xm)
funksiya esa
Ё = {(xj,x2, ..., x„,)e 7?m;xi = cpi(/), x2 =ф2(0, •••> xm = Фт(0}
to'plamda berilgan bo'lib, ular yordamida
/(ф](0, ф2(0,..., ф„,(0) = F(t}, t2,..., tA)
murakkab funksiya hosil qilingan bo'lsin.
4-teorema. Agar x, = ф, (^, t2,..., tk) funksiyalarning har biri
(/ - 1, 2,..., m), (tf, t2,..., M nuqtada differensiallanuvchi
bo'lib, /(%!, x2,..., xm) funksiya mos (x°, x2,..., x®,) nuqtada
VX1 - Ф1 VI ’ ?2 ’ x2 - Фг VI ’ 4 )> ’ Xm ~ Фт VI ’ 4 ))
differensiallanuvchi bo'lsa, u holda murakkab
f (Ф1 (zi > > Ф2 (h > ), Фт (h, tk))
funksiya (/“, t2,..., nuqtada differensiallanuvchi bo'ladi.
65
◄ t%)e M nuqtaning koordinatalariga mos ravishda
AZ], AZ2,AZ* orttirmalar beraylikki, bunda
(z® + AZ!, Z2° + AZ2,tk + &tk) e M ,
bo'lsin. U holda har bir x,- = <p, (Zj, Z2,tk) funksiya (z = l,2,...,m)
ham Ax,- (z = orttirmalarga va nihoyat f(x) funksiya А/
orttirmaga ega bo'ladi.
Shartga ko‘ra х,-= ср,-(z15 Z2,..., Z*) funksiyalarning har biri
(Z1°, Z2°,tk) nuqtada differensiallanuvchi. Demak,
M + °(p),
d/1 dtz dtk
. Эхп a Эх? *. , dx? rv / \
Ax2 = —— + —— AZ2 +... + — Ык + 0(p),
oq o^2 ^k
..................................................... (6)
Ax„, = AZ, + AZ2 +... + + 0(p)
Oq V‘2 v*k
bo'ladi, bunda
(z = l,2,...,m; У = 1,2,...,Л)
xususiy hosilalarning (zf, Z2,..., Z®) nuqtadagi qiymatlari olingan va
p - л/az!2 + AZ2 + ... + AZ^ •
Shartga ko‘ra f (xj, x2,..., x„,) funksiya (x®, x2,x® ) nuqtada
differensiallanuvchi. Demak,
,r df , elf , (If* л л * /'IX
& = -i- AX] + -±-Ax2 +... + -^-/xxm + a.AXj + a2Ax2 +... + a„Axm (7)
ЭХ] Эх2 дхт 2 z m m \ /
bo‘ladi, bunda , (z = 1,2, xususiyhosilalarning (xf, x£,..., x° )
Эх/
nuqtadagi qiymatlari olingan va
Axt -> 0, Ax2 -> 0,..., Axm -» 0 da oq —> 0, a2 —> 0,..., am 0.
(6), (7) munosabatlardan topamiz:
66
А/ = <Г Эх1
dXj Э?]
э*2 L 1
Г <)хг. .
эхт L э?1
Д?! + ~ ДГ2 + ••• + Мк + 0(р) +
1 Эг2 dtk к
+ Эх1д/ -; ... I ЙА'2 1
Э?2 2 dtk •' _
Эх"’ ~2 + ... + ^ Мк +0(р)1 +
Э/2 dtk к
А/2 + ...+ ;i-2 А/^. + 0(р) +...+
^-ДГ] + -—-Д/? + ...+
л л * | Э/ Эх] Э/ Эх2
+ а, Дх, + а, Дх? +... + а,„Дх„, = — —‘ + - - • --- +... +
1,22 т т [Эх! Э?! Эх2 Э?!
+3L .^Улг +
ZAti I I "т" -г ••• i” IZ-Xk^ I • ••
dxm Э?1 I I aXj dt2 dx2 dt2 dxm dt2 )
( df Эх, Э/ Эх2 Э/ Эхт V
^axj dtk dx2 dtk dxm dtk j
( df df э/ \ 4
+ _д_ + +... + -Olpj + ai/Xx, +а,Дх7 + ... + атДх_.
I ЭХ] Эх2 Эхт I
Bu tenglikdan | — + — +... + —O(p) - 0(p).
I 3xj дх2 дхт I
ДГ] -> 0, &t2 -> 0,..., Atk -> 0, ya’ni p 0 da
ДХ; -> 0, Дх2 0,..., Дхт чО va а, ч0,а, ч 0, ..., ат -> О
bo‘lgani sababli
aj ДХ] + а2Лх2 + ... + атДхт = 0(р)
bo‘lishi hamda quyidagi
А = У . —1 + У • —2 + +
J ЭХ] dtj Эх2 dtj дхт dtj (°)
(у = 1,2,...,к) belgilashlar natijasida
Д/ = 4Д?! +A2At2 +... + AmNtm +0(р) (9)
bo‘ladi. Demak, murakkab funksiya t0 nuqtada differensiallanuvchi. ►
Aytaylik,/(x(0) murakkab funksiya yuqoridagi teoremaning shart-
larini qanoatlantirsin. U holda
4A(f) = ^2 + - + + °(P)
Э/1 3^2 otk
67
bo‘iadi. Bu hamda (8), (9) munosabatlardan foydalanib murakkab
funksiyaning xususiy hosilalari quyidagicha
ЗА = Э/ Эх} + э/ Эх2 + + Э/ dxm
Эг, 9xj Э%2 дхт ’
ЗА = ЗА 9xt t Э/ Эх2 ! + ЗА дхт
ЭД ЭХ] д/2 Эх2 д?2 дхт Э/2 ’
ЗА = ЗА 3xt + ЗА + + ЗА Эхст
dtk Эх, Эд Эх2 дхт а1к
bo‘lishini topamiz.
5°. Xususiy hollar, m = 1 bo‘lganda bir o‘zgaruvchili и = f(x')
(x c R, и g R) funksiya hosilasi tushunchasiga kelamiz. Bular ha-
qidagi ma’lumotlar 19—21- ma’ruzalarda bayon etilgan.
m = 2 bo‘lsin. Bu holda ikki o‘zgaruvchili w = /(x,y)
((x, у) e E c R1, и e R) funksiyaning xususiy hosilalari
= lim = lim ,
Эх л«0 Дх дх—>0 Дх
= lim = lim
ay Ду Ду—>0 Ду
hamda quyidagi
ДА = f (x + Дх, у + Ay) - f (x,y) - Alxx + Btxy + oqAx + a2Ay
differensiallanuvchanlik shartiga ega bo‘lamiz.
2- misol. Ushbu f (x, у) = In tg ~
funksiyaning xususiy hosilalari topilsin.
•< Berilgan funksiyaning xususiy hosilalari quyidagicha bo‘Iadi:
1 1 £ ______2___.
x X 2 X v . 2x ’
tg— cos — z у sin--------
У У У
1 ( x A -2
2X v2 2 2x
cos — \ y J у sin--------
У У
68
3- misol. Ushbu
ГТ2^’ agar U5y)*(0,0) bo‘lsa,
f(x,y) = lxz+yz
[ 0 , agar (x,y) = (0,0) bo‘lsa
funksiyaning xususiy hosilalari topilsin.
◄ Aytaylik, (x, у) * (0,0) bo‘lsin. U holda
3/ _ 3 f 2xy 2y(x2+y2)--2xy-2x _ 2y\y2-x2)
dx ~ Tk 1^2 J ^^2 - ’
df _ 3 f 2xy 2x(x2 +y2)-2xy 2y _ 2x(x2-y2)
ду - Црт/ j (^y)2 ~ 7JZ7F
bo‘ladi.
Aytaylik, (x, y) = (0, 0) bo‘lsin. Bu holda ta’rifdan foydalanib topamiz:
3/(0,0) = lim /(0+Ax,0)-/(0,0) = Iim 2ДХ-0 _ 0
Эх Дх—>0 Дх Дх—>0 Дх^
3/(0,0) = Iim /(0,0+Ду)-/(0,0) = Ит 2Ду О _ q
Эу Ду—>0 Ду Ду—>0 Ду3
4- misol. Ushbu f (х, у) = л/х2 + у2 funksiyaning xususiy hosi-
lalari topilsin. )
◄ Aytaylik, (x, у) Ф (0, 0) bo‘lsin. Bu holda
3/ _ 3 Г^. 2 _ 2x _ x
dx 2^x2+y2 y/x^+y2
2^x2+y2 -/х^+У2
bo'ladi.
Aytaylik, (x, y) = (0, 0) bo‘lsin. Ta’rifga ko‘ra
3/(0,0) = lim /(0+Ax,0)-/(0,0) = lim M
Эх Дх—>0 Дх Дх-д0 Дх ’
3/(0,0) = lim /(0,0+Ду)-/(0,0) = lim Ы
Эу Ду-»0 Ду Ду—>0 Ду
bo‘lib, bu limitlar mavjud bo'lmaganligi sababli berilgan funksiya
(0,0) nuqtada xususiy hosilalarga ega bo£lmaydi. ►
69
г- misol. Ushbu
f(x,y) =
х3У
y6 , 2
л -t-y
agar (x,y) * (0,0) bo‘lsa,
0 , agar (x,y) = (0,0) bc‘lsa
funksiyaiKRg (0, 0) nuqtadagi xususiy hosilalari topilsin.
◄ Ta’rifga ko‘ra
0/(0,0) = Hm /(0+Ax,0)-/(0,0) = 0,
Эх Дх->0 AX ’
Э/(0,0) = lim /(0,0+Ду)-/(0,0) = 0
dy Av—>0 Ду
bo‘ladi. Biroq berilgan funksiya (0, 0) nuqtada uzluksiz bo‘lmaydi,
chunk!
6-misol. Ushbu
. Ar . agar (x,v)*(0,0) bohsa,
/(x,y)=
[ 0 , agar (x,y) = (0,0) bo‘lsa
funksiyaning (0, 0) nuqtada xususiy hosilalarining mavjudligi, amnio
shu nuqtada differensiallanuvchi emasligi kohsatilsin.
◄ Ravshanki,
a/(0,0) = lim /(дх,0)-/(0,0) = 0
дх Дх—>0 ЛХ '
э/(0,0) = lim mAy)-/(0,0) = 0
Эу ду->о Ду
Demak, berilgan funksiyaning (0, 0) nuqtada xususiy hosilalari mavjud
va ular 0 ga teng.
Bu funksiya (0, 0) nuqtada differensiallanuvchi bo'lmaydi. Shuni
isbotlaymiz. Teskarisini faraz qilaylik, qaralayotgan funksiya (0,0)
nuqtada differensiallanuvchi bo‘lsin:
70
Э/(0,0) д Э/(0,0) ,
А/ (0,0) = — А-—- Дх + - ——А Ay + cq Дх + а2 Ду -
= cqAx + а2Ду, (Ах 0> Av 0 da oq 0, а2 —* ®)-
Ayni paytda,
А/ (0,0) = / (0 + Дх, 0 + Ду) - / (0,0) = / (Дх, Ду) = -7==^
У Ах2 +Ду2
bo‘ladi. Demak, у = о^Дх + eq Ду.
fhx2+&y2
Bu tenglikdan, Ax = Ду > 0 bo'lganda
1
a, + a, = -t=
1 2 V2
bo'lishi kelib chiqadi. Bu esa Ax = Ay > 0 da oq -> 0, a2 -> 0 bo‘-
lishiga zid. Demak, berilgan funksiya (0, 0) nuqtada differensialla-
nuvchi emas. ►
7-misol. Agar/(x,y) funksiya R2 da differensiallanuvchi bo'lib,
, ¥ Э/ ,
x = rcoscp, у = r sin ср bo Isa, lar topilsin.
◄ Ravshanki,
/(x.y) = /(/• ccs 9, rsinip).
Murakkab funksiyaning xususiy hosilalarini topish qoidasiga ko'ra
ЗГ df dx df dv df df 1 ( df df\ \
dr dx dr dy dr dx V Эу ^Д.2 +^2 Эх dy j
df df dx df dy df df df df .
- A--+ ' - = -r Sin ф — + Г COS ф - = —у — + X — . ►
Э<р Эх Эф dy Эф Эх dy Эх Эу
Mashqlar
1. Ushbu
/(x,y) = (|j\ /(
, , . х+1
х,у) = Insin-^
fy
funksiyalarning xususiy hosilalari topilsin.
71 i
2. Agar
f{x, у) - xsinj? + у sin x, x = ~,y = u-v
bo‘lsa, — lar topilsin.
du dv
3. Aytaylik, /(x) va g(x) funksiyalar U5 (x°) c Rm da aniqlangan
bo‘lib,
1) /(x) funksiya x° nuqtada differensiyallanuvchi va/(x0) = 0,
2) g(x) funksiya x° nuqtada uzluksiz bo‘lsa, f (x) • g(x) funksiyaning
x° nuqtada differensiallanuvchi bo'lishi ko‘rsatilsin.
4. Ushbu /(x,y) = .Jixyj
funksiyaning (0,0) nuqtada differensiallanuvchi emasligi isbotlansin.
60-ma’ruza
O‘rta qiymat haqida teorema. Yo‘nalish bo‘yicha hosila
1°. O‘rta qiymat haqida teorema. Faraz qilaylik, /(x) =
= /(x1,x2,...,xm) funksiya Ec Rm to‘plamda berilgan bo‘lsin. Bu
E to‘plamda shunday
a = (a},a2,...,am), b = (by ,b2,...,bm)
nuqtalarni qaraymizki, bu nuqtalarni birlashtiravchi to‘g‘ri chiziq
kesmasi E to‘plamga tegishli bo‘lsin.
Ravshanki, bu kesma ushbu
К = {(xl,x2,...,xrn)e Rm : X] = Oi -aj),
x2 =a2 +1^ -ai),...,xm =am + t(bm ~am), (0 < t < 1)}
nuqtalar to‘plami bilan ifodalanadi: Kc E.
1- teorema. Agar f (x) funksiya К kesmaning a va b nuqtalarida
uzluksiz bo‘lib, kesmaning qolgan barcha nuqtalarida differensial-
lanuvchi bo‘lsa, u holda Кkesmada shunday c = (q, c2,..., cm) nuqta
topiladiki, bunda
/(Z>) - /(a) - л; (c)(6j - q ) + д; (c)(^ - a2) +... + (c)(im - am) (1)
bo‘ladi.
72
◄ /(x) funksiya K<~ E kesmada quyidagi
/(x) = /(x1,x2,...,xm) =
= /(«i + t(^ -«!>, a2 +1^ -a2),am +t(bm -am)), (0 < t < 1)
kohinishda bo‘ladi. Bu Zo'zgaruvchining funksiyasini F(t) bilan belgi-
laylik:
Ptf = f(ax +t(bi -ax), a2 + t(b2 -a2),am+t(bm
Ravshanki, F(t) funksiya [0, 1] segmentda uzluksiz bo‘lib, (0, 1) da
A(t) = A' (^i - «1) + A, (^2 - «2) + - + A„, (bm - am)
hosilaga ega bo'ladi. Bunda Д' , Д' ,f*m xususiy hosilalaming
(«1 +1^ -gJ, a2 + t(b2 -a2),am+t(bm -am))
nuqtadagi qiymatlari olingan.
Lagranj teoremasidan foydalanib topamiz:
F(l) - F(0) = F'(t0), (0 < t0 < 1). (2)
Agar
F(0) = /(g), f(l) = f(b) (3)
hamda
+^o(4
x(Z>] -a, )+/4 (A +$) (^1-4 )> +'b (4 ), H (4» ~^))x (4)
.x(^-a2)+...+f^ (A +f0 (Z»,-q),+4, (bm -^)) (Z>W
bo‘lishini e’tiborga olsak, so‘ngra ushbu
ai + Qb _ ai) - ci >
«2 + Z0 (^2 - «2 ) = c2 ,
+ ^0 (^m — ) =
belgilashlami bajarsak, u holda
c = c2,cm)e К
bo‘lib, (2), (3) va (4) munosabatlardan
73
f(b) - f(a) = f'{ (c)(6j - q ) + Д (c)(b> - fl2) + ... + /xm (c)(bm - )
bo‘lishi kelib chiqadi. ►
Odatda, (1) formula Lagranjning chekli orttirmalar formulas!
deyiladi.
2°. Xususiy hollar. Yo‘nalish bo‘yicha hosila. m = 1 bo‘lganda
yuqoridagi teoremada keltirilgan formula
/(Z>)-/(fl) = /'(C) (6-fl)
{a g R, b e R, a < c < b) ko‘rinishga keladi. Bu Lagranj teoremasini
ifodalovchi formula bo‘lib, 21- ma’ruzada o‘rganilgan.
m — 2bo‘lganda (1) formula
f(b) - f(a) = A'(c)(^ - 01) + /;(с)(^ - a2 ),
(Z> = , b2) g R2, a = (fl!5 fl2)e R2, c = (q, c2) g R2)
ko'rinishda bo‘ladi.
Ma’lumki, и = f(x), (xe R, u g R) funksiyaning hosilasi f'(x)
shu funksiyaning o‘zgarishini (o‘zgarish tezligini) ifodalar edi.
u = f(x), ((x,y) g R2, и g R) ikki o‘zgaruvchili funksiyaning
/x' (x, y), f' (x, y) xususiy hosilalari funksiyaning mos ravishda OX
hamda OY o‘qlar bo‘yicha o‘zgarish tezligini bildiradi. Boshqacha
aytganda, f(x,y) funksiyaning xususiy hosilalari koordinata o‘qlari
yo'nalishi bo‘yicha hosilalar bo‘ladi.
Endi f(x,y) funksiyaning tekislikdagi ixtiyoriy tayin yo‘nalish
bo‘yicha hosilasi tushunchasini keltiramiz.
Faraz qilaylik, f (x,y) funksiya E a. R2 to‘plamda berilgan bo‘l-
sin. Bu funksiyani Dekart koordinatalar sistemasida tasvirlangan
4)=(xo>ko) nuqtaning U5 (Ao) с: E, (8 > 0) atrofida qaraymiz.
Ushbu A =(x,y) clUs(Ao) nuqtani olib, Ao va A nuqtalar orqali
to‘g‘ri chiziq o‘tkazamiz. Undagi ikki yo‘nalishdan birini musbat
yo‘nalish (26-chizmada ko‘rsatilgandek), ikkinchisini esa manfiy
yo‘nalish deb qabul qilamiz. Bu yo‘nalgan to‘g‘ri chiziqni / bilan
belgilaymiz. Ao va A nuqtalar orasidagi masofa
p = р(4),Л) = 7(x-x0)2+(y-y0)2
74
bo'lib, bu masofa A0A vektorning yo‘nalishi I ning yo'nalishi bilan
bir xil bo'lsa, musbat ishora bilan, aks holda, manfiy ishora bilan
olinadi.
Agar I ning musbat yo'nalishi bilan OX va OY koordinata
o'qlarining musbat yo'nalishlari orasidagi burchakni mos ravishda
a va p deyilsa (26- chizma), u holda '
X-Xn У-Уо a
—-u=cosa, --JA = cosB
P P
bo'lishi topiladi.
1- ta’rif. Agar lim
4-м, p
limit mavjud bo'lsa, bu limit f(x,y) funksiyaning Д, = (x0,y0) nuq-
tadagi / yo'nalish bo'yicha hosilasi deyiladi. Uni
Э/(4) .. Жл)
Э/ y k Э/
э/(Л) r /(W/W
kabi belgilanadi. Demak, -— = Jun ------------------.
1-misol. Ushbu /(х,у) = у[х*у
fimksiyaning (0, 0) nuqtada barcha yo'nalishlar bo'icha hosilalarining
mavjudligi ko'rsatilsin.
75
•4 Aytaylik, а * bo'lsin. Bu holda
у = tg а • х
bo‘lib, _______ ,
/(x,y) = (/%’tga = x(/tga,
p((x,y),(0,0)) = yjx2 + x2 tg2 a = 1x^1 + tg2 a
bo‘ladi. U holda berilgan funksiyaning (0,0) nuqtadagi а ± bo‘lgan
ixtiyoriy yo'nalish bo‘yicha hosilasi, ta’rifga binoan,
Э/(0,0) = Ит f(x,y)-f(Q,0) = ffigq-x
Э/ P^° P Р^°71+1?аЫ
bo‘ladi.
Agar - ^ < a < bo‘lsa, u holda x > 0, Ы = x bo‘lib,
2 2
3/(0,0) _ ytgoc
'ji+tg2 a
bo‘ladi.
Agar 2< a <Т bo‘lsa, u holda x < 0, W = -x bo‘lib,
з/(о,о) _ Vtga
71+tg2~a
bo'ladi.
Aytaylik, a^±y bo‘lsin. Bu holda x = 0, /(0,y) = 0 bo'lib,
bu yo'nalishlar bo‘yicha hosila
3/(0,0) = 0
3/
bo‘ladi. ►
1-teorema. Agar f{x,y) funksiya Д) =(x0,y0) nuqtada diffe-
rensiallanuvchi bo‘Isa, u holda funksiya shu nuqtada har qanday
yo‘nalish bo'yicha hosilaga ega va
3/(4,) _ Э/(х0,у0) _ У(хо,уо) Э/(х0, Уо) R
cos а + cos р
bo‘ladi.
76
◄ Aytaylik, f(x,y) funksiya Aq =(x0,y0) nuqtada differensialla-
nuvchi bo'lsin. U holda
f U) - f (4) = f (x, y) - f (x0 ,y0)
orttirma uchun
/U)-/(4) = ffi^(x-xo) + ^^(y-yo) + O(p)
bo'ladi, bunda p = ^(x - x0 )1 2 * + (y - y0 )z .
Keyingi tenglikning har ikki tomonini p ga bo'lamiz:
/U)-/(4) _ 3/(4). x-xq , 3/(4) y-y0 [ 0(p)
p Эх p dy p p
, , ,, , . x-x0 y-Уо о
Ma’lumki, -------------- = cos a, - = cosp.
P P
Shuni e’tiborga olib, p -> 0 da limitga o'tib topamiz:
f(A)-f(A0) 3/(4) 3/(4) _
lim--------cos a + —A— cos В.
p->0 p 3x dy )
„ . 3/(4) 3/(xn, y0) 3/(x0, y0) J. 4
Demak, —422 = 2Л u 42 cos a + -2_L2_22Z cos В . ► 4
3/ Эх dy
2- misol. Ushbu f (x, y) = %2 + y2
funksiyaning (1,1) nuqtada r = i + 2j vektor yo'nalish bo'yicha hosi-
lasi topilsin.
◄ Ravshanki, bu holda
1 O 2
cos a = -f=, cos p = ,
V5 И V5
Э/(х,у) _ Э(х2+у2) 3/(1,1) _ _
' Эх Эх ’ ' Эх
У(х,у) Э(х2+у2) _ 3/(1,1) _ ?
Эу Эу Эу ~
bo'ladi. (5) formuladan foydalanib topamiz:
3/(1,1)_ 1 2 _ 6
3/ V5
77
Faraz qilaylik, f(x,y) funksiya ochiq Ea Rm to‘plamda differensial-
lanuvchi bo‘lsin. Binobarin, funksiya Eto‘planining har bir (x,y) e E
nuqtasida
df(x,y) df(x,y)
dx ’ dy
xususiy hosilalarga ega bo‘ladi. Koordinatalari shu xususiy hosilalardan
iborat bo‘lgan vektorni tuzamiz:
, (6)
Эх dy
bunda i va j — koordinata o‘qlari bo‘yicha yo'nalgan birlik vektorlar.
(6) vektor f(x,y) funksiyaning gradiyenti deyiladi va gradf kabi bel-
gilanadi:
,r df(x,y) Э/(х,у)
Эх dy
Demak, gradf E to'plamning har bir (x,y) nuqtasiga bitta vektorni
mos qo‘yuvchi qoida, boshqacha aytganda, ikki o'zgaruvchili vektor
funksiya bo‘ladi.
f(x,y) funksiyaning ё = (cos a, cos p) vektor yo‘nalishi bo'yicha
—hosilasini uning gradiyenti orqali ifodalash mumkin. Haqi-
dl
qatan ham, grad/va ё vektorlaming skalyar ko‘paytmasi
jz Э/(х,у) йЭ/(х,у)
e gradf - cos a + cos p — rjx
дх dy v '
bo‘lib, u (5) formulaga ko'ra ga teng bo‘ladi:
Э/(х,у)
e gradf = —.
ax
Ayni paytda, ё nz. gradf vektorlaming skalyar ko‘paytmasi shu
vektor uzunliklari ko‘paytmasining ular orasidagi burchak kosinusiga
ko‘paytirilganiga teng bo‘ladi:
ё gradf = \gradf\ • |ё| • cos (ё , gradf). (8)
Ravshanki, iei = 1. (7) va (8) munosabatlardan
78
= \gradf(x,y)\ -cos(e, gradf(x,у))
bo‘lishi kelib chiqadi.
Keyingi tenglikdan ko‘rinadiki, e hamda gradf(x,y) vektorlar
parallel bo‘lganda —ning qiymati eng katta va u
\gradf (x,y)| = y[ff2 (x.y)+ f'2 (x,yj
ga teng bo'ladi.
Shunday qilib,/(x,y) funksiyaning gradiyenti gradf funksiyaning
(x,y) nuqtadagi eng tez o'sadigan tomonga yo'nalgan bo‘lib, uning
uzunligi shu yo'nalish bo'yicha o'sish tezligiga teng ekan.
3- misol. Ushbu f(x,y) = x2 + 2y2
funksiyaning (1, 1) nuqtada eng tez o'sadigan yo‘nalishi aniqlansin
va shu yo‘nalish bo‘yicha o‘sish tezligi topilsin.
•< Ravshanki,
Э/(х,у) _ э(х2+2у2) _ _
дх дх ’ дх
df(x,y) = д (х2+2у2) . Э/(1,1) = 4
ду ду ’ ду
Л
bo‘lib, gradf (1,1) = 2i+4],
\gradf (1,1)| = л/22 + 42 = 2 45
bo‘ladi. ►
Mashqlar
1. Aytaylik,/(х) funksiya bog‘lamli Ее Rm to‘plamda differen-
siallanuvchi bo‘lsin. Agar Eto‘plamning har bir x e E c Rm nuqtasida
f (x) funksiyaning barcha xususiy hosilalari nolga teng bo‘Isa, funksiya
E to‘plamda o‘zgarmas bo‘lishi isbotlansin.
2. Agar f (x,y) funksiya (0,0) nuqtada barcha yo‘nalishlar bo‘yicha
hosilaga ega bo‘lsa,/(x,y) funksiya (0,0) nuqtada differensiallanuvchi
bo'ladimi?
79
61- ma’ruza
Ko‘p o‘zgaruvchili funksiyaning differensiali
1°. Funksiya differensiali tushunchasi. Faraz qilaylik, f (x) =
= /(x!,x2,...,xm) funksiya Ec-R" da berilgan bo‘lib, x° =
- (xf, x2, •••> 4)e E nuqtada differensiallanuvchi bo‘lsin. U
holda ta’rifga ko‘ra funksiyaning x° nuqtadagi to‘liq orttirmasi
«/•( ol Э/(х°) Э/(х°) Э/(х°) / x
Л/Ьс J = 4----AXi+4—-Ax2 +... + 4-—Axm+o(p) (1)
ОЛ2 ®Хт
bo'ladi. Bu munosabatda
p = ^Axf + Ax2 + ... + Ax^,
bo‘lib, Axj -> 0, Дх2 —> 0,..., Axm 0 da p -> 0 .
l-ta’rif /(x) funksiyaning A/(x°) orttirmasidagi
3/(x°) . Э/(х°) . Э/(х°) .
4-----Axt + 4-----Ax2 + ... + <----Ax
ЭХ! Эх2 Эхто
ifoda /(x) funksiyaning x° nuqtadagi differensiali (to‘liq differensiali)
deyiladi va
#(x°) yoki df(x\, x2,..., x°)
kabi belgilanadi:
,,z Ox э/(х°). э/(х°) . э/(х°).
#(4) = 4—-AXi +-2—-Дх2 Axm.
OAj OX} uXm
Demak,/(x) funksiyaning x° nuqtadagi differensiali AX], Ax2,..., Exm
larga bog'liq va ulaming chiziqli funksiyasi bo‘ladi.
Agar
Ax! = dxr, Ax2 = dx2,..., Axm = dxm
deyilsa, f (x) funksiyaning x° nuqtadagi differensiali ushbu
j/-/ o\ Э/(х°) , Э/(х°) , Э/(х°) .
df(x ) = —dx, + A-—rflx, +... + f------------axm
3Xi 1 Эх2 2 Эхт m
ko‘rinishga keladi. Demak,
80
(2)
V(xo) = #(x°) + O(p).
Keyingi tenglikdan p —> 0 da
A/(x°) = #(x°)
bo‘lishi kelib chiqadi. Bu taqribiy formulaning mohiyati shundaki,
funksiyaning orttirmasi AX[, Дх2,Дхт laming, umuman aytgan-
da, murakkab funksiyasi bo'lgan holda funksiyaning differensiali
AXj, Ax2 ,Axm laming chiziqli funksiyasi bo‘lishidadir.
2°. Murakkab funksiyaning differensiali. Differensial shaklning
invariantligi. Aytaylik,
xi = Ф1 (0 = Ti 0, h, •••, h)»
X2 = (p2 (Z) = ф] (Zj , Z2 , ..., ZA ),
Xm ~ Фт (0 = Ф1 (?1 ’ h > > 4 )
funksiyalarning har biri Mg Rk to'plamda berilgan bo'lib,
E = {(xi,x2,...,xm')e Rm \xx = <p1(Z) = 91(ZI,Z2,..., 4),
x2 = (p2 (Z) = Ф1 (Zj, t2, ..., tk), ..., xm = cpm (t) = ф1 (Z], Z2,tk)}
to'plamda esa f (x1,x2,...,xm) funksiya aniqlangan bo'lsin. Bularyor-
damida
/0(0) = /Oi(0, *2(0, хт(0) = F(tx,t2;..., tk)
murakkab funksiya hosil qilingan bo'lsin.
Ma’lumki, x, = <p,- (z15..., tk) (7=1,2,...,m) funksiyalar Z° = (z®,..., z“)
nuqtada differensiallanuvchi bo'lib, /(x) = /(x1; x2,..., xm) funk-
siya mos x° = (xf, x2,..., x^) nuqtada (x? = q>](Z°),(Z°),
..., x° = <pm (Z0)) differensiallanuvchi bo'lsa, murakkab funksiya
Z° = (z5°,..., tk) nuqtada differensialanuvchi bo'ladi.
Modomiki, /(x(z)) funksiya Zj, Z2,..., tk o'zgaruvchilarga bog'liq
ekan, u holda
81
(3)
bo‘ladi.
Murakkab funksiyaning xususiy hosilalarini hisoblash formulalari-
dan foydalanib topamiz:
У _ У . Эхд + а/ ax2 + t а/ дхт
Sfj ЭХ] Э^ Эх2 ЭГ1 <}хт йГ) ’
У „ а/ . + а/ эх2 + + а/ Эхт
dt2 ЭХ] Э?2 Эх2 Э?2 дхт Э/2 ’
,а/_ _ а/ ах] а/ эх2 + а/ эхт
3х1 dtk дх2 dtk дхт dtk
Bu xususiy hosilalarni (3) ifodadagi —, laming o‘rniga
Э?! dt2 dtk
qo‘yamiz. Natijada
df =
La*! a/j Эх2
Эх2 + _ + У
ah " axm
dt} +
ah J 1
а/ . ад + а/ Эх2 + ! а/
а*! а/2 эх2 dt2 дхт
дхг.
dt2
dt2 + ... +
bo'ladi.
+ - a*l
La%i dtk
¥ a%!
a*! [a?]
ax2 [ a^i
+ +~^dt2 +... + a^Ldt)
dxm dti dt2 2 dtk 1
df dx2
а/ ax,
+ •^ + - + TC-T2L dtk
axw dtk _
dX]
a^
dt2 + ... + ^dtk
dtk k
Эх,
dX2 3tk
dXi , uai ,
+ ~-dt2 + ... + -±dtk
dt2 1 k
^x2
dl2
dxr
dtx
dt2
aq
к
Ravshanki,
Эх| . 3xi , Эх, . .
-~-dt{ + —i dt2 + к dtk = dx.,
az] 1 a?2 dtk k 15
82
df + dt2 +... + dtk = dx2,
df dt2 dtk k 2
^S-df + "1 dt2 +... + ^Ldtk -dxk.
d?i 1 dt2 2 dtk k K
Demak, murakkab funksiyaning differensiali
,z э/ , df , df ,
df = f-dx, + -f-dx2 +... + dxm (4)
9xj 1 Эх2 dxm m
bo'ladi.
Biz yuqorida f (x) hamda f (x(t)) murakkab funksiyaning differen-
siallari uchun (2) va (4) ifodalarni topdik. Bu ifodalami solishtirib,
ulaming shakli (ko'rinishi) bir xil, ya’ni (2) va (4) formulalarda funk-
siyaning differensiali xususiy hosilalaming mos differensiallarga ko'payt-
malaridan tuzilgan yig'indiga teng ekanligini payqaymiz. Bu xossa
differensial shaklining invariantligi deyiladi.
Eslatma./(x) funksiya differensialining (2) ifodasidagi
dx} ,dx2 ,...,dxm lar mos ravishda AX], Дх2 ,...,Ax„, lar bo'lsa,/(x (7))
funksiya differensialidagi dxx, dx2dxm lar f, t2,..., tk o'zgaruvchi-
larning funksiyalari bo‘ladi. Demak, (2) va (4) formulalaming ko'ri-
nishlarigina bir xil bo'ladi.
3°. Sodda qoidalar. Aytaylik,
и = u(xi,x2,...,xm), V = u(x1,x2,...,xm)
funksiyalar R.m to'plamda berilgan bo'lib, x° = (xj°,x£>—>xm)6
nuqtada differensiallanuvchi bo'lsin. U holda:
1) d (u + v) = du + dv,
2) d (u v) = vdu + udv,
-.x j (u\ vdu-udv / ,
3) d - =-----=—, (.v Ф 0)
\vJ v1-
bo'ladi.
Bu munosabatlardan birining, masalan, 3) ning isbotini keltiramiz.
◄ Aytaylik, F =
bo'lsin. Bu holda F funksiya и va v larga hamda и va v lar o'z
83
navbatida x1,x2,...,xm o‘zgaruvchilargabog‘liqbo‘lib, murakkabfunk-
siyaga ega bo‘lamiz. Differensial shaklining invariantlik xossasiga ko‘ra
, j-. dF , dF ,
dF---du+-dv |-
du dv !
bo‘ladi. Ravshanki,
3F = 1 3F = __u_
du v ’ dv v2 '
„ , , „ 1 , и , vdu-udv
Demak, dF = - du- -dv = —-=—,
V V V
, . , /u\ vdu-udv
ya m d - =--------x—
\v) t/
bo‘ladi. ►
4°. Xususiy hollar. Funksiya differensialining geometrik ma’nosi.
Aytaylik, m = 1 bo'lsin. Bu holda и - f (x), (x e R, и e R) funksiya
va uning differensiali
du = df = f'(x)dx
ga ega bo‘lamiz.
Ma’lumki, и = /(x) funksiyaning differensiali shu funksiya tasvir-
langan egri chiziqqa (x0 ,/(x)) nuqtada o‘tkazilgan urinma ordina-
tasining orttirmasini ifodalaydi (27- chizma).
27- chizma.
84
т = 2 bo‘lsin. Bu holda ikki o‘zgaruvchili u = f(x,y),
((x,y)e R2 ,ue R) funksiyaga ega bo‘lib, uning (x0, y0) nuqtadagi
differensiali
du = df (x0,y0) = dx + ’’j dy
bo‘ladi, bunda dx = Ax, dy = Ay .
Дх va Ду lar yetarlicha kichik bo‘lganda
¥(*о>Уо)~ df\x0,y0),
ya’ni f (x0 + Ax, y0 + Ду) ~ f (x0, y0) + дх + ду
oXi dy
taqribiy formula hosil bo‘ladi.
1-misol. Ushbu u=xy
funksiyaning differensiali topilsin.
4 Ravshanki, - wk' 1. ’-= xy Inx.
Эх dy
U holda (5) formulaga ko‘ra
du = yxyAdx + xy In xdy
bo‘ladi. ►
2- misol. Tomonlari x = 6 m va x = 8 m bo‘lgan to‘g‘ri to‘rtburchak
berilgan. Agar bu to‘g‘ri to‘rtburchakning x tomonini 5 sm ga oshi-
rilsa, у tomonini 10 sm ga kamaytirilsa, to‘rtburchakning dioganali
qanchaga o‘zgaradi?
◄ Agar berilgan to‘g‘ri to‘rtburchakning dioganalini и desak, unda
U = y/x2~+ y2
bo‘ladi. Endi
Au (x0, y0) = r-“ - Ax + -7=^2= Ду
v и > л и ) Г 2 2
Vx0 +^о A +h)
bo‘lishini e’tiborga olib, topamiz:
Ди(х0, y0) = • Дх + 2 Ay = .
V^o+Vo vxo+h) Vxo+h)
85
Bu munosabatda
x0 = 6 m, Ax = 0,05 m, y0 = 8 m, txy = -0,10 m
deyilsa, u holda
Aw ~
6 0,06+8 (-0,10)
V36+64
m = -0,05 m
bodishi kelib chiqadi.
Demak, to‘g‘ri to‘rtburchakning diagonali taxminan 5 sm ga
kamayar ekan. ►
Endi f (x, y) funksiya differensialining geometrik ma’nosini kel-
tiramiz.
Aytaylik, г = /(х,у)
funksiya ochiq Ее R2 to‘plamda differensiallnuvchi bo'lsin. Bu funksiya
grafigi R3 fazoda biror r(f) sirtni ifodalasin. Г(/) = {(x,y,z)e R3:
(x,y)e E, z = f(x,y)} sirtda (Wo,*o)e r(/), = /(Ao,y0))!
nuqtani va shu nuqtadan o‘tuvchi, qaralayotgan sirtga tegishli bo‘lgan
silliq
Г = {x = x(t),y = y(t), z = z(t) : a < t < p}
egri chiziqni olamiz. Modomiki, egri chiziq sirtda yotar ekan, u holda
z(t) = /(x(0,y(0),
(ООо)>.УОо), )) = (Wo.Zo). e («,p))
bo‘ladi. Ravshanki,
z(0 = /(x(0,y(0)
murakkab funksiya bo'lib, uning t0 nuqtadagi differensiali, differensial
shaklining invariantlik xossasiga binoan, ushbu
#(x0,y0) = * = ^^dx + ^^°-)dy (6)
ko‘rinishga ega.
Koordinatalari dx,dy, dz bo‘lgan vektor Гegrichiziqqa (x0, y0 ,Zq )
nuqtada o‘tkazilgan urinma vektor bo‘ladi.
Endi koordinatalari
df(x0 ,y0) _ df(x0,y0)
3x ’ dy ’
86
bo‘lgan n vektorni qaraylik. Yuqoridagi (6) munosabat n vektor
urinma vektorga (x0, y0, Zq ) nuqtada ortogonal bo'lishini bildiradi.
Shuning uchun n vektor egri chizjqqa (x0, y0, Zq ) nuqtada ortogonal
deyiladi.
Ma’lumki, Г egri chiziq (x0,y0,Zo) nuqtadan o'tuvchi va Г(/)
sirtda yotuvchi ixtiyoriy egri chiziq edi. Binobarin, n vektor shu
(xo,yo,Zo) nuqtadan o'tuvchi va Г(/) sirtda yotuvchi ixtiyoriy egri
chiziqqa ortogonal bo‘ladi. Shuning uchun n vektor П/) sirtning
(x0, y0, ) nuqtasidagi normal vektori deyiladi.
Sirtning (x0,y0, £o) nuqtasidan o‘tuvchi va sirtning normal vek-
toriga ortogonal bo'lgan tekislik, F(/) sirtga (xo,yo,Zo) nuqtada
o'tkazilgan urinma tekislik deyiladi. Lining tenglamasi
z - (X - x0) + (Y - л)
bo'ladi, bunda (X,Y,Z) urinma tekislikdagi o'zgaruvchi nuqta. Bu
tenglikdan foydalanib,
Z - ъ (* - ^) + О- л)
ifodani olamiz. Keltirilgan tenglik va (6) munosabatdan
df(xQ,yo) = Z~Zq
bo'lishi kelib chiqadi.
87
Shunday qilib, z = f(x,y) funksiyaning (x0, y0) nuqtadagi diffe-
rensiali df(x0,y0) bu funksiya grafigiga (x0, Уо/(хо, y0)) nuqtadagi
urinma tekislik applikatasining orttirmasini ifodalar ekan (28- chizma).
Mashqlar
1. Ushbu /(x2 + y2 ,arctg^j, (x2+y2>0)
funksiyaning differensiali topilsin.
2. Ushbu a = (1,02)3,01 miqdorning taqribiy qiymati topilsin.
62-ma’ruza
Ko‘p o‘zgaruvchili funksiyaning yuqori tartibli hosila va
differensiallari. Teylor formulasi
Г. Yuqori tartibli xususiy hosilalar. Faraz qilaylik, f (x) =
= /(xj ,x2 ,—,xm) funksiya ochiq Ec.Rm to‘plamning har bir
x = (xj, x2,x„,)e E nuqtasida
xususiy hosilalarga ega bo‘lsin. Bu xususiy hosilalar x(, x2, xm
o'zgaruvchilarning funksiyasi bo‘lib, ular ham xususiy hosilalarga ega
bo‘lishi mumkin:
dxk I dx,- J ' '
Bu xususiy hosilalar berilgan /(x) funksiyaning ikkinchi tartibli
xususiy hosilalari deyiladi va
уоИ
kabi belgilanadi:
a2/(x) , ч э fa/(x)A
Эх^Эх,' ЭхЦ Эх, J-
88
Agar i * к bo‘lsa,
Э2/(х)
Эх^Эх,
ikkinchi tartibli xususiy hosila aralash hosila deyiladi.
Agar i = к bo‘lsa, ikkinchi tartibli
Э2/(х)
r)xkdx,
XjXk (%)
xususiy hosilalar quyidagicha yoziladi:
Э2Лх)
Эх2
= ZJ (x).
f (x) funksiyaning uchinchi, to‘rtinchi va h.k. tartibdagi xususiy
hosilalari xuddi yuqoridagiga o‘xshash ta’riflanadi. Umuman,
/(x) = f (xx,x2,...,xm') funksiyaning Xj,xi2 ,—,xin } ,xin o'zgaruvchi-
lar bo‘yicha n- tartibli xususiy hosilasi berilgan funksiyaning (л? — 1)-
tartibli xususiy hosilasi
э"~7(х)
(г, +i2 + + = n- 1)
ning xZi o'zgaruvchi bo‘yicha xususiy hosilasi sifatida ta’riflanadi:
Э"/(х) _____________________________= <) ( Эи-'/(х) '
ЭхЛ-1 •••КУ Эх,Дэх(п1 ...Эх^Эх^ •
Bu holda ham z]; z2, ..., z„ lar bir-biriga teng bohmaganda
ay
эх,п ...Эх,2 Эх,.
aralash hosila deyiladi.
Agar Z[ = z2 = ... - in = к bo‘lsa, n- tartibli xususiy hosilalar qu-
yidagicha yoziladi:
aV(x)
ax;
Ushbu k}
dxkdXj dxidxk
aralash hosilalar funksiyaning turli o‘zgaruvchilari bo‘yicha differen-
siallash tartibi bilan farq qiladi:
89
&f
ЪхкЪх1
da f (x,, x2, •••,xm) funksiyaning awal x, o'zgaruvchi bo'yicha, so'ng-
ra xk o'zgaruvchi bo'yicha xususiy hosilasi hisoblangan bo'lsa,
a2/
i)xfxk
ifodada esa awal xk o'zgaruvchi bo'yicha, so'ngra x, o'zgaruvchi
bo'yicha xususiy hosila hisoblangan. Ular bir-biriga teng ham bo'lishi
mumkin, teng bo'lmasdan qolishi ham mumkin (misollar keyingi
bandda keltiriladi).
Aralash hisilalarning tengligini quyidagi teorema ifodalaydi.
1-teorema. Faraz qilaylik, f (xl,x2,...,xm) funksiya x° =
= (x,°, x2,...,x° ) e E c Rm nuqtada n marta differensiallanuvchi bo'l-
sin. U holda x° nuqtada f (x,, x2,..., xm) funksiya ixtiyoriy n- tartibli
aralash hosilalarining qiymati x„ x2, ..., xm o'zgaruvchilar bo'yicha
qanday tartibda differensiallanishiga bog'liq bo'lmaydi.
◄ Bu teoremaning isboti, keyingi bandda ikki o'zgaruvchili funk-
siya uchun keltiriladigan teorema isboti kabi bo'ladi. ►
2°. Yuqori tartibli differensiallar. Faraz qilaylik, /(x) =
= f (x,, x2,..., xm) funksiya ochiq Rm to'plamda berilgan, xe E
nuqtada ikki marta differensiallanuvchi bo'lsin.
1- ta’rif./(x) funksiya differensiali df(x) ning differensiali berilgan
funksiyaning x nuqtadagi ikkinchi tartibli differensiali deyiladi va d2/(x)
kabi belgilanadi:
d2f(x) = d(df(x)f
Endi funksiya ikkinchi tartibli differensialini uning xususiy hosilalari
orqali ifodalanishini ko'rsatamiz.
Ravshanki,
j/-/ \ df(x) , Э/(х) , Э/(х) ,
df(x) = - - dxy + dx-, + ... + x_x_L dxm
J v 7 Эх, 1 Эх2 2 Эхт m
bo'lib, u x = (x1,x2,...,xm) ga hamda dxx,dx2,...,dxm larga bog'liq
bo'ladi. Bu tenglikda с/х,, dx2,..., dxm lami tayinlangan deb hisoblab,
90
df(x) ni x{, x2, xm o‘zgaruvchilaming funksiyasi sifatida qarab,
uning differensialini topamiz:
= dx.
+ dx2
d(df) = d(^fdxj + xf dx2 + ... + ~~-dxm | =
I C<X| uX^ oX^j J
a p/ A , a ( df A ,
f- • dx2 + - + 5— p- \ dxm
dx2 I ЭХ] I dxm I ЭХ] I
, Э ( df > d ( df A ,
• dx. + — p~ \dx2 + ... + -— —- \dxm +
Эх2 I dX2 I х dXOT I oX2 I
* U
dXj I dx.
ар/
dX] I dX2
dxj [ дхт PX| + Эх2“ [ дхт + - + dXm [ a/m
= a { dxi +rlydxl+... + d-^-dx2m
Эх2 Эх2 Ъх2т
dx,dx3 +... + dx}dx +
Эх^Эхз дх\дхт dx^dx^
+... + dx2dxm + ... + —
3x2dxm 3xm_}dxm
+ dxm
+ 2 —- dx.dx~, +
Эх]Эх2
, , Э2/ , .
dx2dx3 + -—-—dXidxA
2 J Эх2Эх4 i
dXm-\dXm
= fdxx + dx2 +... + dxm} f.
I aXj 0X2 1
Bunda simvolik yozuvdan foydalaniladi. U quyidagicha tushuniladi:
qavs ichidagi yig’indi kvadratga ko‘tarilib, so‘ng/ga «ko'paytiriladi».
K.eyin daraja ko'rsatkichlari xususiy hosilalar tartibi deb hisoblanadi.
Demak, x
d2f(x) = (-3- dx' + dx2 + ... + ~- dxm ) .
I oXj dx2 dxm I
(1)
f (xj funksiyaning x nuqtadagi uchinchi, to‘rtinchi va h.k. tartibdagi
differensiallari ham yuqoridagidek ta’riflanadi.
Umuman,/(x) funksiyaning x nuqtadagi (n— 1)- tartibli differensiali
d n~'f (x) ning differensiali f (x) ning n- tartibli differensiali deyiladi
va dnf(x) kabi belgilanadi:
d"f(x) = rf(J"-7(x)) •
91
Agar f (x) funksiya x nuqtada n marta differensialanuvchi bo'isa,
u holda
bo‘ladi.
3°. Murakkab funksiyaning yuqori tartibli differensiallari. Biz
yuqorida funksiyaning yuqori tartibli differensallarini bayon etdik.
Linda funksiya argument! x13 x2, xm lar erkli o‘zgaruvchilar edi.
Aytaylik,/(x) = f(xx, x2, • ••, funksiyada x„ x2, xm o‘zga-
ruvchilaming har biri tx, t2, tk o‘zgaruvchilarning funksiyalari bo‘l-
sin (x, = Ф,. (Z!,Z2)).
Qaralayotgan /(x) va x,=(p,(i), (z = 1,2,funksiyalar
n marta differensiallanuvchanlik shartlarini bajargan deb, murakkab
/(x(0) funksiyaning yuqori tartibli differensiallarini hisoblaymiz.
Ma’lumki, differensial shaklning invariantligi xossasiga binoan,
murakkab funksiyaning differensiali
Э/ , Э/ , df ,
df = f-dxx + f~dx2 +... + f-dxm
J 3X1 1 Эх2 2 dxm m
bo'ladi. Differensiallash qoidalaridan foydalanib funksiyaning ikkinchi
tartibli differensialini topamiz:
d2 f - d (df) - d( dxx + (>ddx2 +... + f^—dx
v ’ I Эх, 1 dx2 2 dx„,
= d[ — dx, )+ d{^—dx2 )+... + d{f^—dx =
I Эх, J Эх2 J I dx„, J
= d( — Y dx, + — d(dxA + d(dx2 + d (dx2 )+...+
^Эх, J 1 ЭХ1 v 17 ^Эх2 J 2 dx2 v 27
+d[~^~\dXm +drd(dXm^
dXmJ dXm
+ ^d2x} +^d2x2 +...+ ^-d2xm
Эх, Эх2 Эхт
92
Demak,
d2
f = f ^~dx, + dx2 + ... + --- dx„.
I dX] Эх2 oxm
df j2 df >2 df j2
dXi dx2 oxm
.2
(3)
m •
Shu yo‘l bilan berilgan murakkab funksiyaning keyingi tartibdagi
differensiallari topiladi.
1- e s 1 a t m a . (1) va (3) formulalarni solishtirib, ikkinchi tartibli
differensialarda differensial shaklning invariantligi xossasi o‘rinli emas-
ligini ko'ramiz.
2-eslatma. Agar /(x1,x2,...,xm) funksiya argumentlari
Xj,x2, —>xm laming har biri f, t2,..., tk o‘zgaruvchilaming chiziqli
funksiyasi bo‘Isa, u holda f (x) funksiyaning ikkinchi tartibli (umuman,
n- tartibli) differensiali differensial shaklning invariantlik xossasiga
ega bo'ladi.
◄ Aytaylik,
x: = b< +ai^\ + - + aiktk, (z = 1,2,...Д)
bo'lsin. U holda, ravshanki,
d2f = d2t2 = ... - d2tk = 0
bo'lib,
d2x, = aZ[ d2tx + d2t2 + ... + a, d2tk - 0
bo'ladi. (3) formuladan foydalanib topamiz:
d2/ = f ~ dxx + ---dx2 + ... + V .
I dX] dx2 дхт I
Bu esa J2/ning (1) formula ko'rinishiga ega ekanligini bildiradi. ►
4°. Ko‘p o'zgaruvchili funksiyaning Teylor formulas!. Aytaylik,
/(x) = /(xj, x2,..., xm) funksiya ochiq Rm to'plamda berilgan
bo'lib, U5(x°) с E bo'lsin, bunda x° = (x®, x2,..., x° ) va 8 > 0.
Ravshanki,
Vx = (х]|,х2,...,хт)е t7s(x°), x° = (xf
nuqtalarni birlashtiruvchi to'g'ri chiziq kesmasi
,o
93
A = {xf + r(X] - xf), x2° + Z(x2 - x2°),x° + t(xm - x° ); 0 < t < 1}
shu £/s(x°) ga tegishli bo'ladi.
Farazqilaylik, f (x1,x2,...,xm) funksiya f/5(x°) to‘plamda(л+1)
marta differensiallanuvchi bo'lsin. Bu funksiyani A to‘plamda qarasak,
[0, 1] segmentda aniqlangan ushbu
F(t) = /(*1° + t(x} -x?), x2° + t(x2 — x2), x° + t(x„, -x“ ))
funksiyaga ega bo‘lamiz. F(f) funksiya [0, 1] da hosilaga ega bo‘lib,
f= sr hl - )+^ - h: - x?)+... + b. - 4) =
bo‘ladi, bunda/(x) funksiyaning barcha xususiy hosilalari
(xf +t(x! -xf), x2° + t(x2 -x2°),x° +t(xm -x°)) (4)
nuqtada hisoblangan.
Umuman, hosil qilingan F(f) funksiya k- tartibli (k = l,2,...,n+l)
hosilalarga ega va u
= _xo) +JL.(x2 _xo)+ + Э (x^ _хоИ у
I vxl °х2 ®хт )
ga teng, bundagi barcha xususiy hosilalar (4) nuqtada hisoblangan.
Bu munosabatning to‘g‘riligi matematik induksiya usuli yordamida
isbotlanadi.
Shunday qilib, F(t) funksiya F'(t), F"(t),F(n+l\t) hosilalarga
ega bo‘ladi. Teylor formulasiga ko‘ra (qaralsin, 24- ma’ruza) t0 nuqtada
(0<f0<l)
F(0 = F(t0) + F'(?o)(^^) + ^''ao)(^-^o)2 +••• +
bo‘ladi, bunda c = fo+e(f-to),O<0<l.Bu tenglikda tQ = 0, t - 1
deyilsa, u holda
94
F(l) = F(0) + 1 F'(0) +1 F'(0) + ... + Д F(n} (0) + F("+1) (0)
1! 2! nl U+l)!
bo'lishi kelib chiqadi.
Ayni paytda,
F(0) = /(4,x2°,.. .,x°m),
F(l) = f(xi,x2,...,xm),
F(fc)(0) = f4-(x1 -4) + -|-.(x2 -х2°) + ... + -^-- (хт-х®)У (6)
l ОЛ2 ^xm J
(bunda/funksiyaning barcha xususiy hosilalari (xf, x2,..., x° ) nuq-
tada hisoblangan) bo‘lishini e’tiborga olsak, u holda (5) va (6) tenglik-
lardan ushbu
n 1
f (Xj, x2,..., xm) = f (4, x2°,4) + Xp x
k=l
( 3 ( n\ Э I Ot 3 ( oa'I r! о о 0
VX1 - X1 ) + И2 - X2 ) + - + 47“\Xm - /(*! , X2 , ..., x"
г vX\ dX2 dx^ 1
+ г \и[Л(х1-4)) +/ (X2 -ХЛ+ -- + 7 -(л™ '--4)^ x
(л-И)! I 1 7 дх2 дхт v ' I
Xf (4 + 0 (x, - 4), x2° + 0 (x2 - 4 ), ..., X®, + 0 (xm - x°))
(0 < 0 < 1) tenglikka kelamiz. Bu ifoda ko‘p o'zgaruvchili f (X], x2,..., xm)
funksiyaning Lagranj ко ‘rinishidagi qoldiq hadli Teylorformulasi deyiladi.
5°. Xususiy hollar. Aralash hosilaning tengligi haqida teorema.
m = 1 bo‘lsin. Bu holda и = /(x) (x e R, и e R) funksiyaning yuqori
tartibli hosila va differensiallariga kelamiz. Ular 23- ma’ruzada batafsil
bayon etilgan.
m = 2 bo'lganda и =f(x, y), ((x,y) e R2,u& R) ikki o'zgaruvchili
funksiya bo‘lib, uning ikkinchi tartibli xususiy hosilalari (ular 4 ta
bo'ladi) quyidagicha bo'ladi:
Э2/(х,у) = Э (3f(x,y) A 32f(x,y) = 3 hdf(x,y) 3
Эх2 Эх Эх / ЗуЗх Зу ;Эх J
Э2/(х,у) = Э f Э/(х,у) А Э2/(х,у) _ 3 р/(х,у) А
ЗхЗу Эх I Зу Г Зу2 ду I Эу J'
95
1-misol. Ushbu f(x,y) = arctgy, (у * 0)
funksiyaning ikkinchi tartibli xususiy hosilalari topilsin.
◄ Ravshanki,
Э/ _ 1 1 _ у Э/ _ 1 (_ x x
dx x2 У x2+y2 ’ dy x2 I у2 I x2+y2
i+ 7 i+ v ;
У У
bo‘ladi.
Endi ta’rifdan foydalanib, berilgan funksiyaning ikkinchi tartibli
xususiy hosilalarini topamiz:
Э2/ _ Э f у A
Эх2 3*^x2+y2J
2xy
(x2 +y2 )2
a2/ _ a f у a x2- y2
dydx ay^x2+y2J (x2+y2t ’
d2f = a / x A x2- y2
dxdy dx ( X2 +y2 J (x2 +y2 у ’
d2f _ d f x A 2xy
dy2 dy I Х2+У2 I (x2+v2?
2- misol. Ushbu
/U,y) =
x2-y2
xy-^—Y
x+y
0 .
agar x2 +y2 >0 bo‘lsa,
agar x2 + y2 =0 bo‘lsa,
funksiyaning (0, 0) nuqtadagi aralash hosilalari topilsin.
Aytaylik, (x,y)(0,0) bo‘lsin. Bu holda
Э/ = f x2-y2 4x2y2
Эх x2+y2 (x2+;v2)2
df _ (x2 -y2 4x2y2
a2/ _ a p/\_ x2-/
dydx dy\dx) x2+y2
(x2 +У2 ) J
96
э2/ = э С,!' )_ х1-у2.(i + __8х2у2.__ '
ЭхЭу Эх (йу J х2+у2 (х2+у2)2
bo'ladi.
Aytaylik, (х,у) = (0,0) bo'lsin. Bu holda funksiyaning hosilalarini
ta’rifgga ko‘ra hisoblaymiz:
3/(0,0) = lim ./1.w.O) /(().()) = Q
Эх Дх—>o Дх
Э/(0,0) = Ит /(0,Ду)-/(0,0) ()
Эу ду->0 Ду
3/(0,Ду) Э/(0,0)
U Э2/(0,0) AV А -Ду3 ,
- - ' = Iim —ЛХ--------------z\x_ _ llm у _
ЭуЭх Лу-,() Ду Др^О Ду-’
Э/(Дх,0) ,)/(().())
Э2/(0,0) . Ду Ду .. -Ду3
—— = lim----------------~------------— = lim -----. - 1. ►
ЭхЭу ДХ Лх-^0 Дх-
Yuqorida keltirilgan misollardan ko‘rinadiki,/(x,y) funksiyaning
э2/
ЭхЭу ’ dydx
aralash hosilalari bir-biriga teng ham boOishi mumkin, teng bo‘lmasdan
qolishi ham mumkin ekan.
2- teorema. Faraz qilaylik,/(x,y) funksiya (x0, y0) e R2 nuqtaning
^8 ((xo^o)) atrofida
aralash hosilalarga ega bo‘lib, bu hosilalar (хоАо) nuqtada uzluksiz
bo‘lsin. U holda/(x,y) funksiyaning aralash hosilalari (x0,y0) nuqtada
teng bo‘ladi:
Э2 / (xOjy°) = a2/(x0 ,y0)
dydx dxdy
◄ Aytaylik, (x0 + Ax, y0 + Ay), (x0 + Ax, y0), (,x0, y0 + Ay) nuq-
talar (x0,y0) nuqtaning atrofiga tegishli bo‘lsin:
97 ;
(х0 + Лх, у0 + Ду) е U& ((х0,у0)), (*о + Ах, ко) е U& ((х0, у0)),
(х0,у0 + Лу)^иб ((х0,у0)).
Ushbu i
Ф (Лх, Ду) = f (х0 + Лх, у0 + Ду) ~ f (*о + Лх, у0 ) -
-/(*о>ко + Ду) + /(х0,у0),
ф(х) = f (х, у0 + Ay) - f (х, у0 )
funksiyalarni qaraylik.
Ravshanki,
Ф(Лх, Лу) = <р(х0 +Дх)-ф(х0)
bo‘ladi. Bu tenglikning o‘ng tomoniga Lagranj teoremasini ikki marta
qo'llab topamiz:
ф(х0 + Дх)-ф(х0) = ф'(х0 + 0] • Дх) Дх =
а/ (хо+ердх^о+ду)
Эх
Э/(х0 +0J Дх,уо)
Эх
Лх =
= (0<е,,е2 <1).
ЭуЭх
Shartga ko‘ra aralash hosila (х0,у0) nuqtada uzluksiz. Demak,
Лх -» 0, Лу -> 0 da
= э;/(х0.л) + 0(1)
ЭуЭх ЭуЭх
bo‘lib,
Ф (Лх, Ду) = —ДхДу + 0(1) (7)
bo‘ladi.
Endi Ф(Лх, Ду) funksiya bilan birga quyidagi
V(J^) = /(^o + Ax,y)-/(x0,y)
funksiyani qaraymiz. Ravshanki,
Ф (Дх, Ду) = у (y0 + Ду) - у (y0)
bo‘ladi. Yuqoridagidek, bu tenglikning o‘ng tomoniga Lagranj teore-
98
masini ikki marta qo'llab, so'ng aralash hosilaning (x0,y0) nuqtada
uzluksizligidan foydalanib topamiz:
V(y0 i Av) v(r„) =
dy dy
Э2/(хо+е2Ал!уо+О5Лу) Э2/(л-о,Уо) . .
= - ------- AxAy ------------------ AxAy + 0(1),
JAW dXdy
(0<9]', Q'2 < 1, Ax-» 0, Ay->0).
Demak, Ф (Ax, Ay) = AxAy + 0(1). (8)
ЭхЭу
(7) va (8) munosabatlardan
Э2/(х0,у0) = Sj/jxo^o)
ЭхЭу ЭуЭх
bo‘lishi kelib chiqadi. ►
Mashqlar
1. Ushbu и =/(x,y), x = t2 + s2, у = t • v funksiyaning ikkin-
chi tartibli differensiali topilsin.
2. Ushbu и ~ у • <p(x2 -у) funksiya quyidagi
i du 1 du _ U
X dx у dy y2
tenglikni qanoatlantirishi isbotlansin.
63-ma’ruza
Ko‘p o‘zgaruvchili funksiyaning ekstremumlari
1°. Funksiya ekstremumi tushunchasi. Zaruriy shart. Faraz qi-
laylik, f (x) = f (xj, x2,..., xm) funksiya £c Rm to'plamda berilgan
bo'lib, x° = (x]°, xf, .... x° )eE bo'lsin.
1- ta’rif. Agar shunday 5 > 0 son topilsaki,
f/s(x°) с E bo'lib, Vxe t/5(x°) da \/(x) < /(x°)
99
bo‘lsa,/(x) funksiya x° nuqtada lokal maksimumga-, f(x) > f(x°)
bo‘lsa, f(x) funksiya x° nuqtada lokal minimumga erishadi deyiladi.
2- ta’rif. Agar shunday 3 > 0 son topilsaki, t/5(x°) cz E bo‘lib,
Vx e C7g(x°)\{x0} da /(x)< /(x°) bo‘Isa,/(x) funksiya x° nuqta-
da qat’iy lokal maksimumga; f (x) > /(x°) bo‘Isa, /(x) funksiya x°
nuqtada qat’iy lokal minimumga erishadi deyiladi.
Funksiyaning lokal maksimumi, lokal minimum! umumiy nom
bilan funksiyaning lokal ekstremumi deyiladi. Bunda x° nuqta /(x)
funksiyaning lokal ekstremum nuqtasi.flk') ga esa funksiyaning lokal
ekstremum qiymati deyiladi.
Funksiyaning maksimum (minimum) qiymati quyidagicha belgi-
lanadi:
/(x°)= max /(x) , /(x°)= max /(x) .
ae(/s(x°) ( xet/s(.d) ?
Ma’lumki, Hf(x(>) = f (x) - /(x°)
ayirma funksiyaning x° nuqtadagi to‘liq orttirmasi deyilar edi.
/(x) funksiya x° nuqtada lokal maksimumga erishsa, u holda
Vx e t/s(x°) da
Д/(х°)<0
bo‘ladi va aksincha. Shuningdek, /(x) funksiya x° nuqtada lokal
minimumga erishsa, u holda Vx e Us (x°) da
A/(x°)>0
bo‘ladi va aksincha.
1-teorema. Agar /(x) =/(x15 x2,..., xm) funksiya x° = (x®,
x2, x°) nuqtada lokal estrerpumga erishsa va shu nuqtada barcha
(/ = 1,2,...,/и)
dx,
xususiy hosilalarga ega bo‘Isa, u holda
---L = o, (l - 1,2,...,/и)
Эх/
bo‘ladi.
100
◄ Aytaylik, f(x) = f[xi,x1,...,xm) funksiya x° = (x?, x2°,..., x°)
nuqtada lokal minimumga erishsin. U holda
Vx = (x1,x2,...,xm)e f/s(x°) da f(xx ,x2 ,...,xm) > )
tengsizlik bajariladi. Jumladan,
f (xj, x2°, x3°,..., x°) > f (x°, x2°,..., x° )
bo‘ladi. Agar
ф(х1) = /(х1,х2°,х3°,...,х“)
deyilsa, Vxj e (xf - 8, xf + 8) da
ф(х1)>ф(х1°)
bo‘lib, bir o’zgaruvchili cp(X] ) funksiya xf nuqtada lokal minimumga
erishadi. U holda 25- ma’ruzada keltirilgan teoremaga ko‘ra
Ф (xj ) = 0, ya m = 0
bo‘ladi. Xuddi shunga o‘xshash
a/(x°) _Q э/(х°Г Q \
Эх2 ’ dxm
bo‘lishi isbotlanadi. ►
1-eslatma. Agar/(x) funksiya biror x° nuqtada lokal ekstre-
mumga erishsa va shu nuqtada differensiallanuvchi bo‘lsa, u holda
#(x°) = 0
bo‘ladi.
2- e s 1 a t m a. /(x) = f (xj, x2,xm) funksiyaning biror x° nuq-
tada barcha xususiy hosilalarga ega va
= 0, (z = 1,2,...,/и)
bo‘lishidan, berilgan funksiyaning shu nuqtada lokal estremumga eri-
shishi har doim kelib chiqavermaydi (misoliar keyingi bandda kelti-
riladi).
Demak, 1- teorema funksiyaning lokal ekstremumga erishishining
zaruriy shartini ifodalaydi.
101
/(x) funksiya xususiy hosilalarini nolga aylantiradigan nuqtalar
uning statsionar nuqtalari deyiladi.
2°. Funksiya ekstremumga erishishining yetarli sharti. Aytaylik,
/(x) = /(Xj, x2,xm) funksiya x° e Rm nuqtaning biror C/S(x°) atro-
fida berilgan, shu atrofda barcha ikkinchi tartibli uzluksiz xususiy
hosilalarga ega va
d/(x°) n /. , з >.
A-—- 0, (z = 1,2,...,m)
dx,
bo‘lsin. Bu funksiyaning Teylor formulas! (62- ma’ruzada keltirilgan
Teylor formulasida n = 2 bo‘lgan hoi)
——- = 0, (z = 1,2,
dx, '
shartni hisobga olgan holda quyidagicha
/(х) = /(х°) + |£^-Дх,Дхл (1)
z “1 dxi°xk
ko‘rinishda ifodalanadi, bunda ikkinchi tartibli xususiy hosilalar
(x]° + 0 Axt, x2 + 9 • Ax2 ,x° + 9 • Axm)
(0 < 9 < 1) nuqtada hisoblangan va bunda
AXj = Xj -xf, Ax2 =x2 — x2, ..., Axm =xm -x° •
Berilgan f (x) funksiya ikkinchi tartibli xususiy hosilalarining x° statsio-
nar nuqtadagi qiymatlarini
(j,k = l,2,...,m)
dXjdx^
bilan belgilaymiz. Barcha ikkinchi tartibli xususiy hosilalar
Э2/
dXjdXk
laming x° = (x®, x2,x° ) nuqtada uzluksizligidan
aik ~ aki
hamda
102
э2/(х1°+едх1, х“+е-дх2,х°+едхт) э2/(х°)
---------------_— _ —-----1_ (ч. _ д., + ц.,
дх,дхк---------------------------------------dXjdxk К к к
bo‘lishi kelib chiqadi, bunda
kXj -> 0, (z = l,2,...,zz?) da alk -> 0.
Natijada (1) tenglik ushbu
Д/ (x°) = f (x) - f (x°) =
। Гн
~ ^а^Лхк
m
m
+Ха'*Лх'дх^
'Л
ko‘rinishga keladi. Agar
p = ^/Ax2 + Ax2 + ... + Ax2 ,
Ax, = p • (z =
deyilsa, so‘ngra Дх;. 0 (z = 1,2,...,m) da, ya’ni p -> 0 da
У = P2 У <^ik^k = P2 a(p)
; I, i ; i.
(bunda, p -> 0 da a(p) -> 0) bo‘lishini e’tiborga olsak, u holda
дЛх°) = 4
tn
У aij£&k +a(p)
i,k=l
(2)
bo‘lishini topamiz.
Ma’lumki, a^Cx0) =/(x)-/(x°) ayirma 17s(x°) da ishora
saqlasa, ya’ni Vx e U& (x°) da
A/(x°)>0
bo‘lsa, f (x) funksiya x° nuqtada lokal minimumga;
A/(x°)<0
bo'lsa, f (x) funksiya x° nuqtada lokal maksimumga erishadi.
Yuqoridagi (2) tenglikdan ko‘rinadiki, A/(x°) ning ishorasi koefFitsi-
yentlari
a2/6c°) /. 7 1 ~ x
103
bo‘lgan X а1к^Лк (3)
/Л=>
kvadratik shaklga bog‘liq bo'ladi.
2- teorema. Agar (3) kvadratik shakl musbat aniqlangan bo‘lsa,
fix) funksiya x° nuqtada lokal minimumga; manfiy aniqlangan bo‘lsa,
lokal maksimumga erishadi.
Agar (3) kvadratik shakl noaniq bo‘lsa, fix') funksiya x° nuqtada
lokal estremumga erishmaydi.
◄ Bu teorema, keyingi bandda, xususiy holda, ya’ni ikki o‘zga-
ruvchili funksiyalar uchun isbotlanadi. ► (Qaralsin, [1], 13-bob).
3°. Xususiy hollar, m = 1 bo‘lsin. Bu holda и = /(x), (xg R, иe R)
funksiyaning lokal ekstremumlari, ekstremumning zaruriy va yetarli
shartlari kabi tushuncha va tasdiqlarga kelamiz. Ular 25- ma’ruzada
bayon etilgan.
m = 2 bo'lsin. Bu holda и - f (x,y), ((x, y) e R2, и e R) ikki
o‘zgaruvchili funksiyaning lokal ekstremum tushunchalari yuzaga kelib,
bu hoi uchun ulaming ta’riflari quyidagicha bo‘ladi.
Aytaylik, и = f (x,y) funksiya Ec Rm to'plamda berilgan bo‘lib,
(x0,y0) e E bo‘lsin.
Agar 5>0 shunday son topilsaki, [/5((x°,y0)) с E bo‘lib,
V(x,y)e t/§ ((x0,y0)) uchun
/(x,y)>/(x0,y0), (/(x,y)</(x0,y0))
bo‘lsa, f (x,y) funksiya (x0,y0) nuqtada lokal minimumga (lokal mak-
simumga) erishadi deyiladi. (x0,y0) nuqta /(x,y) funksiyaning lokal
minimum (maksitnum) nuqtasi, /(x0,y0) miqdor esa funksiyaning
minimum (maksimum) qiymati deyiladi.
Agar shunday 8 > 0 son topilsaki, Ug((x°,y0)) c E bo‘lib,
V (x, у) g Us ((x0, y0)) \ {(x0, y0)} uchun
/(x,y) > /(x0,y0), (/(x,y) < /(x0,y0))
bo‘lsa,/(x,y) funksiya (x0,y0) nuqtada qat’iy lokal minimumga (qat’iy
lokal maksimumga) erishadi deyiladi.
1- misol. Ushbu f (x,y) = >/l - x2 - y2 funksiyaning (0,0) nuq-
tada qat’iy maksimumga erishishi ko‘rsatilsin.
104
◄ 8 > 0, (0 < 8 < 1) sonni olib, (0,0) nuqtaning Ц((0,0)) atrofini
hosil qilamiz. U holda V(x,y)e U5 ((0,0))\{(0,0)} uchun
f (x, y) = 71--X2 < f (0,0) = 1
bo'ladi. Demak, berilgan funksiya (0,0) nuqtada maksimumga eri-
shadi. ►
Agar /(x,y) funksiya (x0,y0) e E с K8 > 0m nuqtada lokal
ekstremumga erishsa va shu nuqtada
у
dx ’ Эу
xususiy hosilalarga ega bo'lsa, u holda
Э/(хо,Уо) = 0 Э/(х0,у0) =
dx ’ dy
bo'ladi.
Biroq,/(x,y) funksiyaning biror (x*,y*) nuqtada Ц, ~~ xususiy
hosilalari mavjud bo'lib, ular shu nuqtada nolga teng bo'lsa, qara-
layotgan funksiya (x*,y*) nuqtada ekstremumga erishmasdan qolishi
mumkin. Masalan,
J\x,y) = xy
v • У Э/
funksiya ^-У, ^y-x
xususiy hosilalarga ega bo'lib, ular (0,0) nuqtada nolga teng:
э/(0,0) _ Q a/(0,0) _ 0
dx ’ Эу
bo'lsa ham, bu funksiya (0,0) nuqtada ekstremumga erishmaydi (funk-
siya grafigi — giperbolik paraboloidni tasawur qiling).
Aytaylik, f (x,y) funksiya (x0,y0) e R2 nuqtaning biror f/5((x0,y0))
atrofida (8 > 0) berilgan bo'lib, quyidagi shartlarni bajarsin:
1) f{x,y) funksiya t/g((x0,y0)) da uzluksiz va uzluksiz /*, fy, f"2,
fxy, fyi xususiy hosilalarga ega, г>
2) (x0, y0) statsionar nuqta:
fx(xo,yo) = O, /;(xo,yo) = O.
105
Bu f (x) funksiya uchun 2° da yuritilgan mulohazalami qo‘llab
A/(x0,y0) = /U^)-/(x0,y0) =
= |(«цАх2 + 2а12ДхАу + a22Ay2 + осцАх2 + 2ос12ДхДу + а22Ду2) (*)
bo‘lishini topamiz, bunda
all - (x0> Уб), й12 - fxy (^b > %) = fyx (*0 > •%)> ^2 = fyl (ДЬ’ %)
bo‘lib,
Ax -» 0, Ay -> 0 da an -> 0, al2 -> 0, a22 -> 0
bo‘ladi.
3- teorema. Agar
anAx2 + 2a12AxAy + a22 Ay2 (4)
kvadratik shakl musbat aniqlangan, ya’ni
a21
«12
°22
- allfl22 ~ ah > 0
bo‘lsa, f(x,y) funksiya (x0,y0) nuqtada lokal minimumga erishadi,
agar (4) kvadratik shakl manfiy aniqlangan, ya’ni
0ц < 0,
«н
°21
a12
fl22
= alla22 - an >0
bo‘lsa, /(x,y) funkusiya (x0,y0) nuqtada lokal maksimumga erishadi.
◄ Ma’lumki, f (x,y) funksiyaning (xo,yo) nuqtada ekstremumga
erishishi f/s((x0,y0)) da ushbu
ayirmaning ishora saqlashi bilan bog‘liq:
V(x,y)e Us ((x0,y0)) da AfOWo) > 0 bo‘lsa,
(x0,y0) nuqtada lokal minimum; V(xo,J;o)<O bo‘lsa, (x0,y0)
nuqtada lokal maksimum sodir bo‘ladi.
A/" (x0, y0) ayirmaning ishorasini aniqlash qulay bo‘lishi maqsadida
(4) da
Ax = p • cos <p , Ay = p sin tp
106
almashtirish bajaramiz, bunda
p = yjXx2 + Ay2 .
Natijada (*) munosabat ushbu
А/ (x0, y0) = ^2 [(°n cos2 + 2й12 cos (p sin (p + a22 sin2 ф) +
+ (an cos2 ф + 2a12 cos ф sin ф + a22 sin2 ф)^ (5)
ko‘rinishga keladi. Aytaylik,
flll >0, <2ji«22 ~ a12 > 0
bo‘lsin. Ravshanki,
an cos2 ф + 2an cosф8т ф + a22 sin2 ф =
= — Нац cosф + an $тф)2 + (апа22 -а22)• sin2 ф1.
«п L J
Ayni paytda, bu funksiya ф ning funksiyasi sifatida [0,2л] da
uzluksiz bo‘lib, o‘zining eng kichik qiymati (uni m bilan belgilaylik)
m ga ega bo'ladi:
|an cos2 ф + 2a12 cos фsin ф + a22 sin2 ф| > m > 0 .
Ikkinchi tomondan, Ax —> 0, Ay -ч> 0, ya’ni p -> 0 da an -> 0,
a12 0, a22 -> 0 bo‘lganligi sababli, p ning yetarli kichik qiymat-
larida
|аи cos2 ф + 2oc12 cos ф sin ф + a22 sin2 ф| < |ап j + 2 |а121 + |а22| < т
bo‘loladi.
Demak, al} > 0, ana22 - a22 > 0 bo‘lganda (5) tenglikning o‘ng
tomonidagi ifoda musbat bo‘ladi. Binobarin,
>o
bo‘lib, f (x,y) funksiya (x0,y0) nuqtada lokal minimumga erishadi.
Aytaylik, an < 0, ana22 -a22 >0
bo‘lsin. Bu holda (5) tenglikning o‘ng tomonidagi ifoda manfiy bo'ladi.
Binobarin,
ДА(хо,Уо)<О
bo‘lib,/(x,у) funksiya (x0,y0) nuqtada lokal maksimumga erishadi. ►
107
3- e s 1 a t m a. Agar ax j a22 - < 0 bo'lsa, f (x,y) funksiya (x0,y0)
nuqtada ekstremumga erishmaydi.
4- e s 1 a t m a. Agar ax ja22 - cf2 = 0 bo'lsa, f (x,y) funksiya (x0,y0)
nuqtada ekstremumga erishishi ham mumkin, erishmasligi ham
mumkin (qaralsin, [1], 13-bob).
2- misol. Ushbu
f (x,y) - x2 + xy + y2 - 2x - 3y
funksiya ekstremumga tekshirilsin.
◄ Awalo berilgan funksiyaning statsionar nuqtalarini topamiz:
Щх,у) = 2х+y-2, 2x+y-2 = 0, ль=|,
4 (x,y)= x + 2y-3, x+2y-3=0, Уо=|-
/1 4)
Demak, I -, j I — statsionar nuqta. Ravshanki,
(x,y) = 2, f;y (x, y) = 1, /;2 (x, y) = 2.
Demak, au = 2, aI2 = 1, a22=2. Bunda an - 2 > 0 va
7 /14)
йн°22 ~ й12 = 3 > 0 bo'lganligi uchun berilgan funksiya lj,jl
nuqtada lokal minimumga erishadi va
min/(x,?) = /(pi) = -5
bo'ladi. ►
3- misol. Ushbu
/1 (%,y) = x4 +y4,
fl (x,y) = -(x4 +y4),
/3(x,y) = x3+y3
funksiyalar ekstremumga tekshirilsin.
◄ Berilgan funksiyalar uchun (0,0) statsionar nuqta bo'ladi. Bu
funksiyalar uchun
«пй22 -й122 =0
108
bo‘ladi. Ravshanki, (0,0) nuqtada/(x,у) funksiya minimumga,/2(x,y)
funksiya esa maksimumga erishadi. /3(x,y) funksiya (0,0) nuqtada
ekstremumga ega bo'lmaydi. ►
Mashqlar
1. 3- teoremada keltirilgan f(x,y) funksiya uchun (x0,y0) statsionar
nuqtada
fxT- (x0’ko )' fvi (xo > ко) •“ [Zry (^b > ко)] <0
bo‘lsa, j\x,y) funksiya (x0,y0) nuqtada ekstremumga erishmasligi
isbotlansin.
2. Ushbu f (%, у) = (у - x)2 +(y + 2)3 funksiya ekstremumga tek-
shirilsin.
64- ma’ruza
Oshkormas funksiyalar
1°. Oshkormas funksiya tushunchasi. Ma’lumki, x c R, Yc R
to'plamlar va biror/qoida berilgan holda har bir x e Xsonga/qoidaga
ko‘ra bitta у e Y son mos qo‘yilsa, X to'plamda у = /(x) funksiya
aniqlangan deyilar edi.
x va у o'zgaruvchilarni bog'lovchi qoida turlicha, jumladan,
analitik ifodalar yordamida, jadval yordamida, egri chiziq yordamida
bo'lishi mumkin.
Endi x va у o'zgaruvchilar tenglama yordamida bog'langan holda
funksiya yuzaga kelishini ko'rsatamiz.
Aytaylik, x va у o'zgaruvchilarning F(x, y) funksiyasi
E = {(x,y)e R2 : a < x < b, c<y<d]
to'plamda berilgan bo'lsin. Ushbu
/-(x,k) = 0 (1)
teglamani qaraylik. Har bir tayinlangan x = x0 da (1) tenglama у ga
nisbatan tenglamaga aylanadi. Bu tenglama yagona y0 yechimga ega
bo'lsin. Demak,
^(^o,ko) = O.
109
Bunday xususiyatga ega bo‘lgan x0 nuqtalar bir qancha bo'lishi
mumkin. Ulardan tashkil topgan to‘plamni Xdeylik. Ravshanki, bunda
Xc. (a, b) bo‘ladi.
Endi Xto‘plamdan olingan har bir x ga (хе X) (1) tenglamaning
yagona yechimi у ni mos qo‘yaylik. Natijada X da aniqlangan funksiya
hosil bo'ladi. Uni <p(x) deylik. Demak,
cp : x -> у va F(x,<p(x)) - 0 .
Bu cp(x) oshkormas (oshkormas ko‘rinishda berilgan) funksiya
deyiladi.
1- misol. Ushbu
F(x,y) = y\lx2 -1-2 = 0 (2)
tenglama yordamida oshkormas fuksiya aniqlanishi kohsatilsin.
◄ Ravshanki, (2) tenglama har bir xe (-o°,-l)u(l,+«) da yagona
У = ф(%) =
Vx2-1
yechimga ega va
F(x,cp(x)) = 0.
Demak, (2) tenglama oshkormas funksiyani aniqlaydi. ►
2- misol. Ushbu
F(x,y) = x -y + | sin у = 0
tenglama yordamida oshkormas funksiya aniqlanishi kohsatiisin.
◄ Berilgan tenglamani quyidagicha yozib olamiz:
x = y-|siny =a(y), (y e (-oo,+oo))_
Bu a(y) funksiya R da uzuluksiz va oc'(j) = 1 - - cosy > 0 bo‘ladi.
U holda a(y) funksiya (-<», +°°) da teskari у = a-1 (x) funksiyaga ega va
F(x,oT} (x)) = 0
bo‘ladi. Demak, bu tenglama ushbu
<p : x —> a1 (x)
oshkormas funksiyani aniqlaydi. ►
110
3- misol. Ushbu
F (x,y') - x2 + y2 - In у - 0, (у > 0)
tenglama у ni x ning oshkormas funksiyasi sifatida aniqlaydimi?
4 Aniqlamaydi, chunki har bir x g (-°°, +°°) da y2 - In у > 0 bo‘l-
ganligi sababli, yechimga ega emas. ►
Oshkormas funksiyalami o‘rganishda quyidagi masalalar muhimdir:
1) F(x,y) funksiya biror Ec. R2 to‘plamda berilgan holda у = <p(x)
oshkormas funksiya mavjud bo‘ladimi va bu funksiyaning aniqlanish
to‘plami qanday bo‘ladi?
2) (1) tenglama bilan aniqlangan у — <p(x) oshkormas funksiya
qanday xossalarga ega va bu xossalar F(x,y) funksiya xossalari bilan
qanday bog'langan?
2°. Oshkormas funksiyaning mavjudligi.
1- teorema. Faraz qilaylik, F(x,y) funksiya (x0,y0) nuqtaning biror
atrofi
uhk ((-UM = {(*> J) e R2 : x0 - h < x < x0 + h, y0 - к < у < y0 +
da (/? > 0, к > 0) berilgan bo‘lib, quyidagi shartlarni bajarsin:
1) F(x,y) funksiya Uhk ((x0,y0)) da uzluksiz;
2) Har bir tayin x & (x0 - h, x0 + h) da у o‘zgaruvchining funk-
siyasi sifatida o‘suvchi;
3) F(x0,y0) = 0.
U holda (x0,y0) nuqtaning shunday atrofi
((хо,Уо)) = e A2 : x0 -3 < x < x0 + 5, y0 - e < у < y0 + e}
topiladiki (0 < 8 < й, 0 < e < A:) , bunda:
a) Vx e (x0 - 3, x0 + 3) da
tenglama yagona v (y e (y0 - e, y0 + e)) yechimga ega, ya’ni
F(x,y) = 0 tenglama yordamida у = cp(x) oshkormas funksiya
aniqlanadi;
b) ф(А)) = У() bo‘ladi;
d) у - <p(x) funksiya (x0 - 8, x0 + 8) da uzluksiz bo‘ladi.
Ill
◄ ^hk ((лО’>’о)) atrofga tegishli bo‘lgan
(^о,Уо-е); (хо,Уо +e), (0 < e < A:)
nuqtalarni olib, [y0 - e, y(l + e] segmentda
y(y) = F(x0,y)
funksiyani qaraymiz. Teoremaning 2- shartiga ko‘ra \|/(y) o‘suvchi,
3- shartiga ko‘ra v(y0) = F(x0,y0) = 0 bo‘ladi. Bunda esa
v(To -е) = ^(х0,У0 -e)<0,
V(y0 +е) = ^(хо,Уо +e)>0
bo‘lishi kelib chiqadi.
Teoremaning 1- shartiga ko‘ra F[x,y) funksiya Uhk ((x0, y0)) da uzluk-
siz. U holda uzluksiz funksiyaning xossasiga ko‘ra, x0 nuqtaning shunday
(x0 - 8, x0 + 8) atrofi (0 < 8 < A) topiladiki, Vx e (x0 - 8, x0 + 8) da
F(x,y0 - e) < 0,
F (x,y0 +e) > 0 (3)
bo‘ladi. Endi (x0,y0) nuqtaning
U& ((Xo^'oj) = {(x.y)e R2 : x0 - 5< x < x0 +5, y0 -E<y < y0 +e}
atrofida
F(x,y) = 0
tenglama у ni x ning oshkormas funksiyasi sifatida aniqlashini ko‘r-
satamiz.
Ixtiyoriy x’ e (x0 - 8, x0 + 8) nuqtani olib, [y0 -£, y0 + e] da
ushbu
g(y) = F(x* ,y)
funksiyani qaraymiz. Ravshanki, bu funksiya [y0 - e, y0 + e] segment-
da uzluksiz va ayni paytda (3) munosabatga binoan
g(y0 -£) - R(x*,y0 -e) < 0,
§(Уо +e) = ^(x*,y0 +e) > 0
bo‘ladi. U holda Bolsano—Koshi teoremasiga ko‘ra shunday
y* e [y0 -£, y0 +e] nuqta topiladiki, bunda
112
g(y*) = F(x*,y*) = O
bo‘ladi.
Ayni paytda, g(y) funksiya [y0 - e, y0 + e] da o'suvchi (qat’iy
o‘suvchi) bo'lganligi sababli, у shu oraliqda bittadan ortiq nuqtada
nolga aylanmaydi.
Shunday qilib, ixtiyoriy x e (x0 - 8, x0 + 8) uchun yagona
ye (y0 -e,y0 + e) topiladiki, bunda
F(x,y) = 0
bo‘ladi. Bu esa ((x0,y0)) da F(x,y) - 0 tenglama у ni x ning
oshkormas funksiyasi sifatida aniqlashini bildiradi:
у - <p(x): F(x,(p(x)) = 0.
Aytaylik, x = x0 bo'lsin. U holda teoremaning 3- shartiga ko'ra
F(x0, Уо) = 0
bo'ladi. Binobarin, aniqlangan oshkormas funksiyaning x0 nuqtadagi
qiymati (p(x0) = y0 bo'ladi.
Modomiki, Vx e (x0 - 8, x0 + 8) uchun cp(x) ga ko'ra unga mos
keladigan у e (y0 - e, y0 + e) bo'lar ekan, u holda
|x - x01 < 8 => |y - y01 = |<p(X) - ф (x0 )j < 8
bo'ladi. Demak, oshkormas funksiya x0 nuqtada uzluksiz.
Oshkormas funksiyaning Vx* e (x0 - 8, x0 + 8) nuqtada uzluksiz
bo'lishini ko'rsatish bu funksiyaning x0 nuqtada uzluksiz bo'lishini
ko'rsatish kabidir. Demak, mavjudligi ko'rsatilgan oshkormas funksiya
(xq - 8, x0 + 8) da uzluksiz bo'ladi. ►
3°. Oshkormas funksiyaning hosilalari. Oshkormas funksiyaning
hosilasini aniqlaydigan teoremani keltiramiz.
2- teorema. Faraz qilaylik, F(x, y) funksiya (x0, y0) nuqtaning
biror atrofi Uhk ((x0,y0)) da (Л > 0, к > 0) berilgan bo'lib, quyidagi
shartlarni bajarsin:
1) uhk ((*о > fo)) da uzluksiz;
2) Uhk ((x0,y0)) dauzluksiz Fv'(x,y), F'(x,y) xususiyhosilalarga
ega va F;(x0,y0) * 0;
3) F(x0,y0) = 0.
113
U holda (х0, y0) nuqtaning shunday t/& ((x0,y0)) atrofi
(0 < 8 < h, 0 < e < k~) topiladiki, F (x, y) = 0 tenglama у ni x ning
у = <p(x) oshkormas funksiyasi sifatida aniqlaydi va bu у - <p(x)
funksiya (x0 - 5, x0 + 8) da uzluksiz differensiallanuvchi bo‘lib,
0)7x1-
7y(x,<p(x))
bo'ladi.
◄ Teoremaning shartiga ko‘ra F'(x,y) funksiya Uhk ((x0,y0)) da
uzluksiz va F' (x0, y0) Ф 0. Aytaylik, F? (x0, y0) > 0 bo‘lsin. Uzluk-
siz funksiya xossasiga ko‘ra (x0,y0) nuqtaning shunday ((x0,y0))
atrofi (0 < 8 < h, 0 < £ < k) topiladiki, V(x,y)e ((x0,y0)) da
Fy (x, y) > 0 bo‘ladi. Bundan esa har bir tayin x e (x0 - 6, x0 + 8) da
F(x,y) funksiya у o‘zgaruvchining funksiyasi sifatida o‘suvchi bo‘lishi
kelib chiqadi. U holda 1-teoremaga ko‘ra F(x,y)~0 tenglama
(x0 - 8, x0 + 3) da у ni x ning у = cp(x) oshkormas funksiyasi sifatida
aniqlaydi va у = cp(x) oshkormas funksiya x e (x0 - 8, x0 + 8) da
uzluksiz bo‘lib, cp(x0) = yQ bo‘ladi.
Aytaylik, x g (x0 - 8, x0 + 8), x + Дх g (x0 - 8, x0 + 8) bo‘lsin.
Ravshanki,
F(x,y) = 0, F(x + Дх, у + Ду) = 0
bo‘lib, bundan quyidagi ifodani hosil qilamiz:
ДТ(x,y) = F(x + Дх, у + Ду)-F(x,y) = 0. (4)
Teoremaning shartidan F(x,y) funksiyaning (x,y) nuqtada differen-
sialanuvchi bo'lishi kelib chiqadi. Binobarin,
дТ(х,у) = Тх'(х,у)дх + /Дх, у)Ду+а-Дх+р-Ду (5)
bo‘lib, Дх -» 0, Ду -» 0 da а -> 0, р -> 0 bo‘ladi.
(4 ) va (5) munosabatlardan topamiz:
Ay F^(x,y)+a
Дх ТДх,^)+р ’
Keyingi tenglikda Дх -> 0 da limitga o‘tsak, u holda
114
Ч \ ' Л<(Х,У)
ф(х)=у=‘^
hosil bo'ladi. t/& ((х0,у0)) da Fx(x,у), Fy {x,y} xususiy hosilalar
uzluksiz va Fy (x, у) * 0 bo‘lishidan oshkormas funksiyaning tiosilasi
ning (x0 - 8, x0 + 8) da uzluksiz bo‘lishi kelib chiqadi. ►
4- misol. Ushbu
F (x, у) = ey + у sin x - x3 + 7 = 0
tenglama (2, 0) nuqtaning atrofida у ni x ning oshkormas funksiyasi
sifatida aniqlashi va bu oshkormas funksiyaning hosilasi topilsin.
◄ Ravshanki,
F (x,y) = ey + у sin x - x3 + 7
funksiya R2 da aniqlangan va uzluksiz. Binobarin, u (2, 0) nuqtaning
atrofida uzluksiz, F(x,y) funksiyaning xususiy hosilalari quyickgicha
bo'ladi:
HSL’Zl - JL (ey + у sin x - x3 + 7) = у cos x - 3x2,
dx dx
= JL (ey + у sin x - x3 + 7) = ey + sin x.
dy dy
Demak, F(x,y) funksiyaning xususiy hosilalari R2 da, jumUdan,
(2, 0) nuqtaning atrofida uzluksiz.
So'ngra
Э/’(2,0) / у • x 1 • т
—= (еу + sm х)х=2 v=0 = I + sin 2 + 0
dy
Va nihoyat,
/г(2,0) = (ey + у sin x - x3 +7)x=2 y=0 = 0
bo'ladi. U holda 2- teoremaga ko'ra
F (x, у) = ey + у sin x - x3 +7 = 0
tenglama (2, 0) nuqtaning atrofida у ni x ning oshkormas funksiyasi
115
sifatida aniqlaydi va bu oshkormas ip(x) funksiyaning hosilasi quyida-
gicha bo‘ladi:
,, v FZ(x,y) ycosx-3x2
= = >
Fy(x,y) e^+sinx
1-eslatma. Oshkormas funksiyaninghosilasini quyidagichaham
hisoblasa bo‘ladi:
F(x,y) = 0
ni (yo‘zgaruvchi xning fimksiyasi ekanini hisobga olib) differensiallab
topamiz:
F'(x,y) + F'(x, y)y' = 0.
Keyingi tenglikdan esa quyidagi ifoda kelib chiqadi:
, F;(x,y)
y F;(x,y)
Aytaylik, F(x,y) funksiya f/& ((x0, y0)) da uzluksiz ikkinchi tartibli
(x,y), Fx;(x,y), f;2 (x,y)
xususiy hosilalarga ega bo‘lsin. Ma’lumki,
F*(x,y)
У F^x,y)-
Buni differensiallab topamiz:
, _ (Fx' (*,У))х Fy (x, y) - (F' (x, y))x Fx (x y)
(F^x,y))2
Agar (Fx'(x,y))x = F"2 (x,y) + Uj)- У, (6)
(F; (x, y))x = F" (x, y) + FS (x, y) y'
ekanini hisobga olsak. U holda
, _ (F;x(x,y)+F;2 (x,y)-y)FXx,v)-( (X y)+ x У >>)• V _
(f;(x,v))2
116
= л; ;0+[ ( л; у)- %( X ))- &( ^ > ^( ^ >] >
(f;(x,y))2
bo‘ladi. Bu ifodadagi у' ning o‘rniga
Fx(x,y)
fy(x,y)
ni qo‘yib, oshkormas funksiyaning ikkinchi tartibli hosilasi uchun
quyidagi formulaga kelamiz:
TF’ F’ F' -F'2 F"-' -F'2 F’i
* _ ‘ x ‘ у 1 xy 1 у ‘ XL X 1 yl
у .
ГУ
2- e s 1 a t m a. Oshkormas funksiyaning yuqori tartibli hosilalarini
quyidagicha ham hisoblasa bo‘ladi. Yuqorida
F(x,y) = 0
ni dfferensiallab,
г;(х,у) + г;(х,у)-у = 0
bo‘lishini topgan edik. Buni yana bir marta differensiallab topamiz:
[F^x,y) + F/(x,y) •/]* =
= №'(*, У))х + У • (Fy(x, y))x + F'(x, у) - yf = 0 .
Agar (6) munsabatlardan foydalansak, keyingi tenglik ushbu
f;2 (x,y) + 2Fx;(x,y) • у + к (x,y) • /2 + F/(x,y) • r = о
tenglikka keladi. Undan esa
F’i (хУ)+Т.Р”у(х,уУу'+Р’у1 (х,у) У2
У Fy (x,y)
bo‘lishi kelib chiqadi.
5- misol. Ushbu Cl
F(x, y) = xey + ye" -2 = 0
tenglama bilan aniqlanadigan oshkormas funksiyaning ikkinchi tartibli
hosilasi topilsin.
117 I
•4 Differensiallab topamiz:
(F(%,y))x = (xev +yex - 2)x = 0,
ey + yex + (xey + ex) • y' = 0 , (7)
Endi (7) ni yana bir marta differensiallaymiz:
ey • у' + У'ex + уех + ey у' + xeyy' у' + хеу у" + у"ех + у'ех = 0 •
Keyingi tenglikdan
_ 2еуу'+2еху'+хеУ у'2+уех
У _
bo‘lishi kelib chiqadi. Bu tenglikda у' ning o'rniga (8) da ifodalangan
qiymatini qo‘yib, oshkormas funksiyaning ikkinchi tartibli hosilasi
topiladi. ►
Mashqlar
1. Ushbu у5 + У - x = 0
tenglama bilan aniqlangan oshkormas funksiyaning grafigi yasalsin.
2. Ushbu Xy=yx, (x*y)
tenglama bilan aniqlanadigan у = tp(x) oshkormas funksiyaning у'
va у " hosilalari topilsin.
118
14- В О В
FUNKSIONAL KETMA-KETLIK VA QATORLAR
65-ma’ruza
Funksional ketma-ketliklar va ularning tekis
yaqinlashuvchanligi
1°. Funksional ketma-ketlik va limit funksiya tushunchalari. Aytaylik,
har bir natural n songa E c R to‘plamda aniqlangan bitta /„(x)
funksiyani mos qo'yuvchi qoida berilgan bo‘lsin. Bu qoidaga ko‘ra
/j(x),/2(x),...,/„(x),... (1)
to‘plam hosil bo‘ladi. Uni funksionalketma-ketlik deyiladi. £Чо‘р1аш
(1) funksional ketma-ketlikning aniqlanish to‘plami deyiladi.
Odatda, (1) funksional ketma-ketlik, uning n- hadi yordamida
{/„(%)} yoki/„(x) kabi belgilanadi. Masalan,
, v _ n+1 .2 3 n+1
JnW ~ T ’ ~ 2 ’ “ ’ ’ 2 ’ * * * ’
n+x 1+x 2+x n+x
Г , ч . fx . fx fx fx
fn (x) = sin — : sin , sin - ,..., sin —,...
и 1 2 n
lar funksional ketma-ketliklar bo‘ladi va ularning aniqlanish to‘plami
mos ravishda
E — R, E = [0,-н»)
bo‘ladi. Ravshanki, x o‘zgaruvchining biror tayinlangan x = xQ e E
qiymatida ushbu
{/„ (*0 )} fl Oo )> Л (*0 )’•••> fn Oo )> •••
sonlar ketma-ketligiga ega bo‘lamiz.
1- ta'rif. Agar {/„(x0)} sonli ketma-ketlik yaqinlashuvchi (uzoqla-
shuvchi) bo‘lsa, {/„(x)} funksional ketma-ketlik x = x0 nuqtada yaqin-
lashuvchi (uzoqlashuvchi) deyiladi. x0 nuqta esa bu funksional ketma-
ketlikning yaqinlashish (uzoqlashish) nuqtasi deyiladi.
2- ta’rif. {/„(x)} funksional ketma-ketlikning barcha yaqinlashish
nuqtalaridan iborat Eoc. Eto‘plam {/„(x)} funksional ketma-ketlikning
yaqinlashish to‘plami deyiladi.
119
Masalan, ushbu
/„(x) = xn : x,x2,x3,...,x",.„
funksional ketma-ketlik aniqlanish to'plami E — R bo'lib, u Vx e (-1,1]
nuqtada yaqinlashuvchi, xe R \ (-1,1] da uzoqlashuvchi bo'ladi.
Demak, ketma-ketlikning yaqinlashish to'plami Eo — (—1, 1] bo'ladi.
Faraz qilaylik, {/(x0)} funksional ketma-ketlikning yaqinlashish
to'plami Eo (Eo e R) bo'lsin. Ravshanki, bu holda har bir xe Eo da
/i(x), f2(x),..., /,(x),...
ketma-ketlik yaqinlashuvchi, ya’ni
lim/„(x)
n—>«>
mavjud bo'ladi. Endi har bir хе E ga lim f„ (x) ni mos qo'ysak, ushbu
f : x -» lim/„(x)
funksiya hosil bo'ladi. Bu /(x) funksiya {/„(-x())} funksional ketma-
ketlikning limit funksiyasi deyiladi:
lim/Дх) = /(x), (xef’o)-
M-—>oo
Bu munosabat quyidagini anglatadi: ixtiyoriy e > 0 son va har bir
xg Eq uchun shunday natural (e,x) son topiladiki, ixtiyoriy
n > n0 da
\fn(x)~f(x)\ < e,
ya’ni
Ve > О, 3/Ц) = 1% (e,x)e N, : |/(x) -/(x)| < e
bo'ladi.
1- misol. Ushbu /„ (x) = и sin
funksional ketma-ketlikning limit funksiyasi topilsin.
◄ Berilgan funksional ketma-ketlik E = [0, +<») da aniqlangan.
Uning limit funksiyasi
/(x) = lim /„ (x) = lim n sin ~ = lim —JU 4x = 7x
n yjx
П
120
bo‘ladi. Demak, funksional ketma-ketlik E = [0, +<*>) da yaqinlashuv-
chi va
lim n sin — = 4x . ►
It —It
2- misol. Ushbu fn (x) = xn
funksional ketma-ketlikning limit funksiyasi topilsin.
◄ Bu funksional ketma-ketlik E = R da aniqlangan. Ravshanki,
Vx e (l,+~) da lim /„(x) = lim x" = +°o,
4 z Л->оо
Vx e (-1,1) da lim fn (x) = lim xn = 0 ,
И—M—>OO
x = 1 da lim /„ (x) = lim 1 = 1,
Vxe (-оо,-1) da lim /„(x) mavjud emas.
Demak, berilgan funksional ketma-ketlik Ей = (— 1,1] da yaqinlashuv-
chi bo‘lib, uning limit funksiyasi
.. . „ [0, agar -1<x<1 bo‘lsa,
f (x) = hm x" = j
[1, agar x = 1 bo‘lsa
bo‘ladi. ►
3- misol. Ushbu
fn (x) = n2 - "<), (x > 0)
funksional ketma-ketlikning limit funksiyasi topilsin.
◄ Berilgan funksional ketma-ketlikning limit funksiyasi quyida-
gicha topiladi:
/(x) = lim(/„(x)) = lim n2 (Vx - n+¥x) = limn2 (x" -x^) =
И—>oo ft —>oo
)
_L_ / 1—_L_ \ „2 -
= lim n2xn+x \xn 77+1-l/ = lim-x—•—t--------= lnx. ►
2
rr
121
2°. Funksional ketma-ketlikning tekis yaqinlashuvchanligi. Faraz
qilaylik, {/„(x0)}:
/1 (x),/2(x),..., /„(x),...
funksional ketma-ketlik Eo to‘plamda yaqinlashuvchi (ya’ni yaqinla-
shish to‘plami Eq) bo'lib, uning limit funksiyasi f(x) bo‘lsin:
lim/„(x) = /(x).
Ma’lumki, bu munosabat
Ve > 0, 3n0 =Hq(z,x)e N, \fn> Hq-. |/„(x) - /(x)| < e
bo‘lishini anglatadi. Shuni ta’kidlash lozimki, yuqoridagi natural n0
son ixtiyoriy olingan e > 0 son bilan birga qaralayotgan x e Eq nuqtaga
ham bog‘liq bo‘ladi (chunki, x g Eo ning turli qiymatlarida ularga
mos ketma-ketlik, umuman aytganda, turlicha bo‘ladi).
3- ta’rif. Agar Ve > 0 son olinganda ham shu e > 0 gagina bog‘liq
bo‘lgan natural n() = (e) son topilsaki, Vn > «0 va ixtiyoriy xg Eo da
|/„(x)-/(x)| <e
tengsizlik bajarilsa, ya’ni
Ve > 0, Эл0 = «o(e)G N, \/n>nQ, X/xeE0: \fn (x) - ,/'(x) < e
bo‘lsa, {/„(x0)} funksional ketma-ketlik Eo to‘plamda /(x) ga tekis
yaqinlashadi (funksional ketma-ketlik Eo to‘plamda tekis yaqinla-
shuvchi) deyiladi.
Shunday qilib, {/„(x0)} funksional ketma-ketlik EtJ to‘plamda/(x)
limit funksiyaga ega bo‘Isa, uning shu limit funksiyasiga yaqinalishish
ikki xil bo'lar ekan:
l)Ve>0, 3hq = «о (e, x) e N, Vn> : |/„(x) - f(x)\ < e
bo‘lsa, {/„(x)} funksional ketma-ketlik Eo da /(x) ga yaqinlashadi
(oddiy yaqinlashadi). Bu holda
fn(x) f(x), (xeEq)
kabi belgilanadi.
2) Ve > 0, 3nQ=nQ(s.)&N, Vn> i^,Vxc Eq : \f„(x) - /(x)| < e
bo‘lsa, {f„(x)} funksional ketma-ketlik Eo da f (x) ga tekis yaqinlashadi.
Bu holda
/„(x)^/(x), (xg£0)
kabi belgilanadi.
122
29- chizma.
Ravshanki, funksional ketma-ketlik Eo to'plamda f(x)
funksiyaga tekis yaqinlashsa, u ushbu to‘plamda f (x) ga yaqinlashadi:
A(x)^/(x)=i>/„(x)^/(x), (xe£0).
Aytaylik, /„(x)^/(x), (xe£0) f
bo'lsin. Bu holda V« > nQ va Vx e Eo da
\f„ (x) - /(x)| < £, ya’ni /(x) - e < f„ (x) < /(x) + г
bo'ladi. Bu esa {f„(x)} funksional ketama-ketlikning biror hadidan
boshlab, keyingi barcha hadlari /(x) funksiyaning «£-oralig‘i»da
butunlay joylashishini bildiradi (29- chizma)
4- misol. Ushbu
. sin их
funksional ketma-ketlikning R da tekis yaqinlashuvchanligi ko'rsatilsin.
◄ Ravshanki,
lim /„(x) = lim^^ = 0.
Л—»oo fl
Demak, limit funksiya /(x) = 0.
Agar Ve > 0 son plinganda «() =
deyilsa, u holda Vn > n0 va
Vx e A uchun
123
|/„U)-/(x)| =
sin их
n
-0
sin их
и
1 < _L_
и " иь+1
bo‘lishini topamiz. Demak, ta’rifga binoan
sin их _>q
и
bo‘ladi. ►
Faraz qilaylik, funksional ketma-ketlik £0 to‘plamda f(x)
limit funksiyaga ega bo‘lsin.
1- teorema. funksional ketma-ketlik Eo to‘p]amda f(x) funk-
siyaga tekis yaqilashishi uchun
lim sup \fn (x) - /(x)| = 0
« £(l
bo‘lishi zarur va yetarli.
◄ Zarurligi. Aytaylik,
/„(x)^/(x), (xeF0)
bo‘lsin. Ta’rifga binoan
Ve > 0, 3n0=n0(E)e^V, Vn>«0,VxG£0: \fn(x)-/(x)| < e
bo‘ladi. Bu tengsizlikdan
sup )/„(x)-/(x)| < e
bo‘lib, undan
lim sup |/„(x) -/(x)| = 0
n^oa xeEq
bo‘lishi kelib chiqadi.
Yeiarliligi. Aytaylik
lim sup \fn (x) - /(x)| = 0
bo'lsin. Limit ta’rifga ko‘ra
Ve > 0, g N, Чп>щ: sup |/„(x) -/(x)| < e
bo'ladi. Ravshanki
\fn (x) - f(x)\ sup \f„ (x) - /(x)|.
xe£0
U holda Vx g Eo uchun
124
|АО)-/(х)|
bo'ladi. Bundan
(xe Eo)
bo’lishi kelib chiqadi. ►
г
5-misol. Ushbu /„(x)= lx +-y
v ir
funksional ketama-ketlikning Eo = R da tekis yaqinlashuvchiligi ko'r-
satilsin.
◄ Berilgan funksional ketma-ketlikning limit funksiyasi
/(x) = lim fn (x) = lim lx2 + -L = Ixl, (x ё Rj
у Гг
bo'ladi. Endi
ni topamiz:
sup|/„(x)-/(x)|
sup
xx R
- sup
xxR
Demak,
lim sup
»xeR
bo'lib,
(x e R)
ifodaga ega bo'lamiz. ►
Eslatma. Agar funksional ketma-ketlik uchun Ec R
to'plamda
lim sup|/„(x)-/(x)| 0
xeE
bo'lsa, Щх)} funksional ketma-ketlik E da tekis yaniqlashishi shart
emas.
Endi funksional ketma-ketlikning limit funksiyaga ega bo'lishi va
unga tekis yag'inlashishini ifodalovchi teoremani keltiramiz.
125
2- teorema. (Koshi teoremasi.) funksional ketma-ketlik
E to‘plamda limit fimksiyaga ega bo‘lishi va unga tekis yaqinlashishi
uchun Ve > 0 son olinganda ham shunday = л0(Е) g N topilib,
V/? > n0, Vp g N va Vx g E da
\fn+P(x)~ Z;(a )<c ,
ya’ni Ve > 0, 3«0 = w0 (e) g N, in> n0, ip e N va Vx g E da
[fn+pW ~A(x)| < £ (2)
bo‘lishi zarur va yetarli.
-< Zarurligi. Aytaylik, 2йо‘р1апи1а {Z(x)} funksional ketma-ketlik
limit funksiya f (x) ga ega bo‘lib, unga tekis yaqinlashsin:
Z„(x)^/(x), (xeE0).
Tekis yaqinlashish ta’rifiga ko‘ra
Ve > 0, 3«o = «о(е)е 7V, V£>fl0, Vx g E : |Д(х) - /(x)| < |
bo'ladi. Xususan, к = n, n > nn va к = n + p, pt N da
|/„(x)-/(x)| < |, |/„+p(x)-/(x)| < j
tengsizliklar bajarilib, ulardan
\fn+p W - fn (x)| = \fn+p (*) - /(x) - (A (*) - /(x))|
£ \fn+p (x) - /(x)| + \fn (X) - /(x)| < j + | = E
bo'lishi kelib chiqadi. Demak, (2) shart o‘rinli.
Yetarliligi. {Д,(х)} funksional ketma-ketlik uchun (2) shart bajarilsin.
Uni quyidagicha yozamiz:
Ve > 0, 3«0 = п0(е.) g N, \/n>riQ, \/ptN, 'ixt.E da
\fn+p (x) - fn (x)| < | (3)
bo'ladi.
Ravshanki, tayin x0 g E da {ffxf} sonlar ketma-ketligi uchun (3)
shartning bajarilishidan uning fundamental ketma-ketlik ekanligi kelib
chiqadi. Koshi teoremasiga ko‘ra {/„(x0)} yaqinlashuvchi bo‘ladi. Bino-
barin, chekli
126
lim f„ (x0) (4)
П—
limit mavjud.
Modomiki, har bir x e E da (4) limit mavjud bo‘lar ekan, u
holda awal aytganimizdek, E to‘plamda aniqlangan
x->lim/„(x), (xe£)
n—
funksiya hosil bo'ladi. Uni f (x) bilan belgilaymiz. Bu funksiya
funksional ketma-ketlikning limit funksiyasi bo'ladi:
AUW/fx), (xe £)•
Endi (3) tengsizlikda n va x lami tayinlab (и > /?0, x= £) p da
limitga o'tamiz. Natijada
|/(x) - fn (x)| < | < e
hosil bo'ladi. Bu quyidagicha bo'lishini bildiradi:
AU) Z ZU), Ue A>)- ►
6- misol. Ushbu
AU) =
In nx
4nx
funksional ketma-ketlik E = (0,1) to'plamda tekis yaqinlashuvchan-
likka tekshirilsin.
4 Agar ixtiyoriy k& N uchun
, , * 1 1
n = k, p-k=n, x = — = -
к n
deyilsa,
-Ini
In 2
= en
V2 °
bo'ladi. Demak,
3e0 = ^3 \fk e N, Эп>к, Bpt N,
3x* =l6(0,l): |A+/x*)-A(x‘)|>Eo.
Bu esa yuqoridagi teorema shartining bajarilmasligini ko'rsatadi.
Demak, berilgan funksional ketma-ketlik £=(0,1) da tekis yaqinla-
shuvchi emas. ►
127
Aytaylik, {fn(x)} funksional ketma-ketlik £to‘plamda yaqinlashuv-
chi bo‘lib, /(x) funksiya uning limit funksiyasi bo‘lsin:
A(x)-^/(x), (xe£).
Agar
Эе0 > 0, VkeN, Эп>к, Эх* eE: |/„(x‘) -/(x*)| > e0
bo‘lsa, Щх)} funksional ketma-ketlik E to‘plamda /(x) funksiyaga
notekis yaqinlashadi deyiladi.
7- misol. Ushbu f„ (x) = n sin —
nx
funksional ketma-ketlik E= (0, 1) da tekis yaqinlashuvchanlikka tek-
shirilsin.
i
) sin ' 1
◄ Ravshanki, hm /,(x) - lim nsin — = lim -=-^- = -. •
>03 П-ПХ Ц---------><X5 1 X
---X
ПХ
Demak, berilgan funksional ketma-ketlikning limit funksiyasi /(x) = -
bo‘ladi.
Aytaylik, x* = - bo‘lsin. U holda
n
-/(x*)| = |л sin 1 - n\ > 1 -sinl = Eo
munosabat ixtiyoriy ле Nda o‘rinli bo‘ladi.
Demak, /„(x) = л sin^ funksional ketma-ketlik limit funksiya
/(x) = ga E= (0,1) da tekis yaqinlashmaydi. ►
3°. Tekis yaqinlashuvchi funksional ketma-ketlikning xossalari.
Tekis yaqinlashuvchi funksional ketma-ketliklar qator xossalarga ega.
Bu xossalarni keltiramiz.
Aytaylik, {/„(x)}:
/i(x), f2(x),fn(x),...
funksional ketma-ketlik EcR to‘plamda yaqinlashuvchi bo‘lib,/(x)
uning limit funksiyasi bo‘lsin:
AW-^/(x), (xg£).
128
1- xossa. Agar {/„(x)} funksional ketma-ketlikning har bir f„(.x),
(n=l,2,3,...) hadi E to'plamda uzluksiz bo'lib,
bo'lsa, limit funksiya f(x) shu E to'plamda uzluksiz bo'ladi. Demak,
bu holda
lim Him f„ (0) = lim (lim f„ (/))
munosabat o'rinli bo'ladi.
2- xossa. Agar {/„(%)} funksional ketma-ketlikning har bir f„(x),
(«=1,2,3,...) hadi E— [a,b\ da uzluksiz bo'lib,
/„(x) /(x), (xe[a,i]) , л
bo'lsa,
b t>
Г г
lim fn(x)dx - f(x}dx
J *
a a
bo’ladi. Demak, bu holda
* b
lim f /„ (x)dx = f (lim f„ (x)) dx
J J \n—/
a a
munosabat o'rinli bo'ladi.
3- xossa. Agar {/,(x)} funksional ketma-ketlikning har bir
(n=l,2,3,...) hadi E- [a,b] da uzluksiz /Дх), (n = 1,2,3,...) hosi-
lalarga ega bo'lib,
/Дх) / <p(x), (xeM)
bo'lsa,
ф(х) = / (x)
ga ega bo'lamiz.
Shu kabi xossalarga keyinroq o'rganiladigan tekis yaqinlashuvchi
funksional qatorlar ham ega bo'ladi. Ayni paytda, ular bir mulohaza
asosida isbotlanadi. Mazkur xossalaming isbotini funksional qatorlarga
nisbatan keltiramiz.
129
Mashqlar
1. Ushbu fn (x) = n ^x + - - fx J funksional ketma-ketlik
E = (0, +°o) da tekis yaqinlashuvchanlikka tekshirilsin.
2. Aytaylik, /(x) funksiya (a,b) da uzluksiz f'(x) hosilaga ega
bo‘lib,
bo‘lsin. Bu funksional ketma-ketlikning [at, b, ] c (a, Z>) da f'(x) ga
tekis yaqinlashishi isbotlansin.
66- ma’ruza
Funksional qatorlar va ularning tekis
yaqinlashuvchanligi
1°. Funksional qator va uning yig‘indisi. Faraz qilaylik, Ea R
to‘plamda aniqlangan
mJx), w2(x), ..., m„(x),...
funksional ketma-ketlik berilgan bo'lsin. Bu ketma-ketlik hadlari
yordamida tuzilgan quyidagi
ux (x) + w2 (x) + ... + un (x) + ...
ifoda funksional qator deyiladi va ^w„(x) kabi belgilanadi:
n=l
£w„(x) = z/1(x) + «2(x) + ... + m„(x) + ... (1)
n=l
Bunda E— funksional qatorning aniqlanish to‘plami deyiladi. Masalan,
1) Уx"~' = 1 + x + x2 +... + x”-1 +...,
n=l
2) У nenx = ex +2e2x + 3e3x + ... + nenx + ...
n=l
130
funksional qatorlar bo‘lib, ularning aniqlanish to‘plami E = (-oo;+oo)
bo‘ladi. (1) funksional qator hadlaridan ushbu
^(x) = (x),
S2 (x) = «i(x) + u2 (x),
.......................................... (2)
Sn (*) = «1 (*) + «2 (*) + - + Un (x),
yig'indilarni tuzamiz. Ular (1) funksional qatorning qismiy yig'indilari
deyiladi. Demak, (1) funksional qator berilgan holda har doim bu
qatorning (2) qismiy yig‘indilaridan iborat {5„(x)}:
5Пх),*У2(х),...,5п(х),...
funksional ketma-ketlik hosil bo‘ladi. Ravshanki, x = x0 e E nuqtada
{5„(x0)} sonlar ketma-ketligi bo‘ladi.
1- ta’rif. Agar {5„(x0)} yaqinlashuvchi (uzoqlashuvchi) bo‘lsa,
У«„(х) funksional qator x = x0 nuqtada yaqinlashuvchi (uzoqla-
И=1
shuvchi) deyiladi, x0 nuqta funksional qatorning yaqinlashish (uzoq-
lashish) nuqtasi deyiladi.
2- ta’rif. У un (x) funksional qatorning barcha yaqinlashish nuq-
n=l
talaridan iborat E c: Eo to‘plam, funksional qatorning
«=1
yaqinlashish to‘plami deyiladi. Bu holda У un(x) funksional qator
n=l
Eq to‘plain da yaqinlashuvchi deb ham yuritiladi.
Agar Eo to‘plamda ushbu
У \u„ (x)| = |ц (x)| + |w2 (x)| +... + \u„ (x)| + ...
n=l
qator yaqinlashuvchi bo‘lsa, У un (x) funksional qator Eo da absolut
Л7~1
yaqinlashuvchi deyiladi.
131
3-ta’rif funksional qatorning qismiy yig'indilaridan
n=l
iborat {5„(x)} ketma-ketlikning limit funksiyasi S(x): ,
S„(x) S(x), (xeE0),
У»„(х) funksional qator yig‘indisi deyiladi va quyidagicha yoziladi:
Л=1
^«„(x) = 5(x), (xe£0)-
n=l
1- misol. Ushbu xn 1 = 1 + x + x2 +... + xn 1 +...
n=l
funksional qatorning yaqinlashish to'plami va yig'indisi topilsin.
-< Berilgan funksional qatorning aniqlanish to'plami E = R bo'ladi.
Qatorning qismiy yig'indisini topamiz:
(1___x^
1-x-, agar x*l
n , agar x - 1.
Ravshanki, n -» <» da 5„(x) ning limiti x ga bog'liq bo'ladi:
a) x e (-1,1) da lim Sn (x) = lim | J - | = Д- ;
n->°° n->~yl-X 1—X J 1-X
b) X 6 [1, + oo) da lirn S„ (x) = ;
A7~>00
d) x G (—°°, -1] da lim Sn(x) mavjud emas.
n—
Demak, berilgan funksional qatorning yaqinlashish to'plami
Eo=(—1, 1) bo'lib, yig'indisi
1-x
ga teng bo‘ladi. ►
V Xn
2- misol. Ushbu *—ук funksional qatorning yaqinlashish to'p-
, . 1+x
lami topilsm.
132
◄ Sonli qatorlar nazariyasidagi Dalamber alomatidan foydalanib
topamiz:
lim
un+i(x)
u„(x)
= lim
Л?-^оо
xn+l
a) x 6 (-1,1) da lim —
Bu holda berilgan funksional
bo'ladi.
qator (—1,1) da yaqinlashuvchi
b) xe u(l,+o°) da
lim
x(l+x2n)
l+x2"+2*
= lim
n—
1 1
x2"+| + -x
—+i
x2n+2
1
X
bo‘lib, funksional qator x e (-°°,-1)и (l,+°o) da yaqinlashuvchi
bo‘ladi.
d) x - ±1 da berilgan funksional qator mos ravishda ushbu
sonli qatorga aylanadi va ular uzoqlashuvchi bo‘ladi.
Shunday qilib, qaralayotan funksional qatorning yaqinlashish
to‘plami )
Eo = R \ {-1,1} = (-oo,-1) и (-1,1) о (1, чоо)
bo‘ladi. ►
2°. Funksional qatorning tekis yaqinlashuvchanligi. Aytaylik,
^«„(x) = Mj(x) +«2 (x)+ (x) + ...
77-1
funksional qator Eo to‘plamda yaqinlashuvchi (ya’ni qatorning yaqin-
lashish to‘plami Eo) bo‘lib, yig‘indisi S(x) bo‘lsin:
5„(х)-» 5(x), (xe£0), (3)
133
bunda Sn (x) = щ (x) + u2 (x) + ... + «„ (x). (3) munosabat
Ve > 0, VxejE’q, 3«o = Hq (e,x)e jV, V»>^: |5„(x) - 5(x)[ < e
bo‘lishini anglatadi. ;
4- ta’rif. Agar Eo to‘plamda
S„(x) 5(x), (xe£0)
ya’ni
Ve > 0, Вл0=л0(е)еА, V«>w0, Vxe£0: |5„(x)-5(x)| < e
bo‘lsa, ^«„(x) funksional qator to‘plamda tekis yaqinlashuvchi
Л=1
deyiladi. Agar
r„(x) = 5(x)-5„(x)
deyilsa, funksional qatorning Eo to‘plamda tekis yaqinlashuvchanligini
quyidagicha
r„(x)^0, (xe Eq),
ya’ni
Ve > 0, Ел0 = л0(е it N, \fn>riQ, \fx e Eq : |r„ (x)| < e
ko‘rinishda ta’niiash mumkin bo‘ladi. Shunday qilib,
У u„(x) = Щ (x) + u2 (x) + ... + u„(x) + ...
n=l
funksional qator, uning qismiy yighndisi
S„ (x) = Щ (x) + u2 (x) +... + u„ (x)
va yighndisi S(x) uchun
Sn(x) -> S(x), (xe^)
bo‘lsa, funksional qator Eo da yaqinlashuvchi;
Sn(x) S(x), (xe^)
bo‘lsa, funksional qator Eo da tekis yaqinlashuvchi bo‘ladi.
1-teorema. ^«„(x) funksional qator Eo da qator yig‘indisi
Л=1
5(x) funksiyaga tekis yaqinlashishi uchun
134
lim sup 15и (x) - 5(x)| = 0 ,
ya’ni
lim sup |r„(x)| - 0
n~>°° хчЕп
bo‘lishi zarur va yetarli.
◄ Bu teoremaning isboti ravshan (qaralsin, 65- ma’ruza, 1-teo-
rema.) ►
3-misol. Ushbu X(77-„)(i + „+1)
funksional qatorning [0,+°o) da tekis yaqinlashuvchi bo‘lishi isbot-
lansin.
◄ Berilgan funksional qatorning qismiy yighndisini hisoblab, so‘ng-
ra yig'indisini topamiz:
1
S, ( s =_1__ 1_______ ____________
" X (x+l)(x+2) (x+2)(x+3) "И (х+и)(х+л+1)
JL - JL) + ( 1 . JJ +... + ( 1 _ __L J = X
x+1 x+2/ \x+2 x+3/ \x+n х+л+l/ x+l
lim Sn (x) = lim (-L- - ——-) = 1 .
л—n—\x+l x+n+lj x+l
1
Х+Л+1 ’
Demak,
5(x) = J-
x+1
U holda S„ (x) - 5(x) = Ц - -L = - —L
X+l Х+И + 1 X+l Х + И+1
bo‘lib,
sup |5„(x)-5(x)| = -L
xe[0,+~) «+1
ga ega bo‘lamiz. Keyingi tenglikdan
lim sup \Sn (x) - 5(x)| = 0
”-»“xg[0,+-)
bodishi kelib chiqadi. 1-teoremaga ko‘ra berilgan funksional qator
[0, +oo) da tekis yaqinlashuvchi. ►
135;
Eslatma.Agar lim sup |5„(x)-5(x)p 0
xe[O,+~)
bo‘lsa, ^w„(x) funksional qator Eo da tekis yaqinlashuvchi bo‘lishi
n-\
shart emas. Masalan,
£x" 1 =l + x + x2 + ... + x" 1 +...
«=1
funksional qatorning (—1,1) da yaqinlashuvchi, yig‘indisi
S(x)= 1
1-x
bo‘lishini ko'rgan edik. Bu funksional qator uchun
lim sup \Sn(x) - 5(x)( = lim sup
Xn
1-X
bo'ladi. Demak, funksional qator (— 1,1) da tekis yaqinlashuvchi emas.
Faraz qilaylik,
^и„(х) = щ (x) + u2 (x) + ... + «„ (x) +...
n=l
funksional qator to‘plamda berilgan bo‘lsin.
2-teorema. (Koshi teoremasi.) ^w„(x) funksional qator £to‘p-
«=i
lamda tekis yaqinlashuvchi bo‘lishi uchun
Ve > 0, 3«0 = я0(e) e jV, V«>«0, \/peN, Vx e E da
- S„(x)\ = |w„+1(x) + w„+2(x) + ... + w„+p(x)| < e
bo'lishi zarur va yetarli.
Bu tenglamaning isboti 65- ma’ruzadagi 2- teoremadan kelib chiqadi.
3°. Funksional qatorlarning tekis yaqinlashuvchanlik alomatiari.
a) Veyershtrass alomati. Aytaylik, E to‘plamda
^w„(x) = w1(x) + «2(x) + ... + «„(x) + ... (4)
n=l
funksional qator berilgan bo‘lib,
136
1) V« g N, Vx e E da \un (x)| < C„ ,
2) £c„ = Q + C2 +... + Cn +... sonli qator yaqinlashuvchi bo‘l-
n-1
sin. U holda (4) funksional qator E to‘plamda tekis yaqinlashuvchi
bo‘ladi.
4 1- shartga ko‘ra Vn > n0, \/p e N va Vx e E uchun
|«n+i (x) + m„+2 (x) + ... + и„+/,(х)| < |u„+1 (x)| + |w„+2 (x)| +... + \un+p (x)| <
— ^«+1 ^л+2 ••• ^n+/>
bo‘lib, 2-shartdan, ya’ni qatorning yaqinlashuvchanligidan
n=l
Koshi teoremasiga binoan
Ve > 0, 3n0 = n0 (e) e N, Vn> n(j, Vp e N da
^n+l ^-'n+2 + •• + Cn+p <
bo'ladi. Demak,
|wn+i U) + (x)+... + U„+/,(x)}<£.
Yuqoridagi 2-teoremaga ko‘ra ^«n(x) funksional qator £to‘plarnda
/7=1
tekis yaqinlashuvchi bo‘ladi. ►
4-misol. Ushbu У - funksional qator tekis yaqinla-
„=1 Vl+«2 (1 + ПХ2 )
shuvchanlikka tekshirilsin.
◄ Berilgan qatorning aniqlanish to‘plami E = (-°о,+оо) bo'lib,
uning umumiy hadi
^(^ = -^=7--------г;, (« = 1,2,3,...)
bo‘ladi. Ravshanki,
x sin x |x|
Vl + n2 (1 + nx2) -A+n2 (1 + ЛХ2 ) '
137
Endi Vxe (-<»,-в») uchun
И 1
1+nx2 2jn
bo‘lishini e’tiborga olib topamiz:
w r I £ I.
41+n2 (1+nx2) 27«(l+«2 ) 2«3/2
Demak, berilgan funksional qatorning hadlari uchun
Mx)| - ^3/T
bo‘ladi. Ma’lumki, -y/2 qator yaqinlashuvchi. Binobarin, Veyer-
shtrass alomatiga ko'ra berilgan funksional qator (-<*>,+00) da tekis
yaqinlashuvchi bo'ladi. ►
Funksional qatorlaming tekis yaqinlashishini ifodalovchi keyingi
alomatlarini isbotsiz keltiramiz.
b) Dirixle alomati. Aytaylik, Ec R to'plamda aniqlangan un(x)
va vn(x), (« = 1,2,3,...) funksiyalar quyidagi shartlami bajarsin:
1) Vxg E da {u„(x)} ketma-ketlik monoton;
2) {w„(x)} funksional ketma-ketlik £ da 0 ga tekis yaqinlashuvchi:
w,;(x) ^0, (x e £);
3) shunday C e R mavjudki, Mn g TV, Vx g E da
lyi
(x) + v2 (x) +... + vn
n
(x)! = ^d4(x)
k=\
U holda
£i/„(x)v„(x)
И=1
funksional qator E to'plamda tekis yaqinlashuvchi bo'ladi.
Zsinxsinw.v
-------==—
»=1 ^n+x
funksional qator E = [0, +<x>) da tekis yaqinlashuvchiligi isbotlansin.
138
•< Aytaylik,
ы„(х)= -Д=_, vn(x) = sin x sinnx
'Jn+X
bo‘lsin. Bu funksiyalar uchun Dirixle alomatidagi uchta shart baja-
riladi. Haqiqatan ham,
1) Vx e E da w„(x) =
uchun
1 1 _ 4n+\+x-4n+x _ 1
V/г+Х y/n+l+X у/п+Ху/п+1+Х ^(и+х)(и + 1+х)-(7и + 1+Х+л/«+Х
bo‘lganligidan, uning kamayuvchiligi kelib chiqadi;
2) Ravshanki, un (x) = --Д= < -U, n-+ °<> da -4= -> 0.
'J n+x \]n >Jn
Demak, u„(x) 0, (xe £).
3) Bu holda
n
n
^vk(x) = У sin x sin kx
k=\
*=i
т X . ПХ П+1
= 2 cos - sm — • sm —-- x
2 2 2
<2
2
bo‘ladi.
Dirixle alomatiga ko‘ra berilgan funksional qator E - [0,+°o) da
tekis yaqinlashuvchi. ►
d) Abel alomati. Aytaylik, Ec R to‘plamda aniqlangan и„(х) va
vn (x), (n = 1,2,3,...) funksiyalar quyidagi shartlarni bajarsin:
1) Vxg £ da {u„(x)} ketma-ketlik monoton;
2) shunday C g R topiladiki, V« g N, Vx g E da
|M„(x)i<C;
3) vn (x) funksional qator E to‘plamda tekis yaqinlashuvchi.
Л=1
U holda
^U„(x)vn(x)
n=l
funksional qator to‘plamda tekis yaqinlashuvchi bo‘ladi.
139
6- misol. Ushbu x"
?7=1
funksional qatorning £=[0, 1] da tekis yaqinlashuvchi ekanligi isbotlansin.
( n"+1
•< Aytaylik, u„(x) - x”, vn(x) = —-—, (xe [0,1])
bo‘lsin. Bu funksiyalar uchun Abel alomatidagi uchta shart bajariladi
(bu ravshan). U holda Abel alomatiga ko‘ra berilgan funksional qator
[0, 1] da tekis yaqinlashuvchi bo‘ladi. ►
Mashqlar
l .Agar ^м„(х), (хе E) funksional qator E to‘plamda tekis
n=l
yaqinlashuvchi bo‘lsa, {u„(x)} funksional ketma-ketlikning Eto'plamda
0 ga tekis yaqinlashishi isbotlansin.
2 . Ushbu > -—;,-arctg«x, (xe R) funksional qator A da tekis
«=i n+x
yaqinlashuvchi ekanligi isbotlansin.
67- ma’ruza
Tekis yaqinlashuvchi funksional qatorlarning xossalari
1°. Funksional qator yig‘indisining uzluksizligi. Faraz qilaylik,
Ea Ato'plamda
£«„(%) = щ(х) + w2(x) + ... + un(x) + ... (1)
n=l
funksional qator berilgan bo'lib, uning yig‘indisi S(x) bo'Isin.
1- teorema. Aytaylik, (1) qator ushbu shartlami bajarsin:
1) qatorning har bir u„(x), (л = 1,2,3,...) hadi E to‘plamda
uzluksiz;
2) u„ (x) qator E da tekis yaqinlashuvchi. U holda funksional
n=l
qatorning yig‘indisi 5(x) funksiya E to‘plamda uzluksiz bo‘ladi.
140
◄ Aytaylik, x0 e E,
Sn (%) = ux (x) + u2 (x) + ... + «„ (x)
bo'lsin. Teoremaning 2- shartiga ko'ra
5n(x) ^5(x), (xe£)
bo'ladi. Ta’rifga binoan
Ve > 0, 3/?0 = и0(е) e N, \/n > va Vxe E da
|5„(x)-5(x)|< |, (2)
jumladan, |5„ (x0) - )| < | (3)
tengsizliklar bajariladi.
Ravshanki, (2) va (3) tengsizliklar n ning nQ dan katta biror
muayyan nl qiymatida ham o'rinli bo'ladi:
К (x) - 5(x)| < |, (2')
|S„(x0)-S(x0)|< |. (3')
Teoremaning 1- shartidan va chekli sondagi uzluksiz funksiyalar f
yig'indisi yana uzluksiz bo'lishidan
(*) = «1 (*) + «2 (*) + - + \ (*)
funksiyaning Eto'plamda uzluksiz ekanligi kelib chiqadi. Demak, Sn] (x)
funksiya x — da uzluksiz. U holda, ta’rifga binoan Ve >0, 35 = 8(e) > 0,
|x - x01 < 5 tengsizlikni qanoatlantiruvchi barcha x e E da
|5ni(x)-^(x0)|<| (4)
bo'ladi. Yuqoridagi (2'), (3') va (4) tengsizliklardan foydalanib topamiz:
|ад - ж )| = |(5(x) - Sn (X)) + (x) - )) + (5; (x0) - 5 ))| <
< |S(x)-(x)| + (x) -5ni (xq)| +(x0) -5(x0)| < | +1 +1 = e.
Bu esa 5(x) funksiyaning x0 nuqtada uzluksiz bo'lishini bildiradi.
Modomiki, x0 nuqta E to'plamning ixtiyoriy nuqtasi ekan, 5(x)
funksiya E to'plamda uzluksiz bo'ladi. ►
141
Yuqorida keltirilgan teoremaning shartlari bajarilganda uning
tasdig'ini quyidagicha ifodalash mumkin:
lim У un (x) = У ( lim u„ (x) |. !
2°. Funksional qatorlarni hadlab integrallash. Faraz qilaylik, [«, b]
segmentda
У«„(х) = «i(x) +«2 (x)+ (x) + ... (5)
«=1
funksional qator berilgan bo‘lsin.
2- teorema. Aytaylik, (5) qator quyidagi shartlami bajarsin:
1) qatorning har bir u„(x), (n = 1,2,3,...) hadi [o, b} segmentda
uzluksiz;
2) У u„ (x) qator [a, 6] segmentda tekis yaqinlashuvchi;
n=\
3) У«„(х) = 5(х).
n=l
U holda У J un (t)dt = j щ (t)dt + j и2 + ...
«=1 a a a
qator [a, da yaqinlashuvchi va
Уjun(t)dt = ^S(t)dt, (xe[a,A])
w=l a a
bo‘ladi.
◄ Berilgan funksional qatorning qismiy yig‘indisi
5„(x) = Ц (x) + «2 (x) + ••• + U„(x)
ni olamiz. U holda teoremaning 2- va 3- shartlariga ko‘ra
5„(x)-5(x), (xe[a,Z>])
boladi. Tekis yaqinlashish ta’rifiga binoan Ve > 0, 3«0 = пй (e) e N,
Xfn > «о va Vie [a,b] da
142
tengsizlik bajariladi.
Teoremaning 1- shartidan hamda yuqorida isbot etilgan 1- teorema-
dan foydalanib
(n = 1,2,3,...); JS(t)dt
a a
integrallarning mavjudligini topamiz. Ushbu
У Jun(t)dt - Jщ (t)dt + ju2 (t)dt + ... + Jun(t)dt + ...
a a a a
funksional qatomi qaraymiz. Bu qatorning qismiy yighndisi
n x
o„(x) = £ j uk(t)dt, (x g [a, Z>])
*=1 a
bo‘lsin. Ravshanki,
П Xf( 4
у juk^)dt=j у uk (t) \dt .
a a у ^“1 ,
Demak, <yn (x) = J S„ (t)dt.
a
oo x
Endi
„=1 a
funksional qatorning [a, Z>] da tekis yaqinlashuvchi ekanligini ko‘rsa-
tamiz. Quyidagi
]s(t)dt
ayirma uchun
X X
< [\Sn(t)~S(t)\dt<1^idt = 1-£-]-(x-a)<E
J D—Cl J и ~~ Cl
a a
143
bo‘ladi. Demak,
o„(x) ^Js(r)dr, (xe[a,d]).
a
Bu esa
n=l a
funksional qatorning [a,b\ da tekis yaqinlashuvchi va
У= $S(t)dt
«=1 a a
bo'lishini bildiradi. ►
Keltirilgan teoremaning shartlari bajarilganda teoremaning tasdi-
g‘ini quyidagicha ifodalash mumkin:
<жз X X f oo
yj uk (f)dt = j uk(f) \dt.
/c=l a a y£=l )
3°. Funksional qatorlarni hadlab differensiallash. Faraz qilaylik,
[a, b] segmentda
Х«„(х) = и1(х) + и2(х) + ... + и„(х) + ... (6)
n=l
funksional qator berilgan bo‘lsin.
3- teorema. Aytaylik, (6) funksional qator quyidagi shartlami bajarsin:
1) Qatorning har bir un(x), (n = 1,2,3,...) hadi [a, b] segmentda
uzluksiz u'(x), (n = 1,2,3,...) hosilaga ega;
2) Ushbu
У и'(х) - u[(x) + w2 (x) + — + u'„(x) + ...
«=1
funksional qator [a, b] da tekis yaqinlashuvchi;
3) x0 e [a, b\ nuqta mavjudki, bunda
У M„(X) = U] (x0) + u2(x0) + ... + «„(x0) + ...
«=1
144
qator yaqinlashuvchi. U holda
a) ^и„(х) funksional qator |a, b\ da tekis yaqinlashuvchi;
«=i
b) bu qatorning yig‘indisi
5(x) = £и„(х)
/7—1
[a, Z>| da uzluksiz S'(x) hosilaga ega;
d) 5'(x) = J\'(x) bo‘ladi.
n=l
’ oo
◄ Ushbu £«»(x)
/7—1
qatorning yig’indisini a(x) bilan belgilaylik:
o(x) = £«;(x). (7)
n=l
Bu qator tekis yaqinlashuvchi va har bir hadi [a, Z>] da uzluksiz.
Yuqorida keltirilgan 2- teoremaga ko‘ra (7) ni hadlab integrallash
mumkin:
X oo x
J G(x)dx = У J u'„(x)dx,
•4 «=1 x0
bunda x0 e [a, 6]. x e [a,b]. Ayni paytda, (
. x "
У j w'(x) funksional qator [a, Z>] da tekis yaqinlashuvchi.
x0
Ravshanki, J u'n (x)dx = un (x) - un ().
Demak, У (a„ (x) - u„ (x0)) qator [a, b] da tekis yaqinlashuvchi.
Л=1
Shartga ko‘ra
145 <
п=1
qator yaqinlashuvchi (uni [a, b] da f^e^s yaqinlashuvchi deb qarash
mumkin). Shunday qilib
n=l "=I
qatorlar [a, b] da tekis yaqinlashuvclt1^ bo ladi. Bundan esa bu qator-
larning yig‘indisi bo‘lgan
funksional qatorning [a, b] da tekis yaqinlashuvchi ekanligi kelib chi-
qadi. Shuni e’tiborga olib topamiz:
o° oo ' ч
<j(x)dx = = ~~
___1 ^=1
o(x) funksiya har bir hadi uzluk^z’ ° z' te^'s yaqinlashuvchi
qatorning yig‘indisi bo‘lgani uch’J11 1" teoremaga ко ra, [a,b] da
uzluksiz bo‘ladi. U holda keyingi t^nglikdan
(j(x) = (S(x) - 5'(xo)) - б’(x)
bo‘lishi kelib chiqadi. Demak,
n=l
qator yig‘indisi uzluksiz hosilaga e$a va
bo‘ladi. ►
Bu keltirilgan teoremaning sha^ari bajarilganda uning tasdig'ini
quyidagicha yozish mumkin:
146
d
dx
d <
И=1
1- misol. Ushbu
yi„<»y++
•“ «(/7+1 + X)
n-1
funksional qatorning yig'indisi topilsin.
◄ Ma’lumki,
1
s
funksional qator [0, +°°) da tekis yaqinlashuvchi bo‘lib, uning yig‘indisi
ga teng (qaralsin, 66- ma’ruza):
1 . V 1______________
4-х 7Г] («+х)(л+1+х) ’
Ravshanki, bu qatorning har bir hadi [0, +«=) da uzluksiz. Demak,
uni 2- teoremaga ko‘ra hadlab integrallash mumkin:
dt
0 «=1 0
Aniq integrallami hisoblaymiz:
= ln(l + t)|o = ln(l + x),
о
0 4 ' 0
= ln(w +1)|* -ln(« + 1 + Oio = In (" 11.
IU 10 и(и+1+х)
Demak, V In = hi(l + x). ►
" rt(/7+l + x)
147
Mashqlar
1. Ushbu ^пхл, (-1 < x < 1) funksional qatorning yig‘indisi
n=i
topilsin.
2. Ushbu A(x) = (* e R) funksiya funksional qatorni
«=i n +x~
hadlab differensiallash bilan topilsin.
68- ma’ruza
Darajali qatorlar, ularning yaqinlashish radiusi va
yaqinlashish intervallari
1°. Darajali qator tushunchasi. Abel teoremasi. Har bir hadi
(0 = (t -10 )\ (t0 6 A; n = 0,1,2...)
funksiyadan iborat bo‘lgan ushbu
= "o+M^~'o) + «2 (z~4i)2+••• (1)
n=0
funksional qator darajali qator deyiladi, bunda
<2q , Uj, ..., a„,...
haqiqiy sonlar darajali qatorning koeffitsiyentlari deyiladi.
(1) da t - tn = x deyilsa, u quyidagi
апхл = a0 + atx + a^x1 +... + anxn + ..., (x e R) (2)
«=o
ko‘rinishga keladi va biz shu ko‘rinishdagi darajali qatorlarni o‘rga-
namiz.
Ravshanki, (2) qatorning qismiy yig'indisi
S„ (x) = a0 + a{x + g2x2 + ... + anxn
ko‘phaddan iborat. Ayni paytda, x = 0 da Sn (0) = a0 bo‘ladi. Demak,
har qanday (2) ko‘rinishdagi darajali qator x = 0 nuqtada yaqinlashuv-
chi bo‘ladi.
148
1- teorema. (Abel teoremasi). Agar
'^a„xn = a0 +atx + a2X2 + ... + anx" + ...
n=0
darajali qator x = x() ф 0 nuqtada yaqinlashuvchi bo'Isa, ushbu
tengsizlikni qanoatlantiruvchi barcha x larda darajali qator yaqinla-
shuvchi (absolut yaqinlashuvchi) bo‘ladi.
◄ Aytaylik, x ~ x0 * 0 da
r/-0
qator yaqinlashuvchi bo‘lsin. Qator yaqinlashishining zaruriy shartiga
ko‘ra
lim апХц = 0
77—
bo‘ladi. Demak, ketma-ketlik chegaralangan:
3M >0, Vn e N da | < M .
va jx| < |х0| da
Ravshanki,
n
X
x0
bo‘ladi. Demak
(3)
= Я < 1
geometrik qator yaqinlashuvchi. U holda ushbu
n=0 °
qator ham yaqinlashuvchi bo‘ladi. (3) munosabatni e’tiborga olib,
so‘ngra solishtirish teoremasidan foydalanib,
w=0
darajali qatorning yaqinlashishini (absolut yaqinlashishini) topamiz,''►
149
Natija. Agar «„x" = g0 + qx + c2x2 + ... + a„x" + ...
/7—0
darajali qator x = x, nuqtada uzoqlashuvchi ( ushbu i
a„x" = Oq + «jXj + a2x2 + ... + o„xf + ...
n=0
sonli qator uzoqlashuvchi) bo‘lsa, quyidagi
|x| > |X] I
tengsizlikni qanoatlantiruvchi barcha x larda У, a„xn qator uzoqla-
/7=0
shuvchi bo'ladi.
4 Teskarisini faraz qilaylik, ^anxn qator |xj > SxJ tengsizlikni
n=0
qanoatlantiruvchi biror x = x* nuqtada (ix* I > |xj i) yaqinlashuvchi
bo'lsin. U holda Abel teoremasiga ko'ra !xi < )x*i tengsizlikni qano-
atlantiruvchi barcha x larda yaqinlashuvchi, jumladan, Xj nuqtada
ham yaqinlashuvchi bo'lib qoladi. Bu esa shartga ziddir. ►
Abel teoremasi va uning natijasi darajali qatorlarning yaqinlashish
(uzoqlashish) to'plamining strukturasini (tuzilishini) aniqlab beradi.
2°. Darajali qatorning yaqinlashish radiusi va yaqinlashish intervali.
Faraz qilaylik,
У anxn = o0 + «]X + a2x2 + ...+ anxn + ...
/7=0
darajali qator berilgan bo'lsin. Bu qatorning yaqinlashish yoki
uzoqlashish nuqtalari haqida quyidagi uch hoi bo'lishi mumkin:
1) barcha musbat sonlar qatorning yaqinlashish nuqtalari bo'ladi;
2) barcha musbat sonlar qatorning uzoqlashish nuqtalari bo'ladi;
3) shunday musbat sonlar borki, ular qatorning yaqinlashish nuq-
talari bo'ladi, shunday musbat sonlar borki, ular qatorning uzoqla-
shish nuqtalari bo'ladi.
Birinchi holda, Abel teoremasiga ko'ra darajali qator barcha
x e R da yaqinlashuvchi bo'lib, darajali qatorning yaqinlashish to'p-
lami E - (-00,-1-00) bo'ladi. Bunday qatorga ushbu
150
\ ’ 1/7 1 1 2 1/7
> -- X = 1 + X + - X + ... + X + ...
t-fn'. 2! п\
п=0
darajali qator misol bo‘ladi.
Ikkinchi holda, Abel teoremasining natijasiga ko‘ra darajali qator
barcha x e 7?\{0} da uzoqlashuvchi bo‘lib, uning yaqinlashish to‘plami
E = {0} bo‘ladi. Bunday qatorga ushbu
^nlx" = x + 2lx2 + 3!x3 + ... + nlx" + ...
Г7-1
darajali qator misol bo‘loladi.
Endi uchinchi holni qaraymiz. Bu holga ushbu
= 1 + X + x2 +... + xn + ...
к-0
darajali qator misol bo‘ladi. Bu darajali qator barcha xe (0,1) da
yaqinlashuvchi va demak, Abel teoremasiga ko‘ra qator (—1,1) da
yaqinlashadi, barcha x e |l,+°°) da qator uzoqlashuvchi va demak,
Abel teoremasining natijasiga ko‘ra qator (-«=,-1] u [1, +«>) da uzoq-
lashadi. Demak, darajali qatorning yaqinlashish to‘plami £= (—1,1)
bo‘ladi.
Aytaylik, a„xn = a0 + a{x + агх2 + ... + a„xn + ...
??—0
darajali qator t\ nuqtada (/; > 0) yaqinlashuvchi, R- nuqtada (R} > 0)
nuqtada esa uzoqlashuvchi bo‘lsin. Ravshanki,
ri > Ri
bo‘ladi. Agar anxn darajali qator (
n=0 __j
2
nuqtada yaqinlashuvchi bo‘Isa,
„ _ П + ^1 D _ D
r2-----2— ’ ~
deb; uzoqlashuvchi bo‘lsa,
151
Г2 R2=r^
deb r2 va R-, nuqtalarni olamiz. Ravshanki,
/b-fi I
fi 2 r2, Ri > R, va R2 - r2 = ;
bo‘ladi. Bu munosabatdagi r2 va R2 sonlarga ko‘ra r3 va R3 sonlami
yuqoridagiga o‘xshash aniqlaymiz.
Agar a„xn darajali qator
n=0
ri+^i
2
nuqtada yaqinlashuvchi bo‘lsa,
>2+^2
r3=^,
deb; uzoqlashuvchi bo‘lsa,
A3 - R2
r3 = r2 > R3
= r2+R2
2
deb r3 va R3 nuqtalarni olamiz. Bunda quyidagicha bo‘ladi.:
n R\~ri
r2 <r3, R2> R3 va л3 — r3 = .
Bu jarayonni davom ettirib borilsa, X darajali qatorning
Л7-0
yaqinlashish nuqtalaridan iborat {r„}, uzoqlashish nuqtalaridan iborat
{Rn} ketma-ketliklar hosil bo‘ladi. Bunda
/j < r2 < ... < rn < ..., Ri > R2 > ... > Rn > ...,
R — к
va n -» 00 da R„ - r = -----> 0
П /7
bo‘ladi. U holda [1], 3-bob, 8-§ da keltirilgan teoremaga ko‘ra
lim r„ va lim R„ limitlar mavjud va
W-»OO n—
lim rn = lim 7^,
n—
bo'ladi. Uni r bilan belgilaymiz:
152
lim r„ = lim Rn = r .
A?—ft —>oo
Endi x o‘zgaruvchining \x\ < r tengsizlikni qanoatlantiruvchi
ixtiyoriy qiymatini olaylik. U holda
lim r„ = r
bo‘lishidan, shunday z?0 e N topiladiki, bunda
к M <<r
bo‘ladi. Binobarin, berilgan darajali qator nuqtada, demak, qara-
layotgan x nuqtada yaqinlashuvchi bo'ladi.
x o'zgaruvchining |x| > r tenglikni qanoatlantiruvchi ixtiyoriy
qiymatini olaylik. Bunda
lim R„ = r
bo'lishidan, shunday e N topiladiki,
1*1 > Я„, > r
bo'ladi. Binobarin, berilgan darajali qator Rn. nuqtada, demak, qara-
layotgan x nuqtada uzoqlashuvchi bo'ladi.
Demak, 3- holda anx" darajali qator uchun shunday musbat
n-0
r soni mavjud bo'ladiki, |x^ < r , ya’ni Vx e (-r, r) da qator yaqin-
lashuvchi; jx| > r., ya’ni Vx e (г,-н*>) da qator uzoqla-
shuvchi bo'ladi. x = ±r nuqtalarda anxn darajali qator yaqinla-
n=Q
shuvchi ham bo'lishi mumkin, uzoqlashuvchi ham bo'lishi mumkin.
00 I
1-ta’rif. Yuqorida keltirilgan r son darajali qatorning
л=0
yaqinlashish radiusi, (~r,r) interval esa darajali qatorning yaqinlashish
intervali deyiladi.
Eslatma. 1- holdadarajaliqatorningyaqinlashishradiusi r =
deb, 2- holda darajali qatorning yaqinlashish radiusi r— 0 deb olinadi.
153
3°. Darajali qatorning yaqinlashish radiusini topish. Biror
У anxf‘ = a0 + atx + a2x2 + ... + anx" + ...
«-0
darajali qatorni qaraylik. Bu qator koeffitsiyentlaridan tuzilgan {<?„},
(« = 0,1,2,...) ketma-ketlik uchun
1) V« > 0 da a„ * 0 ,
2) limi-^-
!an+i
yaqinlashish radiusi quyidagicha bo'ladi:
mayjud bo‘lsin. U holda У darajali qatorning
л=0
r = lim .
п~>°° an+l
◄ Aytaylik, darajali qator uchun
lim= £, (an * 0, n = 0,1,2,3,...)
O„+1|
bo‘lsin. Qaralayotgan У g„.v" darajali qatorda x ni parametr hisob-
и-0
lab, Dalamber alomatiga ko‘ra uni yaqinlashishga tekshiramiz:
lim
,, vx+1
an+lx
anxn
- lim
an+l
an
•И = И1ш1
1
an+l
Demak, ~ < 1, ya’ni |x| < L
bo‘lganda qator yaqinlashuvchi bo‘ladi;
W i
— > 1, ya’ni jx| > L
bo‘lganda darajali qator uzoqlashuvchi bo‘ladi.
Bundan У a„xn darajali qatorning yaqinlashish radiusi
«=0
154
г = L - lim —
” ->“ an+\
(4)
bo‘lishi kelib chiqadi. ►
1- misol. Ushbu
oo n
У x". (01= 1)
darajali qatorning yaqinlashish radiusi topilsin.
◄ Bu qator uchun
n" («+1Г1
a =----- a„+l = —y———
e n\ er (я+l)!
bo'ladi. Ravshanki,
Demak, berilgan darajali qatorning yaqinlashish radiusi r = I bo‘ladi. ►
Ixtiyoriy darajali qatorning yaqinlashish radiusini aniqlab beradigan
teoremani isbotsiz keltiramiz.
2- teorema. (Koshi—Adamar teoremasi.) Ushbu
o0 + a}x + a2x2 + ... + o„x" + ...
,7=0
darajali qatorning yaqinlashish radiusi
lim^j
bo‘ladi. [I]
Eslatma. Agar Цтя|д„| = bo‘lsa, \a„xn darajali qa-
/7=0
torning yaqinlashish radiusi r= 0 deb; limи]a„ = 0 bo‘lsa, У anxn
л=0
darajali qatorning yaqinlashish radiusi r = +°o deb olinadi.
155
2- misol. Ushbu X 2" x5n darajali qatorning yaqinlashish radiusi
»=o
topilsin.
-< Avvalo 2x5 = t deb olamiz. Natijada berilgan qator quyidagi
^tn =l + / + r2 + ... + tn + ...
и=0
ko‘rinishga keladi. Bu qatorning yaqinlashish radiusi (5) formulaga ko‘ra
bo‘ladi. Demak, |t| < 1 da
uzoqlashuvchi. U holda
|2x51 < 1, ya’ni |x| < 2=
|2x3 j > 1, ya’ni |x| > ~
Berilgan darajali qatorning yaqinlashish radiusi r = bo‘ladi. ►
<2
qator yaqinlashuvchi, jt| > 1 da qator
da berilgan qator yaqinlashuvchi;
da qator uzoqlashuvchi bo‘ladi.
3-misol. Ushbu darajali qatorning yaqinlashish
to3
to‘plami topilsin.
(-1)"
◄ Ravshanki, a„ = -^Гг, a„+] =
3 yjn 3 Vn+1
Berilgan darajali qatorning yaqinlashish radiusini (4) formulaga ko‘ra
topamiz:
r = lim
an
an+l
= lim
»->oo
(-1)" 3"V^+i
= lim3.(HH = 3.
n—>oo \ П
з”-1(-i)"+!
Darajali qator x — — 3 nuqtada ushbu У, ~7= sonli qatorga ayla-
n=l
nadi va bu sonli qator uzoqlashuvchi bo‘ladi. x = 3 nuqtada esa
156
/ 1\И
У 3—2- sonli qator hosil bo‘ladi va bu qator Leybnits teoremasiga
Zi
ko‘ra yaqinlashuvchi bo‘ladi. Demak, berilgan darajali qatorning
yaqinlashish to'plami E — (—3, 3] dan iborat. ►
Mashqlar
1. Agar darajali qatorning yaqinlashish radiusi r > 0
/7—0
bo‘lsa, ushbu
+ l)a„xn,
n=0 n=0
darajali qatorlarning yaqinlashish radiuslari ham r ga teng bo‘lishi
isbotlansin.
2. Ushbu Х(2„)!л/! darajali qatorning yaqinlashish interval!
n=0
topilsin.
69- ma ’ruza
Darajali qatorning tekis yaqinlashishi. Darajali qatorning
xossalari
1°. Darajali qatorning tekis yaqinlashishi. Aytaylik, ushbu
У, anxn = aQ + axx + a2x2 + ... + anxn + ... (1)
И-0
darajali qatorning yaqinlashish radiusi r > 0 bo'lsin.
1-teorema. (1) darajali qator [cc,(3] c (-r,r) da tekis yaqinla-
shuvchi bo‘ladi, bunda a e R, J3 e R .
◄ Ravshanki, (1) darajali qator (-r, r) da absolut yaqinlashuvchi
bo‘ladi.
Aytaylik, ae (0,r) bo‘lsin. U holda Vn > 0 va Vx e [-a,a] da
|д„х^ < jo„a"|
157
bo‘lganligi uchun Veyershtrass alomatiga ko‘ra, (1) qator [-a,a] da
tekis yaqinlashuvchi bo‘ladi. ►
Demak, У anxn darajali qatorning yaqinlashish radiusi r > 0 bo‘l-
n=0
sa, yuqorida keltirilgan teoremaga ko‘ra bu qator [-с, с] c (~r,r) da
tekis yaqinlashuvchi bo‘ladi. Bunda c sonni r songa har qancha yaqin
qilib olish mumkin bo‘lsa-da, qator (-r, r) da tekis yaqinlashmasdan
qolishi mumkin. Masalan, ushbu
У Xя ~ 1 + X + X2 + ... + x" + ...
darajali qatorning yaqinlashish radiusi r = 1, biroq qator (—1,1) da
tekis yaqinlashuvchi emas.
2°. Darajali qatorning xossalari. Ma’lumki, darajali qatorlar funk-
sional qatorlarning xususiy holi. Binobarin, ular tekis yaqinlashuvchi
funksional qatorlarning xossalari kabi xossalarga ega.
2- teorema. Agar
Уa„x” - a() + OjX + a2x2 +... + a„xn + ...
n=0
darajali qatorning yaqinlashish radiusi r > 0 bo ‘lib, yig‘indisi
5(x) = y^x"
n=0
bo‘lsa, S(x) funksiya (~r, r) da uzluksiz bo‘ladi.
◄ Ravshanki, qaralayotgan darajali qator (-r, r) da yaqinlashuvchi
bo‘ladi. Aytaylik, x0 e (-r, r) bo‘lsin. Ushbu
N <C<r
tengsizlikni qanoatlantiruvchi c sonni olaylik. U holda darajali qator
[-c, c] da tekis yaqinlashuvchi bo‘ladi. Tekis yaqinlashuvchi funksional
qatorning xossasiga ko‘ra У anxn darajali qatorning yig‘indisi 5(x)
n=0
funksiya [-c, c] da uzluksiz, jumladan, x0 nuqtada uzluksiz. ►
3- teorema. Aytaylik, darajali qatorning yaqinlashish radiusi r > 0
bo‘lib, yig‘indisi 5(x) bo‘lsin:
158
5(х) = ^а„хп.
Bu qatorni (-г, г) ga tegishli bo‘lgan ixtiyoriy {a, Z>] bo'yicha
([a, Z>] c (-r,r)) hadlab integrallash mumkin:
ь „ (ь
J S(x)dx - janxndx
a ya у
Xususan, Vx g (-r, r) uchun quyidagicha bo'ladi:
(2)
◄ Ravshanki, darajali qator [a,b\ da ([o, />] c (~r,r)) tekis yaqin-
lashuvchi bo'ladi. Tekis yaqinlashuvchi funksional qatorning xossasiga
ko'ra uni hadlab integrallash mumkin. Ayni paytda, (2) qatorning
yaqinlashish radiusi rga teng bo'ladi. Haqiqatan ham, Koshi—Adamar
teoremasiga ko'ra
ifodaga ega bo'lamiz. ►
Natija. Aytaylik, a„xn darajali qator berilgan bo'lib, uning yaqin-
lashish radiusi r > 0 bo'lsin. Bu qatorni [0, x] bo'yicha (Vx0 e (-r, r))
ixtiyoriy marta hadlab integrallash mumkin. Integrallash natijasida
hosil bo'lgan darajali qatorning yaqinlashish radiusi ham r ga teng
bo'ladi.
4- teorema. Faraz qilaylik,
a„xn = Oq + axx + a2x2 + ... + anxn + ...
л=0
darajali qatorning yaqinlashish radiusi r > 0, yig'indisi 5(x) bo'lsin:
= SW-
159
U holda funksiya (-r, r) da S'(x) uzluksiz hosilaga ega va
S\x) = ^na„xnA (3)
Л7-0
bo‘ladi, bunda (3) qatorning yaqinlashish radiusi ham r ga teng.
◄ Berilgan darajali qator |-c, c] da (0 < c < r) tekis yaqinlashuvchi
bo’ladi. Tekis yaqinlashuvchi funksional qatorning xossasiga ko‘ra darajali
qatorni hadlab differensiallash mumkin. Demak, Vx0 e (-r, r) da
S'M = у (a„xn) = У na„x^ .
n=0 w=l
Bu darajali qatorning yaqinlashish radiusi ham r ga teng bo‘lishi
quyidagi munosabatdan kelib chiqadi:
lim^|«a„| = lim (tfn «/Ш) = Ит«/Ы . ►
Natija. Aytaylik, У anxn darajali qator berilgan bo‘lib, uning
и=0
yaqinlashish radiusi r > 0 bo‘lsin. Bu qatorni (~r, r) da ixtiyoriy marta
hadlab differensiallash mumkin. Differensiallash natijasida hosil
bo‘lgan darajali qatorning yaqinlashish radiusi ham rga teng bo'ladi.
5- teorema. Aytaylik,
У anxn - a0 + axx + atx2 +... + anxn +...
«=0
darajali qatorning yaqinlashish radiusi r > 0, yig‘indisi 5(x) bo‘lsin:
У anxn = 5(x). (4)
n=0
U holda V« > 0 da
bo'ladi.
◄ (4) munosabatda x = 0 deb topamiz:
a0 = S(Q).
(4) qatorni hadlab differensiallaymiz:
160
S'(%) = X )' = X ПапхП~Л
и=0 п=0
Bu tenglikda х = 0 deyilsa
ао = $ (0)
bo‘lishi kelib chiqadi. Shu jarayonni davom ettirib
bo‘lishini topamiz. ►
1- misol. Ushbu nxn = x + 2x2 + 3U +... + nxn +...
n=\
darajali qator yig'indisi topilsin.
◄ Ma’lumki, darajali qator (—1, 1) da yaqinlashuvchi va
...... x
unmg yig mdisi ga teng:
Bu qatorni hadlab differensiallab topamiz:
Keying! tenglikning har ikki tomonini x ga ko‘paytirsak,
bo‘lishi kelib chiqadi. ►
2- misol. Ushbu У, x"+1 - ln + x)
л-()
tenglikning to‘g‘riligi isbotlansin.
◄ Ravshanki, ^x" darajali qator (—1,1) da yaqinlashuvchi bo‘-
n=0
lib, uning yig‘indisi —- ga teng:
161
Bu tenglikda x ni — x ga almashtirsak, natijada
У (-l)"x" =
Ь 1+x
tenglik hosil bo'ladi. Uni [0.x] bo'yicha (0 < x < 1) integrallab topamiz:
0 «=0
'"M
0
dt
1+P
£(-1Р ]РЛ = 1П (1 + Pj* ,
«=0 о
n=0
„Л+1
---- = In (1 + x).
n+l
3-misol. Ushbu У, V~rx2”+1
^2w+1
darajali qator yig'indisi topilsin va undan foydalanib
у (-1)" _ Л
2«+l 4
n=Q
bo'lishi ko'rsatilsin.
◄ Ma’lumki,
(-1 < x < 1).
Bu tenglikda x ni — x2 ga almashtiramiz. Natijada У (-1)"x2" =
Zo 1+^
hosil bo'ladi. Uni [0, x] bo'yicha (0 < x < 1) integrallab topamiz:
^(-l)n]t2"dt = arctg^,
м=0 о
162
~ „2и+1
У(-1)"з— = arctg х.
2"+1
Keyingi tenglikda х — 1 deylik. U holda tenglikning chap tomoni
V
" 2и+1
ет=0
sonli qatorga aylanib, u Leybnits teoremasiga ko‘ra, yaqinlashuvchi
bo‘ladi. Demak,
у kP.1
A 2л+1
= arctg 1 = ►
Mashqlar
1. Hadlab differensiallash bilan ushbu
darajali qatorning yig‘indisi topilsin.
2. Hadlab integrallash bilan ushbu
x - 4x2 + 9x3 - 16x4 + ...
darajali qatorning yig‘indisi topilsin.
70- ma’ruza
Teylor qatori
Г. Funksiyaning Teylor qatori. Aytaylik, f(x) funksiya x0 e R
nuqtaning biror
t/5 (x0) - {* e R : x0 - 8 < x < x0 + 8; 8 > 0}
atrofida istalgan tartibdagi hosilaga ega bo‘lsin. Bu hoi /(x) funk-
siyaning Teylor formulasini yozish imkonini beradi:
/(x) = f (x0 ) + (x - X0 ) + (x - Xq )2 + ... +
+ —(x-x0) +r„(x), Г
bunda r„(x) — qoldiq had.
163
Modomiki, /(x) funksiya C/g(x0) da istalgan tartibdagi hosilaga
ega ekan, u holda
+ + + (1)
darajali qatorni qarash mumkin bo‘ladi.
(1) darajali qatorning koeffitsiyentlari sonlar bo‘lib, ular f (x) funk-
siya va uning hosilalarining x0 nuqtadagi qiymatlari orqali ifodalangan.
(1) darajali qator/(x) funksiyaning Teylor qatori deyiladi.
Xususan, x0 = 0 bo‘lganda (1) darajali qator ushbu
Г<0) 2 Z<")(0) „ у. „
/(0) + 7-rT- x + - xz + ... +-x« +... = > x"
1! 2! n\ n\
n=\
ko‘rinishga keladi. Faraz qilaylik,/(x) funksiya biror (~r, r) da (r > 0)
istalgan tartibdagi hosilaga ega bo‘lib, uning x0 = 0 nuqtadagi Teylor
qatori
,zn4 /'(0) /'(0) 2 /(n)(0) „
/(0)+ i x+ x+...+ x+... (2)
bo'lsin. Bu qatorning qoldiq hadini rw(x) deylik:
Л0)^„^...+ ^/ + гМ
1- teorema. (2) darajali qator (-r, r) da f (x) ga yaqinlashishi uchun
ushbu
/(x) =/(0)+|(-x +x + ... + -—— x" +r„(x)
1! 2! nl
Teylor formulasida Vx e (-r, r) uchun
lim r„(x) = 0
bo‘lishi zarar va yetarli.
◄ Zarurligi. Aytaylik, (2) darajali qator (-r, r) da yaqinlashuvchi,
yighndisi f (x) bo'lsin. Ta’rifga binoan
lim S„(x) = /(x), (xe(-r, r))
n--»oo
bo‘ladi, bunda
e / \ Л0) /'(0) 2 /(и)(0)
S„(x) = /(0) + <п-х + 2_—x2 + ... + 2__
164
Ravshanki, Vxe (-г,r) da lim Sn(x) = /(x) bo‘lishidan
lim[/(x) - 5„(x)] = limr„(x) = 0
>c=-c П—>oo
bo‘lishi kelib chiqadi.
Yetarliligi. Aytaylik, Vx e (-r, r) da lim r„ (x) = 0 bo'lsin. U holda
lim[/(x)-5„(x)]= limr„(x) = 0
П—>oo /7—
bo'lib, undan
lim 5„(x) =/(x)
bo'lishi kelib chiqadi. Demak,
/'(о) Л0) 2 /(n)(o)
J (*) = /(0) + x + ' x~ +... + +...
1! 2! n\
bo'ladi. ►
Odatda, bu munosabat o'rinli bo'lsa,/(x) funksiya Teylor qatoriga
yoyilgan deyiladi.
2°. Funksiyani Teylor qatoriga yoyish. Faraz qilaylik,/(x) funksiya
biror (-r, r) da istalgan tartibdagi hosilalarga ega bo'lsin.
2- teorema. Agar BM >0, Vx e (-r, r), \/n > 0 da
\f(n4x)\<M
bo'lsa,/(x) funksiya i-r, r) da Teylor qatoriga yoyiladi:
/Ы = t Л2 v (0) + Л * + Л + + Л’Т" +... (3)
“ n\ 1! 2! n\
n=Q
◄ Ma’lumki,/(x) funksiyaning Lagranj ko'rinishidagi qoldiq hadli
Teylor formulas! quyidagicha bo'ladi:
/(x) . f (0)+ Л X + фх» + ... + Л°Т” + MX) ,
1! 2! n\
bunda rn (x) = —.—x"+1, (0 < 0 < 1).
Teoremaning shartidan foydalanib topamiz:
=
/("> (0x) „+i
(га+1)!
<м •
rn+\
(“n+1)!’
(x 6
165 '
Ravshanki,
n+1
lim —-- = 0 .
n—>05 (/74-1)!
Demak, Vx0 g (-r, r) da (
lim rn (x) = 0
Л—»oo
bo‘lib, undan qaralayotgan/(x) funksiyaning Teylor qatoriga yoyilishi
kelib chiqadi. ►
3°. Elementar funksiyalarni Teylor qatoriga yoyish.
a) Ko‘rsatkichli va giperbolik funksiyalarning Teylor qatorlarini
topamiz. Aytaylik,
/(x) = ex
bo‘lsin. Ravshanki,
/(0) = l, (0) = 1, (we N)
bo‘lib,
Vxe (-a, a) da (a > 0)
0</(x)<e“, U < f(n>(x) < eu
bo‘ladi. Binobarin, 2- teoremaga ko‘ra f (x) = ex funksiya (-a,a) da
Teylor qatoriga yoyiladi va (3) formulada foydalanib topamiz:
°° и 2 ¥1
= 1 + п + + - + + = <4>
Л=хО
a > 0 ixtiyoriy musbat son. Demak, (4) darajali qatorning yaqin-
lashish radiusi r = bo‘ladi.
(4) munosabatda x ni —x ga almashtirib topamiz:
-x "V1 (-Х)" , X X2 / 1\n xn
e => -—-- = l -- + — -... + (-l) • —
n\ 1! 2! n\
n=0
Ma’lumki, giperbolik sinus hamda giperbolik kosinus funksiyalari
quyidagicha ta’riflanar edi:
ex-e x ex+e x
sh x = —-—, ch x - —-—.
2 2
Yuqoridagi
у , x x2 x"
e = t + T7 + + •• + —Г + — !
1! 2! n\
-x 1 x X2 / .ЧП Xя
e =^n + ir-" + W) 71 + -
166
formulalardan foydalanib topamiz:
y „3 2лт+1 ~ 2n+l
Sh X = ~ ~ + ... + 7^-^ + ... = У ~-----;
1! 3! (2w+l) ! 2L(2„+1)!’
k=0
Bu shx. chx funksiyalarining Teylor qatorlari bo‘lib, ular ifoda-
langan darajali qatorlarning yaqinlashish radiuslari r = +«> bo‘ladi.
b) Trigonometrik funksiyalarning Teylor qatorlarini topamiz.
Aytaylik, /(x) = sinx bo‘lsin. Ravshanki, Vx e R, Vue N da
|/(x)|<l, |/(n)(x)|<l
bo‘lib, /(0), /'(0) = 1, /(2n) (0) = 0, /(2"+1) (0) = (-1)" , (we N)
bo‘ladi. Demak, 2-teoremaga ko‘ra /(x) = sinx funksiya Teylor
qatoriga yoyiladi va (3) formulaga binoan
V (-1)” 2л+1 1 3 1
Sin X = > —----— X = X - ~ X + — X
^(2и+1)! 3! 5!
n-u
bo‘ladi. Aytaylik,
/(x) = cosx
bo‘lsin. Bu funksiya uchun Vx e R, Vne N da
|/(X)| < 1, /,'',(x)< 1
bo‘lib,
(5)
/(0) = l, /'(0) = 0, Z(2") (0) = (-!)", /(2”+1) (0) = 0, (we A)
bo‘ladi. U holda 2-teoremaga ko‘ra /(x) = cosx funksiya Teylor
qatoriga yoyiladi va (3) formulaga binoan
V (-1)" 2и i 1 2 1 4
С05Л = Х(Г„тг ='-2!V * * * * X +4!x —• (6)
n=0 K 7
bo‘ladi.
(5) va (6) darajali qatorlarning yaqinlashish radiusi r = bo‘ladi.
d) Logarifmik funksiyaning Teylor qatorini topamiz. Aytaylik,
/(x) = ln(l + x)
Г" 167,
bo‘lsin. Ma’lumki,
(1+х)"
bo‘lib, =
n\ n
bo‘ladi. Bu funksiyaning Teylor formulas!
ln(l + x) = x - у + у - + (-I)"-1 у + r„(x) (7)
qoldiq had uchun
bo‘ladi va
ko'rinishga ega.
/(x) = In (1 + x) funksiyani Teylor qatoriga yoyishda 1 - teorema-
dan foydalanamiz. Buning uchun (7) formulada r„(x) ning 0 ga intili-
shini ko‘rsatish yetarli bo'ladi.
Aytaylik, xe [0,1] bo'lsin. Bu holda Lagranj ko‘rinishida yozilgan
(_ул+1
/^(X)= (0 < 0 < 1)
(tf+l)(l+9x) 1
lim r„(x) = 0
tenglik bajariladi. Aytaylik, x e [-a, 0] bo‘lsin (0 < a < 1). Bu holda
Koshi ko‘rinishida yozilgan
(o<01 < 1)
(i+e^r1 v '
rn(x) =
qoldiq had uchun
g»+1
1-a
bo‘lib, quyidagiga ega bo‘lamiz:
lim r„ (x) - 0 .
n~
Demak, Vx e (-1,1]
lim rn (x) = 0.
168
U holda 1- teoremaga ko'ra
In (1 + x) = У - x - + ^ -... + (-1Г1 -- + ... (8)
n 2 3 n
n=l
bo'ladi.
(8) darajali qatorning yaqinlashish radiusi r = 1 ga teng. Agar
yuqoridagi ln(l + x) ning yoyilmasida x ni —x ga almashtirilsa, u
holda
formula kelib chiqadi.
e) Darajali funksiyaning Teylor qatorini topamiz.
Aytaylik,
\ /(x) = (1 + x)“ , (a e R)
bo'lsin. Ma’lumki,
(x) = a (a - 1) (a - 2)... (a - n + 1) (1 + x)a~"
bo'lib,
(0) = a(a - l)(a - 2)...(a - n + 1)
bo'ladi. Bu funksiyaning Teylor formulasi ushbu
(!«) =1к..tx„ + M
1! 2! nl
ko'rinishga ega.
Endi n -> oo da r„(x) 0 bo'lishini ko'rsatamiz.
Ma’lumki, Teylor formulasidagi qoldiq hadning Koshi ko'rinishi
quyidagicha
r (x) = (ctZ1^zZM^l)Z(zjzJ21 x"a . x (1 + Qx)“ 1 (-Ь® Г ,
" n\ \l+0x/
(0 < 9 < 1) bo'lar edi. Aytaylik, x e (-1,1) bo'lsin. Bu holda:
1) lim Д (a - l)(a - 2)...[(a -1) - (n - l)]x" = 0 bo'ladi,
chunki limit ishorasi ostidagi ifoda yaqinlashuvchi ushbu
169
, V a(a-l)...(oc-n+l) n
1 + \ --------------------x
n\
/7=1
qatorning umumiy hadi;
2) la • x| (1 - jx|)a ' < a • x (1 + 0x)“' < |a x\ (1 + |x|)a 1;
I i-o " i-e
' li+ox " i+ex
< 1 bo‘ladi. Bu munosabatlardan foydalanib,
Vx g (-1,1) da
limr„(x) = 0
bodishini topamiz. 1- teoremaga ko‘ra
(1 + x)“ = 1 + “ X + x2 +... + +... (9)
1! 2! n\
bo‘ladi. Bu darajali qatorning yaqinlashish radiusi a^ 0, a £ 2Vbod-
ganda 1 ga teng: r = 1.
(9 ) munosabatda a = -1 deb olinsa, u holda ushbu
— = У (-l)nx" = 1 — x + x2 -x3 +x4 -,.. + (-l)"x" + ...
1+x
/7=0
formula hosil bo‘ladi. Bu formulada x ni —x ga almashtirib topamiz:
= У (-1)" x" = 1 + x + x2 + ... + x" + ...
1 -ь
1- misol. Ushbu f (x) = In — funksiya Teylor qatoriga yoyilsin.
1—x
◄ Ma’lumki, In — = In (1 + x)- In (1 -x) bo‘ladi.
1-x
Biz yuqorida
ln(l + x) = x-^ + ~-... + (-D',“1
2 3 n
v2 3 n
In (1 - x) = -X - —- - —---------...---------...
2 3 n
bo dish ini ko‘rgan edik. Bu munosabatlardan foydalanib topamiz:
170
„2 „3 П
In (1 + x) - ln(l - x) = X - — + Д-- - ... + (-1) -------+ ...
2 3 n
X x~
1 । у
i—. . 1 i -V А. А A
Demak, In-—-2 x + — - + — + ... + -—-- + ...
kx 3 5 2/3-1
\ /
(10)
(10 ) darajali qatorning yaqinlashish radiusi. r — 1 bo‘lib, yaqin-
lashish to'plami (—1, 1) bo'ladi. ►
2- misol. Ushbu /(%) = J -y- cit funksiya Teylor qatoriga yoyilsin.
о
.3 .5 . .2,4-1
◄ Ma’lumki, sinf = f+ (-1)" -- .
3! 5! (2n-1) !
. ,, sin/ , Г2 /4 z , .«-I ;2"'2 , „
U holda --- = 1 - ту + г? - •• + (-D 7H—TVi + bo ladi.
t 3! 5! (2и-1)!
Bu darajali qatorni hadlab integrallab topamiz:
, ,2n-2
/ < \n-l l
... + (-l) 7----—- +
(2/3-1) !
= X -
3'3+5!5
+ (-l)"4
x^
Ои4)Га^1) + "
Keyingi darajali qatorning yaqinlashish radiusi r = +<« bo‘ladi. ►
2x~l
3- misol. Ushbu /(x) = -------funksiya Teylor qatoriga yoyilsin
x2 +x-6
va bu qatorning yaqinlashish radiusi topilsin.
◄ Awalo f (x) funksiyani quyidagicha yozib olamiz:
- 2x~l 1 1
x2+x-6 x+2 x-3
□ fl 1
2 1 + -x
2
Ma’lumki,
4 . = V (-1)" .xn,
Ux
171
Bu formulalardan foydalanib topamiz:
(r = 2),
Demak, quyidagi Teylor qatorini olamiz:
2x-l v 1 1 V
y2,v X Z,»+l Z^n+l ZJ nn+l Q»+l
x +х-° n=0 2 n=0 J n=(A 2 J )
Bu darajali qatorning yaqinlashish radiusi r = 2 bo'ladi. ►
Mashqlar
1. Ushbu /(x) = sin3x, /(x) = in (1 — x2), /(x) =---------------------y
1+х+хл
funksiyalar Teylor qatoriga yoyilsin.
"V1 x3f!
2. Ushbu > — ~r-„ (x g R) qatorning yig‘indisi topilsin.
" (3«)!
/7=0
71- ma’ruza
Uzluksiz funksiyani ko‘phad bilan yaqinlashtirish.
Veyershtrass teoremasi
1°. Bernshteyn ko‘phadi. Aytaylik,/(x) funksiya [0,1] segmentda
berilgan bo'lsin. Ushbu
X/ (“) Cnxk 0 - = / (0) • (1 - x)" + / (1) C'x(1 - хГ1 +...+/ (1) x"
4=0 ХП
ko'phad/(x) funksiyaning Bernshteyn ko'phadi deyiladi va Bn (/;x)
kabi belgilanadi:
(1-хГ\
4=0 ' '
172
„ , ,-,к и(л-1)(и-2) (п-к+1)
' Bunda С„ =----------------------------.
к'
Demak, Bernshteyn ko‘phadi п- darajali ko‘phad bo‘lib, uning
koeffitsiycntlari f(x) funksiyaning
(k = 0,1,2,...,/?)
n
nuqtalardagi qiymatlari orqali ifodalanadi. Masalan,
51(/;x) = /(0) + [/(l)-/(0)]x,
52(/;x) = /(0) +
2/(l)-2/(0)lx +
/(0)+2/(1) +/О)]*2
bo‘ladi.
2°. Muhim lemma. Ushbu
£с„"хЧ1-хГА=1, (i)
£=0
--x}2 Ckxk(l-x)n'k = ^-*1, (0 < x < 1) (2)
n ) n
ayniyatlar o‘rinli.
◄ Nyuton binomi formulas!
^Ckakbn~k = (a + b)n
k=0
da a = x, b — 1 — x deyilsa, u holda
^Ckxk (1-x)""* =1
£=0
bo‘lishi kelib chiqadi.
(2) ayniyatni isbotlash uchun quyidagi
yig‘indilarni hisoblaymiz.
Bu yig‘indini hisoblashda yuqorida keltirilgan Ck ning ifodasi va
Nyuton binomi formulasidan foydalanamiz:
173
i=l
Demak,
Endi
У к Скхк (1 - х)п~к = Скхк (1 - х)п~к = У Ск2хХк (1 - х)п~к --
к^п ы
= X • У Ск~1Хк~1 (1 - x')n~l~(k~ii =х [х + (1 - х)Г = X. j
^к-Скхк (1-хУ~к =х. (3)
к=0 п
^^Скхк (1-хГк
к=0 п
yig'indini hisoblaymiz:
У "Z1. ск^хк (1 - xTk + У 1 Ck-\xk (1 - xTk =
x-J n n-l " 1 n n 1
A=1 £=1
= x2 у ck:lxk^ (i - xr2'lk-2) +1 xy ck:'xk-1 (i - хГ1^'1’
П k=2 П k=\
= ~ x2 [x + (1 - x)]"'2 +1 x [x + (1 - x)]" 1 = x2 + -- •
Demak, У Ckxk (l-х)" k = x2 + . (4)
Yuqoridagi (1), (3) va (4) munosabatlardan foydalanib topamiz:
-2хУ -Ck (1 - x)"^ + x2 У Ckxk (1 - x)n~k
*=0 n )t=0
2 x(l-x) ~ 2 x(l-x)
= x +------------2x x + x =---------. ►
n n
174
Natija. Vxe [0,1], V«e N uchun
n , , \2 , .
g(M фЧ-хГЧ! (5)
tengsizlik o‘rinli bo‘ladi.
◄ Ravshanki, Vxe [0,1] uchun
x(i-x)<|
bo‘ladi. Bu tengsizlik va (2) munosabatdan (5) tengsizlikning o'rinli
bo‘lishi kelib chiqadi. ►
3°. Uzluksiz funksiyani ко ‘phad bilan yaqinlashtirish.
1-teorema. (Bernshteyn teoremasi.) Agar /(x) funksiya [0, 1]
segmentda uzluksiz bo‘Isa, u holda
lim max l/(x) - B„ (/, x)l = 0
л->оо 0<х<1 1
bo‘ladi, bunda
n . J .
Bn(M = ±f 7\скхк{\-хГк . (6)
◄ (1) va (6) munosabatlardan foydalanib topamiz:
Ckxk (1 - x)"“*
Kantor teoremasiga ko‘ra qaralayotgan /(x) funksiya [0, 1] da
tekis uzluksiz bo'ladi. U holda ta’rifga binoan
Ve > 0, 38 > 0, Vx', x'e[0,1] uchun |x'-x'|<8
bo‘lganda |/(*') - /(x')| < |
tengsizlik bajariladi. Ma’lumki,
5„(/;x)-/(x)
ayirmani ifodalovchi yig‘indida и+l ta had bo‘lib, ular к ning
0,1,2,...,/? qiymatlarida yuzaga keladi. Bu к ning ushbu
kn~x<8, (xe[0,1])
175
tengsizlikni qanoatlantiradigan qiymatlari to‘plamini E„(k) bilan;
(xe[0,l])
tengsizlikni qanoatlantiradigan qiymatlari to‘plamini Fn(k} bilan bel-
gilaylik. Ravshanki,
bo'ladi. Shuni e’tiborga olib, yuqoridagi yig‘indini ikki qismga ajratamiz:
Endi bu yig'indilami baholaymiz./(x) funksiyaning [0, 1] da tekis
uzluksizligidan hamda lemmadan foydalanib topamiz:
= X <(-)- (1 - х)П~к <; X (1 - x)n~k
|w I
n
<|Jc^ (l-хГ* =|.
fc=0
Ravshanki, /(x) funksiya [0, 1] da chegaralangan. U holda
max \f (x)| = M e R bo‘ladi. Shuni e’tiborga olib topamiz:
'kxk (1 - xTk
< X /(^-/(x)C„fcx41~xrfc <
[Л I
<2M X Скхк(1-хГк.
£:|--x|>6
176
Agar
bo'lishini hisobga olsak, u holda lemmaga ko‘ra
Ckxk (1 - xT~k
1
4«82
bo'ladi. Shunday qilib,
Ckxk (1 - x)n~k
£ M
2 + 2«82
bo‘ladi. Agar n > deyilsa, u holda
252e
M 1
—i
252 « 2
bo‘lib, natijada quyidagiga ega bo‘lamiz:
\B„ (/;x)-/(x)| < e
Bu munosabatdan esa
lim max\B„ (/; x) - /(x)| = 0
0<x<] ! ’
bo‘lishi kelib chiqadi. ►
Bu teoremadan n -» oo da
5„(/;x)-/(x), (0 < x < 1)
bo‘lishini topamiz. Demak, [0, 1] da uzluksiz bo‘lgan f(x) funksiya
(/; x) ko‘phad bilan yaqinlashtirildi:
/(x) « У / (-) Ckxk (1 - x)n~k, (0 < x < 1) •
Йо [n/
177
Aytaylik, f(x) funksiya [a, b] segmentda uzluksiz bo‘lsin. Ma’-
lumki, ushbu
. 1 a
1~Ь^аХ'ь^а
chiziqli almashtirish [a,b] segmentni [0,1] segmentga almashtiradi.
Bu almashtirishdan foydalanib ushbu
ф(0 = f(a + (b-a)t), (0 < t < 1) (7)
funksiyani hosil qilamiz. Ravshanki, <p(r) funksiya [0, 1] da uzluksiz
bo'ladi. Yuqoridagi teoremadan foydalanib topamiz:
limmax|/?„ (cp;/)-«>(z)| = 0 , (8)
0<Г<1 1 1
bunda
\ fl /
k=0
(7) va (8) munosabatlardan
lim max
и-»<*=> a<x<b
bo'lishi kelib chiqadi, bunda
Shunday qilib quyidagi teoremaga kelamiz.
2- teorema (Veyershtrass teoremasi.) Agar f (x) funksiya. [a, b]
segmentda uzluksiz bo'lsa,
lim max
w—a<x<b
= 0
bo'ladi.
178
Mashqlar
l.Agar/(x) funksiya [0, 1] segmentda uzluksiz bo'lsa, Vxe [0; 1] da
bo‘lishi isbotlansin.
2. Agar f(x) funksiya [0, 1] segmentda uzluksiz bo‘lsa,
sup x) - /(x)| < I (о[4Л
0<x<l 2 J
bo‘lishi isbotlansin, bunda w(5) — funksiya /(x) ning uzluksiz moduli.,
72- ma’ruza
Furye qatori tushunchasi
1°. Davriy funksiyalar haqida ba’zi ma?Iumotlar. /(x) funksiya
R = (^>o,+«o) to‘plamda berilgan bo‘lsin. Ma’lumki, shunday
T e R \ {0} son topilsaki, Vx e R da
/(х + Г) = /(х)
tenglik bajarilsa, /(x) — davriy funksiya, son esa uning davri
deyilar edi.
Agar f (x) davriy funksiya bo'lib, TV 0 son uning davri bo‘lsa, kT
sonlar (k = ±1,±2,...) ham shu funksiyaning davri bo'ladi.
Agarf (x) va g(x) davriy funksiyalar bo‘lib, TV 0 ulaming davri bo‘lsa,
/(x)±g(x), /(x)g(x), (g(x)^0)
funksiyalar ham davriy bo‘lib, ularning davri Tga teng bo‘ladi.
Aytaylik,/(x) davriy funksiya bo‘lib, uning davri TVodsin. Agar
bu funksiya grafigining tasviri [a, a+T] oraliqda (ae R) ma’lum bo‘lsa,
uni birin-ketin
x = a + kT, (T = ±1,±2,...)
vertikal to‘g‘ri chiziqqa nisbatan simmetrik ko‘chirish natijasida
/(x) ning (-oo, +°o) dagi grafigi hosil bo‘ladi (30- chizma).
Bu jarayonni [a, a+7'| da berilgan funksiyani (-oo, +«) da davriy
davom ettirish deb ham yuritiladi.
179 '
a a+T
30- chizma.
Shuni ta’kidlash lozimki, T davrli /(x) funksiya [a, a+T] da
uzluksiz bo'lsa, uni (-<», +<») ga davriy davom ettirishdan hosil bo'lgan
funksiya (uni ham /(x) deymiz) (-<», +°°) da uzluksiz yoki bo'lakli
uzluksiz (ya’ni x — a + kTnuqtalarda (k = ±1,±2,...) uzilishga ega
bo'lib, boshqa barcha nuqtalarda uzluksiz) bo'lishi mumkin.
Masalan, [0, 1] da berilgan
/(x) = 2^x (1 - x)
funksiyani (-°o, +°°) da davriy davom ettirishdan hosil bo'lgan funksiya
(_oo, +oo) da uzluksiz bo'ladi (31- chizma).
/¥VYY\
-2-1 0 12 3
31- chizma.
[—1, 2] da berilgan
/(x) = x2
funksiyani (-<», H da davriy davom ettirishdan hosil bo'lgan funksiya
(-«>, +00) da bo'lakli uzluksiz bo'ladi (32- chizma):
Lemma. Agar /(x) — davriy funksiya, uning davri T bo'lib,
[a, a+T] da integrallanuvchi bo'lsa, u holda
a+T b+T
J f(x)dx = J f(x)dx, (Z>e 7?)
a b
bo'ladi.
180
32- chizma.
◄ Aniq integral xossasidan foydalanib topamiz:
£7+7' b b+T a+T
j j\x)dx = ^f(x)dx + J /(x)Jx + J f(x)dx. (1)
a a b b+T
a+T
Bu tenglikdagi j f (x)dx
b+T
integralda x = t + T almashtirish bajaramiz. Natijada
a+T b a b
J f(x)dx = \f(t + T)dt = $f(t)dt = -\f(x)dx (2)
b+T a b £7
bo‘ladi. (1) va (2) munosabatlardan
a+T h+T
J f(x)dx = J f(x)dx
a b
bo‘lishi kelib chiqadi. ►
2°. Garmonikalar. Ushbu &
/(x) = Л sin (ax + p) (3)
funksiyani qaraylik, bunda A, a, p — haqiqiy sonlar. Bu davriy
funksiya bo+ib, uning davri
T = —, (a*0)
a
ga teng bo‘ladi.
181
•< Haqiqatan ham,
f(x + —j = A sin^a^x + + p j= A sin (ax + p + 2л) =
= A sin (ax + p) = f (x). ► ’
Odatda, (3) funksiya garmonika deyiladi. Garmonikaning grafigi
у — sinx funksiya grafigini OXva OYo‘qlar bo‘yicha siqish (cho‘zish)
hamda OX o‘q bo‘yicha surish natijasida hosil bo'ladi.
Garmonikani quyidagicha yozish ham mumkin:
/(x) = A sin (ax + p) = A (cos ax sin p + sin ax cos p) =
= A sin p • cos ax + A cos P • sin ax = a cos ax + b sin ax,
bunda
u = ^sinp, Л^/lcosp.
Aksincha,
f (x) = a cos ax + b sin ax
funksiya garmonikani ifodalaydi:
/(x) = a cos ax + 6sinax =
a b
-=== cos ax + - sm ax =
42+b2 4444 )
= A (sin p cos ax + cos p sin ax) = A sin (ax + p),
bunda 4a2 + b2 = A, = sin p, -.4,^ = cos p.
4444 4444
3°. Furye qatorining ta’rifi. Har bir hadi
u„(x) = an cos их + bn sin nx, (n - 0,1,2,...)
garmonikadan iborat ushbu
a0 + (й„ cos nx + bn sin nx) (4)
«=i
funksional qator trigonometrik qator deyiladi. Bunda
a0, Oi, 615 a2, b2,..., a„, b„,...
sonlar trigonometrik qatorning koeffitsiyentlari deyiladi.
182
Odatda, (4) trigonometrik qatorning qismiy yig‘indisi
n
Tn(x) = ай + ^(ak cos kx+ bk sin kx)
k=\
trigonometrik ko‘phad deyiladi.
Aytaylik, /(x) funksiya [-л, л] da berilgan bo‘lib, u shu oraliqda
integrallanuvchi bo‘lsin.
Ravshanki,
/(x)cosnx, /(x)sinwx, (n = 1,2,3,...)
funksiyalar ham integrallanuvchi bo‘ladi. Yuqorida keltirilgan funk-
siyalarning integrallarini quyidagicha belgilaymiz:
«о = - f f(x)dx,
Я J
— 71
1
an = - Г /(x)cosnxdx, (и = 1,2,...) (5)
Я J
-л
Jt
bn = -- Г f (x) sin nxdZx, (« = 1,2,...)
Я J
- к
So‘ng ushbu y-+ (a„ cosnx + Z>„ sinnx) (6)
2 »=i
trigonometrik qatorni tuzamiz.
Ravshanki, (6) trigonometrik qator (5) munosabatlardan topiladigan
a0, «], bi, a2, b2,..., a„, b„,...
sonlar bilan to‘la aniqlanadi.
1- ta’rif. Koeffitsiyentlari (5) munosabatlar bilan aniqlangan (6)
trigonometrik qator f (x) funksiyaning Furye qatori deyiladi. Bunda
a0, ait by, a2, b2,an,b„, ...
sonlar f (x) funksiyaning Furye koeffitsiyentlari deyiladi.
Demak, f (x) funksiyaning Furye qatori shunday trigonometrik
qatorki, uning koeffitsiyentlari (5) formulalar yordamida aniqlanadi.
Shuni e’tiborga olib, funksiyaning Furye qatori quyidagicha yoziladi:
/(x) ~ + У (fl„ cos nx + bn sin ox).
И=1
183
1- misol. Ushbu
/(x) = eax, (-л < x < л, а Ф 0)
funksiyaning Furye qatori topilsin.
◄ (5) formulalardan foydalanib, berilgan funksiyaning Furye koef-
fitsiyentlarini hisoblaymiz:
aQ = i f e^dx = - e~m ) = — sh are,
kJ an an
-71
1 - 1 .71
1 f (П J 1 acos rt-X + rtSin nx ar
an = - e cos nxdx ----------------y—z-------e =
я J я а2+л2 -д
-71
= (-1)" - -2-sh сот, (n = 1,2,...),
П cr+rr
1л 1 7t
j 1 f ал * i 1 asm rtx-rtcos nx ctx
bn - “ H sin nxdx =----------—v—-----------e™ =
я J я ог+лг
-71
= (-1)"'1 --^^yshoOT, (n-1,2,...).
or +n
Demak,
f(x) = e™
funksiyaning Furye qatori
f(x) = em ~ v + («„ cos nx + bn sin nx) =
«=1
2shorn 1 (-1)” ( . x
-------- + x — (a cos nx - nsin nx)
% [2a
bo‘ladi. ►
Aytaylik, ushbu shartlar bajarilsin:
1) Quyidagi
у + У, (an cos nx + bn sin nx)
n=\
(7)
trigonometrik qator [-л, л] da yaqinlashuvchi va uning yig‘indisi
f(x) ga teng:
184
/(х) = °^ + Х (а„ cos их + sin их); (8)
Л=1
2) (8) ifoda hamda uni cosAx va sinAx larga (A=0,l,2,...) ko'pay-
tirishdan hosil bo'lgan
/(x) cos kx - cos kx + У (o„ cos nx cos kx + bn sin nx cos Ax),
n=\
/(x) sin kx = sin kx + V (an cos nx sin kx + bn sin nx sin Ax),
2 n?\
qatorlar [-л, л] da hadlab integrallansin. U holda
aQ, ax, bx, «2, a„, bn,...
sonlar f (x) funksiyaning Furye koeffitsiyentlari bo‘ladi, (7) trigono-
metrik qator esa f (x) funksiyaning Furye qatori bo'ladi. Bu tasdiqning
isboti quyidagi
0 л
- J f (x) cos nxdx + j/(x)cosnxJx -
-n 0
j f(x)dx, J f (x) cos kxdx, J f (x) sinAxcZx
— 7T —7t -It
integrallarni hisoblashdan kelib chiqadi.
4°. Juft va toq funksiyalarning Furye qatori. Faraz qilaylik, /(x)
funksiya [-л, л] da berilgan juft funksiya bo'lib, u shu oraliqda
integrallanuvchi bo'lsin. Bu funksiyaning Furye koeffitsiyentlarini
topamiz:
71
a I f(x) cos nxdx = -
Л J Tt
-Tt
71
= - j/(x)cosnxc7x, (n = 0,1, 2,...),
71 0
71
t>„ = - ( /(x)sin
7Г J
-к
1 Л
- -j/(x)sinnxdx + j/(x)sinnxdx - 0, (n = l,2,...).
71 L о 0
’ o.
и,
nxdx = - J /(x)sin nxdx + J /(x) sin nxdx =
0
П
185
Demak, juft f (x) funksiyaning Furye koeffitsiyentlari
2 K
a„ f(x) cos nxdx, (n = 0,1,2,...)
л о
/>„=0, (/7 = 1,2,...)
bo'lib, Furye qatori
/(x) - 3 +ХЙ« C0SHX
«=1
bo‘ladi.
Aytaylik, /(x) funksiya [-л, тс] da berilgan toq funksiya bo‘lib, u
shu oraliqda integarallanuvchi bo‘lsin. Bu funksiyaning Furye koef-
fitsiyentlarini topamiz:
Я
a - - Г f (x) cos nxdx = -
71 J 7Г
0 Я
| f (x) cos nxdx + j f(x) cos nxdx =
_~Я 0
£
n
-J/(x) cos nxdx - /(x) cos nxdx
0
J Jt
bn = - I /(x) sin nxdx =
7t J 7t
= 0, (« = 0,1,2,...),
0 я
- J /(x) sin nxdx + J /(x) sin nxdx =
^-я 0
Я
//(*) s*n ’ (л = 1,2,...).
Lo
Demak, fix') toq funksiyaning Furye koeffitsiyentlari
a„=0, (n = 0,1,2,...),
2 71
bn = - J/(x)sinrocc7x, (/7 = 1,2,...)
710
bo‘lib, Furye qatori quyidagidan iborat:
/(x) ~ sin roc.
n=l
186
2- misol. Ushbu f (x) = x2, (-л < x < л)
juft funksiyaning Furye qatori topilsin.
< Awalo berilgan funksiyaning Furye koeffitsiyentlarini topamiz:
2 f 2 ,
a0 = I x dx
7t J
0
„ It
й« : „
7t .
0
X cos nx
n
p-
2 Г 2 j
= - x cos nx dx =
7t J
1 Г
— — [cos nx dx = (-1)” •
n J
2 2 8ПШ
-X
7Г
я - *
o n
0
4 Г . ,
----- x sm nx dx =
rar J
о
(« = 1,2,
n
4
m
n
л
о
Demak, /(x) = x2 funksiyaning Furye qatori
/(x) = x2 ~ ~ + 4 V (-1)"
3 Z? n
bo‘ladi. ►
3- misol. Ushbu f (x) = x, (-л < x < л) toq funksiyaning Furye
qatori topilsin.
•< Berilgan funksiyaning Furye koeffitsiyentlarini hisoblaymiz:
, 2 г , 2 x cos nx If ,
b„ = - x sin nx dx = -----+ - cos nx dx
It J 7t П n П J
0 U 0
Demak, /(x) = x funksiyaning Furye qatori
°° П
> /(x) --sin nx
M=1
2C-1)"”1
n
bo’ladi. ►
5°. [—I, Z] oraliqda berilgan funksiyaning Furye qatori. Faraz
qilaylik, f (x) funksiya [—I, /] oraliqda (/ > 0) berilgan bo‘lib, u shu
oraliqda integrallanuvchi bo‘lsin.
Ravshanki, ushbu t = у x almashtirish natijasida [—I, /] oraliq
[-л, л] oraliqqa o‘tadi. Agar
187
/(*) = /(-') = <р(0
\ 7t J
deyilsa, <p(Z) funksiya [-л, тг] oraliqda berilgan va shu oraliqda integral-
lanuvchi funksiya bo‘ladi. lining Furye qatori ;
ф(0 ~ v + V (a„ cos nt + bn sin nt)
2.
n=\
bo‘lib, a„ - i [ <p(t)cosntdt, (n - 0,1,2,...)
7C J
— 71
Л
b„ = - f <p(Z) sin «ZzZz1, (« = 1,2,...)
7t J
-7Г
bo'ladi. Endi t = ~x bo‘lishini e’tiborga olib topamiz:
(7t \ fin V” I 7C r • Я \
7 ; ~ 2 + ” cos n~[x + °n sm и у xl,
«=i v
/
a„ - | f (pfyX^costtyXtZx, (n = 0,1,2,...),
I J \ I ] I
-I
I
= 7 f tp(“x)sin fl-xzZx, (« = 1,2,...).
I J \ I / /
-I
Natijada berilgan f(x) funksiyaning Furye qatori quyidagicha
~ cos-r+bn sin ~t]
bo‘lib, bunda:
i
an = 7 f /(x)cos^zZx, (и = 0,1,2,...)
I J t
-I
I
bn = 7 f /(x)sinxdx, (« = 1,2,...).
I J I
-I
188
,an = J ex cos rmxdx
-i
4- misol. Ushbu f(x) = ex, (-1 < x < 1)
funksiyaning Furye qatori topilsin.
◄ Yuqoridagi formulalardan foydalanib, f (x) = ex funksiyaning
Furye koeffitsiyentilarini topamiz:
i
a0 = j exdx = e - e~l,
-i
i . i
. итгх-cos m.i v
-----------e* =
1+«27T2----_]
= —iz-v (e cos ил - e"1 cos rm) = (-1)" —* _, (n = 1,2, ...),
1+и2л2 1+л2л2 v 7
1 . 1
, г x , sin ratx-ffltcos imx x
b„ = \ e cos rmxdx -----------r-—----e =
j li/rn2
1 I -1 \ ил(-1)" ( -1 1
= —r— erm cos rm + rme cos rm =---------r-—• (e - e) ~
Wir2 V - 7 l + w2!?
= (-l)"+1±±l,
1+n n
Demak,
/(x) = ex, (-1 < x < 1)
funksiyaning Furye qatori quyidagicha
77^1
ko‘rinishda bo'ladi. ►
Mashqlar
1. Usfibu /(x) = 2 sin (2x + 2) garmonikaning grafigi topilsin.
2. Ushbu f (x) = |xi, (-л < x < л) funksiyaning Furye qatori
topilsin.
(-1F (_i),7+1
—cos rm + —y-y rm sin rmx
1+hV l+nV
189
73- ma’ruza
Furye qatorining yaqinlashuvchanligi
1°. Lemmalar. Furye qatorining yaqinlashishini isbotlashda muhim
bo‘lgan lemmalami keltiramiz.
1- Iemma. Agar <p(x) funksiya \a,b\ da integrallanuvchi bo‘lsa,
ь b
lim I <p(x) sin px dx = 0, lim [ cp(x) cos px dx = 0
p__>oo J J
a a
bo‘ladi.
-< Ravshanki, lemmaning shartidan
<p(x) sin px, cp(x) cos px
funksiyalar \a,b} da integrallanuvchi bo‘ladi. [a,b\ segmentda
x0, Xj, x„_,, x„, (a = x0 < Xj < x2 < ... < x„„j < x„ = b)
nuqtalarni olib,
h
J (p(x)sin pxdx
a
ni quyidagicha yozib olamiz:
b n-\
J (p(x) sin px dx - У, j cp(x) sin px dx =
a ^=0
л-l *4+1 n-1 *<+'
= X I [ф(х) _ mk ]sin px dx + mk f sin pxdx, (1)
A'£ ^“0 Xk
bunda mk = inf <p(x), (/< - 0,1,2,..., n-1).
, xt+1 ]
Bu (1) tenglikning o‘ng tomonidagi integrallarni baholaymiz:
„-1
Г [cp(x) - mk ] sin px dx
n-l xk+l n-1
-X J ^kdx = ^^k/\xk,
Xfc A-0
bunda T5k — funksiya cp(x)ning [xk, xfc+1] dagi tebranishi, bxk = xk+1 - xk.
190
Modomiki, cp(x) funksiya \a,b\ da integrallanuvchi ekan, u holda
£п5,Дхл<| (2)
k=0
qilib olinishi mumkin.
Endi (1) tenglikning о‘ng tomonidagi ikkinchi integralni baho-
laymiz:
«—1 xk+l «-1
'^jmk J sinpxdx < |
£=0 xi- &=0
COS pXfr -cos
p
л-l ~ ~ n-l
k=0 И r 11=0
Ravshanki, p ni yetarlicha katta qilib olish hisobiga
jXkl<| (3)
и k=f>
ga erishish mumkin. Natijada (1) , (2) va (3) munosabatlardan
b
Jcp(x)sin pxdx < e
a
bo‘lishi va undan
b
lim f <p(x) sin pxdx = 0
p—»oo J
a
ifoda kelib chiqadi. Xuddi shunga o‘xshash
b
lim f <p(x) cos pxdx = 0
p—>oo J
a
isbotlanadi. ►
Agar [a, />] oraliqni shunday
[o0,OiL fa, a2],[a„_i, a„], (a0=a,a„=b)
bo‘laklarga ajratish mumkin bo‘lsaki, har bir (ak, ak+1) da
(к - 0,1,2,..., n - 1) /(x) funksiya uzluksiz bo‘lib, x = ak nuqtalar-
da chekli о‘ng
191
f(ak+O), (£ = 0,1,2,...,/?-!),
va chap
/(^-0), (£ = 0,1,2,...,/?)
limitlarga ega bo'lsa,/(x) funksiya [a,b] da bo‘lakli uzluksiz deyiladi.
Yuqoridagi lemma <p(x) funksiya [a,b] da bo'lakli uzluksiz funksiya
bo'lgan holda ham o'rinli bo'ladi.
1- lemmadan quyidagi natija kelib chiqadi.
Natija. Agarf (x) funksiya [-я, л] oraliqda bo'lakli uzluksiz bo'lsa,
uning Furye koeffitsiyentlari n ч da nolga intiladi:
7Г
lim a„ = lim - f f(x) cos nx dx = 0,
П—/7—7t J
-7Г
71
lim bn - lim - | f (x) sin nxdx - 0.
А7—Л7-—7C *
-7T
1 « sin(2n+l)^
2- lemma. Ushbu = + cos ~tenglik o'rinli.
k=\ 2 sin-
2
◄ Ravshanki,
1 n
| cos ku
k=l
1
2sin-
2
и
sm - +
n
2 sin у cos ku
k=l
bo'ladi. Agar
1
2 sin | cos
*=i
n
IJ 1
sin! k + -
. , 1\ . / 1\ . и
«-sm £-- и =sm /?+- «-sm-
\ 2/ \ 2) 2
bo'lishini e’tiborga olsak, u holda yuqoridagi tenglikdan
1 A , sin(2w+l)
- + > cos ku = —---------------
2 - и
<t=i 2 sm-
2
tenglikni keltirib chiqaramiz. ►
2°. Furye qatorining qismiy yig'indisi. Dirixle integrali. Funksional
qatorlar nazariyasidan ma’lumki, qatorning yaqinlashishini aniqlashda
192
awalo uning qismiy yig'indisi topilib, so‘ngra bu qismiy yig'indining
limiti o‘rganilar edi.
Funksiya Furye qatorining yaqinlashishini aniqlashda ham awalo
uning qismiy yig'indisi topiladi.
Aytaylik, f (x) funksiya [-л, л] oraliqda integrallanuvchi bo'lsin.
Bu funksiyaning Furye koeffitsiyentlarini topib, uning Furye qatorini
tuzamiz:
ak = i [ f(t)cosktdt, (k - 0,1,2,...),
7t J
-к
П
bk = - f f(t)s'mktdt, (£ = 1,2,...),
7Г J
-л
f(x) ~ у- + X (ak cos + bk sin kx\
fc=i
Ravshanki, bu qatorning qismiy yig'indisi
Fn(f', x) = + X (ak cos kx + bk sin Ax)
bo'ladi. Bu tenglikdagi ak va bk laming o‘miga ularning yuqorida
keltirilgan ifodalarini qo'yib topamiz:
1 r n к
Fn(f-,x) - — Г f(t')dt + 'S' - f /(0[eos£rcosAx + sin£isin kx}dt-
2я J к J
-n ^-1 -л
= ; J /«)
~n
1
- + У cos k(t - x) dt.
2 k=i
Ma’lumki, 2- lemmaga ko‘ra
. n sin(2R+l)^—-
7 + У cos ~
k=i 2 sin—
2
bo‘ladi. U holda Fn (f; x) yig'indi quyidagi ko'rinishga keladi:
193
, * sin(2«+l)---
2 sin---
я 2
(4)
Odatda, (4) tenglikning o‘ng tomonidagi integral f(x) funksiyaning
Dirixle integrali deyiladi.
Fn (/1 *) yig'indining bu ifodasini yanada o‘zgartirib, n <» da
Fn (/; x) ning limitini topishga qulaylik keltiradigan ko‘rinishga olib
kelamiz.
Awalo (4) integralda t — x — и almashtirishni bajaramiz. Bunda
integral ostidagi funksiya 2л davrli bo‘lganligi sababli integrallash
chegarasining o‘zgarmay qolishini e’tiborga olib topamiz:
F„ (f', x) =
. * sin(2«+D-
— f f(x + u)-------7T~du-
2sin|
Bu tenglikni ikki qismga ajratib:
F, ±
Z7C
0 sin(2n+l)^ * sin(2n+l)~
I f(x + u)------—du + I f(x + u)---------du
-n 2 sin- 0 2sin-
o‘ng tomondagi birinchi integralda и ni -u ga almashtirib topamiz:
. n sin(2zi+l)~
Fn (/; x) = -Г[/(х + и) + /(x-m)]--------u^du'
о 2 sin-
Xususan, f (x) s 1 bo‘lganda
bo‘lib, u 1 ga teng bo'ladi.
Haqiqatan ham, 2- lemmadan foydalansak, u holda
194
F„ (!,*)= 1(2
7t J
0
n
У,cosku du~\ +
1
2
2 ” f
- V | cos kudu =
71 *=1 0
bo‘lishi kelib chiqadi. Demak,
• С П
n Sin П+- И
1 = 1 [—A—2J~du. (5)
n J . и
0 2 sin-
s’’. Lokallashtirish prinsipi. f (x) funksiya Furye qatorining qismiy
yig’indisi
( П
it sin n + - In
F„ C/» = - [[/(x + «) + /(x-zz)]—1—-l-d« (6)
0 2sin^
ning bitta muhim xossasini keltiramiz.
Ixtiyoriy 5 sonni (0 < 8 < л) olib, (6) integralni ikkita integralga
ajratamiz:
F„ (f’ J[/(x + «) + /(* ~ “)] - ~du +
K о 2sin—
7t
+| j[/(* + «) + /(* -«)]
8
du =JX (n, 8) + J2 (n, 8).
(7)
1- teorema. n -> °° da /2 (я, 8) ning limiti nolga teng bo’ladi:
lim J2 (n, 8) = 0 .
◄ f(x) funksiya [-л, л] da integrallanuvchi bo’lganligi sababli
ф(«) = —(x + w) + / (* ~ «)]
2sin-
2
195
funksiya ham [8, л] da integrallanuvchi bo'ladi. U holda 1- lemmaga
ko‘ra
7Г
lim J2 (n, 8) = lim - f Г/(х + и) + fix - w)l
dii =
= lim fcp(u)sin(n + -Uudu = 0
ft Л->оо J \ 2 /
bo ‘ladi. ►
(7) munosabat va keltirilgan teoremadan muhim natija kelib chi-
qadi. Ushbu
• ( 1\
5 sm n+~ и
f in, 8) = - [[/ (x + u) + f (x - h)] —idu
о 2 sin-
integralning n~>°° dagi limiti mavjud bo‘lgandagina Fn (/; x) ning
limiti mavjud va
lim F„ (/, x) = lim f (n, 8)
munosabat o‘rinli bo‘ladi.
Ma’lumki, J} in, 8) integralda f funksiyaning [x - 8, x + 8] ora-
liqdagi qiymatlarigina qatnashadi.
Demak, f (x) funksiya Furye qatorining x nuqtada yaqinlashuv-
chanligi yoki uzoqlashuvchanligi bu funksiyaning shu nuqta atrofi
(x - 8, x + 8) dagi qiymatlarigagina bog'liq bo‘ladi. Buni lokallash-
tirish prinsipi deb yuritiladi.
4°. Furye qatorining yaqinlashuvchanligi. Endi funksiya Furye
qatorining yaqinlashishi haqidagi teoremani keltiramiz.
Agar har bir (ak, ak+l) da (к = 0,1,2,..., n -1) f (x) funksiya dif-
ferensiallanuvchi bo‘lib, x = ak nuqtalarda chekli o‘ng
f'(ak+&), (£ = 0,l,2,...,n-l)
va chap
196
f'(ak-O), (к = 0,1>2’'"’^
, .. . , .. . c , . r t>] da bo‘lakli differensial-
hosilalarga ega bo Isa, f (x) funksiya [a<
lanuvchi deyiladi. . M oraUqda Wlakli diffe-
2- teorema. 2л davrh/(x) funksiya F1]rve n„torj
rensiallanuvchi bo‘Isa, u holda bu funksi’ S ГУ 4
/(xb^ + Y^coskx^8^
£=i
[-л, л] da yaqinlashuvchi bo‘lib, uning yi^
/(x+0)+/(x-0)
2
:ja teng bo'ladi.
< (5) tenglikning har ikki tomonini
j[/ (x + 0) + /(x/0^
ga ko‘paytirib, ushbu
Гя(/;х)-1[/(х + 0) + /(х"°И
ayirmani quyidagicha
F.(/;*)-l[/(x + o)+/(x 0)]
• ( и
sin и+- h
1 "г г f ( ч r ( x r ( nx / f (x - 0)1 —*-du
J[/(x + u) + /(x-w)-/(x + 0H J 2sin-
o 2
x .... z>‘ ng tomonidagi integralni
ко nmshda yozib olamiz. Bu tenglikning c
ikkita
197i
integralga ajratamiz. Natijada
^(/;x)-|[/(x + o)+/(x-o)] = j1+j2
bo‘ladi. i
Endi J\ va J2 integrallarni baholaymiz. integralni baholash
uchun awalo ixtiyoriy 8 (0 < 8 < л) sonni olib, ni ikki qismga
ajratib yozamiz:
8
И
0
sin n+- и
1 2 "^4-
2sin^
2
(
л sm n+~ и
У [/ (x + u) - f (x + 0)] —L_J_ du.
8 2 sin-
(8)
Lokallashtirish prinsipiga asosan
8
Demak, Ve > 0, 3«q = я(г,8)е N, da
( и
it sin n+— и
^[/(х + и)-/(х + 0)]-^^-с1и
8 2 sin-
(9)
bo‘ladi. Shartga ko‘ra, /(x) funksiya [-тс, л] da bo‘lakli differen-
siallanuvchi. U holda Vx e [-л, л] da
/(x+o)
u->+0 U V '
mavjud bo‘lib, 33j > 0, 0 < и < 8j da
= сом)
198
tengsizlik o'rinli bo'ladi. Shuningdek, 3S2 > 0, 0 < и < §2 da
u
—< M2, (M2 = const)
sin-
2
tengsizlik bajariladi.
Endi min<5i,82, >=5 deb olamiz. Natijada, V«g
bo'lganda (8) tenglikning o'ng tomonidagi birinchi integral uchun
ushbu
7t J
0 L
U
2 - I 1 \ '
sin in + - udu <
. и \ 2
sm- ' '
2
и
J^du<-M,M28<^-
. U 7t 1 2 2
J sm-
2
bahoga ega bo'lamiz. (8), (9) va (10) munosabatlardan
(10)
)71l= У[/(х + и)-/(х + 0)]
0
• ( И
sin n+~ ki
I 2 Г ,
—v-----'du
- . и
2sm~
2
bo'lishi kelib chiqadi.
J2 integral ham xuddi shunga o'xshash baholanadi va
du
, . и
2 sin
2
5 Г
7t J
0 L
0
u
u
bo'lishi topiladi. Demak,
Fn (/; x)-|[/(x + 0) + /(x-0)]| < 2e
bo'lib, undan
199
lim Fn (/; x) = | [f (x + 0) + f (x - 0)]
bo‘lishi kelib chiqadi. Bu esa f(x) funksiya Furye qatorining yaqinla-
shuvchi va
~ + V (ak cos Ax + bk sin Ax) = |[/(x + 0) + f (x -0)]
2 £i 1 2
bo‘lishini bildiradi. ►
Natija. Agar/funksiya yuqoridagi teoremaning shartlarini bajarib,
x nuqtada uzluksiz bo‘lsa, u holda quyidagi natijaga ega bo'lamiz:
po
5+ cosAx + bk sin Ax) =/(x).
£=1
Misol. Ushbu
/(x) = cosox, (-л < x < n, atnsZ)
funksiyaning Furye qatori topilsin va uni yaqinlashishga tekshirilsin.
◄ Bu funksiyaning Furye koefiitsiyentlarini topamiz. Qaralayotgan
funksiya juft bodgani uchun
bn=0, (n = 1,2,3....)
bo‘lib,
п я
an = ~ j cos ax cos nxdx = j [cos (о - и) x + cos (a + ri) x] dx -
71 о о
= +_L'
n ]_a+n a-n
bo'ladi. Demak,
f{x)
sin ал 1 v ( i \n ( 1 1 \
------ -+> (-1) ----------+------ cos их
л a " \a+n a-n
n=l
Agar /(x) = cos ax funksiya teoremaning hamda natijaning shart-
larini bajarishini e’tiborga olsak, u holda
sin an
cos ax =------------
71
a "
«=1
1 1 j
----+----- COS ИХ
a+n a~nl
bo‘lishini topamiz. ►
200
Keyingi tenglikda x = 0 deyilsa,
-JL_ = l + t(-i)"CL + _l_
sin ал a “ \a+n a-n
И=1
bo‘lishi kelib chiqadi.
(ID
Mashqlar
1. Ushbu
-x, agar - n < x < 0 bo‘lsa,
0 , agar 0 < x < л bo‘lsa
funksiyaning Furye qatori topilsin va uni yaqinlashishga tekshirilsin-
2. Ushbu
/(x) = -ln sin - ,
(x * 2kn, к e Z)
funksiyaning Furye qatori topilsin va uni yaqinlashishga tekshirilsin.
201
15- В О В
PARAMETRGA BOG'LIQ INTEGRALLAR
74-ma’ruza
Ikki o‘zgaruvchili funksiyaning bir o‘zgaruvchisi
bo‘yicha yaqinlashishi
1°. Limit funksiya. Faraz qilaylik, f (x,y) funksiya R2 fazodagi
M - {(x,y) g R2 : a < x < b, у e. E c R}
to'plamda berilgan va y0 e R nuqta Eto'plamning limit nuqtasi bo'lsin.
Ravshanki, har bir tayin x g [a, b] da f (x,y) funksiya у o'zga-
ruvchining funksiyasiga aylanadi. Aytaylik, bu funksiya x g [a, A] da
lim /(x,y)
limitga ega bo'lsin.
Har bir x g [a, b] gaf (x,y) funksiyaning у -> y0 dagi limitini mos
qo'yish natijasida
Ф : x -» lim f (x,y)
У-*Уо
funksiya hosil bo'ladi.
Odatda, bu funksiya f (x,y) funksiyaning у -> y0 dagi limitfunksiyasi
deyiladi:
lim/(x,y) = ф(х), (x6[a,Z>]). (1)
y-O-O
(1) munosabat quyidagicha tushuniladi: Ve > 0 son olinganda
ham shunday 5 = 8(e,x) > 0 son topiladiki, bunda 0 < |y - yoj < 3
tengsizlikni qanoatlantiruvchi Vy e E uchun
|/(x,y)-cp(x)| < £, (xG[a,&])
bo'ladi.
Endi f (x,y) funksiya
M = {(x,y) e R2; x g [a,Z>], у g £ c 7?}
to'plamda berilgan va °° «nuqta» E to'plamning limit nuqtasi bo'lsin.
202
Agar Ve > 0 son olinganda ham shunday 8 = 8 (e, x) > 0 son
topilsaki, |y| > 3 tengsizlikni qanoatlantiruvchi Vy e E uchun
|/(х,у)-ф(х)| < £
tengsizlik bajarilsa, cp(x) funksiya f (x,y) ning у °° dagi limit funksiyasi
deyiladi.
1- misol. Ushbu /(x,y) = xy funksiyani
M = {(x,y)e R2 : 0 < x < 1, ye [0,1]}
to‘plamda qaraylik. Bu funksiyaning у -> y0 = 1 dagi limit funk-
siyasi <p(x) = x bo‘lishi ko‘rsatilsin.
•< Ixtiyoriy e > 0 songa ko‘ra, har bir x e [0,1] uchun 8 = e deb
olinsa, u holda |y - y0| - |y -1| < 3 tengsizlikni qanoatlantiruvchi
ye [0,1] uchun
|/(x, y) - <p(x)| = |xy - x| = |x| |y - 1| < |y -1| < 8 = E
bo'ladi. Demak,
lim xy = x . ►
2- misol. Ushbu f (x, y) - xy, (0° = 0) funksiyani
M = {(x,y)e R2 : 0 < x < 1, ye [0,1]}
to'plamda qaraymiz. Bu funksiyaning у -> y0 =0 dagi limit funk-
siyasi topilsin.
◄ Aytaylik, x = 0 bo‘lsin. Bu holda Vy e [0,1] uchun
/(0,y) = 0
bo‘lib, у -> 0 da /(0,y) -» 0 bo‘ladi.
Aytaylik, x 0 bo‘lsin. Bu holda у -> 0 da
/(x,y) = x* x° =1
bo‘ladi. Haqiqatan ham, ixtiyoriy e > 0 songa ko‘ra 8 = logx (1 - e)
deyilsa (x > 0), u holda |y - y01 = |y - 0| = jy| «с 8 tengsizlikni qanoat-
lantiruvchi ye [0,1] uchun
|/(x,y) - <p(x)| = p -1| = 1 - xy < 1 - xlofo(1“e) = 1 - (1 - e) = E
bo‘ladi. Demak, у -> 0 da f (x, y) = xy funksiyaning limit funksiyasi
203
ф(х) = <
1, agar x 6 (0,1] bo‘lsa,
О, agar x - 0 bo‘lsa
bo‘ladi. ►
2°. Limit funksiyaga tekis yaqinlashish. Faraz qilaylik, f(x,y)
funksiya
M = {(x,y)e R2 : a < x < b, yeEcR}
to‘plamda berilgan bo‘lib, y0 g R nuqta E to‘plamning limit nuqtasi
bo‘lsin. Bu funksiya har bir tayinlangan x g [a,b\ da у o‘zgaravchining
funksiyasi sifatida у -> y0 da limit funksiyaga ega bo‘lsin:
lim /(x,y) = <p(x).
f (x,y) funksiyaning cp(x) ga intilish xarakteri olingan x ga bog‘liq,
chunki x ning turli qiymatlarida f (x,y) funksiya, umuman aytganda,
у o'zgaruvchining turlicha funksiyalari bo‘ladi. Bu vaziyat
lim f(x,y) = <p(x), (xg[u,Z>])
У->Уо
tushunchasidagi ixtiyoriy £ > 0 songa ko‘ra topiladigan 8 > 0 sonning
qaralayotgan x ga bog'liq yoki bog'liq emasligida namoyon bo‘ladi.
Yuqorida keltirilgan misollaming birinchisida 8 = e bo'lib, u faqat
£ > 0 gagina bog'liq, ikkinchisida esa 8 - logx (1 - e) bo'lib, u olingan
e > 0 bilan birga qaralayotgan x ga ham bog!liq ekanini ko‘ramiz.
1- ta’rif. Agar Ve > 0 son olinganda ham shunday 8 = 8(e) > 0
son topilsaki, (y-y0|<8 tengsizlikni qanoatlantiruvchi ye E,
Vxe [a, Z>] uchun
j/(x,y)-<p(x)| <E
tengsizlik bajarilsa, ya’ni
Ve >0, 38 = 8(e) > 0, |y - y01 < 8, у g E,
Vxg [«,&]: |/(x,y) — <p(x)| < e
bo‘lsa, f(x,y) funksiya <p(x) ga [a,Z>] da tekis yaqinlashadi deyiladi.
3-misol. Ushbu /(x,y) = xsiny funksiyani
M = {(x,y) g R2: 0 < x < 1, уб[0,л]}
204
to'plamda qaraylik. Bu funksiyaning у y0 = ~ da limit funksiyasi
topilib, unga [0, 1] da tekis yaqinlashishi ko'rsatilsin.
◄ Ravshanki,
r • V3
lim x sm у = — x.
л 2
y^>-
Demak,
z x V3
<p(x) = — x.
I7C
у - J
< 5 tengsiz-
likni qanoatlantiruvchi ye [0,n] va Vxe [0,1] uchun
|/(*,У)-ф(х)|
- x sin у -
II* • Лг 7Г q
- |x| sm у - sm - < у - j < о = e
bo'ladi. Ta’rifga binoan, у-> j da /(x,y) = xsiny funksiya
J3
<p(x) =-x limit funksiyaga [0,1] da tekis yaqinlashadi. ►
E s 1 a t m a. Aytaylik, lim /(x, у) = <p(x) bo'lsin.
Agar V8 > 0 son olinganda shunday e0 >0, x0 e [a, Z>] va
|y - y0) < 5 tengsizlikni qanoatlantiruvchi y} e E topilsaki, bunda
|/OWi)-~<p(*o)|-eo
bo'lsa, f (x,y) funksiya у -> y0 da limit funksiya cp(x) ga tekis yaqin-
lashmaydi deyiladi. Masalan,
/(x,y) = x\ (0° =0)
funksiya у 0 da limit funksiya
1, agar xe(0,l] bo'lsa,
0, agar x = 0 bo'lsa
<p(x) = -
205 I
ga tekis yaqinlashmaydi. Haqiqatan ham, V3 > 0 son olinganda,
_±
e0 - 1, 0 < V] < 5 tengsizlikni qanoatlantiruvchi y{ va x0 = 2 n
deb olinsa, u holda
|/(^о,У1)-ф(хо)| = 1-^о‘ =1-J = |>eo
bo‘ladi. Faraz qilaylik, f (x,y) funksiya R2 fazodagi
M - {(x,y)e R2 : a < x < b, у e E c R}
to‘plamda berilgan va y0 g R nuqta Eto‘plamning limit nuqtasi bo‘lsin.
Agar E to‘plam y() ga intiluvchi {y„} ketma-ketlikdan iborat bo‘lsa,
f (x,y) funksiyani [a, b] da aniqlangan
/„(x) = /(x,y„)
funksional ketma-ketlik sifatida qarash mumkin. Masalan,
funksiyani Mo = {(x,y)G R2 : xe [0,1], yeE = {l,j,|,„.}| to‘p-
lamda qarasak, u quyidagi
г ! ч 2хи
AW = -ГТ
l+и xz
funksional ketma-ketlikka aylanadi.
1- teorema. Agar у -> y0 da/(x,y) funksiya <p(x) ga [a,b] da tekis
yaqinlashsa, u holda E to'plamdagi y0 ga intiluvchi har bir {>’„} ketma-
ketlikda (y„ с E)
/„ (x) = /(x,y„)
funksional ketma-ketlik ham \a,b\ da cp(x) ga tekis yaqinlashadi.
◄ Aytaylik, f(x,y) funksiya у -> y0 da <p(x) funksiyaga [a,b] da
tekis yaqinlashsin. U holda ta’rifga binoan Ve >0, 38 = 8(e) > 0,
0<|y-y0|<8 tengsizlikni qanoatlantiruvchi ixtiyoriy у g E,
Vxg [«,/>]: |/(x,y) - <p(x)| < e bo‘ladi.
206
Modomiki, {y„} ketma-ketlik y0 ga intilar ekan,
V8 > 0, Bn0 e N, V« > n0: |y„ -y0| < 3
tengsizlik bajariladi. Demak,
Ve>0,33>0, |y„ - yoj < 8,y„6 E, Vxe [«,/>]: |/(x,y„)-ф(х)| < s,
ya’ni,
|/„(х)-ф(х)| <S
bo‘ladi. Bu esa fn(x) funksional ketma-ketlikning [a,b\ da <p(x) funk-
siyaga tekis yaqinlashishini bildiradi. ►
Endi f(x,y) funksiyaning limit funksiyaga ega bo‘lish va unga
tekis yaqinlashishi haqidagi teoremani keltiramiz.
2- teorema. f (x,y) funksiya у —> y0 da limit funksiya <p(x) ga ega
bo‘lishi va unga tekis yaqinlashishi uchun Ve > 0 olinganda ham x ga
bog‘liq bo‘lmagan shunday 38 = 8(e) > 0 topilib, jy - y01 < 8 ,
|y' -y0|<8 tengsizliklarni qanoatlantiruvchi ixtiyoriy у, у'e E
hamda Vx e [a, b] da
!/(^,y)-/(x,y')| < e (2)
tengsizlikning bajarilishi zarar va yetarli.
◄ Zarurligi. Aytaylik, f (x,y) funksiya у -> y0 da limit funksiya
<p(x) ga [a,b\ da tekis yaqinlashsin. U holda ta’rifga binoan
Ve > 0, 38 > 0, |y - y01 < 8, Vy e E,
Vxe [a,b\: |/(х,у)-ф(х)| < j , (3)
jumladan, |y' - y0| < 8, у' e E uchun ham
|/(х,у')-ф(х)| < | (4)
bo'ladi. (3) va (4) munosabatlardan
|/(^,y)-/(x,y')| < £
bo‘lishi kelib chiqadi.
Yetarliligi. Aytaylik, (2) shart bajarilsin. Modomiki, har bir tayin-
langan Vx e [a, va |y - y01 < 8, |y' - y01 < 8 , у e E, у’ e E da
207
ga tekis yaqinlashmaydi. Haqiqatan ham, V3 > 0 son olinganda,
2.
e0 = 1, 0 < y} < 5 tengsizlikni qanoatlantiruvchi уг va x0 = 2 z
deb olinsa, u holda
=i-| = ^>e0
bo‘ladi. Faraz qilaylik, f (x,y) funksiya R2 fazodagi
M = {(x,y)e R2 : a < x < b, у g E c R}
to'plamda berilgan va y0 g R nuqta Eto'plamning limit nuqtasi bo'lsin.
Agar Eto'plam y0 ga intiluvchi {y„} ketma-ketlikdan iborat bo'lsa,
f (x,y) funksiyani [a, b\ da aniqlangan
Л(*) = /(*>л)
funksional ketma-ketlik sifatida qarash mumkin. Masalan,
funksiyani Mo =|(x,y)e R2 : xg [0,1], у e E = jj to'p-
lamda qarasak, u quyidagi .
=
2xn
l+n2x2
funksional ketma-ketlikka aylanadi.
1- teorema. Agar у -> уй da/(x,y) funksiya <p(x) ga [<2,Z>] da tekis
yaqinlashsa, u holda E to'plamdagi y0 ga intiluvchi har bir {yn} ketma-
ketlikda (y„ с E)
f„(x) = f(x,y„)
funksional ketma-ketlik ham [a,b] da cp(x) ga tekis yaqinlashadi.
◄ Aytaylik, f(x,y) funksiya у y0 da ф(х) funksiyaga [a,b] da
tekis yaqinlashsin. U holda ta’rifga binoan Ve >0, 38 = 8(e) > 0,
0<|y-y0|<8 tengsizlikni qanoatlantiruvchi ixtiyoriy ye E,
Vxg[c,Z>]: |/(x,y)--<p(x)| < e bo'ladi.
206
Modomiki, {y„} ketma-ketlik y0 ga intilar ekan,
V8 > 0, Зл0 e N, \/n > n(j: |y„ - y01 < 3
tengsizlik bajariladi. Demak,
Ve>0,38>0, \y„ -y0| < 8,yne E, Vxe [«,&]: |/(x,y„)-ф(х)| < e,
ya’ni,
|Л(*)-Ф(*)| < e
bo‘ladi. Bu esa/„(x) funksional ketma-ketlikning [a,b] da <p(x) funk-
siyaga tekis yaqinlashishini bildiradi. ►
Endi f{x,y) funksiyaning limit funksiyaga ega bo‘lish va unga
tekis yaqinlashishi haqidagi teoremani keltiramiz.
2- teorema. f(x,y) funksiya у -> y0 da limit funksiya <p(x) ga ega
bo‘lishi va unga tekis yaqinlashishi uchun Ve > 0 olinganda ham x ga
bog‘liq bo‘lmagan shunday 38 = 8(e) > 0 topilib, |у-Уо|<3,
|у'-Уо|<3 tengsizliklarni qanoatlantiruvchi ixtiyoriy у, у'e E
hamda Vx e \a, da
\f(x,y)-f(x,y')\ < e (2)
tengsizlikning bajarilishi zarur va yetarli.
◄ Zarurligi. Aytaylik, f (x,y) funksiya у -» y0 da limit funksiya
ф(х) ga [a,b] da tekis yaqinlashsin. U holda ta’rifga binoan
Ve > 0, 38 > 0, jy - 1 < 3, Vy e E,
Vx 6 [a, b]: |/(x, у) - <p(x)| < |, (3)
jumladan, |y' - y0| < 8, у’ e E uchun ham
|/(x,y')-(p(x)| < j (4)
bo‘ladi. (3) va (4) munosabatlardan
|/(*,y)-/(*,/)) <e
bo‘lishi kelib chiqadi.
Yetarliligi. Aytaylik, (2) shart bajarilsin. Modomiki, har bir tayin-
langan Vxe [a,Z>] va |y -y0| < 8, |y'-y0| < 8, ye E, y'e E da
207
\f(x,y)-f(x,y')\<E.
tengsizlik bajarilar ekan, u holda Koshi teoremasiga ko‘ra у -> y0 da
/(x,y) funksiya limitga ega bo‘ladi. Uni <p(x) bilan belgilaylik:
lim /(x,y) = <p(x).
Endi у o'zgaruvchining |y'-y0|<6 tengsizlikni qanoatlantira-
digan qiymatida (2) tengsizlikda у' -» y0 da limitga o‘tib topamiz:
|/(x,y) - cp(x)| < e .
Bu esa у -> yQ da f(x,y) funksiyaning <p(x) ga [a,b] da tekis
yaqinlashishini bildiradi. ►
3- teorema. f (x,y) funksiya uchun quyidagi shartlar bajarilsin:
1) har bir tayin у e E da f(x,y) funksiya [a,b] da x o'zgaruv-
chining funksiyasi sifatida uzluksiz;
2) y-> y0 da f(x,y) funksiya ]a,b] da <p(x) ga tekis yaqinlashsin.
U holda cp(x) funksiya [a,b] da uzluksiz bo‘ladi.
4 E to‘plamda y0 ga intiluvchi ixtiyoriy {y„} ketma-ketlik olib
(y„ e E, n = 1,2,..., yn -> y0) [a,b] segmentda aniqlangan ushbu
/„(x) = /(x,y„)
funksional ketma-ketlikni hosil qilamiz. Teoremaning shartlariga ko‘ra:
1)/„(*) funksional ketma-ketlikning har bir hadi [c,Z>] da uzluksiz
boTadi;
2) mazkur ma’ruzadagi 2- teoremaga binoan у -> y0 da fn(x)
funksional ketma-ketlik <p(x) funksiyaga [a,b] da tekis yaqinlashadi.
U holda <p(x) funksiya [a,Z>] segmentda uzluksiz bo‘ladi (qaralsin,
65- ma’ruza). ►
Mashqlar
1. Ushbu f(x,y) = n
funksiyani M ={(x,m)g jR1 2: xe (0,<*>), ne N} to'plamda qarab,
uning n -> oo dagi limit funksiyasi topilsin.
208
2. Ushbu
I 1 \ 1
f(x,y) = Ml -xy/xy
funksiyani M =](x,y)e RI 2 : xg
|,1 , ye (0,1 И to'plamda qa-
rang. Bu funksiya uchun quyidagi tenglik o'rinli bo'lishi isbotlansin:
lim f (x, y) = 0.
3. Aytaylik, f(x,y) funksiya
M = |(x,y)e R2 : xe[a,b], yeEcRj
to'plamda berilgan va yD e R esa E ning limit nuqtasi bo'lsin. у -> y(t da
f (x,y) funksiyaning cp(x) ga [a,b] da tekis yaqinlashishi uchun E to'p-
lamdagi y0 ga intiluvchi ixtiyoriy {yn} ketma-ketlikda
fn(x) = f(x,y„)
funksional ketma-ketlikning [a,b] da cp(x) ga tekis yaqinlashishi zarur
va yetarli ekani isbotlansin.
75-ma’ruza
Parametrga bog'liq integrallar
Iе. Parametrga bog'liq integral tushunchasi. Aytaylik, f(x,y)
funksiya
M = {(x,y) e R2 : a < x < b, у e E a R]
to'plamda berilgan bo'lsin. Bu funksiya har bir tayinlangan yeE da
x o'zgaruvchining funksiyasi sifatida \a,b\ da integrallanuvchi, ya’ni
b
\f{x,y)dx
a
mavjud deylik. Qaralayotgan integrating qiymati tayinlangan у ga
bog'liq bo'ladi:
b
J(.y) = J f(x,y)dx. (1)
a
209 !
Masalan, у * 0 bo Uganda
о
eyxdx = —
еу
У
у о
у = 0 bo Uganda
1
J e)xdx = 1
о
boUadi. Demak,
/(>) =/ль-fy1’ agar b0‘lsa’
о [ 1, agar у = 0 boUsa.
Odatda, (1) integral parametrga bogUiq integral, у esa parametr
deyiladi.
Ravshanki, J(y) funksiya (parametrga bogUiq integral) berilgan
f(x,y) funksiya orqali aniqlanib, unga bogUiq boUadi.
Parametrga bogUiq integral mavzusida f (x,y) funksiyaning funk-
sional xossalariga ko‘ra J(y) funksiyaning funksional xossalari (limiti,
uzluksizligi, differensiallanuvchanligi, integrallanuvchanligi) o‘rganiladi.
2°. J(y) funksiyaning limiti. Aytaylik, f(x,y) funksiya
M = {(x,y)e R2 : a < x < b, у e E c R}
to‘plamda berilgan boUib, yatR esa E to‘plamning limit nuqtasi
boUsin. Bu funksiya uchun har bir tayin у g E da
b
J(y) = ^f(x,y)dx
a
mavjud boUsin.
1- teorema. Faraz qilaylik, f (x,y) funksiya quyidagi shartlami
bajarsin:
1) har bir tayin ye £ da f(x,y) funksiya x o‘zgaruvchining
funksiyasi sifatida [a,b\ da uzluksiz;
2) У y0 da f (x,y) funksiya limit funksiya cp(x) ga [a,b\ da tekis
yaqinlashsin.
210
U holda у -> у0 da Ду) funksiya limitga ega bo‘lib,
lim /(у) - ср(х)б/х
У~>Уо J
(2)
bo'ladi.
◄ Keltirilgan teorema shartlarining bajarilishidan, 74- ma’ruzadagi
3- teoremaga ko‘ra, limit funksiya <p(x) ning \a,b\ da uzluksiz bo‘lishi
kelib chiqadi. Demak,
integral mavjud.
Ayni paytda, у -> y0 da/(x,y) funksiyaning [a,b] da <p(x) funksiyaga
tekis yaqinlashuvchi bo‘lishidan, ta’rifga binoan,
Ve > 0, 38 > 0, |y-y0| < 8, Vy e E, Ухе [a,b]: [/(x,y)- <p(x)| <
bodishini topamiz. Ushbu
ь
ayirmani qaraylik.
Ravshanki, |y - y01 < 8 tengsizlikni qanoatlantiruvchi ixtiyoriy
у e E uchun
b h b
J(y)- \q(x)dx = | f(x,y)dx - Гcp(x)Jx <
< Г1/(х,у) - ф(х)|/х < f dx = e
b-a J
bo‘ladi. Keyingi munosabatdan
lim J (y) =
bo‘lishi kelib chiqadi. ►
211
(2) munosabatni quyidagicha
lim f f (x,y)dx = f lim f(x,y) dx
ko‘rinishda ham yozish mumkin. Bu integral belgisi ostida limitga
o‘tish qoidasini ifodalaydi.
3°. J(y) funksiyaning uzluksizligi. J(y) funksiyaning uzluksizligini
quyidagi teorema ifodalaydi.
2- teorema. Agar f (x,y) funksiya
Мй = {(x,y)G R2 : a < x < b, с < у < d]
to'plamda uzluksiz bo'lsa, J(y) funksiya [c,d] da uzluksiz bo'ladi.
◄ Ixtiyoriy y0 g [c,d] va y0 + Ay g [c,d] nuqtalarni olib, J(y)
funksiyaning orttirmasini topamiz:
AJ (y0) = J(y0 + Ay)-J(y0) = J[/(x,y0 + Ау)-/(^Уо)]^-
f (x,y) funksiya M(t to'plamda tekis uzluksiz. Unda Ve > 0 uchun
shunday 8 > 0 topiladiki, |Ay| < 3 bo'lganda, Vxe [a,b] uchun
|/(x,y0 + Ay)-/(x,y0)| < 8
bo'ladi. Demak, |Ду| < 8 bo'lganda
b
|A/ (Уо)| = J[/(x>Уо + Ay) - f (*>Уо)]dx < e(/> - a)
bo'ladi. Keyingi munosabatdan
lim Д/ (y0) = 0
bo'lishi kelib chiqadi. Bu esa J(y) funksiyaning ixtiyoriy y0 nuqtada,
binobarin, [c,d\ da uzluksiz bo'lishini bildiradi.
4°. J(y) funksiyani differensiallash. Aytaylik, f(x,y) funksiya Mo
to'plamda berilgan bo'lsin.
3- teorema. Faraz qilaylik, f (x,y) funksiya quyidagi shartlami
bajarsin:
212
1) har bir tayin у e [c, d} da f(x,y) funksiya [a,b] da x o‘zga-
ruvchining funksiyasi sifatida uzluksiz;
2) f (x,y) funksiya Mo to'plamda f' (x, у) xususiy hosilaga ega va
fy'(x,y) funksiya Mo da uzluksiz.
U holda J(y) funksiya [c, d] da hosilaga ega va
b
J\y) = \fy{x,y)dx (3)
a
bo‘ladi.
◄ у g [c, d], у + Ду g [c, d] nuqtalarni olib, topamiz:
J(y+Ay)-/(y) = Г f{x,y+\y)-f{x,y)
Ay J Ay
a
Lagranj teoremasiga ko‘ra
(0<e<1)
bo‘lib,
J (y+S^~J (y>> = \ f'(x,у + QAy)dx, (0 < 0 < 1) (4)
a
bo‘ladi.
fy (x,y) funksiya Mo to‘plamda tekis uzluksiz bo'lganligi sababli
Ve > 0, 38 > 0, |Ay | < 8, Vx g [a, Z>]: \ fy (x,y + 0Ay) - // (x,y)| <
tengsizlik bajariladi. (4) munosobatdan foydalanib
b b
y+x~y ~ i(*’у)dx - jу+ед^) ~ dx <e
a a
bo‘lishini topamiz. Demak,
lim _ f f' (x,y)dx .
A.y-^0 Ay J jy v
a
b
Bii esa /'(y) = J f' (x,y)dx ekanini bildiradi. ►
i
213 1
(3) munosabatni quyidagicha
ь b
-rT-\f^x^y)dx =
ay j j ay
a a
ko‘rinishda ham yozish mumkin. Bu differensiallash amalini integral
belgisi ostiga o'tkazish qoidasini ifodalaydi.
5°. J(y) funksiyani integrallash. Faraz qilaylik, f (x,y) funksiya
Mq to‘plamda berilgan va uzluksiz bo'lsin. U holda 2- teoremaga ko‘ra
b
J (y) = \f (x,y)dx
a
funksiya [c,d\ da uzluksiz bo‘ladi. Binobarin, bu funksiya [c,d] da
integrallanuvchi, ya’ni
d
\j(y)dy
c
mavjud bo‘ladi.
4- teorema. Agar f (x,y) funksiya Mo to'plamda uzluksiz bo'lsa, u
holda quyidagi ifoda o'rinli bo‘ladi:
◄ Vie [c,d] nuqtani olib, ushbu
funksiyalarni qaraymiz. Ravshanki,
b
= ^f(x,t)dx,
a
214
b
Demak, F'(t') = Ф'(0 = J f (x, t) dx
a
bo'lib, uiidan
F(t) = Ф(0 + C, (C = const)
bo'lishi kelib chiqadi. Agar t = c deyilsa,
F(c) = Ф(с) = 0
bo'ladi va keyingi tenglikdan C = 0 bo'lishini topamiz. Demak,
F(t) = <D(t).
Xususan, t = d bo'lganda Fid) = Ф(d) bo'lib,
bo'ladi. ►
Mashqlar
1. Ushbu
"""? ( 1 \ 1
/(x,y) = Ц1-ху/х^
funksiyani
x,y) e R2 : x e
1 je (0,1
to'plamda qaraylik. Bu funksiya uchun
1 1 / x
lim j f (x, y) dx * lim f (x, y)
-v~] -{v-»+o )
2 2
bo'lishi isbotlansin.
2. Agar f (x) funksiya [0,1] segmentda uzluksiz hosilaga ega bo'lsa,
i
J(y) = j f(x)sign sin (xy)dx,
о
(y>0)
funksiyaning hosilasi topilsin.
215
3. Agar /0(у) = - [cos(y cosx)r&, (ye/?)
7C J
0
bo‘Isa. u quyidagi y./f'(y) + /o'(y) + уЛ>(у) = 0 tenglamani qanoat-
lantirishi ko‘rsatilsin.
76- ma’ruza
Chegaralari o‘zgaruvchi parametrga bog‘Iiq integrallar
Faraz qilaylik, f (x,y) funksiya
Л/о = {(x,y)e R2 : a < x < b, с < у < d]
to'plamda berilgan va har bir tayin da f(x,y) funksiya
x o'zgaruvchining funksiyasi sifatida [a,b] da integrallanuvchi bo'lsin.
a(y) va p(y) fiinksiyalaming har bin [c,d\ da berilgan va Vy e [c, o'] uchun
a < a (y) < P(y) < b (1)
tengsizliklar bajarilsin. Ushbu
₽d)
J /(x,y)dx
a(y)
integral, ravshanki, у o‘zgaruvchiga bog‘liq bo‘ladi:
Pd)
J f(x,y)dx. (2)
ad)
2) integral chegaralari ham parametrga bog‘liq integral deyiladi.
Г. Ji(y) funksiyaning uzluksizligi. /j(y) funksiyaning uzluksizligini
quyidagi teorema ifodalaydi.
1- teorema. Faraz qilaylik, f(x,y) funksiya Mo to‘plamda uzluksiz
bo‘lib, a(y) va p(y) funksiyalar esa [c,d] segmentda uzluksiz bo‘lsin.
U holda
₽(y)
Л(У)= j f(x,y)dx
ad)
funksiya [c,d\ da uzluksiz bo‘ladi.
216
◄ Ixtiyoriy y0 G 1C>^1 nuqtani olaylik. Integralning ma’lum xossa-
laridan foydalanib topamiz:
₽(y) Фо) Фо)
Л(у) = j f(x,y)dx = J f(x,y)dx + j f(x,y)dx +
Ф) Ф) фо)
Ф) Фо) ф) Ф)
+ j f{x,y)dx- J f(x,y)dx + J f(x,y)dx- j f(x,y)dx. (3)
фо) Фо) фо) фо)
Фо)
Ravshanki, j f(x,y)dx
Фо)
integral chegarasi o‘zgarmas bo'lgan parametrga bog‘liq integral. Bu
funksiya 75- ma’ruzada keltirilgan 2- teoremaga muvofiq у o‘zgaruv-
chining uzluksiz funksiyasi bo‘ladi. Demak,
POo) фо)
У~*Уоаа j f{x,y)dx-^ j f (x, y0) dx = J} (y0) (4)
Фо) Фо)
bo‘ladi.
f (x,y) funksiya Mo to‘plamda uzluksiz bo‘lganligi sababli у shu
to‘plamda chegaralangan bo'ladi:
|/(x,y)|<C, (C = const).
Shartga ko‘ra a(y) va P(y) funksiyalar segmentda uzluksiz.
Demak:
У -^Уо da a(y)^a(y0),
У ^Уо da р(у)^р(уо)-
Endi
Ф)
j f(x,y)dx
фо)
<Clp(y)-₽(y0)|,
<Ф)
фо)
/(x,y)dr
< С|а(у)-а(у0)|
217
munosabatlardan
₽(Я ₽(/)
У -> y0 da j f(x,y)dx^0, у y0 da j f (х,у)фс0
₽(№) <x(y0) i
bo'lishini topamiz.
(3) tenglikda, у -> y0 da limitga o'tish va unda (4) va (5) muno-
sabatlarni hisobga olish natijasida
У -> Уо da J, (y) -> (y0)
bo'lishi kelib chiqadi. Demak, Jj(y) funksiya [c,d\ da uzluksiz. ►
2°. /](y) funksiyani differensiallash. Faraz qilaylik, f (x,y) funksiya
Мй = {(x,y) e R2 : a < x < b, с < у < d}
to'plamda, a(y) va P(y) funksiyalar esa [c,d] segmentda berilgan bo'-
lib, a(y), P(y) funksiyalar (1) shartni bajarsin, ya’ni Vy e [c,d] uchun
a < a(y) < p(y) < b
bo'lsin.
2-teorema. Aytaylik, f(x,y), a(y) va p(y) funksiyalar quyidagi
shartlarni bajarsin:
1) f(x,y) funksiya Mo to'plamda uzluksiz;
2) f(x,y) funksiya Mo to'plamda uzluksiz f' (x.y) xususiy hosi-
laga ega;
3) a(y) va P(y) funksiyalar [c,d] da a'(y) va p'(y) hosilalarga ega.
U holda
₽(Я
J f(x,y)dx
«(j')
funksiya [c,d] segmentda //(y) hosilaga ega bo'lib,
₽(y)
Л'(у)= J fy {x,y)dx + P'(y)/(P(y),y)-a'(y) /(a(y),y)
a(.y)
bo'ladi.
◄ y0 g [c,d], y0 + Aye [c,d] nuqtalami olib, topamiz:
218 •
/^^oWW^jb) = x
\y Ay
P(j'oW)
а(м+Ду)
/(x,y0 + by)dx-
РЬо)
J f(x,yQ)dx
«(№)
Agar
₽(уо+Ду) ₽(Уо)
j f(x,y0 + Ay)dx = j f(x,y0 + Ay)dx +
а(у0+Ду) а(Уо)
РО'о+АУ) а(у0+Ду)
+ j f(x,y0+^y)dx- j f(x,y0+by)dx
POo) “CM
bo‘lishini e’tiborga olsak, u holda
Ш+Ау)-Ш)
— i-------4/л -f-
АУ------------------------------J s АУ
“(Уо)
₽(л +Ду) «bo +лу)
+ - f /(х>.Уо + [ / (х, у0 + Ду) cfx (6)
J /\у J
Р(уо ) «О'»)
bo‘lishi kelib chiqadi. 75- ma’ruzadagi 1- teoremaga ko‘ra
д>->0 J Ay
“(Л) . 0
г [/(x,y0+Ay)-/(x,y0)j с .
= hm t-----------------------±dx= f (х,у0)dx
J Aj'-^O Ay J
<x(M)) “(Го)
bo‘ladi. 0‘ rta qiymat haqidagi teoremadan foydalanib, topamiz:
Р(уо +Ay)
J /(х,Уо +Ay)dx = f(x',y0 + Ду)[р(у0 +Ду)~Р(у))],
Р(Уо)
а(уо+Ду)
J /(х,У() + Ау)<7х =/(х’,у0+Лу)[а(у0+Лу)-а(у0)].
. а(л)
219
Bunda x' nuqta p(y0), Р(Уо + ду) nuqtalar orasida, x" esa
a(y0), а(Уо + ду) nuqtalar orasida joylashgan. у -> ya da limitga
o'tishi bilan quyidagi tengliklarga kelamiz:
₽(?0+Д1') i
J /(Х,Л+Л^)А =
Pho)
= 2*^0f + ~-°+^ P(—= f (P(%), Уо) P(л)>
а(Уо + Ду)
Й>^ I /(х,Л+ДУ)Л= (8)
<х(Уо)
= lim f (х’,у0 + Ду)= / (а (у0), у0) а (у0).
Ду—>0 Ду
Yuqoridagi (6) munosabatda Ду -> 0 da limitga o‘tib, (7) va (8)
tengliklami e’tiborga olib, ushbu
1 J\ (Уо +Ду)-71 (Уо) ₽(’f f fr / x ,
hm ‘YA <_‘A,.0/ = / (x, y0) rfx +
Ду—>0 Ду J y
а(Уо)
+f (P(Уо),Уо)P'U )-/(«(%), Уо)« U)
tenglikka kelamiz. Demak,
₽ho)
Л'(Уо)= J /;(х,уо)с&с + /(р(уо),уо)р'(у))-/(а(у)),^)а(3б)-►
«ho)
i
Misol. Ushbu J у (y) = J ex |y - x| dx funksiyaning hosilasi topilsin.
о
◄ Aytaylik, у e (-°°,0) bo‘lsin. Bu holda
i i f
Jj (y) = -yjexdx + Jxexdx = у (1 - e) + [e- (e-1)] = (1 - e)y + 1
о о
bo‘lib, (y) = 1 - e ga ega bo‘lamiz.
220
Aytaylik, ye (0,1) bo'lsin. Bu holda
dx-
y i 1
-jxexdx- jyexdx + xexdx-2ey -(e + 1) y-l
о у у
bo'lib, (у) - 2ey - e -1 bo'ladi.
Aytaylik, у e [1,-к») bo'lsin. Bu holda
i i
(у) = У J e*dx - J xexdx = у (e - 1) - [e - (e -1)] = (e - l)y -1
о о
va (у) - e - 1 bo'ladi. Demak,
1-e, agar -o=<y<0,
Л'(у) =
2er-e-l, agar 0 < у < 1,
e -1, agar 1 < у < +«>
bo'ladi. ►
Mashqlar
1. Agar
(0<x<D
bo'lsa, u holda 0 < у < 1 uchun
1 f exdx
о
bo'lishi isbotlansin.
i+y
2. Agar Jx (y) = —5—у bo'lsa, lim Jj (y) topilsin.
J l + XZ+y2 y->0
У
221
77- ma'ruza
Parametrga bog'liq xosmas integrallar
1°. Parametrga bog‘liq xosmas integral tushunchasi. Faraz qilaylik,
f(x,y) funksiya
M = {(x,y) e R2 : x e [a,+°°), ye E a R.}
to'plamda berilgan bo'lsin. Bu funksiya har bir tayin ye E da x o‘z-
gamvchining funksiyasi sifatida |a,H da integrallanuvchi, ya’ni
j/(x,y)t/x
a
xosmas integral yaqinlashuvchi. Ravshanki, integralning qiymati у o'z-
garuvchiga bog'liq bo'ladi:
F(y) = \f(x,y)dx. (1)
a
Masalan, у > 1 bo'lganda
Ч-QC t
f = Hm f— = lim -1) = J-
J t—><x* J уУ t—1—У У—1
bo'ladi. Demak, bu holda
ifoda kelib chiqadi.
(1) integral parametrga bog'liq chegarasi cheksiz xosmas integral,
у esa parametr deyiladi.
Xuddi shunga o'xshash
Fi (y) = j f(x,y)dx, F>(y) = J f(x,y)dx
parametrga bog'liq xosmas integrallar tushunchalari kiritiladi.
Aytaylik, f (x,y) funksiya
M = {(x, у) e R2 : x e [a, E), у e E c R}
222
to‘plamda berilgan bo‘lsin. Bu funksiya har bir tayin ye £ da x o‘zga-
ruvchining funksiyasi sifatida qaralganda uning uchun b maxsus nuqta
bo‘lib, u \a,b] da integrallanuvchi, ya’ni
h
jf(x,y)dx
a
xosmas integral yaqinlashuvchi bo‘lsin. Ravshanki, bu holda ham
integralning qiymati у o‘zgaruvchiga bog‘liq bo‘ladi:
ь
Ф(у) = \f(x,y)dx. (2)
a
Masalan, 0 < у < 1 bo‘lganda
2 t
[——— = lim f (2 — x)~y dx = lim —[(2 - ti~y -1] = ---
' (2-х/ /->2-0 J /->2-0 y-1 1-y
bo‘ladi. Demak, bu holda
®W=X <
bo‘ladi.
(2) integral parametrga bog‘liq, chegaralanmagan funksiyaning
xosmas integrali, у esa parametr deyiladi.
Umumiy holda, parametrga bog‘Iiq, chegaralanmagan funksiyaning
chegarasi cheksiz integrali tushunchasi ham yuqoridagidek kiritiladi.
Parametrga bog‘liq xosmas integrallarning funksional xossalari
(limiti, uzluksizligi, differensiallanishi, integrallanishi)ni
F(y) = J f(x,y)dx
a
integral uchun keltirish bilan kifoyalanamiz.
2°. Integralning tekis yaqinlashishi. Aytaylik, f(x,y) funksiya
M = {(x,y)e R2 : хе [a,+°°), у e E c R]
to‘plamda berilgan bo‘lib, har bir tayin ye E da
F(y) = J f(x,y)dx
223
xosmas integral yaqinlashuvchi bo‘lsin. Ta’rifga binoan
F(y) = [ f (x,y)dx - lim \ f (x,y)dx, (a < t < °°)
a a \
bo‘ladi. Natijada berilgan f (x,y) funksiya yordamida
G(y,t) = jf(x,y)dx, (a<t<°°)
a
F(y) = *J f(x,y)dx
funksiyalar yuzaga keladi va
lim G(y,f) = F(y), (yeE)
t—>+oo
munosabat bajariladi.
Demak, G(y,t) funksiya t -> +°° da limit funksiya F(y) ga ega
bo'ladi.
1- ta’rif. Agar t -> +°° da G(y,t) funksiya limit funksiya F(y) ga
E to‘plamda tekis yaqinlashsa,
F(y)= J f(x,y)dx
a
integral E to‘plamda tekis yaqinlashuvchi deyiladi.
Integralning E to‘plamda tekis yaqinlashuvchanligini quyidagicha
anglash lozim:
1) har bir tayin ye E da J f(x,y)dx xosmas integral yaqin-
a
lashuvchi;
2) Ve > 0 olinganda ham shunday 8 = 3(e) > 0 topiladiki, bunda
Vt > 8 va Vy e E uchun
+oo
J /(x,y)rfx
t
< E
tengsizlik bajariladi.
224
1-misol. Ushbu j e x cosxy dx
о
xosmas integralning (-00, -в») da tekis yaqinlashuvchi ekani ko‘rsatilsin.
◄ Har bir tayin у e (-«>, 4-00) da qaralayotgan xosmas integralning
yaqinlashuvchi ekanligi ravshan.
2
Ve > 0 ga ko‘ra 8 - In deyilsa, u holda Vr > 8 va Vy e (-<», +°°)
uchun
+°° +°° I 2
j e~x cosxy dx < J e~xdx = e~' < e~s = e £ = | < e
t t
bo'ladi. Demak, berilgan integral (-00, -в») da tekis yaqinlashuvchi. ►
2- ta’rif. Agar t -> da G(y,t) funksiya limit funksiya F(y) ga
E to'plamda tekis yaqinlashmasa,
F(y) = j f(x,y)dx
integral E to'plamda tekis yaqinlashmaydi deyiladi.
Integral E to'plamda yaqinlashuvchi, ammo u shu to'plamda
tekis yaqinlashmaydi degani quyidagini anglatadi:
1) har bir tayin у e E da j f (x,y)dx xosmas integral yaqinla-
shuvchi;
2) V8 > 0 olinganda ham shunday e0 > 0, y0 e E va t} > 8
bo'lgan e [«,+^) topiladiki, bunda quyidagi ifoda o'rinli bo'ladi:
J f(x,yi)dx >e0.
2-misol. Ushbu
J yexydx
xosmas integralning (0, в») da tekis yaqinlashmasligi ko'rsatilsin.
225
◄ Ravshanki,
Г ye Xydx = lim Г ye^dx = lim (1 - e 1)1) = 1.
J /—>+=*» J t—>4-00
о 0
Demak, berilgan xosmas integral yaqinlashuvchi. Aytaylik,
у e E = (0, +“) bo‘lsin. Ixtiyoriy musbat 8 sonni olaylik. Agar
e0 = i, t0 > 8 va y0 = — deb olsak, u holda
j tQ
= > | = £0
bo‘ladi. Bu esa J ye dx integral E = (0,+°°) da tekis yaqinlash-
o
masligini bildiradi. ►
4-00
Yuqoridagi F (y) = j f (x, y) dx
a
parametrga bog'liq xosmas integralning parametr у bo'yicha E to‘p-
lamda tekis yaqinlashishini quyidagicha ham ta’riflasa bo‘ladi.
3- ta’rif. Agar
lim sup F (y) - \f (x, y) dx - lim sup | f (x, y) dx - 0
ye£ J f->+~ yEg J
(a < t < +°o) bo'lsa,
+o°
F(y)= j/(x,y)dx
a
xosmas integral to‘plamda tekis yaqinlashuvchi deyiladi.
3- misol. Ushbu F (y) = [ xosmas integralninig E = [2,+°°)
J xy
to‘plamda tekis yaqinlashuvchi ekani ko‘rsatilsin.
226
◄ Ravshanki, 1 < t < +°o uchun
0<
sup -
M2.+-) ' x-
bo‘lib,
lim sup
f — = 0
J хУ
bo'ladi. Demak, berilgan xosmas integral E = [2,+°°) to‘plamda tekis
yaqinlashuvchi. ►
Endi integralning tekis yaqinlashishini ifodalovchi teoremani
keltiramiz.
1-teorema. Ushbu F(y) = | /(x,y)t/x
integralning E to‘plamda tekis yaqinlashuvchi bo‘lishi uchun Ve > 0
olinganda ham у ga bog'liq bo‘lmagan shunday 5 = 8(e) > 0 topilib,
t' > 8, t" > 8 tengsizliklami qanoatlantiruvchi Vf, t" va Vy e E da
J/(x,y)c?x
tengsizlikning bajarilishi zarur va yetarli.
Bu teoremaning isboti ravshan.
3°. Parametrga bog‘liq xosmas integrallarning parametr bo‘yicha
tekis yaqinlashish alomatlari.
2- teorema. (Veyershtrass alomati.) Aytaylik, f (x,y) funksiya
M = {(x,y) e R2 : x e [й,+°°), у e E cz R}
to'plamda berilgan va harbir tayinye Edaf (x,y) funksiya [o,+°°) da
integrallanuvchi bo‘lsin.
Agar da aniqlangan shunday <p(x) funksiya topilsaki,
1) Vx e [й,+°°), Vy g E uchun \f (x,y)| < <p(x) bo‘lsa,
2) ushbu [ q(x)dx xosmas integral yaqinlashuvchi bo‘lsa, u holda
227
F(y)= J f(x,y)dx
integral E to'plamda tekis yaqinlashuvchi bo'ladi.
◄ Modomiki, | <p(x)rfx yaqinlashuvchi ekan, u holda Ve > 0 olin-
ganda ham shunday 8 = 8(e) > 0 topiladiki, t' > 8, t" > 8 bo'lganda
J/(x,y)Jx
tengsizlik bajariladi. Ayni paytda,
, у) dx < J |/ (x, у)| dx < J <p(x)dk, (t' < t”)
bo'lganligi sababli
j/(x,y)rfx
bo'ladi. Yuqorida keltirilgan 1- teoremaga muvofiq
F(y) = | f(x,y)dx
integral E to'plamda tekis yaqinlashuvchi bo'ladi. ►
4- misol. Ushbu f COSX^dx, (у e E - (-<*>,+00))
J 11 v-
0 1+x'
integralning tekis yaqinlashuvchi ekani ko'rsatilsin.
◄ Ravshanki, Vxe [0,+°o) va Vy e uchun
bo'ladi. Ayni paytda,
228
—v dx
xosmas integral yaqinlashuvchi bo‘lganligi sababli Veyershtrass
alomatiga ko‘ra berilgan integral E - (-«>,+«>) da tekis yaqinlashuv-
chi bo‘ladi. ►
Integrallarning tekis yaqinlashishini aniqlashda ko‘p foydala-
niladigan Abel hamda Dirixle alomatlarini isbotsiz keltiramiz.
3- teorema. (Abel alomati.) f (x,y) va g(x,y) funksiyalar
M = {(x,y)e R1 : хе [й,+°°), у e E g 7?}
to‘plamda berilgan bo‘lib, quyidagi shartlar bajarilsin:
1) har bir tayin у e. E da g{x,y) funksiya [a,4o°) da monoton bo‘lsin;
2) V(x,y)e M uchun |g(x,y)|<c, (c = const) bo‘lsin;
3) ushbu f (x,y')dx integral E to'plamda tekis yaqinlashuvchi
boUsin. U holda
J f(x,y)g(x,y)dx
integral E to‘plamda tekis yaqinlashuvchi boUadi.
4- teorema. (Dirixle alomati.) f{x,y) vag(x,y) funksiyalar Mto‘p-
lamda berilgan boUib, quyidagi shartlar bajarilsin:
1) Vt > a hamda Vt e E da
J f (x, y) dx <c, (c = const)
tengsizlik bajarilsin;
2) har bir tayin у e E da g(x,y) funksiya limit funksiya <p(x)=0 ga
tekis yaqinlashsin. U holda
J /(x,y)g(x,y)dx
integral E to‘plamda tekis yaqinlashuvchi boUadi.
229 '
5- misol. Ushbu
jsn^y^ (ye £=[1,2])
о
integral tekis yaqinlashuvchanlikka tekshirilsin.
◄ Berilgan integralda
f(x,y) = sinxy, g(x,y) = ^
deyilsa, u holda
1) VZ >0, Vy e [1,2] uchun
J/(x,y)dx = J sin xy dx
1-cosiy
у
<2,
о
2) x -> +-OO da g(x,y) = ^ funksiya £=[1,2] da nolga tekis
yaqinlashuvchi.
Dirixle alomatiga ko‘ra berilgan integral £ = [1, 2] da tekis yaqin-
lashuvchi bo‘ladi. ►
Mashqlar
Г у cos xyl dx
1. Ushbu----------7— integralning E— [2,10] to‘plamda tekis
J y+xy
yaqinlashishi isbotlansin.
2. Ushbu Г (y > 1) integral tekis yaqinlashishga tekshirilsin.
J l+x-v
3. Aytaylik, f (x) funksiya R da uzluksiz bo‘lib, Vxe R da/(x) > 0
bo‘lsin. Ushbu
+~ о
\f(y-x)dx, J f(y-x)dx
о
integrallaming у parametr bo‘yicha ixtiyoriy chekli \a,b\ a R seg-
mentda tekis yaqinlashuvchi bo‘lishi isbotlansin.
230
78- ma’ruza
Parametrga bog‘liq xosmas integrallaming
funksional xossalari
Ushbu ma’ruzada parametrga bog‘liq xosmas integral
F(y) = f f(x,y)dx
a
ning limiti, uzluksizligi, differensiallanishi hamda integrallanishi
masalalarini bayon etamiz.
1°. F(y) funksiyaning limiti. Aytaylik, f(x,y) funksiya
M - {(x,j/)g R2 : xg [<з,+°°), у g E c R}
to'plamda berilgan, y0& R esa E to‘plamning limit nuqtasi bo‘lsin.
1- teorema. f (x,y) funksiya quyidagi shartlarni bajarsin:
1) har bir tayin у g E da f(x,y) funksiya x o‘zgaruvchining funk-
siyasi sifatida [<?,+<») da uzluksiz;
2) у -> y0 da f(x>y) funksiya ixtiyoriy [а, da (a < t < limit
funksiya <p(x) ga tekis yaqinlashsin;
3) ushbu F(y) = j f(x,y)dx integral Eto'plamda tekis yaqinla-
a
shuvchi bo'lsin. U holda у -» y0 da F(y) funksiya limitga ega va
lim F(y) - I cp(x)Jx
у->Ув J
a
bo'ladi.
◄ Teoremaning 1- va 2- shartlarining bajarilishidan <p(x) funk-
siyaning l<2,+°°) da uzluksiz bo'lishini topamiz. Binobarin, <p(x)
ixtiyoriy [a,t\ da (o < t < integrallanuvchi bo'ladi. Modomiki,
F(y) = J f(x,y)dx
a
integral £ to'plamda tekis yaqinlashuvchi ekan, u holda 77- ma’ruza-
dagi 1- teoremaga ko'ra
Vs > 0, 38 = 8(s)>0, f>8, Г >8, Vf, t”, \/y e E :
t”
jf(x,y)dx
t'
bo‘ladi. Keyingi tengsizlikda, у -> y0 da limitga o‘tsak, u holda
t”
J <p(x)c?x
f
< s
tengsizlik hosil bo‘ladi. Bundan <p(x) funksiyaning [«,+<«) da integ-
rallanuvchanligi kelib chiqadi. Ushbu
-|-eo q-oo
j f (x, y) dx - J 9 (x) dx
a a
ayirmani qaraymiz. Uning uchun quyidagi tengsizlik bajariladi:
J f(x,y)dx - j (p(x)tZx <
(a < t < 00). (1)
Bu tengsizlikning o‘ng tomonidagi qo'shiluvchilarni baholaymiz.
J f (x,y)dx integral E to‘plamda tekis yaqinlashuvchi bo‘lganligi
a
sababli,
Vs > О, З81 = 5i (£) > °’ V/ > 8P Vy e £ :
J f(x,y)dx
t
(2)
bo‘ladi.
j <p(x)c?x
integral yaqinlashuvchi bo'lganligi sababli
232
Ve > 0, Э82 = S2 (e) >0, V/ > 82 :
J q>(x)dx
t
ifodaga ega bo‘lamiz.
Ravshanki, Vi > 80 : (80 = max(8j82)) da (2) va (3) tensizliklar bir
yo‘la bajariladi. Funksiya f(x,y) y-*y0 da [ad] segmentda (7 > 80)
limit funksiya <p(x) ga tekis yaqinlashuvchi bo‘lganligi sababli
Ve > 0,38'= 8'(e) > 0, |y-y0|<8', VyeE, Vxe[a,t], (a<i<oo)
(4)
bo‘ladi. (1), (2), (3) va (4) munosabatlardan
J f {x,y)dx - J (p(x)Jx
a a
< £
bo‘lishi kelib chiqadi. Demak
lim F(y) = lim | f (x,y)dx = Г <р(х)с/х. ►
У->Уо У~>Уо J J
Keyingi tenglikni quyidagicha ham yozish mumkin:
lim f f (x, y) dx = f Г lim f (x, y)l dx.
y-m * J J
a a
- . , TT , , г f -xv sinx , f sinx , , ,
1- misol. Ushbu hm e --------------dx - ------dx tenghk isbot-
y-»+0 J X J X
a a
lansin.
◄ Agar <p(x) = s,^x- funksiyaning x = 0 nuqtadagi qiymatini
<p(0)=l deb olinsa, u holda
Л\ -xv sinx
funksiya {(х,у)е й2 : xe [0,+°o),ye [0,+°°)} to'plamda uzluksiz
bo'ladi.
233
Ravshanki, har bir tayin у e [0, +«>) da f (x,y) funksiya x o'zga-
ruvchining funksiyasi sifatida [0,+«>) da uzluksiz bo‘lib, у -> -к» da
bu funksiya ixtiyoriy [0, 1] da (0 < t < «) <p(x) = s'^- funksiyaga
tekis yaqinlashadi. Endi
f e~*y ™\*dx
j x
0
xosmas integralni parametr у bo‘yicha [0,-и>=) da tekis yaqinlashuvchi
bo‘lishini ko'rsatamiz.
Agar 77-ma’ruzada keltirilgan Abel alomatida f(x,y) funksiya
sifatida gix,y) funksiya sifatida e~xv funksiyalar olinsa, ular
uchun Abel alomati barcha shartlarining o'rinli bo'lishini ko'rsatish
qiyin emas. Demak, alomatga ko'ra
F-xySinx^
J X
о
integral tekis yaqinlashuvchi.
Yuqorida keltirilgan 1- teoremaga binoan
lim f e~xy
y->+0 J X
0
f (lim
J v-»+o x }
, Г -ст smx , f sinx , , ............
bo lib, undan hm e y--------------dx- ---------dx bo lishi kelib
’ y-HO j X J X
о 0
chiqadi. ►
2°. Цу) funksiyaning uzluksizligi. Aytaylik, f(x,y) funksiya
Mo ={(x,y)e A2 : xe [a,4oo), ye[c,rf]}
to'plamda berilgan bo'lsin.
2- teorema. Agar f[x,y) funksiya MQ to'plamda uzluksiz bo'lib,
J f(x,y)dx
a
integral [c,<7] da tekis yaqinlashuvchi bo'lsa, u holda F(y) funksiya
da uzluksiz bo'ladi.
234
◄ Ixtiyoriy yoe[c,J], у0+Ауе[с,</] nuqtalarni olib, F(y)
funksiyaning orttirmasini topamiz:
AF(y0) = ?(Уо + Ay) ~F(y0) = J[/(x,y0 + ty)-f(x,y0)]dx.
a
Shartga ko‘ra J f (x,y)dx integral fc, d\ da tekis yaqinlashuvchi.
U holda
Ve > 0,38 = 8(e) > 0, V/o >8, Vy e [c, d}:
J f(x,y)dx
f0
(5)
e
< 3
bo‘ladi. Ravshanki, f(x,y) funksiya
Mt. R2 : xe [a,Z0], ye[c,<7]}, (a < t0 < +°o)
to‘plamda tekis uzluksiz bo‘ladi. U holda
Ve > 0, 38, = 8I (e) >0, Ay < 8j (e):
|/(x, y0 + Ay) - /(x, y0 )| <
(6)
ga ega bo‘lamiz. Agar 80 = max {8,8]} deyilsa, uning uchun (5) va
(6) tengsizliklar bir yo‘la bajariladi. (5) va (6) munosabatlami e’tiborga
olib topamiz:
|AF(y0)| = J [ЛЗД + Ay)-/(x,y0)]c?x <
a
zo
£ J \f(x, y0 + Ay) - f(x,y0 )dx\ +
a
J f(x,y0 + &y)dx
< e.
Demak, lim AF(y0) = 0 .
A.y-»0
Bu esa F(y) funksiyaning [c, d\ oraliqda uzluksizligini bildiradi. ►
' 2
2-misol. Ushbu F(y)= | e~^x~y^ dx integral у parametrning uz
о
luksiz funksiyasi bo‘lishi ko‘rsatilsin.
235
4 Berilgan integralda x - у = t almashtirish bajaramiz. U holda
F(y) = J e~'2 dt = J e~'2 dt + J e~’2 dt = J e'2 dt + J e~'2 dt
—у -у 0 0 0
bo‘lib, bu yig‘indining har bir qo‘shiluvchisi у ning uzluksiz funksiyasi
bo‘lgani uchun berilgan integral у parametrning uzluksiz funksiyasi
bo‘ladi. ►
3°. F(y) funksiyani differensiallash. Faraz qilaylik, f(x,y) funksiya
Af0 to‘plamda berilgan bo‘lsin.
3- teorema. f (x,y) funksiya quyidagi shartlami qanoatlantirsin:
1) funksiya Mo to‘plamda uzluksiz;
2) fy(x,y) xususiy hosila mavjud va u Mo to‘plamda uzluksiz;
3) Har bir tayin у e [c, d] da
F(y) = J f(x,y)dx
a
integral yaqinlashuvchi;
4) Ushbu J fy{x,y)dx integral [c, d] da tekis yaqinlashuvchi.
a
U holda F(y) funksiya [c, d\ da F(y) hosilaga ega va
4-oo
F\y) = J fy{x,y)dx
a
bo‘ladi.
4 y0 e [c,d], y0 + Ay e [c,rZ] nuqtalarni olib, topamiz:
F(y0+Ay)-F(y0) _ 7 /(х,у0+Ду)-/(х,у0) dx
Ду J Ду
a
Lagranj teoremasiga ko‘ra
ZXJZ J
236
bo'ladi. Demak,
lim , lim 7/-(х,л + . (7)
ду->0 Ay Ду->0 j y °
a
Shartga ko'ra fy(x,y) funksiya Mo to'plamda uzluksiz. Kantor
teoremasiga binoan u
Mt = {(x,y) g R2 : x g [u,t], У 6 [c,</]}, (a < t < oo)
to'plamda tekis uzluksiz bo'ladi. U holda
Ve > 0, 33 - 8(e) > 0, |Ay| < 8(e), Vx e [a, /],
|4'(x,y0 + W) - fy(x> Уо)| < e
bo'ladi. Demak, Ay -> 0 da fy(x,yQ + 9Ay) funksiya //(x,y0) ga
tekis yaqinlashadi. Shartga ko'ra
J fy(x,y0)dx
a
integral tekis yaqinlashuvchi. U holda
Ve > 0, 38 - 8(e) >0, t' > 8, t” > 8, Vt', t", Vy g [c,d}’.
^fy{x,y)dx
f
< £ 5
jumladan,
f
+6Ay)c?x
f
< £
bo'ladi. Keyingi tengsizlikning bajarilishidan esa
4-00
J //(x,y0 + 9Ay)dx:
a
integralning tekis yaqinlashuvchanligi kelib chiqadi. Ushbu ma’ruzada
keltirilgan 1-teoremani (7) tenglikning o'ng tomoniga qo'llab, to-
pamiz:
23?
Hm J f'(x,y0 + 6Ay)dx = J Jim /Дх, y0 + 0Ay)l dx =
a a
= J fy(x,y0)dx.
a
(8)
(7) va (8) munosabatlardan
F'(y0)= j f'(x,y0)dx (9)
a
bo‘lishi kelib chiqadi.
(9) munosabatni quyidagicha ham yozish mumkin:
a ' a
Bu differensiallash amalini integral ostiga o‘tkazish qoidasini ifo-
dalaydi. ►
4°. F(y) funksiyani integrallash. Aytaylik, f (x,y) funksiya
= {(x,y)e R2 : xg [a,+°°)> yG[c,d]}
to‘plamda berilgan bo'lsin.
4- teorema. Agar f (x,y) funksiya Mo to‘plamda uzluksiz va
4-00
F(y) - J f(x,y)dx integral [c, d\ da tekis yaqinlshuvchi bo‘lsa, u
a
holda F(y) funksiya [c, d] da integrallanuvchi va
bo'ladi.
◄ Ravshanki, Ду) funksiya [c, d] da uzluksiz bo'ladi. Binobarin,
u [c, d] da integrallanuvchi. Shartga ko‘ra
F(y) = J /(x,y)dx
a
integral [c, d\ da tekis yaqinlashuvchi. U holda
238
Ve > 0,35 = 5(e) > О, V/ > 5, Vy е [с, d] :
J /(х,у)</х
< е
bo‘ladi. Shu tengsizlik bajariladigan t ni olib topamiz:
4-00 t 4-00
I f(x, y)dx = J f(x,y)dx + J f(x, у) dx.
a a t
Natijada
bo‘ladi. Agar
bo‘lishini e’tiborga olsak, u holda
d
$F(y)dy =
c
bo‘lib,
ekanligi kelib chiqadi. ►
Mashqlar
1. Agar f (x) funksiya (0, da integrallanuvchi bo'lib,
F(y) = J e^f^xjdx
о
239
bo‘lsa,
lim F(y) = lim [
y->+0 y~»+0 J
e ^ftxjdx = J f(x)dx
о
bo'lishi isbotlansin.
7 _ 2
2. Ushbu F(y) = I e y Xydx, (-« < у < +°o) funksiya uzluksiz-
o
likka tekshirilsin.
79- ma’ruza
Ba’zi xosmas integrallarni hisoblash
Parametrga bog'liq integrallar va ularning funksional xossalaridan
foydalanib, ba’zi xosmas integrallarni hisoblaymiz.
Г sin x
1°. ----dx integralni hisoblash. Bu integralning yaqinlashuv-
J X
0
chiligi 77- ma’ruzada keltirilgan. (
Ma’lumki, [ e'*” sin xdx = - Ц-. (1)
J i+/
Bu tenglikdagi
F (y) = J e~xy sin xdx
о
parametrga bog'liq integral у parametr bo'yicha ixtiyoriy [t, J] da
(t > 0) tekis yaqinlashuvchi bo'ladi. Bu tasdiq
sin x| < e 01, j e dx = -
о
bo'lishi hamda Veyershtrass alomatini qo'llashdan kelib chiqadi. (1)
tenglikni integrallab topamiz:
j !
sin x dx dy = ------v
J 1+v2
dy = arctg A - arctg t.
240
Bu tenglikning chap tomonidagi integral uchun
о
e sin xdy
dx -
sin xdx
va Vx > 0 da (sin xj < x bo'lib,
’v i
I -----sinxdx < | e'^dx = ~-
J x J A
0 |o
bo‘ladi. Natijada Л —>+<*> da
it 4. i f -ix sin x ,
- - arctg t=\e ---------dx (2)
2 J x
o
bo‘lishi kelib chiqadi. Endi
lim? = T sinxdx
l->+0 J X J X
о 0
tenglikning o‘rinli ekanini (qaralsin, 78- ma’ruza) e’tiborga olib (2) da
t +0 da limitga o‘tib topamiz:
s +f sinx . it
---- dx = -.
J x 2
o
2°. [ dx integralni hisoblash. Bu integralning (->», +°o) da
* X
0
yaqinlashuvchi bo‘lishi ravshan. Aytaylik, у > 0 bo‘lsin. Bu holda
integralda yx = t almashtirish bajarib topamiz:
1 x J I 2
о 0
Aytaylik, у < 0 bo‘lsin. Bu holda qaralayotgan integralda yx = —t
almashtirish bajarib topamiz:
f sin vx , Г sin/ . л
—— dx = - I ---dt = - -
J x J t 2 •
о 0
241
Aytaylik, у = 0 bo'lsin. Bu holda
sin Ox , n
-----dx = 0
о
bo‘ladi. Demak,
ya’ni
sinvx ,
—— dx =
it
aSar
0, agar
71
aSar
У=0,
у < 0,
sin vx , 7t .
dx = - signy
bo‘ladi.
у > 0
о
о
integralni hisoblash. Awalo bu parametrga bog‘-
о
liq xosmas integralni yaqinlashuvchanlikka tekshiramiz. Buning uchun
berilgan integralni quyidagicha yozib olamiz:
+°° 1
a-l S’ a-l
— dx + Г--------dx.
+x J 1+x
(3)
о 0
Aytaylik, 0 < x < 1 bo‘lsin. Bu holda
xa-1 1
*___ S V<7-1
1+X
bo‘lib, a > 0 da ushbu
i
о
integralning yaqinlashuvchi bo‘lganligidan, a > 0 da
о
integralning ham yaqinlashuvchi bo'lishi kelib chiqadi.
242
Aytaylik, x > 1 bo'lsin. Bu holda
bo'lib, a < 1 da ushbu
J xa~2dx
i
integralning yaqinlashuvchi bo'lganligidan, a < 1 da
integralning ham yaqinlashuvchi bo'lishi kelib chiqadi.
Demak, qaralayotgan
F(a) = ^dx
J 1+x
о
integral 0 < a < 1 da yaqinlashuvchi bo'ladi.
Endi F(a) integralni hisoblaymiz. Ma’lumki, 0 < x < 1 da
J- = y(-i)‘V
s
Bu tenglikdan
Xя
1+X
= ^(-l)*xo+w
k=0
bo'lishini topamiz. Tenglikning o'ng tomonidagi qator [a0, Z>0] da
(0 < aQ < x < Z>0 < 1) tekis yaqinlashuvchi bo'lib, uning qismiy yig'indisi
n-1 , a-l I
ад = £(-D =--4гк
k=£>
bo'ladi. Agar Vrce N, Vxe (0,1) uchun
o-l
243
1
tengsizlikni hamda J xa~ldx, (0 < a < 1) integralning yaqinlashuvchi
о
ekanligini e’tiborga olsak, u holda Veyershtrass alomatiga ko‘ra
i
J Sn(x)dx
о
tekis yaqinlashuvchi bo‘ladi. Demak,
i i
lim I (x)tZx = Г (limS„(x)')dr ,
n—* J \rt—/
о 0
ya’ni
oV*=°
bo‘ladi. Demak,
i
\( «-1
j lim£
J n—^oo
о V A=o
a+k-l
Г хй—1
dx = -—dx
* 1+x
о
a-l
— dx
_+x
0
K-l 1
fc=0 0
.a+k-l
dx =
0 V=° 7
^dx=nt^
h a+k
(4)
Г xa~l 1
Endi J dx integralda x = -
i x r
almashtirish bajarsak, u holda
z(l-a)-l
Ц-------dt
1+f
bo‘lib, yuqoridagi (4) munosabatga ko‘ra
J 1+x a-k
1 k=\
(5)
bo‘ladi. (3), (4) va (5) munosabatlardan
244
Sc-»*
А=1
11'
а+к а-к
bo‘lishi kelib chiqadi. Ma’lumki,
1
- +
a
lt=l
1 1
a+k a-k
jt
sin ait
(0 < a < 1)
(qaralsin, 76-ma’ruza). Demak, quyidagi ifoda kelib chiqadi:
7C
sin an ’
(0<o<l).
4°. J f{ax) JAbx) fa jnjegra|nj foisoblash. Bunda/(x) funksiya
о
+oo
[0,+oo] da uzluksiz, istalgan A > 0 da f — ^-dx integral yaqinla-
* X
A
shuvchi va a > 0, b > 0.
Berilgan integralni quyidagi ikkita integralning limiti deb qaraymiz:
J X 8->0 J X J X
0 L s S
Bu tenglikning о‘ng tomonidagi birinchi integralda ax = t, ikkinchi
integralda bx — t almashtirishlami bajarib topamiz:
4-00 4-00 4-00
Г f(ax)-f{bx) , Г f{t) , r Г f(J) , r Г f(t) ,
———---------dx = hm dt - hni ' Jr = hm dt.
J X 8^0 J t 8->0 J t 8~>0 J t
0 ab Ьд a8
Ravshanki,f(f) —uzluksiz funksiya, у funksiya esa ishora saqlaydi
(chunki a > 0, b > 0, xe (0, + <»)). Demak,
a5
integralda o‘rta qiymat haqidagi teoremani qo‘llash mumkin:
245
Л8 ч Ь8
«8 дЗ
за за
Natijada lim f ^dt = lim/(O = Hm/(^)ln- (7)
8~-^0 * t 8—>0 * t §~^0 G
ad aS
bo'ladi. Modomiki, £, nuqta «3 bilan b8 orasida ekan, 3 -> 0 da -> 0 va
Hm/(£) = /(0) (8)
^->0
bo'ladi. (6), (7) va (8) munosabatlardan
j l^lJS^ldx = /(0)ln|
bo'lishi kelib chiqadi.
5°. Ba’zi xosmas integrallarning qiymatlari. Quyida ba’zi xosmas
integraharning qiymatlarini keltiramiz:
1. =
0
0
f xsinxy , л . -Ы
5. ----5- dx = - signye 11.
n 1+x2 2
T cosxy , n -Ivl
4. I ~-^dx = -e w.
j l+x2 2
+°° . •)
f Sin XZ , 7t
6- dx = -
J x 4
+f sin4 ax-sin4 bx , 3 t a
7. J---x--Л=8|П6-
0
V e-ax ~e~bx b a
8. sin nx dx = arctg— arctg -, (a > 0, b > 0, n * 0)
J x nn ' '
о ' \
9.
e ax~e hx , 1 . b2+n2
---------cos nx dx = - In —у
x--------2. a2 +n2
246
Mashqlar
, т т . , f 1-COS XV _fcr
1. Ushbu ---------- e
j x
0
1 i 11 У I
- In 1 + ~ ,
2 k1
(y > 0, к > 0) tenglik
isbotlansin.
2. Ushbu
ln(l+«2x2) ,
dx,
i b2+xl
(a > 0, b > 0) integral hisoblansin.
3. Ushbu
/4-
0 X *'•
— 71
- 14a ’ > 0) tenglikdan foydalanib,
f —, (« e N)
(x2+a)”+l
integral hisoblansin.
80- ma’ruza
Eyler mtegrallari
Biz 48- ma’ruzada ushbu
i
J xa~x (1 - х)л~' dx
о
xosmas integralning a > 0, b > 0 bo‘lganda yaqinlashuvchi ekanligini,
J xa^exdx
fj о
xosmas integralning esa a > 0 bo‘lganda yaqinlashuvchiligini isbot-
lagan edik.
Ravshanki, bu xosmas integrallar a va b larga bog‘liq, ya’ni para-
metrga bog‘liq xosmas integrallar bo'ladi.
1°. Beta funksiya va uning tekis yaqinlashuvchanligi. Ushbu
i
J x0”1 (1 - x)b-1 dx
.... 0 !
j 24"7
parametrga bog'liq xosmas integral beta funksiya (1-tur Eyler integrali)
deyiladi va B(a,b) kabi belgilanadi:
i
B(a,b) = Jx"-1 (1 - x)*-1 <Zx , (a > 0, b>Q).
о
Demak, beta funksiya
{(a, b)e R2 :ae (0, +°°), b e (0, +<*>)}
to‘plamda aniqlangan funksiya.
1- teorema. Ushbu
i
B{a, b) = J xa-1 (1 - x/’1 dx
о
integral Mo = {(«,b) e R2 : a e [a0, +<*>),be [Z>0, +<*>),a0 > 0,b0 > 0}
to‘plamda tekis yaqinlashuvchi bo'ladi.
◄ B(a, Z>)funksiyani ifodalovchi integralni ikki qismga
i
12 1
J Xй-1 (1 - x)6-1 dx = J Xй'1 (1 - x)*-1 dx + J x°4 (1 - x)6-1 dx
0 0 1
2
ko'rinishda ajratib, har bir integralni tekis yaqinlashishga tekshiramiz.
Parametr a > a0, (aQ > 0), VZ> > 0, Vx e ^0, da
Xй-1 (1 - x)*4 < Xй""1 (1 - х)лч <2хй°-1
va a > 0 bo'lganda
i
2
J xa~xdx
о
integralning yaqinlashuvchi bo'lishidari Veyershtrass alomatiga ko‘ra
i
2
J xa-1 (1 - x)*-1 dx
0
248
integralning a > a0, (a0 > 0) da tekis yaqinlashuvchanligini topa-
miz. Shuningdek, parametr b > b0, (b^ > 0), Vtz > 0, Vx g , 1] da
Xя"1 (1 - x)b-' < хяЧ (1 - x)^’1 < 2 (1 - x?4
i
va b > 0 bo'lganda J(1 - x)64 dx
i
2
integralning yaqinlashuvchi bo'lishidan Veyershtrass alomatiga ko'ra
i
j x°-1 (1 - x)^1 dx
2
integralning b>bti, (b^ >0) da tekis yaqinlashuvchi bo'lishini topa-
miz. Demak,
i
B(a,b) = J xfl4 (1 - хЛ1 dx
о
integral Mo = {(«, b) g R2 : a e [o0, -в»), b e [Z>0, -н»), > 0, Z>0 >0}
to'plamda tekis yaqinlashuvchi bo'ladi. ►
Natija. B(a, b) funksiya
M = {(a, b) g R2 : a e (0,+°°), b e (0, -к»)}
to'plamda uzluksiz bo'ladi.
i
◄ Bu tasdiq j Xя”1 (1 - x)*-1 dx
о
integralning tekis yaqinlashuvchanligi hamda integral ostidagi funksiya-
ning M to'plamda uzluksiz bo'lishidan kelib chiqadi. ►
2°. B(a, b) funksiyaning xossalari. Endi
/" 1
B(a, b) = J Xя'1 (1 - x)h-1 dx
о
funksiyaning xossalarini keltiramiz.
249
1) B(a,b) funksiya a va b argumentlariga nisbatan simmetrik
funksiya, ya’ni:
B(a,b) = B(b,a), (a > 0,Z> > 0).
•< B(a, b) ni ifodalovchi integralda x = 1 — t almashtirish bajarib
topamiz:
i о
B(a, b) = J xal (1 - x)*-1 dx - - j (1 - /Л1 Л1 dt =
о i
i
= ^tb~x (\-t)a~x dt = B(b,a). ►
о
2) B(a, b) funksiyani quyidagicha ifodalash ham mumkin:
B(a,b)= [-J^-j-dt. (1)
J (l+r)a+A
-< B(a, b) ni ifodalovchi integralda x = almashtirish bajarib
topamiz:
B(a,b) = \xa-\l-x)^dx= [ -Ц 1--U -JL=f-_2—
Jo V W (1+ri2 {(1+0о+А
Agar (1) da b = 1 - a , (0 < a < 1) deyilsa, u holda
+oo । \
B(a, 1 - a) = f -— dt = —-—
J 1+/ sin ла
0
bo‘ladi. Xususan: В | -, -1 = n.
\2 2/
3) B(a, b) funksiya uchun ushbu
B(a + l,b) = -^-B{a,b}, (a > 0, b > 0)
formula o'rinli bo‘ladi.
i
◄ Ravshanki, B(a + 1, b) = J^“(l ~ x)b~x dx.
о
250
Bu integralni bo‘laklab integrallaymiz:
= -|xfl(l-x)A
i
+ [xfl(l-x/dx =
b j
о
i
= £jxfl-1(l-x)z’
0
1 1
J x0-1 (1 - x/~‘ dx - J Xя (1 - x/-1
.0 0
dx
= ~B(a,b)-~B(a+l,b).
b b
Natijada
B(a+ \,b) = ~B(a,b)-?-B(a+ \,b) (2)
b b
bo‘lib, undan
B(a + \,b) = -?-B(a,b)
a+b
bo‘lishi kelib chiqadi. ►
B(a, b) funksiya simmetrik bo‘lganligidan
В(а,Ь + 1) = -^В(а,Ь) (3)
ifodani yozish mumkin.
Natija. B(m, n) funksiyaga (m e N, n g N) (2) va (3) formula-
lami takror qo‘llash natijasida
B(m,ri) = - y-
(m+n-1)!
bo‘lishi kelib chiqadi.
3°. Gamma funksiya va uning yaqinlashuvchanligi. Ushbu
j xa~ie~xdx
о
parametrga bog'liq xosmas integral gamma funksiya (2- tur Eyler
integral!) deyiladi va Г(а) kabi belgilanadi:
251
Г(а) = J ха хе Xdx.
о
Demak, gamma funksiya (0, +°°) da aniqlangan funksiya.
2-teorema. Ushbu Г(а) = j xa'xe~xdx
о
integral [a0, fy, ] da (0 < <Ь^ < -н») tekis yaqinlashuvchi bo'ladi.
◄ Г(«) funksiyani ifodalovchi integralni ikki integral yig'indisi
sifatida yozib olamiz:
Г(а) = J xa~xe~xdx + j xa~xe~xdx.
о i
So'ngra ikkala integralning ixtiyoriy [<з0,/>0] segmentda
(0 < «о < 4 < +°°) tekis yaqinlashuvchi bo'lishini ko'rsatamiz. Para-
metr a > aQ (й0 > 0), Vx e (0,1] da
xaX ex < x*' 4
i
va a0 > 0 da Jx^^dx
о
integralning yaqinlashuvchi bo'lishidan Veyershtrass alomatiga ko'ra
i
jx°~xe~xdx
о
integralning a > «0 da tekis yaqinlashuvchi bo'lishi kelib chiqadi.
Shuningdek, parametr a < b<}, Vx e [1,+°°) da
xa'xe~x < x^'1^* va j xA“-1^xdx
i
integralning yaqinlashuvchi bo'lishidan yana Veyershtrass alomatiga
ko'ra
j xa~xe~xdx
1
252
integralning a < b0 da tekis yaqinlashuvchi bo'lishini topamiz. Demak,
Г(а) = J xa~ie~xdx
о
xosmas integral [a0, Z>0] da tekis yaqinlashuvchi bo‘ladi. ►
Natija. Г (я) funksiya (0, -к») da uzluksiz bo‘ladi.
◄ Bu tasdiq
J xaAe~xdx
о
integralning tekis yaqinlashuvchiligi hamda integral ostidagi funk-
siyaning M = {(x,a)e R2 : xg (0, ч-°°), a g (0,+°°)} dauzluksiz bo‘li-
shidan kelib chiqadi. ►
4°. Г(а) funksiyaning xossalari. 1) Gamma funksiya (0, +«=) da
barcha tartibdagi uzluksiz hosilalarga ega va
Г(л)(а)= j xa-1e'x(lnx)n dx , (n = 1,2,3....)
о
bo'ladi.
◄ Ravshanki, Г(а) = j xa~le~xdx
о
integral ostidagi f (x, a) = Xя'1 ex funksiya
M = {(x, a) g R2 : x g (0,+^), a g (0,+°°)}
to‘plamda uzluksiz bo‘lib, uzluksiz
fa(x,a) = xa-1 e~x Inx
hosilaga ega boUadi. Yuqorida aytganimizdek,
i +~
Г(а) = J xa~le~xdx + j xa~le~xdx
о i
tenglikning о‘ng tomonidagi integrallar ixtiyoriy [a0, Z>0] da
(0 < fig < < +o°) tekis yaqinlashuvchi.
253
1 +с*>
Ushbu J xa-1 hi x e~xdx, J xa~l In x • exdx integrallarni qaray-
o i
lik. Bu integrallardan birinchisi, a > a0 > 0 da
i
|хаЧ Inx- e~x| < x0*1'1 |lnx| va Jxa°~' |lnx|dx
о
integral yaqinlashuvchi bo‘lganligidan Veyershtrass alomatiga ko‘ra
tekis yaqinlashuvchi bo'ladi. Shuningdek, ikkinchi integral ham
a < b0 < +°° da
|хйЧ Inx e~x| < Xй0-1 Inx-e~x = x4 • ex va J хйн Inx e~xdx
i
integral yaqinlashuvchi bo'lganligidan yana Veyershtrass alomatiga
ko‘ra tekis yaqinlashuvchi bo‘ladi. Parametrga bog‘liq xosmas integral-
ning parametr bo'yicha differensiallash haqidagi teoremadan foyda-
lanib topamiz:
d r/ \ d
-j-V(a) = —
da da
j*"'*
0
!-l
e dx - [4~(x^ ]e )dx +
j da
о
+ [ (x le )dx - f x^ 1 • In x • e dx.
J da J
1 1
Demak, Г'(а) = j x° 1 -Inx-e Xdx.
о
Г '(a) funksiyaning [o0, Z>0] da uzluksiz bo'lishi ravshan. ;
Xuddi shu yo‘l bilan funksiyaning ikkinchi, uchinchi va hokazo
tartibdagi hosilalarining mavjudligi, uzluksizligi hamda
Г(п)(а) = J xa-le~x(lnxydx
о
bo'lishi ko'rsatiladi. ►
254
2) Г(о) funksiya uchun ushbu
Г(а + 1) - аГ(а) (4)
formula o'rinli bo‘ladi. J
◄ Ravshanki, Г (a) = J xa~xe~xdx.
о
Bu integralni bo'laklab integrallaymiz. Natijada
Г(а +1) = J xae~xdx = - j x?d(e~x} = -x°e-?c| + a J x?Ae~x dx = dT(a,
0 0 0
bo‘ladi. ►
Ma’lumki, ae (0,1] bo‘lsa, a + le (1,2] bo‘ladi. Г(а) funksiya-
ning bu xossasini ifodalovchi (4) munosabat F(o) funksiyaning (0,1]
dagi qiymatlariga ko‘ra uning (1,2] oraliqdagi qiymatlarini, umuman,
ixtiyoriy (n,n+1] dagi qiymatlarini topish imkonini beradi.
Natija. Г(«) funksiyaga (we TV) (4) formulani takror qo‘llash nati-
jasida (Г(1)=1)
Г(л) = (w-l)!
bo‘lishi kelib chiqadi.
3) Г(а) funksiyaning o‘zgarish xarakteri. Ravshanki,
Г(1) = j exdx = 1.
о
Yuqoridagi (4) formulaga ko‘ra
Г(2) = 1 • Г( 1) = 1
bo'ladi. Roll teoremasiga muvofiq, shunday a0 (1 < a0 < 2) nuqta
topiladiki,
Г(яо) = О
bo‘ladi. Ayni paytda, Vae (0,+°°) da
Г'(а) = J xa~le~x In2 xdx > 0
о
bo‘lganligi uchun Г'(a) funksiya (0,+o°) da qat’iy o‘suvchi bo‘ladi.
255
Binobarin, Г '(a) funksiya a0 nuqtadan boshqa nuqtalarda nolga aylan-
maydi. Demak,
Г'(о)= j xa4e~xlnxo5c = 0
о !
tenglama (0,+<«) oraliqda yagona yechimga ega. U holda
0 < a < a0 da Г'(«) < 0,
< a < 4-oo da Г'(о) > 0
bo ‘lib, Г(й) funksiya nuqtada minimumga ega bo'ladi. (a0 =1,4616...,
Г(«о) = minf(a) = 0,8856... bo'lishi topilgan).
Г(а) funksiya a > a0 da o‘suvchi bo'lganligi sababli a > n+1
bo‘lganda Г(а) > Г(п+1) = n! bo‘lib, undan
lim Г(а) =
bo'lishi kelib chiqadi. Agar a -> +0 da Г(а +1) -> Г(1) = 1 hamda
Г(а) = Г(^2
bo‘lishini e’tiborga olsak, u holda
lim Г(а) =
a-++0
ekanligini topamiz.
5°. Beta va gamma funksiyalar orasidagi bog‘Ianish. Beta va gamma
funksiyalar orasidagi bog‘lanishni quyidagi teorema ifodalaydi.
3- teorema. V(a, b) e {(a, b) e R2 : a e (0, +~), b e (0, +<*=)} uchun
B(a,b) =
Г(д)-Г(й)
Г(«+/>)
(5)
formula o‘rinli bo‘ladi.
◄ Ushbu Г(5) = J xs~'e~xdx \
о '
integralda x = (1 + u)t, (t > 0) almashtirish bajarib, s ni a+b ga
almashtiramiz. Natijada
Г(а + b) = J (1 + «)fl+64 ta+h~xe~(1+u},(l + и) dt
о
256
bo‘lib,
Г(а+Ь)
(1+м)0+л
J ta+b-le~(l+u)ldt
о
bo‘ladi.
Endi bu tenglikning har ikki tomonini ua~l ga ko‘paytirib, so‘ngra
(0,+°°)oraliq bo'yicha integrallab topamiz:
4-00
Г(а + b) J
о
(l+a)fl+A
ГА-1е-(1+«)гЛ
ya’ni
Г(а + b) B(a, b) = J
о
e if 1 du.
[1], 17-bob, 8-§da keltirilgan teoremadan foydalanib, keyingi
tenglikning o‘ng tomonidagi integrallarning o‘rinlarini almashtiramiz.
Natijada
bo‘ladi. Integralda ut = у almashtirish bajarib topamiz:
J y“ 1 ? 1 e ' e y dy
о
F(a + b) B(a, b) - J
о
dt =
= J t^e^dt J ya~{e~ydy = Г(/>) • Г(о).
о о
Demak,
Natija. Va e (0,1) uchun
sin®
(6)
bo‘ladi.
257
< (5) tenglikda b = l-a (0 < <7 < 1) deb olinsa, unda
B(a,l-a) =
Г(а)Т(1-д)
Г(1)
bo‘ladi. Ma’lumki,
B(a,l-a) = -^~,
sin an
r(l) = 1.
Demak, Г(а)Г(1 - a) = -Д- , (0 < a < 1). ►
smait
Agar (6) formulada a - deyilsa,
bo‘lishi kelib chiqadi.
1- misol. Ushbu J e~*2 dx integral hisoblansin.
0
•< Bu integralda x2 = t almashtirish bajaramiz. U holda
dx - —L dt = \t 2dt
bo‘lib,
[ e~xldx = [ t 2e~'dt [ t2 e~'dt =lr{-) =
J 2 J 2 J 2 \2/ 2
000
bo‘ladi. ►
f dx
2- misol. Ushbu J -—у integral hisoblansin.
0 1+x
•< Bu integralda 1 + x3 = almashtirish bajaramiz. U holda
4 y
258
Г dx
J 17?
о
x-- 11 Л '
У J У Н
_ 1 в / 2 1 \ 1 [з J [з] _ 1 тг _ л _ 2 тг
= з Ь’зГГ Г<1) 'з'ТТ^'^Т’зТз
з 2
bo'ladi. ►
Mashqlar
На
1. Va е R \ {0,-1,da Г(а) = lim———~—— bo‘li-
И-^ОО a(a+l)...(a+n)
shi isbotlansin.
2. Ushbu
xmdx
(a+bxn)p
(a > 0, b > 0, n > 0) integral beta funksiya
orqali ifodalansin.
3. Quyidagi (Г'(а))2 < Г(а)- Г"(а) tengsizlik isbotlansin.
259
16- в о в
KARRALI INTEGRALLAR
81-ma’ruza
Tekis shaklning yuzi hamda fazodagi jismning
hajmi haqida ba’zi ma’lumotlar
Aniq integralning tatbiqlari mavzusida tekis shaklning yuzi hamda
jismning hajmi haqida ma’lumotlar keltirilgan edi. Bu tushunchalar
karrali integrallar nazariyasida muhimligini inobatga olib, ular to‘g‘ri-
sidagi ta’rif va tasdiqlarni talab darajasida bayon etishni lozim topdik.
1°. Tekis shaklning yuzi va uning mavjudligi. Tekislikda Dekart
koordinatalari sistemasi berilgan bo‘lsin. Bu tekislikda sodda yopiq
chiziq bilan chegaralangan tekislik qismidan tashkil topgan Q shaklni
(tekislik nuqtalari to'plamini) qaraylik. Q shaklning chegarasini (sodda
yopiq chiziqni) 3Q bilan, QudQ ni esa Q bilan belgilaymiz:
Masalan, koordinatalari ushbu
x > 0, у > 0 , x + у < 1
tengsizliklarni qanoatlantiruvchi (x,y) nuqtalardan tashkil topgan
A = {(x, y): x > 0, у > 0, x + у < 1}
to‘plam 33- chizmada tasvirlangan uchburchak shaklini ifodalaydi.
OX o'qdagi birlik kesma
(0 < x < 1) OY o'qdagi birlik kes-
ma (0 < у < 1) hamda (1,0) va
(0,1) nuqtalarni birlashtiruvchi
to‘g‘ri chiziq kesmalari birgalikda
uchburchak shaklining chegarasi
ЭА ni tashkil etadi.
Tekislikda uchburchaklar, yopiq
siniq chiziq bilan chegaralangan te-
kislik qismidan tashkil topgan
ko'pburchaklar yuzaga ega va ular-
ni topish o'quvchiga maktab mate-
matika kursidan ma’lum.
260
Tekislikda Q shakljbilan birga A va В ko'pburchaklarni olaylik.
Agar A ko‘pburchakning har bir nuqtasi Q ga tegishli bo‘lsa, A ko‘p-
burchak Q shaklning ichiga chizilgan deyiladi (bunda A c Q bo‘ladi).
Agar Q ning har bir nuqtasi В ko‘pburchakka tegishli bo‘lsa, В ko‘p-
burchak Q shaklni o‘z ichiga oladi deyiladi (bunda Q с В bo'ladi).
Agar [iA va рБ lar mos ravishda A va В ko‘pburchaklarning yuza-
lari bo‘Isa, u holda
рЛ<рЯ (1)
tengsizlik bajariladi.
Aytaylik, Q shaklning ichiga chizilgan ko'pburchaklardan iborat
to'plam — {A}, Q shaklni o‘z ichiga olgan ko'pburchaklardan iborat
to‘plam {B} bo‘lib, ularning yuzalaridan iborat to‘plam esa mos
ravishda {рЛ} va {p/?} bo‘lsin.
Ravshanki, {рЛ} va {p5} lar sonlar to'plami bo‘lib, {рЛ}
yuqoridan, {p5} esa quyidan chegaralangan to‘plamlar bo‘ladi. U
holda to‘plamning aniq chegaralari haqidagi teoremaga ko‘ra
sup {рЛ} = p.0, inf {/лВ} = n*Q
lar mavjud. Odatda, p*0 son shaklning quyi yuzasi, ц Q son esa Q
shaklning yuqori yuzasi deyiladi.
Tasdiq. p.0 va p*0 miqdorlar uchun
p.0 < P*0 (2)
tengsizlik bajariladi.
Aytaylik, p.0 > ii“Q bo‘lsin. Bu holda, ravshanki, p.0 — p*Q
ayirma musbat bo'ladi. Aniq chegara ta’riflariga ko‘ra Ve > 0, jumladan,
e = |(p.0-p‘0)>O
uchun shunday Ao a Q , Q c Bo ko‘pburchaklar topiladiki,
рЛо > p* Q - e, pB 0 < ]iQ + e
tengsizliklar bajariladi. Bu tengsizliklardan foydalanib topamiz:
p50 - рЛо < p*0 + e - (p.0 - e) = \i*Q - p* Q + 2e =
= p*0 - p.0 + (p.0 - p*0) = o.
Keyingi tengsizlikdan {рЛ0 > p50 bo‘lishi kelib chiqadi. Bu esa
(1) munosabatga zid. Demak, (2) tengsizlik o'rinli bo‘ladi. ►
261
1-ta’rif. Agar ]itQ = y*Q tenglik o'rinli bo‘lsa, Q shakl yuzaga
ega deyiladi. Ushbu = u*Q miqdor Q shaklning yuzi deyiladi.
Uni nQ kabi belgilanadi:
1- teorema. Tekislikdagi shakl yuzaga ega bo‘lishi uchun Ve > 0
soni olinganda ham Q shaklni ichiga joylashgan shunday A ko'pbur-
chak, Q shaklni ichiga olgan shunday В ko‘pburchak topilib, ular uchun
цА - \iB < e (3)
tengsizlikning bajarilishi zarur va yetarli.
◄ Zarurligi. Aytaylik, tekislikdagi Q shakl yuzaga ega bo‘lsin:
Aniq chegara ta’riflariga ko‘ra, Ve > 0 uchun shunday
Ac Q, QcB
ko‘pburchak topiladiki, bunda
p.B<pQ + ~,
ya’ni + |
bo'ladi. Bu tengsizlikdan
цВ - jiA < e
bo‘lishi kelib chiqadi.
Yetarliligi. Aytaylik, A c Q , Q с В ko‘pburchaklar uchun
\xB - цА < e
tengsizlik bajarilsin. Ravshanki,
{iA < p.Q, pfi > p*Q.
Yuqoridagi (2) munosabatdan foydalanib topamiz:
M < p.Q < p*Q < jiB.
Bu va (3) tengsizlikka ko‘ra
- цЛ < e
bo‘ladi. Demak, ц*2 = ц Q. ►
262
Faraz qilaylik, tekislikda I chiziq (u yopiq yo,ki yopiq bo'lmasligi
mumkin) berilgan bo‘lsin.
2- tarif. Agar shunday Ao ko‘pburchak topilsaki,
1) l <= Л,
2) Ve > 0 uchun цЛ0 < e bo‘lsa, I nol yuzali chiziq deyiladi.
Masalan, / chiziq у = f (x) g C[a, Z>] funksiyaning grafigidan
iborat bo'lsa, u nol yuzali chiziq bo'ladi.
•< Ve > 0 sonni olib [a,b] segmentni shunday
(k = O,l,2..,n-l;xo = a,x„ = b) bo'laklarga ajratamizki, har bir
[xk , xr+r ] da f (x) funksiyaning tebranishi
bo'lsin. U holda I chiziqni o'z ichiga olgan Ло ko'pburchakning yuzi
n-1
Mo = У (Mk - mk)(xk+l -xk)
k=0
bo'ladi, bunda
Mk =sup/(x), хе[хьхы], (к = 0,1,...,и- 1),
mk = inf/(x), xe[xt,xw], (k = 0,1,...,и-1).
n-l n-l
Ravshanki, = У олкЬхк < -^—^bock = e.
fc=0 b~a k=0
Demak, Z — nol yuzali chiziq. ►
Bu tushuncha yordamida yuqoridagi 1-teoremani quyidagicha
ifodalasa bo'ladi.
2- teorema. Tekislikdagi Q shakl yuzaga ega bo'lishi uchun uning
chegarasi 3Q nol yuzali chiziq bo'lishi zarur va yetarli.
Natija. Agar tekislikdagi Q shaklning chegarasi dQ , har biri
у = f(x) e C[a,b] yoki x = g(y) e C[a,b]
funksiyalar tasvirlangan bir necha egri chiziqlardan tashkil topgan
bo'lsa, u holda Q shakl yuzaga ega bo'ladi.
Odatda, uzunlikka ega bo'lgan egri chiziq to‘g‘rilanuvchi chiziq
deyiladi. Quyida Q tekis shaklning yuzaga ega bo'lishining yetarli
shartini ifodalovchi teoremani isbotsiz keltiramiz.
263
3- teorema. Agar Q tekis shaklning chegarasi 3Q to'g'rilanuvchi
egri chiziq bo‘lsa, u Q yuzaga ega bo‘ladi.
2° . Yuzaning xossalari. Endi yuzaning asosiy xossalarini keltiramiz.
1) Agar tekislikdagi Q, va Q2 shakllar yuzaga ega bo‘lib, c Q2
bo‘lsa, u holda
Ц01 < [kQ2
bo'ladi.
2) Agar va Q2 tekis shakllar yuzaga ega bo‘lsa, u holda Qv и Q2
ham yuzaga ega va
h(Qi uQ2) < iiQi +ц22
bo‘ladi. Agar bu Qx va Q2 shakllar chegaralaridan boshqa umumiy
nuqtaga ega bo'lmasa, ya’ni Qi n Q2 = 0 bo‘lsa, u holda
u(Q] Q2) = pQ, + pQ2 bo'ladi. Bu yuzaning additivlik xossasi
deyiladi.
3°. Tekis shaklni bo'iaklash. Tekislikda biror yuzaga ega bo‘lgan
Q shakl berilgan bo‘lib,
QxQi -Qn
shakllar uning yuzaga ega bo‘lgan qismiy shakllari, yani
fteg, (Ы,2,...,л)
bo‘lsin. Agar QiQ2...Qn lar uchun
1) Qi ^>Q2 u....uQ„ = Q,
2) ixtiyoriy Qk va £), lar (k = 1,2,...,«; i = 1,2,..., w) umumiy
nuqtaga (chegaralaridagi nuqtalardan boshqa) ega bo'lmasa, u holda
O](22...Q„ lar 0 da bo'iaklashbajaradiyoki Qshakl QiQ2...Q„ shakl-
larga bo‘laklangan deyiladi.
Q shaklni QXQ2 ...Qn larga bo'laklashni P bilan belgilanadi:
P = {Q\Qi-Qn}-
Ushbu d(Qk) = supp((x',y'),(x',y')),
(x',/)eQt, (x", y")e Qk, (k = 1,2,...,и)
miqdorlarning eng kattasi P bo ‘laklashning diametri deyiladi va Xp
kabi belgilanadi:
X =raaxd(Qk).
l<k<n
264
Masalan, ushbu
Qki = {(*>У)e R2 '-xk - x - -^+1 ’y< -У -Ум’}
(к = 0,1,...,n-1; i = 0,1,...,m-1; x0 = a> xn = b> Л = c> Ут =d>
to‘g‘ri to‘rtburchaklar
Q = {(x,y)e R2 :a< x<b,c<y<d\
tekis shaklning P bo‘laklashini hosil qiladi. Bunda
X_ = max у Ax*2 + Ay,2
0<i<m-l
b° 4’dl Л3 fazoda jismning hajmi. R3 fazoda Dekart koordinatalar
sistemasi berilgan bo‘lsin. Bu fazoda, chegaralangan yopiq sirt bilan
(yoki bunday sirtlarning bir nechtasi bilan) o‘ralgan kjismni (Я3 fazo
qismini) qaraylik. Kjismni o‘rab turuvchi sirtni - V, jismning che-
garasini ЭГ bilan, UuOE ni V bilan belgilaymiz:
V =ИиЭИ.
Masalan, koordinatalari ushbu
X2 + y2 + Z2 < 1
tengsizlikni qanoatlantiruvchi (x,y,z)) nuqtalardan tashkil topgan
S = {(x,y,z)e R3 ;x2 +y2 +Z2 <1}
to'plam, markazi (0,0,0), radiusi 1 ga teng bo‘lgan shami - jismni
ifodalaydi. Uning chegarasi esa
35 = {(x,y,z)e R3 :x2 +y2 +z2 =1}
sfera bo‘ladi. Bunday jism - shar hajmga ega va quyidagiga teng:
tz 4
Umuman, fazoda ko‘pyoqliklarning hajmga ega bo‘lishi va uni
topish qoidalari o‘quvchiga o‘rta maktab matematika kursidan ma’lum.
Endi R3 fazoda Г jism bilan birga f va G Wpyoqliklarni qaraylik.
Agar F ko‘pyoqlikning har bir nuqtasi V ga tegishli bo'lsa,
F ko'pyoqlik И jismning ichiga joylashgan deyiladi (bunda Fc V
bo'ladi). Agar V ning har bir nuqtasi G ko'pyoqlikka tegishli bo‘lsa,
G ko‘pyoqlik Kjismni o‘z ichiga oladi deyiladi (bunda у c G).
265
Agar pF va pG lar mos ravishda F va G ko'pyoqliklarning hajm-
lari bo'lsa, u holda
pF < pG
tengsizlik bajariladi.
Aytaylik, V jismda joylashgan ko'pyoqliklar hajmlaridan iborat
{pF} to'plam, V jismni o'z ichiga olgan ko'pyoqliklar hajmlaridan
iborat {pG} to'plam bo'lsin. U holda
sup{p£} = p.K, inf{pG} = pV
lar mavjud.
3- ta’rif. Agar
p*F = pV
tenglik o'rinli bo'lsa, jism hajmga ega deyiladi. Ushbu
Р.Г = pV
miqdor Vjismning hajmi deyiladi. Uni pF kabi belgilanadi:
р,К = р’И^.рИ.
Tekis shaklning yuzi, fazodagi jismning hajmi tushunchalarida
bir-biriga o'xshashlik borligini inobatga olib, jism hajmining mav-
judliligi haqidagi teoremani keltirish bilan kifoyalanamiz.
4- teorema. Fazodagi Fjism hajmga ega bo'lishi uchun Ve > 0
son olinganda ham Kjismning ichida joylashgan shunday Fko'pyoqlik,
Fjismni o'z ichiga olgan shunday G ko'pyoqlik topilib, ular uchun
pG - \iF < e tengsizlikning bajarilishi zarur va yetarli.
Mashqlar
1. Aytaylik, /(x)e C[a,b] bo'lib, Vxe [о,6] da f(x) > 0 bo'l-
sin. Bu funksiya grafigi — x = a, x = A chiziqlar hamda [a, b\ kesma
bilan chegaralangan shakl yuzaga ega bo'lishi isbotlansin.
2. Tekislikda Q shakl berilgan bo'lib, {An} va {B„} ko'pburchaklar
ketma-ketligiuchun An cO , Bn c[) (n = l,2,...) bo'lsin. U holda
Q shakl yuzaga ega bo'lishi lim An - lim Bn tenglikning bajarilishi
orqali ifodalanishi mumkinmi?
266
82-ma’ruza
Ikki karrali integral tushunchasi va
uning mavjudligi
1°. Funksiyaning integral va Darbu yig‘indilari. Faraz qilaylik,
tekislikda yuzaga ega bo‘lgan D shakl (to'plam) berilgan bo'lsin. Bu
to‘plamda f (x, y) funksiya aniqlangan va chegaralangan:
3M = const, 3m = const, V(x, y)&D, m<f(x,y)<M.
D ning biror
P = {D1,D2,.
bo'laklanishi va har bir Dk da ixtiyoriy (&k,nk) e Dk nuqtani (k = 1,
2,...,n) olib quyidagi
k=l
yig'indini tuzamiz.
1-ta ’rif. Ushbu <5 = (£>k, ) \kDk
k=l
yig'indi f(x,y) funksiyaning integral yig'indisi (Riman yig'indisi)
deyiladi.
Keltirilgan ta’rifdan ko'rinadiki, integral yig‘indi/(x,y) funksiyaga,
D to‘plam va uni bo‘laklash usuliga hamda har bir (^ ,'r]A )e Dk
nuqtalarga bog'liq bo‘ladi:
= {f^k^kY
Modomiki, f (x,y) funksiya D da chegaralangan ekan, u har bir
Dk da (k = 1, 2,...,n) ham chegaralangan bo'ladi. Demak,
mk = inf{f(x,y): (x,y)e Dk},
Mk = sup{/(x,y) : (x,y) e Dk}
mavjud. Ayni paytda, V(x, y) e Dk uchun
mk < f(x,y) < Mk (1)
tengsizliklar bajariladi. c
267
2- ta’rif. Ushbu
s = ^mk\iDk, S = ^Mk\iDk \
k=l A=1 ’
yig'indilar mos ravishda Darbuning quyi hamda yuqori yig‘indilari
deyiladi.
Funksiyaning Darbu yig‘indilari f (x,y) funksiyaga, D to'plam va
uning bo'laklashiga bog'liq:
s = sp(f), S=Sp(f)
bo'lib, har doim s<Stengsizlik bajariladi. (1) tengsizlikdan foydalanib
topamiz:
• ^mkiiDk < ^f^k,i\k)y.Dk <^Mk\iDk .
k=\ k=\ k=\
Demak, s < о < S .
2°. Ikki karrali integral ta’riflari. Aytaylik, f(x,y) funksiya yuzaga
ega bo'lgan D to'plamda aniqlangan va chegaralangan bo'lsin. D ning
P = {A,D2,...,Dn}
bo'laklashini olib, berilgan funksiyaning integral yig'indisini tuzamiz:
n
CT = ^f^k^k^Dk .
k=l
3- ta’rif. Agar Ve > 0 son olinganda ham shunday 8 > 0 son
topilsaki, D ning diametri kp < 8 bo'lgan har qanday P bo'laklash
hamda har bir Dk da olingan ixtiyoriy , г|л) lar uchun
|o-/| < e
tengsizlik bajarilsa, /son о yig'indining \,—> 0 dagi limiti deyiladi va
lim (5 = J
kabi belgilanadi.
4-ta’rif. Agar 0 da/(x,y) funksiyaning integral yig'indisi
limiti mavjud va chekli / ga teng bo'lsa, f(x,y) funksiya D da integ-
rallanuvchi deyiladi. /soniga esa/(x,y) funksiyaning D bo'yicha ikki
karrali integral! deyiladi. Uni quyidagicha
\\f(x,y}dxdy
D
268
kabi belgilanadi. Demak,
ff f(x,y)dxdy = lim <5 = lim \ f (f,k ,x\k)\iDk .
Masalan, f(x,y) = C = const bo‘lsin. Bu funksiyaning integral
yig‘indisi
c = ^CiiDk =Cp.D
ti <
bo‘lib, uning ikki karrali integral!
JJ Cdxdy - lim C\xD = C]iD
D
bo‘ladi. Xususan, C = 1 bo‘lganda quyidagiga ega bo'lamiz:
jj\dxdy - \iD.
D
Funksiyaning ikki karrali integrali yuqori hamda quyi integrallar
yordamida ham ta’riflanishi mumkin.
Faraz qilaylik, f(x,y) funksiya yuzaga ega bo‘lgan D to‘plamda
berilgan va chegaralangan bo‘lsin. Dning turli bodaklashlaridan tashkil
topgan to'plamni {/*} deylik: P - {Д, D2,..., Dn }.
Har bir P e {P} bo'laklashga nisbatan f (x,y) funksiyaning Darbu
yig‘indilarini tuzib, ushbu {^(7)}, {5^(7)} to‘plamlarni hosil
qilamiz. Bu to‘plamlar chegaralangan bo‘ladi.
5- ta’rif. pp(/)} to‘plamning aniq yuqori chegarasi f(x,y) funk-
siyaning quyi ikki karrali integrali deyiladi va
D
kabi belgilanadi. Demak,
L = \\f{x,y)dxdy = sup (s (/)) = sup(Y mk\iDk).
p^ip} Pe{p}
6- ta’rif. {5^(7)} to‘plamning aniq quyi chegarasi f(x,y) funk-
siyaning yuqori ikki karrali integrali deyiladi va
269
J = JJ f(x,y)dxdy
D
kabi belgilanadi. Demak, ,
J = \\f(x,y)dxdy = inf (5 (/)) = inf (£ Mkp.Dk).
JJ Pe{?} 7>e{P} “
Demak, chegaralangan f (x,y) funksiyaning har doim quyi hamda
yuqori integrali mavjud bo'ladi.
7- ta’rif. Agar J = J
bo‘lsa,/(x,y) funksiya Dto'plamda integrallanuvchi, ularning umumiy
qiymati J = J =J esa f (x,y) funksiyaning D bo'yicha ikki karrali
integrali deyiladi. Demak,
^f(x,y)dxdy = J = J. L
D
E s I a t m a. Agar J Ф J bo'lsa, f (x,y) funksiya D da integrallan-
maydi.
3°. Darbu yig‘indilarining xossalari. Aytaylik,/(x,y) funksiya yuzaga
ega bo'lgan D to'plamda berilgan va chegaralangan bo'lsin. D to‘p-
lamning bo'laklashlari to'plami P = (P) dagi P = {Д, D2,..., Dn}
bo'laklashga nisbatan f(x,y) funksiyaning integral hamda Darbu
yig'indilarini kiritamiz:
n
GP(f'^k^k) = ^f^k’^k)pDk!,
k=l
n n
sp(f) = Уm^Dk , Mk\kDk ,
k=\ k=l
bunda mk = inf {/(x,y): (x,y) <= Dk],
Mk =sup{/(x,y): (x,y)e Dk}
bo‘lib, V(x,y)eDk uchun quyidagi ifoda o'rinli:
/^ </(x,y) < 34 .
270
Ma’lumki, 33-ma’ruzada /(x) funksiya Darbu yig'indilarining
xossalari keltirilib, ular batafsil isbotlangan edi.
Xuddi shunday xossalar f(x,y) funksiya Darbu yig‘indilari uchun
ham o‘rinli bo‘ladi. Ular awalgidek mulohaza asosida isbotlanishini
e’tiborga olib, mos xossalami keltirish bilan kifoyalanamiz.
1) Ve > 0 olinganda ham (£fe,r|A)e Dk nuqtalarni (£=1,2,
shunday tanlab olish mumkinki,
0<5p(/)-^(/;^,nJ<e,
shuningdek, , t)a ) e Dk nuqtalarni yana shunday tanlab olish mum-
kinki,
bo‘ladi. Bu xossa Darbu yig'indilari integral yig'indi uchun aniq
yuqori va aniq quyi chegara bo‘lishini bildiradi.
2)Aytaylik, P. = {Dl,D2,...,Dk_l,Dk,Dk+y,...,Dn},
lar D to‘plamning bo‘laklashlari bo‘lib,
Dk - D'k u Dk , D'k n D" = 0
bo'lsin. U holda
sn<Sp2(f), 5ft(/)<5A(/)
bo'ladi. Bu xossa D ning bo'laklashdagi bo'laklar soni orta borganda
ularga mos Darbuning quyi yig'indisining kamaymasligi, yuqori yig'in-
disining esa oshmasligini bildiradi.
3) Agar P] va P2 lar D ning ikki bo'laklashi bo'lib, sPi (/), Sn (f)
va sn (/), (f) larf (x,y) funksiyaning shu bo'laklashlarga nisbatan
Darbu yig'indilari bo'lsa, u holda
(/)
bo'ladi.
Bu xossa, D ning bo'laklashlariga nisbatan tuzilgan quyi yig'in-
dilar to'plami {u (/)} ning har bir element! (yuqori yig'indilar to'p-
lami [Sp (/)} ning har bir dementi) yuqori yig'indilari to'plami
{^z>(/)} ning istalgan elementidan (quyi yig'indilar to'plami
p,, (/)} ning istalgan elementidan) katta (kichik) emasligini bildiradi.
271
4) Ushbu
sup { <;//)}< inf {Sj, (/)}
munosobat o‘rinli. Bu xossa f(x,y) funksiyaning quyi ikki karrali
integrali, uning yuqori ikki karrali integralidan katta emasligini bildiradi:
J< J .
5) Ve > 0 olinganda ham shunday 8 > 0 topiladiki, D ning diametri
Xp < 8 bo'lgan barcha bo‘laklashlari uchun
0<5//)-J<e, 0<J-5p(/)<e
bo‘ladi. Bu xossa f (x,y) funksiyaning yuqori hamda quyi integrallari
Xp -> 0 da mos ravishda Darbuning yuqori hamda quyi yig‘indilari-
ning limiti ekanligini bildiradi.
4°. Ikki karrali integralning mavjudligi. f (x,y) funksiyaning Darbu
yig'indilari va ularning xossalaridan foydalanib, ikki karrali integralning
mavjudligi haqidagi teoremani keltiramiz.
Aytaylik, yuzaga ega bo‘lgan D to‘plamda f(x,y) funksiya beril-
gan va chegaralangan bo‘lsin.
1- teorema. f(x,y) funksiya to‘plamda integrallanuvchi bo‘lishi
uchun, Ve > 0 son olinganda ham, shunday 8 > 0 soni topilib, D ning
diametri > 8 bo‘lgan har qanday P bo‘laklashiga nisbatan Darbu
yig‘indilari ushbu
^(/)-5p(/)<£ _ (2)
tengsizlikni qanoatlantirishi zarur va yetarli.
◄ Zarurligi. Faraz qilaylik, f (x,y) funksiya D da integrallanuvchi
bo‘lsin. Ta’rifga ko‘ra J = J =J bo‘ladi, bunda
L = sup(s (/)) = sup(V mkuDk),
p p k?q
J = inf(5p(/)) = inf(^M^).
*=?
Ayni paytda, Darbu yig‘indilarining 5- xossasiga ko‘ra
Ve > 0, 38 > 0, Xp < 8, Vp e (P):
5p(/)-J<|, J-5p(/)<|
272
va J = J = J bo'lgani uchun
/-^(/)<|
tengsizliklar o‘rinli bo'ladi. Keyingi tengsizliklardan
bo'lishi kelib chiqadi.
Yetarliligi. Aytaylik, Ve > 0, 38 > 0, < 5, Vp e (P):
Sp(J)-sp(f)<t
bo'lsin, f (x,y) funksiya D da chegaralanganligi uchun
sup (/)} = J, inf {5p (/)} = J
mavjud bo‘lib, Darbu yig'indilarining 4-xossasiga ko'ra J < J bo'ladi.
Demak,
Bu tengsizliklar va (2) shartdan foydalanib topamiz:
0 < J-J < Sp(f) - sp(f) < £..
Demak, J<J. f(x,y) funksiya D da integrallanuvchi. ►
Aytaylik, D ning P - {DifD2,...,Dn} bo'laklashning Dk bo'la-
gida (k = 1,2,...,») f(x,y) funksiyaning tebranishi
=sup{/(x,y): (x,y)e Dk}-mf {f(x,y): (x,y)e Dk}
bo'lsin. Unda f (x,y) funksiyaning D da integrallanuvchi bo'lish sharti
JcojiZk-CE, (3)
k=l
ya’ni
(4)
ko'rinishlarga keladi.
Demak, f(x,y) funksiyaning D to'plamda integrallanuvchi bo'li-
shini isbotlash uchun (2), (3), (4) shartlardan birining bajarilishini
ko'rsatish yetarli bo'ladi.
273
Mashqlar
1. Ushbu D = {(x,y)e R2 :0<x<l,0<y<l} to'plam (tekislik-
dagi kvadrat)
x = x.=-, i = 1,2,3, ,.,n , у - у,- = -, к - 1,2,3,..,л
n n
chiziqlar yordamida Djk larga bo'laklangan. Shu bo'laklashning diametri
topilsin.
2. Yuqoridagi D to'plam va uning P = {Djk -J, к = 1,2,..., fl} bo‘-
laklashga nisbatan f(x,y) = x2+y2 funksiyaning
a) Darbu yig'indilari,
i к
b) har bir Dik da , T|£ = - deb, integral yig'indisi topilsin.
3. Aytaylik, D — tekislikdagi yuzaga ega bo'lgan to'plam bo'lsin.
Ushbu
. ч [1, agar (x, y) e D, x e Q,y e Q bo'lsa,
P[X, y) = -{
[0, agar (x,y)e D,x va у
laming kamida bittasi irratsional bo'lsa, funksiyaning D da integralla-
nuvchi bo'lmasligi isbotlansin.
4. /(x,y) funksiya yuzaga ega bo'lgan D to'plamda chegaralangan
bo'lib, J va J lar mos ravishda funksiyaning yuqori va quyi ikki
karrali integrallari bo'lsa, / < J bo'lishi isbotlansin.
5. f (x,y) funksiyaning Darbu yig'indilari uchun
limSp(J) = J, limsp(fy=J
^р->0 Лр->0 F
bo'lishi isbotlansin.
83- ma’ruza
Integrallanuvchi funksiyalar sinfi. Integralning asosiy
xossalari
1°. Uzluksiz funksiyalarning integrallanuvchi bo‘lishi. Uzluksiz
funksiyalarning integrallanuvchi bo'lishini quyidagi teorema ifodalaydi.
1- teorema. Agar f (x,y) funksiya chegaralangan yopiq D to'plamda
uzluksiz bo'lsa, u shu to'plamda integrallanuvchi bo'ladi.
274
◄ Ixtiyoriy 8 > 0 sonni olaylik. f(x,y) funksiya chegaralangan
yopiq D da uzluksiz. Binobarin, funksiya D da tekis uzluksiz. U holda
songa ko‘ra, shunday 3 > 0 son topiladiki, D ning diametri Xp > 3
bo‘lgan
р = {д,д,...,ад
bo'laklashning har bir Dkbo'lagida (k = 1,2,...,ri)f(x,y) funksiyaning
tebranishi a>k uchun
tengsizlik bajariladi.
Shunday P bo'laklashlarga nisbatan
n n
*=i M k=\
bo'ladi. Demak, f (x,y) funksiya D da integrallanuvchi.
2°. Uzilishga ega bo'lgan funksiyaning integrallanuvchi bo'lishi.
Ba’zi bir uzilishga ega bo'lgan funksiyalarning integrallanuvchi bo'lishi
haqidagi teoremani keltirishdan awal bitta sodda tasdiqni bayon etamiz.
Aytaylik, tekislikda yuzaga ega bo'lgan D to'plam berilgan bo'lib,
I esa shu to'plamga tegishli nol yuzali chiziq bo'lsin.
Tasdiq. Ve > 0 son olinganda ham shunday 8 > 0 topiladiki, D
ning diametri kp > 3 bo'lgan VP e fP bo'laklash olinganda, bu
bo'laklashning Ichiziq bilan umumiy nuqtaga ega bo'lgan bo'lakchalari
yuzalarining yig'indisi 8 dan kichik bo'ladi.
◄ I chiziq nol yuzali bo'lganligi uchun shunday A ko'pburchak
topiladiki,
1) IcA,
2) Ve > 0 uchun рЛ < e bo'ladi. Aytaylik, I n ЭА = 0 bo'lsin.
I chiziq nuqtalari bilan ЭА nuqtalari orasidagi masofaning eng kichigini
8 (8 > 0) deylik. U holda > 8 bo'lgan VP e fP bo'laklashning
I chiziq bilan umumiy nuqtaga ega bo'lgan burchaklari A ko'pburchak-
ka tegishli bo'ladi. Binobarin, bunday bo'lakchalar yuzalarining yig'in-
disi 8 dan kichik bo'ladi. ►
275
2- teorema. Agar f (x,y) chegaralangan yopiq D da berilgan bo‘lib,
bu to‘plamga tegishli chekli sondagi nol yuzali chiziqlarda uzilishga
ega, qolgan barcha nuqtalarda uzluksiz bo‘lsa, f(x,y) funksiya D da
integrallanuvchi bo'ladi.
•< Soddalik uchun f (x,y) funksiya D dagi bitta nol yuzali I chi-
ziqda uzilishga ega, qolgan barcha nuqtalarda uzluksiz deylik.
Ixtiyoriy e > 0 sonni olamiz. U holda I <z А, цА < e bo'lgan
A ko‘pburchak (A a D) D ni A va D\A qismlarga ajratadi.
Ravshanki, f(x,y) funksiya D\A da tekis uzluksiz. U holda
Ve > 0 ga ko‘ra shunday 3j > 0 topiladiki, D ning diametri > 8,
bo‘lgan P bo‘laklashining har bir bo‘lakchasida f (x,y) funksiyaning
tebranishi quyidagicha bo'ladi:
<f>k < e.
Yuqoridagi tasdiqqa binoan va Ve > 0 ga ko‘ra shunday 82 > 0
topiladiki, D ning diametri Xp > 32 bo‘lgan P bo'laklashining A ko‘p-
burchak bilan umumiy nuqtaga ega bo‘lgan bo'lakchalari yuzalari
yig‘indisi e dan kichik bo‘lishini topamiz.
Endi 8 = min{81,82}
deb, diametri Xp > 8 bo‘lgan D ning
P = {Dt,D2,...,D,}
bo‘laklashini olib, unga nisbatan tuzilgan Darbu yig‘indilari ayirmasi
= (1)
b=l
ni qaraymiz.
(1) tenglikning о‘ng tomonidagi yig‘indi n ta haddan iborat. Uni
ikki qismga ajratamiz:
= ^'(0kiiDk + ^'(oky.Dk ,
k=\
bunda cOfchA ifoda — Pbo'laklash bo‘lakchasi Dk laming Л ko‘p-
burchakdan tashqarisida joylashganlariga mos (1) ning hadlaridan
iborat yig'indi, esa (1) ning qolgan barcha hadlaridan
tashkil topgan yig‘indi.
276
Yuqorida aytilganlami e’tiborga olib topamiz:
+£ ОцД. + Q-2e = e(pZ> + 2Q).
k=l
Bunda Q — funksiya /(x,y)ning D dagi tebranishi. Keyingi tengsizlikdan
Hm=0
x',->0 k=i
bo'lishi kelib chiqadi. Demak, f{x,y) funksiya D da integrallanuvchi. ►
3’. Ikki karrali integralning xossalari. Ikki karrali integral ham
[1], 35- ma’ruzada batafsil bayon etilgan aniq integralning xossalari
singari qator xossalarga ega. Shuni ham aytish kerakki, ulami isbotlash
jarayonlaridagi mulohazalar bir-biriga o'xshash bo'ladi. Shularni
e’tiborga olib, quyida keltiriladigan xossalarning ba’zilarini isbotlash
yo'l-yo'riqlarini, ba’zilarini esa isbotsiz keltirish bilan kifoyalanamiz.
1) Faraz qilaylik, J\x,y) funksiya D to'plamda integrallanuvchi
bo'lsin. Agar D nol yuzali I chiziq bilan umumiy ichki nuqtaga ega
bo'lmagan bog'lamli Dv va D2 to'plamlarga ajralgan bo'lsa, f(x,y)
funksiya har bir D, va D2 larda integrallanuvchi va
fff(x,y)dxdy =
D Oi D2
bo'ladi.
•4 Aytaylik,
lar mos ravishda D{ va D2 laming bo'laklashlari bo'lsin. Bu bo'lak-
lashlar D to'plamning
P = {Z)i(1), , Д(2), ,.., , D<m)]
bo'laklashlarini hosil qiladi. Agar
(/), (/), (/), (/), ^(/), Sp(f)
lar f(x,y) funksiyaning Px, P2, P bo'laklashlariga nisbatan Darbu
yig'indilari bo'lsa, u holda
Dx c D Sn (/) - (/) < Sp (/) - sp (/),
D2 c D (/) - Sp2 (/) < Sp (/) - sp (/)
JJ f(x,y)dxdy + jjf(x,y)dxdy (2)
277
bo'lib, quyidagi ifodaga ega bo‘lamiz:
Sp(f)-sp(f)<£^Spi(f)-sp> (/)<e, Sn(J")-Sp2 (/)<£.
Demak, f(x,y) funksiya D} va D2 to'plamlarda integrallanuvchi. Ushbu
Sp(f) = SPl(f) + SP2(f), sp(f) = Spi(f) + Sp2(f)
tengliklarni e’tiborga olib,
JJ f{x,y)dxdy = JJ f(x,y)dxdy + JJ f(x,y)dxdy
D £>2
bo'lishini topamiz. ►
Yuqoridagi xossaning aksi ham o'rinli, ya’ni f{x,y) funksiya har
bir Dx va D2 to‘plamlarda integrallanuvchi bo‘lsa, u D da integralla-
nuvchi bo'lib, (2) tenglik o‘rinli bo‘ladi.
2) Agar f(x,y) funksiya Dda integrallanuvchi bo‘lsa, cf(x,y) funk-
siya (c = const) ham D da integrallanuvchi va
JJ cf\x,y)dxdy = cJJ f(x,y')dxdy
D D
bo‘ladi. Bu xossaning isboti ushbu
M X № = c lim )p^
tenglikdan kelib chiqadi.
3) Agar f (x,v) va g(x,y) funksiyalar D da integrallanuvchi bo‘lsa,
f (x,y) ± g(x,y) funksiya ham D da integrallanuvchi va
JJ[/(*, У) ± g(x, У)]dxdy = JJ f(x, y)dxdy ± JJg(x, y)dxdy
D D D
bo'ladi.
4) Agar f (x,y) funksiya D da integrallanuvchi bo'lib, V (x, у) e D da
f(x,y) > 0 bo'lsa,
ft f(x,y)dxdy >0
D
ga ega bo'lamiz. Bu xossaning isboti
>o
^°fc=l • .
bo'lishidan kelib chiqadi.
278
5) Agar f (x,y) va g(x,y) funksiyalar D da integralanuvchi bo‘lib,
V(x,y)e D uchun f(x,y) < g(x,y) bo‘lsa, u holda
x, у)dxdy < JJ g(x, у')dxdy Q
D D
bo'ladi.
•4 Bu xossaning isboti g(x,y) - f(x,y) funksiyaga 5- xossani tatbiq
etish va 3- xossadan foydalanish natijasida kelib chiqadi. ►
6) Agar f(x,y) funksiya D da integrallanuvchi bo‘lsa, u holda
\f (*, y)| funksiya ham D da integrallanuvchi va quyidagi ifoda o‘rinli
bo‘ladi:
< jj|/(x,y)|dxdy.
D D
4°. O‘rta qiymat haqidagi teoremalar. Aytaylik, f (x,y) funksiya
yuzaga ega bo‘lgan D to‘plamda berilgan va chegaralangan bo'lsin:
ЭМ = const, Вт = const, V(x,y) e D :
3- teorema. Agar f (x,y) funksiya D da integrallanuvchi bo‘lsa, u
holda, shunday a son (m < a < M) topiladiki, bunda
fff(x,y)dxdy - apZ>
D
bo'ladi.
•< Yuqorida keltirilgan ikki karrali integralning xossalaridan
foydalanib topamiz:
x,y)dxdy = a => Jj/(x,y)drJy = apD,
D
(m < a < M). ►
Bu teoremadan quyidagi natija kelib chiqadi.
Natija. Agar f(x,y) funksiya bog'lamli yopiq D to‘plamda uzluk-
siz bo‘lsa, u holda shunday (£,T|)e D nuqta topiladiki,
Д f(x,y)dxdy - /(£,r|)pZ)
D
bo‘ladi.
279
4- teorema. Agar f (x,y) va g(x,y) funksiyalar D to'plamda integ-
rallanuvchi bo'lib, V(x,y)e D uchun g(x,y) > 0 (yoki g(x,y) < 0)
bo'lsa, u holda shunday a son (m < a < M) topiladiki, bunda
Jjf(x,y)g(x,y)dxdy = affg(x,y)dxdy ।
D D
bo'ladi.
Mashqlar
l. Agar f(x,y) funksiya chegaralangan yopiq D c R2 to'plamda
chegaralanmagan bo'lsa, uning D da integrallanuvchi bo'lmasligi isbot-
lansin.
2. Agarf (x,y) funksiya D cz R2 da integrallanuvchi bo'lsa, \f (x, y)|
funksiyaning ham D da integrallanuvchi bo'lishi ko'rsatilsin.
3. Ma’lumki, ushbu
м [/] = Л JJ f(x, y)dxdy
' d -
miqdor f(x,y) funksiyaning D dagi o'rta qiymati deyiladi.
Quyidagi
f(x, y) = sin2 x sin2 у
funksiyaning D = {(x, y) g R2 : 0 < x < л, 0 < у < л} dagi o'rta qiy-
mati topilsin.
4. Ushbu -j < JJ (x2 -y2)dxdy < 4л tengsizliklar isbotlansin,
D
bunda D - {(x,y) g R2 : x2 +y2 -2x < 0}.
84- ma’ruza
Ikki karrali integralni hisoblash
1°. To‘g‘ri to'rtburchak to'plam bo'yicha ikki karrali integrallarni
hisoblash. f(x,y) funksiya tekislikdagi D = {(x,y) g R2 : a < x < b,
c<y<d} to'plamda berilgan bo'lsin. Bu f(x,y) funksiyaning D
bo'yicha ikki karrali integralini hisoblash masalasini qaraymiz.
280
1- teorema. f (x,y) funksiya quyidagi shartlarni bajarsin:
1) f(x,y) funksiya D da integrallanuvchi;
2) Har bir tayin x & [a,b] da
J(x) = ]f(x,y)dy
integral mavjud.
U holda J(x) funksiya [a,b] da integrallanuvchi, ya’ni
j J(x)dx = j J/(x,y)rZy dx
b{ d
mavjud va
fff(x,y)dxdy = j j f(x,y)dy dx
bo‘ladi.
◄ [a,b\ segmentning
a = x0 < x, < x2 < ... < xn = b ,
\c,d\ segmentning
с = Уо < У1 < У2 < - < Ут = d
nuqtalari yordamida D uchun ushbu
p = {Dik} = {(*>У) 6 R2 xt <x< x,+1, yk < у < y*+J,
0=0,1,2,...,м-1; к = 0,1,2,...,т-1)
bo‘laklashni hosil qilamiz. Uning diametri
kp - max Jax,2 + Ay* >
(Ax,- = x,-+1 -X,-, \yk = уы -yk-i = Q, 1,2,...,n -1; к = 0,1,2,..., m -1)
boUadi. Aytaylik,
mik = inf {/ (x, у): (x, y) e Dik },
Mik = sup {f (x, у): (x, у) e Dik },
(i = 0,1,2, ...,n-l; к = 0,l,2,...,m-l)
boUsin. Ravshanki, V(x,y)e Dik uchun
281
mik <f(x,y)< Mik
Ук+l Ук+l Ук+l
bo‘lib, J mikdy < j f(x,y)dy< J Mikdy,
Ук Ik Ук -
Л+1
ya’ni mik^yk < j f (x,y)dy < Mik&yk
ik
bo‘ladi.
Keyingi tengsizlikni к ning к = 0,l,2,...,w -1 qiymatlari uchun
yozish, so‘ngra ularni hadlab qo'shish natijasida
m-l d m-l
У mik^yk J f(x,y)dy <y MikAyk (2)
k=0 c £=0
d
hosil bo‘ladi. Ushbu jf(x,y)dy
c
d
integral x ning F(x) = J f(x, y)dy
c
funksiyasi bo‘lib, bu funksiya [a,b\ da, jumladan, [x,,xz+1] da che-
garalangan bo‘ladi. Agar
m, = inf {F(x), x e [x,, x,+I ]},
Mj =sup{F(x),xe [x,,x,+1]}, (i = 0,1,2,3,n -1)
deyilsa, (2) munosabatga ko‘ra
У Щк^Ук <1Ц< Mi Mik\yk
k=0 k=0
bo‘lib, undan
m-l
о < M,mi < У (Mik - m* )Лук
л=о
bo‘lishi kelib chiqadi. Bu tengsizlikni Лхк ga ko'paytirib, so‘ngra
282
hosil bo'lgan tengsizlikni i ning i = 0,l,...,«-l qiymatlarida yozib,
ularni hadlab qo'shib topamiz:
к-1 к-l m-1
0 < £(M,. - m,^xk < - ^Dk = Sp(f) - sp(f).
i=0 /=0 A=0
Modomiki, f (x,y) funksiya D da integrallanuvchi ekan, u holda
Xp -> 0 da (max &xk -> 0 j da
K-l
-т, )Дхл-*0
/=o
bo'ladi. Bu esa
d
= Jf(x,y)dy
funskiyaning \a,b\ da integrallanuvchi ekanini bildiradi.
b b
Demak, jF(x,y)flh: = J J/(x,y)d> dx
a a Lc
integral mavjud.
(2) tengsizlikni [x,, x,+1 ] oraliq bo'yicha hadlab integrallab topamiz:
x'+l m-1 Xiy
] J
Xi Xi
d x'+l m-1
\f(x,y)dy dx< J У Mik&ykdx=>
, С _ Xj
п-\ т-\
ЕЕ &ук < J J f(X, у) dy \dx <
;=0 А:=0
я-l w-1
У У Л4Мдд,
/=о А:=0
Ъ
]f(x^y^dy dx<sp(f)
a Le-
~d
ya’ni
munosabatga kelamiz. Ravshanki,
sp(f) < JJ f(x,y)dxdy < Sp(f)
D
(3)
(4)
283
N?k
Sp(f)-sp(f)<z.
d
a
d
U holda (3) va (4) munosabatlardan
b[d
JJ f(x,y)dxdy = J f(x,y)dy dx
bo'lishi kelib chiqadi. ►
2- teorema. f (x,y) funksiya quyidagi shartlarni bajarsin:
1) f(x,y) funksiya D da integrallanuvchi,
2) har bir tayin у e[c,d] da
J(y) = ]f(x,y)dx
integral mavjud.
U holda J(y) funksiya [c,d] da integrallanuvchi, ya’ni
d dTb
= J jf(x,y)dx dy
f/Г ь
mavjud va jjf(x,y)dxdy = J f f(x,y)dx dy
D c _a
bo‘ladi.
◄ Bu teoremaning isboti yuqoridagi teoremaning isboti kabidir. ►
1- natija. f (x,y) quyidagi shartlarni qanoatlantirsin:
1) f(x,y) funksiya D da integrallanuvchi;
2) har bir tayin xe [a,b] da f(x,y)dy integral mavjud;
3) har bir tayin ye [c,d] da f(x,y)dx integral mavjud. U
holda
bTd "I dTb
J jf(x,y)dy dx, J j/(x,y)dx dy
integrallar mavjud va
284
bo'ladi.
2- natija. Agar f(x,y) funksiya D da uzluksiz bo‘lsa, u holda
rF'r 1 d\h
Jj/(x,y)dxdy, j jf(x,y)dy dx, j ^f(x,y)dx dy
D a
a
integrallar mavjud va ular bir-biriga teng bo'ladi. Demak, integrallash
to'plami
D = {(x, y) <= R1 2 : a < x < b, с < у < d}
bo'lgan holda f(x,y) funksiyaning D bo'yicha integrali awal birinchi
argument! (ikkinchi argumentini o'zgarmas deb hisoblab), so'ngra
ikkinchi argument! bo'yicha integrallab topiladi.
1- misol. Ushbu jj x2ydxdy integral hisoblansin, bunda
r , d
D = {(x,y) e R2 : 2 < x < 5, 1 < у < З}.
◄ Integrallanayotgan f(x,y) = x2y funksiya 1- va 2-teorema-
lar shartlarini bajaradi. Ulardan foydalanib topamiz:
3 Г 5 "I 3 z 3 y=5
jj x2ydxdy = j j x2ydx] dy = j — dy =
D 1 L2 J 1 V Л=2
= | j(125y-8yMy =156-
i \ Л
Shuningdek,
dx =
1 /• ( \
= - j(9x2-x2)<ix = 4 у =156
2 \ h
bo'ladi. ►
285
2°. Egri chiziqli trapesiya bo‘yicha ikki karrali integrallarni hi-
soblash. f (x,y) funksiya tekislikdagi
Д = {(%, y) e R2 : a < x < b, (x) < у < <p2 (x)}
to‘plamda berilgan bo‘lsin, bunda <px (x), <p2 (x) funksiyalar [a,b] da
uzluksiz va Vx e (a, b) da <pj (x) < <p2 (x).
3- teorema. f (x,y) funksiya quyidagi shartlarni bajarsin:
1) f(x,y) funksiya D da integrallanuvchi;
2) har bir tayin x e [a, />] da
<p2(x)
J f(x,y)dy
<Pi(x) Л .
integral mavjud. U holda j
b Г'Й (*)
J J f(x,y)dy dx
а [_Ч>1 (*)
mavjud va quyidagi ifoda o'rinli bo'ladi:
b <h(x)
=J J
f(x,y)dy dx.
4 Aytaylik, D = {(x,y) e R2 : a < x < b, с < у < d} to'g'ri to'rt-
burchak Z>! ni o'z ichiga joylashtirsin: I\ c D (34- chizma).
Ushbu
F(x,y) =
/(x,y), agar (x,y)e Dr
0, agar (х,у)б2)\Д
bo'lsa,
bo'lsa
funksiya uchun, ravshanki,
jjf(x,y)dxdy = R(x,y)dxdy (5)
D
tenglik bajariladi.
Agar F{x,y) funksiya har bir tayin x g [a, b\ da у o'zgaruvchining
funksiyasi sifatida qaralsa, u holda teoremaning 2- sharti hamda F{x,y)
funksiyaning tuzilishidan
286
bo‘ladi. Ayni paytda, har bir tayin x e \a,b\ da
d 91 (x) 92 (x) d
jF(x,y)dy = J F(x,y)dy + j F(x,y)dy+ j F(x,y)dy =
С С 91 (%) 92 (x)
92 W 92 (x) (7)
= J F(x,y)dy = J f(x,y)dy
91 (x) 91 (x)
bo'ladi. (5), (6) va (7) munosabatlardan j
^F(x,y)dxdy
д
bo‘lishi kelib chiqadi. ►
Aytaylik, f (x,y) funksiya tekislikdagi
D2 ={(x,y)e R2 : (у) < x < у2 (у), с < у < d]
to‘plamda berilgan bo‘lsin, bunda (y) va v2 O') funksiyalar [c,d] da
uzluksiz va Vy e (c,d) da cpj (y) < <p2 O') •
4- teorema. f(x,y) funksiya quyidagi shartlarni bajarsin:
1) f(x,y) funksiya D2 da integrallanuvchi;
2) har bir tayin у e [c,d] da
92 (y)
J f (x,y)dx
91W
287
integral mavjud. U holda
d Гч<2 (У)
J J f{x,y)dx
dy
mavjud va quyidagi ifoda o'rinli bo'ladi:
V2 O')
jjf(x,y)dxdy = J j f(x,y)dx dy.
Л1О)
◄ Bu teoremaning isboti 3-teoremaning isboti kabidir. ►
Agar f (x,y) funksiya D* da kerakli shartlarni bajarib, integrallash
to'plami D* esa nol yuzali chiziqlar yordamida o'zaro bir-biri bilan
ichki umumiy nuqtaga ega bo'lmasa hamda yuqoridagi teoremalardagi
kabi л
Z)‘= Д* иД и...иД
bo'lsa, u holda quyidagi tenglik kelib chiqadi:
JJ f (x,y) dxdy = JJ f (x, y} dxdy + JJ f (x, y) dxdy
$
^f(x,y)dxdy.
2- misol. Ushbu J = jj -jx + уdxdy
D
integrallar hisoblansin, bunda D — quyidagi
x~ 0, у = 0, x + у = 1
chiziqlar bilan chegaralangan to'plam.
◄ Bu chiziqlar bilan chegaralangan to'plam 35- chizmada tasvir-
langan.
f(x,y) - fie + y funksiya va D to'plam 3- teoremaning shartla-
rini bajaradi. Endi
D ~{(x,y)e R2: 0 < x < 1, 0<y<l-x}
ekanini e’tiborga olib topamiz:
288
3- misol. Ushbu J = JJ (x2 + y2 )dxdy
D
integral hisoblansin, bunda D quyidagi
у = x, у = x + а, у = а, у = За, (a > 0)
chiziqlar bilan chegaralangan to‘plam.
◄ Bu chiziqlar bilan chegaralangan to'plam 36- chizmada tasvir-
langan.
Berilgan integralni hisoblashda 4- teoremadan foydalanamiz:
Sitz4 16 a4 27 a4 a4
~12 ЁГ + ПГ~~ 12
-У у-- + у2 (у - a) dy =
/
~ =14«4. ►
4- misol. Ushbu
quyidagi chiziqlar:
J - JJ dxdy integral hisoblansin, bunda
D -
D
289
у2 = 2x parabola va uning (2; —2) va (8; 4) nuqtalarini birlashti-
ruvchi vatar bilan chegaralangan to'plam.
•4 y2 = 2x parabolaning (2; — 2) va (8; 4) nuqtalarini birlashtiruv-
chi vatar tenglamasi
у = x -4
ko'rinishda bo‘ladi. y2 = 2x va у = x -4 chiziqlar bilan chegaralan-
gan D to'plam 37- chizmada tasvirlangan.
x = 2to‘g‘ri chiziq yordamida D to'plamni ikkita Dx va Z>2 larga
ajratamiz. Bunda:
Д = {(x,y) g R2 : 0 < x < 2, -\/2x < у <-J2x},
D2 - {(x,y)e R2 : 2 < x < 8, x-4<y<y/2x}.
Ikki karrali integralning xossalaridan foydalanib topamiz:
D Д Oj
Bu integrallami hisoblaymiz:
2 8
= ^2у/2хсЬс + ^(J2x - x + 4^dx = №. ►
0 2
290
Mashqlar
1. Ushbu ffsin4j—y-^dxdy integral baholansin, bunda
Jj x- +/ +1
D = {(x, y) e R2 : x2 + y2 < 9}.
2. Ushbu jj f (x,y)dxdy integral takroriy integralga keltirilsin,
D
bunda D to‘plam x2 + y2 = 4 va x2 - 2x + у1 = 0 aylanalar bilan
chegaralangan.
3. Ushbu jj ————у integral hisoblansin, bunda
D (1+x2 +y2 )2
Z> - {(x, y)e R2 : 0 < x < 1, 0 < у < 1 - x}.
85- ma’ruza
Ikki karrali integralda o‘zgaruvchilarni
j almashtirish
, Ikki karrali integrallarni hisoblashda ancha qiyinchiliklarga duch
ijelinadi. Bu qiyinchiliklar:
1) integrallanuvchi funksiyalarning murakkabligi;
! 2) integrallash to'plamining murakkabligi hisobiga sodir bo'ladi.
Ba’zan o'zgaruvchilarni almashtirish natijasida integrallanuvchi
funksiya ham, integrallash to'plami ham soddaroq ko'rinishga (integral-
lash uchun qulay ko'rinishga) keladi va integralni hisoblash osonlashadi.
1°. Tekislikda to‘plamlarni akslantirish haqida. Faraz qilaylik,
tekislikda XOY dekart koordinatalar sistemasiga nisbatan chegara-
langan D to'plam, uOv dekart koordinatalar sistemasiga nisbatan esa
chegaralangan Д to'plam berilgan bo'lib, ularning chegaralari va
ЭД lar bo'lakli-silliq yopiq chiziqlardan iborat bo'lsin (38- chizma).
Aytaylik,
Jx = <p(u, v),
sistema A ni Z>ga akslantirsin. Bu akslantirish quyidagi shartlami bajarsin:
291
38- chizma.
1) bu o‘zaro bir qiymatli akslantirish;
2) <p(w,u) va y(w,y) funksiyalar A to'plamda uzluksiz va uzluksiz
barcha xususiy hosilalarga ega;
3) xususiy hosilalardan tuzilgan
J(«,u)=
dx
du
Эу
du
dx
dv
dv
funksional determinant A da ishora saqlasin va V(«, v) g A da
J(u,v) * 0 bo'lsin.
Odatda, determinant (1) sistemaning yakobiani deyiladi.
Ravshanki, bunday holda (1) akslantirishga teskari
и = cp(x,y),
v = y(x,y)
akslantirish mavjud va u D ni A ga bir qiymatli akslantiradi.
Tasdiq. D to'plamning yuzi
\i.D - JJ | J(u, v)| dudv
Д
bo'ladi (qaralsin, [1], 19-bob, 3-§).
2°. Ikki karrali mtegrallarda o‘zganivchilarm almashtirish.
f (x,y) funksiya D to'plamda berilgan va uzluksiz bo'lsin. Ushbu
292
х = <р(«, и),
1 / \ (2)
у = \у(и,и) 4 '
sistema A ni D ga akslantirib, и Г da keltirilgan 1-3- shartlarni bajarsin.
D ning biror
P& - (Ai, Аг > •••> A„ )
bo'laklanishi olaylik. Bu bo‘laklash (1) akslantirish yordamida D to‘p-
lamning
PD = (z>15z>2,. -M
bo‘laklashlarini hosil qiladi.
Ikki karrali integral ta’rifiga ko‘ra
£=1
bo‘lib,
lim <*= lim ^f(^k,x\k)\kDk = ff/(x,yWy (3)
bo‘ladi.
Г da keltirilgan tasdiqdan foydalanib topamiz:
iiDk = jj \J(u, v)| dudv.
I
O‘rta qiymat haqidagi teoremaga binoan, shunday
(*4X)e A*
nuqta topiladiki, bunda
J\J(u, v)\dudv = г^)|цД-
D
tenglik bajariladi. '
Natijada j\x,y) funksiyaning integral yig‘indisi quyidagi
CT = У f&k >)\j(uk, Vk)jцД*
*=i
ko‘rinishga keladi. {^k,y\k)& Dk nuqtaning ixtiyoriyligidan
293
t=k=(uk,vk), r\k=(uk,vk)
deb olish mumkin. U holda
a = XA<P(«jt > vk), V(uk>vk)\J(uk,v*)|Mfc
k=l
bo'ladi. /(<p(u,t>), y(u,v))|/(w, v)| funksiya A da uzluksiz, bino-
barin, integrallanuvchi. Demak,
Jim o= lim Т/(ф(м;,^),у(^,^)|/(«;,1?;)|цАА =
= JJ/((p(w,v),v(w,v))jJ(w,u)| dudv
Д
bo'ladi. (2) va (3) munosabatlardan
JJ-ЖЯ =JJ f (yp(u,v),y(u,v))\J(u,v)\dudv
d д
(4)
(5)
bo'lishi kelib chiqadi.
(5) ifoda ikki karrali integrallarda o'zgaruvchilarni almashtirish
formulasidir.
1- misol. Ushbu
JJ y^dxdy
D
integral hisoblansin. D quyidagi у = x2, у - 2x2, xy - 1, xy = 2
chiziqlar bilan chegaralangan.
39- chizma.
◄ Berilgan chiziqlar bilan che-
garalangan D to'plam 39- chiz-
mada tasvirlangan.
Ushbu
u = ^~
x2 ’ (x > 0) (6)
u = xy,
akslantirishda D ning aksi:
1 Sw <2,1 <v <1}
294
Ravshanki, (5) akslantirish o‘zaro bir qiymatli akslantirish bo'lib,
unga teskari akslantirish quyidagicha:
_i i
x - и 3u3,
1 I (6')
у = u3v3.
(6) sistemaning yakobianini topamiz:
~u 3u3 3v3
„12 „11
2 з з 2 3 3
J 3W u
“S' l/("’u)l = 5R-
Endi y3 = uv2 ekanini e’tiborga olib, berilgan integralda (6')
almashtirish bajarsak, u holda (5) formulaga ko'ra
Л D D
bo'ladi. Keyingi integralni hisoblaymiz:
2
Jj«v2 = | J J
D D 1^1
[J y3dxdy = ~. ►
D
Demak,
1 /8 _ 1_
313 3
7
9 •
3°. Ikki karrali integralning qutb koordinatalarida ifodalanishi.
Yuqoridagi (1) sistema sifatida ushbu
x - r coscp,
у = r sin cp
(7)
akslantirishni olaylik. Bu tekislikdagi qutb koordinatalari sistemasi
bo'yicha (r,q>) nuqtani dekart koordinatalari sistemasi bo'yicha (x,y)
nuqtaga akslantirishni ifodalaydi.
(7) sistemaning yakobiani
cos ф
-r sin ф
-r sin ф
r cos ф
= r
bo'ladi. XOYtekisligidagi yuzaga ega D to'plamni olaylik.
295
Bu D ning (7) akslantirish yordamida asli (proobrazi)
A c {(/*, <p) e R2 : r > 0, 0 < ф < 2 я} bo‘ladi.
Agar О nuqta (koordinata boshi) D ga tegishli bo‘lmasa, u holda
A ni D ga akslantirish o‘zaro bir qiymatli bo‘lib, sistemaning yakobiani
0 dan farqli bo'ladi.
Agar О nuqta D ga tegishli bo'lsa, u holda (7) akslantirishning
o‘zaro bir qiymatliligi hamda J(r,<p) * 0 shart nol yuzali chiziqlar-
dagina bajarilmaydi.
Demak, f (x,y) funksiya D^jdD da uzluksiz bo'lsa u holda
JJ /(x, y) = JJ /(cos <p, r sin ^rdrda? (8)
D 1) 7" \
formula o'rinli bo‘ladi.
2-misol. Ushbu / = ff—^—y-dxdy
JJ (x2+y2)
integral hisoblansin, bunda D — quyidagi x — 0, у = 0, x + у = a,
x + у = b (0 < a < b) chiziqlar bilan chegaralangan to‘plam.
◄ Berilgan integralda o‘zgaruvchilarni quyidagicha
x = r cos <p, у = r sin <p
ko‘rinsihda almashtiramiz. Unda x2 + y2 = r2 bo‘lib, (8) formulaga
ko‘ra
JJ -i- rdrd cp = JJ -ij- drd <p
d r д r
bo‘ladi. Endi A nitopamiz. fining
tekislikdagi tasviri 40- chizmada
ko'rsatilgan.
Ravshanki, qutb burchagi ф ning
o‘zgarishi 0 bilan orasida bo‘-
ladi: 0 < ф < . (г,ф) nuqta D da
bo‘lishi uchun r qutb radiusi chiz-
V
mada ko‘rsatilgan A nuqta bilan
В nuqta orasida bo‘lishi kerak.
296
A nuqtada x + у = a bo'lgani uchun r coscp + r sincp = a , ya’ni
a
r =----------.--
coscp+sincp ’
В nuqtada x + у = b bo'lgani uchun r cos cp + r sin cp = b , ya’ni
b
coscp+sincp
bo‘lib,
< Г < ГВ
bo'ladi. Demak, A = |(r, cp) & R2 :rA <r <rB, 0 < cp < j
Natijada
ga ega bo'lamiz.
Integrallarni hisoblab topamiz:
к n
2 . . , , 2
г / cos cp+sm cp cos cp+sm cp\ , b-a Г, x ~ b-a .
- —r-------1--------*-----x <Ap = (cos cp + sm <p) d<& =2 —y-. ►
J \ a b ) ab 3 ab
о о
3- misol. Ushbu J - JJ (x + y~)dxdy integral hisoblansin, bunda
D
D to'plam x2 + y2 - 1, x2 + y2 - 4 , у = 0 (Z) da у > 0) chiziqlar
bilan chegaralangan (41- chizma).
(8) formuladan foydalanib topamiz:
J - Jj (x + y)dxdy -jj (r cos (p + r sin cp)t/rJcp.
D D
Ravshanki,
A = {(r, cp) e R2 : 1 < r < 2,0 < ср < n}.
297
Natijada J = 11 r2 (cos <p + sin <p)tZrc?cp -
D
о
я r 2 ' я
= J jr2(coscp + sin cp)dr t/ф = 3 |(созф + sinф)^ = -
° U
ga ega bo‘lamiz. ►
Mashqlar
1. Ushbu xy = 1, xy = 2, x — у — 1 = 0 (x > 0, у > 0) chiziqlar
bilan chegaralangan to'plamni tomonlari koordinatalar o‘qiga parallel
bo‘lgan to‘g‘ri to'rtburchakka o‘tkazuvchi akslantirish topilsin.
2. Ushbu
x2+y2=4x, x2+y2=8x, y = x, у = 2x
chiziqlar bilan chegaralangan.
j-f integral hisoblansin, bunda D quyidagi
86- ma’ruza
Ikki karrali integralning ba’zi bir tatbiqlari
1°. Tekis shaklning yuzi. Tekislikda yuzaga ega bo'lgan D shakl
berilgan bo'lsin. Bu shaklning yuzi
pZ> = JJ(/xdy (1)
D
298
bo‘ladi. Bu tenglikning isboti ikki karrali
integral ta’rifidan kelib chiqadi.
Misol. Tekislikning birinchi chora-
gida ushbu
x2 + y2 = 2ax, y1 =2ax,
x = 2a (o > 0)
chiziqlar bilan chegaralangan shaklning
yuzi topilsin.
◄ Bu shakl 42-chizmada tasvirlan-
gan.
(1) formulaga ko‘ra qaralayotgan
shaklning yuzi
Y.
О a la
42- chizma.
= JJ dxdy
D
bo‘lib, bunda
D = {(x,y) e R2 : 0 < x < 2a, 72 ax-x2 < у < y)2ax\-
Integralni hisoblab, topamiz:
3 2 6
2’. Jismning hajmi. 81-ma’ruzada fazodagi jismning hajmi
tushunchasi va uning mavjudligi sharti bayon etilgan edi.
Endi jism hajmining ikki karrali integral orqali ifodalanishini
ko‘rsatamiz.
Л3 fazoda Dekart koordinatalar sistemasi va unga nisbatan joy-
lashgan V jismni qaraylik. Bu jism yuqoridan z - f (х,У) ifodalagan
sirt, yon tomondan yasovchilari OZo‘qiga parallel silindrik sirt hamda
pastdan ZOhtekisligidagi chegaralangan yopiq D to'plam bilan chegara-
langan jism bo‘lsin. Bunda f (x,y) funksiyani D da uzluksiz deb qaraymiz.
D to‘plamning
299
bo‘laklashlarini olaylik. U holda
mk = inf {/(x,y): (x,y) e Dk},
Mk = sup{/(x,y) : (x,y)e Dk}
mavjud bo'ladi. Ushbu
M = У mk^Dk , = У Mky.Dk
k=l k=}
yig'indilar mos ravishda Ujismning ichiga joylashgan A ko'pyoqlik-
ning hajmi va Kjisrnni o'z ichiga olgan В ko'pyoqlikning hajmi bo'lib,
[kA < ikB
bo'ladi.
D to'plamni turli bo'laklashlar natijasida hosil bo'lgan {рЛ} va
{pZ?} to'plamlarning chegaralanganligidan sup{q/l}, inf{p5} laming
mavjud bo'lishi kelib chiqadi.
f (x,y) funksiya yopiq D to'plamda uzluksiz. Demak, u D da tekis
uzluksiz. U holda Ve > 0 olinganda ham shunday 8 > 0 topiladiki,
D to'plamning k, < 8 bo'lgan ixtiyoriy
P = [Dl,Dl,..Dn}
bo'laklash uchun har bir Dk da (k=l,2,...,n) funksiyaning tebranishi
tengsizlikni qanoatlantiradi. Shularni e’tiborga olib topamiz:
inf W} - sup {рЛ} < p5 - рЛ = У Mk\kDk - У mk\kDk =
k=\ k=l
= ^(Mk-mk^Dk <^Dk=^^D =£-
Demak, 0 < inf {p5} - sup {рЛ} < e .
Keyingi munosabatdan
inf {p5} = sup {рЛ}
bo'lishi kelib chiqadi. Bu esa V jism hajmga ega bo'lishi va uning
hajmi p V ning
300
pF = inf {pf?} = sup {рЛ} (2)
ekanligini bildiradi. Ayni paytda,
sup{p5} = JJ f(x,y)dxdy , inf {рЛ} = JJ f(x,y)dxdy
D D
va (2) tenglikka ko'ra
JJ f{x,y)dxdy = JJ f(x,y)dxdy = JJ f(x,y)dxdy
D D D
(3)
i bo‘ladi. (2) va (3) munosabatlardan
pF = JJ/(x,y)tte/y (4)
D
bo‘lishi kelib chiqadi.
2- misol. Fazodagi Z
x2+y2+z-4 = ® 4
sirt (paraboloid) hamda tekislik bilan
chegaralangan jismning hajmi topilsin. f / \\
◄ Bu jism 43-chizmada tasvirlan- / / \ \
gan bo'lib, D to'plam XOYtekislik- / / |
dagi x2 +y2 <4 doiradan iborat.
Sirtning tenglamasini z = 4-x2-y2 у
ko‘rinishda yozib, (4) formuladan
foydalanib topamiz: x
43- chizma.
pF = JJ(4-x2 -y2)dxdy , (5)
D
bunda D = {(x,y) e R2 : x2 + y2 < 4},
(5) integralda o‘zgaruvchilami quyidagicha
x = r cos ф,
у = r sin cp
ko‘rinishda almashtirib hisoblaymiz:
4 - x2 - y2 - 4 - r2 , /(r,<p) = r, 0<r<2, 0<<р<2тс,
301
2тг / 2 \ 2п/
4 - х2 - у2 )dxdy - j j(4-r2)riZr <Ap= j I 2г2 -
dq> = 8л.
Demak, jismning hajmi pF = 8л ga teng.
3°. Sirtning yuzi. Faraz qilaylik, tekislikda yuzaga ega bo'lgan D
to'plamda z =f(x,y) funksiya berilgan bo'lib, u shu to'plamda uzluksiz
fx(x,y), fy(x,y) hosilalarga ega bo'lsin. Bu funksiyaning grafigi
R3 fazoda 5 sirtni ifodalasin (44- chizma).
Bunday sirtning yuzasi ikki karrali integral orqali quyidagicha
ifodalanadi:
p5 = Jj f*2 (x, y) + fy2 (x, y) dxdy.
(6)
(Z>)
3- misol. Asosining radiusi r, balandligi h ga teng doiraviy konus-
ning yon sirti topilsin.
4 Ma’lumki, konus sirt z = - ^x2 + y2 tenglama bilan ifodala-
nadi. (6) formulaga ko'ra konusning yon sirti
p5 = Jj д/l + (z'x2 (x,y))2 + (z'y2 (x,y))2 dxdy
D
bo'ladi, bunda D = {(x,y) e R2 : x2 + y2 < r2}.
Agar
y r ^x2 +У2 ’
^ + (42(^,n,t))2 +Wy (^,nj)2 =
JJ
D
44- chizma.
ekanini topamiz. ►
302
4°. Ikki karrali integralning mexanikaga tatbiqlari. Aytaylik,
tekislikda massaga ega bo'lgan moddiy D shaklning har bir (x, у) e D
nuqtasidagi zichligi p(x,y) bo'lib, u D da uzluksiz bo'lsin. D shakl-
ning massasini topish talab etilsin.
Ravshanki, p(x, у) = C — const bo'lsa, u holda D shaklning massasi
m = CpD
ga teng bo'ladi. Agar p(x,y) ixtiyoriy (Л=1,2,...,л) uzluksiz funksiya
bo'lsa, D shaklning massasini topish uchun D ning
P = {Д, d2,..d„}
bo'laklashini va har bir Dk da (T=l ,2,...,«) ixtiyoriy ) nuqtani
olamiz: (^,^)е Dk. Har bir Dk da p(x,y) ni o'zgarmas va uni
p(t,k,x\k) ga teng deyilsa, u holda Dk ning massasi taxminan
P(^,t1*)hA
ga teng bo'lib, D shaklning massasi esa taxminan
Xp^hJpA (7)
fc=l
ga teng bo'ladi.
P bo'laklashning diametri —> 0 da (7) yig'indining limiti izla-
nayotgan shaklning massasini ifodalaydi.
Ayni paytda, (7) yig'indi funksiyaning integral yig'indisi va p(x, y)
funksiya D da uzluksiz bo'lganligi sababli bu yig'indining limiti
jjp(x,y)dxdy
D
bo'ladi. Demak, D shaklning massasi
m = Jjp(x,y)dxdy (8)
D
tenglik bilan aniqlanar ekan.
4- misol. Tekislikda a radiusli doiraviy plastinka berilgan bo'lib,
uning har bir A(x,y) nuqtadagi zichligi shu nuqtadan koordinatalar
boshigacha bo'lgan masofaga proporsional. Doiraviy plastinkaning
massasi topilsin.
303
◄ Dekart koordinatalar sistemasining koordinatalar boshiga doi-
raviy plastinkaning markazini joylashtiramiz. U holda plastinkaning
A(x,y) nuqtasidan koordinatalar boshigacha bo'lgan masofa
d - y]x2 + y2
bo'lib, plastinka zichligi
p(x,y) = k^x2 +y2
bo'ladi, bunda к — proporsionallik koeffitsiyenti.
(8) formulaga ko'ra plastinka massasi
m = JJ kyjx2 + y2dxdy
D
bo'ladi, bunda D = {(x,y)e R2 : x2 + y2 <r2}.
Ikki karrali integralda
x = r cos <p,
x = r sin cp
almashtirish bajarib, uni hisoblaymiz:
2n z j y;
JI у I Jcp = - kna3 .
0 \ /)
о
m = j j kyjx + у dxdy - J
d о
Ikki karrali integrallar yordamida statistik momentlar:
Mx = jj yp(x,y)dxdy, (OJf o'qiga nisbatan),
My - JJxp(x,y)dxdy, (OYo'qiga nisbatan),
D
og'irlik markazining koordinatalari:
*» = JJ ’ Л = J^F, JJ ydxdy
D n D D
inersiya momentlari:
Jx = jjy2p(x,y)dxdy, (OXo'qiga nisbatan),
D
304
Jy - JJx2 p (x, у) dxdy, (OYo‘qiga nisbatan).
D
JQ = JJ (x2 + y2) p (x, y) dxdy (koordinatalar boshiga nisbatan)
D
topiladi.
Mashqlar
1. Tekislikda ushbu
y2+a2 y2+b2
x = , x = y—-~ , (0 < a < b)
2a 2b
parabolalar bilan chegaralangan shaklning yuzi topilsin.
2. Fazoda quyidagi
x2 + y2 = 4x, z = x, z= 2x
sirtlar bilan chegaralangan jismning hajmi topilsin.
87- ma’ruza
Uch karrali integrallar
Matematik analiz kursi davomida /(x) funksiyaning R
segment bo‘yicha aniq integrali, f(x,y) funksiyaning De R2 to'plarn
bo‘yicha ikki karrali integrali tushunchalari kiritilib, ular batafsil o‘rga-
nildi.
Xuddi shunga o‘xshash bu tushuncha uch o‘zgaruvchili f (x,y.z)
funksiya uchun ham kiritiladi. Unda, awalgi hollarda keltirilgan
ma’lumotlar va ularni isbotlashda yuritilgan mulohozalar qaytariladi.
Shuni e’tiborga olib, uch karrali integral haqida tushuncha va
tasdiqlarni keltirish bilan chegaralanamiz.
1°. Uch karrali integral tushunchasi. Faraz qilaylik, R2 fazoda
chegaralangan hamda hajmga ega bo'lgan Fjism (to‘plam) da/(x,y,z)
funksiya aniqlangan va chegaralangan bo‘lsin.
m < f(x,y,z) < M, ((x,y,z)eF).
V to‘plamning biror
305
bo'laklashini va har bir Vk da ixtiyoriy ^к,у\к,^к)& Vk nuqtani
(k = 1,2,...,n) olib, ushbu
>1=1
yig'indini tuzamiz. U f(x,y,z) funksiyaning integral yig'indisi deyiladi.
1- ta’rif. Agar Ve > 0 son olinganda ham shunday 8 > 0 son
topilsaki, Kto'plamning diametri ^>8 bo'lgan har qanday Pbo'lak-
lash hamda har bir Vk da olingan ixtiyoriy (£>к,т\к, zk) lar uchun
|o-J| < e
tengsizlik bajarilsa, J son о yig'indining kp > 8 dagi limiti deyiladi va
quyidagicha belgilanadi:
lim c = J.
Xp —>0
2- ta’rif. Agar kp > 8 da /(x,y,z) funksiyaning integral yig'indisi
chekli limitga ega bo'lsa, f(x,y,f) funksiya V to'plamda integralla-
nuvchi, J songa esa f(x,y,z) funksiyaning V to'plam bo'yicha uch
karrali integrali deyiladi va quyidagicha
^f(x,y,z)dxdydz
v
ko'rinishda belgilanadi. Demak,
\\\f(x,y,z)dxdydz = lim
f(x,y,z) funksiya V da chegaralanganligi uchun
mk = inf{/(x, y, z) : (x, y,z)e Kk},
Mk = sup{/(x,y,z): (x,y,z)e KJ
mavjud. Ushbu 5 = У mkpVk , S = ^MkpVk
k=l k=l
yig'indilar mos ravishda Darbuning quyi hamda yuqori yig'indilari
deyiladi.
Ravshanki, s = sp (f), S = Sp (f)
bo'lib, {s = sp(/)}, {A = A’pC/’)} to'plamlar chegaralangan bo'ladi.
306
3-ta’rif. {sp(f)} to‘plamning aniq yuqori chegarasi f(x,y,z}
funksiyaning quyi uch karrali integrali deyiladi va
v
kabi belgilanadi.
4- ta’rif. {Sff ) to‘plamning aniq quyi chegarasi f(x,y,f) funk-
siyaning yuqori uch karrali integrali deyiladi va
/ = ^f(x,y,z)dxdydz
v
kabi belgilanadi.
5- ta’rif Agar J = J bo‘lsa, f(x,y,z) funksiya V to‘plamda in-
tegrallanuvchi, ularning umumiy qiymati
J -J = J
f (x,y,z) funksiyaning Kto‘plam bo'yicha uch karrali integrali deyiladi.
2°. Uch karrali integralning mavjudligi. Quyidagi teorema uch
karrali integralning mavjudligini ifodalaydi.
1- teorema. f(x,y,z) funksiyaning V to‘plamda integrallanuvchi
bo‘lishi uchun Ve > 0 son olinganda ham shunday 3 > 0 son topilib,
V to‘plamning diametri \, > 8 bo‘lgan har qanday P bo‘laklashiga
nisbatan Darbu yig‘indilari ushbu
(1)
tengsizlikni qanoatlantirishi zarur va yetarli.
Agar f(x,y,z) funksiyaning Vk dagi tebranishini coA desak, u holda.
n n
Sp{n-sp(n = ^Mk-mk^Vk=Y^Vk
k=\ k-\
bo‘lib, (1) shart ushbu
J^Vk <£
*=i
ko‘rinishni oladi. Bu holda
n
lim У co JI = °
deyish mumkin.
307
3°. Integrallanuvchi funksiyalar sinfi. Uch o'zgaruvchili f(x,y,z)
funksiyalar ma’lum shartlarni qanoatlantirganda ularning integ-
rallanuvchi bo'lishini ifodalaydigan teoremalarni keltiramiz.
2- teorema. Agar f(x,y,z) funksiya chegaralangan yopiq Иto'plam-
da uzluksiz bo'lsa, u shu to'plamda integrallanuvchi bo'ladi.
Aytaylik, R3 fazoda 5 sirt berilgan bo'lsin.
6- ta’rif. Agar R3 da shunday Ko ko'pyoqlik topilsaki,
l)5cK0,.
2) Ve> 0 uchun цИ0 < e bo'lsa, S nol hajmli sirt deyiladi.
3- teorema. Agar f(x,y,z) funksiya chegaralangan yopiq Hto'plam-
dagi chekli sonda nol hajmli sirtlarda uzilishga ega, qolgan barcha
nuqtalarda uzluksiz bo'lsa, f (x,y,z) funksiya Иto'plamda integralla-
nuvchi bo'ladi.
4°. Uch karrali integralning xossalari. Uch karrali integrallar
ham ikki karrali integralning xossalari kabi xossalarga ega.
1) f(x,y,z) funksiya Kda (Ис R3) integrallanuvchi bo'lsin. Agar
Иto'plam nol hajmli 5sirt bilan umumiy ichki nuqtaga ega bo'lmagan
bog'lamli kj va V2 to'plamlarga ajralgan bo'lsa, f(x,y,z) funksiya har
bir va V2 to'plamlarda integrallanuvchi va quyidagicha bo'ladi:
ffjf(x,y,z)dxdydz = jfjf(x,y,z)dxdydz + Jff f(x,y,z)dxdydz
2) Agar f(x,y,z) funksiya V to'plamda integrallanuvchi bo'lsa,
c f (x,y,z) funksiya (c = const) ham Иto'plamda integrallanuvchi va
V V
bo'ladi.
3) Agar f (x,y,z) va g(x,y,z) funksiyalar И da integrallanuvchi bo'lsa,
f(x,y,z) ± g(x,y,z), /(x,y,z) • g(x,y,z) funksiyalar integralla-
nuvchi va
jjjlf(x,y,z)±g(x,y,z)]dxdydz =
v
= jJJ f(x,y,z)dxdydz ± JJJ f(x,y, z}dxdydz
V V
bo'ladi.
308
4) Agar f(x,y,z) funksiya К to'plamda integrallanuvchi bo‘lib,
V(x,y,z)eK da /(x,y,z) > 0 bo'lsa,
jjj f(x, у ,z) dxdydz > 0
v
bo'ladi.
5) Agar f(x,y,z) funksiya Vto'plamda integrallanuvchi bo'lsa, u
holda |/(x,y,z)| funksiya ham К da integrallanuvchi va
jjj f(x, у, z) dxdydz < jjj \f(x, y, z)| dxdydz
V V
bo'ladi.
6) Agar f(x,y,z) funksiya И to'plamda integrallanuvchi bo'lsa, u
holda shunday a son (m < a < M) topiladiki, bunda
jjj f{x,y,z~)dxdxydz = apK (V(x,y,z) e V : m < /(x,y,z) < M)
v
bo'ladi (o'rta qiymat haqidagi teorema).
5° . Uch karrali integrallarni hisoblash. Uch karrali integrallarni
hisoblash formulalari integrallash to'plamining ko'rinishiga qarab
turlicha bo'ladi.
a) Aytaylik, f(x,y,z) funksiya R3 fazodagi to'plam
V - {(x,y,z) e R3 : a < x < b,c < у < dp < z 2 q}
da (parallelepipedda) uzluksiz bo'lsin. U holda quyidagicha bo'ladi:
jjj/(x,y,z)cto/yafc =
и
b [d( q
A
f(x,y,z)dz) dy
7
dx.
(2)
b) Aytaylik, R3 fazodagi Иto'plam pastdan z = , yuqo-
ridan z = У1(х,у) sirt (bunda D<^R2 to'plam V jismning XOY
tekislikdagi proyeksiyasi) bilan chegaralangan bo'lsin. Agar bu V da
f(x,y,z) uzluksiz, \yx(x,y) va y2(x,y) funksiyalar D da uzluksiz
bo'lsa, u holda quyidagicha bo'ladi.:
Щ f(x,y, z)dxdydz = jj j f(x,y,z)dzdxdy.
(3)
309
d) Aytaylik, b) holdagi D to‘plam quyidagicha
D = {(x,y) e R2 : a < x < b, cpj (x) < у < <p2 (x)}
bo‘lib, <pj va <p2 funksiyalar \a,b\ da uzluksiz bo‘lsin. U holda
ь .. ... ...
^f{x,y,z)dxdydz = J J J j\x,y, z)dz) dy dx
V o|_«pi(x)
4>2 (*)f V2 (*,У)
Vl
bo'ladi.
1- misol. Ushbu J = JJJ(x + У + z)dxdydz integral hisoblansin,
v
bunda V = {(x,y,z) e B3 : 0 < x < 1, 0 < у < 3, 0 < z < 2}.
◄ Yuqoridagi (2) formuladan foydalanib berilgan integralni hi-
soblaymiz:
о Lo
.0 V°
rf
J XZ+ K+y
(Л
2 Y=3
У I
2 Jy=0
г=2
dy dx =
z=o
о
1 Г з
0
1
0
о
2-misol. Ushbu jjj z2dxdydz integral hisoblansin, bunda V —
(n
konus (z = 7%2 +У2 ) va z — h tekislik bilan chegaralangan to‘plam.
◄ V ning XO Y tekislikdagi proyeksiyasi
D - {(x, y) e R2 : x2 +y2 < h2}
bo‘ladi. (3) formuladan foydalanib topamiz:
Keyingi integralda
x - r coscp,
у = r sin cp
310
almashtirish bajarib, uni hisoblaymiz:
\rdr d<y = |тг/г5 .
6°. Uch karrali integrallarda o'zgaruvchilarni almashtirish.
Aytaylik, f(x,y,z) funksiya Ис R3 to'plamda berilgan va uzluksiz
bo'lsin. Ushbu
x = cp(u,u, w),
y = y(w,i>,w),
z = ^(u,v,w')
sistema A c R3 to'plamni Иto'plamga akslantirish bo'lib, bu akslan-
tirish 85- ma’ruzada keltirilgan 1— 3- shartlarni bajarsin. U holda
jff f(x,y,z)dzdydz =
v
= Jjj/(<p(w, v, w), xy(u,v,w'), %(m,U,w))|J| Jirtfodw
Д
bo'ladi, bunda
dx dx dx
du dv dw
J = dy dy dy
du dv dw
dz dz dz
du dv dw
bo'ladi.
Ko'p hollarda dekart koordinatalaridan silindrik hamda sferik koor-
dinatalarga o'tish bilan uch karrali integrallar hisoblanadi.
a) Dekart koordinatalari x, y, z dan silindrik koordinatalar p, <p, z ga
o'tish
x = p cos q>, у = p sin <p, z = z
(0 < p < +°o, 0 < <p < 2n, -oo < z < +°°) formulalar yordamida amal-
ga oshiriladi (45- chizma).
311
45- chizma.
JJJ (P C0S<P> P sin Ф, z)pdpdqdz
Bu almashtirishning yakobiani J = p bo'lib,
JJJ f(x,y,z) dxdydz =
и
ga ega bo'lamiz.
b) Dekart koordinatalari x, y, z dan sferik koordinatalar p, cp, 0 ga
o'tish
x = p sin 0 • cos ср, у = p sin 0 • sin (p , z~ p cos 0
(0 < p < +°o, 0 < ср < 2л, 0 < 0 < л) formulalar yordamida amalga
oshiriladi (46- chizma).
Almashtirish yakobiani J — p2sin0 bo'lib,
f (x,y,z) dxdydz =
0 cos cp, p sin 0 sin <p, p cos B)p2 sin QdpdqdQ
v
bo‘ladi.
3- misol. Ushbu
JJJ zdzdydz
v
integral hisoblansin. Bunda quyidagi
= (h>Q)
r2 h2
konusning yuqori qismi va z = h tekislik bilan chegaralangan to'plam.
312
◄ Berilgan integralda o'zgaruvchini quyidagicha
x = p cos ср, у = p sin <p, z - z.
ko‘rinishda almashtirib topamiz:
x2+y2 _ ? P2 _ z2 x Л
r2 h2 r2 h2
(0 < p < г, 0 < <p < 2л, 0 < 0 < л).
Natijada
г Г2л/ h
bo‘ladi. Keyingi integralni hisoblaymiz:
dp =
nh2 r2 f ( 2 2 \ J 12 (P2 Y ЛЙ2 r2
= r2 j -P )Pdp = iM I у I =-4-.
Demak, J = ►
4
4- misol. Ushbu J = JjJ (x2 + y2 + z2)dxdydz
v
integral hisoblansinki, bunda V to'plam
1 2 2^2
x + yL + z r*
shardan iborat.
•< Bu intervalda
x = p sin 0 • cos <p, у = p sin 0 • sin <p , z = p cos 0
almashtirish bajaramiz. U holda
x2 + y2 + z2 = p2, J = p2 sin 0
bo'lib,
313
О < р < г, 0<<р< 2л, О < 0 < л
bo‘Iadi. Natijada berilgan integral
г я /2л
у2 + z2) dxdydz = Г f f р2р2 sin 0d<p dQ dp
ko‘rinishga keladi. Keyingi integralni hisoblaymiz:
г Г re (lit
J p* sin GzZcp dQ dp = j J (p4 sin 0 • 2л) dQ dp = 4л J p^dp =
4w5
~5~
Demak, J = —y. ►
7°. Uch karrali integrallaming ba’zi tatbiqlari. Uch karrali integral
yordamida R2 fazodagi jismlarning hajmini, massali jismning massasini,
og‘irlik markazini, inersiya momentlarini topish mumkin.
Mashqlar
1. Ushbu
JJJ 7*2 + у2 dxdydz
и
integral hisoblansin, bunda V — fazoda quyidagi
X2 + y2 = z2, z = 1
sirtlar bilan chegaralangan jism (to‘plam).
2. Sferik koordinatalarga o‘tib, ushbu
JJJ -Jx2 + y2 + Z2 dxdydz
integral hisoblansin, bunda V — fazoda
sirt bilan chegaralangan jism (to‘plam).
314
17- В О В
EGRI CHIZIQLI INTEGRALLAR
88- ma’ruza
Egri chiziqlar va ularning uzunliklari haqida
1°. Egri chiziq tushunchasi. Oliy matematikaning dastlabki qismini
o‘rganish mobaynida o‘quvchi egri chiziq va uning tenglamalari,
egri chiziqning uzunligi kabi ma’lumotlar, shuningdek, ba’zi egri
chiziqning tasvirlari bilan tanishgan. Egri chiziqli integrallar naza-
riyasida (shuningdek, keyinchalik o‘rganiladigan kompleks analiz kursida)
egri chiziqlaming muhimligini e’tiborga olib, ular haqida ba’zi ma’lu-
motlarni keltirish lozim topildi. Hozirgi zamon matematikasida egri
chiziq turlicha ta’riflangan bo'lib, ular orasida Jordan tomonidan
keltirilgan ta’rif birmuncha tabiiyroq hisoblanadi. U egri chiziqni
nuqtaning uzluksiz harakati natijasida qoldirgan izi sifatida qaragan.
x(i), y(t) funksiyalar |a,[3] segmentda aniqlangan va uzluksiz bo'l-
sin. Bu funksiyalardan tuzilgan ushbu
x = x(/),
У = y(t)
(a < t < P)
(1)
sistemani qaraylik. Tekislikda dekart koordinatalar sistemasini olib,
x va у larni shu tekislikdagi biror M nuqtaning koordinatalari sifatida
qaraymiz: M = Ravshanki, M nuqta [a,p] dan olingan t ga
bog'liq. Ayni paytda, M nuqta argument t ning (1) akslantirishdagi
aksi (obrazi), t ning o'zi bu akslantirishdagi Mnuqtaning asli (proob-
razi) bo'ladi. Shunday qilib, (1) akslantirish yordamida [a,p] seg-
mentning aksi tekislikda ushbu
Г = {(x,y): x = x(t),y = y(t), te [a,p]}
to'plamni hosil qiladi. Bu Г to'plamga tekislikdagi egri chiziq deyiladi.
Demak, egri chiziq [oc,p] da uzluksiz bo'lgan 2 ta x(t), y(f) funksiyalar
yordamida ta’riflanar ekan. Odatda, egri chiziqning bunday berilishi
uning parametrik ko'rinishda berilishi deyiladi. Bunda t — parametr.
Masalan:
315
X = r cos t,
у = r sin f
(О < t < 2 л, г > 0)
(2)
sistema tekislikda markazi koordinatalar boshida, radiusi r ga teng
bo‘lgan aylanani ifodalaydi. Demak, (2) — aylananing parametrik
tenglamasi.
Ba’zi hollarda egri chiziqning ta’rifini ifodalaydigan Г to‘plam
murakkab bo‘lib, hatto u biz tasawur etadigan egri chiziqqa butunlay
o‘xshamay qolishi mumkin. Masalan, Peano tomonidan [0,1] seg-
mentda uzluksiz bo'lgan shunday x(z), y(r) funksiyalar tuzilgan:
Г to‘plam uchlari (0,0), (1,0), (1,1), (0,1), nuqtalarda bo‘lgan kvad-
ratdan iborat bo‘ladi. Boshqacha qilib aytganda, «Egri chiziq» kvadrat-
ning har bir nuqtasidan o‘tadi. Bu «Egri chiziq» shu bilan xarakter-
lanadiki, bunda parametrning cheksiz ko‘p turli qiymatlarida x(t) va
yit) funksiyalar bir xil qiymatni qabul qiladi.
Aytaylik,
x = x(Z),
У = yit)
(a < Z < p)
(3)
tenglamalar sitemasi biror egri chiziqni aniqlasin, bunda x(f), y(f)
funksiyalar [a,p] da uzluksiz. Agar tv,t2 e [ex,p] da * t2 bo‘lganda
xrij = x(t2), y(tl) = y(t2)
bo‘lsa, u holda egri chiziqning (x(h ),у(^)) va (x(t2 ),y(Z2)) nuqta-
lari uning karrali nuqtalari deyiladi (bu nuqtada egri chiziq o‘zini o‘zi
kesib o‘tadi). karrali nuqtalarga ega bo‘lmagan egri chiziq sodda Jordan
egri chizig‘i deyiladi. Bu holda t parametrning turli tx,t2 (/) Ф t2)
qiyrhatlariga mos keluvehi egri chiziqning (x(^ ),y(i,)), (x(z2 ),y(Z2))
nuqtalari turlicha bo‘ladi. Masalan, \a,b\ segmentda uzluksiz bo‘Igan
у —f(x) funksiya grafigi sodda Jordan egri chizig‘i bo'ladi. Haqiqatan
ham,
x = t,
' У = fit), (y = fix), a<x<b)
deyilsa, u holda turli , t2 (tj tif) uchun Xi Ф x2 (xj = , x2 = t2)
bo‘lishi ravshan. Agar (3) sistema bilan aniqlanadigan egri chiziqda
t parametrning turli t2,t2 * t2) qiymatlariga mos keluvehi egri
316
chiziqning (х(^), у )), (x(i2),y(t2)) nuqtalari ham turiicha bo‘lib,
x(a) = x(P), y(a) = y(P)
bo‘lsa, egri chiziq sodda yopiq egri chiziq deyiladi. Masalan, ushbu
rx = ccost, ,n „ . ,
< (0 < t < 2л, a > 0, b > 0)
|y - bsint
sictema bilan aniqlangan egri chiziq (ellips) sodda yopiq egri chiziq
bo'ladi.
Biror sodda egri chiziq ushbu
x = x(Z),
’ (a < t < P)
b = y(0
tenglamalar sitemasi bilan aniqlanadigan bo'lsin. (x(a),y(a)) - A,
(x(P),y(P)) = В nuqtalar bu egri chiziqning mos rayishda boshi va
oxirgi nuqtalari deyiladi. Bu holda egri chiziqni AB yoy deb ham
yuritiladi.
Parametr t <= [a,P] ning tpt2 (h * t2) qiymatlari hdhftn t\ < t2
bo'lganda egri chiziqning (x(i2 ),y(Z2)) nuqtasi (x^ ),y(t[))
nuqtadan keyin kelishi bilan AB yoyda yo'nalish o'rnatiladi. Bunday
yo'nalish A dan Bga qarab bo'ladi. Agar (3) sistemadagi
x = x(i), y=y(0
funksiyalar [a,p] da uzluksiz y'(f) hosilalarga ega bo'lib,
x'2 (/) + y'2 (7) > 0 bo'lsa, (3) sistema aniqlagan egri chiziq silliq egri
chiziq deyiladi. Agar AB egri chiziq chekli sondagi silliq egri chiziq-
lardan tashkil topgan bo'lsa, uni bo‘lakli silliq egri chiziq deyiladi.
Silliq egri chiziq har bir nuqtasi urinmaga (chetki nuqtalarda bir
tomonli urinmalarga) ega bo'ladi. Bo'lakli silliq egri chiziqlar esa
chekli sondagi nuqtalarda bir tomonli urinmalarga ega bo'lishi mum-
kin. Masalan
x = «cost, _
’ (0 < t < 2л) т
Ь = b sin t
ellips — silliq egri chiziq, siniq chiziq esa bo'lakli silliq egri chiziq
bo'ladi.
317
2°. Egri chiziqning mavjudligi va uning uzunligi. Faraz qilaylik,
AB egri chiziq
lx = x(t),
' (a < Г < P)
Ь = y(0 5
tenglamalar sistemasi bilan aniqlangan bo'lsin, bunda A = (x(a), y(a)),
В = (x(P),y(P)), [a,p] segmentning ixtiyoriy bo'laklanishi
P = Ьо,h ,-4-i An}, bo = tn = P)
ni olamiz. P bo'laklashning bo'luvchi tk (k = 0,1,2,...,/?) nuqtalari
AB egri chiziqda
4 = (*Ь*),уЬА))-> (k = 0,1,2r34 = A, 4, - B)
nuqtalarni hosil qiladi. Bu nuqtalarni bir-biri bilan. to'glri chiziq
kesmalari yordamida birlashtirib, AB egri chiziqqa chizilgan siniq
chiziqni topamiz. Ravshanki, siniq chiziq uzunlikka ega (odatda,
siniq chiziq uzunligi uning periametri deyiladi). Uni L bilan belgilaylik.
Siniq chiziq perimetri L [cc,PJ ning bo'laklanishi Pga bog'liq bo'ladi:
L = L(P). [a,p] segmentning barcha bo'laklashlari to'plami P={P}
ning har bir bo'laklashiga nisbatan egri chiziqqa siniq chiziq chiziladi.
Bunday siniq chiziqlarning perimetrlari {L(P)} to'plamni hosil qiladi.
1- ta’rif. Agar ЩР)} to'plam chegaralangan bo'lsa, AB egri chi-
ziq uzunlikka ega deyiladi. Agar {L(P)} to'plam chegaralanmagan
bo'lsa, AB egri chiziq uzunlikka ega emas deyiladi.
Endi egri chiziqning uzunlikka ega bo'lishini ifodalaydigan teore-
malarni isbotsiz keltiramiz.
Aytaylik, AB egri chiziq ushbu
x = x(0, ,
’ (a < t < p)
b = yb)
tenglamalar sistemasi bilan aniqlangan bo'lsin. [a,p] segmentning ixtiyoriy
P Ь0=«Л=Р)
bo'laklashini olib, quyidagi
4 = У1Ж+1) - x^k )|> s2 = у b*+1) - у (M
k=0 k=0
318
yig'indilarni tuzamiz. Ravshanki, bu yig'indilar P bo'laklashga bog'-
liq bo'ladi:
=51(P), S2 = S2(P).
1- teorema. AB egri chiziq uzunlikka ega bo'lishi uchun [a,p]
segmentning barcha turli bo'laklashlari bo'yicha tuzilgan {S,(P), S2(P)}
to'plamlarning chegaralangan bo'lishi zarur va yetarli.
Xususan, egri chiziq
у = f(x), (a < x < b) (4)
tenglama bilan aniqlangan bo'lib, f(x) funksiya [a,b] segmentda
uzluksiz bo'lsin. [a,b] segmentning ixtiyoriy
Р = {х0,х15...(*o =a,xn = b)
bo'laklashini olib, unga nisbatan ushbu
5(P) = Xl/(^+i)-№)|
k=0
yig'indini hosil qilamiz.
2- teorema. (4) egri chiziq uzunlikka ega bo'lishi uchun [a,b\
segmentning barcha turli bo'laklashlari bo'yicha tuzilgan
= )-№)|
k=0
to'plamning chegaralangan bo'lishi zarur va yetarli.
1-misol. 1. Ushbu
/(*) =
7t
X COS -,
X
°,
agar 0 < x < 1,
agar x = 0
tenglamalar bilan aniqlangan egri chiziq uzunlikka ega emasligi isbot-
lansin.
•< Bu funksiya [0,1] segmentda uzluksiz bo'ladi. segmentining
P = {x0,x1,...,x„_1,x„}
bo'laklashini olaylik, bunda
x0 = u, %1 = -, x2 = wyr -> *n-i = 2’ x« =
319
bo'lsin. Ravshanki,
bOda /(ло) = /(О)=О,
UO da /(Xfc) = x^cos~ = -4nCOs(«-^ + l)K = ^L-r
П—/c+1 rr-K.-rl
bo'lib,
|/(^+1) ~ Ж)| = Ж +
bo‘ladi. Natijada
ЭД = 2Жя)-Л^)|=|/(хО|+|/(л2)-/(хОК--- + |Ж)-Ж-1)Н
111 1 .
- - + —- + - + ... + - +1
n л-I n 2
bo‘lib, bundan S(P) > 1 + | + | +... + - bo‘lishligi kelib chiqadi.
Keying! tengsizlikdan esa S(P) ning chegaralanmaganligini topamiz. ►
2- misol. Ushbu
2 К
X COS ,
• X
0,
Ж =
agar 0 < x < 1,
agar x = 0
tenglama bilan aniqlangan egri chiziq uzunlikka ega bo‘lishi isbot-
lansin.
◄ Bu funksiya [0,1] segmentda uzluksiz bo‘ladi. [0,1] segment-
ning ixtiyoriy
P = {x0, Xr,..., x^^x^
bo'laklashini olib,
S(P) = ^\f( ) - f(xk )|
k=0
yig‘indini qaraymiz. Lagranj teoremasidan foydalanib topamiz:
<1=0
Agar
|/'(x)| = 2xcos^ + rcsin^ < 6, (0 < x < 1)
320
bo'lishini e’tiborga olsak, keyingi munosabatdan
5(P)<6y(xfc+i -xj = 6
A=0
bo‘lishi kelib chiqadi. Demak, qaralayotgan egri chiziq uzunlikka
ega. ►
E s I a t m a. Egri chiziqning uzunlikka ega bo‘lishi va uning uzun-
ligini limit orqali ta’riflash mumkin.
Aytaylik, ushbu
tenglamalar sistemasi Jordan chizig'ining ifodasi bo'lsin, bunda x(f),
y(t) funksiyalar [a,p] da uzluksiz.
[a,{3] segmentning
bo'laklashini olib, so'ngra egri chiziqning
(x(/0), у(Г0)), (x(A), y(A)), (%(/„), y6„))
nuqtalarini to'g'ri chiziq kesmalari yordamida birlashtirib, egri chi-
ziqqa chizilgan siniq chiziqni hosil qilamiz. Uning perimetri
= +№+iW(O2
*=o >
bo'ladi.
2- ta’rif Agar Ve > 0 olinganda ham shunday 8 > 0 son topilsaki,
diametri \, > 8 bo'lgan [a,|3] segmentning ixtiyoriy Pbo'laklashi uchun
|Z(P)-/|<E
tengsizlik bajarilsa, ya’ni
lim L(P) = 1
—>0
bo'lsa, egri chiziq uzunlikka ega deyilib, I esa uning uzunligi deyiladi.
3°. Egri chiziq uzunligini hisoblash formulalari. 40- ma’ruzada
egri chiziq uzunligini hisoblash formulalari bayon etilgan. Egri chiziqli
integrallarda egri chiziqning uzunligi muhimligini e’tiborga olib, tegishli
formulalarni keltiramiz.
321
1) AB egri chiziq у = f (x), (a < x < b) tenglama bilan berilgan
bo'lib, f(x) funksiya [a,b] da uzluksiz va uzluksiz f'(x) hosilaga ega
bo'lsin. U holda AB egri chiziqning uzunligi quyidagiga teng bo'ladi:
ь ___________
I - J 7^ + f '2 (x)dx.
a
2) AB egri chiziq
Г = х(,)- (aS(S₽)
V=ио
tenglamalar sitemasi bilan aniqlansin. Bunda x(t), y(t) funksiyalar
[a,p] segmentda uzluksiz va uzluksiz x '(t), у '(t) hosilalarga ega bo'lib,
Л = (х(а),у(а))> Я = (х(Р),у(Р))
bo'lsin. U holda egri chiziqning uzunligi
₽ __________________________________
/ = J y]x'2(t) + y'2(t)dt
а
bo'ladi.
3) AB egri chiziq qutb koordinatalar sistemasida
p = p(0), (a<0<p)
tenglama bilan aniqlansin, bunda p(0) funksiya [a,p] segmentda uzluk-
siz va uzluksiz p'(9) hosilaga ega. U holda AB egri chiziqning uzunligi
quyidagiga teng bo'ladi:
₽ _____________
/ = J7p,2(e) + pWe-
a
Mashqlar
1. Ushbu /(x) =
x cos -, agar 0 < x < 1 bo'lsa,
X
0 , agar x = 0 bo'lsa
tenglamalar bilan aniqlangan egri chiziqning uzunlikka ega emasligi
isbotlansin.
322
2. Agar AB yoy I uzunlikka ega bo‘lib,
AB ~ AA{ + А^ A2 +... + A^_^ В
bo‘lsa, u holda
-<44 > 44 > •••> 4-i^
yoylar ham Zl5 /n_j uzunliklarga ega va
I = lx +12 +... + ln_x
bo‘lishi isbotlansin (additivlik xossasi).
89- ma’ruza
Birinchi tur egri chiziqli integrallar
Ma’lumki, integral matematik analizning muhim tushunchalaridan
hisoblanadi. Uning umumlashtirishlaridan biri — ma’ruzalarda bayon
etilgan ikki o‘zgaruvchili funksiyaning tekislikdagi to‘plam bo‘yicha
ikki karrali integralidir. Ayni paytda, ikki o'zgaruvchili funksiya
integralini boshqacha umumlashtirish (bu konkret amaliy masalalarni
hal qilishda zarur ekanligidan kelib chiqqan) ham mumkin. Quyida
keltiriladigan egri chiziqli integral shular jumlasidandir.
1°. Birinchi tur egri chiziqli integral tushunchasi. Tekislikda sodda
uzunlikka ega bo‘lgan AB egri chiziqni qaraylik (47- chizma).
Bu egri chiziqda A dan В ga qarab yo‘nalishni musbat yo‘nalish
deb, lining
A0,Al,...,A„_l,An (A^ - A,An - B)
nuqtalar yordamida hosil qilingan
P ~ {4 > 4 > > 4}
bo'laklashini olamiz. Natijada AB
egri chiziq
44+1 (^ = 0,1,2,..., w - 1)
bo'lakchalarga ajraladi. Uning uzun-
ligini Д4 (k = 0,1,2,...,n -1) de-
yilsa, P bo'laklashning diametri
4 - max{A4.} bo'ladi.
323
Aytaylik, bu AB egri chiziqda/(x,y) funksiya aniqlangan bo‘lsin
((x,y)e AB). Har bir Ak Ak+i da ixtiyoriy (£к ,x\k) nuqtani oiib, so'ngra
bu nuqtadagi f{x,y) funksiyaning qiymati f((f>kA\k)') ni \Sk ga
ko‘paytirib ushbu
/7—1
4=0
yig'indini hdsii qilamiz.
Ta’rif. Agar Ve > 0 olinganda ham shunday 3 > 0 son topilsaki,
AB egri chiziqning diametri k„> 0 bo'lgan har qanday Pbo'laklash
uchun tuzilgan о yig'indi ixtiyoriy (^a.,t|a.)g AkAk+x nuqtalarda
|o - J\ < e
tengsizlikni bajarsa,/(x,y) funksiya AB egri chiziq bo'yicha integral-
lanuvchi deyilib, J son esa/(x,y) funksiyaning AB egri chiziq bo‘yicha
birinchi tur egri chiziqli integrali deyiladi. U /
J f(x,y)ds
AB
kabi belgilanadi. Demak,
J f(x,y)ds = lim Y^f(^k,x]k)\Sk .
Keltirilgan ta’rifdan ko'rinadiki, f(x,y) funksiyaning birinchi tur
egri chiziqli integral! AB egri chiziqning yo'nalishiga bog'liq bo'lmaydi:
J f(x,y)ds = J f(x,y)ds.
AB BA
2°. Birinchi tur egri chiziqli integralning mavjudligi va uni hisob-
lash. Birinchi tur egri chiziqli integral ta’rifidan ko'rinadiki, u berilgan
f(x,y) funksiya va AB egri chiziqqa bog'liq bo'ladi.
Faraz qilaylik, AB sodda silliq egri chiziq ushbu
x = x(r),
у = y(0
(a < t < p)
324
tenglamalar sitemasi bilan aniqlangan va
A = (x(a),y(₽)), 5 = (x(P),y(₽))
bo‘lsin. Shu egri chiziqda f(x,y) funksiya berilgan.
Teorema. Agar f (x,y) funksiya AB da uzluksiz bo'lsa, u holda
birinchi tur egri chiziqli integral
J f{x,y)ds
AB
mavjud bo'lib, quyidagi tenglik o'rinli bo'ladi:
₽ __________________________
j f(x, y)ds = j f(x(t),y(t))yjx'2(t) + y'2(t)dl.
- a
AB
◄ [ajij segmentning
J3 = (t0=a, 4=P)
bo'laklashi AB egri chiziqda
4 = (x(tk),y(tk)), (k = 0,1,2,...,«)
nuqtalarni hosil qilib, u o'z navbatida egri chiziqning
р = (Aq=A,A„=B)
bo'laklashini yuzaga keltiradi. Bu bo'laklashga nisbatan quyidagi
° = (1)
fc=0
yig'indini tuzamiz. Bunda ,г|л)е AkAk+l , ASk esa AkAk+1 egri
chiziq uzunligi. Ma’lumki,
= j Jx'2(,f) + y’2 (t)dt
tk
bo'ladi. O'rta qiymat haqidagi teoremadan foydalanib topamiz:
Д4 = 7х'2(6fc) + /2 (Ш
(4 < 4 < 4+i ’ Atk = tk+i -tk).
325
Endi ^=x(Oj, т]л=у(ел)
deb qaraymiz. Ravshanki, (^,qA)e AkAk+i . Modomiki, f(x,y) funk-
siya AB egri chiziqda berilgan ekan, u holda f(x,y) = f(x(t),y(t))
bo‘ladi. Natijada (1) yig'indi ushbu
n-1 ------------------
О = X ), У (e*))V*'2 ) + У'2 <0* (2)
k=0
ko'rinishga keladi.
x(t), y(t) funksiyalar [oc,[3] da uzluksiz bo‘lganligi sababli
max {Atk } -> 0 da - max {/xSk } -> 0
bo‘ladi. Yana
/(x(t), y(t))y/x'(t) + y'2(t)
funksiya [a,[3] da uzluksiz bo‘lganligi uchun u |a,[3| da integralla-
nuvchi bo'ladi.
(2) tenglikda limitga o‘tib topamiz:
n-1
Hm <r= lim У f(x(6k), Ж
Хр->0 max {Л/д. }->0
₽ r_________________________________
=J f (%(o, .vwx/*'2 (eJ+/2 №
a
₽ ____________________________________________
Demak, j f(x,y)ds = J/(x(t), y(t))'jx'2(t) +y'2(t)dt. (3)
AB a
Bu teorema birinchi tur egri chiziqli integralning mavjudligini
ifodalash bilan birga uni hisoblash imkonini ham beradi.
1- natija. Aytaylik, AB egri chiziq у = y(x) (a < x < b) teng-
lama bilan aniqlangan bo‘lib, y(x) funksiya [a,b] da uzluksiz hamda
uzluksiz y'(x) hosilaga ega bo‘lsin (y(a) = A, y(b) = B).
Agar f (x,y) funksiya esa shu AB egri chiziqda uzluksiz bo‘lsa,
j f (x,y)ds birinchi tur egri chiziqli integral mavjud bo‘lib,
AB
326
))J*'2 (6J + /2 (0/tM =
b
j f(x,y)ds = J/(x,y(x))71 + /rW^ (4)
AB a
bo‘ladi.
2- natija. Aytaylik, AB egri chiziq qutb koordinatalari sistema-
sida
p = p(9), (a < 0 < P)
tenglama bilan aniqlangan bo'lsin, bunda p = p(0) funksiya [oc,(3]
segmentda uzluksiz va uzluksiz p' hosilaga ega. Bu egri chiziqda
f(x,y) funksiya aniqlangan va uzluksiz. U holda
J /(xj)*
AB
birinchi tur egri chiziqli integral mavjud bo'lib,
₽ _______________________
j f(x,y)ds = j/(p cos 0, p sin 0)7p2+p'2^0 (5)
AB
bo'ladi.
1- misol. Ushbu > J - f - ds
\ J у
AB
integral hisoblansin, bunda AB egri chiziq p y2 = 2x parabolaning
(1, л/2), (2,2) nuqtalari orasidagi qismi.
◄ (4) formuladan foydalanib topamiz;
2 I 72 V
J - f * Vl + (a/2x) dx ,
J V2x
1
2 .___ 2
J = \^^^dx = \\^bcdx = lA5^►
J 2 J 6 p
327
2- misol. Ushbu J - f 1 cos Qds
J P
c
interal hisoblansin, bunda C — markazi (o,0) nuqtada, radiusi a ga
teng bo'lgan aylana.
◄ Ma’lumki, bu aylananing tenglamasi qutb koordinatalar siste-
masida \
p(0) = 2ocos0,
ko'rinishda bo'ladi. (5) formuladan foydalanib topamiz:
7t П
2 2
j = fcos0 Jp2(e) + p/2(9)de = f de = к. ►
J p J
7Г Л
~2 '•J
3°. Birinchi tur egri chiziqli integraUarning ba’zi tatbiqlari. Birinchi
tur egri chiziqli integrallar yordamida egri chiziqning uzunligini, jism-
ning massasini, og'irlik markazini, inersiya momentlarini topish kabi
masalalar hal etiladi.
1. Tekislikda uzunlikka ega bo'lgan AB egri chiziqning uzunligi ushbu
S = j ds (6)
AB
integral yordamida topiladi.
2. Tekislikda uzunlikka ega bo'lgan AB egri chiziq bo'yicha
massa tarqatilgan bo'lib, uning zichligi p = p(x,y) bo'lsin. Bu egri
chiziqning massasi ushbu
m= J p(x,y)dr
AB
integral yordamida, og'irlik markazining koordinatalari esa
x0 =-J- [ xp(x,y)ds, y0 =~ f yp(x,y)ds (8)
rfl J ПТ J
AB AB
integrallar yordamida topiladi.
328
3. Tekislikda uzunlikka ega bo'lgan AB egri chiziqning OX va
OTkoordinata o‘qlariga nisbatan statik momentlari ushbu
Sx - j" yds, Sy = [ xds (9)
AB AB
formula bilan, shu o‘qlarga nisbatan inersiya momentlari esa quyidagi
Jx = J y2ds, Jy = J x2ds (10)
AB AB
inegrallar yordamida topiladi.
3- misol. Ushbu
x(t) - a cos31, .
- (0<r < 2л)
> |y(r) = asin3r
tenglamalar sistemasi bilan aniqlanadigan AB egri chiziq (astroida)
ning uzunligi topilsin.
◄ Astroida koordinatalari o'qlariga nisbatan simmetrik bo‘lishini
e’tiborga olib, (6) formuladan foydalanib topamiz:
2 _____________ 2 ________________________________:____
5 = j ds = 4J^x'2(t) + y'2(t)dt = j ^(-3acos2 isint)2 + (3asin21 cos t)2 dt
AB 0 0
Itdt =6a jsin 2tdt = 6a . ►
о
4-misol. Chizig‘ining zichligi p(x,y) = |y| bo'lgan AB massali
egri chiziq — y2 =2 px, ^0 < x < у j parabolaning massasi hamda
og‘irlik markazi topilsin.
◄ (7) formulaga ko‘ra parabolaning massasi <
m = j |y| ds
AB
329
bo‘ladi. Endi birinchi tur egri chiziqli integralni (4) formulaga ko'ra
aniq integralga keltirib hisoblaymiz:
P I f p _________ p _____________
m = J И Jl + ^dy = 2 - J yjp* 2 + y2 dy = - J j p2 + y2 d(p2 + y2) =
-p ’ p p о p 0
( 3 *- Y
= 1 (р2+у2)Ц I =b2(2V2-l).
P к 3 Jo J
Qaralayotgan massali parabola og‘irlik markazining koordinata-
larini (8) formuladan foydalanib topamiz:
p
x°= ifx W ds "ify3 Jp2+y2dy >
AB 0
p ________ y2 = u, du - 2ydy
]уЧр2 +Vdy = ---- з =
о УуР" +y2dy = dv, u = j(/+y2)2
= |/(P2 +/) -|(2y(p2 + y2)2 dy = 3Y|£__1.|(/ +y2)2
3 q 3 J 3 3 3
0 0
_2p5(l+V2)
15
Demak, x0 =
1 2p5(V2+l) _ 3 1 2p5(Л+1) _ p3(Зл/2 +5)
« 15 15 - 35
Xuddi shunga o!xshash
Уо = ~ f У M ds = (3V2 + ln( 1 + ^))
ш J Z,o
AB
bo'lishi topiladi.
5- misol. Ushbu C aylana (x2 + y2 = a2) ning uning diametriga
nisbatan inersiya momenti topilsin.
< Berilgan aylananing parametrik tenglamasi
x = о cost,
у - a sin t
(0 < t < 2tc)
330
bo'ladi. Aylana diametrini OX o'qqa joylashtirib, so'ngra (10) fbr-
muladan foydalanib topamiz:
2 л ____________________
Jx = jy2ds = j a2 sin2 t + 7(ocost)'2 + (asint)'2cfr =
с 0
2 it
= a3 J sin2 tdt -na3. ►
о
E slat ma. Aytaylik, AB egri chiziq fazoviy egri chiziq bo'lib,
bu chiziqda f (x,y,z) funksiya berilgan bo'lsin. Yuqoridagidek,/(x,y,z)
funksiyaning AB egri chiziq bo'yicha birinchi tur egri chiziqli integral
tushunchasi kiritiladi va o'rganiladi.
Mashqlar
1. Ushbu у = 1 - In cosx, (O < x < ^) tenglama bilan berilgan
egri chiziqning uzunligi topilsin.
1 ( ~
2. Zichligi p(x,y) = -=- bo'lgan ushbu y = -\ea +e al zanjir
у 2
chiziqning massasi topilsin.
90- ma’ruza
Ikkinchi tur egri chiziqli integrallar
1°. Ikkinchi tur egri chiziqli integral tushunchasi. Tekislikda
(sodda) uzunlikka ega bo'lgan AB egri chiziqni qaraylik (48- chizma).
Bu egri chiziqning biror
P = {4),4,4,...,AJ, (4=л, 4=5)
bo'laklashini olamiz. Natijada AB egri chiziq
44i> (k = 0,1,2,1)
bo'lakchalarga ajraladi. AkAk+x ning OXva OYkoordinatalar o'qlari-
331
dagi proyeksiyalari mos ravishda Axk va Ayk bo‘lsin:
pr0XAkAk+l=bxk, proy AkAk+l = Ayk, (k = 0,l,2,...,n-l).
Aytaylik, AB egri chiziqda f(x,y) funksiya berilgan bo‘lsin. Har
bir AkAk+l da ixtiyoriy ,-q*.) nuqtalarni olib, so'ngra bu nuqtadagi
funksiyaningf(^k,v\k) qiymatini Axk va &yk larga ko'paytirib, quyi-
dagi
«-1 И-1
<*1 = X , Л* Ж , <*2 = £ f&k > )M
k=$ k=f)
yig'indilarni hosil qilamiz. Bu yig‘indilar f(x,y) funksiyaga bog‘liq
bo‘lishi bilan birga AB egri chiziqni bo‘laklashga hamda har bir
ЛЛ+i da olingan (^,т|л) nuqtalarga bog‘liq bo‘ladi.
1- ta’rif. Agar Ve > 0 olinganda ham shunday 3 > 0 son topilsaki,
AB egri chiziqning diametri < 8 bo'lgan har qanday Pbo'laklash
uchun tuzilgan O](o2) yig‘indi ixtiyoriy AkAk+1 nuqtalarda
|o]-Jj|<e, (|o2-J2|<e)
tengsizlik bajarilsa,/(x,y) funksiya AB egri chiziq bo‘yicha integral-
lanuvchi, f son (J2 son) esa f (x,y) funksiyaning ikkinchi tur egri
chiziqli integrali deyiladi. Uni
332
j f(x,y)dx, (j f\x,y)dy)
AB AB
kabi belgilanadi. Demak,
n-1
| f(x,y)dx = ЦтУ/^Л)^,
AB
( I f(x,y)dy = lim У
AB
Keltirilgan ta’rifdan quyidagi xulosalar kelib chiqadi:
1) f (x,y) funksiyaning AB egri chiziq bo'yicha ikkinchi tur egri
chiziqli integrali ikkita bo'ladi:
J f(x,y)dx, §f(x,y)dy.
AB AB
Aytaylik, AB egri chiziqda P(x,y) va Q(x,y) funksiyalar berilgan
bo'lib, J P(x,y)dx, j Q(x,y)dy lar esa ularning ikkinchi tur
AB AB
egri chiziqli integrallar! bo'lsin. Ushbu
j P(x,y)dx+ J Q(x,y)dy
AB AB
yig'indi ikkinchi tur egri chiziqli integralning umumiy ko'rinishi
deyiladi va
J P(x,y)dx + Q(x,y)dy
AB
kabi belgilanadi:
J P(x,y)dx + Q(x,y)dy = J P(x,y)dx + j Q(x,y)dy .
AB AB . AB
333
2) f(x,y) funksiyaning ikkinchi tur egri chiziqli integrallari AB
egri chiziqning yo'nalishiga bog‘liq bo'lib,
J f(x,y)dx = - j f(x,y)dx, J f(x,y)dy = -J f(x,y)dy
BA AB BA AB
bo'ladi.
3) Agar AB egri chiziq OXkoordinata o'qiga (OFkordinata o'qi-
ga) perpendikular bo'lgan to'g'ri chiziq kesmasidan iborat bo'lsa,
ff(x,y)dy = 0, ' J f(x,y)dy = (T
BA AB
bo'ladi.
Aytaylik, K=AB sodda yopiq egri chiziq bo'lsin. Bu holda Ava
В nuqtalar ustma-ust tushadi (49- chizma).
Yopiq egri chiziq К da chizmada ko'rsatilganidek ikki yo'nalish
bo'lib, ulardan biri musbat, ikkinchisi esa manfiy bo'ladi.
Agar kuzatuvchi К chiziq bo'yicha harakatlanganda A'bilan che-
garalangan to'plam har doim chap tomonda qolsa, bunday yo'nalish
musbat bo'ladi, aks holda esa manfiy bo'ladi.
Shu К egri chiziqda f(x,y) funksiya berilgan bo'lsin. К chiziqda
ixtiyoriy^ikki A va_5 nuqtalarni olaylik. Bu nuqtalar К egri chiziqni
ikkita AnB va BmA egri chiziqlarga ajratadi.
Faraz qilaylik, quyidagi
J f\x,y)dx, J f(x,y)dx
AnB BmA
49- chizma.
integrallar mavjud bo'lsin. Ushbu
J f(x,y)dx+ J f(x,y)dx
AnB BmA
yig'indi f(x,y) funksiyaning A'yopiq
egri chiziq bo'yicha ikkinchi tur
egri chiziqli integrali deyiladi. Uni
^f(x,y)dx yoki <§f(x,y)dx
к к
334
kabi belgilanadi. Bu holda К yopiq chiziqning musbat yo‘nalishi
olinadi. Demak,
^f(x,y)dx = J f(x,y)dx + J f(x,y)dx.
K AnB BmA
Xuddi shunga o‘xshash
J/(x,y)Jx
к
hamda umumiy holda
J P(x, y)dx + Q(x, y)dy
к
integrallar ta’riflanadi.
Aytaylik, AB fazodagi sodda uzunlikka ega bo‘lgan egri chiziq
bo‘lib, bu egri chiziqda f (x,y,z) funksiya berilgan bo‘lsin. Yuqoridagi-
dek,/(x,y,z) funksiyaning ikkinchi tur egri chiziqli integrallari ta’rif-
lanadi va ular quyidagicha belgilanadi:
J f(x,y,z)dx, j f(x,y,z)dy, j f(x,y,z)dz,
AB AB AB
j P(x,y,z}dx + Q{x,y,z)dy + R{x,y,z)dz.
AB
2°. Ikkinchi tiir egri chiziqli integralning mavjudligi va uni hisob-
lash. Faraz qilaylik, AB egri chiziq ushbu
x = x(t) ,
У = У(0
(a < / < P)
(1)
tenglamalar sistemasi bilan aniqlangan bo‘lib, x = x(Z) funksiya [a,p] da
uzluksiz, x '(/) hosilaga ega, y(t) funksiya esa [a,p] da uzluksiz hamda
A = (x(a),y(a», 2? = (х(Р),ИР))
bo‘lsin. t parametr a dan p ga qarab o‘zgarganda AB egri chiziqning
(x,y) = (x(Z),y(/)) nuqtasi A dan В ga qarab AB ni chizib borsin.
335
1- teorema. Agar f(x,y) funksiya AB da uzluksiz bo‘lsa, u holda
ikkinchi tur egri chiziqli integral
J f(x,y)dx
AB
mavjud bo'lib, u quyidagiga teng:
₽
j = J7(x(0,y(0)*W' (2)
Xb
◄ [a,₽] segmentning
P = {A,h >’ (n-i An}, (t0 = a, t„ = 0)
bo'laklashi AB egri chiziqda
Л = (x(tk),y(tk)), (£ = 0,1,2,3,..., и)
nuqtalarni hosil qilib, ular o'z navbatida AB egri chiziqning
ГЦ^,...,^}, (Aq = A, A„ ~ B)
bo'laklashini yuzaga keltiradi. Bu bo'laklashga nisbatan quyidagi
n-i
= (3)
k=0
yig'indini tuzamiz. Bunda &xk miqdor AkAk+1 ning OX o'qidagi
proyeksiyasi bo'lib,
&xk = x(tk+l) -x(tk)
bo'ladi. Ayni paytda,
f(^k,i)k) = /(х(тк),у(тк)), (ike[tk , tk+i ])
tenglikka ega bo'lamiz. Endi
<t+i
Axk = J x'(t)dt
>k
bo'lishini e’tiborga olib, (3) tenglikni quyidagi ko'rinishda yozib olamiz:
336
П-l 'Ail л-l 'A+1
<h =^1\хЫ,У^кУ> J x'(t)dt = ^ J f(x(Tk),y(xk))x(t)dt.
k=0 ,k k=0 tk
Ravshanki, ushbu
P
J\ = \f(At},yW)x(f)dt
a
integral mavjud, uni quyidagicha
П-l ‘k+l
j\ J f(x(t),y(t))x'(t)dt
k=0 tk
deb yozib, so‘ngra
Л—1 ‘k+l
<h ~J\ =X J [/(x(TA),y(Tj)-/(x(0,y(t))]x'(0^
*=° tk
ayirmani qaraymiz.
f(x(t), y(fy) funksiya [oc,J3] da uzluksiz. U holda Ve > 0 olinganda
ham shunday 8 > 0 topiladiki, bunda barcha \tk = tk+i - tk lar 8 dan
kichik bo'lganda f(x(t), y(t)) funksiyaning tebranishi s dan kichik
bo'ladi. x'(t~) funksiya esa [a,p] da uzluksiz, demak, chegaralangan:
jx'(O| < M.
Shunday qilib, )
|cq - /j | < eAf (P - a)
bo'ladi. Keyingi munosabatdan
lim о, = Jx
kl, >o
bo'lishi kelib chiqadi. Bu tenglik integralning mavjudligi va (2) teng-
likning o'rinli bo'lishini isbotlaydi. ►
Aytaylik, (1) sistemadagi x(r), y(t) funksiyalar [a,p] da uzluksiz
bo'lib, y(t) funksiya esa uzluksiz у'(/) hosilaga ega bo'lsin.
2- teorema. Agar f(x,y) funksiya AH da uzluksiz bo'lsa, u holda
ikkinchi tur egri chiziqli integral
337
J f(x,y)dx
AB
mavjud bo‘lib, qjuyidagi tenglik o‘rinli bo'ladi:
₽
J f(x,y)dy = j f(x(t),y(J)}y'(t)dt.
AB “
(4)
Aytaylik, (1) sistemadagi x(t), y(t) funksiyalar [cc,j3] da uzluksiz
x'(t), y\f) hosilalarga ega bo‘lsin.
3- teorema. Agar P(x,y) va Q(x,y) funksiyalar AB da uzluksiz
bo‘lsa, u holda egri chiziqli integral
J P(x,y)dx + Q(x,y)dy
AB
mavjud bo‘lib,
j P(x,y)dx+ Q(x,y)dy =
AB
₽
= J [P(x(O, y(t))x'(f) + Q(x(t),y(t))y'(t)]fit (5)
a
bo‘ladi.
Bu teoremalar yuqoridagi 1- teorema kabi isbotlanadi. Keltirilgan
teoremalar ikkinchi tur egri chiziqli integralning mavjudligini isbotlash
bilan birga ularning aniq integrallarga (Riman integrallariga) kelishini
ifodalaydi. Binobarin, egri chiziqli integrallarni hisoblash imkonini
beradi. Egri chiziqli integrallar (2),(4) va (5) formulalar yordamida
hisoblanadi.
Agar AB egri chiziq ushbu
у = y(x), (о < x < b); x = x(y) , (с < у < d)
tenglamalar bilan berilgan bo‘Isa, u holda egri chiziqli integrallar
birmuncha sodda ko‘rinishga ega bo‘ladi. Aytaylik, AB egri chiziq
У - У{х), (a<x<b)
338
tenglama bilan berilgan bo'lib, y(x) funksiya [a,b\ da uzluksiz y'(x)
hosilaga ega bo'lsin. U holda (2) va (5) formulalar quyidagi
b
$ f(x,y)dx = jf(x,y(x))dx, (6)
AB a
b
j P(x,y)dx+ Q(x,y)dy = J[P(x,y(x)) + 2(x,y(x))/(x)]<& (7)
AB a
ko'rinishga keladi. Aytaylik, AB egri chiziq
x = x(y), (c<y < d)
tenglama bilan berilgan bo'lib, x = x(y) funksiya [c,d] da uzluksiz
x'(y) hosilaga ega bo'lsin. U holda (4) va (5) formulalar quyidagi
d
f f(x,y)dy = f f(x(y),y)dy , (8)
AB c
d
j P(x,y)dx + Q(x,y)dy = j[P(x(y),y)x(y) + Q(x(y),y)]dy (9)
AB c
ko'rinishga keladi.
1- misol. Ushbu
Jx = j (x2 -y2~)dx, J2 = j (x2-y2)dy
AB AB
integrallar hisoblansin. Bunda AB egri chiziq у = x2 parabolaning
absissalari x = 0, x = 2 bo'lgan nuqtalari orqasidagi qismi.
◄ AB egri chiziq у = x2 tenglama bilan aniqlanishini e’tiborga
olib, integralni hisoblashda (6) formuladan foydalanamiz:
2
/1= f (x2 -y2)dx - f(x2 -x4)dx =
J J ID
AB 0
J2 integralda integrallash egri chizig'i x2 = у bo'lib, (8) formula-
ga ko'ra quyidagi natijani olamiz: ;
339
1
J2 = J (x2 -y2)dy = J(y -y2)dy = -y.
AB 0
2- misol. Ushbu J y1 dx + x2dy
AB
integral hisoblansin, bunda AB egri chiziq—. + —- = 1 ellipsning
a1 bl
yuqori yarim tekislikdagi qismi.
◄ Bu ellipsning parametrik tenglamasi
x = a cos t,
у - bsmt
bo'ladi. A = (u,0) nuqtaga parametrning t = 0 qiymati, B= (-a,0)
nuqtaga esa t = л qiymati mos kelib, t parametr 0 dan л gacha
o‘zgarganda (x,y) nuqta A dan В ga qarab ellipsning yuqori yarim
tekislikdagi qismini chizadi. Ravshanki,
P(x,y)=y2, Q(x,y) = x2
funksiyalar AB da uzluksiz. Berilgan integralni (5) formuladan foy-
dalanib hisoblaymiz:
71
j y2dx + x2dy = j[b2 sin2 t(-usint) + a2 cos2 tZ>cosf]<# =
ab °
К
= ab^ (a cos31 - b sin3 f)dt = - - ab2. ►
о
3- misol. Ushbu cjj 2xydx - x2dy
к
integral hisoblansin, bunda K— yopiq chiziqning 0(0,0) va /4(2,1)
7 1
nuqtalarini birlashtiruvchi to'g'ri chiziq kesmasi hamda у = ^x
parabola yoyidan tashkil topgan yopiq egri chiziq (50- chizma).
340
50- chizma.
Ravshanki,
<j) 2xydx - x2dy = J 2xydx + x2dy + j 2xydx + x2dy.
k OA AO
OA kesmada x — 2y bo‘lib, (9) formulaga ko‘ra
J 2xydx + x2dy = J[2 • 2y2 2 - 4y2 ]dy = ~
OA 0
natijaga ega bo'lamiz.
OA yoyda x = 2y2 bo‘lib, yana (9) formulaga ko‘ra
1
j 2xydx + x2dy = f[2-2y2 ,y.4 y-4y4]dy =
AO 0
bo‘ladi. Demak, 2xydx + x2dy = ~ - у = -||.
к .
3°. Ikkinchi tur egri chiziqli integralning ba’zi tatbiqlari. Ikkin£J,
tur egri chiziqli integrallar yordamida tekis shaklning yuzi, ku^..
ta’sirida bo‘lgan maydonda bajarilgan ish topiladi hamda boshqa dx
fizik va mexanik masalalar hal etiladi. Tekislikda biror yuzaga
bo‘lgan D shakl berilgan bo‘lib, uning chegarasi to‘g‘rilanuvchi yo^1^
3D chiziqdan iborat bo‘lsin. Bu shaklning yuzi ushbu
p.D-^xdy, \iD = -^ydx, l j xdy- ydx (1^
an an an
formulalar yordamida topiladi.
7
Aytaylik, uzunlikka ega bo‘lgan AB egri chiziq berilgan bo‘lib,
uning har bir (x,y) nuqtasi ushbu
F(x,y) = P(x,y)i +Q(x,y)j
kuch ta’sirida bo‘lsin. U holda A nuqtani В nuqtaga o'tkazishda
bajarilgan ish quyidagicha hisoblanadi:
W = J P(x,y)dx+ Q(x,y)dy. (11)
AB
4- misol. Ushbu
x = acost, .. .
(0 < t < 2л)
у = b sm t
ellips bilan chegaralangan shaklning yuzi topilsin.
◄ Bu shaklning yuzi (10) formulaga ko'ra
| xdy - ydx
Э(П)
bo'ladi. Egri chiziqli integralni hisoblaymiz:
12lt
- J (a cos t b cos t + b sin t • a sin t}dt -
о
1 2л
- -ab Г (cos2/ + sin2/) dt = nab . >
Z *
0
5- misol. AB egri chiziq у - x3 chiziqning (0,0) va (1,1) nuqtalari
orasidagi qismi bo'lib, uning har bir nuqtasi
F(x,y) = 4x6i + xyj
kuch ta’sirida bo'lsin. Bu kuch ta’sirida bajarilgan ish topilsin.
< Izlanayotgan ishni (11) formuladan foydalanib topamiz. Bu holda
P(x,y) = 4x6, Q(x,y) = xy
bo'lishini e’tiborga olsak, u holda bajarilgan ish
i
W - J 4x6dx + xy dy = J (4x6 + x * x’ *3x2 )dx = 1
AB 0
bo'ladi. ►
342
Mashqlar
1. Ikkinchi tur egri chiziqli integrallar ham aniq integral xossalari
kabi xossalarga ega. Bu xossalar keltirilsin va ular isbotlansin.
2. Birinchi va ikkinchi tur egri chiziqli integrallar ushbu
j f(x,y)dx = j f(x,y)cosads, j f(x,y)dy = j /(x, y) cos
AB AB AB AB
j P(x,y)dx + Q(x,y)dy - J [P(x,y)cosa + 0(x,y)cos|3]d5
AB AB
' bog‘lanishda bo‘lishi isbotlansin, bunda a va [3 — mos ravishda OX
va OKo‘qlar bilan urinmaning yoy o‘sishi tomoniga qarab yo‘nalishlari
orasidagi burchaklar.
3. Ushbu J (2a - y)dx + xdy
AB
integral hisoblansin, bunda AB yopiq chiziq quyidagi
Ь = (Os,<27t)
|y = я(1-cost)
sikloidadan iborat.
4. Ushbu (£ , л1, Adx + dy)
рИ+Н
, - - A
integral hisoblansin, bunda К yopiq chiziq uchlari
Л = (1,0), В = (0,1), С = (-1,0), Z) = (0,-l)
nuqtalarda bo‘lgan kvadratdan iborat.
91- ma’ruza
Grin formulas! va uning tatbiqlari
1°. Grin fonnulasi. Tekislikda ushbu
У = У1 (x), у = y2 (x), (a < x < b, Vi (x) < y2 (x))
hamda
343
х = a, x — b
chiziqlar bilan chegaralangan to'pamni olaylik, bunda ^(x) va
y2(x) funksiyalar [a,b\ da uzluksiz (51- chizma).
Ravshanki, Dx ning chegarasi (konturi) dD1 quyidagi I, II, Щ
IV chiziqlarga ajraladi (bunda II va IV chiziqlar nuqtalaiga aylanishi
rnumkin). _
Aytaylik, D = Dl u ЭД da P(x,y) funksiya uzluksiz bo‘lib, u
. 3P(x,y)
uzluksiz xususiy hosilaga ega bo‘lsin. Ushbu
j P(x,y)dx
3z?i
egri chiziqli integralni qaraymiz. Uni quyidagicha
J P(x,y)ah' = JP(x,y)ch-+ jp(x,y)dr + j P(.x,y)dx + J P(x,y)<£
ЭД ’ 1 II III IV
ko'rinishda yozib olamiz. II va IV chiziqlar OXo‘qqa perpendikular
bo'lganligi sababli
j P (x, y) dx = j P (x, y) dx = 0
II IV
bo'lib,
J P(x,y)dx = ^P(x,y)dx+ j P(x,y)dx
3Di i in
bo'ladi. Endi
344
b b
$P(x,y)dx + j P(x,y)dx = P(x,y1(x))dx + $ P(x,y2(x))dx =
I III a a
b b
=/[^^1)-Л^У2)]^ =-f dx =
a a
b У-У1
« Lv=n
9v
bo'lishini e’tiborga olsak, u holda
j P(x,y)dx-^~^ldxdy (1)
ЭД Д
tenglikka ega bo'lamiz.
Faraz qilaylik, tekislikdagi Gto'pam shunday bo'lsinki, uni vertikal
chiziqlar yordamida yuqoridagi kabi Gk (Л = 1,2,3,...) larga ajratish
mumkin bo'lsin (52- chizma).
Bunday to'pam uchun ham (1) formula o'rinli bo'ladi:
J P(x,y)dx = '£ J P(x,y~)dx =
*=!( Gk ) G
Endi tekislikda ushbu
x = Xj(j), x = x2(y), (c<y<d)
hamda у = с, у = d
chiziqlar bilan chegaralangan D2 to'pamni olaylik, bunda x}(y), x2(y)
funksiyalar [c,d] da uzluksiz (53- chizma).
Ravshanki, D2 ning chegarasi (konturi) dD2 quyidagi I, II, III,
IV chiziqlarga ajraladi (bunda II va IV chiziqlar nuqtalarga aylanishi
mumkin).
Faraz qilaylik, D2 = D2 (jdD2 da Q(x,y) funksiya uzluksiz bo'lib,
u uzluksiz xususiy hosilaga ega bo'lsin. Ushbu
345
j Q(x,y)dy
Эбз
egri chiziqli integralni qaraymiz. Uni quyidagicha
j Q(x,y)dy = fQ(x,y)dy + jQ(x,y)dy + j Q(x,y)dy+ j Q(x,y)cfy
dG? I II III IV
ko'rinishda yozib olamiz. II va IV chiziqlar OYo‘qqa perpendikular
bo‘lganligi sababli
J Q(x,y)dy = J 2(x,y)dy = 0
II IV
bo‘lib, J Q(x,y)dy = jQ(x,y)dy + j Q(x,y)dy
dG2 I III
ga ega bo'lamiz. Endi
d
jQ(x,y)<fy + J Q{x,y)dy = (у),у)Ф> +
I III c
+\Q(x2 (y),y)dy = ][2(х15у)-0(%2,у)]^ =
d
= je(x,y)Q^=J
d г
dQ(x,y)
dx
bo‘lishini e’tiborga olib topamiz:
— dxdy
JJ dx
02
346
JJ Эх z
—
Aytaylik, tekislikdagi F to'p-
lam shunday bo'lsaki, uni go-
rizontal chiziqlar yordamida
yuqoridagi Z>2 kabi Fk (£=1,
2,3,...)larga ajratish mumkin q
bo'lsin (54- chizma).
Bunday to'plam uchun ham 54'chizma-
(2) formula o'rinli bo'ladi:
J Q (x,у)dy = У J) Q (x,y )dy = У JJ^^dxdy = JJ d-^^dxd)
dF k=lSFk J G
Faraz qilaylik, tekiclikdagi D to'plam yuqoridagi Dl va D2 lar
xususiyatiga ega bo'lib, unda P(x,y), Q(x,y) funksiyalar uzluksiz va
. dP(x,y) 9Q(x,y) . -
uzluksiz —— xususiy hosilalarga ega bo Ism. U holda
P(x,y) va Q(x,y) funksiyalar uchun bir yo'la (1) va (2) formulalar
o'rinli bo'ladi. Ularni hadlab qo'shib topamiz:
f P(x,y)dx + Q(x,y)dy = [[[ Adxdy. (3)
J JJ l Эх dy I
Bu Grin formulasi deyiladi. Demak, Grin formulas! to'plam
bo'yicha olingan ikki karrali integral bilan shu to'plam chegarasi
bo'yicha olingan egri chiziqli integralning bog'lanishini ifodalaydi.
2°. Grin formulasining ba’zi bir tatbiqlari. Aytaylik, yuqorida
keltirilgan bir bog'lamli D to'plamda P(x,y), Q(x,y) funksiyalar uzluksiz
va uzluksiz xususiy hosilalarga ega bo'lsin. U holda Grin formulasi
(3) o'rinli bo'ladi.
Grin formulasidan foydalanib, tekis shakl yuzining egri chiziqli
integral yordamida ifodalanishini ko'rsatish mumkin.
Aytaylik, P'(x,y). Q\x,y) funksiyalar D to'plamda yuqorida kelti-
rilgan shartlarni qanoatlantirishi bilan birga ushbu
347
shartni ham qanoatlantirsin. U holda
и[<<ы> _ Ъл.ф, u0
JJ l Эх <fy
D 'I
bo'lib, Grm formulasiga ko'ra :
|xZ) = | P*(x, y)dx + Q’(x, y)dy
az>
bo'ladi. Xususan, P*(x,y)---y, Q(x,y) = G yoki
/,‘(x,y) = 0, Q(x,y) = 0, yoki P*(x,y) = -ly, Q(x,y) = ^x
bo'lsa,
dQ*(x,y) _ ЭР*(х,у) = 1
Эх dy
bo'lib, to'plamning yuzi quyidagiga. teng bo'ladi:
pD = -<j) ydx = <j) xdy = у <j) xdy - ydx. (4)
az? az> 2 az>
Mashqlar
1. Grin formuiasidar foydalanib, ushbu
J jx2 + y1 dx + у
i:
xy + In I x + ylx2 + y2 j dy
egri chiziqli integral hisoblansin.
2. Ushbu
x = acosJt, /A „ .
(0 < t < 2n)
у - a sin3 t,
astroida bilan chegaralangan to'plamning yuzi topilsin.
348
Adabiyotlar
1. Azlarov T., Mansurov H. Matematik analiz. 1-tom. Toshkent,
«O‘zbekiston», 1994, 1995.
2. Xudayberganov G., Varisov A., Mansurov H. Matematik analiz.
1- va 2-qismlar. Qarshi, «Nasaf», 2003.
3. Архипов Г., Садовничий'£., Чубариков В. Лекции по мате-
матическому анализу. Москва, «Высшая школа», 1999.
4. Ильин В., Садовничий В., Сендов Б. Математический анализ,
Москва «Наука», 1979.
5. Кудрявцев Л. Курс математического анализа. Т. 1. 1973.
6. PvduH У Основы математического анализа. Москва, «Мир»,
1976.
7. Дороговцев А. Математический анализ. Киев, «Высшая
школа», 1985.
8. Фихтенгольц Г. Курс дифференциального и интегрального
исчисления. Т. I, II. Москва, «Физмат-лит», 2001.
9. Sa’dullayev A., Mansurov И., Xudayberganov G., Varisov А.,
G'ulomov R. Matematik analiz kursidan misol va masalalar
to‘plami. 1- va 2- tomlar. Toshkent, «O!zbekiston», 1993, 1996.
10. Демидович Б. Сборник задач и упражнений по математи-
ческому анализу. Москва, «Наука», 1990.
349
MUNDARIJA
So'zboshi.............................................................
11- bob. Sonli qatorlar (davomi)
53- ma’ruza. Ixtiyoriy hadli qatorlarda yaqinlashish alomatlari...... 4
54- ma’ruza. Cheksiz ko'paytmalar................................... 9
12- bob. Ko‘p o‘zgaruvchili funksiyalar, ularning limiti,
uzluksizligi
55- ma’ruza. Rm fazo. Rm fazoda ochiq va yopiq to'plamlar............16
56- ma’ruza. R”' fazoda ketma-ketlik va uning limiti................25
57- ma’ruza. Ko'p o'zgaruvchili funksiya va uning limiti............33
58- ma’ruza. Ko‘p o'zgaruvchili funksiyaning uzluksizligi.
Tekis uzluksizlik. Kantor teoremasi..................................46
13- bob. Ko‘p o‘zgaruvchili funksiyaning hosila va differensiallari
59- ma’ruza. Ko‘p o‘zgaruvchili funksiyaning xususiy
hosilalari. Funksiyaning differensiallanuvchanligi....59
60- ma’ruza. 0‘ rta qiymat haqida teorema. Yo'nalish bo'yicha
hosila................................................72
61- ma’ruza. Ko‘p o'zgaruvchili funksiyaning differensiali.........80
62- ma’ruza. Ko‘p o'zgaruvchili funksiyaning yuqori tartibli hosila
va differensiallari. Teylor formulasi.................88
63- ma’ruza. Ko‘p o'zgaruvchili funksiyaning ekstremumlari.........99
64- ma’ruza. Oshkormas funksiyalar................................109
14- bob. Funksional ketma-ketlik va qatorlar
65- ma’ruza. Funksional ketma-ketliklar va ularning tekis
yaqinlashuvchanligi................................. 119
66- ma’ruza. Funksional qatorlar va ularning tekis
yaqinlashuvchanligi................................. 130
67- ma’ruza. Tekis yaqinlashuvchi funksional qatorlarning
xossalari........................................... 140
68- ma’ruza. Darajali qatorlar, ularning yaqinlashish radiusi
va yaqinlashish intervallari........................ 148
69- ma’ruza. Darajali qatorning tekis yaqinlashishi.
Darajali qatorning xossalari.......................... 157
70- ma’ruza. Teylor qatori..........................................163
71- ma’ruza. Uzluksiz funksiyani ko‘phad bilan yaqinlashtirish.
Veyershtrass teoremasi.................................172
72- ma’ruza. Furye qatori tushunchasi...............................179
73-ma’ruza. Furye qatorining yaqinlashuvchanligi....................190 -
15- bob. Parametrga bog‘liq integrallar
74- ma’ruza. Ikki o‘zgaruvchili funksiyaning bir o'zgaruvchisi
bo'yicha yaqinlashishi.................................202
75- ma’ruza. Parametrga bog'liq integrallar.........................209
76- ma’ruza. Chegaralari o'zgaruvchi parametrga bog'liq
integrallar............................................216
77- ma’ruza. Parametrga bog‘liq xosmas integrallar..................222
78- ma’ruza. Parametrga bog‘liq xosmas integrallarning
funksional xossalari...................................231
79- ma’ruza. Ba’zi xosmas integrallarni hisoblash...................240
80- ma’ruza. Eyler integrallari.....................................247
16- bob. Karrali integrallar
81- ma’ruza. Tekis shaklning yuzi hamda fazodagi jismning
hajmi haqida ba’zi ma’lumotlar.........................260
82- ma’ruza. Ikki karrali integral tushunchasi va uning mavjudligi.267
83- ma’ruza. Integrallanuvchi funksiyalar sinfi.
Integralning asosiy xossalari.........................................274
84- ma’ruza. Ikki karrali integralni hisoblash......................280
85- ma’ruza. Ikki karrali integralda o'zgaruvchilami almashtirish ... 291
86- ma’ruza. Ikki karrali integralning ba’zi bir tatbiqlari.........298
87- ma’ruza. Uch karrali integrallar.............................. 305
17- bob. Egri chiziqli integrallar
88- ma’ruza. Egri chiziqlar va ularning uzunliklari haqida..........315
89- ma’ruza. Birinchi tur egri chiziqli integrallar.................323
90- ma’ruza. Ikkinchi tur egri chiziqli integrallar.................331
91- ma’ruza. Grin formulas! va uning tatbiqlari.....................343
Adabiyotlar...........................................................349
22.1
М31
Matematik analizdan ma’ruzalar/G. Xudayberganov va boshq.;
taqrizchilar: R.R. Ashurov, R.N. G‘anixo‘jayev; O‘zbekiston Respub-
likasi Oliy va o'rta-maxsus ta’lim vazirligi. — T.: «Voris-nashriyot»,
2010. — 352 b.
1. Xudayberganov G.
ББК22.1Я73
G. Xudayberganov, A.K. Vorisov,
X.T. Mansurov, B.A. Shoimqulov
MATEMATIK ANALIZDAN
MA’RUZALAR
II
5460100—«Matematika», 5440200—«Mexanika» bakalavr
yo‘nalishidagi talabalar uchun o‘quv qo‘llanma
«Voris-nashriyot» MChJ
Tashkent — 2010
Muharrir
Badiiy muharrir
Sahifalovchi
M.Shermatova
B. Ibrohimov
Sh.Rahimqoriyev
Original-maketdan bosishga 23.11.2010 da ruxsat etildi.
Bichimi 60x84'/16. Ofset bosma usulida bosildi. Bosma t. 22,0.
Shartli b.t. 19,0. Adadi 500. Buyurtma № #
«Voris-nashriyot» MChJ, Toshkent, Shiroq ko‘chasi, 100.
MChJ «Noshir» O‘zbekiston-Germaniya qo‘shma korxonasining
bosmaxonasida chop etildi.
Toshkent sh., Navoiy ko‘chasi, pastki savdo rastalari