Курс термодинамики - Ноздрев В.Ф.

Author: Ноздрев В.Ф.

Tags: физика термодинамика

Year: 1967

Similar

Общий курс физики. Термодинамика и молекулярная физика

II. Термодинамика и молекулярная физика

Курс термодинамики

Термодинамика и статистическая физика

Text

В.Ф.НОЗДРЕВ
курс
термодинамики
Издание 2-е,
исправленное
Утверждено
Министерством просвещения РСФСР
в качестве учебного пособия для педа-
педагогических институтов
издательство «просвещение» москва
196 7

ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ. Второе издание
«Курса термодинамики» подверглось небольшим изменениям:
во введении уточнены некоторые исходные представления и
понятия термодинамики;
в первой главе (Уравнения состояния) даны некоторые допол-
дополнения с учетом современного состояния теории реальных газов и
жидкостей;
из второй главы исключен весь материал, относящийся к поня-
понятию тепловой энергии.
Автор
ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ. Настоящий курс
термодинамики возник на основе лекций, читавшихся автором в
течение ряда лет студентам физической специальности в Москов-
Московском областном педагогическом институте им. Н. К. Крупской.
При создании курса учитывались также и некоторые разделы по
технической термодинамике, прочитанные автором для* студентов
теплофизической специальности Московского университета.
Излагая основные положения термодинамики и ее методы, ав-
тор обращал особое внимание на приложение их к решению прак-
практических задач.
С этой целью с термодинамической точки зрения рассматри-
рассматриваются процессы, происходящие в двигателях внутреннего сгорания
и реактивных двигателях, явления в гальванических элементах, во-
вопросы теплоемкости, поверхностного натяжения, поведение вещества
при низких температурах и т. п.
Уяснение студентами неисчерпаемых возможностей использо-
использования методов термодинамики при изучении различных физических
явлений и в практике особенно необходимо в свете задач политех-
политехнической подготовки будущих учителей. Наличие значительного
количества упражнений и задач поможет пользующимся данным
пособием получить ясное представление о конкретном применении
изучаемой науки.
Основываясь в изложении на трех началах термодинамики,
как опытных законах, т. е. излагая феноменологическую термоди-
термодинамику, автор, однако, иногда обращается к рассмотрению внут-
внутреннего молекулярного строения тел. Это имеет место главным
образом в тех случаях, когда подобное рассмотрение естественно
объясняет макроскопические закономерности.
Значительное место в учебнике отводится новым разделам
термодинамики, например принципу термодинамического подобия,
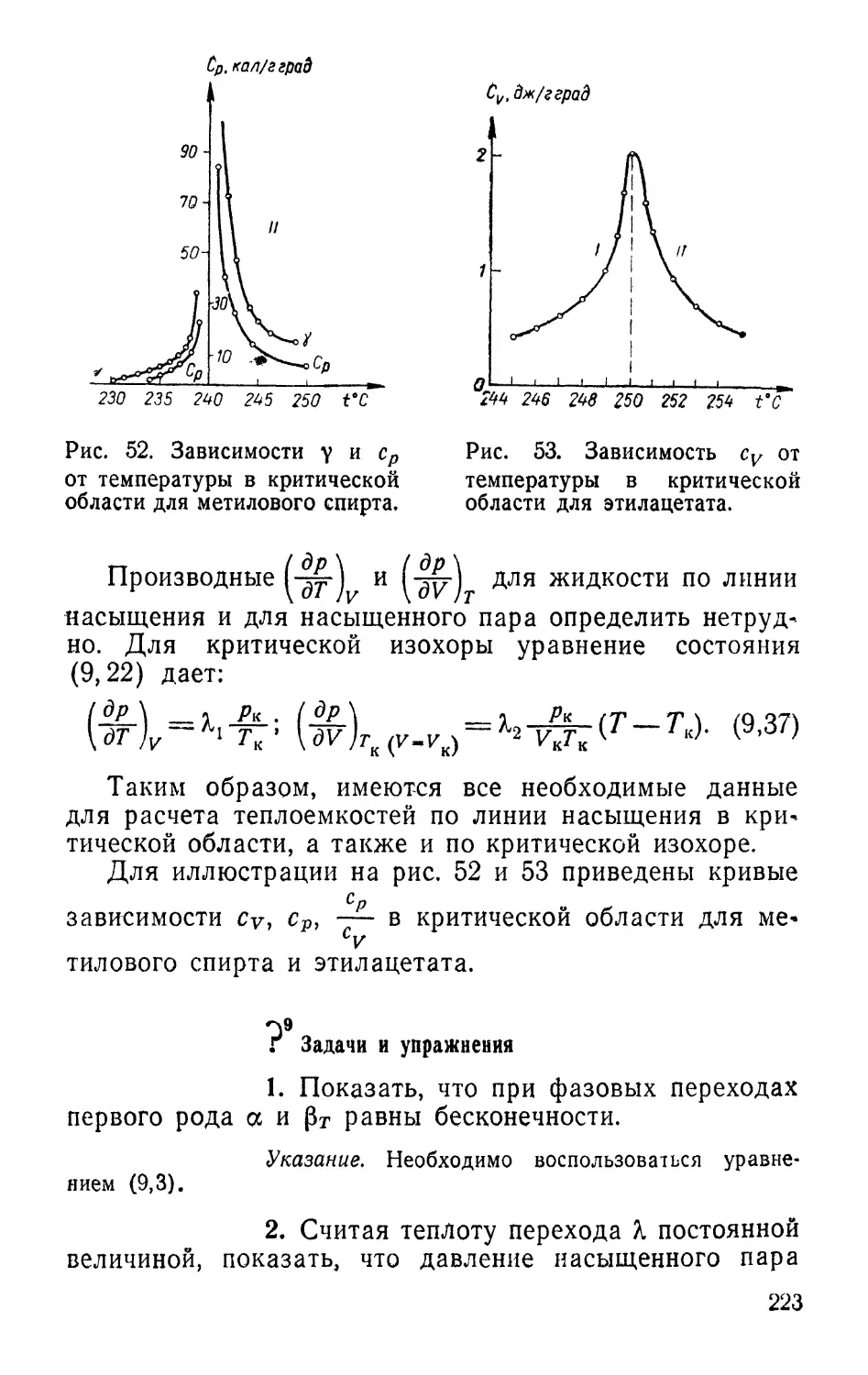
обобщенным критическим явлениям и т. д.
Нам казалось также вполне закономерным и естественным осве*
щать основные методологические вопросы термодинамики по мере
необходимости, в органической связи с основным содержанием курса.
Читатель, желающий углубить свои знания по отдельным во*
просам, затронутым в курсе, может обратиться к спискам рекомен-
рекомендованной литературы, которые даны в конце каждой главы. Одно-
Одновременно в общем списке литературы указывается ряд фундамен*
тальных курсов с широким охватом вопросов излагаемой науки.
1* 3

Считаю своим приятным долгом выразить благодарность, асси-
ассистентам Л. С. Яишной, А. А. Глинскому, Г. Д. Тарантовой за боль*
шую помощь, оказанную мне при подготовке книги к изданию.
Выражаю признательность профессорам М. П. Вукалоеичу,
Я. С. Кудрявцеву и Г. М. Бартеневу за внимательный просмотр
рукописи и ценные замечания.
Автор
ЛИТЕРАТУРА (Ко всему курсу)
!. ВАН-ДЕР-ВААЛЬС.
Термостатика, ч. I, II, Госхимиздат, 1936.
2 А. Б. МЛОДЗЕЕВСКИЙ,
Термодинамика, Учпедгиз, 1948.
3. п. с. эпштейн,
Курс термодинамики, ОГИЗ Гостехиздат, 1948.
4. М. А. ЛЕОНТОВИЧ,
Введение в термодинамику, ГИТТЛ, 1952.
5. в е. микрюков,
Курс термодинамики, Учпедгиз, 1956.
6. к. шефер,
Теория теплоты, ч. I, Гостехиздат, 1939.
7. А. Г. САМОЙЛОВИЧ,
Термодинамика и статистическая физика, Гостехиздат, 1955,
а. м. п. вукалович и и. и. новиков.
Техническая термодинамика, Госэнергоиздат, 1952.
9. И. П. БАЗАРОВ,
Термодинамика, ГИФМЛ, M.t 196I.

введение Предмет и метод
термодинамики. Некоторые
исходные представления
и понятия
Предмет термодинамики. Исторически тер-
термодинамика возникла как наука, изучающая переход
теплоты в механическую работу, что диктовалось прежде
всего необходимостью дать теоретические основы работы
тепловых машин.
Современная термодинамика — это наука, изучаю-
изучающая взаимную связь между различными видами энергии
и влияние этой связи на свойства физических тел. Таким
образом, особенностью термодинамики является рассмо-
рассмотрение процессов, происходящих в природе, с точки зре-
зрения превращений энергии в этих процессах.
Термодинамика есть логическое развитие трех зако-
законов, лежащих в ее основе и являющихся обобщением
огромного человеческого опыта.
Первое начало термодинамики есть закон сохране-
сохранения и превращения энергии.
Второе начало термодинамики характеризует напра-
направление протекания термодинамического процесса.
Третье начало термодинамики утверждает, что абсо-
абсолютный нуль температуры недостижим.
Метод термодинамики. При изучении явле-
явлений природы используются различные методы. Мы ука-
укажем здесь на два исторически сложившихся метода:
1) Введение определенных представлений о строении
вещества и построение на этой основе теории.
2) Построение теории на основе фундаментальных
экспериментальных фактов. Термодинамика относится
к теориям второго типа.
Положив- в основу три основных опытных закона и
привлекая уравнения состояния, полученные из теории
или опыта, термодинамика описывает большой круг яв-
явлений, наблюдаемых в природе и технике. Однако тер*
модинамика не вскрывает их механизма, не отвечает на

вопрос, почему данные процессы происходят именно
таким образом. Она только отвечает на вопрос, как про-
протекает данный процесс. Ответ на вопрос о причине происхо-
происходящих явлений дает молекулярно-кинетическая теория.
Термодинамика имеет свои преимущества и недостат-
недостатки перед молекулярно-кинетической теорией вещества.
Преимущество ее в том, что она не вводит никаких ги-
гипотез, и потому ее положения так же достоверны, как
и законы, на которых она основана.
К недостаткам термодинамики необходимо отнести
отсутствие наглядности и невозможность объяснить с ее
помощью причины происходящих процессов.
Рассмотрим некоторые исходные представления и
понятия термодинамики.
Термодинамические параметры. Любое тело
или группа тел, состоящих из множества частиц, назы-
называется макроскопической системой. Под термодинамиче-
термодинамическими параметрами подразумевают физические величи-
величины, характеризующие макроскопическое состояние тел.
Термодинамические параметры можно разделить на
величины, которые имеют и термодинамический и меха-
механический смысл (объем, давление, энергия), и величины,
которые имеют только статистический смысл (темпера-
(температура) *.
В термодинамике мы часто встречаемся с понятиями
внешних и внутренних параметров. Это разделение впол-
вполне естественно: внутренние параметры характеризуют
изучаемую систему, а внешние — окружающие тела. На-
Например, для газа, заключенного в цилиндре, объем —
внешний параметр (так как он зависит от размеров ци-
цилиндра), а давление газа на стенки цилиндра — вну-
внутренний.
Таким образом, состояние системы зависит и от вну-
внутренних и от внешних параметров. Величины, однознач-
однозначно определяемые заданием этих параметров, называются
функциями состояния.
Число независимых параметров называется числом
степеней свободы системы. Любые термодинамические
* К последним, как мы узнаем в дальнейшем (глава 5), отно-
относится и энтропия,

параметры могут быть выбраны в качестве независимых
переменных. Необходимо, однако, чтобы число их было
равно числу степеней свободы.
Температура. Остановимся на рассмотре-
рассмотрении понятия температуры как специфически термодина-
термодинамическом параметре.
Температура — одно из основных понятий, играющих
важную роль не только в термодинамике, но и в физике
в целом. Температура тела есть мера его нагретости. Ка-
Качественное представление о температуре для нас вполне
привычно. Оно подобно, например, представлению о
длине, массе и т. д., является одним из основных пред-
представлений, которыми мы пользуемся для описания явле-
явлений природы. Однако это качественно легко восприни*
маемое понятие трудно поддается физическому опреде-
определению.
Измерение температуры термометром основано, как
известно, на том опытном факте, что если два тела
порознь находятся в тепловом равновесии с третьим
телом, то все три тела находятся в тепловом равновесии
между собой, т. е. все они имеют одинаковую темпера-
температуру. Следовательно, по показаниям термометра можно
сравнивать температуры различных тел, не приводя их
в непосредственное соприкосновение между собой.
В связи со сказанным возникает ряд вопросов.
Что измеряют приборы, служащие для измерения
температуры? Дают ли они однозначные показания, или
каждый из них дает свое собственное показание? Какое
тело надо выбрать в качестве термометрического? Как
производить градуировку различных термометров, или,
другими словами, какова стандартная шкала темпера-
температур?
Чтобы выработать правильное представление о тем-
температуре, надо выбрать какой-то стандарт для градуи-
градуировки шкалы приборов. Оказывается, с помощью термо*
метров такую шкалу создать нельзя.
Измерение температуры с помощью термометра
основано на расширении тел при нагревании. Для изме-
измерения температуры можно воспользоваться также
свойствами электродвижущей силы термопары, электри-
электрического сопротивления металлов и излучения тел.

Термометр, работающий на принципе расширения
вещества при нагревании, дает различные показания в
зависимости от того, каким веществом он заполнен. На-
Например, если взять два одинаковых термометра, один из
которых заполнен ртутью, а другой — спиртом, отметить
на них две постоянных точки: 0° — температуру таяния
льда и 100° — температуру кипения воды при нормаль-
нормальном давлении, и промежуток между 0 и 100° разделить
на 100 равных делений, каждое из которых будет соот-
соответствовать ^=1°С, то в силу того, что коэффициенты
объемного расширения этих веществ сами зависят от
температуры и притом различным образом для разных
веществ, показания термометров будут, строго говоря,
одинаковы лишь при 0° и при 100°, но не в интервале
между этими температурами. Поэтому деления на шка*
лах этих термометров должны быть различными.
То же самое можно сказать и о термоп'аре: в зависи-
зависимости от того, какие берутся металлы, ее электродвижу-
электродвижущая сила будет различным образом меняться с измене-
изменением разности температур спаев. Таким образом, пока-
показания приборов зависят от природы рабочего тела,
служащего для измерения температуры.
Из предыдущих рассуждений можно сделать следую-
следующий вывод: стандартную шкалу температур можно по-
построить лишь в том случае, если будут найдены веще-
вещества, имеющие постоянный коэффициент объемного
расширения.
Таким веществом является, как известно, идеальный
газ, у которого а = const •= л7~ *„0 . Поскольку, однако,
реальные газы при высоких температурах и низких дав-
давлениях ведут себя практически как идеальный газ, то
любой реальный газ при соответствующих условиях мо-
может служить в качестве рабочего тела для устройства
газового термометра и градуировки по нему шкалы
любого другого термометра.
Таким образом, использование идеального газа в ка-
качестве термометрического тела дает возможность со-
создать стандартную шкалу температур и приводит к по-
понятиям абсолютной температуры и абсолютной шкалы
температур.
В курсе общей физики эти понятия были введены
формально. Применяя последовательно законы Бойля—

Мариотта pV=const и Гей-Люссака V—Vo(l+at) (где
t — температура, показываемая термометром с идеаль-
идеальным газом), при переводе газа из одного состояния в
другое можно получить уравнение вида
Если обозначить const через /?, а (—j-Л через Г, то по-
получаем уже известное уравнение состояния идеального
газа pV — RT, где Т — абсолютная температура, опре-
определяемая из соотношения Г = Л-273,16°. Согласно по-
последнему равенству Г==0 при /=—273,16°С, т. е. нуль
абсолютной шкалы лежит ниже нуля шкалы Цельсия на
273,16°.
Таким образом, абсолютная газовая шкала темпера-
температур вполне может быть принята за эталон, по которому
можно градуировать шкалы других термометров.
Однако выбор такой шкалы в качестве стандарта
еще не дает нам понятия о температуре как величине,
не зависящей от природы термометрического вещества.
Действительно, за определение абсолютной температуры
можно было бы принять определение ее по уравнению
Клапейрона — Менделеева 7| = -~г-, правая часть кото-
которого не зависит от свойств термометрического вещества.
Но этому уравнению в точности подчиняется только
идеальный газ. Для реального газа при любых условиях
имеют место отклонения от этого уравнения, хотя и
незначительные. В то же время такое определение тем-
температуры совершенно не объясняет физического смысла
абсолютного нуля.
Из сказанного можно сделать такой вывод.
Всякое определение температуры при помощи
термометров в сущности не позволяет определить
температуру как некоторую абсолютную величи-
величину, не зависящую от индивидуальных свойств того
или другого вещества.
Только на основании второго начала термодинамики,
как показал впервые Кельвин, можно определить темпе-
температуру как величину, не зависящую от свойств того или
другого вещества (см. § 3, гл. 4).

Давление, как и температура, является од-
одним из основных параметров, характеризующих состоя*
ние тела.
Давление определяется как сила, действующая на
единицу площади. В технике наиболее употребительной
единицей давления, называемой технической атмосфе-
атмосферой, является 1 кГ/см2. В физике за единицу прини-
принимается давление, соответствующее давлению ртутного
столба высотой в 760 мм (физическая атмосфера).
1 техническая атмосфера^ 1,0333 физической атмосферы.
Кинетическая теория материи позволяет установить
связь между давлением и кинетической энергией тепло-
теплового движения молекул вещества.
Таким образом, давление имеет не только механиче-
механический, но и статистический смысл, так как оно связано
функционально с температурой.
Удельный объем, как температура и да-
вление, является термодинамическим параметром, харак*
теризующим макроскопические свойства тел.
Удельный объем (v) есть объем единицы массы. Раз*
мерность удельного объема- [см3-г~1] в абсолютной си-
системе единиц или [мъ-кг~1] — в системе СИ.
Макроскопические свойства тел могут характеризо*
ваться также молярным объемом V.
где М — молекулярный вес.
Когда тело однородно, т. е. плотность его повсюду
одинакова, то
где 1/Общ — общий объем тела, т — масса тела.
При постоянной массе удельный объем пропорциона-
пропорционален общему объему и, следовательно, макроскопические
свойства однородного тела можно характеризовать
общим объемом тела.
Термодинамическая система и термодинами-
термодинамический процесс. Тело или совокупность тел
любой физико-химической природы, полностью характе-
характеризующееся некоторым числом независимых макроско*
10

пических параметров, называется термодинамической
системой. Самой простой термодинамической системой
является газ, характеризуемый давлением /?, объемом V
и температурой Г. Можно легко описать такую систему,
если знать, например, давление как функцию темпера-
температуры Т и Объема V:
Заметим, что значения параметров /?, V и Т предпо*
лагаются одинаковыми во всех частях объема, занимае-
занимаемого газом, т. е. отдельные части системы находятся в
равновесии между собой. В противном случае написан-»
ное выше равенство явно содержало бы зависимость
этих параметров от координат и времени. Поэтому клас-
классическая термодинамика изучает такие процессы, при
которых система проходит через ряд равновесных со-
состояний.
Примером более сложной термодинамической систе-
системы является газ, находящийся в равновесии с жидко-
жидкостью в закрытом сосуде. Если бесконечно медленно по-
повышать температуру, то такая система будет проходить
через ряд равновесных состояний. О таких системах
обычно говорят, что они находятся в условиях динами-
динамического равновесия жидкости и пара.
Еще более сложной термодинамической системой
будет, например, система, состоящая из жидкости, пара
и твердого тела, находящихся в равновесии.
Термодинамические системы могут быть полностью и
частично изолированными. Например, термодинамиче-
термодинамическая система изолирована в тепловом отношении, если
она помещена в не допускающую никакого теплообмена
так называемую адиабатическую оболочку. Но одновре-
одновременно эта система может быть не изолирована в меха-
механическом отношении, если объем ее меняется. Так, если
эта система представляет собой газ в цилиндре с порш-
поршнем, стенки которого абсолютно не проводят тепло, то
возможно изменение механических параметров, описы-
описывающих систему, например изменение объема, занимае-
занимаемого газом, при перемещениях поршня. Такая система
называется частично изолированной термодинамической
системой.
Если система не имеет никаких взаимодействий с
окружающей средой, то ее называют полностью изоли-
II

рованной. Любое изменение в термодинамической си-
системе, связанное с изменением хотя бы одного из ее
термодинамических параметров, называется термодина-
термодинамическим процессом.
Термодинамическое равновесие. Макроскопи-
Макроскопическая система находится в термодинамическом равнове-
равновесии, если состояние ее не меняется с течением времени.
Предполагается при этом, что внешние условия рассма-
рассматриваемой системы остаются неизменными. Следует уточ-
уточнить, что не все макроскопические системы являются
термодинамическими системами, а только те из них, кото-
которые находятся в термодинамическом равновесии. При тер-
термодинамическом равновесии температура и давление во
всех частях системы имеют одно и то же значение *.
Термодинамическое равновесие является одной из
форм теплового движения материи. С точки зрения мо-
лекулярно-кинетической теории при термодинамическом
равновесии остаются постоянными лишь макроскопиче-
макроскопические параметры (величины), характеризующие систему
в целом. Микроскопические же величины будут непо-
непостоянны, так как координаты и скорости молекул при
термодинамическом равновесии меняются с течением
времени.
Равновесные и неравновесные процессы. Под
равновесными процессами в термодинамике понимают
процессы, проходящие через ряд равновесных состояний.
Они протекают таким образом, что изменение параме-
параметров, описывающих систему, за конечный промежуток
времени бесконечно мало.
Рассмотрим пример равновесного процесса. Пусть в
цилиндре под поршнем находится газ. Если бесконечно
медленно повышать температуру газа, то система будет
проходить через ряд равновесных состояний. Для всех
точек системы значения давления р и температуры Т
будут одними и теми же.
* Если система имеет адиабатические перегородки, температу-
температуры частей системы при термодинамическом равновесии могут иметь
различные значения,
12

Неравновесные процессы это такие процессы, при
которых за конечный промежуток времени происходит
конечное изменение параметров системы и, следователь-
следовательно, равновесие системы нарушается.
Примером неравновесного процесса может служить
тот же процесс изменения состояния газа в цилиндре,
когда температура и давление газа изменяются на-
настолько быстро (например, при быстром движении
поршня в цилиндре), что их значения в различных точ-
точках системы в данный момент будут различными.

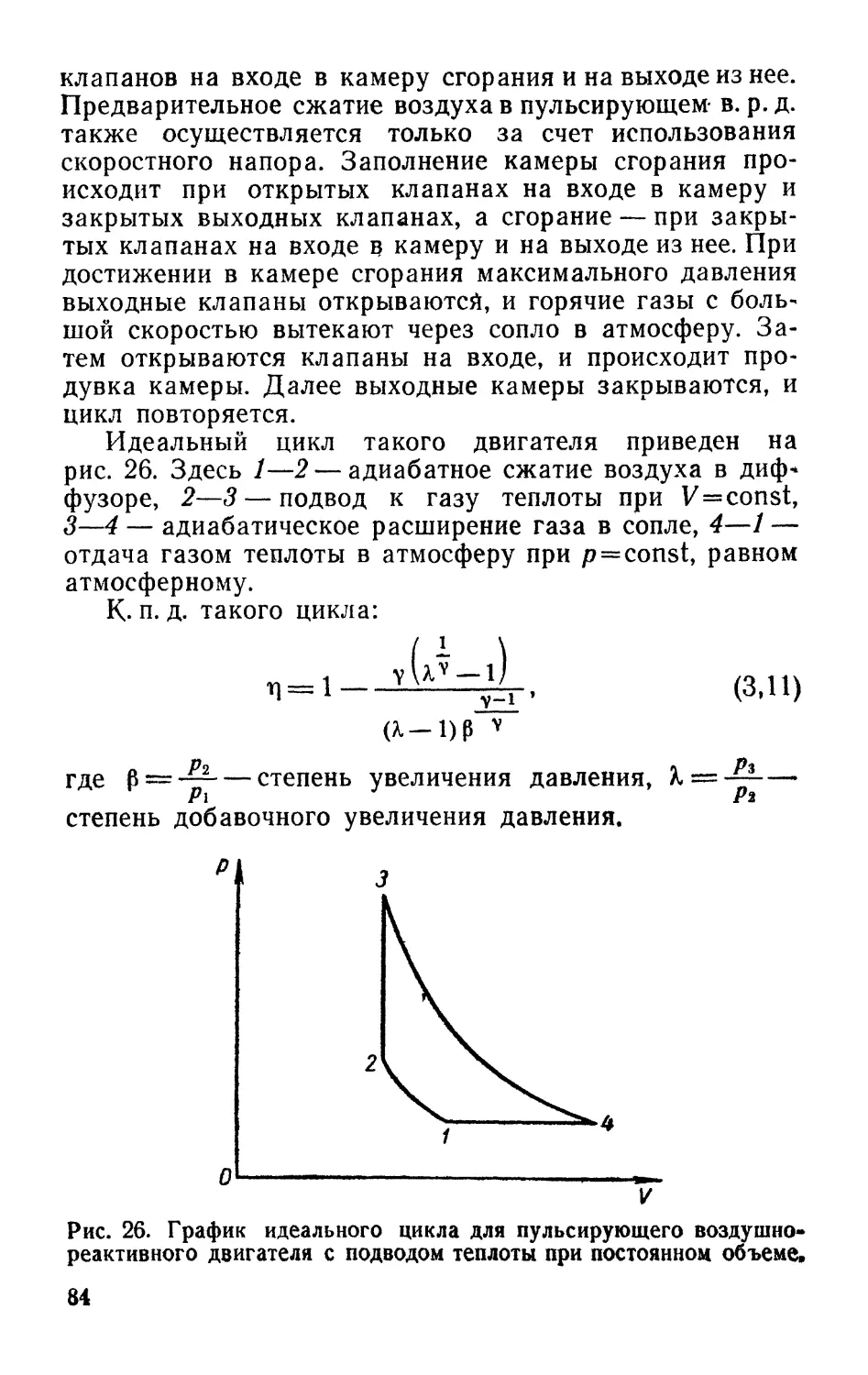
ГЛАВА ПЕРВАЯ
Уравнения состояния
Функциональная зависимость между па-
параметрами простой термодинамической системы — давле*
нием р, объемом V и температурой Т — называется урав-
уравнением состояния.
Эту зависимость в общем виде можно записать так:
F(p,V, Г) = 0, A,1)
где каждая из переменных является функцией двух дру-
других.
Уравнение состояния может быть получено экспери*
ментально и теоретически. Подобное уравнение имеет
смысл только для равновесных систем, в которых тем-
температура и давление одинаковы во всех точках системы.
Находя приращение давления Др из уравнения со-
состояния A, 1), получим:
Пусть Др = 0. Тогда, учитывая, что
из уравнения A,2) можно получить связь между част-
частными производными:
dV
W
Полученное уравнение представляет собой уравнение
состояния в дифференциальной форме. Оно дает воз-
возможность установить связь между коэффициентом объ-
объемного расширения а при постоянном давлении, изотер-
14

мическим коэффициентом сжатия рт и термическим
коэффициентом давления k, имеющими вид:
*-*(*)
Пользуясь этими соотношениями и уравнением со*
стояния A, 3), получаем искомую зависимость в виде:
a==:k$rp. A,5)
При получении дифференциального уравнения состою
яния A,3) не было сделано каких-либо ограничиваю-*
щих предположений относительно вида уравнения со*
стояния A,1). Поэтому соотношение A,3) справедливо
при любом конкретном виде функциональной связи
объема, давления и температуры в уравнении состояния
A,1).
§ Уравнение состояния идеального газа
Для решения большинства термодинами*
ческих задач необходимо знать уравйение состояния в
явном виде. Простейшим уравнением состояния является
уравнение состояния идеального газа, называемое урав-
уравнением Клапейрона — Менделеева. Для одного грамм-*
моля оно имеет вид:
A,6)
где R — универсальная газовая постоянная.
Уравнение A,6) нетрудно получить, используя урав-
уравнения:
/Л/ = const, A,7)
A,8)
Уравнения A,7), A,8) и A,6) получены для идеаль*
ного газа, т. е. газа, в котором молекулы считаются ма-
материальными точками, а силы взаимодействия между
ними равны нулю.
Хотя в природе идеальных газов не существует, в на*
уке и технике, имеющей дело с реальными газами, часто
встречается возможность применить уравнение состоя*
ния идеального газа для расчетов параметров термоди*
15

намической системы. Например, уравнение Клапейро-
Клапейрона— Менделеева применяется при расчетах параметров
рабочих тел реактивных двигателей, хотя в этих случаях
приходится иметь дело с давлением 15—50 атм и тем-
температурами 1500—3000° С.
Для азота при температуре 0°С уравнение состояния
идеального газа применимо до 100 атм, что легко видеть
из приводимых экспериментальных значений давления
р и объема V, а также их произведения pV:
р(атм) 1 100 200 500 1000
V (л) 1 0,009941 0,005241 0,002780 0,0020685
pV (атм-л) 1 0,9941 1,0483 1,3900 2,0685
Для углекислого газа при 0° С уравнение A,6) при-*
менимо только до 10 атм.
Существует определенный критерий применимости
уравнения Клапейрона — Менделеева для реальных га-
газов. Его можно применять к реальным газам при малых
давлениях и температуре выше критической *. При этом
чем выше температура, тем для большего диапазона
давлений действительно уравнение A,6).
Критические температуры для некоторых газов и па-
паров (в °К) для: гелия — 5,2; неона — 44,65; аргона —
150,7; водорода — 33,2; бензола — 561,6; толуола — 593;
четыреххлористого углерода — 556,3; ртути—1723.
Таким образом, для так называемых благородных
газов уравнение Клапейрона — Менделеева применимо
при комнатной температуре, для паров многих органиче-
органических веществ — при температурах выше 500° К, для
паров металлов — при более высоких температурах. Ра-
Разумеется, что приведенные выше границы применимости
уравнения состояния идеальных газов носят качествен-
качественный характер и, следовательно, допустимы отклонения.
§ Уравнения состояния реальных газов
Уравнение Ван-дер-Ваальса. На практике
мы всегда имеем дело с веществами, свойства которых
более или менее отступают от свойств идеальных ве-
веществ. Такие вещества описываются более сложными
уравнениями состояния.
* См. § 3 этой главы.
16

Рассмотрим уравнение Ван-дер-Ваальса, которое ка-
качественно хорошо описывает жидкое и газообразное
состояние систем. Оно для одной грамм-молекулы имеет
вид:
() A,9)
Заметим, что при р^-у? и У^>Ь это уравнение
переходит в уравнение состояния идеального газа
PV=RT.
Уравнение Ван-дер-Ваальса может быть получеыо из
уравнения Клапейрона — Менделеева путем внесения
поправки -ру к величине давления и поправки Ь к объ-
объему.
Поправка Ъ учитывает:
во-первых, объем, занимаемый молекулами реально-
реального газа (в идеальном газе молекулы принимаются за
материальные точки, не занимающие никакого объема);
ва-вторых, так называемое «мертвое пространство»,
куда не могут проникнуть молекулы реального газа при
движении, т. е. объем зазоров между молекулами при
их плотной упаковке.
Таким образом, Ъ = КМол + Узазор-
Поправка к давлению -та- учитывает силы взаимо-
взаимодействия между молекулами реальных газов. Она пред-
представляет внутреннее давление, которое определяется из
следующих простых соображений. Два соседних элемен-
элемента газа будут взаимодействовать с силой, пропорцио-
пропорциональной произведению количеств вещества, заключенных
в этих элементарных объемах. Поэтому внутреннее
давление pi пропорционально квадрату концентра-
концентрации п:
Л~Й2~Р2~~
где р — плотность газа.
Таким образом, общее давление складывается из
внешнего и внутреннего давлений р + А = /?Ч~-у2"«
Учитывая большое значение уравнения Ван-дер-Ва*
альса для описания реальных веществ, остановимся на
2 В. Ф. Ноздрец 47

его характеристике более подробно. Рассмотрим графи*
ческое изображение изотерм Ван-дер-Ваальса на диа-
диаграмме pV (рис. 1).
Как показывает эта диаграмма, вид изотерм меняет*
ся в зависимости от температуры, при которой осущест-
осуществляется изотермический процесс с газом. На изотерме
Ть<Тк одному значению давления р соответствуют три
значения объема Vu V2, V3. Для изотермы Г=ГК (кри«
тическая изотерма) характерно наличие точки переги*
ба /С, в которой Vi = V2—Vzy и на всей изотерме каждо*
му значению давления однозначно соответствует опре*
деленное значение объема. Изотерма TS>TK имеет вид
плавной кривой, совпадающей с изотермой для идеаль-
идеального газа pV~const при высоких температурах.
Проведем сравнение изотерм, рассчитанных по урав-
уравнению Ван-дер-Ваальса (рис. 1) и полученных экспери-
экспериментально в 1868 г. Эндрюсом при исследовании угле-
углекислоты (рис. 2).
Как показывают экспериментальные изотермы, при
Г<ГК переход вещества из одцой фазы в другую со-
совершается при постоянном давлении (АВ — прямая),
поэтому на практике выделить объем V2 невозможно.
Более тщательные опыты дали возможность полу-
получить изображенные на рис. 1 участки изотермы AtB и
Рис. 1. Изотермы
Ван-дер Ваальса.
18

Рис. 2. Изотермы угле- Р
кислого газа, полученные
Эндрюсом.
А2Е. Участок изотерм BE экспериментально обнаружить
не удалось.
Участок А\В описывает перегретую жидкость. Экспе-
Экспериментально его можно получить, если из исследуемой
жидкости предварительно удалить воздух и различные
примеси. Такая «очищенная» жидкость при температуре
кипения некоторое время не переходит в парообразное
состояние, расширяясь по кривой AtB.
Участок изотермы А2Е соответствует перегретому па*
ру. Экспериментально его можно обнаружить, если очи*
стить пар от центров конденсации.
Рассмотренные участки изотермы соответствуют не-
неустойчивым состояниям системы. Малейшее возмуще-*
ние в системе вызывает переход с А{В и А2Е на пря-
мую A iA2.
Уравнение Ван-дер-Ваальса в критической области
удовлетворительно описывает состояние жидкостей и
газов как качественно, так и количественно. Однако в
области температур ниже критической оно дает дляяйщ-
костей только качественное описание состояния системы.
Например, для изотермического коэффициента сжимае*
= —7\~д/Г/ ' и экспеРимент и расчет по
19
мости

уравнению состояния Ван-дер-Ваальса показывают, что
рт с повышением температуры возрастает. Однако раз-
разница в числовых данных может доходить до 100% й
более.
Уравнение состояния Ван-дер-Ваальса играет боль-
большую роль в развитии наших представлений о термоди-
термодинамических свойствах газов и жидкостей. Оно привело
к учению о термодинамически неустойчивых состояниях,
к учению о критическом состоянии вещества и послу-
послужило основой для теории соответственных состояний.
К сожалению, отсутствие строго теоретического обоснова-
обоснования этого уравнения состояния накладывает определен-
определенные ограничения в применении его в теории и практике.
В науке и технике уравнение состояния Ван-дер-
Ваальса обычно используется для качественного ана-
анализа газового и жидкого состояний. Для областей, близ-
близких к условиям идеальности, оно дает и хорошее коли-
количественное соответствие теории и опыта. Часто в технике
используются уравнения состояния, которые в узкой
области изменения параметров состояния дают хорошее
согласие теории с экспериментом.
Дадим краткую характеристику других уравнений
состояния.
Уравнение состоянияКлаузиуса представляет
собой видоизмененное уравнение Ван-дер-Ваальса. По
Клаузиусу, внутреннее давление jpj= т у , .2 , т. е.
внутреннее давление, помимо более сложной зависимо-
зависимости от объема V, зависит также и от температуры. Под-
Подставляя это значение рг- в уравнение Ван-дер-Ваальса,
получим уравнение Клаузиуса:
(U0)
Уравнение Клаузиуса содержит четыре постоянных:
а, Ъ, с, R, значения которых связаны со значениями па-
параметров в критической точке следующим образом:
_ RTK
р« ~ 8 (Ь + с) *
8а
27R(b + с)
20

Рис. 3. Изотермы углекислого
газа, в приведенных перемен-
переменных ф и п (сплошная кривая)
и изотермы Клаузиуса (пунк-
(пунктирная линия).
\
\\
\
Поскольку трех уравнений недостаточно для опреде-
определения четырех постоянных, одну из них (константу с)
обычно определяют из других условий или выбирают
произвольно.
О соответствии уравнения Клаузиуса опытным дан-
данным можно судить по кривой для критической изотермы
р v
углекислоты СО2 (рис. 3), где я = —; <р = -рг-.
График показывает, что для углекислого газа в обла-
области давлений ниже критических опытные данные (сплош-
(сплошная кривая) хорошо совпадают с теоретическими (пунк-
(пунктирная кривая).
Уравнение состояния Бертло также яв-
является видоизменением уравнения состояния Ван-дер-
Ваальса. Положив а=-у-, Бертло пришел к следую-
следующему уравнению состояния:
A,11)
Величины а'9 Ъ и R выражаются через значения рк,
1/к, Тк так:
*' = 3pJKVl; b^Vj * = %^. ОЛЮ
Уравнение Бертло очень хорошо согласуется с дан-
данными опыта при давлениях не выше 5—6 атм и при тем-
температурах выше критической, а также при низких темпе-
температурах в области малых давлений.
21

Анализ этого уравнения показывает, что оно более
точно передает свойства слабо сжатых газов, имеющих
температуры кипения 70—200° К (водород, аргон, кис-
кислород, азот и др.). В критической области и при боль-
большом сжатии уравнение Бертло становится совершенно
непригодным.
Область применимости уравнения состояния Бертло
для различных газов такова (в атм): Не E,2) *,
Н2C3,4)—свыше 200; N2 A26), СО A34,4), Аг A50),
О2 A54,3), NO A79) —от 0 до 200; СН4 A90,6) —от 0
до 100.
Уравнение состояния Камерлинг-Оннеса.
Камерлинг-Оннес предложил уравнение состояния по-
полуэмпирического типа:
Это уравнение учитывает все особенности реальных га-
газов в наиболее полном виде.
Уравнение Камерлинг-Оннеса в общей сложности
имеет 24 постоянных. В нем величина A = RT, а постоян-
постоянные В, Ct D, E, F рассматриваются как эмпирические
функции температуры, например:
^^ р (U3)
Уравнение Камерлинг-Оннеса показывает, к каким
усложнениям необходимо прибегать, чтобы добиться со-
соответствия уравнения опытным данным.
Современная молекулярно-кинетическая теория по-
позволяет получить точное уравнение состояния реального
газа. Такое уравнение было получено Манером и Бого-
Боголюбовым. В самом общем виде оно может быть запи-
записано:
где коэффициент Av]x выражается через потенциал вза-
взаимодействия молекул **.
* В скобках указана критическая температура по Кельвину.
** См.: М. П. Вукалович и И. И. Новиков, Уравнения
состояния реальных газов, Госэнергоиздат, 1948»
22

§'
Критическое состояние вещества
О критическом состоянии вещества и па-
параметрах, характеризующих это состояние, уже говори-
говорилось в настоящем курсе при рассмотрении изотерм Ван-
дер-Ваальса и экспериментальных изотерм Эндрюса.
Из указанных на рис. 1 изотерм Ван-дер-Ваальса
особый интерес вызывает та изотерма, которая отделя-
отделяет волнообразные кривые от монотонно спадающих. Эта
изотерма носит название критической, а соответствую-
соответствующая ей температура — критической температуры (Тк).
Критическая изотерма имеет лишь точку перегиба КУ
в которой выполняются соотношения:
Заштрихованная область на диаграмме pV (рис. 1)
характеризует двухфазное состояние вещества жид-
жидкость— пар, причем точка А{ соответствует жидкому
состоянию, а точка А2 — газообразному состоянию ве-
вещества.
Точку перегиба К можно определить как точку, в ко-
которой исчезает различие между жидким и парообразным
состоянием вещества. Выше критической точки вещество
может находиться лишь в газообразном состоянии. Та-
Таким образом, точка К характеризует особое состояние
вещества, называемое критическим состоянием, а сама
точка К называется критической точкой. Давление и
объем вещества в критическом состоянии называются
критическим давлением (рк) и критическим объемом
(VK).
Учитывая большое значение изучения критического
состояния вещества для теории и практики, мы ближе
познакомимся с относящимися сюда опытными и теоре-
теоретическими исследованиями. Понятие о критической тем-
температуре было впервые введено Д. И. Менделеевым в
1861 году. При исследовании зависимости поверхностно-
поверхностного натяжения жидкости от температуры Д. И. Менде-
Менделеев пришел к выводу, что должна существовать такая
температура, при которой лля данной жидкости по-
поверхностное натяжение становится равно нулю и, сле-
следовательно, исчезают мениск жидкости и различие меж-
между жидкостью и ее насыщенным паром. Эту температуру
23

Д. И. Менделеев назвал «абсолютной точкой кипения».
Он рассматривал ее как температуру, при которой исче-
исчезает поверхностное натяжение жидкости и жидкость пре-
превращается в пар независимо от давления и удельного
объема. К подобным же выводам относительно крити-
критической температуры позднее пришел русский физик
А. Г. Столетов.
Эндрюс, экспериментально исследуя углекислоту,
полностью подтвердил идеи Д. И. Менделеева. Он ука-
указал на наличие такого состояния вещества, когда газо-
газообразная и жидкая фазы делаются неразличимыми одна
от другой. Эндрюс нашел, что для индивидуальных со-
соединений это состояние совпадает с наиболее высоким
давлением и наиболее высокой температурой, при кото-
которой еще возможно одновременное существование газо-
газообразной и жидкой фаз. Эндрюс установил непрерыв-
непрерывность газообразного и жидкого состояний. Оказалось,
что вещество можно перевести из жидкого состояния в
газообразное и наоборот, не пересекая двухфазную об-
область. Пунктирная линия на рис. 1 показывает непрерыв-
непрерывный переход вещества из парообразного состояния / в
жидкое состояние //.
Первые обширные и систематические исследования
критических параметров Гь, /?к, VK ряда веществ были
проведены русским физиком М. П. Авенариусом и его
учениками А. И. Надеждиным, В. И. Зайончевским и
другими в физической лаборатории Киевского универ-
университета в 1873—1895 гг. А. И. Надеждин впервые в
1885 г. определил критическую температуру воды:
Г 374°С
Схематически метод определения критической темпе-
температуры заключается в следующем. В стеклянную трубку
помещают исследуемую жидкость, после чего трубку за-
запаивают. Затем трубку помещают в тепловую баню и
начинают нагревание. Над поверхностью жидкости обра-
образуются насыщенные пары.
Проследим за поведением мениска, отделяющего в
трубке жидкую фазу от газообразной. На мениск влияют
два процесса: с одной стороны, поскольку жидкость при
нагревании расширяется, ее мениск должен повыситься,
а с другой стороны, поскольку испарение жидкости уси-.
ливается и количество жидкости уменьшается, ее мениск
должен понизиться,
24

Какой из этих факторов будет преобладать, зависит
от количества жидкости. Если жидкости много, преоб-
преобладает ее расширение и мениск повышается. Так, жид-
жидкость может заполнить весь объем трубки при темпера-
температуре еще ниже критической. Но если жидкости мало,
то преобладает ее испарение, и паровая фаза также мо-
может заполнить весь объем трубки при температуре тоже
ниже критической. И только при определенном объеме,
равном критическому, мениск не исчезает вплоть до кри-
критической температуры.
По достижении Тк давление насыщенных паров, кото-
которое непрерывно увеличивалось с повышением темпера-
температуры, достигает максимального значения (критическое
давление). В этот момент плотность жидкости стано-
становится равной плотности пара, всякое различие между
жидкостью и паром пропадает и наблюдавшийся ранее
мениск исчезает.
Графически зависимость плотности от температуры
изображена на рис. 4.
Наблюдая за исчезновением мениска в трубке при
постоянном нагревании, можно определить критическую
температуру Тк.
Величина критического объема жидкости, как можно
показать, воспользовавшись уравнением Ван-дер-Вааль-
са, должна составлять 7з величины объема всей трубки.
Однако для многих веществ это соотношение в точности
не выполняется, и критический объем находят опытным
путем.
Рис. 4. Зависимость плотности
жидкости и насыщенного пара
над ней от температуры.

Тщательные исследования критического состояния
вещества привели к более точному определению крити-
критической температуры. Известный русский ученый Б. Б. Го*
лицын впервые отметил, что «температура исчезновения
мениска предшествует критической температуре, хотя и
лежит очень близко к ней».
Действительно, мениск исчезает несколько раньше,
чем вещество достигает критической температуры, т. е.
и после исчезновения мениска вещество продолжает не-
некоторое время находиться в двухфазном состоянии.
Причина этого явления заключается в том, что критиче-
критическое состояние вещества характеризуется мощным раз-
развитием флуктуации плотности (быстрой сменой сгуще*
ний и разрежений) в системе, которые представляют
собой случайные отклонения от среднего (равновесно-
(равновесного) значения плотности. Это вызывает помутнение веще*
ства и исчезновение мениска при температуре несколь-
несколько ниже критической. Одним из самых характерных
признаков критического состояния является опалесцен-
ция — сильное рассеяние света на быстро возникающих
неоднородностях плотности вещества.
Идея Б. Б. Голицына в последнее время A947—-
1950 гг.) была уточнена и развита профессором Москов-
Московского университета В. К. Семенченко, который ввел по-
понятие критической области вещества.
До открытия критического состояния газы пытались
переводить в жидкость одним только сжатием. Таким
методом многие газы (азот, гелий, кислород, водород
и др.) обратить в жидкость не удавалось. Изучение кри-
критического состояния вещества показало, что сжатием
газ можно перевести в жидкое состояние только в том
случае, если его температура ниже критической. В связи
с этим понятно, что, поскольку опыты по сжижению ука-
указанных выше газов проводились райее при комнатной
температуре, а их критические температуры гораздо
ниже 0°С, все эти попытки не имели успеха.
Таким образом, для того чтобы перевести газ сжа-
сжатием в жидкое состояние, надо сначала охладить его до
температуры Т<ТК.
Знание критических параметров позволяет качествен-
качественно установить границы применимости того или иного
уравнения состояния.
26

Наконец, открытие критического состояния привело
к развитию нового раздела термодинамики, особенно
важного для решения прикладных задач, — учения о тер-
термодинамическом подобии.
Принцип термодинамического подобия
Сравнивая свойства различных веществ,
мы обычно берем эти вещества при одинаковых темпера*
турах Ту давлениях р или при каких-то других равных
параметрах. Спрашивается, рациональны ли подобные
способы сравнения? Не следует ли сравнивать свойства
веществ, взяв их в иных, в каком-либо другом смысле
«соответственных» друг другу состояниях?
Открытие критического состояния привело к установ-
установлению закона соответственных состояний, на котором и
базируется принцип термодинамического подобия.
Исходя из уравнения Ван-дер-Ваальса, можно полу*
чить так называемое «приведенное уравнение состоя*
4шя». Запишем уравнение Ван-дер-Ваальса в форме:
_ RT а_ A 15)
Учитывая, что в критической точке имеют место соот-
соотношения A,14), получим:
Шт — ^ + ?=0. 0.16)
к
(Л2л \ ОРТ fi/7
•* I ^Z^ ———————— —— —«—¦ ¦ - i II I I 1 / I
dV2 )T (V — bf V* ' v » ;
Из уравнений A,15), A,16) и A,17) находим:
= J а_. у _3?. т _J а_ /j щ
Соотношения A,18) позволяют определить по крити-
критическим параметрам веществ рк, VK и Гк постоянные Ван-
дер-Ваальса и наоборот.
Пользуясь тем, что каждое вещество имеет вполне
определенные критические параметры Гк, VKt рш можно
ввести новые переменные:
^- = я; -^=q>; ^ = t, A,19)
где я, ф,т-~ приведенные давление, объем, температура.
27

Используя приведенные параметры, можно написать
уравнение состояния Ван-дер-Ваальса так, что в него не
войдут постоянные а и Ьу т. е. будут исключены индиви-
индивидуальные свойства вещества.
Из соотношений A,19) имеем:
Тк = ^; VK = ^; A = ?. A,20)
Подставляя эти соотношения в формулы A,18), по-
получим:
Наконец, подставив выражения A,21) в уравнение
Ван-дер-Ваальса, получим уравнение вида:
1) = 8т. A,22)
Это уравнение называется приведенным уравнением со-
состояния, так как в него входят только приведенные ве-
величины и не входят величины, характеризующие данное
вещество и отличающие его от других веществ. Уравне-
Уравнение A,22) представляет собой уравнение состояния всех
веществ, для которых справедливо уравнение Ван-дер-
Ваальса.
Наличие уравнения A,22) позволяет установить по-
понятие соответственных состояний; состояния двух или не-
нескольких веществ, в которых они имеют одинаковые при*
веденные параметры я, q>, т, называются соответственны-
соответственными состояниями.
Закон соответственных состояний формулируется так:
Если два или несколько веществ, удовлетворяющих
одному и тому же приведенному уравнению состояния,
имеют одинаковые два из трех приведенных параметров
л, ср, т, то можно утверждать, что в этом случае они будут
иметь одинаковый и третий приведенный параметр.
Ясно, что критические состояния веществ (я=1,ф=1,
т=1)—соответственные состояния. Количество взятого
вещества при этом никакой роли не играет.
Наличие закона соответственных состояний позволяет
ввести в термодинамику новое очень важное понятие —
термодинамическое подобие, Термодинамически подоб-
подобными называются вещества, подчиняющиеся закону соот-
28

Рис. 5. Изотермы для трех
различных термодинамически
подобных веществ в перемен-
переменных р, V.
\
Г A,11,1/1)
<Р
Рис. 6. График зависимости между
приведенным давлением п и объе-
объемом ф для всех термодинамически
подобных веществ при неизмен-
неизменной приведенной температуре т.
ветственных состояний и удовлетворяющие одному и то-
тому же приведенному уравнению состояния.
Значение термодинамического подобия заключается в
том, что оно дает представление о свойствах одного ве-
вещества, если известны свойства другого.
Например, в координатах л, (р, т для термодинамиче*
ски подобных веществ мы получим одну кривую. Графи-
Графики же в параметрах р, V, Т будут индивидуальными для
каждого вещества (рис. 5 и 6). Следовательно, зная, на-
например, давление р для одного вещества, можно по зна-
значению приведенного давления найти давление р для лю-
любого другого термодинамически подобного ему вещества,
если известно его рк.
Далее, если известна, например, графическая зависи-
зависимость от температуры коэффициента изотермической
сжимаемости одного вещества, то можно легко подсчи-
подсчитать коэффициент сжимаемости любого другого термо-
термодинамически подобного ему вещества, пользуясь соотно-
соотношением
Pi Р2 Рз /1 С)О\
Рк Рк Рк
если известно хотя бы одно значение р для интересую-
интересующих нас веществ.
29

Не все вещества хорошо подчиняются закону соот-
соответственных состояний. По существу его применяют для
отдельных групп веществ. Так, закон соответственных
состояний хорошо выполним для некоторых групп орга-
органических веществ, как например индивидуальные углево-
углеводороды, и плохо выполняется для ассоциированных ве-
веществ. Но во многих случаях технического применения
Принципа термодинамического подобия эти отступления
можно не учитывать.
Г Задачи и упражнения
1. Для азота при /==20° С и /? = 0,134 атм
а = 0,00368 и /(=0,00368. Вычислить сжимаемость.
Отв. Ь =
2. Показать, что коэффициент объемного
расширения а и коэффициент сжатия рг для идеального
газа равны:
Найти численное значение этих коэффициентов на 1 град
и 1 мм рт. ст. при нормальных условиях: Г = 273°К,
/7 = 760 мм рт. ст.
Отв. а = 0,00368; (Зг = 0,00132.
3. Найти коэффициенты объемного рас*
ширения а и сжатия рт для уравнений Ван-дер-Ваальса
и Бертло.
Отв. а) для уравнения Ван-дер-Ваальса:
а ==¦
y2) Rtv

б) для уравнения Бертло:
V \*
V—b)
4. Пользуясь уравнением Ван-дер-Вааль-
са, определить изотермическую скорость звука.
Указание. Учесть, что, по определению, изотер-
изотермическая скорость звука равна*
\ Ф 1т
где м- — масса одной грамм-молекулы.
5. Вычислить с помощью уравнения
A,18) постоянные Ван-дер-Ваальса а, Ъ и отношение
пользуясь критическими параметрами следующих
(,
веществ:
Метилацетат
Метилформиат
506,9
487,2
рк (атм)
46,33
59,25
227,6
172,0
Отв. Метилацетат:
л2 • атм
а = 10,6-
моль2
Метилформиат:
см*
моль
31

6. Установить связь между критическими
параметрами и постоянными уравнения состояния Берт-
ло A,11), пользуясь формулами A,14).
7. Аналогичным способом установить
связь между критическими параметрами и постоянными
уравнения Клаузиуса A,10).
8. Аналогичным способом установить
связь между критическими параметрами и постоянными
уравнения Дитеричи:
Указание. Когда исчезают первые и вторые про-
производные р, то производные In p также исче-
исчезают.
Отв. рк~
9. Убедиться, что в приведенных пара-
параметрах я, ф, т уравнение состояния Камерлинг-Оннеса
придимает вид:
10. Показать, что для веществ, подчи*
няющихся закону соответственных состояний, справед-»
ливо соотношение
|^ = -^, A,24)
fV2 Ркх
где рг и рг — коэффициенты изотермической сжимае-
сжимаемости двух веществ;
pKi и р —соответственно их критические давления.
Решение. Выразим коэффициент изотер-
изотермической сжимаемости какой-нибудь жидкости
32

через приведенные параметры л, ф и т, связанные с /?,
V, Т соотношениями
где />к, VK, Гк — критическое давление, объем, темпера-
температура.
Отсюда
'» ФА,
Для другой жидкости с критическим давлением PKi
коэффициент изотермической сжимаемости имеет анало-
аналогичный вид:
1 (дц2\
2 ф2Рк2 [дл2)
Если положить ф1 = ф2 (а это следует из того, что
объемы жидкостей хорошо подчиняются закону соответ-
соответственных состояний), то получим соотношение A,24),
т. е. коэффициент рг в соответственных состояниях об«
ратно пропорционален критическим давлениям этих жид-
жидкостей.
11. Показать, что для веществ, подчиняю-
подчиняющихся закону соответственных состояний, справедливо
соотношение:
где ах и а2 — коэффициенты объемного расширения рас-
рассматриваемых веществ,
ГК2 и TKl — соответственно их критические темпера-
температуры.
Решение. Следуя путем, которым мы шли
при решении предыдущей задачи, выразим коэффициент
объемного расширения а = 'уг[~дт~) вещества через
приведенные параметры я, ср, т.
Тогда выражение для а первого вещества примет
вид:
3 В Ф Ноздрев 33

Для второго вещества с критической температурой ГКг
коэффициент объемного расширения запишется анало-
аналогично:
Если оба рассматриваемых вещества подчиняются за
кону соответственных состояний, то для них П\=П2\
«2
ЛИТЕРАТУРА
1. М. П. ВУКАЛОВИЧ и И. И. НОВИКОВ,
Уравнения состояния реальных газов, Госэнергоиздат, 1948»
2. о. д. хвольсон,
Курс физики, т, 3, Госиздат, Берлин, 1923.
3. А. Г. СТОЛЕТОВ,
Избр. соч., т. I, Гостехиздат, 1939,
4. Б. Б. ГОЛИЦЫН,
«ЖРФХО», т. 22, 1890.
5. В. Ф. НОЗДРЕВ,
Применение ультраакустики в молекулярной физике, Гостехиздат*
1958,

глава вторая Первое начало
термодинамики
Первое начало термодинамики — это за«
кон сохранения и превращения энергии. Оно утверж-
утверждает, что определенному количеству теплоты соответст*
вует вполне определенное количество работы: Q=AW,
где А — тепловой эквивалент работы.
Первое начало термодинамики иногда формулируют
так: невозможно построить вечный двигатель первого
рода, т., е. такую периодически действующую машину,
которая бы совершала работу без затраты энергии. По*
строение такой машины невозможно, ибо это противо-
речило бы закону сохранения энергии.
Говоря о первом начале термодинамики, необходимо
подробно остановиться на законе сохранения и превра-
превращения материи и энергии в самом общем его понимании.
Этот закон утверждает, что материя может бесконечно
переходить из одной формы в другую, и эти превращен
ния обязательно сопровождаются энергетическими изме-
нениями.
М. В. Ломоносов, впервые сформулировавший ука-
указанный закон, весьма близко подошел к современному
его пониманию. В своем знаменитом письме к Эйлеру
он писал: «Все перемены, в натуре случающиеся, такого
суть состояния, что сколько чего у одного тела отни-
отнимается, столько же присовокупляется к другому. Так,
ежели где убудет несколько материи, то умножится в
другом месте. Сей всеобщий естественный закон прости-
простирается и в самые правила движения: ибо тело, движу*
щее своей силой другое, столько же оныя у себя теряет,
сколько сообщает другому, которое от него движение
получает».
Закон сохранения материи и энергии, установленный
Ломоносовым, был конкретизирован другими учеными.
Так, акад. Г. Г. Гесс в 1840 г. сформулировал закон со-
сохранения энергии для химических реакций. Ленд в
1844 г. дал формулировку закона сохранения и превра-
превращения энергии для теплового действия электрического
тока.
3* 35

Робертом Майером в 1842 г. впервые было сделано
обобщение количественного соотношения между тепло-
теплотой и работой и высказан принцип взаимопревращае-
взаимопревращаемости теплоты и работы. Для доказательства этого прин-
принципа решающее значение имели опыты Д. Джоуля
A843 г.), измерившего механический эквивалент тепла,
и исследования Г. Гельмгольца «О сохранении силы»
A847 г.).
§ Понятие элементарной работы
Под элементарной работой в механике
понимают произведение силы на бесконечно малое пе-
перемещение точки по направлению этой силы.
В самом общем случае величину элементарной рабо-
работы можно определить так:
d'W — ydx, B,1)
где у — обобщенная сила, а х — обобщенная координата.
В зависимости от характера процесса выражение для
элементарной работы d'W будет различным. Например,
при поднятии тела весом Р на высоту h работа вычис-
вычисляется по формуле d'W = Pdh.
Если работу совершают силы поверхностного натя-
натяжения, то d'W =—odS, где о — коэффициент поверхно-
поверхностного натяжения, a dS — элемент поверхности.
Работа по перенесению заряда в электрическом поле
есть d'W—ydq, где ф — разность потенциалов, a q —
электрический заряд.
Рис. 7. Работа расширения
газа, графически выражае-
выражаемая заштрихованной - пло-
площадью. (При тех же самых
значениях начального Vx я
конечного V2 объемов
работа зависит от формы
кривой ЛВ.)

Если работа совершается на конечном участке, то ее
легко определить графически.
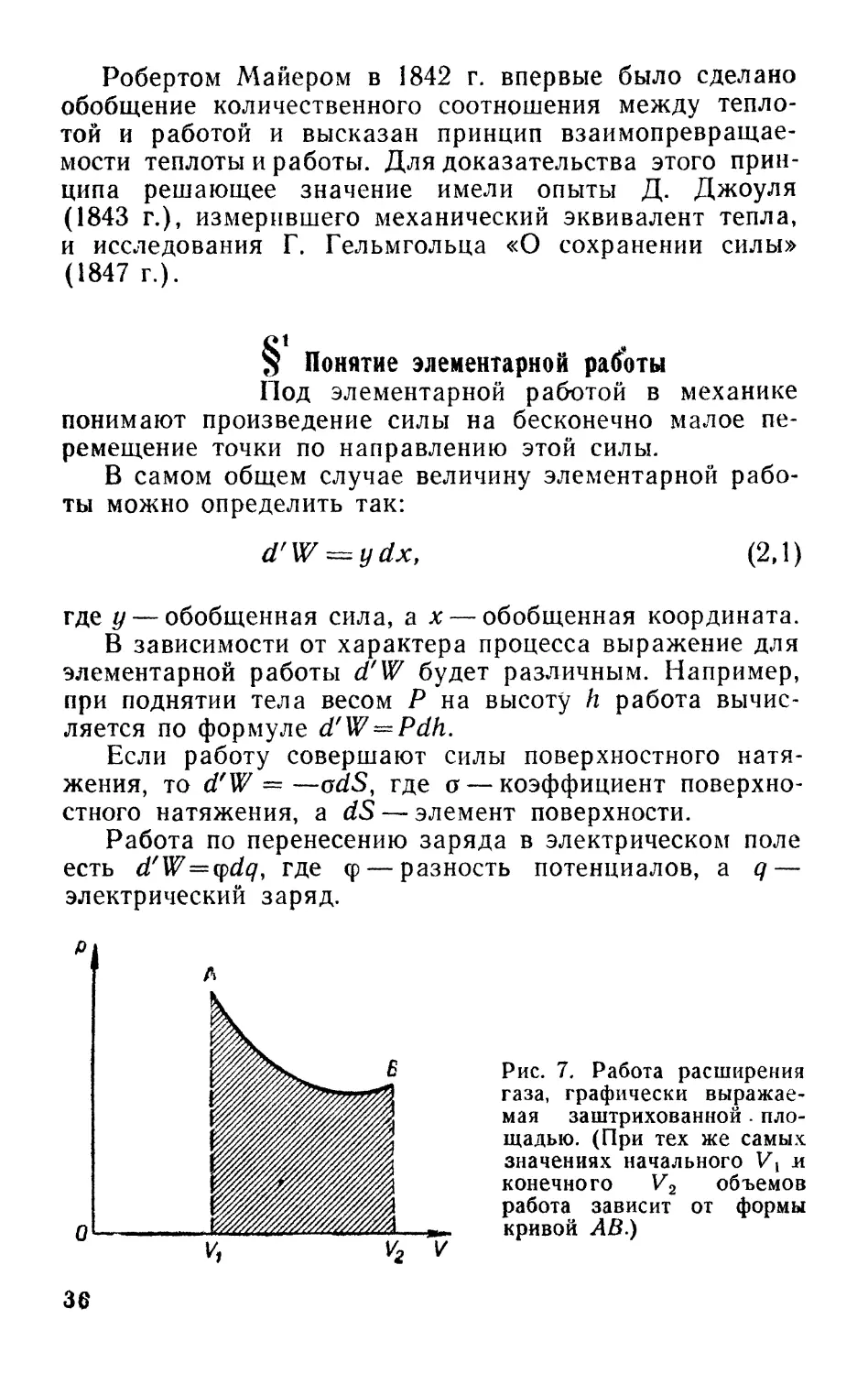
Работа, совершаемая газом, равна площади ABV2Vi
(рис. 7). Аналитически элементарная работа в этом слу-
случае может быть записана в виде:
d'W = pdV. B,2)
Полная работа расширения, совершенная газом в
процессе, который графически изображен на рис. 7 кри-
криволинейным отрезком АВ, равна интегралу от выраже*
ния B, 2):
в
W= \pdV. B,3)
А
Заметим, что для величины работы существенны не
только начальное А и конечное В состояния газа, но и
характер процесса, посредством которого газ переводит-
переводится из одного состояния в другое. Действительно, вели-
величина площади, заштрихованной на рис. 7, зависит от
формы кривой между точками Л и В.
Условие полного дифференциала
Из математического анализа известно,
что дифференциал функции многих переменных F (хи
х2, xz,...) выражается в виде:
Следовательно, для того чтобы выражение
являлось полным дифференциалом некоторой функции
F(xu *2, *з>...)> необходимо, чтобы функции fu /2» /з»-..
являлись частными производными этой функции по со*
ответствующим переменным, т. е. необходимо, чтобы

Поскольку вторая производная по переменным xk n
не зависит от порядка дифференцирования:
д j^jL dF
то для того, чтобы написанное выше линейное диффе-
дифференциальное выражение являлось полным дифференциал
лом некоторой функции F(xu x% Хз»-«-)> нужно, чтобы
выполнялись так называемые соотношения взаимности:
ЖГ^ = Ж^ С*=1. 2, 3, ....л). B,4)
Как показывается в математическом анализе, криво-
криволинейный интеграл по кривой АВ от полного дифферен-
дифференциала не зависит от формы кривой между точками А и
В и равен разности значений функции F в точках В и А:
в
J dF=F{**>, 4fi)> 4B)> • • -)-fWA)' 4A)> 4Д)> • • ¦)• <2'5>
А
Поскольку, как мы видели выше, работа, совершен-
совершенная газом, зависит от формы пути между точками А и
В (рис. 7), элементарная работа не является полным
дифференциалом. Этот факт графически отмечают, ставя
знак «штрих» в выражении элементарной работы d'W*
§•
Внутренняя энергия как функция
состояния
Под полной энергией системы понимает^
ся сумма кинетической, потенциальной и внутренней
энергий:
где ЕКШ1 — кинетическая энергия движения всей системы,
?пот — потенциальная энергия всей системы в поле сил
тяготения, U — внутренняя энергия системы, т. е. та ки-
кинетическая и потенциальная энергия, которой обладает
вся совокупность частиц, составляющих данную систему.
Она зависит от параметров, характеризующие состояние
системы.
В свою очередь, внутренняя энергия системы равна
сумме:
38

где f/кин — энергия движения частиц системы и (Лют —
энергия взаимодействия частиц.
Кинетическая энергия частиц системы состоит из
трех слагаемых: кинетической энергии поступательного
движения частиц, кинетической энергии их вращатель-
вращательного движения и кинетической энергии колебательного
движения частиц:
^кин == ^кин. пост~Т~ Uкин. вр~Т~ ^кин. колеб*
Таков физический смысл внутренней энергии.
В частном случае может быть, что полная энергия
тела или системы равна только ее внутренней энергии,
т. е. Е = U. Такой случай может быть при ?Кин = О;1
?пот = 0, т. е. система находится в покое вне поля сил
тяготения. Этот случай в основном мы и будем рассмат-
рассматривать в курсе термодинамики.
Выясним, обладает ли внутренняя энергия полным
дифференциалом, т. е. является ли она однозначной
функцией состояния.
Предположим, что одному и тому же состоянию си-
стемы соответствуют два различных значения внутрен-
внутренней энергии Ui и U2. Это значит, что часть энергии мо-
можно отнять от системы и при этом никаких изменений
в системе не произойдет. Мы получим источник энергии,
позволяющий построить вечный двигатель первого рода.
Но это противоречит первому началу термодинамики,
следовательно, сама предпосылка неверна, т. е. внутрен-
внутренняя энергия является однозначной функцией состояния.
Таким образом,
2
J dU — U2 — Ux = U(x2, y2i z2) — U(xt, yl9 Zy).
Количество теплоты и теплоемкость.
Термостат
Если две системы с различной темпера*
турой не являются изолированными и приведены в кон-
контакт между собой, то между ними начинает осущест-
осуществляться теплообмен. Система с более высокой темпера-
температурой, охлаждаясь, отдает некоторое количество теплоты
системе с более низкой температурой, которая при этом
39

нагревается. Через некоторое время температуры си-
систем сравняются, и теплообмен прекратится.
Экспериментально установлено, что количество теп-
теплоты, необходимое для нагревания тела, пропорциональ-
пропорционально массе этого тела и разности конечной и начальной
температур:
введя коэффициент пропорциональности с, получим:
b'Q = cm(T2 — Tx), B,6)
отсюда
A'Q I A'Q /97ч
с ' ^П
Коэффициент с имеет размерность [с] = кал/г -град.
Он называется удельной теплоемкостью ве-
вещества и показывает, какое количество теплоты не-
необходимо сообщить телу массой в 1 г, чтобы нагреть его
на 1°С.
Величина с — -—^~-есть средняя удельная теплоем-
теплоемкость. Чтобы получить истинную теплоемкость, надо пе-
перейти к пределу. Тогда получим выражение:
v ~~ m dT '
Однако теплоемкость есть функция процесса, т. е.
будет различной в зависимости от того, ведется ли про-
процесс, например, при постоянном давлении, или объеме,
или температуре и т. д. Это следует учесть. Поэтому точ-
точная, более общая запись величины удельной теплоем-
теплоемкости имеет вид:
с ±(Щ
С*— т\дТ )х'
где х — параметр, остающийся в данном процессе по-
постоянным.
Например, может быть рассмотрена теплоемкость при
постоянном давлении:
СР —In \~W~)P'
Теплоемкость при постоянном объеме:
d'Q
40

Если процесс протекает изотермически, то теплоем-
теплоемкость запишется в виде:
с —ЦЩ
Ст~ т\дТ )т-
Отметим, что теплоемкость при постоянной темпера-
температуре равна бесконечности (ст=±оо), так как прираще-
приращение температуры в этом случае ДГ равно нулю.
Прежде чем пояснить последнее утверждение на при-
примере, введем понятие о термостате как термодина-
термодинамической системе, которая может обмениваться теплотой
с телами без изменения температуры. Практически это
всегда можно осуществить, если взять тело, обладающее
гораздо большей теплоемкостью по сравнению с рабо-
рабочим телом. Так, любое тело является термостатом по
отношению к термометру, измеряющему его температу-
температуру, т. е. теплоемкость тела, температура которого изме-
измеряется, и термометра должны находиться в соотношении
^термост^^термом- Если это условие не соблюдается, то
измерение температуры тела термометром уже приводит
к изменению температуры тела.
Термостат можно осуществить и путем автоматиче-
автоматического регулирования температуры.
Введение понятия о термостате позволяет наглядно
уяснить физический смысл теплоемкости при изотерми-
изотермическом процессе (ст=±оо).
Поставим цилиндр с газом на термостат бесконечной
емкости. Пусть температура в цилиндре с газом и тер-
термостате Т\. Чтобы повысить температуру в цилиндре, на-
прямер, на 1°, надо также повысить и температуру тер-
термостата на 1°. Но так как емкость термостата по усло-
условию бесконечна, то для нагревания цилиндра с газом на
1° требуется бесконечно большое количество теплоты.
Остюда заключаем, что ст — оо.
Чтобы понизить температуру цилиндра на один гра-
градус в этих условиях, необходимо отнять бесконечно
большое количество теплоты от термостата, т. е. тепло-
теплоемкость в этом случае ст— —оо.
Таким образом, о теплоемкости имеет смысл гово-
говорить только в связи с конкретным рассматриваемым про-
процессом.
Так как различных процессов существует бесконеч-
бесконечное множество, а к&ждый процесс характеризуется своей
41

теплоемкостью, то, следовательно, и теплоемкостей
существует бесконечное количество. Значение сх может
пробегать очень широкий интервал значений (от +оо)
до (—оо).
В технике обычно рассматривается ограниченное ко*
личество процессов, а следовательно, и теплоемкостей.
Это будет более подробно рассмотрено в последующих
главах.
§¦
Обратимые и необратимые процессы
Мы уже говорили о равновесных и не«
равновесных процессах. Определение обратимых и необ-
ратимых процессов неразрывно связано с этими поня-
понятиями. Прежде всего необходимо ввести понятие квази-
квазиравновесных, или, как их иначе называют, квазистатиче-
квазистатических, процессов.
Под квазистатическим процессом понимают процесс
с малым отклонением от равновесного состояния. Это
бесконечно медленный процесс, состоящий из ряда по-
последовательных почти равновесных состояний.
Равновесных процессов, по существу, в природе нет,
но квазистатических процессов много, и они имеют боль-
большое практическое значение. Равновесные процессы яв-
являются предельным случаем квазистатических.
Отметим два важных свойства равновесных процес-
процессов.
Во-первых, равновесные процессы можно изображать
графически. Это объясняется тем, что только равновес-
равновесные процессы описываются уравнениями состояния, т. е.
для них можно написать функциональную зависимость
между параметрами /?, V> Г, а всякую функциональную
зависимость можно изобразить графически.
Так, например, на рис. 8 изображен график зависи-
зависимости /?l/=const в случае равновесного процесса.
Во-вторых, равновесные процессы обладают свой-
свойством обратимости. Под обратимыми процессами мы по-
понимаем такие процессы, которые могут проходить как в
прямом, так и в обратном направлениях, причем в по-
последнем случае система проходит через те же состояния,
что и при прямом процессе. При этом ни в окружающей
среде, ни в самой системе не возникает никаких оста-
остаточных изменений.
42

Рис 8 Изотерма идеального
газа
Рис. 9. Схема опыта,
иллюстрирующего равно-
равновесный процесс в газе.
Для более конкретного представления этого процесса
проф. А. Б. Млодзеевский предложил интересную схему
опыта, изображенную на рис. 9.
На поршне М укреплен столик L с песком. Если с по-
последнего снять несколько песчинок на соответствующую
полку Л, поршень станет легче и под действием давле-
давления рабочего тела (газа) поднимется на уровень с дру-
другой полкой. На эту полку можно ёбросить еще несколь-
несколько песчинок, отчего поршень со столиком поднимется к
следующей полке и т. д. Если песчинки бесконечно малы
и полки расположены бесконечно часто, можно считать
подъем поршня бесконечно медленным и изотермиче-
изотермическим, а давление одинаковым во всем объеме газа и
равным внешнему давлению на поршень. Если теперь
проводить процесс в обратном направлении, т. е. бро-
бросать на столик L с каждой полки по бесконечно малой
песчинке, можно утверждать, что система будет прохо-
проходить через те же состояния, что и в прямом направле-
направлении, лри этом никаких изменений ни в самой системе,
ни в окружающей среде не возникает.
Процессы, не удовлетворяющие условиям обратимо-
обратимости, называются необратимыми. С последними мы обыч-
обычно имеем дело в природе и на практике. Если в ранее
рассмотренном примере снять с поршня значительный
груз, то внешнее давление сразу станет меньше давле-
4а

ния газа под поршнем, в результате чего произойдет бы-
быстрое расширение газа, сопровождающееся понижением
его температуры. Кроме того, при быстром движении
поршня часть механической энергии вследствие трения
расходуется на нагревание окружающей среды. Сжимая
газ так же быстро до прежнего объема, мы в связи с по-
потерей части энергии не можем уже вернуть его в перво-
первоначальное состояние. В этом случае также непосред-
непосредственно под поршнем давление будет больше, чем во
всем объеме, и равновесие системы нарушится. Можно
сказать, что всякий равновесный процесс обратим, вся-
всякий неравновесный процесс обязательно необратим.
Обратимые процессы являются абстракцией и в чи-
чистом виде в природе не реализуются. Однако рассмотре-
рассмотрение обратимых процессов играет большую роль в термо-
термодинамике, так как, во-первых, многие процессы в природе
и технике являются практически почти обратимыми. Во-
вторых, обратимые процессы являются наиболее эконо-
экономичными и приводят к максимальному значению коэф-
коэффициента полезного действия для тепловых машин. Изу-
Изучая эти процессы, можно указать, как мы увидим ниже,
пути повышения коэффициента полезного действия ре-
реальных тепловых машин.
§•
Аналитическая формулировка первого
начала термодинамики
Аналитически первое начало термодина*
мики можно записать в виде:
d/Q = dU~\-d'W. B,8)
Теплота, получаемая системой, идет на увеличение
внутренней энергии системы и на совершение работы.
Как видно из равенства B, 8), количество теплоты
d'Q, как сумма полного dU и неполного d'W дифферен-
дифференциалов, не является полным дифференциалом.
Аналитическая формулировка первого начала B, 8),
справедлива как для обратимых, так и для необратимых
процессов.
Для случая расширения идеального газа первое на-
начало термодинамики запишется:
d'Q=zdU+pfdV. B,80
U

Эта запись справедлива для равновесного и для нерав-
неравновесного процессов, ибо р' есть внешнее давление, ока-
оказываемое на газ. Для равновесного процесса внешнее
давление // равно давлению р, и первое начало термо-
термодинамики для этого случая запишется в виде:
d'Q^dU + pdV. B,9)
Поскольку внутренняя энергия обладает полным диф-
дифференциалом dll, она является функцией состояния си-
системы. Работа W, совершаемая системой над внешними
телами, и теплота Q, полученная системой от внешнего
источника, не обладают полными дифференциалами и не
являются, следовательно, функциями состояния. Эти ве-
величины зависят от пути, по которому система переходит
из начального в конечное состояние.
Методологическое значение первого
начала термодинамики—закона
сохранения и превращения энергии
История развития науки показывает, что
вокруг закона сохранения и превращения энергии всегда
велась весьма острая борьба между материализмом и
идеализмом.
Закон сохранения и превращения энергии имеет боль-
большое методологическое значение. Энгельс уделял ему осо-
особое внимание как одному из основных положений диа-
диалектического материализма. Он подчеркивал количест-
количественную и качественную стороны данного закона. Энгельс
писал: «Если еще десять лет тому назад новооткрытый
великий основной закон движения понимался лишь как
закон сохранения энергии, лишь как выражение того,
что движение не может быть уничтожено и создано,
т. е. понимался только с количественной стороны, то
это узкое, отрицательное выражение все более вы-
вытесняется положительным выражением в виде закона
превращения энергии, где впервые вступает в свои права
качественное содержание процесса...» (Анти-Дюринг,
стр. 9, М., Политиздат, 1966.
В своем знаменитом труде «Материализм и эмпирио-
эмпириокритицизм» В. И. Ленин подверг резкой критике возник-
возникший еще в конце XIX —начале XX в. энергетизм Ост-
Оствальда, показав его идеалистическую направленность.
45

Согласно концепции Оствальда, все многообразные яв«
ления природы можно свести к энергетическим измене-
изменениям. Появление такой точки зрения было обусловлено
тем, что к концу XIX в. понятие энергии приобрело зна-
значение важнейшего понятия физики, а закон сохранения
и превращения энергии получил всеобщее признание.
В связи с этим физико-химик Оствальд выдвинул идею
замены понятия материи понятием энергии. Он утвер-
ждал, что под понятие энергии можно подвести «все фи-
физические явления, данные нам в опыте».
«Мы замечаем, — писал он, — что все, происходящее
во внешнем мире, может быть исчерпывающим образом
охарактеризовано, когда указывают род и количество
тех энергий, которые тратятся или превращаются в дан-
ном процессе». (Лекция о натурфилософии, Лейпциг,
1902, стр. 109.)
Здесь ясна попытка оторвать движение от материи и
рассматривать его как нечто совершенно независимое от
последней. Критикуя энергетизм Оствальда, В. И. Ленин
показал, что отрыв движения от материи неизбежно ве-
ведет к устранению материи и, следовательно, к идеализ-
идеализму; признание существования энергии без материи рав-
равносильно признанию мышления без источника мысли.
«Энергетическая физика, — писал Ленин, — есть ж>
точник новых идеалистических попыток мыслить движе-
движение без материи — по случаю разложения считавшихся
дотоле неразложимыми частиц материи и открытия до-
дотоле невиданных форм материального движения» (Ма-
(Материализм и эмпириокритицизм, М., Политиздат, 1965,
стр. 258).
В последнее время замечательное открытие взаимо-
взаимосвязи энергии и массы, выражаемое формулой Е=тс2>
было использовано современным «физическим» идеализ-
идеализмом для возрождения энергетизма Оствальда. Закон
взаимосвязи массы и энергии трактовался идеалистами
как закон превращения массы в энергию, что означало
попытку отмены закона сохранения массы и закона со-
сохранения и превращения энергии и сведение их в один
закон сохранения массы — энергии. Такая явно идеали-
идеалистическая трактовка закона сохранения и превращения
энергии противоречит всей его истории развития.
Тесная связь массы и энергии, даваемая законом
Е=тс2, означает, что в физических процессах всякие из-
46

менения массы должны сопровождаться энергетическими
изменениями.
В действительности имеют место два закона — закон
сохранения и превращения вещества и закон сохранен
ния и превращения энергии. Открытие же тесной связи
между массой и энергией показывает, что, хотя каждый
из этих законов имеет вполне самостоятельное значение,
нельзя их рассматривать независимо друг от друга, по-
поскольку немыслимо никакое материальное превращение
без энергетического, т. е. нет материи без движения, так
же, как нет движения без материи. В этом смысле мож*
но говорить о законе сохранения материи и энергии как
о всеобщем законе. Поскольку еще имеют место попытки
дать идеалистическую трактовку закона сохранения и
превращения энергии, этот вопрос не теряет своего акту-
актуального значения и в настоящее время.
п8
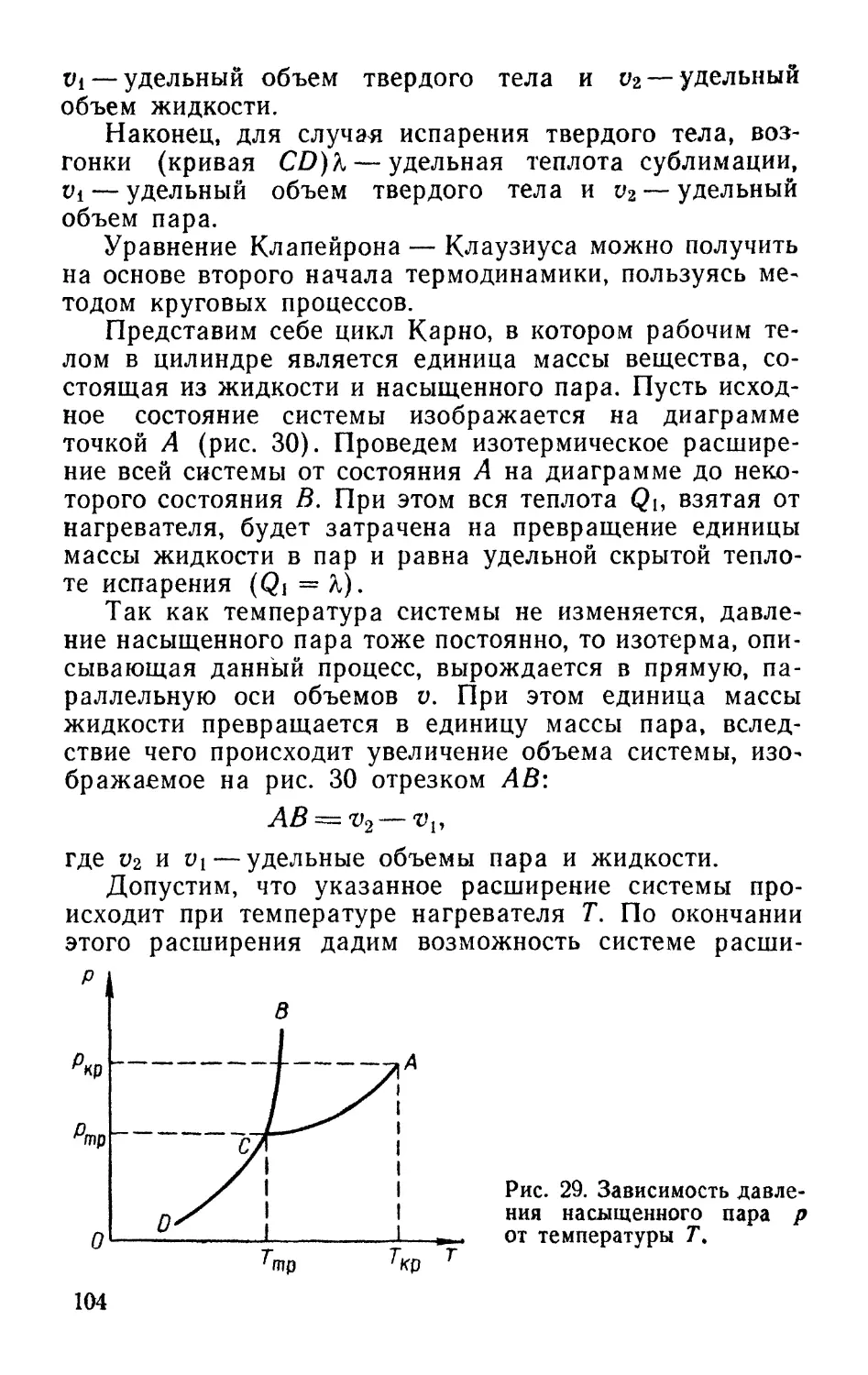
§ Связь между теплоемкостями при
постоянном давлении и постоянном
объеме
Возьмем внутреннюю энергию как функ*
цию объема и температуры:
U = f(V, T). B.10)
Подставим полный дифференциал этой функции
в выражение первого начала термодинамики B, 9):
. B,12)
Предположим, что процесс проходит при постоянном
объеме (dl/ = 0), тогда
B,13)
В этом случае
d'Q = cvdT. B,14)
Из равенств B, 13) и B, 14) следует:
Ш' B,15)
47

т. е. cv есть частная производная внутренней энергии по
температуре при V = const. С учетом равенства B, 15)
соотношение B, 12) принимает вид:
d'Q =(jp) dV+cvdT+pdV. B,16)
Предположив, что процесс идет при постоянном дав-
давлении (/? = const), можем записать:
и уравнение B, 16) примет вид:
или
лт dV I dV \ .
Учитывая, что 7r==l7i") ПРИ P==cons^ оконча-
окончательно получим:
Соотношение B, 17) устанавливает связь между теп-
лоемкостями ср и cv и частными производными:
Следовательно, если из теории или эксперимента изве-
известно уравнение состояния системы и выражение внутрен-
внутренней энергии, то можно найти разность теплоемкостей
cv—cv.
Если предположить, что процесс идет при постоян-
постоянном х, где х — может означать любой постоянный пара-
параметр, то, проводя рассуждения, аналогичные предыду-
предыдущим, получим связь между теплоемкостями и частными
производными внутренней энергии по объему и объема
по температуре в общей форме:
Однако с помощью только первого начала термоди-
термодинамики связь между сх, cv и параметрами состояния в
раскрытом виде может быть получена лишь для простей-
простейших систем.
48

Найдем выражение для внутренней энергии и разно*
сти теплоемкостей ср — cv идеального газа. Полное изме^
нение внутренней энергии равно сумме двух слагаемых:
первое из них (^г) dV обусловлено изменением сил
взаимодействия между молекулами, второе слагаемое
/ dU\ ,~
\дТ) —изменением кинетической энергии молекул.
Так как в идеальном газе силы взаимодействия между
молекулами отсутствуют, то ("зтт/ #у—и, и соотноше*
ние B, 11) упрощается:
-)vdT = cvdT. B,19)
В интегральной форме соотношение B, 19) прини*
мает вид:
U^CyiTs-T,). B,20)
Определим теперь разность теплоемкостей идеально*
го газа. В этом случае ("^тг) =0 и уравнение B, 17)
имеет вид:
(^) B,21)
Объем многих твердых тел, например резины, каучу-
каучука, камня и т. д., лишь незначительно изменяется с по-
повышением температуры. Поэтому в практических рас-
расчетах для этих тел можно принять Су = ср, т. е. что
теплоемкость при постоянном объеме у них равна тепло-
теплоемкости при постоянном давлении. Для металлов и дру-
других тел, объем которых сильно зависит от температуры,
это равенство несправедливо.
u u (dV\
Найдя i-gjH из уравнения состояния идеального га-
газа A, 6) и подставив в равенство B, 21), получим:
cp-cv = R. B,22)
Уравнение B, 22) носит имя Роберта Майера. Оно
показывает, что разность теплоемкостей (ср — cv) иде-
идеального газа есть величина постоянная, равная универ-
универсальной газовой постоянной R.
4 В. Ф. Ноздрев 49

Роберт Майер использовал в свое время уравнение
{2, 22) для определения механического эквивалента теп-
теплоты.
В термодинамике проблема теплоемкостей полного решения не
находит.
Современная теория теплоемкости была создана на основе ста-
статистической физики и квантовой механики. В статистической физике
доказывается равномерное распределение энергии по степеням сво-
свободы. Согласно теории для идеального газа
где i — число степеней свободы, k — постоянная Больцмана.
Тогда
cv = YW)v:=YR- B-23)
Соотношение B,23) показывает, в что согласно классической ста-
статистической физике теплоемкость не "зависит от температуры, а за-
зависит только от числа степеней свободы /. Поскольку число поступа-
поступательных степеней свободы равно трем, то *=3-М', где /'— число
вращательных степеней свободы. Отсюда
B.24я)
.-i±Jl* + *:
Может ли меняться число степеней свободы с ростом темпера-
температуры? Квантовая механика отвечает на этот вопрос утвердительно.
Оказывается, при высокой температуре возникает еще колебатель-
колебательное движение атомов в молекуле, т. е. появляются новые степени
свободы, так что в общем случае выражения для теплоемкостей
B,24а) и B,246) можно записать так:
B.25)
B,26)
где с'(Т)—теплоемкость, связанная с колебательными степенями
свободы *.
Например, в случае двухатомных газов квантовая статистика
дает для с'(Т):
0
С (Т) = (±У eJ . MR. B,27)
U)
* Формулы B,25); и B,26) могут быть записаны в самом об-
общем виде, если учесть зависимость V от Т.
50

В B, 27) 9 — характеристическая температура, равная —г-, где h —
постоянная Планка (/г=6,624• Ш~27 эрг» сек), k — постоянная Больц-
мана (&= 1,38 • 10~23 -<—1, со — собственная частота колебаний.
Таким образом, как видно из B,27), квантовая статистика уста-
устанавливает не только зависимость теплоемкости от температуры, но
и предсказывает принципиально новое явление: неравномерность рас-
распределения энергии по степеням свободы.. При приближении темпе-
температуры тела к абсолютному нулю наступает так называемое «вы-
«вырождение степеней свободы» (постепенно исчезают колебательные
движения атомов в молекуле, затормаживаются вращательные дви*
жения молекул, а при абсолютном нуле прекращаются и поступав
тельные движения молекул.
При Г=0°К теплоемкость равна нулю (см. гл. 10).
Результаты, полученные из квантовой статистики, находятся в
хорошем соответствии с опытными данными.
§•
Применение первого начала
термодинамики к некоторым
термодинамическим процессам
Несмотря на то, что различных термоди*
намических процессов существует весьма много, для ре-
решения теоретических и практических задач достаточно
изучить наиболее типичные из них.
Изобарическим процессом называется про-
процесс, протекающий при постоянном давлении (р = const)«
На диаграмме р, V этот процесс изображается прямой^
параллельной оси объемов (рисч10).
Так как р = const, то выражение элементарной рабо-
работы легко интегрируется.
2 2
\ - Vx\ B,28)
Рис. 10. График изобарического
процесса.
51

о
Рис. 11. График изохорического
процесса.
и первое начало термодинамики для изобарического про-
процесса принимает вид:
dfQ = dU + p(V2-Vx). B,29)
Теплоемкость ср при изобарическом процессе имеет
конечное значение.
Изохорическим процессом называется про-
процесс, протекающий при постоянном объеме (V= const).
Графически этот процесс изображается прямой, парал-
параллельной оси давлений (рис. 11).
Первое начало термодинамики для изобарического
процесса имеет вид:
d'Q = dU. B,30)
Из соотношения B, 30) видно, что теплота, подводи-
подводимая к системе при этом процессе, полностью идет на
повышение внутренней энергии, т. е. система не совер-
совершает работы.
Теплоемкость cv при изохорическом процессе яв-
является также конечной величиной.
Изотермичейшм процессом называется про-
процесс протекающий при постоянной температуре (Т =
= const). В случае идеального газа он описывается урав-
уравнением Бойля — Мариотта и графически на диаграмме
pV изображается гиперболической кривой /?V=const
(рис.8).
52

Запишем первое начало термодинамики для данного
случая:
d'Q = cvdT+pdV. B,31)
Но
dT = 0,
следовательно,
d'Q = pdV. B,32)
Последнее соотношение свидетельствует о том, что в
рассматриваемом случае вся полученная системой теп-
теплота идет на совершение работы. Теплоемкость при изо-
изотермическом процессе сг*=±оо.
Адиабатическим процессом называется про-
процесс, при котором рассматриваемая система не обмени-
обменивается теплом с окружающей средой. Это не значит, что
рассматриваемая система должна находиться в адиаба-
адиабатической оболочке в буквальном смысле этого слова.
К адиабатическим процессам относятся, например, про-
процессы распространения звука в среде и истечения газа
из сопла. В первом случае скорость распространения
звуковой волны настолько велика, что обмен энергией
между волной и средой не успевает произойти и, следо-
следовательно, распространение звуковой волны можно счи-
считать процессом адиабатическим. Истечение газа и^
сопла происходит с большой скоростью, часто превышаю-
превышающей скорость звука, поэтому такой процесс можно счи*
тать практически адиабатическим.
Первое начало термодинамики для адиабатной систе-
системы запишется в виде:
или
dU = — d'W. B,33)
Работа d'W считается положительной, если ее совершает
система, и отрицательной, если работу совершают над
системой.
Выведем уравнение адиабаты для идеального газа.
Для этого воспользуемся первым началом термодинами*
ки и уравнением состояния идеального газа.
Так как
a d'W = p,
53

то соотношение B, 33) для адиабатного процесса будет
иметь вид:
cvdT = — pdV. B,34)
Откуда
Соотношение B, 34) позволяет сделать вывод: если
при адиабатическом процессе происходит расширение
газа, то температура его понижается. Наоборот, сжатие
газа сопровождается повышением температуры.
Продифференцируем уравнение состояния (I, 6):
^RdT. B,35)
На основании равенства B, 34):
^ B,36)
или
cv (р dV + V dp) = - R {p dV). B,37)
По уравнению Роберта Майера: R=cp — cv. Раскрыв
скобки и приведя подобные члены в уравнении B, 37),
получим:
Vd+dV O. B,38)
Разделив полученное выражение на произведение
Су Vp и обозначив отношение ~ через у, получим:
-y- + v4r = a B>39)
Считая теплоемкости ср и cVf а следовательно, и их
отношение y ——— величинами постоянными, после ин-
су
тегрирования уравнения B, 39) найдем:
In р + у In V = In ay
где а — произвольная постоянная.
Или
B,40)
Уравнение B, 40) называется уравнением Пуассона.
Графически описываемая им зависимость изображается
54

Рис. 12. Изотерма pV = const
и адиабата pV^ = const.
кривой, аналогичной изотерме pV=const, но круче спа-
спадающей к оси объемов (см. рис. 12). Теплоемкость при
адиабатическом процессе постоянна и равна нулю:
0
Политропическим процессом называется ирр-
цесс, протекающий при постоянной теплоемкости.
Поскольку политропические процессы имеют большое
практическое значение, на их рассмотрении следует оста*
новиться более подробно. Рассмотренные выше адиаба-
адиабатический и изотермический процессы являются частными
случаями политропического, так как теплоемкости
сг=±оо, сад=0 есть постоянные величины.
При изобарическом и изохорическом процессах теп*
доемкости ср и cv конечны, но меняются, например, с из*
менением температуры; поэтому вообще эти процессы
считать частными случаями политропического процесса
нельзя. Однако, когда ср или cv постоянны, то можно
рассматривать изобарический и изохорический процессы
как частные случаи политропического.
Найдем уравнение политропы в случае идеального
газа. Для этого воспользуемся уравнением Клапейро-
Клапейрона— Менделеева и соотношением теплоемкостей:
сх —
B,41)
DP
Учитывая, что р^-у-, найдем выражение
из соотношения B,41):
дт)х
55

Так как
= ср
то
bl^ B.42)
Разделив переменные в уравнении B,42):
dV с —с.. dT
-=t=^-~ B'43)
и интегрируя уравнение B,43), получим:
In у = ^UhL in T + In a, B,44)
где а = const Или:
ex-ev
с —с
VT p v ^= const. B,45)
Часто пользуются уравнением политропы, выражен-
выраженным через параметры р и V:
pycv~cx = const, B,46)
которое нетрудно получить из уравнения B,45), исполь-
используя уравнение состояния pV = RT.
Последнее уравнение можно записать в виде:
pVn = const. B,46')
Величина п — — называется показателем поли-
полису X
тропы.
Каждый из политропических процессов характери-
характеризуется вполне определенным постоянным значением по-
показателя политропы п. Поэтому теплоемкость сх в этом
случае целесообразно обозначать через сп.
с —-
п — у
п~~~ л —1 ~ п — 1 ^yt
Это и есть выражение теплоемкости политропического
процесса.
56

Рис. 13. Зависимость
теплоемкости сп от
показателя политро-
политропы п.
Какие значения может иметь показатель политропы
л? Рассмотрим три случая.
1) 1 < п < y» где y== ~~^~- В этом случае сп<0> т. е.
cv
при данных условиях теплоемкость является величиной от-
отрицательной. Последнее утверждение говорит о существо-
существовании процессов, при которых для нагревания системы
на 1°С необходимо от системы отнимать тепло. Иными
еловами, наличие отрицательной теплоемкости показы-
показывает, что при некоторых процессах, несмотря на подвод
к системе теплоты, ее температура уменьшается. Про-
Процессы с отрицательной теплоемкостью наблюдаются в
астрофизике (распад звезд), а также при использовании
насыщенных паров в теплотехнике.
2) n=Y- В этом случае сп = 0. Политропический про-
процесс вырождается в частный случай — адиабатический
процесс.
3) При n>Y, cn>0.
Характер зависимости теплоемкости сп от показателя
политропы п изображен на рис. 13.
Рассмотрим изменение температуры в политропиче-
политропическом процессе.
Для политропического процесса в идеальном газе
имеем:
Согласно аналитической записи первого начала тер-
термодинамики B, 8) :
57

Так как
ПСУ~СР „ CP
то
^^=-^4т(Л — ^2). B,47)
Соотношение B,47) показывает, что при политропа
ческом процессе совершение газом работы сопровож-
сопровождается понижением температуры.
§10
Установление связи между
адиабатическим и изотермическим
модулями упругости и скоростью звука
Предварительно выведем уравнение ади*
абаты для общего случая, исходя из уравнений B,16)*
и B,17).
Поскольку рассматривается адиабатический процесс,
то d'Q = Q и уравнение BД6) запишется в виде:
= 0. B,48)
Из уравнения B,17) и B,48) можно получить урав-
уравнение адиабаты для общего случая, выраженное через
независимые переменные Т и V:
). B,49)
Учитывая, что модули упругости связаны с перемен*
ными р и V, найдем уравнение адиабаты в тех же пере-
переменных.
Из уравнения состояния T=f(p, V) определим диф-
дифференциал температуры:
Совместное решение уравнений B,49) и B,50) при-
приводит к выражению адиабаты для общего случая в пе«
ременных р и V:
или
f
др)у
58

По определению адиабатического и изотермического
модулей упругости:
Для случая изотермического процесса (dT—О) урав-
уравнение B, 50) можно записать так:
\дУ)р _ ( dp \ ,9 „ч
7ЕТ~Ы1 B>53)
Е
dp)v
Сравнивая последнее уравнение с уравнением B, 51),
находим:
или, согласно соотношениям B, 52):
B,55)
Учитывая, что величина, обратная упругости, есть коэф-
коэффициент сжимаемости:
Рад = "^7; Риз = ~К^'
получим следующую зависимость коэффициентов сжи-
сжимаемости:
V = fe' B.57)
Теперь установим связь между отношением теплоем*
« ср
костей — и скоростью звука в среде.
Скорость распространения звука в среде определяет-
ся из уравнения ci = -^?~, где р — плотность среды.
Так как плотность среды обратно пропорциональна
удельному объему р^ —, то
B.58)
Распространение звука в среде является адиабатным
процессом^ поэтому
Ш <2-59)
59

Подставляя выражения
I дР \ *
в выражение для скорости звука, получим равенство:
^^"жг BД))
или согласно соотношению B,57):
Наконец, можно установить связь между модулями
упругости и скоростью звука. Подставляя значение
B,57) в формулу скорости звука B,61), окончательно
получим искомое соотношение:
РРиз А из
о2
Г Задачи и упражнения
1. Написать выражение первого начала
для единицы объема непроводящего диэлектрика, поме-
помещенного во внешнее постоянное однородное электриче-
электрическое поле (например, между пластинами конденсатора),
предполагая для простоты векторы Е и D параллельны-
параллельными в каждой точке, а удельный объем постоянным.
Решение. Элементарная электрическая
работа для единицы объема диэлектрика равна
-r^-EdD. Пренебрегая, по условию, работой расшире-
расширения (сжатия) pdV, запишем первое начало в виде:
d'Q
лн 4л '
где d'Q — элементарное количество подводимого тепла;
Uuom — энергия системы, включая энергию электриче-
электрического поля.
->
Введем электрическую поляризацию Р по формуле
-> -> ->
D=E+4nP и выделим из выражения полной энергии

энергию электрического поля в вакууме, положив
Тогда получим: d'Q — dU—EdP.
2. Вычислить работу, совершаемую внеш-
внешним электрическим полем при поляризации диэлектрика.
Решение. В качестве термодинамической
системы возьмем диэлектрик, находящийся между двумя
пластинами плоского конденсатора. Работа, которую
нужно совершить при переносе электрического заряда
dq между двумя точками с разностью потенциалов q>,
равна d'W = —ydq.
Если S — площадь пластины, а а — поверхностная
плотность заряда, то электрический заряд q = So. По-
Поскольку электрическая индукция ? = 4я0, изменение ко-
количества электричества dq = Sdo = S -j—.
Так как потенциал и напряженность электрического
поля связаны соотношением ф=?7, то, подставляя ф и
dq в выражение работы d'W, получим:d'W——j—EdD.
Работа, отнесенная к единице объема 1*^=5/ диэлек-
диэлектрика, будет равна:
Поскольку
то
~
где Р — вектор поляризации единицу объема диэлек-
диэлектрика.
3. Вычислить работу испарения воды,
если при переходе одного моля воды A8 г) в пар при
100° С увеличение объема составляет VB— VA==
= 30 186 смг/моль. Давление в течение процесса постоян-
постоянно и равно р= 1,013-10е дн/см2=1 атм. Отв. W=
= 3,06 кдж.
4. Дан 1 моль газа при нормальных ус-
условиях (Va= Vo=22414 cmz, /7=1 атм). Вычислить ра-
работу, необходимую для уменьшения объема этого газа
61

в 2 раза, считая, что процесс подчиняется закону Бой-
ля — Мариотта:
Отв. 1^^ — 1,57 кдж.
5. В калориметр, содержащий 200 г воды
(начальная температура /i=20°C), бросают куски ме-
металла весом по 300 г, имеющие начальную температуру
?2=Ю0°С. Температура равновесия / равняется: для
алюминия (^=27,0 г) 39,5° С, для железа (р,=55,8 г)
31,9°С, для цинка (ja = 65,4 г) 29,8°С, для серебра (р,=
= 107,9 г) 26,2° С. Найти удельную (суд) и молярную
теплоемкости (С) этих четырех металлов (ц — атомный
вес).
Отв.
для алюминия: суд = 0,21 кал/г• град; С == 5,67 кал/град;
для железа: гуд = 0,116 кал/г-град; С = 6,47 кал/град;
для цинка: сУА = 0,093 кал\г• град; С ж 6,08 нал/град;
для серебра: суя = 0,056 кал/г• град; С « 6,04 кал\град.
6. Стержень длиной / растягивается си-»
лой Р. Считая деформацию упругой (так что длина
стержня является функцией Р и температуры), показать,
что изотермический и адиабатический коэффициенты
удлинения у-gp» связаны соотношением
dl\ _ ct ( dl
'dpL~T^VdP
где ci и сР — теплоемкости стержня при постоянной дли-
длине и постоянном растягивающем усилии соответственно.
Решение. Работа упругих сил стержня
при удлинении на dl равна —PdU поэтому первое начало
термодинамики принимает вид: d'Q = dE — PdU где Е-.
энергия стержня. Запишем равенство B, 12} в перемен*
ных /, Т и в переменных Р, Г, введя обозначение
#)
62

Отсюда по определению сг и сР:
Переписав равенство B,12) в переменных Р, /, полу-»
чаем с помощью соотношения B,63):
Для адиабатического процесса d'Q = 0, откуда
*L\ —-SL \дрп —(dl \ [IL
dPh~ ' *L\ —\дР){
dt
7. Определить работу при изотермиче*
ском расширении газа, подчиняющегося уравнению Ван-
дер-Ваальса.
Решение. Работа расширения газа выра-
выражается интегралом:
2
i
Уравнение Ван-дер-Ваальса A,9), разрешенное отно-
относительно давления р, имеет вид:
_ RT а_
Р— v — b V2 #
Следовательно, работа при изотермическом расшире-
расширении 1 моля газа, подчиняющегося уравнению Ван-дер*
Ваальса, равна:
где Vi и V2 — начальное и конечное значения молярного
объема.
63

8. Определить особенности следующих по-
литропных процессов:
PV°'S = const; pVl>3 = const;
pVlf5 = const.
Коэффициент у принять равным 1,4.
Решение. Процесс р У0*8 = const принадле-
принадлежит к первой группе политропных процессов, так как в
нем n<v.
Коэффициент а = _ = —-=^5^-^ = ^.
В данном процессе при расширении газа к нему под*
водится теплота, одна треть которой идет на увеличе-
увеличение внутренней энергии газа, а две трети — на совер-
совершение внешней работы. Следовательно, температура
газа при его расширении в этом процессе увеличивается.
9. Аналогичным образо.м исследовать
остальные процессы и показать относительное располо-
расположение политроп в /?У-диаграмме.
10. В политропном процессе газ при рас*
ширении получает 10 ккал теплоты. Рассчитать процесс,
если объем газа увеличивается в 10 раз, а давление
уменьшается в 8 раз.
Отв. п = 0,9; а==-^-; Ш'=2 ккал.
11. В процессе сжатия совершается
20 000 кГм работы и от газа отводится 60 ккал теплоты.
Определить п, считая -у—l Д.
Отв. п = 0,9.
12. Показать, что для веществ, подчи-
подчиняющихся закону соответственных состояний, справедлив
во соотношение
Y2
64

где Yi и Y2 — отношение теплоемкостей ~ рассматри-
рассматриваемых веществ,
РаД1 и раДз — коэффициенты адиабатической сжимаемо-
сжимаемости веществ,
Рщ и Рк2 "" их критические давления.
Решение. Пользуясь ранее полученными
соотношениями B,57) и A,24), находим:
откуда
Vl
Y2 Рц
Последнее уравнение можно с успехом применить для
ср
определения — вещества, подчиняющегося закону со-
cv
ответственных состояний, если известны из опыта рад и
отношение теплоемкостей хотя бы для одного вещества,
удовлетворяющего этому закону.
ЛИТЕРАТУРА
1. А. С. ЯСТРЖЕМБСКИЙ,
Техническая термодинамика, Госэнергоиздат, 1953.
2. А. м. литвин,
Техническая термодинамика, Госэнергоиздат, 1956.
3. в. ф. ноздрев,
Применение ультраакустики в молекулярной физике, Гостехиздат,
1958.
4. А. Г. САМОЙЛОВИЧ,
Термодинамика и статистическая физика, Гостехиздат, 1955.
5 В. Ф. Ноздрев 65

ГЛАВА ТРЕТЬЯ
Круговые процессы,
или циклы. Цикл Карно.
Идеальные циклы
тепловых двигателей
Круговые процессы
Основные термодинамические процессы
(изотермический, изобарический, изохорический и др.)
графически изображаются в виде некоторых отрезков
кривых (или прямых) на диаграмме pV (рис. 8, 10, 11),
Заметим, что рабочее тело в начале и в конце не*
замкнутого процесса находится в различных состояниях.
Параметры, определяющие его состояние, имеют различ-
различные значения.
В термодинамике особенно важное значение имеют
такие процессы, когда термодинамическая система в кон-»
це процесса приходит в первоначальное состояние, и па*
раметры, определяющие это состояние, принимают пер-
первоначальные значения. Такие процессы носят название
замкнутых процессов или циклов. Например, процесс,
изображаемый замкнутой кривой ABCDA (рис. 14),
является примером такого замкнутого процесса, или
цикла. Очевидно, работа, совершенная в результате этого
цикла, численно равна плрщади, ограниченной кривой
ABCD.
Итак,
если система, проходя ряд состояний, возвра-
возвращается в свое начальное состояние, то говорят,
что данная система совершает цикл.
О
т
V 1
Рис. 14. Пример замкнутого
процесса или цикла.

Рис. 15. График цикла, сб-
стоящего из изобарического
(АВ)% изохорического (ВС)
и изотермического (С А) про-
процессов.
v9 v
В природе существует бесконечное количество циклов.
Образуем, например, цикл из изобары, изохоры и изо-
изотермы (рис. 15). В этом случае рабочее тело, пройдя
ряд состояний, вернулось в начальное состояние А. По-
Полезная работа такого цикла равна численно площади
ABC.
Возьмем цикл, состоящий из двух изобар (АВУ CD)
и двух изохор (ВС, DA) (рис. 16). Полезная работа та-
такого цикла равна площади ABCD.
Остановимся на некоторых общих особенностях
циклов.
Прямые и обратные циклы.Циклы, в которых
работа совершается за счет затрат теплоты, называются
прямыми циклами. В них линия расширения газа
на диаграмме pV располагается выше линии сжатия.
Прямые циклы совершают все тепловые машины (паро*
вые, двигатели внутреннего сгорания и др.).
Обратными циклами называются циклы, на
осуществление которых расходуется механическая энер*
гия. В них линия расширения лежит ниже линии сжатия.
Обратные циклы используются при создании холодиль*
ных машин.
Рис. 16. График цикла, состо-
состоящего из изобарического (АВ\
изохорического(ВС), изобари-
изобарического (CD) и изохорическо-
изохорического (DA) процессов.
67

Изображенные на рис. 14, 15 и 16 циклы, проходимые
в направлении, указанном стрелкой, являются прямыми.
Цикл Карно. Возникает вопрос: какой
цикл из всего многообразия существующих циклов яв-
является самым экономичным, т. е. имеет наибольший ко-
коэффициент полезного действия? Такой цикл был предло-
предложен французским инженером и ученым Сади Карно в
1824 году.
Представим себе мысленно цикл, состоящий из двух
изотермических и двух адиабатических процессов, чере-
чередующихся между собой (рис. 17).
Чтобы осуществить цикл Карно, необходимо иметь
два термостата и рабочее тело. Упругое тело, совер-
совершающее цикл, будем называть рабочим телом. В каче*
стве рабочего тела возьмем газ в цилиндре с подвижным
поршнем, на который действует внешнее давление.
Боковые стенки цилиндра и его поршень имеют
адиабатную оболочку, дно же такой оболочки не имеет.
Термостаты должны иметь бесконечно большую тепло-
теплоемкость и разные температуры. Термостат, сообщающий
рассматриваемой термодинамической системе теплоту,
будем называть нагревателем, а термостат, принимающий
от рассматриваемой системы теплоту, — холодильником.
Пусть сначала рабочее тело расширяется при посто-
постоянной температуре Т\ по изотерме АВ. Для этого поста*
вим цилиндр с хорошо проводящим тепло дном на тер-
термостат, имеющий температуру Т\ (рис. 18), При изо-
изотермическом расширении от состояния Л до В газ
получит от нагревателя количество теплоты Q\ при тем-
температуре 7\ и, поднимая поршень, совершит положитель*
о
Рис- 17. График цикла Карно,
состоящего из изотермического
расширения (АВ), адиабатиче-
адиабатического расширения (ВС), изо-
изотермического сжатия (CD) н
адиабатического сжатия (DA).
68

Рис.18. Схема, иллюстрирую-
иллюстрирующая реализацию иикла Карно.
ную работу WAB против внешнего давления, численно
равную площади, заключенной между кривой АВ и осью
абсцисс.
В состоянии В давление, объем и температура имеют
значение р2> V2, Tt. Если бы расширение газа осущест-
осуществлялось не бесконечно медленно, то при таком расшире-
расширении температура газа упала бы ниже температуры на-
нагревателя, так как не успевала бы происходить тепло-
теплопередача от термостата к цилиндру. Такой процесс был
бы необратимым. Чтобы процесс расширения газа был
обратимым, необходимо увеличивать его объем беско-
бесконечно медленно.
Далее снимем цилиндр с термостата и закроем дно
термоизолирующей подставкой. Газ за счет внутренней
энергии будет расширяться адиабатически. Температура
его при этом понизится, а давление, упадет. Произойдет
адиабатическое расширение газа. Оно будет продол-
продолжаться до тех пор, пока температура газа сравняется
с температурой холодильника, т. е. до точки С. В этом
состоянии температура, объем и давление газа прини-
принимают значения /?3> Уз, 7V
Чтобы перейти от точки С в точку D изотермически,
надо снова поставить цилиндр на термостат, но с темпе-
температурой Г2. Этот термостат служит холодильником. При
изотермическом сжатии газа внешними силами от со-
состояния С до состояния D газ передает холодильнику
количество тепла Q2.
От точки D до точки А снова совершается адиабатиг
ческий процесс. Для этого цилиндр снимается с термо-
термостата, а его дно закрывается адиабатной заслонкой.
При адиабатическом сжатии системы температура
газа повышается. Когда работающее тело возвращается
69

в исходное положение Л, давление, объем и температура
принимают прежние значения ри Vh 7V Цикл закончен.
Работающее тело получает от нагревателя при рас-
расширении по изотерме АВ количество теплоты Qu а при
сжатии по изотерме CD отдает холодильнику количество
теплоты Q2. При изменении состояния по адиабатам ВС
и DA тело не получает и не теряет теплоту. Таким обра-
образом, в результате цикла тело совершает работу, эквива-
эквивалентную количеству теплоты Qi—Q2. К. п. д. цикла пред-
представляет собой отношение полезно затраченного коли-
количества теплоты к количеству теплоты, полученному от
нагревателя, и выражается отношением:
или Л=
Этот коэффициент показывает, за счет какой доли
получаемой теплоты тепловая машина совершает ра-
работу. На примере цикла Карно мы видим, что работа
совершается не за счет всей теплоты Qu взятой от на-
нагревателя, а толвко за счет части ее Qt—Q2.
Изс^термические и адиабатические процессы, из кото*
рых состоит цикл Карно, — процессы обратимые. Следо-
Следовательно, и весь цикл в целом обратим.
§¦
Цикл Карно с идеальным газом
Рассмотрим цикл Карно, когда рабочим
телом в нем является идеальный газ.
Согласно первому началу термодинамики
d'Q = dU+d'W. C,1)
При изотермическом процессе внутренняя энергия
идеального газа не изменяется. Следовательно, d'Q—d'W.
Выразим элементарную работу идеального газа, исполь-
используя уравнение состояния в виде:
C,2)
_
Следовательно, работу при изотермическом процессе
от состояния ViPi до состояния Vzp2 можно выразить так:
n^. C,3)
70

При адиабатическом процессе система не получает
тепла, и работа расширения происходит за счет убыли
внутренней энергии газа, т. е. на адиабате ВС d'Q = 0.
Работа идеального газа на изотерме CD:
Q2=W2 = RT2ln%L. C,4)
На адиабате DA система не отдает и не получает
теплоту d'Q=0. В результате цикла определим полезную
работу, равную разности количества теплоты, получен-
полученного рабочим телом от нагревателя и отданного холо-
холодильнику:
Ql — Q2=Wl—W2=:RTlln^ — RT2lnQ. C,5)
Чтобы упростить это выражение, покажем, что
Для этого из уравнения адиабаты для идеального газа
получим для точек В и С:
а для точек D и А:
Разделим эти выражения почленно:
РгП
Полученное выражение перепишем в таком виде:
Так как на изотермах АВ и CD (рис. 17) по закону Бой-
ля — Мариотта
и
.то будем иметь:
71

Тогда равенство C,5) можно переписать в виде:
Найдем теперь к. п. д. цикла Карно для идеального
газа:
откуда
t,=Ii^lL. C,6)
Из формулы C,6) следует:
к. п. д. цикла Карно с идеальным газом зависит
только от абсолютных температур нагревателя и
холодильника.
При возрастании температуры нагревателя или при
уменьшении температуры* холодильника к. п. д. цикла
увеличивается. При Ti~T2 к.п.д. цикла Карно равен
нулю. Это означает, что нельзя, затратив теплоту, совер-
совершить работу, если все тела системы находятся в тепло-
тепловом равновесии, т. е. имеют одинаковую температуру.
К. п. д. цикла Карно может быть только меньше еди-
единицы. Равенство к. п. д. единице возможно было бы при
Г2 = 0, что практически нельзя реализовать (см. гл. 4).
Таким образом, получаемую в цикле Карно теплоту
нельзя полностью использовать для совершения работы,
так как совершение работы в этом случае сопровождает-
сопровождается передачей некоторого количества теплоты от нагрева-
нагревателя холодильнику.
Как будет видно дальше, положения, устанавливае-
устанавливаемые при рассмотрении цикла Карно для идеального уаза,
окажутся весьма необходимыми при формулировке вто-
второго начала термодинамики.
Идеальные циклы двигателей
внутреннего сгорания
Одной из важнейших проблем термоди^
намики является проблема совершения работы за счет
подводимой к двигателю теплоты. Задачей теплотехники
72

является создание таких циклов, к. п. д. которых по воз-
возможности приближался бы к к. п. д. цикла Карно. Однако
вследствие конструктивных трудностей до настоящего
времени не удалось построить, например, двигатель вну«
треннего сгорания, в котором сообщение, а также отня*
тие теплоты происходило бы при постоянной темпера*
туре, по изотерме. Реальные двигатели внутреннего его*
рания не работают по циклу Карно.
Сообщение теплоты в поршневых двигателях вну*
треннего сгорания в процессе горения топлива происхо*
дит при постоянном объеме, или постоянном давлении,
или частично при постоянном давлении и частично при
постоянном объеме.
Заметим, что осуществляемые в тепловых двигателях
циклы необратимы и в действительности даже незамкну-
незамкнуты, так как в них рабочее вещество, т. е. сгоревшая
смесь газов, по окончании цикла выбрасывается наружу.
Таким образом, реальные процессы в двигателях вну-
внутреннего сгорания не могут быть изучены методами
термодинамики во всей их действительной сложности.
Строгое и полное количественное исследование возможно
только по отношению к обратимому процессу, а индиви-
индивидуальные особенности реальных процессов, связанные с
их необратимостью, должны быть отражены в форме по-
поправок.
При изучении термодинамического идеального цикла
двигателя внутреннего сгорания будем считать, что, во-
первых, процессы в нем происходят обратимо, и, во-вто-
во-вторых, предположим, что цикл замкнут, т. е. рабочее веще-
вещество не выбрасывается в атмосферу, а возвращается в
первоначальное состояние.
Современные двигатели внутреннего сгорания выпол*
няются в виде поршневых двигателей, газовых турбин и
реактивных двигателей. Они получили широкое распро-
распространение в самых разнообразных отраслях народного
хозяйства. В зависимости от назначения двигателя вну-
внутреннего сгорания созданы самые разнообразные их
типы.
Однако если исходить из используемых в этих двига-
двигателях циклов, то все они могут быть разделены на три
группы:
I — двигатели, использующие циклы с подводом
теплоты при F=const (цикл Отто);
73

II — двигатели, использующие цикл с подводом теп-
теплоты при /?=const (цикл Дизеля);
III — двигатели, использующие так называемый сме-
смешанный цикл с подводом теплоты частично при постоян-
постоянном объеме, частично при постоянном давлении (цикл
Тринклера).
Цикл с подводом теплоты при постоянном
объеме. В качестве горючего в двигателях с подводом теп-
теплоты при V== const применяется легкое топливо, жидкое
или газообразное (бензин, керосин, генераторный или
светильный газы).
Первый такой двигатель был построен в 1876 г. не-
немецким изобретателем Отто.
Основной частью двигателя является один или не-
несколько цилиндров, внутри которых производится сжига-
сжигание топлива.
Внутри цилиндра (рис. 19) перемещается поршень.
Движение поршня из одного крайнего положения
в другое крайнее положение называется тактом. Ра-
Работа двигателя состоит из четырех тактов. Во время
I такта при перемещении поршня в цилиндр двигателя
через впускной клапан / засасывается горючая смесь
бензина с воздухом. При обратном ходе поршня и за*
крытых впускном и выпускном клапанах происходит
сжатие горючей смеси (II такт). Когда поршень дости-»
гает крайнего левого положения, горючая смесь воспла*
меняется от электрической искры. Следующее за этим
расширение продуктов сгорания, сопровождаемое дви*
жением поршня, называется рабочим ходом, поскольку
при этом собственно и производится полезная работа
(III такт). Когда поршень приходит в крайнее положе*
ние, открывается выпускной клапан 2 и, вследствие
вытекания газов в атмосферу, давление в цилиндре резко
падает (IV такт). Четвертый такт происходит при открьь
Рис. 19. Схема двигателя
внутреннего сгорания с
подводом теплоты при
постоянном объеме.

Рис. 20. График идеального
цикла для двигателя внутрен-
внутреннего сгорания с подводом
теплоты при постоянном
объеме.
том выпускном клапане и представляет собой выталки*
вание, или выпуск, оставшихся в цилиндре газов, имею-
имеющих давление, лишь незначительно превышающее атмо*
сферное.
За процессом выпуска вновь начинается процесс вса-*
сывания, в результате чего и осуществляется непрерыв-
непрерывная работа двигателя.
Из сказанного видно, что этот цикл не является
замкнутым: продукты выбрасываются из цилиндра, и по-
последний заполняется новой смесью. Кроме того, этот цикл
не является обратимым (необратимое сжатие смеси, ко-
конечная скорость поршня, теплообмен при конечной раз-
разности температур и т. д.). Кривые расширения и сжатия
являются политропами.
Идеальный цикл такого двигателя, состоящий из двух
изохор и двух адиабат, представлен на рис. 20. Цикл
замкнут. Предполагается, что цилиндр заполнен посто-
постоянной порцией рабочего тела. Все процессы рассматри-
рассматриваются как обратимые. Сгорание топлива здесь происхо-
происходит мгновенно, поэтому принимается, что подвод всего
количества теплоты осуществляется при неподвижном
поршне, а следовательно, при постоянном объеме. Отсю-
Отсюда получил название и весь цикл.
Процесс падения давления в цилиндре вследствие
выпуска продуктов сгорания условно заменяется изохо-
рическим процессом. Рабочее тело практически можно
считать идеальным газом. На рис. 20 сортояние /—2—
адиабатное сжатие горючей смеси, 2—3 — изохорический
подвод теплоты (при горении топлива), 3—4 — адиабат-
адиабатное расширение продуктов горения, 4—/ — изохорический

процесс выхода теплоты, эквивалентный процессу выхло-
выхлопа отработанного газа.
Определяя к. п. д. этого цикла, найдем, что Qi =
= cv(Ts—Г2), так как теплота подводится в процессе при
постоянном объеме (участок 2—3). Далее: Qz—
~cv(Ti—Г1), так как теплота отводится в процессе
D—/) при V—const. Поэтому
f f
' 3 Л 2
Для упрощения этого выражения воспользуемся
уравнением адиабаты расширения C—4) и адиабаты
сжатия A—2). Находим, что
Но по условию цикла 1^4= У\ и l/3= V2.
Следовательно,
или
т4 — тх тх *
Зная последнее соотношение и произведя некоторые
преобразования, найдем:
т3~т2
Величина г = ~ степень сжатия; она показывает»
у 2
во сколько раз сжато рабочее тело перед подводом к
нему теплоты. Как видим, к. п. д. цикла с изохорным
подводом теплоты в основном зависит от степени сжатия
и отношения теплоемкостей.
Возможность повышения степени сжатия, однако,
ограничивается температурой самовоспламенения горю-
76

чей смеси. При высоких степенях сжатия возникает де*
тонация топлива. В связи с этим каждому виду топлива
должна соответствовать определенная степень сжатия.
В зависимости от вида топлива степень сжатия в рас-
рассматриваемых двигателях изменяется в пределах от 4
до 9. Таким образом, в двигателях с горением топлива
при V=const не могут применяться высокие степени
сжатия. Поэтому эти циклы имеют сравнительно низкие
к. п. д.
Цикл с подводом теплоты при постоянном
давлении. В двигателях, работающих по циклу с подводом
теплоты при постоянном давлении, сжатие воздуха и
топлива проводится раздельно: воздух сжимается в ци«
линдре двигателя, а жидкое топливо — в насосе. Такое
проведение процесса позволяет получить высокие степени
сжатия и исключает преждевременные вспышки смеси.
Создание двигателя со сгоранием топлива при /? = const
относится к 1897 г. и не вполне обоснованно связано
с именем немецкого ученого Дизеля, который предлагал
вести сгорание топлива по изотерме. Реальный двигатель
значительно отличался от предложенного Дизелем.
Схематически работа двигателя происходит так: в
цилиндр забирается воздух при первом ходе поршня.
При втором ходе поршня производится сжатие воздуха
до высоких степеней сжатия (порядка 12—20). Давление
воздуха в этом случае достигает 34—36 атму а темпера-
температура поднимается до 600—800° С.
При достижении максимального сжатия через фор*
сунку в цилиндр подается мелкораспыленное топливо.
Так как температура воздуха в цилиндре выше темпера*
туры самовоспламенения топлива, то оно воспламеняется
и горит при /? = const в период работы форсунки. Далее
происходит расширение продуктов горения и выпуск.
Таким образом, весь цикл совершается в четыре так-
такта. Этот цикл можно заменить идеальным, состоящим из
адиабатического сжатия газа, изобарического подвода
к газу теплоты, адиабатического расширения газа и изо-»
хорического отвода теплоты от газа.
На рис. 21 участок /—2 отвечает адиабатическому
сжатию воздуха,, участок 2—3— подводу теплоты при
/?=const, участок 3—4 — адиабатическому расширению
газа, участок 4—/ — отдаче теплоты при V=const
77

Рис. 21. График идеального
цикла для двигателя внутрен-
внутреннего сгорания с подводом
теплоты при постоянном да-
влении.
Для определения к. п. д. этого цикла подсчитаем теп-*
лотуг полученную при сгорании топлива на участке 2—3
и отданную на участке 4—/:
Найдем значения Ти Т2, Ts, Tk и основные параметры
цикла: степень сжатия е=-~- и степень предваритель*
ного расширения р=-тг-.
В точке 2 (рис. 21) 1/2=-^- и согласно уравнению
адиабаты имеют место равенства:
В точке 3 цикла:
Следовательно, температуры Г3 и Г2 связаны соотно-
соотношением:
В точке 4 цикла Vk~Vi и согласно уравнению адиа*
баты
Температуры Г4 и Tt связаны соотношением:
78

Выражения для Qt и Q2 можно преобразовать:
Qi = cp(T3- Т2) = срТ1гУ-Ц9~ 1);
Q2 = cv (ТА - Г,) = cvTt (Pv - 1).
К. п. д. цикла запишется:
или
1—¦
Pv-1
C,8)
К. п. д. цикла с подводом теплоты при р = const увели-
увеличивается с возрастанием степени сжатия г и уменьшает*
ся с возрастанием степени предварительного расшире-
расширения. Так как в этих двигателях е== 12—20, то к. п. д. цикла
с подводом теплоты при р = const значительно выше, чем
с подводом теплоты при V=const.
Цикл со смешанным подводом теплоты (цикл
Тринклера). Двигатель с изобарическим подводом теплоты
имеет ряд недостатков: наличие компрессора, сложное
устройство форсунок и т. п. Стремление упростить
устройство этого двигателя привело к созданию двига-
двигателей, цикл которых является смешанным.
Такой двигатель был построен в 1904 г. русским ин-
инженером Г. В. Тринклером. В смешанном цикле подвод
теплоты производится частично при V—const, а частич-
частично при р =*const.
Распыление топлива происходит в так называемой
предкамере (рис. 22), которая соединена с основным ци-
цилиндром узкими каналами. Сжатие воздуха осуществ-
осуществляется так же, как и в двигателях с подводом- теплоты
при р=const. Высокие степени сжатия обеспечивают
Рис. 22. Схема двигателя вну-
внутреннего сгорания со смешан-
смешанным подводом теплоты: рх —
давление в цилиндре; р2 —
давление в предкамере.
79

Рис. 23. График идеального
цикла для двигателя внутрен-
внутреннего сгорания со смешанным
подводом теплоты.
самовоспламенение. Во время сжатия, вследствие нали-»
чия сопротивления в соединительных каналах, давление
Рх в цилиндре возрастает быстрее, чем давление р2 в
предкамере. В результате разности давлений происходит
интенсивное истечение воздуха из цилиндра в камеру.
Кинетическая энергия воздуха расходуется на распыле-
распыление жидкого топлива, впрыскиваемого в предкамеру.
С момента вспышки в камере устанавливается давление
большее, чем в цилиндре. Процесс горения части топлива
в предкамере можно практически считать изохориче-
ским. Под влиянием быстрого возрастания давления в
предкамере направление потока газов меняется. Из пред-
предкамеры происходит истечение продуктов сгорания, воз-
воздуха и несгоревшего в предкамере топлива, имеющего
температуру 1500—1800° С. Большие скорости истечения
и наличие вихрей обеспечивают хорошее перемешивание
топлива и воздуха. Однородная смесь сгорает в цилиндре
при р = const. Затем происходит адиабатическое расши-
расширение продуктов сгорания и их выпуск. Идеальный цикл
такого двигателя представлен на рис. 23.
Весь цикл состоит из ряда процессов: адиабатическое
сжатие A—2), изохорический подвод теплоты B—3),
изобарический подвод теплоты C—4), адиабатическое
расширение продуктов сгорания D—5), изохорический
отвод теплоты E—/).
Для определения к. п. д. цикла Тринклера подсчитаем
полученную при сгорании топлива на участках 2—3 и
3—4 теплоту Q\ и отданную на участке 5—/ теплоту Q2:
80

Найдем значения температур Гь Г2, Г3, Г4, Т5 и основ-
основные параметры цикла, используя уравнение адиабаты.
Обозначив степень сжатия е = -~, степень повыше-
Р
ния давления Я = -^ и степень предварительного рас-
ширения p = -j~, можно записать:
V2 = ~> P2
5р P5 PiP 5l
С учетом последних соотношений выражения для ко-
количеств теплоты Qi и Q2 примут вид:
1)];
Следовательно, можно определить:
Л=1--тп ^^ • C,9)
Теория смешанного цикла содержит в себе, как част-
частные случаи, результаты, относящиеся к ранее рассмот-
рассмотренным циклам. Если допустить, что Л=1, получим цикл
с подводом теплоты при р = const. Если положить р=1,
получится цикл с подводом теплоты при 1/=const.
К. п. д. смешанного цикла возрастает с увеличением
степени сжатия е и зависит от X и р. Благодаря сравни-
сравнительной простоте устройства и надежности в работе дви-
двигатели, использующие цикл со смешанным подводом
теплоты, нашли широкое применение в промышленности
и на транспорте.
Идеальные циклы воздушно-реактивных
двигателей
Увеличение скорости и высоты полета
самолетов привело к необходимости замены поршневых
авиационных двигателей значительно более мощными
реактивными двигателями.
6 В. Ф. Ноздрев 81

Реактивным двигателем называется такой тепловой
двигатель, в котором химическая энергия топлива пре-
преобразуется в кинетическую энергию газовой струи, а
получающаяся при этом сила реакции непосредственно
используется как сила тяги.
Существует несколько типов реактивных двигателей
в зависимости от вида применяемого топлива и окисли-
окислителя. Мы остановимся на изучении воздушно-реактивных
двигателей (в.р.д.). В этом случае в качестве окисли-
окислителя при сжигании топлива используется кислород из
окружающей атмосферы.
Современные воздушно-реактивные двигатели могут
быть подразделены на бескомпрессорные (прямоточные
и пульсирующие) и турбокомпрессорные.
С термодинамической точки зрения в зависимости от
характера процесса горения топлива они делятся на дви-
двигатели с горением топлива при постоянном давлений
(р = const) и на двигатели с горением топлива при по-
постоянном объеме (К=const).
Воздушно-реактивные двигатели, использую-
использующие цикл с подводом теплоты при р = const Цикл с подво-
подводом теплоты при р=const использован в прямоточном
в. р. д., принцип работы которого весьма прост. При полете
с большой скоростью встречный поток воздуха, набегаю-
набегающий на двигатель, тормозится, в результате чего умень-
уменьшается скорость воздуха и повышается его давление. Это
торможение начинается до входа в двигатель и продол-
продолжается во входном устройстве — диффузоре. При дозву-
дозвуковых скоростях полета торможение воздушной струи
сопровождается увеличением ее площади сечения. В этом
случае входное устройство выполняется в виде расши-
расширяющегося канала. Сжатый во входном диффузоре воз-
воздух поступает в камеру сгорания, в которую через ряд
форсунок впрыскивают топливо (рис.24). Воспламенение
горючей смеси осуществляется электрической искрой.
Температура на выходе из камеры сгорания может
Рис! 24. Схема прямоточного
воздушно-реактивного двига-
двигателя*
82

Рис. 25. График идеального
цикла для прямоточного воз-
воздушно-реактивного двигателя
с подводом теплоты при по-
постоянном давлении.
достигать 2000° С и более. У прямоточных в. р. д. давле-
давление в процессе сгорания меняется незначительно, поэтому
их принято относить к типу двигателей, использующих
цикл с подводом теплоты при р=const. На рис. 25 пред-
представлен график цикла для такого двигателя.
Участок 1—2 соответствует процессу адиабатического
сжатия набегающего потока воздуха в диффузоре, уча-
участок 2—3—процессу подвода теплоты при сгорании
топлива, участок 3—4— процессу адиабатного расшире-
расширения продуктов сгорания в сопле, участок 4—/ — изоба-
изобарическому охлаждению удаленных в атмосферу продук*
тов сгорания до температуры окружающей среды.
К. п. д. такого цикла
4=1 ^г = 1-~г> (ЗЛО)
Р v
где р —-у—степень увеличения давления воздуха в
диффузоре.
При полетах со скоростями 900—1000 км/ч степень
сжатия воздуха в диффузоре очень низкая и tj=3—4%.
Заметим, что цикл турбо-реактивных двигателей ана-
аналогичен циклу прямоточного в. р. д. Разница лишь в том,
что в турбо-реактивном в. р. д. необходимое сжатие, воз-
воздуха обеспечивается компрессором. Поэтому к. п. д. та-
такого двигателя значительно выше.
Воздушно-реактивные двигатели, использую-
использующие цикл с подводом теплоты при V = const. К таким дви-
двигателям относятся пульсирующие в. р. д. Пульсирующий
в. р. д. конструктивно отличается от прямоточного наличием
6* S3

клапанов на входе в камеру сгорания и на выходе из нее.
Предварительное сжатие воздуха в пульсирующем- в. р. д.
также осуществляется только за счет использования
скоростного напора. Заполнение камеры сгорания про-
происходит при открытых клапанах на входе в камеру и
закрытых выходных клапанах, а сгорание — при закры-
закрытых клапанах на входе ъ камеру и на выходе из нее. При
достижении в камере сгорания максимального давления
выходные клапаны открываются и горячие газы с боль-
большой скоростью вытекают через сопло в атмосферу. За-
Затем открываются клапаны на входе, и происходит про-
продувка камеры. Далее выходные камеры закрываются, и
цикл повторяется.
Идеальный цикл такого двигателя приведен на
рис. 26. Здесь /—2 — адиабатное сжатие воздуха в диф*
фузоре, 2—3— подвод к газу теплоты при V=const,
3—4 — адиабатическое расширение газа в сопле, 4—/ —
отдача газом теплоты в атмосферу при р = const, равном
атмосферному.
К- п. д. такого цикла:
C,11)
-1)Р Y
где § = ——степень увеличения давления,
степень добавочного увеличения давления.
Р
О
Рис. 26. График идеального цикла для пульсирующего воздушно-
реактивного двигателя с подводом теплоты при постоянном объеме»
84

Заметим, что не рассмотренные здесь циклы газотур«
бинных установок аналогичны приведенным выше цик-
циклам в. р. д. при F=const и pt
г Задачи и упражнения
1. Рассматривая цикл, состоящий из изо-
хоры, изобары и изотермы, установить связь между теп-
лоемкостями
L p Ly
Решение. Рассмотрим элементарный
цикл, состоящий из изохоры, изобары и изотермы
(рис. 27). По первому началу термодинамики работа W
такого цикла равна:
где
. t dU\ .
Iw) • P—скрытая теплота изотермического рас-
расширения.
Из чертежа видно, что
следовательно,
откуда
дУ
или

Рис, 27. График элементарного
цикла, состоящего из изохори-
ческого, изотермического и
изобарического процессов.
2. Рассчитать цикл Карно (рис. 17), со-
совершаемый при работе 1 кг воздуха, если параметры
точки A: Pi = 20 атм, ^=327° С, а точки С: р3=1,2 атм,
Решение. Для точки А имеем: pi~20 атм>
Ti=27.3°+327°=600° К. Объем газа определится из урав-
уравнения Клапейрона:
Для точек Б и С имеем:
Г2=600°К, рз=1,2 атм, Гз=27°-ь273о=300°К;
R*$ 29,27 • оОО л 7O1
По уравнению адиабаты ВС:
Получаем:
Уравнением изотермы АВ:
_ p{vx _ 20.0,088 _ -о ,
Найдем параметры состояния для точки D. По урав-
уравнению адиабаты DA:

Получаем:
г»4 = 0,088№r = 0,497 м?'кг.
Из уравнения Клапейрона находим /?4:
Р*~ ~— 0,497 — i»" a/lwc-
Определим к. п. д. цикла:
ч =2^=*^» =0,5; л =
Или иначе т] найдем так:
Вычислим количество теплоты, полученное от нагре-
нагревателя:
Тогда количество теплоты, отданное холодильнику:
П ЛОТ in ^ -29,27.300-2,303 ,„ 0,497
Q2 = -^Г81п —= 557 ^0J32- =
= 8 кк,ал\к1.
3. 2 #г воздуха совершают цикл Карно
в следующих пределах:
/>, = 40 атму Тх = 700° К,
Рассчитать цикл.
Замечание. При решении задач мы
пользуемся единицами, которые применяются в техниче-
технической термодинамике. 3(а единицу массы принимаем 1 кг,
за единицу объема 1 ж3. Удельный объем (объем едини-
единицы массы) равен объему одного килограмма в кубиче-
кубических метрах (и=мв/кг). Давление р (кГ/м2, кГ/см2 =
= 10000 кГ/м2 = 1 атм).
4. В идеальном цикле Отто (рис. 20)
определить параметры всех точек, количество теплоты,
переданное рабочему телу, к. п. д., количество теплоты,
затраченное на полезную работу, если дано:
С, А = 1 атм, е==6, Я = 1,6.
87

Теплоемкость принять постоянной. Рабочее тело —¦
воздух.
Расчет ведем для 1 кг рабочего тела.
Решение, В точке /: ^«1 атм, Тх = 100°+^
+273° = 373°К. Начальный удельный объем определится
из выражения:
— RTX;
/гг|_29Д7-а7з_1(Ю ч/
В точке 2: из выражения —i- = c = 6 определяем
1 ПО
v2=~ = 0,182 ^3/кгг.
Конечная температура сжатия определятся из урав-
уравнения:
Т2 = Г, f-^-f"Х = 373 • 6м == 765 °К.
\ V 2 /
Конечное давление сжатия:
г> - RT> - 29'27'765 -12
В точке 3 для изохорического процесса имеем:
^L==Ii- = A,= l,6; Г3=Г2. 1,6 = 765- 1,6 = 1225° К.
Конечный удельный объем:
«03 = *;2 = 0,182 ^3//сг.
Конечное давление:
/>з=12,3. 1,6 = 19,7 aw^c.
В точке 4: удельный объем
^5=^ = 1,09 м2[кг.
Конечная температура расширения находится из
уравнения:

конечное давле«ие:
Т4 1 600 1 ~
А —Ау^ — 1 ' ЗТЗ*^1'6 атя>
к. п. д. цикла:
Подведенное количество теплоты определяем из уравне-
уравнения:
Q{ = cv (Г3 — Т2) = -glgg- A225 — 765) = 79,8 ккал\кг,
а отведенное количество теплоты — из уравнения:
Q2 = cv(TA— Т{) = -^F00 — 373) — 39,4 ккал!кг.
Отсюда полезная теплота:
Qz^Qj —Q2== 79,8—39,4 = 40,4 ккал[кг.
5. В идеальном цикле Дизеля определить
параметры всех точек и к. п. д., если дано: ^i = 47° С,
р!=*0,9 атм, е== 12, р —2. Теплоемкость постоянная. Рабо-
Рабочее тело — воздух.
Решение. В точке / примем Vi=l м3,
^=0,9 атм, rt = 47+ 273 = 320° К.
В точке 2 из отношения
определяем:
К2 = -^ = -1=0,0832
Конечная температура адиабатического сжатия опре-
определяется из уравнения:
ТУГ1 = T2VV\ Т2 = Тх (-p-f = 320 . 12м == 865° К.
Конечное давление адиабатического сжатия опреде-
определится нз уравнения:
/I -—. п I L I -——- О Q • 19 -— OQ О п tti ы
89

Для точки- 3 из отношения
Определяется температура Г3*
Г3 = 865- 2 =1730° К.
Найдем объем из соотношения:
l/3==2V2 = 0,0832- 2 = 0,166 м\
/?з = р2 = 29,2 атм.
В точке 4 V'4=Vi=sl м3. Конечная температура адиа*
батического расширения определится из уравнения:
Г4= Гз^У = 1730 - 0,166м = 845 °К.
Конечное давление расширения можно определить
из уравнения:
А = А ^jV = 29,2 . 0f 166м = 2,38 атм.
К. п. д. идеального двигателя:
"-' - Y(p-7,',v- -'- Mgtlo.'ttH -о-565-
6. Для цикла поршневого двигателя вну«
треннего сгорания при 1/=const (цикл Отто) известны
* 77°C 250°С
Известна также степень сжатия г = _!- — з,5.
' 2
Определить к. п. д. этого цикла и цикла Карно, совер-
совершающегося в том же интервале температур. Рабочее
тело обладает свойствами воздуха.
Отв. т|о=0,394; %=0,595.
7. Рассчитать цивд Тринклера (график
изображен на рис. 23), в котором:
рх — \ атм, ^ = 50° С, е = 10, А, = 1,4; р= 1,7, y = 1,4-
Отв. ч = 0,27.
90

8. Рассчитать цикл пульсирующего реак*
тивного двигателя (рис. 26), если дано: ^ = 17° С,
pt=l атм% 8=4, Qi= 100 ккал/кг, рабочее тело имеет
массу 1 кг.
Отв. rj = 0,493.
9. Показать, что к. п. д. воздушно-реак-
воздушно-реактивных двигателей с подводом теплоты при V=const и
подводом теплоты при /?=const определяются соответ-
соответственно выражениями C,10) и C,11).
ЛИТЕРАТУРА
1. М. П. ВУКАЛОВИЧ и И. И. НОВИКОВ,
Техническая термодинамика, Госэнергоиздат, 1952.
2. А. С. ЯСТРЖЕМБСКИЙ,
Техническая термодинамика, Госэнергоиздат, 1953.
3. а. м. литвин,
Техническая термодинамика, Госэнергоиздат, 1956.
4. И. И. КУЛАГИН,
Тепловые процессы в реактивных двигателях, Оборонгиз, 1949.
б. г. с. жирицкий,
Газовые турбины, Госэнергоиздат, 1948.
6. Е. Ф. БАЛАХОНЦЕВ,
Основы технической термодинамики, М., 1956, гл. VII, стр. 177—213,
7. А. И. ВЕЙНИК,
Техническая термодинамика и основы теплопередачи. Мч 1956,
гл. VI, стр. 201—211.
91

глава четвертая Второе НЗЧаЛО
термодинамики
Пользуясь первым законом термодина*
мики и привлекая уравнение состояния, можно решить
многие термодинамические задачи. Однако первое на-
начало термодинамики совершенно не рассматривает во-
вопроса о направлении происходящих процессов. С точки
зрения первого начала термодинамики любой мыслимый
процесс, который не противоречит закону сохранения
энергии, принципиально возможен в природе.
Например, если имеются два тела, температуры кото-
которых различны, то первому началу термодинамики не
противоречил бы переход теплоты от тела с более низ-
низкой температурой к телу с температурой более высокой.
Единственное ограничение, налагаемое первым началом
термодинамики на этот процесс, заключается в требова-
требовании, чтобы количество теплоты, отданной первым телом,
было равно количеству теплоты, полученной вторым те-
телом (при условии отсутствия работы). В действительно-
действительности, как показывает огромный опытный материал, тепло-
теплота сама собой переходит только от тела, имеющего более
высокую температуру, к телу, имеющему более низкую
температуру. Ответ на вопрос о направлении перехода
теплоты при теплообмене между двумя телами дает вто-
второе начало термодинамики.
Второе начало термодинамики приложимо не только
к явлению теплопередачи, но и ко многим другим явле-
явлениям в природе, связанным с обменом, энергиями. На-
Например, при падении камня на землю потенциальная
энергия переходит, в кинетическую, а в момент удара
о землю механическая энергия переходит во внутреннюю.
С точки зрения первого начала термодинамики ка-
камень за счет энергии может сам подняться на ту же
высоту, если только эта часть внутренней энергии об-
обратно перейдет в механическую энергию. Второе начало
термодинамики утверждает, что такого явления не может
быть, что и подтверждается повседневными наблюде-
наблюдениями.
92

Такцм образом, открытие второго начала термодина-
термодинамики обусловлено исторической необходимостью дать
ответ на вопрос о направлении процессов, происходящих
в природе.
§ Некоторые эквивалентные формулировки
второго начала термодинамики
Содержание второго начала термодина-
термодинамики может быть выражено в нескольких одинаковых по
смыслу формулировках.
Теплота сама собой не может переходить от тела ме-
менее нагретого к телу более нагретому без одновременных
изменений в этих телах или в окружающей среде.
Или: невозможно построить такую периодически дей-
действующую машину, которая бы непрерывно совершала
работу за счет теплоты, выделяемой системой при охла-
охлаждении, причем других изменений в этой системе или в
окружающей ее среде не происходило бы. Другими сло-
словами, невозможно построить вечный двигатель второго
рода.
Остановимся подробнее на второй формулировке.
Согласно первому началу термодинамики всякая ра-
работа производится за счет некоторой затраты энергии,
это значит, что построить такую машину, которая про-
производила бы работу без затраты энергии, т. е. вечный
двигатель первого рода, нельзя. Однако, учитывая, что
при охлаждении всех тел природы выделяется огромное
количество теплоты, можно, казалось бы, построить ма-
машину, работающую за счет этой теплоты. Во всяком
случае первому началу термодинамики построение такой
машины не противоречило бы.
Например, если бы удалось построить двигатель, ра-
работающий за счет выделяющейся при остывании океанов
и морей теплоты, то весь земной шар был бы полностью
обеспечен энергией около 1700 лет, а температура воды
океанов понизилась бы при этом только на 0,01° С. Мы
имели бы, таким образом, вечный двигатель второго
рода.
Однако опыт показывает, что такая машина тоже не
осуществима, построение ее противоречит второму нача*
лу термодинамики. Действительно, пусть нагревателем
машины, работающей по циклу Карно, является океан.
93

Если Qi — количество теплоты, которое машина <берет от
нагревателя, а С?2 — количество теплоты, которое она
отдает холодильнику, то полезная работа; совершаемая
за счет разности этих количеств, равна Qt—Q2. При
этом, так как теплоемкость нагревателя (океана) беско-
бесконечно велика, то температура его практически остается
постоянной, температура же холодильника, имеющего
конечную теплоемкость, будет непрерывно повышаться.
Поэтому рано или поздно должен будет наступить такой
момент, когда температуры нагревателя и холодильника
станут равными и теплообмен прекратится и, следова-
следовательно, машина перестанет работать.
Построение вечного двитателя второго рода было
бы возможно при отсутствии холодильника, когда вся
теплота, полученная от нагревателя, расходовалась бы
на совершение работы. Но, поскольку наличие холодиль-
холодильника в любой периодически действующей машине совер-
совершенно обязательно, это значит, что осуществить вечный
двигатель второго рода нельзя никакими путями.
Прежде чем перейти к формулировке второго начала
термодинамики в аналитической форме, докажем сле-
следующую весьма важную теорему.
Теорема Карно
Из всех периодически действующих теп-
тепловых машин, имеющих одинаковые температуры нагре-
нагревателей^ и холодильников, наибольшим коэффициентом
полезного действия обладают обратимые машины. При
этом к. п. д. обратимых машин, работающих при одина-
одинаковых температурах нагревателей и холодильников, рав-
равны друг другу и не зависят от конструкции машины.
Пусть обе машины, обратимая и необратимая, рабо*
тающие по циклу Карно, берут от нагревателя одинако-
одинаковое количество теплоты, равное Qi. Количество же тепло-
теплоты, отдаваемое холодильнику обратимой и необратимой
машинами, пусть будет различным, равным соответствен-
соответственно Q2 и Q'r Обозначим к. п. д. обратимой машины ц и
необратимой машины х\'.
Тогда
S4

Докажем первую часть теоремы Карно: наибольшим
к. п. д. обладает обратимая машина. Доказательство по-
поведем методом от противного, т. е. предположим, что
т)'>т). Согласно равенствам D,1) это предположение
означает* что Q? < Q2> т. е. количество теплоты, пере-
переданное холодильнику необратимой машиной, меньше
количества теплоты, отданное холодильнику обратимой
машиной. Другими словами, необратимая машина совер-
совершает большую работу за счет того же количества
теплоты.
Для доказательства неверности" последнего утвер-
утверждения цредположим, что необратимая машина совер-
совершает цикл Карно ABCD в прямом направлении (рис. 17),
а обратимая — в обратном.
Согласно принятым обозначениям необратимая ма«
шина должна затратить на совершение полезной работы
количество теплоты W—Qx— Ql2 и обратимая W=
«Qi—Q2. Так как Qx — Q2<QX — Q^ то для передачи
тепла от холодильника нагревателю будет использована
часть полезной работы необратимой машины, превра-
превращаемая в теплоту так, чтобы нагревателю снова возвра-
возвратить количество теплоты Q\. В результате этого процесса
получится работа, эквивалентная количеству теплоты:
Посмотрим теперь, какие изменения произошли в ма-
машине после совершения цикла Карно? Необратимой ма-
машиной было взято от нагревателя количество тепла Q\
н такое же количество теплоты Qi было ему отдано обра-
обратимой машиной; следовательно, в состоянии нагревателя
не произошло никаких изменений.
Холодильнику необратимая машина отдала количе-
количество теплоты* равное Qf2, а обратимая машина взяла от
него количество теплоты, равное Q2. Следовательно, в
холодильнике произошло изменение энергии, равное
Q2-Q2. D,3)
Выражения D,3) и D,2) показывают, что по оконча-
окончании цикла холодильником было потеряно количество
теплоты Qzr-Qi и совершено эквивалентное количество
работы. При этом никаких других изменений в системе
95

и окружающей ее среде не произошло. Таким образом,
мы получили вечный двигатель II рода, что противоре-
противоречит второму началу термодинамики. Следовательно, на-
наше предположение о том, что т]/>г], неверно, т. е.
к. п. д. необратимой машины не может быть боль-
больше к» п. д. обратимой машины, работающей с тем
же нагревателем и тем же холодильником.
Аналогично можно доказать и вторую часть теоремы
Карно.
Принимая к. п. д. двух обратимых машин равными
тO и г) и предполагая, что первая машина работает в
прямом направлении, а вторая — в обратном, докажем
неверность предположения ц'>ц. Затем, пользуясь тем,
что обе машины обратимы, поменяем их местами так,
чтобы вторая машина совершила цикл в прямом направ-
направлении, а первая — в обратном. Тем же методом от про-
противного докажем, что т] не может быть больше ц\
Остается только заключить, что ц—ц'.
На основании теоремы Карно можно получить ана-
аналитическое выражение второго начала термодинамики.
Согласно формулировке этой теоремы к. п. д. всех
обратимых машин, у которых холодильники и нагрева*
тели имеют одинаковые температуры, равны и не зави-
зависят ни от природы рабочих тел, ни от конструкции ма*
шин, т. е.
Л1==Л2 = Пз== ••• D>4)
Последнее соотношение означает, что если известен
к. п. д. хотя бы одной обратимой машины, то тем самым
известен к. п. д. всех обратимых машин, у которых нагре-
нагреватели и холодильники имеют такие же температуры.
Как уже известно, к. п. д. цикла Карно для идеально-,
го газа выражается формулой
где Т\ и Т2 — абсолютные температуры нагревателя п
холодильника.
Так как цикл Карно для идеального газа является
примером обратимой машины, то на основании теоремы
Карно можно записать значение к. п. д. для всех обрати-
96

мых машин, у которых нагреватель имеет температуру
Tiy а холодильник — Т2.
. D,5)
т
Обобщая это выражение для всех обратимых и необ-
необратимых машин, получим:
I D)б)
Это соотношение дает количественную формулировку
второго закона термодинамики для простейшего слу-
случая— машины с нагревателем и одним холодильником.
Покажем, что выражение D,6) является наиболее об-
общим и содержит в себе обе ранее данные формулировки
второго начала термодинамики.
Действительно, пусть теплота переходит от одного
тела к другому без совершения работы. Если Qi — коли-
количество теплоты, отданное одним, и Q2 — количество теп-
теплоты, полученное другим телом, то Qi = Q2 и выражение,
характеризующее второе начало термодинамики для
этого случая, примет вид:
Поскольку, однако, передача тепла есть процесс необра-
необратимый, знак равенства в формуле D,7) следует исклю-
исключить, т. е.
7\ т
0< \х2 . D,8)
Но 7\>0, так как абсолютная температура не может
быть отрицательной.
Поэтому запись второго начала термодинамики в
виде D,8) справедлива только в том случае, если
Тх — Т2 > 0, или Тх > Г2.
Полученное неравенство говорит о том, что темпера-
температура тела, отдающего количество теплоты Q\, должна
быть выше температуры тела, получающего количество
теплоты Q2, т. е. теплота переходит от тела более нагре-
нагретого к телу менее нагретому, но не наоборот.
Одна из формулировок второго начала термодинами-
термодинамики утверждает невозможность построения вечного
7 В. Ф. Ноздрев 97

двигателя II рода. Действительно, построение такого двиг»
гателя означало бы превращение всей теплоты, взятой от
нагревателя, в полезную работу, т. е. имели бы место
равенства W=Q\ и Q2=0.
Для этого случая выражение, характеризующее "вто-
"второе начало термодинамики, можно переписать в виде:
но 7\ и Г2 всегда больше 0. Следовательно —^—— не
может быть больше единицы. Остается единственно воз-
возможный случай:
Il=lLl = i, D,10)
или
7-2 = 0. D,11)
Подытоживая проведенные рассуждения, замечаем,
что вечный двигатель II рода можно было бы построить
при обязательном соблюдении двух условий. Первое —
процесс работы этого двигатеЛя должен быть строго об-
обратимым согласно равенству D,10). Второе — темпера-
температура холодильника такого двигателя должна быть равна
абсолютному нулю. Но так как ни первое, ни второе
условия в природе неосуществимы, то, следовательно,
вечный двигатель II роДа построить невозможно.
§ Абсолютная термодинамическая шкада
температур
Как уже было сказано выше, только на
основании второго начала термодинамики можно опреде-
определить температуру как величину, не зависящую от свойств
того или иного вещества.
Для доказательства этого положения воспользуемся
количественной формулировкой второго начала термо*
динамики:
Qi ~~Фг ^ Т\ — ^2 (л *г>\
Qx ^ 71! V*'1*)
Представим соотношение D,12) в следующем виде:
98

Рис. 28. Представление
произвольного цикла через
элехчентарные циклы Карно
123
В частном случае для обратимого процесса будем
иметь:
Q*-=?. Dt13)
Предположим, что осуществляются циклы Карно в раз-
различных температурных интервалах посредством какого-,
либо рабочего тела.
Графически эти циклы можно получить путем раз-
разбивки сеткой изотерм некоторого большого цикла на
меньшие (рис. 28). Температуры изотерм, входящих в
отдельные циклы Карно, обозначим через Гь Г2, Г3 ...,
Тп, а соответственные им количества теплоты, получае-
получаемой или отдаваемой рабочим телом на этих изотермах,
через Qi, Q2, <2з, . . . , Qn-
Запишем второе начало термодинамики для каждого
цикла. Для первого цикла Qi и Т\ — теплота и темпера-
температура нагревателя, Q2 и Т2 — теплота и температура хо-
холодильника. Тогда второе начало термодинамики для
первого цикла будет иметь вид:
Ql = 1± DU)
V2 * 2
Для второго цикла, согласно его построению, Qz и
Тг — количество отдаваемой теплоты и температура на-
нагревателя, Qz и Г3—количество получаемой теплоты и
температура холодильника. Отсюда
¦§Г = Т7- D.15)
7*

Аналогично для третьего цикла:
ж-к- DЛ6)
Объединяя соотношения D,14), D,15) и D,16) ...,
приходим к равенству:
Q,:Q2:Q3:,..., : Qn = Tr. Т2: Т3:, ..., :Тп, D,17)
которое позволяет сделать следующий важный вывод:
температуры тел можно измерять через соответствую-
соответствующие количества теплоты. А так как последние явно не
зависят от природы рабочего тела, то и измеренные та-
таким способом температуры также не зависят от природы
рабочего вещества. На этом основании температура Г,
входящая в соотношение D,17), была названа термо-
термодинамической температурой.
Отметим, что практически измерять таким образом
температуру трудно, но в отдельных случаях сделать
это можно, например, наблюдая за плавлением какого-
либо вещества. В этом случае, как известно* затрачен-
затраченное количество теплоты Q зависит от удельной теплоты
плавления ЯПл и массы пг плавящегося вещества: Q =
=Япл^ Величина Q в этом случае определяется через
легко измеряемые величины кПл и т.
Второе начало термодинамики не только дает воз-
возможность определить температуру как величину, не за-
зависящую от природы рабочего тела, но и указыва-
указывает принцип построения абсолютной термодинамической
шкалы температуры. Для доказательства последнего
утверждения запишем выражение второго начала термо-
термодинамики для каждого цикла, изображенного на рис, 28,
в виде:
Т\ Qi . 2!l Q2 ¦ ^з (?з /д 1 о\
т2 ~ Q2 ' ть — Q3 f г4 — Q4 • У*>1*>
Применяя правила сложной пропорции к равенствам
D,18), перепишем их в виде:
D.19)
100

После почленного деления последних равенств, при-
принимая во внимание равенства D,18), получим:
Q2-Qs um
2-Qs Т3~Т4 Q8-Q4 А* V ' '
Допустим, что
Tl-T2=T2-T3^T3-Tt=..., D,21)
тогда
Qi_Q2==Q2_Q3=Q3_Q4===... D,22)
Учитывая, что Qi—Q2» Q2—Фз> Q3— Qa и т. д. есть ко-
количества теплот, превращенные в работу, соответственно
в первом, во втором, в третьем и т. д. циклах Карно, из
равенств D,12) и D.22) можно сделать следующий вы-
вывод:
Если циклы Карно будут образованы посредством
равноотстоящих изотерм согласно соотношениям D,21),
то в этих циклах в работу превращается одинаковое ко-
количество теплоты [см. равенства D,22)].
Это свойство цикла Карно и положено в основу по-
построения абсолютной термодинамической шкалы темпе-
температуры. Выделим из всех циклов Карно цикл ABCD
(рис. 17), образованный изотермами То и Гкиш и допу-
допустим, что изотерма Го соответствует температуре таяния
льда, а изотерма Ткш — температуре кипения воды.
Предположим, что в цикле Карно ABCD на работу было
затрачено количество теплоты Q. Тогда, если разбить
площадь ABCD сеткой равноотстоящих изотерм из 100
равных частей, то в каждом из полученных циклов Карно
на работу будет затрачиваться количество теплоты, рав-
равное 0,01 Q. Температурный интервал между изотермами
составит 1° (если Г0 = 0°С и Гкип=100°С).
Этим же методом можно построить изотермы, лежа-
лежащие ниже изотермы То. Естественно возникает вопрос:
как найти предельную изотерму, соответствующую наи-
наименьшей возможной температуре? Используем для этой
цели общее выражение к. п. д. цикла Карно, не завися-
зависящее по теореме Карно от рода вещества:
Из формулы видно, что г| = 1 при Г2=273,
Ш

Допустим, что существует температура Тг2 более низ-
низкая, чем Г2=0^=—273,16°С),
тогдя
^^ yi-^y-^y2j_ 1\ + Г2 ^ j
что противоречит второму началу термодинамики.
Следоватедьно, температура Г=0 (/= —273,16° С)
является наименьшей возможной температурой и может
быть принята за начальную постоянную естественную
точку термодинамической температурной шкалы. Иными
словами, абсолютная температура не может иметь отри-
отрицательных значений.
Второе начало термодинамики раскрывает и физи-
физический смысл абсолютного нуля температур.
Количественное выражение абсолютного нуля для
случая обратимого цикла ~ = ~- показывает, что
Т2=0, если Q2=0. Следовательно, абсолютный нуль тем-
температуры— это такая температура, при которой тепло-
теплота, сообщаемая холодильнику, равна нулю, т. е. вгя
теплота нагревателя переходите полезную работу. При
равенстве температуры холодильника абсолютному нулю
к. п. д. обратимой машины равен единице.
Таким образом, второе начало термодинамики позво-
позволяет определить температуру как величину, не завися-
зависящую от природы рабочего тела, и указывает на возмож-
возможность построения стандартной термодинамической шка-
шкалы температур.
Оказывается, что термодинамические температуры
равнозначны абсолютным температурам, измеряемым
термометром с идеальным газом. Действительно, все рас-
рассуждения мы вели, исходя из аналитического выра-
жения второго начала термодинамики —х Q <С —Чр—~ •
Однако для получения этого выражения мы использова-
ли значение к. п. д. rj = —Ц^—2-, полученное для случая,
1 2
когда рабочим веществом является идеальный газ, под-
подчиняющийся уравнению Клапейрона pV~RTy где Т — аб-
абсолютная температура. Следовательно, можно утвер-
утверждать, что термодинамическая температура равнозначна
абсолютной температуре, измеряемой термометром с
идеальным газом.
102

Таким образом, возможность создания стандартной
абсолютной шкалы температур была найдена еще до
формулирования второго начала* термодинамики благо-
благодаря использованию идеального газа в качестве термо-
термометрического вещества, но понятие температуры и тео-
теоретическое обоснование этой возможности было дано
только на основании второго начала термодинамики.
В настоящее время практически в качестве стандарт-
стандартной шкалы температур используют эмпирическую шкалу
водородного термометра, поскольку водород по своим
свойствам наиболее близок к идеальному газу. Термоди-
Термодинамическую же шкалу температур получают из эмпири-
эмпирической шкалы путем внесения соответствующих поправок.
Уравнение Клапейрона—Клаузиуса
Уравнение Клапейрона — Клаузиуса, ха-
характеризующее изменение давления насыщенного пара р
в зависимости от температуры, имеет вид:
Г^5- = —L—. D,23)
Это уравнение было получено экспериментальным путем.
Оно справедливо лиш*> для процессов, которые проте-
протекают в системе по линии насыщения, т. е. в условиях
равновесия жидкости со своим паром.
Как известно, для данного вещества эти процессы
можно изобразить на диаграмме рТ кривыми, имеющими
одну общую точку (см. рис. 29).
На этом рисунке СА — кривая парообразования, опи-
описывающая равновесие системы жидкость—пар, СВ —
кривая плавления, описывающая равновесие системы
твердое тело — жидкость, и CD — кривая сублимации,
описывающая равновесие системы твердое тело — пар.
Уравнение Клапейрона — Клаузиуса хорошо описы-
описывает все рассматриваемые системы. Однако физический
смысл величин, входящих в это уравнение, в каждом
конкретном случае различен.
В частности, для случая испарения жидкости (кривая
СА) К — удельная теплота парообразования, Vi — удель-
йый объем жидкости и v2 — удельный объем пара.
Для случая плавления твердого тела (кривая СВ)
X представляет собой удельную теплоту плавления,
103

vl — удельный объем твердого тела и v% — удельный
объем жидкости.
Наконец, для случая испарения твердого тела, воз-
возгонки (кривая CD)К — удельная теплота сублимации,
Vi — удельный объем твердого тела и v% — удельный
объем пара.
Уравнение Клапейрона — Клаузиуса можно получить
на основе второго начала термодинамики, пользуясь ме-
методом круговых процессов.
Представим себе цикл Карно, в котором рабочим те-
телом в цилиндре является единица массы вещества, со-
состоящая из жидкости и насыщенного пара. Пусть исход-
исходное состояние системы изображается на диаграмме
точкой А (рис. 30). Проведем изотермическое расшире-
расширение всей системы от состояния А на диаграмме до неко-
некоторого состояния В. При этом вся теплота Qu взятая от
нагревателя, будет затрачена на превращение единицы
массы жидкости в пар и равна удельной скрытой тепло-
теплоте испарения (Q{ = К),
Так как температура системы не изменяется, давле-
давление насыщенного пара тоже постоянно, то изотерма, опи-
описывающая данный процесс, вырождается в прямую, па-
параллельную оси объемов v. При этом единица массы
жидкости превращается в единицу массы пара, вслед-
вследствие чего происходит увеличение объема системы, изо-
изображаемое на рис. 30 отрезком АВ:
где V2 и V\ — удельные объемы пара и жидкости.
Допустим, что указанное расширение системы про-
происходит при температуре нагревателя Т. По окончании
этого расширения дадим возможность системе расши-
расшиРис. 29. Зависимость давле-
давления насыщенного пара р
от температуры 7\

Рис. 30. Цикл Карно для
случая, когда рабочим те-
телом является единица массы
жидкости и насыщенного
пара.
А
\
! о
i
i
в
\
1 С
1
1
1
1
1
ряться адиабатно из состояния, изображаемого точ*
кой В, до бесконечно близкого состояния, изображае-
изображаемого точкой С. При этом бесконечно малая часть жид-'
кости испаряется. Теплота, необходимая для этого
испарения, берется от работающей системы, вследствие
чего температура жидкости и пара понижается на dT^w
в точке С диаграммы становится равной Т — dT. По-
Последнее обстоятельство влечет за собой и понижение
давления пара на величину dp.
Далее, от состояния С совершим изотермическое
сжатие при температуре Т — dT до состояния D и ади-
адиабатное сжатие от состояния D до состояния А. После
этого цикл Карно оказывается законченным. Система
приходит в первоначальное состояние. Таким образом,
на участке ABC происходит переход жидкости в пар,
а на участке CDA — превращение пара в жидкость.
Запишем второе начало термодинамики для рассмот-
рассмотренного случая D,5):
В равенстве D,5) Qi—Q2 — количество теплоты, затра-
затраченное на работу, равное площади цикла ABCD, т. е.
Так как Q\ = Я, Т\ = Г, Т2 — Т—dT, то выражение D,5)
для рассматриваемого случая можно переписать в виде
D,23):
(v2 — vAdp dT
ИЛИ
dT
105

Итак, получено уравнение Клапейрона — Клаузиуса.
Оно дает возможность вычислить удельную теплоту па-
парообразования, если известна зависимость давления на-
dp
сыщенного пара от температуры, или вычислить -т?г»
если известны Г, A, v2 и vu Поскольку удельный объем
пара очень велик по сравнению с удельным объемом
жидкости, величиной v{ во многих случаях можно пре-
пренебречь. Тогда уравнение D, 23) примет вид;
rp dp X
где v — удельный объем пара.
Заметим, что в уравнении Клапейрона — Клаузиуса
во всех трех случаях фазовых равновесий, изображен-
изображенных на диаграмме, А>0, разность же удельных объемов
Vu—DX может быть и положительной, и отрицательной.
В первом случае -^- > 0, т. е. с повышением давле-
давления температура плавления (испарения, возгонки) воз^
растает.
Во втором случае -^?- < 0, т. е. с повышением дав-
давления температура плавления уменьшается. Последний
случай имеет место, например, для системы вода — лед.
§¦
Зависимость поверхностного натяжения
от температуры
Рассмотренный нами прием проведения
мысленных замкнутых процессов можно применить к
нахождению зависимости поверхностного натяжения от
температуры.
Пусть рабочим телом является пленка чистой жид-
жидкости, растягиваемая на проволочной рамке. Хотя прак-
практически такие пленки малоустойчивы, возможность этого
опыта в малом масштабе вполне допустима.
Обозначим поверхность пленки через Si и ее поверх-
поверхностное натяжение через а. На диаграмме oS (рис. 31)
исходное состояние пленки изобразится некоторой точ-
точкой А. Произведем изотермическое растяжение пленки
при температуре Г так, чтобы ее поверхность сделалась
равной S2-
Так как процесс проводится при Г=const, то поверх-
поверхностное натяжение о~о(Т) тоже постоянная величина,
106

Рис. 31. Мысленный цикл, 6
позволяющий установить
зависимость поверхностного
натяжения жидкости от
температуры.
и изотерма вырождается в прямую, параллельную оси 5.
Новое состояние системы будет изображаться на диа-
диаграмме точкой В. Однако, как показывает опыт, увели-
увеличение поверхности жидкой пленки сопровождается ее
охлаждением, поэтому во время процесса на участке АВ
для поддержания постоянной температуры к пленке не-
необходимо подвести от нагревателя количество теплоты,
равное Q\. Далее, от состояния, изображенного точ-
точкой В, будем адиабатно растягивать пленку.
Если ^рассматривать бесконечно близкие состояния,
температура пленки понизится при этом на величину dT,
что влечет за собой повышение поверхностного натяже-
натяжения на da. Новое состояние системы на диаграмме aS
изобразится точкой С. Далее дадим пленке возможность
изотермически сокращаться при температуре Т—dT до
состояния, изображаемого точкой D, причем выделГяю-
щаяся из жидкости теплота Q2 передается холодильни-
холодильнику. И наконец, пусть для завершения цикла на пути DА
пленка сокращается адиабатно до первоначального со-
состояния Л.
Для нахождения зависимости поверхностного натя-
натяжения от температуры воспользуемся количественным
выражением второго начала термодинамики для обрати-
обратимого цикла D, 6). В данном случае работа цикла вы-
выражается площадью ABCD, равной (S2—Si) da,, и выра-
выражение D, 6) можно переписать в виде:
do
dT
T S, —S,
D,24)
D,25)
107

Знак минус в полученной формуле указывает на то,
что положительная работа сокращения пленки сопрово-
сопровождается не поглощением, а выделением теплоты. На-
Наоборот, положительное количество теплоты, получаемое
от нагревателя, поглощается пленкой йри отрицатель*
ной работе растяжения ее внешними силами.
Отношение ~ _^ ¦ определяет количество теплоты,
потлощаемое пленкой при увеличении ее поверхности на
единицу площади, и называется скрытой теплотой
образования поверхности. Если обозначить
эту величину г, то выражение D, 25) примет вид:
Так как скрытая теплота образования поверхности
положительна (г>0), то согласно равенству D,26)
da . г,
< и, т. е. поверхностное натяжение с повышением
температуры уменьшается. Этот вывод хорошо согла-
согласуется с экспериментальными наблюдениями.
О4
Г Задачи и упражнения
1. Показать, что адиабата не может пе-
пересекаться с изотермой более чем в одной точке.
Решение. Предполагая, что адиабата и
изотерма пересекаются в двух точках, получим возмож-
возможность осуществить цикл, при котором теплота термоста-
термостата будет переходить в работу при отсутствии холодиль-
холодильника. Это противоречит второму началу термодинамики.
Следовательно, предположение наше неверно.
2. Показать, что температура вдоль ади-
адиабаты изменяется в одном и том же направлении.
Решение. Предположим, что температура
вдоль адиабаты изменяется не в одном направлении,
а, например, сначала "убывает, а затем начинает возра-
возрастать. Тогда в двух точках адиабаты будет иметь место
одинаковая температура. Но это значит, что в этих двух
точках адиабата пересекается с изотермой. Невозмож-
Невозможность последнего случая была доказана в предыдущем
108

Рис. 32. График цикла Карно
с газом, подчиняющимся урав-
уравнению Ван-дер-Ваальса.
0
упражнении. Следовательно, температура вдоль адиаба*
ты изменяется в одном направлении.
3. Показать, что абсолютная термодина-»
мическая шкала температур совпадает с температурной
шкалой газа, подчиняющегося уравнению Ван-дер-
Ваальса.
Указание. Для доказательства следует рассмотреть
обратимый цикл Карно для случая, когда рабочим телом
является газ, подчиняющийся уравнению Ван-дер-Ва-
Ван-дер-Ваальса.
Решение. Будем рассматривать обрати-
обратимый цикл Карно (рис. 32), в котором рабочим телом яв-
является газ, подчиняющийся уравнению Ван-дер-Ваальса
с постоянными a, b, cv. Воспользовавшись уравнением
и уравнением Ван-дер-Ваальса
_ RT* а_
Р— v — b V2 '
определим количество теплоты, полученной телом от на-
нагревателя на изотерме АВ\ где df*=0:
Количество теплоты, отданное телом холодильнику
на изотерме CD, равно:
109

Найдем отношение этих величин:
ft П ^ «*>
и докажем, что
VC~b _VB~b
VD-b~VA-b'
Напишем для адиабаты ВС уравнение в форме:
Аналогично для адиабаты DA можно написать:
После деления одного уравнения на другое, получим:
b\cv Vc-b VB-b
?^l—c V или —^ — —?
п-ъ-уА-ъ*
Следовательно, уравнение D,27) принимает вид:
В то же время, согласно равенству D,13)
где Г — термодинамическая температура.
Сравнивая уравнения D,28) и D,13), получаем:
г*
1 — "рг I 2-
Таким образом, есл^ гааовую и термодинамическую
шкалы совместить в некоторой произвольной точке, где
r2*==r2, то Т~Т*> т. е. газовая шкала совпадает с абсо-
абсолютной термодинамической шкалой температур.
110

4. Вывести зависимость электродвижу*
щей силы гальванического элемента от температуры,
пользуясь методом круговых процессов.
Решение. Будем рассматривать обрати*
мый гальванический элемент, т. е. такой, в котором сила
тока мала и джоулевым теплом можно пренебречь. Обо-
Обозначим заряд, проходящий по гальванической цепиг
через е, а э. д. с. гальванического элемента — Е.
На диаграмме еЕ исходное состояние системы изо-»
бразится точкой А (см. рис. 33). Будем сначала брать
ток от элемента, сохраняя его температуру постоянной-
В этом случае его э. д. с. тоже остается величиной по-»
стоянной, и изотерма АВ в цикле Карно представится
прямой, параллельной оси абсцисс (ось е). От нагре*
вателя элемент получит количество теплоты Qu равное
согласно первому закону термодинамики выражению:
где U2—Ui — изменение энергии элемента во время изо*
термического процесса, a W — совершенная во время
этого процесса работа.
Из состояния В в состояние С разрядка элемента
происходит адиабатически, что влечет за собой пониже*
ние его температуры от Т до Т—dT.
Далее, от состояния, изображаемого на диаграмме
точкой С, будем пропускать ток через элемент сначала
изотермически при температуре Т—dT до состояния D,
затем адиабатно до состояния Л, завершая цикл. Во
время процесса CD элемент отдает холодильнику коли*
чество теплоты, равное Q%. Следовательно, количество
теплоты, за счет которой совершена работа, равно
Рис. 33. График цикла, прово-
проводимого с гальваническим эле-
элементом.
е
111

разности Qi—Q2 и определяется площадью цикла
ABCD, равной edE:
Q\ Q
Применим к рассматриваемому циклу второе начало
термодинамики D, 5):
edE _ dT
~ Т •
Изменение энергии элемента U2—U\ определяется
тепловым эффектом происходящей в ней химической ре-
реакции. Поэтому
где q — тепловой эффект реакции, сопровождающий
прохождение по цепи единицы заряда.
Знак минус указывает на уменьшение химической
энергии элемента в результате выделения теплоты при
изотермическом процессе.
Величина работы на изотерме АВ на основании фор-
формулы B,1):
Wx = eE.
Следовательно, второе начало термодинамики для
данного кругового процесса можно переписать в виде:
dE dT ~ i т dE
т—^=^г или Е^д + Т^.
Полученное уравнение выражает зависимость э. д. с.
гальванического элемента от температуры и называется
уравнением Гельмгольца.
ЛИТЕРАТУРА
1 Дж. РОБЕРТС,
Теплота и термодинамика, Гостехиздат, М.—Л., 1950.
2. А. С. ЯСТРЖЕМБСКИЙ,
Техническая термодинамика, Госэнергоиздат, 1953.
3. в. с. микрюков,
Курс термодинамики, Учпедгиз, 1956*
4. к. шефер,
Теория теплоты, ч. I, Гостехиздат, 1939,

ГЛАВА ПЯТАЯ
Энтропия
§'
м
Второе начало термодинамики для
случая большого числа нагревателей
и холодильников
Количественное выражение второго на-
начала термодинамики в виде D, 6) было получено для
одного рабочего тела, совершающего цикл с одним на-
нагревателем и одним холодильником.
Обобщим второе начало термодинамики на наиболее
часто встречающийся в природе и практике случай
большого числа нагревателей и холодильников. Запи-
Запишем соотношение D, 6) в несколько измененном виде:
0*2 \ ^2 0*2
~~7~\ -^^ "т* ' * ИЛИ т
VI ' 1 * 2
откуда
Величины Qi и Q2, обозначающие соответственно ко*
личество теплоты, взятое от нагревателя и отданное хо*
лодильнику, имеют разные знаки, поскольку одна из них
берется от нагревателя, другая передается холодильни-
холодильнику. Условимся Qi считать положительным, a Q2 — отри-
дательным. Тогда соотношение E, 1) прихмет вид:
или ТГ + 7Г<°- <5'2>
Величина -у представляет собой теплоту, отнесен-
отнесенную к температуре, и называется приведенной теплотой.
Таким образом, из формулы E, 2) можно заключить,
что для каждого цикла с одним нагревателем и одним
холодильником сумма приведенных теплот меньше либо
равна нулю.
Представим себе теперь несколько работающих тел,
каждое из которых совершает свой цикл. На диаграмме
pV этот сложный процесс можйо представить в виде
8 В. Ф. Ноздреа ИЗ

Рис. 34. График цикла Кар-
но, разделенного сеткой
адиабат и изотерм на эле-
элементарные циклы /, 2, 5,.,.
некоторого цикла Карно, разделенного сеткой изотерм
и адиабат на большое число элементарных циклов
(рис. 34).
Рассмотрим три таких элементарных цикла: 1, 2, 3,
допуская, что все они совершаются рабочими телами в
одном направлении, например по часовой стрелке.
Для каждого из взятых нами циклов можно напи^
сать второе начало термодинамики:
для первого цикла
для
для
второго
третьего
цикла
*?
цикла
1 2
1 _____ ,^* ||
1 1
и т. д.
. д.
Найдем сумму всех полученных соотношений:
E,3)
Легко показать, что в полученной сумме отсутствуют
члены, относящиеся к тем отрезкам изотерм, по кото*
рьш элементарные циклы соприкасаются. Действитёль*
114

но, вдоль этих отрезков изотерм система совершает
процесс в противоположных направлениях. Поэтому
если, например, в первом цикле рабочее тело отдает хо«
лодильнику количество теплоты Qf2, то во втором цикле
оно берет от нагревателя то же количество теплоты
Q2'=SQ\", следовательно, сумма приведенных количеств
теплоты по изотерме равна нулю. Аналогичные рассу*
ждения можно привести и относительно других изотерм.
Учитывая это обстоятельство, можно вместо взятых трех
циклов рассматривать один цикл с одним нагревателем
и одним холодильником.
Рассмотрим теперь цикл произвольной формы, в ко*
тором давление и объем меняются непрерывно (рис. 35)*
Поскольку в таком цикле температура тоже меняется
непрерывно, то для него второе начало термодинамики
в виде E, 3) применить нельзя. В этом случае разобьем
рассматриваемый контур сеткой изотерм и адиабат, из
которых можно составить ступенчатый контур. Для это-
этого последнего второе начало термодинамики можно за-
записать в виде:
E,4)
При бесконечном уменьшении длины каждого звена
ступенчатого контура и соответственно увеличении их
ч(ч
\
л:
Рис. 35. График произвольного циклаЛ разделенного сеткой адиабат
и изотерм на элементарные циклы Карно.
8* 115

числа ступенчатый контур приближается к непрерыв-
непрерывному контуру и выражение E, 4) принимает вид:
E,5)
Выражение E, 5) дает количественную формулиров-
формулировку второго начала термодинамики в самом общем слу-
случае дл-я произвольного замкнутого цикла: криволиней-
dQ
ныи интеграл по замкнутому контуру от величины -^-
равен нулю в случае обратимого процесса и меньше
яуля в случае процесса необратимого.
Рассмотрим выражение E, 5) в применении к изотер-
изотермическому замкнутому обратимому циклу:
Поскольку
Т = const,
то можно записать:
Но так как
то
В данном случае d'Q = 0 и dt/=O, так как рассма-
рассматривается процесс замкнутый. Следовательно, d'W—O.
Это значит, что работа, совершаемая обратимым изо-
изотермическим циклом, равна нулю.
Нами были рассмотрены замкнутые процессы. Од-
Однако в природе встречаются и незамкнутые процессы,
к которым второе начало термодинамики также приме-
применимо. Более общую формулировку второго начала тер-
термодинамики, охватывающую и незамкнутые процессы,
можно получить с помощью введения нового понятия —
энтропии.
116

§ Энтропия
Понятие энтропии является одним из
сложнейших понятий физики. Энтропия в переводе с гре-
греческого (evtpco) означает одностороннее изменение.
Вначале энтропия была введена в науку формально.
Затем на основании рассмотрения большого числа за-
задач было выяснено ее физическое содержание.
Применим второе начало термодинамики к циклу
произвольной формы ADBCA (рис. 36).
Для данного цикла мы можем разбить интеграл в
, Г d'Q
форме I -у*- на два слагаемых, соответствующих двум
частям цикла: АСВ и BDA.
E,6)
где (С) и (D) указывают пути интегрирования. Соотно*
шение E, 6) можно иначе представить в следующем
виде:
E,7)
Допустим, что часть цикла BDA совершается обра-
обратимо, тогда в правой части соотношения E, 7) пределы
интегрирования можно изменить:
в в
Рис. 36. График цикла про»
извольной формы АСВиА.
X
117

Это и будет выражением второго начала термодина-
термодинамики для цикла в самом общем случае.
Рассмотрим теперь только обратимый процесс:
Полученное равенство показывает, что при обрати-
d'Q
мом процессе интеграл от -j?- не зависит от пути ин«
тегрирования, а так как пути АСВ и BDA были нами
выбраны совершенно произвольно, то согласно равен-
в
ству E, 9) J -jr- для обратимого процесса зависит
А
только от начального и конечного состояний системы.
Следовательно, подынтегральное выражение -^ яв-
является полным дифференциалом функции, зависящей
только от состояния системы. Эта однозначная функция
состояния была обозначена S и названа энтропией. Сле-*
довательно,
в в
(С) J *? e (D) J ^Я = SB - SA. E,90
А А
Вернемся к рассмотрению общего случая (см. фор-
формулу 5, 8).
Поскольку интеграл в правой части E, 8) написан
для обратимого процесса, его можно заменить разно-
разностью SB—SA:
в
{D)J*Q.<Sb-Sa, E,10)
А
или, учитывая произвольный выбор цикла:
в
-SA. E,11)
Формула E, 11) выражает собой второй закон тер-
термодинамики для самого общего случая, относящегося не
только к Циклам, но и к любым незамкнутым процессам.
118

Формулу E,5) легко получить из формулы E, И) как
частный случай. Например, для замкнутого процесса
Следовательно,
Оо Ji z==: U И
Второе начало термодинамики в форме E, 11) утвер-
утверждает, что разность энтропии двух состояний системы
d'Q
равна интегралу от —jr- между этими состояниями,
если последний, берется по обратимому пути, и больше
d'Q л
интеграла от -у по необратимому пути.
Это, однако, не означает, что разность энтропии
имеет различное значение в зависимости от того, какой
процесс мы рассматриваем (обратимый или необрати-
необратимый). Энтропия является однозначной функцией состоя-
состояния, и, следовательно, разность энтропии имеет посто-
постоянное значение независимо от характера процесса. Знак-
неравенства в формуле E, \\) указывает на то, что в
случае необратимого процесса интеграл в левой части
ее уже не выражает собой разности энтропии, а меньше
ее. Второе начало термодинамики в дифференциальной
форме имеет вид:
^-<dS. E,12)
Используя количественное выражение первого на-
начала термодинамики B, 8), получим основное уравнение
термодинамики в виде:
Щ^ E,13)
Энтропия изотермических обратимых процес-
процессов. Второе начало термодинамики может быть записано
следующим образом:
2
I «г— === к)% ~"~~" *^1#
J *
1
119

Поскольку при изотермическом процессе Г=const, то
ИЛИ
SjL = S2 — Sx. E,14)
Рассмотрим конкретный пример. Равновесие жид*
кости с ее насыщенным паром при неизменной темпера*
туре Т.
На превращение единицы массы жидкости в пар за*
трачивается некоторое количество теплоты, равное скры-
скрытой теплоте испарения, т. е. Q = A,.
В этом случае уравнение E, 14) имеет вид:
1 _ с с
у — Ь2 — г>{,
где S2 — энтропия парообразного состояния, S{ — энтро*
ПИЯ ЖИДКОГО СОСТОЯНИЯ.
Такое же выражение справедливо для случая равно*
весия фаз жидкость — твердое тело, но только здесь
к — скрытая теплота плавления:
где S2 — энтропия жидкой фазы, Si — энтропия твер*
дого тела.
Таким образом, энтропию можно выразить через кон*
кретные физические величины: скрытую теплоту испаре*
ния, скрытую теплоту плавления и т. д. и температуру.
Энтропия, как видим, не измеряется, а вычисляется с по*
мощью других физических величин, которые легко опре*
делить экспериментально. Однако, зная эти физические
величины, мы можем рассчитать лишь разность энтро*
пий, но не ее абсолютные значения. Вообще, пользуясь
первым и вторым началами термодинамики, можно вы-
вычислить любые функции состояния (в частности, энтро-
энтропию) только с точностью до постоянной, т. е. вычислить
только разность значений этих функций в двух состоя-
состояниях. Вычисление же абсолютных значений функций
состояния возможно лишь с помощью третьего начала
термодинамики.
120

Энтропия идеального газа. Для нахождения
энтропии идеального газа запишем выражение второго
закона термодинамики в дифференциальной форме:
d'Q ,с с Г d'Q
—~- — dS, или 5= J -у-
Г
= J
Знак неравенства в формуле E,12), указывающий на не-
необратимость процесса, можно не учитывать, поскольку
рассчитываемая величина — энтропия — является функ-
функцией состояния и не зависит от характера процесса.
Используя первое начало термодинамики для иде-
идеального газа B,31), перепишем выражение E,12) в виде:
Воспользуемся уравнением состояния идеального га-
газа и зависимостью S = /(/?, V). Поскольку в этой форме
записи энтропия S явно не зависит от температуры,
исключим последнюю из подынтегрального выражения
E,15)*, сделав следующее преобразование:
т pV ит pdV+Vdp
тогда
/. с (ndV-UV dn\-URnrtV
E,16)
cv(pdV+Vdp)
Подставляя в выражение E,16) значение R — cv—cv,
находим S в виде:
Так как теплоемкости ср и cv для идеального газа
постоянны, то
или
E,19)
V. E,20)
Итак, разности энтропии идеального газа можно лег-
легко рассчитать, если известны параметры р и V системы.
121

Энтропия и закон соответственных состояний.
Заменяя в выражении дифференциала энтропии
ds~-~- E,12) величину d'Q на основе первого нача*
ла термодинамики, получим:
OS^dU + pav E21)
Последнее выражение должно являться полным диф*
ференциалом, что налагает определенные требования на
правую часть этого выражения (см. главу 2).
Заменив величину d'Q в выражении E,12) ее значе*
нием из выражений B,12), получим:
Соотношение взаимности B,4) требует, чтобы имело
место равенство:
д г! /ш\ 1 _ д rl (dU\ .
IV[Т [WJylr~~дТ[Т\W)t"^
Рассматривая U как функцию только V и Т и опуская
при дифференцирования значки Т и V при вторых про-
производных, получим:
1 д2и , 1 / dp \ _
Т дТдУ ~*~ Т \ дТ )
Т дУдТ ~ Т дТдУ *~ Т \ дТ )v
или
В интегральной форме выражение E,25) примет вид:
E-26)
Подставляя в последнее равенство приведенные па-*
р а метры
р V Т
Рк ук * к
находим, что частное от деления интеграла на абсо-
абсолютную температуру является универсальной функцией
122

приведенных переменных jt, ф, т. Поэтому можно пола-
полагать, что и все выражение, исключая нулевую энергию,
является подобной функцией:
^k E,27)
RT
Действительно, величина К~ у является универ-
JrK К
сальной функцией приведенных переменных я, ф, т. Это
следует, например, из уравнения состояния Камерлинг-
Оннеса (см. гл. 1, упраж. 9). Аналогично и величина
РкУк Я « л.
--* к = -^- должна являться универсальной функцией
приведенных переменных, так как R — универсальная
постоянная.
Поэтому выражение
^ , ,,,) E,28)
имеет одно и то же значение для различных термодина-
термодинамически подобных веществ в соответственных состоя-
состояниях.
Из равенств E,21), E,27) и E,28) следует, что диф-
дифференциал энтропии также есть универсальная функция
от я, ф, т:
Иными словами: для всех термодинамически подобных
веществ разность молярных энтропии в двух соответ-
соответственных состояниях одинакова.
§ Энтропия адиабатических процессов
Для адиабатического процесса, проте*
кающего без теплообмена с внешней средой, d'Q = 0.
Тогда из выражения E,12) следует:
dS>0. E,29)
Соотношение E,29) указывает, что в. обратимых
адиабатических процессах энтропия не изменяется, а в
необратимых всегда возрастает (dS>0).
Рассмотрим полученный результат более подробно,
Пусть внутри замкнутой адиабатической системы нахо*
дятся два тела: Л, имеющее температуру Т\, и В, имею-»
щее температуру Т2 -(рис. 37).
Ш

Обозначим энтропию тела А через 5Ь энтропию тела
В через S2 и допустим, что Ti>T2.
В рассматриваемом случае, хотя система в целом
адиабатна, внутри нее протекает неадиабатический про-
процесс. Исследуем изменение энтропии всей системы. Из
выражения E,12) для каждого из тел А и В, когда они
еще не соприкасаются следует:
для тела А
dSt=-
для тела В
E,30)
E,31)
Так как Ti>T2, теплота от тела А будет переходить
к телу В и общее изменение энтропии будет равно:
E,32)
Знак минус перед первым членом суммы E,32) ука-
указывает на то, что тело А отдает количество теплоты d'Qi-
В выражении E,32) d'Qi>0 и Т\>Т2 по условию. Следо-
Следовательно, изменение энтропии положительно:
dS>0.
E,33)
Полученное неравенство E,33) доказывает возраста-
возрастание энтропии системы в случае необратимого адиабата*
ческого процесса.
Рис. 37, Схема замкнутой
адиабатической системы, вну-
внутри которой находятся тела Л
и В с температурами Тх и Г2.
124

Рис. 38. Схема опыта по рас-
расширению идеального газа в
пустоту.
Возрастание энтропии при расширении идеаль-
идеального газа в пустоту. Представим себе сосуд, разделенный
перегородкой на две части (рис. 38), и допустим, что
одна часть сосуда (объем Vi) содержит идеальный газ,
а из другой части газ удален до полного вакуума. Если
открыть отверстие в перегородке, то газ с большой ско-
скоростью устремится в пустоту и равномерно заполнит весь
сосуд.
Рассматриваемый процесс необратим, так как каж-
каждое промежуточное состояние газа не является состоя*
нием равновесия, и адиабатен, поскольку скорость его
велика, и обмен энергиями с окружающей средой Ъро*
изойти не успевает. Для такого процесса dS>0.
Покажем справедливость неравенства E,33) для слу*
чая истечения идеального газа в пустоту. Энтропия не
зависит от характера протекающего процесса и является
функцией состояния системы. Запишем ее выражение
для обоих состояний газа.
Энтропия газа в объеме V\ равна:
Sx = Су In p{ 4- cp In Vt + SQ.
Энтропия газа в объеме 1/2 равна:
S2 — Су In р2 + ср In V2 + So»
причем, поскольку газ расширяется,
V2>VX и р2<рх.
Найдем изменение энтропии:
S2 — S{ — cv (In p2 — In /?!) + ср (In V2 — In V{)f
или
E,34)
E,35)
E,36)
E,37)
125

Используя соотношение — = -гг- для идеального га*
Р 1
за, запишем равенство E,37) в виде:
^ ^. E,38)
Но так как V2>Vi E,36), то 52—5i>0, т. е. энтро-
энтропия возрастает.
Все самопроизвольные процессы, аналогичные рас-»
смотренным выше, сопровождаются возрастанием энтро-
энтропии. А так как в природе процессы сорершаются само-
самопроизвольно, то адиабатная система всегда стремится
к состоянию с максимальным значением энтропии.
Энтропия и равновесие системы. Быраже-
ние второго начала термодинамики для адиабатическо-
адиабатического процесса в виде E,29) показывает, что энтропия
является хорошей характеристикой приближения адиа-
адиабатической системы к состоянию равновесия. Действи-
Действительно, так как приближение системы к состоянию
равновесия сопровождается ростом ее энтропии, то чем
больше значение последней, тем ближе система нахо-
находится к состоянию устойчивого равновесия. Если изме-
изменение энтропии системы равно нулю, то система нахо-
находится в состоянии равновесия.
Таким образом, энтропия может быть использована
как для определения состояния равновесия, так и для
определения состояний, близких к равновесию. Если из-
известна энтропия как функция параметров системы, то
можно предсказать, в каком направлении будут проис-
происходить в ней процессы. Можно, например, предсказать ход
химической реакции в адиабатических условиях, если из-
известна энтропия исходных и конечных продуктов реакции.
В неадиабатических условиях все приведенные выше
рассуждения теряют смысл, поскольку не выполняется
соотношение dS^-О. В этом случае роль энтропии играют
другие термодинамические функции (см. гл. 7).
Статистический характер второго начала
термодинамики
Все системы, рассматриваемые в термо-
термодинамике, представляют собой совокупность большого
количества частиц (молекул) одного или нескольких ве*
126

ществ. Обобщение огромного экспериментального мате-
материала по наблюдению над процессами, протекающими в
таких системах, привело к открытию первого и второго
начал термодинамики.
Как известно, опираясь на второе начало термодина-
термодинамики, мсркно определить направление процессов в систе-
системе. Эти процессы протекают таким образом, что система
стремится занять наиболее вероятное состояние, кото-
которому соответствуют одинаковое давление и темпера-
температура во всем объеме данной системы (состояние рав-
равновесия) .
Вернемся к ранее рассмотренному примеру перехода
большой массы газа из одной части сосуда в другую без
совершения работы и притока теплоты извне (рис. 38),
Как только будет открыто отверстие в перегородке,
газ вследствие хаотического движения его молекул зай-
займет весь объем сосуда. Но новое состояние равновесия в
соответствии со вторым законом термодинамики насту-
наступает только тогда, когда давление и температура будут
одинаковыми в каждой точке сосуда.
Допустим теперь, что в том же сосуде находится не-
небольшое число молекул газа (например, 20 молекул).
В этом случае вероятность равномерного распределения
молекул в обеих частях сосуда (по 10 молекул в каждой
части) уменьшается.
Не исключена возможность присутствия в одной из
частей сосуда большинства молекул.
Если в сосуде находятся только две молекулы газа,
то согласно второму началу термодинамики они должны
находиться в разных частях сосуда. Однако вследствие
своего движения., столкновений между собой и со стен-
стенками сосуда, молекулы могут одновременно оказаться в
одной части сосуда, неравномерность же распределения
частиц противоречит второму закону термодинамики.
И наконец, если в сосуде имеется всего одна молекула,
вероятность ее нахождения в одной из частей сосуда
равна Y-
Как видно, уменьшение числа молекул газа влечет за
собой уменьшение вероятности равномерного распреде-
распределения их в сосуде. На практике, когда мы имеем дело
с телами, состоящими из небольшого числа молекул, и
наши наблюдения относятся к сравнительно небольшим
127

промежуткам времени, такие отклонения от второго на-
начала термодинамики возможны, хотя и маловероятны.
Убедительным доказательством проведенных рассу-
рассуждений .являются подсчеты, выполненные польским уче-
ученым Смолуховским. Если рассматривать 1 см3 газа при
нормальных условиях, то лишь один раз в течение
A010I4 лет удаетсязаметить отступление плотности- газа
на 1% от равномерной. Если же взять очень малое ко-
количество газа, например, содержащееся в кубике, ребро
которого равно 0,2 микрона, то такие отступления могут
происходить примерно 1 миллиард раз в секунду.
Другой пример. Если имеются два тела, имеющие
температуру 301 и 300° К, то должен наблюдаться пере-
переход теплоты от первого тела ко второму. Подсчет пока-
показывает, что если в течение определенного промежутка
времени от первого тела ко второму переходит 1 кал те-
теплоты, то на A00010I0 случаев может произойти один
случай, когда переход в нормальном направлении не со-
совершится.
Однако, если такой же подсчет произвести для очень
малого количества теплоты 12 • 10~12 кал, то уже в десяти
случаях из 37 не будет обычного перехода теплоты от
горячего тела к холодному.
Таким образом, второй закон термодинамики в от-
отдельных случаях может не выполняться, но чем значи-
значительнее это отступление от выполнения закона, тем оно
менее вероятно. Отметим, что подобного рода нарушения
закона чаще всего имеют место в критическом состоя-
состоянии вещества, где развиваются сильные флуктуации
плотности.
Сказанное позволяет сделать вывод, что второе нача-
начало термодинамики в отличие от абсолютного закона со-
сохранения и превращения энергии носит статистический
характер и в некоторых случаях может не выполняться.
г
Энтропия и вероятность
Вернемся к рассмотрению замкнутых
термодинамических систем. Как известно, необратимые
процессы в таких системах сопровождаются возраста-
возрастанием энтропии, максимум которой соответствует равно-
равновесному состоянию систем, являющемуся наиболее ве-
вероятным.
128

Таким образом, статистическая причина увеличения
энтропии в необратимых процессах состоит в увеличении
при этом вероятности состояния системы. Следовательно,
энтропия системы есть некоторая функция вероятности
ее состояния. Это основное положение, определяющее
сущность второго начала термодинамики и устанавли-
устанавливающее связь между энтропией и вероятностью, впервые
было высказано Больцманом.
Найдем вид зависимости
где w — вероятность состояния.
Обозначим энтропии и вероятности двух систем соот-
соответственно Si, W\ и S2, w2i а энтропию и вероятность
сложной системы, состоящей из двух первых, S и w.
Тогда на основании предложения Больцмана должны
иметь место зависимости:
S,= /К), E,39)
S2*=f(w& E,40)
S = f(w). E,41)
Учитывая, что энтропия системы обладает свойством
аддитивности, т. е. энтропия системы равна сумме энтро-
энтропии отдельных ее частей *, а вероятность состояния
сложной системы равна произведению вероятностей со-
состояний отдельных систем, запишем:
или
S - f (w{) + f (w2) = f (wxw2). E,42)
Продифференцировав это выражение сначала по W\,
а затем по w2i получим:
f/(wlw2)w2^ff(w{), E,43)
E,44)
Умножим уравнение E,43) на шь а уравнение E,44)
на w2:
f (w,a>2) *®1Щ — V (^i) wv E,45)
ff(wlw2) w^ = f (w2) щ. E,46)
* См. гл. 7.
9 В. Ф. Ноздрев 129

Отсюда
Г(Щ)Щ^Г(Щ)Щ, E,47)
т. е.
р (w) w = const = k. E,48)
С другой стороны, из соотношения E,41) следует, что
Г (•) = ?• <5'49>
Сравнение равенств E,48) и E,49) приводит к соот-
dS k
ношению ~-j— = —, интегрирование которого позволяет
записать выражение энтропии через вероятность состоя-
состояния:
S = k In w + const. E,50)
Соотношение E,50) указывает на пропорциональ*
ность энтропии системы логарифму вероятности состоя-,
ния системы. Как показывает дополнительный анализ
выражения E,50), коэффициент пропорциональности k в
этой формуле есть постоянная Больцмана.
Основываясь на приведенных выше рассуждениях,
Больцман дал такую формулировку второму закону тер*
модинамнки: «Природа стремится от состояний менее
вероятных к состояниям более вероятным».
§•
0 так называемой «тепловой смерти»
вселенной
Неправильное представление о вселенной
как замкнутой системе является причиной появления
теории «тепловой смерти» вселенной. Рассмотрим вопрос
об энтропии в замкнутой системе Как было показано, в
адиабатических системах изменение энтропии либо равно
нулю (в обратимых процессах), либо энтропия возрастает
(в необратимых процессах).
Отсюда Клаузиусом и другими был сделан такой вы-
вывод. Если энтропия замкнутой системы растет, то, пред-
представляя весь мир системой замкнутой, можно к нему
также применить неравенство dS>Ot что говорит о росте
энтропии всего мира. Последнее же означает увеличение
количества обесцененной энергии, которая не может
быть использована для совершения работы и, следова-
следовательно, должна привести к «тепловой смерти» вселенной.
130

Действительно, для одного нагревателя и одного хо-
холодильника в случае обратимого процесса имеет место
соотношение:
Q2
* 2 1
Если температура нагревателя меняется, то
ИЛИ
Последнее равенство говорит о том, что в замкнутом
цикле количество теплоты, передаваемой холодильнику,
увеличивается, т. е. увеличивается количество обесценен*
ной энергии.
Таким образом, развитие мира, по Клаузиусу, идет
неизбежно в таком направлении, что движение материи
утрачивает свою способность к дальнейшим превраще-
превращениям.
Излагая эти взгляды Клаузиуса, Энгельс писал: «Ми*
ровые часы сначала должны быть заведены, затем ежи
идут, пока не придут в состояние равновесия, и только
чудо может вывести их из этого состояния и снова пу*
стать в ход. Потраченная на завод часов энергия исчез*
ла, по крайней мере в качественном отношении, и может
быть восстановлена только путем толчка извне. Значит,
толчок извне был необходим также и вначале; значит,
количество имеющегося во вселенной движения, или
энергии, не всегда одинаково; значит, энергия должна
была быть сотворена; значит, она сотворима, значит, она
уничтожима.
Ad absurdum! (До абсурда)»*
«Теория» Клаузиуса, приводящая в итоге к идее со*
творения мира, т. е. к идеализму, не имеет никаких фи*
зических оснований. Дело в том, что, как показывают
данные астрономии, мир не замкнут в пространстве и
времени и не имеет ни начала, ни конца. Поэтому
распространять на безграничную вселенную вывод о воз-»
растании энтропии в замкнутой системе не правомерно,
*Ф< Энгельс, Диалектика природы^ Госполитиздат, 1949,
стр. 229,
9* 131

так как вывод о возрастании энтропии справедлив только
для замкнутой системы.
Иными словами, исходные позиции «теории» Клаузи-
уса ложны, а следовательно, и вывод относительно «теп-
«тепловой смерти» вселенной является антинаучным.
Впоследствии Больцман, дав статистическое толкова-
толкование второму началу термодинамики* также подверг кри-
критике идеалистические выводы Клаузиуса. Больцман
исходил из того, что бесконечная вселенная в бесконеч-
бесконечное время имеет вероятность значительно отклоняться
от своего среднего наивероятного состояния и только
после этого снова приближается к наивероятному состоя-
состоянию. Хотя идеи Больцмана сыграли неоценимую роль
в разоблачении идеалистических извращений второго
начала термодинамики, их слабым местом является то,
что они предполагают абсолютное равновесие мировой
системы, т. е. «тепловую смерть» вселенной, и признают
отклонение от этого состояния случайным. Ё действи-
действительности, помимо термодинамических стимулов разви-
развития природы, имеется ряд других факторов, приводящих
к тому, что «...в природе, в конце концов, все совершается
диалектически, а не метафизически, что она движется
не в вечно однородном, постоянно сызнова повторяю-
повторяющемся круге, а переживает действительную историю»
(Ф. Энгельс, Анти-Дюринг. Госполитиздат, 1950,
стр. 23).
О5
Г Задачи и упражнения
1. Найти изменение энтропии тела для
случая расширения его при постоянном давлении.
Решение. Имеем:
Учитывая, что
т(й)
< /р
и принимая во внимание, что коэффициент расширения
а— V \дТ)р'
132

получим:
Знак этого выражений Зависит от внака а.
2. Вычислить энтропию газа Ван-дер-Ва-
Ван-дер-Ваал ьса и найти уравнение его адиабаты.
Решение,
-J —7—-J
Разрешая уравнение Ван-дер-Ваальса относительно
давления, получим:
Следовательно,
Поскольку cv слабо зависит от температуры, то
Для того чтобы найти уравнение адиабаты ван-дер-ва-
альсовского газа, приведем выражение B,12) с по-
помощью равенства E,25) к виду:
%) E,51)
Поскольку при адиабатных процессах d'Q — Q, это со-
соотношение E,51) можно упростить следующим образом:
E,52)
Заменив в последнем уравнении производную ущп
ее значением из уравнения Ван-дер-Ваальса, получим:
1 ^ E,53)
133

Для газа, подчиняющегося уравнению Ван -дер- Ви*
альса:
f-gXJ =0, или cv~cv(T).
Действительно, рассматривая энтропию S как функ*
цию температуры Г и объема F, Запишем ее полный
дифференциал:
Если процесс протекает при постоянном объеме
V= const, то
dS
¦. E,55)
\ и л / у л л.
откуда
Взяв производную от с у по объему при Т=const и
воспользовавшись соотношением (см. гл. 7, § 6)
(dS_\
\dv)
получим:
\Ж)Т =
Т W (дг/к^ Т~5F \) Г Ы
откуда следует, что теплоемкость грамм-моля ван-дер*
ваальсовского газа не зависит от объема.
Уравнение E,53) может быть проинтегрировано, если
определена зависимость теплоемкости от температуры,
т. е. Су=Су(Г). Предположим, что газ идеален в смысле
^v-^const и подчиняется уравнению Ван-дер-Ваальса.
Тогда интегрирование равенства E,53) приводит к урав*
нению адиабаты в переменных Т и V в виде:
R
— Ъ)Су = const E,57)
Если в полученном уравнении заменить температуру
Т ее значением из уравнения Ван-дер-Ваальса, получим
уравнение адиабаты в переменных р и V:
134

3. Показать, что энтропия увеличивается,
когда, например, горячая вода отдает теплоту такой же
массе холодной воды и температуры их выравниваются.
Т -4- Т
Решение. Температура смеси Т= !^" *,
изменение энтропии
г т
|^+|4Я, где d'Q^
Следовательно,
так как (i
4. Каждый из двух сосудов содержит по
одному молю идеального газа при температурах еоответ*
ственно Т\ и Г2. Сосуды приводят в соприкосновение и
обоим веществам дают возможность прийти в состояние
равновесия посредством теплопроводящих стенок без
изменения объема.
Подсчитать общую энтропию в исходном и конечном
состояниях и показать, что она увеличивается.
5. Вычислить увеличение энтропии в еле*
дующем процессе: одна грамм-молекула воды A8 г) при
100° С переводится в пар при давлении 1 атм, а пар на-
нагревается при р = const до 650° С.
Отв. А5^33 кал\град.
6. Идеальный газ как рабочее тело уча-
участвует в следующих двух обратимых процессах: а) от
состояния /?i, V\ процесс ведется сначала при р = р\ до
состояния ри V2'y затем при 1/=У2 до состояния ргУъ
б) от состояния ри V\ до состояния р2, Vi при V= Vu за-
затем при р=р2 до состояния р2, V2>
Величины ср и cv постоянны. Показать, что теплоты,
сообщенные системе в этих двух процессах, различны, а
изменение аятропии одно и то же.
Решение. Изобразим рассматриваемые
обратимые процессы графически на диаграмме pV
(рис. 39).
J35

о
Рис. 39. График процессов
перехода от состояния А к со-
стоянию С различными путями:
посредством изобарического
расширения A3 и последую-
последующего изохорического процесса
ВС и посредством изохориче-
ского процесса AD с после-
дующим изобарическим рас-
ширением DC.
Согласно первому началу термодинамики количество
теплоты, сообщаемое идеальному газу в первом процео
се, равно:
Р у(Т,-Т2). E,58)
Аналогично для второго процесса можно написать:
cv(Ta-T1) +
p-TJ. E,59)
Преобразуем выражение для AQ2.
Из закона Шарля для изохор ВС и AD легко полу*
чить соотношения:
откуда
.?L_Za« Pi —/i__
/>2 ^3 P2 TA*
Tg Tx
E,60)
С помощью полученного соотношения E,60) приве*
дем уравнение E,59) к виду:
+ Су(Тг-Т2)^. E,61)
Так как согласно направлениям процессов I и II
Г2>Г3 и Г3>Г4, то из соотношений E,58) и E,61) оче*
видно неравенство:
^Q2<^Ql.
135

Вычислим увеличение энтропии в рассматриваемых
процессах.
В первом случае
Во втором случае
\4
Полученные выражения и соотношение E,60) пока-
показывают, что ASi = A52, т. е. изменение энтропии в обоих
процессах одно и то же.
7. Найти выражение универсальных
функций /i(^, ф, т) и /2(я, ф, т), определенных уравне-
ниями E,27) и E,28) для случая идеального газа.
Отв. fj(rtf ф, т) = ~/?,
8*. Коэффициент объемного расширения
воды а при 4° С меняет знак, будучи при 0°</<4°С ве-
величиной отрицательной. Показать, что в этом интер-
интервале температур вода при адиабатическом сжатии
охлаждается, а не нагревается, как все газы и другие
жидкости.
Решение. В соответствии с первым нача*
лом термодинамики имеем:
Но согласно соотношениям {1ЛУ и A,5)
)
* Задачи 8 и 9, а также их решения предложены автору
И. П. Базаровым.
137

/
\
)
0
Рис. 40. График цикла Карно
с водой в качестве рабочего
вещества.
S
Поэтому
При адиабатическом процессе d'Q = 0, следовательно,
dT = — T—%-dV.
Отсюда видно, что вода в интервале 0°С</<4°С,
когда у нее а<0, при адиабатическом сжатии (dV<0)
охлаждается (dT<0).
9, Показать, что температура ?=4° С не*
достижима для Лды при охлаждении ее с помощью
адиабатического расширения.
Решение. Рассмотрим цикл Карно, в ко*
тором рабочее вещество — вода (рис. 40), причем темпе-
температура нагревателя 7*1—283° К*810° С, а холодильника
Г2=277ОК=4°С.
Для цикла ф-~^ = 0 или
Д51|2 + Д52,3 + Д53>4 + Д54|1 - 0.
Но
Из уравнения первого начала термодинамики
138

Для изотермического процесса при 4° С, когда а=0,
получаем d'Q = 0, поэтому
Таким образом,
что противоречит второму началу термодинамики.
Следовательно, температура 4° С при охлаждении
воды с помощью адиабатического расширения недости-
недостижима.
10. Вычислить разность ср— cv для газа,
подчиняющегося уравнению Ван-дер-Ваальса.
Решение, Используя соотношения E,25)
и A,3), выразим разность теплоемкостей ср—cv ?аза в
следующем виде:
ldV\ — (dp\
\dp)T \dV)T
RT п
Дифференцируя равенство /?== у^ь у* по Г и
находим:
(др \ _ R , (др \ _ RT . 2а
[дТ )v~ V— b* \dV}T~ (V--bJ ~^K3 #
Таким образом,
139

После соответствующих преобразований, оставляя
лишь выражения линейные относительно а и Ь для не
очень плотного газа, получим:
ЛИТЕРАТУРА
1. О. Д. ХВОЛЬСОН,
Курс физики, т. 2, Госиздат, 1923.
2. А. Г. САМОЙЛОВИЧ,
Термодинамика и статистическая физика, Гостехиздат, 1955.
3. В. А. КИРЕЕВ,
Курс физической химии, Госхимиздат, 1951.
4. Л. БОЛЬЦМАН,
Лекции по теории газов, Гостехиздат, 1956.
5. Л. Д. ЛАНДАУ и Е. М. ЛИФШИЦ,
Статистическая физика, изд. 2, Гостехиздат, М. — Л., 1953.
6. А. ЗОММЕРФЕЛЬД,
Термодинамика и статистическая физика, ИЛ, М.—Л., 1955.
7. П. С. ЭПШТЕЙН,
Курс термодинамики, Гостехиздат, 1948.)

глава шестая Термодинамика
и проблемы излучения
Полное рассмотрение вопросов излуче-
излучения требует знания элементов электродинамики, стати-
статистической физики и квантовой механики. Однако с по-
помощью таких общих положений термодинамики, как
понятие о равновесии или второе начало термодинами-
термодинамики, можно объяснить некоторые законы, относящиеся
даже к такой, казалось бы, далекой от термодинамики
области, как излучение.
Равновесное излучение. Всякое нагретое
тело излучает электромагнитные волны. При этом энер-
энергия передается от одного тела к другому без наличия
контакта между ними. Падающие на тело лучи могут им
отражаться или поглощаться. Тело, которое поглощает
все падающие на него лучи, называется абсолютно чер-
черным телом. Излучение, находящееся в термодинамиче-
термодинамическом равновесии с окружающими телами, называется
равновесным.
Температура излучения. Понятие о темпера-
температуре излучения было впервые введено Б. Б. Голицыным.
Поскольку полная плотность энергии излучения пропори
циональна ТА (закон Стефана — Больцмана) и энергия
излучаемых телом электромагнитных колебаний пропор-
пропорциональна квадрату амплитуды, температура излучения
определяется как величина, четвертая степень которой
пропорциональна сумме квадратов амплитуд всех коле-
колебаний. Понятие о температуре излучения можно приме*
нить к равновесному излучению.
Закон Кирхгофа
Для излучения Кирхгоф установил сле«
дующий закон.
Отношение испускательной способности к поглоща-
тельной способности не зависит от природы тела; это
141

отношение для всех тел является одной и той же функ-
функцией длины волны и температуры. Аналитически это за-
записывается так: ~^- = е(Ь, Г), где ех — лучеиспускатель-
лучеиспускательная способность тела, А% — поглощательная способность
тела.
Для доказательства этого закона можно использо-
использовать, например, положение термодинамики о произволь-
произвольном выравнивании температур. Пусть в полости имеется
равновесное излучение. Заменим часть этой полости
произвольным телом при той же температуре. Если отно-
отношение испускательной способности к поглощательной
для этого тела будет другим, то лучистая энергия начнет
переходить от тела к оболочке полости или наоборот, в
результате чего появится разница температур. Но такое
положение противоречит второму началу термодинамики,
следовательно, остается признать справедливость закона
Кирхгофа.
г
v Давление излучения
Рассмотрим- термодинамическое доказа*
тельство наличия давления света, принадлежащее
Б. Б. Голицыну. Цилиндр, стенки которого полностью
отражают тепловые лучи, с обеих сторон закрыт телами
Л и В, имеющими соответственно температуры TY и Г2,
причем Г1>Г2. В цилиндре (рис. 41) перемещаются две
зеркальные пластинки, которые могут вставляться и вы-
выниматься около тел А и В. Сначала помещаем одну пла-
пластинку и при этом так, что весь объем цилиндра будет
заполнен лучистой энергией, излучаемой телом. Л, имею-
имеющим большую температуру. Если эту пластинку переме-
перемещать без трения от тела В к телу Л, то при крайнем
положении весь объем заполнится лучистой энергией,
Рис. 41. Схема мысленного эксперимента, выявляющего наличие
давления излучения.
142

излучаемой телом В, а теплота, излучаемая телом Л,
полностью перейдет в тело В. В результате такого про-
процесса произойдет нагревание тела Л, имевшего более вы-
высокую температуру и охлаждение тела В. Этот процесс
можно повторить много раз, в результате чего теплота
от тела менее нагретого будет передана телу более на-
нагретому. Однако согласно второму началу термодина*
мики это возможно только при совершении работы на
перемещение пластинки. Отсюда следует, что лучистая
энергия, находящаяся с двух сторон от пластинки, про*
изводит на нее давление. Величина светового давления
чрезвычайно мала, поэтому создание П. Н. Лебедевым
прибора, обнаружившего реальное существование давле*
ния света, имело огромное значение в истории развития
физики.
Закон Стефана—Больцмана
Этот закон был сначала эксперимеяталъ*
но установлен Стефаном, а затем теоретически подтвер*
жден Больцманом.
Излучение можно рассматривать как обыкновенную
термодинамическую систему. Внутренняя энергия такой
системы
U = eV9 F,1)
где е(Т)—плотность энергии и V — объем системы.
Дифференциал энтропии для такой системы имеет вид:
tdV + ^dV
F,2)
Поскольку энтропия S(TV) является функцией состо-
состояния и dS полный дифференциал, то дифференцируя по
V, найдем:
д (V дг\дD \ дЪ
)
* В F,2) используется формула для давления изотропного
излучения p-g- {см. А. Б, Млодзеевский «Термодинамика», М.,
Ш48, стр. 83J,
143

Учитывая, что г(Т) зависит только от температуры,
получим уравнение:
решая которое, находим!
е«*оГ4, F,4)
где а=7,64-10~15 эрг/град*-смИши 1,82-10~22 кал/град4 X
X ?Л*3. Выражение F,4) и представляет собой закон
Стефана — Больцмана, согласно которому плотность
энергии излучения пропорциональна четвертой степени
температуры.
§•
Закон Вина
Рассмотрим адиабатическое расширение
шара, заполненного черным излучением и имеющего
идеально отражающие стенки. Если шар расширяется
равномерно и бесконечно медленно, то излечение испы-
испытывает обратимый адиабатический процесс.
Так как стенки шара перемещаются, то длина отра-
отраженных от них световых волн испытывает изменение,
причем измененная длина волны
F,5)
где А/?— увеличение радиуса шара за время А/, так что
скорость расширения шара
Уравнение F,5) можно переписать в виде:
Я ~ 3 ' V f
или
~ 3 V '
где V — объем шара, v — частота излучения.
Интегрируя это уравнение, получим:
vn/ = const. F,60
144

Обозначив частоту до и после расширения соответ*
ственно v и v', а объем — V и V, получим:
или
(
откуда
(v'K у' + 3 (v7J dv'Vr *= v3^ + 3v2 dv V.
Из последних уравнений следует:
V'(v'Jdv'^Vv2dv. F,7)
Пусть объем с идеально отражающими стенками за-
заполнен черным излучением при температуре Т. Обозна-
Обозначив Uvdv энергию единицы объема излучения, частота
которого находится в границах между v и v + dv, опре-
определим Uv.
Энергия излучения в объеме V есть VUvdv. Увеличе-
Увеличение объема на dV сопровождается работой излучения,
причем давление излучения на стенки
p=L(Jvdv. F,8)
В рассматриваемом адиабатическом процессе работа
излучения произведена за счет убыли внутренней энер-
энергии. В конце расширения внутренняя энергия
V'U'v dv = VUV dv — p dV,
ИЛИ
V'U'v* dv = VUV dv — -jUv dv Al/.
Поэтому энергия объема в конце расширения с уче-
учетом уравнения F,7) будет равна:
'vr dv.
Сократив последнее равенство на d\\ получаем:
Отсюда с учетом равенства F,6) получаем:
VUv—jUvAV^VU'v.-}-jUrvAV. F,9)
Но
10 В. Ф. Ноздрев 145

Подставив в последнее равенство Av из равенства
F,6), получим:
Подстановка полученного выражения в равенство
F,9) дает:
Последнее уравнение удовлетворяется решением ви*
да:
{/ F,10)
где F — неопределенная функция.
Выведем зависимость между температурой и объемом
в адиабатическом процессе.
Воспользуемся соотношением F,2), положив в нем
d'Q=0 и подставив е из выражения закона Стефана —
Больцмана F,4):
или, так как е=0Г4,
^L__3il rein
Интегрируя это равенство, получим
\nV = — 3In Г+const,
откуда
V7* = const, F,12)
Перепишем выражение F,10) с учетом последнего
соотношения:
(f) FЛЗ)
Это выражение и представляет собой закон смеще*
ния Вина.
Одни термодинамические методы без дополнительных
предположений не позволяют определить вид функции f.
Если перейти от рассмотрения частот к рассмотрению
длин волн, положив
146

где Exdk-~ энергия единичного объема, заполненного
излучением с длиной волн в границах между А и X+dX,
и поскольку
v — с F —И dv — с П
то формулу закона Вина можно переписать в виде:
5 F,14)
Экспериментальная зависимость Е% от А при фикси-
фиксированной температуре, построенная для разных темпера-
температур, позволяет заключить, что если Амакс — длина волны,
соответствующая максимуму А, то
К*ксТ = const. F,15)
Вскрыть вид функции f в формуле закона Вина
позволяет формула излучения Планка.
г
?5
Формула излучения Планка
На основании методов статистической физики можно показать,
что если имеется большое количество независимых плоскополяри-
зованных гармонических колебаний одинаковой частоты, то наибо-
наиболее вероятно такое распределение осцилляторов, при котором число
их с энергией, находящейся в промежутке между Е и E+dE, есть
Е
Ае~ kT dE, F,16)
где А — константаг Т — абсолютная температура и k — постоянная
Больцмана.
Если приращение энергии dE задать в окрестности значений
?*0, ?=8, ?=2с и т. д.* то количества осцилляторов, обладаю-
обладающих энергией в этих пределах, относятся как
е 2е_
l:e~kT:e kT.
Если N осцилляторов имеют энергию в интервале dE около
нуля, полное число осцилляторов можно представить как
+e~kT +e kT+...). F,17)
Тогда энергия всех этих осцилляторов равна:
F,18)
10* М7

Средняя энергия осциллятора будет равна частному от деле-
деления энергии всех осцилляторов на их число:
F.19)
— 1
Как известно, классическая механика предполагает, что энер-
энергия каждого осциллятора меняется непрерывно. Поэтому, если
е->0, то последнее выражение в классическом приближении дает
kT, что соответствует равномерному распределению энергии по сте-
степеням свободы.
Для дальнейшего важно выяснить число независимых колеба-
колебаний, которые может иметь сплошная среда. Так, например, струна
имеет, как известно, помимо основной частоты ряд обертонов, ка-
каждый из которых независим. Вейль показал, что число независимых
колебаний единицы объема, лежащих в интервале частот между
v и v+rfv, равно
4л -г- v2 dv.
с
Однако, поскольку колебания, поляризованные во взаимно перпен-
перпендикулярных плоскостях, для каждого направления распространения
волн независимы, последнее выражение следует удвоить* Так как
— с
V~~X
и
, с ,.
dv = —р- tf л,
то число независимых колебаний в единице объема пустого про-
пространства, длина волны которых ограничена пределами X и X+dX,
равно
8зтЛ dX,
Правильное решение проблемы излучения может быть получе-
получено лишь на основе квантовых представлений. Планк принял по-
постулат: единственно возможные энергии простого гармонического
колебания, имеющего частоту v, суть
nhvt
где л = 0, 1, 2, 3 ... и h = const; получившая название «постоянной
Планка».
Тогда е в выражении F,19) следует принять равным не кулю,
как в классическом приближении, a hv или -у-.
Поэтому средняя энергия колебания, длина волны которого X,
при температуре Т равна
1 -. F,20)
Не
е ккт — ]
148

Полученное выражение, будучи умножено на общее число ко-
колебаний в единице объема, длина волны которых заключается ме-
между X и X+dX, дает энергию излучения
отсюда
Qt*Us>
F,22)
Это выражение и представляет собой формулу Планка.
Длина волны, отвечающая максимуму кривой распределения,
удовлетворяет соотношению:
=0. F,23)
Лмакс
Дифференцируя формулу Планка, получим:
he
;v+i ^ =li Fi24)
откуда
ж^у = 4,9651;
F>25)
Таким образом, постоянная, стоящая в формуле F,15) спра-
ва* оказалась связанной с постоянной Планка h и постоянной
Болщмана к. Экспериментальное ее определение позволяет опре-
определить из формулы F,25) постоянную Планка.
0е
Г Задачи и упражнения
1. Определить cv, ср, cp — cv, — для
единицы объема равновесного излучения.
Решение. По определению:
Для равновесного излучения:
и /? = -
149

поэтому
<V^4aF3 = 7,3 . 1(Г22Г3 (кал/град ¦ см%
Поскольку давление и температура излучения не не-»
зависимы, то, следовательно, они не определяют состоя-
состояния излучения.
Состояние излучения характеризуется переменными
р и V или Т и V, при этом
Таким образом, из равенства
заключаем, что для равновесного излучения
с —с =оо y==^- = oo
Р ' су
2. Сравнить Су излучения с cv идеаль*
ного газа, используя данные задачи 1.
Отв.
Су
ИЗЛуЧ - , Hft-lS'pZ
3. Найти энтропию равновесного излучения.
Отв. S=ja
ЛИТЕРАТУРА
1. О. Д. ХВОЛЬСОН,
Курс физики, т. III, Госиздат, 1923.
2. Б. Б. ГОЛИЦЫН,
Собр. соч-, т. IV, 1959.
3. М. ПЛАНК,
Термодинамика, Госиздат, 1925.

глава седьмая Термодинамические
функции
Как было показано в главе четвертой,
при решении разнообразных конкретных термодинами-
термодинамических задач может быть использован метод вообра*
жаемых циклов, при условии, что их построение не про*
тиворечит первому и второму законам термодинамики.
В частности, таким путем было получено уравнение
Клапейрона — Клаузиуса D,23). Этот метод приводит
к правильным результатам, однако его применение часто
бывает затруднительным. Причина этих затруднений
состоит в том, что не всегда легко придумать необходи-
необходимый цикл в каждом конкретном случае.
Поэтому в настоящее время вместо метода мыслен-»
ного построения цикла пользуются главным образом
аналитическим методом, впервые примененным Гиббсом.
Предложенные им термодинамические функции обла-
обладают некоторыми важными свойствами.
Если известно аналитическое выражение любой тер*
модинамической функции через независимые параметры
системы, то это позволяет определить в явной форме все
термодинамические величины изучаемой системы. Все
термодинамические функции аддитивны, т. е. значение^
их для сложной системы, состоящей из нескольких неза-
независимых частей, равно сумме значений этих функций для
отдельных частей.
Дифференциалы термодинамических функций яв«
ляются полными дифференциалами, следовательно, сами
термодинамические функции являются функциями со-
состояния.
П|эи равновесии систем термодинамические функции,
каждая при определенных условиях, проходят через
экстремальные значения.
Рассмотрим несколько таких функций, предложенных
Гиббсом.
151

§'
Внутренняя энергия как
термодинамическая функция
На основании первого начала термодина-
термодинамики B,8) можно написать выражение для дифферен-
дифференциала энергии системы:
dU^d'Q — d'W. G,1)
Учитывая выражение второго начала термодинамики
E,12) и формулу B,1) для вычисления элементарной
работы, перепишем равенство G,1) в виде:
dU=TdS — ydx. G,2)
Для частного случая, когда работа, совершаемая си-
системой, есть работа расширения, соотношение G,2) при-»
нимает вид:
dU^TdS — pdV. G,3)
Отсюда следует, что U=U(S, х), или, в частном слу-
случае, U=*U(S, V).
Пользуясь соотношением G,3), найдем значения
частных производных:
(д[1\ Т
или для частного случая:
Полученные частные производные имеют в термоди*
намике большое применение, поскольку они связывают
параметры, характеризующие состояние системы.
Покажем, что внутренняя энергия удовлетворяет и
второму свойству термодинамических функций. Действи-
Действительно, исходя из выражений первого и второго начал
термодинамики E,12) и G,1), легко получить соотно-
соотношение:
dU+ydx—TdS^O, Gt8)
или в частном случае
dU + pdV — TdS^O.
152

Допустим, что изменения объема и энтропии системы
равны нулю, т. е. dV=0[dx=0] и dS = 0.
Тогда соотношение G,8) принимает вид: dU^CO, т. е.
в состоянии равновесия внутренняя энергия про*
ходит через минимум, а при необратимых про*
цессах изменение ее меньше нуля.
Свободная энергия
Термодинамическая функция, получив-
получившая название свободной энергии, записывается в виде:
F^U—TS. G,9)
Так как U, 5, входящие в равенство G,9), являются
функциями состояния, то и свободная энергия F есть
функция состояния, т. е. дифференциал ее является пол*
ным.
Действительно,
G,10)
откуда с учетом равенства G,3) получим:
dF^ — SdT — ydx, G,11)
т. е.
F = F(T, х).
Найдем значения частных производных:
(w)x=-s>
Покажем, что в условиях равновесия системы сво-
свободная энергия при определенных условиях также про-
проходит через минимум.
Воспользуемся соотношением G,8). Если а?л:=О,
dT = Oy то с учетом равенства G,9) имеет место условие:
d(U— 7\S)<0,
или
153

§ Тепловая функция, или энтальпия
Термодинамическая функция, получив-
получившая название энтальпии или тепловой функции, записы-
записывается в виде:
J^U+xy G,14)
или для случая простой системы
J = U+pV. G,15)
Как видно из равенства G,14), тепловая функция
является функцией состояния, ее полный дифференциал
равен:
dJ=.dU+xdy+ydx, G,16)
Используя равенство G,2), получим:
dJ=TdS + xdy, G,17)
откуда
Найдем выражение для частных производных:
№).-*¦ <7-19>
В частном случае для простой системы:
Если в соотношении G,8) положить dS = 0, dy = Q, то
с учетом равенства G,14) получим:
т. е. в состоянии равновесия системы имеет место усло-
условие минимума энтальпии.
Термодинамический потенциал Гиббса
Термодинамическая функция
Ф^и—TS+xy G,20)
получила название термодинамического потенциала
Гиббса. Он также обладает полным дифференциалом,
154

так как все входящие в него параметры являются функ-
функциями состояния:
d<P = dU—TdS — SdT~{-xdy + ydx. G,21)
Принимая во внимание соотношение G,2), можно за*
писать:
G,22)
т. е. Ф = Ф(Т, у).
Значения частных производных:
#), —А Р,23)
или для частного случая системы x—V
дф\ Я
др)т
Если в соотношении G,8) положить dy = O, dT=O, то
с учетом равенства G,20) получим:
d(U-\-xy—TS)^Q> т. е. <2Ф<0.
К рассмотренным четырем функциям (?/, F, /, Ф)
необходимо добавить ранее изученную нами функцию SH
(энтропию), также являющуюся термодинамической
функцией.
С помощью любой из рассмотренных выше термоди*
намических функций можно характеризовать различные
термодинамические процессы. Однако для описания
каждого определенного процесса наиболее подходящей
бывает одна из них. Например, энтропия наиболее под-
подходит для описания адиабатических процессов; свобод-*
ная энергия — для описания изотермических процессов
и т. д.
Как определить, какая термодинамическая функция
наиболее удобна для описания заданного конкретного
термодинамического процесса? Если, например, мы изу*
чаем систему, для которой в условиях термодинамиче*
155

ского равновесия Т=const; р=const, то наиболее подхо-
подходящей термодинамической функцией для описания такой
системы будет потенциал Гиббса Ф, так как
= /G\ р).
§
Химический потенциал
При рассмотрении термодинамических
функций количество вещества в системе считалось неиз-
неизменным. Чтобы учесть изменение этих функций при из-
изменении количества вещества в системе, необходимо
к дифференциалу каждого термодинамического потен-
потенциала добавить член \xdti, где п — число частиц веще-
вещества в системе, a \i — коэффициент пропорциональности.
В этом случае термодинамические функции будут
описывать также и те системы, в которых совершаются
процессы с изменением количества вещества.
Например,
dJ^TdS-{-xdy-{-\xdn, G,25)
отсюда
Так как все рассмотренные функции U, F, /, Ф, S
имеют размерность энергии, то согласно формуле G,26)
коэффициент пропорциональности ^х может быть опре-
определен как энергия, отнесенная к одному молю. Этот ко-
коэффициент получил название химического потенциала.
Таким образом,
химический потенциал характеризует изменение
энергии при изменении количества вещества в си-
системе на один моль.
Выражение G,25) справедливо для системы, состоя-
состоящей из однородных молекул. Если же система состоит
из разнородных веществ, последний член в формуле
G,25) надо представить в виде суммы
23 М*,. G>27)
Здесь
G,28)
4'S,y, nvn2,...t n._v пш
156

характеризует изменение энергии при изменении коли-
количества данного компонента вещества в системе на один
моль.
Понятно, что химический потенциал можно опреде-
определить, исходя не только из выражения тепловой функ-
функции / G,26), но и из выражения любой другой термоди-
термодинамической функции. При этом по определению
Щ —(Щ -1Щ —(??] -и
S Соотношение взаимности41
Если продифференцировать уравнение
G,4) по х при постоянном 5, а уравнение G,5) по 5 при
постоянном х, то в результате сопоставления равенств
GД) и G,5) получим:
(?).--(*).•
Аналогичным образом из уравнений G,12) и G,13)
следует:
dS\ _(ду\
Из уравнений G,18), G,23) и G,24) соответ-
соответственно могут быть получены соотношения:
Уравнения G,30) — G,33) являются соотношениями
взаимности. Они фактически получены из уравнения
G,2) и являются, таким образом, следствиями перво'го
и второго начал термодинамики. Применение уравне-
уравнений G,30) — G,33) весьма упрощает решение многих
термодинамических задач. Покажем это на примере по-
получения уравнения Клапейрона — Клаузиуса.
* См. § 2, гл. 2.
157

Это уравнение было получено нами ранее из рассмо*
трения так называемых круговых процессов. Более про-
просто оно может быть выведено из уравнения G,31).
Положим в нем x=v и #=/?, тогда
Рассмотрим систему жидкость — насыщенный пар в
сосуде постоянного объема. Поскольку превращение
жидкости в пар происходит при Г=const и общий объем
системы не изменяется, соотношение G,34) можно пе-
переписать в следующем виде:
Для рассматриваемой системы
dS=*j*.= *Lm G,36)
Подставив значение dS в уравнение G,34), получим?
— * -" или Т% = -±-. G,37)
Т (v2 — v,) — dT ' """ л dT — v2 — i/,
Разобранный пример убедительно показывает боль*
шие преимущества метода термодинамических функций
перед методом воображаемых круговых процессов.
Как было отмечено выше, каждая из термодинами-*
ческих функций имеет свою область применения. Сво-
Свободная энергия, например, применяется для анализа
изотермических процессов, термодинамический потен-
потенциал Гиббса — при исследовании изотермо-изобариче-
ских процессов и т. п. Однако, чтобы показать пригод-
пригодность какой-либо термодинамической функции для ана-
анализа той или иной системы, необходимо прежде всего
дать подробный анализ самой функции.
В этой главе мы остановимся на подробном анализе
физического содержания и практических применений
свободной энергии и тепловой функции.
В главе 8 такому анализу будут подвергнуты вну-
внутренняя энергия и термодинамический потенциал Гибб-»
са. Энтропия была рассмотрена выше (см. гл. 5).
158

Физический смысл понятия свободной
энергии
Рассмотрим более подробно свободную
энергию как термодинамическую функцию. С этой
целью запишем еще раз выражения для F и dF:
F=U—TS\ dF =
Установим в общем виде связь между свободной
энергией и работой, совершаемой системой. Допустим,
что в замкнутой адиабатической системе В имеется дру*
гая адиабатическая система А (рис. 42). Обозначим их
температуру через Г. Внутри этих систем могут проис-
происходить различные процессы при постоянной темпера-
температуре.
Если обозначить через dU изменение энергии вну*
треннего тела А и через dV— изменение энергии внеш-
внешнего тела — среды В, то по закону сохранения энергии
для всей замкнутой системы:
dU+dU' = Q* G,38)
Согласно второму началу термодинамики
dS+dS'^O, G,39)
где dS — изменение энтропии тела А и dS' — изменение
Штропии среды В.
Предположим, что подсистема А совершает работу
над телами, находящимися в окружающей ее среде В,
и передает последней при этом некоторое количество
теплоты. Тогда согласно первому началу термодинами-
термодинамики определим изменение внутренней энергии среды В:
dUf = TdS'+d'W. G,40)
Поскольку нас интересует свяаь внутренней энергии
тела В с совершаемой им работой, то из соотношений
Рис. 42.
Щ

G,38), G,39) и G,40) следует исключить величины,
относящиеся к внешней системе В. Для этого найдем из
равенства G,38) значение dU' и подставим его в ра-
равенство G,40). Полученное соотношение будет иметь
вид:
— dU^ TdS'+d'W, G,41)
откуда
dS'=~~dU~d'W . G,42)
Решая совместно выражения, находим:
dS ~ > 0. G,43)
Отсюда путем ряда простых преобразований, считая
J*= const, получаем:
dF^ — d'W. G,44)
Соотношение G,44) позволяет раскрыть физический
смысл понятия свободной энергии. Для обратимого про-
процесса оно записывается в виде:
dF^ — d'W, G,45)
или
— dF^d'W. G,450
Из выражений G,45) и G,45/) следует, что измене-
изменение свободной энергии системы равно совершаемой ра-
работе. При этом знак минус в формуле G,45) указывает
на совершение внешней работы над системой, приводя-
приводящей к увеличению ее свободной энергии. В формуле же
G,45') знак минус указывает на совершение работы са-
самой системой за счет ее свободной энергии, в резуль-
результате чего последняя уменьшается.
Подставив в равенстве G,45') значение dF, найден-
найденное из соотношения G,10), получим:
dU — d(TS) = d'W,
или, поскольку процесс протекает изотермически,
d'W^~{dU~T dS). G,46)
160

Наконец, пользуясь равенствами G,45) и G,46), по-
получаем:
dF = dU—TdS. G,47)
Анализ соотношений G,46) и G,47) показывает, что
свободная энергия системы представляет собой часть ее
общей энергии, за счет которой при изотермическом
процессе совершается внешняя работа.
Таким образом, общую энергию системы можно пред-
представить в виде суммы двух слагаемых:
U=(U—TS)+TS, G,48)
где первое слагаемое равно свободной энергии систе*
мы /% а второе слагаемое TS представляет собой ту
часть энергии, которая не может быть использована для
совершения работы и выделяется в виде теплоты. Энер-
Энергию TS согласно ее физическому смыслу Гельмгольц
назвал связанной энергией.
$ Свободная энергия и максимальная работа.
Уравнение Гиббса—Гельмгольца
Для необратимого изотермического про-
процесса соотношение G,44) имеет вид:
dF<—dfW, G,49)
говорящий о том, что увеличение свободной энергии в
этом случае меньше работы, совершаемой над системой.
Если выражение G,45') проинтегрировать между не-
некоторыми начальным и конечным состояниями системы,
то можно определить работу W=Fi—F2, а в случае не-
необратимого процесса
W>F2-FV
Отсюда следует, что
наибольшая работа, которую система может со-
совершить в изотермическом процессе между двумя
данными состояниями, получается при обратимом
процессе между этими состояниями. Максималь-
Максимальная работа равна разности свободных энергий
этих двух состояний:
W F — F
™ макс — * 1 л 2*
11 В. Ф. Ноздрев 161

Найдем уравнение максимальной работы. Для этого
используем уравнение Гиббса — Гельмгольца, которое
легко получается из объединении формул G,9) и G,12)
и имеет вид:
Допустим, что система изотермически переходит из
одного состояния в другое. Тогда % перв&м состоянии:
Л-Ц+г^. GД))
и во втором состоянии:
(^). G,50')
Найдем разность свободной энергии двух состояний,
равную максимальной работе процесса:
W^^F.-F^U.-U.+ T^F.-F^y, G,51)
ИЛИ
Wmm = -A(/+ T (^Р")к , G,52)
где
Так как для изохорического процесса первое начало
термодинамики B,9) имеет вид:
или
Qv^U2~Ui = dU1 G,53)
то, подставляя значение dU в равенство G,51), найдем:
. G,54)
Уравнение G,54) называется уравнением максималь*
ной работы. Оно устанавливает связь между тепловым
эффектом и максимальной работой реакции при посто*
янных Т и V*
162

о9
$ Электродвижущая сила гальванического
элемента
В качестве примера применения свобод*
ной энергии для решения термодинамических задач рас*
смотрим связь электродвижущей силы гальванического
элемента с другими параметрами, характеризующими
состояние системы. Остановимся на рассмотрении слу-
случая обратимого изотермического процесса. Запишем
выражение работы гальванического элемента:
d'W = Ede, G,55)
где Е — электродвижущая сила элемента, е — заряд,
протекающий в цепи за время изотермического процесса.
Принимая во внимание уравнение G,45), получим:
dF = — Ede> G,56)
или
Fx—F2 = Ee, G,57)
т. е. работа, совершаемая гальваническим элементом,
равна разности свободных энергий в первом и во втором
состояниях его. Для нахождения этой разности запишем
уравнение Гиббса — Гельмгольца для обоих состояний:
G,58)
G,59)
\ V* / у
отсюда
fl — P2^=Ul — U2-\-Tw(Fl — F2)v. G,60)
Обозначим
Ul — U2==qe, G,61)
где q — количество теплоты, выделяемой в результате
реакции на единицу заряда.
Уравнение G,60) с учетом равенств G,57) и G,61)
можно переписать так:
ИЛИ
и*

Выразим величины Е и q через разности F4—F2 и
ц1—и2а Из равенства G,57)- имеем:
FF G,63)
E
и из равенства G,61)
д=^=^-. G,64)
Из выражений G,62), G,63), G,64) находим:
дТ)у—С Ч— е е
= }[(Л-^.)-(^-^)]. G,65)
Учитывая, что
F=U— TS,
получим:
или
где S2—5i — разность энтропии в конечном и начальном
состояниях гальванического элемента.
Интегрируя выражение d'Q = TdS при Т = const и
подставляя результат в равенство G,66), окончательно
получаем:
2L\ —Q
WJv — е •
где Q — количество теплоты, полученное элементом от
термостата. Отсюда следует, что если э. д. с. гальвани-
гальванического элемента возрастает, т. е. -^ > 0, то количество
теплоты положительно и, следовательно, работа эле-
элемента совершается за счет его химической энергии и
притока теплоты от термостата.
Если-дтр-<0, то Q<0. В этом случае часть химиче-
химической энергии элемента выделяется в виде теплоты, ухо-
уходящей в термостат.
164

Таким образом, с помощью термодинамического ме-
метода установлена связь между параметрами гальваниче*
ского элемента.
Так как многие химические реакции протекают изо-
изотермически, то свободная энергия особенно часто ис-
используется в химической термодинамике.
§¦
МО
Свободная энергия равновесных систем
Рассмотрим системы, в которых измене-
изменение объема, а следовательно, и внешняя работа равны
нулю. Для них изменение свободной энергии согласно
соотношению G,44)
Отсюда можно заключить, что при неравновесном
процессе свободная энергия системы уменьшается и по
достижении равновесия имеет минимум. Это дает воз-
возможность с успехом изучать изотермические равновесия
системы, а для случая неравновесных процессов опре-
определять, насколько близко или далеко находится система
от состояния равновесия.
Фазовые превращения многих систем происходят изо-
изотермически при постоянном объеме. Например, серое
олово превращается в белое при определенной темпера-
температуре и при F==const. Различие этих модификаций обу-
обусловливается их различным строением, различным вза-
взаимным расположением их молекул. Другой пример.
Кварц при температуре 576° С превращается из ос-моди-
ос-модификации в р-модификацию.
Изучение таких систем удобно производить, исполь-
используя свободную энергию (см. задачу 10, гл. 7).
Поверхностное натяжение и поверхностное
давление. Найдем условие равновесия в системе, состоя-
состоящей из жидкости (I) и пара (II), при F=const и V=const.
В этом случае удобно воспользоваться свободной энергией
как термодинамической функцией.
Выражение для дифференциала свободной энергии
в этом случае будет иметь вид:
dF = — p' dV — f dV"+ о dS G,68)
165

(температура и химические потенциалы жидкости и
пара одинаковы).
При равновесии dF=0, поэтому
adS — p' dV — f dV" = 0. G,69)
Учитывая, что
V' + Vff = V = const,
получим:
4
dS
Величина ~-ту? определяет кривизну поверхности раз-
раздела жидкости и пара.
В случае сферической поверхности
dS 2
(г принято считать положительным, когда кривизна по-
поверхности направлена в жидкость).
В случае произвольной поверхности
dV'
где г\ и г2 — главные радиусы кривизны поверхности.
Итак, при равновесии сферических капель жидкости
с паром давление в капле р' и давление пара р" свя-
связаны условием:
или
Значит, на поверхности раздела капля — пар суще-
существует скачок давления, равный — (при сферической
форме капли) и о( 1 ) (при произвольной форме
поверхности жидкости). Величина — (для сферической
капли) или о(~-\-—\ (при произвольной фарме по-
поверхности жидкости) называется поверхностным
давлением или давлением Лапласа.
166

В случае плоской поверхности (г=оо) раздела жид-»
кости и пара давление Лапласа равно нулю и условием
равновесия системы жидкость — пар при заданных ус*
ловиях будет р'~р".
§¦
Ml
Тепловая функция. Эффект Джоуля—
Томсона
Как известно, внутренняя энергия иде*
ального газа, представляющая собой кинетическую
энергию движения молекул, определяется только тем-»
пературой газа.
Зависимость внутренней энергии реального газа от
объема и давления проверялась Джоулем на следующем
опыте. Брались два сосуда, соединенные трубкой с кра-
краном. В одном из сосудов находился газ при давлении /?,
а в другом был создан вакуум. При открытии крана
воздух необратимо расширялся в пустой сосуд без со-
совершения внешней работы. Оба сосуда находились в ка-
калориметре, и никакого изменения температуры после
открытия крана замечено не было. В связи с этим был
сделан вывод, что внутренняя энергия газа не зависит
от объема. Однако изменение температуры газа в этом
опыте определялось по изменению температуры калори-
калориметра. Поэтому точность этого измерения была очень
низкой.
Позднее этот опыт был повторен Джоулем и Томсо-
ном и привел к установлению зависимости внутренней
энергии от объема.
В новом опыте в соединительную трубку между со-
сосудами помещалась пробка из пористого вещества
(ваты), а разность температур газа определялась с по-
помощью двух чувствительных термометров, помещенных
по разные стороны пробки. Газ протекал по трубке с пе-
перепадом давлений в месте, где была расположена
пробка. Процесс течения газа по-прежнему был необра-
необратимым. При измерении температуры по обе стороны
пробки была обнаружена незначительная разность тем-
температур. Для большинства газов температура с той сто-
стороны пробки, где давление было меньше, оказывалась
ниже. Для водорода изменение температуры оказа-
оказалось обратным. Этот эффект, заключающийся в измене-
изменении температуры газа при расширении, называется
167

Pi
Рис. 43. Схема опыта по выявлению эффекта Джоуля — Томсона.
эффектом Доюоуля — Томсона. Он обусловлен отступле-
отступлением свойств реальных газов от идеальности.
На рис. 43 представлена схема этого опыта. Газ пе-
переходит из объема I с давлением pi в объем II с давле-
давлением /?2. Давление р\ и р2 будем считать постоянным,
что может быть достигнуто введением в рассматривае-
рассматриваемые объемы подвижных поршней Пх и Я2, на которые
действуют постоянные силы. В рассматриваемом случае
стенки сосуда и пробка не проводят тепла.
Если один моль газа перешел через пробку из объ*
ема I в объем II без притока теплоты извне (аГB-=О), то
изменение внутренней энергии газа U2—Ui равно работе
V V2, поэтому
Каждая из частей равенства представляет собой теп*
ловую функцию, и, следовательно, рассматриваемое
течение газа происходит при постоянной энтальпии /.
Выразив дифференциал энтальпии G,17) через перемен-
переменные Тир путем замены dS выражением
получим:
Учитывая, что в данном случае d/=0, можно запи^
сать для изменения температуры газа с изменением
давления следующее выражение:
дТ
168

где значок / при производной обозначает, что произвол*
ная берется при постоянной энтальпии. Из определения
энтропии и теплоемкости при постоянном давлении еле*
(dS\ CP гг
дует, что rjfl — -у Далее, заменяя
др)т~ \дт)р*
получим окончательное выражение:
т
(ЁЦ -
\dpjj-
Производная (-дтг) показывает, насколько изме*
нится температура газа при изменении давления на еди*
ницу, и определяет дифференциальный эффект Джоу-
Джоуля— Томсона. Теплоемкость в нашем случае всегда
меньше нуля, поэтому знак изменения температуры прв*
тивоположен знаку числителя. Зная уравнение состоя-
состояния газа, можно определить величину и знак производи
и (дТ\
Для идеального газа, используя уравнение состоя-
состояния A,6), найдем:
\дТ)р- р '
Следовательно,
Для газа, подчиняющегося уравнению Ван-дер-Ва-*
альса A2,2), найдем выражение ~^- при постоянном
давлении из формулы:
(ГУ \ г" DT Оя т
•«Л \ ^/'Г» I *\* ¦ль* ,т г л
~v~=~b) dr—[(v~by~~T?\dV===0-
Считая, что V^b, RTV^>a, с помощью простых преоб*
разований получим:
2а ь
9,=JV" G>72)
169

Поскольку а и Ь постоянны, то при Т = -щ знак
температурного эффекта должен меняться. Величина
Т = ~ называется температурой или точкой
инверсии и обозначается Тияв. Температура инвер-
инверсии зависит от давления газа. Зависимость Гинв от дав-
. (дТ\
ления называется кривой инверсии, вдоль которой 1-хг)
равно нулю. Эта кривая отделяет положительную об-
область от отрицательной.
Температуры инверсии ряда газов при нормальном
давлении следующие:
Газ
Гелий
Водород
Азот
Кислород
Углекислый газ
Т°К
34
216
865
1040
2050
Т°С
--239
—57
592
763
1777
Температура инверсии гелия и водорода значительно
ниже комнатной, поэтому для этих газов должно наблю-
наблюдаться повышение температуры. Температура инверсии
остальных газов выше комнатной, и при нормальных
условиях должно наблюдаться понижение температуры.
Это свойство азота, кислорода и углекислого газа
используется в холодильной технике для получения низ-
низких температур в так называемой машине Линде, где в
результате многократного расширения газа его темпера-
температура понижается. При этом учитывается интегральный
эффект Джоуля — Томсона:
Рх
§
12
Сопло Лаваля
В технике очень часто приходится иметь
дело. с течением газа или пара по трубам. При этом
всегда стремятся получить поток газа с очень большой
170

скоростью, чтобы использовать его кинетическую энер-
энергию в турбинах или реактивном двигателе. Для случая
течения газа по трубе переменного сечения выполняется
следующее соотношение:
= const, G,74)
где Q(x)—сечение трубы, со(х)—скорость потока газа,
v(x)—удельный объем, х — координата, меняющаяся
вдоль трубы.
Казалось бы, что, уменьшая сечение трубы и увели-
увеличивая давление, можно получать сколь угодно большие
скорости газового потока. Однако с помощью только
суживающейся трубы не удалось получить скорость по-
потока, превышающую «местную» скорость звука в трубе.
Рассмотрим течение газа по трубе с большой ско-
скоростью. Теплообменом со стенками в этом случае можно
пренебречь, т.е. можно считать, что процесс происходит
адиабатически: dS — Q. Но необходимо учитывать также
кинетическую энергию потока газа. Поэтому полная
энергия газа будет равна:
^ ^ G,75)
<В2 (JC)
где —~—кинетическая энергия одного моля газа.
Изменение полной энергии должно равняться нулю,
т. е. учитывая, что dS = 0:
/> 2 Не)
Для адиабатического процесса dp = ^-, где с~-
скорость звука. Тогда связь скорости потока с удельным
объемом будет иметь вид:
Найдя дифференциал от выражения G,74), можно
получить связь удельного объема со скоростью потока и
сечением трубы:
dv
v
171

Из двух последних выражений может быть найдена
связь скорости потока с сечением трубы:
1 t 9 9Ч day с2 du (~ ~а,
-К-с2Oг = ^-ж. G,76)
Исследуем полученное выражение. Рассмотрим сужи-
суживающуюся трубу —г- < 0, считая, что начальная ско.рость
потока меньше скорости звука со<с. Тогда -^ > 0, т. е.
скорость потока при его движении вдоль трубы увеличи-
увеличивается. При этом должен наступить момент, когда эта
скорость CTaHet равной скорости звука: со = с. В правой
части равенства стоит отрицательная величина, для то-
^ d®
го чтобы равенство имело смысл, ~т— должно равняться
±оо. При этом, пока скорость со остается меньше с, про-
происходит ускорение потока, но, как только скорость по-
потока превысит скорость звука, движение переходит в
замедленное. Таким образом, с использованием только
суживающегося сопла нельзя получить скорость потока
больше скорости звука. Скорость потока со = с называет*
ся критической скоростью.
Если в тот момент, когда скорость потока становится
du
равной скорости звука, -j— станет равно нулю, как вид-
видно из уравнения G,76), ~ может оставаться больше
нуля. Если при переходе потока через критическую ско-
скорость сечение трубы в дальнейшем будет увеличиваться,
то скорость потока будет продолжать расти. Поэтому
для получения очень высоких скоростей газового потока
необходимо пользоваться трубой определенной конструк-
конструкции; сначала сужающейся, а затем расширяющейся.
Труба такой формы, применяемая для ускорения газо-
газовых потоков, называется соплом Лаваля. Ускорение га-
газового потока в таком сопле будет происходить только
в том случае, если при -^ = 0 скорость потока будет
точно равна критической скорости. Это достигается спе-
специальным расчетом режима работы сопла Лаваля,
172

Г Задачи и упражнения
1. Пользуясь основным уравнением тер-
термодинамики, установить правило Максвелла: на диа-
диаграмме pV (рис. 44) площадки, образующиеся при
пересечении изотермы Ван-дер-Ваальса эксперименталь-
экспериментальной прямой — изотермой-изобарой, соответствующей
равновесию системы жидкость—пар, одинаковы.
Решение. Первое и второе начало термо-
термодинамики дают:
а в применении к изотермическому циклу:
Т j dS^jdU+j pdV.
Но J dS = 0 и J <Ш=0, поэтому
откуда следует, что площадки 1 и 2 одинаковы.
2. Вычислить термодинамические функ«
ции V, F, J, Ф для равновесного излучения.
Решение. Функции U, F, /, Ф как термо-
термодинамические функции должны быть выражены соответ-
соответственно в переменных:
U=U{S, V), F = F(T, V), / = /(Sf /0, Ф = Ф{Т, р).
Для равновесного излучения U=uV, где и — плот-
плотность энергии, по закону Стефана — Больцмана равная
оТ4, так что U=T4V
Рис. 44. Графики изотермы
Ван-дер-Ваальса и экспери-
экспериментальной прямой изотер-
изотермы-изобары.
V
173

Чтобы представить выражение для V в переменных
S и 1/, необходимо выразить Т через S и V.
Из выражения энтропии излучения S — -joT3V на-
находим:
и
W и
Свободная энергия:
F = U—TS = oT*V— T~-
Энтальпия:
J = U + pV = ~oT*V =TS ^S(?fju.
Термодинамический потенциал Гиббса:
= —±
Отсюда видно, что термодинамический потенциал
Гиббса Ф(Т,Р) не может служить для равновесного из-
излучения термодинамической функцией. Это обусловлено
тем, что р и Т не являются для излучения независимыми
переменными:
1
3, Исходя из того, что dS — полный диф*
ференциал, доказать, что удельные (или молярные) вну*
тренняя энергия и энтальпия идеального газа являются
функциями только температуры.
Указание. При решении задачи удобно восполь-
воспользоваться следующими уравнениями:
dU=* TdS — pdV; dJ=zTdS + V dp.
4. Вычислить химический потенциал \л
идеального газа.
Решение.
174

5. С помощью уравнения термодинамики
G,30) найти изменение температуры при адиабатном
расширении и сжатии тел (для общего случая и для
идеального газа).
Решение. Положив в уравнении G,30)
x=V и */=/?, получим:
dV)s~ \dS)v*
или согласно II началу термодинамики:
dV)s~ l \dQ)v*
Так как правая часть относится к постоянному объ*
ему, то
d'Q dT
дГ
^ L/iL\
или согласно соотношению A,3):
дТ\ Т { др\ (dV
Последнее выражение и является искомым.
Так как \-gy\ <0, т0 знак изменения температуры
противоположен знаку коэффициента теплового расши*
рения а:
В частном случае для идеального газа:
\dT)v— V и \dV)s — ~7^'
6. С помощью уравнения G,30) найти
изменение температуры при адиабатном процессе в галь-
гальваническом элементе.
-(?).—?¦(*).-
175

7. С помощью уравнения G,31) получить
зависимость поверхностного натяжения от температуры.
п да — l (dQ \
8. Показать, что свободная энергия и
термодинамический потенциал идеального газа, у кото-
которого cv « а — ЬТ, равны:
" — ' —ft
9. Показать, что
10. Показать, что при переходе одной
модификации в другую (например, олово или кварц)
удельные свободные энергии обеих модификаций равны
между собой.
Решение. Общая свободная энергия обе-
обеих модификаций при температуре перехода одной моди-
модификации в другую равна:
где Fi и f2 — удельные свободные энергии каждой мо-
модификации.
Так как рассматриваемая система замкнута, то общее
изменение свободной энергии равно нулю, т. е.
dF = Fx dmx -f F2 dm2 = 0. G,77)
При этом масса системы остается неизменной:
m = mx + m2 = const.
Поэтому
или
dmx = — dm2
176

и соотношение G,77) переписывается в виде:
rfm1(F,-JF2) = 0, G,78)
откуда
ft=F2, так как с1т{Ф0.
11. Доказать соотношения:
dV JT—' \dT*Jv
f — Г
dp h~
Указание, Необходимо воспользоваться вторым
началом термодинамики в дифференциальной
форме, определением теплоемкостей и соотноше-
соотношениями взаимности G,31)\ G,33).
12. Показать, что ср—cv — R для идеаль-
идеального газа, пользуясь тепловой функцией.
Решение,
Известно, что
тогда
•(?).-«¦
13. Показать, что ср и cv для идеального
газа не зависят от р и V.
Указание, Необходимо воспользоваться соотно-
соотношениями!
I dV )т ~ XST^/v' \Тр )т==~'
и уравнением состояния *
14. Пользуясь выражением для свобод-
свободной энергии идеального газа (см. задачу 8), найти урав-
уравнение состояния идеального газа.
Указание. Необходимо воспользоваться соотно*
шением G,13}.
12 В. Ф. Ноздрев 177

15. Исходя из уравнения:
и уравнения G,30), вывести соотношение:
16. Найти соотношение между темпера-*
турой инверсии и критической температурой реальных
газов.
Решение. Согласно полученному соотно*
шению G,71):
dp.
СР
Из уравнения Ван-дер-Ваальса
R
дТ )р— р_ а , 2аЬ '
считая, что V^>b и RTV^>at получим выражение G,72)
в виде:
—dpt
P
где ср — молярная изобарная теплоемкость газа.
Так как ??ГИнв=0, то
2а А_п. т — 2а
-5= о — U, 1 инв — -пГ •
*\1 инв ас?
Используя выражение критической температуры для
реальных газов Тк—^-щ- и найДенное выражение для
температуры инверсии, получим:
6,75ГК.
инв = 6,75ГК.
Таким образом, температура инверсии реальных га*
зов (по Ван-дер-Ваальсу) в 6,75 раза больше их крити*
ческой температуры.
178

17. Показать, что изменение кинетиче-
кинетической энергии газового потока при течении по соплу про-»
извольной формы определяется разностью энтальпий на-
начального и конечного состояний газа.
Указание. Следует воспользоваться выражением
G,75).
ЛИТЕРАТУРА
1. Дж. В. ГИББС,
Термодинамические работы, Гостехиздат, 1950.
2. Р. ВЕННЕР,
Термодинамические расчеты, ИЛ, 1950.
3. М. ВУКАЛОВИЧ и И. НОВИКОВ,
Техническая термодинамика, Госэнергонздат, 1962,
4. В. А. КИРЕЕВ,
Курс физической химии, Гостехиздат, 1951.
5. ВАН-ДЕР-ВААЛЬС,
Термостатика, чр. I, Госхимиздат, 1936»
12*

глава восьмая
о термодинамическом
равновесии
в сложных системах
В предыдущих главах рассматривались
в основном только однородные системы с заданным ко-
количеством вещества. Перейдем к установлению условий
равновесия сложных систем. Эти системы делятся в
термодинамике на гомогенные и гетерогенные.
Гомогенной системой называется однородная систе-
система, каждой точке которой в условиях равновесия соот-
соответствуют одинаковые значения давления р, темпера-
температуры Т и концентрации С. К гомогенным системам отно-
относятся все индивидуальные однородные вещества (вода,
спирт, кристаллы соли и др.), смеси разных газов, когда
последние смешиваются в любых пропорциях, жидкие и
твердые растворы в случае полного взаимного смешения
их составных частей.
Гетерогенными системами называют сложные систе-
системы, состоящие из ряда однородных или гомогенных си-
систем. Таковы, например, система лед — вода, растворы
частично растворимых веществ (например, вода — бути-
бутиловый спирт), система лед — вода — пар и т. п.
К гетерогенным системам относятся также суспензии
и эмульсии. Суспензиями называются жидкости, в кото-
которых находятся во взвешенном состоянии частицы твер-
твердого вещества. Такую систему можно получить, если
размешать в воде мелкий порошок какого-либо нерас-
нерастворимого вещества, например глины.
Эмульсиями называют жидкости, в которых находят-
находятся во взвешенном состоянии мельчайшие капельки дру-
другой жидкости. Например, молоко представляет собой
эмульсию мельчайших капелек жира, взвешенных в воде.
Заметим, что многие системы, на первый взгляд ка-
кажущиеся гомогенными, в сущности не являются ими.
Таковы коллоидные растворы, или золи, занимающие
промежуточное положение между истинными растворами
(гомогенные системы) и смесями. В них частицы одного
вещества, распределенные в другом веществе, имеют на-
настолько малые размеры, что обнаружить их можно только
180

при помощи ультрамикроскопа. К коллоидным системам
принадлежит, например, человеческая кровь — входящие
в ее состав эритроциты имеют диаметр 7,5 микрона. Кол-
Коллоидные растворы играют важную роль в химии, биоло-
биологии, медицине, сельском хозяйстве и технологии, поэто-
поэтому изучение их имеет большое значение.
Однородная часть гетерогенной системы, которая
имеет границу раздела и может быть механическим пу-
путем отделена от общей системы, называется фазой. Так,
например, гетерогенная система лед — вода — пары воды
имеет в своем составе три фазы.
Компонентой называется независимая часть физиче-
физической системы, которую можно выделить, не нарушая
условий существования системы. Например, смесь каких-
либо пяти газов состоит из пяти компонентов. В растворе
вода — этиловый спирт две компоненты. Смесь паров
воды, водорода и кислорода при нормальных условиях
имеет три компоненты: Н2О, Н2 и О2.
Если эту систему нагреть до 400° С, то между ком-
компонентами ее возникает химическая реакция: 2Н2О^
ч=^2Н2 4- О и число компонент уменьшится до двух.
В общем случае, если в системе возникли химические
реакции, то компонент будет столько, сколько их было
до реакции, минус число реакций.
Например, обжиг извести сопровождается химиче-
химическим разложением ее на окись кальция и углекислый
газ:
СаСО3-
Такая система рассматривается как состоящая из
любых двух компонент, но не из трех.
Общие условия термодинамического
равновесия гетерогенной системы
Для того чтобы найти условия равнове-
равновесия в сложной термодинамической системе, воспользуем-
воспользуемся тем, что в случае равновесия все термодинамические
функции при определенных условиях проходят через
экстремум (минимум или максимум). Поэтому
(8,1)
Ш

Зная функциональную зависимость термодинамиче-
термодинамических функций от параметров системы, можно найти об-
общие условия равновесия гетерогенной системы.
Для вывода условий равновесия в самом общем слу-
случае воспользуемся внутренней энергией U.
Допустим, что замкнутая гетерогенная система со-
состоит из г фаз и п компонент. Изменение внутренней
энергии для каждой фазы системы по всем ее компонен-
компонентам можно записать так:
dUx = Тх dSx - Pl dVx
dU2 = Т2 dS2 — р2 dV2
(8,2)
-f P> dmf + ... + *x(«) dm[n\
где нижние индексы соответствуют обозначениям фаз, а
верхние — обозначениям компонент.
Сложение равенства (8,2) дает общее изменение
внутренней энергии системы dUt равное в условиях рав«
новесия нулю. Поскольку рассматриваемая система
является замкнутой, имеют место дополнительные усло-
условия, выражающие постоянство энтропии, объема и массы
всей системы:
25 = Ср 2V = C2; Smr = C3. (8,3)
Предположим, что в рассматриваемой системе оста-
остаются неизменными все величины, кроме энтропии первой
и второй фаз. Тогда согласно требованиям (8,3)
dSl = — dS2. (8,4)
Изменение энергии системы:
dU = dUx + dU2 = Тх dS{ + Т2 dS2 = 0 (8,5)
или согласно равенству (8,4):
182

а так
то
как
dSt
= т2.
Если предположить, что в системе меняется только
энтропия второй и третьей фаз, а остальные величины
остаются постоянными, то в результате аналогичных
рассуждений получаем условие T^Tz, затем Г3 = Г4
л т. д.
Следовательно,
при равновесии гетерогенной системы температу-
температуры всех ее фаз равны:
Т^Т2=Т3= ...=ТГ (8,6)
Допустим далее, что в системе меняются только объ*
емы V\ и К2 первой и второй фаз. Тогда изменение
энергии
но так как по условиям (8,3)
то
Но так как
то
А —^2 = 0, или рх=р2.
Аналогичным образом доказываются равенства р2=Рз
и т. д.
Окончательно: /?4~/?2=/?з = - * .=/V- (8,7)
Следовательно,
при равновесии гетерогенной системы давления
во всех ее фазах равны.
Предположим, наконец, что в данной сложной систе-
системе все величины постоянны, кроме количества вещества
первой компоненты в первой фазе и первой компоненты
во второй фазе. Тогда согласно равенству (8,3):
=d^
183

Но так как
то
Если предположить, что изменяется только количе-
количество вещества первой компоненты во второй и третьей
фазах, получим равенство:
|j?) = (lO> И Т. Д.
Таким образом,
в случае равновесия гетерогенной системы для
первой компоненты ее получаем равенство хи-
химических потенциалов компоненты во всех фазах
системы,
Аналогично для всех других компонент доказывается
справедливость следующих уравнений:
(8,8)
Соотношения (8,6) — (8,8) представляют собой уело*
вия равновесия в гетерогенной системе с произвольным
числом фаз и компонент при Т =*const и р = const.
Запишем их вместе:
г, = г2 = ... = тг
Р\ —Pi = ... —рг
(8,9)
Равенство температур Т означает равенство кинети-
кинетических энергий в в фазах сложной системы.
Равенство давлений р в гетерогенной системе свиде-
свидетельствует о наличии в ней механического равновесия.
Равенство химических потенциалов означает, что в
условиях равновесия удельные энергии каждой из ком-
компонент во всех фазах равны.
184

В качестве примера напишем условие равновесия для
трехфазной однокомпонентной системы лед — вода — па-
пары воды:
г = 3; л=1,
Аналогично для двухфазной двухкомпонентной (г = 2,
я = 2) системы, например ненасыщенный раствор NaCl
в воде с учетом паров раствора, условия равновесия
имеют вид:
42
Спрашивается: сколько фаз и компонент в гетероген-
гетерогенной системе могут одновременно находиться в равнове-
равновесии? Ответ на этот вопрос впервые был дан Гиббсом.
§•
?2
Правило фаз Гиббса
Анализ общих условий равновесия (8,9)
показывает, что первые два равенства представляют собой
тождества, остальные — уравнения, так как \i = (-gjjj-1 »
т. е. p, = f(S, V). Число таких уравнений в каждой строке
равно (г— 1), а число строк п. Таким образом, общее
число уравнений п(г—1), а число переменных в системе
(8,9) равно (гп + 2); гп неизвестных химических потен-
потенциалов плюс неизвестные температура и давление. Число
переменных в каждой строке можно сократить на еди-
единицу, если брать вместо абсолютных значений химиче-
химических потенциалов их относительные значения. Тогда
число переменных следует принять равным г(п—1)+2.
Как известно, при решении систем уравнений возмож-
возможны следующие три случая:
1) число переменных равно числу уравнений; систе-
система разрешима;
2) число переменных больше числа уравнений; си-
система совместима, но полностью неразрешима;
3) число переменных меньше числа уравнений; си-
система несовместима.
Нас интересуют первые два случая, т. е. условия:
(г—1)л<г(л—1) + 2,
откуда
2 (8.10)
185

Соотношение (8,10) называется правилом фаз Пгбб-
са, это правило гласит:
для существования равновесия в сложной гете-
гетерогенной системе необходимо, чтобы число фаз
было равно или меньше числа компонент плюс
два.
Число степеней свободы. Для анализа кон-
конкретных систем весьма целесообразно ввести понятие
числа степеней свободы N, определяемого разностью ме-
между числом переменных и числом уравнений:
— (г—1)л;
N = n — г+2.
Число степеней свободы N указывает, сколькими пе-
ременными мы можем распоряжаться свободно. Напри-
Например, вода представляет однофазную однокомпонентную
систему. Для нее iV=l—1+2=2. Это значит, что в такой
системе мы свободно можем менять два любых ее пара-
параметра (например, давление и объем), а вода как фаза
не исчезает.
Для двухфазной однокомпонентной системы (г=2,
я=1), например вода — насыщенный пар воды, iV=I.
Следовательно, в этом случае менять можно свободно
только один параметр. Так, изменение только темпера-
температуры системы хотя и смещает положение равновесия, но
не нарушает его.
Если же одновременно менять два параметра (напри-
(например, давление и температуру), равновесие системы
жидкость — пар нарушится, и это повлечет за собой
быстрое исчезновение одной из фаз системы.
Рассмотрим далее равновесие однокомионентной
трехфазной системы лед — вода — пар. Для нее г=3,
я=1 и N—0. Такая система не имеет ни одной степени
свободы и находится в равновесии только в одной точке,
называемой тройной (рис. 28). В этой точке давление
р=4,575 мм рт.ст. и температура Г=0,0075°С. С изме-
изменением одного из параметров системы (Т или р) одна из
фаз исчезает.
Рассмотрим, наконец, четырехфазную однокомпонент-
однокомпонентсистему (г =М, я= 1). Для нее Af= —1. Это означает,
186

что такая система не может находиться в равновесии ни
в одной точке.
Учитывая, что лед может находиться во многих мо-
модификациях, для воды были экспериментально устано-
установлены условия равновесия ее трех фаз:
Фазы
Лед I — жидкость — пар
Лед I — жидкость — лед III
Лед III —жидкость —лед V
Лед V — жидкость —лед VI
Лед I —лед II — лед Ш
Лед II — лед III — лед V
ГС
0,0075
—22
—17
0,16
-37,7
—24,3
Р
4,575 мм рт. ст.
2П5'кГ/см2
3530 кГ/см2
6380 /cF/cm2
2170 кГ/см2
3510 кГ/см2
Модификация лед IV здесь отсутствует, поскольку
экспериментально она пока не наблюдалась. При задан-
заданных условиях любая из указанных комбинаций фаз
может существовать сколь угодно долго.
В качестве второго примера рассмотрим равновесие
двухкомпонентной системы (д = 2, N~n—г+2=4—г).
Такой системой является раствор поваренной соли в
воде.
1. Если раствор ненасыщенный, система однофазна
(г==1, N==3). Следовательно, в такой системе свободно
можно менять три параметра (давление /?, температур
ру Т и концентрацию С), не нарушая условия равновесия.
2. Для системы ненасыщенный раствор поваренной
соли — пары раствора (г = 2) число степеней свободы
iV=2, т. е. уменьшилось на единицу. В этом случае, не
нарушая условий равновесия, можно изменять два па«
раметра системы.
3. Если в равновесии со своим паром находится на-
насыщенный раствор NaCl (г = 3), то число степеней N=1.
В такой системе свободно можно менять только один из
ее параметров.
4. Наконец, прибавление к только что рассмотренной
системе твердой фазы увеличивает число ее фаз до четы-
четырех (г=4) и уменьшает число степеней свободы до нуля
(N=0). Следовательно, четыре фазы двухкомпонентной
системы могут существовать в равновесии только в од«
ной точке (при определенных темпер-атуре и давлении)*
187

§3
Общие условия равновесия в гомогенной
системе
Как было указано выше, система, со-
состоящая из одной фазы, является гомогенной. К таким
системам принадлежат смеси газов, жидкие и твердые
растворы (при полной взаимной растворимости). Если
рассматриваются смеси или растворы, в которых не про-
протекают химические реакции и состав систем постоянен,
то в таких системах составные части одновременно яв-
являются и компонентами. Например, N2 и HJ, N2, O2 и Аг
и т. д.
Для термодинамики особый интерес представляют
такие гомогенные системы, в которых протекают хими-
химические реакции.
Каковы условия равновесия системы, в которой про-
протекают химические реакции между ее составными ча-
частями? В каком соотношении должны находиться ее
компоненты? Ответы на эти вопросы дает закон дей-
действующих масс, но прежде чем перейти к выводу этого
закона, найдем общие условия равновесия таких систем.
Учитывая, что многие химические реакции протекают
при постоянных значениях температуры и давления,
удобно для вывода условий равновесия гомогенной си-
системы взять термодинамический потенциал Гиббса:
T). (8,11)
Как известно, при равновесной системе
Выражение (8,11) записано для случая, когда масса
компонентов системы остается постоянной. В общем слу-
случае, когда меняется и масса компонентов, будем иметь:
m
ai
= /G\ р, nv n2,
+(<») dP+
188

Если r=const и /? = const, то
Цж^)рТп п dnk=°- (8>12)
В уравнении (8,12) частные производные при dtii яв-
являются химическими потенциалами:
Следовательно, уравнение (8,12) можно коротко за-
записать в следующем виде:
2Мя* = 0. (8,120
Сумма произведений химических потенциалов на из-
изменение массы каждой компоненты равняется нулю.
В последнем равенстве масса выражена в числах мо-
молей компонент реагирующей смеси, в которой протекает
химическая реакция
Изменение числа молей г-го компонента выразится
произведением v dn, где dn — количество грамм-эквива-
грамм-эквивалентов реагирующего вещества. Тогда равенство (8,12')
примет вид:
2 0. (8,12")
Выведем условия равновесия в раскрытом виде для
случая смеси идеальных газов.
Для анализа этой системы необходимо знать конкрет-
конкретные выражения через параметры состояния внутренней
энергии ?/, энтропии S, объема V.
§•
Внутренняя энергия и энтропия смеси
идеальных газов. Закон действующих
масс
Для одной грамм-молекулы идеального
газа внутренняя энергия Ui^CiT, где с% — теплоемкость
при V=const
189

Внутренняя энергия смеси газов выразится поэтому
как сумма:
Это выражение действительно, если имеет место фи-
физическое смешение газов беа химических реакций. Если
при смешении газов между ними возникает реакция, то
внутренняя энергия смеси будет равна:
^ = ЕадГ+2ад,, (8,13)
где под Пг подразумеваются числа грамм-молекул как
исходных газов, так и продуктов реакции, a qt — хими-
химическая энергия, выделенная или поглощенная одним мо-
молем при наличии реакции.
Выражение E,19) энтропии идеального газа запишем
в переменных 7, V для одного моля ?-й компоненты до
смешения:
где hi = ci In
Определим значение энтропии той же компоненты
после смешения.
Каждый газ после смешения занимает объем всего
сосуда У, а одна грамм-молекула каждого газа зани-
v
мает объем V — —.
щ
Известно* что при адиабатическом расширении энтро-
энтропия газа S2 увеличивается по сравнению со значением
энтропии Si до расширения на величину
Пользуясь этой формулой, можно записать выраже-
выражение энтропии одного моля каждой компоненты после
смешения:
или
Преобразуем величину Vf следующим образом:
190

где En* — число молей всех газов, входящих в систему,
величина -ц^Г" —^— объем одной грамм-молекулы лю-
любого газа при данной температуре и данном давлении, а
отношение -jr? = Xi— концентрация газа.
Отсюда
Тогда выражение для S[ принимает вид:
S't = cv\nT+R\nV —RXxiXi + hi. (8,13')
В уравнении (8,13') два первых члена и последний
член справа в сумме дают величину энтропии до смеше-
смешения. Поэтому
Отсюда энтропия всей смеси
или
S = 2 *A — #S**lnjc,. (8,14)
Энтропия после смешения газов изменяется на величину
— R 2 Щ In xp
Но так как
то 1пх<<0, т. е. в результате смешения газов энтропия
системы увеличивается. Этого и следовало ожидать, так
как смешение газов есть адиабатический процесс, кото-
который должен сопровождаться возрастанием энтропии.
Формула C,14) выражает собой так называемый па-
парадокс Гиббса. Он заключается в том, что эта формула
должна быть в принципе применимой к смешению каких
угодно газов. Однако если смешать два одинаковых га-
газа, то в этом случае, как видно из формулы (8,14),
энтропия такой системы останется неизменной,
Ш

Итак, для смеси идеальных газов имеет место:
k k
о = ^2j ^i^i — *\ 2u t^i *П %l*
Пользуясь формулами (8,13) и (8,14) и зная р, V, Т
из опыта, можно определить термодинамический потен-»
циал Гиббса:
0^U— TS + pV.
Закон действующих масс. Для того чтобы
определить условия равновесия идеальной газовой см«-
си, вычислим ее термодинамический потенциал Ф.
Учитывая значения U и S из формул (8,13) и (8,14),
получим:
причем
или
Следовательно, на основании уравнения состояния Кла-
Клапейрона — Менделеева
Подставим этот результат в выражение для термоди*
намического потенциала Ф:
,. (8,15)
Для получения условия равновесия в форме (8,12")
необходимо найти fxf = -^—. Заметим, что во всех чле-
членах выражения (8,15) щ входит в сумму 2/^, умножен*
192

ную на величину, не зависящую от щ. Поэтому в резуль-
результате дифференцирования этих произведений получается
просто соответствующий множитель, так как остальные
величины п от щ не зависят. Исключение составляет член
RT Ъщ In xu поскольку Х{ также зависит от щ:
дщ ^ ' ' дщ
1 + In Л,— In У tlt — У Hi r=— = In Щ— In У nt = In ЛГ/.
В результате дифференцирования Ф по п,- имеем:
Далее, выразив объем v из уравнения Клапейрона —
Менделеева и прологарифмировав, получим равенство:
1пг> = 1п/?Н-1пГ — In/?.
Подставим этот результат в выражение для |л* и обо-
обозначим для краткости Ci + R—hi—R In R = a.
Тогда выражение для |лг- примет вид:
Подставим значение [хг- в уравнение (89l2ff):
^O. (8,16)
Разделим это уравнение на RT:
V/ In Xi = ^y js; +
13 В. Ф. Ноздрев 193

Введем обозначения:
Тогда равенство (8,16) примет вид:
—ejnp. (8,160
После потенцирования получаем:
Ях:^ = аГ^Г*+Vе. (8,17)
или
Як? = *(/>, 7).
где /((/?, Г) —константа химического равновесия.
Это и есть закон действующих масс. Он устанавли-
устанавливает связь между концентрациями х\ газов в смеси, не-
необходимую для существования между ними химического
равновесия при данной температуре и данном давлении.
Изменяя величины, входящие в это соотношение, можно
влиять на ход реакции.
Закон действующих масс, полученный для смесей
идеальных газов, справедлив с некоторыми ограничения-
ограничениями для систем, содержащих газы при низких давлениях;
он применим также к процессам полимеризации и диссо-
диссоциации молекул, к разбавленным растворам и даже к
более сложным системам.
В качестве примера применения закона действующих
масс рассмотрим диссоциацию йодистого водорода.
В этой реакции число молей до и после реакции не ме*
няется:
2HJ±?H2+J2.
Эта реакция может идти в прямом и обратном на-
направлениях.
Требуется определить, при каких условиях будет
равновесие в смеси этих трех газов.
Обычно считают стехиометрические коэффициенты
веществ, вступающих в реакцию; отрицательными, а по-
получающихся при реакции, положительными. В нашем
случае vi=—2, v2=l, V3—I и, следовательно,
в=
194

Но так как все три газа двухатомные, то их молярные
теплоемкости cv равны между собой. Поэтому для Ь по-
получаем:
0.
Закон действующих масс для данной реакции будет
иметь вид:
г~вт
2 u,p
xl
Уравнение (8,12) показывает, что для всех реакций,
при которых 6=2vt=0, т. е. при которых число молекул
до и после реакции остается без изменения, равновесие
в газовой смеси не связано с внешним давлением, а за-
зависит только от температуры.
Рассмотрим теперь примеры, когда число молей до и
после реакции меняется. Тогда степень диссоциации бу-
будет зависеть от давления. К таким реакциям относятся:
О2«±2О; J2«±2J; N2O4«±2NO2;
РС15<±РС13+С12.
Здесь vi = —1, V2=2. Следовательно,
Например, для J2
ъ
тогда
'0 -
Для данной реакции в состоянии химического равно-
равновесия концентрации реагирующих газов зависят от внеш-
внешнего давления и температуры. Если увеличивать давле-
давление, то концентрация х% будет уменьшаться, a Xi — уве-
увеличиваться: реакция будет идти в обратном направлении.
Таким образом, меняя давление, можно влиять на ход
реакции.
Рассмотрим еще один пример, иллюстрирующий при-
применение закона действующих масс.
13* 195

В технике очень большое значение имеет процесс
синтеза аммиака из водорода и азота воздуха. Согласно
уравнению реакции
N2+3H2->2NH3
v, = — 1; v2 = — 3; v3==2; в = — 1 — 3 + 2 = — 2,
u_— CN2~ 3c
О R
Закон действующих масс для рассматриваемого слу-
случая имеет вид:
xl q ~gN2"gH2+2gNH,
3 _ аР"Ш т 3 п2
В данной реакции концентрация NH3 увеличивается
при повышении давления: чем больше давление, тем
меньше концентрации N2 и Н2.
Растворы и смеси. Условия равновесия
разбавленных и идеальных растворов
Термодинамика позволяет дать точное
определение понятия смеси и раствора. Раствор — это
гомогенная система, твердая, жидкая или газообразная,
состоящая из двух или большего числа химических ве-
веществ.
В случае твердого тела, если два вещества взаимно
растворимы, они образуют общую кристаллическую ре-
решетку, в которой узлы частично заняты атомами (или
молекулами) одного вещества, частично — атомами дру-
другого. Если составные части сплава не образуют общей
кристаллической решетки, данный сплав представляет
собой смесь.
Tn=6t,5'C T
!96
I Рис. 45. Зависимость плотно-
I стей для двух смешиваемых
I веществ от температуры пол-
1 ного растворения Тп.

Рис. 46. Кривая растворимости
для системы никотин — вода.
210 и 61° С соответственно
верхняя и нижняя температуры
полного растворения.
Вода
Никотин
200Х
Никотина 100%
Аналогичное положение с жидкостями. Истинным рас*
твором является гомогенная система, характеризую-
характеризующаяся равномерным распределением молекул ее состав-
составляющих частей по всему объему.
В случае газов нет различия между растворами и
смесями, так как почти все газы полностью растворяются
или смешиваются в любых пропорциях. Заметим, одна-
однако, что в последнее время обнаружена ограниченная
растворимость аммиака и водорода, аммиака и метана,
серного газа и азота при давлениях в несколько тысяч
атмосфер.
Для твердых и жидких веществ наблюдается различ*
ная степень растворимости — полная и частичная, а так*
же полная нерастворимость. Для ряда веществ суще-
существуют критические температуры смешивания, выше
которых наблюдается полное взаимное растворение,
т. е. гомогенность системы. Например, смесь метилового
спирта с гексаном при обычной температуре имеет
границу раздела между метиловым спиртом и гекса-
гексаном, т.е. смешение их неполное. При температуре 61,5° С
граница раздела исчезает, наступает полное растворение
(рис. 45).
Температуры, при которых происходит полное раство*
рение, называются критическими температура-
температурами смешения.
14 В. Ф. Ноздрев
197

Опыт показывает, что для некоторых двухфазных
жидких систем исчезновение двух фаз происходит при
понижении температуры. Самая низкая температура, при
которой двухфазная система переходит в однофазную с
понижением температуры, называется нижней кри-
критической температурой смешения. Оказы-
Оказывается, многие системы имеют и верхнюю и нижнюю
критические температуры растворения. Для таких си-
систем кривая растворимости имеет форму овала (рис.46,
система никотин —вода).
Самой простой системой из группы растворов являет-
является разбавленный раствор, т. е. такой раствор, в котором
число молей растворителя значительно больше числа
молей растворенного вещества, т. е. -^<С[1» гДе п —
число молей растворенного вещества, a N— число молей
растворителя. Для разбавленных растворов применим
аакон действующих масс в форме уравнения (8,17).
В процессе получения раствора взаимодействие меж*
ду молекулами различных его составляющих приводит
к различным механическим и тепловым проявлениям.
Так, иногдавыделяется «теплота растворения», поскольку
внутренняя энергия раствора не равняется сумме вну-
внутренних энергий веществ, из которых получается рас*
твор. Нередко пррисходит уменьшение объема при обра-
образовании раствора.
Однако в случае, когда химическое сходство состав*
ляющих компонентов велико, эти эффекты незначи-
незначительны.
Идеальным раствором называется раствор со строго
аддитивными объемами и внутренними энергиями, не
изменяющимися гГри получении раствора. Идеальный
раствор представляет собой полезную абстракцию, так
как свойства многих реальных веществ близки к его
свойствам.
Согласно определению идеального раствора утвер*
ждения, имеющие место для разбавленного раствора,
справедливы и для идеального. В то же время идеаль-
идеальный раствор может и не являться по существу разбав-
разбавленным, т, е. соотношение числа молей растворенного
вещества и растворителя в нем может быть любым.
К идеальным растворам закон действующих масс
применим также в форме (8,17).
198

Г Задачи и упражнения
1. Исходя из общих условий равновесия
(8,9) для однокомпонентной системы, получить уравне-
уравнение Клапейрона— Клаузиуса D,23).
Решение. Запишем условия равновесия
для однокомпонентной трехфазной системы:
/>1=*/>2 = />з> (8,18)
Hl = M<2 = №j.
где
—(ди
Последнее условие равновесия можно переписать в виде:
дих _дий _диъ
Внутренние энергии фаз системы выражаются через
удельные внутренние энергии щ, tfe, us:
Соотношения (8,19) можно заменить равенством
удельных энергий фаз:
ax = u2^uz. (8,20)
Рассмотрим, например, кривую равновесия жид*
кость — твердое тело (рис. 29, кривая СВ). Для некото-
некоторой ^гочки М этой кривой, очевидно, справедливо полу»
ченное равенство (8,20)^
их^щ. (8,21)
Тогда для точки М на этой же кривой с координатами
(p + dp, T-bdT) справедливо равенство:
их + dux = и2 + du2. (8,22)
Из равенств (8,21) и (8,22) получаем:
dux = duv (8,23)
14* 199

Будем рассматривать удельную энергию и как функ-
функцию энтропии и объема системы:
Тогда соотношение (8,23) можно переписать в виде:
или
Как легко убедиться, из соотношений G,6) и G,7)
Тогда равенство (8,24) принимает вид:
G^ — Т2) dS = (рх — р2) dV. (8,25)
Как уже известно: aS = -y*
Следовательно,
Обозначая
получим:
— А,-
ИЛЙ
гр Ар X
1 ~W~ v2 — vl •
2. В закрытом сосуде имеется некоторая
жидкость и ее пар, а также инертный газ. Пусть л —
парциальное давление пара, а р — общее давление. По-
Показать, что
dp v2 '
где Vi — удельный объем жидкости, а и2 — удельный
объем пара.
Решение. В случае равновесия системы
термодинамические потенциалы жидкости и пара дол-
должны быть равны, т. е. Ф\ = Ф% Тогда при Т = const co-
200

гласно равенству G,22) в случае какого-либо увеличен
ция общего давления р на жидкость и соответственного
увеличения парциального давления пара я получаем:
= vldp и d02 —
Если система продолжает оставаться в равновесии, то
Ф{ + йФх = Ф2 + d<t>2 или d0x = tf Ф2,
что приводит непосредственно к требуемому результату.
3. Правило фаз Гиббса установлено в
предположении, что каждая компонента входит во все
фазы. Как изменится правило фаз, если не каждая ком-
компонента входит во все фазы?
4. Вывести правило фаз, пользуясь тер*
модинамическим потенциалом Гиббса.
5. Пользуясь условиями равновесия двух
фаз в однокомпонентной системе, показать, что темпе*
ратура кипения жидкости зависит от давления.
6. Определить температурную зависи-
зависимость давления насыщенного пара над твердыми те-
телами.
Указание. Пар следует рассматривать как идеаль*
ный газ, твердое тело и газ — как тела, обладаю-
обладающие постоянными теплоемкостями. Следует вое*
пользоваться выражениями термодинамического
потенциала:
для пара
Фх = N^ г + ЩЬТ In Р — NicPlT In kT — N№r
и для твердого тела
ф2я F2 = N2E0i2 — N2c2T In kT + N2c2T in to,
где 80 — энергия, отнесенная к одной молекуле,
Ni — число молекул пара, N2 — число молекул
твердого тела, &? — постоянная интегрирования;
h — постоянная Планка, со — «средняя геометри-
геометрическая» частота колебания осцилляторов твердо-
твердого тела.
Ввиду относительной малости давления на-
насыщенного пара величиной pV можно пренебречь
и считать Ф равным ^ь
Отв. р я= const T k e kT
201

7. Определить условия равновесия двух*
фазной системы из разных веществ.
Решение. Пусть рассматриваемой систе*
мой является,* например, система вода — керосин. Энтро-
Энтропия такой системы
Внутренними параметрами системы являются
Nv N2i Vv V2% Uv U2t
удовлетворяющие условиям:
Nx = const; N2 = const;
N\Ui + N2^2 — U = const;
NXVX + N2V2 = V = const.
Таким образом, из шести параметров независимыми
являются два, например 1/4 и 1/ь
Условие равновесия найдем из равенства dS = 0 при
дополнительном условии dN\~dN2=Q:
NldUl-\-N2dU2 = 0;
или
T
^ i V 2 s; • = U,
откуда
Л = 7Y> A = A-
На химические потенциалы никакое условие в дан-
данном случае не накладывается, так как у разных веществ
обмена частицами быть не может.
8. Показать, что закон действующих
масс, выраженный через парциальные давления, имеет
вид:
Пры^Кр{р, Т).
Указание. Учесть, что для идеальных газов
202

9. Показать, что зависимость константы
равновесия от давления определяется уравнением:
[д\пКЛ 2V'
\ dp )т~ р
Решение. Из уравнения (8,17) следует,
что с повышением давления при постоянной температуре
константа химического равновесия может в зависимости
от знака суммы Ev* возрастать, уменьшаться или оста-*
ваться неизменной.
Если реакция идет с уменьшением общего числа мо*
лей:
2H2-f О2ч±2Н2О, то 2v;<0»
т. е. при увеличении давления количество образующихся
веществ конечных продуктов BН2О) реакции будет воз*
растать.
Если реакция проходит с увеличением общего числа
молей, например диссоциация аммиака:
то
т. е. увеличение давления приводит к уменьшению коли-
количества образующихся продуктов реакции.
В случае 2vi=*0 (например, 2HJ;
(д\пКс\ =0
т. е. константа равновесия не зависит от давления.
Логарифмируя равенство (8,17), получим:
\Т—0In/?. При Т — const:
fdlnK\ __?__;
\ др )т р
Р
10. Показать, что зависимость константы
равновесия от температуры при р~const определяется
уравнением:
/ A In К . \ П
(8,26)
203

Решение. Из уравнения (8,17) следует
(д\пКЛ <Ь , b + Q q0 I (%W, VI \
[—df-)p — -RTr^ Г~==Лтг-т~Т\~Ъ ^ZlVi)'
или, после соответствующих преобразований,
Учитывая, что Qp — q + q^ получим:
где Qp — тепловой эффект реакции при постоянном дав-
давлении.
Уравнение (8,26) называется уравнением изобары
реакции.
Изменение температуры при постоянном давлении
приводит согласно уравнению (8,26) к изменению кон-
константы химического равновесия и тем большему, чем
больше тепловой эффект реакции.
Если Qp<0, т. е. реакция сопровождается поглоще-
поглощением тепла (эндотермические реакции), то
и константа равновесия убывает с увеличением темпе-*
ратуры. Напротив, для экзотермической реакции, когда
Qp> 0, то Г -фТ с) > 0,и константа равновесия растет
с температурой.
11. Показать, что зависимость констан-
константы равновесия от температуры при V=const опреде*
ляется уравнением:
(д\пК\ Qv
)
Уравнение (8,27) называется уравнением изохоры
реакции:
12. В реакции образования водяного газа
Н2О + СО 5± СО2+Н2
равновесие наступает при Г=1259°К,
204

Известен молекулярный равновесный состав:
o2 = 0J моля, Мсо = 9,46 моля, Мн2о =9,46 моля,
Ми2 = 80,38- моля.
Определить константу равновесия Кс
Отв. Кс^ 0,628,
13. При температуре Г;=717ОК реакция
образования йодистого водорода
H2+J2^± 2HJ.
достигла равновесия.
Зная начальное число молей йода Mj2 =2,94 моля и
начальное число молей водорода Мц2 = 8,1 моля, опреде-
определить число молей HJ при равновесии. Константа равно-
равновесия реакции /Сс = 50,4 при Г=717°К.
14. В какой пропорции (по числу молей)
следует смешать азот и водород, чтобы получить при
любых заданных температуре Т и давлении р наиболь-
наибольший (равновесный) относительный выход аммиака?
Газы считаются идеальными.
Решение. Введя парциальные давле-
давления ри запишем закон действующих масс для реакции
2 + 2 = 2NH3, или ^
в виде:
= *(/>, Т). (8,28)
Обозначая относительную молярную концентрацию
NH3 (при равновесии) через х, а отношение равновесных
н
концентраций Н2 и N2 — г, т. е. полагая /?nh3 — Рг> -р-1- =г
и имея в виду, что
приведем равенство (8,28) к виду:
205

При фиксированных р и 7 это соотношение опреде-
определяет функцию х(г). Из условия экстремума этой функ-
функции заключаем, что л;макс получается при г=*3. Посколь-
Поскольку газы реагируют также в отношении 1 :3, очевидно,
что ту же пропорцию нужно выбрать и для исходной
смеси.
ЛИТЕРАТУРА
1. Дж. В. ГИББС,
Термодинамические работы, Гостехиздат, 1950.
2. В. А. КИРЕЕВ,
Физическая химия, Госхимиздат, 1951.
3. ВАН-ДЕР-ВААЛЬС,
Термостатика, ч. J и И, Госхимиздат, 193&

глава девятая фаз0ВЫе ПереХОДЫ
первого и второго рода.
Критические явления
Нами были рассмотрены условия равно-
равновесия гетерогенной системы (8,9)» при наличии которых
равновесие в сложной системе может сохраняться сколь
угодно долго. Если нарушается хотя бы одно из условий
равновесия, в системе начинается переход вещества, из
одной фазы в другую, например: переход вещества из
твердого состояния в жидкое, из жидкого в газообраз-
газообразное, из одной кристаллической модификаций в другую
и т. д. Теоретическое и экспериментальное рассмотрение
фазовых превращений позволило разделить их на два
класса: фазовые переходы первого рода и фазовые пере-*
ходы второго рода*
Фазовые переходы первого рода.
Уравнение Клапейрона—Клаузиуса
Под фазовыми переходами первого рода
понимаются фазовые превращения, сопровождающиеся
поглощением или выделением скрытой теплоты и скач-
скачкообразным изменением удельного объема.
Рассматривая фазовые превращения как обратимый
процесс, применим к нему второй закон термодинамики:
л с d'Q
Интегрирование равенства (В, 12) при T=const дает:
где % — скрытая теплота превращения при фазовом пе-
переходе.
Согласно определению фазовых переходов первого
рода ХФО.
Следовательно, 53—Si=?0, т. е. при фазовых переход
дах первого рода энтропия терпит разрыв непрерыв-
непрерывности (рис. 47).
207

Рис. 47. Разрыв непрерывности
энтропии 5 при фазовых пере-
переходах первого рода.
По определению удельные объемы при фазовых пре-
превращениях первого рода также испытывают разрыв не-
непрерывности, т. е. V2—v^O. Графически это представ-
представлено на рисунке 48 для системы жидкость — насыщен-
насыщенный пар. Температура Т\ соответствует температуре
фазового перехода первого рода.
Найдем изменение внутренней энергии при рассмат-*
риваемых превращениях. Согласно равенству G,13)
dU^TdS — pdV = T{S2 — Sl)~ р(У2—Уг).
Так как
то
53 —5,
dl/фО,
и У2 —
Следовательно, внутренняя энергия в данном случае ме-
меняется также скачкообразно. Согласно G,11) изменение
свободной энергии
Так как в случае изотермического процесса dT—0,
то
Аналогично, изменение энтальпии при р = const:
dJ =:
Наконец, изменение термодинамического потенциала
при рассматриваемых условиях (T=const, jt? = const)
равно:
dpSdTtVd^O; Фг — Ф2. (9,1)

Как видим, в отличие от всех известных термодина-
термодинамических функций лишь термодинамический потенциал
Гиббса не имеет разрыва непрерывности при фазовых
переходах первого рода, что делает его весьма полезным
при изучении фазовых превращений.
Возьмем частные производные этой функции по тем-
температуре и давлению для двух фаз гетерогенной системы
и вычтем их одну из другой G,23; 7,24):
= 52 — 5t Ф О, (9,2)
Полученные соотношения указывают, что частные
производные термодинамического потенциала при фа-
фазовых переходах первого рода изменяются скачкооб-
разно.
К фазовым переходам первого рода относятся пре-
превращения в однокомпонентных системах (испарение,
возгонка, переход твердого тела в жидкое), переход из
одной модификации в другую и т. д. Все эти процессы
связаны с выделением или поглощением теплоты и с из-
изменением удельного объема.
Основным уравнением, характеризующим фазовые
переходы первого рода, является уравнение Клапейро-
Клапейрона— Клаузиуса, которое легко получить из условия ра-
равенства химических потенциалов при равновесии двух
фаз:
И'(Р, Г) = И"(/>, Т). (9,3)
Пользуясь равенством (9,3), найдем дифференци-
дифференциальное уравнение кривой равновесия.
Рис. 48. Разрыв непрерыв-
непрерывности удельного объема при
фазовых переходах первого д
рода.
Г
20ft

Действительно, дифференцируя равенство (9,3),
найдем:
</|i'(/>, T) = d\x"(p%T),
или
откуда
(d\i"\
%l\ (d\i\
\др /т \ дР )т
Учитывая, что й\к = — SdT + Vdp, так как с/Ф = 0, полу-
получим:
Уравнение (9,4) является дифференциальным урав-
уравнением кривой равновесия, связывающим теплоту пере-
перехода [так как A,= r(S"—S')], скачок удельного объема
и наклон кривой равновесия в точке перехода. В литера*
туре оно чаще всего встречается в виде:
dp _ X
dT ~~ T(v" — V)
(см., например, главу 4, § 4).
Если на систему действует не сила давления Я, а ка-
какая-нибудь обобщенная сила У, то мы получаем обоб-
обобщенное уравнение (9,4) вида:
dY _ AS
где х"—х/=Длг — скачок внешнего параметра, сопря-
сопряженного обобщенной силе У.
Заметим, что в уравнении Клапейрона — Клаузиуса
во всех случаях фазовых равновесий i>0, разность же
удельных объемов v2—vi может быть как положитель-
положительной, так и отрицательной. В первом случае -А- > О,
т. е. с повышением давления температура плавления
(испарения, возгонки) возрастает. Во втором случае
-gjr < 0, т. е. с повышением давления температура плав*
ления (испарения* возгонки) уменьшается.
210

У большинства тел, например, при плавлении v">v\
поэтому у таких тел -jy- > 0.
Однако у воды, висмута, чугуна объем при плавле-
плавлении твердой фазы уменьшается, так что для них ^- < О,
т. е. точка плавления с увеличением давления пони-
жается.
Теплоемкость при постоянном давлении ср при фазо-
фазовых переходах первого рода равна бесконечности.
Действительно,
ср
_(dQ\
-VST).9
но d'Q=?O, а йГ=0, следовательно, ср = оо,
Воспользовавшись равенством (9,3), легко показать,
что рт и а при фазовых переходах первого рода равны
бесконечности.
г
Фазовые переходы второго рода.
Уравнение Эренфеста
Под фазовыми переходами второго рода
понимают фазовые превращения, происходящие без по-
поглощений щи выделения теплоты и без изменения
удельного объема (d'Q = O, dt>=0).
В этом случае в соответствии с равенством E,12)
изменение энтропии dS=0, S2=Sb т. е. при переходе из
одной фазы в другую энтропия меняется непрерывно.
Изменение термодинамического потенциала Гиббса
так же, как и при фазовых переходах первого рода, рав-
равно нулю:
Поскольку Si=S2, 1>1 = У2, первые производные этой
функции не претерпевают скачка:
211

Но вторые частные производные термодинамического
потенциала терпят разрыв непрерывности. Действитель-
Действительно, согласно G,23) и G,24):
(д2фЛ (д2фЛ _№| 1^Л ^^_1pl-
\ дТ* )р \ дТ* )р — \ дТ 1р \дТ }р~ Т Т —
= т{сРг-ср)Ф0. (9,5)
Аналогично.
_(<РФА _fiM /J!M —
)т \ др> )т — \ др }т \ др )т —
(9,6)
/ д2Ф{ \ ( д2Ф2 \ _ dv{ дц2 _
\dpdT)~\dpW)~'~df дТ —
= axv — a2v = v (a{ — а2) ф 0. (9,7)
Как показывают уравнения (9,5), (9,6) и (9,7), при
фазовых переходах второго рода скачкообразное изме-
изменение испытывают теплоемкость при р = const, изотер-
изотермический коэффициент сжимаемости рг и коэффициент
объемного расширения а.
Связь между этими скачками и наклоном кривой
равновесия в точке перехода определяется уравнениями
Эренфеста.
Для получения этих уравнений воспользуемся урав-
уравнением Клапейрона — Клаузиуса, Правая часть этого
уравнения
dp _ S" — S'
dT ~ v" — v*
в точке фазового перехода второго рода принимает вид
0
неопределенности -д-.
Воспользуемся правилом Лопиталя для раскрытия
этой неопределенности.
Дифференцируя числитель и «знаменатель правой ча*
сти уравнения (9,4) по Т или по р1 получим:
dp _1!Г дТ __ ср-с
р _
dT ~- dv" dv' — t I dv\ ~ T.(dv
212

и
dS" dS'
dp dp dp
4T~ dv" dv7"'
dp dp
или согласно G,33)
dp _.
lf~'
Учитывая равенство A,3), из соотношений (9,8) и
(9,9) получим уравнения Эренфеста:
),• (SU0)
устанавливающие связь между скачками ср, Рт, ос и на-
наклоном кривой равновесия в точке фазового перехода
второго рода.
Если на систему действует не только сила давле-
давления Р, но и какая-либо другая обобщенная сила Y, ко-
торой соответствует внешний параметр х, то уравнения
Эренфеста будут иметь вид:
Л«,— Г(?)Г А (¦?),. (9,12)
Рассмотрим ряд примеров фазовых переходов вто-
второго рода:
1. Фазовым переходом второго рода является пере-
переход вещества из ферромагнитного состояния в парамаг-
парамагнитное (сс-железо в jj-железо) в точке Кюри. Это явле-
явление было обнаружено экспериментально при темпера-
температуре около 679° С; оно сопровождается коренным
изменением структуры металла. Экспериментально было
213

установлено, kfo в этом случае изменение энтропии рав-
равно нулю (AS—0), изменение удельного объема также
равно нулю (Да = 0), а коэффициенты объемного расши-
расширения а, изотермическая сжимаемость (Зт и теплоем-
теплоемкость ср претерпевают скачок.
2. Другой пример — сверхпроводящее состояние ме-
металлов. В 1911 г. Камерлинг— Оннесом было открыто
явление сверхпроводимости, заключающееся в том, что
при некоторой определенной низкой температуре ток по
металлу проходит без выделения теплоты, т. е. омиче-
омическое сопротивление его R становится равным нулю.
Ртуть, например, переходит в сверхпроводящее состоя-
состояние при температуре 4,12° К, цинк — при 0,79° К, кад-
кадмий — при 0,6° К и т. д. В настоящее время сверхпрово-
сверхпроводимость обнаружена примерно у 17 металлов. Открытие
сверхпроводимости имеет большое теоретическое и при-
прикладное значение и относится также к фазовым перехо-
переходам второго рода, так как согласно теории и экспери-
эксперименту переход металла в сверхпроводящее состояние
происходит при AS — 0, Да=0 и при скачкообразном из-
изменении коэффициентов а, рт и ср.
3. Рассмотрим еще один пример фазового перехода
второго рода — явление сверхтекучести.
Явление сверхтекучести состоит в том, что при тем-
температуре 2,9° К жидкий гелий разделяется на две
фазы — Hei и Нец, из которых одна (Нец) не обладает
сдвиговой вязкостью (т)=0).
Последний факт дает возможность путем задержа-
задержания гелия (Hei) отделить одну фазу от другой. Переход
гелия I в гелий II происходит при At> = 0 и скачкообраз-
скачкообразном изменении ср, а и рт, т. е. при соблюдении условий
фазовых переходов второго рода.
Отметим, что в каждом рассмотренном случае фазо-
фазовый переход второго рода происходит не в одной точ-
точке, а в некоторой области вокруг нее, поэтому имеет
смысл говорить об области фазового перехода второго
рода.
Изучение одной из систем, удовлетворяющих усло-
условиям фазовых переходов второго рода, дает возмож-
возможность, выяснив закономерности данного явления, пере-
перенести их на другие процессы, относящиеся к той же
группе явлений. Этим методом успешно пользуется со-
современная термодинамика.
214

§'
Критическое состояние вещества.
Критическая область
Состояние^ равновесия системы жид-
жидкость— пар, как известно, описывается уравнением Кла-
Клапейрона— Клаузиуса и на диаграмме (рис. 49) изобра-
изображается кривой испарения АК. Конечная точка этой кри-
кривой К является критической, здесь происходит полное
превращение жидкости в пар; выше нее вещество может
находиться только в парообразном состоянии. Как было
установлено Д. И. Менделеевым на основании многочис-
многочисленных опытов, превращение жидкости в пар в крити-
критической точке происходит без поглощения или выделения
тепла, т. е. Jt=O. Следовательно,
*^2 — 1 "— "тг* —' ^*
Далее многочисленными экспериментами установле-
установлено, что в этой точке многие физические величины, на-
например: теплоемкость (ср), коэффициент изотермической
сжимаемости, коэффициент объемного расширения, из-
изменяются скачками (рис. 50,51).
Следовательно, критические явления в однокомпо-
нентных веществах можно с полным основанием отнести
к фазовым переходам второго рода.
К подобного рода явлениям относятся и критические
явления в смесях.
Известно, что жидкости могут в зависимости от их
природы либо полностью смешиваться одна с другой
Рис. 49. Кривая испарения для
системы жидкость — пар.
Жидкость
215

при любых температурах, либо растворяться одна в дру-
другой лишь частично и при определенной температуре, об-
образуя растворы, состоящие из отдельных фаз. К таким
системам относятся смеси вода —фенол, метиловый
спирт — гексан и т. д. С повышением температуры рас-
растворимость компонентов этих смесей одного в другом
увеличивается, и двухфазная система постепенно пере-
переходит в однофазную. Наивысшая температура, при ко-
которой этот переход совершается полностью, называется
верхней критической температурой растворения. Оказы-
Оказывается, при критическом переходе двухфазной системы
в однофазную скрытая теплота перехода не поглощается,
и поведение вещества аналогично поведению в крити-
критической области системы жидкость — пар. Поэтому явле-
явления в смесях при критической температуре растворения
также можно отнести к фазовым переходам второго
рода.
Необходимо, однако, отметить, что исследования по-
последних лет позволили установить некоторые различия
между фазовыми переходами II рода и критическими
явлениями: в первом сдучае скачки ср, а, (Зт являются
конечными, в случае же критических явлений они бес-
бесконечны. Если же не учитывать этих различий, то ме-
между фазовыми переходами II рода и критическими яв-
явлениями нет никакой разницы *. Поэтому все эти явле-
явления в последнее время объединяются под одним назва-
названием «обобщенных критических явлений».
Рис. 50. Скачок изотермической
сжимаемости при фазовом пере-
переходе второго рода.
* Учитывая последнее уточнение, переход гелия I в гелий II
необходимо отнести к критическим явлениям.
216

Рис. 51. Скачок теплоемкости ср Ср
при фазовом переходе второго
рода.
Классическая термодинамика рассматривает крити*
ческие явления как точечные, происходящие при Гк, рк,
VK. В действительности же эти явления охватывают не-
некоторую область вокруг критической точки (окрестность
критической точки), обладающую специфическими зако-
закономерностями.
Поэтому вполне целесообразно ввести понятие кри«
тической области для описания свойств термодинамиче-
термодинамической системы в окрестности критической точки.
Последние исследования критических явлений в мно«
гокомпонентных системах жидкость — пар показали*,
что и для этих систем понятие критической области
имеет силу,
Это значительно расширяет возможности термодина-
термодинамической теории обобщенных критических явлений и
теорий термодинамического подобия.
Изучение термодинамики критической области будет
значительно облегчено, если найти для ее описания
уравнение состояния.
Уравнение состояния критической
области
Как уже отмечалось (глава I), в критической точке выпол-
выполняются соотношения;
* В. Ф. Ноздрев, Молекулярная акустика, изд, «Знание»,
217
1964.
15 В. Ф. Ноздрев

Если к первым двум равенствам прибавить уравнение состоя-
состояния в дифференциальной форме:
то решение этих трех уравнений даст параметры критического со-
стояния4
Но можно также обратить задачу: по известным параметрам
критического состояния и условиям (9,14) получить уравнение,
пригодное для описания состояния критической области. Конечно,
такое уравнение будет пригодно только для описания состояния
окрестности критической точки и совершенно не пригодно для со-
состояний, далеких от нее.
Чем дальше мы будем уходить от критической точки, тем ме-
менее будет удовлетворяться уравнение состояния, но в непрерыв-
непрерывности среды, а следовательно, и в значении параметров, характе-
характеризующих эту среду, не произойдет никаких нарушений. Таким
образом, о границах критической области можно говорить только
условно.
Если допустить непрерывность термодинамического потенциа-
потенциала и его производных в окрестности критической точки, то этого
достаточно, чтобы термодинамический потенциал Ф(р, Тг V) пред-
представить в виде степенного ряда от
Р=*р — Рк\ v=*V—VK) t^T — Гк;
где Fv(Vl{, Г), FVv(Vk, T) и т. д. представляют собой значения
производных свободной энергии по объему при V~VK. Они яв-
являются функциями температуры. Уравнение (9, 16) содержит по-
постоянные величины, в которые входят параметры критического со-
состояния, но какова связь этих параметров — неизвестно. Если
найти зависимость коэффициентов от параметров критического со-
состояния, то тем самым задача будет решена полностью. Введем
безразмерные переменные:
_ Т — Р . — V
1 к Рк vk
Подстановка их в равенство (9, 16) даст уравнение;
Т V2
пРк = РптТкх + pfoVJjv + pnVVT -j^. тФ2 +
+ PvwK^+---> (9,17)
218

которое после деления на рк переходит в уравнение критической
области для приведенных переменных:
yЧф + (9Д8)
где индексы V, Т, VVT и т. д. указывают, по какому параметру
берется производная и каков ее порядок.
В уравнении (9, 18) переменные есть величины безразмерные,
поэтому коэффициенты при переменных также являются величи-
величинами безразмерными*
V2T
Pvvt 2рк
~. v If
f
Следовательно,
(9,20)
Таким образом, Уравнение состояния по условиям устойчивого
равновесия по заданным критическим параметрам найдено. Оно
может быть записано в безразмерных переменных:
или в переменных, имеющих размерность:
1 к
или
= Я, -р- (Т - Гк) + %2 ^Zjr- {У - Кк) (Г - Тк
-ft- G - FK)^ (Г - Тк) + Я4 -А_ (у _ у2)з + ... (9,23)
к к к к
219

Для анализа критической области и многих других расчетов
часто необходимо знать
(др\ (др\
Urj/ \w)T>
Пользуясь уравнением (9,23), легко получить эти величины?
$rV-VK)>+... (9,24)
dvJT VJK У К>1Г VlTK A
X (V - VK) (T - TK) + ЗЛ4 -Ь- {V - VK)> + ... (9,25)
§ Теплоемкость в критической области
Термодинамика позволяет рассчитать
теплоемкости ср и Су и отношение ~г~ по известным со-»
1 cv
отношениям:
w
(9J8)
Таким образом, для определения теплоемкостей ср,
cv и их отношения необходимо иметь уравнение состоя-
состояния или экспериментально определить производные, вхо-
входящие в формулы (9,26), (9,27) и (9,28),
Порядок определения величин ср и су следующий,
Из формул
с -
Р2с2
(9,30)
220

Ср
определяются cv и ——, теплоемкость при постоянном
Су
давлении подсчитывается из соотношения:
~ = г (9,31)
Формулы (9,29), (9,30) и (9,31) при наличии экс-
экспериментальных значений скорости звука сильно облег-
облегчают задачу нахождения теплоемкостей и их отношения
в критической области **
Теплоемкость в критической точке системы
жидкость—пар. Для определения Су в критической точке
воспользуемся выражением:
<v=-
р
W
Так как в критической точке
то для CvK будем иметь формулу:
т
Тк
(9,32)
Для расчета сУк необходимо определить гк и [^f) *
Величина гк = рс определяется из эксперимента.
Несколько слов о способе определения
Известно, что
* См.: В. Ф. Ноздрев, Применение ультраакустики в моле-
молекулярной физике, Гостехиздат, 1958,
221

Ho (-gp-j стремится к нулю при Т—Гк->0 (пропор*
dV
ционально уменьшению этой разности), а -^г стремит-
стремится к бесконечности как (Т—Гк)~1/2. Поэтому в пределе
первое слагаемое обращается в нуль и получается:
Для вычисления \-fijA можно воспользоваться ка-
какой-либо эмпирической или теоретической зависимо-
зависимостью р насыщенного пара от температуры.
В качестве достаточного приближения в данном слу-
случае может быть использована формула Ван-дер-Ва-
альса:
?L — i рТк
В критической точке эта формула дает:
Величину ^1 можно определить по эксперименталь-
экспериментальным данным. Для этилового спирта, ft-гексана и дру-
других изученных нами веществ Х\ равна приблизительно 8.
Уравнение Ван-дер-Ваальса дает значение Ai=4, по
уравнению Клаузиуса ^i = 7.
Учитывая, что (-д^) =?0, экспериментальное уста-
установление конечности г является одновременно экспери-
экспериментальным доказательством конечности cv в критиче-
критической точке. Но, как видно из сказанного выше, ультра-
ультраакустика позволяет не только экспериментально
показать конечность cv в критической точке, но и дает
метод числового расчета сУк с достаточной для практики
точностью.
Температурная зависимость теплоемкости
вблизи критической точки. Для расчета теплоемкостей
ср
cv, ср и их отношения — вблизи критической точки
воспользуемся формулами (9,29), (9,30) и (9,31) t
222

Ср. кал/г град
90-
70-
50-
Ov, дж/гград
¦Ю
230 235 240 245 250 t°C
Рис. 52. Зависимости у и ср
от температуры в критической
области для метилового спирта.
Производные i~) и
244 246 248 250 252 254 t'C
Рис. 53. Зависимость cv от
температуры в критической
области для этилацетата.
Ш^ для жидкости по линии
насыщения и для насыщенного пара определить нетруд-
нетрудно. Для критической изохоры уравнение состояния
(9,22) дает:
Таким образом, имеются все необходимые данные
для расчета теплоемкостей по линии насыщения в кри-
критической области, а также и по критической изохоре.
Для иллюстрации на рис. 52 и 53 приведены кривые
зависимости cv, cp, -*- в критической области для ме*
су
тилового спирта и этилацетата.
О9
Г Задачи и упражнения
1. Показать, что при фазовых переходах
первого рода а и рт равны бесконечности.
Указание. Необходимо воспользоваться уравне-
уравнением (9,3).
2. Считая теплоту перехода К постоянной
величиной, показать, что давление насыщенного пара
223

меняется с изменением температуры по экспоненциала
ному закону.
Решение.
W^ T(v2-vx) '
где V\ — объем моля жидкости вдали от критической
точки, v2 — объем моля пара вдали от критической точ*
ки, v2^>vlt
Полагая, что насыщенные пары удовлетворяют урав-
уравнению Клапейрона, уравнение (9,38) Ложно предста*
вить:
dp Хр
~~~9
откуда
р = const. е~Щ-
3. Определить скачок теплоемкости при
переходе проводника (например, олова) из сверхпрово-
сверхпроводящего состояния в нормальное.
Решение, Полагая в уравнении (9,12),
Y = Я, х = М, получим для скачка теплоемкости:
ан\2\(дМ\
Для нормального проводника
ц —-1
для сверхпроводника
поэтому
: = i»(-U.
Таким образом,
1 «ш |л — 1
п
дН ~ 4л • дН ~ 4я '
dMs дМп _ ц
224

Но ц=1+4л:х, а х для парамагнитных и диамагнитных
веществ имеет порядок 10~5—10~6, поэтому
) = —Ш и ^~сд= 41)
Этот результат справедлив только для случая, когда
внешнее поле #с==0. При НСФО превращение проводника
в сверхпроводящее состояние сопровождается тепловым
эффектом, т. е. в этом случае имеет место фазовый пе«
реход I рода, описываемый уравнением Клапейрона —
Клаузиуса.
4. На примере газа Ван-дер-Ваальсаубе*
диться в обращении сжимаемости f-j-) и коэффици*
ента теплового расширения (-gf-j в критической точке
в бесконечность.
5. Показать, что
др _(др\ dV .(др
6. Пользуясь уравнением состояния кри*
тической области (9,22), определить производные
дТ)у и \dV)T
по линии насыщения для жидкости и пара.
7. Показать, что скорость звука в кри-
критической точке имеет конечное значение.
Решение. Из соотношений B,55) я
E,62) можно получить:
(др\ _(др\ Т (др\*
Учитывая, что
225

и заменив
дУ
м
так как v= — ¦ получим:
¦или
дТ )v
С учетом равенства B,55) это дает:
-I
1
к/у
dV
с
1
w-
v\w)T
"(wt
(9,41)
• (9,42)
В критической точке 7 = °°. ("^г) и cf остаются
конечными. Следовательно,
2 _ мтк (др
8. Показать, что коэффициент адиабати-
адиабатической сжимаемости в критической точке имеет конеч-
конечное значение.
Решение. В предыдущей задаче из тер-
термодинамических соотношений мы получили:
Принимая во внимание коэффициент адиабатической
сжимаемости
формулу (9,43) можно записать в виде:
J М_ Т (у
ps — р " су \дт)у
(9,44)
±T • (9>45)
а так как в критической точке y = oo> {"w
225

и Су конечны, то
Следовательно, ps в критической точке действитель-
действительно имеет конечное значение.
ЛИТЕРАТУРА
1. А. Г. СТОЛЕТОВ,
Собр. соч., т. 3* Гостехиздат, 1947,
2. Б. Б. ГОЛИЦЫН,
Собр. соч., т. IV, 1959.
3 В. К. СЕМЕНЧЕНКО,
Сб. «Применение ультраакустики к исследованию вещества», вып. III,
изд. МОПИ, 1957.
4. А. ЗОММЕРФЕЛЬД,
Термодинамика и статистическая физика, ИЛ, М.—Л., 1955.
5. В. А. КИРИЛЛИН и А. Е. ШЕЙНДЛИН,
Основы экспериментальной термодинамики, Госэнергоиздат, 1950.
6. В. Ф. НОЗДРЕВ,
Применение ультраакустики в молекулярной физике, Гостехиздат,
1958,

глава десятая Тепловая теорема Нернста.
Третье начало
термодинамики
S История вопроса. Теорема Неряста
Появление в науке тепловой теоремы
Нернста тесно связано с проблемой измерения химиче-
химического сродства. Под химическим сродством понимают
стремление двух веществ реагировать друг с другом.
Очень важно найти количественную меру химического
сродства. Начальное решение этой проблемы было пред-
предложено Томсоном и Бертло. Поскольку при химических
реакциях во многих случаях выделяется теплота, то эти
авторы высказали предположение^ что количество выде-
выделяющейся при реакции теплоты и является мерой хими-
химического сродства: чем больше выделяется теплоты при
реакции, тем больше сродство между веществами.
Однако эгот принцип оказался непригодным для ре-
решения поставленной проблемы. Дело в том, что наряду
с экзотермическими реакциями существуют реакции
эндотермические, при которых теплота не выделяется,
а поглощается; по Томсону и Бертло, это соответство*
вало бы отрицательному химическому сродству, что бес*
смысленно.
Правильное решение вопроса о химическом сродстве
было дано Вант-Гоффом. Он предложил взять в каче-
качестве количественной меры химического сродства сво-
свободную энергию системы до и после реакции, рассчи-
рассчитанную для определенной массы реагирующих веществ;
Как известно, при наличии химического равновесия эта
разность свободных энергий достигает минимума и рав-
равна максимальной работе при обратимых процессах:
К измерению максимальной работы практически и
сводится определение химического сродства. Однако по-
поскольку первое и второе начало термодинамики не дают
правила вычисления постоянных интегрирования и по-
позволяют найти лишь разности термодинамических вели-
величин, т. е, Ui—U2f Si—S2% Fl—F2, Ф1—Ф2 и т, д., то при
228

расчете абсолютного значения химического сродства не-
необходимо каким-то путем определить эти постоянные
интегрирования. Рассмотрим этот вопрос более подробно.
Исследования химического равновесия привели нас
к уравнениям стр. B04—205):
<*1п/< <L и 1п#=- f JL</r+c, мол)
dT — RT2 и in a— j RT% -r v ;
где Q — тепловой эффект реакции, зависящий от темпе*
ратуры *. __
Так как Q можно представить, опираясь на опыт,
в форме:
Q = QQ + aT + bT* + cT*+ .... A0,2)
где Qo —тепловой эффект при Г=0, то:
A0,3)
После интегрирования получим:
^ ^^ ^^ ... + С. A0,4)
Нас интересует определение максимальной работы Wj
как меры химического сродства.
Известно, что W связано с In К следующим образом:
№=-#Пп/С*\ A0,5)
* В формуле A0,1) и везде ниже дается термохимическое обо-
обозначение (Q) теплоты Q~ —Q.
** В уравнении A0,5) 1п/( можно найти, сделав следующие
преобразования:!
d'W
WdT—Td'W=zQdT.
Делим последнее выражение на Т2 (интегрирующий делитель];
WdT—Td'W Q dT . d (W \QdT
T2 e T2 ' dT [ T j — x2 #
Если сравнить последнее выражение с
d\nK Q
dT e RT2'
TO ПОЛУЧИМ2
229

Поэтому, используя выражения A0,4) и A0,5) получим:
IF=QO — аТ\пТ — ЬТ2 — |Р- ... — CRT. A0,6)
Пользуясь уравнениями A0,5) и A0,6), можно опре-
определить меру химического сродства при любой темпера-
температуре, но лишь при том условии, если известна константа
интегрирования С.
Постоянная интегрирования может быть определена
экспериментальным путем. Для этого необходимо опре-
определить из опыта константу равновесия при какой-либо
температуре и затем по уравнению A0,4) найти посто-
постоянную С. Тогда максимальная работа определится по
уравнению A0,6).
Однако экспериментальные определения химического
равновесия довольно затруднительны. Поэтому теорети-
теоретическое решение этого вопроса имело бы громадное зна-
значение, так как оно позволило бы теоретически, не прибе-
прибегая к опыту, определить меру химического сродства W
при любой температуре.
Как показывает теоретический анализ, только в двух
случаях можно обойтись в определении W без экспери-
эксперимента: во-первых, при WQ=Q0 (cm. уравнение 10,6) и,
d'W n
во-вторых, при ~df-~ 0, т. е., когда максимальная ра-
работа не зависит от температуры.
Действительно, когда
dT
то из равенства
получим: ___
Итак, только в этих двух случаях можно определить
теоретически W как меру химического сродства, во всех
же других случаях, когда W=fcQ> химическое сродство
не может быть определено теоретически вследствие не-
невозможности определения константы интегрирования.
Таким образом, с помощью только первого и второго на-
начал термодинамики нельзя теоретически решить до кон*
230

Рис. 54. Зависимости
максимальной работы W
и теплового эффекта
реакции Q от темпера-
температуры Т вблизи абсолют-
абсолютного нуля.
Q-W
а
да задачу определения химического сродства. Следова-
Следовательно, решение этой задачи требует введения дополни-
дополнительных условий, не вытекающих из первого и второго
начал термодинамики. Тепловая теорема Нернста и яв-
является таким дополнением.
Основываясь на опытных фактах, Нерйст положил,
что для конденсированных систем
f (d'W\
hm( 1
A0,8)
d'W
dT jT_0 -
Действительно, если, по опытным данным, при низ-
низких температурах свойства тел почти не зависят от тем-
температуры, то кривые Q и W около Т — 0 должны быть
горизонтальными, а касательные к кривым Q и W при
температурах, близких к нулю, должны идти параллель-
параллельно оси Т (рис. 54).
Математически это означает, что производные
и -—¦ вблизи Г = 0 должны быть равны нулю, т. е.
Щ =0. A0,80
Соотношения A0,8) дают нам недостающее допол-
дополнительное условие для определения константы интегри-
интегрирования С, входящей в формулу для определения хими-
химического сродства W.
Действительно,
W=:Q0 — аТ\п Г — ЬТ2 — {Р-
откуда
d'W
dT
CRT, A0,9)
п 9hT -~L rT% CD
1<У 4Ы{/ I " pj lx X —— , , , —— Vv /T^ ,
231

При
Но согласно тепловой теореме при 7 = 0 —fif-
Поэтому
Величину коэффициента а можно определить из теп*
ловой теоремы:
Но так как
а = 0.
Следовательно, С также равно нулю (С=0). Окон*
чательно выражение для W имеет вид;
W=Q0 — ЬТ2 — уР— ... A0,10)
Таким образом, с ломощью теоремы Нернста воз-
возможно определить постоянную интегрирования в выра-
выражении для W и, следовательно, возможно определить
максимальную работу W чисто теоретическим путем.
Расширенная формулировка теоремы
Нернста. Третье начало термодинамики
Теорема Нернста дает условия:
[dWu\ tdF\
lim {-—-I =Iim (-^г) —О,
°* 'v Г—О
Iv
НО
поэтому
232

Но известно, что
(ЕЛ __ с
Тогда
a —5J = 0f A0,12)
т. е. в области абсолютного нуля процессы проходят без
изменения энтропии. Между тем, как известно, все про-
процессы? идущие с теплопередачей, сопровождаются изме-
изменением энтропии.
Если же 50 = const, это. означает, что в рассматриваем
мых процессах отсутствует теплопередача. Следователь-
Следовательно, при Г=0 система не передает больше теплоту, т. е/
она не «остывает».
Сказанное позволяет сформулировать следующее по-
положение:
Нельзя достигнуть абсолютного нуля отнятием от
тела теплоты при помощи конечных действитель-
действительных процессов.
Иначе говоря,
нельзя создать машину, способную отнять всю
теплоту от тела, т. е. охладить его до абсолют-
абсолютного нуля.
Соотношение A0,12) может быть получено при
S = const или при So=O. Последнее предположение более
вероятно — оно отвечает отсутствию тепловых движений
при Г=0.
Планк предположил, что
HmS = 0, A0,13)
Г->0
т. е.
при абсолютном нуле энтропия равна нулю.
В такой расширенной формулировке тепловая тео-
теорема позволяет вычислить абсолютное значение энтро-
энтропии и свести задачу, определения энтропии к определе-
определению температурной зависимости теплоемкости. На са-
самом деле, повышая изобарно (ф=0) температуру тела
от 0°К до Г, получаем:
Т cpdT
Т %
о
J6 В. Ф. Ноздре* 233

так как
Аналогично
Таким образом, если из эксперимента известна ср
или cv как функция температуры, то этого достаточно
для определения абсолютного значения энтропии и ее
температурной зависимости.
§¦
Свойства тел вблизи абсолютного нуля
Изучение свойств вещества вблизи абсо-
абсолютного нуля представляет большой интерес для науки
и техники.
Многие свойства вещества, завуалированные при
комнатных температурах тепловыми явлениями (напри-
(например, тепловыми шумами), при понижении температуры
начинают все более и более проявляться, позволяя в чи-
чистом виде изучать закономерности и связи, присущие
данному веществу. Исследование в области низких тем-
температур позволило открыть много новых явлений при-
природы, таких, например, как сверхтекучесть гелия и сверх-
сверхпроводимость металлов.
При низких температурах резко меняются свойства
материалов. Одни металлы при низких температурах
повышают свою прочность, становятся пластичными,
другие становятся хрупкими, как стекло.
Изучение физико-химических свойств при низких тем-
температурах позволит в будущем создать новые вещества
с заранее заданными свойствами. Все это весьма ценно
для конструирования и создания космических кораблей,
станций и приборов.
Известно, что при радиолокационных исследованиях
космических тел принимаемый радиосигнал весьма мал
и его трудно выделить из различных шумов. Созданные
недавно советскими учеными молекулярные генераторы
и усилители работают при весьма низких температурах
и поэтому обладают очень низким уровнем шума.
Низкотемпературные электрические и магнитные
свойства металлов, полупроводников и диэлектриков по-<
234

зволяют разработать принципиально новые радиотехни-
радиотехнические устройства микроскопических размеров.
Сверхнизкие температуры используются для созда-
создания вакуума, необходимого, например, для работы ги-
гигантских ускорителей ядерных частиц.
Посмотрим, что дает термодинамика в изучении
свойств вещества при низких температурах.
Значение (~gf"j ПРИ абсолютном нуле.
В простейшем случае для изотермического процесса:
dF=—pdV; F= J pdV.
v
Продифференцируем это выражение по Т при
V=const:
Но, если Т = 0, то по теореме Нернста
Следовательно,
т. е.
вблизи абсолютного нуля изменение температуры
тела при постоянном объеме не вызывает изме-
изменения давления.
Значение \г^\ при абсолютном нуле.
йЕ (ЛаЛ
дТ)у[др)т>
\дТ}р~~ \дТ)[д)
водна
при Г=0, если
Так как производная [-^) имеет конечное значение
235

т. е.
вблизи абсолютного нуля конденсированные тела
при постоянном давлении в результате изменения
температуры не меняют объем.
Значение теплоемкости при абсолютном нуле.
но при Г=О
1 h
тогда
ср — <у = О,
а так как по теореме Нернста
т. е.
то
Следовательно,
lim cp=lim cv = 0. A0,16)
Свойства твердого тела близи абсолютного
нуля. В общем случае всякая элементарная работа мо*
жет быть представлена выражением:
где У — обобщенная сила, х — переменная, которая из-
изменяется под влиянием этой обобщенной силы,
Ср
/ Рис. 55. Зависимость ср от тем-
/ пературы вблизи абсолютного
/нуля.
236

Полная работа запишется в виде:
Следовательно,
Но так как при Г=0
(—) -О
\дт)х — ^
то
(Ц) =0, A0,17)
г, Г-0
т, е.
при абсолютном нуле и вблизи него ряд свойств
твердых тел перестает зависеть от температуры,
В заключение отметим, что существенное ограниче-
ограничение третьего начала термодинамики состоит в том, что
оно применимо только для простых кристаллических
тел. Однако имеется много путей и методов * для опре*
деления с помощью третьего начала термодинамики
абсолютных значений параметров сложных систем.
§*
Получение низких температур
Еще в прошлом веке были созданы опти-»
мальные установки, позволившие впервые получить жид-
жидкий воздух,
Далее были получены в жидком состоянии аргон,
неон, водород и даже гелий, температура сжижения ко*
торого при атмосферном давлении выше абсолютного
нуля всего на 4,2 градуса.
В дальнейшем, понизив давление паров над жидким
гелием, удалось понизить температуру еще на три с
лишним градуса. Для целей получения низких темпера*
тур в этих случаях использовалось понижение темперу
туры ниже Гк, и сжатие газов, испарение жидкостей
(каскадный метод), дросселирование и расширение ежа*
того газа с совершением внешней работы.
* См,г В, И, Кир ее в, Физическая химия, Химиздат, 1951.
237

Принципиальные основы перечисленных методов из-»
ложены нами в 1-й и 7-й главах этого учебника.
Для достижения более низких температур были ис«
пользованы новые методы охлаждения — методы адиа«
батического и ядерного размагничивания. Известно, что
магнитные моменты атомов и атомных ядер ориентируют-
ориентируются в одну сторону сильным магнитным полем. При вы-
выключении поля магнитные моменты дезориентируются
под действием тепловых колебаний, поглощая теплоту
у тела.
Как мы видели выше, теплоемкость вблизи абсолют-
абсолютного нуля весьма мала, поэтому температура тела при
использовании этих методов сильно понижается.
Методами адиабатного и ядерного размагничивания
в настоящее время достигнуты температуры порядка
ю-5ос.
Рассмотрим термодинамику процесса получения
сверхнизких температур. Воспользуемся для этого теп-
тепловой функцией /, дифференциал которой для парамаг-
парамагнетика, помещенного в магнитное поле, будет равен:
На основании G,32) найдем:
( дТ \ _ _/_<Ш\ /<Ш\
\dHh~ \dS)~ \дТ)
Но
>dS\ 1 [dQ
Следовательно,
/ дТ \ Т /дМ\
) )
Для парамагнетика М=%Н, где по закону Кюри
x = f (*>о).
Учитывая это, получим:
(Ж\ -h(*L\ - Нс
\дт)р>н-"\дт)рИ — ~т?'
238

Следовательно,
(—) — сН ^ о
Таким образом, при размагничивании (dH<0) темпера-
температура понижается (dT<0). Так как при низких темпе-
температурах по закону Дебая
то
1
Следовательно, при низких температурах G<1°К) из-
изменение температуры при размагничивании может быть
очень большим.
О10
Г Задачи и упражнения
1*. Доказать, что теорема Нернста при-
приводит к недостижимости температуры абсолютного нуля*
Доказательство. Рассмотрим цикл Карно
при условии, что температура нагревателя Т\ = Т и тем-
температура холодильника Г2=0.
Согласно II началу термодинамики:
ИЛИ
но ASli2 = y-, AS2K —0 (адиабатический процесс);
AS3,4=0 (по теореме Нернста); AS4,i = 0 (адиабатиче-
(адиабатический процесс). Следовательно, -у- = 0, хотя Q=^=0.
Это противоречие указывает на то, что спуститься
на нулевую изотерму нельзя, т. е. абсолютный нуль не*
достижим.
2. Показать, что вблизи абсолютного
нуля, т. е. при Г=0, поверхностное натяжение не зави-
зависит от температуры.
* Задачи 1 и 4 предложены автору И. П. Базаровым,
239

Указание. Следует воспользоваться соотношением
A0,17)
3. Показать, что вблизи абсолютного
нуля э. д. с. гальванического элемента не зависит от
температуры.
Указание. Следует воспользоваться соотношением
A0,16).
4. Как показывает опыт, при превра-
превращении ромбической серы в моноклиническую внутрен-
внутренняя энергия (тепловой эффект) меняется в зависимости
от температуры по закону:
Определить температуру превращения серы ромби*
ческой в моноклиническую.
Решение. Согласно равенству A0,10)
В точке превращения обе модификации серы нахо«
дятся в равновесии:
Ft = F2; W = Fl — F2 = 0.
Поэтому температуру превращения серы Го можно
найти из условия:
r = Q0 — ?>r2 = 50,4-3,69. 10-47i=0.
Откуда Го = 369,5° К (экспериментально найденное зна«
чение Го=368,4°К).
ЛИТЕРАТУРА
1. В. НЕРНСТ,
Теоретические и опытные основания нового теплового закона, Гос-
Госиздат, М. — Л., 1929.
2. м. планк,
Термодинамика, Госиздат, Л., 1925.
3. В. А. КИРЕЕВ,
Физическая химия, Химиздат, 1951.
4. А. В. РАКОВСКИЙ,
Курс физической химии, 1939,

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
вероятность состояния 129
Вырождение степеней свобо-
свободы 51
/Давление внутреннее 17
— излучения, термодинамиче-
термодинамическое доказательство 142, 143
— критическое 23
¦— поверхностное (давление
Лапласа) 166
-»-, понятие 10
Двигатель воздушно-реактив-
воздушно-реактивный прямоточный 82
$ график 83
, коэффициент полез-
полезного действия 83
¦ г схема 82
¦- пульсирующий 83
* , график 84
• , коэффициент полезно-
полезного действия 84
«Дйидкость перегретая 19
Закон Бойля—Мариотта 8
— Гей-Люссака 9
— Дебая 239
*— действующих масс 194
— Кирхгофа 141
—- соответственных состояний
28
— сохранения и превращения
материи и энергии 35
— Стефана—Больцмана 144
«— (начало) термодинамики
второй 5, 92, 93, 97, 118, 119,
128, 130
первый 5, 35, 44, 92
Закон термодинамики третий
5, 233, 237
/Излучение равновесное 141
Изогерма критическая 21, 23
/Количество теплоты 40
Компонента 181
Коэффициент давления терми-t
ческий 15
— объемного расширения 14
в критической точке
215
— при фазовых перехо-
переходах второго рода 212
„ первого ро-
рода 211
— сжатия изотермический 15,
19, 29
в критической точке
215
при фазовых перехо-
переходах второго рода 212
, „ — первого рода
211
— сжимаемости 59
*— стехиометрический 194
Модуль упругости адиабати-
адиабатический 59
изотермический 59
— — и скорость звука 60
//уль абсолютный температур
ры 102
Область критическая 26, 217
Объем критический 23, 25
— удельный 10, 59
Опалесценция 26
/7'ар перегретый 19
Парадокс Гиббса 191
Параметр макроскопический 12
— микроскопический 12
— термодинамический 6
_ внешний 6
внутренний 6
Переменная приведенная 21
241

Переход фазовый второго ро-
рода 211, 213, 214
первого рода 207, 209
Подобие термодинамическое 28
Показатель политропы 56, 57
Поправка к давлению в урав-
уравнении Ван-дер-Ваальса 17
— — объему в уравнении
Ван-дер-Ваальса 17
Постоянная Больцмана 51
— Планка 51
Постулат Планка 148
Потенциал Гиббса 154, 158
— — при фазовых переходах
второго рода 211
__ первого рода
209
— химический 156
Правило фаз Гиббса 186
Процесс адиабатический 53
— изобарический 51
•— изотермический 52
— изохорическн^ 52
— квазиравновесный (квази-
(квазистатический) 42
— необратимый 43
— неравновесный 13
— политропический 55
— —, изменение температуры
57
Процес равновесный 12
— термодинамический 12
Работа замкнутого цикла 66
—полезная 67
•— по перенесению заряда в
электрическом поле 36
— по поднятию тела 36
— силы поверхностного натя*
жения 36
—/, совершаемая газом 37
— элементарная 36
Равновесие динамическое 11
— термодинамическое 12
Раствор 196
— идеальный 198
— истинный 197
— разбавленный 198
Связь между теплоемкбстями
при постоянном давлении и по-
постоянном объеме 48
Система гетерогенная 180
242
, условия равновесия 183,
184
— гомогенная 180
, условия равновесия 188,
189
— макроскопическая 6
— термодинамическая 11
— — полностью изолирован-
изолированная 11
— — частично изолированная
11
Скорость потока критическая
172
Смесь 196
Соотношение взаимности 157
Сопло Л аваля 172
Состояние вещества критиче-
критическое 23, 215
— соответственное 28
Степень повышения давления 81
— предварительного расшире-
расширения 78
— сжатия 76
Суспензия 180
Уело абсолютно черное 141
— рабочее 68
Температура абсолютная 8, 102
—, измерение 7, 9
— (точка) инверсии 170
—• исчезновения мениска 26
— критическая 23
, метод определения 24
—, понятие 7
— смешения критическая 197
_. верхняя 197, 198
—, нижняя 197, 198
— термодинамическая 100, 102
— фазового перехода первого
рода 208
Теорема Карно 94
— Нернста 231, 232, 233
Теплоемкость вещества удель-
удельная 40
— при постоянном давлении 40
у зависимость от тем-
температуры в критической обла-
области 223
f значение при аб-
абсолютном нуле 236
, значение при изо-
изобарическом процессе 52
—. 1 . фазовых пе-
реходад первого рода 211

• -» -^, изменение при фа-
фазовых переходах второго рода
1 определение в кри-
критической области 221
объеме 40
— — — —t зависимость от
температуры в критической об-
области 223
— — — ~.t значение при аб-
абсолютном нуле 236
— — — —, — — изохориче-
ском процессе 52
^—^ определение в кри-
критической области 220
— политропического процесса
56
Теплообмен 39
Теплота образования поверх-
поверхности скрытая 108
— приведенная ИЗ
Термодинамика, метод 5
—, предмет 5
Термостат 41
Точка кипения абсолютная 24
— критическая 23
Уравнение Гельмгольца 112
— Гиббса—Гельмгольца 162
— изобары реакции 204
— изохоры реакции 204
— Клайперона—Клаузиуса 103,
104, 106, 157, 209
— Клаузиуса 20
— кривой равновесия диффе-
дифференциальное 210
— Майера 49
— максимальной работы 162
— политропы 56
— Пуассона 56
— состояния 14
бертло 21, 22
— — Ван-дер-Ваальса 17, 20
__ — —ч графическое изобра-
изображение изотерм 18
— ¦— идеального газа 9
Камерлинг—Оннеса 22
_ — Клайперона—Менделее-
Клайперона—Менделеева 9
, для одного грамм-
моля 15
,— — — —t критерий приме-
применимости 16
„ _ « критической обла*
сти 219
Майера и Боголюбова 22
— — приведенное 27, 28
— термодинамики основное 119
Уравнения Эренфеста 213
Фаза 181
Флуктуация плотности 26
Формула Планка 149
Функция состояния 6
— термодинамическая 151
, внутренняя энергия 152
— —, свободная энергия 153
— —, термодинамический по*
тенциал Гиббса 154
— —, энтальпия (тепловая
функция) 154
Цикл двигателя внутреннего
сгорания идеальный 73
— Дизеля (с подводом тепло-*
ты при постоянном давлении)
74
, график 80
— —, коэффициент полезного
действия 79
, схема работы двигателя
77
— замкнутый 66
— Карно 68
— —, коэффициент полезного
действия 70
с идеальным газом 70
— — — — —f коэффициент
полезного действия 72
— обратный 67
— Отто (с подводом теплоты
при постоянном объеме) 73
, график 75
— —, коэффициент полезного
действия 76
, схема работы двигателя
74,
— прямой 67
— Тринклера (со смешанным
подводом теплоты) 74
— —, график 80
г_ —9 коэффициент полезного
действия 81
— —, схема работы двигате-
двигателя 79
243

Число степеней свободы 6,186
Шкала абсолютных темпера-
температур 8
¦ газовая 9
— температур абсолютная тер-
термодинамическая 100, 101
«Эмульсия 180
Энергия внутренняя при фа-
фазовых переходах первого рода
208
— свободная 153, 158, 160,161
— — и максимальная работа
161
— связанная 161
— системы внутренняя 38, Я9
полная 38
Энтропия 117
*— адиабатического процесса
123
— и вероятность состояния 130
— — закон соответственных
состояний 122, 123
— — равновесие системы 126
— идеального газа 121
— изотермического обратимо-
обратимого процесса 119, 120
— при фазовых переходах пер-
первого рода 207
Эффект Джоуля — Томпсона
168, 169

ОГЛАВЛЕНИЕ Предисловие 3
Литература 4
Введение 5
Глава первая. УраВНСНИЯ СОСТОЯНИЯ 14
§ 1. Уравнение состояния идеального газа 15
§ 2. Уравнение состояния реальных газов 16
§ 3. Критическое состояние вещества 23
§ 4. Принцип термодинамического подобия 27
Задачи и упражнения 30
глава вторая. Первое начало термодинамики 35
§ 1. Понятие элементарной работы 36
§ 2. Условие полного дифференциала 37
§ 3. Внутренняя энергия как функция состоя-
состояния 38
§ 4, Количество теплоты и теплоемкость. Тер-
Термостат 39
§ 5. Обратимые и необратимые процессы 42
§ 6. Аналитическая формулировка первого на-
начала термодинамики 44
§ 7. Методологическое значение первого начала
термодинамики — закона сохранения и пре-
превращения энергии 45
§ 8. Связь между теплоемкостями при постоян-
постоянном давлении и постоянном объеме 47
§ 9. Применение первого начала термодинамики
к некоторым термодинамическим процес-
процессам 51
§ 10. Установление связи между адиабатическим
и изотермическим модулями упругости и
скоростью звука 58
Задачи и упражнения 60
Глава третья, КруГОВЫе ПрОЦвССЫ ИЛИ ЦИКЛЫ. ЦИКЛ
Карно. Идеальные циклы тепловых дви-
двигателей 66
§ 1. Круговые процессы 66
§ 2. Цикл Карно с идеальным газом 70
§ 3. Идеальные циклы двигателей внутреннего
сгорания 72
§ 4. Идеальные циклы воздушно-реактивных
двигателей 81
Задачи и упражнения 85
Глава четвертая. Второе начало термодинамики
92
§ 1. Некоторые эквивалентные формулировки
второго начала термодинамики 93
§ 2. Теорема Карно 94
§ 3. Абсолютная термодинамическая шкала тем-
температур 98
§ 4, Уравнение Клапейрона — Клаузиуса 103
245

5. Зависимость поверхностного натяжения от
температуры 106
Задачи и упражнения 108
Глава пятая. ЭнТрОПИЯ
113
§ 1. Второе начало термодинамики для случая
большого числа нагревателей и холодиль-
холодильников 113
§ 2. Энтропия 117
§ 3. Энтропия адиабатических процессов 123
§ 4. Статистический характер второго начала
термодинамики 126
§ 5. Энтропия «и вероятность 128
§ 6. О так называемой «тепловой смерти» все-
вселенной 130
Задачи и упражнения 132
Глава шестая.
141
151
Термодинамика и проблема излучения
§ 1. Закон Кирхгофа 141
§ 2. Давление излучения 142
§ 3. Закон Стефана — Больцмаиа 143
§ 4. Закон Вина 144
§ 5. Формула излучения Планка 147
Задачи и упражнения 149
глава седьмая. Термодинамические функции
§ 1. Внутренняя энергия как термодинамиче-
термодинамическая функция 152
§ 2. Свободная энергия 153
§ 3. Тепловая функция или энтальпия 154
§ 4. Термодинамический потенциал Гиббса 154
§ 5. Химический потенциал 156
§ 6. Соотношения взаимности 157
§ 7. Физический смысл понятия свободной энер-
энергии 159
§ 8. Свободная энергия и максимальная рабо-
работа. Уравнение Гиббса — Гельмгольца 161
§ 9. Электродвижущая сила гальванического
элемента 163
§ 10. Свободная энергия равновесных систем 165
§11. Тепловая функция. Эффект Джоуля —
Томсона 167
§ 12. Сопло Лаваля 170
Задачи и упражнения 173
глава восьмая. Учение о термодинамическом равновесии
в сложных системах 180
§ 1. Общие условия термодинамического равно-
равновесия гетерогенной системы 181
§ 2. Правило фаз Гиббса 185
246

§ 3. Общие условий равновесия в гомогенной
системе 188
§ 4. Внутренняя энергия и энтропия смеси иде-
идеальных газов. Закон действующих масс 189
§ 5. Растворы и смеси. Условия равновесия раз-
разбавленных и идеальных растворов 196
Задачи и упражнения 199
глава девятая. Фазовые переходы первого и второго рода.
Критические явления 207
§ 1. Фазовые переходы первого рода. Уравне-
Уравнение Клапейрона — Клаузиуса 207
§ 2. Фазовые переходы второго рода. Уравне-
Уравнение Эренфеста 211
§ 3. Критическое состояние вещества. Критиче-
Критическая область 215
§ 4. Уравнение состояния критической обла-
области 217
§ 5. Теплоемкость в критической области 220
Задачи и упражнения 223
Глава десятая. Тепловая теорема Нернста. Третье начало
термодинамики 228
§ 1. История вопроса. Теорема Нернста 228
§ 2. Расширенная формулировка теоремы Нерн-
Нернста. Третье начало термодинамики 232
§ 3. Свойства тел вблизи абсолютного нуля 234
§ 4. Получение низких температур 237
Задачи и упражнения 239
Предметный указатель 241

Василий Федорович Ноздреа
КУРС ТЕРМОДИНАМИКИ
Редактор В. Л. Климентович.
Художник Л. В. Лысенко.
Художественный редактор Б. А. Мокйн.
Технический редактор В. В. Новоселова.
Корректор М. В. Голубева.
Сдано в набор 30/ХН 1966 г. Подписано к печати 16/VI 1967 г.
84xlO8V82- Типографская М 2. Печ. л. 13,02 G,75).
Уч.-изд. л. 10,99. Тираж 40 000 экз. А04836. Зак. 569.
Издательство «Просвещение» Комитета по печати при Совете
Министров РСФСР. Москва, 3-й проезд Марьиной рощи, 41.
Ленинградская типография № 2 имени Евгении
Соколовой Главполиграфпрома Комитета по печати при
Совете Министров СССР. Измайловский проспект, 29»
Цена без переплета 31 кои., переплет 10 коп.